М. Н. Кирсанов
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
МОСКВА
ФИЗМАТЛИТ
2002

УДК 531@75.8)
К43
ББК 22.21
Кирсанов М. Н. Решебник. Теоретическая механика / Под
ред. А. И. Кириллова. - М.: ФИЗМАТЛИТ, 2002. - 384 с. - ISBN
5-9221-0281-8.
Изложены алгоритмы и примеры решения задач статики, кинематики и
динамики из курса теоретической механики, изучаемого в технических вузах.
Каждой задаче отведен отдельный раздел, содержащий общую постанов-
постановку задачи, план ее решения с необходимыми теоретическими пояснениями и
пример. Кроме того, в раздел включены десять задач для самостоятельного
решения и ответы к ним. Разобраны характерные ошибки и даны ответы на
типичные вопросы, возникающие при решении задач.
Приведены программы решения некоторых задач в системе Maple V.
Книга может быть использована как при очной, так и при дистанционной
формах обучения.
Для студентов и преподавателей технических вузов.
Ил. 187.
© ФИЗМАТЛИТ, 2002
ISBN 5-9221-0281-8	© М. Н. Кирсанов, 2002

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ
I СТАТИКА	и
Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ .	14
1.1.	Простая стержневая система 		14
1.2.	Равновесие цепи		21
1.3.	Теорема о трех силах		26
Глава 2. ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ	31
2.1.	Равновесие тяжелой рамы		31
2.2.	Ферма. Аналитические методы расчета		37
2.3.	Ферма. Графический расчет		45
2.4.	Расчет составной конструкции		54
2.5.	Конструкция с распределенными нагрузками		61
2.6.	Расчет системы трех тел, соединенных шарниром		67
Глава 3. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ ... 74
3.1.	Трение скольжения	 74
3.2.	Трение качения	 80
Глава 4. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ ... 86
4.1.	Пространственная ферма	 86
4.2.	Момент силы относительно оси	 91
4.3.	Равновесие вала	 94
4.4.	Определение усилий в стержнях, поддерживающих плиту . . 101
4.5.	Тело на сферической и стержневых опорах	106
4.6.	Приведение системы сил к простейшему виду 	111
Глава 5. ЦЕНТР ТЯЖЕСТИ	118
5.1.	Центр тяжести плоской фигуры	118
5.2.	Пространственная стержневая система 	122
5.3.	Центр тяжести объемного тела	125

ОГЛАВЛЕНИЕ
п. КИНЕМАТИКА		129
Глава 6. КИНЕМАТИКА ТОЧКИ 		131
6.1.	Движение точки в плоскости 		131
6.2.	Путь, пройденный точкой		136
6.3.	Движение точки в пространстве		137
6.4.	Естественный способ задания движения точки		140
6.5.	Движение точки в полярных координатах		144
Глава 7. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА 		149
7.1.	Вращательное движение тела		149
7.2.	Передача вращения		152
Глава 8. ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА 		158
8.1.	Скорости точек многозвенного механизма 		158
8.2.	Ускорения точек многозвенного механизма		170
8.3.	Уравнение трех угловых скоростей		179
8.4.	Уравнение трех угловых ускорений		183
8.5.	Кинематические уравнения плоского движения		188
Глава 9. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ 		195
9.1.	Сложное движение точки в плоскости		195
9.2.	Сложное движение точки в пространстве		202
9.3.	Движение точки по звену механизма		209
9.4.	Механизм с муфтой		216
Глава 10. СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТЕЛА 		222
10.1. Скорость и ускорение точки тела		222
ш. ДИНАМИКА 		226
Глава 11. ДИНАМИКА ТОЧКИ 		228
11.1.	Постоянные силы		228
11.2.	Переменные силы		232
Глава 12. ДИНАМИКА СИСТЕМЫ		236
12.1.	Теорема о движении центра масс		236
12.2.	Кинетическая энергия механической системы 		241
12.3.	Теорема об изменении кинетической энергии		247
12.4.	Теорема о моменте количества движения системы		253
12.5.	Динамический расчет механизма с неизвестным параметром	257

ОГЛАВЛЕНИЕ
12.6.	Плоское движение системы 		266
12.7.	Динамические реакции в подшипниках ротора		272
Глава 13. АНАЛИТИЧЕСКАЯ МЕХАНИКА		279
13.1.	Принцип возможных скоростей		279
13.2.	Общее уравнение динамики (одна степень свободы)		288
13.3.	Общее уравнение динамики (две степени свободы) 		294
13.4.	Уравнение Лагранжа 2-го рода (две степени свободы) ....	300
13.5.	Уравнение Лагранжа. Нелинейные уравнения движения . . .	307
13.6.	Уравнение Лагранжа 2-го рода для консервативных систем .	318
13.7.	Функция Гамильтона		324
13.8.	Уравнения Гамильтона		326
Глава 14. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ		336
14.1.	Система с двумя степенями свободы		336
14.2.	Колебания узла фермы		343
IV. РЕШЕНИЯ В СИСТЕМЕ MAPLE V .349
Глава 15. ПРОГРАММЫ ПО СТАТИКЕ 		350
15.1.	Расчет фермы		350
15.2.	Центр тяжести плоской фигуры		355
Глава 16. ПРОГРАММЫ ПО КИНЕМАТИКЕ 		358
16.1.	Кинематика точки 		358
16.2.	Механизм с двумя степенями свободы		361
16.3.	Скорости точек плоского механизма		364
Глава 17. ПРОГРАММЫ ПО ДИНАМИКЕ		368
17.1.	Принцип возможных скоростей		368
17.2.	Динамика машины с кулисным приводом		370
17.3.	Колебания системы с двумя степенями свободы		373
СПИСОК ЛИТЕРАТУРЫ		375
ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ		377

ПРЕДИСЛОВИЕ
Теоретическая механика — одна из важнейших дисциплин в тех-
техническом вузе. Решение задач по этой дисциплине всегда представ-
представляет определенную трудность для студента. Вызвано это многооб-
многообразием тем или обилием уравнений и теорем, множеством методов,
уровнем абстракции при решении задач или какими-либо другими
причинами — неизвестно. Скорее всего, для студентов младших
курсов все эти факторы вместе приводят к тому, что, по общему
мнению, теоретическая механика, наряду с математикой и сопротив-
сопротивлением материалов, числится в технических вузах наиболее сложной
дисциплиной.
При столкновении с трудной задачей лучшим помощником для
студента, самостоятельно изучающего науку, является книга. По те-
теоретической механике существует много учебников. Можно рекомен-
рекомендовать, например, изданный большим тиражом краткий курс Тарга
СМ. [19]. Очень хорошо подходит для технических вузов учебник
[5]. В этих учебниках и во многих других после изложения теории да-
дается несколько примеров решения задач. Ознакомление с готовыми
решениями ; — один из способов обучения, но не самый лучший.
Если ставить перед собой цель научиться решать задачи (а не решить
вот эту — конкретную задачу), то лучше всего овладеть секретами
мастерства: алгоритмами и схемами решений, методами и специаль-
специальными приемами. РЕШЕБНИК "Теоретическая механика" ставит пе-
перед собой именно такую цель. Продолжая традиции РЕШЕБНИКА
"Высшая математика" [10] и РЕШЕБНИКА "Высшая математика.
*) В сети Интернет существуют специальные страницы, где приводятся
готовые решения заданий и задач по теоретической механике. Форма и
содержание таких решений часто не удовлетворяют самым скромным за-
запросам, не говоря уже о том, что научить они мало чему смогут.

Специальные разделы" [2], в книге даны, во-первых, четкая поста-
постановка задачи, во-вторых, конкретный план действий и, наконец, при-
пример решения задачи по этому плану. В качестве примеров взяты
задачи из сборника задач Мещерского И.В. [14] или задачи близкие
к ним. В конце каждого параграфа приведены десять задач, кото-
которые могут быть решены студентами самостоятельно, а некоторые,
наиболее сложные, соответствуют по уровню курсовым работам. За
образец для таких работ взяты задания из сборников Яблонского А. А.
[17] и Новожилова И.В., Зацепина М.Ф. [15].
Ко всем задачам даны не только ответы, но и, как правило, проме-
промежуточные результаты. Это упрощает проверку решения. Числовые
ответы приведены с двумя или тремя знаками после запятой, пред-
предполагая, что данные в задаче имеют соответствующую точность.
Там, где это необходимо, после решения задачи даются ответы
на характерные вопросы, возникающие у студентов в процессе реше-
решения. За двадцать лет преподавания теоретической механики автор
накопил достаточное число таких вопросов. Даны также предосте-
предостережения о возможных ошибках в решении задач.
В последней части РЕШЕБНИКА приведены примеры решения за-
задач с использованием универсальной математической системы Maple
V, позволяющей решить задачу в аналитическом виде и изобразить
исследуемое явление, например, движение механизма, на экране ком-
компьютера.
Полные тексты приведенных здесь программ и программы для
решения других задач механики с примерами, подробными поясне-
пояснениями и графическим представлением результатов можно найти на
авторской странице Интернет: www.academiaxxi.ru/solverTM.html.
Ссылка на РЕШЕБНИК "Высшая математика" обозначена как
Решебник ВМ с указанием соответствующего параграфа.
В дополнение к этой книге и к программам для Maple V распро-
распространяется пакет программ РЕШЕБНИК.ТМ, представляющий со-
собой электронную версию РЕШЕБНИКА, разработанную на основе
пакета AcademiaXXI. С помощью пакета программ РЕШЕБНИК.ТМ
студент сможет проще решать многие задачи теоретической меха-
механики, уделяя больше сил и времени разбору сути задачи и физичес-
физического явления, лежащего в основе задачи, предоставляя компьютеру
рутинную часть работы, связанную с математическими выкладками
и численным счетом.
Для преподавателей теоретической механики автор разработал
специальную программу-генератор задач, создающую тексты уело-

10
вий и ответов по 50 темам статики, кинематики и динамики. Тексты
задач и рисунки в формате ЖГ^Х могут быть использованы для оч-
очного и дистанционного обучения. Программа содержит сотни тысяч
вариантов задач и используется автором в его педагогической ра-
работе. По десять задач из почти всех разделов программы-генератора
приведены в этой книге в качестве примеров.
Подробная информация о пакете РЕШЕБНИК.ТМ, программе-
генераторе задач и сами программы размещены на странице Интер-
Интернет: www.academiaxxi.ru/solverTM.html.
Автор будет благодарен всем приславшим свои замечания о
комплексе РЕШЕБНИК "Теоретическая механика" и предложения по
адресу:
111250 Москва, ул. Красноказарменная, д. 17, Московский энер-
энергетический институт (ТУ), кафедра теоретической механики.
E-mail: Kirsanov@termech.mpei.ac.ru.

Часть I
СТАТИКА
В статике изучается равновесие тел под действием сил и свойства
систем сил, необязательно находящихся в равновесии.
Задачи статики можно условно разделить на три типа: задачи
на равновесие системы сходящихся сил, т.е. сил, линии действия ко-
которых пересекаются в одной точке (глава 1), задачи произвольной
плоской системы сил (главы 2,3) и задачи пространственной системы
сил (глава 4).
Нахождение координат центра тяжести (глава 5) тоже считается
задачей статики. Хотя силы в этой задаче явно не присутствуют,
основные формулы задачи следуют из уравнений равновесия системы
параллельных сил.
Искомыми величинами в задачах статики могут быть реакции
опор, усилия в элементах конструкций, геометрические (размеры,
углы) и материальные (вес, коэффициент трения) характеристики
систем. В статически определимых задачах число уравнений равно-
равновесия совпадает с числом неизвестных. Именно такие задачи и будут
рассмотрены в этой части.
Для решения задач статики потребуются понятия проекции силы
на ось и момента силы относительно точки и оси. Напомним, что про-
проекция вектора силы F на ось х определяется по формуле Fx = F cos a,
где а — угол между положительным направлением оси и вектором
силы, отсчитываемый против часовой стрелки. Если угол острый, то
проекция положительная, если тупой — отрицательная.
Общее определение момента Мо силы F относительно точки О
дается векторным произведением
Mo(F) = fQxF,	A)
где г0 — радиус-вектор точки приложения вектора силы относительно
точки О. Модуль момента вычисляем по формуле MO{F) = rQFsin7,

12
где 7 — угол между векторами rQ и F. Направление вектора момента
вычисляется по правилу векторного произведения. Плечо h силы от-
относительно точки О — это кратчайшее расстояние от точки до линии
действия силы; h = r0 sin 7-
Вектор момента перпендикулярен плоскости, в которой распо-
располагаются силы. Поэтому в задачах статики плоской системы сил
момент можно рассматривать как скалярную величину — величину
проекции вектора момента на нормаль к плоскости (ось z). Индекс
z для сокращения записи часто опускают и отождествляют момент
силы Мо относительно точки на плоскости со скалярной величиной
— MQz. Отсюда вытекает практическое правило определения мо-
момента силы относительно точки в плоских задачах статики. Для
вычисления момента силы относительно точки О (рис. 1) сначала
находим проекции силы на оси, а затем момент вычисляем по фор-
формуле MOz(F) = — Fx • у0 + Fy • xQ. Другой способ вычисления мо-
момента: MOz(F) = zbF/г, где h — плечо силы относительно точки О.
У
О
Рис. 2
Рис. 3
Знак определяется по правилу векторного произведения. Если сила
поворачивает тело относительно центра по часовой стрелке — мо-
момент отрицательный, против часовой стрелки — положительный. На
рис. 2 момент силы F относительно точки О отрицательный. Если
сила или линия ее действия пересекает точку, то момент силы отно-
относительно этой точки равен нулю.
При решении задач пространственной статики (§ 4.3 - § 4.6) тре-
требуется вычислять момент силы относительно оси, или, что то же,
проекцию момента силы относительно точки A) на ось, проходящую
через нее. Иногда эту величину удобнее искать как момент проекции
Fn силы на плоскость, перпендикулярную оси, относительно точки
пересечения оси с плоскостью (рис. 3). Знак определяем по направ-
направлению вращения вокруг оси с точки зрения наблюдателя, находяще-
находящегося на конце оси. Если вращение происходит по часовой стрелке, то
момент отрицательный, против часовой стрелки — положительный.

	13
Момент силы относительно оси равен нулю, если сила параллельна
оси или пересекает ее, т.е., если сила и ось лежат в одной плоскости.
Кроме сил в статике рассматриваются и пары сил. Пара — это
совокупность двух равных параллельных противоположно направлен-
направленных сил. Пара характеризуется моментом — суммой моментов ее
сил относительно некоторой точки. Легко показать, что положение
точки не существенно и на величину момента не влияет, поэтому мо-
момент пары является свободным вектором. Напомним, что вектор
силы является вектором скользящим. В зависимости от знака мо-
момента пары на плоскости изображать пару будем изогнутой стрелкой
О или yJ" . He путать эту стрелку с вектором пары! Вектор пары
перпендикулярен ее плоскости.
Решение двух задач статики в системе Maple V приведено в § 15.1,
15.2. Большинство задач статики сводится к решению систем линей-
линейных уравнений. Рутинную часть работы по составлению и решению
уравнений можно поручить Maple V. Простейшая программа может
выглядеть, например, так:
eql:=Ха*2.5+Ya*3.1=20:
eq2:=-Xa*l.5+Ya*10=-12.5:
solve({eql,eq2},{Xa,Ya>);
Записывая уравнение на компьютере, а не на бумаге, вы достига-
достигаете сразу же нескольких целей. Во-первых, компьютер выполняет ма-
математические действия, часто весьма громоздкие. Во-вторых, урав-
уравнение легко поправить и сразу же пересчитать, если вы ошиблись
при составлении уравнения и ответ не сходится. В-третьих, решение
удобно оформить, распечатав его на принтере. Можно вывести гра-
график, таблицу результатов и т.д. Все эти действия можно выполнить
и в других системах, в частности, в пакете AcademiaXXI, представ-
представленном на сайте www.academiaxxi.ru.

Глава 1
ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ
СИЛ
При изучении темы ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
вы научитесь составлять уравнения проекций и решать задачи рав-
равновесия плоских стержневых систем методом вырезания узлов. Этот
метод лежит в основе компьютерной программы расчета ферм (§15.1).
1.1. Простая стержневая система
Постановка задачи. Плоская шарнирно-стержневая конструк-
конструкция закреплена на неподвижном основании и нагружена в шарнирах
силами. Найти усилия в стержнях.
План решения
Рассматриваем равновесие внутренних шарниров системы, не со-
соединенных с неподвижным основанием. Такие шарниры будем на-
называть узлами. Действие каждого стержня заменяем его реакцией
— силой, направленной из узла к стержню. Усилие — это проекция
реакции стержня на внешнюю нормаль к сечению. Если в резуль-
результате решения задачи реакция стержня, приложенная таким образом
к узлу, оказывается отрицательной, то стержень сжат, в противном
случае стержень растянут.
1.	Вырезаем узел, соединенный только с двумя стержнями. Дей-
Действие стержней заменяем их реакциями.
2.	Для полученной системы сходящихся сил составляем уравнения
равновесия в проекциях на выбранные для этого узла оси.
3.	Решаем систему двух линейных уравнений и находим искомые
усилия.
4.	Вырезаем очередной узел системы, тот, к которому подходят
не более двух стержней с неизвестными усилиями. Составляем и ре-
решаем уравнения равновесия в проекциях на оси, выбранные для этого

1.1. Простая стержневая система
15
узла. Этот пункт плана выполняем несколько раз для всех узлов до
нахождения всех усилий.
5. Для проверки решения мысленно отделяем конструкцию от ос-
основания, заменяя действие рассеченных стержней найденными реак-
реакциями. Проверяем выполнение условий равновесия полученной сис-
системы сил.
Замечание 1. Существуют фермы *^ , у которых к каждому узлу
присоединены более двух стержней. Например, на рис. 4 изображена
конструкция (сетчатая ферма В.Г.Шухова), к каждому узлу которой
подходит по три стержня. Диагональные стержни расположены в
разных плоскостях и не пересекаются.
Здесь нельзя определять усилия по предложенной схеме, переходя
от одного узла к другому, так как нет узла, с которого можно начать
расчет. В этом случае сначала составляются уравнения равновесия
отдельных узлов, а потом совместно решается система полученных
уравнений. Систему можно решать любым известным способом (Ре-
шебник ВМ, §2.1).
В
Рис. 4
Рис. 5
Замечание 2. Для упрощения уравнений равновесия одну из осей
координат можно направить вдоль стержня с неизвестным усилием.
Для каждого узла можно выбрать свою систему координат.
Замечание 3. Углы между осями и векторами усилий легче опре-
определять, если проводить через узлы вспомогательные вертикальные
или горизонтальные прямые.
Замечание 4. Усилия в стержнях можно найти с помощью сис-
системы Maple V (Программа 1, с. 350).
*) Шарнирно-стержневая конструкция, нагруженная в шарнирах си-
силами, называется фермой. Весом стержней фермы и трением в шарнирах
пренебрегают.

16
Гл. 1. Плоская система сходящихся сил
Пример. Плоская шарнирно-стержневая конструкция закреплена
на неподвижном основании шарнирами Е, D, С и нагружена в шар-
шарнире А горизонтальной силой Р = 100 кН (рис. 5). Даны углы:
IDFA = 135°, IABD = 60°, IDCB = 60°, LBDC = 30°, LDFE = 30°.
Найти усилия в стержнях.
Решение
Конструкция состоит из шести стержней, соединенных тремя шар-
шарнирами (узлами). Узлы фермы находятся в равновесии. Для каждого
узла А, В, F составляем по два уравнения равновесия в проекциях на
выбранные оси. Из шести уравнений находим шесть искомых усилий.
1.	Решение задачи начинаем с рассмотрения узла А, так как этот
узел соединен только с двумя стержнями АВ и AF. При выреза-
вырезании узла действие каждого стержня заменяем силой, направленной
из шарнира к стержню (рис. 6).
2.	Составляем уравнения равновесия. Для упрощения уравнений
ось у направляем по стержню АВ. Получаем
*?Х{ = SAF cos 15° - Р sin 30° = 0,
Y,Y{ = -SAF sin 15° + SAB + P cos 30° = 0.
где Xi — проекции силы i на ось ж, а У. — проекции силы г на ось
У-
3.	Решаем уравнения. Из первого уравнения системы находим уси-
усилие SAF = 51.76 кН, из второго — усилие SAB = —73.21 кН.
4.	Рассматриваем узел F. К нему подходят три стержня (рис. 7).
Saf
А
Рис. 6
30°
Sfd
Рис. 7
Saf
Усилие в одном из них уже известно SAF = 51.76 кН. Усилия в двух
других находим из уравнений для проекций:

1.1. Простая стержневая система
17
J2 Xi = -SFE sin 30° + SAF cos 45° = 0,
i = ~SFE C0S 30° - SFD
SAF Sin 45° =
Находим SFE = 73.21 кН, SFD = -26.79 кН.
Составляем уравнения равновесия узла В в проекциях на оси, на-
направленные по стержням ВС и BD (рис. 8):
J] У. =
- SAB cos 30° = 0.
Решая уравнения, получаем: SDB = —SAB sin 30° = 73.21 • 0.5 =
= 36.6 кН, SBC = SAB cos 30° = -73.21 • 0.866 = -63.4 кН.
5. Проверка. Рассматриваем равновесие конструкции в целом.
Sab
Sbc
Рис. 8
Sfe
Рис. 9
Горизонтальным сечением отсекаем ферму от основания. Действия
стержней заменяем силами, которые направляем, как и раньше, по
внешним нормалям к сечениям стержней, т.е. вниз (рис. 9).
Система сил, действующих на ферму, не является сходящейся. Для
такой системы справедливы три уравнения равновесия, одно из ко-
которых — уравнение моментов. Составление уравнения моментов —
тема задач статики произвольной плоской или пространственной сис-
системы сил (§2.1 — 3.2). Для того, чтобы не выходить за пределы темы
поставленной задачи, в решении которой используются только урав-
уравнения проекций, составим два уравнения проекций на оси хну всех
сил, действующих на ферму целиком:
{ = -SFE cos 60° - SDB cos 30° + SBC cos 60° + P = 0,
i = ~SFE Sm 60° - SFD ~ SDB Sm 30° - SBC Sm 60° = °'
2 M.H. Кирсанов

18
Гл. 1. Плоская система сходящихся сил
Суммы равны нулю. Это подтверждает правильность решения.
Результаты расчетов в кН заносим в таблицу:
Saf
51.76
Sab
-73.21
Sfe
73.21
Sfd
-26.79
Sdb
36.60
Sbc
-63.40
Условия ЗАДАЧ. Плоская шарнирно-стержневая конструкция
закреплена на неподвижном основании и нагружена в одном шар-
шарнире вертикальной или горизонтальной силой Р. Найти усилия в
стержнях (в кН).
1.
D
Р= 1 кН,
1АСВ=30°, ZABC=30°,
?BDC=4b°, IBCD=4,5°,
ICDE=6O°, ICED=3O°.
2.
P= 2 кН,
ZAOB=45°, ZABC=45°,
IBDC=6O°, IBCD=3O°,
?CDE=30°, lCED=4b°.
3.
В^У^
4. В
С
/е
Р= 3 кН,
IBDC=12O°
ICDE=3O°,
Р= 4 кН,
ICDE=3O°]
ААВС=30°,
, /БС?>=30°
ZCED=90°.
IBCD=3O°\
ICED=12O°

1.1. Простая стержневая система
19
5.
p
6.
7.
В
8.
С
В
Р= 5 кН,
ZARD=60°, IADB=9O°,
ABDC=30°, ABCD=120°,
?CDE=30°, ICED=№°.
P= 6 кН,
IACB=SO°,
IBDC=9O°,
?CDE=60°, ICED=6O°.
P= 7 кН,
?ABD=30°, IADB=SO°,
=6O°, IBCD=3O°,
=±b°, lCED=4b°.
P= 8 кН,
=4b
=4b
=4.5°, LCED=№°.
С
P= 9 кН,
IABD=9O°,
?BDC=4b°,	,
=4,b°, ICED=6O°.
P= 10 кН,
IABD=9O°, IADB=6O°,
?BDC=30°, IBCD=9O°,
?CDE=60°, ICED=9O°.
2*

20
Гл. 1. Плоская система сходящихся сил
Ответы
1
2
3
4
5
6
7
8
9
10
Sab
-1.115
1.414
2.196
2.828
8.660
-5.379
5.715
5.657
9.000
17.321
Sac
-0.816
-1.414
-1.553
—
—
-4.392
—
—
—
—
Sad
—
—
—
-2.828
-10.000
—
-2.092
-5.657
-12.728
-20.000
Sbc
0.966
-1.000
-3.804
2.000
15.000
10.392
2.858
4.000
9.000
20.000
Sbd
-0.558
1.000
2.196
-2.000
-17.321
-7.608
-4.950
-4.000
0.000
-10.000
ScD
-0.472
0.732
5.660
-3.464
7.500
-7.856
-2.475
-3.586
-8.069
-34.641
ScE
-0.106
-1.932
-3.928
2.000
12.990
5.321
1.429
2.928
6.588
40.000
Ответы на типичные вопросы, возникающие при решении задачи
1.	Почему в задаче не указаны длины стержней?
Решение задачи зависит только от углов между стержнями и от
внешних нагрузок. Длины стержней не нужны.
2.	После вырезания узла получилась система двух уравнений с
тремя (или более) неизвестными.
Во-первых, см. Замечание 1. Во-вторых, этого можно избежать,
если рассматривать всякий раз узел с двумя неизвестными реакци-
реакциями. В-третьих, возможно не было замечено, что одно из усилий уже
было найдено.
Предупреждение типичных ошибок
1.	Меняя направление реакции стержня, при переходе от рассмот-
рассмотрения равновесия узла на одном его конце к равновесию другого, не
надо менять знак усилия.
2.	Не надо вырезать опорные шарниры. Из этого ничего не полу-
получится. Реакции основания вы не знаете!
3.	Для метода вырезания узлов характерно накопление ошибок
округления. Поэтому рекомендуем промежуточные результаты по-
получать с повышенной точностью, т.е. с четырьмя-пятью знаками
после запятой.
4.	Не стоит вводить для одного усилия два обозначения, напри-
например, усилие SAB при рассмотрении узла А и S'AB для В. Записывая
(или держа в уме) естественное в этом случае соотношение для про-
противоположно направленных векторов реакций: S'AB = — SAB, можно
по ошибке знак минус отнести и к величинам усилий, хотя на самом
деле это одно и то же значение, а минус уже учтен при изображении
векторов в разные стороны.

1.2. Равновесие цепи	21
1.2. Равновесие цепи
Постановка задачи. Определить положение равновесия плос-
плоского шарнирно-стержневого механизма, состоящего из последова-
последовательно соединенных невесомых стержней. Механизм расположен в
вертикальной плоскости. В крайних точках механизм шарнирно за-
закреплен на неподвижном основании. Средние шарниры нагружены
силами. Найти усилия в стержнях.
Особенностью задачи является необычный для статики объект
исследования — механизм, имеющий возможность двигаться. При
определенном соотношении нагрузок и геометрических параметров
механизм принимает положение равновесия. В качестве искомой ве-
величины может быть угол или какая-либо другая геометрическая ха-
характеристика конструкции.
План решения
1.	Записываем уравнения равновесия узлов системы в проекциях.
2.	Решаем полученную систему уравнений. Определяем усилия в
стержнях и искомый угол.
3.	Проверяем равновесие конструкции в целом, освобождая ее от
внешних связей. Проверочным уравнением может быть уравнение
проекций на какую-либо ось.
Пример *^ . Определить положение равновесия плоского симмет-
симметричного шарнирно-стержневого механизма. Концы А ж Е шарнирно
закреплены на неподвижном основании. Три внутренних шарнира В,
С и D нагружены одинаковой вертикальной нагрузкой Q.
Рис. 10
В положении равновесия а = 60°. Определить угол C и усилия в
стержнях (рис. 10). Весом стержней пренебречь.
*) Задача 2.39 из сборника И.В. Мещерского.

22
Гл. 1. Плоская система сходящихся сил
Решение
Конструкция, данная в условии задачи, представляет собой меха-
механизм, находящийся в равновесии только при некоторых определенных
нагрузках. При изменении направлений и величин нагрузок меняется
и конфигурация конструкции. Одной из неизвестных величин задачи
(помимо усилий в стержнях) является угол C. Для решения задачи
используем метод вырезания узлов (§1.1).
1. Записываем уравнения равновесия узлов системы. Составим
уравнения равновесия узла С (рис.11):
^ Х{ = —SBC cos C + SCD cos /5 = 0,
y. = -Q - SBCsinP - SCDsmC = 0.
A)
B)
Конструкция симметрична, поэтому уравнения равновесия узлов В и
D запишутся одинаково. Рассмотрим равновесие узла В (рис.12).
У
С	_ ж	В
Sbc
Sbc
Sab
Рис. 11	Рис. 12
Для упрощения уравнений направим ось у по стержню АВ, ось х —
перпендикулярно АВ. Тогда, уравнение равновесия в проекции на
ось х содержит только одну неизвестную величину:
C)
D)
i = SBC sin(a — j3) + Q cos a = 0,
Y{ = SBC cos(a -13)- SAB - Q sin a = 0.
2. Решаем систему уравнений A—4). Из A) получаем, что SCD = SBC.
Это равенство объясняется симметрией конструкции и симметрией
нагрузок. Из B) и D) с учетом полученного равенства находим
Q = -2SBCsinf3,
SAB = SBC cos(a — C) — Q sin a.
E)
F)

1.2. Равновесие цепи
23
Выражаем SBC из E) и подставляем в C):
-Q sin(a - 13)/{2 sin/3) + Q cos a = 0.
Так как Q ф 0, то после сокращения на Q получаем уравнение для C:
— sin(a — C) + 2 cos a sin /3 = 0,
или 3tg/3 = tga = \/3, tg/3 = 0.577, /3 = 30°. Из E) получаем усилие
SBC = —Q/Bsin/3) = —Q. Стержень ВС сжат. Из F) находим усилие
SAB = SBCcosF0° - 30°) - Q sin60° = -Qy/З.
В силу симметрии задачи SBC = SCD, SAB = ^^л.
Результаты расчетов заносим в таблицу:
tg/3
0.577
/3
7г/б
-QV3
Sbc
-Q
ScD
-Q
Sde
3. Проверка. Рассмотрим равновесие всей конструкции в целом.
А
D
Sab
Sde
Рис. 13
Отсекая стержни от основания, заменим их действие реакциями, на-
направленными по внешним нормалям к сечениям стержней, т.е. вниз
(рис. 13). Уравнение проекций на ось х составлять не имеет смысла —
в силу симметрии оно лишь подтвердит, что SАв = SDE. Проверяем
равенство нулю суммы проекций всех сил на вертикаль:
У. = -3Q - SAB cos 30° - SDE cos 30° = -3Q +
/о
= 0.

24
Гл. 1. Плоская система сходящихся сил
Задача решена верно.
Условия ЗАДАЧ. Определить положение равновесия плоского
шарнирно-стержневого механизма, состоящего из трех последова-
последовательно соединенных невесомых стержней. Механизм расположен в
вертикальной плоскости. В крайних точках механизм шарнирно за-
закреплен на неподвижном основании. Средние шарниры нагружены
вертикальными или горизонтальными силами или грузом Р. Найти
угол а (в рад) и усилия в стержнях 1, 2, 3 (в кН).
1.
Q
Р = 70 кН, Q = 240 кН.
Р = 90 кН, Q = 30 кН.
3.
Q
Р = 80 кН, Q = 160 кН.
Р = 40 кН, Q = 50 кН.
Р = 45 кН, Q = 20 кН.
Р = 50 кН, Q = 60 кН.

1.2. Равновесие цепи
25
Р = 90 кН, Q = 110 кН.
9.
Р = 30 кН, Q = 40 кН.
10.
Р = 100 кН, Q = 270 кН.
60Р
Р = 20 кН, Q = 10 кН.
Ответы
1
2
3
4
5
6
7
8
9
10
tga
0.589
2.000
0.577
0.962
1.250
0.623
1.078
1.732
1.741
1.732
а
рад
0.533
1.107
0.524
0.766
0.896
0.557
0.823
1.047
1.049
1.047
Si
S3
кН
137.852
67.082
277.128
-103.923
-32.016
-57.735
65.885
-20.000
271.017
17.321
140.000
42.426
160.000
-72.111
-28.284
58.900
-80.692
34.641
190.919
-10.000
121.244
30.000
138.564
-51.962
-20.000
31.132
77.836
17.321
190.919
17.321
Ответы на типичные вопросы, возникающие при решении задачи, и пре-
предупреждение типичных ошибок см. с. 20.

26	.Гл. 1. Плоская система сходящихся сил
1.3. Теорема о трех силах
Постановка задачи. Тело находится в равновесии под дейст-
действием трех сил, одна из которых известна, у другой известно только
направление, а у третьей не известны ни величина, ни направление.
Используя теорему о трех силах, найти неизвестные силы.
План решения
В теореме о трех силах утверждается, что если на тело, находя-
находящееся в равновесии, действуют три непараллельные силы (включая
реакции опор), то они лежат в одной плоскости, и линии их действия
пересекаются в одной точке.
1.	Найдем точку пересечения линий действия двух сил, направ-
направления которых известны. Через эту точку должна пройти и линия
действия третьей силы.
2.	Имея направления векторов трех сил, строим из них силовой
треугольник. Начало одного вектора является концом другого. Если
тело находится в равновесии, то сумма векторов сил, действующих
на него, равна нулю. Следовательно, треугольник сил должен быть
замкнут.
3.	Из условия замкнутости треугольника по направлению задан-
заданной силы определяем направление обхода треугольника и, следова-
следовательно, направления искомых сил.
4.	Находим стороны силового треугольника — искомые силы.
Пример *^ . Горизонтальный невесомый стержень АВ находится
в равновесии под действием трех сил, одна из которых вертикальная
сила F = 5 кН (рис. 14), другая — реакция опорного стержня CD, a
третья — реакция неподвижного шарнира А. Используя теорему о
трех силах, найти неизвестные реакции опор.
АС = 2 м, СВ = 1 м
Задача 2.29 из сборника И.В. Мещерского.

1.3. Теорема о трех силах
27
Решение
1. Найдем точку пересечения линий действия двух сил, направ-
направления которых известны. Определим направление линии действия
третьей силы.
На стержень АВ действуют три силы: заданная сила F, реакция
RA шарнира А и реакция RD стержня CD. При этом линия действия
вектора RD известна. Она совпадает со стержнем CD, так как стер-
стержень нагружен только двумя силами в точках С и D (вес стержня
не учитывается). Согласно аксиоме статики эти силы равны по вели-
величине и направлены вдоль CD в разные стороны. Направление реак-
реакции шарнира А определяем по теореме о трех силах. Линии действия
сил F, RD и RA пересекаются в точке О (рис. 15). Следовательно,
АО — линия действия силы RA. Известны только линии действия
сил RD и RA, поэтому векторы на рис. 15 не изображаем, пока из
силового треугольника не узнаем их направления.
^
С
Рис. 15
2. Строим силовой треугольник. Сумма векторов сил, находя-
находящихся в равновесии, равна нулю, следовательно, треугольник, состав-
составленный из F, RD и RA, должен быть замкнут.
Rd
Рис. 16
Рис. 17
Треугольник строим, начиная с известной силы F (рис. 16). Через
начало и конец вектора F проводим прямые, параллельные направле-
направлениям RD и RA.

28	.Гл. 1. Плоская система сходящихся сил
3.	Из условия замкнутости треугольника по направлению внеш-
внешней силы F определяем направление обхода треугольника и, следова-
следовательно, направления реакций опор.
Замкнутость треугольника сил означает, что начало одной силы
совпадает с концом другой. Отсюда определяем направление обхода
треугольника, которое может быть различным в зависимости от спо-
способа построения силового треугольника (рис. 17 — против часовой
стрелки, рис. 18 — по часовой стрелке). Направления и величины сил
в обоих случаях одни и те же.
Изобразим реакции с учетом найденных направлений (рис. 19).
4.	Определяем длины сторон силового треугольника — величины
реакций опор. Найти стороны треугольника сил означает решить
задачу. В нашем случае известны углы (по построению) и сторона F
треугольника. Две другие стороны находятся по теореме синусов.
С
Рис. 19
Можно поступить иначе, используя свойства подобия. На рис. 15
найдем треугольник подобный силовому. В ряде случаев этот тре-
треугольник очевиден. В общем же, для получения такого треугольника
надо выполнить дополнительные построения: провести линии, про-
проходящие через характерные точки (шарниры, точки приложения сил
и т.п.), параллельно сторонам силового треугольника. Проведем, на-
например, вертикаль СС1. Образуется треугольник СС-^О, подобный
силовому (рис. 15, 17). Подобие следует из условия параллельности
сторон треугольников.
Найдем стороны треугольника ССХО\
ОВ = СВ = 1м, ОС = -ЛСВ = л/2 = 1.414 м.
Из подобия /\АОВ и /\ACC-y имеем соотношения
ACJAO = АС/АВ = CCJOB.
Отсюда вычисляем длины: АО = л/АВ2 + ОВ2 = л/1б, АС1 = 2л/1б/3,
СХО = л/10/3 = 1.054 м, ССг = B/3) ОВ = 0.667 м.

1.3. Теорема о трех силах
29
Из условия подобия треугольника сил и АССгО следует, что
F/CC1 = ЯА/СгО = RD/CO.
Из этих пропорций находим искомые величины:
RA = F- C1O/CC1 = 7.901 кН, RD = F • СО/СС1 = 10.607 кН.
Условия ЗАДАЧ. Тело находится в равновесии под действием
трех сил, одна из которых известный вес тела G или внешняя на-
нагрузка Р, другая — реакция опоры в точке В [гладкая опора или
опорный стержень) с известным направлением, а третья —реакция
неподвижного шарнира А. Используя теорему о трех силах, найти
неизвестные реакции опор (в кН). Размеры указаны в см.
1.
40
Р = 10 кН, АС = 60 см
3'
В
Ы
Р= 30 кН, АВ=ВС
5.
А
С
В
Гзо°
Р = 25 кН, ЪАС = 4.СВ
2.
В//
4^45
1Р
D
Р = 20 кН, AB=BD=CB
4.
С
Р=40 кН, AB=AD, AC=BC
6.	С Р
Р = 35 кН , АВ=ВС=СА

30
Гл. 1. Плоская система сходящихся сил
7.
8.
С
G = 45 кН, 2АВ = ВС
9.
D	С
Р=10 кН, BD=3AD=3DC.
10.
с Р
Р = 90 кН
Р = 70 кН
Ответы
1
2
3
4
5
Ra
-9.600
-28.284
-69.282
-28.284
-16.496
Rb
6.210
20.000
45.826
28.284
13.521
6
7
8
9
10
Ra
34.999
-90.000
4.226
-103.923
-46.667
Rb
60.621
55.769
8.695
187.350
61.734
Предупреждение типичных ошибок
1.	Размеры на чертеже сил, приложенных к телу (рис.15), измеря-
измеряются в единицах длины (м, см), а на силовом треугольнике (рис. 17,
18) в единицах сил (Н, кН). Не надо принимать линейные расстояния
АО, СО и ВО за величины соответствующих сил.
2.	Реакция гладкого основания перпендикулярна поверхности ос-
основания. Реакция гладкой поверхности тела о неподвижную опору
перпендикулярна поверхности тела.
3.	В данной задаче должно быть только три силы. Лишние силы
возникают, если прикладывать вес тела там, где его нет, или если
реакцию в шарнире А раскладывать на составляющие.

Глава 2
ПРОИЗВОЛЬНАЯ ПЛОСКАЯ
СИСТЕМА СИЛ
Изучив в предыдущем разделе систему сходящихся сил и уравне-
уравнения проекций, в разделе ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА
СИЛ вы научитесь составлять уравнения моментов, более эффек-
эффективно находить усилия в стержнях фермы и определять реакции опор
составных конструкций.
Почти все задачи этого раздела заканчиваются решением системы
линейных уравнений. Простейший способ выполнения этой трудоем-
трудоемкой процедуры с помощью Maple V приведен на с. 13.
2.1. Равновесие тяжелой рамы
Постановка задачи. Тяжелая однородная рама расположена
в вертикальной плоскости и опирается на неподвижный шарнир и
наклонный невесомый стержень. К раме приложены внешние сосре-
сосредоточенные силы и моменты. Учитывая погонный вес рамы, найти
реакции опор.
План решения
1.	Согласно аксиоме о связях, освобождаем раму от связей. Дей-
Действие опор заменяем их реакциями. Выбираем систему координат. В
неподвижном шарнире имеются две неизвестные составляющие реак-
реакции (горизонтальная и вертикальная), а в невесомом опорном стержне
— одна неизвестная реакция, направленная вдоль стержня. Все на-
наклонные силы раскладываем на составляющие вдоль осей координат.
2.	К центру каждого участка рамы прикладываем его вес, вычис-
вычисленный по формуле Gk = lkp, где lk — длина участка, р — погонный
вес рамы (вес единицы длины стержня, из которого составлена рама).
3.	Составляем уравнение моментов всех сил, действующих на раму,
относительно неподвижного шарнира. Определяем из этого уравне-
уравнения реакцию опорного стержня.

32
Гл. 2. Произвольная плоская система сил
4.	Составляем уравнения проекций всех сил на оси х и у. Из этих
уравнений определяем составляющие реакции неподвижного шарнира
(горизонтальную и вертикальную).
5.	Выполняем проверку решения, составляя уравнение моментов
относительно какой-либо точки, не лежащей на линиях действия ис-
искомых реакций.
Пример. Тяжелая однородная рама расположена в вертикальной
плоскости и опирается на неподвижный шарнир А и наклонный не-
невесомый стержень Н. К раме приложены внешние сосредоточенные
силы Р = 20 кН, Q = 10 кН и момент М = 100 кНм. Дано: 7 = 60°,
а = 60°, Р = 50°, АВ = 2 м, ВС = 4 м, CD = 6 м, DH = 4 м, КС = 2 м
(рис. 20). Учитывая погонный вес рамы р = 4 кН/м, найти реакции
опор.
Рис. 20
Решение
1.	Освобождаем раму от связей. Действие опор заменяем их ре-
реакциями (рис. 21). Выбираем систему координат с началом в точке
А. В неподвижном шарнире А реакция RA имеет две неизвестные
компоненты ХА и YA. Невесомый опорный стержень в шарнире Н
заменяем на его реакцию, направленную по стержню (т.е. под углом
7 к горизонту).
2.	К центру каждого участка рамы (всего четыре прямолинейных
участка) прикладываем его вес, вычисленный по формуле Gk = lkp,
где — lk, k = 1, ...,4 — длины отрезков рамы АВ, ВС, CD и DH, p
— погонный вес рамы.

2.1. Равновесие тяжелой рамы
33
Qsin/3
D
С
5.196
Gdh
Qcosfl
М
Gdc
Ya
A
3.464
3.464
Gbc
Gab
2
Рис. 21
3. Составляем уравнение моментов относительно шарнира А, вы-
выделяя в нем для удобства счета отдельные слагаемые:
= 0. A)
МА = MA(RH) + МА(Р) + MA(Q) + MA(Gk)
Момент MA(RH) реакции опоры
MA(RH) = RHh = -RH((HD+ CB) sinacos'y+
+ (HD cos a + DC + С В cos a + AB) sin 7),
где h — плечо реакции RH взятое со знаком момента.
Моменты сил Р и Q и момент MA(Gk) сил тяжести участков:
МА(Р) = -P{ND + С В) sin a = -103.923 кНм,
MA(Q) = -QcosCCB sina - Qsin P(KC + СВcosa + AB) =
= -69.282 кНм,
MA(Gk) = GDH{{ND + CB) cos a + DC + AB)+
+ GDC{DC/2 + СБ cos а + AB)+
+ GCB {CB/2 cos а + AB) + GA?> АБ/2.
Вычисляя величины сил тяжести участков
GAB = 2 • 4 = 8 кН, СБС = 4 • 4 = 16 кН,
GDC = 6 • 4 = 24 кН, GDH = 4 • 4 = 16 кН,
3 М.Н. Кирсанов

34
Гл. 2. Произвольная плоская система сил
получаем MA(Gk) = 400 кНм.
В итоге уравнение моментов A) принимает вид
-13.856ДЯ - 103.923 - 69.282 + 400 + 100 = 0.
Отсюда находим реакцию стержня
*-=НИ—н-
4. Реакции ХА и YA определяем из уравнений проекций:
= 0,
ХА = -36.792 кН,
= YA- GAB - GBC - GDC -
YA = 34.915 кН.
Ответы заносим в таблицу. Моменты — в кНм, силы — в кН.
MA(Q)
-69.282
МА(Р)
-103.923
400
h
-13.856
хА
-36.792
Ya
34.915
Rh
23.584
5. Проверка. Составляем сумму моментов всех сил, действующих
на раму, включая найденные реакции опор, относительно произволь-
произвольной точки, например, К. Этот выбор оправдывается тем, что в урав-
уравнение моментов войдут все найденные реакции, а известная сила Q
не войдет (ее проверять не требуется), и уравнение будет на два сла-
слагаемых короче
J2 Мк = -RH • 3.464 cos 7 - RH • 6 sin 7 - P • 1.732 + M + GDH • 5+
G
DC
H
~ GBC ' 3 - GAB
DH
YA ' 6 + XA ' 3'464 =
Условия ЗАДАЧ. Тяжелая однородная рама расположена в вер-
вертикальной плоскости и опирается на неподвижный шарнир А и на-
наклонный невесомый стержень Н. К раме приложены горизонталь-
горизонтальная сила Р, наклонная сила Q и момент М. Учитывая погонный вес
рамы р, найти реакции опор.

2.1. Равновесие тяжелой рамы
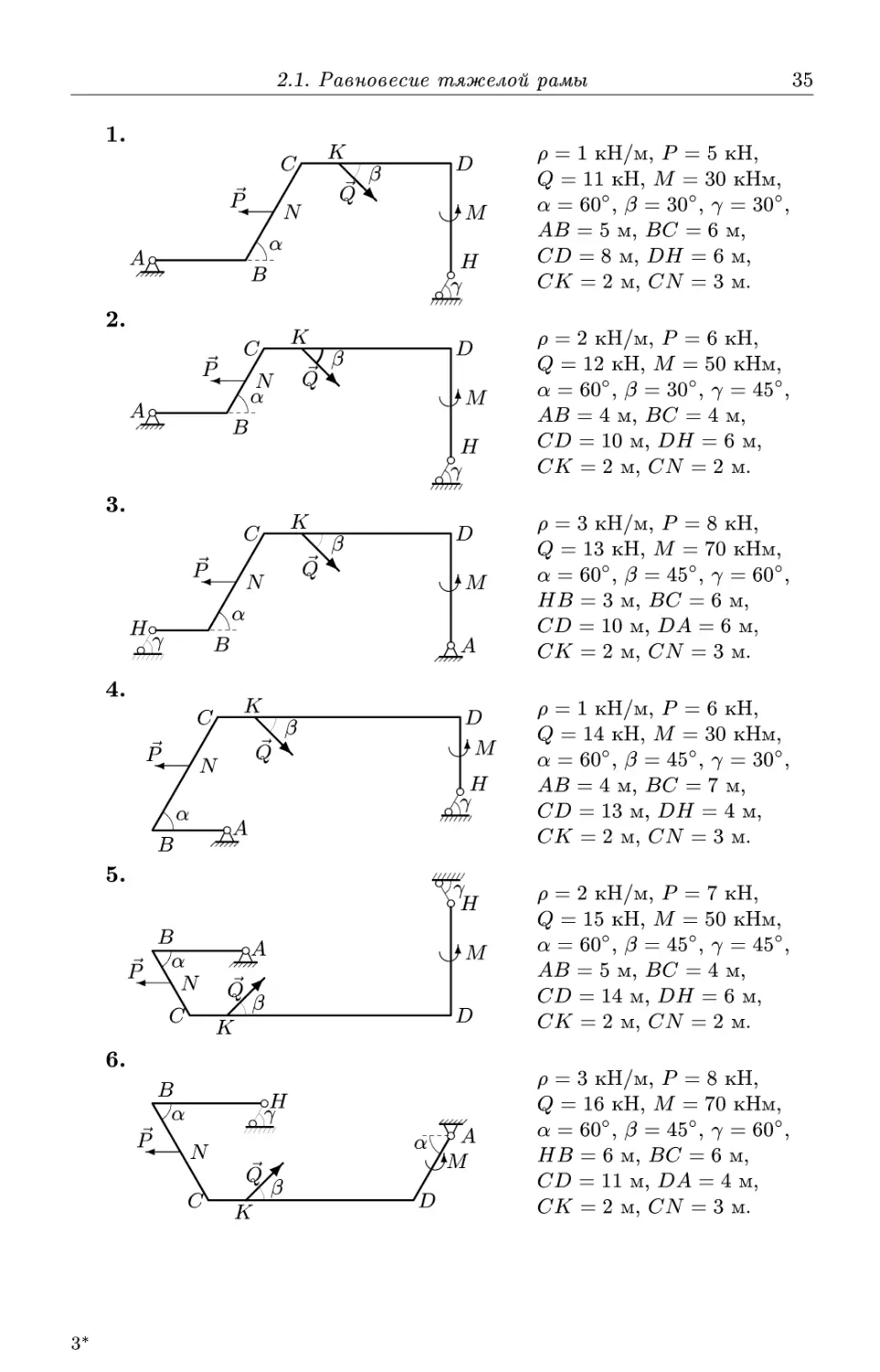
35
5.
6.
Б
7Ь
О/
D
К
р = 1 кН/м, Р = 5 кН,
Q = 11 кН, М = 30 кНм,
а = 60°, /3 = 30°, 7 = 30°,
= 8 м, ?>Я = 6 м,
= 3 м.
р = 2 кН/м, Р = 6 кН,
Q = 12 кН, М = 50 кНм,
а = 60°, /3 = 30°, 7 = 45°,
АВ = 4 м, ВС = 4 м,
CD = 10 м, DH = 6 м,
Cif = 2 м, CiV = 2 м.
р = 3 кН/м, Р = 8 кН,
Q = 13 кН, М = 70 кНм,
а = 60°, /3 = 45°, 7 = 60°,
ЯБ = 3 м, ВС = 6 м,
CD = 10 м, ?>А = 6 м,
СК = 2 м, CN = 3 м.
р = 1 кН/м, Р = 6 кН,
Q = 14 кН, М = 30 кНм,
а = 60°, /3 = 45°, 7 = 30°,
АВ = 4 м, БС = 7 м,
CD = 13 м, DH = 4 м,
Cif = 2 м, CN = 3 м.
р = 2 кН/м, Р = 7 кН,
Q = 15 кН, М = 50 кНм,
а = 60°, /3 = 45°, 7 = 45°,
АВ = 5 м, БС = 4 м,
CD = 14 м, DH = 6 м,
Cif = 2 м, CiV = 2 м.
р = 3 кН/м, Р = 8 кН,
Q = 16 кН, М = 70 кНм,
а = 60°, /3 = 45°, 7 = 60°,
ЯБ = 6 м, БС = 6 м,
= 11 м, DA = 4 м,
= 2 м, CiV = 3 м.
3*

36
Гл. 2. Произвольная плоская система сил
7.
10.
к
р = 1 кН/м, Р = 7 кН,
Q = 17 кН, М = 30 кНм,
а = 60°, /3 = 60°, 7 = 30°,
АВ = 4 м, БС = 11 м,
CD = 6 м, ?># = 6 м,
Б^ = 3 м, CN = 3 м.
р = 2 кН/м, Р = 8 кН,
Q = 18 кН, М = 50 кНм,
а = 60°, /3 = 60°, 7 = 45°,
АВ = 6 м, БС = 10 м,
CD = 6 м, ?># = 5 м,
Б^ = 3 м, CN = 3 м.
р = 3 кН/м, Р = 9 кН,
Q = 19 кН, М = 70 кНм,
а = 60°, /3 = 60°, 7 = 60°,
НВ = 7 м, ВС = 11 м,
= 3 м, C7V = 2 м.
р = 2 кН/м, Р = 8 кН,
Q = 20 кН, М = 50 кНм,
а = 60°, /3 = 60°, 7 = 45°,
АВ = 6 м, ВС = 8 м,
CD = 4 м, ?># = 3 м,
ВК = 2 м, C7V = 2 м.
Ответы
1
2
3
4
5
6
7
8
9
10
Ma(Q)
МА(Р)
EfcMA(Gfc)
кНм
-104.500
-84.000
18.385
-74.862
26.136
-85.259
-44.167
-46.765
131.636
138.564
12.990
10.392
27.215
20.785
-12.124
-6.928
-6.062
-20.785
-15.588
27.713
-243.5
-468.0
487.5
-104.3
-187.0
754.5
-251.5
-487.0
281.3
-313.0
h
м
8.696
13.107
-14.258
4.464
9.571
-9.526
6.500
7.778
-9.526
12.538
ХА
YA
Rh
кН
-34.901
-30.914
-22.341
-28.795
5.480
-41.750
-34.704
-44.868
-24.027
-23.455
12.963
27.478
47.561
23.526
38.307
3.112
20.820
23.720
51.973
19.225
35.074
37.508
42.298
28.746
12.850
76.873
41.805
64.867
49.054
7.714

2.2. Ферма. Аналитические методы расчета	37
Предупреждение типичных ошибок
1.	При вычислении весов участков рамы не надо мельчить участки.
Берите прямолинейные участки от одного изгиба до другого или до
опоры.
2.	Вычисляя момент наклонной силы, учитывайте обе ее состав-
составляющие. Не забывайте, что плечо силы относительно точки равно
расстоянию от точки до линии действия силы, а не до точки прило-
приложения силы.
3.	Знак сосредоточенного момента (пары) в уравнении моментов
не зависит от взаимного расположения точки приложения момента и
точки, относительно которой уравнение составляется. Он определя-
определяется самим моментом (против часовой стрелки "плюс", по часовой
стрелке "минус"). Точка приложения пары не требует точного зада-
задания, так как по свойству пары ее можно переносить в любую точку
тела, не меняя воздействия на тело.
4.	Точку приложения силы можно переносить вдоль линии дейст-
действия силы, не меняя воздействия силы на тело (вектор силы в тео-
теоретической механике является скользящим). Перенеся силу вдоль ее
линии действия поближе к точке, относительно которой вычисляется
ее момент, можно упростить определение момента.
5.	Наклонный стержень одним концом закреплен на неподвижном
шарнире. Часто вместо того, чтобы просто отбросить стержень и
приложить к телу одну силу RH, направленную вдоль стержня, сту-
студент изображает две реакции этого шарнира, после чего в задаче
количество неизвестных становится больше, чем уравнений. Одно-
Одновременно с такой ошибкой возникает вопрос, чему равна длина на-
наклонного опорного стержня? Длина стержня в задаче не дана.
6.	Вес участков рамы учитывайте только в тех задачах, где это
оговорено. В данной задаче рама имеет вес.
2.2. Ферма. Аналитические методы
расчета
Постановка задачи. Плоская ферма опирается на неподвиж-
неподвижный и подвижный шарниры. К узлам фермы приложены нагрузки.
Найти усилия в стержнях фермы методом Риттера*' или мето-
методом вырезания узлов.
*) Август Риттер A826-1906) — немецкий механик.

38	Гл. 2. Произвольная плоская система сил
Эта задача является усложненным вариантом задачи из §1.1, где
усилия в стержнях можно было легко определить только из уравнений
проекций, не находя реакции опор и не привлекая понятие момента
силы. Аналогично можно поступить и в этой задаче, однако поря-
порядок системы линейных уравнений, описывающей равновесие всех уз-
узлов, будет велик, поэтому, во-первых, надежно решить такую систему
можно только с помощью компьютера (§ 15.1, с. 350), во-вторых, та-
таким образом будет проделана лишняя работа, так как система урав-
уравнений содержит усилия всех стержней, в том числе и тех, которые по
условию задачи не требуется определять. Поэтому для решения слож-
сложных ферм, содержащих большое число стержней, применим метод
Риттера, основная идея которого — независимое определение усилий
в стержнях. Эту же идею можно с успехом применять и в других
задачах статики.
План решения
1.	Освобождаем ферму от внешних связей. Действие опорных
шарниров заменяем их реакциями. Для определения реакций опор
составляем три уравнения равновесия.
2.	Проверяем найденные реакции, составляя еще одно уравнение
равновесия фермы.
3.	В тех стержнях, где это возможно, усилия находим методом
Риттера *' . Мысленно разделяем ферму на две части, пересекая три
стержня (сечение Риттера). Действие разрезанных стержней заме-
заменяем их усилиями, направляя соответствующие векторы из узлов в
сторону сечения, предполагая стержни растянутыми.
Рассматриваем равновесие одной из частей фермы (как правило,
где меньше нагрузок). Для стержней, усилия в которых необходимо
определить, находим точки Риттера (моментные точки). Они явля-
являются точками попарного пересечения линий действия сил в рассечен-
рассеченных стержнях. Искомые усилия определяем из уравнений моментов
рассматриваемой части относительно точек Риттера.
Если два стержня в сечении параллельны, то точки Риттера для
третьего стержня не существует, и для определения усилия в нем
необходимо составить уравнение проекций на ось, перпендикулярную
параллельным стержням.
В уравнение метода Риттера всегда входит усилие только одного
стержня. Это позволяет искать усилия независимо одно от другого,
Другие названия — метод сечений, метод моментных точек.

2.2. Ферма. Аналитические методы расчета
39
уменьшая тем самым возможность ошибок и избегал накопления не-
неизбежных погрешностей округления в численных расчетах.
4. Определяем усилия методом вырезания узлов (§ 1.1). Этот ме-
метод применяют в тех случаях, когда сечения Риттера для нужного
стержня не существует. Вырезаем узел фермы, к которому подходит
стержень с искомым усилием. Выбираем оси и составляем уравне-
уравнения равновесия узла в проекциях. Решаем уравнения относительно
искомого усилия. Если к узлу подходит более двух стержней с неиз-
неизвестными усилиями, то метод вырезания узлов можно комбинировать
с методом Риттера.
Пример. Плоская ферма опирается на неподвижный и подвижный
шарниры (рис. 22). К узлам фермы приложены две вертикальные
нагрузки Р = 90 кН и две наклонные Q = 40 кН и F = 38 кН,
а = 55°, C = 15°. Найти усилия в стержнях 1-5.
Рис. 22
Решение
1. Освобождаем ферму от внешних связей. Действие опор заме-
заменяем их реакциями. Левую (неподвижную) шарнирную опору заме-
заменяем двумя составляющими реакции ХА, УА, правую (подвижную)
— одной вертикальной YB (рис. 23). Для определения реакций опор
составляем три уравнения равновесия — уравнение проекций на го-
*)
ризонтальную ось х и два уравнения моментов относительно опор ' :
B = 0,
= 8 P - 8 Q sin P - 4Q cos C + 5 F sin a + 2 P - 10 YA = 0.
*) Уравнение проекций на ось у оставим для проверки реакций Уд и

40
Гл. 2. Произвольная плоская система сил
Система уравнений состоит из трех независимых друг от друга
уравнений, решение которых легко найти, подставив численные зна-
значения нагрузок и углов из условия
УА = 81.827 кН, YB = 118.948 кН, ХА = -60.433 кН.
2. Проверяем найденные вертикальные реакции, составляя урав-
уравнение проекций всех сил на ось у:
P + QsmP-Fsma-P + YB =
= 81.827 -90 + 40 sin 15 - 38 sin 55 - 90 + 118.948 = 0.
Горизонтальную реакцию ХА можно проверить, составив еще одно
уравнение моментов, например относительно точки D.
3. Методом Риттера находим усилия в стержнях 1, 2, 3. Сече-
Сечением I-I (рис. 23) мысленно разделяем ферму на две части, пересекая
три стержня. Действие разрезанных частей заменяем их усилиями.
I	II
I	D I
Ya
Рис. 23
Рассматриваем левую часть (рис. 24), на которую действуют четыре
известных силы ХА, Уд, Р, Q и реакции стержней, направленные
из узлов к сечению. Точки Риттера R1, R2-, R% находятся в точках
попарного пересечения линий действия сил S1^ S2, S3. Номер точки
Риттера соответствует номеру рассеченного стержня, который через
эту точку не проходит.
Точка R2 находится на продолжении стержня 1. Расстояние до
нее легко вычислить, зная угол 7 между стержнем 1 и горизонталью:
tg7 = 1/3.

2.2. Ферма. Аналитические методы расчета
41
ХА
12
Рис. 24
Уравнения метода Риттера имеют вид
J2MRi = -4-Sf1cos7-4-Qcos/3-2-yA = 0,
J2MR2 = -12-S2 cos45 - 4-Q cos/3 - 12-Qsin/3 + 12 • P - 14 • YA = 0,
J2MRs = 3 • S3 - 1 • Qcos/3 - 3 • Qsin/3 + 3 • P - 5 • YA + 3 • XA = 0.
Находим решение системы: S'1 = —83.854 кН, S2 = —40.584 кН,
S3 = -130.04 кН.
4. Методом вырезания узлов определяем S4. Вырезаем узел С
(рис. 23) и составляем уравнение проекций на ось у (рис. 25), из ко-
которого сразу же определяем искомое усилие:
^У. = S4-Fsina = 0, 54 = 31.128 кН.
а
Рис. 25
Рис. 27
Усилие больше нуля, следовательно, стержень 4 растянут. Усилие
в стержне 5 методом Риттера определить нельзя — не существует
сечения, делящего ферму на две части и пересекающего при этом три

42
Гл. 2. Произвольная плоская система сил
стержня. В этом состоит недостаток метода. Поэтому воспользуемся
методом вырезания узлов совместно с методом Риттера. Находим
S5 из условия равновесия узла D. К узлу подходят три стержня с
неизвестными усилиями. Одно из них — S7 легко найти по методу
Риттера. Проводим сечение II—II (рис. 23) и рассматриваем правую
часть фермы (рис. 26). Для определения S7 составляем уравнение
моментов относительно точки Риттера R7:
Находим S7 = —59.474 кН. Заметим, что для определения усилия
S8 по методу Риттера, необходимо составить уравнение проекций на
ось у.
Вырезаем узел D и составляем уравнения равновесия (рис. 27):
Y,Xi = S7- Swcos7 = 0,Y,Yi = ~S5 ~ Swsin7 = 0.
Исключая #10, находим
S10 = #7/cos7, S5 = -S10 sin 7 = -S7tg7 = 19.825 кН.
Результаты расчетов в кН занесем в таблицу:
ХА
-60.433
Уа
81.827
Ув
118.948
Si
-83.854
s2
-40.584
-130.04
31.128
Sb
19.825
Условия ЗАДАЧ. Плоская ферма опирается на неподвижный и
подвижный шарниры. К узлам фермы приложены две вертикальные
нагрузки Р и две наклонные — Q и F. Размеры даны в метрах.
Найти усилия в стержнях 1-5.
Р = 2 кН, Q = 9 кН, F = 9 кН,
а = 60°, /3 = 30°.
Р = 2 кН, Q = 8 кН, F = 10 кН,
а = 60°, р = 15°.

2.2. Ферма. Аналитические методы расчета
43
Р = 3 кН, Q = 7 кН, F = 1 кН,
а = 60°, /3 = 45°.
5.
Р = 4 кН, Q = 4 кН, F = 2 кН,
а = 30°, /3 = 45°.
6.
Р = 5 кН, Q = 5 кН, F = 3 кН,
а = 45°,/3 = 45°.
Р = 6 кН, Q = 6 кН, F = 4 кН,
а = 45°,/3 = 15°.
Р = 7 кН, Q = 7 кН, F = 5 кН,
а = 60°,/3 = 15°.
Р = 8 кН, Q = 3 кН, F = 7 кН,
а = 30°,/3 = 30°.
10.
Р = 8 кН, Q = 5 кН, F = 20 кН,
а = 45°,/3 = 30°.
Р = 3 кН, Q = 6 кН, F = 15 кН,
а = 45°, /3 = 45°.

44
Гл. 2. Произвольная плоская система сил
Ответы
1
2
3
4
5
6
7
8
9
10
Реакции опор
хА
3.294
-12.727
4.450
1.096
-5.657
-8.624
4.261
-3.464
-9.812
-14.849
Уа
4.129
2.563
4.423
2.375
7.942
1.305
12.776
19.485
14.272
5.477
>, кН
Rb
12.165
8.027
7.393
9.453
0.644
11.971
7.366
1.515
18.370
6.886
Si
-1.880
-14.552
0.022
-2.938
-0.429
-0.870
-6.388
16.971
-9.515
2.000
Усилия i
s2
-9.891
-28.897
1.016
8.157
6.161
6.640
-7.219
-26.257
-41.577
-5.496
в стержнях, кН
S3
16.118
41.136
4.084
-4.000
-3.927
4.799
6.458
3.206
51.690
1.886
5.665
8.660
0.866
-3.525
2.121
-2.485
6.602
3.500
7.870
10.607
S5
-2.129
8.027
-3.000
1.583
-3.333
-11.971
7.000
-0.742
8.000
-1.826
Предупреждение типичных ошибок
1.	Следует помнить три основных свойства сечения Риттера:
•	Сечение делит ферму на две части.
•	Сечение пересекает ровно три стержня.
•	Сечение не проходит через шарниры.
Второе свойство имеет исключения. Существуют фермы, которые
одним сечением можно разделить на две, рассекая N > 3 стержней.
При этом для одного из стержней существует точка Риттера — точка
пересечения остальных N — 1 стержней (подумайте, как выглядит
такая ферма).
2.	Сечение Риттера не обязательно должно изображаться непре-
непрерывной линией. В ферме на рис. 4, с. 15 для определения усилия в
стержне АВ надо выполнить разрывное сечение (какое?). Экспери-
Экспериментируя с сечениями, не забывайте про три его основных свойства.
3.	Рассматривая одну из частей рассеченной фермы, забудьте на
время о существовании другой. Иначе в уравнения равновесия вы
можете случайно включить внешние силы или реакции опор отбро-
отброшенной части.
4.	Не стоит беспокоиться, если точка Риттера находится на от-
отрезанной части, располагается где-нибудь далеко или попадает на
шарнир. Ее положение может быть где угодно.
5.	В уравнения метода Риттера (моментов или проекций) должно
войти только одно усилие стержня фермы. В этом основной смысл
метода Риттера. Очень часто встречается следующая ошибка. Со-
Составляя уравнение, студент неправильно выбирает точку Риттера или

2.3. Ферма. Графический расчет	45
составляет не то уравнение, например, уравнение проекций вместо
уравнения моментов. При этом в уравнение кроме одного неизвест-
неизвестного усилия входят и другие, ранее найденные. В принципе такое
уравнение может быть и верно, и ответ получится верным, но это
не метод Риттера, где определение усилий производится независимо
одно от другого во избежание накопления ошибок.
6.	Положение точки Риттера для каждого стержня не зависит от
рассматриваемой части. Однако степень сложности уравнения мо-
моментов для разных частей фермы может существенно отличаться.
Для большей надежности решения уравнение Риттера (в форме урав-
уравнения моментов или уравнения проекций) для одной части может слу-
служить проверочным для другой.
7.	Проверить расчет можно на компьютере. Программа расчета
фермы в системе Maple V приведена на с. 350.
2.3. Ферма. Графический расчет
Постановка задачи. С помощью диаграммы Максвелла-Кремо-
Максвелла-Кремоны*' найти усилил в стержнях фермы.
План решения
Графический метод расчета ферм является дополнением к анали-
аналитическим методам расчета, которые вы изучили в предыдущем па-
параграфе. Диаграмма Максвелла—Кремоны состоит из отдельных си-
силовых многоугольников. Каждый многоугольник соответствует рав-
равновесию какого-либо узла фермы.
1.	Обозначаем усилия в стержнях фермы.
2.	Освобождаем ферму от связей. Действие опор заменяем их ре-
реакциями. Составляем три уравнения равновесия. Находим реакции.
3.	Проверяем найденные реакции, составляя еще одно уравнение
равновесия.
4.	Изображаем все силы, действующие на ферму (включая найден-
найденные аналитически реакции опор), в виде векторов вне фермы. Если
реакция опоры отрицательная, то заменяем ее направление на проти-
противоположное. Для графического способа требуются только реальные
направления реакций.
5.	Обозначаем буквами или цифрами внешние поля — области чер-
чертежа, разделенные силами и стержнями фермы.
*) Джеймс Максвелл A831-1879) — шотландский физик, математик,
астроном. Антонио Кремона A830-1903) — итальянский математик.

46
Гл. 2. Произвольная плоская система сил
6.	Обозначаем буквами или цифрами внутренние поля — области,
ограниченные стержнями фермы.
7.	Внешним нагрузкам и усилиям в стержнях даем новые имена
— по соседним с силой (или стержнем) полям.
8.	Построение диаграммы Максвелла—Кремоны начинаем с мно-
многоугольника внешних сил. Выберем направление обхода фермы (по
часовой стрелке или против). Начинаем с произвольной силы. От-
Откладывая ее в масштабе и соблюдая направление, обозначаем на диа-
диаграмме начальную и конечную точку строчными буквами, соответ-
соответствующими ее новому обозначению по направлению обхода. Следую-
Следующая сила пристраивается к концу первой и т.д. до замыкания много-
многоугольника внешних сил и реакций опор.
9.	Строим точки внутренних полей на диаграмме. Точку, соот-
соответствующую внутреннему полю, можно найти, если у этого поля
построены точки двух соседних с ней полей.
Таким образом, начинать графический расчет можно с поля, у
которого имеется два соседних с ним внешних поля, уже отмечен-
отмеченные на диаграмме. Искомая точка лежит на пересечении прямых,
параллельных стержням, имена которых состоят из имени искомой
точки и точек найденных внешних полей. Этот пункт выполняем
многократно, до полного построения диаграммы. Модули усилий в
стержнях равны длинам соответствующих отрезков на диаграмме.
10.	Определяем знаки усилий. Рассматриваем шарнир фермы,
к которому подходит какая-либо внешняя нагрузка или стержень с
усилием известного знака. Равновесие шарнира изображено на диа-
диаграмме замкнутым силовым многоугольником с заданным направле-
направлением обхода. Сопоставляя направление усилия на диаграмме и его
направление в вырезанном узле, определяем знак усилия. Если на-
направление вектора на многоугольнике совпадает с направлением век-
вектора, приложенного к узлу, то усилие больше нуля. В противном
случае — усилие меньше нуля, т.е. стержень сжат.
Рис. 28

2.3. Ферма. Графический расчет	47
Пример. С помощью диаграммы Максвелла-Кремоны найти уси-
усилия в стержнях фермы (рис. 28). Q = 15 кН, Р = 30 кН, F = 20 кН,
а = 60°, C = 60°. Размеры даны в м.
Решение
1. Обозначаем усилия в стержнях фермы так, как это принято
в строительной механике. Усилия в стержнях верхнего пояса (слева
направо) — О^..., О4, диагонали (раскосы) — D1,..., D4, усилия в
нижнем поясе — U1^U21U?> (рис. 29).
Рис. 29
2. Определяем реакции опор фермы. Реакцию RB направляем
вдоль опорного стержня, т.е. под углом C к горизонту (рис. 29).
Составляем уравнения равновесия:
= ХА - Q + F cos a + RB cos C = 0,
i^5 • 8sin/3 - Р • 6 = 0,
Решаем уравнения и получаем следующие значения:
ХА = -8.32 кН, YA = 24.24 кН, RB = 26.65 кН.
3.	Проверяем вертикальные реакции, составляя уравнение проек-
проекций на вертикальную ось:
^2 У- = УА - F sin а - Р + RB sin/3 = 0.
4.	Изображаем все силы, действующие на ферму. Реакцию ХА,
которая оказалась в результате решения меньше нуля, направляем
в противоположную сторону (рис. 30). Величина этой силы \ХА\ =
= 8.32 кН.
5.	Обозначаем внешние поля — области чертежа, разделенные си-
силами и стержнями фермы, — G, D, E, G, Н, I (рис. 31). Чтобы

Гл. 2. Произвольная плоская система сил
не внести путаницу, не следует использовать буквы А, В, Q, Р, F,
имеющиеся в задаче для обозначения опор и сил.
Q
26.65
24.24
Рис. 30
6. Обозначаем внутренние поля if, L, М, JV, i2 (рис. 31).
G
26.65
24.24
Рис. 31
7. Внешним нагрузкам и усилиям в стержнях даем новые имена
— по соседним с силой (или стержнем) полям. Приведем таблицу
соответствия имен.
F
1С
Р
HI
Q
EG
хА
DE
Ya
CD
Rb
GH
Oi
EK
o2
GK
o3
GN
o4
GR
D1
KL
D2
LM
D3
MN
NR
КС
u2
MI
U3
RH
8. Строим многоугольник внешних сил. Выберем направление об-
обхода фермы по часовой стрелке. Начинаем с произвольной силы, на-
например, F = 20 кН. Откладывая в масштабе эту силу и соблюдая
ее направление, обозначаем начальную и конечную точку строчными
буквами г и с, соответствующими направлению обхода — из поля /
в поле С. Следующая по часовой стрелке нагрузка — вертикальная
реакция опоры YA = 24.24 кН. Строим ее в точке с вслед за силой F.
Конечную точку помечаем буквой d. Обход фермы продолжаем, пока
многоугольник не замкнется. Последней будет сила Р = 30 кН, обо-
обозначенная как HI. Конец ее попадает на исходную точку г (рис. 32).

2.3. Ферма. Графический расчет
49
9. Строим точки внутренних полей на диаграмме. Точку, соот-
соответствующую внутреннему полю, можно найти, если у этого поля
построены два соседних с ним поля. Таким образом, начинать гра-
графический расчет можно с поля R, у которого соседние поля Н и G
определены на диаграмме, или К с известными соседними полями Е
и С (рис. 31). Рассматриваем поле К. По направлению стержней ЕК
и КС проводим линии через точки е и с диаграммы. Точка их пере-
пересечения — к (рис. 33). Длины ек и кс равны абсолютным значениям
усилий в соответствующих стержнях.
Ah
h
Rb
d
Ya
Рис. 33
I /
/\ 9 >
m \ /
kv
h
e
/
i
\
Рис. 34
Рис. 35
На рис. 34—37 показано последовательное получение точек /, т, пи
г. При получении последней точки автоматически выполняется про-
проверка. Так, если точка г строилась на пересечении линий пг и дг, то
проверкой является прямая rh. Если она параллельна соответству-
соответствующему стержню RH, т.е. горизонтальна, то диаграмма построена
4 М.Н. Кирсанов

50
Гл. 2. Произвольная плоская система сил
верно. Заметим, что для ферм с большим числом узлов построение
диаграммы — трудоемкий процесс. Это связано с недостатком ме-
метода вырезания узлов, графической интерпретацией которого явля-
является диаграмма Максвелла—Кремоны. Недостаток вызван неизбеж-
неизбежным накоплением ошибок округления в процессе последовательного
расчета узлов.
Ah
Д/
"V
ал/
h
е
г
\
Рис. 36
Рис. 37
10. Определяем знаки усилий. Рассмотрим, например, усилие О1.
Вырезаем узел А, к которому приложено усилие О1. К этому же узлу
приложены два известных вектора реакций опор и еще одно усилие U-^
с неизвестным знаком. Как обычно, усилия стержней рисуют выходя-
выходящими из узла (рис. 38). Затем на диаграмме Максвелла-Кремоны вы-
выделяется замкнутый многоугольник сил, изображающий равновесие
узла (рис. 39). Направление обхода многоугольника (начало одного
вектора совпадает с концом предыдущего) задается по известной силе
или по усилию в стержне с ранее определенным знаком.
d
24.24
Рис. 38
Рис. 39
Здесь обход cdek против часовой стрелки задает реакция опоры YA =
= 24.24 кН (cd), или ХА = 8.32 кН (de). Если направление вектора

2.3. Ферма. Графический расчет
51
на многоугольнике совпадает с направлением вектора, приложенного
к узлу, то усилие больше нуля — стержень растянут. В противном
случае — усилие Ох (ек) меньше нуля, что соответствует сжатию
стержня. Такие усилия на диаграмме изображаются утолщенными
линиями. Кроме того, получаем U1 > 0. Аналогично определяются
знаки и других усилий. Заметим, что особенно эффективно рассмат-
рассматривать узлы, к которым подходит много стержней и приложена хотя
бы одна внешняя нагрузка.
Окончательные результаты в кН заносим в таблицу:
Oi
-27.10
о2
-9.24
-23.08
о4
-25.80
27.10
D2
-9.79
D3
9.79
D4
25.80
Ui
20.45
u2
29.49
U3
24.87
Замечание 1. Точность, с которой можно получить усилия гра-
графическим способом, обычно невысока. Результаты с тремя знаками
после запятой, данные в таблицах, получены, конечно, не графически,
а из решения задачи аналитическим методом вырезания узлов *' .
Замечание 2. Графический способ расчета ферм в реальной
инженерной практике безнадежно устарел, для расчета пространст-
пространственных ферм он вообще не годится. Однако в учебных целях, для
проверки аналитического решения и как пример изящного и быст-
быстрого определения усилий с помощью карандаша и линейки, диаграмма
Максвелла-Кремоны сохраняет свое значение.
Замечание 3. В качестве необычной задачи программирования,
предлагаем попробовать найти алгоритм автоматического постро-
построения диаграммы Максвелла—Кремоны в системе Maple V, Maple 7,
Mathematica 4 или в любом другом пакете, позволяющем работать с
графикой. Основное требование к программе — не составлять урав-
уравнения равновесия узлов фермы в проекциях. Допустимо найти ана-
аналитическим методом реакции опор.
Условия ЗАДАЧ. С помощью диаграммы Максвелла-Кремоны
найти усилия в стержнях плоской фермы, находящейся под дейст-
действием вертикальной силы Р, наклонной F и горизонтальной Q. Одна
опора фермы — неподвижный шарнир, другая — наклонный опорный
стержень. Размеры даны в метрах, нагрузки — в кН.
*) Программа расчета в системе Maple V приведена на с. 350.

52
Гл. 2. Произвольная плоская система сил
Р = 1, F = 10, Q = 1,
а = 35°,/3 = 30°.
112	2	11
а = 40°,/3 = 30°.
2	2	2	2 11
а = 45°, /3 = 30°.
1111
Р = 4, F = 2, Q = 6,
а = 50°, /3 = 45°.
2 112
р = 5, F = 1, Q = 7,
а = 55°, /3 = 45°.
р = 6, F = 3, Q = 6,
а = 60°, /3 = 45°.
Р = 2, F = 4, Q = 3,
а = 65°, /3 = 45°.
Р = 3, F = 6, Q = 4,
а = 70°,/3 = 60°.

2.3. Ферма. Графический расчет
53
10.
Р = 4, F = 7, Q = 6,
а = 75°, /3 = 60°.
1 1
Р = 5, F = 9, Q = 7,
а = 35°,/3 = 30°.
Ответы
1
2
3
4
5
6
7
8
9
10
Реакции опор, кН
Неподвижный
шарнир
хА
-18.158
-13.820
-13.348
-9.552
-15.772
-16.830
-3.815
-5.527
-10.075
-28.705
Уа
1.559
1.178
6.525
3.266
-2.379
-0.732
6.500
9.548
6.841
1.887
Опорный
стержень
Rb
10.354
8.071
4.263
3.205
11.595
13.195
-1.238
-1.050
4.527
16.550
Усилия в стержнях, кН
Нижний пояс
Ui
19.197
14.998
-1.560
0.000
14.186
16.586
0.000
-0.384
-4.000
-3.333
и2
22.055
14.058
-0.298
0.532
12.875
12.366
-2.875
-5.203
4.916
-19.195
Us
11.555
11.025
-6.823
-6.286
0.027
-1.098
-1.935
-3.586
4.877
-27.446
1
2
3
4
5
6
7
8
9
10
Усилия в стержнях,
Верхний пояс
Oi
-1.874
-1.667
-3.014
-3.205
2.860
0.772
1.238
1.286
5.657
6.009
о2
-4.172
-1.700
-4.263
-4.532
-8.280
-6.536
1.384
1.819
8.000
-0.452
О3
-5.177
-5.820
-10.318
-0.841
2.363
5.196
5.732
8.915
1.672
-3.411
о4
-5.788
-5.707
-9.228
-4.619
0.984
3.674
5.127
7.974
-4.712
-2.268
кН
Раскосы
3.459
0.333
3.014
3.205
2.660
1.407
-0.619
-1.286
-5.657
-5.838
D2
-2.100
2.120
1.228
2.452
3.941
6.597
3.447
5.529
-4.018
-3.821
D3
0.625
2.893
3.386
-2.828
-8.583
-9.521
-6.629
-9.516
5.329
2.456
?>4
5.788
1.141
4.614
4.995
-2.560
-3.674
-2.563
-3.987
3.597
3.565

54	Гл. 2. Произвольная плоская система сил
2.4. Расчет составной конструкции
Постановка задачи. Плоская рама состоит из двух частей,
соединенных одним шарниром. На раму действует момент и силы.
Учитывая погонный вес, найти реакции опор.
План решения
Составная конструкция, состоящая из двух тел, соединенных шар-
шарниром содержит четыре неизвестные реакции опор. Так как для
одного тела под действием плоской системы сил можно составить
только три независимых уравнения равновесия, то для определения
реакций необходимо рассматривать равновесие каждой части состав-
составной конструкции в отдельности.
1-й способ
1.	Разбиваем систему на два тела по сочленяющему шарниру. В
месте разбиения прикладываем реакции отброшенной части. Внеш-
Внешние связи заменяем их реакциями.
2.	Для каждого тела, образованного при разбиении, составляем по
три уравнения равновесия.
3.	Решаем систему шести уравнений. Определяем реакции опор.
4.	Делаем проверку решения, составляя уравнения равновесия це-
целой (нерасчлененной) системы.
2-й способ
1.	Разбиваем систему на два тела по сочленяющему шарниру. В
месте разбиения прикладываем реакции отброшенной части. Внеш-
Внешние связи заменяем их реакциями.
2.	Для каждого тела, образованного при разбиении, составляем
уравнения моментов относительно точки сочленения. Полученные
уравнения дополняем двумя уравнениями равновесия для всей кон-
конструкции в целом.
3.	Решаем систему четырех уравнений. Определяем реакции опор.
4.	Делаем проверку решения, составляя уравнения равновесия це-
целой (нерасчлененной) системы.
Пример. Плоская рама состоит из двух частей, соединенных в
точке С шарниром. На раму действует момент М = 100 кНм, гори-
горизонтальная сила Р = 20 кН и наклонная сила Q = 10 кН. Учитывая по-
погонный вес р = 4 кН/м, найти реакции опор (рис. 40). Дано: а = 60°,
C = 50°, АВ = 4 м, ВС = 6 м, CD = 4 м, DE = 2 м, КС = 2 м,
AN = NB.

2Л. Расчет составной конструкции
55
Решение
1-й способ
1. Разбиваем конструкцию на два тела по сочленяющему шарниру
С. Получаем две части (рис. 41—42). Внешние связи конструкции
заменяем реакциями.
Q
Рис. 40
В точке А прикладываем реакции ХА и YA, в точке Е — реакции ХЕ
и YE. К каждому телу в точке С прикладываем реакции отброшенной
части. Согласно 3-му закону Ньютона, реакции Хс и Yc для разных
частей равны по величине и направлены в противоположные стороны.
В
Qsin/3
К\
Yc
Хс С
Gab
Gbc
М
Yc
,D \E
3.464
Рис. 41
t
Gcd I
Gde
2 | 2
Рис. 42
Система уравнений равновесия двух тел, образованных при раз-
разбиении, замыкается — имеем шесть уравнений равновесия (по три
уравнения на каждую часть) и шесть неизвестных ХА, YA, XE, YE,

56
Гл. 2. Произвольная плоская система сил
2. Для каждой отдельной части составляем по три уравнения рав-
равновесия:
лев) =Ха + Р + Qcos/3 + Хс = О,
лев) = уА + Q gin/3 + ус _ Gab _ Gbc = Qj
^ев) = -XAAB sin a - YA(AB cos a + БС) -
- PNBsina -
A)
B)
cos«
(прав) _
¦хЕ = >
Y^
= 0,
- GDE (DE/2 + CD cos a) - GCD (CD/2) cos a = 0.
3. Решаем систему A—6) относительно неизвестных ХА, У
C)
D)
E)
F)
д,
YE, Хс, Yq. Можно использовать любой способ решения системы ли-
линейных уравнений (Решебник ВЫ, §2.1). Рекомендуем наиболее эф-
эффективный для таких систем метод исключения Гаусса.
Если для решения использовать компьютер, систему лучше запи-
записать в матричном виде, предварительно вычислив правые части сис-
системы A-6) и коэффициенты при неизвестных. Величины сил тяжести
участков вычисляем через погонный вес р по формуле G = pL, где L
— длина соответствующего участка. В нашем случае
GAB = 4 • 4 = 16 кН, GBC = 4 • 6 = 24 кН,
GCD = 4 • 4 = 16 кН, GDE = 4 • 2 = 8 кН.
Система A-6) имеет следующий матричный вид:
Хл	-26.428
32.339
-134.038
Y»	0
-с	24
LC	-60
1
0
-3.464
0
0
0
0
1
-8
0
0
0
0
0
0
1
0
3.464
0
0
0
0
1
4
1
0
0
-1
0
0
0
1
0
0
-
0

2.4. Расчет составной конструкции
57
Результаты расчетов в кН заносим в таблицу:
ХА
73.202
Уа
-14.943
ХЕ
-99.630
YE
71.282
Хс
-99.632
Ус
-47.281
Qsin/3
3.464
3.464
G)
4. Делаем проверку решения, составляя уравнения равновесия для це-
целой (нерасчлененной) системы (рис. 43):
= -YA((AB + CD) cos a + ВС + D?) + M-
-	P(NB + CD) sin a - XA(AB + CD) sina-
-	Q CD sin a cos /3 - Q(KC + CD cos a + DE) sin /
+ Gab ((^^ + CD) cos a -
+ Gbc(BC/2 + CD cos a +
) cos a + D?) + GDE(DE/2) = 0,
:os a + БС + DE) + M+
+ PAN sin a + X^ (AB + CD) sin a+
+ Q ЛБ sin a cos j3 + Q (Ж + ЛБ cos a) sin j3-
-GDE (DE/2 + (AB + CD) cos a + ВС) -
-	GCD((AB + CD/2) cos a + БС)-
-	GBC (ВС/2 + АБ cos a) - GAB (AB/2) cos a = 0.
(8)
Gde
Рис. 43

58
Гл. 2. Произвольная плоская система сил
2-й способ
1.	Разбиваем конструкцию на два тела по сочленяющему шарниру
С. Получаем две части (рис. 41-42). Внешние связи конструкции
заменяем реакциями.
2.	Относительно шарнира С для каждой части конструкции со-
составляем уравнения моментов C) и F). Для всей системы в целом
составляем уравнения моментов G,8) относительно опор А и Е.
3.	Решаем систему четырех уравнений C,6,7,8) относительно че-
четырех неизвестных, замечая, что система распадается на две: урав-
уравнения C) и G) для ХА и УА и уравнения F) и (8) для ХЕ и YE.
4.	Делаем проверку решения, составляя уравнения равновесия це-
целой (нерасчлененной) системы (рис. 43):
Е^(цел) = ХА + Р + Qcos/З + ХЕ = О,
^ У/Цел) = уА + Q gin/3 _ Gab _ Gbc +yE_ о^ _ G^ = a
Условия ЗАДАЧ. Плоская рама состоит из двух частей, соеди-
соединенных в точке С шарниром. На раму действует момент М, гори-
горизонтальная сила Р и наклонная сила Q. Учитывая погонный вес р,
найти реакции опор.
1.
к
в
D
Е
D
Р = 4 кН, Q = 1 кН, М = 3 кНм,
р = 1 кН/м, а = 60°, C = 30°,
АВ = 5 м, ВС = 4 м, CD = 9 м,
DE = 6 м, CN = 2 м, СК = 2 м.
Р = 5 кН, Q = 1 кН, М = 3 кНм,
р = 2 кН/м, а = 60°, /3 = 30°,
АВ = 4 м, ВС = 6 м, CD = 9 м,
DE = 6 м, САГ = 3 м, СК = 2 м.
LD = 2 м
Р = 7 кН, Q = 2 кН, М = 9 кНм,
р = 3 кН/м, а = 60°, /3 = 45°,
АВ = 3 м, ВС = 7 м, CD = 10 м,
= 4 м, САГ = 3 м, СК = 2 м.

2Л. Расчет составной конструкции
59
С К
Р = 5 кН, Q = 2 кН, М = 5 кНм,
р = 1 кН/м, а = 60°, /3 = 45°,
АВ = 4 м, ВС = 4 м, CD = 14 м,
?>? = 6 м, CN = 2 м, СК = 2 м.
Р = 7 кН, Q = 2 кН, М = 6 кНм,
р = 2кН/м, а = 60°,/3 = 60°,
АВ = 5 м, ВС = 6 м, С?> = 13 м,
DE = 4 м, CN = 3 м, СК = 2 м.
LD = 2 м
6.
Р
S-
К
м
Р = 8 кН, Q = 3 кН, М = 9 кНм,
р = ЗкН/м, а = 60°,/3 = 60°,
АБ = 6 м, ВС = 4 м, CD = 12 м,
DE = 4 м, CN = 2 м, СК = 2 м.
Р = 7 кН, Q = 3 кН, М = 9 кНм,
р = 1 кН/м, а = 60°, /3 = 75°,
АВ = 4 м, ВС = 11 м, СТ> = 6 м,
= 6 м, CN = 3 м, ВК = 3 м.
Р = 8 кН, Q = 3 кН, М = 9 кНм,
р = 2 кН/м, а = 60°, /3 = 75°,
АВ = 6 м, ВС = 11 м, СТ> = 4 м,
?>? = 5 м, CN = 2 м, ВК = 3 м.
LC = 7 м.
Р = 9 кН, Q = 4 кН, М = 9 кНм,
р = 3 кН/м, а = 60°, /3 = 75°,
АВ = 4 м, ВС = 11 м, СТ> = 7 м,
= 4 м, САГ = 3 м, ВК = 3 м.
Р = 6 кН, Q = 4 кН, М = 9 кНм,
р = 3 кН/м, а = 60°, /3 = 30°,
АВ = 6 м, ВС = 7 м, С?> = 6 м,
= 3 м, CN = 3 м, ВК = 2 м.

60
Гл. 2. Произвольная плоская система сил
Ответы
1
2
3
4
5
6
7
8
9
10
хА
Уа
ХЕ
YE
Sol
кН
11.062
4.134
—
14.529
6.000
—
10.323
-7.224
-7.965
-9.464
8.270
9.499
9.779
18.835
-5.005
-1.964
4.504
-12.671
144.598
59.348
-7.928
—
5.586
-10.943
—
6.500
-16.547
—
—
-
16.230
-50.005
63.635
7.751
-188.232
77.366
19.598
-5.619
-62.735
8.652
—
91.006
—
—
247.505
—
—
67.392
—
-
МА
МЕ
кНм
—
—
—
—
—
—
—
—
1559.959
415.158
—
—
-376.867
—
—
-684.804
—
—
—
-
Ответы на типичные вопросы, возникающие при решении задачи
1.	Что представляет собой опора в точке Е в варианте 3,6 и в
точке А в варианте 9?
Это жесткая заделка. Реакции заделки — две силы, например,
ХЕ и YE и момент МЕ.
2.	Куда направлять неизвестные реакции? Для двусторонних свя-
связей (не освобождающихся) реакции — силы принято направлять по
положительному направлению осей координат, а моменты — против
часовой стрелки. В данной задаче и везде, где это специально не
оговорено, связи двусторонние.
3.	Какие еще возможны схемы решения задачи?
Можно составить систему из шести уравнений, куда войдут по два
уравнения равновесия для каждой части и два уравнения равновесия
рамы в целом B+2+2). Возможны также варианты 3+2+1, 3+1+2
и другие схемы *^ . Однако, здесь следует проявлять осторожность в
выборе вида уравнений. В частности, если для каждой части и для
рамы в целом составить уравнение проекций на одну и ту же ось
или уравнение моментов относительно одной и той же точки, то три
Х\ ; = 0, z^^i	— 0> 1^Х> } = 0,
будут зависимыми — сумма уравнений для частей дает уравнение для
целой конструкции.
4.	Можно ли разбить раму не по шарниру, а по какой-либо другой
точке, например, по угловой?
*) Невозможно только появление в таких схемах цифры 4, так как для
одного тела в плоской задаче статики более трех независимых уравнений
равновесия не существует.

2.5. Конструкция с распределенными нагрузками	61
Можно, но не нужно, так как при этом, кроме реакций X и У, в
точке разбиения рамы следует добавить еще одну неизвестную вели-
величину — момент. Этот момент удерживает от поворота одну часть от-
относительно другой. В шарнире такой момент отсутствует, поэтому
его и берут за точку разбиения, чтобы не увеличивать число неиз-
неизвестных. Определение внутреннего момента в каждой точке рамы
составляет одну из задач сопротивления материалов и строительной
механики (построение эпюры моментов).
2.5. Конструкция с распределенными
нагрузками
Постановка задачи. Найти реакции опор плоской составной
рамы, находящейся под действием линейно распределенной нагрузки
и нагрузки, равномерно распределенной по дуге окружности.
План решения
1.	Внешние связи заменяем реакциями. Разбиваем систему на два
тела по сочленяющему шарниру. К каждой из образовавшихся час-
частей прикладываем реакции шарнира, помня о том, что части взаи-
взаимодействуют с силами равными по величине и противоположными по
направлению.
2.	Линейную нагрузку с максимальным значением qrnax, распреде-
распределенную по треугольнику, заменяем на сосредоточенную Q в центре
тяжести треугольника A/3 длины участка L нагрузки, считая от
прямого угла). Значение нагрузки вычисляем по формуле площади
треугольника Q = qmaxL/2.
3.	Нагрузку д, равномерно распределенную по дуге окружности
радиусом R с центральным углом 2а, заменим ее равнодействующей
Q = q-2Rsma, направленной по биссектрисе центрального угла ([19],
§21).
4.	Для каждого тела составляем по три уравнения равновесия.
5.	Решаем систему шести уравнений. Определяем реакции опор.
6.	Делаем проверку решения, составляя уравнения равновесия для
целой (нерасчлененной) системы.
Пример. Найти реакции опор плоской составной рамы, находя-
находящейся под действием линейно распределенной нагрузки с максималь-
максимальной интенсивностью q± = 10 кН/м на вертикальном участке рамы А В

62
Гл. 2. Произвольная плоская система сил
и нагрузки с интенсивностью q2 = 2 кН/м, равномерно распределен-
распределенной по дуге С К окружности с центром в точке О (рис. 44). Л5 = 3 м,
ВС = 6 м, DE = 4 м, R = 5 м, СК = тгД/3.
Рис. 44
Решение
1. Внешние связи заменяем реакциями ХА, YA, XE, YE. Число не-
неизвестных реакций больше трех. Следовательно, для решения задачи
необходимо разбить конструкцию на две и рассмотреть равновесие
каждой образовавшейся части (рис. 45—46).
\YC
С
Рис. 45
Рис. 46
При разбиении по шарниру к каждой из частей прикладываем ре-
реакции шарнира, помня о том, что части взаимодействуют с силами,
равными по величине и противоположными по направлению (об этом
шла речь в § 2.4, с. 55).

2.5. Конструкция с распределенными нагрузками	63
2.	Нагрузку, распределенную по линейному закону, заменяем со-
сосредоточенной Q1? приложенной к раме на расстоянии АВ/3 от мак-
максимального значения qx в том же направлении (рис. 45). Величина
равнодействующей Q1 вычисляется по формуле площади прямоуголь-
прямоугольного треугольника с катетами АВ и q^\
Qx = \qxAB = |lO - 3 = 15 кН.
3.	Нагрузку с интенсивностью q2, равномерно распределенную по
дуге СК, заменяем ее равнодействующей
Q2 = q2- 2Rsin (	) = 2 ¦ 2 • 5sinGr/6) = 10 кН,
\2R J
направленной по биссектрисе угла LKOC = 60° (рис. 47). Так как
2i^sinGr/6) = СК, то величина Q2 совпадает со значением равнодей-
равнодействующей нагрузки, равномерно распределенной по хорде СК, той
же интенсивности q2. Воспользуемся тем, что вектор силы в теоре-
теоретической механике является скользящим. Для удобства вычисления
q момента силы Q2 переносим точку ее
приложения вдоль линии действия силы
в центр окружности О. То, что точка О
не принадлежит раме, и сила как-бы "зави-
"зависает" в воздухе, не должно смущать. Твер-
Твердое тело CDE можно мысленно расширить
до точки О, давая, таким образом, силе Q2
реальную точку приложения.
4.	Составляем уравнения равновесия частей рамы:
= ХА (АВ + ВС sin 30°) - YA ВС cos 30° -
- Q^AB/S + ВСsm30°) = 0, A)
E ^(npaB) =YE-YC-Q2 sin 30° = 0,
^рав) = XE(DE + R) + YER- Q2Rsin30° = 0.
5. Решаем систему A) шести уравнений с шестью неизвестными. Ре-
Результаты расчетов в кН заносим в таблицу:

64
Гл. 2. Произвольная плоская система сил
хА
18.322
YA
9.609
хЕ
5.338
Ye
-4.609
*с
-3.322
Yc
9.609
6. Выполняем проверку решения — составляем уравнения момен-
моментов для всей системы в целом (рис. 48):
^ = -XA(R + DE- AB-ВС sm30°)-
-YA(BC cos30° + R) + QX(R + DE - AB/3 - ВС sin 30°)+
+ Q2 cos 30° (# + ?>?) = 0,
J2 М^ел) = XE(R + DE-AB- ?Csin30°)+
+ YE(BCcos30° + R) + B/3H! ЛВ-
- Q2 sin 30°(ВС cos 30° + Д) + Q2 cos 30°(AB
= 0.
Замечание. Можно предложить второй способ решения задачи,
рассмотренный в предыдущем параграфе (с. 54). Для каждого тела,
образованного при разбиении, составляем уравнения моментов от-
относительно точки сочленения С. Полученные уравнения дополняем
двумя уравнениями равновесия для всей конструкции в целом (рис. 48).
Уа
ХА
^Н?>
х
Е ХЕ
5.196
Рис. 48
Для данного примера это уравнения моментов относительно опорных
шарниров А и Е.
Условия ЗАДАЧ. Найти реакции опор плоской составной рамы,
находящейся под действием линейно распределенной нагрузки с мак-
максимальной интенсивностью q± и нагрузки с интенсивностью q2, рав-
равномерно распределенной по дуге окружности. Участок CD пред-
представляет собой четверть окружности радиуса R с центром в О.

2.5. Конструкция с распределенными нагрузками
65
3.
qi = 11 кН/м,	Д = 6м,
q2 = 5 кН/м,	АВ = 6 м,
ВС = 9 м,	Ci^ = ttR/6 м,
= 5 м.
<?i = 8 кН/м,	Л = 8 м,
<?2 = 7 кН/м,	АВ = 8 м,
ВС = 8 м,	1Ж = тгД/3
= 6 м.
gi = 11 кН/м,	Д = 7м,
gr2 = 6 кН/м,	А.В = 6 М,
ВС = 9 м,	DK = тгД/6 м,
= 5 м.
4.
gi = 11 кН/м,	Л = 9 м,
#2 = 5 кН/м,	ЛБ = 7 м,
ВС = 8 м,	СК = тгД/4 м,
= 6 м.
5.
Qi = 9 кН/м,	Л = 6 м,
<?2 = 7 кН/м,	АВ = 6 м,
ВС = 9 м,	Cif = тгЛ/4 м,
DE = 5 м.
5 М.Н. Кирсанов

66
Гл. 2. Произвольная плоская система сил
q\ = 11 кН/м,	Д = 8м,
q2 = 4 кН/м,	АВ = 7 м,
^ ВС = 8 м,	DK = ttR/6 m,
" " = 6 м.
gi=9 кН/м,	Д=7м,
<?2 = 8 кН/м,	АВ = 9 м,
ВС = 9 м,	DK = irR/4: м,
DE = 5 м.
q\ = 11 кН/м, Д = 6м,
<?2 = 5 кН/м, АВ = 6 м,
ВС = 9 м,	(Ж = тгД/6 м,
qx = 12 кН/м,	Л = 7 м,
q2 = 5 кН/м,	АВ = 6 м,
ВС = 9 м,	DK = ttR/6 м,
^ DE = 5 м.
<2i = 8 кН/м,	_R = 7 м,
д2 = 9 кН/м,	АВ = 6 м,
ВС = 9 м,	СК = irR/З м,
= 6 м.

2.6. Расчет системы трех тел, соединенных шарниром
67
Ответы
1
2
3
4
5
6
7
8
9
10
ХА
Уа
YD
ХЕ
YE
кН
-37.019
16.497
13.010
-42.002
-12.302
-34.480
29.021
-4.019
-29.207
31.500
13.882
0.287
-27.675
-37.663
-15.158
-6.584
24.549
-96.489
-43.005
-61.598
4.600
—
—
—
11.191
—
—
-10.875
—
-
—
—
-18.637
10.182
—
-20.020
-85.923
—
24.518
-
-3.482
27.713
15.675
-14.017
6.665
2.297
15.049
89.363
24.505
-16.962
МА
кНм
—
110.646
—
—
—
—
—
—
—
122.290
2.6. Расчет системы трех тел,
соединенных шарниром
Постановка задачи. Определить реакции опор конструкции,
состоящей из трех тел, соединенных в одной точке шарниром.
План решения
1.	Расчленяем конструкцию на три отдельных тела и сочленяющий
шарнир в качестве четвертого тела. Считая, что каждое из трех тел
в точке сочленения взаимодействует только с осью шарнира, действие
оси шарнира на тело заменяем ее реакциями.
2.	Записываем по три уравнения равновесия для каждого из тел и
два уравнения равновесия в проекциях для системы сил, приложенных
к оси шарнира.
3.	Решаем систему 11 уравнений с 11 неизвестными.
4.	Выполняем проверку решения, составляя дополнительное урав-
уравнение равновесия для нерасчлененной конструкции.
Пример. Определить реакции опор конструкции, состоящей из
трех тел, соединенных в точке С шарниром. В точке В конструкция
опирается на неподвижный шарнир, в точках D и Е — подвижные
шарниры, в точке А — горизонтальный опорный стержень. На кон-
конструкцию действуют силы F = 40 кН, Р = 20 кН, Q = 10 кН и
сосредоточенные моменты Мх = 100 кНм, М2 = 30 кНм (рис. 49);
а = 60°, /3 = 30°. Размеры на рисунке указаны в метрах.
5*

68
Гл. 2. Произвольная плоская система сил
D
н
А
с
Е
Рис. 49
Решение
1. Расчленяем конструкцию на три отдельных тела ADC, СВ, СЕ
и сочленяющий шарнир С в качестве четвертого тела. Считая, что
каждое из трех тел в точке сочленения взаимодействует только с осью
шарнира С, действие оси шарнира на тело заменяем ее реакциями
(рис. 50).
Хв
ХА
D
V V V Г^	ТР
-Лз -А. 2 -Al ^	Г
< 4 Щ О	>¦
1
х2
к
с
К.
С
-Уз
2
в
Ye
\
' 4
Е ¦¦
Y2
Рис. 50

2.6. Расчет системы трех тел, соединенных шарниром
69
2. Для каждого из тел (АС, ВС, ЕС) записываем по три урав-
уравнения равновесия — два уравнения проекций и уравнение моментов
относительно точки С *^ . Для системы сил, сходящихся в шарнире
С, составляем два уравнения равновесия в проекциях (рис. 50). По-
Получаем следующую систему уравнений:
=Y1-Psma + YD = 0,
M{CAC) = XA ¦ 4 - YD • 5 + Mx + P ¦ 4cosa = 0,
=X2-Qcosf3
= Y2
sin
B)
= -XB ¦ 4 + YB ¦ 6 + Q • 6sin/3 = 0.
C)
= -x1-x2-x3
= -y1-y2 -y3 =
D)
4. PeniaeM систему 11 уравнений с 11 неизвестными. Результаты рас-
расчетов в кН записываем в таблицу:
хА
-10.90
YD
19.28
Хв
-10.44
Ув
-11.96
YE
5.00
Хг
20.90
?г
-1.96
х2
19.10
Y2
6.96
х3
0
1з
-5.00
5. Выполняем проверку решения, составляя дополнительное урав-
уравнение равновесия для нерасчлененной системы (рис. 51). Моментную
точку К выбираем так, чтобы в уравнения вошли все проверяемые
величины XA,YD, XB,YB,YE:
л) = ХА • 4 + YD • 2 + Мх - М2 + Р • cosa • 4-
- Р • sin а • 7 + Q • sin/5 • 13 + YE • 13 + YB • 13 - ХБ • 4 = 0.
*) В качестве моментной точки можно выбирать любую, в том числе и
не принадлежащую телу.

70
Гл. 2. Произвольная плоская система сил
Замечание. Предложенный способ расчета не является единст-
единственным. Например, если из трех частей, соединенных в одном шар-
шарнире, можно отделить одну, имеющую в качестве опоры подвижный
шарнир (часть СЕ, рис. 50), то получится система двух тел, одно
из которых {СЕ) имеет три неизвестные реакции. Определить эти
реакции можно из системы трех уравнений равновесия этой части.
,YD
К
В
с	в
Хв
Уе 4
\Е
Рис. 51
Затем следует рассмотреть оставшуюся часть, состоящую их двух
еще нерасчлененных тел. В качестве дополнительной нагрузки к ним
будет приложены (в противоположную сторону) две реакции отбро-
отброшенной третьей части.
Условия задач. Определить реакции опор конструкции (в кН),
состоящей из трех тел, соединенных в точке С шарниром. Размеры
указаны в метрах.
1.
А
В	,
С
Е
М
Р = 20 кН,
Q = 30 кН,
F = 70 кН,
М = 100 кНм,
а = 60°.

2.6. Расчет системы трех тел, соединенных шарниром
71
2.
I -> F
/P .
/\a A
,2,2, 4
i T
о
JM
	 D
2 , 1 ,
P-
Q =
F =
M =
a =
30 кН,
40 кН,
60 kH,
= 75 кНм,
60°.
3.
4.
5.
6.
В
\с
1С
Те
4 , 2
Р = 20 кН,
Q = 40 кН,
F = 70 кН,
М = 125 кНм,
а = 30°.
Р = 30 кН,
Q = 50 кН,
F = 90 кН,
М = 175 кНм,
а = 60°.
Р = 20 кН,
Q = 40 кН,
F = 50 кН,
М = 125 кНм,
а = 30°.
Р = 30 кН,
Q = 60 кН,
F = 80 кН,
М = 175 кНм,
а = 60°.

72
Гл. 2. Произвольная плоская система сил
7.
3 , 9
Q
с
Р = 30 кН,
Q = 60 кН,
F = 90 кН,
М = 225 кНм,
а = 30°.
8.
В
Q
С
Р = 30 кН,
Q = 60 кН,
F = 100 кН,
М = 275 кНм,
а = 60°.
9.
Р = 30 кН,
Q = 70 кН,
F = 90 кН,
М = 50 кНм,
а = 60°.
10.
Ы
Р = 40 кН,
Q = 60 кН,
F = 90 кН,
М = 100 кНм,
а = 30°.

2.6. Расчет системы трех тел, соединенных шарниром
73
Ответы
1
2
3
4
5
6
7
8
9
10
ХА
—
-103.529
9.240
—
-40.000
-256.148
-45.000
-267.449
15.000
100.785
Уа
30.000
-47.500
-44.620
100.000
—
—
-10.000
—
50.514
-19.215
Хв
-74.785
—
8.080
—
42.679
—
—
-1.276
—
-66.144
Ув
-97.177
37.500
74.620
-22.500
10.000
10.938
25.000
4.575
25.000
49.215
ХЕ
64.785
88.529
—
-15.000
41.667
154.505
45.000
—
—
-
Уе
9.856
84.019
10.000
-29.286
—
-36.918
—
-30.556
16.667
20.000
xD
—
—
—
—
-151.667
256.643
55.981
213.724
—
-
YD
—
—
—
-114.195
—
—
—
—
41.838
-
Ответы на типичные вопросы, возникающие при решении задачи
1.	К какой части отнести нагрузку, приложенную к шарниру С?
Эту нагрузку можно отнести к любой части.
2.	Чему равна длина опорных стержней, например, горизонталь-
горизонтальных A, D и Е в варианте Ъ?
Для решения задачи длины опорных стержней не нужны. Осво-
Освобождаясь от опор, реакцию опоры прикладываем к телу, в месте
крепления опоры, положение другого конца опорного стержня может
быть неопределено. Для опорного стержня самое главное — это его
направление. Реакцию опорного стержня направляем вдоль него.
3.	В результате решения реакция подвижной опоры оказалась
отрицательной. Означает ли это, что опора отрывается от по-
поверхности скольжения?
Нет. Предполагается, что все связи двусторонние, т.е. предусмот-
предусмотрено некоторое ограничение (на рисунке не показано), не позволяю-
позволяющее подвижным опорам отрываться от поверхности. Более точное
изображение подвижной опоры: Ч?
4.	В условии задачи не указана точка приложения момента М.
Вектор сосредоточенного момента (пары) является свободным.
Его можно прикладывать к любой точке тела, не переносите его
только с одной части составной конструкции в другую.

Глава 3
Равновесие при наличии трения
3.1. Трение скольжения
Постановка задачи. Конструкция состоит из двух шарнирно
соединенных между собой тел. Одна из опор конструкции пред-
представляет собой одностороннюю связь и допускает проскальзывание
с трением. Коэффициент трения, размеры конструкции и часть
внешних нагрузок заданы. Найти пределы изменения одной из внеш-
внешних нагрузок, действующей на конструкцию в условии равновесия.
План решения
1.	Задаем направление возможного движения подвижной опоры,
скользящей с трением. Прикладываем к этой опоре силу трения, на-
направляя ее в сторону противоположную возможному движению. Пре-
Предельное значение силы трения связываем с величиной нормальной ре-
реакции опоры N по формуле Кулона FTp = TV/, где / — коэффициент
трения, зависящий от свойств контактирующих материалов и задан-
заданный в условии задачи.
2.	Решаем задачу о равновесии системы тел. Для этого разбиваем
систему на две отдельные части, для которых составляем и решаем
уравнения равновесия (§ 2.4, § 2.5). Из решения определяем предель-
предельное значение нагрузки для заданного направления скольжения опоры.
3.	Меняем направление возможного движения системы и направ-
направление предельной силы трения. Предыдущий пункт плана выполняем
заново и определяем другое предельное значение нагрузки. Два най-
найденных значения нагрузки определяют ту область ее изменения, при
которой конструкция находится в равновесии.
Пример. Конструкция состоит из двух частей, шарнирно соеди-
соединенных в точке С (рис. 52). Опора В представляет собой односто-
одностороннюю связь и допускает проскальзывание с коэффициентом трения
/ = 0.2, опора А — неподвижный шарнир. К конструкции приложена
пара сил с моментом М = 10 кНм, сила Q = 10 кН под углом а = 60°.

3.1. Трение скольжения
75
Размеры даны в метрах. Найти пределы изменения нагрузки Р, дей-
действующей под углом C = 30° на конструкцию, в условии равновесия.
в
р
С
Рис. 52
Решение
1. Задаем направление возможного движения подвижной опоры,
скользящей с трением Предполагая возможное движение ползуна В
влево, силу трения FT направим направо (рис. 53). Предельное зна-
значение силы трения связываем с нормальной реакцией опоры N по
формуле Кулона:
FTp = Nf,	A)
где / = 0.2 — коэффициент трения.
хА
Ум
А
У А
7
С
6
в л
N
Рис. 53

76
Гл. 3. Равновесие при наличии трения
2. Решаем задачу о равновесии системы тел. Для этого систему
разбиваем по шарниру С на две отдельные части — АС и СВ. Ре-
Реакции шарнира С Хс, Yc для левой и правой части направлены в
противоположные стороны (рис. 54). К точке А прикладываем две
составляющие реакции неподвижного шарнира ХА, YA.
^ш
хА
Q? <Yc
С Y
В
N
Рис. 54
Действие ползуна заменяем нормальной реакцией 7V, направленной
вниз, так как ползун по условию задачи является односторонней свя-
связью, и силой трения FT . Из множества комбинаций уравнений равно-
равновесия (§ 2.4, с. 60) выберем уравнение моментов относительно точки
А для всей системы в целом (рис. 53) и сумму моментов относительно
С для правой части:
л) = _tv . 13 - F • 8 + М - Q • 7 • sina+
- тр
= 0, B)
(прав) = _N QF .4 + p . 6 Sin/5 = 0.
Tp
Уравнения B) вместе с законом Кулона A) образуют замкнутую сис-
систему трех линейных уравнений с тремя неизвестными TV, FT , Р. Ре-
Решение системы имеет вид
я=* P= 3+v
6 + 4/'	0.978 + 0.746/'
C)
При / = 0.2 получаем Рх = 3.015 кН. Эта нагрузка для движения
влево является предельной.

3.1. Трение скольжения
77
3. Меняем направление возможного движения системы и направле-
направление предельной силы трения. Пусть ползун В движется вправо. Силу
FTp направим в противоположную сторону. Очевидно, знак момента
силы FTp в уравнениях B) изменится на противоположный, следова-
следовательно, решение для нового направления движения будет отличаться
от C) только знаком при /. Формально подставляя в C) / = —0.2, по-
получим Р2 = 3.136 кН. Значения Р1 и Р2 являются границами области
равновесия.
Чтобы убедиться, что равновесие соответствует значениям на-
нагрузки между этими числами, определим Р при / = 0. Действи-
Действительно, из C) имеем Рг < Р = 3.066 кН < Р2.
Из выражения C) для N также следует, что при / = ±0.2 нор-
нормальная реакция N > 0, поэтому отрыв ползуна В от поверхности
невозможен. Таким образом, рама находится в равновесии при
Р . < Р < Р ,
mm — — max'
где
Pmin = 3.015 кН, Pmax = 3.136 кН.
Этим нагрузкам соответствуют следующие значения нормальной ре-
акции: iV(min) = 1.330 кН, iV(max) = 1.806 кН.
Замечание. Неравенство АГ,т1ч < iV,m axN не является обязатель-
обязательным.
Условия ЗАДАЧ. Конструкция состоит из двух шарнирно соеди-
соединенных между собой тел. Опора В представляет собой односторон-
одностороннюю связь и допускает проскальзывание с коэффициентом трения f.
Найти пределы изменения нагрузки Р, действующей на конструк-
конструкцию в условии равновесия (в кН). Размеры даны в метрах.
1.
ЩБ
С
-м
D
Q = 30 кН,
М = 10 кНм,
а = 60°, /3 = 30°,
/ = 0.3.

78
Гл.З. Равновесие при наличии трения
2.
С
-М
щв
Я
20
10
3.
с
А
D
v 3
ч<
я
12
4.
с
12
18
5.
С
Q
в
Р	4
Q = 40 кН,
М = 20 кНм,
а = 30°,/3 = 45°,
/ = 0.1.
Q = 50 кН,
М = 30 кНм,
а = 60°, /3 = 45°,
/ = 0.3.
Q = 60 кН,
М = 40 кНм,
а = 45°, /3 = 30°,
/ = 0.1.
Q = 20 кН,
М = 70 кНм,
а = 30°, /3 = 60°,
/ = 0.1.

3.1. Трение скольжения
79
6.
С
e
м А
Q = 20 кН,
М = 70 кНм,
а = 30°,/3 = 60°,
/ = 0.1.
С
Q = 30 кН,
М = 80 кНм,
а = 60°,/3 = 30°,
/ = 0.07.
8.
>Ч
С
Р 4
Q = 40 кН,
М = 90 кНм,
а = 30°, /3 = 45°,
/ = 0.1.
9.
сь
Q = 50 кН,
М = 100 кНм,
а = 60°, /3 = 45°,
/ = 0.3.

80
Гл. 3. Равновесие при наличии трения
10.
м
Q = 60 кН,
М = 120 кНм,
а = 45°, /3 = 30°,
/ = 0.1.
14
Ответы
1
2
3
4
5
6
7
8
9
10
min
35.019
47.392
48.951
14.705
38.807
37.163
67.892
103.805
45.587
2.319
^(min)
28.238
22.726
36.266
66.891
18.191
19.446
61.674
49.694
41.872
18.121
р
max
115.080
54.669
163.360
27.849
41.937
40.139
120.648
112.148
139.065
6.877
^(max)
105.197
27.028
154.415
54.217
22.466
19.216
99.826
58.682
113.924
16.740
3.2. Трение качения
Постановка задачи. Система состоит из двух цилиндров, со-
соединенных стержнем. Цилиндры могут кататься без проскальзыва-
проскальзывания, один цилиндр без сопротивления, другой — с трением качения.
В каких пределах меняется внешний момент, приложенный к одному
из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опор-
опорной поверхности в месте контакта. В результате реакция опоры сме-
смещается в сторону возможного движения на половину длины площадки
контакта и создает момент сопротивления. Плечо этого момента при-
принимают за коэффициент трения качения. Таким образом, МТ = N5,
где N — реакция опоры, 5 — коэффициент трения качения, имею-
имеющий размерность длины. Так в рамках теоретической механики, где
изучается твердое тело, для объяснения явления трения качения вво-
вводят гипотезу деформируемости. Считают, что область деформаций

3.2. Трение качения	81
в теле мала, а глубиной продавливания цилиндра в поверхность (или
величиной смятия цилиндра) пренебрегают. Коэффициент трения
качения зависит не только от свойств материала цилиндра и поверх-
поверхности, но и от радиуса цилиндра.
План решения
1.	Задаем направление возможного движения при достижении усло-
условия предельного равновесия. К катящемуся телу (цилиндру, колесу)
прикладываем момент трения качения, направляя его в сторону, про-
противоположную возможному движению. Не забываем про силу сцепле-
сцепления в точке контакта, направленную вдоль плоскости.
2.	Решаем задачу о равновесии системы тел. Используем метод
разбиения системы на отдельные тела. Внешние и внутренние связи
заменяем их реакциями. Составляем и решаем уравнения равновесия.
Оси координат для уравнения проекций для цилиндрических тел вы-
выбираем вдоль нормальной реакции, а уравнение моментов составляем
относительно точки касания. Из решения системы уравнений равно-
равновесия определяем условие предельного равновесия.
3.	Меняем направление возможного движения системы и направ-
направление момента трения качения. Решаем задачу заново, определяем
второе условие предельного равновесия.
Пример. Система состоит из двух цилиндров весом G± = 20 Н,
и G2 = 30 Н с одинаковыми радиусами R = 50 см, соединенных од-
однородным стержнем веса Gr3 = 40 Н. Цилиндры могут кататься без
проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с
трением качения.
Рис. 55
Коэффициент трения качения 5 = 2 мм. К цилиндру 1 приложена
пара с моментом М. К оси цилиндра 2 приложена наклонная сила
F = 10 Н (рис. 55). В каких пределах меняется момент М в условии
равновесия системы?
6 М.Н. Кирсанов

82
Гл. 3. Равновесие при наличии трения
Решение
1.	Задаем направление возможного движения при достижении усло-
условия предельного равновесия. Пусть за счет достаточно большой, по
сравнению с моментом М, силы F произойдет движение системы
влево. Тогда момент трения качения, приложенный к цилиндру 2,
будет направлен по часовой стрелке (рис. 57). Его величину находим
по формуле Мт = N2 • 5.
2.	Решаем задачу о равновесии системы двух цилиндров и стержня.
Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи за-
заменяем реакциями -Рсц1, АГ1? ^сц2, ^V2-
У\
СЦ1
Рис. 56
Рис. 57
Рис. 58
Реакции ^сц1 и ^сц2 приложены к цилиндрам в точках их касания
поверхностей, вызваны силами сцепления (трения) и обеспечивают
вращение цилиндров. Реакции внутренних связей — Х1? У1? Х2, Y2.
При составлении системы семи уравнений с неизвестными Х1, Y1,
TV-p Х2, Y24 N2, M избегаем уравнения, в которые входят неизвестные
реакции ^сц1 и ^сц2.
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
^ил1) = -X1-R-M = 0.
A)
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
У-(цил2) =Y2 + N2-G2-F sin 45° = 0,
/Г(цил2)
LK2
= -X2.R-MTp
B)

3.2. Трение качения	83
Уравнения равновесия стержня АВ (рис. 58) имеют вид
J2 М^стер) = -Х2 • АВ sin 30° - Y2 • АВ cos 30° -
-G3 {AB/2) cos 30° =0.
Из решения системы уравнений A—3) определяем
V3R FRV2 - S(G3 + 2G2 + Fy/2)
Радиус и коэффициент трения качения переводим в метры R = 0.5 м,
S = 0.002 м. Получаем М = 3.414 Нм. Вычисляем нормальные реакции
опор:
N± = 36.058 Н, N2 = 61.013 Н.
Убеждаемся, что Л^ > 0 и N2 > 0, что соответствует наличию опоры.
Если реакция опоры равна нулю, то это означает отрыв тела от по-
поверхности, отрицательной реакции опоры N < 0 в задаче с односто-
односторонней связью не существует (физически не реализуется).
3. Меняем направление возможного движения системы. Пусть за
счет действия момента М произойдет движение системы вправо. Мо-
Момент трения качения направим против часовой стрелки (рис. 59).
Составляя уравнения равновесия для новой системы сил, заметим,
что отличие от прежней системы про-
проявляется только в знаке Мт во вто-
втором уравнении равновесия B). Так как
Мт = N2 • J, то новое решение для
М будет формально отличаться от D)
только знаком у коэффициента трения
5. Поэтому, не решая (и даже не со-
составляя) системы уравнений равнове-
равновесия типа A-3) для нового направления
возможного движения, записываем ответ, изменяя знаки у 5 в D):
М = ^RFRJ2 + 6(G+2G2 + F^) = ^
2	RV3 -5	V }
Точно так же находим нормальные реакции опор: N± = 35.776 Н,
7V2 = 61.295 Н. При равновесии системы момент, приложенный к
6*

84
Гл. 3. Равновесие при наличии трения
цилиндру 1, изменяется в пределах (в Нм) *'
3.414 < М < 3.658.
Условия задач. Система состоит из двух цилиндров весом Gx
и G2 с одинаковыми радиусами R, соединенных однородным стерж-
стержнем весом G3. Цилиндры могут кататься без проскальзывания, ци-
цилиндр 1 без сопротивления, а цилиндр 2 с трением качения E). В
каких пределах меняется внешний момент М при условии равнове-
равновесия системы?
1.
d = 10 Н, G2 = 23 Н, G3=30 H,
F = 5 Н, R = 35 см, S = 3 мм.
3.
Gi = 5 Н, G2 = 25 Н, С3=10 Н,
F = 30 Н, R = 65 см, S = 5 мм.
2.
Gi = 22 Н, G2 = 23 Н, G3=50 H,
F = 10 Н, R = 50 см, S = 4 мм.
4.
Gi = 24 Н, G2 = 27 Н, G3=20 H,
F = 20 Н, R = 50 см, S = 3 мм.
5.
Gi = 25 Н, G2 = 29 Н, G3=30 H,
F = 25 Н, R = 35 см, S = 1 мм.
6.
Gi = 21 Н, G2 = 26 Н, G3=40 H,
F = 5 Н, R = 25 см, 6 = 2 мм.
*) В задачах, где допускается проскальзывание, необходимо находить
также силы _РСц1 и _РСц2 и проверять условие проскальзывания ^Сц1 =
FTpi < fNi, -РСц2 = FTp2 < fN2, где / — коэффициент трения скольжения.

3.2. Трение качения
85
7.
8.
Gi = 22 Н, G2 = 24 Н, G3=50 H,
F = 10 Н, R = 40 см, S = 3 мм.
9.
d = 24 Н, G2 = 26 Н, G3=50 H,
F = 20 Н, R = 70 см, S = 5 мм.
Gi = 23 Н, G2 = 24 Н, G3=30 H,
F = 15 Н, R = 55 см, 5 = 4 мм.
10.
Gi = 25 Н, G2 = 28 Н, G3=10 H,
F = 25 Н, R = 35 см, S = 1 мм.
Ответы
1
2
3
4
5
6
7
8
9
10
Движение цилиндра 2
по часовой стрелке
^1
Н
64.058
36.095
30.366
53.078
59.996
93.257
9.591
32.909
40.326
25.330
74.888
53.526
47.532
42.872
87.567
140.078
54.537
47.861
69.191
38.168
М
Нм
2.841
11.279
4.896
4.308
8.371
3.211
16.585
0.703
10.516
5.984
Движение цилиндра 2
против часовой стрелки
^1
^2
Н
66.315
36.352
29.638
52.565
60.499
100.988
10.413
32.909
41.303
25.507
77.145
54.023
47.111
42.576
88.438
148.699
55.012
47.461
67.500
38.042
М
Нм
3.297
10.799
4.622
4.456
8.675
4.326
16.395
1.143
9.333
5.922

Глава 4
ПРОСТРАНСТВЕННАЯ СИСТЕМА
СИЛ
4.1. Пространственная ферма
Постановка задачи. Определить усилил в стержнях простран-
пространственной фермы, нагруженной в одном узле силами.
План решения
Задача является естественным обобщением задачи § 1.1, с. 14, в
которой методом вырезания узлов определялись усилия в простейшей
плоской ферме. Этот же метод применим и здесь, единственное от-
отличие — вместо двух уравнений равновесия узла в проекциях на оси
в пространственной задаче будет три уравнения.
Рис. 60
1. Узлы фермы находятся в равновесии. Вырезаем узлы, заменяя
действие стержней их реакциями. Реакцию незагруженного стержня
направляем вдоль его оси. Используя правило знаков, согласно кото-
которому усилие растянутого стержня считается положительным, реак-
реакцию каждого стержня направляем из шарнира по направлению внеш-
внешней нормали сечения стержня. Расчет начинаем с узла, к которому
подходят три стержня с неизвестными усилиями.

4.1. Пространственная ферма
87
2. Для каждого из шарниров составляем по три уравнения равно-
равновесия в проекциях. Решаем полученную систему.
Пример. Найти усилия в стержнях 1—6 пространственной фермы,
нагруженной в одном узле вертикальной силой G = 100 кН и гори-
горизонтальной F = 40 кН. Даны размеры а = 12 м, Ь = 16 м, с = 10 м,
d = 5 м (рис. 60).
Решение
1. Узлы А ж В находятся в равновесии. Вырезаем эти узлы, за-
заменяя действие стержней их реакциями, направленными из узла к
стержню (рис. 61).
Sb
Рис. 61
Стержень 1 является общим для обоих узлов, поэтому на рисунке
есть два противоположно направленных вектора с усилием Sv Один
вектор приложен к узлу Л, другой — к узлу В.
2. Расчет начинаем с узла А, к которому подходят три стержня
с неизвестными усилиями. Составляем уравнения равновесия узла в
проекциях на три оси координат:
(i)
Xi = —S1 cos 7 — 6*2 cos a — S3 = 0,
J2 Zi = S± cos <?? + S2 sin a — G = 0.
Система уравнений A) содержит три неизвестных усилия Sx, S2, S3.

Гл. 4. Пространственная система сил
Вычисляем тригонометрические функции, входящие в уравнения,
sin a =
= = 0.640,
cos а =
= 0.768,
cos C =	= 0.716, cos 7 = , . aL9 . = 0.537,
Va2 + b2 + с2	Vfl2 + b2 + c2
cos <p = —^=
= 0.447.
л/а2 + b2 + c2
Решение системы A):
S± = 55.902 кН, S2 = 117.154 кН, S3 = -120 кН.
Знаки найденных усилий показывают, что стержни 1 и 2 растянуты,
а стержень 3 сжат. Составляем уравнения равновесия узла В:
Xi = S± cos 7 + ?5 sin ^ = 05
У. = 5Х cos/5 - #4 - S5 cos^ - S6 sin(9 = 0,
Z{ = -S± cos y? - 56 cos 0 = 0.
B)
Уравнения B) содержат три неизвестных усилия 54, 55, 56, усилие S±
найдено ранее из условия равновесия узла А. Вычисляем необходимые
тригонометрические функции:
= 0.923,
/а2 + d2
sin в = —?=== = 0.447, cos в =
Решение системы B):
#4 = 65 кН, S5 = -32.5 кН, S6 = -27.951 кН.
Знаки найденных усилий показывают, что стержни 5 и 6 сжаты, а
стержень 4 растянут.
Результаты расчета (в кН) заносим в таблицу:
55.902
s2
117.154
-120.000
65.000
s5
-32.500
-27.951
Условия ЗАДАЧ. Найти усилия в стержнях 1-6 пространст-
пространственной фермы, нагруженной в одном узле вертикальной силой G и
горизонтальной F. Ответ выразить в кН.

4.1. Пространственная ферма
а = 2 м, Ъ = 3 м,
с = 4 м, d = 3 м,
G = 2 кН, F = 1 кН.
а = 4 м, Ъ = 6 м,
с = 5 м, <i = 4 м,
G = 7 кН, F = 6 кН.
а = 5 м, Ъ = 4 м,
с = 3 м, <i = 2 м,
G = 4 кН, F = 2 кН.
а = 7 м, 6 = 6 м,
с = 5 м, d = 4 м,
G = 6 кН, F = 4 кН.

90
Гл. 4. Пространственная система сил
а = 2 м, Ъ = 3 м,
с = 4 м, d = 3 м,
G = 8 кН, F = 5 кН.
а = 4 м, 6 = 6 м,
с = 5 м, d = 3 м,
G = 6 кН, F = 3 кН.
а = 5 м, 6 = 4 м,
с = 3 м, <i = 1 м,
G = 8 кН, F = 4 кН.
а = 7 м, Ъ = 6 м,
с = 5 м, d = 3 м,
G = 7 кН, F = 3 кН.

4.2. Момент силы относительно оси
91
9.
10.
а = 2 м, Ъ = 3 м,
с = 4 м, d = 2 м,
G = 9 кН, F = 8 кН.
а = 4 м, Ъ = 6 м,
с = 5 м, <i = 3 м,
G = 8 кН, F = 7 кН.
Ответы
1
2
3
4
5
6
7
8
9
10
Si
0.000
11.325
5.333
-32.249
0.000
-5.831
4.079
0.000
19.596
-13.606
s2
4.000
5.000
6.667
-26.034
-10.000
3.202
-5.657
-5.244
-17.889
7.470
S3
-4.472
-16.008
-7.775
28.674
11.180
2.500
2.400
2.500
0.000
5.833
s4
2.000
7.211
6.667
6.146
-5.000
-3.606
4.000
4.610
8.000
-8.413
-2.693
-8.964
-9.428
-10.323
6.000
-8.500
0.000
-4.500
-10.062
-8.000
s6
1.500
1.600
7.333
3.733
-10.000
3.202
-8.000
-4.301
4.500
4.667
4.2. Момент силы относительно оси
Постановка задачи. В декартовой системе координат задан
вектор силы. Найти моменты силы относительно осей координат.
План решения
1. Определяем радиус-вектор rQ точки приложения силы.

92
Гл. 4. Пространственная система сил
2. Находим момент силы относительно начала координат как век-
векторное произведение Мо = rQ x F. Моменты силы относительно осей
x,y,z являются компонентами МОж, MQy, MQz вектора Мо *' .
Пример. В декартовой системе координат задан вектор силы F
(рис. 62); F = 20 Н, а = 6 м, Ъ = 11 м, с = 8 м. Найти моменты силы
относительно осей координат ж, у, z.
/ /\
/ /
/
у
/ 771
ч.
с
У
Рис. 62
Рис. 63
Решение
1.	Определяем радиус-вектор г0 точки приложения силы относи-
относительно начала координат (рис. 63): г0 = {а, 6, с}.
2.	Находим момент силы относительно начала координат:
Мо =
х F =
г
а
3
Ъ
к
с
где г, j, к — орты осей ж, г/, z. Так как в явном виде компоненты век-
вектора F не заданы, а известна длина вектора и линия АВ его действия,
представляем F в виде F = FAB/\AB\. Вектор АВ вычисляем как
разность АВ = rB—rQ = {—а, 0, —с}. Длина вектора \АВ\ = ^J а2 + с2.
В результате получаем
F [-a, 0, -с}.
Находим компоненты МОж, МОу, MQz вектора Мо:
МОж = bFz - cFy = -cbF/Va2 + с2 = -176 Нм,
МОу = с^ж - aFz = {-caF + acF)/Va2 + с2 = О,
MOz = aFy - bi^. = abF/Va2 + c2 = 132 Нм.
Модуль вектора момента силы F относительно начала координат:

4.2. Момент силы относительно оси
93
Условия ЗАДАЧ. В декартовой системе координат даны три
силы, приложенные к вершинам параллелепипеда. Найти моменты
этих сил относительно осей координат (в Нм). Размеры на рисун-
рисунках в метрах, силы — в Н.
F, = 1, F2 = 2, F3 = 4.
x = 3, F2 = 4, F3 = 6.
F, = 2, F2 = 2, F3 = 5.
x = 4, F2 = 5, F3 = 6.
F — 1 F — 1 F — 1
x = 2, F2 = 2, F3 = 5.

94
Гл. 4. Пространственная система сил
x = 3, F2 = 3, F3 = 5.
x = 4, F2 = 4, F3 = 5.
, = 2, F2 = 3, F3 = 6.
1
2
3
4
5
6
7
8
9
10
Mlx
0.000
6.000
0.000
-40.000
5.000
6.000
0.000
-20.000
0.000
12.000
Mly
0.000
0.000
0.000
32.000
0.000
0.000
0.000
16.000
0.000
0.000
Mlz
-10.000
0.000
30.000
0.000
0.000
0.000
15.000
0.000
0.000
0.000
M2x
0.000
-4.685
0.000
0.000
0.000
-4.685
0.000
0.000
0.000
0.000
M2y
0.000
3.748
-19.200
-24.000
2.400
3.748
7.200
9.600
-9.600
0.000
M2z
12.494
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
18.741
M3x
0.000
-10.607
-25.456
0.000
4.243
-10.607
-10.607
0.000
21.213
0.000
Мзу
0.000
8.485
20.365
0.000
0.000
8.485
8.485
0.000
0.000
0.000
M3z
0.000
0.000
0.000
0.000
-5.657
0.000
0.000
0.000
-28.284
0.000
4.3. Равновесие вала
Постановка задачи. Горизонтальный вал может вращаться
в цилиндрических шарнирах. К одному шкиву вала приложено нор-
нормальное давление и касательная сила сопротивления, пропорциональ-
пропорциональная давлению. На шкивы вала действуют известные нагрузки. Най-
Найти силу давления и реакции шарниров при условии равновесия вала.

4.3. Равновесие вала
95
План решения
1.	Действие каждой из опор заменяем двумя взаимно перпендику-
перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.
2.	Для определения силы давления составляем уравнение момен-
моментов относительно оси вала. Момент силы натяжения ремня, нити и
т.п. (наклонной или нет) вычисляем как произведение величины силы
на соответствующий радиус со знаком, соответствующим направле-
направлению вращения вокруг вала. Уравнение содержит одну неизвестную,
которую легко найти.
3.	Определяем вертикальные реакции опор вала. Для этого со-
составляем два уравнения моментов относительно осей, совпадающих
с линиями действия горизонтальных реакций шарниров. Решаем эти
уравнения.
4.	Проверяем найденные реакции, составляя уравнение равновесия
в проекции на вертикаль.
5.	Определяем горизонтальные реакции опор вала. Для этого со-
составляем два уравнения моментов относительно осей, совпадающих
с линиями действия вертикальных реакций шарниров.
6.	Проверяем горизонтальные реакции, составляя уравнение рав-
равновесия в проекции на ось вдоль линии действия горизонтальных ре-
реакций.
Пример. Горизонтальный вал весом G = 15 Н может вращаться
в цилиндрических шарнирах А ж В (рис. 64). К шкиву 1 приложено
нормальное давление N и касательная сила сопротивления F = 0.17V.
На шкив 2 действуют силы натяжения ремней Т1 = 30 Н, Т2 = 57 Н.
Груз Q = 18 Н висит на нити, навитой на шкив 3. Определить силу
давления N и реакции шарниров в условии равновесия вала. Учесть
веса шкивов: Рх = 35 Н, Р2 = 10 Н, Р3 = 15 Н. Все нагрузки

96
Гл. 4. Пространственная система сил
действуют в вертикальных плоскостях. Известны радиусы шкивов,
Rx = 26 см, R2 = 10 см, R3 = 11 см и расстояния между характер-
характерными точками вала: а = 22 см, Ъ = 25 см, с = 26 см, б/ = 26 см. Общая
длина вала L = a + b-\-c-\-d; a=30°.
Решение
1. Действие цилиндрических опор А л В заменим реакциями ZA,
ХА и ZB, Хв (рис. 65). Вес вала G приложим в центре. Вес груза
изобразим вектором Q.
У
Рис. 65
2. Для определения силы давления составляем уравнение моментов
относительно оси вала:
^2 Му = FR1 + (Гх - T2)R2 + QR3 = 0.
Уравнение содержит одну неизвестную F. Линии действия остальных
сил пересекают ось у и их моменты относительно оси вала равны
нулю.
Из полученного уравнения находим
R1
По условию N = F/0.1 = 27.692 Н.
3. Определяем вертикальные реакции шарнирных опор вала. Для
этого составляем два уравнения моментов относительно горизонталь-
горизонтальных осей, проходящих через шарниры А и В. Рассматриваем для
удобства проекцию всех сил на плоскость zy (рис. 66). Таким обра-
образом вычисление моментов относительно осей сводим к плоской задаче
вычисления моментов относительно точек А ж В.
Знаки моментов сил определяем как в задачах плоской статики:
момент силы, вращающей тело вокруг моментной точки против часо-

4.3. Равновесие вала
97
вой стрелки считается положительным, по часовой стрелке — отрица-
отрицательным. Моменты сил, перпендикулярных плоскости zy (и поэтому
не изображенных на рис. 66), относительно любой ее точки равны
нулю.
cos a
vP3
Рис. 66
Решая уравнения
cos а ~
с)-
? Mx, = -ZA(a + Ъ) + (Px - F)b - G(L/2 - a - 6) +
+ (T1cosa-P2)c- (P3 + Q)(c + d) = 0,
находим ZA = -11.324 H, ZB = 75.574 H.
4.	Проверяем правильность нахождения вертикальных реакций,
составляя уравнение равновесия в проекции на ось z (рис. 66):
^г = ZA + ^ - Рх + ZB - G + i х COS a - Р2 - Р3 - У =
= -11.324 + 2.769 - 35 + 75.574 - 15 + 30 • 0.866 - 10 - 15 - 18 = 0.
5.	Определяем горизонтальные реакции опор вала. Для этого со-
составляем два уравнения моментов относительно осей, совпадающих с
линиями действия вертикальных реакций шарниров. Рассматриваем
горизонтальную проекцию силовой схемы (рис. 67):
J2MZ(A) = -N -а-Хв(а + Ъ) - (Т± sina + Т2)(а + Ъ + с) = 0,
J2 Mz, =XA(a + b)+Nb- (Tx sin a + Т2)с = 0.
Решая уравнения, находим ХА = 25.100 Н, Хв = -124.792 Н.
6.	Проверяем правильность нахождения горизонтальных реакций,
составляя уравнение равновесия в проекции на ось х вдоль линии
7 М.Н. Кирсанов

98
Гл. 4. Пространственная система сил
действия горизонтальных реакции:
- = ХА + N + Хв
Г2 =
= 25.1 + 27.692 - 124.792 + 15 + 57 = 0.
В
Рис. 67
Результаты расчетов в Н заносим в таблицу:
N
27.692
хА
25.100
ZA
-11.324
Хв
-124.792
ZB
75.574
Условия ЗАДАЧ. Горизонтальный вал весом G может вращаться
в цилиндрических шарнирах А и В. К шкиву 1 приложено нормальное
давление N и касательная сила сопротивления F, пропорциональная
N. На шкив 2 действуют силы натяжения ремней Т± и Т2. Груз Q
висит на нити, навитой на шкив 3. Определить силу давления N
и реакции шарниров в условии равновесия вала (в Н). Учесть веса
шкивов Рр Р2, Р3. Все нагрузки действуют в вертикальной плос-
плоскости. Силы даны в Н, размеры — в см.
1.
Т2
F = 0.17V, Тг = 50,
Т2 = 97, Pi = 16,
Р2 = Ю, Р3 = 14,
Q = 18, G = 25,
а = 30°, Яг = 14,
R2 = 8, R3 = 9,
а = 22, 6 = 25,
с = 26, d=23.

4.3. Равновесие вала
99
2.
3.
F = O.27V, Тг = 70,
Т2 = 136, Pi = 36,
Р2 = 30, Р3 = 34,
Q = 22, G = 35,
а = 60°, Д1 = 18,
Д2 = 12, Я3 = 13,
а = 22, Ъ = 26,
с = 29, d=23.
F = 0.27V, Ti = 30,
Т2 = 56, Pi = 22,
Р2 = Ю, Р3 = 14,
Q = 22, G = 15,
а = 30°, fli =26,
Д2 = 8, Д3 = 9,
а = 22, Ь = 26,
с = 27, d = 26.
4.
F = 0.47V, Ti = 60,
T2 = 117, Pi = 26,
P2 = 10, P3 = 18,
Q = 18, G = 30,
a = 30°, fli =26,
#2 = 8, Д3 = 10,
а = 24, Ъ = 27,
с = 28, d = 28.
5.
F = 0.17V, Ti = 50,
T2 = 26, Pi = 26,
P2 = 20, P3 = 24,
Q = 10, G = 25,
а = 45°, i?i = 16,
R2 = 10, R3 = 11,
а = 22, b = 23,
с = 25, d=23.

100
Гл.4. Пространственная система сил
и х
F = O.27V, Тг = 60,
Т2 = 118, Pi = 38,
Р2 = 30, Р3 = 34,
Q = 14, G = 30,
а = 60°, Д1 =22,
R2 = 12, Д3 = 13,
а = 22, 6 = 24,
с = 27, d = 24.
7.
F = 0.37V, Ti = 40,
Т2 = 78, Pi = 22,
Р2 = Ю, Р3 = 18,
Q = U,G = 20,
а = 30°, Д1 = 18,
Д2 = 8, Д3 = Ю,
а = 24, Ъ = 26,
с = 27, d=26.
F = 0.47V, Тг = 70,
T2 = 136, Pi = 36,
Р2 = 20, Р3 = 28,
Q = 22, G = 35,
а = 45°, i*i =28,
Д2 = Ю, Я3 = 12,
а = 24, Ь = 28,
с = 30, d = 28.
F = 0.17V, Ti = 60,
Т2 = 31, Pi = 16,
Р2 = Ю, Р3 = 14,
Q = 26, G = 30,
а = 30°, i*i = 14,
Д2 = 8, R3 = 9,
а = 22, 6 = 27,
с = 28, d=23.

4.4. Определение усилий в стержнях, поддерживающих плиту 101
10.
N
F = O.27V, Тг = 70,
Т2 = 37, Pi = 20,
Р2 = Ю, Р3 = 14,
Q = 10, G = 35,
а = 30°, #i =22,
Д2 = 8, R3 = 9,
а = 22, Ь = 23,
с = 24, d=25.
Ответы
1
2
3
4
5
6
7
8
9
10
N
194.286
165.000
1.154
34.038
261.250
136.818
29.487
43.214
411.429
100.000
хА
359.986
104.855
-58.706
50.963
7.573
86.784
-38.734
-75.085
46.826
-161.833
ZA
-44.654
84.680
15.924
218.368
-290.264
74.302
77.517
-75.861
647.889
-130.593
Хв
-470.267
-201.855
-24.428
-232.001
36.936
-164.602
-102.395
-153.627
21.164
109.833
ZB
114.726
-3.459
130.614
-165.945
693.129
10.143
56.637
166.078
-90.960
269.971
4.4. Определение усилий в стержнях,
поддерживающих плиту
Постановка задачи. Однородная прямоугольная горизонталь-
горизонтальная плита известного веса опирается на шесть невесомых шарнирно
закрепленных по концам стержней. Вдоль ребра плиты действует
сила. Определить усилия в стержнях.
План решения
1.	Отделяем плиту от стержней, заменяя действие стержней их ре-
реакциями. Реакции направляем вдоль стержней, от плиты. Вес одно-
однородной прямоугольной плиты прикладываем к ее центру вертикально
вниз.
2.	Две оси системы координат направляем вдоль сторон плиты,
третью — перпендикулярно ее плоскости. Начало координат поме-
помещаем в точку, в которой сходится наибольшее число стержней. Со-

102
Гл.4. Пространственная система сил
ставляем уравнения равновесия (три уравнения в проекциях на оси
и три уравнения моментов относительно осей). Решаем полученную
систему.
3. Выполняем проверку решения, подставляя найденные значения
в уравнение моментов относительно какой-либо дополнительной оси.
Пример. Однородная прямоугольная горизонтальная плита весом
G = 20 кН опирается на шесть невесомых шарнирно закрепленных
по концам стержней. Вдоль ребра плиты действует сила F = 10 кН
(рис. 68). Даны размеры: а = 7м, 6 = 8 м, с = 6м. Определить
усилия в стержнях.
Решение
1.	Отделяем плиту от стержней, заменяя действие стержней их ре-
реакциями. Реакции направляем вдоль стержней, от плиты. Вес одно-
однородной прямоугольной плиты прикладываем к ее центру вертикально
вниз (рис. 69).
2.	Выбираем систему координат (рис. 69) и составляем уравне-
уравнения равновесия. В уравнение проекций на ось х не входят силы S1,
$3, *54, $б, F и Gr, лежащие в плоскостях, перпендикулярных Ох. В
уравнение проекций на ось у не входят силы ASf1, *52, *55, SQ и G, лежа-
лежащие в плоскостях, перпендикулярных О у, а в уравнение проекций на
вертикальную ось z входят все силы, кроме горизонтальной F:
Xi = — S2 cos a — S5 cos a = 0.
= 0.
A)
B)

4.4. Определение усилий в стержнях, поддерживающих плиту 103
- #3 sin/3 - S4 sin/3-
- S6 -G = 0.
C)
Линии действия сил S1, #2, S^ пересекают ось ж, поэтому их мо-
моменты относительно этой оси равны нулю. Вычисляя момент силы
S4 относительно оси ж, разложим ее на горизонтальную составляю-
составляющую S4 cos/З с плечом с относительно х и вертикальную — S4 sin/3,
которая пересекает ось и имеет момент равный нулю.
F 7/"
Рис. 69
Аналогично вычисляем моменты других сил и записываем все три
уравнения моментов:
Mxi = -S4 cos/3 • с - S5 sina • b - S6 • b - F • с - G • b/2 = 0,
D)
J2 Mzi = —?3 cos /3 • a + S5 cos a • b = 0.
Находим необходимые значения тригонометрических функций:
с	6
sin a =
= 0.651, cos a = \/l - sin2 a = 0.759,
cos/3 = л/l - sin2 /3 = 0.8.
Решая систему шести уравнений A-4) с шестью неизвестными, полу-
получаем значения усилий, которые заносим в таблицу (в кН):
Si
-2.500
52
3.841
S3
-4.167
54
-16.667
5В
-3.841
56
-5.000

104
Гл.4. Пространственная система сил
3. Выполняем проверку решения, подставляя найденные значения
в уравнение моментов относительно дополнительной оси у"
денной в плоскости плиты параллельно у:
прове-
провеМ ni =
а
S2 sin a • а
sin C • а-\-
+ S5 sin a • a + S6 • a + G • a/2 =
= -2.5 • 7 + 3.841 • 0.651 • 7 - 4.167 • 0.6 • 7-
- 3.841 • 0.651 -7-5-7 +10-7 = 0.
Замечание. Некоторые (или все) уравнения проекций можно за-
заменить на уравнения моментов относительно других осей. Напри-
Например, в нашей задаче вместо сложного уравнения ^Zi = 0, в которое
входят все неизвестные усилия, удобно использовать более простое
уравнение моментов относительно оси у':
Myfi = -
из которого сразу же находится усилие
S4 = -10/0.6 = -16.667 кН,
а уравнение J^ Zi = 0 можно использовать как проверочное, тем бо-
более, что выполнение такой проверки означает правильность сразу
всех найденных усилий.
Условия ЗАДАЧ. Однородная прямоугольная горизонтальная пли-
плита весом G = 25 кН опирается на шесть невесомых шарнирно за-
закрепленных по концам стержней. Вдоль ребра плиты действует
сила F = 10 кН. Определить усилия в стержнях (в кН ).
а = 2м, 6 = 3 м, с = 4м.
а = 2 м, 6 = 3 м, с = 4 м.

4.4. Определение усилий в стержнях, поддерживающих плиту 105
а = 2м, 6 = 3 м, с = 4м.
а = 2м, 6 = 3 м, с = 4м.
а = 3м, 6 = 4 м, с = 3м.
а = 3м, 6 = 4 м, с = 3м.
а = 3м, 6 = 4 м, с = 3м.
а = 3м, 6 = 4 м, с = 3м.
10.
а = 3м, 6 = 4 м, с = 3м
а = 3м, 6 = 4 м, с = 3м.

106
Гл.4. Пространственная система сил
Ответы
1
2
3
4
5
6
7
8
9
10
Si
-8.385
17.702
-12.500
-1.179
13.333
2.500
-28.284
-12.500
31.820
-16.667
s2
-5.000
-20.000
-14.907
-10.000
-39.167
-7.500
7.500
-12.500
-35.000
-2.500
S3
-9.375
-5.208
0.000
-1.389
14.907
0.000
33.333
10.607
20.833
-14.142
s4
0.000
-11.219
16.667
-3.239
-25.833
-5.000
-40.000
-20.000
0.000
-2.500
-13.975
-4.658
-25.833
-15.321
0.000
-10.607
28.284
10.607
-17.678
-14.142
Se
9.375
-5.208
14.907
-1.389
17.951
-14.577
-20.833
0.000
-20.833
19.437
4.5. Тело на сферической и стержневых
опорах
Постановка задачи. Горизонтальная однородная прямоуголь-
прямоугольная полка имеет в одной точке сферическую опору и поддержива-
поддерживается двумя невесомыми, шарнирно закрепленными по концам, стерж-
стержнями (горизонтальным и вертикальным) и наклонной подпоркой. К
полке приложена сила, направленная вдоль одного из ее ребер. Опре-
Определить реакции опор.
План решения
1.	Рассматриваем равновесие полки. Действие на полку опорных
стержней заменяем их реакциями. Реакции стержней направляем
вдоль их осей. Выбираем оси координат с началом в сферической
опоре. Реакцию сферической опоры раскладываем на три составля-
составляющие вдоль выбранных осей.
2.	Составляем систему уравнений равновесия (три уравнения в
проекциях на оси и три уравнения моментов относительно осей). Ре-
Решаем полученную систему.
3.	Выполняем проверку решения, подставляя найденные значения
в уравнение моментов относительно какой-либо дополнительной оси.
Пример. Горизонтальная однородная полка весом G = 6 кН имеет
в точке А сферическую опору и поддерживается двумя невесомыми,
шарнирно закрепленными по концам, стержнями (горизонтальным
и вертикальным) и подпоркой в точке В (рис. 70). К этой же точке

4.5. Тело на сферической и стержневых опорах
107
приложена сила F = 5 кН, направленная вдоль одного из ребер полки.
Даны размеры а = 2м, 6 = 4 м, с = 3м. Определить реакции опор.
	/
А/
Рис. 70
Решение
1. Рассматриваем равновесие полки. Действие на тело опорных
стержней заменяем их реакциями. Реакция V — вертикальная, Н —
горизонтальная вдоль бокового ребра полки.
Усилие S в подпорке направлено вдоль стержня. В сферическом шар-
шарнире А имеется три составляющие реакции XA,YA,ZA, которые на-
направляем по осям координат. Так как полка однородная, ее центр
тяжести совпадает с геометрическим центром. Сюда приложен вес
G. Начало системы координат xyz помещаем в точку А (рис. 71).
2. Составляем систему уравнений равновесия, состоящую из трех

108
Гл.4. Пространственная система сил
уравнении проекции на оси координат всех сил, действующих на пол-
полку, и трех уравнений моментов относительно этих же осей (анало-
(аналогичные уравнения см. § 4.4, с. 103):
A)
+ V -Ssina-G = 0,
S -bsina-G- 6/2 = 0,
i = -H -b- S -
Так как начало координат находится в сферической опоре, система
уравнений равновесия разделяется и становится проще. Из уравне-
уравнений моментов можно найти независимо от других три неизвестные
реакции S, Н и V.
Вычисляем значения тригонометрических функций:
sin a = с/ yb2 + с2 = 3/5 = 0.6, cos a = л/l — sin2 a = 0.8.
Из системы A), находим реакции и заносим их в таблицу (в кН):
хА
-4.5
Уа
-9.0
zA
3.0
н
4.5
V
0
S
-5.0
3. Выполняем проверку решения, подставляя найденные значения
в уравнение моментов относительно дополнительных осей ж'иу', про-
проведенных параллельно соответствующим осям исходной системы ко-
координат:
? Мх, • = -YA • с - ZA • Ъ - V • Ъ + G • Ъ/2 + S • с cos а - F • с = 0,
?М^ = ХА • с - V • a + S • asina + G • a/2 + Я • с = 0.
Замечание. Из решения системы A) получается V = 0. В этом
можно убедиться сразу из уравнения моментов относительно допол-
дополнительной оси и, лежащей на диагонали полки АВ (рис. 71). Дейст-
Действительно, все векторы, кроме У", пересекают эту ось и их моменты
равны нулю. Уравнение принимает простой вид J2 Ми = V • h = 0,
где h — некоторое плечо реакции V относительно оси АВ. Не вы-
вычисляя h ф 0, получаем V = 0.

4.5. Тело на сферической и стержневых опорах
109
Условия ЗАДАЧ. Горизонтальная однородная прямоугольная пол-
полка весом G = 2 кН имеет в точке А сферическую опору и поддер-
поддерживается двумя невесомыми, шарнирно закрепленными по концам,
стержнями (горизонтальным и вертикальным) и подпоркой ВС. К
полке приложена сила F = 3 кН, направленная вдоль одного из ее
ребер. Определить реакции опор (в кН).
а = 2м, Ь = бм, с = 4м.
3.
I	7
а = 5 м, & = 8 м, с = 3 м,
а = 3м, 6 = 8 м, с = 3м.
а = 3м, Ь = 8м, с = 3м.
4.
а = 6 м, 6 = 10 м, с = 4 м,
AD = 5 м.
6.
I	Z
д
а = 3м, 6 = 8 м, с = 3 м,
AD = 4 м.

по
Гл.4. Пространственная система сил
8.
УСА
а = 5м, 6 = 8 м, с = 3 м,
AD = 4 м.
а = 6 м, 6 = 10 м, с = 4 м,
AD = 5 м.
9.
7
а = 6 м, b = 10 м, с = 4 м,
AD = 5 м.
а = 5м, 6 = 8 м, с = 3 м,
1 = 4 м.
Ответы
1
2
3
4
5
6
7
8
9
10
Стержень
горизонтальный
Н
0.500
1.125
-4.667
1.800
-1.125
-4.000
-7.083
-1.500
2.100
-1.333
вертикальный
V
0.000
0.000
0.000
2.000
0.000
0.000
2.000
-1.000
1.000
-1.000
Сферический
шарнир
хА
-3.500
-2.125
0.000
-3.300
0.125
1.000
7.083
-3.000
-3.600
-3.333
Уа
-1.500
-5.667
0.000
-3.000
-0.333
2.667
-5.667
-2.500
-3.000
0.000
zA
1.000
1.000
1.000
-1.000
1.000
1.000
-1.000
2.000
0.000
2.000
Подпорка
ВС
S
-1.803
-3.018
-1.944
-1.803
-3.018
-2.848
-2.848
-3.082
-1.803
-1.944

4.6. Приведение системы сил к простейшему виду	111
4.6. Приведение системы сил к
простейшему виду
Постановка задачи. Систему сил, заданную в прямоугольной
системе координат, привести к началу координат. Найти точку
пересечения центральной винтовой оси с заданной плоскостью.
Привести систему сил к центру О — означает найти главный век-
вектор R и главный момент Мо системы относительно этого центра.
При перемене центра изменяется главный момент. Можно найти
точки, относительно которых получается главный момент, парал-
параллельный главному вектору. Эти точки образуют центральную винто-
винтовую ось (или ось динамы), а совокупность главного вектора и парал-
параллельного ему главного момента называют динамой или динамическим
винтом. Не меняя воздействия на тело, вектор момента можно пере-
переносить параллельно самому себе, поэтому динаму часто изображают
в виде главного вектора и главного момента, лежащими на одной пря-
прямой (на винтовой оси). Если система не уравновешена, то ее можно
привести к трем простейшим вариантам — к динаме, силе (равно-
(равнодействующей), к паре сил.
План решения
1. Вычисляем компоненты главного вектора системы, составляя
суммы проекций всех сил на оси координат:
2.	Находим модуль главного вектора R = \ Щ. + Щ + Щ.
3.	Вычисляем компоненты главного момента системы относительно
начала координат:
4.	Находим модуль главного момента Мо = \/Mqx + Mq + Mqz.
5.	Определяем скалярный инвариант системы. Система сил имеет
две величины, не меняющиеся при перемене центра приведения (инва-
(инварианты) — главный вектор и скалярное произведение главного век-
вектора на главный момент:
I = R.M0 = RxMOx + RyMOy + RzMOz.

112	Гл.4. Пространственная система сил
Если / = 0, то система сил приводится к равнодействующей.
6.	Находим минимальный главный момент М^ = I/R. Проверяем
неравенство М^ < Мо. Если R = 0, то задача решена — система
приводится к паре (или уравновешена, если и Мо = 0.)
7.	Вычисляем шаг винта р = M^/R. Если р < 0, то главный вектор
и главный момент направлены по винтовой оси в разные стороны,
если р > 0 — в одну сторону, а если р = 0, то система приводится к
равнодействующей.
8.	Записываем уравнения центральной винтовой оси *^ :
МОх ~ VRz + zRy = MOy ~ ZRX + xRz = MOz ~ xRy + VRX =
Rx	Ry	Rz
	A)
Индексы в уравнениях образуют круговую перестановку х —>• у —>- z.
Если систему привести к любой точке на центральной винтовой
оси, то главный вектор и главный момент будут лежать на этой оси
и образовывать динаму.
Из трех уравнений A) два являются независимыми.
Если один из компонентов главного вектора равен нулю, напри-
например, Rx = 0, то соответствующее уравнение записывается в другой
форме: МОх - yRz + zRy = 0.
9.	Находим координаты точки А пересечения центральной оси с
плоскостью ху {Решебник ВМ, §1.11). Если прямая параллельна плос-
плоскости жг/, то такой точки не существует. Решая систему A) при
z = 0, получаем у = yA,z = zA. Аналогично можно найти точки пе-
пересечения центральной винтовой оси с плоскостями xz и yz (если они
существуют).
10.	Проверяем решение, приводя систему к любой точке централь-
центральной винтовой оси (например, хА, уА). Для этого новые оси коорди-
координат, параллельные старым, проводим через выбранную точку и по-
повторяем пп. 3—4 плана. Главный момент должен быть равен мини-
минимальному М^.
Пример. Систему сил Fx = 4 Н, F2 = 10 Н, F3 = 21 Н, F4 = 4 Н,
приложенных к вершинам параллелепипеда, привести к началу коор-
координат (рис. 72). Найти координаты точки пересечения центральной
винтовой оси с плоскостью ху. а = 3м, 6 = 5 м, с = 4м.
*) Общие уравнения прямой и каноническая форма уравнения прямой
см. Решебник ВМ, §1.10

4.6. Приведение системы сил к простейшему виду
113
Рис. 72
Решение
1.	Вычисляем компоненты главного вектора системы. Проекции
вектора F4, лежащего на большой диагонали параллелограмма длиной
L = \Лх2 + Ъ2 + с2, вычисляем по формулам
F4* = F4 C0S(F4 Л Ж) = FWL>
F4y = F4 C0S(^4 Л ?/) = F4Ъ/L,
F4z = F4 cos(F4 Az) = -F4c/L.
Определяем компоненты главного вектора:
Rx = Y,Xi = ~Fi ~ F2 + ^4ж = -12.303 H,
Rz = J2Zi = F4z = 2.262 H.
2.	Находим модуль главного вектора:
R =
+Щ
= 22.061 Н.
3. Вычисляем компоненты главного момента системы сил относи-
относительно начала координат:
МОх = EMXi = ~F4yc = -11.314 Нм,
МОу = Т,Муг = -FlC + F4xc = -9.212 Нм,
zi = F±b + F2b - F3a = -7.00 Нм,
MOz =
4. Находим модуль главного момента:
мо =
моу
= 16-182 Нм.
8 М.Н. Кирсанов

114
Гл.4. Пространственная система сил
5. Определяем скалярный инвариант системы:
= R . Мо = RxMOx
RyMOy
RzMOz = 290.745 Н2м.
Скалярный инвариант не равен нулю, следовательно, система сил при-
приводится к динаме.
6. Вычисляем минимальный главный момент системы сил:
Неравенство М^ < MQ = 16.182 Нм выполняется. Точки, относи-
относительно которой момент системы сил меньше М^, не существует.
7.	Находим шаг винта системы сил:
М
р = —^ = 0.597 м.
R
Шаг положительный, следовательно, главный момент и главный век-
вектор направлены по центральной винтовой оси в одну сторону.
8.	Записываем уравнения центральной винтовой оси:
MOx-yRz
MOy-zRx+xRz MOz - xRy + yRx
_MOy
Rx	Ry	Rz
Из этих трех уравнений только два являются независимыми:
2.262 у - 18.172 z - 3.964 = 0,
-2.262 х + 12.303 z + 1.644 = 0.
= р.
B)
9. Находим координаты точки пересечения центральной оси с плос-
плоскостью ху. Решая систему B) при z = 0, получаем, что
у = уА = 1.752 м, х = хА = 0.726 м.
Основные результаты расчета заносим в таблицу:
Rx
Ry
Rz
R
Н
-12.303
-18.172
-2.263
22.061
Мох
Моу
Moz
Мо
Нм
-11.314
-9.212
7.000
16.182
ХА
УА
м
0.726
1.752
10. Проверяем решение, приводя систему к точке А центральной вин-
винтовой оси. Через точку А проводим оси новой системы координат
ж', г/, z;, параллельные исходным осям (рис. 73).

4.6. Приведение системы сил к простейшему виду
115
Z к
1
//\
XA
У А
A
b
\P4
	<4	^
Л
с
/
/Fo
у'
Рис. 73
Получаем моменты заданной системы относительно новых осей
координат и величину главного момента относительно центра А:
МАх, = Е МхЧ = -F4zyA - FAyc = -7.350 Нм,
МАу, = Е Myli = -FlC + F4xc + FizxA = -10.856 Нм,
z4 = (F, + F2)(b - yA) - F4yxA+
+ F4XVa ~ рз(а ~ xa) = -1-352 Нм,
MA =
z/ = 13.179 Нм.
Главный момент системы МА относительно новой точки приведения
совпадает с полученным ранее минимальным М^, что подтверждает
правильность расчетов.
Условия ЗАДАЧ. Систему трех сил, приложенных к вершинам
параллелепипеда, привести к началу координат. Найти координаты
точки пересечения центральной винтовой оси с плоскостью ху. Раз-
Размеры на рисунках даны в м, силы — в Н.
x = 2, F2 = 3, F3 = 5.

116
Гл.4. Пространственная система сил
3.
1
5.
4
/
7 -
8
7
l
/у
У
)
{ Z
= 3, F2 =
к
у/
\
\
)
/F2
5
^F2 /
7
-- 3, F3 = 6.
10
/
л-
Z
о
~ 1
6
4.
8
А ^
У У \
У / ' N
/
1
;
/F2
Fx = 4, F2 =
6.
4
/
/
А2;
1
У У х^4
/ i \
i
i
;—
10
'7
~ X
/
= 5, F3 = 8.
5
\
7
7
3
~ X
F, = 1,F2 = 2, F3 = 4.
7.	A 2?	10
7
\
'А
F± = 4, F2 = 4, F3 = 6.
10.	kZ	5
x = 1, F2 = 2, F3 = 5.
x = 2, F2 = 2, F3 = 3.

4.6. Приведение системы сил к простейшему виду
117
Ответы
1
2
3
4
5
6
7
8
9
10
Rx
Ry
Rz
R
Н
1.756
2.954
5.268
1.402
2.013
4.078
-0.372
2.594
1.228
3.297
2.195
5.878
3.585
5.561
4.390
3.097
3.536
4.243
2.536
2.121
1.849
2.121
2.546
-3.394
-1.697
-2.121
3.279
-4.946
3.321
-1.927
3.364
6.912
6.862
6.664
5.119
5.543
4.836
7.013
4.355
4.369
Мох
Моу
Moz
Mo
Нм
2.657
0.000
-7.028
-9.941
-16.971
-9.292
8.787
-12.728
0.000
-10.000
1.874
12.000
5.622
27.153
13.576
12.233
-26.229
7.782
-9.600
4.800
0.000
-1.259
-12.000
-0.765
2.494
0.000
0.000
20.000
0.000
0.000
3.252
12.066
15.000
28.926
21.876
15.362
27.662
24.951
9.600
11.092
ХА
УА
м
-0.093
-1.721
-3.627
2.848
5.907
5.767
3.574
3.299
1.911
3.805
0.701
-1.978
-0.677
4.228
10.960
4.380
2.215
1.519
0.475
3.146
Замечание. Решение задачи легко проверить в системе Maple V.
Приведем фрагмент программы вычислений *^ .
Введены следующие обозначения: F [1] — сила i^, Т [1] — радиус-
вектор точки приложения силы i*\, R — главный вектор, М — главный
момент, II — скалярный инвариант.
F[3]
F[4]
T[5]
T[2]
Т[4]
F[2]:=vectorC,[-10,0,0]):
with(linalg):
:=vectorC,[-4,0,0]):
:=vectorC,[0,-21,0]):
:=evalmD*normalize(vectorC,[a,b,-c] ))):
=vectorC,[0,0,0]):
=vectorC,[a,b,0]):
=vectorC,[0,0,c]):
T[l]:=vectorC,[0,b,c]):
T[3]:=vectorC,[a,b,0]):
R:=evalm(add(F[i],i=l..N)); R0:=evalf(norm(R,2));
M:=evalm(add(crossprod(T[i],F[i]),i=l..N));
M0:=evalf(norm(M,2));	II:=dotprod(R,M);
Здесь использована библиотека linalg. В последних версиях Maple
6,7,8 существует более совершенный пакет LinearAlgebra. В этом
случае операторы скалярного и векторного произведения необходимо
заменить соответственно на DotProduct и CrossProduct.
*) Полный текст программы размещен на странице сети Интернет
www.academiaxxi.ru/solverTM.html.

Глава 5
ЦЕНТР ТЯЖЕСТИ
5.1. Центр тяжести плоской фигуры
Постановка задачи. Найти площадь и координаты центра тя-
тяжести плоской фигуры.
План решения
1.	Разбиваем фигуру на простые отдельные части, положение цент-
центров тяжести которых известны.
2.	Выбираем систему координат. Вычисляем площади и коорди-
координаты х^ yi центров тяжести отдельных частей. Площади вырезанных
частей берем со знаком минус.
3.	Находим общую площадь фигуры по формуле А = У^ А-.
4.	Определяем координаты центра тяжести фигуры:
Пример. Найти площадь и координаты центра тяжести плос-
плоской фигуры. Криволинейный участок контура является половиной
окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
в метрах.
Рис. 74

5.1. Центр тяжести плоской фигуры
119
Решение
1. Разбиваем фигуру на простые отдельные части, положение цент-
центров тяжести которых известны.
Центр тяжести прямоугольника находится в его геометрическом
центре, положение центра тяжести других фигур, встречающихся в
задачах, изображено на рис. 75.	а
3
1-1
3
Зтг
Зтг
Рис. 75
1-
Рис. 76
Рис. 77
Представляем фигуру в виде двух треугольников 1,2, прямоуголь-
прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в м2) и координаты центра тяжести (в м)
каждого элемента:
Ах = | - 2 • 1 = 1, хх = | • 1 = 0.667, У1 = | • 2 = 1.333,
А2 = ^ • 4 • 1 = 2, ж2 = | • 4 = 2.667, у2 = 2 + | • 1 = 2.333,
А3 = 3 • 2 = 6, а
3.142-I2
4 ~~	2
= 2.5, % = 2 ' 2 = Х'
= -1.571, х4 = 3, у4 =
4- 1
3^
= 0.424.

120
Гл. 5. Центр тяжести
Площадь выреза берем со знаком минус.
3.	Площадь фигуры i = ^^ = l + 2 + 6- 1.571 = 7.429 м2.
4.	Находим координаты центра тяжести всей фигуры:
? А.х. 0.667 • 1 + 2.667 • 2 + 2.5 • 6 - 3 • 1.571 о Лпо
Х=	== 2Л92
А
7Л29=
1-333 • 1 + 2.333 • 2 + 1 • б - 0.424 • 1.571
Вычисления удобно свести в таблицу:
г
1
2
3
4
1
2
6
-1.571
7.429
Xi
0.667
2.667
2.5
3
Уг
1.333
2.333
1
0.424
AiXi
0.667
5.333
15
-4.712
16.288
АгУг
1.333
4.667
6
-0.666
11.333
Сначала заполняем столбцы А^х^у^ затем вычисляем статические
моменты А{х^ А{у{. Внизу записываем суммы столбцов, необходимые
для вычисления координат центра тяжести. Таким образом
16.288 Qioo	11.333
= 2.192 м, ус =
7.429
7.429
= 1.526 м.
Замечание 1. Большинство задач на определение центра тя-
тяжести допускает несколько способов разбиения фигуры. Это можно
использовать для проверки решения. Второй вариант разбиения фи-
фигуры в данном примере состоит из прямоугольника 3 с размерами
4мхЗм и вырезанных из него полукруга 4 и двух треугольников 1 и
2 (рис. 77).
Замечание 2. Решение задачи в системе Maple V методом кон-
контурного интегрирования приведено в § 15.2, с. 355.
Условия ЗАДАЧ. Найти площадь (в м2) и координаты центра
тяжести плоской фигуры (ем). Отметки на осях даны в метрах.
Криволинейный участок контура является дугой половины или чет-
четверти окружности.

5.1. Центр тяжести плоской фигуры
121
2 4 6 8	11
13 4 6
2 4 6 8	11
4-
4 6 7
3 5 7
3 5

122
Гл. 5. Центр тяжести
Замечание 3. Во всех вариантах фигуру можно разбить на пять
частей.
Ответы
1
2
3
4
5
А
40.642
35.642
27.071
26.071
39.783
хс
5.203
4.764
3.887
3.755
4.702
Ус
3.627
3.495
2.492
2.441
3.351
6
7
8
9
10
А
17.858
27.358
19.429
23.929
22.217
хс
2.380
3.582
2.668
2.668
3.593
Ус
2.964
2.653
2.945
3.585
2.950
5.2. Пространственная стержневая
система
Постановка задачи. Найти координаты центра тяжести про-
пространственной фигуры, состоящей из N однородных стержней.
План решения
1.	Разбиваем фигуру на отдельные стержни.
2.	Выбираем систему координат. Вычисляем длины и координаты
xi->Viizii * = 1Э	э ^V" центров тяжести отдельных стержней. Коорди-
Координаты центра прямолинейного однородного стержня вычисляем как
полусумму координат его концов.
N
3.	Находим суммарную длину стержней системы L = у ^ Li.
i=l
4.	Определяем координаты центра тяжести тела по формулам
N
N
N
Пример. Найти координаты центра тяжести пространственной
фигуры, состоящей из шести однородных стержней (рис. 78). Даны
размеры: а = 12 м, Ъ = 16 м, с = 10 м, d = 5 м.
Решение
1.	Разбиваем фигуру на шесть стержней.
2.	Выбираем систему координат (рис. 78). Вычисляем длины и ко-
координаты x^y^z^ г = 1,..., N центров тяжести отдельных стержней.

5.2. Пространственная стержневая система
123
Рис. 78
3. Находим суммарную длину стержней системы:
б
, = 79.162 м.
г=1
Промежуточные результаты удобно занести в таблицу:
г
1
2
3
4
5
6
Va2 + b2 + c2
Va2 + с2
а
d
Vа2 + d2
Vc2 + d2
xi
a/2
a/2
a/2
0
a/2
0
Уг
b/2
b
b
-d/2
-d/2
-d/2
zi
c/2
c/2
0
с
с
c/2
4. Определяем координаты центра тяжести тела по формулам
N
N
Хс = т
N
= 4-774 М, Ус = у
ih= 5.379 м.
= 6-921 М,
Условия ЗАДАЧ. Найти координаты центра тяжести простран-
пространственной фигуры, состоящей из шести однородных стержней (в
метрах). Размеры даны в метрах.

124
Гл. 5. Центр тяжести
а = 3, Ъ = 4, с = 3, d = 2.
а = 6, Ь = 5, с = 4, d = 3.
а = 3, Ь = 4, с = 3, d = 2.
а = 6, Ъ = 5, с = 4, d = 2.
а = 5, 6 = 4, с = 3, d = 2.
а = 4, 6 = 6, с = 5, d = 4.
а = 5, 6 = 4, с = 3, с/ = 1.
а = 4, 6 = 6, с = 5, d = 3.
а = 3, 6 = 4, с = 3, d= 1.
а = 6, 6 = 5, с = 4, d = 2.

5.3. Центр тяжести объемного тела
125
Ответы
1
2
3
4
5
L
24.764
28.065
40.097
38.231
23.933
Хс
1.439
2.945
3.105
2.744
1.124
Ус
0.605
1.929
1.007
2.476
0.556
Zc
1.924
2.216
2.883
3.233
1.939
6
7
8
9
10
L
29.164
30.986
39.460
21.648
31.021
Хс
2.500
1.548
2.000
0.796
2.807
Ус
1.563
2.856
2.680
1.635
2.177
Zc
2.092
2.452
2.957
1.985
3.019
В таблице ответов L — суммарные длины стержней (в м).
5.3. Центр тяжести объемного тела
Постановка задачи. Найти координаты центра тяжести од-
однородного объемного тела.
План решения
1.	Разбиваем тело на простые части, положение центров тяжести
которых известно.
2.	Выбираем систему координат. Вычисляем объемы Vi и коорди-
координаты xi,yi,zi центров тяжести отдельных частей. Объемы вырезан-
вырезанных частей берем со знаком минус.
3.	Находим общий объем тела по формуле V = ^2 V^
4.	Определяем координаты центра тяжести тела:
Пример. Найти координаты центра тяжести однородного объем-
объемного тела (рис. 79); а = 10 м, Ь = 12 м, с = 6 м, d = 8 м, R = d/2.
Рис. 79

126
Гл. 5. Центр тяжести
Решение
1.	Разбиваем тело на пирамиду 1, параллелепипед 2 и половину
цилиндра 3 (рис. 80).
2.	Выбираем систему координат. Вычисляем объемы Vi и коорди-
координаты xi,yi,zi центров тяжестей отдельных частей. Центр тяжести
пирамиды 1 лежит в точке С1? С0С-^ = G0О1/4,
13	5
i = -abc, xx = -а, ^ = -Ь, ^ =
о	о	о
1
тс.
4
Центр тяжести параллелепипеда 2 совпадает с его геометричес-
геометрическим центром:
V2 = abd, x2 = -а, у2 = -Ь, z2 = -d.
Объем половины цилиндра 3 берем со знаком минус:
V3 = -7rR2a/2, х3 = -а, у3 = b - /, z3 = -d,
где I = 4R/Ctt) — расстояние по оси у от оси цилиндра до его центра
тяжести
*)
2
ъ
/
А
Рис. 80
3. Находим общий объем тела:
V =
= 240 + 960 - 251.327 = 948.673 м3.
*) В общем случае объем тела, лежащего в области Q, можно найти,
вычисляя тройной интеграл по области V = J J J dxdy dz, а координаты
о
центра тяжести, например, хс однородного тела можно определить по фор-
формуле хс = —	xdxdydz] см. Решебник ВМ, §12.9.

5.3. Центр тяжести объемного тела
127
4. Определяем координаты центра тяжести тела:
х„ = —
240 • 3.75 + 960 • 5 - 251.327 • 5
948.673
= 4.684 м.
Ус = у
240 • 7.5 + 960 • 6 - 251.327 • 10.302
= 5-240 М.
г=1
240 • 9.5 + 960 • 4 - 251.327 • 4
948.673
= 5.391 м.
Условия ЗАДАЧ. Найти координаты центра тяжести однород-
однородного объемного тела. Размеры даны в метрах.
1.
5
У
4
3
4
/
У
2.
6
У
5
/
\
/¦
4
vr
3.
7
6
") 4
R = 2 см.
4.
9
8
\/
\
6
6
У
5.
к
)
9
\/
\
/
\
/¦
7
\
\
Ч/
/ъ
6
/
У
6.
9 7 5
V
N
/
А
1
6
У

128
Гл. 5. Центр тяжести
7.
14	11
8.
R = 4 см.
9.
10	9	6
10.
Ответы
1
2
3
4
5
V
114.667
180.000
237.699
558.000
490.000
хс
1.744
2.361
2.823
2.903
2.334
Ус
6.872
8.463
9.491
12.129
12.995
1.884
1.741
1.882
3.000
2.893
6
7
8
9
10
V
717.500
1458.000
625.664
816.000
266.667
хс
3.193
3.000
2.500
3.176
2.469
Ус
12.584
14.897
12.131
13.343
12.600
4.263
5.333
3.616
3.608
1.800
В таблице ответов дан объем тела — в м3, координаты центра тя-
тяжести — в м.

Часть II
КИНЕМАТИКА
Кинематика — наука о движении геометрических тел. В ней рас-
рассматривается само движение без изучения причин, вызывающих это
движение. Впервые термин "кинематика" ввел А.Ампер A775—1836),
взяв за основу греческое слово кшгцмх, означающее движение.
Простейшим объектом в кинематике является точка. В кинема-
кинематике точки рассматриваются следующие функции времени t: радиус-
вектор r(t), скорость v(t) и ускорение W(t):
Движение тела в кинематике начинают изучать с поступатель-
поступательного и вращательного движения. Во вращательном движении вво-
вводятся понятия угла поворота тела ip(i), угловой скорости и углового
ускорения. Последние две величины векторные, но для вращатель-
вращательного движения их направление всегда постоянно — по оси враще-
вращения. Поэтому в решении часто используются скалярные величины
uz(t) = </?(?), ?z(t) = ujz(t), имеющие смысл проекций этих векторов
на ось вращения z. Точкой будем обозначать производную по вре-
времени.
В плоском движении тела каждая точка тела движется в плос-
плоскости, параллельной некоторой фиксированной плоскости. Само тело
вовсе не обязательно должно быть плоским. Говорить о скорости тела
или его ускорении в общем случае не имеет смысла: тело состоит из
множества точек, каждая из которых может иметь свою скорость и
ускорение. Исключение составляет поступательное движение тела,
при котором равны скорости и ускорения всех точек. Кроме того,
в некоторых задачах иногда говорят, например, о скорости катяще-
катящегося цилиндра или о скорости автомобиля, подразумевая при этом

130
скорость точек центральной оси цилиндра или скорость кузова авто-
автомобиля, принимая его за точку.
Угловая скорость и ускорение для плоского движения — вектор-
векторные величины, но их направления всегда перпендикулярны плоскости
движения. Введем декартову систему координат, в которой плос-
плоскость ху совпадает с плоскостью движения. Тогда угловая скорость
ой и ускорение е направлены вдоль оси z. В решении задач удобно
использовать скалярные величины — проекции этих векторов на ось
z: UJZ и ez.
Скорость точки А тела при плоском движении вычисляют через
известную скорость какой-либо точки В того же тела, принимаемой
за полюс (рис. 81):
vB = vA + vBA, vBA =ш1х АВ.	A)
Для расчета скоростей точек многозвенного механизма, каждое звено
которого совершает плоское движение, формулу A) применяют
последовательно для всех точек, переходя от од-
одной точки, принимаемой за полюс, к другой.
Схему вычислений в этом случае удобно записы-
записывать в виде структурных формул (графов [15])
А^В,	B)
где над стрелкой указан номер тела или наи-
наитие, ol	менование стержня, которому принадлежат
точки, а снизу — угол <р между осью х и вектором АВ. В проекциях
на оси ж, у граф B) дает уравнения
VBy =VAy+ABuJlz COS (f^
где culz — проекция угловой скорости тела 1 на ось z, перпендику-
перпендикулярную плоскости движения *' . Если вращение происходит против
часовой стрелки, то lj1z = |а;1|, а если — по часовой стрелке, то
Ускорения точек тела при плоском движении связаны формулой
WB = WA + е х АВ + си х vBA.	D)
*) Правило "трех С" для запоминания формулы C): в первом уравнении
(проекции на ось х) "икС", "минуС", "синуС".

Глава 6
КИНЕМАТИКА ТОЧКИ
При изучении темы КИНЕМАТИКА ТОЧКИ вы познакомитесь
с простейшими понятиями кинематики. Этот раздел теоретической
механики наиболее близко примыкает к математике. Умение диффе-
дифференцировать и понимать смысл найденных производных — необхо-
необходимые условия для освоения этой темы.
Проверить и "оживить" решение задачи § 6.1 можно с помощью
программы, написанной для математической системы Maple V (§ 16.1,
с. 358). Аналогичная программа содержится в [13].
6.1. Движение точки в плоскости
Постановка задачи. Точка движется по закону
x = x(t),y = y(t).	A)
Для заданного момента времени найти скорость, ускорение точки
и радиус кривизны траектории.
План решения
1.	Определяем траекторию движения точки, исключая t из закона
движения A).
2.	Дифференцируя A) по времени t, находим проекции скорости
точки на оси ж, у:
Vx =±i Vy= У-	B)
3.	Модуль скорости вычисляем по формуле v =
4.	Дифференцируя B), находим компоненты вектора ускорения
WX=i)X= *> WV=ijy= У-
5.	Определяем модуль ускорения W = \/W% + Wy.
6.	Вычисляем тангенциальное (касательное) ускорение. Диффе-
Дифференцируя скорость v = \/Ух ^~ vy 1 как сложную функцию времени,
9*

132	Гл. 6. Кинематика точки
получаем *'
\v W + v W
\WT\ = х	у у
7.	Вычисляем нормальное ускорение Wn = \/W2 — И7!2.
8.	Нормальное ускорение зависит от скорости точки и радиуса
кривизны траектории:
Отсюда находим радиус кривизны
Пример. Точка движется по закону
ar = 3sin2t, y = 2cos4:t.	C)
Для момента времени t = t1 = тг/12 найти скорость, ускорение точки
и радиус кривизны траектории. Координаты ж, г/ даны в см, время
— вс.
Решение
1. Определяем траекторию движения точки, исключая t из закона
движения C). Параметрическим представлением траектории явля-
является сам закон движения C). Координатную форму уравнения дви-
движения точки получаем, исключая из закона движения C) время:
у = 2A - 2 sin2 2t) = 2A - 2(ж/3J) = 2 - 4ж2/9.	D)
Для того, чтобы окончательно получить ответ на вопрос о траекто-
траектории, необходимо еще выделить область определения функции D). Не
все точки кривой, определяемой этой функцией, являются точками
траектории. При 0 < t < тт/4 имеем
О < х < 3,	E)
*) Эту же формулу можно вывести иначе, исходя из того, что величина
WT равна проекции ускорения на касательную к траектории:
\WT\ = \W-v/v\ = \vxWx+VyWy\/v.

6.1. Движение точки в плоскости	133
т.е. траекторией является правая ветвь параболы D) (рис. 82). Гра-
График строим по точкам (отмечены звездочками), через равные проме-
промежутки времени 0.1 с.
2.	Дифференцируя C) по времени ?, находим проекции скорости
точки на оси ж, у:
vx = х = 6cos2?, vy = у = —8sin4?.	F)
При t = тг/12 имеем следующие численные значения компонентов ско-
скорости:
vx = 6cos(tt/6) = Зл/3 = 5.196 см/с,
Vy = -8sinGr/3) = -4л/3 = -6.928 см/с.
3.	Модуль скорости вычисляем по формуле
v = yjv2x + vl = 5л/3 = 8.66 см/с.	G)
Вектор скорости i7 строим на рисунке в маспгтабе по известным ком-
компонентам vx и v . Если в вычислениях нет ошибок, то вектор ско-
скорости будет направлен по касательной к траектории (рис. 82).
4.	Дифференцируя F), находим компоненты вектора ускорения:
Wx=vx = x = -12 sin 2t,
Wy=vy=y = -32cos4t.
При t = тг/12
Wx = -12sin7r/6 = -6 см/с2,
Wy = -32costt/3 = -16 см/с2.
5.	Определяем модуль ускорения
W = yJw[+W* = v/292 = 17.088 см/с2.
Вектор ускорения строим на чертеже в масштабе ускорений (не обя-
обязательно совпадающем с масштабом скоростей). Вектор ускорения
направлен внутрь вогнутости кривой.
6. Вычисляем тангенциальное ускорение *^ :
46 g 2 /2
=
5уЗ
*) Наличие тангенциального ускорения точки видно уже из рис. 82. Рас-
Расстояние между первыми двумя точками меньше, чем между двумя послед-
последними, хотя интервал времени одинаков. Характеристикой такого измене-
изменения является величина WT = vT.

134
Гл. 6. Кинематика точки
7. Вычисляем нормальное ускорение:
Wn = л/W2 - W? = v/292 - D6/5J = 72/5 = 14.4 см/с2
8. Находим радиус кривизны траектории в указанном положении
точки:
R =
75-5
72
= 5.208 см.
2.0 **
1.5:
1.0 :
0.5 :
0.5
1.0
Рис. 82
1.5
2.0
Центр кривизны траектории лежит на нормали к кривой на рас-
расстоянии R = 5.208 см внутри вогнутости кривой. Окружность ради-
радиусом R с центром в этой точке максимально близко совпадет с кривой
в малой окрестности от нее.
Условия задач. Точка движется по закону х = x(t),y = y(t).
Для момента времени t = t± найти скорость, ускорение точки и
радиус кривизны траектории (х и у даны в см, tx — ее).

6.1. Движение точки в плоскости
135
1.
t± =тг/12.
3. x = 4e2t + 5,
У = e4t/4,
tx = 0.3.
5. x = 6B?-sinB?)),
2/ = 6(l-cosBt)),
^ = 5тг/12.
7.
2. ar = 100/(t-
= 1.1.
9. z = llcosBt)(l-
y = llsinBt)(l-
tx =тг/12.
4. Ж =
^ = 0.4.
6. x =
^ = 0.6.
8. x = D5/(e5t + 1) + l)/9,
2/ = e5t,
^ = 0.08.
10. ж = llsinCt),
у = 21cosCt) + 12,
t± = 5тг/9.
Ответы
1
2
3
4
5
6
7
8
9
10
vx
Vy
V
см/с
3.46
-6.25
14.58
18.49
22.39
-2.37
-10.96
-6.01
-30.05
16.50
-10.39
3.13
3.32
16.42
6.00
-3.68
5.32
7.46
30.05
54.56
10.95
6.99
14.95
24.72
23.18
4.37
12.19
9.58
42.50
57.00
wx
Wy
W
wT
wn
I 2
CM/C
-4.00
3.13
29.15
-37.03
12.00
1.82
17.47
5.93
-82.11
85.74
-24.00
-2.36
13.28
22.16
-20.78
8.28
14.52
37.30
-98.21
-94.50
24.33
3.92
32.04
43.15
24.00
8.48
22.72
37.76
128.01
127.60
21.50
-3.85
31.38
-12.97
6.21
-7.95
-9.37
25.33
-11.39
-65.64
11.38
0.71
6.47
41.16
23.18
2.95
20.69
28.01
127.50
109.42
R
CM
10.54
68.51
34.52
14.85
23.18
6.48
7.17
3.27
14.17
29.69

136	-Гл. 6. Кинематика точки
6.2. Путь, пройденный точкой
Постановка задачи. Точка движется по закону
x = x{t),y = y(t).	A)
Определить длину пути, пройденного точкой за время tx.
План решения
1.	Дифференцируя A) по времени ?, находим проекции скорости
точки на оси ж, у: vx = ж, v = у.
2.	Считая, что время отсчитывается от нуля, находим длину пути *' :
о
Пример. Точка движется по закону
x = at, y = bt2,	B)
где а = 3 м/с, Ъ = 2 м/с2. Определить длину пути, пройденного
точкой за время tx = 1 с.
Решение
1.	Дифференцируя B) по времени ?, находим проекции скорости
точки на оси ж, у:
vx = х = a, v = у = 2Ы.
2.	Считая, что время отсчитывается от нуля, находим длину пути:
t±
S = [л/а2 + АЬЧ2 dt =
о
= A/4) Bt1^fiTW1 + {а)
Подставляя числовые значения t = ^ = 1 с, a = 3 м/с, b = 2 м/с2,
получаем 5 = 5/2 + (9/8) 1пЗ = 3.736 м.
Условия задач. Точка движется по закону х = x(t),y = y(t).
Определить длину пути, пройденного точкой за время tx (x и у даны
в м, tx — ее).
Интегрирование функций см. Решебник ВМ, §7.1-8.6.

6.3. Движение точки в пространстве	137
1. z = 2sin(e*),	2. я? = 2 ln(t + 1),
у = 2 cos(e*) + 2,	j/ = Зу^П,
^ = 1.	^ = 2.
3. ж = Ш3,	4. ж = 3*4+ 5
^ = 0.3.	^ = 0.4.
5. ж = 31п(* + 1),	6. х = C?2
= 1.	^ = 2.
7. х = Dt + 3)/(? + 4),	8. ж = ? sinC?) + 5,
2/ = Et + 4)/(? + 4),	у = tcosCi),
tx = 3.	^ = 2.
9. ж = f2 sin(?2) + 2,	10. ж = ?2cosC?2 + 2),
у = t2 cos(t2) + 3,	у = t2 smCt2 + 2),
^ = 1.	tx = 1.
Ответы
1. 3.437 м. 2. 3.116 м. 3. 0.405 м. 4. 0.488 м. 5. 3.666 м.
6. 1.451 м. 7. 2.209 м. 8. 6.498 м. 9. 1.148 м. 10. 1.884 м.
6.3. Движение точки в пространстве
Постановка задачи. Точка движется по закону
x = x{t), y = y{t), z = z(t).	A)
Определить скорость, ускорение точки и радиус кривизны траек-
траектории в заданный момент времени.
План решения
1. Дифференцируя A) по времени ?, находим проекции скорости
точки на оси ж, у и z:
vx =x, vy = У, vz = z.	B)

138	.Гл. 6. Кинематика точки
2.	Вычисляем модуль скорости v = \/v2 ~^~ vy ~^ v<z-
3.	Дифференцируя B), находим компоненты вектора ускорения:
Wx=i)x = х, Wy = vy = у, Wz=vz = z.
4.	Определяем модуль ускорения W = \/W2 + W2 + W2.
5.	Вычисляем модуль тангенциального ускорения:
6.	Вычисляем нормальное ускорение Wn = \/W2 — W^.
7.	Находим радиус кривизны траектории в указанном положении
точки: R = v2/Wn.
Пример. Точка движется по закону
х = Asinkt, у = Acoskt, z = Bt,	C)
где А = 3 см, к = 2 рад/с, В = 8 см/с. При ? = ?-,_= тг/3 с найти
скорость, ускорение точки и радиус кривизны ее траектории.
Решение
1.	Дифференцируя C) по времени t, находим проекции скорости
точки на оси ж, у и z:
vx = х = Л/с cos kt, v = у = —Ак sin kt, vz = z = В.	D)
2.	Вычисляем модуль скорости
V =
В2.
3.	Дифференцируя D), находим компоненты вектора ускорения:
Wx = х = -Ак2 sin kt, Wy = y = -Ak2 cos kt, Wz = z = 0.
4.	Определяем модуль ускорения:
W = yfWi + Wl + W1 = Ак2.
5. Вычисляем модуль тангенциального ускорения:
|ттг . -А2к3 sin kt cos kt + А2к3 cos H sin kt
\W\ =		=	= 0.
/{AkJ + Б2

6.3. Движение точки в пространстве
139
6. Вычисляем нормальное ускорение:
7. Находим радиус кривизны траектории в указанном положении
точки:
R =
V
w
{AkJ + В2
Ж2
Радиус кривизны в данной задаче не зависит от времени. Кривая
представляет собой винтовую линию постоянной кривизны.
Получаем значения искомых величин при t = тг/3:
v = 10 см/с, W = 12 см/с2, R = 8.333 см.
Ответы занесем в таблицу (скорости — в см/с, ускорения — в
см/с2, радиус кривизны — в см):
vx
-3
Vy
-5.196
Vz
8
V
10
wx
-10.392
Wy
6
Wz
0
w
12
WT
0
Wn
12
R
8.333
Условия задач. Точка движется по закону х = x(t),y = y(i),
z = z(t). Определить скорость, ускорение точки и радиус кривизны
траектории при t = tx (х,у и z даны в см, t utx — ее).
1. х = - s'
2t, у = 12et/2, z= - sin2 4t - 2t, tx = 0.1.
3.	x = b(t + IK/10, y=- sin2 St - At, z = - sin 8^ + 4t, t± = 0.3.
z	z
1	Я
4.	x = b\/U + 5, г/ = - sin4? + bt, z = 	, t1 = 0.4.
Z	T ~~\~ Z
5.	x = 5 In C* + 2), j/ = 16e*/3, z = 7(t + II/5, t± = 0.5.
6.	ж = 3t2 + 3^ + 2, у = 2 In Bt + 2), z = 13e*/4, ^ = 0.2.
7.	ж = -sin2 4^ -4t, у = ^2 + 4^ + 4, z = 31nD? + 2), tx = 0.3.

140
Гл. 6. Кинематика точки
8. я: =
9. х = - s'mSt + 5*, y = 15et/4, z = 6(t + 1K/10, tx
, z = 2Г + 3t + 3, ^ = 0.2.
= 0.4.
*x = 0.1.
10. x = 12e*/2, у = 3(t + 1I/10, z = 3t+]- cos2 8t,
Ответы
1
2
3
4
5
6
7
8
9
10
Vx
Vy
Vz
V
см/с
3.84
-1.04
1.25
3.89
4.29
4.20
-2.65
1.97
1.01
6.31
6.31
-1.04
-7.98
4.94
6.30
1.67
4.60
-1.04
4.14
0.28
-0.57
4.63
1.05
-1.39
1.01
3.42
3.75
3.80
1.42
1.00
7.41
4.86
8.15
6.44
7.69
5.66
6.50
4.41
4.50
6.39
wx
-3.12
1.22
-0.67
-1.18
-3.67
6.00
-11.80
26.55
1.87
3.15
Wy
3.15
1.22
5.60
-8.00
2.10
-1.39
2.00
1.22
1.04
-0.23
Wz
см/с
11.15
1.54
-21.61
1.16
-0.54
0.85
-4.69
4.00
-0.71
0.93
W
2
12.00
2.32
22.34
8.17
4.27
6.22
12.85
26.87
2.25
3.30
wT
0.22
0.95
-8.38
-7.10
-0.40
4.55
3.52
15.05
1.15
3.25
Wn
11.99
2.11
20.71
4.04
4.25
4.23
12.36
22.26
1.94
0.56
R
CM
4.57
11.17
3.21
10.27
13.91
7.58
3.42
0.87
10.44
72.54
6.4. Естественный способ задания
движения точки
Постановка задачи. Точка движется по плоской кривой
У =
A)
с постоянной скоростью v. Определить ускорение точки, радиус
кривизны траектории и косинус угла наклона касательной к траек-
траектории с осью ох, при заданном значении х.
План решения
1. Находим зависимость между компонентами скорости. Диффе-
Дифференцируя A) по t, используя правило дифференцирования сложной
функции y(x(t)), получаем

6.4. Естественный способ задания движения точки	141
где штрихом обозначена производная по координате, у' = dy/dx, a
точкой, как всегда, — по времени, х = dx/dt.
2.	Дополняя B) уравнением v2 -\- v2 = г>2, получаем систему урав-
уравнений, из которой находим компоненты скорости vx и v .
3.	Находим косинус угла наклона касательной к траектории с осью
ox: cos a = vx/v.
4.	Находим зависимость между компонентами ускорения. Диффе-
Дифференцируя B) по ?, получаем
dv'
Wy = -^x + y'x = у"х2 + y'Wx,	C)
где у" = d2y/dx2.
5.	Так как по условию v = const, то тангенциальное ускорение
равно нулю. Отсюда получаем уравнение
\v W +v W \
\W\= ' х х " yl =0,
Т	v2
которое совместно с C) дает систему для определения проекций уско-
ускорения. Решаем систему и находим Wx и W .
6.	Вычисляем модуль ускорения W = \/W2 + Wy.
7.	Согласно п.5, тангенциальное ускорение равно нулю и нормаль-
нормальное ускорение совпадает с полным: Wn = л/W2 — W? = W. Так как
Wn = v2 /R, находим отсюда радиус кривизны траектории:
R = v2/Wn.
Пример. Точка движется по плоской кривой
у = х sin —-—	D)
о
с постоянной скоростью v = 4 м/с. Определить ускорение точки, ра-
радиус кривизны траектории и косинус угла касательной к траектории
с осью ох при х = 1 м.
Решение
1. Находим зависимость между компонентами скорости. Диффе-
Дифференцируем D) по t. Используя правило дифференцирования сложной
функции, получаем
у у = y = y'x = y'vx,	E)

142	Гл. 6. Кинематика точки
где
х-\-1 х х-\-1
+
у = [х sin ——- = sin ——- + - cos
о у	о	о	о
При х = 1 имеем у' = 0.88 и
vy = 0.88?;ж.
2.	Дополняя E) уравнением v2 + v2 = v2, получаем систему урав-
уравнений, из которой находим компоненты скорости vx и vy:
vx = 3.002 м/с, vy = 2.643 м/с
3.	Находим косинус угла касательной к траектории с осью ох:
vx 3.002 п^
cos а = — = 	= 0.751.
v	4
4.	Находим зависимость между компонентами ускорения. Диффе-
Дифференцируя E) по ?, получаем
dv'
г 4 ?/г — и"т2
dv
W — —г 4- ?/г — и"т2 4-
+ + 2 х-\-1 х х + 1
= I sin —	h - cos —— = - cos —	-sin-
где
3 3 3/ 33 9 3
При х = 1 м вычисляем у" = 0.455 м. С учетом ранее найденной
величины х = 3.002, получаем
Wy =4.1 + 0.88И^ж.	F)
5. Из условия v = const следует, что
\v W +v W
Решая это уравнение совместно с F), находим проекции вектора уско-
ускорения:
Wx = -2.035 м/с2, Wy = 2.312 м/с2.
6. Вычисляем модуль ускорения:
W = yfwf+W* = 3.080 м/с2.
7. Находим радиус кривизны траектории:
V2	V2
Л=- = - = 5.195М

6.4. Естественный способ задания движения точки
143
Ответы заносим в таблицу:
у'
0.880
у"
1/м
0.455
Vx
Vy
м/с
3.002
2.643
cos(a)
0.751
wx
Wy
W
м/с2
-2.035
2.312
3.080
R
M
5.195
Замечание. В механике гибких стержней и сопротивлении матери-
материалов для нахождения радиуса кривизны кривой, заданной в форме
у = г/(ж), существует формула
у'2Г2/у".
G)
Решенная задача представляет собой кинематический вывод этой фор-
формулы. Проверку решения можно выполнить, подставив в G) найден-
найденные значения у' и у".
Как и следовало ожидать, радиус кривизны траектории R от ско-
скорости движения точки не зависит, как не зависит, например, форма
рельсового пути от скорости движения трамвая (если, конечно, не
учитывать деформации).
Условия задач. Точка движется по плоской кривой у = у(х)
с постоянной скоростью v. Определить ускорение точки, радиус
кривизны траектории и косинус угла наклона касательной к траек-
траектории с осью ох при заданном значении х.
у = -2ж2 + 5ж + 3,
v = 1 м/с, х = 1 м.
3. 2/ =
v = 5 м/с, х = 3 м.
5. у =
34
v = 8 м/с, х = 5 м.
18
7. 2/ = -
v = 3 м/с, ж = 1 м.
2. 7/ =	\- Sin —,
v = 5 м/с, ж = 2 м.
4. 2/ = Зеж/5 - Зх,
v = 7 м/с, ж = 4 м.
6. 2/ = Зл/Зж + 1,
v = 12 м/с, ж = 6 м.
г> = 4 м/с, ж = 2 м.

144
Гл. 6. Кинематика точки
9. 2/ =
X X
О	5
v = 5 м/с, х = 3 м.
10. г/ = 3 sin2 —Ь cos —,
о	о
v = 4 м/с, ж = 4 м.
Ответы
1
2
3
4
5
6
7
8
9
10
у'
1.000
1.157
1.000
-1.665
-0.694
1.032
-1.047
0.840
0.880
0.133
у"
1/м
-4.000
0.491
-0.200
0.267
0.198
-0.082
0.404
-0.336
0.302
-0.619
vx
Vy
м/с
0.707
3.269
3.536
3.605
6.573
8.349
2.072
3.063
3.753
3.965
0.707
3.784
3.536
-6.001
-4.561
8.619
-2.169
2.573
3.304
0.528
cos(a)
0.707
0.654
0.707
0.515
0.822
0.696
0.691
0.766
0.751
0.991
wx
Wy
W
м/с2
1.000
-2.595
1.250
1.532
4.011
2.839
0.867
1.552
-2.113
1.274
-1.000
2.242
-1.250
0.920
5.781
-2.750
0.828
-1.848
2.400
-9.562
1.414
3.429
1.768
1.787
7.037
3.953
1.199
2.413
3.198
9.646
R
M
0.707
7.291
14.142
27.422
9.095
36.430
7.507
6.629
7.818
1.659
6.5. Движение точки в полярных
координатах
Постановка задачи. Задан закон движения точки в полярных
координатах:
A)
Найти скорость и ускорение точки в полярных, декартовых и ес-
естественных координатах в заданный момент времени.
План решения
1.	Вычисляем полярные координаты точки в заданный момент
времени: р = p(t), (р = (p(t).
2.	Дифференцируя A) по времени ?, находим производные поляр-
полярного радиуса р и полярного угла:
р = dp/dt, ф = dip/dt.	B)
3.	Вычисляем компоненты скорости в полярных координатах:
VP =

6.5. Движение точки в полярных координатах	145
4.	Находим модуль скорости v =
5.	Декартовы ж, у и полярные координаты р, (р связаны соотноше-
соотношениями
у =
Дифференцируя C), вычисляем компоненты скорости точки в декар-
декартовых координатах:
vx =vpcos<p-v(psin(p,
v = v simp-\-v cos (p.
6. Делаем проверку, вычисляя модуль скорости по декартовым
компонентам: v =
7.	Дифференцируя B), находим вторые производные полярного
радиуса р и полярного угла: р = d2p/dt2, ф = d2ip/dt2.
8.	Вычисляем компоненты ускорения точки в полярных координа-
координатах: Wp = p- рф2, W^ = рф + 2рф.
9.	Модуль ускорения вычисляем по формуле W = \/Wp + W2.
10.	Вычисляем компоненты ускорения точки в декартовых коор-
координатах, дважды дифференцируя C):
Wx = W cos (p — W sin <p,
Wy = Wp sin (f + W^ cos (p.
11. Делаем проверку, вычисляя модуль ускорения по декартовым
компонентам: W =
12. Находим модуль тангенциального ускорения,:
|wg = ' х х v yl
и проверяем его по формуле
\v W +v W
\WT\ =
V
13. Вычисляем нормальное ускорение Wn = у rr wT.
Пример. Задан закон движения точки в полярных координатах:
D)
10 М.Н. Кирсанов

146	.Гл. 6. Кинематика точки
Найти скорость и ускорение точки в полярных, декартовых и естес-
естественных координатах при t = 1 с. Радиус дан в метрах.
Решение
1.	Вычисляем полярные координаты точки в заданный момент
времени*^ : р = lsin(l) = 0.141, (р = 1.
2.	Дифференцируя D) по времени ?, находим производные поляр-
полярного радиуса р и полярного угла:
р = sinC?) + 3tcosCt), ф = Ш2.	E)
При t = 1 имеем р = -2.829, ф = 3.
3.	Вычисляем компоненты скорости в полярных координатах:
vp = р = -2.829 м/с, У(р=рф = 0.141 • 3 = 0.423 м/с.
4.	Вычисляем модуль скорости: v = Jv2p + v^ = 2.860 м/с.
5.	Вычисляем компоненты скорости в декартовых координатах:
vx = v cos(p — v sin if = —1.885 м/с,
v =v sin(p-\-v cos<?? = —2.152 м/с.
6.	Делаем проверку, вычисляя модуль скорости по декартовым
компонентам:
v = Jvl +v* = \/l.8852 + 2.1522 = 2.860 м/с.
7. Дифференцируя E), находим вторые производные полярного ра-
радиуса р и полярного угла:
р = d2p/dt2 = 6cosCf) - 9*sinCt),
ф = d2(p/dt2 = 6t.
При t = 1 получаем р = —7.210, «,3 = 6.
8. Вычисляем компоненты ускорения в полярных координатах:
Wp = р - рф2 = -8.480 м/с2, W<f = рф + Трф = -16.126 м/с2.
9. Определяем модуль ускорения: W = \/Wp + W? = 18.220 м/с .
Аргументы тригонометрических функций измеряются в радианах.

6.5. Движение точки в полярных координатах
147
10.	Находим компоненты ускорения в декартовых координатах:
Wx = Wp cos <p-W(psm(p = 8.988 м/с2,
Wy = Wp sin if + W^ cos <p = -15.849 м/с2.
11.	Делаем проверку, вычисляя модуль ускорения по декартовым
компонентам:
W = yJw[+W* = V8.9882 + 15.8492 = 18.220 м/с2.
12. Находим модуль касательного ускорения,
\WT\ = -?—?¦	y—^ = 6.000 м/с2,
и проверяем его по формуле
\Wr\ = W + W\ = 12.829-8.48-а423-16.1261 = ^ ^
13. Вычисляем нормальное ускорение
Wn = л/W2 - W? = 17.204 м/с2.
Ответы заносим в таблицу (скорости — в м/с, ускорения — в
м/с2):
vP
-2.83
0.42
V
2.86
Vx
-1.88
Vy
-2.15
-8.48
-16.13
18.22
Wx
8.99
wy
-15.85
6.0
Wn
17.20
Условия ЗАДАЧ. Задан закон движения точки в полярных коор-
координатах: р = p(t) (в метрах), (р = (f(t). В указанный момент вре-
времени найти скорость и ускорение точки в полярных, декартовых и
естественных координатах*' .
Д,	2. р = 16cos2Gr?/14),
= arccos(?/ll), t = 9 с.	<?> = cos2(tt^/14), t = 10 с.
*) Все кривые, заданные в условиях задач, являются классическими,
имеют свои названия и описаны в справочной литературе [4, §1.3].
10*

148
Гл. 6. Кинематика точки
3. р = 23/A
4. р = Юе"*/7,
= arccos(?/2), t = 1 с.
5.
6.
= cos2(tt?/10), t = 3c.
= ell\ t = 2c.
0.5K, f =
7. р = 8е*/24,
8.	р = 80/t + 10,
(f = t/3, t = Б с.	(р = arccos(?/10), ?
9. p = 5t/4 + 8,	10.	p = llcos(t/10) + l
(^ = arccos(t/8), t = 7 c.	<p = t/10, t = 8c.
Ответы
= 6 с.
1
2
3
4
5
6
7
8
9
10
P
M
0.81
6.22
7.67
7.51
17.37
7.00
9.85
23.33
16.75
19.66
P
м/с
-0.45
3.50
-5.11
-1.07
15.02
-2.63
0.41
-2.22
1.25
-0.79
4>
рад
0.61
0.39
1.05
1.33
0.35
1.00
1.67
0.93
0.51
0.80
Ф
рад/с
-0.16
0.22
-0.58
0.19
-0.30
0.38
0.33
-0.13
-0.26
0.10
vP
v^
V
Vx
Vy
м/с
-0.45
3.50
-5.11
-1.07
15.02
-2.63
0.41
-2.22
1.25
-0.79
-0.13
1.36
-4.43
1.43
-5.19
2.63
3.28
-2.92
-4.32
1.97
0.47
3.76
6.76
1.79
15.89
3.71
3.31
3.67
4.50
2.12
-0.30
2.72
1.28
-1.64
15.89
-3.63
-3.31
1.00
3.19
-1.96
-0.37
2.59
-6.64
-0.70
0.20
-0.79
0.09
-3.53
-3.18
0.80
1
2
3
4
5
6
7
8
9
10
P
м/с2
0.06
0.36
6.81
0.15
22.91
1.31
0.02
0.74
-0.00
-0.08
Ф
рад/с2
-0.04
0.02
-0.19
0.03
0.06
0.09
0.00
-0.01
-0.12
0.00
wp
W
Wx
Wy
\Wr\
Wn
м/с2
0.04
0.06
4.26
-0.12
21.36
0.33
-1.08
0.38
-1.12
-0.27
0.11
1.67
4.43
-0.20
-7.92
-1.31
0.27
0.28
-2.66
-0.16
0.12
1.67
6.14
0.24
22.78
1.35
1.11
0.47
2.89
0.32
-0.03
-0.58
-1.70
0.17
22.78
1.28
-0.17
0.00
0.31
-0.08
0.12
1.57
5.90
-0.16
-0.21
-0.43
-1.10
0.47
-2.87
-0.31
0.07
0.66
6.12
0.09
22.77
1.16
0.14
0.45
2.25
0.04
0.10
1.54
0.56
0.22
0.51
0.70
1.10
0.13
1.81
0.31

Глава 7
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА
При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы
научитесь решать простые задачи кинематики тела. В таких задачах
вводятся векторные величины — угловая скорость uj и угловое уско-
ускорение е. Важно понять, что для вращательного движения тела эти
векторы постоянно направлены по оси вращения. При сферическом
движении (§ 10.1) векторы угловой скорости и углового ускорения
могут лежать на разных прямых, и направления их в общем случае
зависят от времени.
7.1. Вращательное движение тела
Постановка задачи. Твердое тело вращается вокруг неподвиж-
неподвижной оси. Заданы некоторые кинематические характеристики дви-
движения тела и (или) кинематические характеристики движения точ-
точки этого тела. Найти остальные кинематические характеристики
движения тела или точки.
План решения
Пусть тело вращается вокруг оси z. Кинематические характерис-
характеристики движения тела:
—	угол поворота (р;
—	угловая скорость ujz = ф;
—	угловое ускорение ez = ф = ujz.
Кинематические характеристики точки на теле:
—	радиус траектории (расстояние до оси вращения) R;
—	скорость v = ujR, где ио = |u;J;
—	ускорение W = R\fujA + ?2, где е = \ez\.
1. Записываем систему уравнений для всех величин, входящих в
условие задачи. В зависимости от условия возможны три основ-
основных варианта решения.

150	Гл. 7. Вращательное движение тела
— Неизвестный закон вращения. Записываем систему двух
уравнений для скорости v точки, лежащей на расстоянии
R от оси вращения, и ее ускорения W:
A)
Для решения задачи необходимо, чтобы три из пяти ве-
величин (i?, v, И7, ujz, ez), входящих в A), были заданы в
условии.
—	Вращение с постоянной угловой скоростью. Интегрируя
уравнение uoz = d(p/dt, при ujz = const, получаем
<p = uzt + (p0.	B)
Как правило, отсчет ведется от (р0 = 0, поэтому в системе
трех уравнений A-2) содержатся семь величин R, г>, W, ojz,
t, (p, ?z, четыре из которых должны быть заданы в условии
задачи.
—	Вращение с постоянным угловым ускорением. Дважды ин-
интегрируя уравнение
получаем, при (р0 = 0,
где uj — начальная угловая скорость. Совместно с A)
получаем систему четырех уравнений для восьми величин
R, v, W, luz, ez, tp, t, ujz^ четыре из которых должны быть
заданы в условии задачи.
2. Решаем систему. Находим искомые величины.
Замечание. Ряд величин задан в тексте задач неявно. Например,
угол поворота (р может быть задан числом оборотов п = (р/Bтг).
Слова "покой" и "остановка" соответствуют математической записи
ш„ = 0.

7.1. Вращательное движение тела	151
Пример. Диск вращается вокруг неподвижной оси с постоянным
угловым ускорением 0.02 рад /с . Найти ускорение точки, лежащей на
расстоянии 4 см от оси вращения, через 7 с после начала движения
из состояния покоя.
Решение
1. В задаче задано постоянное угловое ускорение. Записываем
систему уравнений для величин, входящих в условие задачи:
По условию задачи диск в начальный момент находился в покое, сле-
следовательно, ujZq = 0. Крс
ez = 0.02 рад/с . Решая
ными uj и W, находим
довательно, ujz = 0. Кроме того, при t = 7 с, даны значения R = 4 см,
?_, = 0.02 рад/с . Решая систему двух уравнений D) с двумя неизвест-
неизвест= 0.02-7 = 0.14 рад/с2,
W = 4\/0.144 + 0.022 = 0.112 см/с .
Ответ. W = 0.112 см/с2.
УСЛОВИЯ ЗАДАЧ
1.	Диск вращается вокруг неподвижной оси с постоянным угловым
ускорением 0.01 рад/с2. На каком расстоянии от оси вращения нахо-
находится точка, ускорение которой через 100 с после начала движения
из состояния покоя достигает 2 см/с2 ?
2.	Твердое тело вращается вокруг неподвижной оси по произволь-
произвольному закону if = ip(i). В момент, когда угловое ускорение тела равно
2 рад/с2, известно ускорение точки, лежащей на расстоянии 4 см от
оси, W =12 см/с2. Чему равна в этот момент угловая скорость тела?
3.	Колесо вращается вокруг неподвижной оси с постоянным угловым
ускорением. На каком расстоянии от оси вращения находится точка,
ускорение которой через 4 с после начала вращения из состояния по-
покоя достигает 9 см/с2, а угловая скорость — 0.3 рад/с?
4.	Твердое тело вращается вокруг неподвижной оси с постоянным
угловым ускорением. Через 34 с после начала движения ускорение
точки М, лежащей на расстоянии 8 см от оси, достигает 39 см/с2.
Сколько оборотов сделает тело за это время?

152	Гл. 7. Вращательное движение тела
5.	Вращаясь с постоянным угловым ускорением, диск радиусом R =
= 6 см делает 50 оборотов за 250 с после начала движения из состо-
состояния покоя. Найти скорость точки, лежащей на его ободе, в этот
момент.
6.	Вращаясь с постоянной угловой скоростью, диск радиусом R =
= 16 см делает 60 оборотов за 36 с после начала движения из состо-
состояния покоя. Найти скорость точки, лежащей на его ободе, в этот
момент.
7.	Колесо вращается с постоянным угловым ускорением. Через ка-
какое время колесо сделает 70 оборотов и разовьет угловую скорость
7 рад/с.
8.	Диск радиусом R = 9 см вращается вокруг неподвижной оси с
постоянным угловым ускорением 1.2 рад/с2 и за некоторое время t
делает 40 оборотов. Начальная угловая скорость диска равна нулю.
Найти скорость точки, лежащей на ободе диска, в этот момент.
9.	Колесо радиусом R = 21 см, вращаясь вокруг неподвижной оси,
увеличивает свою угловую скорость по закону ио = Ы2. Через 1.6 с
угловое ускорение становится равным 6 рад/с2. Найти ускорение
точки, лежащей на ободе колеса, в этот момент.
10.	Имея угловую скорость ио = 8.5 рад/с2, маховик начинает равно-
равномерно тормозить (s = const). После 25 оборотов его угловая скорость
уменьшается вдвое. Найти время торможения до полной остановки
маховика.
Ответы
1. R = 2 см. 2. ujz = 1.5 рад/с. 3. R = 76.82 см. 4. п = 5.97.
5. v = 15.08 см/с. 6. v = 1.68 м/с. 7. t = 125.66 с. 8. v = 2.21 м/с.
9. W = 5 м/с2. 10. t = 24.64 с.
7.2. Передача вращения
Постановка задачи. Механизм состоит из вращающихся на не-
неподвижных осях блоков и поступательно движущихся элементов.
Все элементы находятся во фрикционном, зубчатом или ременном
зацеплениях. Задана какая-либо кинематическая характеристика
одного из тел. Найти кинематические характеристики других тел.

7.2. Передача вращения	153
План решения
1. Определяем кинематические характеристики тела, с заданным
законом движения. Если это тело движется прямолинейно поступа-
поступательно, то скорость и ускорение любой его точки имеет вид
_ da(t)	<Ы$
т~ dt ' т~ dt* '
где a(t) — закон движения тела. При заданном вращательном дви-
движении находим угловую скорость и угловое ускорение:
_d<p(t) Р
где ip(i) — закон вращения тела (зависимость угла поворота в ради-
радианах от времени).
2. Определяем угловую скорость тела, связанного нерастяжимой
нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с
телом, угловая скорость которого известна:
где г1? г2 — радиусы ободов колес (блоков) 1, 2, на которые надет
ремень в случае ременной передачи, или радиусы колес, находящихся
в зацеплении; ujZi,ujZ2 — проекции угловых скоростей колес на ось,
параллельную осям вращения. Знак минус берем при внешнем зацеп-
зацеплении, или крестообразной ременной передаче, когда вращение колес
происходит в разные стороны. При внутреннем зацеплении (рис. 83)
или простой ременной передаче (рис. 84) берем знак плюс. Отно-
Отношение г2/т1 называется передаточным числом от тела 1 к телу 2.
Для зубчатых соединений аналогом A) является соотношение угло-
угловых скоростей
KlUJz1 = ±K2UJZ2,
в которое вместо радиусов г1 и г2 входят числа зубцов К1 и К2,
пропорциональные длинам окружностей шестеренок.
Если поступательное движение тела 1 передается вращательному
движению тела 2 (или наоборот), то связь линейной и угловой ско-
скоростей имеет вид
Vl=r2UJz2^	B)
где г2 — радиус обода, находящегося в контакте с поступательно
движущимся телом.

154	Гл. 7. Вращательное движение тела
3.	Повторяя п.2 для всех пар кинематически связанных тел, со-
составляем и решаем систему уравнений для неизвестных линейных и
угловых скоростей.
4.	Дифференцируя уравнения полученной системы, получаем ана-
аналогичную систему для угловых и линейных ускорений. Например, из
уравнения A) следует, что
Аналогично, из B) следует связь линейного ускорения поступательно
движущегося тела и углового ускорения связанного с ним вращающе-
вращающегося тела:
W, = r2eZ2 = WZ,
где WJ — тангенциальная составляющая ускорения точки вращаю-
вращающегося тела в месте контакта. Было бы ошибкой считать Wx = W2,
так как полное ускорение точки на вращающемся теле включает в
себя и нормальную составляющую W2 = W2 + ^Т-
Решаем систему уравнений для ускорений.
Пример. Механизм состоит из двух колес 1, 3 и блока 2, вращаю-
вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено
ремнем с внутренним ободом блока 2. Внешний обод блока находится
во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзыва-
Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.
Рис. 83	Рис. 84
Задан закон движения ведущего колеса: (рг = t2(t + 2). Стрелкой
указано положительное направление изменения угла <^1; Rx = 40 см,
R2 = 26 см, г2 = 24 см, R3 = 42 см. При t = 0.5 с найти ускорение
точки М, лежащей на ободе колеса 3.
Решение
1. Находим угловую скорость ведущего колеса 1:
"Z1=^ = 3t2 + 4t.	C)

7.2. Передача вращения	155
2.	Определяем угловую скорость блока 2, связанного нерастяжи-
нерастяжимым ремнем с колесом 1:
Rlb>Zl =r2^Z2,	D)
где R± и г2 — радиусы ободов, огибаемые ремнем.
3.	Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в
разные стороны *^ , следовательно
Уравнения C-5) образуют систему, решая которую, при t = 0.5 с,
получаем
u;zi = 2.75 рад/с, с^ = 4.583 рад/с, с^ = -2.837 рад/с.
4. Дифференцируя уравнения системы C—5), получаем аналогич-
аналогичную систему для угловых ускорений:
Решаем систему уравнений для ускорений F) и получаем
ezi = 7 рад/с2, eZ2 = 11.667 рад/с2, eZ3 = -7.222 рад/с2.
Вычисляем ускорение точки М:
W = R3y/s2Z3 +«4 = 42л/7.2222 + 2.8374 = 454.23 см/с2.
Ответ. W = 4.542 м/с2.
Условия ЗАДАЧ. Механизм состоит из двух вращающихся на не-
неподвижных осях блоков, соединенных нерастяжимым ремнем. Блоки
передают движение грузам. Задан закон изменения скорости од-
одного из грузов (в см/с). В указанный момент времени найти ско-
скорость другого груза и ускорение точки М на внутреннем или внеш-
внешнем ободе одного из блоков. Радиусы даны в см, время — ее.
*) В точке контакта скорости точек колес совпадают по величине и по
направлению, чего нельзя сказать об ускорениях.

156
Гл. 7. Вращательное движение тела
В
RA = 20, rA = 16, RB = 15,
rB = 5, vc = 23t2, ti = 1.1.
3. M Л
СП
5.
Ra
= 30, rA
гв =6, ад =
(
\ /7^r //
Л. yjy
\T	\^^
]
RA = 20, rA
гв =5, г»с =
M 4
= 20,
16t4,
>
= 16,
9t3,
Rb =
15,
t! = 1.3.
В
/^—^
Щ
,M
:
Rb = 15,
h = 1.5.
CO
Ra = 30, rA = 20, RB = 15,
rs = 6, vc = 2t2, ti = 1.7.
9.	A
Да = 20, гА = 16, Дв = 15,
тв = 5, ад =t4, ti = 1.9.
Да = 40, га = 30, RB = 25,
гв = Ю, ^с = 36?3, ti = 1.2.
Да = 25, гА = 15, Дв = 10,
гв =8, vc = 7t2, t! = 1.4.
Да = 40, га = 30, RB = 25,
гв = Ю, ад = 10t4, ti = 1.6.
8.
cQ
Ra = 25, rA = 15, RB = 10,
rB =8, »c = 2t3, ti = 1.8.
10.	A
сП
RA = 20, га = 16, RB = 15,
гв = 5, vc = 8?2, ti = 1.1.

7.2. Передача вращения
157
Ответы
1
2
3
4
5
6
7
8
9
10
V
см/с
104.363
207.360
12.186
28.583
113.906
19.661
3.468
15.552
31.277
4.033
WM
см/с2
726.102
687.971
11.137
12.549
864.976
68.719
2.506
9.070
61.141
9.761
189.750
207.360
56.243
19.600
227.813
65.536
10.200
19.440
65.846
22.000
750.486
718.541
57.335
23.273
894.473
94.960
10.503
21.452
89.855
24.068
Предупреждение типичных ошибок
1.	Соотношение v1ujz = =br2c<;z , справедливое для зацепления ко-
колес, вращающихся на неподвижных осях, не используйте для механиз-
механизмов, совершающих плоское движение, например, § 12.3, с. 247.
2.	Ускорение точки М, находящейся на нити, свисающей с блока в
месте ее схода, не совпадает с ускорением точки М', лежащей в этом
же месте на блоке. Точка на нити движется по прямой и ее ускорение
WM. Точка на блоке движется по окружности и ее ускорение имеет
две составляющие: W^, = WM и W^,.
3.	Цилиндры 1 и 2 радиусов г1 и г2 одного блока (на одной оси)
имеют одну и ту же угловую скорость. Иногда по ошибке используют
формулу гги;г1 = v2ujZ2 вместо uozi = uoZ2.

Глава 8
ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА
При изучении темы ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА раздела КИ-
КИНЕМАТИКА, вы научитесь применять аналитические и графические
методы для определения скоростей и ускорений точек тел и механиз-
механизмов. Хотя эти знания имеют самостоятельную ценность, особенно
необходимы они будут для решения задач динамики тела и системы.
В § 16.2, с. 361 и § 16.3 с. 364 приведены программы расчета кине-
кинематики плоского движения в математической системе Maple V. Ани-
Анимационные возможности этой системы делают решение наглядным,
позволяя глубже понять суть задачи.
Методы решения задачи кинематики плоского движения разно-
разнообразны. Выбрать оптимальный путь, который может существенно
упростить решение, помогут примеры, приведенные в этой главе.
8.1. Скорости точек многозвенного
механизма
Постановка задачи. Плоский многозвенный механизм с одной
степенью свободы находится в движении. Известна угловая ско-
скорость какого-либо его звена или скорость одной из точек меха-
механизма. Найти скорости точек механизма и угловые скорости его
звеньев.
План решения
Рассмотрим два простых геометрических способа решения за-
задачи, в которых, в отличие от аналитических методов (§ 8.3, 8.5),
определяются модули скоростей и угловых скоростей. Не оговаривая
отдельно, всякий раз под угловой скоростью uj будем подразумевать
ее модуль \lj\.
1-й способ. Мгновенные центры скоростей
1. Определяем положение мгновенного центра скоростей (МЦС)
каждого звена. МЦС лежит на пересечении перпендикуляров, про-

8.1. Скорости точек многозвенного механизма
159
веденных к скоростям точек, принадлежащих звену (рис. 85). У тех
звеньев, у которых МЦС не существует (скорости двух точек парал-
параллельны и не перпендикулярны отрезку, их соединяющему), угловая
скорость равна нулю, а скорости всех точек равны. Если векторы ско-
скоростей перпендикулярны отрезку их соединяющему, то имеют место
два частных случая положения МЦС (рис. 86, 87).
Если тело (колесо, диск, цилиндр) катится по поверхности без про-
проскальзывания, то МЦС этого тела находится в точке касания.
2. Для каждого звена определяем расстояния от его точек до МЦС
этого звена.
VB + VA ;«? В
Рис. 86
3. Записываем систему уравнений для скоростей N точек звена г,
включая точку с известной скоростью:
Здесь iJji — угловая скорость звена г, Rik — расстояние от МЦС звена
г до точки к. Решаем систему, определяем угловую скорость звена, а
затем скорости всех его точек.
Этот пункт плана выполняем последовательно для всех звеньев
механизма. Очередное звено должно иметь общую точку (шарнир) с
предыдущим, для которого угловая скорость найдена или известна.
2-й способ. План скоростей
1.	Как и в методе МЦС ведем расчет, переходя от одного звена к
другому, шарнирно с ним соединенному.
Построение начинаем с вектора, величина и направление кото-
которого известны или легко вычисляются. Этот вектор в заданном мас-
масштабе откладываем от некоторой произвольной точки О (рис. 91).
Его конец определяет первую точку плана скоростей. Точку плана
скоростей (конец вектора) отмечаем строчной буквой, соответству-
соответствующей точке вектора скорости. Пусть первая точка плана скоростей
обозначена как Ъ.
2.	Рассматриваем очередное звено, на котором имеется точка с
уже известной скоростью. Необходимо, чтобы на этом звене была

160
Гл. 8. Плоское движение тела
еще одна точка с известным направлением вектора скорости (напри-
(например, ползун или точка звена, совершающего вращательное движение).
Пусть эта точка обозначена как С (рис. 88).
Справедливо правило, согласно которому неизменяемые отрезки
механизма, обозначенные прописными буквами, перпендикулярны от-
отрезкам плана скоростей, обозначенными теми же строчными бук-
буквами.
Следующая точка плана скоростей лежит на пересечении двух
прямых. Одна прямая определяется направлением скорости точки
С, вторая перпендикулярна ВС. Длина полученного отрезка Ос яв-
является модулем скорости vc (рис. 91).
Скорости остальных точек этого звена (если таковые имеются)
найдем по правилу подобия неизменяемых фигур механизма и фигур,
обозначенных теми же строчными буквами плана скоростей.
Пункт 2 плана выполняем для всех звеньев механизма (рис. 91—95).
3. После построения плана скоростей определяем угловую ско-
скорость каждого звена по простой формуле ujjj = ij/IJ, где IJ рас-
расстояние между точками / и J звена, ij — длина отрезка на плане
скоростей.
Пример. Плоский многозвенный механизм с одной степенью сво-
свободы приводится в движение кривошипом АВ, который вращается
против часовой стрелки с угловой скоростью шАВ = 2 рад/с (рис. 88).
45°
АВ = 30 см,
ВС = 60 см,
CD = 30 см,
DE = 20 см,
EF = 20 см,
FG = 10 см,
ЕН = 30 см,
FO = 20 см,
СК = 25 см.
Рис. 88
Ползуны С, if, Н движутся горизонтально, BD _l_ DG, DG _l_ FO.
Найти скорости точек В, G, D, E, F, G, i7, К механизма и угловые

8.1. Скорости точек многозвенного механизма
161
скорости его звеньев АВ, BD, DG, EH, FO, СК.
Решение
1-й способ. Мгновенные центры скоростей
1. Определяем положение мгновенного центра скоростей каждого
звена АВ, BD, DG, СК, EH, FO.
МЦС звеньев АВ и FO искать не требуется. Они совершают вра-
вращательное движение вокруг шарниров Аи О соответственно. Можно
условно считать, что там находятся их МЦС.
Вектор vB скорости точки В направим перпендикулярно радиусу
АВ против часовой стрелки (рис. 89). Далее, чтобы узнать положение
МЦС следующего звена надо знать направления векторов скоростей
двух его точек. Следующим звеном будет стержень BD, имеющий
со звеном АВ общую точку В. У него есть три характерные точки
В, С и D. Направление вектора скорости точки D пока неизвестно.
Остается точка С. Ползун С движется строго горизонтально. Век-
Вектор скорости vc направляем по горизонтали налево. Из двух возмож-
возможных горизонтальных направлений мы выбрали этот вариант, исходя
из теоремы о проекции векторов скоростей точек неизменяемого от-
отрезка. Проекции должны быть равны и направлены в одну сторону.
Таким образом, известны направления скоростей двух точек тела.
Это позволяет определить МЦС звена BCD. Находим точку Р1 пере-
пересечения перпендикуляров, проведенных из точек В л С, к векторам
vB и vc (рис. 89). Теперь определяем направление вектора vD. Он
11 М.Н. Кирсанов

162	Гл. 8. Плоское движение тела
будет перпендикулярен радиусу P1D и направлен налево, исходя из
той же теоремы о проекциях скоростей точек отрезка BD.
Со стержнем BCD имеют общие точки два стержня: СК и DG.
Рассмотрим сначала стержень DG. Направление вектора скорости
точки D уже известно. Чтобы определить положение МЦС, надо
знать направление вектора еще одной точки на этом звене. Такой
точкой является F. Вектор ее скорости перпендикулярен радиусу
вращения FO и направлен вертикально. Перпендикуляры к векторам
vD и vF задают положение точки Р2, вокруг которой звено DEFG
совершает мгновенное вращательное движение.
Перпендикулярно радиусам P2G и Р2Е проводим вектора vG и vE.
Переходим к звену ЕН, МЦС которого находим на пересечении
перпендикуляров к vE (продолжение радиуса Р2Е) и к вектору ско-
скорости vH ползуна Н, движущегося горизонтально. Получаем точку
Р3 — МЦС звена ЕН.
И, наконец, рассматриваем звено СК. Скорости vK и vc парал-
параллельны и не перпендикулярны СК. Звено С К совершает мгновенно-
поступательное движение. Условно можно сказать, что МЦС звена
СК находится в бесконечности.
2. Определяем расстояния от МЦС звеньев до тех точек этих
звеньев, скорости которых надо найти.
Звено BCD
РХВ = ВС/ cos45° = 60/0.707 = 84.85 см,
РХС = ВС = 60 см,
PXD = ^P^ + CD2 = 67.08 см.
Звено DEFG. Пользуясь подобием AP±CD ~ AP2DF, находим
iD = ^67-08 = 44-72 см'
Р2Е = ^P2F2 + EF2 = л/202 + 202 = 28.28 см,
P2G = \JP2F2 + FG2 = л/202 + 102 = 25.98 см.
Звено ЕН (рис. 90). Находим расстояния до МЦС:
Р3Е = ЕЬл/2 = 36.74 см,

8.1. Скорости точек многозвенного механизма	163
Р3Н = P3L + LH = P3L + EH cos 60° = 25.98 + 15 = 40.98 см.
3. Записываем систему уравнений для скоростей трех точек звена
BCD, включая точку В с известной скоростью:
ис
UD - ^BD"- 1J
Решаем эту систему. Находим ujbd = vB/P1B = 0.707 рад/с,
vc = 0.707 • 60 = 42.43 см/с, vD = 0.707 • 67.08 = 47.43 см/с.
Система уравнений для скоростей точек звена DEFG имеет вид
vd = uDGP2D,
Е	DG 2 '
G	DG 2
Из первого уравнения вычисляем угловую скорость:
ojdg = vD/P2D = 47.43/44.72 = 1.06 рад/с.
Получаем скорости точек:
vE = 1.06 • 28.28 = 30 см/с,
vF = 1.06 • 20 = 21.21 см/с,
vG = 1.06 • 22.36 = 23.72 см/с.
Система уравнений для скоростей точек звена ЕН имеет вид
vE = ojehP3E,
Н	ЕН 3
Отсюда
ujeh = vE/P3E = 30/36.74 = 0.816 рад/с,
vH = ujehP3H = 0.816 • 40.98 = 33.46 см/с.
Звено СК совершает мгновенно-поступательное движение. Сле-
Следовательно, скорости точек С и К равны: vK = vG = 42.43 см/с.
Угловая скорость этого звена равна нулю *^ .
*) Можно считать, что МЦС звена, движущегося мгновенно-
поступательно, находится в бесконечности. Поэтому, рассуждая фор-
формально, получаем иск = vc/оо = 0.
11*

164
Гл. 8. Плоское движение тела
Частично проверить решение можно графически. Известно, что
концы векторов скоростей точек неизменяемого отрезка лежат на
одной прямой. Убеждаемся в этом, проводя прямую через концы век-
векторов vB, vc и vD, отложенных на чертеже в масштабе (рис. 90).
Рис. 90
Аналогично, проверяем скорости vD, vE, vF и vG. Через их концы
также можно провести прямую. Остались непроверенными скорости
точек Е и Н. Для этого можно воспользоваться методом построения
плана скоростей, см. ниже 2-й способ.
Результаты расчетов помещаем в таблицы. Скорости даны в см/с,
угловые скорости — в рад/с.
Точка
V
В
60.00
с
42.43
D
47.43
Е
30.00
F
21.21
G
23.71
Н
33.46
К
42.43
Звено
ш
АВ
2.000
BD
0.707
DG
1.060
ЕН
0.816
FO
1.060
вк
0
2-й способ. План скоростей
1. Построение начинаем с вектора, величина и направление ко-
которого известны или легко вычисляются. В нашем случае это vB.
Вектор vB в заданном масштабе откладываем от некоторой произ-
произвольной точки О (рис. 91). Все остальные вектора также будем от-
откладывать от этой точки.

8.1. Скорости точек многозвенного механизма
165
Точки плана скоростей (концы векторов) отмечаем соответству-
соответствующими строчными буквами. Таким образом, положение точки Ъ на
плане скоростей известно.
2. Рассматриваем звено BCD (рис. 90), на котором имеется точка
В с известной скоростью. Неизменяемые отрезки механизма, обо-
обозначенные прописными буквами, перпендикулярны отрезкам плана
скоростей, обозначенными теми же строчными буквами, ВС _L be.
Звено механизма ВС горизонтально.
d	d	f
Рис. 91
Рис. 92
Рис. 93
Следовательно, точка с плана скоростей лежит на одной вертикали
с точкой Ъ. Известно направление скорости ползуна С. Точку с на-
находим на пересечении двух прямых. Вектор vc изображен отрезком
Ос плана скоростей (рис. 91). Из правила подобия фигур механизма
и фигур, обозначенных теми же строчными буквами плана скоростей
(в данном случае это отрезки ВС и CD), имеем ВС/CD = bc/cd.
d
f 9
f
Рис. 94
Рис. 95
Так получаем точку d плана скоростей и, следовательно, величину
и направление вектора vD (рис. 92).
Определяем скорость vF. Направление этого вектора известно
— он перпендикулярен радиусу вращения FO. По свойству плана

166
Гл. 8. Плоское движение тела
скоростей DF _L df. Точка d на плане уже есть. Проводим через нее
горизонтальную прямую (перпендикулярную DF) до пересечения с
вертикальным направлением вектора скорости vF. Получаем точку
/ (рис. 93). Соединяя ее с центром О, определяем модуль искомой
скорости vF.
Из соотношения подобия DE/DF = de/df на отрезке df находим
внутри него конец вектора скорости vE и вне отрезка, пользуясь про-
пропорцией DG/DF = dg/df, точку д, определяющую вектор скорости
vG (рис. 94).
Аналогично, определяем скорость vH (рис. 95). Здесь eh JL EH.
Точки к и с на плане скоростей совпадают.
3. Угловые скорости звеньев определяем по простым формулам:
uBD = bd/BD, ludg = dg/DG,
JEH
= eh/EH, uoCK = ck/CK = 0, uoFO = fo/FO.
Условия ЗАДАЧ. Плоский многозвенный механизм с одной сте-
степенью свободы приводится в движение кривошипом, который вра-
вращается против часовой стрелки с постоянной угловой скоростью.
Найти скорости точек механизма (в см/с) и угловые скорости его
звеньев (в рад/с). Размеры даны в см.
1.
а?Ч
= 1 рад/с,
а = 30°,
АВ = 30, ВС = 30,
NB = 60, NF = 15,
CD = 60, EH = 30,
FE = 35, FG = 20,
О А = 30, KG = 25.
= 2 рад/с,
a = 45°,
AB = 30, ВС = 30,
NB = 50, NF = 30,
CD = 50, EH = 30,
FE = 35, FG = 10,
О A = 30, KG = 25.

8.1. Скорости точек многозвенного механизма
167
4.
С
В
А
5.
С
В
N
-А
G
О
О
6.
D
N
D
Н
Е
Н
= 1 рад/с,
а = 30°,
АВ = 10, ВС = 30,
7VB = 50, NF = 40,
CD = 40, ?# = 30,
FE = 15, FG = 10,
О А = 20, KG = 25.
= 3 рад/с,
а = 30°,
АВ = 10, ВС = 30,
DB = 60, ?>F = 30,
NC = 40, ?# = 30,
FE = 15, FG = 30,
ОА = 20, KG = 20.
= 1 рад/с,
а = 30°,
АВ = 30, ВС = 30,
DB = 60, ?>F = 15,
NC = 60, EH = 30,
F? = 35, FG = 20,
OA = 30, KG = 25.
ujoa = 2 рад/с,
a = 30°,
AB = 25, ВС = 10,
BF = 50, 7VF = 50,
CD = 15, EH = 30,
FC = 25, GE = 10,
OA = 30, KG = 25.

168
Гл. 8. Плоское движение тела
10.
О
= 1 рад/с,
а = 45°,
АВ = 20, ВС = 10,
BF = 50, 7VF = 50,
CD = 15, F# = 30,
FG = 25, GE = 10,
ОА = 20, KG = 25.
= 3 рад/с,
а = 30°,
АВ = 20, ВС = 10,
BF = 80, 7VF = 20,
CD = 15, EH = 30,
FG = 25, GE = 10,
OA = 20, KG = 25.
= 1 рад/с,
a = 30°,
AB = 25, ВС = 10,
BF = 50, FD = 50,
7VC = 15, EH = 30,
F? = 55, FG = 10,
О A = 30, if G = 25.
ujoa = 2 рад/с,
a = 30°,
AB = 25, ВС = 10,
BF = 50, FD = 50,
7VC = 15, EH = 30,
FE = 35, FG = 25,
О A = 30, /if G = 25.

8.1. Скорости точек многозвенного механизма
169
Ответы
1
2
3
4
5
6
7
8
9
10
VA
30.000
141.421
31.250
60.000
69.282
60.000
50.000
346.410
17.321
60.000
VB
25.981
100.000
27.063
56.624
62.450
51.962
35.355
300.000
15.203
52.664
vc
30.000
141.421
54.127
51.962
60.000
53.329
39.528
312.250
15.000
51.962
vD
15.000
100.000
46.875
22.500
17.321
12.000
17.678
86.603
2.474
8.571
vE
9.233
218.403
28.641
36.933
35.773
33.407
30.414
77.149
35.746
35.662
vF
6.495
60.000
21.651
34.369
22.913
25.981
17.678
60.000
7.898
27.358
VG
7.500
84.853
25.000
30.000
17.321
30.000
25.000
69.282
8.660
30.000
vH
2.813
150.000
6.250
41.250
41.136
36.000
42.426
83.138
39.280
39.429
1
2
3
4
5
6
7
8
9
10
МАО
1.000
-4.714
-1.563
3.000
2.309
2.000
2.500
17.321
-0.577
2.000
ШАС
0.500
-3.333
1.563
-0.750
0.577
1.200
-1.768
-8.660
-0.247
0.857
UCD
0.433
2.000
0.677
—
—
3.464
2.357
-20.000
—
-
LOBF
0.433
2.000
0.541
0.866
1.000
-0.520
-0.354
3.000
-0.150
-0.520
UGE
-0.188
6.000
-1.250
-0.250
0.433
-0.600
0.707
1.386
0.680
-0.943
UKG
-0.300
-3.394
1.000
1.500
-0.693
-1.200
1.000
-2.771
-0.346
-1.200
шен
-0.250
2.828
0.833
-1.000
-0.577
1.000
0.833
2.309
-0.289
1.000
UCN
—
—
—
1.299
1.000
—
—
—
1.000
3.464
Ответы на типичные вопросы, возникающие при решении задачи
1.	Механизм, изображенный на рисунке не может двигаться. Не
"заклинит77 ли его?
Вполне возможно, что через некоторое время после начала дви-
движения из указанного положения механизм "заклинит". В задаче не
указан интервал изменения времени. Предположите, что он мал или
механизм совершает колебательные движения вокруг указанного со-
состояния. Наша задача найти скорости в данный момент времени.
2.	МЦС оказался очень далеко и лежит за пределами чертежа.
Что делать?
*) В ответах приведены не модули угловых скоростей, а проекции уг-
угловых скоростей на ось z, перпендикулярную чертежу. Знак, определение
которого не входило в условие задачи, дает дополнительную информацию
о направлении вращения звена.

170	.Гл. 8. Плоское движение тела
Уменьшите масштаб длин.
Предупреждение типичных ошибок
1.	Выбирая направление вектора скорости, не проводите вектор
перпендикулярно чему-попало (чаще всего самому звену). Если это
не ползун, у которого направление скорости задается самим ползу-
ползуном, то вектор должен быть перпендикулярен радиусу, соединяю-
соединяющему точку, у которой ищем скорость, с неподвижной или мгновенно-
неподвижной точкой звена, на котором расположена точка.
2.	Распространенная ошибка: определение МЦС как точки пере-
пересечения перпендикуляров к скоростям точек разных звеньев. Будьте
внимательны, при определении МЦС проводите перпендикуляры к
скоростям точек одного звена).
3.	Хорошая проверка записи формулы vN = uJMNPiN: буква или
цифра обозначения точки N должна быть в формуле трижды. Во-
первых, в обозначении самой скорости vN, во-вторых, в индексе угло-
угловой скорости, так как точка принадлежит соответствующему звену,
и, наконец, в наименовании отрезка, соединяющего МЦС звена, на
котором лежит точка и угловая скорость которого используется, с са-
самой точкой. Для большей надежности (но несколько более громоздко)
МЦС можно не нумеровать, а приписывать им буквы соответствую-
соответствующего звена. Тогда появляется еще одна проверка, упреждающая воз-
возможные ошибки. Наименование звена, например M7V, в формуле для
скорости должно появляться дважды: vN = ^MNPMNN.
4.	При построении плана скоростей не надо комбинировать два
метода, строя на плане скорость, направление которой получено при
помощи МЦС. План скоростей полностью независим от метода МЦС
и является его хорошей проверкой *' .
8.2. Ускорения точек многозвенного
механизма
Постановка задачи. Плоский шарнирно-стержневой механизм
состоит из шарнирно соединенных стержней и ползунов. Механизм
приводится в движение кривошипом, который вращается с задан-
заданной угловой скоростью. В указанном положении механизма найти
ускорения всех его шарниров.
*) Существует еще несколько способов проверки вычисления скоростей
точек многозвенного механизма, см. §§ 8.3, 8.5, 16.2, 16.3.

8.2. Ускорения точек многозвенного механизма	171
План решения
1.	Определяем угловые скорости звеньев и скорости точек меха-
механизма (см. § 8.1).
2.	Определяем ускорение шарнира, принадлежащего звену с из-
известным законом движения:
где R — длина звена. Если задан закон изменения угла поворота (p(i),
то си = \dip/dt\, г = duj/dt.
Если угловая скорость звена постоянна, ш = const, то е = 0. Век-
Вектор ускорения в этом случае направляем к центру вращения звена.
3. Для определения ускорения точки В тела, совершающего плос-
плоское движение, воспользуемся векторной формулой
wB = wA + w*A + w%A.	(l)
Здесь WA — известное ускорение точки, выбранной в качестве по-
полюса, W_^ = ujbaAB — центростремительное ускорение условного
движения В вокруг А по окружности с радиусом А В, WBA = sBAAB
— вращательное ускорение.
Возможны три случая определения ускорения по формуле A).
А. Точка В является ползуном, или направление ее вектора уско-
ускорения по каким-либо другим причинам известно. В этом случае фор-
формула A) в проекциях на оси координат представляет собой систему
двух линейных уравнений для неизвестного модуля ускорения ав и
неизвестного углового ускорения звена ?ВА-
Б. В точке В шарнирно соединены звено АВ и звено ВС', где С —
неподвижный шарнир. Таким образом, точка В движется по окруж-
окружности с центром в G, и ее ускорение можно представить в виде век-
векторной суммы нормального и тангенциального ускорения:
WB = W5 + W?.	B)
Величину нормального ускорения WB находим, зная скорость точки
В: WB = vB/BC. Направляем вектор WB по радиусу ВС к центру
вращения С. Вектор WB неизвестен лишь по модулю, направление
его известно — перпендикулярно радиусу ВС.
В результате, система уравнений A-2), записанная в проекциях,
дает четыре уравнения для четырех неизвестных WB, WBx, WBy,
?ВА. Решая ее, находим ускорение WB.

172	Гл. 8. Плоское движение тела
В. Точка В не удовлетворяет случаям А и Б. В этом случае либо
она не является шарниром, либо к ней шарнирно присоединено тело,
совершающее плоское (не вращательное и не поступательное) движе-
движение. Для решения задачи должны быть известны угловая скорость и
угловое ускорение звена, на котором находится точка В. Они могут
быть найдены при вычислении скорости и ускорения других точек
этого звена. При этих условиях уравнение A) является векторным
уравнением для одной неизвестной WB.
Этот пункт плана выполняем последовательно для всех звеньев
механизма. Очередное звено должно иметь общую точку (шарнир) с
предыдущим.
Пример. Плоский шарнирно-стержневой механизм состоит из че-
четырех шарнирно соединенных стержней и горизонтально движуще-
движущегося ползуна С (рис. 96). Механизм приводится в движение кри-
кривошипом ОА, который вращается с постоянной угловой скоростью
иоОА = 2 рад/с. В указанном положении механизма найти ускорения
шарниров А, В, С и точки М. Даны размеры: АО = 2 см, АВ = 5 см,
AM = 2 см, BD = 3 см, ВС = 2 см, а = 30°, C = 30°.
С
А	м
В
Рис. 96
Решение
1. Определяем угловые скорости звеньев и скорости точек меха-
механизма. Находим величину скорости точки А:
vA = uQA . АО = 2-2 = 4 см/с.
Вектор vA направляем перпендикулярно радиусу АО против часовой
стрелки. Вектор скорости vB направлен горизонтально. Мгновенный
центр скоростей Р звена АВ находится на пересечении перпендикуля-
перпендикуляров к векторам скоростей точек Аи. В (рис. 97). Находим расстояния

8.2. Ускорения точек многозвенного механизма
173
от точек А, В, М до МЦС:
АР = АВ/ cos 30° = 5.774 см,
ВР = АР sin 30° = 2.887 см,
МР = \/МВ2 + ВР2 = \/32 + 2.8872 = 4.163 см.
Скорости точек находим из системы уравнений
VA =
В результате решения получаем
иАв = vA/AP = 0.693 рад/с, vB = 2.000 см/с, vM = 2.884 см/с.
_?i
D
Рис. 97
Найти скорость точки С не составит труда. Векторы vB и vc па-
параллельны и не перпендикулярны отрезку ВС. Следовательно, звено
ВС совершает мгновенно-поступательное движение, и скорости всех
его точек в этот момент равны. Отсюда, vc = vB = 2 см/с. Угловая
скорость звена 5G равна нулю.
2. Определяем ускорение шарнира А, принадлежащего звену О А
с известной постоянной угловой скоростью ojoa. Ускорение точки А
состоит только из нормальной составляющей,
WA = и2ОАОА = 4-2 = 8 см/с2,
и направлено вдоль О А к центру О (рис. 98).

174
Гл. 8. Плоское движение тела
в
D
Рис. 98
3. Находим ускорение точки В. Точка В движется по окружности
с центром в неподвижном шарнире Z), и ее ускорение можно предста-
представить в виде векторной суммы нормального и тангенциального уско-
ускорений:
wB = wi + wB.	(з)
С другой стороны, ускорение точки В выражается через ускорение
точки А, лежащей на том же звене АВ. Рассматривая А в качестве
полюса, имеем
WB = WA +
Сравнивая C) и D), получаем, что
wz + wi = wA
W
BA,
wB
D)
A + w^A + wBA.
В проекциях на оси ж, у (рис. 98) векторное уравнение C) дает сис-
систему двух уравнений относительно неизвестных W^ и VF^A:
-WTB = -WA cos 30° -
-W% = -WAsin30° +
E)
где Wg = v%/BD = 4/3 = 1.333 см/с2, W*A = u\BAB = 2.401 см/с2.
Решаем систему E):
WTB = WAcos30° + W^A = 8 • 0.866 + 2.4 = 9.328 см/с2,
WBA = -W% + WA sin 30° = 2.667 см/с2.
Окончательно, величина ускорения точки В
WB =
+ {WD2 = ч/1.3332 + 9.3282 = 9.423 см/с2.

8.2. Ускорения точек многозвенного механизма
175
Вычисление ускорения точки М выполняем по п.ЗВ плана решения.
Действительно, угловая скорость и угловое ускорение звена АВ уже
известны:
иАВ = 0.693 рад/с, гАВ = Wba/ab = 0-533 рад/с2.
Рассматривая А в качестве полюса (рис. 99), записываем векторное
уравнение
*'
wM = wA + wlA + w»MA,	F)
где W^A = шАВАМ = 0.961 см/с2, WljA = ?ЛВАМ = 1.066 см/с2. Из
F) определяем проекции WM на оси координат:
WMx = -H^cos30° - W^A = -7.889 см/с2,
WMy = ~wa sin30° + wma = -2-933 см/с2.
Величина ускорения точки М
WB = y/(WMxy + {WMyY = 8.416 см/с2.
Находим ускорение точки С. Скорости точек В ж С звена ВС, со-
совершающего мгновенно - поступательное движение, равны, однако,
их ускорения различны.
W
МА
4—
м
в
D
Рис. 99
Для определения Wc воспользуемся векторным равенством (полюс
точка В)
*) В качестве полюса можно также брать точку В, ускорение которой
уже найдено.

176
Гл. 8. Плоское движение тела
где W^B = uj^BCB = 0. Вектор WB раскладываем на составляющие
(рис. 100)
Wc =
Векторное уравнение G) содержит две неизвестных величины: WqB
и Wc. Записывая G) в проекциях на оси ху, получаем систему двух
уравнений с двумя неизвестными. Но можно решить задачу проще.
С
w
Рис. 100
Спроецируем G) на ось ?, направленную вдоль стержня ВС. При
этом в уравнение не войдет модуль неизвестного вектора W^B:
-Wccos30° = -W?cos30° -W% sin 30°.
Находим Wc: Wc = WTB + ^tg30° = 10.098 см/с2.
Результаты расчетов помещаем в таблицу (скорости в см/с, уско-
ускорения в см/с2):
VA
4.000
VB
2.000
vc
2.000
VM
2.884
WA
8.000
WB
9.423
We
10.098
WM
8.416
Условия ЗАДАЧ. Плоский шарнирно-стержневой механизм со-
состоит из четырех шарнирно соединенных стержней и горизонтально
или вертикально движущегося ползуна. Механизм приводится в дви-
движение кривошипом, который вращается с заданной постоянной уг-
угловой скоростью. В указанном положении механизма найти ускоре-
ускорения всех его шарниров.

8.2. Ускорения точек многозвенного механизма
177
1.
30°
= 1 рад/с,
О А = 108 см, ?>Б = 14 см,
АВ = 62 см, ВС = 26 см.
2.
_60_°
3.
о
5.
с
ujdb = -4 рад/с,
О А = 29 см, DB = 16 см,
АВ = 37 см, ВС = 29 см.
= 3 рад/с,
О А = 27 см, DB = 12 см,
АВ = 27 см, ВС = 32 см.
= 1 рад/с,
О А = 29 см, БС = 40 см,
DG = 84 см, AG = 40 см,
ВС = 55 см.
= 1 рад/с,
ОА = 28 см, BG = 25 см,
DG = 12 см, AG = 25 см,
ВС = 26 см.
12 М.Н. Кирсанов

178
Гл. 8. Плоское движение тела
6.
9.
10.
= 2 рад/с,
О А = 30 см, DB = 120 см,
АВ = 40 см, ВС = 29 см.
ujoa = -3 рад/с,
О А = 31 см, DB = 16 см,
АВ = 31 см, ВС = 32 см.
ujDB = 2 рад/с,
О А = 32 см, DB = 84 см,
АВ = 40 см, ВС = 55 см.
= 1 рад/с,
О А = 33 см, ВС = 25 см,
DG = 12 см, AG = 25 см,
ВС = 26 см.
= 3 рад/с,
ОА = 27 см, BG = 25 см,
DG = 14 см, AG = 25 см,
ВС = 29 см.

8.3. Уравнение трех угловых скоростей
179
Ответы
1
2
3
4
5
6
7
8
9
10
VA
vB
vc
vG
м/с
1.080
0.370
0.810
0.290
0.208
0.600
0.930
1.680
0.330
0.420
0.624
0.640
0.468
1.046
0.317
0.600
0.930
1.680
0.504
0.420
0.624
1.109
0.468
1.450
0.069
0.600
0.930
1.680
0.330
0.420
—
—
—
0.502
0.120
—
—
—
0.191
0.420
WA
WB
Wc
WG
м/с2
1.080
1.222
2.430
0.290
0.349
1.200
2.790
16.970
0.330
3.378
2.785
2.560
5.434
4.158
0.171
3.459
7.553
3.360
1.489
4.588
2.564
13.859
6.942
21.205
0.504
3.272
4.087
3.360
6.219
8.208
—
—
—
1.936
0.120
—
—
—
0.598
1.260
1
2
3
4
5
6
7
8
9
10
шао
UDB
UDG
uab
шве
рад/с
1.000
-1.274
3.000
1.000
-0.742
2.000
-3.000
-5.250
1.000
-1.556
4.454
-4.000
-3.897
—
—
-0.500
5.813
2.000
—
-
—
—
—
-0.598
1.000
—
—
—
-1.588
3.000
2.011
-1.997
-3.464
1.450
-0.960
-2.121
4.243
-5.940
1.524
0.000
0.000
4.414
0.000
-3.653
1.066
-0.000
-0.000
0.000
-2.931
-2.048
SAB
?вс
рад/с2
2.836
0.834
-0.866
5.143
-0.362
3.439
-6.660
-4.097
2.738
-15.307
-15.106
-33.743
8.054
-38.076
-1.341
-1.195
33.785
-8.640
-25.347
20.356
8.3. Уравнение трех угловых скоростей
Постановка задачи. Подобрать длины звеньев шарнирного че-
тырехзвенника так, чтобы в некоторый момент движения угловые
скорости его звеньев были бы равны заданным. Положение опорных
шарниров четырехзвенника известно.
План решения
Под угловыми скоростями будем понимать проекции соответству-
соответствующих векторов на ось z, перпендикулярную плоскости движения. Ин-
Индекс z дополнительно указывать не будем, принимая uJi = uJiz.
1. Последовательно нумеруем шарниры и звенья механизма. Вы-
Выбираем систему координат, помещая ее начало в один из шарниров
механизма. Определяем координаты шарниров.
12*

180
Гл. 8. Плоское движение тела
2. Записываем уравнения трех угловых скоростей
з ~ Xci)
— 2/2)
/4 — 2/з) = 0>
A)
где x^yi и xi+1,yi+1, г = 1...3, — координаты шарниров на концах
звена, имеющего угловую скорость uji. Шарниры 1 и 4 — опорные.
Все угловые скорости и некоторые координаты даны в условии.
3. Решаем систему A) относительно неизвестных координат. Опре-
Определяем длины звеньев механизма (расстояния между шарнирами) по
формулам
Пример. В положении, изображенном на рис. 101, известны угло-
угловые скорости шарнирного четырехзвенника О ABC: шОА = 2 рад/с,
(jOab = —2 рад/с, швс = 3.5 рад/с. Найти длины звеньев О А и ВС,
AB\\OD. Расстояния даны в см, АВ = 60 см.
20
100
Рис. 101
Рис. 102
Решение
1.	Последовательно нумеруем шарниры и звенья механизма. Но-
Номера шарниров указываем индексами у соответствующих букв. Вы-
Выбираем систему координат, помещая ее начало в шарнир О. Опреде-
Определяем координаты шарниров (рис. 102):
хх =0, у1 = 0, х4 = 100 см, у4 = 20 см.
2.	Записываем уравнения трех угловых скоростей A), где по усло-
условию х3 = х2 + АВ, у2 = у3, иОА =<jjx = 2 рад/с, иАВ = uj2 = -2 рад/с,
*) Уравнения следуют из координатной формы записи векторной фор-
формулы A), на с. 130, для скоростей точек при плоском движении.

8.3. Уравнение трех угловых скоростей
181
ивс ~ ^з = 3-5 рад/с. Система приобретает вид
-1.5ж2 + 20 = 0,
-1.5у2 + 70 = 0.
3. Решаем систему B) относительно ж2, у2- Получаем
х2 = 13.333 см, у2 = у3 = 46.667 см.
^ j
Кроме того, х3 = ж2
длины звеньев:
= 73.333 см, у3 = у2 = 46.667 см. Определяем
= у/(х2-х1J-\-(у2-у1J = 48.533 см,
ВС = ^/(х4 - х3J + (у4 - УзJ = 37.712 см.
Условия ЗАДАЧ. Подобрать длины звеньев (в еж) шарнирного че-
тырехзвенника так, чтобы в некоторый момент движения угловые
скорости его звеньев были бы равны заданным. Положение опорных
шарниров четырехзвенника известно. Расстояния даны в см.
= 1 рад/с,
= 0.2 рад/с,
шве = -0.6 рад/с,
О А = 27 см.
= 4 рад/с,
ujab = -3 рад/с,
= 2 рад/с,
= 29 см.
108
= 3 рад/с,
= -4 рад/с,
= -0.9 рад/с,
О А = 31 см.
124

182
Гл. 8. Плоское движение тела
4.
С
82.5
оооа = -10 рад/с,
uoab = -17 рад/с,
иве = 4 рад/с,
О А = 33 см.
= 1 рад/с,
= 0.4 рад/с,
= 0.3 рад/с,
= 27 см.
6.
Of
174
ujoa = —1.7 рад/с,
шав = 0.2 рад/с,
шве = 2 рад/с,
АБ _L ОС,
АБ = 62 см.
7.
= -1 рад/с,
иав = 5 рад/с,
= 3 рад/с,
_L ОС,
= 31 см.
124
ujoa = 12 рад/с,
^лв = -4 рад/с,
шве = 2 рад/с,
АБ _L ОС,
АБ = 59 см.
145

8.4. Уравнение трех угловых ускорений
183
10.
155
37
= 18 рад/с,
= Ю рад/с,
иве = 3 рад/с,
АВ _L ОС,
АВ = 68 см.
= 4 рад/с,
= —4 рад/с,
= 0.5 рад/с,
О А = 33 см.
132
Ответы
1
2
3
4
5
27.000
29.000
31.000
33.000
27.000
АВ
57.369
41.824
20.397
32.812
141.549
ВС
49.889
47.475
110.910
72.911
114.560
6
7
8
9
10
ОА
98.772
94.283
45.762
44.362
33.000
АВ
62.000
31.000
59.000
68.000
22.531
ВС
86.052
55.886
197.958
189.503
159.049
8.4. Уравнение трех угловых ускорений
Постановка задачи. Многозвенный механизм приводится в
движение кривошипом, вращающимся с известной угловой скорос-
скоростью и известным угловым ускорением. Найти угловые скорости и
угловые ускорения звеньев механизма.
План решения
Под угловыми скоростями и ускорениями будем понимать про-
проекции соответствующих векторов на ось z, перпендикулярную плос-
плоскости движения. Индекс z дополнительно указывать не будем, при-
принимая LUi = UJiz, ?i = ?iz.
1.	Нумеруем шарниры и звенья механизма. Выбираем систему
координат, помещая ее начало в один из шарниров механизма. Опре-
Определяем координаты шарниров.
2.	Выделяем из механизма шарнирные четырехзвенники. Рас-
Рассмотрим четырехзвенник, шарниры которого последовательно обо-
обозначены номерами п1? п2, п3, п4, где п1 и п4 — номера неподвижных

184
Гл. 8. Плоское движение тела
шарниров. Стержни четырехзвенника имеют номера 7?г1, т2, т3. За-
Записываем уравнения трех угловых скоростей:
A)
г=1
г=1
гДе ипы — Уповая скорость гагго звена, хп.,уп., xni+1,yni+1 — ко-
координаты его концов. Номера шарниров п^ г = 1...4, как и номера
звеньев ттг^, г = 1...3, не обязательно должны быть последовательными
числами.
3.	Из решения A) получаем все угловые скорости механизма.
4.	Записываем уравнения трех угловых ускорений для каждого
четырехзвенника
з
г=1
*).
3
~ Е
i=l
3
+ Е
г=1
= о,
B)
где ет — угловое ускорение т-го звена.
5. Решаем B) относительно неизвестных угловых ускорений.
Пример. Многозвенный механизм приводится в движение кри-
кривошипом ОА, вращающимся с угловой скоростью ojoa = 1 рад/с и
угловым ускорением еОА = 2 рад/с2 (рис. 103).
Рис. 103
.?>
Рис. 104
Дано: О А = 50 см, АВ = 70 см, BD = 50 см, АС = 80 см, ЕС = 30 см;
AC _L А В, АВ _L BD. Найти угловые скорости и угловые ускорения
звеньев механизма.
*) Уравнения следуют из координатной формы записи векторной фор-
формулы D), на с. 130, для ускорений точек при плоском движении.

8.4. Уравнение трех угловых ускорений
185
Решение
1. Нумеруем шарниры и звенья механизма (рис. 104). Выбираем
систему координат, помещая ее начало в шарнир О. Определяем ко-
координаты шарниров:
2/1=0,
у2=у4 = OAsina,
у3 = OAsina — АВ,
уъ = OAsina - АВ,
хх = О,
х2 = х3 = О A cos а,
х4 = О A cos a + АС,
хъ = О A cos a-\- BD,
х6 = (ОА - СЕ) cos а + АС, % = (ОА - ЕС) sin a.
2. Выделяем из механизма шарнирные четырехзвенники (рис. 105,
106). Записываем уравнения трех угловых скоростей для четырех-
звенника OABD (рис. 105),
- х2
2 - х3)
- у3)
и для четырехзвенника О АСЕ (рис. 106),
ш1{х1 - х2) + uj4(x2 - х4) + uj5
^iB/i — 2/2) +^4B/2 — 2/4) +^5
3 - хъ) = 0,
-уъ) = 0,
4 - х6) = 0,
4 — 2/6) = °-
C)
D)
3. Решаем систему четырех линейных уравнений C), D). Полу-
Получаем угловые скорости звеньев: uj2 = 0.619 рад/с, ио3 = —0.5 рад/с,
оо4 = 0, uj5 = 1.667 рад/с. Из решения следует, что звено АС движется
мгновенно-поступательно. Этот результат очевиден. Его можно
было получить сразу из условия задачи, не решая ее. Действительно,
ОА\\ЕС, следовательно, векторы скоростей шарниров Аи С также
Рис. 105
Рис. 106

186
Гл. 8. Плоское движение тела
параллельны и не перпендикулярны АС. Мгновенного центра ско-
скоростей звена АС не существует (расположен в "бесконечности"), что
соответствует uj4 = 0.
4. Записываем уравнения трех угловых ускорений для четырех-
звенника OABD (рис. 105),
?3(Ж3 Х^)
~ Уз) - шз(Уз - Уъ) = °>
е\{У\ - 2/2) + ?2(У2 - Уз) + ?з(% - 2/5)+
и для четырехзвенника О АСЕ (рис. 106),
- хъ) = 0,
E)
- 2/2)
^ - у2) - ш\{у2 - у4)
- Уд + ?б0/4 - 2/6)+
- у о) = 0,
F)
- х2
uZ(x2-x4
5. Из решения E,6) получаем угловые ускорения: е2 = 1.773 рад/с2,
?3 = -0.670 рад/с2, е4 = -0.481 рад/с2, еъ = 2.692 рад/с2.
Условия ЗАДАЧ. Многозвенный механизм приводится в движе-
движение кривошипом О А или ВС, вращающимся с известной угловой ско-
скоростью и известным угловым ускорением. Найти угловые скорости
(в рад/с) и угловые ускорения ( в рад/с2) звеньев механизма. Длины
звеньев даны в см. Стержни, положение которых не определено уг-
углом, вертикальны или горизонтальны.
1.
О
2. А
= 2 рад/с, О А = 24,
so a = 2 рад/с2, АВ = 25,
а = 45°,	БС = 22,
/3 = 30°,	BD = 21,
DE = 9.
= 3 рад/с, О А = 24,
= 2 рад/с2, АВ = 54,
а = 45°,	ВС = 27,
/3 = 30°,	BD = 27,
DE = 28.

8.4. Уравнение трех угловых ускорений
187
3.
4. А
5.
6.
7. А
8.
= 4 рад/с,
so а = 1 рад/с2,
а = 45°,
/3 = 60°,
= 1 рад/с,
= 3 рад/с2,
а = 60°,
/3 = 45°,
= 2 рад/с,
= 4 рад/с2,
а = 60°,
/3 = 30°,
БС
О А = 22,
АВ = 53,
34,
28,
24.
26,
72,
27,
25,
32.
18,
17,
31,
ВС
BD
DE
ВС
= 1 рад/с,
= 1 рад/с2,
а = 45°,
/3 = 30°,
= 3 рад/с,
евс = 2 рад/с2,
а = 45°,
/3 = 60°,
= 4 рад/с,
= 3 рад/с2,
а = 60°,
/3 = 45°,
ВС =
БС =
22,
22,
21,
19,
10.
24,
57,
27,
26,
28.
О А
АВ
БС
BD
DE
26,
64,
38,
27,
32.

188
Гл. 8. Плоское движение тела
9. А
°Л
ю.
шве = 1 рад/с, О А = 28,
евс = 4 рад/с2, АВ = 67,
а = 60°,	БС = 29,
/3 = 30°,	Б?> = 24,
= 36.
= 2 рад/с, О А = 30,
евс = 1 рад/с2, АВ = 28,
а = 45°,	БС = 32,
/3 = 30°,	Б?> = 47,
= 37.
Ответы
1
2
3
4
5
6
7
8
9
10
ШОА
2.00
3.00
4.00
1.00
2.00
1.91
-3.37
4.77
1.04
-2.13
ШАВ
-1.66
0.00
1.85
0.00
0.00
-1.65
0.00
2.65
0.00
0.00
шве
1.09
-2.67
2.11
0.96
-1.16
1.00
3.00
4.00
1.00
2.00
швв
-0.00
-1.95
2.22
0.54
-0.66
0.00
2.28
3.98
0.60
1.00
LOBE
2.67
2.31
-1.50
0.59
-0.58
2.10
-1.50
-3.36
0.70
0.90
SOA
2.00
2.00
1.00
3.00
4.00
-9.87
19.27
15.88
4.14
-1.07
SAB
-0.79
10.69
1.12
0.01
6.69
9.42
12.81
5.78
0.02
9.45
SBC
8.01
13.33
-4.33
2.89
-2.32
1.00
2.00
3.00
4.00
1.00
SBD
-2.55
-2.17
0.08
1.26
-1.10
-1.72
-6.43
32.28
2.10
1.57
SDE
23.79
-9.85
2.78
2.03
-1.66
4.41
-4.38
-2.45
2.95
-1.13
8.5. Кинематические уравнения плоского
движения
Постановка задачи. Составить кинематические уравнения
плоского многозвенного механизма.
План решения
1. Составляем кинематические графы механизма, выбирая наи-
наиболее короткие маршруты. Началом и концом графа должна быть
точка с известной скоростью. Кинематические графы должны вклю-
включать в себя все звенья механизма. Некоторые звенья могут входить
в разные графы. Обозначения для графов приведены на с. 130.

8.5. Кинематические уравнения плоского движения
189
2.	Записываем по два кинематических уравнения в проекциях на
оси координат для каждого графа. Получаем систему дифференци-
дифференциальных уравнений.
3.	Упрощаем систему уравнений, используя уравнения связей и
тригонометрические формулы приведения.
Пример 1. Механизм состоит из стержней О А, АВ, CD и пол-
ползунов С и D. Ползун D движется вверх со скоростью vD (рис. 107);
BD = ВС. Составить кинематические уравнения механизма.
Рис. 107
Решение
1. Составляем кинематические графы:
A)
B)
2. Записываем для каждого графа A), B) по два кинематических
уравнения в проекциях на оси координат:
vDx = vOx — фгОА sin (p1 — ф2АВ sinGr + <p2) — фъВЮ sin ip3,
vDy — vOy + ф-^OAcostp-^ + ф2АВcos(tt + <p2) -
VDx =
VDy =
C)
3. Упрощаем систему C), используя уравнения связей, vOx = 0,
и тригонометрические
VOy = U' vDx =
Vcy =

190
Гл. 8. Плоское движение тела
формулы приведения:
0 = —ф± О A sin (р± + ф2 АВ sin (р2 — ф3 BD sin (р3,
vD = фх О A cos ipx — ф2 АВ cos ip2 + ф3 BD cos <^3,
0 = г>с — <^3 CD sin <??3,
vD = ф3 CD cos y?3.
D)
Пример 2. Плоский манипулятор состоит из жесткой детали ОАВ,
стержней ВС, AM, колеса С и захвата М. Даны длины О А = R^
ВС = R2, AM = R3, АВ = R4, и скорость захвата М; АВ _L О Л.
Рис. 108
Составить кинематические уравнения манипулятора *^ .
Решение
1. Составляем кинематические графы:
О
Б
С;
О
М.
E)
2. Записываем по два кинематических уравнения в проекциях на
оси координат для каждого графа E):
vCx
= vOx -
VCy = VOy
L sin (рг — oj1zRa sinC7r/2 -
cos ф1 + ulzRA cosCtt/2 ¦
x sin {px — uj3z R3 sin (p3z,
± cos ipx + uj3z R3 cos (p3z.
l2 sm<^2,
R2 cos<^2,
F)
*) Задание К-3 из сборника [15]. В задании К-3 скорость точки М опре-
определяется из решения дифференциального уравнения так, чтобы манипуля-
манипулятор захватил деталь, движущуюся по известному закону. В рассматривае-
рассматриваемом примере задача захвата не решается, а предполагается, что скорость
М известна из других соображений, в том числе из условия захвата детали.

8.5. Кинематические уравнения плоского движения	191
3. Упрощаем систему F), используя уравнения связей, vOx = О,
vOy = 0, vc = 0, и тригонометрические формулы приведения:
VCx = ~^lz^l Sm ^1 + ^1^4 C0S ^1 "" ^2^2 SH1 ^2'
0 = &lzR1 cos y?1 + ulzR4 sin «^ + &2zR2 cos <^2,
C0S Pi + "з*Д3 C0S Vsz'
Замечание 1. В данной задаче скорости точек механизма можно
найти для некоторого промежутка времени, а не для фиксированного
момента времени, как в аналогичных задачах § 8.1, § 8.3. Решая нели-
нелинейную систему дифференциальных уравнений D), получаем полную
картину движения механизма *^ . Для решения системы D) необхо-
необходимо дополнить ее начальными условиями:
хс@) = хсо, ^@) = <р1о, ^@) = ?>2о, ^з(О) = р3о,	(8)
где константы хс , (рг , <р2 и (р3 определяют начальную конфигура-
конфигурацию механизма. В некоторых численных методах для решения сис-
систему D) требуется привести к форме Коши. Уравнения D) пред-
представляют собой систему четырех алгебраических уравнений относи-
относительно УС)ф1,ф2чФъ- Решая систему, получаем, что
in(^2 ^)),
ф2 = vD sm((p2 + (p3)/BAB cos (p3 sin(^2 - ^J),
ф3 = vD/BBD cos (p3).
Замечание 2. В решении задачи следует использовать наиболее
короткие графы. В данном случае вместо графа B) можно было бы
выбрать граф
Система дифференциальных уравнений изменится, однако в форме
Коши ее вид останется прежним.
*) На странице Интернет кафедры теоретической механики МЭИ
www.termech.mpei.ac.ru можно найти обучающую программу ROBBY2,
разработанную Осадченко Н.В. и Корецким А.В. Программа интегрирует
уравнения D), составленные для задач из сборника [15], анимирует полу-
полученное решение и представляет результаты в виде графиков и таблиц.

192
Гл. 8. Плоское движение тела
Замечание 3. Метод графов широко используется для решения
задач кинематики и динамики. Примеры составления графов пред-
представлены также на с. 243, 244 310, 313, 316, 327, 329.
Условия ЗАДАЧ. Составить кинематические уравнения плоского
многозвенного механизма. Ползуны движутся по горизонтальным
или вертикальным направляющим. Длины стержней известны.

8.5. Кинематические уравнения плоского движения
193
10. АВ = ВО.
С
С
Ответы
Кинематические уравнения
1.
2.
6.
4.
5.
vD =-фгОАвтъ
0 = ф-iOAcosipi +(
vD = -<p3CBsm<p3
0 = фзСВ cos (рз + <
fD = —ф\ОА&\П(р-\
0 = 0iOAcos^i -Ь
vd = —0зСБвт<р
0 = фзСВсоБсрз —
vc = -<PiOAsm<pi
O = 0iOAcos^i +
— Ф2АВ sin y?2 — 04-BD sin y?4,
^2^45 COS (^2 + 04-BD COS <^4,
— 04.В.О8т(^4,
p^BD cos y?4.
04A.DCOS(^4,
3 + 02 AB sin y?2 — 04 AD sin (^4,
02^5 COS y?2 + Фа AD COS y?4.
— 202^5 sin y?2,
202 AB COS y?2,
vD = vc -\- Ф2АВsin(f2 — фзВОъшфз,
0 = — Ф2АВ COS<f2
0 = —20iAB sin (fi
vc = 2ф\АВ cos y?i
г>^ = — 0i AB sin y?
0 = Ф2АВ cos y?i +
vb = —0iO-/lsin(^"
0 = 0iO-Acosc^i —
i?_b = —ф<±DС simp
0 = ф/^DC cos y?4 +
+ фзВОсоъфз.
— 02 AC Sin (^2,
+ 02 AC COS (^2,
1 — 03^Z)sin<^3,
03B?>cos^3.
L + Ф2АВ Sin y?2,
4 — (P3G13 Sill (рз,
0зСБсо8<?з-
13 M.H. Кирсанов

194
Гл. 8. Плоское движение тела
6.
7.
Q
8.
9.
10.
vb = — фгОАзт^
0 = фгОАсоБ^р! -
vr> = фхОС sintpi
0 = —фгОС costpi
0=-ф1О Asian
vd = ^iOAcos^i
0 = — фзСВёт^рз
vd = фзСВ costp3
0=-ф1О Asian
vd = <^iOAcos<?i
0 = —(^3C5sin^3
г;^ = фзСВ costp3
0 = -ф1ОА8ш<р1
vc = (piOA cos (рг
0 = -ф2АВБтр2
1 + <^>2^4-E> sin<^2,
- (^2^4-BcOS(^2,
-^3CDsin^3,
+ фзСБсоъфз.
— ф2АВ&т(р2 — ф^ВИ sin <p4,
+ Ф2АВ COS y?2 + ФаВИ COS y?4,
— ф^ВИ sin y?4,
~h ф^ВТ) cos ^4.
— 0З4 ^4Z) sin LD4.
+ Ф2АВ sin y?2 — ^4^-^D sin y?4,
— Ф2АВ cos y?2 + Фа AD cos (^4.
+ 2(^2^.5 sin y?2,
— 2(^2^.-6 COS y?2,
-(^s^Dsin^s,
vd = vc + Ф2АВ cos y?2 + фзВИ cos (^3.
г>с = — 2(^i A.B sin
0 = 2ф\АВ cos y?i
0=-МВ8Ш»>1
г;^ = Ф2АВ cos y?i
y?i + Ф2АС sm.tp2.
- ф2 AC^cos <p2,
-^s^Dsin^s,
+ фзВИ cos у?з a.
Замечание 4. Для того, чтобы проинтегрировать полученные
кинематические уравнения, необходимо скорости ползунов выразить
через соответствующие координаты, например, vB = xB, задать одну
из пяти функций, входящих в уравнения, и выбрать для остальных
функций начальные условия.
Предупреждение типичных ошибок
1.	Кинематические графы являются ориентированными графами.
Меняя направление маршрута, меняйте и угол. Следующие два графа
эквивалентны: А —> В ; В —> А.
(р	7Г + Ц>
2.	Угловая скорость звена, которому принадлежат точки А и В
графа А —> В , не обязательно равна ф, см., например, с. 243.

Глава 9
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
9.1. Сложное движение точки в плоскости
Постановка задачи. Геометрическая фигура вращается во-
вокруг оси, перпендикулярной ее плоскости по известному закону (f(t).
В канале, расположенном на фигуре, движется точка М по закону
а = a(t). Найти абсолютную скорость и абсолютное ускорение
точки в заданный момент времени t = t1.
План решения
Сложное движение точки М представляется в виде суммы отно-
относительного и переносного. Характерной особенностью этой задачи
является то, что траектории относительного, переносного и абсолют-
абсолютного движения лежат в одной плоскости. Ось z, на которую проекти-
проектируются векторы переносной угловой скорости и переносного углового
ускорения, перпендикулярна этой плоскости и направлена на наблю-
наблюдателя. Угол поворота считается положительным, если со стороны
оси z он виден против часовой стрелки.
Искомые величины получаем из векторных равенств:
W = WOT + Wn + WK,	B)
где ?7от, WOT и г/п, Wn — соответственно относительные и переносные
скорости и ускорения; WK = 2п;и х vOT — ускорение Кориолиса *' .
1.	Вычисляем значение дуговой координаты a(t) при t = t1 и опре-
определяем положение точки в подвижной системе координат.
2.	Дифференцируя a(t) по времени, находим относительную ско-
скорость (скорость точки относительно фигуры):
dt
*) Кориолис Гаспар Гюстав A792-1843) французский механик и мате-
математик.
13*

196	Гл. 9. Сложное движение точки
Вектор vOT направляем по касательной к относительной траектории в
сторону увеличения а, если г?т > 0 и в обратную сторону в противном
случае; vOT = |<т|.
3.	Вычисляем радиус траектории переносного движения Rn — рас-
расстояние от точки М в положении t = tx до оси переносного вращения.
4.	Находим переносную скорость vn = |^п |-Rn, где переносная уг-
угловая скорость
о, = ^
dt '
Вектор vu направляем перпендикулярно Ru в сторону переносного
вращения.
5.	Определяем вектор абсолютной скорости, вычисляя компоненты
г;ж, v векторной суммы A) на произвольно выбранные оси, и модуль
v=
6.	Вычисляем относительное ускорение. В случае криволинейной
относительной траектории
где
от~
W
dt ' от~ R '
R — радиус кривизны относительной траектории в точке М. Для
прямолинейной траектории относительного движения W™T = 0. Век-
Вектор WqT направляем по касательной к относительной траектории,
вектор WqT — к центру кривизны этой же кривой.
7. Вычисляем переносное ускорение:
2 г>	тд/в _	г>	_ 	п^
rtn, vvu — tnrtn, tU — ^ .
Вектор W* направляем перпендикулярно Rn, вектор W? — к оси
переносного вращения (вдоль Ru).
8. Находим ускорение Кориолиса WK. Так как в задачах этого
типа вектор переносной угловой скорости перпендикулярен вектору
относительной скорости, то

9.1. Сложное движение точки в плоскости
197
Направление вектора ускорения Кориолиса можно определить по
правилу Жуковского *' поворотом на 90° вектора относительной ско-
скорости по направлению переносного вращения. В результате вектор
ускорения Кориолиса в таких задачах будет лежать на одной пря-
прямой с WqT при криволинейном относительном движении, а в случае
прямолинейного относительного движения WK перпендикулярен от-
относительной траектории.
9. Вычисляем абсолютное ускорение по формуле B) в проекциях
на оси координат. Модуль абсолютного ускорения W = \/W2 + Wy.
Пример. Прямоугольник ABCD вращается вокруг оси, прохо-
проходящей через вершину А, по закону (ри = t2 + t. Ось вращения пер-
перпендикулярна плоскости прямоугольника (рис. 109). По круговому
каналу радиуса R = 10 см с центром в точке С, расположенному на
прямоугольнике, движется точка М. Дуговая координата точки ме-
меняется по закону КМ = 5тг?3/3 см. Дано: АВ = 12 см, ВС = 15 см.
В
В
Рис. 109
Рис. 110
Найти абсолютную скорость и абсолютное ускорение точки М при
t = t1 = l с.
Решение
Движение точки М представим в виде относительного движения
по круговому каналу и переносного движения вместе с вращающимся
прямоугольником.
1. Вычисляем значение дуговой координаты a(t) = KM, при
*) Жуковский Николай Егорович A847-1921) русский ученый, основопо-
основоположник гидроаэродинамики. Преподавал теоретическую механику в МГУ.
Правило Жуковского для общего случая см. с. 204

198	Гл. 9. Сложное движение точки
t = ?1? и определяем положение точки в подвижной системе коор-
координат. За время tx точка проходит по дуге окружности путь КМ =
= 5тг/3 см. Центральный угол, соответствующий этой дуге,
а = КМ / R = тг/6. Изображаем точку в этом положении (рис.110).
2.	Дифференцируя a(t) по времени, находим относительную ско-
скорость. Находим ее значение при t = 1 с:
vot = ^-KM(t) = 5irt2 = 15.708 см/с.
CVl
Вектор vQT направлен по касательной к окружности.
3.	Вычисляем радиус траектории переносного движения Rn = AM
Rn = ^{АВ - R sin aJ + {ВС - R cos aJ = 9.444 см.
4. Находим переносную скорость vn = |сс;п |Лп. Переносной скорос-
скоростью точки является скорость точки прямоугольника, совпадающей в
данный момент с М *^ . Угловая скорость фигуры, при t = 1 с,
Отсюда vu = \ujUz\Ru = 3 • 9.444 = 28.333 см/с.
5. Определяем вектор абсолютной скорости по формуле A).
Модуль абсолютной скорости v = vQT + vn находим, проецируя
это равенство на неподвижные оси координат ж, у (можно воспользо-
воспользоваться также теоремой косинусов):
vx = vOT sin a — vn sin/5 = —13.141 см/с,
v = — vOT cos a + г>п cos /5 = 5.408 см/с.
Тригонометрические функции угла C вычисляем по формулам
sinC = (АВ - Rsina)/Ru = 0.741,
cos/5 = (ВС - Rcosa)/Ru = 0.671.
Модуль абсолютной скорости v = л/^ж ~^~ vy = 14.211 см/с.
*) Иногда переносная скорость обозначается ve (от французского слова
emporter), реже vtr (от английского слова transport), а относительная —
vr (от английского слова relativ). Эти же индексы используются и для
других компонентов сложного движения.

9.1. Сложное движение точки в плоскости	199
6. Вычисляем относительное ускорение. Ускорение точки, движу-
движущейся относительно прямоугольника по окружности, имеет нормаль-
нормальную и тангенциальную составляющую:
W;T = ^ = Ютг* = 31.416 см/с2, W?T = ^ = 24.674 см/с2.
at	R
Модуль относительного ускорения
WOT = V(W^J + (ВД2 = 39.747 см/с2.
Вектор ускорения W™T направляем по радиусу окружности к точке
С, W?T — по касательной, в сторону увеличения дуги КМ, так как
w;T > о (рис. ш).
7. Вычисляем переносное ускорение Wu = W? + W*. Траектория
переносного движения точки — окружность радиуса Ru с центром
А. Прямоугольник вращается с угловой скоростью иоп = It + 1 и
угловым ускорением
dw	dBt + 1)
Отсюда получаем
W^ = ujIzRu = 84.996 см/с2, W^ = sUzRu = 18.888 см/с2.
Вектор W* направлен против часовой стрелки перпендикулярно ра-
радиусу Ru. Вектор W^ — к центру А. Модуль переносного ускорения
W
rn = \J{W?J + (W?J = л/84.9962 + 18.8882 = 87.069 см/с2.
8. Находим ускорение Кориолиса*' . Модуль вектора ускорения
WK = 2иии х vQT определяем по формуле WK = 2|o;n ||vOT|| sin7|, где
7 — угол между vQT и cJn. Вектор п)и перпендикулярен плоскости
чертежа, следовательно, угол 7 равен 90°. Имеем
WK = 2 • 3 • 15.708 = 94.248 см/с2.
Направление вектора ускорения Кориолиса получаем по правилу
Жуковского — поворотом на 90° вектора относительной скорости
*) Это ускорение называют иногда поворотным, а в англоязычной ли-
литературе — supplementary (дополнительным).

200
Гл. 9. Сложное движение точки
по направлению переносного вращения, т.е. против часовой стрелки
(рис. 112).
В
с
fu
Рис. 111
Рис. 112
9. Вычисляем абсолютное ускорение по формуле B) в проекциях
на оси координат (рис. 111):
Wx = W;T sina + (WonT + WK) cosa- W? cos/3 - W* sin/3 =
Wy = -W0r
= 47.667 см/с2,
= -18.054 см/с2.
Находим модуль ускорения: W = \/W? + Wy = 50.972 см/с .
Ответы заносим в таблицу. Радиус траектории переносного дви-
движения — в см, скорости — в см/с, ускорения — в см/с2.
Дп
9.444
15.708
28.333
V
14.211
Wot
39.747
Wn
87.069
wK
94.248
W
50.972
Условия ЗАДАЧ. Геометрическая фигура вращается вокруг оси,
перпендикулярной ее плоскости. По каналу, расположенному на фи-
фигуре, движется точка М по известному закону cr(t). Найти абсо-
абсолютную скорость и абсолютное ускорение точки при t = tx. Даны
функция o~(t) в см, закон вращения фигуры ipn(i) (или постоянная уг-
угловая скорость uju ), время t1 и размеры фигуры. Углы даны в рад,
угловая скорость — в рад/с, размеры — в см. В задачах 1-4,8,9
длина ВМ или AM — длина дуги окружности.

9.1. Сложное движение точки в плоскости
201
1. unz = 0.05, ВМ = — (t2 + 50),	2. louz = 1.54, AM = -(t3 + 3),
Л = 51,	R = ll,
AB = 2,	А	В AD = 13,
)f_	t = lc.	\[	^ /]	t = 2c.
R!
3. a;nz =0.47, AM = -(t2+i
R = 27,
t = 3c.
4. cjnz = 0.39, ВМ = -(Г + 2)t,
M	Д = 3,
АБ = 8,
t=lc.
5. y?n = O.Olt2, BM = -(t2 + 51), 6. <pn = -0.08t2, DM = -{f + 4),
ЛБ = 28,	AB = 31,
c ВС = 33,
= 2 с.	I	П	t = 3 с.
M С
7. <рп = -0.69Г, ВМ = ^(Г + 2t), 8. cjnz = -0.28, AM = -(Г + 3)t,
6	D
ЛБ = 2,	R= 14,
Б AD = 16,
t = 2c.

202
Гл. 9. Сложное движение точки
9. ujUz = -0.04, ВМ = ^(t2 + 52), 10. <рп = -0.18t2, ВЫ = ^(
R = 61,
АВ = 66,
t = 3 с.
„	М С
| *	=|
АВ = 2,
= lc.
Ответы
1
2
3
4
5
6
7
8
9
10
см
90.072
6.136
27.000
10.159
46.135
40.368
2.404
27.631
110.586
2.828
V
см/с
4.189
9.425
12.566
3.927
2.667
20.250
3.333
7.854
4.712
1.000
4.504
9.449
12.690
3.962
1.845
19.377
3.317
7.737
4.423
1.018
2.316
2.190
12.629
7.151
2.131
12.000
6.211
6.467
8.130
1.865
WOT
W
см/с2
4.203
12.411
6.212
6.974
1.333
13.500
1.667
7.674
1.612
2.000
0.225
14.552
5.964
1.545
0.926
11.323
5.653
2.166
0.177
1.082
0.419
29.028
11.812
3.063
0.213
19.440
9.200
4.398
0.377
0.720
4.076
26.262
4.280
9.851
1.151
15.818
14.862
8.046
1.658
2.990
9.2. Сложное движение точки в
пространстве
Постановка задачи. Геометрическая фигура вращается по за-
заданному закону вокруг неподвижной оси, лежащей в ее плоскости.
По каналу, расположенному на фигуре, движется точка М по из-
известному закону cr{t). Найти абсолютную скорость и абсолютное
ускорение точки.
План решения
Искомые величины получаем из векторных равенств
A)
¦WK,
B)

9.2. Сложное движение точки в пространстве	203
где vOT, WOT и г/п, Wn — соответственно относительные и переносные
скорости и ускорения; WK = 2иии х vQT — ускорение Кориолиса. Ре-
Решение задачи о сложном движении точки в пространстве отличается
от аналогичной задачи, где точка движется в плоскости (с. 195) тем,
что векторные суммы для абсолютных величин вычисляются по трем
компонентам, а ускорение Кориолиса содержит синус угла между век-
вектором переносной угловой скорости и относительной скоростью. От-
Относительная скорость в этих задачах всегда перпендикулярна пере-
переносной, что упрощает вычисление модуля их суммы.
1.	Вычисляем значение дуговой координаты a(t) при t = t1 и опре-
определяем положение точки в подвижной системе координат.
2.	Дифференцируя o~(t) по времени, находим величину относитель-
относительной скорости VqT = do~(t)/dt. Вектор vOT направляем по касательной
к относительной траектории в сторону увеличения а, если г?т > 0 и
в обратную сторону в противном случае; vOT = |г?т .
3.	Вычисляем радиус траектории переносного движения Rn — рас-
расстояние от точки М в расчетном положении до оси переносного вра-
вращения.
4.	Находим модуль переносной скорости vu = |^п |-Rn, где пере-
переносная угловая скорость ujUz = d(pu(t)/dt. Вектор vu располагается в
плоскости перпендикулярной оси вращения и направлен перпендику-
перпендикулярно Ru в сторону переносного вращения.
5.	Определяем величину абсолютной скорости v = y/v%T + v%.
6.	Вычисляем относительное ускорение. В случае криволинейной
относительной траектории
где W?T = dvlT/dt, W™T = vlT/R, R — радиус кривизны относитель-
относительной траектории в точке М. Для прямолинейной траектории относи-
относительного движения WqT = 0. Вектор W?T направляем по касательной
к относительной траектории, вектор W™T — к центру кривизны этой
же кривой.
7.	Вычисляем переносное ускорение:
ТТ/ _ ТТ/Ц , тт^В ТТЛЦ _ , .2 ТЭ	ТД^В _	ТЭ	_ J	IJA.
Вектор W* направляем перпендикулярно Rn, вектор W^ — к оси
переносного вращения (вдоль Rn).
8. Величину вектора ускорения Кориолиса определяем по формуле

204
Гл. 9. Сложное движение точки
Направление вектора ускорения Кориолиса можно определить по
правилу Н.Е. Жуковского поворотом на 90° проекции вектора отно-
относительной скорости на плоскость, перпендикулярную cJn, по направ-
направлению переносного вращения.
9. Вычисляем абсолютное ускорение по формуле B) в проекциях
на оси координат. Ось z направляем по оси вращения. Модуль абсо-
абсолютного ускорения
W=
Пример. Прямоугольник ABCD вращается вокруг неподвижной
оси, проходящей по стороне DC (рис. 113). По круговому каналу
радиуса R = 12 см с центром в точке О, расположенному на прямо-
прямоугольнике, движется точка М по закону ВМ = 7rtBt — 3) см. Найти
абсолютную скорость и абсолютное ускорение точки при t = t1 = 2 с.
ВС = 15 см; (рп = (Ш2.
В
О
IF
А
N
Рис. 113
Рис. 114
Решение
1. Вычисляем значение дуговой координаты <j(t) при t = t± и опре-
определяем положение точки в подвижной системе координат:
сг(^) = ВМ = тг2B • 2 - 3) = 2тг.
Находим центральный угол, соответствующий дуге ВМ:
а = BM/R = 2тг/12 = тг/6.
Изображаем точку в этом положении (рис. 114).

9.2. Сложное движение точки в пространстве	205
2.	Дифференцируя a(t) по времени, находим относительную ско-
скорость:
г?т = ^-^ = ^-irt{2t - 3) = тгD* - 3) = 15.708 см/с.
at at
3.	Траекторией переносного движения является окружность с цент-
центром N. Относительная скорость точки М направлена по касательной
к этой окружности. Траектория лежит в плоскости ху, перпендику-
перпендикулярной к оси вращения DC (ось z). Находим радиус окружности:
MN = Rcosa+OC = Rcosa+BC-R = 12-0.866+15-12 = 13.392 см.
4.	Находим переносную скорость. Вычисляем угловую скорость
вращения прямоугольника ABCD:
Вычисляем переносную скорость
vn = \u;nz \MN = 0.8 • 13.392 = 10.714 см/с.
5. Определяем величину абсолютной скорости. Вектор vQT лежит
в плоскости zy, a vn направлен по оси ж, следовательно, они перпен-
перпендикулярны. Модуль скорости
v =
С = \/10.7142 + 15.7082 = 19.014 см/с.
6. Вычисляем относительное ускорение. Находим нормальную со-
составляющую ускорения точки, движущейся по окружности радиуса
Тангенциальная составляющая
W;T = ^ = ^-wDt - 3) = 4тг = 12.566 см/с2.
Оба вектора лежат в плоскости zy (рис. 115), WJT _L W™T.
7. Вычисляем компоненты переносного ускорения. Прямоуголь-
Прямоугольник вращается с угловой скоростью о;п = OAt рад/с и угловым уско-
ускорением

206
Гл. 9. Сложное движение точки
Получаем
W? = ulzMN = 0.82 • 13.392 = 8.571 см/с2,
W° = ?nzMN = 0.4 • 13.392 = 5.357 см/с2.
Вектор W* направлен по оси ж, вектор W^ — к оси вращения
вдоль оси у.
8. Величину вектора ускорения Кориолиса определяем по формуле
WK = e2\ujn \\vOT\\ sin7|- Вектор сип всегда направлен по оси вращения
в ту сторону, откуда вращение видно против часовой стрелки. В
нашем случае — вверх.
'от,ху
Рис. 115
Рис. 116
Угол 7 между vOT и cJn равен 150°. Определяем
WK = 2 • 0.8 • 15.708 • 0.5 = 12.566 см/с2.
Для того, чтобы найти направление вектора ускорения Кориолиса,
воспользуемся правилом Жуковского (рис. 116). Проецируем вектор
относительной скорости vQT на плоскость перпендикулярную оси вра-
вращения, т.е. на плоскость ху. Повернув проекцию vQT xy по направ-
направлению переносного вращения на 90°, получаем направление вектора
ускорения Кориолиса. Вектор WK лежит на оси х и направлен в сто-
сторону отрицательных значений.
9. Вычисляем абсолютное ускорение по формуле B) в проекциях
на оси координат:
Wx = W* -WK = -7.209 см/с2,
;T sin a + W?T cos a = 32.661 см/с2,

9.2. Сложное движение точки в пространстве
207
Wz = WonT sin a - W;T cos а = -0.601 см/с2.
Окончательно, абсолютное ускорение точки М
W = yjwi + Wl + Wi = \/7.2092 + 32.6612 + 0.6012 = 33.453 см/с2.
Ответы заносим в таблицу. Радиус траектории переносного движе-
движения — в см, скорости — в см/с, ускорения — в см/с2.
Лп
13.392
fOT
15.708
Vn
10.714
V
19.014
wonT
20.562
12.566
w$
8.571
5.357
wK
12.566
W
33.453
Условия ЗАДАЧ. Геометрическая фигура вращается вокруг непо-
неподвижной оси, лежащей в ее плоскости. По каналу, расположенному
на фигуре, движется точка М по известному закону: AM = cr{t)
или ВМ = a(t) (в см). Найти абсолютную скорость и абсолют-
абсолютное ускорение точки при t = t1. Даны функция cr(t), закон вращения
фигуры (fn(i) (или постоянное угловое ускорение ^п ), время t1 и раз-
размеры фигуры. В задачах 1-6, a(t) — дуга окружности.
1. uUz = 0.04, ВМ = j(t2 + 50). 2. cjnz = -1.44, AM = j(t2 + S)t.
R = 51,
AB = 26,
t=lc.
3. uUz = 0.86, AM = -(t2 + At).
4
R = 12,
В
z AB = 12,
t = 2c.
uz = 1.14, AM = ^(t3 + 3)
D

208
Гл. 9. Сложное движение точки
5. ujUz = -0.5, AM = —(t2 + 51). 6. ujUz = 1.21, AM = -(t3 + 2).
о	о
D
7.
= -0.lt2, AM = \(t2 + 2t). 8. <pn = 0.03t2, AM = -(t2 + 3)t.
ЛБ = 28,
a = тг/4,
t=2c.
M
OL
9.
= -O.Olt2, AM = ^{t2 + 52). 10. <pn = 0.14t2, AM = ^(t3 + 3).
AD = 16,
M _^Б Ж7 = 33,
DC = 53,
t = 3c.
cr-
D
AD = 9,
M
= 10,
= 2 с
Ответы
1
2
3
4
5
6
7
8
9
10
-Rn
CM
40.938
4.101
7.286
5.500
8.369
2.598
2.625
18.149
20.658
7.360
t>OT
V
см/с
1.571
11.781
6.283
6.283
8.378
3.142
1.000
2.500
1.500
4.000
1.638
5.905
6.266
6.270
4.184
3.144
0.525
2.178
1.239
4.122
2.269
13.178
8.874
8.876
9.364
4.444
1.129
3.316
1.946
5.744
VV от
WT
VV OT
№\
W
см/с2
0.048
9.914
3.290
3.589
1.276
3.290
0.000
0.000
0.000
0.000
1.571
9.425
1.571
6.283
4.189
6.283
0.500
2.000
0.500
4.000
0.066
8.503
5.389
7.148
2.092
3.804
0.105
0.261
0.074
2.308
0.000
0.000
0.000
0.000
0.000
0.000
0.525
1.089
0.413
2.061
0.089
23.992
10.439
12.406
4.189
7.603
0.200
0.424
0.055
2.004
1.527
24.545
11.215
14.326
5.264
8.647
0.647
2.291
0.672
5.440

9.3. Движение точки по звену механизма	209
9.3. Движение точки по звену механизма
Постановка задачи. Плоский шарнирно-стержневой механизм
приводится в движение кривошипом, который вращается с задан-
заданной угловой скоростью. Вдоль одного из стержней по известному
закону движется точка М. Найти абсолютную скорость и абсо-
абсолютное ускорение точки М.
План решения
Представляем движение точки в виде суммы относительного дви-
движения по звену механизма и переносного движения вместе со звеном.
1.	Вводим неподвижную систему координат ху, совмещая ее на-
начало с положением одного из шарниров механизма в заданный момент
времени. Вдоль стержня, по которому движется точка, располагаем
подвижную ось и, направляя ее в сторону движения точки. Зная за-
закон относительного движения a(t) (он задан в условии), определяем
положение точки относительно звена и неподвижных осей ху в рас-
расчетный момент. Определяем координаты хну шарниров.
2.	Дифференцируя o~{t) по времени, находим проекции относитель-
относительной скорости и относительного ускорения на ось и:
vTOT = do-{t)/dt, W;T = d2a{t)/dt2.
Зная угол между осями ииж, находим проекции векторов vOT и WOT
на оси ху.
3.	Решаем задачу о скоростях точек многозвенного механизма, ис-
используя аналитические методы (§ 8.3, с. 179, § 8.5, с. 188). Вычисляем
вектор скорости той точки механизма, в которой в данный момент
находится подвижная точка М. Эта скорость является переносной
скоростью для точки М.
4.	Определяем вектор абсолютной скорости, v = vO
модуль, v =
5.	Решаем задачу об ускорениях точек многозвенного механизма,
используя аналитические методы (§ 8.4, с. 183, § 8.5, с. 188). Вы-
Вычисляем вектор ускорения той точки механизма, в которой в данный
момент находится подвижная точка М. Это ускорение является пе-
переносным для точки М.
6.	Находим ускорение Кориолиса:
WK = 2о5п х гТот,
14 М.Н. Кирсанов

210
Гл. 9. Сложное движение точки
где п)п = {О, 0,0Jn } — вектор угловой скорости звена, по которому
движется точка.
7. Находим абсолютное ускорение, W = Wu + WOT + W^K, и его
модуль: W =
.
Пример. Плоский шарнирно-стержневой механизм О ABC при-
приводится в движение кривошипом О А =60 см, который вращается с
постоянной угловой скоростью ujOAz = 3 рад/с *^ . Вдоль стержня
АВ движется точка М по закону AM = 1Ы2е1~2 см.
Рис. 117
Рис. 118
Положение механизма при t = t1 = 2 с указано на рис. 117; АВ =120 см,
ВС =80 см, а = 30°. Найти абсолютную скорость и абсолютное уско-
ускорение точки М в этот момент.
Решение
Абсолютное движение точки представляем в виде суммы отно-
относительного движения по звену АВ и переносного движения вместе с
ним. Переносные скорость и ускорение являются соответственно ско-
скоростью и ускорением той точки звена, в которой в данный момент
располагается точка М.
1. Вводим неподвижную систему координат ху, совмещая ее на-
начало с положением шарнира А механизма в заданный момент вре-
времени. Вдоль стержня АВ, по которому движется точка, располагаем
подвижную ось и, направляя ее в сторону движения точки (рис. 118).
Зная закон относительного движения a(t) = 15?2e*~2, определяем по-
положение точки относительно звена при t = 2 с: AM = аB) = 60 см,
т.е. точка находится в центре звена АВ. Определяем координаты
*) Проекция угловой скорости на ось z, перпендикулярную плоскости
чертежа, ujoaz > 0, следовательно, кривошип вращается против часовой
стрелки.

9.3. Движение точки по звену механизма
211
шарниров в неподвижных осях координат:
хо = О,	уо = О А,
хА = 0,	уА = 0,
хв = АВ cos а,	ув = АВ sin а,
хс = Л5 cos а — 5G,	т/с = АВ sin а.
2.	Дифференцируя a(t) по времени, находим проекции относитель-
относительной скорости и относительного ускорения на ось и:
vlT = & = 15et~2Bt + t2) = 120 см/с,
WorT = а = 15е*-2B + At + ?2) = 210 см/с2.
Угол между осями и ж х равен а = 30°. Находим проекции: *'
г>от х = vOT cos a = 103.923 см/с, г>от = ?;от sin a = 60 см/с,
WOT>X = WorT cos а = 181.865 см/с2, WOT>y = WorT sin а = 105 см/с2.
3.	Решаем задачу о скоростях точек многозвенного механизма,
используя уравнения трех угловых скоростей (§ 8.3, с. 179):
^OAzbo - У а) + uABz{yA - у в) + uBCz(yB - yc) = 0,
где по условию MqAz = 3 рад/с. Решаем систему двух уравнений от-
относительно ojABz ж ojBCz. Подставляя численные значения, получаем
00ABz ~ 3 Рад/С> ^BCz ~ 3-897 рад/с. Скорость vM определяем из
равенства
it — it -\- /7) V
Переписываем это равенство в виде
к
°OAz
VM =
г
0
3
0
ха ~хо Уа~Уо
3
о
и;
ABz
хм ~хаУм-Уа 0
A)
Получаем
jAB
AM sin a = 90 см/с,
sAMcosa = 155.886 см/с.
*) Преобразование координат вектора при переходе к новому базису
см. Решебник ВМ, §2.8.
14*

212	Гл. 9. Сложное движение точки
Найденная скорость является переносной скоростью для точки М *^
^п.х ~~ uMxi ип.у — иМу-
Модуль переносной скорости vn = w^iX + v^y = 180 см/с.
4.	Определяем проекции,
vx = Vqt x + 7jn х = 103.923 + 90 = 193.923 см/с,
vy = tjot y + vny = 60 + 155.886 = 215.886 см/с.
и модуль абсолютной скорости: v = д/г;^ + Vy = 290.194 см/с.
5.	Решаем задачу об ускорениях точек многозвенного механизма,
используя уравнения трех угловых ускорений (уравнение B), с. 184),
где ?OAz = 0:
EABz\XA ~ Хв) "I" ?BCz\XB ~ ХС)~
SABzbjA - У в) + ?BCz(Vb - Ус) +
Находим sABz = 4.662 рад/с . Вычисляем вектор ускорения той точки
механизма, в которой в данный момент находится подвижная точка
М. Это ускорение является переносным для точки М. Учитывая,
что ?qaz = 0, записываем векторное равенство
WM = WA + еАВ х AM + ujab x {ujab x AM) =
= йОА х (йОА х О А) + еЛВ xiM + о;АБ х (о;АБ х AM).
Раскрывая векторные произведения по аналогии с A), вычисляем
WMx = -607.504 см/с2, WMy = 512.222 см/с2. Это ускорение яв-
является переносным для точки М:
W = Wn/r , W = Wn/r .
п.ж	Мж' п.у	My
*) Можно выполнить простую геометрическую проверку вычисления
vm • Концы векторов va , vb , vm (построенных в масп1табе) должны лежать
на одной прямой. Векторы va, vb строим перпендикулярно звеньям О А
и ВС соответственно, а их величины вычисляем по известным угловым
скоростям — va = \ujoaz\OA = 180 см/с, vb = \uobcz\BC = 311.769 см/с.

9.3. Движение точки по звену механизма
213
Модуль переносного ускорения Wu = JW^x + W^y = 794.628 см/с .
6. Находим ускорение Кориолиса WK = 2сип х vQT, где п)п — вектор
угловой скорости звена АВ, по которому движется точка:
г
0
3
0
VOT.y
к
^ABz
0
Вычисляем
WK.X = ~^ABzvOTy = -360 см/с2, WKy = 2cuABzvOTX = 623.538 см/с2.
Модуль ускорения Кориолиса *^
|wKl =
*my = 720 см/с2.
7. Вычисляем абсолютное ускорение W = Т^от + Т
Wx = WOT.X + ^п.ж + ^к.ж = -785.639 см/с2,
WK:
W
Umy + WK.y = 1240.76 см/с2
и его модуль W = Jw% + Wy2 = 14.686 м/с2.
Результаты заносим в таблицу. Скорости в м/с, ускорения — в
м/с2, угловая скорость — в рад/с, угловое ускорение — в рад/с2.
3.000
1.200
1.800
V
2.902
Т^от
2.100
Wu
7.946
wK
7.200
14.686
Условия ЗАДАЧ. Плоский шарнирно-стержневой механизм при-
приводится в движение кривошипом О А, который вращается против
часовой стрелки с постоянной угловой скоростью ш. Вдоль стержня
АВ движется точка М по закону AM = a(t) или ВЫ = a(t) (в см).
Положение механизма при t = tx указано на рисунке. Стержни, по-
положение которых не задано углом, горизонтальны или вертикальны.
Найти абсолютную скорость и абсолютное ускорение точки М в
этот момент.
*) Проверка: \WK\ = 2\ujABz\\vOt\ sin90° = 720 см/с2.

214
Гл. 9. Сложное движение точки
1.
ио = 1.4 рад/с, f = 3 с,
4.
О А = 40 см, АВ = 132 см,
ВС = 70 см.
и = 2 рад/с, t = 4c,
= 40 см, ЛВ = 120 см,
ВС = 60 см.
= 1.3 рад/с, ? = 2 с,
О А = 40 см, АБ = 132 см,
ВС = 90 см.
uj = 1.4 рад/с, ? = 2 с,
AM = m + 8sin2GrV4),
ОЛ = 30 см, АВ = 80 см,
ВС = 50 см.
ее; = 2.5 рад/с, ? = 1 с,
ВМ = 10(sinGrV6)+?2),
ОЛ = 10 см, АВ = 30 см,
ВС = 20 см.

9.3. Движение точки по звену механизма
215
7.
8.
9.
М
10.
В
30
= 1.7 рад/с, t = 1 с,
= 30 см, АВ = 80 см,
ВС = 41 см.
и; = 1.8 рад/с, f = 1 с,
= 31 см, АВ = 96 см,
ВС = 51 см.
ее; = 0.7 рад/с, ? = 3 с,
AM = 13(sinGrV6)+?2),
ОЛ = 112 см, АВ = 325 см,
ВС = 128 см.
= 1.5 рад/с, f = 1 с,
с
= 40 см, АВ = 105 см,
ВС = 50 см.
= 2.2 рад/с, f = 1 с,
О А = 30 см, АВ = 90 см,
ВС = 40 см.

216
Гл. 9. Сложное движение точки
Ответы
1
2
3
4
5
6
7
8
9
10
UJnz
рад/с
0.24
0.33
0.20
0.53
0.83
-0.64
0.00
0.00
-0.57
1.27
Sn
рад/с2
-0
-0
-0
0
43
49
61
90
5.72
-1
0
-0
-3
57
58
45
20
3.60
т
-16
41
11
12
т
.00
.02
.00
.00
-24.53
20
24
78
21
-36
.00
.00
.00
.00
.00
Vn
см/с
42.77
73.32
46.87
52.46
27.95
57.02
55.80
78.40
74.94
33.00
V
34.
112.
57.
61.
51.
40.
42.
144.
62.
49
88
52
39
09
14
38
49
25
69.00
4.00
32.06
-22.00
-9.87
-18.63
-40.00
-48.00
22.44
-42.00
18.00
W
(
64
137
36
88
п
zm/c2
86
23
06
28
25.58
150
83
43
214
104
20
11
39
44
04
7.84
27.35
4.33
12.60
40.89
25.50
0.00
0.00
24.00
91.45
W
68.01
178.02
24.17
103.97
33.93
183.65
48.93
64.24
236.39
71.18
Замечание. В таблице ответов относительные скорость и ускорение
даны в проекции на ось АВ.
9.4. Механизм с муфтой
Постановка задачи. Плоский механизм с одной степенью сво-
свободы состоит из шарнирно соединенных стержней и муфты, сколь-
скользящей по направляющему стержню и шарнирно закрепленной на дру-
другом стержне или на неподвижном шарнире. Задана угловая ско-
скорость ведущего звена механизма. Найти скорость муфты относи-
относительно направляющего стержня.
План решения
1.	Представляем движение муфты М в виде суммы относитель-
относительного движения по направляющему стержню механизма и переносного
движения вместе с этим стержнем. Траекторией относительного дви-
движения муфты является прямая. Задачу решаем, используя коорди-
координатную запись векторных соотношений для скоростей при плоском
движении. Выбираем систему координат и определяем координаты
всех шарниров механизма и муфты.
2.	Мысленно снимаем муфту с механизма и находим скорости шар-
шарниров и угловые скорости звеньев получившегося механизма (§ 8.1,
с. 158, § 8.3, с. 179, § 8.5, с. 188).
3. Записываем уравнение сложения скоростей: v = vQrT
где
абсолютная скорость v или относительная скорость vOT выражается

9.4. Механизм с муфтой
217
через скорости шарниров механизма. Составляем уравнение
vN + uNM x NM = vOT + vK + ?KM x fM.	A)
Это векторное уравнение содержит две неизвестные величины. Одна
из них — искомый модуль вектора относительной скорости vQT. На-
Направление этого вектора всегда известно и задается направлением
стержня, по которому скользит муфта *^ . В зависимости от вари-
варианта задачи второй неизвестной может быть угловая скорость uNMz
или шкм , где N и К — точки механизма с известными скоростями.
Если муфта скользит по стержню КМ', угловая скорость ojkm
которого известна, то неизвестной величиной будет угловая скорость
ujnm звена, шарнирно соединяющего муфту с неподвижной точкой
UN
= 0) или с шарниром N механизма с известной скоростью.
Если муфта шарнирно закреплена на стержне NM с известной
угловой скоростью (jOnm , то неизвестной величиной будет угловая
скорость шкм звена, по которому скользит муфта, где точка К не-
неподвижна или является шарниром с известной скоростью.
Если муфта закреплена на неподвижном шарнире, то абсолютная
скорость равна нулю (uNM = 0, vN = 0).
3. Решаем векторное уравнение A). Определяем vQT.
Пример. Плоский механизм с одной степенью свободы состоит из
шарнирно соединенных стержней и муфты Z), скользящей по направ-
направляющему стержню (кривошипу) О А. Муфта шарнирно закреплена на
стержне BD. Кривошип вращается против часовой стрелки с посто-
постоянной угловой скоростью шОА = 3 рад/с. Даны длины: О А = 40 см,
АВ = 111 см, ВС = 43 см, ОС = 62 см. Найти скорость муфты
относительно направляющего стержня в тот момент, когда а = 45°,
а муфта находится на середине кривошипа: OD = О А/2 (рис. 119).
Рис. 119
Рис. 120
*) Направляющий стержень.

218	Гл. 9. Сложное движение точки
Решение
1. Представляем движение муфты М в виде суммы относитель-
относительного движения по направляющему стержню О А и переносного дви-
движения вместе с этим стержнем. Выбираем систему координат и опре-
определяем координаты всех шарниров механизма и муфты. Помещаем
начало координат в точку С (рис. 120) и вычисляем координаты:
хс = 0, ус = 0,	хо = 62 см, уо = 0,
хА = ОС + О A cos а = 90.284 см, уА = О A sin a = 28.284 см,
xD = ОС + OD cos a = 76.142 см, yD = OD sin a = 14.142 см.
Координаты точки В найдем из системы уравнений
{хв - хАJ + {ув - уАJ = АВ2,
Система имеет два решения (задача о точках пересечения двух окруж-
окружностей с радиусами АВ и ВС). Выбираем то решение, у которого
ув > 0: хв = -20.300 см, ув = 37.908 см.
Нелинейную систему уравнений удобно решать на компьютере,
например, в системе Maple V. Программа решения имеет вид
>eqnl:=(ХВ-ХА)~2+(YB-YA)~2=АВ~2;
>eqn2:=(ХВ-ХС)~2+(YB-YC)~2=В(Г2;
>solve({eqnl,eqn2},{XB,YB});
Числа заносятся в десятичной форме: АВ:=111.0 и т.д.
2. Мысленно снимаем муфту с механизма (рис. 120) и находим
скорости шарниров и угловые скорости звеньев получившегося меха-
механизма. Записываем уравнения трех угловых скоростей четырехзвен-
ника О ABC (§8.3, с. 179):
OAz + {УА
(хо - xa)ujOAz + (хА - xb)ujABz + (хв - xc)ujBCz = 0.
При u;OAz = 3 рад/с,
z - 37.91ljBCz = -28.28 • 3,
-110.58u;ABz + 20.30u;BCz = -28.28 • 3.

9.4. Механизм с муфтой	219
Получаем решение: uABz = 1.236 рад/с, uBCz = 2.552 рад/с. Зная
uBCz, находим
хСВ =
О	0	и;
BCz
хв хс Ув Ус О
Компоненты скорости имеют следующие значения:
vBx = -uuBCz(yB - ус) = -2.552C7.908 - 0) = -96.745 см/с,
vBy = u;BCz(xB - хс) = 2.552(-20.3 - 0) = -51.802 см/с.
3. Записываем уравнение сложения скоростей v = vOT + г/п, где аб-
абсолютная скорость v выражается через известную скорость шарнира
В. Составляем векторное уравнение
vB + швп хВЪ = vOT + шОА х ОЪ.	B)
Это уравнение содержит две неизвестные величины. Одна из них
— искомый модуль вектора относительной скорости vQT. Направле-
Направление этого вектора известно и задается направлением стержня О А, по
которому скользит муфта. Вторая неизвестная — угловая скорость
00BD' Подставляем численные значения. Уравнение B) принимает
вид
0.707 <т + 23.766 uoBD = 54.315,
0.707 <т + 96.442 uoBD = 94.232,
где VqT — проекция относительной скорости муфты на ось, направ-
направленную от О к А. Находим решение системы: v^T = 58.361 см/с,
ujbd = 0.549 рад/с. Таким образом, в указанный момент муфта дви-
движется по стержню О А вверх со скоростью vOT = |г?т| = 58.361 см/с.
Замечание. Эту задачу можно решить по крайней мере еще
двумя способами. Во-первых, методами аналитической геометрии
можно найти расстояние SOD(i) от шарнира О до муфты D как функ-
функцию времени. Дифференцируя SOD(i), найдем относительную ско-
скорость. Во-вторых, можно найти скорость стержня О А относительно
муфты. Подвижная система координат будет связана с муфтой. В
этом случае абсолютная скорость точки стержня О А под муфтой —
это скорость точки тела при вращательном движении с угловой ско-
скоростью ojOAz, переносная — скорость муфты, выраженная через ско-
скорость шарнира В.

220
Гл. 9. Сложное движение точки
Условия ЗАДАЧ. Плоский механизм с одной степенью свободы
состоит из шарнирно соединенных стержней и муфты, скользящей
по направляющему стержню и шарнирно закрепленной на другом
стержне или вращающейся на неподвижном шарнире. Кривошип
О А вращается против часовой стрелки с постоянной угловой ско-
скоростью соОА = 2 рад/с. Горизонтальные и вертикальные размеры
на рисунках даны для неподвижных шарниров и для линий движения
ползунов (в см). Найти скорость муфты D [или Е) относительно
направляющего стержня (в см/с).
ОА = 40 см, АВ = 51 см,
ВС = 38 см, OD = ОА/2.
ОА = 30 см, АВ = 30 см,
ВС = 35 см, AD = АВ/2.
ОА = 35 см, АВ = 92 см,
ВС = 69 см, AD = АВ/2.
5. В(
ОА = 40 см, АВ = 75 см,
ВС = 31 см, BD = ВС/2.
О А = 30 см, АВ = 25 см,
ВС = 61 см, OD = ОА/2.
ОА = 35 см, АВ = 42 см,
AD = АВ/2.

9.4. Механизм с муфтой
221
7.
8. в
39
О А = 40 см, АВ = 77 см,
OD = ОА/2.
О А = 30 см, АВ = 65 см,
OD = ОА/2.
9.
О А = 35 см, АВ = 40 см,
ВС = 33 см, AD = АВ/2.
О А = 40 см, АВ = 38 см,
ВС = 50 см, AD = АВ/2.
Ответы
1
2
3
4
5
VA
80.000
60.000
70.000
80.000
60.000
vB
45.296
33.792
54.609
69.994
134.577
vD
40.000
42.283
35.232
34.997
30.000
29.078
24.425
15.291
29.215
28.428
6
7
8
9
10
VA
70.000
80.000
60.000
70.000
80.000
vB
83.975
81.943
58.095
39.044
42.040
vD
74.386
40.000
30.000
48.792
54.572
9.816
0.666
254.043
0.794
46.568
Замечание. В ответах, помимо искомой относительной скорости,
даны промежуточные результаты — скорости точек А, В w. D. При-
Причем в вариантах 1,2,7,8 vD — это скорость той точки направляющего
стержня, в которой в этот момент находится муфта.

Глава 10
СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТЕЛА
10.1. Скорость и ускорение точки тела
Постановка задачи. Твердое тело совершает сферическое дви-
движение по закону, заданному в углах Эйлера ф, (р ив. Найти ско-
скорость и ускорение точки, положение которой дано относительно
подвижных осей координат.
План решения
1.	Воспользуемся кинематическими уравнениями Эйлера для опре-
определения проекций угловой скорости на подвижные оси координат
и;х = ф sin if sin в + в cos (p,
и;у = ф cos (ps'mO — 6 simp,	A)
ujz = ф cos 0 + ф.
2.	Находим проекции скорости v = по х г*, на подвижные оси отно-
относительно которых задан радиус-вектор точки г.
3.	Вычисляем модуль скорости v = Jv*. + Vy + v2z.
4.	Дифференцируя по времени t проекции угловой скорости, по-
получаем компоненты углового ускорения t?= dcu/dt в подвижных осях.
5.	Ускорение точки представляем в виде векторной суммы
W = ex г + uj х v,
где W? =?Xr — вращательное, a W^ = си х v — осестремительное
ускорение.
6.	Находим модуль ускорения W = \/W% + Wy + W%-
Пример. Твердое тело совершает сферическое движение по за-
закону, заданному в углах Эйлера ф = 2?, 0 = тг/6, <р = sinB?). При
t = 1 с найти скорость и ускорение точки, положение которой отно-
относительно подвижных координат задано координатами
х = 1 м, у = 2 м, z = 0.

10.1. Скорость и ускорение точки тела	223
Углы ф, 0 и if даны в рад.
Решение
1. Зная зависимости угла прецессии ф, угла нутации 0 и соб-
собственного вращения (р от времени, воспользуемся кинематическими
уравнениями Эйлера A) для определения проекций угловой скорости
на подвижные оси координат. Подставляя в A) заданные функции,
получаем
ujx = sin(sinB?)),
шу = cos(sinB?)),
При t = 1 вычисляем
ux = 0.789 рад/с, ujy = 0.614 рад/с, ujz = 0.900 рад/с.
Модуль угловой скорости тела
uj = y^x + ^y + Ш1 — 1-345 рад/с.
2. Вычисляем проекции скорости точки на подвижные оси:
vx = ujyZ - ujzy = -1.799 м/с,
v = их - ujz = 0.900 м/с,
vz = и;ху - ujyX = 0.964 м/с.
3.	Модуль скорости точки v = */vx -\- v2, + v2 = 2.231 м/с.
4.	Дифференцируя по ? проекции угловой скорости, получаем ком-
компоненты углового ускорения тела в подвижных осях:
?х ~ ^х ~ 2cos(sinB?)) c
ez = ujz = —
При t = 1 получаем
?ж = -0.511 рад/с2, sy = 0.657 рад/с2, ?_, = -3.637 рад/с2.
Модуль углового ускорения е = Jгх + е* + ^ = 3.731 рад/с2.
5. Ускорение точки представляем в виде векторной суммы:
W = ех г-\- и; х v,

224
Гл. 10. Сферическое движение тела
где W? =exf- вращательное, a W^ = си х v - осестремительное
ускорение. Вычисляем отдельно их проекции на оси ж, у и z:
W?X = ?yz-szy = 7.274 м/с2,
W?y = ezx - exz = -3.637 м/с2,
W?Z=exy-?yx =-1.679 м/с2.
W«x = "yvz ~ "zvy = -0.217 м/с2,
W»y = "zVX ~ "XVZ = -2-379 MA2,
Wu,z = UxVy - UyVx = L815 M/C2'
Компоненты ускорения получаем, суммируя W? и Ww\
Wx = 7.274 - 0.217 = 7.057 м/с2,
Wy = -3.637 - 2.379 = -6.017 м/с2,
Wz = -1.679 + 1.815 = 0.136 м/с2.
6. Модуль ускорения W = Jw* + W? + W2 = 9.275 м/с2. Ответы
занесем в таблицу. Скорости — в м/с, ускорения — в м/с2.
-1.799
Vy
0.900
0.964
V
2.231
7.057
-6.017
wz
0.137
ТУ
9.275
Замечание 1. При сферическом движении тела векторы угловой
скорости и углового ускорения не лежат на одной прямой (шх/ех ф
UJy/?y ^ LUz/?z)i a вект0Р осестремительного ускорения в общем слу-
случае не перпендикулярен вектору вращательного ускорения. В этом
можно убедиться, вычислив скалярное произведение W^ • W? Ф 0.
Замечание 2. Кинематические уравнения Эйлера для опреде-
определения проекций угловой скорости на неподвижные оси координат
имеют вид
ujx, = ф sin ф sin в + в cos ф,
шу1 = —ф cos ф sin в + в sin ф,
uoz, = фсоъв + ф.
Условия ЗАДАЧ. Твердое тело совершает сферическое движе-
движение по закону, заданному в углах Эйлера. При t = 1 с найти скорость

10.1. Скорость и ускорение точки тела
225
и ускорение точки, положение которой дано относительно подвиж-
подвижных осей координат. Углы ф, 0 и (р даны в рад, координаты x,y,z
— ем.
1.	ф = тг/2, в = b/(t + 2), <р = 3(t + 1I/10, x = l,y = l,z = A.
2.	ф = {t/2) sin6t + 3t, в = тг/3, <р = 6/B* + 3), ж = 2, у = 2, я = 1.
3.	ф = b(t + 1K/10, в = 3t2 + At + 2, у? = тг/4, ж = 3, 2/ = 3, z = 2.
4.	ф = тг/3, 0 = (t/2) sin2 4t - 3t, у? = t2 + 3t + 4, ж = 1, у = 2, 2 = 4.
5.	^ = 41nCt + 2), 6> = тг/6, ip = 5^3t + 5, ж = 2, у = 4, z = 3.
6.	ф = 3t2 + 2t + 2, 6> = 2V2t + 2, <p = тг/2, ж = 3, у = 1, 2 = 3.
7.	-0 = тгД 6> = (t/2) sin4t + 3t, у? = 3^4? + 3, ж = 1, у = 2, z = 4.
8.	^ = 5t+(t/2)cos26t, 6> = тг/4, у? = 31nCt + 2), ж = 2, у = 3, 2 = 4.
9.	^ = 4(? + 1K/10, в = 13et/4, у? = тг/3, ж = 3, у = 2, 2 = 2.
10.	ф = тг/6, 6> = 15et/2, у? = 6(t + 1I/10, ж = 1, у = 4, z = 4.
Ответы
1
2
3
4
5
6
7
8
9
10
Vy
Vz
V
м/с
-0.324
-3.075
-11.080
-5.958
-18.938
2.229
-11.283
-17.259
-7.026
-8.553
-2.055
0.174
-17.204
4.406
5.860
2.476
2.831
31.517
-4.334
-48.603
0.595
5.802
42.426
-0.713
4.812
-3.054
1.405
-15.008
14.872
50.742
2.164
6.569
47.104
7.444
20.400
4.520
11.717
38.942
17.010
70.782
wx
0.131
8.339
-313.097
-20.508
-30.306
14.618
-30.351
-120.979
-68.814
-95.343
Wy
м/с
1.050
-32.484
-309.026
-49.249
-96.636
5.558
-8.721
-315.767
-10.565
-645.653
Wz
-1.466
5.135
-176.192
15.896
10.333
-23.280
-22.375
-81.799
-30.878
-583.050
W
1.476
3.538
28.228
21.743
4.454
37.251
27.411
171.495
13.459
39.700
15 M.H. Кирсанов

Часть III
ДИНАМИКА
Динамика *^ — основной раздел теоретической механики. В ди-
динамике изучают механическое движение материальных объектов в
связи с силами, приложенными к ним. Простейшим объектом явля-
является материальная точка — геометрическая точка, наделенная мас-
массой. В главе 11 решаются задачи о движении точки под действием по-
постоянных и переменных сил. Все объекты, о которых там идет речь,
принимаются за материальную точку. Для решения текстовых задач,
приведенных в § 11.1, 11.2, требуется определенный навык прочтения
условия, умение выделить существенное, заметить недосказанное и,
главное, не приписать к условию того, чего там нет. Например, если
в задаче речь идет об автомобиле, который при некоторых условиях
разгоняется за одно время, а при других условиях — за другое, то
естественно предположить, что двигатель в обоих случаях один и тот
же, и все параметры движения, кроме тех о которых явно сказано,
одинаковые. Общий принцип здесь — не вносить в условие дополни-
дополнительных сложностей и использовать все имеющиеся в тексте данные.
Кроме того, для успешного решения этих задач рекомендуем повто-
повторить методы интегрирования (Решебник ВЫ, §7.1-7.10) и методы ре-
решения дифференциальных уравнений {Решебник ВМ, §11.1-11.11).
В § 12.1—12.6 рассматриваются задачи динамики плоского движе-
движения тела и системы тел. В зависимости от постановки задачи приме-
применяются различные методы. В некоторых случаях одну и ту же задачу
можно решить несколькими способами. Так, задачи § 12.3, § 12.5,
§ 12.6 можно решить с помощью теоремы об изменении кинетической
энергии системы, с помощью общего уравнения динамики или урав-
уравнения Лагранжа 2-го рода. Заметим, что большинство трудностей
при решении этих задач связаны с кинематикой. Рекомендуем по-
повторить методы вычисления скоростей (§ 8.1, 8.5) и ускорений (§ 8.2)
*) Название "динамика" ввел Г. Лейбниц в 1690 г.

227
точек тела при плоском движении.
Задача о динамических реакциях подшипников ротора § 12.7 со-
соответствует задаче Д-6 из сборника И.В. Новожилова, М.Ф. Зацепина
[15].
В § 13.1 методами аналитической механики решается задача опре-
определения реакций опор составной конструкции. Здесь в одной задаче
собраны все три раздела механики: методами кинематики находят
возможные скорости, искомая реакция определяется из уравнения
принципа возможных скоростей, а уравнения статики используются
при проверке решения.
Для решения задач динамики системы тел с двумя степенями сво-
свободы применяется общее уравнение динамики (§ 13.3) или уравнение
Лагранжа 2-го рода (§ 13.4).
Особое внимание уделяется задачам, в которых кинетическая энер-
энергия системы зависит от обобщенной координаты. В этом случае ре-
решение ограничивается составлением уравнения движения в форме Ла-
Лагранжа 2-го рода (§ 13.5) или Гамильтона (§ 13.8). При вычислении
обобщенных сил в таких задачах важно знать не только модули ско-
скорости характерных точек (центров масс, точек приложения сил), но
и знаки их проекций. Наибольшие трудности при решении возни-
возникают именно здесь. Именно поэтому в этих задачах рекомендуется
использовать метод кинематических графов. Для численного реше-
решения полученного дифференциального уравнения движения в § 17.2
дана программа для Maple V. С помощью этой программы можно
выполнять задание Д-5 из сборника [15].
В § 14.1 с помощью уравнения Лагранжа 2-го рода решена задача
о собственных колебаниях системы двух тел, совершающих плоское
движение.
Задача колебания узла фермы, разобранная в § 14.2, содержит в
себе элементы теории упругости. Стержни фермы не являются твер-
твердыми телами, для них допускаются продольные деформации. При
определении усилий в стержнях фермы можно воспользоваться про-
программой, написанной для Maple V (§ 15.1).
15*

Глава 11
ДИНАМИКА ТОЧКИ
11.1. Постоянные силы
Постановка задачи. Материальная точка движется по пря-
прямой или по окружности под действием постоянных по величине сил.
Определить закон движения точки или отдельные параметры дви-
движения.
План решения
1.	Выбираем систему координат. Для прямолинейного движения
ось х направляем вдоль линии движения точки. Уравнения движения
под действием сил, главный вектор которых обозначим как F, имеют
вид
тх = Fx, ту = F , mz = Fz.
При движении по окружности используем уравнения движения в
естественных осях:
mv2T/R = Fn, mvT = FT, 0 = Fx.
Нормаль п направлена к центру окружности, г — орт касательной,
направленный в сторону увеличения дуговой координаты a] vT = a.
Ось z — перпендикулярна плоскости окружности.
Прикладываем к точке все действующие на нее силы.
2.	Составляем дифференциальные уравнения движения в проек-
проекциях на оси. В проекции на одну из осей уравнение движения вы-
вырождается в уравнение равновесия. Если в условии задачи есть тре-
трение, то из этого уравнения можно найти силу трения или выразить
ее через другие силы.
3.	Интегрируем дифференциальное уравнение. Константы интег-
интегрирования определяем из начальных условий.
4.	Из полученного закона движения определяем необходимые ве-
величины.

11.1. Постоянные силы
229
Пример. С аэростата сбросили балласт, падение аэростата замед-
замедлилось, и через время tQ он поднялся на ту высоту, с которой сбросили
балласт. Сила сопротивления воздуха R = const, подъемная сила аэ-
аэростата — Т, масса аэростата без балласта — т. Сколько времени
после сброса балласта аэростат опускался?
Решение
1.	Ось у, направим вверх, поместив ее начало в нижней точке тра-
траектории аэростата. При падении на аэростат действуют силы тя-
тяжести G = тд, сила сопротивления воздуха R и подъемная сила Т
(рис. 121). Аэростат принимаем за материальную точку.
2.	Составляем дифференциальное уравнение движения:
ту = Т + R - G.
3.	Дважды интегрируем уравнение движения. Для постоянных сил
интеграл берется просто:
my =
- G)t2/2
C2.
Начальные условия: t = 0, у = Н, у = — vQ. Отсюда находим кон-
константы интегрирования Сх = —mvQ,C2 = mH. Получаем уравнения
y = (T + R-G)t/m-v0,	A)
у = (Т + R - G)t2/{2m) - V + Н.	B)
Аналогично составляем уравнение при подъеме аэростата.
Н
Н
v = 0
У
Рис. 121
v = О
Рис. 122
Сила сопротивления при этом меняет свое направление (рис. 122).
Оставляя ось у прежней, время отсчитываем от нуля с момента подъ-
подъема:
ту = Т - R-G.

230	Гл. 11. Динамика точки
Интегрируя уравнение
ту = (T-R-G)t + C3,	C)
получаем
my=(T-R- G)t2/2 + C3t + С4.	D)
Начальные условия: ? = 0, у = 0, у = 0. Находим константы интегри-
интегрирования: С3 = 0, С2 = 0. Из D) следует
y = (T-R-G)t2/Bm).	E)
4. Находим искомое время падения. Обозначаем его за tv а время
подъема — за t2. По условию t1-\-t2 = t0. Подставляем в A,2) условия:
t = ?1? у = 0, г/ = 0, а в E) t = ?2, г/ = i7. Получаем систему трех
уравнений с неизвестными ?1? i7, v0:
0=(T + i?-G)t1/m-t;o,	F)
0 = (Т + R - G)t\/{2m) - vott + Н,	G)
H = (T-R-G)(to-t1J/Bm).	(8)
Исключая неизвестную высоту Н и неизвестную начальную скорость
г>0, получаем
УСЛОВИЯ ЗАДАЧ
1.	Получив начальную скорость г;0, брусок начал двигаться вверх по
наклонной плоскости и, достигнув максимальной высоты, стал спус-
спускаться вниз. Угол наклона плоскости равен а, коэффициент трения
/. На каком расстоянии от исходной точки окажется брусок за время
спуска равное времени подъема?
2.	Материальная точка массой т движется из состояния покоя по
гладкой направляющей радиусом R, расположенной в горизонталь-
горизонтальной плоскости, под действием силы Q. Определить реакцию направ-
направляющей через время t. Вектор силы направлен внутрь вогнутости
окружности и образует постоянный угол а с вектором скорости.
3.	Тормозной путь автомобиля на горизонтальной дороге при ско-
скорости v0 равен S. Коэффициент трения /. Силу сопротивления воз-
воздуха считать постоянной. Чему равен тормозной путь этого автомо-
автомобиля при той же скорости на спуске а ?

11.1. Постоянные силы	231
4.	В сухую погоду автомобиль проходит закругление на дороге на
предельной скорости г^. Найти предельную скорость прохождения
этого же поворота после дождя, когда коэффициент трения умень-
уменьшается в 4 раза. Считать, что автомобиль не опрокидывается.
5.	Автомобиль начинает движение из состояния покоя по окружности
радиуса R с постоянным ускорением W. Коэффициент трения /.
Через какое время автомобиль соскользнет с окружности?
6.	Автомобиль без груза разгоняется с места до скорости vQ за время
t1. Коэффициент трения /. Какую скорость он разовьет за то же
время с грузом, составляющим 50% массы автомобиля?
7.	Самосвал без груза разгоняется с места до скорости v* за время t*.
Коэффициент трения /. За какое время разгонится до той же ско-
скорости груженый самосвал, масса которого при погрузке увеличилась
вдвое ?
8.	За какое минимальное время автомобиль с постоянной скоростью
объедет квадрат со стороной а, огибая углы по дугам окружности?
Коэффициент трения /. Считать, что на поворотах возможно со-
соскальзывание, но не опрокидывание.
9.	Воздушный шар массой т падает вниз. На высоте Н скорость
шара равна г>0, а ускорение WQ. Какой балласт необходимо сбросить,
чтобы шар мягко (v = 0) приземлился? Силу сопротивления воздуха
считать постоянной.
10.	Тормозной путь автомобиля на горизонтальной дороге при ско-
скорости vQ составляет S. Чему равен тормозной путь этого автомобиля
при той же скорости на спуске а ? Коэффициент трения считать по-
постоянным.
Ответы
1. S = Vq/cos a/(g(f cos a + sin aJ),
2.	N± = (Qt cos aJ/(Rm) - Q sin a, N2 = mg, N = ^N2 + JVf.
3.	Sa = 0.5v2/{g{fcosa- sin a) + Wc), Wc = O.bv2JS - gf.
4.	v2 = vj2.
5.	t = VRfo/W.
6.	v = Bvo-gft1)/3.
7.	t = 2v*t*/(v* -fgt*).
8.	t = 4a/v + 2v(n - 2y/2)/(gf), если v2 < agfл/2/2;
t = 2irv/(gf), если v2 > agfV^/2.

232	Гл. 11. Динамика точки
9. тБ = m{vl + 2W0H)/(v20 + 2gH).
Ю. 5а = vlS/(yl
11.2. Переменные силы
Постановка задачи. Материальная точка движется по пря-
прямой или по окружности под действием переменных сил. Определить
закон движения точки или отдельные параметры движения.
План решения
1.	Выбираем систему координат. Для прямолинейного движения
ось х направляем вдоль линии движения точки. При движении по
окружности используем полярную систему координат с началом в
центре окружности.
Прикладываем к точке все действующие на нее силы.
2.	Составляем дифференциальные уравнения движения в проек-
проекциях на оси.
3.	Интегрируем дифференциальное уравнение.
В зависимости от вида сил, действующих на точку, различают
следующие случаи.
A.	Сила зависит только от времени F = F(t). Решение задачи
сводится к интегрированию функции F(t).
Б. Сила зависит только от координаты точки F = F{x). Вво-
Вводится замена переменной W = vdv/dx, после чего получается
уравнение с разделяющимися переменными.
B.	Сила зависит только от скорости точки F = F(v). Если в
начальных условиях или в вопросе присутствуют время и ско-
скорость, то следует использовать замену W = dv/dt. Если в на-
начальных условиях или в вопросе присутствуют координата и
скорость, то вводят замену переменной W = vdv/dx.
Г. Сила зависит только от скорости точки и от координаты
F = f1(v)f2(x). Если в начальных условиях или в вопросе
присутствуют скорость и координата, то вводят замену пере-
переменной W = vdv/dx. Дифференциальное уравнение допускает
разделение переменных: mvdv/f^v) = f2{x)dx {Решебник ВМ,
§11.2).
Константы интегрирования определяем из начальных условий.
4.	Из полученного закона движения определяем необходимые ве-
величины.

11.2. Переменные силы
233
Пример. Грузовик массой т имеет максимальную скорость г>тах
и разгоняется с места до v^ за время t^. Сила сопротивления про-
пропорциональна скорости. Чему равна средняя сила тяги двигателя
грузовика?
Решение
1. Ось х системы координат принимаем горизонтальной, начало
координат помещаем в начальное положение грузовика. Изображаем
грузовик в некоторый промежуточный момент движения. На него
действует сила тяжести G = mg, сила сопротивления R = kv, про-
пропорциональная скорости г>, с неизвестным пока коэффициентом к,
неизвестная сила тяги F и реакция опоры N (рис. 123).
А 2/
^N
R
v = О
Т°)
G
Рис. 123
2.	Составляем дифференциальное уравнение движения в проекции
на ось х:
тх = F - R.
3.	Дважды интегрируем уравнение движения. Так как правая
часть уравнения является функцией скорости, а в вопросе задачи со-
содержится время, вводим замену v = x и интегрируем уравнение с
разделяющимися переменными t и v:
mdv
F -kv
= dt,
-(m/k)ln(F-kv) = t + Cv
Начальные условия: ? = 0, ж = 0, х = v = 0. Так как в этой задаче не
идет речь о расстояниях, то интегрировать второй раз и использо-
использовать условие на координату х не требуется. Из условия на скорость
находим константу интегрирования Сх = —(т/к) ln(F). Зависимость
скорости от времени движения принимает вид
-(m/k)ln(l-kv/F) = t.
A)

234	Гл. 11. Динамика точки
4. Находим искомую силу тяги F грузовика, считая ее постоян-
постоянной. Для этого используем все имеющиеся в задаче данные. Из-
Известна максимальная скорость v = г>тах. Необходимым условием
экстремума функции v = v(t) является равенство dv/dt = 0 или
тх = F — kvmay. = 0. Отсюда: k = F/vma:ic. Подставляем это со-
соотношение в A), откуда, при t = t^ и v = г^, получаем среднюю силу
тяги грузовика
УСЛОВИЯ ЗАДАЧ
1.	Автомобиль массой т тормозит, двигаясь по горизонтальной пря-
прямой. Сила сопротивления воздуха зависит от скорости, Rc = kv,
коэффициент трения /. За какое время скорость автомобиля умень-
уменьшится с v0 до г^?
2.	Автомобиль массой т разгоняется до некоторой скорости за время
t±. Сила сопротивления пропорциональна скорости, Rc = kv. Чему
будет равно время разгона автомобиля до той же скорости, если его
силу тяги увеличить вдвое?
3.	Материальная точка массой т движется из состояния покоя по
гладкой криволинейной направляющей, расположенной в горизонталь-
горизонтальной плоскости, под действием силы F = Q sin kt. Сила образует по-
постоянный угол а с вектором скорости. Определить скорость точки в
момент времени t.
4.	Сила сопротивления воды при движении катера пропорциональна
скорости, Rc = kxv. При этом максимальная скорость катера г>тах.
Найти предельную скорость этого же катера, если бы сила сопротив-
сопротивления зависела от квадрата скорости, Rc = k2v2.
5.	Автомобиль массой т разгоняется до некоторой скорости за время
t±. Сила сопротивления пропорциональна скорости, Rc = kv. Чему
будет равно время разгона до той же скорости при отсутствии со-
сопротивления?
6.	Брусок А массой т начинает движение из состояния покоя по
горизонтальной поверхности консоли под действием нити, продетой
сквозь неподвижное кольцо О. В начальном по-	А т
ложении брусок находился на расстоянии О А = L
от кольца. Дана толщина консоли Н. Трением и
размерами бруска пренебречь. Натяжение нити	Т ^
F = const. Найти максимальную скорость бруска.

11.2. Переменные силы	235
7.	Воздушный шар плавно (v0 = 0) взлетает вертикально вверх с
начальным ускорением WQ. По мере набора высоты h подъемная сила
F шара уменьшается (за счет охлаждения и уменьшения плотности
атмосферы) по закону F = Fo — kh, где Fo и к известные константы.
Чему равна скорость шара на высоте HI
8.	Автомобиль массой т, имея скорость г>0, начинает тормозить.
Сила торможения постоянна и равна F, сила сопротивления воздуха
пропорциональна квадрату скорости и в момент начала торможения
равна Rc. Найти тормозной путь автомобиля.
9.	Автомобиль массой т1 без груза разгоняется с места до заданной
скорости за время t1. Сопротивление пропорционально скорости. За
какое время разгоняется до той же скорости автомобиль с грузом
т2?
10.	Воздушный шар массой т1 падает вниз. В момент, когда ско-
скорость шара равна г>0, а ускорение Wo, сбросили балласт т2. Сила
сопротивления воздуха пропорциональна скорости, подъемная сила
равна F. Как долго после этого будет продолжаться падение шара?
Ответы
1.	t = (т/к) ln((kv0 + mgf)/(kv1 + mgf)).
2.	t2 = (т/к)(Ы2-.
3.	у = Q/(mk)(l — cos kt) sin a.
5. t = C
6.	v = <s/2F(L - H)/m.
7.	v =
8.	S = mv20/{2Rc)ln{l +
9.	t2 = ^A + m^jm^).
10.	t = (l/fc)(m1 - m2) ln(l - kvo/A), A = (m1 - m2)g -
k = (m1(g-W0)-F)/v0.

Глава 12
ДИНАМИКА СИСТЕМЫ
12.1. Теорема о движении центра масс
Постановка задачи. Механизм, состоящий из п связанных меж-
между собой тел, установлен на призме, находящейся на горизонталь-
горизонтальной плоскости. Трение между призмой и плоскостью отсутствует.
Одно из тел получает перемещение относительно призмы. Куда и
на какое расстояние переместится призма?
План решения
Для решения задачи используем теорему о движении центра масс.
Выбираем систему координат. Одну из осей, например, ось х направ-
направляем перпендикулярно линии действия внешних сил. В проекции на
ось х уравнение движения центра масс принимает вид
тхц = О,	A)
где х — координата центра масс системы, т = X^=i mi — масса
всей системы. Дважды интегрируя A) при условии, что в начальный
момент скорость центра масс была равна нулю, получаем
тхц = const.	B)
Координата центра масс системы вычисляется по формуле
171 г=1
Записывая B) с учетом C) один раз для начального положения сис-
системы (в покое), а другой раз после смещения одного из тел, получаем
формулу, связывающую абсолютные смещения тел системы:
п
,А^=0.	D)

12.1. Теорема о движении центра масс
237
1.	Абсолютное смещение каждого тела представляем как сумму
относительного смещения, зависящего от величины заданного отно-
относительного смещения одного из тел, и неизвестного переносного сме-
смещения А, равного абсолютному смещению того тела, относительно
которого задавалось смещение.
2.	Подставляя абсолютные смещения в D), получаем уравнение для
смещения А. Решение уравнения дает ответ.
Пример. Механизм, состоящий из груза А массой 50 кг, блока
В массой 80 кг (больший радиус R = 30 см, меньший г = 10 см) и
цилиндра С массой 120 кг радиусом Rc = г/2, установлен на призме
D массой 210 кг, находящейся на горизонтальной плоскости. Трение
между призмой и плоскостью отсутствует. Груз А получает переме-
перемещение S = 1.2 м относительно призмы вдоль ее поверхности влево;
а = 75° (рис. 124). Куда и на какое расстояние переместится призма?
Решение
Задаем систему координат. Проекции на горизонтальную ось всех
внешних сил (сил тяжести GA, GB, Gc, GD, реакции опоры TV), дей-
действующих на систему, равны нулю (рис. 125), а трения между приз-
призмой D и опорой по условию нет. Применим к системе следствие из
теоремы о движении центра масс в форме D).
1. Абсолютное смещение тел А, В к С представляем как сумму от-
относительного смещения, зависящего от величины S относительного
смещения груза А, и неизвестного переносного смещения А^, равного
Рис. 124
абсолютному смещению призмы, относительно которой задавалось
смещение S. Обозначаем абсолютные смещения координат центров
масс тел системы А^, Ав, А^, А^. Направление оси х определяет
знаки смещений: налево с минусом, направо с плюсом. Предпола-
Предполагаем, что призма сместится направо. Перемещение центра цилиндра

238	Гл. 12. Динамика системы
С относительно призмы и перемещение груза А связаны так же, как
связаны их скорости.
Цилиндр С совершает плоское движение. Абсолютное смещение
его центра в проекции на ось х равно AD — Sc cos а, где Sc — сме-
смещение центра цилиндра вдоль наклонной поверхности призмы. Вы-
Выразим Sc через S. Для этого свяжем скорости груза А и центра
масс цилиндра С. Мгновенный центр скоростей цилиндра находится
в точке касания призмы, поэтому скорость его центра масс относи-
относительно призмы вдвое меньше скорости нити, накручиваемой на обод.
Скорость груза А выражаем через угловую скорость блока (рис. 132,
с. 249):
vc = 0.5о;Бг, v A = UJBR.	E)
Исключая отсюда иов, имеем связь скоростей: vc = 0.5vAr/R. Интег-
Интегрируя это соотношение при нулевых начальных значениях, получаем
искомую зависимость: Sc = 0.5Sr/R. Находим выражение абсолют-
абсолютных смещений всех тел через AD и S:
AA = AD-S, A5 = AD, Ac = AD-0.5Sr/Rcosa. F)
2. Подставляя абсолютные смещения в D), получаем уравнение
тААА + тпвАв + гпсАс + mDAD = О,
или
mA(AD - S) + mBAD +mc(AD - O.bSr/Rcosa) + mDAD = 0.
Решаем это уравнение относительно AD:
mAS + mc0.5Sr/R cos a
D	mA + mB + mC + mD
Призма D переместится вправо на 14.39 см.
Условия задач. Механизм, состоящий из груза А, блока В
{больший радиус R, меньший г) и цилиндра С радиуса Rc, установ-
установлен на призме D, находящейся на горизонтальной плоскости. Тре-
Трение между призмой и плоскостью отсутствует. Груз А получает
перемещение S = 1 м относительно призмы вдоль ее поверхности
влево или (в тех вариантах, где он висит) по вертикали вниз. Куда
и на какое расстояние переместится призма?

12.1. Теорема о движении центра масс
239
1.
2.
3.
4.
С
гпа = 6 кг, тв = 3 кг,
тс = 11 кг, тв = 40 кг,
R = 16 см, г = 8 см,
Дс = 28 см.
гпа = 9 кг, тв = 6 кг,
тс = 14 кг, тпг) = 51 кг,
R = 24 см, г = 12 см,
Дс = 42 см.
гпа = 6 кг, тв = 3 кг,
шс = 16 кг, тв = 65 кг,
R = 48 см, г = 32 см,
Rc = 24 см.
тпл = 9 кг, тв = 6 кг,
тс = 19 кг, тв = 76 кг,
R = 60 см, г = 40 см,
Дс = 30 см.
гпа = 6 кг, тв = 3 кг,
тс = 21 кг, тпг) = 90 кг,
R = 28 см, г = 16 см,
Дс = 12 см.
гпа = 9 кг, тв = 6 кг,
тс = 24 кг, тв = 51 кг,
i? = 42 см, г = 24 см,
Дс = 18 см.

240
Гл. 12. Динамика системы
7.
8.
10.
7ПА = 6 КГ, ГПв = 3 КГ,
тс = 11 кг, тв = 50 кг,
R = 32 см, г = 16 см,
Re = 56 см.
гпа = 12 кг, тв = 6 кг,
тс = 27 кг, тв = 65 кг,
R = 70 см, г = 40 см,
Дс = 30 см.
гпа = 9 кг, тв = 3 кг,
тс = 14 кг, тпг) = 64 кг,
R = 16 см, г = 8 см,
Дс = 28 см.
гпа = 12 кг, тв = 6 кг,
тс = 22 кг, тв = 80 кг,
Л = 36 см, г = 24 см,
Re = 18 см.
Ответы. 1. 12.887 см. 2. 20.945 см. 3. 13.597 см. 4. 4.986 см.
5. 31.522 см. 6. 27.278 см. 7. 6.760 см. 8. 20.641 см.
9. 11.571 см. 10. 12.981 см.
Предупреждение типичных ошибок
1.	В знаменателе ответа должна стоять сумма масс всех тел сис-
системы. Если вместо суммы масс возникла разность, это значит, что
при вычислении абсолютного смещения получилась ошибка в знаке.
Следите за соответствием направления координатной оси и направ-
направлением перемещения.
2.	Внутренние силы не влияют на решение задачи. Так, если
дополнить условия задач трением качения цилиндров о призму, то

12.2. Кинетическая энергия механической системы	241
коэффициент трения в решение не войдет. А вот малейшее тре-
трение между призмой и неподвижным основанием испортит задачу на-
настолько, что уравнение D) применять будет уже нельзя, так как не
выполняется условие A). Для более ясного представления задачи
можно считать, что призма находится на тонкой пленке воды или
масла на идеально полированном столе.
12.2. Кинетическая энергия механической
системы
Постановка задачи. Выразить кинетическую энергию механи-
механической системы с одной степенью свободы через угловую скорость
одного из тел системы или линейную скорость какой-либо ее точки.
План решения
1.	Составляем кинематические графы системы. Угловые скорости
тел системы и линейные скорости их центров масс выражаем через
заданную скорость (§ 8.5, с. 188).
2.	Вычисляем кинетические энергии отдельных тел системы. Для
тела, совершающего поступательное движение, кинетическая энергия
T=^f,	A)
где т — масса тела, v — скорость любой его точки. Напомним,
что при поступательном движении скорости всех точек тела равны,
а угловая скорость равна нулю. Кинетическая энергия тела, совер-
совершающего вращательное движение с угловой скоростью о;,
J — момент инерции тела относительно оси вращения. Напомним,
что у однородного цилиндра радиуса R момент инерции относительно
оси, проходящей через центр масс, J = mR2/2, однородного стержня
длиной а, относительно середины J = та2/12, а относительно конца
J = Ша2/3.
Моменты инерции тела относительно параллельных осей связаны
соотношением J = J + /г2т, где J — момент инерции относительно
оси, проходящей через центр масс, h — расстояние между осями (см.
также с. 273). Если известен радиус инерции г тела массы т, то его
момент инерции J = mi2.
16 М.Н. Кирсанов

242
Гл. 12. Динамика системы
Кинетическая энергия тела, совершающего плоское движение,
T= mvu
C)
где уц — скорость центра масс тела, Зц — момент инерции тела
относительно оси, проходящей через его центр масс. В частности,
кинетическая энергия однородного цилиндра, катящегося без про-
проскальзывания по неподвижной плоскости, вычисляется по формуле
|
D)
3. Кинетическую энергию системы вычисляем как сумму кинети-
кинетических энергий отдельных тел:
k=i
Пример 1. Выразить кинетическую энергию механической сис-
системы с одной степенью свободы (рис. 126) через угловую скорость ф.
Система состоит из двух однородных цилиндров 1 и 2, радиусом R,
соединенных двухзвенником ABC. Невесомый стержень АВ жестко
Рис. 126
Рис. 127
соединен с цилиндром 1. Массы цилиндров 1 и 2 равны т
однородного стержня ВС — т3- Качение цилиндра происходит без
проскальзывания и сопротивления. На цилиндр 1 действует момент
М, к оси С приложена горизонтальная сила F *^ .
*) Условие задачи содержит избыточные данные — М, F. Они потребу-
потребуются в дальнейшем для составления нелинейного уравнения движения этой
системы в § 13.5, с. 307.

12.2. Кинетическая энергия механической системы	243
Решение
1. Составляем кинематические графы системы:
(р	2тг — (р	ir — (p	Зтг/2
Записываем соответствующие им кинематические уравнения в про-
проекциях на оси х ж у (рис. 127):
vCx = vAx - (pABsimp - uJBCzBCsmB7r - <p),
vCy = vAy + фАВ cos <p + ujBCzBC cosBtt - <p),
VDx = VCx ~ ^BCzCD sinGT - <p),
vDy = ^Cy + uBCzCDcos(tt - y?),
%ж = VCx ~ ^
Точка К является МЦС цилиндра 2. С учетом кинематических связей
vKx = vKy = ^АЖ = vAy = °' ^Су = 0 из системы B) получаем
выражения скоростей точек G, D и угловой скорости uBCz'.
3 . .	1 .
, vDx = --a (p simp, vDy = -cap cos (p.
2. Вычисляем кинетическую энергию тел системы. Цилиндр 1
масса которого т1? а момент инерции относительно оси вращения,
проходящей через центр масс, J1 = m1R2/2, имеет кинетическую
энергию
Кинетическая энергия однородного цилиндра 2, катящегося без про-
проскальзывания по неподвижной поверхности (с. 242),
Т2 = 	—— = Зт2ф2а2 sin2 (p.
Кинетическая энергия плоского движения стержня ВС, центр масс
которого находится в точке D,
9	т	9	/ 2 i 2 \	99
Qt?r> Jтзг^ШTin-, iUo\u'n п^ ^Jlii) ТПп& UJr>r^~,
ГТ1 		О J-J I	.DO DKy Z 		«-> v J-^«b	J-У t// I	^3	DU2
3~^~	2 "	2	24 "
16*

244
Гл. 12. Динамика системы
3. Кинетическую энергию системы вычисляем как сумму кинети-
кинетических энергий отдельных тел:
Т =
Т2 + Г3 = ф2 (а2Cга2 + га3) sin2 <р
га
а2/б) .
Пример 2. Однородный диск 1 массой т1 радиусом R шарнирно
соединен в точке А с вертикально движущимся штоком 2 массой га2.
У	=Г2
Рис. 128
Рис. 129
Диск катится по горизонтальному штоку 3 массой т3 без проскаль-
проскальзывания; О А = а; т1 = т2 = 7гг3 = га. Выразить кинетическую
энергию механической системы (рис. 128) через угловую скорость ф.
Решение
1. Составляем кинематические графы системы: К—>О—> А.
тг/2	<р
К —> О. Записываем соответствующие им кинематические уравне-
уравнения в проекциях на оси хну (рис. 129)
vOx
vAy = vKy
cos(tt/2) + фа cos <p, vOj/ =
cos(tt/2) .
C)
По условию задачи vK = 0 и vAx = 0. Используя эти соотношения
(кинематические связи) получаем из C)
vKx
= ф(Л + asimp).
D)
vAy = фа cos ip, vOx =
2. Вычисляем кинетическую энергию тел системы. Цилиндр 1,
масса которого га1? а момент инерции относительно оси вращения
J1 = rn1R2/2, имеет кинетическую энергию
J-уф2
1 = ^~
Q ф2К2т1
~ = 4
Кинетическая энергия штока 2 — Т2 = тп2у\у/2 = A/2)т2ф2112 cos2 ^,
кинетическая энергия штока 3 — Т3 = m3v2<x/2 = ra3(^2(ii!+asin<?>J/2.

12.2. Кинетическая энергия механической системы
245
3. Кинетическую энергию системы вычисляем как сумму кинети-
кинетических энергий отдельных тел:
Т = Т1 +Г2 +Г3 = 0.5(p2mA.5R2 + (R + asimpJ).
2.
Условия ЗАДАЧ. Выразить кинетическую энергию механической
системы с одной степенью свободы через угловую скорость ф. Все
диски {цилиндры) считать однородными. Качение происходит без
проскальзывания.
pi Механизм приводится в движение
моментом М. Кривошип О А имеет
массу mi, диск С — га2; О А = АВ =
= а, массой ползуна В, стержней АВ
и ВС пренебречь.
Механизм приводится в движение
моментом М. Ползун А считать не-
невесомым, кривошип О А имеет массу
mi, кулиса В — Ш2, диск D — газ,
ползун С — ГП4', О А = а.
Шарнирный параллелограмм приво-
приводится в движение моментом М.
Спарник А А' считать невесомым,
звенья О А и О'А' имеют одинако-
одинаковую массу шь Ползун В вместе со
стержнем ВС имеет массу га,2, масса
диска D — газ, ползуна С — тти;
ОА = а.
4.
Диск О радиусом R массой rai со-
соединен с невесомым стержнем О А =
а, на конце которого закреплен груз
А массой ni2. Груз С имеет массу
газ, шкив D — 1714-

246
Гл. 12. Динамика системы
5.
А[
6.
М
С
9.
F
Ползун А массой mi, скользящий по
гладкой вертикальной поверхности,
соединен с центром цилиндра О не-
невесомым стержнем АО = а. Ци-
Цилиндр О имеет массу га,2, диск D —
7Пз, Груз С 	 7714-
Диск О радиусом R, имеющий массу
rai, соединен с невесомым стержнем
О А. Механизм приводится в движе-
движение моментом М. Массы дисков С
и D гп2 и газ, О А = АВ = а, мас-
массой ползуна В и стержня АВ пренеб-
пренебречь.
Механизм приводится в движение
моментом М. Кривошип О А счи-
считать невесомым. В шарнире А со-
сосредоточена масса тп\. Массы дис-
дисков С и D — ?ri2 и 771з; О А = АВ = а,
массой ползуна В и стержня АВ пре-
пренебречь.
Механизм приводится в движение
моментом М. Кривошип О А счи-
считать невесомым. Ползун А имеет
массу rai, кулиса В — га,2, массы
дисков С и D — 771з и га,4; О А = а.
Однородный диск 1 массой rai ради-
радиусом R шарнирно соединен в точке
А с вертикально движущимся што-
штоком 2 массой га,2. Диск без сопротив-
сопротивления катится по горизонтальному
штоку; О А = а. К горизонтальному
штоку приложена сила F, к диску —
момент М.

12.3. Теорема об изменении кинетической энергии	247
Диск О радиусом R массой тщ соеди-
соединен с однородным стержнем О А = а
массой 77i2. Масса диска D — га3. Мас-
Массой ползуна и стержня ОС пренебречь.
Ответы
1.	Т = ф2а2/2(тг/3 + 6rn2 sin2 ф).
2.	Т = ф2а2/2(тг/3 + (га2 + 3rn3/8 + m4) sin2 у?).
3.	Т = <^2a2/2Bmi/3 + (m2 + ш3/2 + m4) sin2 у?).
4.	Т = ^2/2(Д2(Зш1/2 + ш2 + ш3 + m4/2) + a2rn2 + 2Ram2 sirup).
5.	Т = <^2a2/2(mi + (-mi + 3rn2/2 + 2m3 + 4m4) sin2 ф).
6.	T = <?>2/2(ЗД2т1/2 + (Л + 2a sin фJ(т2 + 3m3/4)/2).
7.	T = ^2a2/2(mi + Bm2 + 3m3/2) sin2 ф).
8.	T = ^2a2/2(mi + (m2 + m3/2 + 3m4/2) sin2 <p).
9.	T = ф2/2{т^2/2 + m2a2 + a2(mi - m2) sin2 y?).
10.	T = ф2/2(Ж2тг/2 + ш2(Д2 + ai^sin^ + a2/3) + 3/8т3й2).
12.3. Теорема об изменении кинетической
энергии
Постановка задачи. Механическая система, находящаяся в по-
покое, под действием внешних сил приходит в движение. За некото-
некоторое время одно из тел системы перемещается на заданное рассто-
расстояние. Найти скорости, приобретенные телами системы.
План решения
1.	Выражаем кинетическую энергию системы через скорость v^
тела, перемещение S^ которого задано.
2.	Вычисляем сумму работ сил, приложенных к системе, на за-
заданном перемещении. Перемещения точек приложения сил и углы
поворота тел, к которым приложены моменты, выражаем через S^.
3.	Из теоремы об изменении кинетической энергии,
>i»	A)
3	3
гДе 2j^/> J2j Aj — работа внешних и внутренних сил, определяем
скорость v^.

248	Гл. 12. Динамика системы
Пример. Механизм, состоящий из груза Л, блока В и цилиндра
С радиусом Rc, установлен на неподвижной призме (рис. 130). Под
действием сил тяжести из состояния покоя механизм пришел в дви-
движение. Даны массы тА = 50 кг, тв = 80 кг, тс = 120 кг, ради-
радиусы R = 30 см, г = 10 см, Rc = г/2, угол а = 75°, радиус инерции
блока г = 15 см, коэффициент трения качения цилиндра о наклонную
плоскость 5 = 2 мм, коэффициент трения скольжения груза о гори-
горизонтальную поверхность / = 0.1. Трения на оси блока В нет. Нити,
соединяющие блок с грузом и цилиндром, параллельны плоскостям,
по которым перемещаются эти тела. Какую скорость развил груз Л,
переместившись на расстояние SA = 1.2 м?
Решение
Применяем теорему об изменении кинетической энергии системы
A). Для рассматриваемой системы, состоящей из твердых тел, соеди-
соединенных нерастяжимыми нитями, работа внутренних сил равна нулю:
^2 ¦ А1, = 0. В начальном положе-
положении все элементы механизма на-
находились в покое, скорости всех
тел были равны нулю, поэтому
То = 0. Кинетическая энер-
энергия Т1? которую получила сис-
система после того, как груз переме-
переместился вдоль горизонтальной по-
поверхности на расстояние SA, за-
Рис. 130	висит от искомой скорости vА.
1. Кинетическую энергию системы, состоящую из трех слагаемых
выражаем через скорость v = vA. Груз А движется поступательно,
следовательно, его кинетическая энергия равна ТА = тАгг/2. Тело
В (блок) вращается относительно неподвижной оси: Тв = JBuoB/2.
Момент инерции блока относительно оси вращения вычисляем через
заданный радиус инерции Jв = гтпв. Угловую скорость ujb необхо-
необходимо выразить через искомую скорость v. Линейная скорость внеш-
внешнего обода блока совпадает со скоростью груза г>, так как обод связан
нерастяжимой нитью с грузом. Для угловой скорости блока записы-
записываем формулу и;в = v/R. Выражаем Тв через скорость v:
_ mBi2v2
в 2Д2 '

12.3. Теорема об изменении кинетической энергии
249
Тело С (цилиндр) совершает плоское движение, поэтому
_ тсус
с~ 2
2 '
vc — скорость центра масс цилиндра, Jc — момент инерции ци-
цилиндра относительно центральной оси:
_ rncR2c _ тс{г/2J _ тсг2
Jc~ 2 " 2 " 8 '
Выражаем vc и иос через v. Точки внутреннего обода блока имеют
скорость гujb или, выражая иов через скорость груза, vr/R (рис.131).
NA
С
УГ
R
Рис. 131
Рис. 132
Рис. 133
Цилиндр катится без проскальзывания, поэтому точка его сопри-
соприкосновения с призмой является мгновенным центром скоростей тела
(рис. 132), отсюда
B)
vr
2RnR
V Г
vc=ujcRc = --.
C)
В результате находим кинетическую энергию цилиндра С:
r.2.,2
о о
mcr v
с =
Кинетическую энергию системы трех тел представляем в виде
,,2
Т1 = ТА + ТВ + ТС =
V
D)

250	Гл. 12. Динамика системы
гДе А^прив = тА + тв^2/-R2 + ^/8 шс г2/R2 — приведенная масса сис-
системы.
2. Находим сумму работ внешних сил. Изображаем действующие
на систему силы (рис. 133). Реакции опор NA,NC и вес GA работы
не совершают, так как они перпендикулярны перемещениям точек их
приложения. Реакции оси Хв, YB и вес GB приложены к неподвиж-
неподвижным точкам, поэтому их работа также равна нулю. Аналогично, ра-
работа силы сцепления, приложенной к цилиндру С в точке касания,
равна нулю. Находим сумму работ остальных сил:
Аз = -
где Sc и (рс — соответственно, смещение центра тяжести и угол
поворота цилиндра С. Находим силу трения скольжения груза А и
момент трения качения цилиндра С. Имеем FTp = NAf, Мтр = NC5,
где NA и Nc соответствующие нормальные реакции. Проекция всех
сил, действующих на тело А, на нормаль к поверхности равна нулю.
Отсюда, NA = GA. Аналогично, из равенства нулю суммы проекций
на нормаль к боковой поверхности призмы всех сил, действующих на
цилиндр, получаем Nc = Gc cos а. В результате
FtP = GAf = mA9f, Мтр = NC5 = mc9S C0S a-
Так как vc = Sc, v = SA, ouc = фс, то интегрируя B) и C) при
нулевых начальных условиях, получаем Sc = SAr/BR), (pc = SA/R.
Суммарную работу выражаем через SA:
3	g r	g
- - тсд5 cos а^-.	E)
3. Кинетическую энергию D) приравниваем сумме работ E):
v2	/	.г	5
mAf + m
Отсюда получаем: v = 2.10 м/с.
Условия задач. Механизм, состоящий из груза А, блока В
(больший радиус R, меньший г) и цилиндра С радиусом Rc, уста-
установлен на призме D, закрепленной на плоскости. Под действием сил

12.3. Теорема об изменении кинетической энергии
251
тяжести из состояния покоя механизм пришел в движение. Между
грузом А и призмой имеется трение (кроме тех вариантов, где груз
висит), качение цилиндра (блока) происходит без проскальзывания.
Коэффициент трения скольжения груза о плоскость f, коэффици-
коэффициент трения качения цилиндра (блока) 5. Трения на неподвижной
оси вращающегося блока (цилиндра) нет. Нити, соединяющие тела,
параллельны плоскостям. Какую скорость развил груз А, перемес-
переместившись на расстояние S = 1 м?
R = 16 см, г = 8 см,
Rc = 28 см, / = 0.01,
г = 13 см, Sa = 1 м,
5 = 0.1 мм, гпа = 6 кг,
тв = 3 кг, тс = 11 кг.
R = 24 см, г = 12 см,
Rc = 42 см, / = 0.02,
г = 19 см, Sa = 2 м,
6 = 0.2 мм, гпа = 9 кг,
тв = 6 кг, тс = 14 кг.
R = 48 см, г = 32 см,
Rc = 24 см, / = 0.03,
г = 41 см, Sa = 1 м,
6 = 0.3 мм, гпа = 6 кг,
тв = 3 кг, тс = 16 кг.
R = 60 см, г = 40 см,
Rc = 30 см, / = 0.04,
г = 51 см, Sa = 2 м,
E = 0.4 мм, гал = 9 кг,
тв = 6 кг, тс = 19 кг.

252
Гл. 12. Динамика системы
5.
С
R = 28 см, г = 16 см,
Rc = 12 см, / = 0.05,
г = 23 см, SU = 1 м,
6 = 0.1 мм, гал = 6 кг,
тв = 3 кг, тс = 21 кг.
6.
R = 42 см, г = 24 см,
Rc = 18 см, / = 0.01,
г = 34 см, SA = 2 м,
E = 0.2 мм, гал = 9 кг,
тв = 6 кг, тс = 24 кг.
7.
Л = 32 см, г = 16 см,
Rc = 56 см, / = 0.02,
г = 25 см, SU = 1 м,
6 = 0.3 мм, гпа = 6 кг,
тв = 3 кг, тс = 11 кг.
8.
R = 70 см, г = 40 см,
Дс = 30 см, / = 0.03,
г = 57 см, SU = 2 м,
E = 0.4 мм, гпа = 12 кг,
тв = 6 кг, тс = 27 кг.
R = 16 см, г = 8 см,
Дс = 28 см, / = 0.04,
г = 14 см, «SU = 1 м,
E = 0.1 ММ, ГПА = 9 КГ,
тв = 3 кг, тс = 14 кг.

12.4. Теорема о моменте количества движения системы
253
10.
С
Ответы
R = 36 см, г = 24 см,
Rc = 18 см, / = 0.05,
г = 32 см, SA = 2 м,
S = 0.2 мм, гпа = 12 кг,
гпв = 6 кг, тс = 22 кг.
1
2
3
4
5
/Лприв
КГ
13.714
55.042
18.855
16.502
108.668
Нм
9.211
4.474
0.350
114.307
177.056
VA
м/с
1.159
0.403
0.193
3.722
1.805
6
7
8
9
10
Мприв
КГ
48.604
13.647
55.192
18.354
20.407
Нм
79.504
40.560
119.894
10.333
5.674
VA
м/с
1.159
0.403
0.193
3.722
1.805
12.4. Теорема о моменте количества
движения системы
Постановка задачи. Горизонтальная платформа, на которой
расположено N материальных точек, свободно вращается вокруг
вертикальной оси. Как изменится угловая скорость платформы,
если в некоторый момент времени точки начнут перемещаться по
платформе вокруг оси вращения с заданными скоростями ? Трением
пренебречь.
План решения
По условию задачи моменты М^ всех внешних сил относительно
оси вращения равен нулю (силы тяжести параллельны вертикальной
оси, а реакции подшипников пересекают ось). Поэтому из теоремы
об изменении момента количества движения системы, записанной в
проекции на ось вращения z,
dt
следует закон сохранения момента количества движения системы
A)

254
Гл. 12. Динамика системы
где Lz0 и Lzl — проекции момента количества движения системы на
ось z до и после относительного движения точек.
1. Вычисляем момент количества движения системы, для случая
неподвижных относительно платформы точек:
N
г=1
B)
где Jz — момент инерции платформы относительно оси z, совпада-
совпадающей с осью вращения, ujz0 — проекция начальной угловой скорости
на ось z\ т^ Щ, г = 1,..., N — массы точек и радиусы окружностей,
на которых они расположены.
2. Вычисляем момент количества движения системы, для случая,
когда точки начали двигаться относительно платформы со скорос-
скоростями Vf
N
г=1
где ujzl — угловая скорость, которую получила платформа.
3. Из уравнения A) находим угловую скорость ojz1.
Пример *^ . Круглая горизонтальная платформа вращается без
трения вокруг вертикальной оси, проходящей через ее центр масс с
постоянной угловой скоростью о;0; при этом на платформе стоят че-
четыре человека: два — на краю платформы, а два на расстояниях
от оси вращения, равных половине радиуса платформы (рис. 134).
Рис. 134
Рис. 135
Как изменится угловая скорость платформы, если люди, стоящие на
краю, будут двигаться по окружности в сторону вращения с отно-
относительной скоростью г>, а люди, стоящие на расстоянии половины
Задача 37.53 из сборника задач И.В. Мещерского [14].

12.4. Теорема о моменте количества движения системы	255
радиуса от оси вращения, будут двигаться по окружности в проти-
противоположную сторону с относительной скоростью 2v? Людей считать
материальными точками одинаковой массы, а платформу — одно-
однородным диском.
Решение
На систему, состоящую из платформы и четырех человек, дейст-
действуют внешние силы. Ось z направим по оси вращения. Моменты сил
тяжести людей E, платформы GQ и реакций подшипника (реакция
X перпендикулярна плоскости чертежа и на рис. 135 не обозначена)
относительно оси z равны нулю (рис. 135). Используем уравнение
сохранения момента количества движения A).
1.	Вычисляем момент количества движения системы, когда люди
стоят неподвижно на платформе:
Lz0 = (Jz + 2mR2 + 2m(R/2J)u;z0 = (Jz + 2.bmR2)u;z0,
где Jz — момент инерции платформы, m — масса каждого человека,
R — радиус платформы.
2.	Вычисляем момент количества движения системы после того,
как люди начали двигаться относительно платформы. У двух чело-
человек на внешнем ободе относительные скорости v и переносные ско-
скорости u;zlR суммируются, v + &zlR, и момент количества движе-
движения вычисляется в виде произведения величины количества движения
m(v + ujz1R) на плечо R. У людей на внутреннем ободе переносная
скорость меньше в два раза, ojz1R/2, направлена в сторону вращения
диска. Относительная же скорость 2v направлена в противополож-
противоположную сторону, поэтому она берется с минусом. В итоге,
Lzl = JzLuzl + 2mR(v+LUzlR)-\-2mR/2(uJzlR/2-2v) = (Jz + 2.5mR2)uzl.
3.	Из равенства LzQ = Lzl следует, что ujz1 = ujzQ, т.е. угловая
скорость вращения платформы не изменилась.
Условия ЗАДАЧ. Однородная горизонтальная платформа ради-
радиусом R = 1 м и массой т0 = 20 кг, на которой расположены три
материальные точки, свободно вращается вокруг вертикальной оси
с угловой скоростью ujz0 = 2 рад/с. Найти угловую скорость плат-
платформы после того, как точки начнут перемещаться по платформе
со скоростями vi, г = 1...3 по окружностям вокруг оси вращения.
Массы даны в кг, относительные скорости — в м/с. Радиус мень-
меньшей окружности г = 0.7 м, радиус большей совпадает с радиусом
платформы. Трением пренебречь.

256
Гл. 12. Динамика системы
V2 ГП2
т\ = 19, 7П2 = 18, тз = 17,
vi = 1, v2 = 2, г>3 = 3.
1711 = 18, 7712 = 16, 7Пз = 14,
vi = 2, г>2 = 3, ^з = 4.
7712	V2
ITli = 17, 7712 = 14, 771з = 11,
г>1 = 3, V2 = 5, г>3 = 6.
TTli = 19, 7712 = 15, 771з = И,
г>1 = 4, г>2 = 6, Уз = 7.
7712
7711 = 19, 7712 = 17, 771з = 16,
vi = 2, ^2 = 4, г>з = 5.
7711 = 18, 7712 = 15, 771з = 13,
vi = 3, г>2 = 4, г>з = 5.
7712	V2
rai = 17, га2 = 13, га3 = 10,
г>1 = 4, г>2 = 6, г>з = 7.
7711 = 16, 7712 = 15, 771з = И,
vi = 1, г>2 = 3, Уз = 4.

12.5. Динамический расчет механизма с неизвестным параметром 257
V2 ТП2
mi = 19, 7П2 = 17, гпз = 14,
vi = 2, v2 = 3, Уз = 4.
i = 18, 7П2 = 15, газ = 11,
= 3, г>2 = 4, ^з = 5.
Ответы. 1. ^ = 0.269 рад/с. 2. ^ = -0.414 рад/с.
3. cjz = 1.725 рад/с. 4. cjz = -0.345 рад/с. 5. ^ = -5.009 рад/с.
6. cjz = 0.407 рад/с. 7. cjz = 2.343 рад/с. 8. cjz = -1.357 рад/с.
9. ^ = 1.058 рад/с. 10. ^ = 2.928 рад/с.
12.5. Динамический расчет механизма с
неизвестным параметром
Постановка задачи. Механическая система с неизвестным па-
параметром под действием внешних сил приходит в движение из со-
состояния покоя. За некоторое время одно из тел системы пере-
перемещается на заданное расстояние и приобретает известную ско-
скорость. Найти неизвестный параметр системы и рассчитать дви-
движение системы в измененных условиях.
План решения
Постановка задачи по сути представляет собой простой вариант
практически важной проблемы идентификации параметров механизма
по наблюдаемым характеристикам его движения. Для решения за-
задачи применим теорему об изменении кинетической энергии.
1.	Выражаем кинетическую энергию каждого тела системы через
известную скорость v0: Tk = /^г>о/2, где fik — приведенная масса к-го
тела. Вычисляем суммарную приведенную массу: //прив = ^^^к-
2.	Записываем теорему об изменении кинетической энергии:
A)
17 М.Н. Кирсанов

258	Гл. 12. Динамика системы
Для неизменяемых систем (твердые тела, нерастяжимые нити) внут-
внутренние силы работу не совершают: J^ . Aj = 0. В начальном состоя-
состоянии система находилась в покое То = 0. Вычисляем работы внешних
сил и записываем A) в форме
B)
Пусть неизвестная характеристика системы содержится в выражении
для работы *' .
3.	Решая уравнение B), определяем неизвестный параметр.
4.	Рассчитываем систему в новых условиях. В соответствии с
ними вычисляем измененное значение работы J^ . А^. Искомую ско-
скорость определяем из равенства
А^при
:рив 2	Z-^ 3*'
Пример. Механическая система состоит из трех тел, соединенных
нитью. Блок А внутренним ободом катится без проскальзывания
по наклонной плоскости, шкив В (однородный цилиндр) вращается
вокруг неподвижной оси. Груз D закреплен пружиной жесткости с
(рис. 136).
Рис. 136
В начальном положении механизм находится в состоянии покоя, а
пружина не напряжена. Переместившись вниз вдоль наклонной плос-
плоскости на расстояние SA = 3 м, блок А приобретает скорость 2.5 м/с.
*) Аналогично решается задача, когда неизвестная характеристика, на-
например масса, содержится в кинетической энергии.

12.5. Динамический расчет механизма с неизвестным параметром 259
Определить коэффициент трения качения блока А о наклонную плос-
плоскость. Учесть момент трения на оси цилиндра Мтр в = 4 Нм, и тре-
трение скольжения груза D о горизонтальную плоскость с коэффициен-
том / = 0.1. Даны радиусы
> тр
= 20 см,
= 30 см,
RA = 40 см, радиус инерции блока г А =24 см. Известны массы тел
тА = 10 кг, тв =90 кг, mD = 36 кг, угол а = 30° и жесткость
пружины с = 20 Н/м.
Чему будет равна скорость блока А на перемещении SA, если ко-
коэффициент трения качения увеличить в 3 раза?
Решение
1. Выражаем кинетическую энергию каждого тела системы через
известную скорость vA центра блока А. Блок А совершает плоское
движение. Кинетическая энергия блока А
Здесь JА = тАг2А — момент инерции блока относительно центра
масс, гА — радиус инерции блока. Вы-
Выражаем угловую скорость блока uja че-
/ ^—^ \	рез скорость центра vА. Блок катится
без проскальзывания, следовательно, его
мгновенный центр скоростей находится
в точке касания внутреннего (меньшего)
радиуса с плоскостью (рис. 137). Таким
образом: и А = vA/rA.
Рис. 137
Кинетическая энергия блока А имеет вид
ТА =
1 +
Приведенная масса (коэффициент при v\/2)
242
1 + ^4=10 1 + =^= 16.4 кг.
Цилиндр В совершает вращательное движение вокруг своей оси,
Тв = JB(jj2B/2, где Jв = mBR2B/2. Угловую скорость цилиндра В вы-
выражаем через скорость точки обода: ujb = vB/RB. Скорость обода vB
цилиндра В совпадает со скоростью внешнего обода блока А, так как
17*

260
Гл. 12. Динамика системы
они связаны нерастяжимой нитью. Расстояние от внешнего обода А
до МЦС блока равно RA — rA (рис. 137). Отсюда получаем выражение
для скорости обода:
— V,
10
L30
3 '
C)
и угловой скорости цилиндра:
3R,
Получаем выражение для кинетической энергии:
mBR2Bv2A rmBv2A
B = A-9R% = T^9~
где приведенная масса \±в = 5 кг.
	 г
D)
ASC
Груз D движется поступательно TD = mj^v^/2. Скорость посту-
поступательного движения груза совпадает с линейной скоростью точек
обода цилиндра В: vD = vB = vA/3. Кинетическая энергия груза D
имеет вид
Л
и 9-2	2
Приведенная масса fiD — 4 кг.
Приведенная масса механизма: /хприв = ЦА + Цв + [iD = 25.4 кг.

12.5. Динамический расчет механизма с неизвестным параметром 261
2. Записываем теорему об изменении кинетической энергии
Вычисляем работу внешних сил (рис. 138). Реакции опор NA и ND
перпендикулярны смещениям точек их приложения и их работы равны
нулю. Так как блок катится без проскальзывания, то сила сцепле-
сцепления FC4 A приложена к МЦС блока и ее работа также равна нулю.
Аналогично не совершают работу реакции Хв, YB, приложенные к
неподвижной точке. Работа силы тяжести блока А, катящегося вниз
AGa = mAgSAsma = 10 • 9.81 • 3 • 0.5 = 147.15 Дж.
Работа момента сил трения на оси В
АВ = ~МТР.ВРВ'
Угол поворота (рв цилиндра В вокруг оси (в радианах) выражаем
через SA, интегрируя D) при нулевых начальных условиях. Получаем
ipB = SA/CRB) = 5, откуда Ав = —4 • 5 = —20 Дж. Работа силы
трения скольжения FTp D груза D на перемещении SD
AD = ~KP.DSD = -mDgfTpSA/3 = -35.32 Дж,
где перемещение SD = SA/3 получаем, интегрируя C) при нулевых
начальных условиях. Работа силы упругости пружины
A
упр	2 '
где Д$с — удлинение пружины, равное перемещению груза D,
ASC = SA/3 = 1 м. Вычисляем: Аупр = -20 • 1/2 = -10 Дж.
3. Определяем коэффициент трения качения 5 блока А. Согласно
E),
V
Мприв у = AGA +AB+AD+ ^упр + As,
где As = —Ms(pA — работа момента сил трения качения Ms на угле
поворота (рА блока А. При vA = 2.5 м/с находим
v2
А5 = Мприв -f ~ Aga -Ab~Ad- ^Упр = -2-45 Дж.

262	Гл. 12. Динамика системы
Момент силы трения качения, Ms = NA5, зависит от свойств сопри-
соприкасающихся тел E) и от реакции 7VA, которую можно найти из урав-
уравнения проекции на нормаль к наклонной плоскости NA = mAg cos a.
Угол поворота (рА = SA/rA = 3/0.3 = 10. В результате получаем
тА д 5 ipA cos a = 10 • 9.815 • 10 • 0.866 = 2.45,
откуда S = 2.45/849.57 = 2.88 • 10~3м = 2.88 мм.
4. Определяем скорость центра блока А в измененных условиях,
при 5^ = 35. Вычисляем работу трения качения при 5^ = 3-2.88-10~3м:
As# = -MbjpA = -тАд(рА5^ cos a = ЗА6 = -7.35 Дж .
Из теоремы об изменении кинетической энергии находим соответ-
соответствующую скорость
v2
Мирив у = AGA + АВ + AD + ^уир + А5* = 74'47-
Вычисляем ответ:
=2Л2 м/с-
Замечание. Для решения задачи можно также использовать ме-
методы аналитической механики: общее уравнение динамики (§ 13.2),
уравнение Лагранжа 2-го рода (§ 13.4) и метод графов для определе-
определения скоростей (§ 8.5).
Условия ЗАДАЧ. Механическая система, состоящая из четырех
тел А, В, С, D и пружины, под действием внешних сил приходит в
движение из состояния покоя. Один из параметров системы [жест-
[жесткость пружины с или момент трения МТ в на оси В) неизвестен.
Учитывается трение скольжения с коэффициентом /т и трение
качения с коэффициентом 5тр. Заданы радиусы цилиндра и блока.
Радиусы инерции даны для блоков, цилиндры считать однородными.
Тело А (груз, цилиндр или блок) опускается вниз или вдоль на-
наклонной плоскости на расстояние SA и приобретает скорость vА.
Чему будет равна скорость vА, если этот же процесс произой-
произойдет для измененного механизма? Условие изменения оговорено в
тексте задач.

264
Гл. 12. Динамика системы
Sa = 1 м, va = 136 см/с,
гпа = 2 кг, тв = 120 кг,
тс = 120 кг, тв = 30 кг,
Дв = 17 см, гс = 16 см,
Rc = 28 см, гс = 20 см,
гв = 16 см, га = 16 см,
Ra = 18 см, га = 17 см,
?тр = 6 мм, с = 410 Н/м.
Условие: момент трения на оси В уменьшить в 8 раз.
6.	с
Sa = 2 м, va = 85 см/с,
га а = 7 кг, шв = 300 кг,
тс = 200 кг, тв = 90 кг,
Rb = 25 см, гс = 24 см,
Rc = 42 см, гс = 28 см,
гА = 22 см, RA = 25 см,
гА = 23 см, Зтр = 9 мм,
Мтр.в = 38 Н • м, /тр = 0.06.
Условие: пружину заменить на четыре такие же, соединенные
последовательно.
7.
Sa = 1 м, va = 49 см/с,
гпа = 7 кг, шв = 4 кг,
гас = 3 кг, тв = 15 кг,
Rb = 25 см, гв = 23 см,
гв = 24 см, гс = 24 см,
Rc = 42 см, гс = 28 см,
га = 23 см, Да = 25 см,
%а = 24 см, EТр = 8 мм,
с = 5 Н/м, /тр = 0.01.
Условие: момент трения на оси В уменьшить в 9 раз.
8.
Sa = 1 м, va = 23 см/с,
гпа = 37 кг, тв = 16 кг,
гас = 12 кг, тв = 5 кг,
Rb = 9 см, гв = 7 см,
iB = 8 см, гс = 8 см,
Дс = 14 см, гс = 12 см,
гв = 6 см, га = 7 см,
?тр = 4 мм, с = 1 Н/м.
Условие: убрать пружину.

12.5. Динамический расчет механизма с неизвестным параметром 265
9.
Sa = 1 м, va = 8 см/с,
гпа = 25 кг, тв = 40 кг,
тс = 120 кг, mD = 120 кг,
Rb = 17 см, гс = 16 см,
Rc = 28 см, гс = 20 см,
Г?> = 22 см, 5Тр = 6 мм,
с = 4 Н/м, /тр = 0.05.
Условие: момент трения на оси В уменьшить в 8 раз.
10.
SA = 1 м, vA = 293 см/с,
тпа = 8 кг, гпв = 4 кг,
тс = 3 кг, rriD = Ю кг,
Дв = 17 см, гс = 16 см,
Rc = 28 см, гс = 20 см,
г^=Лв/2, EТр = 6 мм,
с = 2 Н/м.
Условие: момент трения на оси В уменьшить в 8 раз.
Ответы
1
2
3
4
5
6
7
8
9
10
Мтр.в
Нм
4.000
4.000
1.948
0.989
3.003
38.000
2.994
8.004
5.961
1.967
с
Н/м
3.001
1.013
4.000
13.000
410.000
117.059
5.000
1.000
4.000
2.000
[1А
[IB
кг
8.000
55.500
12.000
18.000
3.784
12.925
13.451
55.500
25.000
8.000
8.711
41.796
50.000
30.000
0.741
2.160
16.056
83.592
20.000
8.000
29.756
229.224
49.954
51.570
0.502
12.089
7.643
55.740
986.667
4.066
126.024
88.163
15.868
5.950
0.073
2.304
4.859
3.689
605.000
15.000
VA
см/с
44.013
33.917
46.611
55.251
158.842
101.365
113.927
23.532
20.951
312.087
В таблице даны момент трения на оси В, жесткость пружины, при-
приведенные массы тел и искомая скорость.
Предупреждение типичных ошибок
1.	В условии задачи имеются величины, выраженные в м, см, мм.
Рекомендуем все величины перевести в м.
2.	Сила трения вычисляется по формуле FTp = TV/. He всегда
N = тпд. Реакцию N надо определять из уравнения проекций сил,
действующих на тело, на нормаль к поверхности.

266
Гл. 12. Динамика системы
12.6. Плоское движение системы
Постановка задачи. Механическая система с одной степенью
свободы состоит из тел, совершающих плоское движение. Соста-
Составить и проинтегрировать дифференциальные уравнения движения
системы.
План решения
1.	Разбиваем систему на отдельные тела. Связи заменяем их ре-
реакциями.
2.	Для каждого тела выбираем систему координат, в которой за-
записываем дифференциальные уравнения движения тела.
3.	Записываем кинематические соотношения между скоростями и
угловыми скоростями отдельных тел. Дифференцируя эти соотноше-
соотношения, находим связь соответствующих ускорений.
4.	Преобразуем и при необходимости интегрируем систему диф-
дифференциальных уравнений движения тел и кинематические соотно-
соотношения.
Пример *' . К барабану ворота радиуса гх и массы т1 приложен
постоянный вращающий момент М (рис. 139). К концу троса, на-
намотанного на барабан, прикреплена ось С колеса массой т2. Колесо
катится без скольжения вверх по наклонной плоскости, расположен-
расположенной под углом а к горизонту. Какую угловую скорость приобретет
барабан, сделав из состояния покоя п оборотов? Барабан и колесо
считать однородными круглыми цилиндрами. Массой троса и тре-
трением пренебречь.
Рис. 139
Рис. 140
Рис. 141
Решение
1. Разбиваем систему на два отдельных тела (рис. 140, 141). Связи
заменяем их реакциями. Действие троса заменяем силой его натя-
натяжения Т, которую прикладываем к барабану и колесу во взаимно
Задача 38.40 из сборника задач И.В. Мещерского [14]

12.6. Плоское движение системы	267
противоположных направлениях. Действие оси, на которой враща-
вращается барабан ворота, заменяем реакциями Хо, YQ. К катящемуся
без проскальзывания колесу С прикладываем силу сцепления FC4 и
нормальную реакцию опоры N. Силу сцепления колеса с наклонной
плоскостью Fc направляем условно вверх (истинное направление бу-
будет известно в результате решения задачи). Прикладываем внешние
силы: веса G1 = m1g и G2 = rn2g.
2. Записываем уравнения вращательного движения барабана мас-
массой т1 в выбранной системе координат
A)
J1(p1 = -M + Trv
Центр масс барабана неподвижен, поэтому первые два уравнения дви-
движения имеют форму уравнений статики.
Рассматриваем движение колеса массой т2 (рис. 141). Система
уравнений движения колеса имеет вид
т2х2 = Т + FC4 — G2 sin a,
B)
Во втором уравнении мы положили у2 = 0.
3. Кинематические связи системы
—ф2Я = х2.
Знак минус возникает из-за того, что положительные направления
углов поворота (против часовой стрелки) колеса и барабана соответ-
соответствуют отрицательной проекции скорости оси колеса. Дифференци-
Дифференцируем C) и получаем соотношения для ускорений
4. Система восьми уравнений A), B), D) содержит восемь неиз-
неизвестных ж2, у31, <?2, Т, FC4, TV, Хо, Уо и разбивается на две. Для
первых пяти неизвестных можно выделить систему пяти уравнений.

268	Гл. 12. Динамика системы
Учитывая, что моменты инерции однородных цилиндров имеют вид
Jx = 7?г1г^/2, J2 = m2R2/2, получаем
т2х2 = Т + FC4 — m2g sin a,
m2RCp2l2 = FC4,
^ =-M/r^+T,	D)
—(p2R = ж2.
Исключал неизвестные Fc , Т, <^2 и х2, находим
.. _ 2(m2gr1sina- M)
Правая часть E) не зависит от времени. Обозначим ее за —А. По-
Получим ф1 = — А, А > 0. Интегрируем E) при условии, что в начале
процесса (t = 0) барабан находился в покое (ф1 = 0), и угол пово-
поворота отсчитывается от нуля (р^ = 0. Получаем уравнения ф-у = —At,
(р-^ = —At2/2, которые записываем для некоторого момента t = t^
когда барабан сделает по часовой стрелке п оборотов и повернется
на отрицательный угол — 2тгп. Угловая скорость барабана при этом
достигнет величины а;, которую надо определить в задаче:
Исключая неизвестное время ^, получаем ответ:
/ /л - /
# = 2л/тгп/А, и = -2л/А7гп =	а 2тгп
Знак минус показывает, что вращение барабана направлено по часо-
часовой стрелке. Анализ подкоренного выражения дает ограничение на
существование решения: М > m2gr1 sin а.
Условия ЗАДАЧ. Механическая система с одной степенью сво-
свободы состоит из тел, совершающих плоское движение. Под дейст-
действием сил тяжести система из состояния покоя приходит в движе-
движение. Какую скорость приобретет груз А, переместившись (вверх
или вниз) на S = 1 м? Качение цилиндра (или блока) происходит без
проскальзывания с коэффициентом трения качения S. Коэффициент
трения скольжения / . Радиусы инерции ic, iD. Внешние радиусы
Rc, RD, внутренние rc, rD.

12.6. Плоское движение системы
269
1.
2.
3.
4.
5.
гс= 12 см,	6= 2 мм,
Rc= 32 см,	гпа= 5 кг,
ъс= 26 см,	тв= 2 кг,
Г?>= 11 см,	тс= 7 кг,
.#?>= 21 см,	rriD= 9 кг.
iD= 16 см,
гс= 14 см,	6= 2 мм,
ifc = 33 см,	тл=12 кг,
гс= 28 см,	тв= 2 кг,
td= 12 см,	тс= 8 кг,
.#?>= 22 см,	mD= 8 кг.
2?>= 17 СМ,
6= 3 мм,
= 16 см, тл=17 кг,
с= 34 см, тв= 3 кг,
= 30 см, тс= 9 кг,
> = П СМ, ГПВ= 7 КГ.
6= 1 мм,
гс= 18 см, гпа= 4 кг,
Дс= 35 см, тв= 2 кг,
ic= 32 см, тс= 5 кг,
Г?> = 13 CM, 7TlD= 6 КГ.
6= 3 мм,
гс= 20 см, тл=20 кг,
Дс= 36 см, тв= 4 кг,
ic= 34 см, ?тгс=11 кг,
Г?>=14 см, rriD= 5 кг.

270
Гл. 12. Динамика системы
6= 4 мм,
rc= 22 см, гпа=19 кг,
Rc= 37 см, тв= 6 кг,
ic= 36 см, тс=П кг,
г^=16 см, rriD= 4 кг.
/тр= 0.7,
гс= 16 см, 6= 2 мм,
Лс= 36 см, гпа= 3 кг,
гс= 30 см, тс= 7 кг,
Г?)=17 см, rriD= 9 кг.
гс= 18 см,	E= 2 мм,
Rc= 32 см,	?тгл=10 кг,
ic= 32 см,	шв= 4 кг,
Г?)= 18 см,	тс= 6 кг,
Д^= 25 см,	rriD= 3 кг.
iD= 23 см,
гс= 14 см,	/тр= 0.2,
Rc= 29 см,	6= 2 мм,
гс= 28 см,	гпа= 6 кг,
г^= 19 см,	тс= 7 кг,
RD= 27 см,	гпв= 4 кг.
г?>= 24 см,
гс= 22 см,	E= 3 мм,
Rc= 38 см,	тА=17 кг,
гс= 36 см,	тв= 6 кг,
Г?)= 20 см,	тс= 9 кг,
_R?,= 28 см,	rriD= 5 кг.
zd= 26 см,

12.6. Плоское движение системы
271
Ответы
1. 2.756 м/с. 2. 1.533 м/с. 3. 1.785 м/с. 4. 3.253 м/с. 5. 1.857 м/с.
6. 2.078 м/с. 7. 1.873 м/с. 8. 2.389 м/с. 9. 1.682 м/с. 10. 1.756 м/с.
Предупреждение типичных ошибок
1.	Составляя уравнения плоского движения тела, не забывайте,
что в уравнении JJp = Мс момент инерции берется относительно
центра масс тела, момент Мс также вычисляется относительно центра
масс.
2.	Характерная ошибка: для катящегося без проскальзывания ци-
цилиндра забывают про силу сцепления.
3.	Не путайте силу сцепления и предельную силу трения, для ко-
которой справедливо соотношение FT = NfT . В данной постановке
задачи проскальзывание не допускается и действует сила сцепления.
4.	Ошибки в знаках кинематических соотношений. Для уменьше-
уменьшения возможности таких ошибок иногда удобно использовать общую
систему координат для всех тел. В любом случае придерживайтесь
одного и того же правила знаков для углов поворота: положительный
угол (и момент!) — против часовой стрелки.
5.	Изображая реакции внутренних связей, не забывайте про 3-й
закон Ньютона ("Силы взаимодействия двух тел равны по модулю и
направлены по одной прямой в противоположные стороны").
6.	Проверку решения можно выполнить с помощью теоремы об
изменении кинетической энергии ( § 12.3, с. 247). Решение при этом
получается значительно проще. Приведем промежуточные ответы
для этого способа решения задачи.
1
2
3
4
5
6
7
8
9
10
ЦС
кг
0.281
11.112
13.547
0.529
12.960
6.000
4.000
6.000
4.621
32.000
31.641
4.180
31.790
29.455
4.861
6.000
6.526
8.078
4.771
5.349
2.625
0.595
7.500
4.243
0.667
0.592
19.009
38.231
АА
Ав
AD
Нм
49.050
117.720
166.770
39.240
196.200
186.390
15.187
98.100
45.088
166.770
7.357
-46.247
-62.539
10.090
-70.632
-58.860
-39.240
-58.860
-0.662
-0.462
-0.936
-0.116
-1.051
-0.825
-0.231
-0.077
-0.474
-1.065
В таблице даны приведенные массы тел. Скорости и угловые ско-
скорости тел выражаются через скорость груза А. Во всех вариантах

272	Гл. 12. Динамика системы
цА = mA. Сумма работ всех сил, приложенных к телу А на заданном
перемещении обозначена как АА. Аналогично Ав и AD — это суммы
работ всех сил, приложенных к телам В и D.
12.7. Динамические реакции в
подшипниках ротора
Постановка задачи. На оси, вращающейся в двух неподвиж-
неподвижных подшипниках под действием постоянного внешнего момента,
закреплен цилиндр и жесткий невесомый стержень с точечной мас-
массой на конце. Ось цилиндра составляет малый угол с осью вращения.
Найти динамические составляющие реакций подшипников.
План решения
Динамические составляющие реакций подшипников ХА, Хв, YA,
YB на подвижные оси, связанные с вращающимся ротором, удовле-
удовлетворяют уравнениям [16]
где m = J2i rni — масса ротора, xc, yc, zc — координаты его центра
масс, Jyz, Jxz — центробежные моменты инерции ротора. Ось z на-
направлена по оси вращения ротора; ujz, ez — угловые скорость и уско-
ускорение ротора в проекции на z; zA, zB — координаты подшипников А
и В.
1. Вводим систему координат. Начало координат помещаем в од-
одном из подшипников, например, А. Ось z направляем по оси враще-
вращения, ось х направляем так, чтобы ось цилиндра лежала в плоскости
xz. Определяем массу т системы двух тел и координаты центра масс
системы:
2	2	2
^2	ХХ	'52	B)
ХА + Х
YA + YB
zAXA +
-zAYA "
В
z
= -rnyt
= mxcsz
BXB =
zBYB =
- m
-Jyz
(
Vc^z
?z -
z^z-
^2ic^ »c	ХХУс«> c
г=1	i=l
где xc.,yc.,zc. — координаты центров масс тел.

12.7. Динамические реакции в подшипниках ротора	273
2. Вычисляем моменты инерции цилиндра, ось ( которого состав-
составляет малый угол с осью вращения z, относительно осей координат:
т(цил)
7(цил)	ГП^2	C)
Jiz =m1yClzCi.
Малый угол а отсчитывается от оси цилиндра ? к положитель-
положительному направлению оси z. Угол берется положительный, если со сто-
стороны оси у поворот оси цилиндра к оси z виден против часовой
стрелки, и отрицательный — если поворот виден по направлению
"	л /г	т(цил) т(цил)	т(цил)
часовой стрелки. Моменты инерции JyZ ', Jlz и Jxz вычислены
по теореме Гюйгенса *^ . Вторые слагаемые в C) представляют со-
собой соответствующие моменты инерции центра масс цилиндра отно-
относительно начала координат.
3.	Вычисляем моменты инерции точечной массы (груза) относи-
относительно осей ж, т/, z
7(груз) _	/о , Г2 \ т(груз) _	т(груз) _
Jzz	— ТП2 [УС2 -\~ ХС2 ), Jxz	— m2Xc2Zc2' JVZ	~
4.	Находим суммарные моменты инерции системы
j —,
Jz^WJI
Лтл)
т(цил)
yz
+
+
т(груз)
<J ZZ 1
т(груз)
JXZ 5
т(груз)
5.	Вычисляем угловое ускорение ротора ez = Mz/Jzz и угловую
скорость ротора в указанный момент t. Если sz = const и сс^(О) = О,
то u;z = ezt.
6.	Искомые реакции находим из решения системы A) при zA = 0.
Пример. На оси, вращающейся в неподвижных подшипниках А
и В под действием постоянного момента Mz = 0.4 Нм, закреплен
ротор, состоящий из цилиндра массой тп1 = 50 кг и жесткого неве-
невесомого стержня длиной L = 21 см с точечной массой тп2 = 6 кг, на
конце (рис. 142). Ось цилиндра составляет угол а = 0.06 рад с осью
*) Христиан Гюйгенс A629-1695) — нидерландский математик, меха-
механик, физик и астроном.
18 М.Н. Кирсанов

274
Гл. 12. Динамика системы
вращения Az. Центр массы цилиндра лежит на оси Az. Стержень
перпендикулярен Az. Найти динамические составляющие реакций
подшипников в момент времени t = 3 с. Ротор вращается из состоя-
состояния покоя.
а = 25 см,
Ъ = 50 см,
z с = 35 см,
Л = 20 см.
Рис. 142
Введены системы координат x^y^z^ г = 1, 2, с осями, параллель-
параллельными ж, г/, z, проходящими через центры масс тел 1 и 2. Ось ( является
осью цилиндра и вместе с осями хх и х2 лежит в плоскости xz. Оси
^ и rj перпендикулярны (.
Решение
1. Вводим систему координат. Начало координат помещаем в под-
подшипнике А, ось z направляем по оси вращения. Ось цилиндра лежит
в плоскости xz. Определяем массу системы т = т1 + т2 = 56 кг и
координаты центра масс системы по формуле B)
хс = -U • 0.2 = 0.0225 м, ус = 0, zc = ^
5о	55
1.1 + 6 • 0.85) = 0.982 м.
2.	Вычисляем моменты инерции цилиндра относительно осей ко-
координат по формулам C), где а > 0
т(цил) -,	о т(цил) г> г^о	о т(цил) г»
Jiz = 1 кг м2, Ji5 = 0.03 кг м2, J^2 = 0.
Угол берется положительный, так как со стороны оси у поворот оси
цилиндра к оси z виден против часовой стрелки.
3.	Вычисляем моменты инерции точечной массы (груза) относи-
относительно осей ж, г/, z
= 0.265 кг м2, j?py3) = 0.945 кг м2, J^py3) = 0.
4. Находим суммарные моменты инерции системы Jzz = 1.265 кг м2,
Jxz = °'975 КГ м2' Jyz = °-

12.7. Динамические реакции в подшипниках ротора
275
5.	Вычисляем угловое ускорение ротора е = Mz/Jzz = 0.316 рад /с
и угловую скорость ротора в момент t = 3 с. Так как е = const и
и@) = 0, то cj = 0.316 • 3 = 0.949 рад/с.
6.	Динамические реакции опор вычисляем, решая систему A) при
zA = 0, zB = а = 0.25 м
*в = -GV + J^w2)/** = -3-512 Н,
ув = (jxzz - v2)/** =L233 н>
ХА = -тусе - тхсш2 - Хв = 2.377 Н,
YA = тхсе - mycuj2 -YB = -2.494 Н.
Условия задач. На оси, вращающейся в подшипниках А и В под
действием постоянного момента Mz, закреплен ротор, состоящий
из цилиндра 1 и жесткого невесомого стержня длиной L с точечной
массой 2 на конце. Ось цилиндра составляет малый угол а с осью
вращения Az. Центр массы цилиндра лежит на оси Az. Стержень
перпендикулярен Az. Найти динамические составляющие реакций
подшипников в момент времени t. Ротор вращается из состоя-
состояния покоя. В центрах масс тел 1 и 2 введены системы координат
xi,yi,zi, г = 1,2 с осями, параллельными x,y,z. Ось ? является осью
цилиндра и вместе с осями х± и х2 лежит в плоскости xz. Оси ? и
rj перпендикулярны ?.
а = 20 см, Ъ = 50 см,
с = 35 см, R = 25 см,
mi = 25 кг, 7П2 = 6 кг,
а = 0.06 рад, L = 10 см,
Mz = 0.3 Нм, t = 3 с.
а = 35 см, Ь = 45 см,
с = 40 см, R = 40 см,
Ш1 = 30 КГ, 7712 = Ю КГ,
а = 0.08 рад, L = 25 см,
Mz = 0.7 Нм, t = 4 с.
18*

276
Гл. 12. Динамика системы
а = 30 см, Ъ = 60 см,
с = 45 см, R = 40 см,
ГГЦ = 55 КГ, 7712 = 14 КГ,
а = 0.1 рад, L = 20 см,
М* = 0.8 Нм, t = 5 с.
а = 35 см, 6 = 65 см,
с = 50 см, Л = 40 см,
mi = 40 кг, 7П2 = 18 кг,
а = 0.12 рад, L = 25 см,
М^ = 0.5 Нм, ? = 6 с.
а = 40 см, 6 = 70 см,
с = 55 см, R = 45 см,
mi = 45 кг, 7П2 = 6 кг,
а = 0.1 рад, L = 30 см,
М^ = 2.5 Нм, t = 3 с.
а = 45 см, Ь = 75 см,
с = 60 см, Д = 50 см,
7711 = 50 КГ, 7712 = Ю КГ,
а = 0.12 рад, L = 35 см,
Mz = 2.2 Нм, ? = 4 с.
2/2

9.
10.
12.7. Динамические реакции в подшипниках ротора	277
а = 35 см, Ъ = 55 см,
с = 45 см, R = 45 см,
TTli = 75 КГ, 7712 = 14 КГ,
а = 0.14 рад, L = 25 см,
Мг = 1.7 Нм, t = 5 с.
а = 35 см, 6 = 65 см,
с = 50 см, Л = 45 см,
mi = 80 кг, 7П2 = 18 кг,
а = 0.16 рад, L = 25 см,
Mz = 1.4 Нм, t = 6 с.
а = 45 см, 6 = 65 см,
с = 55 см, R = 55 см,
7711 = 85 КГ, 7712 = 6 КГ,
а = 0.14 рад, L = 35 см,
Mz = 8.6 Нм, t = 3 с.
а = 45 см, 6 = 75 см,
с = 60 см, Д = 50 см,
7711 = 70 КГ, 7712 = Ю КГ,
а = 0.16 рад, L = 35 см,
М^ = 3.7 Нм, t = 4 с.

278
Гл. 12. Динамика системы
Ответы
1
2
3
4
5
6
7
8
9
10
Jxx
Jxz
Jyy
Jyz
Jzz
кгм2
8.006
14.300
32.665
48.125
25.813
46.875
24.324
55.475
30.901
52.175
0.607
-0.096
-3.560
-0.192
2.742
-0.375
-2.618
0.648
3.210
-0.700
8.066
13.675
33.225
47.000
26.353
45.650
25.199
54.350
31.636
50.950
0.000
-2.000
0.000
-6.750
0.000
6.300
0.000
-6.750
0.000
6.300
0.841
3.025
4.960
4.325
5.096
7.475
8.469
9.225
13.591
9.975
XA
YA
XB
YB
H
0.305
-1.941
-0.752
-0.352
1.501
0.082
1.572
0.196
-0.557
-0.635
-0.095
-6.370
0.186
-1.060
-0.340
2.517
-0.313
-1.964
0.098
4.069
-0.992
1.363
2.573
0.873
-5.399
-1.112
1.954
0.487
-7.010
-0.663
0.309
4.228
-0.638
3.225
1.223
-7.368
-0.389
5.695
1.231
-11.774
Замечание. Есть простое правило для определения знака цент-
центробежного момента цилиндра с наклонной осью. Пусть центр масс
цилиндра находится в начале координат (рис. 143). Ось ? направлена
по оси цилиндра, z — по оси вала. Если цилиндр повернут так, что
все его точки имеют координаты xi^zi одного знака, то Jxz > 0. В
противном случае Jxz < 0 (рис. 144). Если а = 0, то zi = 0 и Jxz = 0.
х	х
Jxz = OL
mR2
mR2
Рис. 143
Рис. 144

Глава 13
АНАЛИТИЧЕСКАЯ МЕХАНИКА
В главе АНАЛИТИЧЕСКАЯ МЕХАНИКА вы научитесь решению
задач статики с помощью принципа возможных скоростей. Вы научи-
научитесь также составлять наиболее универсальные уравнения движения
динамических систем. К ним относятся общее уравнение динамики,
уравнение Лагранжа 2-го рода и уравнения Гамильтона. Первое зна-
знакомство с этой темой немного пугает сложностью: вводятся новые
термины типа "обобщенные координаты" или "виртуальные переме-
перемещения". На самом деле все просто. Обобщенные координаты — это
параметры, однозначно описывающие положение системы, например,
углы поворота или обычные декартовы координаты. Виртуальные
(или возможные) перемещения — это бесконечно малые воображае-
воображаемые перемещения, допускаемые связями. Силы, действующие на сис-
систему, будем делить на активные и реакции связей.
Для успешного составления уравнений движения системы следует
повторить метод кинематических графов вычисления скоростей то-
точек тела при плоском движении (§ 8.5, с. 188).
13.1. Принцип возможных скоростей
Постановка задачи. Плоская система многих тел с идеаль-
идеальными стационарными связями находится в равновесии под дейст-
действием активных нагрузок. Определить реакции опор системы.
План решения
Поставленная задача относится к задачам статики, однако решать
ее методами статики, записывая по три уравнения равновесия для ка-
каждого из тел системы, не удобно и долго, особенно, если по условию
требуется найти только одну реакцию. Используя принцип возмож-
возможных скоростей, эту задачу (независимо от количества тел механичес-
механической системы) можно легко решить, составив одно уравнение.
Связь называют идеальной, если работа ее реакции на любом воз-
возможном перемещении системы равна нулю. Стационарные (или скле-

280	.Гл. 13. Аналитическая механика
рономные) связи не зависят от времени. Будем рассматривать удер-
удерживающие (двусторонние) связи (см. с. 51).
1.	Освобождаем систему от той связи, реакцию которой надо опре-
определить. Действие связи заменяем ее реакцией. Реакция становится
активной силой. Система приобретает одну степень свободы. При-
Прикладываем к системе все активные силы. Реакции идеальных связей
не указываем. Вводим систему координат.
2.	Сообщаем угловую скорость (виртуальную скорость) одному
из тел системы, например, cJ0. Для плоского движения достаточно
задания одной составляющей ujQz. Выражаем скорости точек прило-
приложения сил и угловые скорости тел, к которым приложены моменты,
через ujOz. В некоторых случаях удобнее задавать линейную скорость
какого-либо шарнира механизма.
3.	Неизвестную реакцию определяем из принципа возможных ско-
скоростей. Для системы с N силами (в это число входит и неизвестная
реакция) получаем
г=1
Каждое слагаемое представляет собой мощность силы. Мощность мо-
момента Mi (пары сил) вычисляем как скалярное произведение Mi • uji.
После подстановки в A) кинематических соотношений, заданная ве-
величина ujOz становится общим сомножителем. Сокращая на cuOz ф 0,
получаем уравнение для искомой реакции. Решаем линейное уравне-
уравнение с одной неизвестной, находим реакцию.
Пример 1. Система с идеальными стационарными связями, со-
состоящая из четырех шарнирно соединенных однородных стержней,
расположена в вертикальной плоскости и находится в равновесии под
действием силы F = 20 Н и момента М = 30 Нм (рис. 145). Из-
Известны длины стержней О А = 0.3 м, АВ = 0.55 м, BD = 0.4 м,
ВС = 0.3 м и углы а = 45°, C = 60°. Учитывая погонный вес стерж-
стержней, р = 10 Н/м, определить горизонтальную реакцию опоры С.
Решение
1. Освобождаем систему от горизонтальной связи шарнира С. Не-
Неподвижный шарнир заменяем на подвижный (или ползун) с горизон-
тальнои подвижностью ; . Действие горизонтальной связи заменяем
*) Полученную связь считаем двусторонней и идеальной, т.е. точка С
может без сопротивления двигаться только по горизонтали, не отрываясь
от опорной поверхности.

13.1. Принцип возможных скоростей
281
ее реакцией Хс (рис. 146). Реакция Хс становится активной силой.
Система приобретает одну степень свободы. Прикладываем к центру
каждого стержня его вес Gi = pl^ вычисленный через его длину 1г и
погонный вес р. Вводим прямоугольную систему координат с цент-
центром в шарнире О. Вычисляем проекции сил тяжести на ось у:
GOAy = -3 Н, GABv = -5.5 Н, GCBv = -3 Н, GDBy = -4 Н. B)
VA
A
v.
L
У
D
Ш
Goa
/
ЧЙ
\
GDB\
1
V
Gab
Vc
К 7N
у
vB
_cw_
о
Рис. 145
Рис. 146
2. Сообщаем стержню О А возможную угловую скорость шОА. Вы-
Выражаем скорости точек /, АГ, К, В, G, приложения активных сил и
реакции Хс через шОА. Решаем задачу кинематики многозвенного
механизма (§ 8.3, с. 179), используя уравнение трех угловых скоростей
для четырехзвенника OABD в векторной форме и выражая скорости
одних точек через скорости других. Составляем систему уравнений:
UOA
О А
JBD
BD,
C)
VL = ^OA X 0Li
Vj = uuOA xOA + ujab x AI,
iJB = ?BD x DB,
vR = uBD x DK,
vc = vB+ ujbc x ВС,
vN = vB + cJ5C x Б7У.
Так как шарнир С заменен на горизонтальный ползун (шарнир с го-
горизонтальной подвижностью), то
vcv = О-
D)

282	Гл. 13. Аналитическая механика
Векторы угловых скоростей при плоском движении имеют только
одну составляющую: си = {0, 0, ojz}. Система C), записанная в про-
проекциях на оси ж и у, и уравнение D) содержат пятнадцать уравнений
и пятнадцать неизвестных: двенадцать компонентов скоростей то-
точек В, С, /, JV, К, L и три проекции угловых скоростей на ось z,
перпендикулярную плоскости механизма. Решаем систему C)—D):
vBx
VCx
VKx
VLx
VIx
VNx
ШАЕ
Ш
— -0.3шол,
= -0.819 u;OA,
= -0.15 шОА,
= -0Л5шОА,
= -0-3 ^oa>
= -0.56wOj4,
lz = -0.545 шОА,
-,. = 2u>^ a.
VBy =
VCy =
VKy =
VLy =
vIy =
VNy =
"DBz
-0.
o,
-0.
o,
-0.]
-0.
= -
3^OA>
1ЪшОА
lbuOA
1.061 ш
E)
3. Неизвестную реакцию Хс определяем из принципа возможных
скоростей:
XCVCx + FvBx + GAByVIy + GCByVNy + GDByVKy + M^OA = °'
С учетом E) получаем
-0.819ХсЧ)Л - 0.3FcvOA - 0.15GAByu;OA - 0.lbGCByuOA-
-0.15GDBycoOA + Mu,OA=0.
Сокращаем на и;ОА ф 0, находим, что Хс = 31.569 Н.
Решение задачи в системе Maple V приведено в § 17.1 на с. 368.
Пример 2. В условиях задачи на с. 281 (рис. 145) определить
вертикальную реакцию опоры С.
Решение
1.	Освобождаем систему от вертикальной связи шарнира С. Дей-
Действие связи заменяем ее реакцией Yc (рис. 147). Система приобретает
одну степень свободы. Прикладываем к центру каждого стержня его
вес B).
2.	Сообщаем стержню О А возможную угловую скорость ojoa. Вы-
Выражаем скорости точек А, В, G, /, К, L, N приложения активных сил
и реакции Yc через оиОА. Решая задачу кинематики многозвенного

13.1. Принцип возможных скоростей
283
механизма, составляем систему уравнении, которые не отличаются
от C). Вместо уравнения D) запишем
»с* = О-
F)
Рис. 147
Решаем систему C), F):
vCx = О,
Рис. 148
VBy = -°-
Vcy = -0.473, wOA,
G)
vLx = -0.15 cjoa,	vLy = 0,
vj* = -°-3^oa>	% = -0.15 c^OA,
^лгж = -0.15 ojoa,	vNy = -0.387 ljoa,
^ARr = -0.545cc;n4,	^hr7 = —1.061 o;n4,
^BCz = -1.155 o;OA.
3. Неизвестную реакцию Yc определяем из принципа возможных
скоростей:
YCVCy + FvBx + GAByVIy + GCByVNy + GDByVKy + M^OA = °-
С учетом G) получаем
-0.473Усо;ол - 0.3FwOA - 0.15GAByu;OA - 0.387GCByuOA-

284	Гл. 13. Аналитическая механика
Сокращаем на шОА ф О, находим
Ус = 56.18 Н.
Пример 3. В условиях задачи на с. 281 (рис. 145) определить
горизонтальную реакцию опоры О.
Решение
1.	Освобождаем систему от горизонтальной связи шарнира О. Дей-
Действие связи заменяем ее реакцией Хо (рис. 148, с. 283). Система при-
приобретает одну степень свободы. Прикладываем к центру каждого
стержня его вес.
2.	Сообщаем шарниру О возможную горизонтальную скорость vo.
Решение этого примера оказывается существенно проще предыду-
предыдущих, и связано это с тем, что стержни DB и ВС образуют жесткий
неподвижный треугольник, и скорости всех его точек равны нулю.
Поэтому необходимости в составлении сложной системы кинемати-
кинематических уравнений здесь нет.
Точка А совпадает с МЦС звена О А (§ 8.1, с. 158). Угловая ско-
скорость стержня О А выражается через заданную скорость:
"оа = "о/ОА.	(8)
Скорость vL точки приложения веса стержня О А можно не находить,
так как очевидно, что мощность вертикальной силы с горизонталь-
горизонтальной скоростью точки приложения равна нулю.
3.	Неизвестную реакцию Хо определяем из принципа возможных
скоростей:
С учетом (8) вычисляем
Хо = -М/ОА= -100 Н.
Условия ЗАДАЧ. Система с идеальными стационарными свя-
связями, состоящая из четырех шарнирно соединенных однородных стер-
стержней, расположенных в вертикальной плоскости, находится в рав-
равновесии под действием силы F и момента М. Учитывая погонный
вес стержней р, определить реакции опор (в И).

13.1. Принцип возможных скоростей
285
О А = 108 см, DB = 14 см,
АВ = 62 см, ВС = 26 см.
р = 40 Н/м, М = 8 Нм,
F=20 H.
О А = 26 см, DB = 16 см,
АВ = 37 см, ВС = 29 см.
р = 50 Н/м, М = 10 Нм,
F=40 H.
3.
ОЛ = 27 см, ?>Б = 12 см,
АВ = 27 см, ВС = 32 см.
р = 30 Н/м, М = 11 Нм,
F=10 H.
ОЛ = 28 см, DB = 84 см,
АВ = 40 см, ВС = 55 см.
р = 60 Н/м, М = 13 Нм,
F=60 H.
ОЛ = 26 см, DB = 61 см,
АВ = 30 см, ВС = 23 см.
р = 30 Н/м, М = 6 Нм,
F= 5H.
А 30'

286
Гл. 13. Аналитическая
механика
О А = 30 см, DB = 120 см,
АВ = 40 см, ВС = 29 см.
р = 40 Н/м, М = 13 Нм,
F=60 H.
О А = 31 см, DB = 16 см,
АВ = 31 см, ВС = 32 см.
р = 50 Н/м, М = 17 Нм,
F=50 H.
8.
О А = 32 см, DB = 84 см,
АВ = 40 см, БС = 55 см.
р = 60 Н/м, М = 17 Нм,
F=80 H.
О А = 33 см, DB = 12 см,
АВ = 25 см, ВС = 26 см.
р = 30 Н/м, М = 13 Нм,
F=40 H.
О А = 27 см, ?>Б = 96 см,
АВ = 32 см, ВС = 29 см.
р = 40 Н/м, М = 10 Нм,
F=45 H.

13.1. Принцип возможных скоростей
287
Ответы
1
2
3
4
5
6
7
8
9
10
Хо
50.055
-0.000
50.131
-0.000
-0.000
-0.000
12.054
-0.000
158.213
-0.000
Уо
21.600
-8.958
4.050
66.328
-13.681
65.962
7.750
91.304
4.950
53.284
Хс
-50.055
-91.708
-50.131
25.304
43.081
29.929
-12.054
86.404
-158.213
40.316
Ус
-44.855
98.958
-45.331
-27.328
46.531
57.638
28.878
-69.904
-87.444
46.116
xD
-0.000
91.708
-0.000
-25.304
-38.081
-29.929
-0.000
-86.404
-0.000
-40.316
Yd
87.255
4.000
80.681
25.200
9.150
24.000
68.372
25.200
71.294
19.200
Замечание. С помощью описанного метода можно определить
реакции опор в задачах § 2.4, 2.5. Вычисление реакций заделки, встре-
встречающейся в некоторых вариантах, имеет свою особенность. Заделка
в плоской задаче (рис. 149) имеет три реакции: момент и две силы.
При вычислении момента заделку заменяют на неподвижный шарнир
(рис. 150). Для определения горизонтальной реакции заделку превра-
превращают в скользящую заделку (горизонтальный ползун с жестко соеди-
соединенным с ним стержнем), так, что и момент заделки, и вертикальная
реакция на горизонтальном перемещении образовавшейся связи ра-
работы не совершают (рис. 151). Аналогично поступают и при опреде-
определении вертикальной реакции (рис. 152). Ползун при этом движется
по вертикали.
It*
А
Рис. 149
Рис. 150
Рис. 151
Рис. 152
Ответы на типичные вопросы, возникающие при решении задачи
1.	В какую сторону направлять искомую горизонтальную реак-
реакцию? Налево или направо?
Направляйте в любую сторону. Знак ответа подскажет истинное
направление реакции. Это относится и к вертикальной реакции, и к
моменту в заделке.
2.	Можно ли находить возможные скорости с помощью мгновен-
мгновенных центров скоростей?
Во избежание ошибок со знаками не рекомендуем определять ско-
скорости с помощью МЦС. С помощью этого метода можно определить

288	.Гл. 13. Аналитическая механика
только модули скоростей. В простейших случаях, где знак мощности
очевиден, можно сделать исключение (Пример 3, с. 284).
Предупреждение типичных ошибок
1.	При выборе кинематической схемы следует помнить, что отбра-
отбрасывается только одна связь, и только реакция этой связи на возмож-
возможной скорости будет иметь ненулевую мощность. Реакции остальных
связей, независимо от того, найдены они или еще нет, не должны
иметь мощность. Механизм, полученный из уравновешенной кон-
конструкции отбрасыванием связи, должен иметь одну степень свободы.
2.	Если система, полученная из исходной отбрасыванием одной из
связей, превращается в механизм, содержащий четырехзвенник, то в
качестве виртуальной скорости удобно брать одну из угловых ско-
скоростей четырехзвенника, а остальные угловые скорости определять
с помощью уравнения трех угловых скоростей (§ 8.3).
13.2. Общее уравнение динамики для
системы с одной степенью свободы
Постановка задачи. Плоский шарнирно-стержневой механизм
с одной степенью свободы движется в вертикальной плоскости под
действием сил тяжести и момента М. В неподвижных шарнирах
и ползуне имеется трение, остальные связи идеальные. Известна
угловая скорость одного из звеньев механизма. Для заданного поло-
положения механизма определить величину М.
План решения
1.	Вычисляем угловые скорости звеньев механизма и скорости то-
точек приложения активных сил (§ 8.3, с. 179). В число активных сил
включаем силы трения.
2.	Вычисляем ускорения точек, наделенных массами (§8.4, с. 183).
3.	Вычисляем силы тяжести и силы инерции материальных точек.
Силы трения (сопротивления) направлены в сторону, противополож-
противоположную движению, поэтому записываем их в виде FT = — FT ^/|%|, где
vk — скорость точки приложения силы, FT — модуль силы. Анало-
Аналогично выражаем моменты сопротивления МТ = — Мт ujk/\ujk\.
4.	Записываем общее уравнение динамики:

13.2. Общее уравнение динамики (одна степень свободы)
289
где Fk — активные силы, приложенные к механизму, Фк — силы инер-
инерции. Моменты являются парами сил, которые входят в число актив-
активных сил Fk, однако мощности моментов удобнее вычислять в форме
J2k Мк • cJfc, где сЗк — угловая скорость тела, к которому приложен
момент Мк.
Из полученного уравнения находим искомый момент М.
Пример. Плоский шарнирно-стержневой механизм расположен в
вертикальной плоскости и приводится в движение моментом МОА,
приложенным к звену О А (рис. 153). В узлах Л, В, С и в середине
звена АВ сосредоточены массы тА = 2 кг, тв = 3 кг, тс = 4 кг,
тЕ = 5 кг. Задана постоянная сила сопротивления движению пол-
ползуна, FTp = 10 Н. В шарнирах О ж D имеется момент сил трения
МТ = 15 Нм. Угловая скорость звена О А постоянна и равна 2 рад/с.
А
Е
Пренебрегая массами стержней, определить момент МОА в указан-
указанном положении механизма. Даны размеры: 0А = 0.5 м, АВ = 0.4 м,
АС = 0.45 м, BD = 0.4 м; а = 45°, /3 = 60°.
Решение
1. Вычисляем угловые скорости звеньев механизма и скорости то-
точек А, 5, G, Е. Вводим систему координат xyz (рис. 154). Ось
z перпендикулярна плоскости чертежа. Составляем кинематические
уравнения:
UOA
О А
х АВ + п;
BD
B)
х АС,
х АЕ,
Так как скорость ползуна горизонтальна и vc = 0, система пяти
19 М.Н. Кирсанов

290	.Гл. 13. Аналитическая механика
векторных уравнений (или десяти скалярных уравнений в проекциях
на оси ж, у) содержит десять неизвестных: uABz, uBDz, uACz, vAx,
vAyi vBx> vBy> vEXi vEyi vCx- Решая ее> получаем проекции скоростей,
VAx = VBx
VAy = VBy = VEy = -°'5 M/C> VCx = -1-366 М/С,
и угловые скорости,
^bdz = 2-5 Рад/С> uABz = 0, u;ACz = -1.571 рад/с.
2. Вычисляем ускорения точек Л, В, С', ??. Составляем кинема-
кинематические уравнения с учетом того, что, по условию, стержень О А
вращается равномерно: ?OAz = 0,
х АВ + ?БГ> х BD + cJOA х (cDOA х ОА)+
б х &АВ х АВ) + o;BD х (lubd х Б"Ь) = 0,
= йОА х (ДОА х Ok),
= eBD х ?)Б + o5BD х (<2BD x ?)Б),
АС),
WE = WA + еАВ х АЕ + (JA5 х (о;АБ х
Первое уравнение в этой системе представляет собой векторную
форму записи уравнения трех угловых ускорений четырехзвенника
OABD (§ 8.4, с. 183). Так как вектор ускорения ползуна горизон-
горизонтальный и Wc = 0, система пяти векторных уравнений (или десяти
скалярных в проекциях на ось х и ось у) содержит десять неизвест-
ных: eABz, eBDz, sACz, WAx, WAy, WBx, WBy WEx, WEy, WCx. Решая
систему (З) , получаем проекции ускорений,
WAx = WBx = WEx = l м/с2, WAy = -1.732 м/с2,
WBy = -2.309 м/с2, W^ = -2.021 м/с2, WCx = 0.839 м/с2,
и угловые ускорения,
Zbdz = °-722 Рад/с2,?ABz = -1-443 рад/с2,sACz = -2.974 рад/с2.
Концы векторов ускорений точек неизменяемого отрезка лежат на
одной прямой. Точка Е лежит в центре отрезка АВ. Отсюда следует
простая проверка решения:
WEx = (WAx + WBx)/2, WEy = (WAy + WBy)/2.

13.2. Общее уравнение динамики (одна степень свободы)	291
3.	Вычисляем силы тяжести и силы инерции материальных точек.
Вычисляем силы тяжести:
°АУ = ~тА9 = -19.62 Н, GBy = -mBg = -29.43 Н,
GCy = -mcg = -39.24 Н, GEy = -mEg = -49.05 H.
Вычисляем силы инерции Ф = —mW по Даламберу: *^
фАх = ~mAWAx = -2 Н,	ФАу = -mAWAy = 3.464 Н,
фвх = -mBWBx = -3 Н,	ФВу = -mBWBy = 6.927 Н,
*ех = -™eWEx = -5 Н,	ФЕу = -mEWEy = 10.105 Н,
*сх = -™CWCx = -3.356 Н.
Силу трения направляем в сторону, противоположную движению пол-
ползуна, а моменты трения — в сторону, противоположную вращению
соответствующего кривошипа:
Ртр.х = -FTpVCx/\VCx\>
MtP.BDz = -M^BDzl^BDl Mtp.OAz = -MtP^OAz/\^Oa\-
4.	Записываем общее уравнение динамики
GAyVAy + GByVBy + GCyVCy + GEyVEy + FtP.xVCx + Ф AxV Ax +
ФВу'иВу + Ф ExV Ex + Ф EyV Ey
*CxvCx
Находим из этого уравнения искомый момент: МОА = 140.69 Нм.
Условия ЗАДАЧ. Плоский шарнирно-стержневой механизм с од-
одной степенью свободы движется в вертикальной плоскости под дей-
действием сил тяжести и момента М, который вращает звено О А с
постоянной угловой скоростью шОА. В узлах А, В, С и в центре
Е звена АВ расположены материальные точки. На осях неподвиж-
неподвижных шарниров О и D имеется трение с постоянным моментом Мтр.
Сила сопротивления движению ползуна — FTp; остальные связи иде-
идеальные. Пренебрегая массами стержней, определить величину мо-
момента М.
*) Жан Лерон Даламбер A717-1783) — французский математик, меха-
механик, философ.
19*

292
Гл. 13. Аналитическая механика
1.
А 30
С
ujoaz = 0.8 рад/с,
FTp = 10 Н, Мтр = 5 Нм,
гпа = 1 кг, тв = 2 кг,
тс = 2 кг, гая = 2 кг,
О А = 26 см, DB = 12 см,
АВ = 25 см, ВС = 23 см.
= 0.7 рад/с,
FTp = 20 Н, Мтр = 10 Нм,
гпа = 2 кг, гав = 3 кг,
тс = 3 кг, гпе = 4 кг,
О А = 27 см, DB = 14 см,
АВ = 25 см, ВС = 23 см.
= 1 рад/с,
FTp = 30 Н, Мтр = 15 Нм,
гал = 3 кг, тв = 4 кг,
гас = 4 кг, гпе = 6 кг,
О А = 20 см, DB = 16 см,
АВ = 25 см, ВС = 23 см.
z = 0.3 рад/с,
FTp = 60 Н, Мтр = 20 Нм,
гпа = 4 кг, га# = 5 кг,
гас = 6 кг, гпе = 5 кг,
О А = 60 см, DB = 12 см,
АВ = 25 см, ВС = 26 см.
oooaz = 0.3 рад/с,
FTp = 20 Н, Мтр = 25 Нм,
гал = 1 кг, тв = 2 кг,
гас = 4 кг, гпе = 5 кг,
О А = 70 см, ?>В = 18 см,
АВ = 25 см, ВС = 29 см.

13.2. Общее уравнение динамики (одна степень свободы)
293
6.
А 45
7.
45
С
В 45°
D
= 0.2 рад/с,
FTp = 50 Н, Мтр = 30 Нм,
гпа = 2 кг, тв = 3 кг,
тс = 6 кг, гая = 3 кг,
О А = 120 см, DB = 30 см,
АВ = 66 см, ВС = 32 см.
= 0.6 рад/с,
FTp = 30 Н, Мтр = 35 Нм,
гпа = 3 кг, тв = 5 кг,
тс = 4 кг, га^; = 5 кг,
О А = 32 см, DB = 62 см,
АВ = 30 см, ВС = 23 см.
8.
ш>
Е
зо"
30°
\D
С
ujoaz = 0.6 рад/с,
,ртр = 40 Н, Мтр = 40 Нм,
гпа = 4 кг, гав = 6 кг,
тс = 5 кг, гпе = 7 кг,
О А = 33 см, DB = 63 см,
АВ = 30 см, ВС = 23 см.
9. Ш)
z = 0.7 рад/с,
FTp = 10 Н, Мтр = 10 Нм,
гпа = 1 кг, тв = 3 кг,
гас = 2 кг, гая = 5 кг,
О А = 27 см, DB = 64 см,
АВ = 30 см, ВС = 23 см.
10.
ujoaz = 0.7 рад/с,
FTp = 20 Н, Мтр = 15 Нм,
гпа = 2 кг, тв = 4 кг,
гас = 3 кг, гая = 3 кг,
О А = 28 см, DB = 61 см,
АВ = 30 см, ВС = 23 см.

294
Гл. 13. Аналитическая механика
Ответы
1
2
3
4
5
6
7
8
9
10
VA
VB
vc
VE
м/с
0.208
0.189
0.200
0.180
0.210
0.240
0.192
0.198
0.189
0.196
0.208
0.189
0.200
0.104
0.210
0.240
0.192
0.343
0.327
0.339
0.208
0.189
0.200
0.104
0.210
0.240
0.192
0.343
0.327
0.339
0.208
0.189
0.200
0.104
0.210
0.170
0.136
0.198
0.189
0.196
WA
WB
We
We
м/с2
0.166
0.132
0.200
0.054
0.063
0.048
0.115
0.119
0.132
0.137
0.493
0.332
0.265
0.217
0.394
0.192
0.526
1.264
1.385
1.229
0.024
0.029
0.231
0.042
0.167
0.339
0.582
1.573
2.525
1.105
0.313
0.221
0.229
0.085
0.179
0.098
0.320
0.573
0.758
0.547
М
Нм
0.829
10.537
6.702
60.684
55.255
171.402
24.752
170.651
-8.364
72.748
13.3. Общее уравнение динамики для
системы с двумя степенями свободы
Постановка задачи. Механическая система с идеальными ста-
стационарными связями имеет две степени свободы. К системе прило-
приложены известные активные силы. Найти ускорения тел системы.
План решения
1.	Выбираем две обобщенные координаты. В качестве обобщен-
обобщенных координат можно брать перемещения точек системы или угловые
перемещения тел, однозначно определяющие ее положение.
2.	Ускорения центров масс тел и угловые ускорения тел выражаем
через вторые производные выбранных обобщенных координат (обоб-
(обобщенные ускорения).
3.	Прикладываем к системе активные силы и силы инерции. Век-
Вектор силы инерции вычисляем по формуле Ф = —mW, где W ускорение
центра масс тела. Вектор момента сил инерции находим по формуле
Мф = — Je, где е — угловое ускорение. Реакции идеальных связей не
указываем.
4.	Даем малое приращение (вариацию) одной из обобщенных ко-
координат, фиксируя вторую координату. Составляем первое общее
уравнение динамики, представляющее собой равенство нулю суммы
элементарных работ всех сил, включая силы инерции, на этом прира-
приращении. Так же составляем и второе уравнение, при этом приращение
получает другая обобщенная координата.

13.3. Общее уравнение динамики (две степени свободы)
295
5. Решаем систему двух алгебраических линейных уравнений с
двумя неизвестными обобщенными ускорениями.
Пример. Механическая система с идеальными стационарными
связями имеет две степени свободы и состоит из цилиндра и бруска.
К оси однородного цилиндра мас-
массой т1 приложена горизонталь-
горизонтальная сила F. Цилиндр катится без
проскальзывания по бруску мас-
массой т2. Трение между бруском
и горизонтальным основанием от-
т^ сутствует (рис. 155). Трением ка-
качения пренебречь. Найти ускоре-
ускорение центра масс цилиндра.
Рис. 155
Решение
1. Выбираем две независимые переменные, однозначно описываю-
описывающие положение системы. Пусть переменная хх указывает положение
центра цилиндра по отношению к неподвижной системе отсчета, а
х2 — положение бруска относительно той же неподвижной системы
6X2
иг
2
, 7
i \
>У
1
W?
Рис. 156
Рис. 157
отсчета. Направляем оси хх и х2 в сторону движения, т.е. направо
(рис.156).
2. Ускорения центров масс тел и угловые ускорения тел выражаем
через обобщенные ускорения. Ускорение центра цилиндра Wx = ж1?
ускорение бруска W2 = x2. Для того, чтобы выразить угловое ускоре-
ускорение цилиндра е через ускорения центров бруска и цилиндра, находим
положение мгновенного центра скоростей цилиндра (рис.157). Полу-
Получаем зависимость ujz = — tg7 = — {х± — x2)/R. Дифференцируя ujz по
времени, находим, что ez = — (И^ — W2)/R.

296	.Гл. 13. Аналитическая механика
3.	Прикладываем к системе активные силы G1? G2 и силы инер-
инерции Ф1 и Ф2, проекции которых на ось х вычислены по формулам
Ф1х = —77i1W1, Ф2х = —m2W2, где W± = ж1? И^2 = х2. К цилиндру
прикладываем момент сил инерции. Момент инерции цилиндра от-
относительно центра масс J = m-^R2/2. В проекции на ось z, перпенди-
перпендикулярную рисунку, получаем, что Mf = — Jez = m1R(W1 — W2)/2.
4.	Даем системе малое приращение обобщенной координаты 5хх,
фиксируя координату х2: 5х2 = 0 (брусок неподвижен, цилиндр по-
поворачивается по часовой стрелке на угол S(pz = —Sx-^/R).
Составляем первое общее уравнение динамики как сумму скаляр-
скалярных произведений векторов сил и векторов перемещений:
FSX1 + Ф1аМ + MfS(fz = °>
ИЛИ
W — W Лт
F8Xl - m1W18x1 - J г „ 2-^- = 0.
R R
Сокращаем на 5хг ф 0, тогда
777
F-m1W1--±(W1-W2) = 0.	A)
Второе уравнение получаем в предположении, что 5х2 ф 0, 5х1 = 0.
Цилиндр, имея неподвижную ось, повернется против часовой стрелки
на угол 5х2/R. Получим уравнение Mf5x2/R + Ф2х^х2 = 0> или
W — W Ят
VV I УУ2 ОХ2
J^—-—-—ф - m2W25x2 = 0.
it it
Делим уравнение на 5х2 ф 0,
777
-+(W1-W2)-m2W2=0.	B)
5.	Решаем систему двух алгебраических линейных уравнений A),
B) относительно ускорений. Получаем ускорение центра масс ци-
цилиндра Wx и ускорение бруска W2:
= р m1+2m2	= ^
77г(т7г + 37тг)	7
Зт2
Интересно проанализировать решение. При т2 = 0, т.е. при неве-
невесомом бруске, из выражения для W± следует, что W± = Fjmx. Такое

13.3. Общее уравнение динамики (две степени свободы)
297
ускорение имеет тело массой т1 при поступательном движении под
действием силы F. Таким образом, невесомый брусок, без трения
скользящий по плоскости, выполняет для цилиндра роль идеальной
смазки, в результате чего цилиндр, лишенный зацепления с непо-
неподвижной плоскостью, не вращается, а перемещается поступательно.
Если же устремить массу бруска к бесконечности, то получится прос-
простое решение о качении без проскальзывания однородного цилиндра
по неподвижной плоскости: Wx = 2F/Cm1) *^ .
Условия ЗАДАЧ. Механическая система с идеальными стацио-
стационарными связями имеет две степени свободы и состоит из пяти
тел. Блок {или однородный цилиндр) D катится без проскальзы-
проскальзывания по неподвижной горизонтальной плоскости или по подвиж-
подвижной тележке массой тЕ. Массой колес тележки пренебречь. Грузы
А, В и ось однородного цилиндра Е перемещаются вертикально под
действием сил тяжести. Трением качения пренебречь. Найти уско-
ускорение груза А.
1.
гс= 12 см, гпа= 9 кг,
Rc= 28 см, тв= 4 кг,
гс= 26 см, тс= 4 кг,
Г?)= 19 см, rriD= 5 кг,
гпе= 1 кг.
2.
гс= 14 см, гпа= 4 кг,
Rc= 32 см, тв= 1 кг,
гс= 28 см, тс= 5 кг,
Г?)= 11 CM, mD= 7 КГ,
гпе= 2 кг.
*) Проверим это решение применив, например, теорему об изменении
кинетической энергии (§ 12.3, с. 247). Работа силы F на перемещении х\
равна Fx\. Кинетическая энергия в начальном положении — То, в конеч-
конечном положении — 3?Tiifi/4. Изменение кинетической энергии равно работе
силы: 3?Tiifi/4 — То = Fx\. Дифференцируя это равенство по времени t с
учетом vi = dxi/dt и То = const, получаем искомый ответ.

298
Гл. 13. Аналитическая механика
з.
гс= 16 см,
Rc= 33 см,
гс= 30 см,
гв= 12 см,
RD= 21 см,
Id= 17 см,
гпа= 6 кг,
тв= 2 кг,
тс= 6 кг,
гпв= 6 кг,
гпе= 3 кг.
4.
5.
? В
rc= 18 см,	гпа= 7 кг,
Rc= 37 см,	тв= 3 кг,
гс= 32 см,	тс= 8 кг,
гв= 13 см,	rriD= 8 кг,
.#?> = 23 см,	гпе= 4 кг.
iD= 18 см,
гс= 20 см,	гпа=15 кг,
i?c= 40 см,	тв= 3 кг,
гс= 34 см,	тс= 9 кг,
td= 14 см,	rriD= 9 кг,
.#?>= 24 см,	гпе= 5 кг.
2?>= 19 СМ,
6.
7.
гс= 22 см,	?тгл=26 кг,
_RC= 41 см,	тв= 4 кг,
гс= 36 см,	?тгс=10 кг,
т= 15 см,	гпв= 8 кг,
_R?,= 25 см,	гпе= 6 кг.
zD= 21 см,
гс= 12 см,	?Tiyi=15 кг,
Rc= 30 см,	тв= 5 кг,
гс= 26 см,	тс=Ю кг,
г^= 16 см,	гпв= 7 кг,
Д^= 25 см,	гпе= 7 кг.
zd= 22 см,

13.3. Общее уравнение динамики (две степени свободы)
299
8.
гс= 14 см,
Rc= 28 см,
гс= 28 см,
гв= 17 см,
RD = 24 см,
Id= 23 см,
гс= 18 см,
Rc= 33 см,
гс= 32 см,
т= 18 см,
?тгл=18 кг,
тв= 5 кг,
шс=10 кг,
гпв= 3 кг,
гпе= 8 кг.
гпа=18 кг,
Шв= 6 КГ,
тс=П кг,
гпв= 4 кг,
?>= 26 см, гпе= 9 кг.
>= 25 см,
гс= 20 см, т^= 8 кг,
Rc= 36 см, тв= 4 кг,
гс= 34 см, тс= 4 кг,
Г?>= 19 см, rriD= 5 кг,
гпе= 1 кг.
Ответы
1. 0.780 м/с2. 2. 3.165 м/с2. 3. 4.951 м/с2. 4. 8.763 м/с2.
5. 8.531 м/с2. 6. 8.804 м/с2. 7. 3.473 м/с2. 8. 5.613 м/с2.
9. 8.485 м/с2. 10. 9.198 м/с2.
Ответы на типичные вопросы, возникающие при решении задачи
1.	Радиус цилиндра в задаче не задан. Можно ли решить такую
задачу?
Можно. В процессе решения этот радиус сократится.
2.	Как проверить решение задачи?
Решить задачу, выбрав другие обобщенные координаты, или дру-
другим способом, например, с помощью уравнения Лагранжа 2-го рода
(§ 13.4, 300).
Предупреждение типичных ошибок
1. Особое внимание уделите выбору обобщенных координат. Удач-
Удачный выбор упрощает решение.

300	-Гл. 13. Аналитическая механика
2.	Силы инерции, введенные в общее уравнение динамики, явля-
являются характерной составляющей этого метода. Не вводите силы
инерции в других методах, например, при решении задач динамики
с помощью теоремы об изменении кинетической энергии или в урав-
уравнение Лагранжа 2-го рода.
3.	Не путайте близкие по звучанию, но совершенно разные вели-
величины: момент инерции и момент сил инерции. В первом случае это
физическая характеристика тела, зависящая от распределения масс,
например, J = тВ2/2, для однородного цилиндра относительно его
оси, во втором — динамическая величина, зависящая от вращения
тела: Мф = — Je.
13.4. Уравнение Лагранжа 2-го рода
Постановка задачи. Механическая система с идеальными ста-
стационарными связями имеет две степени свободы. Найти ускорения
тел системы.
План решения. Постановка задачи не отличается от § 13.3. Раз-
Разница только в методе решения.
1.	Выбираем две обобщенные координаты. В качестве обобщен-
обобщенных координат можно брать угловые или линейные перемещения то-
точек систем, однозначно описывающие ее положение.
2.	Вычисляем кинетическую энергию системы.
3.	Вычисляем обобщенные силы. Для этого даем системе малое
приращение одной из обобщенных координат 5q1, фиксируя вторую
координату, 5q2 = 0. Определяем сумму элементарных работ 8А^ всех
сил на этом приращении. Обобщенную силу определяем по формуле
Q1 = 5A1/5q1. Так же находим и другую обобщенную силу.
4.	Записываем систему уравнений Лагранжа 2-го рода *' :
d ( дТ
dt Уд^
d (дТ\ дТ
dt \dq2) dq.
— 42-
5. Решаем систему двух алгебраических линейных уравнений A) с
двумя неизвестными обобщенными ускорениями ^ и q2.
*) Лагранж Жозеф Луи A736 - 1813) — французский математик, меха-
механик, астроном.

13.4. Уравнение Лагранжа 2-го рода (две степени свободы)
301
Пример 1. Рассмотрим задачу на с. 295, рис. 155. Решим ее с
помощью уравнения Лагранжа 2-го рода.
Решение
1. Выбираем две независимые переменные q1 = ж1 и q2 = х2, од-
однозначно описывающие положение системы. Пусть переменная х1
указывает положение центра цилиндра по отношению к неподвиж-
неподвижной системе отсчета, а х2 — положение бруска относительно той же
неподвижной системы отсчета. Направляем оси х2 и хх в сторону
движения, т.е. направо (рис.158).
6X2
Рис. 158
2. Выражаем кинетическую энергию системы через обобщенные
скорости хх = vx и х2 = v2.
Кинетическую энергию всей системы представляем в виде суммы
кинетических энергий цилиндра и бруска: Т = Тх + Т2.
Находим кинетическую энергию цилиндра, совершающего плоское
движение:
,
B)
Угловая скорость о;1 зависит от разности скоростей центра и точки
касания (рис. 157, с. 295). Так как цилиндр катится по бруску без
проскальзывания, скорость точки касания равна скорости бруска v2:
шг = \уг -v2\/R.
Подставляем в B) момент инерции однородного цилиндра относи-
относительно его оси, J = m1 R2/2. В результате получаем выражение для
кинетической энергии цилиндра:

302	Гл. 13. Аналитическая механика
Кинетическая энергия бруска
_ m2v
12 ~ 2
Кинетическая энергия всей системы
3. Обобщенную силу Qx вычисляем по формуле Q1 = SA1/Sx1, где
5АХ — элементарная работа всех сил на перемещении 5хх. При вы-
вычислении элементарной работы 8А1 на приращении обобщенной коор-
координаты ж1 фиксируется другая обобщенная координата, т.е. 5х2 = 0.
Очевидно, что кроме силы F на таком перемещении ни одна сила
работы не совершает, следовательно, 5А± = FSx± и Q1 = F. Анало-
Аналогично, Q2 = 0.
4. Записываем уравнения Лагранжа A) и вычисляем входящие в
них производные:
дТ _	m1	d
dv1 ~ miVl 2 ^ V<2^ dt
дТ _	m1	d f дТ
где Wx = v1^ W2 = v2. В результате уравнения Лагранжа принимают
вид
3W1m1 - W2m1 = 2F,
+ 2m2) = 0.
5. Решаем систему уравнений C):
w =Г wi + 2m2
1 7тг(?77
7тг1(?77,1 + Зт2)' 2 TTij^ + 3?тг2
Пример 2. Механическая система с идеальными стационарными
связями имеет две степени свободы и состоит из груза А и одно-
однородных цилиндров В и С'. Цилиндр С падает вертикально вниз и
передает движение цилиндру В и грузу А, с которыми он связан не-
нерастяжимой нитью. Нить разматывается с цилиндра С. Даны массы
тел тА, тв, тс (рис.159). Найти ускорение груза А.

13.4. Уравнение Лагранжа 2-го рода (две степени свободы)
303
Решение
1. Выбираем две независимые переменные q1 = х и q2 = ip, од-
однозначно описывающие положение системы (рис.160). Переменная х
указывает положение груза по отношению к неподвижной системе
отсчета, а (р — поворот цилиндра С (рис.159).
Рис. 159
Рис. 160
2. Выражаем кинетическую энергию системы через обобщенные
скорости х vl ф.
Кинетическую энергию всей системы представляем в виде суммы
кинетических энергий груза и цилиндров: Т = ТА + Тв + Тс.
Находим кинетическую энергию поступательного движения груза:
Кинетическая энергия вращающегося цилиндра
=
в
= mBR\{xjRBf = твх2
2-2	4 "
Находим кинетическую энергию цилиндра G, совершающего плоское
движение:
rncv
Угловая скорость цилиндра С — ujc = ф. Скорость центра масс
складывается из переносной скорости х и относительной 11сф:
т —
1с -
2	4
Кинетическая энергия всей системы
Т = {1/2)х2{тА + тпв/2 + 777,с) + хфтсЯс

304	Гл. 13. Аналитическая механика
3.	Обобщенную силу Qx вычисляем по формуле Qx = 5Ах/5х, где
5Ах — элементарная работа всех сил на перемещении 5х. Фиксируем
угол поворота цилиндра С: 5(р = 0. Груз А перемещается по гори-
горизонтали на расстояние 5х, цилиндр В поворачивается на некоторый
угол, а цилиндр С поступательно перемещается вниз на расстояние
5х. На этом перемещении работу совершает только сила гпсд, следо-
следовательно, 5Ах = тсд5х и Qx = mcg. Аналогично, фиксируя переме-
перемещение груза Eх = 0), даем приращение углу поворота цилиндра С и
вычисляем Q = mcgRc.
4.	Записываем уравнения Лагранжа A) и вычисляем входящие в
них производные:
ОТ
-—- = х(тА + 0.5гаБ + тс) + фКстс,
СУХ
d_ (дТ\
dt\dx)
) = ^(ША + °'5шБ + mc)
дТ	2	d {дТ\	о
-— = xRcmc + \.b(pRcmc, — I —- I = xRcmc + l.b(pRcmc,
В результате уравнения Лагранжа принимают вид
(тпА + 0.Бтпв + mc)x + mcRc(p =
ж + 1.5mc(pRc =
5. Решаем систему уравнений D) и находим ускорения:
6?77 + Згп + 2т77 '
Згпв + 2т77,с '	Дс(б7тгА + Зтв
Условия ЗАДАЧ. Механическая система с идеальными стацио-
стационарными связями имеет две степени свободы и движется под дей-
действием сил тяжести. Три элемента механизма наделены массами,
кратными некоторой массе т. Трением пренебречь. Подвижные и
неподвижные блоки считать однородными цилиндрами. Найти уско-
ускорение груза А или центра цилиндра А.

13.4. Уравнение Лагранжа 2-го рода (две степени свободы)	305
2.
I с I
3m, тс = 3m.
гпа = 3m, тв = 5m, me = 4m. uia = 5m,
з.
4.
= 4m, тв = 5m, ?nc = 4m. тпл = 5m,
| С |
7m, me = 4m.
гпа = Зт, тв = Зт, тс = 2т. тл = 5т, тв = 4т, тс = Зт.
7.	8.
vaJ l^
AJ Д
С
= 4m, m?j = 6m, me = 7?n. т-^ = Зт, шв == 5?n, тс = 8?n.
20 М.Н. Кирсанов

306
Гл. 13. Аналитическая механика
10.
гпа = Зга, тв = 4га, тс = 5га. га л = 4т, шв = 6т, тс = 7т.
В таблице ответов даны коэффициенты дифференциальных урав-
уравнений движения системы и искомое ускорение. Система (после со-
сокращения на т) имеет вид
а11х1 + &i2^2 = Qii
В качестве обобщенных координат ж1? х2 взяты линейные переме-
перемещения точек ободов цилиндров с неподвижными осями. Координата
хх > 0 соответствует повороту левого цилиндра по часовой стрелке,
х2 > 0 — повороту правого цилиндра против часовой стрелки. Ко-
Коэффициенты afj — безразмерные, Q1? Q2 и WA — в м/с2.
Ответы
1
2
3
4
5
6
7
8
9
10
aii
4.250
6.125
2.875
12.375
2.000
6.750
4.500
4.875
4.750
3.750
«12
1.250
0.375
1.000
0.625
0.500
0.750
0.500
0.625
0.750
0.500
«22
5.250
4.125
5.000
5.875
3.500
5.750
8.500
9.875
5.750
8.500
Qi
-4.905
14.715
19.620
24.525
9.810
14.715
19.620
-4.905
14.715
19.620
Q2
-14.715
-14.715
-19.620
-14.715
-19.620
14.715
19.620
24.525
14.715
19.620
WA
0.355
2.636
1.559
0.305
6.540
2.308
3.098
1.335
2.475
3.490
Ответы на типичные вопросы, возникающие при решении задачи *^
1. Как проверить решение задачи?
Решить задачу, выбрав другие обобщенные координаты или дру-
другим способом, например, с помощью общего уравнения динамики
(§ 13.3, с. 294).
*) См. также ответы на с. 299

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 307
2.	В результате решения получается отрицательное ускорение,
а в ответе оно положительное. Что это значит?
В ответе даны абсолютные величины ускорений.
3.	Как выразить скорость оси цилиндра, подвешенного на двух
нитях и совершающего плоское движение, через скорости нитей
(например, цилиндра А в варианте 10 )?
Если скорости нитей vx и v2 направлены в одну сторону, то ско-
скорость оси цилиндра v = (v1 + i72)/2. Это следует из того, что концы
векторов скоростей точек неизменяемого отрезка (диаметра) лежат
на одной прямой. Угловую скорость легче всего выразить, определив
положение МЦС цилиндра (рис. 87, с. 159).	Получаем:
UJ	=
= (v± — v2)/BR), где R — неизвестный радиус цилиндра (в процессе
решения он сократится и в ответ не войдет). Если скорость v2 на-
направлена в сторону, противоположную гЛр то результаты получаются
те же, но знак у v2 заменится на противоположный.
4.	В условии не дана масса т, через которую выражены осталь-
остальные массы. Какое значение т брать при решении?
Масса т сократится в процессе решения и в ответ не войдет.
13.5. Уравнение Лагранжа. Нелинейные
уравнения движения
Постановка задачи. Механическая система с одной степенью
свободы характеризуется нелинейными кинематическими соотно-
соотношениями. Составить уравнение движения системы.
План решения
1.	Выбираем обобщенную координату. В качестве обобщенной
координаты q можно брать угол поворота одного из тел системы или
декартову координату какой-либо точки, однозначно описывающую
положение системы. Часто обобщенная координата задана в условии
задачи.
2.	Составляем кинематические графы системы. Выражаем через
обобщенную скорость q угловые скорости тел и скорости точек при-
приложения активных сил (§ 8.5, с. 188).
3.	Вычисляем кинетическую энергию системы (§ 12.2, с. 241).
4.	Находим обобщенную силу, вычисляя виртуальные мощности
20*

308	.Гл. 13. Аналитическая механика
активных сил:
5. Находим частные производные dT/dq и dT/dq и записываем
уравнение Лагранжа 2-го рода *^ :
dt{dq) dq~Q-	W
Пример 1. Рассмотрим механическую систему, приведенную в
примере § 12.2. Составим для нее уравнение движения (рис. 126,
с. 242).
Решение
Вычисление скоростей и кинетической энергии, т.е. выполнение
первых трех пунктов плана, подробнее рассмотрены на с. 243.
1.	Выбираем обобщенную координату <р — угол поворота цилиндра
1, соединенного со стержнем А В.
2.	Составляем кинематические графы системы (рис. 127, с. 243) и
получаем выражения для скоростей и угловых скоростей:
vDy =
3. Вычисляем кинетическую энергию системы как сумму кинети-
кинетических энергий цилиндров и стержня (с. 244):
где А л В константы: А = т-^В2/2 + 7тг3а2/3, В = 2а2Cт2 + ш3).
4. Находим обобщенную силу, вычисляя виртуальные мощности
активных сил:
Q = -(С?! • vA + G2 • vc + G3 • vD + M • cJA + F • ?TC).
*) Если кинетическую энергию можно представить в виде Т = 0.5^2
где /(д) — известная функция обобщенной координаты, то уравнение Ла-
Лагранжа 2-го рода имеет вид
qf(.q)+0.5q2f'(q) = Q,
где f'(q) = df/dq.

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 309
Горизонтальная плоскость, по которой катится цилиндр, и шарнир,
на котором закреплен цилиндр 1, являются идеальными связями. Вир-
Виртуальные мощности этих реакций равны нулю, и в выражение для Q
эти силы не входят. Аналогично, не входит в обобщенную силу и
сила трения, приложенная при отсутствии проскальзывания к непо-
неподвижной точке (точке касания поверхности) цилиндра 2. Учитывая
выражения для векторов сил,
Gi = {0, -m.#, 0},г = 1...3, F = {F, 0, 0},
момента М = {0, 0, М}, выражение иоА = {0, 0, ф} и соотношения
B), получаем в результате обобщенную силу:
Q = М — 0.5m3ag cos (р — 2aF sin (p.
5. Находим частные производные
и полную производную по времени
7 / ?)>Jl\
— ( -jrr ) = ф{А + .В sin2 у?) + <^2.Е> sin 2(p.
(JLU \ С/СУ /
Записываем уравнение Лагранжа 2-го рода:
ф{А + .В sin2 у?) + 0.5(^2.В sin 2<?> = М — 0.5т3ад cos (р — 2aF sin <??.
Пример 2. Механическая система с одной степенью свободы
обладает нелинейными кинематическими соотношениями (рис. 161).
Кривошипно-кулисный механизм состоит из маховика 1, кулисы 2,
двигателя со шкивом 3, катка 4 и штока 5. К шкиву 3 приложен
момент двигателя Мдг = Мо — kuo?>z. Каток своим внешним ободом
катится без проскальзывания и без трения качения по горизонталь-
горизонтальной поверхности. Внутренним ободом каток также без проскальзы-
проскальзывания приводит в движение шток, к которому приложена полезная
нагрузка, моделируемая силой FHx = —/лу^х. Трением пальца А в
прорези кулисы 2 пренебрегаем. Шкив 3 считаем однородным ци-
цилиндром, момент инерции маховика 1 вместе с пальцем А, закреп-
закрепленным на нем, равен J1 = 2.5 кгм2. Даны массы: тА = 1 кг,
т2 = 15 кг, т3 = 10 кг, т4 = 16 кг, массу штока 5 считать рав-
равной нулю. Даны радиусы: R± = 0.4 м, ОХА = г± = 0.1 м, R3 = 0.3 м,

310
Гл. 13. Аналитическая механика
г4 = 0.2 м, R4 = 0.41 м; радиус инерции г4 = 0.32 м. Пусковой мо-
момент Мо = — 30 Нм; крутизна статической характеристики двигателя
к = 0.2 Нмс; коэффициент сопротивления /i = 950 Нс/м. Составить
уравнение движения системы *' .
Рис. 161
Решение
1.	Выбираем обобщенную координату (р — угол поворота шкива 1,
отсчитываемый от горизонтальной оси х (направленной, как всегда,
направо) против часовой стрелки.
2.	Составляем кинематические графы системы:
тг/2
'3 '
я/2
ж/2
Точка К является точкой касания внешнего обода блока 4 неподвиж-
неподвижной поверхности, проскальзывание отсутствует, поэтому vK = 0.
Шток 5 касается внутреннего обода блока 4 в точке N, скорость
штока v5x = vNx. Получаем выражения для проекций скоростей:
VAx = ~Г1Ф Sin ?>> VAy = Ггф COS if,
C)
VCx = -
VNx
Нить BD нерастяжимая, отсюда следует кинематическая связь:
vDx = vBx. Вместе с C) это дает uu3z = —(R-^/R^ip, т.е. тела 3 и
1 вращаются в разные стороны. Так как шток 2 кулисы является
жестким, то vAx = vCx. Отсюда находим угловую скорость блока 4
ujAz = (ri/R^cpsmip и скорость штока v5x = — (R4 — r4)r1/R^ sin (p.
3. Вычисляем кинетическую энергию системы как сумму кинети-
кинетических энергий четырех тел. Маховик 1 с моментом инерции J1 и
*) За основу задачи взято задание Д-5 из сборника [15].

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 311
шкив 3 с моментом инерции т31Ц/2 вращаются, каток 4 совершает
плоское движение, а кулиса 2 — поступательное:
2	2 ш3дз	2
+
т4(ггф sin <^J m4i\(r1/R^ sin <^J
2	'	2
Для удобства вычислений представим кинетическую энергию в виде
Г=^-(А + Б8ш2р),	D)
где А = J± + m3Rl/2, В = т2г\ + ш4(г4г1/Д4J + ш4г2.
4. Вычисляем обобщенную силу:
Учитывая выражения для векторов
GA = {0, -шА5, 0},	гГа = {-r^sin^, rllyjcos^, 0},
^я = {-А*"бх» °' °}'	^5 = {"(Д4 " rJrjRttahKp, 0, 0},
Мд = {0, 0, Мо - Ы3г}, ^з = {0, 0, -{RJ
получаем в результате обобщенную силу, которую представляем в
виде суммы Q = QH + QT + QA, где QH = -ц(г^(^ - г4)/R4 sin (рJф,
Qt = -mA9ri C0S(Pi Qa = -(Mo + кф^/R^RjR^.
5. Находим частные производные
дТ	дТ
—- = 0.5ф2В sin 2(р, т— = ф(А + В sin2 у?),
и полную производную по времени
В sin2 у?) + ф2В sin 2y>.
Записываем уравнение Лагранжа 2-го рода:
<р(А + В sin2 ф) + 0.5(^2Б sin 2<p = QT + 0я + 0д.	E)
Полученное нелинейное дифференциальное уравнение движения
системы может быть проинтегрировано численно (§ 17.2).

312
Гл. 13. Аналитическая механика
Пример 3. Механическая система с одной степенью свободы
обладает нелинейными кинематическими соотношениями (рис. 162).
Рис. 162
Система состоит из двух однородных дисков 1, 2 одинакового ради-
радиуса R, невесомого стержня АВ длиной а и поршня 3, перемещающе-
перемещающегося в горизонтальных направляющих. Стержень АВ жестко скреп-
скреплен с диском 1. Диск 1 катается по горизонтальной поверхности, а
диск 2 — по вертикальной поверхности поршня. Качение происходит
без проскальзывания и без трения качения. Массы дисков т1 и т2,
масса поршня т3. К середине стержня приложена сила F, направ-
направленная перпендикулярно АВ. На поршень действует горизонтальная
сила Р, а на диск 2 — пара с моментом М. Составить уравнение
движения системы.
Решение
1. Выбираем обобщенную координату (р — угол поворота стержня
, отсчитываемый от горизонтальной оси х (рис. 163).
У
(
К
/
F
\
С
3
, , Р
Рис. 163
2. Составляем кинематические графы системы. В качестве на-

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 313
чальных и конечных вершин графов берем те точки, скорости кото-
которых необходимо вычислить (Л, В, D) или те, в которых по условию
задачи задана какая-либо кинематическая связь (if, С):
К^А- А^лВ- В^С- A°^D	F)
тг/2 '	Ч>	0	'	у	У J
Записываем уравнения для проекций скоростей, соответствующие
графам F):
VAy = VKy + R(P C0S К/Ъ,
VAx ~ a(P Sin <P>	VBy = VAy + аФ C0S <P>
VCy = VBy + Ru;2z C0S °'
VDy = VAy + °'Ба(Р C0S V-
Точка К является точкой касания обода диска 1 неподвижной поверх-
поверхности, проскальзывание отсутствует, поэтому
*кх = °> vkv = 0-	(8)
Поршень 3 и диск находятся в зацеплении в точке С. Поршень дви-
движется поступательно и вертикальные компоненты всех его точек,
включая и точку G, равны нулю:
vCy = 0-	(9)
С учетом соотношений (8,9) из системы уравнений G) получаем вы-
выражения для скоростей и угловых скоростей:
VAx = -RVi	VAy = О,
-0.5a sin <^?), ^ = O.o^acos^,
cj2z = — ф{а/В) cos<?>,	^Сж = — <^(Д + asin<^).
3. Вычисляем кинетическую энергию системы как сумму кинети-
кинетических энергий трех тел:
Г = Г1 +Т2-\-Т3.
Однородный диск 1 катится без проскальзывания по неподвижной
поверхности и совершает плоское движение (с. 242), поэтому
Т1 = л =	л '

314	Гл. 13. Аналитическая механика
Диск 2 также совершает плоское движение,
_ гп2у2в | J2u%z
12 ~ 2 + 2 '
Момент инерции диска J2 = m2R2/2. С учетом A0) получаем
т2ф2[В? + а2 + 2Да8Ш(^) т2ф2 a2 cos2 (р
Т2 =	2	+	4	'
Кинетическая энергия поступательного движения поршня 3
m^v2^ т3ф2(Я-\-asimpJ
3 = ~^~~ =	2	'
Кинетическую энергию всего механизма для удобства вычислений
представляем в виде
. 2
Т= —(A + Bsm(p + Csin2(p),
где для констант введены обозначения: А = A.57тг1 + т2 + 77Т,3)Д2+
+1.5т2а2, Б = 2Ra(m2 + 7тг3), С = а2(т3 - ш2/2).
4.	Вычисляем обобщенную силу:
Q = -(<?! ¦ vA + G2 • vB + G3 • гГс + F ¦ ^ + Р - гГс + М ¦ а;2).
Учитывая следующие выражения для векторов,
бг = {0, -т1д, 0}, G2 = {0, -т2д, 0},(?3 = {0, -т3д, 0},
F = {Fsin^, -Fcos^, 0}, Р = {-Р, 0, 0}, М = {0, 0, М},
и соотношения A0), получаем в результате обобщенную силу:
Q = —т2 д a cos (р — F @.5а + R sin ф) + Р (R + а sin ф) — М (a/R) cos <p.
5.	Находим частные производные,
9Т
^— = (,3(^ + 5 sin ip -\- С sin2 <
оф

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 315
и полную производную по времени
7 / f\rp \
— ( —т ] =
at \oq J
ф2 (В cos (р + С sin2(p).
Записываем уравнение движения системы:
ф(А + В sin <р + С sin2 ^) + О.Бф2 (В cosp + C sin
= {Pa-FR)sunp- (m2g + М/R)acos(p + PR-O.bFa.
Пример 4. Механическая система с одной степенью свободы с
нелинейными кинематическими соотношениями (рис. 164) состоит
из однородного диска 1 радиусом R, стержня 2 длиной а и невесо-
невесомого штока, двигающегося без трения в вертикальных направляю-
направляющих. Диск 1 вращается на оси, закрепленной в нижней точке штока.
'V
mL
\
i
ч
-A
В
R/ cos (p
R
<Р>С
Рис. 164
Рис. 165
Рис. 166
Стержень 2, вращаясь вокруг неподвижного шарнира А, касается
диска. Диск катится по стержню без сопротивления и проскальзы-
проскальзывания. Шток и шарнир А находятся на одной вертикали. К концу
стержня приложена горизонтальная сила F, к диску — момент М.
Масса диска — 7тг1, масса стержня — т2. Составить уравнение дви-
движения системы.
Решение
1.	Выбираем обобщенную координату (р — угол поворота стержня
2, отсчитываемый от горизонтальной оси х (рис. 165).
2.	Составляем кинематические графы системы:
В-
A1)

316	-Гл. 13. Аналитическая механика
Из треугольника ABC (рис. 166) имеем АС = Rtgip. Записываем
уравнения для проекций скоростей, соответствующие графам A1):
vBx = vAx ~ Rfitgipsmip - Rlu1z sin(<p + тг/2),
vBy = vAy + R(ptg(pcos(p + Ru;lz cos((p + тг/2),
^ж = ^АЖ - °'5a ? Sin ^> ^Dy = VAy + °'5a ? C0S ^
Шарнир А неподвижен: vAx = vA =0; точка .В движется только по
вертикали: vBx = 0. С учетом этих соотношений из системы урав-
уравнений A2) получаем выражения для линейных и угловых скоростей:
y	> vlz = -ф
vDx = -0.5(^asin^,	vDy = О.Бфа cos (p,	A3)
г?Кж = — фа siiKf,	vKy = фа cos (p.
Заметим, что скорость vB можно получить координатным методом,
дифференцируя по времени выражение yB(i) (рис. 166):
_ <кУв _ АУа + Rlcos Ф)
Уву dt	dt	р
3. Вычисляем кинетическую энергию системы как сумму кинети-
кинетических энергий диска и стержня: Т = Тх + Т2. Однородный диск 1
соверпгает плоское движение, поэтому
11	2 + 2 '
Момент инерции диска — J: = 7?г1Д2/2. С учетом A3) получаем
Кинетическая энергия вращения стержня 2 равна Т2 = J2(^2/2, где
J2 = тп2а2/3 — момент инерции стержня относительно конца (точки
А). Отсюда получаем, что Т2 = тп2а2ф2/6. Кинетическую энергию
всего механизма для удобства вычислений представляем в виде

13.5. Уравнение Лагранжа. Нелинейные уравнения движения 317
где для констант вводим обозначения А = т2а2/3, В = m1R2/2.
4.	Вычисляем обобщенную силу Q:
Q=-(G1-vB+G2-vD + F-vK + M- aJx).
Учитывая выражения для векторов
Gx = {0, -ш^, 0}, G2 = {0, -га2#, 0},
F = {-F, 0, 0}, М = {0, 0, М},
и соотношения A3), получаем в результате обобщенную силу:
Q = —т1 gR sin <^?/ cos2 if — 0.5m2ga cos if + Fa sin if — M tg2 <^?.
5.	Кинетическую энергию записываем виде Т = О.Бф f((p), где
+ BC^cosV)sinV_
COS4 ^
В этом случае, согласно примечанию на с. 308, уравнение Лагранжа
2-го рода имеет вид
где
w/ ч = ^/(у) = 4Б C - 2 cos2 у?) sin у?
dip	cos5 у?
В результате получаем уравнение движения системы:
COS4 у?	у/	COS5 if
771 gi?	m9ga cos ip + Fa sin ip — M tg2 y?.
2 у 2
cos
Условия ЗАДАЧ. Механическая система с одной степенью сво-
свободы характеризуется нелинейными кинематическими соотношени-
соотношениями. Составить уравнение движения системы. Рисунки и тексты
вариантов задач приведены на с. 245-247. Даны массы т1 = 6 кг;
т2 = 2 кг7 т3 = 8 кг; т4 = 1 кг.

318	.Гл. 13. Аналитическая механика
Ответы
1.	2фа2A + 6 sin2 ф) + 6ф2а2 sin 2(р = М — Зад cos (р — 4aF sin <??.
2.	2фа2{1 + 3 sin2 у?) + Зф2а2 sin 2у? = М - Зад cos р.
3.	(/За2D + 7sin2 у?) + G/2)ф2а2 sin2<? = М - бадcos<p.
4.	</5Bа2 + 24.5Д2 + 4Да sin ф) + 2<^2аД cos (р = -2ад cos у? - 8#Д.
5.	фа2 F + 17 sin2 ip) + 8.5<?>2а2 sin 2<^ = 2а^C cos ip — sin у?).
6.	ф(9Я2 +4(E + 2asin^J) + 8аф2(R + 2а sin (p) cos (p =
= -M - 4:g(R + 2a sin ф).
7.	2фа2 C + 8 sin2 ф) + 8ф2а2 sin 2(р = —М — Sag sin <?? sin a.
8.	фа2 F + 7.5 sin2 ф) + 3.7Бф2а2 sin 2(р = М — ад sin <?? sin a.
9.	(/3(ЗД2 + 2а2 + 4а2 sin2 ф) + 2ф2а2 sin 2y? =
= М + (R + a sin <?>)F — 2а д cos <??.
10.	фBа2/3 + 2Да sin (р + 14Д2) + <^2Да cos (p = -Зад cos (p.
13.6. Уравнение Лагранжа 2-го рода для
консервативных систем
Постановка задачи. Консервативная механическая система с
идеальными стационарными связями, имеющая две степени свободы,
движется под действием известных сил. Используя уравнение Ла-
Лагранжа 2-го рода для консервативных систем, найти ускорения тел
системы.
План решения. Если все силы, действующие на систему потен-
потенциальны, то такая система называется консервативной. Обобщенные
силы и потенциальная энергия связаны дифференциальными соотно-
соотношениями Qi = —dll/dqi, где qi — обобщенные координаты.
Постановка задачи совпадает с § 13.4. Отличие — в форме урав-
уравнения Лагранжа.
1.	Выбираем две обобщенные координаты.
2.	Вычисляем кинетическую энергию системы Т через обобщен-
обобщенные скорости v± = х1 и v2 = х2.
3.	Вычисляем потенциальную энергию системы 77.

13.6. Уравнение Лагранжа 2-го рода для консервативных систем 319
4.	Определяем функцию Лагранжа L = Т — П *' .
5.	Находим частные производные dL/dvi и dL/дх^ г = 1,2 и за-
записываем систему уравнений Лагранжа 2-го рода в форме
dt \dv2j дх2
6.	Решаем систему алгебраических линейных уравнений A) с двумя
неизвестными — обобщенными ускорениями W1 = ж1 и W2 = х2.
Пример. Консервативная механическая система с идеальными
стационарными связями имеет две степени свободы и представляет
собой механизм, состоя-
состоящий из пяти тел. Груз А
массой тА = 10 кг и од-
однородный цилиндр В мас-
массой тв = 20 кг шарнирно
F соединены жестким неве-
невесомым стержнем. Призма
D массой тD = 40 кг
опирается на пустотелый
Рис. 167	цилиндр (трубу) С и на
колесо Е (однородный цилиндр). Ось колеса соединена с призмой
(рис. 167). Используя уравнение Лагранжа 2-го рода для консерва-
консервативных систем, определить ускорение, которое придает призме гори-
горизонтальная сила F = 100 Н. Трением скольжения и трением качения
пренебречь. Качение происходит без проскальзывания. Масса трубы
тс = 30 кг, колеса тЕ = 5 кг; а = 15°. Нижняя поверхность призмы
параллельна горизонтальному основанию во все время движения.
Решение
1.	Выбираем две независимые переменные, однозначно описываю-
описывающие движение системы. Пусть переменная хх указывает положение
призмы D по отношению к неподвижной системе отсчета, а х2 —
положение оси цилиндра В относительно призмы (рис. 168).
2.	Выражаем кинетическую энергию системы через обобщенные
скорости хх = vx и х2 = v2. Кинетическая энергия всей системы
равна сумме кинетических энергий: Т = ТА + Тв + Тс + TD + ТЕ.
*) Функцию L называют еще кинетическим потенциалом.

320
Гл. 13. Аналитическая механика
Рис. 168
Записываем кинетическую энергию поступательного движения груза
А, имеющего относительную скорость v2 и переносную г^:
(v± + v2 cos аJ + {у2 sin аJ
ТА = ША	2	'
Кинетическая энергия плоского движения цилиндра В
_
1в — тв
|
Угловая скорость иов зависит от скорости относительного движения
иов = v2/RB. Момент инерции однородного цилиндра В относительно
его оси JB = mBRB/2. Кинетическая энергия плоского движения
трубы С
Tc = mc
(V2J
2	2"
Здесь ujc = v1/BRc) — угловая скорость трубы, г^/2 — скорость ее
центра масс; Jc = тсВ?с — момент инерции трубы относительно
ее оси. Кинетическая энергия поступательного движения призмы
TD = mDv2/2. Кинетическая энергия плоского движения колеса Е, у
которого скорость центра масс г;1? имеет вид (см. с. 242)
Т —
1Е —
3v2mE
Кинетическая энергия всей системы
Т =
mA + mB + тпс/2 + ттт,^ + 3mE/2 2
\тпА + mB)v1v2 cos a
ША + ЗШо/2

13.6. Уравнение Лагранжа 2-го рода для консервативных систем 321
3.	Потенциальная энергия системы
П = —хх F — х2 (тА + rnB) g sin a.
4.	Определяем функцию Лагранжа:
_ тА + тв + шс/2 + mD + ЗтЕ/2 2 тА + Зтв/2 2
ь - i - 11 —	^i H	v2-\-
+ (?тгА + тв) v\vi cos а + xi F + Ж2 G?гА "I" 771б) ^ sin a-
5.	Находим частные производные dL/dvi и dL/дх^ г = 1,2 и за-
записываем уравнения Лагранжа A):
/ 771^ 3771 сЛ
Wl[mA+mB+ о +mD^	о	+ Щ(тА + Шб) C0S « = ^
^	2	2 У	. .
cos а + W2 ( ттгА НI
6. Решаем полученную систему двух алгебраических линейных
уравнений с двумя неизвестными ускорениями W1 и W2 и находим
Wx = 0.627 м/с2, W2 = 1.45 м/с2.
Замечание. В правой части B) стоят обобщенные силы, соот-
соответствующие координатам хх и х2. Обобщенные силы можно найти,
вычисляя мощности активных сил на возможных скоростях:
Qj=Nj/xj, J = 1, 2,
где N-± — мощность сил при х2 = 0, a N2 — мощность сил при х1 = 0.
Мощность находим суммируя скалярные произведения N = $^i^ • v^
Fi — силы, vi — скорости точек их приложения. При этом способе
скорости лучше вычислять аналитически (§ 8.5), а скалярные произ-
произведения раскрывать в координатной форме.
Условия ЗАДАЧ. Консервативная механическая система с иде-
идеальными стационарными связями имеет две степени свободы и пред-
представляет собой механизм, состоящий из груза А, блока В {больший
радиус R, меньший г, радиус инерции гв) и цилиндра С радиусом Rc.
Механизм установлен на призме D, закрепленной на осях двух одно-
однородных цилиндров Е. К призме приложена постоянная по величине
горизонтальная сила F. Качение цилиндра С (блока В) и цилиндров
21 М.Н. Кирсанов

322
Гл. 13. Аналитическая механика
Е происходит без проскальзывания. Трением качения и скольжения
пренебречь. Используя уравнение Лагранжа 2-го рода для консерва-
консервативных систем, найти ускорение призмы.
1.
Rb = 16 см,
гв = 8 см,
Re = 28 см,
гв = 13 см,
Re = 29 см,
га л = 6 кг,
тв = 3 кг,
тс = 11 кг,
тв = 1 кг,
тпе = 2 кг,
2.
Дв = 24 см,
гв = 12 см,
Re = 42 см,
гв = 19 см,
Re = 43 см,
гпа = 9 кг,
тв = 6 кг,
тс = 14 кг,
7П?> = 2 КГ,
гая = 3 кг,
F = 15 Н.
3.
Rb = 48 см,
rs = 32 см,
Re = 24 см,
is = 41 см,
Re = 25 см,
гпа = 6 кг,
гав = 3 кг,
тс = 16 кг,
тв = 1 кг,
гпе = 4 кг,
F = 26 Н.
4.
5.
Дв = 60 см,
гв = 40 см,
Re = 30 см,
%в = 51 см,
Re = 31 см,
Дв = 28 см,
гв = 16 см,
Re = 12 см,
%в = 23 см,
Re = 13 см,
гал = 9 кг,
тв = 6 кг,
тс = 19 кг,
тв = 2 кг,
гпе = 5 кг,
F = 63 Н.
гпа = 6 кг,
гав = 3 кг,
гас = 21 кг,
тв = 1 кг,
гпе = 6 кг,
F = 74 Н.

13.6. Уравнение Лагранжа 2-го рода для консервативных систем 323
6.
7.
1-F
RB = 42 см,
тв = 24 см,
Re = 18 см,
iB = 34 см,
Re = 19 см,
Rb = 32 см,
Гв = 16 СМ,
Re = 56 см,
г# = 25 см,
#я = 57 см,
7ПА = 9 КГ,
тв = 6 кг,
тс = 24 кг,
7П?> = 2 КГ,
га# = 2 кг,
F = 2 H.
гал = 6 кг,
тв = 3 кг,
тс = 11 кг,
тг> = 1 кг,
га# = 3 кг,
F = 15 Н.
1-F
Rb = 70 см,
гв = 40 см,
Re = 30 см,
iB = 57 см,
RE = 31 см,
Rb = 16 см,
гв = 8 см,
Дс = 28 см,
is = 14 см,
Ля = 29 см,
Rb = 36 см,
гв = 24 см,
Re = 18 см,
гв = 32 см,
Дя = 19 см,
Систему уравнений Лагранжа записываем в виде
= 12 кг,
: = 6 КГ,
= 27 кг,
= 2 кг,
гпе = 4 кг,
F = 26 Н.
гпа = 9 кг,
шв = 3 кг,
тс = 14 кг,
тв = 1 кг,
гпе = 5 кг,
F = 63 Н.
7ПА = 12 КГ,
Шв = 6 КГ,
тс = 22 кг,
то = 2 кг,
гпе = 6 кг,
F = 74 Н.
21*

324
Гл. 13. Аналитическая механика
где введены обобщенные координаты: хх — горизонтальное смещение
призмы D, х2 — смещение груза относительно призмы. В таблице
приведены инерционные коэффициенты системы ап, а12, а22 в кг,
обобщенные силы Q1? Q2 — в Н и ускорение призмы WD в проекции
на ось х — в м/с2.
Ответы
1
2
3
4
5
6
7
8
9
10
аи
27.00
40.00
38.00
51.00
49.00
47.00
30.00
59.00
42.00
60.00
-7.73
16.76
-12.24
5.48
-37.83
-24.55
4.73
-22.71
-10.41
15.58
&22
13.71
55.04
18.86
16.50
108.67
48.60
13.65
55.19
18.35
20.41
Qi
2.00
-15.00
26.00
-63.00
74.00
2.00
-15.00
26.00
-63.00
74.00
Q2
9.81
3.57
1.35
57.23
180.26
40.57
41.16
61.93
13.87
7.99
WD
0.33
-0.46
0.89
-1.67
3.82
0.65
-1.03
1.04
-1.53
1.41
13.7. Функция Гамильтона
Постановка задачи. Найти функцию Гамильтона*' механи-
механической системы с двумя степенями свободы по известной функции
Лагранжа.
План решения. Для консервативной механической системы можно
ввести функцию Гамильтона
A)
где s = 2 — число степеней свободы, L — функция Лагранжа (§ 13.6),
q- — обобщенные скорости, р- = dL/dq- — обобщенные импульсы.
1. Дифференцируя функцию Лагранжа по q^ и д2, находим обоб-
обобщенные импульсы р± ир2. Получаем два уравнения, связывающие
обобщенные импульсы с обобщенными скоростями и обобщенными
координатами:
Pj^Pjiqj^j), j = 1,2.	B)
*) Гамильтон Уильям Роуан A805-1865) — ирландский математик.

13.7. Функция Гамильтона	325
2.	Решаем систему уравнений B) относительно обобщенных ско-
скоростей:
Qj=Qj(Pj>Qj)> i = 1>2-	C)
3.	Записываем функцию Гамильтона A), в которой обобщенные
скорости заменяем на выражения C).
Пример. Найти функцию Гамильтона механической системы с
двумя степенями свободы по известной функции Лагранжа
L = Qi + Q1Q2 + Q2 — Ъ cos Qi + snl Ъ-
Решение
1.	Дифференцируя функцию Лагранжа по qx и g2, находим обоб-
обобщенные импульсы р-:
Р2 = 9i + 2^2 ~ cos 9i •
2.	Решаем систему D) относительно обобщенных скоростей:
qx = BPl -p2 -cosgJ/3,
3. Записываем функцию Гамильтона A), в которой обобщенные
скорости заменяем на выражения E):
Н=-(р\ - ргр2 + р\ + Bр2 -p1)cosq1 +cos2q1) -sing2.
Замечание. Для стационарных связей функция Гамильтона равна
полной механической энергии Н = Т + П.
Условия ЗАДАЧ. Найти функцию Гамильтона механической сис-
системы с двумя степенями свободы по известной функции Лагранжа;
qly q2 — обобщенные координаты.
1.	L = 6g| + g1g2 + 2(/? + 4(/2.	2. L = 2q21^q1q
3.	L = 2q2 + 2q2+4q2 + 2qiq2.	4. L = Ц2 +Aq2
5.	L = qf + 2q2 + 2^ cos^.	6. L = ^^ + 2g1g1 + 2
7.	L = q\ + ^g2 + 3g2g2.	8. L = 2^ + 6^ + ^g2
9.	L = ^ + ^ + 2g2cosg2.	10. L = 4^+4g| + glg

326	.Гл. 13. Аналитическая механика
Ответы
2.	Я = Plp2 - 2р\ - 3qf -
3.	Я = (l/8)pl + A
4.	Я = Dр? - Plp2 pi)/ Ц,д2
5.	Я = (pf+ рЦ2)/А-р1 cos gx -cos2 gr
6.	H = Plp2 - 2Plq2 - 2p2qx + ±qxq2
7.	H = Plp2 - 3Plq2 -p22 + 6q2p2 -
8.	H = Fp? - Plp2 + 2p2)/47 - 3g2.
9.	H = (p2 + pi)/^ ~~ -P2 cos ^2 "I" cos2
10.	Я = Dp?
13.8. Уравнения Гамильтона
Постановка задачи. Получить уравнения движения в форме
Гамильтона для консервативной механической системы с одной сте-
степенью свободы.
План решения
Для консервативной механической системы с одной степенью сво-
свободы уравнения Гамильтона *^ имеют вид
. он . дн
q= -^—, р = --^—5	I1)
dp	dq
Я — функция Гамильтона (§ 13.7), q, q — обобщенная координата и
ее скорость, р, р — обобщенный импульс и его скорость (§ 13.7).
1.	Выбираем обобщенную координату системы. Определяем кине-
кинетическую энергию системы Т, выражая скорости и угловые скорости
всех тел системы через обобщенную скорость.
2.	Определяем потенциальную энергию Я системы как функцию
обобщенной координаты.
3.	Записываем функцию Лагранжа L = Т — Я.
4.	Записываем функцию Гамильтона Я, выражая в Я = pq — L
обобщенную скорость q через обобщенный импульс р (§ 13.7).
*) Канонические уравнения механики.

13.8. Уравнения Гамильтона
327
5. Вычисляя частные производные функции Гамильтона по обоб-
обобщенному импульсу р и обобщенной координате д, записываем урав-
уравнения движения A).
Пример 1. Получить уравнения движения в форме Гамильтона
для консервативной механической системы с одной степенью сво-
свободы. Система состоит из невесомого стержня АВ длиной 2а и одно-
однородного цилиндра массой т радиусом Я. Под действием вертикаль-
вертикальной силы F стержень скользит по гладкой горизонтальной плоскости,
вращая цилиндр. Между стержнем и цилиндром проскальзывание
отсутствует. Сила F приложена к центру стержня, весом стержня
пренебречь (рис. 169).
В
Рис. 169
Рис. 170
Решение
1. Выбираем угол (р в качестве обобщенной координаты системы.
Определяем кинетическую энергию системы Т, выражая скорости и
угловые скорости всех тел системы через ф.
Для того, чтобы выразить угловую скорость ujz цилиндра через
ф, составляем кинематический граф (§ 8.5, с. 188):
о
??>
Здесь ОС = Л, С А = Rctg(p. В системе координат ху (рис. 170)
этому графу соответствуют кинематические уравнения
VAx =VOx-RuJzSin(
VAV = vOy + Ru;zcos(
¦ тг/2) - Яф ctg (p sin((p + тг),
- 7г/2) + Д(^ Ctg ^ COs((p + 7Г).
B)
Учитывая уравнения связей, vA = 0, vOx = vo =0, из второго
уравнения B) получаем
и = -
(р.
C)

328	.Гл. 13. Аналитическая механика
Первое уравнение системы B) в данной задаче не потребовалось. При
необходимости из него можно найти скорость vAx.
Кинетическую энергию системы, в которой массой обладает только
цилиндр, выражаем через обобщенную скорость:
т= ^ = mR2v2 ctg4 ^
2	4
2.	Определяем потенциальную энергию П системы как функцию
обобщенной координаты (р. При горизонтальном положении стержня
П = 0. Вычисляем работу силы F при перемещении в это положение:
П = Fa sin (p.
3.	Записываем функцию Лагранжа:
4. Записываем функцию Гамильтона Н = pq — L, выражая обоб-
обобщенную скорость q = ф через обобщенный импульс р. Дифферен-
Дифференцируем функцию Лагранжа по обобщенной скорости ф, вычисляем
обобщенный импульс
dL mR2 ф ctg4 (р
Р= =
дф = 2 '
Отсюда находим обобщенную скорость ф = 2ptg4 (р/\тВ?). Функция
Гамильтона приобретает вид
H = pq-L = У \*
5. Вычисляя частные производные функции Гамильтона по обоб-
обобщенному импульсу р и обобщенной координате <р, записываем урав-
уравнения движения A):
дН	дН
op	dip
В результате получаем, что
mR1	mR1 cos5 ^
Интегрирование нелинейной системы дифференциальных уравнений
D) можно выполнить численно. В системе Maple V для этого пред-
предназначен оператор dsolve (с. 373).

13.8. Уравнения Гамильтона	329
Замечание. Кинематическое соотношение C) можно получить
координатным методом. Из АОАС (рис. 170) найдем координату
хА = хо — R/ simp. Дифференцируя жА, с учетом хо = const, полу-
получаем vAx = Rip cos (p/ sin (p. Из равенства проекций скоростей точек
А и С на ось АС имеем vAx cos (p = —ujzR. Отсюда следует C).
Пример 2. Вывести уравнения движения консервативной меха-
механической системы с одной степенью свободы в форме Гамильтона.
Система представляет собой планетарный механизм, расположенный
в вертикальной плоскости (рис. 171). К сателлитам 1 и 2, закреп-
закрепленным на водиле О А длиной 6г1, приложены моменты Мх и М2.
Даны массы т^ т2 и радиусы R± = R2 = 2r1. Массой водила О А и
трением на осях пренебречь. Сателлит 1, блок с радиусом инерции
%х = г-р катится без проскальзывания по внутренней поверхности
неподвижного цилиндра радиусом 8гг Сателлит 2, однородный ци-
цилиндр, находится во внешнем зацеплении с меньшим ободом блока
1.
Решение
1. Выбираем угол (р в качестве обобщенной координаты системы.
Определяем кинетическую энергию системы Т, состоящую из кине-
кинетических энергий тел 1 и 2. Выражаем угловые скорости uj^z, oj2z
сателлитов и скорости их осей через обобщенную скорость ф. Со-
Составляем кинематические графы (§ 8.5, с. 188):
^ ов „ ^ оа . . Яг Тг	/гЧ
О—> В- О—>А; А—>К,	E)
ч>	v	ч>
^С^А.	F)
if	if

330
Гл. 13. Аналитическая механика
Здесь С — точка контакта сателлитов, К — точка контакта сател-
сателлита 1 и неподвижного цилиндра (рис. 172). В системе координат ху
этим графам соответствуют следующие кинематические уравнения:
'> vBy = vOy +ОВф cos if,
vBx = vOx -
Bx
Ox
vAx = vox -
vAx
ox
VKx = VAx - Rl Viz
vAy = vOy + ОАфcos <p
VKy = VAy + Rl "lz C0S
VAx=V
Вх ~ R2 UJ2z Sm ^ ~~ Г1 Ulz Sm
vAy = vBy
(8)
¦ R2 uj2z cos (p + r1 a;lz cos <^?.
Учтем уравнения связей. Точка касания внешнего обода сателлита
1 и неподвижной цилиндрической поверхности при отсутствии про-
проскальзывания является мгновенным центром скоростей, и ее скорость
Рис. 172
равна нулю: vKx = vKy = 0. Кроме того vOx = vOy = 0. В итоге из
уравнений G,8) с учетом соотношений между радиусами, данными в
условии задачи, получаем угловые скорости
A0)
и проекции скоростей:
vAx = Rx uolz sin if = -
vAy = -Rx uj1z cos ip = 6ггф cos (p,
vBx = — ОВф sin if = — 3r1<J3sin <p,
г;в?/ = ОВф cos ^ = Зг-j^^cos <^.
Оба сателлита совершают плоское движение. Кинетическую энергию
системы выражаем через обобщенную скорость ф:
Г =
Т —
12 —
"I
2

13.8. Уравнения Гамильтона	331
Подставляем сюда выражение для момента инерции блока, J1 = тх%\,
однородного цилиндра, J2 = m2R2/2, и соотношения (9,10):
Т = -^гА{Ьт1 + Зш2).	A1)
2. Определяем потенциальную энергию П системы как функцию
обобщенной координаты (р. Находим обобщенную силу:
G1-vA-^G2-v + M-C + M- ш
Ф
По условию моменты М2 и М1 направлены по часовой стрелке, сле-
следовательно проекции их векторов на ось z берем со знаком минус:
М2 = {0, 0, —М2}, М1 = {0, 0, —М1}. Векторы сил тяжести имеют
вид G1 = {0, —т-^д, 0}, G2 = {0, —т2д, 0}. Учитывая (9,10), полу-
получаем обобщенную силу Q:
Q = -ЗМ2 + ЗМ± - 3r1gBm1 + m2) cos (p.
Обобщенная сила и потенциальная энергия связаны дифференциаль-
дифференциальной зависимостью:
«--%¦
Интегрируя A2), получаем
П = ЗМ2(р - ЗМг(р + 3r1gBm1 + m2) sin <p.
Константу интегрирования можно брать произвольной, так как по-
потенциальная энергия вычисляется с точностью до постоянной вели-
величины. В данном случае константа равна нулю, что соответствует
горизонтальному положению водила в нулевом уровне потенциальной
энергии.
3.	Записываем функцию Лагранжа L:
9C2г?
L = Т-П = ——LEm
4.	Записываем функцию Гамильтона Н, выражая в Н = pq — L об-
обобщенную скорость ф через обобщенный импульс р. Дифференцируя
функцию Лагранжа по обобщенной скорости ф, вычисляем обобщен-
обобщенный импульс р:
р = — = 9 г\ ф E т1 + 3 т2).

332	Гл. 13. Аналитическая механика
Отсюда выражаем обобщенную скорость:
.	Р
Функция Гамильтона приобретает вид
5. Вычисляя частные производные функции Гамильтона по обоб-
обобщенному импульсу р и обобщенной координате <р, записываем урав-
уравнения движения A):
. дН . дН
др	д(р
В результате получаем искомую систему дифференциальных уравне-
уравнений для функций if и р:
•	Р
=
^ 9г1(Бт1-\-Зт2)'
р = 3(М1 — М2) — 3r1gBm1 + m2) cos (p.
Замечание. Для определения угловых скоростей сателлитов в пла-
планетарном механизме можно воспользоваться формулой Виллиса [17]:
где к — передаточное число от колеса 1 к колесу 2 (с. 153), п — число
внешних зацеплений между колесами 1 и 2, uo{)z — угловая скорость
водила. В примере 2 во внешнем зацеплении находятся колеса 1 и 2:
("lz ~ "oJ/Ks - "Oz) = ~R2/rn
и во внутреннем — колесо 1 с неподвижным (сс;цил = 0) цилиндром:
К, - "oJ/K-я - "oJ = (ОА + R^/R,.
Отсюда следуют соотношения (9).
Условия ЗАДАЧ. Получить уравнения движения в форме Гамиль-
Гамильтона для консервативной механической системы с одной степенью
свободы. В качестве обобщенной координаты взять угол (р (задачи
1-6, 8-9) или смещение х (задача 7). Качение цилиндров происходит
без проскальзывания, трением ползунов и муфт пренебречь.

13.8. Уравнения Гамильтона
333
1.
5.
М
Однородный цилиндр массой т катится
без сопротивления по горизонтальной по-
поверхности. К цилиндру жестко прикреп-
прикреплен невесомый стержень длиной а, к кото-
которому приложена вертикальная сила F. Ра-
Радиус цилиндра R.
Горизонтально движущийся ползун А мас-
массой т соединен с вертикально движущимся
ползуном В. Массами стержня АВ и пол-
ползуна В пренебречь; АВ = а. На ползун В
действует вертикальная сила F.
К невесомому стержню АВ, скользящему
без сопротивления по ребру опоры, прило-
приложен момент М. Стержень шарнирно со-
соединен с вертикально движущимся ползу-
ползуном массой га.
В шарнире А механизма, состоящего
из двух невесомых стержней одинаковой
длины О А = АВ = а и горизонтально дви-
движущегося ползуна В, сосредоточена масса
В гп. К ползуну приложена горизонтальная
сила F.
Невесомый кривошип О А = а, к которому
приложен момент М, приводит в движение
вертикально движущийся поршень массой
т. Колесико Л, массой и размерами кото-
которого пренебречь, катается без сопротивле-
сопротивления по нижней поверхности поршня.
Шарнирный параллелограмм ОАА'О', со-
состоящий из невесомых стержней, приво-
приводится в движение моментом М. Общая
масса муфты В и горизонтально движуще-
движущегося штока равна т; О А = О' А' = а.

334
Гл. 13. Аналитическая механика
7.
1712
а
8.
9.
10.
в
т
Груз массой гп\ приводится в движение
клином массой 7П2, скользящим без тре-
трения по неподвижной вертикальной поверх-
поверхности и по ребру груза. Дан угол а.
Однородный цилиндр радиуса R, массой
которого можно пренебречь, свободно ка-
катается по горизонтальной плоскости. На
ободе цилиндра помещена точка массой т.
Два одинаковых цилиндра, массой т каж-
каждый, соединены невесомым стержнем дли-
длиной а. Цилиндр А катится без проскаль-
проскальзывания по горизонтальной плоскости, ци-
цилиндр В — по вертикальной. На ось ци-
цилиндра А действует горизонтальная сила
F.
Невесомый стержень АВ = а вращается
вокруг неподвижного шарнира А под дей-
действием вертикальной силы F, приложенной
к его концу В, сообщая горизонтальное
движение параллелепипеду массой т высо-
высотой h. Стержень скользит по ребру парал-
параллелепипеда без трения.
Ответы. Функция Лагранжа L и уравнения Гамильтона
1. L =
J - Fa sin <p,
р = —Facosip.
2. L = (l/2)m(a(psm(pJ - Fa simp,
ф = p/(a2m sin2 <??),
p = cos ip{p2/{ma2 sin3 (p) — Fa).

13.8. Уравнения Гамильтона	335
3.	L = A/2)т(аф/ cos2 (рJ - am gig (р +
у = pcos4 (p/(ma2),
р = р2 sin 2у cos2 (р/(та2) + М — тда/ cos2 у
4.	L = A/2)т(ауJ — mgasimp — 2Facos<^,
^ =р/(а2т),
р = — а(тд cos (р — 2Fsm(p).
Б. L = A/2)т(аф cos (^J - тда sin <p + М(р,
ф = р/(а2т cos2 <р),
р = —р2 sin (р/{та2 cos3 у?) — тда cos <?? + М.
6.	L = (l/2)m(a^sin^J + My?,
<? = р/(а2т sin2 у?),
р = р2 cos (p/(ma2 sin3 у?) + М.
7.	L = A/2)х2(т1 + ?тг2 ctg2 a) + m2 ^ ж ctg a,
ж = р/(т1 + т2 ctg2 a),
8.	L = тA1фJA + sin у?) — Rmgsimp,
ф = р/'BR2m(l + simp)),
р = р2 cos (p/DmR2(I + sin<?>J) — mgR cos (p.
9.	L = C/4:)та2ф2 — amgsunp — Fa cosy,
p = —a(mg cos (p — F sin y?).
10. L = A/2)т(кф/ sin2 yJ - Fa sin <p,
y? = psin4 (p/(mh2),
p = —p2 sin2 у sin 2(p/(mh2) — Fa cos y>.

Глава 14
МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ
В разделе МАЛЫЕ КОЛЕБАНИЯ СИСТЕМБ1 вы научитесь опре-
определять частоты малых собственных колебаний механической системы
с двумя степенями свободы. Другие темы этого раздела, количество
которых так велико, что они могут составить содержание отдельной
книги, остались за пределами РЕШЕБНИКА. Задачи о вынужденных
колебаниях, колебаниях при наличии сопротивления и многие другие
содержатся, например, в [18], [20].
14.1. Система с двумя степенями свободы
Постановка задачи. Механическая система с двумя степенями
свободы состоит из твердых тел, соединенных линейно упругими
пружинами. Определить частоты собственных колебаний системы.
План решения
Задачу решаем с помощью уравнения Лагранжа 2-го рода.
1.	Выбираем две обобщенные координаты ж1? х2.
2.	Вычисляем кинетическую энергию и обобщенные силы. Состав-
Составляем два уравнения Лагранжа 2-го рода.
3.	Записываем полученную систему в стандартной форме уравне-
уравнений колебаний системы с двумя степенями свободы:
CL-1 -I X -1 ~\ d-t су X су ~Т~ С-1 -I X -1 ~\ С-1 су X су 	 U ^
LLcy-i Л/ -|	| (JLcycyJucy | (s-icydu-i	| L^cycyJL/су 	 \J •
где a^,i,j = 1,2, — инерционные коэффициенты, Cij,hj = 1,2, —
обобщенные коэффициенты жесткости тли квазиупругие коэффици-
коэффициенты. Решение системы A) будем искать в форме хх = А± sin(a;^+/?0),
х2 = А2 sm(u;t + /?0), где А±,А2,Р0 — неизвестные постоянные; ио
— круговая частота колебаний. Система A) после сокращения на

14.1. Система с двумя степенями свободы	337
sm(ojt + /30) примет вид
V 11	11 ) 1 V 12	12 ) 2 ~~ '	,^\
(с12 — а12ии2)А1 + (с22 — а22ии2)А2 = 0.	^ '
4.	Условием существования нетривиального решения системы B)
для А-у и А2 является равенство определителя системы нулю. Отсюда
получаем уравнение частот:
5.	Решая C), находим частоты колебаний системы.
Пример. Механическая система с двумя степенями свободы со-
состоит из двух однородных цилиндров и двух линейно упругих пру-
пружин. Цилиндр А массой тА = 50 кг может кататься без проскальзы-
проскальзывания и трения качения по горизонтальной поверхности. Его ось со-
соединена с неподвижной стенкой горизонтальной пружиной 1. Ободы
цилиндров связаны нитью и
пружиной 2. Цилиндр В мас-
I (	^ ( q )	сои тв = ^0 кг вращается во-
вокруг неподвижной оси. Жест-
Жесткость пружин, работающих и
на сжатие и на растяжение,
Рис- 173	одинакова: с = 90 Н/м.
Массой пружин пренебречь. Найти частоты собственных колебаний
системы.
Решение *)
Задачу решим двумя способами. Различие между ними — в вы-
выборе обобщенных координат и форме вычисления обобщенных сил в
уравнении Лагранжа.
1-й способ
1.	В качестве обобщенных координат выбираем удлинения пружин
(рис. 174). Связи предполагаем идеальными и их реакции на рисунке
не показываем.
2.	Кинетическую энергию системы, состоящую из суммы кинети-
кинетических энергий двух тел: Т = ТА + ТВ, выражаем через обобщенные
скорости хх и х2. Кинетическая энергия однородного цилиндра Л,
*) Решение задачи в системе Maple см. § 17.3, с. 373
22 М.Н. Кирсанов

338
Гл. 14. Малые колебания системы
катящегося без проскальзывания по неподвижной плоскости, вычис-
вычисляется по формуле D) на с. 242:
ТА = C/4)mAif.
D)
Кинетическая энергия вращения цилиндра В вокруг неподвижной оси
имеет вид Тв = Jbujb/2, где Jв = mBRB/2.
Рис. 174
Рис. 175
Левый конец пружины 2 движется со скоростью 2х± (рис. 175),
скорость удлинения пружины х2. Скорость правого конца пружины
равна скорости точки обода цилиндра В и равна сумме 2хх + ж2,
отсюда иов = Bх1 + x2)/RB — угловая скорость вращения цилиндра
В. Таким образом получаем Тв = тпвBх1 + х2J/4. Кинетическая
энергия всей системы
Т =
(l/4)mBBir1 + х2J.
Для того, чтобы вычислить обобщенную силу Q1? даем возмож-
возможное перемещение (удлинение) 5хх пружине 1, фиксируя удлинение
пружины 2, или заменяя пружину 2 нерастяжимой нитью (рис. 176).
Рис. 176
Рис. 177
Воспользуемся формулой Q1 = SA1/Sx1, где 8А1 = — ^упр Sxv Так
как ^уПр = сж1? то Q1 = —сж1. Аналогично, фиксируя удлинение
пружины 1, растягиваем пружину 2 на 5х2 (рис. 177) и вычисляем
fe2. Отсюда Q2 = —сж2.
(!L42 = —

14.1. Система с двумя степенями свободы	339
Записываем систему уравнений Лагранжа 2-го рода:
d (дТ\ дТ „
dt \дх1
j
dt \dxj дх2 ~Qt
Вычисляем производные, входящие в уравнения Лагранжа:
дТ	ч дТ
—	= l.bmAx1 + mBBx1 + ar2), — = О,
дТ	дТ
—	=0.5твBх1+х2),	— =0.
Уравнения Лагранжа принимают вид
Bтв + 1.БтА)х1 + твх2 = —сж1?
E)
3. Записываем E) в стандартной форме уравнений колебаний сис-
системы с двумя степенями свободы A). Инерционные коэффициенты
для данного примера имеют вид
ап = 2тв + 1.5тА, а12 = а21 = тБ, а22 = 0.5ттт,б.
Коэффициенты жесткости системы сп = с22 = с, с12 = с21 = 0. Коэф-
Коэффициенты жесткости и инерционные коэффициенты образуют сим-
симметричные матрицы. Предполагая, что каждая обобщенная коорди-
координата меняется по закону гармонических колебаний, решение системы
A) ищем в форме
хх = Ах sin(cc;? + /30), х2 = А2 sin(ujt + /30),
где A1,A2,oj,[3o — неизвестные постоянные. Система E) после со-
сокращения на sm(ojt + /30) принимает вид
(с - Bтв + 1.5шА) а;2)^! - mBJ1A2 = О,
-шБо;2Л1 + (с - О.Бтви;2)А2 = 0.
Из условия существования нетривиального решения этой системы для
Ах и А2 получаем уравнение частот:
-тАтвы4	^	^сш2 + с2 = 0.	G)
22*

340
Гл. 14. Малые колебания системы
Подставляем числовые данные задачи, решаем биквадратное урав-
уравнение G) и находим две частоты собственных колебаний системы:
ии1 = 0.871 рад/с, ии2 = 3.774 рад/с.
2-й способ
1.	В качестве первой обобщенной координаты выбираем смещение
х цилиндра А, а в качестве другой — угол поворота (р цилиндра В
(рис. 178). Таким образом, q± = ж, q2 = (р.
2.	Кинетическую энергию системы, состоящую из суммы кинети-
кинетических энергий двух тел, Т = ТА-\-Тв, выражаем через обобщенные
скорости х ж ф. Кинетическая энергия цилиндра А вычисляется так
же, как и в 1-м способе по формуле D): ТА = ЗтАх /4. Кинетическая
энергия вращения цилиндра В
Тв =
= твф211в/4.
Кинетическая энергия всей системы Т = C/4)тАж2 + т
Для того, чтобы вычислить обобщенные силы находим потенциаль-
потенциальную энергию системы. Силы тяжести работу не совершают, поэтому
вся потенциальная энергия содержится в пружинах. Удлинение пер-
первой пружины равно х. Левый конец пружины 2 смещается на 2ж,
правый — на RB(p в ту же сторону (рис. 179).
Рис. 178
2х
Рис. 179
Удлинение второй пружины равно по модулю \2х—В,вф\. Потенци-
Потенциальная энергия пружин, не имеющих предварительного напряжения,
имеет вид
Обобщенные силы вычисляем по формулам
Qi = —?¦ = ~
= -cR
- 2x).

14.1. Система с двумя степенями свободы	341
Вычисляем производные, входящие в уравнения Лагранжа:
дТ _	.	дТ _
дх	А	дх
дТ	дТ
gT=0.5mBRB<p, — =0.
Уравнения Лагранжа принимают вид
1.ЪтАх = — сEх — 2RBLp),
(8)
0.5mBR23(fi = —cRB(RB(p — 2х).
3. Записываем (8) в стандартной форме уравнений колебаний сис-
системы с двумя степенями свободы A). Инерционные коэффициенты
для данного примера имеют вид
12 = а21 = 0, а22
Коэффициенты жесткости имеют вид сп = 5с, с12 = с21 = —2cRB,
с22 = сД^. Решение системы A) ищем в форме гармонических
колебаний: х = А± sm(u;t + /?0), ^ = ^2 sin(^^ + /^о)' гДе ^-ij^-2'^'^o
— неизвестные постоянные. Система (8) после сокращения на общий
множитель sm(u;t + /?0) принимает вид
Eс - 1.5гаА ou2)A1 - 2cRBA2 = 0,
-2сАх + RB(c - 0.5mBuj2)A2 = 0.
Для неизвестных амплитуд колебаний А± и А2 система (9) яв-
является однородной. Из условия существования нетривиального ре-
решения приравниваем нулю определитель системы и получаем урав-
уравнение частот, в точности совпадающее с G). Таким образом, с
другим набором обобщенных координат мы находим те же частоты:
о;2J = G5 ± Зл/505)/Ю, или ш1 = 0.871 рад/с, ш2 = 3.774 рад/с.
Замечание. Решение задачи равносильно отысканию собствен-
собственных значений матрицы А~^С, где А и С матрицы инерционных и
квазиупругих коэффициентов. Действительно, представим A) в виде
Ах + Сх = 0, где х = {х1,х2}. Умножим это уравнение на обрат-
обратную матрицу А~^. Получаем, что х + А~^Сх = 0. Решение ищем
в форме гармонических колебаний, записываем систему однородных
линейных уравнений для амплитуд колебаний, определитель которой

342
Гл. 14. Малые колебания системы
имеет вид det(—ио2Е + A 1С), где Е — единичная матрица. Таким
образом, квадраты частот равны собственным значениям матрицы
А'1 С (Решебник ВМ, §2.10.)-
Условия ЗАДАЧ. Механическая, система с двумя степенями сво-
свободы состоит из двух однородных цилиндров и нескольких линейно
упругих пружин с одинаковой жесткостью с. Цилиндры катаются
без проскальзывания и сопротивления по горизонтальной поверх-
поверхности, пружины в положении равновесия не имеют предваритель-
предварительного напряжения. Массой пружин пренебречь. Определить час-
частоты собственных колебаний системы.
1. гпа = 9 кг, тв = 6 кг,
с = 1 Н/м.
2. гпа = 7 кг, тв = 4 кг,
с = 3 Н/м.
3. гпа = 5 кг, тв = 6 кг,
с = 5 Н/м.
4. гпа = 3 кг, тв = 6 кг,
с = 7 Н/м.
А
В
5. гпа = 1 кг, тв = 4 кг,
с = 9 Н/м.
А
6. тпл = 10 кг, тв = 3 кг,
с = 6 Н/м.
7. тл = 8 кг, тв = 3 кг,
с = 8 Н/м.
Б
8. тл = 6 кг, тв = 5 кг,
с = 10 Н/м.

14.2. Колебания узла фермы
343
9. VflA = 4 КГ, Г
с = 12 Н/м.
= 1 кг,
10. VflA = 2 КГ, ГПв = 5 КГ,
с = 14 Н/м.
Инерционные коэффициенты системы an, a22 приведены в кг, ко-
коэффициенты жесткости сп, с12, с22 — в Н/м и собственные частоты
в рад/с. В качестве обобщенных координат ж1? ж2 взяты линейные
перемещения осей цилиндров А ж В соответственно. При таком вы-
выборе обобщенных координат а12 = а21 = 0.
Ответы
1
2
3
4
5
6
7
8
9
10
ац
13.5
10.5
7.5
4.5
1.5
15.0
12.0
9.0
6.0
3.0
9.0
6.0
9.0
9.0
6.0
4.5
4.5
7.5
1.5
7.5
си
8
15
20
14
9
30
32
50
12
28
С12
-4
-12
-20
-14
-18
-12
-16
-10
-12
-14
С22
9
24
45
63
72
30
40
60
24
84
001
0.617
0.854
1.065
1.456
1.514
1.257
1.407
2.248
0.968
2.678
0J2
1.101
2.168
2.556
2.827
3.963
2.662
3.094
2.916
4.131
3.655
14.2. Колебания узла фермы
Постановка задачи. В одном из шарниров плоской фермы нахо-
находится точка с массой т. Стержни фермы упругие. Ферма располо-
расположена в горизонтальной плоскости. Пренебрегал массой стержней,
определить частоты собственных малых колебаний шарнира фермы.
План решения. Система имеет две степени свободы. Основные
уравнения задачи следуют из уравнения Лагранжа 2-го рода. В ка-
качестве обобщенных координат принимаем горизонтальные и верти-
вертикальные перемещения узла х1 и х2- Предполагая, что упругие силы
линейно зависят от перемещений, записываем уравнение Лагранжа
2-го рода в матричном виде:
Ах + Сх = 0,
A)

344	Гл. 14. Малые колебания системы
где А — матрица инерции, С — матрица жесткости. Матрица об-
обратная С — матрица податливости В = С, коэффициенты которой
(перемещения от единичных сил) вычисляем по формуле Максвелла-
Мора [20]:
B)
где I — длины стержней, Е и F — модуль упругости и площадь по-
поперечного сечения стержней, S- — безразмерное усилие в стержне
с номером /1 от действия единичной горизонтальной (г = 1) или вер-
вертикальной (г = 2) нагрузки на шарнир с массой. Произведение ЕЕ
называют жесткостью, в данной задаче она считается одинаковой
для всех стержней фермы. Коэффициенты bi j имеют простой фи-
физический смысл: bi ¦ — это перемещение узла в направлении г под
действием единичной силы, действующей в направлении j. Измеря-
Измеряются Ъ- ¦ в м/Н. По теореме взаимности Бетти *^ Ь- ¦ = Ъ- •.
Кинетическая энергия точки имеет вид Т = т(х\ + ж|)/2, следо-
следовательно, матрица инерции является диагональной:
A- I m °
Умножаем A) на В и делаем подстановку х = —о;2ж, что равносильно
замене хх = Ах $m{ujt + /30), х2 = А2 sm(u;t + /30), где АХ,А2 — ам-
амплитуды, uj — частота, /30 — начальная фаза колебаний. Получаем
однородную систему
m<jj2Bx — х = 0,
имеющую ненулевое решение в том случае, если ее определитель равен
нулю. Следовательно, задача свелась к поиску собственных значений
Л = l/{muj2) матрицы В.
1.	К шарниру, наделенному массой, прикладываем единичную (без-
(безразмерную) горизонтальную силу. Определяем усилия в стержнях
*Sf1 , /i = 1,..., п, где п — число стержней фермы.
2.	Прикладываем к этому же шарниру единичную вертикальную
силу. Определяем усилия в стержнях S2 .
Энрико Бетти A823-1892) — итальянский математик.

14.2. Колебания узла фермы
345
3. Используя формулу Максвелла-Мора B), вычисляем коэффици-
коэффициенты податливости Ь{ .. Записываем их в симметричную матрицу
В =
2
4.	Вычисляем собственные значения (Решебник ВМ, §2.10, с. 68)
\12 матрицы В.
5.	Находим частоты собственных колебаний uj1 = 1/д/ттгЛ1,
си2 = 1/у/т\2.
Пример. В шарнире С плоской фермы находится точка с массой
т = 9 кг (рис. 180). Жесткость всех стержней фермы одинакова
EF = 0.1 кН, Z = 1 м. Ферма расположена в горизонтальной плос-
плоскости. Пренебрегая массой стержней, определить частоты собствен-
собственных малых колебаний шарнира.
Решение
1. К шарниру С, наделенному массой, прикладываем единичную
(безразмерную) горизонтальную силу (рис. 181). Методом Риттера
или методом вырезания узлов (§ 2.2, с. 37) определяем усилия в стерж-
стержнях: S± x = S± 2 = S± 4 = S± 5 = 0, S± з = —1. В усилии S± первый ин-
индекс указывает направление приложенной единичной силы.
^0° бо\/
/
Рис. 180
V
/
1/2,
1
l/
С
\2
4
Рис.
3
/
181
/
хв
ХА/
С/
tl
\
Рис.
J-1
/
182
/
Хв
Индекс 1 соответствует горизонтальной единичной силе, 2 — верти-
вертикальной силе. Второй индекс — номер стержня. Номера стержней
указаны на рис. 181.
2. К шарниру С прикладываем единичную вертикальную силу
(рис. 182). Определяем усилия в стержнях: S2 i = 0, 522 = 1.155,
52„ = -0.577, 5,4 = 5,5 = 1.155*).
*) Определение усилий в стержнях с помощью Maple V см. § 15.1, с. 350.

346
Гл. 14. Малые колебания системы
3. По формуле Максвелла-Мора B) находим коэффициенты подат-
податливости bi .. Промежуточные результаты заносим в таблицу:
1
2
3
4
5
0
0
-1
0
0
0
1.155
-0.577
-1.155
-1.155
1
1
1
1
1
/ Я2
0
0
1
0
0
1.000
1/j,Sij/j,S2,ij,
0
0
0.577
0
0
0.577
7 o2
^^2,/Lt
0
1.333
0.333
1.333
1.333
4.333
Суммируя три последних столбца, получаем коэффициенты подат-
податливости, отнесенные к жесткости EF:
Ь1Д = 1.000/(#F), Ъ12 = 0.5
и записываем их в виде симметричной матрицы
В =
0.01 0.00577
0.00577 0.04333
4. Вычисляем собственные значения Л: 2 матрицы В. Приравни-
Приравниваем нулю определитель
ъи-\
Решаем квадратное уравнение и находим собственные значения:
Хг = 0.044305, Л2 = 0.009028.
6. Находим частоты собственных колебаний (круговые частоты):
ш1 = 1/у/шЛ1 = 1.584 рад/с, сс;2 = 1/у/шЛ2 = 3.508 рад/с.
Условия ЗАДАЧ. Б одном из шарниров плоской фермы (на ри-
рисунке выделен) находится точка с массой т. Стержни фермы уп-
упругие. Жесткость стержней EF; I = 1 м. Ферма расположена в
горизонтальной плоскости. Пренебрегал массой стержней, опреде-
определить частоты собственных малых колебаний шарнира фермы.

14.2. Колебания узла фермы
347
1.
EF = 0.9 кН, т = 1 кг.
EF = 1.6 кН, т = 9 кг.
5.
1/2
1/2
EF = 3.6 кН, т = 25 кг.
7.
ZV3/2
EF = 0.9 кН, m = 49 кг.
6.
ZV3/2
= 1.6 кН, т = 4 кг.
= 2.5 кН, m = 16 кг.
EF = 4.9 кН, m = 36 кг.
8.
EF = 1.6 кН, т = 64 кг.

348
Гл. 14. Малые колебания системы
9.
1/2
1/2
EF = 2.5 кН, т = 81 кг.
EF = 3.6 кН, т = 1 кг.
Коэффициенты податливости, умноженные на жесткость EF, даны
в м, частоты — в рад/с. Индекс 1 соответствует горизонтальной еди-
единичной силе, 2 — вертикальной.
Ответы
1
2
3
4
5
6
7
8
9
10
buEF
1.000
1.000
5.828
5.000
2.621
1.889
9.000
1.000
2.775
3.828
b12EF
-1.000
0.000
1.000
2.887
-1.207
-0.321
0.000
0.000
-0.736
0.000
b22EF
3.828
1.732
1.000
3.000
1.207
1.074
1.732
1.000
0.592
1.000
Ml
14.733
15.197
5.431
4.706
6.593
8.250
1.429
5.000
3.208
30.665
36.323
20.000
14.897
12.859
16.718
11.889
3.256
5.000
9.175
60.000

Часть IV
РЕШЕНИЯ В СИСТЕМЕ MAPLE V
Все задачи, приведенные в решебнике, могут быть решены в сис-
системе аналитических вычислений, например, Maple V, Mathematica 4,
Derive. В некоторых случаях такие решения представляют собой
вычисления по формулам, подготовленным вручную, например, ре-
решения систем линейных уравнений, что, конечно, упрощает работу
учащегося, концентрируя его внимание на сути предмета. Однако
преимущества системы аналитических вычислений проявляются наи-
наибольшим образом в совместном применении аналитических возмож-
возможностей системы и эффективных алгоритмов расчетов. Здесь мы при-
приведем несколько программ решения задач статики, кинематики и ди-
динамики, в которых использованы такие алгоритмы.
В качестве условий задач взяты примеры, приведенные в решеб-
решебнике (за исключением задачи Программы 4). К текстам программ
даны краткие пояснения свойств основных операторов Maple V и
некоторые формулы. Более подробные описания системы Maple V
можно найти в книгах [8], [9], [12], [13].
Первой командой каждой программы является команда restart —
очистка памяти и отмена всех ранее назначенных команд и условий.
Все команды в Maple V вводятся после знака > и заканчиваются точ-
точкой с запятой, если результат требуется вывести сразу же на экран,
или двоеточием, если выводить результат не надо. Комментарии за-
записаны на строках без знака > или после знака #.
Качество графики системы Maple V можно повысить, увеличив
масштаб изображения (CTRL 3...CTRL 6), пропорционально умень-
уменьшив при этом шрифт в интерфейсе системы (Format — Styles — С
Maple Input - Modify).
Тексты программ 1—9 (с анимацией, которая в решебнике приво-
приводится не для всех программ) и программы для решения других задач
механики с примерами и подробными пояснениями можно найти на
авторской странице Интернет: www.academiaxxi.ru/solverTM.html.

Глава 15
ПРОГРАММЫ ПО СТАТИКЕ
15.1. Расчет фермы
УСЛОВИЕ ЗАДАЧИ. Определить усилия в стержнях плоской фермы
(рис. 28, с. 46).
Решение
В основу расчета положим метод вырезания узлов *^ . В стати-
статически определимой неизменяемой ферме с N узлами, стержней всего
2N — 3. Для N узлов составляем 2N уравнений проекций на оси ж, у.
Включаем в число стержней три опорные стержня (два для неподвиж-
неподвижной опоры А и один для опоры В, рис. 29). Таким образом, число
уравнений совпадет с числом неизвестных.
Описание программы
Программа (с. 353, 354) состоит из трех блоков.
1. Ввод данных. Задаем число узлов и число стержней фермы,
величины нагрузок (в кН), углы. Оператор evalf переводит символ
Pi, в формат вещественного числа тг.
Для алгоритмизации процесса составления уравнений пронуме-
пронумеруем стержни и узлы (рис. 183). Шарниры 8, 9, 10 необходимы для
ориентации опорных стержней 12, 13, 14. Для этих шарниров урав-
уравнения равновесия не составляются.
Координаты узлов х, у задаем в виде векторов (массивов) с N +
3 компонентами. Начало координат помещаем в опоре А (узел 1).
Вектор заключен в скобки < > , элементы отделены вертикальными
черточками |.
Указываем номера точек приложения (Nbeg) векторов усилий в
стержнях и номера их концов (Nend). Точка приложения выбирается
условно, так как стержень подходит к двум узлам, и в качестве на-
начала вектора усилия можно взять любой из них.
Алгоритм Горячева В.Н., Резунова А.В.

15.1. Расчет фермы
351
2. Рисунок фермы. Для контроля ввода геометрических величин
изображаем ферму средствами графики Maple V. Для этого задейст-
задействуем оператор вывода графических объектов на экран display.
5	ю	6	11	7
Рис. 183
Изображение стержня с номером г присваиваем переменной R[i]
в цикле по числу стержней, включая опорные.
Одна из форм оператора цикла в Maple имеет вид
for i from il by i2 to i3 do ...od.
Шаг by i2 и начальное значение from il по умолчанию приняты
равными 1 и могут опускаться. Оператор PLOT (CURVES ( [[xl,yl] ,
[х2 ,у2] ] )) создает графический объект — отрезок с концами в точ-
точках с координатами (ж1,г/1) и (ж2,г/2).
Для вывода номеров стержней и узлов выбираем шрифт и раз-
размер. Эти значения заносим в переменную Шрифт. В Maple для пе-
переменных можно использовать русские буквы, программы при этом
читаются легче. В отдельных циклах создаются графические объ-
объекты Шарнир [i] — номера узлов, Стержень [i] — номера стержней.
Цвет номеров задает оператор COLOR (HUE, n). Выбор цвета опреде-
определяет дробная часть числа п. Можно также использовать оператор
COLOR (RGB, nl,nl,n3) и выбирать цвет оттенками красного, зеленого
и голубого, 0 < ni < 1.
Оператор для изображения нагрузок — arrow. Параметры стре-
стрелок (толщина стрелки, толщина острия, отношение длины острия к
длине стрелки и цвет) присвоены переменной arw *' .
Чтобы не писать длинный список объектов, для вывода изображе-
изображения используется запись seq(R[i] ,i=l. .M) — краткая форма прос-
*) В пакетах plots и plottools системы Maple 7 оператор arrow опре-
определяется различным образом, поэтому порядок подключения этих пакетов
для решения является существенным.

352	Гл. 15. Программы по статике
того перечисления R[l] , R[2] , . . . , R[M].
В операторе display можно использовать различные режимы (оп-
(опции); scaling=constrained — опция, задающая одинаковый по осям
координат масштаб рисунка. Если после оператора display поста-
поставить не двоеточие, а точку с запятой, то на экране появится изобра-
изображение фермы (рис. 183).
3. Вычисления. Косинус угла усилия S[i], г = 1,...,М с осью ж,
приложенного к узлу j, поместим в переменную типа двумерного мас-
массива G [2 j -1, i] . Косинус угла этого же усилия с осью у — в G [2 j , i] .
Элементы G предварительно обнуляются командой restart.
В теле цикла вычисляются G[i,j]. Каждое из неизвестных уси-
усилий Si входит в систему уравнений дважды: в уравнения равновесия
узлов Nbeg[i] и Nend[i] с разными знаками. Только усилия опорных
стержней с номерами М-2, М-1, М появляются в уравнениях равно-
равновесия по одному разу, отсюда необходимость условного оператора if
< М-2. . . fi*) .
Проекции нагрузки F-x и F , приложенной к узлу j, заносятся
соответственно в элементы 2 j — 1 и 2j вектора В правой части системы
уравнений.
LinearSolve(A,B) — оператор решения системы уравнений с мат-
матрицей А и вектором правой части В. Для того, чтобы этот оператор
работал, необходимо загрузить специальную библиотеку программ
командой with (Linear Algebra). Величины G[i, j] не образуют мат-
матрицу, поэтому для обращения к оператору решения LinearSolve ис-
используем преобразование Matrix(M,G). В результате решения значе-
значения усилий присваиваются элементам вектора S.
Для вывода на печать чисел и символов используем оператор фор-
форматного вывода printf. Сначала указываем формат вывода (список
форматов), потом список чисел. Вместо знака °/0 предполагается ста-
ставить число по формату, следующему за этим знаком. Формат g го-
годится для вывода целых и вещественных чисел. Формат N. Mf отводит
при печати N позиций под вещественное число, включая десятичную
точку и М позиций для дробной части числа. Число на своей позиции
сдвигается вправо. Перевод каретки на новую строку кодируется
как \п.
*) Для завершения цикла и условного оператора допустимо применять
end вместо od и f i.

15.1. Расчет фермы	353
Программа 1. Расчет фермы
>	restart: with(LinearAlgebra):
1.	Ввод данных
N - число узлов, М - число стержней фермы.
Нагрузки (кН), угол наклона опорного стержня
>	N:=7: M:=2*N: P:=30: Q:=15: F:=20:
>	alpha:=evalf(Pi/3): beta:=evalf(Pi/3):
Длина опорных стержней на рисунке
>	d:=l.:
Координаты узлов
>	х:=<0|2|6|81114|7 I-d|О I8-cos(beta)*d>:
>	у:=<0|О I 0|О I 2|2|2|О I-dI-sin(beta)*d>:
Номер узла начала и конца стержня-вектора
>	Nbeg:=<1|2|3|1|2|2|3|3|4|5|6|1|1|4>:
>	Nend:=<2|3|4|5|5|6|6|7|7|6|7|8|9|10>:
2.	Рисунок фермы
>	with(plots):with(plottools):
>	for i to M do
>	R[i]:=PLOT(CURVES([[x[Nbeg[i]],у[Nbeg [i]]],
>	[x[Nend[i]],у[Nend[i]]]])):
>	od:
>	Шрифт:=FONT(TIMES,BOLD,8):
>	for i to N+3 do
>	Шарнир[i]:=PLOT(TEXT([x[i],y[i]+0.3],convert(i,symbol)),
>	Шрифт,С0Ь(Ж(НиЕ,1)):
>	od:
>	for i to M do
>	Стержень[i]:=PL0T(TEXT([(x[Nbeg[i]]+x[Nend[i]])/2,
>	(y[Nbeg[i]]+y[Nend[i]])/2+0.3],
>	convert(i,symbol)),
>	Шрифт,COLOR(HUE,0.3)):
>	od:
Параметры стрелки на рисунке
>	arw:=0.05,0.2,0.2,color=red:
Проекции наклонной силы
>	Fx:=F*cos(alpha): Fy:=-F*sin(alpha):
23 M.H. Кирсанов

354	Гл. 15. Программы по статике
Изображение нагрузок
>	Fl:=arrow([x[2],y[2]],evalm([Fx,Fy]*0.05),arw):
>	Ql:=arrow([x[5],y[5]],evalm([-Q,0]*0.05),arw):
>	PI:=arrow([x[3],у[3]],evalm([0,-P]*0.05),arw):
>	Изображение фермы
>	display(Fl,Ql,Pl,seq(R[i],i=l..M),
>	seqCUIapmip[i],i=l..N+3),
>	Бед(Стержень[1],i=l..M),
>	scaling=constrained,axes=none);
3. Вычисления
Заполнение матрицы
>	for i to M do
>	Lx:=x [Nend[i]]-x[Nbeg[i] ] :
>	Ly:=y[Nend[i]]-y[Nbeg[i]]:
>	L:=evalf(sqrt(Lx~2+Ly~2)):
>	G [2*Nbeg [i]-1,i]:=Lx/L: G [2*Nbeg [i],i]:=Ly/L:
>	if i<M-2 then G[2*Nend[i]-l,i]:=-Lx/L:
>	G [2*Nend[i],i]:=-Ly/L: fi:
>	od:
Правая часть системы - вектор нагрузок
>	В:=<0|0 IFx|Fy|0|-Р|0|0 I-Q|0|0|0|0|0>:
Решение системы
>	S := LinearSolve(Matrix(M,G),-В):
>	printf(ce/.s\nc,c n	S	n	S c);
>	for i to M/2 do
>	printf(co/o3.Of°/09.3f 7o3.Of7o9.3f\nc,
>	2*i-l,S[2*i-l],2*i,S[2*i]);
>	od;
Ответы. Усилия даны в кН.
n
1
3
5
7
9
11
13
S
20.446
24.865
27.102
9.786
-25.804
-23.080
-24.240
n
2
4
6
8
10
12
14
S
29.486
-27.102
-9.786
25.804
-9.240
8.325
-26.651

15.2. Центр тяжести плоской фигуры	355
15.2. Центр тяжести плоской фигуры
Условие ЗАДАЧИ. Определить координаты центра тяжести од-
однородной плоской фигуры (рис. 74, с. 118).
Решение
Применим метод интегрирования по контуру. Для площади фи-
фигуры, ограниченной ломаной L с угловыми точками (х^ У{)^ = 1,..., тг,
существует точная формула ; :
/1 Г
dA=2j
/1 Г	1
dA2j V<1X ХAУ 2
A	(L)	i=1
Аналогично вычисляем координаты центра тяжести:
1 п
г=1
г=1
Принимается обход контура по часовой стрелке, последняя точка сов-
совпадает с первой и имеет номер (п + 1). Пронумеруем угловые точки
контура (рис. 184). Дугу окружности заменяем ломаной. Коорди-
Координаты угловых точек на дуге вычисляем по формулам
Х{ = 3 + Rcos(i7r/N), yi = i?sin(i7r/7V), i = l,...,N, R = 1,
где TV — число точек на окружности. Если фигура двусвязная, то
для использования этого метода необходимо сделать разрез, соеди-
соединяющий внутренний и внешний контур (рис. 185). При обходе фи-
фигуры внутренний контур будет пройден против часовой стрелки, и
его площадь станет отрицательной, а разрез, пройденный дважды в
противоположных направлениях, не внесет добавки в интеграл.
*) Фихтенгольц Г.М. Курс дифференциального и интегрального исчис-
ления.ТШ, М.:1970, с. 35.
23*

356
Гл. 15. Программы по статике
Рис. 184
Рис. 185
Описание программы
Вводим число точек контура без кругового выреза К и число то-
точек на вырезе N. Координаты точек заносим в переменные X,Y и
Xcircl, Ycircl, а затем в матрицу Т.
Программа 2. Центр тяжести
>	restart:
Число точек на дуге и число угловых точек
>	N:=20: K:=4: pi:=evalf(Pi): n:=K+N:
Матрица координат
>	F:=i*pi/N: X:=l,0,4,4: Y:=0,2,3,0:
Точки на дуге
>	Xcircl:=seqC+cos(F),i=l..N):
>	Ycircl:=seq(sin(F),i=l..N):
Матрица координат
>	T:=matrixB,n+1,[X,Xcircl,1,Y,Ycircl,0] ):
>	with(plots):polygonplot(T,scaling=constrained);
Площадь
A:=add(Z,i=l..n)/2;
Координаты центра тяжести
Xc:=add(Z*(T[1,i]+T[1,i+1]),i=l..n)/6/A;
Yc:=add(Z*(T[2,i]+T[2,i+1]),i=l..n)/6/A;
A := 7.435655350
Xc := 2.193077180
Yc := 1.524739473

15.2. Центр тяжести плоской фигуры	357
Первая строка матрицы — координаты ж, вторая — координаты
у. Последняя точка имеет номер K+1+N и совпадает с первой.
Оператор polygonplot строит изображение контура, ограничен-
ограниченного точками, заданными в матрице Т. Рисунок, который выдает
система, совпадает с рис. 74, с. 118 и здесь не приводится. Функция
add(c[i], i=l..n) означает сумму Х^Г=1сг# Точность вычислений
зависит от числа точек на окружности. Три правильных знака после
запятой получаются при N > 100.
Отметим необычную для алгоритмических языков конструкцию.
Значение Z задано вне цикла суммирования. Аналогично, угол F "вы-
"вычислен" до того, как параметру i было присвоено число. Это харак-
характерная особенность оператора присваивания := в пакетах символь-
символьных вычислений.
Замечание. В курсе сопротивления материалов используются
геометрические моменты инерции плоских фигур. Эти характерис-
характеристики можно также вычислить методом контурного интегрирования.
Осевые моменты инерции рассчитываются по формулам
12 Z^*+i + Ук+iVk
fc=i
U fc*+i xk+ixk
k=l
Центробежный момент инерции имеет вид
fc=i
Центральные моменты инерции имеют вид Jxc = Jx — %
J с = J — х\А, Jх с = Jx — xcycA. Главные центральные моменты
инерции имеют вид
J
Радиусы инерции имеют вид гтах = y/J^/A, imhl = л/7~Ц, где А
— площадь фигуры. В динамике используются физические моменты
инерции, зависящие от массы. Они связаны с геометрическими мо-
моментами инерции, и для однородных тел вычисляются по формуле
J = i2777,, где г — соответствующий радиус инерции, найденный, на-
например, с помощью приведенного алгоритма.

Глава 16
ПРОГРАММЫ ПО КИНЕМАТИКЕ
16.1. Кинематика точки
Условие задачи. Точка движется по закону
х = 3 sin 2t, у = 2 cos At.
При t = t1 = тг/12 найти скорость, ускорение и радиус кривизны
траектории. Построить траекторию при 0 < t < 0.4. Координаты
ж, у даны в см, время — в с (§ 6.1, с. 132).
Решение
Для нахождения скорости и ускорения точки применяем оператор
дифференцирования diff. Траекторию строим по ее параметричес-
параметрическому представлению оператором plot. Для наглядности средствами
Maple V на экране компьютера получаем изображение движущейся
точки вместе с изменением векторов скорости и ускорения. Для этого
формируем массив изображений — отдельных кадров движения *^ .
Описание программы
Программа (с. 359) состоит из двух основных частей.
В первой части программы строим траекторию движения точки
и изображаем векторы скорости и ускорения. Количество кадров за-
задаем числом N. В цикле от 1 до N в массиве p[i] создаем N кадров,
показывающих положение вектора скорости v и вектора ускорения W
на траектории; г — радиус-вектор точки. Производные г по времени
вычисляем с помощью оператора дифференцирования diff. Вторая
производная обозначена значком $2. Оператор тар применяет опе-
операцию дифференцирования к каждому элементу вектора и создает
соответствующий вектор скорости или ускорения. Коэффициенты
mv и mw введены для масштабирования изображений векторов и под-
подбираются вручную.
*) Аналогичная программа приведена в [13].

16.1. Кинематика точки	359
Перед построением траектории производим очистку переменной
времени t: =J tJ.
Для того, чтобы при выводе изображения оператором display из-
изображения не накладывались друг на друга, а замещались, создавая
тем самым эффект движения, используем опцию insequence=true.
График параметрически заданной функции (траектории) строим опе-
оператором plot. Время меняем от 0 до Т. Совмещенный вывод изобра-
изображения неподвижной траектории и движущихся стрелок осуществляем
оператором display.
Во второй части программы вычисляем тангенциальное ускоре-
ускорение, нормальное ускорение и радиус кривизны траектории.
Используем пакет линейной алгебры linalg. Сначала находим
модуль вектора скорости norm(v,2). Цифра 2 означает, что норма
вычисляется по формуле v = * /v% + Vy.
Тангенциальное ускорение вычисляем с помощью скалярного про-
произведения dotprod: \WT\ = W • v/v. Выведем аналогичную формулу
для вычисления нормального ускорения. Умножаем векторно равен-
равенство W = WT + Wn на v:
v x W = v x WT -\-vx Wn.
Учитывая, что v x WT = 0 и \v x Wn\ = vWn, получаем
\vx W\ =vWn.
Оператор векторного произведения обозначается как crossprod.
Программа 3. Кинематика точки
>	restart:
Количество кадров анимащш
>	N:=20:
Масштабные множители скорости и ускорения
>	mv:=l/10.: mw:=l/30.:
Закон движения
>	x:=3*sinB*t): у:=2*cosD*t):
Время движения
>	T:=evalf(Pi/12):
>	г:=vector( [x,y]):

360	Гл. 16. Программы по кинематике
Векторы скорости и ускорения
>	v:=map(diff,r,t):
>	W:=map(diff,r,t$2):
>	with(plots): with(plottools):
Параметры стрелок на рисунке
>	arw:=0.02,0.2,0.2:
>	for i to N do
>	t:=i/N*T:
>	Ускорение:=arrow(r,evalm(W*mw),arw,color=red):
>	Скорость:=arrow(r,evalm(v*mv),arw,color=blue):
>	p[i]:=display(Скорость,Ускорение):
>	end:
>	Стрелки:=display(seq(p[i],i=l..N),insequence=true):
>	t:=Jt>:
>	Траектория:=plot([x,у,t=0..T]):
>	display(Стрелки,
>	Траектория,
>	scaling=constrained,
>	title="CKopocTb и ускорение точки");
>	v: =
Модуль скорости
>	with(linalg): V:=norm(v,2):
Тангенциальное ускорение
>	Wt:=dotprod(v,W)/V:
Модуль ускорения
>	W:=norm(W,2):
Нормальное ускорение
>	Wn:=norm(crossprod(v,W),2)/V:
Вывод результатов счета
>	t:=T;
>	' хс=х, с ус=у, ' vc=V;
>	с Wnc=Wn, ( WC=W;
>	с WTc=Wt, croc=V~2/Wn;
t := .2617993878
х = 1.500000000, у = 1.000000000, v = 8.660254038
Wn = 14.40000001, W = 17.08800750
Wt = 9.200000000, го = 5.208333330

16.2. Механизм с двумя степенями свободы
361
16.2. Механизм с двумя степенями
свободы
Условие ЗАДАЧИ. Механизм манипулятора (рис. 186) приводится
в движение двумя независимыми приводами. Задан закон движения
ползуна, s(i) = s0 — vBt, и закон движения руки АС относительно
кривошипа О А: ф = ф0 + ujt. Построить график зависимости ско-
скорости и ускорения захвата С на интервале 0 < t < 1 с; ф0 = тг/6,
ио = Зтг/4 рад/с, АВ = 90 см, АС = 50 см, О А = 80 см, vB = 70 см/с,
s0 = 100 см, i7 = 120 см. Через какое время после начала движения
захват поднимется на высоту HI
Рис. 186
Рис. 187
Решение
Поставленную задачу решаем в системе Maple V координатным
методом. Для этого вычисляем координаты захвата С как функции
времени. Дифференцируя эти функции, находим скорость и ускоре-
ускорение С. Строим графики решений, получаем вид траектории и "ожив-
"оживляем" манипулятор специальными средствами анимации, делающими
решение наглядным.
Описание программы. По теореме косинусов из АОАВ нахо-
находим тригонометрические функции cos (p и sin (p. Вводим систему ко-
координат ж, у с началом в точке О (рис. 187), вычисляем координаты
шарнира А,
хА = О A cos <р, уА = О A simp,
и искомые координаты захвата:
- ф), ус = уА- ACsm((p - ф).

362	Гл. 16. Программы по кинематике
Так как О В = s(t) и ф = ф(?), то полученные координаты за-
зависят от времени. Дифференцируем координаты оператором diff.
Графики скорости и ускорения строим в одних осях разным цветом
color= [black,blue] и разной толщины thickness=[2,3] . Кривые
подписаны с помощью опции legend=["V11, "w"] . Шрифт для меток
на осях координат выбираем опцией axesfont= [TIMES,ROMAN,8] .
Искомое время подъема захвата на высоту Н находим, решая
уравнение yc(t) = Н. Используем оператор численного решения не-
нелинейного уравнения f solve.
Изображение механизма в движении создаем в цикле из К = 24
кадров. На экран изображение выводим оператором display.
Программа 4. Манипулятор
Начальные значения и размеры
>	restart:
>	S0:=l.: AB:=0.9: pi:=evalf(Pi):
>	0А:=0.8: АС:=0.5: phiO:=pi/6:
Скорость ползуна В
>	VB:=-0.7:
Угловая скорость руки АС
>	omega:=3*pi/4:
Угол поворота руки АС
>	phi:=phiO+t*omega:
Закон движения ползуна В s(t)
>	OB:=SO+t*VB:
>	cosp:=cos(phi): sinp:=sin(phi):
Определение тригонометрических функщш
>	cosf:=(-AB~2+0B~2+0A~2)/B*0A*0B):sinf:=sqrt(l-cos:T2) :
Координаты шарнира А
>	xa:=0A*cosf:
>	ya:=0A*sinf:
Координаты захвата С
>	xc:=xa-AC*(cosf*cosp+sinf*sinp):
>	yc:=ya+AC*(sinp*cosf-cosp*sinf):
Скорость точки С
>	vx:=diff(xc,t): vy:=diff(yc,t): v:=sqrt(vx~2+vy~2):
Ускорение точки С
>	Wx:=diff(vx,t): Wy:=diff(vy,t): W:=sqrt(Wx~2+Wy~2):

16.2. Механизм с двумя степенями свободы
363
Графики функций W(t), v(t)
>	plot([v,W],t=0..1.,thickness=[2,3],
>	color=[black,blue],
>	legend=[IIVII,IIWM] ,
>	axesfont=[TIMES,ROMAN,8]);
5-
2-
0.2
0.4
0.6
Legend
V
¦W
>	Time=fsolve(yc=1.2,t);
Time = .8370890321
>	with(plots):
Число кадров анимации
>	К:=24:
>	for i from 0 by 1 to К do
>	t:=i/K:
>	P[i]:=PL0T(CURVES([[0,0],[xa,ya],[0B,0]]),
CURVES([[xa,ya],[xc,ус]]),
>	TEXT([-0.03,0],c0c),
>	TEXT([xc,yc+0.04],CCC),
>	TEXT([xa,ya+0.04],CAC),
>	TEXT([0B+0.03,0.04],CBC)):
>	od:
Изображение механизма в движении
>	display(seq(P[i],i=0..К),insequence=true,thickness=2);

364
Гл. 16. Программы по кинематике
16.3. Скорости точек плоского механизма
Условие задачи. Найти скорости шарниров плоского механизма
(рис. 87, с. 160).
Решение
Представляем механизм в виде отдельных простейших кинема-
кинематических схем. В каждой схеме по одним кинематическим харак-
характеристикам легко определяются другие. Соответствующие решения
оформляем в виде процедур. Для решения поставленной задачи до-
достаточно трех схем *' , которые для наглядности поместим в таблицу
и укажем входные и выходные данные, т.е. известные и искомые
величины. Подразумевается, что координаты точек известны.
Схема
А А
СХЕМА 1 _ / \
VA /
/ Г)
]? Ч vb
vB
СХЕМА 2 ^^У
СХЕМА 3
Известные
величины
VA
<Р, VA
va, шва
Искомые
величины
VB,
шва, шве
vb, шва
vB
Последовательность расчета такова. Сначала вычисляем коорди-
координаты всех точек механизма. Затем последовательно, переходя от од-
одной точки к другой, применяем процедуры СХЕМА 1, СХЕМА2, СХЕМАЗ и
определяем скорости точек.
Алгоритм Резунова А.В., Сафронова B.C.

16.3. Скорости точек плоского механизма	365
Описание программы
Программу разделяем на две, каждую из которых записываем в
отдельный файл. Процедуры СХЕМА 1, СХЕМА2, СХЕМАЗ помещаем в Про-
Программу 5.
В процедуре СХЕМА 1 решаем векторное уравнение
Ча = "ев хСВ + шВА х В А
относительно угловых скоростей locb и ojba. Заметим, что оператор
solve решает систему уравнений, а оператор assign присваивает по-
полученное решение переменным wl и w2.
Скорость шарнира В вычисляем по формуле vB = шсв х СВ.
Аналогичные формулы заложены в процедуры СХЕМА2 и СХЕМАЗ.
Оператор save записывает процедуры и массив угловых скоростей
в файл kine.m. Программа 6 на с. 366 содержит вычисления коорди-
координат точек механизма (начало координат в шарнире В) и вычисления
скоростей с помощью созданных процедур. Процедуры считываются
с диска оператором read. Программа может быть легко дополнена
графическим изображением механизма и вычислением ускорений.
Программа 5. Три кинематические схемы
>	restart: with(linalg):
Угловые скорости звеньев
>	w:=MatrixA..10,1..10,shape=symmetric):
Процедура 1 вычисления скорости шарнира
ib двухзвенника с опорой ic и
известной скоростью конца ia
>	CXEMAl:=proc(ia,ib,ic) local wl,w2,Wcb,Wba,eq,s:
>	global w,V:
>	Wcb:=[0,0,wl]:Wba:=[0,0,w2]:
>	eq:=evalm(-V[ia]+crossprod(Wcb,X[ib]-X[ic])
>	+crossprod(Wba,X[ia]-X[ib])):
>	s:=solve({eq[l],eq[2]},{wl,w2});
>	assign(s);
>	w[ib,ic]:=wl:
>	w[ib,ia]:=w2:
>	V[ib]:=crossprod([0,0,wl],
>	end proc:

366	Гл. 16. Программы по кинематике
Процедура 2 вычисления скорости
ползуна ib (угол Fi)
по известной скорости точки ia
>	CXEMA2:=proc(ia,ib,Fi) local Vb,vb,wl,Wba,eq,s:
>	global V,w:
>	Wba: = [0,0,wl] :
>	Vb:=[vb*cos(Fi),vb*sin(Fi),0]:
>	eq:=evalm(-V[ia]+Vb+crossprod(Wba,X[ia]-X[ib])):
>	s:=solve({eq[l],eq[2]},{vb,wl});
>	assign(s);
>	w[ib,ia]:=wl:
>	V[ib]:=Vb:
>	end proc:
Процедура З вычисления скорости точки ic
по известным скоростям точек ia,ib
>	CXEMA3:=proc(ia,ib,ic) local Wac: global w,V:
>	Wac:=[0,0,w[ia,ib]]:
>	V[ic]:=evalm(V[ia]+crossprod(Wac,X[ic]-X[ia])):
>	end proc:
Запись процедур и массива w на диск
>	save СХЕМА1,СХЕМА2,СХЕМАЗ,w, "С:\\Mapl7\\kine.m";
Программа 6. Скорости точек механизма
> restart:
> with(linalg):
Считываем
процедуры из файла
> read MC:\\Mapl7\\kin€
Размеры
> AB:=30.: BC:=60.:
> DE:=20.: EF:=20.:
> EH:=30.: F0:=20.:
> al:=evalf(Pi/4):
> bt:=evalf(Pi/6):
CD
FG
CK
i.m" :
=30. :
= 10. :
=25. :

16.3. Скорости точек плоского механизма	367
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
2)
3)
4)
5)
6)
7)
8)
9)
Координаты узлов
X:=[[AB*cos(al),-AB*sin(al),0],
[0,0,0],
[ВС,0,0],
[BC+CD,O,O],
[BC+CD,-DE,O],
[BC+CD,-DE-EF,O],
[BC+CD,-DE-EF-FG,O],
#A-1
#B-2
#C-3
#D-4
#E-5
#F-6
#G-7
[BC+CD+EH*cos(bt),-DE-EH*sin(bt)
[BC+CK*cos(bt),CK*sin(bt)
[BC+CD+FO,-DE-EF,0]]:
,0],
Задаем угловую скорость звена
w[l,2]:=2:
Скорости неподвижных шарниров
V[l]: = [0,0,0]: V[10] : = [0,0,0] :
СХЕМАЗA,2,2): # Определяем Vb
СХЕМА2B,3,0): # Определяем Vc
СХЕМАЗB,3,4): # Определяем Vd
СХЕМА1D,6,10):# Определяем Vf
СХЕМАЗD,6,5): # Определяем Ve
СХЕМАЗD,6,7): # Определяем Vg
СХЕМА2E,8,0): # Определяем Vh
СХЕМА2C,9,0): # Определяем Vk
Вывод результатов
printf(с \n vx vy
for i from 2 to 9 do
printf(ce/.l.Of) 7o7.3g 7o7.3g 7.7
(N2)
(N3) -
(N4)
(N6)
(N5)
(N7)
(N8) -
(N9) -
,0],#H-8
#K-9
#0-10
OA
равны нулю
ползун (угол 0)
ползун (угол 0)
ползун (угол 0)
v \n<):
.3g \n'
i,V[i] [1] ,V[i] [2] ,norm(V[i] ,
vx vy v
-42.426 -42.426 60
-42.426 0 42.426
-42.426 21.213 47.434
-21.213 21.213 30
0 21.213 21.213
10.607 21.213 23.717
-33.461 0 33.461
-42.426 0 42.426
2)):od:

Глава 17
ПРОГРАММЫ ПО ДИНАМИКЕ
17.1. Принцип возможных скоростей
Условие задачи. Система, состоящая из четырех однородных
стержней, расположена в вертикальной плоскости. К системе прило-
приложена сила F = 20 Н и момент М = 30 Нм (рис. 145, с. 281). Известны
длины стержней 0А = 0.3 м, АВ = 0.55 м, BD = 0.4 м, ВС = 0.3 м и
углы а = 45°, C = 60°. Учитывая погонный вес стержней р = 10 Н/м,
определить горизонтальную реакцию опоры С.
Решение
Освобождаем конструкцию от горизонтальной связи в шарнире
С, заменяем связь искомой реакцией Хс. Система приобретает одну
степень свободы. Придаем стержню О А возможную (виртуальную)
угловую скорость и;ОА = 1. Скорости точек приложения активных
сил (рис. 146) GOA, GAB, GCB, GDB и F и реакции Хс определяем,
используя три схемы Программы 5 (с. 365).
Реакцию Хс вычисляем из принципа возможных скоростей:
XCVCx + FvBx + GAByVIy + GCByVNy + GDByVKy + M^OA = °'
Описание программы
Процедуры СХЕМА 1, СХЕМА2, СХЕМАЗ Программы 5 считываем из
файла kine.m оператором read. Нагрузки и координаты точек зано-
заносим в векторы F и X. Начало координат находится в точке О. Вве-
Введены обозначения О А = а, АВ = 6, BD = с, ВС = d. Мощности сил
вычисляем с помощью оператора скалярного произведения dotprod
пакета linalg. Мощность момента в общем случае тоже можно вы-
вычислять в виде скалярного произведения, но в данной задаче момент
только один, поэтому, чтобы не вводить векторы угловых скорос-
скоростей и моментов, его мощность вычислим просто в виде произведения
M*w[l,2], учитывая, что момент направлен против часовой стрелки
(в противном случае эту мощность берем со знаком минус).

17.1. Принцип возможных скоростей
369
Программа 7. Применение принципа возможных
скоростей для определения реакций опор конструкции
restart: with(linalg):
read llC:\\Mapl7\\kine.m11:
Размеры
a:=0.3: b:=0.55: c:=0.4: d:=0.3:
al:=evalf(Pi/4): bt:=evalf(Pi/3):
Нагрузки
F:=[[0,0,0], [0,0,0], #0, A
[20,0,0],[0,0,0], #B, С
[0,0,0], [0,-5.5,0],#D, I
[0,-3,0], [0,-4,0], #N, К
[0,-3,0]]: #L
M:=30: #Момент
Координаты точек
X:=[[0,0,0],[0,a,0],[b,a,0], #0,j
[b+d*cos(bt),a+d*sin(bt),0],#C
[b-c*cos(al),a+c*sin(al),0],#D
[b/2,a,0],	#1
[b+d/2*cos(bt),a+d/2*sin(bt),0]
[b-c/2*cos(al),a+c/2*sin(al),0]
[0,a/2,0]]:
#N
#K
#L
Задаем угловую скорость звена 0А
Скорости неподвижных шарниров равны нулю
: = [0,0,0]:V[5]: = [0,0,0]:
Вычисление скоростей
2)
5)
6)
СХЕМАЗA,2
СХЕМА1B,3
СХЕМАЗB,3
#0пределяем Va (N1)
#0пределяем Vb (N3)
#0пределяем Vi (N6) - середина АВ
СХЕМАЗE,3,8): Определяем Vk (N8) - середина DB
СХЕМА2C,4,0): Определяем Vc (N4) - ползун (угол 0)
СХЕМАЗC,4,7): Определяем Vn (N7) - середина ВС
Определение реакщш Хс
Xc:=-(add(dotprod(V[i],F[i]),i=1..8)+M*w[l,2])/V[4] [1];
Хс := 31.56969109
24 М.Н. Кирсанов

370	Гл.17. Программы по динамике
17.2. Динамика машины с кулисным
приводом
Условие ЗАДАЧИ. Проинтегрировать нелинейное дифференци-
дифференциальное уравнение движения механизма с кулисным приводом (при-
(пример 2, с. 310, рис. 161) на интервале времени т = 0.262 с. Построить
графики ip(t) и ujlz(t). Дана угловая скорость шкива 1 в начальный
момент: <^lz@) = 24 рад/с, и начальный угол (р@) = тг/2.
Решение
Уравнение движения E), с. 311, полученное в результате решения
примера, разрешаем относительно углового ускорения:
(p = {QT + QH + QA- О.Бф2В sin 2(p)/(A + В sin2 <р).	A)
Описание программы
Вводим обозначения. Угол поворота if шкива 1 (обобщенная коор-
координата) — phi(t), угловая скорость ф — omega, угловое ускорение ф
обозначаем как eps. Интегрируем уравнение A) используя оператор
dsolve.
Графики phi (t), omega и eps строим с помощью оператора odeplot.
График omega выведен на экран. Для того, чтобы графики phi(t)
и eps также были выведены на экран, необходимо двоеточие после
соответствующих операторов заменить на точку с запятой. В конце
программы для вывода на печать таблиц результатов используем опе-
оператор printf.
Программа 8. Динамика машины с кулисным приводом
> restart:
> МО
> к:
> mu
> 11
> Rl
> 14
:= -30:
=0.2:
:= 950:
:= 2.5:
:=0.4:
:= 0.32
g:=9.81:
Параметры двигателя
# Пусковой момент
# Крутизна статической характеристики
# Коэффициент сопротивления
Инерщюнные параметры
т2:= 15: тЗ:= 10: т4:= 16: та:=1:
Геометрические параметры
rl:=0.1: R3:=0.3: r4:=0.2:
: R4:=0.41:

17.2. Динамика машины с кулисным приводом	371
Начальные значения
>	phiO:=evalf(Pi/2): omegaO:=24:
Время моделирования
>	tau:=0.262:
Угловая скорость
>	omega:=diff(phi(t),t):
>	Обобщенная сила (силы тяжести)
>	Qt:=-ma*g*rl*cos(phi(t)):
Обобщенная сила (нагрузка)
>	Qn:=-mu*omega*(rl*(R4-r4)/R4*sin(phi(t)))~2:
Обобщенная сила (двигатель)
>	Qd:=-(M0+k*omega*Rl/R3)*Rl/R3:
Обобщенная сила
>	Q:=Qd+Qt+Qn:
Коэффициенты дифференциального уравнения
>	A:=Il+m3*Rl~2/2:
>	В:=rl~2*(m2+m4*(i4/R4)~2+m4):
Дифференциальное уравнение
>	eps: = (Q-0.5*B*omega'42*sinB*phi(t)))/(A+B*sin(phi(t))'42) :
>	Уравнение:=diff(omega,t)-eps:
>	НачУсловия:=phi@)=phiO,D(phi)@)=omegaO:
Решение
>	sol:=dsolve({Уравнение,НачУсловия},phi(t),
>	type=numeric,
>	output=listprocedure):
Графики результатов
>	with(plots):
>	odeplot(sol,[t,phi(t)],0..tau,title=cУголс,
>	color=black,
>	thickness=2):
>	odeplot(sol,[t,omega],0..tau,title=cУгловая скоростьс ,
>	color=black,
>	thickness=2);

372
Гл. 17. Программы по динамике
25
24.8^
24.6
24.4
24.2
24
/
/
/
/
0
> odeplot(sol
>
>
>
/
05
.[t.
Угловая скорость
\ / \
\ / \
\ / \
0.1 t 0.15 0.2 0.25
eps],0..tau,title=cУгловое ускорениес ,
color = black,
thickness = 2,
legend=cepsilonc):
Таблица результатов
> N:=12: ff:=subs(sol,phi(t)): ww:=subs(sol,omega):
> printf(" t
> prini
> for :
--F ( "
l from
0 to
fi omega\n"):
\n ) .
N do printf 07,04.2f °/005.3f °/005.3f \n",
> tau/N*i,ff(tau/N*i),ww(tau/N*i)) od:
> prini
t
0.00
0.02
0.04
0.07
0.09
0.11
0.13
0.15
0.17
0.20
0.22
0.24
0.26
--F f»
¦'I V,
fi
1.571
2.096
2.632
3.183
3.738
4.279
4.807
5.334
5.874
6.428
6.981
7.519
8.046
omega
24
24
24
25
25
24
24
24
25
25
25
24
24
000
200
942
483
161
411
033
357
125
518
041
302
046

17.3. Колебания системы с двумя степенями свободы	373
17.3. Колебания системы с двумя
степенями свободы
Условие задачи. Найти частоты колебаний системы, изобра-
изображенной на рис. 173, с. 337. Построить график движения оси цилиндра
А. В начальный момент система находилась в покое, а каждая пру-
пружина получила удлинение 0.1 м.
Решение
Задачу решаем с помощью уравнения Лагранжа 2-го рода. Выби-
Выбираем две обобщенные координаты. Вычисляем кинетическую энер-
энергию и обобщенные силы. Составляем два уравнения Лагранжа 2-го
рода и уравнение частот, решая которое, находим частоты собствен-
собственных колебаний системы. Подробное решение задачи дано на с. 337 -
342.
Описание программы
Обозначаем обобщенные координаты ^=х, q2 =s, и обобщенные
скорости q^ =vx, q2 =vs. Коэффициенты при обобщенных скорос-
скоростях q^ в выражениях dTjdq^ выделяем оператором coeff. Харак-
Характеристическое уравнение численно решаем оператором f solve. По
найденным инерционным коэффициентам составляем систему диф-
дифференциальных уравнений движения. Решаем систему оператором
dsolve. Производные в начальных условиях обозначаются буквой
D. По умолчанию оператор dsolve дает решение в аналитическом
виде, поэтому для получения численного результата указываем оп-
опцию type=numeric. График движения цилиндра строим специальным
оператором odeplot. Для более четкой прорисовки кривой увеличи-
увеличиваем число точек на ней numpoints=150.
Программа 9. Колебания системы с 2 степенями свободы
restart:
ma:=50: mb:=20: # Массы (кг)
с:=90:	# Жесткость пружин (Н/м)
g:=9.81:	# Ускорение свободного падения (м/с2)
Кинетические энергии тел А, В
Ta:=3*ma*vx~2/4:
Tb:=mb*(vs+2*vx)~2/4:

374
Гл. 17. Программы по динамике
Кинетическая энергия системы
>	Т:=Та+ТЬ:
Инерщюнные коэффициенты
>	all:=coeff(diff(T,vx),vx):
>	al2:=coeff(diff(T,vx),vs):
>	a22:=coeff(diff(T,vs),vs):
>	УравнениеЧастот:=
>	(c-all*omg~2) * (c-a22*omg'42) - (al2*omg~2) ~2=0:
Решение уравнения частот
>	sol:=fsolve(УравнениеЧастот,omg=0..infinity);
sol := .8708263224, 3.773812597
Дифференциальные уравнения колебаний
>	eql:=all*diff(x(t),t$2)+al2*diff(s(t),t$2)=-c*x(t):
>	eq2:=al2*diff(x(t),t$2)+a22*diff(s(t),t$2)=-c*s(t):
Численное решение системы с начальными данными
>	г:=dsolve({eql,eq2,s@)=0.1,х@)=0.1,
>	D(s)@)=0,D(x)@)=0},
>	{s(t),x(t)},type=numeric,
>	output=listprocedure):
>	with(plots):
>	T0:=14.3:
>	odeplot(r,[t,x(t)],0..T0,numpoints=150,
>	labels=[t,x],
>	color=black);

Список литературы
1.	Аладъев В.З., Богдлвичус М.А. Maple 6: Решение математических,
статистических и физико-технических задач. — М.: Лаборатория ба-
базовых знаний, 2001.
2.	Афанасьев В.И., Зимина О.В., Кириллов А.И., Петрушко И.М., Саль-
Сальникова Т.А. Решебник.Высшая математика. Специальные разделы. —
М.: ФИЗМАТЛИТ, 2001.
3.	Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика
в примерах и задачах.Т.1. — М.: Наука, 1984.
4.	Бронштейн И.Н., Семендяев К.А. Справочник по математике.— М.:
Наука, 1980.
5.	Бутенин Н.В., Лунц Я.Л., Меркин Д.Р., Курс теоретической меха-
механики. — СПб.:Лань, 1998.
6.	Веретенников В.Г., Карпов И.И., Маркеев А.П. и др. Теоретическая
механика. Вывод и анализ уравнений движения на ЭВМ: учебное по-
пособие для вузов. — М.: Высшая школа, 1990.
7.	Вилъке В.Г. Теоретическая механика. — М.: Изд-во МГУ, 1998.
8.	Говорухин В., Цибулин В. Компьютер в математическом исследовании.
Учебный курс.— СПб.: Питер, 2001.
9.	Дьяконов В.П. MAPLE 7. Учебный курс. — СПб.: Питер, 2002.
10.	Зимина О.В., Кириллов А.И., Сальникова Т.А. Решебник. Высшая ма-
математика. — М.: ФИЗМАТЛИТ, 2001.
11.	Кепе О.Э., Виба Я.А., Грапис О.П. и др. Сборник коротких задач по
теоретической механике. — М.: Высшая школа, 1989.
12.	Манзон Б.М. Maple V Power Edition. — М.: ИИД "Филинъ", 1998.
13.	Матросов А.В. Maple 6. Решение задач высшей математики и меха-
механики. — СПб.:БХВ-Петербург, 2001.
14.	Мещерский И.В. Сборник задач по теоретической механике. — М.: На-
Наука, 1981.

376	СПИСОК ЛИТЕРА ТУРЫ
15.	Новожилов И.В., Зацепин М.Ф. Типовые расчеты по теоретической
механике на базе ЭВМ. — М.: Высшая школа, 1986.
16.	Павловский М.А., Акинфиева Л.Ю., Бойчук О.Ф. Теоретическая ме-
механика. Динамика. — Киев: Выща шк., 1990.
17.	Сборник заданий для курсовых работ по теоретической механике:
Учеб. пособие для техн. вузов / Яблонский А.А., Норейко С.С, Вольф-
сон С.А. и др.; Под ред. А.А.Яблонского.— 3-е изд — М.:Высшая школа,
1972.
18.	Светлицкий В.А., Стасепко И.В. Сборник задач по теории колебаний.
— М.: Высшая школа, 1973.
19.	Тарг СМ. Краткий курс теоретической механики. — М.: Высшая
школа, 1998.
20.	Яблонский А.А., Норейко С.С. Курс теории колебаний. — М.: Высшая
школа, 1975.

Именной и предметный указатель
AcademiaXXI 13
add 117, 357
arrow 351, 354, 360
assign 365
axes 354
axesfont 363
black 374
blue 360
BOLD 353
coeff 374
COLOR 351, 353
constrained 352, 360
convert 353
crossprod 117, 360
CrossProduct 117
CURVES 351
diff 374
display 351, 360, 363
dotprod 117, 360
DotProduct 117
dsolve 371, 374
end 352
evalf 359
evalm 117, 360
for..from..to..do..od 367
fsolve 362, 363, 374
global 365
HUE 351, 353
if ... then 354
infinity 374
insequence 360, 363
labels 374
legend 363, 372
linalg 117, 360
Linear Algebra 117, 352
LinearSolve 352
listprocedure 374
local 365
map 360
Matrix 352, 354, 365
matrix 356
none 354
norm 117, 360, 367
normalize 117
numeric 374
numpoints 374
odeplot 371, 374
output 374
Pi 350
PLOT 351
plots 351, 353, 371
plottools 351, 353
polygonplot 357
printf 352, 367, 372
proc 365
read 365, 366
red 360
restart 349, 352
RGB 351
ROBBY2 191
ROMAN 363
save 365, 366
scaling 352, 360
seq 351, 352, 360
377

378
ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
shape 365
solve 13, 218, 365
sqrt 354
subs 372
symbol 353
symmetric 365
TEXT 363
thickness 363, 371
TIMES 363
title 360
true 360
type 374
vector 117, 359
with 352, 353
www.academiaxxi.ru 13, 117, 349
www.termech.mpei.ac.ru 191
Амплитуда колебаний 341, 344
Анимация 191
Бетти Э. 344
Вал
—	динамические реакции 272
—	равновесие 94
Вектор
—	свободный 13
—	скользящий 13, 37, 63
Верхний пояс 47
Виллиса формула 332
Винт динамический 111
Виртуальные перемещения 279
Внешнее зацепление 153, 332
Внутреннее зацепление 332
Водило 329
Возможные перемещения 279
Гармонические колебания 341
Главный вектор 111
Главный момент 111
Граф 130, 194, 243
Графический расчет фермы 45
Гюйгенс X. 273
Даламбер Ж. 291
Двигатель 309
Движение
—	вращательное 129
—	плоское 129
—	поступательное 129
—	сложное 195
Двусвязная фигура 355
Двухзвенник 242, 365
Декартовы координаты 279
Динама 111
Жесткая заделка 60
Жесткость 344
Жесткость пружины 265
Заделка 60, 287
Закон Кулона 76
Запись на диск 366
Зацепин М.Ф. 9, 191, 227, 376
Зацепление
—	внешнее 153, 332
—	внутреннее 332
—	зубчатое 153
—	фрикционное 153
Знак
—	момента 12, 96
—	пары 37
—	усилия 51
Зубчатое зацепление 153
Интегрирование по контуру 355
Канонические уравнения 326
Каток 309
Кинематические графы 307, 327,
329
Кинематические уравнения
—	Эйлера 222
—	плоского движения 188
Кинетическая энергия 300
—	вращения 248
—	плоского движения 249

ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗА ТЕЛЬ
379
—	системы 327, 329
Колебания гармонические 341
Консервативная система 318, 326
Координаты
—	декартовы 145
—	естественные 144
—	подвижные 222
—	полярные 144
Кориолис Г. 195
Коэффициент
—	податливости 345
—	сопротивления 310
—	трения качения 80, 262
—	трения скольжения 74
Коэффициенты
—	жесткости 339
—	инерционные 324, 339, 374
Кремона А. 45
Кривошип 166, 170
Крутизна статической характерис-
характеристики двигателя 310
Кулиса 309
Кулон Ш. 74
Лагранж Ж. 300
МЦС 158
Максвелл Д. 45
Максвелла-Мора формула 344
Манипулятор 361
Массив двумерный 352
Мгновенно-поступательное движе-
движение 162
Мгновенный центр скоростей 158,
172
Метод
—	Риттера 38
—	вырезания узлов 14, 38, 350
—	графов 130, 188
—	контурного интегрирования 120
—	координатный 329, 361
—	моментных точек 38
—	сечений 38
Механизм
—	кривошипно-кулисный 309
—	многозвенный 166
—	планетарный 329
—	шарнирно-стержневой 170
Мещерский И.В. 9, 21, 26, 254, 266,
375
Минимальный момент М* 112
Многоугольник сил 45
Модуль упругости 344
Момент
—	сил инерции 294
—	количества движения 253
—	статический 120
—	трения 265
—	трения качения 81, 250
Момент инерции
—	геометрический 357
—	главный центральный 357
—	стержня 241
—	физический 357
—	центральный 357
—	центробежный 272, 357
—	цилиндра 241
Момент силы
—	относительно оси 12
—	относительно точки 11
Моментные точки 38
Мощность момента 289
Накопление ошибок 20
Нижний пояс 47
Новожилов И.В. 9, 191, 227, 376
Ньютон И. 55
Обобщенная сила 300, 308, 331
Обобщенная скорость 326
Обобщенные импульсы 324
Обобщенные координаты 300, 318
Обобщенный импульс 326
Обучающая программа 191
Общее уравнение динамики 288
Оператор
—	вывода графики 351
—	присваивания 357

380
ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
—	условный 352
—	цикла 351
Палец 309
Пара сил 13, 73, 111
Передаточное число 332
План скоростей 159
Плечо 12, 108
Плита 101
Погонный вес 31, 58
Подвижная опора 73
Полезная нагрузка 309
Ползун 176
Полюс 130
Поля
—	внешние 45
—	внутренние 46
Потенциальная энергия 328, 331
Потенциальная энергия пружины
340
Потенциальные силы 318
Правило
—	Жуковского 197, 204
—	плана скоростей 160
Приведенная масса 250, 257
Привод 361
Принцип возможных скоростей 280
Проекции силы 11
Процедура 365
Пусковой момент 310
Работа внутренних сил 258
Работа момента трения качения
250
Работа сил 250
Равнодействующая 111
Радиус
—	инерции 248, 357
—	кривизны 132, 196
—	полярный 144
Раскосы 47
Распределенная нагрузка
—	линейная 61
—	по дуге 61
Реакция
—	гладкого основания 30
—	заделки 60
—	неподвижного шарнира 32
—	опорного стержня 31
—	сферической опоры 106
Ременная передача 153
Решебник 112, 126, 136, 211, 226,
232, 345, 375
Риттер А. 37
Сателлиты 329
Связь
—	двусторонняя 60, 73
—	идеальная 279, 318, 337
—	стационарная 279, 318
Сечение Риттера 44
Силовой треугольник 26
Силы инерции 288, 291, 294
Система трех тел 67
Скалярный инвариант 111
Скорость
—	абсолютная 195, 203
—	относительная 196, 203
—	при плоском движении 130
—	угловая 129, 223
Собственные значения 342, 344
Составная конструкция 54
Степень свободы
—	две 294, 300, 318, 324, 336, 343
—	одна 245, 266, 288, 307, 326
Тарг СМ. 61, 376
Теорема
—	Гюйгенса 241, 273
—	взаимности Бетти 344
—	о движении центра масс 236
—	о проекциях векторов скорос-
скоростей 161
—	о трех силах 26
—	об изменении кинетической энер-
энергии 247, 257
—	об изменении момента количества
движения 253

ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗА ТЕЛЬ
381
Точки Риттера 38
Трение
—	качения 80
—	скольжения 74
Угол
—	наклона касательной 140
—	нутации 223
—	полярный 144
—	прецессии 223
—	собственного вращения 223
Узел 14
Уравнение
—	винтовой оси 112
—	динамики общее 288, 294
—	сложения скоростей 219
—	частот 341, 373, 374
Уравнения
—	Гамильтона 326
—	Лагранжа 2-го рода 300, 341
—	канонические 326
—	кинематические 289
—	трех угловых скоростей 180
—	трех угловых ускорений 184
Усилие 14
Ускорение
—	Кориолиса 197, 204
—	абсолютное 195
—	вращательное 222
—	касательное 131
—	нормальное 132, 145, 359
—	осестремительное 222
—	относительное 196, 203
—	переносное 196, 203
—	при плоском движении 130
—	свободного падения 373
—	тангенциальное 131, 145
—	угловое 129, 223
Фаза колебаний начальная 344
Ферма 15
—	Шухова 15
—	колебание узла 343
—	плоская 15, 38, 45, 350
—	пространственная 86
—	сетчатая 15
Фихтенгольц Г.М. 355
Формат вывода 352
Формула
—	Виллиса 332
—	Максвелла-Мора 344
Функция
—	Гамильтона 324, 326
—	Лагранжа 324, 326
Центр масс 236, 241, 272
Центр тяжести
—	параллелепипеда 126
—	пирамиды 126
—	плоской фигуры 118
—	половины цилиндра 126
—	полукруга 119
—	пространственного тела 125
—	прямоугольника 119
—	стержневой фигуры 122
—	треугольника 119
Центральная винтовая ось 111
Цепь 21
Частот уравнение 341
Частоты собственных колебаний
336
Четырехзвенник 179, 290
Число
—	зубцов 153
—	передаточное 153, 332
—	стержней фермы 350
Шаг винта 112
Шарнир 14
Шкив 309
Шток 309
Шухов В.Г. 15
Эйлера углы 222
Энергия
—	полная механическая 325
—	потенциальная 318, 326

THE SOLVER
M. N. KIRSANOV
THEORETICAL MECHANICS
PHYSICS AND MATHEMATICS PUBLISHERS
International Academic Publishing Company "Nauka"
Russian Academy of Sciences
Moscow, 2002, 384 pages
THE SOLVER "Theoretical Mechanics" is the part of tutorial com-
complexes THE SOLVER edited by professor A.I. Kirillov. It is designed for
computer-based education and consists of this book and software package
THE SOLVER TM.
This book contains 4 parts : STATICS, KINEMATICS, DYNAMICS
and SOLUTIONS in MAPLE V and 17 chapters:
Concurrent Force System in a Plane
General Case of Forces in a Plane
Equilibrium with Friction
Forces System in Space
Centre of Gravity
Kinematics of a Particle
Rotational Motion of a Rigid Body
Plane Motion of a Rigid Body
Resultant Motion of a Particle
Motion of a Rigid Body Having One Fixed Point
Particle Dynamics
Dynamics of a System
Analytical Dynamics
Vibration of a System
Solutions in Maple V (Statics)
Solutions in Maple V (Kinematics)
Solutions in Maple V (Dynamics)
The chapter divided into sections. Each section contains one basic
problem with general formulation of the problem, a solution plan, a so-
solution example and ten problems of the same kind. In the most cases

the answers of the problem have not only final result but a intermediate
results too. It is simplify to find possible error in the solution.
THE SOLVER "Theoretical Mechanics" contains new methodical re-
results of the author and new problems and solutions.
Using THE SOLVER, the student can deeply understand how to solve
the basic problems of Theoretical Mechanics because this book concen-
concentrates an attention on the new and the essential.
Tutorial complex is useful for tutors. One part of the software is the
Problem-Generator, designed by author. Problem-Generator can produce
variants of problems with text, figure and answers for test and control in
THE SOLVER "Theoretical Mechanics" can be used at colleges, tech-
technical universities, and for distant education. It enables the student to
study independently.

Учебное издание
КИРСАНОВ Михаил Николаевич
РЕШЕБНИК
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Под редакцией профессора А. И. Кириллова
Редактор М. Б. Козинцова
Оригинал-макет автора
Оформление переплета: А.Л.Логунов
ЛР№ 071930 от 06.07.99
Подписано в печать 12.07.02. Формат 60x90/16
Бумага офсетная № 1. Печать офсетная
Усл. печ. л. 24. Уч.-изд. л. 24. Тираж 5000 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с диапозитивов
в РГУП «Чебоксарская типография № 1»
428019 Чебоксары, пр. И. Яковлева, 15
БВМ 5 -9221 -0281 -8
9 785922 102810