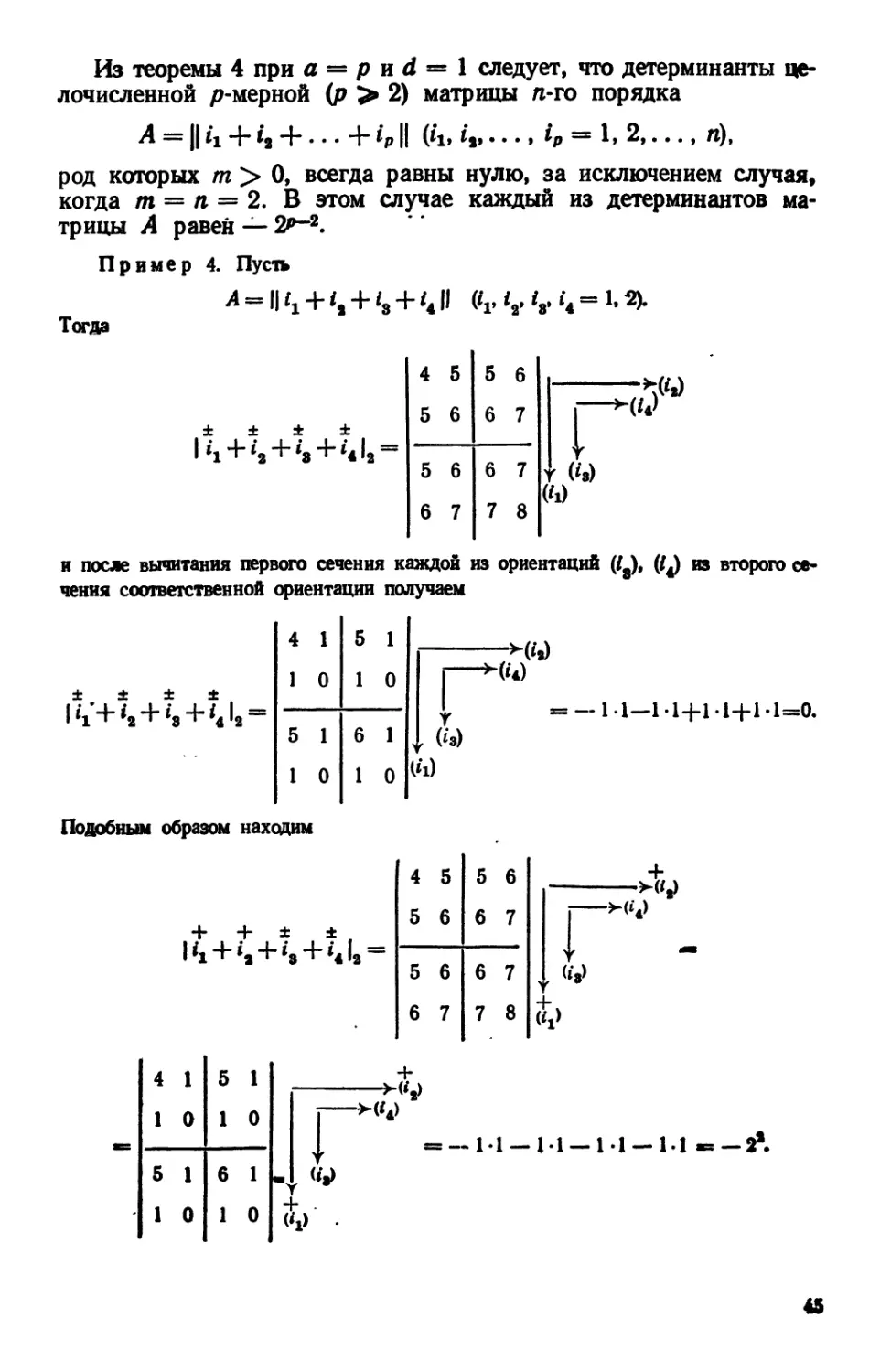
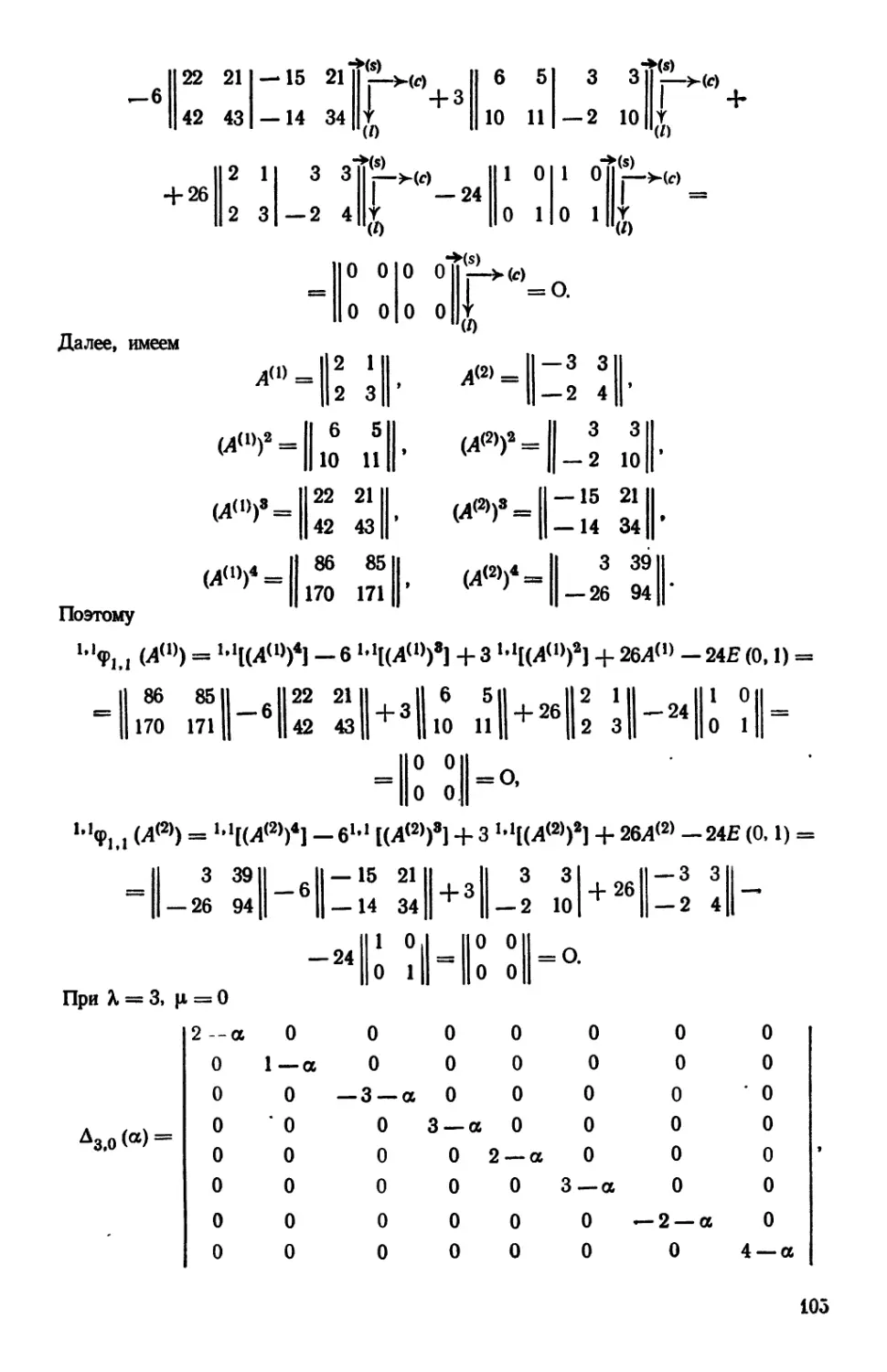
Текст
ВВЕДЕНИЕ
В ТЕОРИЮ
АКАДЕМИЯ НАУК УКРАИНСКОЙ ССР
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ИНСТИТУТ МАТЕМАТИКИ
н. п. соколов
ВВЕДЕНИЕ В ТЕОРИЮ
МНОГОМЕРНЫХ МАТРИЦ
ИЗДАТЕЛЬСТВО «НАУКОВА ДУМКА»
КИЕВ -1972
517.1
C59
УДК 512.8
В монографии излагаются главным образом сведения о многомерных
матрицах. Рассматриваются операции над ними, простейшие матричные уравнения»
полиномиальные многомерные матрицы. Излагаются мультипликативные и
спектральные свойства многомерных матриц с неотрицательными элементами.
Книга предназначена для математиков, а также аспирантов и студентов
старших курсов математических и смежных специальностей.
Ответственный редактор академик АН УССР
Ю. А. Митропольский
Рецензенты:
доктор математических наук В. П. Вельман,
член-корреспондент АН УССР Ю, М. Березанский
Редакция физико-математической литературы
Зав. редакцией Я. В. Евсеенко-Мисюренко
2—2—5
143-72М
ПРЕДИСЛОВИЕ
Теория многомерных матриц является естественным обобщением теории
обычных матриц и находит многочисленные применения при изучении
алгебраических форм и связанных с ними геометрических образов (см. [3]).
Предлагаемая книга служит введением в теорию многомерных матриц,
все еще далекую от полного завершения, и состоит из восьми глав.
В главе I излагаются хорошо известные основные сведения о многомерных
матрицах и порождаемых ими детерминантах. Остальные главы содержат
оригинальные результаты исследований автора в этой области, частью
опубликованные в статьях [4—9], частью излагаемые здесь впервые. В главе II
отмечаются замечательные свойства детерминантов некоторых многомерных матриц.
Устанавливается общее свойство детерминантов с целочисленными элементами
и обобщаются детерминантные тождества Смита и Дьиреша, рассматриваются
детерминанты, порождаемые ганкелевой многомерной матрицей одного
частного вида, и многомерные детерминанты, приводящиеся к обычному
детерминанту Вандермонда. Главы III—VI охватывают вопросы, связанные с
расширением матричных операций, необходимым для устранения тех ограничений
в обобщении многих важных понятий, которые еще встречаются в теории
многомерных матриц и препятствуют ее дальнейшему развитию.
В главе III даются определения основных операций — сложения и
умножения многомерных матриц — в зависимости от операций над
ассоциированными с этими матрицами полилинейными формами. Приведенное здесь
определение умножения соответствует правилам Кэли и Скотта умножения
детерминантов и значительно шире обычного определения умножения многомерных
матриц, вносящего некоторые ограничения в понятия единичной и обратной
матриц. В соответствии с умножением определяются элементарные
преобразования многомерных матриц и устанавливается понятие их эквивалентности.
Упомянутые выше ограничения в понятиях единичной и обратной матриц
высших измерений устраняются введением новых определений для этих матриц,
вытекающих из рассмотрения простейших матричных уравнений, которым
посвящена глава IV. В той же главе дается понятие о характеристических числах
и собственных матрицах для данной многомерной матрицы, которые играют
большую роль при исследовании ее структуры.
Введенная автором операция умножения матриц делает возможным
построение функций, в первую очередь полиномов, от любой многомерной
матрицы. Такие полиномы рассматриваются в главе V, где также вводятся
имеющие фундаментальное значение характеристический и минимальный полиномы
многомерной матрицы и доказывается общая теорема Гамильтона—Кэли.
Глава VI посвящена операциям над полиномиальными многомерными
матрицами. На основе эквивалентности таких матриц обобщается классическая
теория элементарных делителей Вейерштрасса, устанавливаются нормальные
формы многомерных матриц и дается критерий подобия матриц любого числа
измерений. Как частный случай полиномиальных матриц рассматриваются
регулярные и сингулярные пучки многомерных матриц. Указываются канонн-
г
ческие формы этих пучков и приводятся критерии строгой эквивалентности как
регулярных, так и сингулярных пучков.
В главе VII излагаются основные мультипликативные и спектральные
свойства неотрицательных многомерных матриц. Обобщаются теоремы
Перрона и Фробениуса о характеристических числах и собственных векторах
квадратных матриц с положительными и неотрицательными элементами и
указываются специфические особенности примитивных и стохастических
многомерных матриц.
Последняя глава VIII посвящена квазиспектральным свойствам матриц.
В ней по аналогии с обычным матричным спектром вводится понятие
квазиспектра квадратной матрицы, определяется ее квазихарактеристическое число
и соответствующий квазисобственный вектор и указывается применение этих
величин к изучению квазистохастических (в частности, стохастических) матриц.
Далее приводятся критерии квазистохастической эквивалентности и
квазистохастического подобия матриц как частных видов их эквивалентности и
устанавливается квазинормальная форма матрицы, рассматриваемая как
представитель класса квази стохастически эквивалентных (или его подкласса квази
стохастически подобных) матриц. Полученные результаты распространяются затем
на многомерные матрицы.
Автор считает своим приятным долгом выразить благодарность ответст-^
венным редакторам академику АН УССР Ю. А. Митропольскому,
члену-корреспонденту АН УССР Ю. М. Березанскому, а также доктору математических
наук В. П. Вельмину, сделавшим ценные замечания по содержанию
монографии.
ГЛАВА I
ОСНОВНЫЕ СВЕДЕНИЯ О МНОГОМЕРНЫХ МАТРИЦАХ
И ИХ ДЕТЕРМИНАНТАХ
§ 1. СТРУКТУРА МНОГОМЕРНОЙ МАТРИЦЫ
Пусть дано некоторое числовое поле Р. Любая система из пг ... пр
элементов Aixiz„Ap (ia = 1, 2, . . . , па\ а = 1, 2,..., р) поля Р,
расположенных в точках р-мерного пространства, определяемых
координатами ilf t2, . . . , ipt образует р-мерную (пх х п2 х . . . X
X пр)'Матрицу над Р:
А = IIАtxt2...tp И Се = 1,2,... ,п0; а = 1,2,... .р).
Такая матрица, если число ее измерений р можно предполагать
каким угодно целым, большим двух, называется также
пространственной.
Если все числа пъ п2 , . . . , пр, за исключением одного, из них
па (1 < а < Р)> одинаковы, то матрица А называется расширенной
или сжатой в направлении (ia), смотря по тому, будет ли па больше
или меньше одинаковых чисел щ ф = 1, ..., а — 1, а + 1, ... , р).
В дальнейшем рассматриваются главным образом
многомерные матрицы с одинаковыми размерами пг = п2 = . . . = пр. В
этом случае, полагая п = п± = . . . = пР9 имеем р-мерную матрицу
п-го порядка над Р:
Л = ИА...*Р11 (',.'2 <р=1.2 л). (1
состоящую из Пр элементов.
Совокупность элементов матрицы (1) с фиксированным
значением 1а индекса ia (1 < а < р) образует сечение (простое)
ориентации (ia), являющееся (р — 1)-мерной матрицей n-го порядка:
\\\...w«'*»...iPII (tV• • • • '-!• W. {P = 1'2 »>•
Совокупность элементов с фиксированными значениями ia, i^
индексов iat ty (1 < а < р < р) образует сечение (двукратное)
ориентации (iai$), являющееся (р —2)-мерной матрицей n-го порядка:
" * М ... 'a-l'a'a+l • • 'Р--1!Э'Э+1 - 'р"
(*1> • • • > 'а-1' 1а+Г " • • » *Р—1' 10-Н' * * * '*Р = Ь 2, . .. , П)
б
и представляющее совокупность элементов, общих двум сечениям
ориентации (ia), (*э):
И Л,... ^-^э'Э-н ..• h " ^i»" " • *0-i' 'з+1' • • •• 1р e *'2> Л)*
Вообще, совокупность элементов матрицы (1) с
фиксированными значениями Cat, . . . ,\т индексов iai, . . . , fam (1 < m< р—1;
1 < ai < • • • < am< P) образует сечение (т-кратное) ориентации
(i0l . . . ian), являющееся (р — т)-мерной матрицей n-го порядка
и представляющее совокупность элементов, общих т сечениям
ориентации (tcj, . . . , (tam); при т = р — 1 имеем сечение ориентации
0<v • • *ap_i)» которое является одномерной матрицей я-го
порядка, состоящей из элементов, общих р — 1 сечениям ориентации
(Ч)» • • • » (4,_i)» и поэтому называется также строкой
направления (i0p).
В обычной двумерной матрице || Aif || строки и столбцы можно
рассматривать как сечения ориентации (i) и (/) или как строки
направлений (/) и (О-
Пусть
аг...,ат, Pt,. • -,P^_m
— некоторая перестановка из чисел 1,2, . . . , р. Называя тогда
ориентации (i^ . . . i^) и (^. . . hp-m) ^-кратного и (р — т)-крат-
ного сечений матрицы (1) противоположными, будем
подразумевать под соответственными элементами двух m-кратных сечений
одной и той же ориентации (tai . . . i0m) те элементы, которые
принадлежат одному и тому же (р — т)-кратному сечению
противоположной ориентации (^ ... i$p_m)- В частности, соответственными
элементами двух сечений ориентации (ia) (I < a < p) являются
элементы, принадлежащие одной и той же строке направления
(ia), а соответственными элементами двух строк направления (ta)
будут элементы, принадлежащие одному и тому же сечению
ориентации (la).
Два сечения одной и той же ориентации называются
пропорциональными, если элементы одного из них отличаются от
соответственных элементов другого одним и тем же множителем, и
тождественными, если соответственные элементы их равны.
Пользуясь двумерными сечениями, можно записать матрицу (1)
в виде квадратной или прямоугольной таблицы в зависимости от
того, будет ли число измерений ее р четным или нечетным;
двумерные сечения при этом отделяются друг от друга вертикальной или
горизонтальной чертой. Так, например, кубическая матрица
второго порядка \\Aifk\ (i, /', k = 1, 2) с помощью сечений ориентации
(/) может быть записана в виде прямоугольника
б
A\\\ Am
4m A
212
A A
Л121 Л122
A A
Л221 л222
+U)
<*)
<*>
а матрица (1) при /) = 4ип = 2с помощью сечений ориентации
OVi) — в вВДе квадрата
А А
^1111 Л1112
Л1121 л1122
2Ц1 ^2112
4 А
^2121 ^2122
^1211 Л1212
А А
л1221 л1222
2211
2221
^212
4*222
Г
v Y
«1>
Стрелки указывают направление, в котором возрастают
соответствующие индексы.
Элементы матрицы (1), взятые в количестве, не превосходящем
ее порядка п, называются трансверсальными, если ни одна пара
их не принадлежит одному и тому же сечению (простому) какой-
либо ориентации. Совокупность п трансверсальных элементов
матрицы (1), представленная в виде одномерной матрицы п-го
порядка, образует трансверсаль. Число всех трансверсалей
матрицы (1) равно (ШУ"-1. Среди них находятся 2Г1 диагоналей,
образованных элементами, расположенными на прямых,
соединяющих противоположные вершины матрицы. Та из диагоналей,
у которой в каждом элементе значения всех индексов одинаковы,
называется главной, а ее первый элемент Ап . . .г — главным.
Обобщением понятия трансверсали является понятие транс-
версального сечения. Б^дем называть строки данного направления
матрицы (1), взятые в количестве, не превосходящем ее порядка п,
трансверсальными, если ни одна пара их не принадлежит одному
и тому же сечению (простому) какой-либо ориентации.
Совокупность п трансверсальных строк какого-либо направления,
представленная в виде квадратной матрицы л-го порядка, будет
двумерным трансверсальным сечением, соответствующим этому на-
правлению. В матрице (1) число всех двумерных трансверсальных
сечений, соответствующих направлению (ia) (1 < а < р), равно
(п\)°~2. Среди них находятся 2Р~~2 двумерных диагональных сечений.
Одно из них, главное, состоит из элементов с одинаковыми
значениями р — 1 индексов ix, . . ., ta_b i^, . . . , ip. При /?> 3 кроме
двумерных трансверсальных сечений имеются также трансвер-
сальные сечения высших измерений. Будем называть т-кратные
(2 < т < р — 1) сечения данной ориентации (i^ . . . £«,„)» взятые
в количестве, не превосходящем п, трансверсальными, если ни
одна пара их не принадлежит одному и тому же сечению (простому)
какой-либо ориентации. Совокупность п трансверсальных сечений
7
ориентации (i^ . . . tam), являющихся (р — т)-мерными матрицами
n-го порядка, может быть представлена в виде (р — т +
^-мерной матрицы того же порядка, которая и будет трансверсальным
сечением р — т + 1 измерений, соответствующим ориентации
(i0l . . • iam)- Число всех такого рода сечений равно (л!)"1"1. Среди
них находятся 2Ш~1 диагональных сечений р — т + 1 измерений.
То из них, которое состоит из элементов с одинаковыми значениями
индексов iai, . . ., iafn, называется главным сечением. Так, в
четырехмерной матрице второго порядка || 4Mlil/J| (il9 i2, i3, *4= 1, 2)
имеем два трехмерных диагональных сечения, соответствующих
ориентации (*У2):
А А
^1111 ^1112
А А
^1121 ^Ц22
А А
Л2211 ^2212
*2221
4
!222
2111
\
112
А А
^2121 ^2122
А А
^1211 ^1212
А А
1221 ^1222
Первое из них является главным _
Многомерная матрица, у которой все элементы, расположенные
вне главной диаюнали, равны нулю, называется диагональной,
если не все элементы главной диагонали — нули; в противном
случае, когда все элементы матрицы равны нулю, она называется
нулевой. В дальнейшем диагональную матрицу с элементами
главной диагонали Аъ А2, . . . , Ап будем обозначать символом {Alf
Л2, . . . , Ап), а нулевую — через О.
Многомерная матрица называется симметрической относительно
двух индексов, если каждые два элемента ее, получающиеся один из
другого перестановкой этих индексов, одинаковы. Так, кубическая
матрица я-го порядка
Иш11 iU,*=1.2,...fn)
(2)
будет симметрической относительно индексов /, К если
А/* = А*у (i,j,k = l929...9n).
— Кубическая матрица 2-го порядка, симметрическая относительно
индексов /, к, имеет вид
НО
Иш Al2
1А А
| 112 ^122
А А I
Л211 Л212
А А '
^212 ^222
■ ч
1 г
Y
1 (/)
Многомерная матрица называется симметрической
относительно нескольких индексов, если она симметрическая относительно
любой пары из них. Если симметрия имеет место по отношению ко
всем индексам, то матрицу будем называть просто
симметрической. Так, кубическая матрица (2) будет симметрической, если
\ih = Aiki = Aiki ^ А>пк = Аы/ = \и (*• A k = 1» 2,..., п).
*ш
'ikj
Ч*
xiik
w
**/<
8
Симметрическая кубическая матрица второго порядка имеет вид
Mi)
An Am
А А
^112 ^122
А А
Л112 ^122
А А
^122 л222
Г
г
(/)
-^(k)
Число различных элементов у симметрической р-мерной матрицы
/1-го порядка, очевидно, равно C£+P_i.
Многомерная матрица называется кососимметрической
относительно двух индексов, если каждые два элемента ее, получающиеся
один из другого перестановкой этих индексов, отличаются друг
от друга только знаком. Так, кубическая матрица (2) будет косо-
симметрической относительно индексов /, k, если
Aijk ——Aikj
(/,/,/2= 1,2 ,Л).
Отсюда вытекает, что элементы этой матрицы с одинаковыми
значениями индексов /, k равны нулю. Кубическая матрица
второго порядка, кососимметрическая относительно индексов /, kf
имеет, следовательно, вид
О
— А
112
*112
О
О А
-А
мо
212
212
О
->- (k)
Y
</>
Многомерная матрица называется кососимметрической
относительно нескольких индексов, если она кососимметрическая
относительно любой пары из них. Если косая симметрия имеет место по
отношению ко всем индексам, то матрицу будем называть просто
кососимметрической. Элементы кососимметрической матрицы, у
которых не все индексы имеют различные значения, очевидно, равны
нулю. Таким образом, кубическая матрица (2) будет
кососимметрической, если
Aijk = —Aikf = Ajk. = — Ajik = AHl = —Akj. (i9 /\ k = 1,2,..., n).
Кососимметрическая кубическая матрица второго порядка
является, следовательно, нулевой матрицей.
Число не равных нулю и отличных друг от друга не только по
знаку элементов кососимметрической /7-мерной матрицы л-го
порядка равно Сп (при п < р все элементы матрицы равны нулю).
Матрица
*-II4a~i,I
(i'i.*2'---» 1p = 1.2,... .л),
элементы которой связаны с элементами матрицы (1) соотношениями
А = А
4*2 ••• *р ^а2"-сар
где i0l> Ч» • • *» Ч— какая-нибудь перестановка из индексов
*i» ^2» • • • > ip> называется транспонированной относительно ма-
(h *2 •••*? \
трицы (1) соответственно подстановке Wal4 . . . ia /.Этуматрицу
будем обозначать также символом
ДЧЧ - Ч/
_^ Таким образом, матрицы Л<'»''*> и Л<''*»Л, транспонированные
относительно кубической матрицы второго порядка
Л =
All Al2
А21 А*2
J it*0
211 Л212 I > (*)
21
Г
соответственно циклическим подстановкам (i, /, /г) и (i9 fe, /), имеют
эид
г^(0
д<МЛ J
д«.*.Л _
А А 1
Л111 Л121
All ^221 1
14 4
Л111 Л211
\А А
1 ЛП2 Л212
4 4 II
Л112 Л122
4 4
Л212 Л222 ||
\А А 1
Л121 Л221
4 А
1 Л122 Л222 1
Г
г
(/)
>- (Л)
+(0
->- (*>
Точно так же матрицы Л(/,/)» Л</»*), А<'-*\ транспонированные
относительно той же матрицы А по двум индексам, имеют
соответственно вид
A(U) =
А™ =
An Awl
|Аи A12I
Иш А21
4 А
||Л112 Л122
II Аи Ап
IIA21 А21
А А II
Л121 ^122
^221 222 II
An A21I
А12 222II
\А А \\
^112 Л212
4 4
Л122 Л222||
ио
j—>- (*>
I
(/)
•(О
->-(*)
(/)
Mi)
i—>-(*>
(/)
Число всех матриц, транспонированных относительно матрицы
(1), включая последнюю, которую можно рассматривать как тран-
спонированную соответственно тождественной подстановке vW-V»
равно р\
Если матрица (1) симметрическая (кососимметрическая)
относительно т каких-нибудь ее индексов i , i ,
1 ^&
Л (2<m<p), то
»m
10
/'ai'a2"4n \
транспонированная матрица A l f где i^ , la ,..., tp —
какая-нибудь перестановка из индексов L , in ,..., t" , совпадает с
I четная, и отличается от (1)
только знаками соответствующих элементов, если эта подстановка
нечетная.
Возьмем /7-мерную (пг х Щ X . . . X яр)-матрицу
Л==НЛ^2...<„11 Ce=1»2t...ine; a=l,2,...,p),
где среди чисел п^ (а = 1, 2, . . . f р) некоторые или даже все могут
быть одинаковыми.
Пусть ma, v^1 \ v^2),... % v^* — какие-нибудь целые
положительные числа, удовлетворяющие условиям
vi,)+vf + ...+vlm«)=na(« = 1.2.....P).
Разбивая тогда значения 1,2,...,па каждого из индексов ia
(а = 1,2,... ,р) матрицы Л на ma групп так, чтобы первая
группа состояла из чисел 1,2,...,Va\ вторая —из чисел Va° + 1,...
. • •»v^+v? и т. д., а та-я— из чисел va! + • • .+v^B""l)+1,..., ла«
можем представить матрицу Л в виде клеточной (или блочной)
р-мерной (/«! х т2 х ... X тр)-матрицы
л = 11\1Ц2... йр11 0*а = 1,2,,.., ma; a = 1, 2,... ,р),
элементами которой являются клетки (или блоки), представляемые
р-мерными (v{l*l) X v^ X ... X vp p )-матрицами
^i*i2 ••• »р = I' Af\h ••• /р И
a=l,2,...,p).
В частности, если какие-нибудь целые положительные числа
п, т, v,, v2 vm связаны соотношением
Vl + V2 + • ' • + Vm = «.
то р-мерная матрица n-го порядка
А = И,<2... („II (*i. V • • • • 1р = !»2 д>
11
может рассматриваться как клеточная /7-мерная матрица т-го
порядка:
А = 11*11^... ирИ (IV h- • • • 'l*p = ^2- • • *т)>
элементами которой являются клетки, представляемые р-мерными
(% X ^2 X • • • X ^-матрицами
(/a = v, + --- + 4^1 + l,...,v1 + ...+v|la_1+vJla;
a = l,2,...,p).
Диагональные клетки Ж{м (\i = 1,2,..., т) представляются
тогда р-мерными матрицами v^-ro порядка;
Я(Д) = КА... h II (*« = v, + ... + v^ + 1,..., v,+ ... +V-1 +V
a=l,2,...,p).
Если диагональные клетки 9t(1>> 2t(2), . . . , 9l(m) не все равны
0, а все недиагональные клетки состоят целиком из нулей, т. е.
равны 0 все элементы 91ц,ц2.. .цр, у которых по крайней мере два
индекса имеют отличные друг от друга значения, то матрица А
называется клеточно-диагональной и обозначается символом {2t(1),
9t(2),..., %im)].
§ 2. ДЕТЕРМИНАНТЫ, ПОРОЖДАЕМЫЕ МНОГОМЕРНОЙ МАТРИЦЕЙ
Возьмем в матрице (1) какую-нибудь трансверсаль
А (1)М) (1) , A i2) (2) (2) , • • • , А(П) („) in) ,
tj t2 ••• lp ll l2 -• lP ll l2 •- lP
где значения #\ 42\ • • • » *vn> индексов tv (v = 1, 2, . . . , p) в
элементах трансверсали образуют некоторую перестановку из чисел
1, 2, . . . , л, и составим произведение этих элементов
А<1>,<1) Л1) ^,(2).(2) .(2) • . • Алп)(п) (п) • (3)
Ч Н •••*/> М 12 "• h l\ (2 — lp
Пусть т — какое-либо четное неотрицательное число, не
превосходящее р. Выберем из индексов ilf i2t . . . , ip какие-нибудь
т индексов, например il9 i2, . . . , im, и определим число инверсий
/^ в перестановке 4°, $\ . . . , %\ образуемой значениями ин-
12
декса /ц (1 < (л < т). Умножая произведение (3) на дополнитель-
т
ный множитель (—I)»**-1 , получим выражение
т
(— I)**" ^ <1),<1> ,(1) ^,(2) .(2) (2) • • • А(п)Лп) (п) , ^4)
*1 12 ••• *р *1 '2 ••• *р Ч *2 ••• *р
где значения i\l\ 42), . . . , 4п) первого индекса 1Ъ очевидно,
можем предполагать идущими в натуральном порядке. Индексы
*д (\i = 1, 2, . . . , m), от которых зависит тот или иной знак
выражения (4), называются альтернативными, остальные же р — т
индексов tOT+b . . . , ip — неальтернативными*.
Составляя выражения вида (4) для каждой из (я!)"-1 трансвер-
салей матрицы (1) и беря их алгебраическую сумму, получим
р-мерный детерминант п-го порядка \А± ± + + |п с сиена-
1 1 ••• *т 1 т+\ ••• * p
± ± + +
турой (tj... fmfm+1... *р), где альтернативные индексы отмечены
знаком *, а неальтернативные—знаком +. (Число я, стоящее внизу
правой вертикальной линии в обозначении детерминанта, пишем
лишь в том случае, когда желательно обратить внимание на его
порядок).
Имеем, таким образом,
т
= £ (- I)11"' Л <1>4» ... ,(« Л <2>,<2> ... ,<2> • • •
/г
•••Л.(»>,<«> ,(«)» " (5)
«1 t2 ---'р
где суммирование распространено на все возможные комбинации
перестановок $\ 42\ • • • » 4ге) (а = 2, 3, . . . , р) при
фиксированной перестановке i[l\ i\2) ,. . . , tf"\ представляющей ряд
натуральных чисел 1, 2, . . . , п. Слагаемые суммы (5), число которых
равно (и!)р~1, называются членами детерминанта.
Число т альтернативных индексов всегда предполагается
четным, так как тогда и только тогда сохраняется коммутативность
умножения. Это число определяет род р-мерного детерминанта.
У /7-мерной матрицы при р четном существует только один
детерминант наивысшего рода /?, когда все индексы альтернативные
(гипердетерминант). При р нечетном существуют р детерминантов
± ± -ь ± ±
наивысшего рода р — 1 с сигнатурами (ix . . . *a-_it0ta+i . . . ip),
где a = 1, 2, . . . , р. Детерминант наинизшего рода 0, когда все
* Эти определения относятся не только к индексам, но также к строкам
и их направлениям, к сечениям (простым) и их ориентациям и пр.
13
± +
+
индексы неальтернативные, называется перманентом.
Детерминанты, род которых больше нуля и меньше р9 называются
смешанными.
Детерминанты (включая перманент), порождаемые одной и той
же многомерной матрицей, объединяются под общим названием
кодетерминантов. Два кодетерминанта четного числа измерений
будут союзными, если альтернативные индексы одного являются
неальтернативными индексами другого, и наоборот.
Так, например, у четырехмерной матрицы второго порядка
II^Mt/i/JI (кш h> ht & = 1, 2) детерминантом наивысшего рода 4
будет гипердетерминант
И±±±± в А\ 111 2222 ^1112^2221 А\ 12Г*2212 "»" А 122^2211
' _ А21Л122 + А\2\2Г2\2\ + ^122 Ап2 ^1222^2111 '
Союзным кодетерминантом является перманент
Л4-+++ ^ 1111 2222 "т" ^1112^2221 • ^112Г*2212 "•" Al22^2211 '
+ ^1211^2122 "■" ^1212^2121 + ^1221^2112 "«" ^1222^2111 #
Кроме того, имеются три пары союзных кодетерминантов рода
2, из которых отметим пару смешанных детерминантов
|^+±+± = ^1111^2222 ^1112^2221 + Л1121Л2212 Л1122Л22!1
1\^Ъ1А\2_А л , л л _а л .ж А
Л12ЦЛ2122 ^ rk\2\Tk2\2\ ^1221^2112 » ^1222^2111 '
Afc+± + ~ А 111^2222 + ^1112^2221 Al2lA*212 Al22^2211 +
hhhU |2 , л я ,А л _А л _а а
^ /11211/12122 ~ Л1212Л2121 Л122Г12112 ^1222^2111 *
Детерминанты двух матриц, обладающие одной и той же
сигнатурой, называются косигнатурными.
Обозначение детерминантов, порождаемых многомерной
матрицей, можем сделать более подробным, выписывая полностью
элементы матрицы с помощью ее двумерных сечений и заменяя
крайние двойные черты простыми, причем неальтернативные
направления всегда будем отмечать знаком «+»•
Таким образом, детерминанты, порождаемые кубической
матрицей второго порядка || Аф\\ (i, /', k = 1, 2), могут быть
представлены в виде
I HkV
Цк\2
.. . Л
А А
Л111 Л112
^121 ^122
^211 ^212
^221 ^222
. >- (*)
Y
"" АиАйй ^112^221 "^121^212 "Г" ^122^211 ■
14
l±f±
ijk
All A\\2
^211 ^212
A A
л121 л122
^221 ^222
Л
(A)
Y
(0
— А1Л22 ^112^221 + А2Л12 А\22Г2\1 »
-I-
-Hk)
±dtt
i j k 12
A A
Л111 Л121
^211 A
221
л112 л122
Ат А
222
4
(0
(Л
"" ^111^222 "Т" ^цИ221 ^121^212 ^122^11 '
tt
А 12
All Al2
4 А
л121 л122
Л У1
^211 '*212
+
-»<0
^221 А
222
<1>
Y
+
= АША222 + ^112^22i + А2Л12 + A\22A2\i •
Детерминант и перманент обычной матрицы /1-го порядка \\Аа\\
}i, / = 1,2,..., п) также могут быть обозначены символами
А±±\ и IД| , I как двумерные детерминанты с сигнатурами
± ± ++ ^
(i /) и (I /). Таким образом, имеем
АП А\2
А2Х А^
— АЦА22'
AvAn>
К А
22
"" АЛг + ^12^1 •
Замечание 1. В дальнейшем будем говорить об элементах,
сечениях и строках детерминантов многомерной матрицы как о
соответствующих элементах, сечениях и строках этой матрицы.
§ 3. ОСНОВНЫЕ СВОЙСТВА ДЕТЕРМИНАНТОВ
МНОГОМЕРНОЙ МАТРИЦЫ
Характер свойств детерминантов многомерной матрицы зависит от
их рода. Гипердетерминант обладает свойствами, являющимися
обобщением хорошо, известных свойств обычного детерминанта.
Смешанные же детерминанты и перманент наряду со свойствами,
общими всем кодетерминантам, имеют многие своеобразные
свойства, присущие им одним. Детерминант с той или иной сигнатурой
15
{в частности, перманент), число измерений которого можно
предполагать каким угодно целым, большим двух, в дальнейшем
будем называть многомерным.
Свойство I. Многомерный детерминант равен нулю, если одно
из его сечений* состоит из нулей.
Это очевидно, так как в каждый член многомерного
детерминанта, у которого одно сечение состоит из нулей, входит один
элемент из этого сечения.
Свойство II. Детерминанты матрицы A=\[Aili2... /pj| (il9 t2, ...
. . . , ip = 1, 2, . . . , п) связаны с детерминантами
транспонированной относительно А по двум каким-нибудь индексам, например
ix и t2, матрицы AUuU) следующими соотношениями:
м*...|
tt iz.»
где в каждом из равенств многоточиями заменены части сигнатур,
ничем не отличающиеся друг от друга.
Действительно, для каждой пары элементов р-мерных матриц
л-го порядка А и AUlM имеем
it i2. -
\А±+
=
=
м,...
Aduiz)
Л+±
it iz ...
»
'
А++
h iz -
= I
И
A?V? . =А
4*2*3 "• '
¥А-'р vi
My
tp = l,2,...,n)
и все трансверсали транспонированной матрицы Л(/1'/2>,
получающейся из А путем обмена соответственными сечениями ориентации
(*i) и (*a)t находятся среди трансверсалей исходной матрицы Л.
Наоборот, каждая трансверсаль матрицы А является трансвер-
салью матрицы AittM. Таким образом, каждый член детерминанта
матрицы А будет иметь равный себе член среди членов
детерминанта матрицы A{itJz\ обладающего такой же сигнатурой, как и
данный детерминант, или отличающейся от нее лишь знаками над
индексами 1г и i2, смотря по тому, цмеют ли индексы iu i2 один и
тот же или противоположный характер. Так как в каждом из ра-
сматриваемых детерминантов все члены различны, а число их
одно и то же, то эти детерминанты равны.
Следствие 1. Гипердетерминант и перманент не меняются
при любом транспонировании их матриц.
Свойство III. От перестановки двух сечений одной и той же
ориентации многомерный детерминант не меняется, если
ориентация неальтернативная, и только меняет знак, если ориентация
альтернативная.
В самом деле^ трансверсали матрицы Л', в которую переходит
матрица А = || А^ t \\ (lv ir ..., ip = 1,2,..., п) данного
детерминанта при перестановке двух каких-нибудь сечений одной
* Сечения, встречающиеся в § 3, 4, предполагаются простыми.
16
и той же ориентации, например, i^-ro и t'iV)-ro (1 < ji<v<n)
сечений ориентации (ЭД, ничем не отличаются в своей
совокупности от трансверсалей матрицы Л. Возьмем какую-нибудь
трансверсаль Л (1) (1) (1), ..., Д(и)(м (Л,. .., AXv) (v) (v), ...
*i «2 — *p M '2 - lp 4 '2 ••• h
• • •, A (rt) (n> («) матрицы Л. Содержащаяся в ней пара элементов
*1 *2 —'р
A(W*o*)...*(W > ^ (v) (v) (v> занимает в преобразованной матрице А
М 2 р Ч *2 ••• *р
положение, соответствующее положению трансверсальной пары
элементов AXv) <w (w , Л (Jl) (v) (V), тогда как остальные элемен-
*1 ^ — *р 11 *2 ••• *р
ты трансверсали занимают в матрице А то же положение, как и
в матрице А. Таким образом, члену детерминанта матрицы Л,
составленному из произведения элементов рассматриваемой
трансверсали и дополнительного множителя (—1)^, определяемого
сигнатурой детерминанта, соответствует член косигнатурною
детерминанта матрицы Л', составленный из произведения тех же
элементов и дополнительного множителя (—1)^', где N' определяется
той же сигнатурой и имеет ту же четность, как и N, или
противоположную ей, в зависимости от того, будет ли индекс ix
неальтернативным или альтернативным (т. е. в зависимости от того, будет
+ ±
ли сигнатура иметь вид {ix . ..) или {1г . . .)), так как только
перестановки, образуемые значениями индекса ix в элементах обоих
членов, различны и, переходя друг в друга транспозицией (iM,
i{v>), имеют противоположные четности. В первом случае эти члены,
а следовательно, и содержащие их детерминанты, равны, во
втором же случае — лишь отличаются знаком.
Следствие 2. От перестановки двух сечений одной и той
же ориентации перманент не меняется, а гипердетерминант лишь
меняет знак.
Следующие два свойства очевидны, если принять во внимание
свойство III.
Свойство IV. Многомерный детерминант не меняется от
одинакового числа перестановок сечений каждой ориентации.
Свойство V. Если в многомерном детерминанте два сечения
одной и той же ориентации одинаковы, то этот детерминант будет
равен нулю, если ориентация альтернативная, и не будет
необходимо равным нулю, если ориентация неальтернативная.
Следствие 3. Гипердетерминант, у которого два сечения
одной и той же ориентации одинаковы, равен нулю.
Свойство VI. Если все элементы какого-либо сечения в
многомерном детерминанте умножить на некоторое число, то сам
детерминант умножится на это число.
Действительно, пусть все элементы некоторого сечения в
многомерном детерминанте умножены на число t. В каждый член
детерминанта должен войти сомножителем один из элементов рассматри-
2-595
17
ваемого сечения, а следовательно, и число tf т. е. сам детерминант
умножается на t.
Это свойство допускает и такую формулировку: общий
множитель всех элементов какого-либо сечения в многомерном
детерминанте можно вынести за знак детерминанта.
Свойство VII. Если в многомерном детерминанте два сечения
одной и той же ориентации пропорциональны, то этот детерминант
будет равен нулю, если ориентация альтернативная, и не будет
необходимо равным нулю, если ориентация неальтернативная.
В самом деле, пусть в рассматриваемом многомерном
детерминанте элементы некоторого сечения какой-нибудь ориентации
отличаются от соответственных элементов другого сечения той же
ориентации одним и тем же множителем t. Вынося тогда, согласно
свойству VI, общий множитель t за знак детерминанта, получим
детерминант, у которого два сечения одной и той же ориентации
одинаковы и к.которым, следовательно, применимо свойство V.
Следствие 4. Гипердетерминант, у которого два сечения
одной и той же ориентации пропорциональны, равен нулю.
Замечание ^.«Свойство V, а также свойство Г являются, очевидно,
частными случаями свойства VII:
До сих пор мы рассматривали многомерные детерминанты с
одночленными элементами, Обратимся теперь к рассмотрению
многомерных детерминантов с многочленными элементами и установим
принцип разложения их на сумму детерминантов, элементы которых
являются одночленами.
Свойство VIII. Если в р-мерном детерминанте я-го порядка
каждый элемент некоторого сечения какой-нибудь ориентации,
например v-ro (1 < v < п) сечения ориентации (ix), представлен
в ввде алгебраической суммы некоторого числа h слагаемых, т. е.
h
\dv) № = £ АТм /(v> ^2V> •" " • С = Ь 2, ..., л),
2 •" * ц=1 \l2 — h
то этот детерминант равен сумме h косигнатурных детерминантов,
у которых все сечения ориентации (/х), кроме v-ro, такие же, как
и в данном детерминанте, a v-e сечение в (г-м (1 < ц,< А)
детерминанте состоит из элементов Aill\v) <v>.
Действительно, при упомянутом выше условии член р-мерного
детерминанта я-го порядка
(— 1) Д.(1) .(1) Л,,(2) (2) • • • Л (v) (V) • • • А (П) (п) ,
где дополнительный множитель (—1)^ определяется сигнатурой
детерминанта, можно представить в виде
2 (-1>"л,4»... *<»'л*«>... 42) • • • 'V*... 4V) *''Л4П) •• 4П)'
18
г. е. в виде алгебраической суммы ft членов косигнатурных
детерминантов, получающихся из данного заменой каждого элемента
A (v) f(v) в v-м сечении ориентации (У элементом
^K-4V) .(I* = !-2 Л>-
Составляя эти суммы для каждого из (л!)"-1 членов данного
детерминанта и собирая вместе их ji-e слагаемые, получим, очевидно,
ji-й косигнатурный детерминант, отличающийся от данного лишь
тем, что в v-м сечении ориентации (1г) вместо элементов A <v) (v)
стоят элементы A^hv, <v>- Полагая \i последовательно равным
Vi2 /... ip
1, 2, . . . , ft, получим ft косигнатурных детерминантов, сумма
которых будет равна данному детерминанту.
Будем говорить, что v-e (1 < v < п) сечение какой-нибудь
ориентации в многомерном детерминанте л-го порядка есть
линейная комбинация его остальных сечений той же ориентации, если
для всякого ji-ro (|i = 1, . . . , v — 1, v + 1, . . . , п) сечения
можно указать такое число ^, что, умножая ji-e сечение на t^,
а затем складывая все сечения, кроме v-ro, получим v-e сечение
(умножение сечения на какое-нибудь число надо понимать как
умножение всех его элементов на это число, а сложение сечений
одной и той же ориентации — как сложение соответственных
элементов этих сечений). Некоторые из множителей t^ могут быть
равными нулю, т. е. v-e сечение фактически будет линейной
комбинацией не всех п — 1 оставшихся сечений, а лишь некоторых из
них. В частности, если только один из множителей t^ не равен
нулю, получим случай пропорциональности двух сечений.
Наконец, если сечение состоит целиком из нулей, то оно всегда будет
линейной комбинацией остальных сечений, т. е. получим случай
когда все множители t^ равны нулю. Первому из этих частных
случаев соответствует свойство VII, обобщением которого является
следующее.
Свойство IX. Если одно из сечений какой-нибудь ориентации
в многомерном детерминанте есть линейная комбинация его
других сечений той же ориентации, то детерминант будет равен нулю,
если ориентация альтернативная, и не будет необходимо равным
нулю, если ориентация неальтернативная.
В самом деле, пусть в рассматриваемом многомерном
детерминанте п-го порядка некоторое сечение какой-нибудь ориентации,
например v-e (1 < v < n) сечение ориентации (t\), есть линейная
комбинация ft других сечений той же ориентации. Тогда каждый
элемент этого сечения будет алгебраической суммой ft слагаемых,
а потому, на основании свойства VIII, детерминант может быть
представлен в виде суммы ft косигнатурных детерминантов, в
каждом из которых v-e сечение ориентации (ix) будет
пропорционально одному из остальных сечений той же ориентации. По свойству
VII все эти детерминанты равны нулю, если ориентация (У альтер-
2*
19
нативная. В этом случае равен нулю, следовательно, и
рассматриваемый детерминант. Последний, очевидно, не будет необходимо
равным нулю, если ориентация (У неальтернативная.
Следствие 5. Гипердетерминант равен нулю, если одно
из его сечений какой-либо ориентации есть линейная комбинация
других сечений той же ориентации.
Следующее свойство является обобщением теоремы Якоби,
относящейся к обычным детерминантам.
Свойство X. Если в многомерном детерминанте к некоторому
сечению какой-нибудь ориентации прибавляется другое сечение
той же ориентации, умноженное на какое-либо число, то
детерминант не меняется, если ориентация альтернативная, и, вообще
говоря, меняется, если ориентация неальтернативная.
Действительно, пусть в данном многомерном детерминанте к
некоторому сечению какой-нибудь ориентации, например (У,
прибавляется другое сечение той же ориентации, умноженное на
какое-либо число. Тогда по свойству VIII детерминант делается
равным сумме двух косигнатурных детерминантов. Один из них есть
данный детерминант, а другой содержит два пропорциональных
сечения ориентации (У и, согласно свойству VII, будет равен
нулю, если ориентация (У альтернативная. Последнего
заключения, однако, нельзя сделать в силу того же свойства VII, если
ориентация (У неальтернативная.
Следствие 6. Гипердетерминант не меняется, если к
одному из его сечений какой-нибудь ориентации прибавляется дру.
гое сечение той же ориентации, умноженное на какое-либо число-
§ 4. РАЗЛОЖЕНИЕ МНОГОМЕРНЫХ ДЕТЕРМИНАНТОВ
Вычисление детерминантов многомерной матрицы, если
непосредственно применять их определение, становится по мере возрастания
порядка матрицы все более и более громоздким. Существуют
более простые методы вычисления многомерных детерминантов,
основанные на выражении их через детерминанты низшего числа
измерений или через детерминанты низшего порядка.
Рассмотрим сперва случай понижения числа измерений
многомерных детерминантов. Напишем /7-мерную матрицу п-го порядка
А в виде
4 =41А ,, ,, к и\\ (6)
(H = f+1, r + u=m, m + v=p, 2<m</7—1).
Будем рассматривать какие-нибудь т индексов, например, первые
т индексов iv..., ir, j{,..., jt> ju в матрице (6) как один /л-крат-
ный индекс t,... у,... jju и обозначим через
20
одну из (р — т + 1)-мерных матриц л-го порядка, которые
представляют (п\)т-1 трансверсальных сечений р — т + 1 измерений
матрицы (6), соответствующих ориентации (tx . . . irjt . . . jtju).
Каждая из (п\)р-т трансверсалей матрицы (7) является также
трансверсалью матрицы (6), и трансверсалями (и!)"1-1 матриц вида
(7) исчерпывается совокупность всех трансверсалей матрицы (6).
Из упомянутых выше т индексов матрицы (6) какие-нибудь г (0<
< г < т) индексов, например ilt . . . , i,9 будем предполагать
неальтернативными, а остальные и (О < и < т) индексов /lf. . .
• • • t /*t iu — альтернативными. Рассмотрим /7-мерный
детерминант п-то порядка:
И| = |Л+ ++ +± ...I, (8)
I *!-« *r/l ™ ///« I
где многоточием в конце заменена остальная часть сигнатуры,
относящаяся к индексам kl9 . . . , kv. Будем различать два случая
соответственно четности числа и.
В первом случае, когда и — нечетное, положим т-кратный
индекс ix . . . ir]\ . . . jtju в матрице (7) альтернативным по одному
какому-либо из индексов /ь . . . , /t, /ы, например, по индексу
/я. Срставим (р — m + 1)-мерный детерминант /х-го порядка
. ...I, (9)
где многоточием в конце заменена остальная часть сигнатуры,
ничем не отличающаяся от той части сигнатуры детерминанта (8),
которая относится к индексам k1$ . . . , kv. Тогда детерминант (8),
очевидно, может быть разложен на алгебраическую сумму (/г!)т-1
(р — m + 1)-мерных детерминантов вида (9)
И1 = 2(-1)'
t
Ц=1
А ± ...I, (10)
где /д — число инверсий в перестановке $\ $ , . . . , $\
образуемой значениями индекса /ц в элементах каждого члена
детерминанта (9), которые могут быть взяты в такой последовательности,
чтобы значения индекса /„ шли в натуральном порядке.
Во втором случае, когда и — четное (в частности, 0), положим
m-кратный индекс ix . . . irjx . . . ju в матрице (7)
неальтернативным и составим (р — m + 1)-мерный детерминант (в частности,
kv неальтернативные) п-го
I, (П)
[ерманент, если все индексы kl9
Y\T\CtTtVCk
1.ир>1Д|\.а
\А
+
21
где, как и в детерминанте (9), многоточием в конце заменена
остальная часть сигнатуры, тождественная с частью сигнатуры
детерминанта (8), относящейся к индексам klf . . . , kv. Тогда получим
разложение детерминанта (8) на алгебраическую сумму (я!)"*-1
(р — т + 1)-мерных детерминантов (в частности, перманентов)
вида (11)
|Л|=2(-1)'
и
2
(12)
Последняя формула, если и = 0 и все индексы klf. . . , kv
неальтернативные, дает разложение р-мерного перманента и-го
порядка | А\ на сумму (я!)"1-1 (р — т + 1)-мерных перманентов того
же порядка:
Ф (+)
1*1-2* + + + • (13)
ix ... tOTfe, ...kv\
Повторными разложениями детерминантов (в частности,
перманентов), фигурирующих в предыдущих формулах, детерминант
р измерений можно представить в виде алгебраической суммы
косигнатурных детерминантов меньшего числа измерений q. При
этом сигнатура слагаемых детерминантов определяется в
зависимости от того, каким образом р индексов в данном детерминанте
распределены на q групп, представляющих индексы (простые или
кратные) в <7-мерных детерминантах. Именно, каждый из q
индексов будет неальтернативным, если он вовсе не содержит
альтернативных в данном детерминанте индексов или содержит четное
число их (формулы (13), (12)); если же он содержит нечетное число
таких индексов, то будет альтернативным по одному
какому-нибудь из них (формула (10)). В частности, каждый многомерный
детерминант с той или иной сигнатурой разлагается, притом
различными способами, на алгебраическую сумму обычных детерминантов
или перманентов. Такое разложение называется полным.
Для иллюстрации указанного выше способа понижения числа
изменений многомерных детерминантов при их вычислении
приведем разложения четырехмерного гипгрдетерминанта второго
порядка:
±±± ±
h it U U
= £(-d
'l+/«
x +± ±
h it it i4
A A
A A
^1121 ^1122
*2211 ™%
-*</i Q
1212
A A
222l ^2222
Г
Us)
*21U "2112
A A
^2121 ^21221
A A
I?11 IB12
A A
Л1221 ^1222
+
•*> им
I—r (u)
r
(it)
22
б) \А
± ±
it iz
i* U Ь
h+U
A A
11U л1112
A A
-^2221 л2222
+
A A
^2211 ^2212
A A
Л1121 ЛП22
| h it i» i* I2
А А
\2}\ ^1212
4 А
л2121 л2122
^21И ^2112
А А
^1221 Л1222
+ +
it i2iz £4
(+>
А А
л1122 ^2222
(f) (+) <+> <+>
^1121 ^2221
А112 Л:
+
!212
Л2121 Л1221
А А
^2112 ^1212
А2\\\ А
(+)
1211
А А
^2122 ^1222
+
С помощью формул (10), (12), (13) легко доказывается теорема.
Теорема 1. Если р-мерный детерминант п-го порядка с какими-
нибудь т (1 < т < р — 2) неальтернативными индексами, напри-
меР h> /2» • • • у *т> имеет все пт т-кратные сечения ориентации
(ixi2 . . . im) одинаковые, то он равен умноженному на (п\)т
детерминанту (р — т)-мерной матрицы, представляющей одно из
упомянутых выше одинаковых сечений, причем сигнатура этого
детерминанта одинакова с сигнатурой всех индексов данного детерминанта,
отличных от ilt i2, .. . ., im.
Переходя к вопросу о вычислении многомерных детерминантов,
основанном на выражении их через детерминанты низшего
порядка, введем предварительно понятия минора многомерного
детерминанта и его алгебраического дополнения.
Выделим вр-мерной матрице n-го порядка А = ||Ау2..., || (t"lf i2,
h = 1. 2,
п) по v (1 < v < n) каких-нибудь сечений
каждой из ориентации (1г)9 (i2) . . . , (ip). Тогда общие всем
выделенным сечениям элементы, число которых равно v", образуют
минорную р-мерную матрицу порядка v. Ее детерминант М с той или
иной сигнатурой называется минором v-ro порядка косигнатурного
детерминанта | А | основной матрицы Л. В частности, минором
первого порядка детерминанта | А | будет отдельный элемент
детерминанта. Минором п-го порядка является сам детерминант | Л |.
Вычеркивая в детерминанте | А [ те сечения ориентации (tx),
(i2)f . . . , (ip)t которые содержат элементы минора М, получим ко-
сигнатурный детерминант (п.— v)-ro порядка М', называемый до-
полнительным минором для М. Если вычеркнем, наоборот, те
сечения ориентации (h), (i2), . . . , (ip)9 в которых расположены эле-
23
менты минора М', то останется, очевидно, минор М. Таким
образом, М и М' составляют пару взаимно дополнительных миноров
данного детерминанта.
Пусть т (0 < т < р) —род детерминанта | А | и ilt t2, ... , im—
его альтернативные индексы. Если элементы минора М содержатся
в сечениях ориентации (i ) с номерами fjj), tj*>f . . . , fljj> (ц =
= 1, 2, . . . , m), то выражение
ЭП = (— \)гМ\ (14)
где
т
e-J <#> + *?> + ... + #)*. (15)
называется алгебраическим дополнением минора М.
В частности, алгебраическим дополнением какого-либо элемента
Л* ...о а о Детерминанта |Л| будет выражение
т
«1 -атат+\»-ар V ' а1 - ат«т+1 - °Р
™е А1в1... атат+1... ар - дополнительный минор для Л0[... anflm+i... „р.
Докажем теперь лемму, необходимую для вывода формул
разложения любого из детерминантов многомерной матрицы по
какому-нибудь его сечению.
Лемма. Произведение любого минора детерминанта
|Л| =
А± ± + +
*1 — lm 'm-fl
на его алгебраическое дополнение является алгебраической суммой
некоторых членов детерминанта \А\.
Доказательство леммы начнем с частного случая, когда минор
v-ro (1 < v < п — 1) порядка М детерминанта | А |, расположен
в сечениях ориентации (У, (t2), . . . , (ip) с одними и теми же
номерами 1, 2, . . . , v. Тогда дополнительный для М минор М' будет
расположен в сечениях тех же ориентации с одними и теми же
номерами v + 1, v + 2, ..., п и будет, следовательно, также
алгебраическим дополнением минора М. Возьмем произвольный
член минора М:
т
2 '',
(—!) Л (1) .(oA,,^) .(2) ... Aiy) (v), (17)
Но ... 1п 2to «. in v*2 ••• lD
где /^ — число инверсий в перестановке f£l) i(£\ ... ,/{iV)
* Число е, равное сумме номеров альтернативных сечений детерминанта
|Д|, в которых содержатся элементы минора М, можно заменить суммой
номеров альтернативных сечений, в которых содержатся элементы минора М'9
так как обе суммы имеют одинаковую четность.
24
Произвольный член минора М! имеет вид
т
(— !) A,J.i/<V+l> /^+!) A,WV+2> f(V+2) * * * Ап,М /(П) ' ^
VH-K2 ... ip v-j-2f2 ... tp m2 • ip
где /Ji, — число инверсий в перестановке 4v+1),/^+2),... ,$°.
Перемножая члены (17) и (18), получаем
т
(19)
где I = Г^ + Г , очевидно, есть число инверсий в перестановке
/(1) /<v) .(v-H) An)
Произведение же (19) является членом детерминанта |Л|. Этим
доказан рассматриваемый частный случай леммы,
Перейдем теперь к рассмотрению общего случая, когда минор
М расположен в сечениях ориентации ia (а = 1, 2, ...,/?) с
номерами t<J), t<2>, . . , , fwt< идущими в возрастающем порядке.
Переставляя в детерминанте | А | последовательно соседние
сечения каждой из ориентации (t\), (i2), . . . , (ip)t можем перевести
минор М в первые v сечений всех ориентации, не меняя при этом
дополнительного для М минора ЛГ. Для этого понадобятся,
очевидно, (ф— 1) + (*(а2)— 2) + • • • + (i^p— v) перестановок
сечений ориентации (ia) (а = 1, 2, . . . , р). Так как детерминант | А \
по свойству III многомерных детерминантов не меняется от
перестановок сечений ориентации (*m+i), (*m+2J» • • • » (h) и лишь
меняет знак от перестановки двух сечений любой из ориентации
(/д) (|Л = 1, 2, . . . , т), то полученный в результате упомянутых
выше преобразований косигнатурйУй детерминант будет равен
f [(41,-i)+(42)~2)+...+(4v)-v)]
(-1Г1 И1, т. *. (-1)8И|,
где е выражается формулой (15).
В новом детермийанте, по доказанному выше, произведение
ММ' является алгебраической суммой некоторых членов этого
детерминанта..Следовательно, выражение (—1)еЛШ', равное,
согласно формуле (14), произведению минора М на его
алгебраическое дополнение ЗП в детерминанте | Л|, является алгебраической
суммой некоторых членов детерминанта |Л|. Лемма доказана.
Из леммы вытекает правило разложения детерминанта |Л| по
какому-нибудь его сечению.
25
Действительно, произведение какого-либо элемента
Аа а а а детерминанта \А\ на его алгебраическое
дополнение 2t0 a, выражаемое формулой (16), является,
согласно лемме, алгебраической суммой некоторых членов
детерминанта |Л|. Число этих членов равно числу членов минора (п—1)-го
порядка М„ „ „ п , дополнительного для элемента
Ап п п „ , т. е. равно [(и— 1)!]р_1.
Возьмем теперь любое сечение детерминанта \А\ и составим
произведение каждого из гР~"х элементов этого сечения на его
алгебраическое дополнение. Никакой член детерминанта |Л|,
очевидно, не может войти в состав двух разных из числа таких
произведений. С другой стороны, общее число членов детерминанта
)Л|, входящих во все эти произведения, равно
[(n—l)!]p~ln°~1=(n!)p"1,
т. е. этим исчерпываются вообще все члены детерминанта |Л|.
Тем самым доказана соответствующая теореме Безу для
обычных детерминантов следующая теорема.
Теорема 2. Любой из детерминатов многомерной матрицы
равен сумме произведений всех элементов какого-нибудь его сечения
на их алгебраические дополнения.
Из теоремы 2 вытекает соответствующая теореме Вандермонда
для обычных детерминантов следующая теорема.
Теорема 3. Если в многомерном детерминанте все элементы
какого-нибудь сечения альтернативной ориентации умножить на
алгебраические дополнения соответствующих элементов другого
сечения той же ориентации и полученные произведения сложить, то
сумма будет равна нулю.
В самом деле, если в р-мерном детерминанте п-го порядка
заменим (г-е сечение альтернативной ориентации (ia) v-м сечением
той же ориентации (v Ф р; 1 < \i <; и, 1 < v < n; 1 < а < р)9
то составленный таким образом косигнатурный детерминант
будет на основании свойства V многомерных детерминантов равен
нулю. С другой стороны, этот же детерминант, согласно теореме 2,
равен сумме произведений всех элементов упомянутого выше v-ro
сечения ориентации (ia) в исходном детерминанте на алгебраические
дополнения соответствующих элементов ц-го сечения ориентации
(ia) в том же детерминанте. Таким образом, рассматриваемая сумма
равна нулю.
Обобщение теоремы 2 приводит к разложению любого из
детерминантов многомерной матрицы, соответствующему
разложению обычного детерминанта, указанному Лапласом.
Теорема 4. Возьмем любой из детерминантов многомерной
матрицы п-го порядка и выделим в нем произвольно v (1 < v < n — 1)
сечений какой-нибудь ориентации. Тогда сумма произведений всех
26
миноров v-го порядка, расположенных в этих сечениях, на их
алгебраические дополнения будет равна данному детерминанту.
Действительно, произведение какого-либо минора v-ro порядка
М любого детерминанта \А\ р-мерной матрицы л-го порядка А на
алгебраическое дополнение DR этого минора является, согласно
лемме, алгебраической суммой некоторых членов детерминанта
|Л|. Так как минор М содержится Bv(l<v<n — 1) сечениях
каждой из ориентации (/х), (i2), . . . , (ip) детерминанта |Л| , то,
составляя произведения ЛСК для всех миноров v-ro порядка,
расположенных, в одной из этих р групп сечений, будем иметь (C%f~*{
алгебраических сумм некоторых членов детерминанта |Л|, причем
каждая из сумм состоит из (v!)p""1[(n — v)!]p~l членов и ни одна
пара их не имеет общих слагаемых. Таким образом, общее число
членов детерминанта |Л|, входящих в упомянутые выше
произведения ЛШ, равно
(v!)"-1 l(n- v)!]'-1 (СУ1 = (Ш)р-1,
т. е. равно числу всех членов детерминанта |Л|. Следовательно,
сумма всех этих произведений является точным представлением
детерминанта |Л|.
Доказанная теорема с успехом применяется при вычислении
многомерных детерминантов, у которых многие из миноров,
расположенных в некоторых сечениях какой-либо ориентации, равны
нулю.
Так, например, выделяя в нижеследующем кубическом
детерминанте четвертого порядка первые два сечения ориентации (i) и
составляя сумму произведений всех миноров второго порядка,
расположенных в этих сечениях, на их алгебраические дополнения,
получаем
лИ1л112оо
^,22 00
О
о
00
00
4,Л,200
л221Л
,22оо
0 00
0 00
^311^312^313^314
^321 ^322 ^323 ^324
А А А А
^331 ^332 ^333 334
А А А А
Л341 л342 Л343 Л344
А\\\А\\2
А А
121 ^122
А А
А А
Л221 ^2 22
+
->(0
-*№)
(/)
А А
^333 ^334
А А А А
Л411 л412 Л413 Л414
А А А А
Л421Л422 423^424
А А А А
431 ^432 433 ^434
А А А А
/1441Л442Л443Л444
+
►(О
+
(О
-М*)
ЛизЛ<
44
А А
л433 Л434
А А
л443 ^444
I
У
.—> (fe)
С помощью теоремы 4 легко показать, что любой из
детерминантов клеточно-диагональной многомерной матрицы равен
произведению косигнатурных детерминантов ее диагональных клеток.
Из теоремы 4 вытекает соответствующая теореме Коши для
обычных детерминантов следующая теорема.
Теорема 5. Если в многомерном детерминанте порядка п все
миноры v-го порядка, расположенные в каких-нибудь v (1 < v < n—
27
— 1) сечениях альтернативной ориентации, умножить на
алгебраические дополнения соответствующих миноров, расположенных в
других v сечениях той же ориентации, отличающихся от первых
хотя бы одним сечением, и полученные произведения сложить, то
сумма будет равна нулю.
В самом деле, если в многомерном детерминанте п-ro порядка
заменим какие-нибудь v (1 < v < n — 1) сечений альтернативной
ориентации другими v сечениями той же ориентации,
отличающимися от первых хотя бы одним сечением, то составленный таким
образом косигнатурный детерминант будет иметь по крайней мере
два одинаковых сечения альтернативной ориентации и потому, на
основании свойства V многомерных детерминантов, будет равен
нулю. Но этот же детерминант, согласно теореме 4, равен сумме
произведений всех миноров v-ro порядка исходного детерминанта,
расположенных в упомянутых выше заменяющих v сечениях, на
алгебраические дополнения в том же детерминанте соответствующих
миноров, расположенных в заменяемых v сечениях. Таким
образом, рассматриваемая сумма равна нулю.
Заметим, что теорема 3 есть частный случай доказанной
теоремы, если в последней считать v = 1.
Обобщением теоремы 4 является такая теорема.
Теорема 6. Разобьем в р-мерной матрице п-го порядка А п
сечений некоторой ориентации на q (2 < q < n) групп, выделяя в
v-/o (v = 1, 2, . . . , q) группу какие-нибудь nv сечений так, что
я
]g nv = п. Пусть \А\ —любой из детерминантов матрицы А,
v=l
а Му(1 < v < q) — какой-нибудь его минор порядка пу,
составленный из элементов v-й группы. Возьмем некоторую трансверсальную
совокупность миноров Ml9 М2, . . . , Mq, т. е. такую совокупность
их, в которой ни одна пара миноров не содержит элементов
матрицы А, принадлежащих одному и тому же ее сечению какой-либо
ориентации. Вычеркивая в детерминанте \А\ сечения ориентации
(*i)» (У» • • • у (*р)> содержащие элементы миноров Мъ М2, . . . ,
..., Mft(l < fe < ^ — 1)» получим косигнатурный детерминант
M'k порядка п — (пг + п2 + . . . + nh), который назовем
дополнительным минором для Мъ М2, . . . , Mh. Составим теперь
произведение Мг М2 . . . Мя миноров рассматриваемой трансверсальной
Ssft
совокупности и умножим его на (—l)fe=1, где гк — сумма номеров
альтернативных сечений дополнительного минора М^_{, в которых
содержатся элементы минора Mk (M^ = |Л|). Тогда алгебраическая
сумма выражений
(_1)*=i8Vm3...M,,
28
распространенная на все трансверсальные совокупности миноров
детерминанта |Л|, расположенных в q группах сечений, будет
равна детерминанту \А\.
В справедливости теоремы легко убеждаемся, замечая, что
упоминаемые в ней выражения
(_ i)*=i M1M2...Mg,
распространенные на все трансверсальные совокупности миноров
детерминанта |Л|, расположенных в q группах сечений, являются
алгебраическими суммами некоторых членов детерминанта |Л|,
причем число этих сумм равно
(CniCn2 спя—\ У~1 / п* \
У^п ^п-г^ ' ' ' ^n-(n1+n2+...+ng_2V [ nji П2\. .. nq\ )
p-i
<74
каждая из них состоит из (пх\ п2! . . . nq\)P~l членов и ни одна
пара их не имеет общих слагаемых.
§ 5. УМНОЖЕНИЕ МНОГОМЕРНЫХ ДЕТЕРМИНАНТОВ
Правило Кэли — Раиса умножения многомерных
детерминантов одного и того же порядка.
Пусть даны р-мерный и q-мерный детерминанты п-го порядка.
\А\ = И(±)^ ± j±p^ | (ir iv • • •, ip = 1,2,..., n\ 1 < a < p),
'i--*a— l*a*a-H--*p
\Щ = \B j^ ± _<±)о^ | (Д, \v . .., }q = 1 2 n; KP< q\
'1-/0-1 /p/p+l—/g
где символами (±) %» (±) s2, (±) <*ъ (do) <*2 обозначены совокупности
знаков «+», «±» яад соответственными индексами.
Если г?~~х строк альтернативного направления (ia)
детерминанта \А\ умножим на nq~l строк альтернативного направления (/р)
детерминанта \В\ и полученные пр+я~2 произведений примем за
элементы (р + q — 2)-мерного детерминанта п-го порядка с
многочленными элементами
I n
|С| — 2 ^ (±)% (±)s2 В (±)Qi (±)a2
|c=l ^...«a-i^o+l—'p /i—/p-lff/p+l—'^1
(ip ..., ^д^р *a_f_p • • •» *pt /p • • • t /p_p /p_j_i» • • • f /^ === A» ^> • • •» я),
mo
|A|-|B|=|C|. (20)
29
Вывод формулы (20), очевидно, можно ограничить случаем,
когда перемножаемые детерминанты имеют ввд
|Л| = |А++± ±± ±| (r+t = p — 2, 0</</>-2),
iv..irlv.. ltip-\ip
|B| = |fl±±± ±+ +| (0<u<q-2).
Рассматривая первые р—1 индексов в детерминанте |Л| как
один (р— 1)-кратный индекс i{... iflx... ltip__v составим квадратный
детерминант я-го порядка
И f ± ±1. (21)
где (р — 1)-кратный индекс предполагается альтернативным по
индексу i^v
Полное разложение детерминанта |Л| представляется тогда,
согласно формуле (10), алгебраической суммой (п\)р~2 квадратных
детерминантов вида (21):
Hi = S(-i)^Vf * ±|,
где / — число инверсий в перестановке /£> , /Ф, . . . , /<[*>,
образуемой значениями индекса 1^(1 < ji < t) в элементах каждого
члена детерминанта (21), которые берутся в такой
последовательности, чтобы значения индекса ip-\ шли в натуральном порядке.
Подобным образом полное разложение детерминанта |В|
представится алгебраической суммой (и!)*-2 квадратных детерминантов
я-го порядка вида
\В±± |, (22)
где (q — 1)-кратный индекс предполагается альтернативным по
индексу /2. Именно,
и
|B|=S(-ir=i \В±± |,
/1/2m1...mw/tt+3--/\7
где Jv — число инверсий в перестановке т^9 т^\ . . . , т<р\
образуемой значениями индекса mv(l < v < и) в элементах каждого
члена детерминанта (22), взятых в такой последовательности, чтобы
значения индекса /2 шли в натуральном порядке.
30
Согласно правилу умножения обычных детерминантов, имеем
|Л|.|В| = 2(-
/ и
l)|i=l v=i
-\с cj2rnl...muiu+z.
Но правая часть последнего равенства есть полное разложение
(Р + Я — 2)-мерного детерминанта п-то порядка
|С|-
Следовательно,
п 1
2 4+ +± ±± 5 ±± ± + +
И|.|В| = |С|.
Число всех представлений произведения двух многомерных
детерминантов, составленного по правилу Кэли — Раиса, очевидно,
равно произведению чисел, определяющих род этих детерминантов.
Так, произведение кубического детерминанта n-го порядка на
квадратный детерминант тогб же порядка представимо, согласно этому
правилу, четырьмя способами в виде кубического детерминанта
/1-го порядка:
\Ап+\г
НЧз
£л+±в±
\с=1 *iV V
г\*
п
ifln ~
'V2
с=1 V
£ ^+*B±
к3 *«
/»
п
£
с=1
/1
4+ ±В+
То обстоятельство, что перемножаемые строки многомерных
детерминантов альтернативные, является весьма существенным,
так как умножение неальтернативных строк приводит к
детерминанту, не выражающему произведения данных детерминантов, а
умножение альтернативных строк одного детерминанта на
неальтернативные строки другого, вообще, не дает в результате этой
операции какого-либо детерминанта, поскольку число альтернативных
индексов в произведении становится тогда нечетным.
Правило Кэли — Раиса, очевидно, не распространяется на
тот случай, когда хотя бы один из множителей рассматривавшегося
выше произведения является перманентом. Это ограничение
устраняется правилом Скотта — Раиса умножения многомерных
детерминантов одного и того же порядка с любыми сигнатурами.
Правило Скотта—Раиса. Пусть даны р-мерный и q-мерный
детерминанты п-го порядка
1А | = \А (±)Sl (±)s (±)s^ 1 (*р *2«"
',= 1.2,.
, п\ 1 < а < р),
31
|Bl = |5^±)cru(±)a <±)0. | (/,»/2..... 4= 1,2,..., П; 1 <P<9),
/l"-/0-l /p /0+l-/f
где каждый из символов (±) s, (±) cr обозначает любой из знаков
Умножим каждый из п^\ элементов v-го (1 < v < п) сечения
ориентации (ia) детерминанта \А\ на каждый из /г7""1 элементов
v-го сечрния ориентации (/') детерминанта \В\ и полученные пР+ч-2
произведений примем за элементы v-го сечения ориентации (ia)
(р + Я — X)-мерного детерминанта п-го порядка с одночленными
элементами
\С\=\А (±)St (±)g0 (±)s2 В (±)gl (*)0Г2 1
'i—'a-l *а 'а+l—'р /г-/Э-1 Vp+1 —^
(*Р • • • » *р» /p • • • » /p— p /p.}_i» • • • » /^ = *t 2, . . . , n)t
где соединительные индексы *а, /p рассматриваются как один дву:
кратный индекс ур, принимающий п значений 11, 22, . . . , яя,
и знак (±) <*о «яд индексом ia будет «+» ала «±» смотря по тому,
имеют ли индексы ia и L перемножаемых детерминантов один и
тот же или противоположный характер. Тогда
\А\-\В\ = \С\.
Действительно, \А\ \В\ и \С\ содержат одно и то же число
(п!)р+</"*2членов, вообще говоря, различных между собой, причем,
как легко убедиться, каждому члену произведения |4|-|Б|
соответствует один и только один равный ему член детерминанта |С|.
Число всех представлений произведения двух многомерных
детерминантов, составленного по правилу Скотта — Раиса,
очевидно, равно произведению чисел измерений этих детерминантов.
В частности, произведение двух квадратных детерминантов п-го
порядка или произведение квадратного детерминанта /i-го порядка
на квадратный перманент того же порядка представимо, согласно
этому правилу, четырьмя способами в виде кубического
детерминанта порядка п:
lil2 /1/2 «i«2 K2&2 кхк2 кЛк2 К\Яг k\kz
яфъ к9я1
*1*2 Vi T2 ТЗ *1*2 3*2 *1*2 1*3
*1*2 Vl
32
Точно так же произведение двух квадратных перманентов п-го
порядка представимо четырьмя способами в виде кубического
перманента того же порядка:
*= fejfej fejfej к^к^ к^к9 к^к^ /fjftj
3-S9I
ГЛАВА II
ЗАМЕЧАТЕЛЬНЫЕ СВОЙСТВА ДЕТЕРМИНАНТОВ
НЕКОТОРЫХ МНОГОМЕРНЫХ МАТРИЦ
§ 1. ОБЩЕЕ СВОЙСТВО ДЕТЕРМИНАНТОВ,
ПОРОЖДАЕМЫХ ЦЕЛОЧИСЛЕННОЙ МНОГОМЕРНОЙ МАТРИЦЕЙ
Возьмем р-мерную (р > 2) матрицу п-го порядка над некоторым
числовым полем Р:
А = || Ауг.Лр || (tb i%,..., i9 = 1,2,... п).
Пусть т — какое-нибудь четное неотрицательное число, не
превосходящее р. Матрица А порождает С% детерминантов рода т%
имеющих вид
2 V
\А (±)а | = 2(—1) ~ * Аи({) л(1)А2{{2) j^.-.A^n) {nh
ГГ~~? 2 р 2 р 2 р
где символом (±) <* обозначена сигнатура р-мерного детерминанта
и-го порядка, содержащая т альтернативных индексов ^ (1< \i =
=аь а2, . . . , с^ < р), значения которых образуют перестановки
*,?. *? W (^м)
из чисел 1, 2, . . . , п, а /^ — числа инверсий в этих
перестановках; суммирование в правой части последнего равенства
распространено на все возможные комбинации перестановок (Т2), (Т3), . . .
. . . , (Гр), образуемых значениями индексов t2, i3f . . . , iv.
Число детерминантов всех возможных родов, порождаемых
матрицей А, равно
1+С2р + Ср + ...+Срр) = 2р-\
где символом {р} обозначается наибольшее четное число, не
превосходящее целого р. Иначе говоря, число всех кодетерминантов
равно числу диагоналей их матрицы. Найдем сумму Sp всех
кодетерминантов матрицы Л. Пусть
Аиф-лмАф .(2)... Ап.{п)„л(п) (1)
— какой-нибудь член перманента \А++ +1» т* е* того из коде-
терминантов матрицы Л, род которого т = 0. Если все
перестановки (Г2), (Т3)9 . . . , (Тр) в произведении (1) четные, то оно будет
34
членом каждого изт2р-1 кодетерминантов матрицы Л. Если же
среди перестановок (Г2), (73), . . . , (Тр) имеется k (1< k < р — 1)
перестановок нечетных, то число N кодетерминантов, членом
которых является произведение (1), составляет только половину всего
числа кодетерминантов матрицы Л, так как
... + Си (1 + Cp_k + Cp-/; + ... + Cp__fe ),
т. e.
;v = (i + c^+cU+... + c^
__ 2?—fc—i ,2^""1 = г'7"2
Каждый из остальных У""2 кодетерминантов в этом случае
будет иметь своим членом произведение (1), взятое с
противоположным знаком. Следовательно, сумма Sp всех кодетерминантов
матрицы А выражается формулой
SP — 2Р~ 2^1*0>...*0>Лм(2)_г<2) . . . Ап({П) .(Л), (2)
2 р 2 р 2 р
где суммирование распространено на все возможные комбинации
четных перестановок, содержащихся среди перестановок (Г2),
(Т'з)» • • * > (Тр)\ число слагаемых в этой сумме равно —^—.
В частности, когда матрица Л целочисленная, из формулы (2)
получаем
Sp^0(mod2p-1). (3)
Из сравнения (3) вытекает следующая теорема, выражающая
общее свойство детерминантов, порождаемых целочисленной
многомерной матрицей (см. [4], стр. 126).
Теорема 1. Среднее арифметическое всех кодетерминантов
целочисленной р-мерной {р > 2) матрицы есть целое.
Пример 1. Для целочисленной кубической матрицы второго порядка
II Aijk || (U /,/5=1, 2) имеем
И+±±|а + |Л±+±|2 + |Л±± + |а + |Л, , , |2=-
ij k i j k ijk i i k
= АщАт "~ ^112^221~~ Л2И212 + ^122^211 +
+ ^111^222 — ^112^1 +А2И212 ""^122^211 +
+ ^111^222 + ^112^221 — ^121^212 — ^122^211 +
8» 35
+ АщАш + ^112^1 + ^121^212 + ^122^И :
= 4Л пЛ22 = ° (mod 2%
§ 2. ОБОБЩЕННЫЕ ДЕТЕРМИНАНТНЫЕ ТОЖДЕСТВА СМИТА
И ДЬИРЕША
Теорема 2. Пусть А—целочисленная р-мерная (р>3) матрица
п-го порядка:
А = || (iv iv.... *р|| (*V t2,.. •, ip =» 1.2,..., n),
£0* 0i> 4» • • • > *p) — общий наибольший делитель чисел ilf i2, . . .
.. . , ip. Тогда каждый из детерминантов матрицы А, род которых
больше нуля, равен произведению Ф (1) Ф(2) . . . Ф (п), еде Ф (k) —
известная функция Эйлера, указывающая число всех целых,
меньших чем k и взаимно простых с k (k = 1, 2, , . . , п), причем Ф(1) =
= 1 (см. [41, стр. 127).
Действительно, такой детерминант должен иметь по крайней
мере два альтернативных индекса, и так как матрица А —
симметрическая, то все порождаемые ею детерминанты одного и того
же рода одинаковы, и мы можем, не нарушая общности,
ограничиться рассмотрением р-мерного детерминанта /i-го порядка
± ± ± + +
Д Н(*г '*•••. 1т> W'--' У" C't. *я 'р— 1.2 Л),
род которого т — четное положительное число, не
превосходящее р.
Возьмем в матрице А одно из {п\у-2 двумерных трансверсаль-
ных сечений, соответствующих направлению (d):
(2, 1,#>,...,*«>) (2,2,if>,...,f<2>)...(2, n.tp9...9tp)
(п, 1, #>,..., ф (п. 2, *р,..., *W)... (л, п. *<*>,..., *<*>)
где
— некоторая перестановка из чисел 1,2,..., л. Будем
рассматривать последние р— 1 индексов v, Jf>,..., i*v> (v =1,2,..., л) в
элементах квадратной матрицы (4) как один (р—1)-кратный
индекс vi£v>... /£*>. Обозначим детерминант этой матрицы через
.(*)
86
Получим тогда» согласно формуле (10) гл. I, полное разложение
детерминанта Д на алгебраическую сумму (л1У>~2 обычных
детерминантов вида (6)
т
2 'л ± *
Д = 2(-!)»-з |(tlft2,t3,...,y|, (7)
где /ц — число инверсий в перестановке <£>, *<*>, . . . f i№t
образуемой значениями индекса 1ц (3 < ц < т) в элементах каждого
члена детерминанта (6), взятых в такой последовательности, чтобы
значения индекса *2 шли в натуральном порядке.
Входящий в выражение (7) детерминант матрицы (4),
соответствующий значениям
#) = 1, tjf)=2,...,^)=n (X = 3,...,p),
можно переписать в виде детерминанта
|(1,1) (1,2)... (1,11)
(2,1) (2, 2)... (2, л)
|(л, 1) (л,2)...(л,л)(
равного, согласно детерминантному тождеству Смита,
произведению Ф (1) Ф (2) . . . Ф (л). Все же остальные из (л!)*-2
детерминантов, входящих в выражение (7), равны нулю.
В самом деле, в каждом из таких детерминантов по крайней
мере одна из перестановок (5) отлична от перестановки!, 2, ... f л
и любой из них имеет вид
(1,40 (1.<У...(1,4.)
(2,<у (2.<у...(2,4)
(8)
| (л, d2) (л, rfa).. • (л, dn) J
где dv = (v, ф°>..., ^v)) (v=l, 2,..., л), причем по крайней
мере два из чисел dlf d2,..., dn одинаковы, так как в противном
случае вследствие dx = 1 имеем
d2 = 2, dg = 3,..., dn = л,
откуда последовательно находим
#>=...=1<,">=л,
1<зп"° =...=^-1) = л— lf
37
/(2)
*3
.=^ = 2,
что для рассматриваемых детерминантов не может иметь места.
Таким образом, каждый из детерминантов вида (8), имея по
крайней мере два одинаковых столбца, равен нулю. Из выражения
(7) получаем тогда обобщенное детерминантное тождество Смита;
Д = Ф(1)Ф(2)...Ф(л).
Пример 2. Пусть Л = || (iu i2, t3, i4) || (ii, h> H, U = 1. 2» 3) =
(1,1,1,1) (1,1,1,2) (1,1,1,3)
(1.1,2,1) (1,1,2,2) (1,1,2,3)1
(1,1,3,1) (1,1,3,2) (1,1,3,3)
(2,1,1,1) (2,1,1,2) (2,1,1,3)
(2,1,2,1) (2,1,2,2) (2,1,2,3)
(2,1,3,1) (2,1,3,2) (2,1,3,3)
(3,1,1,1) (3,1,1,2) (3,1,1,3)
(3,1,2,1) (3,1,2,2) (3,1,2,3)1
(3,1,3,1) (3,1,3,2) (3,1,3,3)1
(1,2,1,1) (1,2,1,2) (1,2,1,3)
(1,2,2,1) (1,2,2,2) (1,2,2,3)1
(1,2,3,1) (1,2,3,2) (1,2,3,3)
(2,2,1,1) (2,2,1,2) (2,2,1,3)
(2,2,2,1) (2,2,2,2) (2,2,2,3)
(2,2,3,1) (2,2,3,2) (2,2,3,3)
(3,2,1,1) (3,2,1,2) (3,2,1,3)
(3,2,2,1) (3,2,2,2) (3,2,2,3)|
(3,2,3,1).(3,2,3,2) (3,2,3,3)
(1,3,1,1) (1,3,1,2) (1,3,1,3)|
(1,3,2,1) (1,3,2,2) (1,3,2,3)
(1,3,3,1) (1,3,3,2) (1,3,3,3)
(2,3,1,1) (2,3,1,2) (2,3,1,3)|
(2,3,2,1) (2,3,2,2) (2,3,2,3)
(2,3,3,1) (2,3,3,2) (2,3,3,3)
(3,3,1,1) (3,3,1,2) (3,3,1,3)
(3,3,2,1) (3,3,2,2) (3,3,2,3)1
(3,3,3,1) (3,3,3,2) (3,3,3,3)
Тогда
+ + т т
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 2 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1|
1 1 1
1 1 3
+
-Hh)
-(и)
1(h)
(к)
+(и)
Вычитая в последнем детерминанте первое сечение каждой из ориентации (У,
(tA) из второго и третьего соответственной ориентации, получаем
38
+ + ± ±
I (h> h> h> U) |з =
l 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 1 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 2
->■ (h)
(is)
-* (W
= 1-1-2 = 2.
Y
+
(h)
Аналогично находим
± ± ± ±
I (*i, i2> h> h) Is = 2.
С другой стороны, имеем Ф (1) = 1, Ф (2) = 1, Ф (3) = 2 и Ф (1) Ф (2) Ф (3) = 2.
Обобщением теоремы 2 является следующая теорема.
Теорема 3. Пусть
А = II (*'i. if ..., iPYM || (*i, h> • • • э ip = 1, 2,..., я),
где р > 3, r = 0,1,2,..., и пусть
•,«-«^(i-^)(i-^)...(i-4) (*_..» *
•
где б (k) — число простых делителей nv я2,..., n6{k) целого fe,
причем Фг(1) = 1. Тогда каждый из детерминантов матрицы Л»
род которого больше нуля, равен произведению Фг (1) Фг (2)... Ф, (п)
(см. [4], стр. 129).
В самом деле, ограничиваясь, как и при доказательстве теоремы
2, рассмотрением /7-мерного детерминанта n-го порядка
± +
+
Аг — I (tp t2» • • • » *m» 1т+\> • ' • » V I V\* h> * ' ' » *p — 1, 2, . . . , #),
порождаемого матрицей Л, получим полное разложение этого
детерминанта, аналогичное разложению (7):
т
2 V
Детерминант
д. = z(-!)"-» к»р «2 gr+,i
(9)
± ±
|&.Уг+1| (ti, t2=l,2,..., it).
входящий в выражение (9), равен, как показал Дьиреш[14],
произведению Ф, (1) Фг (2)... Фг (п). Любой же из остальных входящих
39
в выражение (9) детерминантов, имея вид
\(ivdt/+1\ (ti,«2 = l,2,..., л),
гле из чисел dv = (v, i£v>,..., i™) (v»l, 2,..., n) по крайней
мере два одинаковы, равен нулю. Имеем, таким образом,
обобщенное детерминантное тождество Дьиреша:
Дг = Фг(1)Фг(2)...Фг(л) (г = 0,1, 2,...)
Следствие. Если г = я— 2, где я— любое простое, большее
чем л, то упоминаемые в теореме 3 детерминанты делятся на
од
я'
*=2
Действительно, при г = п — 2 имеем
ф^2(А) = /^1(яГ1-1)(^1-1)...(ЛбЙ-1) (* = 2,3,,
где /—целое, равное
., л),
¥г-^
Так как по условию теоремы 3 целые я1э я2,..., п^) меньше
простого я, то каждая из разностей яу-"1 — 1 (/ = 1, 2,..., б (*)),
согласно теореме Ферма, делится на я, а потому Фя_2 (Л) делится на nw.
Следовательно, детерминант Дя_2, равный произведению Фя_г(1) X
я
2в<*>
X Фя-2 (2)... Фл^-2 (п), делится на я*=2 .
Пример 3. Пусть А = || tf 1§ *2, i3> i4)41| (*г i2, *8, it = 1, 2, 3) =»
111
111
111
111
111
111
111
111
111
1 1 1
1 1 1
1 11
1 1 1
1 2« 1
1 1 1
1 1 1
1 1 1
1 1 1
11 3*
->&)
-01)
ш
(h)
+ + ± ±
Детерминант | (iv i, tj,* )418 матрицы А после вычитания первого сечения
каждой из ориентации (i9), (»«) из второго и третьего соответственной ориентации
40
делается равным детерминанту
100
0 0 0
0 0 0
10 0
0 0 0
00 0
10 0
00 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
015 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
0 0 0
0 0 0
1 0 0
00 0
0 00
1 0 0
0 0 0
0 080
Аналогично находим
■>(&
-Ни)
Г
у (*з)
h
= 11580 = 1200.
1(1Д41)413 = 1200.
С другой стороны, имеем Ф8 (1) = 1, Ф3 (2) = 15, Ф3 (3
ХФ8(3)=1200. Кроме того,я = 5, б(2) = б(3)=1 и
в:
=80 и Ф8(1) Фз(2)Х
-делитель числа 1200.
§ 3. ДЕТЕРМИНАНТЫ ГАНКЕЛЕВОЙ МНОГОМЕРНОЙ МАТРИЦЫ
ОДНОГО ЧАСТНОГО ВИДА
Теорема 4. Детерминанты, порождаемые р-мерной (р >2)
матрицей п-го порядка
А = Hiitf-i-ll ('г ^ • • •. 'Р =" 1.2,..., п)
с элементами
из некоторого числового поля Р и имеющие род т >0, всегда равны
нулю, за исключением случая, когда т = п = 2. В этом случае
каждый из детерминантов матрицы А равен — 2f>-2d* (см. [4],
стр. 129).
В самом деле, матрица А принадлежит к типу ганкелевых
многомерных матриц, у которых элементы с одной и той же суммой
индексов одинаковы. Последовательные элементы каждой строки
любого направления в матрице А образуют арифметическую
прогрессию с разностью d, и каждое сечение (простое) любой
ориентации в этой матрице получается из предьщущего сечения той же
41
ориентации увеличением соответственных элементов на d. Поэтому,
если п > 2, то вычитая в матрице А из &-го сечения какой-нибудь
альтернативной ориентации (ta)(l<a<p) (k-l)-e сечение той
же ориентации, где k последовательно принимает значения и, п—1,
получим матрицу
В = II 5м,...*р|| &. *2> . . . , *р = 1, 2, . . . , п),
у которой ft-е и (л— 1)-е сечения ориентации (1а) одинаковы.
Следовательно, все детерминанты матрицы В, в элементах которых
индекс ia альтернативный, равны нулю. Эти же детерминанты
ничем не отличаются от косигнатурных детерминантов матрицы А.
Так как матрица А — симметрическая, то доказанным свойством
будет обладать в рассматриваемом случае любой из ее
детерминантов, род которых т > 0.
Пусть теперь п = 2. Тогда, если т > 2, что возможно лишь
при р > 4, не ограничивая общности, можем в виду симметричности
матрицы А предполагать индексы ip_3> ip-ь h-u iP
альтернативными. Вычитая тогда в матрице А из второго сечения каждой из
альтернативных ориентации (tp_3)> О'р-2), (ip-i), (iP) первое сечение
соответственной ориентации, придем к матрице
С = ||С|11я...,р|| (Ц 'р = 1^ я),
имеющей при четном р вид
Н«
] М*д>
(*l)
где
II a + 2kd d
d 0
d 0
11 0 0
(£ = 0, 1,..., 2 2 -~2),
42
1 с°
Сх
2 2 —1
ci
с*
См
2 2
. . .
. . .
СР-4
2 2_i|
СР-4
2 2 |1
С р—2
2 2 -2
d 0
о о
о о
о о
-н
V
^(»р_2)
Y
(«р-3
а при нечетном р — вид
С'о
с\
2 2 —1
1 с;
с;
Ср—Ь
22
. . .
С Р-5
2 2 _!
С'р—5
2 2
С'р-3
2 2 -2
<S
' с;
2 2 — 1
С'
<£
Г" 1
С Р-5
22 1
| . - .
. . .
1 2 2 _,
^Р-5
2 2 J
2 2 -2
ЧУ
■+■ ('»)
i—ии
w
Y
где
cfc =
a + 2Ы d
d 0
d 0
0 0
d 0
0 0
0 0
0 0
('р-з)
j—ну
Y '
<(P-l)
c*=
a + (2fc+l)d
d
d
0
d
0
0
0
d 0
0 0
0 0
0 0
~M'V-2)
-ну
, Pp-l)
('V-s>
p-3_
(* = 0,1,..., 2 2 -2).
В обоих случаях
1С
<±)<*
1 = 0,
где (±) а — любая из возможных сигнатур над индексами 1Ъ .. •
• . . , 1р—4»
Следовательно, и
1 l3v t± ± ± ± '
lv..tp^4 ip—z ip-2 ip—\ip
Таким образом, все детерминанты матрицы Л, род которых
т > 2, равны нулю и при и = 2.
Наконец, в случае, когда т = п = 2, можем без ограничения
общности предполагать индексы tp_i, tp альтернативными. Вычи-
43
тая тогда в матрице А из второго сечения каждой из
альтернативных ориентации (tp_i), (ip) первое сечение соответственной
ориентации, получим матрицу
^ = 11Аа-^р11 (*f<« 'p— 1.2).
которая при четном р имеет вид
1 D°
D1
Рр-2
2 2 -•
°1
°г
2 2
. . .
К-2
2 2 -1
DP~2
2 2
Dp
2
2 -2
-НЧ)
-иу
Y
&)
где
Db =
c + W d
d О
(ft = 0, 1 22 —2),
а при нечетном р — вид
D=
1 °о
D1
2 2 -1
Dl
D2
Op_3
2 2
• •
DP-Z
2 2_,
2 2
DP-.
2 2 -2
Dl
^
1 2 2
°.
D3
DP-3
2 2 +1
"и |
2 2 J]
"и
2 2 +4
|DP-1
2 2 -l||
*(»i)
-Mfe)
Y
w
где
D„ =
a + fed d
d 0
(* = 0,1 2 2 -1).
ID
В обоих случаях
Теорема доказана.
44
+ + ± ±| = -2"-2d2.
'i— 'р_2*р-1*р
Из теоремы 4 при а = р и d = 1 следует, что детерминанты
целочисленной р-мерной (р > 2) матрицы /i-го порядка
A = \\h + i2 + ...+ ip || (i'i, i%9..., lp = 1, 2,..., n),
род которых m > О, всегда равны нулю, за исключением случая,
когда т = п = 2. В этом случае каждый из детерминантов
матрицы А равен — 2?~2.
Тогда
Пример 4. Пусть
Л^\\1г + (% + 13 + 1А1\ dv i2, is> t4= 1,2).
± ± ± ±
К + ^ + 'з + 'Л"
4 5
5 6
5 6
6 7
5 6 1
6 7
6 7
i 7 8
-v(/4)
>&)
и после вычитания первого сечения каждой из ориентации (/8), (tj из второго
сечения соответственной ориентации получаем
± ± ± ±
Подобным образом находим
1 4 1
1 0
5 1
1 0
5 1 1
1 0
6 1
1 0
-НУ
у
11—11+1 1+1-1=0.
+ + ± ±
1<1 + 'з + 'а + '41г =
[ 4
5
5
6
5
6
6
7
5
6
6
7
6
7
7
8
-му
Г"" -
14 1
1 0
5 1
1 0
5 1
1 0
6 1
1 0
(«V
«1>
М —11 —11 —Ы -=—2*.
«i>
45
§ 4. МНОГОМЕРНЫЕ ДЕТЕРМИНАНТЫ, ПРИВОДЯЩИЕСЯ
К ОБЫЧНОМУ ДЕТЕРМИНАНТУ ВАНДЕРМОНДА
ИЛИ СТЕПЕНИ ЭТОГО ДЕТЕРМИНАНТА
Теорема 5. Пусть
А = II 4а-'р-1 II ('о 'Р • • • > *p_i = 1. 2,..., п)
— р-мерная (р > 3) матрица п-го порядка, где \ir..ip_l = rf'iv'M»
причем av а2,..., ап —элементы некоторого числового поля Р и
символом (iv ..., f ) обозначен общий наибольший делитель
чисел il9 . . . , tp_i. Тогда каждый и* детерминантов матрицы А,
в элементах которых индекс ^альтернативный, равен обычному
детерминанту Вандермонда.
V<2) = \J*\ С/о-/i = Ь 2,..., л) =аЛ...ажП («/.-«/.)
/о
(см. [5], стр. 834).
В самом деле, такой детерминант имеет по крайней, мере два
альтернативных индекса, и так как матрица А — симметрическая
относительно индексов ilf . . . , tp_i, то, не нарушая общности,
можно ограничиться рассмотрением /7-мерного детерминанта п-го
порядка рода т:
уф) = | Jy5m-X ~U) j {^ fi *p_! — 1.2 П),
to
где m — четное положительное число, не превосходящее р.
Возьмем одно из (и!)"-2 двумерных трансверсальных сечений
матрицы А, соответствующих направлению (*0):
II <>
г
Г
4»~
.«у>..
4°-
••*А>
■■<£.>
-^
(,f>....
1
а2
^.
*(2) )
Р-Г #
р—1
..«<2) )
Р-Г ,
(п
а
• •в,
(п
.'?>.•
«<«>...
4п)-
-'Г,'
-г,>
■•'&>
где
Ч!}' <12)>---> Ф> (2<Ь<р-1) (П)
— некоторая перестановка из чисел 1, 2, . . . , п.
Рассматривая индексы t<v>, *<v>,..., fjWj (v=l, 2 , n) в
элементах квадратной матрицы (10) как один (р—1)-кратный ин-
46
(10)
деке t<v>Qv>.. Л£>г обозначим детерминант этой матрицы через
• W
±
i.
(12)
Тогда детерминант VlP\ согласно формуле (10) гл. I, представится
алгебраической суммой (п\)р"2 обычных детерминантов вида
т—1
V?} = 2 (—1)й-2 #11
ч
*p-i>
±
(13)
где /^ — число инверсий в перестановке fjj>, ig>,..., ijp, образуемой
значениями индекса i (2 < ja < m — 1) в элементах каждого члена
детерминанта (12), взятых в такой последовательности, чтобы
значения индекса 1Х шли в натуральном порядке.
Входящий в выражение (13) детерминант матрицы (10),
соответствующий значениям
qi> = l, ф = 2,.... qjo=n (X—2,3 Р—1).
очевидно, равен обычному детерминанту Вандермонда
V?-
а{ а\ ... ап{
а2 а\
а%
a di ..
а*
аха2... апП(аи — аи)(\ < j{ < /0< л),
тогда как все остальные из (п\)р~2 детерминантов, входящих в
выражение (13), равны нулю, ибо в каждом из них по крайней мере
одна из перестановок (11) отлична от перестановки 1, 2, . . . , п,
и гакой детерминант имеет вид
(14)
где dv=(v, t£v>,..., *Wj) (v=l, 2,..., n), щшчем, как легко
убедиться, по крайней мере два из чисел dl9 d2,..., dn равны между собой,
и следовательно, по крайней мере два столбца детерминанта (14)
одинаковы.
Из выражения (13) находим тогда V(np) = Vj?,
tf
4
eft
1
a*,.
tf"
d„
adn
adn
n
47
Теорема 6. Пусть
А = || а£+-+'р-. „ (,о, ti ^, - 1.2..... п)
— р-мерная матрица п-го порядка с элементами из некоторого
числового поля Р. Тогда порождаемый этой матрицей р-мерный
детерминант наивысшего рода
WiP) =
<;t*+H М|.....'^,-1.2.....л)
(здесь (±) s есть знак «±» при р четном и знак «+» при р
нечетном) равен (VW1. где
V<2> =
afi
(/о» А = *» 2,..., л)
— обычный детерминант Вандермонда (см. [51, стр. 836).
В справедливости формулы
^-(УГУ
,р—1
(15)
убеждаемся, замечая, что, согласно правилу Скотта — Раиса
умножения многомерных детерминантов (гл. I, § 5), будет
[ИГ0?? =
ui±)*
(*0» *!»•••» *д_2> /о» /i = l> 2, . . . , М) =
± ± ±
I flV*-...+ *р-2д *р—1
(±)« **
± ± ±
(«о> «j,..., «^^j — 1,2,..., л),
где знак (±)s имеет то же значение, что и выше, а (±) а есть знак
с±» при р нечетном и знак «+» при р четном, т. е. имеет место
равенство
и ряд аналогичных равенств
причем
48
Из формулы (15) вытекают очевидные следствия.
1. Если а^ = i0 (i0 = 1, 2,..., л), то
Я^ = (1121... nlf-\
2. Если р — простое и а^ а^ . . . , с^ — целые положительные
числа, не сравнимые с нулем и друг с другом по модулю р, то
W*p)el(modp).
4-595
ГЛАВА III
ОПЕРАЦИИ НАД МНОГОМЕРНЫМИ МАТРИЦАМИ
§ 1. СЛОЖЕНИЕ МНОГОМЕРНЫХ МАТРИЦ.
УМНОЖЕНИЕ МНОГОМЕРНОЙ МАТРИЦЫ НА ЧИСЛО
Рассматривая основные операции над многомерными матрицами —
сложение матриц, умножение матрицы на число и умножение
матриц,— будем определять их в зависимости от операций над
ассоциированными с этими матрицами полилинейными формами,
заданными над некоторым числовым полем Р.
Пусть даны две р-линейные формы:
'г*. <Р=» 1 *
т
зависящие от р рядов переменных
x<v>, 4V)> 4^ •.. (v=l,2,...,p).
Формы F и F' тождественно равны друг другу, если у них число
переменных в каждом из р рядов одно и то же и соответственные
коэффициенты одинаковы. В связи с этим соответствующие
формам F, F' /7-мерные матрицы
А = 1И<Л...<рИ Qv l2> -.^U л),
А = И Л'А-'р И (|"»' *» • ■ • • 'р = *• 2. • • • ■ m)
называются тождественно равными, если они одного и того же
порядка и их соответственные элементы одинаковы, т. е. если
т = п и
^А-'р = ^...«р (*г «2 /р— 1, 2 п).
Сумма двух р-линейных форм
50
Ф= S fly,.V?*P ■■■•"?
м, 'p=l
с соответствующими р-мерными матрицами п-то порядка
А = Ц Лцг.Лр ||, В = || Blllv.Jp || (*,, t2,..., ip = 1, 2 n)
равна р-линейной форме
где ч
CVr-'p = ^i'r-'p + BVr-'p ^V '* • • •, tp = 1, 2,..., /i). (1)
Соответствующая форме *Р р-мерная^матрица я-го порядка
C = \\CtlW..ip\\ (iv «2,-... /p= 1.2,..., n),
элементы которой, определяются формулами (1), называется
суммой матриц А и В. Операция нахождения суммы двух данных
/7-мерных матриц одного и того же порядка называется сложением
этих матриц. Имеем, таким образом,
л+в = с.
Из определения сложения многомерных матриц непосредственно
следует, что оно обладает коммутативным и ассоциативным
свойствами:
А+В=В + А,
(А + В) + С = А + (В + С)9
где А, В, С — любые матрицы одного и того же числа измерений
и одного и того же порядка над полем Р.
Кроме того, принимая во внимание определение нулевой много?
мерной матрицы (гл. I, § 1), имеем
А + 0 = А.
Распространяя упомянутое выше правило сложения двух мат
триц на случай суммы какого угодно числа многомерных матриц,
укажем для любого из детерминантов этой суммы как детерминанта
с многочленными элементами разложение, обобщающее известное
разложение Альбеджиан» для квадратных детерминантов (см. [15],
стр. 83).
Пусть A cs= Л(1) + Л<2) + ... + А{Н) — сумма h р-мерных матриц
п-го порядка
Ат = удэд ip\\(ilti2t'... Jp =1,2,... ,n; a = 1,2,.. * ,Л),
4* 51
т. е.
ь
А - US43. <pll(M2,... Л « 1.2,... ,я).
0=»1
Пусть, далее, \A\-~любой из детерминантов матрицы А и
| Л(а)| — косигнатурные детерминанты матриц А{а) (а = 1,2,..., А).
Обозначим через М{?г\М^ ,... ,М{^{\ <<7<m = min(A, л); 1<
я
< % < а2 < ... < а^ < А) миноры порядков пъ /ц,..., щ, где £ Яу =
= л, детерминантов |Л(а1>|, |Л(а,) |,..., |A(Vj и возьмем
какую-нибудь смешаннуютрансверсальную совокупность миноров M(,ai), M^K ...
.... M(*Q\ т. е. такую их совокупность, в которой ни одна пара
миноров не содержит элементов, входяищх в состав элементов одного
и того же сечения (простого) какой-либо ориентации матрицы А
(при 9 = 1 эта совокупность состоит из одного детерминанта |Л(а1>|).
Обозначим, далее, через Mlt Af2,..., Mq соответственную
трансверсальную совокупность миноров какого-либо из детерминантов
|Л(а)| (а = 1,2,..., А) и составим выражение
rq = (— iy~*k MfpMp*... му,
где гк—сумма номеров альтернативных сечений дополнительного
для Ml9 М2, . . . , Mk-\ минора М\-\, в которых содержатся
элементы минора Мк. Тогда алгебраическая сумма выражений Tq,
распространенная на все смешанные трансверсальные совокупности
миноров детерминантов |Л(а)| (а'= 1, 2, . . . , Л), будет равна
детерминанту \А\>
Действительно, всякий член детерминанта \А\ есть сумма hn
одночленов с одним и тем же знаком. Следовательно, число
одночленных слагаемых в развернутом выражении детерминанта |Л|
равно (л!)*"*1 Ап. С другой стороны, выражение Tq, как легко
убедиться, является алгебраической суммой некоторых Л^ из этих
одночленных слагаемых, где
^f-ni[^-cj»-ir+c;((7-^-...i+(-i)^-^ix
Число N одночленных слагаемых в алгебраической сумме
выражений Т9, распространенной на все смешанные трансверсальные
совокупности миноров детерминантов |Л(а)| (а = 1, 2, .. . , А),
будет равно
52
причем все пары из выражений Tq без общих слагаемых. Принимая
во внимание равенство (2), находим
N = nlZtf-Cl(q-\r + dj,(q-2)n-...+
+ (- \)Я"2С^2-Г + (- D^CJ"1] С2,
откуда после упрощения получаем
N = (n\)p~lhn.
Упомянутая выше алгебраическая сумма выражений Тщ
является, таким образом, точным представлением детерминанта \А\.
Замечание 1. Теорема 6 гл. I есть частный случай обобщенного
разложения Альбеджиани фигурирующего в этой теореме
детерминанта \А\ р-мёрной матрицы л-го порядка Л, если Л рассматривать
как сумму q (2 <: q < п) матриц л-го порядка Л(1\ Л(2), . . , f A{*\
где в каждой из матриц A{v) (v = 1, 2, ... , q) все сечения (простые)
какой-нибудь ориентации нулевые, кроме некоторых Лv (V =
= 1, 2f . . . , q) сечений этой ориентации, элементы которых при-
я
надлежат матрице Л, причем JJ riy = л*
Умножая р-линейную форму
с соответствующей р-мерной матрицей
А = IIЛм,...<р II ('г *2,....',« 1.2 л)
на какое-нибудь число / из поля Р, получим форму
<t.ie *p=l
где
**....*„ - tAi>i>...ip С г Ч,..., tp = 1,2...., л). (3)
Соответствующая форме Ф р-мерная матрица п-го порядка
В = ИВм,.. Jl Vv h> ....'„- 1.2,.... ,*)>
53
элементы которой определяются формулами (3), называется
произведением матрицы А на число t. Имеем, таким образом,
tA = B.
В частности, если t = 1 или t = 0, то 1 • А = А, О-А = 0.
Ясно, что любой из детерминантов матрицы В равен косигна-
турному детерминанту матрицы Л, умноженному на tn.
Из определения умножения многомерной матрицы на число
вытекают следующие свойства этой операции:
t(A+B) = tA + tB,
(t + u)A = tA + uA,
t(uA) = (tu)A,
где Л и В — произвольные матрицы одного и того же числа
измерений и одного и того же порядка над полем Р, a t и и — числа
из поля Р.
Первые два свойства связывают умножение многомерной
матрицы на число со сложением многомерных матриц. Вводя
обозначение
; (-1)А А,
будем иметь также на основании указанных выше свойств:
Л+(-Л) = 0,
(-1)А =-tA,
-(А + В) = -А-В,
-{-А)=А.
Вместо А + (— В) будем сокращенно писать А — В и называть
это выражение разностью матриц Л и В.
§ 2. УМНОЖЕНИЕ МНОГОМЕРНЫХ МАТРИЦ
Пусть р, q — какие-нибудь положительные целые их, 1, ц, v-
неотрицательные целые, удовлетворяющие услозиям
х + Х + р^р, X+\i + v=q. (4)
Возьмем р-мерную матрицу и-го порядка
. А = И Aw»..tjL {iv '2 /р= 1.2 п).
Обозначая через
/ = (/j, /2,,...«/н), s = {Sy s2,..., s^), с = (Cj, с2, • • •»£у)
54
разбиения совокупности индексов ilt t2,..., ip матрицы А, можем
представить эту матрицу в виде
A" UJi.
где каждый из индексов разбиений /, s, с пробегает значения 1.2» ...
..., п.
Ассоциируем с матрицей А р-линейную форму
• 1
и подвергнем ее однородному преобразованию*
Oli ,...,/71^=1
(Sp . . . xS^t £j, . . • , Cp = l> Z, . . . > ft)
с ^-мерной матрицей л-го порядка
II Cj...r|is1...s^mj...mv И »
которую с помощью разбиений с, s и m = (mb . . . , mv)
представим в виде
*-IHUI.
где каждый из индексов разбиений с, s m пробегает значения 1,
2, .... п.
В результате преобразования, принимая во внимание легко
выводимое из условий (4) равенство
K + X + v==p + q — t, (5)
где
г = Я + 2ц,, (6)
получим (p + q— т)-линейную форму
ф = S c/,../Ks,.^,..^11)- ■ ■ *%у% • - • >'М.. - zft
где
я
е\ <ю=1
Ей соответствует (p + q— т)-мерная матрица п-го порядка
*-» = || ^/j...^Sp..s^mj.../Лу || (Zjt . . . , /х, Sp . . . S^, /Яj, . . . , ttlv =* 1» А • • • ffljt
* Преобразования Кремоны являются частным случаем такого типа
преобразований.
55
которую с помощью разбиений /, s, m можно представить также
в виде
С = \\СШ\\9
где
Wsm = 2^ AlscBcsm •
(с) " "
Матрица С называется (\\л)-свернутым произведением матрицы
А на В по индексам разбиений sue (см. [6], стр. 1323).
Обозначая его символом*"11 (АВ), получаем
х,^
(АВ)
(г) "
(7)
В произведении 0) индексы разбиения с, по которым
производится суммирование, называются калиевыми, соединительные
индексы разбиения s — скоттовыми, а индексы разбиений /, ш, не
причастных к свертыванию, — свободными.
Из равенств (4) вытекает, что
0 < X + ц < »,
(8)
где о; = min (p, ?).
Следовательно, число (X, (л)-свернутых произведений матрицы
А на. В, составляемых по формуле (7), при всех значениях А,, у,
удовлетворяющих условию (8), равно
1+2 + ... + (ю+1)-^(Ю+1)(Ю + 2).
Пример 1. Подвергая трилинейную форму
-2Wl + 3W*
-► (s)
с матрицей
Л = М
ISC I
2 1
-1 5
— 3 4
— 2 3
►(О
&
однородному преобразованию
с матрицей
-naaJI-l
11
5
1
— 1
3 —411
: — 1 2 J
►(s)
(m),
получаем трилинейную форму
+ ^iV* - ¥Л + 14**V2
56
е матрицей
С-II С,.» II-
7 1
24 —6
— 13 20
— 9 14
..-*<*>
которая может быть определена по формуле (7) как (К, \i)-свернутое
произведение матрицы Л на В при % = 1, ц = 1:
Ы
(АВ) =
2.1 + 1.5 2.1 + 1. (— 1)
— 1.1 + 5.5 — 1.1+5. (—1)
-а (-4)+4.2
_2.(— 4)+3.2
-*<s)
Mm) =
7 1
24 —6
_3.3 + 4.(— 1)
_2.3 + 3.(— 1)
is)
— 13 20
— 9 14
Mm).
Ь)
Из определения (X, ц)-свернутого произведения матрицы А на
В следует, что в общем случае оно не обладает коммутативным
свойством.
Ассоциативный закон умножения матриц одного и того же
порядка имеет место при условии, что свертываемые совокупности
кэлиевых индексов в разных парах перемножаемых матриц не
пересекаются между собой и с совокупностями скоттовых индексов.
Действительно, рассматривая (А,, ц,)-свернутое произведение
матрицы А на В, имеем, согласно формуле (7),
x,»t
где
(АВ) = ||£АЛОТ^||,
(с) " "
m's'c' = m и s' = (s\t s2,...9 s'k,)f с' = (cj, ^ ..., <£,),
(9)
причал с и с' не пересекаются между собой, а также с 4 и s.
Составим, далее, (X', ц')-свернутое произведение Х',|1'(ВС)
матрицы В на г-мерную матрицу л-го порядка С = || CfS'm" ||, где
ds'm" — натуральная последовательность г индексов матрицы С.
Имеем аналогично предыдущему
•** у ВС) = || J] Bcsm's'c'Cc's'm" ||.
(О ^ ^
Пользуясь формулами (9), (10), находим
^'[*-VLB) q -1| 2 (S AA-w) с;
(С) (с) >—„ ^ 1^
Х»[АК'»\ВС)] = 12 Льг (2 ft-. w (W-r) ||
(10)
■*c's'm*
(с) ic')
откуда следует, что
**'[**»(АВ)С1 = я *[Ак'жфЪЪ
57
Дистрибутивный закон умножения матриц одного и того же
порядка относительно сложения матриц одного и того же числа
измерений и порядка всегда выполняется. Так,
Х'*[А (В + С)]= к» (АВ) + к» (АС),
где матрицы В и С того же порядка, что и матрица Л, и имеют одно
и то же число измерений.
Выражаемое формулой (7) произведение матриц является
правым (Я, ц,)-свернутым произведением матрицы А — \АШ\ на В =
= ||£csm||. К понятию левого (А,, ^-свернутого произведения матрицы
A'=\\A'csHi, транспонированной относительно А соответственно
подстановке (Z, с), на матрицу В' — ||В^<|, транспонированную
относительно В соответственно подстановке (т, с), приходим,
подвергая ассоциированную с матрицей А' р-линейную форму
F' - S^...^,..*,..^ • • • 4|Х • • • *8*р • • • *£>
1
однородному преобразованию
4;> • • • *gy.j> • • • <> = s ^....^...^...-Л...
Y<v)y(l) V(M
• • • •л/»у1 Sj • • • л S^
(£|> • • • » ^p,» ^j, . . . , S^ = 1, Z, . . . , tl)
с ^-мерной матрицей n-го порядка ЦЯ^шЦ.
R результате преобразования получим (р + q — т)-линейную
форму
i
где
л
Cmi...OTvsI...s^/1.../H= Jj BOTl...mvs1...s^f1...CjJlA'1...Cjls1...s^1.../K-
c\ CH=1
Ей соответствует (p + q— т)-мерная матрица /г-го порядка
которую с помощью разбиений m, s, / можно представить в виде
С =|| С/1|,
где
58
Матрица С есть левое (А,, |г)-свернутое произведение матрицы
А' на В' по индексам разбиений s и с. Обозначая его символом ^ЦВ'А'),
получаем
к»(В'А') = \\%В'„^Л81\\.
(И)
(с)
Поскольку матрица С является транспонированной
относительно матрицы С, представляемой формулой (7), соответственно
подстановке (/, /л), то
[к'»(АВ)]' = *"»(В'А').
Пример 2. Подвергая трилинейную форму
F = 2Wl + хгУ1г2 - ду, А + Ьх#гг2 - Зд^у А + 4*^ — 2дуг А + 3Wa
с матрицей
I 2 М
— 1 5
*'-ii4ji-
-*(s)
-23ll(t)
однородному преобразованию
xl¥l = Х?г + X2YV xlVi = ЗХгУг - 4Х/а,
**i-*Xfi-X?V Чъ *1У2 + 2ХЛ
с матрицей
-*(s)
11 11 3—4
||б—lj —1 2
-*<m),
\{с)
ll*«JI~
получаем трилинейную форму
ф = - МуА ♦ 26Х/А + ЗХ/А - 4Х2КА - 7XXYA +
+ 9ХХКА + 8Х2КА - 10Х2УА
с матрицей
J —3 1261—7 „ .. #Л
3_4| 8_ю||(С
'msl I
которая может быть определена по формуле (11) как левое (А,, |л) - свернутое
произведение ^(В'Л') матрицы А' на матрицу
-*<s>
*'-»ll*mJ|-
1 5
1 —1
3 —1
— 4 2
(m)
при А,= 1, |1= 1:
и(В'Л')^
3-4 —ЬЗ
— 4.4 + 2.3
12 + 5- (— 1) 1.1+5-5
1.2 —Ь(—1) L1 — 1.5
Ms)
(т)
■3 26|
3 -.4
3.(—3) —Ь(—2)
_4.(-3) + 2.(-2)
-7 9
8 —101
(т)
59
Замечание 2* При определении (Я, |х)-свернутого произведения
двух матриц для упрощения записи свертывание производилось
по крайним индексам этих матриц. С таким же успехом, однако,
свертывание можно производить по любым упорядоченным
разбиениям индексов, так как всегда можно прийти к рассмотренному
случаю, транспонируя надлежащим образом перемножаемые
матрицы, найти затем их произведение и в полученном результате
обратной операцией восстановить нарушенный порядок индексов.
Число NPtq всех возможных (31, ц)-свернутых произведений
р-мерной матрицы А п-го порадка на ^-мерную матрицу В того же
порядка выражается, согласно неравенствам (8), формулой
#*.* =
чРуЯ
SP* £l_
АЛ уй (р — А,— ц)! А,! |а! (q — к -
|i)!
Например, для кубической матрицы А = || A,f2i31| (*V *V 'з == *» 2,....л)
и квадратной матрицы В = || B/l/21| (/г /2 = 1,2,..., п) имеем (см.
стр. 61).
§ 3. ЧАСТНЫЕ СЛУЧАИ УМНОЖЕНИЯ МНОГОМЕРНЫХ МАТРИЦ
Отметим некоторые частные случаи умножения многомерных
матриц согласно формуле (7).
I. При отсутствии скоттовых индексов, когда X = 0 и т = 2ц,,
произведение (7) переходит в (0, ^-свернутое произведение
о.ц
(АВ) = \\%А1сВст
(с)
(12)
рассматривавшееся Ольденбургером [16], а также Гуарне и
Самюэлем [13].
В частности, если А, = 0 и ц = 1, то т = 2, и (0,1)-свернутое
произведение 0>,(Л, 5) представится в виде (р-\-q — 2)-мерной
матрицы п-го порядка
o.i,
{АВ) =
S V
/p—ic ст2...тд
Ср * * • » fp-i» m2> —t m^ — 1» 2, .... Л).
(13)
Порождаемые матрицей (13) детерминанты являются
произведениями соответствующих детерминантов матриц Л и В,
составленными по правилу Кэли — Раиса (гл. I, § 5):
2 ^ <±>* Я <±>*
f^l /i...fp_ic сШ2...т^
Г ^..Лр_1/р| I iftjmg,
,.та
60
X
j"o]
1
0
2
1
0
м.
~o|
0
1
0
1
2
1
ft"*(AB)
И \^%Втктш H ^P ^ h mV m2=l>2 n>
II \уРшп lb И ^s/Дп И» И ЛмДп И-
н № "• и л/А "•»^A- ii
(/i, /2. «» m = 1» 2, ..., n);
II n II
2j \ljPcm '
|l c—1 ||
ll л II
2j Alxl^mc >
II *=! II
II n ll
2j \cltBcm
|l ^=1 ||
|| n ||
S \cltBcm
|l*=*l II
II n
• П. Л* / Дли II •
l|*-l
II "
» 2j AclJ2Bmc ||
|lc=l
(Zlt /2, m = I, 2,..., л);
И ^А». И И\|ьВм.1И1^Ль11
(/, si, s2 = 1, 2,..., n);
n ||
2j AlscBcs '
«*-l ч—' II
rt ||
2j AsblBcs .
*=1 N—' l|
л ||
2j AtscBsc ,
*-l W II
n ||
2j ЛсАс
*=1 " II
ll n ll
2j AlcsBcs »
II ^—1 w II
ll n II
2j AclsBcs »
ll*=l w II
II n ll
ij AlcsBse »
|lc=l w ||
ll n ll
||c=l w II
II n ||
Zi AslcBcs
|U=i "—' II
II n 1
2j AcsiBcs
\\c=l " ' I
|| n ||
2j AslcBsc
\\c=l ||
ll n ll
2j AcslBsc
II *■*! W II
i
(/,s = l,2 n);
II n 1
II ri,c,=l |
II n
2j Actctfictct
\\CfCr=l
1
\ n 1
1 CX9Cf=\ \
Г
(/ = 1, 2, ..., П)
p!
Х!|*1(Д--Х—Р)!
i
3
3
3
6
3 .
a! 1
X!|i!fa-X-|i)H
i
2
2
1
2
1
w
Для выражения детерминантов, порождаемых (0,1)-свернутым
произведением двух расширенных (или сжатых) многомерных
матриц служит следующее утверждение.
Обобщенная формула Вине — Коти. Пусть
А - ||Д
«V
9 *а— 1» 1а+\> • •'
= 1, 2, ..., п\
to =1.2,
т)
— р-мерная матрица, расширенная (или сжатая) в направлении
(*а) (1 < « < Р), U
В = ||В
/i ••-/0-1/0/0+1—М
V/j» • • • » /p_i» /р+1* • • * » iq == » • • • • » /*» /fl = *» , * • • • » /")
— q-мерная матрица, расширенная (или сжатая) в направлении
(If) 0 < Р < ?)• Умножая пР~х строк направления (ia) матрицы
А на п*-1 строк направления (/р) матрицы В, примем полученные
пр+я-2 произведений за элементы (р + q — 2)-мерной матрицы п-го
порядка
<м,
(АВ) =
s\
С=1
-lrta+i«
.Л
в.
(*V
■•/0-lff/0+l-"/^
/ =1,2,
(14)
.,n),
*а— 1* *a+i' • • • » *р» /р • • • » /0—1» /0+1» • • ' »
представляющей (ОЛ)-свернутое произведение матрицы А на В.
Пусть Г — какое-нибудь сочетание из т элементов 1, 2, . . . , т
по п (без повторений или с повторениями), например
возрастающая последовательность v (1 < v < min (m, n)) целых
положительных чисел а1$ а2, . . . , сц,, не превосходящих т и повторяющихся
соответственно п^, щ,, ... , п? раз (пг + п2 + • • • + ^v = n)- Пусть,
далее, Л(Г) и В(Г) — минорные матрицы п-го порядка, составленные
соответственно из сечений ориентации (ia) матрицы А с номерами,
образующими сочетание Г, и из сечений ориентации (/р) матрицы
В с теми же номерами. Возьмем порождаемые матрицами Л(Г) и
В<Г) р-мерный и q-мерный детерминанты п-го порядка
И(Г,1 =
|в,г,1 =
А(Т) I
*1...*а_1 *а *a+l--*pln
В(Г) I
/0-1 /0 /0+1-
/l—/0-1 /0 /0+1—/V1
с од«ой к той дата сигнатурой (±) s «ad индексами fa, /p и любыми
сигнатурами (±) %, (±) s2 a (±) alf (±) a2 wad остальными
индексами при условии, что число альтернативных индексов в каждом
детерминанте четное. Возьмем также порождаемый матрицей (14)
62
(p + q — 2)-мерный детерминант п-го порядка
| 0.1
(АЩ\ =
2 ^ ji^ (±)s» B (±)<у
<±>**
1^»1 <i...<a_i*c4-l—fp Л—/&-i'/0+i—/«W
в котором сигнатура над несуммируемыми индексами составлена
из сигнатур над соответственными индексами в детерминантах
Л(Г)| и | В(Г)|. Тогда
|°^ЛВ)1 = Ц-^г1л(Г)ыв(Г)1 е^*)' (15>
(Г)
гбв Г пробегает все С£+*-1 сочетаний из т элементов 1, 2, ..., т
по п (с повторениями) и k{V) = пг\п2\... nvl
Формула (15) упрощается в случае, когда индексы ia и i$ в
детерминантах \А{Г)\ и \В{Т)\ альтернативные. Тогда, если т>п,
имеем
ГЧлв)] = £|л<Г>|.|в<Г)|, (16)
(Г)
где суммирование распространено на все С^ сочетаний Г (безповто-
оений). Если же т<^п, то
(17)
Г(АВ)1=0.
При т = п формула (15) вырождается в формулу (20) гл. /
умножения многомерных детерминантов по правилу Кэли — Раиса*.
Для вывода формул (15) — (17) достаточно представить
матрицу (14) в виде суммы т матриц л-го порядка
А В
(с = 1,2, ...,m)
и применить к детерминанту I0»1 (ЛВ)| обобщенное разложение
Альбеджиани, приняв во внимание свойство V многомерных
детерминантов (гл. I, § 3) и теорему 1 гл. I.
Пример 3. Даны матрицы А = || Aiti% \\ (ix = 1, 2, ..., п; f «1,2,..., m)
и В = || By . || (/j. =1,2 /я; /2 = 1, 2, ..., п), каждый элемент которых
равен единице. Тогда
2 4.А
с/*
с=1
('г /2=1,2,
..я)
является квадратной матрицей п-то порядка, каждый элемент которой равен /я.
Ее перманент
* т
с=1 he cft
= /i!mn
* Формула (15) для неальтернативных индексов *а, /р установлена Оль-
денбургером, формула (16) — Гегенбауэром (см. [3], стр. 63, упр. 13, 14).
63
равен, согласно формуле (15),
Следовательно,
у (*!)*
2. ДСП
(Г)
яг«
2- пг\пА ... /ц,! *
(Г)
где пх + п2 +... + nv= n и Г пробегает все сочетания из т элементов 1, 2,..
.... m по л с повторениями.
Пример 4.
1 2
*i*.-
•ат\
•"ml
|а1 Pi II
«2 Р2
а Р
1 m ^m Ч
а1а1 + ваа2 + "- + атата1р1 + аЛ + --•+«!»?
*А + *Л + - + »Ж«Ж 6lPl + *A + -" + 6mPmll"
Поэтому формула (15) дает перманентное тождество, аналогичное детерминантвому
Кош и:
тождеству
(+)
bl«l + b2«2 + - + bm«m *A+*A + -+V,
m
<fikl
1<*<1<т
»*»*
(+> (+> „ (+>
«i P«
где dfc/ —символ Кронекера.
Полагая в этом тождестве с^ = а., Р4 = bt (i = 1, 2,..., m), находим
(+) (+)
о* +4 + ... + <& «Л+^+...+a^
(+)
«Aw
Пример 5.
°lfl2
1<Л</<т
С1С.
<+)
"k "i
■Mil) I
l«l Pill
«2 P2
Г 'II
«in Pn,
.-Hit)
«A + «Л + • • • + om«m "1P1 + aA + • • • + aJm I ciai + c*az + • ••
61«! + »,«,+••• + *m«m *,Pi + »Л + • • • + 6mP» I dl«l + *A ♦ • -
-Hit)
i—MW.
«A+'A+'-' + sA
*A + *A + -+*.A
Поэтому, согласно формуле (16), получаем детерминантное тождество
+ с а
4- d а
1 т т
Y
&А**Л + -+*««т 6А^^Р2 + ---+&тРт
С1а1+С2а2 +•-
.. + с а
1 т т
+ *««« ^А + ^2 + -'+^тР|
+
Mix)
-И/.) :
Y
С.)
- 2
ака1
hbl
■*(h)
ch cl\ 1—M/t>
dHd,
Y
aftP*j
ai h\
II. Если Л, = 1 и |i = О, тот=1и(1, 0)-свернутое произведение
|,0(АВ) представится в виде ip + q—1)-мерной матрицы л-го
порядка:
ЛЩ = ||Л1.../^Дт2...т,|| «I- • • • • '/>-!• * ™2> .«. ^ = L 2, .... л).
^ (18)
Порождаемые матрицей (18) детерминанты являются
произведениями соответствующих детерминантов матриц А'и В,
составленными по правилу Скотта — Раиса (гл. I, § 5):
M±)gi
<1...1рм1
>(±
B(±)a-i*JSL I
Ш| tn2...nXq I
где каждый из символов (±)ст' и (±)а* над индексами /р и тг
обозначает любой из знаков «+*, «±», а символ (±)<т0 над
индексом s будет обозначать знак «+» или «±», смотря по тому,
одинаковы или различны значения символов (±)<х', (±)о".
III. Из равенств (5), (6) следует, что
0<т<р + <7.
Если т=0, то А,=0, ц,=0 и произведение °'°(АВ) без
свертывания * представится в виде (р + ^-мерной матрицы л-го порядка:
* Согласно обозначению Г. Вейля для квадратных матриц, °°(АВ)
записывается как Ах В.
5-595
65
°'°(AB) = \\\l2muJBmi^Mq\\ (lv lv ..., /,, mv mv ..., mq= 1, 2, ..../i).
(19)
Ассоциированная с матрицей (19) (p + ^-линейная форма Ф
является произведением форм
F — VA x{{)x(2) x{p) co = VB 70>7(2) 7(<7)
1 1
с соответствующими матрицами
(/р /2, ..., 1р = 1, 2,..., я),
(тг т2,..., т = 1, 2, .... п).
\l2-h
А
В = 11В
Детерминанты, порождаемые матрицей 0,0{АВ), выражаются
через соответственные детерминанты матриц Л, В в виде
\А (±)s В (±)а I = /г! |
(1Ъ /2, ..., /р, mlf m2, ..., тщ = 1, 2, ..., п).
Действительно, (р + <7)-мерный детерминант и-го порядка
5 (±)g
/И1Ш9.. ./Я-
(20)
Д =
Л (±)S В (±)а
l\h--lp ЩЫ<1—тц \п
является, согласно определению, алгебраической суммой (я!)р+7~!
членов вида
(_ 1)8+ч (Л (1) (1)В (!) (1))(Л(2) ,(2)5(2) и))—И,(п) ,(п)В (п) (и)),
где значения 4°, &2\ . •., /аП) и mjj0, т£2\..., т^п) индексов
1а (а = 1, 2,..., р) к щ ф = 1, 2, ..., q) матриц Л и В образуют
некоторые перестановки из чисел 1, 2,..., л, а г и ц — суммы
чисел инверсий в перестановках, образуемых значениями
альтернативных индексов соответственно в Л и В. Так как указанное выше
выражение общего члена детерминанта А не меняется при любой
перестановке п множителей
BJl> m(1)' BJ2) m(2>» * • • » Bm№ т(П>»
то А можно представить в виде
А = л! £ (—l)4<i> (1)Л(2) (2)...
• • • А.(п) Лп) У (— 1Г# (1) m(DBm(2) (2) • • • В (п) (п),
*j[ ..Лр *-* /rtj .,.m^ /П| ...trig /itj ...m^
66
где первое суммирование распространяется на все возможные
комбинации перестановок $\ 1а\ ..., /ая) (а = 2, 3, ..., р) при
фиксированной перестановке l[l\ lf\ . . . , /^ и дает детерминант
A (±)s I , а второе суммирование распространяется на все возмож-
ные комбинации перестановок т£\ т^\ т^ (р = 2, 3, ..., q)
при фиксированной перестановке т[{К т(2), ..., т[п) и дает
детерминант
В
(±)о
Ш|Ш2.
nq \n
Из равенства (20) находим
Д (±>g
mttn.2* ..тЯп
л!
^ (±)s В (±)о
/|/2..Лр mlm<2...mq
(21>
Таким образом, в дополнение к правилам Кэли—Раиса к
Скотта — Раиса представления произведения двух
детерминантов р н q измерений и пбрядка п в виде детерминантов
измерений p + q—2 и p + q— 1 и того же порядка п мы получили
выражение (21) рассматриваемого произведения через детерминант
p + q измерений и порядка п с сигнатурой, полностью
составленной из сигнатур перемножаемых детерминантов.
В частности, согласно формуле (21), произведение двух
квадратных детерминантов или перманентов n-го порядка представимо
соответственно четырехмерным гипердетерминантом или
перманентом n-го порядка, умноженными на — :
И±±| *|Я±±| =-гИ±±В±±|
I it t2 \n I h h \n I н i» /i /2 \n
Л-н-l -|5++| ==l[r\A++B++\ •
it it \n I /1 /2 I" I H i2 /1 /2 I"
Точно также, произведение квадратного детерминанта n-го
порядка на квадратный перманент того же порядка представимо
смешанным четырехмерным детерминантом n-го порядка, умножен-
1
ным на-^:
А±±\ .|В++| =±\А±±В++\
it i% \n I /i /1 \п Пт | Hh /1 h \n
IV. Если x=p+q, то из равенств (4), (6) следует, что и + К +
4- v = 0, т. е. х = 0, X = 0, v = 0, а потому р = q = ji, и полно-
0,Р(ЛВ) представимо в виде скаляра
AcxC2...c„Bcic<>...c0* (22)
стью свернутое произведение
°'Р(ЛВ) =
2] ^^...Ср^сз...^*
eVc2 Vi
б*
67
Согласно формуле (22), /?-линейная форма F = J] А. . { х^х
X х{р ... х<р) представима в виде полностью свернутого
произведения 0>Р(АХ) р-мерных матриц и-го порядка:
*hiv.^kX-K)*?----«?)ii е..'г-.',-1.2 п).
V. Особо важен случай, когда (А,, (г)-свернутое произведение к^(АВ)
представляется матрицей такого же числа измерений, как у
одного из сомножителей. Очевидно, это будет тогда и только тогда,
когда число измерений другого сомножителя равно т, т. е. Я + 2 ц.
В частности, если обе матрицы А и В имеют одно и то же число
измерений р = X + 2(г, получаем
к*(АВ) = || J Aci0)scil)Bc{l)sc{2) || (ji Ф 0), (23)
^(ABr^\\AslS2,„SpBSlS2.„Sp\\ (,1 = 0),
(24)
О* ¥■<>),
где каждый из индексов разбиений s = (sv s2,..., s^), c<*> == (c<f\
C2fe)» • • •» ^ ПРИ * = °» 1» 2 пробегает значения 1, 2, ..., л.
Если при этом В = Л, то из формул (23)» (24) находим (А,, ц)-
свернутый квадрат матрицы А:
'%4 ) == I J A.(0)sc(lH,(l)sc(2) |
II <«П>> ^ '
^2HHW-J (^ = 0)
и, вообще, (X, ц,)-свернутая u-я степень матрицы А представляется
в виде
П4") = || Е ...
• • • ( S ( S А«№ЬсОЛ<1>«<*>) Лс(2),с<3>) • • • Л(«-»5с(«) || 0* * О),
"V>-II *,*••*» (11-0),
где а —любое положительное целое и каждый из индексов
разбиений s = (s,, s2, ..., s^), с<*> = (с<*>, с<*>, ..., с<*>) при k — О, 1, . ..
..., и пробегает значения 1, 2, ..., п.
Пример 6. Пусть
Ms)
А =
1 2
4 1
3 4
2 3
Г
Или А о В, согласно обозначению Адамара для квадратных матриц.
£8
Тогда
'W =
Ы+2.4
4Л + 1-4
1.2 + 2-1
4.2+L1
3.3 + 4-2 3.4 + 4-3
2.3 + 3-2 2-4 + 3-3
•Hs)
«<2>)
Y
(с(0)>
9 4
8 9
17 24
12 17
Ms)
.(г<2>)
Г
\А*) =
9.1+4-4 9.2 + 4-1
81 + 9-4 8-2 + 91
17.3 + 24-2 17.4 + 24-3
12.3+17-2 12-4+17.3
Г
>(с(3))
25 22
44 25
99
70
140
3,0,
(Л2) =
зд
'(А8)-
1
16
1
64
99
19
И
.(Л
Г"
(г(0))
16 II Г"М*8>
27 64
8 27
У
'(St)
г—Ms»)
I
(Si)
VI. Полагая й фбрмуле (24) каждый элемент матрицы В равным
матрице К любого *й*сйа измерений и порядка, получим прямое
или кронекерово произведение А ф К матрицы А на К:
А® К = ||Л^2...^К|1 {ivi2,... Лр = 1,2,..., л)
в виде клеточной р-мерной Матрицы п-го порядка, клетки которой
составляются из произведений элементов матрицы А на /С.
Очевидно, произведение АЩК есть'диагональная матрица,
если обе матрицы А и К диагональные, и А ® К есть клеточно-
диагональная матрица, если только матрица А диагональная.
Кронекеровым произведением можно Воспользоваться для
символической записи многомерных Матриц *(см. [71, стр. 70). Возьмем
сперва матрицу четного числа измерений
^ = 1Ич^2г1|(^Р^
4*= 1.2,,
,п).
Введем в рассмотрение квадратную матрицу я-го порядка а =
= II^Mtll (h> i*2 = U 2, . . . , п) и составим кронекерово
произведение
I А1га... А1па
афа =
Ап1а... Аппа
e
которое обозначим через а2. Имеем
ЛпЛп • • • AHin
АцАп1 • • • А-иАпп
Ап\А1Х • • • Ап1А1п
An\Ani • • • Ап1Апп
^ln-^ll • • • А1пА1п
Л\пАп1 • • • AinAnn
АппАщ • • • AnnAln
А А A A
(25)
Отсюда видим, что а2 будет символическим представлением
квадратной таблицы из я4 элементов, в виде которой записывается
четырехмерная матрица п-то порядка, если в клеточной матрице
{25) произведения Aixi Aijtii заменить элементами AitititU. Со-
® ®0
ставляя, далее, кронекеровы произведения а ® а2 = а3, ...
. . . , а ® аг-1= аг, придем к символическому представлению w
квадратной таблицы Т2г из п2г элементов, в виде которой
записываемся матрица Л.
Возьмем теперь матрицу нечетного числа измерений
А = || AHv,.i2r || (i, /,,...,^=1,2,..., л).
Вводя в рассмотрение (1 х л)-матрицу а' = ||ЛХ, Л2, .
составим кронекерово произведение
All
а'®аг = || Лх^, Л2а^,..., АпаГ ||. (26)
Последнее будет символическим представлением прямоугольной
(пг х nr+1) -таблицы 7V+1 из я2г+1 элементов, в виде которой
записывается матрица Л, если в (26) произведения АЛ. .... А{ {
заменить элементами Auxi2,%.i2r_xi2r
Транспонируем таблицу Тр, где р = 2г или р = 2г + 1, соот-
-[!]+*<*
= 1,2,
ветственно подстановке . . р. , где а/,
...,Р) и
(1§~~ г если Р и ^ одинаковой четности;
11 1, если р четное и h нечетное;
10, если р нечетное и h четное.
В результате получим таблицу, представляющую двумерную
(я 2 X л ) - матрицу, ассоциированную с матрицей Л.
70
Например, для матрицы А == || Aiilit \\ (t, iv i2 = 1,2) по формуле (26)
находим
Тя =
Аш Am
^121 ^122
^211 Л212
•^221 ^222
-W0
Ч*2>
Г
и, транспонируя Т3 соответственно подстановке (t\ /x), получаем
ассоциированную с А двумерную (2 х 4) -матрицу
^111 ^112 ^121 Ах
^211 ^212 ^221 А2
у
(О
Точно также для матрицы А = || AvW4|| (ib i2, f8. h= 1» 2) находим
n=
^1111 Л1112
^1121 ^1122
Л2Ш Л2112
^2121 ^2122
"ЧаИ Л1212
*1221 ^1222
^2211 ^2212
^2221 ^2222
I
. Y
Y Ut)
(h)
и, транспонируя Т4 соответственно подстановке (t2,is)» получаем
ассоциированную с А двумерную (4 х 4) -матрицу
^1111 ^1112 ^1121 Al22
-^1211 ^1212 ^1221 ^1222
-^2111 ^2112 ^2121 ^2122
^2211 ^2212 ^2221 ^2222
§ 4. СВЕРТЫВАНИЕ И РАЗВЕРТЫВАНИЕ МАТРИЦ *
Возьмем выражаемое формулой (12) (О,|г)-свернутое произведенн»
р-мерной матрицы /1-го порядка
А = || \..1нС1.,.С111| (1г /х, cv .. ., с^ = 1,2,..., л),
где х + (л = р, на q - мерную матрицу того же порядка п
В-ПД
c^...c[im^...nb)j
| (cv с^ mv..., mv = 1,2,..., я),
где n + v = <7.
Полагая в матрице В все элементы равными единице,
рассмотрим два случая, когда l<[i<pHv==0 или р = 0 и v > 1.
В первом случае, когда 1 < ц < р и v == 0, произведение (12)
представится (/? — (л)-мерной матрицей я-го порядка, которую
обозначим через М и назовем ^-свернутой матрицей для А {по ин-
71
дексам съ . . . f c^). Имеем, таким образом,
МЛ = || 2 \.^cv.,»Ulv...,l^=h2 n). (27)
с\ cnel
При \i = р матрица (27) будет полностью свернутой, т. е.
скаляром
л
Число всех свернутых матриц для Л, очевидно, равно
£c5J = 2p-i.
При ц < /? — 2 любой (р —ц)-мерный детерминант n-го
порядка |М|, порождаемый матрицей (27), имеет элементами суммы
г№ элементов матрицы А и может быть вычислен с помощью
обобщенного разложения - Альбеджиани.
Замечание 3. Из формулы (27) следует, что произведение двух
многомерных детерминантов одного и того же порядка, составленное
по правилу Кэли — Раиса, является детерминантом 1-свернутой
(по соответственному индексу) матрицы произведения тех же
детерминантов, составленной^ по правилу Скотта — Раиса, если оба
соединительных индекса чв перемножаемых детерминантах
альтернативные.
Например, произведение детерминантов
|АнН1п, |В±±+ + |„ (28)
может быть представлено по правилу Скотта — Раиса (при
соединительных альтернативных индексах /3, тг) детерминан!ом
Для соответствующей матрицы
II А 1х1фВ sm^mtm, || (l1§ /2, S, /П2, /П3, /И4 = 1, 2, . . . , П)
1 - свернутая (по индексу s) матрица имеет вид
л
I £ &гцР*пюгц || Wb U> ^2» Щ>Щ= 1,2,..., П).
Порождаемый ею детерминант
\%А+±В±++1
72
является произведением детерминантов (28), составленным по
правилу Кэли — Раиса.
Обратимся теперь ко второму случаю, когда |л = 0 и v > 1.
Тогда произведение (12), где, как и в первом случае, все
элементы матрицы В предполагаются равными единице, представится
(Р + v)-MepHoft матрицей п-го порядка, которую обозначим через
ХА и назовем \-развернутой матрицей для А (по индексам тъ . . .
. . . , nty). Имеем, следовательно,
vA = || -А/j.../^mj mv || {lxt • • • • /pt л^... t fl*v = 1,2f..., л), (29)
где
Л/i...f
A i. i
/1.../pm,...mv — --^....p.
Таким образом, в матрице VA все /xv сечений ориентации (ти ..., гщ)
одинаковы.
Каждый (р + г)-мерный детерминант л-го порядка |Vi4|,
порождаемый матрицей (29), согласно свойству V многомерных
детерминантов (гл. 1,,§ 3),! равен нулю, если хотя бы один из индек-
сов тъ . . . , пи, альтернативный, тогда как \VA\ с
неальтернативными индексами тъ ... f ту и любой сигнатурой (±) о над
индексами llt . . . , /р, в соответствии с теоремой 1 (гл. I, § 4),
представляется в виде
/j...lpl71|...f7Iy
/!.../р
Пример 7. Для матрицы
I «All Al2
Г
м/2>
у
имеем
И = И Л\цп Н =
Ац Alt
Ац А22
А\\ Ai2
А%\ i42j
Y
Ut)
H = IH*/l/jmimf||==
Лц Лхг
^21 Л22
Ац А12
An An
Ац A12
%2i A22
Ац A12
An A2t
—Mm»)
-M*t>
Детерминанты |А±±_}_| и \A*±-l+^I» порождаемые этими развернутыми ма-
li 1% tn ti l9jniimt
трицами, представляются в виде
ia;±+i = 2
ltljn
(-
22
Ац Л18|
Aii 4»|
All ^12
Aei ЛО-
73
§ 5. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МНОГОМЕРНЫХ МАТРИЦ
Рассмотренное в предыдущих параграфах умножение многомерных
матриц равносильно цепочке их элементарных преобразований,
понятие которых тесно связывается с двумерными матрицами,
известным образом ассоциированными с многомерными матрицами.
Пусть
/(1) ,(2) ,("*)
C(D Q<2) Jnh
й , о , . . . , д ,
с(,),с(2) с^,
m(1), m(2,,...,m("V)
— расположенные в нормальном порядке совокупности значений
индексов, разбиений /, s, с, т матриц и-го порядка Л = ||Л/$С|| и
£ = ||Б«ОТ||, числа измерений которых соответственно равны р=к+
+ X+\i и q = % + \i + v.
Составим из элементов матрицы А двумерную клеточно-диаго-
нальную матрицу
где диагональные клетки St^o.n (А = 1,2,... f /Iх) — двумерные (лх x
X яд) - матрицы:
«V = || А&ь || (/ = /Ч /»,.... i*"»; г - с(1\ с<2>,.... с^>).
Матрица Якд.и называется (х, А,, Ц,) -ассоциированной с матрицей Л*.
Подобным образом составим матрицу 2Vfa,tV, (|хД, v) -
ассоциированную с матрицей В:
jb^a.v = {s^o.v, a5{i%.v,..., »$to,
где диагональные клетки S3{£o,v (Л = 1,2,.... я*) — двумерные (лд х
X nv) - матрицы:
«g?o.v = II *««» || (с = с(1\ с(2),..., с(яР1); m = m(l), m<2),..., m^),
и матрицу ®х.м» (Х> ^tv)" ассоциированную с матрицей С = ||C/sm||,
представляемой формулой (7):
&x,a,,v == {®x,o,v, ©x.o.v, • •.» ®x,o,v},
* Число Np всех возможных такого рода матриц для данной матрицы А
Р
выражается формулой N9 = \ ^-т . Каждая из них вполне оп-
jLJ Л,! ft! (р—X—11)!
ределяет матрицу Л.
74
где диагональные клетки S^o.v, (А = 1,2,..., л*) — двумерные (пхх
X п*) - матрицы:
«$>.* = || £ As(*)As<>0m|| V = '(1)> *».-. №\ т = т<«, /»»,..., m<"v>).
(с) "
Тогда
- {|| S Asu> As<.w ||. IБ 4* Ал. || • • • ■ • || S VbA*^ || }•
^, - {I s W^ 1И1S As<2) A.2)ffl||..... || S >W^ J-
Следовательно,
, ©*,A,,v = 91хЛ,ц95цД,г. (30)
J
Далее, принимая во внимание формулу (9) и замечая, что
1) матрица 2Сд,ц, транспонированная относительно 91хд,ц, (\i, К
у) -ассоциирована с матрицей А = || Xs/|| , транспонированной
относительно А соответственно подстановке (/, с)\
2) матрица SS^.v, транспонированная относительно вцд,^ (vA,
\i) -ассоциирована с матрицей В = || B'msc ||, транспонированной
относительно В соответственно подстановке (т,с);
3) матрица Cca.v» *ранспонированная относительно (£x,a,,v, (vA
и)-ассоциирована с представляемой формулой (11) матрицей С' =
= || C'msi ||, транспонированной относительно С соответственно
подстановке (1,т), находим подобно предыдущему
<£x,fc,v = ЯЗйЛ.Л«д,ц.
Таким образом, справедлива следующая теорема.
Теорема 1. Матрица, (к,)*, ^-ассоциированная с правым (А,, ц,)-
свернутым произведением матрицы А=*\\Аьс\\на В = \\Bcsrn\\tравна
правому произведению матрицы, (к, К \ь) - ассоциированной с А, на
матрицу, (р, A,, v) - ассоциированную с В.
Точно также матрица, (у, К к)-ассоциированная с левым (А,, \л)-
свернутым произведением матрицы К = || А'ы \\ на В' = || В^с ||,
равна левому произведению матрицы, (ji, А,,х)- ассоциированной с А',
на матрицу, (v, А,, |л) - ассоциированную с В'.
Замечание 4. Если х = (г, т. е. /? = А, + 2щ то (щ A,, р) -
ассоциированную с А = || Л/s, || матрицу 2Гцд,ц будем назьгоать просто (А,, ц)-
ассоццир'ованной с Л и обозначать через ЭД^.ц. Если матрица ЭД^.ц —
— симметрическая, то А называется (А,, |л) - симметрической матрицей
(тогда Aisc = Acsi).
75
Будем называть (х, К (л) - элементарными преобразованиями*
матрицы А = || Aisc || следующие операции над любым ее сечением
ориентации (s), например над сечением Aih)= \\Als(h)c\\(l < ft< пк):
a) умножение какого-либо сечения ориентации (с), например
\\Ais(h)ca) II (1 < / < яц), на произвольное, отличное от нуля число t£P;
b) прибавление к какому-либо сечению ориентации (с), например
II \(Ь)со) II» умноженного на t любого другого сечения той же
ориентации, например || Als{h)cin || (1 < /' < п*\ /' Ф /);
а') умножение на t какого-либо сечения ориентации (/), например
IH/(os<ft>J (1<;<"н);
&') прибавление к какому-либо сечению ориентации (/),
например || ^/<о8 (Mr И» умноженного на / любого другого сечения той же
ориентации, например ||Л цг)8ф)е || (1 < t' < nx, i'j=i).
Эти операции в дальнейшем будем обозначать символами
а)
Ь)
а')
Ь')
1
5<А)с(/>
Usw
^уГ|
1 +
t,
s(ft)c(/')
/(i)s(ft>
1 +
\t.
\?nsih)\
и
t.
Если с помощью одной из операций а), Ь), а'), Ь') можно
перейти от матрицы А к другой матрице В, то, очеввдно, мож^о и
обратно получить матрицу Л из В с помощью операции такого же
типа.
Операциям а), Ъ\ а'), Ъ') соответствуют элементарные
преобразования диагональной клетки З^о.ц матрицы 2Гх#31,ц»(и> К v)m
ассоциированной с матрицей А:
a) умножение /-го столбца на t\
b) прибавление к /-му столбцу умноженного на t /'-го столбца;
а') умножение t-й строки на /;
b') прибавление к t-й строке умноженной на / t'-й строки.
Эти преобразования; очевидно, являются также элементарными
преобразованиями матрицы 9tx % .
Замечание 5. Операциями типов а), Ъ) или а'), Ь') можно пере*
ставить в каком-нибудь сечении ориентации (s) матрицы А =
= || А
lsc I
любые два сечения соответственно ориентации (с) или
(О, поскольку в соответствующей диагональной клетке (х, X, |i)-
ассоциированной с А матрицы %нК11 операциями типов а)% Ъ)
* Или (А,, [л) -элементарными преобразованиями, если х=ц.
76
«ли о'), Ь') можно переставить соответственные столбцы или строки
(см. [21, стр. 152). Так, перестановка /-го и /'-го (1 <: / < /' < п*)
сечений ориентации (с) в /i-m (1 < h < nx) сечении ориентации
(s) Л<*> матрицы А равносильна цепочке (х, К ц)-элементарных
преобразований:
JV»
+
smcin
swcw)
+ I s(AV»
■(-1).
sV>
(-1),
Л(/)
+
S<V>
•(-1),
а перестановка t'-го и t'-ro (1 < i < t" < пк) сечений ориентации
(О в Л<А> равносильна цепочке
/«>s(h>
+
/«'>s<A>
/<'V>
+
iV
•(-1).
/(»')SW
(-1),
/<гУ>
+
/(|'У*»
(-1).
Операции а), Ь) над матрицей 21хЛ равносильны, как
известно (см. [11, стр. 137), умножению ее справа соответственно на
элементарные порядка л*"1"" квадратные матрицы ® , (Sr ',
являющиеся клеточно-диагональными матрицами, у которых все пх
диагональных клеток — единичные матрицы порядка п*\ кроме одной
/i-й клетки, представляющей вdr ' матрицу || (&£' || (£, if) = 1, 2,...У1),
где каждый элемент &£' равен б. (символ Кронекера), кроме
элемента е|;а) = *, а в (5(Ь) — матрицу || 0$ || (£. л = 1, 2,..., яд), где
каждый элемент Щ^ равен 6Сч, кроме элемента Щ.', = f.
Точно также, операции о'), Ь') над матрицей &„»м
равносильны умножению ее слева соответственно на элементарные порядка
«х+х квадратные матрицы @г , От ', являющиеся
клеточно-диагональными матрицами, у которых все лх диагональных клеток —
единичные матрицы порядка п*, кроме одной Л-й клетки,
представляющей в @г ' матрицу ||@i*'|| (£, г\ = 1,2,..., и"), где каж-
~(а') „ ~(а') , а-(Ь')
дый элемент Щ^ равен 6tt), кроме элемента б„ = f, а в <sv —
матрицу || щ^ '|| (£, т| = 1, 2,..., пи), где каждый элемент (^ч
равен 6£ , кроме элемента ($■,,' = f.
77
Аналогично, операции а), Ь) над матрицей А = \\ AISC ||
равносильны (к, (л)-свернутому умножению ее справа соответственно на
(А,, (л)-элементарные матрицы измерений x=%+2\i и порядка п:
£(а, = 11*111. £<6, = 1Ю>
гдет=(т,,т2, ..„т^ и каждый из элементов £^, Е^т равен 8сту
кроме E%s{h)mU)=t и E%sih)min=t.
Точно также операции а'), &') над матрицей Л = || АНс ||
равносильны (Я, х)-свернутому умножению ее слева соответственно на
(Кх)-элементарные матрицы измерены. а = Я+2х и порядка п:
£(a'> = ||£g?||. Е(Ь,) = \\Е&?1
где ^=(^,^2,... ,&х) и каждый из элементов £^\ Ejjj^ равен 8kV
кроме £fc(os<*),(o-r и л*(п,(*)/(0 ~ г"
Отметим, что упомянутые выше матрицы являются
(Я, ^-ассоциированными с £(а), £(6), а матрицы @г \ (г '—(^,х)-
ассоциированными с Е{а'\ Е(Ь'\
Поскольку матрицы @^, как и матрицы @^а \ 6^ ^,
неособенные, матрицы Е{а) и £(Ь) будем называть (А,, ^-неособенными^
а матрицы £(а) и £<6) — (%,к)-неособенными*.
В результате операции а) или Ь) матрица А преобразуется
соответственно в х,м,(Л£(а)) или Х,Д(Л£(6)), с которыми (иД,
^-ассоциируются 21хЛ @г , 21хД„@ , а в результате операции а') или
Ь') над Л получаем соответственно х,х (£(a'U) или Х,Х(Е(М)Л), с
которыми (х, А,, [^-ассоциируются @г Якд ^ @ ^хд.д-
Две р-мерные матрицы я-го порядка А = || Л/5С || и В = || B/sc ||
с элементами из поля Р называются (х,%^)-эквивалентными** над
Р, если от каждой из них можно перейти к другой с помощью
конечного числа (х,Я, (г)-элементарных преобразований.
Пусть матрица В получается из Л с помощью цепочки. (х, К \*>)-
элементарных преобразований, соответствующих (К,
^-элементарным т-мерным матрицам Еъ £2,... Дя и (А,, х)-элементарным
а-мерным матрицам Е\9 Ё^... ,Eq> одного и того же порядка п.
Тогда
В = х Y** (Е,.... Е'&'хА) ЕгЕ2 ...Ея] =
* Вообще, любая т-мерная или 0-мерная матрица порядка п называется
(А, ц)-неособенной или (Я, х)-неособенной, если соответствующая (Я,
|i)-ассоциированная или (Я, у) -ассоциированная матрица неособенная.
** Или (Я, \л)-эквивалентными, если х=|х,
78
= K»lEq-... Е'Я\к*(АЕгЕ%... Eq)\. (31)
Полагая
K* (E1Et ...Eq)=V, к*(Е'д*... Е'тЕ'г) = U,
где У — (А,, |д,)-неособенная т-мерная матрица n-го порядка,
представляющая (А,, |х)-свернутое произведение (А,, ^-неособенных
матриц Еъ Е2,...,Еду a U — (Я,х)-неособенная а-мерная матрица
я-го порядка, представляющая (А,, х)-свернутое произведение (31, х)-
неособенных матриц Ея>,... ,£г, Е[> имеем также
В = к»[к* (JJA) V] = Кк [UKlL(AV)\. (32)
Наоборот, из равенства (32) вытекает равенство (31), так как
каждая т-мерная или а-мерная матрица может быть представлена
соответственно в виде (А,, (х)-свернутого произведения (А,,
^-элементарных т-мерных матриц или в виде (А,, х)-свернутого произведения
(А,, х)-элементарных а-мерных матриц (поскольку соответствующая
(А,, (л)-ассоциированная или (А,, х)-ассоциированная квадратная
матрица представима произведением элементарных квадратных
матриц).
Таким образом, равенства (31) и (32) равносильны, и
предыдущее определение (х, А,, (х)-эквивалентности матриц А и В можно
заменить равносильным ему следующим определением.
Две р-мерные матрицы л-го порядка A =\\Ahc\\ и В =||B/S4I
с элементами из поля Р называются (х, А,, ^-эквивалентными над
Я, если они удовлетворяют соотношению
В = Kll[K" (JJA V] = *"* [UKl1 (AV)l
где V — некоторая (А,, (л)-неособенная т-мерная матрица л-го
порядка, a U — некоторая (А,, х)-неособенная а-мерная матрица того
же порядка» п над Р.
Последнее определение в случае, когда х = ц, формулируется
следующим образом: матрицы А я В называются (А,,
^-эквивалентными над Р, если они удовлетворяют соотношению
В = ^(UAV),
где U, V—некоторые (А,, |л)-неособенные р-мерные матрицы п-го
порядка над Р.
Будем называть (кЛ,\*)-рангом* матрицы Л = ||Л/5С|| и
обозначать через rKkll(A) совокупность рангов г(Я2|в#й), ^(Я2о,ц)» • • •
..., г (И^ диагональных клеток «g0§|l; «g^..., И^ (х> *» Р>
ассоциированной с А матрицы ЯхХ ^г
гм(А - иО'С; '<*&».
* Или (А, у)-рангоя при х = р. Если при этом г (Ж£^,р) ■■ л*1 (А —»1,
2,..., п\ то матрица А будет (А, р)-неособешюй.
79
где
о < г &&J < *min(x,,1) (* = u Д
Очевидно,
где г^Дх (Л(/,с)) есть (цД, х)-ранг матрицы Л(/,с),
транспонированной относительно А соответственно подстановке (/, с).
Из предыдущего следует, что (х, Я, (х)-эквивалентность матриц
А = ||Л /sc || и В = || B/sc|| влечет эквивалентность соответственных
диагональных клеток (х, Я, ^-ассоциированных с Л и В матриц
8(х, л, ц и $Вкл.|& и» наоборот, эквивалентность этих клеток
обусловливает (х, Л, (х)-эквивалентность матриц Л и В. Поэтому,
принимая во внимание известное свойство ранга двумерной матрицы,
легко убеждаемся в справедливости следующей теоремы.
Теорема 2. Если р-мерные матрицы п-го порядка A=\\Aisc\\
и В = ||B/SC|| (х, К (х) -эквивалентны над Р, то они имеют один
и тот же (х, Я, \ь)-ранг и, наоборот, если эти матрицы обладают
одним и тем же (х, К \1)-рангом, то они (х, X, ^-эквивалентны
над Р
Для матрицы C = ||C/sm||, представляющей выражаемое
формулой (7) (Я, (л)-свернутое произведение матрицы Л =||Л/8С|| на
В = IIAsmllt справедлива такая теорема.
Теорема3. (х,К\)-рангrKkv(С) (К.^свернутого произведения
С матрицы Л = ||Л,С8|| на B = ||BtfSm|| не превосходит (хД.р)-
ранга гк % (Л) матрицы А и (\i, Я, \)-ранга гдЛ^ (В) матрицы
В, т. е.
'k,x.v (Q < min Кк» №> гц.м <В»-
Действительно, согласно определению
где г (£(£ofV) — ранг диагональной клетки ©^ v (Л = 1, 2,.... я*)
матрицы ttKfXfV, (х Д, г)-ассоциированной с матрицей C = ||C/sm||f и
>Va.v (5> = С ^v), г (§B^V),..., г (»f0>v)),
где г(*^}0э|1) —ранг диагональной клетки SS(^0,v (Л — If 2,... ,ях)
матрицы »ц,х^» (Iх Д> ^-ассоциированной с матрицей B = ||BCsm||.
Из равенства (30) следует, что
С = СЛл (* - 1. 2 п\ (33)
Отсюда заключаем, что
r(ej»>v) < min(r(5t^i(l),r(^h>v)) (Л = 1, 2,... ,Д
Следовательно,
'xa.v (С) < min(rKtXtJ1(i4)f r^>v (В)).
80
Более точный результат имеет место для случая, когда один из
сомножителей, например В = ||Bcsm||> является т-мерной (Я, ц,)-
неособенной матрицей. Тогда v = fi и (Я, ^-ассоциированная с
В матрица ЯЗ^.ц и все ее диагональные клетки SBo^ (Л = 1, 2, . . .
. . . , пк) будут неособенными квадратными матрицами. Поэтому,
принимая во внимание равенства (33), имеем
т. е.
Таким образом, имеет место следующая теорема.
Теорема 4. (хД, \)-ранг rHtX>v(C) (Ху\1)-свернутого произведе-
дения С р-мерной матрицы п-го порядка A = \\Alsc\\ на х-мерную
(А,, ^-неособенную матрицу п-го порядка B = ||BCSm|| равен (хД,|х)-
рангу rKk (А) матрицы А.
Заметим, что (х, А,, |л)-ранг r„Xfl(A) матрицы А =||Л/5С|| сразу
выявляется, коль скоро она (х, Я, |д)-элементарными
преобразованиями приводится к каноническому виду
7(хД,(г) = ||/Ьс||,
где в каждом сечении ориентации (s) || / (fc) || (А = 1, 2,..., пк)
все элементы—нули, кроме элементов / (fe) {h) {k) = 1 (fe = 1, 2,...,
Cfc e *4*!S>.ii))- Каждая диагональная (/^хл^-клетка Зи,о,ц(л===
= 1, 2,..., п%) (х, Я, ^-ассоциированной с / (х, X, (г) матрицы
Зид.ц имеет канонический вид
1
0
0
0
I о
0 . .
i
о . .
о . .
о . .
.
. 0
. 0
. 1
. 0
. 0
о . .
0 . . ,
0 . .
0 . .
0 . . .
. oil
oil
oil
. о
o|
•(Q*). (34)
(x, X, (л)-элементарные преобразования, с помощью которых
матрица А приводится к / (х, А., (х), соответствуют тем элементарным
преобразованиям диагональных клеток Я{*^ (h = 1, 2, . . . , пх)
(х, К (л)-ассоциированной с А матрицы Ч&хХи » с помощью
которых они приводятся к каноническим видам (34).
хМатрица / (х, A,, (i) может быть рассматриваема как
представитель класса К (х, А,, ц) /7-мерных матриц /1-го порядка, (х, Я, ji)-
эквивалентных матрице А.
6-595
81
ГЛАВА IV
ПРОСТЕЙШИЕ МАТРИЧНЫЕ УРАВНЕНИЯ
§ 1. ЕДИНИЧНЫЕ МАТРИЦЫ
Рассмотрим матричное уравнение
К»(АХ) = Л, (1)
где
А = И Лм,...*рИ ('г *2> .-../р=1.2 л)
— данная /7-мерная матрица я-го порядка над полем Р, а X —
неизвестная матрица того же порядка л.
Так как левая часть уравнения (1), являющаяся (Я,
^-свернутым произведением матрицы А на X, должна иметь то же число
измерений р, как и правая часть этого уравнения, представленная
матрицей Л, то число измерений матрицы X должно равняться
т = % + 2 |i (см. §3, гл. III). Имеем, следовательно,
Х = \\ХЫ^Л Уг/. /,= 1,2,....л).
Представляя матрицы Л и X с помощью разбиений
совокупностей их индексов
/ = (lv /2,... ,ZJ, s = (sv s2,..., sk), с = (cv c2>..., cj,
m = (w1,m2,...,mJA),
где
7i+%+li=Pl (2)
в виде
A = \\AlsC\\, X-\\XC9M\\9
можем переписать уравнение (1), в соответствии с формулой (7)
гл. III, так:
И ^i^lscXcsm К = А (3)
(с) " '
где каждый из индексов разбиений /, s, с, т пробегает независимо
друг от друга значения 1, 2, . . . , п.
Решение X уравнения (1), совпадающее с решением уравнения
(3), является, таким образом, t-мерной матрицей n-го порядка, у
82
которой число свободных индексов, составляющих разбиение тг
равно числу калиевых индексов разбиения с. Такой матрицей,
очевидно, будет х-мерная матрица п-го порядка
E=\\ECsm\\, (4)
в которой каждый элемент Есш равен 8ст (символу Кронекера),
ас, s, m — упоминавшиеся уже разбиения совокупности индексов
/ъ /г» • • • * ]%•
Матрица (4) называется (Я, \1)-единичной матрицей порядка п
и более подробно обозначается через Е (X, \i) (см. [6], стр. 1323).
Как легко убедиться, она перестановочна с любой р-мерной
матрицей п-го порядка А:
К\АЕ) = К\ЕА) = А (5)
Число единиц в матрице £ (Я, \i) равно Ф+*. В частности, в
матрице £ (а, 0) каждый элемент равен единице.
Матрица б^.ц, (Я, ^-ассоциированная с Е (Я, (х), является
единичной квадратной матрицей порядка rfi+i1.
Из равенства (2) имеем ;
и так как 0 < ji< р, то
0< А, + ц,<р
0 < т < 2р.
(6)
(7)
Из неравенств (6), (7) заключаем, что число матриц Е (A, \i),
удовлетворяющих условию (5) при всех возможных значениях
т=М-2ц
0
1
2
2
3
4
X
0
1
0
2
1
0
*
0
0
1
0
1
2
■£<*" «- || Ecsm ||
1
II 1> Ml
li? II
III IN
->(s) 1
10
1° l 1
1 l °
0 0
0 0
1 0
1 0 |—M"<)
0 i Y
U l II (c) J
loil
0 0
0 0
0 1
• V (r \
r \ca)
| Hm2)
Y
(яц)
Y 1
1 {Ct)
6*
83
X, р, равно числу пар (А,, ц), у которых сумма А, + \л пробегает
значения 0, 1, 2, . . . , р% т. е. равно
1 + 2+... + (/>+1) = ~(р + 1)(р + 2).
Например, при р = 2 и и = 2 имеем (см. стр. 83).
При р = 3ил = 2 предыдущий вывод надо дополнить
следующим:
т=А,+2Ц
Е(К Ю=|| *
1 1
1 1
1 1
1 1
-><s2>
г
<st)
-W
i о
0 1
i о
0 1
1 0
0 1
1 0
0 1
(с)
<«l)
-Ms,)
-Mm)
1 l °
0 0
0 0
|l 0
0 1
0 0
0 0
0 1
i о
0 0
0 0
1 0.
0 1
0 0
0 0
0 1
-*<s>
-M*2)
>w
Y
(ct)
1 0
0 0
0 1
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
1 0
0 0
0 1
0 0
0 0
1 0
0 0
0 1
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0 1
1 0
0 0
0 1
-Mc2)
—Mm,)
|—Mm,)
У
(m8)
У
(c*)
Матрица @а,,й второго порядка имеет вид {1, 1, 1, 1} при Л +
+ |i = 2 и {1, 1, 1, 1, 1, 1, 1, 1} при X + |i = 3.
84
§ 2. ОБРАТНЫЕ МАТРИЦЫ
Рассмотрим теперь уравнение
Х*(ЛХ)=Е(Х\|Л (8)
где А = \\Aisc\\ —та же матрица, что и в уравнении (1), а £(А/, \i')
есть (А/, ц/)-единичная %'-мерная матрица порядка п, где
т' = Я/ +2[*',
причем
О < к' + |i' < р.
Неизвестная матрица л-го порядка X = II Xcsm\\ , где т = (т^ /п2,
. . . , mv), в соответствии с формулой (/) гл. III, должна иметь q
измерений, где
q = x' + x-p. (9)
Матрица X, удовлетворяющая уравнению (8), называется (Я, ji)-
обратной матрицей для А относительно Е (X', ц') и обозначается
через Л-1 или более подробно через А-1 (X, ц,) (см. [61, стр. 1323).
Для нахождения элементов матрицы А-1 (Я,, |л) имеем систему
пх' линейных уравнений с лт'+т-р неизвестными X^:
2 A/scXCsm = f/sm» ОФ
где т' индексов совокупности /#п образуют совокупность индексов
сг . . . CpSi. . . s^/Hx. . . /%' матрицы Е (A/, \i'). Существованием
решений этой системы обусловливается существование матрицы
А-ЧК V).
Число уравнений системы (10) равно числу неизвестных, если
р = т. Тогда, согласно формуле (9), q = т', причем -g-p < т' <
< 2 р. В этом случае разбиения Z и с, составленные
соответственно из свободных и кэлиевых индексов матрицы Л, содержат одно
и то же число \i индексов. Обозначим, как и раньше (гл. III),
через /<*>, /<2), . . . , lm>; sO>, s<2\ . . . , s(nM; cO>, c<2>, . . . , с{т>
расположенные в нормальном порядке совокупности значений
индексов каждого из разбиений /, s, с. В совокупности индексов
т = (ть /7^, . . . , пи,) целое v удовлетворяет условию
Детерминант системы уравнений (10) будет тогда равен Д£>|А,
где
85
Представляя произведение (11) nl квадратных детерминантов,
согласно правилу Скотта — Раиса умножения многомерных
детерминантов, в виде (п^+ 1)-мерного детерминанта, получим
д =|Л(±)а +А +...Л .+ |(S = /(1),/(2),...,/(Al,X>;
Vri2....,V=c(1).c<2) **)- О2)
где (±) а есть знак «+» при п четном или «±» при п нечетном.
Можно также, используя формулу (21) гл. III, выразить Д^
через 2 /^-мерный гипердетерминант в виде
Ка = \— М+ +А+ +...Л+ х+ I (13)
ft t C - /(1) /(2) /(яД)- n n n - c(l) c(2) r("^
Если Дя,ц =£ 0, то система уравнений (10) имеет единственное
решение, определяемое по формулам Крамера. Оно и дает искомые
элементы матрицы А~1(к, ц).
Рассмотренная выше матрица А~1 (X, \i) является правой (Я, ji)-
обратной матрицей для А относительно Е (V, \i'). Левая матрица
такого же рода будет решением уравнения
Х'*(КЛ)=£<Я\А О4)
где, как и в уравнении (8), каждая из сумм К + р, А' + ji' не
превосходит р. Ее элементы определяются из системы пх'
линейных уравнений с пх'+х~р неизвестными Y^c
2jYms(Acsl = Emsh (15)
(с)
где индексы msl образуют совокупность индексов матрицы £(А', |i').
Правая и левая (1, (х)-обратные матрицы для А относительно
Е (А/, \ь') в общем случае, очевидно, различны.
Замечание 1. Если А' = Я, ц/ = ц и А + 2 ji = р, то вместо
уравнений (8), (14) имеем соответственно
Х^(АХ) = Я(Я.|*). ^(!M) = £(A,ji)
и системы уравнений (10), (15) принимают вид
2jAisCXcSm = t,iSmt 2j * mscAcsl = ^ms/»
ГДе (с) (С)
/ = (/P /a. • • • • *ц). с = (cp c2,..., <g, m = (/пг/п2,... ,/тг^),
S === (si» s2> * ' ' » SA/#..
86
Легко убедиться, что в этом случае правая и левая (Я,
^-обратные матрицы Л-1 (Я, \i) для (Я, ^-неособенной /7-мерной матрицы
п-го порядка Л = \\Aisc\\ относительно Е (к, \i) одинаковы. Будем
называть тогда Л-1 (к, \i) просто (А,, ^-обратной матрицей для Л.
Имеем, таким образом,
b&i a л-h
(АЛ'1) = ™(A-lA) = Е(к fi).
(16)
Число матриц Л-1 (к, ц,), удовлетворяющих условию (16), равно
числу пар значений к, р» удовлетворяющих равенству к + 2 |л = р,
т. е. равно 1 + Г|-1.
Матрицей, (Я. (л)-ассоциированной с Л"1^^), является
обратная для 91^ матрица 21^, где %kil—неособенная
клеточво-диагональная матрица, (А,, (л)-ассоциированная с Л, причем
диагональным (пдх п*)- клеткам 91^ (Л= 1, 2,... ,п*) матрицы Ях§|1
соответствуют таких же размеров диагональные клетки (StfJJi)"1 (ft =
= 1, 2,. .. 9n^) клеточно-диагональной матрицы SG^, являющиеся
обратными матрицами для неособенных матриц 21^ (Л = 1, 2,...fnx).
Пример 1. Пусть дана кубическая матрица второго порядка
*=м,-н =
Лщ
^211
^112
Л212
-^121
Лаз!
Л122
-^222
!
•Г/1
-(с)
Найдем сперва правую и левую (Я, |х)-обратные матрицы для А относительно
Е (У, |i'), полагая К = 1, jx = 1, V = 3, |i' = 0. Уравнение (8) имеет в этом
случае вид
ы {АХ) =* £ (а 0),
где
—>-(s)
1 И , — Ыт)
Е (3, 0) =
1 Y
1!«(/)
и для нахождения элементов Xcs (с, s, т = 1, 2) правой (1, 1)-обратной
матрицы Л-1 (1,1) относительно £(3,0) получаем из (10) систему линейны»
уравнений
2
2j ^/sAsm —
с=1
находим
Х,п = Хцо = ^212 — Л112
л111 '412 7ГГТ
1«Й1|
Хоц = Хи» = ^111 — ^211
**211 *ж212 , /,ч , i
1 (/, s, m = 1, 2),
V _ у __ ^222 ^122
• л»-х» |Щ-
V у ^121 ^221
■ " KIT*
87
где детерминанты
I л211 -^212 |
1«Й1-
^121 ^122
i422l л222
=i4i21i4222 — Ai2$A<
221
предполагаются отличными от нуля.
Уравнение (14) имеет вид
lA(YA) = £ (3,0)
и для нахождения элементов Y sc (m, s, с = 1, 2) левой (1, 1)-обратной
матрицы Л"-1 (1,1) для А относительно £(3,0) получаем из (15) систему
линейных уравнений
2
2УтшсАси"1 <*.*'-!. 2).
Отсюда, сохраняя предположение, что | 21^ I =£ о, I $1^ I ^= 0, находим
Y V -^212 — -^211 V V -^222 — ^221
Г 111 — Г 211 : 7Т7-; » Г 121 ~ * 221 — ■
|<\| |«Я
0,11
У У Лш — Ац2 у У Л12т — А-122
m"aia шг' —ш~'
Определим теперь (А,, р.)-обратную матрицу Л-1 для А, полагая А/ = А, = 1,
р/ = \i = 1. Имеем тогда, рассматривая Л-1 как правую (1, 1)-обратную
матрицу для Л,
Ы(ЛХ) = £(1, 1),
где
—Ms)
n/. ,v II1 0I1 0 llj—Mm)
E(M)-|1» i|o .I|, •
к iwiewicnivra -л матрииы А
ных уравнений
Для нахождения элементов Xcs матрицы Л иолу чаем из (10) систему линей-
С=1
откуда в предположении неравенства нулю детерминантов | 31^] |, | $tf£\ |
находим
Y ^212 у _ ^112 у ^222 у _ ^122
А А А А
У _ Л211 у HI Y _ ^221 у Ш
211 ~ I *#} | * **« - | И"} | ' A22l ~ | *g| | • Л222 ~ | g£2) | •
Рассматривая же Л-1 как левую (1,1)-обратную матрицу для А, имеем
l-\YA) = E(l,l)
и для нахождения элементов Ymsc (m, s, с = 1, 2) матрицы А 1 получаем из
(15) систему линейных уравнений
2
откуда находим
V ^212 „ ^12 у ^222 у ^122
Ш~К1Г 112= W ш~1*йг 122~ I «gj I •
211 111 221 l2l
^""[«ЙГТ' ^'йодТ' Гш==_Го"' Кг22 = Го
Как видим, соответственные элементы правой и левой упомянутых .выше
обратных матриц одинаковы.
§ 3. УРАВНЕНИЯМ (АХ)=В ИК*(УА)=В
Пусть дано матричное уравнение
^(ЛХ)=В, (17)
где Л, X, В — матрицы р9 q, r измерений и порядка п над полем
Р, а X, \i — неотрицательные целые, сумма которых не превосходит
чисел р, q. Из уравнения (17) вытекает, что г = р + q — т, где т
удовлетворяет неравенствам (7). Следовательно,
(7 = г — р + х. (18)
Отсюда, принимая во внимание неравенства (7), находим
г—p<q<r + p.
Из формулы (18), учитывая, что X + \i < q, получаем также
неравенство
г>р —Ji, (19)
являющееся необходимым условием существования решения
уравнения (17). Предполагая это условие выполненным, допустим, что
известна левая (V, ц/)-обратная матрица А-1 (А/, (*') для А
относительно Е (Я, ц,), удовлетворяющая равенству
k'*'(A-lA) = E(Kii).
Тогда
К^Ж(А~{А) X] = К»(Е (Я, fi) X).
Но по ассоциативному закону умножения матриц, принимая во
внимание уравнение (17), имеем
KY*\A-lA) X] = ™[А-1 *'%4Х)] = »*\А-ХВ).
89
С другой стороны, очевидно,
Следовательно,
X = Х'Ж(А~1В)
(20)
есть решение уравнения (17).
Замечание 2. У матриц А и X как разбиения с (\i кэлиевых
индексов), так и разбиения s (X скоттовых индексов) являются общими.
У матриц А~19 А и В общими являются как разбиения с' (ц/
кэлиевых индексов), так и разбиения s' (Я/ скоттовых индексов).
Вследствие ассоциативного закона умножения матриц разбиения сие'
не должны пересекаться ни между собой, ни с разбиениями s' и s.
Из всех возможных решений уравнения (17), представляемых
формулой (20), отметим те, которые соответствуют 1 + -тН па~
рам значений А/, ц/, удовлетворяющих условию
Я' + 2(1'= р.
(21)
Для каждой из таких пар может существовать только одна
матрица A~l (A/, р'), фигурирующая в формуле (20), и если эта
матрица существует, то при условии (19) рассматриваемое решение
будет единственным.
Пример 2. Решим уравнение (17), полагая
и Я = 1, |&= 1.
Имеем
р = % г = 3.
Следовательно, неравенство (19) выполняется. Кроме того, т = 3, а потому,
согласно формуле (18), q = 4.
Четырехмерную матрицу второго порядка X, удовлетворяющую
уравнению
{>\АХ) = В,
будем искать, выполняя условие (21), дающее две пары значений V, |i':
(0,1) и (2,0).
Левая (0,1)-обратная матрица Л""1 (0,1) для А относительно Е (1,1) имеет
-M*i)
вид
л—1
11^1«.И»1''.^.в1^-тят
Л22 ~~Л12
Л22 "~^11
— i42l ^11
->- (t.)
в предположении, что
|Л| =
^11 ^12
А%1 А22
Ф0.
90
По формуле (20) находим тогда
2
Х = °'1(А-{В) =
Zj Altl2cBcmtm2
c=l
(lv /2, mv m2 = 1,2).
Представляя сечения ориентации (1\12) матрицы для X столбцевыми
матрицами, получаем
1^111 + ^122^211
х =
лт
\Аи\
\лп\
\Ай[
-^211
Мгп
^211
Мги
:5Ш + ^112^211
1^112 + ^112^212
^121 + ^112^221
5122 + ^ 112^222
111
+ ^212^211
ИЛИ
8112 +^212^212
15121 + ^212^221
^122 +^212^222
^12
^12
^12
^12
^22
^22
^22
н22
112
+ А
|-1д
122°212
121 "г л\22"22\
^122 + ^122^222
Х =
А\
VW
"Vlll
*422в112 ~ Л12В212
Л22В121"~>412В221
Л22В122 """ Л12В222
5111 + ^222^211
\ + ^222^212
^121 + ^22^221
5122 + ^222^222
Л22В1и ~~ ^12^211
">- <*2)
У
ill)
I—>- (mt)
У
{тх)
22 112
■АЛЛ
12** 212
Л22б121 ~~ ^12б221
Л22В122 _ Л12б222
^UB2U _ Л21ВШ
Л1В212-Л21ВП2
ЛЛ21_Л21В121
Л11В222
-Л21В122
А11ВЦХ~ АЦВ111
Л11В212-Л21ВШ
ЛиВ2г1-Л21В121
АиВыъ~~Аг1В1ы
I
(mt)
-v a»)
kit)
Левая (2,0)-обратная матрица A l (2,0) для А относительно Е (1, 1) имеет
вид
||^»11^Ч^з=Ь2) =
Л21
1
^12
0 Л
->- (ia)
J
(<i)
ал. на
в предположении, что все элементы матрицы А отличны от нуля.
Формула (20) дает тогда другое решение данного уравнения:
X = 2-°(А~'В)= || Л& BSiSjm || (I, sv V in = 1,2),
т. е.
Х =
^lll^lll ^1115112
л112°121 л112°122
^211^111 ^211^112
^212^121 ^12^122
^121^211 ^121^212
A~]fi
'221
^122^222
^221^211 ^221^212
-^222^221 ^222^222
-V (St)
-<m),
Г
(Si)
91
или
х =
|Bir
Ми
0
0
Вш
Ми
Решение уравнения
В112
^11
0
0
В122
В211
Л21
0
0
В221
^22
В212
^21
0
0
В222
Л22
I
->• (st)
■> (m)
^(УЛ) = В (22)
с теми же матричными коэффициентами А, В, что и в уравнении
(17), находим аналогично по формуле
Y=W\BA-% (23)
где А~1—правая (А/, ц/)"°братная матрица Л-1 (А/, ц,') для Л
относительно £(Я, ц,).
Пример 3. Решим уравнение (22), полагая как и в предыдущем примере,
/41 4а II <'г', - 1. 2). ^ - || *ш§ || (/г /V /• = *•2>
И Х=1, |А == 1.
Неизвестную четырехмерную матрицу второго порядка У, удовлетворяющую
уравнению ]fl(YA) = В, будем искать, выполняя условие (21), дающее те же две
пары значений V, ИЛ как и в предыдущем примере.
Полагая в формуле (23) сперва V = 0, |i' = 1, находим с помощью правой
(О, 1)-обратной матрицы А~{ (О,1) для А относительно £(1,1):
Y = °'l(BA-l) =
А-1
l,fi ^стцпъ
(/r/2,mrm2=l,2).
Представляя сечения ориентации (1\12) матрицы для У столбцевыми
матрицами, получим
К =
1
\А\
1 ^111^22""" ^112^21
Г"ВиИц + В112^и
5иИ22""5П2^21
рш^1.+ виЛ
В*п.\ъ~~ВЫъАъ\
-52lHl2 + 52l24l
В211Л22""5212Л21
|-В211Л12 + 5212Л11
1 В121Л22""В122Л21
-Bl.A«+BuAl
ВШЛ22~"5122Л21
-5121Л12 + В122Л11
522И22~~5222Л21
-5221Л12 + В222Л11
В221Л22 " В222Л21
К522Л2 + В222Л11 1
-v (U)
г
Y
> (tnt)
Ui)
в предположении, что | А \ Ф 0.
Полагая затем в формуле (23) V = 2, ц' = 0, получаем с помощью правой
(2, 0)-обратной матрицы Л"4 (2,0) для Л относительно £(1,1) другое решение
данного уравнения:
Y = 2'° №~1) = || Bls%H А,^ || (/, sv st, m = 1.2),
92
т. е.
В1П
вш
вт
В212
0
0
0
0
0
0
0
0
вш
В1М
В221
222
А-
22
в предположении, что все элементы матрицы А отличны от нуля.
§ 4. ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА И СОБСТВЕННЫЕ МАТРИЦЫ
ДЛЯ ДАННОЙ МНОГОМЕРНОЙ МАТРИЦЫ
При исследовании структуры /7-мерной матрицы п-го порядка А
над Р большую роль играют матрицы п-го порядка X, для которых
^(АХ)=аХ (а€Р, ХфО). (24)
Такие матрицы называются (Я, ^-собственными матрицами
для А, а соответствующие им числа а — (А,,
^-характеристическими числами (или (%, ^-собственными значениями) матрицы А
(см. [6], сгр. 1324).
Обозначая через q число измерений матрицы X, видим из
соотношения (24), что р + Ч—т = ?» т- е- Р = г» гДе t = A,+ 2ji.
Таким образом, q есть произвольное целое, не меньшее, согласно
неравенствам (8) гл. III, чем X + ц,. Вводя в рассмотрение т-мер-
ную (Я, ^-единичную матрицу п-го порядка Е (Я, ц,), можем
переписать соотношение (24) в виде
^(ЛХ)=^(аЕ(Х,^)Х)
или
к* [(А — аЕ (X ji) X] = О. (25)
где О — нулевая ^-мерная матрица п-го порядка.
Матрица А —аЕ (Я, \i) называется (А,, ^-характеристической
матрицей для А.
Представим матрицы Л, £ (Я, \i), X, входящие в уравнение
(25), в виде
A = \\Alx\\,EM = \\Elsci X = \\Xcsm\\,
где каждый из индексов разбиений / = (1Ъ 129. . . , /ц), s = (%, s2, ...
. . . , Sa,), с = (clf c%, . . . , fy), т = (тх, /т^, . . . , т^) пробегает
значения 1, 2 п, причем А, + ц + v = q.
93
j—>- (m)
У
Г
Элементы матрицы X находим тогда, решая систему пк+Р
линейных однородных уравнений с лМ-и неизвестными Ycs = XCSm:
(с)
которую перепишем, используя обозначения § 2 настоящей главы,
в виде
/i= 1,2, ..., /Iх). (26)
Системе уравнений (26) соответствует клеточно-диагональная
матрица
*х.и <«> = <*"i («>• *S («)• • • ■ • «о? («)>• (27)
f(ft)
W1C1JM1 '4 '
ка я'
где клетки Щ,ц (а) (Л = 1,2,..., п ) — квадратные матрицы поряд-
>^ (а) = || Л^(Л)л — абСт| Ц (? = /(1>, /<2>,..., /<^>;
Т1 = с(1),с(2) ...,с(Л. (28)
Матрица (27) — (к, (^-ассоциированная с (Л,
^-характеристической матрицей А—a£(i, \i) для А и является клеточно-диагональ-
яой при 0 < X < р. При % = О, когда р = 2jx, она имеет обычный
вид
IIЛ,- «%,II« = <(1). '<2)> • • •. ^; л - с(1>. <<2) <(пД)).
При Я = р, когда р, = О матрица (27) принимает диагональный
вид
H(0-a^s(2)-a"--V)_ab
Вводя для детерминантов матриц (27) и (28) соответственно
обозначения
\>> Н\д (а) I и Д<>) Н <>) I.
получаем
Vw-flO*)- (29)
Произведение (29) может быть представлено (пк + 1)-мерным
детерминантом наивысшего рода, косигнатурным детерминанту (12):
А^(а) = |Лфа Л ±...Л ± |(^/(1>, /»..... ^>;
94
= C(1) J2) J^h
Л.г,,,...,^^^,^,....^),
где
V\ = AZsW\-a\% (h=l29...yn\
Можно также выразить Д^ (а) через гл^-мерный
гипердетерминант аналогично формуле (13) в виде
Ax,tl (а) = "^Р31"' ^ЧЧК • • • ^Ч* I
(5,. k..., Са =/П)> /<2) ^ ч,. л2 v =
Л.... с**»).
Для существования ненулевого решения системы уравнений
(26) необходимо и достаточно, чтобы
А^(а) = 0. (30)
Уравнение (30), являющееся характеристическим уравнением
матрицы (27), называется (А,, ^-характеристическим уравнением
матрицы А (см. [61, стр. 1325). Корни его, число которых с
учетом их кратностей равно пх+^9 если элементы матрицы А
принадлежат полю комплексных чисел, составляются согласно формуле
(29) из корней характеристических уравнений
Ai*i(o) = 0 (/1=1,2,.... л*") (31)
матриц ИОД = || V>n II « " /U)> **■ ■ • • • ^ П = ^ *". • - -. с{п\
(0, (^-ассоциированных с 2|д,-мерными матрицами я-го порядка
Л(Л) = ||Л/5(А),Ц (/г = 1,2, лгя), (32)
представляющими сечения ориентации (s) матрицы А. Корни
уравнения (30), будучи характеристическими числами матрицы (27),
являются также (Л, \i)-характеристическими числами матрицы Л,
а определяемые корнями уравнений (31) характеристические числа
матриц (28) будут вместе с тем и (0, (л)-характеристическими
числами матриц (32). Таким образом, (Я, (х)-характеристические числа
матрицы А составляются из rih совокупностей (0,
^-характеристических чисел матриц Л<А> (А = 1, 2, ... , пк), определяемых
формулами (32).
Каждому (Я, \i)-характеристическому числу а матрицы Л
соответствует ненулевая ^-мерная (Я, ^-собственная матрица X для
Л, у которой элементы Х^т с одними и теми же индексами cs
одинаковы, т. е. все сечения ориентации (т) в матрице X одинаковы
и, следовательно, X является v-развернутой матрицей VY для
у=\\у«\\-
.95
Из равенства
видим, что прет произвольном q число v также будет произвольным
неотрицательным целым. Матрица Y есть (X, ^-собственная
матрица для А с минимальным числом измерений X + \i (когда v = 0)
и называется фундаментальной (X, \i)-собственной матрицей для Л.
В частном случае, когда X = р и, следовательно, \i = 0, все
пр элементов матрицы А будут (/?, 0)-характеристическими числами
ее. Соответствующая элементу As{h) (1 <Л< пР) р-мерная
фундаментальная (/?, 0)-собственная матрица Y для А имеет все элементы,
равные нулю, кроме элемента Ys{h), равного произвольному,
отличному от нуля числу, и всякого иного элемента Ys(g) (1 < g < nP),
также произвольного, отличного от нуля числа, если Asig) = As{h).
Как иллюстрацию вышеизложенного приведем численный
пример.
Пример 4. Найдем все (Я,, \i) -характеристические числа и
соответствующие им (Я, ц) -собственные матрицы для кубической матрицы второго порядка.
Л = ||Л/8,||(/,5,с = 1,2) =
4—3
2 3
6 9
->- (с)
Г
(/)
Имеем две пары значений X, |i:(l,l) и (3,0), удовлетворяющих условию
К + 2ji = 3.
Пусть X = 1, |i = 1. Тогда (1.1)-характеристическая матрица А — аЕ (1,1)
для А имеет вид
,—МО
Следовательно,
3—а 4
4 —3 —а
3 —а 4
4 —3—а
2 —а 3
6 9 —а
. «&(«> =
Y
(/)
2—а 3
6 9 —а
Им(а) =
3 —а 4
4 —3 —а
2 —а 3
6 9 —а
Приравнивая нулю детерминант Д1л(а) матрицы #1Л (а), получаем
(1,1)-характеристическое уравнение матрицы А:
3 —а
4
2 —а
б
= 0.
96
Корни его ах = 5, «2 =—5, а3 = 0, а4=11 дают (1,1)-характеристические
числа матрицы А.
Элементы фундаментальной (1,1)-собственной матрицы Y = || У^ || (с, s =1,2)
для А соответствующей (1,1)-характеристическому числу а, находим из системы
уравнений
(3 - а) Уп + 4Ya = О, (2 - а) Ylt + ЗКИ = 0,
4Уи_(3+а)К21 = 0, 6У12 + (9-«)У22 = 0.
Получаем соответственно четырем вышеуказанным значениям а четыре
фундаментальные (1,1)-собственные матрицы Y для А:
2а 0
а 0
г
a Oil
— 2а 0
-4-
0 а
0 За
(с, s, m = 1, 2) для Л
где а — произвольное, отличное от нуля число.
Остальные (1,1)-собственные матрицы X = \\Xcsm\
составляются из полученных матриц Y как v-развернутые матрицы VF (v = 1, 2,...)#
Так, например, одноразвернутые матрицы iY для Y имеют вид
2а 0
а 0
-t<m)
2а 0
а 0
(s)
0 — 2-а
(с)
Mm)
а
а
— 2а
°-г*
->-(s)
Y
(f)
0
0
0 а
0 За
а 0
— 2а 0
(с)
Mm)
0 а
0 За
-*is)
(s)
У
(с)
Пусть теперь К = 3, |х = 0.
Тогда (3,0)-характеристическая матрица А — аЕ (3,0) для А имеет вид
3 — а 4 —а
4—а —3—а
2 —а 3
б —а 9 —а
М?г)
а I
-*Ы
(St)
щ0 (а) = {3 — а, 4 — а, 2 — а, 3 — а, 4 — а, — 3 — а, 6 — а, 9 — а}#
Далее, составляем (3,0)-характеристическое уравнение матрицы А, приравнивая
нулю детерминант A3f0(a) диагональной матрицы Щ^((х):
(3 — а)а(4 — а)2(2 — а)(—3—а)(6 —а) (9 — а) = 0.
Шесть различных корней этого уравнения
0^ = 3, а2 = 4, а3 = 2, а4 = — 3, а5 = 6, ав =9
определяют (3,0)-характеристические числа матрицы А
Элементы фундаментальной (3,0)-собственной матрицы Y = \\ YStSiH || (sJf s2,
s3= 1, 2) для Л, соответствующей (3,0)-характеристическому числу а, находим
7-596
97
из системы уравнений
(i4vt"" a) УWs " ° (* V 5з - *• 2>-
Получаем соответственно шести найденным значениям а шесть
фундаментальных (3,0)-собственных матриц для А.
а О
О О
О О
О О
О О
О О
О Ъ
-*- (s«)
о о
а О
О О
•Нн)
О а
Ь О
-*(S8)
о о
о о
г
(Si)
-*■ (s.)
(«i)
о о
О а
М*г)
О О
О О
(S.)
>(s8)
т *-lsei
г
(st)
-WSl)
о о
а О
-М4)
О О
О О
-*(S2)
О О
О а
Г
| (Si)
->-<■■)
где аУЬ — произвольные, отличные от нуля числа.
Остальные (3,0)-собственные матрицы X = || Xsm || (s, m a 1, 2) для Л
найдем, составляя v-развернутые матрицы VY (v = 1,2,...) для К.
ГЛАВА V
ХАРАКТЕРИСТИЧЕСКИЙ И МИНИМАЛЬНЫЙ ПОЛИНОМЫ
МНОГОМЕРНОЙ МАТРИЦЫ
В этой и последующих главах, в целях представления (X,
[^-свернутых произведений и степеней р-мерных матриц в виде матриц
того же числа измерений, ограничимся при рассмотрении такого
рода операций только теми парами неотрицательных целых
значений X, ji, которые удовлетворяют условию X + 2 ц = р. Это
ограничение дает возможность построения полиномов от
многомерной матрицы и установления важных в теории матриц понятий
характеристического и минимального полиномов /7-мерной
матрицы. Исследованию свойств этих полиномов предпошлем
необходимые для дальнейшего основные сведения о полиномах от
многомерной матрицы.
§ 1. ПОЛИНОМЫ ОТ МНОГОМЕРНОЙ МАТРИЦЫ
Рассмотрим р-мерную матрицу и-го порядка над полем Р:
A = \\Alsc\l (1)
где каждый из индексов разбиений
пробегает значения 1, 2, . . . , п.
Пусть
f(a) = а0аи + а^1 + ... + аи (2)
— некоторый полином от а над Р.
Заменяя в полиноме (2) скаляр а матрицей Л, а степени его —
соответственными (X, ц,)-свернутыми степенями матрицы Л,
получим (X, \ь)'Свернутый полином от А:
**Ч(А) - №(Аи) + а^(Аи~1) + ...+аиЕ (X, ц). (3)
Выражение (3) называется также (X, рУзначением полинора f (а) при
а = Л и является, очевидно, р-мерной матрицей rt-го порядка над Р.
7*
99
Возьмем другой полином от а над Р:
9(a) = 60att + &latt-1 + ...+&w (4)
и составим соответствующий (К ц)-свернутый полином от Л:
к'\ (Л) = b№ (Аи) + fi» (Л-1) +...+&„£ (Я, ц). (5)
Обозначая через F(a) и Ф(а) соответственно сумму и
произведение полиномов (2) и (4), имеем
F (а) = (а0 + 60) а" + (ах + 6J а"-' + ... + (ц, + &■),
Ф (а) = а^а* + (а0Ьг + а^) а2""1 + ... + аиЬи.
Далее находим
*-»F (А) = (а0 + bf» (Аи) + (а, + ttf* (A-«)+.. .+(<**+ W Я (X, ц),
Л'*Ф(Л) = ^(Л2*) + («А + аА^М8"-1) + ... + оАЕ (Я, ц).
Составляя затем сумму и (Я, (х)-свернутое произведение матриц
^3) и (5), получаем
^(Л)=я^(Л) + ^ф(Л), (6)
^Ф (А) = *'д Iх* f (Л)^Ф (Л)]. (7)
Равенства (6) и (7) устанавливают, что (А,, (л)-значение суммы
полиномов от а при a = Л равно сумме (Я,ц,)-значений слагаемых,
а (К, ^-значение (Я, ц,)-свернутого произведения полиномов от a
при a = Л равно (X, \i)-свернутому произведению (Я, (х)-значений
сомножителей.
В качестве примера рассмотрим полиномиальное тождество
а2—1 =(а—1)(а+1).
Беря (А,, ^-значения левой и правой части при a = Л, получаем
матричное тождество
х"(Л2)-£(Я, |i) = к»[(А-Е (К v)) (A + E(К v))].
Аналогично, из а3 + 1 = (а + 1) (а2 — а + 1) получаем
к» (Л3) + Е (К V) = Xji [(Л + £ (Я, |i)) (^ (Л2) - Л + Е (К v))l
Вообще, из каждого соотношения между полиномами от а
таким способом получается некоторое матричное тождество.
В частности, из тождества / (а) ф (а) = ф (а) / (а) имеем
х.ц f,»f (Л)х.цф {Д)] = х.ц jx.nv (Д)х.|^ (А)]
Следовательно, (X, ц,)-свернуты£ полиномы от одной и той же
матрицы Л перестановочны друг с другом.
100
Определим теперь матрицу, (X, ^-ассоциированную с р-мерной
матрицей, представляющей выражение (3).
Пусть 3fo,m—квадратная матрица порядка aza,+j\ (К
^-ассоциированная с матрицей А. При \i Ф 0 ЭД^д является клеточно-диаго-
нальной матрицей, состоящей из пк квадратных клеток и^-го
порядка 9$!t (А = 1,2,..., пк); при \i = О матрица 21а,,ц —
диагональная порядка пр. Согласно правилу составления {X, ц,)-свернутого
произведения матриц, квадратная матрица 2$tJl при любом
положительном целом и будет (Я, (^-ассоциированной с р-мерной
матрицей и-го порядка, представляющей (Я, (х)-свернутую м-ю степень
^\Аи) матрицы А. Следовательно, полином от матрицы Sfo.i*
fWb.v) = aj&tn + (h^ti? + • • • + at№k,ix будет квадратной матрицей,
{X, (г)-ассоциированной с р-мерной матрицей ^/(Д). Доказана, таким
образом, следующая теорема.
Теорема У. Если 4&%у11—квадратная матрица, (X,
^-ассоциированная с матрицей А, то полином f (%х,ц) от матрицы 9ta,tJLl
является квадратной матрицей, (X, [^-ассоциированной с р-мерной
матрицей, представляющей (X, \1)-свернутый полином %**f (А) от
матрицы А.
Пример 1. Пусть / (а) = а2 + 2а — 3,
2 111
— 1 3 2—3
4 II г—Мс)
X = 1, |i = 1.
Тогда
ы.
2\ —
) —
3 51
1—5 в|
(1.1) =
9 ■
-811
— 4 171
11 0|1 О"
[0 1
|о 1
:<«>
г
(S)
.—Мс>
I 9
Г
(/)
(с)
Следовательно,
С другой стороны,
Ы/ (А) = Ь,(Л2) + 2Л — ЬЕ (1,1):
4 718 0
—7 И 0 8IГ
(s)
-(с)
О) —
41
I 2 Г
— 1 3
• «-П-П
«ни а- к -л
101
Далее, имеем
■1,4!
Следовательно,
'<*!.!>-*1.1+2*1.1-3«1.
3 511 II 9 —8
— 5 8||' 11—4 17
вм-{1.1.1,1}.
4 7
il-7 11
8 О
О 8
I-
Как видим, / (Щ л) совпадаете матрицей, (1,1 ^ассоциированной с
матрицей ulf(A).
§ 2. ХАРАКТЕРИСТИЧЕСКИЙ ПОЛИНОМ МНОГОМЕРНОЙ МАТРИЦЫ
Полином ф^ц (а) степени пМ-и, корни которого являются (Я, ц,)-
характеристическими числами р-мерной матрицы я-го порядка Л,
представленной в виде (1), называется (X, ^-характеристическим
полиномом матрицы А над Р.
Имеем, следовательно,
ъ# w = (- 1)""+Ч.м («).
где Ая,ц(а) — детерминант матрицы Ях(р(а)' (А,, (^-ассоциированной с
(А, ^-характеристической матрицей А — аЕ (Я,, \i) для А. Таким
образом,
Фя.д. W==а — о{а + ...
... + (_ lf^Sn^a + (- lr^vf*.
(8)
где Sg (g = 1,2.... f nx+|i) есть сумма главных миноров* g-ro
порядка детерминанта Д*,ц (А,, ц,)-а хоциированной с Л матрицы 91*,,ц.
Согласно формуле (29) гл. IV, Да,,ц(а) есть произведение п%
детерминантов Дол* (а) матриц Яо^ (а), (0, (г)-ассоциированных с 2ji-
мерными матрицами л-го порядка Aih) (h = 1,2,... ,пя),
представляющими сечения ориентации (s) матрицы Л.
Обозначая через <pj*£(a) (0, ^-характеристический полином
матрицы Aih\ корни которого являются ее (0,
^-характеристическими числами, имеем
,»дл<м
Следовательно,
Ф^(«)=(-1ГА^(«).
чй(«)-<^"
■SfV"-*
* Т. е. миноров, получаемых вычеркиванием в данном детерминанте строк
и столбцов с одинаковыми номерами. Главный минор наивысшего порядка,
очевидно, совпадает с самим детерминантом.
102
... + ,_ i^-'S^a + (- l)nli S$ (h = 1,2,..., nx) (9)
где S{gh) (g== 1,2,... .л*1) есть сумма главных миноров g-ro
порядка детерминанта Ло% (0, ^-ассоциированной с A{h) матрицы Ч$%.
Таким образом, (к, ц)-характеристический полином (8> матрицы
А разлагается в произведение пк (О, ц)-характеристических
полиномов (9) матриц А{Н) (Л «1,2, ...,/!*):
Ф^(«) = П <i(«). (Ю)
Так как «р^ (а) является также характеристическим
полиномом квадратной матрицы З^.и* то в силу теоремы Гамильтона—Кэли
Но тогда и
*.>ЧрЛ>11(А = 0.
поскольку q^ (ЯХв|1), согласно теореме 1 настоящей главы
представляется матрицей, (А,, ^-ассоциированной с матрицей Х,,*ФХ>Д (Л),
и, следовательно, может быть нулевой лишь одновременно с
последней.
Точно так же убеждаемся, что
°'\Z(Alhh> = ° (Л -1.2, ....А
А тогда, вследствие равенства (10), имеем
х,Ч.цИ(/0)в0 (Л = 1.2....,Л
Нами доказана следующая теорема.
Теорема 2. (Общая теорема Гамильтона—Кэли.) Всякая
матрица А = || Aisc || любого числа измерений p = X + 2\i и все ее
сечения ориентации (s) являются корнями (X, ^-характеристического
полинома матрицы А.
Замечание. Теорема 2 включает в себя классический результат
Гамильтона — Кэли, если X = 0 й ji = 1; если же X = 2 и [л = 0,
то она указывает, что всякая квадратная матрица А = ЦЛ^Н (*./=
= 1,2,... f л) и каждый ее элемент Ац являются корнями (2,0)-ха-
рактеристического полинома матрицы Л, т. е.
2'°Ф2,о(Л) = ° и Ф2,о(Л/)=° (А/— 1.2 я).
Пример 2. Пусть
л =
2 1
2 3
— 3 3
— 2 4
г-мо
I, |А-1.
103
Тогда
|2 —а 1
Д. (а) = л
и1К ' 2 3—а
-3 —а 3 I
— 2 4 —а
«--а; и-1- t
Составляем последовательно
Si = 2 + 3—3+ 4 = 6,
S2 =
2 1
2 3
+
2 0 3 О
+ +
^ О 4Г 0 —3
О —3
= 4 — 6 + 8 — 9+12 — 6 = 3,
О 4 Г
2 1
2 3
О О
0
0
3
+
2 1 0
2 3 0
0 0 4
+
2 0 0
0—3 3
0—2 4
+
3
о —
о —
= — 12 + 16 — 12 — 18 = — 26,
12 1 0 01
2 3 0 0
О 0 —3 3
О 0 —2 4
S4-
= -24.
Следовательно,
Имеем
Фы (а) = а* —6а8 + За2 + 26а — 24,
ыфы (А) = 1.1(Л*) -6М(Л8) + 3М?У) + 26Л -24£
Ы(Л2) =
6 5
10 11
22 21
42 43
86 85
170 171
3 3
— 2 10
tf<s>
— 15 21
— 14 34
3 39
— 26 94
-МО
I
Г
</)
(О
7—МО
Y
(/)
-МО
£(Ы) =
1 0
О !
1 О
О 1
(S)
Г".
Y
а потому
Li
ФЫИ)-
86 85
170 171
3 39
— 26 94|j
ffrs>
-МО
104
^-6
1122
21
II42 43
+ 26
см см
*15 2l|
— 14 341|
1
3
з з]
— 2 4
-(г)
+ 3
(О
j—МО
24
6 5
10 11
1 О
О 1
3 3
— 2 10
is)
-(с)
1 О
О 1
о о
о о
о о
о о
^(s>
Далее, имеем
2 1
2 3
А(\)
<*"Ч1.о ■!
(Л<»)8 =
(с)
О)
Л<2> =
-3 3
(Л<1>)4 =
22 21
42 43
86 85
170 171
(Л<2>)2 =
(Л<2>)3 =
(Л<2>)4 =
— 2 4
U3 3
— 2 10
15 21
14 341|9
3 39
-26 94
Поэтому
ь,Фы М0)) = М[(Л(1))4] — 6 М[(Л(1))8] + 3 и[(Л(1>)2] + 26Л<*> - 24Е (0,1) =
86 8511 1122 2111 11 6 511 л ||2 111 л II1 Oil
170 .7. Н 42 48 +81ю 11 +* 2 3 И* О 1 "
О О
о о
= 0,
•"ф1Л (Лр>) = '•'[(Л2*)*] -б1'11(Л<2>)8] + 3 '• W] + 26Л<2> -24£ (0,1),
=
3
26
При X = 3, \i = 0
дз.о (а) =
2-
0
0
0
0
0
0
0
391
94 J
а
— 6 1
0
1—а
0
* 0
0
0
0
0
— 15 21
— 14 34
-241
1+3
i Ы
0 0
0 0
— 3 —а 0
0 3 —а
0 0
0 0
0 0
0
0
1 3 3
|—2 10
) 01
) 0
0
0
0
0
2 —
0
0
0
1 = 0
а
3
+ 2б|
0
0
0
0
0
— а
0
0
— 3
— 2
0
0
0
0
0
0
-2 —
0
31
4|
а
—
0
0
' 0
0
0
0
0
4 —а
103
Фз.о <а> = «8 — 10а7 + 22ав + 80а» — 395а* + 290а8 + 948а* — 1800а + 864,
3,°Фз,о М) = 3' V) - Ю 3'°(Л7) + 22 3'°(Лв) + 80 3'°(Л6) - 395 3'°(Л4) +
+ 290 3'°(Л8) + 948 3'°(Л2) — 1800Л + 864Е (3,0) =
— 10
256 1
256 6561
128 I
128 2187
6561 6561
256 65536
•tist)
;—Mss)
Y
— 2187 2187
— 128 —163840
■fr<s«)
-^(s.)
Y
(Si)
+
+ 22
64 1
64 729
729 729
64 4096
■fr<s*>
-Ms»)
Г"'+80
-395
16 1
16 81
81 81
Y
(Si)
32 1
32 243
— 243 243
— 32 1024
+(s*)
->-(s.)
j—^ks»j
Y
(Si)
16 256
4s.)
+ 290
(Sl)
8 1
8 27
— 27 27
— 8 64
Tf(s8)
pM«.)
Y
(Si)
+
+ 948
4 1
4 9
9 9
f£<s*>
9 16
+ 864
1 1
1 1
1 1
1 1
p-Ms.)
Y
(Sl)
(Sl)
r~Ms,) _
Y
(Si)
2 li-,3 3l|(^(s,)
-18001| | -
2 3—2 4 Y
1 l(si)
о on о o|(pLHSe)^o
0 0 0 0 Y ""
" '(si)
Кроме того,
Фз,о (2) = 28 —10 -27 + 22 -2е + 80-2б — 395 24 + 290-2s +
+ 948-22 — 1800 -2 + 864 = 0,
ф3 0 (1) = 1 — 10 + 22 + 80 — 395 + 290 + 948 —1800 + 864 = 0,
Фз 0 (— 3) = 38 + 10 -37 + 22 -3e — 80 -36 — 395 34 —
— 290-38 + 948-32 + 1800-3 + 864 = 0,
ф3 0 (3) = 38 — 10 37 + 22 -3e + 80 -36 — 395 34 +
+ 290 33 + 948-32 — 1800.3 + 864 = 0,
Фз.о (—2) =- 2s + 10-27 + 22-26 — 80-26 — 395-24 —
—290-28 + 948-22 + 1800-2 + 864 = 0,
ф3>0 (4) = 48 — KM7 + 22.4е + 80-46 —395-44 +
+ 290-48 + 948-42 — 1800-4 + 864 = 0.
toe
Если ага2, ,..,а^ — все характеристические числа (с учетом
кратностей) квадратной матрицы лАгИа-го порядка 21^, (X,
^-ассоциированной с р-мерной матрицей /г-го порядка Л, а /(а)—
некоторый полином от а, то, как известно (см. [1], стр. 94), /(аД
/(а2),... ,/(a^+Jl) —все характеристические числа матрицы f(\tV)-
Но характеристические числа матрицы %%,» являются также (А,,ц,)-
характеристическими числами матрицы Л, а / (ЭДа,,д) есть (Я,
^-ассоциированная матрица с х,(*/ (Л). Следовательно, справедлива теорема.
Теорема 3. Если ара2,..., а^+ц —все (X, ^-характеристические
числа (с учетом кратностей) р-мерной матрицы п-го порядка Л, а
f (а) — некоторый полином от а, то /(о^), /(а2),... ,/(an^+|i) — все
(Xy\iyхарактеристические числа р-мерной матрицы п-го порядка^
представляющей (%,\1)-свёрнутый полином Х,|1/(Л) от матрицы А.
В частности, если матрица А имеет (А,, ^-характеристические
числа ara2,... ,адА,+и» то (А., (л)-свернутая и-я степень Я,М,(Л")
матрицы Л имеет (X, ^-характеристические числа о^,а£,... ,а^+ц,
(а = 0,1.2,...).
Общая теорема Гамильтона — Кэли позволяет представить (X,\i)-
свернутую н-ю степень Я,М,(Л") матрицы Л где w^/i*"1"**, в виде
(К, ^-свернутого полинома от Л степени меньшей, чем я*"**. Пусть
XeV^ = «J,-iX,V^l) + e^X,^"i)+ .. + а1Л + а0£(А,(г), (11)
где N = n%+».
Если а — одно из (А,, [^-характеристических чисел a^a^ ... ,aN
матрицы Л, а К — соответственная фундаментальная (Я,
^-собственная матрица для Л, то
^(ЛГ)==ссК (12)
Используя равенство (12). можем написать
*'%4V) = а ь|\Л*-|У) = «2 X,V"*P).
откуда, по индукции,
^(Л*К) = aV (13)
для любого положительного целого k.
Далее, из неравенства (11) получаем
^(AUY) = йы_х ^(AN~lY) + aN„2%»(AN~*Y) + ..
... + a1^(AY) + a^Y.
Отсюда, на основании равенства (13), находим
«ЛГ-1^"1 + аЫ-2*"~2 + - + *1<* + % = <*"• <14>
107
Полагая в (14) а последовательно равным ava2,... ,aN, будем
иметь систему N линейных уравнений относительно а0,а{>... >Д#__Г
Из этой системы уравнений, предполагая все (А,,
^-характеристические числа матрицы А различными между собой, находим
где
У =
1 а, а.
1 а2 ай
„N—1
N-1
а2
1 а„ а„ ... а
есть детерминант Вандермонда порядка #, построенный на числах
аьа2, . . . , ад?, а У; получается из У заменой (/ + 1)-го столбца
на столбец
i%
составленный из (Я, ^-характеристических чисел матрицы ^ЦА1*).
С помощью выражений (15) равенства (11) можем представить в
виде
где
Аналогичное равенство, как легко убедиться, имеет место для
всякого (Я, (г)-свернутого полинома *»vf (Д) степени и > iV от
матрицы Л:
7И) = £
К/ Х.|*/*/<
(А
/-о
где Vlf) получается из V заменой (/ + 1)-го столбца на столбец
//(Oi)\
/К)
vM
108
составленный из (к, ^-характеристических чисел матрицы ^/(Л)*.
Пример 3. Пусть
T*(s)
Л =
2 11—3 3
2 3—2 4
-(с)
У
СО
Я= 1, |i = 1,
/(а) = а& — 4а4 + 2а + 1.
Найдем представление (1,1)-свернутого полинома
Ы/(Л) = Ь1 (Л5) — 41Л (Л4) + 2Л + £(1,1)
(1,1)-свернутым полиномом от матрицы А степени ниже четвертой.
Определяем прежде всего из (1,1)-характеристического уравнения матрицы А
|2-а 1 I
I 2 3—а|
ее (1,1)-характеристические числа
— 3 —а 3
— 2 4 —а
= 0,
и вычисляем
«1 =4, а2 = 1, а3 = 3, а4 = — 2
/(а1) = 9, /(а2) = 0, /(а3) = -74, /(а4) = -99.
Затем находим
1 4 16 64|
1111
1 3 9 27
1 _2 4 —8
V =
= -540,
V0 =
Vx =
V* =
9 4 16 64
0 111
-74 3 9 27
-99 —2 4 —8
1 9 16 64
1 Oil
1 —74 9 27
1 _99 4 —8
1 4 9 64
110 1
1 3 — 74 27
1 _2 —99 —8
= — 26460,
= 14040,
= 17280,
* Частный случай, когда p—2, Я=0, |i=l, рассматривался Астином [10].
109
1
1
1
1 -
4 16
1 1
3 9
-2 4
9
0
— 74
— 99
^»e . о л ,J = —48ба
Формула (12), имеющая в этом случае вид
1ЛЖ) = 49Я(1,1) — 26Л — 32м (А2) + 9м (Л3).
Непосредственной проверкой убеждаемся, что левая и правая
части последнего равенства представляют одну и ту же
кубическую матрицу второго порядка:
дает
3 31 — 104 15
6 6 —10 —6
гие>-
(0
§ 3. МИНИМАЛЬНЫЙ ПОЛИНОМ МНОГОМЕРНОЙ МАТРИЦЫ
Пусть fK[i(a) — аннулирующиц полином матрицы 91Лц, (X,
^-ассоциированный с р-мерной матрицей n-го порядка Д представленной в
виде (1), т. е. }к[1 (Ч&К11) = О. Тогда, в силу теоремы 1, имеем
Xi]lfK[i(A)=^0. Поэтому 4|Ц(а) будем называть также (X,
^-аннулирующим полиномом матрицы А. В частности, минимальный полином
^% \к (°0 матрицы %^ т. е. ее аннулирующий полином наименьшей
степени со старшим коэффициентом, равным единице, является
(X. ^-минимальным полиномом матрицы Д будучи при этом
единственным (X, ц)-аннулирующим полиномом наименьшей степени при
выбранных разбиениях /, s, с индексов матрицы А: Согласно
общей теореме Гамильтона — Кэли, (X, |х)-характеристический
полином ф^ (а) матрицы А будет (X, ^-аннулирующим полиномом этой
матрицы. Однако, в общем случае, он не является (X,
^-минимальным. Действительно, ф^^(«) есть также характеристический
полином матрицы %^ и, как известно (см. [1], стр. 100),
Ч\.» =
ЯЧ.ц(«)
(16)
где Dnx+n_i(a)— общий наибольший делитель со старшим
коэффициентом 1 всех миноров порядка rih+v— 1 характеристической
матрицы %иАъ) Для %¥iVL.
Обозначим через D§JL_x(a) общий наибольший делитель со
старшим коэффициентом 1 всех миноров порядка гР—1
характеристической матрицы Я^(а) для 31^ (А = 1, 2, ... ,пк). Тогда,
очевидно
но, £)„&+»_,(<*) будет общим наибольшим делителем произведений
где Фо*д(а) — характеристический полином матрицы Я^,
связанный аналогично формуле (16) с минимальным полиномом ^^(а)
этой матрицы соотношением
ti&W- дУ ^ (А -1.2 я»). (17)
Из (17) имеем
C(«) = D^-i(«)C(a) (*-1.2,..., А
Следовательно,
я*
*W-i («) = © («) П D$-, (a). (18)
где 0(a) — общий наибольший делитель произведений
<>) • • • <^ («)<!">> • • • *M<°> (Л = 1. 2 Л
Подставляя выражение (18) для Dnx+ji_, (a) в формулу (16) и
принимая во внимание формулы (10) и (17), получаем
П О)
Как известно, общее наименьшее кратное двух полиномов от
одной переменной равно произведению этих полиномов, деленному
на их общий наибольший делитель. Обобщая это равенство на
случай нескольких полиномов, легко убедиться, что правая часть
равенства (19) будет общим наименьшим кратным ОД^а), i|#^(a)> ...
..., i|?J*|l) (а)] минимальных полиномов всех матриц И^ (А = 1, 2, ...
..., лх). Имеем, следовательно,
Wa> = 1С (<*>> *£>>. • • • > <С («И- (20)
Принимая во внимание, что фх (а) является также (Л,, ja)-mh-
нимальным полиномом матрицы Л, а я|>(Л)(а) — (0, (г)-минимальным
полиномом 2|х-мерной матрицы A(h\ представляющей А-е сечение
ориентации (s) матрицы A (ft *= 1, 2, ..., л*), заключаем из
равенства (20), что имеет место следующая теорема.
Ш
Теорема 4. (К ^-минимальный полином р-мерной матрицы Л,
представленной в виде (1), равен общему наименьшему кратному
(0; ^-минимальных полиномов всех сечений ориентации (s) матрицы А.
Как иллюстрацию изложенного выше рассмотрим следующий
пример
Пример 4. Пусть
Л =
3 —1110
2 0 0 1
Ms)
-(с)
Y
(/)
X = 1, и = 1.
Тогда
*м («) = {
3 — а —1
2 — а
. «ffi(«) =
1—а 0
0 1—а
3—а —1
2 -all'
1—а 0
0 I—а
Отсюда получаем (1,1)-характеристический полином
Ф1Л(а) = (а-2)(а-1>»
и (1,1)-характеристические числа
ах = 2, а2 = 1» аз=1, а4 = 1
матрицы Л.
Находим затем общий наибольший делитель D8 (a) всех миноров третьего
порядка матрицы 2^ j (a):
A,(a) = (a-1)2.
По формуле (16) получаем тогда (1,1)-минимальный полином фы (а)
матрицы Л:
^ л (а) = а2 — За + 2,
вследствие чего
и% (Л) = *'2 (Л2)-ЗЛ + 2£ (1,1) =
7 —3
6 —2
п.
1 0
0 1
Ms)
-(О
— 3
+ 2
10110
0 10 1
Y
Ms)
3 -1
2 0
1 0
0 1
■*<*)
-(с)
(/)
0 0
0 0
Ms)
0 0 || ,_>.(г)
о о
+
= 0.
(/)
Для минимальных полиномов ty{0\\ (a) и ф^ (а) матриц $1^ , ^2), находим
выражения
i${(a) = a2--3a + 2, ф£> (a) = a - 1.
Их общее наименьшее кратное совпадает с ф1(] (а).
Из соотношения (16) между (К (х)-характеристическим и (К
^-минимальным полиномами матрицы А следует, что степень по-
112
линома \t[Ji(Q) не превосходит степени полинома 9Xjl(a). Так
как корнями полинома ^^(а) служат все различные между собой
корни полинома Фх§|1(<*). то в случае, когда полином фЛц(а) имеет
только простые корни, последними исчерпывается вся совокупность
корней полинома ^^(а), иначе говоря, (Л,, ^-характеристический
полином матрицы А является также ее (Л,, (х)-минимальным
полиномом, если все (ку (л)-характеристические числа матрицы А
различны между собой.
8-695
ГЛАВА VI
ПОЛИНОМИАЛЬНЫЕ МНОГОМЕРНЫЕ МАТРИЦЫ
§ 1. ОСНОВНЫЕ ОПЕРАЦИИ НАД МАТРИЧНЫМИ ПОЛИНОМАМИ
Возьмем полиномиальную /7-мерную матрицу /1-го порядка:
А (а) = || Ahit h (a) || (iv ty ..., ip = 1, 2t ..., л), (1)
элементы которой — полиномы от а над полем Р:
litf'tpx ' *i»i«.»*p м*"»р ■ itis...ip
Матрицу (1) можно представить в ввде полинома с матричными
коэффициентами, расположенного по степеням а:
Л (а) = Да" + Да"-' + ... + Д, (2)
где
Л = 1И!1..^11 <'i.'*-...'p-i.2.....*)
при ft = 0, 1, ..., и,
* Полином (2), коэффициенты которого являются /7-мерными
матрицами /г-го порядка, будем называть р-матричным полиномом
степени и (если Л0 Ф О) и порядка п. Если матрица А0 — (Я, ц,)-
неособенная, то полином (2) называется (Я, ^регулярным.
Пусть даны два /7-матричных полинома одного и того же
порядка Л (а) и В (а). Обозначим через и наибольшую из степеней
этих полиномов и запишем их в виде
Л (а) = Да» + Да"-' + ...+Att9
В(а)=В0а»+В1а»-*+.. .+Ви.
Тогда
A(a)±B(a)=(A0±B0)a» + (A1±B1)a«--i + ...+(Au±Bu)i
т. е. сумма или разность двух /7-матричных полиномов одного и
того же порядка может быть представлена в виде /7-матричного
полинома, степень которого не превосходит наибольшей из степеней
данных полиномов.
Пусть теперь даны два р-матричных полинома Л (а) и В (а)
степеней и и v одного и того же порядка п:
114
Л(а) = Л0а"+Аа"-1 + .. +Аи (Л0^0) (3)
В (а) - В0а" + Вга?-\ + ...+В. (В0Ф О). (4)
Тогда (Я, |л)-свернутое произведение матрицы А (а) = || Atsc (а) || на
В (а) = )| Bcsm (а) ||, где 'индексы разбиений
m = (/Пх, /я2, ...»/Пц)
пробегают значения (1, 2,..., л), можно представить в виде
х*(А(а)В(а)) = *Wo)a"+" + l^CAA) + х*(АЛ)]а"^1 + . ..
...+XJi(AA).
Поскольку всякая р-мерная матрица и (Я, (х)-ассоциированная
с ней квадратная матрица одновременно равны или не равны нулю,
(Я, ^-свернутое произведение Л^ДД) может равняться нулю при
А0 Ф О, В0 Ф О. Однако, если хотя бы одна из матриц А0, В0—
(Я, \i)-неособенная, то из А0 ф О и В0 ф О следует, что ^(А0В0)ф
Ф О. Таким образом, (Я, ц)-свернутое произведение двух р-матрич-
ных полиномов равно р-матричному полиному, степень которого
меньше или равна сумме степеней сомножителей. Если хотя бы
один из сомножителей — (Я, ^-регулярный полином, то степень
(Я, (л)-свернутого произведения в этом случае всегда равна сумме
степеней сомножителей.
Заметим, что (Я, (х)-свернутое произведение р-матричных
полиномов в общем случае не обладает коммутативным свойством.
| Обращаясь к делению полинома (3) на полином (4), будем
предполагать последний (Я, ^-регулярным.
р-матричные полиномы Q (а) и R (а) называем соответственно
правым (Я, \х)'Свернутым частным и правым (Я, \1)-свернутым
остатком при (Я, (л)-делении А (а) на В («), если
A(a) = K»(Q(a)B(a)) + R(a) (5)
и степень R (а) меньше степени В (а) или R (а) г О. Аналогично,
р-матричные полиномы Q (а) и R (а) называем соответственно
левым (Я, \1)-свернутым частным и левым (Я, \\)-свернутым остатком
при (Я, ^-делении А (а) на В (а), если
A(a) = k*(B(*)Q(a)) + R(a) (6)
и степень R (а) меньше степени В (а) или R (а) е=* О.
Из равенств (5) и (6) видим, что полиномы Q (а) и R (а) в общем
/Ч ХЧ
случае не совпадают с полиномами Q (а) и R (а).
[Покажем, что как правое, так и левое (Я, (л)-деление р-матрич-
ных полиномов одного и того же порядка всегда выполнимо и
однозначно, если делитель есть (Я, (х)-регулярный полином.
8* 115
Рассмотрим правое (X, ^-деление Л (а) на 5(a). Если u<v, то
можно положить Q(a)=0 и R(a)=A(a). Если же ы>о, то,
применяя обычную схему деления полиномов, делим старший член
делимого Да" на старший член делителя В0аи. Получаем старший член
правого (X, (л)-свернутого частного*"ll(A0B~l)au~*vy где В~{ есть (X, Ц,)-
обратная матрица для (X, ц.)-неособенной матрицы В0. Составляя
(X, ^-свернутое произведение этого члена на делитель В (а) и
вычитая полученный результат из А (а), находим правый (X,
^-свернутый остаток Ail)(a). Имеем, таким образом,
А (а) = ^V'W) *U-VB (a)] + Л(1) (a). (7)
Представляем остаток Л(1)(а) в виде р-матричного полинома
Л<>) = Л»>а"(,, + ...(Л<'>*0),
степень которого и<!> меньше, чем и. Если а(,) > о, то, повторяя
этот процесс, получаем
Л(,) (а) = *• Y* К'Ч"1) а"0>~°5 («М + ^(2> («)•)
Л<>)=^«"(2, + ...(42)*0), }
где а(2) <и(1), и т. д.
Так как степени полиномов А (а), Л(1) (а), Л(2) (а),... убывают,
то в конце концов придем к правому (X ^-свернутому остатку
R (а), етепень которого меньше, чем и. Тогда справедливо
равенство (5), где R(a) принимает указанное выше значение, а Q(a)
определяется формулой
Q (a) - ПАА") а""0 + ХМЧ~') «""^ + • • •.
как это следует из равенств (7), (8).
Чтобы убедиться в однозначности правого (Х9 ц,)-деления,
допустим, что кроме равенства (5) справедливо также равенство
A (a) = ^ (Q* (а) В (а)) + R* (а), (9)
причем степени р-матричных полиномов R (а) и R* (а) меньше,
чем v.
Вычитая почленно (5) из (9), находим
XJI[(Q («) - Q* (а)) В (а)] = R* (a) - R (а). (10)
Отсюда следует, что
Q(a)-Q*(a)sO,
так как в противном случае ввиду (Я, ^-регулярности полинома
В (а) степень левой части равенства (10) равнялась бы сумме
стене
пеней полиномов В (а) и Q (а) — Q* (а) и потому была бы не
меньше, чем v, тогда как степень правой части равенства (10) меньше,
чем v. Таким образом, Q* (а) = Q (а) и тогда из (10) получим
R* (а) = R (а).
Аналогично устанавливается существование и единственность
левого (А,, [^-свернутого частного и левого (X, ц,)-свернутого
остатка при (Я, ц,)-делении А (а) на В (а). В этом случае находим
старший член левого (ht |л)-свернутого частного k,ll(B^lA0) a"~"°, a
затем из равенства
А (ее) = ^ [В (а)к* (В~1А0) оГ*\ = А(1) (а)
получаем левый (А,, (л)-свернутый остаток
а<1)(а) = ^,)а»(,) + ...А'ЧО).
Повторяя этот процесс, если и(1) > и, находим Л(2) (а) и т. д.,
пока не придем к левому (К (х)-свернутому остатку R (а). Левое
(А, |х)-свернутое частное Q (а) определяем тогда по формуле
$ (а) = ^(В~%) а""0 + ** (ЧГОД *">-+ ...
Пример 1. Пусть
—а3—2а»—3 2а$—2a2+lj
—а3+3а2+7а 5а3+2
is)
Л(а)=
—а3—4а2ф2 7а3+3а2
2а3—ба2 11а3+2а2+1
(s)
(s)
г- Мс)
= а*
1 7I-"1 2
2 11 1-1 Б || J
-НО
+ а2
— 4 3
— 6 2
— 2 —2
-Ю
+ а
В(а) =
010 o|j!L
0|7 oil
Не)
+
= а2
1
— 1
(/)
а2+ 2 За2—1
а2 + 1 2а2 + 1
(?)
2 0
0 1
— 3 1
0 2
0 У
"(О
(S)
1—м*>
I »
Г
(/)
+
[ — 2а2+ 3 а2+1
а2 + 3 а2 —1
(s)
Y
(О
— 2 1
1 1
Г
Y
(с)
И«)
+
2 —1
1 1
3 1
3 —1
(s)
(с)
Полагая К = 1, ji = 1, найдем правые (1,1)-свернутые частное и остаток
от деления А (а) на В (а). Имеем
Ло =
• 1 7
2 11
2 j—ИО
-15||г '
*0 =
1 l 3
1 — 1 2
-2 1]
1 1|
(s)
-И)
117
Далее, последовательно находим
v=
bHV)
1 2
3 1
3 3
-L -£.
3 3
(s)
(0
-<m)
1 1
2 3
bl[!XV) *(«)] =
-a2+4 7a2+l
2a2 + 7 11a2 —2
ll V*'
P"'
'(0
-a8+ 6 2as-l|pi^(f)
-a*+15 5a*-4||r
4iH
-4a2—4a+2 3a2—a
-6a2—7a 2a2+2a+l
-2a2—6a—3 —2a2+a+l ll
(s)
M(f5o"l) =
— 4 3
— 6 2
3a2—8a
— 2 —2
4a+2
"(I)
(s)
-(c)
(0
— 1 3
-2 4
(s)
r(m>.
r
(/)
-4a+l
—4a2+l 3a2+4
—6a2 2a2+6
—2a2—6 —2a*+4|
3a2 ^-3
(s)
(/)
-W
Л(2)(а)«
Следовательно,
Я(а) =
—7a
-a-4
2a-5
— 6a+ 3 a — 3
-8a 4a + 5||r
(s)
-(c)
— 4a + 1 — a — 4
— 7a 2a —5
— 6a + 3 a —3
— 8a 4a+ 5
(s)
т—М*)
(/)
Q (a) - Ь1 (Л fi~i) a +ы (^-l) = a
1 2
3 1
1 1
2 3
(s)
Mm)
Г"+
+
— 1 31 0 —2
— 2 4| — 1 1
(s)
Г
r
(/)
Mm) ll»—1 2a+3
3a —2 a + 4
a a —2
2a—1 3a+ 1
(«)
-*»>
118
При левом (Я, р)-делении А (а) на В (а) находим последовательно
-*(*>
О 1
M(VA>> =
5 "" 5
Ml
1В{аУ'1(В?1А$ш*
5 5
17
— 1 4
56
40
l(m)
-a2--ir 7а*-нг
** —Г "tf—ff
2<»<a) =
17 о о 56
—4а2+ -g-a+2 За2+ -g- a
7 1
-6а2+ -г а 2а2+ -^ а+1
-а2-1 2а2+7
—а2+1 5а2—1
2а2+а—3 —2а2—7а+1
1№
,—МО
[(f)
За2+6а а+2
(s)
,—МО
I t
У
(О
ЭД
0):
— 4 3
— 6 2
— 2 -2
3 0
(s)
г(0,
1-Чв?ЩЪ-
2 0
5 2
Т Т
± 1.
3^3
— 2 1
ЬЧЯ(а)Ь1(^1>)]=г
— 4а2+ 6 За2 —1
(s)
г
(т)
— 6а2 2а2 + 1
19 4
— 2а2+ -3- —2а2 + "з"
3«2 + 4г
(S)
40
|М
Л<2>(а) =
Следовательно,
Я(а) =
17 56
-g-a-4-g-a+l
7 1
28
а—— — 7а--з-
6а—-
И
а— -о-
«
-МО
17 . 56
"5-а^4 —а+1
7 1
28 т 1
*-"Г ~7а-"з"
И 2
6а—-у а—-у
т
\(с)
(S)
,—МО
1(0
ш
Q(a) =
8 19
--g-a + 2 -Ta
1 л 18
5 2
-a+-
4a~T
(s)
-M/)
У
(m)
Возьмем произвольный р-матричный полином степени и и
порядка п:
F(a)=F0a" + F1a"-»+ ..+РЦ. (11)
Подставляя в (11) вместо скалярного аргумента а р-мерную
матрицу я-го порядка Л, получим в результате этой подстановки
правое значение F (Л) полинома F (а) при а = А:
F (А) - ** [F*-* И")] + ",Д l/f (Aa-')\ + ...+F..
(12)
О V* /J I 1-1 V- /j •••■•- „-
Полином (11), однако, можно записать также в виде
F (ее) - <*"/?0 + аи-% + mmm+Fu. (13)
Подставляя в (13) вместо а матрицу Л, получим левое значение
F (А) полинома F (а) при a = Л:
F (А) = X'V V") f ol + *" Y"11 И11"1) fj + ... + ^«. (И)
Полиномы (12) и-(14), вообще говоря, различны, поскольку
(Я, ^-свернутые степени матрицы Л могут не быть
перестановочными с матричными коэффициентами F0iРъ..и,/v_i.
Совершая правое (Я, ц,)-деление полинома F (а) на бином
<х£ (Я, \i) — Л, получим правое (Я, ц,)-свернутое частное:
Q (a) = ^сТ"1 + [*•* (F^) + /\] a""2 +
+^IF0^(AU'1)] +
+ ^lF1^(Au-2)] + ... + Fu_l
и правый (Я, \i -свернутый остаток (независящий от а):
т. е,
R = F(A).
При левом (Я, р)-делении J7 (а) на о£ (Я, ц) — Л находим левое
(Я, (л)-свернутое частное:
3(a) = /-„a""1 + [^(AF0) + Fx] a""2* ... + ^(Au~Vol +
и левый (Я, (х)-свернутый остаток (независящий от а):
£ =^>»(AU)F0\ +K»[k'll(Au-l)F1] + ... + F»
120
т. е.
R=F(A).
Таким образом, справедлива следующая теорема.
Теорема /. (Обобщенная теорема Безу). При правом (или
левом) (Я, ^-делении р-матричного полинома F (а) на р-матричный
бином аЕ (Я, Ц.) — А правый (или левый) (Я, у^-свернутый остаток
равен F (А) (или F (Л)).
Из этой теоремы вытекает важное следствие.
Следствие. Правое (или левое) (Я, ^-деление полинома
F (а) на бином аЕ (Я, \i) — А тогда и только тогда совершается без
остатка, когда F (А) = О (или F (А) = О).
Пример 2. Пусть
^(а) = /(а)£(Я,^)-^/(Л),
где f (а) — полином от а над Р.
Тогда
F(A) = F(A) = 0.
Следовательно, правое и левое (Я, ^-деление F (а) на аЕ (Я, jx)—
— А совершается без остатка.
§ 2. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
ПОЛИНОМИАЛЬНЫХ МНОГОМЕРНЫХ МАТРИЦ
Назовем (Я, ^-элементарными преобразованиями полиномиальной
/7-мерной матрицы л-го порядка (1), представленной в виде
Л(а) = ||4*с(с0||, (15)
где каждый из индексов разбиений
I — (Zl. k> • • • » W. s — (Sb 52, . . . , S))9 С = (сь C2, . . . , Cja)
пробегает значения 1, 2, . . . , л, следующие операции над любым
ее сечением ориентации (s), например, над сечением
1И/$<А>Да)11 (!<*<*):
а) умножение какого-либо сечения ориентации (с), например
\W(h)ca)(a)II (l</<«l*)f на произвольное, отличное от нуля
число *€Р;
б) прибавление к какому-либо сечению ориентации (с),
например II Als(h)c(i) (<z)||. любого другого сечения той же ориентации, напри-
меР II \мс(Г) (а) II (1<У'<лД1 /' «р Л. умноженного на
произвольный полином 9(a) с коэффициентами из поля Р;
а') умножение на t какого-либо сечения ориентации (/), например
IIW)>)II (!<'<**);
121
б') прибавление к какому-либо сечению ориентации (/),
например 1|Л/(0в<Л)г(а)||, умноженного на 0(a) любого другого сечения
той же ориентации, например \\Alinsih)e(a)\\ (1 <{'</!», i'Ф1).
Если с помощью одной из операций а), б), а'), б') можно
перейти от матрицы А (а) к матрице В (а), то, очевидно, можно и
обратно получить матрицу А (а) из В (а) с помощью операции
такого же типа.
Операциям а), б), а'), б') соответствуют элементарные
преобразования диагональной клетки 3t<^ (a) (X, (х)-ассощшрованной с Л (а)
матрицы 91х,ц(а):
a) умножение /-го столбца на t\
b) прибавление к /-му столбцу умноженного на в(а) /'-го
столбца;
а') умножение i-й строки на t\
Ь) прибавление к t-й строке умноженной на в (а) i'-й строки.
Эти преобразования, очевидно, являются также элементарными
преобразованиями матрицы 9fot|Ll(a).
Замечание. Операциями типов а), б) или а'), б') можно
переставить в каком-нибудь сечении ориентации (s) матрицы Л (а) =
= |H/sc(a)|| любые два сечения соответственно ориентации (с) или (/).
Операции а), Ь) над матрицей 21^ (а) равносильны
умножению ее справа соответственно на элементарные квадратные
матрицы порядка пк+%(а\ $ь\ являющиеся клеточно-диагональ-
ными матрицами, у которых все пк диагональных клеток —
единичные матрицы порядка л*\ кроме одной А-й клетки,
представляющей в @(а) матрицу ||^|| (£,rj = 1,2,... ,Д где каждый
элемент в£0 равен 6^, кроме (£^) = tf а в $ь) — матрицу ||<Е^||
(£, л = 1,2,..., лц), где каждый элемент (S& равен 6^, кроме (£^1 =
= 6 (a).
Точно так же, операции а'), Ь') над матрицей ЗСЯЛ1 (а)
равносильны умножению ее слева соответственно на элементарные
квадратные матрицы порядка пк+]1$а'\ @КЬ'), являющиеся
клеточно-диагональными матрицами, у которых все пх диагональных
клеток—единичные матрицы порядка л*\ кроме одной А-й клетки,
представляющей в <g(a') матрицу || Ц*') || (£, т) = 1,2 , л**), где каждый
элемент @^') равен 6^, кроме ©^ = tf а в <£(*') — матрицу
\\&§?\\ (6.4= Ь2» .•-.л'*), где каждый элемент равен 6|1Г кроме
<$,'> = 6 (а).
Аналогично, операции а), б) над матрицей Л (a) = || Aisc (а) ||
равносильны (X, (х)-свернутому умножению ее справа
соответственно на (А,, (^-элементарные матрицы измерений р и порядка п:
122
где m=^(mvm2t... ,/%) и каждый из элементов £<££, ЕсЗп равен
*«.. КР0Ме ^.(*)т(Л = *> E%s(h)mW) = в (а).
Точно так же, операции а'), б') над матрицей Л (ct) == || Л/вс (а) (|
равносильны (X, ц)-свернутому умножению ее слева соответственно
на (Я, (х)-элементарные матрицы измерений р и порядка п
£*>-|J*?||. E^=\\Et?\\,
где k = (&i,&2,♦.♦,£ц) и каждый из элементов ££?, fjfi? равен
6kv кроме £&Wo=='> 4Тп8(Л)/(0==в(а).
Отметим, что упомянутые выше элементарные квадратные
матрицы @(а), (§№\ @(а'\ @^') являются (Я, ^-ассоциированными с
матрицами £(а), £(б), £(а'\ 2J*6'*, причем их детерминанты не
зависят от а и отличны от нуля.
Две полиномиальные р-мерные матрицы я-го порядка А (а)
и В (а) называются (Л, ^-эквивалентными, если от каждой из них
можно перейти к другой с помощью конечного числа (X,
^-элементарных преобразований. Иначе говоря» матрицы А (а) и В (а)
будут (А,, (х)-эквивалентны, если (X, ^-ассоциированные с ними
матрицы 9fo,n(<*) и 83;с,ц(а) эквивалентны.
Пусть матрица В (а) получается из А (а) с помощью цепочки
(А,, ^-элементарных преобразований, соответствующих (X,
^-элементарным р-мерным матрицам д-го порядка: Еъ Ег> ...» Eq,
на которые А (а) умножается справа, и E'v Е'2, . . . , E'qt, на
которые А (а) умножается слева. Тогда
В (а) =я'ц (Е'я<... Я^Л (а) ЕгЕ2 ...Eq) (16)
или
5(а)=^({/(а)Л(а)У(а)), (17)
где
{/ (а) =^ (Я;.... Е'2Е\)У V (а) =^ (£х£2 ...Вщ)
— полиномиальные /7-мерные матрицы л-го порядка, с которыми
(X, ^-ассоциируются полиномиальные квадратные матрицы с
постоянными (т. е. независящими от а) отличными от нуля
детерминантами.
Наоборот, из равенства (17) вытекает равенство (16), так как
каждая полиномиальная р-мерная матрица, с которой (А,,
^-ассоциируется полиномиальная квадратная матрица с постоянным
отличным от нуля детерминантом, может быть представлена в виде
(А,, (х)-свернутого произведения (X, ц)-элементарных р-мерныз( матриц
(поскольку соответствующая (X, (л)-ассоциированная
полиномиальная квадратная матрица с постоянным отличным от нуля
детерминантом представима произведением элементарных квадратных
матриц).
123
Таким образом, равенства (16) и (17) равносильны, и
предыдущее определение (Л, \i)-эквивалентности матриц А (а) и В (а)
можно заменить равносильным ему следующим определением.
Две полиномиальные /7-мерные матрицы я-го порядка А (а) и
В (а) называются (%, ^-эквивалентными, если они удовлетворяют
соотношению
В(а)=^((/(а)Л(а)У(а)),
где U (а), V (а) — некоторые полиномиальные р-мерные матрицы
п-го порядка, с которыми (X, Ц.)-ассоциируются полиномиальные
квадратные матрицы с постоянными отличными от нуля
детерминантами.
(К, \1)-рангом гХ[1 (А(а)) полиномиальной р-мерной матрицы п-го
порядка А (а) = \\ Аис (а) || называется совокупность рангов
г Л И), г(5й^(а)),...,г(91Й(а)) Диагональных клеток «&(«).
2to?n (<*)»•••» SfoV (<*) (^, (А)-ассоциированной с Л (а) матрицы ЭД^.ц (<*):
гя.и И (а)) = (г (И& (а)), г Л (а))..... г («ft (а)).
где
0<г(2С(а))<п* (Л =1,2....,Л
Если г (8ft*|i (а)) = л* (Л = 1,2,..., я*), то матрица Л (а) будет
(Л,, (л)-неособенной.
Равенство (А,, ц,)-рангов полиномиальных р-мерных матриц п-го
порядка Л (а) и В (а) является необходимым, но недостаточным
условием их (X, (л)-эквивалентности.
§ 3. ИНВАРИАНТНЫЕ МНОЖИТЕЛИ И ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
ПОЛИНОМИАЛЬНЫХ МНОГОМЕРНЫХ МАТРИЦ
Из определения (А,, (х)-ранга г^ (А (а)) полиномиальной р-мерной
матрицы л-го порядка А (а), представленной в ввде (15), ясно, что
rK\i(A (а)) является арифметическим инвариантом относительно
(Я, [а)-элементарных преобразований матрицы А (а). Кроме такого
рода инвариантов матрицы А (а) существуют, однако, еще и
другие величины, обладающие инвариантными свойствами.
Обозначим через D^h) (а) общий наибольший делитель (со
старшим коэффициентом 1) всех миноров v-ro порядка (v=l,2,... ,Qh)
диагональной клетки 21^ (а) ранга Qh = г (И^ (а)) (А = 1,2,...
...,лл) матрицы $Г;иц(а). Тогда имеет место следующая теорема.
Теорема 2. Полиномы D^\a) (v = 1, 2, . . ;, qa; h = 1, 2, ...
. . . , Ф) остаются неизменными при (X, ^-элементарных
преобразованиях матрицы А (а).
124
Действительно, (Xt (А)-элементарные преобразования матрицы
А (а) сопровождаются элементарными преобразованиями
полиномиальных квадратных матриц 2lcui(a) (А = 1,2,..., nk)t при которых,
как известно, полиномы D{*} (a) (v = 1,2,..., Qh) остаются
неизменными.
Вместо полиномов D$\a) можно ввести другие инварианты,
которые мы назовем (Xt \х)-инвариантными множителями матрицы
Л (а). Для определения их заметим, что D(vft)(a) делится без
остатка на D^{(a) (v = 1,2,... ,Qh), причем D<h)(a)s 1 (Л = 1,2,...
..., п\ Полученные в результате деления полиномы
где каждый полином ffl (а) служит делителем следующего
полинома d^!(a), являются инвариантными множителями матрицы
«CU») (Л= 1,?,...,лх).
Совокупность полиномов
d\]) (a), 4° И,.... dff («); df> (a), <#> (a),..., 4? (a);...
...;^(а)§4^(а).....|1Й(«)
(A = 1,2,....Д
и будем называть (X, ^-инвариантными множителями матрицы
А (а).
Заметим, что в общем случае (X, ц,)-инвариантные множители
матрицы А (а) не совпадают с инвариантными множителями
матрицы 8fo,n(a).
Так как инвариантные множители полиномиальной
квадратной матрицы остаются неизменными при ее элементарных
преобразованиях, то справедлива такая теорема.
Теорема 3. (X, ^-инвариантные множители полиномиальной
р-мррной матрицы А (а) являются инвариантами относительно
(X, ^-элементарных преобразований этой матрицы.
Также очеввдна следующая теорема.
Теорема 4. Для того чтобы две полиномиальные р-мерные
матрицы п-го порядка А (а) и В (а) были (X, [^-эквивалентны,
необходимо и достаточно, чтобы они имели одни и те же (Х9
^-инвариантные множители.
Таким образом, (X, ц,)-инвариантные множители
полиномиальной р-мерной матрицы образуют полную систему инвариантов
относительно (X, (^-элементарных преобразований этой матрицы.
Так как каждая матрица 8fo!ll(a) (А = 1, 2, . . . , пк) с помощью
конечного числа элементарных преобразований мвжет быть прн-
125
ведена к канонической диагональной матрице
{tf,(a).4i*(a).....dg(a).0i...\0b
то, очевидно, матрица А (а) с помощью конечного числа
соответственных (X, (х)-элементарных преобразований может быть
приведена к каноническому виду
/х.|*(а) = ||/ы(а)||. О»)
где в каждом сечении ориентации (s) || //8(Л)с(а) || (А = 1,2,..., Ф)
все элементы — нули, кроме элементов
VmaMv) («) = dV («) (v = 1,2,. _ , рл).
Каждая диагональная клетка §о?ц(а) (А ^ 1.2,..., п*) (А»,
^-ассоциированной с /Xt|l(a) матрицы Зх,ц(а) имеет канонический вид:
3ji («) = (С («>. 4h) <«). • • •. С <«). о..... о}.
Матрица (18) может быть рассматриваема как представитель
класса /Сх,|д(<*) полиномиальных р-мерных матриц n-го порядка,
(X, (л)-эквивалентных матрице Л (а).
Элементарные делители матрицы 8(x,ji(<*) в поле Р,
совокупность которых получается объединением элементарных делителей
матриц SlojSi (а) (А = 1,2, пк) в том же поле, будем называть
{X, ^-элементарными делителями матрицы А (а) в поле Р (см. [7],
стр. 78).
Отсюда вытекает, что (А,, ^-инвариантные множители матрицы
А (а) вполне определяют ее (А,, (л)-элементарные делители.
Обратное утверждение также справедливо, если известен (А, ц,)-ранг
г%^(А (а)) матрицы А (а). Следовательно, (X, ц,)-элементарные
делители матрицы А (а) будут не только инвариантами, но и
образуют также вместе с (Я, ц,)-рангом г^(А(а)) полную систему
инвариантов относительно (X, ^-элементарных преобразований
матрицы А (а). Имеет место, таким образом, такая теорема.
Теорема 5. Две полиномиальные р-мерные матрицы п-го
порядка тогда и только тогда (X, ^-эквивалентны, когда они
обладают одним и тем же (X, \л)-рангом и (X, ^-элементарные делители
одной из матриц тождественно равны соответствующим
элементарным делителям другой.
Простейшим видом полиномиальных многомерных матриц
является уже рассматривавшаяся в гл. IV (X, ^-характеристическая
матрица А — аЕ (X, \i) для р-мерной матрицы л-го порядка А =*
==f|^/sf|| над Р, где индексы разбиений
/ = (/j, /2,. *,, Z^), s = (Sj, s2, . . . , s^j, с = {Cj, £g> * • • > cij)
126
пробегают значения 1, 2, . . . , п. Матрица А — аЕ (A,, (i)
является (А,, ^-неособенной. Ее (А,, (л)-инвариантные множители
называются (А,, [^-инвариантными множителями матрицы А, а
соответствующие (А,, (х)-элементарные делители в поле Р — (А,,
^-элементарными делителями в поле Р матрицы А.
Следующие теоремы устанавливают связь (X,
^-характеристического и (X, (А)-минимального полиномов матрицы Л с ее (А,,
^-инвариантными множителями.
Теорема 6. (А,, ц,)-характеристический полином q^a) матрицы
А равен произведению всех ее (А,, ^-инвариантных множителей
Действительно, согласно формуле (10) гл. V, <рЯ|11(а)
разлагается в произведение (0, ц,)-характеристических полиномов (^(а)
(А = 1,2,..., пк) сечений Aih) ориентации (s) матрицы А = || Ai8C ||,
а ф^> (а) является также характеристическим полиномом (0,
^-ассоциированной с А{Н) матрицы Яо*|1, который, как известно (см.
[2], стр. 176), равен произведению
^>(а)4Л)(сс)...<^(а)
всех инвариантных множителей этой матрицы.
Теорема 7. (А,, ^-минимальный полином \9VL(&) матрицы А
совпадает с последним ее (X, \1)-инвариантным множителем d^V(a),
если каждый (X, ^-инвариантный множитель d%Tl) (a) будет
делителем d?* (a) (ft = 2,3,...,Д
В самом деле, при выполнении условий теоремы совокупность
инвариантных множителей (Я, ^-ассоциированной с А клеточно-
диагональной матрицы 3fo,n(a) получается объединением
инвариантных множителей диагональных клеток Stolji (a) (h = 1,2,..., пк)
(см. [1], стр. 144), т. е. дает все (А,, ц)-инвариантные множители
матрицы Л, и последний из них d^ * (а) совпадает с минимальным
полиномом матрицы $х,ц(а) (см. [2]. стр. 176), являющимся
также (А,, ^-минимальным полиномом Ф^О*) матрицы А.
Составив элементарные делители матриц Stolli (Л = 1,2,««.-,л^
в поле Р содержащем все характеристические числа их, можем
найти жордановы нормальные формы J^ этих матриц, а затем и
жорданову нормальную форму Jk матрицы %%t[i в виде клеточно-
диагональной (или диагональной, если все элементарные делители
матрицы Stx.i* будут первой степени) матрицы
/ — //(о 7(2) т(п\
127
Тогда р-мерная матрица п-го порядка J (X, \л), с которой (X, \i)-
ассоциирована матрица Д.ц, будет (X, {^-нормальной формой
матрицы А (см. [6], стр. 1325). Число всех (А,, ^-нормальных форм
матрицы А равно 1 + •§" • причем (р, 0)-нормальная форма
матрицы А совпадает с Л, т. е. J (р, 0) = А.
Теорема 8. Матрица А (Х9 \л)-подобна над Р своей (А,,
^-нормальной форме J (X, \i), т. е. существует такая р-мерная матрица п-го
порядка Т над Р, что
^(Г-МТ) = J (X, ц), (19)
где Т-1— (X, ^-обратная матрица для Т.
Действительно, пусть ?о?ц—неособенная квадратная матрица,
преобразующая Sft^ в подобную ей матрицу J^, т. е.
(^r№^ = ^ (*-if2....fД
Тогда
^д-{«41{|.«й*.....«Й?}
является матрицей, преобразующей Sfo.n в подобную ей матрицу
Л ,„ т. е. имеет место соотношение
где
«й - (Л)-, («а)-1 (s$r'}-
Обозначая через Г и Г-1 р-мерные матрицы п-го порядка, с
которыми (X, ^-ассоциированы матрицы З^ц и S^jn. и принимая
во внимание замечание в § 2, гл. IV о составлении (А,, ц,)-
обратной матрицы, легко убеждаемся на основании соотношения (20)
в справедливости равенства (19). Матрица Т будет, таким
образом. (А,, ^-преобразующей матрицей для А.
Следующая теорема выражает критерий подобия двух
многомерных матриц (см. [7], стр. 79).
Теорема 9. Две р-мерные матрицы п-го порядка А и В тогда
и только тогда (А,, \л)-подобны над Р, т. е.
к*(Т-{АТ) = В9
когда они имеют одни и те же (X, ^-элементарные делители в
поле Р.
Действительно, необходимое и достаточное условие подобия
над Р (X, ^-ассоциированных с А и В квадратных матриц Sfo,n и
93а,,ц заключается в том, чтобы они обладали одними и теми же
элементарными делителями в поле Р. Последние же являются
(А,, ^-элементарными делителями матриц А и В, а подобие матриц
%иц и 93а,,ц влечет за собой (X, (х)-подобие матриц А и В.
128
Из теоремы 9 вытекает, что матрица / (X, \i) может быть
рассматриваема как представитель содержащегося в классе К (А,, \л)
матриц, (X, |х)-эквивалентных матрице А, подкласса Кг (X, |х) Рт
мерных матриц л-го порядка, (X, ^-подобных матрице А.
§ 4. ПУЧКИ МНОГОМЕРНЫХ МАТРИЦ
Обратимся теперь к частному, весьма важному случаю, когда все
элементы полиномиальной р- мерной матрицы я-го порядка
представляются линейными полиномами над полем Р. Имеем тогда
пучок /7-мерных матриц я-го порядка
М(а) = Л + аВ,
где матрицы
A = \\At*\\' B=z\\Bisc\\ (/1,...,/(1,s1,....s;i,c1,.,.,^=l,2,..., п)
образуют базис пучка.
Соответствующий пучок квадратных матриц порядка /гх+ц
базисом которого являются (X, ^-ассоциированные с Л и В
матрицы 9lfc,n и ЯЗх.ц, будет (X, ^-ассоциированным с пучком М (а).
Если пучок ЭП&(|д(а) регулярный, т. е. детерминант |9Йх,ц(а)|
не равен тождественно нулю, то пучок М(а) называется (31,
^-регулярным*. Если же пучок Жх.ц(а) сингулярный, т. е. ] SR^.n (а) |==з
s=sO, то пучок М(а) называется (X, ^-сингулярным.
Два пучка р-мерных матриц я-го порядка М (а) = А + аВ и
М (а) = А + аВ назьгеаются строго (X, ^-эквивалентными над
полем Р, если существуют такие (X, ^-неособенные матрицы (/, V
измерений р и порядка п с постоянными, т. е. независящими от а,
элементами из поля Р, что
Kll(UM(a)V) = M(a).
Иначе говоря, пучки М(а) и Л1(а) будут строго (X, \i)-эквивалентны
над полем Р, если (X, ^-ассоциированные с ними пучки ЭП^,ц(а) и
ЭПх,ц(а) строго эквивалентны над Р (см. [11, стр. 331).
Чтобы установить критерий строгой (X, ц.)-эквивалентности
пучков р-мерных матриц, введем в рассмотрение (X,
^-элементарные делители пучка М (а, Р) = рл + аВ, заданного с помощью
«однородных» параметров а, р.
* Это определение несколько шире данного в § 1 наст, главы определения
(К ^-регулярного матричного полинома: для (X, ^-регулярного пучка М (а)
возможно равенство | ©^ ^ | = 0 и даже | Щ^ ц | = | 58^ ц | =* 0.
9-5W
129
Назовем (А,, ^-элементарными делителями пучка М (а, Р) в поле
Р элементарные делители £&(«, Р) (£=1,2,...) в этом поле
(А,, [^-ассоциированного с М(а,Р) пучка ЗИх,ц(а Р), которые
определяются аналогично элементарным делителям ek(a) (fe=1.2,...)
пучка ОД.» (ос) (см. [1], стр. 333). Ясно, что, полагая р = 1 в
£Л(а,Р), вернемся к элементарным делителям ek(a) пучка Жх,ц(а)»
и наоборот, из каждого элементарного делителя ek(a) степени qk
пучка Ш%^(а) получим соответствующий элементарный делитель
ek(a, P) по формуле
Таким способом могут быть получены все элементарные
делители пучка ЭПд,,|д(а, Р) за исключением элементарных делителей
вида р*.
Элементарные делители вида р* существуют в том и только том
случае, когда |93a,,ia| = 0, и носят название «бесконечных»
элементарных делителей пучка ЭПа,,ц (а). Последние называются также
«бесконечными» (X, (^-элементарными делителями пучка М (а).
Остальные (К, ^-элементарные делители пучка М (а) будем
называть «конечными».
Поскольку необходимое и достаточное условие строгой
эквивалентности над полем Р регулярных пучков квадратных матриц
Жк.и(а) == %ки + a ЯЗь.ц и ЭНь.ц (a) = Slx.n + а 2к,ц заключается в
том, чтобы эти пучки имели одни и те же («конечные» и
«бесконечные») элементарные делители в поле Р (см. [1], стр. 334), то,
очевидно, справедлива следующая теорема, дающая критерий
строгой (X, (х)-эквивалентности (А,, ^-регулярных пучков р-мерных
матриц.
Теорема 9. Для того чтобы два (X, ^регулярных пучка р-
*>*
мерных матриц п-го порядка М (а) и М (а) были строго (А,, ц,)-
эквивалентны над полем Pt необходимо и достаточно, чтобы эти
пучки имели одни и те же {«конечные» и «бесконечные») (А,,
{^-элементарные делители в поле Р.
Найдем теперь канонический вид (А,, ^-регулярного пучка М (а).
Пусть р*1 , р*2 ,..., Р\ — «бесконечные» элементарные
делители диагональной клетки Ж^(а) (1 < А< пк) регулярного пучка
ЯЯрии(а). Пусть, далее, JJui — квадратная матрица порядка wh =
= гР—£ tff0» имеЮ1Дая любую нормальную форму (например,
естественную первого рода, второго рода или жорданову).
Обозначим через (Sft единичную квадратную матрицу порядка fe, а через
$k — квадратную матрицу порядка &, у которой элементы первой
наддиагонали равны единице, а все остальные—нули. Далее>
введем обозначения
(т-
130
Тогда, как известно (см. [1], стр. 334), пучок ЭП^ (а) (Л = 1, 2, . . .
. . . , пк), также регулярный, приводится к строго эквивалентному
каноническому клеточно-диагональному виду
К№) = {К}*ы>К}»м>-•■'*%&> С+«ЧК (21>
где первые th диагональных клеток соответствуют «бесконечным»
элементарным делителям пучка OTqjL (<*)> а нормальная форма
последней диагональной клетки У^ + a QtWfi однозначно определя*
ется «конечными» элементарными делителями пучка ЭП^Л (а).
Следовательно, регулярный пучок ЭПд^а) может быть приведен
к строго эквивалентному каноническому клеточно-диагональному
виду:
«х.и(а) = {Яй*(«). Я& (а),..., ЯЙ? <а)Ь
Поэтому, очеввдно, имеет место следующая теорема.
Теорема 10- Произвольный (Я, ^-регулярный пучок М (а) р-
мерных матриц п-го порядка может быть приведен к строго (Я, \л)~
эквивалентному каноническому пучку N(a), с которым (X, \i)-
ассоциирован пучок 92л,|д(а).
Согласно определению, пучок М (а) будет (X, ^-сингулярным,
если хотя бы один из диагональных пучков квадратных матриц
ЯП$&(<*) (Л = 1, 2, . . . , л*) сингулярный.
Как известно (см. [1], стр. 343), всякий сингулярный пучок
2Koji(°0 О < Л< пк) может быть приведен к строго
эквивалентному каноническому клеточно-диагональному виду:
It
^>)=f^0,S$) (*),... Л%(*),&% (a),...
-..2^(«).(?С(«Ц. (22)
где е<** = ... = е<Л> = 0, ejh>, |f..., е<Л> — минимальные индексы для
столбцов, a rjW = ... = r)<h> = 0, rjW p ..., г£Л> — минимальные
индексы для строк пучка, fi*h)'(a)— матрицы, транспонированные
относительно матриц вида
&Л)и =
Га 1 0 .
0 а 1
0 0
.
•
0 0 1
• •
а 1 1
*.
9*
131
и (^oji(a))0 — регулярное «ядро» пучка, имеющее нормальную
форму (21).
Поэтому в самом общем случае пучок Жх,ц(а) приводится к
строго эквивалентному каноническому клеточно-диагональному
ввду %.ц(а), который получается из %,»*(«) заменой
диагональной клетки $Roi(a) клеткой Щ%,(а). определяемой формулой (22),
для каждого сингулярного пучка ^щ%(а) (1 < А<п'А).
Отсюда вытекает следующая теорема.
Теорема 11* Произвольный пучок М{а) р-мерных матриц п-го
порядка может быть приведен к строго (X, ^-эквивалентному кат
ноническому пучку N(a), с которым (Я, ^ассоциирован пучок
Пример. 4. Выпишем каноническую форму N (а) пучка кубических
матриц шестого порядка
М(а) = || Л/5,|| +а|| Blsc\\ (/, а, с-1.2.3. 4, 5, 6),
если известны минимальные индексы и элементарные делители диагональных
клеток 2Й$^ («) (л = h % 3. 4, 5, 6) (Я, ^-ассоциированного с М (а) пучка
%,и («) при Я, = 1. (4 =» 1:
<<>(«)
ч%>
«g|(a»
2R$<a>
JKi1|(a)
«о!!<«>
2Н$(а>
Минимальные индексы
__
—
81=0, T)l=0
8l=0, е2=2, rii=0, Т)2=0
е,=0, е2=0, Л1=0. Л2=1
8! =2, Л1 =2
Элементарные делители
а—1, (а+1)2, (а+2)3
а, а2, Р*
а-4, (а+5)2, Р2
(а-3)2
а+4, Р2
а—5
Составляем сперва по формуле (21) канонические виды 9$| (а) и Ш^\ (а) пучков
2>#i(a) и2К$(а):
^(а):
a —l!
I 0 а + 1 !
|а + 2 1 О
| 0 а + 2 1
|_0 2_jx+_2
132
1
0
0
a 0
1 a
0 I
a 1 j
0 a J
*ft<«>-
Затем находим по формуле (22) канонические виды 91^', (a) —gj^ (а) пучков
"Г!
-|ТТ|
|0_1|
$Й («)=
|а + 5 1 1
| 0 а+б{
а —4
\ —
$£> (а) =
1
а 1 01
0 a lj
|а —3 1
I О а —3
«£} (а) =
0 0 1
1 а
1 a j
о ij '
■«4-4
»й(«)-
а 1 О
О а 1
а О
1 а
О 1
la — 5
Следовательно, каноническая форма Л^! j(a)ny4KaM(a) имеет вид
Кл («> - ii *й («) I *а («) I *ffl («> I а© («) i ЭД} («> i *$ о II ^ •
Рассматривая совокупности минимальных индексов для
столбцов и строк пучков 3R$^(a) (ft = 1, 2, . . . , г&) как (Л,, ц,)-лшаш-
мальные индексы для сечений ориентации (sc) и (Zs) (X,
^-сингулярного пучка М (а) и принимая во внимание, что необходимое
133
и достаточное условие строгой эквивалентности произвольных
пучков квадратных матриц состоит в том, чтобы эти пучки имели одни
и те же минимальные индексы и одни и те же («конечные» и
«бесконечные») элементарные делители, легко убеждаемся в
справедливости следующей теоремы, представляющей критерий строгой (Л,
неэквивалентности произвольных пучков р-мерных матриц п?го
порядка.
Теорема 12. (Общая теорема Кронекера.) Для того чтобы два
произвольных пучка р-мерных матриц п-го порядка М (а) и М (а)
были строго (к, ^-эквивалентны над полем Р, необходимо и
достаточно, чтобы эти пучки имели одни и те же (Xt \i)-минимальные
индексы и одни и те же («конечные» и «бесконечные») (Я,
^-элементарные делители в поле Р.
ГЛАВА VII
О МУЛЬТИПЛИКАТИВНЫХ И СПЕКТРАЛЬНЫХ
СВОЙСТВАХ МНОГОМЕРНЫХ МАТРИЦ
С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
§ 1. ОСНОВНЫЕ МУЛЬТИПЛИКАТИВНЫЕ СВОЙСТВА
НЕОТРИЦАТЕЛЬНЫХ МНОГОМЕРНЫХ МАТРИЦ
Будем рассматривать р- мерную матрицу л-го порядка А над полем
вещественных чисел Р, представленную в виде
i*-||iM. (1)
где каждый из индексов разбиений
/ = (Zp lv..., у, s = (s|f s2, . . . , sx), с = (с,, с2,... сд)
пробегает значения 1, 2, . . . , я.
Матрицу А называем неотрицательной (или положительной),
вводя обозначение А > О (или Л > О), если все элементы матрицы
А неотрицательны (или положительны).
Введем, далее, следующие определения.
Неотрицательная матрица Л, представленная в виде (1),
называется полностью или частично (Я, \1)-разложимой, если
соответственно все или некоторые из диагональных клеток ИЙ£ (ft =
= 1, 2, . . . , пк) (X, \i)-ассоциированной с А клеточно-диагональ-
ной матрицы 21я,ц разложимы, т. е. перестановкой рядов* могут
быть приведены к виду
..«и* «И
где 98(1Л), 8?}— квадратные матрицы. В противном случае, когда
каждая из матриц ЭД^ (Л = 1,2,... f л*) неразложима, т. е. не
может Сыть приведена перестановкой рядов к виду (2), матрица А
называется (К \1)-неразложимой.
Если каждая из матриц 91^ (ft = 1, 2, . . . , я*) покрываемоне-
разложима (см. [121, стр. 577), т.е. min {е + г\] > п», где е(0<
< б < п*) — число строк, а т) (0 < т] < л*1) — число столбцов
матрицы таких, что каждый ее ненулевой элемент принадлежит одной
* Под перестановкой рядов в квадратной матрице подразумевается
соединение перестановки строк с такой же перестановкой столбцов этой матрицы
(см. [1], стр. 352).
я&-
135
из этих строк или одному из этих столбцов, то матрица А
называется (А,, [к)-покрываемонеразложимой.
Теорема 1. Неотрицательная р-мерная матрица п-го порядка
А тогда и только тогда является (X, ^-неразложимой, когда сумма
матрицы А и (X, ^-единичной р-мерной матрицы п-го порядки
Е (X, \i) есть (X, \1)-покрываемонеразложимая матрица.
Теорема очевидна, если принять во внимание, что покрываемая
неразложимость суммы матрицы Sloji и единичной квадратной
матрицы п^-го порядка (£ ц является необходимым и достаточным
условием неразложимости матрицы 8lo!|i (А= 1,2,..., пх) (см. [12],
стр. 577). _
Отметим основные мультипликативные свойства
неотрицательных многомерных матриц (см. [8], стр. 73).
Теорема 2. Если неотрицательная р-мерная матрица п-го
порядка А является (X, \л)-покрываемонеразложимой, то ее (X, \i)-
свернутая (п» — \)-я степень представляет положительную
матрицу, т. е.
^(Ап1Х-г)>0 . (3)
Действительно, по условию теоремы каждая из матрац л^-го
порядка Stojii (Л = 1,2,..., пк) покрываемонеразложима, а тогда,
как известно (см. [12], стр. 577),
<№f*-l>0 (А=1,2,...,лх).
Таким образом, все диагональные клетки клеточно-диагональной
матрицы StX.jJ"1 положительны. Но матрица Их,!*"1! согласно
правилу составления (X, ц,)-свернутого произведения многомерных
матриц, является (X, ^-ассоциированной с р-мерной матрицей л-го
порядка ' (Ап ~~1). Последняя, следовательно, удовлетворяет
неравенству (3).
Из теорем 1 и 2 вытекает очевидное следствие.
Следствие. Если неотрицательная р-мерная матрица п-го
порядка А (X, ^-неразложима, то (Я, ^-свернутая (п» — 1)-я
степень суммы матриц А и Е (X, \i) является положительной
матрицей, т. е.
^l(A + E(Xtli)f-]]>0.
Рассмотрим один частный вид многомерных неотрицательных
(X, (х)-неразложимых матриц, определяемых следующим образом.
Неотрицательная (X, ^-неразложимая р-мерная матрица п-го
порядка Л, представленная в виде (1), называется (X,
^-примитивной, если все матрицы ИЭД (А =1, 2, * . . , пк) примитивны
(см. [1], стр. 377).
136
Следующая теорема устанавливает важное свойство (X,
^-примитивных матриц (см. [81, стр. 77).
Теорема 3. Неотрицательная р-мерная матрица п-го порядка
А тогда и только тогда является (X, \1)-примитивной, когда суще-
ствует целое положительное число q такое, что
Xji(4«)>0. (4)
В справедливости теоремы убеждаемся, замечая, что^необхо-
димое и достаточное условие (А,, ^-примитивности матрицы А
совпадает с необходимыми и достаточными условиями примитивности
матриц 9$}1 (А = 1, 2, . . . , пх). Эти условия, как известно (см.
[1], стр. 377), заключаются в существовании целых
положительных чисел qh таких, что
Тогда будет иметь место неравенство
(зО< > о,
где"а — максимальное из чисел qh(h = 1, 2, . . . , nk).
Следовательно, справедливо и неравенство (4).
Если неотрицательная р-мерная матрица л-го порядка А (Л, (х)-
примитивна, то наименьшее целое положительное число у (А)
такое, что при q > у (А) имеет место неравенство (4), называется
(А,, \л)-показателем матрицы А.
Теорема 4. (А,, [^-показатель у (А) (А,, ^-примитивной р-мер-
ной матрицы п-го порядка А удовлетворяет неравенству
y(A)<(f?-if+l. (5)
Действительно, так как клеточно-диагональная матрица 2$,ц
является (X, (г)-ассоцшфованной с матрицей *"Д(Л*), положительной
при 0>y(4), то диагональные клетки (®о%)я (А = 1, 2,.. , пк)
матрицы 21£,ц положительны. Следовательно, каждая из матриц
лц-го порядка Wtfb (А = 1, 2,..., пк) — примитивная с
показателем y(^(ui), удовлетворяющим, согласно теореме Виландта (см.
[18], стр 648), неравенству
7Л)<(^-1)2+1 (А=1,2,...,Л * (6)
Совокупность же неравенств (6) обусловливает неравенство (5).
137
§ 2. ОСНОВНЫЕ СПЕКТРАЛЬНЫЕ СВОЙСТВА
НЕОТРИЦАТЕЛЬНЫХ МНОГОМЕРНЫХ МАТРИЦ
Многомерные положительные матрицы являются частным видом
(X, ^-неразложимых неотрицательных матриц. Следующая теорема
выражает спектральные свойства положительных многомерных
матриц (см. [81, стр. 73, 74).
Теорема 5. (Общая теорема Перрона). Положительная р-
мерная матрица п-го порядка А, представленная в виде (1), всегда
имеет вещественное и притом положительное (X,
[^-характеристическое число R, которое является g-кратным (1 < g < nfy корнем
(X, \i)-характеристического уравнения этой матрицы и превосходит
модули всех других (Ху ^-характеристических чисел*. Вместе с тем
R есть простой корень (0, ^-характеристических уравнений g
сечений ориентации (s) матрицы А. Числу R соответствует
неотрицательная фундаментальная (X, ^-собственная матрица Y =
= || YcS\\ для А. Положительные элементы матрицы Y образуют
g сечений ориентации (s) этой матрицы, которые представляют
соответствующие числу R фундаментальные (0, ^-собственные
матрицы Yih) = || YcS(h) \\ (ft = ftb 1ц, . . . , hg) для упомянутых
выше сечений матрицы А.
Действительно, так как А > О, то и 21^ > О (ft = 1, 2, . .>..
. . . , лх). Согласно теореме Перрона (см. [1], стр. 354),
положительная матрица 9to!U всегда имеет вещественное и притом
положительное характеристическое число Rh9 которое является простым
корнем ее характеристического уравнения и превосходит модули
всех других характеристических чисел этой матрицы.
Характеристическая матрица для ЭД$ есть матрица рассматривавшейся в
§ 4, гл. IV системы п* линейных однородных уравнений с п*
неизвестными
S (Vbi -a\r)Ynsi* = 0 (С = /(1\ /(2),..., 1{п\ (7)
из которых при a=i?/t определяются координаты соответствующего
числу Rh собственного вектора Ysih) = (Yc{x)s(hhYci2)sih),... ,7^%*))
матрицы 2$ti. Согласно теореме Перрона, все эти координаты
положительны и Ys(h) > 0.
Пусть R—максимальное из чисел Rh (ft = 1 » 2,..., л*) и пусть им
обладают g (1<£<л*) матриц 31^ (h=hv ft2,... hg), а
следовательно, и g сечений ориентации (s) матрицы Д, с которыми (0,|л)-ассоцииро-
ваны эти матрицы и которые представляются матрицами Л(А) = || Alsih)c \\
(ft = Аь А2,..., hg). Тогда /?, являясь также простым корнем (0, ц,)-
* В дальнейшем число R иногда именуется максимальным (Я,
^-характеристическим числом матрицы А.
138
характеристических уравнений матриц A{h) (A = Alf А2, Ag),
будет g-кратным корнем (X, (х)-характеристического уравнения
матрицы Л, и модули всех других (А,, ц,)-характеристических чисел
будут меньше чем R. Соответствующие числу R собственные
векторы Ysih) матриц 21^ (А = Аь А2,... ,Ав), как указано выше,
положительны. Каждый из них является (0, ^-ассоциированным
вектором с (0, ^-собственной матрицей Yih) = || Y^h) || для A{h) (А =
= Ait Л2,... ,Ag). Матрицы У(Л) (А = Аь А2,..., Л*), имеющие
наименьшее число измерений ц,, являются фундаментальными (0,
несобственными матрицами для A{h) (А = Аь А2,... ,he). Эти матрицы,
составленные из тех же элементов, что и векторы Ysih) (А = Ль
Л2,..., Ag), положительны. Каждая из них представляет сечение
ориентации (s) фундаментальной (X, ^-собственной матрицы Y =
= || Усs || Для Л, соответствующей (л, ^-характеристическому
числу Я матрицы Л. Таким образом, g сечений ориентации (s)
матрицы Y положительны. Остальные же сечения этой ориентации —
нулевые, так как при а = R системам линейных однородных
уравнений (7) при значениях А, отличных от Аь А2 , hg%
соответствуют неособенные матрицы, и, следовательно, эти системы уравнений
имеют только нулевое решение. Теорема доказана.
Спектральные свойства (X, ^-неразложимых неотрицательных
многомерных матриц выражаются следующей теоремой,
обобщающей теорему 5 (см. 181, стр. 74, 75).
Теорема 6- (Общая теорема Фробениуса). Представленная в
виде (1) (X, ^-неразложимая неотрицательная р-мерная матрица
п-го порядка А всегда имеет положительное (X,
^-характеристическое число R, которое является g-кратным (1 < g < nK) корнем
(X, ^-характеристического уравнения этой матрицы. Модули всех
других (X, ^-характеристических чисел не превосходят числа R*.
Вместе с тем R есть простой корень (О, ^-характеристических
уравнений g сечений ориентации (s) матрицы А. Числу R
соответствует неотрицательная фундаментальная (X, ^-собственная
матрица Y = || Yes\\ для А. Положительные элементы матрицы Y
образуют g сечений ориентации (s) этой матрицы, которые
представляют соответствующие числу R фундаментальные (О,
^-собственные матрицы Y{h) = \\Yc8(h)\\ (А = Ах, А2, . . . , Ag) для
упомянутых выше сечений матрицы А.
Если при этом А имеет g рядов (X, ^-характеристических
чисел
<>=£, of) a^ (А==А1,А2,...,Аг)
с одним и тем же модулем R, то все числа каждого ряда различны
между собой и являются корнями соответствующего уравнения
ah — Rdh=0 (А = Л1,А2,...,Л|г).
* См. предыдущую сноску.
139
Вообще весь (X, ц,)-спектр а§\ а[Н), . . . , aJJL^ft = 1, 2, . . . , /i*)
матрицы А состоит из (О, \*)-спектров пк сечений ориентации (s)
матрицы А. Рассматриваемый как система точек в комплексной
а-плоскостщ этот спектр переходит сам в себя при повороте
а-плоскости вокруг точки а = О на угол —?- , тогда как каждый
из упомянутых выше (О, \ь)-спектров переходит сам в себя при по-
2я
вороте плоскости на угол -j- (h = 1, 2, . . . , nk), где dh — число
(О, ^-характеристических чисел h-го сечения ориентации (s)
матрицы А с максимальным модулем Rh, ad — общий наибольший
делитель чисел dlf d2, . . . , dnx. При dh > 1 (ft = 1, 2, . . . , Ф)
перестановкой сечений ориентации (I) и такой же перестановкой
сечений ориентации (с) в каждой из матриц A{h) = || Ais(h)c \\ (ft =
= 1,2,..., /Iх), представляющих сечения ориентации (s) матрицы
А, последняя может быть приведена к такой р-мерной матрице,
для которой диагональные клетки (к, ^-ассоциированной с ней
клетошо-диагональной матрицы являются клеточными матрицами
«циклического* вида:
*&А
i °
0
0
«8>
0
0
0
0 • •
■ff ::
0 . .
0 . .
• 0
; о
• adh—\dh
. 0
(8)
где И{г\ Sfi\ ..., Яб^-1«|Л. ^\ — ненулевые матрицы и все
диагональные нулевые клетки—квадратные матрицы.
В самом деле, если А — (X, (л)-неразложимая неотрицательная
матрица, то 8$£ (А = 1, 2, . . . , п%) — неразложимые
неотрицательные матрицы. Согласно теореме Фробениуса (см. [11, стр. 355),
матрица 91^ имеет положительное характеристическое число Rh9
которое является простым корнем ее характеристического
уравнения и которого не превосходят модули всех других
характеристических чисел этой матрицы. Повторяя те же рассуждения, что и
при доказательстве теоремы 5 настоящей главы, нетрудно
убедиться в справедливости первой части доказываемой теоремы.
В справедливости ее второй части убеждаемся, замечая, что,
согласно той же теореме Фробениуса, характеристические числа
матрицы ЭД^ц с одним и тем же максимальным модулем Rh различны
мезвду собой и являются корнями уравнения
adh-Rdhh = 0,
140
где dh — число этих характеристических чисел, и что спектр
а<А>, а(*>,..., a^ матрицы 31^, рассматриваемый как система
точек в комплексной a-плоскости, переходит сам в себя при пово-
роте этой плоскости вокруг точки a = 0 на угол -j-, а также
h
принимая во внимание, что при dh > 1 матрица ЯЙЙ* может быть
приведена к виду (8) перестановкой рядов, чему соответствуют
однотипные перестановки сечений ориентации (/) и (с) в матрице
Am = \\Ab<fl)e\\.
Спектральные свойства (Я, (А)-неразложимых неотрицательных
многомерных матриц не сохраняются при переходе к (Я,
^-разложимым матрицам, однако в ослабленной форме некоторые из этих
свойств имеют место и для (А,, ц,)-разложимых неотрицательных
многомерных матриц. Для произвольных неотрицательных
многомерных матриц укажем на следующую теорему (см. [81, стр. 76).
Теорема 7. Неотрицательная р-мерная матрица п-го
порядка Л, представленная в виде (1), всегда имеет неотрицательное
(X, ^-характеристическое число R такое, что модули всех других
(X, \л)-характеристических чисел матрицы А не превосходят R.
Вместе с тем R есть корень (Я, ^-характеристических уравнений
g (1 < g < nk) сечений ориентации (s) матрицы Л. Числу R
соответствует неотрицательная фундаментальная (А,,
^-собственная матрица Y = || YcsII для А. В матрице Y nk—g сечений
ориентации (s) целиком состоят из нулей, а остальные g сечений
неотрицательны и представляют соответствующие числу R
фундаментальные (О, ^-собственные матрицы Y{h) = ЦК^^Ц (ft = hlt 1ц, ...
. . . , ftg) для упомянутых выше сечений матрицы А.
Доказательство теоремы проводим аналогично доказательствам
предыдущих теорем, принимая во внимание, что неотрицательная
матрица $fil (Л = 1,2, . . . , пк), как известно (см. [11, стр. 365),
всегда имеет неотрицательное характеристическое число Rht
которого не превосходят модули всех других ее характеристических
чисел и которому соответствует отличный от нуля собственный
вектор Ysw = (Yc(\)s(h)9 Yc<2)s(h), . . . , Yc(n^)s{h)) с
неотрицательными координатами.
Замечание 1. Составляя суммы элементов каждой строки
неотрицательной матрицы 3to!»i» т. е. суммы элементов каждого
сечения ориентации (/) матрицы Л(/1), и обозначая наибольшую из
этих сумм через Vh, а наименьшую через vhi можем, как известно
(см. [11, стр. 362, 366), установить границы для величины
максимального характеристического числа Rh матрицы 3$£, а именно
vh<Rk<Vb (А = 1,2,...,Л
откуда заключаем, что максимальное (Я, (х)-характеристическое
число R неотрицательной матрицы Л, являющееся максимальным
141
из чисел Rh (ft = 1, 2, . . . , rfi), содержится в границах
v<R<V (9)
где V — максимальное из чисел Vhi a v — минимальное из чисел
vh (ft = 1, 2, . . . , Ф).
Замечание 2. Для максимального (А,, (л)-характеристического
числа R положительной матрицы А можно указать интервал более
узкий, чем (9). Сохраняя прежние обозначения Rh, Vh, vh в случае,
когда матрица 31^ положительна, обозначим через Nh
минимальный элемент положительной матрицы 91сч1 и положим
Тогда, согласно неравенствам Островского (см. [17], стр. 254),
получим
vh + (±-l)jNH<RH<VH-(\- kh)Nh (A = 1, 2,... Л
откуда
w < R < Wy
где W — максимальное из чисел Vh — (1—kh)Nh> a
w—минимальное из чисел иЛ— (j )\Nh (ft = 1, 2,..., rf).
Будем называть нормальной формой полностью (X,
^-разложимой неотрицательной /7-мерной матрицы n-го порядка Л,
представленной в виде (1), ту форму, которую она принимает при
однотипных перестановках ее сечений ориентации (/) и (с),
соответствующих перестановкам рядов в матрицах ЯГоЩ (ft = 1, 2, ... , л*),
приводящим последние к нормальным формам (см. [1],- стр. 373):
■&-
«}*>
О
о
«I»
e£w «ffw
vh2
О
О
К
о
о
«3U <V,
•&
«&н
О
о
о
о
(10)
, 93^ — квадратные
неразложимые матрицы, а
где»?», SSf...
в каждом ряду
по крайней мере одна из матриц — ненулевая.
Иначе говоря, нормальной формой матрицы А является р-мер-
<^»
ная матрица л-го порядка Л, с которой (X, ^-ассоциирована ма-
*& »&»-, («*='*+! <Ъ>
142
трица
X,|i I 0,|i» 0.Ц* • # # • O.JA /"
Пользуясь нормальной формой полностью (X, ^-разложимой
неотрицательной матрицы А, отметим спектральное свойство этой
матрицы, выражаемое следующей теоремой.
Теорема 8. Максимальному (X, ^-характеристическому числу
R матрицы А, являющемусяg-кратным (1 < g < nk) корнем (X, \i)-
характеристического уравнения этой*матрицы, соответствует не-
отрицательная фундаментальная (А,, ^-собственная матрица Y =
= \\YCS\\ с положительными g сечениями ориентации (s) в том и
только в.том случае, когда в нормальных формах (10) матриц
ЭДола (й = hl9 h2, . . . , hg), имеюших одно и то же максимальное
характеристическое число R, каждая из матриц 93 [Л), ЯЙЛ), • • .
. . . , 95^ имеет число R своим характеристическим числом и (при
h < vh) ни одня и3 матриц 8/*!,,.. . , 93£*} этим свойством не
обладает.
В справедливости теоремы легко убеждаемся, замечая, что
элементы g сечений ориентации (s) матрицы Y = \\YCS\\ являются также
координатами собственных векторов Ysih) = (УС(1)8(Л), Yc(2)s(h), . . .
. . . , Yc(nfl)s(h)) матриц 2$£ (h = 1ц, 1ц, . . . , hg), имеющих одно
и то же максимальное характеристическое число R, а эти векторы,
как известно (см. [II, стр. 374), положительны, если выполняются
условия теоремы. Остальные же сечения ориентации (s) матрицы
Y = || Ycs || нулевые, поскольку при а = R системы линейных
однородных уравнений (7) имеют только нулевое решение, если
h отлично от /*х, А2, . . . , ftg.
Путем аналогичных рассуждений на основании известной
теоремы (см. [1], стр. 376), дающей характеристику неотрицательной
квадратной матрицы, которая вместе со своей транспонированной
матрицей обладает тем свойством, что максимальному
характеристическому числу отвечает положительный собственный вектор,
доказывается следующая теорема.
Теорема 0. Максимальному (X, ^-характеристическому
числу R полностью (X, \i)-разложимой неотрицательной матрицы
А = || AlsC ||, которое является g-кратным (1 < g < nk) корнем
(X, ^-характеристического уравнения этой матрицы, отвечает
неотрицательная фундаментальная (X, ^-собственная матрица
Y = || Ycs || с положительными g сечениями ориентации (s) для А
и такого же типа фундаментальная (X, ^-собственная матрица
для транспонированной относительно А соответственно
подстановке (I, с) матрицы А(1'с) в том и только в том случае, когда
матрица А однотипными перестановками сечений ориентации (/) и
(с) может быть приведена к форме, с которой (X, ^-ассоциирована
клеточно-диагональная матрица
{«I0 «SJ>. «Р.....«» ef"\.... «Sjb
143
где Sj*. 3S£ft),.... »|*f (Л -■= 1, 2,... ,пХ)-квадратные неразложимые
матрицы, каждая из которых имеет число R своим максимальным
характеристическим числом.
Отсюда вытекает очевидное следствие.
Следствие. Если максимальное (X,
^-характеристическое число R неотрицательной матрицы А = || AlsC ||, которое
является g-кратным (1 < g < nk) корнем (А,, (х)-характеристического
уравнения этой матрицы, будет простым корнем (0,
^-характеристических уравнений g сечений ориентации (s) матрицы А и ему
отвечает неотрицательная фундаментальная (Я, ^-собственная
матрица Y = || YC81| с положительными g сечениями ориентации (s)
для А и такого же типа фундаментальная (X, ^-собственная
матрица для транспонированной относительно А соответственно
подстановке (/, с) матрицы А{1,с), то А есть (А,, ^-неразложимая
матрица.
Поскольку, обратно, всякая (А,, (л)-неразложимая
неотрицательная р-мерная матрица обладает свойствами, указанными в
этом следствии, то эти свойства представляют собой спектральную
характеристику такого рода матриц.
Особую разновидность неотрицательных многомерных матриц
представляют (X, \i)-стохастические матрицы, определяемые
следующим образом.
Представленная в виде (1) р-мерная матрица л-го порядка А
называется (А,, ^-стохастической, если она неотрицательна и
сумма элементов каждого ее сечения ориентации (Is) равна единице.
Отметим некоторые специфические свойства (А,,
^-стохастических матриц (см. [8], стр. 78).
Теорема 10. Неотрицательная р-мерная матрица п-го
порядка А, представленная в виде (1), тогда и только тогда будет (X, ц,)-
стохастичрской, когда она имеет фундаментальную (Х9
^-собственную матрицу, все элементы которой равны единице, при
максимальном (X, ^-характеристическом числе 1 кратности не менее
пк, являющемся также простым или кратным максимальным (О, ц,)-
характеристическим числом каждого сечения ориентации (s)
матрицы А.
В самом деле, согласно определению, матрица А будет (X, \i)-
стохастической лишь при соблюдении условий
с'
(п»)
Аф)с > 0 £ Alsih)c = !(/ = /(1\ /(2\ ..., Г\ с = cil), с
...,с<Л А=1,2, .А
когда каждая из матриц 9fо?Д (Л = 1, 2, . . . , пк) стохастическая.
Необходимое и достаточное условие для этого состоит, как
известно (см. [1], стр. 381, 382), в существовании собственных
векторов Ysih) = (У^^л), Y&wh) *V*)s(/t>) c координатами,
144
равными единице, при характеристическом числе 1, которое
является максимальным для стохастических матриц 9$^ (А =
= 1, 2, . . . , /г*). Повторяя далее те же рассуждения, как и при
доказательстве теоремы 5, легко убеждаемся в справедливости
теоремы 10.
Поскольку (Х9 ц,)-характеристические числа и соответствующие
им (А,, |д,)-элементарные делители /7-мерной матрицы я-го порядка
А получаются объединением характеристических чисел и
соответствующих им элементарных делителей матриц Ж$%, (h = I, 2, . . .
. . . , /г*), а также поскольку характеристическому числу 1
стохастической матрицы Stcui, как и всякому ее характеристическому
числу с модулем 1, всегда соответствуют только элементарные
делители первой степени (см. [1], стр. 383), то, очевидно, иадеет место
следующая теорема.
Теорема 11. (К [^-характеристическому числу 1 (X,
[^-стохастической матрицы, как и всякому ее (А,
[^-характеристическому числу с модулем 1, всегда соответствуют только (X,
^-элементарные делители первой степени.
10-595
ГЛАВА VIII
КВАЗИСПЕКТРАЛЬНЫЕ СВОЙСТВА МАТРИЦ
§ 1. КВАЗИСПЕКТРАЛЬНЫЕ СВОЙСТВА КВАДРАТНОЙ МАТРИЦЫ*
Возьмем квадратную матрицу /1-го порядка А =||Л^|| (if j ==»
= 1, 2, . • . , п) над некоторым числовым полем Р и отличный от
нуля вектор х = (хъ хг, . . . , хп) с координатами Хь х^ . . . , хп
из поля Р. Как известно, спектр матрицы А определяется из
соотношения
Ах = аЕ(0Л)х, (1)
где Е (0, 1) — обычная единичная матрица порядка п. Заменим
матрицу Е (0, 1) в равенстве (1) (2, 0)-единичной матрицей E (2, 0)
того же порядка к, все элементы которой равны единице. Получим
соотношение
ut = a£(2,0)x, (2)
определяющее квазиспектр (т. е. квазихарактеристическое число
a(zP и соответствующий квазисобственный вектор х Ф 0)
матрицы А.
Перепишем соотношение (2) в виде
(А— аЕ(2,0))* = 0. (3)
Матрица А :— а£ (2, 0), которая умножается на
квазисобственный вектор х, называется квазихарактеристической матрицей для
А. Приравнивая нулю координаты вектора, стоящего в левой
части равенства (3), будем иметь для определения координат
квазисобственного вектора х систему скалярных уравнений
£(4, —а)*, = 0 (* = 1.2,...,п). (4)
Так как х Ф 0, то среди координат хъ хъ . . . , хп по крайней
мере одна координата должна быть отличной от нуля.
Необходимым и достаточным условием для этого является равенство нулю
детерминанта
Д(а) = |Л„-а| С/ =1,2.. ,,п) (5)
системы линейных однородных уравнений (4).
* См. [9, стр. 67].
146
Квазихарактеристическое число а матрицы А определяется
таким образом из уравнения
Д(а) = 0, (в)
называемого квазихарактеристическим уравнением матрицы А.
Элементарными преобразованиями детерминант (5) приводится
к виду
Д(<х) = Д — аД', (7)
где
Д = |АЛ (*',/= 1,2,...,л), (8)
Д' = И*Л (i\/ = l,2,...,/i-l), (9)
причем элементы детерминанта (9) определяются по формулам
\Ai+U AH-i/+i{
(i,y=l,2,...,n—1).
Следовательно, квазихарактеристическое уравнение (6) равно*
сильно уравнению
Д — аД' = 0,
откуда, если А' Ф О, находим
а = А (10)
д
Как известно (см. [15], стр. 97, 98; [111, стр. 261),
А'= S4, (И)
*./-!
где А*ц — алгебраическое дополнение элемента Ац (i, ] — 1, 2, . . .,
• . . , п) в детерминанте (8). Таким образом, неравенство нулю
суммы элементов матрицы Л* == ЦЛ//Ц (f, / = 1, 2, . . . , п)
является необходимым и достаточным условием существования
определенного конечного квазихарактеристического числа а матрицы
Л, которому соответствует ненулевое решение системы уравнений
(4), определяющее квазисобственный вектор х = (хъ х2, . . . , хп)
матрицы А с точностью до скалярного множителя. Будем говорить
в этом случае, что А есть матрица с квазиспектром.
Замечание. Для неособенной матрицы А формула (10), очевидно,
может быть представлена в ввде
1
а =
24Г°
10« 147
где A^ifl) (i, / =* 1,2,...', ft) — элементы обратной матрицы Л""1 для А.
Булем называть матрицу А = || Аи \\ (i, / = Ц 2,..., п) квази-
стохастинеской S-матрицей, если
£^ = S(i = l,2,...,n), (12)
тде S — некоторое число из поля Р.
При S = 1 будем называть А просто квазистохастической
матрицей. Неотрицательная квазистохастическая матрица, очевидно,
является стохастической.
Теорема /. Квадратная матрица п-го порядка А с
квазиспектром тогда и только тогда является квазистохастической S-мат^
рицей, когда она имеет квазисобственный вектор (1,, 1, . . . , 1)
при квазихарактеристическом числе —.
Достаточность условия теоремы вытекает непосредственно из
системы уравнений (4). Докажем его необходимость.
Пусть А = || A{j\\ (iy j = 1, 2, . . . , п) — квазистохастическая
5-матрица, имеющая определенное конечное
квазихарактеристическое число а. Тогда детерминант Д', определяемый равенством
(9), отличен от нуля. Для детерминанта (8) имеем
п
SA А* ( Д если й = / ..
AnAik = \ / (/ = 1.2,. ...л; 1<&<л).
(О, если кф\
Отсюда, ввиду соотношений (12), следует
A-SJJ^ (/=1.2,. ...я).
Суммируя последние п равенств, находим
откуда, вследствие равенств (И), получаем
А— А
Д' "~ п
(13)
или, на основании формулы (10),
S
а = —
п
При определении квазисобственного вектора х матрицы Л,
соответствующего квазихарактеристическому числу а = —, будем
Ту
ш
различать два случая, в зависимости от того, будет ли S ф О или
5 = 0.
Случай I, когда S Ф 0. Тогда вследствие соотношения
(13) А Ф 0. Переписывая систему уравнений (4) в виде
So
£ЛЛ= — (*' = 1,2, ...,л),
/-=1
п
где а = ][] *j, и полагая
.А...
А« =
•щ
•Л 1-1 1 ^•+Г,,Ал
•A2i-\ l Л t+i • • • А2п
•К 1-х * Ait+i1
(И)
(15)
находим ненулевое решение системы уравнений (14):
SaA.
* = -ST (t = l,2,...,n). (16)
Заменим /-й столбец в детерминанте (15) равным ему столбцом
элементов ■$]£ Au (i = 1,2,... ,п), из которых затем вычтем ум-
/=1i
ноженные на -^ соответственные элементы всех остальных
столбцов. В результате получим
Д< = S" ^ = 1>2'--->Л)>
вследствие чего выражения (16) примут ввд
*i = -j (* = 1.2, ...,л),
(17)
откуда вытекает, что
Xi Хо . .
Таким образом, квазисобственный вектор х Ф 0 матрицы А,
определяемый с точностью до скалярного множителя, равен (1, 1, ...
. . . , 1).
Случай II, когда 5=0. Тогда, вследствие
соотношения (13), А = 0 и система уравнений (4) принимает вид
^rt = 0(i = l,2 п).
/-1
(18)
149
Так как Л' Ф 0, то вследствие равенства (11) по крайней мере
один из элементов матрицы А* отличен от нуля.
Пусть
АмфО (1<й<л, 1</<и).
Переписывая тогда уравнения (18) в виде
(/>*)£ А<& = 0 (i = 1,2,..., л), (19)
где
£/ = */ — ** (/ = 1.2, &— 1.Л+ 1 п),
видим, что система линейных однородных уравнений (19) имеет
только нулевое решение
|; = 0 (/=1,2,...,*—1,*+1,...,я).
Следовательно, система уравнений (18) допускает ненулевое
решение
*1 == «^2 == • • • = *Л
и матрица Л имеет квазисобственный вектор (1, 1, . . . , 1).
Теорема 2. Если неособенная квадратная матрица п-го
порядка А с квазиспектром является квазистохастической S-матри-
цей, то обратная ей матрица Л""1 = || A{[fl) || (i, / = 1, 2, . . . , п)
будет квазистохастической STX-матрицей.
Действительно, при выполнении условия теоремы из
соотношения (13) вытекает, что S Ф 0 и, следовательно, имеют место
равенства (16). С другой стороны, разлагая детерминант (15) по i-му
столбцу, находим
п
А'= %A*ti (i=l,2,...,/i),
вследствие чего равенства (16) принимают вид
п
** = т£4Г° (* = 1,2,...,п). (20)
Сравнивая выражения (17) и (20), получаем
jMir^S-* (t = l,2....,/i).
Следовательно, согласно определению, А"1— квазистохастическая
Я^-матрица.
В частном случае, когда S = 1, из теорем 1 и 2 вытекают оче«
видные следствия.
150
Следствие 1. Неотрицательная квадратная матрица п-го
порядка А с квазиспектром тогда и только тогда будет
стохастической, когда она имеет квазисобственный вектор (1, 1, . . . f 1)
при квазихарактеристическом числе —.
Следствие 2. Если неособенная квадратная матрица А
с квазиспектром является квазистохастической (или дважды
квазистохастической*), то обратная ей матрица Л""1—также квази-
Сгохастическая (или дважды квазистохастическая).
Квазихарактеристическую матрицу А — аЕ (2, 0) для А
можем рассматривать как пучок квадратных матриц, заданный с
помощью параметра а. Пусть г < п — ранг этого пучка, т. е.
наибольший и<* порядков миноров, не равных тождественно нулю.
Согласно общепринятой терминологии (см. [11, стр. 332), пучок
А — аЕ (2, 0) будет регулярным при г = п и сингулярным —
при г < п.
Как легко убедиться, пучок А — аЕ (2, 0) строго эквивалентен
в поле Р одному и только одному из следующих четырех
канонических клеточно-диагональных пучков:
п г Г~Х
Л-Г , ,
{я —г [О, 1, ..,Ь а—а} (I)
с «конечным» элементарным делителем а — а, где а£Р —
квазихарактеристическое число неединичного базиса «ядра» пучка А—
— аЕ (2.0) (т. е. подматрицы порядка г этого пучка матриц) с «бесконе-
чными» элементарными делителями р,... , Р и минимальными
индексами 8/ = 0 (у = 1,2,... ,п — г) для столбцов ить = 0(1'=:
= 1,2,... ,я — г) для строк;
jn-riar М, 1 ll (ii)
с «бесконечными» элементарными делителями р*, Р, ...,Р и теми же
минимальными индексами, что у пучка (I);
{п—г . ( г~х ц
я-МО.Р] 1 И (1И)
г—1
1 I
с «бесконечными» элементарными делителями Р,..., Р и
минимальными индексами ej = 0 (/ = 1,2,..., п — г) для столбцов и тц =
= 0 (/=1,2, . .,л — г— 1), V.r=l Для строк;
{п-г [О, (а 1), 1 1) (IV)
* Т. е. имеющей сумму элементов каждого столбца, так же, как и сумму
•лементов каждой строки, равную единице.
15!
♦
с теми же элементарными делителями, что у пучка (III) и
минимальными индексами
в/.= 0 (/ = 1, 2, . . . , п — г — 1), ert__r = 1 для столбцов и
r\t = 0 (i = 1, 2, . . . , п — г) для строк.
Будем называть квадратные матрицы п-го порядка А и В ква-
зистохастически эквивалентными над полем Я, если существуют
неособенные квазистохастические матрицы п-го порядка U к V над
Р такие, что
B = UAV, (21)
где V — транспонированная матрица относительно V.
Теорема 3. Квадратные матрицы п-го порядка А и В тогда
и только тогда квазистохастически эквивалентны над полем Р,
когда пучки матриц А — аЕ (2, 0) и В — аЕ (2, 0) имеют одни
и те же («конечные» и «бесконечные») элементарные делители в поле
Р и, если они сингулярные, одни и те же минимальные индексы.
В самом деле, пусть матрицы А и В квазистохастически
эквивалентны над Р, т. е. имеет место соотношение (21). Тогда
В— аЕ(2. 0) = UAV — аЕ (2,0)
и так как
E{2,0) = UE{2t0)V't
то
В — аЕ (2,0) = U (Л — аЕ (2,0)) V.
Следовательно, пучки А — аЕ (2, 0) и В — аЕ (2, 0) строго
эквивалентны над Р и потому, согласно теоремам Вейерштрасса
и Кронекера, имеют одни и те же («конечные» и «бесконечные»)
элементарные делители в поле Р и, если они сингулярные, одни
и те же минимальные индексы.
Наоборот, если выполняются условия теоремы, то пучки А —
— а Е (2, 0) и В — аЕ (2, 0) строго, эквивалентны над Р, т. е.
существуют независящие от параметра ,а неособенные квадратные
матрицы п-го порядка
u = \\uu\\*o = \\vu\\ (*,/ = lf2f...,n)
такие, что
В — аЕ (2,0) = и {А — аЕ (2,0)) v\ (22)
где v' — транспонированная матрица относительно v.
Из соотношения (22) имеем
В = uAv\ Е (2, 0) = иЕ (2.0) v'. (23)
Полагая
п п
si = 2 «у. U = 2 ^ (' = 1.2,... .л),
/=l /-1
можем переписать последнее из равенств (23) в виде
£(2,0) = ||s^|| (*,/=!,2,...,/г),
152
откуда следует, что
si==S (i = 1,2, п\ tj
г-i
(/=1,2. ..,я),
где S — некоторое число из поля Р, отличное от нуля.
Представляя теперь первое из равенств (23) в виде
В = S-{uAv'S
и замечая, что матрицы S~lu = U, Sv = V квазистохастические,
приходим к равенству (21). Следовательно, матрицы А и В ква-
зистохастически эквивалентны над Р.
Принимая во внимание указанные выше канонические виды
(I) — (IV) пучка матриц А — аЕ (2, 0), легко установить на
основании теоремы 3, что квадратная матрица я-го порядка Л,
являющаяся одним из базисов пучка А — аЕ (2, 0), ранг которого г < я,
квазистохастически эквивалентна над Р своей квазинормальной
форме У, представимой в одном из следующих клеточно-диагональ-
ных (или диагональных) видов:
**№
i i
i.-i.(-i)2
.<-.>!И-
а а...а
a b...b
ка b...b;
(П
(где аф0, Ь = у + (— 1)г~у) , если пучок А — аЕ(2,0) имеет
«конечный» элементарный делитель а — а и «бесконечные» элемен-
г-1
I I
тарные делители р,..., р а также минимальные индексы е7- — 0
(/== 1,2 л — г) для столбцов и r\i = 0(i = 1,2,... ,я—г) для
строк;
п—г+1
{1,-1д-1)2,...,(-1Г2, о 0}, (in
если пучок А — а£(2,0) имеет «конечный» элементарный делитель
т—\
а, и «бесконечные» элементарные делители р,
мальные индексы, как и в случае (Г);
,Р и те же мини-
—1г]+"
U-D2.
(ПГ)
153
(где е = -% + (— 1)г-^), если пучок А — а£ (2, 0) имеет «бесконеч-
г—2
ные» элементарные делители р2, р,..., р и те же минимальные
индексы, как и в предыдущих случаях;
п—г+Х
г
1
г—1
1... ,1,1
,1 1...Ц
0 0...0
Ч) 0...0>
(IV')
если пучок А — аЕ (2, 0) имеет «бесконечные» элементарные делите-
1 i
ли р,..., р и минимальные индексы в/ = 0 (/ = 1, 2,.. , л—г) для
столбцов и r\i = 0 (i = 1, 2,..., л —г — 1), т^_, = 1 для строк;
п— г+1
(V)
1 0... 0>
если пучок Л — аЕ (2, 0) имеет те же элементарные делители, как
и в случае (IV), и минимальные индексы р; = 0 (/ = 1, 2,..., л—
— г— 1), ert_r = 1 для столбцов и i\i = 0(i = 1,2,..., л—г) для
строк.
Квазинормальная форма / может быть рассматриваема как
представитель класса К матриц, квазистохастически
эквивалентных матрице А.
Будем говорить, что квадратные матрицы л-го порядка А
и В квазистохастически (точнее: дважды квазистохастически)
подобны над полем Р, если существует неособенная дважды
квазистохастическая матрица п-го порядка W над Р такая, что
В = WAW
-i
(24)
где W~~ — обратная матрица для W.
Теорема 4. Квадратные матрицы п-го порядка А и В тогда
и только тогда квазистохастически подобны над полем Р, когда
они обладают одними и теми же элементарными делителями в
поле Р и когда при этом пучки матриц А — <х£ (2, 0) и В —
— аЕ (2, 0) имеют одни и те же («конечные* и «бесконечные») эле-
*54
ментарные делители и, если они сингулярные, одни и те же
минимальные индексы.
Действительно, квазистохастически подобные матрицы Л и В,
согласно определению, являются одновременно подобными и
квазистохастически эквивалентными, так как W~~l по следствию 2
одновременно с W будет дважды квазистохастической матрицей
и потому соотношение (24) представляет частный случай
соотношения (21). Для подобия же матриц Л и В, как известно, необходимо
и достаточно, чтобы их элементарные делители в поле Р были одни
и те же, тогда как для квазистохастической эквивалентности
матриц А и 5, согласно теореме 3, необходимо и достаточно, чтобы
пучки А — аЕ (2, 0) и В — аЕ (2, 0) имели' одни и те же
(«конечные» и «бесконечные») элементарные делители в поле Р и, если
они сингулярные, одни и те же минимальные индексы.
На основании теоремы 4 заключаем, что квадратная матрица
я-го порядка Л, являющаяся общим базисом пучков Л — аЕ (2, 0)
и Л —аЕ (0, 1), квазистохастически подобна над Р той же
квазинормальной форме /, представленной в одном из ввдов (Г) — (V'),
если пучок Л — аЕ(29 0) ранга г < п имеет, соответствующие этому
виду элементарные делители и минимальные индексы, указанные
выше для пучков I — IV, а элементарные делители матрицы Л
те же, что у матрицы J*, т. е.
г—2 г—2
__2 2
а — 1,,..,а— 1, а+ 1, ...,а+ 1,
п—г
, I 1
— У 4 (п— г) + 5), а,..., а (при г четном)
или
г—1 г—1
2 2
1 i i i
а— 1,... ,а— 1,а+1,...,а + 1, а —
п—г
1 1
— (п—г+ 1)а, а,... ,а (приг нечетном)
а— 1,..., а — 1, а + 1,..., а + 1, а,..., а в случае (ПО;
* Предполагается, что поле Р содержит не только элементы матрицы /,
ко и все характеристические числа ее.
!»•
[ в случае (Г);
155
г—2
2
а— 1,... ,<х— 1, а+ 1,... ,а + 1, а-
п—г
I I
— (л — г + 1), а,. ., а (при г четном)
или
г—г
2
г—1
2
а — 1,... ,а— 1, а+ 1,... ,а+ 1, а —
-1(1 + У*(п-г) + 5), а-1(1-
— J/ 4 (п — г)+5), а,... ,а (при г нечетном)
в случае (НГ);
п—т
I 1
а— 1,...,а — 1, а,. .,ав случаях (IV), (V').
Таблица 1
Порядок
матриц
п
2
J
\ а а \
1 а 0 |
{ОфаеР)
1 1 0 1
0 0
1—1 0
0 1
\ а а \
(аеР)
111
| 0 0 |
1 1 0
10
J-aE(2,0)
Ранг
г
2
2
2
1
1
1
Элементарные
делители
а—а, Р
а, (3
р*
а—а
—
—
Минимальные
индексы
—
—
—
8l=0, tj1=0
8l=0, Tl^l
8!=!, % —0
Элементарные делители
матрицы
о*
J
а—г(/5 + 1),
а—1, а
а—1, а+1
а—2а, а
а—1, а
а—1, а
156
Таблица II
Порядок
матриц
п
3
1
J
11 0 0 II
0—10
1 0 0 a I
(а£Р)
I —1 0 0 II
0 11
1 0 1 0 ||
а а а II
а 0 0
1 а ° ° 1
(Офа £ Р)
1 10 0 ||
0 0 0
1 ° ° ° 1
II —1 0 0 1
0 11
II ° * l I
I] 10 0 1
0 11
II ооо J
II 10 0 |
0 10
|| 0 10 J
|| а а а 1
а а а
а а а
(а£Р)
II 111 I
0 0 0
II 0 0 0 |
11 10 0 |
10 0
|| 1 0 0 |
Х-аЯ(2,0) _|
Ранг
1 r I
3
3
2
2
2
2
2
1
1
1
Элементарные
делители |
а—а,
Р. Р
Р2. Р
а—а, Р :
а. Р
Р*
Р
Р
а—а
—
—
Минимальные
индексы J
—
—
ег=0,
ти=0
ei=0,
8i=0,
8!=0,
81= Ь
Tii=0
61=62=0,
81=82=0,
^ = 0,^=1
8!=0, 82=Ь
Т11=Л2=0
Элементарные делители 1
матрицы I
/>* 1
а—1, а+1, а—а
а+1, а~т(|/5+1),
а—-2а, а+а, а
а—1, а, а
| а—2, а+1, а
а—1, а—1, а
а—1, а—1, а
а—За, а, а
а—1, а, а
а—1, а, а
157
Таблица III
Порядок I
матриц 1
1 п 1
4
I
J
1 1 000 II
0—100
[о Оаа
1 0 ОаО II
(ОфаеР)
1—10 0 Oil
01 0 0
0 0—10
1 00 0111
1 1 00 0 ||
0—100
0 0 10
II ° 00° II
1 * 00° II
0—100
0 Оаа
У 0 Оаа II
(аеР)
|| — 1 000 1
0 111
0100
(J 0 1 0 01
|| 1 0 0 0 1
0 10 0
0 0 11
|| 0 0 0 0 |
|| 1 0 0 0 |
0 10 0
0 0 10
|| 0 0 1 0 |
1 7-аЕ<2,0) |
Ранг 1
г 1
4
4
4
3
3
3
3
Элемечтар-1
ные I
делители |
а—а,
Р. Р. Р
Р*, Р. Р
а, Р,
р. р
а—а,
р. р
р*. р
р. р
р. р
Мвнималь- 1
ные I
индексы 1
—
—
8х=0,
8i=0,
щ«0
б!=0,
111=1
8i=l,
Элементарные делители I
матрицы I
**** 1
J |
а—1, а+1, I
*—Y(Vb +1)
а+у(К5 - 1)
а—1, а—1, а+1, а+1
а—1, а—1, а, а+1
а—1, а+1, а—2а, а
а—2, а+1, а+1, а
а—1, а—1, а—1, а
а—1, а—1, а—1, а
158
Продолжение табл. Ill
Порядок 1
матриц I
п I
4
*>*
J
а а а а
\ а 0 0 0
\\ а 0 0 0
1 а 0 0 0 ||
(О^аеР)
|| 1 0 0 0 11
0 0 0 0
0 0 0 0
|| 0 0 0 0 ||
II —1000||
0 111
0 111
| 0 1 1 11|
II 1 0 0 0 II
0 111
0 0 0 0
|| 0 0 0 0 |
|| 1 0 0 0 II
0 10 0
0 10 0
|| 0 1 0 0 |
|| а а а а |
11 а а а а 1
а а а а
а а а в
(аеР)
|| 1 1 1 1 [
0 0 0 0
0 0 0 0
I 0 0 0 0 |
1 7--а£(2,0)
Ранг
1 г
2
2
2
2
2
"1
1
Элементарные
делители
ос—а, р,!
а» р
Р*
Р
Р
а—а
—
Минимальные
индексы
е1=82=0,
К|1==1Г|2=0
е1=82=0,
%=112=0
81=82=s0,
11l=1l2=0
е1==е2=0,
4i=0, Л2=1
е^О, еа=Ь
111=112=0
81=82=?8s=0»
1 'П1=,П2=
=TJ8=0
81=82=
=83=0,
Л1=т|2==о,
Т1з=1
Элементарные делители 1
матрицы
J
a—5-(KT3"+l),
о+-|-оаз"-1),
ОС» ОС
ОС—1, ОС, ОС» ОС
ос—3, ос» ос» ос4-1 1
ос—1» ос—1» ос» ос 1
ос—1, ос—1» ос» ос 1
ос—4а, а» а» а
ос—1» ос» ос» ос
150
Продолжение таблицы III
Порядок
матриц
п
4
J
II 1 0 0 0 II
10 0 0
10 0 0
1 1 о о о II
| 7— а£(2,0)
Ранг
1 г
1
Элементарные
делители
—
Минимальные
индексы
81=82=0,
е3=1,
41=112=
=Лз=0
Элементарные делители 1
матрицы 1
J
СС—'1 у СС, 06 » СС 1
Таким образом, при указанных выше условиях
квазинормальную форму / можно рассматривать как представителя матриц,
квазистохастически подобных матрице А и образующих в своей
совокупности пересечение К (] Кг класса К матриц,
квазистохастически эквивалентных матрице Л, и класса К\ матриц, подобных матри-
це А. В табл. I — III указаны представители J классов
квазистохастически эквивалентных (или их подклассов квазистохастически
подобных) матриц порядков 2,3,4.
Пользуясь таблицами (I—III), можно определить, какому классу
квазистохастически эквивалентных (или подклассу
квазистохастически подобных) матриц принадлежит данная матрица А порядка
п<4.
Примеры.
1. Дана матрица
Пучок матриц
Л —а£(2,0) =
А\
J1 — 1 — 1
1—2—2
0 2 1
|1 —1 —1
11 — а — 1 — а
1 — а —2 —а
— а 2 — а
|1— а
— 1—а
— 1 1
— 1
1
0
•
— 1—а
— 2 —а
1—а
— 1
— а
— 1—а
— 1—а
1 -а
— а
ранг которого равен 4, строго эквивалентен пучку
{1, 1.1.06-1}
и имеет элементарные делители
а-1,р,р,р.
160
1
0
0
0
0 0 01
— 1 0 0 |
Oil
0 101
Из табл. III видим, что теми же элементарными делителями обладает пу-
чок / — а£ (2,0), где
/==
причем элементарные делители матрицы /
а —1. а+1, а-уО/5+1), а + ^О^-!)
отличаются от элементарных делителей матрицы А% так как ни один из них
не является делителем характеристического полинома этой матрицы,
имеющего вид
1_а_1 _i __i
|Л-а£(0,1)| =
1 —2 —а —2 —1
0 2 1—а 1
1 —1 —1 —а
а4 + 3а2 — 2а+1.
Следовательно, матрица А квазистохастически эквивалентна своей
квазинормальной форме
II 0 0 01
/ =
0 —1 0 0
0 0 11
|о о 1 о I
Это подтверждается также равенством
vaV = 7,
где квазистохастические матрицы U, V имеют вид
U:
2. Дана матрица
1
0
0
0
— 1 0
11
1 1 — ll
0 1 0
0 0 1]
л =
2
3
4
3
2
3
1
3
• V =
2
3
2
""3
1
~~ 3
1
3 ~
1 0
1 —1
0—1 1 1
0 0—1 2
10 0 0 1
0 1
1 —1
0 —1
1 1
Ц-595
161
Пучок матриц
А — аЕ (2,0)
у —а з"—а —а
1 —а
2^
3
4 2
"о" — а —*о" —а 1—а —1—а
~о"—а —"о" — а —а — 1 — а
т~а
-%-— а —1 —а 1«— а
ранг которого равен 4, строго эквивалентен пучку
{l.l.l.a-l}.
имеющему те же элементарные делители
ех-1,р,р,р,
что и пучок /—аЕ (2,0), где
" ] 1 0 0 0
J =
0—100
0 0 11
0 0 10
Для характеристического полинома матрицы А находим выражение
2
3 "
4
3
2
3
1
3
-а
2
3
2
~ 3
1
~ 3
1
3
— а
0
1
а
.1
1
— 1
— 1
1—а
,а*_ аз_ 2а2 + а+ 1
= (а-1)(а+1)[а-у(1^5+1)][а + у(/5-1)"|,
откуда видим, что элементарные делители матрицы А те же, что у матрицы /.
Следовательно, матрица А квазистохастически подобна своей
квазинормальной форме
0 0 0
«100
0 1 1
0 1 0
162
Это подтверждается также равенством
WAW~X = 7,
где дважды квазистохастическая матрица W и обратная ей матрица W~~~{ имеют
вид
W =
1
— 1
0
1 -
0 1 —1
1 0 1
1 —1 1
-1 1 0
w~l =
1
3
2
3
1
3
1
3
1
-~т
1
3
2
3
1
3
2
3
1
3
1
~~ 3
1
3
1
3
1
""3
1
3
2
3
§ 2. КВАЗИСПЕКТРАЛЬНЫЕ СВОЙСТВА МНОГОМЕРНЫХ МАТРИЦ *
Полученные в § 1, гл. VIII результаты распространим на
многомерные матрицы.
Возьмем р-мерную (р > 2) матрицу n-го порядка А над Р,
представленную в виде
i» = ||iM. (25)
где каждый из индексов разбиений
/ = (/р /2» • • • > У» 5 = (Sp S2« . . , SjJ, С = (Cj, Cg, • • . , Сц )
пробегает значения 1,2,..., л.
Пусть У = || Yes || — ненулевая матрица К + |л измерений и
порядка п, удовлетворяющая соотношению
к*(АУ) = к*(оЕ{р,0)У),
(26)
где а£Р и Е (р, 0) есть (р, 0)-единичная /7-мерная матрица порядка
/г, все элементы которой равны единице. Матрица Y называется
фундаментальной (Я, [1)-квазисобственной матрицей для А,
соответствующей (X, \л)-квазихарактеристическому числу а.
Перепишем соотношение (26) в виде
^[(Л-а£(р,0))Г]=О,
(27)
где О — нулевая матрица Я + \i измерений и порядка п. Матрица
А — аЕ (р, 0) называется (X, \ь)-квазихарактеристической матрицей
для Л. Принимая во внимание правило составления (Я,
^-свернутого произведения многомерных матриц, находим из соотношения
* См. [9], стр. 75.
11*
163
(27) элементы матрицы Г, решая систему п»+ь линейных
однородных уравнений, с л*+д неизвестными
£(^-a)Kcs=0. (28)
(О
Сохраняя обозначения § 4, гл. IV, перепишем систему
уравнений (28) в виде
£ (\№, -а)У№)=0 (? = /(1),/(2)....,/<">; А= 1,2,...,Л
^" feS Т] Т]5
(29)
Системе уравнений (29) соответствует квадратная клеточно-
диагональная матрица
К» w = <*С («)• «ft «*>. • • • ■ «J? (<*»*
где
«J!i(«) = ll^a^-a||(C-^i»...../^;
при А = 1,2,... ,п*\
Детерминант А&*»(а) матрицы йо*д(«) определяется, согласно
формуле (7), равенством
Ai*i(a) = Ai*i-c^(Ai*i)'f
где Ао^—детерминант матрицы
«S-IIVb,n G = '(V2) ^: л-с», с» С("\
являющейся диагональной клеткой (Я, (^-ассоциированной с А кле-
точно-диагональной матрицы
91 =Ш(1) 2t(2) Я(пХЧ
(Асы*)' — определяемая соответственно формуле (9) сумма
элементов матрицы (Яо*£)*, составленной из алгебраических дополнений
элементов детерминанта А^, ад — квазихарактеристическое число
матрицы ИЭД (ft = 1,2,..., hK).
Следовательно, квазихарактеристическое уравнение матрицы
21^ имеет вид
164
и если (Д&1)' Ф 0, то
ал = 77Ш^ (Л=1.2,....л*). (30)
Детерминант AXt(l(a) матрицы \t|Ll(a), очевидно, равен
произведению детерминантов До*м,(а) матриц
Оа) (Л —1.2 ....п\ т. е. Ах.ц(а) = П Оа)>
h=i
и система линейных однородных уравнений (29) тогда и только
тогда имеет* .'ненулевое решение, когда
Д^(а) = 0. (31)
Уравнение (31) называется (Яг, (л)-квазихарактеристическим
уравнением для матрицы А Если сумма элементов каждой из матриц
Л)* (Л = 1,2,.... /Iх) отлична от нуля, т. е. (Д$)' =£0 (А = 1,
2,...,^), то уравнение (31) имеет я* корней, определяемых
формулами (30), причем среди этих корней могут быть и одинаковые
Таким образом, совокупность [X (л)-квазихарактеристических чисел
матрицы А состоит из п^ квазихарактеристических чисел матриц
Яо*д (А = 1, 2 , пк). которые являются в то же время (0, ц.)-ква-
зихарактеристическйми числами 2|х-мерных матриц Aih) =\\A (Л) ||
(Л = 1,2,..., л^), представляющих сечения ориентации (s)
матрицы А. Каждому квазихарактеристическому числу ah матрицы Я^
соответствует ее квазисобственный вектор У^ = (У^щн), ^c(2)s(/i), ...
• ••.У и. ihO» (0, (^-ассоциированный с фундаментальной (0,|х)-ква-
зисобственной матрицей У{Н) = || У {Н) || для Л(/1) (А = 1,2,..., п\
представляющей А-е сечение ориентации (s) фундаментальной (КрУ
квазисобственной матрицы У для А. В случае, когда все числа
(ДолО' (А = 1,2,..., /Iх) отличны от нуля, будем говорить, что А
есть матрица с (Я,ц)-квазиспектром.
Будем называть матрицу Л, представленную в виде (25),
(А,, \1)-квазистохастической S-матрицей, если сумма элементов
каждого ее сечения ориентации (Is) равна S £ Р, т. е. если (X,
^-ассоциированная с А матрица 21^(М, есть квазистохастическая 5-ма-
трица.
При S>:= 1 будем называть А просто (К \1)-квазистохастической
матрицей, являющейся (К, (г)-стохаспической, если А > О.
Теорема 5. р-мерная матрица п-го порядка А с (X, \ь)-квази-
спектром тогда и только тогда будет (X, \1)-квазистохастической
S-матрицей, когда она имеет фундаментальную (А,, \х)-квазисоб-
165
ственную матрицу, все элементы которой равны единице, при
(X, \1)-квазихарактеристическом числе — кратности лх, являющемся
также простым (О, [х)-квазихарактеристическим числом каждого
сечения ориентации (s) матрицы А.
В справедливости теоремы нетрудно убедиться, замечая, что
А, согласно определению, является (X, ц,)-квазистохастической S-
матрицей лишь при существовании равенств
V A{h) =S(£ = /(1\/(2>,...,/(n); ft=l,2,...,A
когда каждая из матриц Stojl (Л = 1, 2, . . . , я*) порядка яц будет
квазистохастической S-матрицей, и что необходимое и достаточное
условие для этого, согласно теореме 1, состоит в существовании
квазисобственного вектора матрицы $<$, (ft = 1, 2, . . . , я*), все
я** координат которого равны единице, при квазихар актер истиче-
5
ском числе —-.
п»
Теорема 6. Если (А., ^-неособенная р-мерная матрица п-го
порядка А с (X, \х)-квазиспектром является (X, \1)-квазистохасти-
ческой S-матрицей, то (X, \л)-обратная матрица А"1 (X, у) для А
будет (Я, \хУквазистохастической ST]-матрицей.
Действительно, согласно замечанию в § 2, гл. IV, (А,;
[^-ассоциированной с Л"~! (Я,, и») будет матрица
«G=<Ю~1* Ю~1> • ■ • ■ К*Т1},
где (ЭДо^Г*1 — обратная матрица для 8$^ (А = 1,2,..., я*).
Так как при выполнении условия теоремы каждая из матриц
^1 (А = 1,2,..., я*) является квазистохастической S-матрицей, то
каждая из матриц (3toU)~l (ft = 1,2,... ,яЛ), согласно теореме 2,
будет квазистохастической S^-матрицей. Следовательно, А~х (X, \i)
есть (X, [л)-квазистохастическая ^-матрица.
Из теорем 5, 6 вытекают очевидные следствия.
Следствие 1. Неотрицательная р-мерная матрица я-го
порядка А с (X, \i)-квазиспектром тогда и только тогда будет
(X, (^-стохастической, когда она имеет фундаментальную (X, \i)-
квазисобственную матрицу, все элементы которой равны единице,
при (X, ц,)-квазихарактеристическом числе — кратности лх,
являющемся также простым (0, (л)-квазихарактеристическим числом
каждого сечения ориентации (s) матрицы А.
Следствие 2. Если (X, (л)-неособенная р-мерная матрица
А с (X, н^-квазиспектром является (А,, р,)-квазистохастической (или
166
дважды (Я, |*)-квазистохастической*), то (X, |л)-обратная матрица
А~{(Х, (л) для А также будет (А,, (г)-квазистохастической (или
дважды (А,, ц)-квазистохастической).
Будем называть /7-мерные матрицы n-го порядка А = || Alsc || и
В = || Blsc || (А,, \х)-квазистохастически эквивалентными над полем
Р, если существуют (А,, \х)-неособенные (X, ^)-квазистохастические
матрицы л-го порядка (/ = \\и18С\\ и V = |l^8c|| над Р такие, что
B = %*(UAV{l'c\
где V(/*с) — транспонированная матрица относительно V,
получающаяся из V путем обмена соответственными сечениями
ориентации (0 и (с).
Составим пучки квадратных матриц 91^— а£(2,0) (ft=l,2,...
•.., л*), где (2,0)-единичная матрица Я (2, 0) того же порядка лд,
как и матрица Яо^, и будем рассматривать совокупность
элементарных делителей этих пучков как (X, [1)-элементарные делители
пучка р-мерных матриц п-го порядка Л —а£(р, 0), а совокупность
минимальных индексов для столбцов и строк пучков ИЗД — а£(2,0)
(h = 1,2,..., пк) — как (X, ^-минимальные индексы для сенений
ориентации (sc) и ориентации (Is) пучка А — аЕ(р,0). Сделаем то
же самое в отношении другого пучка р-мерных матриц л-го
порядка В — аЕ(р,0) Тогда, как легко убедиться, имеет место теорема.
Теорема 7. Две р-мерные матрицы п-го порядка А и В тогда
и только тогда (X, \1)-квазистохастически эквивалентны над полем
Р, когда пучки матриц А — аЕ (р> 0) и В — аЕ (р, 0) имеют
одни и те же («конечные» и «бесконечные») (X, ^-элементарные
делители в поле Р и\ если они (X, ^-сингулярные, одни и те же (X,
^-минимальные индексы.
Будем говорить, далее, что р-мерные матрицы л-го порядка
А и В (X, р)-квазиетохастически (точнее: дважды (X, \х)-квазисто-
хастически) подобны над полем Р, если существует (X,
^-неособенная дважды (X, (л)-квазистохастическая матрица л-го порядка W
над Р такая, что ~
B = ^(WAW-\
где W1 есть (X, (х)-обратная матрица для fc.
Объединяя элементарные делители квадратных матриц StJIIi (^
= 1, 2, . . . , л*) в совокупность (X, ^-элементарных делителей
р-мерной матрицы п-го порядка А и аналогично поступая с
другой р-мерной матрицей л-го порядка В, нетрудно установить
необходимые и достаточные условия (X, ц,)-квазистохастического
подобия матриц Л и В, выражаемые следующей теоремой.
* Т. е. имеющей сумму элементов каждого сечения ориентации (cs),
так же, как и сумму элементов каждого сечения ориентации (ls)t равную
единице.
167
Теорема 8. Две р-мерные матрицы п-го порядка А и В тогда
и только тогда (А,, \1)-квазистохастически подобны над полем Р,
когда они обладают одними и теми же (X, ^-элементарными дели-
телями в поле Р и когда при этом пучки матриц А — аЕ (р, 0)
и В — аЕ (/?, 0) имеют одни и те же («конечные» и «бесконечные»)
(X, ^-элементарные делители и, если они (X, ^-сингулярные, одни
и те же (X, ^-минимальные индексы.
Отметим в заключение, что /7-мерная матрица я-го порядка А
(X, (х)-квазистохастически эквивалентна (или (X, ц.)-квазистохасти-
чески подобна) над Р своей (X, \1)-квазинормальной форме J (X, \i),
определяемой как р-мерная матрица п-го порядка, с которой (X, |л)-
ассоциирована квазинормальная форма
7 _i7<» У<2> У(п\
матрицы ЗДХ , где jf^ (h = 1,2,..., nk) — представленные в видах,
аналогичных типам (Г) — (V) в § 1, квазинормальные формы
диагональных клеток Я^ (А = 1, 2,..., я*) матрицы 21^.
л».
(X, |х)-квазинормальная форма / (X, (л) может быть рассматриваема
как представитель класса К (X, \i) матриц, {X, (л)-квазистохасти-
чески эквивалентных матрице А или, при известных условиях, как
представитель множества матриц, (X, ц,)-квазистохастически
подобных матрице А и образующих в своей совокупности
пересечение К (X, |д) f| Кг (X, \х) класса К (X, у,) и класса К% (А,, у) матриц
(Я, (х)-подобных матрице А.
Примеры.
1. Дана кубическая матрица второго порядка
Л =
•* (s)
1 316 4
1 2 3 2
—>- (О
Y
(О
Положим X = 1, \i = 1.
Пучок кубических матриц второго порядка
II1 — а 3 — а
Л-а£;(3.0) =
II 1 — a z-—a.
а 4 —а
3-а 2-а|||
(Г0
строго (1,1)-экБивалентный пучку
1 0 |1 0||_^(с)
0 а — 1 0 а I
(/)
имеет (1, 1)-элементарные делители а — 1, 0; а, р.
168
где
Теми же (1, 1)-элементарными делителями обладает пучок / (1, 1) — аЕ (3,0),
/(1,1) =
1 1
1 0
-*<s)
о о°|||"
(/)
(*>
При этом (1, 1)-элементарные делители матрицы /(1, 1)
a-yf/S+l), a + j(/5-l); а, а
отличаются от (1,1)-элементарных делителей матрицы А
у(/13 + 3), а + \
а-Т(/13 + 3), а + т(]ЛЗ-3); а,а —8.
Следовательно, матрица А (1,1)-квазистохастически эквивалентна своей (1,1)
квазинормальной форме
/(1,1) =
1 111 0
1 0 0 0
Ms)
I—>- (с)
Y
(/)
Это подтверждается также равенством
1,1 (UAVil,c)) = 7(1,1),
где
*/ =
1 21—2 3
0 1—1 2
г—>- (с)
Y
(О
U)
■*ч;_:|
-3 —2
4 3
>(s)
-У (с)
2. Дана кубическая матрица второго порядка
Л =
II
""ЗГ Т ,—мо
4 5 у
Положим X = 1, р. в 1.
169
Пучок кубических матриц второго порядка
А — а£ (3,0) =
5 ~~а "" 5 ~"а
5
6 4
-Ms)
~~ з "~а з""~а
"""Т""06 з""~а
-> (О
строго (1,1 ^эквивалентный пучку
->(s)
1 Oil all ^
0 a|0 l|||
(/)
(с)
имеет (1,1)-элементарные делители а, р, р2.
Теми же (1, 1)-элементарными делителями обладает пучок / (1,1) — a£(3,0)
где
/(Ы) =
1 01 — 1 0
0 0 0 1
► (S)
, >~ (с)
г
(Л
При этом матрицы А и /(1, 1) имеют одни и те же (1, 1)-элементарные
делители a — 1, a; a — 1, a + 1.
Следовательно, эти матрицы (1,1)-квази стохастически подобны.
Это подтверждается также равенством
lA(WAW^l)^7(h\),
где дважды (1,1)-квазистохастическая матрица
трица W~~l имеют вид
и (1,1)-обратная для W ма-
-><s)
3
— 21
2
— 2 3 J — 1
=
1 3 2
5 5
2 3
1 5 5
2
3
1
3
— 1
2
Иг
Al
(Ь
! Г
т
2
з 1
Ms)
|—
1
Г
(/)
->-w
>W
ЛИТЕРАТУРА
1. ГантмахерФ. Р. Теория матриц. «Наука», М., 1966.
2. Мальцев А. И. Основы линейной алгебры. Гостехиздат, М.— Л., 1948.
3. Соколов Н. П. Пространственные матрицы и их приложения. Физмат-
гиз, М., 1960.
4. СоколовН. П.— УМЖ, 1964, 16, 1.
5. С о к о л о в Н. П.— УМЖ, 1964, 16, 6.
6. СоколовН. П.— ДАН СССР, 1965, 163, 6.
7. СоколовН. П.—УМЖ, 1965, 17,5.
8. СоколовН. П.— УМЖ, 1966, 18, 4.
9. СоколовН. П.— УМЖ, 1967, 19, 4.
10. A s t i n J.— Math. Gaz., 1965, 49, 370.
11. Bicknell Marjorie R.— Amer. Math. Monthly, 1965, 72, 3.
12. Dulmage A. L., Mendelsohn N. S.—Duke Math. Journ., 1964, 31.
13. Gouarne R., Samuel I.—Cahiers de Physique, 1962, 140.
14. G у i г е s Bel a.— Pubis math., 1957, 5, 1—2.
15. Muir Tom as.— A treatise on the theory of determinants. Dover, New
York, 1960.
16. Oldenburger R.— Ann. Math., 1934, 35, 3.
17. О s t г о w s k i A.— Journ. of London Math. Soc, 1952, 27.
18. W i e 1 a n d t H.~ Math. Zeitschr., 1950, 52.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебраическое дополнение 24
Взаимно дополнительные миноры 24
Гипердетерминант 13
Детерминант косигнатурный 14
— многомерный 16
— р-мерный 13
— смешанный 14
Диагональ 7
— главная 7
Диагональное сечение 7
главное 7
Дополнительный минор 23
Индексы альтернативные 13
— кэлиевы 13
— неальтернативные 56
— свободные 56
— скоттовы 56
Канонический вид многомерной
матрицы 81
пучка многомерных матриц 132
Квазинормальная форма матрицы 153,
168
Квазисобственный вектор 146
Квазистохастически подобные
матрицы 154, 168
— эквивалентные матрицы 152, 167
Квазихарактеристическое уравнение
матрицы 147, 165
— число 146, 163
Кодетерминанты 14
— союзные 14
Критерий квазистохастического
подобия матриц 154, 168
— квазистохастической
эквивалентности матриц 152, 167
— (х, Я, \i) -эквивалентности
многомерных матриц 78, 79
— (Я, ц)-неразложимости
неотрицательной многомерной матрицы 135
подобия многомерных матриц
128
примитивности многомерных
матриц 136
эквивалентности
полиномиальных многомерных матриц 125, 126
— строгой (Я, \х) -эквивалентности
(Я,|л)-регулярных пучков
многомерных матриц 130
(Я, ц)-сингулярных
пучков многомерных матриц 129, 133
Кронекерово произведение
многомерных матриц 69
(х, Я, |ы)-ранг многомерной матрицы
79
— эквивалентные многомерные
матрицы 79
— элементарные преобразования
многомерной матрицы 76
(Я, ц) -ассоциированный пучок матриц
129
— инвариантные множители
многомерной матрицы 127
полиномиальной
матрицы 125
— минимальные индексы (Я,
^-сингулярного пучка многомерных
матриц 133
— минимальный полином
многомерной матрицы ПО
— нормальная форма многомерной
матрицы 128
— подобные многомерные матрицы
128
— показатель многомерной матрицы
137
— ранг многомерной матрицы 79
полиномиальной матрицы 124
— свернутое произведение
многомерных матриц 56, 58
частное 115
— свернутый остаток 115
полином от многомерной
матрицы 99
— эквивалентные многомерные
матрицы 78
полиномиальные матрицы
123, 124
172
— элементарные делители
многомерной матрицы 127
полиномиальной матрицы
126
пучка многомерных матриц
130
— элементарные преобразования
многомерной полиномиальной
матрицы 121
— характеристический полином
многомерной матрицы 102
— характеристическое уравнение
многомерной матрицы 95
число (собственное значение)
многомерной матрицы 93
Матрица дважды стохастическая 151,
167
квазистохастическая 151, 167
— диагональная 8
— квазистохастическая 148, 165
— квазихарактеристическая 146, 163
— клеточно-диагональная 12
— кососимметрнческая 9
относительно нескольких
индексов 9
— (х, Я, ц) -ассоциированная 74
— (Я, ^-ассоциированная 75
единичная 83
неособенная 78
неразложимая 135
обратная 85, 87
левая 86
правая 86
покрываемонеразложимая 136
примитивная 136
разложимая (полностью или
частично) 135
симметрическая 75
собственная 93
стохастическая 144
характеристическая 93
— минорная 28
— ц-свернутая 71
— неотрицательная 135
— нулевая 8
— v-развернутая 73
— р-мерная 5
— положительная 135
— пространственная 5
— расширенная 5
— сжатая 5
— симметрическая 8
относительно нескольких
индексов 8
— с квазиспектром 147
— транспонированная 10
— фундаментальная (Я, ц)
-собственная 96
(Я, ja) -квазисобственная 163
Минор многомерного детерминанта
Нормальная форма полностью (Я,
неразложимой неотрицательной
многомерной матрицы 142
Обобщенная теорема Лапласа 28
— формула Бине-Коши 62
Обобщенное детерминантное
тождество Дьиреша 40
Смита 38
— разложение Альбеджиани 51
Общая теорема Безу 121
Гамильтона — Кэли 103
Кронекера 134
Перрона 138
Фробениуса 139
Перманент 14
Полностью свернутое произведение
многомерных матриц 67
Правило Кэли — Раиса умножения
детерминантов 29
— Скотта—Раиса умножения
детерминантов 31
Произведение многомерных матриц
без свертывания 65
Пучок многомерных матриц 129
р-матричный полином 114
(Я, ji) -регулярный 114
Разность многомерных матриц 54
Род детерминанта 13
Сечение (простое или кратное)
матрицы 5, 6
Сигнатура детерминанта 13
Сложение многомерных матриц 51
Строго (Я, и) -эквивалентные пучки
многомерных матриц 129
Сумма многомерных матриц 51
Теорема Безу 26
— Вандермонда 26
— Лапласа 26
— Коши 27
Тождественно равные матрицы 50
Трансверсаль 7
Трансверсальные сечения матрицы 7
— строки матрицы 7
— элементы матрицы 7
Третье правило составления
произведения детерминантов 67
Член детерминанта 13
ОГЛАВЛЕНИЕ
Предисловие 3
Глава I. Основные сведения о многомерных матрицах и их детерминантах 5
§ 1. Структура многомерной матрицы 5
§ 2. Детерминанты, порождаемые многомерной матрицей . . . .12
§ 3. Основные свойства детерминантов многомерной матрицы . . . 15
§ 4. Разложение многомерных детерминантов 20
§ 5. Умножение многомерных детерминантов 29
Глава II. Замечательные свойства детерминантов некоторых
многомерных матриц 34
§ 1. Общее свойство детерминантов, порождаемых целочисленной
многомерной матрицей 34
§ 2. Обобщенные детерминантные тождества Смита и Дьиреша . . 36
§ 3. Детерминанты ганкелевой многомерной матрицы одного
частного вида 41
§ 4. Многомерные детерминанты, приводящие к обычному
детерминанту Вандермонда или степени этого детерминанта 46
Глава" III. Операции над многомерными матрицами 50
§ 1. Сложение многомерных матриц. Умножение многомерной
матрицы на число , 50
§ 2. Умножение многомерных матриц 54
§ 3. Частные случая умножения многомерных матриц 60
§ 4. Свертывание и развертывание матриц 71
§ 5. Элементарные преобразования многомерных матриц .... 74
Глава IV. Простейшие матричные уравнения 82
§ 1. Единичные матрицы 82
§ 2. Обратные матрицы 85
§ 3. Уравнения К»(АХ)=В и А'Д(УЛ)=Я 89
§ 4. Характеристические числа и собственные матрицы для данной
многомерной матрицы 93
Глава V. Характеристический и минимальный полиномы многомерной
матрицы 99
§ 1. Полиномы от многомерной матрицы 99
§ 2. Характеристический полином многомерной матрицы . . . .102
§ 3. Минимальный полином многомерной матрицы 110
Глава VI. Полиномиальные многомерные матрицы 114
§ 1. Основные операции над матричными полиномами 114
§ 2. Элементарные преобразования полиномиальных многомерных
матриц 121
174
§ 3. Инвариантные множители и элементарные делители
полиномиальных многомерных матриц 124
§ 4. Пучки многомерных матриц 129
Глава VII. О мультипликативных и спектральных свойствах
многомерных матриц с неотрицательными элементами 135
§ 1. Основные мультипликативные свойства неотрицательных
многомерных матриц 135
§ 2 Основные спектральные свойства неотрицательных многомерных
матриц 138
Глава VIII. Квазиспектральные свойства матриц 146
§ 1. Квазиспектральные свойства квадратной матрицы 146
§ 2. Квазиспектральные свойства многомерных матриц . . . .163
Литература 171
Предметный указатель . 172
Соколов Николай Петрович
ВВЕДЕНИЕ В ТЕОРИЮ МНОГОМЕРНЫХ МАТРИЦ
Печатается по постановлению ученого совета Института математики АН УССР
Редактор Н. М. Игнатович
Художественный редактор К. Г. Лычаковский
Оформление художника В. Г. Самсонова
Технические редакторы И. Е. Немченко, Т. Я. Смолякова
Корректор Л. М. Тищенко
Сдано в набор 21.11. 1971 г. Подписано к печати 14.111. 1972 г. БФ 17900.
Зак. № 595. Изд. № 260. Бумага № 1. Формат 60X90Vi6- Условн. печ. листов 11.
Учетно-изд. листов 9,86. Тираж 1800. Цена 1 руб. 14 коп.
Издательство «Наукова думка»,
Киев, Репина, 3.
Киевская книжная типография № 5 Комитета по печати
при Совете Министров УССР, Киев, Репина, 4.