Текст
В.К.Кобушкин
МЕТОДИКА РЕШЕНИЯ ААДАЧ ПО ФИЗИКЕ
Изд-во ЛГУ, 1972, 247 с.
Цель книги — довести до читателя некоторые весьма общие методы решения задач по элементарной физике, основанные на возможности общего подхода к решению различных задач, а также на том широко известном факте, что все явления описываются небольшим числом основных уравнений.
Книга состоит наследующих разделов: «Механика», «Механические колебания и волны», «Термодинамика», каждому из которых предпослан необходимый теоретический материал. С целью расширения представлений учащихся о возможных методах решения ряд задач решен несколькими способами. При решении многих из них широко использованы элементы векторной алгебры.
Книга предназначена для учащихся старших классов средних школ, а также для студентов педагогических вузов и преподавателей физики.
СОДЕРЖАНИЕ
От автора 3
Часть I. Механика
1. Элементы векторной алгебры 5
2. Примерная схема решения задач 12
3. Кинематика материальной точки 12
4. Динамика материальной точки (собственно законы Ньютона) 24
5. Закон изменения количества движения системы тел и закон его 54
сохранения
6. Движение тела переменной массы 59
7. Работа, энергия, мощность 66
8. Столкновение тел 75
9. Тяготение 85
10. Динамика движения материальной точки по окружности 94
И. Статика 109
12. Гидроаэростатика 121
13. Движение заряженных частиц в силовых полях 135
14. К обоснованию выбранного способа решения задачи 145
Часть II. Механические колебания и волны
1. Основные понятия 155
2. Замечания к решению задач 161
3. Сводка формул для гармонических колебаний 163
4. Задачи к разделу «Колебания и волны» 164
Часть III. Термодинамика
1. Идеальный газ (основные понятия) 188
2. Задачи к разделу «Идеальный газ и пар» 192
3. Энергия, работа, теплота 224
4. Задачи к разделу «Энергия, работа, теплота и агрегатные переходы» 229 5. Замечания к разделу «Термодинамика» 245
ОТ АВТОРА
Данная книга задумана как методическое пособие для учителей физики, студентов младших курсов вузов (прежде всего педагогических), а также для учащихся старших классов средних школ (особенно школ физико-математического профиля). Для школьников на первых порах книга может показаться трудной (в основном, однако, из-за непривычности векторного изложения). Тем не менее достаточно упорные учащиеся, надо полагать, почерпнут для себя много полезного.
Автор старался везде придерживаться единого метода решения задач, в основе которого лежит использование небольшого количества фундаментальных законов физики с привлечением по мере надобности незначительного количества вспомогательных формул.
Для большей ясности изложения каждому разделу предпосланы основные теоретические положения.
В книге нет обстоятельного ответа на вопрос «как научить учеников» решать задачи, ибо это уже вопрос преподавания. Автор сомневается в необходимости подчеркивания ответа на этот вопрос в книге, посвященной непосредственно подходу к решению и самому решению задач с возможно большей строгостью.
Задачи в основном составлены автором. Целый ряд задач нарочито дан в весьма «размытой» формулировке с целью научить школьников мыслить общими положениями, без излишней привязанности к конкретным данным. С этой же целью в некоторых задачах указаны не все данные, необходимые для отыскания ответа; решающий такую задачу должен сам ввести недостающие данные, когда ему станет очевидной их необходимость.
1*
3
Большое внимание уделяется оговоркам о том, какие допущения делаются при решении данной задачи, в каком приближении опа решается. Исследуется решение ряда задач. В некоторых случаях из результата решения задачи общего типа получаются решения более частных задач. Такой элемент исследования автор считает безусловно важным для развития физического мышления.
Изложенный метод решения задач апробирован автором в нескольких обычных средних и специализированных физико-математических школах Ленинграда, а также излагался на семинаре учителей физики средних школ Ленинграда.
Автор благодарен Александре Васильевне Тиморевой, Елене Федоровне Яруниной и Евгению Ивановичу Бутикову за ряд критических замечаний» которые, разумеется, были учтены.
ЧАСТЬ I
МЕХАНИКА
1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
В курсе элементарной физики, как известно, приходится оперировать двумя категориями величин — скалярными и векторными.
Существенным отличием вектора от скаляра является направленность вектора, чем и обусловлены особые правила действий над ними, носящие геометрически й характер. д
Поскольку действия над век- Себер
торами по существу учащимся i i
известны плохо, то представляет- '
ся необходимым рассмотреть про- А
стекшие операции над векторами перед изложением основного ма-териала этой книги. Необходи-мость этих предпосылок объяс- А
няется еще и тем, что векторная Юг
запись многих уравнений физики Ряс- 1-
более полно отображает соответствующие процессы и является более простой и компактной.
Вектор определяется абсолютной величиной (модулем) и направлением и на чертежах изображается направленным отрезком, длина которого в определенном масштабе характеризует абсолютную величину вектора. Так, движение какого-либо тела на северо-восток со скоростью 30 м/сек может быть изображено отрезком, направленным на северо-восток (и только туда!) и имеющим длину, определяемую масштабом; например, при масштабе в 1 см 10 м/сек длина отрезка О А должна быть 3 см, а при масштабе в 1 см 15 м/сек — —• 2 см и т. д. (рис. 1). Точка О называется началом вектора, точка А — его концом.
Принято для отличия векторов от скаляров обозначать в тексте векторы жирными буквами или над буквами ставить черту или стрелку. Например: a, v, Е или a, v, Е, или a, V, Ё и т. д.
5
Абсолютные значения векторов обозначают теми же буквами, но без всякого выделения их, например: a, v, Е или в виде |а|, ) vI, iЁ! •
Формально векторные равенства имеют тот же вид, что и скалярные, например, а -4-Ь = с. Стрелки же над буквами означают, что мы имеем дело с векторами и, значит, операции над ними производятся по особым правилам, о которых речь будет идти в дальнейшем. В частности, такая запись означает, что если а — 2 и 6 = 3, то с не обязательно будет равно 5.
а) умножение вектора на скаляр
Умножение вектора а на какой-либо положительный скаляр дает вектор того же направления, что и вектор а, но в п раз больший по величине (рис. 2).
Рис. 3.
Рис. 2.
Умножение вектора а на отрицательный скаляр т дает вектор противоположного вектору а направления и в \т\ раз больший по величине (рис. 3).
б) сложение векторов
Сложить несколько векторов — это значит заменить несколько на самом деле имеющихся векторов таким одним, который был бы
Рис. 4.
эквивалентен всем замененным. Результирующий вектор находят как замыкающую той ломаной линии, звеньями которой являются составляющие векторы. Например, надо сложить изображенные на рис. 4 векторы а, Ь, с и d. Для этого пристраивают в любом порядке к концу одного (предыдущего) вектора начало другого (последующего).
Результирующий вектор f направлен от начала первого слагаемого к концу последнего. При этом имеет место коммутати
вность, т. е. то, что от перестановки составляющих сумма не
6
меняется. Из рисунка видно, например, что a-{-b -\-c-\-d ~ = b-\- a “I- d, с.
В частном случае сложения двух векторов при построении получается треугольник, две стороны которого — составляющие, а третья — результирующий вектор.
в) вычитание векторов
Как и в случае скаляров, вычитание векторов есть действие, сложению. Рассмотрим вычитание на примере двух
обратное векторов.
Пусть надо из вектора с вычесть вектор а и тем найти их разность Ь = с — а. Чтобы найти разность двух векторов сна, надо к вектору с
прибавить вектор (—а), т. е. вектором Ь = с — а будет вектор, направленный от начала вектора с к концу вектора (—а) (рис. 5).
На рис. 6 показаны два вектора а и Ь, их сумма с = а-\-Ь, разности d — = b — а и f = a — b-
Из рис. 7 видно, что в параллелограмме, построенном на векторах а и b как на сторонах, одна диагональ (с) имеет смысл суммы, а другая (3) — разности векторов b и а.
7
В процессе изменения вектора могут меняться обе характеристики вектора: и его величина (модуль) и направление. На рис, 8 показан некоторый вектор, изменившийся от и0 ДО V, а также До — полное изменение вектора с учетом изменения его по величине (Лит) и по направлению (Доп). Легко видеть, что
До — До. Доп.
г) разложение вектора на составляющие
Часто бывает необходимо заменить один вектор такими несколькими, которые в сумме своей были бы эквивалентны этому замененному. Такая операция называется разложением вектора на составляющие векторы. Рассмотрим три случая, когда составляющих векторов должно получиться два:
1. Известны кроме раскладываемого вектора направления составляющих. Подлежат нахождению величины составляющих векторов. Очевидно, геометрически задача сводится к построению треугольника по одной из сторон и прилежащим к ней двум углам и нахождению сторон получив-b____________________________шегося треугольника (или
jj х*/ параллелограмма).
-1 I 2. Известен кроме раскла-
\л Ус /ах"^ / Дываемого вектора один из
/^Х*^ составляющих векторов. Надо
ь найти второй составляющий
рис g вектор. Геометрически задача
сводится к построению треугольника по двум сторонам и углу между ними (или к построению параллелограмма по диагонали, одной из сторон и углу между ними), определению третьей стороны треугольника и угла, составляемого этой стороной с одной из заданных сторон (или соответствующих элементов параллелограмма).
3. Известны кроме раскладываемого вектора величины составляющих векторов. Надо найти их направления. Геометрически задача сводится к построению треугольника по трем сторонам (или параллелограмма по диагонали и сторонам) с последующим определением углов треугольника (или параллелограмма).
На рис. 9 пояснены эти три случая. Первому случаю соответствует построение параллелограмма или треугольника по известным с, а. и {3 с последующим определением а и Ь. Второму случаю — построение по заданным с, а и р (или с, b и а) с последующим определением b и а (или а и р). Третьему случаю — построение по известным с, а, b с последующим определением а и р, •
8
д) решение векторных т реуго льников
Решение векторных многоугольников, т. е. /аких, сторонами которых являются векторы, производится по тем же правилам, что и решение обычных многоугольников,
В том частном случае, когда получившаяся фигура является
косоугольным треугольником, се решение сводится к применению
теоремы косинусов п теоремы синусов (и редко теоремы тангенсов).
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Так, для случая, изображенного на рис. 10, имеем:
с2 — а2 Ь'2 — 2ab cos 7;
а2 = с2 У1 — 2cb cos а;
Ь‘2 = а2 4- с2 — 2ас cos р.
ТеЬрема синусов: -стороны треугольника пропорциональны сину-
сам противолежащих этим сторонам углов.
Для случая, изображенного на рис. 10, имеем
a sin a a sin a b sin 8
-г- —-т-7-; -=-— И
о sin р ’ с sin 7 с sin 7
В том случае, когда треугольник получается прямоугольным, решение упрощается. Рассматривать этот случай мы не будем.
е) проекции вектора на оси координат и сопоставление векторному равенству скалярных равенств
Воспользовавшись сказанным в пункте 4 (случай 1), можно ввести понятие о проекциях вектора на оси координат.
Пусть на плоскости задан век юр с. Введем в этой же плоскости две взаимоперпендикулярные оси координат х и у, положительные направления которых указаны стрелками. Тогда вектор с определится своей величиной с и углом, который он составл5!ет с какой-либо осью, например, осью х (рис. 11).
Разложим вектор с на векторы а и Ь, направленные вдоль осей х и у, и спроектируем их на оси координат. Тогда проекции этих векторов будут одновременно и проекциями вектора с на оси координат. Проекция вектора считается положительной, если соответствующая составляющая вектора направлена в сторону положительного направления оси, и наоборот. Например, на
9
рис. 11 сх и Су положительны, так как соответствующие им составляющие вектора с (а или b) направлены в стороны положительных значений х и у.
На рис. 12 проекция сх положительна (так как соответствующая ей составляющая
Проектируя все векторы
вектора с направлена вдоль положительных значений оси х), а проекция Су отрицательна (так как соответствующая ей составляющая вектора с направлена в сторону, противоположную положительному направлению оси у).
Очевидно, что задание вектора его величиной и углом, который он составляет с какой-либо осью, совершенно эквивалентно заданию проекций этого вектора на оси. Действительно, зная с и а, можно найти cx = ccosa и су — = с sin а. Верно и обратное: зная проекции вектора, можно найти его величину и направление, а именно
С—"КИ tga = ^. сх
Пусть теперь нам задано векторное равенство a b — с. Изобразим три этих вектора в соответствии со сказанным в пункте 2. на оси координат (рис. 13), получим
очевидные равенства
cx — ax-}-bx или cx = acosa4~ & cos Р;
Cy = ay-}-by или Су = a sin сх. —& sin р, т. е. по проекциям векторов а и b легко находятся проекции суммарного вектора с. Но проекции вектора вполне определяют сам вектор, именно
и tgi—г-^Х
10
Таким образом, всякому векторному равенству вида
оb — с k = I f — ... h (1)
можно сопоставить на плоскости два скалярных равенства проекций векторов
ах-}~Ьх— Cx-f- kx = /х-f- fx—Fix’, (2)
ay~^~by — cy-|~ ••• — (3)
При этом полученная система совершенно эквивалентна исходному векторному равенству в том смысле, что позволяет определить проекции интересующего нас вектора по проекциям остальных векторов.
В случае, если векторы лежат не в одной плоскости, то к двум равенствам проекций на оси. х и у добавляют третье равенство проекций векторов на ось г, ибо в трехмерном случае вектор определяется тремя проекциями на оси.
Примечание. Решение векторных равенств, как видно, может быть сделано как с помощью теорем синусов и косинусов, так и с помощью сопоставления векторному равенству равенств скалярных. Первый способ удобен в том случае, если в векторном треугольнике задан один из углов. В случае же, если все углы задаются по отношению к одному и тому же направлению, удобен второй способ.
На чертежах часто замененные векторы помечают волнистой черточкой. Например, на рис. 12 вектор с разложен на составляющие векторы а и b (т. е. заменен ими), поэтому он помечен такой черточкой. Эти пометки не обязательны, но в случаях, могущих вызвать недоразумение, полезны.
Надо запомнить, что знаки, стоящие в равенствах (2) и (3), никакого отношения к знакам проекций векторов не имеют и означают лишь те действия, которые производят с векторами и их проекциями. Эти знаки просто переносятся из векторного равенства (1) в (2) и (3); о знаках же проекций следует судить по сказанному в пояснении к рис. 11 и 12.
Отметим, что для сокращения записи проекций векторов на оси координат, которым они параллельны, мы в тексте обозначаем их ±а, ± & и т. д. вместо, например, ах, Ьх и т. д. Но при этом помним, что ах = а или bx = b при affox и ~b ft ох, если же af|ox или 6f|ox, то ах = — а и Ьх = — Ь. Иными словами, мы сразу учитываем тот факт, что вектор, параллельный какой-либо оси, проектируется на нее плюс-минус модулем (а на остальные оси, разумеется, он спроектируется нулями).
Часто в тех случаях, когда направление вектора очевидно, мы указываем только его модуль.
2. ПРИМЕРНАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ
Разумеется, общего рецепта для решения задач нет, но придерживаться какой-либо схемы желательно. Автор считает полезной следующую схему:
1. Установить в общих чертах условия задачи.
2. Сделать краткую запись условий.
3. Сделать чертеж, схему, рисунок, поясняющие описанный в задаче процесс.
4. Написать уравнение или систему уравнений, отображающих происходящий процесс.
5. Если равенства векторные, то им сопоставить скалярные равенства.
^^Используя условия задачи и чертеж, преобразовать исход-ньюравенства так, чтобы в конечном виде в них входили лишь упомянутые в условиях задачи величины и табличные данные.
7. В случае необходимости исследовать полученные решения.
8. Все величины перевести в одну систему единиц.
9. Произвести вычисления.
Первые задачи в этой книге решены достаточно подробно, а ряд последующих — более сжато, с опущенными очевидностями. Наиболее трудные задачи помечены звездочкой. В параграфе 14 проведено обоснование подхода к решению ряда задач по механике и даны вариации в их решениях.
3. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Кинематика — это раздел механики, изучающий различные движения тел без рассмотрения тех причин, которые вызывают это движение. Если размеры тела в данной задаче несущественны (часто это означает, что линейные размеры тел много меньше расстояний между ними и вращения тел отсутствуют), то такое тело называется материальной точкой.
Движение материальной точки считается известным, если известно ее положение относительно выбранной системы отсчета в любой момент времени, или, что все равно, если мы знаем, как изменяется положение материальной точки в пространстве со временем.
Введем понятие радиус-вектора г точки N как вектора, соединяющего начало координат с интересующей нас точкой N (рис. 14). Очевидно, что проекции конца этого вектора есть координаты точки. Очевидно также, что задания положения точки ее координатами (х, у и г) или радиус-вектором (г) эквивалентны друг другу.
При движении материальной точки ее координаты (а значит и ее радиус-вектор) будут меняться. Задачей кинематики является
12
установление зависимости г от времени t, или, как говорят, установление зависимости г=г(/), или зависимостей
x=x(t\, y==y(t); 2 = 2(t).
Эти уравнения называются кинематическими уравнениями движения материальной точки.
Если в результате движения вдоль какой-то кривой материальная точка переместилась за время А/ из положения, определяемого радиус-вектором г0, в положение, определяемое радиусом-вектором г, то вектор Дг = г — гп называется перемещением материальной точки, а длина части кривой между конечной и исходной точками — путем As (рис. 15).
Надо четко себе представить разницу между перемещением Дг и путем As: Дг— вектор; Дз — скаляр; |Дг| — измеряется попрямей между исходным и конечным положениями точки; As — измеряется вдоль траектории. Очевидно, Дз^|Дг|. В двух случаях между .| Аг | и Д$ нет разницы: 1) движение прямолинейное, в одну
13
сторону; 2) движение криволинейное, но два соседних положения материальной точки 1 и 2 столь близки, что нет возможности отличить дугу &s от хорды | Дг| (рис. 16).
В соответствии со сказанным можно ввести понятие о сред-
„ - Дг
ней скорости перемещения уср = ^- и средней скорости прохо-г Д$ »—» “* г о
ждения пути уср = ^, При этом уср и уср отличаются в той же
мере друг от друга, что и Дг от Дз.
Часто учащиеся склонны считать среднюю скорость движения в виде
___vl + + ••• + Vn
^ср — п
где щ....v„ — скорости движения на 1, 2, ..., n-м участках.
Это ошибочное мнение.
Средняя скорость, по определению, есть отношение общего перемещения Дг к тому промежутку времени Д/, за который это перемещение произошло, т. е.
"* Дг 1 -4- Ап 4- ... -4- АгЛ » Д$£ -4- As® -4- ... -4- А$Л
а) результирующее и относительное движение
Рассмотрим два случая одновременного движения двух тел.
1. Одно из тел движется по другому телу, в свою очередь тоже движущемуся. Например, человек движется по кораблю, движущемуся относительно берегов без вращения, т. е. поступательно. __
Пусть при этом Дг1 — перемещение корабля относительно берега и Дг2 — перемещение человека относительно корабля.
Тогда по закону независимости движений перемещение человека относительно берега Дгрез — результирующее перемещение — будет складываться из Дп и Дг2, т. е.
ДГрез = д71 4- Дг2.
Деля обе части равенства на Д/ — время, за которое произошли эти перемещения, получим
ДГрез
или
Урез = У1 + Vi.
Другим примером является движение лодки относительно берегов в случае, если гребец перемещает лодку относительно воды, а вода перемещается относительно берегов (рис. 17).
14
Таким образом, результирующие Дг и v изображаются геометрической суммой составляющих Дг и v. Аналогичное соотношение имеет место для ускорений (если нет вращений).
2. Два тела движутся независимо друг от друга в некоторой системе отсчета. Как определяется их движение друг относительно друга?
Рассмотрим этот случай на примере двух кораблей, движущихся относительно берега. Пусть из некоторой точки А (рис. 18) выходят два корабля, и один из них удаляется от А на расстояние Дг1( а другой — на расстояние Дга- Очевидно, относительное
Рис. 18.
их перемещение определяется взаимным расстоянием Дг01Н. И, значит, относительное перемещение равно разности Д/ч и Дг4. При этом перемещение 1-го относительно 2-го
Дг12=Дг1 — Дг2,
а перемещение 2-го относительно 1-го
Дга, j = Дл2 — ДгР
Очевидно, что
Д Г1, а = — Дга, 1.
Деля перемещения на время, за которое они произошли, имеем
Дгь а_Дг( Дг8 Zra,, ___Ar j Аг,
Д< Д< Д£ ’ Д< Д£ Д< ’
ИЛИ
V1:2 = V1-Vi, Vgl=Vg—Ур
Аналогично ар g = ai — а.2 и «а, i = ae— щ (если нет вращения), где щ и «а — ускорения 1-го и 2-го кораблей относительно берега.
Таким образом, относительные перемещение и скорость двух тел определяются векторной разностью их перемещений и скоростей, заданных по отношению к одной и той же системе отсчета.
15
б) равномерное движение
Равномерным называется движение с постоянной скоростью, т. е. с v = const Ясно, что при таком движении (по его определению) ни модуль, ни направление скорости не меняются.
Задача 1
Первую половину времени тело движется со скоростью oi = 20 м/сек под углом а1 = 60° к заданному направлению, а вторую половину времени — под углом а4=120° к тому же направлению со скоростью v.> = 40 м/сек. Найти среднюю скорость движения t'cp (рис. 19).
Решение
Так как тело совершило два перемещения, то суммарное перемещение определится равенством
Дг = ДГ1 -j-* Дгi.
откуда
Сопоставляя этому векторному равенству два скалярных, получим
Уср* _ = _ 5 м/сек.
= = 15 /з м/сек.
Задача 2
Тело совершает два последовательных, одинаковых по величине перемещения со скоростями щ = 20 м/сек под углом at — 60° и у2 = 40 м/сек под углом а2=120° к заданному направлению. Найти среднюю скорость уср (рис. 20).
16
Решение .
Как и в.предыдущей задаче, Дг = Art-|-Дг2, или Уср# = сГЛ4-4-пЛ, откуда
7Г +
Уср— I ,
ИЛИ
- Аг, -и, —1 + V, 1 vt ~ 3
Дг8
V-3
&Г1 , ДГ2 V, -t" vs
А так как Дг1 = Дг2, то по сокращении на него имеем
-1,-1
- _Viv; + v*v~
Vz?~ 1 । 1
Vt + vs
или в проекциях на выбранные направления
V. cos а.----1- cos а» —
___ vt cos at + cos a2
УсрА. j—-у — —T 1 :
Vt ' О, ®a
-1—1^ "Г -3—2^ Sinai + Sill
УсР>-“ 1,1 ~ 1,1
Vt ' V2 «I Vs
Подставляя численные значения, получим
1/1}
^cpA. = 0; yCPj, = 20 ig- м/сек.
Задача 3
Два корабля движутся со скоростями Vt и под углом я друг к другу. Найти скорость первого корабля относительно второго (рис. 21).
Решение
Здесь речь идет об относительной скорости, поэтому У1,2= ?1 —t>2.
17
Так как здесь упомянут угол я между th и у2, то удобно вое. пользоваться теоремами синусов и косинусов
У1,9 = Vv'{ -f- v% — 2vit>g cos a.
Направление vlfS определим, напри мер, углом Р; тогда из
sin р_sin а
V, «1,>
Имеем
. п sin а sin₽=—-Vi =
Ul) 2
__ sin а
+ V* — COS a
Задача 4
Лодка передвигается относительно воды в реке со скоростью v под углом я к течению, скорость которого равна и. Найти скорость лодки относительно берега (рис. 22).
Рис. 22.
Решение
Очевидно, что искомая скорость t»pe3 =v и. Так как углы я и р являются одновременно и углами параллелограмма и углами, заданными по отношению к одному и тому же направлению, то решать полученное равенство можно любым из двух способов.
Пользуясь теоремами косинусов и синусов, получим
— — 2uv cos (180 —я) = + w2 + 2uy cos я;
sin (180 — а)sin р
откуда
. n V sin а
Sin В = ==.
У Vs + иа 4- 2uv cos а
18
В проекциях же на оси хну получим из vpes = t»4' и v^x~vcosa.-\-u-,
УреЗу == V Sin Я.
Покажем, что второе решение тождественно первому
Орез = j/~и2резх + Пре3>1 = V COS2 Я —U2 —%VU C0S я 4~ 51П'2 я =
= [/u't (sin2 а 4~ cos2я) 4~ и'2 4- 2уи cos а = Ко2 а2 4~ 2ou cos я, . п UPe3v v sin а
SIП р =----- = 7..- _— - -- .
ирез у v~ + 11~ + 2.VU COS а
Таким образом, оба решения эквивалентны, как и должно быть.
в) равнопеременное движение
При движении тела скорость его может изменяться. Для характеристики быстроты этого изменения вводят понятие среднего ускорения для промежутка времени Д/
— Ли v — V(, а^~ Tt~ ' д/ >
откуда
v = у0 -}- асрДЕ
Поскольку Д/ = /— /0, то
0 = Уо + <2ср (/ — /о).
Если включать часы в момент /о = О, то
у(/) = о04-аср (/) t.
Движение, при котором а = const, называется равнопеременным. В этом случае аср = а и, значит,
V — Vo-}-at.
Покажем, что при таком движении
или, что все равно,
®оу + »у
УсРл:- 2 ’ UcPj'--- 2
Для доказательства этого построим графики зависимостей vx = Vox-}-axt-, vy — voy}-a^.
1»
Известно, что на таких графиках (рис. 23) заштрихованная площадь численно равна соответствующей проекции перемещения, происшедшего за время t. Но в таком случае
. vox + vx
Lx —----2-----А# = ~ 2~'~ (*>
(Дх и Ly подсчитаны как площади трапеций). С другой стороны, из Дг = уср/ имеем
Дх = уср^; Ly = vcPyt.
Поэтому, пользуясь равенством (*), получим
Сокращая в обоих равенствах t, получим
V0X Т" VX 4“ vy
V^PX— 2 ’ г'ч’у— 2
или, что все равно,
Рис. 23.
Используем полученный результат для вывода другой основной формулы равнопеременного движения.
Гг = vept = t = t = v.t + .
Эту формулу можно вывести и иначе, подставив сразу в (*) значения vx и vy. Тогда axt* avt~
Дх — W4-—; ДУ =уо/+-2~, что эквивалентно формуле
” 4. I ot2 &г = v^t -j—2 •
20
Полученные формулы
позволяют решить любую кинематическую задачу на равнопеременное движение.
Задача 5
Из ямы глубиной h бросают тело под углом а0 к горизонту со скоростью vQ. Найти положение и скорость тела через время t (рис. 24)
Рис. 24.
Решение Проектируя уравнение
—v^t -\-Ц-на выбранные оси, получим
X — хп = Vat cos а0;
, . eta
у — у,== sin а0 —
и учитывая, что хй = 0 и у0 =— h, найдем
X — Vot cosao;
у = — h vot sin «о — §2-. Аналогично находим скорость из
После проектирования на оси получаем
vx = Vo COS а0; vy = v0 sin а0 — gt.
21
Задача 6
Тело брошено под углом я0 к горизонту со скоростью t'O наточки с координатами х0, уп. Найти зависимость у = у(х), т. е. получить уравнение траектории (см. рис. 24).
Решение
Из уравнения
Дг==У0/-]-^-
получим в проекциях на оси
X — Хп = Vot COS «0. у — Уй = sin «0 — или, исключая из этих уравнений время t,
у — у9 = S i В — 0f-~ ,
J Y»cos “° ^v»cos “°
откуда окончательно
С > У ~ У° + (х *o)tg<X() ^2 cos8 а •
С)' -7 '-’”0 VUO Уд
Задача 7
Найти максимальную высоту подъема утак и наибольшую дальность полета хтах для тела, брошенного под углом а0 к горизонту со скоростью п0.
Решение
Максимальной дальности полета хтах соответствует у = 0 (тело упало). Но тогда, полагая в уравнении
У=У» + (х — х0) tg я0 — £-Uq CUo Uq у = 0, получим
О 2 . 2 „ {Xmax Xo)lg®o У» — и.
Л. U 0 LU& Яд
Решая это уравнение относительно (xmax — х«), найдем затем И Хтах-
Задача упрощается при уо = 0- Тогда
По сокращении на (хтах — х0) и упрощении получим v _________________________sin 2<х0 ।
Атах — ~ "т* л0*
22
Отсюда видно, что при заданных х0 и пп дальность полета будет наибольшей при а0 = 45°. (При у0 У- у результат будет другим).
Найдем //щах исходя из того соображения, что в наивысшей точке траектории vy — 0. Тогда из
у — £/0 = yo/sina0 — O = vosinao — gt,
2ga
исключая время t, получим
Vo sin а0 gvl sin2 a, f/tnax — ya = y0Sin a0-° °- — -----
s откуда после приведения подобных членов
Ч; sin2 «о , 1/тах- 2^ Н У'1'
Очевидно, что при заданных и у0 высота уюяк будет наибольшей при ао = 9О°.
Задача 8
Два тела брошены одновременно из некоторой точки. Найти уравнения относительного движения их (рис. 25).
Решение
Очевидно, что подлежат нахождению
Дг12 = Дг1— Дг2
и vt, 2 = ni — v%,
т. е. относительное перемещение и относительная скорость этих тел.
Но из
ДГ1 = По1/-(~ U)
Дг2 = п02/-|-~р (2)
после вычитания (2) из (1) получим
ДГ1, «=(?«! — Vn)t.
Аналогично из
Vi = v01 -j-gt и На = Vfn 4- gt
имеем
П1, а = — ^оа-
23
Таким образом, тела, брошенные в поле тяжести одновременно, движутся до своего падения друг относительно друга равномерно и прямолинейно, т. е. с 2 = цотн = const
4. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ (собственно законы Ньютона)
Решение задач на законы Ньютона предполагает, естественно, использование всех трех законов в своей совокупности независимо от конкретного вида задачи. Разъясним это.
1. Любое описание любого механического движения имеет смысл лишь при указании той системы отсчета, по отношению к которой измерены положение, скорость и ускорение интересующего нас тела, а также силы, действующие на это тело.
И так как в средней школе рассматриваются только инерциальные системы отсчета (т. е. те, о которых говорится в первом законе), решение задачи, естественно, нужно начинать с фиксирования некоторой инерциальной системы отсчета, за которую приближенно можно принять, при небольших продолжительностях движения тел по земле, землю или любое тело, движущееся относительно нее равномерно.
Таким образом, ссылка на первый закон очевидна.
2. Определить характер движения тела невозможно без анализа сил, действующих на него. Но силы — это мера взаимодействия тел. Это означает, что без рассмотрения взаимодействия интересующего нас тела с другими телами задача решена быть не может. Взаимодействие же, а значит, и определение всех сил, действующих ыа исследуемое тело, немыслимо без пользования третьим законом.
3. Так как изменение скорости тела определяется ускорением тела, а величина его определяется из второго закона, то ясна и его необходимость при решении механических задач.
Необходимо отчетливо представить себе эту взаимосвязь всех трех законов Ньютона, бессмысленность их использования в отрыве друг от друга.
Рассмотрим несколько примеров в общем виде с тем, чтобы проиллюстрировать сказанное выше.
Пример 1. Лошадь везет в гору воз, движение которого нас интересует.
1. Естественно за систему отсчета взять землю, дорогу или гору и связать с ней систему координат (рис. 26).
2. На воз существенным образом действуют: а) Земля с силой тяготения Р, направленной вертикально вниз; б) деформированная, «прогнувшаяся» опора (дорога) в направлении, перпендикулярном к себе с силой Q; в) сила тяги со стороны лошади вдоль горы вверх; г) сила трения Етр вдоль дороги вниз и
24
обусловленная микро- и макрошероховатостями (с точки зрения механики) дороги.
Естественно, на воз действует бесчисленное множество других сил, но их действие несущественно в данном случае.
3. Результат рассмотрения сил позволяет написать второй закон в виде
т
Пример 2. Камень, лежащий на руке, подбрасывают вверх (рис. 27, А).
1. За систему отсчета берем землю и связываем с вел систему координат, начало которой располагаем в любой близкой к камню точке.
2. На камень действуют: а) рука с силой Q; б) Земля с силой Р; в) сопротивление воздуха с силой Fc. Остальные силы несущественны.
3. Второй закон записываем в виде
ПримерЗ. Подброшенный камень летит вверх (рис. 27, Б).
1. То же, что и в предыдущем примере. .
2. На камень действуют: а) сила тяжести Р со стороны Земли, б) сила сопротивления воздуха Fconp; эти силы направлены вертикально вниз.
Необходимо отметить, что учащиеся склонны в подобных случаях еще приписывать к перечисленным уже силам «силу
25
инерции», «силу движения» и т. д. Нужно уяснить, что по третьему закону силы «порождаются» только телами и никак не скоростью, инерцией и т. д.
В нашем примере существенных сил только две — Р и КСОПр.
3. Второй закон для этого случая имеет вид
а — с011р
т
Отметим еще один случай, часто приводящий учащихся в смущение. Речь идет о силах, действующих на «самодвижу-щиеся» тела — автомобили, поезда, животных.
Учащиеся склонны считать, что движущей силой в случае автомобиля является сила тяги мотора. Это, строго говоря, неверно! Тело не может само себе сообщить ускорение. Это
и
могут сделать лишь другие тела. Каково же происхождение этой силы тяги, движущей силы, сообщающей автомобилю ускорение?
При включенном двигателе соответствующие механизмы (трансмиссия) передают возникающее в цилиндрах мотора усилие на колеса. Колеса, воздействуя на землю, отталкивают ее с силой F3. а (рис. 28). По третьему закону, земля толкает колеса, а значит, и автомобиль с силой, равной и противоположной по направлению Ра з. Этим и обусловлена сила тяги. Она — ответ, реакция на действие колес на землю. Если исключить сцепление колес с землей, то двигатель ускорения автомобилю не сообщит.
Можно сказать, что автомобиль приводится в движение силой движущего трения. (Не путать его с трением тормозящим!)
Несколько слов о силе трения. Величина силы тормозящего трения при движении тел подсчитывается по формуле
Р тр
где Q — сила, с которой тела прижаты друг к другу; она направлена перпендикулярно к поверхности соприкасающихся тел. Сила Ктр направлена в сторону, противоположную относительной ско
26
рости движения. Сила же движущего трения направлена в сторону движения и является чаще всего силой трения покоя. Сила трения покоя не может быть подсчитана по формуле FTp = &$, так как при одних и тех же k и Q Лр. пок может иметь самсе различное значение. Поэтому подсчитывать силу трения покоя можно лишь исходя из второго закона Ньютона — именно FTp. пок
всегда равна и противоположна той силе, которая, действуя по касательной к поверхности, «стремится» сдвинуть тело.
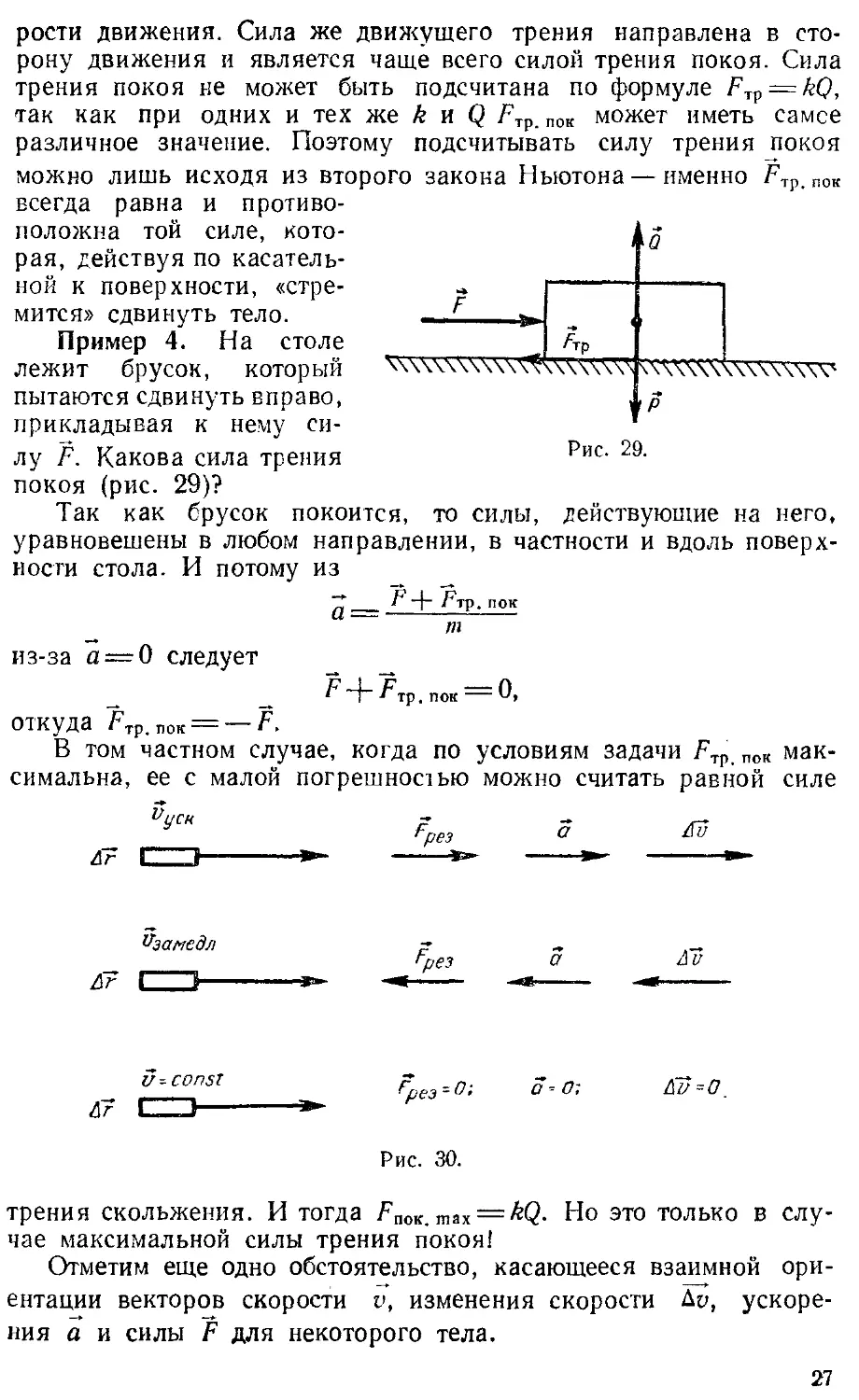
Пример 4. На столе лежит брусок, который пытаются сдвинуть вправо, прикладывая к нему силу F. Какова сила трения покоя (рис. 29)?
Так как брусок покоится, то силы, действующие на него, уравновешены в любом направлении, в частности и вдоль поверхности стола. И потому из
д F + Рту . пок
m
из-за а —0 следует
_ _ F + FTp. по» — О,
откуда FTp noK = —F,
В том частном случае, когда по условиям задачи FTp пок максимальна, ее с малой погрешностью можно считать равной силе
^замедл
Ррез
~ @ - О
Рис. 30.
трения скольжения. И тогда Люк. max —Но это только в случае максимальной силы трения покоя!
Отметим еще одно обстоятельство, касающееся взаимной ориентации векторов скорости v, изменения скорости До, ускорения а и силы F для некоторого тела.
27
Векторы Ду, а и F направлены в одну сторону и не обязательно совпадают по направлению с и и Дг. Пояснения даны на рис. 30 и 31.
Из сказанного следует, в частности, что скорость под действием как свою величину, так и направление.
В случае криволинейного движения второй закон Ньютона можно записать как обычно в виде
силы можег менять
Рис. 31.
или, вводя направление по движению (t-направление) и ему пер-перпендикулярное («-направление), в виде
at =
" т ’
где at и Ft—проекции ускорения и силы на /-направление; ап и Fn — проекции ускорения и силы на «-направление (рис. 32).
При этом at показывает, на сколько изменилась скорость за единицу времени по величине (тангециальное или касательное ускорения); ап—изменение скорости по направлению за единицу времени (нормальное или центростремительное ускорение).
а) движение одной материальной точки под действием постоянных во времени сил
Поскольку силы, действующие на тело, постоянны, то в соответствии со вторым законом Ньютона и ускорение будет постоянным. Это означает, что мы вправе пользоваться, когда это необходимо, формулами
v — у0 at, at*
Дг = vot -f- -J
О)
(2)
28
Весьма удобными являются и формулы
vi — 0^ = 2ахДЛ; (3)
Vy— vly = 2ay&v, (4)
которые в случае прямолинейного движения можно свести к одной о2 — vl — 2a&s. (5)
Надо иметь в виду, что формулы (3), (4) и (5) связывают между собой скалярные величины.
Указанные формулы (1) — (5) используются совместно со вторым законом Ньютона в тех случаях, когда в условиях задачи необязательно упоминается ускорение, но упоминаются v, или I.
Задача 9
На тело массой 2 кг действуют силы F-, = 3«и/72 = 4« под углами 60° и 120° к начальной скорости по = 2О MjceK. Найти
ускорение тела, его скорость и перемещение к концу 10-й секунды движения (рис. 33).
Решение
Так как силы, действующие на тело, постоянны, то и ускорение будет постоянным
т
Выбирая оси координат вдоль о0 (ось х) и перпендикулярно к о0 (ось у), получим
= F.cosa. + ^cosa, = _ 3
х т , I >
^ = ./?1Sin a1 + FaSinaa^3 м/секК
29
Так как а — const, то
v—ve-{-~ai
или
vx — vax-}-axt;
vy = vOy 4- ayt\
и так как v0x = y0 и w0y = 0, то
vx~Vb-{-axt‘,
vy = ayt.
Поскольку ax и ау уже найдены, то, подставляя их значения, получим ^=17,5 м/сек-, vy — 3Q м/сек.
Аналогично найдем и перемещение
__ _ -Л ’ л~* “* . t at
Ьг = и^-\—2",
или в проекциях на оси
Дх = vMt + -^4-; Ду = v№yt 4- -*-.
В силу того, что о0х = о0 и vay — Q, имеем Ь.х— 187,5 м;
150 м.
Задача 10
Брусок весом Р тянут по горизонтальной поверхности, прикладывая силу F под углом а к горизонту. При этом брусок
за время t изменил свою скорость от до v, двигаясь ускоренно в одну сторону. Найти коэффициент трения бруска о поверхность k (рис. 34).
30
Решение
Силы, действующие на брусок, очевидны. Полезно заметить, что Q<^P (это будет отчетливо видно из решения).
По второму закону
т
Так как в условиях задачи ускорение не фигурирует, a v, v0 и t упомянуты, то естественно использование формулы
V —t/Q -ф- Clt.
Исключая из этих формул ускорение, получим
v-va ^P + F+Q + F-rp t т
Проектируя все векторы на оси х и у и учитывая при этом, что vx=v и Vgx — Vg (так как движение происходит вдоль оси х), получим систему
{У — Уо F cos а — FTp
t т ’
I 0 ~ р + Z7 sin « + Q
I т
р
Так как FTp = ^Q, т = —, то
i у — у0__Fcosa — kQ
J t P
I 0 = — P F sin a -ф- Q.
Выражая из второго равенства Q = P — Asina (о том, что в этой задаче Q<^P, указывалось выше) и подставляя его значение в первое равенство, получим
V — У„__F COS а — k (Р — F sin a)
- g,
откуда
Р — F sill a
Задача 11
Автомобиль, имевший у основания горы с углом наклона a скорость Vg, движется вверх с выключенным двигателем. Считая коэффициент трения равным k, найти изменение высоты автомобиля над основанием горы за время t (рис. 35).
31
Решение
Очевидно, что
___P + Q-F Fтр. т ’
V" -, , «/3
Дг — v$t -|—2~,
Исключая отсюда а,
получим
Р 4~ Q Ч~ ~Ртр 2Дг — 2V(ft
т t1
или, проектируя все векторы на оси к и у,
— mg sin а — Гтр 2Дх — 2»0£ т 1?
— mg cos « + 0 Q
т
(ибо по оси у ускорения нет). Так как F-^ — kQ, а из второго равенства Q — mg cos а, то
Сокращая слева на т и замечая, что Д/г = Дх51ла, получим
/ | г , \ «111 и /
g (sin а 4- « cos а) = —i--------------,
откуда
Д/г = ~ sin а.
32
Задача 12
Автомобиль весом Р, двигаясь в гору с углом наклона а, на пути As увеличивает свою скорость от до и. Считая коэффициент тормозящего трения равным k, найти силу движущего трения (рис. 36).
Решение
Очевидно, что происходящие с автомобилем механические процессы описываются в данной задаче уравнениями
- Ap + Q+Ap + P.
а~ т ’ а~ 2As *
Так как во вторую формулу входит величина ускорения, а в первую — вектор ускорения, то исключать ускорение нельзя до тех пор, пока первому равенству не сопоставлены скалярные, именно:
__ — Ртр /тр — Р sin а т *
0 = Q — Pcosa;
2As
Здесь учтено, что ау — 0 и, значит, ах — а. Учитывая, чтоFip=&Q р
и т — ~ и исключая из системы Q и а, получим
Vs — vl — kP COS а -р /Тр — Р sin а
2As ~ Р
откуда
^p==(?ir7+&cosa+sina)р*
2 В, К. Кобушкин
33
Задача 13
На нити, выдерживающей натяжение не более Ттях, поднимают груз весом Р из состояния покоя вертикально вверх. Считая силу сопротивления среды равной Рсопр, найти наибольшую высоту, на которую можно под- нять груз за время t (рис. 37).
Решение
I. - Очевидны равенства
г + Р + Аопр. m ’
л । at'2 Дг = Vot + ~-•-----------О ...- .. . — >» ‘t
\р х или в проекциях на вертикаль,
¥ с учетом По = О и исключая а,
получим
Рис. 37. Т — Р — Fconp 2 Ду
m Р '
Предельная высота определяется в данном случае прочностью нити, т. е. при = Т = Тт!Я. Поэтому
т — р — F 2h 2 max г ‘ сопр „___‘щах
Р р ,
откуда
т ______Р — F Р
Ь ______ им сопр ~
"щах--- р g •
Задача 14
Цилиндрическое ведро с водой поднимают равноускоренно и за время t скорость его изменяют от до v. Зная, что масса воды равна ш, а площадь основания _
ведра S, найти давление воды на дно (рис. 38). ---„ .
Решение Z_—~ Ц“
Очевидно, что движение воды опре- _ _____
деляется равенствами __ ____ _ _____
V — Оо + at,
- О,
из которых следует по исключении а
Q + P у —V о ''
m t ’ Рис. 38.
34
или в проекции на вертикаль
откуда
Q — mg v — v0
т t ’
Q = ,:,(s+^\
\ b 1
Но по третьему закону Qt —-Q или в Qi=Q-
Учитывая, что
проекции на вертикаль
окончательно имеем
Р — Ро\
t 1
Задача 15
Камень весом Р, падая с высоты /zi и попадая в снег, пробивает в нем яму глубиной Считая движение в воздухе и в снегу равнопеременным, силу сопротивления в воздухе равной Flt найти силу сопротивления движению в снегу Fi (рис. 39).
Рис. 39.
Решение
Очевидно, что движение камня распадается на два этапа (в воздухе и в снегу), и потому
и
2*
3’-
Учитывая, что t>M = 0, у2 = 0, vl = vt№ = v и считая направление вниз положительным, имеем
Р — F,
«1 =—рЧ, (1)
V2 /04
«I 57^; (2)
Р — F.
— а^ = —р-^ g; (3)
__С,2===Д!. (4)
Z/Д, ' ’
В уравнениях взято со знаком «минус», ибо а2 направлено вверх при выборе положительного направления вниз.
Исключая из (1) и (2) ах и из (3) и (4) а«, получим
о8 Р - Л Vs 2Л, — р g h 2hs
g.
Р
Деля эти равенства одно на другое и упрощая, получаем fl = p(s+1)-f'S-
Задача 16
Каксе наибольшее количество вагонов может паровоз везти в гору с уклоном 0,025 (sin а = 0,025), если известно, что 1) вес паровоза в три раза больше веса вагона; 2) коэффициент максимального трения покоя /?•> = 0,1; 3) коэффициент трения качения ki = 0,001?
Решение
На состав действуют (рис. 40): 1) сила тяжести
Рссст ~ Рваг-У Рпар — Рваг (N 3);
2) сила тормозящего трения
Р тр ^iQcoctj
3) сила движущего трения
f = k'iQnap-
Считая движение состава вверх -равномерным, получим
Qcoct f “К РГОСТ “К Ртр = О
или в проекциях на 7- и п-направления
f — Рсоса sin а — Гтр = 0;
Qcoct РCOCT COS (X — 0.
36
ТаК КаК FTp— ^iQcoctj & f — ^jQnap
^‘iQnap Pсост^1П CC ^iQcoct —~ Oj
^coct Fcoct COS CC 0.
Исключая QC0CT и учитывая, что Qnap = ЗРваг cos а, получим
fc$3PBar COS a — (*v -j- 3) Psar sin a — ki (N -J- 3) PBar cos a = 0,
откуда
д,_____3 [(Й3 — kt) COS a — sin a]_________g
sin a kt COS a
Интересно сравнить это число с тем числом вагонов, которое вез бы паровоз по горизонтальной дороге (т. е. а = 0)
N' 3 (^ — fet). 297>
Отсюда видно, как сильно сказывается даже малый уклон на числе N.
Задача 17
По наклонной плоскости с углом наклона а и коэффициентом трения k движется под действием силы F, составляющей угол [3 с направлением вверх вдоль наклонной плоскости, тело массой т. Тело двигалось вверх замедленно, имея начальную скорость о0. Через какое время t от начала наблюдения тело будет иметь скорость v уже при движении вниз?
37
Решение
При движении тела вверх (рис. 41, А) тё + ^тР1 4~ Q 4- F — тай (1)
П1
где v'— конечная при движении вверх и начальная при движении вниз скорость.
Рис. 41.
При движении вниз (рис. 41, Б)
mg Ч- ^трг 4* Q + F = тай (3)
Исключая О] из (1) и (2) и о2 из (3) и (4), получим с учетом v'~ О
4- ^тР14-Q4-^ == ~
mg 4- FTPs4- Q 4- F = т^.
Проектируя все векторы на оси, получим с учетом F-^ — kQ
mg sin а 4- kQ — F cos p = ;
— mg cos а 4- Q 4~ F sin $ — 0;
mg sin а — kQ — F cos 8 ~ ~
38
или, исключая из этих равенств Q,
mg sin i-y-k (mg cos a — F sin (!) — F cos $ = (5)
mg sin a — k(mg cos a — F sin (3) — F cos p = ^-. (6)
Выражая из (5) Л, а из (6) и складывая их, найдем после очевидных преобразований
I _ _____________"'Ро________________!
mg (sin a k cos a) — ?' (cos p 4- k sin P) ‘
।_______________mv
‘ mg (sin a — k cos a) — F (cos ? — k sin 3) ’
б) движение системы материальных точек, связанных нерастяжимыми невесомыми нитями, и тел, имеющих взаимные ускорения
В принципе решение задач этого параграфа не отличается от решения задач предыдущего параграфа: надо рассматривать силы, действующие на каждое из интересующих нас тел, и, написав второй закон для каждого из них, решать систему уравнений.
6
Рис. 42.
В тех случаях, когда нас не интересуют силы, возникающие в нитях, можно рассматривать систему совместно движущихся тел как одно тело.
Выражение «натяжение нити в данном месте» означает силу, с которой одна часть нити действует на другую в данном сечении (рис. 42, Л). По третьему закону | 7\ 2| = | 11, и потому
мы обозначим величину натяжения нити буквой Т без индексов.
Покажем, что величина силы натяжения по всей нити одинакова, если нить невесома и если на нить не действуют никакие внешние силы, приложенные к поверхности нити вдоль ее оси. Для этого выделим мысленно любой кусочек нити А/ (рис. 42, Б). На него действуют 7\ и fi.
39
По второму закону ЛТа = Д/п • а. Так как Д;п = 0 (нить невесома), то 1\ =— f2 и, значит, 17\ | = | Та | = 7" = const по всей нити.
Аналогично доказывается, что силы, действующие на любое невесомое тело, дают в сумме пуль. В частности, это относится к невесомым блокам, упоминающимся в задачах.
Естественно, понятие «невесомое» тело означает лишь то, что его масса ничтожно мала по сравнению с массами любых других тел, упомянутых в задаче.
Если тела движутся с ускорениями относительно друг друга, то для решения задачи часто необходимо бывает эти ускорения связать друг с другом, для чего надо иметь в виду, что орез = =a1-\-ai и щ <> = £! — (в соответствии со сказанным в параграфе 3, п. а).
Задача 18
На два бруска массами и тг, связанных нерастяжимой питью, действуют силы Fx и Еа под углами cq <^90° и а2^>90о
Рис. 43.
к направлению движения. Найти ускорение системы, если коэффициент трения между брусками и горизонтальной плоскостью равен k (рис. 43). Бруски от плоскости не отрываются.
Решение
Так как ускорения обоих тел одинаковы и силы натяжения нас не интересуют, можно рассматривать всю систему как одно тело. Тогда
—__Ai Qt + Ттр1 + ^*1 + ft + Ттр2 +
т1 4“
Считая направление вдоль движения положительным и учитывая, что ал = 0 (и, следовательно, at = a), получим
Л cos at — Д.гр| + COS аа - FTpa .
а rnt ms ’
0 = sin й] —|— Qi — Pi "4“ Qa —j- Eg sin ctg — Pg.
40
А так как FTp = FTPl + FTPs = ^ (Qi+<?а)< т0
____Ft cos a, + F3 cos aa — fe <Qt -j- Q2) °___mt + m2
0 = Fi sin ai — Pi F'i sin a2 — P> -j- (Qi 4- Qi)-
Исключая отсюда (Qi4~Q4 и учитывая, что P = mg, получим
___F\ cos g, F3 cos a2 — fe (mig w2g — Fr sin at — F-. sin a2) a___nii-\- ms
При этом так как а2>90°, то cosa4<^0 и F2 cos а2 <0.
Задача 19
На горизонтальной поверхности с коэффициентом трения k движется брусок весом Р2, соединенный нитью со свисающим бруском весом Pi. Найти натяжение нити и силу давления на ось невесомого блока (рис. 44).
Решение
Здесь 71,б — сила натяжения нити, действующая между блоком и первым телом; 7\ 6— сила натяжения нити между вторым телом и блоком. Очевидно, что
Рис. 44.
—* Ps + 7тр + Фг+ П, б ---------------------•
Надо иметь в виду, что здесь at и а2 векторы, чи-
сленные значения которых равны, но направления разные. Поэтому но \oi j = Ja4j = a. То же и с натяжением нити:
ТУб^Пб, но \ fi.6\ = \7\6\==T.
В данном случае удобно все векторы проектировать на t- и п-направления, и так как ап = 0 (направление скорости движения тел не меняется), то at — a.
41
Поэтому равенства в проекциях на t- и n-направления (вдоль и поперек движения) будут иметь вид:
a = a = 0 = _pa + Q2.
Исключая из этой системы а и Q2, получим после несложных преобразований
т_Р1-Ра(1 + й) Pi + Pa •
Для нахождения силы давления на ось блока учтем, что (рис. 45)
Тб, 1 + Т&, 2 Qe — Д
т. е. тот факт, что блок находится в равновесии. Здесь T$,i и Тб, а — силы натяжения нити, действующие между блоком и первым
и вторым телами соответственно (при этом 7\ i==T6,2 = 7); <?б— сила, действующая на ось блока со стороны подставки. Проектируя силы на горизонтальное и вертикальное направления, получим
(—Т + Qe cos 45° = 0; (7 = Q6cos 450;
(—Т Qs sin 45° = 0 ИЛИ | 7 = Q6sin45°.
Возводя в квадрат каждое из равенств этой системы и складывая их, получим
2Г = Q! (cos2 45° 4-sin* 45°) или 272 = Qi, откуда
Q6 = r/2.
42
Q6 можно было найти и иначе. Заменяя T^s-f-T^.i на их результирующую F, получим F-]-Q6 = 0 или Q6 =— F. Но, как видно из прямоугольника, F — TV2. Значит, и Q — TV2.
Задача 20
По шероховатой (при наличии трения) горизонтальной поверхности под действием горизонтальной силы F движется однородный постоянного сечения брусок длиной I. Найти натяжение в бруске как функцию расстояния от его заднего края (рис. 46).
Решение
Разобьем мысленно брусок сечением АВ на две части. Так как брусок движется как одно целое, то о1 = о2 = о и тогда для двух частей бруска
_ +t1i2 + q1+p
а=---------:
mt ’
— g 4" F-rn, + + Qa
0=---------—-----------
тг
Проектируя все векторы на t- и n-направлеиия, получим, учитывая, что Fip = ^Q и Ti,s = 7\i — Т-.
a^~kQy-T + P. mt ’
0 = —+
_feQa+ Г mt ’ о = — -Ф- Qs’
(1)
(2)
(3)
(4)
43
Исключая из (1) и (2) Q1( а из (3) и (4) Q3, имеем
— kniig — 7 + F а —---------------------!—I
771, ’
Исключая а, получим
— kmsg + Т т3
откуда
Но
Т , F __ . . Т
mt~^~ nii m2
mt pV, ps(l — x) I
ma plA psx x
« —
Подставляя это значение в выражение для Т, получаем
оконча-
тельно
T—j-x.
Задача 21
По клину, грани которого составляют углы at и а2 с горизонтом, движутся два бруска, массы которых и та. Связываю-
щая их нить перекинута через блок. Зная коэффициенты трения брусков о клин ki и ki, найти (рис. 47): а) ускорения тел; б) натяжение нити; в) силу давления на ось блока.
Решение
Силы, действующие на бруски, очевидны, и поэтому miS ~Ь Qi 4~ ^тр! = mia\;
4~ Т,, б Qa ^трз = т^а^,
44
Считая указанные направления t и п положительными и учитывая, что величина натяжения по всей нити одинакова и равна Т, получим в проекциях на оси с учетом а1 = а2 = а
triig sin ctj — Т — AiQi = пца; (1)
— nitg cos aj -f- Qi — 0; (2)
— ttiig sin a2 T — k.,Q> — m,a\ (3)
— m2gcosa2-|-Q2 = 0. (4)
Исключая из (1) и (2) Qb а из (3) и (4) Q2, будем иметь ni\g sin aj — T — kitriig cos оц = TTZiC;
— mig sin «2 Г — cos a2 — nW, откуда после решения системы находим
____ (от, sin a, — m2 sin а2) — (ЙЦ/Ц cos + k2m2 cos а2) a_g “OTi
Что касается силы давления на ось блока, то, поскольку блок ускорения не имеет (рис. 48),
Qg Н- Уб, 1 + Уб. 2 = 0 или
Q64-F = 0, по
F = VГ2 4-Г-2Г cos (Я1 + а2) = Т/2[1—cos (оц-Ю] =
= 2ПпьЦ^2.
Поскольку Т уже найдено, то тем и исчерпывается решение задачи.
45
Задача 22
На горизонтальной плоскости лежит брусок массой М, на котором помещен другой брусок массой т. Зная, что коэффици-
ент трения между бруском и плоскостью равен klt а между брусками — /г», найти силу, которую надо приложить к нижнему бруску, чтобы верхний брусок соскользнул (рис. 49).
Решение
Очевидно, что
Сьа4~Ртр~гQi. пл Р =/Ищ, ITlg —|— Qg, 1 4“ ^*2,1 ——ЩО-jj
или в проекциях с учетом Fjp — kQ
— kiQi—k.>Qz-\-F ~ Май (1)
-M^-Q3 + Qi = 0; (2)
к^ = тай (3)
— mg4-Q3 = 0, (4)
где Qi — |Qi,n|; Qa— = iQa.il•
Подставляя из (4) в первые три уравнения, а загем Qt из (2) в (1), получим
— М (М — k.mg ф- F — Май
k^g = с3.
46
Так как для соскальзывания бруска tn необходимо ai^>a2, то
F — S [fejM 4~ (fei ~Ь feg)ffl]
откуда искомая сила
* Задача 23
Система грузов с т1( тг и т3 изображена на рис. 50. Блоки А и В и нити невесомы; mi^> m24~ tn3 и m2^>m3. Найти
ускорение грузов относительно земли и натяжение нитей.
Решение
Силы, действующие на тела, очевидны, поэтому
т1§ ~'г ?1>А — т1а1> (1) |
Т в, а 4~ Т в, j-J- Т в, з = Швав", (2;
- § т<£-\-Ть в = т3а3; (3) *
Т3, в = т3оз. (4) |
О;
Очевидно, что эти равенства дадут В в проекциях четыре скалярных ра- | венства, а подлежат нахождению <§ пять величин: ait а3, а3, Ti и Т3. Необходимо еще одно равенство. Получим его из того, что
а3 = о.в 4~ fij;
5 = 54-5,
Рис. 50.
где ав — ускорение блока В относительно земли; а3 и а3 — ускорения 2-го и 3-го тела, относительно блока В. Но
йв= — at, поэтому
5 = —214-5;
5 = -54-5-
Учитывая, что а3 = -~а'3, получим, складывая эти равенства, 54-5=—25- (5)
Пусть направление вниз будет положительным. Тогда 5 из-за 4-пг3) направлено вниз. Чго касается 5 и а3, то а3
41
обязательно направлено при этом вверх из-за m2^>m3. О направлении а} ничего сказать нельзя до конца решения задачи. Будем пока предполагать направленным вниз.
Проектируя равенства (1) —- (5) на вертикаль, получим (с учетом того, что TltA = T13A — Ti и в = Гд 2 = 7\ в = = ТВ13 — Тг, а также с учетом mB = Q)
rriig — Т1 = т1а1‘, (6)
Т1-2Тг = 0‘, (7)
niig — Т2 = m-ia-i. (8)
m3g — Т\— ~тм (9)
а.2 — а3— — 2at (Ю)
или с учетом Ti = 27\ по (7)
2/, at — g (11)
(12)
«. (13)
— 2ai = а2 — а3. (14)
Складывая (12) и (13), получим
#3 2g — Т2 ( 1 . ь 1 mJ (15)
Подставляя а2 из (11) в (14), получим
г> । 4 г, а2 а3= 2g-\-m-. (16)
Приравнивая правые части (15) и (16), после преобразований имеем
Зная находим по (11), (12) и (13) (8 \ / 4 \
1 — 4 _1_ m‘ I °2 ~SI тг ]: 7)
<1 Ч---г- — । I -----1- 1 Ч---I
1 / \ tnt J
{ 4 Л
3 s 4т, т, t
\ mt т3 /
Выясним направление а>. Мы считали его направленным вниз, т. е. полагали его проекцию а2 положительной. Но для а2^>0 необходимо по (17)
Mi т3
48
т. е. массы ть тг и
т3 должны удовлетворить соотношению
т,т.
tn3<Z~y——i—
в противном случае а3 направлено вверх.
* Задача 24
По клину с углом наклона а и массой М, движущемуся по горизонтальной поверхности без трения, скользит вниз брусок
Рис. 51.
массой т. Считая коэффициент трения между клином и бруском равным /г, найти ускорение клина а3 и ускорение бруска а относительно земли (рис. 51).
Решение
Силы, действующие на тела, очевидны. Тогда
Mg 4~ Qi, 2 Qi. п Ч- Ртр1,2 — Мац-mg Ч~ Р тр2> 1Ч- Qa, 1 та.
Или в проекциях на выбранные направления с учетом
а$у — 0, Qi, з — Qa,1 — Qi, Qi, п — Qa» Ртр1,2 — Ртр2,1 — ^Q;
— Qi sin а Ч~ kQi cos а — — Май\ (1)
— Mg — Qi cos а Ч- Qa — sin а = 0*, (2)
— А(?1С08аЧ-(218ша = тая; (3)
— mgkQt sin a.-\-Qt cos а.=тау. (4)
Очевидно, четырех уравнений для решения задачи недостаточно, ибо неизвестных пять.
49
Найдем пятое уравнение, связав аа, а и а', где а' — ускорение бруска относительно клина; имеем
а = аа а'.
Поскольку Ох и а’ направлено вдоль клина вниз, то в проекциях на оси имеем
ах — — я0 4~ a'cos а; ау =— а'sin а.
Исключая отсюда величину относительного ускорения а', получим ау = — (a04-ax)tga. (5)
При этом й0^>0, ах~^>0 и ау<^0.
Складывая (1) и (3), получим
тах — Май = 0. (6}
Исключая Qi из (1) и (4), получим
I k sin a 4- COS a .. tnav — — mg----;----г--- Mat
y ° 1 sin a — k COS a u
ИЛИ
n — ct I Л1а,> k a + 1 /7\
ay — -g+—------[gaTTF- <7>
Исключая ay из (5) и (7), имеем
Л4<20 k tg a 1 i
g~~^~~tga—=^ + 4v)tga. (8)
Решая систему (6) и (8), находим
Для нахождения ау подставим в (5) ах = —из (6), а потом уже найденное ай. Тогда
ГМ ,
/ М\ ~ \ т + tg а
ау— ~ (ай-ах) tga= - ) tga = tg2 а 7 ------.
т tg a — 1г +fsa
Ясно, что решение для а0, ах и ау имеет смысл лишь при tga^>^.
Полученные результаты полезно исследовать для случаев М^т, т^М, k — Q, a = 0, a = 90.
50
Задача 25
С каким ускорением должен ехать вниз~заводной автомобиль массой т по доске массой М, лежащей на неподвижном клине с углом наклона а, чтобы доска равномерно скользила вверх по клину? Коэффициент трения автомобиля о доску равен klt доски о клин — ki (рис. 52).
Ркс. 52.
Решение
Имеем в проекциях на оси:
/Ц-mg sin а — F1 = ma; (1)
Qi — mg cos а = 0; (2)
Pi 4-Pi 4" Mg sin а— / = 0; (3)
Qi — Qi — Algcosa — 0, (4)
где f = fb2 = f2ll — сила движущего трения; F1 = F12 = F2>1 — тормозящее трение между автомобилем и доской; Р2 — тормозящее трение между доской и клином.
Складывая (1) с (3) и (2) с (4), находим
g(m-{--M) sin а 4~ Ра = ma;
Q2 — g (М 4- m) cos a = 0.
Учитывая, что
Ft — k2Q2, имеем из (5)
g (m 4- Л4) sin a -f- A’2Q2 = ma.
(5)
(6)
Подставляя сюда Q2, выраженное из (6), получаем g (т 4- Л4) sin a 4- ktg (Л4 m) cos a — ma, откуда
a — g(l + (sin a-f-^cos a).
51
Видно, что а не зависит от kt, т. е. от трения между автомобилем и доской в том смысле, что оно может быть любым, но отличным от нуля (в противном случае / = 0 и доска вверх скользить не сможет).
Задача 26
На краях тележки массой М и длиной I находятся два человека массами nil и т.2. Коэффициент трения тележки о горизонтальную поверхность равен k. С каким ускорением а будет двигаться тележка, если люди пойдут навстречу друг другу с ускорениями Oj и а2 по отношению к земле (рис. 53)?
Решение
Очевидно, на тела действуют, помимо сил тяжести и реакций опор, силы трения. При этом на каждого человека и на тележку действуют и силы движущего (f) и силы тормозящего (С) трения. Имеем сразу в проекциях на линию движения с учетом F^ = kQ
fi — Fi = miar,
— = —ГПчйг,
— fi -ф- Fi -ф- f2 — Fi — kQ =. Ma.
При этом знак а неизвестен. Складывая эти равенства и учитывая, что
Q = Mg -ф- Qi -ф- Qi = (Л1 mi -ф- m.>) g, получаем
— k (Л4 -ф- ту -ф- m-i) g — Matniai — т2а2,
52
откуда
а —
msa, — midi — k (M -f- m{ + g Л1
Отсюда видно, что аД>0, т. e. тележка будет иметь ускорение в сторону t — (вправо) лишь при
/?г. а.2 4> r/Zj«i 4- k (М 4- mi 4- т2) g. (*)
Задача 27
Считая, что в предыдущей задаче известно ускорение тележки а и что ускорения людей относительно тележки равны и противоположны (т. е. а[ = — щ), найти ускорения людей относительно земли.
Решение
Очевидно, что решение этой задачи даст как и в предыдущей
— k (м 4- mi 4- s — Ма 4~ (**)
Для нахождения at и необходимо еще одно уравнение, связывающее a, ai и а3. По условию задачи
-Н2, но щ = а 4~ 4 и я., — а 4' откуда
щ — а — — (а-2 — а) или
щ 4-«2 = 2а.
Считая, что а и at направлены вправо, а а3 — влево, получим в проекциях на линию движения
zzj ““ (###)
Решая (**) и (***) совместно, находим
„ ____ a (2от2 + М) + k (М + mt + тг) g
ai —---------------------------------------------
т.г — mt
a + M) + k (M + mx + m2) g ----------------------------------------
и., — mt
Отсюда видно, что при а>0 (что имеет место при условии (*) предыдущей задачи), знаки и аа определяются соотношением между Ш! и при наше предположение о направлениях щ и а2 справедливо; при — нет.
53
5. ЗАКОН ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ ТЕЛ И ЗАКОН ЕГО СОХРАНЕНИЯ
Часто тела взаимодействуют столь сложным образом, что решение задачи с использованием второго закона Ньютона становится затруднительным. Но если в такого рода задачах нас не интересуют ускорения и координаты взаимодействующих тел, то разумно воспользоваться законом изменения количества движения системы тел:
? А/ = 4-... 4- w„un) — + • • • 4 «гл)-
Здесь F — результирующая всех внешних сил, действующих на систему; т^; — количество движения Pro тела до начала действия сил; пцщ— то же после воздействия сил.
Как всегда, этому векторному равенству можно сопоставить три скалярных:
Fx-M = (miihx +... -J- — (mxvix 4- • 4~ mnvnx);
Fy-M = {пциу 4- • • 4- mnuny) — (miViy 4" • • • + mnvny)-, Ft-M= (гщи^ 4- ... 4- тпипг) — (пци1г 4-... 4- mnvrix).
Если в каком-либо направлении внешние силы на систему не действуют, то система в этом направлении своего количества движения не меняет.
Если ?А/ = 0, то система вообще не меняет своего количества движения. Естественно, таких систем в природе не бывает, но бывают такие системы тел, для которых Г-Д/^О. Такие системы почти не меняют своего количества движения за время А/ в том смысле, что изменение общего количества движения системы много меньше того количества движения, которым система обладала до воздействия внешних сил. При этом К-А/ может быть близко к нулю как за счет F 0 при большом Д/, так и за счет Д/^«0 при большой F.
Система, на которую не действуют внешние силы в каком-либо направлении, называется замкнутой в этом направлении.
Рассмотрим несколько примеров.
1. Несколько шаров падают в воздухе. Очевидно, что по вертикали система не замкнута, а в горизонтальной плоскости ведет себя как замкнутая.
2. На неподвижной горизонтальной шероховатой поверхности двигается несколько шаров. Здесь положение как раз обратное: по вертикали силы, действующие на систему, уравновешены и в этом направлении система ведет себя как замкнутая; но в горизонтальной плоскости действуют, вообще говоря, неуравновешенные силы, и поэтому в этой плоскости система не замкнута.
3. Два шара сталкиваются в воздухе. Во время столкновения на шары действуют и силы тяжести и силы сопротивления, по-
54
этому система не замкнута. Но так как время удара весьма мало, ю за время удара количество движения системы существенно не изменится. Поэтому во время удара система
мало отличается от замкнутой.
4. Мальчик, стоя на льду, бросает камень под углом к горизонту, причем лезвия коньков расположены в плоскости бросания. Ясно, что в направлении z, перпендикулярном к этой плоскости, система замкнута (рис. 54).
В направлении х система не замкнута благодаря силам сопротивления, в направлении у система тоже не замкнута благодаря силам сопротивления
и силам, действующим на систему
со стороны земли (тяготение и опора).
При этом степень нарушения замкнутости системы в направлениях х и у зависит от угла бросания а.
Если, однако, трение мало, то во время броска система в направлении х мало отличается от замкнутой. В направ-
лении же у она замкнута лишь при а = 0.
Рис. 55.
Задача 28
Две одинаковые лодки двигались со скоростями 01 и Vi под углами и аа к некоторому направлению. Когда лодки оказались на очень близком расстоянии, пассажиры лодок одновременно обменялись
одинаковыми мешками с грузом так аккуратно, что при отделении мешка от «своей» лодки скорость лодки и мешка не изменилась. Считая массу каждой из лодок вместе с пассажиром в п раз большей массы мешка, найти скорости лодок после обмена мешками (рис. 55).
Решение
После отделения мешков от лодок лодки имели импульсы Mi’i и Mvit а мешки mvt и то2.
55
При соединении лодок с мешками имеем, пренебрегая импульсом внешних сил:
-j- mu2 ~ (М т) иг', Mvi -J- mv! = (М т) и2.
Будем искать не величины скоростей и} и «2 и определяющие их направления углы Pi и р2, а проекции скоростей uJX, и1у, uix и Ччу. Тогда в проекциях на оси получим:
' Л1У! cos а2 4- mv.2 cos а2== (Л4 4- т) и1х;
Mvt sin oq-j-nws sin а2 = (Л1 -J-/л) uiy;
Mv.2 cos a2 4“ cos «1 — (M 4- tn) utx;
Mv3 sin a2 4- 4iVi sin оц = (M 4~ m) uiy.
Так как M — mn (по условию), то
nV, COS a. + V5 COS aa
-----„+Т------;
__________________________nVi sin a, -|- v2 sin a2
u'y~~ «4-1 ‘ ’’
_ tlV„ COS as + VL COS a, ;
_____nv2 sin a2 -|- Vt sin at uiy — •
Задача 29
Определить скорости лодок после обмена мешками (задача 28), если сперва был переложен первый мешок, а потом второй.
Решение
Пренебрегая импульсом внешних сил, получим для случая перекладывания первого мешка во вторую лодку:
(Л14- т) о2 4- mvt = (М 4- 2т) и.2
или в проекциях
(М т) и2 cos a2 -4 mVi cos сч = (Л14- 2m) uix-,
(M 4- m) sin a2 -4 mvx sin = (M 4- 2m) uiy,
откуда с учетом M = m • n
__(n -|- 1) v3 COS a2 + Vi COS a,
Uix — n + 2 ;
(n + 1) v.2 sin a2 + Vi sin a, u-y ~~ F+i •
53
При подсчете скорости первой лодки после перекладывания в неэ мешка со второй надо учесть, что мешок теперь имеет скорость и2, поэтому
Мщ ти^ — (М -t- т) Ut или
Mvt cos 04 -f- niuix = (М «О «i.v'>
Alt’i sin Я] 4~ muiy — (Л1 4~ tn) uiy, откуда
__nv, cos a, + и., v
U1 v--------;—;-- \
iX n 4- 1
__ nvx sin aj + a >_jj
UV — r+'l •
Читателю предоставляется самому сопоставить и исследовать причины различных решений этой и предыдущей задач.
* Задача 30
Из орудия, установленного па платформе массой М, производится выстрел снарядом массой т, который получает скорость v под углом а к горизонту. Платформа в результате отдачи приходит в движение. Сколько времени платформа находилась в движении, если коэффициент трения о рельсы равен k и М^>т?
Решение
Очевидно, что Д/ складывается из Д4 и Д/2, где ДЛ —время ускоренного движения платформы в момент выстрела, ЛА2 — время замедленного движения платформы после выстрела. На чертеже/4, с и 7*4 п —— силы взаимодействия снаряда и платформы.
Для первого этапа движения платформы (рис. 56, А)
(Al^ + Fn,c4-Q14-FTpi)A/ = Mu~Mu0 (*)
или с учетом того, что «о = О, получим в проекциях на оси
( (F„, с cos a — kQi) Mi = /Ии;
I — Mg — F„, c sin a 4- Qi = 0.
Исключая Qi, получим
(Fn, c cos a — kMg — kF„, c sin a) Д4 = Mu. (1)
Для снаряда с учетом mg^FZt п получим:
?с, пМ — mv — mvo или с учетом о0 = 0
( Fz, п cos аД/j — mv cos а; (2)
1 FCl п sin aAZi = me’ sina. (3)
57
Учитывая, что Fn Z=FC n = F, получим, подставляя (2) и (3) в (1),
mv cos а — kMg^ti — knw sin а — Ми, откуда
. , mv (cos а — k sin а) и
' — kMg kg'
Для второго этапа движения платформы (рис. 56, Б) найдем (W + Q.2 4-fTp2) М. = Ми'-Ми, (**)
где и' —0 (конечная скорость платформы).
В проекциях на оси будем иметь
| — kQt-^t=—Mir,
1 -Mg + Q2 = 0,
58
откуда после исключения Q2 получим
Тогда
Д^ =
и
kg'
Л , . , । л г и , mv (cos а — k sm а)
= Zifo -4— --- -----h- --------t-t-z--------
Z 1 kg 1 kMg
ll
kg'
Окончательно найдем
mv (cos a — k sin a)
kMg
Замечания. Угол наклона орудия а не равен углу, под которым вылетает снаряд. Действительно, гс = vc> п + и (см. рис. 56, А).
Здесь « — скорость платформы относительно земли, vCl п — скорость снаряда относительно платформы (она и составляет угол а с горизонтом), vc — скорость снаряда относительно земли. Она составляет угол а-|-Да с гори
зонтом. Ясно, что Да —» О при —» О,
что и имеет место в нашем случае.
Задачу можно было бы начинать решать со сложения уравнений (*) и ;**) с последующим проектированием векторов на оси.
6. ДВИЖЕНИЕ ТЕЛА ПЕРЕДАННОЙ МАССЫ
Если при движении тела его масса меняется, то производить расчеты по формуле а ——становится затруднительным. Удобной является формула Мещерского
та — ? + рс,
где F — результирующая всех внешних сил, действующих на тело; р — изменение массы в единицу времени, обусловленное выбросом или присоединением частиц к движущемуся телу; р^>0, если частицы присоединяются к телу (масса тела увеличивается); р<^0, если частицы покидают тело (и масса тела убывает); с —скорость частиц относительно тела основной массы (например, ракеты); рс— реактивная сила. Очевидно, рс направлена в сторону с при Р>0 и противоположна с при р<^0 (см. рис. 57, А).
В случае F — const движение тела не будет равнопеременным при pc = const из-за const. Но если за время движения масса тела существенно не изменилась, то можно считать, что при F = const и pc = const ускорение тоже постоянно, т. е. а = const, и движение будет практически равнопеременным, так что можно использовать при решении задач, где это необходимо, кинематические формулы для равнопеременного движения. При этом в формуле Мещерского считаем р<^0, если частицы покидают ракету, и р>0, если частицы присоединяются к ракете.
59
Уравнение Мещерского является следствием закона изменения количества движения системы тел. Сделаем вывод его.
Пусть некоторое тело (рис. 57, Б) имело количество движения mv и к нему за малое время А/ присоединилась некая малая масса Ат, имевшая до присоединения скорость v1: а значит, и
Рис. 57.
количество движения ^mvt. Обозначая количество движения системы тело — частица буквой р, получим до присоединения Ат
Ро — mv -J-
после присоединения
р = (т -|- Ат) (и -|- Дц),
так как в результате вполне неупругого удара (присоединения) масса образовавшегося тела стала равной (m-j-Am)- а скорость, изменившись на Ду, стала равной (р-)~Дц). Так как
Р — Ро = F • А/, то
(т4- Ат) (оДо) —(то4~&mvi) = FM,
откуда по раскрытии скобок и пренебрежении членом ДтЛо найдем
Ьт (v — vi) = FM
или после деления на А/ получим
та 4~ Iх (° — Pi)=F-
Так как Vt— v = c есть скорость присоединяющегося тела малой массы относительно основного тела массы т, то в соответствии со сказанным в начале этого параграфа
та — F 4~
60
Задача 31
Космический корабль влетает со скоростью v в облако космической пыли плотностью р2. Чтобы скорость корабля не уменьшилась, включили двигатель. Какова плотность вытекающих из
сопла сечения Si газов, если скорость их вытекания относительно корабля равна и, а сечение корабля S2? Пылинки после удара прилипают к обшивке корабля (рис. 58).
Решение
Возьмем за систему отсчета корабль. Так как корабль ускорения не имеет, то пли
Л-Л = 0, но „ Д/?г ₽1ДР1 PiSjA/i о о о Г1 = и = и = и — UDtSill = PtStiT.
Аналогично и тогда откуда
F8 = p2S2n9, piSjiz® — p2S2?/3 = О,
Задача 32
Реактивная тележка с массой М движется вверх по наклонной плоскости с углом наклона я и коэффициентом трения k за счет выброса под углом р к поверхности наклонной плоскости струи сжатого воздуха. Считая скорость воздуха относительно
61
тележки равной с, его массу, выброшенную за время движения, равной Дт и малой по сравнению с М, определить время, за которое тележка изменила свою скорость от п0 До v (рис. 59).
Рис. 59.
Решение
Так как все силы постоянны и Л1^> Ат, то a — const и поюму ( Mn = Mi4-FTP + Q + ^P;
[ v = По —at
или
M~^=Mf+AP+Q+4
И в проекциях на оси Тип
М Г ~ =— Mg sin а — kQ-'~-~-^-c cos P;
0 = — Mg cos a Q — c sin p.
Исключая Q, получим
Л1 —= — Mg sin a — k [Mg cos a c sin pj c cos p,
отсюда
___cAffi (cos ft — fe sin ft) — M (v — v0) Mg-(sin a 4-fc COS a)
При решении этой задачи считалось, что скорость тележки v мала по сравнению с величиной с и, значит, скорость движения струи воздуха относительно земли и практически совпадает с с.
62
* Задача 33
В тележку весом Р, имеющую форму параллелепипеда с площадью дна Sue отверстием в дне площадью Si, движущуюся по горизонтальной Роверхности с коэффициентом трения k, льет дождь плотности р под углом а к вертикали. Найти условие, при котором скорость тележки постоянна, и найти эту скорость, если скорость капель дождя равна v (рис. 60), а масса воды в тележке Л4В.
Рис. 60.
Решение
Так как ускорение тележки равно нулю, то
р 4~ 4- ЛР 4- Q 4- 4- рс=о, (1)
где Р — вес тележки; — вес находящейся в тележке воды; Q — сила реакции опоры; — сила трения; р.с— сила со стороны дождя; р. — масса воды, попадающей в тележку в единицу времени; ~FB — y.BvB— сила реакции вытекающей из тележки воды, где vB — скорость воды относительно тележки (причем, очевидно, что vB = V2gh), а цв— быстрота вытекания воды.
Поскольку
P^pSA,; h = ^, Op
ТО
^в = Р-вУв = р51О1 = 2Мв§^. (2)
Скорость капель дождя относительно тележки
с — v — и или в проекциях:
Cjc=y.sina — и; cy = vcosa., (*)
где и — скорость тележки относительно земли.
63
Берем проекции уравнения (1) па вертикаль и горизонталь — Р — M3g -4- Q + Fa — р. су = 0; (3)
— — 0- (4)
Исключая Q из (3) и (4), получим с учетом (2) и (*) после преобразований:
Л1В,Ц1—2^—Ц----------k----vcosaj^~p = 0. (5)
Поскольку Si, S, v, а, и, k, Pn^ — pSc— величины постоянные, то Л1В = const, что приводит К р=рв.
Но из р = рв следует, что
pSCy =PS1]/2g^-, откуда
Необходимое с| подставляем из (*).
При выполнении условия (6) скорость тележки может оказаться постоянной. Величину этой скорости находим из уравнения (5)
U — V (sin а — COS а)-- (I — 2^-t~Pl.
p- L \ 6 / j
Если условие (6) не выполнено, то скорость тележки не может быть постоянной. Таким образом, масса воды в тележке не должна быть иной, чем указано в (6).
* Задача 34
Вагон длиной I и массой М движется по рельсам с коэффициентом трения k. На вагон вертикально вниз сыплется песок
с высоты Н. Считая, что вагон двигался во время погрузки недолго, а значит почти равнозамедленно, и изменил свою ско-рость от оо до v, наити скорость погрузки песка р. = -гт (рис. 61).
АС
64
Решение
На вагон действуют очевидные силы Mg,— р.с, и Q. При этом только сила Mg постоянна, остальные переменны. Учитывая оговорку о равнопеременном движении вагона, можем считать
- с„ 4- с
Р-Сср — р 2 >
р ___F<> + F .
г то — 2 ’
(Л14-Д/И)ср = ^Ч-Л1;
7) __Qo + Q
ыср — 2 •
По закону изменения импульса системы
[(«+^!);+1‘Md+^+a4a]"=
— ^M-\-&M^v — Mv9. (*)
Помня, что с —и — v, где и — скорость песка относительно земли перед падением в вагон; v — скорость вагона относительно земли, найдем
с» + с (и — ©о) + (и - v) р v„ 4- V 2 ~ 2 — и 2 '
Проектируя (*) на 7- и «-направления получим с учетом Fjp —-
р = + &M)v — Mv9-,
— (Л1 4- ДМ ) g — [Ш 4- = °-
Исключая отсюда , получим
— [(Л 4- k f M 4- g -4- M = (m 4- дм) и - MOo.
Учитывая, что в нашем случае
и что
u=V2gH, а также, что
?/
т
3 В. к. Кобушкин
65
получим
= — (м -|—=х~'j v 4- /Иуо .
\ 1 wo + w/ 1
Откуда после преобразований и упрощения найдем
|Х =-----------i----------------------1
1 (3W + Wo)+* ’
J \ v -f- va/
Читатель может исследовать результат для частных случаев: |i = 0, k — 0, уо = О, ц = 0, k= 0 и v — 0.
7. РАБОТА, ЭНЕРГИЯ, МОЩНОСТЬ
Если уравнение F = ma спроектировать на направление движения, то
F cos a —mat. (1)
Если Feos а = const, то at — const и справедлива формула
Но тогда, исключая из (1) и (2) касательное ускорение, получим г • mv'2 mv’i
FAscOSa ——g------g-5. (3)
Это важное равенство называется законом изменения кинетической энергии и позволяет решать многие задачи механики в тех случаях, когда непосредственное применение второго закона Ньютона затруднительно. В частности, этим равенством (3) разумно пользоваться, когда ускорения нас не интересуют. Надо четко представлять себе, что равенство (3) — скалярное.
Величина FAscosa называется величиной работы и обозначается буквой А, т. е.
А = FA s cos а.
При Fcosa^>0 работа положительна; при Fcosa<^0 — отрицательна. Или, что все равно, работа силы положительна, если эта сила имеет составляющую, направленную по скорости; если же сила имеет составляющую, направленную навстречу скорости, то ее работа отрицательна.
Среди сил есть такие, значение которых зависит от скорости движения (например, силы сопротивления, электромагнитные силы). Работа этих сил зависит от формы траектории.
Силы, значение которых зависит только от координат тела, его положения (например, силы тяжести) или от его формы
66
(упругие силы) и работа которых (и это главное) не зависит от формы траектории, а определяется только начальным и конечным положением, называются потенциальными.
Потенциальным силам можно сопоставить понятие потенциальной энергии (или энергии положения).
При этом &Wn — —FnAscosa или &Wn = — Лп или Л„ =—&Wn, т. е. работа, совершаемая потенциальными силами, равна убыли потенциальной энергии этих сил.
Разделим все силы, способные действовать на интересующее нас тело, на силы сопротивления Fconp, потенциальные силы Fa и все прочие, которые мы будем называть F.
Тогда закон изменения энергии может быть записан в виде ТСОпр As cos а 4- F„ As cos p 4- F bs cos 7 = A IFK,
где а, p и 7 — углы между перемещением Аг и соответствующими силами.
Учитывая, что /7nAscos|3 =— AUZ„, получим
ДсопР+л=дгк4-д«7п
или
Л 4- Лсопр = ДГ,
где Дсопр — работа сил сопротивления; А — работа всех прочих сил, кроме потенциальных и сил сопротивления; A IF — изменение полной механической энергии тела или системы тел.
Если Л = 0 и Лсопр = 0, то AIF=O или IF = const, т. е. получаем закон сохранения энергии.
Считается известным, что потенциальная энергия тела, высота центра тяжести которого равна h, определяется Wg = mgh (для случая, когда уровню отсчета энергии соответствует /г = 0). Потенциальная энергия деформированного тела
пу — упр — ~~2~ >
где k — коэффициент жесткости, показывающий, какую силу надо приложить к телу, чтобы вызвать у него единичную деформацию; х — величина деформации (удлинение, укорочение, прогиб и т. д.); при этом деформация отсчитывается от состояния свободного, недеформированного тела.
Задача 35
Какова жесткость k буферных пружин вагона, если при скорости ц0 он останавливается на пути s при столкновении его с опорой? Масса вагона равна М, буферных
пружин две (рис. 62). Рис. 62.
3«
67
Решение
Очевидно, кинетическая энергия вагона перешла в потенциальную энергию пружин. По закону энергии для системы вагон — пружина имеем
л + лсмр = дгк + дгп
и так как А ~ Лсопр — 0, то
__/Mvs , п M’S3_
U — ^-5 Tj~^Z\'2 ~TJ-
Учитывая, что s0 = O и v = 0, получим
k= Д'М 2s2
Задача 3S
Цилиндрическая труба высотой Н и толщиной стенок b построена из материалов плотностью р. Считая, что сечение трубы есть кольцо с внутренним радиусом R, найти работу силы тяжести при постройке трубы.
Решение
Работа силы тяжести равна убыли потенциальной энергии тела, поэтому
лтяж=-дгп
или
л тяж = — (mgh — mgh9),
где h9 и h — высота центра тяжести материалов до и после постройки.
Так как h9 — 0, h — ~ и т — рУ, то
ЛТЯж = — pVg у. и так как
V = SH = к И (/?| — Rl) =*H[(R + b)* — /?2], то
л _ (2# + 6) „
''ТЯЖ 2 S*
Знак минус означает, что работа силы тяжести отрицательна, т. е. при перемещении материалов вверх сила тяжести действовала навстречу, т. е. вниз.
68
Задача 37
Тело массой т брошено со скоростью под углом а0 к горизонту. Найти его потенциальную и кинетическую энергии спустя время t.
Решение
Задача сводится к нахождению v и у для тела, брошенною под углом к горизонту, но
V- — v\- 4- Vy — vl cos’2 a0 4- (o0 sin a9 — gtf —
— v'i coss sto4~ Op sin’2 я0 — 2v9gl sin a0 4- gW — — vl4* ~ sin a()
и
IP к = у (По 4- — Zvogt sin ЯО).
Так как г
y~v0! sina0 —~,
то /
\Vg = mg [vot sin a0 — ,
Очевидно,
Г„4-^ = ^о«-
Убедимся в этом:
™ 2t'<’Tz sin + mS (44 sin ao — —
/vi > g't' , 1 , g‘ts\ "tv«
= m (д 4- ------o0g( sm a0 4- vogt sin a0 — = -g-C
Задача 38
Тело массой m, брошенное под углом к горизонту, упало па расстоянии s от места бросания. Зная, что максимальная высот, достигнутая телом, равна Н, найти работу бросания. Сопротив-
ление воздуха не учитывать (рис. 63).
Примечание. Работа бросания — это работа, совершенная силой F, сообщившей брошенному телу запас энергии для полета.
нуля до Wlt поэтому А = Wt.
Решение
на
Во время броска тело действовала сила F, изменившая энергию тела от
Во время полета на тело действовала только потенциальная сила mgH W =const вовсе время полета. Поэтому WZj— и А — или
.69
Но
s V*=2i>
где t — время подъема или время опускания. Из И = следует, что
следовательно,
Л = ^(/7 + ^).
Задача 39
Планер массой т, имевший на высоте ht скорость vt, по некоторой кривой длиной / снизился до высоты й8, погасив скорость до v-г. Найти силу сопротивления воздуха, считая ее постоянной.
Решение
Поддерживающая планер подъемная сила Q перпендикулярна к скорости и работы не совершает. Поэтому <4 = 0 и Лсопр = Д)Г;
— Ло,1р/ = \mghi (mgh, 4- ,
откуда
mg (Л2 — hg + (vl - v\) р —___________________f________
•* сопр- [ •
Задача 40
Тело массой т поднимают медленно по желобу высотой h и длиной основания Ь. Считая коэффициент трения равным k, найти работу внешней силы (силы тяги), работу силы тяжести, работу силы трения и силы нормальной реакции (рис. 64).
Решение
Силы, действующие на тело, очевидны. Так как тело движется под действием переменных сил (движение криволинейное), то путь s надо разбить на столь малые участки As,, которые
70
были бы неотличимы от отрезков прямых.. Тогда
дАоп»г = Атр/ д$/ (— 1) = — kQi &$t = — kmg cos a-i &$i = — king b.bf ‘^сопр == Д-Aonpj “I- • • 4~ Д^сопрп ==
= —kmg (Aftj 4-... 4- A&n) == — kmgb\
^Ag.= mg &St cos Р/ = — mg Д/г;;
A^ — mg (ДА 4-... 4- Дйп) = — mgh
или. так как 1ТОП = 0 (на высоте, равной нулю), то
— mgh = — (W — й7„) = Д^г и Ае = — ДГС?
(как уже отмечалось во вводной части).
Сила Q работы не совершает, так как она составляет угол 90° с направлением движения. Для работы силы F имеем
ДЛг = Fi Д$г (4- 1) = (FTpj 4- mg sin аг) Д$г =
= (kgm cos a-i 4- mg sin аг) Дз; = kmg hbi 4* mg &hi = = mg (k t^bt 4- Д/1г) и
A = kmgb 4- mgh.
Этот же результат можно было получить из закона изменения энергии
Д4-Лсопр = Д^п4-д^к-
Так как v = const, то
ДП7к = 0 и А — — Асопр 4- = kmgb 4- mgh.
Надо обратить внимание на то, что если работа силы F на участке Де равна ДА, то работа ДЛ2 против этой силы, т. е. силы, равной и противоположной силе F, будет отличаться от ДЛ] лишь по знаку.
71
Действительно, поскольку Л, = — Д2 и As, = Д$2, то Fx As, = = — F2As2 или ДА, =—АЛ2. Поэюму работа силы тяжести в нашей задаче
Ag = —mgh.
Работа внешней силы, преодолевающей силу тяжести:
А внеш “ High.
Аналогично, работа силы трения АСОпр =— kmgb, работа же силы, преодолевающей силу трения, равна + kmgb.
* Задача 41
Две очень тонкие пластины, массы которых т, и т.2, скреплены невесомой пружиной с коэффициентом жесткости k (рис. 65).
11 "Н
Рис. 65.
С какой силой F надо надавить на верхнюю пластину, чтобы, двигаясь вверх по окончании действия силы F, она приподняла нижнюю?
Решение
1. Если к первой пластине приложить искомую силу, то она будет в равновесии под действием сил F и упругой силы
Аупр = — k(xA -F Ах).
Тогда в проекции на вертикаль получим
+ F = kx{ 4- kbx. (*)
Перед сжатием пружины силой F первая пластина была в равновесии под действием сил mg и упругой силы —Аг,, т. е.
mgg = kxt, (**)
и, значит, искомая сила определится равенством F = k&x.
72
Для нахождения Дх надо сопоставить, учитывая условия задачи, состояние пружины при наличии F и состояние пружины в момент отрыва второй пластины. Но из первого состояния во второе система переходит под действием переменных сил, и потому удобно воспользоваться законом энергии.
Будем отсчитывать энергии тел от уровня, определяемого верхним концом недеформированной пружины. При этом высота, а значит, и или mgh<^Q в зависимости от того выше
или ниже уровня отсчета находится тело.
При действии на верхнюю пластину искомой силы пружина сожмется дополнительно на Дх, и система пластина — пружина будет обладать энергией по отношению к уровню, определяемому высотой недеформированной пружины
IT 0 = — ™ig (Xj 4- Дх) — m>gla 4--.
2. Если предположить, что первая пластина, поднимаясь вверх, растянет пружину так, что вторая пластина не оторвется от опоры, то энергия системы будет в этот момент
W — OTigXs — niiglo 4- .
Так как при движении первой пластины — то
/ I л , I k <Xt 4- Д-Х)а I kxj
— mig (Xi 4- Дх) 4- —— m,gxt 4- .
Необходимые Xj и х8 найдем из условия равновесия первой пластины до начала действия силы F и второй пластины в момент, когда она перестает давить на опору. Именно
т ig = kxi; = kx<i.
Тогда
!
~r 2 \ k ' 7 —m-iS ~r2 ’
откуда
Ar — ("'1 + x~ k
и
k^x — (mi-\-mi) g.
Ho k^x—F и окончательно
/=’ = (mi4-ma) g.
Для уверенного отрыва второй пластины необходимо, чтобы
E'>E=(mi4-ma)g.
73
* Задача 42.
По условиям предыдущей задачи, при F = g, опре-
делить: 1) характер движения первой пластины по окончании действия силы; 2) характер изменения сил, действующих на вторую пластину при движении первой пластины.
Решение
1. Характер движения тела определяется ускорением тела. Будем считать направление вверх положительным. Тогда с учетом того, что в пружине возникает при деформации Fynp = =—kx, приложенная к телу пц, получим
msg+Fynp __ m,g—kx
т1 пц
или в проекции на выбранную ось
+ kx _ । kx
d ----------- - - g -Ч---
при /<Ч0, x^>0, и потому
При движении пластин вверх а убывает, но а^>0 до тех пор, m.g п „ а
пока ±2-; при х — —а = 0, и в дальнейшем при 0<_ К п
<х< а<^0. При х = 0 а = — g и далее х<^0, поэтому
\kx\ а =— g------!,
ь т. It ft I I ttlv&r
так как | х | растет, то а уоывает и при |х| = —а достигает наименьшего значения (а по модулю — наибольшего).
Значит, тело mi из исходного положения до положения х =движется ускоренно (а^>0) со все убывающим уско-рением; от положения х = -~^ до положения |х| = —тело движется замедленно (а<^0) со все возрастающим замедлением.
Скорость тела в положениях исходном и конечном равна tll\g
нулю; в положении х = -~ она максимальна, ибо до этого положения тело шло ускоренно, а после него — замедленно.
2. На нижнюю пластину действуют силы m^g, — kx? и реакция подставки Q. х?— координата нижнего конца пружины по отношению к верхнему; ясно, что х? ——х.
74
Так как пластина все время в покое, то
nhg — kx! 4~^? = О
или с учетом / ——х
m^g 4~ kx Q = 0.
В проекции на вертикаль
— m^g И- kx ~|— Q = 0,
откуда Q = m<>g — kx.
Сила m<ig постоянна, сила kx, а значит, и Q переменны.
Сила —kx' — kx направлена для нижнего тела вниз при сжатой пружине и вверх при растянутой пружине (/^>/в).
Это значит, что при (т. е. х^>0)
Q=m3g-[-\kx\'^>tnig;
при 1 = 10 (т. е. х = 0)
Q = niig;
при 1^> /о (т. е х<0)
Q = rriig — | kx ]
и в верхнем положении первой пластины tritg = \kx\, т. е. Q = 0.
8. СТОЛКНОВЕНИЕ ТЕЛ
Задачи на эту тему решаются исходя из законов сохранения количества движения и энергии. В том случае, если внешних сил нет или они малы и массы тел не меняются, то
4" 4“ • • • 4~ mnVn = /721И1 4~ tTlnll-1 ~+~ • • • 4“ mnUi
И
<mnvn_mia\ , , тпип ,п
2 -Г • • • -Г 2 — 2 "Г • • • "Г 2 ' k
Здесь через v{ обозначены скорости тел до удара, через «, — после удара. Изменением высоты тел во время удара и, значит, изменением потенциальной энергии поля тяжести пренебрегаем. Q — тепло, выделившееся при ударе или прибыль внутренней энергии тела за счет убыли энергии механической. (Подробнее о термине «выделившееся при ударе тепло» см. в задаче 39, ч. III.)
Задача 43
Доказать, что при абсолютно упругом ударе шарика о стенку угол отражения равен углу падения, а у0 и v лежат в одной плоскости с перпендикуляром к стенке, восстановленным из точки падения (рис. 66).
75
Решение
sin а0 = —
НО ИЗ
т v2
следует, что vl = v2 или о0 = о.
Так как сил трения между упругости удара), то ах = 0, т.
Vx и sina = —, v ’
mvl
шариком и стенкой нет (из-за е.
но тогда
Vex = V.
vox __ Чу уй v
и, значит, sina0 = sina.
Поскольку а0 и a — острые углы, то из sina0 = sina следует, что a = a0.
Так как касательных не могло
сил при ударе нет, то у шарика появиться составляющей скорости, перпендикулярной к плоскости vay. Это означает, что и v будет лежать в той же плоскости.
л>г,г?,
до удара
(т, +тг) и
—s»- после удара
Рис. 67.
Задача 44
Два глиняных комка массами mi и та, летящие со скоростями Vt и навстречу друг другу, неупруго соударяются. Найти количество выделившегося тепла Q (рис. 67).
Решение
Очевидно
и
miUi mtVt = (mj Ц- m2) и
miv{ । m2vl (mj-f-ffijiu2 , 2 "r 2 — 2 "•
у
76
Считая направление вправо положительным, имеем
mtVi — тг1ь — (mi -f- т^) и; т^1 , mav'i __(nit 4- tna) и8 ,
2 "Г 2 — 2. т4,
Исключая отсюда и, получим
miV'i I mavl__(mj 4- — т.2у.,У‘ , Л
2 "Г 2 — 2(mi4-/n8)‘
откуда
___nitvl । mav‘i (nilvl — msvs)‘
2 I 2 2 (m, 4" m>)
или, раскрывая скобки и приводя подобные члены, получим р__ трл8 4- v.2)s
4 2 (m, 4- тг)
Задача 45
Решить предыдущую задачу между скоростями комков до
Решение
Опять
miVi 4- m2Vg= (mi 4- nh) и и
tnsVj | nw; (nil 4- mJ ц8
Величину и® найдем из векторного треугольника по теореме косинусов. Именно
[(/7/14- mi) «Г=miv'i 4- т&1 — — 2,7zIy1msz?8-cos(180—tz), (2)
для случая, когда угол удара равен а. (рис. 68).
тогда при подстановке ы® из (2) в (1) найдем nitvl । m2vi__________ m‘iv'1 4- tnr2vl — 2mlvimavs cos (180° — a) , n
' 2(/rtl4-ms) ( <•
Откуда после преобразования получим
X.__ ОТД/Ц |t>i Pg 4- 2t>jPs cos (180° — a)]
2(ml+nia)
Очевидно, при а. = 180° из этого решения последует решение предыдущей задачи. При а —0 (комки легят один за другим)
Z)__ «И/Иа (vt —vs)a
V— 2(Wl4-zns) ’
при a — 90°
___ CTifflj (of 4-t>f)
4 2 (Wj 4- mt) °
77
Задача 46
Два костяных шарика одинаковых масс налетают друг на друга со скоростями и v3 под углом а и разлетаются после абсолютно упругого удара со скоростями щ и ы2. Найти угол разлета р (т. е. угол между скоростями щ. и н2) (рис. 69).
Решение
Очевидно, что по законам сохранения
m«i тщ = tnuj 4~ m«2; mv'; । tnvi _muj ( mui
. ~T +"2^ ~ ~ 4" 2
или после сокращения на т
f vi 4“ Щ -j- u>;
I vi + vi — щ 4-
Ho m | щ -(- v-г | и суть величины диагоналей векторных
параллелограммов, причем т | 4~y«l ~т I “i 4~ и* 1> а тогда по теореме косинусов
т2| с? — 2ощ2со8 (180° — а) | =
= т8 |Н1 4~ на ~ 2«i«3cos (180° — Р) | или
о? 4- и* — 2«i02cos (180° — а) = «14-«а — 2«1«2 cos (180° — р).
Так как
«14- — и{ 4-то
— 2О;cos(180° — а.)— — 2«i«gcos (180° — Р) или
COS tx = U1U-2 COS р, откуда о 0,4» COS а
COS Р = ——-----.
г щиа
78
Задача' 47
При абсолютно упругом ударе двух шаров, налетавших под углом а друг к другу, скорость одного из шаров по величине не изменилась (рис. 69). Найти угол разлета р (массы шаров разные).
Решение
Очевидно
tniVi -f- т%иг = miUi 4- тг«2;
~2 Г~2~ — ~ I —*
Из второго равенства в силу о1 = и1 вытекает, что Vt = u*. По теореме косинусов
tnfui mfvl — cos (180° — a) =
= m[u[ 4~ mluf — 2m1m.2u1«2 cos (180° — P), откуда вытекает
Vjt’2 COS a — UlUi COS p
ИЛИ
cos tx = COS p
(В силу C’it’2 = «iUs).
Задача 48
В известной демонстрации на и энергии при ударе (рис. 70) шаров, сколько налетает, объяснить это.
законы сохранения импульса всегда отскакивает столько
Решение
Пусть налетают /о шаров, двигающихся совместно (слитно) со скоростью vit отскочат А’2 шаров со скоростью
Рис. 70.
г4. По законам сохранения
k^mvi = k^mvi', kitnvl__ksmv'i
~2" — —2^’
По сокращении на массу получим
kiV^kiVi, (*)
kiv'i — kiV^.
79
Возводя равенство (*) в квадрат и деля полученное на равенство
<**), получим k\ = ki, что и требовалось показать.
Деля (**) на (*), получим vl — u2.
* Задача 49
На чашку пружинных весов падает с высоты Н кусок мягкой глины массой т. Зная, что масса чашки М, а коэффициент жесткости пружины k, найти зависимость скорости системы от величины деформации пружинки (рис. 71). Удар считать абсолютно неупругим.
Решение
В первое мгновенье после удара система обладает энергией
Ц70 — <-т + М) и*_
где х отсчитывается от уровня нижнего края недеформированной пружинки. В последующие моменты
iv/ 1т 4-М) и1 . , ... . kx*
W =4-^-2---------(m_|_ /W)grX-b -у-.
Так как при движении системы внешних непотенциальных сил кет, то
или
-|" + *1> “! - (т + Л1) gx, + 41 =
= (" + м>“'_(,,, + M)gx + ^. (,)
Скорость Ио находится из уравнения сохранения импульса при ударе глины о чашку
mv = (т -ф- М) и#,
где v определяется
Таким образом,
из того, что
U MV* mgH =~2~.
___ mv ____т fogH и<>~т + М. т + М
(**)
80
Хо определяется из условия равновесия чашки весов до удара, т. е.
Mg = kxo (***)
Подставляя (**) и (***) в (*), получим после очевидных преобразований
.81О ... , . g2Al .... о ч । 2m^gH , M2ga
- kx1 + 2gx (M + m) - (M + 2m) + Г
------------------------------------—________
u M + m
Задача 50
Какой минимальной скоростью п0 должен обладать кубик с ребром I на расстоянии $(«;>/) от преграды, чтобы при
Рис. 72.
уларе о нее он перевернулся? Коэффициент трения о подставку равен k. Потеря механической энергии при ударе о преграду составляет п-ю часть от кинетической энергии перед ударом (рис. 72).
Решение
Чтобы куб перевернулся, его энергия перед ударом о пре-, те th’ — h) , ,,
граду должна быть не меньше - _ —-, где h и п — высота
центра тяжести кубика до и во время переворачивания.
Поскольку непотенциальная сила работы не совершает (Q ± v), то из
А + А имеем — kmgs Очевидно, h = -< Учитывая это, получаем kgs^ откуда mg (h’ — Л) mvl 1 — п 2 / и //2 Г И h ~ 2 • 1 (K2~-l)g 2 1 - п
81
* Задача 51
Чашка пружинных весов массой М с лежащим на ней шариком массой т оттянута вниз силой F и отпущена. На какие после отрыва от чашки шарик и чашка (рис. 73)? Каков при этом характер движения тел? Коэффициент жесткости пружины равен k.
Решение
Движение шарика складывается из трех этапов: 1) ускоренного движения вместе с чашкой до положения равновесия, определяемого уравнением
(Мт) g — kx\ (1)
2) замедленного движения вместе с чашкой с \а | g до момента отрыва, происходящего в том положении, где шарик и чашка уже не давят друг на друга, и, значит, они движутся с a = g (очевидно, в этот момент пружина недеформи-рована); 3) оторвавшийся шарик движется вверх с ускорением а = g (замедленно) под действием только
силы тяжести (чашка же из-за возникшей деформации в пружине движется замедленно с a->^>g).
Очевидно для последнего этапа, который, собственно, нас интересует по условиям задачи, имеем
(2)
где Н отсчитывается от положения отрыва (и, значит, от положения нижнего конца недеформированной пружины).
Из (2) получаем
Для определения воспользуемся тем, что при движении системы от нижнего положения до момента отрыва энергия системы не менялась, т. е.
< ъл । \ (Л4 + т) vs ..
~2---(/H-i-m)gXo= (4)
Необходимое находится из условия равновесия системы в ниж-
нем положении
(M-(-m)g-f-F = kx0. (5)
82
Решая совместно (3), (4), (5), получим
2k (Л4 4- т) g '
(6)
Для нахождения высоты поднятия чашки h после отрыва шарикз имеем
Мча .. , , kh?
— = W + ^->
а так как по (3)
vi = ‘2gH, то
MgH=Mgh + k^,
Подставляя сюда значение И из (6), получим окончательна, с учетом того, что h^>0,
,_____ Mg [ -i f M*g* , Mg [Л2 — (Л-I + т)г g2] ~
k ' У ka ' fea (M +,n) S
* Задача 52
С какой по величине и направлению скоростью должен прыгнуть человек массой т, стоявший на краю тележки массой М и длиной I, чтобы попасть на другой ее конец к моменту оста
Рис. 74.
новки тележки? Коэффициент трения тележки о подставку равен k, временем взаимодействия человека с тележкой пренебречь по сравнению с временем его полета. Где снова остановится тележка после того, как закончится ее движение вместе с человеком (рис. 74)?
83
Решение
Если тележка за время полета человека переместилась на Г, то человек переместился по горизонтали на Дх = / — Г (все перемещения по отношению к земле). При мальиая дальность полета и, значит,
L w? sin 2а
Перемещение тележки I' определим из ческая работу
энергия после взаимодействия с против сил трения, т. е.
kMgl' = ^,
этом Дх — это макси-
(1)
того, что ее кииетп-человеком пошла на
(2)
находим из сохранения горизонтальной составляющей импульса человека и тележки при прыжке человека, т. е. из
77W0COS а = Ml-lt). (3)
Необходимый угол а определим из того, что время движения тележки t равно времени полета человека 2Г, где f — время его подъема или опускания. Но
где и0
kg
поэтому
— 2п0 sin а (из / = 2Г).
(4)
и
__Vo sin а
“ g
Решая совместно (3) и (4), получим
- т
Исключая и0 из (2) и (3), получим, считая а известным из (*),
COS3 а
1 ~ 2kgM2 •
Подставляя это значение Г в (1), найдем после очевидных преобразований
v = _________‘Я_________
0 т2 cos3 а .
2А1аЛ + Sm 2а
Найдем новое перемещение тележки после опускания человека на тележку. Очевидно, что кинетическая энергия тележки и чело-
«4
века пошла на совершение работы против силы трения, поэтому k (М 4- m) gl' = +2т)-и", (5)
где и — скорость тележки и человека сразу по опускании. Она находится из того, что
mv0 cos а = (М -}-т) и. (6)
Поскольку и0 и а уже найдены, то решение (5) и (6) дает ,, _ m'2v2 cos2 х
1 ~ 2kg (Л1 + т)1'
Очевидно, что тележка остановится на расстоянии Г — Г от первого своего (исходного) положения.
Рекомендуем читателю равенства (3) и (6), записанные уже в проекциях на направление движения, получить из общей формы закона изменения импульса в векторной форме.
9. ТЯГОТЕНИЕ
Закон всемирного тяготения для двух материальных точек в векторной форме имеет вид
где сила F и единичный радиус-вектор г0 (орт) направлены от притягиваемого тела к притягивающему. Этот закон позволяет формальным образом решать любые задачи на гравитационное взаимодействие, т. е. изучать и описывать движение тел под действием вышеупомянутой силы.
Природу же этого взаимодействия закон не вскрывает. Это в некоторой степени сделано в теории тяготения Эйнштейна. Известно, что всякое взаимодействие осуществляется посредством некоего агента — поля. Одним из таких полей и является гравитационное поле.
Как видно из закона тяготения, Fr9 зависит для данных двух тел только от их взаимного расположения. Это приводит к тому, что работа этих сил по изменению взаимных расположений этих тел не зависит от того, как это изменение происходило, или (пользуясь понятием поля) работа по перемещению одного тела в гравитационном поле другого не зависит от формы пути.
Это позволяет приписать каждой точке гравитационного поля некоторую энергетическую характеристику, называемую потенциалом <р, такую, что работа сил поля при перемещении в нем тела массой т определится равенством
Л,а = — т (?а — <pi). (*)
85
Величину mv называют потенциальной энергией тела в поле тяжести. Если за уровень отсчета этой энергии взять энергию тела на поверхности земли, то при h((R3 y = где g —ускорение свободного падения, Тогда
Л 1,2 = — т (ghi — ghi), или
/41,2 = mghi — mghv.
Поля, работа которых от «формы пути» не зависит, называются потенциальными. Другим примером такого поля является электрическое поле неподвижных зарядов — кулоновское поле, описываемое формально законом
г2
Магнитное поле этим свойством независимости работы от «формы пути», вообще говоря, не обладает. Поэтому его нельзя охарактеризовать понятием потенциала и приписывать телу, находящемуся в нем, понятие потенциальной энергии.
Поскольку потенциальная энергия определена как энергия взаимодействия, то естественно положить ее равной нулю там, где тела существенно взаимодействовать не могут, т. е, на бесконечном удалении тел друг от друга. Это означает, что потенциал поля в бесконечно удаленной от тела, создающего это поле, точке полагают равным нулю.
В этом случае равенство (*) можно, полагая © = 0, переписать в виде Ai,oo = m?i, где AijCO — работа, которую совершает гравитационная сила при удалении тела изданной точки в бесконечность.
Если тело уходит на бесконечность под действием некоторой силы, в каждый данный момент уравновешивающей гравитационную силу, то, очевидно, из Егр =— F следует, что
Агр = — Ар, и тогда
(А1,оо)/= = —/и?, откуда можно определить потенциал данной точки поля как ______________________ (^l.oo)rp (^-l.co)/5
* т т ’
т. е. как величину, численно равную той работе, которую совершает гравитационная сила (или — с точностью до знака — уравновешивания ее сила) по перемещению тела единичной массы из данной точки в бесконечность.
Поскольку mtp в соответствии со сказанным можно определить как запас потенциальной энергии тела в данной точке, то <Р =—1 есть величина, численно равная потенциальной энергии
86
тела единичной массы в данной точке. Этим и обусловлено название термина «потенциал».
Для описания всякого силового поля (в том числе и непотенциального) вводят силовую его характеристику.
В случае гравитационного поля такой характеристикой явля-_> л
ется напряженность g==-₽, численно равная силе, действующей
в данной точке со стороны гравитационного поля на тело единичной массы. Тот удивительный факт, что в случае именно гравитационного поля ускорение силы тяжести (свободного падения)
и напряженность поля совпадают, есть следствие эквивалентности инертной массы, входящей во второй закон Ньютона, и гравитационной, или тяжелой, массы, входящей в закон тяготения. (Именно эта эквивалентность и легла в основу теории пространства, времени и тяготения, фундамент которой заложил Эйнштейн.)
Итак, всякое тело создает вокруг себя силовое поле тяготения, которое характеризуется в каждой точке напряженностью g (силовая характеристика поля тяготения) и ская характеристика)
- F ё т’
потенциалом ср (энергетиче-
<2 =---------------------
' т
Wa т ’
где т — масса пробного тела, которым исследуют интересующее нас поле; F — сила, которая действует на пробное тело в данной точке со стороны поля; — работа, которую необходимо совершить, чтобы пробное тело равномерно и в отсутствии сил сопротивления унесли из данной точки в бесконечность. Очевидно, эта работа численно равна той потенциальной энергии lFn, которой обладает тело т в данной точке.
Если исследуемое поле создается материальной точкой (рис. 75), то
Знак «минус» в формуле для <р означает, что всякое тело обладает в поле, созданном телом т0, отрицательной потенциальной энергией по отношению к бесконечности.
87
Надо помнить, что g — вектор, а ф — скаляр. И если в некоторой точке нас интересует поле, созданное несколькими телами, то
S — Si • • • 4- ёп> ? — ?i ••• + ?/»•
Однородный шар или шаровой слой создают вокруг себя такое гравитационное поле, как если бы этот шар или слой сжался бы без изменения массы в свой центр.
Задача 53
Доказать, что внутри однородного шарового слоя g —О (рис. 76).
Д5,
Рис. 76.
Решение
Выбрав внутри шарового слоя некоторую точку, проведем из нее два малых конуса, которые, пересекая слой, вырежут на нем поверхности Д£1 и Д£а.
88
Если конусы очень узки, то Д/тг( и Д/п.2 можно рассматривать как материальные точки и, значит,
— I уг Г01 4* I уг Г02, НО
Дт = Dh&s = D!i ,
cos а ’
где ASn построена перпендикулярно к оси конуса; D — плотность; h — толщина слоя.
Поэтому
д£ = ^Ьг''|,, + 4гМ-Так как
Д£о .
= Дда
г2
(по определению телесного угла), то
Д£ = I (Д®1 ''м + Д^‘2Ла)
и из-за = (вертикальные углы равны) получаем
, - Dlikw
— l------
• cos a
( foi И- ros)
Поскольку r0I =— Гоа (как противоположные орты), то го1Ц-Го2=О. и поэтому Ag = 0.
Поскольку такой же вклад в общее поле дают и остальные подобные пары элементов Д/п, то внутри однородного шаровою
слоя действительно g = O в любой точке.
Задача 54
Найти зависимость g = g(r) внутри однородного шара (рис. 77).
Решение
Выбрав произвольную точку N внутри шара, проводим через нее сферу, концентрическую с шаром.
Рис. 77.
По доказанному в предыдущей задаче, слой h поля в точке Л' не создает. Остальная же часть шара создает вне себя поле
т - з ' - 4
S = I р ''0 = I—р— 0= и ^DV = kr,
т. е. g внутри шара пропорционально расстоянию до центра шара и направлено по радиусу к центру шара.
89
Задача 55
Доказать, что внутри произвольной сферической полости, сделанной в однородном шаре, g = const, т. е. поле однородно (рис. 78).
Рис. 78.
Решение
Очевидно, что не будь полости, поле в точке N было бы равно g-t—kri. Наличие же подсети меняет это поле на величину g^ — kr^. При этом искомое поле g таково, что поле (g-\-gi) должно быть равно полю сплошного шара g\, т. е.
+ откуда
g = —g2 = /7(n — r2) = kd.
Но г। — r2 = d численно равно расстоянию между центрами шара и полости и есть величина постоянная, а потому и g = Ы = const.
Задача 56
Найти вторую космическую скорость, т. е. ту минимальную скорость относительно центра Земли, которую должно иметь тело для того, чтобы выйти за пределы земного тяготения. Сопротивление среды не учитывать (рис. 79).
90
Решение
Поскольку движение тела происходит под действием переменных сил, то воспользуемся законом энергии
А + ЛСОПР = ДГ.
Считая двигатель выключенным и сопротивление отсутствующим. получим ДГ = 0 или Го=Гю, здесь Го—полная механическая энергия тела в той точке, где ей сообщили искомую скорость, а Гео —энергия
тела на бесконечности, равная, очевидно, нулю. Но тогда и Го —0 или
mva тМ, п -----Т---- =0, 2----1 г ’
ci куда
0 = /2^.
Это выражение можно преобразовать
• у —
Здесь r = R3-\-h, где h — высота той точки над поверхностью Земли, где тело получило искомую скорость.
Задача 57
Какую минимальную работу надо совершить по удалению тела массой т с поверхности Земли в бесконечность, если работа сил сопротивления составляет п-ю часть искомой работы?
Решение
По закону изменения энергии
Л + ЛопР = ДГ.
Поскольку ЛСОПр и А противоположных знаков, то
А~ -=ДГ п
91
или с учетом, что ДЦ/К = О (мы ищем минимальную работу) н
откуда
л _ „ тМ
7 ч / . I
Задача 58
Две звезды с массами тх и т2 находятся на расстоянии I. Найти напряженность поля и его потенциал в точке, находящейся на расстоянии и и rt от первой и второй звезд соответственно (рис. 80).
А'
Рис. 80.
Решение
Из рисунка видно, что такие точки лежат на окружности в плоскости, перпендикулярной к прямой, соединяющей эти звезды. Рассмотрим задачу для произвольной точки А этой окружности Тогда
S = gi±gi-
Из векторных треугольников получаем
==^i + gi + 2g1g«cos а;
/2 = г\ — 2/V2 cos а,
исключая отсюда cos а, получим g1 = fii + gi —
92
Подставляя значения gt и g^, находим
Зная g, найдем и его направление, определяемое, например, углом ₽
О _ §2 - g1 2 - gl
C0Sp“--------2^-----•
Потенциал в точке А определяется алгебраической суммой <?i и <ра
Задача 59
Найти работу по переносу тела массой т с одной планеты на другую в отсутствие сил сопротивления. Массы и радиусы планет известны, расстояние между ними велико (рис. 81). При переносе величина скорости тела не меняется.
Рис. 81.
Решение
Очевидно, что А Лсопр = Д1ГП + Д1РК. По условию ЛСОПр = 0; будем считать и Д1Гк = 0. Тогда
А — т — <р0, где <pi и <ра создаются обеими планетами, т. е.
<Pi = и ? 2 = <р' .
Тогда
или
Л Г / 1 1 \ | ! 1 1
1 1 - 1
и гак как к- и много больше -у-, то
93
Задача 60
Какова скорость истечения газа из сопла двигателя космического корабля при старте, если он получает ускорение а в направлении, противоположном ускорению свободного падения g?
Сечение сопла S, плотность газов р, массы корабля т и планеты М, а также расстояние до ее центра г и сила сопротивления атмосферы Fz известны (рис. 82).
Решение
На корабль действуют /',реакт, сила тяжести mg и сила сопро>
тивления Fz mg + Fc 4- та
или в проекции на направление g ' i i) , mg -j- Fz — jxc = — ma, v
так как
то th Л4 । г-» о я T-pr + ^c “ pSc2 = — ma,
откуда T r3 A-Fz + ma c—r ?S
10. ДИНАМИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО окружности
Задачи этого типа в принципе не отличаются от задач, рассмотренных ранее. Исходным равенством является второй закон Ньютона
а = - (1)
т ' 7
94
или в проекции на v- и r-направления (т. е. по касательной и по радиусу)
При этом
ar = ~ = nFr = 4^г —(3)
где г — радиус-вектор материальной точки (радиус окружности); v — линейная скорость движения; «> — угловая скорость вращения радиус-вектора; f — частота вращения; Т — период оборота.
Формула (3) справедлива для любых видов движения материальной точки. Что же касается av, то оно не всегда может быть выражено просто через v, ш, Т и f. Поэтому в тех случаях, когда а7, ф 0 (т. е. движение происходит с переменной по величине скоростью), вместо уравнения (1) для решения задачи пишут в дополнение к (2) закон изменения энергии
4 + 4conp = AUZ, (4)
при этом аг выражают через V, ибо именно v и входит в уравнение (4).
В формуле (2) Fr— это суммарная проекция всех сил, действующих на тело, на направление радиус-вектора г.
Часто учащиеся склонны придумывать различные «и еще центростремительные силы», кроме Fr. Надо помнить, что в соответствии с третьим законом Ньютона каждая сила, действующая на тело, — это результат взаимодействия этого тела с каким-то другим телом.
Поясним это на примерах.
1. Спутник движется по круговой орбите вокруг Земли. Если он находится за пределами атмосферы и двигатель не работает, то на спутник действует только сила тяжести, которая одновременно есть и Fr и Ецс (центростремительная).
2) Конический маятник (рис. 83) вращается в горизонтальной плоскости с ш = const. На грузик m действуют сила тяжести mg и натяжение нити Т. Их результирующая и есть Fr или Ецс.
И никаких «и еще центростремительных сил» не существует. Это будет отчетлива видно в дальнейшем при решении задач.
95
При движении тела по окружности результирующая сила не обязательно направлена в центр окружности, по обязательно во внутрь ее. Результирующая сила направлена в центр окружности лишь при | = const (или ш = const), т. е. когда величина скорости не меняется.
Если не все силы лежат в одной плоскости (как, например, в случае движения конического маятника), второй закон в проекциях имеет вид:
где п направлен нормально к той плоскости, в которой происходит вращение.
Если вращение происходит в плоскости с постоянным угловым ускорением, то имеют место равенства
л , > У2
Л? -- ;
(U =в)0-|-
где Д<р — угол, на который повернулся радиус-вектор г (в радианах) за время t~, ш — угловая скорость вращения; р — величина углового ускорения вращения; причем Р>0 для ускоренного, а р<^0 для замедленного вращения.
Угловые и линейные характеристики вращения связаны равенствами
Д/ = Д®-г; v=wr, av = fi-r.
Задача 61
Конический маятник массой т вращается в горизонтальной плоскости, отстоящей на расстоянии h от точки подвеса, с постоянной по величине скоростью (рис. 83). Найти частоту вра
щения маятника.
Силы, действующие
I или
и, так как
то
Решение
на маятник, очевидны mg -}-Т = та
Т sin а — т4т^*г, — mg 4- cos<*=о
, , , sin а
r = h tg а = п--,
° COS а ’
Т sin а = m4tctfth ; ' cos а
Т cos а = mg.
96
Деля одно из этих равенегвла-^другое, получим
Задача 62
Конический маятник, длина нити которого равна I с периодом
вращается в горизонтальной плоскости угол а, который составляет нить маятника с вертикалью, и силу натяжения нити (рис.
и масса т, Т. Найти
84).
Рис. 85.
Реше н ие
Как и в предыдущей задаче, получим г- и /г-направления
„ . 4тс8г
Qsina = /n
, Г’ ’
. Q cos я = mg.
сразу в проекциях на
Учитывая, что r = /sina, получим ____________________________т4л8/.
J W J'S »
I Q cos я — mg.
Из (*) сразу <2 = туГ. Деля (**) на (*), получаем cosa=b/-
(*)
Задача 63
Найти первую космическую скорость, т. е. ту скорость, которую должно иметь тело на круговой орбите на высоте h от поверхности планеты массой М и радиусом Д (рис. 85).
4 В, К. Кобушкив
97
Решение
Очевидно, на тело действует только сила тяжести и она перпендикулярна скорости (орбита круговая), поэтому
Frp = та или
Лр = та„
или
тМ Vs
т —у- — т — 1 г3 г
так как г = /?-}-/г, то окончательно
Задача 64
В лифте, движущемся вертикально вверх с ускорением Оо, находится вращающийся с частотой f горизонтальный столик, на котором лежит маленький коробок. Зная, что коэффициент трения коробка о столик ра-вен k, найти то максимальное расстояние коробка от оси вращения, при котором он еще I k j будет удерживаться на столике.
Найти ускорение коробка относительно земли (рис. 86).
Решение г 6g--------
-•—------ Очевидно, коробок удержи-
I I вается на столике силой тре-
ния. По второму закону
J' m^4-FTp + Q = ma.
Проектируя равенство на вертикаль и на г, получим
—mg-\-Q — man‘, kQ — mar, где ап — ай и аг — 4п*рг.
Исключая Q, получаем km (До g) = т.4к‘2}'г, откуда
А (а0 + g)
Рис. 86. 4л3/*
98
Ускорение коробка относительно Земли
а= Оо4-аг
или
— ^0» ^гориз —
так как ап = const, а аг вращается (аг = 4л:2рг направлено по вращающемуся г), то а будет описывать коническую поверхность вокруг вертикали (рис. 87). При этом а составляет с вертикалью угол, определяемый равен-
ством
k(a0 + g)_!J. , g\
— а0 ' \^ааГ
Задача 65
Каким должен быть минимальный коэффициент трения скольжения, чтобы автомобиль, идущий со скоростью v, мог сделать поворот с радиусом кривизны г (рис. 88)?
Решение
Имеем в проекциях и п-
направления ( kQ='^-,
откуда
лучаем
I Q = mg, по исключении Q
на
по-
k = ~. rg
Задача 66
Автомобиль массой т движется с постоянной по величине скоростью, описывая окружность радиуса г по поверхности с коэффициентом трения k. Какова при этих условиях мощность двигателя автомобиля, если малейшее увеличение подачи топлива в двигатель приводит к скольжению (рис. 89)?
4*
99
Решение
Так как по условию автомобиль движется на «пределе» трения покоя, то можно считать движущее трение и трение,
удерживающее автомобиль на окружности, одинаковыми. Тогда N = fjpV = kQv-, г — f тр —
mg = Q.
Исключая Q, получаем
W — kmgv, mv2 , —— = kmg.
Исключая отсюда v, найдем
N = т
* Задача 67
Автомобиль, движущийся по окружности, равномерно увеличил свою скорость от v0 до v, сделав при этом один оборот. Считая силы движущего и «заворачивающего» трения одинаковыми и превышающими к концу оборота силу тормозящего трения в п раз, найти это п. Какой угол составила при скорости у результирующая сила со скоростью (рис, 90)?
100
Решение
Силы, действующие на автомобиль, очевидны. По второму закону Ньютона имеем
7дв ^торм + Аав Q 4- mS — та
или в проекциях на и-, г- и «-направления /дв Fтори "— tTlCtvt Fзав ПШГ>
nig — Q = 0.
С учетом av = —получим
f -р ==mS22-^. т
I цв 1 тори ’ '*)
г tnvs
^зав п • (2)
Деля (1) на (2), получаем с учетом = п и f№~ F33a * тори
откуда
(3)
Из чертежа видно, что
1 „
, /дв ^торм , I V9
С tg а = ------Г.---— = 1----------= —;--------,
/"зав П 4п
(4)
Интересно заметить, что максимальное значение п равно единице. При этом из (3) р = рв> т. е. движение «равномерное», и тогда из (4) ctga = 0 или а = 90°, т. е. результирующая сила при v — const направлена в центр окружности. Но только при ц== = const!
Задача 68
Невесомый стержень длиной / с грузом на конце подвешен другим концом к потолку и отклонен на угол а0 от вертикали, а затем отпущен. Найти зависимость угловой скорости стержня w от переменного угла а между стержнем и вертикалью (рис. 91).
101
Решение
Движение груза происходит под действием переменных сил (натяжение стержня меняется и по величине и по направлению).
Поэтому воспользуемся законом энергии
Л4-Лсопр=Д^, так как сила натяжения стержня работы не совершает (из-за Г_[_о), а сил сопротивления нет, то с учетом о0 = 0
О = mgh ---------mSho
или
и так как
| Д/l | = I (COS а — COS а0), a v = и/, то
, , X <o2Za
gl (cos Я — COS Я0) — -у , откуда
_ 1 /~2g (cos а — cos gp)
Задача 69
По условиям предыдущей задачи найти Т = Т (я), если масса грузика равна т. Считая нить малорастяжимой с коэффициентом жесткости k, найти удлинение нити Д/ = Д/(я) (рис. 91).
Ю2
Решение
1. По второму закону имеем в проекции на ^направление гр, mv2
Т — mg cos а — -j-.
Кроме того, как и в предыдущей задаче (однако при Д/ < /),
У = gl (cos а — COS а0).
Исключая из этих равенств v\ получим
Т — mg (3 cos а — 2 cos а0).
2. Так как T = kM, то
> , mg (3 cos а — 2 cos а0)
Задача 70
Какую максимальную скорость может развить велосипедист, движущийся по окружности радиуса г, если коэффициент максимального трения покоя равен k? Под каким углом к вертикали
будет при этом наклонен велосипедист (рис. 92)?
Решение
Силы, действующие на велосипедиста, очевидны. Имеем в проекциях на г- и «-направления (ц-на-правление нас не интересует, поскольку модуль скорости не меняется)
г- т®8 I л л
FTp = —; — mg-]-Q = 0,
так как FyP = kQ, то получим из системы
v = V kgr.
Можно показать, что велосипедист своим телом должен быть ориентирован так, чтобы суммарная реакция опоры F действовала вдоль линии, проходящей через центр тяжести тела. Но тогда
tga =
Стр kQ
103
* Задача 71
Найти зависимость силы движущею трения от угла а (рис. 93) для автомобиля, идущего с постоянной скоростью по выпуклому мосту радиуса г. Коэффициент трения качения равен k, масса автомобиля равна т.
Рис. ез.
Решение
Возможны два случая: I) автомобиль поднимается на мост и 2) авюмобиль спускается с моста.
В проекциях на г- и и-направления получим:
I) mgcosa — Q = ;
/дв — Лор» — mg sin a — 0;
2) mg cos a — Q = ~-.
f дв Fторы ~F mg sin a — 0.
С учетом /^торм — kQ получим:
1) fдв = m [g cos a — y) + g sin a];
[/ 1
k \g COS a — yj — gsinaj.
Проанализируем оба результата.
1) При ^gcosa — у^ = 0 получается формально
f№ — ±mg sin a.
104
Но очевидно, что этого быть не может, ибо если geos а — у = 0,
то, согласно (1), Q = 0. Но если Q = 0, то движущее трение тоже равно нулю, как и всякое другое трение.
2) В случае спуска автомобиля с моста при
/ \ k lg COS а — у I <^g sin а
получится /дв <^0, что означает вращение колес в обратную сторону, т. е. трение «движущее» становится «тормозящим».
В чем же казус?
Очевидно, задача сформулирована некорректно. Надо было четко сформулировать, при каких углах a v — const. Действительно, не может же автомобиль двигаться, да еще с постоянной скоростью вертикально, что должно было бы произойти при а = 90°.
Значит, при больших а задача теряет смысл. Очевидно, задача обретает определенность при geos а—-^>0 или npHcosaj> —, т. е. при достаточно малых а.
Кроме того, чтобы было действительно движущим, т. е. U>0 и при спуске с моста, необходимо
к (g cos a — у I g sin a, что приводит к требованию
Значит, должно быть: 1) угол а достаточно мал; 2) трение качения достаточно большим: 3) скорость автомобиля достаточно малой; 4) радиус кривизны моста достаточно велик.
Вот сколько надо было сделать оговорок, чтобы задача стала определенной и не получилось бы казуса!
Задача 72
С вершины полусферы сколь- Рис. 94.
зит шайба без трения. Показать,
исходя из второго закона Ньютона, что шайба оторвется, не доходя до горизонтального диаметра (рис. 94),
105
Решение
Отрыв шайбы означает Q = 0. В проекции на г имеем mgcosa. — Q = ^-. (I)
При движении шайбы возрастает, mg cos а убывает. Чтобы возрастало, необходимо, чтобы разность (mg cos а— Q) тоже возрастала, несмотря на убывание mg cos а. Но это возможно лишь при убывании Q более быстром, чем mg cos а. Так как mg cos а обращается в нуль лишь при а = 90°, то Q должно обратиться в нуль раньше, ибо разность (mg cos а — Q) должна из-за быть всегда положительной.
Для нахождения места отрыва необходимо знать и. Так как движение происходит под действием переменных сил, то и найдем из закона энергии, который в данном случае (Q работы не совершает, трения нет) имеет вид
Fo = W или mg/i = ^~. (2)
Решая (1) и (2) совместно, получим при Q = 0
2р-Л gcosa=-y-, и так как г — h . г cos а —----------------------, то п = -5-.
г ’ 3
Задача 73
Шайба массой m скользит без трения с высоты Н по желобу, переходящему в петлю радиуса г. Найти силу давления Q шайбы
на опору в точке, определенной углом а (рис. 95). При каком значении а произойдет отрыв?
106
Решение
Очевидно, что
। г, mg sin a -j-Q =---
mgn = mgr -f-sin a)-g-.
Исключая отсюда ц8, находим
Гг> Н — Г (1 + sin a) 1
Q = mg 2------44------- — sin a .
Так как условие отрыва Q — 0, то
sina =
Задача 74
С каким угловым ускорением в вертикальной плоскости должен вращаться невесомый стержень с массой т на конце, чтобы он разорвался, проходя нижнее положение через время t от начала движения (рис. 96) из нижнего же положения? Стержень выдерживает усилие не больше Тпред = nmg. Длина стержня /, он мало растяжим, вращение равноускоренное.
Решение
Так как стержень практически не растяжим, то г = / = const. В проекции на г имеем в нижнем положении
mg (п—\ ') = ти?г и с» = р/,
и так как шо = О, то^(п— 1) —р9/8/, откуда _______
i-l) It*
Видно,
что ответ не зависит
п
от массы груза т, но зависит от
Т'пред
~~Р~ •
Задача 75
звезды массами тх и /п2 находятся на постоянном рас-
Две _ _
стоянии I друг от друга. Каков характер их движения (рис. 97)?
107
Решение
Так как между звездами действуют силы взаимного притяжения, то каждая из них должна двигаться ускоренно. Но так как
по условию расстояние между ними постоянно, то ускорение
должно быть нормальным к их скоростям и, значит, каждая из
звезд должна двигаться по окружности, причем обе окружности должны иметь общий центр (называемый центром масс систем).
Найдем его положение и периоды обращения звезд, считая систему замкнутой.
Очевидно, что имеем в проекции на /
F\ = т^!; Fi = гп&, так как Fl=Fi (по третьему закону), то или
или nitty________________тага
"Г? — -ц •
Рис. 97. Но чтобы звезды были
все время на одинаковом расстоянии /, проходящем через центр масс, необходимо 7\~Тъ и тогда miri = m2r2.
Так как — то получим
тг1 tnL + тг ’
mJ nit + тг'
Легко видеть, что у звезды с большей массой радиус вращения меньший. Пусть т^п^. Тогда из последних равенств видно, что г2>Г1, т. е. звезда с большей массой почти «топчется» на месте (и очень мало), а звезда с малой массой движется по окружности г2г=«/, т. е. практически звезда с малой массой вращается вокруг практически неподвижной звезды с большой массой.
Поскольку на эти звезды внешние силы не действуют, то, естественно, их общее количество движения не меняется, а это значит, что совместно с их взаимным вращением звезды могут двигаться так, что их центр масс имеет скорость о = const, 108
Зная и и Гъ, нетрудно найти 7\ = 7\. Например, для первой звезды из /ф = гп^ получаем
tn^ma 4лаг.
Т-)Н=/И1-ур-!-,
откуда
1\
или, учитывая, что
найдем
т,1
+ т, ’
]/___________
Г 1 (rnt + т3) ’
т. е. период обращения зависит лишь от их взаимного расстояния и суммы масс и не зависит от соотношения масс.
11. СТАТИКА
Статика — это тот раздел механики, который изучает условия
равновесия твердого тела, т. е. такого тела, которое под действием внешних сил своей формы существенным образом не меняет, Введем понятие центра
масс сишемы тел как той точки, в которую сжалась бы вся система тел, если бы между частями системы появились бесконечно большие гравитационные силы. Положение центра масс системы (рис. 98) определяется равенством
- ___TiWi4-...4-rnOTn
с + -.. + тп ’
где ri, ..., г — радиус-
векторы отдельных малых
тел системы в некоторой (любой) системе отсчета; тъ ..., т„ — массы этих малых тел; гс — радиус-вектор центра массы системы.
Если система тел находится в однородном гравитационном поле, то центр масс системы одновременно является центром тяжести системы.
Центры масс однородных простой формы тел находятся: 1) в стержне постоянного сечения, в цилиндре, шаре, сфере, параллелепипеде — в центре; 2) в треугольнике — на пересечении медиан; 3) в правильной пирамиде на одной трети высоты от ее основания.
109
При нахождении центра тяжести тела сложной формы его разбивают мысленно на тела простой формы, гс которых известны.
При этом, если имеется некоторое однородное плотностью р тело с полостью внутри, то при нахождении гс тела полость можно формально считать телом отрицательной плотности —р, а тело сплошным (без выреза).
Введем еще одно понятие — понятие о величине момента силы, как величины, определяемой равенством
M — Fr sin а,
где F— сила, действующая на тело; г — радиус-вектор ее точки приложения; а —- угол между F и г (рис. 99).
В дальнейшем мы будем рассматривать только тот случай, когда все силы лежат в плоскости, перпендикулярной к оси вращения, причем моменты сил, вращающих тело по часовой стрелке, будем считать поло-\ жительными, против часовой
стрелки — отрицательными.
Теперь можно сформули-ровать основную теорему статики для этого простейшего случая.
Рис- "• Чтобы твердое тело на-
ходилось в равновесии, необходимо и достаточно, чтобы геометрическая сумма сил, действующих на тело, была равна нулю (при этом центр массы тела не будет иметь ускорения) и алгебраическая сумма моментов этих сил относительно любой точки плоскости, в которой лежат силы, была равна нулю (при этом тело не будет иметь углового ускорения).
В математической форме эту теорему можно выразить так.
Для ас — 0 необходимо ?i4-.,.4-fn = 0 и для {3 = 0 необходимо Mi 4~... 4~ Мп = 0.
Сформулированная теорема есть просто второй закон Ньютона для частного случая а = 0 и р = 0.
Можно показать, что сколько бы ни было у тела опор, независимых уравнений моментов будет только одно. Однако иногда бывает выгодно написать два-три таких уравнения (вместо, разумеется, каких-то других); но надо помнить, что они будут не независимыми, а следствием каких-то других уравнений (см. задачи 82 и 83.)
Задача 76
Найти центр масс однородной пластины постоянной толщины, размеры которой указаны на рис. 100.
110
Решение
Разобьем пластину на три части и введем оси координат, как показано на рис. 100 (с началом в центре тяжести первой части).
Тогда
7 — nwi+7awa + r3m3 с Wj + ms + т3
или в проекциях на оси х и у
___-^1^1 4-хата + ^8и8-с mt 4- mt + т3 ’ +b«s +^»«»
Ус та 4- та + т3 •
Учитывая, что т; = рУ{ = рй5г и л. л. а , I — а I / Ь Ь — с\ с
0; z/i 0, Хг 2 4* 2 У’ ("г Т~/--------Т»
*з = у + (I — а) + j = I — у 4- j; уз — — j;
получим
рЛ [4 (Z _ 0) (» _ е) 4-(z_|4-|). .*.(»_,) Л
хс -— ---------------i_____,____I-----------J •
рЛ аЬ 4- (I — а) (й — с) 4- у (Ь — с) d j
рйГу (Z — а)(Ь — с) + ~ • у (Ь — с) <zl
ус =------j=----------------7---------г .
рй I аЬ 4- (Z — а) (Ъ — с) 4- у (Ь - с) <ZJ
Сокращая на рй, видим, что от толщины пластины й и ее плотности р положение центра масс не зависит и определяется только формой пластины.
Рис. 100.
Рис. 101.
Задача 77
Найти центр масс однородной пластины постоянного сечения с вырезом в виде круга радиуса (рис. 101).
111
Решение
Взяв за начало отсчета центр прямоугольника, получим в проекциях на оси с учетом того, что ркруга =— р
(- рп/?’Л) (d-
(— -p ?ab/i — nA'3 -p ab ’
(-рп/?2Л){~—
(—ртх/4Л)-|-p«Z»/; —nRs + ab '
здесь учтено, что х-я координата центра круга отрицательна.
1У
Рис. 102.
шара с одной из осей вдоль координату ус — 0). Тогда
Задача 78
Найти центр масс однородного шара радиуса R с шаровой полостью Rt внутри, если расстояние между центрами шара и полости равно а (рис. 102).
Решение
Расположим шар так, чтобы прямая а была в плоскости чертежа (тогда не придется считать гс), и выберем начало отсчета в центре а (и, значит, не придется считать
/ 4 \
(—Р -д it/?’) (—а) хс== 4 4
-р-д-^ + р-з
Rsta т-яг
Очевидно, что хс лежит на прямой х в стороне, противоположной той, где находится полость, ибо из R^>Ri следует хс>0.
0 12 3 М-1 N
|« g .X g.-Д. _?_>Ц ------------------X -?-»]
Рис. 103.
Задача 79
W материальных точек с массами h?i = /7?0, /л4 = 2/л0, ... , mN=Nm^ расположены на одинаковом расстоянии а одна от другой вдоль одной прямой. Найти центр масс этой системы (рис. 103). 112
Решение
Возьмем за систему отсчета точку, лежащую слева от первого тела на расстоянии а, тогда
т,а -|- nit2a + ... + nt^Na т0 (а + 2 • “2а + ... + N • /Уд)
с т । + • + 111 д' т о (1 + 2 + • • • + W)
а(12 + 22 + ...-рЛП a?V(/V+1) (2W+1) 2 „«(2^+1)
(I+24-...4-Л') ~ 6 ’A+V+1)"- 3
Очевидно, что можно было взять за начало отсчета любую другую точку, тогда расчет был бы несколько сложней.
Задача 80
На концах тележки человека массами mi и
длиной I и массой М находятся два т2. Как изменится положение тележки
по отношению к земле, если люди поменяются местами (рис. 104)? Трением тележки о пол пренебречь и считать mi>m2.
Решение
Исходим из того, что поскольку тележка раньше была в покое и внешние силы уравновешены во время движения, то положение центра масс измениться не могло, т. е. л0, = хс. Очевидно, что те
Рис. 104
лежка переместится в сторону, где был раньше человек с массой mi. Возьмем за начало отсчета точку, в которой находился центр тележки до перемещения людей. Тогда до перемещения тележки
I , I — -2- + и3 2-
Л! + /щ + /я3
I т, — т1
2 М + nil + w2 ’
(1)
После перемещения тележки
Л4 + mt + «3
(2)
ИЗ
Сравнивая (1) и (2), получаем
—= —Д/) — МЫ — тг {^-\-Ы
откуда
А/ = 1(т'~
М + т, + та"
Видно, что Д/)>0. Зто означает, что наше предположение о передвижении тележки влево правильно. В противном случае получилось бы Д/<^0.
* Задача 81
Два человека, о которых говорилось в предыдущей задаче,
положение тележки не изменилось. Где остановится человек большей массы mlt если человек меньшей массы гпч дойдет до края тележки (рис. 105)?
Решение
Поскольку положение тележки не изменилось, то можно производить расчет положений относительно ее центра. Очевидно, кроме того,
двигались одновременно так, что
что тележка это то тело, через которое два человека взаимодействовали (т. е. в принципе не отличается от каната, который тянут два человека, стоя на гладком льду). То тогда, по третьему закону Ньютона,
F1>g = -F8tI
или в проекциях на линию движения
Г1, s = Д8,1
и с учетом F = ma получим
tniai =
Если считать движение людей равноускоренным при разгоне их и равнозамедленным при их торможении, то, обозначая их перемещения при разгоне через I, а при торможении через L, а времена разгона и торможения через tr и ts, получим
2/, 2Z2 2L, 2£,
или
/zii/i =/п8/8; tn^Lfy
114
складывая эти равенства, получим
но Ц -f- Li = &xt есть перемещение людей относительно земли или тележки, поэтому
mi Д%1 = т9Дх9,
и так как по условию Дх9=/, то . ml Д%1 = —.
Ответ получен при упрощающем предположении о равнопеременном движении людей. Но и без этого предположения результат был бы тот же.
Задача 82
A В
Балка весом Р, нагруженная силами Fi и Ft, как показано на рис. 106, находится в равновесии. Найти реакции опор Qt и Q3, считая I, a, b, Fi, Ft 04 и си известными.
Решение
Будем искать проекции сил Qi на оси х и у. Условие неподвижности центра масс балки дает
Fi COS Я] -J" Qix 4~ Qix — — /4 cos я., = 0; (1)
Fi sin СЦ 4- Qiy — p 4" Q.iy 4"
4- Ft sin Я9 == 0. (2)
Кроме того, считая возможными не обязательно, но упрощает отсутствия вращения балки
Fi sin Я1Я 4~ Р sin 90° — а\ — Qiy (I — a — b) —
— Ft sin я9 (I — a) = 0. (3)
Fi sin ai (I — b) 4- Qij (I — a — b) — P sin 90° — b^ —
— Ft sin я96 = 0. (4)
P
Рис. 106.
точками вращения А и В (это расчет), получим из условия
(Ясно, что уравнения (2) — (4) не являются независимыми, и читатель может сам показать, что одно из них есть следствие двух других.)
115
Из любой пары уравнений (2), (3) и (4) можно найти Qly и
Для определения же Qix и мы имеем одно уравнение (Г), из которого можно найти лишь
Qu Qix = f i COS аз — Fi COS Otj.
Поскольку все условия равновесия исчерпаны, то порознь Qlx и Qix не найти, что естественно, поскольку искомых было пять при четырех уравнениях. Таким образом, задача однозначного решения не имеет.
Если, однако, предположить, что х-е проекции сил пропорциональны нормальному давлению на опоры, т. е.
\Qlx\ = kQiy и \Qix\ = kQiy
(5)
или
Qix I_Qi?
Qsx I
то это пятое уравнение
Рис. 107.
позволит однозначно решить задачу. Но дело в том, что (5) имеет место далеко не всегда.
Надо обратить внимание на то, что силы реакции Qi и Q* направлены необязательно вертикально вверх. В данной задаче Qi и Qi вертикальны лишь при а1 = а2==90° (при этом, естественно, QIJf = Q2jf = 0).
Задача 83
Однородный диск подвешен на нити так, что касается вертикальной стены. Диск находится в равновесии. Зная угол а, найти вес диска Р, силу натяжения нити Т, силу тре-
ния покоя F и силу нормальной реакции Q со стороны стены
(рис. 107).
Решение
Неподвижность центра массы диска дает в проекциях
— Р -f- F 4- Т cos а = 0; Q — Т sin а = 0.
(1)
(2)
не
Отсутствие вращения вокруг центра диска и вокруг точки касания о стену соответственно дают
FR — TR = Q; (3)
PR — Т sin ^90 — cos у — 0. (4)
Из (3) получаем F — T, а тогда из (1) и (2) следует, что
Т (1 4- cos я) = Р и Q=Tsina. (5)
Из (4) и (5) после преобразований получаем
1 cos я —2 cos2 у, что имеет место всегда.
Таким образом, можно найти лишь связь между Р, F, Q и Т, однозначно их значения определить нельзя, хотя уравнений было четыре. В чем же дело? Дело в том, что наши четыре уравнения не являются независимыми. Именно уравнение (4) есть следствие (1) и (3). Действительно, (4) дает
P = 2rcos2y,
а (I) и (3) дают
Р — Т(\ 4-cos я), что равносильно.
В чем же физическая подоплека этого казуса? Она заключается в следующем:
1) поскольку ни одна из сил не задана, то нельзя ни одну из них выразить только через угол, данный в условиях, ибо динамические величины через кинематические и наоборот не выражаются;
2) силы Т, Q, F пропорциональны Р;
3) легко видеть, что задание одной из сил (например, Р) делает сразу задачу однозначной.
Задача 84
Доска весом 7% и длиной I имеет ось вращения на расстоянии ~ от нижнего края (рис. 108). Какой минимальной скоростью у основания доски должен обладать брусок весом Р, чтобы при подъеме бруска по доске доска повернулась вокруг оси? Угол между доской и горизонталью равен я, коэффициент трения бруска о доску равен k.
117
Решение
Для поворота доски необходимо, чтобы момент сил, вращающих доску против часовой стрелки, был не меньше момента сил,
удерживающих доску, т. е. чтобы брусок прошел влево за ось вращения настолько, чтобы
Рх sin (90° — а) = Р() -sin (90° — а)
или
х~ Р~1[п 2 Г W
Величину х можно найти из условия движения бруска по доске, например из
Д + Дсопр = •
Или в раскрытом виде, с учетом А = 0, v — 0 и Ло = 0,
Г / / , \ п«, Р Й
— FT0----х\ —Ph---------£
тр \ п ' J g 2
ИЛИ
— kPcosa^ + х) =Р ^ + ^)sina-y (**)
Сокращая на Р и исключая х из (*) и (**), находим
Vo = ]/2g/ (k cos a + sin a) .
Задача 85
Какова реакция оси доски при скорости бруска несколько большей, чем найденная в предыдущей задаче (рис. 109)?
Решение
Считаем, что брусок едва-едва перешел за положение, определенное равенством (*) предыдущей задачи. Тогда правый край
118
доски перестанет взаимодействовать с спорой, а доска практически ускорения иметь не будет. Значит, для нее имеем
Q + Ро + Q1 + FTp = О, (1)
где Q1 и Ртр —силы, действующие на доску со стороны бруска. В проекциях на оси
получаем
Qjc — ^тр cos а = 0;
— Q1-Fo + Fipsina +
+ Q>- = 0 или с учетом
FTp = kP cos a найдем
= Qi&P cos2 a;
Qy = P о + . n f k sin 2a\
+ P^cosa----------)•
Если брусок не дойдет до указанного в начале решения положения, то надо учитывать силу, действующую на доску
со стороны опоры справа.
Если брусок пройдет значительное расстояние сверх указанного, то появится большой вращательный момент против
часовой стрелки, доска будет иметь ускорение и исходное
равенство (1) будет несправедливо.
Задача 86
Равнобочный клин (рис. НО) находится в равновесии, если сила W, действующая поперек обуха, в п раз меньше силы Q, действующей поперек щеки клина. Зная п, найти угол клина a и коэффициент трения k клина о бревно, в котором он едва удерживается.
Решение
Будем считать, что клин выдвигают из бревна. Тогда силы
трения и F2, действующие на клин, будут направлены, как
указано на рис. ПО (если бы клин вдвигали в бревно, то Flt F2 и были бы направлены в обратные изображенным на ри
119
сунке стороны). В проекциях на оси получим учетом Ft=kQ и /д = kQ'j
®— 2kQ cos a -|-2Q sin a = 0; (!)
Q cos a— Q COS a kQ sin a— £Qsina = 0; (2)
из (1) получим
-i- — 2 (k COSa — sin a),
a (2) дает тождественный нуль и решение неопределенно, ибо из одного равенства (I) два неизвестных найти однозначно нельзя.
Надо заметить, однако, что пока клин в покое и не находится в состоянии «вот-вот» начнет ползти, о коэффициенте трения покоя k можно говорить лишь весьма условно (в соответствии со сказанным на стр. 26).
Можно говорить лишь о коэффициенте максимального трения
покоя, который часто близок по
Рис. 111.
своему значению коэффициенту трения скольжения. Если материалы клина и бревна заданы, то k можно взять из таблицы, а тогда а сразу определяется из (1).
Задача 87
Как должна меняться в зависимости от положения столба сила F, приложенная перпендикулярно к оси столба в конце его, чтобы столб равномерно
поворачивался из горизонтального положения в вертикальное вокруг другого конца (рис. 111)? Вес столба равен Р. Какова при этом реакция Земли Q?
Решение
Для равномерного вращения столба вокруг его конца необходимо равенство нулю суммарного момента сил, т. е.
Р sin р — FI — 0,
или cos a— Fl — Q, (*)
откуда Г Р COS a F~~ 2 •
120
Так как силы уравновешены (ускорение центра масс практически равно нулю при медленном повороте), то
Qy-[- F cos а — Р = 0;
Qx — F sin а - 0, г Р cos а откуда с учетом г = —’ получаем
„ __Р sin 2а
Чх — 4 •
12.ГИДРО АЭРОСТАТИКА
Ничего принципиально нового в задачах на этот раздел по сравнению с задачами на другие разделы механики нет. Все формулы этого раздела есть рядовые следствия законов Ньютона, а потому и все задачи этого раздела в принципе могут быть решены исходя из этих законов.
Напомним некоторые положения гидроаэростатики.
]. Закон Паскаля: внешнее давление, производимое на жидкость или газ, находящиеся в равновесии, передается ими во все стороны без изменения.
2. Гидростатическое давление жидкости, обусловленное силой тяжести на глубине h, определяется формулой p = dh = pgh. и не зависит, согласно закону Паскаля, от ориентации площадки, на которую оказывается давление.
3. Жидкость находится в равновесии, если на любой элемент ее действуют уравновешенные силы.
4. Закон Архимеда:
Fa = ~ Хыт,
где Рвыт — вес жидкости (или газа) в объеме погруженной части тела, на которое действует интересующая нас FA.
* Задача 88
В изогнутой трубке, изображенной на рис. 112, находится известная жидкость. Вес поршня Р и сила F, действующая на него, известны. Найти распределение давления р — р (/), если все необходимые размеры трубки заданы.
Решение
Прежде всего отметим, что на одинаковых уровнях давления в обоих коленах трубки с однородной жидкостью одинаковы, иначе жидкость не находилась бы в равновесии. Кроме того,
121
любой элемент жидкости находится тоже в равновесии. Рассмотрим условие равновесия какого-нибудь элемента. Учитывая, что по условию задачи нужно найти р = р (/) и тот факт, что давление на уровне Н находится просто, приходим к выводу, что интересным элементом является заштрихованный кусочек.
По второму закону Ньютона
лр+Л + Fb + q. + q^o,
где ДР — вес заштрихованной части жидкости; Рв и FB — сила давления на эту часть снизу и сверху со стороны остальной части жидкости; Qt и Q2 — силы давления на выделенный элемент жидкости со стороны стенок сосуда.
В проекции на вертикаль получим
?gS (I — Я) 4- pBS — PeS = 0
или
ре = ра — Pg(l — Н).
Так как ра равно давлению под поршнем, то
где So—-сечение поршня.
Окончательно искомое давление
Р = Рв = ^Ф^~РЙ-(/~Я). (*)
Строго говоря, давление под поршнем надо было бы находить так. Из условия равновесия поршня
Р F — Qn, ж — О, откуда
Рп.ж = Р + Р.
Но, по третьему закону Ньютона, силы взаимодействия поршня и жидкости равны, т. е.
I Qn,»1== (— Q«, п |== Q, и окончательно
<2 P + F
Читатель может исследовать (*), давая I различные значения. 122
Задача 89
В изображенные на рис. 113 сосуды кость до одинакового для всех сосудов
налита одинаковая жид-уровня. Найти соотно-
шение между силой давления жидкости на дно Qt и ее весом Pt для каждого сосуда в пренебрежении внешним давлением.
Решение
a) Qi = pSi = dhSi^>dVX1 = Ръ так как hSi^>VXi. б) Qt = pS$ = dhSi = dVK.i = Рг, так как hS^— ]7Ж2. в) <2з = pS3~dhS3<ZdVX3 = Pit так как /153<РЖз.
Задача 90
В сосуд, изображенный на рис. 114, налиты три несмешива-ющиеся жидкости. Зная удельные веса первых двух жидкостей di и dit а также вес третьей жидкости Р3) определить разность
уровней второй жидкости ДЛ, если угол а, площадь поперечного сечения правой трубки S и высота столба первой жидкости hi известны. Внешние давления на поверхности жидкостей одинаковы.
123
Решение
Поскольку жидкости в равновесии, то на одинаковых уровнях одной и той же жидкости давления одинаковы. Так как нас интересует Д/г, то разумно приравнивать давления на уровне ht. Тогда на этом уровне
Рправ--Рлев*
Но каждое из давлений складывается из внешнего давления и давлений столбов выше расположенных жидкостей; поэтому
Рвиешы 4~ ^3 Рвпешн 4~ 4” ^8
Так как
, , • К.
й3 = /3 sin а = sin а, О
где 14— объем третьей жидкости, то с учетом равенства внешних давлений
sin а = dihi
или
р
-Д sin а = rfjAj 4- rfjA/i, откуда
Р3 sin а — Sd^
Задача 91
В сосуд высотой h налита жидкость с удельным весом d. Какова площадь клапана S, если при коэффициенте жесткости его пружины k и величине сжа-
Рис. 115.
тия ее х жидкость начинает выливаться через клапан лишь тогда, когда доходит до краев сосуда (рис. 115)? Вес клапана равен Р.
Решение
Очевидно, клапан открывается, когда сила, действующая на
него вниз, не меньше силы, действующей вверх, т. е.
или
откуда
F 4-P>F
1 д I 1 1 упр
dhS 4- Р ss kx,
S
kx- Р dll
124
* Задача 92
В сообщающиеся сосуды с площадями поперечного сечения Si и S8 была налита жидкость d0. При этом уровни в обоих сосудах оказались на одной высоте. Какова будет разность уровней этой жидкости, если в правый сосуд налить Р.> легкой жидкости? Коэффициент жесткости пружины равен k. Правый сосуд открыт (рис. 116). Поршень все время соприкасается с жидкостью.
Решение
Исходим из того, что на уровне h’ давления одинаковы, т. е.
Рправ — Рлев ИЛИ
Рвнешн. прав —dh, —- Рвнешн. лев~Рdo&ll, где рввеши. пГа, —ЭТО давление окружающей сосуды среды;
Рвнешн. лев складывается из давления окружающей среды и , где Q — сила взаимодействия поршня и жидкости.
Обозначая давление среды р0, имеем
Ро Н- dh — ро -j- -j- do&h,
но
dh = !’2, 02
a Q = P — Fy„v (из условия равновесия поршня), поэтому
Р — kx
d<Ah.
(1)
Видно, что для ответа на вопрос необходимо найти х. Найдем х на основании следующих соображений.
Новая деформация пружины х меньше той х», которая была до наливания второй жидкости на Д/гь где Д/г( — увеличение уровня жидкости в левом сосуде, т. е.
X — Хо — Д/11 или X = — Д/lj
(2)
125
^поскольку уровни жидкости были на одинаковой высоте, то сила взаимодействия поршня и жидкости была равна нулю, поэтому х0 = ^. Так как
Д/ггххД^ + Д/г, и ДУ1 = ДУа, (3)
где Д/г2 — опускание уровня первой жидкости в правом сосуде, a AVj и ДУ2 — количество первой жидкости, перешедшей из правого сосуда в левый при наливании второй жидкости, и поскольку ДИ/ = 5гДй/, то из (3) получим
Д/ii =
ДЛ
Подставляя найденное Д/г( в (2), потом значение х из (2) в (1),
получим
(р \
—Ц—--^h
откуда
,(A’i ~Ь Ss) Si
Замечание. Уравнение (1) написано в том предположении, что пружина после доливания жидкости осталась растянутой, но в меньшей мере, чем была; если бы Ps было достаточно велико, то пружина могла оказаться сжатой и вместо уравнения (1) имело бы место уравнение (Г)
а вместо уравнения (2) — уравнение (2') Л? р
•Г = ДЛ1—Т’ (Z)
1 и результат решения не изменился бы. 7г,
Задача 93
L В цилиндрический сосуд, радиус основания которого равен R, налиты две несмешивающиеся жидкости с удель-
Рис. 117. ными весами d( и d2. Зная высоту стол-
ба нижней жидкости ht и высоту столба верхней жидкости hi, найти отношение п силы давления жидкостей на малые одинаковые площадку дна и боковую вертикальную полоску стенки сосуда (рис. 117).
126
Решение
Очевидно, что вертикальная полоска цилиндра должна быть такой узкой, чтобы она мало отличалась от куска плоскости. Тогда сила, действующая на эту полоску, будет иметь одинаковое направление для всех элементов этой полоски. Получаем
__ ДфоСН __ AQoCH _____________ Росн ’ A*S0CH
А(?бок &Q1 бок Н- бок + Р^
При этом
Д£( -|- Д£8 = AS0CH.
Но
ASi 4- ASa = /tiAZ -|-Л2Д/,
где Д/ — ширина вертикальной полоски. С учетом этого, а также того, что
Росн — Рввешн Ч~ -f"
Рср2--Рвнешн
2 ’
и । j k ।
Pcpi Рвнешн “Г U2/I2 ~| >
получим
__ ________(Рвнешв (^j ________
(рвнешн + h1М + ( рввеша + ^1\ h^l
что по сокращении на Д/ и даст ответ.
Задача 94
На границе раздела двух несмешивающихся жидкостей d( и dt плавает полый шар, удельный вес вещества которого равен у d. Каков объем полости шара, если отношение объемов р* по-'2 груженных в жидкости частей шара равно п и У2 известно (рис. 118)?
Решение
Так как шар в равновесии, то
Р + 4 = 0 или
P = Fa.
Но
P = d(V — ДУ), где V — внешний объем шара, а ДV — объем полости.
127
По закону Архимеда FA = Pt -f- Pt, где Pt и Р3 — вес жидкостей в объеме погруженных в жидкости частей шара У4 и И3.
Рис. 118.
С учетом сказанного имеем
d(V — Wj^dtVt + dtVt, или
d (Vi -f- Vs — ДИ) = dtVt dtV3.
Учитывая Vi = nVt, получим
d (nV%^2 — ДИ) = (din dt) V8>
откуда
Д |/ ==: (tl О — (^ln ~V
Задача 95
С какой силой давят друг па друга дно сосуда и кирпич с удельным весом d, площадью основания S и высотой h, если в сосуд налита жидкость dM до высоты Н (рис. 119)?
Решение
Возможны два случая: 1) кирпич неплотно прилегает ко дну сосуда; 2) кирпич «прилип» ко дну сосуда так, что жидкости между дном сосуда и кирпичом нет. - •
128
1. Давление снизу на кирпич есть, и оно больше давления сверху. За счет разницы этих давлений и появляется РА.
Тогда
Р + ?а + & = Ъ,
или
Р — dxvx — Q1 = O,
или
dSh — d„Sh — Q, = О,
откуда
Qi = (d — d1K) Sh.
2. Давления жидкости снизу нет и FA = 0, давление же сверху есть и создает добавочную силу Fa = dM(H — h) S.
В этом случае
P + ?b + Qs = 0 пли
d Sh + (Н — h) S — Q4 — 0, откуда
Qi — S [(d — dx) h dxH],
Замечание. Первую часть можно было бы решать, не прибегая к понятию Ед (рис. 120).
Именно, считая силу давления жидкости снизу Fu, а сверху FB, получим условие равновесия кирпича в виде
?+^н+Л + 51 = о или
dhS - dxHS + </ж (Н — h) S - Q = 0, откуда
Qi = (rf — б(ж) Sh.
Ь В. К. Кобушкин
129
Задача 96
Как зависит архимедова сила, действующая на тело, от глубины погружения тела?
Решение
р __ р __и ]/ __л Рт___Ск р
‘ А — * ж — * т — иж $ — 1 т •
С ростом глубины погружения из-за сжатия жидкости и тела d№ и dr возрастают в какой-то мере, а Рт = const.
Если жидкость более сжимаема, чем погружаемое тело, то с ростом h растет, если наоборот, то убывает с возрастанием h. Соответственно растет пли убывает FA. Если жидкость и тело одинаково сжимаемы, то FA^£FA(h), ибо = const ,
Задача 97
Тело плавает внутри жидкости во взвешенном состоянии. Каков вид равновесия этого тела?
Решение
Очевидно, РЛ = Р или dxVr = diVt, т. е. ^=1 (па данной глубине!). т
Рис. 121.
1. Если жидкость более сжимаема, чем тело, то с увеличением ft 2> 1 илн Fa^>P, ас уменьшением h ^<^1 или FA<pp, т. е. при выводе тела из равновесия, оно вновь в него возвращается (рис. 121),
130
2. Если тело более сжимается, чем жидкость, то с ростом h Fa<C.P,c. уменьшением й Fa^>P, т. е. тело, выведенное -.;з равно-
весия, уходит от него все дальше, и равновесие неустойчиво (рис. 122).
3. Жидкость и тело одинаково сжимаемы — тогда Fa = P и равновесие безразличное.
Задача 98
Известно, что при движении шарика в жидкости сила сопротивления при небольших скоростях пропорциональна Rn, где IsSnsSS, и скорости V. Исходя из этого, доказать, что чем больше радиус шарика, тем с большей скоростью он будет падать в жидкости (рис. 123).
Решение
При достижении достаточно большой скорости v шарик будет падать равномерно. Значит,
Р = Ра 4- Есопр или
^R3(d-dK) = kRnu
О
(k — коэффициент пропорциональности). И, значит,
__ рЗ-п
так как п<^3, то чем больше R, тем больше v.
5*
131
Задача 99
На какую глубину h* в жидкость плотности рж погрузится упавшее с высоты hi над ее поверхностью тело плотности р, если средняя сила сопротивления в жидкости составляет 1/zi-io часть веса тела? Сопротивлением воздуха пренебречь и считать р<рж (рис. 124).
Решение
Движение тела складывается из двух этапов — в воздухе и в жидкости. Для первого этапа Р — таг, для второго Р-т-АдН-4~ Рс — та*
В проекции на 7-направление имеем с учетом того, что конечная скорость тела в воздухе равна начальной скорости тела в жидкости
г?
,, те v2
mg-p^gV--------
132
Или с учетом И —
т
Р
g (1 —
S \ р
V'1
2h3-
« /
Исключая на, получим
Задача 100
Какую работу совершает выталкивающая сила при погружении в жидкость плотности р вертикально ориентированного цилиндра высотой Н и радиусом R?
Решение
Поскольку при погружении тела выталкивающая сила меняется, то
А — FC0As cos а.
Так как FA пропорциональна объему погруженной части тела, а в данном случае V = ~R'2h, то в силу Fa~Q
р _F+F0_F_Pg^H гСр— 2 — 2 — 2 1
Поскольку перемещение цилиндра антипараллельно выталкивающей силе, то cos а = — 1. Окончательно имеем с учетом hs = H:
А — ~
Задача 101
Найти выражение потенциальной энергии для тела, погруженного в жидкость.
Решение
По определению потенциальной силы и ее энергии имеем
А пот:== пот.
В нашем случае роль потенциальной силы играет (?д-|-Р) или в проекции на вертикаль (Р — FA). Если тело опустилось под
133
действием этой силы с высоты /ц до высоты h> от дна сосуда, го (Р - FA) (ht -h,) = — (IF2 - IFOkot, откуда
й\от - Й\от = (P~ FA) hi-(P- Fa) h,.
Считая IF пот = 0 на высоте /z = 0, получим
Wln„ = (P-FA)hi, Wtn<n = (P — FA)hi. И вообще
№пот = (P-FA)h = (P-P1K) gVh,
где h отсчитывается, например, от дна сосуда.
Задача 102
Два шарика весом Pj и Р8 и радиусами Ri и /?3 соединены штангой весом Р, объемом V и длиной I. Эта система погружена в жидкость плотностью р. Где надо поместить точку опоры, чтобы система находилась в равновесии (рис. 125)?
Рис. 125.
Решение
Поскольку речь идет о равновесии тела, имеющего ось вращения, то на основании правила моментов имеем
(FA1 - Р^ (4 - х + Rt) + (Р - F А) х +
+ (Р2-Дд2) (4 + * + ^) ==о
(4 “RiPg — Р1^ — х-{- Ri^ (Р ~ pgV) X
+ ( Р-2 —з ^Rlpg^ [^2 ~Т х ~г = 0> откуда можно найти х.
134
13. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В СИЛОВЫХ ПОЛЯХ
существенно излучают энергию, но частиц малыми, а тогда их излуче-
Рис. 126.
Поскольку не очень малые заряженные частицы подчиняются законам механики не хуже, чем незаряженные, то методика решения задач остается прежней. Правда, при очень больших ускорениях заряженные частицы мы будем считать ускорения нием можно пренебречь.
Сила, действующая на частицу с зарядом q, в электрическом поле (кулонова сила Л<) подсчитывается по формуле
F;< = qE.
Сила, действующая на эту же частицу в магнитном поле (лоренцева сила ?л) — по формуле
Fn = qvB sin an.
Здесь Е — напряженность электрического поля, числен
но равная силе, действующей на единичный положительный точечный (т. е. сосредоточенный на малом теле) заряд, помещенный в ту течку поля, где нас интересует F; и —скорость движения заряда; В — величина вектора индукции магнитного поля, численно равная силе, действующей на единичный положительный точечный заряд, движущийся с единичной скоростью перпендикулярно к магнитному полю; a — угол между v и В; п — единичный вектор, направленный перпендикулярно к плоскости, в которой лежат v и В, в сторону, определенную правилом левой руки или правилом буравчика (рис. 126), причем вращение производят по кратчайшему угловому пути.
Естественно, сила, действующая на отрицательный заряд в данных полях Е и В, будет направлена в сторону, противоположную той, в которую направлена сила, действующая на положительный заряд в этих же полях.
Формально теория электростатического поля построена так же, как и теория гравитационного поля (классическая, разумеется), ибо основной закон электростатики (закон Кулона) имеет вид, аналогичный закону тяготения Ньютона, а именно — для двух точечных зарядов
?к = А^г
135
и, значит, для случая поля, созданного точечным зарядом Q,
имеем
E = k^ 7, Га >
где г проведен от Q в интересующую нас точку (рис, 127); k — некоторый коэффициент пропорциональности, зависящий от среды, . в которой создано £, и выбора еди-
Е V ниц.
» г\ Электрический (кулонов) потенциал
\ <рк в данной точке определяется фор-
0 0 му лой
у© Q _ W?
Рис. 127. Чк — —-,
т. е. численно равен потенциальной энергии й7, которой обладает д = -|-1 в данной точке.
В случае поля, созданного точечным зарядом,
, Q
<?к = Ь^,
где г — расстояние от Q до интересующей нас точки. Очевидно, что при движении заряда q
= q Дфк,
Сила, действующая на заряд со стороны магнитного поля, всегда перпендикулярна к направлению движения и поэтому работы не совершает, а лишь изменяет направление скорости частицы. Силовые линии магнитного поля суть замкнутые кривые. (Такое поле называется вихревым.)
Во всех рассматриваемых задачах мы будем считать магнитное поле однородным, т. е. постоянным по всему рассматриваемому пространству, и постоянным во времени.
Какие причины определяют В и по какому закону она подсчитывается, мы рассматривать не будем.
Задача 103
Частица массой т, несущая положительный заряд q, брошена со скоростью Го под углом а0 к горизонту в однородном электрическом поле напряженностью Е, которая составляет угол ₽ с вертикалью (рис. 128
в) уравнение траектории, т. е. у — у(х).
. Найти: а) г — /•(/); б) v — v (/);
136
Решение
Очевидно, что движение частицы будет происходить с а'~ const (поскольку действующие на нее силы постоянны), поэтому имеем
mg -f- Fk — та;
v t’o “I- crt;
—► —» —* п / 2
r — ro 4~ 4~ “2~.
где г и r0 проведены, естественно, из начала отсчета, которое, разумеется, мы можем взять в любой точке. Исключая из этих равенств ускорение а, получим
~ mg+qE . v — ----т
или в проекциях на оси х и у
, qE sin В , vx — ve cos а0 + ——-1;
vy = Vo sin a0 -|- —t;
x = vo 4- vat cos a0 4~ qE^n • у; (*)
У = Уь+ий1 sina04-~"'g + gCcos- (**)
Исключая из (*) и (**) время t, можно получить уравнение траектории. Не будем этого делать из-за громоздких вычислений,
тем более что сразу видно, что уравнение у — у{х) будет уравнением параболы.
Задача 104
От неподвижного шара радиуса R с равномерно распределенным по нему зарядом объемной плотности рэл
движется частица массой т и зарядом q, имевшая па расстоянии гй от его центра скорость v0. Пренебрегая всеми силами, кроме кулоновой, определить расстояние г, на котором частица будет иметь скорость v (рис. 129).
137
Решение
Так как частица движется под действием переменной силы Fk = Fk (г), а в задаче фигурируют скорости и положения частицы, то очевидно, что надо воспользоваться законом энергии
/1 + Лсопр = ДГкЧ-ДГп.
И поскольку непотенциальных сил нет, то
Д№к+МГп = 0 или с учетом
Q = Рэ.Л = рэл4Я^’>
« (V* - vl) + kq 4 ^Зрэл (L _ Д = о,
° V 'О/
откуда легко находим г.
Задача 105
В однородное магнитное поле с индукцией В, направленное перпендикулярно к этому листу от нас, влетает частица массой т и отрицательным зарядом q со скоростью и, лежащей в плоскости этого листа (рис. 130). Как будет двигаться частица, если пренебречь всеми силами, кроме ло-ренцевой?
Решен ие
Так как В и v направлены, по условию, взаимно-перпендикулярно, то
Гл = | q | vB
и Ел все время перпендикулярна к и и В (ибо Гд всегда направлена так).
Но это означает, что Гл будет _ менять только направление ско-
рости, т. е. Гл есть сила, вызывающая центростремительное ускорение аг. Поэтому частица будет двигаться по окружности радиуса г в плоскости чертежа и
I I п №'’ |<7|цВ = —-
откуда
mv
138
Время оборота Т с учетом о = -у будет
<г__ Чпт
\Я\В
и не зависит от скорости частицы. Очевидно, что вращение положительной частицы происходило бы в обратном направлении, т. е. против часовой стрелки.
Задача 103
Отрицательно заряженная частица движется прямолинейно (рис. 131), в полях (однородных) Е и В, направленных, как показано на этом же рисунке. Найти скорость частицы. Силой тяжести пренебречь. п
Решение
Направления /ж и Е-\ очевидны, и поскольку частица движется прямолинейно и равномерно, то
или
откуда
Лл+Л = о
| q | Е — | q | vB = 0,
Задача 107
Важной характеристикой заряженной частицы является отношение заряда частицы к ее массе, т. е. Как зависят ст — отклонения А// частиц от оси х, вдоль которой они двигались с одинаковой начальной скоростью ц0, если электрическое поле направлено вдоль оси у и равно £? Все частицы проходят одинаковое расстояние вдоль оси х (рис. 132). Силой тяжести пренебречь.
139
Решение
Очевидно, что на положительные частицы действует сила, направленная вниз, а на отрицательные — вверх, соответственно и отклонения будут противоположными. Поскольку поле Е постоянно и однородно, то, например, для положительной частицы с учетом /\ = 0 и T’Ov = 0 получим
х — Vat; кц——Е^-.
“ ’ » т 2
Исключая отсюда t, получаем
V 2vf т •
Из этого соотношения, если необходимо, можно найти — для частиц по их отклонениям Дг/.
* Задача 108
Шарик массой тис положительным зарядом q подвешен на нерастяжимой нити длиной I в горизонтальном электрическом
Рис. 133.
поле Е. Нить отклонили на угол а от вертикали и отпустили. Каково будет ее натяжение Т в момент прохождения шариком равновесного положения (рис. 133)?
Решение
Очевидно, что прежде всего надо определить положение равновесия, например, найдя угол а0. который составляет нить с вертикалью при равновесии сил FK, Та и Р.
140
Из
mg + To 4- FK = O или из
— To sin a0 4-(?£ = О,
Ta cos a0 — mg — 0 находим
Для нахождения T, т. е. той силы, с которой будет растянута нить при движении шарика, имеем
4-fK = .w; (1)
Д4-Лсопр = ДГк + Д1^ + Д^Е. (2)
Поскольку движение происходит по окружности, имеет смысл написать (1) в проекции на радиус вращения, т. е.
— cos а0Т — qE sin гй = —(3)
Поскольку T_\_v, то Л—0, а поскольку силы сопротивления в задаче не упомянуты, то и ЛС0Пр —0. Равенство (2) перепишем поэтому в виде
0 = Д- (^ — nJ) 4. mg (у.2 — yt) qE (х3 — х$. (4)
Так как vt— скорость шарика в положении а равна нулю, а
Уч — У\ = — I (cos а0 — cos а), (5)
и
х3— x1==/(sina0— sin а), (6)
то совместное решение (3) и (4), т. е. исключение из (3) и (4) н|, дает с учетом (5) и (6)
Т — mg (3 cos а0 — 2 cos а) 4~ (2 sin а — sin я0).
Задача 109
Конический маятник массой m и положительным зарядом у вращается в g и Е полях, причем Е направлено горизонтально. Зная длину нити маятника /, найти угол а, составленный нитью с нормалью к плоскости вращения, и угол 0 между этой нормалью и вертикалью (рис. 134).
141
Решение
Очевидно, маятник будет находиться в устойчивом движении
г лругу, если результирующая
Рис. 134.
сил qE и mg будет перпендикулярна к плоскости орбиты (подобно тому как конический маятник, вращающийся только в поле тяжести, будет в устойчивом вращении лишь при v_Lg, т. е. при горизонтальной пло-
скости вращения). При этом получим в проекции на радиус вращения г и нормаль п
Т sin а=m4vtf1r;
сткуда с учетом r = Z-sina
/^g3 + <?2£3
Угол В находится, очевидно, из того, чго (qE-\-mg) параллельно п и, значит,
tgp = ^-. ° “ mg
Задача ПО
Считая, что электрон вращается в атоме водорода вокруг ядра по круговой орбите, найти отношение потенциальной энергии электрона к его кинетической энергии (рис. 135).
142
Решение
Очевидно,
-kq*
Wr, г
U7K — mtf_
2
(1)
(знак „минус11 обусловлен тем, что заряды ядра и электрона противоположны по знаку), и так как
Ек = та
или
kq3 _ mvs
~г3~~~Г~'
то, подставляя из (2) в
(1) значение
ivlt
v“, получим
2.
Очевидно такое же спутников, движущихся
соотношение
по круговым орбитам.
получится для планет пли
Задача 111
В вертикальной абсолютно гладкой трубке находятся дза одинаковых заряженных шарика массами т с положительными зарядами q и радиусами R (рис. 136). В начальный момент шарики находились вплотную друг к другу, а затем были отпущены. Как они будут двигаться, если отпустить: а) оба шарика, б) только нижний, в) только верхний? Считать силы трения ничтожными и заряды во время движения неизменными.
Решение
а) Если расстояние между шариками г, то они взаимодействуют с силой
р — г~ г3 '
Центр масс системы движется вниз с ускорением g, а ускорение шариков друг относительно друга составляет
Uoia— тг‘ '
Рис. 136.
143
б) Шарик будет двигаться вниз с ускорением
« = г4
/г<?8
г2 in ’
в) Если т, q и R таковы, что в начальный момент mg^qE, то верхний шарик в движение не придет. Но если mg<"qE в начальный момент, то шарик пойдет вверх сперва ускоренно до положения Г], определяемого уравнением
mg
kq‘‘ "г2,
а затем замедленно. В некоторой точке, на расстоянии г между центрами, шарик остановится, потом
пойдет вниз и будет колебаться. Положение г найдем с учетом ио = п = О из
HWg 4- Д1ГЕ = 0
или
mg (г — г0) 4-
ИЛИ
mg(r — r0)— rn), • ' о
откуда с учетом ra~2R получаем
2Rmg'
Задача 112
определяемой углом сравнению
с I (рис.
а
137).
Два одинаковых по величине и противоположных по знаку заряда находятся на расстоянии I друг от друга. Найти Е и <рк в точке, 90° на расстоянии г, очень большом по
Решение
В силу того, что
fi rit
то
Е^Е>,
г^>1, угол между rt и га мал. И так как а Е составляет с 7 угол, практически рав-
ный 90°. Величину же Е найдем следующим образом.-
144
Откладывая на и величину г.2) получим треугольник со сторонами л>, Г] и АВ, подобный треугольнику со сторонами Е1, Еа и Е, и тогда
а так как
то
Е I sin а
Г 2
С _____ } Я \
--- ---Q--- >
Г3
Е^Е,
, I sin п k | q | I sin a r——~^----s-
Что касается срк, то с учетом разных знаков зарядов имеем
fe; ? I (г2 — г а
?к — ?! 4“
k | q ] I cos a
rs
14. К ОБОСНОВАНИЮ ВЫБРАННОГО СПОСОБА РЕШЕНИЯ ЗАДАЧИ
Часто учащиеся при решении задачи выписывают чуть ли не все формулы, которые они знают, и затем пытаются как-то их скомбинировать для получения ответа. Такое «решение» задачи вряд ли является целесообразным, тем более что даже при получении верного ответа смысл хода решения ускользает, уверенности в правильности его нет и у учащегося остается неприятное чувство неудовлетворенности. О наличии же логики, стройности и завершенности решения при таком методе не может быть и речи.
Как же приступить к решению задачи и проводить его?
Во-первых, надо придерживаться примерной схемы решения, приведенной в разделе II настоящего пособия.
Во-вторых, и это очень важно, не надо пытаться сразу детализировать задачу, задаваться вопросами, куда девать те или иные данные задачи или откуда взять недостающие.
В-третьих, надо правильно выбрать исходное равенство или равенства. Выясним последнее.
В принципе, если мы умеем связывать между собой ускорение, скорость и перемещение тела со временем при любом движении, го для решения любой задачи динамики достаточно только знания законов Ньютона. Но учащиеся средней школы умеют связывать указанные кинематические величины лишь для случая равнопеременного движения. Отсюда следует, что во всех других случаях, т. е. когда действующие на тела силы являются непостоянными, использование при решении задачи второго закона Ньютона становится затруднительным, особенно при криволинейном движении. На помощь в этих случаях и приходят законы
145
изменения импульса и энергии (или в частных случаях законы сохранения). Поэтому, если в задаче упоминаются постоянные силы и ничего не говорится о работе, энергии, мощности, исходным уравнением может служить второй закон Ньютона.
Если в процессе, описываемом в задаче, действуют переменные силы и из кинематических характеристик движения фигурируют только скорости, разумно исходить из закона изменения импульса, а если его для решения недостаточно, то использовать закон изменения энергии (как в случае, например, ударов тел).
Если при наличии переменных сил задаются положения тел и их скорости, но не упоминаются ускорения, исходным равенством является закон изменения энергии.
Рис. 138.
Естественно, при упоминании в задаче работы или мощности за исходное надо брать соответствующие формулы
N = ~ или А — F As cos a = F, As. t 1
При этом надо помнить, что формула А — Ft As справедлива лишь при постоянной Ft; если же сила переменная, то надо пользоваться законом изменения энергии или усреднять Ft.
Естественно, что в более сложных задачах приходится прибегать и к комбинациям нескольких формул.
Рассмотрим несколько примеров для пояснения сказанного в этом разделе.
Пример 1. Брусок соскальзывает с вершины наклонной плоскости высотой й0 и углом а при с'о = О. Найти скорость бруска у подножья плоскости, если коэффициент трения равен k (рис. 138). Сделав чертеж и рассмотрев силы, действующие на брусок, убеждаемся в том, что они постоянны, и за исходное берем второй закон Ньютона
Кроме того,
146
Проектируя векторы на оси х и у, получим с учетом Flv = kQ, ау — 0 и ах — а
rngixm — kQ — mcr,
— mg cos a Q = 0;
Откуда по исключении Qua получим
—J = g(sina— я cos a), и так как
sin a ’
TO
sin a — g (sin a — k COS a), ZZZ0
откуда с учетом no = O получим
v = ]/"2g/i0(l —kctga).
С другой стороны, в задаче упомянуты положения тела и его скорости. Поэтому можно исходить из закона изменения энергии
Л Лсопр = AIV7.
Так как QJ_o, то Л = 0 и, значит, „ fmv3 . ,> [mvl , , \
— TTPs = mgh) — [-^ 4- mghoj.
Так как FTp = kQ, о0 = 0 и /г = 0, то
— kQs=™-------mgha.
Для нахождения Q надо учесть, что поперек плоскости у бруска ускорения нет, т. е.
Q — mg cos a = 0.
С учетом
sin a
получим
, Ло mt/9 ,
—/emg cos = ------------mgh0,
откуда опять
v = V2gha (1 — k ctg a).
147
Эту же задачу можно решить и исходя из закона изменения импульса тела
(mg + ?тр 4- Q) Л/ = mv — mvQ,
s 2s 2s
что в проекциях с учетом ив = 0, FTp = kQ и М = — = -х—= -^ср I ^0
дает
2s
(mg sin а — kQ) — = mv;
—mg cos a Q — 0.
Откуда, исключая Q и учитывая s = -^, получим
v — /2g/z0 (1 — fcctga).
Естественно, что эти решения все эквивалентны, но первый способ с использованием только второго закона Ньютона несколько
проще.
Легко видеть, что масса бруска не играет роли в данном случае, так что не надо задумываться, как это часто бывает
с учащимися, над тем, откуда ее брать.
Нужно помнить, что часто необходимые на первый взгляд величины потом так или иначе при решении уходят, подобно массе бруска в этой задаче.
Пример 2. С кривого желоба ВЫСОТОЙ Йо и длиной I соскальзывает брусок массой т. Начальная скорость бруска с’о, конечная v. на брусок при его движе-
Рис. 139.
Найти силу трения, действующую нии (рис. 139).
Очевидно, что на брусок наряду с постоянной силой mg действуют переменные по величине и по направлению Q и FTp. С другой стороны, в задаче упомянуты положение тела и его скорости, поэтому разумно применить закон изменения энергии.
Л + А0,,Р = А1Е.
Так как Q_J_y все время, то 4 = 0. Сила трения все время направлена против скорости, т. е. угол между Етр и v равен 180°. Но величина Етр меняется из-за изменения величины Q. Поэтому 148
можно найти только среднюю силу трения Fcp. Учитывая это,
получим
— ЛСр/ — 4- mghj — 4- mgh^,
откуда с учетом ft —О находим
Fv> =(^о 4
2 Г
Пример 3. Кувалда массой т падает свободно с высоты й0 па кол массой М и забивает его на А/ в землю. Считая удар кувалды о кол абсолютно неупругим и мгновенным, найти сред-
нюю силу сопротивления грунта (рис. 140).
Очевидно, здесь имеют место следующие три основных для данной задачи процесса: 1) падение груза т под действием силы mg', 2) неупругий удар тел; 3) совместное движение тел под действием переменных сил.
Первый процесс вполне описывается любым из уравнений:
F = ma; kp = FM
и Л + Лопр = ДИ7.
Второй процесс описывается законом сохранения импульса (ибо из-за мгновенности удара импульс внешних сил равен нулю).
Третий процесс описывается, как и первый, ибо хотя сила сопротивления и переменная, но направлена все время в одну сторону, и уравнения имеют вид:
Fcp = macp; kp — FcpM и А 4~ Лс01ф = .
Уже говорилось, что удобнее при наличии переменных сил пользоваться законом изменения энергии. Им тем более можно пользоваться и при действии постоянных сил. Поэтому опишем первый и третий процессы законом изменения энергии, а второй— законом изменения импульса. Тогда
Л] 4* Лсопр1 — Д1ТТ;
Дрг — 0;
Лз 4~ Лсопр3 — AlFg.
Так как по условию
Л] = Лсопр1 = Л з = О, то
IV'oi— Poi— Pi, ^сопрз — — IT’os.
149
Раскрывая эти равенства, получим
, . mvi, , , mv'',
mgh^ + m^hl +
mvoi —(т-^-М) V/,
-ЛсрД/ = (т + М) (gh3 +£)_(т + М) (gh^ + .
Учитывая, что v01 = г?3 = 0; р1 = у02 = р; ца = г03 = и; hn = h0’, hi=h® = Ы и Л3 = 0, имеем
^0 = ^/4-у;
mv= (т 4-Л4)«;
- РсрД/ = - (т + М) [gM + .
Исключая отсюда и и и, найдем
Аср = (т + M)g4- g-
ср ' I ! S I (ет _j_ Д/J) д; S
Пример 4. Два глиняных шарика с массами mi и т2 привязаны в одной точке потолка длинными нитями /1 = (2 = /. Их
отводят в сторону так, что нити образуют углы и оч с вертикалью в плоскости чертежа, и отпускают. На какой угол они отклонятся при их неупругом ударе в нижней точке (рис. 141)?
Можно было бы решать эту задачу подобно предыдущей: выписать сразу все уравнения, отображающие интересующие нас процессы. Но учащиеся не всегда могут это сделать. Поэтому выберем иной ход решения.
Нас интересует именно угол отклонения нити а. Из чертежа видно, что
/г = /(1 — cosa). (1)
150
Для нахождения а необходимо знать h. 'Но высота поднятия h есть результат того, что шарики имели в нижней точке скорость и. Так как из нижней точки движение происходило под действием переменных сил, то очевидно использование закона энергии в виде
(,я,+ ")“*= (та+ (2)
комбинируя (1) и (2), получим
— —cos о). (?)
А теперь необходимо знать и. Но и есть скорость тел после неупругого удара в нижней точке. Значит,
тМ m3v.2 — (т3 т3) и.
Считая направление вправо положительным, имеем
mi Hi — m~v, — {rn,i -j- m3) u. (4)
Исключая из (3) и (4) и, получим
^^^g = Z(l-cosa). (5)
("'1 И т2>
Необходимые 14 и v3 находят из того, что при движении шариков к нижней точке энергии их не меняются,и значит
niigni = -^- и m3gh3 = —(6)
Тогда (5) будет иметь вид ... .
и так как ht = l(i—cosaj), h3 = l(\—cosa2), то
[/И, V‘2gl (1 — cosaj - ms/2gZ (1 — cos a»)]'3 _Z/1 _Л
+ C0Sa'-
По сокращении на 2gl получим
(/Я, У 1 — COS a( — m,Vl — COS as )3 .
——-------H—i—4=---------— = 1 — cos a. (7)
Учитывая, что 1—cosa; = 2sin2-g-, и извлекая корень квадратный из равенства (7), получим а, mt sin Д — т« sin 2 2 .а
--------i-------= SIH тг.
nit -f- та 2
151
Этот способ решения хорош тем, что каждое предыдущее действие со всей необходимостью указывает, что надо делать дальше.
Действительно, из равенства (1) вытекает необходимость нахождения h и I. Поскольку I брать неоткуда, оно до поры до времени будет переходить из предыдущих равенств в последующие и, может быть, так или иначе уйдет. Что касается /?, то оно находится из уравнения (2). Но из (2) вытекает необходимость определения и, что приводит к (4), а (4) к (6) и т. д.
Для развития навыков в решении задач необходимо комбинировать различные способы решения как в пределах одной задачи (пример I), так и при решении различных задач (примеры III и IV).
Полезно решить задачу каким-либо способом и хотя бы набросать ход решения другим способом.
Очень полезной является тренировка на составление уравнений, отображающих процессы, о которых говорится в данной задаче. Поскольку доведение до численного результата здесь необязательно, это значительно экономит время, а с другой стороны — приучает учащихся шире смотреть на происходящие явления, вырабатывает у них свободный, смелый подход к решению задач. При этом, если есть возможность решить задачу несколькими способами, следует выбрать наиболее рациональный и при этом, конечно, мотивировать свой выбор. (Правда, такую работу без учителя выполнять трудно, по отчего бы и не попробовать, особенно если занимается совместно группа учащихся.)
Поясним сказанное примерами.
Пример 5. Брусок соскальзывает с наклонной плоскости и у ее подножия неупруго соударяется с другим бруском. Описать происходящие процессы с точки зрения механики.
Разбор. Очевидно, что «напрашиваются» три этапа в данной задаче.
I. Движение бруска по плоскости. Оно описывается любым из уравнений:
F — тег,
F&t = mtv1 —
А Д- Лс0:1р = ДГ.
Какое из исходных равенств лучше, с помощью какого проще решается задача, здесь сказать нельзя, ибо задача сформулирована в очень общем виде.
2. Соударение. Очевидно, что единственным исходным равенством является уравнение
FM ----- (tnt Д- Ото) и — тщь
ибо при ударе действуют между телами переменные силы столь сложного характера, что воспользоваться вторым законом нет возможности. Так как удар происходит достаточно быстро, то вме
152
сто закона изменения импульса нужно воспользоваться законом его сохранения.
3 Совместное движение брусков описывается, как и иа первом этапе, любым из трех уравнений, но написанных уже для тела массой (т, -ф- ma).
Пример 6. Несколько связанных нитями брусков движутся под действием постоянных внешних сил по некоторой поверхности. Сколько тел необходимо рассматривать, сколько уравнений второго закона надо написать?
Разбор. Очевидно, что на вопрос так сформулированной задачи ответить нельзя: необходимо задачу конкретизировать.
1. Если натяжения нитей нас не интересуют, то можно (и разумно) рассматривать систему брусков как единое тело. При этом, если движение происходит не по одной прямой, а по нескольким (например, по двойной наклонной плоскости при наличии блока, через который перекинута нить), то достаточно написать второй закон для системы тел, но не в векторной форме (ускорения брусков неодинаковы!), а в проекциях на t- и «-направления.
2. Если натяжения нитей или силы, действующие на блоки, через которые нити перекинуты, нас интересуют, то надо считать систему, состоящей из (М-ф-1) тел, где N — число интересующих нас нитей или блоков, и писать соответственно второй закон для (N-ф- 1) тел порознь.
Естественно, можно писать и в любом случае столько уравнений второго закона, сколько брусков имеется в системе, но не всегда это целесообразно
Пример 7. Несколько брусков движутся один по отношению к другому с ускорениями.
Разбор. Очевидно, что при любой конкретизации этой задачи, надо писать столько уравнений второго закона, сколько движущихся тел упомянуто в задаче. При этом необходимы еще дополнительные уравнения, связывающие между собой ускорения тел.
Разумеется, что если в задаче упомянуты энергия или работа, то для решения задачи понадобится обязательно закон изменения энергии.
Пример 8. Брусок движется по кривой поверхности. Конкретизировать задачу настолько, чтобы был однозначно ясен выбор способа решения.
Разбор. Пусть нас интересует сила нормальной реакции поверхности Q (см. рис. 139). Естественно, необходимо будет воспользоваться вторым законом для г-направления, т. е.
Q — Р cos а_Vs
т ~ г ‘
Отсюда видно, что проще всего задать Р, a, v и г. Можно усложнить задачу, задав не v, а высоту /г0, с которой сколь
153
зило тело, скорость его в этом месте и работу силы трения. Тогда необходимое Q найдется из
„ mv3
Q — mg cosa = — и
Лтр = (mgh0 4- — [mgh 4- .
Конечно, все эти примеры достаточно расплывчаты. Но можно подобные тренировки в разборе задач проводить на любых задачах из любого задачника.
И наконец, очень полезным является составление задач учащимися с последующим, разумеется, решением этих задач самими же учащимися. Поскольку это является делом трудным с непривычки, то начинать разумно с вариаций уже сформулированных задач. Эти вариации могут заключаться как в усложнениях и упрощениях задачи, так и в замене одних данных другими.
ЧАСТЬ II
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
1. ОСНОВНЫЕ ПОНЯТИЯ
Если в процессе своего изменения некоторая величина при-
нимает повторяющиеся значения (через равные или неравные промежутки времени), то говорят, что она колеблется. Суще-
ствуют колебания более или менее сложные. На рис. 1 представлены графики различно колеблющейся величины 2 = 2(1).
Наиболее простым видом колебания является такое, при котором колеблющаяся величина изменяется по закону синуса или косинуса. Такое колебание называется гармоническим. Примером его может служить колебание проекции радиус-вектора, вращающегося с постоянной угловой скоростью ш (рис. 2):
х = R cos <? — R cos (ш/ -f- <р0) = X cos (mt -J- <p0),
y — R sin © = R sin (mt — Y sin ?0).
155
Величина /? = Л = У/ имеет смысл модуля наибольшей проекции радиус-вектора на какую-либо ось и называется амплитудой колебания данной проекции. Величина
2л
<р = wt -ф- <р0 = 2т.[( <ро = ~|_ То
(здесь f — частота, а Т — период вращения радиус-вектора R) называется фазой гармонического колебания. Смысл фазы в том, чю она указывает состояние колебательного процесса: зная фазу <р, мы можем узнать из уравнения z — Z sin <р относительное значение колеблющейся величины, а также характер ее изменения. Например, если фаза <р равна ~, то это означает, что 2
г = у и в данный момент времени г возрастает (это следует из того, что при ? = -g- функция sin® ведет себя именно так.^ Но знание значения колеблющейся величины и скорости ее изменения вполне определяют состояние колебания. Отсюда и важность понятия фазы колебания.
Чем дольше происходят колебания, тем больше фаза. При Z = 0 ® = и тогда, например, 2 = Zsin<p0> т. е. начальная фаза характеризует состояние, из которого величина г начала свои колебания Например, если фо = О, то колебания начались из состояния, когда значение колеблющейся величины было равно нулю; если р0 = ±-^-, то колебания начались из состояния, когда значение колеблющейся величины г было равно плюс или минус амплитуде; при ср0 = у—из состояния, при котором колеблющаяся величина имела исходное значение в половину амплитуды, и т. д.
Если ?о = О, то о = — 2r.ft = 2r.N, откуда N — ~ т. е. фаза деления на 2т. показывает число колебаний, сделанных за время t.
Из определения фазы следует, что с течением времени она растет п может стать сколь угодно большой.
То, что сказано про колебания проекций радиус-вектора R, в равной мере может быть отнесено к любым колеблющимся по закону синуса (или косинуса) величинам. При этом колебаться могут и скалярные и векторные величины. Если имеется в виду последнее, то надо заранее оговорить, какое направление взято за положительное.
Пусть, например, по окружности радиуса R движется материальная точка с постоянной по модулю скоростью. Очевидно, для случая, когда начало координат взято в центре окружности, имеем (рис. 2)
x — R cos <f> = X cos <р = X cos (wZ -|- tp0), y = R sin — Y sin p — X sin (<<>/ po).
156
Для проекций скорости имеем (рис. 3)
vx = — V sin ? = — V sin (и/ <р0).
vy = V cos ? — V cos (wt -|- <р0)
Для проекций радиального ускорения материальной точки получаем (рис. 4)
ах —— /5cos? =—A cos (со/ ?0), ау= — A sin ? = — A sin (w/ -j- ?0).
Поскольку две проекции вектора на оси координат в случае плоского движения вполне определяют вектор, то можно ска-
зать, что равномерное вращение радиус-вектора R эквивалентно двум гармоническим колебаниям его проекций на оси координат и наоборот. Это особенно отчетливо будет видно, если вектор R записать в виде суммы его составляющих на i и / направления (т. е. вдоль положительных направлений осей координат ох и оу):
R — xi-\- yj = X cos (u>t <p0) •»+ Y sin (utf ?0) • j-
Обозначая Xi = Rt и Yj= Rj, получим
Д = Ri COS (wt <P0) + Rj sin + To)-
Таким образом, равномерное вращение вектора R эквивалентно двум гармоническим колебаниям взаимно-перпендикуляр-иых, одинаковых по модулю векторов; при этом колебания этих векторов сдвинуты по фазе на у (именно так сдвинуты тригонометрические функции cos? и sin?).
157
Все сказанное относительно /? вполне относится и к скорости v и ускорению а материальной точки, движущейся по окружности с постоянной по величине скоростью.
Можно показать, что если материальная точка движется под действием силы, пропорциональной смещению и обратно ему направленной, т. е. под действием силы
/’ = — А: Дг,
то ее движение будет гармоническим. Это означает, что смещение Аг материальной точки, ее скорость и, ускорение а и сила F будут меняться в соответствии с уравнением
z = Z cos (w/ + 'fo) или z = Zsin(utf
где под z понимается какая-либо из перечисленных величин Дг, v, а или F. Примером такого движения может быть движение
Рис. 5.
гирьки на пружине (рис. 5) в отсутствие сил сопротивления при малых смещениях Дг (столь малых, чго даже величина максимального смещения Дг? много меньше длины пружины) и при условии невесомости пружины (т. е. масса пружины ничтожна по сравнению с массой гирьки). Такого типа колебания, происходящие под действием сил F==— йДг, называются малыми собственными колебаниями. Оказывается при этом, что Дг колеблется гармонично, т. е. Дг — Д/? cos (и/ -|- ?») или ^r~^Rsin\ X (“^ ~i~ ?#), а частота этих колебаний определяется формулой
j/" т илн более компактной <o=J/r~ , где« = 2к/—циклическая или круговая частота колебаний.
В формуле F = — kAr знак «минус» означает, что в любой момент времени смещение материальной точки Дг и действующая на нее сила F направлены навстречу друг другу.
Поскольку сила F всегда направлена к положению устойчивого равновесия, то ее называют возвращающей (в равновесие) силой.
158
Полезно отметить, что при указанных колебаниях материальной точки ее кинетическая энергия и потенциальная энергия деформированной пружины, равные соответственно
р ___mvs р __kx3
Д к — ~2 И п — "2“ *
тоже колеблются гармонично, но с удвоенной частотой. Действительно, если например v = V cos (otf-j- <р0), то
с mv3 mV3 2. , . \ tnV2 1-ф cos (2<о/-ф 2ср0)
А к — — = ~2~ cos + 'то) = ~2----------!----2--=
mV- . mV- /о v [ о \
= — Н—— cos (2w/-1-2<р0).
При этом колебания £к происходят около значения £ср = ^—. Аналогично обстоит дело и с потенциальной энергией Еп колеблющейся гармонично системы.
По гармоничному закону колеблются в электрической сети ток и напряжение. В простом колебательном контуре (состоящем из индуктивности L, емкости С и ничтожного сопротивления Д) по такому же закону колеблются ток, напряжение на конденсаторе, заряды на его обкладках, э. д. с. самоиндукции. В излучаемых таким контуром волнах по тому же закону колеблются напряженность электрического поля Е и индукция магнитного поля В.
Подавляющее число колебательных процессов в природе, конечно, происходит не по гармоническому закону, но можно показать (что делается в так называемом гармоническом анализе), что сколь угодно сложное колебание может быть представлено как какой-то набор простых (гармонических) колебаний разных частот (монохром). Отсюда ясно, что изучив простые (монохроматические) колебания, легко понять и сколь угодно сложные.
Поскольку колебательные процессы распространены в природе исключительно широко (если не подавляюще широко), то очевидна важность изучения этих процессов. Важно понимать, что независимо от их природы все простые колебания описываются одинаковыми уравнениями
z = Z cos (и/ <р0) = Z cos (2tc/Z 4- ?о),
где z мгновенное (в момент времени /) значение колеблющейся величины; Z — ее максимальное (амплитудное) значение.
В случае гармонических колебаний векторов
z = Z cos (ш/ -f- <р0) = Z cos (2л// 4- <р0),
где / — частота колебаний; ш — циклическая или круговая частота (это просто обычная частота f, умноженная на 2л).
159
Колебания могут распространяться в среде в виде возмущений, которые называются волнами. Простые колебания порождают простые волны, а сложные колебания — сложные волны.
Простейшая волна — это
плоская монохроматическая волна.
Плоская — значит ее фронт (т. е. та поверхность, до которой к данному моменту времени дошло возмущение) есть плоскость; монохроматическая — значит в породившем ее источнике происходят гармонические колебания.
Чем дальше от источ-
ника находится интересующая нас точка, тем меньшее время она колеблется, тем меньше ее фаза. Очевидно, что время колебания в этой точке t' — t—, где г — радиус-вектор, проведенный от источника до этой точки;
и — скорость распространения волн в среде; а — угол между г и и
(рис. 6). Но в таком случае для чин имеем при = О (^о = О формул)
г = Z cos и/' =
v , г COS а
= Z COS (ОЙ--------------
\ и
Это и есть уравнение монохроматической волны, в которой колебания происходят с круговой (циклической) частотой и.
Очевидно, уравнение волны показывает, как колеблется некоторая величина в точке, удаленной от источника на расстояние г. Для плоской волны Z —const, а для сферической Z — , где Zo — амплитуда
волны на расстоянии г0 от источника. Расстояние, которое проходит монохроматическая волна за период, называется длиной волны. Отсюда Х = «7 — 4 =Очевидно такие, что к — это кратчайшее расстояние между точками, колебания в которых
колеблющихся гармонично вели-положено для упрощения вида
Рис. 7.
160
происходят со сдвигом по фазе в 2к. С учетом этого имеем для уравнения монохроматической волны
•7 / t г cos а \ лу / г» г cos а \
Z = Z COS ш/ — 0)---- = Z cos mt — 2л —;—).
\ « / \ Л /
При этом для сферической волны а = 0 (рис. 7).
Нормаль к фронту волны называется лучом. Направление луча и скорости распространения фронта волны совпадают.
2. ЗАМЕЧАНИЯ К РЕШЕНИЮ ЗАДАЧ
Задачи на колебания, конечно, столь же разнообразны, как и задачи на другие разделы физики, но из тех задач, которые основываются па школьном материале, наиболее интересны задачи на определение периода гармонических колебаний.
Методика их решения весьма проста—для нахождения периода таких колебаний надо согласно формуле T = 2xj/ ™ найти коэффициент возвращающей силы /г. Это делается следующим образом: 1) способное колебаться оноэо положения устойчивого равновесия тело смещается на небольшое расстояние Дг из этого положе! ия; 2) рассматриваются действующие на это тело силы (в этом смещенном положении); 3) находится составляющая всех сил па направление к равновесию (т. е. на направление — Дг) — возвращающая сила F.
Полученное для возвращающей силы значение во всех рассматриваемых в этой книжке случаях окажется пропорциональным смещению — Дг. Стоящая перед — Дг величина и есть коэффициент возвращающей силы k. (В некоторых случаях положение равновесия «не бросается в глаза», его надо еще определить). В соответствии со вторым законом Ньютона условием равновесия является. равенство нулю суммы сил, действующих на тело. Из этого условия и определяется положение равновесия (см. задачу 4).
Если колеблющееся тело участвует вместе с подставкой, подвеской или иной опорой в ускоренном движении, то надо найти положение «равновесия», т. е. то положение, около которого будут происходить качания маятника по отношению к подставке. Опять же это «равновесное» положение находят из того, что покоящееся относительно подставки тело должно под действием сил, приложенных к нему, иметь то же ускорение, что и подставка (например, задача 7).
Из сказанного ясно (а решения последующих задач помогут это уяснить еще более), что в принципе задачи на нахождение периода колебаний тела суть задачи все на то же использование все тех же законов Ньютона (можно показать, что сама формула Т = 2л l/'-j есть результат применения законов Ньютона к спо-
6 В. К. Кобушкин
161
собному колебаться телу). Поэтому и подход к решению задач и само решение мало отличаются от тех, что рассматривались в разделе «Механика».
Существенно новым здесь является лишь указанный выше способ нахождения Fx, основанный на анализе сил, возникающих при малом смещении тела из равновесия.
Задачи на волны уже мало похожи на задачи о движении материальной точки. Оно и понятно — волна есть объект, существенно отличающийся от материальной точки — другие свойства, другие закономерности, другие уравнения. Но некоторые общие черты есть. Это, прежде всего, указанная схема проведения решения. Кроме того, волна — это распространение колебаний в среде, т. е. процесс передачи движения (импульса и энергии) от одних точек среды к другим. Таким образом, упругая волна в ряде случаев может рассматриваться как совокупность отдельных вибраторов (маятников), связанных друг с другом непрерывным взаимодействием. Таксе рассмотрение волны позволяет легко ввести понятие плотности энергии в волне, понятие вектора переноса энергии и т. д.
Все остальное о поведении волн — на примерах задач 18—25.
При решении задач желательно во всех случаях придерживаться какой-нибудь схемы, последовательности действий.
Мы будем придерживаться примерно такой схемы:
1. Усвоение условий задачи в общих чертах.
2. Построение чертежа, рисунка, схемы, поясняющих смысл задачи.
3. Написание уравнения или уравнений, отображающих процесс, на который делается упор в задаче.
4. С помощью чертежа и различных вспомогательных соотношений — сведение уравнения к виду, в котором фигурируют лишь упомянутые в задаче и табличные величины.
5. Исследование полученных выражений (в случае необходимости).
6. Если заданы числовые значения, производятся вычисления.
Сделаем еще одно существенное замечание: рассмотрев решение одной-двух задач, изложенное в книжке, необходимо попытаться решить следующую задачу собственными усилиями. Если это не получится — сделать попытку на последующей задаче и т. д. Но эти попытки необходимы.
Далее, рассматривая изложенное в книжке решение той или иной задачи, необходимо отдавать себе отчет, что именно делается и зачем. Пассивное восприятие решения не научает решать, а способствует развитию умственной лености, привычки к зазубриванию и т. д. Разобравшись в решении задачи, надо попробовать изложить его самому и желательно наиболее кратко. Если удастся, то найти самому более удобное решение. (Заметим для тех, кто знаком с принципом эквивалентности, что введение 162
в движущейся равноускоренно системе дополнительной «тяжести» — та значительно упрощает решение ряда задач.)
Закончив рассмотрение задач раздела, надо попытаться обнаружить нечто общее в способе решения этих задач. Если это удастся сделать, значит в общих чертах методика решения понятна.
3. СВОДКА ФОРМУЛ ДЛЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
1. Уравнение колебания
2 = Z cos (ut-j- ?о) или 2 = Z sin (w/?())•
2. Для собственных механических колебаний период колеба
ния Т = 2тс 1/ где т — масса материальной точки; k— коэф
фициент возвращающей силы, определяемой уравнением F.=— kbr. Если начало отсчета выбрано в положении равновесия, то Fx = —kr, где г — радиус-вектор колеблющейся точки.
3. Связь между характеристиками колебаний и волн
к = 1,7- = 1 = ^.
/ “
4. Уравнение монохроматической волны, распространяющейся со скоростью и, для случая <?0 —0:
2 = Z COS О) [t — —°s а-^ ИЛИ 2 — Z sin 0) U — —, \ и \ и г
где t — время колебаний в источнике; г — радиус-вектор интересующей нас точки, проведенный от месторасположения источника; ш — циклическая частота колебаний в источнике (значит, и в любом другом месте, куда пришли колебания от этого источника).
5. При отражении волны лучи упавший и отраженный составляют одинаковые углы с нормалью к границе раздела в точке падения, т. е. аотр = апад (рис. 8) и «отр = ипад.
6. При прохождении волны из одной среды в другую происходит изменение и величины и направления скорости распространения, при этом (рис. 8)
Sin аПад_^пад
Sin ®прел ^отр
Частота колебаний в волне при отражении и преломлении не меняется.
6*
Е63
4. ЗАДАЧИ К РАЗДЕЛУ «КОЛЕБАНИЯ И ВОЛНЫ»
Задача I
Показать, что свободные малые колебания нитяного маятника в отсутствие сопротивления будут гармоническими.
Решение
Как было сказано раньше, механические колебания гармоничны, если они происходят под действием силы, пропорциональной смещению и обратно ему направленной. Значит, если
мы покажем, что при малых смещениях возникающая сила подчиняется уравнению F =— k\r, то тем самым задача и будет решена.
На наш маятник (т. е. на материальную точку, подвешенную
на невесомой и нерастяжимой
нити) действуют сила тяжести mg и натяжение нити Q. Их результирующая Fpe3 изображена на рис. 9. Так как материальная точка движется по кривой, то Fpe3 направлена куда-то во внутрь кривой, как и изображено на рис. 9. Здесь же указано и смещение Дг. Видно, ЧТО Лрез и Дг, как будто бы почти антипараллельны... Но! Если смещение равно нулю, ?рез не равна нулю и направлена к центру дуги, по которой движется материальная точ
ка. При Дг^О Fpe3 практически перпендикулярна Дг и лишь в крайних точках Fpes и Дг практически противоположны по направлению. Итак, Fpe3 не удовлетворяет условию F = — /еАг. Поэтому нитяной маятник колеблется не гармонично! Тем не менее бытует утверждение как раз обратное. Как же их примирить? Довольно просто. Разложим Ррез на две составляющие: Ft — по нити и — по ка-
сательной к ней. Тогда, очевидно, имеем в проекциях на I и т
направления F; — Q — mg cos а, | Fx | — mg sin а. F; ответственна за сообщение радиального (центростремительного) ускорения, a Fx—
за касательное ускорение.
Поскольку при малых углах синус угла и сам угол в радианной мере равны друг другу, то при |Дг|<<Д (т. е. при малых
Д^ Д/" t I 1ft
колебаниях) sina^a = yA»y. Но тогда |/\ | = ing sin лаь
^mg~. С учетом же F, Дг получим FT = — Дг*
164
Итак, для касательной, составляющей вектора Fpe3 и смещения Аг имеет место равенство Лт — — k&r, что и является необходимым и достаточным условием того, чтобы Дг, v, и F, колебались гармонично с частотой
=1/^=1/-ft
f т f I • т V I
Обычно при колебаниях нитяного маятника интересуются именно колебаниями проекций векторов Дг, a, v и F на касательное направление к траектории, т. е. величинами Дг, и, а, и Fr.
Легко, однако, видеть, что величины ah Ек и Еп колеблются с частотой 2«>. Для этого надо учесть, что
и2 mv! г- k&r3
ai = j, FK = -^- и Еп = —
и воспользоваться сказанным в параграфе 1 относительно колебаний кинетической энергии гирьки.
Таким образом, колебания нитяного маятника характеризуются колебаниями с частотами со (для Дг, v, ат, Fx) и 2<о (для о,, Ек, £„), а такие колебания, строго говоря, не являются гармоническими. Для большей точности следует, говоря о колеба-
ниях в системе, указывать, какая из характеристик движения нас интересует.
Задача 2
Найти период малых колебаний величин смещения и скорости бруска, который может без трения скользить по внутренней части обруча радиуса R (рис. 10).
Решение
Очевидно, движение та-
кого бруска не отличается
в принципе от качаний нитяного маятника. Только роль связи (опоры) играет не пить, а обруч.
При малых колебаниях подобного рода Т = 2л НО о
предыдущей задаче показано, что гт =--f кг, т. е. роль коэф-
фициента k играет величина у? (или для обруча ^). В соответствии с этим
165
Задача 3
Найти период малых собственных колебаний Дг и v маленького заряженного шарика, колеблющегося в однородных полях
Рис. 11.
Очевидно, для численного массу шарика т, его заряд < ческого поля Е и длину нит1
g и Е, совпадающих по направлению (рис. 11).
Решение
Период таких колебаний будет найден, если определим коэффициент возвращающей силы. Из рис. 11 видно, что \FZ\ — (mg -f- qE) sin а или при малых углах отклонения |РТ | — 1 дг I, а с учетом
противоположности направлений Ft и Дг =
Отсюда k = и, значит,
ответа на вопрос задачи надо знать ; величину напряженности электри-[ I.
Задача 4
Определить частоту малых собственных колебаний касательных характеристик движения (Дг, v, а. и Ет) шарика колеблющегося па нити во взаимо-перпендикулярных полях g и Е (рис. 12).
Решение
Решение сводится к нахождению коэффициента возвращающей силы k. Здесь уместно еще раз отметить, что k= показывает, какая возвращающая сила возникает при единичном смещении тела из положения устойчивого равновесия. В предыдущих задачах положение равновесия определялось «само собой», а в этой задаче его еще надо определить.
.Из рис. 12 видно, что положение равновесия определится из условия mg -ф- qE -ф- <2о = 0.
В проекциях на т и I направления получим:
— mg sin а0 -ф- qE cos а0 = О,
— mg cos а0 — qE sin а0 -j- Q = 0.
166
Первое равенство дает tga0 = ^| (а из второго можно было бы определить натяжение Qo в равновесном положении).
На маятник в любом положении, кроме переменной силы Q, действует сила F — tng-\- qEy постоянная по величине и направ
ленная всегда под углом а0 к направлению g. Касательная составляющая этой силы,
Fx и обуславливает интересующие нас колебания. Если вывести маятник из равновесия на малый угол {3, то, как видно из рис. 13, возникает сила | Fx | — F sin [3 или | Л, | = -у | Дг где F = V(mgy-[-(qEy. Но тогда
f —11/ А =
' 2т: у т
__£ 1 Л/(Mg)a + (<?£)а
2~ У ml
Рис. 18.
Задача 5
Найти связь между баний математического
углом отклонения а и фазой малых коле-нитяного маятника (рис. 14).
167
Решение
Совершенно очевидно, что единственно, что можно по этому поводу написать, так это уравнение
|Дг| — |Д/?| sin (to/4- ?0),
где Д/? — амплитудное значение смещения.
В исходное равенство вошли Дг и Д/?, которые не фигури-
руют в условиях, а угол отклонения Но из рис. 14 видно, что для малых отклонений |Дг| I -а |Д/?[ • атах
(а берется в радианной мере). Подстановка этих значений |Дг| и |Д/?| в исходное равенство приводит после сокращения на I к искомой зависимости
Sin (<1>/4-ср0).
Видно, что угол отклонения от вертикали колеблется гармонически, как и смещение Дг.
не вошел в равенство.
Задача 6
В цилиндрическом ведре массой М, высотой Н и сечением S насыпан песок плотности р. Расстояние от точки подвеса до дна ведра I. Считая дно ведра невесомым, найти зависимость частоты малых собственных колебаний получившегося маятника от уровня песка в ведре (рис. 15).
Решение
Если бы вместо описанной системы качалась материальная точка, то решение было бы тривиальным. Но материальная точка в данном случае отличается от ведра с песком тем, что массы
168
ведра и песка ге сосредоточены в малом объеме, т. е. систему нельзя считать материальной точкой Но если бы наша система сжалась в точку, расположенную в центре масс системы, то период качаний никак те изменился бы (сопротивления нет, поэтому размеры системы роли не играют). Отсюда вывод — заменить имеющуюся у нас систему материальной точкой, расположенной в центре масс системы. Тогда f = , где Г—расстояние от
точки подвеса до центра масс системы (так называемая приведен' ная длина физического маятника, т. е. качающегося протяженного тела).
Но Г находим по формуле для центра масс системы, взяв за начало отсчета точку подвеса (с учетом того, что из-за симметрии системы относительно линии точка подвеса — ось ведра центр масс находится на этой линии):
_ Л1/в + Л1,,/п Л1 + Л'1п
где /в и /п— расстояния от точки подвеса до центра масс ведра и песка соответственно: /Ип — масса песка, равная p|Z = pS/i.
/V h
Так как 1а — 1—и 1а = 1 — — , то
I Н\ / (Г
MU- " +р«Л / - £ Z~——'^+75/
(*)
Подставляя (*) в формулу для частоты, получим ответ.
Очевидно, что при малых размерах ведра (т. е. при Н I) получим Г = 1, как и должно быть, ибо в этом случае ведро можно рассматривать как материальную точку.
Читатель, возможно, захочет исследовать результат для различных случаев, например, И — I, h = И, h = ^, h = 0, Л-1 )> pSh и т. д.
Видно, что в числитель (*) входит Л3, а в знаменатель h. Это означает, что при изменении h числитель и знаменатель меняются неодинаково. Поэтому если h меняется от Н до 0, то дробь сперва растет от и----до некоторой величины, а потом
начинает опять убывать до I/---? .
Физически это ясно: когда ведро полно песку (т. е. h = H\, центры масс ведра и песка совпадают и I =1—Когда песок высыпается, то его центр масс опускается и /' сперва растет. Но когда песок высыплется (т. е. Л —0), то качаться будет ., , н
лишь ведро и / — I—
Задача 7
По наклонной плоскости с углом наклона а идет с ускорением а тележка, на которой подвешен маятник длиной I (рис. 16,а). Найти положение равновесия маятника и период малых собственных колебаний.
б 3
Рис. 16.
Решение
Как уже говорилось, все задачи такого типа сводятся к нахождению коэффициента возвращающей силы k. Для нахождения его прежде всего определяют положение равновесия маятника, то т. е. то положение, около которого происходят качания. Поскольку наш маятник находится на ускоренно движущейся тележке, то «равновесным» положением будет такое, при котором маятник будет неподвижен относительно тележки, т. е. будет иметь относительно наклонной плоскости скорость и ускорение такие же, как у тележки.
Найдем это положение, определяемое, например, углом р0, который составляет нить с осью оу (очевидно, при этом нить составит с вертикалью угол а Д- р0).
170
Из mg -FQ9 = ma получим в проекциях на оси ох и оу mg sin a -f- Qo sin р0 = та, — mg cos а -j- Qo cos = 0.
(В искомом состоянии «равновесия» ax = a и ay = Q, ибо тележка, а значит, и маятник не имеют ускорения в направлении, перпендикулярном плоскости.)
Исключая отсюда Qo, получим
tg 80 = —-----tg а.
to ГУ geos а ь
Это равенство позволяет найти при желании угол р0.
Теперь надо вспомнить, что коэффициент k определяет возвращающую силу, возникающую при единичном смещении из положения равновесия. (В нашем случае это — «равновесие», ибо маятник вместе с тележкой движется ускоренно).
Натяжение нити Q не дает возвращающей силы, ибо при любых малых смещениях Q будет перпендикулярно им. Значит, надо найти прирост соответствующей составляющей силы trig.
При этом надо учесть, что mg одной из своих составляющих должна участвовать в создании постоянного ускорения а, а другой — создавать возвращающую силу.
Отсюда ясно, что mg надо раскладывать в «равновесии» по направлениям а и —Qo, как это показано на рис. 16, б (на F —— Qo и та). При этом составляющая F уравновесит силу Qo, а составляющая вдоль наклонной плоскости сообщит шарику постоянное ускорение а. В этом положении «равновесия» сила F играет ту же роль, что и сила mg в задаче 1.
Сила F при малом выводе маятника из «равновесия» будет своей составляющей, перпендикулярной к Q, давать возвращающую силу (подобно тому, как это происходило с mg в первой задаче или с силой (mg-FqF) в задачах 3 и 4.
Очевидно, что при выводе маятника из равновесия на малый угол Ду (через у обозначен для краткости угол а-(-₽о), возникнет |/\| = у|Дг| (рис. 16, в) и значит k = ~. Но, как видно из рис. 16, б,
F — Y(mg)2 (та)2 — 2mg та cos (90° — а) = — mYg2 а3 — 2ag sin а. .
Для периода колебаний будем иметь
Л Г Kg2 + о2 — 2ag sin а
171
Полезно исследовать результат при разных а и а.
Например, при а = 0 получим Т = 2к . При скольжении тележки по наклонной плоскости без трения (т. е. при a — g sin а) Т — 2 к |/ При а = ±у Т — 2к L а При свободном па/ евии тележки, т. е. при a = g (а, значит, a — g), формально Т = 2г 1/ —- * сю.
Г g-Д
Таким образом, в решении заключены ответы на определение Т маятника во всех тех случаях, когда он колеблется па подвеске, движущейся с произвольным постоянным ускорением.
Решим эту задачу, пользуясь принципом эквивалентности сил инерции и силы тяжести. Он означает в данном случае, что движение тележки и шарика с ускорением а эквивалентно тому, что па шарик, кроме сил mg и Q, действует еще сила инерции — та (с точки зрения наблюдателя, связанногос тележкой, т. е. с веинерциальной системой отсчета). Сила mg’ = mg— та эквивалентна новой тяжести. Но в таком случае наша задача сводится к задаче 1, только роль mg играет в этой задаче новая «тяжесть» mg’ —mg — та и. значит, Т— 2п |/"^. Но теперь задача сводится к нахождению g'. Из рис. 16, г видно, что
(mg')* — К(mgY' -j- (та)* — 2mgrna cos (90° — a),
откуда g' = У g1 -j- as — 2ag cos (90° — a) , а потому
T = 2^i/ - l-—=.
У У g2 + a2 — 2ag sin a
Результат решения, естественно, тот же, но получен он несравненно более простым способом.
Читатель может попробовать усложнить задачу, введя в условия заряд шарика q и электрическое поле Е, составляющее с g некоторый угол р. Из полученного при этом решения можно будет получить решения всех предыдущих задач как частные случаи.
Задача 8
Цилиндрический брусок (рис. 17) находится в вертикальном положении на границе раздела двух жидкостей и делится этой границей на две равные части. Найги период малых вертикальных колебаний бруска в пренебрежении силами трения.
172
Решение
Решение задачи сводится к нахождению коэффициента возвращающей силы k. Если из равновесного положения сместить брусок на Дг, например вниз, то возникнет возвращающая сила, направленная вверх и обусловленная изменением выталкивающей силы.
Действительно,
?= (7^+mg) —
(FВЫТ “Ф ^g) BUT*
Но Д/фЬ1Т складывается из Д/д и Д7.2, так как брусок плавает в двух жидкостях. При этом Д7\ — это прибыль архимедовой силы со стороны пижвей жидкости и направлена вверх (навстречу Дг), а Д7.2 — убыль архимедовой силы со стороны верхней жидкости и направлена в сторону Дг (см. рис. 17). Поэтому
F = А^выт = — И?5Дг-’-^ -ф дг = — gS (pi — р4) Дг,
откуда k = gS (pi — р.2).
Для периода качаний имеем 7 = 2*1/"' = 2* 1/\--т-----; .
Т k у gSfp, —р2)
Массу бруска определим из условия равновесии бруска
т8 + Л + = 0.
или в проекции на направление тяжесш с учетом Vt = V,2—
И V „ mg — Pig у — P-ig = °,
откуда (pi-ф р2) у или /п = (pi-ф рй) у.
Подставляя это значение т в формулу для Т, получим
7 = 2*
1Л1 (pi + рд
Г 2g(₽1 - ₽8) •
При pi = р2 7 ->со, что означает отсутствие колебании.
Ясно, что для численного ответа на вопрос задачи необходимо задание входящих в решение величин.
173
Задача 9
Сформулировать зависимость полной энергии математического маятника от амплитуды малых собственных колебаний и частоты. Связать частоту колебаний с максимальной скоростью маятника.
Решение
Поскольку колебания малы, то, как показано в задаче 1, Дт =— k^r. Но это означает, что потенциальная энергия выра-жается формулой ьп = —^~,
В крайней точке | Дг | — и, значит, в этой точке Еп = = —2~. Поскольку в крайней точке скорость маятника, а значит, и его кинетическая энергия равны нулю, то полная механическая энергия равна потенциальной:
р —р р —р —kM?
^мех —“ J~,n — 2 * *
Поскольку при гармонических колебаниях смещения Дг ш =
-я Г k , » гл с k\R2 m<A2\R3
= 1/ то й = тг. Но тогда Еяех=-^~ = —2—•
В положении равновесия Еп = 0 и Ewex = EK. Поскольку энергия маятника не меняется (сопротивления нет и колебания собственные), то из того, что потенциальная энергия в крайней точке равна кинетической в равновесном (наинизшем) положении, следует—— =—2—> 0ТКУда утах = юД/? или V — <йДК, где V — cmas — амплитуда колебания скорости.
Задача 10
Найти время, необходимое математическому маятнику для прохождения расстояния от Д^ до Дл2,
Решение
Время движения маятника и смещение Дг входят лишь в уравнение Дг = Д/? sin (со/-|-ср0), откуда через смещение Дг время А/-
движения выражается формулой art 4-<р0 — arcsin или t = . Дг Л
arcsin — <Ро
Для нашего случая искомое Д/ = /2 —где f2 и — время движения маятника от начального положения до положений Дг2 и Дп соответственно. Но тогда
. Дга . ДГ[
arcsin -г-Д — arcsin -г-Д
Д/ = t2 - 4=-----------.
* * г.\ "
174
Задача 11
Какова начальная фаза гармонических колебаний скорости маятника, если v = va при t = 0, а максимальная скорость равна V? Выразить результат через амплитуду смещения А/? и частоту колебаний ш. Каков ответ для случая нитяного маятника, колеблющегося под действием тяжести?
Решение
Для гармонических колебаний величины скорости имеем у — = V sin (со^ —?«)• Для момента / = 0 имеем y0=l/sin©0, поэтому ®о — arcsinp. Поскольку, как показано в задаче 10, амплитудное (или максимальное) значение скорости связано с амплитудой колебания смещения и частотой по формуле = то ?0== = arcsin^.
Для указанного в условии задачи маятника ш=='|/'у, а потому
«о ®o = arcsin —~.
Задача 12
Нитяной маятник колеблется гармонично под действием тяжести, Как изменится амплитуда колебаний, если нить укоротить от /1 до 1г, не меняя при этом энергии маятника?
Решение
Так как энергия маятника Ь =—2-------> то 113 E1 = Ei (по
условию задачи энергия не изменилась) следует —i =
/Т gARi bR'i
и так как ш = I/ ~ , тсг^-— = или = откуда
1 /~1г видно, что = У .
Задача 13
Если в Земле прорыть тоннель (рис. 18), то в таком тоннеле при отсутствии трения тело могло бы совершать гармонические колебания. Убедиться в этом расчетом и найти период таких колебаний в зависимости от длины тоннеля. Считать известным, что внутри однородного сплошного шара напряженность поля
175
тяготения пропорциональна расстоянию до центра шара и напран-лена в центр, т. е. g ——сг, где с — некоторая константа. Вращение Земли не учитывать.
Решение
Из соображен i”i симметрии следует сразу, что положение равновесия будет в точке А. Если сместить тело на расстояние Дг от равновесия, то возникает возвращающая сила | I = tng sina
(сила Q не внесет вклада в Fx, поскольку она всегда нормальна к скорости тела).
Поскольку нас интересует зависимость Fx от смещения Дг, то,
выражая г через Дг, получим г — (рис. 18). Но тогда
IF,I = mg sin a = mg---=mc I Дг I или = — tricar, что и является
J T I О О I i I '
условием гармоничности колебаний тела; при этом поскольку тс есть некоторая константа, то Т = 2гс j/~'^ тоже вели-
чина, не зависящая от местоположения и длины тоннеля.
Это и естественно, ибо при гармонических колебаниях период колебания пе зависит от амплитуды.
Задача 14
Математический маятник массой т и длиной / совершает малые собственные колебания без сопротивления. Какую работу совершит возвращающая сила за время t, считая от момента выхода из равновесия? Амплитуда колебаний равна Д/?.
Решение
Поскольку возвращающая сила пропорциональна смещению, то ее работа, как уже показывалось, определяется по формуле
, . r. fk^r'i k^rl\ . пл
А = — Д£п = —----------Tl’ а ПРИ А =-----2^-
176
Поскольку фо = О, а для математического маятника, колеблю-, те / е .
щегося под действием тяжести, к — и со = I/ “ , то А —
]/~f t.
Если записать выражение для А через период колебаний Т, то А — — ^yA/?2sin2^. Отсюда видно, что работа, произведен-
, пТ
пая за время, например, i = где п — целое, равна нулю. Почему так? Потому что при движении маятника от положения равновесия сила 7\ совершает отрицательную работу (ибо р), а при движении тела к положению равновесия — положительную (ибо F\ р). Эти работы численно равны и противоположны по знаку, а в сумме за ^=|- или = работа возвращающей силы и будет равна нулю.
Задача 15
Лифт движется по вертикали сперва с ускорением at, а потом с «замедлением» в течение времени h и Ц соответственно. В лифте находится маятник длиной I. Сколько колебаний он сделает за время движения?
Решение
Очевидно, число колебаний за время / = будет равно N ----- Ni -р А^. Но как показано в задаче 7, в таком лифте 7\ — = 2я ]/ и Т, = У , поэтому N = + N, = £ +
. С I7 £ + «1 + / Я — а8
О 2 л |//
Задача 16
Найти отношение потенциальной энергии к кинетической при гармоническом колебании материальной точки как функцию времени.
Решение
Искомое отношение имеет вид
£п __feAr2 __MR3 sin2 (at + <f0)
EK mv3 Г.к mV3 sin2 (at -|- <p') 1
где <pi — начальная фаза колебаний скорости; <f>0 — начальная фаза колебаний смещения.
177
Но как показано во вводной части этого раздела, если смещение колеблется по закону синуса, то скорость изменяется по закону косинуса или что все равно и отличаются на у (когда смещение равно нулю, скорость максимальна и наоборот).
Е„ k&R* sin2 (ы/ 4- ю0) kARs , „о , , , .
Поэтому 777 2 , , 7 Щ — —ттт tg- (ш/ 4- <₽о) и поскольку
} Ек mVs cos2 (о4 -j- ср0) mV- ° ' 1 т' J
k — ты- и У = то
t=
Если тело вышло в момент tu — 0 из равновесия, то ср0 = 0 и
—tg2w/. Если же оно вышло из крайней точки, то =
— ±ту и, значит, 7# — tg21 ± тг — ctg'W и т. д.
Задача 17
Точечный вибратор, колеблющийся с частотой ш, создает на поверхности жидкости круговые волны, распространяющиеся со скоростью и. Найти: а) сдвиг по фазе колебаний точек, определяемых радиус-векторами ri и п, проведенными от источника S; б) относительное смещение поплавков, находящихся в этих точках; в) относительную скорость этих поплавков.
Решение
Если начало отсчета помещено в источник, то фаза сферической волны ср = сро — Но тогда а) ср3 — = (rs — п)
(не путать п — ri — | г-> | — | п | с | — н |, ибо разность модулей и модуль разности — разные понятия!);
б) поплавки, как и частицы жидкости, колеблются в данном случае по вертикали. Обозначая смещение поплавка через h и считая, что волна от источника идет «горбом» (т. е. <ро = О), получим
М> = Sinш [t - _ "еsin с» It - ;
" г2 \ и] rt \ и) ’
в) как уже указывалось, скорость частицы колеблется, опережая смещение на у, поэтому для скоростей поплавков имеем
Д о-2,1 — Vi — Vi = V ого
COS ш
га
COS a It — ~ \ и
Г1
178
В б) и в) Н и V — амплитудные значения колеблющихся величин приняты направленными вверх (волна идет «горбом» вперед).
Очевидно, без задания Но, V» и г0 численные значения интересующих нас величин получить нельзя.
Задача 18
Написать явное выражение вектора Умова — Пойнтинга через амплитуду колебаний волны, частоту колебаний и плотность среды (см. рис. 19).
Вектором Умова—Пойнтинга называется величина, показывающая, какое количество энергии переносит волна за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Решени е
Если за время М через площадку Д5И, поперечную волне, будет перенесено энергии ДЕ, то из определения вектора Умова
ДЕ
имеем, что его величина определится отношением , а так как вектор этот направлен в сторону переноса энергии (по скорости волны), то, обозначая этот вектор буквой Р, получим
Т,__ ДЕ и
М Д8Я и '
— \Е —
Поскольку «Д^ = Дг, то Р = ; ~ и, а так как Д5иДг=ДЕ—
Д р
объем, который заполняется волнами за время Д/, то Р = ~и.
Если ДЕ трактовать как количество энергии колебаний, запол-др
няющих объем ДЕ, то -^=w — есть объемная плотность энергии. Поэтому P=wu. Под w можно понимать энергию всех осцилляторов (т. е. вибраторов или колеблющихся частичек), находящихся в единице объема, т. е. щ = еп, где е — энергия одного осциллятора, ап — число осцилляторов в единице объема. Поскольку, как показано в задаче 9, s = fflc0^ , то Р =
ягш2ДЕ2 - —
— —2—и поскольку пгп есть плотность среды р, то окончательно
P = ^-l.
179
Задача 19
Исходя из решения предыдущей задачи, показать, что в однородной изотропной непоглощающей среде для сферической волны амплитуда колебаний обратно пропорциональна расстоянию до источника.
Решение
Окружим источник двумя концентричными сферами радиусов Го и г (рис. 20).
Поскольку среда однородна и изотропна, то волны будут сферическими, а так как среда не поглощает, то Л£0 = Д£, т. е. сколько энергии пройдет через поверхность сферы So, столько
пройдет и через поверхность S. Поскольку поток энергии Д£ через поверхность равен P&SU, то из Д£0 = Д£ или из
Р.ДЗ^РДЗ (*) получим —a>-^"«4ivro= р- и4т.г, откуда Д£ =—а тогда, как и указано в водной части к этому разделу, уравнение сферической волны будет иметь следующий вид для случая колебания смещения частиц:
. Д/?„г0 „ ! , . <ог\
ДГсиегц = COS ~ J •
Заметим, что из («) вытекает для случая сферических воли Р04тсг(® — Р4пг и, значит, Р =
Повторяя рассуждения для случая плоской волны, читатель может убедиться в том, что в плоской волне Д/^ = и Р — Ри.
Задача 20
Интерференцией волн называется явление наложения волн друг на друга, приводящее к тому, что амплитуда результирующей волны может быть той или иной в зависимости от того, каков сдвиг по фазе между колебаниями в волнах.
Принимая, что амплитуда результирующего колебания максимальна, если сдвиг по фазе у соответствующих колебаний равен 2/гтс, и минимальна при Дер = (2k -j- 1)«, найти геометрические места точек, в которых амплитуда колебаний от двух точечных источников максимальна и минимальна (рис. 21).
180
Решение
Поскольку Дер = —'рь где ?2 и — фазы встречающихся волн, тс
Дса = [шЛ 4- сроз — 2 л— (<’Х ?ot — 2ffi -у-j =
= — wi) t Дсро — 2« — -Ji-).
Видно, что Дэ оказался зависящим от времени, а это означает, что положение интересующих нас максимумов и минимумов колебаний будет меняться со временем. Такое непостоянное во времени распределение амплитуд результирующих колебаний
Рис. 21.
называется неустойчивой интерференционной картиной, а сами источники и волны — иекогерентными (несогласованными).
Но если <o.2 = a)1 = u), то (с учетом того, что при этом и Ла =
Дер— Л То —2л-у—.
Поскольку условием максимума колебаний является Д<р = 26л, Дг
то 2/г- = Аро — 2л -у-, откуда соответствующая разность хода
Дг == k\
1
В том частном случае, когда в источниках колебания происходят со сдвигом фаз A<p0 = 2ivn, получим hr — (k — п)\ = тХ = ~ (целое число) При зафиксированном (k— п) имеем, что Дг = const, т. е. разность расстояний от точек местоположения максимумов до источников есть величина постоянная и, значит, они лежат на гиперболах, фокусы которых находятся в источниках.
Итак, все максимумы находятся на семействе гипербол Дг — — где т — целое число.
181
Очевидно, все минимумы лежат на семействе гипербол Дг = = (2m-J-1)-^-. Ясно, что в случае когерентных источников (т. е. таких, у которых Дер Дер (/)) положения максимумов и минимумов со временем не меняются. Такая интерференционная картина называется устойчивой.
Задача 21
Какое количество энергии волн «падает» за единицу времени на единичную площадку от точечного источника волн мощностью Л\ находящегося в однородной, изотропной и непоглощающей среде на расстоянии г от площадки; нормаль площадки составляет угол а с вектором Умова.
Решение
ДР
По смыслу вопроса нас интересует величина Р' = ,
отличающаяся от величины вектора Умова лишь тем, что в знаменателе стоит вместо нормальной к вектору Р площадки AS;i площадка AS, расположенная под каким-то углом а к Р.
Для достаточно удаленного источника (когда линейные размеры «освещаемой» области малы по сравнению с г) и и г.3 мало отличаются друг от друга (рис. 22). Делая циркулем засечку радиусом г из местоположения источника, получим равнобедренный треугольник со сторонами ri, п и а. Равные углы при этом будут мало отличаться от прямых (ибо из-за г^а угол ₽«=«0). Но тогда угол у₽«90° и, значит, AS„ = AScosa.
Из определения вектора Умова следует, что его величина
р__
SSa •
Интересующая же нас величина Р' выразится как
ДЕ ДЕ г> , ,
Р= -ДГД5 = AFAS7C0Sa = Pc0Sa- «
Зависимость Р'=Р'(а) вскрыта. Теперь надо связать Р' с N и г. Из определения Р= . Лс следует, что в однородной, изотроп
182
ной и непоглощающей среде для сферической волны в силу перпендикулярности поверхности сферы лучу
р____ &Е____Ag ______ N
AS,t At 4тсг4 4-rJ ’
где Д£— энергия, прошедшая за время Д/ через сферу радиуса г.
С учетом этого и (*) P^-^j-cosa.
Заметим, что величину 7 = -^-, показывающую, какая мощность излучается в единицу телесного угла, называют иногда силой излучения источника (в данном случае изотропного).
Для случая световых волн величину N называют световым потоком от источника, J — средней силой света, величину Р' — освещенностью площадки, а соотношение Р — —rcosa = 4кГ
J
— — cos а — законом освещенности, создаваемой точечным источником в однородной, изотропной и непоглощающей среде.
Если источник неизотропный, т. е. излучает различно в разных направлениях, то вводят понятие силы излучения в данном направлении J — где ДД— мощность, посылаемая источником в телесный угол Д2.
Задача 22
На расстоянии h от точечного источника мощностью N, находящегося в однородной, изотропной и непоглощающей среде, находится идеально отражающая волны плоскость. Найти Р = ~Р (г), где г — расстояние от источника до интересующей нас точки.
Решение
В интересующую нас точку энергия будет попадать как непосредственно от источника, так и после отражения от плоскости. Из рис. 23 (построенного с учетом того, что угол отражения луча
183
равен углу его падения) видно, что геометрически отражение волны от плоскости эквивалентно ее распространению от точки S'— мнимого изображения источника S. Поскольку по условию плоскость отражает волны без поглощения их энергии, то это эквивалентно тому, что в точку А энергия приносится от источников S и S' одинаковой мощности. При этом, как видно из рисунка, h’ = h.
в
^-стрела дуги, радиуса- н (зеркала) осг-стрела дуги, радиуса d, /тронта, упавшей на зеркало болны )
Хц-стрели дуги радиуса f (фронта, отраженной волны)
Проводя плоскость через прямую h’h и точку А и располагая данный лист в этой плоскости, получим картину, изображенную
... _ _ _ N и
на рис. 23. Так как Pve3 = P —Р', или /?рез= • ~и Н-
I то с учетом одинаковой направленности г с и и г'
' 4лг' 11
с и’ получим
р __л L 'рез 4,, I Г*
где г и г’ — расстояния от источника S и его «изображения» S' до точки А.
184
Пусть начало отсчета находится в точке S и пусть, например, положение точки А задано координатами х и у. Тогда задача сводится к нахождению г' или, что все равно, его проекций гх н г,,. Но из рис. 23 видно, что г^ = гЛ = х, a ry = h-ф-h' — = г/-]-2й.
При этом г'3 — (Гд-2 -1- ГуУ1* — [х2 4- (У + 2/г)2]3/2.
Расписывая равенство (*) в проекциях, получим
Р — N I х , ___________________х )
Грезл — + + [Х8 + (3, + 2Л)Т''2/’
Р — N / У , УА-М \
Г^У— 47\(х24-Л-а)’/2 । [х* + (.у + 2Лр]^ •
Задача 23
На вогнутую сферическую поверхность радиуса /? падает волна от точечного источника J, находящегося на расстоянии d от поверхности (рис. 24). Найти положение изображения источника, т. е. точку, в которую «сойдется» волна после отражения от поверхности. Среда однородна и изотропна.
Решение
Поскольку среда, в которой распространяется волна, однородна и изотропна, то волна, идущая от источника J, будет сферической. Пусть для определенности d^>R. В некоторый момент времени фронт упавшей волны имеет около отражающей поверхности вид. указанный пунктиром на рис. 24, а. В то время как точки А и В фронта уже коснулись поверхности, точка С еще до нее не дошла, и к тому моменту, когда точка С дойдет до зеркала, точки фронта А и В переместятся после отражения в положения А' и В'.
По определению фронта волны времена прохождения волной расстояний Л/4', ВВ' и СС одинаковы и сами эти расстояния одинаковы (какое расстояние Xi пройдет падающая волна от С до С, такое же расстояние Xi = AA’ за это врямя пройдет отразившаяся часть фронта волны). Из рисунка видно, что |х4| — — | X] | -ф-1 х21-4-1 х31. Но так как | х31 = A A’ cos р — | Xi | cos р, то | Х4 | = | Xi | (1 4- cos р) 4-1 х21.
Если пучок волн, падающий иа поверхность, узкий (т. е. а->0), то р->0 и
I xi I — 2 | Xi | 4~ I х21.
Поскольку х2 соответствует падающей волне, а х4 и 2xi — отраженной, то они должны быть противоположных знаков, а потому —Xt= —2х1~4х2, или
2xi = Xi -j- х*.
185
Известно, что при малых высотах сегмента имеет место связь (рис. 24, б). Поэтому равенство (*) (с учетом того, что при а->0 имеет место hi^hs^h3 = h) примет вид
2 1 I 1 I X
Это соотношение называется формулой для сферического зеркала. Она пригодна и для вогнутого и для выпуклого зеркала, но при пользовании ею (существенно псмнить правило знаков:
Расстояния d и f измеряют в последовательности источник — зеркало — изображение. При этом расстояния, отсчитанные по ходу волны, положительны, а против хода — отрицательны. R положительно для вогнутого зеркала и отрицательно для выпуклого.
В нашем случае все расстояния положительны.
р
Полагая в (**) d->oo, получим f = -^-. Эту величину обозначают буквой F, а тогда (**) примет вид
F f'd'
Очевидно, F равно расстоянию от зеркала до той точки, где собираются лучи от бесконечно удаленного источника.
Формула зеркала, как видно из вывода, является приближенной, но тем более точной, чем меньше угол а.
Задача 24
Силой излучения источника волн в данном направлении назы-, XN ХЕ
вается величина j =-Г7г==т7-г?;, показывающая, какая энергия волн пронизывает за единицу времени в единичном телесном угле любое его сечение. Если источник и среда изотропны, то сила
т N
излучения одинакова по всем направлениям и J = == ,
как и указывалось в задаче 21.
Найти силу излучения изображения источника, даваемого сферической вогнутой поверхностью, поглощающей п-ю часть упавшей на нее энергии от источника силой J, находящегося на расстоянии а от полюса сферической поверхности радиуса R (рис. 25).
Р ешение
Напомним, прежде всего, что телесный угол Д2 определяется отношением части сферической поверхности, на которую он опи-
ДЗп /
рается, к квадрату радиуса этой сферы, т. е. Д2 = —(подобно
186
тому как центральный линейный угол измеряется отношением дуги, на которую он опирается, к радиусу дуги, т. е. Да = -^2^.
Проведя от источника J узкий конус с углом Д2 к отражающей поверхности и произведя построение отраженных крайних лучей конуса в соответствии с законом отражения лучей, получим изображение источника J'. Из рис. 25 видно, что волны, шедшие от J в телесном угле Д2, после отражения сходятся к J', а потом расходятся от него в конусе с углом Д2'.
Рис. 25.
По условию задачи n-я часть энергии при отражении теряется. Это значит, что Д£' - ДЕ (1 — п) или &N’ = ДУ (1 — п), где — мощность падающих волн, а ДУ' — отраженных. Но ДА' — J&Q иДУ' = /'Д2', поэтому <7'Д2'=/Д2 (1—п). Поскольку Д2=-^|^
и Д2 =—~-,to J (1 — «), откуда J' = J±—dJJ .
Rd
Так как f = -^s—5- (см. задачу 24), то окончательно J’= — /у
J (2d — •
Полученный результат справедлив лишь для узких пучков, лежащих вблизи оси симметрии картины. Вообще говоря, изображение J' не является изотропным «источником». У него наибольшая сила излучения вдоль оси симметрии. Именно для этой силы излучения и справедлив полученный результат.
ЧАСТЬ III
ТЕРМОДИНАМИКА
Процессы, рассматриваемые в этом разделе физики, существенно отличаются от тех, которые рассматриваются в механике. Они гораздо более сложны и многообразны. Описываются они, естественно, другими уравнениями; важнейшими характеристиками движения здесь уже являются не перемещения, скорость и сила, а другие (какие именно, будет видно в дальнейшем). Есть и общие для всех видов движения характеристики, такие, как энергия, понятие о которой необходимо, однако, обобщить и на немеханические виды движения.
Несмотря, однако, на существенное различие механического и немеханического движений, метод его исследования, а значит, и метод решения тех или иных задач в главных своих чертах остается прежним, хотя, конечно, проявляются и особенности, обусловленные спецификой данного вида движения.
Поэтому мы и в дальнейшем будем придерживаться в общих чертах той схемы, которая изложена во введении к разделу «Колебания и волны».
1. ИДЕАЛЬНЫЙ ГАЗ (основные понятия)
Идеальный газ — это простейшая система, рассматриваемая в термодинамике и молекулярной физике. В этот термин вкладывается следующее содержание. Известно, что между молекулами вещества, находящегося в любом агрегатном состоянии (твердом, жидком, газообразном), существуют как силы притяжения, так и силы отталкивания, которые весьма быстро убывают с увеличением расстояния между молекулами. При достаточно больших расстояниях между молекулами эти силы ничтожно малы и молекулы большую часть времени при своем движении практически не взаимодействуют, и их движение можно рассматривать как
188
свободное от одного удара о стенку сосуда (если глаз заключен в сосуд) до другого Такой газ мы и называем идеальным. Очевидно, что необходимым условием применимости такого рассмотрения для реального газа является его разряженность. Такой газ можно рассматривать как множество материальных точек, подавляющую часть времени движения не взаимодействующих между собой. Естественно, такое рассмотрение не является правомерным при уплотненных состояниях газа.
В случае идеального газа (т. е. достаточно разреженного реального газа) его состояние определяется заданием четырех из следующих пяти величин: М — масса газа, р — молекулярный вес, р — давление газа на стенки сосуда, IZ — объем, занимаемый газом, Т — абсолютная температура газа.
Между этими величинами существует связь, устанавливаемая уравнением состояния идеального газа
pV = ^RT или pV = ZRT (1)
(уравнение Клапейрона — Менделеева), которая позволяет по четырем величинам найти пятую. Здесь R — универсальная газовая постоянная, численное значение которой определяется выбором „ М
системы единиц, Z = — — число молей газа в сосуде.
Если в сосуде имеется смесь газов, то по закону Дальтона
Р — Pl + Pi + • • + Pi + • • • + Piv (2)
где pi — вклад в общее давление, вносимый г-м газом (парциальное давление); р — суммарное давление газа на стенки сосуда. Поскольку
PiV = ^RTh (3)
Г/
то уравнение Клапейрона — Менделеева в случае смеси газов можно записать в отличном от (1) виде. Именно, домножая (2) на объем сосуда V, получим pV — (piV-|-...-f-piV), или с учетом (3) PV — ~RT-]-~^RT. Вынося RT за скобку, получаем
/^=(г+---+?0/?Л \ Hi гп /
Обычно в задачах фигурируют данные о двух состояниях газа — первоначальном и конечном. Тогда при решении задачи надо соответственно написать уравнение (1) или (в случае смеси газов (4)) дважды: для начального и конечного состояний.
В тех случаях, когда объем газа может меняться за счет подвижности пробки, клапана или поршня, давление газа определяют из условия движения этих подвижных «закрывашек». В слу
189
чае их покоя это условие означает равенство нулю геометрической суммы сил, действующих на «закрывашку».
Поскольку в уравнении (1) содержатся все частные газовые законы (Бойля-Мариотта, Гей-Люссака и Шарля), то отдельно их рассматривать мы не будем и всегда будем пользоваться (1), хотя во многих случаях для упрощения записи можно было бы воспользоваться частными законами.
В уравнение (1) входят пять переменных величин: р, V, М, у и Т (у может меняться, если в газе протекают реакции). На плоском же графике можно изобразить только зависимость между двумя переменными. При этом надо оговаривать, как себя ведут остальные переменные. Например в случае, когда
М, у и Т меняются, но так, что при этом --T = const, необхо-р*
димо сделать на графике оговорку, что —Т — const (рис. 1). р
Возможны, естественно, такие процессы, когда — Т Ф const, р.
Тогда надо, повторяем, указать, как ведут себя М, у и Т. Это не сделано на рис. 2, на котором следовало бы указать, что на участках 0—1 и 2 — 3 (сплошной график) const, у = const и Т — const, а на участке 1 — 2 М const из-за конденсации пара.
Уравнение (1) можно рассматривать как следствие основного уравнения кинетической теории идеального газа
р = nkT, (5)
где п — число молекул в единице объема; k — постоянная Больцмана. Но п = где — N— число молекул в сосуде. Если одна грамм-молекула газа содержит NA = 6,23 1023 молекул (число Авогадро), то Z грамм-молекул содержат N = NAZ молекул. Поскольку Z = то (5) примет вид Обозначая
NAk = R, получим pV = — RT.
р*
190
Если в сосуде смесь газов, то вместо (5) надо написать уравнение
р = Р14-..- + рл или p = kT (П14-... + ««)•
Повторяя рассуждения в отношении пг, придем к уравнению (4).
Пар и газ — это в принципе одинаковые состояния вещества, и различие между ними чисто условное. Именно, мы называем в быту паром газообразное состояние тех веществ, которые при обычных температурах мы видим и в жидком (или твердом) состоянии. Газом же называют пары тех веществ, которые в жидком или твердом состояниях находятся при очень низких температурах. Так, газ воды или ртути мы называем паром, а пар кислорода, азота и т. д. — газом.
Из сказанного вытекает, что пар должен подчиняться уравнению Клапейрона — Менделеева в той же мере, что и любой газ.
Следует, однако, сделать следующую оговорку: при достаточно низких температурах (ниже критической) пар может частично конденсироваться. Для каждого данного пара существует предельно возможное содержание его в данном объеме при данной температуре. Такой пар называется насыщающим, и его плотность определяется для данного пара только температурой. Существуют таблицы, где указаны эти зависимости.
Пар из ненасыщающего может быть превращен в насыщающий понижением температуры или уменьшением объема. Верно и обратное— увеличение температуры или объема, занимаемого паром, делает его ненасыщающим (если, однако, вся жидкость при этом будет исчерпана — испарится).
На рис. 2 приведены зависимости давления пара от объема при Т — const и р. = const. Видно, что в области V^>Vi имеет место р, в области имеет место рт^р(К), а
в области К24>^ сжимается жидкость. Для сравнения пунктиром изображен график p — p(V) при Т const и р. = const для некон-денсирующегося пара (идеальный газ).
При V^> Vi масса пара не меняется и пар подчиняется закону Бойля-Мариотта. При V2<C^<C^i пар конденсируется, и его масса убывает. Поэтому закону Бойля-Л^ариотта он не подчиняется. При V<^Vi практически весь пар сконденсировался в жидкость.
Очевидно, при увеличении объема в области Vi<^V <^Vi количество пара будет возрастать.
Можно ли пользоваться уравнением Клапейрона — Менделеева в области V2<^V <Vi? Можно, но надо знать М — массу пара, содержащегося в сосуде, что не всегда удается установить без соответствующих таблиц. Поэтому в области V2<^V в случае необходимости М надо найти с помощью этих таблиц. При
191
этом, естественно, Л4 = р„1/, где рн — плотность пара, насыщающего пространства при данной температуре (табличная величина); V — объем, занимаемый паром.
В случае водяного пара его плотность часто называют абсолютной влажностью, а отношение / — -— относительной влаж-Рн
костью. Здесь р — плотность пара, имеющегося в пространстве.
Из всего вышесказанного следует, что, решая задачу о паре, находящемся в состоянии, близком ' к состоянию насыщения, надо выяснить, является ли пар насыщающим или нет (а следовательно, постоянна его масса при изменении состояния или нет). Полезно знать, что под изогнутой поверхностью существует дав-2а лепие (Лапласово). В случае сферической поверхности рл = ,
<де а — коэффициент поверхностного натяжения (зависящий ог температуры); R— радиус кривизны сферы. Очевидно, тонкую пленку ограничивают две поверхности практически одинакового радиуса. Поэтому в случае, например, мыльного пузыря рл=^. При этом сила давления направлена во внутрь поверхности.
Т я жестью газа мы везде в задачах пренебрегаем.
2. ЗАДАЧИ К РАЗДЕЛУ «ИДЕАЛЬНЫЙ ГАЗ И ПАР»
Задача 1
В узкой, закрытой с одного конца трубке находится газ, запертый столбиком ртути длиною Н. Если трубку наклонить под углом а к вертикали, то длина столбика воздуха будет равна I. Каково внешнее давление, если при переворачивании трубки открытым концом вниз верхний кран столбика ртути переместился на А/ и при этом за счет выливания ртути столбик ртути укоротился на А/7? Считать, что температура газа во время переворачивания не изменилась, капиллярными явлениями и трением пренебречь (рис. 3).
Решение
Так как в задаче говорится о двух различных состояниях газа, то пишем уравнения Клапейрона — Менделеева для каждого из них
p.V^ZiRT., р*У9=г^Тг.
Поскольку Ti = 7\ (по условиям задачи) и Z| = Z3 (масса газа не изменилась), то получаем при делении исходных равенств pl(/1 = p9V'a (что можно было бы написать и сразу).
С учетом того, что = Sl^ и = имеем
Pili = рЛ- (1)
192
Давления pt и pt найдем из условия равновесия столбиков ртути. Именно, проектируя все силы на ось трубки, получим
Fai + mig COS а — Fl = 0, (2)
— F al ~T mlg "F Ft == 0,
где Fax и Fai — модули сил, действующих на столбики ртути со стороны внешней среды (атмосферы); Fx и F2 — модули сил давления газа на ртуть изнутри; rtii и т-2— массы столбиков ртути.
Поскольку Fai = Fai~paS, Fi — p{S, Fi = p.lS, mi = ?HiS и = то уравнения (2) примут вид (с учетом t~h — H и
Ра$ + P'SHg COS а — PiS = 0,
— Ра$ “И рЗ (Д — ДД) g -ф- P-2S — 0,
где р — плотность ртути.
Выражая из этих равенств давления р2 и р-2:
Pi=Pa-F 9gH COS а,
Рг^Ра — ?g(H — ЬН), и подставляя эти значения р2 и р2 в (1), получим (с учетом /1 = / И /2 = /Д-Д/)
(Pa + pgH C0S7.) / ==|ра — ?g (Н — -j-ДД
откуда легко находится внешнее давление ра:
Pa=fi [Hl cos а-}-(// — кН)(1 4- Д/)|.
При этом полагаем, что плотность ртути мало отличается от табличного значения, даваемого при
1 В. к. Коб>шкип
193
Задача 2
Бак в виде прямоугольного параллелепипеда движется в направлении, перпендикулярном одной из его стенок (рис. 4). Найти разность плотностей (р3 — р„) у его задней и передней стенок,
Рис. 4.
если бак находится достаточно долго в движении с ускорением а. Плотность покоящегося газа р0, его масса М, температура Т и длина бака I известны. Силой тяжести, действующей на газ, пренебречь.
Решение
Для нахождения р3 и р„ рассмотрим весьма тонкие около стенок, такие, чтобы в пределах этого слоя газа была практически постоянна. Тогда уравнения газа дадут
• _ДЛ4, RT
Рз~Ы3 [X ’
_ДЛ4П RT Рп~ДИп‘ р. ’
слои газа плотность состояния
(1)
(2)
где рп и р3 — давление газа у передней и задней стенок бака. Поскольку ^1 = Рз и ^р^ = рп, то, вычитая (2) из (1), получим
Рз Рп-----(рз Рп) >
откуда
Видно, что для ответа на вопрос задачи необходимо знать разность давлений газа у передней и задней стенок бака. Эта разность найдется, естественно, из уравнения движений газа как целого. Именно полагаем, что за длительное время движения колебания газа затухнут из-за внутреннего трения и все части газа будут иметь одинаковое ускорение а. Тогда по второму закону механики
Ма = Р3 + Л. (4)
где F3 и Р„ — силы, действующие на газ со стороны задней и передней стенок бака.
194
Проектируя (4) на направление движения, получим с учетом того, что F3 = p3S и Fn = pnS
Ma — (р3 — ра) S.
Так как М = р0/<$, то (4) примет вид
ро/а = (р3 —рп)- (5)
Исключая из (3) и (5) разность давлений (р3 — р„), получим
Задача 3
В цилиндре (рис. 5), закрытом поршнем весом Р, находится газ с молекулярным весом р. и массой М. К середине поршня приделан шток В, соединенный рычагом I с шарниром А. Газ
равномерно нагревают. Чтобы поршень при этом покоился, грузик т приходится передвигать влево. Найти положение грузика т как функцию времени. Высота поршня над дном сосуда равна Л, атмосферное давление и трение считать ничтожными.
Решение
Очевидно, что нагрев газа приводит к росту давления и увеличению силы, действующей со стороны газа на поршень. Если груз т не передвигать вле
во, то равновесие системы нарушится. Чтобы оно не нарушилось, необходимо равенство нулю суммы моментов, вращающих рычаг относительно, например, точки Д. Это приводит к равенству
Р1 — pSl -|- mgr = 0.
Входящее сюда давление газа на поршень определится из формулы
pV=MRT'
Подставляя выраженное отсюда давление р в исходное равенство, получим
MRTSI , п -----i-mgr =
7*
195
Учтя,
S 1 что приходим к уравнению
/Ш’Г \ рА
I mg ’
. По условиям задачи газ нагревают равномерно, т е. его температура Т растет со временем по линейному закону: Т = Тн„ч-\-const (/ — /вач). Подставляя это значение в предыдущее равенство, получаем решение задачи в виде:
г = (7 нам + const ДО — Р]^.
Задача 4.
По условиям предыдущей задачи найти скорость движения д/ грузика гп, если скорость нагрева известна.
Решение
п Дг
По определению величины скорости движения грузика v= где Да —(г— гиач) — перемещение грузика за время Д/.
п Д7
Но определению скорость нагрева есть величина , где Д7' = (7'— Твач) — изменение температурь) за время Д/.
Но по условиям предыдущей задачи Т = Ткач -ф- const Д/. Отсюда Т — Тцач — const Д/, а = const, т е. —const есть именно та константа, которая фигурирует в решении предыдущей задачи.
Поскольку из решения предыдущей же задачи
Г M1R У I , д .. Г Г RtR 'Г I
г — Гнач == U чач 4~ COIlSt Дг) — /-----—г / вач — " — =
вач [ рЛ ' 11,14 1 ’ J mg L J mg
MR . Л, /
= —г const Д/ — , [хЛ mg’
Ьг
то, выражая отсюда д^, получим
Дг MR . I
-г-. = —г const — .
Дг рл mg
г &г Д7
С учетом = v и const = получим
MR Д7 /
V — ; д7 — .
р.Л ДГ mg
1S&
Задача 5
процессы происходят
Показать, что при отсутствии трения поршня о стенки цилин- • дра (рис. 6) давление газа под поршнем есть линейная функция от объема газа, независимо от того, каки с газом, лишь бы его сжатие или расширение происходили равномерно. Наружное давление ра постоянно.
Решение
Поскольку в задаче не фигурируют какие-либо характеристики состояния газа, то исходить при решении задачи из уравнения состояния газа нерационально. С другой стороны, в задаче явно делается упор на равномерное движение поршня (равномерное сжатие или расширение газа означает равномерное движение поршня). Но в таком случае сумма сил, действующих на поршень, равна нулю, т. е.
mg + Ра + ^упр + ^газа-О*
Положим для определенности, что в некотором состоянии пружина сжата. Тогда в проекции на вертикаль получим mg + PaS 4- kx — pS = 0, где x— величина деформации пружины, отсчитанная от недефор-мированного ее состояния (этот уровень отмечен пунктиром).
Из полученного уравнения следует , mg + kx
Р = Ра+~^—-
Но x — h — h0 — 1/(1, где Vo — объем газа при недеформирован-
ной пружине, а V — при деформированной на х.
Тогда _________„ , , k (^~ Н) _ _ I mg kV,s . kV Р Ра-\~ $ -V Pa~t~ s S2 ~T S2 •
Так как в правой части равенства все величины, кроме объема газа V, постоянны, то можно записать p = a-}-bV, что и означает линейную зависимость давления газа от его объема.
Задача 6
В баллоне находится смесь газов в количествах М\, М^,..., Mt.... М„ с молекулярными весами ць |х«,..., р.(,..., при
температуре Т. Каков молекулярный вес смеси (т. е. молекуляр
197
ный вес такого газа, который, заменив собой имеющуюся смесь, де изменил бы давления газа на стенки сосуда при той же температуре)?
Решение
Для смеси газов имеем
pV = RT
\Р1 ' 1 Рп 1
Для «заменяющего» газа
pV = RT-. р
Приравнивая правые части равенств, получим
м = м, . ч.
Р Pl ‘ ”Г" Рп ’
Отсюда с учетом М. = Mi -|-... М.п получим
___Mi 4~ мд
^“М!, ,М„*
---г •*» И-
Н Рт2
Задача 7
В закрытом баллоне объемом V была смесь кислорода и водорода в количествах Мк и Мв соответственно. В результате реакции весь водород вступил в соединение с кислородом. Температура при этом возросла от Т до Т'. Какое было давление смеси газов до реакции и после нее, если конденсации водяных паров не произошло?
Решение
До реакции pV = RT f— ), откуда сразу находим р.
\рк Рв /
После реакции
/м' м \
p'V — RT’ ,
\Рк 1 Ри/
где Mi — масса оставшегося кислорода; Мп — масса получившихся паров воды; рп— молекулярный вес пара.
Очевидно, Mi = (Мк-j-Мв) — Мп, а Мп = Мв-]-8Мв (так как в водяном паре на каждую весовую часть водорода приходится 8 частей кислорода).
Подстановка этих значений Mi и Мп в (*) после очевидных преобразований даст
.__RT' (Мк-Шв , 9МВ\
Р ~ V \ Рк Ри Г
198
Задача 8
В баллоне был некоторый газ. При выпуске из баллона части газа температура газа уменьшилась в п раз, давление — в k раз. Какая часть газа выпущена?
Решение
До выпуска газа ptVi == —! RTt. После выпуска газа для оставшейся части газа имеем р?У i =RT<i.
Деля равенства друг на друга и учитывая, что = (объем баллона), получим = — или с учетом того, что — — k,
Pl All / ! Pl
Г8 ил лл л лл a Mi — ДА! , Л ДМ\
и —ДЛ4, получим k— м----------п, или k = (1 — м~]п'
ДМ , k
откуда часть вышедшего газа определится равенством -гт- = 1------.
/vll ft
Поскольку то, безусловно, 1 и k<Cji^
Задача 9
Сферические сосуды 1 и 2 объемами Vj и Ка соединены трубкой сечения S, в которой находится ртуть. Начальное положение ртути указано на рис. 7 жирным пунктиром. В результате
изменения температуры вокруг сосудов уровни ртути в обеих частях трубки стали одинаковыми. Зная исходную разность уровней ртути, найти первоначальные и конечные давления газов в сосудах, а также отношение конечной температуры к начальной. Капиллярностью, давлением паров ртути и ее расширением пренебречь.
Решение
Поскольку в задаче фигурируют четыре состояния газа, то необходимо написать уравнение Клапейрона—Менделеева для каждого из них.
199
Для газа, находящегося в левом сосуде I, ptV, = ^RTt, p'iV'i = ^RTi.
Р-1
(1)
(2)
Для второго газа, находящегося в сосуде 2,
PiV^^RTi, (3)
p2V2=^RT2. (4)
Р-2
Неизвестные и неинтересующие нас — и -- сразу исключаем pl Р-2
делением (1) на (2) и (3) на (4). Учитывая, что температура газов в сосудах равна температуре окружающей среды, т е. 7\ = Т° — Тн Т\ — Т'2 = Т', получаем в результате указанного деления
где штрихом помечены конечные состояния газов.
В два уравнения (5) и (6) входят пять интересующих нас Т'
величин pi, pit pi, р2 и . Необходимы дополнительные уравнения. Они получаются при рассмотрении равновесия ртути в начальном и конечном состояниях. Равновесие всей ртути в конечном состоянии (уровни ее слева и справа на одной высоте) дает
Р1 = Р\- (7)
Очевидно также, что в результате изменения температуры давление газа в сосуде / увеличилось, а в сосуде 2 уменьшилось на АЛ
одну и ту же величину pg (высоты уровнен ртути изменялись
Д/Л ~
на у). Ото приводит к । дл
Pi = Pl + pg 2 . (8)
' ДЛ /п,
Pi = Pt — pg 2 . (9)
Учет изменения объемов газов дает
yi==y1 + S^t (Ю)
V2=Vi-S^. (11)
200
Решение системы семи уравнений (5) —(И) дает ответ на вопросы задачи. Именно, приравнивая левые части уравнений (5) и (6) и учитывая (7), получим
Р1К Р-2
(12)
V[ ~ К ’
Сравнивая правые части (8) и (9), получим Pi = pi + Pg^h.
Подставляя теперь (10), (11) и (13) в (12), получим Р.П (Pi + pgAA) IA И + -j- т
Отсюда находим pit что при подстановке в (13), (8) и (9) дает возможность найти р\ и pi. Подставляя найденные значе-
Т' ния, например, в (5), найдем у задачи. Из-за громоздкости ответа мы его не приводим.
Ясно, что при решении задачи плотность ртути полагалась не зависящей от температуры, что возможно лишь при небольших отличиях температур Т и Т' от температурыГо = 273° К, при которой обычно и приводятся табличные данные величин, зависящих от температуры.
(13)
Задача 10
В сосуд (рис. 8) налита ртуть, запирающая находящийся в закрытом левом колене воздух. Площадь сечения левой части сосуда 5Л, правой части сосуда — Snp. Зная высоту стол-
ба воздуха I, а также его массу и разность уровней ртути ->Н. Атмосферное давление Капиллярными явлениями, давлением паров ртути мостью плотности ртути от температуры пренебречь.
температуру системы, найти равно ра. зависи-
и
Решение
Состояние воздуха описывается уравнением
pV = ~ RT. (1)
Причем давление р находится из условия равновесия ртути. Так как нас интересует АН, то разумно рассмотреть равновесие
8 В. К. Кобушкин
201
именно этого столба жидкости. При этом надо учесть, что на одинаковых уровнях в сообщающихся сосудах давление жидкости одинаково, т. е. интересующее нас давление газа р на поверхность жидкости слева равно давлению в жидкости на соответствующем уровне справа.
С учетом сказанного имеем в проекции на вертикаль
-j- Ра^пр р5Пр--0.
Так как масса столба ртути m = pA/YSnp, то
p&HSnp g -|- PaSnp — рЗПр = 0. (2)
Сокращая на Snp и исключая р из (2) с помощью (1), получим л и । MRT п PW + Pa-W=0-
Полагая плотность ртути р равной табличному значению при 7" = 273° К, т. е. пренебрегая тем, что р = р(Т), найдем отсюда &Н.
Задача 11
На рис. 34 изображены диаграммы процессов, протекающих с газом Определить по этим диаграммам: в каком состоянии
Рис. 9.
объем, занимаемый газом, максимален и минимален (рис. 9, а), как изменилась масса газа при переходе из состояния 1 в состояние 2 (рис. 9, б), как изменилась температура газа (рис. 9, в)?
Решение
На координатной плоскости р и Т, V и Т или р и V состояние газа задается точкой (при известном, конечно, уравнении состояния газа). Если с газом происходит какой-либо процесс, то точка, определяющая состояние газа, описывает некоторую кривую, уравнение которой не противоречит равенству
pV = -RT. (*)
202
В случае а) нас интересует объем газа при -= const.
Тогда из (*) и рис. 34, а имеем
V = - R - = const - = const • ctg а, и Р Р ь
где а — угол, составленный прямой, проведенной из интересующей нас точки в начало координат, с осью Т. Очевидно, Vi соответствующий наименьшему значению ctgа, будет наименьшим, a У2, соответствующий наибольшему значению ctg а, — наибольшим.
В случае б) нас интересует масса газа при р — const и Р = const, поэтому из (*) и рис. 34, б получаем
М V = const ~ = const • tg а. Ki 1
Отсюда следует, что при переходе газа из состояния 1 в состояние 2 его масса уменьшилась, ибо tga уменьшился.
В случае в) Т = pV • = const • pV, где pV — площадь
прямоугольника, ограниченного осями р, V и перпендикулярами, опущенными на них из интересующей нас точки. Видно, что p^V^piVi, значит Л>Л, т. е. газ нагрелся.
Задача 12
В сосуде объемом V находится пар при температуре Т и давлении р. Сколько жидкости может выпасть в осадок при понижении температуры на ДГ?
Решение
Очевидно, если осадок выпадает, то его масса определится равенством
= — = V (Pg — Pi) = V (ра_
где — масса оставшегося в сосуде насыщающего пара; р2 — его плотность при температуре Г — ДГ; — масса бывшего в сосуде пара; Pi — его плотность при температуре Г.
Величина Pi берется из таблицы, как плотность насыщающего пара при температуре Г2=Г — ДГ.
Если Д/эт^>0, осадка не было и оставшийся пар еще не стал насыщающим. Если Д/п<0, осадок был. Если Д/п = 0 —граничный случай: осадка не было, но оставшийся пар стал насыщающим.
Задача 13
В цилиндре под поршнем находится пар, занимающий объем V при температуре Т. Пар сжимают, причем его температура оказывается равной Г'<Гкр. Каков наименьший объем V', который займет вещество под поршнем?
8*
203
Решение
Оговорка о том, что окончательная температура системы меньше критической, сразу приводит к мысли о том, что весь пар сконденсируется в жидкость, которая и займет объем V. Пренебрегая зависимостью объема жидкости от давления, но учитывая более сильную зависимость объема жидкости от температуры, получаем
К» = Ко» (1 + “О,
но УОж=-^, а тж = Мп, а потому Рож
Г=Уж==-^(1+аО, (*)
Рож
Плотность жидкости при t = Q°C и коэффициент ее расширения а — табличные данные, а необходимую для решения задачи массу пара находим из уравнения Клапейрона— Менделеева для начального состояния газа
Исключая из (*) и (**) массу пара, получаем ответ на вопрос
задачи
У'
рУр Рож^Г
(1 + 0,
где Г = Г — 273°К.
Задача 14
В манометрическую лась. Найти ее массу
трубку попала капелька воды и испари-тв, зная показания этого и исправного
манометров (Ян и Н„), пренебрегая тепловым расширением стекла и ртути (рис. 10). Сечение трубки манометра равно S, длина ее части, выступающей над уровнем ртути в сосуде, равна /.
204
Решение
В исправном манометре над поверхностью ртути давление практически равно нулю из-за малой летучести ртути. Поэтому ртутный столбик находится в равновесии под действием внешней силы давления paS и силы тяжести m^g. Поэтому для исправного манометра получаем в проекции на вертикаль
m^g — paS — 0. (1)
Над ртутью же неисправного манометра находится пар, и условие равновесия столба ртути неисправного манометра приводит к равенству
mprg'4-р.,5 — paS = 0. (2)
Поскольку
_ Л4„ RT _ тв RT
Рп ~ Рв И ~~ |хв ‘ S (Z - На) > W
то, исключая из (1), (2) и (3) величину pBS и давление ра, получим
, \ mBRT
(ШрТ mpT) g — _
и так как /прт —ppiS//H и тг,г~р?Т8На, то окончательно т Ррт 5 (//и — /7Н) . „
«В — -2-----------g (I — Ян) |Х.
Решение, конечно, можно было начать с написания уравнения состояния пара над ртутью в неисправном манометре (3), а потом написать условие равновесия столба ртути в нем (2), куда недостающее давление ра нужно было бы взять из условия равновесия столба ртути в исправном манометре (1). Но сама постановка задачи о сравнении показаний манометров по существу говорит о сравнении положений столбов ртути в них под действием каких-то сил, а эта задача уже механическая. Поэтому мы и проводим решение в указанном порядке. Ясно, что результат решения от способа решения зависеть не может (если, разумеется, решение проводится верно).
Задача 15
В наклоненном под углом а к горизонту цилиндре длиною L (рис. 11) находится смесь газов и поршень весом Р, не проницаемый для одного из газов, находящихся в левом отсеке. Молекулярный вес этого газа равен р. Поршень находится у верхнего основания цилиндра. Где он установится, если его отпустить? Трение поршня о стенки весьма мало. Температура системы Т, масса непроходящего сквозь поршень газа равна М.
205
Решение
Поскольку поршень проницаем для всех газов, кроме одного, то состояние всех этих газов на равновесии поршня никак не скажется — он является для этих газов «решетом». Поэтому принимать их во внимание не следует. Газ же, для которого поршень непроницаем, при движении поршня вниз будет сжиматься
и при каком-то давлении его р поршень окажется в равновесии (после некоторого числа колебаний, которые из-за трения о
стенки и в газе затухнут). Тогда по второму закону механики без учета трения поршня о стенки получим Р -j- Q = О, а в проекции на ось цилиндра
Р sin а — pS = 0. (1)
Уравнение состояния для непроникающего через поршень газа дает с учетом V = SI:
MRT р~~ •
Из уравнений (1) и (2) следует
Рр. sin а '
(2)
Видно, что при а = 0 / обращается в бесконечность, что является бессмыслицей, ибо длина всего цилиндра L конечна. В чем же дело? Дело в том, что если бы цилиндр был справа неограничен, то поршень действительно ушел бы как угодно далеко. На самом же деле поршень дойдет до правого днища цилиндра и там упрется в стенку, со стороны которой на него будет действовать сила, не учтенная нами в решении, поскольку рассматривали поршень на некотором расстоянии (L — /) от нее. Таким образом, ничего парадоксального в решении нет.
Задача 16
В сосуде (рис. 12) находится под поршнем весом Р газ в количестве М с молекулярным весом р при температуре Т. Газ начинают греть, и поршень идет равноускоренно вверх. Считая среднюю силу сопротивления со стороны внешнего давления и стенок трубки равной F, найти зависимость температуры газа от времени. Сечение трубки равно S, ускорение поршня — а. Считать движение поршня очень медленным.
206
Решение
Закон движения поршня в проекции на вертикаль имеет вид
-P + pS-F = ya. (1)
И поскольку Р, F и а постоянны, то постоянно и давление газа р. Но в таком случае для двух последовательных состояний
газа имеем
pV' = ^-RT', г р
pV = ~RT, г р
что дает при вычитании
pkV ~ — R (Т'~ Т), (2)
р
где ДУ = £Д/, a A/ = -y в силу равнопеременного движения поршня из состояния с уо = О. С учетом этого уравнение (2) примет вид pS ~ R (Т' — Т), что совместно с (1) приводит к
При решении задачи мы как будто бы нигде не использовали оговорки о медленном движении поршня. И что значит «медленно»? Оказывается оговорка весьма существенна Дело в том, что если поршень движется с большой скоростью, то в разных частях сосуда давление р и температура Т будут разными и тогда совершенно неясно, какое же давление и какую температуру надо подставлять в уравнение pV = — RT. Чтобы задача стала опре-р
деленной, необходимо быть уверенным в том, что р и Т от места к месту не меняются, т. е. при движении поршня они успевали бы выравниваться. Отсюда ясно, что надо понимать под словами «поршень движется очень медленно». Он должен двигаться столь медленно, чтобы выравнивание р и Т действительно бы происходило.
Задача 17
В цилиндрической тонкостенной пробирке весом Р и сечением S находится газ с молекулярным весом р. в количестве М. Пробирка снизу закрыта тонким поршнем массы т, привязанным ниткой ко дну сосуда, заполненного жидкостью плотностью р.
207
Верхний край пробирки находится на глубине hB. Температура среды Т и атмосферное давление ра известны. Найти натяжение нити Q (рис. 13).
Решение
Поскольку в задаче больше говорится о механическом состоянии системы, чем о термодинамическом состоянии газа в пробирке, то начнем решение задачи с рассмотрения механического равновесия поршня и пробирки. Второй закон механики даст в этом случае для поршня и пробирки соответственно (в проекции на вертикаль)
mg pS + Q —
Р 4“ (Pg^B 4“ Ра) S — pS — О, (2) откуда, складывая и преобразуя, получим
Q — Р£(ЛН —- ha) S — Р — mg или
Q = PgV — P — mg. (3) Видно, что нахождения Q необходимо знать V. Но из уравнения состояния газа
(4) до v '
и потому
Q = ^L-P-mg.
Р-Р
Подстановка в это равенство давления р из (2) приводит к ответу Q =____________________KMRTS _р_тд
Задача 18
В горизонтальном цилиндре, разделенном поршнем, проницаемым для газа с молекулярным весом находятся еще и газы с молекулярными весами lu и Газы щ и а» химически Л4„
реагируют в отношении -~ = п, образуя новый газ с молекулярным весом р' = р-2 —Газы р3 и р3 были вначале слева от
208
поршня, а газ р.2— справа. Количество первого и третьего газа соответственно было Mi и М3. Второй газ нацело реагирует с первым. Найти отношение объемов, на которые разделится сосуд поршнем по прошествии длительного времени.
Решение
Поскольку для газа [-и поршень не преграда («решето»), то он будет перетекать довольно легко из одной части сосуда в другую. Попадая в отделение с газом [л2, он вступает в реакцию, давая новый газ с молекулярным весом р/ = р.2 -j- Так будет продолжаться до тех пор, пока газ нацело прореагирует. Результат: с одной стороны поршня газ р3, с другой — р/ — р3-|--f-fyii; газ же рь проходя сквозь поршень, будет в обоих отделениях создавать в силу этого одинаковые давления справа и слева. Положение поршня поэтому будет обусловлено давлениями газов р3 и р' = ра -j- fepi. По прошествии достаточного времени температуры и давления выравниваются.
Поскольку для левого и правого газов имеем соответственно
Вз
„у _____ + пМ1 рт
Рпр^пр— К/ пр,
то, деля эти равенства одно на другое, получим с учетом равенства давлений и температур слева и справа
К,___ М,з (Ра +
% м-а(1 •
Задача 19
Цилиндр разделен подвижным с ничтожным трением поршнем массой т и сечением S на части Vi и У.2 с газами pi и р2 в количествах Mi и М3. Температура системы Т, поршень в равновесии. Цилиндр приходит в равноускоренное движение и за длительное время t набирает скорость v. Из-за трения о воздух температура повышается на Д7\ Найти новые объемы V[ и V2, на которые поршень разделит цилиндр.
Решение
Поскольку движение происходит длительное время, то колебания, вызванные выводом поршня из равновесия, затухнут, а температура и давления станут постоянными (не зависящими от времени).
209
Уравнения состояния газов дадут:
p'iVi = ^R<T-^M), (1)
Г1
Р^ = ^/?(Т + ДГ). (2)
rS
Уравнение движения поршня в проекции на направление движения дает с учетом F[=p'lS и Р'ъ = р'£
(p't — p't) S — та. (3)
Выражая из (1) и (2) разность давления (p.j — pi) и приравнивая ее к (р'г — pi), выраженной из (3), получим с учетом того, Л v
что из-за fo = O ускорение поршня равно у
(-^г — ^R(T-^^T) = ^. (4)
Кроме того,
УЛ-у^у,-^. (5)
Полученная система (4) и (5) решает задачу.
При решении не учитывалось то, что давление газа в каждой секции не постоянно вдоль ускорения а, подобно тому, как при решении задач на газ в вертикальных цилиндрах не учитывается изменение давления газа вдоль g.
Задача 20
В сосуде объемом У находилась при температуре Т вода в количестве т. В результате нагрева на ДТ вода испарилась. Найти давление ее паров до и после нагрева.
Решение
Первоначальное состояние пара описывается уравнением
Р1(у-ув) = ^/?т. (1)
г
При этом пар был насыщающим, ибо находился достаточно долго в сосуде одновременно с водой и, значит,
Л4 = Рн(У-Ув). (2)
Исключая из (1) и (2) массу пара Л4, получим pi = — При
I1
этом рн берется из таблиц. Можно, конечно, определить pi сразу из таблиц, если есть таковые.
Для конечного состояния системы (после испарения воды) имеем
рзу = -^Т). (3)
Iх
210
Подстановка сюда необходимого М из (2) приводит к уравнению
= Ри + т R(T-\- ДГ), f* ¥
где IZ т т /1 I А '/в = — = — (1 НВ Ро В
Роа и а — табличные данные, a t = T — 273° К (температура воды по Цельсию перед нагревом).
При решении не учитывалась зависимость плотности воды от давления и изменения объема сосуда при изменении температуры.
Задача 21
В пробирке (рис. 14) находится газ при температуре Т. При нагреве до Т' газ расширяется и выходит из пробирки в количестве ДМ. Плотность жидкости р, а указанные на рисунке размеры и атмосферное давление рй известны. Найти первоначальную массу газа М в пробирке. Капиллярность пренебречь.
Рис. 14.
Решение
Очевидно, состояния газа описываются уравнениями pV = — RT и p'V' = ^-RT'.
i1- i1-
Деля эти равенства одно на другое и учитывая, что М' = М — — ДМ, получим
pV _ мт p'V~ (М- Ш) Т"
211
Поскольку = ТО
pl _ мт , .
p'(l + a + b)~ (М-ДЛ1) V
Давление p найдем из условия равновесия столбика жидкости (а-\-Ь), которое приводит к уравнению
pS + p(a + &)Sg— (ра-f~ pga) <$ — О, откуда
p = pa — pgb. (2)
Давление же р' есть просто давление в жидкости на глубине а, т. е.
p' = Pa + pga- (3)
Подставляя (2) и (3) в (1), получим
(Pa~?gb)l _ AIT
<Ра + fg«) (l + a + b)— (Л4 — ДМ) T > откуда без труда и находим М.
Задача 22
В комнате объемом V при понижении температуры от 7\ до 7% выпало ДМ росы. Какова была плотность водяного пара (абсолютная влажность) и относительная влажность его до понижения температуры?
Решение
Очевидно, ДМ = М2 —Mi или ДМ = V (р4 — pt). Но р2 есть плотность насыщающего пара при температуре 7\, т. е. табличное данное; тогда из ДМ — V (р2и — pi) следует очевидное pi = р2н — —.
По определению относительной влажности
Подставляя сюда найденное pi и табличное значение р1н, получаем
Задача 23
В замкнутом сосуде объемом Vc содержится m жидкости при температуре 7\. При повышении температуры до Т2 жидкость испарилась. Построить примерные графики зависимости абсолютной и относительной влажности от температуры, т. е. графики р = р (Т) и f = Начальная масса пара мала.
212
Решение
По определению абсолютной влажности р = ^, где Л1„ — масса пара, a Vn—предоставленный ему объем. Поскольку УП=УС—Уж, ТО р=^ _Р ис
Пока в сосуде есть жидкость, пар будет близок к насыщению и с ростом Т величина р будет возрастать из-за прибыли Ма (жидкость переходит в пар). Некоторое увеличение знаменателя
Рис. 15.
из-за уменьшения VK сказывается мало. Итак, р растет с ростом Т до тех пор, пока в сосуде есть жидкость. После испарения всей жидкости при некоторой температуре Т' величина р будет оставаться постоянной. Но это означает, что р, возрастая, стремится
m гч
к пределу ртах = -77~- это в свою очередь означает зависимость "с
р = р(Т) примерно такую, как на рис. 15, а.
Поскольку при медленном нагреве пар, как сказано выше, будет практически насыщающим вплоть до Т', то с ростом темпе
2
Рн
ратуры вплоть до Т' относительная влажность / =
Рн ___ |
Рн
При Т^>Т' из-за испарения всей жидкости р = const, а рн растет,
поэтому f = — будет убывать, стремясь при очень высокой Т Рп
к нулю. Примерный график f = f(T) и изображен на рис. 24,6.
Задача 24
В вертикальном замкнутом цилиндре сечением S находится газ с молекулярным весом р. Способный без трения перемещаться поршень массы tn делит объем, занимаемый газом, на части Vi и Vi. Температура всей системы неизменна и равна Т. Зная, что период колебания поршня равен т, найти массу газа в цилиндре, считая, что над и под поршнем масса газа одинакова.
213
Решение
Сразу видно, что это задача на колебательное движение, а точнее на определение коэффициента возвращающей силы k. Поэтому, рассматривая силы, действующие на поршень (рис. 16), находящийся в равновесии, получим в проекции на направление тяжести
— pi)S=O.
Если сместить поршень, например, вниз на Дг, то давле-
ние внизу возрастет на Др2 и станет равным pi, а сверху уменьшится на Др1 и станет равным p'v
Поскольку mg при этом не изменится, то возвращающая сила будет обусловлена изменением давлений pi и р2, т. е.
=—(ра — р^ s 4- (р; — р4 s.
В соответствии с уравнением состояния идеального газа р = ^--~^-. Поэтому, подставляя значения pi, pj, р2 и p.j в предыдущую формулу, получим
т и L \е2 vs) 1
_ MRT f V2 - W2 . Vt - Vt
I* \ -r
Вводя обозначения Vi —• = ДЕ2 и V[ — Vi —
— Д1Л и учитывая, что ДЕ1 =— ДУ2 (на-Рис' сколько увеличился объем сверху, настолько
уменьшился он снизу) и что при малом смещении Vi^&Vi и приходим к следующему выражению:
F.
MRT/ДУ.
|Л ( У/
MRT/ДУ^ ДЕЛ,
i) о м#т( 1
Г/ Г W
MRT / 1
И
С учетом же взаимных направлений векторов F,. и Дг получим
MRTS2 /1 । 1 \ |Л VI)
кг.
MRTS2 / 1 1 \
Отсюда ясно, что k = —-—VgJ’ где М — половина всей массы газа.
214
Подставляя найденное значение k в формулу для периода, получим
Т = 2к у = 2тс уГ MRrS2 / 1 1 \ >
Г |Л + Vlj
откуда и находим М.
Если бы в условии вместо Vi и фигурировали высоты частей цилиндра /ii и hi, то можно было бы обойтись без сечения S: именно, с учетом V = Sh получили бы
Задача 25
В цилиндрическую капиллярную трубку, погруженную в полностью смачивающую ее жидкость, как указано на рис. 17, впустили столько же (и такого же) газа, сколько в ней уже содержалось. Насколько изменится длина воздушного столба в результате этого?
Рис. 17<
Решить задачу в достаточно общем случае, сделав, однако, необходимые допущения, и выяснить, какие данные необходимы для решения задачи. Получив решение, сделать максимальное упрощение за счет одного допущения.
Решение
Поскольку в задаче говорится о двух состояниях газа, то, очевидно, необходимо написать два раза уравнение Клапейрона — Менделеева: ..
PV=^-RT, p'V’ = ^RT'. С*
215
В задаче сказано, что М' = 2М, поэтому с учетом V' = V AV получим
pV = ^-RT,
p'(V + bV) = ^RT', Г
Чтобы привлечь минимум необходимых для решения задачи данных, надо избавиться от наибольшего числа входящих в равенство величин. Если мы разделим равенства одно на другое, то избавимся от необходимости знать М и сечение трубки S (ибо V = Sl). Деление равенств с учетом сказанного приводит к уравнению
——— = (О
р'(/-|-Д/) 2Г"
Поскольку столб жидкости внутри трубки подвижный, то для нахождения давлений р и р’ необходимо рассмотреть условия равновесия этого столба в начальном и конечном состояниях. При этом надо учесть факт смачиваемости трубки жидкостью. Действительно, в задаче сказано, что жидкость смачивающая, значит этот факт необходимо учесть. Но что означает в данном случае смачиваемость? Очевидно то, что поверхность жидкости в трубке будет искривленной, что приводит к появлению Лапласова давления под ее поверхностью и отклонению формы воздушного столба от цилиндрической. Последним можно пренебречь, если т. е. если радиус трубки мал. Но именно малость радиуса трубки заставляет учесть первый эффект — появление Лапласова давления. Поскольку жидкость полностью смачивающая, а трубка цилиндрическая, то мениск будет сферическим и 2а
Рл = у •
С учетом сказанного рассмотрение сил, действующих на столбики жидкости (рис. 17, а и 17, б), приводит к уравнениям (в проекции на направление g)
pS-\-pghS-^S-paS = O, (2)
p'Spgh'S— у S — paS — O. (3)
Здесь учтено, что изменились только высота столба жидкости h и давление р. Остальные, входящие в эти равенства величины, не изменились. Ясно, что давления р и р' не удастся найти, если неизвестны все входящие в условия задачи величины. Едва ли все они будут заданы. Значит, надо искать дополнительные связи между ними. Найдем их. Во-первых, на глубине Н в жидкости давление определяется формулой = + Во-вторых, из рис. 17, а и 17,6 видно, что h' = h — Ы.
216
Подставляя эти значения в (2) и (3), получим после сокращения на S и группировки членов
p-^ + ?g(h-H)-Pi = 0, (4)
Pr~7 + Pg(h-M-H)-pa=0. (&)
Входящие сюда, кроме р и р’, величины в условии задачи не фигурируют, «значит их надо ввести самим. Необходимо также ввести -отношение температур в (1).
Подставляя в (1) р и р' из (4) и (5), получим
Fy+^a-Pg'CA-^)1/ т
.12----------------J-----= ^, (6)
откуда и найдем Д/. Ответ, безусловно, будет громоздким. Не будем его выписывать. Но в условиях задачи рекомендовано сделать весьма упрощающее допущение. Каково оно? Очевидно, самое упрощающее допущение должно привести к тому, что состояние газа вообще не изменилось и, значит, Д/ = 0. Но это возможно лишь в случае М' = М, р' — р и т. д. В задаче же ясно сказано, что М' = 2М. Но в таком случае, чтобы Д/ = 0 при р' = р, необ-
Т 7*
ходимо Т'—7. Значит, при М' = 2М и Т' = -7- будет Д/ = 0 (если, конечно, р' — р, что возможно, если с трубкой и жидкостью ничего не делали). Это сразу видно будет из уравнений состояния для начального и конечного состояний газа.
Но положим в решении (6) Т = 2Т. После очевидных упрощений получим для Д/ два значения: 1) что вполне
согласуется со сказанным выше, и 2) Д/2 = — (/ -f* h — Н).
Второй ответ явно несуразный. Как же он мог получиться? Для выяснения этого перепишем второй ответ в виде
7 + р.-Р^(/ + й-Я)-Р^Д/4 = 0. (7)
Заметим, что величина — (см. рис. 17, в) есть длина части трубки, выступающей над уровнем жидкости. Но тогда, умножив (7) на S, получим
(7 + Pa)S-pg(/ + A-tf)S-pgA/3 = 0. (8)
Рассмотрим теперь равновесие столба жидкости (/-j-й — Н) в трубке (рис. 17, в). В проекции на g получим
(y + Pa)S-pg(Z + /i-//)S-pS = O. (9)
9 В. К. Кобушкац
217
Но если высота столба жидкости равна (I h— Н), то это значит, что вся трубка заполнена жидкостью (мениском мы при-небрегли) и в ней нет газа. Но тогда д> = 0. Сравнивая при этом условии (9) и (8), приходим к выводу, что Д/а = 0. Таким образом, никакой несуразицы во втором ответе не содержится. Он относится к случаю, когда М' = 2М =0, т. е. когда газа в трубке не было. В этом случае ответ 1) означает, что жидкость заполнит всю трубку, а 2) есть просто условие равновесия этой жидкости.
Отметим еще одну тонкость. Мы не учитывали объем пространства около мениска, что справедливо лишь при /^> г. Но если вся трубка заполнена жидкостью, то условие / ^> г не выполняется и решение становится неверным. В какой мере эта неверность т скажется на ответе при сделанном нами предположении Т =-^ ? В случае, когда газа в трубке не было, ответ тоже будет Д/2 = 0. Но! ... Когда трубка заполнена жидкостью так, что края мениска коснутся верха трубки, радиус кривизны мениска будет больше, чем г, и станет равным такому К, чтобы
р+Ра-р^(/ + Л-Я) = 0.
Это следует непосредственно из того, что столб жидкости все-таки будет в равновесии под действием сил Рл — ^tS, Fa = paS и mg = pg (l + h — H)S.
Если бы жидкость касалась всей своей поверхностью верхнего края трубки, то мениска не было бы, но на жидкость действовали бы силы paS, pgS(l-]-h—Н) и сила давления верхнего края трубки. При этом
PaS — pgS (l + h — Н) — Q = 0.
Задача 26
Из металлического баллона объемом V, содержавшего воздух при давлении р, сделали // откачиваний и N накачиваний насосом с рабочим объемом v. Считая наружные условия заданными (ра и Т), найти изменение массы воздуха в сосуде, если все процессы происходили достаточно медленно.
Решение
Медленность процессов в данном случае означает, с учетом металличности баллона, что температура системы все время мало отличается от температуры окружающего воздуха и равна Т. Очевидно также, что
^М = М' — М = (М'-\-пг) — М, (*)
где М’ — масса воздуха после откачки; М' — конечная масса воздуха в баллоне; М — начальная масса воздуха в баллоне;
218
tn — масса накачанного воздуха; &М — изменение массы воздуха за весь процесс. Но
т — m3N = pvN vN,
(**)
где т» — порция воздуха, забираемая насосом за один раз извне, причем в силу неизменности внешних условий все та одинаковы.
При откачке протекание процесса существенно меняется. Поскольку объем насоса неизменен, а при откачке каждый раз давление в сосуде все уменьшается, то порции откачиваемого воздуха не равны меж собой. Это надо учесть при нахождении М'.
Именно
М' ==~Бт’> (#**)
где р'— давление газа в конце откачки. Его надо находить поэтапно (в силу сказанного выше).
Для серии откачиваний имеем (с учетом постоянства температуры и массы газа при расширении)
1) PV^Pl(V + v),
2) piV = pi (Уо),
3) piV — p3(V-\-v),
N) Pn-iV = pn(V + t>).
Эта система равенств приводит при их перемножении и делении на pt-pt- ... • Pt • ... • Pn-\ к уравнению
/ I/ \ЛГ
PN = P\y^] •
Поскольку давление р^ и есть р', то уравнение (***) примет вид |ЛИ / V \N ,
м ~ rtp \y+v) * (****)
Подставляя М' из (****), т из (**) в (*), получим
а.М [pV (рт^)" + p.vN-pV ].
Задача 27
Из адиабатически изолированного жесткого баллона, содержащего газ при давлении р и температуре Т, производится N откачиваний насосом с рабочим объемом v. Зная, что объем баллона V и что давление газа в баллоне упало до рм найти конечную температуру газа Т^.
9'
219
Решение
Адиабатичность баллона означает, что температура газа после каждого выброса газа при откачке, т. е. от конца k-vo откачивания до начала (k-\- 1)-го, не меняется.
С учетом этого и того, что во время расширения газа его масса не меняется, имеем для серии откачиваний
п рУ______Р1 (У'+р)
г 71
2) PjV р* (У'+р)
Л/Ч РкУ_Рк<У+^‘ IV ) т гр .
1 N-1 1 N
Перемножая эти равенства друг на друга, а потом сокращая р, Pi Pn~\
на ~ • — ... у—, получим
Pn __ Р I v \N
TN — T\V-\-vj >
что и дает ответ на вопрос задачи.
Задача 28
Два сосуда объемами Vi и Ve соединены капилляром с краном.. Левый сосуд содержит газ при условиях pi и Д а правый — при и 7\. Кран откры-. • ;\ вают и давления выравни-ваются, становясь равны-
—Т. . I. • ’| ми р'. Найти это р' (рис. 18).
' г —т . *
‘ ‘J Решение
‘ Пренебрегаем объемом
Рис. 18. капилляра и тем, что
вдоль него имеет место перепад температур от Л слева до 1\ справа. При этих условиях можно считать, что левый и правый сосуды разделены легким поршеньком, находящимся в равновесии. Это приводит к тому, что в конце процесса давления на поршенек (т. е. в левом и правом сосудах) равны. Уравнения состояния газов в левом и правом сосудах дадут соответственно
и = (1)
Соответственно до открытия краника с учетом неравных справа и слева давлений
PiVi^RTi и ptV^^RTi. (2)
Г* I1- - - .
220.
При этом
(3)
Выражая из (1) Л4) и M’it а из (2) Mi и Ма и подставляя эти значения в (3), получим
Iх [PiVi ] (p'Vi i p'V%\
R\ Л Г Tt]~R\Tl^ Tj'
откуда и находим р'. В решении учтено, что объемы сосудов не менялись, т. е. У1 = У£ и Уа=Уа.
Задача 29
Теплонепроницаемый поршенек делит сосуд на две равные части. Левую часть нагревают на ДТ, а правую охлаждают на МГ. Зная первоначальные объемы V и температуру Т, определить
двигаться вправо и левая
часть газа расширится на Рис. 19.
ДУ, а правая сожмется
на ДУ. Давления же справа и слева будут одинаковыми и равными сперва р, а потом р'. По уравнению состояния для левой половины имеем до и после изменения Т
PV=^RT и p^V + W^^-RtT + MT). Г* Р
Откуда
_________= _Л_ Ш р'(ин-ди) г-удг Of
Для правой половины аналогично
____?*.__= , /2) р'(И-ДИ) Г-ДГ' О/
Деля (1) на (2), получим
и-ди___г—дг
И+ДИ~Г+ДГ’
откуда и определится ДУ.
221
Задача 30
В капилляре (рис. 20) при температуре Т находится столбик
ртути. На сколько градусов надо нагреть его, чтобы вся ртуть
вышла? Все размеры указаны на чертеже. Несма-чиванием пренебречь.
Решение
Очевидно,
или
ра__р'. . Т~ 7'4-ДГ >
рг — это конечное давле-
ние газа в капилляре.
Поскольку ртути в нем не остается, то р' = ря. Исходное же давление р находим из условия равновесия столбика ртути.
Именно в проекции на ось трубки имеем
pS -j- pgSb sin а — paS = 0.
Подставляя отсюда значение р
, \ (Ра — Pgb sin а) а
в (*), получим —---------— =
~^г+~д^’ откуда и находим ДР (при известном ра)<
Задача 31
Закрытый сверху капилляр опущен в ртуть так, что над ртутью остается часть длиной а, а уровень ртути в капилляре на b ниже наружного уровня. Атмосферное давление равно ря. Какой будет длина столба воз-
духа в капилляре, если его пол-
ностью вытащить из ртути? Несмачиванием пренебречь, длина капилляра L, температура неизменна (рис. 21).
Решение
Очевидно, piVi = paVa или с учетом S1 = <Sa Pi (a-\-b) — p»h
222
pi — это давление в жидкости на глубине b и, значит, pi — рл -ф* -ф- Pgb. Pi найдется из условия равновесия ртутного столба. Именно
Р£ (L — l)-\- Pi — Ра = 0.
Подстановка значений pi и р.> в равенство (*) дает
{Ра + pgb) (a-[-b) = [ра — Pg (L — /)] I,
откуда и находим /.
Задача 32
В цилиндре, закрытом поршнем, подвешенном на пружине,
находится газ.
Найти зависимость объема газа от температуры при очень медленном ее изменении. Трение поршня о стенки считать ничтожным (рис. 22).
Решение
Поскольку температура, а значит, и давление газа меняются очень медленно, то поршень заметного ускорения не имеет и потому в проекции на вертикаль при расширении получим
mg -ф- kx -ф- ра8 — рЗ = 0.
Кроме того,
pV = — RT.
Исключая из этих равенств р и учитывая, что х=- gV*-(где V — объем газа в рассматриваемый момент, а — в момент, когда пружина была недеформирована), получим
„ . , V- Vo I с М RT с п mg -ф- k |~ paS — — • —у 3 — 0, откуда
|^ + (w + PaS-^T-^/?ST = 0, или
aV^-j-bV — сТ = 0, откуда
у__— + 4ac Т
V ' 2а •
где ради краткости введены обозначения
а = b = [mS-\-PlL3-^ и р = ^/?3.
223
3. ЭНЕРГИЯ, РАБОТА, ТЕПЛОТА
Вся термодинамика построена на трех законах (началах), подобно тому, как вся классическая механика построена на трех законах Ньютона.
Так же как в механике, любая задача решается с помощью законов Ньютона и кинематических уравнений, так и любая задача собственно термодинамики решается с помощью трех начал и уравнений состояния вещества.
Мы здесь сформулируем первое начало термодинамики в довольно общем виде, второе — в частном, третьего вообще формулировать не будем, поскольку оно нам не понадобится. Что касается уравнения состояния вещества, то оно выглядит очень просто лишь в случае идеального газа и нами уже сформулировано. Это уравнение Клапейрона—Менделеева. Других уравнений состояния мы рассматривать не будем.
Поскольку могут встречаться комбинированные задачи на тепломеханические процессы (удары, перемещения тел и т. д.), то могут понадобиться, естественно, и основные положения из механики, что будет видно из решения задач.
Первое начало термодинамики — это наиболее общая формулировка закона изменения и превращения энергии. Оно является результатом обобщения колоссального числа опытов и ни из каких других законов выведено быть не может.
Прежде чем его формулировать, расширим понятие энергии системы.
Известно, что энергия — это наиболее общая характеристика, наиболее общая мера всех видов движения, в том числе молекулярных, атомарных, волновых и т. д. Она характеризует в этом смысле состояние, в котором находится интересующая нас система тел.
Именно, зная функциональную зависимость энергии системы от своих аргументов, можно очень просто получить все характеристики, все свойства этой системы. Поэтому знание такой зависимости эквивалентно полной информации о состоянии системы. В этом и заключена важность понятия энергии системы.
Принято называть энергию тела, обусловленную взаимодействием его с другими телами и движением тела как целого, механической, а энергию, обусловленную внутренним состоянием тела, — внутренней. Очевидно, внутренняя энергия тела — это кинетическая энергия движения его частиц (молекул, атомов, электронов, нуклонов, фотонов и других частиц) и потенциальная энергия их взаимодействия. Правда, деление энергии на механическую и внутреннюю довольно условно и не всегда это деление можно провести однозначно.
Например, часто говорят, что внутренняя энергия тела зависит от температуры, а механическая — нет. Но это явно не так. Если зело, лежащее на подставке, нагрезь, то центр массы тела 224
может! подняться из-за расширения тела, а это значит, что с изменением температуры тела изменилась его механическая энергия. Правда, та часть энергии, которую принято называть внутренней, изменится при этом сильнее, чем та часть, которую принято называть механической. Изменится в этом случае энергия системы в целом. Аналогично обстоит дело, например, при плавлении тела — меняется и внутренняя и механическая энергия. Эти и другие примеры позволяют прийти к выводу об относительности деления энергии на внутреннюю и механическую.
До тех пор, пока тело или система тел не обмениваются движением с другими телами или системами, его энергия не меняется. Если же обмен движением есть, то энергия системы не остается, вообще говоря, постоянной.
Очевидно, система может обмениваться с другими телами как макроскопическим движением (раздвинуть, например, другие тела, передать им часть своей механической энергии), так и микроскопическим (нагреть, расплавить, излучить свет и т. п.).
Изменение энергии системы за счет обмена макроскопическим движением (т. е. такой обмен, который связан с механическим перемещением каких-то тел или изменением их формы и объема) называется механической работой.Изменение же энергии системы за счет обмена с другими телами микроскопическим (хаотическим) движением называется теплообменом или коротко — теплотой.
Первое начало термодинамики утверждает, что только за счет этих обменов и происходит изменение энергии системы. При этом
LE' = A+Q,
где ^Е' = Д£вН + ДДмех —• убыль полной энергии системы; А — работа, совершенная системой над внешними телами, мешающими системе менять свою форму или объем; Q' — теплота, переданная системой внешним телам.
Если мы сумеем измерить работу А, совершенную системой, и теплоту Q', отданную этой системой другим телам, то мы сможем подсчитать изменение энергии системы. В этом смысле первое начало термодинамики есть определение энергии, которое можно сформулировать так: энергия — это такая функция состояния системы (т. е. такая характеристика состояния системы), об изменении которой можно судить по работе, совершенной системой над окружением, и по переданному ею окружающей среде теплоте в соответствии с равенством &E' = A-\-Q'.
Удобнее, однако, вместо тепла Q', отданного системой, иметь дело с Q —— Q', т. е. теплом, которое система получила, и с ДЕ =— ДЕ', т. е. с прибылью энергии системы вместо ее убыли. Тогда первое начало будет иметь вид — &Е = А— Q или
(? = ДЕ4-Л,
т. е. тепло, полученное системой, идет на изменение полной
225
энергии системы и на работу, которую система совершает над внешними телами при своем расширении.
Обратим внимание на то, что в первое начало не входит работа диссипативных сил в явном виде: она входит в ДЕВИ, подобно тому, как работа потенциальных сил входит в Это надо учитывать при решении задач.
Договоримся о знаках величин Q, ДЕ и A. Q^>0, если система получает тепло, Q<^0, когда она его отдает; ДЕ^>0 — при возрастании энергии системы, ДЕ<0 при убывании ее; А^>0 при расширении системы, А<^0 при ее сжатии.
Очевидно, что если система замкнута (с другими телами существенно не взаимодействует), то Q = 0, А=0, а тогда и Д£ = 0— полная энергия системы не меняется, хотя превращения энергии внутри системы могут иметь место, но так, чтобы ЬЕ„а -|-Д£’мсх = 0, т. е. убыль механической энергии ведет к прибыли внутренней или наоборот.
При очень быстрых процессах, происходящих в системе, она не успевает в существенной мере обменяться запасом своего движения с окружением и потому ее можно в таких случаях считать замкнутой. Примером таких процессов могут быть удары и взрывы.
Если система меняет свой объем при постоянном внешнем давлении, то работа, совершенная ею, подсчитывается по формуле Л = /?Д1/.
Мы будем давление всегда считать положительным (не будем рассматривать растянутых тел), а тогда знак работы определяется знаком ДЕ: при расширении ДУ^>0, при сжатии ДУ<^0.
Изменение внутренней (в основном внутренней) энергии системы происходит при изменении температуры, плавлении и отвердевании, испарении и конденсации, при химических реакциях и т. п.
При нагреве, плавлении и испарении энергия растет, а при обратных процессах уменьшается. Химических реакций и других сложных процессов мы рассматривать не будем. Кроме того, считаем, что в системе одновременно все эти процессы не идут, а сменяют один другой (без этого упрощения нам задачи решать было бы очень трудно).
Расширением твердых и жидких тел при изменении их состояния, как правило, мы будем пренебрегать во всех случаях, кроме оговоренных особо.
Введем понятия теплоемкости и удельных теплот плавления, испарения и сгорания.
Величина С — называется теплоемкостью системы и показы-ДГ
вает, сколько тепла надо сообщить системе для изменения ее температуры на один градус. Величина c = ^f называется удельной теплоемкостью вещества и показывает, сколько тепла надо
226
сообщить единице массы вещества для изменения ее температуры на единицу. Величина С = ^|у— молярная теплоемкость—показывает, сколько тепла надо сообщить одному молю вещества, чтобы его температуру изменить на единицу.
Легко видеть, что все эти теплоемкости связаны между собой равенством
С = ст = CZ.
Величина Х=-^5— называется удельной теплотой плавления вещества и показывает, сколько тепла надо сообщить единице массы вещества, чтобы его расплавить.
Величина г—т-О- называется удельной теплотой испарения и численно равна теплоте, находимой для испарения единицы массы вещества.
Величина q = -~- называется удельной теплотворной способностью вещества (теплотворностью топлива) и показывает, сколько тепла выделяется при полном сгорании единицы массы топлива.
Здесь величины т, Дтпл, Д/тгисп и Дтсг означают соответственно массы нагреваемого, плавящегося, испаряющегося или сгорающего вещества. Стоящая в числителе вышенаписанных дробей величина Q есть тепло, которое поглощено или выделено при соответствующих процессах нагрева, плавления, испарения и горения.
Следует заметить, что величины С, с, С, X и г для данной системы, тела или вещества не есть величины постоянные. Они зависят и от температуры, и от давления в системе, и, кроме того, от характера процесса, происходящего в системе. Во избежание недоразумений необходимо, говоря об этих величинах, делать оговорки о том, при каких условиях в системе они нас интересуют.
Принято у этих величин ставить внизу индекс, обозначающий, какая величина в системе остается неизменной при интересующем нас процессе. Так, величины ср, кр, гр означают, что нас интересуют удельные теплоемкость, теплота плавления и испарения при неизменном давлении в системе. При этом ср Ф cv^ сТ, \р ГрфГуф ГТ и т. д.
Будем величины с, X, г и q считать положительными; остальные же величины могут быть и отрицательными. Дтпл^>0 (при плавлении), но Д/потв<^0 (при отвердевании), Дш„ц>0 (при испарении), но ДщКОнд <С О (ПРИ конденсации), Дпгсг всегда положительно.
Из первого начала видно, что при А —О и Д£мех = 0 имеет место <) = Д£ВН, поэтому величины СДТ, ХД/ипл и гДщисп можно рассматривать как величины, равные изменению внутренней энергии
227
системы при соответствующих процессах. Но это лишь в слуг чае А — 0 и ДЕмех — 0- Чаще всего это означает-пренебрежение работой по расширению системы, т. е. при pAV-^Afi", что при небольших р означает V = const. В этом случае
А£вн == СрАГ, Д/?вн -^'1/Д^ПЛ» А/Гвн = Г^АШисп,
где Су — теплоемкость системы при постоянном объеме; и rv—удельные теплоты плавления и испарения при постоянном объеме.
С учетом сказанного первое начало можно записать в развернутом виде так:
Q = Cj/A71 4-^-иАЩпл 4~ fv^mazn 4~ А£мех 4~ pAJZ.
В таблицах же фигурируют Су, "Кт и гт. В указанном приближении (рАИ<^А£), однако, имеем
Q = А£ = Су&Т -{- Хт'Ащпл /*/' А/цисп.
Второе начало термодинамики утверждает, что невозможно всю внутреннюю энергию системы превратить в механическую, а также нельзя при повторяющихся процессах (циклах) всю подведенную к машине теплоту превратить в работу.
Введем понятие коэффициента полезного действия цикла равенством
т1 = 9н79-- или 71 = 4,
где т]—к. п. д. цикла; QH — тепло, полученное рабочим телом от нагревателя; Qx — тепло, отданное рабочим телом холодильнику; С?н —Qx — теплота, превращенная в работу.
Из того, что вся теплота QH не может быть превращена в работу (или, что все равно, нельзя не отдать часть тепла холодильнику), следует, что для любых циклов. Это и есть одна из возможных формулировок второго начала термодинамики.
Часто используют понятие коэффициента полезного действия машины в несколько ином смысле. Именно, если к машине за некоторое время" подведено количество тепла Q или энергии Д£, а целенаправленно удалось использовать Qn0J1, ^Епол (или Лпол), то величину
— _ ОпоЛ _ Д^ПОЛ _ Лпол _ А^ПОЛ
Q ~ ДЕ — А ~ N
и называют коэффициентом полезного действия машины. Ясно, что и в этом случае ц 0.
Считается известной зависимость объема тела от температуры при постоянном давлении:
228
где Vo — объем тела при / = 0°С (именно при /==0°С, а не первоначальный объем, как ошибочно иногда считают); V — объем тела при температуре /; 0— термический (температурный) коэффициент объемного расширения.
4. ЗАДАЧИ К РАЗДЕЛУ «ЭНЕРГИЯ, РАБОТА, ТЕПЛОТА И АГРЕГАТНЫЕ ПЕРЕХОДЫ ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ»
Задача 33
Z молям газа сообщили Q тепла при постоянном давлении. Определить:
1) изменение температуры газа,
2) изменение внутренней энергии газа,
3) совершенную газом работу,
4) связь между Ср и Cv для идеального газа.
Решение
Первое начало можно записать в данном случае в виде Q = ZCKA7,4-pAV + A£Mex.
Вообще говоря, при нагреве газа в цилиндре с подвижным поршнем газ будет двигать поршень и, значит, при этом у газа несколько изменится кинетическая энергия. Кроме того, при расширении газа центр массы его меняет свое положение, что приводит к изменению его потенциальной энергии в поле тяжести. По если этим изменением механической энергии пренебречь, то
Q=ZCyA£-}-pAV. (1)
Видно, что для ответа хотя бы на один вопрос задачи одного уравнения (1) — недостаточно — слишком много в нем фигурирует величин, не упомянутых в условиях. Но очевидно, что в данном случае поможет уравнение состояния идеального газа, написанное для случая начального и конечного состояний:
pV = ZRT, (2)
p'V' = ZRT'. (3)
По условиям задачи нас интересует не состояние газа, а его изменение. Поэтому, вычитая (2) из (3), получим с учетом р — р’-.
pW = ZR&T. (4)
Исключая из (1) и (4) величину pAV, приходим к равенству
Q=Z(Cv + R)bT, (5)
откуда находим АТ.
229
В предпосылке к этому разделу говорилось, что разделение энергии системы на внутреннюю и механическую весьма условно. Но в данной задаче мы решили изменением механической энергии пренебречь, поэтому в (1) первое слагаемое означает изменение внутренней энергии газа. Но тогда
Д£ВН = 2СИДТ,
куда ДТ подставляем из (5).
Для ответа на третий вопрос задачи надо учесть, что работа газа phV найдется из (1) при известном Q и найденном из (5) ДГ. Именно,
рДV = Q- Д£вн = Q - ZCvbT = Q fl - Си \
\ Cy-t-ff'
Из определения молярной теплоемкости следует, что С = Но из (5) Q = Z (Си4~^) А?1 и> значит,
2(Су + Р)ЛТ_ ь — "гьт —
Поскольку, однако, (5) отображает процесс при р = const, то С —Ср и, значит, Ср — Cv-\-R.
Физически результат понятен: при V — const тепло идет только на изменение энергии (ибо Л —0), а при p — const еще и на работу по расширению, что и означает Qp^>Qy, а потому и CP>CV.
Задача 34
Переохлажденная на ДТ ниже точки замерзания жидкость при встряхивании частично замерзла за очень короткое время. Зная ДТ и количество жидкости т, найти количество затвердевшей жидкости Д/л, если окончательная температура системы стала равна нормальной точке замерзания.
Решение
Поскольку процесс теплообмена со средой стема не совершила; случае вид
протекал очень быстро, то существенного не произошло и существенной работы си-поэтому первое начало имеет в данном
0 = сгщДТ -[-^Дпг,
т. е. энергия, выделившаяся при затвердевании, была поглощена нагревшейся до точки замерзания жидкости. При небольших ДТ удельная теплота плавления практически постоянна, т. е. X const, и можно считать ее равной Хг.
230
Из вышенаписанного уравнения в этом случае следует
Л сг«ДГ
кт —------;--.
Л
Так как у->0, а ДГ^>0 (жидкость нагрелась), то Дт<^0, что и соответствует согласно нашей договоренности отвердеванию.
Задача 35
На тележку массой М, идущую без трения со скоростью о» по горизонтальным рельсам, неупруго падает с высоты h мешок массой т. Сколько тепла выделилось после удара?
Решение
Произошел удар, т. е. кратковременное взаимодействие тележки и мешка. Поэтому за время удара существенного обмена энергий со средой не произошло. Значит, первое начало с учетом Q = 0 и Л —О имеет вид
0= Д£вн 4~ А£мех- (1)
Но
+ <2)
где и — скорость мешка и тележки после удара. Она, очевидно, найдется из закона изменения импульса системы (количества движения тележки и мешка) при ударе. Именно,
(М-\-т)и— Л1у0 — mv — (QMgnig) kt. (3)
Поскольку все силы и скорость мешка направлены по вертикали, то в проекции на горизонталь (на направление движения тележки) получим
(М-}-т)и— Мщ = 0. (4)
Подставляя отсюда и в (2), получим после очевидных преобразований
др __ Mvl .
кЕ№е11 — 2 + 2 mgh,
а по упрощении л п mMvl ,
Д^мех — — 2(М + т) ~ msft"
Подставляя это значение ДЕ„еХ в (1), получим
ДЕвн
mMvl
2 (Л1 + w)
\-mgh.
Поскольку величины т, М, v9, g и h положительны, то Д/зим <^0, а Д^вн > 0, т. е. во время удара внутренняя энергия системы воз-
231
росла за счет убыли ее мёханической энергии. Очевидно, что температура системы повысилась и могла стать выше температуры среды.
После удара имеем
Q = ДЕВН -J- ДЕмех
или, пренебрегая сопротивлением движению тележки с мешком, а значит и изменением механической энергии,
(? = ДЕВН.
Если считать, что начальная температура системы до удара и окончательная (значительно после него) одна и та же, то без большой ошибки мы можем считать, что ДЕВН =— &ЕВВ, т. е. насколько внутренняя энергия системы увеличилась при ударе (нагрев), настолько она убыла при теплообмене со средой (остывание) после удара. Значит,
Q = ДЕМ = -ДЕвн = Д.Еме![ = - -mSh-
То, что Q<\0, означает отдачу системой тепла среде. Надо, однако, учесть, что ДЕВН =— ДЕВН верно лишь при указанном предположении о температуре системы и среды.
Если тележка после удара переехала в область, температура которой выше температуры тележки, то система могла не остывать, а нагреваться и соответственно не отдавать энергию, а по-
лучать ее.
задачу можно
Рис. 23.
В указанном предположении о температуре тележки и мешка
было бы решить и несколько более сокращенно. Именно, полагая очевидным, что изменение механической энергии системы (убыль ее) перешла во внутреннюю энергию системы с последующей отдачей ее в виде тепла среде, сразу можно написать Q = ДЕмех> где ДЕмех находится, как и указано выше.
При таком решении несколько сократилась запись, но ход решения (проведенный частично мысленно) остался, естественно, тем же самым.
Задача 36
В цилиндре, закрытом поршнем весом Р и сечением S, находится 1 молей известного газа. Поршень подсоединен к недеформиро-ванной пружине (рис. 23). Сколько тепла
надо сообщить газу, чтобы он нагрелся на ДЕ, а пружина сжалась на Д/? Теплоемкостью цилиндра и
поршня пренебречь.
232
Решение
Очевидно, что здесь происходит не только изменение внутренней энергии газа, но и изменение энергии поршня и пружины. Включим в нашу систему не только газ, но и поршень с пружиной. Тогда, в пренебрежении изменением кинетической энергии системы
Q = ZC Т + + Р Д/ + раД V,
где второе слагаемое — изменение потенциальной энергии газа из-за повышения на у его центра тяжести при нагреве. Слагаемое pa&V— это работа нашей системы против внешних сил, т. е. против силы атмосферного давления.
Можно было бы не включать в систему поршень и пружину. Но тогда внешней силой, против которой газ совершал бы работу, была бы переменная сила F = Р -ф- paS -ф- kx и решение несколько усложнилось бы. Читатель может убедиться в том, что результат получился бы тот же, если считать Fcp = Р -ф- p^S -ф- .
Задача 37
Сколько тепла надо сообщить куску металла для увеличения его объема на AV при атмосферном давлении?
Решение
Если считать, что центр массы бруска положения существенно не изменил, то первое начало имеет в данном случае вид
Q = cl/mA7’ ф-раДУ.
Из формулы же расширения тела при р = const имеем
ДЕ = уорд; = Еордт
(температура по Цельсию t не равна температуре по Кельвину Т, но разности их равны, что видно из связи СТ = £-ф-273).
Подставляя из этой формулы ДЕ в исходную формулу, получим
Q = с7т^ + раДК.
Атак как -^- = р0 — табличная плотность металла при Z = O°C, то
Читатель, пользуясь таблицами, легко найдет, что—^^Pi, поэтому работой при расширении твердых (да и жидких) тел при неболь
233
ших давлениях можно вполне пренебречь по сравнению с изменением их энергии при нагреве или агрегатном переходе. Поэтому
в данном случае с большой точностью Q зависит от величины объема куска металла.
=!—р—Ди. Ответ не Читателю предоста-
вляется возможность подумать над этим.
Формальный ответ можно усмотреть из приведенного здесь решения, стоит лишь сопоставить первые две формулы.
А как дать ответ «на пальцах»?
Задача 38
Автомобиль весом Р идет в гору с уклоном а и на расстоянии / увеличивает скорость от о0 до v. Считая известными коэффициент трения автомобиля о дорогу k, коэффициент полезного действия двигателя т]1 и трансмиссии (механизма, передающего усилие двигателя к колесам) а также род топлива q, найти еже-секундный расход топлива, т. е. величину =т0 (где Д/—время, за которое израсходовано Д/n топлива).
Решение
Поскольку в задаче фигурирует к. п.д., то удобно решение и начинать с того факта, что все тепло, выделившееся при сгорании топлива, превратить в работу не удалось, т. е. начинать А
с уравнения 7i = ^-
Далее, поскольку к. п. д. сложной машины, составленной из включенных последовательно машин, равен произведению к. п. д. отдельных звеньев, то = Очевидно также, что Q = q\m = — qmaM, где m0 — скорость сгорания топлива (ежесекундный расход).
Работа же А есть та работа, которую совершил «самодвижу-щийся» экипаж (см. часть I — „Механика"). Она пошла на увеличение механической энергии автомобиля и на работу против силы сопротивления, т. е.
А==3..^^1^Р^А-/гР cosa-Z.
Но в таком случае исходное равенство примет вид
V3 — vfl
7|17)2 = Р
{-1 sin a + kl COS a
qm^bt
Для ответа на вопрос задачи надо знать Д/. Поскольку все силы, действующие на автомобиль, практически постоянны, а масса его из-за сгорания топлива существенно не изменилась, то уско-
234
рение автомобиля практически постоянно. Но в таком случае v„ 4- v I 'll
= — и, значит, Д/ — — =—:—. С учетом этого имеем
F I ®ср ®о +v
f»2 _
—2—4 + I (sin я + k cos я)
W = P----------------21-------’
<?m0--j—
откуда и находится m0.
Задача 39
Брусок соскальзывает с горки высотой ho и углом наклона а. Считая, что «т;-я часть выделившегося тепла идет на нагрев бруска», найти на сколько градусов он нагрелся, если скорость бруска изменилась от р0 до V.
Решение
Прежде всего разъясним смысл устоявшегося термина «т|-я часть выделившегося тепла пошла на нагрев». Это выражение сродни бытующему «сколько тепла выделилось при ударе», только еще хуже. При скольжении бруска часть его механической энергии из-за трения переходит во внутреннюю энергию и бруска и подставки. Изменение внутренней энергии бруска часто и называют «теплотой, пошедшей на нагрев бруска». Из смысла первого начала ясно, что если и говорить о выделившейся в данном случае теплоте, так она пошла никак не на нагрев бруска, а наоборот — из-за отдачи бруском в виде тепла в окружающую среду части доставшейся ему внутренней энергии — на нагрев среды (и, естественно, привело к остыванию бруска). Величина ц, фигурирующая в условии, обозначается той же буквой, что и к.п.д., но не является к. п. д. Она просто показывает, какая доля изменения внутренней энергии системы брусок — плоскость досталась бруску. При решении же задач она формально фигурирует как к.п.д., а потому
(1)
сист
Очевидно, по условию задачи LEn„^ — cvm^T. Что касается Д£вн.сист, то из первого начала для бруска и подставки (в пренебрежении обменом энергий со средой и работой по расширению твердых тел) имеем
О == Д£вн. СИСТ A£Mex jJp или
А£вВ. СИСТ == А£ыех. бр, (2)
235
т. е. прибыль внутренней энергии системы равна-убыди механической энергии системы. У подставки она не изменилась, а у бруска
мех. бр = у-”1 + (0 - mghj. (3)
с„ДТ
Комбинируя (1), (2) и (3), получим -q ——5—, откуда
и находим ДТ.
Задача 40
Какое количество известной жидкости испарится за время Д/, если тепловая отдача нагревателя равна ц, его мощность N, количество жидкости т и теплоемкость сосуда, в который она налита, Cv известны?
Решение
Тепловая отдача нагревателя -ц — характеристика, несколько сходная с к. п. д. двигателя. Тепловая отдача нагревателя показывает, какая доля тепла, выделяемая им, может быть использована целенаправленно. Считая, что в данном случае все тепло, используемое целенаправленно, отдается сосуду и жидкости, получим
СКД7'+СЖтД7' + ГТДтисп+М1Л
NM
Последнее слагаемое в числителе есть работа по расширению пара. Ею уже пренебречь нельзя, как в случае работы по расширению твердых и жидких тел. Считая, что внешнее давление при испарении жидкости не меняется, получим из уравнения Клапейрона — Менделеева
TZ Д^ИСП7?7" п V-P ’
где Дтисп— масса пара, равная массе испарившейся жидкости. Поскольку ДУ — это изменение объема вещества при переходе его из жидкого состояния в газообразное, то ДУ = УП— Уж, и так как Vn^>V«, то ДУ?«УП. Окончательно имеем
(ск+тжсж) дг+(гт + пг1Атисп
п—-______________i_____L______
откуда и получим ответ, взяв из таблиц сж, гт и Т = ТКИп для известной жидкости и задав То или ДТ. В решении не учтена работа по расширению сосуда и жидкости, а также зависимость теплоемкостей и теплоты испарения от температуры.
236
Задача 65
Сколько тепла выделится при превращении в жидкость насыщающего пара, если температура среды постоянна и равна Т, а начальный объем пара V?
Решение
Очевидно, Q = rrAmK0IU4- p^V, где р — давление насыщающего пара при температуре конденсации Т. Поскольку ^пгкояя — — рнК (весь пар конденсировался) и ДК = КЖ—V, то с учетом того, что по уравнению Клапейрона — Менделеева
_ MRT____М RT___ RT
Р И ‘ (л Р“ И ’
имеем
(2 = -ГгРнК-ЬРн^(Кж-К). (*)
Г
Объем жидкости Кж, получившейся при конденсации пара, найдется по формуле
Кж=~ж- = ^(1 + ^). ГЖ г О Ж
Так как /пж = тп, а тп = рнК, то Кж — , что при под-
становке в (*) дает
Q = Vp Гт_^^ГРн1£+М_ i'll
Ч ИН I т ' (X L Рож J)
Видно, что Q<^0. Это и означает в соответствии с договоренностью о знаках в уравнении первого начала выделение тепла. Вообще говоря, возможно формально и Q 0 при рн (1 -ф- $t) рОж, что как будто противоречит выделению тепла при конденсации. Но дело в том, что рн(1 + ?О^>Рож лишь при t настолько больших, что ^>/крит, т. е. когда конденсации не может произойти. Кроме того, формула рж = ]-7р^ справедлива лишь при небольших значениях t. Поэтому в нашем случае обязательно Q<^0.
Задача 41
В стакан теплоемкостью Cv налито тж жидкости с удельной теплоемкостью сж и брошен кусок льда массой тя. По прошествии некоторого времени вся система пришла в равновесие со средой при температуре 9, большей температуры таяния льда Тпл. Зная исходные температуры стакана Тст, жидкости Тж и льда Тд, найти количество тепла Q, которым обменялась система с внешней средой.
237
Решение
Поскольку об испарении речи нет, то работой по расширению системы пренебрежем, равно как и изменением механической энергии системы из-за ее расширения. Тогда
(2 = Д£СТ4-ДЕЖ + Д£Л или
Q — Су (9 — Тст) -J- сжтж (9 — Тж) слтл (Тпл — Тл)
X уДШпл СЖШВ (9 Тпл), где последние три слагаемые отображают нагрев льда до точки плавления, плавление и нагрев получившейся изо льда воды от точки плавления до температуры 9.
Очевидно, знак Q зависит от соотношения между слагаемыми в правой части. Нужно только помнить, что в случае плавления А/Япл^>0. В данном случае Атпл — тл, ибо лед весь растаял (по условию задачи 9^>ТПЛ).
Задача 42
В цилиндре объемом V находится Mi воздуха и М3 воды при температуре, близкой к замерзанию. Цилиндр выдерживает давление не большее рпред. Сколько топлива с калорийностью q надо сжечь, чтобы цилиндр взорвался, если т]-я часть выделяющегося при сгорании тепла передается цилиндру с содержимым? Теплоемкость цилиндра Cv. К моменту взрыва вода испарилась целиком.
Решение
Первое начало написать для этого случая в конечном виде трудно, ибо при нагреве происходило испарение жидкости, расширение пара и газа, изменение теплоемкостей и теплоты испарения.
Но если пренебречь работой по расширению пара и газа, а также зависимостью С и г от температуры, то полезная теплота пошла на нагрев цилиндра, воздуха и пара от температуры таяния льда Т„л до температуры Т, при которой произошел взрыв, а также на испарение воды. Полагая (еще одно упрощение), что вода испарилась при температуре, близкой к Тпл, получим
Q = Су (Т - Тпл) + CVl + CyJ (Т - Тпл) + ггДтисп, где Д/тгисп = М2— количество пара, получившегося из воды.
Температура взрыва Т определяется давлением, при котором он происходит. Но по уравнению Клапейрона—Менделеева для смеси паров и воздуха имеем
п — , МАЯТ
Л<ред —Т у •
238
Необходимое для решения задачи количество тепла Q находится из условия, что только т)-я часть тепла, выделившегося при сгорании топлива есть Q, т. е. из уравнения
Q
(**)
Подставляя в исходное равенство величины Т ные из (*) и (**), получим
и Q, выражен-
Гпл
откуда и находим Дтсг.
Задача 43
Покоившийся снаряд взорвался при сгорании в нем m пороха с колорийностыо q. Оценить кинетическую энергию осколков в начальный момент.
Решение
Если считать, что порох сгорает полностью и быстро в малом объеме, то с некоторой ошибкой можно полагать всю внутреннюю энергию пороха перешедшей в механическую энергию осколков.
Считая порох источником энергии для оболочки снаряда, имеем
q&tticv — Д.£?к,
где Дтсг = т, а \ЕК~ЕК.
Здесь не учтен ряд многих эффектов, в частности то, что оболочка снаряда и сам порох нагревались. Поэтому оценка, конечно, весьма груба.
Задача 44
Какую работу надо совершить для равномерного увеличения радиуса мыльного пузыря на небольшую величину Д^? Поверхностное натяжение а, внешнее давление р и радиус пузыря R известны, а температура системы существенно при расширении не менялась.
Решение
Поскольку изменение радиуса пузыря невелико, то и давление, производимое пленкой на газ внутри пузыря, практически постоянно. Поэтому Д = рДУ, где р—давление внутри пузыря.
239
Поскольку пузырь раздувается равномерно, то каждый малый участок его поверхности находится в равновесии, поэтому
рДЗ = (р
внешн + рл) Д5 или
Р == Рвнешн Рд и, значит,
А = (Рвнешн “j- Рл) Д V = -ф- ‘
Так как ДК = 4к/?2Д/?, то
Л==(ра4-^)4к/?2Д/?.
Расчет справедлив лишь для ^R^R, ибо только тогда рл^ const и ДУ = 4к/?2ДЯ
Задача 45
Как изменится температура известной жидкости, если в нее опустить капиллярную трубку, теплоемкостью которой можно пренебречь? Наружная стенка трубки к смачиванию безразлична, а внутренняя полностью смачиваема или, наоборот, абсолютно несмачиваема. Объем жидкости V известен. За время процесса жидкость получила Q тепла. Каким будет ответ в случае замкнутости системы?
Решение
При погружении трубки в жидкость последняя будет или опускаться или подниматься по внутренней части трубки до тех пор, пока не наступит равновесие, определяемое тем, что силы, действующие на поднявшийся столб, дадут в сумме нуль. Из этого условия равновесия столба (ря p^S — (pgh -ф- ра) S следует Р« = Pgh.
Поскольку жидкость полностью смачивает (или не смачивает) трубку, мениск будет полусферой с радиусом, равным радиусу трубки. Поэтому рл = ^ и, значит,
2а , • 2а .
#=Pgh или h = ^g, (*)
где R — радиус трубки.
Первое начало дает (в пренебрежении работой расширения жидкости)
Q = с ДТ -ф- MgWic,
где Д/гс — изменение высоты центра тяжести жидкости. Очевидно, что из-за малости объема капилляра по сравнению с объемом жидкости можно считать, что изменилось положение центра тяжести 240
только у той части жидкости, которая вошла в трубку. Но это значит, что Mg^hc mg у, где т — масса вошедшей в трубку жидкости, h—высота этого столба.
С учетом сказанного имеем
Q^cv?V^T±^Rihg^,
что совместно с (*) дает
Q^c^plZATzb^.
Г о
Знак «Ц-» соответствует смачиванию (жидкость поднимается), знак «—» — несмачиванию (жидкость опускается).
Если система замкнута, то Q = 0 и
ДГ = —
2о8 \ м2Н-
(**)
Из этой формулы видно, что смачивающая жидкость будет охлаждаться (ДТ<^0), а несмачивающая — нагреваться (ДТ^>0).
Коэффициент а зависит от температуры, а мы считали его постоянным. Но допущенная ошибка, очевидно, невелика при Утрубки «С V. Действительно из (**) следует, что АТ р и ДГ при большом V очень мало, что означает const, а значит и а const.
Задача 46
Найти работу при замкнутом процессе (цикле), представляющем в координатах р и V окружность с центром в точке р0, Ко, а максимальные объем и давле
ние равны соответственно Ктах и Ртах (рис. 24).
Решение
Элементарная работа ДЛ равна рДК. При этом расширению соответствует положительная, а сжатию — отрицательная работа.
Очевидно Ait 2,3— работа расширения газа — будет равна площади под кривой 1—2—3, з Л, 4,1 — работа сжатия — пло-
щади под кривой 3—4—1.
Полезная работа за цикл Л = Л1,2, з + A,4.i численно равна в координатах pV площади, охватываемой кривой 1—2—3—4,
которая в нашем случае есть окружность, поэтому
А - S = TtR^—Tt (pfflax — рв) (Кшах — Vfi)-
241
Задача 47
Показать на примере мыльного пузыря, что коэффициент поверхностного натяжения аг численно равен работе, необходимой для увеличения поверхности пленки на единицу при изотермическом процессе.
Р е ше н и е
Элементарная работа по расширению пузыря (см. задачу 69) подсчитывается по формуле
ДЛ = (Рвиешн + Рл) 4кК2ДК = 4ат
= РвИеши4^Д7? + -^4^Д^
Работа по растяжению пленки — это второе слагаемое. Поэтому ДАа = 2а • SnRhR. Но 8nRhR — изменение поверхности сферы при малом изменении ее радиуса на Д/?, следовательно, ДДа = 2атД5. Так как у пузыря две поверхности, то 2Д5 есть изменение полной поверхности. Значит,
г —2AS ДУПОЛН’ что и требовалось показать.
Задача 48
Какую работу надо совершить для равномерного изотермического раздувания мыльного пузыря от Rt до Rt при наружном давлении р8Нешн?
Решение
Очевидно, искомая работа складывается из работы против внешнего давления и работы по изотермическому увеличению пленки, а потому
А = Двн Дз — Рвнешн^ К “И атД5 = j = Рвнешн 4 * (Rl - R1) + М* (RI ~ RI).
Задача 49
В калориметре теплоемкостью Cv находится nti льда при температуре Тя <С 273° К. В калориметр впускают та водяного пара при температуре ГП^>373°К. Найти температуру 9, установившуюся в калориметре по прошествии достаточно большого времени.
242
Решение
Задача, как сразу видно, сформулирована недостаточно конкретно: не сказано, что получилось в конце концов в калориметре— лед, вода, пар или смесь.
Сделаем предположение, что в конце процесса получилась вода при температуре 6 и небольшое количество насыщающего пара при той же температуре. Тогда, пренебрегая теплообменом системы со средой, получим
О = ДЕкал -j- ДЕЛ Д£п -ф- /7СрДV
или
О = Cv (0 - Тл) + [с.,тл (273 - Тл) + ХтДщпл -J- свтл (0 - 273)] +
4 [сптп (373 — Тп) -|~ /'тДшконд свтп (9 — 373)] -j- Pcp^V. (*)
Согласно договоренности о знаках в данном случае Дтпл^>0> а Дт«Оид<С0> а именно Дщпл = тл и ДтК0Нд = —т„. Что касается слагаемого рсрДУ, то его можно только оценить, ибо в условиях задачи не сказано, как происходил процесс конденсации пара (т. е. как при этом менялось давление с температурой). Положим рср^/>нач2+/> (что, вообще говоря, верно лишь при р = рНач4~ 4-const Т, в чем у нас уверенности нет).
Изменение же объема пара при конденсации ДУ = (14— V„)^ а» — Уп. В этом случае
рсрд17^-е-^ уп.
Если пренебречь конечным давлением пара, что возможно при Тп, значительно больше, чем 373° К, то
РерДЕ^-Л^Н.
Но по уравнению состояния plta4V„ — — RTn и, значит, р
рсрд1/№_^.
Видно, что эта работа отрицательна, и это находится в соответствии с нашей договоренностью о знаках величин, входящих в первое начало термодинамики.
Подставляя найденное значение рсрД17 в (*), получим уравнение, из которого и найдем 0. Правда, оценка последнего слагаемого в (*) довольно груба, но она едва ли несет в решение большую ошибку, чем неучет теплообмена системы со средой.
Кроме этих неточностей, в решении имеются и другие, обусловленные тем, что мы не учитывали зависимости Су, гт и. Хт от
243
температуры и будем брать их из таблиц при Т = 273°К и Г —373° К. И, наконец, мы полагали, что процессы нагрева льда, его таяния, нагрева получившейся воды и т. д. сменяют один другой, в то время как они идут все совместно, сразу.
Задача 50
С какой скоростью должен влететь в земную атмосферу метеорит, чтобы он смог испариться?
Решение
Метеорит может изменить свое агрегатное состояние за счет убыли своей механической энергии. При этом некоторая доля (1—4 этой убыли будет отдана окружающей среде в основном в виде тепла (метеориту же достанется tq-я доля изменения этой анергии).
Имеем
Q— 4“ Д^мех + РсрДР-
По нашему предложению
Q = (I — «]) Д£мех.
Но тогда исходное равенство запишется в виде
(!—»]) Д£мех = Д£вн + Д£мех + РсРдУ или по приведении подобных членов
т]Д£мех = Д£вн РсрДР •
Полагая, что метеорит пришел из бесконечности со скоростью и взорвался где-то на высоте h, имея уже малую скорость, полу-с тМ,
чим с учетом сп = —
Д£мех = Д£к + ДЕП = (о - 4-
+b4M=-'”('?+i4U Подставляя это значение в предыдущее равенство, получим, раскрывая подробно выражение для Д£вн,
т/n 4~ Т _|1 = cTBm (Тпл — Т9) ~4 ^гД^пл
—С1ЕШ (Ткип Тпл) j - ГтД/Иисп “4 (Т Ткип) “4 РсрДР•
Вместо суммы величин Хт 4~ сж (TKHn — Тпл) 4~ г г может быть взята удельная теплота сублимации (возгонки) I, тогда, учитывая А/ипл = Дтисп = т, получим
ч +.7 = Ств (Гпя “ Гв) +1 + с“(Г “ Тыа} +
244
Работу по расширению можно оценить как и в предыдущей задаче (только здесь ДК^>0). Окончательное учетом малости начальной температуры (То мало по сравнению Тпл, Ткип и Т) имеем
ч (т + ~ +/+Сп (Г - ТКип)+
Отсюда можно найти ц0- Конечно, это оценочное и довольно грубое значение для г0.
5. ЗАМЕЧАНИЯ К РАЗДЕЛУ «ТЕРМОДИНАМИКА»
Как показывает опыт, существенную помощь в обучении решения задач на этот раздел может оказать тренировка в решении, а потом и составлении самими учащимися задач в общих чертах, в наметках, без особой детализации и доведения до конкретного ответа.
Приведем несколько примеров.
Пример 1. Написать идентичные уравнения, отображающие неполноту использования теплоты и энергии: а) в нагревательном приборе, б) в двигателе автомобиля, в) в кузнечном прессе.
Решение. Поскольку неполнота использования энергии в машинах характеризуется в первую очередь их коэффициентом полезного действия, то искомые уравнения имеют вид
а)
б)
в)
п Фполезн Фна нагрев
Фподвед ^2подвед
•С Ополезн _ А
Ч Оподвед ^2подвед
п — Сполезн ^на деформ, детали
ч Фподвед Уподвед
Пример 2. Конкретизировать предыдущую задачу для случаев: а) за счет сгорания топлива нагревается некоторый предмет; б) за счет энергии топлива автомобиль идет по горизонтальной дороге без ускорения;
в) пресс известной мощности деформирует деталь при среднем
давлении рср. Решение. . сткТ б) > ‘ qLm,c в) Т— В' Л~ N-t •
Пример 3. Написать первое начало термодинамики для случая, когда в идеальном калориметре за счет остывания бруска плавится лед (без предварительного нагрева) и получается теплая вода.
245
Решение. Если калориметр идеальный, то систему, заключенную в нем, можно считать замкнутой, и тогда первое начало будет иметь вид \
0 = ДЕвн-|- ДЕмех.
Поскольку никакие механические процессы в системе не происходят, то ДЕмек = 0, а потому и ДЕВН = О или более подробно ДЕЛ-j-ДЕВ + Д£бР = 0 и окончательно
О — ^тД/Ипл + (Т — 273) 4“ Сбр^бр (Т — Го 6р).
При этом Дтпл —тл = тв, ибо весь лед растаял.
Пример 4. Написать уравнение, отображающее нагрев камня, упавшего с некоторой высоты.
Решение. Очевидно, камень нагрелся за счет убыли части своей механической энергии, поэтому (см. задачу 75)
cvm^T cvm&T Су^Т
~ — АД’мех — mgMi — g(Q — h) gh •
Ясно, что эти примеры можно рассматривать как некоторые наметки. Возможны самые различные вариации и конкретизации их.
Чем хороши подобного рода задачи? Они отучают ученика от извечной заботы: откуда взять недостающие в условиях величины и куда пристроить имеющиеся, от фетишированной привязанности к конкретным данным задачи. Конечно, эта забота должна быть, но она не должна давлеть над учеником. Гораздо важнее то, что ученик научается определенным процессам сопоставлять определенные уравнения в общем виде, а потом уже конкретизирует их вид в соответствии с конкретными величинами, фигурирующими в условиях.
В этом отношении термодинамика очень «удобна», ибо имеется изрядное количество таких процессов, которые описываются с помощью начал и уравнений состояния с большими возможностями в варьировании условий. При этом, как показывает опыт, учащиеся довольно легко с подобными задачами справляются, а потом этот метод переносят и на другие разделы, т. е. у них действительно вырабатывается метод в подходе к решению и его проведению.
Весьма полезно вести занятия по решению задач примерно в такой последовательности:
1. Решение некоторых конкретных «обычных» задач.
2. Примерные решения задач с «размытыми» условиями типа примеров 1—4.
3. Решение конкретных задач с учетом метода решения задач малоконкретизированных, т. е. решение опять же «обычных» задач, но с более общих позиций, единым методом.
Сказанное здесь в большей мере относится и к другим разделам физики, но в термодинамике это психологически проще воспринимается.
СОДЕРЖАНИЕ
Стр.
От автора ....................................................... 3
Часть I. Механика
1. Элементы векторной алгебры.................................... 6
2. Примерная схема решения задач ............................... 12
3. Кинематика материальной точки ................................ —
4. Динамика материальной точки (собственно законы Ньютона) ... 24
5. Закон изменения количества движения системы тел и закон его сохранения...................................................... 54
6. Движение тела переменной массы............................... 59
7. Работа, энергия, мощность .................................. 66
8. Столкновение тел............................................. 75
9. Тяготение.................................................... 85
10. Динамика движения материальной точки по окружности......... 94
11. Статика.................................................... 109
12. Гидроаэростатика........................................... 121
13. Движение заряженных частиц в силовых полях ............. 135
14. К обоснованию выбранного способа решения задачи ........... 145
Часть И. Механические колебания и волны
1. Основные понятия ........................................... 155
2. Замечания к решению задач................................... 161
3. Сводка формул для гармонических колебаний................... 163
4. Задачи к разделу «Колебания и волны»........................ 164
Часть III. Термодинамика
1. Идеальный газ (основные понятия) ........................... 188
2. Задачи к разделу «Идеальный газ и пар»...................... 192
3. Энергия, работа, теплота.................................... 224
4. Задачи к разделу «Энергия, работа, тейлота и агрегатные переходы термодинамических систем»...................................... 229
5. Замечания к разделу «Термодинамика»........................ 245