Текст
С. Г. ШВХЦНЦКИ11
АНИЗОТРОПНЫЕ
ПЛАСТИНКИ
Сканировал и обрабатывал
Лукин А.О.
О ГИЗ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
ИЭСКЗА—1947—ЛЗНПЯГРАД
Редактер П. А*. Снитко.
Технический редактор Ахламов С. U.
Подписано к печати 6/II 1917 г. 22,25 печ. ла 20,75 уч.-авт. л. 38 000 тип.
зн. в печ. л. Тираж 5000 экз. А-02222. Цена книги 13 р. Переплет 1 р. 50 к.
Зак. 719.
16-я типография треста «Полигрэфкнига» ОГИЗа при Совете Министров СССР
Москва, Трёхпрудный, 9.
ПРЕДИСЛОВИЕ
В современной технике, и особенно в самолётостроении,
находят применение в качестве элементов конструкций
анизотропные пластинки, т. е. пластинки, у которых со-
противление механическим воздействиям различно для раз-
ных направлений. К таким пластинкам относятся плас-
тинки, изготовленные из авиационной фанеры, текстолита
и некоторых других авиационных материалов. Экспери-
ментальные исследования такого материала, как фанера,
показывают большое различие между модулями упругости
для основных направлений—^доль волокон рубашки и по-
перёк волокон; есть фанера, у которой модули относятся,
как 2:1, а есть и такая, у которой отношение модулей
равно 12:1. Ясно, что рассчитывать фанерные пластинки на
прочность по формулам, выведенным для изотропного тела,
неправильно, и для расчёта приходится выводить специаль-
ные формулы на основании теории упругости анизотропного
тела. Как анизотропные можно рассматривать и такие плас-
тинки, у которых искусственно создано различие между
жёсткостями изгиба для разных направлений —пластинки
гофрированные или усиленные гофром, пластинки, усилен-
ные часто поставленными параллельными рёбрами жёстко-
сти и т. д. G подсчётом напряжений и деформаций в
анизотропных пластинках приходится сталкиваться не толь-
ко авиаконструктору, но и физику, работающему с плас-
тинками, вырезанными из кристаллов, например, с квар-
цевыми пластинками.
Литература по вопросам, связанным с прочностью ани-
зотропных пластинок, в настоящее время ещё очень огра-
ничена, так как эти вопросы ещё недостаточно разработаны.
Литература сводится к ряду отдельных журнальных статей
советских и иностранных авторов, опубликованных в раз-
личных журналах и трудах научно-исследовательских инсти-
тутов, и к нескольким небольшим книжкам по отдельным воп-
росам прочности анизотропных пластинок. Некоторые из
з
работ нашли своё отражение в справочниках и руководствах,
большая же часть остаётся неизвестной широкому кругу
инженерно-технических работников. Такой книги, где были
бы систематически изложены вопросы, связанные с раз-
личного рода деформациями и прочностью анизотропных
пластинок, где лица, интересующиеся по роду своей ра-
боты расчетом анизотропных пластинок на прочность,
могли бы найти необходимые им сведения,—до сих пор
не существовало. Автор настоящей работы поставил своей
задачей восполнить этот пробел и создать такую книгу,
которая охватывала бы по возможности большинство сов-
ременных исследований по вопросам деформации анизо-
тропных пластинок и могла бы служить пособием для
инженера, авиаконструктора, физика и других специали-
стов, работающих с анизотропными пластинками.
В настоящей книге отражены три основные темы:
обобщённое плоское напряжённое состояние анизотроп-
ных пластинок (главы 2 — 7); изгиб анизотропных пла-
стинок (главы 8 — 10) п устойчивость анизотропных пла-
стинок (главы 12 —15). Большинство решений, изложенных
в книге (особенно в главах, посвящённых плоской
задаче), принадлежит самому автору и представляет
собой результат двенадцатилетней работы в области теории
упругости анизотропного тела.
Все изложенные вопросы касаются лишь малых упру-
гих деформаций пластинок. Вопросы, связанные с пла-
стическими деформациями пластинок, с поведением пласти-
нок после потери устойчивости, с температурными и
остаточными напряжениями в пластинках и т. п., в кни-
ге не отражены; по этим вопросам автору неизвест-
ны какие-либо исследования, за исключением несколь-
ких экспериментальных работ. Эти вопросы ещё ждут
своих исследователей. Очень мало изучены вопросы ди-
намики анизотропных пластинок; известный автору мате-
риал по вопросу о поперечных колебаниях пластинок со-
бран в главе 11.
Принимая во внимание довольно большой материал
и малый объём книги, автор стремился сделать изложение
по возможности сжатым. Основное внимание обращено на
практическую сторону излагаемых решений; формулы и
заключения, представляющие чисто теоретический интерес,
в большинстве случаев даны без вывода с указанием лите-
ратуры, где интересующиеся могут найти подробное изло-
жение и доказательства. В тех случаях, где это представ-
ля л ось возможным и интересным для практики, резуль-
таты доведены до расчётных формул, графиков или таблиц.
Весь материал, изложенный в книге, разбит на пят-
надцать глав и 89 параграфов. Приводимые формулы
и уравнения занумерованы, причём первая цифра указы-
вает параграф книжки, а вторая — номер формулы по
порядку в данном параграфе. В конце приведён перечень
литературы по вопросам деформации анизотропных пла-
стинок; туда же включены некоторые основные руководства
и работы по теории упругости, используемые в книге.
Ссылаясь на литературу, мы указываем номер работы,
по прилагаемому списку, в квадратных скобках.
Май 1944 г.
С. Г, Лехницкий
ОГЛАВЛЕНИЕ
Глава I. Основные уравнения теории упругости анизо-
тропного тела................................ 11
1. Напряжённое состояние сплошного тела. ...... 11
2. Обобщённый закон Гука . . ......... 15
3. Основные уравнения и основные задачи теории упру-
гости .............................................. 20
4. Криволинейная анизотропия...................... 23
Глава II. Плоская задача теории упругости анизотропного
тела................................................ 26
5. Обобщённое плоское напряжённое состояние.......... 26
6. Плоская деформация.............................. 30
7. Общие выражения для функции напряжений............ 32
8. Связь плоской задачи теории упругости с теорией
функций комплексного переменного ......... 35
9. Лист фанеры, как анизотропная пластинка ...... 39
10. Пересчёт модулей упругости при переходе к новым
осям .......................................... . 41
И. Пересчёт комплексных параметров при переходе к
новым осям .................................... 45
12. Примеры преобразования упругих постоянных и ком-
плексных параметров.................................. 47
13. Обобщённое плоское напряжённое состояние в плас-
тинке с цилиндрической анизотропией............. . 49
Глава III. Изгиб анизотропных балок и кривых брусьев. 52
14. Простейшие случаи распределения напряжений в
плоской пластинке................................... 52
15. Изгиб консольной балки поперечной силой.......... 55
16. Изгиб балки равномерно распределённой нагрузкой . 57
17. Изгиб балки произвольной нагрузкой............... 59
18. Изгиб клинообразной консоли силой, приложенной к
вершине.............................................. 62
19. Изгиб клинообразной консоли моментом............. 65
20. Изгиб клинообразной консоли распределённой нагруз-
кой . . ........................................... 67
6
21. Чистый изгиб кривого криволинейно-анизотропного
бруса............................................... 70
22. Изгиб кривого криволинейно-анизотропного бруса попе-
речной силой......................................... 72
23. Распределение напряжений в криволинейно-анизо-
тропной трубе ........................................ 74
Глава IV. Распределение напряжений в бесконечной уп-
ругой среде ........................................• . • 76
24. Упругая полуплоскость, нагруженная вдоль границы . 76
25. Действие сосредоточенной силы, приложенной к гра-
нице .................................................. 80
26. Действие сосредоточенной силы, приложенной вну-
три неограниченной среды ............................. 85
Глава V. Концентрация напряжений около эллиптиче-
ского и кругового отверстия................................ 88
27. Определение напряжений в пластинке с эллиптическим
отверстием............................................. 88
28. Частные случаи................................... 92
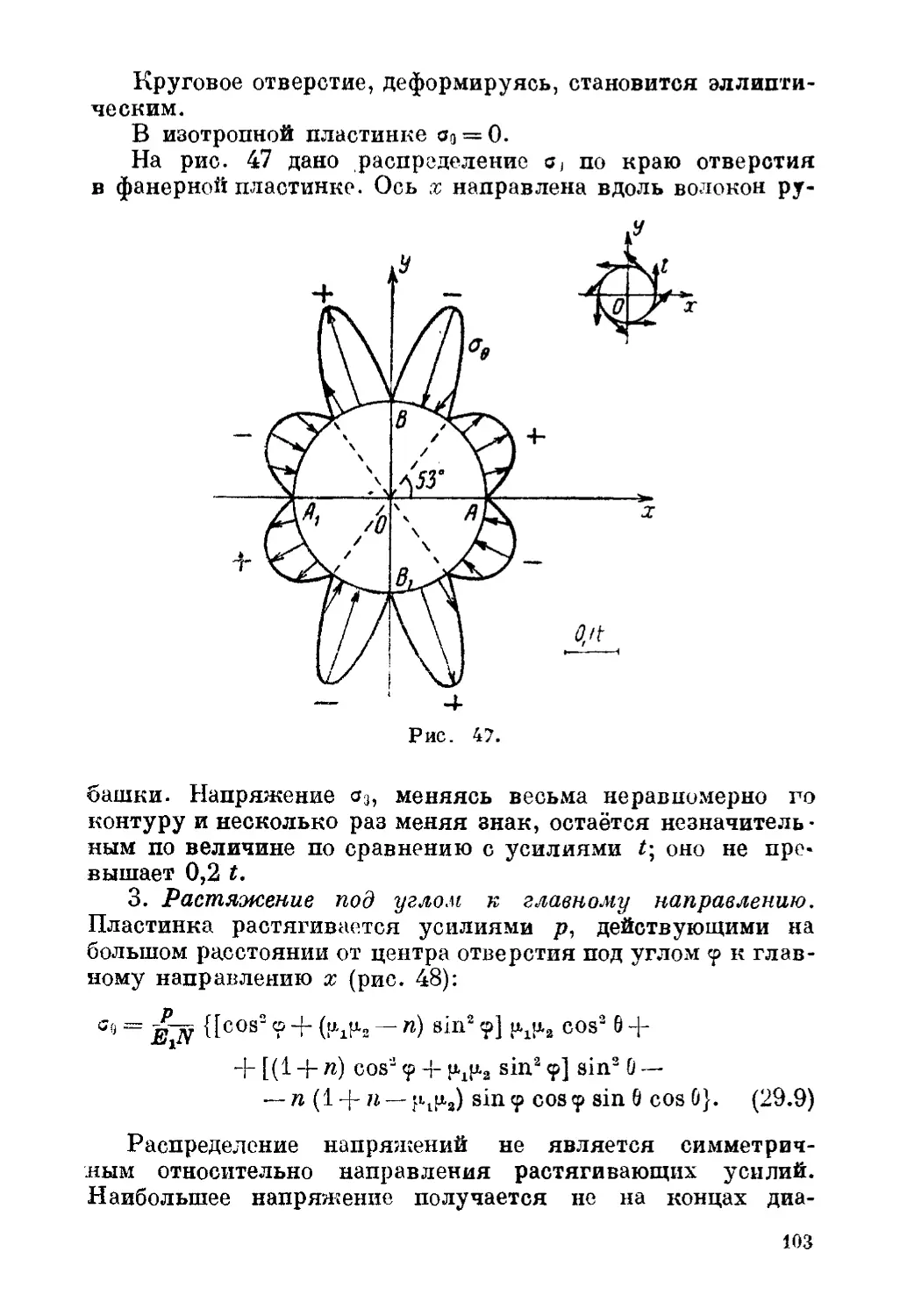
29. Распределение напряжений в ортотропной пластинке с
круговым отверстием при заданных внешних усилиях 100
30. Распределение напряжений в ортотропной пластинке с
круговым отверстием при заданных смещениях . . . 113
Глава VI. Распределение напряжений в эллиптической
пластинке и круглом диске............................. , 119
31. Распределение напряжений в нагружённой эллипти-
ческой пластинке ........................... ........ 119
32. Распределение напряжений во вращающейся эллипти-
ческой пластинке и круглом диске . . ................. 123
33. Распределение напряжений во вращающемся криво-
линейно-анизотропном диске............................ 126
Глава VII. Приближённый способ определения напряже-
ний в пластинке со слабо выраженной анизо-
тропией ... ........................................ . 127
34. Плоская задача для слабо анизотропной пластинки . 127
з5. Распределение напряжений в пластинке, ослабленной
отверстием............................................ 132
36. Растяжение пластинки с отверстием, близким к квад-
ратному ............................................. 134
37. . Распределение напряжений в однородном кольце, сжа-
том равномерным давлением............................. 137
7
Глава VIII. Теория изгиба анизотропных пл&стппок . . . 139
38. Приближённая теория изгиба анизотропных пла*
стилок (тонких плит) ..............•................. 139
39. Уравнение изогнутой поверхности............. . 146
40. Уравнение изогнутой поверхности с учётом про-
дольных сил. Пластинка па упругом основании .... 149
41. Связь теории изгиба с теорией функций комплексно-
го переменного .................................... 154
42. Определение жёсткостей изгиба и кручения различных
ортотропных пластинок ............................. 158
43. Определение жёсткостей многослойных пластинок . . 162
44. Определение жёсткостей для пластинок с модулями
упругости, меняющимися но толщине................... 107
45. Вычисление жёсткостей для произвольных направле-
ний ............................................... 170
46. Изгиб пластинки, обладающей цилиндрической анизо-
тропией ........................................... 172
Глава IX. Изгиб пластинок нормальной нагрузкой. . . . 175
47. Простейшие случаи изгиба ................... . . 175
48. Изгиб ортотропной прямоугольной пластинки с опёрты-
ми сторонами...................................... 179
49. Изгиб ортотропной прямоугольной пластинки с Двумя
опёртыми сторонами .................................. 182
50. Изгиб прямоугольной ортотропной пластинки равно-
мерно рапределёпной нагрузкой ....................... 186
51. Изгиб полосы с опёртыми сторонами * . ........... 193
52. Приложения теории изгиба ортотропной полосы . . . 198
53. И-гиб эллиптической и круглой пластинки, заделан-
ной по краю ..................................... . . 202
54. Изгиб круглой криволинейно-анизотропной пластинки 205
55. Приближённый метод определения прогибов анизо-
тропной пластинки . » •............................. 212
Глава X. Изгиб пластинок нагрузкой, распределённой по
краю......................................«......... 217
56. Местные напряжения около прямолинейного края . . 217
57. Действие сосредоточенного момента.............. 220
58. Изгиб пластинки с эллиптическим отверстием .... 223
59. Чистый изгиб пластинки, ослабленной круговым отвер-
стием .......................................... . . 226
Глава XI. Поперечные колебания пластинки................ 232
60. Свободные колебания пластинки.................... 232
61. Определение частот прямоугольной пластинки «... 236
8
62, Приближённые методы определения частот ...... 239
63. Примеры определения частот в первом приближении . 242
64. Вынужденные колебания пластинки ............... 244
Глава XII. Основы теории устойчивости пластинок .... 246
65. Общая постановка задач об устойчивости пластинок . 246
66. Основные методы определения критической нагрузки 248
67. Работа внешних усилий.......................... 252
Глава ХШ, Устойчивость прямоугольной пластинки и по-
лосы при распределённой нагрузке ... ... 254
68. Устойчивость прямоугольной опёртой пластинки, сжа-
той в главном нап равлении......................... 254
69. Устойчивость опёртых фанерных пластинок, сжатых в
главном направлении ............................ ... 258
70. Устойчивость прямоугольной пластинки с двумя
опёртыми сторонами при сжатии в главном направ-
лении ......... .................................... 263
71. Устойчивость пластинки, сжатой по двум направ-
лениям ............................................. 268
72. Устойчивость пластинки, нагруженной нормальными
усилиями, рапределёнными по линейному закону • . 272
73. Устойчивость прямоугольной пластинки под дей-
ствием касательных усилий.......................... 277
74. Устойчивость бесконечной полосы под действием ка-
сательных усилий.................................... 280
75. Устойчивость пластинки при совместном действии
нормальной и касательной нагрузки .............. 285
Глава XIV. Устойчивость пластинок, сжатых сосредото-
ченными силами ................ 290
76. Устойчивость прямоугольной пластинки, нагруженной
сосредоточенными силами..................<.......... 290
77. Метод функций влияния........................... 293
78. Функции влияния для ортотропной пластинки с опёр-
тыми сторонами.................................... 295
79. Сжатие пластинки двумя силами.................. 300
80. Сжатие пластинки четырьмя силами............. . 304
Глава XV. Устойчивость пластппок, подкреплённых рёб-
рами жёсткости..................................... 308
81. Устойчивость пластинки с продольными рёбрами,
сжатой равномерно распределённой нагрузкой . * . . 308
9
82. Случай одного продольного ребра .......... 312
83. Устойчивость пластинки с поперечными рёбрами
сжатой равномерно распределённой нагрузкой .... 318
84. Случай одного поперечного ребра........... 323
85. Устойчивость пластинки, усиленной рёбрами жёстко-
сти, под действием сил, приложенных по концам рёбер 327
86. Метод функций влияния.................... 330
87. Устойчивость пластинки с одним ребром..... 337
88. Устойчивость прямоугольной пластинки, усиленной
рёбрами по двум сторонам...................... 340
89. Пластинка, усиленная одинаковыми рёбрами но двум
сторонам................................... 343
Литература.................................... 349
Именной указатель ........................... 353
Предметный указатель . ....................... 354
ГЛАВА I.
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
АНИЗОТРОПНОГО ТЕЛА.
1. Напряжённое состояние сплошного тела.
Напряжённое состояние сплошного тела, находящегося
в равновесии или движении под действием внешних сил,
характеризуется, как известно, шестью составляющими
напряжения, которые действуют на трёх взаимно-перпен-
дикулярных площадках, проведённых через данную точку
тела и ориентированных по отношению к некоторой системе
прямоугольных коорди-
нат. Чаще всего, изу-
чая равновесие или ко-
лебания сплошного те-
ла, последнее относят к
системе прямоугольных
декартовых координат
ж, у, z и рассматрива-
ют составляющие на-
пряжения на площад-
ках, перпендикулярных Рис 1
к осям координат. На
рис. 1 показаны эти составляющие. На площадке, перпенди-
кулярной к оси х, мы имеем составляющие (нормальное на-
пряжение) и т:;сс (касательные напряжения); на площадке,
перпендикулярной к оси?/, — составляющие ххЮ а на
площадке, перепендикулярной к оси z, — составляющие
, Нормальные составляющие принято обозначать
буквой а со значком, указывающим ориентацию площадок,
на которых эти составляющие действуют; касательные
составляющие обозначают буквой т с двумя значками, из
которых второй указывает направление площадки, а пер-
вый—направление самой составляющей. Как известно из
И
механики сплошной среды, всегда "-у™^,
и вообще с^ = ту.
Наряду с декартовой системой координат мы иногда
будем пользоваться цилиндрической системой координат
г, 0, 2, у которой ось z совпадает с осью z декартово:!
системы, а угол 0 отсчитывается от оси я, принимаемо:!
за полярную ось.
Составляющие напряжения на площадках, перпен-
дикулярных к координатным направлениям г, 0, z цилин-
дрической системы, показаны на том же рис. 1; они обоз-
начаются, соответственно: Gr, TrQ, gj? tz0; тГ2, az.
Переход от составляющих напряжения в декартовых ко-
ординатах к составляющим в цилиндрических координатах
совершается по формулам, выводимым в механике сплош-
ной среды:
ar ~ ах cos2 0 4~ Gy sin2 6 -}- 2тХу sin 0 cos 0, !
Gj = sin2 0 + Gy cos2 0 — 2хху sin 0 cos О,
V)==(°!7- aj sin 0 cos 0 + (cos20 — sin2 G),
Gr = Gz ' * '
xrz — tx. cos 0 4~ Ty; sin 0,
= — Xxz sin 0 4- Xyz COS 0.
Составляющие напряжения в сплошной среде, находя-
щейся в состоянии равновесия, удовлетворяют уравнениям
равновесия:
—ч-^+—+-Х = 0
dx dy CZ
Щ + + у = о
dx Уу 1 dz ‘
I 4- 4. Z = О,
дх ду dz ' ’
(1.2)
Tzx '— ^XZt ^zy — ^yzt ^yx — Txy
(в декартовой системе координат) или
. 1 dr "г г ^ri . chrs ^r+li7 -J + B = o, 1
c'V , 1 dr г da<i . o*0 dz + Д - + 0 —0,
dr r d*0 ' dz t “ r -+Z-0 z
Ъг* TJr = Tr5
(1.3)
12
(в цилиндрической системе координат). В уравнёнйях (1.2)
и (1.3) обозначено: X, У, Z; К, 9, Z — проекции объёмных
сил, отнесённых к единице объёма, на координатные на-
правления Ху у, z и г, 0, z.
Уравнения движения сплошной среды отличаются от ура-
внений равновесия только инерционными членами,
которые нужно поставить в правых частях (1.2) и (1.3)
вместо нулей.
Для уравнений в декартовой системе координат инер-
ционные члены имеют вид: pwx, ptv, (где р — плотность,
а wz — проекции ускорения па координат-
ные направления); для уравнений в цилиндрической си-
стеме инерционные члены будут соответственно: рщг,
PvVq, p(Vz.
В зависимости от того, какими переменными мы поль-
зуемся при изучении движения сплошной среды — пере-
менными Эйлера, Лагранжа, или какими-либо другими,
проекции ускорения можно выразить через проекции ско-
рости или через проекции перемещения частиц. На этом
вопросе мы останавливаться не будем, так как в даль-
нейшем будем изучать преимущественно вопросы равно-
весия.
Деформированное состояние сплошной среды характери-
зуется шестью составляющими деформации.
Составляющие деформации в декартовой системе коор-
динат обозначают через sx, щ (относительные удли-
нения бесконечно малых отрезков, направленных до де-
формации параллельно осям х, гл z) и уу2, ухг, yxg (от-
носительные сдвиги, т. е. изменения углов между
отрезками, которые до деформации были параллельны
ОСЯМ Ху у у z).
Составляющие деформации в цилиндрической системе
координат обозначают через эг, sj, (относительные
удлинения отрезков, направления которых до деформации
совпадали с координатными направлениями г, 0, z) и
yrz, Тю (относительные сдвиги —изменения углов между
вышеуказанными отрезками).
Составляющие деформации s.v, . . . , ух.у связаны с
проекциями смещения частиц среды на координатные направ-
ления Ху уу z —-Uy х)у Wy а составляющие ег, э«, .. . , угз вы-
ражаются через проекции смещения на координатные
направления г, 0, z— ur, uz.
Если никаких ограничений на величину деформа-
ций не накладывается, то связь м^жду sT, уХ1) и ?г, и, (V
13
выражается формулами:
8,=/i+2g+(gy+(g)-+(gy-i,
'=/1+2S+(S)‘+C3!+G)!-1-
dv dw .ди
. dz + dy dy * dz' dy dz'dy' dz
81nY»z“ (By+1) (., + 1)
du । dw . du du . dv dv ^dw
. dz ’ dx dx dz ‘ dx dz dx dz *
3111 Ysz = (s.x + 1) (».+ 1)
du t _1JU -L-^V
. du dx ' dx dy ‘ dx dy ’ dx dy
81П Yx» '' fe+lHSy+l) '
(1.4)
Эти формулы упрощаются в случае малых деформаций,
когда производные от смещений суть величины малые по
сравнению с единицей, и принимают вид:
__du _dv dw
dx ’ Чу; dk'dy9
_dv _ди . dw
dy ’ 4xz dz'dx9 >
__dw _du . dv
£z dz * Чху dy^~ dx*
(1.5)
Связь между er, e9, ... , угб и wr, u3, uz в случае малых
деформаций даётся уравнениями:
дит
£r=Z ~дг ’
1
£j ~ г at)
ди0
Sz~~~dz 9
1 duz t
4^z "r dft gz
v
*rz dz * dr 9
v -1
Чг* r dO * dr
' (1.6)
J
Приведённые здесь формулы и уравнения справедливы
для всякого сплошного тела, упругого или неупругого1).
Для изучения вопросов равновесия и движения упру-
гого тела необходимо знать зависимость между составляю-
щими напряжения.
г) Затронутые здесь вопросы подробно изложены, например, у
Трефтца ([47], гл. II и III), и у Лява ([2в], гл. I и II).
14
2. Обобщенный закон Гука»
Упругое тело называется изотропным, если его упру-
гие свойства одинаковы для всех направлений, и анизо-
тропным, если его упругие свойства различны для раз-
ных направлений. При изучении вопросов равновесия и
движения упругого тела, испытывающего малые деформа-
ции, обычно полагают, что тело следует обобщённому
закону Гука, согласно которому составляющие деформа-
ции являются линейными функциями составляющих на-
пряжения. Во всех случаях, разбираемых в настоящей
книге, мы будем считать, что для упругого тела имеет
место обобщённый закон Гука. Приведём аналитические
выражения этого закона для однородного тела, у которого
упругие свойства одинаковы для всех параллельных
направлений, проведённых через любые точки, или, иначе,
все одинаковые элементы в виде прямоугольных параллеле-
пипедов с взаимно параллельными гранями, выделенные
в различных местах тела, обладают одинаковыми упру-
гими свойствами.
Отнеся тело к прямоугольной декартовой системе
координат, мы можем в самом общем случае анизотро-
пии, когда какие-либо элементы упругой симметрии от-
сутствуют, записать выражения обобщённого закона Гу-
ка в виде:
£У = ^iaCo; “b “Ь................................ 4“ >
4~...........................+
(2Л)
Здесь a1L, а12, ... , а60 — упругие постоянные (коэффициенты
деформации); число различных постоянных в общем слу-
чае равно 21.
Если в теле наблюдается симметрия внутреннего
строения, то и в упругих свойствах проявляется симме-
трия; эта «упругая симметрия», как её обычно называют,
сказывается в том, что симметричные направления ока-
зываются эквивалентными в отношении упругих свойств.
При наличии упругой симметрии выражения обобщённого
закона Гука упрощаются. Упругая симметрия наблюдается
в кристаллах, а также в фанерных и текстолитовых пла-
стинках и в других анизотропных телах. По характеру
15
уцругой симметрии все кристаллы могут быть разбиты на
девять классов1).
Мы не будем останавливаться на различных случаях
симметрии, характерной для кристаллов, а укажем выра-
жения обобщённого закона Гука для наиболее важных
случаев упругой симметрии, которая может наблюдаться
не только в кристаллах, но и в других анизотропных
телах.
1. Плоскость упругой симметрии. Пусть в каждой
точке тела имеется плоскость, обладающая тем свойством,
что любые два направления, симметричные относительно
этой плоскости, являются эквивалентными в отношении
упругих свойств (в однородном теле все эти плоскости,
проведённые чере^ любые точки, параллельны). В этом
случае уравнения обобщённого закона Гука, записанные
для координатной системы с осью и, перпендикулярной
плоскости упругой симметрии, будут иметь вид:
4 4 j
£У = 'Г ^23^2 4~ ^2еТХ<Р I
SZ “ 4“ ^2зау 4 ^83^2 4 *
Yyz “ ^44Xyz 4 ^45^X2?
4^2e®y 4 4 >
(2.2)
Число независимых упругих постоянных сокращается
до 13. Можно получить более наглядное представление о
свойствах тела с плоскостью упругй симметрии на осно-
вании следующего примера. Предположим, что из тела
выделен элемент в виде прямоугольного параллелепипеда,
у которого две грани параллельны плоскостям упругой
симметрии, и к этим граням приложены растягивающие
или сжимающие нормальные напряжения az (рис. 2).
Деформация элемента будет характеризоваться составляю-
щими, которые мы получим из уравнений (2.2):
Yff3 = 0,
гу==®23®2> Тхг = ^>
е„ —й33<зг, Yxy“^3e^z* >
(2-3)
См. [2в], гл. VL стр. 170—172, и [4] — (с), стр. 427. В указан*
пых работах Лика и Бехтерева подробно разбираются вопросы,
связанные с упругой симметрией кристаллов и других анизотропных
тел.
16
Эти равенства показывают, что при простом растя-
жении-сжатии в направлении, перпендикулярном к пло-
скости упругой симметрии, углы меж-
ду направлением растяжения — сжатия
и направлениями и, лежащими в плос-
кости упругой симметрии, не искажа-
ются, остаются прямыми.
Направления, перпендикулярные к
плоскостям упругой симметрии, мы бу-
дем называть главными направлени-
ями упругости, или, короче, главны-
ми направлениями. Для рас-
сматриваемого случая симметрии —че-
рез каждую точку тела проходит одно
главное направление.
2. Три плоскости упругой симметрии. Если через каж-
дую точку однородного тела проходят три взаимно пер-
пендикулярные плоскости упругой симметрии, то уравне-
ния обобщённого закона Гука, отнесенные к осям х> т/, г,
перпендикулярным к этим плоскостям, принимают вид:
ех “ Yy: “ й44Ту;7
£у “ “к ^22^у Ч ZX “ ?
£z Н" ®2з°у 4~ J Yxy ~ J
(2.4)
Число независимых упругих постоянных равно девяти.
Тело, однородное и обладающее в каждой точке тремя
взаимно перпендикулярными плоскостями упругой симме-
трии, называют ортогонально-анизотропным, или, коро-
че, ортотропным. Уравнениям (2.4) удобнее придать
иную форму, записав нх в виде1 2):
1 vol ч31
е* ~ Е\ °х “ Е3 °-’
___ 'Чз I 1 v32
Е, х 1 Е2 у Е.3
SZ= — ELSn— ^/9+ 'E3°z'
Yff! Q )
1
1
YiB — 6i2 X«X'
(2-5)
Здесь Ev E2, -Z?3 —модули Юнга для растяжения —сжа-
тия вдоль главных направлений упругости х, у, г;
v12 —коэффициент Пуассона, характеризующий сокращение
в направлении у при растяжении в направлениях х]
v21 —коэффициент Пуассона, характеризующий сокращение
-1) См., например, [зэ], стр. 8.
2 С. Г. Лохиицкий
17
в направлении х при растяжении в направлении у и т. д.;
£23, G13, —модули сдвига, характеризующие изменения
углов между главными направлениями г/ и z, я и г, х пу,
Между модулями Юнга и коэффициентами Пуассона су-
ществуют зависимости:
^'1'*’21 ” ^2^125 ^2^32 ^23> ^3^13 (2л 6)
3. Плоскость изотропии. Если через каждую точку
тела проходит плоскость, в которой все направления
являются упруго эквивалентными, то уравнения обобщён-
ного закона Гука для системы координат с осью г, пер-
пендикулярной к плоскости изотропии, и осями х и у,
лежащими в этой плоскости, запишутся так:
4“ 4" ^13^2*
eff “ ^12^1 4" 4"
SZ “ ^1з(^х4“ $у) 4“ ^38®Z)
7yz —
^zx~^^^xzi >
Чху — 2 (au a12) tair.
(2.7)
Число различных упругих постоянных сводится к
пяти. Тело с анизотропией этого вида называют транс-
вер с а л ьно-и зотропным1). Направление, перпенди-
кулярное к плоскости изотропии, и все направления в
самой этой плоскости являются главными.
Другая форма уравнений (2.7):
ея “ JE? ” Е' az1 4vz ~ G'
1 , \ v' 1
£У~ $ \*у ™х) Е'0^ 4zx— Qi^ZXt
v' ( . ч 1 2(14-V)
— ft'(ax 4” су) 4“ j£/ azJ Чху— ft Хху
(2.8)
I
J
Здесь Е — модуль Юнга для направлений в плоскости
изотропии; 2?' —модуль Юнга для направлений, перпен-
дикулярных к этой плоскости; V—-коэффициент Пуассона,
характеризующий сокращение в плоскости изотропии, при
растяжении в этой же плоскости; v' — коэффициент Пуас-
сона, характеризующий сокращение в плоскости изотропии,
при растяжении в направлении, перпендикулярном к
этой плоскости; G' — модуль сдвига, характеризующий
искажение углов между направлениями в плоскости изо-
тропии и направлением, перпендикулярным к ней.
х) См. [23], стр. 172.
18
4. Полная симметрия—изотропное тело. У изотроп-
ного тела любая плоскость есть плоскость упругой симметрии
и любое направление — главное. Уравнения обобщённого
закона Гука для изотропного тела имеют вид:
es= i С5» - *(»* + «.-)],
ez = [°z v (ea; C»)L
YPZ“ Q XyZ)
1 YzX ~Q (2.9)
1
Yx» Q 'xv
Здесь E — модуль Юнга, v — коэффициент Пуассона и
л Е
С^г[г+?)“модуль сдаига-
Если, изучая деформации изотропного тела, перейти
от системы координат ж, у, z к какой-либо другой прямо-
угольной системе я/, у', z\ то вид уравнений (2.9) не
изменится, и упругие постоянные Е и у сохранят свои
значения и в новой системе. В случае анизотропного тела
переход от системы координат к другой влечёт за собой
необходимость перехода к новым упругим постоянным.
Некоторые вопросы, связанные с пересчётом упругих по-
стоянных прй переходе к новым осям, будут освещены в
дальнейшем (п° 10).
Деформируясь, упругое тело накопляет запас потен-
циальной энергии. Выражение потенциальной энергии
деформации, отнесённой к единице объёма, можно в самом
общем случае анизотропии записать в виде:
+ ^гз^х^г 4* ^i5CxTzx ^le^x^xp *J“
+ 4^°*+ a34?zxyz+ aMy +
2 ^4^TPz ^i&xyzxzx + ^ie^ffz^xp "b
+ ^56^XZ^XP ’b
+ |a..4e- (2-10)
Отсюда легко получить выражение для V и в любом
частном случае анизотропии. Кроме того, V можно предста-
2* 19
вить в так называемой билинейной форме, которая оди*
каково пригодна как в случае изотропного, так и любого
анизотропного тела х):
|/ z= — (ахед. + ау~у + CLSr "F jtf)’ (2.11)
Потенциальная энергия деформации V для всего тела
найдётся путем интегрирования по всему объёму тела:
V dx dy dz.
(2.12)
3. Основные уравнения и основные задачи теории
упругости.
Напряжённо-деформированное состояние тела будет
известным, если будут известны в любой точке составляю-
щие напряжения ах, . . . , *саП и проекции смещения
а, у, tv; если рассматривается задача о движении тела,
то эти величины должны быть известными в любой точке
в любой момент времени. Для определения девяти функций
ау, ... , ?г, г, tv нужно иметь девять независимых
уравнений.
Присоединяя к уравнениям равновесия (1.2) уравнения
обобщённого закона Гука (2.1) (или, соответственно, (2.2),
(2.4) и т. д.), получим основную систему уравнений равно-
весия анизотропного упругого тела:
I I c'zxz [ у______п
£Х 4~ ”1” ^13^2 ~Ь ^X^yz ^15^X2 + >
^2 2®У ............... 4“ ^26^2 У>
(3.1)
1ху й16^х4“ ^2б^У~1“ ..................J
Девять функций, определяющих напряжённо-деформи-
рованное состояние тела, находящегося в равновесии под
действием внешних усилий, должны быть найдены путём
интегрирования основной системы (3.1) (или системы,
эквивалентной основной) с учётом условий на поверхности
*) См. гл. Ill, и Г7], стр. 34.
20
тела (граничных условий), В зависимости от того, что
именно задаётся на границах, различают первую основ-
ную задачу, вторую основную задачу и задачи смешанно-
го типа.
Первая основная задача. На поверхности задаётся внеш-
няя нагрузка, а также объёмные силы. Обозначая через
Xn, %п проекции внешних поверхностных усилий,
отнесённых к единице поверхности, на оси х, г/, z и через
п —направление внешней нормали к поверхности тела,
можно записать условия на поверхности в виде:
cos (и, я) + cos (и, у) + 7rz cos (n, z) = Хп,
Хух cos (n, х) + ау cos (п, у) Ц- тИ2 cos (и, г) = Г„, >
т.хс°8 (л, rr) + r.ycos (п, у) 4-а, соз(д, z) = Zn.
(3.2)
Вторая основная задача. На поверхности задаются сме-
щения, кроме того, задаются объёмные силы. В этом
случае граничные условия имеют вид:
u = u*, d —и*, w = (3.3)
где и*, и*, w* —заданные на поверхности тела составляю-
щие смещения в направлении осей х, у, z.
С задачами смешанного типа мы встречаемся в слу-
чаях, когда на поверхности задаются частично усилия
И частично смещения.
Вопрос о единственности состояния равновесия тела
под действием заданных нагрузок (иначе говоря, вопрос
о единственности решения уравнений равновесия упругого
тела) решается теоремой Кирхгофа, согласно которой
состояние равновесия является единственным, пока внеш-
ние нагрузки не превышают критических значенийг).
По этой теореме, основная система (3.1), соответствующая
малым деформациям, когда составляющие деформации
выражаются через проекции смещения линейно, имеет
единственное решение как в случае первой и второй
задачи, так и в случае смешанных задач.
Несколько иначе ставятся задачи об устойчивости
упругих тел в виде стержней, пластинок или оболочек:
основная часть задачи сводится к определению крити-
ческих нагрузок, при которых основная форма равновесия,
х) См. [4Т], стр. 45,
21
имеющая место при малых нагрузках, перестаёт быть един-
ственной и устойчивой формой равновесия.
Основную систему уравнений движения упругого ани-
зотропного тела получим из системы (3.1), заменяя в
ней уравнения равновесия сплошной среды уравнения-
ми движения, т. е. вводя в рассмотрение инерцион-
ные члены.
В тех случаях, когда точное решение задачи о равно-
весии получить не удаётся (когда интегрирование основной
системы или уравнений, вытекающих из неё, затрудни-
тельно), часто удаётся получить приближённое реше-
ние на основании теорем теории упругости о минимуме
работы.
При изучении изгиба пластинок мы используем теорему,
касающуюся возможных перемещений. Под возможными
перемещениями подразумеваются такие перемещения
в теле, при которых тело остаётся сплошным, и выпол-
няются граничные условия на тех частях поверхности,
где задаются смещения.
Составим сначала выражение Z7, равное потенциальной
энергии деформации тела минус работа внешних усилий,
поверхностных и объёмных:
U = V dx dy dz — (Xnw + Ynv + Znw) dS -
— dxdydz (3.4)
(тройные интегралы распространены на весь объём тела,
двойной интеграл берётся по поверхности тела). Теорему
о возможных перемещениях теперь можно сформулировать
следующим образом.
Если рассматривается выражение £7(3.4), в котором
под и, и, w подразумеваются возможные смещения, то дей-
ствительные смещения в теле (при переходе от начального
состояния в состояние упругого равновесия) отличаются
от всех возможных тем, что они сообщают выражению U
минимальное значение *).
Можно получать приближённые решения задач о рав-
новесии тела, задаваясь выражениями для смещений
в виде сумм с неопределёнными коэффициентами и под-
бирая члены сумм так, чтобы они удовлетворяли усло-
виям непрерывности и граничным условиям. Коэффици-
*) См. [47], гл. V, стр. 45.
22
енты определяют, требуя, чтобы выражение U получило
минимальное значение; задача сводится к отысканию
минимума целой алгебраической функции второй степени
относительно коэффициентов.
4. Криволинейная анизотропия
Однородное анизотропное упругое тело, рассмотренное
в § 2, характеризуется тем, что у него эквивалентными
являются параллельные направления, проведённые через
разные точки. Можно представить себе тело (и такие
тела, действительно, существуют в природе) с анизотро-
пией иного рода, при которой эквивалентными являются
не параллельные направления, проведённые через разные
точки, а направления, образующие некоторые углы друг
с другом. Если выбрать систему криволинейных коорди-
нат так, чтобы в разных точках тела эквивалентные на-
правления совпадали с координатными направлениями,
то элементы тела, выделенные в разных местах тремя
парами координатных поверхностей, будут обладать оди-
наковыми упругими свойствами. В однородном теле та-
кими элементами являлись прямоугольные параллелепи-
педы Со взаимно параллельными гранями; в рассматри-
ваемом случае анизотропии элементы в виде параллеле-
пипедов уже не будут обладать одинаковыми упругими
свойствами. Анизотропия, которая характеризуется тем,
что эквивалентными направлениями в теле являются на-
правления непараллельные, называется криволиней-
ной1). Число возможных видов криволинейной анизотропии
практически ничем не ограничено, но наиболее инте-
ресным для практики и наичаще встречающимся яв-
ляется вид криволинейной анизотропии, который мы бу-
дем в дальнейшем называть «цилиндрической анизо-
тропией»2).
Цилиндрическая анизотропия характеризуется следую-
щими свойствами. С телом неизменно связана прямая
g —ось айизотропии; все направления, пересекающие эту
ось под прямым углом, являются эквивалентными. Все
элементы Д, Л2, ..., выделенные из тела тремя парами
поверхностей: а) двумя плоскостями, проходящими через
х) См. [26], гл. VI, стр. 172, 173.
й) На этот вид анизотропии обратили внимание ещё Сен-Вещш
(см. [м]) и Фохт (см. [77]).
ось анизотропии и образующими бесконечно малый угол,
б) двумя бесконечно-близкими плоскостями, перпендику-
лярными к оси анизотропии, и в) двумя бесконечно близ-
кими поверхностями круговых коаксиальных цилиндров
зотропией, отнесённые к
иметь вид:
с осью, направленной по оси ани-
зотропии, обладают одинаковыми
упругими свойствами (рис. 3).
При этом ось анизотропии может
проходить как внутри тела, так
и лежать вне его. При изучении
вопросов равновесия и движения
тела с цилиндрической анизотро-
пией естественно пользоваться
цилиндрической системой коор-
динат г, б, и, направляя ось z по
оси анизотропии, а полярную ось,
от которой отсчитываются углы
6 — произвольно.
Уравнения обобщённого за-
кона Гука для общего слу-
чая тела с цилиндрической ани-
указанной системе г, 0, z, будут
8, •— 4" ^22®^ ~Н....................“Г
• • •...........................*................7
yr3 #iear -р а26а8 +.......................+йввтгд.
(4.1)
Коэффициенты —упругие постоянные; число различных
постоянных не может быть больше 21. Не лишним будет
отметить, что если уравнения обобщённого закона Гука
для однородного тела с прямолинейной анизотропией
отнести к цилиндрической системе координат, то в общем
случае они будут иметь вид (4.1), только коэффициенты
acj уже не будут постоянными, а будут зависеть от угла 0.
В теле с цилиндрической анизотропией также возможно
существование различных элементов упругой симмет-
рии. Если в каждой точке тела имеется плоскость упру-
гой симметрии, перпендикулярная оси анизотропии, то
уравнения (4.1) принимают форму такую же, как (2.2),
24
так как
014 — 6Z24 — й15 — ^85 — ^34 — ^35 — ^46 ^66 — (4*2)
Если в каждой точке имеются три плоскости упру-
гой симметрии, из которых одна перпендикулярна оси
анизотропии, а вторая проходит через ось анизотро-
пии, то уравнения обобщённого закона Гука принима-
ют вид:
Sr — а115Г + ai2°J + ai3CZ, Yf)Z =
S9 ” -f- й2аС 9 4" ^23^5? Yzr ~
ZZ “ ai3Gr 4” a23a9 4“ a33Cz5 Yr9 = a86Tr9*
(4.3)
В этом случае тело уместно назвать ортотропным
телом, обладающим цилиндрической анизотропией.
Примером тела с цилиндрической анизотропией может
служить деревянный1 брусок с правильными годичными
слоями (поскольку
дело касается упру-
гих его деформаций).
Сердцевина играет
роль оси анизотропии (рис. 4). Тело с цилиндрической
анизотропией можно образовать искусственно, построив
его из однородных анизотропных элементов. Представим
себе большое количество анизотропных однородных «кир-
пичиков», одинаковых по упругим свойствам, у которых
две противоположные грани образуют малый угол. Если из
этих «кирпичиков» построить свод, как на рис. 5, то этот
свод в целом будет обладать свойствами тела с цилин-
дрической анизотропией. Осевые направления элементов,
эквивалентные между собой, в своде будут радиальными
направлениями.
К этому виду анизотропии мы еще вернёмся в гла-
вах II, III, VIII и IX.
25
ГЛАВА II,
ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
АНИЗОТРОПНОГО ТЕЛА.
5. Обобщённое плоское напряжённое состояние.
Рассмотрим упругую однородную анизотропную плоскую
пластинку постоянной толщины, находящуюся в равнове-
сии под действием сил, распределённых по краю, и объём-
ных сил. Мы будем предполагать,- что: 1) в каждой точке
пластинки имеется плоскость упругой симметрии, парал-
лельная срединной плоскости; 2) приложенные к краю
усилия и объёмные силы действуют в плоскостях, парал-
лельных срединной, распределены симметрично относи-
тельно срединной плоскости и незначительно меняются
по толщине; 3) деформации пластинки малы. Напряжённое
состояние пластинки, работающей в указанных условиях,
называют обобщённым плоским напряжённым состоянием.
Срединная поверхность при де-
формации её не искривляется,
остаётся плоской.
Примем срединную плос-
кость за координатную плос-
кость ху, поместив начало в
произвольной точке О и оси х
и у, направив произвольно
(рис. 6). Обозначим через h тол-
щину пластинки, Хп, Yn — проекции усилий, распределён-
ных по краю, на единицу площади, X, У —проекции
объёмных сил на единицу объёма (Zn = Z = 0 по условию),
ai2f ••• ^вв —упругие постоянные материала, отне-
сённые к системе координат х, у, z. Изучая обобщённое
плоское напряжённое состояние, вводят в рассмотрение
средние по толщине составляющие напряжения и смеще-
ния:— тар, и, и, определяя эти величины, как
интегралы от соответствующих напряжений или смещений
по толщине, делённые на толщину:
h/Z
П/2
h/2
-Л/2
Л/2
°» =
*v-"h J
~hfZ
-h/2
u = 4 f u dz, v
h *
-hpl
Z h *1,9
— /1/2
Л/2
> (5.1)
26
В дальнейшем величиной пренебрегают по сравне-
нию о и Для этих средних величин легко полу-
чить из основной системы уравнений равновесия 5 урав-
нений по числу неизвестных функций. Умножая первое
и второе уравнения (1.2) на dzjh, интегрируем обе части
уравнений в пределах толщины пластинки (от — Л/2 до
Л/2); то же самое проделываем с первым, вторым и шестым
уравнениями обобщённого закона Рука [которые в данном
случае нужно взять в форме (2.2)]. Тогда получаем урав-
нения, которым удовлетворяют средние величины х):
дх &у
I I У = О;
дх ' ду~
SX ~ а11^Х 4"
-f- а22ву -J-
Yxs ” 4* 4“ >
Здесь
h/2
Х = Xdz,
-h]’Z
hj'Z
У = 4 Ydz
Л J
-Л/2
суть средние по толщине объёмные силы, а ех, ед и со-
ответственно равны:
ди - dv — ди , dv
дх ’ Sff ду ’ ду~^~ дх* ( * )
Если на краю пластинки заданы внешние усилия, то
граничные условия получим из условий (3.2); осредняя их,
получим:
ах cos (и, х) соз (и, у} =~Хп, |
zXB cos (га, х) + ау cos (и, у) = Yn. I
Здесь
Л/2 h/2
Xn = 4 $ Xndz, Yn=~^Yndz.
-h/z -hrz
Предположим, что объёмные силы имеют потенциал U (х, у).
1) См. наши работы [10] и [п]
27
через который выражаются по формулам:
Х=-~, Y=-^. (5.6)
dx ’ dy ' '
Уравнениям равновесия мы удовлетворим, введя функ-
цию напряжений F (х, у), полагая
д*Е . тт ~ д21? , тт - д*Е .(
+ аО ~ <^ + ^’ 'С®9 дх dy • С5'7)
Исключая путём дифференцирования смещения u, v из
равенств (5.4), получим условие совместности деформаций:
d2sx | „ П ft Q\
</f/2 + гъ,2 dxdrj “U)
а подставляя сюда выражения ex, etf, у1Уиз уравнений (5.3)
и выражая составляющие напряжения через F, получим
дифференциальное уравнение, которому удовлетворяет
функция напряжений:
d*F 0/у дЧ? . Л)/7 . х d*F . d*F _
^22 дх* 26 дх3 ду * ' 12 ' ^бе' 0х2ду2 1в дх ду* 11 ду*
/ ч d2U , , . ч d2U . . ч d2U m
= - (а12 + о24) + («хе + а2в) 57^ - («12 + Яц) • (5.9)
Если объёмные силы отсутствуют или не учитываются,
то вместо (5.9) имеем однородное уравнение:
л b*F 9/7 _L
°22^ " Zfl26 с/х3 ду
1/Г) I \ Oz, I /Е ЛЛ\
+ (2а13 + ас6) — 2а1в - 0. (5.10)
В частности, для ортотропной пластинки, совмещая
направления осей х и у с главными направлениями упру-
гости, получим уравнение:
1 2М °*F I 1 дЧ? -О (5 1П
Ej дх2ду2 ' * 4
Здесь Ех, Е2 —модули Юнга для растяжения — сжатия по
главным направлениям хи у; G = 613 — модуль сдвига,
характеризующий изменение углов между главными на-
28
Правлениями х, у; vx v12 — коэффициент Пуассона, харак-
теризующий сокращение в направлении упри растяжении —
сжатии в направлении х [см. уравнения (2.5)]. Для изу-
чения напряжений и деформаций ортотропной пластинки,
которая имеет девять упругих постоянных, достаточно
знать только четыре: Е„ Е2, v15 G. В дальнейшем оси х и у,
направления которых соответствуют главным направле-
ниям ортотропной пластинки, мы будем называть i лавными
осями.
У изотропной пластинки Ех = Е2 = Е, G =- Е]2 (1 v),
и уравнение (5.11) переходит в бигармоническое:
V2V2F = 0, (5.12)
где
о»х2 ‘ ду2-
Что касается гра-
ничных условий (пе-
реходящих в данном
случае в условия на
контуре плоской фи-
гуры & на плоскости
ху), то они, при
заданных внешних
усилиях, могут быть
сведены к заданию
Р Г
Рис. 7.
первых производных
функций напряжений. Пусть S — область пластинки, ограни-
ченная внешним контуром и одним или несколькими вну-
тренними контурами (для общности будем полагать, что
пластинка имеет одно или несколько отверстий). Уравне-
ния контуров будем задавать в параметрическом виде,
принимая за параметр дугу контура $, отсчитываемую от
начальной точки (О' на внешнем контуре, О" —на вну-
треннем):
z = z(s), y = y(s). (5.13)
Положительными направлениями отсчёта дуг будем счи-
тать направления, показанные на рис. 7 стрелками.
♦) Подробнее:
0W дЧ?
дх* <ух2 ду2 ду*
(см., например, [2в], гл. IX, стр. 215).
29
Тогда для внешнего и внутреннего контура
cos (п, х) = сов (п,у)=-^.
Подставляя в условия (5.5) и интегрируя по дуге $
от начальной точки контура до переменной точки, полу-
чим граничные условия при заданных внешних усилиях
Хп, Yn в виде:
S л
^=-\(Yn + Ux')ds + clt ~=\(Xn-Uy')ds+Ci (5.14)
О о
((\, с2 —постоянные, которые можно произвольно зафи-
ксировать на одном контуре).
После того, как напряжения будут найдены, смещения
определятся путём интегрирования уравнений (5.3),
В дальнейшем для простоты записи мы будем опу-
скать чёрточки над символами для напряжений и сме-
щений, и, рассматривая какую-либо задачу о плоском
напряжённом состоянии пластинки, будем под ах, aff,
и, и подразумевать средние по толщине пластинки зна-
чения этих величин.
6. Плоская деформация.
С задачей об обобщённом плоском напряжённом со-
стоянии пластинки имеет много общего задача о плоской
деформации, также приводящаяся
к плоской задаче (т. е. к задаче
двух измерений). Пусть имеется
однородное анизотропное тело в
виде цилиндра произвольного се-
чения, находящееся в равновесии
под действием усилий, распреде-
лённых по боковой поверхности.
Предположим, что: 1) усилия
действуют в плоскостях, нормаль-
ных к образующей, и не меня-
ются вдоль образующей (длина
которой предполагается большой
го сравнению с размерами поперечного сечения); 2) в
каждой точке тела имеется плоскость упругой симмет-
рии, перпендикулярная к образующей; 3) деформации малы.
Примем плоскость какого-нибудь поперечного сечения
за плоскость ху, направив ось z параллельно образующей,
за
а оси x и у—-произвольно (рис. 8). Сечения, удалённые
от концов цилиндра, можно считать плоскими.
Полагая
и = к(я, у), и = и(х, у), (v = 0,
получим:
ди dv ди . dv /а л\
дх ’ ду ’ 1 ду^~ дх ' *
ez “ “ Yxz — 0.
Из основной системы (3.1) выводим уравнения х):
^+^г+Х=О,
Г 7 (6-2)
^+^+У = 0;
дх 1 ду ’
гх ~ Ри^х4* 1
£Q = Pr2ax“h 4" PseTW ? (6.3)
Yxy “ pieax'”h p26av 4“ PeeTXff» J
(а1зояг4- 4* ^зв^ар)? ^yz~ ^xz^^(6*4)
где — коэффициенты, связанные с упругими постоян-
ными следующими формулами:
(Z, / = 1, 2, 6).
имеют потенциал,
у- _ди
ду ’
т. е.
(6-5)
(6.6)
аналогич-
R , — п _^i3aj3
Ро “ iJ «зз ’
Полагая, что объёмные силы
х=-~,
ах 7
приходим к формулам и уравнениям, вполне
ным тем, какие были получены в предыдущем параграфе:
дгР . d*F . тт <>*F ,с
в1 = Тт+^1 °о~TTf+ *'> тхп=----L" * » (6-7)
о dtF gp d*I? . i p \ d*I? np d*]? .
Pa2 ~d^ zp2e ~д^Г ^ P12 Pe6' дх2 dy* "" ZPie dxdyz
+ ₽n = - (P.. + ₽..) S +(?.. + ₽..) ^ -
-(?,.+₽..)^. (S-8)
Граничные условия сводятся к условиям на контуре
сечения и по форме совпадают с условиями для пла-
стинки, находящейся в обобщённом плоском напряжённом
состоянии [(5.14) при заданных внешних усилиях].
х) См. наши работы [10] и [и].
3<
Приведённые здесь формулы и уравнения нё учиты-
ваю!1 условий на концах цилиндра. В случае свободных
концов можно учесть влияние их на распределение напря-
жений приближённо на основании принципа Сен-Венана
(согласно которому статически эквивалентные нагрузки,
приложенные к концу стержня, вызывают одинаковое
действие во всех частях его, за исключением областей
вблизи концов), путём введения поправочного члена.
Предположим, что область сечения цилиндра конечна,
начало координат помещено в центре тяжести сечения и
оси х и у направлены по главным осям инерции сечения.
Определив напряжения мы по формуле (6.4)
получим — нормальное напряжение в поперечных сече-
ниях. В самом общем случае найденное az приведётся
в каждом поперечном сечении к центрально приложенной
силе Р, направленной параллельно образующей, и к мо-
менту с составляющими тх и ту относительно осей х и ?/.
Тогда, желая учесть условия на свободных концах, мы
должны к напряжению вычисленному по формуле (6.4),
добавить поправку:
, Р . тх т1{
Oz=(6.9)
1 Д. Л у
(А — площадь поперечного сечения, —моменты инерции
сечения относительно главных осей инерции х и у).
Ввиду почти полного совпадения основных уравнений
для плоского напряжённого состояния и для плоской де;
формации (разница лишь в коэффициентах), обе задачи
решаются одинаковыми методами. Получив решение для
плоского напряжённого состояния, мы тем самым полу-
чаем решение и для случая плоской деформации.
7. Общие выражения для функции напряжений.
При отсутствии объёмных сил задача об обобщённом
плоском напряжённом состоянии плоской пластинки сво-
дится к определению в области 5 на плоскости ху функ-
ции напряжений F (х, у), удовлетворяющей уравнению
Л (PF г, Л । / 9 п ! \ ё4 F
Ягг ~~ 26128 ~dj? Оу' + ^Я1а "т" дх? Оу1 ~
9 &Р I ^Р Л Л Л\
— 2а1в + w = 0 (7А)
дх ду3 * 11 ду* х 7
и граничным условиям па контурах, ограничивающих
32
область. Уравнение (7.1) можно проинтегрировать в общем
виде, предварительно записав его символически с по-
мощью четырёх линейных дифференциальных операторов
таким образом:
(7.2)
Здесь символ Dk обозначает операцию:
д (i о к
D, = ----[хА. -- , (/.3)
А <jy ‘ h дх х
где рЛ. —корни характеристического уравнения:
аи[? — 2«хв!13 + (2а1а + аев) и2 — 2а3,р. а22 = 0. (7.4)
В своих работах автор показал, что характеристиче-
ское уравнение для всякого идеально упругого тела может
иметь либо комплексные, либо чисто-мнимые корни, а
вещественных корней получиться не может1). Таким обра-
зом, рЛ. всегда либо комплексные, либо чисто мнимые
числа, которые можно принять за числа, характеризую-
щие анизотропию тела. Эти числа мы будем обозначать
далее через р2, и называть комплексными пара-
метрами плоского напряжённого состояния. В зависимо-
сти от соотношения между упругими постоянными, воз-
можны два случая:
1) комплексные параметры все различны:
~ a -J- ?/, р2 ~ Y + Pi = а •— Р2 = Y — (7.5)
(а, р, у, о — вещественные числа, В > 0, о > 0) и
2) комплексные параметры попарно равны:
pL = р.2 = а + $1, = <л2 = а —4*k‘ (3 > 0). (7.6)
Ко второму случаю относится случай изотропной пла-
стинки; у такой пластинки
’Ч = i, p-i = р2 = — /, а = 0, 3 1.
Представив уравнение (7.1) в виде (7.2), мы можем
свести интегрирование его к интегрированию четырёх
уравнений в частных производных первого порядка.
3j См. раб(.ты [И] и [Х2].
С. Г. ЛехнипкнК 33
Действительно, полагая
DtF^^, DtDtDJF^^r (7.7)
получаем уравнение:
Л?15ф^=0. Р-8)
Интегрируя, находим:
Тх = Л (« 4-Р-9)
где Д —произвольная функция переменного #4-s\y. Далее,
ив (7.7) получаем уравнения:
др д1? __ „
ди '*2 дх J
Интегрируя эти уравнения по порядку, приходим
к следующим выражениям для F:
1) в случае различных комплексных параметров:
F = F1(x + н?/) -I- F.2 (х 4- «2?/) 4- Fs (т 4-й,у) +
+ F\ (х + [л2?/) (7-11)
(F,, F2, F\- произвольные функции переменных % + pi:y*
х’ + р-л?/);
2) в случае попарно равных комплексных параметров
А = F\ (х 4- fxj/) 4- (х 4- F.. (х 4- ^у) 4-
4- F, (х 4- ^у) 4- (х 4- wj) Ft (х 4-\у). (7.12)
Переменные я комплексные, но не обычного
типа а усложнённые; вводя для них обозначения::
~1 = ж4-111г/, г2 = х4-и2у, z^x + ^y, ~z2^= x-'f-n2y, (7.13)
и учитывая, что функция напряжений должна быть веще-
ственной функцией, можем выражения (7.11) и (7Л2) за-
писать иначе:
J) в случае различных комплексных параметров:
F = 2Re[F,(21) + F2(z2)]; (7.14).
?-4
2) в случае попарно равных комплексных параметров:
F-2Re[F1(.l) + FiFs (zj] (7.15)
(Re — обозначение для вещественной части какого-либо
комплексного выражения).
_ В частности, для изотропного тела = x + iy— z-,
— x — iy — 2; изменяя обозначения произвольных функ-
ций. получим известное выражение1):
F^Rek?(3) + x(3)]. (7.16)
8. Связь плоской задачи теории упругости с теорией
функций комплексного переменного.
Как показывают формулы (7.14) —(7.15), функция на-
пряжений выражается через две произвольные функции
комплексных переменных: х + Р1У, -2“ (в слу-
чае неравных комплексных параметров; при равных пара-
метрах получаем одну комплексную переменную
Зная выражение для функции F, легко найти выра-
жения и для составляющих напряжения, а путём инте-
грирования уравнений (5.3) получить формулы и для сме-
щений. Вводя обозначения
«МЛ = ^, = = (8.1)
<41 U Л 2 “ 1 *' 2
получим, в случае различных комплексных параметров
при отсутствии объёмных сил, следующие формулы 2):
сх.= 2Ке[^Ф;с1) + ^Ф;(^)], ]
Sf = 2Re'p;(zHW], М
= ~2Re [а, ф; (л) + ‘КСЛ; J
« = 2Re[/71®1(z1)-|-M’i(3!!)l-«>//-r «о, 1
г = 2Re[9A(^)H-+ + J
Здесь
;^==«11^ + а12-а1.ь, ]
а / (Ь>4)
= Wi + ~ Я* |
6 См. lss], §31, стр. 105.
Ь См. нашу работу Р2], стр. 81.
35
a co, zz0, t\ — произвольные постоянные, характеризующие
«жёсткое» перемещение пластинки, т. е. перемещение в пло-
скости ху без деформации (ш характеризует поворот,
а и0, и0 —поступательное перемещение).
Составляющие напряжения на площадке с произвольно
направленной нормалью п —нормальная сп и касательная
тл —найдутся по формулам:
сл — аг cos2 (/г, х) 4- ау cos2 (?z, у) 4-
+ 2-cxycos (тг, rr)cos (/г,у),
ах) cos (?z, <т) cos (/?, у) 4-
+ ~Ху (П> •*') - с <|S' (И, iO], >
пли, на основании (8.2),
у., = 2Re { [cos (лг, у) — cos (п, а:)]2 Ф{ (zx) + 1
4- [cos (п, г/) — u2 cos (n, а)]2Ф{ (з„)}, I
tn = 2Re {[cos (/г, у) — cos (n, a)] x v
X [cos (n, a’) 4-}^ cos (и, у)] ФЩ) 4-
4- jcos (n, y) — [i2 cos (и, a:)] X
X [cos (n, j.) 4- U2 COS (n, у)] Ф{ (z2)]. j
Граничные условия принимают форму, при заданных
внешних усилиях Хп, Yn [см. формулы (5.14)]:
2Re [Фх (21) 4- Ф3 (О] = - Ylt ds 4- еп
о V
s
2Re [pjl\ (zx) 4- (z3)] = A4>ds + c2-
о
(8.7)
при заданных смещениях zt*, ?;*:
2Re [p/l\ (zx) 4- Л'К CO] — + "о = г1‘, ]
2Re (zj 4- ?„Ф2 (О] 4- шс 4- = c*. J
Приведённые равенства показывают связь составляющих
напряжения и смещения с функциями комплексных пере-
менных. Если ввести обозначения:
а-х = а:4- ау, уг = ^у, а"а = • с + ?.</, = (8-9)
то функции Фх и Ф2 можно рассматривать, как функции
36
комплексных переменных обычного тлта:
Щ — Xt | I '/ t, — X% 4" ^//2 •
Но при этом, если область пластинки 5, то областями,
в которых меняются функции <1\ и Ф2, будут некоторые
области Л\ и 52, полученные из S путём так называемого
афинного преобразования [преобразования с помощью
формул (8.9)]. На рис. 9 даётся представление о том,
Par. 9.
как получаются области 5Х и вз области пластинки 5.
Таким образом, плоскую задачу можно рассматривать,
как задачу определения двух функций Ф} (zx) и Ф2 (z2)
в областях 5Х и 53, удовлетворяклцих граничным усло-
виям (в соответствующих точках контуров областей 5t
и iSs) — (8.7) или (8.8). Задача эта представляется доста-
точно сложной в общем случае, хотя в частных случаях
удачно решается.
Исследование показывает, что функции Фг и Ф3 дол-
жны внутри своих областей удовлетворять следующим
условиям 1):
1) если область пластинки 5 односвязна гпластпнка
не имеет отверстий), то функции Ф3 и Ф2 оломорфны)
и‘ однозначны в своих областях и 6Т2;
2) если область пластинки ограничена несколькими
контурами (пластинка ослаблена отверстиями), но при
этом главный вектор (равнодействующая) усилий, прило-
женных к каждому из контуров, равен пулю, то функции
Фх и Фо — голоморфны и однозначны в своих областях
52; “
3) если область пластинки S ограничена несколькими
контурами (пластинка имеет отверстия), и хотя бы на
х) См. liaaiy работу рЧ- стр, 83— 87.
37
одном контуре усилия приводятся к равнодействующей,
то функции Ф1Э Ф2 будут многозначными. Если, например,
в пластинке имеется одно отверстие, и на краю отверстия
действуют усилия, приводящиеся к равнодействующей
с проекциями Рх и то функции Фг и Ф2, при обходе
по любому замкнутому контуру, окружающему отверстие,
получат приращения Дп Д2, которые найдутся из урав-
нений ’):
1
д1+д2Н-д1 + д2 = ^,
1 y
J 3 2~ h ?
д ___ __ (11Ъ X__ а i 2
2 h alt h ’
-1 д1 + ±дз +
Fl Из |At fig ^23 h аЭ2
Для изотропной пластинки, на основании
ния (7.16), получаются следующие формулы 2):
+ 2^ГТ/ - 2 [2?" (2) + 9' Ш )
°Х + °и = 4Re [?' (z)], /
(8.10)
выраже-
(8.11)
2р. (a -f- iv) — zco (s) — гср' (z) — 0 (s)
[здесь 9(z) = x'(z), ?' (z), Ф(г) —функции, сопряжённые
с <p'(z) и Ф(г); a —G —модуль сдвига; х = v—коэф-
фициент Пуассона].
При заданных внешних усилиях Хп, Кп, граничные
условия для функций о и 0 принимают вид:
в
ср (z) + ztp' (z) + Ф (z) = (iXn — YIt) ds -j- c
0
(с —постоянная).
(8.13)
г) Определитель этой системы уравнений равен:
Я АЧА К«-Т)в + Ш-а)* * * В 91 . [(а — т)а + (3 + «И
d = ---------________
В случае неравных комплексных параметров, очевидно, всегда d > 9.
’) См. [’»], п° 32, стр. 106, 108; н° 41, стр. 136—137.
Если на контуре заданы смещения, то граничные усло-
вия можно записать следующим образом:
пр (z) —zy' (z) — Ф (z) = (я* + zr*). (8.14)
Здесь мы не разбираем случай попарно равных ком-
плексных параметров; путём замены переменной и изме-
нения контура области, в которой надо определить функ-
ции комплексного переменного, он сводится к случаю
изотропного тела.
Вопросы существования и единственности решения пло-
ской задачи теории упругости анизотропного тела иссле-
дованы С. Г. Михлиным х), Г. Н. Савиным г) и Д. И. Шер-
маном 3). G. Г. Михлин рассмотрел случай конечной
односвязной области, для которой свёл плоскую задачу
к системе интегральных уравнений. Г. Н. Савин рассмо-
трел случай бесконечной области с отверстием, а Д. И. Шер-
ман-случай конечной многосвязной области; эти авторы
также свели задачу к системе интегральных уравнений.
Сведение плоской задачи к интегральным уравнениям
дало возможность доказать существование и единствен-
ность её решения и наметить общие методы её решения
в любом случае. Те решения для простых областей, кото-
рые мы излагаем ниже, получены сравнительно элемен-
тарными приёмами, не связанными с интегральными урав-
нениями.
9, Лист фанеры, как анизотропная пластинка.
Из пластинок, которые на практике при расчётах рас-
сматриваются обычно как однородные и анизотропные,
отметим пластинки, вырезанные из листов авиационной
фанеры. Обычно лист фанеры изготовляется из нечётного
числа слоёв древесины (3, 5, 7 и т. д.), которые склеи-
ваются каким-либо склеивающим веществом,—белковыми
клеями, бакелитовой плёнкой и др. Волокна смежных
слоёв располагают под прямым углом так, что волокна
внешних слоев или, как говорят, волокна рубашки ока-
зываются параллельными. Фанерная пластинка, строго
говоря, есть тело неоднородное, но, изучая деформации
фанерных листов, у которых размеры велики по сравне-
нию с толщиной, можно рассматривать их как однородные,
Ъ См. [28
2) См. [*7
3) См. [51
30
анизотропные и притом ортотропные пластинки. У этих
пластинок одна из трёх ортогональных плоскостей упругой
симметрии параллельна срединной плоскости, вторая же
перпендикулярна к волокнам рубашки. Упругие постоян-
ные фанерной пластинки (которые, строго говоря, явля-
ются средними по толщине значениями) обнаруживают
большую разницу в величинах для направлений вдоль
волокон рубашки и поперёк волокон.
В нашей работе некоторые задачи иллюстрированы:
вычислениями, проделанными для фанеры двух типов.
Фанера, которую мы в дальнейшем условимся называть
«фанерой первого типа», имеет, согласно американским
данным, следующие упругие постоянные: модули Юнга
для направлений вдоль волокон рубашки и поперёк воло-
кон— 1,4 • 105 /гг/елг и 1,4/12 • 105 кг/см2; коэффициенты
Пуассона — 0,46 и 0,46/12; модуль сдвига для главных
направлений упругости —0,12 • 10б яа/слг. Эта фанера,
склеенная из трёх или пяти слоёв берёзовой древесины,
была впервые в русской литературе рассмотрена Я-М. Се-
керж-Зеньковичем *), который исследовал устойчивость
прямоугольной фанерной пластинки под действием каса-
тельных усилий. Следует отметить некоторую неточность
в определении модулей для этой фанеры: модули Юнга
определены из опытов на изгиб, другие постоянные — из
иных опытов.
Если, решая плоскую задачу для пластинки из фанеры
первого типа, направить ось ,т вдоль волокон рубашки,
то в уравнениях (2.5) и (5.11) надо положить:,
f / 1 Гг- 77 1,4 п .а 0,46
1,4 * 10', Е > = • 10', --0,4b, v2 = -р- ?
Комплексные параметры получаются такими:
3,08г, [Л2 = 1,12гГ.‘
Если направить ось х поперёк волокон рубашки, то
надо положить:
^ = 1^.10% Ех = 1,4 • 10% у. = 0,46,
L’z ' “ 7 7 1 12’“
G = 0,12-105,
У См. стр. 15.
40
Для комплексных параметров получаем новые значениям
^ = 0,321% у 2 — 0,89 Л
Другой тип фанеры, которую мы условимся в дальней-
шем называть «фанерой второго типа», это —трёх- и пяти-
слойная берёзовая фанера, склеенная бакелитовой плёнкой.
Некоторые данные для неё имеются в «Справочнике авио-
конструктора», часть III г), а именно: модули Юнга для
направлений вдоль и поперёк волокон рубашки—1,2- 10б кг/см*
и 0,6-10*кг/см\ модуль Юнга для направления под углом 45э
к волокнам рубашки 0,24 * 10s кг'см\ модуль сдвига для
главных направлений упругости — 0,7 • 105 кг/см2, модуль
сдвига для направлений под углом в 45° к главным —
0,39 • 10б кг[см2. Коэффициенты Пуассона не даны, но, на
основании имеющихся данных, их можно определить по фор-
мулам, выведенным в следующем § 10; на основании этих
формул, они получились равными 0,071 и 0,036, что мм
и примем. Направляя ось х вдоль волокон рубашки, имеем:
7% -1,2- 10% Ег - 0,6 • 10% - 0,071, у2 = 0,036,
<7 = 0,07 • 105, |^ = 2, -^ = 4,11/, у.2 = 0,343Л
Если направить ось х поперёк волокон рубашки, то будем
иметь:
Е. = 0,6 • 10% Е2 = 1,12 • 10% - 0,036, v2 - 0,07 J,
<7-0,07 • 10% н = 0,243/ ;л2 = 2,91/.
х> о
10. Пересчёт модулей упругости при переходе к ногым
осям.
При изучении плоского напряжённого состояния анизо-
тропной пластинки часто можно встретиться с такой зада-
чей: известны упругие постоянные и комплексные параметры
для некоторой системы координат х, у, и требуется найти
упругие постоянные и комплексные параметры для новой
системы координат я% yf, повёрнутой по отношению к пер-
вой на угол ср (рис. 10). Для ортотропной пластинки, как,
например, фанерной, обычно задаются упругие постоянные
для главных направлений; однако, может оказаться, что этой
главной системой на практике пользоваться неудобно,
и тогда мы встречаемся с указанной задачей.
% См. таблица 63 на стр. 325.
Формулы для пересчёта упругих постоянных можно полу-
чить следующим образом1). Пусть а —упругие постоян-
ные для координатной системы х, у и — упругие постоян-
ные для новых осей х\ у', повёрнутых по отношению
к первым на угол <р вокруг начала. Полагая, что главных
направлений в плоскости нет, имеем уравнения обобщён-
ного закона Гука и выражение для упругого потенциала:
®х==Лиах4 ai$ay + ai3Xxy*
= ^12ах 4-4" z (10.1)
Yx.V ” J
+^13^оу4-«1взхтгЭ+-а.2а^ +
4“ 4" *О* "xtf• (Ю.«)
Для новой системы х', у' имеем:
®Х “ ^11^Х 4~ 4“ й1вТХУ’ 1
~ 4~ Z (10.о)
Y-У “ aiG^X 4~ 4“ ^вв*Л1/’ J
F = 2 4- + 4 a^'y +
+ a^a'a^B + ja^r (10-4)
0 Этот вопрос разобран в книге Лява [а#], стр. 163, 164; у Геке-
лера [57j> етр. 412, и очень подробно у П. Бехтерева!4] (с) и И. Г. Чен-
цова f50].
Выражая через o', g', по формулам:
ax = g^. cos1 2 sin2 9 — 2^gsin 9 005 9,
ay~Gx sin2 9 4- cos2 9 + 2^ sin 9 cos 9,
SB = « “ °y) sin ? cos 9 + x'XG (cos2 9 — sin2 9),
(10.5)
подставляем эти значения в выражение потенциально й
энергии (10.2) и сравниваем с (10.4). Отсюда находим
искомые формулы:
«к = аи cos4 9 + (2л12 + а66) sin2 9 cos2 9 4-
+ а22 sin* 9 4- («1в cos2 9 4- aS6 s n2 9) sin 29, |
zz'2 = alY sin4 9 4- (2«12 4" «ee) sin2 ? cos2 9 +
4* «22 cos4 9 — («le sin2 94-^28 cos2 ?) s'n 29,
= («и + «22 — 2a13 — «ee) sin2 9 cos2 9 4~ «12 4~
+ 4 (а2в^а1б) sin 2? cos 29,
<« = 4 («11 + — 2«12 — a8e) sin2 9 cos2 9 4- «ee +
4- 2 (a2S — а1й) sin 29 cos 29, ^(10.6)
*«'6 = [«22 sin2 9 — aLl cos294*4(2«i2+«e6) cos 2э] sin 29+ j
4- «16 cos3 9 (cos2 9 — 3 sin2 9) 4-
4-«as sin2 ? (3 cos29 —sin2 9),
= [«22 cos2 9—«X1 sin2 9~4(2«12+«бб) cos 29] sin 294-
4- «16 sin2 9 (3 cos2 9 — sin2 9) 4 !
4- a2e cos2 9 (cos2 9 — 3 sin2 9). j
В частности, для ортотропной пластинки уравнения
обобщённого закона Гука, связывающие средние значения
составляющих напряжения и деформации, отнесённые
м главным осям, имеют вид:
(10.7)
1 v,
s-v~ b\Ojc
1
Yxff ~~ Q ~Х!Г 1
Перейдя к новым осям х', у', йолучим уравнения
обобщённого закона Гука:
/ 1 ' **3 л , / 'I
с ь;с.<- E'asi/ ' аЛ!'’ J
£> + + ? (10.8)
' I ' 1 1 '
7й» “ аА; ' i у
где ^ — модули Юнга для новых направлений х', у'г
у', у' — коэффициенты Пуассона; G' —модуль сдвига Для
новых направлений; а1? а2 —побочные коэффициенты, про-
падающие в главной системе. Новые модули и коэффи-
циенты определятся по формулам, следующим из (10.6):
1 cos4 ? + -й) sin2 cos2 ф+АпП i ‘ + E, ’
L sin4 3 < 1 sin2 ф , cos4
£. I cos2
Е’~ Е, J ? r e2 '
_1 _ ' и + •*1 , 1 + -G -2Л sin2 2?,
G' ' G ' ( 1 G )
V 1 —‘ -^1 [ л ЁГ — А Л k Е, +х J G -) sin2 2? 1,
,Е'2
v- —
(10.9>
Отметим две инвариантные величины, сохраняющие*
свои значения при повороте осей:
1 ( 1 2v't
1
G' Ё[
Ei 1 Е.3
1 4-?, .
G В/
(10.10)
На практике может возникнуть и такой вопрос: в орто-
тропной пластинке известны упругие постоянные Е'^ Ё'2,
у', v2, &’ •> ai и а2? отнесённые к системе координат х', у',
не совпадающей с главной; требуется определить 1лавные
направления и постоянные, отнесённые к главным направ-
лениям.
Вопрос решается на основании двух последних фор-
мул (10.6). Приравнивая а1в и аав нулю, получим после
преобразований два уравнения, которым удовлетворяет
угол ср наклона главной оси х к оси хг\
tg 2<р = -р2—, I
° ‘ М-А 1+va *
Е[ G')
Эти уравнения будут иметь общие решения при выпол-
нении условия:
Если последнее условие не выполняется, то главных
направлений не существует, и пластинка не является
ортотропной.
11. Пересчёт комплексных параметров при переходе
к новым осям.
Если известны комплексные параметры р* и р2, вычис-
ленные для осей х и у, и требуется найти комплексные
параметры и' и р' для новых осей х\ у’, то можно посту-
пить следующим образом. Запишем уравнение для функции
напряжений F в символическом виде; в системе т, у имеем:
(11.1)
где
Dr = ~-{xk-, (11.2)
к 1 h ах* К
а р;. — корни уравнения
— 2я1ви3 + (2«i2 + «,.) Г — 2aasu + а2г = 0. (11.3)
Произведём замену переменных на основании формул
(рис. 10):
х' = х cos фЧ-г/ sin «р, ] 4)
у' = — х sin <f> + y СО8^>, J
и выразим производные по у и по х через производные
во у' и по х'. Получим:
д д д . v
= + 'I
д <? . , д f
V =--------Т~/ 81П Q + COS <?.
дх ду' т 1 дя' т )
(11.5/
Тогда, по сокращении на постоянный множитель, мы
запишем уравнение (11.1) в виде:
d;/xd;d;f-o, (и.б)
где
р = о _ x.eos, s;„. <?_
Л ду' cos t? 4- |л/г s m ъ дх' V л
Отсюда пол х чаем формулы для пересчёта комплексных
параметров при переходе к новым осям:
. Hi cos?— sin в , р.а cos ? — sins 1
u = .. 1 -------. 1. U — — *---------: — (
• 1 cos ? 4- |1Х sin с? 1 - cos ? -r l-l2 sm z ’ ।
Pi cos? — sin? ___ p-2 cos ? —sin ? f (11.8)
‘ 1 cos ? 4- |ix sin ? ’ cos ? 4- Pa sin ¥ J
Отметим некоторые свойства комплексных параметров^
обнаруживающиеся в результате анализа формул (11.8):
1) Если параметры и jt2 Для какой-нибудь системы
координат х, у оказались неравными, то они останутся нерав-
ными в любой другой системе координат х’, у’, повёрну-
той по отношению к первой на произвольный yi ол ф.
2) Если для какой-нибудь системы координат х, у пара-
метры и а2 являются комплексными числами, то и для;
любой системы х', z/', повёрнутой по отношению к первой,
параметры р.[, а' будут комплексными (или в частном слу-
чае чисто-мнимыми) числами. Наоборот, если бы в
какой-нибудь системе координат для и у.2 получились
вещественные значения, то и в любой другой повёрнутой
системе параметры будут вещественными числами (этот
случай, как указано выше, невозможен для упругой ани-
зотропной пластинки).
3) Если для какой-нибудь системы координат получи-
лось: = то и для любой повёрнутой системы
комплексные параметры будут иметь те же значения:
— /, Это — случай трансверсально-изотропного тела
с плоскостями изотропии, параллельными хул или пол-
ностью изотропного тела.
46
12. Примеры преобразования упругих поетоянных-
и комплексных параметров.
Поясним изложенное в §§ 10 и Г1 двумя численными
примерами.
1. Требуется определить упругие постоянные и ком-
плексные параметры пластинки из фанеры первого типа
для осей х', у', образующих углы в 45° с главными осями.
Для главных осей имеем:
£х = 1,4 • Ю6 KejcM*, • 10’ кг/см-,
G=0,12 • 106л-й/сл<г, vx = 0,46, >2 = °;26’
рх = 3,08/, pa=l,12i, рх=—3,08i, jl2=— l,12i.
Полагая <р=45°, получаем по формулам (10.9):
jfe-sH (i+4+г-- 2г)"4’24'1^*,
н-нстчь°'»7-10
1=^+1* + *^ = 9,94- 10-’,
“.-“.-4(y-x) = 3,9310-.
Отсюда1)
= 0,236 • Ю’кг/сл2, >; = v' = - 0,017,
G' = 0.101 • 10sA-a,W.
Г6
По формулам (11.8) получаем:
01113+°’994‘>
= 0,809 - 0,587/,
^ = 0,113-0,994/.
J) Коэффициенты Пуассона получились отрицательными; это зна-
чит, что при растяжении пластинки, вырезанной из фанерного листа
под углом в 45° к главным направлениям, материал будет не сжи-
маться, а расширяться в направлении, перпендикулярном к растя-
гивающим усилиям. Возможно, что такой мало убедительный ре-
зультат получился вследствие неточного определения постоян-
ных фанеры.
47
2. Для анизотропно# пластинки, находящейся в обоб-
щённом плоском напряжённом состоянии, найдены следую-
щие значения упругих постоянных, отнесённых к некоторой
^системе координат:
.^ = 0,781 • 10“% 1,531 * 10“% я12 = — 0,006 • 10“%
«66 = 2,575 10"% а1в= - 0,541 • 10"% я..в - -0,758 • 10“%
требуется определить главные направления (если они суще-
ствуют) и вычислить упругие постоянные и комплексные
параметры для главных направлений.
Угол, образованный одним из главных направлений
«с осью х, определится одновременно из двух уравнений
(10.11); если эти два уравнения имеют общие решения, то
главные направления существуют.
В нашем случае уравнения (10.11) принимают вил:
tg 2«р= 1,732,
tg 4ср = —1,732.
Из первого находим: ср = 30°, 120°, 210е, 30.0 и т. д.;
яти же значения удовлетворяют и второму уравнению.
^Следовательно, главные направления существуют, и одна
из них образует с направлением оси х угол <р - 30°.
По формулам (10.6) находим упругие постоянные для
главных направлений:
«А = /б 19й11 + 3 (2й1з 4- + «.»] + “g-O»!. + аи) =
= 0,5 • 10"*,
= 1llflu + 3 (2а12 + йв«) + 9«за] —%5 (01, + За,,) =
= 2,0 10"%
= 1 б ^11 °2г 2й12 йв.) й12 4 g~ (й2в Я1в) ~
= -0,1 • 10"*,
Йв6 (й11 4“ ®22 йв.) ~Ь 0». 4 о (й26 - ®1«) =
= 2,2 • 10"*,
= "V («22 Заи -I- 2д12 4- aj +=? = 0,
й26 ~ % (Зй22 0Ц 2й12 — as«) 4“ V — 0;
2% = 2 - 105 .KejcM-, Ег = 0,5 • Ю5 кг.}слг,
v,=O,2, v2 = 0,05, 6=0,455 • 10* кг/см\
48
Характеристическое уравнение для главных осей при-
нимает вид:
0,5р.* 4 + 2а2+ 2-0.
Корни этого уравнения— комплексные параметры, по-
парно равные:
Hi ^2 = 1^2 • 1,41/,
Й1 = = --1^2 • *
13. Обобщённое плоское напряжённое состояние в пла-
стинке с цилиндрической анизотропией.
В предыдущих §§ 5 — 12 были рассмотрены однородные
пластинки, у которых эквивалентными являются парал-
лельные направления, проведённые через разные точки.
В этом § 13 мы выведем общие уравнения плоской задачи
Для тела с цилиндрической анизотропией1).
Рассмотрим упругое равновесие пластинки постоянной
толщины, обладающей цилиндрической анизотропией, под
действием усилий, распределённых по краю, и объёмных
сил. Относительно упругих свойств мы будем предполагать
следующее:
1) ось анизотропии нормальна к срединной плоскости
пластинки (точка пересечения срединной плоскости с осью
анизотропии, которую мы будем называть полюсом анизо-
тропии, может лежать внутри или .у
вне пластинки, это не играет роли); *_
2) в каждой точке имеется плос- Xх*;
кость упругой симметрии, параллель- ( : \ z
ная срединной плоскости. —4
Рассмотрим тот случай, когда / .
усилия — поверхностные и объём- #
ные — параллельны срединной пло- у /
скости, распределены симметрично 1г
относительно этой плоскости и не- р н
значительно меняются по толщи-
не пластинки. Деформации будем считать малыми.
Примем ось анизотропии g за ось z цилиндрической
системы координат, направив полярную ось х произвольно
в срединной плоскости (рис. 11).
Обозначим через h — толщину пластинки, R, в — проекции
объёмных сил (на единицу объёма) на координатные на-
правления г, О (Z = 0) и, как в случае однородной пластинки,
1 См. нашу работу р*|, стр. 144.
4 С. Г. Лехнипкий
49
введём в рассмотрение средние по толщине значения со-
ставляющих напряжения и проекций смещения:
h/г л/г
“’•"’Т С,^4’ 5 a‘dz’
-h/г -h/г
h/г h/г
1 С 1 С
\ u/iz-
rij ri J
-h/2 -h/2
Введем ещё обозначения:
h/г h/з
B = y \lldz, ё = ~- ^e«?z; (13.2)
-h/2 -h/2
— d c/.Un jt — 4 Щ л
Trt = 7^+~-7(lM>
и рассмотрим тот случай, когда объёмные силы имеют по-
тенциал U (г, 0), т. е. определяются формулами:
Ъ К 1 и /1О /ч
Я= -аР е=~7^- (13'4>
Уравнения для величин с9 иг щ мы получим,
произведя операции осреднения над уравнениями равновесия
в цилиндрических координатах (1.3) и уравнениями обоб-
щённого закона Гука.
В результате получим:
! t f °r fffl .
4 d0) 2т1Ч .
dr * г с/0 г ‘
R = О/
0 = 0,,
ег = аи°г 4 «1»«з + «1.^0,
Yr3 ®ie®r “I” ^ae*^u ^ee^r^* j
(13.5)
(13,6)
Исключая смещения из выражений для составляющих
деформации (13.3), получаем уравнение совместности:
. /8<^> . дг^>) Г^г п. ,13<7>
£>Q2 * (>ГЙ <7Г с?9 0Т (
50
Уравнениям равновесия (13.5) мы удовлетворим, введя
функцию напряжений F (г, &), полагая:
— 1 1 '_П
®г— г дг +г» 30s и'
cFF . Т7
Qp-й ~Ь
з2
ТгЭ — ЭгЗО V г ) •
(13.8)
На основании уравнения совместности (13.7) и вави-
оимостей (13.6) и' (13.8), получаем дифференциальное
уравнение, которому удовлетворяет функция напряжений F:
dip ‘Уп А д'р л.Пп । « \ A д'р 1 &F ,
a"dF 28 Г Зг’ЗО*' \““12 1 а»«1г2 0Г2ЭД2 ^aUjA дтд№ ‘
, 1 W , пя 1 d*F (Г)„ , „ ч 1 W ,
+ ан r4 5Q4 + гЯ2» r dr* (zai2 + ate) fA дгд№ "А
. 1 d5F „ 1 32F „ , I Л ч 1 ,
+ ^aie ,л дй* 011 Г* dr* 2 'a« ' a**' Iя dr 38 "*
+ (2вц + 2e1S + ael) ~ + an 73 + 2 (aie + «2e) ;r fy =
. . x d-u . . . . 1 O-U . . x 1 347
» (^ie"b^26/ r Qr (^12 “Ь бц) ya ^((2
(2^22 • ~Г ^12)“ "Г (я1в 4~ #2б) ~2 • (13.9)
Ото .уравнение соответствует уравнению (5.9) для одно-
родной пластинки.
В частном случае, когда пластинка с цилиндрической
анизотропией является одновременно и ортотропной (пло-
скости упругой симметрии проходят через ось антзотро-
I ии z), уравнения обобщённого закона Гука (13.6) ? ожно
записать так1):
1 - У1-
~~ I?/1*'
®! “ ~SLs’-+^°э’ Yri = М-
* J
Здесь Er^ Е — модули Юнга для растяжения — сжатия
в главных направлениях г, 0;.vr, v3 — коэффициенты Пуас-
сона; G —модуль сдвига для главных направлений г, 0.
х) Опп получаются из уравнещ й (4.3) путём осреднения. В
дальней ли*м чё'точим над символами напряжений и деформаций
будем опускать.
4* 51
(13.10)
Для этого случая уравнение (13.9) упрощается и принимает
следующий вид:
I &F , / 1 2vr\ 1 1 1 dlF .
We dr‘+<G 'Er) r* Er ’ ? <>0* "Г
2 1 d*F C 1 _ 2vr\ 1 ifiF _ 1_ 2.
+ Eo ' У № <G E~J 7» Or MF Er ' r1 Ji» h
+ <Er + G ErJ r* MP ‘ Er ' r* dr ~
Г1—7,1 .(>w 4. £z2r 1 :j*u
L * or2 Er * r2 d>62
, n„L+v±^ 1
+ Er J r dr J ‘
(13.11)
Граничные условия при заданных усилиях по краю
пластинки могут быть сведены к заданию на контуре пла-
стинки первых производных функции напряжений — dFjdr.
<1F /дЬ. Теория интегрирования уравнений (13.9) и (13.11)
пока ещё, повидимому, недостаточно разработана, и общгю
выражения функции F, соответствующие выражениям
(7.14) и (7.15), не известны.
Задача об обобщённом плоском напряжённом состоянии
совершенно аналогична задаче о плоской деформации. Если
тело, изображённое на рис. 8 (§6), обладает цилиндрической
анизотропией с осью анизотропии z, направленной па-
раллельно образующей, то для него справедливы уравне-
ния (13.5) — (13.9), в которых нужно только заменить
коэффициенты a j величинами
р а (/,/=1,2,6). (13.12)
ГЛАВА III.
ИЗГИБ АНИЗОТРОПНЫХ БАЛОК И КРИВЫХ БРУСЬЕВ.
14. Простейшие случаи распределения напряжений
в плоской пластинке.
В этой главе мы рассмотрим некоторые случаи распре-
деления напряжений под действием изгибающих нагрузок
в прямоугольной плоской пластинке, в клинообразной
консоли прямоугольного сечения и в кривом брусе, пред-
ставляющем собой часть плоского кругового кольца. Во
52
всех случаях мы будем предполагать, что в каждой точке
пластинки, консоли и кривого бруса имеется плоскость
упругой симметрии, параллельная срединной плоскости.
Рассмотрим предварительно простейшие случаи равно-
весия однородной анизотропной прямоугольной пластинки
постоянной толщины Л, находящейся в обобщённом плоском
напряжённом состоянии под действием усилий, распределён-
ных по краям. Во всех случаях этого параграфа, а также
и других параграфов настоящей главы, срединная плоскость
принимается за плоскость ху, и уравнения обобщённого
закона Гука, связывающие средние значения составляющих
напряжения и деформации, имеют вид:
“Г Й12ау 4“ )
Sy = <Z12<JX -р -f-
Yory ~ 4“ 4“ Й66Т»У J
Упругие постоянные « у считаем известными. В частном
случае, когда пластинка является ортотропной, и глав-
ные направления приняты за направления осей ж и у.
коэффициенты а1ъ и а26 равны нулю, а остальные выража-
ются через главные упругие постоянные:
— 1 m 1
аи—Е^
__ 21 __ 71 л____L
12~ ~Е1 Ёг' ° ~G
(14.2)
Решения для всех случаев глементарны, и мы их
приводим без вывода.
1) Растяжение. Прямоугольная пластинка растя-
гивается нормальными усилия-
ми р, равномерно распреде-
лёнными по двум противопо-
ложным сторонам (рис. 12) •.
= ff» = ^a = 0, F = ^y2 }
(14.3) (р — интенсивность рас-
тягивающих усилий — усилие Рис. 12.
на единицу площа;и).
Распределение напряжений—такое же, как и в изо-
тропной пластинке, а деформации определяются из
53
уравнений (14.1):
~ (14.4)
Неортотропная пластинка под действием растягивающих
усилий удлиняется в направлении усилий, укорачивается
в перпендикулярном направлении (если а13 < 0) и перека-
шивается в плоскости ху\ перекос определяется постоян-
ной а1в (см. пунктирную линию на рис. 12). Ортотропная
цластинка, деформируясь, сохраняет форму прямоуголь-
ного параллелепипеда.
2) Сдвиг. По краям прямоугольной пластинки распре-
делены равномерно касательные усилия t на единицу
площади (рис. 13). Имеем:
= = = F=—txy, (14.5)
ех — гв — "(хд — (14.*-')
Неортотропная пластинка под. действием касательных
усилий испытывает не только сдвиг в плоскости
Рис. 13.
Рас.
определяемый постоянной азв, но и удлинения или укоро-
чения сторон, в зависимости от знаков а1в и а2в. Ортотроп-
ная пластинка испытывает один сдвиг.
3) Чистый изгиб. По двум сторонам пластинки рас-
пределены усилия, приводящиеся к моментам М (в кг см\
(рис. 14). Имеем:
'г^У, ав = гхй = о, F=™-y*', (/ (14.7)
Распределение напряжений такое же, как и в изотроп-
ной балке (если не учитывать местных напряжений около
загруженных частей балки, которые, согласно принци-
пу Сен-Веиана практически не оказывают влияния на
напряжения в частях, удалённых от загруженных поверх-
ностей).
54
Перемещения частиц балки равны:
и=Т (а1гху + у^') — 0>г/4-и0, 1
М > (14.8)
U =21(а^У^а11Х )+шЯ Г V0J J
где со. н0, v0 —постоянные, выражающие «жёсткое» пере-
мещение балки в её срединной плоскости. Первое из
выражений показывает, что сечения неортотропной балки
не остаются плоскими; искривление зависит от постоян-
ной а1Ъ.
Сечения ортотропной балки при деформации не искрх^-
еляются.
Уравнение изогнутой оси при неподвижных концах
х = 1 имеет вид:
Ag.ii (fa ___ (14.9)
где у)—ордината изогнутой оси.
Кривизна изогнутой оси равна:
(14.10)
Зависимость между кривизной изогнутой оси и изги-
бающим моментом такая же, как у изотропной балки,
Только вместо модуля Юнга Е (одинакового для всех на-
правлений у изотропной балки) нужно подразумевать мо-
дуль Юнга Е\ для растяжения —
сжатия вдоль оси балки. ___________И if
15. Изгиб консольной 'Т Ч-*
балки поперечной силой. v 7 L
__ р -лр 1 £
Балка с сечением в виде узко-
го прямоугольника заделана од-
ним концом и изгибается поперечной силой Р, прило-
женной к другому концу (рис. 15).
Решение получается с помощью функции напряжений F
fa виде полинома четвёртой степени1):
?=И_И„^+аС^-0]. (15-1)
*) См. нашу работу [и], с;р. 159.—160.
56
Составляющие напряжения определяются по формулам:
«в = о, } (15.2)
Из этих формул видно, что в ортотропной пластинке, у
которой главным направлением является осевое направле-
ние ж, распределение напряжений получается таким же,
как и в изотропной балке '):
/ (1 - •<-) */> ]
^ = 0, > (15.3)
Р 2-\
21 Ст-2/ ) J
Для балки, у которой коэффициет а1в не равен нулю
(случай неортотропной балки или ортотропной балки, у
которой осевое направление х не является главным) f
Рис. in.
распределение нормальных
напряжений по сечению под-
чиняется параболическому
закону. График распределе-
ния напряжения охпо сечению
представлен (в произвольном
масштабе для а1в > 0) на
рис. 16; пунктирная пря-
мая — распределение напря-
Наибольшее нормальное
у — Ь / 2 или у = — b I 2)
жения в изотропной балке,
напряжение (в месте заделки, при
равно по величине:
(для «12 > 0; напряжение сжимающее), или
(для а1в < 0; напряжение растягивающее).
*) См., например, С. П. Тимошенко t48], стр. 45. На рис.*15
напей работы оси направлены иначе, чем у Тимопенко.
Заметим, что формула для кривизны изогнутой оси
балки (безразлично, ортотропной или неортотропной)
имеет такой же вид, что и в случае чистого изгиба, т. е.:
₽=^=У’ (1516)
только в данном случае изгибающий момент М меняется
по длине балки и равен
М=~Р(1~х).
(15.7)
Параболической закон распределения напряжений по
сечению не отражается на уравнении изогнутой оси балки,
которое имеет такой же вид, как в случае изотропной
балки:
4=^(3/^-я8). (15.8)
16. Изгиб балки равномерно распределённой нагрузкой.
Балка с сечением в виде узкого прямоугольника (балка-
пластинка) лежит на двух опо-
рах и изгибается равномерно
распределённой нормальной на-
грузкой q на единицу длины
(рис. 17).
Распределение напряжений
получается с помощью функ-
ции напряжений в виде полинома пятой
4
ь
Т-— I
-----: ZL
I —-
•у
Рис.
\у
17.
степени г):
। ? Г __ «и t :
Т* h |_ ап b \ 2 i
2Л1й + а66 \ f V* УЛ
J <563 “ 106/
। 1 (16 п
’ ” у V563 10&7 4 *46 J ' '
Составляющие напряжения определяются по формулам:
а*
*) См. налу работу [п], стр. 163.
57
В частности, для ортотропной балки, у которой главным
является направление оси получим:
Отсюда видно, что распределение напряжений и в
ортотропной балке не отличается от распределения в йзо-
трспной балке. Закон распре-
деления нормальных напряже-
ний ах по сечению— такой же,
как в изотропной балке, только
коэффициент при втором члене
— 2v1} равный для изотроп-
ной балки двум, здесь имеет
иное значение ’1). Для балки,
РиС. 18.
и изгибаемой равномерно распре-
заделанной одним концом
делённой нагрузкой (рис. 18), получаем формулы для на-
пряжений, напоминающие (16.3):
Составляющие перемещения и и и в обоих случаях най-
дём путём интегрирования уравнений (14.1). Заметим, что
закон пропорциональности кривизны изогнутой оси изгибаю-
щему моменту для балок, нагруженных равномерно распре-
делённым давлением,, не имеет места.
Аналогичным путём, используя функцию напряжений в
виде целого полинома, можно получить распределение на-
пряжений в балке под действием собственного веса. Решая
от у задачу, приходим к следующему заключению:
См., начример, С. П. Тимошенко [43], стр. 50,
58
Распределение напряжений ах и для балок по рис. 17
и 18 получается точно таким же, как если бы эти балки
изгибались равномерно распределённой по верхней грани
нагрузкой интенсивностью q^-^bh (на единицу длины), где
у — удельный вес материала. Что касается нормальных
напряжений а у впродольных сечениях, выражающих действие
продольных слоёв балки друг на друга, то они в обоих
случаях распределяются по закону:
ав= (16.5)
17. Изгиб балки произвольной нагрузкой.!
С помощью функций напряжений в виде целых полино-
мов можно всегда определить распределение напряжений
в однородной балке под действием нагрузки, распределён-
ной по всей длине по закону:
v
<7=?о + 2 С7-1)
Л-1
Если нагрузка распределяется по более сложному закону,
особенно в тех случаях, когда загружена только часть про-
лёта балки, распределение напряжений можно получить с
помощью рядов Фурье. Мы рассмотрим порядок применения
этого метода на примере балки, лежащей на двух опорах
и нагруженной нормальней нагрузкой, распределённой сим-
метрично относительно середины по произвольному закону.
Другие случаи однопролётной балки —балки консольной в
балки на двух спорах, нагруженной несимметричной на-
грузкой, могут быть исследованы тем же методом, с
соответствующими несущественными изменениями в
деталях г).
Балка из однородного анизотропного материала лежит
на двух опорах и подвергается действию нормальной на-
грузки, распределённой симметрично относительно центра
балки по произвольному закону. Предполагается, что балка
является ортотрспнсй, и плоскости упругой симметрии её
параллельны граням, а следовательно, осевое направление
-является главным.
/) Задача об изгибе изотропной балки с » о мощью дядоз Фугьэ
ре галась Рибьером, Файловом, Блгйхом и др. (литература г.о этому
вопросу указана у С. П. Тимошенко [43], стр. 56—63).
59
Расположив оси координат, как показано на рис. 19,
обозначим через ‘11 — длину, через Ь — высоту и через
Л —толщину балки. Нужно подобрать такое решение
уравнения
+- —=0 (17 21
Ег дх*'\6 Е1)дхъдуг^гЕ1д^ U’
которое даст возможность точно удовлетворить условиям
L на длинных сторонах балки.
и приближённо — на корот-
ких.
Разложим нагрузку qr
как функцию х, в ряд Фу-
рье на интервале ( — Z, Z),
РИС< pj, на котором эта нагрузка
задана. Ряд будет содер-
жать только косинусы и постоянный член:
?==?.+ 2 ^cos "г» ем
где
i i
iLif С т 2 f* A.7ux г
у \ 0*== у \ ? cos у dx.
о о
Граничные условия на длинных сторонах имеют вид:
при у = ~ ^=0, ^^0;
, 00 , (17.4)
_ b X? к^х Л '
При 7/=-’ -у ^CCS "Г ’ Х^==0’
7с—1 J
Функция напряжений, соответствующая постоянному
члену разложения нагрузки, нам известна [формула (16.1)]у
а функцию, дающую распределение напряжений от нагруз-
ки ?дсоз^, будем искать в виде:
^ = /л(2/)соз^р. (17.5)
Подставляя в уравнение (17.2), получаем обыкновенное
уравнение для функции fk (у):
(?)’«+
60
Вид функции /л. зависит от корней характеристического
уравнения:
(17.7)
лЩ «17 "2 '
Здесь возможны три случая:
Случай I. Корни вещественные, неравные; обозначим
их:
± S1J ± 52 (tS'l t<f2 0).
Случай II. Корни вещественные, равные’.
± s (s > 0).
Случай III. Корни комплексные; обозначим их:
$ ± ti, — $ ± Н (s > 0, t > 0).
Чисто мнимых корней получиться не может, так как
сходное уравнение
не имеет вещественных корней т).
В случае I функция напряжений Fk имеет вид:
Fk = (Ak ch -f Вк sh 4- С\ ch +
+ Z)fcsh^)cos~ (17.9)
{Ак, Вк, Ск, Dk — произвольные постоянные).
В случае 11:
Fk = [ (Ак + Вку) ch s-^ + (Ск+Dky) sh ] cos . (17.10)
В случае III Fk можно представить так:
F«= [ В,:^) С».^ +
+ (С„ ч- л. sh ’4’4 sin Чя 1 o»s . (17.11)
Беря функцию F в виде суммы выражения (16.1)
и выражений (17.9) [или соответственно (17.10) или (17.11)],
г) Числа sL и $а связаны с комплексными параметрами плоского
напряжённого состояния и ца зависимостями: —Фь $2 = —
61
по формулам (5.7) определяем напряжения и из условий
(17.4) находим постоянные D^. В результате
получаем формулы для напряжений в виде рядов довольно
сложной структуры. Напряжение по концам балки может
привестись к моменту, от которого мы избавимся наложе-
нием решения для случая чистого изгиба.
Этого рода задачи до численных результатов для анизо-
тропной балки, пзвидимому, пока не доведены.
18. Изгиб клинообразной консоли силой, приложенной
к вершине.
Рассмотрим упругое равновесие клинообразной консоли
прямоугольного сечения; широкий конец неограниченно
далеко от вершины заделан неподвижно, а к вершине при-
ложена сила Р. Мы будем предполагать, что материал кон-
соли является одно-
родным и анизотроп-
ным, но вообще не
- г ~ °г ортотропным (суще-
0 | ; ствование плоскостей
/7^----------------*---1----------- упру гей симметрии,
! параллельных сре-
/ длиной плоскости,
^*4^. / мы всегда предпола-
/ гаем).
. К вершине клина
приложена сила Р,
20’ действующая под про-
извольным углом к
оси клина. Примем вершину клина за начало координат
и направим ось х произвольно в срединной плоскости
(рис. 20); будем пользоваться полярными координатами,
отсчитывая полярные углы 0 от оси х. Обозначим углы
наклона граней к оси х через и % (Уг°л при вер-
шине равен, очевидно, + угол наклона силы к оси х
через
Задача состоит в выборе такого решения уравнения
(5.10), которое позволит удовлетворить условиям на гранях
клина:
при 0=—-фх и 6— % = —0, (18.1)
условиям равновесия части клина под действием силы
@2
Р и определит составляющие напряжения, стремящиеся
к нулю по мере удаления от вершины.
Как покапывает исследование '), функция напряжений,
дающая решение задачи, имеет вид:
Г-гФ^б), (18.2)
где Ф1 — функция одного только полярного угла, которая
определится из уравнения (5.10). Для определения функ-
ции Фх полезно записать уравнение (5.10) в символической
форме:
(18-3)
где dk — линейные операторы, пропорциональные операто-
рам Dk и в полярных координатах имеющие вид:
dk = (cos 6 -- pi sin б) — — (sin б + pi cos б) у , (18.4)
a pi— корни уравнения
a22j*'4 — 2a26u.'3 + (2a12 + aee) ц'* — 2aie!i/ -j- au = 0. (18.5>
Корни последнего уравнения по величине обратны кор-
ням ранее рассмотренного уравнения (7.4) и также не могут
быть вещественными.
С помощью символического представления уравнения
(18.3) функция Ф* определится в четыре приёма, путём
последовательного интегрирования четырёх уравнений пер-
вого псрядка. В результате, на основании равенств (13.8),
мы получаем формулы для определения напряжений в клине
от силы Р:
где
L (б) ~ a22 sin4 б “ 2a2e sin8 0 cos 0 4-
4 (2a134-a66)sin2Gcos20~-2aissin Ocos’fl-t au cos4 0. (18,7)
Произвольные постоянные А и В определяются из условий
равновесия части клина, вырезанной круговым сечением
произвольного радиуса г, описанным из вершины, как из
х) См. нашу работу [п], где этот вопрос рассмотрен более
детально.
о4
центра (пунктир на рис. 20). Получим1.
фз фа X
. С cos20 . г» С sin 0 cos 0 Р |
А \ -Y-^rdd + B \ —d0= — —roosw, I
J Z(0) J b(u) a22h I
-> “'i'1 . > (18.8)
фз фа ' 7
. Г sin 0 cos 0 тй . » C sin2 0 Р я.
А \ —/>н\— м + В \ <79^ —-—г sin ш
J L (0) J L (0) 1?23Л
-ф1 -ф1 7
(Л —толщина клина).
Вычисления упрощаются, если консоль является орто-
тропной и направление оси х совпадает с главным. Тогда
L W = ~Ё7 + <0 “ ЁГ) S1Q' 9 008 9 - • (18/Э)
Заметим, что в данном случае L(9) есть величина, обрат-
ная модулю Юнга для радиального направления [см. фор-
мулу (10.9)].
Относительно общего характера распределения напря-
жений необходимо отметить следующее. Распределение
напряжений в клине является «радиальным» или «луче-
образным»; напряжение аг в любой точке является глав-
ным и направлено вдоль луча, проведённого из вершины
в данную точку. В зависимости от соотношения между
упругими постоянными и углом наклона силы о>, возможны
три случая: 1) все части клина сжаты, 2) все части клина
растянуты, 3) в области клина имеется нейтральная линия,
по которой напряжения равны нулю; по одну сторону ней-
тральной линии материал сжат, по другую сторону — рас-
тянут (рис. 21, а, Ь, с).
Положение нейтральной линии определяется углом 90,
для которого
tg 00 = - (18.10)
*) Интегралы, входящие в уравнения (18.8) вычислены для
разных случаев корней нл в нашей работе [п] (стр. 178—179).
64
Точки, где главное напряжение вг имеет одинаковую
величину а0, положительную плп отрицательную, распола-
гаются на кривых четвёртого порядка; по одну сторону ней-
тральной линии располагаются точки, соответствующие сжи-
мающим напряжениям (отрицательным а0); по другую сто-
рону — точки,соответствующие растягивающим напряжениям
(положительным с0). Уравнение семейства кривых одинако-
вых напряжений имеет вид (в декартовых координатах):
<7]ГС —2бг;бж3?/+ (2а12 4 «66) х'у"— 2а2вху3 +
+ 4 By) = 0. (18.11)
Кривые эти —всегда замкнутые, хотя в область клина
попадают только некоторые их дуги; все кривые проходят
через вершину. С подобными кривыми мы ещё встретимся
в следующей главе.
Для консоли из изотропного материала L(0) Соста-
вляющие напряжения найдутся по формулам (ось х напра-
влена по оси симметрии, угол при вершине — 2'^):
2Р / cos со cos 0 . sin (О sin 0 \ л п .« о .
^-=0’ ^=°- (18Л2>
Кривые одинаковых напряжений превращаются в окруж-
ности, проходящие че-
рез вершину.
19. Изгиб клинообраз-
ной консоли моментом.
Клинообразная кон-
соль, рассмотренная в
§ 18, изгибается момен-
том М, приложенным к
вершине.
Направим ось х (по-
лярную ось) по оси
симметрии клина; угол
при вершине обозна-
чим через 2Ф (рис. 22).
Рпс. 22.
В этом случае па гранях должны выполняться условия:
при 9 = ± Ф ^9 — 0, — 0;
(19.1)
кроме того, составляющие напряжения должны стремиться
5 С. Г. Лехнпцкии
к нулю по мере удаления от вершины. Функция напряже-
ний, которая даёт возможность удовлетворить этим усло-
виям п условиям равновесия, имеет вид х):
(19.2)
(она не зависит от г). С помощью символического предста-
вления уравнения (18.3) эта функция определяется в не-
сколько приёмов путем интегрирования уравнений первого
порядна.
В результате для составляющих напряжения, удовле-
творяющих условиям (19.1), получаем формулы:
Г 2 sin 20 . , (0)1 \
°-- - L -т^-+c°s 20 -cos He? J'
sj = O, > (19.3)
_ Л<722 cos 20— cos 2Л
're -- Г(0) • }
Здесь
L (9) a22 sin4 9— 2a.is sin3 Seos 9-|-|
4- (2a,3 4- ae„) sin'* 2 6 cos'2 9— |
— 2ale sin 9 eus3 9 + cos4 9 ) (19.4)
Z/(') J
Постоянная А определяется из условий равновесия части
клина, вырезанной круговым сечением (рис. 22), п оказы-
вается равной:
. М t
Л = ~- • 5----------
А а 9 ? ?
Г cos 20 —cos 2ф ,п /ш г\
\---П8)—(19-0
В случае ортотропной консоли удобнее совместить
направление оси х с главным направлением. Если главное
направление не совпадает с направлением оси клипа, то фор-
мулы (19.3) несколько усложняются ").
Относительно общего характера распределения напряже-
ний следует отметить, что в случае изгиба моментом распре-
г) См. нашу работу [п], где данный вопрос разобран иол се под-
робно.
2) Значения интегралов, черв) которые вьцажаклся постоянные
в формулах для напряжений в ортотропной консоли, приведены
в нашей работе [11].
66
деление уже не будет «радиальным». Если в случае изгиба
силон напряжения убывали обратно пропорционально рас-
стоянию от точки приложения силы, то в случае момента
убывание будет более быстрое: напряжения меняются в клине
обратно пропорционально квадрату расстояния от точки при-
ложения момента.
В изотропной консоли распределение напряжений опре-
деляется формулами:
sin 20
sin 2-i>— 2ipcos 2ф hr2
__ М res 20 — cos 2’р
r9 sin 2ip— 20 cos 20 hr2
2.М
(19.6)
20. Изгиб клинообразной консоли распределённой
нагрузкой.
Составляющие напряжения в клинообразной консоли из
однородного анизотропного материала, изгибаемой нагруз-
кой, распределённой по всей длине грани по алгебраиче-
скому закону:
(20.1)
можно получить, комбинируя функции напряжений вида:
Е^г™Фт(6), (20.2)
о
Рис. 2:
на
В частности, для консоли, изгибаемой равномерно рас-
пределённой нагрузкой q
(рис. 23), распределение на-
пряженийнайдётсяс помощью
функции напряжений вида х):
F - г2Ф2 (6). (20.3)
Если направить ось х
произвольно XI обозначить
углы наклона гранен клина к
осн х через и то условия
сать следующим образом:
при 0= —<!\ 3,~0,
при 6 —=
((/-—нагрузка на единицу длины).
У См. начту рабсту [п].
гранях можно запп-
(20.4)
_ 7
h ’
= о
67
Для функции Ф3 получается выражение:
Ф3 (0) Л cos 20 4- В sin 20 4- Со (0) + D. (20.5)
Здесь Л, В, С, D — произвольные постоянные, а о (0) --
функция довольно сложной структуры. В общем случае
неортотропной консоли, когда корни уравнения
a22p/‘-2a26/3 + (2ai24-aJ ^-2^' + ^-0 (20.6)
имеют вид:
Аг = ® ± А А = Y ± А (-0.7)
для функции 9 получается выражение:
о (0) = В8{(а — у) sin2 0 + (а2 — у2 + р2—о2) sin 0 cos Он~[у (а24-р2) —
— а(у2 + о2)] cos2 0} X In
sin20 4- 2а sin 0 cos 0 4- (а2 4- p2) cos2 0
sin2 0 4- 2y sin 0 cos 0 4- (y2 4~<S2) cos (1
— 8 {4 (z - y) P2 (sin 0 4- a cos O) cos 0 + [(a - y)2 4- 82 — p2] x
X [sin2 04-2z sin6 cos G+(x2—p2) cos2 01} x arctg —v—4.
1 1 i \ i / n о sin Q a cos (J *
4- P {4 (a — y) 82 (sin 0 4- у cos G) cos G —
— [(* — Y)24-p2 — S2] [s*n2 &4"2ysin Geos 0 + (y2—82) cos2 &]} x
X arctg
3 cos9
sin 0 4- у cos 0
(20.8)
Общие формулы для составляющих напряжения имеют
вид:
аг - - 2Л cos 20 - 2В sin 20 4- С (2<? + </') 4- D,
— 2 (Л cos 20 + В sin 20 + С? + 6)),
тг9 — 2Л sin 20 — 2В cos 20 — С?'.
(20.9)
Постоянные Л, В, С, D все определяются из гранич-
ных условий; окончательные выражения сложны, и мы их
приводить не будем.
Характерной особенностью приведённого решения яв-
ляется независимость напряжений от расстояния г.
6S
В случае изотропной консоли а = *' = 0, 3 - о = 1, и вы-
ражение для <р чрезвычайно упрощается; функция напря-
жений, дающая распределение напряжений в изотропной
консоли, имеет вид:
F - (A cos 26 + В sin 29 + СО + D) r\
Из других случаев изгиба консоли распределённой на-
грузкой отметим изгиб нагрузкой, меняющейся по линей-
ному закону: q = qrx (рис. 24). В этом случае распреде-
ление напряжений’в анизотропной
консоли, независимо от того, бу-
дет ли консоль ортотропной или
нет, в точности совпадает с рас-
пределением напряжений в изо-
тропной консоли под действием
такой же нагрузки х). Так же и
распределение напряжений в ани-
зотропной консоли от собственного
Рис. 24.
веса совпадает с распределением
в изотропной консоли (при любом направлении силы тя-
жести по отношению к граням, если только срединная пло-
скость консоли вертикальна).
Формулы для напряжений можно найти, например, у
Лява2), почему мы их и неприводим. Что касается дефор-
маций анизотропной консоли, то они, разумеется, будут
отличаться от деформаций консоли из изотропного мате-
риала.
Общий случай изгиба клинообразной консоли, рассма-
триваемой как клин неограниченной длины, под действием
нагрузки, распределённой по грани по любому закону или
заданной в виде сосредоточенных сил, изучен В. М. Абра-
мовым [х]. Решение получено в общем виде с помощью
интеграла Меллина, однако до численных результатов его
довести не удалось.
г) Функция напряжений, дающая распре деление напряжений в
изотропией консоли, загруженной по схеме рис. 24, есть целый по-
лином третьей степени:
F = Л xs + Lx 2у + Сху2 4~ Dy3.
Очевидно, эта функция при любых значениях постоянных будет ре-
шением пе толькой бигармонпческого yj авнения, но и более общего
уравнения (5.10). Отсюда следует вышесказанное.
2) См. [26], стр. 223—224.
6 С
21, Чистый изгиб кривого кринолин: йно-
анизотропного бруса.
Рассмотрим упругое равновесие кривого бруса в вида
части плоского кругового кольца под действием усилий,
приложенных к концам и приводящихся к моменту. Пред-
полагаем, что брус обладает цилиндрической анизотропп-
х
ей, причём полюс ани-
зот ропии находится в
общем центре кругов,
дуги которых образуют
внешний и внутренний
контуры бруса. Ника-
ких элементов упругой
симметрии, кроме плос-
костей упругой симмет-
рии, параллельных сре-
динной плоскости, не
предполагаем. На рис.
25 изображено сечение
бруса срединной пло-
скостью; в этом сече-
нии полюс анизотропии
принят за начало координат, полярная ось х направлена
по оси симметрии. Обозначим через б/, 6 —внутренний и
внешний радиусы, с = у, Л —толщину бруса, М — вели-
чину моментов. Составляющие деформации и напряжения
связаны уравнениями обобщённого закона Гука в форме
(13.6). Услоеия на линиях, составляющих контур бруса,
очевидны: на кривых напряжения равны нулю, на кон-
цах напряжения должны привестись к моментам Л/.
Решение получается с помощью функции напряжений
F(r), удовлетворяющей уравнению (13.9) (в котором ?/~~0)
и не зависящей от полярного угла 0 г). Вид этой функ-
ции таков:
F (г) - А + Br2 + (7г1 +* + (21.1)
где
х) Решение имеется в на пей работе [19]. стр.14 7—Г*8.
70
(причём Е'г. Е'} суть модули Юнга для растяжения — сжатия
в радиальном и тангенциальном направлениях).
После определения постоянных из граничных условий
получаем следующие выражения для составляющих на-
пряжения (средних по толщине):
М Г, 1 —
'r~ Wig L1 1—О )
~ О*
1—С3 k (Г-С**1)2 kc2 (l-C^1)2
2“ Л-pi* 1 —с2* 1— с2Л
(21.3)
Распределение напряжений получается одинаковым для
всех радиальных сечений; нормальное напряжение в сече-
ниях не следует ни линейному, ни гиперболическому за-
кону.
На внешнем и внутреннем контурах бруса нормальные
напряжения равны:
Wb =
М 1 — к + 2/,'Ct+1 —(1 -j- Ai е-к
b^Tg' 1— с2к
, ч _ М (1 + //)
&2//g* 1—С2Л
(21.4)
(21.5)
Одно из этих значений будет по величине наибольшим
для всего бруса, но какое именно — нельзя заранее ска-
зать, не зная величины А.
Перемещения бруса пг, в радиальном и тангенци-
альном направлениях можно легко определить из урав-
нений обобщённого закона Гука (13.6).
Заметим, что в случае, когда ап~а33, т. е. E'r~E'h
к = 1, формулы для напряжений совпадают в точности
71
с формулами для изотропного бруса 3):
Cr=-b^g{ с“1пс (l-c* 2)ln|),j
°-==-^{1-c2+c21nc[1+G/]- <21-6)
- (1- с2) In
з — 0;
g= 0~т~У—сЧ1пс)2’ (-1-7)
22. Изгиб кривого криюлинейно-анизотропного бруса
поперечной силой.
Кривой брус в виде части плоского кругового кольца за-
делан одним концом и деформируется силой/*, приложенной
к другому концу. Брус обладает цилиндрической анизо-
тропией с полюсом
в центре ограничива-
ющих дуг, а, кро-
ме того, каждое ра-
диальное сечение яв-
ляется плоскостью
упругой симметрии2).
Направим ось х со-
гласно рис. 26 и обо-
значим через ад угол
наклона силы к пло-
скости сечения, где
она приложена (в цен-
тре сечения). Величи-
на угла между концевыми сечениями не имеет значения;
важно, чтобы она была меньше 2тг.
В данном случае а1в = а26~0. Для определения функ-
ции F послужит уравнение (13.11), в котором надо поло-
жить £7 — 0. Решение получается с помощью функции на-
пряжений вида:
F (г) cos 0 + <Pi (/’) s in 0 = (Лг1+п + 2?г1~п + С,г +-
+ Dr In г) cos 0-|- (Л'гНп_р £'г1- n_|_ Q'r jyr ]n sin Q. (22.1)
См. С. П. Тимошенко [43], стр. 72.
2) Это ограничение, которое не являлось необходимым в случае
чистого изгиба, в данном случае довольно существенно. Решение
рассматриваемой задачи имеется в работе [13] на стр. 149—151 [в фор-
мулах (7, 8) на стр. 151 есть опечатки].
Здесь
п= + = l/l+§ (l-2vr)4-^- (22.2)
f <7 2 2 * & T U
Определив постоянные Л, В, ... , D' из условий на ду-
гах кругов, где ог — тг9 = 0, и требуя, чтобы напряжения
на свободном конце привелись к силе Р, получим:
°г=4; • 7-[(0n-t-cn(r)n-1-cn]sin<9+w)’
°3==^'>’[(1 + ге)(0 + (22.3)
X А X п *1 4 7
+ (1 — л) сп (у J — 1 — сп I sin (0 4-а>),
= | (1-Cn) +(l + cn)lnc. (22.4)
Нормальные напряжения получаются наибольшими по
величине в сечениях бруса, перпендикулярных к линии дей-
ствия силы; в этих сечениях касательные напряжения рав-
ны нулю. Касательные напряжения достигают наибольших
по величине значений в сечениях на линии действия силы;
нормальные напряжения там равны нулю. Нормальное
напряжение в произвольном сечении 9 —90 получается наи-
большим по величине на внутренней поверхности:
> _ />sin(0o+e>) n(1—с”) р9 г )
Если упругие постоянные удовлетворяют условию:
g(l-27r) + |’ = 3, (22.6)
то п --2, и распределение напряжений будет в точности1
таким же, какое получается в изотропном брусе г):
= [т + с2 (т-)3- О + О sin (° + “+ 1
(1 + с2>г] 8*п(° + ш)’ (22-7>
= [у Нг(т')3“(1 + сг)7’]со8(0 + <п); '
^=1-с2 + (П-сг)1пс. (22.8)-
л) У Тимоленко в [4;] приводится решение доя случая радиаль-
ной силы, направленной внутрь fo> ^тг, стр. 84—86).
73:
23. Распределение напряжений в криволинейпо-
анизотроппой трубе.
Рассмотрим упругое равновесие пластинки, имеющей
форму полного кругового концетрического кольца, сжатого
по внешнему и по внутреннему контурам равномерно рас-
пределёнными нормальными усилиями. Будем полагать, что
пластинка обладает цилиндрической анизотропией, причём
полюс лежит в центре кольца, п никаких элементов упру-
гой симметрии, кроме
плоскостей, парал-
лельных срединной г
нет. Решив эту зада-
чу, мы тем самым
получим решение и
аналогичной задачи
о распределении на-
пряжений в трубе из
X материала, обладаю-
щего цилиндрической
анизотропией, под
действием внутрен-
него и внешнего дав-
лений х).
Приняв полюс
анизотропии (центр
кольца) за начало
_ координат, направим
Рис* 2/' полярную ось произ-
вольно (рис. 27) и обозначим через р и q величины вну-
треннего и внешнего давлений на единицу поверхности,
и через а и b — внутренний и внешний радиус кольца.
Распределение напряжений найдётся с помощью функ-
ции напряжений (21.1), не зависящей от 6, и представится
формулами:
_ + 1 — q / г
м = 0.
р—1
1-са» С
) р—9с*"1
i
(23.1)
г} Эта задача для тела с цилиндрической анизотропией частного
вида была решена ещё Сен-Венаном [в8] и Фохтом [7Т]. В нашей
работе [19] решение дано для иеортотропной трубы. А. Н. Митинский
определил напряжения в деревянной тр бе, рассматривая её как те-
ло с цилиндрической анизотропией (работа р7])-
74
Здесь
Ъ ’
Распределение напряжений одинаково для любых ради-
альных сечений и зависит только от отношения модулей
Юнга для растяжения — сжатия в тангенциальном направле-
нии; распределение получается одним и тем же, независимо
от того, является ли кольцо (или, соответственно, тру-
ба) ортотропным или нет. Влияние радиальных плоскостей
упругой симметрии сказывается лишь на деформации: если
плоскости эти имеются, то радиальные сечения остаются
плоскими, если же указанных плоскостей пет, то ради-
альные сечения искривляются.
Для анизотропного материала с одинаковыми моду-
лями Юнга для радиального и тангенциального направ-
лений распределение напряжений получается таким же,
как в изотропном кольце (трубе). Полагая & = из фор-
мул (23.1) получаем известное решение Ляме1):
р^ — д р — д
г 1—с2
1 —с-
(23.2)
Рс
в*=~-
ТГ5 — 0.
Заслуживает упоминания один частный случай. Если
в формулах (23.1) положить с — 0 и = то получится
распределение напряжений в сплошном криволинейно-
анизотропном диске, сжатом по ободу усилиями q:
тн-О. (23.3)
В изотропном диске материал будет равномерно
сжат, но в криволинейно-анизотропном напряжение будет
меняться по диаметру. Для дисков из материалов, у ко-
торых Е'л > Е'г, к > 1, напряжения убывают по мере при-
ближения к ценгру, и в центре обращаются в нуль. Но
если Е\ < Б?, то к < 1 и, как видно из формул (23.3),
будет происходить концентрация напряжений около центра
диска. Кривые, дающие представление о распределении
напряжениГт аг или по диаметру диска, даны на рис, 28
для к = 1, к > 1 и к < 1.
См. [43], Стр. 69.
75
ГЛАВА IV.
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В БЕСКОНЕЧНОЙ
УПРУГОЙ СРЕДЕ.
24. Упругая полуплоскость, нагруженная вдоль границы.
В этой главе мы рассмотрим основные случаи распре-
деления напряжений в плоской упругой среде («упругая
полуплоскость»), нагруженной вдоль границы, и в не-
ограниченной плоской среде, под действием сосредоточен-
ной силы.
Рассмотрим упругую однородную анизотропную пла-
стинку с прямолинейным краем, по которому распределены
усилия, действующие в срединной плоскости. Если размеры
пластинки вдоль прямолинейного края и в других напра-
влениях велики по сравнению с длиной загруженного
участка края, то можно получить представление о рас-
пределении напряжений, упрощая задачу, а именно, рас*
сматривая пластинку, как бесконечно простирающуюся
плоскую упругую среду с прямолинейной границей,,
иначе-как «упругую полуплоскость».
Поставленную задачу можно решить различными мето-
дами, пз которых укажем один, основанный на применении
интегралов Фурье. Для простоты мы примем следующие
76
ограничения: 1) среда является ортотропной, причём глав-
ными являются направления, параллельные и перпенди-
кулярные к прямолинейной границе; 2) нагрузка приложена
к конечному участку границы, распределена симметрично
относительно середины загруженного участка и приводится
к конечно!^ равнодействующей1).
Примем середину загруженного участка границы за
начало координат, направим ось у вдоль границы, а ось
.а; —внутрь полуплоскости (рис. 29). Обозначим нормаль-
ную и касательную составляющие нагрузки, рассчитанные
на единицу длины, через N и Т; N (у) будет чётной функ-
цией от у, а Т (у) — нечётной функцией. В выбранной
системе координат функция напряжений удовлетворяет
уравнению:
1 . /" 1 2vr\ иЧ? . 1 д*Е п п
(объёмные силы не рассматриваем). Представим функции N
и Т интегралами Фурье; так как N чётная функция, а
Т нечётная, то мы получим2):
со со
Л'(у)=,2 ф (а) сов а ?/da, Т (у) = 2 х (а) sift «ydv., (24.2)
0 II
где
оо со
0 (х) — N (tj) cos ат] dr^ / (а) = Т (^) sin dr^ (24.3)
о о
]) Задача решается и без этих ограничений, но решение значи-
тельно сложнее нижеприведённого.
2) Смирнов В. И. Курс высшей математики, т. 2, 1932, стр. 431.
77
По мере удаления от границы напряжения дол;кнь®
стремиться к нулю, а па самой границе, т. е. при z = 0
аХ fa (Z/) 5 "'XU ' “ ^ ^ (//) ’
(24.4)-
Решение полупится с помощью функции напряжений
в форме:
F — \ Ф (a, z) cos а?/ da.
(24.5)
Вид функции Ф (a, z) зависит от корней уравнения J):
4-6г-й->= +к“°- (24'6)
Возможны следующие три случая:
Случай I. Корни уравнения вещественные, неравные:
± ± U2 (111 > 0? 112 > 0).
Случай II. Корни вещественные, попарно равные ме-
жду собою:
± и (и > 0).
Случай III. Корни комплексные:
и Jh i v, — и ~* L io.
в случае I: Ф (a, х) = Ae^v^x+Be~v-ax. (24.7>
в случае II: Ф (а, х) = (Л -+ Вх)е~г1ЛХ . (24.8>
в случае III:
Ф (а, z) — (Л cos vaz + В sin vaa)e ~УЛХ. (24.9)-
| Постоянные А и В надо считать зависящими от па-
раметра а. Удовлетворяя граничным условиям, полу-
*) Корни уравнения (24.6) ± ?/2 свяваны с кохмплексными
i i
параметрами .зависимостями: щ— —, ,
78
чпм для случая I г):
оо
2 С
} [O(a)(u2e-«1--Mie-^)-
и
— 7. (а) (е-«1а* — е~и*ах)] cos v.y dn,
СО
tl;j 5 t't’ W «1“2 (- «xe- ',1ах 4 и2е~и^х) +
О
J>(24.10>
+ X (а) ui°-x — и*е~и2*х)] cos ху dx,
[6 (а) iijiz (с“'и1СЖ — eU2ax)~
U
“ X (а) (иле и1ЛХ ~ и2е’*,4*ах)] sin ау <2а.
Чтобы подсчитать напряжения по этим формулам npir
заданном распределении нагрузки, нужно вычислить инте-
гралы ф (а) и х (а) и> подставив найденные величины в (24.10),
произвести интегрирование. При простом законе распреде-
ления нагрузки вычисление интегралов не встречает осо-
бых затруднений.
Формулы для случаев II и III можно получить из (24.10У
путём предельного перехода.
Решение для случая антисимметричной нагрузки, когда
N (у) — нечётная и Т (у) — чётная функция у, находится со-
вершенно аналогичным путём с помощью функции напряже-
ний вида:
со
F ~ Ф (а, х) sin а у dx. (24.11)
о
Функция имеет точно такую же структуру, что и
функция Ф; она, в зависимости от того, какой случай кор-
ней имеет место, определяется по формуле (24.7), (24.8)>
или (24.9).
Другие методы решения рассматриваемо!! задачи осно-
ваны на использовании представления напряжений с по-
мощью двух функций Ф1(с1) иФ2(:2) и на применении
аппарата теории функций комплексного переменного: инте-
гралов типа Коши и интеграла Шварца * 2).
х) См. нашу работу [п], стр. 167,
2) Решение задачи с помощью интеграла Шварца получена
Г. Н. Савиным в работе [39].
7‘Э
25. Действие сосредоточенной силы, приложенной
к границе.
От нагрузки, распределённой по некоторому участку
границы, нетрудно перейти к сосрэдоточенной силе, при-
ложенной в точке границы. Желая получить распределе-
ние напряжений от
нормальной силы Р,
приложенной в точ-
ке О (рис. 30), рас-
смотрим сначала
действие нагрузки,
распределённойрав-
У номерно по малому
участку около точ-
ки (7, длиной 2s, с
равнодействующей,
равной силе Р. Все
интегралы, входя-
щие в формулы
(24.10), легко вы-
числяются; резуль-
тат будет зависеть
от величины s. Уст-
ремляя затем г к
Рис. зо. г
нулю, получим в
пределе следующие формулы для определения напряжений,
вызванных сосредоточенной силой *):
= __ 0'1 + »2) . ______________я3______________
izh (у2 4- г/|х2] 1у'2 -р ’
__ Риги2 (ил Н- w2) ГС?/ "
{У2 -Г ujx2) (№4- ti'zx') ’
__ Pit^i* + а3) _______xsy_____________
Тл'?г’“ rp + (?у24--
Это решение выведено для случая I [неравных корней
уравнения (24.6)]. Решение для случая II получим из
*) См. нашу работу [“], стр. 169 н следующие. Задача о дей-
ствии сосредоточенной силы, приложенной к границе плоской среды,
рассматривалась также Вольфом в работе [79] для среды с анизо-
тропией частного вида и Окубо Хаюми в работе [8в].
-30
(25.1), полагая ux = ut = u, и решение для случая Ш,
полагая uz — u — vi.
Перейдя к полярным координатам, получим, выразив
и и2 через упругие постоянные:
_____Р (аг 4-и2) соз 6 А
вг— Kh ‘ rL(0) ’ }• (25.2)
«о = Ог tra = 0. J
Здесь
т /£А sin*9 , / 1 2v X . 2 fi 2С , cos4 0
Л (0)« -g- 4- ) am* 0 cos’ 0 + -g- . (25.3)
Как уже отмечалось, функция £(б) имеет определён*
ный физический смысл: это величина, обратная модулю
Юнга для растяжения — сжатия по радиальному напра-
влению, под углом 0 к линии Действия силы [см. форму-
лы (10.9)].
Как видно из формул (25.2), распределение на-
пряжений является «радиальным», «лучеобразным»1). На-
пряжение сг, которое является главным, убывает об-
ратно пропорционально расстоянию г, а при заданном г
меняется с изменением угла 6 по довольно сложному
закону.
Точки, в которых напряжение аг имеет одну и ту же
величину а0, располагаются на кривых четвёртого порядка;
уравнение семейства этих кривых имеет вид:
-^+^x{x* + y*) = Q. (25,4)
Эти кривые —линии одинаковых напряжений —все зам-
кнуты, симметричны относительно оси х (линии действия
силы) и проходят через точку приложения силы.
Исследование выражения (25.2) и уравнения (25.4)
приводит к следующим результатам.
х) Этот вывод вполне согласуется с тем, что изложено в § 18;
очевидно, полуплоскость есть «клин» с углом при вершине, рав-
ным 180°.
6 С. Г. ЛехпицкиЙ
81
Напряжение аг достигает максимального (по абсо-
лютной величине) значения на линии действия силы 6=»0j
если 1 2vt . 3 1 . .
или если О Еа~ 2 Et [0'
и одновременно 4->0. (6') jQ-j JCJ} ' '
Если, кроме условий (а) или (6) и (6')> постоянные среды
удовлетворяют ещё двум условиям:
JL_2vi Jl
G Ех> Ех >
( 1 2V. + 4A* 4/2 4*1 + 3Л-^л
<G Е, ) Еа\6 ) > и»
(с)
(с')
то, кроме направления действия силы, существуют ещё два
направления, для которых | сгг | достигает максимальных
значений; углы, определяющие эти «опасные» направления
в среде, найдутся из уравнения:
ta 9= 4 /2 4yi+3\
6 2 V G Ел \G Ez ) Ei VO" £i J’
(25.5)
Если условия (с) и (с') не выполняются (или хотя бы
одно из них не имеет места), то максимум | аР | на линии
действия силы будет единственным.
Два значения угла 0, при которых |аг| достигает мини-
мума, найдутся из уравнения:
tgfi= ± * Н.М. (25.6)
х ж « Ла * \tr Ла / ЛаХСг Лх /
Если постоянные среды удовлетворяют условию;
JL____2vt . 3 1
G Е\ 3 £/]
(d)
«2
или удовлетворяют
одновременно двум условиям;
1 _ 2Vj _ £ J_
G j?! 2 jb’i ?
8
О,
(е)
(И
то напряжение <зг на линии действия силы достигает
не максимального, а м и н и- Р
мального по величине зна~ I
чения. В этом случае суще- ofy
ствуют два угла, отвечающие "у
максимуму |ог|; найдутся они
из уравнения (25.5).
В соответствии с этими ре-
зультатами можно, отметить
три типа линий одинаковых
напряжений, которые могут
быть в ортотропной среде. Кри-
вые первого типа, имеющие
место, когда выполняются ус-
ловия (а) или (6) —(6'), но ус-
ловия (с), (с') не выполня-
ются, изображены на рис. 31.
Кривые второго тгпа получаются, если выполняются одно-
временно условия (а) [или (6), (6')] и (с)? (с7)]* Они пока*
Рис. 31.
Рис. 32. Рис. 33.
заны на рис. 32. Боковые отростки соответствуют опасным
направлениям, по которым | аг | достигает добавочных
£*
83
максимальных значений. Кривые третьего типа, показан-
ные на рис. 33, получаются при выполнении условий
или (е), (е').
Линии одинаковых напряжений дают возможность со-
о том, как распределяются
напряжения, вызванные
сосредоточенной силой. В
частных случаях кривые
могут выродиться в эллип-
сы и в окружности. В слу-
чае изотропной среды,
ставить ясное представление
Рис. 34. Рис. 35.
когда их — ua 1, получаем известное решение Фламана X)S
2Р COS 0 л л /ПК. *7\
aJ== 0, м = 0; (25.7)
линии одинаковых напряжений превращаются в окружно-
сти (рис. 34).
В случае силы, направленной произвольно, общий харак-
тер напряжённого состояния, разумеется, остаётся прежним,
а напряжение определяется по формуле:
а
г
Р{иг+и2)
кЬ. YЕкЕ2
COS U) COS 0 -р
/Ei . . л
SIU а) 81П О
2
rL (0)
(25.8)
X
(ю — угол, образованный линией действия силы с нормалью
к границе —см. рис. 35). В этом случае внутри полупло-
скости образуется нейтральная линия, на которой на-
пряжения равны нулю; уравнение нейтральной линии:
tg 9 = — ctg ш. (25.9)
*) См., например, l*3], стр. 97.
84
Нейтральная линия вообще не перпендикулярна к ли-
нии действия силы, образуя с ней острый угол, если
Ех > и тупой, если Ех < Е2. По одну сторону нейтраль-
ной линии среда сжата, по другую растянута. Линии
одинаковых напряжений представляются в виде кривых
четвёртого порядка, сходных с кривыми (25.4).
26. Действие сосредоточенной силы, приложенной
внутри неограниченной среды.
К задаче определения напряжений в анизотропной пла-
стинке, вызванных сосредоточенной силой, приложенной
к внутренней точке, достаточно удалённой от края, мож-
но подойти следующим образом. Будем рассматривать пла-
стинку, как безграничную упругую плоскую среду, к од-
ной из точек которой приложена сосредоточенная сила Р.
Самое сосредоточенную силу можно рассматривать, как не»-
которую нагрузку, распределённую каким-либо образом по
краю бесконечно малого отверстия, приводящуюся к рав-
нодействующей силе Р 1).
Примем точку приложения силы О за начало коорди-
нат, оси х и у направим произвольно (рис. 36) и будем
считать известными постоянные, отнесённые к зтим осям;
пластинку будем полагать вообще неортотропной. Для ре-
*) Решение рассматриваемой задачи дано в нашей работе [12].
85
шения задачи воспользуемся выражениями для составляю-
щих напряжения через две функции ФД^) и Фа (и2) (см.
§ 8). Так как около точки О предполагается отверстие,
хотя и бесконечно малых размеров, то функции Фх и Ф2
должны быть многозначными, причём их приращения при
обходе по любому замкнутому контуру у, окружающему
отверстие, должны удовлетворять уравнениям (8.10),
где надо положить Px-Pcosu>, Pff==Psino) (рис. 38).
Составляющее напряжения должны стремиться к ну-
лю по мере удаления от точки приложения силы.
Всем этим условиям позволяют удовлетворить функ-
ции вида:
(^1) In I .
Ф2(2а)«В1П2г, / (2бЛ)
где Л, Б —постоянные, вообще комплексные, которые оп-
ределятся из уравнений (8.10).
Обозначая через А и В величины, сопряжённые с А
и В, получаем, на основании (8.10), уравнения для опре-
деления Л, j3, А п В:
а+в-а-в^р4^,
' 2^/it ’
Ap.i + Вра - 4ax — = — Р-^~-,
Л pl -И -Bpl — — В^2 = . (26 2)
_ а1в Р cos о а12 Р sin со
an 2t:Ai au ’
л 1 , в 1 “7 1 б 1
А—г В------Л_---В “ =
Hi Нз
_________а12 Р cos ш Р sin со
аа2 2^/U ~^~а22 >
Здесь р1? р2 — комплексные параметры —корни уравнения
(7.4), предполагаемые различными.
Составляющие напряжения определятся по форм улам;
(26.3)
86
В общем случае эти выражения получаются очень слож-
ными. Мы приведём только формулы для составляющих
напряжения в полярных координатах, по которым эти вели-
чины вычисляются в случае ортотропной пластинки, когда
направления осей х vl у совпадают с главными, а сила
действует в направлении оси х-
а Г X
г 2^(14-14’)
.. созЭГ. .. ..
(1 4- Hi) sin* 0 4- |4
cos’ 0 — |л1 sine О
— itt fl — V sin*Q + ni
IS ( ati) соз2 у — Ц» sin10
____P . 1 + ^2^11^3 , cos 9
2n/t ' f (Hi. 4- H2) r ’
____P 1 + ~»,aP-iP-a sin 9
2яЛ i (Щ 4- щ) r '
. (26.4)
В данном случае комплексные параметры p.t и щ явля-
ются корнями уравнения:
s+G-ftk+i,-0- <ад
Хотя в выражения (26.4) входит мнимая единица
е —1, темне менее все три выражения — вещественные:
для ортотропной пластинки р-ар.а и i (р.х + р2) — всегда веще-
ственные числа.
Обращает на себя внимание очень простой закон рас-
пределения напряжений gq и тг° и очень сложная зависи-
мость от 6 напряжения аг. От расстояния г все напряже-
ния зависят так же, как и в случае силы, приложенной
к границе полуплоскости.
Путём предельного перехода, полагая ~ Из “ Ь полу-
чим распределение напряжений в изотропной среде (v —
коэффициент Пуассона) г):
_ ___3 -Н Р cos 6
4тсЛ г
1—V Р cos О
Г
1—v Р sin 0
Тг5 Mi ' г
(26.6)
Ъ См. ["], стр. 126,
87
ГЛАВА V.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО
ЭЛЛИПТИЧЕСКОГО И КРУГОВОГО ОТВЕРСТИЯ.
27. Определение напряжений в пластинке с эллиптическим
отверстием.
В настоящей главе рассматриваются вопросы, связан-
пые с определением напряжений в пластинке, ослабленной
отверстием и деформируемой усилиями, действующими
в срединной плоскости. Известно, что в изотропной пла-
стинке влияние отверстия сказывается в повышении напря-
жений около отверстия по сравнению с пластинкой сплош-
ной, неослабленной. Это явление носит название концен-
трации напряжений. Вопрос о концентрации напряжений
в изотропной пластинке разработан достаточно полно; изуче-
ны случаи отверстий разных форм 1). В случае анизотроп-
ного материала хорошо изучен лишь вопрос о распределе-
нии напряжений в пластинке, ослабленной эллиптическим
или круговым отверстием. Ниже приводятся решения ряда
задач из этой области.
Рассмотрим анизотропную пластинку (вообще неортотроп-
ную) какой-либо формы, ослабленную эллиптическим отвер-
стием, деформируемую усилиями, которые распределены по
краю отверстия и действуют в срединной плоскости. Ес-
ли размеры отверстия малы по сравнению с размерами
пластинки и оно не находится вблизи края пластин-
ки, то можно упростить задачу, полагая пластинку беско-
нечной и пренебрегая, следовательно, влиянием внеш-
них краёв. В такой постановке мы и будем рассматри-
вать задачу.
Направим оси х, у по главным осям эллипса (рис. 37)
и обозначим: а, —упругие постоянные материала для вы-
бранных осей координат (мы их будем считать известными);
а, Ь — длины полуосей эллипса; Хп, Уп —проекции усилий^
действующих на краю отверстия (на единицу площади);
Рх, Ру — проекции главного вектора (равнодействующей)
этих усилий. Уравнение контура возьмём в параметрц-
х) Краткий обвор литературы по вопросу о концентрации напря-
жений в изотропных пластинках имеется, например, у С. П. Тимо»
шенко (см. [**], § 28).
88
ческом виде:
а: = асов», у = b sin»,
(27.1)
и заданные усилия будем считать функциями параметра О,
который, при обходе по контуру отверстия, меняется от О
до 2я.
Воспользуемся комплексным представлением напряжений
через две функции Фх (лх) и Ф2 (z2) [см. § 8, формулы (8.2) —
(8.6)]. Функции Ф! и Ф2 должны удовлетворять граничным
Рис. 37.
условиям (8.7). Считая заданными проекции усилий Хп>
Yn, разложим их в ряды Фурье (по параметру &); выражая
величины J Xnds, J Ynds через », можно записать условия
(8.7) в виде:
2Ве[Ф1(21) + Фа(2а)] =
СО
=thа+а*+2 (w™+
2Re [р^Ф, (zj + р.2Ф2 (z,)] -
СО
= - th& + +2 с?****'+₽*«"***)-
Здесь аЛ, — известные коэффициенты, вообще комплекс-
ные, зависящие от распределения усилий; аА, р;. — вели-
чины, сопряжённые с первыми; а0, р0 — произвольные по-
стоянные. По мере удаления от отверстия составляющие
напряжения должны стремиться к нулю.
У?
Решение получается с помощью функций *):
Ату ;Л)
Hi — Ha I
_ > (27.3)
Ф.&) - В. 4- 51nC, - VА~ЪЯ» С*’
n-i 14 ~1‘’ )
Здесь
г St + i/^-gtZ^p г_ +
1- a—l^b ’ a-i^b
суть функции, которые на краю отверстия принимают
значение ем; А0 Во— произвольные постоянные, а А,В —
постоянные, определяемые из уравнений:
Л+В-Л-В=^,
Ла, + Ва, - - S«, = - Лт,
'Ы+м-лй -ад=-^4-^
A A I R J_Д 1_R А = Д1а . JoX л . g2ft .
Hi На |лЛ ра я82 2яЛ< а2а
Явных выражений А и В мы не приводим ввиду их слож-
ности.
Производные Ф; (zj и Фд (z2) равны:
(27.6)
Составляющие напряжения определятся по формулам
(8.2), а проекции смещения — по формулам (8.3). Отметим
ещё одну формулу, которой в дальнейшем мы часто будем
г) См. наш у работу [м], где дан вывод и обоснование решения.
Все эти формулы и последующие выведены для случая, когда щ .
Для случая равных комплексных параметров соогветствующие фор-
мулы можно получить путём предельного перехода, устремляя щ
к Ра-
90
пользоваться. Напряжение а* на площадках, нормальных
к краю отверстия, у самого края отверстия равно *):
__ 2 J I ([Аг a sin &4-& cos О)2
a2 sin2 & 4- 62 cos2 & t a sin 0 —- щ b cos &
у< Л-ьХЧР*-1*8“* е-А&Л — * а sin ° + Ь 003 6)* У
+ 1Ч-1Ч ) а sin 0 — щ & cos 9 Х
(27.7)
Если на краю отверстия заданы смещения u*, v*
00
«* = «о + 2 (ял еШ + *.< е-*8’),
А-1
оо
(27.8)
v*=₽.+2(M'tW+M-AW)
Л«=1
и проекции равнодействующей усилий (распределение
которых неизвестно), то функции Фх и Ф2 имеют вид:
(zi) = 40 + Л In + £ ах7а — рхра +
+ | ® (г bqt + apt) 1 ~ + ~- s - ч * ,
’Х А=2
ф» (2г) = Во + В In — Рхрх +
4-lo>(i’6g1+ep1)] oY3—7) ^49i — hPi)^tk •
3 k=2
(27.9)
Здесь 40, Bo — произвольные постоянные, не влияющие
на распределение напряжений; Л, В — постоянные, опреде-
ляемые из уравнений (27.5), /?а, qlt q2 — постоянные;
!) См. формулу первую (8.6). В данном случае:
, . л sin & z —Ъ cos 6
COS (П, x) = • ......... , , , > COS (n, y) = • / ..
'yf a2 sin2 6 + b2 cos* 6 }/ a2 sin & + 68 uose S
94
определяем формулами (8.4):
= (27.10)
ш — постоянная, выражающая поворот пластинки в пло-
скости ху, для определения которой нужно сформулировать
дополнительные условия (во всех рассмотренных ниже
случаях (о = 0).
Приведённые здесь формулы соответствуют самому
общему случаю загружения края отверстия. В следующих
параграфах мы более подробно останавливаемся на частных
случаях, представляющих практический интерес1).
28. Частные случаи.
Приведём решения для нескольких частных случаев
распределения напряжений в пластинке с эллиптическим
отверстием2). Мы ограничимся лишь указанием функций
Фх и Ф2, коэффициентов а*, и напряжения с^по всему
контуру и в отдельных его точках; формулы для по
контуру мы оставляем в комплексной форме, так как
отделение вещественной части (т. е. фактическое выполне-
ние действий, которые подразумевает символ Re) приводит
*) Ре пение рассмотренной в § 27 задачи иным путём, с по-
мощью интеграла Шварца, было получено Г. Н. Савиным в работе
[38]; способ, предложенный Г. Н. Савиным, приводит, разумеется,
к тем же результатам.
а) Эти случаи рассмотрены в наших работах [15] и Р].
92
к выражениям чрезвычайно громоздким, занимающим
много места, но не представляющим особого интереса* Во
всех случаях функции Фх и Ф3 состоят только из одного
члена. Комплексные параметры полагаем вообще нерав-
ными:
5*1 = « + ₽?, F-s = Y + Sf' (Р > 0, 8>0).
1. Равномерное давление по контуру отверстия. Край
отверстия сжат нормальными усилиями q (на единицу
площади), распределёнными равномерно (рис. 38).
ФДг)1 = ^~|,,В1- 4> <М«»)= (28.1)
п Pi—ь v И1-1*. С» ' '
<=-%, Р1=-5т; (28.2)
с ________Я______т>р J____________
& aasina&4-d2cos2B [ (a gin 0—|лх &cos §) (a sin 0—pa6cos0)
X [аРчРч~— Фз^) a3sin3&4-i (рула —2)a2feasin2 &cos& +
+ (2^1 “ 1) л2 Ь2 sin & cos2 & -f-
4 + —td) fc8cos3&] J . (28.3>
В точках А и At на концах большой оси (рис. 38),
где 0 = 0, 0 = тг:
в& = ? [ (^ + Д(£+а2)+ Т (?'+Ка + -FM0 ] * (28,
В изотропной пластинке в тех же точках
=« = ^(-1 + у)- (28.5)
В точках В и Вх на концах малой оси (рис. 38),
где & = у, 0 = -|«:
а8 = д[аТ-р§ + | (? + &)]. (28.6)
В изотропной пластинке в тех же точках
а, = ?(-1 + 2|). (28.7)
93
Распределение напряжений у края отверстия полу-
чается, в общем случае неортотрспной властинки, симмет-
ричным относительно центра О, и лишь в случае ортотроп-
ной пластинки, когда направления главных осей эллипса
совпадают с главными направлениями упругости, стано-
вится симметричным и относительно этих осей,
2. Касательные усилия, равномерно распределённые по
контуру (рис. 39). Фх и Фа имеют вид (28.1), но в дан-
ном случае
«1 = Т. ?1=—% (28.8)
где г —интенсивность усилий, а
°* a* sin® 0 + fc2 cos2 0 б * I (а sin Ь — fccos 0) (а sin 0—jAaicosO)^
X [(ар-х + ар.2 4- ifcPiPs) a3 * * sin8&4- (2 —|\u2) a3b sin2 0 cos 8 4-
-b (2р4Р2 — 1) ab* i sin & cos2 & +
+ (a ib Pj 4- ib p2) b3 cos3 0] J . (28.9)
3. Растяжение. Пластинка растягивается усилиями р,
приложенными на достаточно далёком расстоянии от отвер-
стия (в теории— на бесконечности) и действующими под
углом <р к большой оси а (рис. 40); на краю отверстия
никаких внешних усилий нет.
94
Составляющие напряжения найдутся путём суммирова-
ния напряжений в пластинке сплошной, равномерно рас-
тянутой:
вх = р cos2 <р, Иц = р sin2 у, TxU — р sin cos <р (28.10)
в напряжений, получаемых с помощью функций Ф, и Ф,
вида (28.1), где
ai — — —v*¥ (в sin у — ib cos ?), 1
* / (28.11)
= — (asin<p — ib сов ?). I
Приведём выражение для напряжения в том слу-
чае, когда пластинка растягивается в направлении оси
х (<р = 0) (см. рис. 41):
— a2 sin2 ft рЪ
Р а2 sin2 0 + Ъ2 cos2 ft * a2 sin2 ft~p b2 cos2 0
1(а sin ft— |лх b cos 0) (a sin ft—b cos 0) s*n
+ (2 — |rjAa) a*b sin2 9 cos & + b* cos’ &]| . (28.12)
95
В «очках А и Лх (рис. 41)
Ofh = Р (а4 + ?а) (та + «2) ’ (28‘
в изотропией пластинке в тех же точках а» = — р.
В точках В и Bt
ав = ^[1 + |(? + 8)] ; (28.14)
в изотропной пластинке в тех же точках
зе = р(1 + 2|). (28.15)
4. Сдвиг. Прямоугольная пластинка с эллиптическим
отверстием в середине деформируется касательными уси-
лиями с интенсивностью s, распределёнными равномерно
по сторонам; большая ось отверстия образует с одной ив
сторон угол ф.
При малых размерах отверстия (по сравнению с разме-
рами сторон) пластинку можно считать бесконечной, и
усилия s — действующими на бесконечности (рис. 42). Рас-
пределение напряжений получим, суммируя напряжения в
сплошной пластинке:
— — ssin 2<?, ay —ssin2cp, = scos2<p, (28.16)
и напряжения, получаемые с помощью функций вида
(28.1), где
ах = у (— a sin-2^+iЬ cos 2<?),
= ~ (я сов 2^ + ib sin 2<р)*
(28.17)
$6
Рис. 43.
В частности, при <р = 0 (рис. 43) получаем следующий
закон распределения напряжения по краю отверстия:
__ аЬ sin 20 . s
ф Cog2 sin2 aJ cos^O
у J{e / ________________ie ---------------- - X
Л [ (a sin В — соз &)(<г sin 0- cos 0)
X [(ap-i + au2 — a* sin3 fl -f- (2 — a2b sin2 fl cos fl +
4- i (1 — 2 P4PS) #6a sin & cos8 fl4я
4~(a — 44b — ф2ft) ft’cos3fl]| . (28.18)
7 С. Г. Лехницкий
97
5. Изгиб. Прямоугольная пластинка, с косо прорезан-
ным эллиптическим отверстием в центре, изгибается момен-
тами М (рис. 44). При малых размерах отверстия пластинку
полагаем бесконечной, и напряжения в ней получаем, сумми-
руя напряжения в сплошной пластинке, соответствующие
чистому изгибу1):
а" — — \У cos ? — х 81П ф) cos~ ?? I
Af I
= -j (у cos © — x sin <p) sin2 ср, у (28.19^
"xtj cos cp — x sin <p) sin <p cos 9, I
и напряжения, получаемые с помощью функций вида:
fta —tutxa 1
Ф2(^)= . *
2ks' Hl—
(28.20)
где
jVf SIH ® • у о ° 2*4 t ' 1 * О \
a4 ----------gj-1-(0 cos~ 9 — as snr 9 + iabam 2cp),
pa = ——x. cos^ cp — a2 sin2 <p4“ iab sin 2<p).
(28.21)
*) I—момент инерции поперечного сечения сплошной, неослаб-
ленной пластинки (подразумевается, конечно, первоначально данная
пластинка, которую мы, далее, условно рассматриваем как беско-
нечную).
98
В частности, если оси отверстия параллельны сторонам
пластинки, т. е. ? —О (рис. 45), получаем:
____Mb a2 sin2 0 1 v
°*- ~Г ' лгз1паЭ4-ЬаС082В+-27 aasina» + bacosa» Х
ИГ™
xlcX(a8in ®—HjftcosS) (а sin 0—(ij&cos 9) '' 1'Г1 "т“2/ “ s*n
+ (2 — a*b sin2 & cos & + b3 cos3 &]}. (28.22)
В точках А и Д на концах большой оси эллипса (рис. 45)
<28-23)
тогда как в изотропной пластинке в этих местах 09 = 0.
В точках В и
^=±^(1 + у--Чг)’ (28-24>
а в тех же точках у изотропной пластинки
+ (28.25)
с эллиптическим отверстием при постоянной перерезывающей
силе1).
*) Работа [зв].
Распределение напряжений по краю отверстия ани-
зотропной и притом неортотрспной пластинки подчиняется
гораздо более сложным законам по сравнению с распреде-
лением в изотропной пластинке.
В разобранных случаях распределение напряжений а»
симметрично относительно центра отверстия, но вообще
несимметрично относительно е о осей. Формулы для напря-
жений в точках на концах осей эллипса А, Z?, Bt
дают представление о концентрации напряжений (по край-
ней мере для ортотропной пластинки, у которой главные
направления упругости параллельны направлениям осей
отверстия). Все формулы пригодны и в случае кругового
отверстия, когда
29. Распределение напряжении в ортотропной пластинке
с круговым отверстием при заданных внешних усилиях.
В этом параграфе ив следующем рассмотрены некоторые,
наиболее интересные случаи распределения напряжений в
ортотропной пластинке, ослабленной круговым отверстием
радиуса а1).
Во всех случаях начало координат помещено в центре
отверстия, а за направления осей х и у взяты глав-
нын направления упругости. Мы пользуемся обозначе-
ниями, часть которых уже встречалась ранее, а именно:
Е^ /?2—-модули Юнга; у15 у3 — коэффициенты Пуассона;
G — модуль сдвига — всё для главных направлений; <л17 р3 —
комплексные параметры —корни уравнения
(29л)
— г (!\ + р.г);
N (0) — величина, обратная модулю Юнга для растяжения —
сжатия в направлении касательной к контуру отверстия 2):
sin* 0 , /1 SvA . . cos* 9
N ^==~ET+Cg'~W1) Sin’6cos'& + -^-• (29.2)
l) Приведённые в этом параграфе решения изложены в наших
работах [1а] и [1в].
2) См. формулы (10.9).
100
Отметим попутно формулы, которые будут использо-
ваны в дальнейшем:
1*»ь= —'I
H: + rf = 2vt-§, У (29.3)
п= —i i fi2)= |/2 + • >
Мы приводим ниже формулы для напряжения дч по
краю отверстия и в отдельных его точках, а также числен-
ные значения с, и графики изменения его по контуру отвер-
стия в зависимости от полярного угла 6, для пластинки,
изготовленной из фанеры первого типа. На графиках зна-
чения отложеныпо продолжениям радиусов круга с отсчё-
том от контура круга; положительные величины обозна-
чаются стрелками, направленными от центра, отрицатель-
ные —стрелками, направленными к центру. На каждом
чертеже справа вверху показывается схема нагрузки. На-
поминаем, что для фанеры первого типа
[1^3,08 /, = 1,12 и ~4,2,
если ось х направлена вдоль волокон рубашки, и
р.1==0,32 z, = 0,89 г, п—1,21,
если ось х направлена поперёк волокон рубашки. В этом
и следующем параграфах пластинку, изготовленную из фа-
неры первого типа, мы, для краткости, будем называть про-
сто «фанерной пластинкой». На графиках изменения a j
в фанерной пластинке пунктиром показаны кривые изме-
нения аз в изотропной пластинке, деформируемой теми
же усилиями.
1. Равномерное давление но краю отверстия. По краю
отверстия распределены равномерно нормальные усилия q
на единицу площади (рис. 46):
°з = [ W 4- П (sin8 0 - cos’ 6) +
+ (1 + :W + hD sin20]- (29.4)
В случае изотропной пластинки аз = ?-
В ортотропной пластинке напряжение меняется по до-
}е .ьни сложному закону, но отклонения напряжения от
среднего значения невелики.
101
В точках 0 = О и 9 = те на главной оси х
в точках 0 = на главной оси у
(29.5)
(29.6)
Круговое отверстие деформируется в эллиптическое
с полуосями а', Ь'.
(29.7)
На рис. 46 показано распределение напряжения в) по
краю отверстия в фанерной пластинке; ось х параллельна
Рис. 46.
волокнам рубашки. Наибольшее значение eg не превышает
1,2 наименьшее (в точках В и равно 0,75 q.
2. Касательные усилия, равномерно распределённые по
краю отверстия. По краю отверстия равномерно распреде-
лены усилия t (на единицу площади) (рис. 47):
°’= 2F7v sin 26 ^1!*’ — 1 + n G + №) +
1 +(1 + ^(1+^) cos 26]. (29.8)
Круговое отверстие, деформируясь, становится эллипти-
ческим.
В изотропной пластинке а9 = 0.
На рис. 47 дано распределение по краю отверстия
в фанерной пластинке. Ось х направлена вдоль волокон ру-
башки. Напряжение меняясь весьма неравномерно го
контуру и несколько раз меняя знак, остаётся незначитель-
ным по величине по сравнению с усилиями /; оно не пре-
вышает 0,2 t,
3. Растяжение под углом к главному направлению.
Пластинка растягивается усилиями р, действующими на
большом расстоянии от центра отверстия под углом 9 к глав-
ному направлению х (рис. 48):
{[cos2 9 + — п) sin2 9] pbJXg cos2 6 +
+ [(1 + п) cos2 9 + ^p-2 sin2 9] sin2 0 —
— n (1 + и —РчНа) sin 9 cos 9 sin 9 cos 0}. (29.9)
Распределение напряжений не является симметрич-
ным относительно направления растягивающих усилий.
Наибольшее напряжение получается не на концах диа-
юз
метра, перпендикулярного к растягивающим усилиям,
а в двух других точках, симметричных относительно
центра.
В изотропной пластинке
р [1 — 2сов 2 (0 —ф)].
(29.10)
На рис. 49 показано изменение а, вдоль края отверстия
в фанерной пластинке при растяжении под углом 45° к глав-
ному направлению. Ось х
параллельна волокнам ру-
башки. Точки, где я* = 0.
определяются углами 9 »
-33°, 87 :, 213° и 267°. Наи-
большее напряжение полу-
чается при 9 -- 110° и 290
и составляет 3,9 р; сле-
довательно, коэффициент
концентрации напряжения а?
в этом случае к = 3,9, тог-
да как в изотропной пла-
стинке к - 3.
4. Растяжение в главном направлении. Пластинка растя-
гивается усилиями р (на единицу площади); направление
усилий совпадает с одним из главных направлений (х на
рис. 50).
Из формулы (29.9), полагая <р 0, получим:
= cos2 0-Ь (i 4- /г) sin2 G].
(29.11)
Здесь распределение напряжений симметрично относи-
тельно главных направлений. Наибольшее напряжение полу-
чается в точках контура на главной оси.
В точках А и
; (29.12)
в точках В н Вг
Ъ = р (l-f-n).
(29.13)
В точках А и Ах на концах диаметра, параллельного
усилиям, напряжение — сжимающее, а в точках В и Вг на
концах диаметра, перпендикулярного к усилиям,— растяги-
вающее. Может оказаться (и это мы показываем на примере),
104
что сжимающее напряжение по величине будет ббльшим
растягивающего.
Круговое отверстие деформируется в эллиптическое
с полуосями
< Ve^eJ J
(29.14)
На рис. 51 дано изменение о вдоль края отверстия
в фанерной пластинке, когда последняя растягивается вдоль
Рис. 51.
волокон рубашки (ось х направлена вдоль волокон рубашки).
В точках А и At
а9 = -0,29 />; (29.15)
ж точках В и Вг
ай = 5,2 р. (29.16)
J06
Коэффициент концентрации к = 5,2. Точки, где oJ = 0?
получаются при 9 — ± 39°, ± 141°.
Рис. 52.
Иная картина получается в пластинке, растягиваемой
поперёк волокон рубашки (рис. 52; ось х направлена
перпендикулярно к волокнам).
В этом случае в точках А и At
О^-3,4р; (29.17)
в точках В п Вг
= 2,2 р. (29.18)
Растягивающие напряжения получаются меньше (по ве-
личине) сжимающих. Точки, для которых с9 = 0, определя-
ются углами в = ± 20°, ± 160°.
Для пластинки, растягиваемой в направлении оси у,
------------_____— [sin2 б + — n) cos2 9]« (29.19)
у ВгВ2 * Л
5. Всестороннее растяжение. Если пластинка растяги-
вается по двум главным направлениям одинаковыми уси-
107
лиями р (а это эквивалентно всестороннему растяжению)^ то
°'=~cos2 е+0+п)sin* бь с29-20)'
ISfjZr
В случае изотропной пластинки — 2р.
Рис, 53.
На рис. 53 дано распределение по краю отверстия’
в фанерной пластинке; ось х направлена вдоль, волокон ру-
башки. Наибольшее напряжение получается нс на главных:
осях; оно не превышает 2,2 р.
6. Стеснённое сжатие. Если прямоугольная ортотропная
пластинка с отверстием сжимается в главном направлении,
108
но не может расширяться в поперечном направлении (бла-
годаря жёстким стенкам — рис. 54), то, рассматривая пла-
стинку как бесконечную, сжатую усилиями р и pv2 2), полу-
чаем:
•« > = — {№ Г1 + (№ — «)] cos* 8 +
+ (1 + n + V^p.,) sin4 8}. (29.21}
В Изотропной пластинке
C;j = - p[i + v - 2 (1 - v) cos 20], (29.22)
где v —коэффициент Пуассона.
На рис. 55 изображён график с?э по контуру отвер-
стия для фанерной пластин-
ки , сжатой вдоль вол о ко н
рубашки.
В тонких А и
ав-0,2 р; (29.23)
в точках В и Вг
с _ „5,07 р. (29.24)
Пунктиром показана кри-
вая изменения в изо-
тропной пластинке с коэф-
фициентом Пуассона v =
— 0,25; для этой пластинки
в точках А и А1
~ 0,25 р,
в точках В и Bt
—2,75 р.
7. Сдвиг. Пластинка де-
формируется приложенными
вдали от отверстия равно-
мерно распределёнными ка-
сательными усилиями $ на
единицу площади, параллельными главным направлениям
х) Если Ву — О, то из второго уравнения (5.3) (при а2в = 0) сле-
дует:
а22
109
(рис. 56, верхняя схема):
п С1 + п“ HiHa) sin 26. (29.25)
В изотропной пластинке
= —4s sin 26. (29.26)
В ортотропной пластинке afJ обращается в нуль в четырёх
точках контура на главных осях и достигает наибольших
Рис. 5G.
до величине значений в четырёх точках, симметричных
относительно главных направлений.
На рис. 56 показано распределение ад по краю отвер-
стия в фанерной пластинке; ось х направлена вдоль во-
локон рубашки. Наибольшее напряжение в фанерной
пластинке равно 5,8s, тогда как в изотропной пластин-
не 4s.
1Ю
8. Нагиб. Прямоугольная пластинка с отверстием изги-
бается моментом М (см. рис. 57, где направления осей ж
Рис. 57.
и у совпадают с главными). Рассматривая пластинку, как
бесконечную, получаем:
= Вт[f + №-(1_^ + «)соа 26]. (29.27>
В точках Л иЛ^д-О, а в точках В и Вг
а5 = ±^2(14-2 ) * (29.28>
Напряжение обращается й нуль в шести симметрия*
пых точках контура, участки которого между нулевыми
точками попеременно растянуты и сжаты.
В изотропной пластинке
sin 0 cos 20. (29.29)
Если фанерная пластинка изгибается так, что напра-
вление оси х соответствует направлению волокон рубашки,
то распределение напряжений имеет вид, как на рис. 58.
В точках В и Вх
=9= ±3,1^; (29.30>
нулевые точки при 6 = 0°, 180°, ±53°, ±127°.
Для фанерной пластинки, у которой ось х направле-
на поперёк волокон рубашки, а моменты приложены так,
как на верхней схеме рис. 59, распределение сц по краю
отверстия показано на том же рис. 59. В этом случае в
точках В и Вх
а8 = ±1,6^-, (29.31)
Рис. 53. Рис. 59.
тогда как на боковых участках напряжение по величине
л t Ма
почти такое же —1,5 у.
В изотропной пластинке в точках В и Вг
________। 9
би = ± 2 -7-
(29.32)
наибольшее напряжение на боковых участках равно
0,54 Ма/1.
30. Распределение напряжений в ортотропной пластинке
с круговым отверстием при заданных смещениях.
В этом параграфе рассмотрены некоторые случаи рас-
пределения напряжений в ортотропной пластинке, ослаблен-
ной круговым отверстием, когда задаются не усилия, а сме-
щения края отверстия *). Направления осей х пу, так же как
и в § 29, соответствуют главным направлениям упру-
гости.
Для каждого случая приводятся графики распределения
напряжений по краю отверстия в пластинке, изготовлен-
ной из фанеры первого типа, которую мы для сокраще-
ния называем «фанерной пластинкой».
1. Действие жёсткого стержня, вогнанного в отверстие
с натяжением. В отверстие вогнан жёсткий стержень, диа-
метр которого несколько больше диаметра отверстия; диа-
метр отверстия 2а, диаметр стержня 2(а4-е); поверхность
края стержня шероховата, вследствие чего скольжение
материала пластинки по поверхности стержня невозможно.
Это—случай, когда краю отверстия сообщены радиальные
смещения, равные е (рис. 60). Решение получается с по-
мощью функций Фг и Фа вида [см. §27, формулы (27.9) —
(27.10)]:
(30.1)
х) Приводимые в этом параграфе решения для случаев 1 и 2 изло-
жены в нашей работе [1в].
lit
8 С. Г. Лехницкий
Нормальное давление аг и касательные усилия ^го по по-
верхности края отверстия распределяются по закону:
(30.2)
где
п= — г(н+ _
g=1-^_..+A |/5i,
6 Et ~G V Ег j
(30.3)
Эти формулы показывают, что стержень передаёт пла-
стинке давление, распределённое неравномерно; кроме того,
между поверхностью стержня и пластинкой развираются
силы трения. Наибольшей величины давление достигает в
точках пересечения контура с главными направлениями, а
касательные усилия— на биссектрисах углов между глав-
ными направлениями.
В точках Л и Ах (рис. 60)
+ ^=°: <304)
w& L " -^2 J
и4
в точках В и
о’=-«и/й+"_,,1’ ,',=с' <ад
Наибольшее касательное усилие
е
(30.6)
Напряжение ад на площадках, нормальных к краю от-
верстия, определится по гораздо более сложной формуле,
которую мы не приводим; укажем лишь значения в
точках Л, Лг В. Bt.
В точках А и Лх
= <3°-7>
в точках В я Вг
(30.8)
В случае изотропной пластинки с модулем Юнга Е и
коэффициентом Пуассона v для края отверстия:
аг =----nm, °o = -7§-4’ тг9 = 0. (30.9)
г a(l + v) 7 а (1-{- у) '
На рис. 61 показан закон распределения давлений и
сил трения в фанерной пластинке; ось х параллельна во-*
локнам рубашки.
В точках 4 и Д
. 105 .0,594; (30.10)
в точках В и
- - | . 105 * 0,244; (30.11)
тМрх= Юв‘ 0,175. (30.12)
На рис. 61— пунктирная окружность —среднее давле-»
ние по контуру, равное ~ • 106 • 0,419.
В рассматриваемой пластинке наибольшее отклонение
давления от среднего составляет 42%.
8*
115
2. Скручивание пластинки в её плоскости. Краю отвер-
стия сообщён поворот на малый угол а (тангенциальные
смещения ах); по внешнему контуру, который мы в теории
относим в бесконечность, пластинка закреплена неподвиж-
но (рис. 62). Этот случай можно себе представить так: край
отверстия зажат между двумя жёсткими круговыми шай-
бами, которые поворачиваются на угол а, или, иначе, в от-
верстие ввинчен жёсткий стержень, который затем повора-
чивается, увлекая за собой и край отверстия.
Функции Фх и Фа, дающие распределение напряжений,
имеют вид:
фх(^)=-В (ЗОЛЗ)
На краю отверстия развиваются нормальные и касатель-
ные усилий аг и тгв; они распределяются неравномерно:
аг=— | (1- у/" sin 9 cos б,
г.= - | [ 1//Г^-Л + «(со82б+ sin2 6) ].
(30.14)
Наибольшие касательные усилия развиваются в точках
пересечения контура с главными направлениями, а наи-
большие нормальные усилия — ца биссектрисах углов между
главными направлениями. Сопоставляя этот случай с пре-
дыдущим, можно заметить, что нормальные п касательные
усилия как бы меняются местами. Понятие о распределе-
нии нормальных и касательных усилий даёт график рис. 61,
если оси х и у поменять местами; внешняя кривая
даст закон изменения тгд, а внутренняя — закон изменения аг.
В изотропной пластинке на краю отверстия:
аг = ае = 0, (30.15)
3. Растяжение пластинки с жёстким круговым ядром.
Представим себе, что в круговое отверстие в пластинке впа-
ян, вклеен или ввинчен без натяга жёсткий стержень (яд-
ро), и пластинка растягивается в главном направлении
усилиями р на единицу площади (в теории пластинку, как
и раньше, считаем бесконечной, а усилия —приложенными
на бесконечности). При достаточно тщательной склейке,
спайке и т. п. ядро не даёт возможности краю отверстия
116
117
деформироваться под действием растягивающих усилий,
и контур сохраняет свою форму и размер. Схема этого
случая дана на рис. 63; направление осей х и у соответ-
ствует главным направлениям упругости.
На краю отверстия появляются нормальные и касатель-
ные усилия:
9* * f {IG “ й) +к+/ж 1С08’0+
, р Г vi(i + n) 1__, (
r’ g L V'E.E, Ег Еа*
+ — Sin Seos 6. ,
Л! J г J )
(30.16)
В точках А и Aj
°'=s / и^+ж+/®.в'.] ’ (30-17>
’•=7-3;/у;(®‘-’.+ /в;+")- <3018>
В точках В и Bt
°r=A [ i~v*(1+re\]’ ”°rV <3o-19>
В случае изотропной пластинки, работающей в тех же
условиях, получим следующее распределение напряжений
вдоль края отверстия:
vr~p(г~г—Но 2— cos26^) ,
г г \14-v * 3—v / ’
2
ae = arv, sin 29.
(30.20)
118
Формулы для случая сжимающих усилий получим из
(30.16) — (30.20), изменив знак у р. Если сжимаемая пла-
стинка лишена возможности расширяться в поперечном
направлении (например, потому, что на некотором рас-
стоянии от ядра имеются жёсткие неподатливые стенки,—
Рис. 641.
рис. 64), то на контуре отверстия развиваются нормаль-
ные и касательные усилия, равные:
°г--р{(1 + у /|)С088 е+_ j
+ |\ + |(/g-vi)]sin*O}r > (30.21)
Тг1 = /? |1-V2 +J [vj-l- —1)]J Sin0COS0, I
причём
, 1 — V>
E.
ГЛАВА VI.
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИИ В ЭЛЛИПТИЧЕСКОЙ
ПЛАСТИНКЕ И КРУГЛОМ ДИСКЕ.
31. Распределение напряжений в нагруженной
эллиптической пластинке.
В настоящей главе рассматриваются задачи о распреде-
лении напряжений в эллиптической пластинке, нагружен-
ной вдоль края, а также во вращающейся эллиптической
пластинке и круглом диске. Начнём с эллиптической пла-
стинки.
119
Рассмотрим эллиптическую пластинку из однородного
анизотропного материала, находящуюся в равновесии под
действием усилий, распределённых по краю по произволь-
ному закону. В общем случае мы будем считать пластинку
неортотропной; направив оси х и у по главным осям эллип-
са (рис. 65), будем иметь такие уравнения, связывающие
средние по толщине составляющие напряжения и деформа-
ции:
ех ~ Н- “1“ ?
== а12<* *Х + «2 + a26TXff’ '
(31.1)
Рис. 65.
Постоянные an, a12, . . . , aee будем считать известными.
Обозначим проекции усилий, действующих на краю пла-
стинки, отнесённые к
единице площади, че-
рез Хп, Yn; длины по-
луосей эллипса — а и Ь,
Объёмными силами бу-
дем пренебрегать. Си-
лы Xn, Yn находятся
в равновесии, т. е.
главный вектор их и
главный момент равны
нулю.
Эта задача для изо-
тропной пластинки ре-
шена Н. И. Мусхелишвили *). Решение для анизотропной
пластинки излагаемым здесь методом получено автором 2)
и другим методом — П. П. Куфаревым3).
Уравнение контура пластинки возьмём в параметриче-
ском виде:
х ~ a cos &,
y~b sin Э;
(31.2)
усилия, заданные на контуре, рассматриваем как функ-
ции переменной & (меняющейся от 0 до 2т).
Ч См. [»], § 62, стр. 222 — 228.
*) Си. |WJ.
’) См. [•]•
120
Для решения задачи воспользуемся комплексными пред-
ставлениями функции напряжений и самих напряжений
через функции Фх и Фа (см. §8). Функции Фг и Ф, должны
удовлетворять граничным условиям (8.7). В соответствии
с этими условиями разложим заданные усилия Хп, Yn в
ряды Фурье и составим выражения—Ynds и Xnds;
последние представятся также в виде рядов:
- 00 -
— \ ynds = ae + 2 («*«** + «*«“***)>
> (31.3)
JXndS = ₽0+2(^W + ₽Ae-,£A<)> I
k-i )
где ak, p* —известные коэффициенты, зависящие от закона
распределения нагрузки; ak, рЛ. — сопряжённые величины;
а0, ро — произвольные постоянные.
Для равновесия необходимо выполнение условия:
= . (31.4)
bi а 4 '
Решение задачи для самого общего случая распределения
нагрузки получается с помощью функций Ф* и Ф3 в виде:
ф1 &) - Ав + + 2 AkPlk (zx), I
*=* ’ (31.5)
Ф.(г2) = Вв-ЬВ1г2 + 2влр»*(;г*)- !
Здесь Р1к и Р2к — целые полиномы степени к относи*
тельно переменных и zt, имеющие вид:
Р1к &) = [& + / - а2 - 4- j
+&-i/^-«2-^2)*], I 3
P2ft (z2) = __ [(2а + Vе zf—a2 — +
+ 62)*].
121
Постоянные А, Вк для к = 2, 3,... и сопряжённые
с ними А в Вк определятся из уравнений г):
где
к + А*1 + Вк1 г = ~ «А,
АР» + ^к?» + AM* + ~ — ?А,
М++А + вл = - А»
АРч**++ АЙ + Ар-» = — Ра,
^i, ^ — сопряжённые постоянные; постоянные At и Bt опре-
делятся из уравнений:
Ай!+ВД+Ай + Ай,
А+А+А+А-’-4#’ ' <31>9)
Afh + АР» + АР1 + Ан» = ~~bt “ 1 • •
Линейные члены функций — Atz± и BjZ2 определяют постоян
ные напряжения в диске, равные
-о___ai 4“ ai о _ ai — ai______
а»---------- “
(31.10)
постоянные Ло, BQ остаются произвольными, а члены рядов
(31.5), начиная с к -- 2, определят напряжения, меняющиеся
по площади пластинки.
Таким путём можно получить формулы для подсчёта
напряжений в любом случае распределения усилий; ряды-
(31.5), после того как Ак и Вк будут определены из урав-
нений (31.7), окажутся сходящимися абсолютно и рав-
номерно как в случае распределённых нагрузок, так
и в случае нагрузок сосредоточенных. Фактическое осу-
ществление вычислений сопряжено вообще со значитель-
ными трудностями, избежать которые пока не представ-
ляется возможным.
*) Эта система всегда имеет решение в случае неравных комп-
лексных параметров, так как определитель её не равен нулю.
122
Интересно отметить, что в случае диска, когда 6 - а
и & = 0, никаких существенных упрощений не получается.
Задачи о равновесии эллиптической пластинки и кругового
диска оказываются задачами примерно одинаковой труд-
ности.
Иначе обстоит дело в случае изотропной пластинки;
задача о распределении напряжений в круглой пластинке
оказывается гораздо проще такой же задачи для эллипти-
ческой пластинки.
32. Распределение напряжений во вращающейся
эллиптической пластинке и круглом диске.
Предположим, что эллиптическая однородная пластинка
вращается с постоянной угловой скоростью о вокруг оси,
проходящей через центр и нормальной к плоскости пла-
стинки. Ось предполагается идеальной — математической
прямой. Решение для этого случая— очень простое и может
быть найдено элементарным путём.
Направим оси х и у, как указано на рис. 66. Не
предполагая, что пластинка ортотропная, имеем зависи-
мости (31.1).
Составляющие напряжения (средние по толщине) опре-
деляются формулами:
(32.1)
423
(32.2)
Здесь у —удельный вес материала, g — ускорение силы
тяжести,
л L4p2_________________giic* 4- 2а1ас2 4- aZi_,
° 3auc* + (2а12 + aee) с2 + За2а
с = а}Ь.
Это распределение напряжений удовлетворяет всем урав-
нениям плоской задачи ^в которых объёмные силы равны
соответственно '—х и — и соответствует отсутствию
внешних усилий на поверхности края пластинки.
Элементарное исследование приводит к следующему
заключению. Наибольшее напряжение на площадках,
уц)2
£
нормальных к краю (растягивающее), получается на концах
малой оси эллипса:
- ___Т0*8 г2р2 gnc4 4~ 2а12е2 4~ Д2а_ /оп о\
°® g За11С*+(2а11 + ам)С» + За„ ’
Напряжение в центре (наибольшее для всей пластинки,
если авв > 4а12) равно:
р,2 8 gllc4 + ~2 a66c2 + g22
ба = — {2ala + a„)C» + 3aM ’ <32'4)
Распределение напряжений в круговом диске радиуса а,
вращающемся вокруг идеальной оси, проходящей через
центр (рис. 67), получим, полагая Ь~а и с — 1. Состав-
124
ляющие напряжения в полярных координатах оказываются
зависящими только от расстояния г от центра вращения:
м - 0; )
. _ • <Хц 4- 2ях1 + а„
Злхх "Ь 4“ Зам
(32.5)
(32.6)
В случае изотропного кругового диска, вращающегося
вокруг оси, проходящей через центр (рис. 67), получаем
известное распределение напряжений *):
(32.7)
тго — 0.
Все вышеприведённые формулы дают возможность вы-
числить средние по толщине напряжения. В действитель-
ности напряжения меняются по толщине, т. е. зависят ещё
от координаты z, отсчитываемой от срединной плоскости
в перпендикулярном направлении. Если обозначить черев
вх, истинные напряжения в пластинке, а ои, txy —
средние по толщине напряжения, то формулы, учиты-
вающие изменение напряжений по толщине А, можно пред-
ставить таким образом:
°г = ^г = тВг = 0.
(32.8)
Постоянные В, С, D для эллиптической однородной, но
неортотропной пластинки определяются ив следующих
1) См., например, С. П. Тимошенко [43], стр, 81.
126
уравнений:
Т £*^12 "4“ *^^16
” За* (а19с2 + За2з) ” “з (а1з + ’
Ва^ + Са22 +^26 —
= зр(3а- + “28)-4(^2 + а23),
^^18 Н“ ^^28 “Ь = ^а2^Й^3 6*
(32.9)
В частности, для эллиптической изотропной пластинки,
когда
1 __ v
Л11_____________________________^22 = £ 1 а19 “ Й23 “ ^13 ~_?
2(1 4. у)
двв — __ , ^ie — а2в — — О,
получаем:
2м (с4 + с2+2) (1+ 2м) 4-с2 (Зе2 4-1} v
Л"~ 3(1 — м2) 3с*4-2са4-3 ’ |
с 2м (2с* 4- с2 + 1) (1 -}- 2v) -f (с2 + 3) v > (32.10)
G 3 (1 — м2) 3с*4-2с24-3 ’ I
£> = 0. )
33. Распред/леоне напряжений во вращающемся
криволинейно-анизотропном диске.
Легко получить также распределение напряжений
в диске с цилиндрической анизотропией, вращающемся
с постоянной угловсй скоростью е> вокруг идеальной оси,
проходящей через центр.
Пусть диск, изображённый на рис. 67, обладает цилин-
дрической анизотропией с полюсом в центре <?; предполо-
жим, кроме того, для простоты, что диск одновременно
является и ортотропным (с радиальными плоскостями
упругой симметрии). Решение этой задачи было найдено
Г. С. Глушковым в работе [’], который рассмотрел также
случай диска с отверстием в центре, т. е. вращающегося
кольца.
126
-р2а2 3 + 7cavr
°r~~g~ S — k*
к
~ "~7~ ’
(33.1)
Распределение напряжений зависит только от расстоя-
ния г и определяется формулами1):
GF-GF '
(3+лч)(4у-‘-
_ft(l + 3vr) (£)’],
тг3 = 0.
/Ёв
Здесь к —у Er, Е— модули Юнга для растяжения —
сжатия в радиальном и тангенциальном направлении;
^ — коэффициент Пуассона [см. § 13, уравнения (13.10)].
При к ®= 1 получаем распределение напряжений в изо-
тропном диске [см. (32.7)]. Для материалов, у которых
к > 1, т. е. E.j > Ет, составляющие напряжения обраща-
ются в нуль в центре диска, и оа достигает наибольшей
величины у обода:
~g----з+Г~- <33-2>
Для материалов, у которых к < 1, т. е. £о<£г, по
мере приближения к центру напряжения должны возрас-
тать, что видно из формул (ЗЗЛ); в этих случаях около
полюса анизотропии должна происходить концентрация
напряжений, подобная концентрации в диске, равномерно
сжатом по ободу (йя. § 23).
ГЛАВА VII.
ПРИБЛИЖЁННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ
НАПРЯЖЕНИЙ В ПЛАСТИНКЕ СО СЛАБО
ВЫРАЖЕННОЙ АНИЗОТРОПИЕЙ.
34. Плоская задача для слабо анизотропной пластинки.
Приведённые в главах III — VI решения плоской задачи
для однородного анизотропного тела показывают, что основ-
ными величинами, от которых зависит закон распределения
напряжений, являются комплексные параметры и ^2-
х) Эти формулы по существу совпадают с формулами Г. С. Глуш-
кова (работа [7]J; мы пользуемся несколько иными обозначениями.
127
Эти величины входят во многие формулы для напря-
жений, от них зависит наибольшее напряжение, концен-
трация напряжений и т. д. В изотропной пластинке
= л = — 1. Если представить комплексные пара-
метры однородной анизотропной пластинки в виде:
Рч = / (1 + ^1)^_ Р-2 = + ^2)^ 1
- г(1 + \), рй= -f(l + ka), } (б4Л)
то числа Х2 (вообще комплексные) можно рассматри-
вать как величины, характеризующие отклонение пла-
стинки от изотропной, иначе говоря, как величины, харак-
теризующие анизотропию. Чем меньше | Хх | и |Х2| по срав-
нению с единицей, тем ближе пластинка приближается по
своим упругим свойствам к изотропной.
Под «слабо анизотропной» мы будем подразумевать пла-
стинку, у которой |XJ и |Х2| малы по сравнению с еди-
ницей настолько, что можно пренебрегать высшими степе-
нями и произведениями этих величин по сравнению с пер-
выми и вторыми степенями. Мы ограничимся исследова-
нием напряжений в слабо анизотропной ортотропной
пластинке во втором приближении, разыскивая функцию
напряжений в виде ряда, расположенного по степеням
>4 и Х2, и пренебрегая степенями этих величин, начиная
с третьей. Заметим, что подобный приём разложения по
степеням малых параметров с отбрасыв^ние^м высших сте-
пеней неоднократно применялся для приближённого опре-
деления напряжений в таких телах, как слабо изогнутый
брус, брус, мало отличающийся от призматического
и т. п.
Рассмотрим случай, когда объёмные силы отсутствуют1).
Составляющие напряжения определяются по формулам:
d*F _#*F __ dzF
dyz ’ dxz ’ дх dy * (34.2)
В уравнении, которому удовлетворяет функция напря-
жений (5.11), выразим коэффициенты через комплексные
параметры и р.а, являющиеся корнями уравнения
х+О-йУ+к-0’ Р4-3’
1) См. нашу работу [20].
128
а и pt2 выразим через и Х2 и отбросим степени кх и Х2
выше второй.
Тогда получим:
TTF + (2Хх + 2Х8 + X’ 4- Х|) VF + 4Х,Х2 = 0, (34.4)
где
v2=^+±2 .
дх* ‘ ду“
Разыскивая функцию F в виде
F = Foa + (Хх + Х2) Fl0 + (Х“ + XI) F20 + Х^, (34.5)
заключаем, что функции Рф входящие в (34.5), удовле-
творяют уравнениям:
V2V2F00 = 0, |
WF10=-2^V2F00,
,2 > (34.6)
WF20=-^V2(2F10 + F00),
^2^2 p _ __ 4 (^2 p ! ,
Y V гюТ ^.2 J
Интегрируя эти уравнения последовательно, находим
следующие общие выражения х):
Fqq — Re 2^р00 (z) + Zoo (^)L
F10 = Re z?10 (z) + xl0 (г) - -J- ? ?'o (z) ] ,
F20 = Re z <p20 (z) + X20 (2) — 4 22 Ф10 (2) +
+ A 23 f ОТ (2) + 4 2a ?0’o (z) ] ,
Fu = Re [ (z) + Xu (2) - 4 22 tio (z> +
+ 4 Z3 ?OT (2) - 4 22 Xo'o(2) ] . л
Здесь
z = x 4- iy, z = x — iy.
(34.7)
*) Величины Ai + A2, Л^ + Я|, AXA2 — всегда вещественные числа,
а потому и для F получается вещественное выражение (34.5). Зная,
нак выражается бигармоническая функция Foo> получим для Z^30
неоднородное уравнение, легко интегрируемое, и т. д.
9 С. Г. Лехницкий
129
Z / (3) ~ произвольные аналитические функции ком-
плексного переменного z. Далее будем пользоваться сокра-
щёнными обозначениями:
Т./ = Т</(г), 9.J = Z//(Z), T./ = T./(z), 9.7 = £,(z) я т.п.
Па основании выражений (34.7) получим общие фор-
мулы для первых производных от F и составляющих на-
пряжения, которые удобно представить в комплексном виде:
dF . . dF —, — . ,
дх **" 1 ~ду ~ Z'?00 + 9оо Too +
+(>ч+м [ 2?;0+910+?ю - 4 (22?w+2й:з ] +
4* G4 + ^а) [ z?ao + 9ао + Та о Т C^Tio 4~ 2z<p'o) 4"
4" 8 ( з Too 4" Z2 Too 4" 2’?оо 4- 2z?00^ J +
4- W [ z?; 4- 9„ 4- ?11 -1 (z2?” + 2Г?;0) +
4-1 (з ?o'o - z29;; 4-z2?;; - 219;.) ]; (34.8)
° в - 4- 2г = 2 (zf” 4- 9 J 4-
+ (^1 4“ ^a) 2 (Zfi' 4 9io) — -у Фм' — Too J 4-
4- (4 4- K) 2 (z<Pa^ 4 9ao) Tio' — ¥10 4-
4- J2 4- <f>w 4- у ?w 4* 4 Too ] 4^
4- [ 2 (z?" 4- 9JJ — Z2<p"' - 2a>;0 4-
4- jo ¥0^ 4~ 9oo ~1~ 2 Too ~2 ^00] ’ (34.9)
4- Oy = Re [ 4?;0 + (Хх 4- Xt) (4?;o — 2l<p") 4-
4- (4 4- M) —2z<Piu 4- -у- ?o.7 4- zip'0 4-
4-' Л - 4z^;.' 4- — —z 9” ]. (34.W)
130
Аналогичны >, но божсложны , выражения Получа-
ются для перемещений1).
Если на границе заданы внешние усилия А\, Yn, то
граничные условия запишутся следующим образом2):
5 Ух'-у'№+с- (34.11)
G
Если распределение усилий по краю пластинки не
зависит от упругих свойств материала, то на основании
(34.8) и (34.11) мы получаем следующие граничныэ условия
для определения функций <р^ и ф.р
- " V
z?oo+9oo + ?оо= ) GA'a-yjds + Coo,
G
z'?io + 9io + ?10 = V (z2^o + 2z?oo) + C10>
z?i>+^«o + ®20= 4 (z’?lo+2z®;t)—4 (z <?"' +
_4 (34.12)
+ Z8 %o + z4uu + 2z?Q + C20 ’
zfii+’Fn + ?n=- -4(^0+2z?;e) ~4
- z* + 22Ф00 — 2z <jQ 4- c „
(C00 + (^1 4 MC10 T + ^)сяо+ M‘A1 c).
Функции 900 и дают распределение напряжений
в изотропной пластинке той же формы, что и слабо ани-
зотропная, и нагруженной теми же усилиями XTli Yn; их
мы можем определить, применяя методы, разработанные
Н. И. Мусхелишвили. Найдя функции ф00 и Фоо, на осно-
вании условий (34.12) (вторая строчка) определяем <р10, 61О;
эти функции дают распределение напряжений в изо-
тропной пластинке той же формы, что и слабо анизотроп-
ная, но нагруженной усилиями, закон распределения ко-
торых зависит от вида функций <р00 и йе0. Найдя <р10 к <Ь10/на
*) См. [20], L стр. 435, формулу (2.8).
См. условия (5.14).
9*
131
основании условий (34.12) (третья и четвёртая строчки) опре-
деляем функции <р20, <Ь20 и ф1Х; эти функции также
дают распределение напряжений в изотропной пластинке
той же формы, на которую действуют некоторые усилия,
зависящие от вида найденных функций <р00, Фоо и <р10, О10.
Таким образом, для определения напряжений в слабо ани-
зотропной пластинке во втором приближении нужно ре-
шить четыре задачи о распределении напряжений в изо-
тропной пластинке такой же формы, что и пластинка
слабо анизотропная, и нагруженной некоторыми усилиями
по краю. Теория плоской задачи для изотропного тела хо-
рошо разработана (благодаря, главным образом, трудам
Г. В. Колосова и Н. И. Мусхелишвили); выработаны эф-
фективные методы для решения этой задачи (метод рядов,
методы, основанные на применении конформного отобра-
жения и интегралов типа Коши, и др.) х).
Применение изложенного способа определения напря-
жений в слабо анизотропной пластинке мы покажем ниже
на двух примерах.
35. Распределение напряжений в пластинке, ослабленной
отверстием.
Рассмотрим слабо анизотропную пластинку с отвер-
стием, находящуюся в равновесии под действием усилий,
приложенных к внешнему краю и к краю отверстия;
в теории будем считать пластинку бесконечной. Предпо-
ложим, что главный вектор усилий, распределённых по
краю отверстия, равен нулю. Далее, рассмотрим беско-
нечную область на плоскости комплексного переменного С,
внешнюю по отношению к кругу с радиусом, равным еди-
нице («внешность единичного круга»), и отобразим кон-
формно эту область на область пластинки («бесконечная
плоскость с вырезом заданной формы»). Пусть функция,
совершающая это конформное отображение, имеет вид:
(Q. (35.1)
Если р, q, t — известные нам значения напряжений
(Уд., и на бесконечности, то функции и как
г) Эти методы изложены в известной книге Н. И. Мусхели-
швили [29], главы 2—4.
132
легко показать, представятся в виде:
?оо (2)=£4-?z + /00 (z),
910 (Z) = /10 (z)> ?so (z) ~ /20 (z), ?ll(z) = /ll (z),.
ho (z) = 4 (9 - P + 2t7) z 4- Foo (z); > (35.2)
ho (z) = “4^ “ + Fio(z)> ho (z)“ P^4 z + F20(z), Ф11 (z) = 4 (? - P - 2i0 z -1- Fn (z). '
Здесь fn (z), F.j (z) — функции, которым соответствуют
напряжения, стремящиеся к нулю по мере удаления от
отверстия.
Введём обозначения:
/г/(*) = /,гМ9] = М)’
hi (2) — иij (Qj
Л/' (-) = G)>
FiM ”
(35.3)
Из условий (34.12), путём замены переменной = а> («)],
получим условия, которым должны удовлетворять ФП-(С)
и Ф/;- (С) — функции, голоморфные и однозначные вне единич-
ного круга | С| — 1, на контуре этого круга.
Методы определения функций Фгу- и Ф,/ достаточно раз-
работаны. Если функция ко (Q является алгебраической,
то Ф// и Ф/у можно определять в виде степенных рядов:
ф;(ч --<?,+ 2 I
? (33-4)
«Г./Я=в;,+
JfI '
133
в некоторых случаях более удобным сказывается аппарат
интегралов типа Коши1).
Ксгла все функции будут спределены, составляющие
напряжения получим по формулам (34.9) и (34.10). Напря-
жение на площадках, нормальных к контуру отверстия,
у самого контура определится в общем случае по формуле:
°э = - + Р + Q + 4R? (а)] +
+ 01 + ' s) Re [ 4w10 (а) — 2ш ъ-00 (а) J +
+ (К3. + Х=) Re !4»80 (а) + « (у) [ vOo(°) ~
- 2г10 (а) + (у) «’со (а) ] | +
+ XjX.Re 14wn (а) + а) (у) £ _ Уоо (0) —
<v00(a)]}.(35.5)
Здесь —нормальное напряжение, действующее на
краю отверстия (величина известная), а —& — поляр-
ный угол, определяющий положение точек на контуре еди-
ничного круга (и тем самым, на основании зависимости
(35.1), положение точек на контуре отверстия), со — ве’
личина, сопряжённая с <о(сг). В следующем параграфе
мы рассмотрим более подробно распределение нгпряже-
Н1Ш в растянутей пластинке с отверстием, близким к
квадратному.
36. Растяжение пластинки с отверстием, близким
к квадратному.
Слабо анизотропная ортотропная прямоугольная пла-
стинка ослаблена в центре малым отверстием и растяги-
вается усилиями р (на единицу площади), распределён-
ными равномерно по двум внешним сторонам; главные на-
правления параллельны внешним сторонам, и растяжение
производится в главном направлении. Поместив начало
координат в центре отверстия и совместив направления
осей с главными, рассмотрим отверстие такой формы, ко-
торой соответствует параметрическое уравнение:
х~а (cos& + b cos 3&), у~ a (sin& — b sin 39) (36.1) 9
9 См. нашу работу [20]_. II.
131
Q0 — параметр, меняющийся от 0 до 2г, а, Ь — постоянные
коэффициенты, причём а > 0, |6|<4- ) . Пластинку рас-
сматриваем как бесконечную, и усилия относим на
бесконечность.
Путём надлежащего подбора коэффициента Ъ можно
получить фигуры, мало отличающиеся от квадрата с за-
круглёнными углами.
При положительных Ь «квадрат» расположен как на
рис. 68, а, и растяжение производи!ся в направлении диа-
гонали; при отрица-
тельных b положение
отверстия соответству-
ет рис. 68, Ь.
Задача о распреде-
лении напряжений в
изотропной пластинке,
ослабленной отверсти-
ем, близким по форме
к кв а др атному, рас-
сматривалась П. А. Со-
коловым г) (растяже-
ние, сдвиг), Г. Н. Сави-
ным 2) (растяжение, из-
гиб) иМ. И. Найманом8)
(изгиб). Беря урав-
нение контура в виде рие оа
(36.1), М. Й. Найман
1 1
полагал b - ~, а Г. Н. Савин Ь — ± ; последний рао
9 Ь * 7
сматривал также контуры с более сложными уравнениями,
дающими лучшее приближение к квадрату.
Ход решения задачи был показан в § 35. Функция,
производящая конформное отображение, имеет вид:
to (Q = а . (36.2)
В формулах, приведённых в § 35, надо положить
q = t = an=Q. Функции Ф/7- и Ч?'оо, которые необходимо
Ч См. [«].
2) См. [36р
8) СМ. [«О].
135
внать для определения напряжения около отверстия, по-
лучаются следующими ’):
,-ь' $ I?) ’
«•.. я= О ])-» (
ф..й= -тНйгш(')+
. раЬ* Г.3 , 106*-|-36 —2 £ 4Ьа(1 —&) , 6 ~| ,
+8(1-6)' 4 i-ь ’ i ~~ ?* f c’J
+ д’ w (у) Е ^В1° 2В°° (9 “ (1; ) v°a (9 J ’
фц (<) = - цёгь) I362 (i + ft) +1 - ft] «> (Q+
. Pab2 Ггз । 136*4-36—2 1 46*(1 — 6) , 6 Л .
*8(Ьб) LC + 1-6—-У-—VT--M +
*441) [8“‘°(Q+2£Zee (9-44) v»« (9 ] •
(36.3)
Полагая в этих выражениях С = а = и подставляя
в (35.5), получим распределение напряжений у контура
отверстия.
В точках на концах диаметра, перпендикулярного к рас-
тягивающим усилиям (В и Вг на рис. 68а и 686), получаем:
= (1-6Н1-36) [3 + 26-3d*-НМ Х2) (1 + 46-66*-
-36*) + (к* + к*) 2(^-(-5 + 56 + 3262 - 336* + 126‘) +
+ \ х2 Т(4бГ (1-86 + 6* 4- 386s - 216* + 36’) ]. (36.4)
При растяжении в направлении диагоналей (рис. 68, а)
получаем: для 6 -- ^ :
cr» = z47,8 + (kx + ks)3,57-(kf+k‘) 0,15 —кх к2 • 0,03]; (36.5)
Для ft = у :
с» = Р (5,37 + (Хх + Х2) 2,31 - (к* + к2) 0,05 + кх к, • 0,02]. (36.6)
*) Эти функции найдены методом Н. И. Мусхелишвили, осно-
ванным на применении интегралов типа Коши; подробнее—см. нашу
работу f2®], II, стр. 844—847.
136
При растяжении в направлении сторон «квадрата»
(рис. 68, Ь) для 6= — -g-:
= р [ 1,47 + (Ч + Х2) 0,10 - (Х| + X*) 0,03 - X, Х2 • 0,09]; (36.7)
, 1
для 6 = — :
р [1,85 + (Хх+Х2) 0,32-(X* 4 X*) 0,02 + Хх Х2 0,06]. (36.8)
При 6 = 0 получаем круговое отверстие радиуса а.
В точках на концах диаметра, перпендикулярного к рас-
тягивающим усилиям, получаем по формуле (36.4):
aft = p(3 + X1+X2), (36.9)
Этот результат совпал (случайно) с точным [см. фор-
мулу (29.13)].
37. Распределение напряжений в однородном кольце,
сжатом равномерным давлением.
В § 23 рассмотрено решение задачи о распределении
напряжений в кольце, обладающем цилиндрической анизо-
тропией, сжатом по внешнему и внутреннему контуру.
Решение имеет очень простую форму; радиальные направ-
ления являются эквивалентными, и вследствие этого соста-
вляющие напряжения зависят только от расстояния г. Та
же задача для однородного кольца представляется значи-
тельно более сложной, хотя бы потому, что радиальные
направления в этом кольце не являются эквивалентными,
и, следовательно, нет оснований ожидать, что напряжения
не будут зависеть от полярного угла 6. Точное решение
этой задачи ещё не найдено. Мы приводим здесь решение
для слабо анизотропного ортотропного кольца во втором
приближении.
Помещая начало координат в центре кольца, примем
главные направления упругости за направления осей х и у
(см. «рис. 27 в § 23); обозначим через а и b внутренний
и внешний радиусы кольца, через c — a{b отношение ра-
диусов и через р и q величины внутреннего и внешнего
давлений на единицу поверхности.
Обратимся к формулам (34.8) — (34.12). Функции ср00 и %0,
определяющие напряжения в изотропном кольце, известны,
137
они равны '):
рс* — д (7 —p)c2£>3 . 1
too 2(1 —с2) ’ ‘°0’ 1—са Z ’
(37.1)
Остальные функции <р10, ф10, <?20, ф20, срп, находим эле-
ментарным путём, по известным ?ео и о00: разыскиваем
функции в виде полиномов с положительными и отрица-
тельными степенями г и коэффициенты их определяем из
граничных условий (34.12).
В результате оказывается, что <р10 — $10 — <р20 — ф20 = О,
и только <рХ1 и 61Х отличны от нуля. Опуская все проме-
жуточные вычисления, совершенно элементарные, укажем
результат. Составляющие напряжения аг, а}, на площад-
ках, перпендикулярных к радиус-вектору г и проходящих
через радиус-вектор, определяются формулами:
Здесь:
4=^-(14-е2), - (3 + 4сг + 3с‘),
С = -5* С + <* + 5с= + с<)’ Р с* С + 4с’ + с<)>
8 = 14- 4с2 + Юс* 4- 4с’ 4- с’.
(37.3)
*) См. [29], § 51а, стр. 179.
138
Формулы (37.2), да ющио распределение напряжений
в однородном слабо анизотропном кольце во втором при-
ближении, содержат только произведения Х^ и не содер-
жат первых степеней и квадратов Хх и Х2. Отсюда следует,
что распределение напряжений в рассматриваемом кольце
в первом приближении совпадает с распределением на-
пряжений в кольце из изотропного материала; поправки на
анизотропию — величины второго порядка малости. Если
для данного материала один из комплексных параметров
равен /, т. е. одна из величин ХгХ2 равна нулю, то распре-
деление в слабо анизотропном кольце совпадает с распреде-
лением в изотропном кольце и во втором приближении г).
Далее, из формул (37.2) следует, что в кольце, сжатом
давлениями одинаковой интенсивности (q = р), а также
в диске, сжатом давлением, равномерно распределённым
по краю (р ~ 0, с 0), устанавливается однородное поле
напряжений:
аг = о 5 = — q, тг1 — 0, (37.4)
такое же, какое получается в изотропном кольце и диске.
Заметим, что в этих двух случаях формулы (37.4), следующие
из формул второго приближения, оказываются точными, и
притом не только для тела со слабой анизотропией, но и
для любого однородного упругого кольца или диска.
Применяя метод малых параметров, изложенный в на-
стоящей главе, легко получить во втором приближении
напряжения в однородном слабо анизотропном кольце и для
общего случая, когда кольцо деформируется усилиями,
как угодно распределёнными по контурам.
ГЛАВА VIII.
ТЕОРИЯ ИЗГИБА АНИЗОТРОПНЫХ ПЛАСТИНОК.
38. Приближённая теория изгиба анизотропных пластинок
(тонких плит).
Рассмотренные в главах II —VII случаи деформации
анизотропной пластинки характерны тем, что срединная
х) Более детальное исследование показывает, что в особом слу-
чае, когда ftsi, а —любое комплексное число, распределение
напряжений в однородном анизотропном кольце в точности совпадает
с распределением в кольце из упругого изотропного материала.
139
поверхность пластинки остаётся плоской. В настоящей
главе рассматривается общая теория деформаций анизо-
тропных пластинок, при которых срединная поверхность
искривляется, т. е. теория изгиба. Здесь мы остана-
вливаемся исключительно на той категории пластинок,
какая известна под названием «тонких плит», и рассма-
триваем приближённую теорию тонких плит. Для изотроп-
ных пластинок разработана также и строгая теория изгиба,
но для анизотропных пластинок в настоящее время раз-
работана лишь приближённая теория, почему нам и при-
ходится ею ограничиться.
В теории упругости тонкой плитой называют пластинку,
толщина которой мала по сравнению с другими размерами,
работающую на изгиб и испытывающую малые, по срав-
нению с толщиной, прогибы (во всяком случае, не пре-
вышающие толщины).
Так как в пределах настоящей работы мы будем иметь
дело только с тонкими плитами, то в дальнейшем будем
называть их просто «пластинками».
Рассмотрим упругое, равновесие плоской однородной
анизотропной пластинки постоянной толщины, закреплён-
ной по всему краю или по части его и деформируемой
изгибающей нагрузкой.
Изгибающая нагрузка в общем случае состоит из
нагрузки q кг[см\ распределённой по плоским поверх-
ностям и нормальной к срединной плоскости в недефор-
мированном её состоянии, и из нагрузок, распреде-
лённых по краю в виде изгибающих моментов т и сил
р, нормальных к недеформированной срединной поверх-
ности; последние могут быть заданными, а могут быть
и реактивными моментами и усилиями, возникающими
в местах закреплений.
Предположим, что в общем случае пластинка не яв-
ляется ортотропной, но имеет в каждой точке одну пло-
скость упругой симметрии, параллельную срединной пло-
скости.
Примем срединную плоскость недеформированной пла-
стинки за плоскость ху\ поместив начало в произволь-
ной точке О, направим ось z в сторону ненагруженной
внешней поверхности (рис. 69). Объёмными силами бу-
дем пренебрегать. В силу сделанного предположения отно-
сительно упругих свойств, будем считать справедливы-
ми для пластинки уравнения обобщённого закона Гука
в форме (2.2).
1'10
Приближенная теория изгиба пластинок (тонких плит)
строится на следующих двух предположениях:
1) прямолинейные отрезки, которые в недеформирован-
ном состоянии пластинки были нормальны к её плоской
срединной поверхности, при изгибе остаются прямолиней-
ными и нормальными к
ности («гипотеза прямых
нормалей»);
2) давление слоёв, па-
раллельных срединной
плоскости (напряжение
az), — величина, малая по
сравнению с напряжени-
ями в поперечных сечени-
ЯХ ах, Sg И
Обозначим через h
толщину пластинки, не-
изогнутой срединной поверх-
рез u, v перемещения
любых точек в направлении осей х и у, а через w (х, у)
прогиб срединной плоскости, т. е. перемещение в напра-
влении оси z частиц пластинки, лежащих на срединной
плоскости; вид функции w определит форму изогнутой
срединной поверхности.
Из первого предположения следует, что:
и =
дю
— Z —, v ~
дх 7
дю
— z
<>у
(38.1)
(дю п д^ю /ОО
(38.2)
Полагая, что для пластинки
обобщённого закона Гука (2.2),
(пренебрегая gz):
справедливы уравнения
используем три из них
” #11 $Х 4“ #12 “Ь #1в
— ai2 6t22 Gy 6f2e
#16 4~ #20 #66 ^ХУ*
(38.3)
Ч Основы теории изгиба анизотропных пластинок были зало-
жены в работах Геринга [58] и Буссинеска [б5]. Приближённая
теория изгиба анизотропных пластинок разработана, главным образом,
благодаря работам Губера [в0], [е1]> [п].
141
Решая эти уравнения отшситсльно составляющих на-
пряжения, получим:
6.
, П t OR
^2+ ^12 ^+2^16
37=+-B2t^+-p««
^ + /?se^ + 2Bee
dx Оу
d*w
Эх ду
d2w
дх ду
(38.4)
Постоянные выражаются черев а именно:
^11 Д’ (й22 ^ве Л2ё)? -®22 :
Д12 Д (flie aS6 “ С Е12 ЙСб)э ^68
-Die — д (^12 Я2в Л 22 ^ieh ^28
1 ^115 ^125 ^18
Д " ^22J ^2® •
1 ^1в> ^28 ’ ^В8
д (Gn ^8 #ie)>
= д' (^11 ^22 #12) )
= y(«i»o1.-e«®».)> > <38-5>
Составляющие и xyz определяем из уравнений рав-
новесия:
О,
dx dy ' dz
।. I ^Tyg _ a
dx dy * dz ’
(38.6)
учитывая, что на внешних поверхностях
Получаем:
[Bng+3B,.s-.7-T
V -2 -4‘) [ S + <B- + 2B-> +
(38.7)
Если выделить в пластинке площадки, нор ml
к первоначальной срединной поверхности с
ЛЬПЫО
высотой.
^ху ~ z
yz ~ 0.
1
142
pai.ной толщине пластинки, и с основаниями dx, dy, то
составляющие напряжения аж, су, хху приведутся к момен-
там Mydx, Hxydx и Mxdy, Hyxdy, а т;ж, *с;у к силам
-Nxdy, Nydx. Величины Мх, Му называют изгибающими
моментами, Нау — скручивающими моментами, a Nx, Ny~
перерезывающими силами (все они относятся к единице
длины). Очевидно,
П/2
Мх — <зл.z dz,
Л/2
= ^„zdz,
-h/2
h/2
Mу== &y 2 dz, 11 xy = HухI
~'hw w 1(38.8)
x= ,izxdzi Ny— ( x.gdz. I
-h/2 -h/2 }
Отсюда и из (38.4) и (38.7) вытекают зависимости:
Afv= — ,
а^4а/^+зл.-^+ j
+ {Dli + 2Dts)^i + L
-[^.°S+(^t + 2^.)
+ 3Dtt^-2 + L
d^ dyz 1
(38.9)
(38.10)
b*w
дх2 ду
> &*w
°
Постоянные Dsj связаны c Btf
D^B^.
(38.11)
По аналогии с изотропной пластинкой, для которой вве-
дено понятие «жёсткости», назовём постоянные жёст-
костями анизотропией пластинки, именно: Z>u, D2i — жёст-
кости изгиба вокруг осей у и х; /)вв —жёсткость кручения
для осей х и у* /?16 и Р26— побочные жёсткости; отноше-
ния Z>ia/.Z>22 “ Yn ^12/^11 ™ Ь уместно назвать, учитывая
143
формулы для ортотропной пластинки (которые будут приве-
дены ниже), приведёнными коэффициентами Пуассона.
Между составляющими напряжения, моментами и пере-
резывающими силами существуют, как это следует из выше-
приведённых формул, простые зависимости:
(38.12)
На рис. 70, а показаны составляющие напряжения на пло-
щадках, нормальных к осям х и ?/, а на рис. 70, b — моменты
и перерезывающие силы, к которым приводятся напря-
жения.
Если пластинка ортотропна и направления осей х и у
совмещены с главными направлениями упругости, то,
144
вместо уравнений (38.3), (38.9) и (38.10) будем иметь:
гх— (ах vi°y)’ sy E2^° vaax)> Yxy— Q Txy? (38.13)
n f l)2w , (72(v\ 1
Mx 1)1 (.51? -j-v‘ dy*) ’ (
д, Гч f d2w . d2w\ rr nn ^2(V t
N.-^^D^ + D,3-^,}, ]
x dr \ 1 cU2 1 3 dy2 J ’ I
Nv=Md,^D^. I
° <>У\ 3 r^2 oty2y '
(38.14)
(38.15)
Здесь E^ vx, v2, G — модули Юнга, коэффициенты
Пуассона и модуль сдвига для главных направлений;
п ___ п __ Е2 h2 J-. Gh2 /qq
12(1~^у3) ’ D2 “ 12 (1 —v±v2) ’ ^“12 (38Л6)
— жёсткости изгиба и жёсткость кручения для главных
направлений упругости, или главные жёсткости,
= + 2Л; (38.17)
побочные жёсткости исчезают. В случае изотропной пла-
стинки Ех = Е2 = Е, v^Va^v, G = jE/2(14-v), и все жёст-
кости сводятся к одной:
Приведём выражения потенциальной энергии изгиба для
неортотропной и ортотропной пластинок [вытекающие из
выражений (2.11)— (2.12), если пренебречь txz, xyz и cz]:
+P„(^)+4C..(^)- +
^4m^sy+2c‘’-s-^+
+D^y+iD^S’Suy}d^« t38-1’)
(интегралы берутся по области, занятой пластинкой).
10 С- Г. Лехницк! й Н5
Кроме составляющих напряжения, моментов й перере-
зывающих сил, действующих на элементы пластинки, пер-
пендикулярные к осям х и у, нам иногда придётся рассма-
тривать составляющие напряжения а/;, xzn на площадке
с произвольно направленной нормалью п, соответ стт у ющие
изгибающий и крутящий моменты —Htn и перерезыва-
ющую силу Nn (рис. 70). Последние определяются по фор-
мулам *):
Мп ~ Мх cos2 (ft, х} + Му cos2 (ft, у) 4- \
4- 2Н:iy cos (ft, х) cos (ft, у),
H= (Му -- MJ CCS (ft, x) cos (n, y) + >
+ HX у [cos2 (ft, x) — COS2 (ft, y)],
Nn = Nx cos (Л, x) 4- Nv cos (ft, y);
(38.20)
°n
h* z’
~ дз “ hs 4 * J *
(38.21)
Знаки моментов и перерезывающих сил мы будем
определять в связи с формулами (38.12) и (38.21): поло-
жительными будем считать моменты и перерезывающие
силы, которые создаются положительными при г > 0 на-
пряжениями.
39. Уравнение изогнутой поверхности.
Как видно из формул предыдущего параграфа, моменты
и перерезывающие силы (а следовательно, и напряжения)
выражаются через прогиб срединной поверхности w. Сама
эта функция удовлетворяет дифференциальному уравне-
нию четвёртого порядка, которое мы получим, рассматри-
вая равновесие элемента пластинки в виде прямоугольно-
го параллелепипеда с рёбрами dx, dy, h. Схема такого
элемента вместе с действующими на него усилиями и
моментами показана на рис. 71 (толщина h не изобра-
жена, так как она не играет роли: моменты и перерезы-
вающие силы относятся к единице длины срединной пло-
скости).
Условия равновесия элемента (сумма проекций усилий
на ось z равна нулю, и суммы моментов относительно
См. формулы перехода (8.5).
146
осей х\ у', параллельных осям х и
вид:
дх 1 ду 1 *
V _ дМх . дНАу
х дх ' ду ’
лг — дМу । (^^ху
у> равны нулю) имеют
(39.1)
Здесь £ —нагрузка на единицу площади, распределён-
ная по внешней поверхности.
Подставляя в первое уравнение выражения для пере-
резывающих сил (38.10), получим уравнение прогибов не-
ортотропной пластинки:
*g + 4Dle + 2 (Z)12 + 2Z)e6) ^2+
+ 4^6^ + ^ = <Л (ЗЭ-2)
В частности, для ортотропной пластинки, совмещая
направления осей х и у с главными, получим:
D ^ + 2Z)3.44^2 + D
xt)x4 ‘ 3dx2dz/2 1
d*w___
2 ду^
(39.3)
У изотропной пластинки
1 2 8 2(1—№) ’
10*
147
и уравнение (39.3) принимает вид 1):
DVzTw = q. (39.4)
Задача определения прогибов и напряжений в однород-
ной пластинке, изгибаемой какими-либо усилиями, сводится
к интегрированию уравнения (39.2) [или, соответственно,
(39.3) или (39.4)]. При интегрировании необходимо учиты-
вать, что прогиб w должен удог летворять граничным усло-
виям, которые зависят от способа закрепления или загрузки
края пластинки. Приведём граничные условия для пяти
основных случаев закрепления или загрузки края пла-
стинки, который в обшем случае будем считать криволи-
нейным, с нормалью /ц направленной произвольно по отно-
шению к осям я, у 2):
1) край жёстко заделан (защемлён):
<39-5)
2) край опёрт (шарнирно закреплён):
w = Q, М„-0; (39.6)
3) край свободен:
М„ = 0, JVn + ^ = O (39.7)
(d/ds — производная по дуге s контура);
4) край нагружен заданными изгибающими моментами
и усилиями, величины которых на единицу длины соответ-
ственно тир:
Мп = т, Nn + d-^ = p- (39.8)
5) край деформирован, причём известен прогиб края w*
и угол наклона а* изогнутой поверхности к плоскости ху:
(39-9)
В условиях (39.8) и (39.9) известные правые части
равенств предполагаются заданными либо в виде функций
дуги контура $, либо функций какой-нибудь другой пере-
менной, определяющей положение точки на контуре.
9 Вывод уравнений теории изгиба для анизотропной пластинки
имеется, например, в работе Губера [62] и в нашей работе [21],
а для изотропной пластшпиг-в книге акад. Б. Г. Галеркина [5]
и в курсе С. П. Тимошенко [44], ч. II, § 49.
2) См., например, [2в], стр. 478—481 и [441, стр. 270--275.
148
40. Уравнение изогнутой поверхности с учётом
продольных сил. Пластинка на упругом основании.
Предположим, что однородная анизотропная пластинка
нагружена силами, вызывающими изгиб (рассмотренными
в § 38 — 39) и, кроме того, силами, действующими в сре-
динной плоскости (продольными силами). Если действуют
только первые силы, то в пластинке развивается распре-
деление напряжений, соответствующее изгибу; если дей-
ствуют только продольные силы, то напряжённое состояние
пластинки будет обобщённым плоским.
При совместном же действии этих сил неправильно
определять напряжения путём простого суммирования
напряжений от изгиба и напряжений, соответствующих
плоскому напряжённому состоянию; продольные силы ока-
зывают влияние на прогиб, и уравнения (39.2) —(39.4)
перестают быть верными.
Изучая (приближённо) совместное действие изгибающих
нагрузок и продольных сил, полагают, что составляющие
напряжения в пластинке складываются из двух частей:
°х^°х + <4
° У ~
~ "хУ 4"
"yz ~ ТУ.” |
)
(40.1)
Здесь сГд,, ау, —средние по толщине значения напря-
жений, вызванных одними продольными силами; а^, ау, ^хУ —
напряжения, пропорциональные z и определяемые по фор-
мулам (38.12) и (38.9). Чтобы получить уравнение, кото-
рому в данном случае должен удовлетворять прогиб w,
введём в рассмотрение величины Тх, Sxy, Syx — продоль-
ные и касательные усилия на единицу длины:
Л/2
Тх — =
— Л/2
Л/2
-h/2
Л/2
~ л/2
(40.2)
149
Очевидно, ТТу, SxU удовлетворяют уравнениям рав-
новесия ')
Ф + ^ = О, ^ + ^i = 0; (40.3)
дх оу 1 ох ду ’ ' •
чъобы определить их, нужно решить для пластинки плоскую
задачу.
Выделим из пластинки элемент в виде прямоугольного
параллелепипеда с рёбрами dx, dy и h и рассмотрим его
равновесие. На этот элемент, кроме сил и моментов, пока-
занных на рис. 71, будут действовать продольные усилия,
изображённые отдельно на рис. 72 и 73. Учитывая, что
при деформации элемент искривляется, и усилия Т Tyj Sxy
в деформированной пластинке уже не будут лежать в пло-
скости ху, получаем составляющую этих усилий в направ-
лении оси z:
z - (?45+S;+т^~) d* (40/‘>
или, на единицу площади,
7 = Тж^+25хвЛ~4-7’и^. (40.5)
х dxs ‘ Х®дхду v ду2 7
Это усилие Z нужно присоединить к нагрузке q в уравне-
ниях § 39, и мы получим для иеортотропной пластинки:
D„ g + iD„ + 2 (Д„ + 2D..) + 40,. +
+ о„ + Т, + 2S„ + Т, g? (40.6)
и для ортотропной пластинки:
D I 7? №?-
1 дх1+ 3 дх* ду* 2 ду* “
= ? + Л:й + 251г, Д+Т/Д. (40.7)
* 1 х дх* хи Эх ду " ду* v ’
Задача об изгибе пластинки с учётом продольных уси-
лий значительно усложняется, если нет оснований считать
прогиб малым по сравнению с толщиной. В этом случае
прогиб и функция напряжений определятся из системы
двух нелинейных уравнений.
!) При отсутствии объемных сил.
150
151
Эта система для изотропной пластинки была выведена
Карманом. Приведём краткий вывод соответствующей си-
стемы для ортотропной пластинки.
Полагаем, что составляющие напряжений определяются
по формулам (40.1), а составляющие деформации скла-
дываются также из Двух частей:
£х — sx“hex? еу — еу4“еу, Yxy Yxp (40.8)
Величины ех, еу, уху —составляющие деформации срединной
плоскости; они зависят не только от смещений и и и, но
и от прогиба tv. Из общих выражений (1.4) получаем, рас-
кладывая их в ряды и сохраняя первые степени производ-
ных от и и v и вторые степени производных от w\
х дх' 2 \дхJ ’
- __dv 1 / 2
£у oty 2 \ ду) ’ ।
___ди .dv dw дю I
ду дх • дх ду * I
(40.9)
Исключая и и и путём дифференцирования, получим:
= ( <^w У d*w
ду2 ""Г" дх2 дх ду \дх ду) дх2
д2ю
(40.10)
Слагаемые si, Y^y зависят от изгиба пластинки и
определяются по формулам (38.2). Полные напряжения ах,
оу, приведутся по толщине пластинки к продольным
силам Тх, Ту, Sxy [см. (40.2)] и к моментам Му, Нху,
а напряжения txz, туг приведутся к перерезывающим силам
Nx, Ny [см. (38.14) и (38.15)]. Напряжения ох, тху
удовлетворяют уравнениям равновесия:
<^х_ । __ л __п
дх иу ’ дх ду ’
(40.11)
откуда следует, что они выражаются через функцию напря-
жений F:
d*F - a*F - _ d*F .,п 1(П
ах'~ dyi‘> Txv Hxdy’
152
Эти напряжения связаны с деформациями уравнениями
обобщённого закона Гука:
ех — jg»1 (ах viGy)> ” V2Gx) 5 (40.13)
- _ £-
Yxy ~ Q T*P’
Перерезывающие и продольные силы удовлетворяют урав-
нению
ф++ + т +25 + г = о,
дх 1 ду х дх2 1 дх ду * оу2
(40.14)
которое получается из рассмотрения равновесия прямоуголь-
ного элемента пластинки, изображённого на рис. 71, с учё-
том составляющих сил в направлении оси z, вызванных
продольными силами (рис. 72 и 73).
Подставим в уравнение (40.10) выражения (40.13) и за-
меним напряжения через функцию F; подставим, кроме
того, в уравнения (40.14) выражения для перерезывающих
сил (38.15) и заменим продольные усилия через функцию F.
Тогда получим систему из двух нелинейных уравнений,
которым удовлетворяют функция напряжений и прогиб:
* (7 Z* I [ л. -1 *1 Д о Г | л и г
Б], dZ*’+\O~E1J дх3ду3 Ё1~ду*~
Г> — 4- 2D д** 4- Л
11 'дх* + 3 дх3 ду3 3 ду*
, , /d3F d3w „ d3F
= q + hl — — 2
2 d2w d2w
дх2 dy2
dx ду дх ду
d2w , d2F d2w
dx2 dy2.
j> (40.15)
J
Эти уравнения выведены Г. Г. Ростовцевым1).
Интегрирование их, вследствие присутствия нелиней-
ных членов в первом уравнении, сопряжено с большими
трудностями; точное решение уравнений пока неизвестно
ни для одного случая изгиба.
При малых прогибах нелинейным выражением можно
пренебречь, и тогда функция напряжений определится не-
зависимо от прогиба.
2) См. работу f34].
153
Если однородная пластинка лежит на сплошном упругом
основании и изгибается нагрузкой причём прогиб её мал
по сравнению с толщиной, то уравнение прогиба мы можем
получить, полагая, по Винклеру, что реакция основания 7?
в данном месте пластинки пропорциональна прогибу в
этом же месте1):
R^kw (40.16)
(к — коэффициент упругости основания, иначе — коэффи-
циент постели). Уравнение пластинки на упругом основании
мы получим таким же путём, как и для пластинки, не
лежащей на упругом основании; нужно только учесть, что
на элемент, изображённый на рис. 71, действует в данном
случае нагрузка q — kw. В результате получаем уравнение
для неортотропной пластинки:
Л,5+ 4В..^ + 2<°.. + 2'>..) JX- +
+ <40-17)
для ортотропной пластинки:
Ag + 22>. (40.18)
Если на пластинку, лежащую на упругом основании, дей-
ствуют не только нагрузка q, но и продольные силы, то
уравнение прогибов получим из (40.6) и (40.7), добавляя
к левым частям члены kw.
41. Связь теории изгиба с теорией функций
комплексного переменного.
Уравнение прогибов анизотропной пластинки (39.2) того же
типа, что и уравнение для функции напряжений (5.9)
в теории плоского напряжённого состояния. Общее выра-
жение для функции ер известно; оно зависит от корней
p-i, р.2, р,х, характеристического уравнения
DttV.* + 4O2.U’ -ь 2 (Dlt + 2Z>„) + 4/)16|л -b D„ = 0. (41.1)
Это уравнение для любого упругого однородного мате-
риала, как было нами показано, не может иметь веществен-
ных корней2). Комплексные или чисто мнимые числа
х) См. [в], стр. 149.
2) См. нашу работу [21]. стр. 187. Приведённые ниже формулы,
выводятся в той же работе.
is;
= а 4- pZ и р2 = у + oz назовём комплексными параметрами
изгиба; они вообще отличаются от комплексных параметров
плоского напряжённого состояния для той же пластинки,
и только в случае изотропного материала и те и другие
равны i.
Общее выражение для прогибов имеет вид1):
1) в случае различных комплексных параметров (р2 #= р.г)
<v = «'04-2ReX(z1)4-«’2(z2)]; (41-2)
2) в случае одинаковых комплексных параметров
(р« = th)
+ 2Re [я\ (zj + Z1<v2 (z2)]. (41.3)
Здесь <v0 — частное решение неоднородного уравнения
(39.2), вид которого зависит от распределения нагрузки q
по поверхности, w1? (v2 —произвольные аналитические функ-
ции комплексных переменных — х + и z2 — х + р2г/.
На основании формул (38.9) и (38.10) получаем общие
выражения для моментов и перерезывающих сил (для слу-
чая Ф P.J:
Мх = М°х — 2Re [р^\ (ZJ 4- ptwt (za)], )
Му — Мд-2Rc[gX (Zi)4-?2< (z,)], } (41.4)
^T,, = H^-2Re [rX (zt)4-rX (ze)]; J
^X ~ NX- 2Re [u.JS1W’1 (zt) 4- P-2^2^2 Cj)]( 1 /XI e\
^=2V»4-2Re[SX"C1)4-sI<"(^). J 1 *
Здесь Mb My, .. ., моменты и перерезывающие силы,
соответствующие функции w0 [они определяются по фор-
мулам (38.9) и (38.10)];
Pi “ 791Г -'р 7912р^ 4' 2771буп р2 = + 7912^2 И- 2Z)leu2,
(71 “ + ^2зК“Ь 27926|\, g2 Р13 4-Z?a2uJ + 2Z)2ey*2,
ri — +^2бРч + 2Dse^15 г2 == £\б + -^2бН-2 + 279бв|ха,
S1 = + 3D„ 4- (O1S + 2Z)ee) 4- D2X,
D 9 <41-6)
^2 — ~ + 3D16+(Z)12 4- 2Z)ee) a2 + D2ep.2,
H-2
__r — El g ____ p ~
1 2 2 14’
4’^= (71[л s2 + r2 = q2^2*
*) Формулы (41.2) — (41.3) выводятся так жр. как и общие выра-
жения для функции напряжений 2^(см. § 7).
155
Остановимся на случае, когда пластинка изгибается толь-
ко усилиями и моментами, распределёнными по краю (q =б).
Уравнения (39.2) —(39.4) становятся однородными, и в
формулах (41.2) —(41.5) надо положить wQ = М* — М2 =
= Я»„ = 2У« = 2У» = О.
Если по краю пластинки заданы изгибающие моменты
m(s) и силы p(s) (на единицу длины), как функции дуги
s, то граничные условия (39.8) преобразуются в условия
для функций w'i и J):
2Re Г^(^) + fs^(22)l= 1
L Hi Иг J
s
(mdy + f dx) — Cx-^-C^
° < (41.7)
2Re [g1w'1(z1) + ?X(z»)] =
s
== ^ ( — mdx + f dy) + Cy + Ct.
o J
s
Здесь С, неопределённые постоянные, /= pds\
о
интегралы берутся по дуге контура от начальной точки до
переменной точки.
При заданной деформации края отверстия, вызванной
неизвестными усилиями [когда заданы ер* ($) и а* ($)], гра-
ничные условия (39.9) принимают вид:
2Re[«-i (zj + w2 (z2)] - — cos («, y) + a* cos (ra, x), ]
dtv* }(41-8)
2Re[uX (zx) + у-Х (z2)] = -^- cos (и, x) + a* cos (n, y) j
(n —направление внешней нормали к контуру пластинки).
Внутри области пластинки, изгибаемой усилиями, рас-
пределёнными по краю, функции ер' и ер' должны удовле-
творять ряду условий, которые выведены в нашей работе
[21], а именно:
1) если область пластинки односвязная (пластинка не
имеет отверстий), то функции ер' (zj и ер' (z2) должны быть
голоморфными и однозначными в своих областях и 52
(см. § 8, рис. 9);
См. нашу работу [21], стр. 191.
156
2) если область пластинки имеет отверстия, но при
этом усилия, распределённые по краям отверстий, уравно-
вешиваются на каждом из них (главный вектор и главный
момент равны нулю), то функции w'(zj и (v'(z2) голо-
морфны и однозначны в своих областях и S2;
3) если область пластинки ограничена несколькими кон-
турами (пластинка имеет отверстия) и при этом, хотя бы
для одного контура, главный вектор и главный момент
усилий не равны нулю, то функции wj(zx) и w'2(z2) будут
многозначными.
Пусть, например, в пластинке имеется одно отверстие,
и на краю этого отверстия действуют усилия и моменты,
приводящиеся к равнодействующей (главному вектору) Pz
и к моменту с составляющими тх и Тогда, при обходе
по любому замкнутому контуру, окружающему отверстие,
функции ф' и w' получат приращения Д' и Д', а производ-
ные их (V* и % (т. е. вторые производные функций и
уравне-
(V,) — приращения Д* и Д*, которые определятся
ний х):
2
А + ^1 + ^1 + Дз“ о,
"Т ^2*^2 4“ HlAi 4” 9,
ьйд;+йд:^о,
А д'1 + А д:^А
1*1 Из
из
(41.9)
1
Из
)
д; + д: х д; + д: - о,
Ml + м1+ ^1=0,
^д; + ^д; + <4д;+ р*д;= -
А д;+Ад;+А д; + Ад;_
Hi Н 11Х
тх
У?*
•^22
ХР3
Рц -^н
(41.10)
На основании вышесказанного, природа функций ^(zj
и w2(z2) становится ясной. Мы видим, что задача об изгибе
пластинки нагрузкой, распределённой по краю, имеет много
общего с плоской задачей и вместе с тем таит в себе те
же трудности, связанные с определением функций разных
комплексных переменных zt и z2, что и плоская задача.
Для простых контуров, когда пластинка имеет форму
4 Определитель этих систем для неравных комплексных параме-
тров всегда не равен нулю (см. примечание в §8).
157
Прямоугольника, полосы или круга, задача в ряде случаев
решается просто, без комплексного представления, но в
более сложных случаях комплексное представление может
оказаться весьма полезным. Укажем ещё формулы для
изотропной пластинки, аналогичные формулам плоской
задачих):
w = w0+ 2Re (z) + zw2 (z)];
Му - Мх + 2ШХУ - МS - М2 + ЖУ +
4 4D (1 —>) [< (*) + *% (z)],
Мх + Му - М°х + Му - 8D (1 + v) Re [w\ (z)];
(41.11)
(41.12)
— = (41.13)
где
n Eh* . -
Благодаря такому комплексному представлению яв-
ляется возможным при решении задач об изгибе изотроп-
ных пластинок применение всех тех методов, которые
разработаны для плоской задачи в трудах Г. В. Колосова,
Н. И. Мусхелишвили и др. и изложены в книге
Н. И. Мусхелишвили [ав].
42. Определение жёсткостей изгиба и кручения
различных ортотропных пластинок.
Основными величинами, характеризующими упругие
свойства однородной ортотропной пластинки при изгибе,
являются её главные жёсткости Dr, D2, Dk и коэффициенты
Пуассона vx, v2. Для вычисления жёсткостей изгиба и
кручения однородной ортотропной пластинки необходимо
знать её толщину Л* и главные упругие постоянные
Е„ Е2, v1? v2, G.
Заметим, что жёсткости можно представить в виде:
= D-~^’ D‘ = GI’
h*
где I = 12 — момент инерции балки прямоугольного сечения,
вырезанной из пластинки, имеющей высоту пластинки h
и основание, равное единице.
х) См. на ну работу [*А], ч. 11.
158
йа практике можно рассматривать приближенно, как од-
нородные и ортотропные, и такие пластинки, которые со-
ставлены из ряда слоёв (фанера), а также пластинки из
изотропного материала, гофрированные и ‘усиленные гоф-
ром или часто поставленными рёбрами жёсткости. Приве-
дём примеры опреде *ения главных жёсткостей некоторых
таких пластинок.
1. Фанерные пластинки. Хотя фанерная пластинка пред-
ставляет собой, строго говоря, неоднородное тело, она
обычно, при расчётах, рассматривается, как однородная
и ортотропная; одна из плоскостей упругой симметрии па-
раллельна срединной плоскости, вторая из трёх перпенди-
кулярна к волокнам рубашки. Значения главных упругих
постоянных (средних по толщине) длц фанеры двух типов
указаны в § 9; зная эти постоянные, легко определить и
жёсткости [по формулам (38.16) или (42.1)].
Для фанеры первого типа х) направляя ось х парал-
лельно волокнам рубашки, получаем:
£\ = 1,425 • 10s g, £>„ = 0,119 • 10‘g,
Г. Л Л-1 0,46
£>, = 0Л2 106- , =-i2 ’»
комплексные параметры равны:
-0,701 + 1,72/, р2=-0,701 + 1,72/. .
Для той же фанеры, направляя ось х поперёк волокон
рубашки, получаем:
£\ = 0,119-106g, Z>2 = 1,425 10s g, £>*=--0,12- 10s g,
va = 0,46; ^ = 0,2024-0,4981, ^=-0,202 + 0,4981.
Для фанеры втсфого типа имеем:
£)х = 1,203 • 10s g , Dt = 0,602 106 g, Dk = 0,07 • 10s g ,
vs = 0,036; = 0,745 4- 0,928i, = -0,7454- 0,928i
(ось x параллельна волокнам рубашки), или
D, = 0,602 • 10s g , £>а = 1,203 • 10s • g , ££ = 0,07 • 10s g ,
v, = 0,071; = 0,527 4- 0,6561, p, = - 0,527 + 0,656i
(ось x перпендикулярна к волокнам рубашки),
1> См.
159
2. Гофрированные пластинки. Гофрированную пластин-
ку из изотропного материала, т. е. пластинку, кото-
рой придана волнистость в одном направлении, можно рас-
сматривать приближённо как ортотропную и однородную
(если, конечно, число волн гофра вдоль стороны достаточ-
но велико, или, иначе, дли-
на хорды гофра мала по
сравнению с длиной стороны
пластинки).
Определение жёсткости
гофрированной пластинки,
а также пластинки, усилен-
ной часто поставленными
параллельными рёбрами
жёсткости, сводится к под-
счёту моментов инерции, от-
несённых к единице длины,
для основных сечений [см.
формулы (42.1)].
Рассмотрим гофрирован-
ную пластинку, изображён-
ную на рис. 74. Главными
будут направления образующей гофра и перпендикуляр-
ные к нему (х и у на рис. 74). Полагая, что осевая линия
сечения, гофра есть синусоида
2 = T/siny, (42.2)
введём обозначения: Z — длина хорды одной полуволны,
$ — длина дуги одной полуволны, Л —толщина пластинки,
£*, V —модуль Юнга и коэффициент Пуассона материала.
Приближённые формулы для жёсткостей, по Зейделю, име-
ют вид х):
D =1 . Da = EI, Da = (42.3)
1 s 12 (1 — v2)’ а ’ 3 I 12 (l-J-v) ’ 4 '
где / — средний момент инерции сечения пластинки пло-
скостью xz на единицу длины, равный:
I = 0,5W! [ 1-----1 ' (42Л)
1 1
х) См. работу [?2] или [8], стр. 254.
160
3. Пластинки, усиленные часто поставленными рёбра-
ми жесткости. Для изотропной пластинки, усиленной
с двух сторон параллельными рёбрами жёсткости типа й&о-
бражённой на рис. 75, жёсткости определятся по фор-
мулам:
12'1—v2)
л __ Eh* хЕ^
1 2 ”12(1— v2)+ d 1
(42.5)
где 7 — момент инерции сечения ребра относительно оси,
лежащей в срединной плоскости; Е, v — модуль Юнга и ко-
эффициент Пуассона
материала пластинки;
Е’— модуль Юнга ма-
териала, из которого
изготовлены рёбра; d —
расстояния между рёб-
рами г).
Если
ложены
стороны
моменты инерции сече-
ний нужно вычислять
относительно линии,
проходящей через центр
тяжести сечений, кото-
рый не будет лежать
на срединной плоскости.
Рис. 75.
рёбра распо-
лишь с одной
пластинки, то
Для пластинки, усиленной в двух направлениях вза-
имно перпендикулярными рёбрами, расположенными сим-
метрично по обе стороны срединной плоскости, жёсткости
можно подсчитывать по формулам:
_ Eh* Е'Ц
_ Eh* EVa
2 12(1 —v2)*
D =^hz .
’ 12 (1 —ча) •
(42.6)
x) Рёбра предполагаются одинаковыми и расположенными на
одинаковых расстояниях друг от друга—d,
11 С. Г. Лехницкий
Предполагается, что оси рёбер параллельны главным
направлениям; Е', Е” — модули Юнга материалов, из ко-
торых изготовлены рёбра, параллельные осям у и z; 11У
Ц — моменты инерции сечений этих рёбер относительно
линий, проходящих через центры тяжести сечений и
лежащих, в силу симметрии, в срединных плоскостях;
dx, d2 —расстояния между рёбрами, параллельными оси у
и осиа\
43. Определение жёсткостей многослойных
пластинок.
Для определения жёсткостей многослойной пластинкщ
построенной симметрично из ряда слоёв, можно в первом
приближений использовать формулы для однородной ани-
зотропной пластинки, подставив в них средние по тол-
щине значения упругих постоянные. Но если известны
упругие постоянные для каждого слоя в отдельности, то
можно получить более точные формулы для жёсткостей из-
гиба и кручения, а также для напряжений в каждом слое.
Вопрос этот подробно исследован в нашей работе [22];
здесь мы ограничимся указанием основных выводов для
пластинки, построенной из симметрично расположенных
ортотропных и изотропных слоёв, отсылая интересующихся
к указанной нашей статье.
Пусть имеется многослойная пластинка, построенная
из нечётного числа однородных ортотропных слоёв, рас-
положенных симметрично относительно среднего слоя *).
Именно, к среднему слою с обеих сторон примыкают
два' слоя одинаковой толщины и с одинаковыми упру-
гими свойствами; к внешним поверхностям этих слоёв
примыкают ещё два одинаковых слоя и т. д. Пред-
полагается, что все слои ортотропны, и плоскости упру-
гой симметрии у них взаимно параллельны, причём одна
из плоскостей упругой -симметрии в каждом слое парал-
лельна срединной плоскости слоя и всей пластинки
в целом.
Предполагается, кроме того, что скольжение слоёв
друг по другу невозможно, так как слои склеены или
спаяны друг с другом по поверхностям соприкосновения
и при деформировании работают совместно.
I) В нашей работе [22] рассмотрен также более общий случай,
когда слои не являются ортотропными.
162
Примем срединную плоскость среднего слоя (она же
срединная плоскость всей пластинки) за плоскость ху,
совместим направления осей с главными направлениями
среднего слоя и введём следующие обозначения: 2п + 1 —
число слоёв (крайние слои имеют номера 1 и 2п +1,
средний является пн- 1— т по счёту); h — полная толщина
пластинки; /г2, . .., Лп+1— расстояния от срединной
плоскости до границ слоёв (рис. 76); Е™, Я™, у™, v™, Gm —
Рис -
модули Юнга, коэффициенты Пуассона и модуль сдвига для
слоя с номером т (Е[ = Е\ = Е*\ Е^ — Е^-^ и т. д,;
это касается и прочих постоянных).
Результаты сводятся к следующему.
Пластинка в целом изгибается, как однородная и ор-
тотропная, именно: моменты и перерезы! ающие силы в
ней определяются по тем же формулам (38.14) и (38 Л5),
какие имеют место для однородной ортотропной пластин-
ки, а прогиб срединной плоскости w удовлетворяет урав-
нению (39.3).
Что касается жёсткостей Z>2, Dk и величины, иг-
рающей роль коэффициента Пуассона vx, то они опреде-
11*
163
ляются по формулам;
л = 2[ , V
П1 = 1
л _ 2 г
* з L 1—v;*4£+1
п
1-2
т=1
Л;; = 4[С"+‘Л’+1
п
+ 2Gm (Л’т-^М)
ш=1
>(43.1)
Граничные условия на краю многослойной пластин-
ки не отличаются от условий на краю изотропной пла-
стинки.
Составляющие напряжения уже не будут связаны такими
простыми зависимостями с моментами и перерезывающими
силами, какие имели место в однородной плите [см.
(38.12)]. В многослойной плите для каждого слоя
имеются особые формулы для определения напряже-
ний. Составляющие напряжения в слое номер т опреде-
ляются по формулам:
бу = — Z
„ z
ху
1 — у™у™ ‘ а с*у* )
_Е?
1 — у™у™ ‘ 1 J
dx ду'
тт _ С. ±Г —®. ( Е^” . 2Г"Л — 1
Т«— 2 dz|_ 1 —дхг -Г < 1—//Ч1 “ V J дуг J
д Г <<т I (Гт _L ‘)fm\ 1
- г L1 и + ,б) J
+ — 1-
2 ду [ < 1 —vjb/™ u J дх* 1 —vj»-/® ду2 J
г (О ^гг^^+с-"—1
2 Ну L + ZGe*' + аа <^Уг J
(43.2)
>(43.3)
]
164
Здесь
1 __ -®1 ГЧ______ -®2
11 |------vlvl 5 J----yl-yl ’
C\2
ЕЫ
1 —v’vj
C^G1;
для т > 1:
E?h*n
Cm = — r ---------r- z
° и Л21 i—vF*F
A-=l
m— 1
•Elli
-C'l /> 4
.-□M” l^A
sim __J;
- Д2
rm_l Г E”Wh*
V““A2 11 — v?v?
E?hl V
—r^J
Л=1
m—1
T71 A'
^2_____(Ъ*
Wh
JS7?v3*
l-v*v«
m-1
Г-1
Напряжения в симметричных слоях распределяются
симметрично.
Если пластинка составлена из симметричных изотроп-
ных слоёв, то она изгибается, как изотропная с жёстко-
стью D и с коэффициентом Пуассона v, которые опреде-
лятся по формулам:
п
l_(y» + ip
JE?/n
1__(yWja ^rn+1) J j
2. Г En^n*lhn^ i V E”^m /7,3
V 3D L 1 — (-vll + 1)2 "1~ 2j i_(y>«)aVzm
m=l
(43.5)
Здесь Em, vm —модуль Юнга и коэффициент Пуассона
для слоя с номером т (симметрично расположенные слои
имеют одинаковые модули Юнга и коэффициенты Пуас-
сона). Состаьляющие напряжения в слое с номером т
165
определятся по формулам:
Ет z'дга>
~~ ~~Z 1—(v™)3 V dya ) ’
Е”‘ fdaw . md»2w\
°» — 3 1—(v”*)2 \дуа V дха ) ’
Ет ()*<»
<гП1 - __ , •
ху 1 4- дх ду 9
(43.6)
, / т .2-^Ст ]yV4
1 — (vwt)2 J дх 1
ют -1 а
.21_____h2Cm U-V2w
l-(v^)2 ПЬ J дуУ >
(43 7 )
__
' ~ 1—(V1)2 ’
Г E™h*m
' ~~ ha L i—(v'">*
m-t
+ 2 1 —(V^J5 ~ ] .
Л=1
(43.8)
Пр имер. Пластинка построена из трёх симметричных
по упругим свойствам слоёв постоянной толщины Л/3.
Если слои ортотропны, то жёсткости определятся по
формулам:
п _ JL < * Y < 2бЕ1 . ^‘1
1 12 < 3 ) <1 — 4^2 't"l —v’v» J ’
. =1<AY ( 2бДз
’ 12 V 3 ) <1 — ф} "П—vjv2 J
Dk = Y2(iy ^ + G2).
(43.9)
Эти выражения можно записать в более наглядной фор-
ме, если обозначить через Z)}, D]z жёсткости крайних
слоёв и через DI, Dlf — жёсткости среднего слоя, а
именно:
Z)x-26Z)1 + ^5 )
D^26Di + Dl, I (43.10)
Dk = 2eDl + D^ J
Если все слои изотропны, то
D = 26D1 + D\
v = ^(26Z)V + Z)V),
(43.11)
где Л1, V1 —жёсткость и коэффициент Пуассона крайних
слоёв, Р2, V3 —то же для среднего слоя.
166
44. Определение жёсткостёй для пластинок с модулями
упругости, меняющимися по толщине.
Если пластинка является неоднородной в том смысле,
что модули упругости её меняются по толщине, и притом
симметрично (точкам, симметричным относительно средин-
ной плоскости, отвечают одни и те же значения упругих
постоянных), то в первом приближении можно определить
её жёсткости по формулам (38.16), подставляя, вместо
Е1У Е2, ух, у2 и средние по толщине значения модулей
Юнга, коэффициентов Пуассона и модуля сдвига. Но в этом
случае есть возможность получить более точные резуль-
V2
Рис. 77.
таты. Вопрос об изгибе указанных пластинок подробно
разобран в уже упомянутой нашей работе [22]; ограничимся
здесь лишь важнейшими окончательными результатами для
ортотропной неоднородной пластинки.
Пусть пластинка постоянной толщины h является орто-
тропной, но притом неоднородной: модули её одинаковы
для всех точек на плоскости, параллельной срединной, но
меняются по толщине, и притом симметрично. В каждой
точке имеются три плоскости упругой симметрии, причем
одна из них параллельна срединной плоскости, и в разных
точках соответствующие плоскости упругой симметрии
имеют одно и то же направление. Примем срединную пло-
скость за плоскость ху и, как обычно, совместим направ-
ления осей х и у с главными направлениями упругости
(рис. 77). Обозначим через Ег Е^ vx, v2, G главные модули
упругости и коэффициенты Пуассона. В данном случае эти
величины будут чётными функциями от z\
E1( — z) = E1(z), Et( — z) — Et{z), v, ( — z) = v/(z),
va( — z)=v2(z), (7( —z)=G(z).
Будем считать эти функции заданными. Относительно не-
прерывности этих функций не будем делать никаких пред-
положений; функции могут быть непрорывными, но могут
быть и разрывными.
167
Результаты в основном сводятся к следующему.
Изучаемая неоднородная пластинка изгибается, как од-
нородная ортотропная; моменты и перерезывающие силы
её вычисляются по формулам (38.14) и (38.15), а прогиб
срединной плоскости w определяется из уравнения (39.3).
Жёсткости находятся по формулам:
hfZ
Егг2
1~
dz,
h/2
Рг = 2( — ’ — dz,
О >
(44.1)
Dk = 2 Gz2dz,
о
(vx — величина, соответствующая коэффициенту Пуассона
однородной пластинки).
Составляющие напряжения определяются по формулам:
EjZ / d2w d^w \
1—^2 ~^Va ty2 )
— ViVa ’ 1 dx2 J
d2w
дх dy'
(44.2)
& Гд2и> Г E,z . ,
Тг* <)x Lo1»2 J 1 — vf/g
-h/2
d2» Г Y
~ ^Уг J ^1—v1V
- It/2
> (44.3)
168
В частности, для пластинки неоднородной, но обладаю-
щей свойством изотропии, у которой
Et = El — E(z), vs = v1 = v(2), G(z) = 2^),
получаем такой результат: пластинка изгибается как изо-
тропная, с жёсткостью D и коэффициентом Пуассона у,
которые вычисляются по формулам:
D
у
Л/2
= 2 (
J 1—V2 ’
о
h/2
2 С Svz2 ,
-- Fi \ Л 2* diZ»
D J 1 — v2
О
Составляющие напряжения определятся по формулам:
___ Ez /c*2w . д2ю \
“ 1 — V2 Veto2 ду2 J1
___ Ez ( d2w d2w \
r=^5A<ityr + v ЙГ2')'
__ Ez .
“ i-f-v ctocty’ ,
Z
д -a C Ez ,
Tza = тг- V2cv \ -----r dz,
** 0X JI — v2
-h/2
z
д n2 C Ez *
—tt V w \ ~—r dz.
vz dy J 1—-v2
-h/2
(44.6)
Пример. Имеется пластинка изотропная, но неоднород-
ная; коэффициент Пуассона её v — постоянная величина
для любого места пластинки, а модуль Юнга меняется
по толщине по квадратичному закону:
E = E. + E.z\ (44.7)
Эта пластинка изгибается, как однородная изотропная,
имеющая коэффициент Пуассона, равный у, и жёсткость 7),
вычисляемую по формуле:
я = ^&)(‘ + о.15§0' (44-8)
169
45. Вычисление жёсткостей для произвольных
направлений*
Жёсткости анизотропнойпластинки являются величи-
нами, зависящими от направления выбранных осей коор-
динат; изменяя направление осей координат, т. е. переходя
от одной системы координат х, у, z к другой —а/, у\ zf,
мы изменим и жёсткости Dл. Рассмотрим формулы для
пересчёта жёсткостей при переходе от одной системы коор-
динат к другой (аналогичные формулам, выведенным в § 10
для упругих постоянных).
Пусть в системе координат ж, ?/, z жёсткости пластинки,
вообще неортотропной, равны Z)22, Z>12, Z>66, D10 и T)2e,
а в системе х’, yf, zf, повёрнутой по отношению к первой
на угол 9 вокруг , оси z (рис. 10), жёсткости равны
D'1? Z)'2, Д2, Z>'e, /)'в и Z)'e. Для вывода формул пересчёта
жёсткостей рассмотрим выражение потенциальной энергии
деформации на единицу объёма; если в выражении (38.18)
производные от прогибов заменить составляющими дефор-
мации ех, £у, то получится:
в системе ж, ?/, z:
v = I [ Ал: + + D^v +
+ АЛ+2(А.®Л + А,ев) Тх1Г] , (45.1)
а в системе х\ у\ z*\
V = Is [ 4- 2D»; + Азе; + Dt+
+ 2(Аз<+А.№]- (45.2)
Составляющие деформации гх, ед, ужВ и гх, s;, ^'хУ свя-
заны зависимостями 2):
гх = <соза? +easin’? — sin 9 cos ф, j
eB = e^. sin3 ф 4-GOS2 <p +sin <p cos <p, > (45.3)
Гх» = 2 (< — sin ф cos ф 4- y;b (cos2 ф — sin2 ф). j
*) Эти формулы выводятся в механике сплошной среды.
170
Подставляя эти выражения в (45.1) и сравнивая
с (45.2), получаем искомые формулы преобразования:
= Dix cos* 9 + 2 (°i8 + 2^вб) sin° 9 cos3 9 + >
+ D2i sin* 9 4-2 (Z>le cos'2 9 + D2i sin2 9) sin 2<p,
= sin1 9+2 (Z)12+2Dee) sin2 <p cos3 <p-i-Z>22 cos1 9 —
— 2 (Z>le sin2 tp -|- -O2e cos2 9) sin 29,
/>n = -Dis 4- 1Л1 + Aa — 2 (Ла + 2Z>6J] sin2 9 cos29 4-
+ (A6 —Ae) cos 29 sin 29,
D'e. = + Pn4- ^>22 — 2 (£>n + 2AJ] sin2 9 cos2 9 4-
4- (Z)2e — D16) cos 29 sin 2?,
/>й== у [i>22 sin2 9 —1>11 cos2 9 4-
4" + 2-^ee) cos 29 ] sin2<p+ j
+ Z>16 cos2 9 (cos2 9 — 3 sin2 9) 4-
+ D2e sin2 cp (3 cos2 <p -sin3 cp),
Z>,e = ~ ^Z)a2 cos2 <p — Dtl sin2 <p —
— (Z)12 J-2/)GG) cos sin 2<p f-
4- Z)1(t sin3 9 (3 cos2 <p — sin2 cp) 4-
+ Z>26 cos2 <p (cos2 9 — 3 sin2 <?). >
Рассмотрим также случай ортотропной пластинки. Пусть
направления осей х и у совпадают с главными, а главные
жёсткости равны Z)i? /)2, ^к, &з —
Если требуется перейти к новей системе координат
х', у', повёрнутой на произвольный угол ср, то в этой
новой системе уравнение прогибов будет иметь такой вид:
/>й й + 40й г, Z 4-2 (/>й + 2^й) т-?4-2 4
11 дх 4 ’ 16 дх 3 (Уу 1 \ 12 1 66/ f^x ^oy 2
4-4O;6 - >3- 4- Дй (45.5)
1 28 (Ух ду3 ду 1 \ /
а выражения для моментов и перерезывающих сил полу-
чим в виде (38.9) и (38.10) (куда вместо надо под-
ставить D'ij). Жёсткости изгиба вокруг новых осей —
^22? жёсткость кручения _D'e и приведённый коэффи-
171
циент Пуассона ух — D'lltID'ti определяются по формулам,
вытекающим из (45.4):
D’IX — Dx cos* <p-|-2.D8 sin2 <p cos2 <p + Z>2 sin4 <p, )
D'j = Dx sin4 <p 4- 2D8 sin2 <p cos2 <p + D2 cos4 <p, I
P^^H^x + ^-^sin^cos2?, [ (45.6)
у1 = ^[Л''1 + (Л + Л!--2.Е>1!) sin2 <? cos2 <p].J
Побочные жёсткости Z>'e и D'^ которые исчезают
в главной системе #, z, равны:
£>'в = А (£>2 sin2 <р — Р1 cos3 tp + D3 cos 2<р) sin
1 . (45-7)
T)2e = у (D2 cos2 9 — Dk sm2 <p — D3 cos 2<p) sin 2<p. j
Отметим, что выражения D'j -|-jD'2 + 2Z)'2 и Z>'a — £)'a
сохраняют свою величину в любой системе координат:
2)п + Z)33 + 2/)р2 “Dj + Z>2 4“ 2Z)2v1?
(45.8)
Комплексны? параметры изгиба ux и u2 при переходе
к новым осям преобразуются по формулам, в точности
совпадающим с формулами преобразования комплексных
параметров плоского напряженного состояния [см. (11.8)].
46. Изгиб пластинки, обладающей цилиндрической
анизотропией.
Вводя те же предположения и упрощения, какими поль-
зуются при построении приближённой теории изгиба одно-
родных пластинок (тонких плит), легко построить и
теорию изгиба пластинок, криволинейно-анизотропных
и, в частности, пластинок, обладающих цилиндрической
анизотропией. На этом типе пластинок мы и остановимся
вкратце.
Предположим для простоты, что пластинка с цилинд-
рической анизотропией является одновременно и ортотроп-
ной, причём плоскостями упругой симметрии являются
все радиальные плоскости, проходящие через ось анизо-
тропии g. Полюс анизотропии — точка пересечения оси
анизотропии и срединной плоскости (которая к этой оси
предполагается перпендикулярной) может лежать внутри
172
пластинки или вне её. Как обычно, примем полюс анизо-
тропии за начало цилиндрической системы координат г, 6, z,
ось z направим по оси анизотропии, ось х — полярную
ось—-произвольно в срединной плоскости. В этой система
координат уравнения обобщённого закона Гука будут
иметь вид (4.3).
Порядок вывода уравнений теории изгиба такой же,
как и для однородной пластинки. Пренебрегая запи-
шем три из уравнений обобщённого закона Гука в виде:
®d=^ (33 —> (46Л)
I
G V )
Здесь Er, Ез — модули Юнга для растяжения— сжа-
тия в радиальном направлении г и в тангенциальном
03
направлении 0; vr, v.j — главные коэффициенты Пуассона
(ErVi = E^r)] G — модуль сдвига для направлений г и 8
(главных). На основании «гипотезы прямых нормалей»
получаем выражения для смещений точки в направлениях
г и 9--ur и zzj—-через прогиб срединной поверхности
w (г, 6):
0W 1 //г?
(46.2)
Далее определяем ег, Из уравнений (46.1) нахо-
дим аг, оj, тг9; из уравнений равновесия [см. первое и вто-
рое уравнения (1.3); при отсутствии объёмных сил
R = 0 = 0] находим составляющие тг2 и Напряжения
ar, Gj приведутся к изгибающим моментам Mrl Мнапря-
жение тг3 — к скручивающему моменту Hri и напряжения
тг2, т2—-к перерезывающим силам NT и Лго- Схема распре-
деления напряжений около некоторой точки пластинки
показана на рис. 78 (вверху); схема моментов и перере-
зывающих сил, к которым приводятся напряжения, изо-
бражена на нижней части рис. 78.
Для составляющих напряжения, моментов и перерезы-
вающих сил получаются формулы:
Г2Мг
— Л3 г>
_ 6.vr / А2
— А3 к 4
п Г I /1^.1 I
Л/г — дг2 + Vo р dr + Г2 дда J J »
Al j “ -Jj§ у ---1---1---- I
L т dr2 г 7,2 ^0 J
»-=»«=
(46.3)
(46.4)
(46.5)
174
Здесь Dr, Da — жёсткости изгиба вокруг осей 0 и г, про-
ведённых через данную точку; Dk—жёсткость кручения;
D Erh*........ I
r 12Ц-^у) ’ |
D -
’ - 12 •
Z)r3 = Z>rvj + 2Z>A,
Е Ji3
г\ __ ______i______
42 (1 —vrva)
(46.6)
Прогиб w определяется из уравнения г):
n । on 1 , п 1 । on 1 on 1
1 d2w . п/гч I гл ч 1 <^w , гл 1 ( Гч //а
’”Ay2^- + 2(Po4-Prj)rT5jjr+^J73—= 0. (г> 6)> (46./)
где #—интенсивность нормальной нагрузки, распределён-
ной по внешней поверхности.
В случае изотропного материала
Eh&
ВГ~ВЬ — ~D — 12 (i—^2) ’
Уравнение (46.7) принимает вид:
DTTw = q(r, 6),
(46.8)
где д2 —оператор Лапласа в полярных координатах:
V2 — — _±_ J ф 1 £
dr2 * г2 <?0а ~ г дг '
ГЛАВА IX.
ИЗГИБ ПЛАСТИНОК НОРМАЛЬНОЙ НАГРУЗКОЙ.
47. Простейшие случаи изгиба»
В этой главе мы рассмотрим ряд конкретных задач
об изгибе однородной, а также криволинейно-анизотроп-
ной прямоугольной пластинки, полосы, эллиптической
и круглей пластинки.
Это уравнение получается из условия равновесия элемента
пластинки, аналогичного элементу, изображённому на рис. 71,
только в цилиндрических координатах.
175
Простейшими случаями изгиба однородной пластинки
являются: 1) чистый изгиб, 2) чистое кручение, 3) изгиб
по цилиндрической поверхности. Прогибы, моменты, пере-
резывающие силы и напряжения в этих случаях нахо^
дятся элементарным путём, и мы приводим формулы без
вывода. Во всех случаях мы полагаем, что пластинка
однородна, но не ортотропна, так что уравнение прогиба,
отнесённое к выбранным осям х и у, имеет вид (39.2),
а выражения для моментов и перерезывающих сил —(38.9)
и (38.10).
1. Чистый изгиб. Прямоугольная пластинка изгибается
моментами Мг (на единицу длины), распределёнными рав-
номерно по двум сторонам, и моментами (на единицу
Рис. 79.
длины), равномерно распределёнными по двум остальным
сторонам.
Обозначая длины сторон черев а и Ь и направляя осп
вдоль сторон (рис. 79), получим:
МХ = М^ Му-М^ = (47.1)
W = 4- Вху 4- Су* 4- ctx4- Cty 4- Са, (47.2)
где А, В, С —постоянные, определяемые из уравнений:
AD^ + BD^ + CD^ -4' ’ I
ADlt + BDie + CDtt=-^, <47-3)
ADlt±BDtt + CDtt = 0-, )
a Cv Ci > "-постоянные, которые найдутся из условий за-
176
крепления. Например, для пластинки, закреплённой в трёх
углах (0, 0), (а, 0), (0, fe):
w = А {х* — ах) -р Вху + С{у*-~ by). {VIA)
Другой случай чистого изгиба —изгиб пластинки про-
извольной формы моментами М (на единицу длины),
2
Рис. 80:
распределёнными равномерно по всему краю (рис. 80).
В этом случае для любого элемента с нормалью п
Мп = М, Nn = Q (47.5)
2. Чистое кручение. Прямоугольная пластинка дефор-
мируется крутящими моментами Н (на единицу длины),
распределёнными равномерно по всем сторонам (рис. 81).
В этом случае
Мх = М„ = 0, НХ„~Н, ДГЖ = ДГВ = О. (47.6)
42 с. Г. Лехнлцнпй
177
Прогиб w имеет вид (47.2), но постоянные А, В, С опре-
деляются из уравнений:
ЛРи4-£7)1в + СЛ12 = 0, 1
— 0, j. у)
AD„+BD„ + CDtt^-~. J
Другой вариант чистого кручения — деформация пла-
стинки, опёртой по двум противоположным углам, силами
Рис. 83.
2Н, приложенными к свободным углам (рис. 82). Для
этого варианта справедливы те же формулы (47,6),
(47.7), (47.2).
3. Изгиб по цилиндрической поверхности. Пластинка
в виде длинного прямоугольника однородно закреплена по
длинным сторонам, произвольно закреплена по коротким
сторонам и деформируется нагрузкой, не меняющейся
вдоль длинных сторон.
В этом случае в мес-
тах, удалённых от ко-
ротких сторон, изогну-
тая поверхность плас-
тинки будет близка к ци-
линдрической; поверх-
ность будет строго ци-
линдрической для пла-
стинки бесконечной
длины.
длинной стороне вдали
ось х вдоль длинной
стороны (рис. 83), мы можем считать прогиб w — w(y)
функцией только у.
178
Помещая начало координат на
от коротких сторон и к направляя
Тогда
Мх^ — Му = — D22w\ Uxv~ — D2*w’f,
Nx~ D2q^ , Ny= -D22w
Прогиб определится из уравнения:
D^=q(y). (47.9)
Это уравнение совпадает с уравнением прогиба балки
с жёсткостью/>22, изгибаемой произвольной нормальной на-
грузкой величины Му и Ny определятся как изгибающий
момент и перерезывающая сила в этой балке. Закрепление
концов балки должно соответствовать закреплению длин-
ных сторон пластинки. Таким образом, задача об изгибе
пластинки по цилиндрической поверхности сводится к за-
даче об изгибе балки, решаемой элементарной теорией
изгиба. Лишние силовые факторы — МХУ Н2У и Nx, кото-
рых в балке нет, легко определятся по найденному про-
гибу. Для ортотропной пластинки, у которой главные
направления параллельны сторонам, НхУ == Nx ~ 0.
(47.8)
48. Изгиб ортотропной прямоугольной пластинки
с опёртыми сторонами.
Прямоугольная ортотропная пластинка, у которой глав-
ные направления параллельны направлениям сторон,
опёрта (шарнирно закрепле-
на) по всем четырём сторо-
нам и изгибается нормаль-
ной нагрузкой, распределён-
ной по произвольному за-
кону.
Направим оси х и у вдоль
сторон (рис. 84) и обозна-
чим через а, Ъ длины сторон
пластинки и л —их отноше-
ние: с = а/6. Уравнение
Рис. 84.
будет (39.3); его надо
прогибов
проинтегрировать, учитывая граничные условия;
при х — 0, х = a w = Мх = 0;
при у " 0, у = b Му = 0.
(48.1)
12*
179
Все эти условия будут удовлетворены, если восполь-
зоваться решением уравнения (39.3) в виде ряда
СО со
V^ Vi л • tmzx . ппу
W = 2j Лпп8*П-а- 81И-^.
n=l
(48.2)
Для определения коэффициентов Атп разложим функ-
цию q (х, у) в двойной ряд Фурье '):
00 со
? = 2 2a^sm—81ПУ’
т=1 П = 1
(48.3)
где
а Ь
4 Г Г . тпх . ппу 7 _ /го /\
«тп = аЬ} \ ? В1П — 81П dx dy. (48.4)
0 0
Подставляя выражения (48.2) и (48.3) в уравнение
(39.3) и сравнивая коэффициенты при одинаковых синусах
в левой и правой частях, получаем выражение для прогиба:
т = 1
(48.5)
Это решение аналогично решению Навье для изотроп-
ной пластинки * 2):
W — —.
. ттзх . пт/
sin-----sin
(48.6)
(D — жёсткость изотропной пластинки). В выражение (48.5)
нужно подставить значения коэффициентов ат1, которые
зависят от закона распределения нагрузки. Так, для слу-
х) Представление функции д (я, у) в виде ряда Фурье возможно
в случае, когда эта функция удовлетворяет условиям Дирихле (как
в отношении переменной х, так и в отношении у). Практически
всякую нагрузку, сплошную или заданную в виде сосредоточенных
сил, можно представить двойным рядом Фурье.
2) См. [44], § 54, или стр. 137—139.
180
(48.7)
чая нагрузки, распределённой равномерно по всей пло-
щади, получаем:
«тп=5г • дан т, п» 1,3,5,...
атп — О ДЛЙ всех прочих т, п
(р — нагрузка на единицу площади).
Для сосредоточенной силы Р, приложенной в точке (?, ?]):
S (48.8)
7п=1, 2, 3, ..и=1, 2, 3, •..
Моменты и перерезывающие силы определятся по фор-
мулам (38.14) — (38.15) и также представятся в виде двой-
ных рядов.
Решение в форме двойных рядов представляет теорети-
ческий интерес, но неудобно для применения на практике.
Хотя ряды, через которые выражаются прогиб, моменты
И перерезывающие силы, практически всегда сходятся, но
сходятся довольно медленно; для вычислений приходится
брать много членов рядов. Поэтому в тех случаях, когда
Можно обойтись без двой-
ных рядов, предпочитают
иметь дело с решениями
в форме простых рядов,
Сходимость которых гораз-
до лучше (об этих реше-
ниях будет сказано ни*
же).
Если по сторонам плас-
тинки, изгибаемой произ-
вольной нагрузкой q (48.3),
распределены равномерно
нормальные силы рг и р2 (рис. 85), то вместо уравнения
(30.3) будем иметь уравнение вида (40.7), где надо положить
Тх — Ри Ту = р2, Sxy = 0.
И в этом случае прогиб легко определяется в виде ряда;
4V =
X
. mnx . nnv
sin----sin—~-
a b
+
(48.9)
2n’
184
Если усилия растягивающие, то > 0 и р*> 0;
знаменатели всех членов ряда положительны и боль-
ше соответствующих знаменателей ряда (48.5). Отсюда
ясно, что добавление растягивающих усилий, распреде-
лённых по сторонам, уменьшает прогиб; пластинка ста-
новится как бы более жёсткой. Если усилия сжимающие,
то Pi <0, < 0, и знаменатели выражения (48.9) бу-
дут представлять собой разности положительных величин.
Добавление сжимающих усилий увеличивает прогиб или,
иначе, уменьшает жёсткость пластинки. При сжи-
мающих усилиях возможны и такие случаи, когда
один или несколько знаменателей выражения (48.9) обра-
щается в нуль, и прогиб под действием нагрузки q,
вследствие этого, становится теоретически бесконечно
большим. Это означает, что пластинка, сжатая одни-
ми усилиями рх и р2? находится в неустойчивом равно-
весии.
Вопросы устойчивости пластинки подробно исследуются
в главах XII-XV.
49. Изгиб ортотропной прямоугольной пластинки с двумя
опёртыми сторонами.
Прямоугольная ортотропная пластинка, у которой две
противоположные стороны опёрты, а две другие как угодно
закреплены, изгибается
нормальной нагрузкой qr
Мы рассмотрим случай,
когда нагрузка не меня-
ется вдоль опёртых сто-
рон. Более общий случай
будет разобран в § 52.
Для указанной пластинки
можно получить решение
в виде простых рядов, ко-
торое является обобщени-
ем известного решения Мориса Леви на случай ортотроп-
ной пластинки 1).
Поместим начало координат в середине опёртой стороны
и направим ось х вдоль опёртой стороны, а ось у—пер-
пендикулярно к ней (рис. 86, а).
Решение для изотропной пластинки см. в [44], § 55, стр. 292-
298, или [®], стр. 139—142.
182
Уравнение прогибов будет иметь вид:
^S+2^J^+^==^), (*9Л>
где q (у) — заданная функция. Функция w, определяемая
из этого уравнения, должна удовлетворять условиям на
опёртых сторонах (при у = 0, у ~ Ь):
дга> , дги> „ ;>п п\
W ~ ду* + V1 дх* ~~ ® (49*2)
и четырём условиям на прочих сторонах. Будем искать
решение в виде суммы:
«* = «,»(У) + (ж, у). (49.3)
Здесь iv0 (у) —функция, удовлетворяющая уравнению
Dtw^ = q (у) (4QA)
и условиям
(0) = < (0) = we (Ь) = < (&) = 0; (49.5)
это —прогиб балки о жёсткостью, равной Dt) длиной 6,
опёртой своими концами и нагружённой нагрузкой q
(рис. 86, Ь). Функция удовлетворяет однородному урав-
нению
Л + 2Р.л4тг5 + = 0, (49.6)
1 дх* * и ду* 7 ' '
условиям (49.2) и подбирается так, чтобы иметь возмож-
ность удовлетворить условиям на сторонах Х“±а/2.
Функцию яр0 для многих случаев нагрузки можно опре-
делить в конечном виде методами теории сопротивления
материалов, но для того, чтобы удовлетворить условиям на
сторонах х = необходимо представить её в виде ряда
Фурье, расположенного по синусам. Этот ряд будет иметь
вид:
w» = о S 8in П-Т- > (49.7)
• Р2тг п* Ъ 7 v '
л*= 1
где
ап = у 9 Sin r^- dy (49.8)
о
183
— коэффициенты разложения в ряд Фурье функции q (у),
представляющей закон распределения нагрузки. Функцию
разыскиваем В виде ряда:
СО
(49-9>
Полный прогиб (V —+ будет удовлетворять усло-
виям на опёртых сторонах, и нам останется удовлетворить
условиям лишь на сторонах х — ± а/2, что всегда возможно.
Для функции Хп получается уравнение:
(™уХп=о. (49.10)
Вид функции Хп зависит от корней характеристиче-
ского уравнения *):
- 2D3sz + D2 ^0. (49.11)
В зависимости от соотношения между величинами жёст-
костей пластинки, возможны три случая:
Случай I. Корни уравнения (49.11) вещественные >
неравные*.
± ± ($i >0? 0).
Случай IL Корни уравнения (49.11) вещественные t
равные попарно:
± $ (* > 0).
Случай IIL Корни уравнения (4941) комплексные:
s i ti, —s -l~ ti.
В случае I:
Xn = An ch ^4- £nsh 4 Cn ch »4-Dn sh™ .(49.12)
В случае II:
Xn = (Л 4- Bn x) ch 4- (Cn 4- Da x) sh . (49.13)
x} Корни этого уравнения связаны с комплексными параметрами
< *
изгиба Hi, На вависимостями ^®= —, $а = — .
184
В случае Шг
„ / . nntx . „ . nntx'X , »wsx
Xn = (An cos-y +Bnsm -y J ch -y +
MtX t yx . 7l7Ctz\ тПШ ,Zrt ,,x
Cn COB -y + Dn sin -y J sh -y , (49.14)
где Лп, Bn, Cn, ^ — произвольные постоянные.
Таким образом, получаем.
В случае I:
w = Vf^L + Anchn-^+Bnsh^ +
VPjTc4»4 * л Ъ * п о 1
Л = 1
+ sin W . (49.15)
В случае II:
«-2[^+14.+в.»)Л^+
п-1
+ (Сп + Dn х) sh ] sin . (49.16)
В случае III:
СО
V4 Г аП^Л I / л nntLr: I п • nnt%\ 1 nnsx .
w=2 И"008 —+Bn8m ~ь~)ch -г+
n— 1
, f nntx . r. . n7ii#\ . /iTcsz'l . nity . 7V
+ (J7n cos + Dn sin — ) Sh J sin ~ . (49.17)
Множитель при каждом синусе содержит четыре произ-
вольных постоянных и столько же мы имеем условий на
сторонах х = ± а/2; этим условиям мы можем удовлетворить
при любом их закреплении.
В дальнейшем нет необходимости подробно анализиро-
вать все три случая —I, II, III. Достаточно рассмотреть
случай I; решения для остальных случаёв определят-
ся путём предельного перехода при $х = $а = $, либо пу-
тём отделения вещественной части комплексного выра-
жения, которое получается, если положить Щ
— s — ti.
185.
В случае четырёх опёртых сторон получаем:
со
«’ = «'. X
•br27t ft *2 J
П«=1
(' „ , птад.ж e , nitsa \
s? ch —J— sjch ? -\
л b 1 b | . птиу
--------------------8in .
, nns,c , П7г$,е / b
ch -Г" ch ~T~ /
Для пластинки, у которой стороны х = ± а/2 заделаны:
«• = «'. W+zgrSsx
n-i
Sa 8h те ch _ Sl sh ch
X-------------------------------— sin^ . (49.19)
_ nnS'C , nns9c . птс$9с , mrs.c b 4 '
SiSh --^ch-y^ — ^sh -—-ch-j2-
Зная выражение для прогибов, по формулам (38.14)
и (38.15) определим моменты и перерезывающие силы,
а по ним и напряжения.
Ряды типа (49.18) значительно удобнее для вычисления,
чем двойные ряды предыдущего параграфа; члены их обычно
быстро убывают, и для вычисления прогибов и напряже-
ний в данных точках, с достаточной для практики точно-
стью, можно ограничиться лишь небольшим числом членов
ряда.
50. Изгиб прямоугольной ортотропной пластинки
равномерно распределённой нагрузкой.
Если нагрузка q распределена по пластинке, рассмо-
тренной в предыдущем пара-
графе, равномерно (рис. 87),
то
W’« = 24k +
2 (50.1)
‘ Яп = ^ для п=1, 3, 5,...,
61 " {0 * га = 2, 4, 6, ...
(50.2)
Ряды (49.18) и (49.19) будут содержать только члены
с нечётными п.
186
Рассмотрим более подробно два случая;
1. Пластинка с четырьмя опёртыми сторонами. Скру-
чивающий момент и перерезывающие силы определятся
по формулам (38.14) и (38.15). Для прогиба и изгибаю-
щих моментов получаем следующие формулы:
4сьп-^\
1( *---Ь-_------А_ sin^
\ ch —~ ch —]
(50.3)
47b2 DL 1
* ~3 Z>a s2—sf
. nny
sm/,
Ch n™3-'
SJ(v $») ------
i \ a a/ nns^c
ch — J
(50.4)
Мд=~1(уг-Ьу) +
47 &2 1_____
7t3 s\ — si
л==1,3, 5,..
£
n3
chre^
s« (1 _y1SJ) ---b—
ch —A-
b
s’ (1 ~ visa)
14 . Тт$2с
oh —
. nw
sin
О
Наибольший прогиб и наибольшие изгибающие момен-
ты получаются в центре и могут быть представлены таким
образом:
И'шах = 384 2)^ (50.5)
(J/Jmax = Г, (Мв)Юлх = ?. (50.6)
187
«, Р' и р представляют собой поправочные коэффициен-
ты, учитывающие влияние боковых стороп х ~ ±п/2. При
больших отношениях сторон c^ajb эти коэффициенты
можно принять следующими: а~1, p' = vn р = 1, и тогда
мы будем иметь дело с изгибом по цилиндрический по-
верхности.
Как определяются а, Р', р для конечных отношений с в
случае I, ясно ив формул (50.3) — (50.4). Мы приведём
значения коэффициентов для случая III, имеющего наи-
больший практический интерес, так как комплексные корни
уравнения (49.11) получаются для фанеры первого и вто-
рого типов.
1,004 V, (— 1) 2
st
3,5,...
X £ 2s/ ch cos
0, , 1,032
₽=vi + -7f- 1
п-1,3, 5,
.2Х 1 zitcsc . nntc
Hsh-y-sin-^-
(-1) 2 „
п’$п Х
[/St й । 1 TlltSC * H/TZtC
(s! -Н — v»s + V ) sh -у- Sin —j—
n= 1,3, 5,.
o . nnsc птЛс 1
— 2v2 st ch -2- cos,—g-
n-1
П’йп X
(50.7)
(vxs’ 4- Vx/‘ — 8 + / ) sh -g- sin —---
— 2 st ch -y cos -y- J
Sn — chzmsc + cos nntc.
Эти ряды имеют хорошую сходимость (по крайней ме-
ре, для пластинок из таких материалов, как фанера пер-
вого и второго типов); члены их быстро убывают, и для
вычисления моментов, с достаточной для практики точно-
стью, можно взять 2 — 3 члена ряда, а при вычисле-
нии прогибов можно ограничиться даже одним первым
членом.
188
Формулы для случая П получим из вышеприведённых,
путём предельного перехода, полагая t=0.
Изгиб пластинки с четырьмя опёртыми сторожами под
действием равномерно распределённой нагрузки был деталь-
но изучен Губером для случая, когда жёсткости удов-
летворяют условию: Dt = DtDt (случай II). Губер даёт
таблицы для вычисления «наибольшего прогиба tvmax> наи-
больших моментов (Л/^тах, (ЛГу)тах, а также и других ве-
личин, представляющих интерес для расчёта на прочность,
цак-то: 1) наибольших перерезывающих сил (TVJmax, (Л^шах,
которые получаются в серединах сторон; 2) наибольших
значений опорных реакций (Bjmax, (Rt)max, получающихся
в тех же местах; 3) полного давления пластинки на
опоры ±а/2 и 7Г. на опоры у = 0, у = b; i) реакций R
в углах пластинки. Все эти величины рассматриваются
как функции отношения
8 =
Dt
О,
(«>*);
(50.8)
они определяются по формулам:
(50.9)
(50.10)
(в середине пластинки х = 0, у — Ь/2)-
(AQmax— [Р-111 + Н1М + |
(^i)max = [ Pin + P122 (v, + J
(50.11)
(в точках £=±«/2, т. e. в серединах сторон 6);
£ Р'заз 4 Hii2 (^vi+|
(^г)тах ~ £ Paas 4" P'na 4" j/^p^ j
189
(в точках x = Q, у = 0 и х — 0., у — Ь, т. е. в серединах
сторон а);
К** ГHiq-r ’ )
^1— [Имя + Рщ ]
(50.14$
Приводим таблвду Губера для, коэффициентов
|л,а, ... , Нц в зависимости от отношений е1).
Таблица а.
Значения коэффициентов из формул (50.9)—(50.14)
• I * i J Ни Р-22 Р-111 Р122 р.222 Р-112 J p-’lll Р-'122 Ц’222 Р-’из Р-*12
1 0,00407 0,0368 0,0368 0,219 0,119 0,219 0,119 0,157 0,093 0,157 0,093 0,9466
1,5 0,00772 0,0280 0,0728 0,199 0,164 0,335 0,089 0,145 0,122 0,241 0,081 0,0611
2 ^01018 0,0174 0,0964 0,189 0,181 0,410 0,055 т 0,138 0,133 0,299 0,066 0,0663
2,6 0,01150 0,0099 0,1100 0,188 0,183 0,453 । 0,031J 0,137 1 0,134 0,338 0,054 0,0670
8 0,01213 0,0055 0,1172 0,187 0,185 0,476 0,017 С,136 ОД?5 0,865 0,045 0,Сб75
5 .0,01297 0,0004 0,Г45 0,186 0,186 0,499 0,U01 0,136 0,136 0,419 0,027 О,С679
со 0,01302 0,0000 0,1251 0,186 0,186 0,500 0,000 0,136 ,136 0,500 0,000 0,0679
2. Пластинка с двумя опёртыми и двумя заделанными
сторонами. Прогиб и изгибающие моменты определяются
по формулам:
w=WD^~2bya+b^
4#* у _2_
' Zi п»Дп Х
п=1,?, 6Д..
(. П735йс . НГЯуХ . nr.S.C ^riKS«X\ . пку /ел ,гх
Mh—гр- ch—~--sjsh—ch—] sin—— ; (50.15)
х) См. [м], стр. 74—75. Коэффициенты рп, р22, р'13 представляют
собой значения вторых производных от прогиба, коэффициенты с тре-
мя индексами пропорциональны значениям третьих производных.
Таблица приводится в сокращённом виде.
190
Mx = %(by-y'} +
4?Ьа D. v _1 Гл, . о-Ло ок пта»с „к n*«i*
*^• 2), 2d n’A„L( a sJSi.Sh-y-СИ-j--
n-=i,3,5,...
-(y.-^s.sh^ch^jsm^, (50.16>
мв~{-(Ьу-уг) +
1 n4J(l-y^S1^ch^
п «=1,3,5,...
-(l-M^sh^nh^-'] sin = ;
* , п7С51с л nits<,c , wksaC v rmStC
An = s1sh—ch -y^ — s,sh —f- ch—.
Наибольший прогиб получится, естественно, в центре;
представим его в виде:
^max — 3847j* а-
(50.17)
Что касается изгибающих моментов, то наибольшие их
значения в изотропной пластинке получаются на середи-
нах заделанных сторон; в случае ортотропной пластинки
не исключена возможность, что наибольших величин изги-
бающие моменты достигнут в центре» Обозначая через Мх^
М9й изгибающие моменты в центре и через Л/аЬ, М9Ь
изгибающие моменты в середине заделанной стороны, пред-
ставим эти величины формулами:
^«0 = ^', Л/В0 = ^Р,
(50.181
При больших отношениях c = a[b'.
a^l, fL' = vu ₽ = 1, =
191
Мы ограничимся указанием формул для коэффици-
ентов а, Р, К и только для случая III:
ет п-1 )
«-4-2,008 J Цй7~х
П“1, 8,5,...
С. nrcsc . nntc , . , nnsc птисЛ
SCh—2-sxn24-ish-^-C°8— J,
?'-.,-2,0в4й 2
п»1,Г, 5,...
Г . я .1ч , ТфЗО . nntc .
х ^(v, — s’—г’)sch-~-ein——h
i / । 9 i л I n^tsc Tiictc "1
+ (v. + S +12) t Sh —2- 60S — J ,
П—1
CO -g-
₽ -1-2,064 2
n-1,3, 5,...
rz. a .24 , ixnsc . nntc ,
X 1 (l — v^8 —v/2)sch^-sin—+
4- (1 + v1s> + v^*) t sh cos — J ,
(50.19)
Pi = 1,032 i/^l v
v D» п»Дп X
n—1, 8, 5,...
X (t sh nnsc — s sin nntc),
___ ю n-1
P1-1,032., /a 2
л«»1.8,5,..Л
X (fshntcsc—sinnwZc),
Дл = t sh nizsc + 5 sin’nTrfc.
Члены рядов, входящих в формулы (50.19), в случае
пластинок из фанеры первого и второго типов убывают
довольно быстро, а поэтому при вычислении, с достаточной
для практики точностью, можно ограничиться небольшим
числом членов1).
*) При малых отношениях с Сходимость рядов ухудшается.
192
51. Изгиб полосы с опёртыми сторонами;
Значительный практический интерес представляет за-
дача об изгибе длинной прямоугольной ортотропной пла-
стинки с опёртыми сторонами, под действием нагрузки,
распределённой по ограниченной части её поверхности
(в теории такая пластинка рассматривается, как беско-
нечная полоса с опёртыми сторонами). Эта задача в об-
щем видё и для многочисленных частных случаев была ре-
шена М. Т. Губером. Мы приводим здесь основные резуль-
таты Губера, не останавливаясь на детальном их обосно-
вании и изложении1).
1. Полоса, нагруженная вдоль отрезка прямой. Беско-
нечная полоса шириной Ъ с опёртыми сторонами* подвер-
гается действию йагрувки, pac^
нределённой произвольно по
отрезку прямой, перпендику-
лярной к сторонам. Предпола-
гается, что главные направле-
ния упругости параллельны и
перпендикулярны к направле- |2
ниям сторон. Направляя ось Рис 88
х вдоль стороны? а ось у по и • .
загруженному отрезку» как на
рис. 8Й, равЛОжим заданную нагрузку #'(^) (на единицу
длины) в ряд Фурье; получим:
01.1)
Выражения для прогибов будут зависеть от корней
характеристического уравнения (4u.il) и могут быть запи-
саны следующим образом для положительных х (т. е. для
частей пластинки по правую сторону загруженного отрезка):
в случае I (см. § 49):
1
фр —_________ .
Зя3 *1
(51.2)
х) См. [в®], § 5, стр. 38 — 56.
13 С. Г. Лехякцкий
1<>3
в случае 41;
Й1П ;
ь
(51.3)
й. в случае III:
&8 х
W ~~ 4 г.»
со mwc_
х? «Н / 1 ПТЛХ , 1 . n7tt-c\ к . ПТ.11
x2n’(7cosT+7sin“Tje sin7 • (51-4>
л=1
Вираже нйя 'для ПрбНйба по левую сторону от загружен-
ного отрезка получим, заменяя — х На х1).
В каждом данном частном случае необходимо найти
коэффициенты разложения в ряд Фурье ап и подставить
их в формулы (51.2) — (51.4). Зная, как выражается
прогиб, найдём изгибающий
и скручивающий моменты
и перерезывающие силы по
формулам (38.14) — (38.15),
а по ним и напряжения.
Заметим, что формулы
для случаев II и III полу-
чаются из формул bi (51.2)
путём предельного перехо-
Рис. 89.
да; в дальнейшем мы ограничимся указанием лишь вы-
ражения для прогиба, соответствующего случаю 1.
Если нагрузка qf распределена равномерно по участку
оси у длиной Ьи середина которого находится на расстоя-
нии 71 от начала координат (рис. 89), то
4(7 ' . П7Г&1 . nrvn
ап=^-^~ 81П Sin .,
п пп 2b Ь
<51.5)
2g'&8 1
LV - ------ . --- V
*1—*t
х 2^8in"sr8in"'F(Sie 6 — s2e b ')sin^F
n=l
(для x > 0).
J) См. [ea], стр. 40.
194
В частности, если пластинка загружена нагрузкой
q*, распределённой равномерно со вйёй ширине {b^b,
т) -±а fe/2 — рис. 90), то для частей по правую сторону от на-
груженного отрезка получаем:
si-s»
°° Z' _ птс$1Х
X ’S b ~~s*e ъ (51.7)
1,3,5—
Исследование этого .случая приводит к следующим
результатам
Наибольший прогиб получается в.точкел соответствую-
щей середине загруженного участка — я = 0, у = 6/2 —
Рис. 90.
и определяется по формуле (независимо от того, какой слу-
чай корней имеет место):
9'&3
0,989
(51.8)
Наибольшие изгибающие моменты получаются в той же
точке:
(^ х)шах
(Л/Р)тнх = 0,0929
(51.9)
*) См. [ва], стр. 44 и 49.
13*
195
Если загружен не весь отрезок 6, а только часть его,
длиной (с центром в точке х~0, gr=<fe/2)> то наи-
большие моменты определяются по формулам, кото-
рые отличаются от (51.9) лишь численным коэффициен-
том, стоящим после знака равенства. Коэффициент полу-
чается больше чем 0,0929 и зависит от отношения bjb;
чем меньше это отношение, тем больше коэффициент, или,
иначе, тем больше концентрация напряжений. Так, по
Губеру, при отношениях
2. Полосу наг/у&сен~
нйя си-
Лдй (grid* 91). Сосредото-
ченную силу можно рас-
сматривать, как предель-
ный случай нагрузки,
имеющей конечную равно-
't z
Рис. 91.
действующую и распределённой по бесконечно малому отрез-
ку. Обозначая через Р величину силы, полагая q’b^ — P, и
переходя к пределу при — получим из (51.6) формулу
для прогиба по правую сторону от точки приложения силы:
P&s _J_
со — nrzs »х - птсэдх
х SisinVL(S1<? Ь Ъ Jsinnr- (51Л°)
Прогиб быстро убывает по мере удаления от точки при-
ложения силы. Губер указывает, что прогиб на практике
можно считать равным нулю уже на конечном расстоянии
от точки приложения сил&
(51.11)
где Ьир —приведённая ширина— определяется, по Губеру,
следующим образом:
в случае I:
(51.12)
1%
в- случае II:
в случае III:
(51.13)
(51.14)
Если сила приложена на одинаковом расстоянии от сто-
рон (г}= £/2), то прогиб под силой равен1):
- 0,01696 — - ,....' .. = . (61.15)
г 2D/ 2 V D2
От сосредоточенной силы легко перейти к нагрузкеk рас-
пределённой по площади любой фигуры S в плоскости
полосы. Решение получится на основе решения (51.10)
путём суммирования прогибов, вызванных бесконечно малы-
ми силами, и выводится следующим образом. Пусть
у\ 7]) —прогиб в точке (я, у) от сосредоточенной силы,
пряложёйяой в точке (0, т}); тогда Прогйб в точке (х, у)
от силы, приложенной в точке ($, tj), представится функ-
цией Р<?(х— у; т|). Если на пластинку действует нагрузка
Р{х^у}ч распределённая по некоторой площади 5, то на-
грузку р (5? т|) d? сЬ], приходящуюся *на элемент площади
можно рассматривать, как сосредоточенную силу;
прогиб от этой силы в точке (я, у) будет равен:
Р (2, *)) ? (х — с> У, ч) d? di].
Прогиб? вызванный всей нагрузкой, получим, интегрируя
предыдущее выражение по площади 5:
w = 55 р & ?
(51.16)
»> У, ifid'dii.
Некоторые случаи распределённой нагрузки были
детально изучены Губером; в частности, исследован случай
нагрузки, распределённой равномерно по площади прямо-
угольника 2).
>) См. [в2], стр. 42 — 45.
2) См. Г2], стр. 55.
197
52. Приложения теории изгиба ортотропной полосы.
С помощью решения для ортотропной полосы, изгибае-
мой заданной нормальной нагрузкой, можно получить реше-
ние задачи об изгибе прямоугольной ортотропной пластинки
с двумя, тремя и четырьмя опёртыми сторонами, под дей-
ствием произвольной нагрузки (в § 49 — 50 мы рассматри-
вали только нагрузку, которая не меняется вдоль опёртых
сторон). Это решение получается следующим образом *).
Желая определить прогиб, моменты и перерезывающие силы
в пластинке длиной а и шириной 6, у которой стороны
а опёрты, рассматриваем вспомогательную фиктивную пла-
стинку в виде бесконечной полосы той же ширины
b с опёртыми сторонами. Прямыми, перйендикулярными
к сторонам, мы разбиваем полосу на ряд одинаковых прямо-
угольных полей длины а, равных по площади исследуемой
пластинке, а затем загружаем эти поля нагрузками, свя-
занными определённым образом с той, которая действует
на пластинку. Распределяя по полям нагрузку различным
образом, как будет указано ниже, можно создать на гра-
ницах полей те же условия, какие имеют место на сторонах
исследуемой пластинки.
Решение задачи для полосы, нагруженной произволь-
ной нагрузкой, известно [оно получается из решения для
случая сосредоточенной силы, — см. формулу (51.16)],
а поэтому и решение для прямоугольной пластинки можно
найти в любом случае распределения нагрузки. Задача
сводится к суммированию прогибов полосы, вызванных
периодически повторяющейся нагрузкой, а с математической
стороны это сводится к суммированию рядов вида
2 что легко выполняется. Рассмотрим три основ-
п
ных случая закрепления сторон прямоугольной пластинки,
изгибаемой заданной нагрузкой.
1, Две стороны опёрты, две заделаны. На сторонах
пластинки длиной Ь должны выполняться условия:
и’=0’ 2=°- (52Л>
Рассматривая вспомогательную полосу, разбитую на
поля, соответствующие данной пластинке, распределим
нагрузку следующим образом: одно из полей, которое
мы будем считать первым, нагрузим усилиями q (теми,
!) См. [в8Ь стр. 56-58.
198
которые действуют ца исследуемую пластинку); соседнее,
второе, поле нагрузим усилиями распределёнными сим-
метрично с усилиями q по отношению к линии раздела
полей; третье поле нагрузим опять усилиями q\ четвёр-
тое—усилиями ит. д., как показано на рис. 92. Под
Рис- 92.
действием этих усилий полоса прогнется, и сечение изо-
гнутой поверхности будет иметь вид, как на нижнем рис. 92;
в силу симметрии на линиях раздела полей будет выпол-
нено второе условие (52.1). Далее распределим по линиям
раздела нагрузки q\ и q->y направленные вверх и представ-
ленные в виде рядов с неопределёнными коэффициентами:
оо оо
= sin “Г ’ ?2 = 2i sm IT •
n=l n=1
(52.2)
Полный прогиб в любом месте полосы представится
в виде суммы прогиба wt от нагрузок q и и прогиба
от нагрузок q\ и д':
(Р=
(52.3)
Требуя, чтобы на линиях раздела выполнялись условия
мы определяем коэффициенты ап и Ьп и сам прогиб
w. Условия на границе первого поля теперь будут в точ-
ности соответствовать условиям на краях пластинки
а поэтому прогиб этого поля будет равен прогибу в соот-
ветствующем месте пластинки.
199
2. Все содремы опёрты. На сторонах Ь пластинки .в этом
случае должны выполняться условия:
Л dlW , Яг№ „ ,са
«*=-0, ^ + ^-^ = 0. (52.4>
Нагрузим первое поле вспомогательной полосы усилиями
д, действующими на изучаемую пластинку; второе поле —
усилиями —д\ симметричными с первыми относительно
линии раздела, но направленными в противоположную*
сторону; третье поле нагрузим опять усилиями q, и т. д.
(рис. 93). Сечение изогнутой поверхности будет иметь вид^
как на нижнем рис. 93. Очевидно, первые условия (52.4)
Рис. 93.
на границах полей будут выполнены. Легко показать, что
и вторые условия будут выполнены. Действительно, линиям
раздела соответствуют точки перегиб а сечения изогнутой
поверхности, в которых вторая производная от w по х
обращается в нуль; производная d^wjdy2 обращается в нуль.
в тех же местах, где w = 0, следовательно, на линиях раз-
C^(V z~\
дела полей 4-v2 ~-~ === 0. Отсюда ясно, что первое поле
можно рассматривать, как изолированную пластинку с опёрт
тыми сторонами.
3. Три стороны опёрты, одна заделана. Если одна из
сторон Ь пластинки опёрта, а другая, противоположная,
заделана, то на первой должны выполняться условия
(52.4), а на второй — условия (52.1). В этом случае пер-
вое поле вспомогательной полосы нагрузим теми же уси-
лиями q, какие действуют на пластинку; второе поле —
усилиями д’, симметричными относительно линии раздела;
третье поле — усилиями — д, распределёнными так же, как
д, но направленными в противоположную сторону; четвёр-
тое поле — нагрузкой — д’, симметричной относительно линии
200
равдвве; пятое поле—натрузной д, и т. д. (рис. 94). Рас-
сматривал сечение «вогнутей поверхности (нижний рис. 94)>
замечаем, что на одной и8 линий, ограничивающей первое
поле, выполнены условия (52.4), а на другой линии»
Рис. 94.
только одно условие dWjdx — O. Чтобы добиться выполне-
ния ясах условий, распределим по линиям раздела попере-
менно нагрузки д( и д?, которые будем представлять в виде
рядов (52.2). Полный прогиб полосы складывается из про-
гиба tv, под действием нагрузок д’, —д, — д* и из про-
гиба «'г под действием нагрузок gi и д?;
w = и/14-и'2.
(52.5>
Неизвестные коэффициенты ап и Ьп определяем, требуя,,
чтобы на линиях раздела полей прогиб равнялся нулю.
Этим способом Губер получил решение задачи об изгибе-
пластинки с опёртыми сторонами под действием сосредото-
ченной силы Р и под дей-
ствием сил, расположен-
ных в Шахматном порядке ,
а также исследовал ряд
случаев изгиба пластинок
с двумя, тремя и четырьмя
опёртыми сторонами под
действием различных рас-
пределённых нагрузок. Не
имея возможности разоб-
рать все случаи, приведём
решение лишь для случая сосредоточенной силы, приложен-
ной в точке (5, т)) пластинки, опёртой по всем четырём сторо-
нам (рис. 95).
2015
ВиД выражения для прогиба получается различным
в зависимости о® того, какой из трёх случаев — I, II или
III—имеет место, ВТ случае I получается 1):
для :
«’ = w(aj, а — 5, у) =
SiSh^Mo-4)
ЧРЪ1
т.3 ]/~D[d72
1
---sh—
Ь о
, nns^a
Sh-T~
, nnsA (а—. пк$.х э
sn sh-------sh—r~
* о о
"sh^! ~
sin-^; (52.6)
для $ < x a:
tv _ w (a -- x, $, y).
Выражения для w в случае равпых и комплексных
корней характеристического уравнения (49.11) легко полу*
чаются из выражений (52.6) путём предельного перехода
я ли отделения вещественной части комплексного выраже-
ния.
53. Изгиб эллиптической и круглой пластинки,
заделанной по краю.
Рассмотрим эллиптическу ю
заделанную по всему краю,
однородную пластинку,
изгибаемую нормальной на-
грузкой q кг)см\ распреде-
лённой равномерно по всей
площади. Для этого случая
изгиба можно получить эле-
ментарным путём точное ре-
шение, которое мы и приве-
дём, Мы будем предполагать
в общем случае, что плас-
тинка не является ортотроп-
ной.
Рис. %.
Направим оси х и у по главным осям эллипса (рис. 96)
м обозначим через а и b величины главных полуосей его
и с^=а/Ь, Уравнение прогиба в общем случае неортотроп-
Ч См. [«], стр. 59—60.
202
ной: пластинки будет иметь нид:
+ + Ь2Овв)^,+
+ 4fl»W + fl>$ = ?- (53.1)
В правой части — постоянная величина. Жёсткости
1)ц считаем известными. Задача сводится к определенно
такого решения уравнения (53,1), которое удовлетворяет
граничным условиям:
м dw дю , ч . dw t
«' = 0, d^ = №cos(”’ х) + rfycos(я’у) =0 о3л
(n—направление внутренней нормали к контуру пла-
стинки). Таким решением, как легко проверить, является
полином четвёртой степени:
—<53-3>
где
Z)' - 1 [3Z)2ac‘ + 2 (Dia + 2Z)e6) с- + 3Z)U], (53.4)
Зная прогиб, по формулам (38.9) найдём моменты,
которые, очевидно, будут полиномами второй степени отно-
сительно х и у, а по формулам (38.10) —перерезывающие
силы, которые будут линейными функциями хну. Опре-
деление мест, где получаются наибольшие напряжения, не
представляет труда. Наибольший прогиб получается в
центре:
^max~6W' * (53.5)
Остановимся более подробно на решении для пластинки
из ортотропного материала, у которой главные направле-
ния параллельны направлениям главных осей эллипса. В
этом случае
^11 “ ^1? ^28 — ^21 -^18 'Ь = Z?8, £)1Л = D26 = ОД
I (53.6)
D'^tfD^ + lD^ + ZDJ. J
203
Моменты и перерезывающие силы определятся по фор-
мулам:
М.= -^l[^3 + v^) + g(l + 3^)-l-v^] ,
Mv = - [ g (3?! + c2) 4-g (*x + 3c2) - Л - r ] ,
> (53.7)
H - goW* .^n-
П** 16J>' аЬхУ>
) (538>
.v, •-ig>ie.Ks-**)+WH J
Наибольший изгибающий момент получается на концах
большой оси или на концах малой оси.
Если
то
= <53-9>
у-0 ° "
если ясе
то
Ми^-\Ми\^^ - (53.10)
у ь
Прогиб пластинки на изотропного материала, жёсткость
которой равна найдём по известно11 фор-
муле *):
Для однородной круглой пластинки радиуса а решение
получается как частный случай вышеприведённых реше-
ний при Ь — а и с®1. Так, например, в случае орто-
тропной пластинки, у которой оси х и у совмещены с
*) См. курс С. П. Тимошенко [И], ч. II, § 52, стр. 277, или [•]>
стр. 137.
201»
главными осцми упругости,
D' = ~(3Di + 2Ds + 3Ds), (53.12)
-6-^0-5У; ^13)
К1 + vs) (Г2 - а2) 4- 2 (х2 + У.У Е)1. ]
Мв "S' к1 + <г2 ~а^ + 2(**х* + ys)b! <53Л4>
H*v = — ib? I
^х=-^(3/)д + ^,)х, 1
+ ЗРа)у, | (53-15)
(г =у х'1 + if). J
Заметим, что привздённыэ решения можно обобщить
на случай более сложной нагрузки, распределённой по
закону целой алгебраической функции:
9 « 2 ^тп хт Уп- (53-16)
т-0л=0
В этом случае выражение для прогиба нужно искать
в форме
2 X
W = (1 —— -р)' 2 2Л,п"-х’т//"• (53.17)
m-О п-- 0
Такая функция удовлетворяет граничным условиям
(53.2) при любых значениях коэффициентов Атп, а коэффи-
циенты все определятся на основании уравнения (53.1).
Более сложной представляется задача об изгибе пластинки
•с опёртым краем; решение иока rte найдено даже ДЛЯ
круглой ортотропной пластинки.
54. Изгиб круглой криволинейно-анизотропной пластинки.
Все ранее рассмотренные случаи изгиба относились- it
однородным анизотропным пластинкам. В настоящем пара-
графе мы рассматриваем некоторые основные случай изгиба
круглой пластинки, обладающей цилиндрической анизо-
тропией. Поставим задачу следующим образом.
205
Имеется круглая пластинка радиуса а и постоянной
толщины Л из материала, обладающего цилиндрической
анизотропией и при этом ортотропного. Предполагается,
что ось анизотропии проходит через центр и перпендику-
лярна к плоскости пластинки и что плоскости, параллель-
ные срединной, а, также плоскости, проходящие через ось
анизотропии, являются плоскостями упругой симметрии
(иначе говоря, в каждой точке имеются три главных на-
правления — нормальное, радиальное и тангенциальное).
На пластинку, край которой заделан или опёрт на всём
протяжении, действует нормальная нагрузка, распределён-
ная симметрично относительно оси анизотропии (оси вра-
щения); эта нагрузка, очевидно, вызывает изгиб по поверх-
ности вращения. Требуется определить прогиб, моменты
и все прочие величины, необходимые для расчёта на-
прочность.
Примем точку пересечения оси анизотропии и средин-
ной плоскости — полюс анизотропии — за начало, а ось.
анизотропии — за ось z цилиндрической системы координат;
произвольное радиальное направление примем за направле-
ние полярной оси, от которой отсчитываются углы 0 (см4
рис. 97). В этой системе координат уравнения обобщён-
ного закона Гука будут иметь вид (46Л)Г а уравнения
теории .изгиба пластинок будут (46.3)— (46.7). Нагрузка q
есть функция одного г и прогиб w, который определив
поверхность вращения, есть также функциц одного г* На?
основании этого, формулы (46,4) — (46.5) и уравнение
206
^4в«7) запишутся следующем образом:
MT=-DT(w" + ^W'y
Мц — — D* (уг<р"4- у ,
Nr = -Dr( w"' + у «>") +D.t ± w',
Hr^Q, 2Ve = 0;
1
(54-1)
(54.2)
При к =*'l уравнение (54;2) совпадает с уравнением-
прогибов изотропной пластинки с жёсткостью Ьгх). Общее
выражение для прогиба — общий интеграл уравнения (54.2)^
для к #= 1 имеет вид:
w - А + Вг2 + Сг^к + Ег^к+^0(г), (54.3)
где wQ (г) — частное решение уравнения (54.2), зависящее
от того, по какому закону распределена нагрузка q вдоль
радиуса; Л, В, С, Е — произвольные постоянные, которые
определятся из граничных условий на краю пластинки^
и из условий в центре. Граничные условия будут
иметь вид:
заделанный край:
при г—a w - 0, w' = 0; (54.4)
опёртый край:
при r = a w = 0, w"+~,w' = 0; (54.5)
свободный край:
при г = а ^4~рМи' = 0, wf,f + — “2= 0. (54.6)
Условия в центре г —0 сводятся к требованиям огра-
ниченности прогиба и отсутствия угловой точки у изо-
гнутой поверхности (^'(0)~0), ИДИ, в других случаях, в:
зависимости от нагрузки, к требованиям ограниченности
моментов и перерезывающих сил.
*) См. [**], § 53, стр. 282, или [•], стр. 132.
207
Рассмотрим два основных случая изгиба: изгиб нагруз-
кой, распределённой равномерно по всей площади пла-
стинки, и изгиб сосредоточенной в пентре силой, Реше-
ния этих задач для изотропной пластинки хорошо изве-
стны *), решения для криволипей .о-анизотропнэй рассма-
чрййаемой пластинки получаются также просто.
1. Изгиб равномерно распределённой нагрузкой (рис. 97).
В этом случае q ~ const. Полагая, что к не равно 1 или 3,
.получаем:
W = А + Cfi+k + 8(9-9£)Д7 ’ <54^
постоянные В и Е нужно положить равными нулю, так
как в противном случае прогиб и перерезывающая сила
в центре будут равны бесконечности. После определения
постоянных А п С из условий на краю полученные выра-
жения ДЛЯ прогиба, моментов и перерезывающей силы
(будут справедливы И в том случае, когда к = 1 ия* & = 3.
Если край пластинки заделан, то:
Е3-*-4 СО1 +
+ (’+<-')'] ; (М.8)
[<*+'> аг-’з+«->ш1 i
i (М-9>
V __ _Уг I
Наибольший прогиб (в центр?):
W'mnx = Я(3 + к) [i + k; br ’ (5Z‘•1 °}
Изгибающие моменты у края пластинки равны:
* —И&Г rfra’b <«•“>
Величина изгибающих моментов в центре существен-
ным образом зависит от отношения жёсткостей А/Д, илй,
что то Же самое, Модулей Юнга Ё /Ёг> т. е. от вели-
чины к.
См. [«], § 52, стр. 281 — 284, идя [*J, стр. 132—135.
208
При к > 1,, Е> > Ег в центре Мг = Мз = 0; тогда наи-
большее значение изгибающего момента получается у края:
Л/тах — I г-а
да*
2(3 + ЛГ
(54.12)
При к < 1, Ej < Ег моменты, по мере приближения к
центру, неограниченно возрастают; в этом случае в цент-
ре происходит концентрация напряжений, и теоретически
в этом месте Мг = Мз = оо.
При к = 1 получаем прогиб изотропной пластинки:
(54.13)
В случае опёртого края
да* г(3 —Zt)(4 + *4-v9) * (3 + у0)
W~ 8(9-Л*)рД (14-Л) (A + voj (Ц-А) (Л + у9) Х
*GF+G)‘b
мт — 9(3+ *,)<? 2(9 — It*) [GF-OT
М,= qk*a* Г 2(9—A2) L
Nr = 2 * (54.15)
Наибольший прогиб (в центре)
фа4 4 4- Л +
И'тах = 8(3 + Л) DT ' (1 +Л) (*+*,) '
У края
л/г —0, Мз— 2(3 + Л)’ Л + У,
(54.1(5)
(54.17)
И в этом случае при к > 1 в центре Jfr = Afa = O, а
при к < 1 моменты неограниченно возрастают по мере
приближения к центру.
Для изотропной пластинки
= |~5 + v 2(3 + у) / г \» . / гМ1
64DL14-V 14-v \Л/’\й/,г
14 с. Г. ЛехиЕцкий
(54.18)
209
2. Изгиб сосредоточенной силой (рис. 98). В этом
случае w0 ~ 0; постоянную Е нужно положить равной нулю,
иначе в центре получим угловую точку изогнутой поверх-
ности, тогда как должно быть w' (0) = 0. Из условий на
краю получим два уравнения для определения постоян-
ных Л, В, С. Недостающее уравнение получим, вырезая из
пластинки часть в форме круга произвольного радиуса г
и рассматривая её равновесие. Очевидно, перерезывающие
силы, распределённые по краю вырезанной части, должны
уравновесить силу Р и, следовательно,
= (54.19)
откуда
В = . .. Р.мп . (54.20)
4тс(1 — к*)Ог ' ’
Выражение для прогиба принимает вид:
“ = йчТ^)р/’+Л + С'-,+''- <54-21’
Заметим, что в рассматриваемом случае нет оснований
требовать ограниченности напряжений в центре, где при-
ложена сосредоточенная сила; наоборот, там естественно
ожидать концентрации напряжений.
Если к£ай пластйнки заделан, то выражения для про-
гиба и моментов, после определения Л и С, принимают
210
вид (предполагается, что к #= 1):
W = 4я(1 —**)(! + /() D, [ 1 Л «О ~
-2(01+,С]; (54.22)
^’•_2тС(1 — /с») + V“) С « ) U + vj)] ,
м* = [ (1+Ьг) (1 - (1+vr) ],
N — — Р- ,
Nr 2кг
Наибольший прогиб (в центре):
_ Ра»
<Vmax ” 4т: (1 + Л)»Р, ’
)
(54.23)
(54.24)
Следует отметить, что при Л > 1, Еъ> Ет изгибающие
моменты в центре получаются' конечными, а при Л<1
Е^^ЕГ неограниченно возрастают по мере приближения
к центру. Перерезывающая сила при приближении к цен-
тру неограниченно возрастает, независимо от того, какова
величина отношения Е>1ЕГ,
Для изотропной пластинки с жёсткостью D:
(54.25)
В случае опёртого края:
Ра* Г (2 + * + vj) <1—
W = 4к(1 —*»)Д. L (1+ *)(* + •*(,) +
w Рк» Г(1 + ч() (Avr+1) z fSi-j I
Afj- 2«(J-A») L k + ^ U) "I (5427)
- (l + vr)].
Nr = 2w ’
Pa» 2 + *+ve
W’max 4re(l + *)»jDr’ * + v4 ’ (5.4.28)
14*
211
Относительно моментов можно высказать те же замеча-
ния, что и в случае заделанной пластинки.
Для изотропной пластинки
»=^{^[‘-ау]+2тм}- (ь4.29)
Сделаем ещё одно замечание относительно общего ха-
рактера распределения напряжений и деформаций. Про-
гибы, моменты и перерезывающие силы в рассматриваемом
случае криволинейно-анизотропной пластинки, изгиба-
ющейся по поверхности вращения, зависят только от мо-
дулей Юнга и коэффициента Пуассона, но не зависят от
модуля сдвига. Если у пластинки модули Юнга и коэффи-
циенты Пуассона соответственно равны, то отсюда ещё не
следует, что пластинка изотропная. Однако для такой ани-
зотропной пластинки распределение моментов, перерезыва-
ющих сил и деформаций получается точно таким же, как
и в изотропной пластинке.
Не представляет никакого труда получить решение за-
дачи об изгибе криволинейно-анизотропной пластинки по
поверхности вращения и в том случае, когда в центре
имеется круговое отверстие. К условиям на внешнем краю
добавятся , условия на краю отверстия, и число условий
будет равйо числу постоянных в выражении для прогиба
(54.3); это даёт возможность определить все постоянные
Л- В, С, Е.
65, Приближённый метод определения прогибов
анизотропной пластинки.
Очень частно на практике приходится иметь дело с та-
кими случаями изгиба, для которых точное решение неиз-
вестно. Точное решение пока ещё не йайдено даже для
однородной анизотропной круглой пластинки, опёртой по
краю, и прямоугольной анизотропной пластинки с заделан-
ными краями, не говоря уже о пластинках более сложных
очертаний. Для анизотропных пластинок можно указать
приближённый метод определения прогибов, аналогичный
методу, который успешно применяется для решения задач
об изгибе изотропных пластинок; этот метод основан на
теореме теории упругости о минимуме энергии. Если обо-
значить через w возможные прогибы пластинки, т. е. про-
гибы, при которых пластинка остаётся сплошной, и нуж-
ные граничные условия удовлетворяются, то только что
212
названная теорема (см. п° 3) в применении к пластинке
может быть сформулирована следующим образом: действи-
тельный прогиб пластинки, соответствующий данным гра-
ничным условиям и нагрузке, отличается от всех возмож-
ных тем, что он сообщает минимальное значение выраже-
нию
+4D-GSJ+4
— 2qw~^dxdy. (55.1)
Здесь интеграл берется по площади пластинки.
Н амечается следующий ход приближённого решения
задачи об изгибе (методом Ритца).
Задаёмся выражением для возможных прогибов в виде
суммы
«'=2S*4mnW'mn’ (55,2)
ш п
гДе Функции, удовлетворяющие граничным условиям,
непрерывные, дающие гладкую поверхность и зависящие
от двух параметров т и п, а Атп — неопределённые коэф-
фициенты. Подставляя это выражение в (55.1), получаем £7,
как квадратичную функцию (полином второй степени) коэф-
фициентов Далее определяем минимальное значение
этой функции, для чего составляем и решаем уравнения
Заметим, что при удачном выборе функции wmn можно
получить результат с достаточной для практики точностью,
взяв небольшое число членов суммы (55.2) —два, три чле-
на, а иногда (по крайней мере для изотропной пластинки)
даже один член (первое приближение)1).
Приведём решение в первом приближении для пла-
стинки прямоугольной, ортотропной, с главными направ-
х) Много приближённых решений для изотропной пластинки име-
ется уФеппля в книге [48] (см. §§ 19— 21, стр. 153—170). Приведён-
ный в этой книге подробный анализ разных решений позволяет су-
дить о точности первых приближений для изотропной пластинки.
213
лениями, параллельными направлениям сторон, заделан-
ной по краю и изгибаемой равномерно распределённой на-
грузкой. Направим оси х и у по осям симметрии (рис. 99)
п стороны обозначим через а и Ъ.
Рис. 99,
Выражение (55.1) в случае ортотропной пластинки при-
нимает вид:
Л/2 fr/2
5 S [<£)*+^.£•£+*(£?)*+
-а/2 -Ь/2
С55-4*
Изогнутая поверхность должна быть симметричной от*
носительно осей х и у, не должна иметь разрывов, изло-
мов и волнистости; в центре ордината её должна иметь
наибольшее значение, а по мере приближения к краям
должна плавно (монотонно) убывать до нуля.
На сторонах, параллельных оси г/, должны выполняться
условия;
w=^ = 0; (55.5)
&Х х 7
на сторонах, параллельных оси z, —условия:
= —= 0. (ээ.о)
Можно указать целый ряд выражений для wm/n которые
являются непрерывными функциями и удовлетворяют всем
214
указанным нужным условиям. Можно, например, предста-
вить wmn в виде целого полинома
y(y*-biy ^туп (55-7)
(т = 0, 1, 2, ... , n = 0, 1, 2, ...),
который, очевидно, удовлетворяет всем нужным граничным
условиям. Полагая, в первом приближении,
w = , (55.8)
получим:
U-aS> [^7Д5* + 4Р,аЧ’4-7Р,а<)--Л{.] . (55.9)
Минимальное значение получится при
А = Т ’ 7Z)1b‘ + 42)s«2&a+7P1ai ’ (55.10)
Отсюда приближённое выражение для прогиба:
W~ 8 7D1644-4D,a2ba4-7Z),a* (55.11)
Прогиб в центре равен:
*max = 0,003418
1
Р»
^PiP,
(55.12)
а
где с = у
В частности, для изотропной пластинки с жёсткостью/):
^х-0.ООМ18вг+олЯ4?+г-- (65ЛЗ>
Во втором приближении надо положить:
W = (х* - у У (у* - у У(Л00 + Амхг + Л„у‘)> (55.14)
215
Можно также построить выражение для w с помощью
тригонометрических функций, полагая:
«’тп=[1-(-1)’псов?^] [l-(-l)"cos2^] (55.15)
(т = 1, 2, 3, ... , га= 1, 2, 3, ...).
В первом приближении
Получим:
w — A ^l-J-cos—^ (1 + cos^^) .
л = га*_____________?___________
4it* З^ + гРэС’ + ЗР.с*
(1+cos^)(l+coS2-^)
4л ’ 3Dt + 2Р3са + ЗР,с4
Прогиб в центре:
^тах =
=0,003422
Vnj)2
(55.16)
(55.17)
(55.18)
(55.19)
^* + 0,6667
д
/ад
В частности, для изотропной пластинких)
^шах — 0,003422 • j-^0)6667c2-j-с4 * (55.20)
Заранее сказать, какое из двух выражений —(55.12)
или (55.19)— точнее, нельзя, не зная точного решения.
Можно, однако, утверждать, что лба выражения сравни-
тельно мало отличаются друг от друга. Проще всего это
показать на примере изотропной квадратной пластинки.
По формуле (55.13) получается:
я^ах = 0,00133^, (55.21)
а по формуле (55.20)
«-max = 0,00128“ (55.22)
Результаты совпадают с точностью до двух значащих
цифр: сохраняя в обоих случаях две значащие цифры
получаем один и тот же коэффициент —0,0013.
х) См. [е], стр. 443.
216
ГЛАВА X
ИЗГИБ ПЛАСТИНОК НАГРУЗКОЙ, РАСПРЕДЕЛЁННОЙ
ПО КРАЮ.
В настоящей главе рассматриваются некоторые случаи
изгиба однородной анизотропной пластинки нагрузкой
в виде изгибающих моментов и усилий, распределённых
по краю.
56. Местные напряжения около прямолинейного края.
В настоящее время исследованы два случая изгиба
не считая элементарных случаев чистого изгиба и круче-
ния: изгиб ортотропной пластинки с прямолинейным краем
под действием нагрузки, распределённой по краю, и изгиб
пластинки с эллиптическим или круговым отверстием под
действием нагрузки, распределённой по краю отверстия и
по внешнему краю (который в теории полагается беско-
нечно удалённым от отверстия).
Рассмотрим однородную анизотропную пластинку, кон-
тур которой имеет прямолинейный участок. Предположим,
что пластинка изгибается нагрузкой, распределённой по
небольшой части прямолинейного участка границы. Отно-
сительно упругих свойств мы будем предполагать, что
пластинка является ортотропной, причём главные напра-
вления параллельны и перпендикулярны к прямолинейному
участку края.
Приближённые формулы для определения моментов и
перерезывающих сил вблизи загруженной части прямо-
линейной границы мы получим, рассматривая пластинку,
как бесконечную, как «упругую полуплоскость». Метод.,
которым решается эта задача, имеет много общего с мето-
дом, применённым для исследования плоского напряжён-
ного состояния «упругой полуплоскости» и изложенным
в главе IV1).
Ограничиваясь для простоты случаем, когда загружен
конечный участок прямолинейной границы изгибающими
моментами и нормальными силами, распределёнными сим-
метрично относительно середины участка, примем середину
загруженного участка за начало координат, ось у напра-
х) Решение этой задачи имеется в нашей работе [21].
217
вим вдоль границы, а ось х внутрь полуплоскости (рис. 100).
Уравнение прогибов будет однородным (? = 0):
+ + = (56.1)
1 дх* 1 9 дх9 ду9 3 ду^ 4 '
Обозначим через т(у) изгибающие моменты и р(у)
изгибающие нормальные усилия на единицу длины— за-
данные функции у (чётные в силу симметричного распре-
деления). Условия на границе:
= Nx-\-
= Р (у)-
(56.2)
Представим заданные моменты и усилия в виде инте-
гралов Фурье:
ОО оо
m (у) — (а) cos ay da, р (у) = — X (а) 003 аУ ^а> (56.3)
и о
где
оо оо
W (а) = m (?]) cos ат) diq, X (а) ~ Р 01)003 аЧ (56.4)
о о
:и отыщем'решение уравнения (56.1) в виде:
оо
w — Ф (а, х) cos ay da.
о
(56.5)
218
Вид функций Ф будет зависеть от корней уравнения
D^* — 2Dss’ + Z>2 = 0,
(56.6)
которое уже рассматривалось в § 49.
Учитывая, что, по мере удаления от края, составляю-
щие напряжения ах, св, должны стремиться к нулю,
получим:
случай I: Ф = Ac-81®® + Be~SiW; (56.7)
случай II: Ф = (А-|-Вг)г‘и; (56.8)
случай III:
Ф = (Асоз tax + Bs,inta,x)e-slx. (56.9)
Удовлетворяя граничным условиям, получаем следую-
щие выражения для моментов и перерезывающих сил
в случае неравных корней (sx Ф s»)=
ОО
Ж = Рх [A (va - s’) е-«1«= +
+ В (v, — sx) е~е1**] cos лу du,
М9 — Ьг [А (1 — vxsj) e-s*0® +
о
+ В (1 —>!«!) е-’»’*] сое wy da,
(56.10)
Ця^ — —2Dk \ (As^-’i®® 4-Bsse~8i"®) sin «у da;
+ B(Dts’ —D.JSje-’^Jacosayda, >
Л[A (7>3s’ - A) +
о
(56.11)
sj — Ps) e-’1*® ] a sin ay da,,
219
где
Л . 24 _ х
X [ Ф (a) s, (D^l-D —2Dk} +
Ч.Х£) Di {sl _Ve)] _А_,
1
(56.12)
^Dth»^Et + iG^ -Jj)
X [w(a)S1(P1S;-P,-2DJ +
Определение моментов и перерезывающих сил в каж-
дом конкретном случае сводится. к вычислению интегра-
лов W(a) и х (а) и интегралов в формулах (56.10), (56.11).
При простом законе распределения нагрузки все инте-
гралы вычисляются без особого труда, и выражения для
Мх, Му, i . . , Ny получаются в конечном виде.
Решения для случая II можно найти путём перехода
к пределу при — решение для случая комплекс-
ных корней можно получить • из вышеприведенного, полагая
$* = $4-^ и $s — $— ti и отделяя вещественную часть ком-
плексного выражения.
57» Действие сосредоточенного момента.
Предположим, что в точке О прямоугольного края
пластинки (которую мы рассматриваем как бесконеч-
ную) приложен сосредоточенный момент М\ требуется
определить местные напряжения, вызванные этим момен-
том (рис. 101).
Заменяя сосредоточенный момент М статически экви-
валентными ему моментами с интенсивностью т
распределёнными равномерно по малому участку гра-
ницы 2е, получим:
ЧГ(а) = у-8-£“, Z(a) = 0. (57.1)
220
Подставляя эти выражения в (56.12) и далее в (56.10) —
(56.11) и переходя к пределу, когда длина участка 2в
стремится к нулю, получим интегралы, которые легко вы-
числяются. В результате получим следующее распреде-
ление моментов Мх, Му, НхУ, вызванное сосредоточенным
моментом1):
* м к +2PjX23/2 + Д1!/4 >
М — Мк_________ху*—
ш у МК + VDxx*y* + О1У* ’
И - М к- 20
Л хв - Л + 2ОаХгу, + D1J/* •
(57.2)
Здесь
»!.+ *» _.
В.+ 4О/®.
(57.3)
Для определения перерезывающих сил можно восполь-
зоваться формулами:
х ах 1 ду ’ * ду 1 дх
(57.4)
= /Д»-Р.
Моменты Мп Нгъ отнесённые к полярным коор-
динатам (точка приложения момента М — полюс, ось я —
х) См. нашу работу [21]. В этой работе применены несколько
иные обозначения.
221
полярная ось), определятся по формулам:
Мт = ~ cos О {2G(1 + у,) + \Ег - 26(1+?,)] cos 20},
= °’ ш. > (57.5)
~ sin 6 -''*)+£»+
+ [Я2-26(1 + у2)] cos 20}. .
Здесь
А = Dx sin4 6 + 22)э sin2 0 cos2 0 + Dz cos4 0 (57.6)
— жёсткость изгиба вокруг оси, имеющей радиальное на-
правление г [см. формулы (45.6)].
Приведённые выражения показывают, что изгибающие
и крутящие моменты убывают по мере удаления от точки
приложения сосредоточенного момента О, меняясь об-
ратно пропорционально расстоянию г; по такому же за-
кону меняются и напряжения ах, ау, и аг, Пере-
резывающие силы меняются обратно пропорционально
квадрату расстояния г; так же меняются и касательные
напряжения тх2, tFz. В самой точке О мы получаем
(в теории) бесконечно большие напряжения. На опреде-
лённом расстоянии г от точки О момент Мг достигает
наибольшей величины на нормали к краю пластинки, а
скручивающий момент Нгз там обращается в нуль: изги-
бающий момент обращается в нуль у края пластинки»
В изотропной пластинке получаем распределение:
я, 2М 1 + v cos 6
лг=о,
17 1 siD в
те 3 -|- v г
(57.7)
Из этих формул легко заметить, что точки, где ради-
альный момент Мт имеет одну и ту же величину, распо-
лагаются на окружностях с центрами на нормали к гра-
нице (на оси х), проходящих через точку приложения
момента О (эти окружности уже встречались в теории
плоской задачи, — см. § 25, рис. 34). Линии одинаковых
скручивающих моментов Яго представляют собой окруж-
ности, ортогональные к первым; они проходят через
точку приложения сосредоточенного момента, а центры
их лежат на краю пластинки. В анизотропной пластинке
линии одинаковых моментов будут более сложными кри-
выми 4-го порядка.
58. Изгиб пластинки с эллиптическим отверстием.
Рассмотрим анизотропную, однородную, но вообще не
ортотропную пластинку произвольной формы, имеющую*
эллиптическое отверстие и изгибаемую усилиями и момен-
тами, которые распределены по внешнему краю и по краю
отверстия.
Вопрос о влиянии эллиптического и кругового отвер-
стия на распределение напряжений хорошо изучен для
случая обобщённого плоского напряжённого состояния
(по крайней мере для малого отверстия, удалённого от
внешнего края, см. § 27 — 30). Комплексное представле-
ние прогиба, моментов и перерезывающих сил с помощью
двух функций и w2 даёт возможность изучить этот
вопрос и в случае изгиба х).
Полагая, что размеры отверстия малы по сравнению
с размерами пластинки и оно удалено от края, мы будем
рассматривать пластинку, как бесконечную, как «упругую
Рис. 102.
плоскость с эллиптическим вырезом». Рассмотрим случай^
когда нагрузка в виде изгибающих моментов т и изги-
бающих нормальных усилий р распределена только по
краю отверстия.
Примем срединную плоскость за плоскость ху, на-
чало коор; инат поместим в центре отверстия, а оси
х й у направим по главным осям эллипса (рис. 102)
Ч Этот вопрос подробно разбирается в нашей работе
223
и будем считать известными все жёсткости для
осей х и у. Уравнение контура эллипса возьмём в па-
раметрическом виде:
x = acos&, y = 6sin&;
(58.1)
т и р будут функциями 9. В общем случае будем пред-
полагать, что нагрузка, распределённая по краю отверстия,
приводится к силе Pz и к моментам тх и тр (относительно
осей х и у).
Моменты и перерезывающие силы выражаются через
две функции ^(zj и w>3(za) комплексных переменных
z^x + y^y и z2 = ^ + u2?y [см. формулы (41.4) и (41.5)];
производные функций и w' удовлетворяют на краю
отверстия условиям (41.7). Составив выражения, входящие
в правые части граничных условий (41.7), в общем случае
распределения нагрузки получим:
8
\ (тЖ/ + /<М = ^&со8&-^М4-ав +
+ 2 (а* «*в<+
/с==1
+S(f, «*•'+?« •-*«>.
A-l
(58.2)
Здесь
Рл* —коэффициенты, зависящие от закона распределения
нагрузки [их мы получим, раскладывая т и р в ряды
Фурье по переменной 0 и интегрируя, как предусматри-
вается формулами (58.2)]; afc, — коэффициенты, сопря-
жённые о первыми.
124
Решение получается с помощь» функций »*':
(z,) = (A,z1 + Л) In Ct + At +
4-5r[b?»«i-A₽i-f (M»e+M0] £ +
+ J- 2 - а?*)
wt (Z.) = (B'z2 + B) In Cg + B„ -
[mi«i-aFi-4(Mi«+a*o]
- a* 2 ~ a₽*> •
Здесь C1, С* —функции zx и zt:
r = >1 + /gf-a»-|1»fr*
41 a — i^b
a a — i^b
<*=A?»h»—a?ia;
(58.3)
(584)
(58»5)
А, В, А', В' — постоянные, определяемые не уравнений
[см. § 41, уравнения (41.9) —(41.10)]:
А’+ В'- А' — В' = 0,
{‘lA' + t^B' — f^A' — р,В' ~ О,
^А' + ^В'-ЙА'-ЙЯ'^О,
- А' + - В'-- А' --В’ = А- ;
Fi Ft Hi pg ’
A+ B- A- B = 0,
H A + р.» В — p, A — [i, В = 0,
p.JA + p.9aB-‘p?A-p.;B= -2Кш?,’
1 A I 1 О A 1 *D m9
—AH—B— — A----*
Fi Fi |11 p ir^Da
(58.61
(58,7)
Постоянную С мы определим, требуя, чтобы прониб w
представлялся однозначной функцией.
С. Г. Лехкицкий
Если на контуре отверстия действует уравновешенная
нагрузка, т. е. Pz~mx^ ту~ 0, то тогда Л' == В' ~ 0г
Л = В = 0, и решение упрощается.
Существенные упрощения получаются в том случае,
когда пластинка является ортотропной»
Приведённые общие формулы позволяют учесть (правда,
после довольно объёмистой вычислительной работы) влия-
ние отверстия в любом случае распределения нагрузки.
Если нагрузка действует и на внешнем крае, то распре-
деление напряжений получим, складывая напряжения
в сплошной, неослабленной пластинке, с напряжениями
в бесконечной пластинке с эллиптическим отверстием.
Распределение напряжений в пластинке с круговым отвер-
стием радиуса а найдём из общих формул, полагая Ь^а
и 8 = 6 (полярный угол). Мы рассмотрим подробно только
один частный случай изгиба, именно, выведем формулы,
учитывающие ослабление круговым отверстием ортотропной
пластинки при чистом изгибе.
59» Чистый изгиб пластинки, ослабленной круговым
отверстием.
•Прямоугольная ортотропная пластинка, ослабленная
круговым отверстием в центре, изгибается моментами
распределёнными равномерно по двум внешним сторонам;
на краю отверстия
нагрузки нет. Пред-
J&y S полагается, что глав-
'7?' ные направления х
и У паР алдельны
sQC сторонам пластинки
s < М и что диаметР отвер-
—-------стия мал по сравне*-
✓у нию с размерами сто-
рон (рис. 103).
Рис. 103. Решение получим,
складывая моменты
и перерезывающие силы в сплошной пластинке при чистом
изгибе:
М* Му = Нху - Nx = Ns - 0 (59.1)
и моменты и перерезывающие силы в бесконечной пластин*
ке с круговым отверстием, загруженной усилиями и момент
гае-
теми по краю отверстия '). Последние должны быть выбраны
»ак, чтобы на краю отверстия удовлетворялись условия:
Мг = 0, ЛГг4-А^’ = 0. (59.2)
Добавочные моменты и перерезывающие силы определятся
с помощью функций:
__Mai РчЦ292 а,'_____ Mai
W' ~^d • — ’ ----~2d----~ ‘ ( У ’
Важнее всего изучить распределение напряжений у края
отверстия, так как там должна быть концентрация напря-
жений.
После ряда довольно громоздких преобразований цолу-
коорди-
чаем моменты М, и Яга (отнесённые к полярным
натам) у края отверстия:
М9 =М Г1 + --!^^ - х
L /^, + 40
3*п* “Ь sin* 9 cos* 9 4- ffAcos* 0 ~|
Dr СП J ’
____ jg j/"* * о c sin* 9 *4“ cos2 9
rd = M * - - sin 6 cos 6 —i--n~7fiT---
УЕ^ + Ю Dr (9)
[Mr -0].
Здесь
Dr — cos4 6 2J9a sin2 6 cos’ 0 4- sin4 в
(59.4)
(59.5)
— жёсткость изгиба вокруг оси, касательной к контуру
отверстия ’),
а0 = Е2п,
аг = /ад Etn* + {4G (1 + v.) - Я,] (1 + л),
а. = /адад-4С (1 + Vi) j/j,
а, - (2Gv. ад) (1 + п) - 2G / J, (59‘6)
Г "1
в, = /ад + 2с(1-п-л« ) ,
n = — i (Uj +11,);
х) См. нашу работу [17] или [21]> стр. 202—203.
*) См, формулы (45.6).
15*
227
Eu **» V», G — главные упругие постоянные; р, —
комплексные параметры изгиба, являющиеся корнями урав?
нения
2>tl?4-2Dtt? 4-Z>1 = 0. (59.7)
Наибольшей концентрации нормальных напряжений
(определяемых моментами естественно ожидать на глав-
ных осях у края отверстия.
В точках А и (рис. 103):
я-=0’ <59-8>
в точках В и Вх (рис. 103):
Мо = М + , Яг0 = 0. (59.9)
/JS^ + 40 '
Крутящие моменты получаются наибольшими на бис-
сектрисах углов между главными направлениями.
Для пластинки из изотропного материала получаем
у края отверстия:
ДГ. = М (l-2|±^cos20),
Яг9= -Af^-sin 28.
34-v •»
В точках А и (рис. 103):
в точках В и Вг (рис. 103):
(59.10)
(59.11)
(59.12)
Мь = М^
О ~Г" »
На рис. 104 показано распределение моментов по краю
отверстия в пластинке из фанеры 1-го типа х); направле-
г) На графиках рис. 104—106 положительные и отрицательные
величины отложены от окружностей по продолжениям радиусов;
положительные величины изображаются стрелками, направлен-
ными от центра, отрицательные—стрелками, направленными к центру.
223
ние волокон рубашки соответствует направлению оси х;
нагружены края, перпендикулярные к волокнам рубашки.
У
РИС. 10..'
В точках А и момент Мй равен
Мч = 0,11 М-, (59.13)
в точках В и В±:
Л/е-2,58 М. (59.14)
Наибольший скручивающий момент
(Hrt)max = 0,5 м. (59.15)
На рис. 105 дано распределение моментов по краю отвер-
стия в пластинке из фанеры 1-го типа в случае, когда
ось х направлена поперёк волокон рубашки; нагружены
стороны, параллельные волокнам рубашки.
229
В точках Л и At:
Me = 1,33 М;
в точках В и В^.
M0 = lj46 М.
Наибольший скручивающий момент
(Hr3)max = O,9 М.
(59.16)
(59.17)
(59.18)
В первом случае получается большая концентрация на-
пряжений од и значительная разница в величине напряже-
ний'в точках A, At и В, В/, наибольшее нормальное напря-
жение (в точках В и BJ таково:
»тах = 1-^Л/* (59.19)
Во втором случае концентрация напряжений меньше,
но зато разница между напряжениями в. точках Л, Аг и В,
Вг незначительна.
Наибольшее нормальное напряжение (в точках В и
оюах = ^-М. (59.20)
230
На рис. 106 для сравнения изображено распределение
моментов по краю отверстия в изотропной пластинке о ко-
эффициентом Пуассона v = 0,3. Здесь в точкам Л и
ЛГ) = 0,21 И, (59.21)
в точках В и Вг = (59.22) (#,«)»« = 0,6 М-, (59.23) ®тах = ^Л/. (59.24)
Сопоставление всех приведённых графиков даёт нагляд-
ное представление о том, как влияет анизотропия мате-
риала на распределение напряжений при изгибе в пла-
стинке, ослабленной круговым отверстием.
231
ГЛАВА XI.
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ПЛАСТИНКИ.
60. Свободные колебания пластинки.
Во всех ранее рассмотренных случаях предполагалось,
что пластинки деформируются статической нагрузкой. Зада-
ча исследования деформаций и напряжений в анизотропной
пластинке значительно усложняется, если нагрузки меня-
ются о течением времени или прикладываются внезапно, т. е.
являются динамическими. Динамические задачи тесно свя-
заны с вопросами колебаний пластинок. В настоящей главе
мы очень кратко остановимся на некоторых вопросах попе-
речных колебаний анизотропных пластинок, которые харак-
теризуются искривлением срединной поверхности. Вообще
следует отметить, что вопросы динамики анизотропных пла-
стинок ещё мало изучены.
Рассмотрим пластинку произвольной формы; анизотроп-
ную и однородную, но вообще неортотропную, с произ-
вольно закреплённым или свободным краем. Предположим,
что некоторые усилия, распределённые по поверхности,
сообщают частицам, расположенным на срединной поверх-
ности, прогибы и скорости, направленные перпендикулярно
к первоначальной (не деформированной) срединной поверх-
ности, и в момент времени, который принимается за на-
чальный, пластинка внезапно разгружается от всех внеш-
них нагрузок. Получив начальную деформацию и скорость,
пластинка, будучи разгружена, колеблется, причём части-
цы, лежавшие на срединной, плоскости, перемещаются
перпендикулярно к ней, в результате чего пластинка
в любой момент времени представляется изогнутой. Та-
кого рода колебания называют свободными поперечными
колебаниями.
Дифференциальное уравнение колебаний мы полу-
чим, составив уравнение движения элемента в виде пря-
моугольного параллелепипеда с высотой h и основа-
нием dxdy.
Пусть у —удельный вес материала, w (х, у, г) —прогиб
срединной плоскости; остальное обозначения для жёстко-
стей, моментов и перерезывающих сил оставим прёжйими.
Обратимся к рис. 71 (нагрузку ? надо считать отсут-
ствующей).
232
Вместо первого уравнения равновесия (39.1) мы полу-
чаем, учитывая силы инерции, уравнение движения:
(^+^)dxdy^dxdyd^^ <60Л>
ИЛИ
£+£ [я.. S+ (А.+^..)5Й?+
+ (60.2)
В частности, для ортотропной пластинки получается
уравнение
(60.3)
а для ивотропной пластинки с жёсткостью D — уравнение
V’^ = Q. (60.4)
Прогиб w должен удовлетворять граничным условиям,
зависящим от способа закрепления края пластинки (эти
условия при заделанном, опёртом и свободном крае не от*
личаются от условий в случае равновесия), и начальным
условиям:
при ; = о w = w9(x, у), ~£=vt(x, у), (60.5)
где w9i v9 — заданные начальный изгиб и начальная ско-
рость для точки (ж, у).
Полное исследование вопроса о свободных колебаниях
должно привести к определению прогиба в любой точке
и в любой момент времени, но важнейшей частью задачи
является определение частот собственных колебаний и соб-
ственных функций. В вопросах динамики пластинок частоты
собственных колебаний играют важную роль; знание их
необходимо для определения динамических напряжений,
вызванных переменной нагрузкой.
Укажем кратко ход решения задачи о свободных попереч-
ных колебаниях методом Фурье.
233-
Введём (ради сокращения записи) оператор £:
I" А.',+«.. + 2(O.= + 2O..)j5?+
+ 4с-.^.+о-.^‘- <60-6>
Тогда уравнение (60.2) запишется сокращённо так:
5 + ^^ = 0. (60.7)
Ищем решение этого уравнения в виде произведения:
w ь= (Л cos pt4- В sin pt) W (x, у), (60.8)
тде p —-частота собственного колебания пластинки, под-
лежащая определению х).
Подставляя в (60.7), получим для W уравнение:
LW-p^W = 0. (60.9)
Далее, ищем решение этого уравнения, удовлетворяю-
щее граничным условиям (условия для W в случае заде-
ланного, опёртого или свободного края не будут отличаться
от условий для w). Для простых контуров, например, для
^прямоугольной пластинки, можно заранее подобрать выра-
жение для W9 которое позволит удовлетворить граничным
условиям или уже им удовлетворяет; выражение это будет
содержать произвольные постоянные. Требуя, чтобы функ-
ция W удовлетворяла граничным условиям и была реше*
нием уравнения (60.7), получаем систему однородных
уравнений для неизвестных постоянных; эта система
имеет решения, отличные от нуля, только в том случае,
когда её определитель Д (р) равен нулю. Отсюда полу-
чаем уравнение частот:
Д(р) = 0. (60.10)
Уравнение это будет иметь бесконечное множество реше-
ний, которые составляют спектр частот для данной пла-
стинки. Частоты вообще будут зависеть от двух парамет-
ров—иг и п 1, 2, 3, ..., п—1, 2, 3, ...). Наимень-
шая частота называется частотой основного тона, прочие
частоты — частотами высших порядков, или частотами обер-
тонов.
Точнее, р—круговая частота—величина, связанная с периодом
колебания Т зависимостью: р^2п/Т,
234
каждой частоте ртп соответствует функция (ж, у),
которая, на основании однородной системы уравнений,
определится с точностью до постоянного множителя (этот
множитель можно отнести за счёт постоянных А и В). Функ-
ции называемые собственными функциями, опреде-
ляют формы колебаний (т. е» формы изогнутой поверхно-
сти, соответствующие колебаниям с частотами ртп).
Если желательно решить задачу до конца, т. е. опре-
делить прогиб w (х, г/, t) в любой точке и в любой момент
времени, то поступают следующим образом. Раскладывают
заданные начальный прогиб и начальную скорость в ряды
по собственным функциям Wmn, т. е. представляют их
в виде^
оо оо со со.
*0 - 2 2 и»=2 2 w™ <60Л1)
m=lп=1 т=1п~1
ж берут решение уравнения (60.7) в виде суммы всех ре-
шений вида (60.8):
Если коэффициенты amn, Pmn удаётся определить, то
определение постоянных А я В не представляет никакого
труда. В результате получается:
СО оо
*=2 2 (атлС08 pmnf + ^8in W^. (60.12)
т=1n=l
Полный прогиб в любом месте представляется^ как ре-
зультат наложения бесконечного ряда прогибов, меняю-
щихся с течением времени по закону простых гармониче-
ских колебаний с частотами ртп.
Уравнение свободных поперечных колебаний в общем
случае, когда пластинка лежит на сплошном упругом ос-
новании с коэффициентом упругости к и подвергается
действию продольных усилий Тх, Ту, 5ху, не меняющихся
•с течением времени, имеет вид:
^.+ L(Lw + kW-Tx^-2SxV^. -Туд-^)=0. (60.13)
</t2 Лу х. х дх2 xvdxay »ду2 J v 1
Для определения частот собственных колебаний и собствен-
ных функций в этом случае можно применить тот же ме-
тод Фурье, который приводит, естественно, к более слож-
ному, по сравнению с (60.9), уравнению для функции ТУ.
23 &
61, Определение частот прямоугольной пластинки.
Дана прямоугольная однородная ортотропная пластинка*
у которой главные направления упругости параллельны
Рис. 107.
длины сторон. Функция W
удовлетворять условиям:
направлениям сторон; тре-
г буется определить частоты
собственных колебаний. Эта
задача полностью решена
только для ортотропной пла-
стинки с четырьмя опёрты-
ми сторонами.
Направим оси вдоль сто-
рон пластинки (рис. 107}
и обозначим через а и Ъ
[см. формулу (60.8)] должна
при г = 0, х — а И = ^£=0; (61.1)
1 3 ду*
при у = 0, у = Ь ^ = ^+>/-^=0. (61.2)
Этим условиям, очевидно, будет удовлетворять выражение
тт, . nVKX . ппу
W = sin-------sin —
а и
(61.3)
где т и п —целые числа. Потребуем, чтобы это выраже-
ние было решением уравнения (60.9), которое в случае
ортотропной пластинки принимает вид:
1 дх* 1 3 дх*ду* 1 * ду* g '
Подставляя в левую часть функцию (61.3) и приравнивая
результат нулю, получим:
D, (=)‘+2О. (=£)’+ D, (61.5)
Отсюда находим частоты р — р^-
/»,С")‘+2D."' (тУ+Р.»*. (61-6)
где е-а/Ь.
азе
Частота основного тона равна:
В частности, для квадратной пластинки со стороной о:
Pmn = ^Y ^j/D^ + W^+D.n*, = D1 + 2Dt + Dt. (61.8) (61.9)
Если пластинка изотропна *)? то
(61.10)
Данной частоте pmri соответствует прогиб
Рис. 108.
= Итп COS ртп t + sin р^ t) sin 8Ш . (61.11)
Собственные функции = sin sin определя-
ют формы колебаний, т. е. формы изогнутой поверхности
пластинки, соверша-
ющей колебания с дан-
ными частотами ртп.
На рис. 108,а показан
жид изогнутой поверх-
ности в произвольный
момент времени для
пластинки, совершаю-
щей колебания основ-
ного тона, с частотой
место наибольшего
отклонения, или пуч-
ность, находится в сере-
дине. На рис. 108, b и
108, с показаны изогну-
тые поверхности пла-
стинки, совершающей
колебания с частота-
ми и р21; в каждом
а одна из осей симметрии остаётся неподвижной, т. е.
является узловой линией.
Полный прогиб пластинки, получившей произвольное
начальное отклонение tv0 и начальную скорость vt, пред-
случае имеются две пучности,
1) См.» например, [*5], § 56, стр. 308.
13?
ставится как результат наложения бесконечного ряда
прогибов вида (61.11);
«'==2 2 (am* cos Ann * + sinsin ^sin^-
m«*i n=l
.12)
Здесь a^, Pmn —коэффициенты разложения начального
Прогиба и начальной скорости в ряды по собственным функ-
циям (см. предыдущий параграф); в данном случае это —
двойные ряды Фурье, коэффициенты которых определяются
по формулам:
а ъ \
«тп = Sin sin dx dy,
I ь° ? (61.13>
₽4 С Г . ткх . птш , , I
ob j J v° sin “ sin "ТГ dxdy*
0 0 J
Для пластинки, у которой две стороны х = 0, х = &
опёрты, а другие закреплены как угодно или свободны,
выражение для функции W имеет вид;
w = (с„ -=2й- + С,„ оо» -==!* + С,„ +
+ Cm0h2=b»-),in = , (61.14)
где
к,
p4v(al Da
2 g-rthn* D2 ’
Dl-D1Di+Di-^^-
• * a 1 2 girm* 1 D.
> (61.15)
Эта функция удовлетворяет условиям на опёртых сто-
ронах. Из условий на других сторонах получается система
четырёх однородных уравнений с четырьмя неизвест-
ными: (7im, C2mi Сът, С4т] частоты определятся из урав*
нения, которое получится, если приравнять определитель
однородной системы нулю. Каждому значению т == 1, 2, 3,...
соответствует бесконечный ряд частот ртп, так как урав-
нение Д (/?) — 0 получается трансцендентным и имеет бес-
конечное число решений. В частном случае, когда все
стороны пластинки опёрты, мы получаем формулу (6Lfi)
для частот.
238
62. Приближённые методы определения частот.
Точное определение частот пластинки (за исключением
пластинки прямоугольной с двумя или четырьмя опёртыми
сторонами) сопряжено со значительными трудностями, свя-
занными с интегрированием уравнения 4-го порядка (60.9)
или (61.4).
На практике могут оказаться полезными приближённые
методы определения частоты основного тона, аналогичные-
методам, применяемым при изучении собственных коле-
баний балок. Существует целый ряд приближённых мето-
дов определения частот поперечных колебаний балок, поз-
воляющих быстро, без интегрирования дифференциальдых
уравнений, определять частотых) (преимущественно частоты
основных тонов, представляющие наибольший практический:
интерес). Эти методы легко обобщаются и на случай плас-
тинки.
Мы рассмотрим здесь один из них —метод Релея<-Ритца
и с помощью его определим приближённо частоту основ-
ного тона для пластинки прямоугольной с заделанными,
краями и круглей пластинки, заделанной по ободу.
Применяя этот метод, рассматривают упругое тело, со-
вершающее свободные колебания с частотой основного тона
(в нашем случае пластинку), как систему с одной степенью*
свободы, состояние которой в любой момент времени опре-
деляется одной обобщённой координатой gr(Z).
В случае пластинки полагают, что прогиб в любой мо-
мент времени имеет вид:
w=q{t)W (х, у), (62Л)
где W— непрерывная функция, удовлетворяющая гранич-
ным условиям (зависящим от способов закрепления краёв)
и представляющая приближённо форму изогнутой поверх-
ности колеблющейся пластинки. Далее составляют урав-
нение движения системы, используя известные уравнения
Лагранжа. В данном случае получается только одно урав-
нение, соответственно числу степеней свободы, имеющее
вид:
4- — —+^ = о, (62.2)
dt \dqJ dq'dq^ \ '
*) По этому вопросу см. С. П. Тимошенко [45], § 48, 49 и 56,
и книгу С. А . Бернштейна [8], гл. V, где различные приближённые
методы определения частот балок рассмотрены очень подробно и ил-
люстрируются многими примерами.
где Т — кинетическая и V — потенциальная энергия си-
стемы. Для пластинки ортотропной и однородной
► (62.3)
т = £ • W2 dx dy
t(y— удельный вес, h — толщина).
Обозначим выражение для V сокращённо таким обра-
зом:
V = g4^ V (W) dx dy. (62.4)
Уравнение Лагранжа после подстановки выражений. Т
си V принимает вид:
9" + раЗ=О, (62.5)
тде р —частота, для которой получается формула:
2g ! \V{W}dxdy
Р hy ^WtdxdV *
Выражение для прогиба получается в виде:
w — (Л cos pt 4- В sin pt) W. (62.7)
Точность определения частот в значительной мере за-
висит от удачного выбора выражения W. Для простых
контуров подбор функций этих не представляет особого
труда; иногда удаётся сразу указать несколько различных
выражений для них. Можно, например, в качестве первого
приближения для функции W взять выражение, пропор-
циональное статическому прогибу пластинки с теми же
условиями закрепления края под действием равномерно
распределённой нормальной нагрузки. Это равносильно
предположению, что поверхность пластинки, совершающей
колебания основного тона, имеет ту же форму, что и по-
верхность пластинки, изгибаемой равномерным давлением.
Задаваясь заранее формой изогнутой поверхности, по
существу рассматривают не пластинку, частоты которой
нужно определить, а близкую к ней более жёсткую систему.
Поэтому приближённое значение частоты (по крайней мере
£40
для изотропных пластинок и балок), найденное указанным
способом, получается больше истинного значения. Учиты-
вая это, можно задачу поставить таким образом: опреде-
лить функцию W, при которой выражение для р* (62.6)
получает минимальное значение, и найти это минимальное
значение.
Приближённое решение этой вариационной задачи можно
получить методом Ритца. Порядок применения этого ме-
тода—обычный: задаются выражением для W в форме
суммы с неопределёнными коэффициентами:
W^A^,
т п
(62.8)
где — непрерывные функции, зависящие от двух па-
раметров т и п и удовлетворяющие всем граничным усло-
виям.
Тогда р” представится в виде дроби
п2 —
(62.9)
числитель и знаменатель которой — однородные квадратич-
ные функции коэффициентов Лтп. Далее ищут минимум
этой функции, т. е. составляют производные др*)дАтп
и приравнивают их нулю. Очевидно,
17 Л тп
1
Л * ^Лтп
1 f дМ. 2
(62.10)
Отсюда ясно, что задача отыскания минимума дроби
(62.9) равносильна задаче отыскания минимума выражения
5 = (62.11)
или, в старых обозначениях, выражения:
5==$ 5 dxdy- (62.12)
Подставляя сюда значение W (62.8), получают S в виде
однородной квадратичной функции коэффициентов
Далее, ищут минимум функции S и получают систему одно-
родных уравнений первой степени для коэффициентов
требуя, чтобы по крайней мере один из коэффициентов
был отличен от нуля, приравнивают нулю определитель
С* Г. Лехшщкнй
241
системы и получают уравнение частот:
Д(/0 = О. (62.13)
Наименьшее решение, отличное от нуля, и будет прибли-
жённым значением частоты основного тона.
63. Примеры определения частот в первом приблиясении.
Рассмотрим два примера.
1. Частота прямоугольной пластинки с заделанными
сторонами. Пусть требуется определить частоту основного
тона прямоугольной ортотропной пластинки, у которой
все четыре стороны заделаны (рис. 109).
Точное решение этой задачи пока неизвестно, а прибли-
жённой можно получить, полагая, например,
у (г - v)2 (63.1)
где яг, п —целые числа.
Очевидно, все эти функции (и функция W в целом)
будут удовлетворять условиям
на сторонах:
при X = ±—
^ = 0, (63.2)
, г>
при v/ = ±y
^ = ^=0. (63.3)
В качестве первого приближения возьмём только первый
член суммы (62.8):
W = A(x*-^) {У-h)- <63-4>
Подставляя в выражение (62.6) и производя интегриро-
вание, получим:
= /% + 0,571 ^ + Р2. (63.5)
В частности, для i вадратней изотропной пластинки
с жёсткостью D
а2 V Лт '
(63.6)
242
Можно указать и иное выражение для WmH:
Wmn = [l-(-l)mcoS2-^] • [l-(_ipcos^],(63.7)
которое, очевидно, также удовлетворяет всем граничным
условиям. Первое приближение для частоты основного
тона получим, полагая
И’ = Л^1-гсоз ^14-cos yQ. (63.8)
В результате всех вычислений находим:
Л. = 4?- /TF (63.9)
Для изотропной квадратной пластинки из этой формулы
получаем:
37,2 9/gD
а2 V by
(63.10)
Разница между выражениями (63.6) и (63.10) невелика;
она составляет 3*/8% по отношению к меньшей из двух
величин.
2. Частота круглой пластинки с заделанным краем.
Требуется определить частоту основного тона круглой
ортотропной однородной пластинки, заделанной по краю
(рис. 110, где направления осей х и у совмещены с главными
направлениями упругости).
н*
243
Для получения первого приближения воспользуемся
выражением для статического прогиба под действием рав-
номерно распределённой нагрузки, выведенным в § 53.
Полагая
W = (63.11)
получим:
А1 = 3Й5 /ЗА + 2Р, + 32).«=
= /Л + 0,667Л.+А. (63.12)
В частности, для такой же пластинки из изотропного
материала *):
а2 V hy ’
(63.13)
64. Вынужденные колебания пластинки.
Уравнение вынужденных колебаний, т. е. уравнение
движения пластинки под действием переменной нагрузки
*/(#,у, О? выводится так же, как и в случае свободных
колебаний, только при выводе нужно принять во внимание
нормальную нагрузку q (см. рис. 71).
Для неортотропной пластинки получится уравнение
(64Л>
а для ортотропной —уравнение
z+^(".g+2'>.^.-+^. Z) -№ ** <м-2>
Задача сводится к определению решения уравнения (64.1)
или (64.2), удовлетворяющего граничным и начальным
условиям. Для определения точного решения можно при-
менить следующий способ.
Сначала решаем задачу о свободных колебаниях и опре-
деляем частоты собственных колебаний ртп и собствен-
ные функции JTjnn- Затем представляем нагрузку q как
х) См., например, [45]. стр. 313. Формула (62.13) даёт первое
приближение; во втором приближении для изотропной пластинки
10,21, / gD f .
^7“ у (СМ. там же).
а»
244
функцию х и у в виде ряда, расположенного по соб-
ственным функциям:
со оо
?=2 2а™ Wwi (х> с64-3^
m^l п=1
в ищем решение в форме:
со со
w=2 2 у}-
Л1=1 п = 1
Для функции Т„щ получается уравнение
Тmn 4~ PnuiT-mri — атп (0, (64.5)
етауда
У тп ~ -^тп COS ртп£-{~ Втп 81П РтдР 4~ (0? (64.6)
ОО ОО
"S Мтл Pmrf ~Г -®mn Ртп^ 4" Tmn (01 Wynn* (64./)
n-1
Здесь — частное решение неоднородного уравнения
(64.5); вид его зависит от атп, т. е. от закона изменения
нагрузки с течением времени. Постоянные и В)пп
определяются из начальных условий так же, как и в слу-
чае свободных колебаний.
Укажем решение для одного частного случая.
Пусть нагрузка, действующая на прямоугольную опёр-
тую пластинку, задана в виде функции:
Q = 7. (х, у) cos pt, (64.8)
т. е. распределение её по поверхности пластинки остаётся
неизменным, а величина в каждой точке меняется по
закону простого гармонического колебания с частотой р.
Полагая, что в начальный момент пластинка находится
в покое, получаем:
СО СО
w=Д 2 2 <cos pt ~008 Рт^sin sin "F ’ t64,9)
zn=l n=^l
fj b
4 С ( * AH ТТЛ- • TlTtl-J -j j ,nf л (\\
C'rnn ab H 7° Sm ~ SB1 dX ЛУ' (64Л°)
G 0
Если частота нагрузки р совпадает с какой-нибудь из
частот собственных колебаний пластинки, то пластинка
будет колебаться в состоянии резонанса. Так, если для
каких-либо т и п имеем: р — то соответствующий член
ряда (64.9) принимает неопределённый вид 0/0; раскры-
вая неопределённость, получаем:
Wmn=Д' ir *sin Ртп 1 sin т1гsin ’-Т • <64-1
Это движение представляет собой колебание с ампли-
тудой, неограниченно возрастающей с течением времени
(пропорционально времени). Впрочем, этот результат мы
получаем, совершенно не учитывая сопротивлений —сопро-
тивления внешней среды и внутреннего трения, а между
тем эти факторы оказывают существенное влияние на
процесс колебаний; благодаря им колебания получаются
с ограниченной амплитудой.
На практике опасным может быть резонанс в основном
тоне, когда колебания основного тона, характери-
зующиеся пучностью в середине пластинки, при резонансе
усиливаются, и это может привести к явлениям, опасным
для прочности пластинки.
ГЛАВА XII.
ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ ПЛАСТИНОК.
65. Общая остановка задач об устойчивости пластинок*).
В этой главе мы даём формулировку задач об устой-
чивости пластинок, указываем основные методы определе-
ния критических нагрузок и приводим некоторые общие
формулы, имеющие отношение к задаче об устойчивости.
Состояние равновесия пластинки, деформируемой уси-
лиями, действующими в срединной плоскости, является
единственным, и равновесие является устойчивым, пока
усилия достаточно малы по величине. Единственная
и устойчивая форма равновесия, соответствующая доста-
точно малым нагрузкам, характеризуется тем, что средин-
ная поверхность пластинки остаётся плоской; эту фор-
х) См., например, [а], § 20, и [в], § 81, стр. 236—238.
24G'
му равновесия мы в дальнейшем будем называть основ-
ной. Если, не меняя закона распределения усилий по
краю пластинки, увеличивать их, то может наступить
такой момент, когда основная форма равновесия пере-
станет быть единственной и устойчивой и, кроме неб,
становятся возможными другие формы, для которых ха-
рактерно искривление срединной поверхности. Плоская
форма становится неустойчивой, и пластинка, деформиро-
ванная усилиями, под действием самого незначительного
поперечного усилия перейдёт от неустойчивой формы
к устойчивой, с искривлением срединной поверхности.
В таких случаях говорят, что пластинка теряет устой-
чивость. В большинстве случаев потеря устойчивости
элемента конструкции в виде пластинки есть явление
нежелательное; оно может привести к нарушению правиль-
ной работы конструкции и даже к разрушению ее. По-
этому, при расчёте на прочность элементов тонкостенных
конструкций в виде пластинок, нужно обращать серьёзное
внимание на ту часть расчёта, которая имеет целью
подобрать размеры или величины действующих усилий
таким образом, чтобы при работе конструкции явление
потери устойчивости не могло иметь места.
Задаче об устойчивости плоской пластинки в её общей
постановке можно дать следующую развёрнутую форму-
лировку.
Имеется пластинка данной формы, к которой прило-
жены внешние усилия, действующие в срединной пло-
скости. В общем случае предполагается, что пагрузка со-
стоит из двух частей: из нагрузки, закон распределения
которой по краю и величина остаются неизменными, и из
нагрузки, заданной с точностью до множителя X; послед-
нее значит, что закон распределения усилий по краю
задан, а величина их может меняться от 0 и до произ-
вольно больших значений. Предполагается, что при Х = 0
пластинка находится в устойчивом равновесии (обобщённое
плоское напряжённое состояние), при увеличении же X
может наступить момент, когда единственность равновесия
нарушится. Требуется определить такие значения X == Хп
Х2, Х8, ..при которых происходит разветвление равно-
весия, т. е., кроме плоской формы, становится воз-
можным существование других форм равновесия (в общем
•случае имеется бесконечный ряд таких значений). Наи-
меньшее значение X, при котором основная форма равно-
весия перестаёт быть единственной и устойчивой формой,
247
называют критическим, и нагрузки, соответствующие этому
значению, — критическими.
Хотя исследование всех возможных форм равновесия
пластинки представляет большой теоретический интерес,
на практике обычно ограничиваются определением крити-
ческой нагрузки и той формы равновесия пластинки,
которая становится тозможной наряду с плоской, когда
нагрузка равна критической. Получение точного решения
задачи о различных формах равновесия и об устойчивости
сопряжено с большими математическими трудностями;
приходится решать нелинейные уравнения теории упру-
гости, учитывая большие деформации.
Поэтому на практике почти всегда ограничиваются
приближённым решением.
66. Основные методы опр< деления критической нагрузки х).
Из различных методов приближённого определения
критических нагрузок, известных в настоящее время,
отметим три метода: 1) статический метод, 2) энергетиче-
ский метод и 3) динамический метод.
1. Статический метод. Рассматривая равновесие пла-
стинки, нагруженной усилиями, действующими в средин-
ной плоскости (из которых часть останется постоянной,
а другая часть задаётся с точностью до множителя X),
полагают, что при некотором значении X становится воз-
можным небольшое искривление срединной поверхности.
Составляют дифференциальное уравнение изогнутой по-
верхности, с учётом продольных усилий, вызванных внеш-
ней нагрузкой. Некоторые из коэффициентов этого урав-
нения будут содержать множитель X как параметр. Далее
ищут решение полученного уравнения, удовлетворяющее
всем граничным условиям (в зависимости от того, как
закреплены края пластинки), не равное тождественно нулю.
Такое решение существует не при всяких значениях X,
а лишь при определённых значениях — Хп Х2, Х3,... (харак-
теристические числа); наименьшее из этих значений, не
равное нулю, и будет критическим —XFP.
Уравнение изогнутой поверхности получится из урав-
нений (40.6) или (40.7), г;е нужно положить ^ = 0 и под-
ставить значения продольных усилий Для
определения продольных усилий нужно решить плоскую
х) См., например, [44], § 20.
248
8» да чу; в результате получится:
тя=тх+хт;, гв=т.4-хт;, sa„=s+xs', (вел)
и уравнение изогнутой поверхности для ортотропной пла-
стинки примет вид:
Д ^+2Р, + Ра (Д + КГ')
1 дх* * 3 дх^ду* 1 2 ду* 4 1 17 ОХ3
В зависимости от вида контура пластинки и закрепле-
ния её края, ищут решение уравнения прогибов в такой
форме, которая позволит удовлетворить граничным усло-
виям или уже им удовлетворяет. Решение — функция:
tv (х, у) — будет содержать произвольные постоянные. Удо-
влетворяя граничным условиям, получают систему одно-
родных уравнений относительно постоянных, которая
имеет решение, отличное от нуля, только тогда, когда
определитель её равен нулю. Приравнивая нулю опреде-
литель системы, получают уравнение для к. Из всего’
бесконечного ряда решений (уравнение обычно получается:
трансцендентным) нужно взять наименьшее, не равное'
нулю. Когда критическое значение Хкр найдено, выражение
для прогиба будет определено с точностью до произволь-
ного постоянного множителя *).
2. Энергетический метод основан на общих теоремах
о равновесии механической системы.
Как известно из механики, потенциальная энергия
системы в положении равновесия имеет экстремальное
значение. Равновесие будет устойчивым, если потенциальная
энергия в положении равновесия имеет минимальное зна-
чение (по сравнению со значениями, соответствующими
любым возможным малым отклонениям от положения рав-
новесия); неустойчивым, если энергия имеет максималь-
ное значение, и безразличным, если в положении равно-
весия энергия не имеет ни максимума, ни минимума. При-*
2) Произвольный постоянный множитель указывает на то, что
состояние равновесия пластинки будет безразличным, что и имеет
место, когда нагрузка в точности равна критической. В частности,
формой равновесия будет плоская форма, соответствующая множи-
телю, равному нулю.
меняя этот критерий к пластинке, поступают следующим
образом.
Рассматривают два состояния пластинки — состояние
равновесия под действием данной нагрузки, при которой
срединная поверхность остаётся плоской, и смежное состо-
яние, при котором срединная поверхность слегка искрив-
лена, вследствие сообщённых пластинке малых возможных
перемещений. Пусть 70 —потенциальная энергия в поло-
жении равновесия и 7 —потенциальная энергия в смежном
состоянии. Равновесие будет устойчивым, если для всех
возможных малых отклонений (т. е. прогибов w) Уо < V,
неустойчивым, если Vo > V, и безразличным, если =
Если пластинке даются малые прогибы, то потенциальная
энергия увеличивается за счёт энергии изгиба РиЗГ и умень-
шается за счёт работы А, произведённой внешними уси-
лиями при искривлении срединной поверхности. Для без-
различного равновесия
И-7о+7изг-А (66.3)
или
УЙЗГ = А(к). (66.4)
Таким образом, для определения критического значе-
ния к нужно приравнять потенциальную энергию изгиба,
соответствующую малым искривлениям срединной поверх-
ности, работе, совершённой внешними усилиями.
Применяя энергетический метод на практике, обычна
поступают следующим образом. В зависимости от формы
пластинки и закрепления её края задаются подходящим
выражением для прогиба в виде суммы с неопределёнными
коэффициентами:
= 2 2 (66.5)
т п
где wmn — непрерывные функции, удовлетворяющие всем
условиям на контуре. Подставляя это выражение в урав-
нение (66.4), находят К в виде дроби, числитель и зна-
менатель которой зависят от коэффициентов Атп:
[Лтп)
Если в выражении для w взят только один член
то в формуле (66.6) коэффициент сокращается,
250
(66.6)
суммы,
и по-
ручается приближенно? значение Хкр, зависящее от т
и п, соответствующее безразличному равновесию пла-
стинки. Если выражение (66.5) взято в вице суммы двух,
трёх и более членов, то коэффициенты Лт1 в формуле
(66. >) не сократятся. Имея в вицу получить наименьшее
из всех возможных X, ищут минимум дроби (66.6).
а это равносильно отысканию минимума разности1).
(66.7)
В результате получают систему однородных уравнений
относительно коэффициентов и, приравнивая нулю её
определитель, получают уравнение для К; наименьшее из
всех решений, не равное нулю, и будет Хкр.
3. Динамический метод. Если пластинку, находящуюся
в состоянии равновесия под действием внешних усилий
(при плоской форме срединной поверхности), вывести из
состояния равновесия, сообщив её частицам малые началь-
ные смещения и скорости в поперечном направлении, то
пластинка будет двигаться, и характер движения будет
зависеть от того, каким было равновесие — устойчивым,
неустойчивым или безразличным. Пластинка, выведенная
начальным возмущением из положения устойчивого равно-
весия, будет стремиться вернуться в это положение, т. е.
выпрямиться; идеально упругая пластинка будет совер-
шать незатухающие колебания около положения равнове-
сия. Если же равновесие было неустойчивым, то пластинка
не будет стремиться вернуться в положение равновесия,
а будет отходить от него далее, всё более изгибаясь.
Применяя динамический метод, полагают, что пластинке,
находившейся в состоянии равновесия, сообщается произ-
вольное начальное отклонение и начальная скорость в попе-
речном направлении. Составляют дифференциальное урав-
нение движения, т. е. уравнение поперечных колебаний
с учётом продольных сил [см. уравнение (60.13)]; в состав
этого уравнения войдёт X как параметр. Далее, опреде-
ляют частоты собственных колебаний пластинки ртп,
которые будут зависеть от размеров и упругих постоянных
пластинки и от X. Рассматривая выражение для частот
(или уравнение, из которого они определяются), подме-
чают следующее. Пока величина X мала, все частоты по-
J) См. § 62 настоящей книги, формулы (62.9)—(62,11).
251
л у чаются вещественными, и прогиб пластинки предста-
вится как результат наложения прогибов вида;
^тп — Ишп COS pmnt 4" Btnn Pmnty ^тп* (66.8)
Это значит, что пластинка будет совершать колебание
еколо положения равновесия, и равновесие было устой-
чивым. С увеличением X для некоторых частот могут
получиться мнимые или нулевые значения: Ртп — ip'mn или
Аил —0; тогда соответствующие выражения типа (66.7),
из которых составляется прогиб, должны быть заменены
членами, неограниченно возрастающими с течением вре-
мени:
= GO" р;»и‘ + Wm„ (66.9)
или
(66.10)
Благодаря присутствию членов этого типа полный про-
гиб будет стремиться неограниченно возрастать с течением
времени, и, следовательно, при таких значениях X плоская
форма пластинки является неустойчивой (или безраз-
личной).
Наименьшее не равное нулю значение X, соответствующее
переходу от незатухающих колебаний (66.8) к движению,
которое характеризуется неограниченнно возрастающими
отклонениями от плоской формы, и будет критическим-
В дальнейшем мы будем пользоваться только статиче-
ским и энергетическим методами.
67. Работа внешних усилий.
При решении задач об устойчивости пластинок энерге-
тическим методом нам придётся иметь дело с выражением
для работы внешних усилий Л, совершаемой при малых
отклонениях от плоской формы. Выведем это выражение-
При выводе предполагается, что срединная поверх-
ность искривляется, не претерпевая растяжений или сжа-
тий; вследствие этого, при изгибе края пластинки сбли-
жаются, и продольные усилия производят работу.
Пусть на элементы срединной плоскости, перпендику-
лярные к осям х и г/, действуют снижающие усилия рхг
ру и касательные усилия t (на единицу длины):
Т х~ рхч Ту = ру7 SXy^= t. (67.1)
252
Выделим из пластинки полоску, параллельную оси х„
шириной dy, и на ней элемент длиной dx. Сближение
концов этого элемента по рис. 111 равно:
йД — dx — dx cos а = 4 dx sin2 а = у dx (jj-Q • (67.2)
Работа усилий равна:
dAl = pxdy - dx(j^y. (67.3)
Работу усилий для всей пластинки получим, инте-
грируя выражение (67.3) по всей площади пластинки:
А = 4 $ $ Рх (jt) *dx dy- (&7-4)
Аналогично, работа усилий pv равна
=4 ($£)****- (67-5>
Для вычисления работы касательных усилий рас-
смотрим такой же элемент dx dy, показанный на том же
рис. 111. Под действием касательных усилий элемент йере-
25а
ьашивается и в проекции на плоскость ху принимает
форму параллелограмма, причём:
^3 = YaBrfy- (67.6)
Так как срединная плоскость нерастяжима, то отно-
сительный сдвиг у1Р по шестой формуле (1.4) равен *):
* ду ’ (67.7)
следовательно,
(67.8)
и работа касательных усилий на перемещении с/8 равна:
dA3 — tdr-i~; -^dy. (67.9)
Работа касательных усилий для всей пластинки:
<67ЛО>
Суммируя выражения Л1? Л2 и Л3, [получим работу
продольных усилий при малом искривлении пластинки:
л л (□’+* ао+21 s • £ w <в7-“>
ГЛАВА XIII.
УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ
И ПОЛОСЫ ПРИ РАСПРЕДЕЛЁННОЙ НАГРУЗКЕ.
68. Устойчивость прямоугольной опёртой пластинки,
сжатой в главном направлении.
Из различных задач об устойчивости анизотропных
пластинок, представляющих практический интерес, лишь
сравнительно немногие подробно изучены и доведены до
численных результатов. Из них в первую очередь нужно
упомянуть о задачах об устойчивости прямоугольной орто-
тропной пластинки и пластинки в виде бесконечной
х) Здесь мы сохраняем члены 2-го порядка малости и отбрасываем
члены высших порядков.
254
волосы, деформируемой усилиями, распределёнными по
краям по простому закону. Известны решения лишь для
случаев нормальной нагрузки, равномерно распределённой
ио линейному закону, равномерно распределённой каса-
тельной нагрузки и для случая одновременного действия
нормальной и касательной нагрузки. Эти решения и рас-
сматриваются в настоящей главе.
Начнём с рассмотрения устойчивости прямоугольной
опёртой пластинки, сжатой в главном направлении.
Имеется прямоугольная ортотропная пластинка, у ко-
торой все стороны спёрты; по двум сторонам распределены
равномерно нормальные сжимающие усилия. Предпола-
гается, что главные направления в пластинке параллельны
её краям. Требуется опреде-
лить критическое значение
усилий />цР, при котором пло-
ская форма равновесия нереста- у
ёт быть единственной и устой- $
чивой формой (пластинка те- i
ряет устойчивость). I
Обозначим через а и b дли-
ны сторон пластинки, через
с — а/Ь — отношение сторон и че-
рез р—величину усилия на
единицу длины и направим оси координат по сторонам
пластинки (рис. 112).
До потери устойчивости напряжённое состояние пла-
стинки является плоским, причём Тх=^—р, Ty = Sxy^O~
Решение задачи легко получается с помощью любого
из трёх основных методов, изложенных в § 66. Мы пред-
почтём статический метод *).
Уравнение изогнутой поверхности будет:
дх* + ду* + °’
(68.1)
Нужно найти решение этого уравнения, отличное от нуляг
удовлетворяющее условиям на сторонах:
при х==0 и х = а w = 0, + (68.2)
при у —О и у=Ь w =0, 4-Vj ^ = 0, (68.3>
1) См. нашу книгу Р4], стр. 34—37. Решение этой задачи-
имеется также у Губера в книге [в2], стр. ИЗ—117.
25$
Этим граничным условиям удовлетворяет любое ив выра-
жений:
л . тт.х . плу
«' = Лтп81п — аш-уК,
(68.4)
где Лтп — постоянный коэффициент, а т и п —целые числа.
Будем искать решение уравнения (68.1) в такой форме
•(68.4). Подставляя в уравнение (68.1), получаем:
{«• [Л(")‘+2О, (=)ЧС. -
=°- (68.6)
Так как нас интересует решение, не равное нулю, то
надо приравнять нулю выражение в фигурной скобке.
Отсюда находим:
я» /Z),jDs Г ( т \ = 2Р,
------г^-' IV оЛ~) +Уг5
Постоянная Атп остаётся неопределённой. Формула
(68.6) даёт все значения р, соответствующие значениям
jh = 1, 2, 3, ..п = 1, 2, 3, ..., при которых становится
возможным искривление вида (68.4). Из всей совокупности
значений р надо выбирать наименьшее; оно и будет кри-
тическим. Очевидно, наименьшее значение р получится
при п = 1, чему соответствует искривление в направлении
стороны b по одной полуволне синусоиды. Далее нужно
определить, при каком т выражение для р, соответствую-
щее данному отношению сторон с, будет наименьшим, и
найти это наименьшее значение.
При п=1 формула для р принимает вид:
Не останавливаясь на подробностях элементарного ис-
следования выражения (68.7), приведём основные резуль-
таты.
556
1) Если отношение сторон с удовлетворяет условию.
C = (68.8)
где тп' —целое число, то в выражении (68.7) надо положить
m == и для критической нагрузки получается формула1):
(в8.9)
Это значение будет наименьшим из всех определяемых
по формуле (68.7).
2) Если
с = , (68.10)
где m — какое-нибудь целое число, то при одной и той же
критической нагрузке оказываются возможными две формы
равновесия:
с т полуволнами в направлении стороны а:
w = Ат1 sm ~ sin -A; (68.11)
с т + 1-ой полуволной:
w = Дп+1,1 Sin X------sm . (68.12)
На основании формулы (68.10) легко установить число
полуволн т9 соответствующее данному отношению с.
Именно:
если 0 < с < 1,41 , то тп = 1,
если 1,41 |Z&<c< 2,45 l/^i, то т = 2,
г г Х/а j
если 2,451/ < с < 3,46 ]/", то т = 3, J
(68.13)
и Т. д.
3) При произвольно заданном отношении сторон с кри-
тическая нагрузка определяется таким образом: устанав-
*) Эта формула выведена Ямала (см. [и]).
17 с. Г. Лехнпцкий
257
ливается число т, соответствующее данному с [на осно-
вании вышенаписанных неравенств или формулы (68.10)];
найденное значение т подставляется в формулу (68.7),
которая и даёт величину критической нагрузки. При
больших отношениях сторон е > 3 критическую нагрузку
можно определять по формуле (68.9).
Деля величину критической нагрузки на толщину
пластинки, получаем нагрузку на единицу площади, или
критическое напряжение
°кр —
(68.14)
В частном случае, когда пластинка изготовлена из
изотропного материала, = D2 = D3 = D, и критическая
нагрузка определится по формуле *)
?- = ¥("+йУ <68-15>
(для произвольного отношения с). Отношения г, при кото-
рых совершается переход от in полуволн в направлении
оси х к ?п-|-1-й полуволне, равны
с = j/m (т+1). (68.16),
Если г —число целое, то т = и
(68.17)
69* Устойчивость опёртых фанерных пластинокг
сжатых в главном направлении.
Приведём численные результаты для прямоугольных
пластинок с опёртыми сторонами, изготовленных из фанеры
и сжимаемых в одном направлении распределёнными нор-
мальными усилиями * 2). Предполагаем, как и раньше, что-
главные направления параллельны сторонам, и сжатие*
следовательно, производится в главном направлении.
2) См„ например, С. П. Тимошенко [м], стр. 320, или книгу
С. В. Серенсена [40], стр. 164.
2) См. нашу книгу [24], § 15, стр. 37— 40.
258
Формулу для критической нагрузки можно представить
в виДе:
= (69.1)
где к — коэффициент, зависящий от отношения сторон и от
отношений жёсткостей.
1) Ф а н е р а 1-гот и п а *). Если пластинка изготовлена
из фанеры 1-го типа и сжимается в направлении волокон
рубашки, то предельные отношения сторон, соответствую-
щие переходу от т полуволн в направлении сжимающих
усилий, к m+1-й полуволне, будут:
c~|/m(m + l) • 1,86. (69.2)
Отсюда получаем:
если 0 < С < 2,63, то тп = 1
если 2,63 <; е < 4,56, то тп~ 2
если 4,56 < с < 6,45, то тп = 3,
(69.3)
и т. д. Наименьшее значение коэффициента к равно:
к = 3,43; (69.4)
оно соответствует отношениям с = тп' 1,86, где т' —целое
число.
Для пластинки, сжимаемой поперёк волокон, предель-
ные отношения с определятся по формуле:
с = ]/ m (тп -|- 1) * 0,54. (69.5)
Отсюда находим:
если 0- < с < С 0,76, то тп = 1
если 0,76 : < с < - 1,31, то тп = 2
если 1,31 • < с < : 1,86, то тп = 3
если 1,86 < с < С 2,41, то тп = 4
(69.6)
и т. д. Наименьшее значение коэффициента /сив этом случае
к = 3,43; (69.7)
оно получается при с = 0,54 m', где тп'— целое число.
9 См. § 9 настоящей работы.
17*
259
В таблице 2 даны значения коэффициента к для
некоторых отношений с и указано соответствующее число
полуволн.
Т аблица 2
Значения коэффициента к для разных отношений с
(сжатие в главном направлении; фанера 1-го типа)
Сжатие вдоль волокон рубашки
с к т 0,5 15,4 1 1 5,19 1 1,86 3,43 1 2 3,45 1 2,63 3,93 1—2 3 3,62 2 со 3,43
Сжатие поперёк волокон рубашки
с
к
т
0,5
3,45
1
0,54
3,43
1
0,76
3,92
1—2
1
3,45
2
1,31
3,59
2—3
1,62
3,43
3
1,86
3,47
3-4
3,45
4
оо
3,43
Таблица показывает, что при увеличении отношения с
коэффициенты к стремятся к своим наименьшим значениям
3,43.
На рис. 113 дан график изменения к с изменением
отношения сторон с прл сжатии вдоль волокон пластинки
260
перпендикуляр до пересе-
из фанеры 1-го типа; на рис. 114 —график к для той же
пластинки, сжимаемой поперёк волокон рубашки. Эти гра-
фики состоят из отрезков кривых /с = / (с, т), соответствую-
щих разным целым значениям т. Желая по графику
определить коэффициент к для данного отношения сторон,
нужно отметить на оси абсцисс данное значение с и из
полученной точки восстановить
чения о ближайшей кривой;
длина отрезка от оси абсцисс
до ближайшей кривой даст зна-
чение А, а сама кривая ука-
жет, какое т соответствует
критической нагрузке. Напри-
мер , на рис. 113 видно, что
перпендикуляр, восставленный
из точки с = 2,63 на оси абс-
цисс, попадает в точку пере-
сечения кривых с параметра-
ми тп=1 и тп = 2; следователь-
но, при с = 2,63 возможны два
значения: тп = 1 и тлг = 2, кото-
рые соответствуют коэффици-
енту к = 3,93. Если же взять,
например, отношение с = 3,72,
то ближайшей кривой будет
кривая, соответствующая тп=2;
это даёт нам две полуволны в
направлении сжимающих уси-
лий и к = 3,43. При взгляде на графики становится понятной
неравномерность изменения к при изменении с.
Пластинка, сжатая вдоль длинных сторон, после потери
устойчивости образует ряд полуволн в направлении сжи-
мающих усилий. Таблица и графики показывают, что число
полуволн, на которые разбивается пластинка, сжимаемая
поперёк волокон, получается, как правило, значительно
большим, чем при сжатии вдоль волокон (при тех же раз-
мерах). Возьмём, например, две пластинки из фанеры
1-го типа с отношением сторон с = 2; у одной — волокна
рубашки параллельны длинным сторонам, у другой—
параллельны коротким сторонам. При сжатии вдоль
длинных сторон первая пластинка образует одну полу-
волну в направлении длинных сторон, тогда как вторая
пластинка, потеряв устойчивость, разобьётся на четыре
полуволны.
261
При больших отношениях сторон критическую нагрузку
можно считать не зависящей от с и определять по формуле
Р«р = Ь2 -3,43, (69.8)
которая пригодна как в случае сжатия вдоль волокон,
так и в случае сжатия поперёк волокон.
2) Фанера 2-го типа. Для пластинки, изготовлен-
ной из фанеры 2-го типа, получаем аналогичные резуль-
таты, только изменяются численные значения коэффици-
ентов. При сжатии вдоль волокон предельны? определятся по формуле с = ]/ т (т +1) • 1,18; значения с (69.9)
отсюда следует, что
если 0 < с < 1,66, то иг=1; 1 если 1,66 < с < 2,88, то т = 2; 1 если 2,88<с<4,08, то т = 3? | (69.10)
и т. д. При сжатии поперёк волокон рубашки отношение с равно предельное
с = у т (т г 1) -0,84; (69.11)
отсюда получаем числа полуволн:
если 0 < с < 1,19, то т = 1; 1 если 1,19 < с < 2,05, то т —2; 1 если 2,05<с<2,91 то тп = 3; j если 2,91 < с < 3,77 то /лг — 4, j (69.12)
и т. д.
Наименьшее значение коэффициента к из формулы (69.1)
к — 2,43 (69.13)
при сжатии как вдоль, так и поперёк волокон; соответ-
ствующее значение с при сжатии вдоль волокон с —1,18 т',
а при сжатии поперёк волокон с —0,84 пг'.
В таблице 3 приведены значения к для некоторых
отношений с.
262
Таблица 3
Значения коэффициента к для разных отношений с
(сжатие в главном направлении; фанера 2-го тина).
Сжатие вдоль волокон рубашки
с 0,5 1 1,18 1,66 2 2,36 2,88 3 оо
к 6,26 2,55 2,43 2,89 2,55 2,43 2,58 2,55 2,43
т 1 1 1 1—2 2 2 2—3 3 —-
Сжатие поперёк волокон рубашки
с 0,5 0,84 1 1,19 1,68 2 2,05 3 оо
к 3,61 2,43 2,55 2,93 2,43 2,55 2,59 2,48 2,43
! т 1 1 1 1 1—2 2 2 2—3 4 —
?0. Устойчивость прямоугольной пластинки с двумя
опёртыми сторонами при сжатии в главном направлении»
Если у пластинки, изображённой на рис. 112, нагру-
женные стороны х = 0 и х — а опёрты, а стороны г/ = 0,
у~Ь закреплены как угодно или свободны, то решение
уравнения (68.1) следует искать в форме:
^ = /(у)81п^. (70.1)
Это выражение удовлетворяет условиям на опёртых
сторонах. Подставляя выражение (70.1) в (68.1), получим
уравнение для определения /:
A/lv-2 = (70J)
Обозначим корни характеристического уравнения
_2 (7)SP,s2 + 7Л Р (7)’ = о (70.3)
соответственно через ± ±*Л25 где
(70.4)
263
Выражение для прогибов принимает вид:
w = (A ch + кгу+С cos к2у ~\-D sin Лйу) sin . (70.5)
Постоянные A, J5, С, D определяются из условий на
сторонах а. На каждой из сторон имеем по два условия, а
всего четыре условия; столько же мы имеем неизвестных ко-
эффициентов. Следовательно, мы можем удовлетворить усло-
виям на сторонах а при любом способе их закрепления.
Выполняя это, получим однородную систему из четырёх
уравнений для А, В, С, D; приравнивая нулю определи-
тель этой системы, получим уравнение для определения
р. Из всех решений последнего надо взять наименьшее, не
равное нулю, которое и будет критической нагрузкой рКр.
В настоящее время до численных результатов доведён,
невидимому, только один случай, когда обе стороны = 0
и у — Ь заделаны (не считая случая четырёх опёртых сторон,
разобранного в § 68). Результаты можно сформулировать
следующим образом1):
1) критическая нагрузка определится из уравнения
th kJ tg kJ = (1 —. * . , Л (70.6)
(которое, разумеется, неразрешимо относительно р);
2) для длинных пластинок, у которых отношения с >
критическую нагрузку можно считать не зависящей от с.
Для длинной пластинки, изготовленной из фанеры 1-го
типа, при сжатии вдоль волокон и поперёк волокон,
^ = "**^6,34. (70.7)
Сравнение этой формулы с формулой для опёртой по всем
четырём сторонам фанерной пластинки показывает, что за-
делка продольных сторон увеличивает критическую нагруз-
ку почти вдвое.
Для изотропной пластинки2)
7- (70.8)
Точное определение критической нагрузки для пластинки
с двумя опёртыми сторонами связано с решением сложно-
2) См. [*], стр. 25—26, или [42], стр. 244.
я) См. [“], § 65, стр. 349.
264
го трансцендентного уравнения1). С помощью энергетиче-
ского метода можно получить приближённые формулы для
определения критической нагрузки.
Полагая, что после потери устойчивости пластинка
(сжатая в главном направлении) изогнётся по синусоиде я
направлении сжимающей нагрузки, будем искать выраже-
ние для прогиба в форме (70.1).
Потенциальная энергия при искривлении пластинки
увеличится за счет энергии изгиба, которая определяется
по формуле (38.19), и ц данном случае равна
- A/SS. j [ /- - 2 (™)' j/g fl-+
+С?)‘/%'+(W
При искривлении пластинки сжимающие усилия произве-
дут работу, равную *):
Л = ( fdy.
О
Приравнивая выражения (70.9) и (70.10), получим::
___ ь _____ _
р~ т^тг / Rff+
о
<7ол1>
Далее подберём выражение для функции /, удовлетво-
ряющее условиям на сторонах а и дающее гладкую поверх-
ность, в виде суммы с неопределёнными коэффициентами:
/= 2 (70.12>
*) Исключение составляет только случай пластинки с четырьмя
опёртыми сторонами (см. п° 68)
») См. (67.11).
265.
Подставляя это выражение в формулу (70.11), ищем ми-
нимум р, а это, как было указано в § 62, равносильно
разысканию минимума выражения:
v- 5 ХтХ/I«'+Ст)I-
+ (п™\- Р---2 f- 1 dy. (70.13)
Для пластинки с заделанными сторонами у-^0, у^Ь
можно положить:
/n(2/)=l-cosln'2/, (70.14)
/ = ^ Ип (1 - cos . (70.15)
71
Остановимся более подробно на первом приближении.
В первом приближении для пластинки с двумя опёртыми
и двумя заделанными сторонами примем:
/ = л( l-cos^y-Q , (70.16)
где /2 -целое число, которое надлежит далее определить.
Подставляя в формулу (70.11), получим:
+ <7ол7)
Очевидно, наименьшее значение р будет при п==1, и,
^следовательно, критическая нагрузка определится по фор-
.муле: __
+з'зз/йХЛ (7ол8>
Далее, надо установить число полуволн в направле-
нии сжимающих усилий которые образует пластинка,
потерявшая устойчивость.
256
Результаты исследования формулы (70.18)^ которое про-
водится так же, как для пластинки с четырьмя опёртыми
сторонами, сводятся к следующему:
1) Если отношения сторон удовлетворяют условию:
с = 0,658
(70.19)
где т" — целое число, то т-т'. и
^£^2,67 (1,73 + р^-). (70.20)
Это значение будет наименьшим из всех, определяемых
по формуле (70.18).
2) Если
е
= 0,658 |7 т (т ~|~ 1)
(70.21)
где гп — целое число, то при одной и той же критической
нагрузке возможны в направлении оси х формы равновесия
с т полуволнами и с т + 1-й полуволной:
. / . 2ю/ \ . ткх.
w = А ( 1 — cos Jsin ---
(70.22)
tv — A fl — cos ~
\ 7
. (т 41) к.г
SIH '-—~
(70.23)
Для отношений с, не удовлетворяющих условиям (70.19)
или (70.21), число полуволн определяется на основании
нижеследующих неравенств:
то т = 1; )
то т=‘2; [ (70.24)
то т = 3,
II т. д.
3) Для определения критической нагрузки при задан-
ном отношении сторон определяем число т на основании
неравенств (70.24), т. е. устанавливаем, в какой строке
находится данное отношение, а найдя т, находим ркр.
по формуле (70.18). Для больших отношений сторон
критическую нагрузку можно определять по форму-
ле (70.20).
Для длинной изотропной пластинки в первом прибли-
жении
^р = ^Е^1Ь7,29, (70.25)
тогда как в точдой формуле (70.8) стоит коэффициент 7.
Погрешность первого приближения доставляет около 4%.
Для длинной пластинки из фанеры 1-го типа в первом
приближении
?kp = "2Eljl£?6,54. (70.26)
Рис. 115.
Если принять, что формула (70.7) является точной, то
погрешности первого приближения (70.26) составит 3,2%.
Заметим, что в первом приближении мы получаем преуве-
личенные критические нагрузки (по сравнению с более
точными значениями), так как по
Р существу заменяем исследуемую
Л пластинку более жёсткой систе-
мой.
71. Устойчивость пластинки,,
сжатой по двум направлениям.
Прямоугольная ортотропная
пластинка, у которой главные на-
правления параллельны сторо-
нам, сжимается нагрузкой рх, распределённой равномерно
по двум сторонам, и нагрузкой pff, распределённой равно-
мерно по другим сторонам (рис. 115). Задача об устой-
чивости такой пластинки решена для случая всех че-
тырёх опёртых сторон; для получения решения удобно
использовать статический метод г).
х) Приведённые* в этом параграфе решения имеются в нашей ра-
боте [24], j стр. 43-45.
268
Уравнение прогибов будет иметь вид:
+ ^D* dx*dt/2 + ^2ду* + Р*Эх* + Р”ду*
Ищем решение в форме
л . тпх . ппу >^4
W = Лта81» — 81П -^ . (71.2)
Требуя, чтобы выражение (71.2) было решением уравне-
ния (71.1), получаем зависимость:
О’МЯ=
=’'’[°1(т)‘+22’.(а?)’+й-(^)‘] • (7L3>
Далее, для определённости задачи необходимо задать
дополнительные условия для усилий рх и pff, указав, как
эти величины связаны между собой. Связь, разумеется,
может быть различной; одно из усилий может быть по-
Ч5тоянным, а другое переменным, или отношение усилий
остаётся постоянным и т. п. Если одно из усилий растя-
гивающее, его в уравнении (71.3) нужно взять со знаком
минус.
Рассмотрим подробнее несколько частных случаев рас-
пределения усилий.
1) Усилия рх и pv меняются, но отношение их вели-
чин остаётся постоянным:
/>« = *, рв = Ха.
Критическое значение X определяется на основания
формулы:
Дальнейшая задача состоит в отыскании значений m
я и, которым соответствует наименьшее к, и самого кри-
тического значения. Если усилия р0 растягивающие, то
нужно взять а со знаком минус.
26»
Приведём некоторые результаты для квадратной пла-
стинки, изготовленной из фанеры 2-го типа.
а) Квадратная пластинка сжата усилиями, распреде-
лёнными равномерно по всем сторонам (рх = ру = К, 7.^1):
• 1,28, w=l, л=1. (7J.5)
Потеряв устойчивость, эта пластинка образует по од-
ной полуволне в направлении сторон.
б) Квадратная пластинка сжимается усилиями, равно-
мерно распределёнными по двум сторонам, и растягивает-
ся усилиями той же величины, равномерно распределён-
ными по другим сторонам
= \ э.= -1).
При сжатии вдоль волокон рубашки и растяжении по-
перёк волокон
Х/р=^А.8,35, т = 2, п=1. (71.6)
При сжатии поперёк волокон и растяжении вдоль во-
локон
• 4,82, m = 2, п = 1. (71.7)
В первом случае пластинка более устойчива; критическое
значение Хкр больше той же величины для второю случая
примерно в 1,7 раз. В обоих случаях при потере устой-
чивости образуются две полуволны в направлении сжи-
мающих усилий и одна полуволна в направлении растя-
гивающих усилий.
Для опёртой изотропной пластинки с произвольным от-
ношением сторон е, сжатой усилиями К, распределёнными
равномерно по четырём сторонам, получается х):
= «=1- <71.8).
’) См. (“], § 61, стр. 325.
270
2) Вдоль сторон я —О, х = а распределены равномерно
сжимающие усилия X, а по сторонам ^ = 0, у — Ь — растя-
гивающие усилия /?; сжимающие усилия могут меняться
по величине, а растягивающие остаются неизменными. Тре-
буется оценить влияние дополнительных растягивающих
усилий на величину критической сжимающей нагрузки.
В формуле (71.3) надо положить />х=^Х, — р; тогда
Z>2 •
рЬ2п-
Наименьшее значение X получится, очевидно, прип=1,
когда в направлении растягивающих усилий образуется
одна полуволна. Результат дальнейшего исследования вы-
ражения (71.9) моя но сформулировать таким образом^
а) Если отношение сторон с удовлетворяет условию
(71.10),
1/ I fib
V
где т' —целое число, то критическое значение X равно:
= 1+^+^^=), (71.11)
Это значение будет наименьшим из всех, определяемых
по формуле (71.9), а отношения сторон (71.10) будут
невыгоднейшими. Дополнительные растягивающие усилия,
как и следует ожидать, увеличивают критическую нагруз-
ку, т. е. повышают устойчивость пластинки.
б) Предельные отношения сторон, при которых проис-
ходит переход от т полуволн в направлении сжимающих
усилий к m + 1-й полуволне, равны:
yf т (т 4- 1)
?/
V Dy
(71.12)
При хаких отношениях сторон пластинка наиболее'
устойчива.
Рис. 116.
Ч-i. Устойчивость пластянви, нагруженной нормальными
усилиями, распределёнными по линейному закону.
Прямоугольная ортотропная пластинка деформируется
усилиями, распределёнными по двум сторонам по линей-
ному закону (рис. 116):
? = к(1-“69 . (72.1)
Главные направления параллельны сторонам. Критиче-
ское значение Хкр опре-
делено приближённо
для случая, когда все
четыре стороны опёрты
(что мы и будем пред-
полагать) *).
Уравнение прогибов
будет в данном случае
иметь переменный коэф-
фициент, и интегриро-
в ание его оказывается
затруднительным. Для
решения задачи удобнее применить энергетический метод,
не связанный с интегрированием каких-либо уравнений.
Если пластинка получит малые прогибы, то внешние
усилия произведут работу, равную 2)
а Ъ
о о
Потенциальная энергия изгиба определится
ле (38.19). Из уравнения
изг = А
дюлучаем:
(72.2)
по форму-
(72.3)
(72.4)
а b
1) Решение этой задачи имеется в нашей работе [м]. $ 13,
-стр. 46—50.
*) См. формулу (67.11).
-272
где
л-n , on . , n . zn f d*w V
1 V®2/ Qch/V + Ы>к\&хду) ’
Выражение для прогибов, удовлетворяющее всем усло-
виям на сторонах, можно взять в виде:
Xi V' а • m7Z% • игсу
=2а 281П ~8Ш Т
(72.5)
тп п
Подставляя это выражение в формулу (72.4) и произ-
ведя указанные там действия, мы в результате получим
дробь, числитель и знаменатель которой—однородные
квадратичные функции коэффициентов Атп.
Все интегралы, с которыми придётся иметь дело, све-
дутся к нижеследующим:
а
. ТППХ . J С 7П7С.Г Ых > л
sin—sm—dx = \cos—cos—ах = 0 для i
a a J a a ’
и
a
C o mnx T a
\ cos2 dx~ — ,
J CL &
b
cos cos ^dy = 0 для j #= n,
О
а
С . й тпх ,
\ sin2---dx
J а
о
ъ
С . пт/ . jm/ 1
\ sm -^sin^—aw
J Ъ b &
и
sin2 r~ dy^
и
472.6)
и
5со»-7^-А;
О
(для n ± /
нечётных), /79 7\
(для n ±/
чётных)
Ь . / 4ab nj
0 ~a^) S^nT^ = у (и2—72)2
(72.8)
Мы ограничимся приближённым решением задачи. В пер-
вом приближении положим
ф = Лт1йш -— sm -у-
а Ъ
(72.9)
w
а
38 С. Г. ЛехницкпЙ
273
и получим:
+ )’]• (72Ло>
Это значение отличается от ХкР для пластинки, сжатой в
одном направлении равномерно распределённой нагрузкой,
лишь делителем 1 — ~ , а потому все выводы из формулы
(68*7) применимы и в данном случае. Иначе говоря, в пер-
вом приближении критическая нагрузка для пластинки
со сторонами а, Ь и отношением с определяется, как для
пластинки со сторонами а yf и 6 рЛ 1--^, сжатой
равномерно в одном направлении. Для изотропной пла-
стинки первое приближение даёт удовлетворительные ре-
зультаты лишь при а < 0,6, когда преобладают сжимаю-
щие усилия. Формула теряет смысл, когда а — 2, т. е.
имеет место чистый изгиб.
Второе приближение получим, взяв в выражении (72.5)
два члена:
(Anisin ^ + Лт2sin sin^ . (72.11)
Коэффициенты Ат1 и Лт2 нуж.но подобрать так, чтобы
для X получилось наименьшее значение. Задача отыска-
ния минимума дроби равносильна задаче отыскания ми-
нимума интеграла г):
а Ъ
о о
+ (£)]*^.(72.12)
После подстановки и интегрирования получаем:
у [ami-k'(l-у)] +
. (72.13)
х) См. § 62, формулы (62.8)—(62.12).
274
Здесь введены сокращённые обозначения:
Составляя производные от U по ЛтиЛт8и приравни-
вая их нулю, получаем уравнения:
16 аЛ'_Л
“9^ ~U’
- + [aml->/ (1 -] =0. ,
(72.15)
Приравнивая нулю определитель этой системы, полу-
чаем две серии значений к:
Дальнейшая работа сведётся к отысканию числа тп1,
которому, при данном отношении сторон, соответствует
наименьшее К, и отысканию этого наименьшего значения,
которое и будет, во втором приближении, критическим.
Задача доведена до численных результатов для пла-
стинки из фанеры 1-го и 2-го типа, работающей при чистом
изгибе (а = 2; на одной половине стороны b действуют
сжимающие усилия, на другой — растягивающие). Если
обозначить через М момент усилий, то критическое
значение изгибающего момента 7Икр определится, как
наименьшее значение выражения
М ~ — |/ад • / (72.17)
18*
275
Формулу для критического момента представим в виде:
к.
(72.18)
Критическое напряжение в крайних волокнах пла-
стинки равно:
тс2 к
Ь2 ' h'
(72.19)
Значения коэффициента к для фанерных пластинок
приведены в таблице 4; там же помечено число полуволн т,
на которые разбивается пластинка, потерявшая устойчивость.
Таблица 4
Значения коэффициента к для фанерных пластинок
(изгиб моментом)
Фанера 1-го типа Фанера 2-го типа
Волокна перпендику- лярны к нагружен- ным сторонам Волокна парал- лельны нагру- женным сторо- нам Волокна пер- пендикулярны к нагружен- ным сторонам Волокна парал- лельны нагру- женным сторо- нам
с к 1 1 Тп к т к ' 1 т 7с т
0,5 49,5 1 23,5 1 22,2 1 16,9 1
1 23,5 1 22,2 3 16,9 1 16,9 2
2 23,5 2 21,9 5 16,9 2 16,5 3
3 22,2 2 24,9 7 16,5 3 16,3 5
Дальнейшие уточнения коэффициента к получим, взяв
третье приближение:
w = (4ni sin у + Атг sin + Дпз sin v) sin (72<2°)
Для изотропной пластинки, изгибаемой моментами, кри-
тическое напряжение во втором приближении определится
по формуле *):
°гф = зг5?(1 + с2И1 + 4с2)- (72-21)
1) См. [44], стр. 332, или [40], стр. 169.
276
73. Устойчивость прямоугольной пластинки под
действием касательных усилий.
Прямоугольная ортотропная пластинка деформируется
касательными усилиями £, распределёнными равномерно по
всем четырём сторонам (рис. 117). Главные направления
параллельны сторонам; все стороны опёрты. Требуется
определить критические у си-
лия ^р, при которых пла-
стинка потеряет устойчивость, г-
Эта задача решена прибли- |
жённо энергетическим методом. .
Работа касательных усилий, & |
соответствующая малым про-
гибам, равна1):
о
t
— а —
Рис. 117.
а Ъ
(’ЗЛ>
о о
Приравнивая эту работу потенциальной энергии изгиба,
получаем:
а Ъ
о и
a b
о 0
(73.2)
где
1 z
‘ 1 (Jy~
Выражение для прогиба ей, удовлетворяющее всем
условиям на сторонах, можно взять в виде суммы:
»’=22^"=i"“Ista-7- <73-3>
m п
При вычислении интегралов следует учесть равен-
ства (72.6) —(72.7), а также следующее:
« /2а
Г . wittz inx , | —
। sin — cos —dx = 2 «
J (0
(для тп ± i нечётных)
(для тп ± i чётных).
*) См. формулу (67.11).
277
Дальнейший ход решения задачи в общем такой же,
как и в случае нормальной нагрузки, распределенной по
линейному закону (см. § 72).
Задача доведена до численных результатов и расчёт-
ных формул для пластинки из фанеры 1-го типа
Я. И. Секерж-Зеньковичем *). Укажем важнейшие резуль-
таты.
Если волокна рубашки параллельны длинным сторонам,
то достаточная для практики точность достигается, если
взять выражение для прогиба в виде суммы пяти членов.
А1 81П - + 81П — J 81П f 4- Q Аз Sin - 4-
. i . ЗзыА . Зпу . . . 2тгх' . 2tzj
4-Аз sin— J 81П-^4-Л22 Sin— sin (73.5)
Для постоянных Ad получается система из пяти однород-
ных уравнений, определитель которой зависит от t и
должен равняться нулю.
Рассматривая пластинку, у которой волокна рубашки
параллельны коротким сторонам, упомянутый автор, желая
получить ту же точность, брал различное число членов
суммы (73.3) в зависимости от отношения сторон. Для
квадратной пластинки выражение для w бралось в виде
(73.5). Для пластинки с отношением сторон с — 2 полагалось:
w = (Л1 sin 2~~ 4- Ах sin sin ^ +
4- (Аз sin 4- Аз sin sin . (73.6)
Для пластинки с отношением сторон с~ 3 было принято:
»=(л. sin V+-4.1 sin v) sin'i +
+ (Л, sin + Л., sin sin 5.’. (73.7)
Критическая нагрузка определяется по формуле:
(73.8)
где к — коэффициент, зависящий от отношения сторон.
х) См. работу [39].
273
Критическое касательное напряжение получим, деля
нагрузку на толщину h:
ткр=10‘ (4)**- (73.9)
В следующей таблице приведены численные значения
коэффициента к для некоторых отношений с.
Таблица 5
Значение коэффициента к для разных отношений с
(касательные усилия; фанера 1-го типа).
Для пластинки из фанеры 1-го типа предложены также
следующие приближённые формулы х):
а) волокна рубашки параллельны длинной стороне:
. . 2,08ч.
^ = -^0,664 + ^--);
(73.10)
б) волокна рубашки параллельны коротк,ой стороне:
^ = ^3(2,3 + °4-6). (73.11)
В этих формулах с = а / 6, а > Ь; Е'— модуль Юнга
для направлений, параллельных волокнам рубашки.
Первая формула даёт погрешность не более 4%, вто-
рая—до 2%.
См. [42], стр. 246.
279
74. Устойчивость бесконечной полосы под действием
касательных усилий.
Z
Рис. 118.
Если отношение сторон велико (с >4), то можно пре-
небречь влиянием коротких сторон и рассматривать пря-
моугольную пластинку, как бесконечную полосу.
Рассмотрим бесконечную полосу, по сторонам которой
распределены равномерно касательные усилия t на единицу
длины (рис. 118). Строгое ре-
шение задачи об устойчивости
получено Зейделем для орто-
тропной полосы с главными
направлениями, параллельными
и перпендикулярными к сторо-
нам, в случае опёртых и за-
деланных сторон; решение най-
дено с помощью статического
метода х).
Viiuvricivi ьирагцс, tian получено это решение, и приведём
основные результаты.
Уравнение прогибов имеет вид:
+ ^. + ^+2^ = 0. (74.1)
Требуется найти решение, этого уравнения, неравное
нулю и удовлетворяющее условиям:
а) на опёртых сторонах
дуг 1 дх*
б) на заделанных сторонах
* = % = 0.
<>у
Решение ищется в форме
«, = /(у)е«'Я! (/ = ]/^Л).
Для функции / получается уравнение
Dtfv-2D, (^Уг + it %f+Dt (^у /==0,
(74.2)
(74.3)
(74.4)
(74,5)
*) Работы [’°] — [”].
280
общий интеграл которого зависит от корней характери-
стического уравнения:
- 2D, (£)2 s2 + it % s + А У = 0. (74.6)
bs
Введя новую величину ? = получим для неё урав-
нение
f^W-Ciyg^ + ^O. (74.7)
Корни этого уравнения имеют вид:
^ = а(1 + п), ₽, = а(1-и), |
Р8 = а(-1 + т), pt = a(-l — пг), J '
где а — вещественное число, т и п —вещественные или
комплексные числа.
Выражение для прогибов получается в таком виде:
iu 2-^ in w «Л
w = e* \С1еъ У + С2е^ У+ Съе* Л (74.9)
На основании граничных условий (74.2) или (74.3) по-
лучаем четыре однородных уравнения для постоянных
С„ С„ С4 и, приравнивая нулю определитель, получаем
уравнение для определения критического усилия £кр.
Нагрузка t, при которой становится возможным искрив-
ление, получается, как функция величины х. Далее, нужно
определить х, при которой получается наименьшее значе-
ние ?, и само это наименьшее значение, которое и будет £кр.
Потеряв устойчивость, пластинка образует ряд волн,
идущих под углом к сторонам; длина волн характеризуется
параметром х.
Зейдель вводит величину & = и приводит резуль-
таты вычисления критической нагрузки в зависимости от
величины 0.
Для пластинок, у которых & лежит в пределах от 1 до оо,
получаем:
= (74.10)
'-C'AVs.- <’4-“)
значения коэффициентов Са и С' приведены в таблице 6.
281
Значения коэффициентов Са и
Таблица 6
Стороны , ъ У = ±т опёрты Стороны 1/ = ±У заделаны
_ 0 Са 1 С'а Са 1 С'а
1 13,17 2,49 22,15 1,66
2 10,8 2,28 18,75 1,54
3 9,95 2,16 17,55 1,48
5 i 9,25 2,13 16,6 1,44
10 8,7 2,68 15,85 1,41
20 8,4 15,45 ——
30 II 2,05 1,38
40 8,25 — 15,25 ——
со 8,125 —— 15,071 1 ""
Для пластинок, у которых & лежит в пределах от 0 до 1,
(74.12)
«=с;|/й- <74ЛЗ>
Значения коэффициентов Съ и С'ъ приведены в таблице 7 .
Таблица 7
Значения коэффициентов Сь и С’ъ
Стороны 1/=±~Г опёрты С тороны У = ± 2 заделаны
0 Сь Съ Съ C'b
0 11,71 1 18,59
0,05 — 1,92 — 1,16
0,2 11,8 1,94 18,85 1,20
0,5 12,2 ! 2,07 19,9 1,36
1 13,17 2,49 22,15 1,66
282
Для полосы с опёртыми сторонами, которая может и не
быть ортотропной, можно получить приближённое решение
по методу С. П. Тимошенко.
Рассмотрим сначала ортотропную пластинку, у которой
главные направления параллельны и перпендикулярны
сторонам.
Направим оси не так, как на рис. 118, а несколько
ин аче: примем к аку ю-нибудь точку на стороне полосы
за начало координат, а ось х направим по стороне. Будем
искать приближённое решение уравнения (74.1) в форме
tv = Л sin у sin $ (гс — у tg ф). (74.14)
Это выражение удовлетворяет нужным граничным у ело-
виям и представляет собой уравнение поверхности с косыми
волнами, длина которых в направлении оси х равна s,
а угол наклона к оси у равен ф. Точного решения в такой
форме не существует, но можно подобрать величины s, t
и ф, так что выражение (74.14) будет приближённым реше-
нием уравнения (74.1). Воспользуемся приёмом С. П. Тимо-
шенко х), а именно*, подставим выражение (74.14) в левую
часть уравнения (74.1), результаты подстановки умножим
на sin у sin у {х — у tg ф) dxdy и проинтегрируем по у
в пределах от 0 до Ь и по х в пределах от 0 до 5. Замечая,
что
Ъ 8
5 5 sin7сое у sin у (ж— г/cos 7 (ж — ylgtydxdy^Q,
О о
тогда как
ь s
sin2 у sin2 у (z — у tg ф) dx dy =# О,
о б
приравняем нулю коэффициент при последнем интеграле.
Тогда получим:
+ + + <74.15)
См. [44], § 63д стр. 339.
283
Здесь обозначено:
Y=(y)* 2> a=tg<[>. (74.16)
Ищем минимум выражения (74.15), которое является
функцией- двух переменных а и у, по обычным правилам,
т. е. решаем уравнения:
Я-0- «->°- (74Л7>
Подставляя найденные отсюда а и у в формулу (74.15),
получаем искомое критическое усилие.
Сложная формула, определяющая критическое каса-
тельное усилие, может быть упрощена для пластинок
с резко выраженной анизотропией, когда жёсткость в одном
направлении в несколько раз больше жёсткости в другом
направлении (такими являются, например, пластинки из
фанеры 1-го типа). Для этих пластинок критические каса-
тельное усилия можно определять по следующей прибли-
жённой формуле х):
4 + + (74.18)
В случае заделанных сторон полосы, изготовленной из
фанеры t-го типа, критическая нагрузка определится по
формуле 2):
f __3,45тс2 1/гР2Р3 , / / I 3 » D3 .г* г
Указанным выше приёмом можно получить приближён-
ное решение и для ортотропных пластинок с главными
направлениями, не параллельными сторонам. В этих
случаях, направляя ось х вдоль стороны и ось у перпен-
дикулярно к сторонам, нужно предварительно вычислить
жёсткости Dn, . .., Dee для направлений х и у
[по формулам (45.6)] и вместо уравнения (74.1) рассмотреть
х) См. работу [2], стр. 31.
2) Эта формула получается таким же путём, vto и (74.18),
и является приближённой. Она следует из формулы (47) в работе [2],
стр. 33.
?84
уравнение:
D„ + 40ie + 2 (Dlt + 2Dtt) +
11 дх* хв дх? ду ' 18 6в/ дх2 ду2
+ 4D26 Д^ + Л82^+2*Х^- = 0- (74.20)
26 дхду* 1 3 ду* 1 дх ду ' '
Приведём численные результаты для полосы из фанеры
первого типа, у которой волокйа идут под углом в 45°
к сторонам *). Если усилия по отношению — __
к волокнам действуют, как показано па
рис. 119, а («сдвиг под углом в 45°»),
то
fKp = 10* • 9,21. (74.21)
Если усилия действуют так, как по-
казано на рис. 119, b («сдвиг под углом
в 135е»), то для этого случая
«1<Р = 10‘ • 50,66 . (74.22) Рис- 119-
В последнем случае полоса оказывается значительно
более устойчивой, чем при «сдвиге под углом в 45°»,—кри-
тическая нагрузка в 5г/а раз больше. Формулы (74.21)
и (74.22) применимы к пла-
стинке, у которой отношение
сторон не меньше 4.
75. Устойчивость пластинки
при совместном действии
нормальной и касательной
нагрузки.
Рассмотрим прямоуголь-
ную пластинку с опёртыми
сторонами, которая дефор-
мируется нормальными усилиями р (на единицу длины),
распределёнными равномерно по двум сторонам, и касатель-
ными усилиями t, распределёнными равномерно по всем
четырём сторонам (рис. 120). Пусть требуется определить
критические значения усилий.
х) См. работу [8], стр. 35, или [42], стр. 247.
28'5
В настоящее время известно лишь приближённое реше-
ние для бесконечной полосы, сжатой вдоль сторон, и дефор-
мируемой также касательными усилиями (с™ со). Это
решение найдено Л. И. Балабухом по предложенному
G. П. Тимошенко методу, использованному в предыдущем
§ 74 Ч.
В случае ортотропной полосы с главными направле-
ниями, параллельными и перпендикулярными сторонам,
уравнение изогнутой поверхности имеет вид:
d*w , d*w . d*w , d2w п. d2w л
ZX -л—! -4- 2ZL т—й й 4- D» -7Г-1 4- р ъ~8 — — 0* (* 6.1)
1 дх* 1 3 ох2 ду2 1 2 ду* г дх2 дх ду v '
Приближённое решение этого уравнения, удовлетворяю-
щее условиям на сторонах, ищем в форме:
w = A sin у sin ~ (я -- г/ tg ^). (75.2)
Подставим выражение (75.2) в левую часть уравне-
ния (75.1), умножим результат подстановки на
sin у sin у (х — у tg <р) dx dy,
проинтегрируем по у от 0 до Ь и по х от 0 до s и потре-
буем, чтобы результат был равен нулю. Тогда получим
зависимость:
I 1 Ь2 1 + j/^(a‘Y + 6x2+ |)]+2a*, (75.3)
где a==tg^ (75-4)
Считая временно усилия t постоянными, будем искать
минимум /?, как функции двух переменных а и у. Из урав-
нений
д_Р
да
О,
(75.5).
См. работу [2].
286
получаем зависимости:
(75.6)
_ Г D2
D^ + W^ + D^'
Подставляя значение у в (75.3) и первую формулу (75.6)
получаем:
(75.7)
Эти равенства дают в параметрическом виде зависимость
между р и при выполнении которой наступает потеря
устойчивости; они получают
наглядность, если дать им сле-
дующее геометрическое истол-
кование.
Если изменять параметр а
от 0 до бесконечности и откла-
дывать соответствующие зна-
чения р по оси абсцисс, а зна-
чения t по оси ординат, то
получится кривая, напоми-
нающая квадратную параболу
(рис. 121). Отрезок на оси
абсцисс от начала координат
равен по величине критиче-
скому сжимающему усилию р^ при отсутствии касатель-
ных усилий, а отрезки, образуемые кривой на оси ординат,
равны по величине критическому касательному усилию
при отсутствии нормальных усилий х). Принимая кривую
за квадратную параболу, можно представить зависимость
между р и t в виде:
+ 4- = 1.
^кр *кр
(75.8)
1) График имеется в курсе [8], § 93, стр. 263.
287
Так как р’кр и <кп мы определять умеем (см. §§ 68 и 74),
то из уравнения (75.8) всегда можем найти критическую
нормальную нагрузку при заданных касательных усилиях
или критические касательные усилия при заданных нор-
мальных усилиях, или, наконец, критическое значение Хкр,
если нормальные и касательные усилия заданы с точ-
ностью до множителя X (т. е. если задано отношение их
величин).
Критическая нормальная нагрузка РкР для ортотропной
полосы равна: ___
+ (75.9)
Критическая касательная нагрузка рассматривалась
в предыдущем § 74. Для таких пластинок, у которых
жёсткости для главных направлений сильно разнятся друг
от друга (например, для фанеры 1-го типа), можно восполь-
зоваться приближённой формулой:
<75ЛО>
где акр и х™ напряжения: критическое нормальное и каса-
тельное х).
Уравнением (75.8) можно пользоваться и в случае заде-
ланных сторон полосы. В этом случае для фанеры 1-го типа
нужно /?нр взять по формуле (70.7), а ^р по формуле (74.19).
Для фанеры 1-го типа и ей подобных материалов
вместо (75.10) будем иметь уравнение * 2).
°кр
*с2
3, 5тС2
b'2h
(/ад+Л)- (75.11)
7? (>. + ».
Задача усложняется, если главные направления идут
под углом к сторонам пластинки. Л. И. Балабух довёл
до численных результатов решение задачи для пластинки
из фанеры 1-го типа, опёртой, у которой волокна рубашки
идут под углом в 45° к сторонам. Эти результаты сводятся
к следующему.
х) См. работу [2], стр. 31. Мы пользуемся несколько иными
обозначениями.
2) Работа [*], стр. 33. Уравнение (75.11) — приближённое; оно
даёт преуменьшённые значения критических напряжений.
288
Условимся считать положительными касательные уси-
лия, производящие сдвиг под углом в 45° (рис. 119, а),
а отрицательными — касательные усилия, производящие
сдвиг под углом в 135° (см. рис. 119, 6), й обозначим через
^кр и ^кр величины критических касательных усилий, произ-
водящих сдвиг под углом в 45° и в 135° при отсутствии
нормальной нагрузки. Для критических значений р и t нор-
мальной и касательной нагрузок, действующих совместно,
получается параметрическое представление такого же типа,
что и (75.6), только с более сложными выражениями, зави-
сящими от а. Анализируя эту зависимость, удалось под-
метить следующее. Если давать параметру а различные
значения и откладывать соответствующие р по оси абсцисс
и t по оси ординат, то получится кривая, напоминающая
параболу х). Эта кривая образует на оси абсцисс отре-
зок Ркр, равный по величине критической сжимающей
нагрузке для сжатия под углом в 45° к волокнам рубашки.
Принимая кривую за параболу, представим (приближённо)
зависимость между р и t в виде уравнения:
<7S-12>
Значения и *кр приведены в § 74 для фане-
ры 1-го типа; критическая сжимающая нагрузка
при сжатии под углом в 45° к волокнам рубашки,
по Л. И. Балабуху, приблизительно равна критиче-
ской нагрузке при сжатии вдоль и поперёк волокон ру-
башки.
Уравнение (75.12) позволяет определять критическую
сжимающую нагрузку при заданных касательных усилиях,
критические касательные усилия при заданных растяги-
вающих или сжимающих усилиях и т. д.
Интересно отметить, что при положительных каса-
тельных усилиях величина критической сжимающей
нагрузки уменьшается, а при отрицательных касатель-
ных усилиях —увеличивается по сравнению с усилиями
при отсутствии касательной нагрузкиа). Таким об-
разом, оказывается возможным увеличить устойчивость
сжатой полосы путём распределения по её краям каса-
тельных усилий.
*) Ом. [а1, стр. 35.
а) См. [*], стр. 36.
19 С. Г. Лехницкии 28$
ГЛАВА XIV.
УСТОЙЧИВОСТЬ ПЛАСТИНОК, СЖАТЫХ
СОСРЕДОТОЧЕННЫМИ СИЛАМИ.
76. Устойчивость прямоугольной пластинки, нагруженной
сосредоточенными силами.
В настоящей главе рассматриваются некоторые случаи
устойчивости анизотропных пластинок, когда нагрузка
задана в виде сосредоточенных сил.
Рассмотрим сначала анизотропную однородную прямо-
угольную пластинку, у которой две противоположные сторо-
ны закреплены произвольно или свободны, а две другие
опёрты и подвергаются дей-
ствию нормальных сосредото-
ченных сил К, кР2? . . ., кРх,
сгруппированных попарно (рис.
122). Силы заданы с точностью
до множителя к; требуется оп-
ределить критическое значение
Хкр. Мы ограничимся иссле-
дованием устойчивости орто-
тропной пластинки с главными
направлениями, параллельны-
ми направлениям сторон.
Направим оси вдоль сторон
пластинки и обозначим через
а и 6, как обычно, длины сто-
рон и через т]2, .. —ор-
динаты точек приложения сил; обозначения для главных
упругих постоянных и жёсткостей оставим прежними (эти
величины считаем известными).
Решаем задачу энергетическим методом х). Предположим,
что пластинке сообщены малые прогибы. Линии действия
сил разбивают пластинку на прямоугольные участки, число
которых N +1; обозначим прогибы этих участков через (Рх,
При искривлении срединной поверхности
силы произведут работу, равную 2):
N а
<76Л>
Решение имеется в нашей книге [я1], § 23, стр. 60—63.
*) См. формулу (67.11).
250
приравнивая
получаем:
эту работу потенциальной энергии изгиба.
N+1 т а
i=-l Tii—1 О
dx dy
(76.2)
где
•--а (Э)‘+2й-’-Э 'Э+».(*?)’+«><££)•
(в этом равенстве т]о = О, P^l).
Будем искать выражения для прогибов в форме, кото-
рая обеспечивает удовлетворение условиям на опёртых
(нагруженных) сторонах:
wl = fi (У) sin par, (76.3)
где £==--, т —целое число. Функции Д (у) и /дг-м (у)
должны удовлетворять условиям на сторонах у ~ 0 и?/ = 4,
в зависимости от способа их закрепления; например:
/ = /' = 0 (76.4)
— на заделанной стороне,
/ = Л = 0 (76.5)
— на опёртой стороне и т. д. Кроме того, на линии дей-
ствия сил функции fi должны удовлетворять условиям,
вытекающим из вполне естественного требования непре-
рывности изогнутой поверхности и отсутствия у ней из-
ломов:
Л+1(^) = Л(^), 1
(i = l, 2, ..., N). j
(76.6)
Имея в виду определение наименьшего значения X, не
равного 0, поставим задачу следующим образом: найти
функции /1? /8, ../n+i, удовлетворяющие условиям (76.6)
и условиям на сторонах у = 0, у = Ъ, при которых выра-
жение (76.2) получает минимальное значение.
19*
291
Задача отыскания Минимума дроби (76.2) равносильна
задаче отыскания минимума выражения х):
N+l Tjf
и = 2 $ +т+W2/';) dy -
i-1 1Q£-1
(76.7)
i-1
Решаем эту задачу по правилам вариационного исчис-
ления: составляем вариацию U — W и приравниваем её
нулю, учитывая условия (76.6) и условия на сторонах а.
После ряда промежуточных вычислений получаем сле-
дующий результат.
Функции удовлетворяют уравнению:
DJ™ - 2D^f{ + = 0 (76.8)
и условиям: а) на сторонах у = 0, у =Ь — условиям, соот-
ветствующим способу закрепления этих сторон; Ъ) на ли-
ниях действия сил у = ^1^
/i+ito<) =ft to),
/:+i to,) = Л to,),
/'+1to.) = /; to.), (76.9)
Dtf^ to,) -M' м = to).-, I
(Z=l, 2, ..., N, Pt = l). J
Каждая из функций /* (у) содержит четыре произволь-
ных постоянных; всего имеется 42V + 4 постоянных. Столь-
ко же получается и условий для функций (4 условия на
сторонах а и 47V условий на линиях 2/ = ^.), Удовлетворяя
этим условиям, мы получим систему из 47V + 4 однородных
уравнений с таким же числом Неизвестных, а приравнивая
нулю определитель этой системы, получим уравнение (алге-
браическое, TV-й степени) 'для определения X.
Применяя метод функций влияния, изложенный в следую-
щем параграфе, можно задачу определения Хкр значительно
упростить, сведя её к решению не 47V4-4 уравнений, а толь-
ко N однородных уравнений.
!) См. § С6—2 или G2.
292
Рис. 123.
у которой концы также
77. Метод функций влияния.
Рассматривая уравнения для функций Д- и условия для
них, легко подметить аналогию с балкой. Именно, урав-
нение (76.8) можно истолковать, как уравнение прогибов
участков балки (с жёсткостью изгиба/)2), лежащей на сплош-
ном упругом основании (коэф-
фициент упругости которого
к == p4Z\), растянутой продоль-
ной силой Т = 2/)зр2 и изги-
баемой сосредоточенными си-
лами Qu Qi, ..., прило-
женными в точках у — т]1,
У = у - (ось у направ-
лена по оси балки,— рис. 123).
Пластинке, у которой сто-
роны у = 0, у =Ь опёрты или
заделаны, соответствует балка,
опёрты или заделаны х).
Будем обозначать прогибы указанной фиктивной балки
просто через / (у), без индекса. При изгибе сосредоточен-
ными силами сама функция / и её производные /' и /*
непрерывны по всей длине балки, а третья производная
испытывает разрывы непрерывности в точках приложения
сил, причём
+ = (* = 1, 2, . N). (77.1)
Сравнивая эти равенства с четвёртыми условиями (76.9),
заключаем, что силы, изгибающие фиктивную балку, долж-
ны быть пропорциональны прогибам:
& = М, Qt = Ы, •> <?№ (w). (77.2)
Установив эту аналогию, мы можем дальше отвлечься
от пластинки и решать задачу об изгибе балки, на кото-
рую действуют силы, пропорциональные прогибам —(77.2).
Обозначим через 8 (vj, у) функцию влияния для про-
гиба, т. е. прогиб в точке у от силы, равной единице и при-
ложенной в точке т); значения этих функций при т] = т]/
и y — y\j обозначим через 80-:
= ^)- (77.3)
См. [24], § 24, стр. 63—64.
?93
Тогда полный прогиб балки представится в виде суммы-’
Л'
Ш = 2 (77.4)
7с= 1
Так как изгибающие силы Ql; должны удовлетворять
условиям (77.2), то мы получаем систему однородных
уравнений для определения Qk и К:
Qi (1 - *PS8„) - R4 - • • • - <2.v^23№ = 0, )
+ Q. (I - *фгЛ8„) - • • - = о, I {77 5)
-£Х₽’Рл81№
- (1 - >.₽2РЛ8Л]У) = 0.
Приравнивая нулю определитель этой системы, полу-
чаем уравнение, из которого определится ккр:
^11 9 °21 ’ • • 8;vi
8 5 1 ft
18’ ЛЗа^2 * ’ ’ 0;V2
= 0. (77.6)
S1N
8aiV •••
Отсюда получим вообще N различных значений К, каж-
дое из которых будет зависеть от т. Наименьшее из всех
значений К, не равное нулю, и будет критическим ккр.
Основной частью задачи является построение функций
влияния для данного способа закрепления концов балки.
Задачу можно значительно облегчить, составив таблицы
значений функций влияния 8Ч- (Р) для разных р = в точ-
ках, взятых через определённые интервалы; ясно, что чем
больше этих точек, тем лучше, тем большее число задач
мы смой.ем решить с их помощью. Например, составив
таблицы В,-/ для значений vj и у, взятых через у 6, мы смо-
жем с их помощью решить задачу об устойчивости пла-
стинки, сжатой любым числом спаренных сил —от одной
до семи. Относительная величина сил может быть какой
угодно; некоторые из сил могут быть и растягивающими
(для растягивающих сил множители надо взять со зна-
ком минус). Заметим, что функции влияния для анизо-
тропной пластинки зависят от упругих постоянных мате-
риала (точнее, от комплексных параметров изгиба), а по-
этому для каждого материала будут особые таблицы. Однако,
работа по составлению таблиц функций влияния оправ-
дает себя, если необходимо производить расчёт на устой-
чивость целой серии пластинок из одного материала.
78. Функции влияния для ортотропной пластинки
с опёртыми сторонами г).
Функции влияния 8 (>], у) можно представить в виде
8h’ y} = ^Vs^sh' (78Л)
Безразмерную функцию g удобно представлять с по-
мощью двух различных аналитических выражений, из кото-
рых одно даёт форму изогнутой оси по левую сторону от
силы, а другое —по правую сторону:
, ДЛяО<у<7|,
8 7)’ lg« (у) для 7)<у <Ь.
Обе эти функции удовлетворяют уравнению
D^-2D^Y + D^g = Q (78.3)
и условиям:
§2 (Ti) = gi 01)» ga fa) = gi 01)» _ )
ga W = gi (g) , ga' h) = g7 h)+4?s j/"gt (ц). / (78,4)
Кроме того, gr должна удовлетворять условиям на
конце у = 0, a ga — условиям на конце у —Ь. Вид этих
функций зависит от корней уравнения:
DjP - 2D.uz + Dx = 0. (78.5)
Обращаясь к § 49, заметим, что корни этого уравне-
ния по величине обратны корням уравнения (49.11)2).
Здесь также возможны три случая корней.
х) См. [24], § 25, стр. 65—72.
3) Корни уравнения (73.5) связаны с комплексными параметрами
изгиба и у.2 зависимостями: u2=—t[x2.
295
Случай I. Корни уравнения (78.5) вещественные
неравные:
±гг1? ± и2 (их>0, иа>0).
Случай II. Корни —вещественные равные:
+ и (и > 0).
Случай III. Корни комплексные:
и ± /и, —и ± io.
Для пластинки с четырьмя опёртыми сторонами (кото-
рой соответствует балка, опёртая по концам) функцию g
в случае комплексных корней уравнения (78.5) можно пред-
ставить в таком виде:
Для 0<2/<7]
2
8 I7!» у} 81 (у) и [chtyub — cos2pv6)
X |[shpu (26 — т]) sin рит] — sh Put] sin Ви (26 — т])] x
X — sh $uy cos fivy + ch fiuy sin py +
+ [ch Put] cos Pv (26 — 7]) — ch pu (26 — tj) cos putj} x
X G~ ch $uy sin $vy — sh $uy cos Poy^ | ; (78.6)
ДЛЯ 7]<y< b
S С7!» У) ~ ёа (?/) u (oh2pub — cos 2ftob)
X |[shpu (b — tj) sinpu (6 + 7]) — sh pw (6 + 7)) sinpu (b —•»])] X
X [ ~ sh ри (y — b) cos Pv (y — &) +
+ chpii {y — b) sinpu(y — b) j +
+ [ch pu (b 4~ 7]) cos pu (b — 7j) - ch ри (b — tj) cos Pn (b + т])] X
X [ sh pu (y — b) sin p» (y — b) —
— sh ри (у — b) sin Pu (y + b) ] } . (78.7)
2 96
Функцию g (v]? у) для пластинки с опёртыми сторонами
можно представить ещё иначе, в виде ряда:
, ч 8 (md}* ГDr
§ h, 2/) = -V-y х
. птстп . ппу
00 sin—* sin ~
х2т-----------лт. гв.......*7в-\Т1------ (78'8>
А [»+(-!§] +[гНЮ К1,
Здесь и в дальнейших формулах d = b/a.
Для изотропной пластинки получаем ряд:
СО Ф 717СТП . nntj
gb, У)= 8-^ 2 Sin~d~S-- A . (78.9)
П=1 [n2 + (md)2]2
Для других случаев закрепления сторон выражения
получаются более сложными, и мы их не приводим.
Укажем ещё вид функций g для пластинки в виде бес-
конечной полосы (с опёртыми сторонами):
Случай I.
„ 1 5- -’Л — и8е₽ц11»-’|>]
W1 — W3
, X ДЛЯ — ОО < у < тп,
g h, у) =) 1
-а-..„а - в8е₽"11ч-»)]
| ua
i Для 7] <y < oo.
Случай II.
g Cl, У) =
-1 еМв-ч) [1— pu(y— »])] для —oo<y<7),
-i gMii-B) [1 — fJu (tj — у)] для •»] -С у < oo.
Случай III.
еМв-’i) £ A cos 8в (y — 7]) — -i- sin pu (y — •»)) J
для —OO<y<7],
еЗиС1!-») £ cos Рг (t] — y) 4- ~ sin Pc (•»]—y) J
k для 7]<y<oo.
(78.10)
(78.11)
(78.12)
Далее мы приводим таблицы функций §(т],у) для пла-
стинки с четырьмя опёртыми сторонами, изготовленной
?97
ив изотропного материала и из фанеры 2-го типа (табли-
цы 8, 9 и 10). Значения функций вычислены для т] и г/,
Таблица 8
Функции д для опёртой пластинки. Изотропный материал.
>1 то\ /=1 6/8 2 6/4 2 36/8 4 6/2 5 56/8 6 36/4 7 76/8
4=1 6/8 0,5 1 1,5 2 2,5 3 0,0437 0,180 0,328 0,464 0,581 0,677 0,0694 0,259 0,413 0,509 0,557 0,570 0,0783 0,258 0,348 0,355 0,319 0,266 0,0749 0,223 0,259 0,220 0,165 0,115 0,0618 0,172 0,174 0,125 0,0882 0,0454 0,0449 0,115 0,105 0,0651 0,0339 0,0157 0,0233 0,0576 0,0486 0,0272 0,0121 0,00413
2 6/4 0,5 1 1,5 2 2,5 3 &31=&12 0,122 0,438 0,676 0,818 0,899 0,943 0,144 0,480 0,664 0,715 0,697 0,650 0,141 0,430 0,522 0,479 0,397 0,312 0,120 0,340 0,367 0,295 0,215 0,157 0,0861 0,230 0,222 0,1^3 0,0903 0,0497 Sil" §19
3 36/8 0,5 1 1,5 2 2,5 3 &32 £аЗ 0,185 0,610 0,850 0,944 0,977 0,988 0,189 0,595 0,767 0,780 0,731 0,665 0,165 0,488 0,570 0,507 0,409 0,316 ^8б“^2Б
4 6/2 0,5 1 1,5 2 2,5 #41“ £14 #42“ #24 #43=£з4 0,208 0,667 0,898 0,971 0,990 0,992 £45~£з4 #24
1
взятых черев интервалы, равные —
Ъ. Для опёртой пла-
стинки функции g явля ются симметричными:
кроме того:
ё\п”&7,8-п» Sin ” &6,8—Лэ • • • ) = ё^.б-п»
Так, например,
#5б ~ S g- ь, у b} — g38 = g Qg- 6, g- b) ,
= b,^b^=gli = g^b,~ by
gii = gjtl
(78.13)
(78.14)
Функции g зависят не только от tq и у, но ещё и от
произведения md. которое входит, как параметр. В наших
298
Таблица 9
Функции д для опёртой пластинки. Фанера 2-го типа. Сжатие в направлении волокон рубашки.
1 md 7 = 1 6/8 2 Ь/4 3 36/8 7 6/2 5 56/8 6 35/4 7 1 75/8
i=l 6/8 0,5 1 1,5 2 2,5 3 0,0724 0,289 0,500 0,690 0,839 0,944 0,117 0,415 0,590 0,664 0,651 0,583 0,134 0,413 0,453 0,374 0,255 0,144 0,130 0,349 0,279 0,147 0,0483 —0,0165 0,123 0,261 0,143 0,0310 —0,0124 —0,0164 0,0818 0,170 0,061 —0,00858 —0,0164 —0,00836 0,0415 0,0829 0,197 —0,011 —0,00844 —0,0033
2 i 6/4 0,5 1 1,5 2 2,5 3 £ai“£i2 0,207 0,810 0,953 1,06 1,09 1,09 0,248 0,763 0,869 0,811 0,699 0,582 0,245 0,674 0,596 0,405 0,242 0,128 0,210 0,521 0,346 0,153 0,0592 0,0348 0,152 0,452 0,163 0,0201 —0,0207 —0,0193 £s7~£16 ।
3 36/8 0,5 1 1,5 2 2,5 3 £з1==£1В £з2 = £23 0,317 0,963 1,10 1,10 1,08 1,07 0,327 0,933 0,930 0,802 0,683 0,573 0,286 0,769 0,616 0,394 0,234 0,124 £36=£25 £87“ £15
4 6/2 0,5 1 1,5 2 2,5 3 #41 = £14 £<а”£а4 £<8~£з4 0,359 1,05 1,12 1,08 1,07 1,07 £45 ”£84 £дв=£а4 £47==£14
таблицах для каждой пары значений и у приводятся
шесть значений g — для m<Z = 0,5, 1, 1,5, 2, 2,5 и 3.
Функции g яля. бесконечной полосы имеются в таблицах
14, 15, 16 (§ 87).
Перейдём далее к основным частным случаям распре-
деления сил.
Таблица 10
Функция g для опёртой пластинки. Фанера 2-го типа.
Сжатие поперёк волокон рубашки.
/=1 6/8 6/4 3 3&/8 4 6/2 5 5 6/8 6 3 6/4 7 7 &/8
i = 1 Ь/8 0,5 1 1,5 2 2,5 3 0,0403 0,226 0,446 0,657 0,858 1,03 0,0661 0,353 0,624 0,803 0,936 0,944 0,0769 0,389 0,606 0,646 0 593 0,490 0,0754 0,364 0,497 0,424 1,293 0,168 0,0647 0,299 0,361 0,238 0,105 —0,0213 0,0469 0,211 0,229 0,114 0,0186 -0,0199 0,0246 0,109 0,111 0,043 -0,0044 -0,0171
2 6/4 0,5 1 1,5 2 2,5 3 £21“£12 0,117 0,615 1,05 1,30 1,45 1,52 0,142 0,717 1,12 1,23 1,20 1,11 0,142 0,680 0,966 0,884 0,698 0,511 0,123 0,576 0,728 0,546 0,326 0,172 0,0893 0,408 0,470 0,281 0,100 0,0042 £г7=£16
3 3&/8 0,5 1 1,5 2 2,5 3 £з1~£13 £з2 ==£зЗ 0,182 0,915 1,41 1,54 1,56 1,54 0,189 0,928 1,35 1,34 1,22 1,09 0,166 0,797 1,08 0,927 0,694 0,494 £36==£25 £з7±=£15
4 Ь/2 0,5 1 1,5 2 2,5 3 £11 “£14 £42 = £24 £43“£з4 0,207 1,02 1,52 1,58 1,55 1,53 £45“£з4 с £48 “£24 £47“£14
79. Сжатие пластинки двумя силами.
Прямоугольная ортотропная пластинка сжимается двумя
силами, приложенными на расстоянии т] от одной из сторон;
стороны, где приложены силы, опёрты; остальные закреп-
лены как угодно г) (рис. 124).
*) Решение этой задачи см. в нашей работе [24], § 26, стр. 72—75.
300
В этом случае
w = Q6 (т), у) sin рх.
Вместо определителя (77.6) получаем уравнение:
8ц
откуда ___
. 1 4л )/ DiD^ т
Т'®п « ' 1) ‘
(79.1)
(79.2)
(79.3)
Критическое значение ХЕр представим таким образом:
XKP=4^f-lgj-&- (79.4)
Коэффициент к — наименьшее зна-
чение отношения m/gu, которое лег-
ко установить, используя таблицы
функций g (если, конечно, они для
данного материала имеются).
В таблице 11 приведены зна-
чения к для пластинки изотропной
if
Рис. 124.
и изготовленной из фанеры 2-го типа
и указаны соответ-
ствующие т (число полуволн, на которые разбивается в
Таблица 11
Значения коэффициента к для пластинки, сжатой двумя силами
d fl=b!8 т) = Ь/4 тд = 3&/8 1 4 = 6/2
_Ll т к 1 т к 1 т к | т
Изотропный ма- 0,5 8,61 5 4,44 3 3,28 2 3,00 2
териал 1 4,31 2 2,28 1 1,64 1 1,49 1
2 2,16 1 1,22 1 1,06 1 1,03 1
3 1,48 1 1,06 1 1,01 1 1,01 1
Фанера 2-го ти- 0,5 5,80 4 2,47 2 2,08 2 1,91 2
па, сжатие 1 2,90 2 1,23 1 1,04 1 0,956 1
вдоль волокон 2 1,45 1 0,940 1 0,912 1 0,923 1
рубашки 3 1,06 1 0,918 1 0,933 1 0,935 1
Фанера 2-го ти- 0,5 5,81 6 2,85 3 2,12 3 1,96 2
па, сжатие по- 1 2,90 3 1,53 2 1,09 1 0,978 1
перёк волокон 2 1,52 1 0,767 1 0,649 1 0.631 1
рубашки 3 0,968 1 0,657 1 0,648 1 0,654 1
301
направлении действия сил пластинка, потерявшая устой-
чивость).
Приводим также формулы для коэффициента к для
пластинки, сжатой силами, действующими по оси сим-
метрии *).
Случай I:
а) все стороны опёрты:
б)
7 II ч ~ Ни • * ГН . /
Л =—Ц:—i min /----------------------т\ ; (79
2 ( ,, тпи, а ттш.а ) ’ '
< «1 th 2^--и a th 2" '
стороны, где приложены силы, опёрты, остальные
заделаны:
ь ц1—4
Л 2
т
Хтш
тки-, d ,, m~u9d
“ith------i/2 th-
~ ?1Иа
, rmtu. d , rmtu* d k й 4 x 2
ch—ch—
Случай II:
а) все стороны опёрты:
mTcu^d
Г"
(79.6)
(79.7)
к = и min
т
тпи d rmtud
th—---------------у
2 о , 2 rmtud
2ch “2~
б) стороны, где приложены силы, опёрты, остальные
заделаны:
7 и . Г" sh тпи d 4- rmw d "j /-7П q\
к ~ У min m • (79-8)
L Sh 2-------
Случай III:
а) все стороны опёрты:
7 . Г ch тпн d 4- cos тгл d 1 n\
ft = iwmin m—г------------------т ! (7У.У)
L v sh mnu d — и sin rmtv a J
б) стороны, где приложены силы, опёрты, остальные
заделаны:
7 1 . г- v sh mmi d 4- и sin rmtv d
k^uv -a tmn Г m----------------------
2 о T&rmtud _ . „ rmtu
L Vй sh2—------t*2sin2—£
(79.10)
A) В формулах (79.5)—(79.10) имеются в Виду минимальные значе-
ния выражений, не равные нулю, соответствующие целому числу т.
302
Из формулы (79.7) при и-1 получаем значение коэф-
фициента А, найденное С. П. Тимошенко для изотропной
пластинки с опёртыми сторонами, сжатой по оси сим-
метрии *).
Решение задачи об устойчивости изотропной прямоуголь-
ной пластинки с двумя опёртыми и двумя заделанными
сторонами при сжатии двумя сосредоточенными силами
было получено А. П. Филипповым 2) и другим методом
А. И. Лурье 3). Результаты А. П. Филиппова и А. И, Лурье
получаются из вышеприведённых формул (79.7) и (79.8)
при u = 1.
Вопрос о том, при каком т выражения в скоб-
ках (79.5) —(79.10) получают минимальные значения, со-
ответствующие данному отношению сторон d = bja, ре-
шается путём вычислений; заранее определить число
полуволн для пластинки с произвольным отношением
сторон (исключая бесконечную полосу), невидимому,
нельзя.
В таблице 12 приведены значения коэффициента к из
формул (79.9) и (79.10) для пластинок из фанеры 1-го типа,
сжатых по оси симметрии.
Таблица 12
Значении коэффициента к для прямоугольной пластинки, сжатой
вдоль оси симметрии (фанера 1-го типа).
Сжатие вдоль волокон рубашки Сжатие поперёк волокон рубашки
Стороны а опёрты Стороны а заделаны Стороны а опёрты Стороны а заделаны
d л- 1 т к 1 т к т _А__J m
0,5 1 2 3 2,61 1,75 1,72 1,72 1 1 1 1 3,87 1,94 1,72 1,72 2 1 1 1 2,59 1,29 0,646 0,498 4 2 1 1 3,73 1,87 1,05 0,498 6 3 2 1
г) См. [44], § 64, стр* 341*
2) СМ* [49].
8) См* [25]. А. И. Лурье дал метод решения также более общей
задачи об устойчивости- пластинки произвольной формы, обладающей
по крайней мере одной осью симметрии, при сжатии вдоль оси сим-
метрии.
303
Для бесконечной полосы, сжатой силами X (рис. 125):
Х~Р = Т т = 1 (79.11)
[в случае неравных корней уравнения (78.5)] или
Хкр=4М^Л.и> т=1 (79.12)
(для равных или комплексных корней).
Критическая сила для изотропной полосы (Z)1=:Z>2 = Z),
и — 1) найдена Зоммерфельдом х).
Просматривая приведённые табли-
цы, можно отметить, что пластинка,
сжатая поперёк волокон, т. е. в на-
правлении, для которого модуль Юнга
наименьший, стремится, потеряв устой-
чивость, образовать ряд волн в на-
правлении линии действия сил; число
волн тем больше, чем длиннее плас-
тинка, т. е. чем меньше d. Пластинка
с отношением сторон tf , сжатая
вдоль волокон (в направлении, для
которого модуль Юнга наибольший),
теряя устойчивость, образует только одну-две полуволны
в направлении сжимающих сил.
80. Сжатие пластинки четырьмя силами.
Прямоугольная пластинка деформируется четырьмя
силами, приложенными к двум сторонам, как показано
на рис. 126; нагруженные стороны опёрты; остальные
закреплены как угодно 2).
Пусть величины действующих сил — X и ХР. Критическое
значение К определится из уравнения:
U11 °22
й) Решение этой задачи см. в нашей работе [24], § 27,
стр. 75 — 78.
304
откуда после несложных преобразований получены две
серии значений к:
} , 4- / PJ),
а
------------------------- - , (80.2)
b^+yTQ^y+feuea
= кп У~Р,Р3 ________ т. .... ...... (80.3)
8Ц±£и_
Из этих двух серий значений нужно выбрать наимень-
шее; работа облегчается, если имеются таблицы функ-
ций g для данного материала.
Рассмотрим подробнее два случая.
1) Все силы—сжимающие, равны по величине и при-
ложены в симметричных точках: у = Ь-— т], у = т) (см.
рис. 127); все стороны опёрты.
В этом случае
V = ^ур3р^ т , (80.4)
а gll + gu 4 1
, (80.5)
« gn—ga ' '
Значениям к' соответствует симметричная форма изо-
гнутой срединной поверхности пластинки (см. рис. 128а,
где изображен примерный вид поверхности при яг=1).
Значениям kff соответствует антисимметричная форма
20 с. Г. Лехницкий 305
изогнутой поверхности (рис. 1286, где также взято
т= 1).
К какой из двух серий к принадлежит наименьшее
ккр, — заранее сказать нельзя; вопрос решается путём вычис-
лений, которые значительно облегчаются, если имеются
таблицы функций g.
Формула для определения критического значеция будет
иметь вид:
ккрС= к (80.6)
В таблице 13 приведены значения коэффициента к для
изотропной пластинки с четырьмя опёртыми сторонами,
изготовленной из фанеры 2-го типа; коэффициенты к вычис-
лены с помощью таблиц функций g. Вычисления показы-
вают, что во всех рассмотренных случаях, кроме двух,
изогнутая поверхность пластинки, потерявшей устойчи-
вость, должна быть симметричной относительно линии
г/=6/2; исключения из этого правила, помеченные в таб-
лице 13 ввёздочками, объясняются, может быть, недоста-
303
Таблица 13
Значения коэффициента к для прямоугольной пластинки, сжатей
четырьмя силами
d ь ^ = -8 ъ 4=4- 1 = ЗЬ = 8
к 1 т * 1 т к | т
Изотропный мате- 0,5 7,96 3 2,99 2 1,82 2
риал 1 4 07 2 1.50 1 0,911 1
2 2,04 1 1,03 1 0,689 1
3 1,47 1 1,01 1 0,767 1
Фанера 2го типа. 0,5 4,30 3 1,58 2 1,16 2
Сжатие вдоль во- 1 2,69 1 0,792 1 0,577 1
локон рубашки 2 1,47 1 0 923 1 0,671 1
3 1,06 1 0,903* 1 0,836 1
Фанера 2-го типч. 0,5 5,39 3 1,96 2 1,17 2
Сжатие поперёк 1 2,84 2 0,978 1 0 584 1
волокон рубашки 2 1 43 1 0 631 1 0 405 1 1
3 0,952* 1 0,655 1 0,491 1 i
точной точностью таблиц или неточностью в определении
упругих постоянных фанеры.
2) Все силы, действующие на пластинку, одинаковы
по величине и приложены в симметричных точках; две
силы — сжимающие и две — рас-
тягивающие (рис. 129).
Критическое значение Хкр
определится по формуле
(80.6), где
Л = min Г(80.7)
К У gh — S12 >
Формулу для критического
значения Хкр можно написать
и иначе:
Хкр = min j/X' X", (80.8)
где X' и X" определяются из формул (80.4) и (80.5) пре-
дыдущего случая.
20*
307
ГЛАВА XV.
УСТОЙЧИВОСТЬ ПЛАСТИНОК, ПОДКРЕПЛЁННЫХ
РЁБРАМИ ЖЁСТКОСТИ.
81. Устойчивость пластинки с продольными рёбрами,
сжатой равномерно распределённой нагрузкой.
Пластинку с часто поставленными параллельными рёб-
рами жёсткости можно рассматривать, как ортотропную и
однородную; как определяются жёсткости такой пла-
стинки, было указано в § 42. Если пластинка подкре-
плена малым числом рёбер, например, одним или двумя
рёбрами, то нет оснований рассматривать её, как одно-
родную и ортотропную, а нужно учитывать совместную
работу пластинки и рёбер. В настоящей главе мы рас-
сматриваем вопросы устойчивости прямоугольных орто-
тропных пластинок с продольными и поперечна ми рёб-
рами, сжатых нормальной нагрузкой, равномерно распре-
делённой по сторонам, или сосредоточенными силами, при-
ложенными к концам рёбер.
Рассмотрим сначала о; нородную ортотропную прямо-
угольную пластинку с главными направлениями, параллель-
ными направлениям сторон, усиленную несколькими парал-
лельными рёбрами жёсткости. Пусть на пластинку действу-
ет сжимающая нагрузка р, равномерно распределённая по
сторонам, перпендикулярным к рёбрам. Предполагается, что
Рис. 130.
стороны, на которых укрепле-
ны концы рёбер, опёрта, другие
стороны закреплены произволь-
но, концы рёбер также опёрты и
закреплены против поворота
вокруг осей рёбер. Предпола-
гается далее, что рёбра жёстко
скреплены с пластинкой, а сече-
ния их имеют оси симметрии,
перпендикулярные к недефор-
мированной срединной поверх-
ности пластинки. Требуется
определить критическое значе-
ние сжимающей нагрузки /Ър, при которой пластинка,
усиленная рёбрами, потеряет устойчивость.
Направим оси координат вдоль сторон пластинки (ось
х параллельно рёбрам,— рис. 130) и введём обозначения:
308
Dk, vx, v2 — жёсткости и коэффициенты Пуассона
пластинки; 2?х —модуль Юнга пластинки пля направлений,
параллельных рёбрам; а, Ь — длины сторон пластинки;
TV —число рёбер; Е\ . . . , — модули Юнга рёбер;
Е1„ ЕЦ, . . . , EIn — жёсткости изгиба рёбер в плоско-
стях, перпендикулярных к плоскости пластинки; Сх, . .,
, . . , CN — жёсткости кручения рёбер; F„ F2, . . . , F#~
площади поперечных сечений рёбер, 7|х, т]2, . . . , —рас-
стояния рёбер от нижней кромки пластинки;
8 y-~- ~ х Ъ
< = 2> 3, •••)•
(81.1)
Приближённое решение задачи об устойчивости изо-
тропной пластинки с продольными рёбрами получено
С. П. Тимошенко с помощью энергетического метода х).
Применяя энергетический метод, легко получить при-
ближённое решение задачи и для анизотропией пластинки
совершенно аналогичным путём; на этом приближённом ре-
шении мы и остановимся в этом и следующих параграфах.
До потери устойчивости пластинка находится в пло-
ском напряжённом состоянии, а рёбра — в состоянии про-
стого сжатия в; оль их осей. Сжимающие силы при-
ходящиеся на кониы рёбер, мы легко определим, если до-
пустим, что относительное сжатие пластинки
относительному сжатию еХ1. любого ребра.
Очевидно,
е ________________IL е ______ .
х Я1’ xi FiEi ’
ех равно
(81.2)
но бд, — ехГ, следовательно,
(81-3)
Приступая к решению зада* и, предположим, что вся
система получила малые отклонения от плоской формы;
пластинка прогнулась, а рёбра прогнулись и закрутились.
Обозначая через w (и, у), w (х), bf(z) — прогибы пластинки
и рёбер и углы закручивания рёбер, имеем, в силу жёст-
х) См. [45] или курс С. П. Тимошенко, [44], ч. II, § €6,
стр. 850—853.
309
кого соединения пластинки с рёбрами:
wi(x) = w(x,tit), 0< (a:) = (^Y_T • (St4)
Потенциальная, энергия системы при этом увеличивается
на величину
а Ь
^иэг=4 5 +2£>1V*
о о
о*ха ду* ~г" *\.ду*) ’
+ 4D-< (j^xdy +
Na а
+42 lEI>\Mtdx+Ci («*>•<**] <81-5)
i=l О 0
и уменьшается за счёт работы, произведённой внешними
силами:
а Ъ Na
Л==^ И (Й)2</жсГ2/ + у2Р< 5 {81-6)
00 t=l о
Условиям на опёртых (нагруженных) сторонах пла-
стинкц и на концах рёбер мы удовлетворим, полагая:
(V = / (у) sin ₽г,
^z==/(^z) sin
6Z = /' (tjJ sin ря.
(81.7)
Из уравнения
(81.8)
получаем выражение для нагрузки р, которая может
вызвать искривление системы:
ь N
ФЛу+ь^ГМ+’чРГМ}
Р = \Го^ °----, (81.9)
р» [ ( гау + ьУб^сщ}]
L 0 i-i
где _ _ _
ф 2?ч /а а-+?-/%/•+
ЗЮ
кого соединения пластинки с рёбрами:
= (81.4)
Потенциальная энергия системы при этом увеличивается
на величину
а b
Гизг=|^ + 2Д*а ——2
О о
+4^Gr^-)2]rfa:^+
+ 42 l£/< ^'i’ydx + C, 5 (6D’ л>] (81.5)
t = l L О О
и уменьшается за счёт работы, произведённой внешними
силами:
A==i \ $ $ ^dx- <81-6)
0 0 1 = 1 о
Условиям на опёртых (нагруженных) сторонах пла-
стинки и на концах рёбер мы удовлетворим, полагая:
(V ®= / (у) sin [Зге, 1
<vz — / (?]) sin ₽я, б = /' (yj ) sin J (81.7)
Из уравнения
ГИЗГ=Л (81.8)
получаем выражение для нагрузки р, которая может
вызвать искривление системы:
ь N
Р = /ад -------N, (81.9)
[Р [ Р<1у + ьУ^(Щ
L 0 1=1
где _ _ __
ф = /£. /-> _ 2?ч /§//+?++ 7=5/
310
Далее можно пойти таким путём: подобрать выраже-
ние для функции f(y) в виде суммы с неопределёнными
коэффициентами
/=2Дш./п(у),
п
(81.10)
где /л ~ непрерывные функции, удовлетворяющие усло-
виям на сторонах у = 0, у = Ь* подставить это выражение
в формулу (81.9) и определить минимальное значение р,
как функции коэффициентов Лтп. Задача отыскания ми-
нимума дроби (81.9) равносильна задаче отыскания мини-
мума выражения 1):
о 1 2 3
+ 0ь)+*.₽’/'*(ъ)]}-
V ViJJz у *
b N
-р?1 Ц fdy+b 2мг(ъ)] . (81.11)
L О i = l
Это выражение представляется в виде однородной квад-
ратичной функции коэффициентов Amri; разыскивая мини-
мум (7, т. е. полагая
J*L = q J*L^o
0Aml v’ <^ma v’ • • • ’
(81.12)
получим систему однородных уравнений, определитель
которой должен равняться нулю. Отсюда получаем
уравнение
Д (р) = 0, (81.13)
наименьший корень которого и даст величину критиче-
ской нагрузки.
Рассматривая пластинку с рёбрами, расположенными
симметрично относительно линии y~bf2} можно в первом
приближении принять:
9 См. § 66.2 или 62 настоящей книги.
311
а) для пластинки с опёртыми сторонами а:
/ = 2^8^^; (81.14)
б) для пластинки с заделанными сторонами а:
f = Ami (1- соз^) ; (81.15)
в) для пластинки со свободными сторонами а:
f — Атп ^v1m24~4n2c’— vxm2 cos^^Q . (81.16)
Если же рёбра расположены несимметрично, то после
потери устойчивости изогнутая поверхность будет несим-
метричной относительно линии у ~ Ь/2, а потому первое
приблин ение может дать величину критической нагрузки
с недостаточной для практики точностью. В этих случа-
ях, сообразуясь с числом и расположением рёбер, сле-
дует принять выражение для / в виде суммы нескольких
членов.
В дальнейшем, рассматривая пластинки с симметрич-
ными рёбрами, мы ограничимся определением критической
нагрузки лишь в первом приближении. Для изотропной
пластинки, подкреплённой несколькими равноудалёнными
рёбрами одинаковой жёсткости, как указывает G. П. Ти-
мошенко, первое приближение даёт вполне удовлетвори-
тельные результаты, в других слу-
р чаях первое приближение даёт,
’Т* по С. П. Тимошенко, вполне удо-
22 влетворительные результаты для
22 2Z длинных изотропных пластинок,
___ Р у которых с > 2 г).
* — 82. Случай одного продольного
, т ребра.
а -—~ Пластинка, подкреплённая реб-
Рис. 131. ром я ёсткости, направленным по
оси симметрии, сжимается нормаль-
ной нагрузкой, распределённой равномерно по сторонам,
перпендикулярным к ребру (рис. 131).
!) Cm.[w], стр. 5, и [**], стр. 354.
312
нельзя; это зависит от величины отношений
х, 8, у.
Введём сокращённые обозначения:
Представим формулу для критической нагрузки в виде
к. (82.6)
Результаты исследования, довольно элементарного,
можно свести к следующему:
1) если отношение сторон пластинки удовлетворяет
условию
с “ т'г^ (82.7)
где т’ — целое число, то ти = 7п',
к =
(82.8)
2) если отношение сторон удовлетворяет уравнению
с==4 т'
то = т',
(82.9)
(82.10)
314
3) для больших отношений сторон О 3
или
/с = Л:1, если kt <
к-к^ если > къ.
(82.11)
Эти результаты удобно расположить в виде таблицы,
в которой помещены значения с и соответствующие к и т
(при n—1 и п = 2).
Сводная таблица иоэффицие itob к для случая опёртых сторон
стей DJD2 и у и требуется найти критическую нагруз-
ку для пластинки с данным отношением сторон с. Что*
бы определить соответствующее Л, устанавливаем, в ка-
ком месте таблицы находится данное отношение с при
л—1 и при п = Определив строчки, в которых на-
ходится с, из колонки для к берём соответствующие
значения этого коэффициента; из найденных двух значе-
ний нужно взять меньшее (какое из двух значений бу-
315
дет меньшим — зависит от соотношения между парамет-
рами пластинки).
Пусть, например, для квадратной пластинки (с= 1)
найдено: ^ = 1,5, г2 = 1?2, и требуется определить /с.
Данное отношение сторон находится в 1-й строке таблицы,
соответствующей и—1, и в 4-й строке таблицы для м = 2.
Следовательно, можно принять одно из двух значений:
к — к±1 или к ~ кщ именно то, которое меньше. В зависимости
от соотношения между параметрами пластинки, возможно
одно из двух: 1) пластинка образует одну полуволну
в направлении нагрузки (оси х) и одну полуволну в на-
правлении оси у; к — Zcn; 2) пластинка образует две полу-
волны в направлении оси х и две полуволны в напра-
влении оси г/; к—к22х),
2. Стороны г/= 0 иг/=Ь заделаны.
Полагая
(82.12)
получаем на основании общей формулы (81.9):
(/Й + 2.66У (”)’ + 2,вв7„- +
+ 5,333»' /§(£)’ (82.13)
(для п=1, 3, 5, ...);
р- /Й(™)’+2’в67“‘
+ S,333n‘]/5Q)’] (82.14)
(для ?г=2, 4, 6, . . .).
Очевидно, наименьшее значение р из первой формулы
будет при и=1, а из второй —при п=2.
х) В последнем случае ребро остаётся прямолинейным, но при
этом закручивается.
316
Формулу для критической нагрузки представим в виде
(82.Ь). Введём сокращённые обозначения:
*~>=7+^й{(/5 + 2.6в7т) (”)’ +
4-2,667 4-5,333 l/-Y} ,
Ь' „— 1 Л-0! Л ™ V I 1Л fifi7 „ _1_
2
(82.15)
- 1^3 + 87 + v'Dtt
At—2,667 14-2,еб7в ’
^10,^3+^.
Результаты сводятся к следующему:
1) Если отношение сторон с удовлетворяет условию
где тп' —целое число, то тп~т',
к — к[;
2) если отношение сторон равно
1 ,
с=— т
4 4
то т—тп7,
к=кг,
3) для больших отношений сторон
к — к{, если Л1 < ks;
к=к'3, если ki > kt.
(82.16)
(82.17)
(82.18)
(82.19)
(82.20)
317
Сводная таблица коэффициентов к для случая заделанных
Пользоваться этой таблицей нужно так же, как и в слу-
чае опёртых сторон.
83. Устойчивость пластинки с поперечными рёбрами,
сжатой равномерно распределённой нагрузкой.
Рассмотрим прямоугольную однородную ортотропную
пластинку, подкреплённую параллельными рёбрами жёст-
кости, сжатую нагрузкох! /?, распределённой равномерно
по сторонам, параллельным рёбрам. Предполагается, что
стороны, по которым распределены сжимающие усилия,
опёрты, а другие стороны закреплены произвольно. Рёбра
жёстко скреплены с пластинкой, сечения их имеют оси
симметрии, перпендикулярные к первоначальной срединной
плоскости пластинки.
Требуется определить критическое значение сжимающих
усилий.
318
Направим оси х и у по сторонам пластинки (рис. 132).
Сохраним обозначения, принятые в § 81, и введём новые:
у ?№расстояния рёбер
от одной из нагруженных сторон,
f'i= - Е/1 - , *1= — - (83.1)
‘ а VаУDJ>2 ’
Задача об устойчивости изо-
тропной пластинки с поперечны-
ми рёбрами решена приближённо
с помошью энергетического метода
С. П. Тимошенко1); приближённое
решение такой же задачи для
ортотропной пластинки мы получим аналогичным путём,
также пользуясь энергетическим методом.
Потенциальная энергия изгиба системы, получившей
малые отклонения от плоской формы, равна
^паг—2 + • ^« + -°8Сг/а/ +
l> 0
+4^ +
+ i 5 [ EJt 5 w dy+Ct $(65)’dy ] ’(83,2)
i=l о 0
где
а, й, »<=Q),.t/
Усилия p при искривлении системы произведут работу:
а Ъ
A=iV\(^ydxdy’ (8з-з>
о о
Для пластинки с произвольно располоя енными рёбра-
ми выражение для прогиба моялю взять в виде:
(83-4)
_____________ т
*) См. работу С. П, Тимошенко [4в], стр. 15—23, и курс I44], §66,
стр. 358—359.
31^
и далее, определяя р из равенства 7Изг=Д нужно подо-
брать функции fm так, чтобы они удовлетворяли условиям
на сторонах ?/=0, у^Ь и давали наименьшее значение
для р.
Но если рёбра расположены симметрично, -то есть
основания предполагать, что, рассекая плоскостью, парал-
лельной xzr поверхность потерявшей устойчивость пла-
стинки, получим синусоиду с определённым числом полу-
волн т; по крайней мере для изотропной пластинки, как
указывает С. П. Тимошенко, это предположение обычно
даёт удовлетворительную точность1).
В дальнейшем мы рассмотрим только случай, когда
рёбра расположены симметрично относительно оси сим-
метрии пластинки х — a/2t и рёбра, находящиеся на оди-
наковых расстояниях от этой оси, имеют одинаковые жёст-
кости изгиба и кручения. В этом случае
?№в — ?N-I=a —В, И т. д.
Полагая
w=f(y) sinfta:, (83.5)
находим:
ь n ь
Ф1 dy + 2^ <btdy
р = 1—------<=*J------, (83.6)
О
где
ф, _ /..-2., ₽//' + /5Г +
Ф2 = Yt iffZ sin8 + Y* /'s cos3
Рассмотрим случаи опёртых и заделанных сторон.
1) Стороны у=0, у = Ь опёрты; концы рёбер опёрты и
закреплены против поворота вокруг осей рёбер:
Положим
/=4^111^. (83.7)
*) См. [«]. стр. 20, и [«] § 66, стр. 359.
320
Подставляя эту функцию в (83.6), находим:
___ N
[^ат,+2„.с.(_^+2«;оо^)+
N
+£<У%+22*™,=?)]- (83.8)
1’-1
Очевидно, наименьшее значение р получится при л=1:
Г-- Г— N
[ /gm.+2c. ( ^_+2«;со8- =Ь) +
/•*1
+ &(/§+22г;в1п,!?)]- (83.9)
Этим усилиям соответствует изогнутая поверхность
(V=Лт1 sin ^sin . (83.10)
Введём далее сокращённое обозначение:
Гт№ l/^X
г х/2
X xjsin(2/ге + -у pinJ +(2да + 1)*+
+ 2(2т+1)|/Г^ 2 —
N p ₽1
— m (m -j- 1) 2 * i sin (2m +1) у sin — I :
i=l j
r ff
: pm + 1 + 2 |/ ^2 t'i [(w + l)*sin*^-
- m* sin* J j | . (83.11)
С. Г. Лехнидкий
321
Вопрос о числе полуволн т, соответствующих крити-
ческой нагруеке, решается, как показывает элементарное
исследование, следующим образом.
Предельные отношения сторон с, при которых проис-
ходит переход от т полуволн к m-f-l-fi полуволне,
равны:
Если
с=]/т(тА1) •’ rniN,
(83.12)
О < с < j/2 г1Л-, то
если 2 < с < }/6г2Л-, то
если ]/6 г,Л < с < }/12 гах, то
т=1;
т=2;
771 = 3.
(83.13)
и т. д.
Если исвестны величины DJDt, "fa Sr, то число
полуволн, соответствующих данному отношению с, опре-
деляется на основании предыдущих неравенств; когда
число т установлено, то критическая нагрузка опреде-
лится по формуле (83.9).
2) Стороны у = 0, у = Ь заделаны;. концы рёбер заделаны
и закреплены от поворота вокруг осей рёбер.
В этом случае вместо формулы (83.13) имеем:
Р-[ /Si "+2.667С- cos" +
r 1 8 /=1
+ 5,333^(/а + 22т;«т"!=1')]; (83.14)
i«=l
sm -J- Ql — cos J . (83.15)
Предельные отношения с, при которых совершается
переход от т ткяувът кт-j 1-й полуволне, находятся по
формуле:
с = | /т(т+1) smN, (83.16)
822
где
х
(Гт («+!) 2 (2m + l)—‘sin—‘1* + 3(2т+1)» +
„ . „ mrL
I» sin® —
а
N
—m(/n + l) xi sin <2/u + 7isin‘T
; 2m+1 + 2
_ N
M
_zn,sin»H+.1)^
a
(83.17)
л т/ 2 . )
Если 0<с<Л2“^1у, то тп—1; |
если < с < Xj— s3N, то т = 2; J (83.18)
/б /12 о I
если s2Jy < с < -у- s8y, то ?n = a, I
и т. д.
84. Случай одного поперечного ребра.
Пластинка, подкреплённая одним ребром по оси симмет-
рии, сжимается в направлении, перпендикулярном к реб-
ру (рис. 133). В этом случае 7V=1, . Введём обо-
значения:
, _ El 1
Y ’’ I
> О [
а/ДРа I
(84.1)
21*
323
Для критической нагрузки получаются различные
выражения — для нечётных т я для чётных т.
Разберём два случая
закрепления сторон, на которых
укреплены концы рёбер.
1) Стороны г/ = 0, г/ == 6
опёрты.
Для нечётного числа полу-
волн т получаем:
+ 2с2
+ &(/157+2y')] ’ (8412)
Если отношение сторон с
удовлетворяет условию
т'
(84.3)
где т' —нечётное число, то т~ т',
1 + 2//а+1/А_).; (84.4)
Для чётного числа полуволн
(84.5)
Еолз отношение сторон удовлетворяет условию:
(84.6)
где тп‘- чётное число, то1) /п = т',
+ (84.7)
*) Езди т — число чётное, то при потере устойчивости ре-
бро остаётся неподвижный и прямолинейным и ли-пь закручи-
вается.
324
Число полуволн тп, на которое разобьётся пластинка
при данном отношении сторон, найдётся на основании
неравенств, приведённых в § 83,
В рассматриваемом случае tw — rmi
(84.8)
в т. д.
Если известны величины у', х', то на осно-
вании неравенств (83.13) легко установить число тп, со-
ответствующее данному отношению сторон с; если по-
лучится нечётное тп, нужно для определения критиче-
ской силы воспользоваться формулой (84.2); если по-
лучится чётное тп, надо ргр определять из формулы
(84.5). Формулы (84.4) и (84.7) дают наименьшие зна-
чения критических нагрузок (по сравнению со всеми
величинами, определяемыми по формулам (84.2) и (84.5);
отношения (84.3) и (84.6) являются наименее выгодными
в смысле устойчивости пластинок. Для больших отно-
шений с > 3 критическая нагрузка определится либо
по формуле (84.4), либо по формуле (84.7), в зависимости
от того, какая из них даёт меньшее значение р.
325
2) Стороны у = 0, у — Ь заделаны.
Для нечётных т
р - [ /5 "’+2'6в7с’ рй; +
+ 5,333^,(/3 + 2Т-)]. (84.9)
В частности, при
где т'— нечётное число, тп —тп' и
тс2
Ркр=-~
&а
2,6в7(/3|/ (84 И)
Для чётных тп*)
Ц?°-' [/&,"'+2’«ет'’(кй+’<')
зззйКвП- (М-
В частности, при
2 V D, ’
(84.13)
где тп'—чётное число, тп=тп' и
Т’кр=--^^-2,667 (j/З- 4-х' ) . (84.14)
ч. у Х/|Л^2
*) При чётных т ребро после потери устойчивости остаётся я а
подвижными прямолинейным, но закручивается.
326
Число полуволн определяется из неравенств (83.13), где
W"-5mi5
85. Устойчивость пластинки, усиленной рёбрами жёстко-
сти, под действием сил, приложенных по концам ребер.
Ео всех рассмотренных в настоящей главе случаях
предполагалось, что нагрузка, действующая на подкреплён-
ную пластинку, распределена по двум сторонам равномер-
но. Перейдём сейчас к случаям деформации пластинкй с
рёбрами под действием сосредоточенных сил, приложенных
по концам рёбер.
Поставим задачу следующим образом. Имеется прямо-
угольная ортотропная пластинка о главными направле-
ниями упругости, параллельными направлениям сторон,
усиленная рёбрами жёсткости, параллельными двум сто-
ронам. Рёбра жёстко связаны с пластинкой; стороны, на
которых укреплены концы рёбер, опёрты, другие стороны
как угодно закреплены; концы рёбер опёрты и закреплены
от поворота. По концам рёбер действуют осевые силы,
заданные с точностью до множителя X; требуется опреде-
лить критическое значение Хкр.
Направим оси х и у по сторонам пластинки (рис. 134)
и введём обозначения: а, Ъ — длины сторон пластинки;
327
Du Dk, vn vt — главные жёсткости и коэффициенты
Пуассона пластинки; TV —число ребер; X* г? * * * ? U^-
силы, деформирующие систему; EIh С£ —жёсткости изгиба
и кручения рёбер; 0== — , m= 1, 2, 3, ... ; т)п т]2,... , t|N —
расстояния рёбер от нижней кром-
ки пластинки (от оси х).
Задачу удобно решать, исхо-
дя из энергетического метода так
же. как и задачу об устойчивости
неподкреплённых пластинок, сжа-
тых сосредоточенными силами.
Предположим, что система по-
лучила малые отклонения от плос-
кой формы; пластинка получила
прогибы, а рёбра —прогибы и за-
кручивание. Линии рёбер раз-
бивают всю пластинку на ряд участков, число которых N +1.
Обозначим прогибы участков пластинки через у); тог-
да, в силу жёсткой связи пластинки и рёбер, прогибы рёбер
будут wf(x, т),), а углы их закручивания 9Х =
При искривлении силы произведут работу, равную
dx.
(85.1)
К потенциальной энергии системы прибавится энергия
изгиба УИ8Г, которая складывается из энергии изгиба уча-
стков пластинки и из энергии изгиба и кручения рёбер.
Из уравнения
ГИ8Г-А (85.2)
находим;
, 1М а
<-1 О
+^(J^y]dxdv+
N а
N а
: 2 4 о?);.,/* (85’з>
>28
Разыскиваем выражения для прогибов пластин-
ки, удовлетворяющие условиям на сторонах ж —
в виде:
wlsin (85 4)
прогибы и узлы закручивания рёбер будут, соответственно,
Л (vji) sin Рх, /;(7)f)sin^.
Задача сводится к определению функций (у), со-
общающих выражению (85.3) минимальное значение*
а это равносильно задаче отыскания минимума выра-
жения1):
N4-1 т
и= 2 (иы? - +w) dy+
Ч(-1
N
+ + (85.5 >
4=1
Решая эту задачу методами вариационного исчисления,
получаем следующий результат.
Функции ft (у) удовлетворяют (в любой точке соответ-
ствующего участка между рёбрами или между ребром и
внешним краем) уравнению:
Л/Г-22>,₽’/;+Л?‘/,=0 (85.6)
и условиям: а) на сторонах у=0 и у=Ь — в зависимости от
способа закрепления их; б) на границах между участками
(г=1, 2, ... , N), т. е. на линиях рёбер:
fi+iM=fi СпО,
л/ж(^1)-л//(^)=с₽2/:ы,
л/;;; ю-ад" ммхл-ег^ ₽•/, ь )
0=1, 2.............N).
1
г (85.7)-
Каждая из функций определяемых из уравнения
(85.6), содержит четыре произвольных постоянных. Усло-
вия для дают систему 47V-|-4 однородных уравнений
со столькими же неизвестными. Как и в случае сжатия
пластинки без рёбер, можно задачу значительно упро-
стить, воспользовавшись балочной аналогией и функциями
влияния.
х) См. § 66.2 или § 62 настоящей работы.
329
86. Метод функций влияния.
Уравнение (85.6) и условия (85.7) можно истолковать,
как уравнение и условия для участков балки (длина ко-
торой b и жёсткость Z)a), лежащей на сплошном упругом
основании (коэффициент упругости A—Z)^4), растянутой
Рис. 135.
осевой силой Т=22)зр2 и изгибаемой силами Qt и момента-
ми Mi9 приложенными в точках у—(см. рис. 135, где
изображённые силы и моменты считаются положительными).
У такой балки прогиб f(y) есть непрерывная функция
вместе с цервой производной, а вторая и третья производ-
ные в точках приложения сил и моментов испытывают
разрывы вида:
W+Q)-W-OM(, )
Сопоставляя эти равенства и условия (85.7), получаем
связь между моментами, силами и прогибами балкц:
Mt=ctrr^),
<2, г (86.2)
MN=CN^j' (T)N),
Ввёдем далее функции влияния: 8 (т), у) — прогиб балки
в точке у от единичной силы, приложенной в точке т), и
Д(т), у} — прогиб в точке у от единичного момента, прило-
ззо
ценного в точке и обозначим:
ti — 8 (vj , ^l/)) А j — Л (^/, ?]/),
= T)J
Тогда прогиб балки f (у) можно представить в
(86.3)
виде:
/=2 [Qi8 у^>+Mi д Сп.’ • (86-4>
г-И
Подставляя в (86.2), получаем систему из 2N уравнений
для определения Qi и Mt'.
Л/х ^Ди+ Л/2 Д21 + • • '+ЛГ?/Длч +
+ Sli "Ь (?й 82i + • • '+Qa8.vi“0,
Л/\ Д12 + М2 ^Д‘22 — + • • • +Л/#Дя2 4-
4" Qx 812 + (?2 °22 + * ' • 4“ Qn 8ns — О,
Мг Дш 4- м2 Д^ + • • ’4-Мл(д5до-^) +
4“ (?i8'in4-<?282n4- • • • 4-(?№nn —0, s (86-5)
M± Д11 + М2 Д214“ • • •
4- — Хзй~^/г ftQ + Qi 8n + ' ' * 4-<2n8^ = 0,
Ml Д124"М2 Д2г4“ • • * 4~Л^Д#24“
4“ C?1812 “Г C22 2P2 82^_EI2 P40 4“ * * * 4*^n8 №“0,
Мг ДххЧ- M2 Д2х4~ • • • 4~jW\vAnw +
+<?! 8ix+e. w • • • +ew(w - й>7^=£17^)=oj
Решим первые N этих уравнений относительно момен-
тов; тогда получим выражения вида:
N N 2V
^1 = 2 Q>y^ ... , MN^^\QiqiN. (86.6)
<“1 i=l >«=1
Далее подставим найденные значения моментов в остав*
331
шиеся уравнения и получим N уравнений, которые будут
содержать, кроме К, только Q,:
Qi ‘ ‘ ’ +Qn кщ — о»
Qiklt + Qt (^kti — ‘ '+<?w^jy» = O,
QJc1N+Qt ktN + • • • +Qn (jcNN — Jp—==0-
(86.7)
Здесь обозначено сокращённо:
N
klj = Zij+'Vqillbni.
n = l
(86,8)
Приравнивая нулю определитель системы, получим уравне-
ние для определения X:
I,____1 ъ
11 А?4—Е1Х ’ 41 ’
ъ I.1
14 ’ 44
. . kNt
. kjfz
к1н , kaN •kxN-lpNy_EIjry
= 0.
(86.9)
Это уравнение степени TV;
значений X, каждое ив которых
оно определит вообще N
будет зависеть от mi
\ (т), X,(т), , ХЛ (т).
Из этих N серий значений нужно выбрать наименьшее,
не равное нулю; оно и будет критическим.
Выражение для Хкр будет содержать значения четырёх
функций —8fj, Дф 81/, Д</. Заметим, что функции Д, о' и
Д' определятся путём простого дифференцирования, если
известны выражения для функций 8(т), у).
Это вытекает из следующего основного свойства функ-
ций влияния.
Если представить единичный момент, приложенный в
точке т|, как предельный случай двух равных и противо-
332
положных сил Qt приложенных в точках т] и
причём Qdy — 1, то легко получить зависимость:
(8640)
Таким образом, зная 8, легко получить и остальные
три функции.
Функции 8, Д и их производные удобно выразить
через безразмерные функции g и Л:
в(’|’г)=17гЫе(,|’’)’ A(’1’")=4?F5X4l’1’s>’
8' “ 4?у*д,д,s' А' (’ь у)=ггтЫ ,
(8641)
Здесь и в дальнейшем штрихи означают дифференцирова-
ние по у. В дальнейшем будем пользоваться сокращён-
ными обозначениями:
git = g Kz, ч), h,tj = h (7]л 7);), 1
gii = g'^t^> k'n-h' Cb,^)- J
(86.12)
Выражения функций g (tq, у) для конечной опёртой
пластинки и для бесконечной полосы о опёртыми сторо-
нами приведены в § 78; зная g, легко находим, дифферен-
цируя, g't h и Отметим, что для бесконечной полосы
g' (ЯъУ) = А (т), у) = — (86.13)
В приводимых нитке таблицах 14, 15, 16 даны значе-
ния функций g) hvi h' для изотропной полосы и для полосы
из фанеры 1-го и 2-го типа. Значения этик функций вы-
числены при произвольной точке приложения единичной
силы или момента т) для точек балки y = 7j-|-(Z — 1) £ ,
(4 = 1, 2, . •., 13), иначе говоря, таблицы содержат зна-
чения gih„ и h’j. Другие значения — gih hq и
не включённые в таблицы, найдутся по табличным дан-
ным на основании следующих соотношений, которые легко
333
Таблица 14
Функции g9 h, h' для бесконечной по-
лосы. Изотропный материал.
У g h h'
7] 1 0 —1
ffi 4- я/4 0,814 -0,358 —0,0978
+ а/2 0,535 -0,327 0,119
т] 4- За/4 0,318 -0,223 0.129
») + а 0,179 -0,136 0,0925
1) + 5а/4 0,0971 -0,0774 0,0577
») + За/2 0,0513 -0,0423 0,0334
ij + 7а/4 0,0266 -0,0225 0,0184
7} -{• 2а 0,0136 -0,0117 0,0099
7j 4- 9а/4 0,0069 -0,0060 0,0052
71 4- 5а/2 0,0034 -0,0031 0,0027
у, 4- Иа/4 0,0017 -0,0015 0,0014
4- За । 0,0008 -0,0008 0,0007
установить, рассматривая изгиб бесконечной растянутой
балки на упругом основании:
gn= £»а= • • • = ''
£12 £зз--------- * * * - 1+1?
Sin Si»n-^i - • • • 1 >
А л /^22 :z= ’ * * — ii 6.
Лх8 = Лаэ” ’ * * = 1+1,
^in~^2+i+~: ' ’ * A/,n+i-lJ
h 2 = • • • = hir
Л12== /123= ’ ' • — hl, i + i,
/11Z1 = h%t 71T 1 = • • * == /1ц tt j-i-l»
(86.14)
На рио. 186 показаны графики функций g, к и h' для
изотропной полосы; на рис. 137 —графики тех же фунн-
334
Таблица 15
Функции g, h, hf rslsl бесконечной полосы. Фанера 1-го типа.
У Сжатие вдоль волокон Сжатие поперёк волокон
£ h h' S Л | h'
ъ 0,581 0 -2,01 2,01 0 -0,581
У -Г «/4 0,321 -0,388 -0,224 1,87 -0,306 -0,236
1) 4- а/2 0,103 -0,172 0,234 1,58 -0,409 -0,0494
Ч + За/4 0,0239 -0,0497 1 0,0882 1,25 -0,406 0,0420
Ч + а 0,0036 -0,0104 0,0232 0,949 -0,355 1 0,0787
Ч + ба/4 0,0000 -0,0013 0,0044 0,696 -0,289 0,0858
Ч + За/2 -0,0002 0,0001 0,0004 0,496 -0,224 0,0787
Ч + la/b -0,0001 0,0001 -0,0001 0,343 -0,166 0,0658
т) +'2а 0,0000 0,0000 -0,0001 0,233 -0,120 0,0521
т) 4- 9а/4 0,0000 0,0000 0,0000 0,153 -0.084 0,0393
- 7] 4- 5а/2 0,0000 0,0000 0,0000 0,0979 -0,0574 0,0287
т] 4- 11а/4 0,0000 0,0000 0,0000 0,0609 -0,0382 0,0204
Ч 4- За 0,0000 0,0000 0,0000 0,0368 -0,0249 0,0141
Таблица 16
Функции gf h, Л* для бесконечной полосы. Фанера 2-го типа.
У Сжатие вдоль волокон Сжатие поперёк волокон
S 1 Л 1 h' « 1 h 1 h'
ч 1,09 0 -1,54 1,54 0 -1,09
Ч + а/4 0,799 -0,545 -0,110 1,30 -0,492 -0,269
ЧЧ-в/2 0,388 -0,438 -0,268 0,876 -0,538 0,0912
т) 4- За/4 0,125 -0,226 0,241 0,492 -0,413 0,196
щ4- а 0,097 -0,0797 0,132 0,225 -0,260 0,182
7) 4- 5а/4 -0,0217 -0,0115 0,0497 0,0697 -0,137 0,129
7) 4- За/2 -0,0198 -0,0093 0,0934 -0,0045 -0,0570 0,0762
т) 4- 7а/4 -0,0109 0,0102 -0,0040 -0,0301 -0,0135 0,0373
т)4-2а -0,0041 0,0059 -0,0054 -0,0314 0,0056 0,0136
• т)4-9а/4 -0,0008 0,0025 -0,0034 -0,0236 0,0109 0.0016
т)4-5а/2 0,0004 0,0006 -0.0015 -0,0146 0.0100 -0,0031
' т)4-11а/4 0,0005 -0,0001 -0,0004 -0 0076 0,0070 -0,0040
7) 4-За 0,0003 И -0,0003 0,0000 -0,0003 II 0,0042 -0,0033
336
ций для полосы с постоянными фанеры 1-го типа для
случая, когда ось х направлена вдоль волокон рубашки
и на рис. 138 —то же для случая, когда ось х направлена
перпендикулярно к волокнам рубашки.
87. Устойчивость пластинки с одним ребром.
Прямоугольная пластинка, подкреплённая одним реб-
ром, сжимается осевыми силами X, приложенными к кон-
цам ребра (рис. 139). В общем случае полагаем, что ось
ребра не совпадает с осью симметрии пластинки.
Обозначим через EI и С— жёсткости изгиба (в пло-
скости, перпендикулярной к ху) и кручения ребра и
Ста
22чС. Г. ЛехннцкиП
337
В рассматриваемом случае для конечной пластинки
N = i, ?), = •»»,
/=<2s('*i, у)+м Mw)-
(87Л)
Уравнения (86.5) принимают вид:
М Гаи— Foa")+(?Sh = 0, )
> IX } (87.2)
МДи + <? (\i ~ ^г~ —0- |
Отсюда
(87'3>
у Е1пгтг 4-/д2 т 1 (874)
в gn, clhigu tn
1— ------- • —
cmhx — 1 gxx
и здесь остаётся пока неопределённым.
Если имеются таблицы функций
g, h и hf, то для определения т
можно использовать эти таблицы.
В частном случае, при ничтож-
ной жёсткости кручения, когда ребро
сопротивляется только изгибу и не
сопротивляется закручиванию,
а а £ц
Число полуволн
k
где
случае же бесконечной жест-
не может закручиваться.
В
кости кручения, когда ребро
а может только изгибаться:
, 4т:}/ 1
+ а (87.6)
^ii
Не делая каких-либо дополнительных предположений
относительно жёсткостей ребра; рассмотрим кратко два
случая.
338
1) Симметричное ребро. Если ребро направлено
по оси симметрии пластинки, то, как легко видеть,
8J1 = £н=0,
_____________________ А У
। , т /ду ------
аа а Ян’ ' ’ )
где £Х1=£(Ь/2, Ь/2; т). Число по- 0 * X
луволн определяется с помощью —* —— ------------►
таблиц функций влияния (в тех
случаях, когда такие таблицы име-
ются). Из формулы (87.7) вид-
но, что критическая сила для Е77
пластинки с ребром, направленным
по оси симметрии, не зависит от рис* 140-
жёсткости кручения ребра, а толь-
ко от жёсткости изгиба его (и, разумеется, от жёсткостей
пластинки).
2) Полоса с одним ребром. Для бесконечной
полосы с одним ребром (рис. 140):
g'll = A11 = g (Ъ7)) = Л(71,7)) = 0, )
, Ч 1,14 г (87.8>
g11 = gt'b'»)) = 2’(«i + “2), j
где их, «а — корни уравнения
P2w‘ — 2£>3гг2 +£, = (). (87.9)
Получаем:
Х = :^-‘ + 2-^1-1т(и14-и2). (87.10)
Очевидно, наименьшее значение X получится при m = i,
и окончательно
. Е1п* 2лDjD, , . ч /О« ...
*кр = -^—F—LTJ-“(«x + «»)- (87.41)
Формула годится для любого из трёх возможных слу-
чаев корней I, II, III (см. § 78). Интересно отметить, что
критическая сила для полосы с поперечным ребром полу-
чается в виде суммы эйлеровой критической силы для
22*
33*
а -—-----
Рас. 141.
ребра (т. е. для стержня с опёртыми концами, сжатого
осевыми силами) и из критической силы для полосы, сжа-
той двумя противоположными силами (см. §79).
88. Устойчивость прямоугольной пластинки, усиленной
рёбрами по двум сторонам.
Рассмотрим прямоугольную ортотропную пластинку с
главными направлениями, параллельными направлениям
сторон, у которой две стороны подкреплены рёбрами
жёсткости. Система деформируется двумя равными про-
тивоположными силами к, приложенными по концам одного
ребра, и двумя сила-
ми XjP, приложенны-
ми к концам другого
ребра;, требуется оп-
ределить критичес-
кое значение акр. Сто-
роны, некоторых ук-
реплены концы рё-
бер, предполагаются
опёртыми; концы рё-
бер предполаг аются
опёртыми и закреп-
лёнными против по-
ворота.
Направим ось Ох вдоль усиленной стороны (рис. 141)
и введём обозначения: EI^ Е12— жёсткости изгиба рёбер
в плоскостях, перпендикулярных к первоначальной пло-
скости пластинки ху* эти плоскости предполагаются глав-
ными плоскостями изгиба рёбер; С„ Съ — жёсткости кручения
рёбер; а, Ь — размеры сторон пластинки; d^=bja^ fi-mn/a
(тп=Л,. 2, 3, ...).
Будем решать задачу энергетическим методом. Пред-
положим, что система получила малое искривление: пла-
стинка изогнулась, а рёбра изогнулись и закрутились.
Обозначим через w (я, у) прогиб пластинки; = w (х, 0),
- w - прогибы рёбер; 91== 62 = -
углы закручивания рёбер. Потенциальная энергия изгиба
^изг будет складываться из потенциальной энергии пла-
стинки [см. (38.19)] и из потенциальной энергии рёбер
а
{ЕЦW + C, (0'х)8 + G (9'2)3] dx. (88.1)
340
При искривлении системы силы произведут работу:
а
о
(88.2)
Из уравнения Уизг “ А находим:
а Ъ
^ц^у—ч^у^
> = —------;------------------------+
[(«-;i2+-p («;>’] dx
о
[EI, + Eit (»>;)» + 0» (01)2 + 0, (01)4 dx
+ "-------------------------------; (88.3)
^[(и'1)2 + Р(«’1)2] dx
О
Задаёмся выражением для Щ, удовлетворяющим условиям
на опёртых сторонах г’ — О, х=^а в виде:
w = / (у) sin рх; (88.4)
тогда
«’1 = /(O)siri₽x, = / (b) sin pz, |
= /' (0) sin 02 = /' (6) sin p#. i
Подставляя в (88.3), будем искать функцию f(y\ сообщаю-
щую X минимальное значение. Эту задачу сводим к
задаче определения минимума выражения1):
и = $ (Z>2/"2 - 2D^-fr + + 4 А т dy +
+ (ЕЦГ - X) Р2/2 (0) + (Е1г р2 - ХР) В2/2 (6) +
+ [A/'a(0) + Gf2(O]P2- (88-6)
*) См. f 66.2 или § 62 настоящей книги.
341
Решая её по правилам вариационного исчисления, полу-
чаем следующие результаты.
Функция / удовлетворяет уравнению
- 2/у Т + Dpf = 0 (88.7)
и условиям:
/*(0)—мхр*/(О) —% р»/'(0) ==0-'
—О,
/ 4П Л 1 }(в8.8)
(0) - (\+ ) ₽7' (0)+я (EI& - X) (0) = о,
Г” (6) - (Ч + Р7' (6) - ± (ЕЦУ - хр)?7 (Л)=0.
Общий интеграл уравнения (88.7) зависит от корней уже
встречавшегося характеристического уравнения:
(88.9)
и запишется различно в зависимости от того, какой из
трёх случаев корней имеет место (см. § 78).
Случай I. Вещественные неравные корни ±ux, ±иа:
/ = A ch $игу + В sh fapj + C ch $upj-\-D sh Puay. (88.10)
Случай II. Вещественные, равные корни±и:
f = (A-[-By) ch fiuy + (C + Zty) sh fiuy. (88.11)
Случай III. Комплексные корни u^iv, — u^iv:
f = (A cosfivy-j-B sin Poy)chpuy + (£ cos +
4-D sin pvt/) sh риу. (88.12)
На основании условий (88.8) получаем систему из че-
тырёх однородных уравнений для А,В, приравнивая
нулю определитель этой системы, получаем уравнение
для X. Последнее уравнение —второй степени; оно даст
две серии значений — (т) и Ха(т). Далее, необходимо
Я42
установить число полуволн в направлении рёбер — иг, ко*
торому соответствует наименьшее X, не равное нулю, и само
вто наименьшее значение.
89. Пластинка, усиленная одинаковыми рёбрами
по двум сторонам.
Остановимся более подробно на случае симметричной
системы, когда рёбра имеют одинаковые жёсткости и силы
одинаковы.
В этом случае
Е1г = ЕЦ = ЕЦ С^С^С, Р = 1.
Здесь возможны две основные формы искривления пла-
стинки после потери устойчивости; первая характеризуется
тем, что пластинка, потеряв устойчивость, выпучится, об-
разуя поверхность, симметричную относительно оси у~ Ь/2,
вторая характеризуется антисимметричной изогнутой по-
верхностью. Исследуем каждую из этих форм; общее
исследование будем вести для случая I (неравных корней
характеристического уравнения), а потом укажем резуль-
таты и для других двух случаев —II и III.
1) Симметричная форма.
Уравнение симметричной изогнутой поверхности пла-
стинки имеет вид1):
/ =A ch К (у-6 /2) + В ch ₽wa (у — Ь/ 2).’ (89.1)
Условия (88.8)- сведутся к двум:
Г(0)-*1₽7(0)-Д₽в/'(0) =о,
Г (0) - (Ч + ₽7' (0)+± (EIF -1) ₽7 (0)» 0.'
(89.2)
Подставляя значения
условия, получаем два
А Г. /*, при у —о в эти
однородных уравнения для
*) Эта функция, очевидно, есть частный случай функции (88.10).
343
постоянных Л и В, а приравнивая нулю определитель
этой системы, получим после несложных преобразований:
. _ Е1^т* .
аа +
+ д / Д Д2
а
(89.3)
Входящие в эту формулу величины lm, ет, sm являют-
ся функциями отношения d = b / а и зависят от т, которое
равно числу полуволн в направлении сил.
В случае I (неравные вещественные корни —см. §88)
эти величины имеют вид:
= i (uj-w’)ch^^ch—
em = £(u1ch^8h^-Ksch^sh^),
s - -1- /„» . gh mmt'd nh mTC1<2rf
rT , mnu.d i тт.иЛ л m~u^d , mnuyd
Hm ~ sh —ch —r=-if2 sh —ch —.
(89.4)
Та же формула Для k (89.3) получается в случае II и
в случае III, только ет и sm будут иметь другой вид,
В случае II:
= ту- 2u (ch mitud +1),
т
ет ” тГ~ (3^ m>Kllc^ —
л т >
1 I
sm = 2и (ch maud — 1), I
|
Нт — sh mnud + mnud. I
В случае III:
= 7— (ch mitad + cos m^vd),
tt~ (sh mnud — ~ sin ттгу(/),
sm = ту- 2u (ch mKud — cos
m
Ят = вЬ mnud sinzwrrtf).
(89.5)
(89.6)
344
Для больших отношений d можно принять
1; 1т — sm Ui4~Wj (89.7)
(или соответственно lm = зт = 2и).
2) Антисимметричная форма.
Полагая
/ = АвЬ -bl 2) + В sh ?ws(y-6/2), (89.8)
опять сводим условия (88.8) к двум (89.2). Приравнивая
нулю определитель системы уравнений для Аи В, полу-
ченной из условий (89.2), находим:
, Е1п* 1 * * *тг .
«р\ V° Vem'V
"Г а т , яС
+ тет
Исследование полученных
позволяет сделать следующие
заключения:
1) При любых конечных
отношениях сторон должна
иметь место симметричная фор-
ма потери устойчивости с Одной
полуволной (т=1) в направ-
лении сжимающих сил, и толь-
ко для больших отношений
d (в теории для d~ ос) симмет-
ричная и антисимметричная
формы становятся равновоз-
формул (89.3) и (89.9)
можными. Вид симметричной
и антисимметричной поверхности показан на рис. 142 для
7П = 1.
2) Критическая нагрузка определяется по формуле:
где
(89.10)
(89.11)
345
Критическая нагрузка, как видно из этих формул,
складывается из эйлеровой критической силы и из допол-
нительной силы, зависящей от свойств пластинки. При
EI — С~ 0 получим критическую нагрузку для пластинки
без рёбер с двумя свободными и двумя опёртыми сторо-
нами, сжатой силами, приложенными вблизи её свободных
краёв:
(89Л2>
3) Для больших отношений сторон d можно принять
4) Для пластинки с рёбрами, у которых жёсткость
кручения С = 0, получаем:
(89Л4)
Этот случай равносилен случаю пластинки, не скреп-
лённой с рёбрами жёстко, а свободно опёртой на рёбра,
так как равенство 67 = 0 можно рассматривать как условие
свободного поворота краёв пластинки вокруг осей рёбер.
5) Для пластинки с бесконечной жёсткостью кручения
(89.15)
физически это значит, что рёбра могут только прогибаться,
но не могут скручиваться (благодаря, например, особым
боковым закреплениям).
34П
Расчёт на устойчивость пластинок, усиленных рёбрами
вблизи краёв, значительно облегчается, если имеются
таблицы величин Z15 en sv Такие таблицы мы приводим ниже
(таблицы 17, 18, 19) для изотропной пластинки и для
Таблица 17
Функции 1Х) eif $г для изотропной
пластинки
d
0,25 2,81 0,0503 0.393
0,5 1,81 0 189 0,661
0,75 1,67 0,379 1,14
1 1,71 0,572 1,44
2 1,96 0.954 1,95
3 2,00 0,997 2,00
оо 2.00 1.00 2,00
у
О 0.5 / 1,5 2 2,5 3
пластинки из фанеры 1-го и 2-го типов. Желая получить Хкр
для пластинки с данным отношением сторон d, берём
соответствующую таблицу и найденные из таблицы 1Х, $х,
подставляем в формулы (89.10) —(89.11). Значения этих
величин для отношений, не вошедших в таблицу, можно
определять приближённо путэм интерполирования, так
как функции lx (tf), е, (<Z), представляются, достаточно
плавными кривыми. На рис. 143 показаны графики функ-
ций для изотропной пластинки; на рис. 144 —графики
тех же функций для
пластинки из фанеры
1-го типа, сжимаемой
вдоль волокон рубашки
(рёбра усиливают сто-
роны, параллельные во-
локнам, ось х направ-
лена вдоль волокон).
На рис. 145 показа-
ны графики тех же
функций для пластин-
ки из фанеры 1-го
рубашки (рёбра скрепл
ными к волокнам, ось х направлена перпендикулярно
к волокнам). Разница между графиками рис. 144 и 145
Рис. 145.
типа, сжатой поперёк волокон
ны со сторонами, перпендикуляр-
347
весьма заметна; это вполне понятно, так как разница
между упругими свойствами файеры 1-го типа в напра-
влении волокон и в направлении, перпендикулярном к
волокнам, довольно значительна.
Таблица 18
Функции Zlf elf si для пластинки из фанеры 1-го типа
d Сжатие вдоль волокон С 4 1 !жатие.поперёк волокон
1 ₽1 *1 5i
0,25 0,5 0,75 1 3,25 2,84 3,16 3,36 I __J 0,169 0,545 0,844 0,965 1,35 2,52 3,18 3,40 j ' ! 2,61 1,39 1,03 0,879 1 0,0177 0,0615 0,131 0,223 0,114 0,227 0,340 0,450
сч со 8 3,44 3,44 3,44 1,00 1,00 1.00 3,44 3,44 3.44 0,851 0 986 0,996 0,660 0,992 1,00 0,808 0 998 0,996
Таблица 19
Функции 119 е19 для пластинки пз фанеры 2-го типа
d Сжатие вдоль волокон с 11 жатие поперёк волокон
61 1
0,25 2,65 0.0746 0,557 2,60 0,0382 0,279
0,5 1,55 0,281 1,10 1,39 0,145 0,555
0,75 0,885 0,566 2,10 1,07 0,312 0,819
1 । 1,57 0.824 1,83 1,00 0,511 1,04
2 1,87 1,01 1,87 1,28 1,01 1,36
з !, 1 1,86 0,999 1,86 1,32 1,01 1,32
оо \ ! 1,86 1.00 1,86 1.31 1.00 1,31
ЛИТЕРАТУРА
3. Абрамов В. М, Распределение напряжений в плоском безгранич-
ном клине при произвольной нагрузке. «Труды Конференции по
оптическому методу изучения напряжений НИИММ ЛГУ и
НИИМех МГУ», ОНТИ, 1937.
2. Балабух Л. И, Устойчивость фанерных пластинок. «Техника воз-
душного флота», № 9, 1937.
3. Бернштейн С, Л. Основа динамики сооружений. Госстройиздат,
1933.
4. Бехтерев П. Аналитическое исследование обобщённого закона
Гука, части 1 и 2. а) Ленинград, издание автора (литографирован-
ное), 1925; в) «Журнал русского физико-химического общества»,
VII, вып. 3—4; с) то же, VIII, вып. 3, 1926.
5. Галеркин Б. Г. Упругие тонкие плиты. Госстройиздат, 1933.
б. Гекелер И. В. Статика упругого тела, ГТТИ, ОНТИ, 1934.
7. Глушков Г. С. Определение напряжений во вращающемся диске
при различных упругих свойствах материала в двух направлениях.
«Труды Московского станко-инструментального ин-та», сбор-
ник III, 1939.
8. Кан С. Н. и Свердлов И. А. Расчёт самолёта на прочность, Москва,
Оборонгиз, 1940, гл. X.
9. Куфарев П> П. Определение напряжений в эллиптической анизо-
тропной пластинке. «Доклады Академии Наук СССР», т. XXIII,
№ 3, 1939.
10. Лехницкий С. Г. К вопросу о влиянии сосредоточенной силы на
распределение напряжений в упругой анизотропной среде. «При-
кладная математика и механика», т. Ill, № 1, 1936.
11. Лехницкий С. Г. Некоторые случаи плоской задачи теории упру-
гости анизотропного тела. Сборник «Экспериментальные методы
определения напряжений и деформаций в упругой и пластической
зонах», ОНТИ, 1935.
12. Лехницкий С. Г. Плоская статическая задача теории упругости
анизотропного тела. «Прикладная математика и механика»,
новая серия, т. 1, вып. 1, 1937.
13. Лехницкий С. Г. Концентрация напряжений вблизи эллиптического
и кругового отверстия в растягиваемой анизотропной пластинке.
«Вестник инженеров и техников», № 5, 1936.
14. Лехницкий С. Г. Напряжения в неограниченной анизотропной пла-
стинке, ослайнежной Эллиптическим отверстием. «Доклады Акаде-
мии Наук.СССР*, т. IV (XIII), № 3 (107), 1936»
15. Лехницкий С. Г. Теоретическое исследование напряжённого со-
стояния анизотропной пластинки ,<оел&(йшнной эллиптическим или
круговым отверстием. «Труды' Конференции по оптическому методу
изучения напряжений НИИММ ЛГУ и НИИМех МГУ»; ОНТИ,
1937.
349
16. Лехницкий С. Г. Некоторые случаи распределения напряжений
в анизотропной пластинке с круговым отверстием. «Учёные записки
Ленинградского гос. университета», серия математических наук
(механика), вып. 8, 1939.
17. Лехницкий С. Г. О напряжениях вблизи кругового отверстия в ани-
зотропной пластинке при изгибе. «Вестник инженеров и техников».
№ 4, 1937.
18. Лехницкий С. Г. Решение плоской задачи теории упругости анизо-
тропного тела для сплошного эллипса. «Доклады Академии Наук
СССР», т. XV, № 9, 1937.
19. Лехницкий С. Г. Плоская задача теории упругости для тела с ци-
линдрической анизотропией. «Учёные записки Саратовского гос.
университета», т. I, (XIV), серия физ.-мат., вып. 2, 1938.
20. Лехницкий С. Г. Плоская задача теории упругости для среды со
слабо выраженной анизотропией, 1, II, «Доклады Академии Наук
СССР», т. XXXI, № 5 и № 9, 1941.
21. Лехницкий С. Г. О некоторых вопросах, связанных с теорией изгиба
тонких плит. «Прикладная математика и механика», новая серия,
т. II, вып. 2, 1938.
22. Лехницкий С. Г. Изгиб неоднородных анизотропных тонких плит
симметричного строения. Прикладная математика и механика,
т. V, № 1, 1941.
23. Лехницкий С. Г. К расчёту на устойчивость ортотропной пластинки.
«Вестник инженеров и техников», № 1, 1941.
24. Лехницкий С, Г. Устойчивость анизотропных пластинок. Пособие
для авиаконструкторов. ОГИЗ, Гостехиздат, 1943.
25. Лурье А. И. Устойчивость пластинки, сжатой сосредоточенными
силами. «Труды Ленинградского индустриального института»,
1939, № 3, раздел физ.-мат. наук, № 1.
26. Ляв А. Математическая теория упругости. ОНТИ, 1935.
27. Митинский А, Н. Расчёт напряжений в деревянной сверлёной
трубе.
«Вестник инженеров и техников», № 5, 1936.
28. Михлин С. Г. Плоская деформация в анизотропной среде. «Труды
Сейсмологического института АН СССР», № 76, 1936.
29. Мусхелигивили Н. И. Некоторые основные задачи математической
теории упругости, изд. Академии Наук СССР, 1935.
30. Найман М. И. Распределение напряжений в пластинках, ослаблен-
ных отверстиями. «Труды ЦАРИ», вып. 313, 1937.
3'1 . «Прочность и устойчивость тонкостенных конструкций в самолёто-
строении». Сборник под ред. А. А. Уманского и П. М. Знаменского,
изд. ЦАГИ, 1937.
32. Ростовцев Г. Г. Приведённая ширина изотропной и анизотропной
пластинки. «Труды Ленинградского института инженеров граждан-
ского воздушного флота», № 6, 1936.
33. Ростовцев Г. Г, К вопросу о приведённой ширине ортотропной
пластинки. «Техника воздушного флота», № 10, 1937.
34. Ростовцев Г, Г. Расчёт тонкой плоской обшивки, подкреплённой
рёбрами жёсткости. «Труды Ленинградского ин-та инженеров
гражданского воздушного флота», вып. 20, 1940.
35. Савин Г. Н. Распределение напряжений в плоском поле, ослаблен-
ном каким-либо отверстием. «Труды Днепропетровского инженерно-
строительного ин -та», сообщение 10, 1936.
36. Савин Г. Н. Изгиб анизотропной балки с постоянной перерезываю-
щей силой, ослабленной эллиптическим и круговым отверстием.
«Вестник инженеров и техников», № 4, 1938.
359
37, Савин Г, Н. Основная плоская статическая задача теории упруго-
сти для анизотропной среды. «Труды Ин-та строительной механики.
УАН», № 32, 1938,
38. Савин Г, Н. Некоторые задачи теории упругости анизотропной
среды. «Доклады Академии Наук СССР», т. ХХШ, № з, 1939-
39. Секерж-Зенъкович Я. И, К расчёту на устойчивость листа фанеры,
как анизотропной пластинки. «Труды ЦАГИ», №76, 1931.
40. Сервисен С. В. Основы технической теории упругости. ГН.ТИ
Украины, 1934.
41. Соколова. А. Распределение напряжений в плоском поле, ослаб-
ленном отверстиями. «Бюллетень научно-техн, комитета УВМС
РККА, вып. 1, IV, 1930.
42. «Справочник .авиаконструктора», том III. Прочность самолёта.
Изд. ЦАГИ, 1939.
43. Тимошенко С. П. Теория упругости, ОНТИ, 1937.
44. Тимошенко С. П. Курс теории упругости, часть II. Стержни и
пластинки, Петроград, 1916.
45. Тимошенко С. П. Теория колебаний в инженерном деле. ГНТИГ
1932.
46. Тимошенко С. П. Об устойчивости пластинок, подкреплённых
жёсткими рёбрами. Изд. Ин-та инж. путей сообщения, Петро гр ад^
1914.
47. Трефтц Е. Математическая теория упругости, ГТТИ, 1932.
48. Феппль А Сила и деформация, ч. I, ОНТИ, 1933.
49. Филиппов А. П. Stabilitat rechteckiger Platten, die durch Einzel-
krafte gedruckt werden. «Известия Академии Наук СССР» (OMEH)r
№ 7, 1933.
50. Ченцов Н. Г. Исследование фанеры, как ортотропной пластинки.
«Технические заметки ЦАГИ», № 91, 1936.
51. Шерман Д. И. Плоская задача теории упругости для анизотропной
среды. «ТрудыСейсмологического ин’Та АН СССР», .№ 86, 1938.
52. Шу лежко П. Г. Уравнения движения и равновесия анизотропной
неоднородной тонкой плиты переменной толщины.
а) «Труды Харьковского ин-та сооружений», 1941; б) «Прикладная
математика и Механика», т. VI, вып./ 2—3, 1942.
53. Auerbach F. Elastizitat der Kristalle. Handbuch der physika-
lischen und technischen Mechanik, B. Ill, Leipzig, 1927.
54. Bergman S. u. Reissner h. Neue Probleme aus der Flugzeugstatik.
Zeitschr. Flugtechn. Motorluftsch. a) t. 20, № 18, 1929, b) t. 21
№ 12, 1930.
55. Boussinesque M. I. Compl6ments h une etude sur la theorie de
l’6quilibre et du mouvement des solides elastiques. Journ. de Math,
pures et appl., 3 sdr., t. 5, 1879.
56. Cox H. L. Summary of the present state of knowledge regarding
sheet-metal construction. Aeron, Res. Comm. Rep. and Mem.,
London, 1933, p. 1553.
57. Geckeler I. Elastizitatstheorie anisotroper KOrper. Handbuch der
Physik, В. VI, Berlin, 1928.
58. Gehring F. De aequationibus differentialibus quibus aequilibrium et
motus laminae crystallinae definitur, Berlin, 1860.
59. heck O. u. Ebner. Tafeln und Berechnungen fur die Festigkeit von
Platten-u. Schalenkonstruktionen im Flugzeugbau.Luftfahrforschung,
B. 11, № 8, 1935.
60. huber M. T. Teorja plyt. Lwow, 1921.
61. Huber M. T. Einige Anwendungen der Biegungstheorie orthotroper
Platten. Zeitschr. f. Angew. Math u. Meeh. B. 6, H. 3» 1926.
951
62. Huber M. T. Probleme der Statik technisch wichtiger orthotroper
Flatten. Warszawa, 1929.
€3. Lechnitski S. Sur quelques ргоЫётез de I’elasticitd des corps aniso-
tropes. Comptes Rendus (Paris), t 20$, 1936.
64. Leitz H. Eisenbewehrte Flatten bei allgemeinem Biegungszustand.
Bautechnik, 1923.
65. Leitz H. Zur Anisotropie kreuzweise bewehrten Be to ns, Zeitschr. f.
Angew. Math. u. Meeh., B. 6, H. 3, 1926.
66. Okubo Hafumi . General expression of stresses components in two
dimensions in an aeralotropic substance. Sei. Rep. Tohoku Univ.,
I, s. 25, 1937.
67. Saint-Venant B. Me mo ire sur la distribution d’elasticite. Journ. de
Math, pures et appl. (Liouville), s6r. 2, t. 8, 1863.
68. Saint ’Venant В. Memoire sur les divers genres d’homog£neite des
corps solides. Journ. de Math, pures et appl. (Liouville), t. 10, 1865.
69. Schmieden C. Das Ausknicken versteifter Blech unter Schubbean-
spruchung. Zeitschr. Flugtechn. Motorluft. T. 21, H. 3, 1930.
70. Seydel E. Beitrag zur Frage des Auabeulens von versteiften Flatten
bei Schubbeanspruchung. DVL.-Bericht. Luftfahrforschung, t. 8,
№ 3, 1930.
71. Seydel E. Uber das Ausbeulen von rechteckigen iso tropen Oder ortho -
gonal-anisotropen Flatten bei Schubbeanspruchung. Ingenieur
Archiv, t. 4, № 2, 1933.
72. Seydel E. Schubknickversuche mit Welblechtafeln. DVL.-Bericht,
1931.
73. Seydel E. AusbeuLSchubblast rechteckiger Flatten. Z. Flugtechn.
Motorluftsch., t. 24, № 33, 1933.
74. Sommerfeld Л. Uber die Knicksicherheit der Stege von Walzenpro-
fielen. Zeitschr- f. Math. u. Physik, t. 54, 1906.
75. Tu.zt. M. Effect of a circular Hoile. Philos. Magazine 9, № 56, 1930.
76. Voigt. W. Lehrbuch der Kristallphysik. VerL Teubner, 1910.
77. Voigt. IF. Uber die Elasticitatsverhaltnisse cylindrisch aufgebauter
Kdrper. Nachrichten v. d. Konigl. Ges. der Wiss. zu Gottingen,
1886, № 16.
78. Wagner H. Sheet-Metal Airplane Construction. Aeron. Eng., t. 3,
№ 4, 1931.
79. Wolf K. Ausbreitung der Kraft in der Halbebene und in Halbraum
bei anisotropem Material. Zeitsch. f. Angew. Math. u. Meeh., B. 15,
H. 5, 1935.
80. Yamana M. On the Elastic Stability of Aeroplane Structures,
I. Fac. Eng. Tokyo Univ., t. 20, № 8, 1933.
ИМЕННОЙ УКАЗАТЕЛЬ
Абрамов В. М. 69, 349
Ауэрбах Ф. (Auerbach F.) 361
Балабух Л. И. 286, 288, 349
Бергман G. (Bergmann S.) 351
Бернштейн С. А. 239, 349
Бехтерев П. 42, 349
БлеЙх 58
БуссинескМ. (BoussinesqM.) 141,
351
Вагнер Г. (Wagner Н.) 352
Вольф К. (Wolf К.) 81, 352
Галеркин Б. Г. 148, 349
Геки О.(Heck О.) 351
Геккелер И. (Geckeler I.) 349,351
Геринг Ф. (Gehring F.) 351
Глушков Г. С. 126, 127, 349
Губер М. (Huber М.) 141, 148,
189, 193, 197, 351
Зейдель Е. (Seydel Е.) 281, 352
Зоммерфельд A. (Sommerfeld Д.)
304, 352
Нан С. Н. 349
КуфаревП. П. 120, 349
Кокс Г. (Сох Н.) 351
Колосов Г. В. 132
Леви М. 182
Лейтц Г. (Leitz Н. 71) 351
Лехницкий С. Г. 349, 350, 351
Лурье А. И. 303, 350
Ляв A. (Love А.) 42, 350
Митинский А. Н. 75, 350
Михлин С. Г. 39
Мусхелишвили Н. И. 120, 131,
132,350
Найман М. И. 135,350
ОкубоХагоми (OkuboHajumi)81,
Рейснер Г. (Reissner Н.) 351
Рибьер 58
Ростовцев Г. Г. 153, 350
Савин Н. Г, 19,39, 99, 135, 350
Свердлов И. А. 349
Секерж-Зенькович Я. М. 40, 278,
350
Сен-Венан Б. (Saint Venant В.)
352
Серенсен С. В. 258, 350
Соколов П.А. 135, 350
Тимошенко С. П. 58, 71, 73, 88,
148, 239, 258, 283, 286, 303, 309
312, 319, 320, 351
Трефтц Е. (Trefftz Е.) 351
Туци (Tuzi) 352
Файлон (Filon) 58
Фёппль A. (Foppl А.) 351
Филиппов А. П. 303, 351
Фламан 84
Фойгт В. (Voigt W.) 75, 352
Ченцов Н. Г. 42, 351
Шерман Д. И. 39, 351
ШмиденК. (Schmieden С.) 352
Шулежко П. Г. 351
Эбнер (Ebner) 351
Ямана М. (lamana М.) 352
23 Лехнин лай
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Анизотропия криволинейная 23
— цилиндрическая 23, 25, 49, 71,
72, 74
Балка, заделанная одним концом
58
— консольная 55, 58
— на двух опорах 58
— на упругом основании 293, 330
— однопролётная 58
— однородная 58
— ортотропная 55, 56, 57, 58
плоская 52
Брус кривой 52
— криволинейно-анизотропный
кривой 70, 72
Гипотеза Прямых нормалей 141,
Деформация плоская 30
Диск изотропный 75
— криволинейно-анизотропный
186
— круглый 123
Жёсткости анизотропной пла-
стинки 143, 162, 167,170
Жёсткость главная 158
— изгиба 143, 158
— кручения 143, 158
— побочная 143
Задача плоская 37
— для слабо анизотропной пла-
стинки 127
ЗАкон Гука обобщённый 15, 24,
S3, 142
Изгиб балки плоской 52, 55,
57, 58
— бруса кривого 52, 70, 72
— консоли клинообразной 62,
65, 67
354
Изгиб пластинки 139,178,182
— чистый 54
Колебания пластинки вынужден-
ные 244
— поперечные 232
— свободные 232
Кольцо однородное 137
Консоль анизотропная 69
— изотропная 67, 69
— клинообразная 62, 65,67
— ортотропная 64, 66, 69
Концентрация напряжений 88
Коэффициент Пуассона 17
— приведённый 144
Лист фанерный 39
Модуль сдвига 18
— Юнга 17
Нагрузка критическая 248, 257,
259, 262, 264, 266, 268, 278
Направления главные 17
Напряжения местные 217
Ось анизотропии 49
Отверстие круговое 88
— эллиптическое 88, 92, 96, 98
Параметры комплексные 33, 45,
155
Перемещения возможные 22
Пластинка анизотропная 39, 85,
88,139
— гофрированная 159, 160
— изотропная 29, 38
— криволинейно - анизотропная
205
— круглая, заделанная по краю
204
— многослойная 162
— на упругом основании 149
— нагруженная нормальными
усилиями 272
Пластинка ортотропная 28, 40,
41, 51, 53, 94
— однородная 76
Пластинка подкреплённая ребром
159, 161, 308, 312, 323, 327, 337
— прямоугольная 176, 177
— под действием касательных
усилий 277
— с косопрорезанным эллипти-
ческим отверстием 98
— с опёртыми сторонами 178,
182, 258, 263, 268, 272, 277,
285, 295
•— с равномерно распределённой
нагрузкой 186
— с жёстким круговым ядром 116
—• с круговым отверстием 100,
113,226
— с модулями упругости, меняю-
щимися по толщине 167
— с отверстием, близким к квад-
ратному 134
— со слабо выраженной анизотро-
пией 127
— с цилиндрической анизотро-
пией 49, 173
— с эллиптическим отверстием
88, 92, 96, 223
— сжатая в главном направлении
258
— — по двум направлениям 268,
304
— слабо анизотропная 132
— усиленная гофром 159
-----рёбрами жёсткости 159,161,
308, 312, 327, 337
— усиленная рёбрами по двум
сторонам 340, 343
— фанерная 39, 101, 115, 258
— эллиптическая 120
-----вращающаяся 123
-----заделанная по краю 202
Плита многослойная 164
— тонкая 140
Плоскость изотропии 18
— упругой симметрии 16,49
Поверхность средняя 26
Полоса бесконечная 280
Полоса с опёртыми сторонами 193
Полуплоскость упругая 76
Полюс анизотропии 49
Симметрия упругая 15,24
Состояние напряжённое 11
— — плоское обобщённое 26, 49
Среда бесконечная упругая 76
— упругая плоская 76
Тело анизотропное 15
-----однородное 23
— изотропное 15
— ортогонально-анизотропное 17
— ортотропное 25
— трансверсально-изотропное 18,
46
Теорема возможных перемещений
22
— Кирхгофа 21
Труба криволинейно-анизотроп-
ная
Устойчивость пластинки 246, 255,
258, 263, 268, 272, 277, 285, 29©,
308, 318, 327, 337, 340, 343
— полосы бесконечной 280
Фанера второго типа 41, 159, 262
263, 270, 275, 298, 299, 300, 3 01
336, 347, 348
•— первого типа 40, 101, 159, 259,
260, 275, 279, 288, 303, 336, 347,
348
Функция влияния 293, 295, 330
— напряжений 32
Частоты колебаний, приближён-
ные методы определения 239
— собственных колебаний пря-
моугольной пластинки 236
Энергия деформации потенциаль-
ная 19