МАТЕМАТИКА
Большой справочник
для школьников и поступающих
в вузы
Краткое изложение школьного курса
математики
ш
Задачи по основным разделам школьного
курса математики
ш
Контрольные и проверочные работы
по математике.
Тесты
ш
Справочные материалы
ш
Подготовка к экзаменам
Москва • Издательский дом «Дрофа» •1998

УДК 373.167.1:51(03)
ББК22.1я2
М34
Серия основана в 1998 году
Авторы разделов:
Д. И. Аверьянов, П. И. Алтынов, И. И. Баврин, Л. О. Денищева,
Г. В. Дорофеев» Л. И. Звавич, Н. В. Карюхина, В. С. Крамор, Г. М. Кузнецова»
А. И. Медяник, Т. М. Мищенко, Ю. В. Нестеренко, С. Н. Олехник, В. А. Попов,
М. К. Потапов, А. Р. Рязановский, Е. А. Седова, В. К. Смирнова,
Л. Я. Шляпочник, Б. В. Юрченко, Ел. В. Юрченко
Математика: Большой справочник для школьников и поступающих в вузы/Д. И. Аверьянов,
М34 П. И. Алтынов, И. И. Баврин и др. — М.: Дрофа, 1998. — 864 с: ил. — (Большие справочники
для школьников и поступающих в вузы).
ISBN 5—7107—2093—3
Справочник является уникальным учебным пособием по математике, содержащим теоретический материал
школьных курсов математики (5—6 кл.), алгебры (7—11 кл.), геометрии (7—11 кл.), примеры решения типовых задач и
задачи для самостоятельного решения, контрольные и проверочные работы, тесты, различные справочные
материалы.
Кроме того, в справочнике представлены обширные материалы для подготовки к выпускным экзаменам по
математике в 9 и 11 классах, к вступительным экзаменам по математике в высшие учебные заведения.
Содержание книги охватывает почти десять школьных учебников по математике для 5—11 классов и около
двух десятков обычных изданий справочно-методической литературы. Книга адресована учащимся, учителям,
родителям, абитуриентам, студентам педвузов.
УДК 373.167.1:51(03)
ББК 22.1я2
ISBN 5—7107—2093—3 © «Дрофа», 1998

Содержание
Предисловие 4
Краткое изложение школьного курса математики
Математика. 5—б классы (П. И. Алтынов) 7
Алгебра. 7—11 классы (Е. В. Юрченко, Ел. В. Юрченко, В. С. Крамор, В. А. Попов) ... 43
Геометрия. 7—9 классы (И. И. Баврин) 119
Геометрия. 10—11 классы (И. И. Баврин) 183
Задачи по основным разделам Школьного курса математики
Математика. 5—6 классы (J7. И. Алтынов) 231
Алгебра. 7—9 классы (Л. И. Звавич, Л. Я. Шляпочник) 241
Алгебра и начала анализа. 10—11 классы (Л. И. Звавич, Л. Я. Шляпочник). ...... 255
Геометрия. 7—9 классы (П. И. Алтынов) 263
Геометрия. 10—11 классы (П. И. Алтынов) 275
Контрольные и проверочные работы по математике. Тесты
Контрольные и проверочные работы
Математика. 5—6 классы (П. Я. Алтынов) 285
Алгебра. 7—9 классы (Л. И. Звавич, Л. Я. Шляпочник) 289
Алгебра и начала анализа. 10—11 классы (Л. И. Звавич, Л. Я. Шляпочник) 297
Геометрия. 7—9 классы (А. И. Медяник) 301
Геометрия. 10—11 классы (А. И. Afедяник) 307
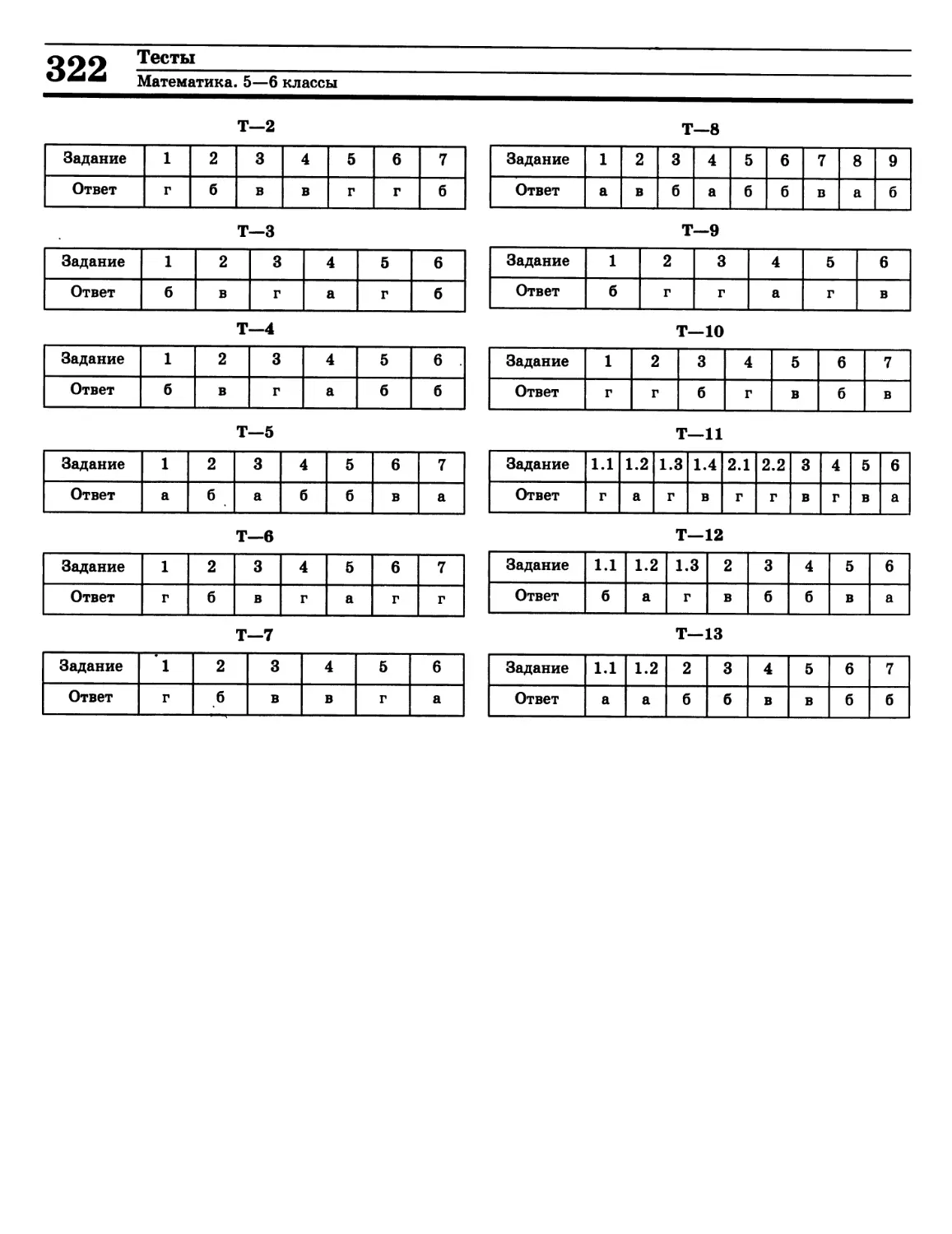
Тесты
Математика. 5—6 классы (Е. В. Юрченко, Ел. В. Юрченко) 312
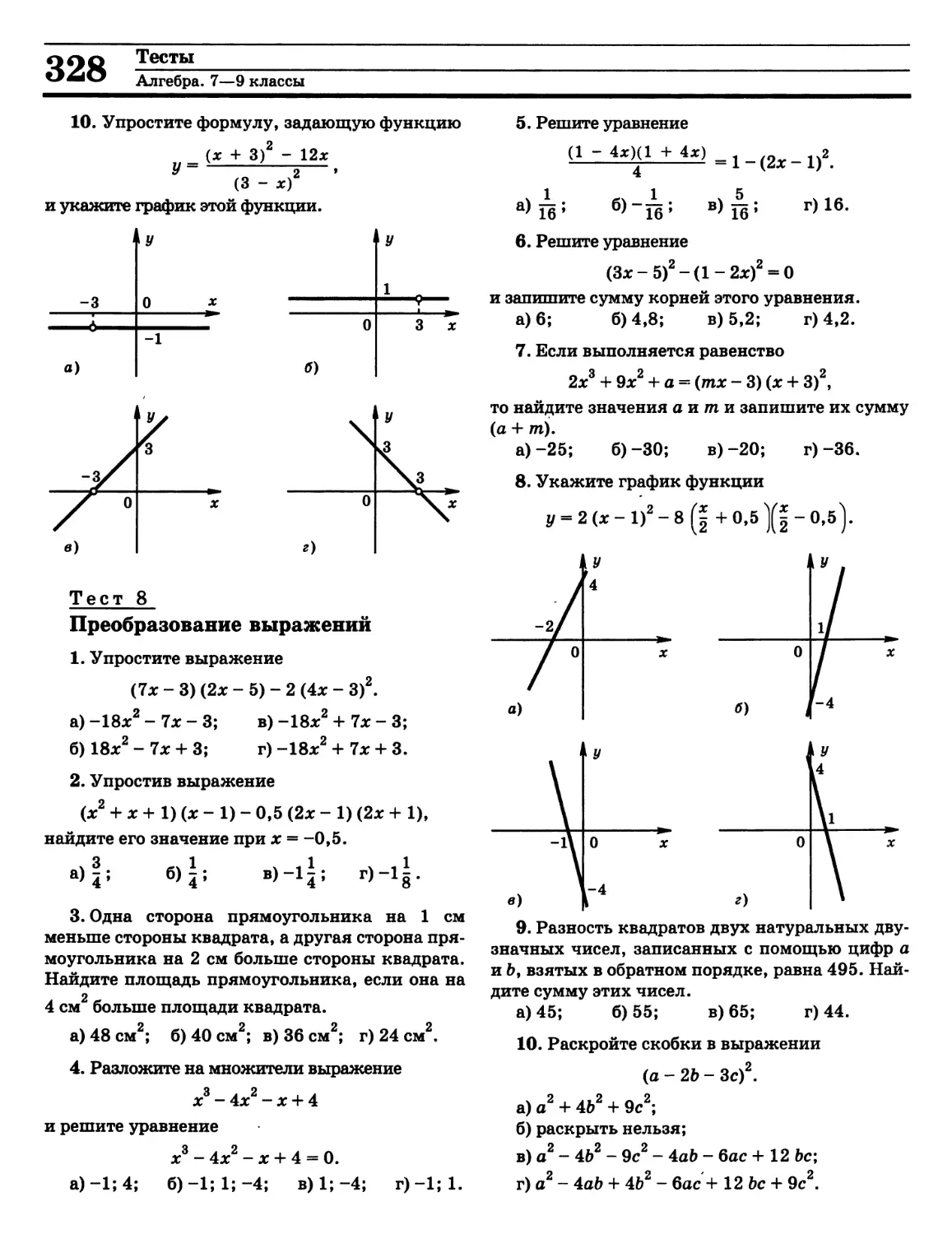
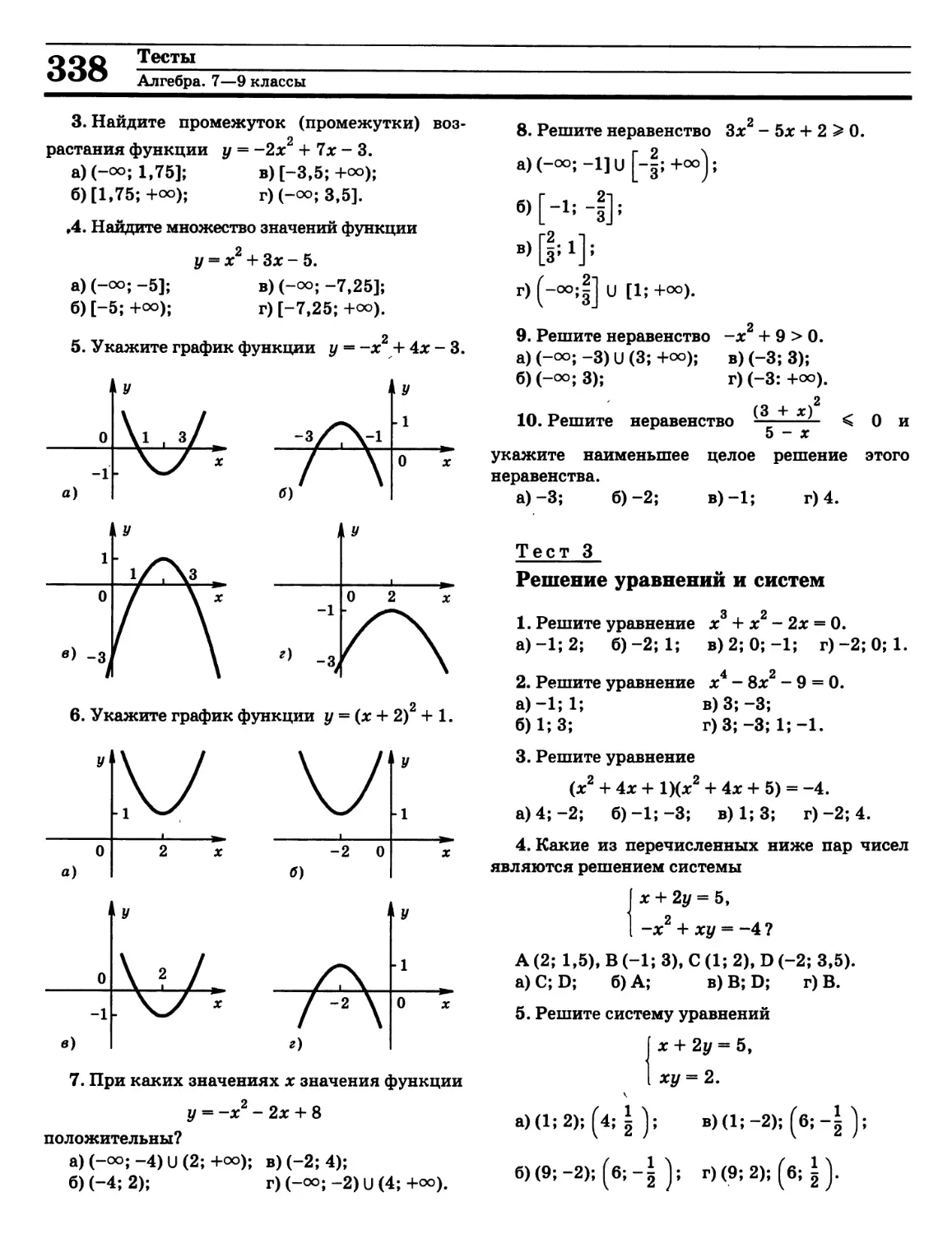
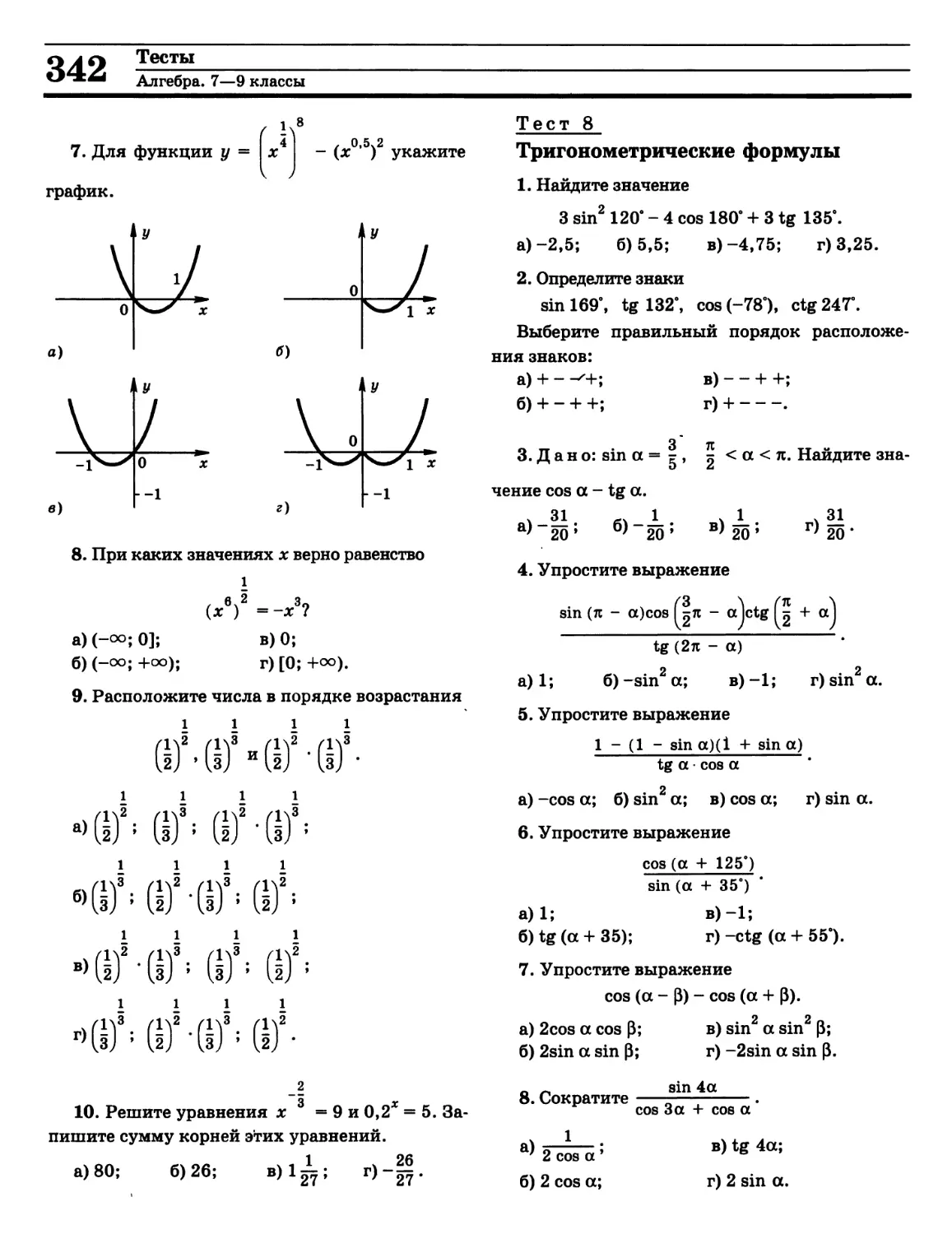
Алгебра. 7—9 классы (П. И. Алтынов) 323
Алгебра и начала анализа. 10—11 классы (П. И. Алтынов) 347
Геометрия. 7—9 классы (П. И. Алтынов) 364
Геометрия. 10—11 классы (Я. Я. Алтынов) 380
Справочные материалы
Краткий справочник по математике (Я. Я. Баврин) 395
Алгебра в таблицах (Л. Я. Звавич, А. Р. Рязановский) 475
Геометрия в таблицах (Л. Я. Звавич, А. Р. Рязановский) 537
Математика в формулах 620
Подготовка к экзаменам
9 класс
Примерные билеты и ответы к устному экзамену по геометрии (Г. В. Дорофеев,
Т. М. Мищенко) 639
11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа (Л. Я. Звавич,
Д. И. Аверьянов, В. К. Смирнова) 675
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
(Л. О. Денищева, Н. В. Карюхина, Г. М. Кузнецова) 723
Примерные билеты и ответы к устному экзамену по геометрии (Г. В. Дорофеев,
Е. А. Седова) 777
Для поступающих в вузы
Задачи и решения письменных экзаменов по математике (М. К. Потапов,
С. Н. Олехник, Ю. В. Нестеренко) 819
Предметно-тематический указатель
К разделу * Краткое изложение школьного курса математики» 850
К разделам «Задачи...» и «Контрольные и проверочные работы. Тесты» 853
К разделу «Справочные материалы» 855

Предисловие
Перед вами необычный учебный справочник.
Его уникальность в том, что он объединяет
практически все, что относится к изучению и
преподаванию школьного курса математики. Впервые
заинтересованный читатель (ученик, учитель,
родитель, репетитор) получает книгу, 9 которой
так полно отражены все основные этапы и все
виды деятельности при обучении математике.
Содержание справочника охватывает почти
десять школьных учебников по математике для
5—11 классов и около двух десятков обычных
изданий справочно-методической литературы.
В справочнике пять разделов, соответствующих
основным формам обучения: усвоению теории,
решению задач, подготовке к контрольным
работам и тестированию, работе со справочными
материалами, подготовке к экзаменам.
Структура всех разделов, кроме справочного,
соответствует традиционному делению школьной
математики по предметам и классам.
Первый раздел «Краткое изложение
школьного курса математики» предназначен для
самостоятельного повторения материала школьной
программы. В очень сжатой форме в полном
соответствии с действующими учебниками
изложена теория и даны примеры решения задач.
Материал второго раздела «Задачи» и
третьего «Контрольные и проверочные работы.
Тесты» можно использовать для закрепления
навыков решения задач, для самопроверки и для
подготовки к контрольным работам и тестированию
в школе. Задачи, контрольные работы и тесты
скомпонованы по классам и основным темам в
соответствии с самыми распространенными
учебниками. Ко всем заданиям даны ответы, более
сложные задания традиционно отмечены
звездочками.
Следующий раздел составляют различные
справочные материалы. «Краткий справочник
по математике» содержит математические
понятия, предложения, формулы по основным
разделам школьного курса математики и примеры
применения теории к решению задач, а также
сведения, значительно расширяющие
общеобразовательный курс.
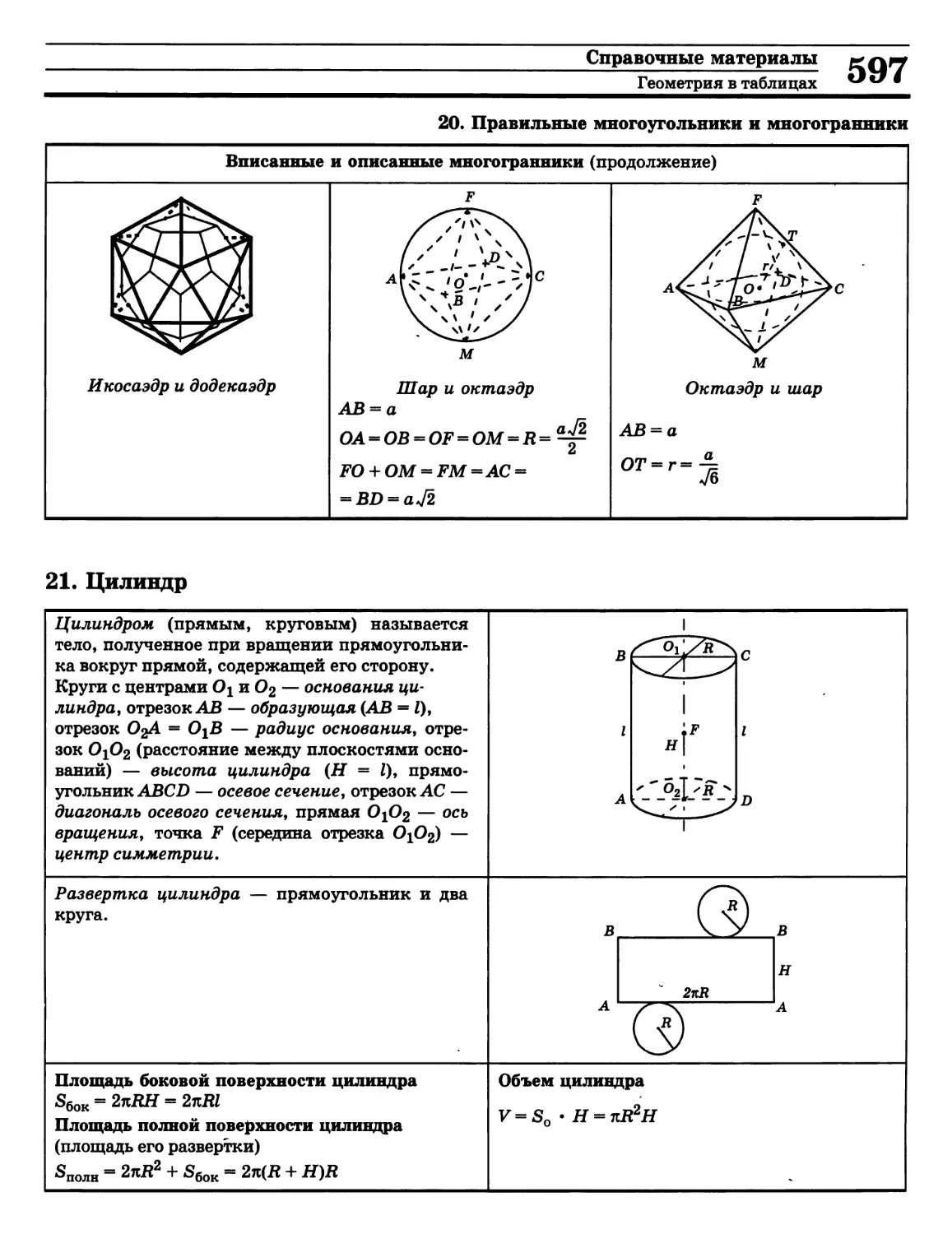
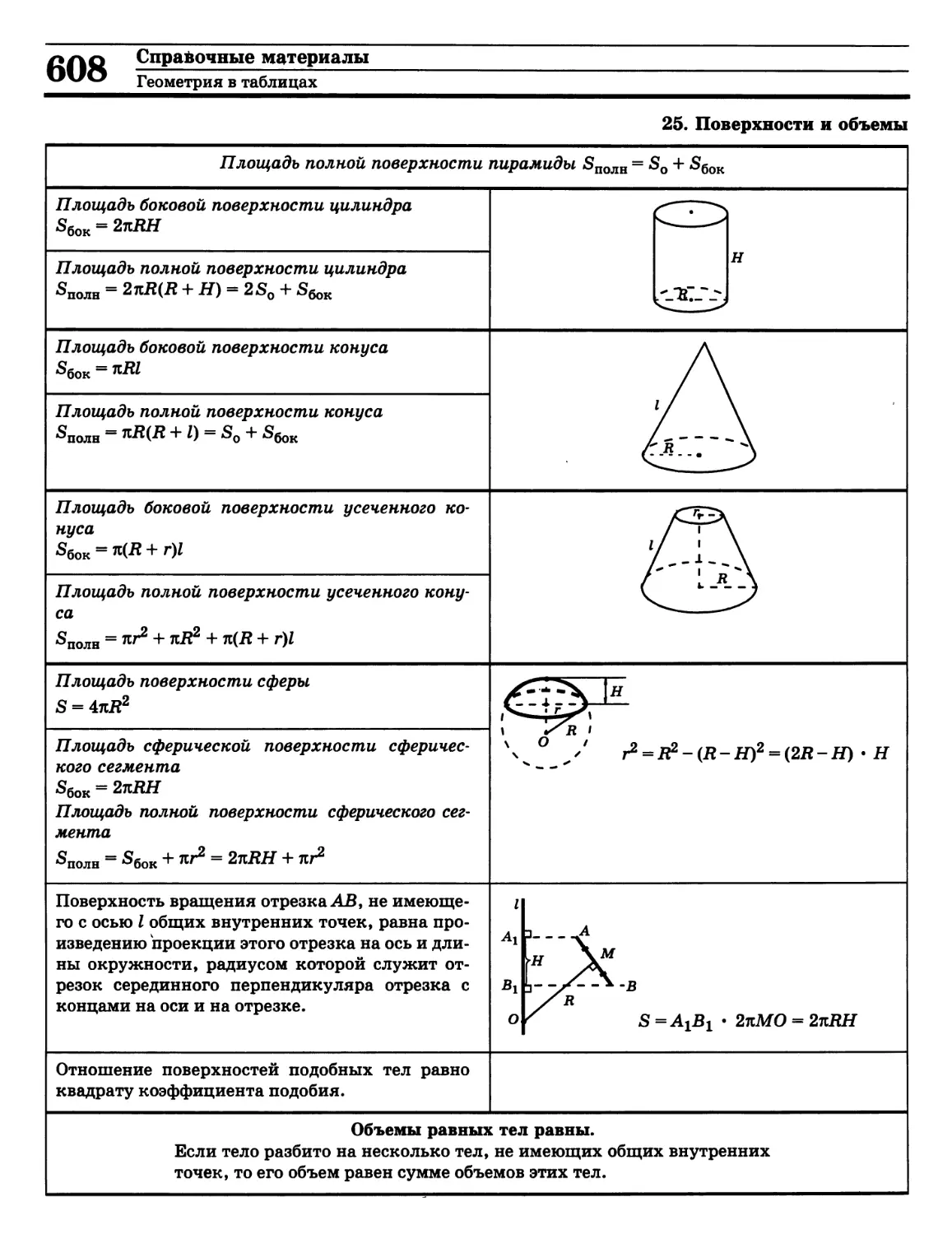
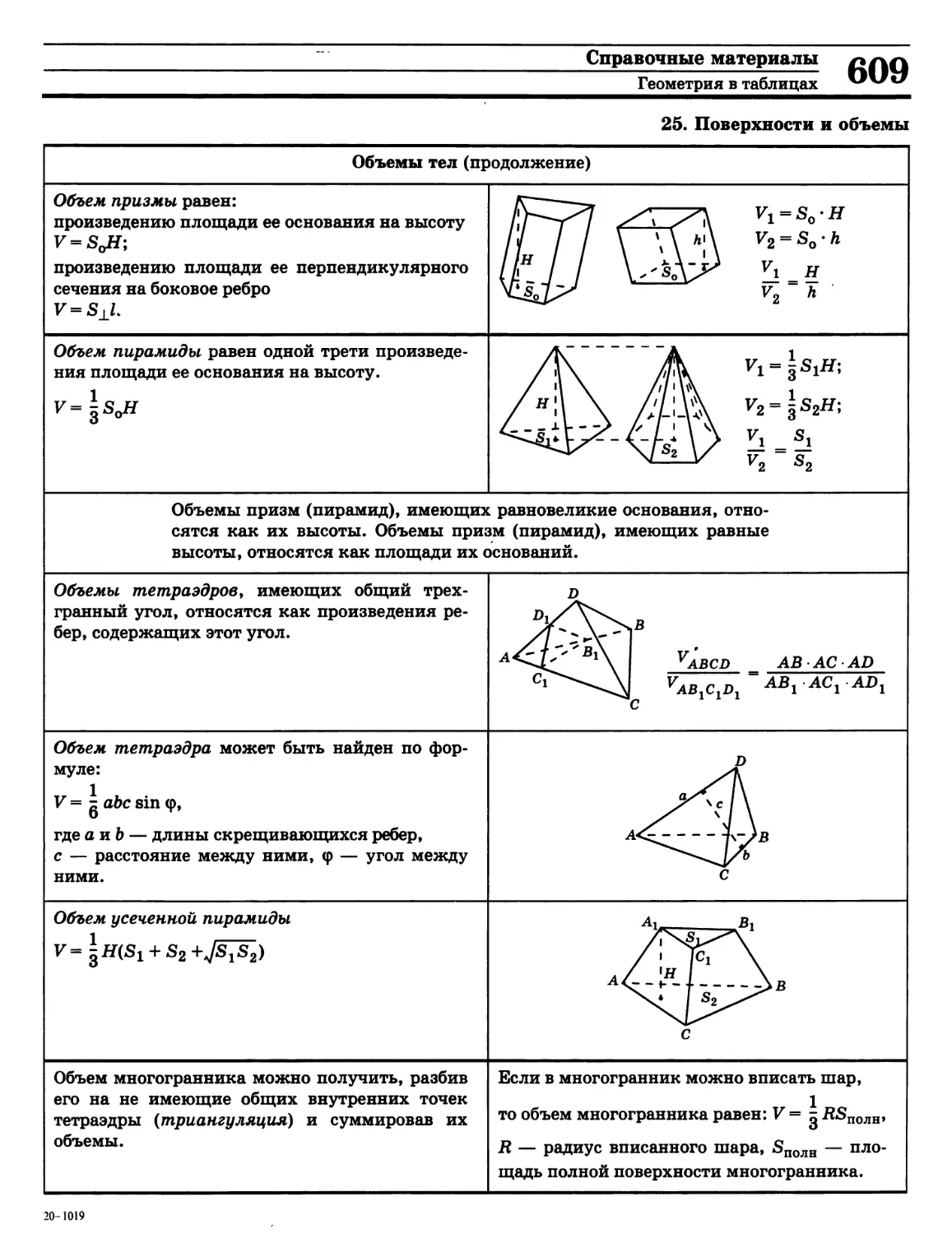
Справочные материалы «Алгебра в таблицах»
и «Геометрия в таблицах» отличаются
краткостью изложения теории и наглядностью.
Определения, теоремы, формулы, рисунки, примеры
решения задач сгруппированы в тематические
таблицы по всем наиболее важным темам
школьного курса математики.
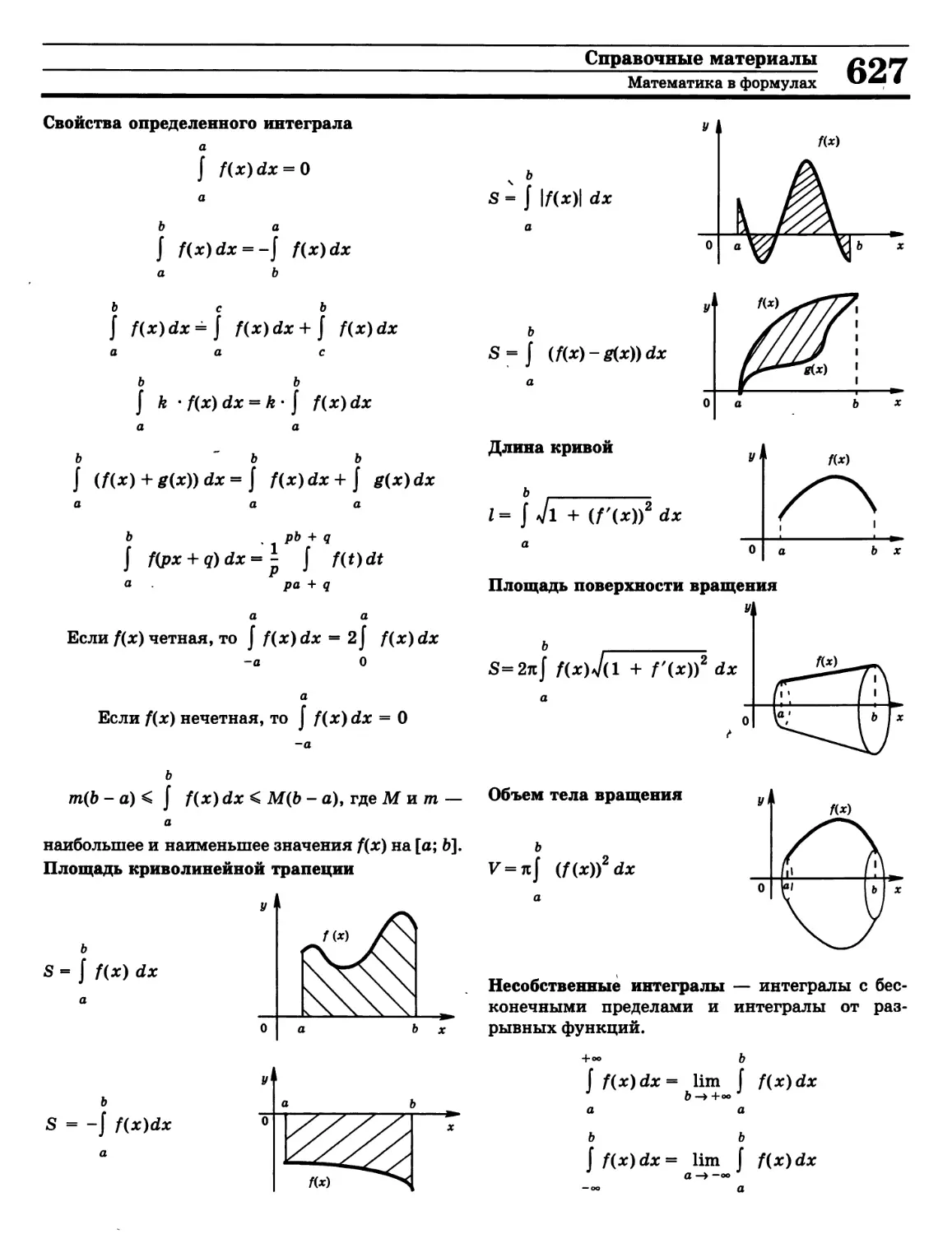
Название самых оперативных и кратких
справочных материалов — «Математика в
формулах» (точнее, школьный курс математики в
формулах) — является точной характеристикой
содержания этой части справочника.
Заключительный раздел книги содержит
материалы для подготовки к экзаменам по
математике: варианты экзаменационных работ
письменного экзамена по алгебре и началам анализа в
11 классе с разобранными решениями,
примерные билеты и ответы для устной итоговой
аттестации выпускников 9 и 11 классов по
геометрии, алгебре и началам анализа, варианты
экзаменационных работ с решениями по математике
для поступающих в вузы.
Учебный справочник объемлет все этапы
учебного процесса, и любой читатель найдет в нем
полезную и необходимую информацию.
Учащийся, не очень уверенно чувствующий себя в
математике, сможет восполнить пробелы в теории и
научиться решать задачи с помощью первого
раздела справочника. Тот, кто хочет
потренироваться решать задачи или проверить свои
знания, воспользуется вторым и третьим
разделами. Необходимые формулы проще всего найти в
справочных материалах «Математика в
формулах», определения, теоремы, свойства — в
таблицах, а если возникли вопросы, выходящие за
рамки школьной программы, то можно
заглянуть в «Краткий справочник».
Нужную информацию — разъяснение
термина, теоретические сведения по конкретному
вопросу, задачи или тесты на определенную тему —
поможет найти в книге предметно-тематический
указатель.

Краткое изложение
школьного курса
математики
поможет быстро и эффективно
повторить весь изученный материал

Краткий курс
математики содержит
теоретические сведения
и типовые задачи
с решениями по предметам
«Математика», «Алгебра»
и «Геометрия», изложенные
кратко и доступно.
Он позволит в оптимальные
сроки повторить весь
изученный материал,
поможет быстро
и эффективно
подготовиться
к контрольным работам,
выпускным
и вступительным
экзаменам.

Математика. 5—6 классы
НАТУРАЛЬНЫЕ ЧИСЛА
И ДЕЙСТВИЯ НАД НИМИ
Понятие о натуральном числе
Числа, употребляемые для счета предметов,
называют натуральными. Любое натуральное
число можно записать с помощью десяти цифр:
О, 1,2,3,4,5,6, 7,8,9.
Такую запись чисел называют десятичной.
Нужно запомнить, что число 0 натуральным не
является.
Для чтения натуральных чисел их
разбивают, начиная справа, на группы по три цифры в
каждой (самая левая группа может состоять из
одной или двух цифр). Три первые цифры
справа составляют класс единиц, три следующие —
класс тысяч, далее идут классы миллионов,
миллиардов и т. д.
1 миллион (1 млн) = 1 000 000
1 миллиард (1 млрд) = 1 000 000 000
1 триллион (1 трлн) = 1 000 000 000 000
Например, число 23 078 000 104. Его читают:
23 миллиарда 78 миллионов 104.
Классы
Разряды
Число

Миллиарды
с
Д
2
е
3

Миллионы
с
0
Д
7
е
8
Тысячи
с
0
Д
0
е
0

Единицы
с
1
д
0
е
4J
с — сотни, д — десятки, е — единицы
Примеры:
а) Число 100 005 читается так: сто тысяч пять.
б) Число 1 000 050 читается так: один миллион
пятьдесят.
в) Число 10 000 005 000 читается так: десять
миллиардов пять тысяч.
Сложение натуральных чисел
Если прибавить к натуральному числу
единицу, то получится следующее за ним число.
Например, 8 + 1 = 9; 53 + 1 = 54; 399 + 1 = 400.
Таким образом, сложить, например, 9 и 4
означает: прибавить к 9 четыре раза единицу.
Получим: 9 + 4 = 9 + 1 + 1 + 1 + 1 = 13.
Естественно, что это записывают короче:
9 + 4 = 13.
Числа, которые складывают, называют
слагаемыми; число, получающееся при сложении
этих чисел, называют их суммой.
В записи 9 + 4 = 13 числа 9 и 4 — слагаемые,
число 13 — сумма.
Если сложение обозначить буквами, то
а +& = с
слагаемые сумма
При сложении многозначных чисел
употребляют способ сложения столбиком.
Примеры:
а) 3198 б) 183487
+ 457 + 59794
870 243281
4525
При устном счете можно складывать числа
поразрядно.
Примеры:
а) 58 + 74 = (50 + 70) + (8 + 4) = 120 + 12 = 132;
б) 453 + 865 = (400 + 800) + (50 + 60) + (3 + 5) =
= 1200 + 110 + 8 = 1318.
Вычитание натуральных чисел
Действие, с помощью которого по сумме и
одному из слагаемых находят другое слагаемое,
называют вычитанием.
Вычитание — это действие, обратное сложению.
То есть: «из 7 вычесть 3» означает: «найти
такое число, которое в сумме с 3 дает в
результате 7».
7-3 = х, х + 3 = 7, х = 4.
Итак, 7-3 = 4.
Число, из которого вычитают, называют
уменьшаемым, а число, которое вычитают, —
вычитаемым. Результат вычитания называют
разностью.
18 - 13 = 5
уменьшаемое вычитаемое разность
а - Ь = С,
т. е. с + Ъ = а.

8
Краткое изложение школьного курса математики
Математика. 5—б классы
При действиях с натуральными числами
уменьшаемое не может быть меньше
вычитаемого.
Разность двух чисел показывает, на сколько
первое число больше второго или на сколько
второе число меньше первого.
Примеры:
а) 101 - 13 = 88, так как 88 + 13 = 101;
б) 34 - 0 = 34, так как 34 + 0 = 34;
в) 573 - 573 = 0, так как 0 + 573 = 573.
При вычитании многозначных чисел
результат удобно находить столбиком:
27384
542
-128
414
-9298
18086
Умножение натуральных чисел
Правило: Умножить число т на
натуральное число п значит найти сумму п слагаемых,
каждое из которых равно т.
Выражение т • п и значение этого
выражения называют произведением чисел тип.
Числа т и п называют множителями.
Примеры:
а) 5-4 = 5 + 5 + 5 + 5 = 20;
б) 7 • 1 = 7.
Очевидно, что 5*4 = 4*5, что ясно из
рисунка:
*****
*****
*****
*****
* * * *
* * * *
и * * * *
* * * *
* * * *
При письменном умножении результат
удобно получать столбиком.
а)
в)
Примеры:
„58
б)
37
+ 406
174
2146
2640
5700
1848
1320
15048000
г)
257
Х 39
2313
+ 771
10023
439
308
3512
Ч317
135212
1) при умножении на 10 в результате к числу
справа приписывается 0:
48 • 10 = 480;
2) при умножении на 100 в результате
приписываются справа два 0:
576 • 100 = 57 600
и т. д.;
3) при умножении на 15 число сначала
умножают на 10, а затем прибавляют половину
полученного числа:
496 • 15 = 4960 + 2480 = 7440;
4) при умножении на 5 число сначала
умножают на 10, а затем берут половину полученного
числа:
38 • 5 = 380 : 2 = 190;
5) при умножении на 25 число сначала
умножают на 100, а затем берут четверть
полученного числа:
17 • 25 = 1700:4 = 425;
6) при умножении на 50 число умножают на
100, а затем берут половину полученного числа:
435 • 50 = 43 500 : 2 = 21 750.
Нужно очень хорошо запомнить, что
0=0,а•1=а
При устном умножении нужно знать, что:
Для обозначения действия умножения
применяют два знака: • и х. Знак х впервые
использовал в своих работах в качестве знака,
обозначающего умножение, Оутред. Знак • появился в
1698 г. Его ввел немецкий математик Готфрид
Вильгельм Лейбниц.
Деление натуральных чисел
Деление — действие, обратное умножению.
Его смысл заключен в нахождении одного из
двух множителей, если известны произведение
и другой множитель.
Таким образом, «24 разделить на 8 — значит
найти такое число, что при умножении его на 8
получается 24», т. е.
24 : 8 = х, х • 8 = 24, х = 3.
Итак, 24:8 = 3.

Краткое изложение школьного курса математики
Математика. 5—6 классы
9
Примеры:
а) 105 : 15 = 7, так как 7 • 15 = 105;
б) 0 : 8 = 0, так кдк 0*8 = 0.
Особо нужно запомнить, что
0 : а = 0, если а * 0
а : 0 — нельзя!
Итак, а :Ь = с, причем с • Ъ = а; а — делимое,
& — делитель, с — частное.
Пример: 48 : 6 = 8, 48 — делимое, 6 —
делитель, 8 — частное.
Знак деления : впервые появился в 1202 г, в
работах Леонардо Пизанского. Однако есть еще один
знак деления —, впервые введенный У. Джонсом
в 1633 г. Таким образом, записи 76
1П 76
19 и jg
означают одно и то же. Преимущества записи
деления через черту вы увидите чуть позже.
Итак,
. h - а
Примеры:
а) 90 : 5 = (50 + 40): 5 = 50 : 5 + 40 : 5 = 10 + 8 =
= 18;
б) 165 : 3 - (150 + 15): 3 = 150 : 3 + 15 : 3 = 50 +
+ 5 = 55.
Если делимое оканчивается нулем, то
сначала делится число без нуля на делитель, но в
частном к результату приписывают нуль.
Если и делимое и делитель оканчиваются
нулем, то деление проводят без последних нулей.
Примеры:
а) 480 : 12 = 40, так как 48 : 12 = 4;
6)460:230 = 46:23 = 2;
в) 800 : 40 = 80 : 4 - 20.
Однако при делении натурального числа а на
натуральное число Ъ может случиться, что нет
такого натурального числа с, что с • Ъ = а,
например 15 ; 7. В этом случае речь идет о делении
с остатком. Тогда запись ведется следующим
образом:
15:7 = 2 (ост. 1) или 660 : 50 = 13 (ост. 10).
Обратите внимание на наличие нуля в остатке
во втором примере.
Нужно запомнить, что если а — делимое,
Ъ — делитель, с — неполное частное, г —
остаток, то а = с • Ъ + г. Причем остаток всегда
меньше делителя, т.е. г <Ъ. Следовательно, при
делении, например, на число 7 возможны
только остатки; 0, 1, 2, 3, 4, 5, 6.
Примеры:
а) 48 : 7 = 6 (ост. 6);
6)81: 7 = 11 (ост. 4).
Если в остатке получилось число 0, то
говорят, что одно число разделилось на другое
нацело. Например, 35 : 7 = 5 (ост. 0), пишем просто
35:7 = 5.
Примеры:
а)
_15в|18
13 [12
26
0
156:13 = 12
б) _ 1428|14
14 |102
28
28
0
1428 : 14 = 102
Свойства действий над числами
Переместительное свойство
Правило: Сумма чисел не изменяется при
перестановке слагаемых.
a +b =b + а
Пример: 308 + 1427 = 1427 + 308.
При любом способе сложения результат
равен 1735.
Правило: Произведение чисел не
изменяется при перестановке множителей.
Пример: 14 •
+ 1
14
а •Ъ = Ь • а
108 = 108 • 14.
14 108
08 14
12 + 432
108
1512 1512
Сочетательное свойство
Правило: Чтобы прибавить к сумме двух
чисел третье число, можно к первому числу
прибавить сумму второго и третьего.
(a+b) + c =а+(Ь +с)
Примеры:
а) (327 + 84) + 116 = 327 + (84 + 116) = 327 + 200 =
= 527;

10
Краткое изложение школьного курса математики
Математика. 5—б классы
б) (4083 + 576) + 5917 = (576 + 4083) + 5917 =
= 576 + (4083 + 5917) = 576 + 10 000 = 10 576.
Правило: Чтобы умножить произведение
двух чисел на третье число, можно первое число
умножить на произведение второго и третьего.
(а • Ь) • с = а • (Ь • с)
Примеры:
а) (7 • 25) • 8 = 7 • (25 • 8) = 7 • 200 - 1400;
б) (50 • 23) • 40 = (23 • 50) • 40 = 23 • (50 • 40) =
= 23 • 2000 = 46 000.
Распределительное свойство
Правило: Для того чтобы умножить сумму
двух чисел на число, можно умножить на это
число каждое слагаемое и сложить
получившиеся произведения.
(а +Ь) • с = а • с + 6 • с
Примеры:
а) (17 + 8) • 5 = 17 • 5 + 8 • 5 = 85 + 40 = 125;
б) 24 • 19 + 76 • 19 = (24 + 76) • 19 = 100 • 19 =
=1900.
Правило: Для того чтобы умножить
разность двух чисел на число, можно умножить
на это число уменьшаемое и вычитаемое и из
первого произведения вычесть второе.
(а-Ь)*с=а*с~-Ь
Примеры:
а) (28 - 19) • 3 = 28 • 3 - 19 • 3 = 84 - 57 = 27;
6)317 • 213-217 • 213 = (317-217) • 213 =
= 100 • 213 = 21300.
ДЕЛИМОСТЬ ЧИСЕЛ.
ДЕЛИТЕЛИ И КРАТНЫЕ
Делители числа
Делителем натурального числа а называют
натуральное число, на которое а делится без
остатка.
Примеры:
а) число 18 имеет шесть делителей: 1, 2, 3, 6, 9,
18;
б) число 25 имеет 3 делителя; 1, 5, 25;
в) число 73 имеет 2 делителя: 1 и 73.
Число 1 является делителем любого
натурального числа.
Если числа а и b оба делятся на число с, то с
называется общим делителем чисел а и Ь.
Примеры:
а) число 28 делится на 4 и 48 делится на 4,
следовательно, 4 — общий делитель чисел 28 и 48;
б) 20 делится на 5, а 53 не делится на 5,
следовательно, 5 не является общим делителем чисел
20 и 53.
Найдем общие делители чисел 48 и 60.
Для числа 48 делителями являются: 1., 2, 3,
4,6,8,12,16,24,48.
Для числа 60 делителями являются: 1, 2, 3,
4,5,6,10,12,15,20,30,60.
Общими делителями являются числа: 1, 2, 3,
4, 6, 12.
Из них 12 — наибольший общий делитель.
Наибольшее натуральное число, на которое
делятся без остатка числа а и Ъ, называют
наибольшим общим делителем этих чисел.
Признаки делимости
на 2, 3, 4, 5, 6, 9, 10
Правило: Если запись натурального числа
оканчивается цифрой 0, то это число делится
без остатка на 10.
Если запись натурального числа
оканчивается другой цифрой, то оно не делится без
остатка на 10.
Примеры:
а) 680 делится на 10;
б) 104 не делится на 10.
Правило: Если запись натурального числа
оканчивается цифрами 0 или 5, то это число
делится без остатка на 5.
Если же запись числа оканчивается иной
цифрой, то число без остатка на 5 не делится.
Примеры:
а) 370 и 1485 делятся без остатка на 5;
б) числа 537 и 4008 без остатка на 5 не делятся.
Цифры 0, 2, 4, 6, 8 называют четными, а
цифры 1, 3, 5, 7, 9 — нечетными.
Натуральные числа называют четными, если
они оканчиваются четной цифрой, и
нечетными, если они оканчиваются нечетной цифрой.
Правило: Если запись натурального числа
оканчивается четной цифрой, то это число
делится без остатка на 2, а если нечетной
цифрой, то число без остатка не делится на 2.

Краткое изложение школьного курса математики
Математика. 5—б классы
11
Короче говоря, четное число делится на 2,
нечетное не делится на 2.
Примеры:
а) 8, 60, 574 — делятся на 2;
б) 13, 25, 1001 — не делятся на 2.
Правило: Если сумма цифр числа делится на
3, то и число делится на 3. Если сумма цифр не
делится на 3, то и число не делится на 3.
Примеры:
а) 276 делится на 3, так как 2 + 7 + 6 = 15, а 15
делится на 3;
б) 563 не делится на 3, так как 5 + 6 + 3 = 14, а
14 не делится на 3.
Правило: Если сумма цифр числа делится
на 9, то и само число делится на 9. Если
сумма цифр числа не делится на 9, то и число не
делится на 9.
Примеры:
а) 5787 делится на 9, так как 5 + 7 + 8 + 7 = 27, а
27 делится на 9;
б) 359 не делится на 9, так как 3 + 5 + 9 = 17, а
17 не делится на 9.
Правило: Число делится на 4, если число,
составленное из двух последних цифр данного
числа, делится на 4.
Примеры:
а) 78 536 делится на 4, так как 36 делится на 4;
б) 8422 не делится на 4, так как 22 не делится на 4.
Правило: Число делится на 6, если оно
делится одновременно на 2 и на 3. В противном
случае оно на 6 не делится.
Примеры:
а) 2862 делится на 6, так как 2862 делится и на
2, и на 3;
б) 3754 не делится на 6, так как 3754 не делится
наЗ.
Простые и составные числа
Натуральное число называют простым, если
оно имеет только два делителя: единицу и само
это число.
Натуральное число называют составным,
если оно имеет более двух делителей.
Примеры:
а) число 9 имеет три делителя (1, 3 и 9),
следовательно, оно составное;
б) число 17 имеет два делителя, значит, оно
простое;
в) число 1 имеет только один делитель — само
это число, поэтому оно не является ни
составным, ни простым.
Правило: Разложить составное число на
простые множители означает записать
данное число в виде произведения простых чисел,
которые являются делителями данного числа.
При любом способе записи получается одно и
то же разложение, если не учитывать порядка
множителей.
Примеры:
а) 180 = 2 • 2 • 3- 3 • 5;
б) 1368 = 2 • 2 • 2 • 3 • 3 • 19.
180
90
45
15
5
1
2
2
3
3
5
1368
684
342
171
57
19
1
2
2
2
3
3
19
Разложение числа на простые множители
помогает решить задачу отыскания наибольшего
общего делителя двух или более чисел.
Наибольший общий делитель (НОД)
Правило: Чтобы найти наибольший общий
делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать те множители, которые
входят в разложение каждого из чисел;
3) найти произведение этих множителей.
Примеры:
а) Найти НОД (6600; 6300):
6600 = 2 • 2 • 2 • 3 • 5 • 5 • 11,
6300 = 2 -2-3-3-5-5-7,
НОД (6600; 6300) = 2 • 2 • 3 • 5 • 5 = 300;
б) Найти НОД (34 398; 1260; 6552):
34398 = 2 • 3 • 3 • 3 • 7 • 7 • 13,
1260 = 2 • 2 • 3 • 3 • 5 • 7,
6552 = 2 • 2 • 2 • 8 • 3 • 7 • 18,
НОД (34 398; 1260; 6552) = 2 • 3 • 3 • 7 =
= 126.
При нахождении наибольшего общего
делителя двух чисел полезно знать еще одно
правило, называемое ^алгоритм Евклида*.

Краткое изложение школьного
Математика. 5—6 классы
Пример: Найти НОД (270; 186). Разделим
270 на 186 с остатком:
270 : 186 = 1 (ост. 84).
Далее разделим делитель на остаток и т. д.:
186 : 84 = 2 (ост. 18),
84: 18 = 4 (ост. 12),
18 : 12 = 1 (ост. 6),
12:6 = 2 (ост. 0).
Наибольшим общим делителем чисел 270 и
186 является последний ненулевой остаток, т. е.
число 6.
Пример: Найти НОД (234; 180).
1) 234 : 180 = 1 (ост. 54),
2) 180 : 54 = 3 (ост. 18),
3) 54 : 18 = 3 (ост. 0).
Следовательно, НОД (234; 180) = 18.
Натуральные числа называют взаимно
простыми, если их наибольший общий делитель
равен единице.
Примеры:
а) 75 и 14 — взаимно простые числа, так как
НОД (75; 14) - 1;
б) 20, 9 и 77 взаимно простые числа, так как
НОД (20; 9; 77) = 1.
Кратные числа
Кратным натуральному числу а называют
натуральное число, которое делится на а без
остатка.
Примеры:
а) для числа 18 кратными являются числа: 18,
36, 54, 72, 90, 108, 126 и т. д.;
б) для числа 7 кратными являются числа: 7, 14,
21, 28, 35, 42, 49 и т. д.
Итак, нужно запомнить:
1) любое число имеет бесконечное число
кратных;
2) наименьшим кратным для числа является
само это число.
Общим кратным для двух и более чисел
будет число, которое является кратным для
каждого из этих чисел.
Примеры:
а) Для числа 8 кратные: 8; 16; 24; 32; 40; 48;
56; ... . Для числа 12 кратные: 12; 24; 36; 48; 60;
(а} ... .
математики
Таким образом, общими кратными для чисел
8 и 12 являются числа: 24; 48; 72; ... .
б) Для числа 7 кратные: 7; 14; 21; 28; 35; 42;
49; ... . Для числа 3 кратные: 3; 6; 9; 12; 15; 18;
21; 24;... .
Общими кратными чисел 3 и 7 являются
числа: 21; 42; 63 и т. д.
Наименьшее общее кратное (НОК)
Из общих кратных двух (или нескольких)
чисел особо выделяют то, которое является
наименьшим общим кратным этих чисел.
Примеры: наименьшее общее кратное чисел
8 и 12 равно 24, а наименьшее общее кратное
чисел 3 и 7 равно 21.
Наименьшим общим кратным натуральных
чисел а и Ъ называют наименьшее натуральное
число, которое кратно и а, и Ь.
Нужно запомнить:
1) если одно из двух натуральных чисел
делится на другое число, то большее из этих двух чисел
является их наименьшим общим кратным;
2) если два (или более двух) числа являются
взаимно простыми, то наименьшее общее
кратное этих чисел равно их произведению.
Примеры:
а) НОК (9; 18) = 18;
б) НОК (2; 8; 16) = 16, так как 8 делится на 2, а
16 делится на 8;
в) НОК (7; 10) = 70, так как 7 и 10 — взаимно
простые числа;
г) НОК (5; 9; 11) = 495, так как 5,9,11—
взаимно простые числа и 5 • 9 • 11 = 495.
В некоторых случаях наименьшее кратное
двух чисел находят устно.
Примеры:
а) НОК (12; 18) = 36;
б) НОК (18; 30) = 90;
в) НОК (5; 10; 12) = 60;
г) НОК (14; 8) = 56.
Однако устно, например, не так просто найти
наименьшее общее кратное чисел 360 и 825.
Правило: Чтобы найти наименьшее общее
кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в
разложение (лучше наиболее длинное) одного из чисел;

Краткое изложение школьного курса математики
Математика. 5—6 классы
13
3) добавить к ним недостающие
множители из разложений остальных чисел;
4) найти произведение получившихся
множителей.
Пример: Найдем наименьшее общее кратное
чисел 360 и 825, придерживаясь этого правила.
1) 360 = 2 • 2 • 2 • 3 • 3 • 5,
825 = 3 • 5 • 5 • 11;
360
180
90
45
15
5
1
8251
275
55
11
1
12
2
2
3
3
5
3
5
5
11
2) выпишем наиболее длинное разложение:
2 • 2 • 2 • 3 • 3 • 5;
3) добавим к нему недостающие множители из
второго разложения: 5 и 11;
4) НОК (360; 825) = 2-2-2'3-3-5-5«11 =
= 19 800.
Заметим, что нет необходимости перемножать
все числа, так как 2'2*2«3«3'5 = 360 и
нужно просто выполнить умножение 360 • 55.
Пример: Найти наименьшее общее кратное
чисел 2940; 550 и 63.
2940 = 2-2-3-5'7-7,
2940
14701
735
245
49
71
1
550 = 2 • 5 • 5 • 11,
"550|
275
551
11
1
2
5
5
11
63 = 3 • 3 • 7;
63
21
7|
1
НОК (2940; 550; 63) =
= 2 • 2 • 3 • 5 • 7-7 • 5 • 11 • 3 = 485 100.
Кроме правил нахождения наибольшего
общего делителя и наименьшего общего кратного
двух чисел полезно знать, что произведение
наименьшего общего кратного двух чисел и
наибольшего общего делителя этих чисел равно
произведению самих этих чисел, т. е.
НОК (о; Ь) • НОД (а;Ь) = а • Ь
или
Н0К<а'&>=нсщЬг
Примеры:
а) Найти НОК (20; 48).
Так как очевидно, что НОД (20; 48) = 4, то
НОК (20; 48) = ^-^ = 240.
б) Найти НОК (72; 60).
НОД (72; 60) = 12, тогда
НОК (72; 60) = 'ЩР
360.
II
III
ДРОБИ
(обыкновенные и десятичные).
ОБОЗНАЧЕНИЕ ЧИСЕЛ
НА КООРДИНАТНОМ ЛУЧЕ
Обыкновенные дроби
Если пирог разрезать на 8 равных частей, то
каждая из этих частей называется долей. Так
как пирог был разрезан на 8 частей, то каждая
доля равна g пирога. Если бы пирог был
разрезан на Ючастей, то каждая доля была бы равна
1
т~ пирога.
Дробью называется число, состоящее из
нескольких долей единицы (в том числе и из одной
доли).
Например, если в обед съели 5 долей пирога,
это означает, что съедено было g пирога, а оста-
3 13
лось g пирога. Запись -g-
означает, что имеется в виду один
8
пирог, состоящий из g пирога,
5
а также g другого такого же
13 ,5
пирога, т. е. -g- ■» lg.

14
Краткое изложение школьного курса математики
Математика. 5—6 классы
Итак, любая дробь записывается в виде —,
где т называется числителем дроби, an —
знаменателем дроби.
Если числитель меньше знаменателя, то
дробь называется правильной; если числитель
равен знаменателю или больше его, то дробь
называется неправильной.
Например, дроби т= и. - правильные дро-
5 23
би, g и -g- — неправильные дроби.
Число lg называется смешанным числом.
Причем 1 называется целой частью числа, a g —
дробной частью числа. Запись неправильной
дроби в виде смешанного числа называется
выделением целой части числа. Эта запись
получается в результате деления числителя на
знаменатель (здесь надо вспомнить, что знаки — и :
означают одно и то же).
Правило: Чтобы из неправильной дроби
выделить целую часть, надо:
1) разделить с остатком числитель на
знаменатель;
2) в качестве целой части взять неполное
частное;
3) остаток (если он есть) дает числитель,
а делитель — знаменатель дробной части.
Примеры:
23
а) Записать дробь -g- в виде смешанного числа.
23 5
23 : 6 = 3 (ост. 5), тогда -g- = 3g;
б) Ш - 28*, так как 200 : 7 = 28 (ост. 4);
20
в) _. =4, так как 20 : 5 = 4 (ост. 0).
о
Если числитель равен знаменателю
(естественно, не равны нулю), то дробь равна 1.
Примеры:
ч 2 . *х 5 - ч 10 - ч 23 1
a) g = 1; б) g - 1; в) ^ = 1; г) 5а = 1.
10
23
Правило: Чтобы представить смешанное
число в виде неправильной дроби, нужно:
1) умножить его целую часть на
знаменатель дробной части и к полученному
произведению прибавить числитель дробной части;
2) записать полученную сумму числителем
дроби, а знаменатель оставить без изменения.
Примеры:
а) 5г те -g-, так как 5*8 + 3 = 43;
б) 2g « g, так как 2-3 + 1 = 7.
Любое натуральное число можно записать в
виде неправильной дроби с любым
знаменателем.
ft 0 2 4 6 8
Пример: 2=j=2=g=jHT. д.
Десятичные дроби
Рассмотрим числа 7г^;
8 417
100 ; Ь1000 *
Числа со
знаменателями 10, 100, 1000 и т. д. условились
записывать без знаменателя. Сначала пишут
целую часть, а потом числитель дробной части.
Целую часть отделяют от дробной части запятой.
Если дробь правильная, то перед запятой пишут
0, а количество знаков (цифр) после запятой
должно равняться числу нулей в знаменателе.
Такую запись дробей называют десятичной, а
сами дроби — десятичными.
Примеры: 7тт: = 7,3;
10
8
100
= 0,08; 5
417
1000
= 5,417;
147
10
= 14^ - 14,7;
3_
50
6
= loo = °'06;
54 =510б =5'75'
Изображение чисел
на координатном луче.
Сравнение чисел
Отметим на луче ОХ точку и обозначим ее,
например, Е. Напишем над началом луча
(точкой О) число 0, а над точкой Е число 1. Отрезок
ОЕ называют единичным отрезком. Отложим
отрезок ЕА, равный единичному отрезку, и над
точкой А напишем число 2. Так, шаг за шагом
получаем бесконечную шкалу. Ее называют ко
ординатным лучом. Числа 0, 1, 2 называют ко
ординатами точек О, Е, А. Пишут О(0), Е(1)
А(2). В свою очередь, каждый из отрезков ОЕ
ЕА и т. д. можно разбить на любое число равных
отрезков. Это дает возможность отмечать на
координатном луче дробные числа.

Краткое изложение школьного курса математики
Математика. 5—6 классы
15
О 0,25 g 0,8 1
ljl.4
•!
I I I I I I I 1 I I 1 I I I I 1 1 1 I 1 I 1 1 I -
О
0,5
Е
1,75 А
Равные числа отмечаются на координатном луче
одной точкой. Из двух чисел больше то,
которое правее на координатном луче, а меньше
то9 которое левее.
ДЕЙСТВИЯ
С ОБЫКНОВЕННЫМИ ДРОБЯМИ
Основное свойство дроби,
сравнение и сокращение дробей
Правило (основное свойство дроби): Если
числитель и знаменатель дроби умножить
или разделить на одно и то же натуральное
число, то получится равная ей дробь.
Примеры:
а)
б)
в)
г)
4
7
2
3
8
20
42
56 '
4-2
: 7 2
2 3
: 3 3
8:2
20:2
42:2
56:2 :
8 4
: 14 ; 7 =
6 2
: 9; 3
4
10
21 42
28 ; 56
4 5
"75
2 10
3 10
4:2
10:2
42:7
~56:7
20
" 35'
20
= 30*
2
5'
6
8;
т. е.
т. е.
42
: 56 =
8
14
6
9
20
35
20
: 30 ;
42:14
" 56:14
>
3
4
Нужно запомнить, что две равные дроби
являются различными записями одного и того же
числа. Например, число, получающееся при де-
4
лении 4:8, можно записать в виде дроби «, а
1 4 1 „ Q к 3 6
можно 2 > так как о = н • 5 * 16"
Таким образом, используя основное свойство,
можно заменять дроби равными дробями с
большими или меньшими знаменателями.
Деление числителя и знаменателя на их
общий делитель, отличный от единицы, называют
сокращением дроби. Другими словами:
сокращение дроби — это замена данйой дроби равной
дробью с меньшими, чем были, числителем и
знаменателем.
В простых случаях дробь сокращают устно.
Примеры:
. 12 _ 4
а)15 ~ 5;
В последнем примере дробь можно сократить
по-разному, но дробь ~ больше сократить
нельзя — такую дробь называют несократимой.
В большинстве случаев задание «сократить дробь»
означает представить ее в виде несократимой
дроби.
Примеры: Сократить дробь.
77 7 11 _ 7
9;
а)
99
^24 2
б)ёов
в)
105
9 11
12 =
5 12
7 15
2
5;
J7_
20
300 20 15
Однако иногда дробь устно сократить бывает
252
трудно, например дробь «=« . В этих случаях
нужно найти наибольший общий делитель
числителя и знаменателя и разделить на него числа
252 и 378. НОД (252; 378) = 126, тогда 252 : 126 -
252 2
= 2, 378 : 126 = 3. Следовательно, o=g в 5 •
При выполнении многих заданий с двумя и
более дробями их нужно заменить равными
дробями с одинаковыми знаменателями. Такая
замена называется приведением дробей к общему
знаменателю. Чаще всего дроби приводят к
наименьшему общему знаменателю.
Правило: Чтобы привести дроби к
наименьшему общему знаменателю, надо:
1) найти наименьшее общее кратное
знаменателей этих дробей, оно и будет их
наименьшим общим знаменателем;
2) разделить наименьший общий
знаменатель на знаменатели данных дробей,
(получившиеся числа называют дополнительными
множителями для дробей);
3) умножить числитель и знаменатель
каждой дроби на ее дополнительный множитель.
Например, приведем дроби « и g к
наименьшему общему знаменателю.
Для этого:
1) найдем наименьшее общее кратное (можно
просто общее кратное) чисел 8 и 6. Оно равно 24.
2) выполним деление 24 : 8 = 3 и 24 : 6 = 4.
Получившиеся числа 3 и 4 называют
дополнительными множителями соответственно к дро-

16
Краткое изложение школьного курса математики
Математика. 5—6 классы
Примеры: Привести дроби к общему
знаменателю.
а) 12 И 20 *
НОК(12;20) = 60.
60:12 = 5,60:20 = 3.
7-5
12 5
Значит, т~ =
к\ A L 4
°' 18 ; 10 и 9 *
НОК (18; 10; 9) = 90.
35
60'
9^
20
9 3
20 3
27
60
90 : 18 = 5, 90 :10 = 9, 90 : 9 = 10.
5 55 25 7 79
значит, 18 18 5 до5 10 10 9
4 4 10 40
9 9 10 90 *
63 .
90 ;
Одним из применений приведения дробей к
общему знаменателю является сравнение
дробей. Например, при сравнении дробей из
предыдущего примера получаем, что je
^ 4 ^ 7
<д <1б>так
25
как90
40 63
90 90 *
Примеры: Сравнить дроби.
ч 2
а>3И
2
3
5
7*
14 5 15 _ 14 ^
2Ти7=21-ТаККаК2Т <
б)15И18-
8
15
ч 7
в) g и
7
9
48 11 55. 8
90 И 18 90 ' 15
20
27*
20
: «г»следовательно,
<м-
7 20
9 27
15
21
2 5
Т03<Г
Сложение и вычитание обыкновенных
дробей и смешанных чисел
Правило: Чтобы сложить (вычесть) дроби с
разными знаменателями, надо:
1) привести данные дроби к наименьшему
общему знаменателю;
2) сложить (вычесть) полученные дроби.
5 7
Например, сложим дроби 5 и ?2 * Приведем
оа 5 20 7 21
их к общему знаменателю 36: g = 57» и jo = оа •
5 , 7 20 , 21 41 1 5
Теперь получаем: § + и = м + ш = g6 = Х36 •
9
(3 (7
27-7
20
42
10
21
Пример: п -g - 42
Правило: Чтобы сложить смешанные
числа, надо:
1) привести дробные части этих чисел к
наименьшему общему знаменателю;
2) отдельно выполнить сложение целых
частей и отдельно дробных частей; результаты
сложить;
3) если при сложении дробных частей
получилась неправильная дробь, то, выделить
целую часть из этой дроби и прибавить ее к
полученной целой части.
Пример: 19g + 24^ = (19 + 24) + g + Aj =
=43+(ii + g)=43+li=43+i24=44-
Правило: Чтобы выполнить вычитание
смешанных чисел, надо:
1) привести дробные части этих чисел к
наименьшему общему знаменателю; если
дробная часть уменьшаемого меньше дробной
части вычитаемого, превратить ее в
неправильную дробь, уменьшив на единицу целую часть
уменьшаемого;
2) отдельно выполнить вычитание целых
частей и отдельно дробных частей;
результаты сложить.
Пример: 16^ - 7 А = 16| - 7§jj = (16 - 7) +
Чбо 6oJ * во *боф
Умножение обыкновенных дробей
Правило: Чтобы умножить дробь на дробь,
надо:
1) найти произведение числителей этих
дробей и произведение их знаменателей;
2) первое произведение записать
числителем, а второе — знаменателем;
3) если возможно, сократить дробь.
а)
Примеры:
2 5 2 5
3 " 7 3 7 =
а т
Ъ' п =
10
= 21 ;
а т
Ь п

Краткое изложение школьного курса математики
Математика. 5—6 классы
17
°'8 ' 21 8 21
112
168
2
3
В последнем примере для простоты
сокращения дроби можно поступить так:
7
8
16 7 16 7 2 12 2
21 8 21 1 21 13 3*
Правило: Для того чтобы выполнить
умножение смешанных чисел, надо записать их в
виде неправильных дробей, а затем
воспользоваться правилом умножения дробей.
Примеры:
.„5 „3 41
а>218 'Ч = Т8
^А5 О2 29
б>46 -25=Т( •
1А5'
»)2§.1|.5|-
18 41 18 41 1
5 18 5 5 55;
12 29 12 29 2 58
5 6 5 5 5
8 15 27 8 15 27
3 " 8 ' 5 3 8 5
= 27.
Правило: Чтобы умножить смешанное
число на целое число, надо целое число записать в
виде дроби со знаменателем 1, смешанное
число записать в виде неправильной дроби и
перемножить получившиеся дроби.
Примеры:
6
а)3§ ■
« 17
« 53
•б=12
= ±°2.=20^
6
1
5
53 6
12 1
'5
53
2 1
2 ZD2
-j
-5-1
з 1ф
В последнем примере произведение чисел g и
3 оказалось равным единице. Два числа,
произведение которых равно единице, называются
взаимно обратными.
Примеры:
а) g иЬ взаимно обратные числа, так как
5 -1 5 6 =1.
6 ' Х5 6*5 i;
tfxol 3 - 01 3
б) 2« и = взаимно обратны, так как 2« • = =
7 3
3 " 7
1;
в) для числа г обратным является число « > или
i2 3 5 1
lg » так как г • = — 1.
Таким образом, чтобы для числа,
записанного дробью, найти обратное число, достаточно
поменять местами числитель и знаменатель.
Например, для j обратным будет число « > а для
,5 12 Л 7
1 = = -=- обратным является число т^ .
Деление обыкновенных дробей
Правило: Чтобы разделить одну дробь на
другую, надо делимое умножить на число,
обратное делителю.
а)
Примеры:
3 5 3 6
8 * 6
1
8
3 6
8-5
_.. 03 9 11 9
б>42:24~2 :Т = 2
18 Л1_
11 Х11;
3 3 _ 9 .
4 5 20'
А = 9 4 = 9 2
11 2 11 1 11
в) 5:
г)3|
Д)1:
e)3|
За1
Ф
:8
4
5
• 4
5
1
15
4
»1 •
: 3
8
: 1
5
4
2 °4
5
1
15
4
ф
15
4
3
10
1
• —
8
9
2 :
=
=
27
4
5 3
1 10
15 1
4 8
15
4
13
12
15
32 ;
3
2
27
15 9 4 ^ 15 1 1 = 5 =91
4 2 27 12 3 2 2
ДЕЙСТВИЯ
С ДЕСЯТИЧНЫМИ ДРОБЯМИ
Сравнение десятичных дробей
Правило: Если в конце десятичной дроби
приписать нуль (или несколько нулей) или
отбросить нуль (или несколько нулей), то
получится дробь, равная данной.
Примеры: 5,70 = 5,7; 18,3400 = 18,34; 163,1 =
= 163,10; 0,35 = 0,3500; 17,0 = 17.

18
Краткое изложение школьного курса математики
Математика. 5—6 классы
Так же как и натуральное число,
десятичную дробь можно разложить по разрядам.
Например, 23,5708 = 23 + 0,5 + 0,07 + 0,0008.
Цифра, стоящая на первом месте после
запятой, относится к разряду «десятых», на втором
месте — к разряду «сотых», на третьем
месте— к разряду «тысячных», на четвертом
месте— к разряду «десятитысячных». Число
23,5708 читается: 23 целых 5 тысяч 708
десятитысячных.
Правило: Для того чтобы, сравнить две
десятичные дроби, надо сначала сравнить целые
части дробей; в случае их равенства
последовательно сравнивают цифры, стоящие в
разряде «десятых*; в случае их равенства
сравниваются цифры следующего разряда — «сотых*
и т. д.
В случае разного числа цифр после запятой у
сравниваемых чисел их уравнивают
приписыванием справа необходимого количества нулей.
Примеры:
а) 78,001 > 13,7859, так как 78 > 13;
б) 14,387 < 14,5082, так как целые части равны,
а в разряде десятых 3 < 5;
в) 0,47 > 0,09;
г) 1,537 > 1,5369, так как 1,5370 > 1,5369;
д) 18,34 < 18,343, так как 18,340 < 18,343.
Сложение
и вычитание десятичных дробей
Правило: Чтобы сложить (вычесть)
десятичные дроби, надо:
1) уравнять в этих дробях количество
знаков после запятой;
2) записать их друг под другом так, чтобы
запятая была записана под запятой;
3) выполнить сложение (вычитание), не
обращая внимания на запятую;
4) поставить в ответе запятую под
запятой в данных дробях.
Примеры:
а) 23,756 + 4,8 = 23,756 + 4,800 - 28,556.
23,756
+ 4,800
28,556
б) 0,017 + 23,24 = 0,017 + 23,240 = 23,257.
в) 75 + 1,248 - 75,000 + 1,248 = 76,248.
75,000
+ 1,248
76,248
г) 90,04 - 7,518 - 90,040 - 7,518 = 82,522.
90,040
~ 7,518
Д)5-
- 0,04 -
е) 24,87 - 5
5,00 -i
- 24,87
0,04 =
-5,00
82,522
4,96.
5,00
0,04
4,96
= 19,87.
24,87
5,00
19,87
Умножение десятичных дробей
Правило: Чтобы умножить десятичную
дробь на натуральное число, надо:
1) умножить ее на это число, не обращая
внимания на запятую;
2) в полученном произведении отделить
запятой столько цифр справа, сколько их
отделено запятой в десятичной дроби.
Примеры:
а) 7,84 • 92 = 721,28;' 7,84
х 92
6)14,3 • 39 = 557,7.
1568
7056
721,28
х14*'о
39
1287
429
557,7
+
0,017
23,240
23,257
Правило: Чтобы умножить десятичную
дробь на 10, 100, 1000 и т. д., надо в этой
дроби перенести запятую на столько цифр
вправо, сколько нулей стоит в множителе после
единицы.
Примеры:
а) 16,48 • 10 = 164,8;
6)1,0073 • 100 = 100,73;
в) 74,235 • 1000 = 74 235.
Правило: Чтобы перемножить две
десятичные дроби, надо:

Краткое изложение школьного курса математики
Математика. 5—б классы
19
1) выполнить умножение, не обращая
внимания на запятые',
2) отделить в полученном произведении
запятой столько цифр справа, сколько их стоит
после запятой в обоих множителях вместе.
в) 2978,4 : 73 = 40,8;
Примеры:
а) 7,38 • 0,4 = 2,952;
6)9,45 • 0,012 = 0,1134;
в) 24,079 • 1,5 = 36,1185.
+
7,38
Х 0,4
2,952
х 9,45
0,012
1890
945
0,11340
24,079
1£
120395
24079
36,1185
Правило: Для того чтобы умножить
десятичную дробь на 0,1, надо запятую перенести в
дроби влево на одну единицу; на 0,01 —
перенести запятую влево на две единицы; на 0,001 —
перенести влево на три единицы и т. д.
Примеры:
а) 78,3 • 0,1 = 7,83;
б) 0,056 • 0,01 = 0,00056.
Деление десятичных дробей
Правило: Чтобы разделить десятичную
дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая
внимания на запятую;
2) поставить в частном запятую, когда
закончится деление целой части.
Примеры:
а) 1825,2: 234 = 7,8; 1825.21234
1638 (73~
_1872
1872
6)95,41 : 47 = 2,03;
0
95,41147
94 |2^3
_141
141
0
2978,4173
292 (40^8
_584
584
г) 3,2 : 8 = 0,4.
Правило: Чтобы разделить десятичную
дробь на 10, 100, 1000 и т. д. надо перенести
запятую в этой дроби на столько цифр влево,
сколько нулей стоит после единицы в
делителе.
Примеры:
а) 47,4 : 10 = 4,74;
б) 8,92 : 100 = 0,0892.
Правило: С помощью деления находят
десятичную дробь, равную данной обыкновенной
дроби. Для этого надо поделить числитель
этой дроби на знаменатель.
Примеры:
a) g = 7 : 8 = 0,875;
_ 7,0 0018
0 |0,875
70
64
60
56
40
40
0
б) ~ = 0,15; в) | = 1,5; г) ~ = 0,025.
Правило: Чтобы разделить число на
десятичную дробь, надо:
1) в делимом и делителе перенести
запятую вправо на столько цифр, сколько их после
запятой в делителе;
2) после этого выполнить деление на
натуральное число.
Примеры:
а) 160,23 : 4,9 = 1602,3 : 49 = 32,7;
1602,3149
147 f
132
98
343
343
32,7

20
Краткое изложение школьного курса математики
Математика. 5—6 классы
б) 0,05 : 0,004 = 50 : 4 = 12,5;
в) 40 : 0,25 = 4000 : 25 = 160.
Правило: Чтобы разделить десятичную
дробь на 0,1; 0,01; 0,001 и т.д., надо
перенести в ней запятую вправо на столько цифр,
сколько в делителе стоит нулей перед
единицей. (То есть, другими словами, разделить на
0,1; 0,01; 0,001 и т. д. — это то же самое, что
умножить число на 10,100,1000 и т. д.)
Пример: 7,23 : 0,1 = 72,3.
Приближенные значения чисел.
Округление чисел
Если данное число заменяется на другое
число, близкое ему по значению, то получаем
приближенное значение данного числа.
Например:
17,23 - 17, 0,0028 - 0, 199 » 200,
g « 0,3, 24,5043 - 24,5, 37,92 » 37,9.
Замену числа ближайшим к нему
натуральным числом или нулем называют округлением
этого числа до целых.
Примеры: 27,4 « 27; 239,7 « 240; 4,1589 « 4.
Числа можно округлять до любого разряда:
до десятых, до сотых, до тысячных и т. д.
Правило: Если число округляют до какого-
нибудь разряда, то все следующие за этим
разрядом цифры заменяют нулями, а если они
стоят после запятой, то их отбрасывают.
При этом если первая отброшенная или
замененная нулем цифра равна 5, 6, 7, 8 или 9, то
стоящую перед ней цифру увеличивают на 1.
Если же первая отброшенная или замененная
нулем цифра равна 0, 1, 2, 3 или 4, то
стоящую перед ней цифру оставляют без
изменения.
Примеры:
а) Округлить числа 89,6289; 113,251; 9,97 до
десятых:
89,6289 « 89,6; 113,251 - 113,3;
9,97=10,0.
б) Округлить числа до целых:
236,48 « 236; 18,713 * 19; 89,545 - 90.
ЕДИНИЦЫ ИЗМЕРЕНИЯ ВЕЛИЧИН.
СООТНОШЕНИЯ МЕЖДУ
ЕДИНИЦАМИ ИЗМЕРЕНИЯ
ОДНОЙ И ТОЙ ЖЕ ВЕЛИЧИНЫ
Значения десятичных приставок
При обозначении единиц разных величин
используются приставки, показывающие, во
сколько раз увеличилась или уменьшилась
основная единица измерения величины.
Приставки увеличения и их краткие
обозначения:
дека — в 10 раз больше да;
гекто — в 100 раз больше г;
, кило — в 1000 раз больше к;
мега — в 1 000 000 раз больше М.
Приставки уменьшения:
деци — в 10 раз меньше д;
санти — в 100 раз меньше с;
милли — в 1000 раз меньше м;
микро — в 1 000 000 раз меньше мк.
Например, декалитр — это величина, в 10
раз большая, чем 1 литр. Тогда если вспомнить,
что 1 литр кратко обозначается 1 л, а краткая
запись приставки дека — да, то получается
следующая запись: 1 дал = 10 л или 1 л = 0,1 дал.
Другой пример. Миллиметр — это величина,
в 1000 раз меньшая, чем 1 метр. Так как один
метр имеет краткую запись 1м, а приставка
милли кратко обозначается также м, то
получается, что 1 мм = 0,001 ж,а1л= 1000 мм.
Единицы измерения длины
Основной единицей измерения длины
является метр. Метр кратко обозначается м, т. е.
1 метр записывается 1 м.
1 м = 10 дм = 100 см = 1000 мм = 1 000 000 мкм.
Напомним, что последняя запись означает,
например, что 1 метр равен 1 000 000 микронов.
Из этой цепочки следует, что:
1 дм = 10 см = 100 мм = 100 000 мкм;
1 см = 10 мм = 10 000 мкм;
1 мм = 1000 мкм.
Эти соотношения можно записать
по-другому:
1 мкм = 0,000001 м = 0,00001 дм =
= 0,0001 см = 0,001 мм;
1мм = 0,001 м = 0,01 дм = 0,1 см;

Краткое изложение школьного курса математики
Математика. 5—6 классы
21
1 см = 0,01 м = 0,1 дм;
1 дм =0,1 м.
Длину большей величины обычно
записывают в километрах, краткая запись — 1 км.
1 км = 1000 м = 10000 дм = 100 000 см =
= 1 000 000 мм = 1 000 000 000 мкм,
т. е.
1 мкм - 0,000000001 ?СЛ1,
1 лсл* = 0,000001 км, \см= 0,00001 км,
\дм = 0,0001 км, 1 ле = 0,001 км.
Очень мелкие величины измеряются в
ангстремах:
1 ангстрем = 0,0001 мкм.
Единицы измерения массы
Основной единицей измерения массы
является грамм, краткое обозначение — г. При
обозначении других единиц массы обычно
используются приставки милли и кило (другие
приставки используются редко).
1 г = 1000 мг или 1 мг = 0,001 г,
1 кг = 1000 г или 1 г = 0,001 кг,
1кг = 1 000 000 мг или 1 мг = 0,000001 к:г.
Крупные по массе величины измеряют в
тоннах (т) и центнерах (ц):
1 т = 10 ц = 1000 кг = 1 000 000 г или
114 = 0,1т, 1 кг =0,001 т,
1 г = 0,000001 /п, 1 ц = 100 кг = 100 000 г или
1 кг = 0,01 ц, 1 г = 0,00001 ц.
Единицы измерения площади
Основная единица измерения площади —
квадратный метр: обозначается м .
1 м = 100 дм = 10000 см = 1 000 000 мм,
т. е. 1 ел*2 = 0,0001 м, 1 дл*2 = 0,01 м,
1 еж2 = 0,01 дм, 1 еж2 = 100 мм2,
1 лш2 = 0,01 см2, 1км2 = 1 000 000 м,
\м2 = 0,000001 км2.
При измерении земельных участков часто
используются единицы измерения ар и гектар
(краткая запись a is. га).
1 а= 100 м = 1 000 000 см, т. е. 1 м = 0,01 а.
Другое название ара — сотка. 1 сотка — это и
2
есть 1 ар, или 100 м .
1 га = 100 а = 10 000 л*2 или 1 а = 0,01 га, a
1л2 = 0,0001 га.
Единицы измерения объема
Основной единицей измерения объемов явля-
ется кубический дециметр; обозначается дм .
з
Для 1 дм имеется другое название — 1 литр. То
з
есть иными словами 1 дм = 1 л.
Тысячная часть литра обозначается
миллилитр, т. е. 1 л - 1000 мл, а 1 мл = 0,001 л.
1 л = 1 дм3 = 1 000 000 лш3,
1 мм3 = 0,000001 л.
3 3
Таким образом, 1 мл — 1000 жж , а 1 лги =
3 * 3
= 0,001 л!Л. Так как 1 см = 1000 лш , то 1 мл =
= 1 см .
Крупные объемы измеряются в декалитрах
з
(дал): 1 дал = 10 л; и кубических метрах (м ):
1 м = 1000 л, т. е. 1 м = 100 дал.
Единицы измерения времени
Самой мелкой единицей времени является
секунда. При записях единиц времени
приставки обычно не используются (хотя, например,
можно измерять время в миллисекундах, т. е. в
тысячных долях секунды).
1 MUH = 60 С, 1 С = rg мин,
1 ч = 60 мин = 3600 с,
1 __L- 1 - -L
1 с ~ 3600 ч> * "*"*w "" 60 ч*
1 сут = 24 ч = 1440 лшн = 86 400 с,
Т. е. 1 Ч = «Г сУт> 1 мин = JTJq С1/7П.
Перевод одних единиц времени в другие
связан не с десятичными дробями, а с
обыкновенными.
Например, 5 мин = gn ч = То ч>
Нужно запомнить, что 30 мин = 0,5 ч = ~ ч;
1 3
15 мин = 74= 0,25 ч; 45 мин = т ч = 0,75 ч;

22
Краткое изложение школьного курса математики
Математика. 5—6 классы
20 мин = g ч; 6 ч = j сут; 8 ч = ^ q/m; 12 ч =
= 1
! 2 c#m-
Единицы измерения скорости
Задача. Бегун пробежал 100 м за 10 с.
Очевидно, что он бежал со скоростью 10 метров в
секунду. Это записывается 10 м/с. Велосипедист
за 1 ч проехал 36 км — естественно, его скорость
36 км/ч.
Вопрос: У кого скорость передвижения была
больше? Давайте разберемся.
10 м/с = 36 000 м/ч = 36 км/ч
(так как 1 ч = 3600 с, а 1 км = 1000 м).
Можно по-другому: 36 км/ч = 36 000 м/ч =
= 10 м/с.
Получается, что скорость у них была
одинаковая.
Примеры:
а) Перевести 15 км/ч в м/мин:
(15 • 1000 - 15 000) (15000 : 60 = 250
15 км/ч = 15 000лс/ч
= 250 м/мин;
б) 4 км/с перевести в м/мин. 4 км/с =
= 4000 м/с = 240 000 м/мин.
В 1972 г. на Олимпиаде в Мюнхене в
плавании на 400 м два спортсмена — швед Г. Ларссон
и американец Т. Макки — показали
одинаковое время: 4 мин 31,98 с. С какой скоростью
(м/с) они двигались? Ответ: 400 : 271,98 =
« 1,47 м/с (так как 4 мин = 240 с, 240 + 31 =
= 271 с).
Кого наградить золотой медалью? Один из
секундомеров зафиксировал, что Ларссон на 0,001 с
раньше коснулся стенки бассейна (в тот момент
пальцы Макки были в 1 мм от стенки). Вот вам
и 0,001 с.
Для любознательных
Старинные русские меры
Меры длины:
1 верста = 1,067 км;
1 сажень = 3 аршина = 7 футов = 2,134 м;
1 аршин = 16 вершков = 0,711 м = 71,1 см;
1 вершок — 4,445 см (оказывается, что «от
горшка два вершка» — это 9 см).
Самое любопытное в том, что были меры
«линия» и «точка»:
1 линия = 10 точкам = 2,54 мм;
1 точка = 0,254 мм.
Меры массы:
1 пуд = 40 фунтов = 16,38 кг;
1 фунт = 0,41 кг = 410 г;
1 лот = 12,8 г;
1 золотник = 4,26 г; '
1 доля = 44,4 жг.
Меры объема:
1 бочка = 40 ведер = 492 л;
1 ведро =10 штофов = 20 бутылок = 12,3 л;
1 штоф = 10 чарок — 1,23 л;
1 чарка = 0,123 л — 123 жл;
1 бутылка = 0,615 л = 615 мл.
Английские старинные меры
Меры длины:
1 миля = 1609 м;
1 ярд = 91 см;
1 ф1//п = 30,5 см;
1 дкшл* = 2,54 см;
1 морская миля, = 1853 ж;
1 кабельтов = 185 ж.
Меры массы:
1 англ. фунт = 0,454 «:г = 454 г (английский
фунт на 44 г больше русского фунта);
1 унция = 28,3 г (1 аптекарская унция =
= 31,1 г).
Меры объема:
1 галлон = 4,55 л;
1 кварта = 1,14 л;
1 пинта = 0,57 л.
Для любителей читать Ж. Верна
Формула для перевода градусов Цельсия в
градусы Фаренгейта: F = 1,8 • С + 32. Например, по
Цельсию t = 20°. По Фаренгейту t = 1,8 • 20 +
+ 32 = 68°. Другой пример: по Цельсию t = -10°,
а по Фаренгейту t = 1,8 • (-10) + 32 = 14°.
Обратная формула (перевод градусов
Фаренгейта в градусы Цельсия):
С = 1 .(^-32).
Например, по Фаренгейту 95°, тогда по
Цельсию 35°.

Краткое изложение школьного курса математики
Математика. 5—6 классы
23
ПРОЦЕНТЫ
Что такое процент
Сотую часть рубля называют копейкой,
сотую часть доллара называют центом (от
латинского слова centum — сто), сотую часть метра —
сантиметром (обратите внимание на значение и
произношение приставки санти), сотую часть
гектара — аром (а по-народному — сотка).
Принято называть сотую часть любой
величины или числа процентом.
Значит, 1 копейка — один процент рубля,
1 см —- 1 процент метра, 1 цент — 1 процент
доллара, 1а — 1 процент гектара, а число 0,05 —
1 процент от 5. Для краткости слово «процент»
1
после числа заменяют знаком %, т.е. 1% =
100
= 0,01.
Понятие процента неразрывно связано с
десятичными дробями.
Правило: Чтобы обратить десятичную
дробь в проценты, ее надо умножить на 100.
Чтобы перевести проценты в десятичную
дробь, надо число процентов разделить на 100.
Примеры:
а) Записать десятичные дроби в процентах.
0,25 - 25% (т. к. 0,25 • 100 =25);
0,5 = 50% (т. к. 0,5 • 100 = 50);
0,003 = 0,3% (т. к. 0,003 • 100 = 0,3);
0,0158 - 1,58% (т. к. 0,0158 • 100 = 1,58);
1,538 - 153,8% (т. к. 1,538 • 100 = 153,8).
б) Записать проценты в виде десятичных дробей.
40% = 0,4 (т. к. 40 : 100 = 0,4);
63% = 0,63 (т. к. 63 : 100 = 0,63);
1,5% = 0,015 (т. к. 1,5 : 100 = 0,015);
0,08% = 0,0008 (т. к. 0,08 : 100 = 0,0008);
110% = 1,1 (т. к. 110 : 100 = 1,1);
200% = 2 (т. к. 200 : 100 = 2).
Основные задачи на проценты
Задача 1. В школе 800 учеников. Из них
46% приняли участие в математической
олимпиаде. Сколько человек приняли участие в
олимпиаде?
Решение: 1) Найдем 1% учеников школы:
800 : 100 = 8 (уч.).
2) Найдем 46%:
8 • 46 = 368 (уч.).
Ответ: 368 учеников.
Решение задачи можно оформить короче, если
перевести 46% в десятичную дробь: 46% = 0,46,
а затем число всех учеников умножить на
полученную десятичную дробь, т. е.
800 • 0,46 = 368.
Правило: Для того чтобы найти р
процентов от данного числа а, надо:
1) перевести р процентов в десятичную дробь;
2) умножить число а на получившуюся
десятичную дробь.
Примеры:
а) Найти 17% от 32.
17% =0,17,32 • 0,17 = 5,44.
б) Найти 30% от 1,8.
1,8 • 0,3 = 0,54.
в) Найти 145% от 76.
76 • 1,45 = 110,2.
Задача 2. На городскую олимпиаду
школьников по математике из всех школ приехали
140 человек, что составило 3,5% всех желавших
принять в ней участие. Сколько всего человек
хотели принять участие в олимпиаде?
Решение: 1) Найдем сначала 1% всех
желавших:
140 : 3,6 = 40 (чел.).
2) Найдем количество всех желавших:
40 • 100 = 4000 (чел.).
Ответ: 4000 человек.
Можно было поступить по-другому:
перевести 3,5% в десятичную дробь (3,5% = 0,035), а
затем число учеников, принявших участие в
олимпиаде, разделить на полученную
десятичную дробь, т. е. 140 : 0,035 = 4000.
Правило: Для того чтобы найти все число
по известной части Ь и числу
соответствующих процентов р, надо:
1) перевести р процентов в десятичную
дробь;
2) разделить Ь на полученную десятичную
дробь.
Примеры:
а) Найти число, если 12% его составляют 66.
66:0,12 = 550.

24
Краткое изложение школьного курса математики
Математика. 5—6 классы
б) Найти число, если 150% его равны 960.
960: 1,5 = 640.
в) Найти число, если 0,2% его равны 5.
5 : 0,002 = 2500.
г) Вкладчик положил в банк некоторую сумму
денег под 80% в год. Через год он получил
прибыль в 30 000 рублей. Найти величину
вклада.
30 000: 0,8 = 37 500 (р.).
Задача 3. В финале Всероссийской
математической олимпиады приняли участие 160
школьников, из них 24 человека стали призерами.
Какой процент школьников стал призерами
олимпиады?
Решение: 1) Найдем 1% всех школьников:
160: 100 =1,6 (чел.).
2) Найдем процент призеров:
24:1,6=15%.
Ответ: 15% всех участников стали призерами.
Однако можно рассуждать по-другому: най-
24
дем дробь r-jwj и умножим ее на 100, чтобы
перевести ее в процент, т. е.
24 2400
160 " 10°-Тб0- ~15/о-
Правило: Чтобы найти процент числа Ь
от числа а, надо дробь - умножить на 100.
Примеры:
а) Найти, сколько процентов составляет число
15,57 от числа 90.
15,57 |100и1ММ00иШв1Ш|
ПОЛОЖИТЕЛЬНЫЕ
И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА
Координатная прямая
Точка О на прямой АВ разбивает эту
прямую на два дополнительных луча О А и ОВ.
Выберем единичный отрезок и примем точку О за
начало отсчета. Тогда положение точки на
каждом из двух лучей задается ее координатой.
Чтобы отличить друг от друга координаты на этих
двух лучах, условились ставить перед
координатами на одном луче знак «+» (обычно на правом
или верхнем луче), а перед координатами на
другом луче знак «-» (обычно на левом или
нижнем луче).
-5 -4 -3 -2 -1 0
■ч 1 1 1 1 н-
+1 +2 +3 +4 +5
—I 1 1 1 м
В
О
Числа со знаком «+» перед ними называют
положительными. Часто знак «+» опускают. На-
2 2
пример, вместо +7 пишут 7. То есть +2g = 2g,
+4,3 = 4,3.
Числа со знаком «-» перед ними называют
5
отрицательными. Пишут: -1; -6; -= , -2,6 и
читают «минус один», «минус шесть», «минус
пять седьмых» и т. д.
Начало отсчета (или начало координат) —
точка О — изображает число нуль (0). Само
число нуль не является ни положительным, ни
отрицательным. Оно отделяет положительные
числа от отрицательных.
-3-
-+-+-
-2,6
Н—I—ь
-1
—н
0
-4-
«S
ч—н-
4,3
-44 Н
90
90
9
О
б) Найти, сколько процентов составляет число
150 от числа 120.
150
15 000
120 # 10° 120
- 125%
в) Найти, сколько процентов составляет число
0,3 от 1,9.
0,3 «м-0.3-100 „300 _1(Л5 «-«о.
Прямую с выбранными на ней началом
отсчета, единичным отрезком и положительным
направлением (помечается стрелкой на прямой)
называют координатной прямой. Число,
показывающее положение точки на прямой,
называют координатой этой точки.
Например, координата точки С равна -2,6.
Записывается; С(-2,6). Координата точки D
равна +4,3. Записывается D(+4,3), или D(4,3).

Краткое изложение школьного курса математики
Математика. 5—б классы
25
Противоположные числа.
Целые числа. Модуль числа
Два числа, отличающиеся друг от друга
только знаками, называют противоположными.
-5 -4 -2,5 -1 0 +1
—н 1 1—i—i 1 1 н
+2,5 +4 +5
I i I 1 h-^-
Например, +1 и -1 — противоположные числа;
2,5 и -2,5 — противоположные числа;
4 4
-6 ц и6? —противоположные числа.
Для каждого числа есть только одно
противоположное число. Число 0 противоположно
самому себе.
Натуральные числа, противоположные им
числа и число нуль называют целыми числами.
Например, про числа -15; -3; 0; 1; +5; 10 014
можно сказать, что они целые. А про числа -7,5;
1 5
-2 g ; 1,1; 15 5 нужно сказать, что они целыми не
являются. Числа 5; +17; 106 являются и
натуральными, и целыми, а числа -3; -19; 0; -101
целыми являются, а натуральными — нет.
Модулем числа а называют расстояние (в
единичных отрезках) от начала координат до точки
А(а).
1
-4,7
-3
—н
l I 1
-Н—h
А О
Вместо слова «модуль» в записи используют
символ | |. Например, запись «найти |-3|»
означает, что надо найти модуль числа -3. Из
определения модуля следует, что |-3| = 3, так как
число -3 находится на расстоянии трех
единичных отрезков от начала отсчета.
Л
= 15 > так как расстояние от нуля до
числа l| равно \\ . |3| = 3; |-4,7| = 4,7.
Заметим, что |0| = 0.
Правило: Модуль числа не может быть
отрицательным (так как расстояние не может
быть отрицательным). Для положительного
числа и нуля он равен самому этому числу, а
для отрицательного числа модуль равен
противоположному числу.
Противоположные числа имеют равные
модули, так как они находятся на равных
расстояниях от начала отсчета. Например, |-10| = 10 и
|10| = 10, следовательно, |-10| = |10|.
а)
б)
в)
Примеры:
1-12,6| = 12,6; г) |23| = 23;
0| = 0; д)|1|-1;
5 е)|-1| = 1.
4
= 7
6*
Сравнение положительных
и отрицательных чисел
-5 -4 -2,75 -1 0 1
4,5
l 1 I I
III —
Правило: Из двух чисел, отмеченных на
координатной прямой, больше то, которое
лежит правее, и меньше то, которое лежит
левее.
Примеры:
а) 4,5 > -5, так как число 4,5 расположено
правее, чем -5;
б) -4 > -5, так как -4 расположено правее, чем
-5;
в) -2,75 < -2g , так как -2,75 на координатной
прямой левее, чем -2^ .
Правило: Любое отрицательное число
меньше любого положительного числа.
Из двух отрицательных чисел меньше то,
модуль которого больше.
Нуль больше любого отрицательного числа,
но меньше любого положительного.
Примеры:
1
а) -100 < g
б) 1,4 >-14;
в)-7д <-6, так как
-7
= 7| и|~6| = 6,а7| >6.
Значит, число -7g расположено дальше от
нуля, чем число -6;
г) -7,5 < -6, так как 7,5 > 6;
д) 0 > -80;
е) -4,9 < 0;
ж)3^ >0.

26
Краткое изложение школьного курса математики
Математика. 5—6 классы
Сложение чисел с помощью
координатной прямой
Правило: Прибавить к числу а число Ь
значит изменить число а на Ь единиц. Причем
если Ъ — число положительное, то число а
увеличивается; если же Ь — отрицательное
число, то число а уменьшается.
Примеры:
а) -8 + 3 = -5;
б)-8 + (-3) = -11;
Г
+з
А
-8
н—ь
-5
Л h
-3
-11
Л
н—н
-8
в) -2 + 4 = 2;
г)3 + (-4) = -1.
+4
-4
Г
Л
г
Л
\ 1 1—ь
-2
-1
При сложении двух положительных чисел
суммой является положительное число.
Сложение двух отрицательных чисел дает в
результате отрицательное число,
Сумма положительного и отрицательного
чисел может быть как положительной, так и
отрицательной (смотри примеры а) и в)).
При сложении двух противоположных чисел
суммой является число 0.
Например, -3 + 3 = 0; 4,9 + (-4,9) = 0. В
общем виде:
а + (-а) = 0
От прибавления нуля число не изменяется.
Например, -13 + 0 = -13; -2,8 + 0 = -2,8.
Сложение положительных
и отрицательных чисел
Правило: Чтобы сложить два
отрицательных числа, надо:
1) сложить их модули;
2) поставить перед полученным числом
знак «-».
Примеры:
а) -6 + (-4) = -10 (так как |-6| + |-4| = 6 + 4 = 10
и перед этим числом ставится знак «-*);
б) -3,2 + (-!) = -4,2.
Правило: Чтобы сложить два числа с
разными знаками, надо:
1) определить больший модуль из модулей
этих чисел;
2) из большего модуля вычесть меньший;
3) поставить перед полученным числом знак
того слагаемого, модуль которого больше.
Примеры:
а) Нужно сложить -4 и 9. Для этого:
1)|-4| = 4,|9| = 9и4<9;
2) 9 - 4 = 5;
3) так как |9| > |-4|, то ответ положительный,
т. е.-4 + 9 = 5.
б) Сложим 3 и -10.
1) |3| = 3, |-10| = 10 и 3 < 10;
2) 10 - 3 > 7;
3) так как |-10| > |3|, то ответ отрицательный,
т. е. 3 + (-10) = -7.
.»
(3
= -1140-21=-11^
11 24 1X24#
г) -3,7 + (-10,12) = -(3,7 + 10,12) = -13,82.
д)-4,5 + 1,2 =-3,3.
ж)-12,5 +5 = -7,5.
Вычитание положительных
и отрицательных чисел
Правило: Чтобы из данного числа вычесть
другое число, надо к уменьшаемому прибавить
число, противоположное вычитаемому:
а -Ъ = а + (-&)
Примеры:
а) 14-19 = 14+ (-19) = -5;
б) -9,2 - 3 = -9,2 + (-3) = -12,2;
в) -3-(-4)= -3 + 4 =1.
а - Ь а+{-Ъ)
При выполнении примеров типа т - (-п)
нужно очень хорошо помнить, что
т - (-п) = т + п.
Примеры:
а) 4 -(-2,1) = 4 + 2,1 = 6,1;
б) -9,8 - (-5,7) = -9,8 + 5,7 = -4,1.
Разность двух чисел положительна, если
уменьшаемое больше вычитаемого, и
отрицательна, если уменьшаемое меньше вычитаемого.

Краткое изложение школьного курса математики
Математика. 5—б классы
27
Если уменьшаемое и вычитаемое равны, то
их разность равна нулю.
Примеры:
а) -4 - 3 < 0, так как -4 < -3 (-4 - 3 = -7).
б) -2g - (-8) > 0, так как -2g > -8 f-2g - (-8) -
-•й-
в) 5 - (-9) > 0, так как 5 > -9 (5 - (-9) = 14).
г) 12 - 13,8 < 0, так как 12 < 13,8(12-13,8 =
- ~1,8).
Умножение и деление положительных
и отрицательных чисел
Правило: Чтобы перемножить два числа с
разными знаками, надо перемножить модули
этих чисел и поставить перед полученным
числом знак «-».
Примеры:
а)-2,4 • 5 = -(2,4 • 5) =-12;
6)6 • (-0,7) = -(6 • 0,7) = -4,2.
Правило: Чтобы перемножить два
отрицательных числа, надо перемножить их модули.
Примеры:
1 (1\, 11 1.
а' 2A3je2#3e6;
б) -2 • (-0,4) = 2 • 0,4 = 0,8.
При умножении чисел полезно помнить
такую таблицу (правило знаков):
(+)•(+) = (+) (-)•(+>-<-)
(+) •(-)-(-> (-)•(-)-<+)
'Правило: При делении чисел с разными
знаками надо разделить модуль делимого на
модуль делителя и поставить перед частным
знак «-».
Примеры:
5 2 (Ъ 2\ =_5_3 =_5 =,1.
а) 6 : 3 [б:3) 6 2 4 Х4*
б) £ -(-^--{г^^-ГЪ ="3'
Правило: Чтобы разделить
отрицательное число на отрицательное, надо разделить
модуль делимого на модуль делителя.
Примеры:
а) -2,4 : (-0,4) = 2,4 : 0,4 = 6;
б>-2:(-§Н:Ь16-
Правило знаков при делении чисел то же, что
и при умножении: при умножении (делении)
чисел с одинаковыми знаками результат
положителен; при умножении (делении) чисел с
противоположными знаками результат
отрицателен.
ЗАДАЧИ НА ВСЕ ДЕЙСТВИЯ
Порядок выполнения действий
Сложение и вычитание чисел называют
действиями первой ступени, а умножение и деление
чисел — действиями второй ступени.
Правило: 1) Если в выражении нет скобок и
оно содержит действия только одной ступени,
то их выполняют по порядку слева направо.
2) Если выражение содержит действия
первой и второй ступени и в нем нет скобок, то
сначала выполняют действия второй
ступени, а потом действия первой ступени.
3) Если в выражении есть скобки, то
сначала выполняют действия в скобках (учитывая
при этом правила 1 и 2).
Примеры:
Ф @
а) 20,3 - 0,6 + 1,4 = 21,1;
1)20,3-0,6 = 19,7,
2)19,7 + 1,4 = 21,1;
© Ф
6)17,8 - 0,8 • 5 = 13,8;
1)0,8 -5 = 4,
2)17,8-4=13,8;
2 ® 5 ® ( 1 ® 5\ 2
x>4i -1! -ai -1! -a + Ci -1) -ai-
.5
2)2
8
92 =21 §
CZ 8 3
7,
3)lo| "7 = 3?;
r>9i : {ч + ч) • 5=9:
1>88+2§-БЯ«
Z)y2 18 2 : 18 2 ' 95 5 * 5'
3)1;
5 =
= 9.

28
Краткое изложение школьного курса математики
Математика. 5—б классы
В выражениях типа а + Ъ - с разрешается
сначала выполнить вычитание Ь - с, а затем
разность сложить с а.
В выражениях типа а • Ь : с можно сначала
выполнить деление Ь : с (или а : с), а затем
умножить получившееся частное на а (или на Ь).
Примеры:
а) 17,6+ 24,8-3,8 = 38,6;
1)24,8-3,8 = 21,
2)17,6 + 21 = 38,6;
6)24^ • 4? :2| =49;
1)4|:2|=2,
2)24^ • 2 = 49;
4,8-1,5
в)
1,6
= 3 • 1,5 = 4,5.
При выполнении совместных действий с
обыкновенными и десятичными дробями
нужно учитывать рациональность выбора: иногда
лучше действия выполнить в обыкновенных
дробях, а в других случаях — в десятичных.
Примеры:
а) 0,4
6)2^ :0,36 =
It =0,4 • 1,5 = 0,6;
100
36
21
4 °4*
14
B)2g -0,21 = 3 " Ш=25-
Совместные действия
с положительными
и отрицательными числами
Вычисления в примерах, содержащих
несколько действий, можно проводить двумя
способами:
1) просто выполнять отдельно все действия
по порядку;
2) выполнять действия цепочкой.
Примеры:
® ф ®
а)-16,4 - 5,2 : (-0,4) + 1,5 = 1,9;
по действиям:
1)5,2: (-0,4) = -13,
2)-16,4-(-13) = -3,4,
3)-3,4 + 1,5 = -1,9;
цепочкой:
-16,4 - 5,2 : (-0,4) +1,5 = -16,4 - (-13) +1,5 =
= -16,4 + 13 + 1,5 = -16,4 + 14,5 = -1,9;
б)-2
! Ф 5 ® ® ®
-2 : 0,5 + 7,2 = 0,4;
по действиям:'
1) *Ъ * 6 3 5 5 Z,5>
2)2:0,5 = 4,
3)-2,8-4 = -6,8,
4) -6,8 + 7,2 = 0,4;
цепочкой:
-2g : g -2:0,5 + 7,2 = -^-| -4 + 7,2 = -2,8 +
+ 3,2 = 0,4;
@ Ф ®
в) 5 - 4,8 : (-0,3) • 0,75 = 17;
по действиям:
1)4,8: (-0,3) = -16,
2)-16 • 0,75 = -12,
3)5-(-12) = 17;
цепочкой:
5 - 4,8 : (-0,3) • 0,75 = 5 + 16 • 0,75 = 5 + 12 =
= 17.
Степень
Запись ал, где а — любое число, п —
натуральное число, называют степенью. Причем
число п называют показателем степени, а —
основанием степени.
Запись ап означает произведение п
множителей, каждый из которых равен а, т. е.
а = а • а • а
а,
л раз
Примеры:
а) 43 = 4 • 4 • 4 = 64;
б) 0,35 = 0,3 • 0,3 • 0,3 • 0,3 • 0,3 = 0,00243;
B)UJ = 5 5 " 25 »
.ЗУ*
2\2 2 2 _ 4
5) 5 5
«(->!)■-'? И)И)-т ■(-¥)■(-¥)-
1000 „314
343 ^343*
2 2
Не надо путать записи типа (-0,4) и -0,4 ,
так как (-0,4)2 = (-0,4) • (-0,4) = 0,16, а -0,42 =
= -(0,4 • 0,4) = -0,16, а также f g 1 и j, так как

Краткое изложение школьного курса математики
Математика. 5—б классы
29
(й-
? Ё 2 ?=!*! ±L = 2 2 2 2
3*3*3*3 81* а 3 3
16 Л
= Т=5з-
При выполнении примеров, содержащих
степени, в первую очередь выполняется возведение
в степень, а затем все остальные действия.
Примеры:
Ю-2. 1.8»-^—2.1.69- °-4г -
= - 3,38 - 0,008 = -3,388;
б) [\ + I)2 - 50 • ОД3 = [I)2 - 50 • 0,001 -
(5 (9
__25_n25V _JL/ 125 - 9 _ 116 _
36 ' 36 20 180 180
29
45*
Правило: При возведении в степень
отрицательных чисел ответ будет
положительным, если показатель степени — четное
число, и отрицательным, если показатель —
нечетное число.
Примеры:
;-о,и2 = о,с
б) (-0Д)4 = 0,0001; г) (-0Д)5 = -0,00001.
а) (-0Д)2 = 0,01; в) (-0Д)3 - -0,001;
ПРЕОБРАЗОВАНИЕ
БУКВЕННЫХ ВЫРАЖЕНИЙ
Раскрытие скобок
Выражение а + (Ь + с) можно записать без
скобок: а 4- (Ь + с) = а + Ъ + с. Эту операцию
называют раскрытием скобок.
Правило: Если перед скобками стоит знак
«+», то можно опустить скобки и этот знак
«+», сохранив знаки слагаемых, стоящих в
скобках. Если первое слагаемое в скобках
записано без знака, то его надо записать со
знаком «+».
Например, а+(&-с+2) = а+&-с + 2 или
(т - п) + (-4 + а) = т-я-4 + а.
Правило: Чтобы раскрыть скобки, перед
которыми стоит знак «-», надо опустить
скобки и этот знак «-», поменяв знаки всех
слагаемых в скобках на противоположные.
Если первое слагаемое в скобках записано без
знака, то его надо записать со знаком «-».
Например, -(а - Ъ) = -а + Ъ или х - (-у + 5) =
= х + у - 5.
Примеры:
а) (х - у) - (-у + 8) = х - у + у - 8 = х - 8, так
как -у + I/ = 0;
б) -(а + &) + (3 - с) = -а - Ъ + 3 - с = -а - & - с + 3;
в) 8,2 - (4,5 - а) = 8,2 - 4,5 + а = 3,7 + а;
г) (6 - х) - (-9+у) -20 = 6-x + 9-i/-20 =
= -х - у - 5.
Коэффициент.
Раскрытие скобок с применением
распределительного свойства
Если выражение является произведением
числа и одной или нескольких букв, то это
число называют числовым коэффициентом (или
просто коэффициентом).
Например, в выражении -8,5а —
коэффициент равен -8,5; 4ху • 5 = 20ху — коэффициент
равен 20; -тп = -1т — коэффициент равен -1; х =
= 1х — коэффициент равен 1; -т • 6я • (-За) =
= ISmna — коэффициент равен 18.
Правило: Если перед скобками стоит
множитель со знаком «+», то можно опустить
скобки, умножив каждое слагаемое скобок на
этот множитель, сохранив при этом знаки
всех слагаемых.
Например, 7 + 2 • (а - 4) = 7 + 2а - 8 = 2а - 1;
Зх • (-8 - у) = Зх(-8) + Зх(-у) = -24* - Зху.
Правило: Если перед скобками стоит
множитель со знаком «-», то этот знак нужно
заменить на «+», изменив при этом знаки
всех слагаемых в скобках. Далее необходимо
воспользоваться предыдущим правилом.
Например,
-3 • (4 - 5а) = +3 • (-4 + 5а) = -12 + 15а;
18 - 4с • (3+2а) = 18 + 4с • (-3 - 2а) -
= 18-12с-8ас.
Примеры:
а) 4 • (Зх - 2) - 2 • (-Ьу - 1) = 4 • (3* - 2) +
+ 2 • (Ъу + 1) - 12* - 8 + 10у + 2 = 12* + 10у - 6;
б) -6а • (-* + 7) + х • (3 - у) - +6а • (х - 7) +
+ х(3 - у) = бале - 42а + Зх - ху.
Подобные слагаемые. Вынесение
общего множителя за скобки
Слагаемые, имеющие одинаковую буквенную
часть, называют подобными слагаемыми.

30
Краткое изложение школьного курса математики
Математика. 5—б классы
Например, -2а и 0,4а — подобные
слагаемые; х и -5л: — подобные слагаемые, слагаемые
86 и 8а — подобными не являются; подобными
2
также не являются слагаемые ах и ay; х и х .
С подобными слагаемыми можно
производить арифметические действия. Сложение и
вычитание подобных слагаемых называется
приведением подобных слагаемых.
Правило: Чтобы привести подобные
слагаемые, надо сложить их коэффициенты и
результат умножить на общую буквенную часть.
Примеры:
а) -6л: + 8л: = (-6 + 8)л: - 2х;
б) а - Та + 2а = (1 - 7 + 2)х = -4а;
ч 5 7,1 с (Ь 7 , 1\ к
в)^-8^ + 4^"5х=18"8Ч- ij -У-6х =
= 0 •у Ьх = -5л\
Правило: Если слагаемые имеют общий
множитель, то его можно вынести за скобки.
В скобках останется сумма других
множителей.
Примеры:
а) Ъх + 8х = (5 + 8) • х = 13л:;
б)5х + 5у = Ь{х+у);
в) g ах + з &х = g л:(а + 6);
г) л: + дс = х + х • л: = х • (1 + л:).
Примеры преобразования выражений
1. Привести подобные слагаемые:
а) Ч$# - 1х + ц - 10* - 2 = -7у - 17л: - 2;
б) 2£ + 4F- а - 5*Р~За + 26 - 4 = -5а + 6-4.
2. Раскрыть скобки и привести подобные
слагаемые:
а) -8 • (2 - 2у) + 4 • (3 - 4у) = +8 • (-2 + 2у) +
+ 4 • (3-4i/)=z16+ Jt«i/ +12- Jtfli/ =-4;
б) 7л: - 0,5 • (-2л: + 4) - (10 - л:) = 7л: + 0,5 • (2л: -
-4)-10 + л: = 7х + х-2 -10 + х = 9л: - 12;
в) 5 • (|* - 0,7)-3 • (|* - 0,2)= 5 • (j* - 0,7)+
+ з(-|х + 0,2) = 2*-3,5 -£ + 0,6 = х -2,9.
3. Упростить выражение:
1 - 0,5 • (-6л: + Зу - 4) + (Юл: - бу - 5) • (-0,3) =
= 1 + 0,5 • (6л: - Зу + 4) + 0,3 • (-Юл: + 6у + 5) =
= ! + ЗдГ-115£ + 2- 3*Г + l,8t/ + 1,5 = 0,3у + 4,5.
4. Найти значение выражения:
а) -0,4 • (2л: + Зу) + 0,5 • (-Зл: + 5у), при х = -0,5,
У—1.
Сначала упростим выражение:
-0,4 • (2л: + 3i/) + 0,5 • (-Зл: + Ьу) = -0,8л: -
- 1,2у - 1,5л: + 2,6у = -2,3л: + 1,3у.
Теперь подставим значения х и у:
-2,3 • (-0,5)+ 1,3 • (-1) = 1,15-1,3 = -0,15;
б) -4 • (5 - 0,3л:) + 2 • (4,5л: + 10), при х = -0,1.
-4 • (5 - 0,3л:) + 2 • (4,5л: + 10) = +4 • (-5 +
+ 0,3л:) + 2 • (4,5л: + 10) = - Ш +\,2х + 9л: +
+ J2T = 10,2л:;
10,2 • (-0,1) = -1,02.
УРАВНЕНИЯ.
РЕШЕНИЕ УРАВНЕНИЙ
Что такое уравнение
Уравнением называют равенство, в котором
неизвестное обозначено буквой. Значение
буквы, при котором из уравнения получается
верное числовое равенство, называют корнем
уравнения.
Решить уравнение — значит найти все его
корни (или убедиться, что это уравнение не
имеет ни одного корня).
Примеры:
а) Зл: = 21; л: = 7 — корень уравнения, так как
3-7 = 21 (верное равенство);
б) 0,8 + х = 0,5; х = -0,3 — корень уравнения,
так как 0,8 + (-0,3) = 0,5 (верное равенство);
в) Зл: + х = -2; х = -0,5 — корень уравнения,
так как 3 • (-0,5) + (-0,5) = -2 (верное
равенство);
г) уравнение 5 : х = 0 не имеет корней (делить на
0 нельзя, а при делении числа 5 на другие
числа в частном 0 не получится).
Основные правила
решения уравнений
Правило 1: Чтобы найти неизвестное
слагаемое, надо из суммы вычесть известное
слагаемое (если а + х = Ь, то х = Ъ - а).
Примеры:
а) 7 + х = 23; х = 23 - 7; х = 16;
б) х + 0,2 = 1; х = 1 - 0,2; х = 0,8;
в) 1,8 + х = 0,5; х = 0,5 - 1,8; х = -1,3;
г) -3 + х = -2; х = -2 - (-3); х = -2 + 3; х = 1.

Краткое изложение школьного курса математики
Математика. 5—б классы
31
Правило 2: Чтобы найти неизвестное
уменьшаемое, надо сложить вычитаемое и
разность (если х - а = Ъ, то х = а + Ь).
Примеры:
а) х - 8 = 5; х = 8 + 5; х = 13;
б) х - 1,4 = -6; х = 1,4 + (-6); х = -4,6;
в) х - (-2) = -1; х = -2 + (-1); х - -3.
Правило 3: Чтобы найти неизвестное
вычитаемое, надо из уменьшаемого вычесть
разность (если а - х = Ь, то х = а - &).
Примеры:
а) 9 - х = 1,3; х = 9 - 1,3; х = 7,7;
1 _ =5, 1 _ 5;. =_1.
0)2 х g; х g б;* 3;
в) -3 - х = -7; х = -3 - (-7); х = 4.
Правило 4: Чтобы найти неизвестный
множитель, надо произведение разделить на
известный множитель (если ах—Ь, то х = Ъ : а,
или х = - I .
Примеры:
а) 0,2х = 6 б)3х = 0,4 в)-^х=0,4
*-0,4:(-})
х - 0,4 • (-7)
х =-2,8
Правило 5: Чтобы найти неизвестное
делимое, надо частное умножить на делитель
(если х : а = Ъ, или - = Ь, то х = аЬ).
Примеры:
а) х : 0,3 = 4 б) х : (-2,5) = 2 в) j^ = -3
х = 4 • 0,3 х = 2 • (-2,5) х' = -3 • 1,2
х = 1,2 х=-5 х = -3,6
Правило 6: Чтобы найти неизвестный
делитель, надо делимое разделить на частное (если
а : х = Ъ, то х = а : Ъ, или если - = Ъ, то х = г ].
Примеры:
а)0,8:х=-5 б) ? =-0,7 в) J : * = 2
X 4
*=0,8:(-5) *=-о^7 * = !:2
х = 6:0,2
х = 30
0,4
4
* 30
2
* = 15
х=-0,16
*="Т
х =-8
60
Г
4
1
* = 4
Другие правила решения уравнений
Правило 1: Корни уравнения не изменятся,
если какое-нибудь слагаемое перенести из
одной части уравнения в другую, изменив при
этом его знак.
Примеры:
а) Зх - 8 = х - 14 б) -2(3х + 4) = -10 - 8х
Зх - х = -14 + 8 - 6х - 8 = -10 - 8х
2х = -6 - 6х + 8х = -10 + 8
х = -6 : 2 2х = -2
х = -3 х = -1
в) -0,1(х - 0,5) = 0,2(3 - 5х)
-0,1х+ 0,05 = 0,6-х
-0,1х + х =0,6-0,05
0,9х = 0,55
0,55
х =
х =
0,9
55
90
11
Х 18
Правило 2: Корни уравнения не изменятся,
если обе его части умножить или разделить
на одно и то же число, не равное нулю.
Примеры:
а)10х-120 = 30х-40
Разделим каждое слагаемое обеих частей
уравнения на 10.
х - 12 = Зх-4
-2х = 8
х=-4
fi 1 _!=JL_8
' 2х 3 18 9*
Умножим каждое слагаемое обеих частей
уравнения на число 18.
18 _ 18 = 5 18 _ 8 18
2*3 18 9 Х
9х-6 = 5- 16х
9х + 16х = 5 + 6
25х=11
х = 0,44
Пропорции
Частное двух чисел называют отношением,
этих чисел. Например, 5:7==, частное = можно
назвать отношением чисел 5 и 7. Отношением
чисел 1 и 0,25 является число 4, так как 1 : 0,25 = 4.

32
Краткое изложение школьного курса математики
Математика. 5—б классы
Равенство двух отношений называют
пропорцией. Например, равенство 20 : 4 = 0,5 : 0,1
является пропорцией. Эта пропорция является
верной, так как 20 : 4 = 5 и 0,5 : 0,1 = 5, а вот
пропорция 7 : 2 = 10:3 неверная, так как 7:2 =
= 3,5, а 10 : 3 = Зд . В общем виде пропорция за-
l ^ ас
писывается так: а : о = с : а, или г в з •
Числа and называют крайними членами
пропорции, Ъ и с — средними членами пропорции.
Например, в пропорции 7 : 5 = 3,5 : 2,5 числа
7 и 2,5 — крайние члены, а 5 и 3,5 — средние, а
8 3 Q
в пропорции - = - члены 8 и х являются
крайними, а и 2 — средними.
Правило: В верной пропорции произведение
крайних членов равно произведению средних
членов. Верно и обратное: если произведение
крайних членов равно произведению средних
членов пропорции^ то пропорция верна.
Например, 0,4 : 8 = 1 : 20 — верная
пропорция, тогда 0,4 • 20 = 8 • 1 — также верно.
Другой пример: равенство 5 • 6 = 2 • 15 — верно,
тогда 5:15 = 2:6 — верная пропорция.
Часто в пропорции один (или несколько) из
ее членов неизвестен. Например, 6 : х = 2 : 7.
Найдем неизвестный член пропорции. Для этого
воспользуемся свойством пропорции:
6 • 7 = 2 • х
42 = 2 • х
х = 42 : 2
л: = 21.
Примеры:
а) х : 0,2 = 5 : 7
Jx = 5 • 0,2 4 • 5 - 3*
7х = 1 20 = 3*
лч 4 - х
б)3~5
в)
х =
0,46
х =
20
х
7,2 18
0,46 • 18 = 7,2л:
0,46-18
г)
*=63
х - 2 1 - 5х
х =
х =
7,2
4,6-18
72
л: = 1,15
3 4
(х - 2) • 4 = (1 - 5х) • 3
4л:-8 = 3-15л:
4х + 15х = 3 + 8
19* =11
= 11
х 19
д) 0,2 : х = 3 : (х + 2)
0,2 • (х + 2) = Зх
0,2л: + 0,4 = Зл:
0,2л: -Зл: = -0,4
-2,8л: = -0,4
1
х = =
е)
х =
5 3
8 : 4
5 2
SX 7
х =
х =
3
4
2 3 5
7 " 4 : 8
2 3 8
7 4 5
х =
2 3 2
7 5
12
* 35
ФОРМУЛЫ
Путь, скорость, время
Обозначим путь буквой S, скорость — буквой
и, а время — буквой t. Тогда
S = v • t — формула цути,
v = т — формула скорости,
f = _ — формула времени.
Примеры:
а) Автомобиль двигается со скоростью 92 км/ч.
Какой путь проедет он за 5 ч?
S = 92 • 5 = 460 (кл).
б) Турист за 4 ч прошел 18 км. С какой
скоростью шел турист?
и = 18 : 4 = 4,5 (км/ч).
в) Расстояние между Москвой и Новосибирском
2800 км. За какое время самолет преодолеет
это расстояние, если он летит со скоростью
800 км/ч?
t = 2800 : 800 = 3,5 (ч).
При решении таких задач надо внимательно
следить за тем, в каких единицах измеряются
величины. Например, велосипедист за 45 мин
проехал 30 км. С какой скоростью ехал
велосипедист?
v = S : t, t = 45 мин9 S = 30 км. Тогда v изме-
2
ряется в км/мин, т. е. v = 30 : 45 - g (км/мин).
Если же мы хотим получить скорость v в км/ч,
то 45 мин = go ч = j ч* Тогда v = 30 : ^ =
= 30 • g = 40 jcjk/ч.

Краткое изложение школьного курса математики
Математика. 5—6 классы
33
Задача. Марафонец бежал со скоростью 5 м/с.
Какой путь преодолел марафонец за 30 мин?
Решение: v = 5 (м/с) = 5 • 60 (м/мин) =
= 300 (м/мин). Тогда S = 300 • 30 = 9000 (м) =
= 9 (км).
Ответ: за 30 мин марафонец пробежал 9 км.
Среднее арифметическое
Средним арифметическим нескольких чисел
называют частное от деления суммы этих чисел на
число слагаемых. Например, средним арифмети-
а + Ь
ческим двух чисел а и о является число с = —«— ,
а средним арифметическим трех чисел х.уиг-
х + у + г
число с = f .
Примеры: Найти среднее арифметическое:
а) 5,2 и 8: (5,2 + 8): 2 = 13,2 : 2 = 6,6;
б) 1,4, 6 и 7: (1,4 + 6 + 7): 3 = 14,4 : 3 - 4,8.
Задача. Первый час пешеход шел со
скоростью 5 км/ч, второй час со скоростью 4,5 км/ч, а
третий час — 4,3 км/ч. Найти среднюю скорость
пешехода.
5 + 4,5 + 4,3
Решение: vcp =
= 4,6 (км/ч).
Периметр
Сумма длин всех сторон многоугольника
называется периметром. Периметр фигуры,
изображенной на рисунке 1, равен: Р = а +Ъ +с + d + е.
Для прямоугольника формула периметра: Р =
= (а + Ь) • 2 (рис. 2).
Для квадрата (рис. 3) формула периметра: Р =
= 4 • а.
Задача 1. Найти периметр прямоугольника
со сторонами 2,8см и 4 еж.
Решение: Р = (2,8 + 4) • 2 = 13,6 см.
Ответ: 13,6 см.
Задача 2. Одна из сторон прямоугольника
равна 7,3 см, а его периметр равен 30,2 см.
Найти другую сторону прямоугольника.
Решение: Обозначим неизвестную сторону
прямоугольника через х. Тогда по формуле
периметра прямоугольника имеем:
(7,3 + х) • 2 - 30,2
7,3 + х = 15,1
х = 15,1 -7,3
л: = 7,8
Ответ: неизвестная сторона прямоугольника
равна 7,8 см.
Движение по реке
В задачах на движение по реке приходится
иметь дело с собственной скоростью в стоячей
воде (vc)9 скоростью течения реки (vm),
скоростью по течению реки (vno т) и скоростью против
течения реки (vnp т).
Vno m = vc+vm>
Vnp. т = »с- vm'>
vnp. m~vnom~2 vm'
Ко m = %. m + 2vm>
"c = (Vno m + vnp. m) ' *>
"m = ^no m ~ vnp. m> '• 2-
Задача 1. Скорость катера по течению
21,8 км/ч, а против течения 17,2 км/ч. Найти
собственную скорость катера и скорость течения
реки.
Решение:
1) vm - (21,8 - 17,2): 2 = 4,6 : 2 = 2,3 (км/ч);
2) vc = 17,2 + 2,3 = 19,5 (км/ч).
Задача 2. Моторная лодка двигалась по
течению реки со скоростью 15 км/ч. Найти скорость
лодки против течения, если скорость течения
реки 1,8 км/ч.
Решение: v
пр. т
15-2 • 1,8 = 11,4(км/ч).
Площадь
За единицу измерения площа-
2 2 2 v/ & '/Л
дей принимают 1 мм , 1 см ,1м 1Дсм J 1см
2
и другие. Например, 1 см — это
площадь квадрата со стороной
1 см.
Рис. 1
Рис. 2
Рис. 3
2- 1019

34
Краткое изложение школьного курса математики
Математика. 5—б классы
Площадь фигуры, изображенной на рисунке 4,
равна 5 см , а площадь треугольника, изобра-
2
женного на рисунке 5, равна 2 см (подумай
почему).
Формула площади прямоугольника: S = а • Ь,
а квадрата S ^а •а = а .
Задача 1. Найти площадь прямоугольника,
если одна из его сторон равна 7 см, а другая на
2,5 см меньше.
Решение: 1) 7 - 2,5 = 4,5 (см) — сторона.
2
2) 7 • 4,5 = 31,5 (см ) — площадь.
2
Ответ: S = 31,5 см .
Задача 2. Найти периметр земельного
участка прямоугольной формы, если его площадь
равна 8 а, а одна из сторон 16 м.
2
Решение: 1) 8 а = 800 м .
2) 800 : 16 = 50 (м) — неизвестная сторона.
3) (16 + 50) • 2 = 132 (м) — периметр.
Ответ: Р = 132 м.
Объем прямоугольного
параллелепипеда
и площадь его поверхности
Фигуры типа спичечного коробка, кирпича,
молочного пакета имеют форму прямоугольного
параллелепипеда.
Длина, ширина и высота прямоугольного
параллелепипеда называются его измерениями.
Поверхность прямоугольного параллелепипеда
состоит из шести попарно равных
прямоугольников.
Бели все три измерения параллелепипеда
равны, то он называется кубом. Поверхность
куба состоит из шести одинаковых квадратов.
Формула объема прямоугольного
параллелепипеда:
V = а • Ъ • с.
Формула объема куба:
V = а .
Площадь поверхности прямоугольного
параллелепипеда вычисляется по формуле:
S = 2 • (аЬ + ас + be).
Площадь поверхности куба можно вычис-
лить по формуле: S = 6а .
Например, если измерения прямоугольного
параллелепипеда а = 4,5 см, Ь = 8 см, с = 12 см,
то объем его равен:
К = 4,5 ■ 8 • 12 = 432 ел*3,
а его площадь поверхности равна:
S = 2 • (4,5 • 8 + 4,5 • 12 + 8 • 12) =
= 2 • (36 + 54 + 96) = 372 см2.
Площадь круга и длина окружности
Большое значение при вычислении площади
круга и длины окружности имеет число я,
открытое древнегреческим математиком
Пифагором. Оно показывает, во сколько раз длина
окружности больше диаметра. Обычно при вычис-
1см
1см
Рис. 4
1см
1см
S = а*Ь
а
Рис. 6

Краткое изложение школьного курса математики
Математика. 5—6 классы
35
лениях используют значение тс = 3,14. Более
точно я =3,14159.
Формула длины окружности:
С = nd, или С = 2nR.
Формула площади круга:
S = nR2, или S = (nd2): 4.
Задача 1. Радиус окружности равен 8,5 еж.
Найти длину окружности и площадь
соответствующего круга.
Решение:
С = 2яД - 2 • 3,14 • 8,5 - 53,38 = 53,4 {см);
S = nR2 « 3,14 • 8,52 = 3,14 • 72,25 -
« 226,9 (см2).
Задача 2. Длина Московской кольцевой
автодороги примерно равна 110 км. Вычислите
приближенное значение площади, занимаемой
Москвой.
Решение:
1) С = 2яД;
2) S = nR ;
110 = 2 • 3,14 • R; S = 3,14 • 17,5 ;
110 = 6,28 • R; S « 962 (км2).
R = 110: 6,28;
R= 17,5 (км);
Ответ: S « 962 (кле2).
ЗАДАЧИ
Задачи на сравнение величин
Нужно запомнить: фраза «величина а на с
единиц больше Ь* на языке уравнений означает,
что а ~-Ь = с, или а -Ь Л- с, или Ъ - а - с.
Например, если «* на 8 больше 12», то * - 12 =
= 8, или х = 12 + 8, или 12 = х - 8. Решая любое
из этих уравнений, получим х = 20.
Задача 1. Известно, что выражение 2х - 3 на
7 меньше, чем Ъх + 8. Найти значение *.
Решение: Из условия следует, что:
(5* + 8) - (2* - 3) = 7
Ъх + 8 - 2* +3 = 7
3* + 11 = 7
3* = -4
4
* = ~3
Задача 2. Масса 9 кирпичей на 20 кг больше,
чем масса одного кирпича. Найти массу одного
кирпича.
Решение: Обозначим массу одного кирпича
через х (кг), тогда масса 9 кирпичей равна 9л: (кг).
Из условия задачи следует, что:
9* - х = 20
8* = 20
х = 2,5
Ответ: масса одного кирпича 2,5 кг.
Нужно запомнить: фраза «величина а в с раз
больше величины Ь> на языке уравнений означает,
что а : о = с, т. е. г = с, или а : с = &, т. е. - = о,
о с
или а =Ь • с.
Например, если ав5 раз больше, чем 2,4»,
то х : 2,4 = 5, или х : 5 = 2,4, или х = 2,4 • 5.
Решая любое из этих уравнений, получим х = 12.
Задача 3. Известно, что выражение 4 - 3* в
1,5 раза меньше, чем 2,5* + 8. Найти значение
переменной х
Решение: Из условия задачи следует, что
(4-3*) • 1,5 = 2,5* + 8
6-4,5* = 2,5*+ 8
-7* = 2
2
*=-,.
Задача 4. За день Ира прочитала в 3,5 раза
страниц больше, чем Маша. Сколько страниц
прочитала каждая девочка, если Маша
прочитала на 40 страниц меньше Иры?
Решение: Число страниц, прочитанных
Машей, обозначим через *. Тогда Ира прочитала
3,5* (е.). По смыслу задачи
3,5* -х =40
2,5* = 40
* = 16
3,5 • 16 = 56 (с.)
Ответ: Маша — 16с, Ира — 56 с.
Задача 5. Маша и Катя решили испечь к
празднику каждая одинаковое число
пирожков. Но обе очень старались, поэтому Катя
испекла на 6 пирожков больше, чем задумано, а
Маша даже на 13 пирожков больше. В итоге

36
Краткое изложение школьного курса математики
Математика. 5—6 классы
оказалось, что Маша испекла в 1,5 раза больше
пирожков, чем Катя, Сколько пирожков хотела
испечь каждая девочка?
Решение: Каждая девочка хотела испечь по х
пирожков. Но Катя испекла х + 6, а Маша х + 13
пирожков. По условию задачи:
(х + 6) • 1,5 = х + 13
1,5х + 9 = л: + 13
0,5л: = 4
х=8
Ответ: каждая девочка хотела испечь по 8
пирожков.
Задача 6. На одной стоянке стояло в 2 раза
больше автомашин, чем на другой. Когда с
первой стоянки переехало 30 автомашин на вторую,
то на второй стоянке оказалось в 3 раза больше
машин, чем на первой. Сколько автомашин
было на каждой стоянке?
Решение:
было машин стало машин
1 стоянка 2х 2х - 30
2 стоянка х х + 30
По условию задачи х + 30 в 3 раза больше,
чем 2х - 30. Составим уравнение:
(2х - 30) • 3 = х + 30
6л: - 90 = х + 30
Ьх = 120
х = 24
24 • 2 = 48 (м).
Ответ: На первой стоянке было 48
автомашин; на второй — 24 автомашины.
Задача 7. Вася и Коля вместе собрали 91
белый гриб. Более удачливый Вася собрал в 2,5
раза грибов больше, чем Коля. Сколько грибов
собрал каждый мальчик?
Решение:
1-й способ Составим уравнение:
Коля — х (грибов) х + 2,5л: = 91
Вася — 2,5л: (грибов) 3,5л: = 91
Вместе — 91 гриб х = 91 : 3,5
л: = 26
26 • 2,5 = 65(гр.)
2-й способ Составим уравнение;
Коля — х (грибов) 91 - х = 2,5л:
Вася — 91 - х (грибов) 91 = 3,5л:
91 - х в 2,5 раза х = 26
больше, чем х 91 - 26 = 65 (гр.)
Ответ: Коля собрал 26 грибов, Вася собрал 65
грибов.
Задачи на нахождение дроби
от числа и числа по его дроби
Правило: Чтобы найти дробь от числа,
надо это число умножить на данную дробь.
Примеры:
7 7
а) Найти g от числа 360. 360 • ^ = 280.
б) Найти 0,4 от 120. 120 • 0,4 = 48.
Правило: Чтобы найти все число по
данному значению его дроби, надо это значение
разделить на дробь.
Пример: Найти число х, если г этого числа
равны 30. 30 : g = —«— = 50.
Можно оформить решение в виде уравнения:
| х = 30, х = 30 : |, х = 50.
Задача 1. Найти площадь поля, если
известно, что скосили 0,7 всего поля, а осталось неско-
2
шенным 5400 м .
Решение:
1)1-0,7 = 0,3 — нескошенная часть поля;
2) 5400 : 0,3 = 18 000 (м ) — площадь всего поля.
Ответ: 18 000 м.
Задача 2. Турист был в пути 3 дня. В первый
1
день он прошел т всего пути, во второй день —
5
9
оставшегося пути, а в третий день —
последние 16 км. Найти весь путь туриста.
Решение: Пусть весь путь туриста равен х (км).
Тогда в первый день он прошел -г х (км), во вто-
5, 1 ч 5 3 5 ^
рои день — о (* "" Z *) ~ о * i*^!^** к как в
третий день он прошел 16 км, то:
jx + Тох+ 16 = лг
jx + Тох" х = ""16
-§*~1в
х = 48
Ответ: Весь путь туриста равен 48 км.

Краткое изложение школьного курса математики
Математика. 5—6 классы
37
Задача 3. На выполнение домашнего
задания (математика, литература и география)
Миша потратил 90 мин. На литературу он потратил
3
2 того времени, что затратил на математику, а
на географию на 10 мин меньше, чем на
литературу. Сколько времени затратил Миша на
математику, сколько на литературу и сколько на
географию?
Решение: Пусть х (мин) он затратил на мате-
матику, тогда т х (мин) ушло на литературу, а
на географию было потрачено т х - 10 минут.
Так как всего на домашние уроки он затратил
90 мин, то:
4 4
\х = 100
Две величины обратно пропорциональны,
если при увеличении (уменьшении) одной из них в
несколько раз другая уменьшается
(увеличивается) во столько же раз.
Задача 2. Четыре комбайна могут убрать
пшеницу с поля за 10 дней. За сколько дней
уберут это поле пять таких же комбайнов?
Решение: Очевидно, что во сколько раз
больше комбайнов, то во столько же раз меньше
потребуется времени для уборки поля. То есть
можно сказать, что число (п) комбайнов,
убирающих поле, находится в обратной
пропорциональной зависимости от времени уборки (t).
пг = 4 комб. tx = 10 дн.
п2 = 5 комб. t2 = х дн.
TOT»^eVT-e-6
* ^ 4 10 Q
гтс. Отсюда х = 5 = 8.
Ответ: 5 комбайнов уберут поле за 8 дней.
х = 100 : g
х =40
Итак, на математику ушло 40 мин, на литера-
3
туру 2 • 40 = 30 (мин), а на географию 30 - 10 =
= 20 (мин).
Ответ: 40 мин, 30 мин, 20 мин.
Прямая и обратная
пропорциональные зависимости
Две величины прямо пропорциональны,
если при увеличении (уменьшении) одной из них в
несколько раз другая увеличивается
(уменьшается) во столько же раз.
з
Задача 1. Стальной шарик объемом 6 см
имеет массу 46,8 г. Какова масса шарика из той
же стали, если его объем 2,5 см ?
Решение: Очевидно, что, во сколько раз
меньше объем шарика, во столько же раз
меньше его масса. Следовательно, объем шарика (V)
и масса шарика (т) находятся в прямой
пропорциональной зависимости. Решим задачу с
помощью пропорции:
Уг - 6 см тг = 46,8 г У
ТПЛ
V2 = 2,5 см тп2 = х (г)
771л
6 46,8
2,5 х Х
= 19,5.
Ответ: 19,5 г.
46,8-2,
6
1
46,8-
24
И)
468
24
Задачи на деление числа на части,
пропорциональные данным числам
Задача 1. Сережа собрал в саду 2,4 кг
клубники. Четыре части он отдал сестре Наташе, три
части — брату Коле, а одну часть оставил себе.
Сколько килограмм клубники получил каждый
из детей?
Решение: Обозначим массу одной части через
х (кг), тогда масса трех частей — Зх (кг), а масса
четырех частей — 4л: (кг). Так как всего было
2,4 кг клубники, то:
х + Зх + Ах = 2,4
8* = 2,4
х = 0,3 (Сережа)
1) 3 • 0,3 =? 0,9 (кг) — получил Коля;
2) 4 • 0,3 = 1,2 (кг) — получила Наташа.
Ответ: 1,2 кг, 0,9 кг, 0,3 кг.
Задача 2. Для приготовления компота нужна
вода, ягоды и сахар, масса которых должна быть
пропорциональна числам 4, 3 и 2 соответственно.
Сколько нужно взять воды, ягод и сахара (по
массе) для приготовления 13,5 кг компота?
Решение: Пусть для приготовления компота
требуется а (кг) воды, Ь (кг) ягод, с (кг) сахара.
Тогда а:4 = Ь:3 = с:2, или J = з = 2 ' ^Усть ка"
__ 468 _ ждое из отношений равно числу х. Тогда т = х,
Ъ с
5 = х, о = х. Отсюда а = 4#, Ъ - Зх, с = 2х. По
условию задачи а+Ь+с = 13,5(к;г), тогда

38
Краткое изложение школьного курса математики
Математика. 5—6 классы
4* + Зх 4- 2х = 13,5
9* = 13,5
х = 1,5
1) 4 • 1,5 = 6 (кг) — воды;
2) 3 • 1,5 = 4,5 (кг) — ягод;
3) 2 • 1,5 = 3 (кг) — сахара.
Ответ: 6 кг, 4,5 кг, 3 кг.
Задачи «на масштаб»
Отношение длины отрезка на карте к длине
соответствующего отрезка на местности
называют масштабом. То есть запись 1:500000 нужно
понимать так: отрезок на карте в 500000 раз
меньше, чем на местности. Можно сказать и
так: отрезок на местности в 500000 раз больше
соответствующего отрезка на карте.
Например, на такой карте расстояние между
городами А и В равно 8 см. Тогда на местности
(т. е. настоящее расстояние) расстояние между
городами А и Б равно 8 см • 500 000 =
4 000 000 см =40 км.
Наоборот, если известно, что на местности
расстояние между городами С и D равно 300 км, то на
этой карте расстояние между ними будет равно:
300 км : 500 000 = 30 000 000 см : 500 000 = 60 см.
Задача 1. Найти масштаб карты, если
расстояние на местности между городами М и N
140 км, а на карте это выражено отрезком 7 см.
Решение:
7 см : 140 км = 7 см : 14000000 см =
= 1:2000000.
Ответ: Масштаб карты 1 : 2 000000.
Задача 2. Между городами X и У расстояние
на местности 200 км, а на карте 5 см. Каким
отрезком на этой карте будет выражено
расстояние 700 км?
Решение: Эту задачу можно решить через
нахождение масштаба карты, а можно
по-другому — с помощью пропорции. Обозначим
искомый отрезок через х, тогда
5 200
х 700 ' Х "
Ответ: 17,5 см.
5 700
= ' 200
= 17,5 см
Разные задачи
Задача 1. Витя и Толя любят собирать
авиамодели. На сборку одной и той же модели Витя
тратит 4 ч, а Толя — 3 ч. Однажды мальчики
решили собирать модель вместе. Сколько времени
они потратили на сборку?
Решение: 1) За один час Витя может собрать
1
2 часть всей модели;
2) за один час Толя собирает « часть всей
модели;
3) вместе за 1 час они делают: 1 + о = То (час_
тей);
4) тогда, разделив всю работу 1 = т« натл,
получим ответ:
12 7 12 12 12 ,5 , . - AQ
12 : 12 =ТГТ =У =l7(4)=l443 MUH-
Ответ: 1= ч.
Задача 2. Веревку длиной 63 м разрезали на
2 куска так, что 40% длины первого куска были
равны 30% длины второго куска. Найти длину
каждого куска веревки.
Решение: Пусть первый кусок имеет длину
х (м), а второй кусок тогда имеет длину 63-х (м).
По условию задачи 0,4* равны 0,3 • (63 - х).
Составим уравнение:
0,4* = 0,3 • (63-х)
0,4х = 18,9-0,Зх
0,7х = 18,9
х = 18,9: 0,7
х = 27 (первый кусок)
63 - 27 — 36 (м) — второй кусок.
Ответ: 27 ми 36 м.
Задача 3. В растворе содержится 40% соли.
Если добавить 120 г соли, то в растворе будет
содержаться 70% соли. Сколько граммов соли
было в растворе первоначально?
Решение: Пусть общая масса раствора была
первоначально х (г). Тогда соли в нем было
0,4х (г). Если добавить 120 г соли, то масса
раствора будет х + 120, а соли в нем будет 0,4х + 120.
Так как по условию задачи соли стало
содержаться в растворе 70%, то:
0,4х+120 = 0,7 • (х + 120)
0,4x4-120 = 0,7x4-84
О,4х-0,7х = 84-120
-0,3х = -36
х = 120
0,4 • 120 = 48 (г)
Ответ: Первоначально в растворе было 48, г
соли.

Краткое изложение школьного курса математики
Математика. 5—6 классы
39
Задача 4. В клетке находятся фазаны и
кролики. Известно, что у них 35 голов и 94 ноги.
Узнайте число фазанов и число кроликов.
Решение: Представим, что все кролики
встали на задние лапки. Сколько ног в этот момент
будет стоять на земле?
1) 35 • 2 - 70.
Но в условии даны 94 ноги; передние лапы
кроликов не посчитаны. Сколько их?
2) 94 - 70 = 24.
3) 24 : 2 = 12 (кроликов).
4) 35 - 12 = 23 (фазана).
Ответ: 23 фазана, 12 кроликов.
ОТРЕЗОК, ПРЯМАЯ,
ЛУЧ, УГОЛ
Отрезок и прямая
Если к точкам А и В приложить линейку и
по ней провести от А к Б линию, тр получится
отрезок АВ. Тот же отрезок можно обозначить
ВА. Точки А и В называют концами отрезка
(рис. 8).
А В
в т
Рис, 8
Любые две точки можно соединить только
одним отрезком. Длину отрезка АВ также
называют расстоянием между точками А и В.
Если два отрезка CD и MN имеют
одинаковую длину, то отрезки равны (рис. 9).
Записывают CD = MN. Если длина отрезка АВ больше
длины отрезка КЕ, то это записывают так: АВ > КЕ,
илиКЕ <АВ.
Прямую обозначают заглавными
(прописными) буквами: прямая АВ, или одной маленькой
(строчной) буквой: прямая т. Прямая не имеет
длины.
Отрезки и прямые могут пересекаться, а
могут и не пересекаться (рис. 11).
В
х
Q
Рис. 11
Задача. На рисунке 12 можно увидеть три
отрезка: АВ, ВС, АС. Сколько отрезков можно
увидеть на рисунке 13?
В
В С
D Е
Рис. 12 Рис. 13
Ответ: 15 отрезков.
Луч и угол
Точка О разделила прямую АВ на две части
ОА и ОВ, каждая из которых называется лучом
(полупрямой). Точка О называется началом этих
лучей (рис. 14).
О
В
N
Рис. 9
Если начертить отрезок АВ и продолжить его
по линейке бесконечно в обе стороны, то
получим прямую (рис. 10). Через любые две точки
проходит единственная прямая.
Рис. 14
Луч кратко обозначается двумя заглавными
буквами, причем на первом месте пишется
буква, обозначающая начало луча.
Например, на рисунке 15 изображены лучи
CEhDK.
В
Рис. 10
Рис. 15

40
Краткое изложение школьного курса математики
Математика. 5—6 классы
Нужно хорошо запомнить, что у любого луча
есть начало, но нет конца. Так же как отрезки и
прямые, лучи могут пересекаться, а могут и не
пересекаться (рис. 16).
Лучи, на которые точка разбивает прямую,
называются дополнительными лучами.
Например, на рисунке 17 лучи ЕМ и EN —
дополнительные лучи.
М
Е
—•—
N
Рис. 17
Каждая точка прямой разбивает прямую на
два различных луча, две точки — на четыре
различных луча, а три точки — на шесть
различных лучей. Например, на рисунке 18 лучей с
началом в точке А — два, лучей с началом в точке
В — два, лучей с началом в точке С — два. Всего
шесть лучей. Если вам покажется, что их
больше, вы ошибаетесь. Ведь, например, луч АВ и
луч АС — это один и тот же луч.
В
Рис. 18
Запомните! Обозначение АВ может
относиться и к отрезку, и к прямой, и к лучу.
Обычно все можно понять, посмотрев на
рисунок.
Углом называют фигуру, образованную двумя
лучами, выходящими из одной точки. Лучи,
образующие угол, называют сторонами угла, а
точку, из которой они выходят, — вершиной угла.
На рисунке 19 изображен угол CDK или
кратко: ZCDK. Обратите внимание: в середине
обязательно пишется буква, обозначающая
вершину угла.
Если на рисунке нет больше углов с данной
вершиной, то угол можно обозначить только
этой вершиной: ZD, т. е. ZCDK = ZD.
Задача. Сколько углов вы видите на рисун-
ке^20?
В
Рис. 19
О^ С
Рис. 20
На рисунке изображены три угла с
вершиной О : ZAOC, ZAOB и ZBOC.
Два угла равны, если при наложении одного
угла на другой они совпадут. Например, на
рисунке 21 ZBOK = ZCED.
JBL
Рис. 21
Виды углов. Измерение углов
Два дополнительных друг другу луча
образуют развернутый угол. На рисунке 22 ZABC —
развернутый.
В
Рис. 22
Для измерения углов применяют
транспортир. Шкала транспортира располагается на
полуокружности и поделена на 180 равных частей.
Каждая часть называется градусом, т. е.
градус — это ygg доля развернутого угла.
Градусы обозначают знаком °. Величина
развернутого угла равна 180°.
Можно сказать, что ZAOB < ZCED, а
Z РКМ > Z CED (рис. 23).

Краткое изложение школьного курса математики
Математика. 5—6 классы
41
Z АОВ = 53°
Е D
Z CED - 90°
Рис. 23
К М
Z РКМ = 130°
Прямым углом называют половину
развернутого угла. Величина прямого угла равна 90°.
Углы, меньшие прямого, называют острыми
(ZAOB = 53° — острый угол). Величина любого
острого угла меньше 90°.
Углы, большие прямого угла, но меньшие
развернутого, называют тупыми углами (Z РКМ =
== 130° — тупой угол). Величина любого тупого
угла больше 90°, но меньше 180°.
Задача. Какой угол образуют минутная и
часовая стрелки: а) в 6 часов; б) в 3 часа; в) в 16
часов; г) в половину шестого; д) без пяти минут
двенадцать?
Ответ: а) 180°; б) 90°; в) 120°; г) 16°; д) 27,5°.
Биссектрисой угла называется луч,
выходящий из вершины угла и делящий угол на две
равные части.
ZAOB = 58°
ZAOC = Z ВОС = 29°
ОС — биссектриса Z АОВ (рис. 24).
Перпендикулярные
и параллельные прямые
Две прямые j образующие при пересечении
прямые углы, называют перпендикулярными.
На рисунке 25: АВ и CD —
перпендикулярные прямые. Пишут: АВ ± CD. Также можно
записать: CD 1 АВ.
Отрезки (или лучи), лежащие на
перпендикулярных прямых, называют
перпендикулярными отрезками (или лучами) (рис. 26).
М N
MN 1РК
К
Р
луч EF перпендикулярен
лучу ОТ
Рис. 26
Отрезок CD (рис. 27) называется
перпендикуляром, проведенным из точки В к прямой АВ.
Точка С называется основанием перпендикуляра.
С
Рис. 27
В
Через данную точку можно провести
единственный перпендикуляр к данной прямой.
Две прямые на плоскости называются
параллельными, если они не пересекаются.
Пишут: АВ || CD (прямая АВ параллельна
прямой CD на рис. 28).
Рис. 28
Отрезки (лучи), лежащие на параллельных
прямых, называют параллельными отрезками
(лучами).
На рисунке 29 отрезок АВ параллелен
отрезку МК; луч EF параллелен лучу СО.
К
М
Рис. 29
Рис. 24
Рис. 25
Если две прямые на плоскости
перпендикулярны третьей прямой, то они параллельны.
Если прямые п и I перпендикулярны прямой
/п, тогда прямые пи! — параллельны (рис. 30).
Краткая запись: если п ± т и I ± /п, то п \\ I.

42
Краткое изложение школьного курса математики
Математика. 5—6 классы
Через каждую точку плоскости, не
лежащую на данной прямой, можно провести
только одну прямую, параллельную данной прямой
(рис. 31).
т
Рис. 30
Рис. 31
Координатная плоскость
Проведем на плоскости две
перпендикулярные прямые х и у, которые пересекаются в
точке О. Выберем на каждой из прямых х и у
положительное направление и единичный отрезок;
точка О — начало отсчета. Эти прямые называют
системой координат на плоскости, а точку О —
началом координат. Плоскость, на которой
выбрана система координат, называют
координатной плоскостью. Прямую х называют осью
абсцисс; прямую у называют осью ординат.
хЭ •
-5 -4 -3 -2 -1
■ i i i i
О
С
1
- о
-4
-3
-2
о1!
-1
—2-
-3
-4
-5
2 3 4
4 |
D •
i
i
«
А
X
Рис. 32
Каждой точке плоскости соответствуют
координаты. Их записывают после точки в скобках,
на первом месте координату по оси х, на
втором — координату по оси у. Координата по
оси х называется абсциссой, а координата по
оси у — ординатой.
Например, у точки А на рисунке 32
координаты (4; -2), В (-3; 5), С (0; -4), D (2; 0).
У любой точки, лежащей на оси х (оси
абсцисс), вторая координата (ордината) равна
нулю, а у любой точки, лежащей на оси у (оси
ординат), первая координата (абсцисса) равна
нулю.
Задание. Начертить отрезки АВ и CD, если
А(-4; 2), Б(3; -5), С(-5; -7), Я(4; -1).
Найти: а) координаты точки Е —
пересечения отрезков АВ и CD;
б) координаты точки К — пересечения
отрезка АВ с осью х;
в) координаты точки Р — пересечения
отрезка АВ с осью у.
Рис. 33
Ответ: Е (1; -3), К (-2; 0), Р(0; -2).

Алгебра. 7—11 классы
Этот раздел предназначен для быстрого и
эффективного повторения начал алгебры
школьного курса математики.
Теоретический материал разбит на главы,
соответствующие основным темам.
СТЕПЕНИ И КОРНИ
Степень с натуральным показателем.
Свойства степеней.
Степень с целым показателем
1. Степень с натуральным показателем
Степенью действительного числа а с
натуральным показателем п называется произведение
п сомножителей, каждый из которых равен а.
п
а = а*атат... • а
(а ) = а .
4. При возведении в степень произведения
двух чисел, каждое число возводят в эту
степень, а результаты перемножают:
(а •«"-а11-б".
5. Если в степень возводится частное двух
чисел, то в эту степень возводят числитель и
знаменатель, а результаты делят друг на друга.
(а\п = а^
п раз
Число а называется основанием степени,
число п — показателем степени.
Пример 1. 0,23 = 0,2 • 0,2 • 0,2 = 0,008.
Пр„»ер2.(-1)в-(-1)-Н)-(-1)-Н)х
Х Г§] Ч~з] = 729'
Пример З.Ь = Ъ • Ъ • b • Ъ.
2. Свойства степеней
1. При умножении степеней с одинаковыми
основаниями основание оставляют прежним, а
показатели степеней складывают:
т п т + п
а *а = а
2. При делении степеней с одинаковыми
основаниями основание оставляют прежним, а из
показателя степени делимого вычитают
показатель степени делителя:
т п т~п
а : а = а
3. При возведении степени в степень
основание степени оставляют прежним, а показатели
перемножают:
6. Если а > Ь и Ъ > 0, то ап > Ьп.
Пример 1. 0,54 = 0,5-0,5* 0,5* 0,5 = 0,0625
(по определению).
Пример 2. (-5) *(-5) =(-5) (свойство 1).
/ 1*\8 ( 1\14 ( 1\22
Пример 3.( lgl 413) =1*з] (свойство 1).
Пример 4. (|)10 : (J)3 = (j)10 ' = (j)7
(свойство 2).
Пример 5.0,46 : 0,44 = 0,42 = 0,16 (свойство 2).
Пример 6. ((-2)5)2 = (-2)5'2 = (-2)10 = 1024
(свойство 3).
1\4
Пример 7. (о,2-|) =0,24-(д) =
= 0,0016 • ^ = зТШоО (свойство 4>-
Пример 8. [-5•„-] =(-5) •(„-) (свойство4).
Пример 9. (-fj = -^- = ~i = 2401 <свой-
ство 5).
Пример 10. Что больше: 2 или 3 ?
Используя свойства степени, преобразуем
данные выражения:
о300 = 23 • 100 = /о3\100 — Q100

44
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
«200 = «2*100 _ .«2Л00 = Q100
Показатели степеней равны, а основания
связаны неравенством 8 < 9, поэтому, согласно
и о300 ^ о200
свойству о, 2 < 3
3. Степень с целым показателем
Степень действительного числа с целым
отрицательным показателем определяется
следующим образом:
ап = — , где а * 0 и п > 0.
а
Пример 1. (-8)"3 = -^j = -qY2 •
6Г4 Г5\* 625
ТТ^леер 2. (l|)"4 = (I)"4 = (|)4 =
1296*
Любое отличное от нуля число в нулевой
степени равно единице.
а = 1, гдеа*0.
Нуль в нулевой степени не определен, т. е.
выражение 0 не имеет смысла.
Для степеней с целыми показателями
выполняются те же свойства, что и для степеней с
натуральными показателями.
Арифметический квадратный
корень и его свойства
1. Арифметический квадратный корень
Арифметическим квадратным корнем из
неотрицательного числа а называется такое
неотрицательное число Ь9 квадрат которого равен
числу а.
Обозначение: Ja = b. Такая запись означает,
что Ь = аиЬ>0.
Знак 7~ называется знаком радикала.
Пример 1. Vl6 = 4, так как 4 = 16 и 4 > 0.
Пример 2. 75781 = 0,9, так как 0,92 = 0,81 и
0,9 > 0.
Основные тождества, следующие из
определения квадратного корня:
1. л/а = \а\
2. (л/а) =а.
или
а = а при а > 0,
а = -а при а < 0.
2. Свойства арифметического
квадратного корня
1. Корень из произведения двух
неотрицательных чисел равен произведению корней из
этих чисел:
J а • Ъ = Ja • Jb, где а > 0 и Ь > 0.
2. Корень из частного двух чисел равен
частному корней из этих чисел:
J=|,rflea>0,&>0.
Jb
3. Внесение множителя под знак квадратного
корня:
а) Ъ • Та =
= л/ь • а при & :
>0;
б) Ъ • л/а = -*Jb • а при Ъ < 0.
4. Вынесение множителя из-под знака корня:
а) 4ь • а
б) л/ь2 • а
В общем:
Пример
- 8^2.
Пример ,
27 *
Пример
Пример
= & • л/а при & > 0;
= -& • л/а при & < 0.
виде:
л/гЛх =|&1*
1. VI28 =
2 ГбО" _ л/50
* V729 7729
3. лДб*3 =7?
4.\ЛГа=Л
»л/а.
764^2
л/25^2
2 2
• X • X :
• 54а =
= 764
• 7S-
725'72
27
-4-Н-
Тба.
Jx.
Пример 5. Пусть х < 2, тогда V(* - 2) • 3 =
= |ж-2|-73 =(2-ж)-73.
Пример 6. Пусть а > 1, тогда
(1
х)-л/(а- I)3 =-л/(а - D5.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
45
Пример 7. Упростить:
4Я -2V104 +3^ = ]Ш* -2Л04 +
+ Je*y = Л04 -2л/104 + 726 =
= л/26 -л/104 =л/26 -л/4-26 =726 -2726 =
= -726.
Пример 8*. Избавиться от
иррациональности в знаменателе (т. е. от знаков корней в
знаменателе):
10 _
75-Л0 + л/20 + 740-780~
10 10
75(1 -72 + 2 + 272-4) 75(72 - 1)
= 1075(72 + 1) = 1075(72 + 1) =
(75)2(72 - 1)(72 + 1) 5((72)2 - I2)
= 275(72 + 1).
В последнем примере числитель и
знаменатель дроби домножены на одно и то же
выражение д/б (72 +1), при этом дробное выражение не
изменилось. Далее использована формула со-
2 2
кращенного умножения (а + b)(a - b) = a -ft и
тождество (2).
Если выражение а - ft умножается на
выражение а + ft, то такое преобразование в алгебре
называется домножением на сопряженное.
Арифметический корень п-н степени.
Действия с радикалами
1. Определение арифметического корня
/1-й степени
Арифметическим корнем п-й степени из
неотрицательного числа а называется такое
неотрицательное число ft, которое при возведении в
степень п дает число а.
Число п называется показателем степени
корня, число а — подкоренным выражением.
Обозначение: nJa = ft, что означает по
определению Ъп = а и ft > 0.
Пример 1. 378 = 2, так как 23 = 8 и 2 > 0.
Пример 2. 67729 = 3, так как З6 = 729 и 3 > 0.
Напоминаем, что только квадратный корень
записывается без показателя степени корня.
2. Корень нечетной степени
из отрицательного числа
Корнем нечетной степени из
отрицательного числа а называется такое отрицательное
число ft, которое, будучи возведено в эту нечетную
степень, равно числу а. Как правило, корень
нечетной степени из отрицательного числа не
называют арифметическим.
Во многих современных школьных курсах
алгебры корень нечетной степени из
отрицательных чисел не рассматривается. Это
приводит к путанице, особенно при решении
некоторых задач. Выход здесь такой: при решении
конкретной задачи каждый раз оговаривать
отдельно — какое определение вы используете.
Пример 1. 37-27 = -3, поскольку (-3)3 = -27
и -3 < 0.
Пример 2. 5/-—
и-2<0.
V"32 "~ 2 • ТаК КаК ( 2 J " 32
3. Свойства арифметического корня
/1-й степени
1. Корень степени п из корня степени k:
п& = пкЛ.
Пример 1. V7729 = 67729 = 3.
Пример 2. 5л/37-32 768 = 157-32 768 = -2.
2. Корень п-й степени из числа а,
возведенного в натуральную степень k:
Пример 3. лб1 = (,/9)3 = З3 = 27.
Пример 4. 5|^j)3 = [ьЩ = {-If = -|.
3. Корень п-й степени из произведения двух
чисел:
l/ab = nJ~a • nJb.
Пример 5. V16 • 81 = 4Лб • V81 =2-3 = 6.

46
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пример 6. V625 « !/125 • 5 - У125 • У5 -
- 537б.
4. Корень л-й степени из частного двух чисел:
216 37216 6 ,1
Пример 7. з/— =
125 У125 5 S
Пример 8
• Т243
57^32
V243
5. Вынесение множителя из-под знака корня:
nJ^~a=\b\-nJ~a.
При & > О это тождество имеет вид
При & < 0 и а > 0 тождество примет вид
*а/ь" • а = -&-"7а.
Пример 9. V250 = V?" 2 = 5372 .
Пример 10. 5л/(-2)8 • 3 = -2 57§.
6. Внесение множителя под знак корня:
1. &• "Та = "л/&"• а при6 > 0.
2.b-nJa = -"7&"-а при Ь < 0.
Пример 11. 2 V5 = Зл/23 • 5 - V40 .
Пример 12. -572 = -л/5^- 2 = -Тбб.
ОСНОВНЫЕ ТОЖДЕСТВА
1. ("Та)" =а.
•Л"-|а|.
Пример 13*. Избавиться от кррациональнос-
1
ти в знаменателе дроои
Решение.
V5 - V2 (V5 - V5)(VS + V2)
(V5)2 - (V2)2 ^ - Я '
Умножив числитель и знаменатель дро
сначала на (1/5 + 1/2), а потом на(Jb + J2)
воспользовавшись формулой сокращенного у
2 2
ножения (а- Ь)'(а + Ь) - а - Ь , а также при]
денными выше тождествами, получим:
(Уб + 4/2)(75 4 72) = (VB + У2)(Л + Л)
(Л - Л)(Л + 72) (ТЕ)2 - (72)2
_ (47Е + 472)(75 4- 72)
3
Пример 14*. Преобразовать выражение
Уб72 - 7 • 7з + 272.
Решение. 37б72 - 7 • 7з + 272 =
= 37б72 - 7 • л/l + 272 + (72)2 =
= 37б72 - 7 • 7(1 + 72)2 =
= (1 + 72)37572 - 7 =37f572 - 7)(1 + 72)'
= 37(572 - 7)(572 + 7) = 3л/(572)2 - 72 =
= 3./Ь~0 - 49 =1.
3 2
Здесь мы использовали формулу а + За
+ За&2 + Ь3 - (а 4- Ь)3.
Пример 15*. Доказать тождество
V8 - V§7 • V8 + 737 =■• 3.
Решение. Имеем:
37в"- V§7 • V8 + л/37 =
= V(8 - 737)(8 4- л/37) = Уб4 - 37 = \/Z7
Степень с рациональным показате
Степенью положительного числа а с р
ональным показателем г = — (т — целое чи
п — натуральное число) называется корень
пени
л из а , т. е, а = а = уа , где а > 0.
973 = \[оП2 =/3/97^2 = Q2 = «
Пример 1. 21 = V27* =(ty27) =3

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
47
Пример 2. 8~3 = V8"2 = 3 Л = \к = I •
/8
64
Свойства степеней с целыми показателями
верны и для степеней с рациональными
показателями:
\.а
г, + г0
Г1 Г2 Г1 ~ Г2
2. а * : а 2 = а 1 2
Г, '2
1Г2
3. (а !) = а
4. (аЬ)г = аг*Ьг.
4 3 1
5 5 5
= —— = — (свойства 5, 3, 2 и 1).
до
до
Рациональные
и иррациональные числа.
Понятие действительного числа
1. Рациональные числа
Рациональными числами называются числа
р
вида - , гдер — целое, q — натуральное.
Целые и дробные числа являются
рациональными.
Примеры.
з
1) а • а
1 i
г = а (свойство 1).
2
3
1 + 1 1 + -
2) а Ъ •а/'1' = а Ь = а Ь (свойст-
Пример 1.0= г
-8.1—8^"
-31
10
во 1).
5 1
оч 7 5
3) а : а = а
5 __ 1
7 5
18
35
= а (свойство 2).
1 1
4) а Ь
(свойство 2).
з
1
1 1 1-(Л)
8,з з 8 .2 i з; Л,
а о = а о = а о
1 5
24 ,6
/ i.\5 J..? JL
5)
15
а
v )
15 5 25 , оч
= а = а (свойство 3).
( 1
6)
3 1^
а - а
\
= а
^
1 1
о 3 2 , 2
- 2а а + а
ь2
= а -2а + а (свойства 3 и 1).
1 1\5
5 ,8
7) а • Ь
ва 4 и 3).
з
I *
8)
/' Ьз
а
v J
hi A J.
15, 12 ,
= а Ь (своист-
з
i к6;
з
з
а
/ ±\5
аЬ
4 3
3*5
а
3 13
5^6*5
а Ь
з \_
5,10
а 6
Сумма, разность, произведение, частное
двух рациональных чисел, а также результат
возведения в степень рационального числа есть
число рациональное.
Г IV f 5(3 1(1°V»
Пример 2.(2,5-1) ■' {2 + Го ~3 ) =
2. Иррациональные числа
Наряду с рациональными существуют числа,
которые нельзя представить в виде дроби - .
Например, число я, равное отношению длины
окружности к ее диаметру, к « 3,1415...
Длина диагонали квадрата со стороной,
равной 1, является иррациональным числом J2 .
Иррациональными являются также числа
7з , Jb , 7б и множество других. (Однако
число л/i не является
иррациональным, так как 7i = 2 =
т — рациональное число.)
1
Сумма, разность,
произведение, частное рационального
и иррационального чисел есть
число иррациональное.

48
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Г" г 1 V9
Например, числа 1+ J2, 2*Jb, --=; -5
иррациональные.
Сумма, разность, произведение, частное
двух иррациональных чисел, а также результат
возведения иррационального числа в степень
может быть как иррациональным, так и
рациональным числом.
Примеры. 1) (1 + 72) + (1 - 72) = 2;
2) (2- 73)2 = 4-473 +9 = 13-473.
Решение. В периоде данного числа — два зна-
2
ка. Рассмотрим разность числа 10 г и данного:
_ ЮОг = 37,373737...
2= 0,373737...
37
992 = 37,000000... = 37, откуда г = ^ .
Иррациональные числа можно представить
в виде бесконечных непериодических дробей:
Л =1,4142135...
тс = 3,1415926536...
и т. д.
3. Действительные числа.
Обращение рациональных чисел
в бесконечные десятичные дроби
Рациональные и иррациональные числа
составляют множество действительных чисел.
5
Пример 1. g — рациональное число.
Разделим 5 на 8 «уголком»: 5018
Итак « = 0,625. Мы получили
конечную десятичную дробь.
50
48
_20
16
0,625
40
"40
0
Пример 2. Представить ту в виде
десятичной дроби.
Решение. Разделим 7 на 11: 70111
Мы получили бесконечную
десятичную дробь.
Повторяющаяся комбинация цифр называется
ее периодом. Обозначение (63),
т. е. ~ = 0,(63).
6610,636.
_40
33
70
Любое рациональное число можно
представить в виде конечной или бесконечной
периодической десятичной дроби.
Например,
-3 = -3,(0); g=0,(6); -fg =-1,2(7).
Верно и обратное: любая бесконечная
периодическая десятичная дробь является записью
рационального числа.
Пример 3. Представить число г = 0,(37) в
виде рационального числа.
РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Общие сведения
о рациональных уравнениях
1. Равенства и уравнения. Корни уравнения
Два выражения, числовые или буквенные,
соединенные знаком «=», образуют числовое
или буквенное равенство.
Любое верное числовое равенство, а также
любое буквенное равенство, справедливое при
всех числовых значениях входящих в него букв,
называется тождеством.
Пример 1. Числовое тождество:
5-7-6= 20 + 9.
Пример 2. Буквенное тождество:
(а + Ъ)3 - а3 + За2Ъ + ЗаЬ2 + Ь3.
Равенство, содержащее неизвестные
буквенные величины и не являющееся тождеством,
называется уравнением. Уравнение называется
буквенным, если некоторые известные
величины, входящие в него, выражены буквами, в
противном случае уравнение называется числовым.
Неизвестные величины принято обозначать
последними буквами латинского алфавита: х, у,
z, t, и, и, w. По числу неизвестных уравнения
разделяются на уравнения с одним, двумя,
тремя и т. д. неизвестными.
Решением уравнения называется такой
буквенный или числовой набор неизвестных,
который обращает его в тождество (соответственно,
числовое или буквенное). Часто решение
уравнения называют также его корнем.
Пример 3. Решением числового уравнения
3 2
Зх + 2х - 4л: - 1 = 0 является число 1.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
49
Решением буквенного уравнения х - ах +
2
Л-ах-а = 0 является выражение а.
Решить уравнение — значит найти* все его
решения или доказать, что их нет.
Уравнение вида апхп + ап _ гхп ~ + ... + агх +
+ а0 = О, где ап * 0 называется целым
рациональным уравнением степени п с одним
неизвестным. Далее речь идет именно о таких
уравнениях. Числа ал, ап_г ... а0 называются
коэффициентами этого уравнения, а коэффициент а0 часто
называют свободным членом уравнения.
Утверждение 1. Любое уравнение степени п
с одним неизвестным имеет не более п корней.
Утверждение 2. Любое уравнение нечетной
степени с одним неизвестным имеет по крайней
мере один действительный корень.
2. Равносильные уравнения
Два уравнения Рг(х) = Qi(x) и Р2(х) = Q2(x)
называются равносильными, если совпадают
множества их решений.
Обозначение: Рг(х) = Qx(x) <=» Р2(х) = Q2(x).
2 2
Пример 1. Уравнения х +2*-3 = 0ил: +
+ х - 3 - х — равносильны, поскольку имеют
одинаковые корни х = 1 и х = -3.
2 2
Пример 2. Уравнение х + 1 = 0 <=> х +3 = 0,
так как оба они не имеют решений на множестве
действительных чисел.
Равносильные уравнения иногда называют
эквивалентными.
Если уравнения Рг(х) = Qx(x) и Р2(х) = Q2(x)
имеют одинаковые решения на некотором
числовом множестве X, то они называются
равносильными на множестве X.
2 2
Пример 3. Уравнения х -5# + 6 = 0ил: +
+ 2л: —15 = 0 равносильны на числовом
множестве х > 2, поскольку имеют на этом множестве
один корень х = 3. На множестве всех
действительных чисел эти уравнения неравносильны,
так как корнями первого уравнения являются
числа 2 и 3, а второго — числа 3 и -5.
1) перенос любого члена уравнения из одной
части уравнения в другую с противоположным
знаком;
2) умножение и деление обеих частей
уравнения на одно и то же, отличное от нуля, число;
3) умножение и деление уравнения на одно и
то же алгебраическое выражение, определенное
при любых значениях входящих в него букв,
которое не обращается в нуль.
Равносильных (как и неравносильных)
преобразований существует великое множество.
Наиболее часто встречающиеся будут
рассмотрены в следующих параграфах.
2
Пример 1. Зах + Ьх = сх - d <=>
<=» Зах2 + (Ъ - с)х + d = 0.
Пример 2.4х2 + 2х - 2 = 0 <=» 2х2 + х - 1 = 0 <=>
Пример 3. х3 + 2х - х2 - 2 = Зх2 + 6 <=>
<=> х\х - 1) + 2(х - 1) - 3(х2 + 2) <=>
<=» (х2 + 2)(х - 1) - 3(х2 + 2) <=> х - 1 = 3.
В последнем примере обе части уравнения,
разложенного на множители, разделены на вы-
ражение х +2, которое определено для любого
действительного числа и ни при каком значении
х не обращается в нуль (более того, х + 2 > 2
для любого числового значения х).
Решение линейных, квадратных
и биквадратных уравнений.
Теорема Виета.
Разложение квадратного трехчлена
на множители
1. Линейное уравнение
Линейным уравнением с одним неизвестным
называется уравнение вида ах + Ь = с, где а * 0.
Это уравнение всегда имеет единственное реше-
с - Ь
ние х = .
Пример 1. Зх + 2 = 5 <=> х = 1.
3. Равносильные преобразования
К равносильным уравнениям приводят
равносильные преобразования. Например, такие:
Пример 2. 2Ъх +1 = 3<=>x=t;.
Пример 3. Засх - а = 2с <=> х — —^ ,

50
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
2 Ь
Пример 4. 5а х + 6 = 0 <=> х = ^
5а
2. Квадратное уравнение
Квадратным уравнением с одним
неизвестным называется уравнение вида
ах + Ьлг 4- с = 0, где а * 0.
Дискриминантом квадратного уравнения
называется число
D = b2- 4ас.
Справедливы следующие утверждения:
1. Если D < О, то уравнение решений не имеет.
2. Если D = 0, то уравнение имеет единствен-
Ь
ное решение х = -=- .
3. Если D > 0, то уравнение имеет два
решения:
хл =
-Ъ - JD
-Ъ + Jd
"1 2сГ^ " ~2 2а
Обе эти формулы часто записывают в виде
-Ь ± л/ь - 4ас
*1 «> = —on— или X* о =
4,2
2а
4,2
2а
Пример 1.x - Ах + 3 = 0.
Решение. Имеем а = 1, Ь = -4, с = 3.
Я = Ь2 - 4ас = (-4)2 -4-1-3 = 4.
*i =
-(-4) - 2
= 1,
Хо =
_ -(-4) + 2
= 3.
Пример 2. 2х + х + 3 = 0.
Решение. Имеем: а = 2, Ь = 1,с = 3.
D = &2 - 4ас = 1-4-2-3 = -23.
Так как D = -23 < 0, то данное уравнение
решений не имеет.
2
Пример 3. 4л: + 4л: + 1 = 0.
Решение. Имеем а = 4, & = 4, с = 1.
D = &2 - 4ас = 42 - 4 • 4 • 1 = 0, так как D = 0,
то уравнение имеет единственное решение
* 2а 8 2'
При решении примера 3 можно не
использовать формулу корней квадратного уравнения,
2 2
заметив, что 4л: + 4л: + 1= (2х + 1) , а квадрат
числа (выражения) может быть равен нулю
только в случае, когда само это число
(выражение) равно нулю.
3. Неполное квадратное уравнение
Неполным квадратным уравнением
называется квадратное уравнение, в котором хотя бы
один из коэффициентов Ъ или с равен нулю.
При с = 0, уравнение принимает вид:
2
ах + Ъх = 0, или х(ах + Ь) = 0,
т. е. либо х = 0, либо ал: 4- Ь = 0, откуда
л: = 0 и л: = -- .
a
2
При b = 0 уравнение имеет вид: ах + с = 0, то
2 с ,, с л
есть л: = -- . Если выражение -- < 0, то
уравнение решений не имеет, если с = 0, то решение
единственное: л: = 0; если же -- > 0, то решений
два:
<1=Я и *2—Л
4. Приведенное квадратное уравнение.
Теорема Виета
Приведенным квадратным уравнением на-
2
зывается уравнение вида х + рл: + g = 0, т. е.
квадратное уравнение, в котором первый
коэффициент равен единице.
Любое квадратное уравнение можно сделать
приведенным. Для этого достаточно каждый
коэффициент данного уравнения разделить на
первый коэффициент, т. е. на а.
ТЕОРЕМА ВИЕТА
Если приведенное квадратное уравнение
имеет действительные корни, то их сумма
равна второму коэффициенту, взятому со
знаком минус, т. е. -р, а их произведение —
свободному члену q.
ТЕОРЕМА, ОБРАТНАЯ ТЕОРЕМЕ ВИЕТА
Если сумма двух чисел хг и х2 равна числу
-р, а их произведение равно числу q, то они
являются корнями приведенного
квадратного уравнения
х2 + рх + q = 0.
* Теорема Виета в расширенном виде справедлива
для уравнений более высоких степеней, чем вторая.
В множестве комплексных чисел часть формулировки
теоремы — «если у уравнения есть действительные
корни» — является лишней.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
51
Пример 1. Определить знаки корней
уравнения х - 136л: + 29 = О, не решая его.
Решение. Имеем: D = (-136)2 - 4 • 1 • 29 > О,
следовательно, уравнение имеет
действительные корни. По теореме Виета произведение
корней данного уравнения равно 29, то есть
положительно. Значит, корни имеют одинаковые
знаки — либо оба положительные, либо оба
отрицательные. Но по этой же теореме их сумма
равна -(-136) = 136, т. е. тоже положительна, а
сумма отрицательных чисел не может быть
положительной. Значит, оба корня положительны.
Пример 2. Используя теорему, обратную
теореме Виета, найти корни уравнения
х2 + Зх + 2 = 0.
Решение. Это уравнение имеет целые корни,
причем ххх2 = 2, а хг + х2 = -3. Корни легко
угадать: это хг = - 1 и х2 = -2. Действительно:
(-1) • (-2) = 2 и (-1) + (-2) = -3. Значит, числа
-1 и -2 являются корнями данного уравнения.
Пример 3. Найти значение выражения
2 , 2
хг + х2 , где хг и х2 — корни уравнения
Зх2- 39* -17 = 0.
Решение. Запишем данное уравнение в приве-
2 1Q 17 п
денном виде: х - 13л: - -=- = О.
Имеем: D = (-13)2 - 4 • 1 • f-y] > 0,
следовательно, применима теорема Виета.
2 2
Преобразуем выражение хг + х2.
2,2_20 ,2_о -
Х-* т* Хп — X* i CtX-\X2 "Г Х2 &ХлХ2 —
= (*i + х2)2 - 2хгх2.
Это очень важное тождественное
преобразование называется выделением полного
квадрата (к исходному выражению добавили и вычли
одну и ту же величину 2ххх2).
Но по теореме Виета хх + х2 = -(-13),
2 2
следовательно, (хг + х2) = 13 = 169,
17
а 2хгх2 = -2 • -=-, т. е. окончательно получаем
Пример 4*. Решить уравнение
1997х2 + 1937* - 60 = 0.
Решение. Решать данное уравнение,
используя общие формулы, достаточно трудно.
Заметим, однако, что число -1 является корнем
(1997 - 1937 - 60 = 0), следовательно, по
теореме Виета, найти второй корень легко:
= 60
*2 1997
(не забывайте, что уравнение должно быть
приведенным, т. е. его коэффициенты нужно
разделить на 1997).
Замечание. Если сумма коэффициентов
квадратного уравнения равна нулю, то есть а + Ь + с =
= 0, тр х = 1 является его корнем, а если а~-Ь + с =
= 0, то этим корнем является число х = -1, в
обоих случаях второй корень легко находится по
теореме Виета.
4
Пример 5*. Найти значение выражения хх +
+ х2 , где хх и х2 — корни уравнения
х -17л:- 31=0.
Решение. Используя тот же прием, что и в
примере 3, т. е. выделяя полный квадрат,
преобразуем данное выражение (не забудьте
проверить предварительно, что D > 0!).
4 4_ 492 2 *_92 2 _
Хл Т* Хп X л т CiX-t Хп ~Г Хп СкХл Хп
_, 2 2\2_9 2 2_
= (х\ + 2ххх2 + х\- 2хгх2)2 - 2(хгх2)2 =
= ((хг + х2)2 - 2xxx2f - 2(xlx2)2 =
= (172 - 2 • (-31))2 - 2 • (-31)2 =
= 3512-2-961 = 121 279.
5. Биквадратное уравнение
Уравнение вида ах + Ъх + с = 0 называется
биквадратным.
Такое уравнение решается методом замены
переменной. Обозначим х = t, тогда х = (х ) =
2 2
= t . Заметим, что / > 0, так как t = х . Исходное
уравнение примет вид
at2 + bt + с = 0,
т. е. является обыкновенным квадратным
уравнением, которсъ решается по приведенной выше
схеме.

52
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пусть tx и t2 — корни полученного
квадратного уравнения. Если ^ > 0 и f2 > 0 исходное
биквадратное уравнение имеет четыре корня:
Если одно из чисел £х или t2 отрицательно, а
другое неотрицательно, то имеем два корня,
либо один (х = 0).
Введение нового переменного — наиболее
распространенный метод решения самых
разных уравнений.
Пример 1. Решить уравнение
х4 -13л:2 + 36 = 0.
Решение. Обозначим х = t и заметим, что
t > 0(*).
Тогда исходное уравнение примет вид:
t2 - 13* + 36 = 0.
Имеем: а = 1, Ъ = -13, с = 36; D = Ъ2 - 4ас =
= (-13)2 - 4 • 1 • 36 = 25. Так как D > 0, то
полученное квадратное уравнение имеет два корня
^ = 9и*2 = 4.
Оба эти корня удовлетворяют условию (*),
следовательно, уравнение имеет четыре
действительных решения.
2 2
х = 4, откуда *! = 2, л:2 = -2, и х = 9, откуда
*з в 3> *4 = —3.
Пример 2. (х + 7)4 - (* + 7)2 - 2 = 0.
Решение. Обозначим (х + 7)2 = *, заметим, что
t > 0 (**). Исходное уравнение принимает вид
t - * - 2 = 0. Решая его как обычное квадратное
уравнение, получим следующие корни: tx = -1,
*2 = 2. Первый из корней не удовлетворяет усло-
вию (**), следовательно, (х + 7) = 2, откуда # =
= -7 + л/2 , либо х = -7 - */2 .
6. Разложение квадратного трехчлена
на множители
Из теоремы Виета следует очень важное
утверждение: теорема о разложении квадратного
трехчлена на множители.
ТЕОРЕМА
Если квадратное уравнение ах + Ьх + с = 0
имеет действительные корни xt и х2, то
квадратный трехчлен ах + Ьх + с
раскладывается на множители следующим образом:
> 2
аре +Ъх + с = а(* - JCjHx - *2)«
Пример 1. Разложить на множители квад-
2
ратный трехчлен р(х) = 2х + Ьх - 3.
Решение. Вычислим дискриминант квадрат-
2
ного уравнения 2х + 5л: - 3 = 0 и решим его.
Корни хг = -3 и х2 = о •
Следовательно, р(х) — 2(л: + 3)( х - = )•
Зя — 5л: — 2
Пример 2. Сократить дробь: —= .
х + 2х - 8
Решение. Разложим на множители
трехчлены, стоящие в числителе и в знаменателе:
Зх2 - Ьх - 2 - в(х + g )(* ~ 2),
*2 + 2л: - 8 = (х + 4) (я - 2).
Следовательно, дробь примет вид
з(* + 1){х"2)
(х + 4)(х - 2) '
Сокращая на один и тот же сомножитель (л: - 2)
в числителе и в знаменателе, окончательно
получим
3(* + 1)*-2) 8* + 1
(л: + 4)(л: - 2) х + 4 "
Заметим, что сокращение можно производить
только в случае, когда х - 2 * 0. Если же л: - 2 =
= 0, то исходная дробь не имеет смысла и
сократить числитель и знаменатель на х - 2 нельзя.
Специальные типы рациональных
уравнений и методы их решения
1. Метод введения новой переменной
Пример 1. Решить уравнение:
(х2 - 7х + 13)2 - (л: - 3)(л: - 4) = 1.
Решение. Перемножив две последние скобки
данного уравнения, заметим, что полученный
результат (л: - 7х + 12) лишь на 1 отличается от
выражения в первой скобке.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
53
Введем новую переменную t = х - 7х + 12;
тогда х2 - 7х + 13 = t + 1. Имеем:
(t + I)2 - t = 1 <=» t2 + t = 0 <=» t(t + 1) = О,
откуда f = 0 или t = -1. Приходим к
совокупности двух уравнений. Напомним, что
совокупность обозначается квадратными скобками: они
означают, что выполняется одно из уравнений
(условий), стоящих внутри этих скобок.
Итак,
2
[V-7*+12 = 0, ^[^ = 3,
L*2-7* + 12 = -l; L* = 4.
Ответ: 3; 4.
Пример 2. Решить уравнение
*(х+1)(*-1)(* + 2) = 24.
Решение. Рассмотрев отдельно произведения
*(* + 1) и (х - 1)(х + 2), получим
х(х + 1) = х2 + х, (х- 1)(х + 2) - х2 + х- 2.
Заметим, что в этих выражениях есть
одинаковая сумма х + х. Выбрав ее в качестве нового
неизвестного, получаем достаточно простое
квадратное уравнение.
Еще удобнее выбрать следующее неизвест-
2
ное: t = х + х - 1, тогда
х2 + х = * + 1, x2 + x-2 = f- 1.
Исходное уравнение принимает вид
(* + 1)(* - 1) - 24,
Г = 25
откуда получаем совокупность
л: +*- 1 = 5,
У + х-1=-5;
L* = -5,
ость
Г* = 2,
|_* = -3.
2. Симметрическое уравнение
Рассмотрим преобразование, на которое
будем в дальнейшем неоднократно ссылаться.
/ 1\2 2 11
Пример 1. I * + ; 1 =*+2л:*-+-2 =
= х2 + 2 + ^ .
откуда
'+?-(*+$-*■
(*)
или
/ 1\2 2 1
Пример 2.\х — I = х — 2 Н—g ,
Пример 3. х + ~~i= [х + 2\ ""2 =
(**Ч
(***\
Симметрическим уравнением третьей
степени называется уравнение вида
3 2
ах +Ъх +&х + а = 0, а*0.
Заметим, что
ах3 + &л: + Ъх + а = (х + \)(ах + (& - а)л: + а),
следовательно, решение этого уравнения
равносильно совокупности
Гх + 1 = 0,
L ах + (Ь - а)л: + а = 0.
Пример 4. Решить уравнение
х3 + 6х2 + 6* + 1 = 0.
Решение. Имеем:
з 2 Гл: +1 = 0,
я +6x+6x+l = 0 <=> 2 <=>
L* +5*+1 =0;
*--1,
-5 + л/21
л: =
х =
-5 - 721
(1)
(2)
Симметрическим уравнением четвертой
степени называется любое из следующих двух
уравнений:
ах +Ьх -Ьсх + Ъх + а = 0,
ах* + Ъх + сх2-Ьл: + а = 0,
где а * 0.
Число лг = 0 не является корнем этих
уравнений. Разделим каждое из них на одну и ту же
величину х . После приведения подобных членов
получим:
а(х>+±)+ь(х-1)+с = 0.

54
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Для решения первого их этих уравнений вве-
, 1
дем новую переменную у = х + - , а для решения
второго — переменную г = х
1

Воспользовавшись соотношениями (*) и (**), имеем
а{у2-2) + Ъу + с = 0 и a(z2 + 2) + 6z + c = 0,
т. е. получены обыкновенные квадратные
уравнения.
Пример 5. Решить уравнение
3x4-8x3- |х2-8л: + 3 = 0.
Решение. Это симметрическое уравнение чет-
2
вертой степени. Разделив все его члены нал: и
сгруппировав первый член с последним, второй
с предпоследним, получим уравнение
•е* ?)-(*♦ §)-!-•■
Обозначим t = х + - и воспользуемся
преобразованием (*):
3(*2 - 2) - 8* - | - 0 <=> 9t2 - 24* - 20 = 0.
Корни этого уравнения t = -g- и t = - = .
Следовательно, имеем совокупность двух уравнений
х+ - = -5-;
х 3
х = 3,
*-8"
Первое уравнение совокупности решений не
имеет.
3. Некоторые специальные типы
рациональных уравнений
I. Уравнения вида
(х - а){х - Ь)(х - с)(х - d) = А.
Если a 4- & = с + d, то это уравнение сводится
к квадратному. Для этого нужно перемножить
первую пару скобок, затем вторую пару и ввести
2
новую переменную t = х - (а + &)х.
И. Уравнения вида
(ах2 + Ьх + с)(алг2 + d.r + с) = Ах2.
2
Разделив обе части этого уравнения на х ,
получим
(ах + Ь+ ^) [ах + d + £) = А.
Вводя новую переменную £ = ах + - , сведем
уравнение к квадратному.
4 4
III. Уравнения вида (х- а) + (х - Ь) = А.
Эти уравнения сводятся к биквадратным
заменой t = х о— . Выполнив указанную
замену и раскрыв скобки, т. е. возведя каждую
скобку в четвертую степень, видим, что перед
членами с нечетными степенями стоят одинаковые по
величине, но противоположные по знаку
коэффициенты.
Последний пример есть элемент более общего
метода решений уравнений — метода
симметризации.
ФУНКЦИИ
Определение функции
1. Постоянные и переменные величины
Примеры постоянных величин.
1. Количество граммов в килограмме есть
величина постоянная, равная 1000.
2. Количество миллиметров в сантиметре
есть величина постоянная, равная 10.
3. Сумма внутренних углов треугольника
есть величина постоянная, равная 180°, для
любого треугольника.
4. Отношение длины окружности к ее
диаметру есть величина постоянная для любой
окружности, равная -3,14. (Гипотезу о
постоянстве этого отношения высказал Пифагор, в его
честь это число обозначают греческой буквой я.)
5. Количество молекул в 1 моле вещества есть
23
число постоянное, равное 6,02 • 10 . Оно
называется число Авогадро и обозначается NA.
Примеры переменных величин.
1. Сила, действующая на пружину, изменяется
прямо пропорционально растяжению пружины.
2. Время, затраченное на прохождение
данного расстояния, обратно пропорционально
скорости движения.
3. При постоянной температуре давление
газа на стенки сосуда обратно пропорционально
занимаемому газом объему.
2. Определение функции
Две переменные величины х и у связаны
функциональной зависимостью, если каждому

Краткое
значению, которое может принимать
переменная *, соответствует одно и только одно
значение переменной у.
Переменная х называется независимой
переменной или аргументом функции, а
переменная у — зависимой переменной или функцией.
Пример 1. г = 5, где а — сторона квадрата
(независимая переменная), г — радиус
вписанной в квадрат окружности (зависимая
переменная).
2
Пример 2. s = gt /2, где t — время
свободного падения тела, имеющего начальную нулевую
скорость (независимая переменная), s — путь,
пройденный свободно падающим телом
(зависимая переменная), g — постоянная величина —
ускорение свободного падения.
Пример 3. v = s/t, где t — время движения
(независимая переменная), v — скорость
движения (зависимая переменная).
Наиболее распространенные обозначения
функциональной зависимости переменной у от
переменной х таковы: у = f(x) или у = и(х). Если
задано конкретное значение независимой
переменной х = х0, то у0 = f(x0) называют значением
функции / в точке х0.
х
Пример 4. у = f(x) = г .
*ов1»0овЛ*о)в 5 =0,2,
2
Пример 5. 2 = z(t) = -т ; t0 = 2; z0 = z(*0) = -1.
3. Область определения
и область значений функции
Областью определения функции f(x)
называется множество всех действительных значений
независимой переменной х, при которых
функция определена (имеет смысл).
Обозначение: D(f) (англ. define —
определять).
Пример 1. Функция f(x) = ——г определена
для всех действительных значений х9
удовлетворяющих условию л:+1*0,т.е.л:*-1. Поэтому
W)-(-°o;-l)U(-l;oo).
школьного курса математики
Алгебра. 7—11 классы
2
Пример 2. Функция s(t) = gt /2 определена
для всех действительных значений. Однако
если рассматривать ее как физическую
зависимость пути (s) от времени (t) свободного падения
тела, то, учитывая физический смысл, функция
s будет определена только для t > 0, т. е. D(s) =
= [0; оо).
Пример 3. Функция f(x) = Jx - 2,5
определена для всех действительных значений х>
удовлетворяющих условию х - 2,5 > 0, так как
арифметический квадратный корень определен лишь
для неотрицательных чисел, поэтому D(f) =
= [2,5;оо).
Областью значений функции у = f(x)
называется множество всех действительных
значений, которые принимает зависимая переменная у.
Обозначение: E(f) (англ. exist —
существовать).
2 2
Пример 4. у = х — 2jc •+- 10; так как х - 2х 4-
2 2
4-10 = х - 2х 4- 1 4- 9 = (х - 1) 4- 9, то
наименьшее значение переменной у = 9 при х = 1,
поэтому Е(у) = [9; оо).
Пример 5. у = ^2,5 - л: ; так как 2,5 - л: > 0,
то наименьшее значение функции i/ = 0 при лг =
= 2,5. Тогда Е(у) = [0;оо).
2
Пример 6. у = -х 4-11. Поскольку при лю-
2 2
бом действительном значении х > 0, то -х 4-
4-11 < 11, откуда наибольшее значение
переменной у = 11, поэтому £(i/) = (-°°; 11].
Способы задания функции
Функциональная зависимость задана, если
заданы область определения и правило,
устанавливающее, какое число у ставится в
соответствие числу х, принадлежащему области
определения функции.
1. Аналитический способ задания функции
Функция задается формулой, позволяющей
получить значение зависимой переменной (z/),
подставив конкретное числовое значение
аргумента (х).
Пример 1. Зависимость площади круга от
длины его радиуса выражается формулой: S =
= пг . Согласно геометрическому смыслу задачи

56
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
D(S) = [0; оо). Переменная S может принимать
любые неотрицательные значения, значит,
Я(5) = [0;оо).
Пример 2. у = х - Ьх + 6; D(y) = (-оо; оо),
Е(у) - [-0,25; оо), так как х - Ьх + 6 = (х - 2,5)2 -
- 0,25 > -0,25 при любом х € D(y).
Пример З.у = -Зх2 + 17* - 10; D(i/) - (-оо; оо),
Е(у) = (-со; 14-^1, так как -Зх2 + 17* - 10 =
/ 17Л2 1 1
= -3( дг- -g-J +14j2 < 14^2 при любом л: еДу).
Пример 4.у= 4х - 3 ; D(i/) = [3; оо), так как
л/jc - 3 имеет смысл при jc - 3 > 0, т. е. л: > 3,
£(у) = [0; оо) при любом значении jc е D(i/).
2
Пример 5. у= х + 5
U (-5; оо), так как дробь
ли х + 5 Ф 0, т. е. х * -5 при любом х е D(y). Так
2
; DO/) = (-<*>;-5) и
2
имеет смысл, ес-
как дробь
может принимать любые значе-
f х, пр
I -л: ,:
л: + 5
ния, кроме 0, то Е(у) = (-оо; 0) U (0; оо).
Пример 6.
при х>0,
при х < 0.
ЭД - (-°°; °°). ВД - (-°°; °°).
Пример 7.
{х2, если л: € (-оо; 3],
12 - х, если х € (3; 6],
-х2 + 12* - 30, если х € (6; оо).
D(y) = (-со; оо); Е(у) - (-оо; оо) (См. рис. 5 на
с. 57).
Пример 8*. у = J2x - 1 + Vl - 2л:.
Поскольку квадратный корень имеет смысл только
для неотрицательных чисел, то область
определения данной функции D(y) является решением
системы неравенств:
1
2х - 1 > 0,
1 - 2х > 0;
Д(У)
-ш-
<=> х =
2'
значит,
Область значений Е(у) - {0}, так как у Г^1 = 0.
гт лФ (** - 5х + 6)(х + 2) Q
Пример 9*. у = 5 " " • Задан-
(х2 - 4)(х - 3)
ная функция определена при любых значениях
переменной х, кроме обращающих знаменатель
в нуль, т. е. х2-4*0их-3*0. Таким образом
D(y) - (-оо; -2) U (-2; 2) U (2; 3) U (3; оо).
Преобразуем выражение, задающее функцию:
(х2 - Ьх + 6)(* + 2) = (х - 2)(х - 3)(дс 4- 2) = j
(х2 - 4)(х - 3) (* " 2)(* + 2){х - 3)
при любом х е D(y)9 т. е. Е(у) = {1} при любом
х € D(y). (График этой функции изображен на
рис. 6.)
2. Табличный способ задания функции
При этом способе задания функции
заполняется таблица, в верхней строке которой
указываются значения независимой переменной (х), в
нижней — соответствующие значения
зависимой переменной (у).
Этот способ задания функциональной
зависимости удобен для записи результатов
наблюдений и измерений в процессе опытов.
Пример 1. Измерение температуры (Т) тела
больного в зависимости от времени: Т = f(t).
Время суток
*,ч
Температура
тела Т9 °С
8
39,3
12
38,3
14
37,8
16
37,8
20
38,6
24
37,0
Пример 2. Зависимость скорости
распространения сейсмических волн в толще земной коры
от глубины: v = /(А).
Глубина
Л, км
Скорость волн
v9 км/с
20
3,2
45
3,5
1300
6,9
2400
7,5
Таблицы значений чаще составляют для
построения графиков функций, заданных
формулами. При этом для нескольких, произвольно
выбранных, значений независимой переменной
вычисляют соответствующие значения
зависимой переменной.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
57
Например, график функции из примера 1
состоит из шести точек (рис. 1).
Пример 3. у =
X
2
У = х
-2
4
= х .
-1
1
0
0
1
1
2
4
На основании данных таблицы строится
график функции ( рис. 2).
Пример 4.у= л/2 ~ х.
X
у- J2 - х
2
0
1
1
0
Л
-1
7з
-2
2
-7
3
-9
Л!
График функции на рисунке 3.
3. Графический способ задания функции
Пример 1. График изменения напряжения
аккумулятора при заряде и при разряде (рис. 4).
Пример 2. График функциональной
зависимости, заданной формулой
У = \
х , если хе (-оо; 3];
12 - х9 еслихе (3; 6];
2
[ -х + 12* - 30, если х € (6; оо) (рис. 5).
Пример 3. График функциональной
зависимости, заданной формулой
_,_(*2 - 5х + 6)(* + 2)
У о »
(хл - 4)(ж - 3)
ЩУ) = (-оо; -2) U (-2; 2) U (2; 3) U (3; оо),
Е(у) — Ш при любом х е D{y) (рис. 6).
7\°С|
39-
38-
37-
i
г -t
I 1
1
: ,_ _^ ^ .,
- 1 1 1 1
1 III
1 1 1 1 1 1 1 1 1
т
1
1
1
1—1—
1
1—ь-
—^-
2 4 6 8 10 12 14 16 18 20 22 24 t, ч
Рис. 1
У=12-*
3<*<6
у,
1
1 1 1 1 1 1 1 1 1
0
!_
■
1
^
X
Рис.3
*>6
Рис. 2
1
1,8
1,6
1,4
1,2
1
0,8
0,6
i
—i—i—i—i—i—i—i—i—»-
0,51 1,5 22,5 3 3,5 4 *, ч
Рис.4
yi
1
?
1
1
Д 1
-2
-1
0
i
i
1
9
1
i
6
2
?
1
i
5
3
X
Рис. 5
Рис. 6

58
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Отметим, что графический способ задания
функции отличается наглядностью, он удобен
при изучении свойств функции.
Свойства функций
1. Промежутки знакопостоянства
Если функция f(x) > 0 или f(x) < 0 при любом
значении аргумента х е (а; Ь), то говорят, что
функция у = f(x) на числовом интервале (а; Ь) не
меняет знак.
Интервал (а; Ь) С D(f) называют интервалом
знакопостоянства функции f(x).
Пример 1, f(x) = х , f(x) > 0, если х > 0;
fix) < 0, если х < 0 (рис. 7).
Точка х = 0 является точкой изменения
знака функции, т. е. при переходе графика
функции через эту точку значения функции меняют
знак на противоположный.
Пример 2. Значения функции у = х + 2
положительны при любом х (рис. 8), т. е. интервал
знакопостоянства функции: (-°о; оо).
2. Монотонная функция
Функция у = f(x) называется возрастающей
на числовом интервале (а; Ь) С D(f), если для
любых хг и х2 таких, что а < хх < х2 < Ь,
выполняется неравенство /(jcx) < f(x2), т. е. большему
значению аргумента соответствует большее
значение функции.
Функция у = f(x) называется убывающей на
числовом интервале (а; Ь) С D(f), если для любых
хг и х2 таких, что а < хг < х2 < Ь9 выполняется
неравенство f(xx) > f(x2), т. е. меньшему
значению аргумента соответствует большее
значение функции.
Если значения функции связаны нестрогим
неравенством, то говорят, что функция нестрого
возрастает, или, соответственно, нестрого убывает.
Возрастающая (убывающая) на интервале
(а; Ь) функция f(x) называется монотонной на
интервале (а; Ь) С D(f).
Функция, график которой изображен на
рисунке 9, убывает на [-4; 2], постоянна на [2; 4] и
возрастает на [4; 9].
3. Четная и нечетная функции
Функция у = f(x) называется четной, если
для любого х е D(y) выполняется равенство
f(-x) = f(x), при этом -х € D(y).
Ось ординат является осью симметрии
графика четной функции (рис. 10).
Функция у = f(x) называется нечетной, если
для любого х е D(y) выполняется равенство
f(-x) = ~f(x), при этом -х е D(y).
Начало координат является центром
симметрии графика нечетной функции (рис. 11).
у<
1
, , .о
Г
1
:)
/
1
\"
3
= х
х
Ук
1/'"''
1L
——' ■■
0 1 х
Рис. 7
Рис.8
»,
Г'
' Л-*)-
J
-/(*)
X
Рис. 11

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
59
4*. Точки минимума и максимума функции
Пусть функция у = f(x) определена во всех
точках интервала (а; Ь) и х0 е (а; Ь). Если для
всех точек х е (а; 6), таких что х * х09
выполняется неравенство f(x) < f(x0)9 то х0 называется
точкой максимума функции у = f(x)9
значение у0 = f(x0) называется максимумом
функции у = f(x). Обозначение: i/max.
Если же выполняется неравенство f(x) > f(x0)9
то х0 называется точкой минимума функции
у — f{x)9 значение yQ = f(x0) называется
минимумом функции у = f(x). Обозначение: ymin.
Пример. Точки х09 х2, хъ являются точками
максимума функции, график которой
изображен на рисунке 12; точки xv лгб — точками
минимума. Любая точка отрезка [х3\ х4], согласно
определению, является точкой нестрогого
минимума, так как заданная функция постоянна
при любом х е [х3; *4].
Простейшие преобразования графиков
Пусть задан график функции у = f(x).
Покажем, как с помощью графических
преобразований можно с его помощью получить график
функции у = а • f(kx + I) + Ь, где а, k9l9b —
постоянные числа.
1. График функции у = f(kx)
График функции у = f(kx)9 где k > О,
получается из графика функции у = f(x) сжатием к
оси Оу в k раз при k > 1 или растяжением от
оси Оувт раз при 0 < k < 1 (рис. 13).
График функции у = f(-kx)9 где k > О,
получается из графика функции у = f(kx) при помощи
осевой симметрии относительно оси Оу
(рис. 14).
2. График функции у = f(x + I)
График функции у = f(x + Z) получается из
графика у = f(x) параллельным переносом вдоль
оси Ох.
Если I > О, то график у = /(я) переносится
влево параллельно оси Ох на расстояние 19 если
Z < 0, то вправо на расстояние -I (рис. 15).
3. График функции у = а • /(*)
График функции у = a* f(x)9 где а > 0,
получается из графика функции i/ = f(x) растяжени-
Рис. 12
У
y = f(-kx) *k y = f(kx)
yi
0
~ / Л /л, Л^^чА уЧ Л
л
Рис. 13
У-Л*" 4)
Рис. 14
Рис. 15

60
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
ем от оси Ох в а раз при а > 1 (рис. 16) и
сжатием к оси Ох в - раз при 0 < а < 1 (рис. 17).
График функции у = ~-а* f(x), а > О,
получается из графика функции у = а • f(x) осевой
симметрией относительно оси Ох (рис. 17).
4. График функции у = f(x) + Ь
График функции у = f(x) + Ь получается из
графика функции у = /(я) параллельным
переносом вдоль оси Оу.
Если Ь > О, то график i/ = Длг) переносится
вверх вдоль оси Оу на расстояние Ь, если & < О,
то вниз на расстояние -Ь (рис. 18).
5. График функции у = a/(fc* + I) + Ь
Итак, график функции у = а* f(kx + l) + b9 где
a, ft > 0, получается из графика у = /(*) с
помощью следующих преобразований:
— сжатием к оси Оу в ft раз (ft > 1) или
растяжением от оси Оувт раз (0 < ft < 1),
— параллельным переносом вдоль оси Ох на I
единиц,
— растяжением от оси Ох в а раз (а > 1) или
сжатием к оси Ох в - раз (0 < а < 1),
— Параллельным переносом вдоль оси Оу на
Ьединиц.
Элементарные функции
школьного курса
1. Прямая пропорциональность (у = kx)
Функция, задаваемая формулой у = kxf где
х — переменная, ft — число, называется прямой
пропорциональностью. Число ft называется
коэффициентом пропорциональности.
График прямой пропорциональности —
прямая, проходящая через начало координат под
углом а к оси абсцисс (в курсе тригонометрии
X класса доказывают, что tg a — ft).
Коэффициент ft называют также угловым коэффициентом
прямой.
D(y) = (~°°; °°); если ft * 0, то Е(у) = (-оо; оо).
Пример 1. у = 2х (рис. 19).
X
У
0
0
1
2
Для построения прямой линии достаточно
знать координаты двух любых ее точек. Так как
график прямой пропорциональности проходит
через начало координат, значит, нужна еще
одна точка.
При ft > 0 функция у — kx возрастает на всей
области определения, при ft < 0 — убывает.
Интервалы знакопостоянства:
если х е (-°°; 0), то у < О,
если х е (0; оо), то у > 0.
Поскольку у(-х) = ft • (~jc) = -kx = -у(х), то
у = kx — функция нечетная, график
симметричен относительно начала координат.
Пример 2.y = --zx (рис. 20).
х °
у1
0
у
/I
' V = 2f(x)
А .
\ *
\у = /(*)
У = fix) + 5
Рис. 16
Рис. 17
У = fix)
y = fix)-3
Рис. 18
У|
2
1
/1
/ i
Г 1
01
'у- 2*
л
Рис. 19

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
6i
2. Линейная функция (у = kx + I)
Функция, заданная формулой у = kx + I, где
ft, I — числа, х и у — переменные, называется
линейной. График линейной функции —
прямая линия, D(y) = (-оо; со), Е(у) = (-со; оо).
Прямая у = kx + I пересекает ось ординат в
точке (0; I) и ось абсцисс в точке (-г ; 0). Число
k — угловой коэффициент прямой.
Пример 1. Дано уравнение -2л: + Зу = 6.
Выразим переменную у через х. Имеем линейную
2 2
функцию: у = 5 х + 2 (ft = о »* = 2).
X
У
0
2
-3
0
Интервалы знакопостоянства:
если х е (-оо; -3), то у < О,
если л: е (-3; со), то у > 0.
2 2
Так как k = 5 > 0, то функция i/ = 5 * + 2
возрастает на всей области определения (рис. 21).
2 11
Пример 2. ^х + 4у=1; У = "хОл:"Н4
(»~и"-П
лс
У
0
1
4
41
0
Интервалы знакопостоянства:
если х е [ -оо; 2 ^ L то у > О,
если х е (2 ^ ; °°), то у < 0.
Так как k = -т^ < 0, то функция у = —tq х + I
убывает на всей области определения (рис. 22).
Замечание 1. Функция прямая
пропорциональность у = kx является частным случаем
функции y = kx + l (при I = 0).
Замечание 2. Графиком линейной функции
у = J (ft = 0, х е (-со; оо)) является прямая,
параллельная оси абсцисс, пересекающая ось
ординат в точке (0; I).
Пример 3.у = -2 (рис. 23).
Замечание 3. Графиком уравнения х — а
является прямая, параллельная оси Оу,
пересекающая ось абсцисс в точке (а; 0).
Подчеркнем, что уравнение х = а не является
функцией, поскольку нарушается условие
однозначности при определении функции —
каждому значению х должно соответствовать
единственное значение у.
Пример 4. х = 5 (рис. 24).
У[
v. 1
0
i
1
i
у -
1
"2Х
X
Рис. 20
У\
0
-1
-2
1
i
1
X
у = -2
* е Л
Рис. 21
»*
*1
1 _,_ 1
У - "ТО* + 4
0
1
-1
12 3 х
* = 5
1/6 Д
Рис. 22
Рис. 23
Рис. 24

62
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
3. Обратная пропорциональность (у = - J
k
Функция, заданная формулой у = - , где k —
некоторое постоянное число (k Ф 0), называется
обратной пропорциональностью,
Щу) = (-°°; 0) и (0; °°)> так как х Ф 0.
Е(У) = (-°°; 0) U (0; °°), так как у Ф 0
(уравнение 0 = - не имеет решения).
График функции у = - не пересекает осей
координат. Этот график называется гиперболой;
части графика — ветвями гиперболы.
k
Функция у = - при k > 0 убывает при
х е (-оо; 0) и при х е (0; оо),
Интервалы знакопостоянстга:
если х е к1); *">), то у > 0,
если х е (-оо; 0), то у < 0.
Так как у(-х) = — = -- = -у(*), то функция
у = нечетная. График симметричен
относительно начала координат и расположен в I и
III координатных четвертях.
Пример 1.у = - (рис. 25).
fe<0
ft
При k < 0 функция I/ = - возрастает при
х е (-оо; 0) и при X g (0; оо).
Интервалы знакопостоянства:
если х е (-°°; 0), то у > 0;
если х е (0; оо), То у < 0.
Функция нечетная, график симметричен
относительно начала координат и расположен во
II и IV координатных четвертях.
Пример 2. у = -- (рис. 26).
X
У
-6
1
2
-3
1
-1
3
1
2
6
1
2
-6
1
-3
3
-1
6
1
2
X
У
-5
-1
-2,5
-2
-2
-2,5
-1
-5
1
5
2
2,5
2,5
2
5
1
Замечание. Отметим, что грубой ошибкой
является утверждение, что функция у = --
является возрастающей на всей области
определения, т. е. у возрастает при х е (-°°; 0) и (0; оо),
например, при хг = - 3 и при х2 = 3 х2 > xv
однако, у(х2) < у(хх)> так как у(хг) = 1, а у(х2) = -1.
4. Квадратичная функция (у = ах + Ьх + с)
2
Функция, заданная формулой у = ах + Ьл: +
+ с, где а, 6, с — числа и а * 0, называется
квадратичной функцией.
График квадратичной функции называется
параболой. D(y) = (-о°; °о).
_j i i i 1_
Рис. 25
Рис. 26

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
63
Функция у = х (а = 1, Ь = с = 0)
Составим таблицу значений и построим
график функции (рис. 27).
X
2
у = х
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
Ду) = (-°°;00);
2
Е(у) = [0; оо), так как х > 0 при любом
действительном значении лг;
функция I/ = # убывает при х е (-°о; 0] и
возрастает при х е [0; °°);
2
график функции у = х симметричен
относительно оси ординат, так как у(-х) = (-х) = х =
2
= у(х), т. е. у = х — четная функция;
наименьшее значение функции у = х равно
нулю при х = 0.
Точка пересечения параболы с ее осью
симметрии называется вершиной параболы.
Функция у = ах (Ь = с = 0)
D(y) = (-оо; оо).
1)а>0
Е(У) = [0; °°)t так как * ^ 0 ПРИ любом
х € D(i/);
2
график функции у = ах получается из
графика функции у = х сжатием к оси Ох> если
О < а < 1, или растяжением от оси Ох9 если
а > 1;
2
функция у = ах убывает при х е (-оо; 0] и
возрастает при л: е [0; оо);
наименьшее значение у(0) = 0 достигается в
вершине параболы — точке (0; 0);
при а > 0 ветви параболы направлены вверх,
ось Оу является осью симметрии параболы
(рис. 28).
2)а<0
ВД = (-°°;0];
2
график функции у = ах , где а < 0,
получается из графика функции у = |а|х осевой
симметрией относительно оси Ох (рис. 28);
ветви параболы при а < 0 направлены вниз;
функция возрастает при х е (-оо; 0],
функция убывает при х е [0; оо).
2
График функции у - ах + Ьх + с
Графиком любой квадратичной функции у =
2
= ах + foe 4- с, а * 0, является парабола с
вершиной в некоторой точке (х0; у0) и осью
симметрии, проходящей через точку х0 параллельно
оси Оу (рис. 29).
Вычислим координаты вершины параболы.
Для этого преобразуем многочлен ах + Ьх + с,
выделив полный квадрат:
L2 Л t2
/2,ЬЧ1 f 2 ^ п Ь , & 1 Ь
а(х +-х) + с-а\х + 2н~лН о "" т~
v а I 2а 4fl2j 4а
= a(*+-^J +—la" =a(*+2^J + 4а">
где D = & - 4ас. (Число D называют дискрими-
2
нантом квадратного трехчлена ах + &;е + с.)
2
Тогда график функции у = ах +Ъх + с
получается из графика у = ах параллельным пере-
у-2*1
-3-2-10 12 3*
Рис. 27
Рис. 28
Рис. 29

64
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
носом вдоль оси Ох на -«- единиц, вдоль оси Оу
D
на-т- единиц.
2
Следовательно, вершина параболы у = ах +
+ Ьх + с задается координатами х0 = -5-»#о =
= - j- . Осью симметрии параболы является пря-
мая х = х0, т. е. х = -х- » параллельная оси Оу.
При а < 0 ветви параболы направлены вниз и
значение у = у0 является наибольшим
значением функции, т. е. Е(у) = (-оо; у0];
при а > 0 ветви параболы направлены вверх и
значение у = у0 является наименьшим
значением функции, т. е. Е(у) = [у0; со).
2
Если D — b - 4ас < 0, то парабола не
пересекает ось абсцисс, если D = 0, то парабола
касается оси Ох в вершине (л:0; 0), если D > 0, то
парабола пересекает ось Ох в точках (хх; 0) и (х2; 0)»
-Ь - л/D -Ь + л/D
где*!- 2fl их2= 2g .
Парабола пересекает ось Оу в точке с
координатами (0; с).
Пример 1. Построить график функции
• у = 8х2-2х-1.
Решение, а = 8 > 0 (ветви параболы
направлены вверх), Ъ = -2, с = -1;
D = Ь2 - 4ас = (-2)2 - 4 • 8 • (-1) - 36 > 0
(парабола пересекает ось Ох в двух точках);
Ь 1 D
вершина параболы х0 = -х- = r ♦ ^о = ""Т~ =
= -1 £; ось симметрии параболы — прямая
1
3) у = 0 при хх = - j или х2 = g ;
4) у > 0, если я е (-со; - j ) U (g ; оо);
i/<0, если л: е (-^ ; g);
5) функция убывает при л: е (-со; -19
возрастает при лее Г о; °° )•
Пример 2. Построить график функции
у = -2х2 + Зх - 5.
Решение, а = -2 < 0 (ветви параболы
направлены вниз), Ь = 3, с = -5;
D = Ь2 - 4ас - З2 - 4-(-2)-(-5) - -31 < 0,
значит, парабола не пересекает оси Ох;
* Ь 3 D
вершина параболы: *о = ~~<Г* = 4 • ^° = ~~4~ =
7 3
= -3 g ; ось симметрии параболы — прямая х = т ;
точка пересечения параболы с осью Oi/ —
(0; -5).
Строим график (рис. 31).
2
Исследование функции у = -2х + Зл: - 5 по
графику:
l)D(l/) = (-00;00);
/ 7т 7
2) #(i/) = [-со; -3g|, так как у0 = -3g ;
3) интервалы знакопостоянства:
если х е (-°°; °°), то у < 0;
4) функция возрастает при х е (-оо; -1,
убывает при jc е Г т ; со J.
X =
8'
точки пересечения с осью Ох (хг; 0) и (лг2; 0),
поскольку D > 0, xlf 2 =
1
-b±jD = 2_±6
2а 16
; *i - 4;
*2 * 2 •
точка пересечения с осью Оу (0; -1).
Учитывая все вышесказанное, строим
график (рис. 30).
Исследование функции по графику:
l)D(l/) = (-00;00);
2) Е(у) = Г-lg ; со^ так как у0 = -lg ;
у - -2* + 3* - 5
Рис. 30
Рис. 31

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
65
Замечание. По графику квадратичной
функции можно решать заданное квадратичное
неравенство, определяя интервалы знакопостоянства.
Например, неравенство ~-2х + Зл: - 5 > О не
имеет решения, т. к. при любом х е D(y) у < 0.
2
Неравенство 8* - 2х - 1 < 0 имеет решение —
отрезок Г-j ; ~ 1 (рис. 30).
5. Степенная функция (у = хр)
Функция, заданная формулой у = х*
называется степенной функцией.
1) р = 1 (рис. 32).
2) р — натуральное, четное, р = 2д (п е N)
D(y) = (-ОО; ОО); Е(у) = [0; ОО);
если х е D(y), тоу>0;
функция убывает при х е (-°°; 0] и
возрастает при х е [0; оо);
функция четная, так как у(-х) = (-х) п = х п =
график симметричен относительно оси Оу
(рис. 33).
2
Частный случай: у = х.
3) р — натуральное, нечетное, р = 2п + 1 (л € ЛГ)
D(y) = (-ОО; ОО); Е(у) = (-ОО; ОО);
если х е (-°°; 0), то у < 0; если jc е (0; оо), то
У > 0; функция возрастает на всей области
определения; функция нечетная, так как у(-х) =
= ~У(х)\ график симметричен относительно
начала координат (рис. 34).
Частный случай: у = х.
4) р — целое, отрицательное, нечетное
Пусть р = -п (п е N). Тогда по определению
степени с отрицательным показателем имеем:
-п 1
У -* --.
D(y) = (-оо; 0) U (0; оо);
Е(у) = (-оо; 0) U (0; оо);
при х е (-оо; 0) у < 0; при х <= (0; оо) у > 0;
функция убывает при х е (-оо; 0) и при х е
е (0; оо); функция нечетная.
График — гипербола, симметричная
относительно начала координат, расположенная в I и
III координатных четвертях (рис. 35).
5) р — целое, отрицательное, четное
Пустьр = -п(пе N)y = х~п = — ,
D(y) = (-°o;0)U(0;oo);
Е(у) = (0; оо);
у > 0 при любом х е D(y),
функция возрастает при х е (-оо; 0), убывает
при х е (0; оо); функция четная; график —
гипербола, симметричная относительно оси Оу (рис. 36).
6) р — дробное, положительное
Из определения степени с дробным
показателем следует, что степенная функция определена
при х > 0, еслир > 0 и при х > 0 еслир < 0.
Рис. 32
-и 1
у = Х = -
X
(Р - 2д)
Рис. 33
и = х = —
9 п
Рис. 34
I, п — четно
Рис. 35
Ы019

66
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пример 1.р= § » У = х = Jx .
Щу) = [0; оо); Я(У) = [0; оо);
У(0) = 0;
у > 0 при л: € (0; оо);
функция возрастает при х е [0; оо);
график — ветвь параболы (рис. 37).
1
Пример 2.р= о » У = х = 3Jx.
Z)(i/) = [0; оо), Я(у) = [0; оо);
У(О) = 0;
у > 0 при л: е (0; оо),
функция возрастает при х е [0; оо);
график — ветвь параболы (рис. 38).
7)р = 0
о -
у — х = 1 определена для всех значении х,
кроме х = 0 (выражение 0 — не имеет смысла).
D(y) = (-оо; 0) U (0; оо); Е(у) = {1} (рис. 39).
6*. Дробно-линейная функция (у = ——-1
Функция, заданная формулой у = — , где
сх + а
a, b9c9d — некоторые числа, причем с * 0,
называется дробно-линейной функцией.
Дробно-линейная функция определена для
d
всех действительных значении лг, кроме х = -- .
Преобразуем выражение, задающее функцию:
( ^d\ ^ и ad
а\х + -\ + Ъ
+ Ь \ с) с
Рассмотрим случай, когда be - ad = 0, тогда
получим функцию у = - , определенную для
любого х9 кроме х = -- .
Если be - ad * 0, график дробно-линейной
функции можно получить из графика функции
k , be - ad
у = - , где k = 5— параллельным переносом
* с
вдоль оси Ох на — единиц, вдоль оси Оу на -
единиц, т. е. графиком дробно-рациональной
функции является гипербола.
Пример 1. Построить график функции
х - 1
У =
(a-c-l,6--l,d-8).
х + 3
Решение. Преобразуем дробь
х - 1 = (х + 3) - 4 = «
л: + 3
х + 3
л + 3
Построим гиперболу у = --, затем
параллельным переносом вдоль Ох на -3 единицы и
вдоль Оу на 1 получим график заданной
функции (рис. 40).
D(y) = (-оо; -3) U (-3; оо), так как дробь
х - 1
х + 3
имеет смысл при х * -3.
Е(У) = ("°°; 1) и (1; °°)t так как —— * 0 при
X "г о
любом X € D(i/),
i/ = 0, если 1 - ;
= 0; отсюда х + 3 = 4; х = 1,
*/ =
с* + d
Ьс - ad
{- ♦ S)
= ?+^
л: +
л + 3
т. е. гипербола пересекает ось Ох в точке (1; 0);
интервалы знакопостоянства:
если х е (-оо; -3) U (1; оо), то у > 0,
если х е (-3; 1), то у < 0;
функция возрастает, если jc е (-°°; -3) и если
х е (-3; оо);
2
1
0
1 1
у - * - V*
' i i
1 4
л
2
i
0
1 1
1
i
8
лс
у,
1
<
0
1
У-1
i
1 л:
Рис. 37
Рис. 38
Рис. 39

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
67
гипербола пересекает ось Оу в точке [ 0; -= 1.
1остроить график функции
(а = 3,6 = l,c = 2,d = -5).
3)у =
Пример 2. Построить график функции
3* + 1
У =
2х - 5
х + Jx + 3
Решение. у(1) =
1
при л: = 1.
1
1
3*
Решение. Преобразуем дробь
Зх + 1
2* - 5
2* + 2 2
\( Ъ\ 17
>1* " 2) + Т
л -
2+ .1-
* - 2н
Построим гиперболу у = —, затем
параллельным переносом вдоль оси Ох на 2 « единиц
и вдоль оси Оу на 15 » получим график (рис. 41)
заданной функции.
Задачи, связанные с понятием
функции
Пример 1. Найти значение функции в
заданной точке.
2
1) У(х) = Зх - х при х = 1.
Решение. у(\) = 3 • 1 - I2 = 2. Ответ: у{\) = 2.
2) I/ = *]х -5 при л: = 3.
Решение. у(3) = л/32 - 5 = Vi = 2. Ответ:
№ = 2.
1 + JTT~3 1 + 2
Ответ: i/(l)= g.
Пример 2. При каких значениях
независимой переменной х данная функция принимает
данное значение?
1)р- -2* + 5; у = -3.
Решение. -3 = -2л: + 5 <=> -2х = -3 - 5 <=> х = 4.
2) I/ = я2 - Зх; i/ = -2.
Решение. -2 = х2 - Зх <=> х2 - Зх + 2 = 0 <=>
|_х = 2.
Данная функция принимает значение -2 при
двух значениях: х = 1 и х = 2.
3)i/= Vl7 + х; i/ = 5.
Решение. 5 = л/17 + х =>52 = 17 + х=>х =
= 52 -17 = 8.
32
4)i/ =
х + 1
, i/ = 4.
32 28
Решение.4 = <=>4х + 4 = 32<=»х=-г-=7.
х + 1 4
Заметим, что ответ на последние вопросы
сводится к решению соответствующих уравнений.
Пример 3. Принадлежит ли графику данной
функции точка с указанными координатами?
!)?-*+л/5; М(4;6).
2х - 5
Рис. 40
Рис. 41

68
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Решение. Найдем у(4) = 4 + Vi = 6 «=> М(4; 6)
принадлежит графику данной функции.
1) t(x) = х +
2)»-пгЦ:5 Mf1;i)'
л: + Jx v *у
Решение. Найдем у(1) =
1 1
4* + 13
Решение. Нули функции определяются
равенством £(л:) = 0, т. е.
_,_ 3 Л 4*2 + 13* + 3 Л
л: + —■—— =0 <=> — =0 <=>
12 + Л 1 + 1 2'
Так как g * j, то точка М не принадлежит
графику данной функции.
о
Пример 4. Дана функция /(х) = 2х - 8.
Найти /(1 + Л) + /а - Л).
Решение. Имеем:
/(1 + Л) = 2 • (1 + Л )2 - 8 = 2(1 + 2 Л + 5) - 8 =
= 4 + 475.
/(1 - Л ) = 2 • (1 - Л )2 - 8 = 2(1 - 2 75 + 5) - 8 =
= 4-475.
/(1 + 75) +/(1 - 75) = 4 + 475 + 4 - 475 = 8.
Зг — 1
Пример 5. Дана функция t(z) = — 2-2.
Доказать, что *(0,8) - t(l,25) = 0.
Q Л Q _ <
Решение. Найдем *(0,8) = g-g 2 - 0,8 =
4л: + 13
<=»
J 4х2 + 13л: + 3 = 0, ^
I 4л:+ 13*0;
4л: + 13
* = ~4'
х = -3.
2,4 - 1
0,8
2,8 = -1,05.
*(1,25) = [1ъ - 2 - 1,25 = 2,2 - 3,25 =
= -1,05.
*(0,8) - *(1,25) = - 1,05 - (-1,05) = 0.
Пример 6. Дана функция л:(*) = Ы - - .
Найти все такие числа р, что х{р) = х( - J.
Решение. Имеем: х{р) = 5р - - ; л:(-J = 5• - -
-?-5-8р.
1 Р
Р
с 3 5 0 0 8 2 -
5р — = Зр <=> 8р = - <=» р = 1 <=»
Р Р. Р
**Ь—1.
Ответ: исходное равенство верно при р = 1
илир = -1.
Пример 7. Найти нули функции, т. е. такие
значения независимой переменной, при
которых значение функции равно 0.
. Ответ: нули функции в точках л: = -3ил: = -т.
2)р(2) = (22-25)(г-Г5+Н
Решение. Нули функции определяются
уравнением р(з) = 0. Данная функция является
произведением двух алгебраических выражений.
Справедливо утверждение: произведение двух
выражений равно нулю, когда хотя бы одно из
них равно нулю, а другое при этом не теряет
смысла.
Первая скобка имеет смысл (определена) при
любом значении z, вторая — при любом z, кроме
г = -5 и г = 0. Таким образом, либо г - 25 = 0,
2 1
либо + - = 0, при условии, ЧТО 2 * -5 и
г *0 (*).
Решая полученные два уравнения, с учетом
5
условия (*), получим 2 = 5 либо 2 = -= .
Ответ: 5; -=.
Пример 8. Найти область определения
функции.
1)У =
(3 - x)j7x - 3
х + 1
Решение. Область определения данной
функции задается системой неравенств:
7х - 3 > 0,
л:+1*0;
3
<=> S
^ 3
л:*-1;
<=> х -.
Ответ: Г= ; °о ).
(t2 - 9)j2t + 3
t - 3
2)2(0 =
Решение. [2\^\l^
Ответ: Г-|; з! и (3; оо).
t *3.
2'

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
69
3) y(t) = Jt - 1 + 75 ~ t,
Решение.
О, Г*>1,
0; U<5;
Ответ: [1; 5].
{Г-1,;?:-{«i;-••»•»
2)17ах be;
4)3jc-7i/-(-2i/).
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Многочлены.
Действия с многочленами
1. Одночлен и многочлен
Одночленом называется выражение, в
котором числа и буквы связаны только двумя
действиями — умножением и возведением в степень с
натуральным показателем.
Пример 1.
1) -аЪ\
3)^х2уг;
В этом примере одночлены 1), 2) и 3)
записаны в стандартном виде, т. е. первый
сомножитель — число, называемое коэффициентом
одночлена, и каждый буквенный сомножитель
входит в одночлен только один раз.
Приведем одночлен 4) к стандартному виду:
3x-7i/-(-2i/) = 3-7-(-2)-x-i/-i/ = -42xi/2.
Чтобы умножить одночлен на одночлен,
нужно перемножить их коэффициенты и степени с
одинаковыми основаниями.
Пример 2. Привести одночлен к
стандартному виду.
1х2у • (-8*У) = 7 • (~3)х2х7уу3 - -21*У.
2 3
Пример 3. Перемножить одночлены -Ъх t а
и g х tb.
/ ег 2^3 ч (2 5., "\ t сч 2 2 5.3а .
(-5* * а) • I 5 х Й>1 = (-5) • g х х t tab =
= -r^-x f ab.
Многочленом называется сумма нескольких
одночленов .
Одночлены, из которых состоит многочлен,
называются членами многочлена.
Пример 4.1)2х + Заху + Ь;
2) а + &;
3) 5 + х;
4) 17* у г + Зху - Паху г.
2. Приведение подобных слагаемых
Одночлены называются подобными, если,
записанные в стандартном виде, они одинаковы
или различаются лишь коэффициентами.
2
Пример 1.1) Одночлен -Зх у подобен
одночлену Ьх у, так как буквенные сомножители у
них одинаковые;
2 12
2) ab t подобен г b at;
3) 2х подобен Зле;
4) 51 подобен 137;
5) -7и х а подобен 2а и х ;
2 2
6) одночлен 2* i/ не подобен одночлену 2ху ,
так как буквенные сомножители у них разные
(они состоят из одних и тех же букв, но эти
буквы возведены в разные степени).
Рассмотрим сумму подобных слагаемых:
о 2 о 2 , 2
3* а - 2х а + ах .
Вынесем общий множитель за скобки:
А(3 - 2 + 1) - 2 А.
Эта операция называется приведением
подобных членов.
Пример 2.
1) 4t2y + 2ху2 - 3yt2 + у2х - t2y + 3i/2*.
2) 2 + Зх + 5х2 + 2ху - х - х2 + \ ху - 7 =
2 7
= 2л: + Ах + о*У ~" 5.
* В дальнейшем будем считать, что составляющие
любой многочлен одночлены уже приведены к
стандартному виду.
3. Сложение и вычитание многочленов.
Умножение многочленов
Многочлен, все члены которого являются
одночленами стандартного вида, называется
многочленом стандартного вида.
Сумму (разность) многочленов можно привести
к многочлену стандартного вида. Для этого нужно
раскрыть скобки и привести подобные члены.
При раскрытии скобок действует правило:
если перед скобкой стоит знак «+», то скобки
опускаются, а знаки, стоящие перед каждым
членом внутри скобок, остаются прежними.
Если же перед скобкой стоит знак «-», то этот

70
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
«минус» и скобки опускаются, знаки перед
всеми членами многочлена меняются на
противоположные.
Пример 1. (а2 + 15а + 14) - (а2 + 10а - 1) -
- а2 + 15а + 14 - а2 - 10а + 1 = 5а + 15.
Чтобы умножить многочлен на одночлен,
нужно каждый член многочлена умножить на
этот одночлен.
Пример 2.
1) 3x(2x2 - Зху + Ьу2) = б*3 - 9х2у + 1Ьху2;
2) -7а*(2а + 3* - at2 - 4*) = -14а2* - 21а*2 +
+ 7а2*3 + 28а*2 = -14а2* + 7а*2 + 7а2*3.
Чтобы умножить многочлен А на многочлен
В, нужно:
1) первый одночлен многочлена А умножить
на все члены многочлена В подряд и записать
результаты этого действия. Затем второй
одночлен многочлена А умножить на все члены В и
т.д.;
2) привести все подобные члены и записать
результат.
Пример 3.
(За3 - 2а2& + а&2)(2а2 - ab - 5&2) = 6а5
За4Ь-
- 15аУ -4а4&+2аУ + ЮаУ + 2аУ - aV -
- 5аЬ4 = 6а5 - 7а4& - llaV + 9а V - 5а&4.
4. Формулы сокращенного умножения
При возведении двучлена в степень,
умножении многочленов, разложении их на множители
и других тождественных преобразованиях
многочленов применяются специальные формулы,
которые называются формулами сокращенного
умножения.
1) (а + Ь)2 = а2 + 2аЬ + Ь2;
2) (а - Ъ)2 = а2 - 2а& + Ь2;
3) а2 - Ъ2 = (а - Ь){а + Ь);
4) (а + bf = а3 + За2Ь + За&2 + Ь3;
5) (а - Ь)3 = а3 - За2& + За&2 - Ь3;
6) а3 - Ь3 = (а - Ь)(а2 + аЬ + Ь2);
7) а3 + Ь3 = (а + Ь)(а2 - а& + &2);
8)* (а + Ь + с)2 = а2 + &2 + с2 + 2а& + 2ас + 2Ьс;
9)* (а + Ь)4 = а4 + 4а36 + 6aV + 4а&3 + &4;
10)* (а - Ь)4 = а4 - 4а3Ь + 6а V - 4ab3 + b4.
Устно эти формулы произносятся
следующим образом:
1) квадрат суммы двух чисел равен сумме
квадратов этих чисел, сложенной с их
удвоенным произведением;
3) разность квадратов двух чисел равна
произведению разности этих чисел на их сумму;
6) разность кубов двух чисел равна разности
этих чисел, умноженной на неполный квадрат
2 2
их суммы (выражение a + ab + b называется
неполным квадратом суммы двух чисел, а вы-
2 2
ражение a - ab + b —* неполным квадратом
разности).
Пример 1. Устно умножить 41 • 39.
41 • 39 - (40 + 1)(40 - 1) = 402 - I2 = 1599.
2
Пример 2. Устно вычислить 49 .
492 = (50 - I)2 - 502 - 2 • 50 + I2 - 2500 - 100 +
+ 1 = 2401.
Пример 3. Преобразовать выражение
(1 - а)(1 - а + а2)(1 + а + а2)(1 + а).
Произведение первой скобки на третью — это
произведение разности чисел 1 и а на неполный
квадрат их суммы, т. е. можно применить
формулу разности кубов (формула 6):
(l-a)(l+a + a2) = l3-a3.
Произведение четвертого сомножителя и
второго равно сумме кубов чисел 1 и а (формула 7).
Следовательно,
(1 - а)(1 + а + а2)(1 - а + а2)(1 + а) =
= (1-а3)(1+а3).
Произведение разности чисел 1 и а на их же
сумму равно разности квадратов этих чисел
(формула 3):
(1 - а3)(1 + а3) - 1 - (а3)2 = 1 - а6.
Пример 4. Доказать, что справедливо
равенство
а/7 + 473 + 77 - 4л/3 = 4.
Преобразуем подкоренные выражения,
используя формулы сокращенного умножения и
тождество (Та) = а при а > 0.
Итак, 7 + 4л/3 = 3 + 4л/3 + 4 -
= (73)2 + 2-2-лУз +22 = (73 +2)2.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
71
Аналогично, 7-4^3 = 4 - 4^3 +3 =
= 22 - 2 • 2 73 + (73 )2 = (2 - 73 )2.
Имеем: л/7 + 4^3 = 7(2 + 73)2 = 2 + 7з;
77 - 473 - 7(2 ~ 73)2 =2-73.
Следовательно,
77 + 47з + 77 - 47з = 7з+2 + 2-7з=4,
что и требовалось доказать.
Использование формул сокращенного
умножения — постоянная необходимость в
алгебраических преобразованиях, поэтому формулы
следует знать наизусть.
5. Разложение многочленов на множители
Разложить многочлен (алгебраическое
выражение) на множители значит представить его в
виде произведения двух (или более) других
многочленов. При этом используются формулы
сокращенного умножения и некоторые
специальные приемы разложения на множители.
Пример 1. 4 -р2 = 22 -р2 = (2 -р)(2 + р).
Пример 2. 9q2 - 64л:2 = (3q)2 - (8л:)2 =
= (3q - 8л:)(3д + 8л:).
Пример 3. 4л:2 + 4л: + 1 = (2л:)2 + 2 • 2л: • 1 + I2 =
= (2л: + 1)2.
Метод выделения полного квадрата
Пример 1.x +4. Выделим полный квадрат,
сделав тождественное преобразование —
прибавим и вычтем одно и то же выражение: 4х .
Имеем:
х + 4 = л: + 4л: + 4 - 4л: =
= (л:2)2 + 2 • 2л:2 + 22 - 4л:2 = (л:2 + 2)2 - 4л:2 =
= (л:2 + 2)2 - (2л:)2 = (л:2 + 2 - 2л:)(л:2 + 2 + 2л:).
Пример 2*. 1 + а + а . Заметим, что а =
= (а ) . Выделим полный квадрат — прибавим
и вычтем а . Имеем:
-1.4,8 -,4,8.4 4
1 + а +а = 1 + а + а + а -а =
- 1 + 2а4 + (а4)2 - а = (1 + а4)2 - а =
= (1+а4-а2)(1+а4 + а2).
Вторую скобку в полученном выражении при
необходимости также можно разложить на
множители:
1 + а + а = 1 + 2а2 + а - а = (1+ а2)2 - а =
= (1+а2-а)(1 + а2 + а).
Здесь также добавили и вычли одно и то же
2
выражение — а — выделив тем самым полный
квадрат суммы, а затем воспользовались
формулой сокращенного умножения (л: - у)(х + у) =
2 2
= х - у . Таким образом, конечный результат
можно записать в виде:
1 + а4+ а8= (1+а4 - а2)(1 + а2 - а)(1 + а2 + а).
Пример З.р-q, где р > 0, g > 0.
Это выражение можно разложить на
множители несколькими способами (эти разложения
не будут состоять из многочленов, но будут
алгебраическими выражениями).
а)р-д = (л/р)2-(7д)2 = (л/р - Jq)(Jp + 7g).
6)*p-9 = (Vp)3-(^)3 = (Vp-V^)(3Vp"2 +
в)*р - 9 = (ifp )4 - (4^ )4 - {{Mi )Y - « V5 )Y -
- ((4^)2 - (V?)2)((Vp)2 + (V5)2) - (Vp -Vg)x
Пример 4*. х10 - 10хьу* + 25i/16 - л:12 +
+ 4*V - 4i/16 - (х5)2 - 2 • 5» V + (5у8)2 - ((x6)2 -
- 2 • 2y V + (2y8)2 - (x5 - 5y8)2 - (x6 - 2y8)2 =
= (л:5 - by8 - x6 + 2у8)(л:5 - 5i/ + л: - 2y8) =
Метод группировки
2
Пример 1.3x -ах + Зх-а. Группируем
первый и третий члены многочлена: их общий
множитель Зл:, и второй и четвертый — их общий
множитель (-а). Имеем:
Зл:2 + Зл: - ах - а = Зл:(л: + 1) - а(х + 1) =
= (Зл: - а){х + 1).
Общий множитель (х + 1) также выносится
за скобки.
3 2 2 2 2 4
Пример 2.р х ~-2q х ~-2q р+р . Группируем
первый и четвертый члены (их общий множитель
3 2
р ) и второй и третий (общий множитель (~-2q )).
32. 4 о22 о2
рл: +р -2q х -2q р =
= р V + р) - 2д V + р) = (х2 + р)(р3 - 2(?2).

72
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Разложение квадратногб трехчлена на множители
ТЕОРЕМА
2
Если квадратное уравнение ах + Ьх + с = О
имеет действительные корни хг и х2, то
2
ах +Ъх + с = а(х - хЖл: - х2).
члена Р(х)9 а другой — F(x) — частным от
деления Р(л:) на Q(x).
Пример 1.2х - Ьх + 5л: - 2 =
= (л:2-Зл: + 2)(2л:2 + л:-1).
Заметим, что сумма степеней делителя и
частного равна степени делимого многочлена.
Пример 1. Разложить на множители выра- ТЕОРЕМА О ДЕЛЕНИИ МНОГОЧЛЕНОВ С ОСТАТКОМ
жение Зл: + Ьх - 2.
2
Решение. Найдем корни уравнения Зл: + Ьх -
- 2 = 0. Х) = 52-4-3-(-2) = 49;л:1>2= ~5у*в;
л^ = -2, л:2 = « . По теореме о разложении
квадратного трехчлена на множители имеем:
Зл:2 + Ьх - 2 = 3(л: + 2)(х - J ).
Пример 2*. Разложить на множители выра-
жение Зл: - 2а х + Зх а -2а .
Решение. Обозначим х = t, тогда л: = (л: ) = t
и многочлен примет вид: 3t + *(3а - 2а) - 2а .
Рассматривая это выражение как квадратный
трехчлен относительно *, найдем корни
соответствующего квадратного уравнения, то есть
уравнения З*2 + *(3а4 - 2а2) - 2а = 0.
А. 9 9
Дискриминант уравнения D = (За - 2а ) -
в 4. 2 2
-4*3* (-2а ) = (За + 2а ) , откуда корни
j. 22 ^ 4
* = 5 а и * — ~а •
Имеем:
2 2V
3fl
= (Зл:7 - 2а2)(л:7 + а4).
З*2 + *(3а4 - 2а2) - 2а6 = 3(t - | a2)(t + а4) =
6*. Делимость многочленов
от одной переменной. Теорема Безу
Делимость многочленов от одной переменной
Выражение вида
Р(х) = апхп + ап _ гхп " + ... + a^-ha0,
где ад * 0, ад _ v ..., а0 — произвольные
действительные числа, называется многочленом
степени п от переменной х.
Если многочлен Р(л:) можно представить в
виде произведения двух других многочленов Р(х) =
= Q(x)F(x), то один из этих двух многочленов,
например Q(x)9 называется делителем много-
Для любых двух многочленов Р(х) и Q(x)
существуют единственные многочлены F(x)
и R(x) такие, что выполняются следующие
условия:
1) Р(х) = Q(x) -F(x) + R(x);
2) степень многочлена R(x) меньше
степени многочлена-делителя.
Многочлен R(x) называется остатком от
деления многочлена Р(х) на Q(x).
Пример 2.
л:3 + Зл:2 - 16л: + 5 - (л: + 7)(л:2 - 4л: + 12) - 79.
В этом примере делителем является
многочлен первой степени Q(x) = х + 7. Остатком
является многочлен нулевой степени — число -79
(с точки зрения действий с многочленами,
любое действительное число — это многочлен
нулевой степени). Степень остатка на единицу
меньше, чем степень многочлена-делителя, что
согласуется с вышеприведенной теоремой.
Алгоритм деления многочленов «уголком»
При делении многочленов на практике
используют тот же алгоритм, что и при делении
натуральных чисел «уголком».
Рассмотрим конкретный пример деления
многочленов «уголком», а затем опишем
алгоритм этого деления.
Пример. Выполнить деление многочлена
Р(х) = х* - Зх3 + л:2 - Ьх + 4 на многочлен Q(x) =
- л:2 + л: + 1.
Решение.
х* - Зх3 + х2 - 5х + 4
— 4 , 3 , 2
X + X + X
л:2 + х + 1
х - 4л: + 4
- 4л:* - Ьх2
- 4л: - 4л: - 4л:
4л:* - х + 4
4x2+4x+j4
Таким образом,
-Ьх
л:4 - Зл:3 + л:2 - Ьх + 4 -

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
73
= (х2 + х + 1)(л:2 - 4л: + 4) --5л:.
Остатком от деления является многочлен
первой степени R(x) = -5л:.
Алгоритм деления «уголком»
1. Найти такой одночлен, который при
умножении на первый член многочлена-делителя
равен первому члену многочлена-делимого (в рас-
2Ч
смотренном примере это х ), затем каждый член
делителя умножают на найденный одночлен, а
сам одночлен записывают под чертой «уголка».
2. Результат умножения записывают под
многочленом-делимым, начиная со старшего члена
(в данном случае с х ).
Далее — провести черту и под ней записать
разность полученных многочленов (для
краткости записывают не все члены этой разности).
3. В результате под чертой получаем
многочлен, степень которого на единицу меньше
исходного. С ним повторяются операции,
описанные в п. 1 и п. 2.
4. Процесс заканчивают, когда под чертой
окажется многочлен, степень которого на
единицу меньше степени делителя. Этот многочлен
и является остатком от деления двух
многочленов. Многочлен, который получился под чертой
«уголка», является частным от деления
исходных многочленов.
Следствия из теоремы о делимости многочленов
Следствие 1 (теорема Безу). Если многочлен
Р(х) разделить на двучлен (л: - а), то остатком от
деления будет число, равное значению
многочлена Р(х) при х = а, т. е. Р(а):
Р(х) = (х - a)Q(x) + Р(а).
Пример 1. Найти остаток от деления
многочлена Р(х) = х - Зл: + 5л: - 7х + 11 на двучлен
jc-2.
Решение. Используя следствие 1 (теорему
Безу), получим:
Р(2) = 24 - 3 • 23 + 5 • 22 -7-2 + 11 = 16- 24 +
+ 20-14+11-9.
Следствие 2. Если число а является корнем
многочлена Р(х), то многочлен Р(х) делится на
двучлен (л: - а) нацело (т. е. остаток от деления
равен нулю).
Пример 2. Известно, что число 3 является
3 2
корнем многочлена Р(х) = х - 8л: + х + 42.
Найти остальные корни этого многочлена.
Решение. Разделим многочлен Р(х) на
двучлен л:- 3:
х3-8х2 + х + 42
— 3 0 2
х - Зх
-Ьх* + х
х-3
х - Ьх-
-5х2 + 15*
-14х + 42
-Ых + 42
•14
о
Таким образом, Р(х) = (х - 3) (х2 - 5л: - 14).
Чтобы найти оставшиеся корни многочлена
Р(лг), необходимо решить квадратное уравнение
2
х -5л: -14 = 0. Используя формулу корней,
находим х = 7 и х = -2.
Следствие 3» Если многочлен Р(х) с целыми
коэффициентами имеет целый корень, то этот
корень является делителем свободного члена.
Это следствие особенно важно на практике.
з
Пример 3. Решить уравнение х +л:-10 = 0.
Решение. Используя следствие 3, найдем
целый корень уравнения (если он существует!).
Для этого выпишем все делители свободного
члена уравнения: 1, -1, 2, -2, 5, -5, 10, -10.
Последовательно подставляя эти числа в исходное
уравнение, устанавливаем, что число 2 является
з
его корнем, ■к-ак как 2 + 2 - 10 = 0
з
Разделив теперь многочлен Р(л:) = х + х - 10
на двучлен х - 2, получим частное от деления —
2
многочлен Q(x) = х + 2л: + 5.
Уравнение Q(x) = 0 решений не имеет,
поскольку его дискриминант отрицателен.
Следовательно, исходное уравнение имеет
единственный действительный корень х = 2.
Алгебраические дроби
и действия с ними
1. Алгебраические выражения
Алгебраическим выражением называется
выражение, в котором числа и буквы соединены
четырьмя арифметическими действиями, а
также операциями возведения в целую степень и
извлечения арифметического корня.
Выражение, не содержащее операции
извлечения корня из переменной, называется
рациональным.

74
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Выражение, не содержащее операций
деления на переменную и извлечения корня,
называется целым.
Выражение, которое содержит деление на
переменную, называется дробным (или
алгебраической дробью).
Пример 1.
3 7 С —2
1) Выражение 13а • Ъ • к • Ь — целое;
2)
3)
/ 7 , Q5 За
л/ос + р - = нерациональное;
2с
2 3
+ Ъ • а - 4а& — дробное.
Ь + с
Выражения 1) и 3) являются также
рациональными.
Каждая буква, входящая в алгебраическое
выражение, может принимать произвольное
значение. Целое выражение имеет смысл для
любых значений входящих в него переменных.
Дробное алгебраическое выражение (или
содержащее корень) имеет смысл не для всех
значений переменных.
Пример 2.
1) г — имеет смысл при любых значениях
переменных кроме Ъ = О, так как деление на
нуль не определено;
2) *Ja - b — имеет смысл при любых
значениях переменных, удовлетворяющих условию
а - Ъ > О, так как арифметический квадратный
корень определен только для неотрицательных
чисел;
Ъ Г~2
3) - + ыЬ + с — имеет смысл при
одновременном выполнении двух условий:
f с*0,
1 Ъ2 + с > 0;
4) Ja + *fb + J а - Ъ — имеет смысл для
значений переменных, удовлетворяющих
(а>0,
системе: 1 Ь > 0,
[а-Ь>0;
5) J~-a + л/а — имеет смысл только при
а = 0, так как
f а>09
{ а< 0;
Пример 3. Преобразовать выражение
<=> а = 0.
Решение. Данное выражение имеет смысл,
если:
Г а- 1 >0,
\ 1-а>0,
[а-2>0.
Решение первых двух неравенств —
единственное число а = 1, но это число не
удовлетворяет третьему неравенству, поэтому данное
алгебраическое выражение не имеет смысла.
Преобразования производить нельзя, так как они
приведут к неверному результату.
Пример 4. Вычислить значение дроби
п - 1 1
-= при п = 1.
п - Зп + 2
Решение. Выражение имеет смысл, если
п2-Зи + 2*0.
2
Но при п = 1 выражение п - Зп + 2 = 0, т. е.
при я = 1 это выражение не имеет смысла.
Наиболее распространенная ошибка при
решении вышеприведенной задачи выглядит так:
не определив значений переменных, при
которых выражение имеет смысл, раскладывают
знаменатель данной дроби на множители:
п - Зп + 2 = (л - 1)(п - 2).
После чего производят сокращение
одинаковых сомножителей в числителе и знаменателе:
п - 1 = п - 1 = 1
п2-Зд + 2 (n-lKn-2) п-2'
Последнее выражение при п = 1 имеет
значение -1. Это грубо ошибочное решение.
2. Дробно-рациональные алгебраические
выражения
Алгебраической дробью называется
выражение вида д, где А и В — алгебраические
выражения.
Дробно-рациональным называется выражение
р
вида q , где Р и Q — алгебраические многочлены.
Дробно-рациональное выражение
представляет из себя частный случай алгебраической дроби.
Пример. 1) т
х2 + 1
2х4
Зу + 3
2 1
-б/ - Зу + ?
(Va - 1 +Vl - <*)• лА* - 2,
алгебраические дроби, являющиеся
дробно-рациональными выражениями;

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
75
2)
X
1 . (Л + Л) (Л - Л)
— ал-
гебраические дроби, не являющиеся
дробно-рациональными выражениями.
3. Умножение и деление
алгебраических дробей
Так как в числителе и знаменателе любой
алгебраической дроби стоят алгебраические
выражения, то выполнение арифметических
операций с ними весьма трудоемко. Поэтому прежде
чем приступать к выполнению действий с
алгебраическими дробями, следует:
1) разложить на множители числитель и
знаменатель каждой алгебраической дроби, с которой
проводится данная арифметическая операция;
2) выписать систему неравенств для значений
переменных, при которых дроби имеют смысл;
3) одинаковые сомножители в числителе и
знаменателе каждой дроби сократить.
Умножение алгебраических дробей
производится по тому же правилу, что и умножение
обыкновенных дробей:
В% В0
А1 'А2
вг*в2
'1 "г
Но перед тем как производить умножение
выражений (многочленов), стоящих в числителе
и знаменателе, необходимо одинаковые
сомножители, если они есть, сократить. Полученное
выражение можно оставить в виде дроби, где
числитель и знаменатель разложены на
множители, либо произвести умножение, что зависит
от конкретной задачи.
Пример 1. Выполнить умножение
х - 4 х
Зх(х - 2) 2 + х
Решение. Разложим числитель первой дроби
на множители, пользуясь формулой разности
квадратов:
1х~~-Ъ](х + 2) т х
BxtiL^Z) * 2 + х
Сх^И-2)' х
X
3
Целение алгебраических дробей сводится к
умножению:
Вл
Вл
АГ*2
Вг-А2
2 1
X — 1
Пример 2. —z
х + 2х + 4
х (1 - х)
*3-8
= (х - 1)(х + 1) 9 (х - 2)(х + 2х + 4) =
х + 2х + 4
-х\х - 1)
{х—Г)(х + 1)(х - 2)jxt-±-2*-+-*7 =
(х + 1)(х - 2)
Xx£-^*r-h-*)*2ix Г)
4. Сложение (вычитание)
алгебраических дробей
Сложение (вычитание) алгебраических
дробей с одинаковыми знаменателями
выполняется аналогично сложению (вычитанию)
обыкновенных дробей с одинаковыми знаменателями:
Aj А2 >Ц 4- А2
В * В
В
При сложении (вычитании) алгебраических
дробей с разными знаменателями нужно
привести их к общему знаменателю.
Алгоритм нахождения общего знаменателя
алгебраических дробей аналогичен
соответствующему алгоритму для обыкновенных дробей с
той разницей, что в знаменателях
алгебраических дробей стоят не числа, а алгебраические
выражения:
1) разложить знаменатель каждой
алгебраической дроби на возможно большее количество
многочленов-сомножителей;
2) в общий знаменатель вынести все
различные сомножители данных знаменателей с
наибольшим показателем степени.
Пример 1. Найти общий знаменатель
алгебраических дробей.
. 2 .
14 х + а 1
*2-а2И3*-3<Г
2 2
Имеем: х -а = (х - а)(х + а); Зл: - За =
= 3(х - а). Значит, общий знаменатель будет
иметь вид: 3(л: - а)(х + а).
пч 5 Чх-р
4) 2 3И 4
(х + р) (х - 2) (х + р) (* - 2)
Общий знаменатель: (х + р) (лг - 2) .
л - 7а 2х + 1
3)
и
3(* " 1)(*2 + а2) 5(* - 1)3(* - р)
3 2 2
Общий знаменатель: 15(лг - 1) (х + а )(х -р).

76
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
4)
(х3 - 1)(х2 + 2)
и
Зх + 1
7(х - 1)(х + 2)
4 - х
3(х + х + 1)
Знаменатель первой дроби можно разложить
на множители:
(я3 - 1)(х2 + 2) - (я - 1)(х2 + х + 1)(х2 + 2).
Наименьший общий знаменатель:
3 • 7 • (я - 1)(х2 + х + 1)(х2 + 2).
Алгоритм сложения (вычитания)
дробно-рациональных выражений
1) Разложить на множители числитель и
знаменатель каждой алгебраической дроби.
2) Одинаковые сомножители в числителе и
знаменателе каждой дроби сократить.
3) Найти и записать общий знаменатель
дробей.
4 4) Найти и записать дополнительные
множители для каждой алгебраической дроби.
5) Записать сумму (разность) произведений
числителей и дополнительных множителей,
учитывая знаки.
6) Упростить (если возможно) полученную
дробь.
В результате мы получим алгебраическую
дробь, у которой числитель и знаменатель
разложены на множители, причем у числителя и
знаменателя общих множителей нет. Ее можно
оставить в таком виде либо произвести
умножение и привести подобные члены. Это зависит от
конкретной задачи.
Пример 2. Выполнить действия:
х2-4 * + 2'
Решение.
±_+^L_ = I +
_ 4 х + 2 (* ~ 2)(* + 2)
^-2
х
1 + х
- 2х = (х - 1)
х Л- 2 ~" (х - 2)(х + 2) " (х - 2)(х + 2)
Пример 3.
х + а
х - а
х + а
2 2
_ *(х + fl) + Д(х ~ Д) х + ад: + ах - а
(х - а)(х + а)
х" + 2ах - а
(х - а)(х + а)
2
"J
2
а
шы»ч* *. 2 i 2 2 -
(а - Ь) а - Ъ
а + Ь а - b
_ а + ЗЬ а - ЗЬ
(а - Ь)2 <а " «<« +
+ аЬ + ЗаЬ + ЗЬ2 + а - аЪ
(а - Ь)2(а + Ь)
2а + 6Ь2
Ь)
- ЗаЬ + ЗЬ2
(а - Ь) (а + Ь)
Пример 5. Преобразовать выражение
Ь + 2х
3d - Ь
Ъ* - dx
ЗЬ - Зх 2Ь - 2d
(х - а)(х + а)
Ь - bd + dx - Ьх
Знаменатели первых двух дробей легко
раскладываются на множители. Попробуем
разложить на множители знаменатель третьей дроби:
b2-bd + dx-bx = Ь(Ь -d)- х(Ь - d) =
= (Ь - d)(b - х).
Имеем:
3(6 -х) ^
3d - Ь Ь2 - dx =
3(Ь - х) 2(Ь - d) (6 - d)(6 - х)
_2(Ь - d)(b + 2х)-3(Ь - x)(3d - Ь) + 6(Ь2 - dx)
6(Ь - х)(Ь - d)
= lib2 + bx - llbd - dx
6(Ь - х)(Ь - d)
5*. Действия с алгебраическими дробями,
содержащими знак радикала
При выполнении действий с
алгебраическими дробями, содержащими знак радикала,
существенно помогает прием (если его удается
применить) введения новых переменных,
которые превратят алгебраическую дробь в
дробно-рациональное выражение.
Пример. Преобразовать выражение
а - Jab
. (Ma + *Jab + i/b)(ifa - Mob + Mb)
*J7b-b

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
77
Решение. Обозначим s*Ja = х, sJb = у, тогда
\[а = х ;i/b = у ; Ja = х ; Jh =у ; Jab = х у ;
4/~3 6 8,8
Vfl =x;a = x;b = y.
Учитывая это, имеем:
(х + у)2 + (х - у)2 .
8 4 4
Л - Л I/
. (* + *|/ + У )(х ~ ху + у ) =
6 2 8
X у - У
2(х2 + у2) . (х2 + ху + у2)(х2 - ху Л- у2) =
4, 4 4 * 2, 6 6Ч
х (х - I/ ) У (х - у )
2(УЧ^Д)
х4(х*-к#Ь(х2 -1/ )
2 2 2 2
. (х + ху + у )(х - ху + у ) =
2, 3 Зч, 3 , Зч
у (л - у )(х + у )
4, 2 2Ч
^ (Л - у )
у2(х - у)ГЯ*-^~-*у-^-#Ь(* + у)Т^-—*y^Mul
4, 2 2 * 2, 2 2Л
х (х - у ) у (х - у )
_ 2(х^А2 _2у2 _2УЬ
х40с^6 х4 JS *
Иногда в алгебраической дроби, содержащей
радикалы, приходится вводить не две, а три,
четыре новых переменных — все это лишь затем,
чтобы превратить алгебраическую дробь в
дробно-рациональное выражение, обращаться с
которым значительно проще.
УРАВНЕНИЯ
И СИСТЕМЫ УРАВНЕНИЙ
Дробно-рациональные уравнения
Рациональным алгебраическим уравнением
Р(х) Л ш ч
уравнение вида ^^ = 0, где Р(х) и
называется
Q(x) — многочлены.
Выражение т^-т — имеет смысл только в
ЧуХ)
том случае, если выполняется условие Q(x) * 0.
Значит, рациональное уравнение
Г Р(х) - 0,
имеет решение при условии i q, v q
P(x)
Q(x)
= 0
Пример 1. Решить уравнение:
3 + x = 5x
2x - 4 x - 2
Решение.
3 + л:
5л:
3
4Ф
х- 2
3
2(х - 2) л: - 2 4
2(3 + х) - 20х + 3(х - 2) _„ _ -15л:
4(х - 2) ~ " 4(х-2)
Ответ: 0.
= 0 <=>
= 0<=>
Пример 2. Решить уравнение
2х + 5 2 Зх
л:
2 к
л: -f л:
Решение.
2х + 5
х(х + 1)
2л: + 5 - 2(х + 1) - Зл:
х + 1
х + 1
2
л:
2
= 0.
Зл:
х + 1
х(х + 1)
л -Зл: +3
= 0<=> —: гтт =0<=>
х(х + 1)
2
х -
х(х
zi_=0<=>{*2-i = 0;
+ 1) I х(х+1)*0;
<=>
ГГх.= 1,
J L«—1;
I **0,
I л:*-1;
Ответ: 1.
<=> х= 1.
Пример 3. Решить уравнение:
3,2 1
2 " + 2
х^ - 2х + 1 1 - хг
х + 1
Решение.
3
(х - I)2
+
2 1_
(1 - Х)(1 + X) х + 1
= 0
2 2
Замечание. (л: - 1) = (1 - х) .
Получим уравнение:
-х + Зх + 4
(1 - х)2(х + 1)
2
= 0 <=>
f х - Зх - 4 = 0,
1(1-х)2(*+1)*0;
х - Зх - 4
(1 - х)2(х + 1)
Г*--1,
U = 4;
= 0<=>
х*1,
х*-1;
<=> х = 4.
Ответ: 4.

78
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пример 4*. Решить уравнение:
1
Решение.
х(х + 2)
1
(х + 1)
1
12*
-п-°-
х + 2х х + 2х + 1
Применим метод замены переменной. Пусть
у = х + 2л:, тогда исходное уравнение примет
вид:
12(у + 1) Д2у. У(У + 1)
1
У У + 1
12(у + 1) - 12у
12у(у + 1)
*fc±i}_o <=>
У2 + У - 12 =0<=>| И + г/-12 = 0,
12у(у + 1) 1 i/(i/+l)^0;
Откуда
f х2 + 2* = -4,
t*2 + 2x=3.
Первое уравнение л: 4- 2л: 4- 4 = 0 не имеет
решения, так как D = -12 < 0.
Решим второе уравнение: х + 2х - 3 = 0 <=>
Ответ: -3; 1.
Системы уравнений и методы
их решения
1. Графический способ решения
систем уравнений
Система уравнений состоит из двух или более
алгебраических уравнений.
Решением системы называется такой набор
значений переменных, который при
подстановке обращает каждое уравнение системы в
числовое или буквенное тождество.
Решить систему — значит найти все ее
решения или доказать, что их нет.
Пример 1.
У = х,
х + у = 2.
Решение. Каждое уравнение системы задает
линейную функцию. Построим графики этих
уравнений в одной системе координат (рис. 42).
Координаты точки пересечения графиков
обращают оба уравнения системы в верные
равенства. Решением системы является пара
значений переменных: х = 1, у = 1. Ответ можно
записать так: (1; 1).
Графический способ решения систем
уравнений состоит в следующем:
1) строятся графики каждого уравнения
системы;
2) определяются точки пересечения графиков;
3) записывается ответ: координаты точек
пересечения построенных графиков.
Пример 2.
(У = х,
\у-х3 = 0,
[х = -у.
Решение. Графики первого и третьего
уравнений — прямые; график второго уравнения —
кубическая парабола (рис. 43). Из трех точек
пересечения только одна является общей для всех
графиков уравнений системы.
Ответ: (0; 0).
Графический способ решения систем
уравнений в большинстве случаев не дает точного
решения системы, однако он может быть полезен
для наглядной иллюстрации рассуждений.
Пример 3.
f 2 , 2 л
) х +у =4,
U = 3.
Решение. Графиком первого уравнения
системы является окружность с центром в начале
координат и радиусом 2. График второго уравне-
Рис. 42
Рис. 43

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
79
ния — прямая, параллельная оси Ох9
проходящая через точку (0; 3) (рис. 44).
Ответ: нет решений.
2. Решение систем линейных уравнений
Системой двух линейных уравнений с двумя
неизвестными называется система вида:
Г alx-¥bly = cv
| а2х + Ъ2у = с2,
где av а2, bv Ъ2> cv с2 — коэффициенты, причем
хотя бы один из коэффициентов ах или Ъх не
равен нулю и хотя бы один из коэффициентов а2 и
Ъ2 не равен нулю.
График каждого из уравнений системы — это
прямая линия на координатной плоскости. Две
прямые на плоскости либо пересекаются в одной
точке, либо параллельны, либо совпадают.
Следовательно, система двух линейных
уравнений с двумя неизвестными:
1) либо имеет единственное решение: пару
значений переменных, являющихся
координатами точки пересечения прямых (это возможно
тогда и только тогда, когда выполнено условие
ai&2 ~ а2&1 * 0) (Рис- 45, а);
2) либо не имеет решений; прямые
параллельны (существует такое число ft, что
одновременно выполняются условия: а2 = kav Ъ2 == kbv
с2 * ftcj) (рис. 45, б);
3) либо имеет бесконечно много решений;
прямые совпадают; любое решение есть пара
чисел (х; у), удовлетворяющая уравнению прямой
(это возможно, если существует такое число ft,«
что одновременно выполнены условия: а2 = kav
Ъ2 = kbv с2 = kcv т. е. все коэффициенты
пропорциональны) (рис. 45, в).
Практически системы уравнений решаются
аналитическими способами при помощи
тождественных преобразований уравнений, входящих
в систему.
Рассмотрим подробнее различные методы
решения систем уравнений.
3. Метод подстановки
Пример I.
f 2 л. 3 к
}зд;-2у = 1.
Решение. Из первого уравнения выразим х
через у:
2 с 3 3/е 3 ч
3* = 5~4У ^ Х= 2(5~ 4У)'
Подставив полученное выражение во второе
уравнение системы, получим уравнение с одним
неизвестным:
3-|-(5-|i/)-2i/ = l<=>
^2 '5~~2 -1У-2У=1<*У = *-
Подставив это число в выражение
получим: х = 3.
Ответ: (3; 4).
Пример 2.
3/к 3 ч
*-у = 5,
х + ху + 3 = 0.
Ук
f у = з
iL^ + H-4
Ч \
—\ ' ) ш-
0 1 / х
У
Уо
/ 0
. агх + Ьгу - сг
/|\
i \
а2х + Ь2у = с2
а)
б)
в)
Рис.44
Рис. 45

80
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Решение. Выразим из первого уравнения у
через х:
У = *-5.
Полученное выражение подставим во второе
уравнение системы:
x2 + x(x-5) + 3 = 0 <=> 2x2-5x + 3 = 0<=>
х 2
Тогда при jc = 1,i/=1-5 = -4, а при х = ^
находим У = ~2-
3 7
Ответ: (1;-4), (^-«р-
Пример, 3.
*'i/-10i/ = -8,
2
I х -у=1.
Решение. Выразим из второго уравнения у
через х:
1/ = * -1.
Подставив в первое уравнение, получим:
х\х2 - 1) - 10(х2 - 1) - -8 « я4 - Их2 + 18 - 0.
Это стандартное биквадратное уравнение.
2
Обозначим t = х . Тогда
Л2
m + i8 = o «=>
L*-2.
V = 9,
_*2 = 2;
"х = 3,
* = -3,
*= 72,
L* = -72.
Но I/ = х2 - 1, тогда при х = J2 и д: = -72,
у = 2-1 = 1, а при х = 3 и при л: = -3, i/ =
= 9-1 = 8.
Ответ: (72 ; 1), (-72 ; 1), (3;8), (-3; 8).
Алгоритм решения систем уравнений методом
подстановки
1) Из одного уравнения системы одна
переменная выражается через другую.
2) Полученное выражение подставляется во
второе уравнение системы.
3) Решается полученное после подстановки
уравнение.
4) Полученное решение подставляется в
выражение из пункта 1).
5) Если при решении последнего уравнения
получается тождество 0 = 0, то это означает, что
исходная система имеет бесконечно много
решений вида (х; у), каждое из которых
удовлетворяет первому уравнению системы. Если же при
тождественных преобразованиях последнего
уравнения получится неверное числовое равенство,
то система решений не имеет.
4. Метод сложения
Пример 2.
f 2х + Ъу = 4,
I -3* - 2у = 5.
Решение. Домножим первое уравнение
системы на 3, а второе — на 2. Сложим
получившиеся уравнения почленно и запишем результат
вместо второго уравнения системы.
2х + Ъу = 4
-Зх - 2у = 5
хЗ
х2
, 6*+15i/=12
-6*- 4у=10
0* х -hlli/ = 22
f 2х + by = 4, f 2х + 5 • 2 = 4, f * = - 3,
I Hi/= 22; ^11/ = 2; *Mi/ = 2.
Ответ: (-3; 2).
Числа, на которые домножают уравнения
перед сложением, выбираются так, чтобы при
суммировании коэффициент перед одной из
переменных стал равен нулю.
В результате преобразований уравнений
системы и замены одного из уравнений результатом
суммирования других получены равносильные
системы.
Две системы называются равносильными,
если каждое решение одной системы является
решением другой системы, и наоборот.
Вопрос о равносильных преобразованиях
систем — достаточно сложен и в данном пособии
обсуждаться не будет. Перечислим лишь
несколько простейших преобразований,
приводящих к системам, равносильным заданной.
1) Если одно или несколько уравнений
системы заменяются равносильными уравнениями,
то полученная система уравнений равносильна
исходной.
2) Если два или более уравнений системы
складываются и результат записывается вместо
одного из использованных в этой операции
уравнений, то получается система, равносильная
исходной.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
81
3) Если одно из уравнений системы
равносильно совокупности двух уравнений, то
исходная система равносильна совокупности двух
систем. Если Р(х, у) = 0 <=>
ГРг(х9у)-0,
[р2(х,1/) = 0,
то
1Р(х,у) = 0,
I Q(*. У) = 0;
Рг(х, у) - 0,
Q(x, у) = 0;
[ Р2(х, у) = 0,
Q(x, у) = 0.
Пример 2*.
Г х + Зу + 4г = 6,
J Зх - 5у - 22 = 4,
[ -5* + 2у + 52 = 3.
х(-3) |
х5
Решение. Первое уравнение системы
умножим на число (-3), сложим со вторым и результат
сложения запишем на месте второго уравнения.
Затем все то же первое уравнение умножим
на 5, сложим с третьим и результат сложения
запишем на месте третьего уравнения (числа, на
которые производилось умножение,
записываются через вертикальную черту рядом с
уравнением). В итоге получим систему, равносильную
данной.
Г х + Зу + 42 = 6,
J -14i/ - 142 = - 14, <=>
|l7i/ + 252 = 33;
(х + Зу + 42 = 6,
y + 2 = l, | x(-17)
17y + 252 = 33.
В полученной системе два последних
уравнения содержат только два неизвестных, так как
числа, на которые домножалось первое
уравнение, подобраны таким образом, чтобы при
суммировании коэффициент при х стал равен нулю.
Действуя аналогично, умножим второе
уравнение системы на (-17), сложим с третьим
уравнением и результат запишем на месте третьего
уравнения. Получим равносильную систему:
(х + Зу + 42 = 6,
Z/ + 2 = l,
82 = 16.
Из последнего уравнения: 2 = 2. Подставляя
это значение г во второе уравнение, найдем, что
у = -1; подставляя найденные значения у и г в
первое уравнение, найдем: х = 1.
Ответ:(1;-1;2).
Изложенный метод называется методом
Гаусса решения систем линейных уравнений или
методом последовательного исключения неизвестных.
5*. Метод введения новой переменной
При решении систем нелинейных уравнений
как правило применяются различные
комбинации нескольких методов решения систем.
Пример 1.
х 16
ху-~у=Т>
ху
у =2
х 2
Решение. Отметим, что выражения,
объединенные в систему, имеют смысл лишь при
выполнении условий:
f х*0,
\у*о.
Обозначим t = ху; г = - ; тогда - = - . Введя
у X Z
новые переменные, получим систему уравнений:
16
3 '
9
*-2 =
'-I-2-
16
Из первого уравнения: t = г + -г-. Подставим
это выражение во второе уравнение,
преобразуем его, проведя тождественные преобразования,
и решим.
_, 16 1 9
*+у-; = 2
1
6г
&
2г.
е
1 , 16 9 л
2 - ; + т"2 = 0<=>
6г - 6 + 32г - 272 л
<=> — =0»
,1б22 +
I 2*0;
6г
Ьг - 6 = 0,
г=3»
2 = -;
2*
гр . 16 2 . 2 , 16 л
Так как t = г + -=-, то при 2 = 5 > * = о +"о" = ",
3 , 3 ^ 16 23 „
а при 2 = ""о'2 Т =7Г# Получаем Две
системы:
2= -
3 ' либо ^
t = 6,
* = "2'
Г 6 *

82
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Возвращаясь к начальным обозначениям,
получим:
f - = --
либо < у
I 23
Выражая в этих системах х через у из
первого уравнения и подставляя во второе, будем
иметь:
У 3'
ху = 6;
х =
2 2 а
ЪУ =6;
либо <
х = ~2у>
3 2 23
Отметим, что второе уравнение второй
системы не имеет решений, поскольку слева от знака
равенства стоит отрицательное число, а справа —
положительное. Следовательно, вторая система
не имеет решений. Решая первую, получим
У =<Г6 = 9Ч*/ = -3.
При I/ = 3, х = 2, а при у = -3, х = -2.
Ответ: (2; 3), (-2; -3).
Пример 2.
х
У
у = 5
2 2 с
I * -# =5.
Решение. Первое выражение имеет смысл лишь
при выполнении условий:
Рассмотрим сначала только первое уравнение
системы. Обозначим t = -, тогда \ = - и урав-
нение примет вид:
, 1 5
|б*2-
1**0;
- 5* - 6 = О,
3
2*
2
3*
Возвращаясь к первоначальным
обозначениям, получим две системы уравнений:
х
У
3
2'
2 2 е
* -у =5;
х
У
2
2 2 с
х -у = 5;
1 f3 Y* 2 -
"в"'
Li(-f»rv-
Вторая из полученных систем решений не
имеет, а решая первую, будем иметь:
3 Г 3
2 4 е
» =5'5;
ГУ = 2,
Ответ: (3; 2), (-3; -2).
Преобразования систем совершаются с целью
упростить систему так, чтобы легко можно
было воспользоваться тем или другим методом
решения. Еще раз перечислим основные
преобразования:
1) тождественно преобразовав каждое из
уравнений системы, выразить какую-либо
комбинацию неизвестных из одного уравнения и
подставить во второе;
2) умножить одно уравнение системы на
число kv другое на число k2 и сложить;
3) разделить одно уравнение системы на
другое;
4) ввести новые переменные.
Пример 3.
} х-у = 19
13 3 „
\ х -у = 7.
Решение. Преобразуем второе уравнение
системы, воспользовавшись формулой
сокращенного умножения:
х3 - у3 = (х - у)(х2 + ху + у2).
Из первого уравнения системы х - у = 1;
подставим 1 во второе уравнение. Запишем
получившуюся систему:
} х-у = 1,
12, , 2 „
I х + ху + у = 7.
К этой системе уже вполне применим метод —
выразить одно неизвестное из первого
уравнения системы и подставить во второе:
f х = у + 1,
I (I/ -h l)2 -h (i/ Ч-1)1/ + i/2 = 7; ^
Г*-р+1,
li/2 + i/-2 = <i;
[ х--2 + 1,
L 5/ = —2;
I f *=1 + 1,
Lu = i.
Ответ: (-1;-2), (2; 1).

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
83
Пример 4.
|*4 + И = 82,
I ху = 3.
Решение. Преобразуем первое уравнение
системы, выделив полный квадрат:
4, 4 4 , 0 2 2 , 4 0 22
х +у = х + 2х у +у -2х у =
t 2 , 2Ч2 о 2 2
= (х +у ) -2х у .
2 2 2
Но х i/ = (ху) и, используя второе уравнение
системы, приведем первое к виду:
(х2 + у2)2 - 2 • З2 = 82 <=> (х2 + i/2)2 = ЮО <=>
Гх2 + 1/2 = 10,
Lx2 + i/2 = -io.
Второе уравнение этой системы не имеет
решений, следовательно, имеем единственную
систему:
j*2 + i/2 = 10,
I ху = 3.
Вновь выделим полный квадрат в первом
уравнении и используем второе:
х + у2 = х + 2*1/ + i/2 - 2*1/ - (л: + у)2 - 2 • 3.
Получим две системы:
f х + i/ = 4, J х + i/ = -4,
by-8, либ01^ = 3.
К каждой из полученных систем применим
первый метод — выразить одно неизвестное
через другое из первого уравнения и подставить во
второе. Проделав это (либо использовав теорему,
обратную теореме Виета) получим результат.
Ответ: (3; 1), (1; 3), (-3; -1), (-1; -3).
Пример 5.
I х у + ху =10,
2,2
х +у
5.
Решение. Первое уравнение системы
разделим на второе уравнение, получим:
ху(х2 + у2) = 10
2 _l 2 5 *
X + у
Откуда ху = 2. Следовательно, имеем систему:
ху = 2,
I х Л-у = 5; I
f ху = 2,
1(* + */)2 =
(х + у) -2*1/= 5;
Со вторым уравнением здесь проведено то же
самое преобразование, что и в предыдущем
примере — выделение полного квадрата и
использование первого уравнения ху = 2. В итоге
получим две системы, подобные которым
рассматривались выше:
f ху = 2, \ ху = 2,
1х + у = 3, либ0Ь + у = -3.
Решив эти системы, придем к результату.
Ответ: (1; 2), (2; 1), (-1; -2), (-2; -1).
Пример 6.
fx2 + xy + 2y2 = 37,
1 2х2 + 2*1/ + i/2 = 26.
Решение. Умножим первое уравнение на (-2)
и сложим со вторым:
-2(х2 + ху + 2j/2) + 2х2 + 2xj/ + у2 = (-2) • 37 + 26 <=>
Откуда получим две системы, решение
которых не представляет труда:
fy = 4, /У = -4,
"< 9 9 ЛИОО "So о
I х2 + ху + 2у2 - 37, I jc2 + ху + 2yz = 37.
Ответ: (1; 4), (-5; 4), (5; -4), (-1; -4).
Пример 7.
j x + i/ + ху = 5,
I 2 2
I X -hi/ + xy = 7.
Решение. Преобразуем второе уравнение
системы, выделив полный квадрат:
х2 + у2 + ху = х + i/2 + 2*1/ - xi/ = (х + i/)2 - xi/.
тт f х + у + ху = 5,
Имеем: < 9
I (х + z/Г - *у = 7.
Обозначим * = x + y,z = xy. Тогда
I *2-z = 7, ^ I *2 -(5 -t) = 7.
Решая эту систему и возвращаясь к прежним
неизвестным, получим:
f х + у = 3, л J х + у = -4,
\ху = 2, либоЬу = 9.
Ответ: (2; 1), (1; 2).
Уравнение, содержащее переменную
под знаком модуля
Модулем числа х называется само это число,
если оно неотрицательно, либо число -х, если
число х отрицательно. Обозначение: |х|.

84
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Формальная запись этого определения такова:
. , _ Г л: при л: > О,
1*'"~|_-*прих<0.
Примеры. 1) |0,1| = 0,1, так как 0,1 > 0;
2) |-3| = -(-3) = 3, так как -3 < 0;
3) |0| = 0, так как 0 > 0.
При решении уравнений, содержащих
переменную под знаком модуля, используется
определение модуля.
Пример 1. Решить уравнение \х - 1| = -2х.
Решение. По определению модуля:
. , Г х- 1, если х- 1 > 0, т. е. х > 1;
I* " 1' ~ \_-х + 1» если х - К 0, т. е. х < 1.
Говорят, что выражение под модулем меняет
свой знак в точке х = 1, поэтому все множество
чисел разбивается на два числовых промежутка.
а) При х > 1 исходное уравнение принимает
вид:
х- 1 = -2х <=> х + 2х = \ <^> *=з*
Так как « < 1> то это решение не
принадлежит рассматриваемому промежутку, т. е. не
является корнем первоначального уравнения.
б) При х < 1 исходное уравнение принимает
вид:
-х+1 = -2л: <=> -х + 2л: = -1 <=> х = -1.
Поскольку -1 < 1, то найденное решение
принадлежит рассматриваемому промежутку и,
значит, является корнем исходного уравнения.
Ответ: -1.
Пример 2. Решить уравнение
|х + 1| + |2*-6| = 4 + х.
Решение. Найдем точки, в которых
выражения под знаком модуля меняют свой знак.
если х + 1 > 0, т. е. х > -1,
если х + 1 < 0, т. е. х < - 1;
- 6, если х > 3,
если х < 3.
Первое выражение меняет знак в точке х = -1,
второе — в точке х = 3. Поэтому числовая
прямая разобьется на три области.
а) При х < -1 имеем \х + 1| = -х - 1 и \2х - 6| =
= -2х + 6. Исходное уравнение принимает вид:
-х - 1 - 2х + 6 = 4 + х.
. . Гх+1,е(
|2ж-6| = |__2лг + 6)|
Решая его, получим х = т . Так как -г > - 1,
то найденное решение не является корнем
исходного уравнения.
б)При-1<х<3имеем\х + 1| = х + 1; \2х-6| =
= ~-2х + 6. Уравнение примет вид:
х+1-2л: + 6 = 4 + л: <=» х=*.
Поскольку -I < 5 < 3, то полученное
решение является корнем исходного уравнения.
в) При х > 3 имеем \х + 1| = х + 1; |2л: - 6| =
= 2х- 6.
Имеем:
х+1 + 2л:-6 = 4 + л: <=> л: = к .
Так как ~ > 3, то полученное решение
является корнем исходного уравнения.
Ответ: ^; ^.
Пример 3*. Решить уравнение
\х2 - х - 2| = х + 2.
Решение. Чтобы узнать, в каких точках
выражение под знаком модуля меняет знак, решим
квадратное уравнение:
«•-.-«-o-f;:;1-
Построив схематично график параболы
(рис. 46), легко определить, что х - х - 2 > 0
при х е (-оо; -1] и [2; оо) и х2 - л: - 2 < 0 при
* 6 (-1;2).
а) При х е (~оо; - 1] и [2; оо) имеем:
\х - х-2\ = х - х-2.
Исходное уравнение примет вид:
х2-х-2 = х + 2 <=> x2-2x-4 = 0«=>
JjC-1+л/б,
L*-l- 75.
Рис. 46

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
85
Так как 1 + 75 > 2, а 1 - УВ < - 1, что легко
показать, то оба эти числа принадлежат
объединению промежутков. Значит, оба они являются
корнями первоначального уравнения.
б) При - 1 < х < 2 имеем:
\х2 - х - 2| - -(я2 -x-2) = -x2 + x + 2h
уравнение примет вид: -х +х + 2 = л: + 2<=»л: = 0.
Так как число 0 е (-1; 2), то оно является
корнем исходного уравнения.
Ответ: 1 - Jb , 0, 1 + Jb .
Иррациональные уравнения
1. Уравнения, содержащие один знак
радикала второй степени
Возведение обеих частей уравнения в степень
При возведении обеих частей уравнения в
четную степень (в частности, в квадрат),
получается уравнение, неравносильное исходному.
Кроме корней исходного уравнения могут
появиться посторонние корни, т. е. числа,
являющиеся решениями возведенного в четную
степень уравнения, но не являющиеся корнями
исходного уравнения.
Избавиться от посторонних корней помогает
непосредственная проверка полученных корней
в исходном уравнении, т. е. корни поочередно
подставляют в начальное уравнение и
проверяют, верное ли получается числовое равенство.
Пример 1. Решить уравнение Jx -\- 2 = х.
Решение. Возведем обе части уравнения в
квадрат. Имеем:
(Jx + 2) = х2 <=> х + 2 = л:2 <=>
о x2-x-2 = 0~[XxZ~2h
Проверка. При х = -1 Jx + 2 = J-1 + 2 =
= 1, но 1 * -1, следовательно, корень х = - 1 —
посторонний.
При х = 2 Jx Л- 2 = л/2 + 2 = 2. Так как
2 = 2, то проверяемое число действительно
является корнем исходного уравнения.
Ответ: 2.
Равенство нулю произведения (частного) двух
выражений
Произведение двух выражений равно нулю,
если хотя бы одно из выражений равно нулю, а
другое при этом имеет смысл.
Формально это записывается так:
f А(*) = 0,
I х е ЩВ);
А(х)-В(х) = 0<*
f В(х) = О,
х е D(A).
Частное от деление двух выражений равно
нулю, если числитель выражения равен нулю, а
знаменатель не равен нулю и имеет смысл
(иногда говорят — определен).
Формальная запись:
[А(*) = 0,
^§-0« \В(х)*0,
В{х) [ х е D(B).
Пример 2. Решить уравнение
(х2-4)- Jx + 1 =0.
Решение. Воспользуемся первым
утверждением:
(x2-4)-Jx + 1 = 0 <=>
Г *-2 = 0,
I х + 1>0,
f х + 2 = 0,
I х+1>0,
|*2-4 = 0,
I х -hi > 0,
L х+1=0.
Г* = 2,
L* = -i.
L х + 1 = 0.
Ответ: 2; -1.
Метод введения новой переменной
Пример 3. Решить уравнение х - Jx + 1 = 5.
Решение. Обозначим t = Jx + 1 . Заметим,
что: a) t > 0 по определению арифметического
2 2
корня; б) t =х + 1, т. е. х = t -1.
Уравнение примет вид:
*2-1-* = 5 <=> t2-t-6 <=> [Jl?2
Корень * = - 2 не удовлетворяет условию (а),
следовательно, не является корнем исходного
уравнения.
Рассмотрим t = 3, откуда Jx + 1 = 3 или,
после возведения последнего уравнения в
квадрат, *+1 = 9<=>х = 8.
Мы возводили обе части уравнения Jx 4- 1=3
в квадрат, следовательно, -могли появиться
посторонние корни, и формально необходима
проверка.
Следующее утверждение позволяет во
многих случаях обходится без формальной провер-

86
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
ки корней, полученных после возведения обеих
частей уравнения в квадрат:
I g(x) > 0.
g(x)
2. Уравнения, содержащие два (три)
знака радикала второй степени
Возведение в квадрат обеих частей уравнения
При непосредственном возведении в квадрат
обеих частей уравнения уравнение должно быть
сначала преобразовано так, чтобы в одной части
стояли только радикалы, а в другой —
остальные члены исходного уравнения. Так
поступают, если радикалов в уравнении два. Если же их
три, то два из них оставляют в одной части
уравнения, а третий переносят в другую. Затем обе
части уравнения возводятся в квадрат и
проводятся необходимые преобразования (приведение
подобных и т. п.). Далее все члены уравнения,
не содержащие радикалов, снова переносятся в
одну сторону уравнения, а оставшийся радикал
(теперь он будет только один!) — в другую.
Полученное уравнение вновь возводят в квадрат, и
в итоге получается уравнение, не содержащее
радикалов.
Пример 1. Решить уравнение
л/3* + 1 - Jx + 4 = 1.
Решение. Возводим обе части исходного
уравнения в квадрат:
(J3x + 1 - Jx + 4)2 = I2 <=> (JSx + l)2 -
-2j3x + 1 • л/лГ+~4 + (Jx + 4)2 =!<=>
<=>3х +1-27(3* + 1)(х + 4) +х + 4«1.
Отсюда
4x + 4 = 2V(3x + 1)(х + 4)
или, после деления обеих частей уравнения на 2,
2х + 2 = J(3x + 1)(х + 4).
Вновь возводим обе части полученного
уравнения в квадрат:
(2х + 2)2 = (7(3* + 1)(х + 4))2 <=>
«=> 4х2 + 8* + 4 - (3* + 1)(х + 4) <=> х2 - Ъх = 0.
Откуда х = 0 либо х = 5.
Проверка, а) При х = 0 J3x + 1 - Jx + 4 =
= VI - л/i = -1.-1*1, следовательно, л: = 0 —
посторонний корень.
б) При л: = 5 л/Зх + 1 - V* + 4 =
= л/3 • 5 + 1 - л/5 + 4 = 4 - 3 = 1, так как
1 = 1 — тождество, то л: = 5 — корень
исходного уравнения.
Ответ: 5.
Пример 2. Решить уравнение
Jx + 1 + л/4* + 13 = 73х + 12.
Решение. Возводим обе части уравнения в
квадрат:
х+1 + 27* + 1 • л/4х + 13 +4*+ 13 = 3*+12.
Откуда J(x + 1)(4х + 13) = -1 - *.
Еще раз возводим обе части уравнения в
квадрат и получаем:
(J(x + 1)(4* + 13)) = (- 1 - л:)2 <=>
<=>jc2 + 5jc + 4 = 0<=>[^IJ;
Делая проверку, устанавливаем, что х = - 1
является корнем первоначального уравнения, а
х = - 4 — посторонний корень (при л: = -4
первое подкоренное выражение отрицательно, т. е.
это число не входит в область определения
первого подкоренного выражения).
Ответ: -1.
Введение новой переменной
Пример 3. Решить уравнение
J2x + 6 - л/лГТТ = 2.
Решение. Обозначим t =■ Jx + 1. Заметим,
что: а) О 0 по определению арифметического
эня;б)* = х+1, откуда
Уравнение примет вид:
2 2
корня; б) t = х+ 1, откуда х = t -1
л/2(*2 -1) + 6 -1 = 2, или л/2*2 + 4 « t + 2.
Возводим обе части этого уравнения в
квадрат:
(ht2 + 4)2 =(* + 2)2 <=> 2*2 + 4 = 4 + 4* + *2<=>
<=>*2-4* = 0 <=> *(*74) = 0<=> [JlJ
Значит, либо V* + 1 — 0» откуда л: = -1, либо
Jx + 1 = 4, откуда л: + 1 = 16, т. е. л: = 15.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
87
Проверка, а) При х = -1 */2х + 6 - Jx + 1 =
= 72 -(-1) + 6 - V-1 + 1 = 2. Так как 2 = 2 —
тождество, то л: = -1 — корень исходного
уравнения.
б) При х =15 J2x + 6 - V* + 1 =
= л/2 • 15 + 6 - Vl5 + 1 = 2, так как 2 = 2 —
тождество, то х = 15 также является корнем
исходного уравнения.
Ответ: -1; 15.
Пример 4*. Решить уравнение
а/*2 + х + 4 + V*2 + х + 1 = л/2*2 + 2х + 9,
2
Решение. Обозначим t = x + х + 4, тогда
х2 + л: + 1 = * - 3,
2х2 + 2х + 9 = 2(х2 + л: + 4) + 1 = 2* + 1.
Уравнение примет вид:
Ji + V* - 3 = л/2* + 1.
Возводим его в квадрат:
t + 2/t • V* - 3 + *-3 = 2*+1<=>
(1)
<=» л/*(* - 3) =2.
Это уравнение также возводим в квадрат:
t
-3*-4 = 0 <* [J."1'
Проверка. Полученные значения t мы
должны проверить в уравнении (1), так как именно
оно возводилось в квадрат. Проверка
показывает, что t = -1 — посторонний корень, a t = 4 —
действительно корень уравнения (1). Отсюда
получим:
х2 + х + 4 = 4 <=> х2 + х = 0 <=> [*I?i#
Ответ: 0; -1.
3*. Уравнения, содержащие радикалы
третьей и более высоких степеней
При решении уравнений, содержащих
радикалы третьей степени, бывает полезно
пользоваться следующими тождествами:
(а + Ъ)3 = а3 + За2Ь + ЗаЬ2 + Ь3 = а3 + Ь3 + За&(а + Ь);
(а - Ь)3 = а3 - За2& + За&2 - Ь3 = а3 - Ь3 - За&(а - &).
Пример 1. Решить уравнение
У2х + 17 - V2* - 2 = 1.
Решение 1. Возведем обе части этого
уравнения в третью степень и воспользуемся выше
приведенным тождеством:
(ty2* + 17 - У2х - 2)3 = 13<=>2x + 17-2x +
+ 2-ЗУ2* + 17 -372л: - 2(У2х + 17 -
- \]2х - 2)=1.
Заметим, что выражение, стоящее в скобках,
равно 1, что следует из первоначального
уравнения. Учитывая это и приводя подобные члены,
получим:
6= У(2х 4- 17)(2х - 2) «
<=» 63 = (2x+17)(2x-2).
Раскроем скобки, приведем подобные члены
и решим квадратное уравнение. Его корни х = 5
и^ = -у. Если считать (по определению), что
корень нечетной степени можно извлекать и из
отрицательных чисел, то оба полученных числа
являются решениями исходного уравнения.
Ответ: 5, --«г.
Решение 2. Введем две новых переменных
у = Ц2х + 17 и г = У2х ~ 2 , тогда у3 = 2х + 17,
2 = 2х - 2. Заметим, что
у3 -z3 = 2* + 17 -2* + 2 = 19.
В итоге мы получим систему уравнений:
( У-2=1, f 1/-2=1,
U3-23 = 19; l(i/-2)(i/2 + i/2 + 22) =
19.
Используя первое уравнение системы,
преобразуем второе, заменив первую скобку
единицей, а во вторую подставим вместо неизвестного
у выражение у = г + 1, также полученное из
первого уравнения:
(г + I)2 + (г + 1)2 + г2 = 19.
Приведем подобные члены, раскрыв
предварительно скобки и решим полученное
квадратное уравнение. Его корни г = 2 и 2 = -3.
Вернемся теперь к начальной подстановке и получим
искомые решения:
\/2х - 2 =2,
_V2x - 2 =-3.
Решив эти уравнения, найдем корни х = 5 и
25
z = Зл/2х - 2

88
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Если уравнение содержит радикалы более
высоких степеней, то наиболее часто
используемый способ их решения — введение нового
(новых) неизвестного.
Пример 2. Решить уравнение
Jx + 5 + \Jx + 5 -12 = 0.
Решение. Обозначим t , тогда:
a) t > 0 по определению корня четной
степени; б) t2 - {Мх + 5) = Jx + 5 .
Уравнение примет вид:
*2 + *-12 = 0 о [Jl?4
Корень * = -4 не удовлетворяет условию (а).
Следовательно, Мх + 5 = 3 <=» (V* + 5) = 3 <=>
<=>х=76.
Ответ: 76.
Уравнение с параметром
Пример 1. При каких значениях а уравнение
2 2
ах + (а + 2)л: -На -6а+ 1=0 имеет два корня,
один из которых больше 1, а другой меньше?
Решение. Рассмотрим функцию
у = ах2 + (а + 2)х + а2 - 6а + 1
и построим эскиз ее графика. При а = 0
функция становится линейной и двух точек
пересечения с осью Ох (корней уравнения у = 0) иметь не
может.
При а > 0 графиком функции является
парабола, ветви которой направлены вверх.
Необходимым и достаточным условием существования
корней хг и х2 таких, что хг < 1, а х2 > 1 в, этом
случае является единственное условие: у(1) < 0
(рис. 47).
Если же а < 0, то условие, соответственно,
1/(1) > 0 (рис. 48).
Итак, решение задачи формально задается
совокупностью:
f а>0,
1а2-4
4а + 3 < 0;
f а>0,
Ь(1)<0;
I f а < 0, I f а < 0,
Lb(l)>0; |_1а2-4а + 3>0;
Гае(1;3),
**\_aG (-оо; 0).
Ответ: а е (-оо; 0) U (1; 3).
Пример 2. При каких значениях а уравнение
2
ах + 8 + л: =0 имеет два различных корня,
каждый из которых больше 2?
2
Решение. Рассмотрим функцию у = х + ах +
+ 8. Ее графиком является парабола, ветви
которой направлены вверх. Чтобы корни
существовали и были больше 2, необходимо и
достаточно выполнения следующих условий:
(D>0,
}х0>29
[ У(2) > 0.
Первое неравенство системы определяет
существование двух различных корней, второе и
третье выполнение условия задачи, третье —
направленность вверх ветвей параболы (рис. 49).
Решим эту систему неравенств.
а2 - 32 > 0,
-1>2'
f (а-472)(а + 4л/2)>0,
» i а < -4,
4 + 2а + 8>0; 1 а > "6>
Решая эту систему простейших неравенств,
получим результат.
Ответ: а е (-6; -472).
Пример 3. При каких значениях а уравнение
х - Зал: + а + 2 = 0 имеет два различных корня,
один из которых меньше 1, а другой больше 2?
2
Решение. Рассмотрим функцию у = х - Зал: +
+ а 4- 2. Ее графиком является парабола, ветви
которой йаправлены вверх. Для того чтобы одна
точка пересечения графика с осью Ох была ле-
Рис. 47
Рис. 48
Рис. 49

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
89
вее 1, а вторая правее 2 (рис. 50), необходимо и
достаточно выполнения только двух условий:
- За + а + 2 < 0,
- 6а + а + 2 < 0; **
<=>а >
Ответ: ае N;
Пример 4. При каких значениях а уравнение
2л:2 4- бах + 1 = 0 имеет два различных корня, не
превосходящих по модулю единицы?
2
Решение. Рассмотрим функцию у = 2х + бах +
+ 1. Ее графиком является парабола, ветви
которой направлены вверх (рис. 51). Для выполнения
поставленных в задании условий необходимо и
достаточно решить следующую систему неравенств:
2 + 6а + 1 > 0,
2 - 6а + 1 > 0,
6а - <=>
4
ГУ(1)>0,
J уЫ) > о,
К х0 < 1,
-1<-^<1,
ID>0;
1
»<
-2<а<
Л
а>т,
а<~Т
1
36а - 8 > 0;
°—=«(-i'-£)u(f i)
Графическое представление уравнений и
систем часто существенно помогает досконально
разобраться в решении параметрических задач
и наглядно представить решение.
Пример 5. При каких значениях а система
уравнений
j*2 + i/2 = 4,
I \х - а\ - у = 0
имеет единственное решение?
Решение. Графиком первого уравнения
системы является окружность радиуса R = 2 с
центром в начале координат (рис. 52). Второе
уравнение представим в виде у = \х - а\ и построим
его график. Это будет график функции у = |л:|
(рис. 53), сдвинутый на а вдоль оси Ох (рис. 54),
то есть параметр а «управляет» движением
графика вдоль оси Ох. В общем случае (рис. 55)
система может не иметь решения или иметь два
решения. Единственное же решение система будет
иметь только в случае, когда график у = \х - а\
2 2
касается окружности х + у = 4 (рис. 56).
В этом случае имеем прямоугольный и
равнобедренный треугольник ОАВ, катет которого
R = 2, гипотенуза ОВ = 2 J2 .
Рис. 50
Рис. 51
У -1* - *1
\ 2
-2la 0
-2
1
\/у - \х - а\
1 уч /
1 l ^^
1 h а
X
-2 \
2
1
0
-2
Рис
2,2 .
Л 4- у — 4
1 у2 х
;.52
^j
0
i
у-Н/
/V5°
Л
Рис
.53
У « I* - а|
~2\
*>|
^Т
о
-2
1
Ч J/4*-a|
>>^ /
J2B х
Рис. 54
Рис. 55
Рис. 56

90
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Ответ: система имеет единственное решение
при а = 2 V2 либо при а = -2 J2 .
Иногда при решении параметрических задач,
связанных с квадратным уравнением, бывает
полезна теорема Виета.
Пример 6. При каких значениях Ь квадрат-
ный трехчлен (Ь - 2)х - 2Ьх + 2Ь - 3 имеет два
различных корня одного знака?
Решение. Заметим, что при Ъ = 2 исходное
уравнение имеет единственный корень,
следовательно, это значение Ъ не удовлетворяет
условию задачи. При Ь * 2 исходное уравнение будет
равносильно уравнению:
2
л: -
2Ь
х +
2Ь
= 0.
(1)
Ь - 2 ~ ' Ь - 2
Для того чтобы исходное уравнение имело
два различных корня, необходимо и достаточно,
чтобы его дискриминант был положителен. С
другой стороны, если корни приведенного
квадратного уравнения (1) имеют один знак, то их
произведение должно быть положительным.
Произведение же корней приведенного
квадратного уравнения по теореме Виета равно
свободному члену уравнения.
Таким образом, система необходимых и
достаточных условий для данной задачи будет
иметь вид:
&*2,
&*2,
Ъ2-(Ъ- 2)(2Ь - 3) > 0,
2Ь
>0;
1<&<6,
>0.
Ь ~ 2 \ Ь - 2
Решим последнее неравенство системы
методом интервалов:
3>
be [-оо; !) U(2;oo).
У/////////////"Г
о
~<*^$SSS^m
Решением системы неравенств будет
пересечение решений всех неравенств системы:
У/////////////
>!»
6 ь
Ответ: be (l; |] и (2; 6).
НЕРАВЕНСТВА
Свойства числовых неравенств
1. Основные определения и свойства
Определение. Число а > Ь, если а - b > 0 (а > Ь,
если а - b > 0); число а < &, если а - b < 0 (а < &,
если а - b < 0).
Пример 1. -0,5 < 0,2; -0,1 > -0,9.
Свойства неравенств
1) Если a>b,mo Ь<а.
Пример 2. Если g > q ' то 8 < 3 *
если л/3 < л/5 , то л/5 > л/3.
2) Ясли а>Ь и Ь> с, то а> с.
Пример 3. Если -5 > -8 и -8 > -15, то
-5>-15.
Если 2^ >l| nl| >-5, то2д >-5.
3)Если a>b и с — любое число, то
а + с > & + с.
Пример 4. Если х-3>2, тох-3 + 3>2 + 3,
т. е. лг > 5 (к обеим частям неравенства
прибавили 3).
Если х + 1,5 < 7, то х < 5,5 (к обеим частям
неравенства прибавили -1,5).
4) Если а > b и О 0, то ас> be;
если а>Ь и с < 0, то ас <Ьс.
Четвертое свойство формулируется так: если
обе части данного неравенства умножить на
положительное число, то знак неравенства не
изменится, если же обе части неравенства
умножить на отрицательное число, то знак
неравенства изменится на противоположный.
При делении неравенства на число действует
то же правило, что и при умножении, поскольку
разделить обе части неравенства на число с, это
1
все равно, что умножить их на число - .
Пример 5. Если Зх < 1,8, то х < 0,6 (обе
части неравенства умножили на =) •
Если -5л: < 4,5, то х > -0,9 [обе части
неравенства умножили на -•= ].
5) Если а > b и О d, то а + о b + d, т. е.
неравенства одинакового знака можно складывать.
Пример 6. Если -5 > -8 и 10 > -3, то 5 > -11.
Если х + by < 2 и х - Зу < -1, то 2х + 2у < 1.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
91
6) Если а > Ъ > О и о d > О, то ас > bd.
Пример 7. Если Jb > JZ и 14 > 8, то
14^5 >873.
Если (х + I)2 > 9 и уА > 16, то (х + 1)У > 144.
2. Некоторые важные неравенства
Модуль суммы двух действительных чисел
не превосходит суммы модулей этих Чисел:
\а + Ь\< \а\ + |Ь|.
Пример 1. Если а = -7,2, Ь = 5, то
\а + Ь\ = |-7,2 + 5| = |-2,2| = 2,2,
Н + W = |-7,2| + |5| = 7,2 + 5 = 12,2.
Действительно, 2,2 < 12,2.
Пример 2. Если а — -=, Ъ = -=, то
\а + Ъ\ =
W + М =
"I * ("И -
_8| _8_
'1б| 15'
_1| + L1I = 1 + 1 = 1
3 5 3 5 15*
тт 8 8
Получим верное равенство: Те = т*•
Модуль разности двух действительных чисел
не меньше модуля разности модулей этих чисел:
\а-Ь\>\\а\-\Ь\\.
Пример 3. Если а = -5, Ь = 2, то
|а - &| - |-5 - 2| = |-7| = 7,
И-М-Н|-|2||-|б-2|-|8|-8.
Действительно, 7 > 3.
Пример 4. Если а
|а-Ь| =
,2
13,Ь = 32,ТО
1?-3^
13 32
-1
W-M-
л
II
= 1
в*
.51
Получим верное равенство: 1 g = 1 g .
Решение неравенств
и систем неравенств
1. Линейное неравенство
Линейным неравенством называется
неравенство вида
ах + Ь>0, ах + Ь<0, ах + Ь>09 ах + Ь<0,
где аиЬ действительные числа, а •*■ 0.
Решить неравенство — значит найти все
значения переменной, при которых неравенство
обращается в верное числовое неравенство.
При решении неравенств используются их
свойства.
Пример 1.2х - 3,2 < 0;
2л: < 3,2;
х< 1,6.
Ответ: х е (-оо; 1,6).
1
Пример 2-~х + 7 > 0
х<56.
Ответ: л: е (~°°; 56].
Пример 3.1,5(х - 8) - 2(0,75* + 5) < 0;
1,5л: -12 -1,5л:- 10 < 0;
0 • х - 22 < 0 — верно при любом
действительном х.
Ответ: х е (-<*>; °о).
Пример 4.1,5(х - 8) - 2(0,75л: + 5) > 0;
0 • х - 22 > 0 — ложно при любом
действительном х.
Ответ: нет решения.
2. Система линейных неравенств
Решением системы линейных неравенств
называется пересечение множеств решений этих
неравенств, т. е. те значения переменной,
которые одновременно удовлетворяют всем
неравенствам системы.
Пример 1.
f 7л: + 4 > 2л: - 1,5, \ 5х> -5,5,
I 0,3л: - 18 < 0; ^1 0,3л: < 18; ^
Г *>-1Д,
I х < 60.
На числовой прямой решение каждого
неравенства показывают штриховкой
соответствующего числового промежутка, тогда решение
системы — пересечение заштрихованных
промежутков:
-1,1 60 ь
Ответ: х е (-1,1; 60].
Пример 2.
(2,5л: + 1 > 4,3л: - 2, [ -1,8* > -3,
2л:-3<Зл:-5^; <=>|-лг<-2^; ^

92
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
х<
3'
х>2\.
///////////Ш%
4
Ответ: нет решений.
Пример 3.
|lx + 8<-l + !*t f-|*<-4.^
I 4(jc - 0,75) < 5(x + 1); [ -x < 8;
J *>16,
\ x > -8.
-8
<=»
16
Ответ: x e [16; oo).
3. Квадратное неравенство
2 2
Неравенство вида ах + блг + с > 0 или ах +
+ Ьл: + с < 0 называется квадратным
неравенством.
Выражение слева от знака неравенства
можно рассматривать как квадратичную функцию,
тогда решение исходного неравенства сводится
к нахождению промежутков знакопостоянства
соответствующей квадратичной функции (т. е.
промежутков, на которых значения функции
положительны или отрицательны).
2
Пример 1.x > 0.
Парабола у = х расположена выше оси Ох
при любом х * 0 (рис. 57).
Ответ: х € (-оо; 0) U (0; оо).
2
Пример 2.-х > 2.
Так как -х < 0 при любом действительном
значении х, то неравенство не имеет решений.
2 1
Пример 3.x < g ;
* " 9 < °"
Решение. Изобразим схематично график
функции I/ = х - 5 . Для этого найдем нули функции
(т. е. точки, в которых у = 0).
2-!=п. 2=1. =1 г^-1
Ветви параболы направлены вверх, так как
а = 1 > 0 (рис. 58).
2 1
Неравенство х - g < 0 выполняется при
*е Г~3; 3 Г Концы промежутка включаются,
так как задано нестрогое неравенство.
Ответ: х е
[ з;з}
Пример 4. -2х - \\х + 21< 0.
2
Решение. Рассмотрим функцию у = - 2х -
- 11* + 21 (а = - 2; Ъ = - 11; с = 21). Построим
эскиз параболы.
Ветви параболы направлены вниз, так как
а <0.
Найдем точки пересечения параболы с осью
Ох:
-2х - 11* + 21= 0,
J - 4ас
-b±J3 11±17
D = Ь2 - 4ас = (-11)2 - 4 • (-2) • 21 = 289,
х =
2а
-4
* = -7,
3
По эскизу (рис. 59) найдем решение
неравенства -2х - 11л: + 21< 0.
Ответ: х е (-оо; -7) U ( ^ ; оо \
Рис. 59

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
93
Решение неравенств методом
интервалов
Пример 1. (х + Ь)(х - 1)х > 0.
Решение. Отметим на числовой прямой все
точки, в которых левая часть данного
неравенства обращается в 0. Эти точки разбивают
числовую прямую на промежутки. Найдем знак
произведения в левой части неравенства на
каждом промежутке.
+ - +
-5
0 1
При х > 1 каждый множитель произведения
положителен, следовательно, их произведение
также будет положительным (что отмечается
знаком «+» над соответствующим промежутком).
При х е (0; 1) второй множитель становится
отрицательным, другие же множители остаются
положительными, следовательно, произведение
будет отрицательным.
Аналогично определим знаки произведения
на промежутках (-5; 0) и (-оо; -5).
Решение неравенства — объединение
промежутков, на которых значение произведения в
левой части данного неравенства положительно.
Ответ: х е (-5; 0) U (1; оо).
2
Пример 2.x - 2х - 15 < 0.
Решение. Разложим квадратный трехчлен в
левой части неравенства на множители,
пользуясь теоремой Виета:
хг + х2 = 2,
Х-уХ2 ~ """ 10,
Г*!--8,
|_*2 = 5'
х - 2х - 15 = (х + 3)(х - 5) < 0.
Далее решение неравенства будет аналогично
приведенному выше. Записываем ответ с учетом
того, что данное неравенство нестрогое (т. е.
включая концы промежутков).
Отметим, что если степень выражения четная,
то значение выражения неотрицательно и,
следовательно, знак всего произведения зависит от
выражений, возведенных в нечетную степень.
+ + - - +
-5
-1 0
Ответ: х е [-5; 0] U {2} U [4; оо).
Точка 2 включена в ответ, так как значение
выражения в ней равно 0.
Пример 4. (Зх + 5)(2 - Зх)(2л: - 7) > 0.
Решение. Это неравенство отличается от
предыдущих тем, что коэффициенты при
переменной отличны от единицы. Вынесем эти
коэффициенты за скобки:
'(
3 лс +
>0.
Разделим неравенство на 3 • (-3) • 2 = - 18.
Далее решение стандартно:
7
2
Oraer:*6(-oo;-|]u(s;|).
Решение дробно-рациональных неравенств
Пример 5. -—^т~ < 0.
Решение. Отметим на числовой прямой
точки, в которых дробь равна 0, и точки, в которых
выражение не имеет смысла (на прямой
отмечено пустым кружком).
j(* + 3)2 = 0, «I*-""8'
-3 5 х
Ответ: х € [-3; 5].
Пример 3.
(х + Ъ)\х + l)V(x - 2)\х - 4)5 > 0.
Решение. Отметим на числовой прямой
точки, в которых левая часть неравенства
обращается в нуль.
-3 1 х
Далее решение данного неравенства
проводится аналогично вышеприведенным. Так как
2
(х + 3) > 0 при всех х9 то знак дроби зависит от
знака знаменателя.
Ответ: (-оо; 1).
Вообще, частное от деления двух функций
(выражений) имеет тот же знак, что и их
произведение.

94
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Отсюда непосредственно следует, что
следующие два неравенства равносильны (т. е. имеют
одинаковые решения):
8{х)
> О <=> f(x)g(x) > 0.
В случае нестрогих неравенств решения этих
неравенств будут совпадать во всех точках,
кроме тех, в которых g(x) = 0. Таким образом:
/(*)>0tJ £(*)/(*)> о,
Пример 6*. Решить неравенство
(3 - 2х)(х - 4)3(* + 2)4
(х2 - 9)(х2 + х + 1)
>0.
Решение. Преобразуем данное неравенство:
3>
-2(* - fj(x - 4)3(* + 2)4
>0.
(х - 3)(* + 3)(х + х + 1)
Разделив обе части неравенства на -2 и заме-
тив, что х + х + 1 > 0 (что легко показать, выделив
П2 . 3
полный квадрат ^
: х + х + 1 = (я + ^] + \ > 0),
получим, что данное неравенство равносильно
следующему:
(х - |)(* - 4)8(* + 2)4
<0.
(я - 3)(х + 3)
Отметим на числовой прямой точки, в
которых либо числитель, либо знаменатель левой
части неравенства обращается в нуль (не
забудем, что точки, в которых знаменатель
обращается в нуль, следует обвести кружком) и
расставим знаки над соответствующими промежутками:
+ -
о «-
+
-3 -2
3 4 х
Ответ: х е [-3; 11 U (3; 4].
-1.
3(* + 4) - 21 - 7(х - 2) + (* + 4)(х - 2)
(х + 4)(* - 2)
>0;
х* - 2х - 3
>0.
(х + 4)(* - 2)
Согласно теореме о разложении квадратного
трехчлена на множители:
х - 2х - 3 = (х + 1)(х - 3), тогда
(х + 1)(х - 3) >0
(х - 2)(х + 4)
. Далее решение неравенства аналогично
предыдущему примеру.
Решение неравенств,
содержащих модуль
К простейшим неравенствам, содержащим
знак модуля, относятся два типа неравенств:
1) неравенства вида \f(x)\ < g(x)\ такое
неравенство равносильно системе неравенств
tf(x)<Ax)9
I f(x) > -£(*);
2) неравенства вида |/(л:)| > g(x). Решением
такого неравенства является объединение
решений двух неравенств: f(x) > g(x) и f(x) < -g(x),
или
ff(x)>g(x)9
Lf(x)<-g(x).
Пример 1. \Sx - 5| > Ix - 6.
Решение. Данное неравенство равносильно
совокупности неравенств:
Г3х-5>7л:-6, Г-4х>-1,
|_Зж-5<-7ж + 6; ~ |_Ю*<11;
<=>
От]
1х^ 1о;
нет: х е (-оо; — 1
Пример 2. Решить неравенство
2х + 1
<3.
х - 1
Решение. Данное неравенство равносильно
системе неравенств:
х - 2 (х + 4)(х - 2) х + 4
2* + 1
х - 1
2* + 1
х - 1
<3,
>-8;
-х + 4
л: - 1
Ъх - 2
<0,
>0;

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
95
>о,
*м
*_б
>0.
х - 1
Решим неравенства системы методом
интервалов. Покажем штриховкой решение первого
неравенства системы над числовой прямой,
решение второго неравенства — под числовой
прямой:
+ - +
♦|>
Решение системы неравенств — пересечение
полученных промежутков. На рисунке решение
системы отмечено двойной штриховкой.
2
Ответ: х е (-оо; g ] U (4; оо).
Пример 3. Решить неравенство:
2х + 1
>3.
х - 1
Решение. Данное неравенство равносильно
совокупности:
~ х - 4
2х + 1
х - 1
2х + 1
L х - 1
>3,
<-3;
х - 1
2
*"5
Lx - 1
<0,
<0.
Ответ: х е Г|;1^и(1;4].
Пример 4. \3х + 1| - |2 - 5х\ > 0.
Решение. Обозначим выражения, стоящие
под знаком модуля, (1) и (2) и отметим на
числовой прямой точки, в которых эти выражения
обращаются в 0. Определим знаки этих
выражений в полученных числовых интервалах:
(1-)(2+) (1+И2+) (1+М2-)
Таким образом, можно решать данное
неравенство на трех множествах, на каждом из
которых раскрывать знак модуля согласно
определению модуля.
1) Если х е (-оо; -«), то исходное
неравенство равносильно неравенству
-Зх- 1 - (2 - 5х) > 0 <=> 2х - 3 > 0 «=> х> g ,
т.е. х е
И-)
Так как полученный интервал не имеет с
рассматриваемым промежутком общих точек, то на
И -i)
исходное неравенство не
интервале
имеет решения.
[1 2 \
- 5 ; с I то исходное неравенство
равносильно неравенству Зл: + 1 - (2 - 5л:) > 0 <=>
«=>8х-1>0«л:>д,т. е. хе ( g ; °° \
Решением будет пересечение двух
промежутков: полученного [ « ; оо J и рассматриваемого
№)■
Получаем х е ( g ; g j.
3) Если х е г ; оо J, то исходное неравенство
равносильно неравенству Зл: + 1 + 2-5л:>0 <=>
3 / 3\
<=>-2х + 3>0 <=> х< g, т. е. хе f-oo; -j.
Решением данного неравенства на
рассматриваемом промежутке будет пересечение интерва-
лов[|;оо)и(-оо;|).
mmmmmmmm™™*'
Получим хе N; 2).
Объединяя решения, полученные на
соответствующих множествах числовой прямой,
получим ответ:
Ответ: х е
(1Л)
\8* 2)'

96
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Доказательство неравенств
Чтобы доказать неравенство, надо показать,
что оно справедливо для всех допустимых
значений входящих в него переменных (или: на
заданном множестве значений переменной).
Говорят, что неравенство (2) следует из
неравенства (1), если из истинности неравенства (1)
следует истинность неравенства (2).
Обозначение: (1) => (2).
Неравенства (1) и (2) называются
равносильными, если (1) => (2) и (2) => (1).
Пример 1. Доказать, что сумма
положительного числа и обратного к нему не меньше 2:
а + - > 2 (а > 0).
а
Доказательство.
а+->2 «=> а+ - -2>0 <=>
а а
а а
Дробь положительна, если числитель и
знаменатель имеют одинаковые знаки. Так как
(а - I)2 > 0 при любом действительном
значении а и а > 0 по условию, то полученное
неравенство (а значит, и исходное) верно для всех
а > 0.
Отметим, что равенство достигается только в
случае а = 1.
Пример 2. Доказать, что среднее
геометрическое двух неотрицательных действительных
чисел не превосходит их среднего арифметического:
Jab < ^Цр (а > 0, Ъ > 0).
(Jab называется средним геометрическим,
—5 средним арифметическим чисел а и Ь.)
Доказательство.
Jab <
а + Ь
«=> 2 Jab < a + b <=>
<=> {Ja)2 - 2 Jab + (Jb)2 )0o (Ja - Jb)2 > 0,
что справедливо для любых неотрицательных
чисел а и Ь.
Отметим, что равенство достигается только
при а = Ь.
Замечание. Среднее геометрическое п
неотрицательных чисел не превосходит их среднего
арифметического для любого конечного набора
чисел:
Ф\*2
а„ <
h + «2 + аз +
+ а„
Пример 3. Доказать, что
2 2 2
а + b + с > ab + ас + Ьс.
Доказательство. Рассмотрим разность левой
и правой частей неравенства
2 ^ *2 , 2
а + b + с
1 2
(ab + ас + bc) = г (а
2а& + &) +
+ |(&2-2&с + с2) + ^ (с2 - 2ас + а2) = |(а-&)2 +
+ \{Ъ-с)2+\{с-а)2>0.
Полученное неравенство истинно, так как
2 2 2
(а- Ь) > 0, (Ь - с) > 0, (с - а) > 0 при любых
действительных значениях а, Ь, с. Поскольку
2 2
разность выражений неотрицательна, то а + b +
+ с > ab + ас + Ьс, что и требовалось доказать.
Заметим, что один из методов доказательства
неравенств таков: с помощью равносильных
неравенств привести данное неравенство к
очевидному или к ранее доказанному неравенству.
Пример 4. Доказать, что 10а > 3& + 14, если
а>ЬиЬ>2.
Доказательство. По свойству неравенств,
а >&иЬ>2=>а>2.
10а > 3& + 14 <=> 10а - (3& + 14) > 0 <=>
<=> 3(а - Ь) + 7(а - 2) > 0,
что истинно, поскольку а > &, т. е. а - & > 0 и
а > 2, т. е. а-2 > 0.
2
Пример 5. Доказать, что 4а < а +5 при
любом действительном значении а.
Доказательство.
4а < а2+ 5 <=> а2 - 4а + 5 > 0 <=>
о (а2 - 4а + 4) + 1 > 0 «=> (а - 2)2 + 1 > 0,
что истинно при любом действительном значе-
нии а, потому что (а - 2) > 0 при любом
действительном значении а.
Пример 6*. Доказать, что
Г-2 <а<-0,5,
Зт - 2Л 3'
если /
-1 <т<
3*
-5 < h < -2
4*

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
97
Доказательство.
2
-1</п<5 «=> - 3 < Зтп < 2 (обе части
неравенства умножили на 3 > 0),
-5 < А < -2 ^ » 4 о < -2А < 10 (неравенство
умножили на -2 < 0).
При сложении неравенств получим
1|<8ш-2*<12,торда^<—4ГД<|.
Умножив это неравенство почленно на
неравенство 5 < -а < 2, получим
ш < z^h-h < §'тогда з^Ьа >_i-
Пример 7. Сравнить: 72 + У7 и 75 + 2.
Решение. Докажем, что J2 + Jl < Jb +2<г>
<=>(72 + V7)2 <(VB + 2)2<=>
«=>2 + 2л/14 +7< 5 + 475 +4»
<=>9 + 2л/П <9 + 4л/5 «2714 <475 <=>
<=> 7П < 275 *=> (7П)2 < (275)2 <=> 14 < 20.
Последнее неравенство истинно, значит,
72 + 77 < 75 + 2 истинно.
Замечание. При доказательстве было
использовано одно важное свойство: если а > Ь > 0, то
а > Ь <=> а2 > Ь2.
НАЧАЛА ТРИГОНОМЕТРИИ
Измерение углов.
Тригонометрические функции
в прямоугольном треугольнике.
Основное тригонометрическое
тождество
1. Измерение углов. Градус и радиан
Центральным углом называется угол,
вершина которого лежит в центре окружности, а
стороны пересекают окружность.
Если окружность разбить на 360 равных дуг,
то углом в 1° называется центральный угол,
опирающийся на одну из таких дуг (рис. 60).
jwj часть угла в 1° называется углом в одну
градусную минуту; обозначение: 1';
gTj часть угла в 1' называется углом в одну
градусную секунду; обозначение: 1".
Измерение углов в радианах основано на
следующем геометрическом факте: отношение
длины дуги, на которую опирается центральный
угол, к радиусу окружности есть число
постоянное для данного угла, не зависящее от радиуса
окружности. Это число и называется радианной
мерой данного угла (рис. 61).
I
U
1 '2
Ф — радианная мера угла АОВ.
Углом в 1 радиан называется центральный
угол, опирающийся на дугу, равную радиусу
окружности.
Соотношение между радианной
и градусной мерой угла
Длина окружности равна L = 2nR. Отсюда от-
L о
ношение ^ = 2я есть радианная мера полного
угла, т. е. угла в 360°.
360° = 2я радиан;
1° = щ радиан;
1 180 кто
1 радиан = — ~ 57°.
Замечание. Число п — константа, равная
отношению длины окружности к ее диаметру, п —
иррациональное число, п ~ 3,141592.
Таблица соответствия
градусной и радианной мер углов
Градусная
мера
Радианная
мера
360°
2я
270°
Зя
2
180°
Я
120°
2я
3
90°
Я
2
60°
я
3
45°
я
4
30°
я
6
Рис. 61
4-1019

98
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
2. Тригонометрические функции
в прямоугольном треугольнике
Синусом угла а называется отношение длины
противолежащего этому углу катета к длине
гипотенузы (рис. 62). Обозначение sin а.
Косинусом угла а называется отношение
длины прилежащего катета к длине гипотенузы.
Обозначение: cos а.
Тангенсом угла а называется отношение
длин противолежащего катета к прилежащему.
Обозначение: tg а.
Котангенсом угла а называется отношение
длин прилежащего катета к противолежащему.
Обозначение: ctg а.
_ , sin а , cos а
Отметим, что tg а = ^^ » с*£ а =
sin а
cos а
8
17
15
' 17
8-^?
.И--15
8
15*
cos а
sin а
3. Основное тригонометрическое тождество
Поскольку sin а = -, cos а = -, то
• 2 _, 2 (ау , (by
sin а + cos oc=^-J +(^J =
2 . ,2
а + Ь
2 2 2
но по теореме Пифагора а +Ь = с , отсюда
2 2
sin а + cos а = 1.
„ 8
Пример. Пусть а — острый угол и sin а = р= .
Найти cos a, tg а, ctg а.
Решение. Воспользуемся основным
тригонометрическим тождеством:
. 2
in а
8 \2
2 2
sin cc + cos а= 1;
( 8 У 2
I p=J +cos а= 1;
2 - 64
cos а=1"289;
2 225
cos а=289;
15
cos а = yf ;
tgcc =
1 15-7
ctg а = г— = -=- =1з.
ь tgcc 8 8
Тригонометрическая окружность.
Решение простейших
тригонометрических уравнений
1. Тригонометрическая окружность
Тригонометрической окружностью (кругом)
называется окружность на координатной
плоскости с центром в начале координат, радиус
которой равен 1. (Другое название: единичная
окружность.)
Пусть Р0— точка тригонометрической
окружности с координатами (1; 0); Ра— точка,
полученная поворотом точки Р0 вокруг начала
координат на угол а (рис. 63).
Если точка Ра получена поворотом точки Р0
против часовой стрелки, то угол а считается
положительным, если же поворот происходит по
часовой стрелке, то угол а считается
отрицательным.
2. Определение тригонометрических
функций
Если точка Ра получена поворотом точки Р0
тригонометрического круга на угол а, то
синусом угла называется ордината точки JPa, а
косинусом — абсцисса этой точки (рис. 64).
sin a = х; cos a = у.
Замечание. Эти определения согласуются с
определениями тригонометрических функций в
прямоугольном треугольнике: sin a = ^ = | = у;
cos a = 5 = т = х.
а Ь
sin ae- cos a = -
с с
tgo- I
ctg a = -
"i
/s
1 **
\ °
Aa
cos a
Y*
a,o)m
X
Рис. 62
Рис. 63
Рис. 64

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
99
Тангенсом угла называется отношение
синуса этого угла к его косинусу.
, sin а
tg а = .
& cos а
Рассмотрим касательную к единичной
окружности в точке Р0 (рис. 65). Из подобия
треугольников имеем:
sina _ ^о
cos а "~ 1 *
то есть АР0 = tg а. Таким образом значения
тангенсов углов отмечаются на касательной к
единичной окружности в точке Р0. Эта касательная
называется линией тангенсов. Значения
тангенсов, отмеченные выше оси Ох, —
положительны, ниже — отрицательны.
Котангенсом угла называется отношение
косинуса угла к его синусу.
, cos а
Ctff ее = —— .
й sina
Значения котангенсов углов отмечаются на
касательной к единичной окружности в точке
Рп (рис. 66). Справа от оси Оу расположены ПО-
ложительные значения котангенсов, слева —
отрицательные.
3. Значения тригонометрических функций
некоторых углов
Продолжение
а°
ос,
рад
sina
cos а
0°
0
0
1
30°
я
6
1
2
Л
2
45°
к
4
72
2
Л
2
60°
я
3
Л-
2
1
2
90°
я
2
1
0
180°
я
0
-1
270°
Зя
2
-1
0
tga
ctga
0
не
опр.
1
73
Л
1
1
Л
1
л
не
опр.
0
0
не
опр.
не
опр.
0
Пример 1. Вычислить sin 405°.
Решение. Поворот на угол 405° можно
заменить одним полным оборотом и поворотом на угол
45° (рис. 67). То есть sin 405° = sin (360° + 45°) =
= sin45°=^.
Пример 2. Вычислить cos 1440°.
cos 1440° = cos (360° • 4) = cos 0° = 1.
Поворот на угол 1440° можно заменить
четырьмя полными оборотами точки Р0.
4. Решение простейших
тригонометрических уравнений
Пример 1. Решить уравнение cos х = 0.
Решение. Нулю равны абсциссы точек
пересечения единичной окружности с осью ординат,
т. е. абсциссы точек Рп и Р к (рис. 68). Точке
2 ~2
Рл соответствуют углы
2
5; 5+360°; 5+720°;....
Точке Р п соответствуют углы:
"2
-5; -5+360°; -5+720°;....
Решение уравнения можно записать в общем
виде:
к
х = +0 + 360°я, где п — любое целое число.
у\
/о
/ с
1 и
\ °
1
-^V
/\ ^ i
А
8
Ь0
+»
Ро
_
X
vi
г
к.
li2 ♦
2 ctga
А.
J ■
( с
^
1
~X405'
*f ar°
/
X
Рис. 65
Рис. 66
Рис. 67
Рис. 68

100
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пример 2. Решить уравнение sin х = ~ •
Решение. Рассмотрим точки единичной
окружности, ординаты которых равны ^ (рис. 69).
Точке Ра соответствуют углы:
g; g +360°; I +720°;....
В общем виде: g + 360°я.
Точка JPp симметрична точке Ра относительно
оси ординат. Из равенства углов, отмеченных на
рисунке 69, следует, что р = 180° - 30° = 150°.
Таким образом, точке Рр соответствуют углы:
Ц;Ц +360°; ^+720°;....
5 я
В общем виде: -g- + 360°п.
Пример 3. tg х = 7з .
Решение. 7з — табличное значение тангенса
угла, равного g • Найдем общий вид углов,
имеющий тангенс, равный 7з. Рассмотрим
единичную окружность и линию тангенсов. Отметим на
линии тангенсов число 7з « 1,7 (рис. 70).
Ответ: х = g + ял.
Формулы приведения. Основные
тригонометрические формулы
1. Формулы приведения
Для упрощения вычислений и выполнения
преобразований тригонометрические функции
любых углов часто приводят к
тригонометрическим функциям острых углов. Для этого
1
( °
рь\
1 1
Р-У
Ла i
'7з
Р» X
используются формулы приведения. Наглядной
иллюстрацией формул приведения служит
тригонометрическая окружность.
Отложим на тригонометрической
окружности точку Ра так, чтобы угол Р0ОРа = а был
острым. Рассмотрим А ОРаС, катеты которого
равны cos а и sin а. Затем отложим угол -у + а, где
1 < п < 3, и также рассмотрим треугольник, ка-
I • ^яп , Л
теты которого равны по величине sin [ -=- + а I
и cos
(т +а)
Замечая равенство
построенных треугольников, записываем, с учетом
знака, равенство соответствующих катетов.
Пример.
<р-gic-jx
Рис. 69
Рис. 70
ОС = cos а;
РаС = sin а;
ОСх = sin (у - а);
ОСг = ОС; sin ( y — ex J == -cos а.
Запишем также формулы приведения в виде
тождеств.
Углы первой четверти
cos (а + 360°) = cos а;
sin (а + 360°) = sin а;
tg (а + 360°) - tg а;
ctg (а + 360°) = ctg а.
Углы четвертой
четверти
cos (-а) = cos а;
sin (-а) = -sin а;
tg (-а) = -tg а;
ctg (-а) = -ctg а.
Углы третьей четверти
cos (а+180°) =
= -cos а;
sin (а + 180°) =
= -sin а;
tg (а+ 180°) = tga;
ctg (а + 180°) = ctg а.
[ctg а
/sin а
\ ^
?
-1зо8 а
tga
X
-ctg а
^^ina
1 о
Vsina
1
S)a\
^Ч-а
ctg а
Kg а
1 х
ptga
»,
/sin а
/-cos a
1 1 of
Лх + 180*
1
cos a
-sine/
ctg a
4ga
X

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
101
Углы второй четверти
cos (а + 90°) =
= -sin а;
sin (а + 90°) *»
= cos а;
tg (а + 90°) =
= -ctg а;
ctg (а+ 90°) =
= -tg а.
ctg (а+ 90°)
tg(a + 90°)
Запишем формулы приведения в виде
таблицы 1, используя радианную меру углов.
2. Основные тригонометрические формулы
Основное тригонометрическое тождество
2 2
cos a + sin a = 1
При выполнении преобразований
тригонометрических выражений используются также
формулы, являющиеся следствиями основного
тригонометрического тождества:
2 - . 2 .2 - 2
cos a = 1- sin a; sin a — 1 - cos a;
Формулы двойного угла
2 2 2
cos 2a — cos a - sin a — 2 cos a - 1 =
= 1-2 sin2 a;
sin 2a — 2 sin a cos a;
. rt 2tga к ,
tg 2a = 2-5-, a Ф 5 + nn-
1 - tg a
Формулы половинного угла
cos
a =+ /l + cos a
2 ~V 2 ;
a , /l - cos a
m2=±J 2 ;
sin
. a sin a
tgo =
1 - cos a
sin a
, a*nk.
l + tg2a= X
2 '
cos a
1 + ctg' a -
1
. 2 '
sin a
Приведем также еще одну полезную формулу:
tgaectga=l.
Формулы суммы и разности углов
cos (a + Р) — cos a cos p - sin a sin p;
cos (a - p) — cos a cos p + sin a sin p;
sin (a + P) = sin a cos P + cos a sin P;
sin (a - P) = sin a cos p - cos a sin p;
*<■+"»-r^sift'
2 1 + cos a
Формулы преобразования суммы (разности)
в произведение
_L-a o-a + P a - Р
sin a + sin р = 2 sin —=-£ cos —g-^;
. a 0.a-p a + P
sin a - sin p = 2 sin —5-*- cos —g-1-;
an a + P a-p
cos a + cos p = 2 cos —^"^ cos —g-1-;
Q 0 . a + p . a - p
cos a - cos p — -2 sin —s-^ sin —^ ;
sin a cos P = 9 (s*n (a + P) + s*n (a " P))»
sin a sin p = 5 (cos (a-p) - cos (a + p));
cos a cos p = 5 (cos (a + P) + cos (a - P)).
Дополнительные формулы
2 tga Л ^
sin a = 5 , a Ф к + 2кп, n € Z,
1J. 2CX
(«-J
+ яп, P Ф ^ + nn9 a + p Ф I + nn J.
cos a =
1 -tg 2
Л . 4. 2(X
1 +tg 2
, a Ф к + 2яп, ne Z.
Таблица 1
Ф
8Шф
СОЭф
tg<P
ctgcp
a + 27c/i
sin a
cos a
tga
ctg a
-a
-sin a
cos a
-tga
-ctg a
rc-a
sin a
-cos a
-tga
-ctg a
тс + а
-sin a
-cos a
tga
ctg a
к
« — a
2
cos a
sin a
ctg a
tga
2+a
cos a
-sin a
-ctg a
-tga
Зл
-z— a
2
-cos a
-sin a
ctg a
tga
371 ^
-cos a
sin a
-ctg a
-tga

102
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Доказательство тригонометрических
тождеств. Вычисление значений
тригонометрических выражений
Тригонометрические тождества доказывают
с помощью тождественных преобразований
следующими способами:
1) преобразуют одну часть равенства до тех
пор, пока она не станет формально (побуквенно)
равна другой части равенства;
2) преобразуют обе части равенства, пока не
придут к одному результату;
3) рассматривают разность между правой и
левой частью равенства и доказывают, что при
любых допустимых значениях входящих туда
тригонометрических функций эта разность
равна нулю.
Пример 1. (sin а - cos а) = 1 - sin 2а.
Решение. Преобразуем только левую часть:
2 2 2
(sin а - cos а) = sin а - 2sin а cos а + cos а =
2 2
= sin а + cos а - sin 2а = 1 - sin 2а. Мы
получили буквальное совпадение выражений в левой
и правой частях равенства, значит, тождество
доказано.
пРимеР 2- (sh " *е «Xssh + tg °0 =
= 2 cos2a - cos 2a.
Решение. Заметим, что данное выражение
имеет смысл только при cos а Ф 0, т. е. при
a* п + ял-
Тождественно преобразуем левую часть
равенства:
(_L- -tga¥^- +tf aW-Ц* -tg2a =
I cos а ъ Л cos a 6 ) \qosol) 6
Решение. Рассмотрим разность между левой
и правой частью равенства и преобразуем ее:
sin6 + ") 1 +
cos(i + а)
sin 2а
cos 2а
.я тс .
sin 2 cos а + cos т sin а
тс . тс .
cos 7 cos а - sin т sin а
4 4
cos а + sin а
-5-(cosa + sin а)
-«-(cosa - sin а)
1 + sin 2а
2 2
cos а - sin а
1 + sin 2а
(cos а - sina)(cosa + sin а)
(cos а + sin а) - (1 + sin 2а)
(cos а - sina)(cosa + sin а)
2 2
cos a + 2 cos a sin a + sin a - 1 - sin 2 a
2 2
cos a - sin a
1 + sin 2 a - 1 - sin 2 a
= 0.
2
cos a
. 2
sin a
2
cos a
. 2
sin a
2
cos a
2
cos a
2
cos a
= 1.
Значит, левая часть равна 1 для любых
допустимых значений а. Преобразуем правую часть:
2 2 2
2 cos a - cos 2a = 2 cos a - (2 cos a - 1) —
= 2 cos 2 a - 2 cos 2 a + 1 = 1.
Правая часть равна 1 при любых значениях а.
Следовательно, исходное равенство есть
тождество для всех допустимых значений а.
Пример 3. tg ( 2 + а)=
1 + sin 2а
cos 2а
cos 2 а
Разность выражений равна 0, значит, данное
равенство действительно является тожеством
для любых значений а, кроме тех, при которых
cos 2а = 0 или cos (| + а ] = 0.
Замечание. При выполнении данного
примера использовались следующие формулы алгебры
*
и тригонометрии .
1) sin I 2 + a 1 = sin 7 cos a + cos I sin a —
синус суммы двух углов.
лч (Ъ . "\ Я .71.
2) cos (т + a I = cos т cos a - sin т sin a —
косинус суммы двух углов.
2 2
3) cos 2a = cos a - sin a — косинус
удвоенного угла.
.v . тс тс J2
4) sin 2 = cos 7 = "5 значение
тригонометрической функции для угла т (45°).
*При записи доказательства конкретного
тождества ни перечисления, ни ссылок на стандартные
формулы не требуется.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
103
5) cos2ot - sin2ot = (cos а - sin a)(cos a + sin a) —
2 2
формула сокращенного умножения: a - b =
= (a - b)(a + b).
6) (cos a + sin a)2 = cos2 a + 2 cos a sin a + sin a.
2
Формула сокращенного умножения (a + 6) =
= a2 + 2ab + b2.
2 2
7) cos a + sin a = 1 — основное
тригонометрическое тождество.
8) 2 sin a cos a = sin 2a — формула синуса
удвоенного угла.
Пример 4.
2
sin a + 2 sin 3a + sin 5a = 4 sin 3a cos a.
Решение. Преобразуем левую часть
равенства при помощи формулы суммы синусов для
первого и третьего слагаемых,
sin a + 2 sin 3a + sin 5a = sin a + sin 5a + 2 sin 3a =
a + 5a 5a - a
= 2 sin
cos
+ 2 sin 3a =
2 wo 2
= 2 sin 3a cos 2a + 2 sin 3a = 2 sin 3a (cos 2a + 1) =
= 2 sin 3a (2 cos 2 a - 1 + 1) = 4 sin 3a • cos a.
Тождество доказано.
Пример 5. Упростить выражение
4 1
4 cos х - 2 cos 2л: - 5 cos ^Хт
Решение. Воспользуемся формулами:
2 1 + cos 2х л о 2 0 -
cos х= 5 * cos4x = 2cos 2х-1.
Имеем:
f\ + сов2лЛ2
<!
, - 2 cos 2х - | (2 cos2 2х - 1) =
= 1 + 2res^£ + соН^ае - "2тяиь2о: - co§^2jc +
т2 2#
__ ^ -7 1 + sin 4a - cos 4a
Пример 6. Упростить :—— .
г г 1 н- cos4a н- sin4a
Решение. Первое преобразование:
1 + sin 4a = 1 + 2 sin 2a cos 2a =
2 2
= sin 2a + cos 2a + 2 sin 2a cos 2a =
2
= (sin 2a + cos 2a) .
Второе преобразование:
2 2
cos 4a = cos 2a - sin 2a —
(cos 2a + sin 2a)(cos 2a - sin 2a).
Таким образом,
1 + sin 4a - cos 4a _
1 + cos 4a + sin 4a
2 2 2
(sin 2a + cos 2a) - (cos 2a - sin 2a)
2 2 2
(sin2a + cos2a) + (cos 2a - sin 2a)
2
(sin 2 a+cos 2 a) -(cos 2 a-I-sin 2 a) (cos 2 a - sin 2a) _
2 ~~
(sin 2a + cos2a) +(cos2a + sin2a)(cos2a - sin 2a)
(flinflq I roygpQ(sin2a-l-iuo&gtr-xeggtr+3in2a)
juiiiflu I HMifli^(£»r^+cos2a+cos2a-..flia-gTr)
2 sin 2a , rt
= 75 яг = tg 2a.
2 cos 2a ь
Пример 7. Упростить
sin 3 a
1 - 2sin
(i - -)
-cos
(«♦»■
1 к
Решение. Заметим, что 1 = 2 • « = 2 sin g .
Тогда знаменатель дроби можно представить в виде:
2 sin g - 2 sin Г | - 2a J =
= 2( sin g - sin f g - 2a J J = 2 • 2 sin a cos ( g - a j.
Преобразуем числитель:
sin 3a = sin (a + 2a) = sin a cos 2a + cos a sin 2a =
= sin a (cos 2a + 2 cos a).
Имеем:
sin 3 a
1 - 2sin
__ si»tt(co8 2a + 2 cos a) _
fg - 2a] 4si*rtfcos(~ - a]
4 cos a - 1
4 cos
(i-)
2
m 4cos a - 1 / , л \
Тогда --cos(a+gJ =
4cosU " aJ
4cos a - 1 - 4cos(a + gjcosfg - a]
4 cos
4 cos'
(s -a)
'a - 1 - 2[ cos 5 -f cos 2a j
4 cos
S-)
= 4cos a - 1 - 1 - 2(2cos a - 1) =Q
4coe(g - a)

104
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Пример 8. Вычислить значение выражения.
. 5л , . 2я
sin jo + sin-Q- 2 sin
5л 2л
COSJq + cos-g-
2 cos
5л 2л 5л _2яГ
18 + 9 18^9
~2~с>2~
5л 2л 5л
18 9 1
—2—у^ 2
2 suit
2 cost
-1.
Пример 9*. Вычислить sin a sin За, если
cos 2а =-« .
Имеем:
sin а sin За = 5 (cos (За ~ «) - cos (За + а)) =
1 12
= 5 (cos 2сх - cos 4а) = ~ (cos 2а - (2 cos 2а - 1)) =
«g(coe2a-2coe22a+l)«g(-J -2-g +l)-g.
5 - 4 cos а
Пример 10*. Вычислить
( • а о аЛ2
(юп2 - 2cosgJ
если tg g в""2 *
, a sinl 1 а 0 . а
tg 2 = ""о = "I » сое g - -2вш 5 =*
cos g
. а 0 а . а 0/ 0 . а Л с . а
=> sin « - 2 cos g = sin g - 21 -2 sin g J = 5 sin g •
Имеем:
к л 5 - 4(l - 2sin2|l
5 - 4cosa v */
(sing - 2cosg] (5sing]
1 + 8sin2g
oc . 2a
25 sin g
i. 2a
tg2
2 5 sin
n2
^8 .2a
- + gg, но sin g =
H)
1 + tg
2a
1 +
1\2
H)
Toi*aS + s =si
ЧИСЛОВЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
1. Числовые последовательности
Конечной числовой последовательностью
является любой конечный набор действительных
чисел, каждое из которых имеет свой номер, то
есть натуральное число, поставленное в
соответствие данному действительному.
Если таких номеров конечное число, то
последовательность конечна.
Если же любому натуральному числу
поставлено в соответствие некоторое действительное
число (единственное), то последовательность
является бесконечной.
Способы задания числовых последовательностей.
1) Табличным способом задаются конечные
числовые последовательности: составляется
таблица, в одной строке которой записываются
натуральные числа — номера членов
последовательности, в другой — действительные числа,
поставленные в соответствие данным
натуральным (значения членов последовательности).
Такое задание числовой последовательности
происходит при заполнении большинства карт
наблюдений, результатов эксперимента и т. п.
Пример 1. Ученик решил узнать среднюю
температуру воздуха первой недели июля. Для
этого он измерял температуру каждый день с
1 по 7 июля, а результаты заносил в таблицу:
Дни недели
Температура
1
26
2
28
3
31
4
29
5
32
6
26
7
24
Таким образом, средняя температура воздуха
равна t = -=- = 28.
2) Функциональный способ задания числовой
последовательности: каждый член
последовательности задается как функция своего номера.
1 2
Примеры. 1) ап = - ; 2) ап = 2л - Зп;
В)ап-(-1)п; 4)0» = cos п.
В приведенных примерах л - 1, 2, 3, 4, ....
Подставляя конкретное значение п в формулу,
можно определить значение члена
последовательности с соответствующим номером.

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
105
Например, четвертый член
последовательности 2) равен ап = 2 • 4 - 3 • 4 = 20;
последовательность 1) имеет следующие члены:
1.1.1.1.
х» 2' 3' 4' ""
3*) Рекуррентный способ задания числовой
последовательности: каждый член
последовательности, начиная с некоторого, задается как
функция от одного или нескольких
предыдущих членов.
Примеры. 1) ап + г = Зап + 7;
Свойства последовательностей
(*) Последовательность называется
ограниченной сверху, если существует такое число А,
что для любого номера п верно неравенство
ап < А, то есть любой член последовательности
не превосходит некоторого числа.
Соответственно, числовая
последовательность ограничена снизу, если существует такое
число В, что для любого номера п выполняется
неравенство ап > В.
Числовая последовательность называется
ограниченной, если она ограничена и сверху, и
снизу.
Пример 1. Последовательность ап = -п
ограничена сверху, так как любой ее член ап < - 1.
Пример 2. Последовательность ап = 2л + 1
ограничена снизу, так как любой ее член ап > 3.
Пример 3. Последовательность ап = (-1)п
ограничена, так как для любого ее члена верно
неравенство -1 < ап < 1.
Последовательность называется монотонно
возрастающей, если любой ее член, начиная с
некоторого номера, не меньше предыдущего, то
есть ап + ! > ап. (Если же выполняется строгое
неравенство ап + г > ап, то последовательность
называется строго монотонно возрастающей.)
Соответственно, когда любой член
последовательности, начиная с некоторого номера, не
превосходит предыдущего, то последовательность
называется монотонно убывающей (то есть,
если, начиная с определенного номера,
выполняется неравенство ап + г < ап).
Пример 4*. Доказать, что последовательность
= Зп " 1
°п Ъп + 4
монотонно возрастающая и
ограниченная.
Решение. Рассмотрим два соседних члена
последовательности сЛ + 1исли докажем, что
выполняется неравенство сп + г > сп.
3(л + 1) - 1 Зл + 2.
Зл
°п Ъп + 4 '
n + 1 5(л + 1) + 4 Ъп + 9*
Рассмотрим разность:
5л + 4 5л + 9
= Зп + 2 _ Зл - 1 ^
°л + 1 °п Ъп + 9 Ъп + 4
= (Зл + 2)(5л Н- 4) - (Зл - 1)(5л + 9) =
(5л + 9)(5л + 4)
15л2 + 22л + 8 - (15л2 + 22л - 9) =
(5л + 9)(5л + 4)
= 17
(5л + 9)(5л + 4)'
Так как в числителе полученной дроби
положительное число 17 и в знаменателе при любом
натуральном л также положительное число, то
сп + 1-сп>0 *> Сп + 1>сп-
Значит, эта последовательность строго
монотонно возрастающая. Снизу она ограничена чис-
3-1-1 2
ЛОМС1=5ТП=9*
Докажем, что эта последовательность ограни-
3
чена сверху числом g ,
&
Действительно, с„ - ■= — -——
п о 5л + 4
5л + 4
3
5
15л - 5 - 15л - 12
-17
5(5л + 4) 5(5л + 4)
Полученное выражение при любом
натуральном п отрицательно, то есть
cn-g<0 <=> cn<g. Итак, g < с < g .
Мы показали, что данная последовательность
ограничена снизу и сверху, следовательно, она
просто ограничена.
2. Арифметическая прогрессия
Числовая последовательность называется
арифметической прогрессией, если любой ее

106
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
член, начиная со второго, равен предыдущему,
сложенному с одним и тем же числом d * 0.
Число d называется разностью
арифметической прогрессии.
Название «разность прогрессии» происходит
от того, что для любых двух последовательных
членов прогрессии их разность является
постоянным числом d, то есть ап + 1- ап = d.
Примеры. 1) 2; 20; 38; 56; 74 — конечная
возрастающая арифметическая прогрессия;
аг = 2;d = 18;
2) 4,2; 0; -4,2; -8,4; ... — бесконечная
убывающая арифметическая прогрессия; аг = 4,2;
d =-4,2;
S)-l;
8' 4' 8
8' 4'"
— бесконечная
возрастающая арифметическая прогрессия;
1 а 1
ai " "2;d=8-
Формула 71-го члена арифметической прогрессии:
Пример 1. Дана арифметическая прогрессия
13; 11; 9; ... Найти, чему равен 31-й член этой
прогрессии.
Решение. Найдем разность этой прогрессии:
11-13 = -2.
Первый член прогрессии а1 = 13,
следовательно, по формуле л-го члена, имеем:
а31 - ах + (31 - 1) • (-2) - 13 + 30 • (-2) = -47.
Ответ: а31 = -47.
Свойство членов арифметической прогрессии
Каждый член арифметической прогрессии,
начиная со второго, равен среднему
арифметическому двух соседних с ним:
ап-1 + ап + 1 /1Ч
<*„ 2 • (1)
(Благодаря этому свойству
последовательность и называется арифметической прогрессией.)
Верно и обратное утверждение: если все
члены некоторой числовой последовательности,
начиная со второго, удовлетворяют условию (1), то
эта последовательность является
арифметической прогрессией.
Пример 2. Дано два числа: -11 и 35. Какое
число, лежащее между ними, нужно выбрать,
чтобы полученные три числа составляли
арифметическую прогрессию?
Решение. Учитывая утверждение, обратное
сформулированному свойству членов
арифметической прогрессии, найдем нужное число:
-11 + 35 1П л л л*
а2 = g = *2, т. е. три числа: -11; 12;
35 составляют арифметическую прогрессию.
Ответ: число 12.
Формула суммы первых п членов
арифметической прогрессии
Сумма первых п членов арифметической
прогрессии равна среднему арифметическому
первого и л-го члена этой прогрессии, умноженному
на их количество.
Sn = al + a2 + -+an==
а1 +ад
41.
(2)
Из формулы (2) следует и другая формула
для Sn:
2а* + d(n - 1)
Sn=-±—2 п.
(3)
Пример 3. Найти сумму первых 17-и членов
арифметической прогрессии -7; -5; ... .
Решение. Найдем разность этой прогрессии
d = -5 - (-7) = 2. По формуле (3) найдем сумму
первых 17-и членов:
_ 2-(-7) + 2*(17 - 1)
Ответ: S17 = 153.
•17 = 153.
Пример 4*. Сумма первых 13-и членов
арифметической прогрессии равна 65, а сумма
членов с 10-го по 20-й равна 429. Найти сумму
членов этой прогрессии, начиная с 7-го по 23-й
включительно.
Решение. Пусть d — разность этой
прогрессии, аг — ее первый член. Воспользуемся
формулой (3) для суммы прогрессии. Имеем:
2ал + (13 - l)d
S13 - — g 13 = 65'
откуда 2аг + 12d = 10.
Члены исходной прогрессии с 10-го по 20-й
представляют из себя также арифметическую
прогрессию с той же разностью d, но только
первым членом этой прогрессии является число а10,
а количество членов, составляющих сумму,
данную в условии задачи, равно 11. Используем
формулу (2):
аю + а20
•11 = 429 <=> а1П + а9П = 78
ю
*20"

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
107
Учитывая, что
a10 = a1 + (10-l)d;
a2o = ai + (21 - l)d;
a10 + a20 — 2ax + 29d;
имеем систему:
f 2ax + 12d = 10, f 2ax + 12d = 10,
f 2ax + 12d =
t 17d = 68;
[ 2аг + 29d = 78;
f d = 4,
^ja^-19.
Найдем теперь сумму, начиная с 7-го по 23-й
член прогрессии.
а7 = аг + (7 - 1) • 4 = -19 + 24 = 5.
а23 = аг + (23 - 1) • 4 = -19 + 88 = 69.
Искомая сумма:
а7 + а
2 -(23 - 7) = Ц-69 .16 = 37-16 =
= 592.
Ответ: 592.
3. Геометрическая прогрессия
Геометрическая прогрессия — это числовая
последовательность, каждый член которой,
начиная со второго, равен предыдущему,
умноженному на одно и то же число д, называемое
знаменателем геометрической прогрессии,
причем q Ф 0, \q\ Ф 1.
Примеры. 1) 2; 7; 24,5; 85,75 — конечная
возрастающая геометрическая прогрессия;
Ьх = 2; д = 3,5.
2) -3; 9; -27; 81; -243; ... — бесконечная
геометрическая прогрессия; Ьг = -3; q = -3. Эта
последовательность не является ни возрастающей,
ни убывающей.
3) 2; 1; £ ; 7 ; 8 ; ,,# — бесконечная
убывающая геометрическая прогрессия; Ьг = 2; q = ~ •
Формула л-го члена геометрической прогрессии:
Пример 1. Дана геометрическая прогрессия:
т ; г ; 1; ••• Найти ее 9-й член.
Решение. Найдем знаменатель прогрессии:
4
Первый член прогрессии Ъх = т .
По формуле п-го члена: Ь9 — bxg ~ = т • 2 =
- 26 - 64.
Ответ: Ь9 = 64.
Свойство геометрической прогрессии
Каждый член геометрической прогрессии,
начиная со второго, есть среднее геометрическое
двух соседних с ним:
Верно и обратное утверждение: если все
члены числовой последовательности, начиная со
второго, удовлетворяют равенству (4), то данная
последовательность является геометрической
прогрессией.
Пример 2. Какое число нужно поместить
между числами 3 и 243, чтобы три числа составляли
геометрическую прогрессию?
Решение. Воспользовавшись
сформулированным выше условием, найдем такое число. Пусть
Ьг = 3, Ь3 = 243, тогда
62= V3 • 243 =27.
Три числа: 3; 27; 243 составляют
геометрическую прогрессию.
Ответ: Ь2 - 27.
Формула суммы первых п членов
геометрической прогрессии
Пример 3. Найти сумму первых 8-ми членов
1 1 1
прогрессии ^7 5 уд > I' **• *
Решение. В данной прогрессии Ьг = тгт ;
1 1 А
g = т^ : ^7 = 4, следовательно,
с _ 1 1 - 48 21845
Ответ:
'8 64 1-4
21845
64 *
64
Пример 4*. Известно, что восьмой член
геометрической прогрессии в восемь раз больше
пятого ее члена, а шестой член на 15 больше второ-

108
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
го. Найти сумму членов прогрессии со второго
по девятый включительно.
Решение. Пусть Ьх — первый член данной
прогрессии, a q — ее знаменатель. Тогда, по
формуле л-го члена, можем записать:
7 А *»
bS = ь\9 » ЬЪ = b\Q > b6 e biQ '> Ь2 = biQ-
По условию:
Ьл b+q «
г2=8=>-Ц=8«*д=8«*д = 2.
*5 bxq*
По условию:
&6-&2 = 15 => М5-Ь1д= 15<=>
<=>bxg(g - 1) = 15.
Тогда&1-2-(24-1) = 15 <=> &х - \ .
Последовательность Ь2> &з> Ь4> •••» ^9 — также
является геометрической прогрессией с тем же
знаменателем q = 2, а ее первый член — число
&2 = 1. По формуле суммы:
откуда
1 -28 8
S = 1 • V—Т = 2 ~ 1 = 255.
Ответ: 255.
Бесконечно убывающая геометрическая
прогрессия — это бесконечная геометрическая
прогрессия, знаменатель которой q по модулю
меньше 1, т. е. \q\ < 1.
Сумма всех членов бесконечной прогрессии
S = &х + Ъ2 + &з + ••• + К + —
есть конечное число, определяемое формулой:
Пример 5. Найти сумму бесконечно
убывающей геометрической прогрессии
3-1- 1-1 .
Решение. Первый член этой прогрессии
Ьг = 3, знаменатель g = 5 > тогда
1 9
КРАТКИЕ СВЕДЕНИЯ КУРСА
АЛГЕБРЫ 10-11 КЛАССОВ
Показательная функция
1. В курсе средней школы принимается без
доказательства, что положительное число а
можно возводить и в иррациональную степень х;
х хп
а приблизительно равно а , где хп —
рациональное число. Причем это приближение может
быть сколь угодко точным при достаточной
точности приближения иррационального числа х
рациональным числом хп. Функция, заданная
формулой вида у = ах, где а — некоторое
положительное число, не равное единице,
называется показательной.
2. Функция у = а* при а > 0 обладает
следующими свойствами, которые иллюстрируются ее
графиком (рис. 71, 72):
а)Я(/) = Я,£(Я = (0;оо).
б) Функция возрастает при а > 1; функция
убывает при 0 < а < 1.
Показательные уравнения
и неравенства
1. Решением уравнения а* = Ъ служит х =
= loga Ь. Уравнение а/(х) = а*х) (где а > 0, а * 1)
равносильно уравнению f(x) = g(x).
2. Уравнение вида Аа + Вах + С = 0 с
помощью подстановки а* = у сводится к
квадратному уравнению Ay + By + С = 0.
Примеры. Решить уравнения:
1)52х-6-5х+5 = 0;
2)3-16х + 2-81х = 5-36х.
S = 3 + 1 + ... = 3<
Ответ: S = «
1 3

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
109
1) Положим 5х = у. Тогда 5 х = (5х) = у и
2
данное уравнение примет вид у - 6у + 5 — 0,
откуда уг = 1, i/2 = 5» *1 = 0, х2 = 1.
2) Разделив части уравнения на 36х Ф О, полу-
-»•(ЙГ*"(ЙГ-»-ЙГ+*-(!Г-*
х 2
Положим (4/9) = у. Тогда имеем Зу + - =5;
Зг/2 - Ъу + 2 - 0; ух = 1; i/2 = \ 5 (§)* - 1; *i - 0;
(4Л* 2 1
Ы 3;Х2 2 е
3. Решение показательных неравенств вида
af(x) < а^(х) ^где а > о, а ^ 1) основано на
следующих утверждениях:
если а > 1, то afM < а*х) <=* /(*) < g(x);
если 0 < а < 1, то а/(х) < а*х) «► /(*) > g(x).
4. Примеры. Решить неравенства:
1)3Х< |; 2) (0,25)6х"х2 >0,255;
3) 4х - 6 • 2х + 8 < 0.
1) Замечая, что 1/9 = 3~2, перепишем данное
х —2
неравенство в виде 3 < 3 . Так как основание
степени больше 1, то х < -2. Получаем ответ:
(-<*>; -2).
2) Поскольку 0 < 0,25 < 1, заданное
неравенство равносильно неравенству 6х - х < 5, т. е.
(х - 1)(х - 5) > 0. Решая последнее, получаем
ответ: (-оо; 1) и (5; оо).
3) Положим 2х = у; тогда 4х = (2х) = у и дан-
ное неравенство примет вид у - 6у + 8 < 0. Решая
это неравенство, находим 2 < у < 4 или
2 < 2х < 22, откуда К х < 2.
Итак, (1; 2) — решение данного неравенства.
Логарифм и его свойства
1. Логарифмом числа Ъ по основанию а (где
а > 0, а Ф 1) называется показатель степени, в
которую надо возвести а, чтобы получить число
Ъ. Логарифм числа Ь по основанию а
обозначается символом loga Ь.
2. Если а > 0, а * 1, то loga Ъ по определению
есть показатель степени, в которую надо
возвести число а, чтобы получить число Ь. Поэтому ра-
logab
венство а — о есть тождество, которое
называют основным логарифмическим тождеством.
Например, 3 =5.
3. Для обозначения десятичных логарифмов
(логарифмов по основанию 10) принята
специальная запись: вместо log10 6, где Ъ —
произвольное положительное число, пишут \g Ъ.
Логарифм по основанию е (е = 2,712828...)
называется натуральным логарифмом и
обозначается In Ь.
4. Логарифмы существуют только для
положительных чисел, т. е. loga N (где a > 0 и а Ф 1)
существует, если N>0.
5. При основании а > 1 логарифмы чисел N > 1
положительны, а логарифмы чисел 0 < N < 1
отрицательны.
Например, log2 5 > 0, log3 5 < 0.
6. При основании 0 < а < 1 логарифмы чисел
N > 1 отрицательны, а логарифмы чисел 0 < N < 1
положительны.
Например, log1/2 5 < 0, log1/3 5 > 0.
7. Логарифм единицы по любому основанию
(а > 0, а * 1) равен нулю, т. е. loga 1 =» 0.
8. Логарифм самого основания равен 1, т. е.
logaa = l.
Логарифмическая функция
1. Так как показательная функция у — ах (где
a > 0, а Ф 1) является монотонной
(возрастающей при a > 1 и убывающей при 0 < а < 1), то
она имеет обратную функцию. Чтобы найти эту
обратную функцию, нужно из формулы у = а
выразить х через у: х — loga у, а затем поменять
обозначения х на i/ и i/ на х; тогда получим i/ =
= loga х. Функция у — loga л: (где а > 0, a * 1)
называется логарифмической.
Итак, показательная и логарифмическая
функции при одном и том же основании
являются взаимно обратными функциями.
2. График логарифмической функции у =
= loga х можно построить, воспользовавшись
тем, что функция у = loga х обратна
показательной функции у = ах. Поэтому достаточно постро-

110
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
ить график функции у = а , а затем отобразить
его симметрично относительно прямой у = х.
На рисунке 73 изображен график функции
у = loga х при а > 1, а на рисунке 74 — график
функции у = loga х при 0 < а < 1.
3. Отметим свойства функции у = loga х при
а > 1:
а)1>(/) = Д+ = (0;оо);
б) функция возрастает при а > 1, функция
убывает при 0 < а < 1.
Теоремы о логарифме произведения,
частного и степени. Формула
перехода к новому основанию
1. Логарифм произведения двух или
нескольких положительных чисел равен сумме
логарифмов сомножителей, т. е.
loga (NXN2... Nk) - loga Nx + loga N2 + ... + loga iVft.
2. Логарифм частного положительных чисел
равен разности логарифмов делимого и
делителя, т. е.
loga^- =logaiV1-logaiV2.
3. Логарифм степени равен произведению
показателя степени на логарифм ее основания,
т. е. loga № = cloga N.
Замечание.
Если N < 0, а с — четное число, то
справедлива формула loga № = cloga \N\.
Например, loga (-3) = 41oga 3.
4. Формула перехода от основания Ь к
основанию а имеет вид
logaAT
У = loga х
0<а<1
Рис. 73
Рис. 74
5. Если а = N, то формула перехода примет
вид logb а = jjjjp-g , или 1 = \ogba \ogab.
6. Если основание логарифма и число,
стоящее под знаком логарифма, возвести в одну и ту
же степень, отличную от нуля, то значение
логарифма не изменится, т. е.
loga N = log с №;
а
log kN = logaNk =—%-.
Например, log8 Ъ = « log2 b; log^ Ъ = 21og2 Ъ.
7. Пример. Найти:
l-llog549 9 1-41о*549 2-llog549
25 4 = (52) = 5
Преобразуем теперь показатель степени:
1
2 - \ log5 49 - 21og5 5 - log5 492 - log5 52 -
25 2-glog549
- log5 7 = log5 ^ • Следовательно, 5 =
i 25
KlogsT 25 , .
= 5 = -=- (в силу основного
логарифмического тождества).
Логарифмическое уравнение
1. Уравнение, содержащее переменную под
знаком логарифма, называется
логарифмическим. Простейшим примером
логарифмического уравнения служит уравнение loga х = Ъ (где
а > 0, а Ф 1). Его решение х = а .
2. Решение логарифмического уравнения
вида loga f(x) — loga g(x) основано на том, что такое
уравнение равносильно уравнению f(x) = g(x)
при дополнительных условиях f(x) > 0, g(x) > 0.
3. Примеры. Решить уравнения:
Dlog37i (*-1) = 6;
2) log3 (х2 - 4х - 5) = log3 (7 - Зх).
Решение.
1) Согласно определению логарифма имеем
2
х - 1 - (tyl)6, х - 1 - (23)6; х - 1 = 24, х = 17.
2
2) Данное уравнение сводится к уравнению х -
- 4х - 5 = 7 - 3*, откуда получаем х - х - 12 = 0,

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
in
т. е. хх = 4, х2 — -3. Подставим в неравенства,
задающие область определения уравнения
7 - Зх> 0, х - 4дг - 5 > 0. Этой системе
удовлетворяет только х = -3.
4. При решении логарифмических уравнений
применяется метод введения новой переменной,
а также логарифмирование обеих частей
уравнения.
Пример. Решить уравнения:
l)logx575 -l,25 = log*V5; 2) х^ - (Jif.
Решение.
3-5 2
1) Полагая logx 5 = у, получаем "^ "" 4 = 4
или г/2 - 6у + 5 = 0, откуда уг = 1; у2 = 5. Из
первого уравнения находим хх — 5, а из второго х2 = л/5 .
2) Логарифмируем обе части по основанию 10:
Jxlgх = хlg Jx; л/jc lgx = g***x»
5 л/х (2 - V*) lg * = 0. Так как из условия
следует, что х > 0, то последнее уравнение
равносильно совокупности уравнений 2 - Jx = 0;
lg х = 0. Первое из них имеет корень хг = 4, а
второе — корень х2 = 1. Проверка показывает,
что оба корня удовлетворяют данному
уравнению.
Логарифмическое неравенство
1. Неравенство, содержащее переменную
только под знаком логарифма, называется
логарифмическим. При решении логарифмических
неравенств следует учитывать общие свойства
неравенств, свойство монотонности
логарифмической функции и область ее определения.
2. Неравенство loga f(x) > loga g(x)
равносильно системе f(x) > g(x) > 0 при a > 1 и системе 0 <
< f(x) < g(x) при 0 < a < 1.
3. Пример 1. Решить неравенство:
togo,*
Ъх - 3
>1.
»5 х + 2
Решение. Это неравенство равносильно системе:
Ъх - 3
х + 2
Ъх - 3
х + 2
>0,
<0,5.
Первое неравенство характеризует область
определения логарифмической функции, а
второе — условие ее убывания при основании
0 < 0,5 < 1. Далее имеем
Ъх - 3
>0,
х + 2
Ъх - 3 - 0,5(* + 2)
х + 2
<0;
* + 2
*G(-oo;-2)u(|;oo)t
Найдя пересечение указанных в последней
системе множеств, получаем ответ: (3/5; 8/9).
Пример 2. log2 (2х - l)log2 (2х + 1-2)< 2.
Решение. Так как 2х - 2 = 2(2Х - 1), то
данное неравенство можно записать в виде
log2 (2х - l)(log2 2 + log2 (2х - 1» < 2 «
~ log2 (2х - 1)(1 + log2 (2х - 1)) < 2.
Полагая log2 (2х - 1) = у, получим
неравенство у{\ + I/) < 2, или$/ + I/- 2 < 0, откуда-2<у <
< 1. Возвращаясь к переменной х, получим
2"2<2х-1<2; ^ < 2х < 3; log2 \<х< log2 3.
Итак, решением данного неравенства служит
интервал (log2 5/4; log2 3).
Функция у = sin х
1. Отметим основные свойства функции у =
= sinx:
а) область определения — вся числовая
прямая, т. е. D(sin) — R;
б) множество значений — отрезок [-1; 1],
т. е. £(sin) = [-l; 1];
в) функция нечетная: sin(-x) = -sin х для
всех х е R;
г) функция периодическая с наименьшим
положительным периодом 2л, т. е. sin(jc + 2л) =
= sin х для всех х е R;
д) sin х = 0 при х = nk, где ke Z;
е) sin х > 0 для всех х е (2nk; л + 2nk), ke Z;
ж) sin х < 0 для всех х е (л + 2лЛ; 2л + 2лЛ),
*€Z;
з) функция возрастает от -1 до 1 в
промежутках I -5 + 2л£; о + 2л* I, k е Z;

112
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
и) функция убывает от 1 до -1 в промежутках
[jj +2тсй; у +2irt],*eZ;
к) функция принимает наибольшее значение,
равное 1, в точках х = « + 2rcft, ft е Z;
л) функция принимает наименьшее значение,
равное -1, в точках х — -у + 2rcft, ke Z.
2. Все перечисленные свойства синуса
позволяют построить его график на промежутке [-я; тс].
Так как функция у = sin х имеет период 2я, то ее
график на [-я + 2пк; к + 2лЛ] получается из
графика на [-тс; я] с помощью параллельного
переноса (рис. 75).
Функция у = arcsin х
1. Функция у = sin х на отрезке I -= ; « В03"
растает и принимает все значения из отрезка
[-1; 1]. Поэтому функция у — sin х на отрезке
обратима: т. е. имеет обратную функцию, которая
называется арксинусом и обозначается arcsin х.
Геометрически arcsin х означает величину угла
(дуги): заключенного в промежутке I-^ ; ^ L
синус которого равен х.
2. График функции у = arcsin х изображен на
рисунке 76. Этот график симметричен графику
функции у = sin л:, х е 1-=; «J относительно
прямой у — х.
3. Отметим свойства функции у = arcsin х:
a) D(arcsin) = [-1; 1];
6)£(arcsin) = [-5; 5 J.
в) функция нечетная, т. е.
arcsin (-х) = -arcsin х;
г) функция возрастающая.
4. Приведем основные значения функции
arcsin х:
arcsin 1=9»
. л/2 к
arcsin "о" = 7 >
arcsin 0 = 0,
arcsin [—о"J ="
arcsin(-l) = -2
к
~4'
. л/3 тс
arcsin ^ = з'
. 1 тс
arcsin к = g ,
areata (-|)"~g'
. ( Л\ к
агсвш(-т)--§,
Функция у = COS X
1. Отметим основные свойства функции
у — cos х:
а) область определения — вся числовая
прямая: т. е. D(cos) = R;
б) множество значений — отрезок [-1; 1],
т. е. E(cos) = [-1; 1]; значит, косинус —
функция ограниченная;
в) функция четная: cos (-х) = cos х для всех
х е Я;
г) функция периодическая с наименьшим
положительным периодом 2я, т. е. cos (х + 2тс) =
= cos х для всех х е R;
д) cos х = 0 при х = 2 + rcft, ke Z;
е) cos л: > 0 для всех х е (- = + 2лЛ; ~ + 2rcft J,
ft eZ;
ж) cos jc < 0 для всех х е [ « + 2rcft; -х- + 2rcft J,
ft € Z;
з) функция убывает от 1 до -1 в промежутках
[2тсА; я + 2тсЛ], ft € Z;
и) функция возрастает от -1 до 1 в
промежутках [-я + 2nk; 2rcft], ke Z;
к) функция принимает наибольшее значение,
равное 1, в точках х = 2nft, ke Z;
»,
-1/1
/
i5 У"
0 1*
я
Г 2
arcsin х
Зя\
2
■
<2L/
l
/ 0
-i
i
- 2
,
К л
/Ъъ~х
2
Рис. 75
Рис. 76
Рис. 77

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
113
л) функция принимает наименьшее
значение, равное -1, в точках х = я + 2яА, A € Z.
2. Все перечисленные свойства косинуса
позволяют построить его график на промежутке
[-я; я]. Ввиду того что период функции у =
= cos х равен 2я, ее график на [-л + 2яА, я + 2яА]
получается из графика на [-я; я] с помощью
параллельного переноса (рис. 77).
Функция у = arccos х
1. Функция у = cos х на отрезке [0; я] убывает
и принимает все значения из отрезка [-1; 1].
Поэтому функция у = cos х на отрезке [0; я]
обратима, т. е. имеет обратную функцию, которая
называется арккосинусом и обозначается у =
= arccos х. Геометрически arccos х означает
величину угла (дуги), заключенного в промежутке
[0; тс], косинус которого равен х.
2. График функции у = arccos х изображен на
рисунке 78. Этот график симметричен графику
функции у = cos дг, х € [0; я] относительно
прямой у = х.
3. Отметим свойства функции у = arccos х:
а) D(arccos) = [-1; 1];
б) E(arccos) = [0; тс];
в) arccos (-х) = тс - arccos х;
г) функция убывающая.
4. Приведем основные значения функции
arccos х:
arccos 0 =
2'
arccos
arccos 1 = 0,
72_
7з
arccos
тс
4'
arccos "у = ё »
1 тс
arccos g = з'
у = arccos х
Зтс
2
y = tex
SiT
72>
{ 2) 3 '
. ( Jb\ 5тс
arccis [-TJ = т ,
Рис. 78
Рис. 79
( *J2\ Зтс
arccos [-Y) = Т '
arccos (-1) = тс.
Функция у = tg X
1. Отметим основные свойства функции
У = tgx:
а) область определения — множество всех
тс .
действительных чисел, кроме чисел вида х — ~ +
+ ЯА, А € Z;
б) множество значений — вся числовая
прямая, т. е. E(tg) = R;
в) функция нечетная tg (-х) — -tg х для всех
х € D(tg);
г) функция периодическая с наименьшим
положительным периодом тс, т. е. tg (х + тс) = tg х
для всех х € D(tg);
Д) tg х = 0 при х = яА, А € Z;
е) tg х > 0 для всех х € (яА; ~ + яА), ft € Z;
ж) tg х < 0 для всех х е [ -= + яА; яА J, А € Z;
з) функция возрастает на каждом
промежутке f-g + яА; | + nk j, A e Z.
2. Все перечисленные свойства тангенса
позволяют построить его график на промежутке
(~2; 2 г **ВИДУ того что пеРи°Д функции у =
= tg х равен я, ее график на [-= + яА; т> + яА)
получается из графика на(~о• 2 )с помоЩью
параллельного переноса (рис. 79).
Функция у = arctg х
1. На промежутке (~о ' 5 ) тангенс
возрастает и принимает все числовые значения, т. е.
£(tg) — (-°°; °°). Поэтому функция у = tgx на
промежутке (-о» 5 ) Тратима, т.е. имеет
обратную функцию, которая называется
арктангенсом и обозначается у = arctg х.
Геометрически arctg х означает величину угла (дуги), за-
ключенного в промежутке I-= ; « I» тангенс
которого равен х.

114
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
2. График функции у = arctg х изображен на
рисунке 80.
Этот график симметричен графику функции
y = tgx,xe 1""о; 2 Jотносительно прямой у = х.
3., Отметим свойства функции у = arctg х:
a)Z>(arctg) = (-oo;oo);
б) £(arctg) =(-£;£)
в) функция нечетная, т. е.
arctg (-х) = -arctg х;
г) функция возрастающая.
4. Приведем основные значения функции
arctg х:
arctg 73 = д ,
arctg JL =5,
arctg 1 = 4 '
arctg 0 = 0,
arctg (--тг) = -g , arctg (-1) = -J ,
arctg (-73) = -g.
Функция I/ = ctg #
1. Отметим основные свойства функции у =
= ctgx:
а) область определения — множество всех
действительных чисел, кроме чисел вида nk,
k € Z;
б) множество значений — вся числовая
прямая, т. е. E(ctg) = R;
в) функция нечетная: ctg(-x) = -ctgx для
всех х е D(ctg);
г) функция периодическая с наименьшим
положительным периодом п, т. е. ctg (х + к) = ctg х
для всех х € D(ctg);
д) ctg х = 0 при л: = 5 + л£> ke Z;
е) ctg x > 0 для всех x e (rcfc; ~ + nk), ke Z;
ж) ctg x < 0 для всех x e f-= + rcft; rcfc J, ft e Z;
з) функция убывает на каждом промежутке
(nk; к + nk), k е Z.
2. Все перечисленные свойства котангенса
позволяют построить его график на промежутке
(0; тс), т. е. на промежутке, длина которого равна
периоду функции. Потому график функции у =
= ctg х на (nk; п + nk) получается из графика на
(0; тс) с помощью параллельного переноса
(рис. 81).
Функция у = arcctg х
1. На промежутке (0; п) котангенс убывает и
принимает все числовые значения, т. е. E(ctg) =
= (-оо; оо). Поэтому функция у = ctg х на
промежутке (0; п) обратима, т. е. имеет обратную
функцию, которая называется арккотангенсом
и обозначается у = arcctg х. Геометрически
arcctg х означает величину угла (дуги),
заключенного в промежутке (0; л), котангенс которого
равен х.
2. График функции у = arcctg х изображен на
рисунке 82.
Этот график симметричен графику функции
у = ctg х, х е (0; п) относительно прямой у — х.
3. Отметим свойства функции у = arcctg х:
а) D(arcctg) = (-оо; ОО);
б) Е(arcctg) = (0; тс);
в) функция убывающая;
г) arcctg (-х) = п - arcctg х.
4. Приведем основные значения функции
arcctg х:
arcctg 7з = ^ ,
6'
arcctg 1
4'
1
к
2
я
2
1
/у = arctg х
0 х
-2к\
У к y = ctg*
I ч
I ч
*>|
К
2
1
К
V у = arcctg дг
0 х
Рис. 80
Рис. 81
Рис. 82

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
115
аГСС g J3 = 8 *
arcctg (-j=) = f,
arcctg (~л/3) = -g-.
arcctg 0=2»
arcctg (-1) = -j-,
Решение простейших
тригонометрических уравнений
sin х = a, cos jc = а, tg jc = а, ctg jc = а.
Замена переменной
в тригонометрическом уравнении
1. Формула для корней уравнения sin х = а (где
\а\ < 1) имеет вид
и
х = (-1) arcsin а + nk, k е Z.
2. Частные случаи:
а) sin л: = 0 *=* х = 7сЛ, ke Z;
б) sin х = 1 » х = | + 2тс*, * € Z;
в) sin х = -1 <=> х = -g + 2лЛ, k € Z.
3. Формула корней уравнения cos х = а (где
|а| < 1) имеет вид
х — ±arccosа + 2яЛ, keZ.
4. Частные случаи:
а) cos Jt = 0^Jt=2 + rcft, ft е Z;
б) cos jc = 1 » x = 2лЛ, * € Z;
в) cos Jt = -l<=>Jt = 7i + 2rcft, ke Z.
5. Формула для корней уравнения tgx = а
имеет вид
л: = arctg а + я&, k е Z.
6. Формула для корней уравнения ctg х — а
имеет вид
х = arcctg а + rcfc, ke Z.
7. Одним из основных методов решения
тригонометрических уравнений, так же как и
других видов уравнений, является метод замены
переменной.
Пример. Решить уравнение
2 sin х + 7 cos х - 5 — 0.
2 2
Решение. Так как sin х — 1 - cos х, то
уравнение можно переписать следующим образом:
2(1 - cos2 х) + 7 cos х - 5 = 0, т. е. 2 cos х - 7 cos х +
-1-3 = 0. Полагая cos х = у, приходим к квадрат-
2 1
ному уравнению 2у - 7i/ + 3 = 0, откуда 1/1=9»
i/2 = 3, и получаем совокупность двух
простейших уравнений cos х — ~ » cos * = 3. Первое из
них имеет решения л: — ± « + 2яЛ, Л € Z, а второе
решений не имеет.
Методы решения
тригонометрических уравнений
1. Тригонометрическое уравнение вида
a0sin х + a1sin xcos х +
Л - 2 2 Л
+ a2sin xcos jc + ... + a^cos х — 0,
все члены которого имеют одну и ту же k-ю
степень относительно синуса и косинуса,
называется однородным. Однородное уравнение легко
сводится к уравнению относительно tgx, если
все его члены разделить на cos х. При этом если
а0 Ф 0, то такое деление не приведет к потере
решений, поскольку значение cos х = 0 не
удовлетворяет уравнению. Если же а0 = 0, то cos х
выносится за скобки.
Пример. Решить уравнение
о . 2 2 Л
2 sin х - sin х cos х - cos x = 0.
Решение. Разделив все члены уравнения на
2 2
cos х, получим 2tg jc - tg jc - 1 = 0; tg x = 1,
tg x — -5 ; xx = 7 + rcft, ke Z\ x2 = -arctg 5 + тел,
n e Z.
2. Уравнение вида acos x + ftsin x — с
равносильно
уравнению rsin (x + <p), где г = *Ja + 6 ,
Ф — arcsm -.
Пример.
1 /4 1
sin x + л/3 cos x = 1 » 5 sin x + -g- cos x = ^ ^
<=>sinfjc+gj=2 ^ * + g = С""1)" g + ля, л e Z;
x = -5 + (-1) g + тел, ne Z.
3. Наиболее часто применяется метод,
состоящий в том, что все члены уравнения,
стоящие в правой части, переносятся в левую часть;

116
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
После чего левая часть уравнения разлагается на
множители. При этом применяются формулы
разложения тригонометрических функций в
произведение, формулы понижения степени,
формулы преобразования произведения
тригонометрических функций в сумму.
Пример. Решить уравнение sin Зх = sin х.
Решение. Имеем sin Зх - sin х = 0 *=*
*=* 2sin х cos 2х = 0. Значит, либо sin х = 0,
откуда х = кп, пе Z, либо cos 2х = 0, откуда х — т +
+ y > п е z-
Предел функции и непрерывность.
Приращение функции
1. Число Ъ называется пределом функции fix)
при х, стремящемся к а, если для любого
положительного 8 найдется такое положительное
число S, что при всех х Ф а, удовлетворяющих
неравенству \х - а\ < 8, справедливо неравенство
\f(x) - b\ < е. При этом употребляют запись
lim f(x) = b.
х->а
2. Если функция fix) имеет предел при х -» а,
то этот предел — единственный.
3. Теоремы о пределе суммы, произведения и
частного. Если при х —> а существуют пределы
функций / и g, то:
1) lim (/(*) +£(*))= lim/(x) + lim£(x);
х-> а х->а х->а
2) lim f(x)g(x) = lim f(x) lim g(x);
x->a x->a x-)o
/r . lim f{x)
4) lim kfix) = * lim /(x), где k — постоянный
x-> а х-» a
множитель.
4. Пример.
lim *L±i = Iim (« + !)<«'-« + D .
x->-l x + 1 x-»-l X + 1
- lim (x2-x+l) = l + l + l = 3.
x-> -1
5. Функция fix) называется непрерывной в
точке х0, если она определена в некоторой
окрестности этой точки и если предел функции
при х -» х0 равен значению функции в этой
точке, т. е.
Шп/(х) = /(х0).
х""**0
6. Приращением функции fix) в точке х
называется величина А/(х) = fix + Ах) - /(х), где
Ах — приращение аргумента (произвольное
число). Например, fix) = х , тогда
fix) = (х + Ах)2 - х2 = 2хАх - Ах2.
Функция называется возрастающей, если
А/(х) > 0 при любых Ах > 0. Функция
называется убывающей, если А/(х) < 0 при любых Ах > 0.
Производная
и правила ее вычисления
1. Производной функции fix) в точке х
называется предел отношения приращения А/
функции в точке х к приращению Ах аргумента,
когда последнее стремится к нулю. Это можно
записать так: lim т- = fix) = у' = lim т^ .
д*->оАх v * д*-»оДх
2. Пример. Найти производную функции
т* / 1. Aw ,. Jx + Ах - л/х
Решение, у = lim т* = lim т =
* Дх-»оАх Дх-»0 Av
Ах
= lim
х + Ах
= lim
A*->°Ax(V* + Ах + Jx)
1 11
д*->°7х + Ах + Jx Jx + Jx 2jx'
3. Пусть иии — две функции, определенные
на одном и том же промежутке. Тогда
производная суммы этих функций равна сумме их
производных, т. е.
iuix) + vix))' = и\х) + v'ix).
4. Производная постоянной равна нулю:
(С)' =0.
5. Производная произведения двух функций
иии вычисляется по формуле
iu • v)' = u'v + uv'.
6. Если функции иии имеют в точке х
производные и если vix) Ф 0, то в этой точке существу-
u
ет производная из частного - , которая
вычисляется по формуле
(и\ _ uv - UV
7. Производная от сложной функции А(х) =
= gifix)) находится по формуле

Краткое изложение школьного курса математики
Алгебра. 7—11 классы
117
т. е. производная сложной функции равна
произведению производных ее составляющих.
8. Пример. Найти производную сложной функ-
/о с , 2Л00
ции у = (3 - ЭХ + X ) .
Решение, у' = 100(3 - 5* + *2)"(3 - 5х + х2)' =
= 100 (3 - Ъх + х2)"(-5 + 2х).
Производные основных функций
1. Производная степенной функции х , где
k € Я, х > 0, равна произведению показателя к
на степень х , т. е.
(дг ) = кх .
2. Производные тригонометрических
функций вычисляются по следующим формулам:
(sin х)' = cos х9 (cos х)' = -sin х,
(tg*)' =
1
2 '
COS X
(ctg*)' = -
. 2 #
sin Jt
3. Производная показательной функции у = а*
вычисляется по формуле (ах)' = ах1п а, в
частности (ех)' = <?х.
4. Производная логарифмической функции
у = loga х находится по формуле (loga х)' = ^^ .
В частности, производная натурального
логарифма вычисляется по формуле (In х)' = - .
Касательная к графику функции
1. Касательной к кривой в данной точке М
называется предельное положение секущей
NM, когда точка N стремится вдоль кривой к
точке М.
2. Угловой коэффициент касательной к
графику функции равен значению производной
этой функции в точке касания х0:
ft = tg<p = lim -~ =f(x0).
В этом заключается смысл производной.
3. Уравнение касательной к кривой у = f(x) в
заданной точке имеет вид:
У ~ Уо = f (*о)(* - хо)>
ще(х0;у0) —координаты точки касания, (х; у) —
текущие координаты, т. е. координаты любой
точки, принадлежащей касательной, а f(x0) = к =
= tg ф — угловой коэффициент касательной.
Интервалы монотонности.
Максимум и минимум функции
1. Теорема. Если функция / имеет
положительную производную в каждой точке
интервала (а; Ь), то функция возрастает на этом
интервале. Если функция / имеет отрицательную
производную в каждой точке интервала (а; &), то
функция убывает на этом интервале.
2. Внутренние точки области определения
функции, в которых производная функции
равна нулю или не существует, называются
критическими.
3. Точка х0 из области определения функции
/ называется точкой минимума
(максимума) этой функции, если найдется 5-окрестность
(х0 - 8; х0 + 8) точки х0 такая, что для всех х Ф х0
из этой окрестности выполняется неравенство
f(x) > f(x0) (в случае максимума — f(x) < f(x0)).
4. Точки минимума и максимума называются
точками экстремума данной функции, а
значения функции в этих точках — соответственно
минимумом и максимумом функции (или
экстремумом функции).
5. Необходимое условие существования
экстремума.
ТЕОРЕМА ФЕРМА
Если точка х0 является точкой
экстремума функции f(x) и в этой точке
существует производная функции f(x), то она равна
нулю, т. е. f(x) = 0.
6. Достаточные условия существования
экстремума. Пусть функция непрерывна и
имеет производную f(x) в некоторой окрестности
точки х0. Тогда:
если f\x) < 0 на интервале (а; х0) и f'(x) > 0
на интервале (х0; Ь) (т. е. производная меняет
знак с минуса на плюс), то х0 — точка
минимума функции f(x);
если f\x) > 0 на интервале (а; х0) и f\x) < 0
на интервале (х0; Ь) (т. е. производная меняет
знак с плюса на минус), то х0 — точка
максимума функции f(x).

118
Краткое изложение школьного курса математики
Алгебра. 7—11 классы
Исследование функции
1 4
Пример. Исследовать функцию у = jx -
1 3 2 .
- 5 х " х и построить ее график.
Решение.
1) Здесь £>(/) = R.
2) Функция не является ни четной, ни
нечетной, ни периодической.
3) Найдем точки пересечения с осью Ох (т. е.
корни функции): jx - ъх ~ х =0<=>лг1 = 0,
х2 = -1,4, х3 = 2,8.
3 2
4) Находим производную: f\x) = х - х -2х =
= х(х - х - 2) = (х + 1)дг(х - 2). Приравняв
производную нулю, получим критические точки:
х = - 1, х = 0, х = 2.
5) Найденные критические точки разбивают
числовую прямую на четыре промежутка (-о°; -1),
(-1;0),(0;2)и(2;оо).
Составим таблицу.
X
(-оо5 -1)
-1
<-1;0)
0
(0; 2)
2
(2; оо)
Г(х)
-
0
+
0
-
0
+
Л*)
\у убыв.
5
"12 тШ
/ возр.
0 max
""V убыв.
-| min
/ возр.
6) Используя результаты исследования,
строим график функции (рис. 83).
Задачи на нахождение наибольшего
и наименьшего значений функции
1. Для отыскания наименьшего и
наибольшего значений функции, дифференцируемой на
промежутке, следует найти все критические
точки функции, лежащие внутри промежутка,
вычислить значения функции в этих точках и
на концах промежутка, а затем из всех
полученных таким образом чисел выбрать наименьшее и
наибольшее.
2. Пример. Найти наибольшее и наименьшее
значения функции у = -2х3 - Зх2 + 4 на
промежутке^;-0,5].
Решение. Находим критические точки функ-
ции. Так как у' = - 6х - 6х = - 6х(х + 1), то
имеются две критические точки: х = 0их = -1.На
промежутке лежит одна из критических точек:
х = -1. Так как у(-2) = 8, у(-1) = 3, у(-0,5) = 3,5,
то наименьшее значение функции достигается в
точке х = -1 и равно 3, а наибольшее — в точке
х = -2 и равно 8.
Кратко это можно записать так:
min i/(x) = i/(-l) = 3, max у(х) = у(-2) = 8.
[-2;-0,5] [-2;-0,5]
3. Пример. Вписать в круг радиуса R
прямоугольник наибольшей площади.
Решение. Обозначим длину одной из сторон
прямоугольника через х; тогда длина другой
стороны равна
Ля2 - х ■
а площадь равна
S(x) = x*j4R2 - х2.
Наибольшее значение функции S(x) на
отрезке [0; 2R] достигается при х = R*j2, т. е.
искомым прямоугольником служит квадрат.
Рис. 83

Геометрия. 7—9 классы
ВВЕДЕНИЕ
Геометрия — наука о свойствах
геометрических фигур. К числу геометрических фигур
относятся, например, треугольник, квадрат, круг,
сфера и т. д.
Слово «геометрия» греческое, в переводе на
русский язык означает «землемерие».
Школьная геометрия состоит из двух частей:
планиметрии и стереометрии.
Планиметрия — это раздел геометрии, в
котором изучаются геометрические фигуры на
плоскости. Стереометрия — это раздел геометрии, в
котором изучаются фигуры в пространстве.
Основными геометрическими фигурами на
плоскости являются точка и прямая. Точка не
имеет размеров. Точки обозначаются
прописными (заглавными) латинскими буквами: А, Б,
С, ... . Прямую можно мысленно продолжить в
обе стороны безгранично. Прямые обозначаются
строчными латинскими буквами: а, 6, с, ... .
Прямую можно обозначать также двумя
буквами, соответствующими точкам, лежащим на
ней. На рисунке 1 изображены точка А, прямые
а и АВ. Свойства геометрической фигуры
выражаются в виде предложений.
Рассуждение, устанавливающее какое-либо
свойство, называется доказательством.
Доказываемое свойство называется теоремой. При
доказательстве теоремы мы опираемся на ранее
установленные свойства. Некоторые из них, в
свою очередь, являются теоремами, некоторые
же считаются в геометрии основными и
принимаются без доказательства. Последние
называются аксиомами. Мы не будем приводить всех
аксиом и ограничимся некоторыми из них.
В
Точка А
Прямые а, АВ
Рис.1
Отрезок АВ
Рис. 2
Аксиома 1. Для любой прямой
существуют точки, принадлежащие прямой, и точки,
не принадлежащие прямой.
Если А — точка и а — прямая, то либо А
принадлежит а, либо А не принадлежит а. В первом
случае говорят, что прямая а проходит через
точку А, во втором случае — прямая а не
проходит через точку А.
Аксиома 2. Через любые две различные
точки проходит одна и только одна прямая.
Отсюда следует, что две различные прямые
имеют не более одной общей точки.
Говорят, что две прямые пересекаются, если
они имеют только одну общую точку.
Аксиома 3. Если две точки прямой
принадлежат некоторой плоскости, то прямая
принадлежит этой плоскости.
Предложение, которое вытекает (получается)
из теоремы или аксиомы, называется
следствием. Например, из аксиомы 2, как уже
отмечалось, вытекает, что две различные прямые
имеют не более одной общей точки.
Некоторые понятия в геометрии мы
принимаем за начальные, их содержание можно
выяснить только из опыта. К таким понятиям
относятся, например, точка и прямая. Все остальные
понятия мы выясняем, опираясь на начальные.
Такие объяснения называются определениями.
Каждое определение опирается либо
непосредственно на начальные понятия, либо на понятия,
определенные прежде.
ОТРЕЗОК, ЛУЧ, УГОЛ
Отрезок
Отрезком называется часть прямой,
ограниченная двумя точками А и В, включая эти точки
(рис. 2).
Точки, ограничивающие отрезок,
называются его концами. Отрезок содержит точки А и Б и
все точки, лежащие между ними. Обозначается
отрезок АВ или ВА.
Два отрезка называются равными, если они
могут быть наложены один на другой так, что их

120
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
концы совпадут. На рисунке 3, а изображены два
отрезка. Чтобы установить, равны они или нет,
наложим один отрезок на другой так, чтобы
конец одного отрезка совместился с концом другого
(рис. 3, б). Если при этом два других конца
также совместятся, то отрезки полностью
совместятся и, значит, они равны. Если же два других
конца не совместятся, то меньшим считается
тот отрезок, который составляет часть другого.
На рисунке 3, в отрезок АС составляет часть
отрезка АВ, поэтому отрезок АС меньше отрезка
АВ (пишут так: АС < АВ).
Точка отрезка, делящая его пополам, т. е. на
два равных отрезка, называется серединой
отрезка. На рисунке 4 точка С — середина отрезка АВ.
Чтобы на какой-нибудь прямой отложить
отрезок, равный данному, используют циркуль.
Луч и полуплоскость
Если провести прямую и отметить на ней точку О
(рис. 5), то она разделит прямую на две части,
каждая из которых называется лучом,
исходящим из точки О (эти лучи называют
дополнительными). Точка О называется началом луча.
Луч обозначается строчными латинскими
буквами (например, луч а на рисунке 6, а) либо двумя
большими латинскими буквами, первая из
которых обозначает начало луча, а вторая — какую-
нибудь точку на луче (например, луч АВ на
рисунке 6, б).
Прямая а разбивает плоскость на две
полуплоскости. Если концы какого-нибудь отрезка
принадлежат одной полуплоскости, то отрезок
не пересекается с прямой а (границей
полуплоскости). Если концы отрезка принадлежат разным
полуплоскостям, то отрезок пересекается с
прямой а (рис. 7).
Угол
Углом называется фигура, которая состоит из
двух различных лучей с общим началом. Эта
начальная точка называется вершиной угла, а
лучи — сторонами угла. Если стороны угла
являются дополнительными лучами одной
прямой, то угол называется развернутым (рис. 8).
Слово «угол» иногда заменяют значком А.
Угол можно обозначить тремя способами: ZAOB,
ZOyZab (рис. 9).
Говорят, что луч с началом в вершине угла
АОВ проходит между сторонами этого угла, если
он пересекает какой-нибудь отрезок с концами
на сторонах угла (рис. 10). В случае
развернутого угла будем считать, что любой луч с началом
в вершине угла, отличный от его сторон,
проходит между сторонами угла.
Два угла считаются равными, если при
наложении они могут совместиться.
а)
А
б)
Сравнение отрезков
Рис.3
С
АС<АВ
в)
В
А
Точка С
С В
АС = СВ
— середина отрезка АВ
Рис.4
#1
а) -
«4-
В
Лучи дополнительные
Лучи а, АВ
Прямая а разбивает плоскость
на две полуплоскости
Рис. 5
Рис.6
Рис. 7

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
121
На рисунке 11, а изображены неразвернутые
углы 1 и 2. Чтобы установить, равны они или
нет, наложим один угол на другой так, чтобы
сторона одного угла совместилась со стороной
другого, а две другие оказались по одну сторону от
совместившихся сторон (рис. 11,6). Если две
другие стороны также совместятся, то углы
полностью совместятся и, значит, они равны. Если же
эти стороны не совместятся, то меньшим
считается тот угол, который составляет часть другого. На
рисунке 11,6 угол 1 составляет часть угла 2,
поэтому Z 1 < Z 2.
Неразвернутый угол составляет часть
развернутого (рис. 12, угол СОВ составляет часть угла
АОВ), поэтому развернутый угол больше
неразвернутого угла. Любые два развернутых угла,
очевидно, равны.
Луч, исходящий из вершины угла и
делящий его на два равных угла, называется
биссектрисой угла.
На рисунке 13 луч I — биссектриса угла hk.
Измерение отрезков
На практике часто приходится измерять
отрезки, т. е. находить их длины.
Измерить отрезок — это значит сравнить его
с некоторым отрезком, принятым за единицу
измерения (его называют также масштабным
отрезком).
Если, например, за единицу измерения
принят сантиметр, то для определения длины
отрезка узнают, сколько раз в этом отрезке
укладывается сантиметр. На рисунке 14 в отрезке АВ
сантиметр укладывается ровно два раза. Это
означает, что длина отрезка АВ равна 2 см. Обычно
говорят кратко: «Отрезок АВ равен 2 см» — и
пишут: АВ = 2 см.
Может оказаться, что отрезок, принятый за
единицу измерения, не укладывается целое
число раз в измеряемом отрезке — получается
остаток. Тогда единицу измерения делят на равные
части, обычно на 10 равных частей, и
определяют, сколько раз одна такая часть укладывается в
остатке. Например, на рисунке 14 в отрезке АС
сантиметр укладывается 3 раза и в остатке
ровно 4 раза укладывается одна десятая часть
сантиметра (миллиметр), поэтому длина отрезка АС
равна 3,4 см. Но возможно, что и взятая часть
единицы измерения (в данном случае
миллиметр) не укладывается в остатке целое число
раз, и получается новый остаток. Так будет,
например, с отрезком AD на рисунке 14, в котором
Угол развернутый
Рис.8
Угол АОВ
Рис.9
Луч с проходит
между сторонами
угла АОВ
Рис. 10
а)
б)
Рис. 11
Неразвернутый угол СОВ
составляет часть
развернутого угла АОВ
Рис. 12
/ — биссектриса угла О
Рис. 13
1 см
А В
АВ - 2 см; АС - 3,4 см
Рис. 14

122
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
сантиметр укладывается три раза с остатком, а в
остатке миллиметр укладывается восемь раз
вновь с остатком. В таком случае говорят, что
длина отрезка AD приближенно равна 3,8 см.
Для более точного измерения этого отрезка
указанную часть единицы измерения (миллиметр)
можно разделить на 10 равных частей и
продолжить процесс измерения. Мысленно этот
процесс Можно продолжать и дальше, измеряя
длину отрезка со все большей точностью. На
практике, однако, пользуются приближенными
значениями длин отрезков.
За единицу измерения можно принимать не
только сантиметр, но и любой другой отрезок.
Выбрав единицу измерения, можно
измерить любой отрезок, т. е. выразить его длину
некоторым положительным числом.
Это число показывает, сколько раз единица
измерения и ее части укладываются в
измеряемом отрезке.
Если два отрезка равны, то единица
измерения и ее части укладываются в этих отрезках
одинаковое число раз, т. е. равные отрезки
имеют равные длины. Если же один отрезок
меньше другого, то единица измерения (или ее часть)
укладывается в этом отрезке меньшее число раз,
чем в другом, т. е. меньший отрезок имеет
меньшую длину.
На рисунке 15 изображен отрезок АВ. Точка
С делит его на два отрезка: АС и СВ. Мы видим,
что АС — 3 см, СВ = 2,7 см, АВ = 5,7 см. Таким
образом, АС + СВ = АВ. Также и во всех
случаях, когда точка делит отрезок на два отрезка,
длина всего отрезка равна сумме длин этих двух
отрезков.
Длина отрезка называется также
расстоянием между концами этого отрезка.
Пример 1. Точка С — середина отрезка АВ.
Найти длину отрезка АС, если длина отрезка АВ
равна 32 см.
Решение. Имеем: АС + СВ = АВ или АС +
+ СВ = 32. Так как С — середина отрезка АВ, то
АС = СВ и, значит, 2АС = 32, откуда АС = 16 (см).
Пример 2. Точка С — середина отрезка АВ,
точка О — середина отрезка АС. Найти АС, СВ,
АО и ОВ, если АВ = 2 см.
Решение. Так как С — середина отрезка АВ,
то, как и в предыдущем примере, АС = СВ =
= 2AS* или АС = св = 2 "2 = * *см)# Так как
точка О — середина отрезка АС = 1 см, то АО =
= ОС = 0,5 см. Наконец, ОВ = ОС + СВ = 0,5 + 1 =
= 1,5 (см).
Пример 3. Лежат ли точки А, В и С на одной
прямой, если АС — 5 см, АВ = 3 см, ВС = 4 см?
Решение. Если точки А, В и С лежат на одной
прямой, то больший из отрезков АВ, ВС и АС
равен сумме двух других. По условию больший из
данных отрезков (отрезок АС) равен 5 см, а
сумма двух других (АВ + ВС) равна 7 см. Поэтому
точки А, В и С не лежат на одной прямой.
Измерение углов
Измерение углов основано на сравнении их с
углом, принятым за единицу измерения. Обычно за
единицу измерения углов принимают градус —
« 1
угол, равный Tqj: части развернутого угла.
Положительное число, которое показывает,
сколько раз градус и его части укладываются в
данном угле, называется градусной мерой угла.
Для измерения углов используется транспортир
(рис. 16).
В
||111||||||||||||||||1111|1111|||||||||||М11|1111|||||||||||
0 12 3 4 5 6
АС + СВ=АВ
Рис. 15
10 0 10 30 50 70 90 100
Транспортир
Рис. 16

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
123
На рисунке 17 изображен угол АОВ,
градусная мера которого равна 150°. Обычно
говорят кратко: «Угол АОВ равен 150°» — и пишут:
ZAOB = 150°.
1 . 1
~~ часть градуса называется минутой, а ^
часть минуты — секундой. Минуты обозначают
знаком «'», а секунды— знаком «"». Например,
угол в 68 градусов, 32 минуты и 27 секунд
обозначается так: 68°32'27".
Если два угла равны, то градус и его части
укладываются в этих углах одинаковое число
раз, т. е. равные углы имеют равные градусные
меры. Если же один угол меньше другого, то в
нем градус (или его часть) укладывается
меньшее число раз, чем в другом угле, т. е. меньший
угол имеет меньшую градусную меру.
Так как градус составляет т^ часть
развернутого угла, то развернутый угол равен 180°.
Неразвернутый угол меньше 180°, так как он
меньше развернутого.
На рисунке 18 изображены лучи с началом
в точке О. Луч ОС делит угол АОВ на два угла:
АОС и СОВ. Мы видим, что
ZAOC = 40°, Z СОВ = 120°, А АОВ = 160°.
Таким образом,
ZAOC + Z СОВ = ZАОВ.
Ясно, что и во всех других случаях,
когда луч делит угол на два угла, градусная
мера всего угла равна сумме градусных мер
этих углов.
Угол называется:
прямым, если он равен 90° (рис. 19, а);
острым, если он меньше 90°, т. е. меньше
прямого угла (рис. 19, б);
тупым, если он больше 90°, но меньше 180°,
т. е. больше прямого, но меньше развернутого
угла (рис. 19, в).
Пример 1. Луч I — биссектриса угла hk,
равного 50°. Найти градусные меры углов hi и Ik.
Решение. Так как I — биссектриса угла hk, то
градусные меры каждого из углов hi и Ik равны.
Обозначим градусную меру одного из них через
х. Тогда 2х = 50°, откуда х = 25°.
Итак, градусные меры каждого из углов hi и
Ik равны 25° и 25°.
Пример 2. Луч ОС делит угол АОВ на два
угла. Найти угол АОС, если Z АОВ = 155° и угол
АОС на 15° больше угла СОВ.
Решение. Обозначим градусную меру угла
АОС через х. Тогда градусная мера угла СОВ
будет х - 15°. Теперь согласно условию
х + х - 15° = 155°, или 2х = 170°,
откуда х — 85°.
Пример 3. Между сторонами угла cd,
равного 120°, проходит луч а. Найти углы са и ad,
если их градусные меры относятся как 4:2.
Решение. Луч а проходит между сторонами
угла cd, значит, Zca + Zad = Zed.
Так как градусные меры Z са и Zad
относятся как 4 : 2, то
Zca =
120°
6
4 = 80°, Zad =
120°
6
2 = 40°
Смежные и вертикальные углы.
Перпендикулярные прямые
Два угла называются смежными, если у них
одна сторона общая, а другие стороны этих углов
ZAOC = 40°, ZCOB = 120°,
ZAOB = 160°
Рис. 18
Прямой угол Острый угол
а) б)
Рис. 19
Тупой угол
в)

124
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
являются дополнительными лучами. На
рисунке 20 углы АОВ и ВОС смежные.
ТЕОРЕМА 1
Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис. 20)
проходит между сторонами развернутого угла.
Поэтому
ZAOB + ZBOC- 180°.
Из теоремы 1 следует, что если два угла
равны, то смежные с ними углы равны.
Два угла называются вертикальными, если
стороны одного угла являются дополнительными
лучами сторон другого. Углы АОВ и COD, BOD и
АОС, образованные при пересечении двух
прямых, являются вертикальными (рис. 21).
ТЕОРЕМА 2
Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные
углы АОВ и COD (см. рис. 21). Угол BOD
является смежным для каждого из углов АОВ и COD.
По теореме 1
ZАОВ + Z BOD - 180°, Z COD + Z BOD = 180°.
Отсюда заключаем, что Z АОВ = Z COD.
Следствие. Угол, смежный с прямым углом,
. есть прямой угол.
Рассмотрим две пересекающиеся прямые АС
и BD (рис. 22). Они образуют четыре угла. Если
один из них прямой (угол 1 на рис. 22), то
остальные углы также прямые (углы 1 и 2,1 и 4 —
смежные, углы 1 и 3 — вертикальные). В этом
случае говорят, что эти прямые пересекаются
под прямым углом и называются
перпендикулярными (или взаимно перпендикулярными).
Перпендикулярность прямых АС и BD обозначается
так: АС 1BD.
Серединным перпендикуляром к отрезку
называется прямая, перпендикулярная к этому
отрезку и проходящая через его середину.
Рассмотрим прямую а и точку А, не
лежащую на ней (рис. 23). Соединим точку А
отрезком с точкой Н прямой а. Отрезок АН
называется перпендикуляром, проведенным из точки А
к прямой а, если прямые АН и а
перпендикулярны. Точка Н называется основанием
перпендикуляра.
Справедлива следующая теорема.
ТЕОРЕМА 3
Из всякой точки, не лежащей на прямой,
можно провести перпендикуляр к этой
прямой, и притом только один.
Для проведения на чертеже перпендикуляра
из точки к прямой используют чертежный
угольник (рис. 24).
В
^L
.Сумма смежных
углов равна 180°
Рис. 20
В
и
-d
я
Вертикальные
углы равны
Рис. 21
В
Прямые АС и BD —
перпендикулярные
Рис. 22
АН — перпендикуляр
к прямой
Чертежный
угольник
Рис. 23
Рис. 24

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
125
Замечание. Формулировка теоремы обычно
состоит из двух частей. В одной части говорится
о том, что дано. Эта часть называется условием
теоремы. В другой части говорится о том, что
должно быть доказано. Эта часть называется
заключением теоремы. Например, условие
теоремы 2 — углы вертикальные; заключение — эти
углы равны.
Всякую теорему можно подробно выразить
словами так, что ее условие будет начинаться
словом «если», а заключение— словом «то».
Например, теорему 2 можно подробно высказать
так: «Если два угла вертикальные, то они
равны».
Пример 1. Один из смежных углов равен
44°. Чему равен другой?
Решение. Обозначим градусную меру другого
угла через х, тогда согласно теореме 1
44° + х = 180°.
Решая полученное уравнение, находим, что
х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD
равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ
вертикальные, следовательно, по теореме 2 они равны, т. е.
Z АОВ = 45°. Угол АОС смежный с углом COD,
значит, по теореме 1
А АОС = 180° - Z COD = 180° - 45° = 135°.
Пример 3. Найти смежные углы, если один
из них в 3 раза больше другого.
Решение. Обозначим градусную меру
меньшего угла через х. Тогда градусная мера
большего угла будет Зх.
Так как сумма смежных углов равна 180°
(теорема 1), то
х + Зх « 180°,
откуда х — 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов
равна 100°. Найти величину каждого из четырех
углов.
Решение. Пусть условию задачи отвечает
рисунок 21. Вертикальные углы COD и АОВ
равны (теорема 2), значит, равны и их градусные
меры. Поэтому A COD = Z АОВ = 50° (их сумма
по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по
теореме 1 Z BOD = ZAOC - 180° - 50° = 130°.
Контрольные вопросы
1. Объясните, что такое отрезок с концами А
и В. Как он обозначается?
2. Какие отрезки называются равными?
3. Объясните, как сравнить два отрезка.
4. Какая точка называется серединой отрезка?
5. Объясните, что такое луч. Как
обозначаются лучи? Какие лучи называются
дополнительными?
6. Какая фигура называется углом?
Объясните, что такое вершина и стороны угла. Как
обозначается угол?
7. Какой угол называется развернутым?
8. Какие углы считаются равными?
9. Объясните, как сравнить два угла.
10. Какой луч называется биссектрисой угла?
11. Точка С делит отрезок АВ на два отрезка.
Как найти длину отрезка АВ, если известны
длины отрезков АС и СВ?
12. Что такое градусная мера угла?
13. Луч ОС делит угол АОВ на два угла. Как
найти градусную меру угла АОВ, если известны
градусные меры углов АОС и СОВ?
14. Какой угол называется острым? прямым?
тупым?
15. Какие углы называются смежными?
16. Докажите, что сумма смежных углов
равна 180°.
17. Какие углы называются вертикальными?
18. Докажите, что вертикальные углы равны.
19. Какие прямые называются
перпендикулярными?
20. Что называется серединным
перпендикуляром к отрезку?
21. Объясните, какой отрезок называется
перпендикуляром, проведенным из данной
точки к данной прямой.
22. Сформулируйте теорему о перпендикуляре,
проведенном из данной точки к данной прямой.
Упражнения
1. Точка В делит отрезок АС на два отрезка.
Найдите длину отрезка АС, если АВ - 3 дм, ВС =
= 5 дм.
2. Точка В делит отрезок АС на два отрезка.
Найдите длину отрезка ВС, если АВ = 2,7 см,
АС = 5,2 см.

126
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
3. Точки А, Ву С лежат на одной прямой.
Известно, что АВ = 11 см, ВС = 12,5 см. Какой
может быть длина отрезка АС?
4. Точка С — середина отрезка АВ, равного
64 см. На луче С А отмечена точка D так, что
CD = 15 см. Найдите длины отрезков BD и DA.
5. Луч ОС делит угол АОВ на два угла.
Найдите Z АОВ, если Z АОС = 44°, Z СОВ = 76°.
6. Луч ОС делит угол АОВ на два угла.
Найдите угол СОВ, если А АОВ = 75°, а угол АОС на
15° меньше угла ВОС.
7. Луч ОС является биссектрисой
неразвернутого угла АОВ. Может ли угол АОВ быть
прямым или тупым?
8. Найдите угол, смежный с углом ABC, если:
1) Z ABC = 110°; 2) Z ABC - 80°; 3) A ABC - 16°.
9. Один из смежных углов больше другого на
31°. Вычислите эти углы.
10. На прямой АВ взята точка С и из нее
проведен луч CD так, что Z ACD в 4 раза
больше Z BCD. Найдите эти углы.
11. Один из углов, образованных двумя
пересекающимися прямыми, равен 90°. Чему равны
остальные углы?
12. Один из углов, образованных при
пересечении двух прямых, равен 54°. Найдите
остальные углы.
13. Сумма двух вертикальных углов равна
80°. Найдите каждый из полученных четырех
углов.
ТРЕУГОЛЬНИК
Треугольник и его элементы
Пусть А, В, С — три произвольные точки, не
лежащие на одной прямой. Фигура, состоящая из
трех отрезков АВ, ВС, АС (рис. 25), называется
треугольником ABC (обозначается: А ABC).
Треугольником также называют часть плоскости,
ограниченную отрезками АВ, ВС, АС (плоский
треугольник). Точки А, В, С — вершины,
отрезки АВ, ВС, АС — стороны треугольника. Сумма
длин трех сторон треугольника называется его
периметром.
Углом (или внутренним углом) треугольника
ABC при вершине А называется угол,
образованный лучами АВ и АС. Так же определяются
углы треугольника при вершинах В и С.
Углы CAB, ABC, ВС А треугольника ABC
часто обозначают одной буквой (А, В, С
соответственно) или греческими буквами а, р, у (при этом
внутри углов рисуют дуги, см. рис. 25). Говорят,
что угол А противолежит стороне ВС или
сторона ВС противолежит углу А; так же угол В и
сторона АС, угол С и сторона АВ противолежат
(друг другу).
Угол, смежный с каким-нибудь углом
треугольника, называется внешним углом этого
треугольника. Таков, например, угол BCD (рис. 26).
При каждом угле треугольника можно
построить по два внешних угла (продолжив одну или
другую сторону угла). Эти два угла равны как
углы вертикальные.
Отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой
противолежащей стороны, называется
биссектрисой треугольника (рис. 27).
Любой треугольник имеет три биссектрисы.
Отрезок, соединяющий вершину
треугольника с серединой противолежащей стороны,
называется медианой треугольника (рис. 28).
Любой треугольник имеет три медианы.
Перпендикуляр, проведенный из вершины
треугольника к прямой, содержащей противо-
Z BCD — внешний угол
треугольника ABC
ААХ — биссектриса
треугольника ABC
С М В
AM — медиана
треугольника ABC
Рис. 25
Рис. 26
Рис. 27
Рис. 28

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
127
лежащую сторону, называется высотой
треугольника (рис. 29).
Любой треугольник имеет три высоты.
Если один из углов треугольника прямой, то
треугольник прямоугольный (рис. 30, а); если
один из углов тупой — тупоугольный (рис. 30, б);
если все три угла острые — остроугольный
(рис. 30, в).
В прямоугольном треугольнике сторона,
лежащая против прямого угла, называется
гипотенузой, две другие стороны — катетами.
Треугольник, две стороны которого равны,
называется равнобедренным (АС = ВС на
рисунке 31, а). Третья сторона— основание, равные
стороны — боковые стороны.
Треугольник, три стороны которого равны
(АС = ВС = АВ на рис. 31,6), называется
равносторонним.
Пример 1. Периметр равнобедренного
треугольника равен 50 м, боковая сторона — 15 м.
Найти основание.
Решение. Обозначим основание через х.
Тогда периметр треугольника составит
х+15 + 15.
По условию эта сумма равна 50 м, т. е.
х + 30 = 50,
откуда х — 20.
Итак, основание равно 20 м.
Пример 2. Периметр равнобедренного
треугольника равен 70 м. Боковая сторона больше
основания на 5 м. Найти стороны треугольника.
Решение. Воспользуемся рисунком 31, а.
Обозначим АВ через х, тогда ВС =АС через х + 5.
Тогда периметр треугольника составит
(х + 5) + (х + 5) + х.
По условию эта сумма равна 70, т. е.
Зх + 10 = 70, или х = 20.
Следовательно, стороны треугольника 20 см,
25 см и 25 см.
Пример 3. Треугольник, периметр которого
равен 24 см, делится высотой на два
треугольника, периметры которых равны 12 см и 20 см.
Найти высоту треугольника.
Решение. Пусть условию задачи отвечает
рисунок 29. Обозначим периметры треугольников
ABC, АВН и АСН соответственно через Р, Рх и
Рг. Из рисунка 29 видно, что
РХ + Р2 = Р + 2АН,
или
12 + 20 = 24 + 2АН,
откуда. АН = 4.
Признаки равенства треугольников
Два треугольника называются равными, если их
можно совместить наложением. На рисунке 32
В Н С
АН — высота треугольника ABC
Рис. 29
катет
Треугольник:
а) прямоугольный б) тупоугольный
Рис. 30
в) остроугольный
Треугольник:
а) равнобедренный б) равносторонний
ААВС = АА1В1С1
В Ах
Рис. 31
Рис. 32

128
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
изображены равные треугольники ABC и
А1В1С1. Каждый из этих треугольников можно
наложить на другой так, что они полностью
совместятся, т. е. попарно совместятся их
вершины и стороны. Ясно, что при этом совместятся
попарно и углы этих треугольников.
Таким образом, если два треугольника
равны, то элементы (т. е. стороны и углы) одного
треугольника соответственно равны элементам
другого треугольника. Отметим, что
в равных треугольниках против
соответственно равных сторон (т. е. совмещающихся при
наложении) лежат равные углы, и обратно:
против соответственно равных углов лежат
равные стороны.
Так, например, в равных треугольниках ABC
иА1В1С1у изображенных на рисунке 32, против
соответственно равных сторон АВ и АгВг лежат
равные углы С и Сг. Равенство треугольников
ABC и А1В1С1 будем обозначать так: Л ABC =
= АА1В1С1.
Оказывается, что равенство двух
треугольников можно установить, сравнивая некоторые их
элементы.
ТЕОРЕМА 1
первый признак равенства треугольников
Если две стороны и угол между ними
одного треугольника соответственно равны
двум сторонам и углу между ними другого
треугольника, то такие треугольники
равны.
Доказательство. Рассмотрим
треугольники ABC и AXBXCV у которых АВ = АгВг, АС =
= AtCv ZA = Z Ах (рис. 33). Докажем, что А ABC =
= АА1В1С1.
Так как Z А — Z Аг, то треугольник ABC
можно наложить на треугольник А1В1С1 так, что
вершина А совместится с вершиной Ах, а
стороны АВ и АС наложатся соответственно на лучи
АгВг hAjCj. Поскольку АВ = АгВг, АС — АгС1$ то
сторона АВ совместится со стороной A1BV а
сторона АС — со стороной АХСХ; в частности,
совместятся точки В и Bv С и Cv Следовательно,
совместятся стороны ВС и BXCV Итак,
треугольники ABC и А1В1С1 полностью совместятся,
значит, они равны.
Аналогично методом наложения
доказывается теорема 2.
ТЕОРЕМА 2
второй признак равенства треугольников
Если сторона и два прилежащих к ней
угла одного треугольника соответственно
равны стороне и двум прилежащим к ней углам
другого треугольника, то такие
треугольники равны.
Пример 1. В треугольниках ABC и DEF
(рис. 35) А А = Z Е, АВ = 20 см, АС = 18 см, DE =
= 18 см, EF = 20 см. Сравнить треугольники
ABC и DEF. Какой угол в треугольнике DEF
равен углу В?
Рис. 33
Рис. 34
Рис. 35

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
129
Решение. Данные треугольники равны по
первому признаку. Угол F треугольника DEF
равен углу В треугольника ABC, так как эти
углы лежат против соответственно равных сторон
DE и АС.
Пример 2. Отрезки АВ и CD (рис. 36)
пересекаются в точке О, которая является серединой
каждого из них.
Чему равен отрезок BD, если отрезок АС равен
6 м?
Решение. Треугольники АОС и BOD равны
(по первому признаку): Z АОС = Z BOD
(вертикальные), АО = ОВу СО = OD (по условию).
Из равенства этих треугольников следует
равенство их сторон, т. е. АС = BD. Но так как по
условию АС = 6 м, то и BD = 6м.
Пример 3. В треугольниках ABC и DEF (см.
рис. 35)АВ = EF, ZA = ZE,ZB = ZF. Сравнить
эти треугольники. Какие стороны в
треугольнике DEF равны соответственно сторонам ВС и
СА?
Решение. Треугольники ABC и DEF равны по
второму признаку. Стороны DF и DE
треугольника DEF равны соответственно сторонам ВС и СА
треугольника ABC, так как стороны DF и ВС (DE
и СА) лежат против равных углов Е и A (F и В).
Пример 4. На рисунке 37 углы DAB и СВА,
CAB и DBA равны, СА = 13 м. Найти DB.
Решение. Треугольники АСВ и ADB имеют
одну общую сторону АВ и по два равных угла,
которые прилежат к этой стороне.
Следовательно, треугольники АСВ и ADB равны (по второму
признаку).
Из равенства этих треугольников следует
равенство сторон BD и АС, т. е. BD = 13 м.
Замечание. На основе теоремы 1
устанавливается теорема 3.
ТЕОРЕМА 3
Сумма любых двух внутренних углов
треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
TEOPElflA4
Внешний угол треугольника больше
любого внутреннего угла, не смежного с ним.
Свойства равнобедренного
треугольника. Третий признак
равенства треугольников
Свойства равнобедренного треугольника
выражают следующие теоремы.
ТЕОРЕМА 1
В равнобедренном треугольнике углы при
основании равны.
ТЕОРЕМА 2
В равнобедренном треугольнике биссектри-
са, проведенная к основанию, является
медианой и высотой.
ТЕОРЕМА 3
В равнобедренном треугольнике медиана,
проведенная к основанию, является
биссектрисой и высотой.
Докажем одну из них, например теорему 1.
Доказательство. Рассмотрим
равнобедренный треугольник ABC с основанием ВС и
докажем, что Z В = Z С. Пусть AD — биссектриса
треугольника ABC (рис. 38). Треугольники ABD
и ACD равны по первому признаку равенства
Рис. 36
Рис. 37
5-1019

130
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
треугольников (АВ =АС по условию, AD —
общая сторона, Z 1 = Z 2, так как AD —
биссектриса). Из равенства этих треугольников
следует, что Z В = ZC. Теорема доказана.
С использованием теоремы 1
устанавливается следующая теорема.
ТЕОРЕМА 4
третий признак равенства треугольников
Если три стороны одного треугольника
соответственно равны трем сторонам
другого треугольника, то такие треугольники
равны (рис. 39).
Пример 1. Доказать, что точка плоскости,
равноудаленная от концов отрезка, лежит на
серединном перпендикуляре к этому отрезку.
Решение. Пусть точка М равноудалена от
концов отрезка АВ (рис. 40), т. е. AM = ВМ. Тогда
ААМВ равнобедренный. Проведем через точку М
и середину О отрезка АВ прямую/?. Отрезок МО
по построению есть медиана равнобедренного
треугольника АМВ, а следовательно (теорема 3),
и высота, т. е. прямая МО есть серединный
перпендикуляр к отрезку АВ.
Пример 2. Доказать, что каждая точка
серединного перпендикуляра к отрезку
равноудалена от его концов.
Решение. Пусть р — серединный
перпендикуляр к отрезку АВ и точка О — середина
отрезка АВ (см. рис. 40).
Рассмотрим произвольную точку М,
лежащую на прямой р. Проведем отрезки AM и ВМ.
Треугольники АОМ и ВОМ равны, так как у
них углы при вершине О прямые, катет ОМ
общий, а катет О А равен катету ОВ по условию. Из
равенства треугольников АОМ и ВОМ следует,
что AM — ВМ.
Замечание. Предложения, установленные в
примерах 1 и 2, выражают свойства серединного
перпендикуляра к отрезку. Из этих предложений
следует, что серединные перпендикуляры к
сторонам треугольника пересекаются в одной точке.
Пример 3. В треугольнике ABC (см. рис. 35)
АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике
DEF DE = 7 см, EF = 10 см, FD = 9 см. Сравнить
треугольники ABC и DEF. Найти в них
соответственно равные углы.
Решение. Данные треугольники равны по
третьему признаку. Соответственно равные
углы: А и Е (лежат против равных сторон ВС и FD),
BnF (лежат против равных сторон АС и DE)y С
и D (лежат против равных сторон АВ и EF).
Пример 4. На рисунке 41 АВ = DC, ВС =
= AD, ZB = 100°. Найти угол D.
Решение. Рассмотрим треугольники ABC и
ADC. Они равны по третьему признаку (АВ =
= DC, ВС = AD по условию и сторона АС —
общая). Из равенства этих треугольников
следует, что Z В = Z D, но угол В равен 100°, значит, и
угол D равен 100°.
Контрольные вопросы
1. Какая фигура называется треугольником?
Начертите треугольник и покажите его
стороны, вершины и углы. Что такое периметр
треугольника?
2. Какой угол называется внешним углом
треугольника?
3. Какой отрезок называется биссектрисой
треугольника? Сколько биссектрис имеет
треугольник?
4. Какой отрезок называется медианой
треугольника? Сколько медиан имеет треугольник?
5. Какой отрезок называется высотой
треугольника? Сколько высот имеет треугольник?
Рис. 39
В
A D
Рис. 41

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
131
6. Какой треугольник называется
остроугольным? Какой треугольник называется
тупоугольным?
7. Какой треугольник называется
прямоугольным? Как называются стороны
прямоугольного треугольника?
8. Какой треугольник называется
равнобедренным? Как называются его стороны?
9. Какой треугольник называется
равносторонним?
10. Какие треугольники называются равными?
11. Сформулируйте и докажите первый
признак равенства треугольников.
12. Сформулируйте второй признак
равенства треугольников.
13. Сформулируйте теорему о сумме двух
внутренних углов треугольника.
14. Сформулируйте теорему о соотношении
внешнего угла треугольника с его внутренним
углом, не смежным с этим внешним.
15. Докажите, что углы при основании
равнобедренного треугольника равны.
16. Сформулируйте теорему о биссектрисе
равнобедренного треугольника, проведенной к
основанию.
17. Сформулируйте третий признак
равенства треугольников.
Упражнения
1. Периметр равнобедренного треугольника
равен 2 м, основание равно 0,8 м. Найдите
боковую сторону.
2. Треугольник, периметр которого равен
22 см, делится медианой на два треугольника с
периметрами 16 см и 12 см. Найдите длину
медианы.
3. Периметр равнобедренного треугольника
равен 15,6 м. Найдите его стороны, если
основание меньше боковой стороны на 3 м.
4. Отрезки АВ и CD пересекаются в точке О,
которая является серединой каждого из них.
Чему равен отрезок DB, если отрезок АС равен 8 дм?
5. Отрезки АВ и CD пересекаются в точке О.
Докажите равенство треугольников АСО и DBO,
если известно, что угол АСО равен углу DBO и
ВО - ОС.
6. В равнобедренном треугольнике
биссектриса, проведенная к основанию, равна 5 см,
периметр одного из отсеченных ею треугольников
равен 30 см. Найдите периметр равнобедренного
треугольника.
7. Треугольники ABC иАВСг равнобедренные
с общим основанием АВ. Докажите равенство
треугольников АССг и BCCV
8. По данным рисунка 42: а) докажите, что
BD = CD; б) найдите Z С, если Z В = 53°;
в) найдите DC, если DB = 14 мм.
ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ
ПОСТРОЕНИЯ
Окружность
Окружностью называется фигура, которая
состоит из всех точек плоскости,
равноудаленных от данной точки. Эта точка называется
центром окружности.
Расстояние от точек окружности до ее центра
называется радиусом окружности. Радиусом
называется также любой отрезок, соединяющий
точку окружности с ее центром (рис. 43).
Прямая, проходящая через какие-нибудь
две точки окружности, называется секущей.
Отрезок, соединяющий какие-нибудь две
точки окружности, называется хордой. Хорда,
проходящая через центр окружности, называется
диаметром. На рисунке 44 FE — секущая,
ВС — хорда, AD — диаметр.
О — центр
окружности
Рис. 42
Рис. 43
Рис. 44

132
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Пример. Из точки А окружности с центром О
(рис. 45) проведены диаметр длиной 4 см и
хорда АВ. Найти периметр треугольника АВО, если
хорда равна радиусу.
Решение. Треугольник AfiO равносторонний
(ОА и О В — радиусы, АВ — хорда, равная
радиусу). Радиус окружности равен 2 см, так как
длина ее диаметра по условию 4 см.
Следовательно, периметр треугольника АВО равен 6 см.
Основные задачи на построение
В задачах на построение будем рассматривать
построение геометрической фигуры, которое можно
выполнить с помощью линейки и циркуля.
С помощью линейки можно провести:
произвольную прямую;
произвольную прямую, проходящую через
данную точку;
прямую, проходящую через две данные точки.
С помощью циркуля можно описать из
данного центра окружность данного радиуса.
Циркулем можно отложить отрезок на
данной прямой от данной точки.
Рассмотрим основные задачи на построение.
Задача 1. Построить треугольник с данными
сторонами а, 6, с (рис. 46).
Решение. С помощью линейки проведем
произвольную прямую и возьмем на ней
произвольную точку В. Раствором циркуля, равным а,
описываем окружность с центром В и радиусом а.
Пусть С — точка ее пересечения с прямой.
Раствором циркуля, равным с, описываем
окружность из центра В, а раствором циркуля, равным
Ь, — окружность из центра С. Пусть А — точка
пересечения этих окружностей. Треугольник
ABC имеет стороны, равные а,Ь, с.
Замечание. Чтобы три отрезка прямой могли
служить сторонами треугольника, необходимо,
чтобы больший из них был меньше суммы двух
остальных (а < Ь + с).
Задача 2. Отложить от данного луча угол,
равный данному.
Решение. Данный угол с вершиной А и луч
ОМ изображены на рисунке 47. Проведем
произвольную окружность с центром в вершине А
данного угла. Пусть В и С — точки пересечения
окружности со сторонами угла (рис. 48, а).
Радиусом АВ проведем окружность с центром в точке
О — начальной точке данного луча (рис. 48,
лоточку пересечения этой окружности с данным
лучом обозначим Сг. Опишем окружность с
центром Сх и радиусом ВС. Точка Вх
пересечения двух окружностей лежит на стороне
искомого угла. Это следует из равенства А ABC =
= А ОВ1С1 (третий признак равенства
треугольников).
Задача 3, Построить биссектрису данного
угла (рис. 49).
Рис. 45
Рис. 46
Рис. 47
Рис. 48
Построение биссектрисы угла
Рис. 49

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
133
Решение. Из вершины А данного угла, как из
центра, проводим окружность произвольного
радиуса. Пусть В и С — точки ее пересечения со
сторонами угла. Из точек В и С тем же радиусом
описываем окружности. Пусть D — точка их
пересечения, отличная от А. Луч AD делит угол А
пополам. Это следует из равенства A ABD = AACD
(третий признак равенства треугольников).
Задача 4. Провести серединный
перпендикуляр к данному отрезку (рис. 50).
Решение. Произвольным, но одинаковым
раствором циркуля (большим т> АВ) описываем
две дуги с центрами в точках А и В, которые
пересекутся между собой в некоторых точках С и
D. Прямая CD будет искомым
перпендикуляром. Действительно, как видно из построения,
каждая из точек С и D одинаково удалена от А и
В; следовательно, эти точки должны лежать на
серединном перпендикуляре к отрезку АВ.
Задача 5. Разделить данный отрезок пополам.
Решается так же, как и задача 4 (см. рис. 50).
Задача 6. Через данную точку провести
прямую, перпендикулярную данной прямой.
Решение. Возможны два случая:
1) данная точка О лежит на данной прямой а
(рис. 51).
Из точки О проводим произвольным
радиусом окружность. Она пересекает прямую а в
двух точках А и В. Из точек А и В проводим
окружности радиусом АВ. Пусть С — точка их
пересечения. Получаем ОС ± АВ. В самом деле,
А АСВ — равнобедренный, СА = СВ. Отрезок СО
есть медиана этого треугольника, а
следовательно, и высота;
2) данная точка О не лежит на данной прямой
а (рис. 52).
Из точки О проводим произвольным
радиусом окружность, пересекающую прямую а в
точках А и В. Из точек А и В тем же радиусом
проводим окружности. Пусть Ог — точка их
пересечения, отличная от О. Получаем ООг ± АВ.
В самом деле, точки О и 01 равноудалены от
концов отрезка АВ и, следовательно, лежат на
серединном перпендикуляре к этому отрезку.
Контрольные вопросы
1. Какая геометрическая фигура называется
окружностью? Что называется радиусом
окружности?
2. Что такое секущая, хорда окружности?
Какая хорда называется диаметром?
3. Объясните, как построить треугольник по
трем сторонам.
4. Объясните, как отложить от данного луча
угол, равный данному углу.
5. Объясните, как построить биссектрису
данного угла.
6. Объясните, как провести серединный
перпендикуляр к данному отрезку.
7. Объясните, как разделить данный отрезок
пополам.
8. Объясните, как через данную точку
провести прямую, перпендикулярную данной
прямой.
Построение серединного
перпендикуляра к отрезку АВ
В а
Проведение перпендикулярной прямой
к данной прямой
Рис. 50
Рис. 51
Рис. 52

134
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Упражнения
1. Какие из отрезков, изображенных на
рисунке 53, являются: а) хордами окружности;
б) диаметрами окружности; в) радиусами
окружности; г) секущими окружности?
2. Дана окружность радиуса 3 дм. Какую
длину имеет наибольшая ее хорда?
3. Можно ли из точки А, лежащей на
окружности радиуса R = 3 см, провести хорду длиной
7 см?
4. Отрезки АВ и CD — диаметры
окружности с центром О. Найдите периметр
треугольника AOD, если известно, что СВ = 13 см, АВ —
= 16 см.
5. Отрезок МК — диаметр окружности с
центром О, a MP и РК — равные хорды этой
окружности. Найдите Z РОМ.
6. Найдите радиусы двух окружностей,
имеющих общий центр, если диаметр большей
окружности делится меньшей окружностью на
3 части, равные 9 м, 12 м, 9 м.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Определение параллельных прямых
Две различные прямые либо имеют только одну
общую точку, либо не имеют ни одной общей
точки. В первом случае говорят, что прямые
пересекаются, во втором случае — прямые не
пересекаются.
Две прямые на плоскости называются
параллельными, если они не пересекаются.
Параллельность прямых а и Ь обозначается
так:
а\\Ъ.
Пусть две прямые а и Ъ пересечены третьей
прямой с (рис. 54). Прямая с называется
секущей по отношению к прямым а и ft, если она
пересекает их в двух различных точках. При
пересечении прямых а и ft секущей с образуется
восемь углов, которые на рисунке 54 отмечены
цифрами. Определенные пары углов имеют
специальные названия:
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3
и 7;
накрест лежащие углы: 3 и 5, 4 и 6
(внутренние), 1 и 7, 2 и 8 (внешние);
односторонние углы: 4 и 5, 3 и 6
(внутренние), 1 и 8, 2 и 7 (внешние).
Признаки параллельности
двух прямых.
Свойства параллельных прямых
ТЕОРЕМА 1
Если при пересечении двух прямых секу-
щей:
1) накрест лежащие углы равны, или
2) соответственные углы равны, или
3) сумма односторонних углов равна 180°,
то прямые параллельны (рис. 55).
Доказательство. Ограничимся
доказательством случая 1).
Пусть при пересечении прямых а и Ъ
секущей АВ накрест лежащие углы равны.
Например, Z 4 = Z 6. Докажем, что а || Ъ.
Предположим, что прямые а и & не
параллельны. Тогда они пересекаются в некоторой
точке М и, следовательно, один из углов 4 или 6
будет внешним углом треугольника АВМ. Пусть
для определенности Z 4 — внешний угол тре-
м
1 и 5, 4 и 8, 2 и 6, 3 и 7
соответственные углы
Признаки параллельности
двух прямых
Рис. 53
Рис. 54
Рис. 55

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
135
угольника ABM, a Z 6 — внутренний. Из
теоремы о внешнем угле треугольника следует, что Z 4
больше Z 6, а это противоречит условию, значит,
прямые а и & не могут пересекаться, поэтому они
параллельны.
Следствие. Две различные прямые на
плоскости, перпендикулярные одной и той же
прямой, параллельны (рис. 56).
Замечание. Способ, которым мы только что
доказали случай 1) теоремы 1, называется
методом доказательства от противного, или
приведением к нелепости. Первое название этот
способ получил потому, что в начале
рассуждения делается предположение, противное
(противоположное) тому, что требуется доказать.
Приведением к нелепости он называется вследствие
того, что, рассуждая на основании сделанного
предположения, мы приходим к нелепому
выводу (к абсурду). Получение такого вывода
заставляет нас отвергнуть сделанное вначале
допущение и принять то, которое требовалось
доказать.
Задача. Построить прямую, проходящую
через данную точку М и параллельную данной
прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р
перпендикулярно прямой а (задача 6 § 3) (рис. 57).
Затем проводим через точку М прямую Ь
перпендикулярно прямой р. Прямая Ъ параллельна
прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный
вывод:
через точку, не лежащую на данной прямой,
всегда можно провести прямую, параллельную
данной.
Основное свойство параллельных прямых
состоит в следующем.
Аксиома параллельных прямых.
Через данную точку, не лежащую на данной
прямой, проходит только одна прямая,
параллельная данной.
Рассмотрим некоторые свойства
параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и
другую (рис. 58).
2) Если две различные прямые параллельны
третьей прямой, то они параллельны (рис. 59).
Справедлива и следующая теорема 2.
ТЕОРЕМА 2
Если две параллельные прямые
пересечены секущей, то
1) накрест лежащие углы равны;
2) соответственные углы равны;
3) сумма односторонних углов равна 180°.
Следствие. Если прямая перпендикулярна к
одной из двух параллельных прямых, то она
перпендикулярна и к другой (см. рис. 56).
Замечание. Теорема 2 называется обратной
теореме 1. Заключение теоремы 1 является
условием теоремы 2. А условие теоремы 1 является
заключением теоремы 2. Не всякая теорема
имеет обратную, т. е. если данная теорема верна, то
обратная теорема может быть неверна. Поясним
это на примере теоремы о вертикальных углах.
Эту теорему можно сформулировать так: если два
угла вертикальные, то они равны. Обратная ей
теорема была бы такой: если два угла равны, то
они вертикальные. А это, конечно, неверно. Два
равных угла вовсе не обязаны быть
вертикальными.
Пример 1. Две параллельные прямые
пересечены третьей. Известно, что разность двух
внутренних односторонних углов равна 30°. Найти
эти углы.
Решение. Пусть условию отвечает рисунок 60.
Углы 1 и 2 внутренние односторонние, их
сумма равна 180°, т. е.
Zl + Z2 = 180°. (1)
ь
а
М
P
V
Л
Рис. 56
Рис. 57
Рис. 58
Рис. 59
Рис. 60

136
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Обозначим градусную меру угла 1 через х. По
условию Z 2 - х = 30°, или Z 2 = 30° + х.
Подставим в равенство (1) значения углов 1 и
2, получим /
х + 30 + х= 180.
Решая это уравнение, получим х = 75°, т. е.
Z 1 = 75°, a Z 2 - 180° - 75° = 105°.
Пример 2. Две параллельные прямые
пересечены третьей. Известно, что сумма двух
внутренних накрест лежащих углов равна 150°.
Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи
соответствует рисунок 61.
Углы 1 и 2 внутренние накрест лежащие,
следовательно, они равны. Сумма этих углов по
условию задачи равна 150°, тогда Z 1 = Z 2 — 75°.
Найдем остальные углы (рис. 62): Z 1 = Z 3 =
= 75° и Z 2 = Z 7 = 75° (вертикальные). Углы 4 и
5, 6 и 8 равны как вертикальные, a Z 5 = Z 6 как
внутренние накрест лежащие. Все
перечисленные углы 4, 5, 6 и 8 равны между собой и
равны по 105°, так как Z 4 + Z 3 = 180°, a Z 4 =
= 180° - Z 3.
Получили четыре угла по 75°, четыре угла по
105°.
Контрольные вопросы
1. Какие прямые называются параллельными?
2. Что такое секущая по отношению к двум
прямым?
3. Какие углы называются накрест
лежащими?
4. Какие углы называются соответственными?
5. Объясните, какие углы называются
односторонними.
6. Сформулируйте признаки параллельности
прямых.
7. Каково взаимное расположение двух
прямых, перпендикулярных одной и той же
прямой?
8. Сформулируйте аксиому параллельных
прямых.
9. Можно ли утверждать, что две различные
прямые, параллельные третьей, параллельны
между собой?
10. Сформулируйте теорему об углах,
образованных двумя параллельными прямыми и
секущей.
Упражнения
1. Один из углов, которые образуются при
пересечении двух параллельных прямых секущей,
равен 72°. Найдите остальные семь углов.
2. Две параллельные прямые пересечены
третьей. Известно, что разность двух
внутренних односторонних углов равна 40°. Найдите
эти углы.
3. Две параллельные прямые пересечены
третьей.'Известно, что сумма двух внутренних
накрест лежащих углов равна 160°. Чему равны
эти углы?
4. Две параллельные прямые пересечены
третьей прямой так, что один из
образовавшихся углов равен 120°. Под какими углами его
биссектриса пересекает вторую параллельную
прямую?
СУММА УГЛОВ ТРЕУГОЛЬНИКА
Теорема о сумме углов треугольника
ТЕОРЕМА
Сумма углов треугольника равна 180°.
Доказательство. Рассмотрим
произвольный треугольник ABC и докажем, что
ZA + ZB + ZC = 180°.
Проведем через вершину В прямую а,
параллельную стороне АС (рис. 63). Углы 1 и 4
являются накрест лежащими углами при
пересечении параллельных прямых а и АС секущей АВ>
а углы 3 и 5 — накрест лежащими углами при
пересечении тех же параллельных прямых
секущей ВС. Поэтому
Z4 = Z1,Z5 = Z3. (1)
Очевидно, сумма углов 4, 2 и 5 равна
развернутому углу с вершиной В, т. е.
Z4+Z2+Z5= 180°.
4/3
В а
Рис. 61
1/5
6/2
7/8
Рис. 62
А
Х^\
а з\
с
Рис. 63

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
137
Отсюда, учитывая равенства (1), получаем:
Z 1 + Z 2 + Z 3 = 18 0 °, ил и Z А + Z В + Z С = 180°.
Теорема доказана.
Следствия.
1) Сумма острых углов прямоугольного
треугольника равна 90°.
2) В равнобедренном прямоугольном
треугольнике каждый острый угол равен 45°.
3) В равностороннем треугольнике каждый
угол равен 60°.
4) В любом треугольнике либо все углы
острые, либо два угла острые, а третий тупой
или прямой.
5) Внешний угол треугольника равен сумме
двух внутренних углов, не смежных с ним.
Доказательство. Из равенств Z 4 + Z 3 —
= 180° hZ1+Z2 + Z3 = 180° (рис. 64)
получаем, что Z4 = Z1 + Z2.
Пример 1. Два угла треугольника равны 27°
и 41°. Найти третий угол и определить вид
треугольника.
Решение. Так как сумма двух углов
треугольника равна 68°, то по теореме о сумме углов
треугольника третий угол равен 180° - 68° = 112° и,
значит, данный треугольник тупоугольный.
Пример 2. Какой вид имеет треугольник, в
котором один угол равен сумме двух других
углов?
Решение. Обозначим через х градусную меру
того угла треугольника, который равен сумме
двух других углов. Тогда, так как сумма углов
треугольника равна 180°, то 2х = 180°, откуда
х = 90°, т. е. треугольник прямоугольный.
Пример 3. Найти углы треугольника ABC,
зная, что угол С на 15° больше, а угол В на 30°
меньше угла А.
Решение. Обозначим градусную меру угла А
через х, тогда градусная мера угла С равна х +
-I-15°, а угол В - х - 30° (рис. 65).
Так как сумма внутренних углов
треугольника равна 180°, то получаем уравнение
х + (х +15) + (х -30) = 180.
Решая его, получаем х = 65°.
Таким образом,
ZA = 65°, ZB = 35° и ZC = 80°.
Пример 4. В треугольнике ABC (рис. 66)
А А = 60°, Z В = 80°. Биссектриса AD этого
треугольника отсекает от него треугольник ACD.
Найти углы этого треугольника.
Решение. Z DAB = 30°, так как AD —
биссектриса угла A, Z ADC = 30° + 80°= 110° как
внешний угол треугольника ABD (следствие 5), Z С =
= 180° - (110° + 30°) = 40° по теореме о сумме
углов треугольника ACD.
Соотношения между сторонами
и углами треугольника.
Неравенство треугольника
ТЕОРЕМА 1
В треугольнике против большей стороны
лежит больший угол.
Доказательство. Пусть в треугольнике ABC
сторона АВ больше стороны АС (рис. 67, а).
Докажем, что Z С > Z В. Отложим на стороне АВ
отрезок AD, равный стороне АС (рис. 67, б). Так
как AD < АВ, то точка D лежит между точками
А и В. Следовательно, угол 1 является частью
угла С и, значит, Z С > Z 1. Угол 2 — внешний
угол треугольника BDC9 поэтому Z 2 > Z В.
Углы 1 и 2 равны как углы при основании
равнобедренного треугольника ADC. Таким образом,
ZOZ1, Z1 = Z2,Z2>ZB. Отсюда следует,
что Z С > Z В.
Справедлива и обратная теорема (ее
доказательство проводится методом от противного).
Рис. 64
Рис. 65
Рис. 66

138
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
ТЕОРЕМА 2
В треугольнике против большего угла
лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника
равны, то треугольник равнобедренный
(признак равнобедренного треугольника).
Доказательство следствия проводится
методом от противного.
Из следствия 1 следует, что если три угла
треугольника равны, то треугольник
равносторонний.
Из теоремы 2 получаем
Следствие 2. В прямоугольном
треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается
ТЕОРЕМА 3
Каждая сторона треугольника меньше
суммы двух других сторон.
Следствие 3. Для любых трех точек А, В и
С, не лежащих на одной прямой, справедливы
неравенства:
АВ<АС + СВ, АС<АВ + ВС, ВС<ВА + АС.
Каждое из этих неравенств называется
неравенством треугольника.
Пример 1. Сравнить углы треугольника ABC
и выяснить, может ли быть угол А тупым, если
АВ > ВС > АС.
Решение. Согласно теореме 1 имеем: ZC>ZA>
>ZB. Угол А тупым быть не может, так как
тогда Z С тоже тупой и, значит, ZA + ZB + ZC>
> 180°, что невозможно (п. 1, теорема).
Пример 2. Сравнить стороны треугольника
ABC, если ZA> ZB> ZC.
Решение. Согласно теореме 2 имеем: ВС > АС >
>АВ.
Пример 3. Две стороны равнобедренного
треугольника равны б и 2. Чему равна третья
сторона?
Решение. Так как каждая сторона
треугольника меньше суммы двух других сторон
(теорема 3), то третья сторона может быть равной
только 6.
Пример 4. Одна сторона треугольника равна
1>5» другая— 0,7. Определить третью сторону,
зная, что она выражается натуральным числом.
Решение. Обозначим третью сторону
треугольника через х. Тогда х < 1,5 + 0,7 = 2,2
(теорема 3). Отсюда, учитывая, что эта сторона
выражается натуральным числом, следует, что
дг = 2 или х= 1.
Расстояние от точки до прямой
Пусть ВА — перпендикуляр, опущенный из
точки В на прямую а, и С — любая точка на прямой
а, отличная от А. Отрезок ВС называется
наклонной, проведенной из точки В к прямой а
(рис. 68). Точка С называется основанием
наклонной, а отрезок АС — проекцией наклонной.
Из прямоугольного треугольника ВАС с прямым
углом А видим, что наклонная больше
перпендикуляра. В этом треугольнике наклонная
является гипотенузой, а перпендикуляр — катетом.
Расстоянием от точки В до прямой а, не
проходящей через точку В, называется длина
перпендикуляра, опущенного из точки В на
прямую а.
Так как перпендикуляр меньше наклонной,
проведенной из той же точки, то расстояние от
точки В до прямой а является наименьшим из
расстояний от точки В до любой из точек
прямой а.
Пример. Из точки В вне прямой а проведена
наклонная, составляющая с прямой угол в 45°.
Найти расстояние от точки В до прямой а, если
проекция наклонной на эту прямую равна 1 см.
Решение. Пусть условию задачи отвечает
рисунок 68. Треугольник ВАС — прямоугольный и
равнобедренный: ВА — перпендикуляр, Z ВСА —
= 45° (условие) и, значит, угол СВА тоже равен
45°, так как сумма острых углов прямоугольно-
С А
ВА J. а, ВС — наклонная, АС — проекция
Рис. 68

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
139
го треугольника равна 90° (п. 1, следствие 1).
Поэтому искомое расстояние ВА — АС = 1 см.
Признаки равенства
прямоугольных треугольников
Так как в прямоугольном треугольнике угол
между двумя катетами прямой, а любые два
прямых угла равны, то из первого признака
равенства треугольников следует:
если катеты одного прямоугольного
треугольника соответственно равны катетам
другого, то такие треугольники равны.
Далее, из второго признака равенства
треугольников следует:
если катет и прилежащий к нему острый
угол одного прямоугольного треугольника
соответственно равны катету и прилежащему к
нему острому углу другого, то такие
треугольники равны.
Рассмотрим еще два признака равенства
прямоугольных треугольников.
ТЕОРЕМА 1
Если гипотенуза и острый угол одного
прямоугольного треугольника
соответственно равны гипотенузе и острому углу
другого, то такие треугольники равны.
Доказательство. Из следствия 1 (п. 1)
следует, что в таких треугольниках два других
острых угла также равны, поэтому треугольники
равны по второму признаку равенства
треугольников. Теорема доказана.
ТЕОРЕМА 2
Если гипотенуза и катет одного
прямоугольного треугольника соответственно
равны гипотенузе и катету другого, то такие
треугольники равны (рис. 69).
Пример 1. Доказать, что каждая точка
биссектрисы угла равноудалена от его сторон.
Решение. Пусть I — биссектриса Z АОВ
(рис. 70).
Рассмотрим произвольную точку М,
лежащую на луче I. Опустим из точки М
перпендикуляры МС и MD на стороны угла АОВ.
Прямоугольные треугольники ОМС и OMD равны по
теореме 1: у них гипотенуза ОМ общая, а углы
СОМ и DOM равны по условию. Отсюда следует,
что МС = MD.
Пример 2. Доказать, что точка плоскости,
равноудаленная от сторон угла, лежит на
биссектрисе этого угла.
Решение. Пусть точка М равноудалена от
сторон угла АОВ (см. рис. 70), т. е.
перпендикуляры МС и MD к сторонам угла равны. Тогда
А ОМС = A OMD по теореме 2. Отсюда Z СОМ =
= A DOM, и, следовательно, луч ОМ является
биссектрисой угла АОВ.
Замечание. Предложения, установленные в
примерах 1 и 2, выражают свойства
биссектрисы угла. Из этих предложений следует, что
биссектрисы треугольника пересекаются в одной
точке.
Пример 3. Доказать, что в прямоугольном
треугольнике с углом 30° катет,
противолежащий этому углу, равен половине гипотенузы.
Решение. Пусть ABC — прямоугольный
треугольник с прямым углом С и острым углом В,
равным 30° (рис. 71). Отложим на продолжении
стороны АС отрезок CD, равный АС.
Прямоугольные треугольники АСВ и DCB
(углы при вершине С прямые) равны по двум ка-
Рис. 70

140
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
тетам (сторона ВС общая, а. АС = CD по
построению).
Из равенства треугольников следует, что Z D =
= ZA = 60°, Z CBD - Z СВА = 30°, а
значит, ZABD = 60°. Отсюда следует,-что
треугольник ABD равносторонний. Поэтому АС = т> AD =
= 2 АВ, что и требовалось доказать.
Контрольные вопросы
1. Докажите теорему о сумме углов
треугольника.
2. Чему равна сумма острых углов
прямоугольного треугольника?
• 3. Чему равен каждый острый угол
равнобедренного прямоугольного треугольника?
4. Чему равны углы равностороннего
треугольника?
5. Какими могут быть углы в любом
треугольнике?
6. Докажите, что внешний угол
треугольника равен сумме двух внутренних углов, не
смежных с ним.
7. Докажите, что в треугольнике против
большей стороны лежит больший угол.
Сформулируйте обратную теорему.
8. Сформулируйте признак равнобедренного
треугольника.
9. Что такое неравенство треугольника?
10. Что называется расстоянием от точки до
прямой?
11. Сформулируйте два признака равенства
прямоугольных треугольников,
непосредственно следующих из первого и второго признаков
равенства треугольников.
12. Докажите признак равенства
прямоугольных треугольников по гипотенузе и острому углу.
13. Сформулируйте признак равенства
прямоугольных треугольников по гипотенузе и
катету.
Упражнения
1. В треугольнике один из углов равен 30°,
другой равен 75°. Найдите третий угол
треугольника.
2. В равнобедренном треугольнике угол при
вершине равен 42°. Найдите углы при
основании.
3. В равнобедренном треугольнике угол при
основании равен 40°. Найдите угол при вершине.
4. Один из внешних углов равнобедренного
треугольника равен 100°. Найдите внутренние
углы треугольника.
5. В прямоугольном треугольнике один из
двух острых углов в 2 раза больше другого.
Найдите эти углы.
6. В треугольнике один из углов 50°, а
разность двух других 10°. Найдите эти углы
треугольника.
7. Найдите сумму внешних углов
треугольника, взятых по одному при каждой вершине.
8. В прямоугольном треугольнике один
острый угол равен 45°. Найдите катеты, если их
сумма равна 36 м.
9. В прямоугольном треугольнике острый
угол равен 45°. Найдите гипотенузу, если в
сумме с опущенной на нее высотой она составляет
12 м.
10. Сравните стороны треугольника ABC,
ecnnZA<ZB<ZC.
11. Две стороны равнобедренного
треугольника равны 3 и 1. Чему равна третья сторона?
12. Докажите, что в равнобедренном
треугольнике высоты, проведенные из вершин
основания, равны.
13. Докажите, что треугольник
равнобедренный, если он имеет две равные высоты.
14. Из точки вне прямой проведена наклонная,
составляющая с прямой угол в 45°. Найти
расстояние от этой точки до прямой, если проекция
наклонной на эту прямую равна 3 см.
ЧЕТЫРЕХУГОЛЬНИК
Определение четырехугольника
Четырехугольником называется фигура,
которая состоит из четырех точек и четырех
последовательно соединяющих их отрезков. При
этом никакие три из данных точек не должны
лежать на одной прямой, а соединяющие их
отрезки не должны пересекаться.
Данные точки называются вершинами
четырехугольника, а соединяющие их отрезки —
сторонами четырехугольника.
Вершины четырехугольника (рис. 72)
называются соседними 9 если они являются концами
одной и той же его стороны. Вершины, не являю-

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
141
щиеся соседними, называются
противолежащими. Отрезки, соединяющие
противолежащие вершины четырехугольника, называются
диагоналями. На рисунке 72 диагоналями
являются отрезки АС и BD.
Стороны четырехугольника, исходящие из
одной вершины, называются смежными
сторонами. Стороны, не имеющие общего конца,
называются противоположными сторонами.
Четырехугольник называется выпуклым (см. рис. 72),
если он лежит по одну сторону относительно
прямой, содержащей любую его сторону.
Параллелограмм. Расстояние между
параллельными прямыми
Параллелограммом называется
четырехугольник, у которого противоположные
стороны параллельны, т. е. лежат на параллельных
прямых (рис. 73).
ТЕОРЕМА 1
о свойстве сторон и углов параллелограмма
В параллелограмме противоположные
стороны равны, противоположные углы
равны и сумма углов, прилежащих к одной
стороне параллелограмма, равна 180°.
Доказательство. В данном
параллелограмме ABCD проведем диагональ АС и получим два
треугольника ABC nADC (рис. 74). Эти
треугольники равны, так как Z 1 = Z 4, Z 2 = Z 3 (накрест
лежащие углы при параллельных прямых), а
сторона АС общая. Из равенства Д ABC = Л ADC
следует, что АВ = CD, ВС = AD, ZB = ZD.
Сумма углов, прилежащих к одной стороне,
например углов А и D, равна 180° как односторонних
при параллельных прямых. Теорема доказана.
Замечание. Равенство противоположных
сторон параллелограмма означает, что отрезки
параллельных, отсекаемых параллельными, равны.
Следствие. Если две прямые параллельны,
то все точки одной прямой находятся на
одном и том же расстоянии от другой прямой.
Доказательство. В самом деле, пусть а \\ Ъ
(рис. 75). Проведем из каких-нибудь двух точек
Б и С прямой Ъ перпендикуляры ВА и CD к
прямой а. Так как АВ || CD, то фигура ABCD —
параллелограмм, и следовательно, АВ = CD.
Расстоянием между двумя параллельными
прямыми называется расстояние от
произвольной точки одной из прямых до другой прямой.
По доказанному оно равно длине
перпендикуляра, проведенного из какой-нибудь точки одной
из параллельных прямых к другой прямой.
Пример 1. Периметр параллелограмма равен
122 см. Одна из его сторон больше другой на
25 см. Найти стороны параллелограмма.
Решение. По теореме 1 противоположные
стороны параллелограмма равны. Обозначим
одну сторону параллелограмма через х, другую
через у. Тогда по условию
2x + 2i/ = 122,
х-у = 25.
Решая эту систему, получим х = 43, у = 18.
Таким образом, стороны параллелограмма
равны 18, 43, 18 и 43 см.
Пример 2. Четырехугольник ABCD —
параллелограмм с периметром 10 см. Найти
диагональ BD, зная, что периметр треугольника
ABD равен 8 см.
Решение. Пусть условию задачи отвечает
рисунок 76. Обозначим АВ через х, а ВС через у.
По условию периметр параллелограмма
равен 10 см, т. е.
2(* + у) = 10, или х + у = 5.
Периметр треугольника ABD равен 8 см. А так
как
AB+AD = x + i/ = 5,
тоЯО = 8-5 = 3.
Итак, BD - 3 см.
В
A D
Рис. 72
В
A D
Параллелограмм
Рис. 73
В
Рис. 74
Ъ В
£_h
EL
Рис. 75
В У С
A D
Рис. 76

142
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Пример 3. Найти углы параллелограмма,
зная, что один из них больше другого на 50°.
Решение. Пусть условию задачи отвечает
рисунок 77.
Обозначим градусную меру угла А через х.
Тогда градусная мера угла D равна х + 50°.
Углы BAD и ADC внутренние односторонние
при параллельных прямых АВ и DC и секущей
AD. Тогда сумма этих названных углов составит
180°, т. е.
х + х + 50° = 180°, или х = 65°.
Таким образом,
ZA = ZC = 65°, a ZB = ZD = 115°.
Пример 4. Стороны параллелограмма равны
4,5 дм и 1,2 дм. Из вершины острого угла
проведена биссектриса. На какие части делит она
большую сторону параллелограмма?
Решение. Пусть условию задачи отвечает
рисунок 78.
АЕ — биссектриса острого угла
параллелограмма. Следовательно, Z 1 = Z 2.
ВС || AD, АЕ — секущая, следовательно, Z 2 =
= Z 3, т. е. Z 1 = Z 3. А это означает, что
треугольник ABE равнобедренный, следовательно,
АВ = ВЯ = 1,2 дм.
ЕС = ВС-BE = 3,3 дм.
Пример 5. Прямая АВ параллельна прямой
CD (рис. 79). Найти расстояние между этими
прямыми, если ZADC = 45°, CD =1,6 см.
Решение. Искомое расстояние равно длине
перпендикуляра АС. Треугольник ACD —
прямоугольный и равнобедренный (АС —
перпендикуляр, Z ADC = 45° по условию, значит,
и Z CAD = 45°, ибо в прямоугольном
треугольнике сумма острых углов равна 90°. Следовательно,
АС = CD =1,6 см.
ТЕОРЕМА 2
свойство диагоналей параллелограмма
Диагонали параллелограмма
пересекаются и точкой пересечения делятся пополам.
Следующая теорема выражает признаки
параллелограмма.
ТЕОРЕМА 3
Если в выпуклом четырехугольнике:
1) противоположные стороны равны между
собой, или
2) две противоположные стороны равны и
параллельны, или
3) диагонали точкой пересечения делятся
пополам,
то такой четырехугольник — параллелограмм.
Доказательство проведем для одного из
этих признаков, например для признака 1).
Пусть ABCD — четырехугольник, у которого
АВ = CD, ВС = AD (рис. 80). Докажем, что
ABCD — параллелограмм, т. е. что АВ \\ CD,
ВС || AD. Проведем диагональ АС и получим два
треугольника ABC и ADC. Так как АС — общая
сторона, АВ = CD, ВС = AD (по условию), то
А ABC = A ADC. Поэтому Z 1 = Z 2, Z 4 = Z 3, а
из равенства накрест лежащих углов следует
параллельность прямых: ВС || AD, АВ \\ CD.
Пример 6. Диагональ BD параллелограмма
ABCD (рис. 81) равна 8 см. Найти длину
медианы к стороне АС в треугольнике ABC.
Решение. Согласно теореме 2 диагонали
параллелограмма пересекаются и точкой
пересечения делятся пополам. Поэтому ВО — медиана
треугольника ABC к стороне АС и ВО = т> BD =
= | -8 = 4(см).
Прямоугольник, ромб, квадрат
Прямоугольником называется параллелограмм,
у которого все углы прямые (рис. 82).
Прямоугольник обладает всеми свойствами
параллелограмма.
В
В
В
л
ST
\
С D
Рис. 79
/ ^>У
1)*Г 1
A D
Рис. 80
I
L
А
/ъ^7
^<Ы
D
Рис. 81

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
143
ТЕОРЕМА 1
Диагонали прямоугольника равны.
Доказательство. Обратимся к рисунку 83,
на котором изображен прямоугольник ABCD с
диагоналями АС и BD. Прямоугольные
треугольники ACD и DBA равны по двум катетам
(CD = ВА9 AD — общий катет). Отсюда следует,
что гипотенузы этих треугольников равны, т. е.
АС = BD, что и требовалось доказать.
Справедлива и обратная теорема 2.
ТЕОРЕМА 2
признак .прямоугольника
Если в параллелограмме диагонали равны,
то этот параллелограмм — прямоугольник.
Пример 1. Найти длины диагоналей
прямоугольника ABCD (рис. 83), если периметр его
равен 34 см, а периметр одного из
треугольников, на которые диагональ АС разделила
прямоугольник, равен 30 см.
Решение. Обозначим периметр
прямоугольника ABCD через р, а периметр треугольника
ABC — через рг. Треугольники ABC и ADC
равны (третий признак равенства треугольников),
значит, равны и их периметры. Имеем
2рг-р = ЧАС, или 60 - 34 = 2АС,
откуда АС = 13 см, значит (теорема 1), и
диагональ BD равна 13 см.
Пример 2. Биссектриса одного из углов
прямоугольника делит сторону прямоугольника
пополам. Найти периметр прямоугольника, если
его меньшая сторона равна 10.
Решение. Условию задачи отвечает рисунок 84.
BE = ЕС по условию.
Треугольник ABE прямоугольный и
равнобедренный. Следовательно, АВ — BE — 10.
ВС - 2 • BE - 2 ■ 10 = 20.
Периметр прямоугольника ABCD состоит из
суммы всех его сторон и равен
2(АБ + ВС) = 2(10 + 20) = 60.
Ромбом называется параллелограмм, все
стороны которого равны (рис. 85). Ромб
обладает всеми свойствами параллелограмма.
Рассмотрим особое свойство ромба.
ТЕОРЕМА 3
Диагонали ромба взаимно
перпендикулярны и делят его углы пополам.
Доказательство. Рассмотрим ромб ABCD
(рис. 86). Требуется доказать, что AC ± BD и
каждая диагональ делит соответствующие углы
ромба пополам. Докажем, например, что Z ВАС =
= £DAC.
По определению ромба АВ = AD, поэтому
треугольник BAD равнобедренный. Так как ромб —
параллелограмм, то его диагонали точкой О
делятся пополам. Следовательно, АО —
медиана равнобедренного треугольника BAD, а
значит, высота и биссектриса этого треугольника.
Поэтому АС 1BD и Z ВАС = Z DAC, что и
требовалось доказать.
Пример 3. Определить углы ромба ABCD
(рис. 87) при условии, что его меньшая
диагональ АС равна стороне ромба.
Прямоугольник
Рис. 82
В EG

144
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Решение. Так как по условию диагональ АС
равна стороне ромба (а в ромбе все стороны
равны), то треугольник ABC — равносторонний и,
значит, Z ABC = 60°. Тогда (§ 6, п. 2, теорема 1)
Z BAD = 120°. Наконец, по той же теореме 1 Z D —
- Z В - 60° и Z BCD = Z BAD = 120°.
Пример 4. Сторона ромба составляет с его
диагоналями два угла, из которых один больше
другого на 50%. Вычислить углы ромба.
Решение. Пусть условию задачи удовлетворяет
рисунок 86. Обозначим градусную меру угла АВО
через ху тогда Z ВАО = х + 0,5* = 1,5*. В силу
теоремы 3 треугольник АОВ — прямоугольный и,
значит,
х+1,5х = 90о,
откуда х = 36°. Теперь согласно той же теореме
имеем:
ZABC = 36°-2 = 72°,
следовательно,
Z BAD = 180° - 72° = 108°.
Наконец,
ZADC = Z ABC = 72° и Z BCD - Z BAD = 108°.
Квадратом называется прямоугольник, все
стороны которого равны (рис. 88, а).
Квадрат является ромбом, поэтому обладает
свойствами прямоугольника и ромба. Основные
свойства квадрата:
1) все углы квадрата прямые (см. рис. 88, а);
2) диагонали квадрата равны, взаимно
перпендикулярны, точкой пересечения делятся
пополам и делят его углы пополам (рис. 88, б).
Пример 5. В квадрате ABCD (рис. 89)
расстояние от точки пересечения диагоналей до
одной из сторон равно 1 дм. Определить периметр
квадрата.
Решение. В силу основных свойств квадрата
треугольник ВОС — прямоугольный и
равнобедренный. Отсюда и из того, что по условию ОЕ —
перпендикуляр, следует, что треугольники ВЕО
и СЕО — прямоугольные, равнобедренные и
равные.
Значит,
откуда
ОЕ = ВЕ= |ВС,
ВС - 20Е
и, значит, ВС = 2 дм.
Следовательно, периметр квадрата равен 8 дм.
Теорема Фалеса.
Средняя линия треугольника
ТЕОРЕМА 1
теорема Фалеса*
Если параллельные прямые, пересекающие
стороны угла, отсекают на одной его
стороне равные отрезки, то они отсекают равные
отрезки и на другой его стороне.
Доказательство. Пусть Av А2, А3 — точки
пересечения параллельных прямых с одной из
сторон угла и А2 лежит между Аг и А3 (рис. 90).
Пусть Bv В2> В3 — соответствующие точки
пересечения этих прямых с другой стороной угла.
Докажем, что если АХА2 = А^А^ то ВгВ2 = В2В3.
Проведем через точку В2 прямую EF,
параллельную прямой АгА3. По свойству
параллелограмма
А1А2 = ^Б2, А^^В^Е.
И так как АгА2 = AgAg, то FB2 — В^Е*
Треугольники B2BXF и В2В3Е равны по
второму признаку. У них B2F — В2Е по доказанному.
*Фалес Милетский — древнегреческий ученый,
живший в VI в. до н. э.
ВЕС
а) б)
Основные свойства
квадрата
Рис. 88
т
Рис. 89
Рис. 90

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
145
Углы при вершине В2 равны как вертикальные,
а углы B2FB1 и В2ЕВ3 равны как внутренние
накрест лежащие при параллельных АгВг и А3Вг и
секущей EF. Из равенства треугольников
следует равенство сторон: ВХВ2 = В2В3. Теорема
доказана.
Пример 1. Разделить данный отрезок на
четыре равные части.
Решение. Пусть АВ — данный отрезок
(рис. 91), который надо разделить на 4 равйые
части.
Для этого через точку А проведем
произвольную полупрямую а и отложим на ней
последовательно четыре равных между собой отрезка АС,
CD, DE, ЕК.
Соединим точки В и К отрезком. Проведем
через оставшиеся точки С, D, Е прямые,
параллельные прямой ВК, так, чтобы они пересекли
отрезок АВ.
Согласно теореме Фалеса отрезок АВ
разделится на четыре равные части.
Средней линией треугольника называется
отрезок, соединяющий середины двух его сторон.
На рисунке 92 отрезок ED — средняя линия
треугольника ABC.
С использованием теоремы 1
устанавливается следующая теорема:
ТЕОРЕМА 2
Средняя линия треугольника параллельна
третьей стороне и равна ее половине.
Пример 2. Диагональ прямоугольника равна
а. Чему равен периметр четырехугольника,
вершины которого являются серединами сторон
прямоугольника?
Решение. Пусть условию задачи отвечает
рисунок 93. Тогда EF — средняя линия
треугольника ABC и, значит, по теореме 2
Аналогично
hg=|ac=|, EH=±BD=%,
и, следовательно, периметр четырехугольника
EFGH равен 2а.
Пример 3. Стороны треугольника равны 2 см,
3 см и 4 см, а вершины его — середины сторон
другого треугольника. Найти периметр большого
треугольника.
Решение. Пусть условию задачи отвечает
рисунок 94. Отрезки АВ, ВС, АС — средние линии
треугольника DEF. Следовательно, согласно
теореме 2
АВ=|я*\ £С=~2)Я, AC=\DF
или
2=\EF, 3=±1Ж, 4=|Z)F,
откуда
EF = 4, DE = 6, DF - 8
и, значит, периметр треугольника DEF равен
18t5M.
Пример 4. В прямоугольном треугольнике
через середину его гипотенузы проведены
прямые, параллельные его катетам. Найти периметр
образовавшегося прямоугольника, если катеты
треугольника равны 10 и 8 см.
Деление отрезка
на четыре равные части
Рис. 91
ED — средняя линия
треугольника ABC
Рис. 92

146
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Решение. В треугольнике ABC (рис. 95) Z А
прямой, АВ = 10 см, АС = 8 см, KD и MD —
средние линии треугольника ABC, откуда
KD= g АС = 4 см,
ЛП>= g АВ = 5 см.
Периметр прямоугольника KDMA равен 18 см.
Трапеция
Трацецией называется четырехугольник, у
которого только две противоположные стороны
параллельны (рис. 96).
Эти параллельные стороны называются
основаниями трапеции. Две другие стороны
называются боковыми сторонами.
Отрезок, соединяющий середины ее боковых
сторон, называется средней линией трапеции.
На рисунке 97 отрезок EF — средняя линия
трапеции ABCD.
Трапеция, у которой боковые стороны равны,
называется равнобокой или равнобедренной
(рис. 98, а).
Трапеция, один из углов которой прямой,
называется прямоугольной (рис. 98, б).
С использованием теоремы 2 предыдущего
пункта устанавливается
ТЕОРЕМА
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Пример 1. В равнобедренной трапеции
перпендикуляр, проведенный из вершины тупого
угла, делит большее основание на отрезки 10 см
и 20 см. Найти меньшее основание.
Решение. Пусть условию задачи отвечает
рисунок 99, а. Проведем второй перпендикуляр из
вершины второго тупого угла (рис. 99, б).
Получили два равных прямоугольных треугольника
ABE и CDF. Из равенства этих треугольников
следует, что FD — 10 см. Значит, EF = 20 - 10 —
= 10 (см). Четырехугольник EBCF —
прямоугольник. Следовательно, ВС = EF = 10 см.
Пример 2. Средняя линия трапеции равна 7 м,
а одно из оснований больше другого на 4 м.
Найти основания трапеции.
Решение. Обозначим длину меньшего
основания через х. Тогда длина большего основания
будет х + 4. Теперь согласно теореме о средней
линии трапеции получаем уравнение
х + х + 4
= 7,
решая которое находим х = 5. Следовательно,
основания трапеции 5 м и 9 м.
Трапеция
Рис. 96
EF — средняя линия трапеции
Рис. 97
Трапеция
а) равнобедренная б) прямоугольная
Рис. 98
Рис. 99

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
147
Центральная
и осевая симметрии
Две точки А и Ах называются симметричными
относительно точки О, если О — середина
отрезка ААХ (рис. 100). Точка О считается
симметричной самой себе.
Фигура называется симметричной
относительно точки О, если для каждой точки
фигуры симметричная ей точка относительно точки
О также принадлежит этой фигуре. Точка О
называется центром симметрии фигуры.
Говорят также, что фигура обладает
центральной симметрией. Примерами фигур,
обладающих центральной симметрией, являются
окружность и параллелограмм (рис. 101). Центром
симметрии окружности является центр
окружности, а центром симметрии параллелограмма —
точка пересечения его диагоналей. Прямая
также обладает центральной симметрией, однако в
отличие от окружности и параллелограмма,
которые имеют только один центр симметрии
(точка О на рисунке 101), у прямой их бесконечно
много — любая точка прямой является ее
центром симметрии.
Две точки АиАг называются
симметричными относительно прямой а, если эта прямая
проходит через середину отрезка ААг и
перпендикулярна к нему (рис. 102). Каждая точка
прямой а считается симметричной самой себе.
Фигура называется симметричной
относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно
прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии
фигуры. Примеры таких фигур и их оси симметрии
изображены на рисунке 103. Заметим, что у
окружности любая прямая, проходящая через ее
центр, является осью симметрии.
Пропорциональные отрезки
Отношением отрезков АВ и CD называется от-
АВ „
ношение их длин, т. е. ~~ . Говорят, что
отрезки АВ и CD пропорциональны отрезкам АХВХ и
CXDV если
АВ CD
АгВг
СЛ
Например, отрезки АВ и CD, длины которых
равны 2 см и 1 см, пропорциональны отрезкам
АгВг и CXDV длины которых равны 3 см и 1,5 см.
В самом деле,
АВ
АгВг
CD
СгВг
2
3 #
Понятие пропорциональности вводится и для
большего числа отрезков. Так, например, три
О
Точки А и А1 —
симметричные
относительно О
Рис. 100
Фигуры, обладающие
центральной симметрией
Рис. 101
Точки А и Ах — симметричные
относительно прямой а
Рис. 102
Рис. 103

148
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
отрезка АВ, CD и EF пропорциональны трем
отрезкам AXBV CXDX и EXFV если
АВ
АгВг
CD
CXDX
EF
EXFX
ТЕОРЕМА
Параллельные прямые, пересекающие сто-
роны угла, отсекают от сторон угла
пропорциональные отрезки.
Доказательство. Пусть стороны угла А
пересекаются параллельными прямыми в точках
В, С и Вх, Сх соответственно (рис. 104). Теоремой
утверждается, что
АСг
АС
АВг
АВ
(1)
Пусть существует такой отрезок длины е,
который укладывается целое число раз и на
отрезке АС, и на отрезке ACV Пусть
АС = пе, АСг = тг (п > т). (2)
Разобьем отрезок АС на п равных частей
(длины г). При этом точка Сх будет одной из точек
деления. Проведем через точки деления прямые,
параллельные прямой ВС. По теореме Фалеса
эти прямые разбивают отрезок АВ на равные
отрезки некоторой длины г{. Имеем:
АВ = пгх, АВ1 = /пе1.
Отсюда и из (2)
т. АС-!
АВг
АВ
= — и
АС
т
п
Значит,
АСЛ
АВЛ
—11 = *
АС АВ '
Однако не для любых отрезков АС и АСХ
существует такой отрезок е, который в каждом из
отрезков АС и АСХ укладывается целое число раз
без остатка. Но и в этом случае можно доказать,
что равенство (1) выполняется. Теорема доказана.
Задача. Даны отрезки а, Ь, с. Построить
отрезок
be
х = —.
а
Решение. Строим любой неразвернутый угол
с вершиной О (рис. 105). Откладываем на одной
стороне угла отрезки ОА = ои ОВ = 6, а на
другой стороне отрезок ОС = с. Соединяем точки А и
С прямой и проводим параллельную ей прямую
BD через точку В. Отрезок OD = х.
Действительно, по теореме о
пропорциональных отрезках
ОА
ОВ
ОС
OD'
откуда
OD =
ОВ-ОС
ОА
be
а
Примечание. Построенный отрезок х
называется четвертым пропорциональным. Такое
название связано с тем, что он является четвертым
членом пропорции а : Ь = с : х.
Контрольные вопросы
1. Какая фигура называется
четырехугольником?
2. Какие вершины четырехугольника
называются соседними, какие — противолежащими?
3. Что такое диагонали четырехугольника?
4. Какие стороны четырехугольника
называются смежными? Какие называются
противоположными?
5. Что такое параллелограмм?
6. Сформулируйте и докажите свойство
сторон и углов параллелограмма.
7. Что называется расстоянием между
параллельными прямыми?
ОА
ОВ "
OD
Рис. 104
Рис. 105

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
149
8. Сформулируйте свойство диагоналей
параллелограмма.
9. Сформулируйте признаки
параллелограмма.
10. Какой параллелограмм называется
прямоугольником?
11. Докажите, что диагонали
прямоугольника равны.
12. Сформулируйте признак прямоугольника.
13. Какой параллелограмм называется
ромбом? Докажите, что диагонали ромба взаимно
перпендикулярны и делят его углы пополам.
14. Какой прямоугольник называется
квадратом? Сформулируйте основные свойства
квадрата.
15. Сформулируйте и докажите теорему Фа-
леса.
16. Какой отрезок называется средней
линией треугольника? Сформулируйте теорему о
средней линии треугольника.
17. Какой четырехугольник называется
трапецией?
18. Как называются стороны трапеции?
19. Какая трапеция называется
равнобедренной, какая — прямоугольной?
20. Какой отрезок называется средней
линией трапеции? Сформулируйте теорему о средней
линии трапеции.
21. Какие две точки называются
симметричными относительно данной точки?
22. Какая фигура называется симметричной
относительно данной точки?
23. Какие две точки называются
симметричными относительно данной прямой?
24. Какая фигура называется симметричной
относительно данной прямой? Приведите
примеры фигур, обладающих: а) центральной
симметрией; б) осевой симметрией; в) и
центральной, и осевой симметрией.
25. Что называется отношением двух
отрезков? В каком случае отрезки АВ и CD
пропорциональны отрезкам АгВг и С^^
Упражнения
1. Угол параллелограмма равен 36°. Найдите
остальные углы.
2. Параллелограмм делится одной из его
диагоналей на два треугольника, периметр каждого
равен 6,21 м, а периметр параллелограмма
равен 7,12 м. Найдите длину этой диагонали.
3. Биссектриса одного из углов
прямоугольника делит сторону прямоугольника пополам.
Найдите периметр прямоугольника, если его
меньшая сторона равна 20 см.
4. Найдите длину диагонали
прямоугольника, в котором острый угол между диагоналями
равен 60°, а расстояние от точки их пересечения
до большей стороны равно 1,25 м.
5. Дан ромб с углом 120° и стороной, равной
3 м. Найдите меньшую диагональ ромба.
6. Через вершины квадрата проведены
прямые, параллельные его диагоналям. Определите
вид четырехугольника, образованного этими
прямыми.
7. Разделите данный отрезок на пять равных
частей.
8. Стороны треугольника равны 8 см, 10 см,
12 см. Найдите стороны треугольника,
вершинами которого являются середины сторон
данного треугольника.
9. Средняя линия равнобедренного
треугольника, параллельная основанию, равна 3 см.
Найдите стороны треугольника, если его
периметр равен 16см.
10. В равнобедренной трапеции
перпендикуляр, проведенный из вершины тупого угла,
делит большее основание на отрезки 6 м и 30 м.
Найдите меньшее основание и среднюю линию
трапеции.
11. Основания трапеции равны 4 м и 10 м.
Найдите длины отрезков, на которые делит
среднюю линию этой трапеции одна из ее диагоналей.
12. Имеют ли центр симметрии: 1) отрезок;
2) луч; 3) квадрат?
13. Какие из следующих букв имеют центр
симметрии: А, О, М, X?
14. Сколько осей симметрии имеет: 1)
отрезок; 2) прямая; 3) луч?
15. Какие из следующих букв имеют ось
симметрии: А, Б, Г, Е, О?
16. Отрезок длиной в 35 см разделен на две
части в отношении 3:4. Найдите длину каждой
части отрезка.
17. Стороны угла ВАСг пересечены
параллельными прямыми ВВг и ССХ так, что В и С — на
одной стороне угла, а Вх и Сх — на другой.
Найдите длину отрезка ABV если АВ — 5 см, ВС =
= 6 см и ВгСг = 9 см.

150
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ОСТРОГО УГЛА.
ТЕОРЕМА ПИФАГОРА
Определения
Пусть ABC — прямоугольный треугольник с
прямым углом С и острым углом при вершине А,
равным а (рис. 106).
Косинусом угла а (обозначается cos а)
называется отношение прилежащего катета АС к
гипотенузе АВ:
cosa =
АС
АВ'
(1)
Синусом угла а (обозначается sin а)
называется отношение противолежащего катета ВС к
гипотенузе АВ:
ВС (2)
sina =
АВ
Тангенсом угла а (обозначается tg а)
называется отношение противолежащего катета ВС к
прилежащему катету АС:
ВС
(3)
Косинус, синус и тангенс угла зависят
только от величины угла. Поэтому cos a, sin а и tg a
являются функциями угла а. Эти функции
называются тригонометрическими.
Так как в прямоугольном треугольнике
гипотенуза больше катета (§ 5, п. 2, следствие 2), то
cosa< 1 и sin a < 1.
Для sin a, cos a и tg a составлены
специальные таблицы. Эти таблицы позволяют по данному
углу а найти sin a, cos а и tg а или по значениям
sin a, cos a и tg a найти соответствующий угол.
Для этой цели используют также и
микрокалькуляторы.
Теорема Пифагора
ТЕОРЕМА
теорема Пифагора*
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Доказательство. Пусть ABC — данный
прямоугольный треугольник с прямым углом С.
Проведем высоту CD из вершины прямого угла
С (рис. 107). Получили два прямоугольных
треугольника. По определению косинуса угла А
запишем:
Л _AD _АС
C0SA АС АВ'
Отсюда АВ AD=AC2.
BD ВС
Аналогично cos В = -g^ = jg .
Отсюда АВ BD = ВС2.
Складывая полученные равенства почленно и
учитывая, что AD + DB =АВ, получим:
AC2 + BC2=AB(AD + DB) = АВ2.
Теорема доказана.
Пример 1. В прямоугольнике ACBD (рис. 108)
стороны равны 5 см и 12 см. Чему равна
диагональ АВ?
Решение. Из прямоугольного треугольника
АСВ согласно теореме Пифагора имеем:
АВ2=АС2 + ВС2,
или АВ2 - 122 + 52 = 169
и, значит, АВ = 13 (см).
Пример 2. Диагонали ромба ABCD (рис. 109)
равны 24 м и 70 м. Найти его сторону.
* Пифагор — древнегреческий ученый, живший в
VI в. до н. э.
\а
ВС
АВ
АС
АВ
С tga = |§
В sin a =
cos a =
Рис. 106
D В
АВ2 = AC2 + ВС2
Рис. 107
Рис. 108

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
151
Решение. Как известно (см. § 6, п. 3,
теорема 3), диагонали ромба взаимно
перпендикулярны и делят его углы пополам. Поэтому
треугольник АОВ (рис. 109) прямоугольный с катетами
12 м и 35 м и, значит, по теореме Пифагора
АВ - Vl22 + 352 - л/144 + 1225 =
= л/1369 = 37 (м).
Пример 3. Основание равнобедренного
треугольника а, боковая сторона Ъ. Найти
биссектрису, проведенную из вершины,
противолежащей основанию.
Решение. Пусть ABC — равнобедренный
треугольник с основанием АВ и CD — его
биссектриса (рис. 110). Эта биссектриса является
одновременно медианой и высотой. Поэтому AD —
= о АВ и треугольник ADC прямоугольный с
прямым углом D. По теореме Пифагора
AC2=AD2 + DC2,
-(§г
+ D&
Отсюда
DC
-F^i
Основные тригонометрические
тождества
Используя равенства (1), (2) и (3), имеем:
sin а*
1 = ВС АВ = ВС =
cos а АВ АС АС
sin а
tgoc.
Итак, tg ос — . Это равенство есть
тождество. Оно верно для любого острого угла а.
Далее, используя теорему Пифагора (см.
рис. 106), находим:
. 2 ^ 2 ВС2 ^ АС2
sin (X + cos а = —« + —5 —
АВ2 АВ2
ВС2 + АС2 АВ2
= 1.
АВ АВ
Итак, имеем тождество:
2 2
sin ot + cos а= 1.
Используя тождество (4), получаем:
.2 2 , . 2
- , , 2 - . sin a cos а + sin а
1 + tg а = 1 +
(4)
2
cos а
2
cos а
2 '
cos а
Таким образом:
l + tg2ct= *
2 '
cos а
Аналогично выводится тождество:
1 1
1 +
2 2 '
tg a sin а
Полученные тождества позволяют, зная одну
из величин sin a, cos а или tg а, найти другие.
Пример 1. Вычислить значение cos а и tg а,
1
если sin ос = g •
2 2
Решение. Так как sin a + cos а=1,то
cos
o-Vl -sin2a = Jl -(T)2=^,
tga =
sin a
1-2
7з
cos a 2 • Л Л
Пример 2. Вычислить значения sin а и tg a,
3
если cos ct = g .
Решение. Имеем
sina= л/1 - cos a = /l - f g j = ^ ,
4-5 4
Значения тригонометрических
функций некоторых углов
ТЕОРЕМА
Для любого острого угла a
sin (90° - a) = cos a, cos (90° - a) = sin a.

152
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Доказательство. Пусть ABC —
прямоугольный треугольник с острым углом а при вершине
А (рис. 106). Тогда острый угол при вершине В
равен 90° - а. Согласно определению
AC ЯГ
sin (90° - а) - ||, cos (90° - а) = ||
или, с учетом формул (1) и (2),
sin (90° - а) = cos а, cos (90° - а) = sin а.
Теорема доказана.
Пример 1. Найти значения sin 45°, cos 45° и
tg45°.
Решение. Рассмотрим равнобедренный
прямоугольный треугольник (рис. 1.11). В нем
каждый острый угол равен 45°. Пусть его катеты
равны а. По теореме Пифагора его гипотенуза
равна а Л . Теперь по определению имеем:
sin 45° =
cos 45° =
а _ 1 _ Л
аЛ Л 2 ;
аЛ Л 2 ;
1*45°-£-1.
Пример 2. Найти значения sin 30°, cos 30° и
tg30°.
Решение. Рассмотрим прямоугольный
треугольник, у которого один из острых углов
равен 30° (рис. 112). Пусть его гипотенуза равна
с. Так как катет, лежащий против угла 30°, равен
половине гипотенузы (§ 5, пункт 4, пример 3), то
с 1
sin 30° = о-т~ = о и» значит> с учетом примера 1
л * л
предыдущего пункта cos 30° = -у , tg 30° = -у .
Пример 3. Найти значения sin 60° и tg 60°.
Решение. Согласно установленной выше
теореме имеем:
. sin 60° = sin (90° - 30°) = cos 30° = ^ '
cos 60° - cos (90° - 30°) = sin 30° - ^ .
Отсюда
+« «no - sin 60° - ^'2 _ /«
Зависимости между
сторонами и углами
прямоугольного треугольника
Из равенств (2), (1) и (3) получаем
ВС =АВ sin а, AC =АВ cos а, BC=ACtgct.(5)
Пусть ВС = а, АС = 6, АВ *= с. Тогда равенства
(5) перепишутся в виде
а = csin а, Ъ = ccos а, а = big а, (6)
т. е. катет равен гипотенузе, умноженной на
синус противолежащего (этому катету)* угла или
на косинус прилежащего (этому катету) угла;
катет равен другому катету, умноженному на
тангенс угла, противолежащего определяемому
катету.
Далее из равенств (6) находим
с —
sin а
с =
cos or
т. е. гипотенуза равна катету, деленному на
синус противолежащего (этому катету) угла или
на косинус прилежащего (этому катету) угла.
Решение прямоугольных
треугольников
Решить прямоугольный треугольник — значит
вычислить все его стороны и углы по
каким-либо данным, определяющим этот треугольник.
Рассмотрим основные случаи решения
прямоугольного треугольника.
1. По гипотенузе и острому углу.
Дано: Гипотенуза с и острый угол А. Найти
катеты а и 6, острый угол В.
Имеем: а = csin А, Ъ = ccos A, Z В = 90° - ZA.
Рис. 112
* Слова «этому катету*, взятые в скобки, обычно
опускаются.

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
153
2. По катету и острому углу.
Дано: а и Z А. Найти с, Ъ и Z В.
Имеем: с = -Д-г , & = г^7 , Z Б = 90° - Z А.
sin A tg А
3. По гипотенузе и катету.
Дано: с и а. Найти b, Z AnZ В.
Имеем: b= *Jc - а ,
sin А = — , cos В = — .
с с
4. По двум катетам.
Дано: а и &. Найти с, Z А и Z В.
Имеем:
с=л/а2 + Ь2» tgA=~, tgB=-.
Пример 1. Дано: с = 18,2, Z А = 32°20'.
Найти а, & и Z В.
Решение, а = 18,2 • sin 32°20' « 18,2 • 0,5349 «
«9,74;
& = 18,2 • cos 32°20'« 18,2 • 0,8450 « 15,4;
Z В = 90° - 32°20' = 57°40'.
Пример 2. Дано: а = 18, Z А = 47°. Найти
с, &hZB.
18
Решение. Z В = 90° - 47° = 43°; с =
sin 47°
18
0,7314
= 24,61;
& =
18
18
tg47# ~ 1,0724
-18 0,9325 «16,79.
Пример 3. Дано: с = 65, а = 16. Найти &,
ZAhZB.
Решение.
& - л/б52 - 162 = л/(65 + 16)(65 - 16) -
16
= V81 49 = 9 • 7 = 63; sin А = ^ » 0,2461,
отсюда Z А » 14°15'; Z В » 90° - 14°15' = 75°45'.
Пример 4. Дано: а = 12, & = 15. Найти с,
ZAylZB.
Решение, с = Vl22 + 152 = л/144 + 225 -
= 7369 «19,2;
12
tg А = j| = 0,8, отсюда Z А = 38°39'
и Z В - 90° - 38°39' = 51°21'.
Контрольные вопросы
1. Что называется косинусом, синусом и
тангенсом острого угла прямоугольного
треугольника?
2. Сформулируйте и докажите теорему
Пифагора.
3. Приведите основные тригонометрические
тождества.
4. Чему равны значения синуса, косинуса и
тангенса для углов 30°, 45°, 60°?
5. Как выражается катет прямоугольного
треугольника через гипотенузу и острый угол?
6. Как выражается катет прямоугольного
треугольника через другой катет и острый угол?
7. В чем состоит решение прямоугольного
треугольника?
- 8. Каковы основные случаи решения
прямоугольного треугольника?
Упражнения
1. Заполните таблицу:
а
5
Ъ
12
с
13
sin А
cos А
где а, & — катеты, с — гипотенуза прямоугольного
треугольника ABC (Z А противолежит катету а).
2. Заполните таблицу:
а
3
8
Ъ
4
15
tgA
где а, & — катеты (Z А противолежит
катету а).
3. Найдите гипотенузу прямоугольного
треугольника, катеты которого: 1) 6 см и 8 см;
2) 2,1 сми 2 см.
4. Найдите катет прямоугольного
треугольника, если гипотенуза и другой катет
соответственно равны 29 см и 21 см.
5. В прямоугольном треугольнике один из
углов равен 60°, сумма гипотенузы и меньшего
катета 45 м. Найдите гипотенузу.
6. В прямоугольном треугольнике один
острый угол равен 45°. Найдите катеты, если их
сумма равна 36 м.

154
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
Координатная ось
Координатной осью называется прямая, на
которой отмечена точка О (начало отсчета или
начало координат), выбран масштаб, т. е. указан
отрезок единичной длины для измерения расстояний
(единичный или масштабный отрезок), и задано
положительное направление. Так, на рисунке 113
единичный отрезок на координатной оси Ох
обозначен ОЕ, направление от точки О к точке Е
считается положительным (показано стрелкой).
Начало координат О делит координатную ось на
два луча: положительную полуось (которой
принадлежит точка Е) и отрицательную полуось.
Координатой точки Р, лежащей на оси Ох,
называется число х = ±ОР (где ОР означает
длину отрезка ОР), взятое со знаком плюс, если
точка Р лежит на положительной полуоси, и со
знаком минус, если эта точка лежит на
отрицательной полуоси. Координату точки обычно
указывают в скобках рядом с обозначением
точки: Р(х). Между точками на числовой оси и
их координатами имеется взаимно однозначное
соответствие. Расстояние между двумя точками
Р1(х1) и Р2(х2) на оси Ох выражается формулой
1*Л1 - ki - *J.
т. е. оно равно модулю разности
соответствующих координат.
Прямоугольная система координат
на плоскости
Прямоугольная (или декартова) система
координат на плоскости задается парой взаимно
перпендикулярных координатных осей,
имеющих общее начало в точке О и одинаковый
масштаб (рис. 114). Оси координат на плоскости
обычно обозначают Ох и Оу (оси абсцисс и
ординат соответственно). Координатную плоскость
обозначают хОу.
Координатные оси делят плоскость хОу
на четыре квадранта (или четверти): I, II, III,
IV. Пусть точка Р лежит на плоскости хОу (см.
рис. 114). Опустим из этой точки
перпендикуляры на координатные оси; основания
перпендикуляров обозначим Рх и Ру. Абсциссой точки Р
называется координата х точки Рх на оси Ох,
ординатой — координата у точки Ру на оси Оу.
Координаты точки обычно указывают в скобках
рядом с обозначением точки: Р(х; у). Между
точками на плоскости и их координатами имеется
взаимно однозначное соответствие.
Расстояние между точками
Пусть на плоскости хОу даны две точки: Аг с
координатами хг, уг й А2 с координатами х2, у2.
Выразим расстояние между точками Ах и А2
через координаты этих точек.
Рассмотрим сначала случай, когда хг Ф х2 и
уг Ф у2. Проведем через точки Аг и А2 прямые,
параллельные осям координат, и обозначим
точку их пересечения буквой А (рис. 115).
Расстояние между точками А и Аг равно \ух - у2\, а
расстояние между точками А и А2 равно \хг - х2\.
Применяя к прямоугольному треугольнику
ААгА2 теорему Пифагора, получим:
АгА2 = ААг + АА2 , откуда
где d — расстояние между точками Аг иА2.
О Е Р х
Координатная ось
Vl
II
РУ
О
III
1
I
IV
-*р
1
1
1
рх
Рис.113
Прямоугольная система координат
Рис. 114
УЬ
Уг-
Ух-
хх х2
Рис. 115

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
155
Хотя формула (1) для расстояния меяеду
точками выведена нами в предположении хг ф х2, уг ф у2,
она остается верной и в других случаях.
Действительно, если хх = х2, У\ Ф Учу то d равно \ух - у2\.
Тот же результат дает и формула (1).
Аналогично рассматривается случай, когда хх Ф х2, уг — у2.
При хг = х2, уг = у2 точки Аг и А2 совпадают и
формула (1) дает d = 0.
Пример. Найти расстояние между точка-
миА(-1;-2)иВ(-4;2).
Решение. По формуле (1) имеем:
:=АВ= V(-4 + I)2 + (2 + 2)2 -
- л/9 + 16 - 725 =5.
Аналогично получим:
Уг +У2
У=—5—
(3)
Примечание. Формулы (2) и (3) верны и при
любом расположении точек А и Б.
Пример. Даны две вершины
параллелограмма ABCD: А(1; 0), С (3; 2). Найти косфдинаты
точки пересечения диагоналей.
Решение. Точка пересечения диагоналей
является серединой каждой из них. Поэтому она
является серединой отрезка АС и имеет
координаты
1+3 0 0+2 t
х=—ту— =2, у=—к— =1.
Координаты середины отрезка
Пусть А(хг; ух) и В(х2; у2) — две произвольные
точки и С(х; у) — середина отрезка АВ. Найдем
координаты х, у точки С. Рассмотрим сначала
случай, когда отрезок АВ не параллелен оси Оу,
т. е. хх Ф х2. Проведем через точки А, В, С
прямые, параллельные оси Оу (рис. 116). Они
пересекут ось Ох в точках Аг(хг; 0), Вг(х2; 0), Сг(х; 0).
По теореме Фалеса точка Сг будет серединой
отрезка АгВг.
Так как точка Сг — середина отрезка AXBV то
АХСХ = CXBV При выбранном расположении
точек имеем:
и, значит, х - хг = дг2 - х,
откуда
дг =
*1 + *2
(2)
Определение тригонометрических
функций для любого угла
от 0° до 180°
До сих пор значения синуса, косинуса и
тангенса были определены только для острых углов.
Теперь мы определим их для любого угла от 0°
до 180°. Возьмем окружность на плоскости хОу
с центром в начале координат и радиусом R
(рис. 117). Пусть ос — острый угол, который
образует радиус ОА с положительной полуосью
Ох. Пусть х и у — координаты точки А.
Значения sin a, cos а и tg а для острого угла а
выражаются через координаты точки А, а именно:
У х л. У
sma=|, cos a = -д , tg a = ^ .
Определим теперь значения sin a, cos а и tg a
для любого угла а. (Для tg а угол a = 90°
исключается.)
У i
о
{ А
А
X
*1
Li С
С
X
'1
ч»
Е
*2
h
X
X —
У =
*1+*2
2
У1+У2
Vi
/у
\ °
1
у
Ла
1
Мх; у)
С / *
sin a = ^
cos a = р
tg a
= 2
x
Рис. 116
Рис. 117

156
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Имеем:
sin 90° - ^ - 1, cos 90° - | - 0,
sin 180° =|=0, cos 180° = -f = -1.
Считая, что совпадающие лучи образуют угол
0°, будем иметь:
sin0° = 0, cos0° = l, tg0° = 0.
ТЕОРЕМА
Для любого угла а, 0° < а < 180°,
sin (180° - а) = sin а,
cos (180° - а) = -cos а.
Для угла а * 90° tg (180° - а) = -tg а.
Доказательство. Треугольники ОАВ и ОАгВг
равны по гипотенузе и острому углу (рис. 118). Из
равенства треугольников следует, что АВ — AXBV
т. е. у — yv OB = OBv следовательно, х = -xv
Поэтому
У\ и
sin (180° - «) = -д e § = sin а,
cos (180° - а) = -jj- = -£ = -cos а.
Разделив почленно равенство sin (180° - а) =
= sin а на равенство cos (180° - а) — -cos а,
получаем:
tg(180°-ct) = -tga.
Теорема доказана.
Пример. Вычислить: 1) sin 135°; 2) cos 135°;
3)tgl50°.
Решение. Согласно только что доказанной
теореме
1) sin 135° = sin(180° - 45°) = sin 45°;
2) cos 135° = cos(180° - 45°) = -cos 45°;
3) tg 150° - tg(180° - 30°) = -tg 30°.
Ai(*v У\\
A{x; y)
Рис. 118
Hosin45°=Y> cos 45° = ^ , tg 30° = j= .
Следовательно,
sin 135° - £ , cos 135° - ~ , tg 135° - ~ .
Контрольные вопросы
1. Что называется координатной осью?
2. Что называется координатой точки,
лежащей на оси Ох?
3. Объясните, как вводится прямоугольная
система координат на плоскости.
4. Приведите формулу для вычисления
расстояния между двумя точками по их
координатам.
5. Напишите формулы координат середины
отрезка.
6. Дайте определения синуса, косинуса и
тангенса для любого угла от 0° до 180°.
7. Докажите, что для любого угла а, 0° <
< а < 180°, sin(180° - а) = sin a, cos(180° - а) =
= -cos а.
Упражнения
1. Найдите расстояние от точки (-3; 4) до
оси: 1) Ох; 2) Оу.
2. Найдите расстояние между точками А(-1; -2)
иБ(-4;2).
3. Найдите координаты середины отрезка
АВ, если А(1; -2), Б(5; 6).
4. Вычислите синусы углов: 1) 120°; 2) 150°.
5. Вычислите косинусы углов: 1) 120°; 2) 150°.
6. Вычислите тангенсы углов: 1) 135°; 2) 120°.
ВЕКТОРЫ
Понятие вектора
Вектором называется направленный отрезок,
имеющий определенную длину, т. е. отрезок
определенной длины, у которого одна из
ограничивающих его точек принимается за начало, а
вторая — за конец. Бели А — начало вектора и
В — его конец, то вектор обозначается символом
АВ (или АВ). Обычно векторы обозначают
одной малой латинской буквой со стрелкой (или_с
чертой) либо выделяют жирным шрифтом: а, а,

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
157
а. Вектор изображается отрезком со стрелкой на
конце (рис. 119).
Длина вектора АВ называется его
абсолютной величиной или модулем и обозначается
символом \АВ |.
Вектор 2, у которого \а\ = 1, называется
единичным.
Вектор называется нулевым (обозначается О
или О), если начало и конец его совпадают.
Нулевой вектор не имеет определенного
направления и имеет длину, равную нулю.
Векторы а и Ьу расположенные на одной
прямой или на параллельных прямых, называются
коллинеарными. Нулевой вектор коллинеарен
любому вектору.
Два вектора а иЬ называются равными, если
они коллинеарны, имеют одинаковую длину и
одинаковое направление. В этом случае пишут
а = Ь. Все нулевые векторы считаются равными.
Из определения равенства векторов
непосредственно следует, что, каковы бы ни были вектор
а и точка Р, существует, и притом
единственный, вектор PQ с началом в точке Р, равный
вектору а. В самом деле, существует лишь одна
прямая, проходящая через точку Р и
параллельная той прямой, на которой лежит вектор а. На
указанной прямой существует единственная
точка Q такая, что отрезок PQ имеет длину,
равную длине вектора а, и направлен в ту же
сторону, что и вектор а. Таким образом, вектор
можно переносить параллельно самому себе,
помещая его начало в любую точку плоскости.
Пример 1. Рассмотрим квадрат ABCD
(рис. 120). На основании определения равенства
векторов можно записать AD = ВС и АВ =
= DC, но АВ * AD, ВС * DC, хотя \АВ | = \AD \ =
= |БС| = |Бс|.
Пример 2. Какой вид имеет
четырехугольник ABCD, если известно, что AD = ВС ?
Решение. Из равенства AD = ВС следует, что
стороны AD и ВС в четырехугольнике равны и
параллельны и, значит (§ 6, пункт 2, теорема 3), он
параллелограмм.
Два коллинеарных вектора (отличные от
нулевых векторов), имеющие равные модули, но
противоположно направленные, называются
противоположными.
Вектор, противоположный вектору а,
обозначается -а. Для вектора АВ противоположным
является вектор ВА.
Сложение и вычитание векторов,
умножение вектора на число
Пусть а и Ь — два вектора (рис. 121, а). Возьмем
произвольную точку О и построим вектор О А = а.
Затем от точки А отложим вектор АВ = Ъ.
Вектор ОВ , соединяющий начало первого
слагаемого вектора с концом второго (рис. 121, б), называ^
ется суммой этих векторов и обозначается а + b
(правило треугольника).
Ту же самую сумму векторов можно
получить иным способом. Отложим от точки О
векторы ОА =ои ОС = b (рис. 121, в). Построим на
этих векторах как на сторонах параллелограмм
Вектор АВ
Рис. 119
\АВ\ = \AD\ = \ВС\ = \DC\
Рис. 120
О й + Ь
б)
Сложение двух векторов
Рис. 121

158
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
ОАВС. Вектор ОВ, служащий диагональю этого
параллелограмма, проведенной из вершины О,
является, очевидно, суммой векторов а + Ъ
(правило параллелограмма). Из рисунка 121, в
непосредственно следует, что сумма двух векторов
обладает переместите л ьным свойством:
3 + ft = ft + 3.
—»
Действительно, каждый из векторов а + b и
ft + 3 равен одному и тому же вектору ОВ.
Пример 1. В треугольнике ABC АВ = 3, ВС =
= 4, В = 90°. Найти: а) \АВ | + \ВС |; б) \АВ + ВС |.
Решение, а) Имеем: |АВ| = АВ, |ВС| = ВС и,
значит, |АВ| + |ВС | = 7.
б) Так как АВ + ВС= АС, то \АВ + ВС\ =
НАС |= АС.
Теперь, применяя теорему Пифагора,
находим
ас = Jab2 + вс2 - 7э + 16 - 5,
т.е. |АВ + ВС| = 5.
Понятие суммы векторов можно обобщить на
случай любого конечного числа слагаемых
векторов.
Пусть, например, даны три вектора 3, & и с
(рис. 122). Построив сначала сумму векторов а +
+ ft, а затем прибавив к этой сумме вектор с,
получим вектор (3 + ft) + с. На рисунке 122
ОА =а,АВ = ft, ОВ = 3 + ft, ВС = с
и
ОС = ОВ + ВС = (а + ft) + с.
& .
А 5 в
/аЛхЧЛг
/ Z^^ ^S4^ \
О с
Сложение трех векторов
Рис. 122
а/->
О
/ ^s^ j>
1 ^4*
ь 'в
ь
Вычитание векторов
Рис. 123
Из рисунка 122 видно, что тот же вектор ОС
мы получим, если к вектору О А = а прибавим
вектор АВ = ft + с. Таким образом,
(а + ft) + с = а + (ft + с),
т. е. сумма векторов обладает сочетательным
свойством. Поэтому сумму трех векторов а,Ь,с
записывают просто а + ft + с.
Разностью двух векторов 3 и & называется
третий вектор с = а - ft, сумма которого с
вычитаемым вектором & дает вектор 3. Таким
образом, если с = 3 - ft, то с + ft = 3.
Из определения суммы двух векторов
вытекает правило построения вектора-разности
(рис. 123). Откладываем векторы ОА = 3 и ОВ =
= ft из общей точки О. Вектор ВА, соединяющий
концы уменьшаемого вектора 3 и вычитаемого
вектора & и направленный от вычитаемого к
уменьшаемому, является разностью с — 3 - ft.
Действительно, до правилу сложения векторов
ОВ + ВА = ОА, или ft + с = 3.
Пример 2. Сторона равностороннего
треугольника ABC равна а. Найти: а) |ВА - ВС |;
б)|АВ -АС|.
Решение, а) Так как ВА - ВС = СА, а |СА | =
= а, то|ВА -ВС| = а.
б) Так как АВ - АС = СВ , а |СВ | = а, то |АВ -
-АС| = а.
Произведением вектора 3 (обозначается Ал
или ЗА,) на действительное число X, называется
вектор ft, коллинеарный вектору 3, имеющий
длину, равную |А|3|, и то же направление, что и
вектор 3, если А, > 0, и направление,
противоположное направлению вектора 3, если А, < 0. Так,
например, 23 есть вектор, имеющий то же
направление, что и вектор 3, а длину, вдвое
большую, чем вектор 3 (рис. 124). В случае,
когда X = 0 или 3=0, произведение Ал
представляет собой нулевой вектор. Противоположный

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
159
вектор -а можно рассматривать как результат
умножения вектора 3 на X = -1 (см. рис. 124):
-3 = (-1)3.
Очевидно, что 3 + (-3) = 0.
Пример 3. Доказать, что если О, А, В и С —
произвольные точки, то ОА + АВ + ВС + СО —
= 0.
Решение. Сумма векторов ОА + АВ + СВ =
= ОС, вектор СО — противоположный вектору
ОС. Поэтому ОС + СО = 0 .
Пусть дан вектор а. Рассмотрим единичный
вектор 30, коллинеарный вектору а и одинаково
с ним направленный. Из определения
умножения вектора на число следует, что
а = |3|30,
т. е. каждый вектор равен произведению его
модуля на единичный вектор того же направления.
£алее из того же определения следует, что если
6 = Ал, где а — ненулевой вектор, то векторы 3 и
6 коллинеарны. Очевидно^ что и обратно, из
коллинеарности векторов а и 6 следует, что 6 = Ха.
Таким образом,
два вектора а то коллинеарны тогда и
только тогда, когда имеет место равенство
Ь =Ха.
Умножение вектора на число обладает
следующими основными свойствами:
Для любых чисел k>lu любых векторов а, Ь
справедливы равенства:
1. (kl)a — k(la) (сочетательный закон).
2. (k + l)a = ka + la (первый
распределительный закон).
3. k(a + Ъ) — ka + kb (второй
распределительный закон).
Рисунок 125 иллюстрирует сочетательный
закон. На этом рисунке представлен случай,
когда * ■■ 2,1 = 3.
Рисунок 126 иллюстрирует первый
распределительный закон. На этом рисунке представлен
случай, когда k = 3,1 = 2.
Примечание. Рассмотренные свойства
действий над векторами позволяют в выражениях,
содержащих суммы, разности векторов и
произведения векторов на числа, выполнять
преобразования по тем же правилам, что и в числовых
выражениях. Например, выражение
р = 2(3 - 6) + (с + а) - 3(6 - с + 3)
можно преобразовать так:
р = 23 - 26 + с + 3 - 36 + Зс - 33 = - 56 + 4с.
Пример 4. Коллинеарны ли векторы 23 и -3?
Решение. Имеем 23 — -2(-3). Значит, данные
векторы коллинеарны.
Пример 5. Дан треугольник ABC. Выразите
через векторы 3 = АВ и 6 = АС следующие
векторы: а) ВА; б) СВ ; в) СВ + ВА.
Решение, а) Векторы ВА и АВ —
противоположные, поэтому В А = - АВ , или В А = -3.
б) По правилу треугольника СВ = С А + АВ.
Но С А = -АС, поэтому
СВ = АВ +(-АС) = АВ-АС =3-6.
в) СВ + ВА = СА - -АС - - 6.
а
ч-»ч—»-
В
Умножение вектора на число
Рис. 124
ОВ - 20А - 2(33);
ОВ = 63 = (2 3)3
Рис. 125
OA = fe3; АВ - la; OB = (fc+Z)3 = fe3+/3
Рис. 126

160
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Координаты вектора
Обозначим через i и у единичные векторы,
отложенные от точки О в положительных
направлениях на осях Ох и Оу прямоугольной системы
координат (рис. 127).
Пусть а — любой вектор на плоскости хОу.
Тогда вектор а можно представить в виде
a = xi + y] (1)
и притом единственным образом.
Если вектор а представлен в виде а = xi+ yj,
то говорят, что а разложен по векторам i и/.
Векторы ах = xi и ау = у] называют
составляющими вектора а по осям Ох и Оу.
Коэффициенты х и у разложения вектора а по единичным
векторам i и у называют координатами вектора
а в данной системе координат и записывают а
ведению соответствующей координаты
этого вектора на число k.
Доказательство. Пусть
а = хг1 + yj, b = x2i + y2j.
Пользуясь свойствами сложения векторов и
умножения вектора на число, получим
а + Ъ = (xxi + y^j) + (x2i + y2j) =
= (хг + x2)i + (уг + у2)].
Аналогично доказывается:
ha - k(xxi + уг]) = (kxx)i + (fti/x)/.
Значит, координаты вектора а + Ъ равны хг +
+ дг2 и ух + у2, координаты вектора ka равны kxx
и kyv Теорема доказана.
Следствие. Координаты вектора АВ,
заданного двумя точками А(хг; уг) и В(х2; у2),
равны разностям соответствующих
координат точек А и В.
Доказательство. Имеем АВ = ОВ - ОА
(рис. 128). Так как ОА {хг; уг}> ОВ {х2; у2}> то
по теореме
АВ {х2 - хг; у2 - уг}.
Пример 1. Найти координаты вектора с —
- а - 3&, если а {3; 2}, Ь {-3; 1}.
Решение. Согласно полученной теореме
х = 3 - 3 • (-3) = -6, у = 2 - 3 • 1 = -1.
Каждая координата суммы векторов а и Пример 2. Найти координаты вектора а =
{х; у}. Тогда \а\ = *]х + у .
Из единственности представления (1)
следует, что равные векторы имеют равные
соответствующие координаты, и обратно, если у векторов
соответствующие координаты равны, то
векторы равны.
Пусть дана точка М(х; у). Тогда
г = ОМ = xi + у],
где х и у — координаты точки М, т. е. г {х; у},
|я|=77772.
ТЕОРЕМА
Ь равна сумме соответствующих
координат этих векторов; каждая координата
произведения вектора а на число k равна произ-
= АВ , если А(1; 3) и В(5; 8).
Решение. Согласно следствию
х = 5-1 =4, i/ = 8-3 = 5.
А(хг; уг) В(х2; у2)
Рис. 127
Скалярное произведение векторов
Скалярным произведением векторов а {хг; уг) и
Ь {*2> У2) (обозначается аЪ) называется число
ххх2 + уху2. Скалярное произведение аа
обозначается а . Очевидно, а = \а\ .
Из определения скалярного произведения
векторов следует, что для любых векторов а {хг; ух}>
Ь {х2; у2}> с {х3; у3}
(а + Ь)с = ас + be.

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
lei
Действительно, левая часть равенства есть
(*! + х2)х3 + (ух + у2)у3, а правая хгх3 + угу3 +
+ х2хз + УгУзи Очевидно, они равны.
Углом между ненулевыми векторами АВ и
АС называется угол ВАС (рис. 129). Углом
между любыми двумя ненулевыми векторами a nb
называется угол между равными им векторами с
общим началом. Угол между одинаково
направленными векторами считается равным нулю.
ТЕОРЕМА
Скалярное произведение векторов равно
произведению их абсолютных величин на
косинус угла между ними.
Из этой теоремы следует, что
если векторы перпендикулярны, то их
скалярное произведение равно нулю. И обратно,
если скалярное произведение отличных от
нуля векторов равно нулю, то векторы
перпендикулярны.
Пример. Даны векторы й{1; 0} и 6{1; 1}.
Найти такое число А,, чтобы вектор а + ХЬ был
перпендикулярен вектору а.
Решение. Имеем: а(а + АЛ) = 0, а + ЦаЬ) = 0.
Отсюда А, = -=> = ~"7 =""1-
ab 1
Контрольные вопросы
1. Что называется вектором?
2. Что называется абсолютной величиной
вектора?
3. Какой вектор называется единичным?
4. Какой вектор называется нулевым?
5. Какие векторы называются коллинеар-
ными?
6. Дайте определение равных векторов.
7. Какие векторы называются
противоположными?
8. Какой вектор называется суммой двух
векторов?
9. Какой вектор называется разностью двух
векторов?
10. Какой вектор называется произведением
данного вектора и данного действительного
числа?
11. В чем состоит разложение вектора по
осям Ох и Оу?
12. Что называют координатами вектора?
13. Сформулируйте правила нахождения
координат суммы и разности векторов, а также
произведения вектора на число по заданным
координатам векторов.
14. Что такое скалярное произведение двух
векторов?
15. Как определяется угол между векторами?
16. Чему равно скалярное произведение
перпендикулярных векторов?
Упражнения
1. В прямоугольнике ABCD АВ = 3 см, ВС =
= 4 см. Найдите длины векторов: 1) В А; 2) АС.
2. В параллелограмме ABCD диагонали
пересекаются в точке О. Равны ли векторы: 1) АВ и
CD; 2) ВС и AD; 3) АО и ОС; 4) АС и ОС ?
3. ABCD — параллелограмм. Докажите
равенство ВС + DC =АС.
->->*
4. Коллинеарны ли векторы За - 2а (а Ф 0)?
5. Дан вектор a {3k; 4ft}, где k > 0. Выразите
длину вектора а через k.
6. Даны векторы а {3; 4}, Ь {-1; 2}. Найдите
координаты векторов: 1) а 4- 2Ь; 2) За - Ъ.
7. Найдите координаты вектора а = АВ , если
А (2; 7) и В (-2; 7).
8. Найдите скалярное произведение
векторов а {4; 1}и& {2;-8}.
Рис. 129
6-1019

162
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
ПОДОБИЕ
Определение подобных
треугольников
Треугольники ABC и A^B-fi-^ (рис. 130)
называются подобными, если
ZA=ZAV ZB = ZBV ZC = ZCX*
и
АВ
АгВг
ВС
вгсг
СА
СгАг
т. е. углы одного треугольника соответственно
равны углам другого треугольника и стороны
одного пропорциональны сходственным
сторонам другого.
Если треугольники ABC и А1В1С1 подобны, то
пишут Л ABC ™ A AlBlCv
Лемма. Прямая, параллельная какой-нибудь
стороне треугольника и пересекающая две
другие стороны, отсекает от него треугольник,
подобный данному (рис. 131).
Доказательство леммы проводится с помощью
теоремы о пропорциональных отрезках (§ 6, п. 7).
Признаки подобия треугольников
ТЕОРЕМА 1
первый признак подобия треугольников
Если два угла одного треугольника
соответственно равны двум углам другого, то
такие треугольники подобны.
* В этом случае стороны АВ кА1В1, ВС и BXCVAC и
АХСХ называются сходственными.
Доказательство. Пусть ABC и А1В1С1 —
треугольники, у которых Z А = ZAX, ZB = Z Вх,
и следовательно, Z С = Z Сх. Докажем, что
А ABC го AAlBlCl (рис. 132). Отложим на ВА от
точки В отрезок ВА2, равный отрезку АХВХ, и
через точку А2 проведем прямую, параллельную
прямой АС. Эта прямая пересечет ВС в некоторой
точке С2. Треугольники AlBlCl и А2ВС2 равны:
АХВХ = А2В по построению, Z В = Z Вх по
условию и Z Аг — Z А2, так как Z Ах — Z А по условию
и Z А = Z А2 как соответственные углы. По лемме
о подобных треугольниках имеем: А А2ВС2 ™
го Д ABC, и значит, А ABC го АА1В1С1. Теорема
доказана.
По аналогичной схеме устанавливаются
теоремы 2 и 3.
ТЕОРЕМА 2
второй признак подобия треугольников
Если две стороны одного треугольника
соответственно пропорциональны двум
сторонам другого треугольника и углы между
этими сторонами равны, то треугольники
подобны.
ТЕОРЕМА 3
третий признак подобия треугольников
Если три стороны одного треугольника
пропорциональны трем сторонам другого
треугольника, то такие треугольники
подобны.
ААВС со ААХВХСХ
Рис. 130
ВЛ
ZA = ZAUZB
С
ZBX=*A ABC со Л AlBlCl
Рис. 132
MN || АС
AMBN со ААВС

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
163
Пример 1. Подобны ли два равносторонних
треугольника?
Решение. Так как в равностороннем
треугольнике каждый внутренний угол равен 60°
(§ 5, п. 1, следствие 3), то два равносторонних
треугольника подобны по первому признаку.
Пример 2. В треугольниках ABC и А1В1С1
известно, что Z А = ZAV Z В = Z Bv АВ = 5 м, ВС =
= 7 м, АгВг = 10 м, АгСг = 8 м. Найти
неизвестные стороны треугольников.
Решение. Треугольники, определенные
условием задачи, подобны по первому признаку
подобия.
Из подобия треугольников следует:
АВ ВС АС
АгВг
вхсх
АгСг
(1)
Подставив в равенство (1) данные из условия
задачи, получим:
А « 7 _АС
8 *
10
вгсг
(2)
Из равенства (2) составим две пропорции
7
10
вгсг
10
АС
8 '
откуда ВхСг = 14 (м), АС = 4 (м).
Пример 3. Углы В и Вг треугольников ABC и
А1В1С1 равны. Стороны АВ и ВС треугольника
ABC в 2,5 раза больше сторон АгВг и ВХСХ
треугольника А1В1С1. Найти АС и АХСХ, если их
сумма равна 4,2 м.
Решение. Пусть условию задачи отвечает
рисунок 133.
Из условия задачи:
1)ZB = ZBX;
2)
АВ
АгВх
ВС
вхсг
= 2,5;
3)АС+А1С1 = 4,2м.
Следовательно, A ABC ™ АА1В1С1. Из подобия
этих треугольников следует
4^т =2,5, или АС - 2,5-AjC,.
Так как АС = 2,5 -АгС19 то АС +АхСг = 2,5 х
х АгСг + АгСг = 4,2, откуда АхСг = 1,2 (м), АС =
= 3 (м).
Пример 4. Подобны ли треугольники ABC и
AlB1Cv если АВ = 3 см, ВС — 5 см, АС = 7 см,
АгВг = 4,5 см, ВгСг = 7,5 см, АХСХ = 10,5 см?
Решение. Имеем:
АВ
АгВг
г 1 вс б
4,5 1,5' ВгСг 7,5
АС 7 1
АгСг 10,5 1,5'
1
1,5'
Следовательно, треугольники подобны по
третьему признаку.
Пример 5. Доказать, что медианы
треугольника пересекаются в одной точке, которая делит
каждую медиану в отношении 2:1, считая от
вершины.
Решение. Рассмотрим произвольный
треугольник ABC. Обозначим буквой О точку
пересечения его медиан ААХ и ВВг и проведем
среднюю линию АгВг этого треугольника (рис. 134).
Отрезок АхВг параллелен стороне АВ,
поэтому Z1=Z2hZ3 = Z4. Следовательно,
треугольники АОВ иАгОВх подобны по двум углам,
и, значит, их стороны пропорциональны:
АО ВО
АгО
ВгО
АВ
АгВг
Вл
Рис. 133
Рис. 134

164
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Но АВ = 2A1Blt поэтому АО = 2АгО и ВО =
- 2БхО.
Аналогично доказывается, что точка
пересечения медиан ВВг и ССХ делит каждую из них в
отношении 2:1, считая от вершины, и,
следовательно, совпадает с точкой О.
Итак, все три медианы треугольника ABC
пересекаются в точке О и делятся ею в отношении
2:1, считая от вершины.
Замечание. Ранее отмечалось, что
биссектрисы треугольника пересекаются в одной точке,
серединные перпендикуляры к сторонам
треугольника пересекаются в одной точке. На
основе последнего утверждения устанавливается,
что и высоты треугольника (или их
продолжения) пересекаются в одной точке. Эти три точки
и точка пересечения медиан называются
замечательными точками треугольника.
Подобие произвольных фигур.
Преобразование фигур
Понятие подобия можно ввести не только для
треугольников, но и для произвольных фигур.
Фигуры F и Fx называются подобными, если
каждой точке фигуры F можно сопоставить точку
фигуры Fx так, что для любых двух точекMsiN
фигуры F и сопоставленных им точек Мх и Nx
фигуры Fx выполняется условие MN = k, где
k — одно и то же положительное число для всех
точек. При этом предполагается, что каждая
точка фигуры Fx оказывается сопоставленной
какой-то точке фигуры F. Число k называется
коэффициентом подобия фигур F и Fv
На рисунке 135 представлен способ
построения фигуры Fv подобной данной фигуре F.
Каждой точке М фигуры F сопоставляется точка Мг
плоскости так, что точки М и Мх лежат на луче
с началом в некоторой фиксированной точке О,
причем ОМх = k • ОМ (на рисунке 135 k = 3).
В результате такого сопоставления получается
фигура Fv подобная фигуре F.
Этот способ построения фигуры Fv подобной
фигуре F, называется центрально-подобным
преобразованием фигуры F в фигуру Fv или
гомотетией, а фигуры F и Fx —
центрально-подобными или гомотетичными.
Можно доказать, что для треугольников
общее определение подобия равносильно
определению, данному в п. 1.
Примерами подобных четырехугольников
являются любые два квадрата (рис. 136, а), а также
два прямоугольника, у которых две смежные
стороны одного пропорциональны двум смежным
сторонам другого (рис. 136, б).
Если каждую точку Данной фигуры сместить
каким-нибудь образом, то мы получим новую
фигуру. Говорят, что эта фигура получена
преобразованием из данной.
Гомотетия и рассмотренные ранее
центральная симметрия и осевая симметрия — примеры
преобразований фигур.
Рассмотрим еще один пример
преобразования фигуры — параллельный перенос.
Преобразование фигуры F, при котором
каждай ее точка X (х; у) переходит в точку X'
(х + а; у + Ь), а и Ъ постоянные, называется
параллельным переносом (рис. 137).
Параллельный перенос задается формулами
х' = х + а, у = у + Ь.
Эти формулы выражают координаты х\ у
точки, в которую переходит точка (х; у) при
параллельном переносе.
ОМх = k ОМ
Рис. 135
I I а = *1
Ь Ьх
а) б)
Рис. 136
х = х + а, у'' — у + Ь
Рис. 137

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
165
Название «параллельный перенос»
оправдывается тем, что при параллельном переносе
точки смещаются по параллельным (или
совпадающим) прямым на одно и то же расстояние.
Заметим также, что при параллельном
переносе прямая переходит в параллельную прямую
(или в себя).
Пример. При параллельном переносе точка
(1; 1) переходит в точку (-1; 0). В какую точку
переходит начало координат?
Решение. Любой параллельный перенос
задается формулами х' = х + а, у' « у + Ъ. Так как
точка (1; 1) переходит в точку (-1; 0), то -1 = 1 + а,
0 = 1 + Ъ. Отсюда а = -2, Ь = -1. Таким образом,
наш параллельный перенос, переводящий точку
(1; 1) в (-1; 0), задается формулами х' = х - 2,
у'*=у-1. Подставляя в эти формулы координаты
начала (х = 0; у = 0), получим: х' = -2, у' - - 1.
Итак, начало координат переходит в
точку^;-!).
Контрольные вопросы
1. Какие треугольники называются
подобными?
2. Сформулируйте и докажите первый
признак подобия треугольников.
3. Сформулируйте второй признак подобия
треугольников.
4. Сформулируйте третий признак подобия
треугольников.
5. Какие четыре точки называют
замечательными точками треугольника?
6. Какие две фигуры называются подобными?
7. Что называется коэффициентом подобия?
8. Что называется гомотетией?
9. Какие фигуры называются гомотетичными?
10. Что такое параллельный перенос?
Упражнения
1. В треугольниках ABC и А1В1С1 ZA = ZAX
и Z В = Z Вг. Найдите длины сторон АгВг и
BXCV если АВ = 3,5 см, ВС = 2,5 см, АС = 5 см,
АгСг = 4 см.
2. В треугольниках ABC и А1В1С1 АВ = 42 см,
ВС = 63 см, Ad = 36 см, АгВг = 28 см, ВгСг -
= 42 см, АхСг = 24 см. Подобны ли эти
треугольники?
3. В треугольнике ABC сторона АВ = 16 см,
АС = 24 см; в треугольнике А1В1С1 сторона
АгВг = 12 см, АгСг = 18 см. Будут ли эти
треугольники подобны, если ZA = ZAX1
4. В треугольниках ABC и AlBlCl АВ = 4 см,
А1В1 =3см, Z А - Z Аг = 48°, Z В - Z Вх = 78°.
Найдите коэффициент подобия этих
треугольников.
5. Параллельный перенос задается формулами
х' = х + 1, у' = у - 1. В какие точки при этом
параллельном переносе переходят точки: 1) (0; 0);
2)(1;0);8)<0;2)?
ОКРУЖНОСТЬ
Касательная к окружности
Прямая, проходящая через точку окружности
перпендикулярно к радиусу, проведенному в эту
точку, называется касательной. При этом
данная точка окружности называется точкой
касания. На рисунке 138 прямая а проведена через
точку А окружности перпендикулярно к радиусу
ОА. Прямая а является касательной к
окружности. Точка А является точкой касания. Можно
сказать также, что окружность касается
прямой а в точке А.
ТЕОРЕМА
Касательная к окружности не имеет с
ней других общих точек, кроме точки
касания.
Доказательство. Пусть а — касательная к
окружности в точке А (рис. 139). Допустим, что
касательная а и окружность имеют, кроме точки
А, общую точку В, отличную от А. Треугольник
АОВ равнобедренный (ОА и ОВ — радиусы
окружности) и, значит, ZA = ZB. Но угол А —
Рис. 138

166
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
прямой, следовательно, и угол В — прямой, что
невозможно. Теорема доказана.
Говорят, что две окружности, имеющие
общую точку, касаются в этой точке, если они
имеют в этой точке общую касательную (рис. 140).
Касание окружностей называется внутренним,
если центры окружностей лежат по одну
сторону от их общей касательной (рис. 140, а).
Касание окружностей называется внешним, если
центры окружностей лежат по разные стороны
от их общей касательной (рис. 140, б).
Пример 1. Построить окружность данного
радиуса, касающуюся данной прямой в данной
точке.
Решение. Касательная к окружности
перпендикулярна к радиусу, проведенному в точку
касания. Поэтому центр искомой окружности
лежит на перпендикуляре к данной прямой,
проходящем через данную точку, и находится от
данной точки на расстоянии, равном радиусу.
Задача имеет два решения — две окружности,
симметричные друг другу относительно данной
прямой (рис. 141).
Пример 2. Две окружности диаметром 4 и
8 см касаются внешним образом. Чему равно
расстояние между центрами этих окружностей?
Решение. Радиусы окружностей
перпендикулярны их общей касательной (см. рис. 140, б).
Поэтому искомое расстояние равно сумме их
радиусов, т. е. 2 + 4 = 6 (см).
Центральные и вписанные углы
Угол разбивает плоскость на две части. Каждая
из частей называется плоским углом. На
рисунке 142 заштрихован один из плоских углов со
сторонами а и Ь. Плоские углы с общими
сторонами называются дополнительными.
Если плоский угол является частью
полуплоскости, то его градусной мерой называется
градусная мера обычного угла с теми же
сторонами. Если плоский угол содержит
полуплоскость, то его градусная мера принимается
равной 360° - а, где а — градусная мера
дополнительного плоского угла (рис. 143).
Центральным углом в окружности
называется плоский угол с вершиной в ее центре. Часть
окружности, расположенная внутри . плоского
угла, называется дугой окружности,
соответствующей этому центральному углу (рис. 144).
Градусной мерой дуги окружности называется
градусная мера соответствующего центрального
угла.
Угол, вершина которого лежит на
окружности, а стороны пересекают эту окружность,
называется вписанным в окружность. Угол ВАС
на рисунке 145 вписан в окружность. Его вер-
а) касание
внутреннее
б) касание
внешнее
Угол разбивает
плоскость на две
части
Рис. 140
Рис. 141
Рис. 142
Рис. 143
Центральный угол
Рис. 144
Z ВОС — центральный
Z ВАС — вписанный
в окружность
Рис. 145

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
167
шина А лежит на окружности, а стороны
пересекают окружность в точках В и С. Говорят
также, что угол А опирается на хорду ВС. Прямая
ВС разбивает окружность на две дуги.
Центральный угол, соответствующий той из этих
дуг, которая не содержит точку А, называется
центральным углом, соответствующим
данному вписанному углу.
ТЕОРЕМА
Угол, вписанный в окружность, равен
половине соответствующего центрального угла.
Доказательство. Рассмотрим частный
случай, когда одна из сторон угла проходит через
центр окружности (рис. 146). Треугольник АОВ
равнобедренный, так как у него стороны О А и
ОВ равны как радиусы. Поэтому углы АиВ
треугольника равны. А так как их сумма равна
внешнему углу треугольника при вершине О, то
угол В треугольника равен половине угла АОС,
что и требовалось доказать.
Пример 1. Точки А, В, С лежат на
окружности с центром О; угол ABC равен 66°. Найти
центральный угол, соответствующий углу ABC.
Решение. Пусть условию задачи отвечает
рисунок 146. Угол ABC вписан в окружность.
Поэтому согласно теореме о вписанном угле Z ABC =
= | ZAOC или ZAOC = 2ZABC. Ho ZABC = 66°
и, значит, ZAOC = 132°.
Пример 2. Точки А, В, С лежат на
окружности. Чему равна хорда АС> если угол ABC равен
30°, а диаметр окружности 10 см?
Решение. Пусть условию задачи отвечает
рисунок 147, где Z ABC = 30°.
Так как вписанный угол ABC равен « Z АОС,
но ZAOC = 60°. Следовательно, треугольник АОС
равносторонний, и, значит, хорда АС равна
радиусу данной окружности. А так как диаметр
равен 10 см, то радиус равен 5 см.
Следствие. Вписанные углы, стороны
которых проходят через точки АиВ окружности,
а вершины лежат по одну сторону от прямой
АВ, равны (рис. 148).
В частности, углы, опирающиеся на
диаметр, прямые.
Вписанная и описанная окружности
Окружность называется вписанной в
треугольник, если она касается всех его сторон.
Окружность называется описанной около
треугольника, если она проходит через все его
вершины.
ТЕОРЕМА 1
Центр окружности, вписанной в
треугольник, является точкой пересечения его
биссектрис.
Доказательство. Пусть ABC — данный
треугольник, О — центр вписанной в него
окружности, D, Е и F — точки касания окружности со
сторонами (рис. 149). Прямоугольные
треугольники AOD и АОЕ равны по гипотенузе и катету.
У них гипотенуза АО общая, а катеты OD и ОЕ
равны как радиусы. Из равенства
треугольников следует равенство углов OAD и ОАЕ. А это
значит, что точка О лежит на биссектрисе
треугольника, проведенной из вершины А. Точно
так же доказывается, что точка О лежит на двух
других биссектрисах треугольника. Теорема
доказана.
ZABC = ±ZAOC
Рис. 146
Рис. 147
Рис. 148
Рис. 149

168
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
В случае описанной окружности имеет место
следующая теорема.
ТЕОРЕМА 2
Центр окружности, описанной около
треугольника, лежит на пересечении серединных
перпендикуляров к сторонам треугольника
(рис. 150).
Пример 1. Найти радиус окружности г,
вписанной в равносторонний треугольник ABC со
стороной а.
Решение. В силу теоремы 2 из п. 3 § 2 в
равностороннем треугольнике каждая биссектриса
является одновременно медианой и высотой.
Поэтому центр О вписанной окружности лежит
в точке пересечения медиан, которая делит
каждую медиану в отношении 2:1, считая от
вершины (см. § 10, п. 2, пример 5). Из
прямоугольного треугольника ACD (рис. 151) согласно
теореме Пифагора имеем:
AC2=AD2 + CD2,
или
2
CD2=AC2-AD2,
лп2 2 а За
откуда CD = а - -j- = -j-
и, значит, CD = -5- . Поэтому г = -g- .
Пример 2. В прямоугольном треугольнике
катеты равны 12 и 16 см. Вычислить радиус
описанной окружности.
Решение. Центр описанной около
прямоугольного треугольника окружности совпадает с
серединой гипотенузы, откуда радиус
описанной окружности R = -кАВ (рис. 152). По теореме
Пифагора
АВ2 =АС2 + СВ2, или АВ2 = 162 + 122 - 400,
откуда АВ = л/400 = 20 и, значит, R = 10 (см).
Пропорциональность отрезков хорд
и секущих окружности
Задача. Доказать, что если хорды АВ и CD
окружности пересекаются в точке S, то
ASBS = CS- DS.
Доказательство. Докажем сначала, что
треугольники ASD и CSB подобны (рис. 153).
Вписанные углы DCB и DAB равны по следствию из
пункта 2. Углы ASD и BSC равны как
вертикальные. Из равенства указанных углов
следует, что треугольники ASD и CSB подобны.
Из подобия треугольников следует
пропорция
DS
BS
AS
CS'
Отсюда
AS BS = CSDS,
что и требовалось доказать.
Аналогично устанавливается:
1) если из точки Р (рис. 154), лежащей вне
окружности, проведены к ней две секущие, пе-
Рис. 150
Рис. 153
Рис. 152

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
169
ресекающие окружность в точках А, В и С, D
соответственно, то
АР BP = CPDP;
2) если из точки Р (рис. 155), лежащей вне
окружности, проведены к ней секущая,
пересекающая окружность в точках А и Б, и
касательная PC, то
РА • РВ = PC2.
Пример 1. Хорды АВ и CD пересекаются в
точке Е. Найти ED, если АЕ - 5 см, BE = 2 см,
СЕ = 2,5 см.
Решение. Имеем: АЕ • БЕ = ED • СЕ (задача),
или 5 • 2 = 2,5 • ED, откуда ED = ^ = "25" =
= 4 (см).
Пример 2. Из точки А, лежащей вне
окружности, проведены две секущие. Внутренний
отрезок первой равен 47 м, а внешний 9 м;
внутренний отрезок второй секущей на 72 м больше
внешнего ее отрезка. Найти внешний отрезок
второй секущей.
Решение. Обозначим через х длину внешнего
отрезка второй секущей. Тогда согласно
условию задачи длина внутреннего отрезка второй
секущей будет х + 72. Теперь согласно
утверждению 1) имеем:
х(х + х + 72) = 9(9 + 47),
или
х(2х + 72) = 9 • 56.
Решая это уравнение, находим х = 6.
Пример 3. Из точки Р проведены к
окружности касательная PC = 12 м и секущая РВ = 16 м.
Найти внешнюю часть секущей АР.
Решение. Обозначим через х длину внешнего
отрезка секущей. Тогда согласно утверждению
2) имеем:
л2
откуда
х-16 = 12'
х = 9.
Контрольные вопросы
1. Какая прямая называется касательной к
окружности?
2. Что значит: окружности касаются в
данной точке?
3. Какое касание окружностей называется
внутренним, какое — внешним?
4. Что называется плоским углом?
5. Какой угол называется центральным?
6. Какой угол называется вписанным в
окружность?
7. Докажите, что вписанный в окружность
угол равен половине соответствующего
центрального угла.
8. Какая окружность называется вписанной
в треугольник?
9. Докажите, что центр окружности,
вписанной в треугольник, является точкой
пересечения его биссектрис.
10. Какая окружность называется описанной
около треугольника?
11. ГДе лежит центр окружности, описанной
около треугольника?
Упражнения
1. Окружности с радиусами 30 см и 40 см
касаются. Найдите расстояние между центрами
окружностей в случаях внешнего и внутреннего
касания.
2. Найдите дополнительные плоские углы,
зная, что один из них в 5 раз больше другого.
3. Точки М, К, Р лежат на окружности с
центром О; угол МКР равен 33°. Найдите
центральный угол, соответствующий углу МКР.
4. Хорды окружности AD и ВС пересекаются.
Угол ABC равен 50°, угол ACD равен 80°.
Найдите угол CAD.
5. Медиана прямоугольного треугольника,
проведенная к гипотенузе, равна 6 м. Найдите
гипотенузу.
6. Точка касания окружности, вписанной в
равнобедренный треугольник, делит одну из
боковых сторон на отрезки, равные 5 см и 6 см, счи-
Рис. 155

170
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
тая от основания. Найдите периметр
треугольника.
7. Угол при вершине равнобедренного
треугольника равен 120°, боковая сторона — 2 см.
Найдите радиус описанной окружности.
8. Две хорды окружности пересекаются в
точке М. Отрезки одной хорды равны 3 м и 12 м.
Отрезки второй хорды равны между собой.
Найдите отрезки второй хорды.
9. Из точки, лежащей вне окружности,
проведены две секущие. Внутренний отрезок первой
секущей равен 78 см, а внешний — 6 см.
Внешний отрезок второй секущей равен 9 см. Найдите
внутренний отрезок второй секущей.
10. Из точки Р к окружности проведены
касательная PC (С — точка касания) и секущая.
Внешняя часть секущей равна 9 дм, а
внутренняя — 7 дм. Найдите отрезок PC касательной.
РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
Будем обозначать стороны треугольника через
а, Ь, с, а противолежащие им углы через а, р, у.
Теорема синусов и теорема косинусов
ТЕОРЕМА 1 ^
теорема синусов
Стороны треугольника пропорциональны
синусам противолежащих углов.
Доказательство. Пусть ABC — треугольник
со сторонами а, Ь, с и противолежащими углами
ос, Р, у (рис. 156, а). Докажем, что
sin а
Ь
sin (3
с
sin у'
Опустим из вершины С высоту CD. Из
прямоугольного треугольника ACDy если угол а
острый, получаем: CD = Ь sin а (рис. 156, б). Если
угол а тупой, то CD = Ъ sin(180° - а) = b sin а
(рис. 156, в). Так же из треугольника BCD
получаем: CD = a sin р. Итак, a sin р = Ъ sin а. Отсюда
а = Ъ
sin a sin Р *
Аналогично доказывается равенство
Ь = с
sin Р sin у'
Для доказательства надо провести высоту
треугольника из вершины А. Теорема доказана.
Справедлива и следующая
ТЕОРЕМА 2
теорема косинусов
Квадрат любой стороны треугольника
равен сумме квадратов двух других сторон без
удвоенного произведения этих сторон на
косинус угла между ними. Например,
2 2 2
а = Ъ + с - 2Ъс cos а.
Пример 1. В треугольнике ABC угол а равен
30°, угол р равен 30°. Найти отношение а : с.
Решение. По теореме синусов
_2 _£_ (1)
sin a sin у" v '
Используя теорему о сумме внутренних углов
треугольника, имеем
у= 180° - (30° + 30°) = 120°.
Так как
sin 120° = sin(180° - 60°) - sin 60° - ^ »
а _£_
1 S Л к
то -г = -7Г- > или а : с — 1 : л/3 .
Пример 2. В треугольнике две стороны 20 м
и 21 м, а синус острого угла а между ними равен
0,6. Найти третью сторону а.
Решение. Угол а острый, следовательно, cos а >
2
>0. Найдем его, используя тождество sin а +
+ cos2ot= 1:
Рис. 156
cos
а = л/1^- sin2ct = Vl - 0,36 = 0,8.

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
171
Теперь по теореме косинусов имеем:
а = 202 + 212 - 2 • 20 • 21 • 0,8 - 169,
откуда а = 13 м.
Пример 3. Доказать, что сумма квадратов
диагоналей параллелограмма равна сумме
квадратов всех его сторон.
Доказательство. Пусть ABCD —
параллелограмм (рис. 157). Применим теорему
косинусов к треугольникам ABC и ABD. Получим
АС2 = АВ2 + ВС2 - 2АВ • ВС • cos Р;
BD2=AB2 +AD2 - 2АВ AD • cos а.
Так как р = 180° - а, то, складывая эти
равенства и замечая, что cos Р = cos (180° - а) = -cos а,
АВ = CD, ВС = AD, получим
АС2 + BD2=AB2 + ВС2 + CD2 + AD2.
Решение треугольников
Решение треугольников состоит в нахождении
неизвестных сторон и углов треугольника по
известным его углам и сторонам.
Пример 1. В треугольнике даны сторона а = 5
и два угла р = 30°, у = 45°. Найти третий угол и
остальные две стороны.
Решение. Так как сумма углов треугольника
равна 180°, то третий угол а находим:
а - 180° - р - у = 180° - 30° - 45° = 105°.
Зная сторону и все три угла, по теореме
синусов находим две остальные стороны:
sin В
» — а • ——- =
sin а
sin 30°
sin 105°
«5
0,500
0,966
2,59;
Sin Y _
с — a* —.—- =5 • 1ЛС
sin a sin 105
-45-^.0407^^
0,966
Пример 2. В треугольнике даны две стороны
а = 12, Ъ — 8 и угол между ними у = 60°. Найти
остальные два угла и третью сторону.
Решение. Третью сторону находим по теореме
косинусов
7 2 2
а + Ь - 2ab cosy =
= л/144 + 64 - 2 • 12 • 8 • 0,500 = VTl2 « 10,6.
Теперь, имея три стороны, по теореме
косинусов находим косинус одного из неизвестных
углов, например cos а и сам угол а и, значит,
угол р:
и2 . 2 2
о + с —а л.,оЛ
cos а = j7- « 0,189,
откуда а * 79°, р = 180° - а - у« 180° - 79° - 60° =
= 41°.
Пример 3. В треугольнике даны две стороны
а = 6, Ъ = 8 и угол а = 30°. Найти остальные два
угла и третью сторону.
Решение. По теореме синусов имеем:
h Я Я 1
sin р = - • sin а - ^ • sin 30° = 77 • ^ я 0,667.
Этому значению синуса соответствуют два уг-
ла:р1«42°ир2=138°.
Рассмотрим сначала угол рх « 42°. По нему
находим третий угол Yi = 180° - а - р = 108° и по
теореме синусов третью сторону:
а sin п sin 108° 0,951
С sin а ss°' sin 30° в°' 0,500 ~ Х1'4'
Аналогично по углу Р2 * 138° находим у2 *
«12°ис2«2,49.
Примечание. Видим, что эта задача в
отличие от предыдущих имеет два решения. При
других числовых данных, например при а > 90°,
задача может иметь лишь одно решение или
вовсе не иметь.
Пример 4. Даны три стороны треугольника:
а = 2, Ъ = 3, с = 4. Найти его углы.
Решение. Углы находятся по теореме
косинусов:
и2 . 2 2 п
Ь + с - а 7 л огус
cos а = ^ = g = 0,875,
откуда а = 29°.
Аналогично находится cos Р = 0,688, откуда
р « 47° и у « 180° - 47° - 29° = 104°.
Рис. 157

172
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Контрольные вопросы
1. Сформулируйте и докажите теорему
синусов.
2. Сформулируйте теорему косинусов.
3. В чем состоит решение треугольников?
4. Каковы основные случаи решения
треугольников?
Упражнения
1. В треугольнике ABC угол А равен 30°, угол В
ВС ВС
равен 30°. Найдите отношение: 1) -г^ ; 2) -^;
3)А1Г
2. Стороны треугольника 5 м, 6 м, 7 м.
Найдите косинусы углов треугольника.
3. В треугольнике две стороны 20 м и 21 м, а
синус тупого угла между ними равен 0,6.
Найдите третью сторону.
4. В треугольнике ABC стороны АВ — 5,1 м,
ВС = 6,2 м, АС = 7,3 м. Какой из углов
треугольника наибольший, какой — наименьший?
МНОГОУГОЛЬНИКИ.
ДЛИНА ОКРУЖНОСТИ
Ломаная
Пусть на плоскости имеется конечная
последовательность отрезков; у каждого отрезка один
из концов назовем началом. Если начало
второго отрезка совпадает с концом первого, начало
третьего — с концом второго и т. д., то
совокупность (объединение) этих отрезков называется
ломаной (при этом предполагается, что никакие
два соседних отрезка не лежат на одной
прямой). Отрезки, составляющие ломаную, —
звенья, концы отрезков — вершины ломаной
(ломаная АгА2..Л8 на рисунке 158, а). Ломаная
называется простой, если она не имеет
самопересечений; замкнутой, если конец последнего отрезка
совпадает с началом первого отрезка (рис. 158, б).
Многоугольник
Многоугольник — это простая замкнутая
ломаная. Звенья ломаной— стороны, вершины
ломаной — вершины многоугольника.
Многоугольник с п сторонами называется п-угольником.
Многоугольником также называется часть
плоскости, ограниченная простой замкнутой
ломаной (плоский многоугольник). Периметр
многоугольника — сумма длин его сторон.
Многоугольник называется выпуклым
(рис. 159), если он лежит по одну сторону
относительно прямой, содержащей любую его
сторону.
Углы (внутренние) выпуклого
многоугольника — это углы, образованные соседними
сторонами. Число углов многоугольника равно
числу сторон и числу вершин. Среди углов
невыпуклого многоугольника имеется хотя бы один
угол, больший 180°.
ТЕОРЕМА
Сумма углов выпуклого п-угольника равна
(п - 2)180°.
Доказательство. Соединим диагоналями
вершину Ах выпуклого n-угольника (рис. 160) с
другими вершинами. Получим п - 2
треугольника, сумма углов которых равна сумме углов
п-угольника. Сумма углов каждого треугольни-
Ломаная Простая замкнутая
ломаная
а) б)
Рис. 158
Многоугольник
выпуклый
Рис. 159
Рис. 160

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
173
ка равна 180°, поэтому сумма углов
многоугольника АхА2..Лп равна (п - 2) • 180°.
Теорема доказана.
Пример 1. Найти сумму углов выпуклого
семиугольника.
Решение. По доказанной теореме искомая
сумма равна
(7 - 2)180° = 5 • 180° - 900°.
Пример 2. Найти углы выпуклого
пятиугольника, если они пропорциональны числам
1,3,5,7,11.
Решение. Сумма углов выпуклого
пятиугольника равна
(5 - 2) • 180° = 3 • 180° = 540°.
Приняв за х меньший из углов, составим
уравнение:
х + Зх + Ъх + 1х + Их = 540,
откуда х = 20. Таким образом, углы
пятиугольника равны 20°, 60°, 100°, 140°, 220°.
Многоугольник называется вписанным в
окружность, если все его вершины лежат на
некоторой окружности. В этом случае также
говорят: «Окружность описана около
многоугольника» (рис. 161, а).
Многоугольник называется описанным
около окружности, если все его стороны касаются
некоторой окружности. В этом случае также
говорят: «Окружность вписана в многоугольник»
(рис. 161, б).
Правильный многоугольник
Правильным многоугольником называется
выпуклый многоугольник, у которого все углы
равны и все стороны равны.
Примеры правильных многоугольников:
правильный (или равносторонний) треугольник,
квадрат, правильные пятиугольник,
шестиугольник и т. д. На рисунке 162 изображены
правильные пятиугольник и шестиугольник.
Так как сумма внутренних углов выпуклого
л-угольника равна (л - 2)180°, то каждый
внутренний угол правильного л-угольника равен
п - 2
180°
Пример 1. Сколько сторон имеет
правильный многоугольник, каждый из внутренних
углов которого равен 135°?
Решение. По условию задачи составим
уравнение
п - 2
180 = 135,
или
(п -2)180 = 135л,
откуда 45л = 360 и, значит, л = 8.
Для выпуклых правильных
многоугольников справедлива следующая теорема:
ТЕОРЕМА
Если выпуклый многоугольник
правильный, то:
1) около него можно описать окружность;
2) в него можно вписать окружность, причем
центры описанной и вписанной окружностей
совпадают. Эта точка называется центром
правильного многоугольника.
Приведем формулы для радиуса R описанной
окружности и радиуса г вписанной окружности
для правильного л-угольника со стороной а:
а
Д =
2 sin
180°
(1)
Окружность описана
около многоугольника
а)
Окружность вписана
в многоугольник
б)
Правильные пятиугольник
и шестиугольник
Рис. 161
Рис. 162

174
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
г =
2tg
180°
(2)
Пример 2. Для правильного (равносторонне-
180°
го) треугольника (п = 3, —«— = 60°)
2 sin 60° 73; Г 2tg60° 273*
Пример 3. Для правильного
четырехугольника, т. е. квадрата {п = 4,
180°
= 45°),
2 sin 45° J2 ' Г 2tg45°
Пример 4. Для правильного шестиугольника
1 ЯП0
(л - 6, ±^- = 30°)
Д =
2 sin 30°
= = а = а^ (Я\
а; Г 2 tg 30° 2 * w
Из формул (1) и (2) получаем:
180°
а = 2R sin
и
а = 2г tg
180°
(4)
(5)
Пример 5. Сторона правильного вписанного
в окружность треугольника равна 3. Найти
сторону квадрата, вписанного в эту окружность.
Решение. Согласно примеру 2
7з
Если а — сторона квадрата, вписанного в ту
же окружность, то согласно формуле (4)
а - 2 • 73 • sin 45° = Щ^ - 7б .
С=* 2яД
Длина окружности
Наглядное представление о длине окружности
получается следующим образом. Представим
себе нить в форме окружности. Разрежем ее и
растянем за концы. Длина полученного отрезка
и есть длина окружности. Как найти длину
окружности, зная ее радиус? При
неограниченном увеличении числа сторон вписанного в
окружность правильного многоугольника его
периметр неограниченно приближается к длине
окружности (рис. 163). Это используется при
доказательстве следующей теоремы.
ТЕОРЕМА
Отношение длины окружности к ее
диаметру не зависит от окружности, т. е. одно
и то же для любых двух окружностей.
Отношение длины окружности к ее диаметру
принято обозначать греческой буквой к
(читается «пи»):
2Д п$
(6)
Рис. 163
где С — длина окружности, R — ее радиус.
Число тс иррациональное, его приближенное
значение я ~ 3,1416.
Из равенства (6) имеем
С = 2тсД, (7)
т. е. длина окружности радиуса R вычисляется
по формуле (7). Например, длина окружности
радиуса 12 м равна 2тс • 12 = 24л м.
Пример 1. На сколько изменится длина
окружности, если радиус увеличится на 1 м?
Решение. Пусть радиус первоначальной
окружности был Rv тогда длина этой
окружности С = 2kRv
По условию радиус первоначальной
окружности увеличивается на 1 м, т. е. R2 = (Ri + 1)>
тогда длина новой окружности
С2 = 2nR2 = 2n(Rx + 1).
Найдем разность:
С2-Сг = 2n(Rt + 1) - 2nR1 = 2тс.
Итак, С2 - Сг = 2тс« 6,28 (м).
Пример 2. Точки М nN делят окружность на
две дуги, разность градусных мер которых равна
90°. Чему равны градусные меры каждой из дуг?

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
175
Решение. Сумма градусных мер дуг равна
360°, а разность равна 90°. Обозначим
градусные меры этих дуг х и у. Имеем:
х + у = 360,
х-у = 90.
Решая эту систему, получим х = 225°, у =
= 135°.
Пример 3. Сторона квадрата равна 4 см.
Вычислить длину окружности: 1) вписанной в
него; 2) описанной около него.
Решение. 1) Радиус вписанной в квадрат
окружности равен 2 см, тогда длина окружности
равна С = 2яД, т. е. С = 4я см.
2) Радиус окружности, описанной около
CL 4 А~*
квадрата, равен -= . Поэтому R — -= = 2 J2 , а
длина окружности равна С = 4 л/2 я см.
Длина дуги окружности.
Радианная мера угла
Найдем длину дуги окружности радиуса R,
отвечающей центральному углу в п° (рис. 164).
Развернутому углу соответствует длина
полуокружности nR. Следовательно, углу в 1° соответствует
kR
дуга длины щ,
длины
•, а углу в п° соответствует дуга
1 180п'
(8)
Например, длина дуги окружности радиуса
12 м, отвечающей центральному углу в 30°, есть
Пример 1. По данной хорде k найти длину ее
дуги, если она соответствует центральному углу
в 60° (рис. 165).
Решение. Так как АО = ВО = R (R — радиус
окружности) и Z АОВ = 60°, то треугольник АОВ
равносторонний: R = АВ = k. Теперь согласно
формуле (8) имеем:
г =
nR
180
■»-Т'
Радианной мерой угла называется
отношение длины соответствующей дуги к радиусу
окружности. Из формулы для длины дуги
окружности следует, что
I
R
180
л,
т. е. радианная мера угла получается из гра-
* та
дуснои умножением на т™ . В частности,
радианная мера угла 180° равна я, радианная мера
я
прямого угла равна т> •
Единицей радианной меры углов является
радиан. Угол в один радиан — это центральный
угол, у которого длина дуги равна радиусу
(рис. 166). Градусная мера угла в один радиан
180°
равна
<57°
Пример 2. Найти радианные меры углов
параллелограмма ABCD, если^А = 36°.
Решение. Радианная мера угла А равна
36° • tqq3 — к > а радианная мера угла В равна
я 4я
я - •=• = -г-, так как в параллелограмме сумма
углов, прилежащих к одной стороне, равна 180°
(§ 6; пункт 2, теорема 1). Наконец, радианные
г, тл я 4я
меры углов С и D соответственно равны ^ и -г-
(в параллелограмме противоположные углы
равны).
Контрольные вопросы
1. Что такое ломаная?
2. Что такое многоугольник?
3. Какой многоугольник называется
выпуклым?
4. Чему равна сумма углов выпуклого п-уголь-
ника?
. яД
/=180л
Рис. 164
о^—в
Рис. 166

176
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
5. Какой многоугольник называется
вписанным в окружность?
6. Какой многоугольник называется
описанным около окружности?
7. Какой многоугольник называется
правильным?
8. Приведите формулы для радиусов
вписанной и описанной окружностей правильного
л-угольника.
9. Найдите радиусы вписанной и описанной
окружностей для правильного треугольника,
четырехугольника (квадрата), шестиугольника.
10. По какой формуле вычисляется длина
окружности?
11. По какой формуле вычисляется длина
дуги окружности?
12. Что такое радианная мера угла?
13. Чему равны радианные меры
развернутого и прямого углов?
Упражнения
1. Чему равна сумма внутренних углов
выпуклого: 1) четырехугольника; 2)
пятиугольника; 3) шестиугольника?
2. Сколько сторон имеет многоугольник, у
которого сумма внутренних углов равна 1260°?
3. Найдите углы выпуклого
четырехугольника, если они пропорциональны числам 1, 2, 2, 4.
4. Может ли сумма внутренних углов
многоугольника равняться 740°?
5. Чему равен каждый внутренний угол
правильного: 1) восьмиугольника; 2)
десятиугольника?
6. Диаметр окружности равен 10 см. Найдите
сторону правильного четырехугольника,
описанного около этой окружности.
7. Найдите отношение сторон правильного
вписанного в окружность шестиугольника и
квадрата, описанного около той же окружности.
Выпуклый плоский
многоугольник
Рис. 167
8. Отношение числа сторон двух правильных
многоугольников равно 2 : 3, а отношение пары
внутренних углов этих многоугольников равно
6:7. Определите число сторон каждого
многоугольника.
9. Найдите длину окружности махового
колеса, радиус которого равен 150 см.
10. Радиус окружности увеличен на 5 см.
Как изменилась длина окружности?
11. Окружность разделена двумя точками на
две дуги. Найдите градусную меру каждой дуги,
если одна из них в девять раз больше другой.
12. Найдите длину дуги окружности радиуса
3 см, если градусная мера дуги равна: 1) 30°;
2) 60°; 3) 90°.
13. По данной хорде k найдите длину ее дуги,
если она соответствует центральному углу 90°.
14. Найдите радианную меру углов: 1) 30°;
2) 135°; 3) 120°.
15. Найдите радианную меру углов
равнобедренного прямоугольного треугольника.
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Понятие площади
Геометрическая фигура называется простой, если
ее можно разбить на конечное число плоских
треугольников. Примером простой фигуры является
выпуклый плоский многоугольник (рис. 167).
В данном параграфе рассматриваются только
плоские многоугольники.
Дадим определение площади для простых
фигур.
Площадь простой фигуры — это
положительная величина, численное значение которой
обладает следующими свойствами:
1. Равные фигуры имеют равные площади.
2. Если фигура разбивается на части,
являющиеся простыми фигурами, то площадь этой
фигуры равна сумме площадей ее частей.
3. Площадь квадрата со стороной, равной
единице измерения, равна единице.
Фигуры, имеющие равные площади, принято
называть равновеликими.
Площадь прямоугольника
Условимся одну из сторон параллелограмма
называть его основанием, а перпендикуляр,
опущенный на эту сторону из какой-нибудь точки

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
177
противоположной стороны параллелограмма, —
высотой.
В прямоугольнике за высоту можно взять
сторону, перпендикулярную к той, которая
принята за основание. В трапеции высота — общий
перпендикуляр между основаниями. Основание
и высота прямоугольника называются его
измерениями.
ТЕОРЕМА
Площадь прямоугольника раена
произведению его измерений.
Доказательство. 1. Пусть измерения
прямоугольника — натуральные числа тип. Разобьем
прямоугольник на единичные квадраты (как
показано на рисунке 168, где измерения
прямоугольника 5 и 3 единиц). Очевидно, на
прямоугольнике уложится тп единичных квадратов.
По второму свойству площадей площадь
прямоугольника будет равна тп квадратных единиц.
2. Пусть измерения прямоугольника —
рациональные числа аиЬ. Приведем дроби а и & к
общему знаменателю. Пусть а = — и Ь == — , где
тп, п и q — натуральные числа. Разобьем теперь
прямоугольник на такие единичные квадраты,
1
что длина стороны каждого из них равна —
части единицы длины. Прямоугольник будет
содержать тп таких квадратов. Так как площадь
квадрата со стороной — равна -^
4 Я
части
прежнего площадь S
прямого единичного квадрата,
угольника равна
0 1 771 71 L
q2 Я Я
Теорема доказана для случая, когда
измерения прямоугольника — рациональные числа.
Можно доказать, что эта теорема верна и в том
случае, когда хотя бы одно измерение есть
иррациональное число.
Пример 1. Сравнить площадь
прямоугольника со сторонами 48 см и 27 см с площадью
квадрата со стороной 36 см.
Решение. Искомые площади прямоугольника и
квадрата соответственно равны: 48•27 = 1296 (см )
2 2
и 36 = 1296 (см ), т. е. площади этих фигур
одинаковы.
Пример 2. Найти площадь квадрата по его
диагонали, равной 4 м.
Решение. Обозначим сторону квадрата через
х. По теореме Пифагора
х + х — 4 , или 2х — 16,
2 2
откуда х = 8, т. е. площадь квадрата равна 8 м .
Пример 3. Как изменится площадь
прямоугольника, если его основание увеличить на
50%, а высоту уменьшить на 50% ?
Решение. Если основание прямоугольника
принять за х, а высоту за у, то его площадь будет
равна S = ху.
Основание увеличили на 50%, т. е. оно стало
1,5л:. Высоту уменьшили на 50%, т. е. она стала
0,5i/. Поэтому
St = 1,5* • 0,5i/ = 0,75jh/.
Следовательно, площадь прямоугольника
уменьшится на 25%.
Площадь параллелограмма
ТЕОРЕМА
Площадь параллелограмма равна
произведению основания на высоту.
Доказательство. Опустим перпендикуляры
АЕ и BF из вершин А и В параллелограмма ABCD
(рис. 169) на прямую CD. Тогда площадь
трапеции АВСЕ с одной стороны равна сумме
площадей параллелограмма ABCD и треугольника
ADE, а с другой — сумме площадей
прямоугольника ABFE и треугольника BCF. Но так как эти
треугольники равны (значит, имеют равные
площади), то площадь S параллелограмма ABCD
равна площади прямоугольника ABFE, т. е.
S=ABBF,
т
S = тп
>ис. 168
Е D f
S = DC-BF
Рис. 169
С

178
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
или
S = DC- BF.
Пример 1. Основание параллелограмма
равно 35 см, а боковая сторона — 20 см. Найти
площадь параллелограмма, если боковая сторона
образует с высотой, опущенной на основание, угол в
60°.
Решение. Пусть условию задачи отвечает
рисунок 169. Тогда Z BCF = 90° - 60° = 30° и,
значит, катет BF = | ВС = 20 ^ =10 (см) (§ 5, п. 4,
пример 3). Следовательно, искомая площадь
S = 35 10 = 350 (см2).
Пример 2. Дан параллелограмм ABCD со
стороной АВ = 12 см и диагональю АС =16 см.
Вершина D удалена от диагонали АС на 4 см.
Вычислить расстояние от точки D до прямой АВ.
2
Решение. S^cd = 2SAADC = АС • DM = 64 см
(рис. 170), а так как вдд^ = АВ • DK, то DK =
64
12,т,е
DK «5,33 см.
Площадь треугольника и ромба
. ТЕОРЕМА
Площадь треугольника равна половине
произведения его стороны на высоту,
проведенную к этой стороне.
Доказательство. Треугольник ABC (рис. 171)
дополним до параллелограмма ABCD (как
указано на рисунке 171), площадь которого равна
АВ • А. Но площадь S треугольника ABC
составляет половину площади параллелограмма ABCD
(ибо треугольники ABC и CDA равны);
следовательно,
S^^AB -А.
Следствие 1. Площадь прямоугольного
треугольника равна половине произведения его
катетов (так как один катет можно взять за
основание, другой — за высоту).
Следствие 2. Площадь ромба равна
половине произведения его диагоналей.
Пример 1. Найти площадь равнобедренного
прямоугольного треугольника, если его
гипотенуза равна 8 см.
Решение. Обозначив один из катетов данного
треугольника через ху согласно теореме
Пифагора будем иметь:
х2 + х2 = 64, или х2 = 32,
2
откуда у = 16 и, значит, на основании следствия
1 искомая площадь равна 16 см .
Пример 2. В равнобедренном треугольнике
основание равно 30 м, а высота, опущенная на
основание, равна 20 м. Найти высоту,
опущенную на боковую сторону.
Решение. Пусть условию задачи отвечает
рисунок 172. Тогда в треугольнике ABC основание
АС = 30 м, высота BD = 20 м, следовательно,
можно найти площадь этого треугольника:
Площадь этого треугольника можно найти и
1 2S
по-другому: S = «ВС -АЕ, откуда АЕ = ^ (ВС
можно найти из прямоугольного треугольника
В DC по теореме Пифагора), или
АД =
20-30
F^m'
т. е. АЕ = 24 (м).
Пример 3. Вычислить площадь ромба,
диагонали которого равны 6 см и 3,5 см.
Решение. Согласно следствию 2 искомая
площадь равна
S = 6-3,5:2 = 10,5(cm2).

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
179
Пример 4. Найти площадь ромба, если его
высота 10 м, а острый угол 30°.
Решение. Пусть ABCD — ромб, где Z BAD —
= 30°, BE LAD и BE = 10 м (рис. 173).
Из прямоугольного Л ABE найдем АВ:
BE = g АВ (как катет, лежащий против угла
в 30°) и, значит, АВ = 2ВЕ = 2 • 10 = 20 (м).
Так как АВ = AD, то площадь ромба
S = BE AD = 200 (м2).
Площадь трапеции
ТЕОРЕМА
Площадь трапеции равна произведению
полусуммы оснований на высоту.
Доказательство. Проведя в трапеции ABCD
(рис. 174) диагональ DB9 можно рассматривать
ее площадь S как сумму площадей двух
треугольников BCD nADB. Поэтому
S - \DC • h + ~АВ • Л = |(DC + АВ) А,
где А — высота трапеции.
Пример 1. Стекла фонаря имеют вид
трапеции, параллельные стороны которой равны 22 см
и 18 см, а расстояние между ними — 10 см. Как
велика площадь каждого стекла?
Решение. Согласно только что доказанной
теореме, искомая площадь
S = \ (22 + 18)10 = 20 • 10 = 200 (см2).
Пример 2. Найти площадь трапеции,
параллельные стороны которой равны 16 м и 44 м, а
непараллельные — 17 м и 25 м.
Решение. Пусть ABCD — трапеция,
отвечающая условию задачи, тогда AD = 44, ВС = 16
(рис. 175). Следовательно, АЕ + KD = 28 (BE и
СК — высоты).
Обозначим АЕ через х, тогда KD = 28 - х.
По условию АВ =17, CD = 25. Значит, из
прямоугольного треугольника ABE
ВЯ2 = 172-*2.
Из прямоугольного треугольника CKD
согласно теореме Пифагора запишем:
СК2 - 252 - (28 - х)2.
Так как BE = СК9 то
172-*2 = 252-(28-х)2,
откуда х = 8.
Тогда
BE = 7l72 - х2 = 15 (м).
Площадь трапеции
16 + 44 2
S *» 1D Z -15 = 450(м2).
Площадь правильного
многоугольника
ТЕОРЕМА
Площадь правильного многоугольника
равна половине произведения его периметра на
радиус вписанной окружности:
В-**.
(1)
где Р — периметр многоугольника, а г —
радиус вписанной в него окружности.
Пример 1. Вычислить площадь правильного
шестиугольника, периметр которого равен 30 дм.
Решение. Так как периметр данного
правильного шестиугольника равен 30 дм, то его
сторона равна 5 дм. Отсюда радиус вписанной в него
Рис. 173
S = j(DC+ AB)h
Рис. 174
Рис. 175

180
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
5л/3
окружности г = -£- (§ 13, п. 3, формула (3)) и,
значит, согласно формуле (1) искомая площадь
S =2 * 30 • -g- = —j- * 65 (дм ).
Пример 2. Найти площадь равностороннего
треугольника со стороной а.
Решение. Периметр данного треугольника
равен За; радиус вписанной в него окружности
равен —^ (§ *<*, п. 3, пример 2). Следовательно,
согласно формуле (1) искомая площадь
0 1 о а За2 73 2
2 273 473 4
Площадь круга и кругового сектора
Кругом называется фигура, состоящая из всех
точек плоскости, расстояние от которых до
данной точки не больше данного (рис. 176).
Эта точка называется центром круга, а
данное расстояние — радиусом круга. Границей
круга является окружность с тем же центром и
радиусом.
Из наглядных соображений будем считать,
что площадь круга сколь угодно мало отличается
от площади вписанного в нее выпуклого
многоугольника с достаточно малыми сторонами.
Пусть R — радиус круга, а С — длина его
окружности. Впишем в окружность правильный
л-угольник с достаточно большим числом сторон
п. Площадь этого п-угольника
где Р — периметр n-угольника, а г — радиус
вписанной в него окружности (формула (1) п. 6).
При возрастании числа его сторон п периметр Р
сколь угодно мало отличается от числа С, а
радиус г — от числа R. Говорят, что при
возрастании п периметр Р стремится к длине окружности,
а площадь Sn — к площади круга S. Поэтому
S=±CR=^ • 2kR • R = kR2.
Итак, площадь круга вычисляется по формуле
S = лД2,
где R — радиус круга.
Пример 1. Найти площадь круга, если длина
окружности равна ft.
Решение. Длина окружности находится по
формуле С = 2nR. Так как С — ft, то ft = 2яД, или
R — о" > и> значит, площадь круга:
S - uRT = к
2 (k\2 %k2 k2
Ш2
Круговым сектором называется часть круга,
лежащая внутри соответствующего
центрального угла (рис. 177).
Площадь сектора, дуга которого содержит
один градус, равна ^ площади круга. Поэтому
площадь сектора, дуга которого содержит а гра-
дусов, равна обба- Итак, площадь кругового
сектора вычисляется по формуле
(2)
о- kR
Ь~ 360 а'
Рис. 176
Рис. 177
где R — радиус круга, а — градусная мера
соответствующего центрального угла.
Пример 2. В равностороннем треугольнике ABC
со стороной а (рис. 178) дуги КМ и LM — дуги
окружностей радиусов -к. Найти площадь
заштрихованной части треугольника ABC.
Решение. Площадь треугольника ABC равна
^- а (п. 6, пример 2), площадь каждого из
секторов АКМ и CML согласно формуле (2) равна
<f)2-60 яа2
360
24 •

Краткое изложение школьного курса математики
Геометрия. 7—9 классы
181
Поэтому искомая площадь
Контрольные вопросы
1. Сформулируйте свойства площади для
простых фигур.
2. Докажите теорему о вычислении площади
параллелограмма.
3. Докажите теорему о вычислении площади
треугольника.
4. Какие вам известны формулы для
площади прямоугольного треугольника и ромба?
5. Докажите теорему о площади трапеции.
6. Сформулируйте теорему о площади
правильного многоугольника.
7. Чему равна площадь круга?
8. Чему равна площадь сектора?
Упражнения
1. Найдите площадь прямоугольника,
стороны которого 6 дм и 15 см.
2. Как изменится площадь квадрата, если
каждую его сторону увеличить в 3 раза?
3. Периметр прямоугольника равен 50 см, а
его основание — 15 см. Найдите площадь
прямоугольника.
4. В прямоугольнике ABCD одна из сторон
равна 24 см, диагональ 2,5 дм. Вычислите
площадь этого прямоугольника.
2
5. Площадь параллелограмма 120 см ,
основание — 15 см. Найдите высоту, опущенную на
основание.
6. Основание параллелограмма равно 52,5 см,
а боковая сторона 3 дм. Найдите площадь
параллелограмма, если боковая сторона его образует с
высотой, опущенной на основание, угол, равный
60°.
7. Две стороны треугольника равны 30 см и
18 см. Высота, опущенная на первую сторону,
равна 12 см. Найдите высоту, опущенную на
вторую сторону.
8. Найдите площадь равнобедренного
прямоугольного треугольника, если его гипотенуза
равна 3,4 м.
9. Периметр ромба равен 28 дм, а высота —
5 дм. Найдите площадь ромба.
10. Найдите площадь ромба, если его высота
10 см, а острый угол 60°.
11. Стекла фонаря имеют вид трапеции,
параллельные стороны которой — 22 см и 18 см, а
расстояние между ними — 10 см. Как велика
площадь каждого стекла?
12. У равнобедренной трапеции меньшее
основание равно 10 м, боковая сторона 6 м, острый
угол 60°. Найдите площадь трапеции.
13. Сторона правильного вписанного в
окружность треугольника равна 3 см. Найдите
площадь квадрата, вписанного в эту
окружность.
14. Вычислите площадь правильного
шестиугольника, сторона которого 10 см.
15. Диаметр окружности основания
царь-колокола, находящегося в Московском Кремле,
равен 6,6 м. Определите площадь основания
этого колокола.
16. В круг вписан прямоугольник со
сторонами 3 м и 4 м. Найдите площадь этого круга.
17. Из круга, радиус которого 10 см, вырезан
сектор с дугой в 60°. Найдите площадь этого
сектора.
ОТВЕТЫ И УКАЗАНИЯ
Отрезок, луч, угол
1. 8 дм. 2. 2,5 см. 3. 23,5 см или 1,5 см. 4. 47 см
и 17 см. 5. 120°. 6. 45°. 7. Не может. 8. 1) 70°;
2) 100°; 3) 164°. 9. 74,5°, 105,5°. 10. 36° и 144°.
11. 90°, 90°, 90°. 12. 126°, 54°, 126°. 13. 40°, 40°,
140°, 140°.
Треугольник
1. 0,6 м. Я. 3 см. 3. 3,2 м, 6,2 м, 6,2 м. 4. 8 дм.
5. Указание. Используйте второй признак
равенства треугольников. 6. 50 см. 7. Указание.
Используйте третий признак равенства треугольников.
8. а) Равенство BD - CD следует из равенства
треугольников ABD и ACD (первый признак); б) Z С -
- 53°; в) DC - 14 мм.
Основные геометрические
построения
1. a) CD, MN9 АВ; б) АВ; в) OP, OB, ОА; г) EF.
2. 6 дм. 3. Нельзя. 4. 29 см. 5. 90°. 6.15 м и 6 м.

182
Краткое изложение школьного курса математики
Геометрия. 7—9 классы
Параллельные прямые
1. Три угла по 72°, а четыре угла по 108°. 2.110°
и 70°. 3. 80° и 80°. 4. 60° и 120°.
Сумма углов треугольника
1. 75°. 2.69°, 69°. 3.100°. 4.80°, 50°, 50° или 80°,
80°, 20°. б. 30° и 60°. 6.70°, 60°. 7.360°. 8.18 м, 18 м.
9.8 м. 10. ВС <АС <АВ. 11. 3 см. 12. Указание.
Равенство высот следует, например, из равенства
прямоугольных треугольников с общей гипотенузой
(основанием равнобедренного треугольника) и равными
острыми углами при основании этого треугольника.
13. Указание. Следует рассмотреть те же
прямоугольные треугольники, что и в задаче 12 (указание),
которые теперь будут равны по гипотенузе и катету.
14. 3 см.
Четырехугольники
1. 144°, 144°, 36°. 2. 2,65 м. 3. 120 см. 4. 5 м.
5. 3 м. 6. Квадрат. 7. Указание. Решается, как и
задача в примере 1 из пункта 4 § 6. 8.4 см, 5 см, 6 см.
9. 6 см, 5 см, 5 см. 10. 24 м и 30 м. 11. 2 м и 5 м.
12.1) Да; 2) нет; 3) да. 13. О и X. 14. 1) Две;
2) бесконечное множество: любая прямая,
перпендикулярная к данной, а также сама прямая; 3)
одну. 15. А, Е, 0.16.15 см и 20 см. 17. 7,5 см.
Тригонометрические функции
острого угла. Теорема Пифагора
с 12 Ч Я
1. sin А - т£ , cos А - j« • 2- 4 ; 15 • 3. 1) 10 см;
2) 2,9 см. 4. 20 см. 5. 30 м. 6.18 м, 18 м.
Прямоугольные координаты
1.1) 4; 2) 3. 2. 5. 3. 3; 2. 4.1) ^ ; 2) |. 5.1) -\ ;
2)-^.в.1)-1;2)-7§.
Векторы
1. 1) 3 см; 2) 5 см. 2. 1) Нет; 2) да; 3) да; 4) нет.
4. Да. 5. 5*. 6.1) 1; 8; 2) 10; 10. 7. -4; 0. 8. 0.
Подобные фигуры
1. 2,8 см и 2 см. 2. Подобны. 3. Подобны.
АгВг
3
4. ^ - ~ . 5.1) (1; -1); 2) (2; -1); 3) (1; 1).
Окружность
1. 70 см и 10 см. 2. 60° и 300°. 3. 66°. 4. 50°.
5. 12 м. 6. 32 см. 7. 2 см. 8. 6 м и 6 м. 9. 47 см.
10. 12 дм.
Решение треугольников
1. 1) 1:73; 2) 1 : 1; 3) 1.J3. 2. |; J|; |.
3. V1513 м. 4. Наибольший угол треугольника В,
наименьший — С.
Многоугольники. Длина окружности
1. 1) 360°; 2) 540°; 3) 720°. 2. 9. 3. 40°, 80°, 80°,
160°. 4. Не может. 5.1) 135°; 2) 144°. 6.10 см. 7. |.
8. Шестиугольник и девятиугольник. 9. « 9,42 см.
10. Увеличилась на 10ясм. 11.36° и 324°. 12.1) ^ см;
2) я см; 3) g я см. 13. —= . 14. 1) ^ ; 2) j я; 3) ^ я.
6
1К 1 1 1
2 ' 4 ' 4
Площади плоских фигур
1. 9 дм2. 2. Увеличится в 9 раз. 3. 1,5 дм .
4. 168 см2. 5. 8 см. 6. 787,5 см2. 7. 20 см. 8. 2,89 м2.
9.35 дм2. 10. ^? см2. 11. 200 см2. 12. 39 УЗ м2.
л/3
13. 6 см2. 14.15073 см2. 15.» 34,2 м2. 16. 6,25я м2.
17. «52 см2.

Геометрия. 10—11 классы
ВВЕДЕНИЕ
1. Стереометрия — это раздел геометрии, в
котором изучаются фигуры в пространстве.
Свойства геометрических фигур
устанавливаются путем доказательства соответствующих
теорем. При этом отправными являются свойства
простейших геометрических фигур,
выражаемые аксиомами. Основными геометрическими
фигурами в пространстве являются точка,
прямая и плоскость.
Плоскости обозначаются строчными
греческими буквами:
а, р, у, ... .
На рисунке 1 изображены плоскость а,
прямые а и 6 и точки А, В и С. Про точку А и
прямую а говорят, что они лежат в плоскости а
или принадлежат ей. Про точки Б и С и
прямую Ъ — что они не лежат в плоскости а или
не принадлежат ей.
Аксиомы стереометрии состоят из аксиом
планиметрии и следующих аксиом,
выражающих основные свойства плоскостей в
пространстве.
1) Для любой плоскости существуют
точки, принадлежащие этой плоскости, и точки,
не принадлежащие ей.
2) Если две различные плоскости имеют
общую точку, то они пересекаются по прямой,
проходящей через эту точку.
3) Если две различные прямые имеют
общую точку, то через них можно провести
плоскость и притом только одну.
Из аксиом стереометрии следует, что:
а) через прямую и не лежащую на ней точку
можно провести плоскость и притом только
одну;
б) если две точки прямой принадлежат
плоскости, то вся прямая принадлежит этой
плоскости;
в) плоскость и не лежащая на ней прямая
либо не пересекаются, либо пересекаются в
одной точке;
г) через три точки, не лежащие на прямой,
можно провести плоскость и притом только
одну.
2. Все построения, выполнявшиеся в
планиметрии, проводились в одной плоскости с
помощью чертежных инструментов, которые для
построений в пространстве становятся
непригодными, так как чертить фигуры в пространстве
невозможно. Кроме того, при построениях в
пространстве появляется новый элемент —
плоскость, построение которой в пространстве
нельзя выполнять столь простыми средствами,
как построение прямой на плоскости.
(Плоскость на чертеже принято изображать в виде
параллелограмма, хотя возможно ее изображение
и как, например, на рисунках 31, 49, 65.)
Поэтому при построениях в пространстве необходимо
точно определить, что значит выполнить то или
иное построение и, в частности, что значит
построить плоскость в пространстве. Во всех
построениях в пространстве мы будем
предполагать, что:
1) плоскость может быть построена, если
найдены элементы, определяющие ее положение в
пространстве;
2) если даны две пересекающиеся плоскости,
то дана и линия их пересечения, т. е. умеем
найти линию пересечения двух плоскостей;
3) если в пространстве дана плоскость, то
можем выполнять в ней все построения, которые
выполнялись в планиметрии.
Выполнить какое-либо построение в
пространстве — это значит свести его к конечному
числу только что указанных основных
построений.
/^0**^а
а '
Рис.1

Краткое изложение школьного
Геометрия. 10—11 классы
ПРЯМЫЕ И ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
Параллельность
и перпендикулярность
прямых в пространстве
Две различные прямые в пространстве либо
лежат в одной плоскости и имеют только одну
общую точку, т. е. пересекаются, либо лежат в
одной плоскости и не имеют общих точек, т. е.
не пересекаются, либо лежат в разных
плоскостях.
Две прямые в пространстве называются
параллельными , если они лежат в одной плоскости
и не пересекаются. Параллельность прямых а и Ъ
обозначается как и в случае плоскости: а II Ъ.
Две прямые в пространстве называются
скрещивающимися, если они лежат в разных
плоскостях.
Итак, две прямые в пространстве либо
пересекаются, либо параллельны, либо скрещиваются.
На рисунке 2 прямые а и Ъ пересекаются,
прямые а, с и d параллельны, прямые 6 и d
скрещиваются.
Задача 1. Через данную точку А (рис. 3)
пространства, не лежащую на данной прямой а,
провести прямую, параллельную данной
прямой.
Решение. Через прямую а и точку А
проводим плоскость а, в которой строим прямую av
параллельную прямой а.
Задача имеет единственное решение. В самом
деле, искомая прямая должна лежать с прямой а
в одной плоскости. В этой же плоскости должна
находиться точка А, через которую проходит
искомая прямая. Значит, эта плоскость должна
совпадать с плоскостью а. Но в плоскости а через
точку А можно провести только одну прямую,
параллельную прямой а.
Рис. 2 Рис. 3
математики
Задача 2. Найти точку пересечения данной
прямой а с данной плоскостью а (рис. 4).
Решение. Возьмем на плоскости а
какую-либо точку А. Через точку А и прямую а проводим
плоскость р. Она пересекает плоскость а по
некоторой прямой Ь. В плоскости Р находим точку
пересечения прямых а и Ъ. Эта точка искомая.
Если прямые а иЬ окажутся параллельными, то
задача не будет иметь решения.
Справедлива следующая теорема,
аналогичная случаю для плоскости.
ТЕОРЕМА 1
Признак параллельности прямых
Если две прямые параллельны третьей
прямой, то они параллельны.
Пример 1. Доказать, что середины сторон
пространственного четырехугольника
являются вершинами параллелограмма.
Решение. Пусть ABCD — данный
пространственный четырехугольник (вершины
четырехугольника не лежат в одной плоскости) (рис. 5).
Пусть Аг, Bv Сх, £>! — середины его сторон.
Тогда АгВх — средняя линия треугольника ABC,
параллельная стороне AC; CXDX — средняя
линия треугольника ACD, тоже параллельная
стороне АС. Значит, прямые АгВг и CxDt
параллельны и потому лежат в одной плоскости.
Точно так же доказывается параллельность прямых
A1D1nB1Cv
Итак, четырехугольник A1B1C1D1 лежит в
одной плоскости и его противолежащие стороны
параллельны. Следовательно, он — параллелограмм.
Как и на плоскости, две прямые в
пространстве называются перпендикулярными (взаимно
перпендикулярными), если они пересекаются
под прямым углом. Перпендикулярность
прямых а и Ъ обозначается как и в случае
плоскости: a Lb.

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
185
Пример 2. Доказать, что через любую точку
прямой в пространстве можно провести
перпендикулярную ей прямую.
Решение. Пусть а — данная прямая и А —
точка на ней (рис. 6). Возьмем любую точку М
вне прямой а и проведем через эту точку и
прямую а плоскость а (Введение, п. 1, а). В
плоскости а через точку А можно провести прямую 6,
перпендикулярную прямой а. Что и требовалось
доказать.
Параллельность
и перпендикулярность прямой
и плоскости.
Параллельность плоскостей
Прямая и плоскость называются
параллельными, если они не пересекаются.
Параллельность прямой а и плоскости а
обозначается так: а || а.
Прямая, пересекающая плоскость,
называется перпендикулярной этой плоскости, если она
перпендикулярна любой прямой в плоскости,
проходящей через точку пересечения данной
прямой и плоскости. В этом случае говорят
также, что плоскость перпендикулярна прямой.
Перпендикулярность прямой а и плоскости а
обозначается так: а _1_ а.
На рисунке 7 прямая а перпендикулярна
плоскости а.
Две плоскости называются параллельными,
если они не пересекаются. Параллельность
плоскостей аир обозначается так: а II (3.
ТЕОРЕМА 1
Признак параллельности прямой и плоскости
Плоскость и не лежащая на ней прямая
параллельны, если в данной плоскости
найдется прямая, параллельная данной прямой
(рис. 8).
ТЕОРЕМА 2
Признак перпендикулярности прямой и плоскости
Если прямая, пересекающая плоскость,
перпендикулярна двум пересекающимся
прямым, лежащим в плоскости, то она
перпендикулярна этой плоскости (рис. 9).
ТЕОРЕМА 3
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
пересекающимся прямым другой плоскости,
то эти плоскости параллельны (рис. 10).
Ограничимся доказательством теоремы 1.
Доказательство. Пусть а — плоскость, а —
не лежащая на ней прямая и аг — прямая в
плоскости а, параллельная прямой а. Проведем
плоскость а1 через прямые а и аг (рис. 11). Она
отлична от а, так как прямая а не лежит в
плоскости а. Плоскости а и ах пересекаются по
прямой аг. Если бы прямая а пересекала плоскость
а, то точка пересечения принадлежала бы
прямой av Но это невозможно, так как прямые а и
Рис.9
Рис. 10
Рис. 11

186
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
аг параллельны. Итак, прямая а не пересекает
плоскость а, а значит, параллельна плоскости а.
Теорема доказана.
Пример. Доказать, что через любую из двух
скрещивающихся прямых можно провести
плоскость, параллельную другой прямой.
Решение. Пусть а и Ъ — две скрещивающиеся
прямые (рис. 12). Возьмем на прямой а любую
точку и проведем через нее прямую &',
параллельную прямой Ъ. Проведем через прямые а и V
плоскость а. По теореме 1 она будет параллельна
прямой Ь.
Задача 1. Даны две скрещивающиеся
прямые. Как провести через них две параллельные
плоскости?
Решение. Пусть а и Ъ — данные
скрещивающиеся прямые (рис. 13). Через произвольную
точку прямой а проведем прямую Ъ\
параллельную 6, а через произвольную точку прямой Ъ
проведем прямую а', параллельную а. Теперь
проведем две плоскости — одну через прямые а
и &', а другую через прямые & и а'. По теореме 3
эти плоскости параллельны. В первой из них
лежит прямая а, а во второй — прямая Ь.
Теорема 2 приводит к теоремам 4 и 5 о
зависимости между параллельностью и
перпендикулярностью прямых и плоскостей.
ТЕОРЕМА 4
Если плоскость перпендикулярна одной из
двух параллельных прямых, то она
перпендикулярна и другой (рис. 14). Обратно, если
две прямые перпендикулярны одной и той же
плоскости, то они параллельны (рис. 14).
ТЕОРЕМА 5
Если прямая перпендикулярна одной из
двух параллельных плоскостей, то она
перпендикулярна и другой (рис. 15). Обратно,
если две плоскости перпендикулярны одной и
той же прямой, то они параллельны (рис. 15).
Свойства параллельных плоскостей
выражают следующие две теоремы:
ТЕОРЕМА 6
Если две параллельные плоскости
пересекаются третьей плоскостью, то прямые
пересечения параллельны (рис. 16).
Доказательство. Действительно, прямые
пересечения находятся в одной плоскости; они
не могут пересечься, так как в противном случае
пересекались бы данные плоскости. Теорема
доказана.
ТЕОРЕМА 7
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
Доказательство. Пусть аг и а2 —
параллельные плоскости, АгА2 и ВгВ2 —
пересекающие их параллельные прямые (рис. 17). Через
эти прямые проведем плоскость: она пересечет
Рис. 12
Рис. 13
±^
zr^
rr
Рис. 14
^~:
Рис. 15
Рис. 16
Рис. 17

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
187
плоскости аг и ос2 по параллельным прямым АгВг
и А2В2 (теорема 6); следовательно, фигура
А1В1В2А2 — параллелограмм, и потому АХА2 =
= ВгВ2. Теорема доказана.
Задача 2. Через данную точку А пространства
провести прямую, перпендикулярную данной
плоскости а.
Решение. Проведем в плоскости а две
пересекающиеся прямые бис (рис. 18). Через точку
их пересечения проведем плоскости Р и у,
перпендикулярные прямым Ь и с соответственно.
Они пересекаются по некоторой прямой а.
Прямая а перпендикулярна прямым & и с, значит
(теорема 2), и плоскости а. Проведем теперь
через точку А прямую d, параллельную а. По
теореме 4 она перпендикулярна плоскости а.
Задача имеет единственное решение.
Действительно, предположим, что через точку А
проходит еще одна прямая (обозначим ее через d1),
перпендикулярная плоскости а. Тогда по теореме 4
dx || d, что невозможно, так как прямые dx и d
пересекаются в точке А. Следовательно, через
каждую точку в пространстве можно провести
одну и только одну прямую,
перпендикулярную данной плоскости.
Задача 3. Через данную точку А
пространства провести плоскость, перпендикулярную
данной прямой а.
Решение. Проведем через прямую а какие-
нибудь две плоскости аир так, чтобы точка А
принадлежала плоскости а (рис. 19). В
плоскости а через точку А проведем прямую/?,
перпендикулярную прямой а, а в плоскости р через
точку пересечения прямых р и а проведем
прямую д, перпендикулярную прямой а. Так как
плоскость у проходит через прямые р и д, то в
силу теоремы 2 она искомая.
Задача имеет единственное решение. В самом
деле, предположим, что через точку А проходит
еще одна плоскость ух, перпендикулярная
прямой а. Тогда плоскости у и уг согласно теореме 5
параллельны, что невозможно, так как эти
плоскости имеют общую точку А и, значит,
пересекаются по прямой, проходящей через эту
точку.
Примечание. На рисунке 19 изображен тот
случай, когда точка А не лежит на прямой а.
Однако приведенное решение задачи пригодно и для
того случая, когда точка А лежит на прямой а.
Задача 4. Через данную точку А (рис. 20)
пространства, не лежащую на данной плоскости
а, провести плоскость, параллельную данной
плоскости.
Решение. Проведем в данной плоскости а
какие-нибудь две пересекающиеся прямые а и Ъ
(рис. 20). Через данную точку А проведем
параллельные им прямые аг и Ьг. Плоскость р,
проходящая через прямые аг и bv согласно
теореме 3 параллельна плоскости а.
Задача имеет единственное решение.
Действительно, предположим, что через точку А
проходят две различные плоскости Р и рх,
параллельные плоскости а (рис. 21). В плоскости р
выберем некоторую точку В, не принадлежащую
плоскости pj. Через точки А, В и некоторую
точку С, принадлежащую плоскости а, проведем
плоскость у. Она пересечет плоскости а, р и Рх по
некоторым прямым с, d и dr По теореме 6 имеем:
с || d и с || dv Значит, d II dv что невозможно,
так как прямые d и dx пересекаются в точке А.
Рис. 18
Рис. 19
Рис. 20
Рис. 21

188
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
Изображение пространственных
фигур на плоскости
Для изображения пространственных фигур
на плоскости обычно пользуются параллельным
проектированием. Этот способ изображения
фигуры состоит в следующем. Берем произвольную
прямую А, пересекающую плоскость чертежа а,
и проводим через произвольную точку А фигуры
прямую, параллельную Л. Точка Аг пересечения
этой прямой с плоскостью чертежа будет
изображением точки А (рис. 22). Построив таким
образом изображение каждой точки фигуры,
получим изображение самой фигуры. Такой способ
изображения пространственной фигуры на
плоскости соответствует зрительному восприятию
фигуры при рассматривании ее издали.
Пример 1. Доказать, чтЬ при параллельном
проектировании прямолинейные отрезки
фигуры, не параллельные направлению
проектирования, изображаются на плоскости чертежа
отрезками.
Решение. Пусть АС — прямолинейный
отрезок фигуры, не параллельный направлению
проектирования (рис. 23). Все прямые,
проектирующие точки отрезка АС, лежат в одной
плоскости, пересекающей плоскость чертежа а по
прямой А1С1. Произвольная точка В отрезка АС
изображается точкой Вг отрезка АгСг.
Пример 2. Доказать, что при параллельном
проектировании параллельные отрезки фигуры,
не параллельные направлению проектирования,
изображаются на плоскости чертежа
параллельными отрезками.
Решение. Пусть АС и А'С — параллельные
отрезки фигуры (рис. 24), не параллельные
направлению проектирования. Прямые АгСг и
Аг'Сг' параллельны, так как они получаются
при пересечении параллельных плоскостей с
плоскостью а.
Пример 3. Доказать, что при параллельном
проектировании отношение отрезков одной
прямой (не параллельной направлению
проектирования) или параллельных прямых (не
параллельных направлению проектирования)
сохраняется.
Решение. Покажем например, что (рис. 25)
АВ
ВС
АгВг
ВгСг
(1)
Для этого проведем через точку В прямую
А2С2, параллельную АгСг. Треугольники ВАА2 и
ВСС2 подобны (первый признак подобия
треугольников). Из подобия этих треугольников
следует, что
АВ
ВС
А£
ВС'
откуда получаем искомое отношение (1).
Пример 4. Дана параллельная проекция
треугольника. Как построить проекции медиан
этого треугольника?
Решение. Так как при параллельном
проектировании сохраняется отношение отрезков прямой
(пример 3), то середина стороны треугольника
проектируется в середину проекции этой
стороны. Следовательно, проекции медиан
треугольника будут медианами его проекции.
Перпендикуляр и наклонная
Пусть а — плоскость, А — точка, не
лежащая в плоскости а, и В — точка плоскости а
(рис. 26). Отрезок АВ называется
перпендикулярно. 22
Рис. 23
Рис. 24
Рис. 25

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
189
ром у проведенным из точки А к плоскости а,
если прямая АВ перпендикулярна плоскости а.
Длина отрезка АВ называется расстоянием от
точки А до плоскости ос.
Пусть С — точка плоскости а, отличная от В.
Отрезок АС называется наклонной, проведенной
из точки А к плоскости а. Отрезок ВС
называется проекцией наклонной.
Пример 1. Доказать, что если прямая
параллельна плоскости, то все ее точки находятся на
одинаковом расстоянии от плоскости.
Решение. Пусть а — данная прямая и а —
данная плоскость (рис. 27). Возьмем на прямой
а две произвольные точки М и N. Их
расстояния до плоскости а — это длины
перпендикуляров ММг и NNV опущенных на эту плоскость.
По теореме 4 из п. 2 прямые ММг и NN1
параллельны и, значит, лежат в одной плоскости,
которая пересекает плоскость а по прямой MXNV
Прямая а параллельна прямой MXNV так как не
пересекает содержащую ее плоскость а. Таким
образом, у четырехугольника MMXNXN
противолежащие стороны параллельны, т. е. он
параллелограмм и, следовательно, ММХ = NNV
что и требовалось доказать.
Расстоянием от прямой до параллельной ей
плоскости называется расстояние от любой
точки этой прямой до плоскости.
Расстоянием между двумя
скрещивающимися прямыми называется расстояние между
одной из этих прямых и плоскостью,
проведенной через другую прямую параллельно первой.
В решении примера 1 доказывается, что
расстояния от любых двух точек плоскости до
параллельной плоскости равны. Поэтому
расстоянием между параллельными плоскостями
называется расстояние от любой точки одной
плоскости до другой плоскости. Отсюда следует, что
расстояние между скрещивающимися
прямыми равно расстоянию между параллельными
плоскостями, проходящими через эти прямые.,
Пример 2. Точка отстоит от плоскости на
36 см; из нее проведена к плоскости наклонная,
равная 85 см. Чему равна проекция этой
наклонной?
Решение. Пусть условию задачи отвечает
рисунок 26. Треугольник ABC — прямоугольный
с прямым углом В. Поэтому в силу теоремы
Пифагора
ВС = J АС2 - АВ2
-Л
852 -
36" -
= V(85 + 36)(85 - 36) -
= V121 • 49 = 11-7 = 77.
Итак, искомая проекция равна 77 см.
Пример 3. Из точки к плоскости проведены
две наклонные, равные 10 см и 17 см. Разность
проекций этих наклонных равна 9 см. Найти
проекции наклонных.
Решение. Пусть условию задачи отвечает
рисунок 28, где АС = 10 см и AD = 17 см.
Обозначим длины проекций наклонных AC nAD
соответственно через х и у. По условию задачи
имеем:
у-х=9. (2)
Далее из прямоугольных треугольников ABC
nABD согласно теореме Пифагора находим:
100 - х2 = 289 - у2,
или с учетом равенства (2):
100 - х2 = 289 - ( 9 + х)2,
откудах = 6и, значит, у = 15.
Пример 4. Отрезки двух прямых,
заключенных между двумя параллельными плоскостями,
равны 51 см и 53 см, а их проекции на одну из
Рис. 26
Рис. 27
Рис. 28

190
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
этих плоскостей относятся как 6:7. Определить
расстояние между данными плоскостями.
Решение. Пусть условию задачи отвечает
рисунок 29. Обозначим одну часть через х, тогда
проекции отрезков АВ и CD на плоскость р
будут 6х и 7х. Теперь из прямоугольных
треугольников ABE и CDF находим:
ае - Jab2 - be2 = V512 - збх2,
CF = J(
CD2 - DF2 - л/бЗ2 - 49x2.
Но АЕ = CF (расстояния от любых двух точек
плоскости до параллельной плоскости равны) и
потому
512 - 36х2 - 532 - 49х2, или 13х2 - 208,
откуда х = 4 и, значит,
АЕ - л/б12 - 36-16 = V2025 - 45.
Следовательно, расстояние между данными
плоскостями равно 45 см.
ТЕОРЕМА
Теорема о трех перпендикулярах
Прямая, проведенная на плоскости через
основание наклонной перпендикулярно ее
проекции, перпендикулярна и самой
наклонной. И обратно, если прямая на плоскости
перпендикулярна наклонной, то она
перпендикулярна и проекции наклонной.
Доказательство. Пусть АВ —
перпендикуляр к плоскости а, АС — наклонная и с —
прямая в плоскости а, проходящая через основание
С наклонной (рис. 30). Проведем прямую СА\
перпендикулярную плоскости а. Она
параллельна прямой АВ (п. 2, теорема 4). Проведем через
прямые АВ и\А'С плоскость р. Прямая с
перпендикулярна прямой СА\ Если она
перпендикулярна прямой С£, то она перпендикулярна
плоскости (3, а значит, и прямой АС.
Аналогично, если прямая с перпендикулярна
наклонной СА, то она, будучи перпендикулярна
и прямой СА\ перпендикулярна плоскости (3, а
значит, и проекции наклонной ВС. Теорема
доказана.
Пример 5. В равнобедренном треугольнике
ABC основание ВС равно 12 м, боковая сторона
10 м. Из вершины А проведен отрезок AD,
равный 6 м и перпендикулярный плоскости
треугольника ABC. Найти расстояние от точки D до
стороны ВС.
Решение. В треугольнике ABC проведем
биссектрису АН. Тогда АН — медиана и высота.
Соединим точки D и Н отрезком (рис. 31). DH 1
_1_ ВС по теореме о трех перпендикулярах, так
как АН _1_ ВС, и, значит, DH — искомое
расстояние.
Из прямоугольного треугольника ADH имеем:
DH2=AD2+AH2,
где AD = 6.
Из прямоугольного треугольника АСН
получаем, что
АН2 =АС2 - СН2 = 102 - б2 = 64 = 82.
Тогда DH2 = б2 + 82 - 100, DH = 10 (м).
Пример 6. Через центр вписанной в
треугольник окружности проведена прямая,
перпендикулярная плоскости треугольника.
Доказать, что каждая точка этой прямой
равноудалена от сторон треугольника.
Решение. Пусть А, В, С — точки касания
сторон треугольника с окружностью, О — центр
окружности и S — точка на перпендикуляре
Рис. 29
Рис. 30
Рис. 31

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
191
(рис. 32). Так как радиус ОА перпендикулярен
стороне треугольника, содержащей точку А, то по
теореме о трех перпендикулярах отрезок SA есть
перпендикуляр к этой стороне, а его длина —
расстояние от точки S до стороны треугольника. По
теореме Пифагора
SA = J л
'АО* + OS2 = Jr2 + OS2,
где г — радиус вписанной окружности.
Аналогично находим:
SB = л/г2 + OS2 , SC = л/г2 + OS2 ,
т. е. все расстояния от точки S до сторон
треугольника равны.
Перпендикулярность плоскостей
Две пересекающиеся плоскости называются
перпендикулярными, если какая-либо плоскость,
перпендикулярная прямой пересечения этих
плоскостей, пересекает их по перпендикулярным
прямым.
Перпендикулярность плоскостей аир
обозначается так: a J_ р.
На рисунке 33 изображены две длоскости а и
р, которые пересекаются по прямой а.
Плоскость у перпендикулярна прямой а и пересекает
аир. При этом плоскость у пересекает
плоскость а по прямой с, а плоскость р — по прямой
d, причем с J_ d, т. е. по определению а _1_ р.
ТЕОРЕМА
Признак перпендикулярности плоскостей
Если плоскость проходит через прямую,
перпендикулярную другой плоскости, то эти
плоскости перпендикулярны.
Доказательство. Пусть а — плоскость, Ъ —
перпендикулярная ей прямая, р — плоскость,
проходящая через прямую Ъ, и с — прямая, по
которой пересекаются плоскости а и Р (рис. 34).
Докажем, что плоскости аир
перпендикулярны. Проведем в плоскости а прямую а через
точку пересечения прямой Ъ с плоскостью а,
перпендикулярную прямой с. Проведем через
прямые а и Ь плоскость у. Она перпендикулярна
прямой с, ибо прямая с перпендикулярна
прямым а и Ъ. Так как прямые а и Ъ
перпендикулярны, то плоскости аир перпендикулярны.
Теорема доказана.
Задача. Даны прямая а и плоскость а.
Провести через прямую а плоскость,
перпендикулярную плоскости а.
Решение. Через произвольную точку прямой
а проводим прямую Ъ (рис. 35),
перпендикулярную плоскости а (п. 2, задача 2). Через прямые
а и Ъ проводим плоскость р. Плоскость Р
перпендикулярна плоскости а по только что
доказанной теореме.
Пример. Точка М находится на расстояниях
а и & от двух перпендикулярных плоскостей.
Найти расстояние от этой точки М до прямой I
пересечения плоскостей.
Решение. Проведем через точку М
плоскость, перпендикулярную прямой I. Она
пересечет прямую I в точке С. Опустим
перпендикуляры МА и MB (рис. 36), тогда МАСВ —
прямоугольник со сторонами MA = a, MB = &, в
котором СМ — диагональ, т. е. искомое расстояние.
Найдем МС из прямоугольного
треугольника АМС по теореме Пифагора:
МС
= *Ja
г*ьг.
А
Лъ . Р
| а ,
X
Рис. 32
Рис. 33
Рис. 34
Ъ\
Рис. 36

Краткое изложение школьного
Геометрия. 10—11 классы
Контрольные вопросы
1. Каково может быть взаимное
расположение двух различных прямых в пространстве?
2. Какие прямые в пространстве называются
параллельными?
3. Какие прямые называются
скрещивающимися?
4. Сформулируйте признак параллельных
прямых.
5. Какие прямые в пространстве называются
перпендикулярными?
6. Дайте определение параллельности
прямой и плоскости.
7. Дайте определение перпендикулярности
прямой и плоскости.
8. Какие плоскости называются
параллельными?
9. Сформулируйте и докажите признак
параллельности прямой и плоскости.
10. Сформулируйте признак
перпендикулярности прямой и плоскости.
11. Сформулируйте признак параллельности
двух плоскостей.
12. Сформулируйте одну из теорем о
зависимости между параллельностью и
перпендикулярностью прямых и плоскостей.
13. Сформулируйте и докажите теорему о
пересечении двух параллельных плоскостей
третьей плоскостью.
14. Сформулируйте и докажите теорему об
отрезках параллельных прямых, заключенных
между параллельными плоскостями.
15. Перечислите свойства параллельного
проектирования.
16. Что такое перпендикуляр, проведенный
из данной точки на плоскость?
17. Что называется расстоянием от точки до
плоскости?
Рис. 36
математики
18. Что такое наклонная, проведенная из
данной точки к плоскости? Что такое проекция
наклонной?
19. Что называется расстоянием от прямой
до параллельной ей плоскости?
20. Что называется расстоянием между
двумя скрещивающимися прямыми?
21. Что называется расстоянием между
параллельными плоскостями?
22. Сформулируйте и докажите теорему о
трех перпендикулярах.
23. Какие плоскости называются
перпендикулярными?
24. Сформулируйте и докажите признак
перпендикулярности плоскостей.
Упражнения
1. Докажите, что все прямые, пересекающие
две данные параллельные прямые, лежат в
одной плоскости.
2. Плоскости аир параллельны плоскости у.
Могут ли плоскости аир пересекаться?
3. Точка отстоит от плоскости на 20 см; из
нее проведена к плоскости наклонная, проекция
которой равна 15 см. Какова длина наклонной?
4. Точка А отстоит от плоскости на 5 см;
наклонные АВ и АС равны каждая 10 см, а их
проекции образуют между собой угол в 120°.
Найдите расстояние ВС.
5. Из точки к плоскости проведены две
наклонные. Найдите длины наклонных, если одна
из них на 26 см больше другой, а их проекции
равны 12 см и 40 см.
6. Плоскости аир параллельны. Из точек А
и В плоскости а проведены к плоскости Р
наклонные: АС — 37 м и BD = 125 м. Проекция
наклонной АС на одну из плоскостей равна 12 м.
Чему равна проекция наклонной BD1
7. В треугольнике ABC угол В прямой и
катет ВС равен а. Из вершины А проведен отрезок
AD, перпендикулярный плоскости
треугольника, так, что расстояние между точками D и С
равно Ъ. Найдите расстояние от точки D до
катета ВС.
8. Катеты прямоугольного треугольника ABC
равны 15 ми 20 м. Из вершины прямого угла С
проведен отрезок CD, перпендикулярный
плоскости этого треугольника; CD — 35 м. Найдите
расстояние от точки D до гипотенузы АВ.

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
193
9. Из точек А и В, лежащих в двух
перпендикулярных плоскостях, опущены
перпендикуляры АС и BD на прямую пересечения плоскостей.
Найдите длину отрезка АВ, если: а) АС = Зм,
BD = 4 м, CD = 12 м; б) AD = 4 м, ВС =7 м,
CD = 1м; в) AD = ВС = 5 м, CD = 1 м.
УГЛЫ МЕЖДУ ПРЯМЫМИ
и плоскостями.
МНОГОГРАННЫЕ УГЛЫ
Угол между скрещивающимися
прямыми
Две пересекающиеся прямые образуют
смежные и вертикальные углы. Вертикальные углы
равны, а смежные углы дополняют друг друга до
180°. Угловая мера меньшего из них называется
углом между прямыми. Угол между
перпендикулярными прямыми равен 90° по определению.
Угол между параллельными прямыми считаем
равным нулю.
Углом между скрещивающимися прямыми
называется угол между пересекающимися
параллельными им прямыми. Его угловую меру а
выбирают в границах 0° < ос < 90°; она не
зависит от того, какие взяты пересекающиеся
прямые.
По данному ранее определению
перпендикулярными называются прямые, пересекающиеся
под прямым углом. Однако иногда
скрещивающиеся прямые тоже называют
перпендикулярными, если угол между ними равен 90°.
Пример. Прямая а параллельна диагонали
BD ромба ABCD и не лежит в плоскости ромба.
Найти угол меяеду прямыми а и AD, если Z BAD =
= 72° (рис. 37).
Решение. Прямые а и AD —
скрещивающиеся, и, значит, искомый угол равен Z BDA. Так
как треугольник BAD равнобедренный (АВ =
= AD как стороны ромба) и угол при его
вершине по условию равен 72°, то
ZBDA = \ (180°-72°) = 54°.
Угол между прямой и плоскостью
Определим понятие угла между прямой и
плоскостью. Пусть а — плоскость и а —
пересекающая ее прямая (рис. 38). Основания
перпендикуляров, опущенных из точек прямой а на
плоскость а, лежат на прямой Ъ. Эта прямая
называется проекцией прямой а на плоскость а. Углом
между прямой а и плоскостью а называется
угол между этой прямой и ее проекцией на
плоскость а. Его угловую меру со выбирают в
границах 0° < со < 90°. Если прямая параллельна
плоскости, то угол между ними считается
равным нулю.
Пример 1. Точка А отстоит от плоскости на
расстояние А. Найти длину наклонной,
проведенной из этой точки под углом 60° к плоскости.
Решение. Опустим перпендикуляр АА' на
плоскость (рис. 39). Треугольник АА'В—
прямоугольный с прямым углом при вершине А'.
Острый угол этого треугольника, противолежащий
катету АА7, равен 60°. Поэтому наклонная АВ =
= АА' = ?л
sin60° 73'
Пример 2. Отрезок длиной 10 м пересекает
плоскость, концы его находятся на расстоянии
2 м и 3 м от плоскости. Найти угол между
данным отрезком и плоскостью.
Решение. АА' 1 у, ВВ' _1_ у, значит, АА' \\ ВВ'
(рис. 40). Проведем плоскость (J, содержащую
прямые АА' и ВВ'. Рассмотрим Д ВВ'М в плос-
* аА 17
Рис. 37
Рис. 38
Рис. 39
Рис. 40

194
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
кости р. ВВ' = 3, Z В' = 90°, a Z ВМВ' = а —
искомый.
Проводим AC _L ВВ'. В прямоугольном
треугольнике ABC
АВ = 10, ВС = ВВ' + В'С = ВВ' + АА' - 5.
Искомый угол
а = ZBMB' = ZBAC, since = fi =0,5.
АВ
Следовательцо, а = 30°
Угол между плоскостями
Определим понятие угла между
плоскостями. Угол между параллельными плоскостями
считается равным нулю. Пусть аир —
плоскости, пересекающиеся по прямой с (рис. 41).
Проведем плоскость у, перпендикулярную
прямой с. Она пересечет плоскости а и р по прямым
а и Ь. Углом между плоскостями а и $
называется угол между прямыми а и Ь. Этот угол не
зависит от выбора плоскости у.
Пример 1. Две плоскости пересекаются под
углом 30°. Точка А, лежащая в одной из этих
плоскостей, отстоит от второй плоскости на
расстояние а. Найти расстояние от этой точки до
прямой пересечения плоскостей.
Решение. Пусть аир — данные плоскости и
А — точка, лежащая в плоскости а (рис. 42).
Опустим перпендикуляр АА' на плоскость р и
перпендикуляр АВ на прямую с, по которой
пересекаются плоскости. По теореме о трех
перпендикулярах А'В _1_ с. Угол при вершине В
прямоугольного треугольника ABA' равен 301 Имеем:
Расстояние от точки А до прямой с равно 2а.
Пример 2. Через сторону АВ треугольника
ABC проведена плоскость а, образующая с
плоскостью треугольника угол ф. Из вершины С
опущен перпендикуляр ССг на плоскость а. Найти
площадь треугольника АВСХ, если площадь
треугольника ABC равна k.
Решение. Проведем высоту CD треугольника
ABC (рис. 43), тогда
SABC = \AB-CD=k.
По теореме о трех перпендикулярах
Проекция CXD будет высотой треугольника АВСХ, а
угол CDCj будет равен углу между плоскостями
ABC и а, т. е. A CDCX = <р.
Из прямоугольного треугольника CDCX
найдем высоту CXD = CD • cos <р, поэтому площадь
треугольника АВСХ будет равна:
S = g АВ • CXD =2 АВ • CD • cos <р = k cos <р.
Двугранные и трехгранные углы
Двугранным углом называется фигура,
образованная двумя полуплоскостями с общей
ограничивающей их прямой (рис. 44). Полуплоскости
называются гранями, а ограничивающая их
прямая — ребром двугранного угла.
Плоскость, перпендикулярная ребру
двугранного угла, пересекает его грани по двум
полупрямым. Угол, образованный этими полупрямыми,
называется линейным углом двугранного угла.
За меру двугранного угла принимается мера
соответствующего ему линейного угла. Все линейные
углы двугранного угла совмещаются
параллельным переносом, а значит, равны. Поэтому мера
двугранного угла не зависит от выбора
линейного угла.
Рассмотрим три луча а, Ь, с, исходящих из
одной точки и не лежащих в одной плоскости.
Рис. 41
Рис. 42
Рис. 43
Рис. 44

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
195
Трехгранным углом аЪс называется фигура,
составленная из трех плоских углов: ab, Ьс и ас
(рис. 45). Эти углы называются гранями
трехгранного угла, а их стороны — ребрами. Общая
вершина плоских углов называется вершиной
трехгранного угла. Двугранные углы,
образованные гранями трехгранного угла, называются
двугранными углами трехгранного угла.
Аналогично определяется понятие
многогранного угла (рис. 46).
Пример 1. На грани двугранного угла в 30°
дана точка С, удаленная от ребра на расстояние I.
Найти расстояние от этой точки до другой грани.
Решение. Условию задачи удовлетворяет
рисунок 47.
Проведем С В _1_ а и CD ± а, где В
принадлежит плоскости a, a D — ребру а двугранного угла.
По теореме о трех перпендикулярах отрезок
BD перпендикулярен ребру а. Тогда Z BDC —
линейный угол данного двугранного угла, и по
условию CD = l, Z BDC = 30°.
Из прямоугольного треугольника BDC
имеем:
Обозначив ВС = х, АВ = Зх, по теореме
Пифагора из треугольника ABC получим
BC = CD
sin 30°= ^
и есть искомое расстояние.
Пример 2. Треугольник ABC с прямым
углом АСБ и катетом АС, принадлежащим
плоскости а, образует с этой плоскостью двугранный
угол, равный 45°. Найти расстояние от вершины
В до плоскости а, если АС = 20 см и АВ : ВС =
= 3:1 (рис. 48).
Решение. По условию
АВ .ВС = 3:1,
АС = 20 см.
откуда
(Зх)2 = 202 + х2,
х2 = 50, т. е. ВС2 = 50.
Из точки В проведем BE _L а (рис. 48),
соединим Е и С. По теореме о трех
перпендикулярах АС _1_ СЕ у так как АС _1_ ВС. Следовательно,
Z ВСЕ — линейный угол данного двугранного
угла, равного по условию 45°. В треугольнике
СВЕ имеем Z ВСЕ = 45°, Z ВЕС = 90°, поэтому
BE = СЕ, т. е. 2ВЕ2 = ВС2 (по теореме
Пифагора), откуда
2ВЕ2 = 50, BE = 5 (см).
Пример 3. Определить величину
двугранного угла, если точка, взятая на одной из граней,
отстоит от ребра вдвое дальше, чем от другой
грани.
Решение. Воспользуемся рисунком 47. Угол
BDC — линейный угол данного двугранного
угла. Обозначим этот линейный угол через (р. Со-
ВС 1 1
гласно условию задачи я~ = 5 , т. е. sin 9 = 5-
Отсюда ф = 30° и, значит, данный двугранный
угол равен 30°.
Пример 4. В трехгранном угле ЕАВС
плоский угол ВЕС прямой, а два других угла АБВ и
АЕС содержат по 60°. Плоскость а проведена
так, что отсекает от ребер три равных отрезка
ЕВ, ЕА и ЕС. Найдите двугранный угол при
ребре ВС.
Решение. Условию задачи отвечает рисунок 49.
Треугольник ВЕС — прямоугольный и равно-
Рис. 48
Рис. 49

196
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
бедренный. Поэтому углы при его основании
равны по 45°. Так как BE = ЕА и Z ВЕА = 60°,
следовательно, треугольник ABE
равносторонний, значит, BE — ВА. Аналогично
доказывается, что ЕА =АС, тогда
ЕА=ЕВ= ЕС =АВ = АС.
Построим линейный угол двугранного угла
при ребре ВС. Для этого из вершины Е проведем
ED _1_ ВС и точку D соединим с точкой А. Так
как AD 1_ ВС, то утолАЛЕ и есть линейный угол
искомого двугранного угла.
Рассмотрим прямоугольные треугольники
EDB hADB. Они равны по гипотенузе и катету.
Отсюда AD = ED = BD. Тогда треугольники
EDB и EDA равны по третьему признаку
равенства треугольников и, значит, угол EDA
прямой, следовательно, и двугранный угол при
ребре ВС прямой.
Контрольные вопросы
1. Дайте определение угла между
скрещивающимися прямыми.
2. Какие скрещивающиеся прямые называют
перпендикулярными?
3. Дайте определение угла меэеду прямой и
плоскостью.
4. Дайте определение угла между
плоскостями.
5. Что такое двугранный угол (грань угла,
ребро угла)?
6. Что такое линейный угол двугранного угла?
7. Что такое трехгранный угол (грани и ребра
трехгранного угла)?
8. Что такое плоские и двугранные углы
трехгранного угла?
Упражнения
1. Прямые а, Ь, с параллельны одной и той
же плоскости. Чему равен угол между прямыми
& и с, если углы этих прямых с прямой а равны
50° и 70°?
2. Прямая а параллельна стороне ВС
параллелограмма ABCD и не лежит в плоскости
параллелограмма. Найдите угол между прямыми
а и CD, если один из углов параллелограмма
равен: а) 50°; б) 121°.
3. Точка А отстоит от плоскости на
расстояние А. Найдите длины наклонных, проведенных
из этой точки под следующими углами к
плоскости: а) 30°; б) 45°.
4. Из точки, отстоящей от плоскости а на
расстояние а, проведены две наклонные,
образующие с плоскостью углы 45° и 30°, а между
собой — прямой угол. Найдите расстояние
между концами наклонных.
5. Через катет равнобедренного
прямоугольного треугольника проведена плоскость под
углом 45° ко второму катету. Найдите угол между
гипотенузой и этой плоскостью.
6. Из точки, взятой внутри двугранного угла,
опущен перпендикуляр на ребро; он образует с
гранями углы 38°24' и 71° 36'. Найдите
величину двугранного угла.
7. Точка, взятая внутри двугранного угла в
60°, удалена от обеих граней на а. Найдите ее
расстояние от ребра.
8. В трехгранном углу два плоских угла по
45°, двугранный угол между ними прямой.
Найдите третий плоский угол.
МНОГОГРАННИКИ
Понятие многогранника
В стереометрии изучаются фигуры в
пространстве, называемые телами. Наглядно
геометрическое тело (или просто тело) надо представлять
себе как часть пространства, занимаемую
предметом. Геометрическое тело отделяется от
окружающего его пространства поверхностью —
границей тела.
Многогранником называется
геометрическое тело, граница которого состоит из
конечного числа плоских многоугольников (рис. 50).
Многоугольники, ограничивающие
многогранник, называются гранями, их стороны —
ребрами, а вершины — вершинами многогранника.
\ * - \
а)
Рис. 50. Многоп
/^Л
Г < \ и
♦
А
/
/
б)
ранники
7

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
197
Многогранник называется выпуклым, если он
лежит по одну сторону от плоскости,
содержащей любую его грань (рис. 50, а). Гранями
выпуклого многогранника могут быть только
выпуклые многоугольники. Отрезок,
соединяющий две вершины, не принадлежащие одной
грани, называется диагональю многогранника.
Призма и ее площадь поверхности
Пусть а и аг — две параллельные плоскости,
Q — плоский многоугольник в плоскости а, а —
прямая, не параллельная а (рис. 51). Проведем
через произвольную точку М этого
многоугольника прямую, параллельную а. Отрезок
ММХ этой прямой между плоскостями а и а1
обозначим через ам. Когда точка М описывает
плоский многоугольник Q, отрезки ам заполняют
некоторое тело. Это тело называется призмой.
Грани призмы, лежащие в параллельных
плоскостях а и аг, называются основаниями
призмы. Другие грани называются боковыми
гранями. Все боковые грани — параллелограммы.
Ребра призмы, соединяющие вершины
оснований, называются боковыми ребрами. Все
боковые ребра призмы параллельны и равны.
На рисунке 51 изображена призма.
Основаниями призмы являются многоугольник Q и
равный ему многоугольник Q1 в плоскости аг.
Боковыми гранями призмы являются
параллелограммы АВВгАг, ВССгВг, ..., ЕАА1Е1. Боковыми
ребрами призмы являются отрезки ААХ, BBV ..., EEV
Высотой призмы называется отрезок,
заключенный между ее основаниями и
перпендикулярный им. (Высотой призмы называют и
длину этого отрезка.)
Отрезок, соединяющий две вершины, не
принадлежащие одной грани, называется
диагональю призмы. Диагональным сечением призмы
называется сечение плоскостью, проходящей
через два боковых ребра, не принадлежащих
одной грани.
На рисунке 52, а дано изображение призмы
ABCDAlB1C1Dv где ВгК — ее высота, DXB —
одна из ее диагоналей. Сечение АССгАг является
одним из диагональных сечений этой призмы.
Призма называется прямой, если ее боковые
ребра перпендикулярны основаниям. В
противном случае призма называется наклонной.
Прямая призма называется правильной, если
ее основаниями являются правильные
многоугольники.
На рисунке 52, а изображена наклонная
призма, а на рисунке 52, б — прямая, здесь ребро АА}
перпендикулярно основаниям призмы. На
рисунке 53 изображены правильные призмы, у них
основаниями являются соответственно
правильный треугольник, квадрат, правильный
шестиугольник.
Плоскость, перпендикулярная боковому ребру
призмы, пересекает ее грани. Полученный в
сечении многоугольник называется
перпендикулярным сечением призмы. Стороны этого
многоугольника перпендикулярны ребрам (§ 1, п. 2,
теорема 4).
Пример 1. В треугольной наклонной призме
два двугранных угла между боковыми гранями
равны 20°43'28" и 105°27'32". Чему равен
третий угол?
а)
ВЛ
А
-J
в
с
^1
А
^^к
i
i
i
в1-.
<п
пЛ
■)
D
шот
111 f\\
б)
Рис. 51
Рис. 52. Призма:
а) наклонная; б) прямая
Рис. 53. Призмы правильные

198
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
Решение. Проведем перпендикулярное
сечение ABC призмы (рис. 54). Оно представляет
собой треугольник, внутренние углы которого
являются линейными углами соответствующих
двугранных углов между боковыми гранями
призмы. Так как за меру двугранного угла
принимается мера соответствующего ему линейного
угла, то в треугольнике ABC два из трех его
внутренних углов содержат 20°43'28" и
105°27'32". Сумма же внутренних углов
треугольника равна 180°. Поэтому третий его
внутренний угол равен
180°- (20°43'28" + 105°27'32") = 53°49'',
и, значит, искомый двугранный угол равен
53°49'.
Пример 2. Основанием призмы является
правильный шестиугольник со стороной а, а
боковые грани — квадраты. Найти диагонали
призмы и площади ее диагональных сечений.
Решение. Диагональные сечения призмы
представляют собой прямоугольники (рис. 55),
у которых основаниями являются диагонали
оснований призмы, а высотой — высота призмы.
Диагонали основания равны: большая 2а и
меньшая а Л (меньшую диагональ находим из
прямоугольного треугольника ACD' по теореме
Пифагора). Так как высота призмы равна
стороне основания а, то площади диагональных сече-
ний равны 2а и a +J3 . Диагонали призмы
являются диагоналями диагональных сечений. По
теореме Пифагора диагонали призмы равны
л/(2а)2 + а2 - аЛ, л/(а</3)2 + а2 - 2а.
Площадь боковой поверхности призмы —
это сумма площадей всех ее боковых граней.
Рис. 54
Рис. 55
Площадь полной поверхности призмы — это
сумма площадей всех ее граней.
ТЕОРЕМА 1
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы.
Доказательство. Боковые грани прямой
призмы — прямоугольники, основания
которых — стороны основания призмы, а высоты
равны высоте Н призмы. Отсюда площадь
боковой поверхности призмы S6oK равна сумме
произведений сторон основания на высоту if.
Вынося множитель Н за скобки, получим в скобках
его периметр Р. Итак, S6oK = PH. Теорема
доказана.
Аналогично устанавливается
ТЕОРЕМА 2
Площадь боковой поверхности призмы
равна произведению периметра
перпендикулярного сечения на боковое ребро.
Пример 3. В треугольной наклонной призме
расстояния между боковыми ребрами 37см,
13 см и 40 см, а боковое ребро равно 15 см.
Найти площадь ее боковой поверхности.
Решение. Расстояния между боковыми
ребрами являются высотами боковых граней
параллелограммов с основанием 15см. Площадь же
параллелограмма равна произведению
основания на высоту. Поэтому площадь боковой
поверхности данной призмы
S6oK = 37 • 15 + 13 • 15 + 40 • 15 =
- 555 + 195 + 600 = 1350 (см2).
Пример 4. По стороне основания а и
боковому ребру Ь определить полную поверхность
правильной шестиугольной призмы.
Решение. Как известно (см. [1], § 14, п. 6),
площадь правильного многоугольника равна
половине произведения его периметра на радиус
вписанной окружности. Для правильного
шестиугольника этот радиус равен -=- (см. [1],
§ 13, п. 3); следовательно, площадь основания
призмы равна
1 Л аЛ За2Л

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
199
Боковые грани призмы — прямоугольники со
сторонами а и Ь.
Таким образом, искомая площадь
Snojm - 6ab + 2 • ^7^ = 6а& + За2 Л .
Параллелепипед. Куб
Если основания призмы —
параллелограммы, то она называется параллелепипедом. У
параллелепипеда все шесть граней —
параллелограммы. На рисунке 52, а изображен
наклонный параллелепипед, а на рисунке 52, б —
прямой.
У прямого параллелепипеда четыре боковые
грани — прямоугольники, а два основания —
параллелограммы.
Грани параллелепипеда, не имеющие общих
вершин, называются противолежащими. На
рисунке 52, а грани АВВ1А1 и CDD1C1
противолежащие.
ТЕОРЕМА 1
Свойства граней и диагоналей параллелепипеда
В параллелепипеде: 1) противолежащие
грани параллельны и равны; 2) все четыре
диагонали пересекаются в одной точке и
делятся ею пополам.
Эти свойства наглядно иллюстрируются
рисунком 56.
Прямой параллелепипед, основание
которого прямоугольник, называется прямоугольным
параллелепипедом. У прямоугольного
параллелепипеда все грани — прямоугольники.
Длины непараллельных ребер прямоугольного
параллелепипеда называются его измерениями.
У прямоугольного параллелепипеда три
измерения.
Прямоугольный параллелепипед, все ребра
которого равны, называется кубом.
ТЕОРЕМА 2
В прямоугольном параллелепипеде
квадрат любой диагонали равен сумме квадратов
трех его измерений.
Доказательство. Рассмотрим
прямоугольный параллелепипед ABCDAB'CD' (рис. 57). Из
прямоугольного треугольника АС С по теореме
Пифагора получаем:
АС'2=АС2 + СС'2.
Из прямоугольного треугольника АСВ по той
же теореме получаем:
АС2=АВ2 + ВС2.
Следовательно,
АС'2=АВ2 + ВС2 + СС'2.
Следствие. В прямоугольном
параллелепипеде все диагонали равны.
Пример 1. Определить диагонали прямого
параллелепипеда, если его боковое ребро равно
5 м, стороны основания равны 6 м и 8 м и одна
из диагоналей основания равна 12 м.
Решение. Согласно теореме Пифагора одна из
диагоналей данного параллелепипеда равна
л/5 + 12 = V169 =13 (м). Обозначим вторую
диагональ основания через х. Так как в
параллелограмме сумма квадратов диагоналей равна
сумме квадратов всех его сторон (см. [1], § 12,
п. 1, пример 3), то
х2 + 144 = 2 • 36 + 2 • 64,
2
откуда х — 56 и, значит, по теореме Пифагора
другая диагональ параллелепипеда равна
л/56 + 25 - 781 = 9 (м).
Пример 2. В прямом параллелепипеде
стороны оснований равны 3 см и 5 см, а одна из
диагоналей основания 4 см. Найдите большую
диагональ параллелепипеда, зная, что меньшая диа-
п
D
»
С
\~1\
А
\
1 , 1
/
■А;?
В'
В
Рис. 57

200
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
гональ образует с плоскостью основания угол
60° (рис. 58).
Решение. НахЬдим вторую диагональ
основания. Так как основанием служит
параллелограмм, а у параллелограмма сумма квадратов
диагоналей равна сумме квадратов всех его
сторон, то вторая диагональ основания равна
h • З2 + 2 • 52 - 42 = V52 > 4.
Боковое ребро равно 4tg60° = 4л/3. Большая
диагональ параллелепипеда равна
л/(л/52)2 + (473)2 = 10 (см).
Пример 3. У параллелепипеда три грани
2 2 2
имеют площади 1 м , 2 м и 3 м . Чему равна
полная поверхность параллелепипеда?
Решение. Так как у параллелепипеда
противолежащие грани равны, а следовательно, имеют
равные площади, то у данного параллелепипеда
есть две грани площадью по 1 м , две грани — по
2 2
2 м и две грани — по 3 м . Так как у
параллелепипеда ровно шесть граней, то его полная
поверхность равна
2-1 +2-2+ 2-3 = 12 (м2).
Пример 4. В прямом параллелепипеде
стороны основания равны 6 м и 8 м и образуют угол в
30°; боковое ребро равно 5 м. Определить
полную поверхность этого параллелепипеда.
Решение. Высота основания, проведенная из
вершины тупого угла к стороне, равной 8 м,
равна 3 м (как катет, лежащий против угла в 30°).
Поэтому площадь основания параллелепипеда
равна 24 м и, значит, полная поверхность
данного параллелепипеда равна
2 • 24 + 5(2 • 6 + 2 • 8) = 188 (м2).
Пример 5. Определить диагональ
прямоугольного параллелепипеда по трем его
измерениям: 1) 8, 9, 12; 2) 12, 16, 21.
Решение. Искомая диагональ согласно
теореме 2 равна:
1) л/в2 + 92 + 122 = 7289 = 17;
2) л/122 + 162 + 212 = 7841 = 29.
Пример 6. Диагонали трех граней
прямоугольного параллелепипеда, сходящиеся в
одной вершине, равны а, Ь, с. Найдите измерения
параллелепипеда.
Решение. Обозначим через х, у, г измерения
параллелепипеда (рис. 59). Имеем:
2,2 22,2 2
* +» ШС,» +2 ЯС,
2,2 ,2
Почленно складывая первые два уравнения и
вычитая третье, получим:
о 2 2,2 ,2
2у =с +а -6 .
/I 2 2 2
Отсюда у = А2^0 + а - Ъ ). Аналогично
находим:
/1/.2 , 2 2Г Д/ 2 , ,2 гГ
Пример 7. В прямоугольном
параллелепипеде стороны основания равны 7 дм, 24 дм, а
высота параллелепипеда равна 8 дм. Определить
площадь диагонального сечения.
Решение. Согласно теореме Пифагора
диагональ основания равна
Рис. 59
л/72 + 242 - 7625 = 25,
и, значит, площадь диагонального сечения равна
25 • 8 = 200 (дм2).
Пример 8. Определить полную поверхность
прямоугольного параллелепипеда по трем его
измерениям: 10 см, 22 см и 16 см.

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
201
Решение. Искомая площадь равна
2 • 10 • 22 + 2 • 10 • 16 + 2 • 22 • 16 =
= 440 + 320 + 704 = 1464 (см2).
Пример 9. Определить ребра прямоугольного
параллелепипеда, если они относятся как 3:7:8,
2
а полная поверхность содержит 808 м .
Решение. Обозначим через х линейную меру
одной части. Тогда ребра параллелепипеда
соответственно содержат Зх, 7х и 8* и, значит,
2 • Зх • 7х + 2 • Зх • 8х + 2 • 7х • 8х = 808,
или
202*2 = 808,
откуда х = 2. Следовательно, ребра
параллелепипеда равны 6 м, 14 м и 16 м.
Пример 10. По ребру куба а определить
диагональ этого куба и площадь его диагонального
сечения.
Решение. Согласно теореме 2 диагональ куба
4а + а + а = а«/3. Для
равна *4а + а~ + а = а+1'6 . для нахождения
площади его диагонального сечения найдем
диагональ основания куба. По теореме Пифагора
она равна л/а + а = aj2. Отсюда
площадь равна a J2 .
искомая
Пример 11. Определить полную поверхность
куба по его диагонали I.
Решение. Обозначим через х ребро куба.
Согласно теореме 2 имеем:
,2
о 2 ,2 2 /
ЗХ = I , ИЛИ X = тг ,
I2 2
откуда искомая площадь равна ■=• • 6 = 21 .
ной пирамиды. Высотой пирамиды называется
отрезок перпендикуляра, проведенного через
вершину к плоскости ее основания; концами этого
отрезка являются вершина пирамиды и
основание перпендикуляра; на рисунке 60 SH —
высота пирамиды. (Высотой пирамиды называют и
длину этого отрезка.) Пусть А, В, С, ..., -ДГ—
вершины многоугольника Q, лежащего в основании
пирамиды. Тогда треугольники ASB, BSC, ...,
KSA называются боковыми гранями пирамиды,
а отрезки AS, BS, CS,..., KS боковыми ребрами.
Сечение пирамиды, проходящее через
вершину и диагональ основания, называется
диагональным сечением пирамиды. Например,
треугольник ASC (см. рис. 60) — диагональное се:
чение пирамиды.
Пирамида называется правильной, если
основанием ее является правильный многоугольник,
а основание высоты совпадает с центром этого
многоугольника (центром основания). Осью
правильной пирамиды называется прямая,
содержащая ее высоту.
Высота боковой грани правильной
пирамиды, проведенная из вершины пирамиды,
называется апофемой пирамиды (обозначение /t6oK).
Все апофемы правильной пирамиды равны
между собой.
На рисунке 61 изображена правильная
треугольная пирамида, где SO — высота, a SD —
апофема.
Часть пирамиды, заключенная между
основанием и секущей плоскостью, параллельной
основанию, называется усеченной пирамидой
(рис. 62). Параллельные грани ABC и А1В1С1
называются основаниями, а отрезок
перпендикуляра ООv опущенного из какой-нибудь точки Ох
верхнего основания на нижнее основание, — вы-
Пирамида и ее площадь поверхности
Пусть Q — плоский многоугольник в
плоскости а и S — точка, не принадлежащая
плоскости а. Соединим каждую точку М
многоугольника Q с точкой S отрезком MS. Отрезки MS
заполняют некоторый многогранник. Этот
многогранник называется пирамидой (рис. 60).
Пирамида называется п-угольнощ если Q —
д-угольник. Треугольная пирамида называется
также тетраэдром. Многоугольник Q
называется основанием пирамиды, а точка S — верши-
Рис. 60

202
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
сотой усеченной пирамиды. Усеченная пирамида
называется правильной, если она составляет
часть правильной пирамиды. Бе ось — прямая,
проходящая через центры оснований. Боковые
грани правильной усеченной пирамиды —
равные равнобочные трапеции; их высоты
называются апофемами.
Пример 1. Определить боковое ребро
правильной четырехугольной пирамиды, если ее
высота равна 7 см, а сторона основания равна
8 см.
Решение. Пусть условию задачи отвечает
рисунок 63. Из прямоугольного треугольника
ADC согласно теореме Пифагора имеем:
АС = JAD2 + DC2
= Л2 + 82 =8^2
и, значит, АО = 4 л/2 . Наконец, из
прямоугольного треугольника AOS согласно той же теореме
находим:
AS = JAO2 + SO2 = л/32 + 49 = л/81 = 9,
т. е. боковое ребро пирамиды равно 9 см.
Пример' 2. Сторона основания правильной
четырехугольной пирамиды равна 14 м, а пло-
2
щадь диагонального сечения — 14 м . Найдите
боковое ребро пирамиды.
Решение. Пусть условию задачи отвечает
рисунок 63.
Рассмотрим диагональное сечение ASC, где
SO — высота пирамиды. Согласно известной
формуле для площади треугольника (см. [1],
§ 14, п. 4)
lAC-SO = 14.
В силу теоремы Пифагора АС = 14 л/2 и,
значит, SO = л/2.
Теперь из прямоугольного треугольника ASO
по теореме Пифагора находим
AS= IsO2 + №) = л/2 + 49 • 2 = 10.
Итак, боковое ребро пирамиды равно 10 м.
Пример 3. По данной стороне основания а и
боковому ребру Ь определите высоту
правильной треугольной пирамиды.
Решение. Так как пирамида правильная, то
основание ее высоты О совпадает с центром
правильного треугольника ABC — основания
пирамиды (см. рис. 61). Поэтому отрезок ВО равен
радиусу окружности, описанной около
треугольника ABC, и, значит, ВО = -= . Теперь из
л/3
прямоугольного треугольника BOS по теореме
Пифагора получаем:
so = Jbs2 - ВО2
-№■
Пример 4. В правильной четырехугольной
усеченной пирамиде (рис. 64) площади нижнего
и верхнего оснований соответственно равны В и
Ь, а боковое ребро составляет с плоскостью
нижнего основания угол в 45°. Определить площадь
диагонального сечения.
Решение. Стороны оснований равны JB и
л/Ь . Отсюда по теореме Пифагора основания
диагонального сечения, которым является
равнобочная трапеция, равны J2B и J2b . Далее, так как
угол при основании этой трапеции равен 45°, то
Рис. 62
Рис. 63
Рис. 64

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
203
72Б - Ш
ее высота равна «
искомого сечения
и, значит, площадь на
а2Л
Отсюда площадь полной поверхности
J2B + J2b J2B - J2b 2В - 2Ъ В - Ь
ТЕОРЕМА 1
Площадь боковой поверхности правильной
пирамиды равна произведению
полупериметра основания на апофему.
Доказательство. Площадь одной боковой
грани правильной д-угольной пирамиды равна
2 а^бок» гДе а — сторона основания, Абок —
апофема пирамиды. Поэтому
Q _ а/1бок _ап __Р
°бок 2~ 2 " бок"" 2 бок'
где Р — периметр основания пирамиды.
Итак,
^бок = 2 ^*бок"
Теорема доказана.
Площадь полной поверхности правильной
пирамиды (обозначение 5П0ЛН) состоит из площади
боковой поверхности и площади основания.
Поэтому Sn0JIH = S^ + S^ = g ^бок + 2 Рг'
где г — радиус окружности, вписанной в
основание пирамиды.
Аналогично теореме 1 устанавливается
ТЕОРЕМА 2
Площадь боковой поверхности правильной
усеченной пирамиды равна произведению
полусуммы периметров обоих оснований на
апофему.
Пример 5. Найти площадь полной
поверхности тетраэдра с ребром а.
Решение. Каждая из четырех граней данного
тетраэдра — равносторонний треугольник со
стороной а, площадь которого, как было
установлено ранее (см. [1],§14,п.6, пример 2), рав-
тетраэдра с ребром а равна a JS .
Пример 6. Найти площадь боковой
поверхности правильной треугольной пирамиды, если
сторона основания равна 10 м, а апофема — 15 м.
Решение. Согласно условию основанием
данной пирамиды является равносторонний
треугольник со стороной 10 м, и, значит, периметр
основания пирамиды равен 30 м. Теперь по
формуле (1) искомая площадь
5бок=^-30.15 = 225(м2).
Пример 7. Площадь боковой поверхности
правильной четырехугольной пирамиды равна
2
60 м , апофема — 5 м. Найти сторону
основания.
Решение. Подставляя данные условия задачи
в формулу (1), получаем:
60=| -Р.5,
откуда Р = 24 и, значит, сторона основания
равна 6 м.
Пример 8. Найти боковую поверхность
пирамиды, площадь основания которой Q, а
двугранные углы при основании равны ср.
Решение. Пусть А1А2 ... Ап — многоугольник
в основании пирамиды (рис. 65). Проведем
высоту пирамиды МО и высоту MB грани МАХА2.
По теореме о трех перпендикулярах (см. § 1, п. 4)
ОВ — высота треугольника ОАгА2. Имеем:
МВ =
ОВ
coscp'
Рис. 65

204
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
Отсюда
о Ал А9 • MB = о Ал А9 • ,
2 1 2 2 l z coscp'
или
'ДА^М
ъЬАхА20
СОЗф
AAgAgO
Аналогично получаем: S^^m = содф ,
5ДА3А40
saa3a4m = С08ф и т- Д- Складывая эти
равенства почленно, в левой части получим боковую
поверхность пирамиды, а в правой — площадь
основания Q, деленную на cos ср.
Итак, площадь боковой поверхности пирами-
Q
ды равна
СОЗф
Пример 9. Найти площадь боковой
поверхности правильной треугольной усеченной
пирамиды, у которой стороны оснований равны
24 см и 20 см, а апофема равна 18 см.
Решение. Используя условие задачи,
согласно теореме 2 имеем:
5^=1(24-3+ 20-3)-18 =
= (72 + 60) • 9 = 132 • 9 - 1188 (см2).
Итак, искомая площадь равна 1188 см .
Пример 10. Стороны оснований правильной
треугольной усеченной пирамиды равны 4 дм и
2 дм, а боковое ребро равно 2 дм. Найти
площадь боковой поверхности пирамиды.
Решение. Пусть условию задачи отвечает
рисунок 62. Тогда каждая боковая грань данной
пирамиды — равнобочная трапеция, основания
которой равны 4 дм и 2 дм, а боковые стороны
равны по 2 дм. Отсюда катет DC в
прямоугольном треугольнике CtDC равен 1 дм, и, значит,
по теореме Пифагора апофема пирамиды равна
л/3 дм. Теперь находим площадь ее боковой
поверхности согласно теореме 2:
S6ok~
4-3+2-3
- 73 =9л/3 (дм2).
Правильные многогранники
Правильный многогранник — выпуклый
мйогогранник, все грани которого — равные
правильные многоугольники и все
многогранные углы которого равны (таков, например,
куб). Из этого определения следует, что в
правильных многогранниках равны все плоские
углы, все двугранные углы и все ребра.
Существует всего пять типов правильных
многогранников.
1) Правильный четырехгранник, или
правильный тетраэдр (рис. 66), поверхность
которого составлена из четырех правильных
треугольников. Он имеет 4 грани, 6 ребер и 4
вершины.
2) Правильный шестигранник, или гексаэдр,
или куб (рис. 67), поверхность которого
составлена из шести квадратов. Он имеет 6 граней, 12
ребер и 8 вершин.
3) Правильный восьмигранник, или октаэдр
(рис. 68), поверхность которого составлена из
8 правильных треугольников. Он имеет 8 граней,
12 ребер и 6 вершин.
4) Правильный двенадцатигранник, или
додекаэдр (рис. 69), поверхность которого
составлена из 12 правильных пятиугольников. Он имеет
12 граней, 30 ребер и 20 вершин.
5) Правильный двадцатигранник, или
икосаэдр (рис. 70), поверхность которого составлена из
20 правильных треугольников. Он имеет 20
граней, 30 ребер и 12 вершин.
К1^
Рис. 66
Рис. 67
Рис. 68
Рис. 69
Рис. 70

Краткое
Контрольные вопросы
1. Что такое многогранник?
2. Что такое грань многогранника, ребро,
вершина?
3. Какой многогранник называется
выпуклым?
4. Что такое призма?
5. Что такое основания призмы, боковые
грани, боковые ребра?
6. Что называется высотой призмы?
7. Что называется диагональю призмы?
8. Что называется диагональным сечением
призмы?
9. Какая призма называется прямой, какая —
наклонной?
10. Какая призма называется правильной?
11. Что называется перпендикулярным
сечением призмы?
12. Что называется площадью боковой
поверхности призмы и что — площадью полной ее
поверхности?
13. Докажите, что площадь боковой
поверхности прямой призмы равна произведению
периметра основания на высоту призмы.
14. Что такое параллелепипед?
15. Сформулируйте теорему о свойствах
граней и диагоналей параллелепипеда.
16. Какой параллелепипед называется
прямоугольным?
17. Что такое измерения прямоугольного
параллелепипеда?
18. Какой прямоугольный пераллелепипед
называется кубом?
19. Докажите, что в прямоугольном
параллелепипеде квадрат любой диагонали равен сумме
квадратов трех его измерений.
20. Что такое пирамида (основание
пирамиды, высота, боковые грани, ребра)?
21. Что называется диагональным сечением
пирамиды?
22. Какая пирамида называется правильной?
23. Что называется осью правильной
пирамиды?
24. Что называется апофемой правильной
пирамиды?
25. Что называется усеченной пирамидой?
26. Докажите, что площадь боковой
поверхности правильной пирамиды равна
произведению полу периметра основания на апофему.
школьного курса математики
Геометрия. 10—11 классы
27. Сформулируйте теорему о площади боковой
поверхности правильной усеченной пирамиды.
28. Какой многогранник называется
правильным?
29. Перечислите пять типов правильных
многогранников и опишите их.
Упражнения
1. Боковое ребро наклонной призмы равно
15 см и наклонено к плоскости основания под
углом 30°. Найдите высоту призмы.
2. В правильной четырехугольной призме
площадь боковой грани равна Q. Найдите
площадь диагонального сечения.
3. В наклонной треугольной призме
расстояния между боковыми ребрами равны: 37 см,
15 см и 26 см, а боковое ребро равно 2 см.
Найдите площадь ее боковой поверхности.
4. В прямой треугольной призме все ребра
равны. Боковая поверхность равна 12 м.
Найдите высоту призмы.
5. По стороне основания а и боковому ребру Ъ
найдите полную поверхность правильной
призмы: а) треугольной; б) четырехугольной.
6. Найдите диагонали прямого
параллелепипеда, каждое ребро которого равно а, а угол
основания равен 60°.
7. Измерения прямоугольного
параллелепипеда равны 6м,4ми12м. Найдите диагональ
параллелепипеда.
8. Основание прямого параллелепипеда —
ромб с диагоналями в 6 см и 8 см; диагональ
боковой грани равна 13 см. Найдите площадь
полной поверхности этого параллелепипеда.
9. Площадь полной поверхности
прямоугольного параллелепипеда равна 352 м . Найдите
его измерения, если они относятся как 1:2:3.
10. Диагональ куба больше диагонали его
грани на ml Определите ребро куба.
11. Если ребро куба увеличить на 2 см, то
площадь его полной поверхности увеличится на
96 см . Чему равно ребро куба?
12. Определите боковое ребро правильной
треугольной пирамиды, если ее высота равна
1 см, а сторона основания равна 12 см.
13. По данной стороне основания а и
боковому ребру Ь определите высоту правильной
шестиугольной пирамиды.
14. В правильной четырехугольной пирамиде
сторона основания 14 см, а боковое ребро 10 см.
Найдите площадь диагонального сечения.

206
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
15. В правильной треугольной пирамиде по
стороне Основания а и боковому ребру Ъ
определите площадь сечения, проведенного через
боковое ребро и высоту пирамиды.
16. В правильной четырехугольной
усеченной пирамиде высота равна 63 см, апофема —
65 см, а стороны оснований относятся как 7 : 3.
Определите эти стороны.
17. В правильной треугольной усеченной
пирамиде определите площадь сечения,
проведенного через боковое ребро и ось, если боковое ребро
образует с плоскостью нижнего основания угол в
45°, а стороны оснований а и 6.
18. Как изменится площадь полной
поверхности тетраэдра с ребром а, если его ребро
увеличить в четыре раза?
19. По стороне основания а и высоте А найдите
полную поверхность правильной четырехугольной
пирамиды.
20. Определите площадь боковой
поверхности правильной треугольной пирамиды, если ее
высота равна 4 см, а апофема равна 8 см.
21. Основание пирамиды — ромб, диагонали
которого 12 м и 16 м. Высота пирамиды
проходит через точку пересечения диагоналей и равна
6,4 м. Найдите площадь полной поверхности
пирамиды.
22. Определите высоту правильной
треугольной пирамиды, если сторона основания а, а
боковая поверхность вдвое больше площади
основания.
23. В правильной четырехугольной пирамиде
площадь боковой поверхности равна 14,76 м , а
площадь ее полной поверхности равна 18 м .
Определите сторону основания и высоту пирамиды.
24. В правильной четырехугольной
усеченной пирамиде апофема равна 12 см, боковое
ребро равно 13 см и боковая поверхность равна
720 см . Определите стороны оснований.
ТЕЛА ВРАЩЕНИЯ
Цилиндр и его площадь поверхности
Пусть а и аг — две параллельные плоскости,
Р — круг в плоскости а (рис. 71). Проведем
через произвольную точку М круга Р прямую,
перпендикулярную плоскости а. Отрезок ММХ
этой прямой между плоскостями а и ах
обозначим через ам. Когда точка М описывает круг Р,
отрезки ам заполняют некоторое тело. Это тело
называется прямым круговым цилиндром или
просто цилиндром.
Граница цилиндра состоит из круга Р,
равного ему круга Рх в плоскости ах и боковой
поверхности. Боковая поверхность цилиндра
описывается отрезком ам, когда точка М пробегает
окружность круга Р. При этом сами отрезки ам
называются образующими цилиндра. Круги Р и Рг
называются основаниями цилиндра.
Длина образующей называется высотой
цилиндра, радиус основания —радиусом цилиндра.
Прямая, проходящая через центр основания
цилиндра параллельно его образующим,
называется осью цилиндра.
Сечение цилиндра плоскостью, проходящей
через его ось (осевое сечение), представляет
собой прямоугольник (рис. 72), две
противоположные стороны которого — образующие
цилиндра, а две другие — диаметры оснований
цилиндра. Цилиндр, осевое сечение которого
квадрат, называется равносторонним цилиндром.
Сечение цилиндра плоскостью,
перпендикулярной его оси и проходящей между основаниями
(поперечное сечение), — круг (рис. 73) того же
радиуса, что и основания цилиндра с центром на
оси цилиндра.
Пример 1. Радиус цилиндра 2 м, высота 3 м.
Найти диагональ осевого сечения.
Рис. 71
Рис. 72
Рис. 73
Рис. 74

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
207
Решение. Пусть условию задачи отвечает
рисунок 74. Осевое сечение АА'В'В —
прямоугольник, основание которого равно диаметру
основания цилиндра, т. е. 4 м, а высота — 3 м.
Из прямоугольного треугольника АВ'В согласно
теореме Пифагора получаем:
ав' = Jab2 + в'в2 = V42 + з2 =
= Vl6 + 9 = V25 =5.
Итак, диагональ осевого сечения равна 5 м.
Пример 2. Осевое сечение равностороннего
цилиндра равно д. Найти площадь основания
цилиндра.
Решение. Осевым сечением цилиндра
является квадрат, площадь которого по условию зада-
-чи равна q. Значит, сторона этого квадрата
равна Jq. С другой стороны, диаметр основания
цилиндра равен стороне этого квадрата, т. е. Jq =
= 2R , где R — радиус цилиндра. Отсюда R = -£
и, следовательно, площадь основания цилиндра
„2 nq
равна kR = -£.
Пример 3. В цилиндре проведено сечение
через две образующие. Высота цилиндра Я,
радиус R. Сечение отсекает от окружностей
оснований дуги по 60°. Найти площадь сечения.
Решение. Искомое сечение (рис. 75) —
прямоугольник EDCK, площадь которого
S=ED'CD=H-ED.
Угол EOD = 60°, следовательно, треугольник
EOD — равносторонний и потому ED = R. Отсюда
S = R • Я.
Круговой цилиндр можно рассматривать как
тело, полученное при вращении
прямоугольника ABCD вокруг одной из его сторон — оси
вращения (рис. 76). При этом сторона,
параллельная оси, описывает боковую поверхность
цилиндра и является его образующей. Смежные к оси
стороны описывают круги — основания
цилиндра. Прямая, содержащая сторону
прямоугольника, вокруг которой происходит вращение,
является осью цилиндра.
Боковая поверхность цилиндра — кривая
поверхность. Но ее можно, «разгибая», превратить
в плоскую (т. е. положить на плоскость,
развернуть). Если развернуть боковую поверхность
цилиндра, то получится прямоугольник, длина
основания которого равна длине окружности
основания цилиндра, а высота — высоте цилиндра
(рис. 77). Этот прямоугольник называется
разверткой боковой поверхности цилиндра.
За площадь боковой поверхности цилиндра
принимается площадь ее развертки.
Следовательно, справедлива такая теорема:
ТЕОРЕМА
Площадь боковой поверхности цилиндра
вычисляется по формуле
S6ok
где R — радиус цилиндра
линдра.
= 2тсЯЯ, (1)
Н — высота ци-
Площадью полной поверхности цилиндра
(обозначение Sn0JIH) называется сумма площадей
его боковой поверхности и двух оснований. С
учетом этой теоремы площадь полной поверхности
цилиндра равна
«полн = 2*Д2 + в*. = 2тсД2 + 2тсД. Я,
(2)
Я
i
i
i
- L
I
Я
2nR
Рис. 75
Рис. 76
Рис. 77

208
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
или
= 2nR(R + Н).
Пример 4. Чему равно отношение площадей
боковой поверхности и осевого сечения
цилиндра?
Решение. Обозначим через R и Н
соответственно радиус и высоту цилиндра. Тогда площадь
боковой поверхности цилиндра согласно формуле
(1) будет 2nR • Н, а площадь осевого сечения (как
прямоугольника с основанием 2Д и высотой Н) —
2R • Н и, значит, искомое отношение запишется:
2nR-H
2R-H
= 7С.
Пример 5. Радиус цилиндра равен Д,
площадь его боковой поверхности равна сумме
площадей оснований. Найти высоту цилиндра.
Решение. Площадь боковой поверхности
цилиндра равна 2nR • Н9 где Н — его высота; сум-
2
ма площадей оснований равна 2nR . В силу
условия задачи имеем равенство
2гсД.# = 2яД2,
откуда Н = R.
Пример 6. Площадь основания цилиндра
равна А, а площадь осевого сечения — М (рис. 78).
Чему равна площадь полной поверхности
цилиндра?
Решение. Искомую площадь полной
поверхности цилиндра можно вычислить по формуле (2).
Таким образом, задача будет решена, если
найдем R и Н. Согласно условию задачи имеем:
nR =А,
Тогда Япол
Sce4 = BE-ED = 2R'H=M.
= 2nR' + 2nR-H = 2A + кМ —
искомая площадь поверхности.
Конус и его площадь поверхности
Пусть а — плоскость, SO — отрезок
перпендикуляра, опущенного из точки S на плоскость а,
Р — круг в плоскости а с центром О (рис. 79).
Соединим произвольную точку М круга Р
отрезком MS с точкой S. Когда точка М описывает
круг Р, отрезки MS заполняют некоторое тело.
Это тело называется прямым круговым конусом
или просто конусом.
Граница конуса состоит из круга Р —
основания конуса и боковой поверхности. Боковую
поверхность конуса описывает отрезок ам, когда
точка М пробегает окружность круга Р. Точка S
называется вершиной конуса. Отрезки,
соединяющие вершину конуса с точками окружности
его основания, называются образующими конуса.
Прямая OS называется осью конуса, а отрезок OS
между вершиной и центром основания —
высотой конуса.
Сечение конуса плоскостью, проходящей
через его ось (осевое сечение), представляет собой
равнобедренный треугольник (рис. 80),
основание которого — диаметр основания конуса, а
боковые стороны — образующие конуса. Конус,
осевое сечение которого — равносторонний
треугольник, называется равносторонним
конусом.
Сечение конуса плоскостью,
перпендикулярной его оси и проходящей между вершиной и
основанием (поперечное сечение), — круг (рис. 81)
с центром на оси конуса.
Часть конуса, заключенная между
основанием конуса и его поперечным сечением,
называется усеченным конусом (рис. 82).
Пример 1. Радиус основания конуса равен
3 м, образующая — 5 м. Найти площадь осевого
сечения.
Рис. 78
Рис. 79
Рис. 80
Рис. 81
Рис. 82

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
209
Решение. Пусть условию задачи отвечает
рисунок 83. Из прямоугольного треугольника BOD
по теореме Пифагора находим высоту конуса:
OD = JBD2 - ВО2 = л/б2 - З2 =
= V25 - 9 = л/16 =4.
Осевое сечение ADB — равнобедренный
треугольник, основание которого — диаметр
основания конуса и, значит, равно 6 м. Высота этого
треугольника — высота конуса, т. е. равна 4 м.
Отсюда площадь осевого сечения равна
6-4 = 12 (м').
Пример 2. Высота конуса равна радиусу
основания R. Через его вершину проведена
плоскость сечения, отсекающая дугу 60°. Найти
площадь сечения.
Решение. Секущая плоскость пересекается с
поверхностью конуса по образующим ЕА и ЕВ и
хорде АВ (рис. 84).
Искомая площадь есть площадь
треугольника ЛЕВ.
Основание АВ треугольника АОВ стягивает
дугу 60°, следовательно, АВ = R.
Высота сечения ЕС является гипотенузой
треугольника ЕОС, в котором ЕО = R, а ОС =
р Jo
= —j- (радиус вписанной в правильный
шестиугольник окружности — см. [1], § 13, п. 3).
Поэтому
Дл/7
ЕС = Л
ЕО' + СО'
-F
+
!«•-
и, значит, площадь треугольника ABE равна
±AB-EC = ^fi.
Пример 3. Конус пересечен плоскостью,
параллельной основанию, на расстоянии d от
вершины. Найдите площадь сечения, если радиус
основания конуса R, а высота Н.
Решение. Обозначим через г радиус круга в
сечении. Проведем осевое сечение конуса (рис. 85).
Из подобия треугольников SAO и SA101
получаем:
АгОг
SO,
АО SO "
Так как АО = Д, АгОх = rfOS = Н, OxS = d, то
R Я'г
Rd
Н '
Итак, площадь сечения кг = к\ -=• I .
Круговой конус можно рассматривать как
тело, полученное от вращения прямоугольного
треугольника AOS вокруг его катета OS (рис. 86).
При этом гипотенуза AS описывает боковую
поверхность конуса, а катет ОА — круг
(основание конуса). Прямая, содержащая катет, вокруг
которого происходит вращение, является осью
конуса.
Разверткой боковой поверхности конуса
является круговой сектор (рис. 87), радиус
которого равен образующей конуса, а длина дуги
сектора — длине окружности основания конуса.
2nR
Рис. 86
Рис. 87

210
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
За площадь боковой поверхности конуса
принимается площадь ее развертки. Значит,
площадь боковой поверхности конуса равна
площади сектора SAB:
&Л/«|. —
kL а
бок 360 9
где L — длина образующей SA9 а — величина
(в градусах) угла ASB (см. [1], § 14, п. 7). Дуга
АВ имеет длину (см. [1], § 13, п. 5) I = -^ .
Поэтому
2 * <
Ъбок - 360 " 180 " 2 " '' 2 '
Но длина I дуги АВ равна длине окружности
основания конуса, значит, I = 2яД, где R —
радиус основания конуса. Отсюда
S6ok " * • 5 = 2kR '2 =nR'L-
Итак,
S6oK=7ciM,, (3)
где Д — радиус основания конуса, L — длина
образующей конуса.
Таким образом, приходим к следующей
теореме.
ТЕОРЕМА
Площадь боковой поверхности конуса
равна половине произведения длины
окружности его основания на образующую.
Площадью полной поверхности конуса
(обозначение Sn(WIH) называется сумма площадей его
боковой поверхности и основания. С учетом этой
теоремы площадь полной поверхности конуса
равна
= SfiaK + S0CH = nR'L+nR ,
7полн °бок
ИЛИ
SU0JlH=nR(R+L).
(4)
Пример 4. Образующая конуса равна 10 см, а
площадь боковой поверхности больше площади
2
основания на 21 к см . Определить радиус
основания.
Решение. Обозначим радиус основания
конуса через R. Тогда площадь основания конуса
равна icir, а площадь боковой поверхности конуса
равна 10kR. Теперь в силу условия задачи
можно записать уравнение
. uR2 + 21я = ЮяД, или R2 - 10R + 21=0,
решая которое, находим: R = 7 см или R = 3 см.
Пример 5. Образующая конуса L составляет
с основанием угол 60°. Найти площади боковой
и полной поверхностей конуса.
Решение. Пусть условию задачи отвечает
рисунок 88. В силу условия задачи в
прямоугольном треугольнике АОВ угол АВО равен 30°
(ибо по условию образующая составляет с
основанием угол 60°) и, значит, АО = « » т. е. радиус
основания Д = п . Теперь согласно формулам (3)
и (4) имеем:
S6ok = nR'L =
kL
Sm-iW+L)-*§(§ + l)-
3nL'
Пример 6. Равнобедренный треугольник
вращается около своей высоты, проведенной к
основанию. Определить стороны этого
треугольника, если его периметр равен 30 см, а площадь
полной поверхности тела вращения равна
60л см .
Решение. Пусть ABC — равнобедренный
треугольник (АВ = ВС), удовлетворяющий условию
задачи (рис. 89). Треугольники ADB и CDB
равны (по гипотенузе и катету). Поэтому AD = DC.
В силу условия задачи имеем:
f АС + 2ЛВ = 30,
Рис. 88
Рис. 89

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
211
ИЛИ
откуда
или
2АВ = 30-АС,
AC2 + 2АВ АС = 240,
AC2 + 30АС-АС2 = 240, АС = 8
и, значит, АВ = ВС = 11.
Итак, стороны треугольника равны 8 см, 11 см
и 11 см.
Пример 7. Найти площадь боковой
поверхности усеченного конуса, радиусы оснований
которого Rx и R2 (R2 < Rx)9 а образующая L.
Решение. Дополним данный усеченный конус
до полного (рис. 90). Пусть х — его образующая.
Площадь боковой поверхности усеченного конуса
равна разности площадей боковых поверхностей
двух полных конусов: одного — с радиусом
основания Rx и образующей х, другого — с радиусом
основания R2 и образующей х - L. Далее, из
подобия треугольников (см. рис. 90) имеем:
~ R+
х - L
Отсюда
х =
RXL
Ri " R2
поверхности усеченного
Площадь боковой
конуса равна
S6oK = nRxx - nR2(x - L) = nx(Rx - R2) + kR2L =
RXL(RX - R2)
= 7C-
*1-
+ nR2L = nL(Rx +R2).
Пример 8. Найти площадь полной
поверхности усеченного конуса из примера 7.
Решение. С учетом примера 7 площадь полной
поверхности усеченного конуса выразится так:
5Полн= *R\ + nRl + kL(ri + R2>>
, = 7С( R2X + R22 + RXL + i*2L).
Вписанная и описанная призмы,
вписанная и описанная пирамиды
Призмой, вписанной в цилиндр, называется
такая призма, основания которой — равные
многоугольники, вписанные в основания цилиндра. Ее
боковые ребра являются образующими
цилиндра (рис. 91).
Пример 1. В цилиндр вписана правильная
шестиугольная призма. Найти угол между
диагональю ее боковой грани и осью цилиндра, если
радиус основания равен высоте цилиндра.
Решение. Боковые грани призмы — квадраты,
так как сторона правильного шестиугольника,
вписанного в окружность, равна радиусу (рис. 92).
Ребра призмы параллельны оси цилиндра,
поэтому угол между диагональю грани и осью
цилиндра равен углу между диагональю грани и
боковым ребром. А этот угол равен 45°, так как
грани — квадраты.
Плоскость, проходящая через образующую
цилиндра и перпендикулярная осевому
сечению, проведенному через эту образующую,
называется касательной плоскостью цилиндра
(рис. 93).
Призма называется описанной около
цилиндра, если ее основания — равные
многоугольники, описанные около оснований цилиндра.
Плоскости ее граней касаются боковой
поверхности цилиндра (рис. 94).
Пример 2. Найти площадь боковой
поверхности цилиндра, вписанного в правильную
шестиугольную призму, каждое ребро которой равно а.
Рис. 90
Рис. 91
Рис. 92
Рис. 93
Рис. 94

212
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
2я^77- -а= ка л/3 .
Решение. Радиус цилиндра г равен радиусу
окружности, вписанной в правильный
шестиугольник, сторона которого а, и, значит, г =
= -s-. Высота цилиндра равна ребру призмы.
Следовательно, искомая площадь равна
_Ол/3
2
Пирамидой, вписанной в конус, называется
такая пирамида, основание которой есть
многоугольник, вписанный в окружность основания
конуса, а вершиной является вершина конуса
(рис. 95). Боковые ребра пирамиды, вписанной в
конус, являются образующими конуса.
Пример 3. У пирамиды все боковые ребра
равны. Доказать, что она является вписанной в
некоторый конус.
Решение. Опустим перпендикуляр SO из
вершины пирамиды на плоскость основания (рис. 96)
и обозначим длину бокового ребра пирамиды
через Z. Вершины основания удалены от точки О
на одно и то же расстояние
R = л//2 - OS2
Отсюда следует, что эта пирамида вписана в
конус, вершиной которого является вершина
пирамиды, а основание — круг с центром О и
радиусом R.
Плоскость, проходящая через образующую
конуса и перпендикулярная осевому сечению,
проведенному через эту образующую,
называется касательной плоскостью конуса (рис. 97).
Пирамида называется описанной около
конуса, если ее основанием является многоугольник,
описанный около основания конуса, а вершина
совпадает с вершиной конуса (рис. 98).
Плоскости боковых граней описанной пирамиды
являются касательными плоскостями конуса.
Пример 4. Найти площадь боковой
поверхности конуса, вписанного в правильный
тетраэдр с ребром а.
Решение. Радиус основания конуса г равен
радиусу окружности, вписанной в правильный
а
треугольник со стороной а, и, значит, г = —j=.
Образующая конуса L равна высоте этого
треугольника, площадь которого, как известно ([1],
§ 14, п.6), равна
венство
откуда
а2Л
Следовательно, имеем ра-
1 Т а2Л
о аЬ = —-А—
L =
аЛ
Тогда искомая площадь равна
кгЬ =п
2Л
2
па
4
Шар и его площадь поверхности
Шаром называется тело, которое состоит из
всех точек пространства, находящихся на
расстоянии, не большем данного, от данной точки.
Эта точка называется центром шара, а данное
расстояние — радиусом шара и обозначается
буквой R. Граница шара называется шаровой
поверхностью, или сферой (рис. 99). Таким
образом, точками сферы являются все те точки ша-
Рис. 95
Рис. 96
Рис. 97
Рис. 98
Рис. 99

Краткое изложение школьного курса! математики
Геометрия. 10—11 классы
213
ра, которые удалены от его центра, называемого
также центром сферы, на расстояние, равное
радиусу шара, называемому также радиусом
сферы. Любой отрезок, соединяющий центр
шара с точкой шаровой поверхности, также
называется радиусом сферы (шара). Отрезок,
соединяющий две точки шаровой поверхности и
проходящий через центр шара (сферы), называется
диаметром сферы (шара). Концы любого
диаметра называются диаметрально
противоположными точками сферы (шара).
В сечении шара любой плоскостью а
получается круг; центр Ог этого круга есть основание
перпендикуляра, опущенного из центра шара О
на секущую плоскость (рис. 100), а его радиус г,
используя теорему Пифагора, можно вычислить
по формуле
г = Jr2 - оо\.
(5)
Если секущая плоскость проходит через центр
шара (диаметральная плоскость), то в сечении
получается круг, радиус которого равен радиусу
шара. Такой круг называется большим кругом.
Пример 1. Шар, радиус которого 15 см,
пересечен плоскостью на расстоянии 9 см от его
центра. Найти площадь сечения.
Решение. Пусть условию задачи отвечает
рисунок 100. Сечение шара плоскостью есть круг,
радиус которого находится по формуле (5).
Согласно условию задачи R = 15 см и ОО\ = 9 см.
Следовательно,
r=Vl52 - 92 = 7225 - 81 = 7Ш
и площадь сечения равна 144л см .
12
Пример 2. Через середину радиуса шара
проведена перпендикулярная ему плоскость.
Как относится площадь полученного сечения к
площади большого круга?
Решение. Пусть радиус шара R — радиус
круга в сечении АОх (рис. 101).
Треугольник ООхА прямоугольный, Z ООхА =
= 90°. Найдем радиус сечения:
Отношение площади этого круга к площади
большего круга равно:
v2
тсД'
3
4"
Шар, так же как цилиндр и конус, является
телом вращения.
Его можно получить, вращая полукруг
вокруг его диаметра как оси. При этом
полуокружность описывает шаровую поверхность, или
сферу (рис. 102).
Справедлива теорема:
ТЕОРЕМА
Площадь поверхности шара (сферы) равна
учетверенной площади большого круга, т. е.
S = 4яЯ2,
где R — радиус шара.
Пример 3. Как изменится площадь
поверхности шара, если его радиус увеличить: а) в 4 раза;
б) в 5 раз?
Решение. Пусть R — радиус шара. Тогда
площадь его поверхности S = 4яД . Если теперь
радиус шара увеличить в 4 раза, то будем иметь:
2 2
4n(4R) = 16 -4nR = 16S, т. е. площадь его
поверхности увеличится в 16 раз. Если же радиус
шара увеличить в 5 раз, то
4тс(5Д)2 = 25 • 4лД2 = 25S,
В
Рис. 100
Рис. 101
Рис. 102

214
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
т. е. площадь его поверхности увеличится в
25 раз.
Пример 4. Радиусы трех шаров равны 3 см,
4 см и 5 см. Определить радиус шара, площадь
поверхности которого равна сумме площадей их
поверхностей.
Решение. Имеем:
4я.32 + 47С.42 + 4тс-52 =
= 4тс(32 + 42 + 52) = 4тс • 50 = 4тс( 750 )2.
Отсюда следует, что искомый радиус равен
л/50 см.
Пример 5. Шар пересечен плоскостью,
расстояние которой от центра шара на 2 дм меньше
радиуса шара (рис. 103). Радиус круга,
полученного в сечении, равен 6 дм. Найти площадь
поверхности шара.
Решение. Пусть R — радиус шара. Тогда
расстояние секущей плоскости от центра шара
будет R - 2. Теперь из прямоугольного
треугольника АО'О согласно теореме Пифагора имеем:
(R - 2)2 + 36 = R2,
или
Д2-4Д + 4 + 36 = Д2,
откуда R = 10 и, значит, площадь поверхности
2
шара равна 400л дм .
Пример 6. Доказать, что площадь
поверхности тела, образованного вращением квадрата
вокруг стороны, равна площади поверхности
шара, радиус которого равен стороне квадрата.
Решение. Пусть а — сторона квадрата
(рис. 104). При вращении квадрата вокруг
стороны АВ получим цилиндр, радиус и высота
которого равны а. Поэтому площадь его полной
поверхности равна
2
2па(а + а) = Ana ,
т. е. равна площади поверхности шара, радиус
которого равен стороне квадрата.
Вписанный и описанный
многогранники
Плоскость, проходящая через точку А сферы
и перпендикулярная ее радиусу, проведенному в
эту точку, называется касательной плоскостью
к сфере. Точка А называется точкой касания
(рис. 105) сферы и плоскости.
Имеет место теорема, аналогичная теореме о
касательной к окружности ([1], § 11, п. 1).
ТЕОРЕМА
Касательная плоскость имеет с шаром
только одну общую точку — точку касания.
Пример 1. Радиус шара равен 16 см. Точка
находится на касательной плоскости на
расстоянии 63 см от точки касания. Найти ее
кратчайшее расстояние от поверхности шара.
Решение. Пусть условию задачи отвечает
рисунок 106. Так как касательная плоскость
перпендикулярна радиусу, проведенному в точку
касания, то треугольник ОАМ прямоугольный, в
котором ОА = 16 см, AM = 63 см. По теореме
Пифагора
ОМ
= а/162 + 632 = 7256 + 3969 =
= 74225 =65.
Рис. 103
Рис. 104
Рис. 105
Рис. 106

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
215
Теперь находим искомое кратчайшее
расстояние МК, где К — точка пересечения
отрезка ОМ с поверхностью шара. Имеем:
МК = ОМ - ОК = 65 - 16 = 49 (см).
Многогранник называется вписанным в шар
(сферу), если все его вершины лежат на
поверхности шара. Многогранник называется
описанным около шара (сферы), если все его грани
касаются поверхности шара.
Пример 2. В шар радиуса 4 см вписана
прямая треугольная призма. Основанием призмы
служит прямоугольный треугольник с углом а =
= 45°, и наибольшая ее боковая грань есть
квадрат. Найти площадь боковой поверхности
призмы.
Решение. Плоскости, содержащие основания
ВАС и В1А1С1 призмы, пересекают сферу по
окружностям (рис. 107).
Прямоугольные треугольники ABC и А1В1С1
вписаны в эти окружности. Поэтому гипотенузы
АВ и АгВг являются диаметрами окружностей.
Плоскость АВВгАх проходит через центр
шара. Так как по условию АВВХАХ есть квадрат, то
H=AAx=AB=Rj2 -4л/2.
Из прямоугольного треугольника ABC
найдем ВС и СА соответственно:
4W*o_4V2_V2 =
ВС =АВ sin а = 4^2 sin 45° =
AC =АВ cos а = 4^2 cos 45°= 4.
= 4,
Найдем площадь боковой поверхности
призмы:
S6oK = (ВС + СА + АВ) • ААХ = (4 + 4 + 4 J2) 4 J2 =
= 16(2+72)72 =16(272 +2) = 32(1+72) (см2).
Пример 3. Найти площадь поверхности
куба, описанного около шара, площадь поверхно-
2
сти которого равна 36я дм (рис. 108).
Решение. Обозначим радиус шара через R.
Тогда согласно условию задачи 4nR = 36я,
откуда R = 3 и, значит, диаметр шара равен 6 дм.
Его длина совпадает с длиной стороны куба, и
потому площадь поверхности куба равна 6-6 =
= 216 (дм2).
Контрольные вопросы
1. Объясните, что такое прямой круговой
цилиндр. Что такое боковая поверхность,
образующие, основания, высота, радиус, ось цилиндра?
2. Что представляет собой сечение цилиндра,
если секущая плоскость проходит через ось
цилиндра? Как называется такое сечение?
3. Что представляет собой сечение цилиндра,
если секущая плоскость перпендикулярна оси
цилиндра? Как называется такое сечение?
4. Объясните, что такое развертка боковой
поверхности цилиндра. Что принимается за
площадь боковой поверхности цилиндра?
5. Докажите, что площадь боковой
поверхности цилиндра равна произведению длины
окружности основания на высоту цилиндра.
6. Что называется площадью полной
поверхности цилиндра? Как ее вычислить, если даны
радиус и высота цилиндра?
7. Объясните, что такое прямой круговой
конус. Что такое основание, боковая поверхность,
вершина, образущие, ось и высота конуса?
8. Что представляет собой сечение конуса,
если секущая плоскость проходит через его ось?
Как называется такое сечение?
9. Что представляет собой сечение конуса,
если секущая плоскость перпендикулярна его
оси? Как называется такое сечение?
10. Что такое усеченный конус?
11. Объясните, что такое развертка боковой
поверхности конуса. Что принимается за
площадь боковой поверхности конуса?
12. Докажите, что площадь боковой
поверхности конуса равна половине произведения
длины окружности его основания на образующую.
13. Что называется площадью полной
поверхности конуса? Как ее вычислить, если даны
радиус его основания и образующая?
Г>г^
\
• + ^ 1
L ч ' \
Рис. 107
Рис. 108

Краткое изложение школьного
Геометрия. 10—11 классы
14. Как вычислить площадь боковой
поверхности усеченного конуса, если даны радиусы его
оснований и образующая?
15. Какая призма называется вписанной в
цилиндр?
16. Что называется касательной плоскостью
к цилиндру? Какая призма называется
описанной около цилиндра?
17. Какая пирамида называется вписанной в
конус?
18. Что называется касательной плоскостью
к конусу? Какая пирамида называется
описанной около конуса?
19. Какое тело называется шаром? Что такое
центр шара и его радиус?
20. Что такое шар и шаровая поверхность
(сфера); центр, радиус, диаметр шара (сферы)?
Какие точки сферы (шара) называются
диаметрально противоположными?
21. Что представляет собой сечение шара
плоскостью?
22. Какая плоскость называется
диаметральной плоскостью? Что такое большой круг шара?
23. По какой формуле находится площадь
поверхности шара? Во сколько раз эта величина
больше площади большого круга?
24. Какая плоскость называется касательной
к сфере? Какая точка называется точкой
касания сферы и плоскости?
25. Сформулируйте теорему о свойстве
касательной плоскости к шару.
26. Какой многогранник называется
вписанным в шар (сферу)?
27. Какой многогранник называется
описанным около шара (сферы)?
Упражнения
1. Высота цилиндра 6 см, радиус цилиндра
5 см. Найдите площадь сечения, проведенного
параллельно оси цилиндра на расстоянии 4 см
от нее.
2. Высота цилиндра 8 дм, радиус цилиндра
5 дм. Цилиндр пересечен плоскостью
параллельно оси так, что в сечении получился
квадрат. Найдите расстояние от этого сечения до
оси.
3. Радиус цилиндра 2 м, высота 3 м. Найдите
диагональ осевого сечения.
4. В цилиндре проведена параллельно оси
плоскость, отсекающая от окружности основа-
математики
ния дугу в 120°. Высота цилиндра равна 10 см,
расстояние от оси до секущей плоскости 2 см.
Найдите площадь сечения.
5. В цилиндре радиуса 5 см проведено
параллельное оси сечение, отстоящее от нее на
расстояние 3 см. Найдите высоту цилиндра, если
площадь указанного сечения равна 64 см .
6. Высота цилиндра на 10 см больше его
радиуса, а площадь полной поверхности равна
144я см . Найдите радиус цилиндра и его высоту.
7. Вычислите площадь полной поверхности
цилиндра, если радиус цилиндра равен 3 см, а
высота равна 4 см.
8. Какой высоты должен быть цилиндр, чтобы
площадь его боковой поверхности была в 3 раза
больше площади основания?
9. Полуцилиндрический свод подвала имеет
6 м в длину и 5,8 м в диаметре. Найдите
площадь полной поверхности подвала.
10. Радиус основания конуса 3 м, высота 4 м.
Найдите образующую и площадь осевого
сечения.
11. Образующая конуса I наклонена к
плоскости основания под углом 30°. Найдите высоту
и площадь осевого сечения.
12. Радиусы оснований усеченного конуса
равны 3 м и 7 м, образующая 5 м. Найдите
площадь осевого сечения.
13. Как относятся площади основания,
боковой поверхности и полной поверхности
равностороннего конуса?
14. По высоте Н равностороннего конуса
определите площадь его полной поверхности.
15. Площадь основания конуса Q и площадь
его осевого сечения М. Определите площадь
боковой поверхности конуса.
16. Радиусы оснований усеченного конуса
равны 3 м и 7 м, образующая 5 м. Найдите
площадь его полной поверхности.
17. Радиусы оснований усеченного конуса
равны йиг, образующая составляет с
плоскостью основания 45°. Найдите площадь его
полной поверхности.
18. В цилиндр вписан прямоугольный
параллелепипед. Найдите отношение площади
боковой поверхности цилиндра к площади
диагонального сечения параллелепипеда.
19. Вычислите площадь боковой поверхности
цилиндра, вписанного в куб с ребром а.

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
217
20. В равносторонний конус вписана
правильная четырехугольная пирамида. Как
относятся их боковые поверхности?
21. Определите боковую поверхность конуса,
вписанного в правильный тетраэдр с ребром а.
22. Шар, радиус которого 41 дм, пересечен
плоскостью на расстоянии 9 дм от центра.
Найдите площадь сечения.
23. Радиус шара R. Через конец радиуса
проведена плоскость под углом 60° к нему. Найдите
площадь сечения.
24. Радиус земного шара R. Чему равна
длина параллели, если ее широта 60°?
25. Площадь большего круга равца 1 м .
Найдите площадь поверхности шара.
26. Дан полушар радиуса R. Найдите
площадь его полной поверхности.
27. Гипотенуза и катеты служат радиусами
трех шаров. Какая существует зависимость
между площадями их поверхностей?
28. Во сколько раз нужно увеличить радиус
сферы, чтобы увеличить площадь сферы в
16 раз?
29. Найдите радиус шара, описанного около
куба со стороной а.
30. Измерения прямоугольного
параллелепипеда 2 см, 3 см и 6 см. Найдите радиус
описанного около него шара.
31. Около шара радиуса R описана
правильная шестиугольная призма. Определите ее
полную поверхность.
ОБЪЕМЫ МНОГОГРАННИКОВ
И ТЕЛ ВРАЩЕНИЯ
Понятие объема
Тело называется простым, если его можно
разбить на конечное число тетраэдров.
Примером простого тела является любой выпуклый
многогранник.
Дадим определение объема простых тел.
Объем простого тела — это положительная
величина, численное значение которой обладает
следующими свойствами:
1. Равные тела имеют равные объемы.
2. Если тело разбито на части,
являющиеся простыми телами, то объем этого тела
равен сумме объемов его частей.
3. Объем куба, ребро которого равно единице
длины, равен единице.
Если куб, о котором идет речь в определении,
имеет ребро 1 см, то объем будет в кубических
сантиметрах; если ребро куба равно 1 м, то объем
будет в кубических метрах.
Объем прямоугольного
параллелепипеда
Аналогично теореме о площади
прямоугольника (см. [1], § 14, п. 2) доказывается
следующая теорема:
ТЕОРЕМА
Объем прямоугольного параллелепипеда
равен произведению трех его измерений.
Следствие. Объем прямоугольного
параллелепипеда равен произведению площади его
основания на высоту.
Пример 1. Если каждое ребро куба увели-
о
чить на 2 см, то его объем увеличится на 98 см .
Чему равно ребро куба?
Решение. Обозначим ребро куба через х,
тогда
(х + 2)3 - х3 = 98, т. е. х2 + 2х - 15 = 0.
Уравнение имеет два корня: х = 3, х = -5.
Геометрический смысл имеет только
положительный корень. Итак, ребро куба равно 3 см.
Пример 2. Площадь полной поверхности ку-
ба равна 6 м . Найти его объем.
Решение. Так как площадь полной поверхно-
2
сти куба равна 6м , то площадь одной грани,
представляющей собой квадрат, равна 1м и,
значит, ребро куба равно 1 м. Отсюда объем куба
равен 1 м .
Пример 3. Площади трех граней прямо-
2 2
угольного параллелепипеда равны 2 м , 3 м и
2
6 м . Найти объем параллелепипеда.
Решение. Пусть х, у, г — измерения
параллелепипеда. Тогда в силу условия задачи имеем:
ху = 2,уг = 3, хг = 6,
откуда
(xy)-(yz)-(xz) = 2-3.6,
или
(хуг)2 = 36

218
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
и, значит, xyz = 6, т. е. объем параллелепипеда
а 3
равен о м .
Пример 4. Ребра прямоугольного
параллелепипеда относятся как 3:4:5. Определить его
2
объем, если его полная поверхность равна 94 ед .
Решение. Обозначим линейную долю одной
части через *. Тогда ребра прямоугольного
параллелепипеда содержат соответственно 3*, 4*,
Ъх. Согласно условию задачи имеем уравнение:
2(3* • Ах) + 2(4* • Ъх) + 2(3* • 5*) = 94,
или
94* = 94,
откуда * = 1 (* = -1 условию задачи не
удовлетворяет) и, значит, ребра параллелепипеда
соответственно равны 3, 4, 5. Следовательно, его
о
объем равен 60 ед .
Объем призмы
Предложение, сформулированное в следст-*
вии пункта 2, распространяется и на случай
любой призмы, а именно справедлива такая
теорема.
ТЕОРЕМА
Объем любой призмы равен произведению
площади ее основания на высоту:
V = SMH-H,
(1)
где SOCH— площадь основания и Н — ее
высота.
В случае прямой призмы высота равна длине
ее бокового ребра и объем прямой призмы равен
произведению площади основания на боковое
ребро.
Рис. 109
Пример 1. В прямом параллелепипеде
стороны основания а и Ъ образуют угол 30°. Боковая
поверхность равна S. Найти его объем.
Решение. Обозначим высоту
параллелепипеда через *, а высоту его основания, проведенную
к стороне Ь, — через у (рис. 109). Тогда
S = 2ах + 26*
и у = « (как катет, противолежащий углу в 30°).
Отсюда
= S
* 2(а + Ь)'
аЬ
а площадь основания параллелепипеда равна у
и, значит, согласно формуле (1) его объем равен
abS
4(а + Ь)'
Пример 2. Определить объем правильной
треугольной призмы, сторона основания
которой а, а боковая поверхность равновелика сумме
оснований.
Решение. Так как основанием призмы
является правильный треугольник со стороной а, то
его площадь равна —г— (см. [1], § 14, п.6).
Обозначим высоту призмы через Н; тогда согласно
условию задачи будем иметь:
тт <*<УЗ
откуда Н = -g- и, значит,
V =
а л/3 а*/3 а
6
8
Пример 3. Найти объем правильной
шестиугольной призмы, у которой наибольшая
диагональ равна d, а боковые грани — квадраты.
Решение. Обозначим длину стороны
основания призмы через а (рис. 110) и найдем
площадь основания. Как известно ([1], § 14, п.6),
площадь правильного многоугольника равна
половине произведения его периметра на радиус
вписанной окружности. Для правильного шес-
тиугольника этот радиус равен -у (см. [1], § 13,
п. 3); следовательно, площадь основания
с 1 *„ а& ЗТЗ 2
Soch=2 '6а'~ =~а '

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
219
Из прямоугольного треугольника ADDX по
теореме Пифагора получаем
AD\ = AD2 + dd\,
т. е.
j2 А 2 . 2 с 2 d
d =4а + а =5а,а = -т=,
л/5
и, значит, искомый объем
„ зТз 2 ъЛ ,з ЗЛ5 ,з
2 1075 50
Объем пирамиды
Справедлива следующая теорема.
ТЕОРЕМА
Объем, пирамиды равен одной трети
произведения площади ее основания на высоту:
v = з Soch ' н>
(2)
где S0CH — площадь основания и Н — ее
высота.
Примечание. Формула для вычисления
объема усеченной пирамиды имеет вид:
V=\h(Sx + S2+ JS^~S~2), (3)
где Н — высота пирамиды, Sx и S2 — площади
оснований.
Пример 1. Площадь основания пирамиды
равна 4,5 м . Найти объем этой пирамиды, если
ее высота равна 2 м.
Решение. Согласно формуле (2) в силу
условия задачи
F=|.4,5.2 = 3(M3).
о
Итак, объем данной пирамиды равен 3 м .
Пример 2. Периметр основания правильной
четырехугольной пирамиды равен 12 м, высота —
5 м. Найти объем этой пирамиды.
Решение. Основанием данной пирамиды
является квадрат, периметр которого по условию
равен 12 м. Значит, его сторона равна 3 м, а пло-
щадь 9 м . Теперь согласно формуле (2) находим
объем данной пирамиды:
V= | .9-5 = 15 (м3).
Пример 3. Объем правильной четырехуголь-
ной пирамиды равен 125 см , высота пирамиды —
15 см. Найти сторону основания пирамиды.
Решение. Из формулы (2) находим
S -^
°осн ft •
Согласно последней формуле в силу условия
задачи получаем
е 3 125 ок, 2,
Soch = -fg"" = 25 (СМ )f
а так как основанием пирамиды служит
квадрат, то сторона основания пирамиды равна 5 см.
Пример 4. Найти объем правильного
тетраэдра с ребром а.
Решение. Рассмотрим прямоугольный
треугольник SOC, где SO — высота тетраэдра
(рис. 111). По теореме Пифагора
so = Jsc2 - ОС2.
Но SC = а, ОС = -= (как радиус описанной
V3
окружности, [1], § 13, п.З) и потому
rv-i /га аЛ
so = r -"т/г
7з
Далее, так как площадь равностороннего тре-
2
а
-27з
угольника ABC равна . , то объем данного
тетраэдра
1 а2Л аЛ а Л
V =
Л 12
Пример 5. Сколько литров воды вмещает
водоем, имеющий форму правильной четырех-

220
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
угольной усеченной пирамиды, если глубина его
равна 1,2 м, а стороны оснований — 10 м и 5 м?
Решение. Так как основания усеченной пи-
2
рамиды — квадраты, то их площади 100 м и
25 м . Теперь согласно формуле (3) имеем:
V= | -1,2(100 + 25+ 7100-25) =
= 0,4-175 = 70 (м*),
или
V = 70 000 дм*.
Учитывая, что удельный вес воды равен 1,
заключаем, что водоем вмещает 70 000 л воды.
Объем цилиндра, конуса и шара
Как известно (см. [1], § 14, п. 7), при
неограниченном увеличении числа сторон вписанного
в окружность правильного многоугольника его
площадь стремится к площади круга,
ограниченного этой окружностью. Это, в частности,
используется при установлении теорем 1 и 2.
ТЕОРЕМА 1
Объем цилиндра равен произведению
площади его основания на высоту, т. е.
V = S-H = nR'H,
(4)
где R — радиус цилиндра и Н — его высота.
ТЕОРЕМА 2
Объем конуса равен одной трети
произведения площади его основания на высоту, т. е.
v=\soch*h=\kr2h,
(5)
где R — радиус основания конуса и Н — его
высота.
Справедлива и следующая теорема:
ТЕОРЕМА 3
Объем шара равен произведению площади
его поверхности на треть радиуса, т. е.
Г=|тсЯ3,
(6)
где R — радиус шара.
Пример 1. Во сколько раз объем одного
цилиндра больше объема другого, если при
одинаковых высотах радиус первого цилиндра вдвое
больше радиуса второго?
Решение. Согласно формуле (4) имеем:
V1 = nR21H, V2 = kR22H.
Так как Rx = 2Д2» то
V1 = 4nRlH
и
4kR22H
%r\ Н
= 4.
Итак, объем первого цилиндра больше
объема второго цилиндра в 4 раза.
Пример 2. Цилиндрическое ведро имеет
внутренний диаметр 25 см и высоту 40 см.
Сколько литров воды оно вмещает?
Решение. Объем ведра
у = п(Щ • 40 = 6250л (см3),
или
V = 6,25 • тс (дм3) ~ 20 (дм3).
Так как удельный вес воды равен 1, то ведро
вмещает 20 л.
Пример 3. В цилиндр вписана правильная
треугольная призма (рис. 112). Найти
отношение объема цилиндра к объему призмы.
Решение. Так как цилиндр и призма имеют
одинаковую высоту, то отношение их объемов
(эти объемы обозначим соответственно через Vx
и V2) равно отношению площадей оснований
(эти площади обозначим соответственно через Sx
hS2):
Рис. 112

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
221
Далее имеем:
Si = kR ,
где R — радиус цилиндра;
где а — сторона правильного треугольника,
вписанного в окружность радиуса R.
2
Но R = -= и, значит, St = 71-5- . Следовательно,
II = J*ZL ^2 4
Пример 4. Найти объем цилиндра,
вписанного в правильную шестиугольную призму,
каждое ребро которой равно а.
Решение. Высота цилиндра равна боковому
ребру призмы, т.е. Н = а.
Радиус цилиндра равен радиусу окружности,
вписанной в правильный шестиугольник со
стороной а, т. е.
г =
1л/3
Объем цилиндра:
лг а2 3 3 з
Пример 5. Высота конуса равна 4, а диаметр
основания — 6. Определить объем конуса.
Решение. Так как диаметр основания конуса
равен 6, то его радиус равен 3. Теперь согласно
формуле (5) имеем:
V= g -9я-4 = 12тс.
Пример 6. Осевым сечением конуса служит
равнобедренный прямоугольный треугольник,
площадь которого равна 9 м . Найти объем
конуса.
Решение. Обозначим через R радиус
основания конуса, а через Н — высоту конуса. Так как
осевое сечение конуса — равнобедренный
прямоугольный треугольник, то угол ВСО (рис. 113)
равен 45° и, значит, прямоугольный
треугольник ВОС — равнобедренный. Поэтому R = Н.
Теперь согласно условию задачи
2Д-Л
откуда R = 3 и, следовательно, искомый объем
V= | -я-32-3 = 9л(м3).
Пример 7. Найти объем усеченного конуса,
радиусы основания которого Rx и R2 (R2 < R\), а
высота Н.
Решение. Дополним данный усеченный
конус до полного (рис. 114). Пусть х — его высота.
Объем усеченного конуса равен разности
объемов двух полных конусов: одного — с радиусом
основания Rx у. высотой х, другого — с радиусом
основания R2 и высотой х - Н. Далее, из
подобия треугольников (рис. 114) имеем:
X Rl
RXH
х — Н R2 R\ ~~ R2
Объем усеченного конуса равен
к 3
2 R\H 2
я р _ -_- _ kR9
{ Ч - *2 2
( RiH
,Д1 " R2
д3 - я3
Пример 8. Площадь поверхности шара равна
2
225л м . Определить его объем.
Решение. Пусть R — радиус шара. Согласно
условию задачи имеем:
S = 4яЯ* = 2257С,
15
откуда R = у и, значит, согласно формуле (6)
искомый объем равен
т. 4 fl5\8 1125 , з,
v=3n[Y) -—*<м).
= 9,
Рис. 113
Рис. 114

222
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
Пример 9. Радиусы трех шаров равны 3 см,
4 см и 5 см. Определить радиус шара, объем
которого равен сумме объемов этих шаров.
Решение. Найдем сумму объемов шаров с
радиусами 3 см, 4 см и 5 см. Имеем:
|тс.33-Н |тс43-!- |тс53= |тс-27Ч-
+ | я-64+ | • 125=|я. 216=| тс-б3.
Отсюда следует, что искомый радиус равен
6 см.
Пример 10. Доказать, что если радиусы трех
шаров относятся как 1 : 2 : 3, то объем большего
шара в 3 раза больше суммы объемов двух
меньших шаров.
Решение. Пусть Нг — радиус меньшего из
данных трех шаров. Тогда радиусы второго и
третьего шаров будут 2RX и 3RX и, значит,
объемы трех шаров выразятся следующим образом:
vx - t **\ >v2 = t п(2Яг)3 , V3 = | ШЗЯ,)3 .
Отсюда
30^ + V2) = g7i(3i*f + 24Д3) =
= |tc.27*i = |tc (3^)3 =F3,
что и требовалось доказать.
Контрольные вопросы
1. Сформулируйте свойства объема для
простых тел.
2. Как вычислить объем прямоугольного
параллелепипеда, если даны: а) три его
измерения; б) площадь его основания и высота?
3. Напишите формулу для объема: а) любой
призмы; б) пирамиды; в) усеченной пирамиды.
Объясните смысл входящих в каждую из
формул букв.
4. По какой формуле вычисляют объем: а)
цилиндра; б) конуса; в) шара? Объясните смысл
входящих в каждую из формул букв.
Упражнения
1. Если каждое ребро куба уменьшить на
3 см, то его объем уменьшится на 117 см . Чему
равно ребро куба?
2. Поверхность куба равна 54 дм .
Определите объем куба.
3. Площади трех граней прямоугольного па-
2 2
раллелепипеда равны 750 см , 1800 см и
540 см . Найдите объем параллелепипеда.
4. Определите объем прямоугольного
параллелепипеда, если его диагональ равна 35 см, а
ребра относятся как 2:3:6.
5. Основанием прямого параллелепипеда
является ромб, площадь которого S. Площади
диагональных сечений Sx и S2. Найдите объем
параллелепипеда.
6. Основанием наклонной призмы является
равносторонний треугольник со стороной а;
одна из боковых граней перпендикулярна
основанию и является ромбом, у которого меньшая
диагональ равна с. Найдите объем призмы.
7. По стороне основания а и боковому ребру b
определите объем правильной призмы: а)
треугольной; б) четырехугольной; в)
шестиугольной.
8. Определите объем правильной
треугольной призмы, если ее боковое ребро равно высоте
основания, а площадь сечения, проведенного
через них, равна Q.
9. По стороне основания а и боковому ребру Ъ
определите объем правильной пирамиды: а)
треугольной; б) четырехугольной; в)
шестиугольной.
10. Основание пирамиды — прямоугольник
со сторонами 9 м и 12 м, все боковые ребра
равны 12,5 м. Найдите объем пирамиды.
11. Боковое ребро правильной
шестиугольной пирамиды равно 1,4 м. Сторона ее
основания равна 0,2 м. Найдите объем пирамиды.
12. Найдите высоту усеченной пирамиды, ес-
ли ее объем равен 310 см , а площади оснований
32 см и 98 см .
13. Высота усеченной пирамиды равна 15 см;
ее объем равен 475 см ; площади оснований
относятся как 4:9. Найдите эти площади.
14. Определите объем цилиндра, если его
боковая поверхность равна Р, а длина окружности
основания равна с.
15. Радиус цилиндра равен 4 см, площадь осе-
вого сечения 72 см . Найдите объем цилиндра.
16. В цилиндр вписана правильная
треугольная призма, а в призму вписан цилиндр.
Найдите отношение объемов цилиндров.

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
223
17. Осевым сечением конуса служит
равнобедренный прямоугольный треугольник, площадь
которого равна 9 м . Найдите объем конуса.
18. В конус вписана правильная
четырехугольная пирамида, а в пирамиду вписан конус.
Найдите отношение объемов конусов.
19. Объем усеченного конуса равен 584я см ,
а радиусы 10 см и 7 см. Определите высоту
конуса.
20. В усеченном конусе найдите радиусы
оснований и образующую, если они относятся как
4:11: 25, а объем равен 181л м .
21. Как изменится объем шара, если его
радиус увеличить: а) в 4 раза; б) в 5 раз?
22. По объему А шара определите его
поверхность.
23. Площади поверхностей двух шаров
относятся как т : п. Как относятся их объемы?
24. Сосуд имеет форму полушара радиуса Я,
дополненного цилиндром. Какой высоты должна
быть цилиндрическая часть, чтобы сосуд имел
объем А?
ПРЯМОУГОЛЬНАЯ СИСТЕМА
КООРДИНАТ И ВЕКТОРЫ
В ПРОСТРАНСТВЕ
Прямоугольная система координат
в пространстве
Прямоугольная (или декартова) система
координат в пространстве задается тройкой
попарно перпендикулярных координатных осей,
имеющих общее начало в точке О и одинаковый
масштаб. Оси координат в пространстве обычно
обозначают Ох, Оу, Ог. В пространстве
возможны правые (рис. 115, а) и левые (рис. 115, б)
системы координат; мы будем использовать правую
систему координат.
Координатные плоскости хОу, уОг, хОг
делят пространство на восемь октантов.
Координаты х, у, г точки Р в пространстве
определяются аналогично координатам на
плоскости: это координаты (на соответствующих осях)
оснований Рх, Ру, Рг перпендикуляров,
опущенных из точки Р на оси Ох, Оу, Ог, —
соответственно абсцисса, ордината и аппликата.
Координаты обычно указывают в скобках: Р(х; у; г).
Между точками в пространстве и тройками их
координат имеется взаимно однозначное соответствие.
Расстояние между двумя точками А(хх\ уг; гг)
и В(х2; у2; *2) в пространстве определяется с
помощью теоремы Пифагора:
АВ -J(xx - х2)2 + (уг - у2)2 + (гг - г2)2. (1)
В частности, расстояние от любой точки Р(х;
у; г) до начала координат равно
РО
-I
2,2,2
х + у + г .
(2)
Если А (хг; уг; гг) и В (х2; у2; г2) — две
произвольные точки пространства и С (х; у; г) —
середина отрезка АВ, то аналогично случаю
плоскости (см. [1], § 8, п.4) координаты точки С
определяются по формулам
Уг +^2
X =
h + *2
У =
г =
21 + 22
(3)
Пример 1. Даны точки А (1; 2; 3), В (0; 1; 2),
С (0; 0; 3) и D (1; 2; 0). Какие из этих точек
лежат: а) в плоскости хОу; б) в плоскости уОг; в) на
осиОг?
Решение, а) У точек плоскости хОу
координата г равна нулю (рис. 116). Поэтому только
точка D лежит в плоскости хОу.
sx
\р„
а)
б)
Рис. 115
Рис. 116

224
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
б) У точек плоскости уОг координата х равна
нулю. Поэтому точки В и С лежат в плоскости
уОг.
в) У точек оси Ог две координаты х и у равны
нулю. Поэтому только точка С лежит на оси Ог.
Пример 2. Найти расстояние от точки (1; 2; -3)
до: а) координатных плоскостей; б) осей
координат; в) начала координат.
Решение, а) Пусть А (1; 2; -3) и ААХ —
расстояние от А до плоскости хОу, т. е. Аг (1; 2; 0),
так как ААХ ± хОу и Ах принадлежит плоскости
хОу. Тогда по формуле (1)
ААХ = л/(1 - I)2 + (2 - 2)2 + (0 + З)2 = 3.
Аналогично
ААо = & > -""3 =
б) Пусть ААХ — расстояние от А до оси Ох,
тогда Ах (1; 0; 0), откуда
ААХ = л/о2 + (-2)2 + З2 = ЛЗ.
Аналогично
ААу = л/10 , ААг = л/5 .
в) Так как О(0; 0; 0), то согласно формуле (2)
АО = д/l2 + 22 + (-3)2 = л/П.
Пример 3. Найдите точку D (х; у; 0),
лежащую в плоскости хОу и равноудаленную от
трех данных точек:
А (0; 1; -1), В (-1; 0; 1), С (0; -1; 0).
Решение. Имеем:
AD2 = (х - О)2 + (у - I)2 + (0 + I)2,
BD2 = (х + I)2 + (у - О)2 + (0 - I)2,
CD2 = (х - О)2 + (I/ + I)2 + (0 - О)2.
Приравнивая первые два расстояния
третьему, получим два уравнения для определения х
и у:
-4у +1 = 0, 2х - 2у + 1 = 0.
Отсюда у = j » х = ~7 " искомая точка D (-т ;
i;0).
Пример 4. Найти координаты вершины 2>
параллелограмма ABCD, если координаты трех
других его вершин известны:
А (2; 3; 2), В (0; 2; 4) и С (4; 1; 0).
Решение. Найдем координаты точки М
середины АС по формулам (3)
v - 2 + 4 - я „ - 3 + * - 9 , - 2 + ° - 1
х = —2— = о, у g Z, г = —g— = 1,
т. е. М(3; 2; 1).
Диагонали параллелограмма пересекаются и
точкой пересечения делятся пополам, т. е. точка
М принадлежит также BD и ВМ = MD; тогда,
используя формулы для нахождения координат
середины BD, получим:
0 + Хг
,2 =
2 + VD
,1 =
4 + z.
2 '" 2
т. е. xD = 6, i/д = 2, 2D = -2.
Следовательно, D (6; 2; -2).
Пример 5. Доказать, что четырехугольник
ABCD с вершинами в точках
А (1; 3; 2), В (0; 2; 4), С (1; 1; 4), D (2; 2; 2) -
параллелограмм.
Решение. Как мы знаем, четырехугольник, у
которого диагонали пересекаются и точкой
пересечения делятся пополам, есть
параллелограмм. Воспользуемся этим для решения
задачи. Координатами середины отрезка АС будут:
1+1 , 3+1 0 2+4 Q
х = -g- = 1, у = -g- =2,2 = —$- = 3.
Координатами середины отрезка BD будут:
0 + 2 ; 2 + 2 0 4 + 2 Q
х = —£- =l,i/ = —£- =29г = —$- = 3.
Мы видим, что координаты середин отрезков
АС и BD равны. Значит, эти отрезки
пересекаются и точкой пересечения делятся пополам.
Следовательно, четырехугольник ABCD —
параллелограмм.
Преобразования фигур
в пространстве
Понятие преобразования фигур в пространстве
определяется так же, как и на плоскости (см. [1],
§ 10, п. 3). Так же как и на плоскости,
определяются преобразования симметрии относительно
точки и прямой ([1], § 6, п. 6), гомотетия и
преобразование подобия ([1], § 10, п. 3).
Кроме симметрии относительно точки и
прямой в пространстве рассматривается еще один
вид симметрии: точки М и М' называются
симметричными относительно плоскости ос, если
отрезок ММ' перпендикулярен этой плоскости

Краткое изложение школьного курса математики
Геометрия. 10—11 классы
225
и делится пополам в точке пересечения с ней
(рис. 117).
Фигура F симметрична фигуре F
относительно плоскости ос, если все точки F
симметричны точкам JF" относительно этой плоскости
(см. рис. 117), которая называется плоскостью
симметрии. Примеры таких фигур: шар, куб,
цилиндр, прямая призма.
Пример 1. Дана точка (1; 2; 3). Найти точку,
симметричную данной относительно
координатной плоскости хОу.
Решение. Точка, симметричная точке (1; 2; 3)
относительно плоскости хОу, лежит на прямой,
перпендикулярной плоскости хОу. Поэтому у
нее те же координаты х и у: х = 1, у = 2.
Симметричная точка находится на том же
расстоянии от плоскости хОу по другую сторону от нее.
Поэтому координата г у нее отличается только
знаком, т. е. z = -3.
Итак, точка, симметричная точке (1; 2; 3)
относительно плоскости хОу, будет (1; 2; -3).
Параллельным переносом в пространстве
называется такое преобразование, при котором
произвольная точка (х; у; г) фигуры переходит в
точку (х + а; у + Ь; г + с), где а, Ъ, с —
постоянные. Параллельный перенос в пространстве
задается формулами
х' = х + а, у' = у + 6, z' = z +с, (4)
выражающими координаты х', г/, г' точки, в
которую переходит точка (х; у; г) при параллельном
переносе. Так же как и на плоскости ([1], § 10,
п. 3), имеют место следующие свойства
параллельного переноса:
1. При параллельном переносе точки
смещаются по параллельным (или совпадающим)
прямым на одно и то же расстояние.
2. При параллельном переносе каждая
прямая переходит в параллельную ей прямую (или
в себя).
Пример 2. Найти значения а, Ь, с в
формулах параллельного переноса (4), если при этом
параллельном переносе точка А(1; 0; 2)
переходит в точку А'(2; 1; 0).
Решение. Подставляя в формулы (4)
координаты точек А и А', т. е. х = 1, у =0, г = 2, х' = 2,
у' = 1, г' = 0, получим уравнения, из которых
определяются а, Ь, с:
2 = 1 +а, 1 =* 0 + 6, 0 = 2 +с.
Отсюда а = 1, b = 1, с = -2.
Новым для параллельного переноса в
пространстве является следующее свойство:
При параллельном переносе в пространстве
каждая плоскость переходит либо в себя, либо
в параллельную ей плоскость.
Доказательство. Пусть а — произвольная
плоскость. Проведем в этой плоскости две
пересекающиеся прямые а и Ь. При параллельном
переносе прямые а и Ъ переходят либо в себя,
либо в параллельные прямые а' и V. Плоскость
а переходит в некоторую плоскость а',
проходящую через прямые а' и V. Если плоскость а' не
совпадает с а, то по теореме 3 из п. 2 § 1 она
параллельна а. Утверждение доказано.
Векторы в пространстве
Вектор в пространстве определяется точно
так же, как и на плоскости (см. [1], § 9).
Основные понятия для векторов в пространстве
(например, абсолютная величина вектора,
равенство векторов), а также действия сложения и
вычитания векторов и умножения вектора на
число определяются без каких-либо изменений по
сравнению с этими определениями для векторов
на плоскости.
Как и для векторов на плоскости, в
пространстве имеет место разложение
а = xi + yj + zk, (5)
где i, у, k — единичные векторы, имеющие
направления координатных осей, причем
коэффициенты в равенстве (5) (числа х, у и г)
определяются единственным образом и называются
координатами вектора 3, что записывают в виде
3{х; У\ г}. При этом
|3|-Л
х2 +
2 . 2
У + 2 ,
(6)
8-1019

226
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
—> Пример 3. Найти длину вектора 3{2; 3; -6}.
Координаты вектора АВ, заданного двумя Решение. По формуле (6) получаем:
точками А (хх\ уг; гг) и В (х2; у2; г2), равны разно-
стям соответствующих координат точек А и В и, 131 = ^22 + З2 + (-б)2 =
значит,
\ав\ -
= V4 + 9 + 36 = 749 = 7.
1 /7~ ^ .2 2 2 Пример 4. Найти длину вектора АВ, если
-</(*«- *i> + (lf2 *i)+(*2 ^i)-(7> А(3;5;1)иВ(5;6;3).
Скалярным произведением векторов а{хг; уг; Решение. Применяя формулу (7), найдем:
гх} и Ъ{х2\ у2\ z2l (обозначение а Ъ) называется
число
♦ JAB| = л/(5 - З)2 + (6 - 5)2 + (3 - I)2 =
т. е.
*i*2 + ViVs + «А. = 74 + 1+4 = Л = 3.
a ft = лг1лг2 + У1У2 + з^г- (8) Пример 5. Найти единичный вектор, колли-
Так же как и на плоскости, скалярное произ- неарный вектору 3{2; 1;-2} и одинаково с ним
ведение векторов равно произведению их абсо- направленный.
лютных величин на косинус угла между вектора- Решение. Единичный вектор, коллинеарный
ми т е вектору а и одинаково с ним направленный, оп-
аЪ = \а\ \Ъ\ cos а, (9) а „ ,-,
1111 _ ределяется равенством а0 = щ. Но | а \ =
где а — угол между векторами а и Ъ. 1а1
Пример 1. Даны три точки А (1; 0; 1), В (-1; = 74 + 1+4 = 3. Следовательно, искомый
1; 2), С (0; 2; -1). Найдите точку D (х; у; г), если _ (2 1 21
т£ ТГХ ^ вектор есть а0 i «; «; -я [ -
известно, что: а) векторы АВ и CD равны; б) сум- \* 6 6)
ма векторов АВ и CD равна нулевому вектору. Пример 6. При каком значении k данные
Решение. Имеем: , векторы а{2; -1; 3} и ft{l; 3; k) перпендикуляр-
_> -U ны?
MB {-1 - 1; 1 - 0; 2 - 1}, CD {х - 0; у - 2; 2 + 1}, Решение. Условие перпендикулярности^двух
или векторов а и & определяется равенством aft = 0
АВ {-2; 1; 1}, CD {х; у - 2; г + 1}. или в СИЛУ Формулы (8) равенством
) _> 2-1+(-l)-3 + 3-fc =0,
а) Равенство CD = АВ означает, что х =-29
i/-2 = l,г + 1 = 1; таким образом, искомая точ- откуда k = g .
KaD(-2;3;0).
б) Равенство АВ + CD = 0 означает, что х - ПРимеР 7г Най™, ска? я^ое произведение
-2-0,х-2;(у-2)+1-0,у-15(ж + 1) + 1- векторов а и Ь, если |а| = 4, 6| = 6, аугол меж-
= 0, г = -2; следовательно, D (2; 1; -2). д* э™ми векторами равен 45 .
Решение. По формуле (9) имеем:
Пример 2. Три точки А, В и М удовлетворя-
— — v _^_» /2 у—
ют условию AM = ХМВ (X * 0). Доказать, что а& = 4 • 6 • cos 45° = 24 • у = 12 V2 .
эти точки лежат на одной прямой.
Решение. Из равенства AM = ХМ В следует, Контрольные вопросы
что векторы AM и MB коллинеарны, поэтому 1. Что значит задать прямоугольную систему
прямые AM и MB либо параллельны, либо сов- координат в пространстве?
падают, и, следовательно, точки А, В и М лежат 2. Как определяются координаты точки в
на одной прямой. пространстве? Как они называются?

Краткое изложение школьного курса математики
' * Геометрия. 10—11 классы
227
3. Напишите формулу расстояния между
двумя точками в пространстве.
4. Напишите формулы для вычисления
координат середины отрезка по координатам его
концов.
5. Какие две точки называются
симметричными относительно плоскости?
6. Какие фигуры называются
симметричными относительно плоскости? Приведите
примеры фигур, обладающих плоскостью симметрии.
7. Что такое параллельный перенос в про-,
странстве?
8. Перечислите свойства параллельного
переноса в пространстве, отметив среди них новое
свойство по сравнению со случаем плоскости.
9. Что называют координатами вектора в
пространстве?
10. Как выражается модуль вектора в
пространстве через его координаты?
11. Чему равны координаты вектора в
пространстве, заданного двумя точками?
12. Что называется скалярным
произведением двух векторов в пространстве, заданных
своими координатами?
Упражнения
1. Как расположены относительно системы
координат точки А(2; 0; 0), В(0; -5; 0), С(0; 0; -1),
Я(0; 2; 2), Д(5;-5; 0)?
2. На оси Оу найдите точку, равноудаленную
от точек Л(1; -3; 7) и Б(5; 7; -3).
3. На оси Oz найдите точку, равноудаленную
от точек А(4; -1; 2)иВ(0; 2; -1).
4. Найдите длину отрезка, начало которого в
начале координат, а конец — в точке (6; -2; 3).
5. Найдите длину отрезка, соединяющего
точки А(2; 0; -1) и В(3; -2; 1).
6. Даны координаты одного конца отрезка
А(2; 3; -1) и его середины С(1; 1; 1). Найдите
координаты второго конца отрезка В(х; у; г).
7. Даны три последовательные вершины
параллелограмма А(1; 1; 4), В(2; 3; -1), С(-2; 2; 0).
Найдите четвертую вершину D.
8. Докажите, что четырехугольник ABCD
является параллелограммом, если: 1) А(0; 2; -3),
В(-1; 1; 1), С(2; -2; -1), D(3; -1; -5); 2) А(2; 1; 3),
В(1;0;7),С(-2;1;5),Я(-1;2;1).
9. Даны вершины А(3; 2; -1), В(5; -4; 7) и
С(-1; 1; 2) треугольника ABC. Вычислите длину
медианы, проведенной из вершины С.
i 10. Дана точка (4; -3; 1). Найдите точку,
симметричную данной относительно
координатной плоскости хОг.
11. При параллельном переносе точка А(2; 1;
-1) переходит в точку Ах(1; -1; 0). В какую
точку переходит, начало координат?
12. Даны четыре точки: А(2; 7; -3), В(1; 0; 3),
С(-3; -4; 5), D(-2; 3; -1). Укажите среди
векторов АВ , ВС, DC, АС и BD равные векторы.
13. Даны векторы а{-3; -1; 2} и с{5; -2; 7}.
Найдите координаты векторов: а) 2а; б) -3 + Зс.
14. Выясните, принадлежат ли точки А(2; -3;
5), В(4; 7; -9), С(1; -8; 12) одной прямой.
15. Найдите длины векторов: а) а{1;-1;1};
б) &{2; 1; -3}; в) с{0; 1; -1}; г) d{0; -2; 0}.
16. Найдите единичный вектор, коллинеар-
ный вектору 3{3; 4; 0} и противоположно с ним
направленный.
17. Найдите скалярное произведение
векторов а{-2; 3;Ч} и &{5; 7; -4}.
18. Перпендикулярны ли векторы: а) а{-2; 1; 3}
и &{6; -5; 7}; б) с{6; 0; 12} и d{-8; 13; 4}.
19. Найдите скалярное произведение
векторов а и Ь, если \а\ =3, |&| =5,а угол между
этими векторами равен: а) 135°; б) 90°; в) 180°.
20. Найдите косинус угла между векторами
а{-1;2;-2}иЬ{6;3;-6}.
ОТВЕТЫ И УКАЗАНИЯ
Прямые и плоскости в пространстве
1.Указание. Прямая, пересекающая две
данные параллельные прямые, имеет с плоскостью,
проходящей через эти параллельные прямые, две
общие точки. 2. Указание. Используйте задачу
4 из п. 2 § 1. 3. 25 см. 4. 15 см. 5. 15 см и 41 см.
6.120 м. 7.
в) 7 м.
/72 2
*1Ъ - а
8. 37 м. 9. а) 13 м; б) 8 м;
Углы между прямыми
и плоскостями.
Многогранные углы
1. 60°. 2. а) 50°; б) 59°. 3. a) 2h; б) hjl. 4. а Л ,
5. 30°. 6. 110°. 7. 2а. 8.60°.

228
Краткое изложение школьного курса математики
Геометрия. 10—11 классы
Многогранники
1. 7,5 см. 2. Qj2. 3. 156 см2. 4. 2 м. 5. a) Sab +
2 к
+ ^-^ ; б) 4аЬ + 2а2. 6. aj2, 2а. 7.14 м. 8. 288 см2.
9. 4 м, 8 м, 12 м. 10. т(7з + 72). 11. 3 см. 12. 7 см.
13. л/b2 - а2 . 14.14 см2.15. | л/зь2 - а2 .16. 56 см
2- Ь2
и 24 см. 17. —-j . 18. Увеличится в 16 раз.
19. ал/4Л2+ а2 + а2. 20. 288 см2. 21. 256 м2. 22. \ .
23.1,8 м и 4 м. 24. 20 см и 10 см.
Тела вращения
1. 36 см2. 2. 3 дм. 3. 5 м. 4. 40 «/З см2. 5. 8 см.
6. 4 см и 14 см. 7. 42я см2. 8. Я - | А 9. » 116 м2.
2 г~
10. 5 м, 12 м2. 11. ^, -Ь^ . 12. 30м? 13. 1: 2:3.
Объемы многогранников
и тел вращения
1. 5 см. 2. 27 дм3. 3. 27 000 см3 = 27 дм3.
4.4500см3. 5.V- /—i^?. 6. \acjl2a2 - Зс2.
т, v Л/3 2, -V 2, v Зл/3 2, О Л /Q Л ч Л
7. а) ^ а &; б) а &; в) — а Ь. 8. ЯД . 9. a) jg х
х л/з&2 - а2 ; б)»-л/4Ь2-2а2; в) у л/з(Ь2-а2).
10. 360 м3. 11. 48 дм3. 12. 5 см. 13. 20 см2 и 45 см2.
14. ^. 15. 114л см3. 16. 4 : 1. 17. 9 тем3. 18. 2 : 1.
4Л
19. 8 см. 20. 2 м, 5» м, 12^ м. 21. Увеличится а) в
64 раза; б) в 125 раз. 22. 3д/зблА2. 23.
:*}п , или mjm : njn . 24.—5 ~ 5 А
лД2 3
Г1
14. лЯ? 15. >Jq2+k2M2. 16. 108л м2. 17. л(Д* +
+ г2) + 72я(Д* - г2). 18. л. 19. ла2. 20. л : 77.
2 „2
21. л^. 22. 16л м2. 23. Щ-. 24. лА 25. 4 м2.
4 4
26. ЗлД . 27. Площадь большей поверхности равна
сумме двух других площадей. 28. В 4 раза.
29. \ajl. 30. 3,5 см. 31.12Д27з .
Прямоугольная система координат
и векторы в пространстве
1. Точка А лежит на оси Ох, В — на оси Оу, С —
на оси Oz, D — на плоскости уОг, Е — на
плоскости хОу. 2. (0;jj;0). 3. (0;0;|). 4. 7. 5. 3
6.(0;-1; 3). 7. D(0; 0; 5). 9. Тзб. 10. (4; 3; 1)
11. (-1; -2; 1). 12. АВ , DC . 13. а) -6; -2; 4; б) 18; -5
19. 14. АВ = -2АС; да. 15. а) J3; б) УП; в) Л
г) 2. 16. -pi - ft J-|; -|; о|. 17. 7. 18. а) Нет; б)
19. а) -Цр ; б) 0; в) - 15. 20. \ .
да,

Задачи
по основным разделам
школьного
курса математики
помогут повторить материал,
изученный на уроке

Разнообразные задачи
и упражнения,
охватывающие все
основные разделы
математики, алгебры
и начал анализа, геометрии,
помогут закрепить
навыки решения задач
и повторить материал,
изученный в средней
школе.

Математика. 5—6 классы
5 КЛАСС
Отрезок, прямая, луч.
Числовой луч
1. Начертите отрезок АВ. Измерьте его.
Отметьте на нем точку С. Измерьте отрезки АС и
ВС. С помощью сложения найдите длину
отрезка АВ.
2. Постройте отрезок КР = 3 см 7 мм.
Начертите луч ОС. На луче ОС отложите отрезок ОМ,
равный КР.
3. На рисунке
изображены отрезок АВ, прямая CD и
луч MN. Пересекаются ли:
а) отрезок АВ и прямая
CD;
б) прямая CD и луч MN;
в) луч MN и отрезок АВ?
4. На координатном
луче, единичный отрезок которого равен длине
половины клетки, отметьте точки А(2), D(5),
РЦО).
5. Сколько различных отрезков можно
назвать, глядя на рисунок?
В F Е S
6. Сколько натуральных чисел расположено
между числами 27 и 83?
Сложение и вычитание
натуральных чисел
7. Выполните действия:
а) 3 756 478 + 19 354 793;
б) 50 247 653 - 7 457 748;
в) 27 538-16 379+ 13 621.
Выберите из трех полученных ответов
наибольшее число. Запишите его.
8. Туристы были в походе три дня. Во второй
день они прошли 18 км, что на 5 км меньше, чем в
первый день, а в третий день они прошли на 19 км
меньше, чем за два первых дня. Сколько
километров прошли туристы за три дня?
9. Вася и Коля собирали белые грибы. Вася
нашел 43 белых гриба, а Коля на а белых грибов
больше. Сколько всего белых грибов нашли
мальчики?
Составьте буквенное выражение. Найдите
его значение при а = 7; 16.
10. Одна сторона прямоугольника 29 см, а
вторая в 2 раза больше. Найдите периметр
прямоугольника.
11. Два робота делают 2 детали за 2 ч.
Сколько деталей сделают четыре таких робота за 4 ч?
12. Запишите в виде математического
равенства предложение:
«Число т на с больше числа пь.
Буквенные выражения
13. Решите уравнение:
а) 320-*= 176;
б) т + 294 = 501;
в) (i/ + 383) -479 = 332.
14. Упростите выражение:
а) 376 + у + 128; б) 573 - (а + 173).
15. На автостоянке было х машин. Когда с
нее уехало 27 машин и приехало 19, то стало
63 машины. Сколько машин было на
автостоянке первоначально?
16. Если к числу а прибавить 13, то эта сумма
будет на 27 меньше числа 50. Найдите число а.
17. Уменьшаемое на 15 больше разности.
Чему равно вычитаемое?
18. Миша спросил Ваню: «Сколько подъездов
в твоем доме?» Ваня ответил: «Если к моему
подъезду подходить слева, то он по счету будет
седьмой, а если справа, то пятый». Так сколько
же подъездов в доме Вани?
Умножение и деление
натуральных чисел
19. Вычислите:
а) 37 • 908-8816:29;
6)22 378-1378:13 • 97.

Задачи
Математика. 5—6 классы
20. Упростите выражение:
а) 96 • т • 5; б) а • 280 • 40.
21. Решите уравнение:
а) 9826 : х = 34; б) Зх - 432;
в) 8* -34 = 118.
22. Два взрослых медведя и пять медвежат
вместе имеют массу 635 кг. Найдите массу
одного взрослого медведя, если масса одного
медвежонка 35 кг.
23. Сумма чисел хи516на219 больше
разности чисел 1023 и 639. Найдите число х.
24. Угадайте корень уравнения
х • х- 5 • х = 0.
Все действия
с натуральными числами
25. Найдите значение выражения:
32 002 - 509 • 37 + 8816 : 29.
26. Решите уравнение:
а) 3* + 9х = 372;
б) 2Ъу -9у + 78 = 350;
в) 208 : (91 - а) = 4.
27. Упростите выражение и найдите его
значение при т = 20; 38:
256 + 87/п - 29т.
28. У Саши в двух карманах лежат орехи.
Всего 70 штук, причем в правом кармане в 4 раза
больше, чем в левом. Сколько орехов лежит у
Саши в левом кармане?
29. При каком значении х верно равенство
(8 - 5) • х = 8 • х - 5 • 4?
30. Незнайка решает задачу:
На сколько меньше произведение чисел а и 6,
чем произведение чисел а + 1 и Ы
Помогите Незнайке решить эту задачу.
Делимость натуральных чисел
31. Укажите, какие из чисел 7514, 12 570,
256068 и 2055 делятся на 2, 3, 4, 5, 6, 9, 10.
32. Запишите все делители числа 14.
Запишите все делители числа 35.
Есть ли у них общие делители? Какой из
общих делителей можно назвать наибольшим
общим делителем чисел 14 и 35?
33. Для числа 12 запишите все его
двузначные кратные.
34. Выполните деление с остатком числа
22 860 на число 56.
35. Незнайке нужно найти число, которое
делилось бы на 6, на 9 и на 10. Помогите Незнайке
найти это число.
36. Число а разделили на 8. В частном
получили 13, а в остатке 6. Найдите делимое а.
Формулы
37. а) Найдите путь s, если скорость v = 24 км/ч
и время t = 4 ч.
б) Найдите время t9 если путь s = 3 км и
скорость v = 20 м/с.
в) Найдите объем куба, если его сторона b =
= 6 см.
38. Длина футбольного поля 100 м, а ширина
на 40 м меньше. Найдите площадь футбольного
поля.
39. Длина прямоугольного параллелепипеда
равна 8 см, ширина на 2 см меньше, чем длина,
а высота в 2 раза больше, чем ширина. Найдите
объем прямоугольного параллелепипеда.
40. Переведите:
2
а) в квадратные метры 200 000 см ; 20 а;
б) в килограммы 20 т; 3 ц; 60 000 г;
в) в часы 2 недели.
41. Числа а и Ъ связаны формулой
& = 3 • а + 19.
Найдите:
а) 6, если а = 17;
б) а, если Ъ = 46.
42. Число х разделили на 5. Получившееся
частное умножили на 10, а полученное
произведение разделили на 4. Как и во сколько раз
изменилось число х1
Доли и дроби
43. Начертите координатный луч. За
единичный отрезок возьмите 6 клеток. Отметьте точки
А(0), В(1), С(2), л(|), -Eg), F[\),K[ly
Сравните дроби:

Задачи
Математика. 5—6 классы
233
ч 1 2
а) § и з;
«ч 1 1
б) з и g
44. Рабочим нужно отремонтировать
участок дороги длиной 60 км. За первый месяц они
отремонтировали jo Дороги. Сколько
километров дороги было отремонтировано за первый
месяц?
45. В туристический поход отправились 20 пя-
4
тиклассников, что составило ■= всех учащихся
класса. Сколько всего человек в классе?
46. а) Какую часть гектара составляют 1 а;
623 м2?
б) Какую часть часа составляют 7 мин; 23 с?
в) Какую часть от 3 м составляют 29 см?
г) Какую часть суток составляют 30 мин?
47. При каких натуральных значениях п
дробь —= правильная?
48. Кубический метр разрезали на
кубические сантиметры и поставили их друг на друга.
Какой высоты получилась башня?
Сложение и вычитание
обыкновенных дробей.
Смешанные числа
49. Выполните действия:
. П _ _5 _3^
а' 13 13 13'
6)12f7-(5f7 + 3^);
8 «12,fi4
В)719"319 +619-
50. Путешествуя по травяным джунглям, Ка-
рик и Валя должны были пройти 30 м до ручья.
В первый день они прошли 12 о» м, а во второй
7
день Ю од м. Какое расстояние им осталось
пройти?
51. Решите уравнение:
а) - = 5;
б)х + 5± =Ц +6±.
52. Маленькая Маша никак не может
разделить число 30 на 7. Помогите ей.
53. Миша купил несколько апельсинов и
угостил ими своих пятерых товарищей. Каждому
3
из его товарищей досталось по 2 г апельсина.
Сколько апельсинов купил Миша?
54. Некоторое число больше своей половины
на 7. Найдите это число.
Сложение и вычитание
десятичных дробей
55. Начертите координатный луч. За
единичный отрезок возьмите 10 клеток. Отметьте
точки А(0), В(1), С(0,3), 2)(0,65), #(0,5), Я(М),
М(g). Сравните дроби 0,5 и « •
56. Сравните:
а) 0,63 и 0,6284; б) 12,067 и 12,1.
57. Выполните действия:
а) 23,47-19,584+ 10,2;
б) 401 - (0,83 + 81,2 - 12,163).
58. Скорость ветра 2,85 м/с. Чайка летит по
ветру со скоростью 8,3 м/с. С какой скоростью
она будет лететь против ветра?
59. Можно ли назвать такое число х, чтобы
выполнялось неравенство
0,32 <х< 0,33?
Если можно, назовите такое число. Если
нельзя, объясните.
60. Упростите выражение
х +0,4*+ 0,5*- \х.
Умножение и деление
десятичных дробей
61. Выполните действия:
а) 0,604 • 87; б) 29,082 • 75;
в) 19,773: 39; г) 9 : 20.
62. Вычислите 80,3 - 4,2 : 25 • 40.
63. 4 моржа и 3 морских льва имеют массу
5,85 т. Найдите массу моржа, если масса
морского льва равна 0,35 т.
64. Решите уравнение:
а) 39,5 - 4х = 23,8; б) (х - 6,7): 8 = 5,03.

234
Задачи
Математика. 5—6 классы
65. Юра живет в 3 км от парка. Обычно он
ходит со скоростью 4 км/ч. Сможет ли он дойти до
парка за 40 мин?
1
= 4.
66. Решите уравнение
Все действия
с десятичными дробями
67. Выполните действия:
а) 57,08 • 3,9; б) 0,043 • 20,8;
в) 33,947 : 8,3; г) 0,13 : 0,052.
68. Вычислите
(30,09-23,6) -4,5-7: 12,5.
69. Из двух городов навстречу друг другу
одновременно вышли два поезда, причем скорость
одного из них 102,5 км/ч, а скорость другого на
8,2 км/ч меньше, чем скорость первого. Через
сколько часов после начала движения поезда
встретятся, если расстояние между городами
492 км?
70. Решите уравнение
3,9+ 5,2*-1,6*= 18,48.
71. Скорость моторной лодки по течению реки
15,2 км/ч, а против течения 13,5 км/ч. Найдите
собственную скорость моторной лодки и
скорость течения реки.
72. В каком случае результат будет больше и
во сколько раз, если некоторое число поделить
на 0,6 или если это же число поделить на 0,3?
Проценты
i
\ 73. Шахматистам на проведение партии
дается 4 ч. Через некоторое время шахматистов
предупредили, что до конца партии осталось 30%
времени. Сколько времени уже длится эта
партия?
74. Нина читает книгу. Когда она прочитала
35 страниц, она подсчитала, что это составляет
14% всей книги. Сколько всего страниц в книге?
\ 175. Мише надо было решить 20 задач, из них
ощуже решил 13 задач. Сколько процентов всех
задач уже решил Миша?
76. Что больше: 2% от 4 или 0,4% от 1?
77. Число а на 50% больше числа Ъ. Во
сколько раз число а больше, чем число Ь?
78. Запишите в виде десятичной дроби 2 т %.
Измерение углов
79. На рисунке изображен Z.AOB.
а) Определите величину угла АОВ «на глаз».
б) Измерьте этот угол с помощью
транспортира.
в) Найдите разность между двумя
результатами.
г) Что вы можете сказать про свой глазомер?
В
80. Постройте с помощью транспортира
/L COD = 118° и /L MAN, который на 28° меньше,
чем Z. COD.
81. Найдите величину угла РЕК, если
известно, что он равен -g прямого угла. Постройте
Z. РЕК и проведите в нем биссектрису ЕН.
82. Луч ВК делит развернутый угол АВМ на
два угла: /.АВК и Z КВМ, причем Z АВК в
5 раз меньше, чем Z. КВМ. Найдите эти углы.
83. Какой угол составляют часовая и минутная
стрелки, когда часы показывают ровно 8 часов?
84. Сколько процентов развернутого угла
составляет половина прямого угла?
Масштаб.
Среднее арифметическое
85. Расстояние между Москвой и Киевом
равно 820 км. Какой длины будет отрезок на
карте, выражающий расстояние между
городами, если масштаб карты 1 : 4 000 000?
86. На карте расстояние между островом
Пасхи и побережьем Южной Америки
выражается отрезком длиной 3,1 см. Найдите
расстояние на местности от острова Пасхи до берега
Южной Америки, если масштаб карты равен
1 : 95 000 000.

Задачи
Математика. 5—6 классы
235
87. Первое число равно 5,2. Второе число
составляет 40% первого числа. Найдите среднее
арифметическое этих двух чисел.
88. Автомобилист ехал 3 ч со скоростью
85 км/ч, 2 ч со скоростью 90 км/ч и 5 ч со
скоростью 80 км/ч. Найдите среднюю скорость
автомобиля.
89. Первое число равно х, второе число —
7,2, а третье число — 8,4. Среднее
арифметическое этих трех чисел равно 8. Найдите число х.
90. 40% некоторого числа меньше, чем само
это число, на 9. Найдите это число.
6 КЛАСС
Разложение на простые множители.
Наибольший общий делитель.
Наименьшее общее кратное
1. Найдите значение выражения
80,1 -75,48: (40 -21,5) • 7,6.
2. Разложите на простые множители число
4680.
3. Найдите наибольший общий делитель
чисел 1260 и 7800.
4. Найдите наименьшее общее кратное чисел
48 и 90.
5. Приведите пример числа, которое имеет
ровно 5 делителей.
6. Применив алгоритм Евклида, найдите
наибольший общий делитель чисел 800 и 60.
Найдите наименьшее общее кратное этих чисел.
Сложение и вычитание дробей
с разными знаменателями
7. Приведите дроби к наименьшему общему
знаменателю:
ч 5 7
а' 8 и 12 ;
*ч 6 9 ч 3 5 2
б)^ип; в) z ; g и £ .
4' 6 "9
8. Сократите дробь:
f\ 15 •
б)225'
. 21
аЧо;
в>^
9. Сравните дроби:
ч 3 4 _ 8 11
а>5И7; б)15 и20;
10. Выполните действия:
Л±4 лч 7 2 ч 5 , 13
а>6+5; б)10-5; В>9+Г5;
р)1?+2|; Д)17}-8|; е)12£-8§+б|.
11. На приготовление уроков Коля затратил
2 ч. Из них на математику т^ ч, на русский
язык л ч и : ч на устные предметы. Остальное
время Коля просто смотрел в окно. Сколько
времени Коля смотрел в окно?
12. Решите уравнение
1
Х~2
= 2.
Умножение
обыкновенных дробей
13. Выполните действия:
ч 9 2
а)16 * 3'
б)|-2; в)б| • 1^.
14. Найдите значение выражения
л1 д. 2 я6 *3
42+3 #37-54-
2 1
15. Упростите выражение ~ * + 11 х + 0>5х и
найдите его значение при х = 10.
16. Решите уравнение:
а>18П-*-в15;
б) 19 : (х - 4g) = 6.
17. Турист шел 0,2 ч со скоростью 4,5 км/ч и
5 ч со скоростью 5 о км/ч. Сколько всего
километров прошел турист?
18. Найдите хотя бы одно число х такое, что:
0,5 <х< g.
Действия с обыкновенными дробями.
Нахождение части от числа
в)з и 0,3.
19. Найдите значение выражения:
а) 8,25-зЦ; 6)0,12 • 4^; B)(l,5 - |] • 2

236
Задачи
Математика. 5—6 классы
20. Найдите:
5 3
а) ^ отЗО^;
6)32% отЗ^,
21. Ира собирала клубнику. За первый час
она собрала 3 г кг, что вЬ раза меньше, чем за
7
второй час. Ягоды Ира отнесла бабушке, a ttj кг
собранной клубники съела. Сколько
килограммов клубники Ира отдала бабушке?
22. Упростите выражение
0,6 • 2^*+ уХ.
23. В магазин привезли 480 кг яблок. В
первый день продали ц всего количества яблок, во
второй день 75% оставшихся, остальные яблоки
продали в третий день. Сколько килограммов
яблок продали в третий день?
24. Решите уравнение
1
х +
= 0,8.
Деление обыкновенных дробей
25. Выполните деление:
а' 15 ' 35 '
6>ФФ
чл 6
г>4:1з-
в)6^ : 5;
26. Найдите значение выражения
«!*Ф(»й-»1)->1-
всего выстрелов сделал Толя и сколько раз он
попал в цель?
30. Число а увеличили на 2 g %. Во сколько
раз увеличилось число а?
Все действия с дробями
31 Найдите значение выражения
0,8: 2| - 0,12
| 1,26 + 0,08
32. Сколько процентов составляет число « от
числа g ?
33. Велотрасса состоит из трех участков:
равнинного, подъема в гору и дороги под уклон.
Длина участка под уклон составляет 75% от
длины подъема в гору, а равнинный участок в
2 з раза длиннее, чем участок трассы под уклон.
Найдите длину каждого участка, если длина
всей велотрассы 74 км.
34. Кирилл собирает модель корабля за 3 ч, а
его брЬт Антон может собрать эту модель за 5 ч. За
какое время Антон и Кирилл могут собрать эту
модель, работая вместе?
35. Длина отрезка АС составляет 26% длины
отрезка АВ. Найдите длину отрезка АВ, если ВС
больше АС на 2,4 м.
А
С
—•—
В
27. Решите уравнение:
a)2g :*=lg;
в)|* + 0,5* = б|
б>5*-21*
28. В ноябре средняя продолжительность дня
3
составляет г от продолжительности ночи.
Сколько времени в ноябре длится день и
сколько ночь?
29. Толя был в тире, g всех его выстрелов
были точными, а 20 раз он промахнулся. Сколько
36. Сравните g числа 31 и число 25,83.
Пропорция.
Прямая и обратная
пропорциональности
37. Решите уравнение:
3* 8-2-
67 14
а) 2,4 : х = 0,3 : 5,6; б) -\ = -^ .
33

Задачи
Математика. 5—6 классы
237
38. Какую часть составляет разность чисел «
и 0,25 от их суммы?
39. На пошив 7 платьев для кукол пошло 2 ~ м
ткани. Сколько метров ткани уйдет на пошив
9 таких же платьев?
40. Если путешественник будет идти от
деревни А до города В со скоростью 4,5 км/ч, то он
затратит на весь путь 2,5 ч. Сколько времени
пробудет в пути путешественник, если ой пойдет
со скоростью 3 км/ч?
Ответ запишите в часах и минутах.
41. В бидоне было 5,5 л молока. Из него
отлили некоторое количество молока. Отношение
оставшейся части молока к его первоначальному
количеству равно 0,4. Сколько литров молока
отлили?
42. На сколько процентов число 120 меньше
числа 150? На сколько процентов число 150
больше, чем число 120?
Окружность и круг
43. Найдите значение выражения
,2>
16-1?
44. Сравните:
и я;
а>2+3
(l2,2 - lo|) : 0,25.
в>2 и |:8.
45. Радиус круга равен 8,4 см. Найдите
площадь круга и длину соответствующей
окружности.
(Значение числа к и результаты вычислений
округлите до сотых.)
46. Длина окружности, ограничивающей аре-
цу цирка, равна 81,64 м. Найдите площадь
арены. (п~ 3,14.)
47. На сколько метров увеличится длина
окружности, если радиус окружности увеличить
на 1 м?
48. Шаг шестиклассника на 20% короче
шага десятиклассника, но в единицу времени он
делает на 20% шагов больше, чем
десятиклассник. Кто из них раньше придет в школу, если
они живут в одном доме и выходят в школу
одновременно?
Положительные
и отрицательные числа.
Модуль числа
49. Отметьте на координатной прямой точки
М(6), К(-2), £(-5,5), С(2). Какие из отмеченных
точек имеют противоположные координаты?
Можете ли вы назвать какую-нибудь точку с
координатой меньшей, чем -5,5?
50. Сравните числа:
а) 5,9 и -5,93; б)-12,08 и -12,8;
в)-71
и
«I
51. Найдите значение выражения:
а)
: |0,2|;
б)
-15^
-8
52. С помощью координатной прямой
сложите числа:
а) 3 и -5; б) -4 и -3; в) -5,5 и 8.
53. Назовите число х такое, что
-1<х<-1-
54. Сколько целых чисел расположено
между числами -39 и 54?
Сложение и вычитание
положительных
и отрицательных чисел
55. Выполните действия:
а)-4,3+ 1,6;
b)7|-9J;
6)-2g -(-3);
г)-4,13-2,1;
д)-1,5-(-0,3)+ 1,7.
56. Найдите значение выражения:
("4 + 3g]-(-2,8-0,8).
57. Решите уравнение:
а) х-4,7--12; 6)lg -у-2§.
58. Найдите расстояние между точками:
а)С(-5) и D(lfj;
б)М(-2,3) и N(-4,08).
59. Найдите значение выражения
1-2 + 3-4 + 5-6 + 7-8 + 9-10 + 11-12.

238
Задачи
Математика. 5—6 классы
60. Решите уравнение
|*-3| = 2.
Умножение и деление
положительных
и отрицательных чисел
61. Выполните действия:
а)-0,4 • (-0,65); б) в| • (-0,5);
Ч А 5 ( 1 3 "\ Ч ~0'25
в)-4?:[-1п]; г)-^.
62. Найдите значение выражения
-1,7-21,06: (-5,2)-8 • 1,3.
63. Решите уравнение:
а) 2*+ 0,7 = 0;
б)-3*-5^ =0.
2
64. Разность между числами -«их равна
разности между числами -8,6 и -5,4. Найдите
число *.
65. Решите уравнение:
ч 2 4 Л
а) * -д^О;
б)|*|-|*|я.
66. При каких значениях * верна запись
|*|--х?
Раскрытие скобок.
Решение задач
с помощью уравнений
67. Раскройте скобки и найдите значение
выражения
23,4 - (-5,6 + 7,4) + (-13,6 - 1).
68. Упростите выражение:
а)-2,5 • * • | -2§ • ОД*;
б) -3,5 • (4а - 26) + 2,4 • (-За - 5,26).
69. Решите уравнение:
а) -8* - 3 = -6* + 10;
б) 2,5 ■ (3* - 2) - 4 • (2* + 0,5) = -4.
70. Маша и Даша собирали вишню. Маша
собрала в 4 раза больше, чем Даша. Но когда она
отдала 3,9 кг вишни Даше, ягод у девочек стало
поровну. Сколько килограммов вишни собрала
каждая девочка?
71. Моторная лодка шла 0,4 ч по озеру и 0,3 ч
по течению реки, скорость течения которой
2 км/ч. Всего моторная лодка прошла 9 км.
Найдите ее собственную скорость.
72. Если от данного числа отнять 2, то g
получившегося числа будет равна данному числу.
Найдите данное число.
Решение задач
с помощью уравнений
73. Решите уравнение
0,5 • (3* - 5) = 8 - 0,4 • (6 - 2,5*).
74. Сумма двух чисел равна 7. Найдите эти
два числа, если 60% одного из них равны ^
другого числа.
75. От куска материи длиной 30 м отрезали
несколько метров, а затем еще g оставшейся
части. Сколько метров отрезали в первый раз,
если всего отрезали 22 м?
76. Ребята были в туристическом походе три
дня. В первый день они прошли 40% всего мар-
5
шрута, во второй день g оставшегося пути, а в
третий день последние 13,5 км. Найдите
расстояние, пройденное ребятами за три дня.
77. При каком значении * верна пропорция
* + з\ 2* - ъ\
4 7 '
78. Число а разбили на два слагаемых,
причем первое слагаемое составляет 40% числа а.
На сколько процентов второе слагаемое больше
первого?
Пересечение прямых.
Координатная плоскость
79. Начертите в тетради прямую АВ и
отметьте точку С как показано на рисунке.
Проведите через точку С прямую Z, параллельную пря-

Задачи
Математика. 5—6 классы
239
мой АВ, и прямую т, перпендикулярную
прямой АВ.
— 9. 42. Уменьшилось в 2 раза. 44. 25 км. 45. 25
человек. 46. а)
623
7 23
29
1
В
80. Постройте угол МКР, равный 120°.
Отметьте внутри угла МКР точку А так, чтобы
угол АКМ был прямым. Найдите величину угла
АКР.
81. Постройте угол С2Ж, равный 45°. На луче
DC отметьте точку В. Через точку В проведите
прямую, параллельную стороне DE.
82. Отметьте на координатной плоскости
точки А(0; 5), В(-9; -1), С(2; -7) и £>(-5; 0).
Проведите прямые АВ if CD. Найдите координаты
точки пересечения прямых АВ и CD.
83. Найдите величину угла, равного 5%
развернутого угла.
84. Какую часть развернутого угла
составляют 30% прямого угла?
ОТВЕТЫ
5 класс
5. Шесть отрезков. 6. 82 - 27 — 55 чисел.
7. а) 23 111 271; б) 42 789 905; в) 24 780. 8. 63 км.
9. 43 + (43 + а); при а — 7 всего 93 гриба; при а = 16
всего 102 гриба. 10. Р = 174 см. 11. Роботов станет в
2 раза больше, и время увеличится в 2 раза, значит,
число деталей увеличится в 4 раза: 2 • 4 — 8 деталей.
12. т- с = п или т = с + п или т-п — с. 13. а) х — 144;
б) т = 207; в) у = 428.14. а) у + 504; б) 400 - а. 15. 71
машина. 16. а = 10.17.15.18.11 подъездов. 19. а) 33 292;
б) 12 096. 20. а) 480 т; б) 11 200 а. 21. а) х = 289; б) х =
= 144; в) х - 19. 22. 230 кг. 23. х = 87. 24. х = 0 или х =
= 5. 25. 13 473. 26. а) х - 31; б) у - 17; в) а - 39.
27. 256 + 58т; при т = 20 значение выражения равно
1416, при т - 38 равно 2460. 28.14 орехов. 29. При х =
= 4. 30. На 6. 31. На i делятся 7514, 12 570, 256 068;
на 3 — числа 12 570, 256 068 и 2055, на 4 — число
256 068, на 5 — числа 12 570 и 2055, на 6 — числа
12 570 и 256 068, на 9 — число 256 068, на 10 —
число 12 570. 32. Общие делители 1 и 7. Наибольший
общий делитель 7. 33.12; 24; 36; 48; 60; 72; 84; 96.34.408
и 12 в остатке. 35. Например, число 90. 36. а — 8 • 13 +
+ 6 = 110. 37. а) 96 км; б) 150 с - 2 мин 30 с; в) 216 см3.
38. 6000 м2. 39. 576 см3. 40. а) 20 м2; 2000 м2;
б) 20 000 кг; 300 кг; 60 кг; в) 336 ч. 41. а) Ь = 70; б) а =
100 ' 10000 ; б)60 ; 3600 ; в) 300 ; г) 48 "
47. При п = 1, 2, 3. 48. 1 м3 = 1 000 000 см3, высота
9 3
башни равна 1 000 000 см = 10 км. 49. а) =-= ; б) Зз-= ;
в) 10. 50. 7^ м. 51. а) х = 11; б) х = 5^. 52. 4^.
3 13
53. 2 г = -г-, значит, 13 апельсинов поделили на
5 человек. 54. х - ~ х = 7, тогда х = 14. 57. а) 14,086;
б) 331,133. 58. 2,6 м/с. 59. Например, х = 0,327.
60. 1,4 х. 61. а) 52,548; б) 2181,15; в) 0,507; г) 0,45.
62. 73,58. 63. 1,2 т. 64. а) х = 3,925; б) х = 46,94.
65. 3 : 4 = 0,75 ч = 45 мин. Не сможет. 66. х = 0,55.
67. а) 222,612; б) 0,8944; в) 4,09; г) 2,5. 68. 28,645.
69. Через 2,5 ч. 70. х = 4,05. 71. Собственная скорость
лодки 14,35 км/ч, скорость течения реки 0,85 км/ч.
72. Результат будет больше в 2 раза, если число
поделить на 0,3. 73. 2,8 ч или 2 ч 48 мин. 74. 250 страниц.
75. 65%. 76. Больше 2% от 4. 77. а = Ь + 0,5Ь - 1,56,
т. е. число а больше Ь в 1,5 раза. 78. 2 т % = 2,25% =
= 0,0225. 81. Z РЕК = 72°. 82. Z. АВК = 30°,
45 1
<LKBM = 150°. 83. 120°. 84. ^ = j = 0,25 = 25%.
85. 20,5 см. 86. 2945 км. 87. 3,64. 88. 83,5 км/ч.
89. (х + 7,2 + 8,4): 3 = 8, х - 8,4. 90. х - 0,4* - 9, х -
= 15.
6 класс
1. 49,092. 2. 2 • 2 • 2 • 3 • 3 • 5 • 13. 3. 60.
4. 720. 5. Например, 16 = 24. 6. 800 : 60 = 13 (ост.
20); 60 : 20 - 3 (ост. 0), НОД (800; 60) = 20;
нок(800; щ = нодТаоо^бО) - 240°- 7- а) U и
14 66 63 .2730 JL я \ _L м -L
24 ; б) 77 И 77 ; В) 36 ' 36 И 36 " а) 20 ; } 15 ;
3 348111 29
в)20-9а)5>7:б)Т5<20:в)3>0'3-10-а)30:
3 19 17 7 7 1
б)Т0;в)145;г)456;д)89;е)1424-П130 Ч ИЛИ
1 ч 2 мин. 12. х = 3. 13. а) |; б) 1 ^ ; в) 10. 14. 1 ^ .
15. 2^2 х - 24g . 16. а) х = 6|g ; б) х = 7\ . 17. 2 j-g км.
5 11
18. Например, х = 0,6. 19. а) 4ут>; б) « '> в) 3§ "
20. а) 21^; б) 1^. 21. 8^ кг. 22. 2х. 23. 48 кг.

240
Задачи
Математика. 5—6 классы
24. х = ~ . 25. a) 4g ; б) д ; в) 1 \ ; г) ъ\ . 26. 10— .
2 2
27. а) х - 2g ; б) х = 65 ; в) х - 8. 28. 9ч — день, 15ч —
ночь. 29. Всего 45 выстрелов, 25 из них — в цель.
613
13
13
9
30.102g : 100 = ш = \ш. В 1Ш раза. 31. ^
или 0,225. 32. 80%. 33. Длина равнинного участка
39 км, подъема в гору — 20 км, а участка под уклон —
7 5
15 км. 34. За 1 g ч. 35. АВ = 5 м. 36. g числа 31 равны
25^ = 25,833... > 25,83. 37. а) х = 44,8; б) х = 7^ .
38. = часть. 39. 3 м. 40. 3,75 ч или 3 ч 45 мин. 41. 3,3 л.
42. tjq - °>8> т- е- 12° меньше 150 на 20%; j^ =
-1,25, т. е. 150 больше 120 на 25%. 43. 4,5.
44. а) | + g < я; б) т > g : 3. 45. 221,6 см2 и 52,8 см.
46. 530,66 м2. 47. 2л(Д + 1) = 2nR + 2к > 2лД на
2л ~ 6,28 м. 48. Пусть шаг десятиклассника равен х, а в
единицу времени он делает п шагов. Тогда за это время
он проходит расстояние х% п. Шаг шестиклассника
равен 0,8х, а число шагов 1,2и, тогда пройденное им
расстояние равно 1,2и • 0,8х в 0,96хи < хп. Поэтому
раньше в школу придет десятиклассник. 49. Точки К
и С. 50. а) 5,9 > -5,93; б) -12,08 > -12,8; в) -7j < -7g
51. а) 11; б) 6 j|. 52. а) -2; б) - 7; в) 2,5. 53. Напри
мер, х = -0,4. 54. 92 числа: 38 отрицательных, 53
5 5
положительных и число 0. 55. а) -2,7; б) ^ ; в) -1^
г) -6,23; д) 0,5. 56. 2^ . 57. а) х - -7,3; б) у - ~
58. а) б|; б) 1,78. 59. -6.60. х = 5 или х - 1. 61. а) 0,26
б) -4g; в) 3~; г) -~ или 0,3125. 62. -16,15
63. а) х - -0,35; б) х = -1 j|. 64. 2~ . 65. а) х - |
о
или х = -5;б)х = 1,х = -1,х = 0.66. При х < 0. 67. 7.
68. а) -1 jg х; б) -21,2а - 5,48Ь. 69. а) х = -6,5; б) х =
= -6. 70. 10,4 кг и 2,6 кг. 71. 12 км/ч. 72. -1. 73. х -
= 16,2. 74. 4,5 и 2,5. 75. 18 м. 76. 60 км. 77. При х =
= 45,5. 78. Первое слагаемое — 0,4а, второе — 0,6а.
0,6а
0,4а
= 1,5, следовательно, второе слагаемое больше
первого на 50%. 80. L АКР - 30°. 82. (-6; 1). 83. 9°.
84. 15% или 5q .

Алгебра- 7—9 классы
7 КЛАСС
Повторение
1. Вычислите:
а)13^ -9g; б)5±-1^;
в) 3,5 - 4,8 + (-21,7) - (-13,5);
г) 0,3036: (-0,23); д)5,5-1^ :(l3|-9g).
2. Решите уравнение:
а) х + 0,7 = 0,53; б) 0,83 - у = 1;
в) 0,083 •* = 83; г) ± =-|;
д) 2х + Зх = 20; е) (х - 3): 2 = 11;
ж) i -(16-у) = 4.
3. Найдите:
а) 23% от числа 15;
б) число, 45% которого равны 50,25;
в) какой процент составляет 25 от 400.
4. В двух вагонах поезда 60 человек. Сколько
человек в каждом, если в первом вагоне на 12
человек больше, чем во втором?
5. Решите пропорцию 15 : х = 12 : 8.
6. В семи одинаковых мешках содержится
343 кг картофеля. Сколько весит картофель в
четырех мешках?
7*. На координатной плоскости отметьте
точки М(0; 8), N(-3; 0), jST(3; 2) и найдите длину
отрезка оси ординат внутри треугольника MNK.
Числовые выражения
8. Найдите значение выражения 5х + Ту:
ч 3 4 «ч 4 3
а) при х = g, у = ^ ; б) при х = ^, у = g .
9. Сравните значения выражений:
v _7_ _ (1_ _ 2\ J_ (2 _ 1\
*' 39 ЦЗ 3) И 39 [З 13J'
б)5+8 :4HU + 8j:4-
10. Упростите выражение, раскрыв скобки:
а) (76 + За) + (8& - 5а) - 106 + 2а;
б) 8а + (За - 2) - (5а - 2); в) 7 + 2(3* - 4).
11. Найдите число, которое, при увеличении
его на 17, увеличивается в 10 раз.
12. Периметр прямоугольника Р см, а одна
из его сторон 0,17 Р.
а) Найдите другую сторону этого
прямоугольника.
б) Чему равны стороны прямоугольника,
если Р = 50?
13*. Какова должна быть последняя цифра
пятизначного числа, делящегося на 13, если
первые четыре цифры этого числа четверки?
Линейные уравнения
14. Решите уравнение:
а) \х = 13; б) 8* +0,15 = 2,1;
в) 2,1 = 8* + 0,5; г) 13* - 15 = 1х - 5;
д)15-(3*-1) = 40;
е) 8* - (2х + 4) = 2(3* - 2).
15. Среди чисел 1, 2, 3, -1 выберите корни
2
уравнения х - 2х - 3 = 0.
16. При каких значениях т выражения
Зт + 7 и 5 - 7т принимают одно и то же
значение? Для каждого такого т найдите это
значение выражений.
17. Мастер за час делает на 4 единицы
продукции больше, чем ученик. После того, как
ученик проработал 6 часов, а мастер 8, они
изготовили 200 деталей.
а) Сколько деталей в час делает мастер и
сколько ученик?
б) Какой процент заработанных денег
причитается ученику?
18*. Найдите координаты вершин квадрата
со стороной 8, если две его стороны лежат на
осях координат, а одна из вершин имеет
координаты, произведение которых положительное
число (рассмотрите два случая).

242
Задачи
Алгебра. 7—9 классы
Линейная функция
19. Найдите значение функции:
2
а) у = х - Ъх + 3 при х = -1;
*ч 3* + 2 . 1
б)!/=бГ^Г при'=з-
20. При каком значении х функция у =4х - 1
принимает значение, равное 11?
21. Постройте график функции у = 2# - 3 и
укажите с его помощью абсциссу точки графика с
ординатой -7.
22. Постройте на одном чертеже графики
функций у = -3, у =х, у = 2 - х.
23. Укажите координаты вершин
треугольника, стороны которого лежат на прямых в
задании 4.
24*. Найдите координаты точки графика
функции у = 7х - 5:
а) с одинаковыми координатами;
б) сумма координат которой равна 19.
25*. Точка В лежит на отрезке АС, длина
которого равна 8. Постройте график зависимости
длины у отрезка ВС от длины х отрезка АВ
(0 < х < 8) и укажите точку, соответствующую
середине отрезка АС.
Степень с натуральным показателем.
Функция у = х .
Умножение одночленов
и их степень
26. Запишите пропущенные показатели
степеней в правой части равенства:
a) bn-6m = 6D; 6)6*: ^ = 6°;
28. Упростите выражение:
а) 269 • .J б5; б) (2 • б17)3; в) (-5а4)2;
г)За3&2-(-2а63);д)(1|б)3-^б)3.
29. Заполните таблицу и, используя ее,
постройте график функции у = х .
X
х2
0
1
2
1
4
3
?
8
3
3
Используя график и результаты таблицы,
найдите:
а) значение у при х = -1,5;
б) при каких значениях х значение у = 4;
в) сравните значения у при #=-2,Зи*=-3,2.
30*. Пусть а = 25 • З6 • 711, 6 = З5 • 5 • 713.
Найдите:
а) наибольший общий делитель чисел а и Ь;
б) наименьшее общее кратное чисел аиЬ;
в) сколько натуральных делителей у числа а.
31*. Пусть а = 1,3 • 106, Ъ = 2,6 • 105. Найдите
а + Ь; а - Ь; а • Ь; а : Ь.
Действия с многочленами
32. Упростите выражение:
а) (2а + 36с - 1) - (а - 36с - 1);
б) 2а (а - 5) + 9а7.
33. Разложите на множители:
а) 5а6 - Зас; б) 2а26 + 12а62; в) 8а3 + 4а2.
34. Решите уравнение —«
2х - 7 х + 2
=1.
в)(ЬУ=Ь°;
д) ат : Ьт = (а : 6) .
г) 6 с = (6 • с) ;
27. Вычислите:
2Y3 . MY2 *ч 3'
•»(••)*• (и)* • л»* = <мЛ °>^?-
°>ни-а2:«й;
в)гп;
35. Моторная лодка прошла 7 ч по течению
реки и 6 ч против течения. Определите скорость
течения реки, если скорость лодки в стоячей
воде 10 км/ч и за все путешествие лодка прошла
132 км.
36*. Решите уравнение 5х + Зх = 6, если
один из его корней -0,6.
37*. Укажите такие точки графика функции
2
у = х , ордината каждой из которых равна ее
абсциссе, умноженной на 7.

Задачи
Алгебра. 7—9 классы
243
Действия с многочленами
38. Представьте в виде суммы одночленов
выражение:
а) (За - 1)(2а + 7); б) (5& + 2)(3 - 26);
в) (7* + у)(у - 7х); г) (а + 2)(а2 - 2а + 5).
39. Разложите на множители:
а) (5а + 3)*Ь + (5а+ 3)* с;
б) (5а + 3)*6 + 5а+ 3;
в) 5а& + 46 + Бас + 4с.
40. Упростите выражение:
а) (2а + Зх)(5а - х) - (а + *)(10а - 3*);
б) (7х + 1)(х - 5) + (Зх - 2)(2* + 7);
b)-0,1*(2*2 + 6)(5-4*2).
41. Решите уравнение:
а) (4х + 1)(х + 5) - (2х + 1)(2* - 3) = 58;
б*) (4* + 1)(х + 5) = (4х + 1)(3* +2).
42*. Рабочий проработал сначала t ч с
производительностью а деталей в час, а затем на 2 ч
меньше с производительностью на 3 детали в час
больше, чем раньше. За все это время было
изготовлено 169 деталей. Найдите:
а) время всей работы, если первоначальная
производительность 20 деталей в час;
б) начальную производительность, если t =
Формулы сокращенного умножения
43. Преобразуйте выражение:
а) (За - 2&)2; б) (2а + ЗЬ)2;
в) (Зх4 - 5)2; г) (2а - 3)(2а + 3);
д)(5а + 6)(Ь-5а);
1 2 „VI 2
е) ( g ХУ2 ~ За)( 2 ху2 + За )•
44. Разложите на множители:
а) 4х - 9;
в) 25 - 49д2;
д) 16а4-81;
б)4а2 + 12аЫ-962;
ч .. 2 2 п 4
г) 4х у -9а ;
ч 1 з з
е>27* 'У'
45. Решите уравнение
(Зх - I)2 + (4* + 2)2 = (5х - 1)(5* + 1).
46. Сторона первого квадрата на 2 см больше
* л 2
стороны второго, а площадь первого на 12 см
больше площади второго. Найдите периметры
этих квадратов.
47. Вычислите, используя формулы
сокращенного умножения:
а) 1432 - 1422;
б)1572 + 2-157-43 + 432;
в)1732 + 2-173-73 + 732.
48*. Разложите на множители:
а) а - Ъ - 2Ъс - с ;
б)4&2-462+1-с2;
в) 16 (jc - i/)2 - 25 (д: + I/ )2.
49*. Докажите, что сумма кубов чисел 1713 и
3287 оканчивается тремя нулями.
Все действия с многочленами
50. Упростите выражение:
а)2(х-3)2+ 12х;
б) (2х + 3)(3х + 2) - 13(х - 1);
в)(2х2-1)2 + (*2 + 2)2;
г) (4х + З)2 - (2х - 1)(2х + 1).
51. Разложите на множители:
а) х + бху + 9у ; б) х - 6х у + 9ху ;
в) а+ 2аЬ + Ь2 - 4с2; г) (а2 + а) - (б2 + 6);
ч 1.2 2
д) аЪ -ас ;
е) -2*2 + \ху - 2у2.
52. Решите уравнение
(2х + 3)(3* + 1) + (5х + 2)(2х + 5) = (4х - I)2.
53. Найдите значение выражения
9х2 - 24xi/ + 16у2
при x = 2g,i/ = l|.
54. Постройте график функции
у = (2х - I)2 + (х - 2)2 - 5х2.
55*. Вычислите
(22 + 1)(24 + 1)(28 + 1)(216 + 1)(232 + 1) х
х(264 + 1)-1.2128.
56*. Докажите, что
(а + Ь) = а + 4а£
4 4
и упростите выражение (х + 2) + (х - 2) .
(а + &)4 = а4 + 4а3& + 6aV + 4а63 + б4,

244
Задачи
Алгебра. 7—9 классы
Системы линейных уравнений
57. Решите систему уравнений:
Гу=2* + 7,
' \у = 5-х;
Зу + х = 5,
13i/-2x = 11
\2х + Ьу = 13,
' \Zx- Ъу =-\Ъ;
)Пх + 5у =
= 17,
5.
58. Прямая у = ах + Ь проходит через точки
А(1; 5), Б(-2; -1). Найдите числа а и & и
запишите уравнение этой прямой.
59. Сумма двух чисел равна 1,3, а их разность
равна 7,1. Найдите произведение этих чисел.
60. Найдите такие числа а и 6, что равенство
4* + 5 = а(х - 1) + Ь(х - 4)
выполняется одновременно при х = 1 и при
х=-1.
61*. Решите систему уравнений
х у
- * У
62*. Для системы уравнений
Г 2x-3i/ = 2а2 -6а + 2,
1 Зх + 2у = За2 + 4а + 3
определите, при каком значении параметра а
сумма х + у принимает наименьшее значение.
63*. Найдите все пары чисел хиу,
удовлетворяющие равенству
(2х - у + I)2 + х2 + 4xi/ + 4i/2 = 0.
Упражнения,
содержащие параметры
64. Определите, при каких значениях а
число 5 является корнем уравнения:
а) ах = 7; б) 2х = За;
в) (5а - 1)х = 2а + 3;
г) (3 - а)х = 2 - 5а;
д)(3а + 7)х = 15а+ 35.
65. При каких значениях b имеют общий
корень уравнения:
а) Зх + 7 = 0 и 2х - b = 0;
б) 2х - 36 - 1 и Зх - 56 + 7?
66. При каких значениях а и 6 система
уравнений:
Г Зх - Ъу - а, Г ах + &i/ = 2,
' I 2х + у = 6; ' \ 5х + 6i/ = 3 + а
имеет решение x = 3,i/ = -l?
67. При каких значениях а и 6 прямая
у = ах + Ъ
проходит через точки М(1; 5) и N(-5; -3)?
68. При каких значениях а системе
уравнений
3x + 2i/ = 15a,
-x + i/ = 9
a *
удовлетворяет пара равных чисел? Для каждого
такого а найдите решение системы.
69. При каких значениях а сумма чисел,
удовлетворяющих системе
Г Зх - 2у = -2а + 12а + 3,
1 х + Ъу = За2 - 10а - 2,
наименьшая?
70. Для каждого значения Ъ решите уравнение
(б2 - 9)х = Ъ + 3.
71. При каком значении а уравнение
(Зх - а)2 + (4х + I)2 = (5х - I)2
не имеет решений?
72. При ^саких значениях а и 6 уравнение
(2х - а)(18х + 1) = (6х - I)2 + Ъ
имеет не менее трех различных корней?
8 КЛАСС
Сложение и вычитание
алгебраических дробей
1. При каких значениях х определено
выражение:
ч 2 _ 2
а) z—о; б)
х - 3
х - 3 Зх - 1
Зх + 1 ч Зх + 1
; в)
Зх - 1
2. Сократите дробь:
лл 5 4
ач 14* У .
7х у
б)
Зх -I- бу;
2х + 4у'

Задачи
Алгебра. 7—9 классы
245
2 2 2
х + ху + х. * - у
V + *y + / }2х + 2у-
3. Выполните действия:
ч 2 х + 3 -ч 7х + 5 , Зх + 6
а) —гт —гт; б) +
х + 1 х + 1
ч 2 Зх - 2
* х + 1 '
4 1 1
1-х х - 1 '
Г) -5 + 7 + ~;
х2 + х * + 1 *
Д)х2-4 * ~ 2 * + 2 *
4*. Постройте график функции
о 2 - 2
9х - 1 х - х
У =
Зх + 1 х
4 2 + 1
5*. Сократите дробь —= •
X + X + 1
6*. Найдите такие а и 6, при которых для
всех допустимых значений х верно
ах - Зх - Ъ
х - 1
= 2х-1.
Умножение и деление
алгебраических дробей.
Все действия с дробями
7. Найдите произведение дробей:
,2 2
ч ао с
а):т'^;
б)
х2 + Зх х2 - 1
х - 1 * х + 3
8. Найдите частное дробей:
ь3 2и
ч ао а о
а>-2:"^;
/71
9. Упростите:
б)
х + 4х + 4 х + 2
х - 3 ' 2 _
х - 9
2х Л2 /xz - 2х + 1
)■-,
. f 7 5х Л и Зх - 1
В' Ux - 1 2х - 1) '' 4х2 _ г
3_ . 2х ^ 4х + 2х + 6
7
х2-1
1 2 1
10*. Пусть х + - =3. Найдите х + -g .
х х
11*. Пусть - =3. Найдите значение выражения
2 2
Зу - 2ху + х
2 2 "
* + ху + у
Квадратные корни
12. Вычислите:
а) 372;
б)(-37Г;
в) Л369;
г) VI36 000 ; д) ЛзГбЭ ; е) л/0,001369 .
13. Найдите значение выражения:
а) 7^25; б) 7(-9)(-25); в) ^ ;
г) 73^75; rtjSJ;
ж) л/152 + л/(-13)2 - (л/7)2 - 7(-5)2
/ 2 , , 2
л/а + &
14. Сравните значения выражений
иа + 6 при а = 5, & = 12.
15. Найдите значение выражения *]х + у
при данных хиу.
X
У
/2,2
| л/Х + у
3
0
0
-7
4
-3
-5
12
8
-6
7з
1
77
3
-772
772
16*. Вычислите наиболее рациональным
способом:
а)
в)
ш
.1 „2 . (п2\2
+ 2-7|-8| + (в|) ; б) V852 - 842;
Ш
+ 2-3|-78 + (75)!-
Свойства квадратных корней
17. Внесите множитель под знак радикала:
а)2л/7; б) ijb; в)3^2|; г) g 775.
18. Вынесите множитель из-под знака
радикала и упростите выражение
2л/18 + 5750 - \ 732 - 7л/2 .
19. Сократите дробь:
2 г 2 г"
ч 5 - а -ч 2 - л/а v 4х + 4хл/а + а
а) -= ; б) ; в)
75 - а ' ~' а - 4
20. Вычислите:
а)(2лУ§ - 1)(ЗлУз + 5) - 7лУ§;
б)(2л/3 + 5)2 + (10 - л/3)2.
2х + Та

246
Задачи
Алгебра. 7—9 классы
21. Сравните по величине (без использования
таблиц и микрокалькулятора):
а) 7Л и 8л/б ; б) Л + Л и До .
22. Упростите выражение
а + л/а , а - \ 0 г-
^7= + F - 2 л/а •
1 + Л* 1 + Л*
23. Постройте график функции:
а)у = 2х- 1;
6)y=(j2x - 1) ;
в)
tf = V!
(2* - 1)'.
Квадратные уравнения
24. Решите неполное квадратное уравнение:
а) х2 - Зх = 0; б) 7х2 - 28 = 0; в) 5*2 + 3 = 0.
25. Решите уравнение по формуле
-b±*jb - 4ac
*1,2~~
2а
a) jc2 - 13* + 22 = 0; б) Зх2 + х - 30 = 0;
в) х2 - х - 1 - 0.
26.Решите уравнение:
а) 2х2 - х +11 - 0; б) 9х2 - 42* + 49 = 0;
в) Зх2 - 75х + 140 л/Ш - 0.
27. Найдите корни уравнения
(Зх + 4)2 + (5х - I)2 = 38 + х.
28. Для всякого а решите уравнение
х2 -(2а + 1)х + 2а = 0.
2
29*. При каких Ъ уравнение Зх + Ъх + 12 = 0
имеет один корень? Для каждого такого Ь
найдите этот корень.
Дробно-рациональные уравнения.
Теоремы Виета
30. Решите уравнение:
х + 4 х - 1
а)
х + 3 х - 5'
-ч х + 1 с
' * * + 1
31. Не решая уравнение, найдите хг +х2 и
хг * х2 (т*е- СУММУ и произведение его корней):
а) х2 + 7х - 11 - 0; б) З*2 - 5х - 9 =0.
32. Постарайтесь найти корни уравнения
подбором (используя теоремы Виета):
а)*2-(5+ 8)* + 5-8 = 0;
б) х2 - Зх + 2 = 0;
в)х2-(7з +2)х + 27§ =0;
г) х + (а2 - 3)х -За2 = 0.
33. Составьте какое-либо квадратное
уравнение с корнями 8 и -7.
34. При каком значении р один из корней
уравнения х2 - рх + 6 = 0 равен единице? В этом
случае найдите второй корень.
35. Решите уравнение
*2-8х= 7272-8-727.
36. При каком значении а уравнение
х - Зх + 2
х - а
= 0
имеет один корень?
Текстовые задачи, приводящие
к квадратным уравнениям
37. Площадь прямоугольника, одна из
сторон которого на 4 см больше другой, равна
о
32 см . Найдите стороны и периметр
прямоугольника.
38. Скорость моторной лодки в стоячей воде
10 км/ч. Время, затраченное на движение лодки
на 24 км по течению и на 24 км против течения,
равно 5 ч. Найдите скорость течения реки.
39*. Мастер, работая один, тратит на всю
работу на 3 дня меньше, чем ученик, работающий
один, и на один день больше, чем работая вместе
с учеником. За сколько дней выполняет всю
работу мастер, работая один?
40*. За два месяца вклад, сделанный в банк,
увеличился на 21%. Сколько процентов в месяц
банк платит вкладчику? (Проценты по договору
начисляются каждый месяц.)
Числовые неравенства и их свойства
41. Найдите корень уравнения х - 1х - 8 =
= 0, удовлетворяющий неравенству Ъх - 11 > 0.

Задачи
Алгебра. 7—9 классы
247
42. Между какими двумя соседними целыми
числами находится число л/б1 ? К какому из них
оно ближе?
43. Сколько целых чисел удовлетворяет
неравенству:
а)11,7< 117,1; б) -117,1 < Ь < -11,7;
в)-11,7<с< 117,1?
44. Пусть 1 < а < 3. В каких пределах
изменяется:
а) За; б) За - 2; в) 2 - За?
45. Напишите какие-либо два числа, удовле-
31 . 32
творяющие неравенству ™ ^ х < зз •
46. Сравните (без использования таблиц и
микрокалькулятора):
а) 11733-11731и117322;
. 378 563
0) 379 И 565 '
в) ТЗТЭ + 7571 и 4;
ч (23\11 /13У7
r435J "ImJ '
Решение линейных неравенств
47. Решите неравенство:
а) 3* - 1 > 7;
б)5-11х< 2;
ч 8х + 1 . 7х - 5
в) —-— <
г)
3^4
Зх - 1 Ъх + 1
< х-2.
2 3
48. При каких значениях х имеет смысл
выражение:
2 - х 0
a) V3 - Ьх\
б)
Jx - 11
49*. Найдите наибольшее целое число,
удовлетворяющее неравенству 5 - 3* > 105.
50*. Найдите наименьшее целое число,
удовлетворяющее неравенству 2х > л/328 .
51*. При каких значениях а выполняется
неравенство (а2 + 6)(3а - 7) > 0?
52*. При каких значениях Ъ уравнение
3*2-5х + Ь = 0
имеет два различных корня (рассмотрите его
дискриминант)?
Системы линейных неравенств
53. Решите систему неравенств:
«Л*>7' *Л2*>18'
а}1*<9; Ь)\-Ъх>-21\
Г -Ъх < -35,
в)
\ -х > -9:
Г> 1 ! > 4,5.
54. При каких значениях х определено
выражение:
8
а) Зл/5 - 2х + */х; б)
J3x - 1
•xjl - jc?
55. Найдите все значения а, при которых
За-8<5-а< 10а- 1.
56. Дана функция у = 2х - 8. Найдите, при
каких значениях х величина у принимает:
а) положительные значения;
б) отрицательные значения;
в) значения из множества [-8; 2].
2 2
57. Даны уравнения х = а + 7 и х =3-2а.
При каких значениях а:
а) оба уравнения имеют корни;
б) уравнение х = а + 7 имеет корни, а уравне-
ние х = 3 - 2а не имеет корней;
в) оба уравнения не имеют корней?
Степень с целым показателем
58. Вычислите:
59. Найдите значение выражения:
а)(2-уз;
в)(2_1+з2)_1;
б) 2"1 • З2) 1;
гхг^-з"1^)-1.
60. Сравните значения выражений:
а)3"1-7"1и21"1; б) 2"1 + 3_1и 5"1;
в) (ТЗ)"1 и 7F1;

248
Задачи
Алгебра. 7—9 классы
61. Вынесите за скобку х в наименьшей из
данных степеней:
ч 2 о з
, а) х - Зх ;
в) х - Зх ;
б)х 2-Зх 3;
г) х~2 - 3.
62. Упростите выражение:
63. Решите уравнение
3-х 2- 5-л: 4 2 = 0.
64. Решите неравенство (-——- ) < 2.
Упражнения,
содержащие параметры
65. При каких значениях а один из корней
уравнения Зх - Ъх + а = 0 равен 2? Для данного
значения а найдите остальные корни
уравнения.
66. Для каких значений Ъ уравнение
х2 - Ьх + 2Ь - 3 = 0
имеет один корень?
67. Для каждого m решите уравнение:
ч х - Зх - А Л
а) — 1— = 0;
б)
х - m
2 2
х - (2m - 1)х + m - m __
х + 4
= 0.
68. Для каждого а найдите число различных
корней уравнения
(3* - 1)(ах2 + 3* - 2) = 0.
69. При каких значениях а уравнение имеет
три различных корня:
(х2 - (За + 1)jc + 2а2 + а)(х2 + (2а - 1)х - За2 + а) =
= 0? ,
70. При каких значениях р имеют общий
корень уравнения:
а) х + 2* - 3 = 0 ирх2 - х - 1 = 0;
б) х + Зх - р = 0 и 2х2 + х + р - 7 =0?
9 КЛАСС
Решение квадратных уравнений
различными способами
2. 2х - х - 3 = 0.
Решите уравнения:
1. х2 + 7х =0.
3. Ъх2 + 4х - 28 = 0. 4. 5х2 + 4х + 28 = 0.
5. *2-(2+ 73)х+ 2л/3 =0.
6. 2х2 - 2* - 1 = 0.
7. (Зх + 2)(5х + 4) = 0.
8. (Зх + 2)(5х+4) = 1.
9. (Зх + 2)(5х + 4) = 5х + 4.
10. (Зх + 2)(5х + 4) = (Зх + 2)2.
11.
х + 3
=0. 12.
х - 6
= 0.
13 Зх +11*-14=0
9х + 45х + 14
14. (х2 -Ъх- 6)(х2 + 7х - 8) = 0.
Квадратный трехчлен
15. Найдите корни квадратного трехчлена:
а) х2 - 5х - 24; б) -Зх2 - х + 14;
16. Разложите на множители квадратный
трехчлен:
а) 2х2 + Зх;
2
в) х -Ъх- 24;
б) 8xz - 2;
г) Зх2 + х - 14;
д) 9х2 + Зх - 42; е) -х2 - Зх + 4.
лп /-, * 2х2 + х - 3
17. Сократите дробь —$ .
хг - 2х + 1
18. Найдите наименьшее значение
выражения:
а)(х-3)2 + 1; б)4х2 + 4х-1.
19. Найдите наибольшее значение
выражения:
а)-3(х+1)2 + 5; б)-х2 + 6х.
20. Напишите два каких-либо различных
квадратных трехчлена, имеющих корнями
числа-3 и 8.
21*. При каких Ъ квадратный трехчлен
х2-4х + 6
можно разложить на линейные множители?

Задачи
Алгебра. 7—9 классы
249
22*. При каких значениях Ъ в разложении
2 2
квадратных трехчленов 2х - х- 1 и * +4*-6
может быть один и тот же линейный
множитель?
Основные свойства
квадратичной функции
23. Найдите нули функции:
а) у = х2 - 6х - 16; б) у - х2 - Зх + 7.
24. Дана функция /(*) = jc - 4х - 5. Не
производя построения графика, найдите:
а) координаты точек пересечения графика с
осью абсцисс;
б) координаты точки пересечения графика с
осью ординат;
в) координаты точек пересечения графика с
прямой у = 2х - 5;
г) наименьшее значение функции.
25. Напишите промежутки возрастания и
2
убывания функции у = -3* *
26. Постройте в одной системе координат
графики функций
у = х2, у = х -1, у = (х-1) .
27*. При каких значениях k графики
функций
у = х и у = 2х + k
а) не имеют общих точек;
б) имеют одну общую точку;
в) имеют две общие точки;
г) имеют более двух общих точек?
28*. Найдите наименьшее расстояние между
2 о
линиями у = х иу = -2.
29*. Найдите такое значение а, при котором
отрезок прямой х = а, концы которого лежат на
2 2
линиях у = х и у = -(х - 2) , имеет
наименьшую длину.
Квадратичная функция и ее график
30. 1) Определите вид графика. 2) Найдите
координаты вершины параболы. 3) Найдите
значения функции в нескольких точках. 4) Постройте
график функции и укажите:
а) область определения;
б) множество значений;
в) нули функции и промежутки знакопосто-
янства;
г) промежутки возрастания и убывания;
наибольшее и наименьшее значения функции.
30.1. у = х - 2х - 3.
30.2. у = х + 2х.
30.3. у = -х2 + 4х - 3.
30.4. у - -х2 - 2х + 8.
30.5. у = 2х2 - 4х.
30.6.i/ = -|jc2 + jc.
30.7. у = х2 - 6х + 7.
30.8.i/ = (jc-1)(x-3).
Квадратные неравенства
и системы неравенств
31. Решите неравенство:
а)х2-4*-5<0; б) х2 > 16;
в) Зх2 < х; г) х + 6х + 19 < 0;
д) х2 + 6х + 19 > 0; е*) 2х2 + х - 8 > 0.
32. Дана функция f(x) = х - 2х. Найдите,
при каких значениях х
а) / (х) > 0; б) / (х) > 0;
в) / (х) < 0; г) / (х) < 0;
д)/(х)>-1; e)f(x)>-l;
ж)/(х)<-1; з)/(*)<-1.
33. Решите систему неравенств:
х - 4х - 5 < 0,
х>0;
а)|*2~"4*"5<0' б)|
U>-2; I.
вч J х2 - 4х - 5 < 0, г\ J х - 4х - 5 < 0,
1*>в; 1х>5.
34*. При каких значениях Ъ определено
выражение
1
i
100 - 6 +
Ль + 1)(ь - з)
35*. При каких значениях параметра а
уравнение Здс +ах + а-3 = 0 имеет два различных
корня?
36*. Для каждого значения Ь решите систему
| х - Ъх + 4 > 0,
\х>Ъ.

250
Задачи
Алгебра. 7—9 классы
Метод интервалов
при решении неравенств
37. Решите неравенство методом интервалов:
а) х (х - 1)(х + 2) < 0; б) *L±i > 0; в) - < 1.
х — 5 х
2
38. Пусть f(x) = х (х - 1). При каких
значениях х
а) / (х) > 0; б) / (х) > 0;
в) / (х) < 0; г) / (*) < 0?
39. При каких значениях Ъ определено
выражение
Ъ2 -4.
40*. Решите неравенство
(*2-3*-1)2<(*2 + 7х + 1)2.
41*. Для каждого значения а решите
неравенство
х - а
х - 1
<0.
Уравнения, сводящиеся
к квадратным.
Системы уравнений
42. Решите биквадратное уравнение:
a) 2jc4 - Зх2 + 1 = 0; б) х4 - Зх2 - 4 - 0.
43. Решите систему уравнений:
й)\х + у = 5;
Г jc-j/ = 6,
б)\2х-у=11;
Г 3* + у = 4,
[х +у = 2.
44. Длина диагонали прямоугольника равна
5, а его площадь 12. Найдите стороны
прямоугольника.
45*. Решите уравнение
(*2+3*)(*2 + Зх-3) = 4.
46*. Решите систему уравнений
f х + ху = 3,
I у2 - ху = 2.
о 1 Ч
47*. Решите уравнение х Н—5 +3* + - = 2.
Арифметическая прогрессия
48. В арифметической прогрессии
ап = Ъп + 3.
Найдите а1? d, а13.
49. В арифметической прогрессии ах = 3,
d = 7. Напишите формулу общего члена
прогрессии и найдите а19.
50. Найдите сумму первых двадцати членов
арифметической прогрессии, если а2 = 7, а4 = 13.
51. Найдите х, при котором числа х - 1, 2* - 1,
х - 5 составляют арифметическую прогрессию.
52*. В арифметической прогрессии
ап = 18 - Зп.
а) Найдите сумму первых 20 членов.
б) При каком количестве членов прогрессии
(начиная с первого) их сумма наибольшая?
53*. Найдите наименьший член
последовательности
2
ап = п -42п - 2.
54*. Найдите арифметическую прогрессию
(ал), если
| а\ + а\ = 58,
I а9 + аА= 14.
Геометрическая прогрессия
55. В геометрической прогрессии Ьп = 3 • 2 .
Найдите bv q,b5.
56. В геометрической прогрессии Ьг = ^»
g = 3. Напишите формулу общего члена
прогрессии и найдите Ь7.
57. Найдите сумму первых шести членов гео-
метрической прогрессии, если Ь2 = 4, q = -5 •
58. Найдите значение *, при котором числа
t - 1, 2*, 4* + 6 составляют геометрическую
прогрессию.
59*. Три числа являются последовательными
членами арифметической прогрессии. Если
второе и третье уменьшить на 1, а первое оставить

Задачи
Алгебра. 7—9 классы
251
без изменений, то полученные числа будут
составлять геометрическую прогрессию со
знаменателем 2. Найдите эти числа.
Степень с рациональным
показателем
и корни произвольной степени
60. Вычислите:
4\2
,1V1
a) V27 - tyf=32) + 725 ; б) ({) + (l|)~ ;
»?
в) 3УП~/2• VT7VS; г)(|) -(2|) ;
д)72.372-в72;
е) (V^)' + */5? •
61. Упростите выражение
1 1 у-З
2 2
т - п т + 2т п + п
1 1
, 2 2
771 -г /71 71
1 1
2 2
771 + 771 П
62. При каких значениях х определено
выражение
Зх2 + (2 - х) 3?
63. Решите уравнение:
а) УЗх - 1 - -1; б) V3x - 1 - -1;
2 1
в) хЬ - 3 • хЬ + 2 - 0.
64. Постройте графики функций у = Jx и
1
у=х и укажите абсциссы точек первого
графика, расположенных выше соответствующих
точек второго.
Тригонометрические функции
65. Найдите значение тригонометрической
функции:
Зя
a) sin 30°; б) cos 90°; в) sin -у ;
г) tg j ; д) sin g ;
e)cos 17я.
66. Сравните с нулем значение выражения:
a) cos 115°; б) sin 179°; u)tg^;
г) cos (-31°); д) sin (-200°).
X
67. Пусть /(х) = cos х + sin 2л: + tg ~ • Найдите
значение данной функции при:
а) х = g ; б) х = 2я; в) х - g .
68. Используя тригонометрическую
окружность, сравните величины:
a) cos 100° и cos 101°; б) sin 200° и sin 201°;
в) tg 300° и tg 301°.
69*. Какие числовые значения может прини-
2 - 3cos а
мать выражение
, гдеаей?
Основные тригонометрические
тождества
70. Упростите выражение:
ч 1 - sin а . , ч2
a) g (cos а # ** а) »
cos а
б) (sin 2а + 3 cos 2а)2 + (cos 2а - 3 sin 2а)2;
ч 1 - 2 sin х cos х ,
в) —: Ь cos х.
sinx - cos*
71. Найдите sin а, если cos а = -г и а — угол
третьей четверти.
12
72. Найдите cos а, если tg а = --g- иа — угол
четвертой четверти.
73. Докажите тождество
2 2
1 - 4sin а • cos а
- 2 cos а • sin (-а) = 1.
(sin а + cos а)
74*. Найдите значение выражения
3 cos ос + 2 sin а
5 cos а - sin а
, если tga = 3.
75*. Пусть sin а - cos а = «• Найдите
sin a • cos a.
76*. Найдите sin a и a, если
2 ТС
2 cos a - 3 sin а = 0и0<а< «•

252
Задачи
Алгебра. 7—9 классы
Формулы сложения
77. Преобразуйте выражение в
тригонометрические функции угла а:
a) cos Г -у + a ]; б) sin (я -а); в) tg ( « + а J.
78. Упростите выражение:
cos (а + р) + 2 sin а «sin р.
*' cos (а - р) ;
g. cos (а + 32°) + cos (а - 28°)
' sin(88° - а)
79. Пусть а и Р углы первой четверти.
Известно, что cos а = « » cos Р = г . Найдите:
a) cos 2а; б) sin 2а; в) cos(a + Р).
ол о - sina + sin За
80. Сократите дробь r-j- .
Упражнения,
содержащие параметры
81. При каких значениях а неравенство
х - Ъх + a > 0
а) справедливо при всех х;
б) справедливо при х > 3;
в) справедливо при х < 7?
82. Для каждого значения а решите
неравенство
х2-(2 + а)х + 2а < 0.
83. При каких значениях Ъ наименьшее
значение функции у = х -Ах - Ь равно 13?
84. При каких значениях а функция
у = -Зх2-ах + 7
убывает на промежутке (-°°; 7]?
85. Для каждого значения а решите систему
\х + у = 2,
12,2
I* +i/ =а.
2
86. Постройте график функции у = х и для
каждого а найдите ее наибольшее и наименьшее
значения на промежутке [-2; а] (а > -2).
87. При каких значениях а три корня урав-
нейия (х - а)(х - Ъх + 4) = 0 различны и,
взятые в некотором порядке, составляют
а) арифметическую прогрессию;
б) геометрическую прогрессию?
ОТВЕТЫ
7 класс
1. а) 3 Yi ; б) 6; в) -9,5; г) -1,32; д) 1 ^ . 2. а) 0,46;
б) -0,17; в) 1000; г) -5; д) 4; е) 25; ж) 8. 3. а) 3,45;
б) 1111; в)6,25%. 4.36; 24. 5.10.6.196 кг. 7. 7. 8. а) 7;
2
б) 7«к • 9. а) Равны; б) первое больше. 10. а) ЪЬ; б) 6а;
в) 6х-1.11. ^ . 12. а) 0,33 Р; б) 8,5; 16,5.13. 7.14. а) 65;
б) 0,2; в) 0,2; г) « ; д) ~8; е) х — любое число. 15. -1; 3.
16. т "-'-« ; значение 6,4. 17. а) 16 деталей; 12
деталей; б) 36%. 18. (0; 0), (0; 8), (8; 8), (8; 0) или (0; 0),
(-8; 0), (-8; -8), (0; -8). 19. а) 9; б) 3. 20. 3. 21. -2.
23. (-3; 3), (1; 1), (5; -3). 24. а) [|; | ]; б) (3; 16).
25. у - 8 - х; (4; 4). 26. а) Ьп + т; б) Ьч ~р; в) Ь^; г) (Ъс)х;
д) (Ц71.27. а) ^ ; б) 9; в) 1; г) 1; д) 16; е) 16. 28. а) \ Ь14;
б) 8Ь51; в) 25д8; г) -6aV; д) Ь6. 29. а) 2,25; б) -2; 2;
в) у(-2,3) < у(-3,2). 30. а) Зб-7П; б) 25-Зв-5-713;
в)6• 7• 12 - 504. 31. а + Ь - 15,6• 105; а-Ъ =10,4• 105;
а • Ь - 3,38 • 1011; а : Ь - 5. 32. а) a + 66с; б) a7(2a2 - 1).
33. а) а(ЪЬ - Зс); б) 2ab(a + 6b); в) 4a2(2a + 1). 34. 26.
35. 2 км/ч. 36. *! - -0,6, х2 = 0. 37. (0; 0), (7; 49).
38. а) 6а2 + 19а - 7; б) -10Ь2 + lib + 6; в) у2 - 49х2;
г) а + а + 10. 39. а) (5а + 3)(6 + с); б) (5а + 3)(Ь + 1);
в) (6+с)(5а+4). 40. а) бах; б) 13х2 - 17* - 19;
в) 0,8х2 + 1,4х3 - Зх. 41. а) 2; б) -0,25; 1,5. 42. а) 5 ч;
б) 63 детали в час. 43. а) 9а2 - 12аЫ- 4Ь2; б) 4а2 + 12аЬ +
+ 9&2; в) 9х8 - ЗОх4 + 25; г) 4а2 - 9; д) Ъ2 - 25а2;
е) ^ *У - 9а2. 44. а) (2х - 3)(2х + 3); б) (2а + ЗЬ)2;
в) (5 - 7дК5 + 7q); г) (2ху - За2)(2ху + За2); д) (4а2 - 9) х
х(4а2 + 9); е) (|* - у^\х2 + \ху + у2) .45. -0,6.
46. 16 см; 8 см. 47. а) 285; б) 40 000; в) 10 000.
48. а) (а + Ь + с)(а - Ъ - с); б) (2Ь2 - 1 - с)(2Ь2 - 1 + с);
в) -(9* + у)(х + 9у). 49. 17133 + 32873 - (1713 +
+ 3287) (...) = 5000 (...). 50. а) 2х2 + 18; б) 6х2 + 19;
в)5(х4 + 1); г) 12х2 + 24* + 10. 51. а) (х + Зу)2;
б) х(х - Зу)2; в) (а + Ь + 2с)(а + Ь - 2с); г) (а - Ь) х
х (а + Ь + 1); д) а(& + с)(Ь - с); е) -2(х - у)2. 52. -|.

Задачи
Алгебра. 7—9 классы
253
53. 0. 55. -g. 56. 2(х4 + 24х2 + 16). 57. а) х = -|,
17 ^ 32 21 ч Л 13 ч 76
y-y^x-jg.y-^^x-O.y-ysiOx-gj,
y = -gY". 58. а = 2, Ь=3, у = 2х+3. 59. -12,18.
60. а - 7, Ь - -3. 61. х - 1, у - 1. 62. а - -1. 63. х =
7 10 8
= -0,4, у = 0,2. 64. а) ^ ; б) у ; в) 2з ; г) 0; д) а е R.
65. а) -у ; б) -17. 66. а) а - 14, 6 = 5; б) а - 3,5,
Ь = 8,5. 67. а = |, 6 = у . 68. а = 2, х - у - 6.
69. а = -1. 70. Для 6 * 3, Ь * -3 х = , для Ь = -3
О — о
7
х е R, для Ь = 3 нет решений. 71. а = 3. 72. а = ^,
л- 16
8 класс
l.a)xe (-oo;3)U(3;+oo);6)x6 (-оо; | ^и (у ; з)и
U (3; +оо); в) х б (-оо- 1 ^ и (J ; +оо). 2.,а) Ц ; б) |;
v х 1 1 0 ч ч ^ 4х - 1 ч Зх2 + 2
в) -; г) 5* - «У ■ 3* а) "1; б) " Т 5 в)
у' 1; 2Л 24
2 * х + х
2х + 5 ч -2 . п 1 ЛС2
г)-о ;д) .4.у = 2х, х*-р,х*0. 5. х -х +
X + X * + z d
Ь Ь
+1. 6. а - 2, Ь - -1. 7. а) ^; б) х(х + 1). 8. а) —;
с ат
б)(х + 2)(х + 3). 9. а)х2-3х + 1;б) \ ; в) 2_ 10ж
* ох — 1
22
10. 7. 11. j|. 12. а) 1369; б) 1369; в) 37; г) 370;
д) 3,7; е) 0,037. 13. а) 15; б) 15; в) 5; г) 15; д) |; е) \ ;
/~~2 2
ж) 16. 14. л/а + Ъ < а + Ь. 15. См. таблицу.
X
У
Г~2~~л 2
V* + У
3
0
3
0
-7
7
4
-3
5
-5
12
13
8
-6
10
7з
1
2
77
3
4
-772
772
14
16. а) /(7g + 8g) -16; б) 13; в) 4.17. а) 728 ; б) 7235 ;
в) 721; г) 73 . 18. 2372 . 19. а) 75 + а ; б) —= ;
2 + J а
в) 2х + Та . 20. а) 13; б) 140.21. а) 778 > 87б ; б) 7з +
+ 72 < 7Гб. 22. -1. 24. а) 0; 3; б) 2; -2; в) 0. 25. а) 2;
11; б) - у ; 3; в) ^-^ ; ^у^ ; 26. а) 0; б) \ ; в) 0.
21 1 1
27. -1; от . 28. Для а = « х = 1; для а * г х = 1 или
х = 2а. 29. Для Ь = 12 х = -2; для 6 » -12 х - 2.
17 1
30. а) -у ; б) 3; 2; в) -^ ; 1. 31 а) хг + х2 - -7; хх • х2 =
5
= -11; б)хх + х2 = «^ *Г*2 = ~3- 32. а) 5; 8; б) 1; 2;
в) 73; 2; г) 3; а2. 33. Например, х2 - х - 56 « 0.
34. р - 7; х = 6. 35. 727; -719. 36. а = 1 или а = 2.
37. 8 см и 4 см; периметр 24 см. 38. 2 км/ч. 39. За
3 дня. 40. На 10%. 41. 8. 42. 7 < 7б1 < 8; ближе к 8.
43. а) 106; б) 106; в) 129.44. а) 3 < За < 9; б) 1 < (За - 2) <
< 7; в) -7 < (2 - За) < -1. 45. ||; ||. 46. а) 11 733 х
х11731<117322;б) р| > Ц|; в) л/3~9 + ТО <4;
в) (-«>; -1 £ ]; г) [1; +оо). 48. а) (-оо; | ]; б) (11; +оо).
49. -34.50.10.51. Г21; +оо \ 52. (-оо; 2 -^ \ 53. а) [7; 9);
б) 0; в) (-оо; 7); г) [9; +оо). 54. а) [о; \ ]; б) (|; 7].
55. [~; у ). 56. а) (4; +оо); б) (-оо; 4); в) [0; 5].
57. а) [-7; f } б) (§ ; +«>} в) 0. 58. a) g ; б) 4; в) -\ ;
г) 0. 59. а) 8; б) у ; в) ^ ; г) -|. 60. а) З"1 • 7"1 - 21"1;
б) 2"1 + З"1 > 5"1; в) (ТЗ)"1 = Тз11; г) (JJ" - (|) >
> (§" s)"1 •61-а) *2(1"Зх); б) х 3(JC"3); в) х"2(1" 3*5);
г) х"2(1 - Зх2). 62. а) -1; б) 1. 63. 1; |. 64. (-оо; i ) и
U (з ; ll 65. а = -2; х2 = -^ . 66. 6; 2. 67. а) Для m 6
€ (-оо; -1) и (-1; 4) U (4; +оо) х = 4 и х - -1; для m - 4
х = -1; для m = -1 х = 4; б) для m 6 (-оо; -4) U (-4; -3) U
U (-3; +оо) х = тих=т-1; для т — -4 х = -5; для
т = -3 х = -3.68. Для а е [ -оо; - - J один корень; для
ае \~Q9^9^\ 2 различных корня; для а е I -g ; 0 J U
U (0; 9) U (9; +оо) з различных корня. 69. а е (-оо; -1) и

254
Задачи
Алгебра. 7—9 классы
U(-l;0)u(0;|)u(l;+oo].ma)p--§;p-2; 44.3;4.45.1;-4; ^Ц^ . =Ц_^ ^ (_ЗЛ . £ у
б)р=-^;р-4. (*Л._Лу{1;ъ{-1.,-ц.4В.-2-Л:-* + Л.
48. а^ 8, d = 5, а13 = 68. 49. ап = 7и - 4, а19=129.
9 КЛаСС 50- 520 " 65°- 51- * - -1 или х - 4. 52. a) S20 = -270;
б) п = 5 или л = 6. 53. а21 = -443. 54. ап = 2и + 1 или
1. 0; -7. 2. -1; 1,5. 3. -2,8; 2. 4. 0. 5. 73; 2. 1 п.х
- _ а =5/1-8. 55.Ь1-б,д-2,Ь6-96.5в.Ьл = ~ -Зл \
. 1 -Л 1 + 73 2 4 2 4 1 * 1 ,« в п 27
О. 0 , 0 . #. 0 , с • о» А» о • «*■ к t о
2 ' 2 " '""З^б'0, ,"3"v""5,"3' Ь7=27. 57. S6 = -5,25. 58.3. 59.1, 3, 5. 60. a) 10;
Ю.-1;-|. 11.-1; 6. 12.-1. 13.1. 14.-8;-1; 1; 6. 6) \ ; в)-1; г) 2,5; д) 2; e) 18. 61. \ . 62. [0; 2).
15. a) 8; -3; 6) 2; -\ . 16. a) x(2x + 3); 6) 2 (2x - 1) x 63. a) x - 0; 6) 0; в) x - 1, x - 32. 64. x > 1. 65. a) \ ;
x(2x + 1); в) (x - 8)(x + 3); r) (x - 2)(3x + 7); -
w owo u.014 wi v J.л^ i* 2x + 3 6)0;B)-l;r)l;fl)^-;e)-1.66.a)cosll5°<0;6)sinl79°>
д) (x - 2)(9x + 21); e) (1 - x)(x + 4). 17. — . 2
X " 57C
18. a) 1; 6) -2.19. a) 5; 6) 9. 20. Например, x2 - 5x - 24 > 0; в) tg -j > 0; r) cos (-31°) > 0; д) sin (-200°) > 0.
67. a) 3 *6 ; 6)1; в)1. 68. a) cos 101° < cos 100°;
6) sin 201° < sin 200°; в) tg 301° > tg 300°. 69. [-g ; 1].
2
7
и 6x* - 30x - 144. 21. b < 4. 22. 5; -^ . 23. a) 8; -2
б) нулей нет. 24. a) (5; 0), (-1; 0); б)(0; 5); (0; -1)
в) (0; -5); (6; 7); г) -9. 25. Возрастает на (-оо; 0], убы
вает на [0; +оо). 27. а)&<-1; 6)fe--l; в) k > -1
г) 0. 28. 2. 29. 1. 31. а) (-1; 5); б) (-оо; -4] U [4; +оо):
xfix 1 \ ч ~ ч, , ч ч ( -1 - л/65 1 ,, 70. a) cos 2а; б) 10; в) sin х. 71. -= . 72. т^ • 73. Верно.
НО; з ]; г)0; д)(-оо; +оо); е)(-оо; ^— и 5 13
5 1 я
г-1 + 7б5 Л 74.4,5. 75. 75- 76. sin а = « , а = 5 . 77. a) sin а;
ul 4V° ; +оо). 32. а) (-оо; 0) U (2; +оо); '18 2' 6
6)(-oo;0]U[2;+oo); В)(0; 2); г) [0; 2]; д)(-оо;1) и . B4_ctffa 78 п. б) /g 79 *'_!. б) W?.
и(1;+оо);е)хбЛ;ж)0;з){1}.ЗЗ.а)(-1;5);б)(О;5); б) sm а' в) <*ga. 7». а) 1, 0)V* . 7». а) д , О) д ,
в)0; г) {5}. 34. [-10;-1) U (3; 10]. 35. <-<ю; 6) U «
U (6; +оо). 36. При Ь < 1 хе(Ь; 1) и (4; +оо), приКЬ< в) тт(2 - Зл/2). 80. —«- . 81. а) а > 6,25; б) a > 6;
< 4 х е (4; +оо), при Ь > 4 х е (Ь; +оо). 37. а) (-оо; -2) и 1£> cosza
U (0; 1); б) (-оо; -3] U (5; +оо); в) (-оо; 0) U (3; +оо). в) а > 6,25. 82. При а < 2 х е [а; 2]; при а = 2 х - 2;
38. а) (1; +оо); б) [1; +оо) U {0}; в) (-оо; 0) U (0; 1); приа>2 xg [2; а]. 83. Ь =-17.84. 0.85. При а < 2 0;
г) (-оо; 1]. 39. [-2; 0) U [2; +оо). 40. [-2; \ ) U [0; +оо). щшв-2(1;1);щша>2(1 + Jf^l ; 1 - J|^~l )
41. При а > 1 х 6 (1; а], при а = 1 нет решений, при
4; #;б)-2;2. (l - ^ ; 1 + Д7^ } 86.-2 <а < 0: 4; а2;0-
о < 1 * е [а; 1). 42. а) 1; -1; ~ ; у ; б) -2; 2
43. а)(3; 2), (2; 3); б)(6; 1), (-\ ; -12); в)(1; 1), (1,4; -0,2). а е <_«,. Х) и (1; 4) и (4. +оо). а) _2; 2->5; 7; б) 0,25; 2; 16
1 < а < 2: 4; 0; a > 2: a2; 0. 87. Корни различны при

Алгебра и начала анализа. 10—11 классы
10 КЛАСС
Тригонометрические функции
числового аргумента
1. Упростите выражение:
ч 2Я . 2Я
а) cos g - sin g ;
— . я 4я , я 4я
б) Sin = • COS 7v7 + COS = • Sin K7 J
В)
cos За - cos а
sin За + sin а '
2. Постройте часть графика функции:
а) у = cos х на [-я, я];
б) у = sin * на Г^ ; g + 2я"|;
ч х f Я Зя Л
B)i/=tg*Ha[- gJ у }
3. Пусть f(x) = cos 2jc - 3 sin x. Найдите:
a)/(0); 6)/g); B)/g).
4*. Запишите следующие числа в порядке
возрастания:
71 х 1/ч/ъо . 2я я 0 . 17я
sin = ; tg 100°; sm у ; cos ~ ; 2 + cos -г- .
era. гл л Я 2Я Я 7Я
5*. Среди чисел "» я» 5 » т » g » т укажите
решения уравнения 2 cos 2х + cos * + 0,5 = 0.
6*. Докажите, что при всех значениях х
-8 < 3 cos х + 5 sin х < 8.
7*. Найдите наибольшее значение выражения
3 cos х + 5 sin х.
Основные свойства функций
8. Найдите область определения функции:
3 6)f(x)=j3 - х.
9. Найдите нули функции:
10. При каких значениях t функция у = 2t - 1
принимает отрицательные значения?
11. Пусть f(x) = х + - . Сравните:
а)/(3)и/(|);
б)/(-5) и/(-0,2);
в)/(-37,4) и-/(37,4).
12. Найдите множество значений функции:
2
а) у = х ;
в) Ф(0 = sin 2t;
б) f(x) = cos х\
г) i/= 3 cos g - 1.
a) i/ = 3* + l;
6)i/=x -9.
13*. Пусть /(3) = -5, a /(-4) = 3. Найдите /(-3)
и /(4), если:
а) f(x) — четная функция;
б) f(x) — нечетная функция;
в) f(x) — периодическая функция с периодом
Г = 2.
14*. Какое значение функция у = cos х
принимает на [0; 2я] ровно один раз?
Функции
15. Дана функция у = /(х), определенная на
[-6; 6].
1) Найдите по графику (с. 12):
а) /(3); /(-1); /(5);
б) те значения х, при которых значение
функции равно 1.
2) Исследуйте функцию. Укажите:
а) множество значений функции;
б) координаты пересечения графика с осями
координат;
в) промежутки знакопостоянства;
г) промежутки монотонности (промежутки
убывания и возрастания);
д) точки экстремума, вид экстремума,
экстремумы;
е) является функция четной или нечетной.
3) Для каждого а найдите число корней
уравнения f(x) = а.
4) Найдите все такие 6, при которых данная
функция убывает на отрезке [Ь; Ь + 1].

256
Задачи
Алгебра и начала анализа. 10—11 классы
15.1.
15.2.
1 1 1 1 1 |yj | | | | | |
—Ы—Ы——[4 /lv—н——\—
itttti/TktttF
+^j4Wf
т/иимггг
V 4 3 2
У
4
2
if
4
J
f
0]
J
f
f
\
\
\
■w
L 2 3 4 5 6x
15.3.
15.4.
1 1 1 1 1 lyl 1 1 1 1 1 1 1 1 1 1 1 1 1 ly{ 1 1 1 1 1 1 1
У/г f\ M
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 LiHl 1 iJ 1 1 1 L/f 1 1
L и J n Kh-kt
14 1 \\\\y\ 1 И И г MM Ml
6 N1 1 l-KRS^L 1 1/1 6x| | 6 5 4 3 2 io| i 2 3 4 5 6x|
i 1 rlnn1! rrlTI iIIiiiiimiiiiiiI
15.5.
15.6.
1 1 1 1 1 |y| 1 1 1 1 1 1 1 1 1 1 1 1 1 |y| 1 i 1 1 1 1 1
Ьпч пчмтпммТП
iJ4 ГК n n42J
1111 \V\a\ 1 l\l, и 111 T\l 1111J
11 IfiT и hi им |'Гн -tmI
Y\—\—\-\ 4]——————— —Ш——\-\ 4-1—I—1—I—I—k-J-J
/H 5 LJ_L_L_L_LJ 5
15.7.
15.8.
(
J I
з ;
i :
У
L 0
1
i :
2 3
„^5 (
>x
| | | || lyi 1 1 1 1 1 1
1 L M HJ
IfN r Tin
V\\ 1 \ f 111 П
65432\l0|/l23456x
1 1 1 1 1 Nk 1 1 1 1 1 1
Простейшие тригонометрические
уравнения и системы уравнений
Решите уравнение:
16. a) sin х = п ; б) sin 2х = « ;
ч . х 1
B>sln2 =2'
17. a) cos х = -у ; б) cos | = -у;
в) cos 2jc - - -=-.
18,
a)tgx = l; 6)t£(x- g)-l; B)tgx = -1.
19. a) sin 3x = 2; 6) cos j = - */3 ;
в) tg jc (2 - cos jc) = 0.
20*. Решите систему уравнений
f sin (x + y) =0,
1 cos i/= 1.
21*. Решите уравнение:
a) tg n (cos jc + 1) = 0; 6)
sin*
Л
= 0.
4к - x
Типы тригонометрических
уравнений
22. Решите уравнение, упростив левую часть:
ч 2 .2 7з
а) cos х - sin х = -=-;
б) 2 sin jc cos 2jc = 1;
в)sin3jc• cos (jc + j ) + cos 3jc• sin (jc + j J = 0.
23. Решите уравнение, сделав подстановку:
а) 2 sin2 jc - 5 sin x + 2 = 0;
б) 2 cos jc + 5 sin jc - 4 = 0;
в) cos 2jc + 5 sin jc - 3 = 0;
r)2tgjc + 2ctgx = 5.
24*. Решите уравнение методом разложения
на множители:
а) 5 sin jc + 3 sin 2jc = 0; 6) sin 7jc - sin jc = 0.
25*. Решите уравнение, используя
однородность:
а) sin jc - 7з cos jc = 0;
2 2
б) sin jc - 3 sin jc cos jc + 2 cos jc = 0;
в) sin jc • cos jc - 7з cos jc = 0;
2 2
r) 3 sin jc - 3 sin jc cos x + 4 cos jc = 0.
Простейшие
тригонометрические неравенства
26. Решите неравенство:
a)cosjc>0; 6)sinjc<0; B)tgjc>l.
27. Найдите какой-либо корень уравнения
cos jc = о »удовлетворяющий неравенству sin jc> 0.

Задачи ОКГТ
Алгебра и начала анализа. 10—11 классы ™*J •
28. Найдите какое-либо решение неравенства Метод интервалов ,
cos х> 0, удовлетворяющее уравнению sin х = g. 35 Решите неравенство:
х +
29*. При каких значениях а неравенство а) (х - 3)(х + 2) < 0; б) > 0;
х — 4
sin jc < а
(ний;
б) выполняется при любых х;
3 2 Зх ~ 1
а) не имеет решений; в) (х - 2) jc (jc + 1) > 0; г) — < 0;
х + 1
в) имеет одним из своих решений число ^; 36. Пусть f(x) = х (х - 3). Найдите те
значения х9 для которых:
г) не имеет среди своих решений числа т ? a) /(jc) > 0; б) f(x) < 0;
в) f(x) > 0; г) f(x) < 0.
Техника дифференцирования 37*" Решите неравенство:
о
х — 2jc "~ 3 х -- 5 2х "~ 4
30. Найдите производную функции в точке jc0: а) £ < 0; б) —— > ——- .
X X + 4 X + О
а) I/ = Зх , х0 = 1; б) у = cos х, х0 - g ; gg* найдите область допустимых значений
в) I/ = -2 sin jc, jc0 = j ; г) у = 2 + Jx , jc0 = 4.
31. Приведя функцию к виду kxm (т е Z),
функции:
а>Л*>= /~Ч; 6)Лх)-а/9х- х3;
Vx - 7
3
X
найдите производную: в)/(х)= / * - Зл/эх -
2 3 2 Vx - 7
a) i/ = Зх х ; б) I/ = -о ;
* х2 + 1
5 39*. Пусть f(x) = . Найдите все х, удов-
) = — • Ъ = —
в'^ д 5' г'^ 175" летворяющиеусловию:
а)Дх) = 0; б)/'(х)>0; в) f (х) < 0.
32. Используя формулу производной от
суммы, найдите производную функции:
2 i Касательная
а) у = х - 5х + - ;
2 40. Напишите уравнение касательной к гра-
б) у = х (х - 5х + 1); фику функции i/ = f(x) в точке х0:
3 2
В) у = * ~ 5* + * . а) /(*) = х2, Х0 = -1; б) /(*) = cos х, х0 = 0.
33*. Используя формулы производной произ- 41 Напишите уравнение касательной к гра-
ведения или частного, найдите производную фику функции у — 2х - х , параллельной оси
функции: абсцисс.
2
а) у = х cos х; б) i/ = * . 42. Найдите все общие точки графика функ-
1 + X 3 2
ции у = х - Зх и касательной к этому графику
34*. Используя правило дифференцирования в точке с абсциссой х = 0.
сложной функции, найдите производную
функции: 43*. Найдите общую точку касательных к гра-
а) у = (х2 - Зх + I)7; б) у = *Jx2 - Зх + 1; ФИКУ У = *2 " 4* + 3> °Дна из которых касается
графика в точке с абсциссой 3, другая в точке с
в) у = tg [ Зх - ^ ) г) у = cos х. абсциссой 1.
9-1019

258
Задачи
Алгебра и начала анализа. 10—11 классы
44*. Напишите уравнение всех касательных
к графику функции у = х , проходящих через
точку М(-1; 0).
Исследование функции
при помощи производной
45. Найдите критические точки функции,
определенной на множестве действительных
чисел:
a) f(x) - Зх + 5; б) f(x) = х2 - 5х - 1;
b)/(*) = *3 + *2-5*+4.
46. Найдите промежутки возрастания и
убывания функции и определите ее точки экстремума:
a) f(x) = Зх + 6; б) f(x) = х2 - Ъх + 5;
B)f(x) = xB + x2-5x- 3.
47*. Найдите экстремумы функции:
а) /(*) = *2 (х - 3); б) /(х) = х3 (х - 4).
48*. При каких значениях Ъ один из экстре-
мумов функции у = х - Зх + Ъ равен 7?
Исследование функции
и построение графика
49. Для данной функции у = f(x) найдите:
1) Область определения D (/).
2) Производную и критические точки.
3) Промежутки монотонности.
4) Точки экстремума и экстремумы.
5) Точку пересечения с осью Оу и несколько
точек графика.
6) Постройте график функции и определите:
а) множество значений Е (/) функции;
б) корни функции (можно приближенно).
7) Найдите число корней уравнения f(x) = 3.
49.1.
49.2.
49.3.
49.4.
49.5.
49.6.
у = х - 12*.
у = 6х - 2х3.
у = 2х -Зх .
у - Зх2 + 2х3.
у - -jc3 + Зх + 5.
I/ = 2х3 - 6* + 4.
49.8.
49.9.
У" х + 1
*/ =
2х3 + х2 + 1
49.7.
0-
*2 + 4
Нахождение наибольшего
и наименьшего значений функции
50. Для графиков функций из предыдущего
задания:
1) Укажите критические точки функции.
2) Найдите наибольшее и наименьшее
значения функции на отрезке:
а) [-6; 6]; б) [-6; 0]; б) [-6; 0].
3) Укажите какой-либо отрезок, на котором
наименьшее значение функции принимается
на его конце.
4) Укажите какой-либо отрезок, на котором
наибольшее значение функции принимается
в критической точке.
5) Укажите какой-либо отрезок, на котором
наибольшее значение принимается более чем
в одной точке.
6) Найдите все такие 6, при которых
для вариантов 1, 2, 4, 5, 8 min f(x) = /(0);
[0;Ь]
для вариантов 3, 6, 7 тах/(я) = /(0).
[0;Ъ]
7) Для каждого а (-6 < а < 6) найдите max f(x)
на отрезке [-6; а].
Наибольшее и наименьшее
значения функции на отрезке
51. Найдите наибольшее и наименьшее
значения функции f(x) на отрезке:
а)/(*) = 3х- 1на[-1;2];
б)/(*) = " *2 на [-1; 2];
в) f(x) = 2х-х2 на [-2; 0];
г) f(x) = Зх - х3 на [-3; 0].
52. Периметр прямоугольника 20 м.
Обозначим одну из его сторон за х и рассмотрим те
прямоугольники, для которых х е [2; 8]. Найдите
среди них прямоугольник с наибольшей
площадью и прямоугольник с наименьшей площадью.
Укажите площади этих прямоугольников.

Задачи
Алгебра и начала анализа. 10—11 классы
259
53*. Для функции у = х - 3* - 2 найдите все
такие Ъ (Ъ > -1), при которых наибольшее
значение функции на отрезке [-1; 6] равно нулю.
54*. По возможности не производя
вычислений, докажите, что:
max [ х + 4х + Зх + 11 \>
[-7;3]v ;
)■
> max
[
iax ( х + л/:
l;2]v
хл + Зх + 11
Упражнения,
содержащие параметры
55. При каких значениях а функция
у = х +3х + ах - 1
не имеет критических точек?
56. При каких значениях Ъ уравнение
cos2 х - (3 + 26) cos х + 66 = 0
не имеет корней?
57. При каких значениях р уравнение cos х = р
Г к 5я1о
имеет ровно три корня на промежутке ~ 5 ; ~3~
58. При каких значениях т функция
у=х3-Зт2х + 1
имеет ровно одну точку экстремума на отрезке
[-2; 7]?
2
59. Пусть f(x) = х -7х + а. При каких
значениях а
min f(x) = 2?
[3;4]
60. Пусть f(x) = х . При каких значениях 6
(Ь > -3)
max f(x) = 9?
[-3;6]v
61. При каких значениях р функция у =рх +
+ cos Зх не имеет точек экстремума?
62. При каких значениях а уравнение
х - Зх = а
имеет ровно два различных корня?
63. Для всякого 6 найдите число корней
уравнения
4х + - = 6.
х
64. Для каждого значения р найдите число
корней уравнения sin х = « на отрезке [р;р + тс].
11 КЛАСС
Первообразная
и определенный интеграл
1. Найдите общий вид первообразных F(x)
функции у = f(x) на указанном промежутке:
а) f(x) = Зх - 1 на R;
б) f(x) = х + cos х на R;
в) f(x) = \ на (- оо; 0) или на (0; - оо).
X
2. Найдите ту первообразную функции
/(*) = 3*2 + 2*-1,
график которой проходит через начало координат.
3. Вычислите:
з о
2
a) jx dx;
б) J (х2 + 4х - l)dx;
в) J (3jc2 - 2x)dx; г) J sinxdx.
4*. Пусть F(x) — та первообразная функции
f(x) = 4jc — 1, график которой имеет с графиком
функции f(x) общую точку на оси ординат.
Найдите все общие точки графиков функций f(x) и F(x).
5*. Пусть F(x) — первообразная функции у =
= х - 4х. Найдите промежутки монотонности и
точки экстремума функции F(x).
а
6*. Найдите все такие а, что j2xdx > 3.
Вычисление площади
криволинейной трапеции
с помощью определенного интеграла
7. Найдите площадь фигуры (предварительно
сделайте рисунок), ограниченной:
1) графиком функции у = 4х - х и осью
абсцисс;

260
Задачи
Алгебра и начала анализа. 10—11 классы
2) графиком функции у = 4х - х , осью
ординат и прямой у = 4;
3) графиком функции у = cos х9 осью абсцисс
я я
И ПРЯМЫМИ X = д , X = 5 ;
2 2
4) графиками функций i/ = л: иу = 4х-3х ;
5) графиками функций у=*/х9у = 2-хи
осью абсцисс.
Обобщение понятия степени.
Иррациональные уравнения
и неравенства
8. Упростите:
а) 72 -V2 -V2 +(V5)5;
б)
1 - х
12
+
1 - X
36
1 , 36 ,
1 + х л- х
&
1 + X
9. Решите уравнение:
а) УЗх - 1 = -5; б) л/Зх - 1 = -5;
в) V3x - 1 = 5;
г) л/Зх - 1 = л/х + х - 4;
д) V3x - 1 = 1 - Зх; е) л/Зх + 1 = х - 3;
ж)х - 3*/* +2 = 0.
10*. Решите неравенство:
a) Jx - 2 > 3; б) Jx - 2 < 3;
в) Jx - 2 > -2; г) Jx - 2 < -2;
д) Jx - 2 > J3 - х.
Логарифмы.
Показательные уравнения
и неравенства
11. Вычислите:
a) log327 + log2\ - log15«/15 ; б) lg 2 + lg 5;
в)
log332
522 1UB15*
log32 •
12. Решите уравнение:
а) 2х = 32; б) 3* =7;
в) 3х + 3х + Х = 4; г) Ъ2х - 6 • 5х + 5 = 0.
а)2х> J;
13. Решите неравенство:
•»ег**(1Г""-
14*. Найдите все такие *, что
9* + 5 • З2' > 4* + 3 • 22'.
15*. При каких значениях а уравнение
4*-(а + 1)-2* + 2а-2=0
имеет ровно один корень?
Логарифмические уравнения
и неравенства
16. Решите уравнение:
a)log1(3x-5) = -l;
2
6)log1(3x-5)=log1(JC2-3);
2 2
B)log2(x2-3*) = 2;
г) log2* + log2 (x - 3) = 2;
fl)lg2x-21gx-3 = 0.
17. Решите неравенство:
a) log4(2* ~l)>\; 6) log4(2* - 1) > -1;
в) log2 x - 3 \og2x - 4 < 0;
r) log3(5* - 1) > log3(2 - 3x).
18*. Решите систему уравнений
f log2(x + y) = l,
jlog3(*-i/) = 2.
19*. Для каждого а решите уравнение
log3(x - 3) = log3(2x + a).
Показательная
и логарифмическая функции
20. Найдите производную функции:
а) у = 2х - ех; б) у = х2 + 3 • In х.
21. Найдите множество первообразных
функции на заданном промежутке:
а) у = - на (0; +оо); б) у - 2х + е* на Д.

Задачи
Алгебра и начала анализа. 10—11 классы
261
22. Найдите область определения,
критические точки, промежутки монотонности, точки
экстремума и экстремумы функции:
х 2
&)у = х-е ; б)у = 0,5* - In х.
23*. Вычислите площадь фигуры, ограничен-
2 Q
ной линиями у= - и у = 3 - X.
24*. Докажите, что уравнение ех - 1 = х
имеет ровно один корень, и найдите этот корень.
Исследование функций
и построение графикой
(допустимо использование
микрокалькуляторов)
25. 1) Найдите область D(f) определения
данной функции f(x).
2) Найдите f(х) и D(f).
3) Найдите критические точки, исследуйте
функцию на монотонность и определите точки
экстремума функции.
4) Найдите экстремумы функции.
5) Определите точку пересечения графика
функции с осью Оу.
6) Исследуйте функцию на четность и
нечетность.
7) Найдите значения функции в нескольких
дополнительных точках.
8) Постройте график функций.
9) Определите множество E(f) значений
функции f(x).
10) Укажите какой-либо отрезок [а; &],
такой, что
а) тах/(*) = /(а); б) min f(x) = /(a).
[а;Ъ] [а;Ъ]
25.1.
25.2.
25.3.
25.4.
25.5.
f{x) = х - е + 2.
f(x) = х - In X.
1
f(x) = x-2x2.
f(x) = ex-x.
fix) = 2 In x - x
Упражнения,
содержащие параметры
26. При каких значениях а первообразная
F(x) функции f(x) = х - 2х + а возрастает на
множестве действительных чисел?
27. Для каждого значения а решите уравнение
log2(3* - 1) = log2(x + a).
28. При каких значениях а уравнение
4*-(3a + 7)-2* + 21a = 0
имеет ровно один корень?
29. При каких значениях а функция у = х • е х
возрастает на [а - 3; а + 4]?
30. При каких значениях а график функции
у = ах + 1 является касательной к графику
функции у = In JC?
31. При каких значениях а число 2
удовлетворяет неравенству loga(3* - 1) < 3?
32. При каком целом значении Ъ решением
неравенства (х - Ь)(х - log27) < 0 будет отрезок
наименьшей длины?
33. При каком значении а площадь, ограни-
ченная линиями квх,*-а,хяа + 3,у = 0,
принимает наименьшее значение?
34. При каком положительном значении Ь
прямая х = б делит площадь фигуры,
ограниченной линиями у = - 9у = 0, * = 4, * = Ь + 6, на
две равные части?
35. Найдите площадь фигуры, ограниченной
2
графиком функции у = Зх , осью абсцисс и
прямыми х=а-1и#=а + 1, где а е R. При каком
значении а эта площадь наименьшая?
ОТВЕТЫ
10 класс
/о /о
1.а)^-; б)^р B)-tga. З.а)1; б)-4; в)-1.
л j. -ЛЛО п . п . 2я п , 17я _ к 7л
4. tg 100°; COS5 ; sin= ; sin-=-; 2 + cos-r- . 5. « ; -3- •
7. JU.S. а) (-oo; -7) U (-7; +oo); б) (-oo; 3]. 9. а) -|;
б) 3; -3. ЮЛ < \ . 11. а) /(3) > /( § ) б) «-5) = fl-0,2);
в) /(-37,4) = -/(37,4). 12. а) [0; +оо); б) [-1; 1]; в) [-1; 1];
г) [-4; 2]. 13. а)«-3) = -5; /(4) = 3; б) /(-3) = 5;
/(4) = -3; в) Я-3) = -5; /(4) = 3. 14. Значение у - -1
прих = я.16.а)(-1)*-5 +nk,keZ; б)(-1)*-^ +у,

262
Задачи
Алгебра и начала анализа. 10—11 классы
k е Z; в) (-1) • « + 2nk, k е Z. 17. а) ±т + 2пп, -« ; 1 , точка максимума х — -« , точка минимума
Зя я тс х = 1. 47. а) 0 — максимум, -4 — минимум; б) -27 —
п е Z; б) ±-j- + бтт, п е Z; в) ^ ± g + яп, т* € Z. минимум. 48. 5; 9. 51. а) 5; -4; б) 0; -4; в) 0; -8;
iq в\ к л. «г, „ ^ *. к\ 7п -и ^ „ ^ *. „\ п л. ™ г) 185 "2- 52- Прямоугольники: 5 х 5 м, 2 х 8 м; 25 м ,
1о. а) т + ял» ^ ^ Z; о) -Гп + я^» п е Z\ в) — 7 + ял, о
* Л ЧТТ Ч мх „4 ч 16 м2. 53. (-1; 2]. 55.а>3. 56. Ь € (-оо; -0,5) U
neZ. 19. а) Нет решении; б) нет решении; в )т% у +оо) = Q>5 5g m е ^ _2) у (2; ?] ^ а _
т* е Z. 20. х = яд, у - 2я*; п € Z; Л € Z. 21. а) 2лл, = 14>25. 60. Ь е (-3; 3]. 61. р е (-оо; -3] U [3; +оо).
п 6 Z; б) -я; 0; я. 22. а) ±£ + ят*, п е Z; б) J + ? , 62- * е <Т* ?>■ «■ Д™ Ь е <-°°5 "4> " <4; +°°>/ва К°Р"
12 8 2 ня, для Ь 6 {-4; 4} один корень, для о е (-4; 4) нет кор-
Я 1ZTI Л Я Г тс 5я П
п б Z; в) - у^ + -£-, п € Z. 23. а) (-1) • g + яЛ, Ней. 64. Дляр е [-g + 2nk; -у + 2я*|, Л е Z два корня,
*eZ;6)(-l)*-g +nk,keZ; в)(-1)*. £ +я*, * е Z; дляре^ + 2Ш; у + 2я/]и[^ + 2nZ; ^ + 2я/),
г) arctg 2 + я*, arctg Г ^\ + яп, k,neZ. 2А. &)m,neZ; leZ один корень, для р е [ -g- + 2я/п; -у + 2ят J,
J (Ь\\^* и и ~ «,* .,** ™ и * те Z корней нет.
±1 я - arccosl g I I + 2я&, k е Z; б) g + -7-, -=- , k е Z,
7i е Z. 25.a)g + ят*, TieZ; б) j + ят*, агс1£2 + яЛ, И КЛаСС
п е Z, Л е Z; в) « + яд, л g Z; « + ял, Л е Z; г) т + ял, Зх2 „ ^ х6 , , Л ч 1 , „
. z rf 4 1. а) -я х + С; б) -£- + sin х + С; в) -- + С.
/ я Я Л z D *
arctg 2 + яЛ, 71 g Z, Л е Z. 26. а) - о + 2яЛ; « + 2яЛ , « 9 12
f\ 2 2 ) 2..Р(х) = х3 + х2-х.3.а)б5;б)-2=;в)0;г)0,5.4.(0;-1),
(К К \ О О
k е Z; б) (я + 2яЛ; 2я + 2яЛ), k е Z; в) ^ + nk; ^ + nk J, (2,5; 9). 5. Возрастает на (-оо; 0], [4; +оо), убывает
на
я ЛЛ „ я
[0; 4]; 0 и 4 — точки экстремума. 6. (-оо; -2], [2; +оо).
keZ.27. Например, ^ . 28. Например, ^v. 29. а) (-оо; -1]; ,-
7.а) f ; б) |; в) ^-i ; г) |; д) 1 g . 8. а) 7; б) 2.
9. а) -411; б) 0; в) в|; г) 3; д) g; е) 8; ж) 1; 4.
10. а) (11; +оо); б) [2; 11); в) [2; +оо); г) 0; д) (2,5; 3].
32. а) 2х -5- \; б)3х2-10х + 1; в) 2х - 5 - \. П' а> ^5' б> ^ в> 5' 12' а> 5' б> 1о^ в) 0; г) 1; 0.
б) (1; +оо); в) (|;+°°); г) (-оо; ^ ]. 30. а) 6; б) -\ ;
в) -л/2 ; г) |. 31. а) 15х4; б) -4х~3; в) -^ х-6; г) ^х4.
х
33. a) cos х - х sin х; б) ^ • 3** а) 7(^2 ""3* +
13. а) (-2; +оо); б) (3; +оо); в) [-3; 1]. 14. {-\ ; +оо j
(1 + х)а 15.(-оо;1]и{3}.16.а)2|;б)2;в)-1;4;г)4;д)0,1;1000.
**.* — 3 3
+ 1)0(2Х_3); <°2-У*"-8* + 15 B)cos2(3*-^; 17.а)[1,5;+оо);б)(0,5;1,5);в)(0(5;16);г)(|;|)
г) -sin 2х. 35. а) [-2; 3]; б) (-°°; -3) и (4; +оо);
18. (5,5; -3,5). 19. При о < -6 х = -о - 3, при о > -6
в) (-оо; -1) и (2; +оо); Г) (-1; 1). 36. а) (3; +оо); ний нет< 20. а) 2 - ех; б) 2х + - . 21. а) 2 In х + С;
б) (-оо; 0) U (0; 3); в) {0} U [3; +оо); г) (-оо; 3]. *
37. а) (-оо; -1) и (0; 3); б) (-5; -4). 38. а) (-°о; 0] и б) J + е* + с> 22> а) Щу) _ я> критическая точка
39(?aW°?; I»- б! Г-1 и и1- Sov Й/ТЬЖ? * * " °' В03раСТаеТ М "^ °]' *—" На [°; + <Х>)'
43. (2; -2). 44. у = 0 у = -4^ - 4. 45. а) Критических =f' +00>' критическая точках = 1, возрастает на[1; -К»),
к к убьшаетна(0; 1], х = 1—точкаэкстремума, 0,5 —экс-
точек нет; б) g ; в) 1; -д . 46. a) f(x) возрастает на Я, тремум. 23. 1,5 - 2 In 2. 24. х - 0. 26. [1; +оо). 27. На
точек экстремума нет; б) f(x) возрастает на N ; +°° J, [~°°a> 3 J Решений нет» на ("з ; +°° J Х = 2 "
убывает на (-оо; - 1 точка минимума х = ^; в) f(x) 28. (-00; 0] U \ П. 29. (-оо; -3]. 30. е~2. 31. (0; 1) U
возрастает на (-оо; -- ] и на [1; +oo)f убывает на у (3/g ; +оо). 32. 3. 33. -1,5. 34. 3.

Геометрия. 7—9 классы
7 КЛАСС
Аксиомы планиметрии
1. Точки А, В и С лежат на одной прямой,
причем длина отрезка ВС больше длины отрезка
АС в 3 раза, а длина АВ меньше длины ВС на
3,6 см. Найдите длину отрезка АС.
2. Угол между лучами тис равен 157°, а
угол между лучами п и с на 39° больше угла
между лучами тип. Найдите А(пс), если луч п
проходит между лучами тис.
3. На плоскости отмечены пять точек: А, В,
С, D, Е. Прямая т разделила плоскость так, что
две из данных точек оказались в одной
полуплоскости, а три другие в другой. Сколько раз
ломаная ABCDE может пересекать прямую ml
4. Сколько можно начертить треугольников,
равных данному, если две вершины этих
треугольников совпадают с двумя вершинами
данного треугольника, лежащими на прямой Z?
I
5. Точки К, Р и М лежат на одной прямой,
причем МК = 5,4 см, КР = 8 см. Найдите MP.
6. Сколько всего треугольников можно
обнаружить на рисунке?
7. На прямой отмечены шесть точек: А, В, С,
D9 Е, F. Сколько различных отрезков с концами
в этих точках можно составить?
8. На сколько частей могут разбить
плоскость 3 различные прямые?
Углы
9. Углы АОВ и ВОС — смежные. Найдите угол
АОВ, если угол ВОС в 1,5 раза меньше угла АОВ.
10. Прямые MN и КР пересекаются в точке
О, причем сумма углов КОМ и NOP равна 134°.
Найдите величину угла KON.
11. Прямая АВ разбивает плоскость на две
полуплоскости. Из точки О, принадлежащей
прямой АБ, в разные полуплоскости проведены лучи
ОС и OD, причем угол AOD в 3 раза больше
угла АОС. Найдите угол АОС, если A BOD = 126°.
12. Угол NOK в 3 раза больше угла DOM, а
угол DOK на 12° больше угла NOK. Найдите
угол CON.
Р\
13. Углы АОМ и СОМ — смежные. ОК —
биссектриса угла АОМ, причем угол АОК в 4 раза
меньше, чем угол СОМ. Найдите угол КОМ.
14. Дано: Z. ВОС - 148°, ОМ 1 ОС, ОК —
биссектриса A СОВ.
Найти: /.КОМ.
15. Прямые АВ и CD пересекаются в точке О.
ОК — биссектриса угла AOD, А. СОК - 118°.
Найдите угол BOD.
16. Дано: A COD - A KOD - 61°,
A COD - А КОС = 53°.
Найти: A COD.

264
Задачи
Геометрия. 7—9 классы
Равенство треугольников.
Медиана, высота и биссектриса
треугольника
17. Известно, что BD — медиана треугольника
ABC, DE = DB и что АВ = 5,8 см, ВС = 7,4 см,
АС = 9 см. Найдите СЕ.
В
18. ОМ и ON — высоты треугольников АОВ и
COD, причем ОМ = ON. Найдите CD, если АО =
= 6,5 см, AM = 4,2 см и DN = 5,6 см.
19. Дано: А МРС = A DAB, MP - 12 см, СР =
- 8 см, /. А = 73°.
Какое из высказываний верное?
а) DB = 8 см, АВ - 12 см;
б) Z. М = 73°, АВ = 8 см;
b)AD = 12 см, /.Р = 73°;
в)АВ = 12 см, /LP = 73°.
20. Треугольник ABC равен треугольнику
А1В1С1. Периметр треугольника ABC равен 39 см.
Сторона АгВх треугольника АгВгСг в 1,5 раза
меньше стороны В1С1, а АгСг на 3 см меньше
стороны АгВг. Найдите большую сторону
треугольника ABC.
21. В треугольниках МРК и BDE проведены
биссектрисы PC и DN; А МРС = A BDN.
Найдите отрезок NE, если ЛГЙГ = 8 см, a BN < NE
на 2,4 см.
22. Прямая АВ разбивает плоскость на две
полуплоскости. Из точек А и Б в разные
полуплоскости проведены равные отрезки AD и ВС,
причем /. BAD = /. ABC.
Какие из высказываний верные:
1) A CAD = ABDA; 3) А БАО - АБАС;
2) /.DBA = /.CAB; 4)ААОБ = АБСА?
23. Сколько пар равных треугольников на
рисунке?
/S7
24. На какое наибольшее число равных
треугольников может разделить прямоугольник
ломаная, состоящая из трех звеньев?
Равнобедренный треугольник
25. Периметр равнобедренного треугольника
41 см, причем боковая сторона на 3,5 см меньше
основания. Найдите основание треугольника.
26. Периметр равнобедренного треугольника
CDE равен 26 см; СЕ — основание, DB —
биссектриса этого треугольника, периметр
треугольника DBE равен 20 см. Найдите DB.
27. В треугольнике ABC угол А равен углу С,
а высота AD делит сторону ВС пополам. Найдите
АС, если BD = 7,8 см.
28. В треугольнике МРЕ проведена медиана
РК, причем РК = MP и Z. М - 54°. Найдите
угол РКЕ.
29. Какие из перечисленных высказываний
верные?
1) Если медиана и высота, проведенные из
одной вершины треугольника, не совпадают, то
этот треугольник не является равнобедренным.
2) Если биссектриса треугольника делит
противоположную сторону на равные отрезки, то
этот треугольник равнобедренный.
3) Если треугольник равносторонний, то
длина любой его высоты равна длине любой его
биссектрисы.
4) Если треугольник равнобедренный, то
наименьшей из сторон является его основание.
30. В прямоугольнике ABCD сторона АВ
вдвое короче ВС. Найдите угол AKD, где К —
середина ВС.
31. На какое наибольшее число
равнобедренных треугольников можно разделить данный
равнобедренный треугольник тремя отрезками?

Задачи
32. Сколько всего равнобедренных
треугольников можно заметить на рисунке?
Параллельные прямые
33. Прямая MN пересекает параллельные
прямые АВ и CD (М € АВ, N € CD). Сумма углов
AMN и CNM равна 136°. Какие из
высказываний верные?
1) Точки А и D лежат в разных
полуплоскостях относительно прямой MN.
2) Точки В и С лежат в одной полуплоскости
относительно прямой MN.
3) Сумма углов AMN и DNM равна 180°.
4) Угол BMN равен 112°.
34. Прямая ЕК является секущей для
прямых CD и MN (Е ZCD, К € MN). Угол DEK
равен 65°. При каком значении угла NKE прямые
CD и MN могут быть параллельны?
35. Один из внутренних односторонних
углов, образованных параллельными прямыми а и
Ь и секущей с, равен 53°. На сколько градусов
этот угол меньше другого внутреннего
одностороннего с ним угла?
36. Разность между двумя внутренними
односторонними углами при параллельных а и & и
секущей с равна 24°. Найдите больший из этих
углов.
37. Дано: а II Ь, с — секущая, KD и КЕ —
биссектрисы смежных углов, образованных
прямыми бис; DE = 9,6 см.
Найти: КР.
Геометрия. 7—9 классы
Найти: А АСЕ.
В
А
^^ К
AND £~
265
39. Дано:AF \\ BE, АО \\ BD, A OAF = 36°,
Z. ABO в 2 раза больше Z. CBD.
Найти: Z.OBC.
40. В треугольнике ABC ZA= 37°, Z. С = 65°.
Через вершину В проведена прямая MN II АС.
Найдите угол MBD, где BD — биссектриса угла
ABC.
Сумма углов треугольника
41. В треугольнике ABC угол В в 1,5 раза
больше угла А, а угол С на 12° больше угла В.
Найдите угол В.
42. В равнобедренном треугольнике ABC /.С -
= 104°. AM — высота треугольника. Найдите
угол МАВ.
43. В равнобедренном треугольнике
биссектрисы углов при основании образуют при
пересечении угол, равный 52°. Найдите угол при
вершине этого треугольника.
44. В треугольнике МКР медиана МС равна
половине стороны КР. Найдите угол М
треугольника МКР.
45. Один из внешних углов треугольника в
2 раза больше другого внешнего угла. Найдите
разность между этими внешними углами, если
внутренний угол треугольника, не смежный с
указанными внешними углами, равен 45°.
46. Дано: А ABC — прямоугольный (А С =
= 90°), А В - 27°, CD — высота, СК —
биссектриса угла АС В.
Найти: Z.DCK.
А^
38. Дано: CD _L АК, MN _L АК, A AMN - 28°,
СЕ — биссектриса Z BCD.

266
Задачи
Геометрия. 7—9 классы
47. Дано: А ABC — прямоугольный (/. С =
= 90°), ВС = 7,8 см, CD — высота.
Найти: CD.
1205
В
48. Найдите сумму внутренних углов
пятиугольника CDEFK.
Окружность
49. Центр описанной окружности около
любого треугольника — это...
а) точка пересечения высот;
б) точка пересечения биссектрис;
в) точка пересечения серединных
перпендикуляров к сторонам треугольника;
г) точка пересечения медиан.
50. Медиана прямоугольного треугольника,
проведенная к гипотенузе, равна 14 см. Найдите
диаметр описанной окружности.
51. К окружности с радиусом 8 см и центром
О из точки А проведена касательная АВ, причем
расстояние между точками А и О равно 16 см.
Найдите угол АОВ.
52. Хорды MN и МК окружности равны по
18 см, а угол KMN равен 120°. Найдите диаметр
этой окружности.
53. Расстояние от центра О окружности до
хорды CD равно 9 см. Угол OCD равен 45°. Точка
К принадлежит хорде CD, причем С К = 3KD.
Найдите длину отрезка СК.
54. Радиусы двух пересекающихся
окружностей равны 7,8 см и 5,7 см, расстояние меяеду
центрами окружностей 9,6 см. Найдите длину
отрезка АВ.
55. Дано: А ABC — равнобедренный, АВ = ВС,
Z. В = 76°, О — центр вписанной окружности,
OD и ОЕ — радиусы этой окружности (D € АВ,
Е € АС).
Найти: A DOE.
56. Диаметр окружности, описанной около
равностороннего треугольника, равен 48 см.
Найдите радиус окружности, вписанной в этот
треугольник.
Повторение
57. Величины смежных углов
пропорциональны числам 5 и 7. Найдите разность между
этими углами.
58. В прямоугольном треугольнике ABC
/.С = 90°, Z. А = 30°, AC = 10 см, CD ± АВ,
DE _L АС.
Найдите АЕ.
В.
D
59. Прямые а и Ь параллельные, с —
секущая. Разность двух углов, образованных этими
прямыми, равна 130°. Найдите отношение
большего из этих углов к меньшему.
60. Периметр равнобедренного треугольника
равен 13 см, а одна из его сторон на 4 см меньше
другой. Найдите сумму боковых сторон этого
треугольника.
61. Назовите верные высказывания:
А: Треугольник равносторонний, если он
равнобедренный и один из углов равен 60°.
В: Если сумма двух углов равна 180°, то эти
углы смежные.
С: Высота треугольника обладает свойством:
все ее точки равноудалены от сторон угла, из
которого она проведена.
D: Если медиана треугольника равна
половине стороны, к которой она проведена, то
треугольник является прямоугольным.
62. Хорда АВ равна 18 см. ОА и ОВ —
радиусы окружности, причем Z. АОВ — 90°. Найдите
расстояние от точки О до хорды АВ.

Задачи
Геометрия. 7—9 классы
267
63. В треугольнике МРК угол Р составляет
60% угла К, а угол М на 4° больше угла Р.
Найдите угол Р.
64. На каком из рисунков сумма расстояний
АО и ОВ является наименьшей?
а)
в)
б)
А
1
п
т
L
>
г)
1 1 1 1 1 1 1 1 1г
1 1 I 1 1 TiJ
U1
1 1*1 1 1 II 1 1
Ь1
f
1
1 1 1 1 1 1 1 1г
Ti.
\л 1
•р-Т 1 1 1 1 1 1
ом
>
'
8 КЛАСС
Параллелограмм.
Прямоугольник. Ромб
1. Стороны параллелограмма
пропорциональны числам 4 и 5. Найдите большую сторону, если
периметр параллелограмма равен 10,8 см.
2. Один из углов ромба равен 150°, а его
высота равна 3,5 см. Найдите периметр ромба.
3. В прямоугольнике ABCD проведена
биссектриса угла А, которая пересекает сторону ВС
в точке М, причем ВМ : МС = 2:3. Найдите ВС,
если периметр ABCD равен 56 см.
4. В параллелограмме MNPK проведена
высота NE, причем угол NME в 5 раз больше угла
MNE. Найдите угол MNP.
5. Какие из высказываний верные?
А: Если диагонали четырехугольника
равны, то он прямоугольник.
В: Если противоположные стороны
четырехугольника попарно равны, то он
параллелограмм.
С: Если диагонали четырехугольника
перпендикулярны, то он ромб.
D: Диагонали прямоугольника являются
биссектрисами его углов.
6. В прямоугольнике один из углов,
образованных диагоналями, равен 120°, а меньшая
сторона прямоугольника равна 9 см. Найдите
диагональ прямоугольника.
7. В параллелограмме ABCD диагонали
пересекаются в точке О, причем Z. СОВ = 126°,
Z. CAD = 28° и длина отрезка BD вдвое больше
стороны АВ. Найдите угол D параллелограмма.
8. Сколько параллелограммов с вершинами в
трех данных точках, не лежащих на одной
прямой, можно построить?
Теорема Фалеса.
Средняя линия треугольника.
Трапеция
9. Дано: Z.(mn), АВ \\ АгВг || А^2 II А3В3 II А4В4,
ОА = ААг = АгА2 - AaAg - А^А4. ВВ4 - В2В3 -
- 10 см.
Найти: ОВ4.
10. Средняя линия треугольника на 3,6 см
меньше основания треугольника. Найдите
сумму средней линии треугольника и основания.
11. В параллелограмме ABCD периметр равен
56 см, a A D - 120°, BD = AD. Найдите
периметр треугольника CMN, где М — середина ВС,
а N — середина CD.
12. В равнобедренной трапеции ABCD (ВС \\ AD)
Z.B = 135°, ВС = 10 см, AD = 18 см. Найдите
высоту трапеции DE.
13. ABCD — трапеция, AD = 23 см, ВС = 18 см,
МК — средняя линия. Найдите EF.
В С
14. В трапеции МРКЕ (РК II ME) РК - 12 см,
ME = 21 см. Параллельно основаниям
проведены отрезки АВ и CD, причем А и С
принадлежат стороне MP, а В и D — стороне КЕ.
Найдите АВ, если РА=АС = СМ.

268
Задачи
Геометрия. 7—9 классы
15. В трапеции три стороны равны по 4 см, а
четвертая сторона 8 см. Найдите наибольший
угол трапеции.
16. Отрезок АВ пересекает прямую Z, причем
точка А удалена от прямой I на 28 см, а точка В на
21 см. Точка С середина отрезка АВ. На каком
расстоянии от прямой I находится точка С?
Теорема Пифагора
17. Один из катетов прямоугольного тре-
12 щ
угольника равен т~ дм, а гипотенуза равна 10 см.
Найдите второй катет.
18. Периметр прямоугольника равен 62 см, а
точка пересечения диагоналей удалена от одной
из его сторон на 12 см. Найдите длину
диагонали прямоугольника.
19. Периметр ромба 68 см, а одна из его
диагоналей равна 30 см. Найдите длину другой
диагонали ромба.
20. Гипотенуза АВ прямоугольного
треугольника ABC равна 2 722 см, а катет ВС равен 6 см.
Найдите длину медианы ВК.
21. Сторона равностороннего треугольника
равна 18^3 см. Найдите биссектрису этого
треугольника.
22. В треугольнике CDE CD = 15 см, DE =
= 13 см, СЕ = 14 см. Найдите высоту DM.
23. Дано: A ABC, /. С = 90°, CD LAB, АС =
— 15 см, AD — 9 см.
Найти: АВ.
24. На сторонах прямоугольного
треугольника ABC (/-С = 90°) построены квадраты, причем
2 2
Sx - S2 — 112 см , a S3 = 400 см . Найдите
периметр треугольника ABC.
Определение синуса,
косинуса, тангенса, котангенса
25. В треугольнике ABC А С = 90°, Z. А = 37°,
ВС = 8 см. Найдите АС.
26. В равнобедренном треугольника CDE (CD =
= DE) Z_D = 84°, СЕ = 15 см. Найдите CD.
27. Периметр прямоугольника равен 50 см.
Найдите сторону а.
28. Известно, что sin а = т« . Найдите tg а.
29. Вычислите значение выражения
sin2 60° - 3tg 45°.
30. Расположите в порядке возрастания:
cos 17°, sin 56°, cos 62°.
31. На сколько дециметров КР больше СР?
К»
С Р
32. Дано: ABCD — ромб, Z ABC = 38°, АС =
= 10 см.
Найти: высоту ромба.
С

Задачи
Геометрия. 7—9 классы
269
Уравнения прямой
и окружности
33. Точки А и В имеют координаты:
А(-3;-1), В(2;-4).
Найдите отрезок АВ.
34. ABCD — параллелограмм. Координаты
его вершин:
А(-3;-1), В(-2;4), С(6;-1).
Найдите координаты (х; у) вершины D.
35. Дано: А МРК, М(-5; -3), Р(-3; 5), К(Ъ; -1).
Найти: медиану PC.
36. Запишите уравнение окружности,
изображенной на рисунке.
4
37. В каких точках окружность
(*-l)2 + (i/ + 2)2 = 8
пересекает ось 0x1
38. Запишите уравнение прямой АВ, если
А(-3;4) и В(-1;-2).
39. Даны уравнения двух прямых:
-2х - 1у + 1 = 0 и Зх + 4у + 5 = 0.
Найдите координаты (х0; у0) точки
пересечения этих прямых.
40. Найдите радиус окружности, если ее
уравнение
х2 + у2 + 6х - 8у + 5 = 0.
Преобразования плоскости
41. Какое из высказываний верное?
А: Прямоугольник имеет две оси симметрии,
это две его диагонали.
В: Прямоугольник имеет две оси симметрии,
это два серединных перпендикуляра к его
сторонам.
С: Прямоугольник имеет четыре оси
симметрии.
D: Все высказывания А, В и С — неверные.
42. Сколько осей симметрии имеет отрезок?
43. Известно, что при некоторой центральной
симметрии точка А переходит в точку С, а В —
в D (центр симметрии не принадлежит АВ).
Назовите верные высказывания:
А: Длина отрезка AD равна длине отрезка ВС.
В: Фигура, составленная из отрезков АВ, ВС,
CDnAD, является параллелограммом.
С: Величина угла ABC равна величине угла
CBD.
D: Длина отрезка АВ равна длине CD.
44. Назовите верные высказывания:
А: При осевой симметрии два
соответственных отрезка параллельны.
В: При центральной симметрии два
соответственных луча сонаправленны.
С: Центр поворота, при котором точка А
переходит в точку В, лежит на серединном
перпендикуляре к отрезку АВ.
D: Любой пятиугольник не имеет центра
симметрии.
45. Сторона равностороннего треугольника
ABC равна 12 см, BD — медиана. При
параллельном переносе на направленный отрезок AD
треугольник ABC отобразился на треугольник
DBlCv Найдите периметр фигуры СКВгСг, где
К — точка пересечения ВС и DBV
46. При параллельном переносе точка А(-3; 4)
переходит в Ах(1; -1). Найдите координаты
точки Bv в которую переходит точка В(2; -3).
47. А(-2,4; 3,7), Ах — симметричная ей точка
относительно оси Ох, точка А2 — симметричная
точке Ах относительно оси Оу. Найдите
координаты точки А2.
48. /L ABC - 38°. При гомотетии с
коэффициентом, равным 2, угол ABC переходит в угол
А1В1С1. Найдите величину угла А1В1С1.
Векторы
49. ABCD — параллелограмм. О — точка
пересечения диагоналей АС и BD. Назовите
вектор, равный ВС + ОА .
50. РЕ — медиана треугольника МРК.
Назовите вектор, равный ЕК - MP .
51. А(-3; 2), В(-1; 1). Найдите |АВ |.

270
Задачи
Геометрия. 7—9 классы
52. Дано: а(4;-3), \Ха\ - 15.
Найти: X.
53. ABCD — параллелограмм, О — точка
пересечения диагоналей, К — середина отрезка
АО. Выразите DK через АВ и AD .
54. Дано: а(4; -1), Ь(-2; -5).
Найти: а • &.
55. Дано: AMNP, М(-3; -2), АГ(1; 4), Р(2; -1).
Найти: Z. М.
—> —>
56. При каком значении а векторы АВ и CD
коллинеарны, если
А(2;-1), В(-4;3), С(5;-1), 2>(1;а)?
Повторение
57. ABCD — прямоугольник, О — точка
пересечения диагоналей АС и BD. Сумма расстояний
от точки О до сторон AD и CD равна 15 см, а
сторона АВ меньше ВС на 4 см. Найдите
диагональ прямоугольника.
58. ABCD — трапеция, AD \\ ВС, АВ 1 AD,
Z. D = 60°. Найдите основание ВС, если CD = 7 см,
АС 1 CD.
59. В прямоугольном треугольнике ABC /.С =
= 90°, ВС =* 5 см, а АВ на 1 см больше АС.
Найдите tg Z. В.
60. Дано: А ABC — прямоугольный, Z. С
Z А - а, ВС - а, CD J_ АВ.
Найти: CD.
90°,
61. АВ — диаметр окружности. Напишите
уравнение этой окружности, если А(1; 2), В(3; -4).
62. Прямая I проходит через точки М(8; 3) и
N(-4; -6) и пересекает ось Ох в точке А, а ось Оу
в точке В. Найдите периметр треугольника
ОАВ, где О — начало координат.
63. ABCD — параллелограмм, АВ - а, AD =
= £ . Выразите через векторы а и & вектор КМ ,
если Я" — середина AD, М делит Б2> в отношении
1:3, считая от точки В.
64. С(-3; -1), 2>(4; у), А(-1; 4), В(2; -1). При
каком значении у векторы CD и АВ
перпендикулярны?
9 КЛАСС
Подобие треугольников
1. Треугольник ABC подобен треугольнику
A1B1CV BD и BXDX — медианы, причем AD в 3
раза больше А^рх. Найдите отношение периметров
треугольников ABC и А1В1С1.
2. В треугольнике ABC проведены высоты AF
и СЕ, О — точка пересечения высот. Какие из
высказываний верные?
1) АЕВС со A FBA; 3) А ABC со А АОС;
2) A AFC со д СЕА; 4) А АЕО со д CFO.
3. В прямоугольном треугольнике ABC /.С =
= 90°, АС = 6 см, АВ = 9 см, CD — высота.
Найдите BD.
4. Высоты параллелограмма равны 6 дм и
10 дм, а периметр параллелограмма равен 48 дм.
Найдите разность между смежными сторонами
параллелограмма.
5. В треугольнике МКР MP = 24 см, отрезок
DE || MP, причем D € МК, Е € РК. Найдите
МК, если DM - 6 см, a DE - 20 см.
6. В трапеции ABCD (ВС IIAD) ВС = 9 см, AD -
= 16 см, BD = 18 см. О — точка пересечения
АС и BD. Найдите ОВ.
7. Два треугольника подобны. Стороны
одного равны 6 см, 8 см и 13 см, а другого — 12 см, 9 см
и х см. Найдите х.
8. Дано: ААВС, Z. ВКС = Z. СМБ - 90°.
Найти: верное высказывание
a)AMA#co ДМОЛГ;
б) ABAC со ДМАЯ;
в)ДЯАМсо ДМСЖ;
г) ДABC со ДАДМ.
А

Вписанные углы.
Соотношения между хордами
и касательными
9. Угол АС В на 38° меньше угла АОВ.
Найдите сумму углов АОВ и АС В.
10. MP — диаметр, О — центр окружности.
ОМ = ОК= МК. Найдите угол РКО.
м
11. Угол ABC — вписанный, угол АОС —
центральный. Найдите угол ABC, если Z. АОС — 126°.
12. KD и МС — хорды одной окружности,
причем Е — точка их пересечения. Найдите
угол CDE, если угол DEM в 4 раза больше угла
DEC, а угол СМК на 26° больше угла DEC.
13. Дано: KB = 12 см, КС = 30 см, РАКВ = 28 см.
Найти: PCKD.
D
14. Д а н о: КМ и CD — хорды, Е — точка их
пересечения; СЕ = 6 см, ED = 8 см, КЕ на 8 см
меньше ЕМ.
Найти: КМ.
Задачи
Геометрия. 7—9 классы
15. Д ано: АВ - 20 см, АС = 4 см, АЕ =- 16 см.
Найти: 1>Д.
D
16. АВ — касательная к окружности. Найдите
AD, если АВ = 6 дм, CD — 5 дм.
Теоремы
синусов и косинусов
17. Стороны треугольника 5 см и 3 см, а угол
между ними 60°. Найдите третью сторону
треугольника.
18. Стороны треугольника равны 7 см, 8 см и
10 см. Найдите косинус наибольшего угла этого
треугольника.
19. Стороны параллелограмма 5 J2 см и 6 см,
а один из углов параллелограмма равен 45°.
Найдите большую диагональ параллелограмма.
20. Найдите сторону треугольника, лежащую
против угла в 30°.
21. Дано: А ABC, АВ = 5 см, АС = 12 см,
Z. С - 30°.
Найти: Z. В.
22. В треугольнике одна из сторон равна 8 л/3 см,
а противоположный угол равен 60°. Найдите
радиус окружности, описанной около треугольника.
23. В треугольнике CDE CD = 12 см, DE =
= 15 см, СЕ = 18 см, DK — биссектриса угла D.
Найдите разность длин отрезков КЕ и СК.

272
Задачи
Геометрия. 7—9 классы
24. ABCD — трапеция. Найдите основание AD.
В 2 см с
Теоремы синусов и косинусов.
Подобие треугольников.
Вписанные углы
25. Известно, что АВ = 6 см, ВС = 9 см, DE =
= 13 см. Найдите AD.
26. В треугольнике ABC угол А равен 60°, сто-
АС
рона ВС в 1,5 раза больше АВ. Найдите -гъ •
В
27. CD = СЕ, О — центр окружности. Угол р
на 105° больше угла у. Найдите угол а.
28. Найдите сторону ВС треугольника ABC.
Вл
29. Стороны параллелограмма равны 6 дм и
10 дм, а одна из его диагоналей равна 13 дм.
Найдите вторую диагональ параллелограмма.
30. О — центр окружности, ОА, ОВ и ОС —
радиусы. Угол ВОС в 2 раза больше угла АОС, а
угол АОВ в 1,5 раза больше угла ВОС. Причем
сумма всех трех углов равна 360°. Найдите ВС,
если АВ = 8 см.
31. Угол АСБ — вписанный в окружность. О —
центр окружности. Хорда АВ = т, a Z. АС В = « .
Найдите радиус окружности.
32. ME и PC — высоты треугольника МКР.
MP = 9л/2 см, КЕ = л/12 см; СЕ = 37§ .
Найдите отрезок МК,
Многоугольники
33. Один из внутренних углов правильного
n-угольника равен 150°. Найдите число сторон
многоугольника.
34. Величины углов выпуклого
пятиугольника пропорциональны числам 2:3:4:5:6.
Найдите величину большего из углов.
35. Периметр равностороннего треугольника
равен 6 73 см. Найдите радиус описанной
окружности.
36. Около квадрата описана окружность, и в
квадрат вписана окружность. Найдите радиус
вписанной окружности, если радиус описанной
окружности равен Юл/2 см.
37. Внешний угол правильного
многоугольника меньше внутреннего угла на 140°. Найдите
сумму углов данного многоугольника.
38. Меньшая диагональ правильного
шестиугольника равна 5л/3 см. Найдите периметр
шестиугольника.
39. В некотором многоугольнике можно
провести 20 диагоналей. Найдите число сторон этого
многоугольника.
40. Радиус окружности, описанной около
правильного восьмиугольника, равен 1 дм. Найдите
сторону восьмиугольника.

Задачи
Геометрия. 7—9 классы
273
Площади фигур
41. Стороны параллелограмма 6 см и 5 см, а
один из углов параллелограмма равен 150°.
Найдите площадь параллелограмма.
42. Сторона ромба равна 20 см, а одна из
диагоналей равна 24 см. Найдите площадь ромба.
43. Угол при основании равнобедренного
треугольника равен 30°, а площадь треугольника
равна 9</3 см . Найдите боковую сторону
треугольника.
44. Стороны треугольника равны 8 см, 6 см,
4 см. Найдите меньшую высоту треугольника.
45. Диагональ квадрата равна 7^3 см.
Найдите его площадь.
46. Высота правильного треугольника равна
h. Найдите площадь этого треугольника.
47. В равнобедренной трапеции диагональ
перпендикулярна боковой стороне. Найдите
площадь трапеции, если большее основание
равно 16л/3 , а один из углов трапеции равен 60°.
48. Боковая сторона равнобедренного
треугольника равна 24 см. При каком значении
высоты площадь треугольника наибольшая?
Повторение
49. Дано: Окружность с центром О, /. ВАС =
= 45°, диаметр равен 16 см.
Найти: хорду ВС.
50. ABCD — параллелограмм, О — точка
пересечения его диагоналей. Найдите площадь
параллелограмма, если площадь треугольника
2
АВО равна 7,5 см .
51. Стороны параллелограмма равны 3 дм и
5 дм, а одна из его диагоналей равна 4 см.
Найдите длины высот параллелограмма,
проведенных из одной вершины.
52. Трапеция ABCD вписана в окружность
(ВС II AD), АВ = 6 см, a BD 1 АВ, BD = 8 см.
Найдите площадь круга, ограниченного этой
окружностью.
53. Вычислите синус угла правильного
восьмиугольника.
54. Стороны треугольника равны 14 см, 16 см
и 18 см. Найдите радиус вписанной окружности.
55. Дано: А ABC — прямоугольный, АС =
= 90°, ВС = 8 см, АВ = 10 см, CD — высота.
Найти:
JABDC
*AADC
56. Даны уравнения двух прямых:
2jc + i/ + 1 = 0 и * - i/ + 8 = 0.
Найдите площадь треугольника ABC, где А и
В — точки пересечения прямых с осью Ох, а. С —
точка пересечения этих прямых.
57. Треугольник ABC — прямоугольный, /.С =
= 90°, CD — высота. Найдите катет ВС, если
^А = 60°, CD = 673.
58. ABCD — трапеция, ВС \\ AD, О — точка
пересечения ее диагоналей, причем AC J. BD;
'двое
= 16л/2 см2, S
&AOD
36л/2 см2, АВ -
= CD. Найдите площадь треугольника АОВ.
59. Даны точки С(-3; 2) и £>(1; 8), точка М
лежит на оси Ох и равноудалена от точек С и D.
Найдите абсциссу точки М.
60. В треугольнике ABC DE \\ AC, S^^ -
2 2
- 4 см , SADEC = 5 см ; DE — 7 см. Найдите АС.
61. ABCD — трапеция, ВА 1 AD, ВС \\ AD,
ВС = 6 см, АС 1 CD и АС - 10 см. Найдите
площадь трапеции.
В С

274
Задачи
Геометрия. 7—9 классы
62. В треугольнике CDK CD = 8 см, KD = 6 см
и СК = 4 см. Найдите медиану DM.
63. ABCD — параллелограмм. Выразите
через векторы АВ =- а и AD = Ъ вектор МК,
где М — середина CD и ВК : КС = 2 : 1.
64. Стороны угла АСБ, равного 60°, касаются
двух окружностей с центрами Ог и 02,
касающихся одна другой, причем СОх = 12 см.
Найдите радиус окружности с центром 02.
А
ОТВЕТЫ
7 класс
1. 3,6 см. 2. 98°. 3.1, 2, 3, 4 раза. 4. 3. 5. 2,6 см или
13,4 см. 6. 10. 7. 15. 8. 4, 6, 7 частей. 9. 108°. 10. 113°.
11.18°. 12. 24°. 13.30°. 14.16°. 15. 56°. 16.158°. 17. 5,8 см.
18.9,8 см. 19. AD - 12 см, Z. Р = 73°. 20.18 см. 21.5,2 см.
22. 2; 4. 23. 4. 24. 4. 25. 16 см. 26. 7 см. 27. 15,6 см.
28.126°. 29. 2; 3. 30. 90°. 31. 4. 32. 16. 33. 2; 3; 4. 34. 65°
или 115°. 35. 74°. 36. 102°. 37. 4,8 см. 38. 104°. 39. 84°.
40. 76° или 104°. 41. 63°. 42. 52°. 43. 76°. 44. 90°. 45. 75°.
46. 18°. 47. 3,9 см. 48. 540°. 50. 28 см. 51. 60°. 52. 36 см.
53. 13,5 см. 54. 3,9 см. 55. 128°. 56. 12 см. 57. 30°.
58. 7,5 см. 59.6,2. 60.11 g см. 61. A, D. 62. 9 см. 63.48°.
8 класс
1.3 см. 2. 28 см. 3. 20 см. 4.105°. 5. В. 6.12 см. 7.98°.
о
8.3.9.16 g см. 10.10,8 см. 11. 21 см. 12.4 см. 13.2,5 см.
14. 15 см. 15. 120°. 16. 3,5 см. 17. тъ дм. 18. 25 см.
19.16 см. 20.7 см. 21.27 см. 22.12 см. 23.25 см. 24.48 см.
8 ЛЛ 7,5
25.
tg37°
26.
cos 48°
1 — COS CL
30. cos 62°, sin 56°, cos 17°. 31. Л-^= . 32.10 ■ sin 71°.
sin a
33. 734 .34. -1. 35. 758 . 36. (x - 4)2 + (y + 2)2 = 9. 37. 2.
38. у = -3x - 5. 39. -2. 40. 2 Jl. 41. B. 42. 2. 43. A, B, D.
44. C, D. 45. 30 см. 46. (6; -8). 47. (2,4; -3,7). 48. 38°.
49. BO . 50. PE . 51. Л . 52.3 или-3. 53. j AB -| AD.
54. -3. 55. 45°. 56. l|. 57. 7458 см. 58. 10,5 см.
59. 2,4. 60. a cos a. 61. (x - 2)2 + (y + l)2 = 10. 62.12 см.
63. fa- \b. 64. 3,2.
4 4
9 класс
1. 3. 2. 1; 4. 3. 5 см. 4. 6 дм. 5. 36 см. 6. 6,48 см.
7.19,5 см. 8. ABAC со д МАК. 9.114°. 10. 30°. 11.117°.
12. 62°. 13. 70 см. 14. 16 см. 15. 11 см. 16. 4 дм.
1 О 1
17. Л9 см. 18. YY2 ' 19' J™*' 2а Т ДМ' 21' ре"
шения нет. 22. 8 см. 23. 2 см. 24. 7 см. 25. 5 см.
1 + л
26.
:. 27. 100°. 28. 6л/б см. 29. ЛОЗ дм.
30.473 см. 31.
т
2sin X
32. 6 Л см. 33. 12. 34. 162°.
35. 2 см. 36. 10 см. 37. 2880°. 38. 30 см. 39. 8.
40. Л ~ Л дм. 41. 15 см2. 42. 384 см2. 43. 6 см.
44. | Л5 см. 45. 73,5 см2. 46. ^Цр . 47. 144^3 см2.
48. 12^2 см. 49. 87? см. 50. 30 см2. 51. 6,4 дм.
52. 25л см2. 53. ^ • 54- 2*& см. 55. lg. 56. 18,75.
57.1273 .58.2472 см2.59.6,5.60.10,5см. 61.90^ см2.
62. 746 см. 63. о a - g S. 64. 2 см.

Геометрия. 10—11 классы
10 КЛАСС
Аксиомы стереометрии.
Следствия из аксиом
1. В пространстве даны три точки: А, В и С
такие, что АВ = 14 см, ВС = 16 см и АС = 18 см.
Найдите площадь треугольника ABC.
2. Треугольник МКР — равносторонний со
стороной, равной 12 см. Точка А лежит вне
плоскости треугольника МКР, причем АК = АР =
= 4 7з см, a AM = 10 см. Найдите косинус угла,
образованного высотами ME и АЕ
соответственно треугольников МКР и АКР.
3. В плоскости а лежат точки Б и С, точка А
лежит вне плоскости а. Найдите расстояние от
точки А до отрезка ВС, если АВ = 5 см, АС = 7 см,
ВС = 6 см.
4. Даны пять точек пространства. Через
каждые две из них проведена прямая. Сколько
различных прямых Существует при этих условиях?
Рассмотрите различные случаи расположения
точек.
5. Проведены четыре различные плоскости.
Известно, что каждые две из них пересекаются.
Найдите наибольшее число прямых пдпарного
пересечения плоскостей.
6. Некоторая окружность касается двух
пересекающихся прямых в пространстве. Диаметр
этой окружности равен 2 л/3 дм, а расстояние от
центра окружности до точки пересечения
прямых равно л/б см. Найдите угол между этими
прямыми.
7. Четыре точки пространства А, В, С и D
образуют прямоугольник ABCD. Найдите площадь
круга, описанного около этого прямоугольника,
если АВ = -j- см, a AD = ~ см.
8. Прямые аиЬ пересекаются в точке О,
прямая с также проходит через точку О. Через
каждые две из данных трех прямых проведена
плоскость. Сколько всего различных плоскостей
может быть проведено?
Параллельность
в пространстве
9. Плоскость а пересекает АВ и ВС
треугольника ABC в точках D и Е соответственно,
причем АС II а. Найдите АС, если BD : AD = 3 : 4 и
DE = 10 см.
10. Отрезок АВ пересекает плоскость а, точка
С — середина АВ. Через точки А, В и С
проведены параллельные прямые, пересекающие
плоскость а в точках Av Вг и Cv Найдите CCV если
ААг = -= дм и ВВХ = л/2 дм.
11. Сторону CD треугольника CDE
пересекают плоскости а и Р, параллельные стороне СЕ
соответственно в точках К и Р, а сторону DE — в
точках MnN, причем DK вдвое меньше РК, а СР
вдвое больше РК. Найдите СЕ, если КМ = 6 см.
12. ABCDA1B1C1D1 — прямоугольный
параллелепипед, АВ =AD = 8 дм, ААг = 2 дм. Найдите
площадь сечения BMKD, где М — середина
ВХСХ и К — середина C1D1.
l^.ABCDAlBlClDl — куб. Точки Е и F —
середины ребер ААХ и ССХ соответственно.
Определите число сторон сечения плоскостью, которая
определяется точками В, Е nF.
14. MCDN — ромб, длина стороны которого
4 см; MNKP — параллелограмм. Найдите
периметр четырехугольника CDKP, если NK = 8 см и
ZCMP = 60°.
15. В треугольной пирамиде МАВС все ребра
равны 6 см. Найдите периметр сечения,
проведенного параллельно стороне ВС и проходящего
через точки А и К, где К — середина ВМ.
16. ABCDAlBlClDl — куб. К — середина AD,
М — середина CD. В каком отношении, считая
от точки А, делит ребро ААХ плоскость,
проходящая через точки Вх, К и М?

27fi Задачи
™ • " Геометрия. 10—11 классы
Перпендикулярность
в пространстве
VJ.ABCD — квадрат, ВМ ± (ABC). Найдите
отрезок DM, если АВ = л/12 см, а ВМ = 5 см.
18. КО — перпендикуляр к плоскости а, КМ
и КР — наклонные к плоскости а, ОМ и ОР —
проекции наклонных, причем сумма их длин
равна 15 см. Найдите расстояние от точки К до
плоскости а, если КМ = 15 см и КР = 10 7з см.
19. В треугольнике АКС АК _1_ СК; точка М
не принадлежит плоскости АКС и МК J_ СК.
Какие высказывания верны?
\)АК ±(СКМ); 3)АК±МК;
2) СК ± (АКМ); 4) СК 1 AM.
20. Треугольник ABC — прямоугольный, Z С =
= 90°, АС = 8 см, ВС = 6 см. Отрезок CD —
перпендикуляр к плоскости ABC. Найдите CD, если
расстояние от точки D до стороны АВ равно 5 см.
21. Треугольник MKN равносторонний со
стороной, равной 18 см. Точка С удалена от
вершин треугольника MKN на 12 см. Найдите
расстояние от точки С до плоскости MKN.
22. ABCD — квадрат. Точка М удалена от
сторон квадрата на Зл/2 см. Найдите периметр
квадрата, если точка М удалена от плоскости
ABC на V2 см.
23. Плоскость а перпендикулярна плоскости
р. Точка А принадлежит плоскости а. Отрезок
ААХ — перпендикуляр к плоскости |$, точка В
принадлежит плоскости р и ВВХ,
перпендикуляр к плоскости а. Найдите АВ, если ААХ = 8 см,
ВВХ = 12 см, АгВг = 4 72 см.
24. ABCDAlB1C1D1 — куб. Найдите
расстояние между прямыми АВг и ВС, если ребро куба
равно 2л/2 см.
Параллельность
и перпендикулярность в пространстве
25. ABCDA1B1C1D1 — прямоугольный
параллелепипед. Найдите площадь сечения,
проведенного через точки А, Вг и D, если АВ = 4 см,
ААХ = 4 72 см и AD = 2 V3 см.
26. Пусть ABCDA1B1C1D1 — куб и К —
середина АВ, М — середина AD. Укажите верные
высказывания:
1) А АВХС = 90°; 2) КМ II ВХС.
27. Плоскости равностороннего треугольника
ABC и квадрата BCDE перпендикулярны.
Найдите расстояние от точки А до стороны DE, если
АВ = 4 см.
28. Прямая т параллельна стороне АВ
треугольника ABC. Расстояние от прямой т до
плоскости ABC равно ~ см, а расстояние от т до
АВ равно 3 см. Найдите расстояние от точки С
до прямой т, если Z АСВ = 90°, ВС= */3 см, АС =
= 1 см.
29. Плоскость а проходит через сторону CD
ромба CDEK, причем а перпендикулярна
плоскости ромба. В плоскости а проведена прямая III CD.
Найдите расстояние между прямыми КЕ и I,
если СК = 8 см, Z KED = 30° и расстояние между
прямыми I и CD равно 3 см.
30. Ребро куба ABCDA1B1C1D1 равно 16 см.
Найдите расстояние между прямыми АгВ и BXCV
31. Плоскости равностороннего треугольника
ABC и треугольника ABD перпендикулярны.
Найдите длину отрезка CD, если АВ — 12 см, BD — 8 см
иАО =10 см.
32. Точка М лежит вне плоскости
равнобедренной трапеции ABCD (ВС || AD) и удалена от ее
вершин на 7 см. Найдите расстояние от точки М
до плоскости трапеции, если АВ = 6 см, ВС = 8 см
иАО=12см.
Координаты в пространстве
33. А(3; -2; -4). Найдите сумму расстояний от
точки А до оси Оу и от точки А до плоскости хОг.
34. Известны координаты вершин
треугольника ABC: А(2; -1; -3), В (-3; 5; 2), С(-2; 3; -5).
ВМ — медиана треугольника ABC. Найдите
длину ВМ.
35. CDEF — параллелограмм: С(-4; 1; 5),
D(-5; 4; 2), Е(3; -2; -1), F(x; у; г). Найдите
координаты точки F.
36. Координаты точек: А(4; -3; 2), В(-1; -5; 4).
Найдите сумму координат точки С, лежащей на
оси Оу и равноудаленной от точек А и Б.

Задачи
Геометрия. 10—11 классы
277
37. А(3; 1; -4). Точка В — симметрична точке
А относительно плоскости хОу9 а точка С
симметрична точке В относительно оси Оу. Найдите
расстояние между точками А и С. ,
38. При параллельном переносе точка
М(-3; 2; -5) переходит в точку Мг(1; -3; -2).
Найдите координаты точки Kv в которую при
этом параллельном переносе переходит точка
#(1;-2;-5).
39. Треугольник ABC — равнобедренный,
АВ = ВС. А(2; -3; 5), Щх; у; г), С(4; 0; -1).
Выберите уравнение относительно х, у, г,
удовлетворяющее условиям задачи.
а) Зх - 2у + 18г + 35 = 0;
б) 5х + Зу + 4г + 25 = 0;
в) 2х - Зу + Ъг - 40 = 0;
т)4х + 6у- 122 + 21 = 0.
40. Найдите площадь треугольника АВС9 если
А(3; 0; 0), 5(0; -4; 0), С(0; 0; -1).
Углы между прямыми
и плоскостями
41. Треугольник ABC — равнобедренный, АС =
= ВС = 8</б см, ZC = 90°. Плоскость а
проходит через сторону АС, причем сторона АВ
образует с плоскостью а угол 30°. Найдите
расстояние от вершины В до плоскости а.
42. Плоскость а проходит через сторону СК
квадрата CDEK, причем диагональ DK образует
Л
с плоскостью а угол, синус которого равен -^-.
Найдите угол, который образует с плоскостью а
сторона CD.
43. В треугольнике МКР МК = 12 см, Z М =
= 30°, Z Р = 90°. Плоскость а проходит через
сторону MP и образует с плоскостью МКР угол 60°.
Найдите расстояние от точки К до плоскости а.
44. Треугольники ABC и ABD —
равнобедренные, причем АС = ВС = 15 см, АВ = 18 см, ZADB =
= 90°. Найдите косинус угла между плоскостями
ABC и ABD, если CD = 6 см.
45. ABCDAlBxClDl — куб. Найдите угол
между АВХ и BDV
46. Угол между плоскостями
равностороннего треугольника АВК и квадрата ABCD равен
30°. Найдите расстояние KD, если АВ = 6 м.
47. ABC — равносторонний треугольник,
через сторону АВ проведена плоскость а под углом
45° к плоскости треугольника ABC. Отрезок СО —
перпендикуляр к плоскости а. Найдите АВ,
если площадь треугольника АОВ равна 12 </б см .
48. Угол между плоскостями аир равен 60°.
Точка А находится на расстоянии 2 см от
плоскости аи(73 - 1)смот плоскости р. Найдите
расстояние от точки А до прямой пересечения
плоскостей а и р.
Векторы
49. ABCDA1B1C1D1 — куб. Найдите вектор,
равный ААХ + ВХС - CXDX .
bQ.ABCDAlBlClDl — куб; AD = а, АВ = Ь,
ААг = с. Выразите через векторы а, бис вектор
МК , если М — середина AtDx и К — середина
CCV
51. Даны координаты точек:
А(-3; 2; -1), В(2; -1; -3), С(1; -4; 3), Щ-1; 2; -2).
Найдите |2АВ +3CD\.
52. Даны координаты точек:
С(3; -2; 1), D(-l; 2; 1), М(2; -3; 3), N(-1; 1; -2).
Найдите косинус угла между векторами CD
nMN.
53. При каком значении (значениях) k
векторы 3(6 - k; k; 2) и &(-3; 5 + 5ft; -9)
перпендикулярны?
54. При каком значении а векторы АВ и
CD коллинеарны, если А(-2; -1; 2), Б(4; -3; 6),
С(-1;а-1;1),2)(-4;-1;а)?
55. Дано: |3| = 4, |Ь| = 1, Z (а, Ъ) = 60°. Найдите
cos а, где а — угол между векторами а-Ъ и Ъ.
56. Найдите длину вектора a + b-с, если \а\ =
= 1, |б| = 2, \с\ = 3, Z (а, Ъ) = 90°, Z (Ь, с) = 60°,
Z (а, с) = 120°.

Задачи
Геометрия. 10—11 классы
Повторение
57. Отрезок АВ не пересекает плоскость a, a
точка С делит его в отношении 2:3, считая от
точки А. Через точки А, Б и С проведены
параллельные прямые, пересекающие а соответственно
в точках Av Вг и Сг. Найдите длину отрезка CCV
если ААг = 5 см, а ВВг = 8 см.
58. Плоскости треугольника АВК и ромба
ABCD перпендикулярны, причем ZABK = 90°,
Z ABC = 135°, АК - 12 см и ВК = 8 см. Найдите
расстояние от точки К до прямой CD.
59. Треугольник ABC — прямоугольный, ZC =
= 90°. Точка D, лежащая вне плоскости
треугольника, равноудалена от вершин треугольника
ABC на 8 см. Найдите расстояние от точки D до
плоскости ABC, если АС = 12 см и Z ВАС = 30°.
60. Плоскость а проходит через сторону AD
треугольника ABD. Сторона АВ образует с
плоскостью а угол 30°. Найдите синус угла между
плоскостями а и ABD, если AD = 3 см, АВ = 5 см,
BD = 4 см.
61. Треугольник ABC — равносторонний со
стороной 8 см, a BCDE — параллелограмм, СВЕ =
= 60°, CD = 10 см. Найдите косинус угла между
плоскостями треугольника ABC и
параллелограммом BCDE, если расстояние от точки А до
прямой DE равно Тзз см.
62. Точка А(-3; 4; 6). Точка В — основание
перпендикуляра АБ, проведенного к оси Ог.С —
основание перпендикуляра АС к плоскости хОу.
Найдите сумму расстояний АВ и АС.
63. \а\ = 1, |Ь| = 3, |3| = 5, Z (а, 6) = 60°, Z (Ь, с) =
- 90°, Z (а, с) = 120. Найдите \а - Ь + с\.
64. ABCDA1B1C1Dl — куб. М — середина CD.
Найдите площадь сечения куба плоскостью,
проходящей через точки А, Вг и М, если ребро
куба равно 8 см.
11 КЛАСС
Двугранные и линейные углы.
Многогранные углы
1. Двугранный угол, образованный
полуплоскостями а и (J, равен 90°. Точка А удалена от
граней двугранного угла на 8 см и 6 см. Найдите
расстояние от точки А до ребра двугранного угла.
2. Треугольник ABC — прямоугольный, Z С =
= 90°, треугольник DBE — равносторонний.
Найдите линейный угол между плоскостями
треугольников, если стороны АС и DE
параллельны, расстояние между ними 7з см, а ВС =
= DE = 2 см.
3. Плоскости треугольника МКР и ромба
MKEF образуют угол 60°, один из углов ромба
равен 45°, а МК = 3 72 см, MP = 2 7з см и РК =
= 7б см. Найдите расстояние от точки Р до
прямой FE.
4. Плоскость а проходит через сторону AD
квадрата ABCD. Диагональ BD образует с
плоскостью а угол 45°. Найдите угол между
плоскостью квадрата и плоскостью а.
5. Дан трехгранный угол с вершиной А.
Плоскость а пересекает его ребра в точках В, С и D
так, что АВ = АС = CD. Найдите угол BAD, если
Z ВАС = Z BCD = 90° и Z CAD = 60°.
6. ABCDA1B1C1D1 — куб. Найдите угол
между плоскостью, проходящей через точки В, D и
Cv и плоскостью основания.
7. Три плоских угла трехгранного угла с
вершиной О — прямые. Плоскость а пересекает
ребра трехгранного угла в точках С, D и Е9 причем
Sacod = ^i» S&DOE ~ $2 и &АСОЕ = ^2« Найдите
длину отрезка OD.
8. ABCD — ромб, СК — перпендикуляр к
плоскости ромба, причем СК = 2 л/3 см, АВ = 4 см и
ZBAD - 60°. Найдите угол между плоскостью
ABjST и плоскостью ромба.
Параллелепипед
и призма
9. Площадь диагонального сечения куба равна
8 72 см . Найдите площадь поверхности куба.
10. Длины диагоналей трех граней
прямоугольного параллелепипеда, имеющие общую
вершину, равны 5 см, 2л/1з смиЗ-Уб см.
Найдите диагональ параллелепипеда.

11. Стороны основания прямого
параллелепипеда равны 1 см и 3 см, а синус угла между
Л
ними равен -д- . Найдите угол, который образует
большая диагональ параллелепипеда с
основанием, если боковое ребро параллелепипеда
равно «/14 см.
12. Площади двух диагональных сечений пря-
2 2
мого параллелепипеда равны 48 см и 30 см , а
'боковое ребро равно 6 см. Найдите площадь
основания параллелепипеда, если оно является
ромбом.
13. Сторона основания правильной
шестиугольной призмы равна 4 см, а большая
диагональ призмы образует с основанием угол,
равный 60°. Найдите площадь полной поверхности
призмы.
14. АВСА1В1С1 — наклонная треугольная
призма. Двугранный угол при ребре ААХ равен
90°. Расстояния от ребра ААг до ребер ВВХ и
ССХ равны соответственно 4 см и 3 см. Найдите
площадь боковой поверхности призмы, если ее
высота равна 4 Jb см и боковое ребро образует с
основанием угол 60°.
15. АВСА1В1С1 — правильная треугольная
призма. Через ребро АгВг и точку М — середину
АС проведено сечение, площадь которого равна
0,75 Jl см . Найдите высоту призмы, если
сторона ее основания равна 2 см.
16. ABCDA1B1C1D1 — прямоугольный
параллелепипед. Причем АВ = а см, ВС = 2а см, ВВХ =
= 4а см. Через точки А, Вх и С проведена
плоскость. Найдите тангенс угла между
плоскостями АВгС и ABC.
Пирамида.
Усеченная пирамида
17. Все ребра правильной треугольной
пирамиды равны между собой. Найдите косинус угла
между боковой гранью и плоскостью основания.
18. Найдите высоту треугольной пирамиды,
если все ее боковые ребра по */40 см, а стороны
основания равны 10 см, 10 см и 12 см.
Задачи
Геометрия. 10—11 классы
19. Найдите площадь боковой поверхности
правильной четырехугольной пирамиды, если
диагональное сечение пирамиды —
прямоугольный треугольник, площадь которого равна 32 см .
20. Основание пирамиды — ромб, каждая
боковая грань образует с плоскостью основания
угол, равный 60°. Найдите площадь основания
пирамиды, если высота пирамиды 9 см, а один из
углов ромба 45°.
21. Основание пирамиды MABCDEF —
правильный шестиугольник ABCDEF со стороной
8 см. Ребро AM перпендикулярно основанию и
равно 8 см. Найдите двугранный угол между
гранью MED и плоскостью основания.
22. Стороны оснований правильной
усеченной четырехугольной пирамиды равны 4 см и
6 см. Найдите площадь диагонального сечения,
если боковое ребро образует с большим
основанием угол, равный 45°.
23. Стороны оснований правильной
треугольной усеченной пирамиды равны 6 см и 12 см.
Угол между плоскостями боковой грани и
основания равен 30°. Найдите площадь боковой
поверхности данной усеченной пирамиды.
24. KABCD — правильная четырехугольная
пирамида. Точки М nN — середины ребер KB и
КС. Найдите периметр сечения пирамиды
плоскостью, параллельной грани AKD и проходящей
через точки MhN, если сторона основания
пирамиды 16 см, а высота пирамиды 4 см.
Цилиндр. Конус. Шар
25. Осевое сечение цилиндра — квадрат,
длина диагонали которого равна 20 см. Найдите
радиус основания цилиндра.
26. Площадь осевого сечения цилиндра равна
6 л/тс дм , а площадь основания цилиндра равна
25 дм . Найдите высоту цилиндра.
27. Отрезок АВ равен 13 см, точки А и В
лежат на разных окружностях оснований
цилиндра. Найдите расстояние от отрезка АВ до оси
цилиндра, если его высота равна 5 см, а радиус
основания равен 10 см.
28. Длина образующей конуса равна 2 7з см,
а угол при вершине осевого сечения конуса
равен 120°. Найдите площадь основания конуса.

Задачи
Геометрия. 10—11 классы
29. Радиус основания конуса 3 72 см.
Найдите наибольшую возможную площадь осевого
сечения данного конуса.
30. Отрезок АВ — хорда основания конуса,
которая удалена от оси конуса на 3 см. МО —
высота конуса, причем МО = 6 */2 см, где М —
вершина конуса. Найдите расстояние от точки О
до плоскости, проходящей через точки А, ВиМ.
31. Сфера w проходит через вершины
квадрата ABCD, сторона которого равна 1.2 см. Найдите
расстояние от центра сферы — точки О до
плоскости квадрата, если радиус OD образует с
плоскостью квадрата угол, равный 60°.
32. Стороны треугольника ABC касаются
шара. Найдите радиус шара, если АВ = 8 см, ВС =
= 10 см, АС = 12 см и расстояние от центра шара
О до плоскости треугольника ABC равно J2 см.
Объемы многогранников
33. Диагональ куба равна 12 см. Найдите
объем куба.
34. Стороны основания прямого
параллелепипеда равны 1 дм и 2 л/2 дм, а угол между ними
45°. Найдите объем параллелепипеда, если
площадь его меньшего диагонального сечения
равна У1б дм .
35. Все ребра наклонного параллелепипеда
равны, причем боковое ребро образует с
плоскостью основания угол, равный 30°. Большая
диагональ основания равна 6 см, а один из углов
основания 120°. Найдите объем параллелепипеда,
если большее диагональное сечение
перпендикулярно основанию.
36. Диагональ боковой грани правильной
треугольной призмы образует с основанием
угол, равный 60°. Найдите объем призмы, если
площадь боковой поверхности призмы равна
36 73 см2.
37. В основании прямой призмы AECDA^B^^D
лежит равнобедренная трапеция, ВС || AD, при-
' чем АВ = 3 см, AD = 5 см. Диагональ призмы BXD
образует с плоскостью основания угол, равный
45°, а плоскости АА1Б1 и BXBD
перпендикулярны. Найдите объем призмы.
38. Диагональное сечение правильной
четырехугольной пирамиды является
равносторонним треугольником, площадь которого равна
бл/З см . Найдите объем пирамиды.
39. В треугольной пирамиде КАВС АК _L ВК
и ВК.]_ СК, a ZAKC = 30°. Найдите объем
пирамиды, если АК = 8 см, ВК = 12 см и СК = 10 см.
40. Через точку А бокового ребра пирамиды
проведена плоскость, параллельная плоскости
основания, причем точка А делит ребро на два
отрезка, длины которых находятся в отношении
1:3, считая от вершины. Найдите объем
пирамиды, если объем образовавшейся усеченной
пирамиды равен 315 см .
Объемы тел вращения
41. Отрезок АВ, концы которого лежат на
разных окружностях оснований цилиндра,
пересекает ось цилиндра под углом 30°. Найдите объем
цилиндра, если длина отрезка АВ равна 4 */3 см.
о
42. Объем цилиндра равен 63я см , а пло-
щадь осевого сечения 18 см . Найдите радиус
основания цилиндра.
43. Плоскость, проходящая через вершину
конуса и хорду АВ основания, образует с высотой
конуса угол 30° и удалена от центра основания на
3 дм. Найдите объем конуса, если длина хорды
АВ равна 2 дм.
44. Объем конуса равен 9 л/3 тс см . Найдите
высоту конуса, если его осевое сечение —
равносторонний треугольник.
45. На поверхности шара даны три точки: А, В
и С такие, что АВ = 8 см, ВС = 15 см, АС = 17 см.
Центр шара — точка О находится йа расстоянии
735
■—- см от плоскости, проходящей через точки
А, В и С. Найдите объем шара.
46. Прямоугольный треугольник с катетами,
равными 3 см и </3 см, вращается вокруг оси,
содержащей его гипотенузу. Найдите объем
фигуры вращения.
47. Чугунное ядро радиусом 1 дм
переплавили в равновеликий конус, образующая которого

л/б дм. Найдите высоту конуса, если она не
менее 1 дм.
48. В углу комнаты, имеющей форму
прямоугольного параллелепипеда, лежит шар объе-
мом 36л дм , который касается трех граней этой
комнаты, имеющих общую точку. Найдите
расстояние от центра шара до этой точки (вершины
угла комнаты).
Комбинации фигур
49. Куб с ребром, равным J2 дм, вписан в
шар. Найдите площадь поверхности шара.
50. Площадь поверхности правильного
тетраэдра равна 12л/3 см . Найдите площадь
поверхности конуса, вписанного в этот тетраэдр.
51. Основанием прямого параллелепипеда
является ромб, один из углов которого а.
Найдите площадь боковой поверхности
цилиндра, вписанного в данный параллелепипед, если
площадь боковой поверхности параллелепипеда
равна S.
52. Около правильной треугольной
пирамиды со стороной основания 6 см и высотой 8 см
описан шар. Найдите радиус шара.
53. В правильную четырехугольную пирамиду
4 з
вписан шар объемом « я см . Найдите объем
пирамиды, если ее высота 5 см.
54. В полу шар вписан цилиндр, причем одно
из оснований цилиндра лежит в плоскости
диаметрального круга полушара, а высота
цилиндра вдвое меньше радиуса полушара. Найдите
отношение объема цилиндра к объему полушара.
55. Прямоугольная трапеция ABCD (ВС || AD и
Z.D = 90°) вращается вокруг оси, содержащей
сторону ВС. Найдите объем фигуры вращения,
если ВС = 6 см, диагональ АС = 8 см и ZACB =
= 60°.
56. В конус, высота которого равна 4 </2 дм,
а радиус основания 2 дм, вписан куб, четыре
вершины принадлежат основанию, а четыре
другие вершины — боковой поверхности.
Найдите ребро куба.
Задачи
Геометрия. 10—11 классы
Повторение
57. Найдите косинус угла между
плоскостями квадрата ABCD и равностороннего
треугольника АВМ, если диагональ квадрата равна
4 72 см и расстояние от точки М до стороны DC
равно 5 см.
58. Основание пирамиды — трапеция,
основания которой равны 3 см и 5 см. Найдите объем
пирамиды, если все ее боковые грани
составляют с основанием равные двугранные углы по
45°, а высота пирамиды равна л/б см.
59. Около куба описан цилиндр. Найдите
полную площадь поверхности цилиндра, если
поверхность куба равна S.
60. В конусе проведено сечение, проходящее
через вершину конуса и две его образующие.
Найдите расстояние от центра основания до
плоскости сечения, если образующая составляет
с плоскостью основания угол а, плоскость
сечения образует с плоскостью основания угол |3, а
радиус основания R.
61. Стороны основания наклонного
параллелепипеда 3 см и 5 см, а угол между ними 120°.
Большее диагональное сечение, являющееся
ромбом, перпендикулярно плоскости основания.
Найдите объем параллелепипеда, если боковое
ребро образует с основанием угол, равный 60°.
62д Дано: \а\ = 1, |Ь| = 2, \с\ = 3, Z (а, Ь) = 60°,
Z (6, с) = 90°, Z (а, с) = 120°. Найдите косинус
угла между векторами а-Ъ-с и 6.
63. На поверхности шара даны три точки А,
В и С, причем АВ = 2 см, ВС = 3 см и АС = 4 см.
Расстояние от центра шара до плоскости сече-
4
пия ABC равно -= см. Найдите площадь поверх-
V3
ности шара.
64. Основание прямоугольного
параллелепипеда ABCDA1B1C1D1 — квадрат ABCD со
стороной Jb см, длина ребра ААХ = 2*fb. Найдите
площадь сечения, проведенного через точки С, Р и
М, где Р — середина AD и М — середина ВВг.
65. В основании четырехугольной пирамиды
лежит ромб, причем один из его углов равен a, a
его сторона равна 6. Плоскости двух боковых
граней перпендикулярны плоскости основания.

ООО Задачи
™ОА Геометрия. 10—11 классы
Найдите угол наклона двух других боковых гра- 19 2; 4 2о. 1,4 см. 21. 6 см. 22. 32 см. 23. 4 Лб см.
ней к основанию, если высота пирамиды равна а. 2 _
24. 2 см. 25. 24 см . 26. верных нет. 27. 277 см.
66. В основании наклонной призмы
ABCD^C^ лежит трапеция ABCD, причем 28. Щ или ^ • 29. 5 см. 30. 872 см. 31.7154 см.
AD || ВС иАО = 31 см, CD = 17 см, АВ = ВС = * *
= 10 см. Плоскость диагонального сечения приз- 32- 0>&747,5 см- ^ 7- 84. 761. 35.1. 36. -3,25. 37.6.
мы, проходящая через вершину А, перпендику- 38. -4. 39. 4х + 6у - \2г + 21 = 0. 40. 6,5. 41. 87з см.
лярна основанию и равна 20л/Го см . Найдите лл ол0 лп _ /= АА 7 Att лл. лл 0 /=
* ^ 42. 30. 43. 3V3 см. 44. 5. 45. 90. 46. 372 см.
объем призмы. о
67. Апофема правильного тетраэдра равна 47.47б см. 48. 272 см. 49. АС. 50. \а + Ь - \с.
673 см. Через середину одного из ребер прове- -
дена плоскость, параллельная плоскости одной 51.7521. 52. 0,7. 53. 2; -3,6. 54. -1. 55. -j=
из граней тетраэдра. Найдите объем образовав-
71з
шейся усеченной пирамиды. ^ д~х 57 б 2 см 58 2^ см. 59.4 см. 60 J . 61. |.
68. ABCDAtВлC*D* — прямоугольный парал- _ 2
ли л лъ о 62.11. 63.3 73. 64. 72 см2,
лелепипед, причем АВ = 4 см, AD = 8 см и
ААг = 12 см. Найдите длину отрезка КМ, где
точки К и М принадлежат соответственно отрезкам \\ класс
ССг и BXD, причем СгК : КС = 2 : 1 и ВХМ : MD =
= 3:1. 1. 10 см. 2. arccos ^ . 3. 77 см. 4. 90°. 5. 120°.
69. Сфера с центром в точке А (-2; 3; -1) и . о
пересекает ось Ог в точках В (0; 0; zt) и С (0; 0; 22). 6. arctg 72 . 7. /—^—- . 8.45°. 9.48 см2.10. 7б1 см.
Найдите г2, если гг = 3. ' W з
„ „ „ 11. 45°. 12. 20 см2. 13. 240 73 см2. 14. 96 см2. 15.1 см.
70. В шар вписан равносторонний цилиндр.
Найдите отношение объема шара к объему <л ft /= „_ 1 „0 7l5 *л *, /5 2 ол -ло'/п 2
16.275.17. о-18. :lt- см. 19.6473 см .20.10872 см .
цилиндра. 3 4
71.ABCDA1B1C1Z>1 — куб, ребро которого 21. 30°. 22. 10 см2. 23. 54 см2. 24. 36 см. 25. 5 72 см.
равно а. Через точки Bv D и К (точка К — сере- 26.0,6л дм. 27.8 см. 28. 9л см2. 29.18 см2. 30. 272 см.
дина ребра AXDX) проведена плоскость. Наедите 31. 67б см. 32. 3 см. 33. 192 7з см3. 34. 273 дм3.
площадь сечения плоскостью, параллельной плос- з л ~ г- з ™ лл -л з лл «, л /?: з
о тмг о . 35.18 см . 36. 1873 см . 37. 30,72 см . 38. 1272 см .
кости BXDK и проходящей через вершину Av v
39.80 см3.40.320 см3.41.18л см3. 42. 7 см. 43. 26л дм3.
72. Площадь боковой поверхности конуса 3 лп « ш /^ _ з
равна 4 73 л см . Найдите наибольшее возмож-
44. ЗТЗ см. 45. 972л см3. 46. 1,б73л см3. 47. 2 дм.
ное значение объема этого конуса. 48. ЗТЗ дм. 49. 6л см . 50. 4л см . 51. т-
ОТВЕТЫ
52.4,75 см. 53. ^р см3.54. ~. 55.224л см3.56. ^р дм.
Ю класс *7- й' 58'16 см3' 59' 8п(1еЛ) ■ «■R * а cos *
1. 4875 см2. 2. А . з. 276 см. 4.1, 5, 6, 8,10. 5. 6. 61. 78,75 см3. 62. -^= . 63. ^ см2. 64. б| см2.
6. 90°. 7. ^- см2. 8. 1 или 3.9. 235 см. 10.72 дм. 65. arctg,. ? . 66. 41072 см3. 67.12672 см3.
04 о °о sin а
11. 42 см. 12. 12 7б см2. 13. 5. 14. 8(1 + 7з) см. - ^2 /g g /^
15.3(273 + 1) см. 16. 1:2. 17. 7 см. 18. 1072 см. 68. Ш см. 69. -5. 70. — . 71. —j— .72. —g— см .

Контрольные
и проверочные работы
по математике.
Тесты
помогут успешно подготовиться ко всем видам
контрольных работ

Контрольные
и проверочные работы
и тесты охватывают все
разделы математики,
алгебры и начал анализа
и геометрии,
предусмотренные школьной
программой.
Их можно использовать
для проверки
знаний по основным темам
школьной программы
независимо от учебника,
по которому ведется
преподавание.

Контрольные и проверочные работы
Математика. 5—6 классы
5 КЛАСС
Контрольная работа 1
1. Выполните действия:
а) 786 495 + 37 526; б) 51 406 - 23 598;
в) 307 • 794; г) 396 648 : 56.
2. Нильс с дикими гусями был в полете три
дня. В первый день они пролетели 46 км, что на
8 км больше, чем во второй день, а в третий день
они пролетели в 3 раза меньше, чем за два
первых дня вместе. Сколько километров пролетел
Нильс с дикими гусями за три дня?
3. Решите уравнение:
а) 9104-х = 3627;
б) 49 587 + у = 70 427 + 13 586.
4. У Люды были три альбома с марками. В
первом было 534 марки, во втором — х марок, а в
третьем альбоме 420 марок. Люда подарила
брату 185 марок. Сколько марок осталось у Люды?
Составьте буквенное выражение. Найдите его
значение при х = 389.
5. На рисунке изображены 4 линии. Какие из
них пересекаются?
В
8. Сколько треугольников можно заметить на
рисунке?
Контрольная работа 2
1. Вычислите
3686 + 91 476 : (14 191 - 13 894) • 53.
2. Решите уравнение:
а) 13*-4*+ 97 = 700;
б) (301-*) • 54 = 10 962.
3. Упростите выражение и найдите его
значение:
а) а + а + За + 194 - 25, при а = 0;
б) 14х + 25* + 31 - 10х, при х = 10.
4. Персик тяжелее абрикоса в 3 раза.
Найдите массу абрикоса и массу персика, если абрикос
легче персика на 140 г.
5. Запишите все делители числа 30. Найдите
их сумму.
6. Выпишите несколько кратных для числа
12 и несколько кратных для числа 16. Есть ли у
чисел 12 и 16 общие кратные?
Контрольная работа 3
1. Для выполнения разряда по плаванию
Славе надо проплыть 400 м за 16 мин 30 с.
Выполнит ли Слава разряд, если будет плыть со
скоростью 25 м/мин?
2. Известному туристу Колобку нужно
пройти маршрут из деревни Теремок до деревни Про-
стоквашино через Цветочный город. От Теремка
13
до Цветочного города IS™ км, а от Цветочного
города до Простоквашино на 1 ^ км больше. За
17
первый день Колобок прошел 18ng км-
Сколько километров Колобку осталось до
Простоквашино?
3. Площадь участка прямоугольной формы
8 а, причем ширина 16 м. Найдите периметр
участка.
4. Андрей собирал модель самолета. За 6 ч он
выполнил « всей работы. Сколько еще времени
нужно Андрею, чтобы собрать модель
полностью?
5. Часы показывают половину первого ночи.
Какая часть суток прошла?

286
Контрольные и проверочные работы
Математика. 5—6 классы
6. При каких натуральных значениях п дробь
2л
п + 3
— правильная? Запишите эти дроби.
Контрольная работа 4
1. Найдите значение выражения:
а) 12-0,62 • 8,3;
6)27,2-18,91 : (2,48 + 3,72).
2. Найдите:
а) 3% от 12;
б) сколько процентов от 28 составляет число 7.
3. Синеглазка и Снежинка собирали
землянику. Синеглазке удалось собрать в 1,2 раза
больше, чем Снежинке. Сколько килограммов
земляники собрала каждая из них, если вместе
они собрали 10,56 кг?
4. Ребята пошли в двухдневный поход. В
первый день они прошли 24 км, что составило 60%
всего маршрута. Сколько километров они
должны пройти во второй день?
5. Сравните:
a) g и 0,48;
1
б) I и 1,4.
6. По телевидению диктор сообщил: «В
городе N завод увеличил выпуск продукции за месяц
на 50% ». Во сколько раз завод увеличил
выпуск продукции за месяц?
Контрольная работа 5
1. Найдите значение выражения
8-0,026:0,4 + 0,16 • 4,5.
2. Упростите выражение
* + 0,5 • (2,3* - 0,4*)
и найдите его значение при х = 0,1.
3. Решите уравнение:
а) 15| - а = 7| + 4|; б) 1,2* + 5 = 5,72.
4. Туристы были в пути три дня. В первый
1Q 4
день они прошли 18 км, что составило g всего
пути. Во второй день — в 1,5 раза меньше, чем в
первый день. Сколько километров туристы
прошли в третий день?
5. В двух бидонах всего 7,8 л молока.
Сколько молока в каждом бидоне, если во втором на
2,4 л больше, чем в первом?
6. Угол ABC — прямой, угол DEK составляет
20% qt угла ABC, а величина угла MON равна
среднему арифметическому углов ABC и DEK.
Найдите величину каждого из трех углов и
постройте их с помощью транспортира.
•6 КЛАСС
Контрольная работа 1
1. Найдите значение выражения
18-10|.lg+eA.
$. Сравните числа 0,4, То и on • Расположите
их в порядке возрастания.
3. Упростите выражение
12 2
g*+ ^jc-0,75 • £*
и найдите его значение при х = 7.
4. Решите уравнение:
а)7|-* = 3^;
8
12
5. Ира решила помочь маме. Четверть часа
2
она мыла посуду, « часа она подметала пол в
квартире. На уборку своей комнаты она
затратила в 1,5 раза больше времени, чем;на
подметание пола. Сколько всего времени помогала Ира
маме?
Ответ выразите в часах и минутах.
6. Сколько всего различных трехзначных
чисел можно составить из цифр 5, 7, 8, если
каждая цифра используется только один раз?
Контрольная работа 2
1. Найдите значение выражения
57 *\Z *3 Ч 9 Z6j'

Контрольные и проверочные работы
Математика. 5—6 классы
287
2. Найдите:
а) 0,3 от 17g ;
6)4,5% от 12;
2 7
в) число jc, если g числа х равны т« •
3. Решите уравнение
Ф(5Г4-*)=2*Г
4. В трех пакетах лежит крупа: гречка,
пшено и рис. Всего 6 кг. Пшено составляет 30% всей
крупы, гречки в Ь раза больше, чем пшена.
Сколько килограммов каждой крупы лежит в
пакетах?
2
5. Сколько процентов от числа 2 g составляет
число 1,2?
6. Два тракториста могут вспахать поле за 6 ч.
Если поле будет вспахивать один тракторист, то
он его вспашет за 10 ч. За сколько часов может
вспахать поле другой тракторист?
Контрольная работа 3
1. Найдите значение выражения:
а) -12,3 + 8,5-1,9;
б) (з| - if - 5|) :(-2,5).
2. Решите уравнение:
а)-2^ -* = -2,3 + 6,5;
б)-0,4:*=^:6?.
3. На изготовление 5 деталей требуется 3« кг
металла. Сколько килограммов металла
потребуется на изготовление 14 таких деталей?
4. Диаметр окружности равен 15 см. Найдите
длину окружности.
Ответ запишите в дециметрах и округлите
его до единиц, (я = 3,14.)
5. Если из числа 5 вычесть некоторое число,
то отношение получившейся разности к числу 5
равно 0,3. Найдите число, которое вычли из
числа 5.
6. Решите уравнение
\х\ + 4 = 0.
Контрольная работа
4
1. Найдите значение выражения
*7'14
0,2 - 0,2- 1,4*
2. Решите уравнение:
а)-1,2* + 5 = 3-0,4х;
б) 8л:- | • (4,5х-5) = 5-х;
В) х 5 '
3. В квартире три комнаты. Площадь первой
комнаты составляет 40% площади всех трех
9
комнат, площадь второй комнаты равна ту
площади первой комнаты, а площадь третьей ком-
2
наты 15 м. Найдите площадь всех трех комнат.
4. Игорь загадал число а и разделил его на 3,
а Ваня прибавил к а число 2,5 и разделил
сумму на 4. В итоге у Игоря и Вани получился
одинаковый результат. Какое число загадал Игорь?
4
5. На сколько процентов число 0,8 больше 5 ?
6. Что больше: а или 2а? Приведите примеры.
Контрольная работа 5
1. Найдите значение выражения
°-6 -I - (з§ - 2п): 9>6-
2. Решите уравнение
8-1,5-(3* + 2)= | (4-6jc).
3. Сумма трех чисел равна 24,6. Второе число
составляет 48% от первого числа, а третье число
составляет х второго числа. Найдите каждое из
трех чисел.
4. У Димы и Сережи было 12 000 р. Они
купили себе по одинаковой книге, причем на ее по-

288
Контрольные и проверочные работы
Математика. 5—6 классы
купку Дима истратил « своих денег, а Сережа
40% своих денег. Сколько рублей было у Димы
Ъ сколько у Сережи?
5. Найдите неизвестный член пропорции
з| : л: = l| :0,75.
6. Число а увеличили На 30%, а затем
получившееся число уменьшили на 25%. Сравните
последнее число с числом а. Ответ объясните.
К—5
1
1.8,655.2.0,195.3. а) а = 3 g ; б) х - 0,6.4.10,5 км.
5. В первом бидоне 2,7 л, а во втором — 5,1 л. 6. £АВС =
- 90°; L DEK - 18°; L MON - 54°.
6 класс
к—1
1.9^.2. g;0f4;§.8. ^х - § . 4. а) х - зЦ;
б) х - 3,5. 5. 1 Гп ч или 1 ч 55 мин. 6. Шесть чисел.
ОТВЕТЫ
5 класс
к—1
1. а) 824021; б) 27808; в) 243 758; г) 7083. 2.112 км.
3. а) х - 5477; б) у = 34 426. 4. 769 + х, при х - 389
значение выражения равно 1158. 5. АВ и CD; МК и EF. 6.
12 треугольников.
К—2
1. 20 010. 2. а) х - 67; б) х - 98. 3. а) 5а + 169, при
а = 0 значение выражения равно 169; б) 29* + 31, при
х — 10 значение выражения равно 321. 4. Абрикос
весит 70 г, персик — 210 г. 5.1+ 2 + 3 + 5 + 6 + 10 + 15 +
+ 30 - 72. 6. Есть, например 48.
К—3
19 1
1. Да. 2. 13 2« км. 3. 132 м. 4. 3 ч. 5. ^ часть
2 4>
(2 4\
суток. 6. При п - 1, 2 I 7 и 5 J
К—4
1. а) 6,854; б) 24,15. 2. а) 0,36; б) 25%. 3.
Синеглазка собрала 5,76 кг земляники, а Снежинка 4,8 кг.
4. 16 км. 5. ^ > 0,48; j < 1,4. 6. 150 : 100 - 1,5. В 1,5
раза.
К—2
1. 13g. 2. а) 5,25; б) 0,54; в) х = |. 3. х = з||.
2
4.1,8 кг пшена, 3 кг гречки и 1,2 кг риса. 5. 1,2 : 2» х
Х100 = | • | • 100 = 45%. 6. J - £ = ^.
следовательно, второй вспашет поле за 15 ч.
К—3
1. а) -5,7; б) 11. 2. а) х = -6|J ; б) х = -4. 3. в| кг.
4. = 5 дм. 5. 3,5. 6. Нет корней.
К—4
4 6 2
1. -150. 2. а) х - 2,5; б) х - g ; в) х - jj . 3. 55 м .
4
4. а - 7,5. 5. 0,8 : g " 1>8, следовательно, 0,8 больше
| на80%. 6. К 2 • 1; 0 = 2-0; -1 > 2 • (-1).
К—5
1. gj . 2. х - 4 jj. 3.15; 7,2 и 2,4.4.4500 р. и 7500 р.
5. х = 1 р . 6. Число а увеличили на 30%, получили
1,3а. Затем уменьшили на 25%, получили 1,3а • 0,75 =
= 0,975а. Следовательно, число а уменьшилось.

Алгебра. 7—9 классы
7 КЛАСС
Контрольная работа 1
Действия с многочленами
Выполните действия (упростите).
1. Сложение и вычитание:
а) (За2 - 2а6 + 562) + (7а2 + 2 аЬ - 462);
» б) (8т2 + 3 тп - 7) - (5т2 + 2тп - 1);
^ в) (5а2 - За6 - Ъ2) - ((2а2 - За6 + Ь2) - (а2 - 262)).
2. Умножение и возведение в степень:
а)(-За26)3-(-2а&5)2;
2
б) тп(3/п - Ът + 1);
v в) (п - 2т + 1)(3и + т - 2);
v г) (За - 2р)2;
д)(7а + 3д)2;
е)(5а + 36)(5а - 36).
3. Совместные действия:
а) (Зт - 2п)2 - (2т - Зп)2;
, б) (2т + Зп)(Ът -1) - (Зп + 2)(т + и);
в) (а + 1)(а2 + 1)(а4 + 1 )(а - 1);
г) (Зп + 1)(2п - 1) - (п - 2)2 + (3 - п)(5 + п).
Контрольная работа 2
Разложение на множители
1. Разложите на множители вынесением
общего множителя за скобку:
а) За + 126; б)7а26 - 14а62 + 7а6.
2. Разложите на множители, используя
метод группировки и вынесения общего
множителя за скобку:
а) 2а + 26 + а2 + аб;
б) т + тп - т - mq - nq + q;
в) 2(3а2 + 6с) + а (46 + Зс).
3. Разложите на множители, используя
формулы сокращенного умножения:
10-1019
а)9а2-1662;
б) 4а2 - 4а6 + б2;
в) 25а2 + 70а6 + 4962.
4. Разложите на множители, используя
различные способы:
а) 5а - 125а6 ;
б) а2 - 2а6 + б2 - ас + be;
в) (с - а)(с + а) - 6(6 - 2а).
5. Вычислите:
a) 1432 - 1422;
б)1572 + 2;157 -43 + 432;
ч 0,6 0,8 + 0,6 1,2
в> 2 2 •
0,22 - 0,42
6. Разложите на множители, используя
различные приемы:
а) х2 - Зх + 2; б) а - ЗаЪ + 262;
в)х4 + 5*2+9.
7*. Найдите все такие пары чисел а и 6, при
которых значение данного выражения равно нулю:
а) 2а + Заб; б) а - 36 - 3 + аб;
в) а 6 - 46.
8*. Докажите, что число 370 • 371 • 372 • 373 + 1
можно представить как произведение двух
одинаковых натуральных чисел.
Контрольная работа 3
Уравнения
1. Решите уравнение:
а) Зх + 5 =7;
б) (2х + 3) - 2(5* - 1) = (1х - 1) - 2(3* +11);
ч 2х + 7 х - 3 л
в)—з 2~=*х;
г) (2 - Зх)2 + (1 + 4х)2 = (5х - 1)(5х + 1).
2. При каком а значение выражения
ах + 5а - х
при х = 3 равно 7?

290
Контрольные и проверочные работы
Алгебра. 7—9 классы
3. При каких Ъ график функции у = Ьх - Зх +
+ 2 - Ь проходит через точку М(2; 1)?
4. При каких значениях р уравнения
Зх - 7 = 2ирх2 + Зх-1 = 0
имеют общий корень?
5. Решите графически уравнение:
а) 2х - 1 = 5 - х; б) х = 2х + 3.
Контрольная работа 4
Системы линейных уравнений
1. Решите систему уравнений, используя
метод подстановки:
Л i/-3i/=7, f x + 7i/ = 9,
а' J 2х + Зу =23; °' 1 5* + Зу =13;
в)
{
2х + у=11,
Зх - у = 4.
2. Решите систему уравнений, используя
метод алгебраического сложения:
Ьх - 2у =7,
5*-11$/= -2;
{
3x + 5i/ = 21,
5x-3z/ = 1.
3. Решите систему уравнений удобным для
вас способом:
а)
| х + у = 23,
I дс — j/ — 37;
Л 7* + Ъу - 22,
М 31* - 9i/ =22;
б)
г)
3x-i/ = 5,
2х + 7i/ = 34;
Зх - I/ - 5,
[ х - I/ =5.
4*. При каких значениях р система
уравнений не имеет решений:
а) 1х + 2у = 3,
1 * - г/ = р;
» тЛ J
2х + у = 7?
5*. Решите систему уравнений:
v * - у - р;
■Л**8»-1' 2
' 1 х + 3i/ = 3 + р2;
бЛ 2х - Зу = 5,
' \2x-3y =р;
Г) J 8ж + ру- 1,
а)
б)
Зх + 1у +
3x + 7i/
8х + у
2
8х + у
х+ i/ + г = 5,
х+ i/+ * = 6,
х + z + * = 0,
х+ *+ г = 1.
= 3,
= 1;
6*. При каких значениях а и Ъ система
уравнений
f ax + 3i/ = 96, f х = 1,
t 5х - ai/ =6 имеет Решение | у « -17
Контрольная работа 5
Алгебра в арифметике
1. Вычислите:
а)35012-34992;
^ 5372 - 5332
б' 2 2;
536 - 534
в>(4 + А)2 - (51 - А)2;
г) 7,22 + 2-7,2-2,8-f 2,82;
Д)3П#5Й+3Й#6А;
е)(з|)5-(У)8;
ж)(7|)4:(з|)4;
з>(13!)2 -141*121-
2. Вычислите значение выражения
а - Ь2 - Ъа + 56
приа = 3^, 6=1^.
3. Докажите, что число 1728 - 703 делится
на 25 без остатка.
4. Сравните числа 135 787 • 135 789 и
135 7882.
Контрольная работа 6
Итоговая
= 4-х.
1. Решите уравнение
Зх - 5 _ 2х - 3
2 3
2. Упростите выражение:
а) (За + Ъ)(2а - ЪЬ) - 6(а - б)2;
б)(-2а36)3-(-5а26)2.

Контрольные и проверочные работы
Алгебра. 7—9 классы
291
3. Разложите на множители:
а) ab + ас- а;
б) 4а2 - Ъ2 + 2а - Ь.
4. Постройте график функции у = 2х - 1 и
укажите координаты точек его пересечения с
осями координат.
5. Решите систему уравнений
Г 3* - 2у = 14,
I 2* + i/=7.
6. Пешеход сначала шел в горку со скоростью
3 км/ч, а затем спускался с нее со скоростью
5 км/ч. Найдите общий путь, проделанный
пешеходом, если дорога в горку на 1 км длиннее
спуска, а затраченное на весь путь время равно 3 ч.
7*. Для каждого значения а решите
уравнение
(а + 1)(а-1) *х = а + 1.
Контрольная работа 7
Итоговая
2
1. Найдите значение выражения 9т - ЗОтп +
2 2
+ 25п при т = 5« , п = 1,4.
2. Решите уравнение:
а) (Зх - I)2 - 8(х + I)2 = (х + 2)(х - 2);
_ 7х - 1 Зх - 7 д
б>—5 — -в-*-
3. Упростите выражение:
а) (2а - 6)(а + 6 - с) - (а + 26)(а - 6 + с) +
+ Зс(а + 6);
б)(-2а&5с)3-("3а5&с3)2.
4. Постройте в одной системе координат гра-
фики функций у = х и i/ = 5х - 6 и найдите
(графически) координаты точек пересечения.
5. Разложите на множители:
а) а2 - Ъ2 - 26с - с2; б) Ъ2(а + 1) - а2(6 + 1).
6. Найдите такую пару чисел,
удовлетворяющую уравнению 5х + 17у = 61, сумма которых
равна 5.
7. Одна из сторон равнобедренного
треугольника на 8 см меньше другой. Найдите стороны
этого треугольника, если его периметр 44 см.
8*. Для всякого значения Ь решите
уравнение
(6-5)(6 + 3)-х = 62-25.
9*. Разложите на множители х + Зх +4.
8 КЛАСС
Контрольная работа 1
Действия
с алгебраическими дробями
1. При каких значениях х определено
выражение:
3 7
а)
х + 2'
б)
(2 - х)(3х + 5)
2. Сократите дробь
2 л 2
х - 4а
2 , Л АЛ2'
х + 4ах + 4а
3. Выполните действия:
v 9*у ( _аЬ_>|2
Контрольная работа 2
Действия с квадратными корнями
1. Вычислите:
а) л/0, 49 • 64 ;
б) 74, 9 • 6,4 ;
в) 725 +(737)2 -7н5?;
г) л/3(7з + 727 + 748).
2. Найдите значение выражения
(Vi + у) • (7^ - У)
прих = 17,1, I/ = 0,1.
3. Пусть * = л/3-2, у = л/3 + 2. Найдите:
а) х2; б) х2 - у2; в) х • у; г) хл/у2 ; д) yjx2 .

292
Контрольные и проверочные работы
Алгебра. 7—9 классы
4. Упростите выражение
х - у _ х + 4*/ху + 4у
Jx + Jy Jx + 2л/^
1
и вычислите его значение при * = 1,1, У = к
5. Между какими последовательными
натуральными числами находится число 0,5 л/б8 ?
6. Расположите следующие числа в порядке
возрастания: </3; -2л/§; 2^5; 1; V0, 7; «/15;
0,7.
7*. Упростите выражение
(л/3 + I)2 + («/§- 2)2 +
+ л/27 + л/4 + 273 + л/7 - 4л/3.
Контрольная работа 3
Квадратные уравнения
1. Решите уравнение:
а) 2*2 - * = 0; б) 9 - х2 = 0;
2 X2
в)2х-х-1-0; г):-=Н;=1;
х + 6
Д)
х + 2х = 3
х - 1 х - 1 '
ч 5 ^ 4
х+1 х-2 х-3
2. Решите графически уравнение х = 3 -2х.
3. При каких значениях а корень уравнения
х(а + 3) = 9х - а равен 1?
Контрольная работа 4
Текстовые задачи
1. Найдите стороны прямоугольника, если
его периметр 18 м, а площадь 20 м .
2. Пешеход должен был пройти 10 км с
некоторой скоростью, но, увеличив эту скорость на
1 км/ч, он прошел 10 км на 20 мин быстрее.
Найдите истинную скорость пешехода.
3. Ученик делает некоторую работу на 4 ч
медленнее, чем мастер. Работая вместе, они
затратили на эту работу 2 ч 6 мин. За какое время
мастер, работая один, выполнит эту работу?
4. Двузначное число на 14 больше
произведения своих цифр и на 45 меньше числа,
записанного теми же цифрами, но в обратном, порядке.
Найдите это число.
Контрольная работа 5
Линейные неравенства и их системы
1. Решите неравенство:
а)х + 3>5; б)х-8<3;
в) -2х > 7;
ч 5 - Зх . Ъх + 1
г)—5— >—о —
д)(х + 7)2 + (2х+1)2<5х2.
2. Решите систему неравенств:
-х > 3,
х
а)
и >~3'9
2х - 3 < 0,
2х - 1 > 0;
Г Зх - 22 < 0,
в) 1 8 -х < 0;
/*2>о,
I Зх + 1 < 0.
г)
3. Не решая уравнения Зх + 11х-13 = 0,
сравните хх + х2 и хх • х2, где хх и х2 — корни
уравнения.
4. Найдите наибольшее целое число,
удовлетворяющее неравенству
х(2 - JI) > 7, 7 • (2 - л/5).
5. Решите двойное неравенство:
а) 4 < 4х < 7;
б)КЗх-4<5;
в)-К2-Зх<2.
6. Сколько целых решений имеет неравенство
5000 < 53* < 10 000?
Контрольная работа 6
Итоговая
2
1. Решите уравнение Зх + х - 30 =0.

Контрольные и проверочные работы
Алгебра. 7—9 классы
293
2. Решите неравенство:
Ъх - 1 2х + 3
а)
<1;
3 5
б)(1 - 7з)*>1 - 7з.
3. При каких значениях х определено
выражение л/5 - 2х + J7x - 14 ?
4. Преобразуйте выражение:
(л + 3* + х\ ( 1 у V1
5. Найдите два соседних натуральных числа,
сумма квадратов которых равна 365.
6. При каких значениях а уравнение
Зх2 - Ъх + 2а = О
а) имеет корень, равный 3;
б) имеет два различных корня;
в) имеет только положительные корни;
г) не имеет отрицательных корней?
Контрольная работа 7
Итоговая
1. Решите неравенство
Зх + 7 2х + 1 7 - х
5 3
2. Решите уравнение:
а) л/5 • jc2 - 4jc - Jb =0;
ЛЧ Зх , 2х - 1 , 3 - х
О) — Н :—:—К
6
х - 1
X + 1 х - 1
3. При каких значениях х определено
выражение
Jb^Tx + %=^±l
л/х - 7
4. Преобразуйте выражение:
(1+Jm + П . Л+Jm _ ^V1 +(73)4.
I 1 + т т) \ т 1 + т) v '
5. Поезд должен был пройти 840 км в
определенное время. На половине пути он был
задержан на 30 мин из-за технической
неисправности. Чтобы прибыть вовремя, ему пришлось
увеличить скорость на 2 км/ч. Сколько времени
поезд находился в пути?
6. Вычислите
2
(злТ^)-»-*-»-
7. При каких значениях Ъ уравнение
х2 + (4Ь + 3)х + ЗЬ2 + ЗЬ
х - 2
= 0
а) имеет один корень;
б) имеет только отрицательные корни?
8. Составьте уравнение, корнями которого
будут числа хг + 2, х2 +2, где хг, х2 — корни урав-
2
нения х - Зх - 1=0.
9 КЛАСС
Контрольная работа 1
Прогрессии
1. Пусть ах и ап соответственно первый и и-й
члены арифметической прогрессии, d —
разность прогрессии. Известно, что аг = 8, ап = 104,
d = 3. Найдите п — число членов
арифметической прогрессии nSn — сумму п первых членов.
2. Пусть Ьг— первый член геометрической
прогрессии, q — знаменатель прогрессии. Из-
2
вестно, что &! = 243, q = -я. Найдите шестой
член геометрической прогрессии и сумму шести
первых членов.
3. Банк дает сбоим вкладчикам 25%
годовых. Чему станет равен вклад 100 000 р. через
два года?
4. В арифметической прогрессии
ая= 37,7 -0,3и.
Найдите наибольший отрицательный член
прогрессии.
2
5. При каких значениях х числа 1 + х, х + 4,
2х + 9, 9х являются четырьмя
последовательными членами арифметической прогрессии?
6*. Последовательность (ап) задана форму-
Зп + 1
лои своего n-го члена: а„ =
п 2п + 5
Найдите а5 и
12
номер члена последовательности, равного 1 «=

294
Контрольные и проверочные работы
Алгебра. 7—9 классы
Контрольная работа 2
Преобразование выражений
1. Вычислите наиболее удобным способом
(l|| -9,12- 7,4-(-б|)): б|.
2. Упростите выражение
I1 " а + 2ъ) *' U + 2Ь' { + а - 2bj)*
3. Выполните указанные действия:
7о704 - (77 - 272)(78 + 77).
л гл sin3a
4. Существует ли выражение
sin 4 a + sin 2 a
при каждом из указанных значений а:
а)а=^;б)а=^;в)а=к?
5. Дано: tga=5»0<a<o- Найдите
6. Упростите выражение
г \
1
sin a.
1 +
*"8+«).
. 2
'Sin a.
Контрольная работа 3
Уравнения и системы уравнений
1. Решите уравнение
Зх - 1 2х - 1
= - -1
14 1в
2. Найдите все неотрицательные решения
X X
уравнения + = х.
х + 1 х - 3
3. Решите систему уравнений
Г х + Зу - 7,
I 7* + у « 1.
4. Решите систему уравнений
Г(* + 1)(2у-1)-0,
1 4xi/ - jc - 2i/ = 1.
5. Напишите формулу д-го члена и суммы п
первых членов арифметической прогрессии, если
а2 + аь= 41, 0^3=144.
6. Товарный поезд был задержан в пути на
18 мин, а затем на расстоянии 60 км наверстал
это время, увеличив скорость на 10 км/ч.
Найдите первоначальную скорость поезда.
Контрольная работа 4
Неравенства
1. Решите неравенство
Зх + 7 _ 2х + 1 > 1 + х
8 3^2'
2. Решите неравенство
(х + 2)(2 - х) > (х + 2)(х +4).
3. Найдите область допустимых значений ар-
У= л/з^"
гумента функции у = л/3 - 5х - 2х
4. Решите систему неравенств
-Зх2 + 8* +3 > О,
7 - 2* л:
—5-<2+1-
5. Найдите все значения х, при которых
выражение xjx — 7jc — 18 имеет смысл, а также
все значения х, при которых значение этого
выражения равно нулю.
6. В арифметической прогрессии 59, 55, 51,...
найдите сумму всех ее положительных членов.
7. Определите знак sin а, если:
а) a =134°; б) a =1048°;
9л
в) a = у ;
г)ос =
110я
13 '
Контрольная работа 5
Функции и квадратный трехчлен
1. Постройте график функции у = х -4х - 5
и укажите интервалы ее знакопостоянства.
2. Найдите корни квадратного трехчлена
3*2-11*- 34
и разложите его на линейные множители.
3. Расположите в порядке возрастания
sin 30°, sin 60°, sin 210°.

Контрольные и проверочные работы
Алгебра. 7—9 классы
295
4. Определите наибольшее и наименьшее зна-
3 + 7cosa
чение выражения гт* .
5. Найдите координаты точек графика функ-
3
ции у = х + - , отстоящих от оси ординат на 1,5.
6. Решите графически уравнение
7. Изобразите фигуру, ограниченную графи-
ками функций у = х и i/ = 2х + 3 (выделите ее
штриховкой; точки границы фигуры считайте
принадлежащими фигуре). Укажите
координаты точки этой фигуры, имеющей наибольшую
ординату.
ОТВЕТЫ.
7 класс
2 -2Ч
К—1
1. а) 10а2 + Ъ2; б) Зт2 + тп - 6; в) Ца - Ь6)
2. а) - 108aV3; б) Зт3 - 5т2 + т; в) Зп - Ътп - 2т2 +
+ п + 5т - 2; г) 9а2 - 12ар + 4р2; д) 49а2 + 42ад +
2 2Ч
2 о 2
+ 9д ; е) 25а2 - 9Ъ. 3. а) 5(/п - п); б) 10т -Зп +
+ 12тп - 4т -Ъп; в) а - 1; г) 4п2 + и + 10.
К—2
1. а) 3(а + Щ; б) 7аЬ(а - 2Ъ + 1). 2. а) (2 + а)(а + 6);
б) (т - д)(т + п - 1); в) (2а + с)(3а + 2Ь). 3. а) (За - 4Ь) х
х(3а + 4Ь); б) (2а - Ь)2; в) (5а +7Ь)2. 4. a) 5a(a - ЪЬ) х
х (а + 5Ь); б) (а - Ь)(а - Ь - с); в) (с - а + Ь)(с + а - Ъ).
5. а) 285; б) 40 000; в) -10.6. а) (х - 2Кх - 1); б) (а - 2Ь) х
х (а - Ь); в) (х2 + 3 - х)(х2 + 3 +х). 7. а) (0; Ь), где Ь -
любое число; (a; -« )» гДе а ~~ любое число; б) (3; Ь),
где 6 — любое число; (а; -1), где а — любое число;
в) (2; Ь), (-2; Ь), где Ь — любое число; (а; 0), где а —
любое число. 8. Указание. а(а + 1)(а + 2)(а + 3) + 1 -
= (а2 + За + 2)(а2 + За) + 1 - ((а2 + За +1) + Ща + За +
+ 1) - 1) +1 = (а2 + За + I)2. В нашем случае a - 370.
К—3
l.a)|;6)f в)1;г)|.2.2.3.|.4.-|5.а)2;
б)х1--1,х2 = 3.
К—4
1. а) х - jj , у - 7 jj ; б) ж - 2, у = 1; в) ж - 3,
17 31 9
у - 5. 2. а) х - у , у = у ; б) х = g, у - 1; в) х = 2,
154
S/ - 3. 3. а) х = 30, у = -7; б) х = 3, у « 4; в) х = щ ,
264
У = Jqq ; г) х = 1, у = -2. 4. а) 0; б) р * 5; в) р ей;
3 к ч 12 10 *ч О Л о
г)р - g 5. а) х - gg , у = gg; б) х - 3, у = 4, z = -2,
f --1.6. а --6, Ь --1.
К—5
1. а) 14 000; б) 2; в) 4; г) 100; д) 37; е) 32; ж) 16;
з) 1. 2. 0. 3. Указание. Используйте равенство
1728-703-1025. 4. Указание. 135 787-135 789 =
- (135 788 - 1)(135 788 + 1).
К—6
13, 5
1. 3. 2. а) -Ь(а + lib); б) -200а Ь° 3. а)а(Ъ+с- 1);
б) (2а - Ь)(2а +6 + 1). 4. (^ ; 0), (0; -1). 5. х - 4, у = -1.
6. 11 км. 7. Для а * 1 иа^-1 для а « -1 хей, для
а = 1 нет решений.
К—7
1.100. 2. а)-^; 6)3. 3. а) а2 + Ь2 + 2&с;
б)-72а13Ь17Л 4. (2; 4), (3; 9). 5. а) (а-Ъ-с)х
x(a+fc+c); б) (Ъ-а)(аЪ+Ь+а). 6. х - 2; у « 3.
7.12; 12; 20 см или 9g, 17g, 17g см. 8. Для Ь * -3 и
& + 5
Ъ * 5 х - г £ Для Ь - 5 х € Л, для Ь - -3 нет реше-
Ь + 3
ний. 9. (х2 - х + 2)(*2 +* +2).
8 класс
к—1
l.a)(-oo;-2)u(-2; + oo);6)(-oo;-|)u(-g;2)u
в)
2ху
2 2
х - у
К—2
1. а) 5,6; б) 5,6; в) 36; г) 6. 2.17,09. 3. а) 7 - 4л/3 ;
б) -873 ; в) -1; г) -1; д) 1. 4. -1. 5. 4; 5. 6. -2^3 ; 0,7;
7ЬТ7;1; 73; 7ТВ; 275.7. 14 + 7з.

296
Контрольные и проверочные работы
Алгебра. 7—9 классы
к—3 9 класс
1. а) 0; \ ; б) 3; -3; в) 1; -|; г) 3; -2; д) -3; е) 1; 4. К-1
2.1;-3.3.-3; 2. 1.д-33, S-1848. 2. Ьв—32, Se-133. 3.156 250 р.
4. -0,1. 5. 2. 6. а5= 1 ^ . п - 16.
К—4 15
1. 4 м; 5 м. 2. 5 км/ч. 3. За 3 ч. 4. 38. К—2
К—5 1- 7,4. 2. - а L4. 3. 1,2. 4. а) Существует; б) не
2(а — о)
1. а) (2; +оо); б) (-оо; Ц); в) [-3,5; +оо); г) Г-оо; — 1; существует; в) не существует. 5. sin а = 0,8. 6. tg2 а.
д) f-co; -8 J ]. 2. a) [-„; -3]; б) [0,5; 1,5); в) 0; х. |. 2.0; 2 + ^ ; 2 - 7~5 • 3. [-\ ; £ } 4. (-1; -1).
r)(4;0)u(0;+oo).3^1 + x2>^.x2.4.7.5.a)[l;^]; 1ДЛ ^ _ ^ + «|i(j( _ 1}> ^ _ ^ + «j! х
б)[|;з)в)(0;1].6.94. ж^^, либо а„-5П+3, Sn = (»» + »>».
R_6 6. 40 км/ч.
10 ^ 29 Л —
1.-т, 8. 2. .)(-«; й ) в (-со;!). 8. [2; 2.6]. ^ < ^ <2._2<х <_1.3.-3<,< | .4J <х <3.
4. —^—. 5. 13; 14. 6. а) -6; б) (-со- ^ \ „) (0; §? 1; 5- Определено при * е (-«>; -9] и [2; +оо), равно ну-
* + 1 ^ 24 ^ ' ^ 24 J Лю при л; = -9 или х = 2. 6.465. 7. a) sin 134° >0;
Г) 10: +0О)' б) sin 1048° < 0; в) sinfy ) < 0; г) sin(^) > 0.
-/5 К_5
1. [1;+°°). 2. а) -^; ТЕ; б) 2. 3. 0. 4. 10. 5. 21ч. 1.у>0 при х е (-оо; -1)и(5; +оо), у<0при
17
3 1 2 *€(-1;5). г.хх - т, х2=-2; (* +2)(3х - 17).
6.22.7. а) - = ; -5 ; 2. б) (-°°; -1). 8. Например, * - 7t + d
23 3. sin 210° < sin 30° < sin 60°. 4.1;-0,4. 5. (-1,5;-3,5),
+ 9 = 0. (1,5; 3,5). 6. x = 1,8. 7. (3; 9).

Алгебра и начала анализа. 10—11 классы
10 КЛАСС
Контрольная работа 1
Тригонометрические уравнения
и неравенства
1. Решите уравнение:
1
б) sin g =-1;
a) cos х = г ;
в) tg (2х - j J = 1; г) 2 sin х = 1 + cos х;
2 2
д) sin х - 5 sin х cos * + 4 cos * = 0;
е) cos 2x + cos x = 0.
2. Укажите на тригонометрической
окружности все точки, удовлетворяющие неравенству:
a) sin х > 0; б) cos х < 0; в) cos х < ^ •
3. Укажите какое-либо число,
удовлетворяющее всем трем неравенствам задания 2
одновременно.
Контрольная работа 2
Техника решения
тригонометрических уравнений
Решите уравнение.
1. cos Зх = 5 -
о х J*
2. sin 2 =—2".
3. tg f * + 5 ] - 73 . 4. 2 sin2 х - sin * - 1 = 0.
5. 3tgx + 2ctg* = 5.
6. cos -g— 5 cos 5 -2 = 0.
7. cos 2jc + 4л/2 sin x - 4 = 0.
8. cos x - 3 sin x = 0.
9. sin 2x - cos x = 0.
10*. y cos * - g sin * = cos 3x.
ll*.(2cos*- 1)-V-sinx =0.
2sinx - 72
13*. sin2 * + sin2 2x + sin2 3x + sin2 4*
14*. sin x + cos x = 1.
15*. cos 2x + cos 7x - 2.
Контрольная работа 3
Итоговая
1. Найдите критические точки функции
у = х - 2sin jc.
on 3* + 1 ^ л
2. Решите неравенство ч 1.
3 2
3. Исследуйте функцию у = х -Зх -1и
постройте ее график.
Для этого найдите:
а) область определения D (у);
б) производную и критические точки;
в) промежутки монотонности;
г) точки экстремума и экстремумы;
д) точку пересечения графика с осью Оу и
еще несколько точек графика;
е) множество значений Е(у) функции;
ж) нули функции (можно приближенно).
4. Найдите наибольшее и наименьшее
значения функции у = х + - на отрезке I « ; 4J.
Контрольная работа 4
Итоговая
12*.
2cosjc + л/2
= 0.
1. Решите уравнение:
а) 2 cos х + 1 = 0;
2 2
б) sin х - 3 sin х cos х + 2 cos х = 0.
2. Решите неравенство х(х - 9) < 0.
3. Пусть I/ = х3- Зх - 5. Исследуйте
функцию и постройте ее график.
Для этого найдите:
а) область определения D(y);
б) производную и критические точки;
в) промежутки монотонности;
г) точки экстремума и экстремумы;

298
Контрольные и проверочные работы
Алгебра и начала анализа. 10—11 классы
д) точку пересечения графика с осью Оу и
еще несколько точек графика;
е) множество значений Е(у) функции;
ж) нули функции (можно приближенно).
Найдите наибольшее и наименьшее значения
этой функции на отрезке [0; 3].
4*. Найдите критические точки функции
у = 0,5 sin 2х + sin х.
5*. Найдите промежутки возрастания функции
5-3
у = х - Ъх .
6*. Напишите уравнение касательной к
графику функции
i/ = Jx +х
в точке с абсциссой 4.
11 КЛАСС
Контрольная работа 1
Уравнения
1. Решите тригонометрическое уравнение:
х
а) 2 sin 5 - 1 = 0; б) 2 cos х • cos 2х + cos х = 0;
2х
в) sin х - cos х = 0; г*) cos 2х + cos ~ =0,25.
2. Решите иррациональное уравнение:
2х + Зх - 10 =2;
а) Л
6*)V2x2 + Зх - 10 =х;
в*) Jx + Jx + 3 = 3.
3. Решите показательное уравнение:
а) 2х + * = 4; б) 2х = 7;
_ 1
в*)4* 2 -5-2*_1 + 2 = 0.
4. Решите логарифмическое уравнение:
a) log1(5x-3) = -l;
2
6)log2(*2-l) = log2(2x-l);
в*) log5(3x - 1) - 2 log5(2x + 1) = logj 3.
з
5*. Решите трансцендентное уравнение
O2cosx .COSX 1
3 -4 -g.
Контрольная работа 2
Неравенства
Решите неравенства.
1. 3jc + 5 < 2.
х + 1
5.23х>72.
2. х - 6х - 7 > 0.
4. log2(3* - 1) < 0.
6*.*2(3*-1)>0.
7*. (5 - 2*),/* < 0. 8*. lg2* - 2 lg х < 0.
9*. Jx + 2 >х. - 10*. sin * < g •
Контрольная работа 3
Функции и производная
1. Найдите область определения функции
1
f(x) = Jl - х + х7.
2. Найдите производную заданной функции:
a) f(x) = хв + ех- cos Зх; б) f(x) = Jx - 2 In *;
в*) Л*>-*•*"*; r*>rt*>=frf-
3. Найдите промежутки монотонности, точки
экстремума и экстремумы функции:
а)/(*) = 3*-х3 + 2; б*) f(x) = х • In х.
4. Найдите наибольшее и наименьшее
значения функции:
a) f(x) = х2 - 6х + 1 на [2; 4];
б*)/(*) = *•<?"* на [0; 2].
5*. При каких значениях а (а > 0) наиболь-
о
шее значение функции f(x) = х - 6* + 1 на [0; а]
равно 1?
Контрольная работа 4
Итоговая
1. Решите уравнение:
a) cos 2х = 5 ;
в) 7зх2 - 5 = 2.
/1\1 - *
2. Решите неравенство I « I
6)log2(2x + l) = 3;
>2.

Контрольные и проверочные работы
Алгебра и начала анализа. 10—11 классы
299
3. Найдите промежутки монотонности, точки
экстремумов и экстремумы функции
у - 2х - х2.
4. Найдите площадь, ограниченную графи-
2
ком функции у = 2х - х и осью абсцисс.
5. При каких а уравнение
2 sin Зх = а
не имеет решений?
Контрольная работа 5
Итоговая
1. Решите уравнение:
а) cos 2х = cos х -1;
б) log^jc2* 5*-4) = -1;
2
в) ДхГ^~2 = #.
2. Решите неравенство:
б)2х + 2*+1<6.
4. Найдите абсциссы тех точек графика
функции
у = sin jc cos х,
ординаты которых равны 0,25.
5. Найдите промежутки монотонности функ-
3 2
ции у = х (Зх - 5) и точки ее экстремумов.
Контрольная работа 7
Итоговая
1. Найдите абсциссы всех точек пересечения
графиков функций у = хиу=1 + *[х + 5.
2. Вычислите
3. Найдите промежутки монотонности, точки
экстремума и экстремумы функции у = х - 12jc.
4. Найдите площадь фигуры, ограниченной
о
графиком функции у = х - 12л: и прямыми х = 0,
x = -2,i/ = 0.
5. При каких значениях а функция
у = 2е* + ах - 3
не имеет критических точек?
Контрольная работа 6
Итоговая
1. Вычислите значение выражения
V2-V2 о
412
2. Решите уравнение
log2(2x - 1) + log2(3.r - 2) = 0.
l
3. Решите неравенство 3х < 9.
3Jlog72(2sinl) + log72(cosI)'
3. Решите неравенство 2х > 0,5*
4. Найдите площадь фигуры, ограниченной
линиями у = (х - 2)(3 - 2jc) и i/ = 0.
5. На промежутке [-2; 2] исследуйте функцию
1 2
~2Х
f(x) = хе
и постройте ее график.
ОТВЕТЫ
10 класс
к—1
я тс кп
L а) ±д + 2кп, п е Z; б) Зя + 4я&, Л 6 Z; в) j + -у ,
я я
п б Z; г) ±5 + 2ят1, я + 2я£, л, Л е Z; д) т +ял, arctg 4 +
я
+ nk, п б Z, Л е Z; е) ±g + 2ял, я + 2я£, n9k е Z. 3. На-
2я
пример, -«- .
К—2
. ,я , 2я/1 «л , -vin + i 2я , Л
1. х = ±д + -g- , л б Z. 2. х = (-1) ~з" 2шя»
я я
m 6 Z. 3. х = 77 + nkt k 6 Z. 4. х = 5 + 2яЛ, k е Z;x =
= (-l)m + * • g + nmt m e Z. 5. x = j + я*, fe € Z; x =

300
Контрольные и проверочные работы
Алгебра и начала анализа. 10—11 классы
2 К—2
: arctg g + яд, п 6 Z. 6. х - ± 2я + 6яЛ, k е Z.7.X = ^ (_оо; -1). 2. (-оо; -1] и [7; +оо). з. (-оо; -1) и (2; +оо).
- (-1 )* • \ + nk, k б Z. 8. х - arctg | + я*, Л e Z. 9. x = 4. ( |; 115. ( g ;+oo 16.
-jjj + я&,*€^х = (-1)т-| + ят. m € Z. 10. x = j^ + 8.(1; 100). 9. [-2; 2). 10. j
+ nk, k e Z; x - -gj + ^ , n € Z. 11. x - яЛ, Л € Z; К—3
[|;+~)u{0}.7.{0}U[2,5;+oo).
я . Л „ ,Л я
1. [0; 1]. 2. а) Зх2 + ех + 3 sin Зх; б) -Ц - \;
х=-£ + 2wi. it е Z. 12. х - J + 2як, * € Z. 18. х - *• ^ ** --'"* '" . « ™ «*. w, ^ % ,
« «ь «... ч -«/-. ч ч ~3(х + l)»sin3x - cos3x 0 ч _
= ^+f,fteZ;*-f,neZ.14.x=*ft,fteZ; в>' А-**')-* ^77? •*••>*-
я растает на [-1; 1], убывает на (-°°; -1] и на [1; +°°),
х = g + 2^Л, Л е Z. 15. х = 2яи, п е Z. -1; 1 — точки экстремума, 0; 4 — экстремумы; б)
возрастает на - ; +°о L убывает на (0; - I, х = - — точ-
К—3 L в / V € J £
1. х = ±5 + 2я*. ft € Z. 2. Г- J ; 0 \ 3. а) 2>(у) - Я; ка экстремума, - - - экстремум. 4. а) -7; -8; б) - ; 0.
2 3 L 2 ^ 6.(0; 6].
б) у = Зх - 6х, х=0их = 2;в)у возрастает на (-°°; 0] и
на [2; +°о), убывает на [0; 2]; г) 0 и 2 — точки экстре- ^—*
Г.^^Т^лЙ*: "1; в,вд"* '• ■> *8♦■"■•« *»>•* * -л, Л. i » -..
3. Возрастает на (-оо; 1], убывает на [1; +оо), х в 1 — точ-
К—4 4
2П п ка экстремума, 1 — экстремум. 4. «• 5. (-оо; -2) U (2; +оо).
1. а) ±-=- + 2яЛ, k € Z; б) j +nk,k е Z, arctg 2 + яд,
neZ.2. (-оо; -3] и [0; 3]. 3. а)2> ($/) = Я; 6)i/' = 3x2-3, к я
х = 1 и х=-1; в) у возрастает на (-оо; -1] и на 1- а) £ + кЛ; *з + ^Ш' ** п е %> б) 1; ~5; в) 2; 1.
[1; +°°), убывает на [-1; 1]; г) -1 и 1 — точки экстре- 2. а) (-оо; -1) и (3; +оо); б) (-оо; -1). 3. Возрастает на
мума, -3 и -7 — экстремумы; д)х=0, у = -5; (-оо; -2] и на [2; +оо), убывает на [-2; 2], -2; 2 — точки
е) Е(у) - R; ж) х - 2,2, max у = 13, min у = -7.4. я + 2яЛ, экстремума, 16; -16 — экстремумы. 4. 20. 5. [0; -И»),
я /-
Л е Z, ±g + 2яп, п е Z.S.y возрастает на (-оо; -73 ] и К—6
на[73;+оо).6.у -1.25х + 1. L le 2. 1. 3. (-оо; 0) U [|5 +оо). 4. (-1)*-^ + у,
k е Z. 5. Возрастает на (-оо; -1] и на [1; +оо), убывает
на [-1; 1], точки экстремумов х = -1 и х = 1.
11 класс
К—7
К""1 1. 4. 2. -1. 3. (0; 1] U [3: +оо). 4. ^ . 5. Функция
1. а) (-1) g + 3яп, п € Z; б) g +яп;±^ + яЛ, л, нечетная, непрерывная на [-2; 2], возрастает на [-1; 1],
убывает на [-2; -1] и на [1; 2], при -2 < х < 0 /(х) < 0,
k е Z; в) 5 +я/, / е Z;r)±g +2яЛ;±агссо8 (-| ] + 2я/; при 0 < х < 2 /(х) > 0, при х =0 /(х)-0; х - -1 -
?, „ft4ft 7^vrt4^ovrt^^41 ^ЧЛЛ точка минимума; min -—р, х - 1 — точка макси-
k, I е Z. 2. а) 2; ~2 ; б) 2; в) 1. 3. а) -2; 1; б) log27; в)0; 2. Те
4.а)1;б)2;в)2;|.5.±у + 2я*, * * Z. мума; max =-^ .

Геометрия. 7—9 классы
7 КЛАСС
Контрольная работа 1
Установочная контрольная работа
1. Нарисуйте от руки какой-нибудь луч.
Отметьте точку и постройте с помощью линейки
два луча с началом в этой точке.
2. Какая фигура изображена на рисунке 1?
Контрольная работа 2
Измерение отрезков и углов
1. Три точки Р, Q и R лежат на одной прямой.
Какая из этих точек лежит между двумя
другими, если PQ = 5 см, PR = 7 м, QR = 12 см?
2. <Между сторонами угла (ас), равного 80°,
проходит луч Ь. Найдите углы (ab) и (be), если
угол (ab) в четыре раза больше угла (be).
Контрольная работа 3
Равенство отрезков, углов
и треугольников
1. Дан треугольник ABC, у которого АВ = 7 дм,
ВС =15 дм, А В = 40°. На стороне ВС отмечена
точка D так, что CD = АВ. Чему равны угол В и
прилежащие к нему стороны в треугольнике ABD?
2. Укажите равные трезпгольники на рисунке 2.
Контрольная работа 5
Смежные углы
1. Найдите угол, если смежный с ним угол в
6 раз меньше угла, смежного с прямым углом.
2. Данный острый угол в два раза меньше
данного тупого угла. Найдите эти углы, если
один из смежных им углов равен 130°.
Контрольная работа 6
Доказательство от противного
1. Докажите, что если два угла не равны один
другому, то смежные с ними углы тоже не
равны друг другу.
2. Докажите, что если угол, смежный с
данным углом прямой, то данный угол тоже прямой.
Контрольная работа 7
Углы
1. Найдите углы, которые получаются при
пересечении двух прямых, если сумма трех из
этих углов равна 200°.
2. Известно, что АВ = 4 дм, ВС = 5 дм, АС =
= 3 дм. Докажите способом от противного, что
точки А, Б и С не лежат на одной прямой.
3. ВМ — биссектриса угла ABC. Найдите
угол ABC, если угол СВМ равен 57°.
Контрольная работа 4
Основные свойства простейших
геометрических фигур
1. Даны прямая и четыре точки А, Б, С и D,
не лежащие на ней. Пересекает ли данную
прямую отрезок АВ, если отрезки BD и CD
пересекают эту прямую, а отрезок АС не пересекает?
Объясните ответ.
2. Точки А, Б и С лежат на одной прямой.
Принадлежит ли точка С отрезку АВ, если АВ =
= 7,5 см, ВС = 7,8 см, АС = 0,3 см?
3. Между сторонами угла (аЬ), равного 75°,
проходит луч с. Угол (be) в два раза больше угла
(ас). Найдите эти углы.
Контрольная работа 8
Первый и второй признаки
равенства треугольников
1. Докажите равенство двух пар
треугольников, изображенных на рисунке 3.
Рис.1
Рис. 2

302
Контрольные и проверочные работы
Геометрия. 7—9 классы
2. Докажите равенство двух пар
треугольников, изображенных на рисунке 4.
Контрольная работа 9
Признаки равенства треугольников
1. Периметр равнобедренного треугольника
равен 3,2 м, основание меньше боковой стороны
на 1 м. Найдите стороны данного
равнобедренного треугольника.
2. Треугольники ABC и ABD равны, причем
отрезок CD пересекает отрезок АВ в точке О.
Докажите, что СО ± АВ.
3. Даны два равнобедренных треугольника
ABC и ABD с общим основанием АВ. Докажите,
что прямые АВ и CD перпендикулярны в случае,
когда точки С и D лежат по одну сторону от
прямой АВ.
Контрольная работа 10
Признаки параллельности прямых
1. Отрезки АВ и CD пересекаются. Для
прямых AD и ВС и секущей АС назовите пару
внутренних односторонних углов и докажите, что
они действительно являются внутренними
односторонними.
2. Треугольники ACD и CAB равны, причем
точки В и D лежат по разные стороны от прямой
АС. Докажите, что прямые АВ и CD параллельны.
Контрольная работа 11
Равенство прямоугольных
треугольников
1. Докажите равенство двух пар
прямоугольных треугольников, изображенных на рисунке 5.
2. Докажите равенство двух пар
прямоугольных треугольников, изображенных на рисунке 6.
Контрольная работа 12
Сумма углов треугольника
1. Один из углов, которые получаются при
пересечении двух параллельных прямых
секущей, равен 45°. Найдите остальные 7 углов.
2. Найдите острые углы прямоугольного
треугольника, если известно, что биссектриса этого
треугольника, проведенная из вершины острого
угла, образует с противолежащей стороной углы
60° и 120°.
3. Дан треугольник ABC. Докажите, что его
вершины равноудалены от прямой, проходящей
через середины сторон АВ и АС.
Контрольная работа 13
Задачи на построение
1. Постройте треугольник по стороне,
прилежащему к ней углу и биссектрисе второго угла,
прилежащего к этой стороне.
2. Даны параллельные прямые а и Ь и точка В
на прямой Ь. Постройте окружность, которая
касается прямой Ь в точке В и прямой Л.
3. Даны две точки Л и В и прямая а,
проходящая через точку Л. Постройте окружность,
которая касается прямой а в точке А и проходит
через точку В.
Контрольная работа 14
Итоговая (годовая)
контрольная работа
1. Найдите все углы, которые получаются
при пересечении двух прямых, если сумма трех
их них равна 320°.
2. Докажите, что в равностороннем
треугольнике любые две высоты равны.
Рис. 4
Рис.6

Контрольные и проверочные работы
Геометрия. 7—9 классы
303
3. Через середину О отрезка АВ проведена
прямая CD, причем Z. OAD = Z. ОВС. Докажите,
что точка О — середина отрезка CD.
8 КЛАСС
Контрольная работа 1
Установочная контрольная работа
1. Начертите какой-нибудь прямоугольный
треугольник ABC. Постройте равный ему
треугольник, измерив в треугольнике ABC лишь
два элемента — катет и острый угол. Объясните,
почему построенный треугольник равен
треугольнику ABC.
2. Один из углов равнобедренного
треугольника равен 92°. Найдите остальные углы этого
треугольника.
Контрольная работа 2
Квадрат
1. Через вершины квадрата проведены
прямые, перпендикулярные исходящим из них
диагоналям квадрата, которые пересекаются в
четырех различных точках. Докажите, что эти
точки являются вершинами квадрата.
2. Докажите, что около квадрата можно
описать окружность, т. е. что существует
окружность, проходящая через все вершины квадрата.
Чему равен ее радиус?
Контрольная работа 3
Четырехугольники
1. Сумма двух углов параллелограмма равна
90°. Найдите все углы этого параллелограмма.
2. Диагонали прямоугольника ABCD
пересекаются в точке О. Точки Av Bv Сх и Dx
являются серединами отрезков АО, ВО, СО и DO
соответственно. Докажите, что четырехугольник
A1B1C1D1 также является прямоугольником.
3. Боковая сторона треугольника разделена
на 3 равные части и из точек деления
проведены к другой боковой стороне отрезки,
параллельные основанию треугольника. Найдите эти
отрезки, если основание треугольника равно
6 см.
Контрольная работа 4
Неравенство треугольника
1. Могут ли стороны треугольника быть
пропорциональными числам 14, 28 и 42?
2* Стороны прямоугольника ABCD равны
5 см и 12 см. Расстояния точки М от вершин
прямоугольника А и С равны соответственно
5 см и 8 см. Докажите, что точка М лежит на
диагонали АС.
Контрольная работа 5
Теорема Пифагора
1. Докажите, что периметр параллелограмма
меньше удвоенной суммы длин его диагоналей.
2. В прямоугольном треугольнике ABC (Z. С =
= 90°) проведена высота CD. Известно, что CD =
= 8 см, AD =15 см. Найдите стороны
треугольника ABC.
3. Найдите катет и острые углы
прямоугольного треугольника по гипотенузе с = 18 см и
катету а = 4 см.
Контрольная работа 6
Координаты середины отрезка.
Расстояние между точками
Определите вид четырехугольника ABCD
(параллелограмм, прямоугольник, ромб, квадрат),
если:
1) А(0; 8), Б(-6; 0), С(2; -6), Я(8; 2);
2)A(0;l),B(i;2),C(2;2),I>(l;0).
Контрольная работа 7
Декартовы координаты на плоскости
1. В треугольнике ABC с вершинами в точках
А(2; -3), 5(-2; 3) и С(6; -3) проведена средняя
линия ВхСг, параллельная стороне ВС. Найдите
длину ВгСг и составьте уравнение прямой,
содержащей эту среднюю линию.
2. Составьте уравнение окружности,
касающейся осей х и у и прямой х = -4.
3. Используя геометрические соображения,
докажите, что прямая у = 3 не пересекает окруж-
2 2
ность, задаваемую уравнением х + (у + 3) =25.

304
Контрольные и проверочные работы
Геометрия. 7—9 классы
Контрольная руабота 8
Симметрия
1. Известны три первые вершины
параллелограмма ABCD. Постройте его четвертую
вершину D. Однозначно ли определяется точка D
условиями задачи?
2. Сколько осей симметрии имеет ромб, не
являющийся квадратом? Ответ объясните.
Контрольная работа 9
Свойства параллельного переноса
1. При параллельном переносе точки А и В
переходят соответственно в точки Аг и Bv не
лежащие на прямой АВ. Пересекаются ли прямые
ААг и ВВ{1
2. Докажите, что при параллельном переносе
прямоугольник переходит в прямоугольник.
Контрольная работа 10
Движение
1. Докажите, что при симметрии
относительно точки прямая переходит в параллельную ей
прямую (или в себя).
2. Дана трапеция ABCD (АВ II CD). Постройте
фигуру, в которую она переходит при
симметрии относительно прямой CD.
3. При параллельном переносе точка (5; 5)
переходит в точку (-2; 12). В какую точку переходит
при этом параллельном переносе точка (-1; 3)?
Контрольная работа 11
Равенство векторов
1. Даны вектор АС и точка В(1; 1). Постройте
вектор BD, равный вектору АС. Построение
обоснуйте.
2. Дана равнобокая трапеция KLMN с
основаниями KN и LM. Равны ли векторы KL и NM ?
Почему?
Контрольная работа 12
Векторы
1. Дан ромб EFKL. Найдите сумму векторов:
a)EF иЕЬ;б)КЬ и¥к.
2. Найдите угол F треугольника FGH, если
JX2;0),G(-6;0),tf(0;2V3).
3. Даны векторы а(1; 4) и &(-3; 2). Найдите
такое число А,, чтобы вектор а был перпен-
дикулярен вектору а.
Контрольная работа 13
Итоговая (годовая) контрольная
работа
1. Дана равнобокая трапеция, основания
которой равны 1 дм и 4,2 дм. Найдите боковую
сторону трапеции, если расстояние между ее
основаниями равно 3 дм.
2. Дан треугольник ABC, у которого известны
два угла: А А - 60°, Z. С = 45° — и сторона АВ -
= 4 дм. Найдите сторону АС этого треугольника.
3. Дан четырехугольник ABCD с вершинами в
точках А(0; 8), Б(-6; 0), С(2; -6), Щ8; 2).
Докажите, что этот четырехугольник является ромбом.
9 КЛАСС
Контрольная работа 1
Установочная контрольная работа
1. Дан равнобедренный треугольник ABC с
основанием АС. Постройте равный ему
треугольник ADC, вершина D которого находится
относительно прямой АС в полуплоскости, отличной
от той, где лежит точка В. Докажите, что
четырехугольник ABCD является ромбом.
2. В прямоугольном треугольнике CDE с
прямым углом С проведена средняя линия CxDt
(точки Сг и Dx лежат на отрезках ЕС и ED
соответственно). Найдите CXDV если ED = 13 дм,
ССг - 2,5 дм.
Контрольная работа 2
Подобие прямоугольных
треугольников
1. Катеты СМ и CN прямоугольного
треугольника MCN соответственно равны 9 дм и 40 дм.
Найдите высоту этого треугольника,
опущенную на гипотенузу.

Контрольные и проверочные работы
Геометрия. 7—9 классы
305
2. Высота СМ прямоугольного треугольника
QRC, опущенная на гипотенузу RQf равна
13
11пг дм, а проекция катета CQ на гипотенузу
равна 3«= дм. Найдите все стороны этого
треугольника.
Контрольная работа 3
Углы, вписанные в окружность
1. Хорды окружности АВ и CD пересекаются.
Найдите угол АСВ, если Z BAD = 40°, /LABD = 30°.
2. Постройте треугольник по стороне,
противолежащему ей углу и медиане, проведенной из
вершины этого угла.
Контрольная работа 4
Подобие фигур
1. Докажите, что при гомотетии прямая
переходит в параллельную ей прямую (или в себя).
2. В треугольниках ABC и DEF проведены
биссектрисы ВАг и EDV Докажите, что если
треугольники ВАгС и EDtF подобны, то подобны и
данные треугольники ABC и DEF.
3. У треугольника ABC АВ = 15 м, АС - 20 м,
ВС = 30 м. На стороне АВ отложен отрезок AD =
= 8 м, а на стороне АС — отрезок АЕ = 6 м.
Найдите длину отрезка ED.
Контрольная работа 5
Решение треугольников
1. Стороны треугольника равны 3,3 см, 5,6 см
и 6,5 см. Не вычисляя углы треугольника,
определите его вид.
2. В треугольнике ABC АС = 8 дм, ВС =11 дм.
Может ли sin В = 0,75?
3. Докажите, что больше та из диагоналей
параллелограмма, которая соединяет вершины его
острых углов.
2. Постройте правильный восьмиугольник,
описанный около данной окружности.
Обоснуйте построение.
Контрольная работа 7
Многоугольники
1. Найдите длину окружности, описанной
около прямоугольного треугольника с катетами
3 дм и 4 дм.
2. Сторона правильного восьмиугольника
ABCDEFGH равна с. Найдите его диагональ AD.
3. Радиус окружности равен 6 дм. Чему равна
длина дуги этой окружности, соответствующей
центральному углу в 40°?
Контрольная работа 8
Площадь треугольника
1. В треугольнике ABC проведены медианы
ААг и ВВг, пересекающиеся в точке О.
Докажите, что треугольники АОВг и ВОАг имеют
равные площади.
2. Найдите радиусы описанной и вписанной
окружностей для треугольника со сторонами
17 см, 65 см и 80 см.
Контрольная работа 9
Площади фигур
1. Диагонали параллелограмма ABCD
пересекаются в точке О. Докажите, что треугольники
ВСО и DCO имеют равные площади.
2. Основания трапеции равны 10 м и 20 м.
Диагональ трапеции отсекает от нее
прямоугольный равнобедренный треугольник,
гипотенузой которого является меньшее основание
трапеции. Найдите площадь трапеции.
3. В равнобокую трапецию с боковой
стороной 3 м вписан круг, касающийся всех ее
сторон. Найдите площадь круга, если площадь тра-
пеции равна 6 м .
Контрольная работа 6
Правильные многоугольники
1. Радиус окружности, вписанной в
правильный шестиугольник, равен 6 см. Найдите радиус
окружности, описанной около этого треугольника.
Контрольная работа 10
Итоговая (годовая)
контрольная работа
1. Диагональ трапеции делит ее на два
подобных треугольника. Докажите, что эта диагональ

306
Контрольные и проверочные работы
Геометрия. 7—9 классы
есть среднее пропорциональное между
основаниями данной трапеции.
2. Даны две стороны треугольника а = 5 см и
Ь = 8 см, а также угол а = 35°. Найдите его
третью сторону и два угла.
3. Найдите площадь круга, вписанного в
правильный шестиугольник со стороной а.
К—7
1. ВХСХ = 5, Зх + 4у = 0. 2. (х + 2)2 + (у ± 2)2 = 4.
К—8
1. Однозначно. 2. Две.
К—9
1. ААХ || BBV
ОТВЕТЫ
7 класс
к—1
2. Прямая.
К—2
1. Точка Р. 2. £(аЬ) = 64°, Z.(bc) = 16°.
К—3
1. АВ = 40°, АВ = 7 дм, BD = 8 дм. 2. ААВС = ACDA.
К—5
1. 165°. 2. 50° и 100°.
jf у
1. 20°, 20°, 160° и 160°. 3. 114°.
К—9
1. 0,4 м, 1,4 м, 1,4 м.
К—10
1. А ВСА и A DAC.
К—12
1. Три угла по 45° и четыре по 135°. 2. 60° и 30°.
К—14
1. Два угла по 40° и два угла по 140°.
8 класс
к—1
2. 44° и 44°.
К—2
2. Половине диагонали квадрата.
К—3
1. Два угла по 45° и два по 135°. 3. 2 см и 4 см.
К—4
1. Не могут.
К—5
4 1
2. АВ = 19тт см, ВС = 9тт см, АС = 17 см. 3. Ь «
15 15
« 17,55 см, а « 12°50', р = 77о10\
К—6
1. Квадрат. 2. Параллелограмм (но не ромб и не
прямоугольник).
К—10
3. (-8; 10).
К—11
1. Не равны.
К—12
17
1. а) ЕК\ б) FL. 2. 60°. 3. X = -у
К—13
1. 3,4 дм. 2. АС = 2 л/3 +2 дм.
9 класс
к—1
2. 6 дм.
К—2
32
1. 8 jj дм. 2. Qfl = 37 дм, CQ = 12 дм, СЛ = 35 дм.
К—3
1. 70°.
К—4
3. ED = 12 м.
К—5
1. Прямоугольный. 2. Не может.
К—6
1. 4л/3 см.
К—7
4я
1. « 15,7 дм. 2. с (1 + 72 ). 3. у дм.
К—8
со с
2. Л = 76 =2 см, г = 3 g см.
К—9
2. 75 м2. 3. к м2.
К—10
2. Задача имеет два решения: 1) с «8,54 см,
р«66°36', у«78°24'; 2) с = 4,57 см, р«113°24',
2
у« 31°36'. 3.
Зла

Геометрия. 10—11 классы
10 КЛАСС
Контрольная работа 1
Установочная контрольная работа
Даны треугольники ABC и A1BlCv лежащие
в различных плоскостях, у которых /LA = Z. Av
АВ = АгВг и АС = AXCV Если бы эти
треугольники лежали в одной плоскости, то они были бы
равны по первому признаку равенства
треугольников. Ответьте на вопросы к предлагаемому
ниже доказательству этого признака для
пространства (рис. 1).
Доказательство. Пусть АгВ2С2 —
треугольник, равный треугольнику ABC, с вершиной В2
на луче АгВг и вершиной С2 в той же
полуплоскости относительно прямой А1Б1, где лежит
вершина Сг (см. вопрос 1).
Так как АгВг — АгВ2, то вершина В2
совпадает с вершиной Bv Так как Z. BlAlCl = Z. В^А^2%
то луч АгС2 совпадает с лучом АгСг. Так как АгСг =
= АХС2, то вершина С2 совпадает с вершиной Сг
(см. вопрос 2).
Итак, треугольник А1В1С1 совпадает с
треугольником АгВ2С2, значит, равен треугольнику
ABC, что и требовалось доказать.
Вопрос 1. Существует ли треугольник АгВ2С2,
равный треугольнику ABC, у которого вершина
В2 лежит на луче AXBV а вершина С2 — в той же
полуплоскости относительно прямой А1Б1, что и
вершина Сг треугольника А1Б1С1? Объясните
ответ, используя аксиомы стереометрии.
Рис.1
Вопрос 2. Почему совпадают вершина В2 с
вершиной Бх, луч АгС2 — с лучом AXCV вершина
С2 — с вершиной Сх?
Контрольная работа 2
Аксиомы стереометрии
и их простейшие следствия
1. Прямые а, Ъ и с проходят через точку S.
Плоскость, не проходящая через точку S,
пересекает прямые а, Ь и с в точках, не лежащих на
одной прямой. Докажите, что прямые а, Ъ и с не
лежат в одной плоскости.
2. Прямые /п и п не лежат в одной
плоскости. Прямые а и Ь пересекают каждую из
прямых /п и п. Докажите, что прямые а и & не
пересекаются.
3. Плоскости ос и Р пересекаются по прямой с.
Докажите, что через прямую с можно провести
еще хотя бы одну плоскость, отличную от ос и р.
Контрольная работа 3
Скрещивающиеся прямые
1. Прямые а и & пересекают прямые с и d в
четырех различных точках. Докажите, что если
прямые а и & скрещивающиеся, то прямые end
тоже скрещивающиеся.
2. Докажите, что противолежащие стороны
пространственного четырехугольника лежат на
скрещивающихся прямых.
Контрольная работа 4
Свойства параллельного
проектирования
1. Может ли при параллельном
проектировании параллелограмма получиться выпуклый
четырехугольник с углами 60°, 80°, 100° и 120°?
Ответ объясните.
2. У равнобокой трапеции ABCD с
основаниями AD и ВС диагональ АС перпендикулярна
боковой стороне CD. Точки Av Вг и Сх,
являющиеся параллельными проекциями вершин А, Б и С

308
Контрольные и проверочные работы
Геометрия. 10—11 классы
трапеции, известны. Постройте параллельную
проекцию вершины D, если точки Av Вг и Сг не
лежат на одной прямой.
Контрольная работа 5
Параллельные прямые и плоскости
1. Даны скрещивающиеся прямые а, Ъ и
прямая с, не параллельная прямой а. Проведите
прямую, пересекающую обе скрещивающиеся
прямые а и Ъ так, чтобы она была параллельна
прямой с. Всегда ли это возможно?
2. Через концы отрезка АВ и его середину О
проведены параллельные прямые,
пересекающие некоторую плоскость Р в точках Av Вх и Ог
соответственно. Известно, что ААг = 3,4 дм, ВВг —
= 5,6 дм. Найдите длину отрезка OOv если
отрезок АВ пересекает плоскость р.
3. Даны параллельные плоскости а и р. Через
вершины треугольника ABC, лежащего в
плоскости а, проведены параллельные прямые,
пересекающие плоскость Р в точках Av Вг и Сг
соответственно. Найдите медиану треугольника
A1B1CV проведенную к стороне АгВг, если АВ =
= 12 дм, DC = 10 дм, АС = 10 дм.
Контрольная работа 6
Параллельность и
перпендикулярность в пространстве
1. Через вершину А ромба ACBD проведена
прямая а, перпендикулярная прямым АВ и AD.
Докажите, что прямая CD перпендикулярна
плоскости прямых а и АВ.
2. Плоскость, проходящая через сторону АВ
четырехугольника ABQP, перпендикулярна
прямым АР и BQ. Докажите, что если АР = BQ, то
четырехугольник ABQP — прямоугольник.
Контрольная работа 7
Перпендикуляр и наклонная
1. Два отрезка длиной 13 см и 20 см
упираются своими концами в параллельные плоскости.
Найдите расстояние между этими плоскостями,
если разность длин проекций данных отрезков
на эти плоскости равна 11 см.
2. Точка S находится на расстоянии 16 см от
вершин треугольника и на расстоянии 10 см от
его сторон. Найдите расстояние от точки S до
плоскости треугольника.
Контрольная работа 8
Расстояние между
скрещивающимися прямыми
1. В плоскости а дана окружность с центром
О и радиусом R. Через точку С окружности
проведена прямая с, перпендикулярная плоскости
а. Прямая а, лежащая в плоскости а, касается
данной окружности в точке А. Чему равно
расстояние между прямыми а и с, если Z. АОС =
=120°?
2. Через вершину А квадрата ABCD со
стороной d проведена плоскость у, перпендикулярная
прямой АС. Докажите, что если расстояние
между прямой BD и прямой с, лежащей в
плоскости у, больше -= , то BD || с.
Контрольная работа 9
Перпендикулярность прямых
и плоскостей
1. Докажите, что если прямая
перпендикулярна одной из параллельных плоскостей, то
она перпендикулярна и другой плоскости.
2. Через гипотенузу DE прямоугольного
треугольника CDE проведена плоскость у, расстоя-
g
ние от точки С до которой равно 4 г« дм. Катеты
треугольника CDE равны 15 дм и 20 дм.
Найдите расстояние между прямой DE и прямой с,
перпендикулярной плоскости у и проходящей
через точку С.
3. Точка О равноудалена от вершин квадрата
ABCD. Докажите, что если ОА — АВ, то прямые
ОА и ОС перпендикулярны, прямые ОВ и OD
тоже перпендикулярны.
Контрольная работа 10
Площадь ортогональной проекции
многоугольника
1. Дан прямоугольный треугольник ABC с
катетами АС = 15 дм, ВС = 8 дм. Его
ортогональной проекцией на плоскость у является тре-

Контрольные и проверочные работы
Геометрия. 10—11 классы
309
угольник АВСг. Найдите площадь треугольника
ABCV если катет ВС образует с плоскостью у
угол 60°.
2. Ортогональной проекцией треугольника,
ЛЛ 2
площадь которого равна 90 дм , на некоторую
плоскость является треугольник со сторонами
6,5 дм, 15 дм и 18,5 дм. Чему равен угол между
плоскостями этих треугольников?
Контрольная работа 11
Декартовы координаты
и векторы в пространстве
1. Из центра О правильного шестиугольника
ABCDEF восставлен перпендикуляр ОК к его
плоскости. Точка К соединена с серединой М
стороны ВС шестиугольника. Докажите, что
прямые КМ и AD перпендикулярны.
2. Через катет равнобедренного
прямоугольного треугольника проведена плоскость под
углом а ко второму катету. Найдите угол между
гипотенузой и этой плоскостью.
3. Угол между плоскостями равностороннего
треугольника ABC и квадрата BCDE равен 30°.
Найдите расстояние от точки А до вершин
квадрата DhE, если ВС = л/2 см.
Контрольная работа 12
Итоговая (годовая)
контрольная работа
1. Даны два прямоугольника ABCD и ABEF,
не лежащие в одной плоскости. Докажите, что
четырехугольник CEFD также является
прямоугольником.
2. Из центра О окружности, вписанной в
треугольник, восставлен перпендикуляр OS к
плоскости этого треугольника. Найдите радиус
окружности, если расстояния от точки S до одной
из сторон треугольника и до плоскости
треугольника равны 1,2 м и 1,3 м.
3. Из одной точки к плоскости проведены
перпендикуляр и две наклонные, длины
которых равны 10 м и 11 м. Найдите длину
перпендикуляра, если проекции наклонных относятся
как 2:5.
11 КЛАСС
Контрольная работа 1
Установочная контрольная работа
1. Через касательную а к окружности
радиуса R проведена плоскость а, перпендикулярная
плоскости, в которой находятся окружность и
касательная к ней. Чему равно расстояние от
центра данной окружности до плоскости а?
2. Дан равнобедренный прямоугольный
треугольник ABC с прямым углом С. Из вершины В
восставлен перпендикуляр BD = л/3 см к
плоскости треугольника. Чему равно расстояние от
точки D до вершин А и С треугольника, если
расстояния от концов перпендикуляра BD до
прямой АС относятся как 2:1?
Контрольная работа 2
Построение плоских сечений
многогранников
1. Дана четырехугольная призма ABCDA1B1C1DV
Постройте сечение этой призмы плоскостью,
проходящей через вершину А призмы, точку R,
лежащую на ребре А1Б1, и точку Р на ребре ВС.
2. Может ли сечение куба плоскостью быть
прямоугольником (не являющимся квадратом)?
А ромбом (тоже не являющимся квадратом)?
Контрольная работа 3
Параллелепипед
1. Основанием прямого параллелепипеда
служит ромб. Чему равна площадь боковой
поверхности параллелепипеда, если площади его
диагональных сечений равны St и S2?
2. Диагонали трех граней прямоугольного
параллелепипеда, сходящиеся в одной вершине,
равны 8 м, 10 м и 12 м. Найдите линейные
размеры этого параллелепипеда.
Контрольная работа 4
Пирамида
1. Основанием пирамиды является равнобо-
кая трапеция. Докажите, что если двугранные
углы при всех ребрах основания пирамиды
равны, то основание высоты пирамиды не может

310
Контрольные и проверочные работы
Геометрия. 10—11 классы
совпадать с точкой пересечения диагоналей
трапеции.
2. Плоскость боковой грани правильной
треугольной пирамиды образует с плоскостью
основания угол 30°. Радиус окружности, описанной
около основания, равен 12 дм. Найдите площадь
боковой поверхности пирамиды.
центром основания данного конуса, тоже равен
JR. На расстоянии т> от вершины конуса
проведена плоскость, параллельная его основанию.
Найдите площадь части сечения, заключенной
между боковой поверхностью конуса и
поверхностью шара.
Контрольная работа 5
Многогранники
1. Основанием призмы является правильный
шестиугольник, ее боковые грани — квадраты.
Наибольшая диагональ призмы равна 10 дм.
Найдите сторону основания призмы.
2. Диагональ прямоугольного
параллелепипеда равна 22 дм. Найдите ребра
параллелепипеда, если его линейные измерения относятся
как 2:6:9.
3. В правильной треугольной пирамиде угол
между апофемами равен 60°. Докажите, что
боковые грани этой пирамиды являются
равнобедренными прямоугольными треугольниками.
Контрольная работа 6
Шар и сфера
1. Радиус шара равен 3,4 дм. Найдите
площадь сечения шара плоскостью, находящейся
на расстоянии 3 дм от его центра.
2. Диаметр сферы равен d. Плоскость,
проходящая через конец диаметра сферы под углом Р
к этому диаметру, пересекает сферу. Найдите
длину линии пересечения сферы с данной
плоскостью.
Контрольная работа 7
Тела вращения
1. Все стороны правильного треугольника
касаются сферы радиуса 20 см. Найдите
расстояние от центра сферы до плоскости треугольника,
если его сторона равна 60 см.
2. Основание прямой призмы —
равнобедренный прямоугольный треугольник. Найдите
радиус основания цилиндра, описанного около
призмы, если высота призмы 5 см, а ее боковая
поверхность равна 10 см .
3. Высота конуса равна радиусу R его
основания. Радиус шара с центром, совпадающим с
Контрольная работа 8
Объем наклонного параллелепипеда
1. Основанием наклонного параллелепипеда
служит ромб со стороной 2 см и острым углом,
равным 60°. Боковое ребро параллелепипеда,
исходящее из вершины угла в 60°, равно 2 см и
образует со сторонами основания углы, также
равные 60°. Найдите объем данного наклонного
параллелепипеда.
2. Основание наклонного параллелепипеда —
квадрат со стороной а. Две его противолежащие
боковые грани также являются квадратами.
Найдите объем этого параллелепипеда, если
острый угол его граней, квадратами не
являющихся, равен а.
Контрольная работа 9
Объемы многогранников
1. Площади трех граней прямоугольного парал-
2 2 2
лелепипеда равны 12 дм , 15 дм и 20 дм .
Найдите его объем.
2. Основанием призмы является трапеция.
Докажите, что плоскость, проходящая через
середины оснований трапеции параллельно
боковым ребрам призмы, разбивает ее на две
равновеликие четырехугольные призмы.
3. Высота основания правильной треугольной
пирамиды равна 6 дм, а боковое ребро образует с
высотой пирамиды угол 60°. Найдите объем
пирамиды.
Контрольная работа 10
Объемы и поверхности
тел вращения
1. В цилиндр вписана правильная
треугольная призма, сторона основания которой равна а,
а боковое ребро — Ь. Найдите площадь боковой
поверхности цилиндра и его объем.

Контрольные и проверочные работы
Геометрия. 10—11 классы
311
2. Равнобедренный треугольник с боковой
стороной d и углом при основании 30°, вращается
вокруг оси, содержащей его боковую сторону.
Найдите объем полученного тела вращения.
3. Дан шар радиуса R. Плоскость,
пересекающая диаметр шара под углом 60°, делит этот
диаметр в отношении 3:1. На какие части (по
площади) разделилась при этом поверхность
шара?
К—10
1. 2733 дм2. 2. 60°.
К—11
sina _ л
2. arcsin —=- .3. 1 см.
Л
К—12
2. 0,5 м. 3.4 л/б м.
Контрольная работа 11
Итоговая (годовая)
контрольная работа
1. В полушар радиуса R вписан цилиндр, вы-
R
сота которого равна -=. Найдите объем этого
цилиндра.
2. Дан конус, образующая которого
наклонена к плоскости основания под углом 45°.
Найдите объем конуса, если длина образующей равна
6 см.
3. Дана правильная треугольная пирамида
SABC с основанием ABC. Докажите, что сечение
этой пирамиды, проходящее через ее высоту и
боковое ребро SA> перпендикулярно прямой ВС.
ОТВЕТЫ
10 класс
к—1
1. Существует (по аксиоме VIII).
К—4
1. Не может.
К—5
1. Не всегда. 2. ООг =1,1 дм. 3. 8 дм.
к-
1.
к-
1.
к
2.
-7
12 см.
-8
R
2'
-9
"п
.2.
дм
473
•
см.
11 класс
к—1
1. R. 2. CD = 2 см, AD = Jb см.
К—2
2. Прямоугольником, не являющимся квадратом, —
может; ромбом, не являющимся квадратом, —
может.
К—3
1. 2 Jsl + S\ . 2. Л0 м, Зл/Тб м, Зл/6 м.
К—4
2. 216 дм2.
К—5
1. 2 Jb дм. 2. 4 дм, 12 дм и 18 дм.
К—6
1. 2,56ядм2. 2. rcdcosp.
К—7
KR2
1. 10 см. 2. Л - 1 см. 3. -g- .
К—8
1. 472 см3. 2. a3 sin а.
К—9
1. 60 дм3. 3. 16 дм3.
К—10
1. Jgaft и \а2Ъ. 2.\d\ 3. 2ntf (l + f ) и
2**2(l"f }
К—11
„з
1. ^=.2. 18 л/2 я см3.
272

Тесты
Математика. 5—6 классы
5 КЛАСС
Тест 1
Запись и чтение натуральных чисел
1. Сколько тысяч в числе 1389213?
а) 389; . в) 1389213;
б) 300; г) 1389.
2. Сколько сотен тысяч в числе, полученном
при сложении чисел 999999 и111111?
а) Сто одиннадцать; в) 11;
б) 1; г) тысяча сто одиннадцать.
3. Как правильно записать цифрами число:
два миллиарда пятьсот тринадцать
миллионов триста пятьдесят шесть тысяч
восемьсот!
а) 25133568; в) 2513356800;
б) 250013300568; г) 20513035608.
4. Запишите три раза подряд число 87 и три
раза подряд число 13. Сложите полученные
числа. В результате будет:
а) один миллион десять тысяч сто;
б) сто одна тысяча сто;
в) десять миллионов сто одна тысяча;
г) сто одиннадцать тысяч сто.
5. Какое из чисел больше
20000 + 9000 + 900 + 90 + 9
или
30000 + 1000 + 100 + 10 + 1?
а) Второе; в) числа равны;
б) первое; г) не знаю.
6. Какое из четырех чисел самое большое?
1)1234567890;
2)987654321;
3)10203040506070809;
4)90807060504030201.
а) 1); в) 3);
6)2); г) 4).
7. На сколько отличается число
50000 + 4000 + 200 + 30 + 5
от числа
40000 + 3000 + 100 + 20 + 4?
а) На 1111;
б)на 1;
Тест 2
в) на 11;
г) на 11111.
Действия
с натуральными числами
1. Выполните действия и отметьте
правильный результат.
1) 105 -38 + 23
а) 3990;
б) 4003;
2)17 (377 + 233)
а) 610;
б) 1037;
3) (231643+ 7112):
а) 4341;
б) 21 705;
4) (132: 11+ 12 8)
а) 96;
6)11;
в) 4013;
г) 40 030.
в) 1370;
г) 10 370.
55
в) 238 755;
г) 238 705.
:12
в) 9;
г) 24.
2. Выпишите все двузначные числа, которые
можно записать с помощью цифр 1, 0 и 3,
используя каждую цифру только один раз.
Найдите сумму этих чисел.
а) 40; в) 84;
б) 53; г) 74.
3. Скорость велосипедиста 20 км/ч, а
скорость мотоциклиста 60 км/ч. Во сколько раз
скорость мотоциклиста больше скорости
велосипедиста?
а) В 2 раза; в) в 4 раза;
б) в 3 раза; г) на 40 км/ч.
4. Из цифр 1, 3, 5 составляются
всевозможные трехзначные числа. Найдите разность
самого большого и самого маленького из них.
(В любом числе каждая цифра используется
один раз.)
а) 396; в) 144;
б) 216; г) 478.

Тесты
Математика. 5—6 классы
313
5*. Из четырех цифр 1, 2, 3, 4 составьте два
различных двузначных числа, произведение
которых будет наибольшим. Найдите это
произведение.
а) 1300; в) 903;
б) 1312; г) 1462.
Тест 3
Единицы измерений
1. Длина земельного участка равна 1 км
150 м. Выразите эту длину в метрах.
а) 1150 м; в) 150 м;
б) 10150 м; г) 100050 м.
2. Длина отрезка равна 1 м 3 дм 9 см 5 мм.
Выразите длину этого отрезка в миллиметрах.
а) 10395 мм; в) 1395 мм;
б) 1003095 мм; г) 13950 мм.
3. Выразите в килограммах 3 т 2 ц 17 кг.
а) 302017 кг; в) 30217 кг;
б) 32017 кг; г) 3217 кг.
4. Если к 1 т молока сначала добавить 3 ц, а
затем отлить 125 кг, то в результате получится:
а) 1185 кг; в) 1175 кг;
б) 1275 кг; г) 1075 кг.
5. Автомобиль ехал 1 ч со скоростью 60 км/ч
и 2 ч со скоростью, на 10 км/ч большей.
Расстояние, которое он проехал, равно:
а) 180 км; в) 130 км;
б) 200000 м; г) 190000 м.
6*. Длина экватора Земли 40 000 км, а длина
экватора на школьном глобусе 1 м. Сколько
километров земного экватора в 1 см глобуса?
а) 4 км; б) 40 км; в) 400 км; г) 4000 км.
7*. Сколько секунд в сутках?
а) 3600 с; в) 24000 с;
б) 36000 с; г) 86400 с.
Тест 4
Периметр и площадь
1. Одна сторона треугольника равна 10 см,
вторая на 2 см длиннее, а третья на 2 см короче.
Чему равен периметр треугольника?
а) 18 см; б) 20 см; в) 14 см; г) 30 см.
2. Одна сторона прямоугольника вдвое
больше другой, а его периметр равен 12 см. Чему
равна меньшая сторона прямоугольника?
а) 3 см; б) 4 см; в) 2 см; г) 6 см.
3. Одна сторона прямоугольника равна 3 м, а
другая на 2 м больше. Чему равна площадь
прямоугольника?
а) 6 м2; б) 15 м2; в) Юм2; г) 25 м2.
2
4. Два одинаковых квадрата, площадью 1 см
каждый, сложили так, ч*о получился
прямоугольник. Чему равен его периметр?
а) 2 см; б) 1 см; в) 4 см; г) 6 см.
5. Прямоугольник, длины сторон которого
равны 3 см и 6 см, разрезали на два квадрата.
Чему равна сумма периметров получившихся
квадратов?
а) 18 см; б) 24 см; в) 9 см; г) 12 см.
6. От квадрата со стороной 6 см отрезали с
помощью двух разрезов квадрат со стороной 4 см.
Чему равен периметр оставшейся фигуры?
а) 24 см; б) 20 см; в) 16 см; г) 12 см.
2
7*. Площадь прямоугольника равна 24 см , а
длины его сторон — натуральные числа. Может
ли периметр прямоугольника быть равен:
а) 21 см; б) 28 см; в) 24 см; г) 48 см?
8*. Прямоугольник разрезали на три
одинаковых квадрата, сумма периметров которых 24 см.
Найдите площадь исходного прямоугольника.
а) 16 см2; б) 6 см2; в) 18 см2; г) 12 см2.
Тест 5
Сравнение натуральных чисел
1. Укажите такой порядок расположения
чисел, чтобы каждое последующее число было
меньше предыдущего (порядок убывания).
1)3221; 2)4537; 3)3400; 4)4527.
а)(2;3;4;1); в)(2;4;3;1);
б)(4;2;1;3); г)(2;4;1;3).
2. Дано 5 чисел: 837; 132; 1003; 598; 999.
Наибольшее значение суммы двух из этих чисел
равно:
а) 1597; 6)1840; в) 2566; г) 2002.

314
Тесты
Математика. 5—6 классы
3. Укажите цифры, которые можно
поставить вместо звездочек так, чтобы были верны
неравенства:
*321 > 4*47 > 43*2 > *501.
а)(4;3;2;9); в)(6;9;3;1);
б) (5; 7; 9; 4); г)(3;2;1;1).
4. В четырех коробочках лежат красные,
зеленые и желтые кружки.
Коробка
• 1
2
3
4
Кружки
Зеленые
47
51
32
21
Желтые
23
17
44
27
Красные
39
24
37
30
В какой коробочке больше зеленых и
красных кружков?
а)1; 6)3; в) 4; г) 2.
5. На первой чашке весов 3 гири по 1 кг, 2 по
500 г и 4 по 250 г. На второй — 2 гири по 1 кг, 4
по 500 г и 5 по 250 г. Если с первой чашки снять
гирю в 1 кг, а со второй 5 гирь по 250 г, то:
а) положение чашек не изменится;
б) вторая чашка перевесит;
в) чашки уравновесятся;
г) первая чашка перевесит.
6. Отрезок АВ можно разбить на четыре
отрезка по 10 см, шесть отрезков по 5 см и
одиннадцать по 2 см. Отрезок CD можно разбить на
пять отрезков по 10 см, девять по 5 см и десять
по 2 см. Если к АВ прибавить один отрезок
длиной 10 см, а к CD шесть по 2 см, то:
а) длины отрезков станут равны;
б)АВ будет длиннее;
в) CD будет длиннее;
г) точно ответить нельзя.
7*. Заданные тройки чисел — длины
отрезков. Найдите среди них такие, из которых
нельзя построить треугольник.
а) (5; 7; 8); в) (11; 12; 20);
б)(3;7;9); г) (7; 8; 16).
Тест 6
Решение уравнений
1. Решите уравнение 56 - 2х = 36.
а) х = 46; б) х = 20; в) х = 5; г) х = 10.
2. Решите уравнение 34 - 2 • (2х - 9) = 28.
а) х = 3; б) х = 12; в) х = 6; г) х = 8.
3. Пройденный пешеходом путь s, его
скорость и и время движения t связаны
соотношением s = vt. Если пешеход за 4 ч прошел 24 км,
то его скорость равна:
а) 12 км/ч; в) 96 км/ч;
б) 6 км/ч; г) 8 км/ч.
4. Известно, что 2 • (8 + х) + Зу = 50. Найдите
х, если у = 10.
а) х = 20; б) х = 10; в) х = 12; г) х = 2.
5. На трех полках 130 книг. На второй полке
втрое больше книг, чем на первой, а на третьей —
на 10 книг меньше, чем на второй. Сколько книг
на третьей полке?
а) 40; 6)10; в) 50; г) 60.
6. На отрезке АВ, равном 24 см, выбрана
точка К так, что АК = 18 см, и точка М так, что
ВМ — 20 см. Найдите отрезок КМ.
а) 18 см; б) 14 см; в) 20 см; г) 4 см.
Тест 7
Обыкновенные дроби
421
1. Выделите целую часть дроби -^-.
а) 25; 6)16; в) 15; г) 27.
21
2. Превратите 4jg в неправильную дробь.
172
а)
43 '
-ч 193 , 421
б)1Г; В)43";
ч 25
Г>43
5 4
3. Вычислите 13 з-= - 2 р=.
a) 15j|; 6)11^; b)10j§; г) 12 j|
4. Вычислите 12jg - Ытп + 6jg ].
а)3^; 6)1^; в)6^; г)9^.
19'
е /- * 8-75-77
5. Сократите дробь 68 .10.22
19
. 10
а)у;
б)33'
В)55;
*§■
6. Решите уравнение 3 т^ - 2х - 1 ^д •
a)8f|; 6)2Й; в)1^; г)2^
19'
19'
19

Тесты
Математика. 5—6 классы
315
7*. Известно, что - = 3, а Ъу - х = 28. Найдите х.
а) х = 3; б) х = 23; в) х = 7; г) х = 2.
Тест 8
Десятичные дроби
1. Вычислите 3,57 + 2,23 - 4,8.
а) 10,7; 6)1; в) 5,79; г) 1,3.
2. Вычислите 5,508 : 0,27 - 5,3.
а) 20,4; 6)16,1; в) 15,1; г) 15,4.
3. Вычислите (17,28 : 3,2 + 1,4 • 2,5): 89 + 1,9.
а) 1,1; 6)2; в) 2,9; г) 11,9.
4. Решите уравнение 1,5* -1,15 = 1,1.
а)* = 2,25; в)х = 2,16;
б)* = 0,75; т)х= 1,5.
5. Решите уравнение
2,7z/ + 5,31z/ - 2,81z/ - 2,6 = 0.
а) у = 2; в) у = 5;
б) у =0,5; г) у-2,5.
6. Некоторое число увеличили в 2,5 раза, а
затем вычли половину исходного числа, после
чего получилось число, на 1,99 большее
исходного. Найдите исходное число. .
а) 2; 6)7,96; в) 1,4; г) 1,99.
Тест 9
Периметр, площадь, объем
1. Пол комнаты имеет форму
прямоугольника со сторонами 6 м и 4 м. Сколько квадратных
паркетных шашек со стороной 20 см
потребуется для покрытия этого пола?
а) 24; б) 596; в) 384; г) 600.
2. Стороны квадратов, составляющих фигуры,
2
равны 1 см. Укажите фигуры с площадью 7 см .
а)
с)
N
N
Ь)
d)
3. Одна сторона прямоугольника равна 6 см,
а его площадь 42 см . Чему равна другая
сторона прямоугольника?
а) 15 см; б) 9 см; в) 7 см; г) 8 см.
4. Периметр прямоугольника равен 32 см, а
одна его сторона в три раза больше другой. Чему
равна площадь прямоугольника?
а) 64 см2; б) 48 см2; в) 32 см2; г) 40 см2.
5. Комната имеет форму прямоугольного
параллелепипеда. Одна сторона его основания
равна 3 м, вторая вдвое больше, а высота на 2 м
меньше второй стороны основания. Чему равен
объем комнаты?
а) 54 м3; 6) 18 м3; в) 22 м3; г) 72 м3.
з
6*. Объем бассейна равен 100 м , стороны
основания 10 м и 5 м. Сколько квадратных метров
кафельной плитки ушло на облицовку
бассейна?
а) 60 м2; б) 110 м2; в) 160 м2; г) 90 м2.
7*. Из кирпичей, длина которых 30 см,
ширина 10 см и высота 5 см, сложили куб, ребро
которого равно 120 см. Сколько кирпичей на это
было затрачено?
а) 64; б) 1728; в) 1152; г) 1056.
Тест 10
а) а и Ь; б) d;
в) cud; г) с.
Доли и части
2
1. Чему равны « от числа 30 + 60?
а) 20; 6)40; в) 60; г) 30.
3 2
2. На сколько больше г от числа 115, чем =
от числа 147?
а) На 27; б) на 2; в) на 32; г) на 51.
3. От рулона материи, в котором было 120 м,
сначала отрезали ц , а потом j остатка. Сколько
материи осталось в рулоне?
а) 72 м; б) 54 м; в) 18 м; г) 48 м.
2
4. Турист проехал на велосипеде « пути, а
оставшиеся 6 км прошел пешком. Чему равен весь
путь туриста?
а) 12 км; б) 16 км; в) 18 км; г) 10 км.

316
Тесты
Математика. 5—6 классы
5. В слитке, масса которого 1 кг, содержится
3
2 меди и в равных количествах пять других
металлов, один из которых — магний. Сколько
магния содержится в слитке?
а) 250 г; б) 50 г; в) 100 г; г) 20 г.
Тест 11
Уравнения и задачи
по составлению уравнений
2
1. Решите уравнение « * - 7 = 11.
а)х = 18; в)* = 27;
б) х = 54; г) х = 12.
2. Решите уравнение 2~У + ЬъУ "" 2 = 3.
а) у = 5;
б) у = 7;
5
г) У = 7 •
3. Расстояние между городами А и В вдвое
больше расстояния между В и С. Автомобиль,
двигаясь со скоростью 60 км/ч, преодолел путь
из А в С за 6 ч. Найдите расстояние от Л до Б.
а) 360 км; в) 120 км;
б) 240 км; г) 180 км.
4. В трех коробках лежит 70 карандашей,
причем во второй их вдвое больше, чем в
первой, а в третьей — вчетверо меньше, чем во
второй. Сколько карандашей лежит в третьей
коробке?
а) 20; в) 50;
б) 40; г) 10.
5. Велосипедист был в пути 3 ч, причем
каждый следующий час он проезжал расстояние
вдвое меньшее, чем за предыдущий. Какое
расстояние проехал велосипедист за последний час,
если весь путь составил 49 км?
а) 14 км; б) 28 км; в) 7 км; г) 21 км.
6*. Решите уравнение
((((i(, + *)+x)}+,)i+,)i+,)i-!.
а)* = 0; б)х = 2; в)* = 1; г)х=4.
6 КЛАСС
Тест 1
Признаки делимости
1. Из данных чисел выберите число, которое
делится на 2 и на 5.
а) 8016; б) 195; в) 4050; г) 1113.
2. Из данных чисел выберите число, которое
делится на 3 и на 5.
а) 1113; б) 914; в) 3040; г) 7035.
3. Из данных чисел выберите число, которое
делится на 2 и на 3.
а) 2894; б) 405; в) 2802; г) 785.
4. Какую цифру нужно поставить вместо * в
числе 5*62, чтобы полученное число делилось
на 9?
а) 0; б) 2; в) 9; г) 5.
5. Какое число, кратное 25, удовлетворяет
неравенству 430 < х < 460?
а)л: = 445; б)х =450; в)л: =440; г)* = 455.
6*. Запись натурального числа состоит из
двенадцати единиц и тринадцати нулей. Может ли
это число быть квадратом другого натурального
числа?
а) Может;
б) не может;
в) может, если последняя цифра 1;
г) может, если последняя цифра 0.
Тест 2
Наибольший общий делитель
и наименьшее общее кратное
1. Укажите произведение, которое является
разложением числа на простые множители.
1)2-8-11;
2)16-3-11;
8)2-2-2-8-11;
4) 2 • 3 • 4 • 9.
а) 2); 6)1); в) 4); г) 3).
2. Укажите среди данных произведений
разложение числа 54 на простые множители.
1)9-6;
2) 2 • 3 • 3 • 3;
3) 2 • 3 • 6;
4) 2 • 3 • 9.
а)1); 6)2); в) 3); г) 4).

Тесты
Математика. 5—б классы
317
3. Укажите наибольший простой делитель
числа 5460.
а) 21; 6)17; в) 13; г) 15.
4. Найдите наибольший общий делитель
чисел 555 и 275.
а)3; 6)7; в) 5; г) 15.
5. Найдите наименьшее общее кратное чисел
70, 60 и 90.
а) 5400; в) 4200;
б) 1260; г) 3780.
6. Найдите наибольший общий делитель
чисел 180,270 и 450.
а) 10; 6)45; в) 18; г) 90.
7*. Лист картона со сторонами 54 см и 36 см
надо разрезать без отходов на равные квадраты.
Найдите площадь наибольшего квадрата,
который можно получить из этого листа.
а) 16 см ;
б) 324 см2;
Тест 3
в) 81 см ;
г) 36 см2.
Сравнение обыкновенных дробей
1. Укажите наибольшую дробь.
а) 63 ; 0) 315 ; В) 105 ; Г' 126 '
1 2
2. Укажите дробь, большую g , но меньшую з .
,2 .,1 ч 1 ч 1
a)g; б)^; в) р г) ^.
3. Расположите дроби 1) =q ; 2) 57 '> 3) on в по"
рядке убывания.
а) 1,8, 2; 6)1,2,3; в) 3,2,1; г) 2, 3,1.
1 7
4. Что больше: t1 = 7 ч или t2 = те ч?
&)t1<t2; 6)t1>t2; B)tt = t2; r)tt<ta.
5. Укажите, на каком рисунке верно
изображены точки м( j2 )'» N[ 9 J; Т[ 2l ) •
а)
б)
N М Т
М N Т
в)
г)
М Т N
Т М N
35
6. Площадь Чудского озера составляет д~
площади Онежского озера; площадь озера
Ханка — од пл°Щади Онежского озера. Какое из
двух озер больше — Чудское или Ханка?
а) Чудское; в) одинаковы;
б) Ханка; г) Онеэчское.
Тест 4
Сложение и вычитание
обыкновенных дробей
1.Выполните сложение 7я + §6'
а) 144; °' 144; в) 7; Г) 12
2. Выполните вычитание gn "" J5 •
v 2 J_ \1L. л A
a' 675 * ' *-* ' B' i яп » r' 1 к •
45'
180' '15'
17 /1,5
3. Выполните действия 24 "" ( 5 "^ 24 )•
.23 21 11 _3^
a' 53 ' °' 19 ; B) 19 ' r' 10 '
4. Сравните Px = ^ "*" 3 "^4 ^г^+^+ёГ
a)Px>P2;
6)P2>PX;
в)Р2 = Рх;
г) нет решения.
(' 3 5 \
5. Найдите значение выражения ( g + J2 J ^*
a) 9,6; 6)19; в) 16; г) 24.
4 4
6. Решите уравнение д* + ^л: = 12.
а)х = 11 g ;
б) * - 18;
в)х =9g;
r)x = li;

318
Тесты
Математика. 5—6 классы
Тест 5
Умножение и деление
обыкновенных дробей
1. Умножьте дробь на целое число 23 • т^ .
а) 2^; б)|; в) 2^; г)1±.
9 5
2. Вычислите ttj * н •
ч 19 _ 3 ч 15 ч 42
а>18; б)4; В)60; Г)60-
3. Укажите число, обратное 1,4.
5 7
а)=; б)-1,4; в) з; г) 4,1.
4. Выполните деление То : 24 •
а)|; 6)10; в) 2,5; г) |.
5. Вычислите наиболее простым способом
a)gj 6)14^; в)^; г) у.
6. Найдите значение числового выражения
о.5 _3 . 1
^8 4 2-
a)l|; б)|; в)|; r)l|.
7. Найдите значение числового выражения
удобным способом То * IT + 8 : "б" *
ч 17 *ч 2 \ х ч 5
а)44; б)П; В)2; Г)12'
Тест б
Действия со смешанными числами
1. Запишите смешанное число 2тй в виде
неправильной дроби.
19 21 24 30
а) 13 ; °' 13 ; в' 13 ; Г) 13 '
\ л & -ч - 13 v 1 1 v 16
а)4тг» б)1?^: в)1?^; г>
3. Вычислите (3 j= + 4~т J — 1 =-= .
л)бЩ; б)б|; в) 6^; г)в|.
4. Решите уравнение х + ■= + g = 2g.
ч 13
а>*=15;
6)* = -^;
в) л: =4д;
ч 9
3 1
5. Решите уравнение * + 4g = 12«
а) л: = 8g;
б)х = 17;
в)х = 8^;
г)х-1б|.
6. Чтобы получить сплав для пайки металлов,
9 1 2
сплавили yq кг олова, 1 ~ кг свинца и 2 г кг
висмута. Определите вес полученного сплава.
11 4
а) 5 g кг; б) 4 g кг; в) 6 кг; г) 4 g кг.
7. Скорость слабого ветра 2 т м/с,
умеренного — в 2 раза больше, скорость сильного ветра в
1« раза больше скорости слабого и умеренного
ветров вместе. Определите скорость сильного
ветра.
3 1
a) 3j м/с; б) 6 м/с; в) 6« м/с; г) 9 м/с.
Тест 7
2. Вычислите 4
2 2
3 5
Нахождение части от числа
1. Опыливая растения, вертолет совершает
каждый круг в среднем за jtj ч. Сколько минут
длится каждый круг вертолета?
а) Больше 6 мин; в) 10 мин;
б) меньше 6 мин; г) 6 мин.
2. Найдите g от суммы чисел 3g иЬ.
ч 1 *ч 7 J ч 2
а) о; б)5; в)й; г)
8'
6
3

Тесты
Математика. 5—б классы
319
3. Длина прямоугольника 5,6 см, ширина
составляет g длины. Найдите периметр
прямоугольника.
а) 10,5 см; в) 21 см;
б) 49 см; г) 15,4 см.
4. Стороны прямоугольника относятся как
2:3. Найдите отношение периметра
прямоугольника к меньшей стороне.
а)3^; в) 5;
6)3,5; г) 2,5.
5. Сцеплены две шестерни, одна из них имеет
24 зубца, вторая — 8. Вторая шестерня сделала
два полных оборота. Какую часть полного
оборота сделала за это время первая шестерня?
а)1; б)^; в) g;
■»!•
6. Спортсмен прыгнул в высоту 2 т м, что
в 1 ~п раза выше его роста. Определите рост
спортсмена,
а) 1 м 85 см;
6)125 м;
Тест 8
BHgoM;
г) 1 м 75 см.
Проценты
1. Найдите 25% от 56.
а) 14; 6)22,04; в) 20; г) 25.
2. Найдите число, если 1% его равен 75.
а) 0,75; б) 7,5; в) 7500; г) 750.
3. Клубника содержит 6% сахара. Сколько
килограммов сахара в 27 кг клубники?
а) 1,82 кг; в) 2,24 кг;
б) 1,62 кг; г) 2,42 кг.
4. Книга стоила 25 р. После повышения цены
она стоит 30,25 р. На сколько процентов
возросла стоимость книги?
а) На 21%; в) на 24%;
б) на 20%; г) на 25%.
5. Найдите число, 34% которого равны 170.
а) 57,8; 6)500; в) 56,5; г) 510.
6. На математической олимпиаде 32%
участников получили грамоты. Сколько
школьников приняло участие в олимпиаде, если
наградили 416 человек?
а) 932; 6) 1300; в) 133,1; г) 1340.
7*. Число уменьшили на 20%. На сколько
процентов надо увеличить полученное число,
чтобы получить данное число?
а) На 20%; в) на 25%;
б) на 40%; г) на 30%.
8*. Число 56 составляет 80% от некоторого
числа. Найдите среднее арифметическое этих
чисел.
а) 63; 6)44,8; в) 126; г) 56.
9*. Сторону квадрата уменьшили на 20%. На
сколько процентов уменьшилась его площадь?
а) На 20%; в) на 10%;
б) на 36%; г) на 40%.
Тест 9
Отношения и пропорции
1. Укажите верную пропорцию.
а) 2 : 3 = 5 : 10; в) 5 : 10 = 8 : 4;
6)2:3 = 10:15; г) 12 : 18 = 3 : 2.
2. Найдите неизвестный член пропорции
7,5:3,5 = * :14.
а) 19,6; 6)3; в) 7; г) 30.
3. Три ученика пропололи грядку за 4 ч. За
сколько часов выполнят работу два ученика?
а) 2 ч 40 мин; б) 8 ч; в) 10 ч; г) 6 ч.
4. Со 125 гусей можно получить 4 кг пуха.
Сколько пуха можно получить с 875 гусей?
а) 28 кг; б) 57,4 кг; в) 21,8 кг; г) 25 кг.
5. Из 1,75 т золотоносного песка намывают в
среднем 0,7 г золота. Сколько золота можно
намыть из 2170 т золотоносного песка?
а) 564,5 г; б) 542,5 г; в) 642 г; г) 868 г.
2х - 1 Зх + 5
6. Решите уравнение —j
пользуя основное свойство пропорции.
, ис-
а) х = -6;
б) х = 2^;
ъ)х =4^;
т)х^З-2

320
Тесты
Математика. 5—6 классы
Тест 10
Отрицательные числа.
Модуль
1. Сколько целых чисел удовлетворяют
неравенству -8 < х < 4?
а) 12; 6)10; в) 9; г) 11.
2. Укажите наименьшее по модулю число,
а)-13,97; 6)6,3; в) 53,8; r)-2g.
3. Вычислите |5,2 - 7,7|.
а)-2,5; 6)2,5; в) 12,9; г)-12,9.
4. Вычислите (|-7,3| + |-2,б|): |-9|.
а) 13; 6)-1,1; в) 5?; г) 1,1.
5. Вычислите |-4,5|: |-0,9| + |-3|: |2|.
а)-7,5; 6)3,5; в) 6,5; г)-6,5.
а) л: = -7,7;
б)х = 7,7;
в) л: =-2,7;
г) л: =2,7.
6. Вычислите
|-2,1|-|-0,4|
|24|. |-3,5| •
а)-0,1; 6)0,01; в)-0,01; г) 0,1.
7*. Найдите решения уравнения 2 • \х - 3| = 5.
а) 5,5 и -5,5; в) 5,5 и 0,5;
б) 0,5 и -0,5; г) 3,5 и -3,5.
Тест 11
Сложение и вычитание
положительных
и отрицательных чисел
1. Выполните действия:
1)-19 + 40
а) 59; 6)-59; в)-21; г) 21.
2)-3,4+ 5,7
а) 2,3; 6)-2,3; в) 9,1; г)-9,1.
3)-2l-4|
а) -2^; б)2±; в) 7; г)-7.
, 4)-4,7-(-8,5)
а)-12,2; 6)4,8; в) 3,8; г)-13,2.
2. Решите уравнение:
1)7,1 +у =-1,8
а) у = -5,3; в) у = 5,3;
б) у = 8,9; r)z/=-8,9.
2)-5±+*=-2^
3. Вычислите -5,6 + (-3,5 + 5,6).
а) 3,5; 6)2,5; в) -3,5; г)-2,5.
4. Вычислите -6,5 - (4,2 - 6,5).
а) 4,2; 6) 2,4; в) -2,4; г) -4,2.
5. Найдите сумму всех целых чисел,
расположенных между числами -5,6 и 3,5.
а)3; 6)-11; в)-9; г)-15.
6. Скорость лодки по течению реки 15,3 км/ч.
Найдите скорость лодки против течения реки и
собственную скорость лодки, если скорость
течения реки 4,5 км/ч.
а) 6,3 км/ч; 10,8 км/ч;
б) 19,8 км/ч; 10,8 км/ч;
в) 4,5 км/ч; 6,3 км/ч;
г) 5,4 км/ч; 10,8 км/ч.
Тест 12
Умножение и деление
положительных
и отрицательных чисел
1. Выполните действия:
1)-3,6-3
а) -1,2; 6) -10,8; в) 1,08; г) 10,08.
2)-18: (-0,3)
а) 60; 6)54; в) 6; г) 5,4.
a,-|.(-i!)
&)-l\; б)-1^; в)1; г) 1,25.
5 4
2. Вычислите -3,7 ' д ~ § ' ^Д*
а) 3,7; б)-26,95; в)-3,7; г)-29,05.
3. Решите уравнение -6,5у = 130,65.
а) у = -10,2; в) у = 1,02;
б) у =-20,1; г) у = 2,01.
4. Выполните действия -8 • (-3 + 12): 36 + 2.
а)4; 6)0; в) -11; г)б|.
^ п 11 11
5. Решите уравнение ~~тУ ~ ~ёГ •
2 ,. 32 2 . 32
а)у = з; б)у=-^; в)у = -з; r)j/ = ^.

Тесты
Математика. 5—6 классы
321
6. Выполните действия (~4+8J:(~*4r
Т—3
ч 1 «Ч 9
а)"2; б)"10;
в)|;
Тест 13
Решение уравнений
1. Решите уравнение
1)2,6у = -3,51
а) у =-1,35;
6>y-igg;
260
В)У = 351;
г) у = 0,52
ч 9
Г)10
2) -0,2х • (-4) = -0,08
а)х=-0,1; б)х=0,1; в)х=0,01; г)х = 1.
2. Решите уравнение (6,4 - 10х): 4 = 1,1.
а) х = 5,6; б) х =0,2; в)х = |; г) х = 0,506.
3. Решите уравнение (0,56 - х): 0,01 = 8.
а) х = 13; б) х = 0,48; в) х = 0,64; г) х = 1,36.
4. Решите уравнение 3(х -1) = 2(2-х) + 6.
\ 7 -ч л ч 13 ч 4
а) х = g ; б) х = 4; в) х = у ; г) х = g.
5. Решите уравнение г х + 2 « = 3 г.
а) х = 7,5; б) х = -g ; в) х = 4g ; г) х = g .
3 1
6. Решите уравнение 4g : 5т= х : 12.
а)х = 2,5; б)х = 10; в)х = 14,4; г)х = 15.
/о Л 3
7. Решите уравнение 3lgX+3j-gX=8.
a)x = lg; 6)x = -lg; B)x=-g; r)x = -2g.
ОТВЕТЫ
5 класс
т—l
Задание
Ответ
1
г
1 2
в
1 8
в
4
а
5 1
а
6 1
г
7
г
Т—2
Задание
Ответ
1.1
в
1.2
г
1.3
а
1.4
в
2
в
3
б
4
а
5
б
6 класс
Задание
Ответ
1 Х
а
2
в
1 3
г
1 4 1
в
5
б
6
в
I 7
г
Т—4
Задание
Ответ
1
г
2
в
3
б
4
г
5
б
6
а
7
б
1 8
г
Т—5
Задание
Ответ
1 1
в
2
г
3
в
1 4 1
а
5
в
6
в
1 7 1
г
Т—6
Задание
Ответ
1
г
1 2
в
3
б
4
г
5 1
в
6 1
б
Т—7
Задание
Ответ
1 1
в
2
б
3
б
4 1
б
5
а
6
в
1 7 1
г
Т—8
Задание
Ответ
1
б
1 2
в
3
б
4
г
5 1
б
6 1
г
Т—9
Задание
Ответ
1
г
2
б
3
в
1 4 1
б
5
г
6
б
1 7 1
в
Т—10
Задание
Ответ
1
в
1 2 1
а
3
в
1 4 1
в
5 1
б
Т—11
Задание
Ответ
1 1
в
1 2
в
3
б
4
г
5 1
в
6 1
а
Задание
Ответ
1
в
Т
2
г
—1
3
в
4
г
5
б
6
б
11-1019

322
Тесты
Математика. 5—6 классы
Т—2
Задание
Ответ
1
г
2
б
3
в
4
в
5
г
6
г
7
б
Задание
Ответ
1
б
Т
2
в
-3
3
г
4
а
5
г
6
б
Задание
Ответ
1
б
Т
2
в
—4
3
г
4
а
5
б
6 .
б
Т—5
Задание
Ответ
1
а
2
б
3
а
4
б
5
б
6
в
7
а
Т—6
Задание
Ответ
1
г
2
б
3
в
4
г
б
а
6
г
7
г
Задание
Ответ
1
г
Т
2
б
—7
3
в
4
в
б
г
6
а
Т—8
Задание
Ответ
1
а
2
в
3
б
4
а
5
б
6
б
7
в
8
а
"эП
б
Т—9
Задание
Ответ
1
б
2
г
3
г
4
а
5
г
6
в
Задание
Ответ
1
г
2
г
Г—10
3
б
4
г
5
в
6
б
7
в
Т—11
Задание
Ответ
1.1
г
1.2
а
1.3
г
1.4
в
2.1
г
2.2
г
3
в
4
г
5
в
б"
а
Т—12
Задание
Ответ
1.1
б
1.2
а
1.3
г
2
в
3
б
4
б
5
в
6
а
Т—13
Задание
Ответ
1.1
а
1.2
а
2
б
3
б
4
в
5
в
6
б
7
б

Алгебра. 7—9 классы
7 КЛАСС
Тест 1
Выражения с переменными
1. Вычислите значение выражения а - Ь + с,
если
а = ~11~41' *> = -4:0,2 и c = 2,25-j|.
к 1 1 1Q
а)-9~; б) 15^; в) -13^; г)14±|.
2. Найдите значение выражения
2
._ -0,6* - 1 0 л ,
М = — -— , если * = -2,1/ = -0,4.
1 - 2у
a)-l|; б)-2,5; в)-1^; г)1^.
3. Упростите выражение
3 (* - 2z/) - 0,5 (2* + 3z/) - 4,5*.
а) 2,5* + 7у; в) -2,5* + 7,5у;
б) 2,5* - 7z/; г) -2,5* - 7,5 у.
4. Решите уравнение
а) 0,6;
-т* + 5 = 1,5 - 9*.
4
б)~; в)-0,4; г)-0,6.
5. При * = -0,3 найдите значения выражений
M = 0,4*,N = -*2 и Р=^
*
и расположите значения этих выражений в
порядке убывания.
а) Р, N, М; б) М, N, ,Р; в) N, М, Р; г) М, Р, N.
6. 75% числа а на 10 больше, чем « числа а.
Найдите число а.
а) 12; 6)24; в) 36; г) 18.
7. Число 6,1 разбили на три слагаемых,
причем второе слагаемое на 20% больше первого, а
третье слагаемое на 1 больше второго. Найдите
первое слагаемое.
а) 1,5; 6)2,5; в) 0,5; г) 1,25.
8. Решите уравнения
^*-2 = 0и-0,7*-5 = 0
и найдите произведение корней этих уравнений,
а) -10; б) 40,3; в) -20,6; г) -100.
9. Найдите число, которое на 30% меньше
корня уравнения г * = 9.
а) 12; 6)10,5; в) 12,5; г) 9.
10. Корнем уравнения k • * = 3 является число
0,4. Найдите корень уравнения *•* = -!.
а)
15'
б>-Й'
в)
5'
Г>А
Тест 2
Линейная функция
1. Дана функция у = -х -4*+ 5.
Вычислите значения этой функции при * = -2
и * = -6. Запишите сумму получившихся
значений.
а) 2; 6)2,5; в) 0,5; г) 1,8.
2. Для функции у = -0,5* + 3 найдите
значение *, при котором значение у = -1.
а) 10,2; 6)7,5; в) 8; г) 6.
3. Дана функция у = 2* - 5. Какой из
приведенных ниже графиков является графиком этой
функции?

324
Тесты
Алгебра. 7—9 классы
4. Укажите координаты точки пересечения
графиков функций у = -0,5* + 2 и у = -3 + 2х.
а) (-2; -1); б) (-2; 1); в) (2; 1); г) (2; -1).
5. Дан график функции у = ах + Ь. Подберите
формулу, задающую эту функцию.
a)i/ = 3x+l;
б)у= з*+1;
в)у = -дХ + 1;
r)i/ = -3x + 1.
6. Найдите координаты точки пересечения
графика у = -jX-12c осью абсцисс.
а) (-16; 0); б) (-^ ; 0); в) (-8; 0); г) (-12; 0).
7. В одной системе координат построены
графики функций у = 0,5* и z/ = -2.
Определите по графику координаты точки их
пересечения и запишите сумму этих координат.
Тест 3
Степень. Свойства степени
1. Найдите значение выражения
(2\2 Л .2
-3.(1)' -0.5*
а)-ф
б)-1^; в)-1^; r)lj|.
2. Упростите выражение
4 2 6
т • (т )
ч 10 «ч 4 ч > 2 ч 8
а) /п ; б) /п ; в) т ; г) /п .
3. Вычислите
93 274
81
а)3;
6)9;
Л ч 1
в>3; Г)9
У*
о
-2
0,5
j
-3 0
У
у^Л
V-
-2 х
а)-2,5; б)-1,5; в)-5; г)-6.
8. Мастер за три дня изготовил 48 деталей,
причем количество деталей, которое он сделал за
первый, второй и третий день, пропорционально
числам 5, 4 и 3. Сколько деталей он сделал за
два первых дня?
а) 40; 6)36; в) 24; г) 30.
9. Найдите значение углового коэффициента
k для функции у = kx - 2, если ее график
проходит через точку В (-3; 4).
а)|; 6)-i; в)-2; г) 2.
10. График функции у = (а + 1)х + а-1
пересекает ось абсцисс в точке (-2; 0). Найдите
значение а.
а) 0,5; 6)-0,5; в) 3; г)-3.
4. Упростите (0,4* у ) g х у.
а) 0,02х9/; в) 0,02а:1 V;
^ч л г» Ю 9
б) 0,2* у ;
г)0,2*У.
5. Упростив выражение
2 я з о 2
(2а V) -(0,5аЬ )
(3aV)4
вычислите его значение при а=1иЬ = 6^.
Л _ 1 ч 1 ч 2
a)g; 6)g; B)g; г) g.
6. Найдите значение выражения А, если
о 4 3 , л 2 6 0 2
-Зх у =А-9ху и х = -2 и у = д .
а) 6,5; 6)-6,5; в)-4,5; г)-1,5.
2
7. С помощью графиков функций у = х и i/ =
2
= * решите уравнение х = х.
а)-1;1; б)0;1; в>1; г) 0.
о
8. Найдите значение у, если у = -5* + 2х + 3 и
* = -0,4.
а) 1,4; 6)1,2; в) 2,4; г) 1,8.
2
9. Дана функция у = я . Известно, что
произведение абсциссы и ординаты некоторой точки

Тесты
Алгебра. 7—9 классы
325
графика этой функции равно -125. Найдите
сумму абсциссы и ординаты этой точки,
а) 18; 6)24; в) 10; г) 20.
з
10. С помощью графиков функций у = х и у =
з
= 0,5л: + 7 решите уравнение х = 0,5л: + 7 и,
обозначив корень уравнения через х0, найдите зна-
чение-3х0 + 2.
а)-12,5; б)-12; в)-8; г)-10.
Тест 4
Действия с многочленами
1. Найдите значение выражения
-2,5*(-|+ з),
если х = 3.
а)-11,25; б)-10,5; в) 10,5; г) 11,25.
2. Упростите выражение
-Зл:(2л: + 1/)-41/(Зл:-21/)
и вычислите значение выражения при х = -0,1 и
i/ = 0,2.
а) -0,26; б) 0,46; в) 0,56; г) 0,36.
3. Решите уравнение
3 - 2х __ 1 + 4*
4 6
= 2.
а)114; б)114; в*"1!*5 г)_1Та
14
14
4. Упростите выражение
(2* - Ьу)(4х + Зу) - (х + 2у)(5х - 6у).
а) Зл:2 + 18ху - 27i/2; в) За:2 - 16ху - 3z/2;
б) Зл:2 - 18ху - 3z/2; г) Зх2 - 18*1/ - 27у2.
5. Решите уравнение л:(л: + 1) - (х - 2)(х - 3) = 4.
а)-^; 6)12; в^13; г^"13'
6. Разложите на множители выражение
18*У-24*У-30х21/6.
а) 6х2у(3ху* - 4х2у - 5уЬ);
б)6ху2(Зху2-Ах-5у*);
в)6х2у\3х2у2-4х2-5у3);
т)6х2у\Зху2-4х2-Ьу3).
7. Задумали четыре натуральных числа.
Второе число на 3 больше первого, третье — на 1
больше второго, а четвертое — на 5 больше
третьего. Известно, что отношения второго числа
к первому и четвертого числа к третьему равны.
Найдите первое число.
а) 6; 6)2; в) 4; г) 8.
8. Известно, что
(Зл: + а)(х - 4) = Зл:2 - 2л: - 4а.
Найдите значение а и вычислите значение
выражения Зл: - 2л: - 4а при х = -2.
а)-18; б)-24; в)-20; г) 18.
9. Катер проплыл по озеру на 5 км больше,
чем по реке против течения, затратив на путь по
реке на 15 мин больше, чем по озеру. Найдите
расстояние, которое проплыл катер по реке, если
его скорость по озеру 10 км/ч, а по реке 8 км/ч.
а) 24 км; б) 20 км; в) 30 км; г) 36 км.
10. Найдите многочлен М, если известно, что
х3 - Зл:2 - 2л: + 6 = (х2 - 2) • М,
и вычислите значение многочлена М при х=1.
а) 4; б)-4; в)-1; г)-2.
Тест 5
Итоговый 1
1. Найдите значение выражения
а -4&с,
еслиа = 6, 6 = -11, с = -10.
а) 452; б) -202; в) -404; г) 476.
2. Упростив выражение
-0,5(3*-4)-1,5(6 + 5*),
найдите его значение при х = -0,8.
а)-0,4; 6)0,2; в) 0,4; г)-0,2.
3. Решите уравнение
5 - 2(3* - 4) = 4л: - 3.
а) 1,6; б)-1,6; в)^; г)-^.
8'
8
4. Две машинистки напечатали рукопись,
состоящую из 97 страниц. Причем первая
машинистка работала 4 ч, а вторая — 5 ч. Сколько
страниц в час печатала вторая машинистка,
если вместе за 1 ч они печатали 22 страницы?
а) 14 с; б) 13 с; в) 9 с; г) 8 с.

326
Тесты
Алгебра. 7—9 классы
5. Упростите выражение
2 3 з 4
(-1,5*2у) (2ху3)
a)-l,5xz/ ;
6)-2,5*4z/n;
(6*У)2
Ч 1С611
в)-l,5xz/ ;
г)-1,5* у .
6. Решите уравнение
2х -
li - 5* + 2 -q
а)-^; б)-12,25; в)-11,5; г) 12,25.
7. Упростите выражение
(Зх - 2)(2х - 1) - (5* + 2)(3х - 4).
а) -9х2 + 7л: - 10; в) -9х2 + 7* + 10;
б) -9х2 - 7х + 10; г) -9х2 - 7х - 10.
8. Дана функция z/ = -0,5* - 2.
Какой из изображенных ниже графиков
является ее графиком?
меньше. Найдите путь, пройденный дачником
до магазина и обратно, если лесная дорога на 2 км
короче проселочной.
а) 12 км; б) 6 км; в) 8 км; г) 10 км.
Тест 6
9. Дана функция у = « +2. График этой
функции пересекает ось абсцисс в точке (т; 0) и
ось ординат в точке (0; п). Найдите т + п.
а) 6; 6)4; в)-2; г)-4.
10. Дачник шел от дачи до магазина
проселочной дорогой со скоростью 5 км/ч, а возвращался
обратно лесной дорогой со скоростью 3 км/ч,
причем на обратную дорогу он затратил на 8 мин
Формулы сокращенного умножения
1. Раскройте скобки
\2
[1-олу)
а) -j -0,8ху + 0,16у ;
2
б)^ -0Аху + 1,6у;
2
в)|- - 0,2ху + 0,16у2;
X2 2
г) ^-0,4*1/+ 0,161/.
2. Упростите выражение
(!+0.5*)(0.5*-|).
2 2
а)2,5*2-^; в) \ -0,25*;
2 а
б) 0,25*2 - ^- ; г) ^ + 0,25х2
3. Известно, что
9
(i"3^)2=l6+&^2 + 9^
Найдите число Ь.
а) 2,5; б)-2,5; в)-1,5; г) 1,5.
4. Разложите на множители выражение
25х
- 0,0016у4.
a)(f*3-0,4/)(f*3 + 0,4«,2);
6)(|x»-oV)(|*, + oV);
в) (J*3 - 0,04j/2) [|jc3 + 0,04j/2);
г) разложить нельзя.

Тесты
Алгебра. 7—9 классы
327
5. Упростите выражение
( 2 Ь\(Ь2 , аЬ , 4Л
,3 ,3 ,2 ,3
а) а - -g-; б) а + g-; в) а - -j ; г) а + -j-.
6. Разложите на множители выражение
6
-0,064х3 + JL.
2 4
б) (0,4* - у (^ + Д ху2 + 0,16*2);
в) разложить нельзя;
«tf-M.xtf-av+o.ite').
7. Упростите выражение
(а - З)2 - (2 - а)2,
а) 2а -5; б) 5 - 2а; в) 5 + 2а; г) -5 - 2а.
8. Разложите на множители
(*-2)3-1.
а) (х - 3)(*2 - 3* + 3); в) (х - 3)(х2 - 5);
б) (х - 3)(х2 - 6х - 3); г) разложить нельзя.
9. Разложите на множители выражение
(х - 5)2 + (х - 5) (х + 5).
а) 2* (* + 5); в) 2х (х - 5);
б) х(х- 5); г)(х-5)(2 + *).
10. Найдите значение выражения
(* - 2)2 - 2(х - 2)(х + 2) + (* + 2)2 при х = -|.
а) 12;
Тест 7
6)16;
в) 14; г) 18.
Формулы
сокращенного умножения
1. Упростите выражение
(Зх - 2)(3х +2) - (1 + х)(х - 1).
а) 8х2 - 3; 6) 8х2 + 3; в) 9*2 - 3; г) 8х2 - 5.
2. Упростите выражение
6а-(4а-3)2.
а) 8а2 + 18а - 9; в) 16а2 - 30а + 9;
б) 8а2 - 12а + 6; г) -16а2 + 30а - 9.
3. Решите уравнение
(х - 5)2 = Ъх2 - (2х - 1)(2* + 1).
а) — ; 6)2,4; в) -2,4; г) А.
4. Известно, что 3(2* + а)2 = 12х2 + 60* + За2.
Найдите а и вычислите значение выражения
о
3(2* + а) при х = -4.
а)-24; б)-27; в) 27; г) 24.
5. Разложите на множители выражение
9x2-4z/2 + 4z/-l.
a)(3*-2z/-l)(3x + 2z/+l);
6)(3x-2j/)(3x + 2z/)(4i/-l);
в) разложить нельзя;
r)(3x-2z/ + l)(3x + 2y-l).
6. Найдите многочлен М, если известно, что
*3-8 = (*-2)М.
Вычислите значение многочлена М при х = -1.
а)3; 6)5; в)-3; г) 1.
7. Если от квадрата со стороной х см отрезать
полосу шириной 2 см, то площадь получившего-
2
ся прямоугольника будет на 14 см меньше
площади квадрата. Найдите периметр квадрата,
а) 36 см; б) 32 см; в) 24 см; г) 28 см.
8. Разложите на множители выражение
юш
а)-
б)
[ИТ<
-2;
-2;
3 2
X +х
г уравнение
3 . 2
X + х -
2;
-1;2;
'■-4х-
4*-4
в) 2;
г>-1;
4
= 0
1.
9. Найдите координаты точки пересечения
графиков
у = (х + 4) и у = х .
Запишите произведение этих координат,
а)-12; б)-6; в)-8; г)-10.

328
Тесты
Алгебра. 7—9 классы
10. Упростите формулу, задающую функцию
У =
(х + 3) - 12*
(3 - х)
и укажите график этой функции.
J
-3
А
а)
^У
0 х
-1
i
0
б)
1 „
9
3 х
Тест 8
Преобразование выражений
1. Упростите выражение
(7* - 3) (2х - 5) - 2 (4* - З)2.
а) -18*2 - 7* - 3; в) -18л:2 + 7х - 3;
б) 18х2 - 7* + 3; г) -18л:2 + 7х + 3.
2. Упростив выражение
(х2 + х + 1) (х - 1) - 0,5 (2* - 1) (2х + 1),
найдите его значение при х = -0,5.
а) 4''
6)j;
в)-ф r)-l|.
3. Одна сторона прямоугольника на 1 см
меньше стороны квадрата, а другая сторона
прямоугольника на 2 см больше стороны квадрата.
Найдите площадь прямоугольника, если она на
4 см больше площади квадрата.
а) 48 см2; б) 40 см2; в) 36 см2; г) 24 см2.
4. Разложите на множители выражение
х3-4х2-х + 4
и решите уравнение
xz - 4х2 - х + 4 = 0.
а)-1;4; б)-1;1;-4; в) 1;-4; г)-1;1.
5. Решите уравнение
(1 - 4х)(1 + Ах)
^Тб;
б>-
16'
в)
= 1-(2*-1)
5
16'
г) 16.
6. Решите уравнение
(3*-5)2-(1-2х)2 = 0
и запишите сумму корней этого уравнения,
а) 6; 6)4,8; в) 5,2; г) 4,2.
7. Если выполняется равенство
2*3 + 9х2 + а = (пгх - 3) (х + З)2,
то найдите значения аи/пи запишите их сумму
(а + /п).
а)-25; б)-30; в)-20; г)-36.
8. Укажите график функции
z/ = 2(jc-l)2-8g+0,5](|-0,5).
ky
в) l ' г)
9. Разность квадратов двух натуральных
двузначных чисел, записанных с помощью цифр а
и Ь, взятых в обратном порядке, равна 495.
Найдите сумму этих чисел.
а) 45; 6)55; в) 65; г) 44.
10. Раскройте скобки в выражении
(а - 2Ь - Зс)2.
а) а2 + 4Ь2 + 9с2;
б) раскрыть нельзя;
в) а2 - 4Ь2 - 9с2 - 4аЬ - бас + 12 Ьс;
г) а2 - 4аЬ + 4Ь2
6ас+12Ьс + 9с

Тесты
Алгебра. 7—9 классы
329
Тест 9
Системы уравнений
1. Решите способом сложения систему
уравнений
2х - у - 1,
х + у - -4
и, обозначив (т; п) решение системы, вычисли-
2,2
те значение выражения т + п .
а) 17; 6)5;
в) 13; г) 10.
2. Дано уравнение qX - 0,4i/ = 2. Выразите
переменную у через дс.
а) г/ = -1 g -5;
b)i/= 1«х-5;
r)z/= g* +5.
б) у = g х - 5;
3. Решите систему уравнений
2 3 и'
2х - у = 2
и, обозначив (т; п) решение системы,
вычислите значение выражения т + п.
а) 10; 6)8; в) 6; г) 12.
4. Гриша работал за станком 3 ч, а Толя
работал 4 ч. Вместе Они сделали 44 детали. Сколько
деталей сделал каждый из них, если за 1 ч
работы они вместе сделали 13 деталей?
а) 18 и 26; в) 16 и 28;
б) 24 и 20; г) 23 и 21.
5. Дана система
2х - ау = 6,
х + Зу = 10.
При каком значении а решением системы
является пара чисел (2/п; т)1
а)-2; 6)2; в)-1; г) 1.
6. Напишите формулу для функции y = kx + b,
если график этой функции проходит через точку
А (-3; k) и число Ь больше числа k на 6.
а) у = 2х + 8; в) у = х + 8;
б) у = 2х + 4; г) у = х + 4.
7. Какой из графиков является графиком
уравнения 2х - 0,5i/ = 3?
8. График функции у = kx + I проходит через
точки А (2; -3) и Б (1; 2). Напишите формулу,
задающую эту функцию.
a)z/ =
2;
в) I/ = -5* + 7;
б) у = Ьх - 2; г) z/ = 5х - 7.
9. Некоторое двузначное число на 9 больше
суммы его цифр, а квадрат этого числа на 180
больше квадрата его второй цифры. Найдите
квадрат этого числа.
а) 196; 6) 144; в) 256; г) 100.
10. При каком значении а система
\2х - у - 5,
х + ау = 2
решений не имеет?
а)-2; б) -0,5; в) 0,5; г) 2.
Тест 10
Итоговый 2
1. Найдите значение
За2
0,5Ь
1 и 1
если а = -g иЬ= g .
a)g; б)п;
выражения
- 26
- 2а*
в) А.
в; 13*
г)
5
16
2. Решите уравнение
-0,4(1,Ъх - 2) = 1 - 0,5(2* + 1).
а)-
4'
б) 4;
в)1
3'
г)-1|

330
Тесты
Алгебра. 7—9 классы
3* Определите формулу
для функции, график
которой изображен на рисунке.
а) у = -2х + 3;
6)z/ = 1,5* -4,5;
в) у = 1,5* + 3;
г)у = Зх-2.
4. Упростите выражение
2 2 ^
( 2 2 Y л ~ 5
Г 3х у) '1,5ху
" q о 3
(0,5* у£)
а)5§-4;в)в|-«1;в)4|.^;Р)б|-^.
X * X X
5. Упростите выражение
-0,5*(2* - 3) - (4* + 3X1 - 2*).
а) -7*2 + 2,5* - 5; в) -9*2 - 2,5* - 3;
б)7*2-2,5* + 3; г) 7*2 + 3,5* - 3.
6. Решите уравнение
(5 - З*)2 - 0,5(2* - 3)(2* + 3) = 7*2 + 2,5.
а) 1,5; 6)0,9; в) -0,9; г)-1,5.
7. Разложите выражение (Ах - 3) - 16 на
множители и решите уравнение
(4*-З)2-16 = 0.
а)-0,25; 1,75; в) 2; 4;
6)0,5; 1,5;
г; 3 , 1 3
8. Решите систему уравнений
'£+J - У-±1 . о
4 2 и'
|3х + у - 1.
а) (8;-4); б)(-1;2); в)(1;-2); г) (-8; 4).
9. 25% суммы чисел а и Ь равны 125%
разности чисел а и Ь. Найдите сумму чисел а и Ь, если
разность между утроенным числом а и половиной
числа Ъ равна 32.
а) 36; 6)20; в) 28; г) 18.
10. Графики функций
у = ах + 3 и i/ = (2 - а)х + а
пересекаются в точке с абсциссой, равной -1.
Запишите ординату точки их пересечения.
а)
3'
б>-§5
в)-1
3'
v)l\.
8 КЛАСС
Тест 1
Рациональные выражения
1. Найдите значение выражения
5а2 - 2а
1 - 4а
при а = -0,2.
а)ф 6)3; в)|; i)-6.
2. Найдите допустимые значения переменной
в выражении
Зх + 6
1,7 - 2х'
а)**-2; б)**0,85; в)х*1^; г)**-0,85.
3. Сократите дробь
За - 27
18 - 6а *
v а + 3 _ а + 3
а)-2~; б) —
4. Сократите дробь
; в)-5 -1,5; г)
-а + 3
2 '
х + у + 2ху
2х2 + 2у2
в)ху;
а' 2 , 2 '
X + у
6) 2 у ; г) сократить нельзя.
5. Упростите выражение
(а - Ь)(а + Ь) - (а - ft)2
aft - ft2
ч 2 йч 2 . 0 ч 2а
ft" ft
6. Упростите выражение
а ft
а - Ъ
2 . ь2
.а + &
а) 2 ,2 ;
а - Ь
п1 (Д + »)' ,
'2 .2 »
а - ft
а ■
- ft
а + ft*
б)-1;
ч а - ft
г)—Ь

Тесты
Алгебра. 7—9 классы
331
. v 4 - а\ 2а - 5
7. Упростите выражение + .
а — о 3 — а ,
а) ; б) 3; в) -3; г) .
а — 3 а — 6
8. Упростите выражение
5 3
4-
а)1;
g, 4х - 6
о) -« ;
х + 2 *
4х - 3
в)
х + 2х
г)
4х2 + 6х + 6
(х + 2)х
9. Известно, что = 4. Найдите -—т ..
а) 5; б)-4; в)-2; г) 3.
10. При каких значениях m и а верно
сокращена дробь
х - Зх + m
х + а
= х-5?
а)а = -1, m = -6; в) а = -2, m = 10;
б)а=1, /п = -5; г) а = 2, /п =-10.
Тест 2
Преобразование
рациональных выражений
1. Выполните умножение
7х2 х2 - 9
3 - х 14х3 '
3-х ^v х - 3 v х + 3 vx + 3
а) -or-; б) -от-' в> "^тТ- I г> "
2х
2х
7х
2х '
2. Выполните деление
х2 + 10х + 25 х2 - 25
х + 5х
з
\ х *\ х ч х + 5 ч х
a)7TV б>"5; в>^; Г)7ТЪ-
3. Выполните действия
а)
х + 1'
(* + *2):(l + i).
б) х ; в)х; г)х + 1.
4. Выполните действия
/ 2 .. ЗХ2 + 6'Х
(х - 4): я
12
4 - 4х + х
2 '
v 2х -, 2х v 4х - 1 v 4х
&)-—2'' б)—2;В)ТП;Т)—2
5. Упростите выражение
4х - 2 3-х
(х - I)2 (1 - х)2
ч 5 *ч 5 ч 5 ч Зх - 5
а) 2 ; б> Г-Т » в) г-: 5 г>
(1-х)" * ~ *
6. Упростите выражение
1 - х
(х - 1)
( 5 х J *"*
\*^J ^— V х2 + 6х + 9
ч х -/З _ 3-х . 1 ч 2-х
а)ГТз; б)з-Гх; в)Гх> г>—х
7. Выполните действия
(•♦и*)
Зх - 18х + 27
х2 - 36
ч х - 3 -,х + 6 . х + 6 ч 3
а) т-г2; б) —о—» в) -—п; г)
х + 6 ' ~' 3
8. Упростите
5 [ х - 4
х - 3
16
х + 6
! + * U2 + 4х 16 - х2
х
ч 4х ЛЧ 5 ч 5 v 4х
а) ; б) ——т; в) -—- ; г)
х - 4
х + 4:
х - 4'
х + 4
9. Упростите выражение
а - 2а + 1
ЫУ
а)
а - 1
а- IV5
<"Я =
«>tr^
г)
а + 1
10. Если 2а + ЗЬ - 0,6(5а + 3&), то найдите
а + ЗаЬ
значение выражения
а) 8,2; 6)1,28; в) 3,6; г) 5,04.

332
Тесты
Алгебра. 7—9 классы
Тест 3
Определение арифметического
квадратного корня
* 1. Вычислите
ЬЩ - Тодю + л/з2 + 42.
а) 7,5; 6)6,1; в) 5,1; г) 4,8.
2. Найдите значение выражения
(273)2 - 1
\2
а) 18;
6)24;
в) 12;
г) 22.
3. Решите уравнение 0,4* -2 = 0.
а) Л;-Л; в)Л;0;
б) Л', г) нет корней.
4. Решите уравнение 8 - 2 Ja = 0.
а) нет корней; в) 2;
б) 4; г) 16.
5. Вычислите значение выражения
Ш-Ш-
а)-|;
б)-|;
в)-|;
г)-
8
6. При каких значениях х имеет смысл
выражение
а)* 5*0; б)х<0; в)*<0; г)*>0.
7. Упростите выражение
7(а - Ъ)2 + лДба2 , если а < 0 < Ь.
а) -За + Ь; в) Ъа - Ь;
б) -Ь - 5а; г) Ь - 5а.
8. Какие из перечисленных ниже точек
принадлежат графику функции у — Jx:
А(0,4;0,2);Б(18;372);С(3;-73);1>(|;^)?
а) Б; б) С; в)2>; г) А.
9. С помощью графиков функций
j/= Jx иу = х-2
найдите координаты точки их пересечения.
Запишите произведение этих координат.
а) 4; в) 8;
б) 6; г) графики не пересекаются.
10. При каком значении а графики функций
1/=л/хи1/ = ах-3
не пересекаются?
а) а < 0; б) а = 1; в) а > 0; г) а ^ 0.
Тест 4
Свойства арифметического
квадратного корня
1. Найдите значение выражения
(з7^5)2-7з • 70Д2 + J.
а) 67,4; б) 66,8; в) 28,4; г) 80,6.
2. Внесите множитель под знак корня: j Тва.
a)V2a2; б)л/2аа; в) J|-; г)
3. Упростите выражение
л/48 + V75 - УП)8.
а)3л/3; б)27§; в)5л/3; г)-7з,
4. Выполните действия
(4-73)2-(275 -1)(2л/5 +1).
а)87§; в)-б73;
б)-873; г)27з.
5. Сократите дробь
JTbx - Л
Зх - 1
а) 75х - л/5 ; в)
б) Л + Л; г)
V5
73^ - 1'
V5
73х + 1 "
6. Расположите числа в порядке возрастания:
0,7, Ж& и ^.

Тесты
Алгебра. 7—9 классы
333
а) 7075 ; 0,7; ^ г в) JU* ; ^ ; 0,7;
6)0,7; ^;7оТВ; г) ^ ; 0,7; 70^5.
7. Избавьтесь от знака корни в знаменателе
дроби
*2-4
Jx + 2*
а) 7* - 4 ; в) * - 72 ;
б) (х - 2) л/* + 2 ; г) невозможно.
8. Упростите выражение
72 + 1 _ 72 - 1
7з + i 7з - Г
а) 272; б) 7з + 72 ; в) 7з - 72 ; г)27з.
9. Вынесите множитель из-под знака корня:
Ль5.
а) -ЪЪ.РЪЪ; б) 2Ь72Ь ; в) -2b72b ; r^bT1^ ■
10. Укажите верное равенство:
а) 73 - 272 = 1 - 72;
б) 73 - 272 = 72-1;
в) 73 - 272 = 1 + 72;
г) верного равенства нет.
Тест 5
Квадратные уравнения.
Теоремы Виета
1. Решите уравнение
Ьх- = х =0.
а)А; б)0;А; в>17'5' г) 0; 17,5.
2. Решите уравнение
(х - 5)2 = 5(9 - 2х).
а) о и 720; в)-720;7й0;
б) 720 ; г) нет корней.
3. Решите уравнение
(4 - Зх)2 = 25.
a)-g;3; б) |; -3; в) 3; г) 3;-3.
4. Решите уравнение
Зх2 - 2х - 5 = 0.
а) 1,5; -2,5; б) 1 \ ; -\ ; в) 11; -1; г) -1,5; 2,5.
5. При каких значениях т уравнение
4х + 2х - /п = 0
имеет единственный корень?
а) 0,5; б)-0,25; в) 0,25; г)-0,5.
6. При каких значениях k и р корнями
уравнения
kx2+px + 3 = 0
являются числа 1 и -3?
а) А = 1,р = 2; в)£ = -1,р = 2;
6)fe = -l,p = -2; r)fe = l,p = -2.
7. Составьте квадратное уравнение с корнями
72 и-7§.
а) х2 + 72 х - 4 - 0; в) х2 - 72 х - 16;
б)*2- 72*-4; г)
составить нельзя.
8. Решите уравнение —«— = —g
а)-1;1,6; 6)1; -1,6; в) 2;-3,2; г)-2; 3,2.
9. Один из корней уравнения
Зх2 + Ьх + 4 = 0
равен 1, а второй корень совпадает с корнем
уравнения 2х - 3 = т. Найдите т.
а)~~3; б)3; в)~~3; г)
10. Дано уравнение
2
3
х - ах - х + а = 0 (а * 1).
Найдите сумму квадратов корней этого
уравнения.
а) 4 + 4а2: б) 2; в) 2 + 2а2; г) 1 + а2.
Тест 6
Решение дробно-рациональных
уравнений
1. Решите уравнение
2х2 - Зх - 14
х + 2
а) 7;-2; 6)7; в) 3,5; г) 3,5;-2.
= 0.

334
Тесты
Алгебра. 7—9 классы
2. Решите уравнение
х - 3 _ 2х - 1
х х + 24 "
а) 2; 9; б) 4; 18; в)-4;-18; г) 8; 36.
3. Решите уравнение
—Ц -х + 1 = 0.
х - 1
а) 0; 2; б) 0; -2; в) -2; г) 2.
4. Решите уравнение
1_2х2-х-6=0
2-х
а) Корней нет; б) -2; 2; в) 2; г) -2.
5. Произведение двух последовательных
натуральных чисел равно 182. Найдите сумму
этих чисел.
а) 27; 6)36; в) 24; г) 42.
6. Диагональ квадрата равна 6 см. Найдите'
площадь квадрата.
а) 12 см2; б) 36 см2; в) 18 см2; г) 24 см2.
7. Периметр прямоугольника равен 7 см, а его
площадь равна 3 см . Найдите диагональ
прямоугольника.
а) 5 см; б) 2,5 см: в) 3 см; г) 4 см.
8. Моторная лодка прошла 10 км по озеру и
4 км против течения реки, затратив на весь путь
1 ч. Найдите собственную скорость лодки, если
скорость течения реки равна 3 км/ч.
а) 15 км/ч или 2 км/ч;
б) 15 км/ч;
в) 30 км/ч;
г) правильного ответа нет.
9. Через первую соковыжималку можно
приготовить сок на 1 ч быстрее, чем через вторую. А
через вторую на 3 ч быстрее, чем через третью.
За какое время можно приготовить сок,
пользуясь первой соковыжималкой, если это время
равно времени, за которое можно приготовить
сок, пользуясь второй и третьей
соковыжималками вместе?
а)1; 6)3; в) 4; г) 2.
10. При каком значении (или значениях) а
уравнение
х2 - (а + 3) • х + а + 5 = 0
имеет два положительных корня, один из
которых в 2 раза больше другого?
а) а = 2 или а = -0,5; в) а = 3;
б) а = 2; г) а = -0,5.
Тест 7
Неравенства и их свойства
1. Если -2m > g , то какие из перечисленных
неравенств верны?
®т<-п; @т>-2;
(§) 8/7i<-2л.
m<-j;
a) A; 6)BhD; в) В; г) С.
2. Если -6а > -2& + 12, то какие из
перечисленных неравенств верны?
®а<?-2;
®а-1>| -3;
(g)a>|-2; (§)a + 3<g+l.
a) A; 6)AhD; в) В и С; г) В.
3. Если а > &, 0 «'- &, с < Ь, 0 > с, то
расположите в порядке возрастания числа a, Ь, с и 0.
а) с, &, 0, а; в) с, 0, &, а;
б) а, Ь9 0, с; г) 0, с, Ь, а.
4. Даны выражения
M = 6a-(a + 3)2 и N = (2а - 3) (2а + 3).
Какое из высказываний верно?
a)M>N; 6)M>N; b)M<N; t)M<N.
5. Сравните выражения Л и Б, если
2
А = 4wnиВ = (т + л) .
а)А>Б; б)А>В; в)А<В; г)А<В.
6. Если -3 < х < 2, то какое из высказываний
верно:
®4<*2<9; ®0<х2<9;
®0<хЧ4; (§)9<х2<4?
а) С; 6)D; в) А; г) В.
7. Оцените значение выражения 2 - Зх, если
4^х<6.
а) 14 < 2 - Зх < 20; в) 10 < 2 - Зх ^ 16;
б) -14 < 2 - Зх ^ -8; г) -16 < 2 - Зх < -10.

Тесты
Алгебра. 7—9 классы
335
8.Известно, что 5<х<8и1<1/<2.
Л Зх - Ъу
Оцените значение выражения ——-^ .
а)2,8<^Ц^5; В)2<?^^<7;
X ~ О X ~ О
б) 1 ^ 3х~5У < 9,5; г) 2,5 < 3* " *у < 3,8.
х — 3 х ~ о
9. Если а < Ь < т< п, то найдите (а; т) П (Ь; п).
(Укажите правильный промежуток.)
а) (а; л); в) (-оо; т) и (&; +°°);
б) (Ь; т)\ г) (т; л).
10. Найдите сумму натуральных чисел,
удовлетворяющих области допустимых значений
выражения л/7 - 2у.
а) 7; 6)6; в) 3; г) 10.
Тест 8
Решение неравенств
и систем
1. Какие из чисел-0,5, -1, 1 и 0,5
являются решением неравенства
-3*-4>х-1?
а)0,5;1; в) 1;
б)-1;-0,5; г)-0,5; 1; 0,5.
2. Укажите наименьшее целое число, которое
является решением неравенства
-н<°-
а)-1; б)-2; в) 1; г) 2.
3. Решите неравенство
0,5х-3<2х-1.
a)(-lj;+oo) B)(l};+oo)
6)(-oo;-l|) г)(-оо;2|)
4. Решите неравенство
2х + 1 ^ 4* - 3
х -
3
а)(-оо;1,5]; в) [-1,5; +оо);
б) [-0,9; +оо); г) (-оо; 0,9].
5. При каких значениях с уравнение
2х2 - Ъх + с = 0
не имеет действительных корней?
а>[3ё;+°°) B)(3g;+oo);
б)(оо;8|) г)(-8|;+оо)
6. При каких значениях т имеет смысл
выражение
Vo
/0,8 - 3/п
а)(з|;+оо) в)(-оо;^)
б)(Д;+оо) г)[Д;+оо)
7. Решите систему неравенств
f 3*-2<5х-1,5,
а) (-оо; -15] и (-0,25; +°°); в) (-0,25; 15];
б) [-15;-0,25]; г) 0.
8. Найдите область допустимых значений
переменной в выражении
I
0,7 + \ + 5
4 J2 - 0,4* '
a)[~i5;5) в)[-2,8; 0,2);
б) [-2,8; 5); г) (-оо;-2,8] U (5;+оо).
9. Решите двойное неравенство -3 < 1 - 2х < 4.
а)[-1;2,5]; в)[-2,5;1];
б) [-2; 1,5]; г) [-1,5; 2].
10. Решите неравенство Ьх - 2ах - б < 0
при условии, что а > 3.
Тест 9
Степень с целым показателем.
Стандартный вид числа
1. Найдите значение выражения
(-2)-2 + 0А-г-(Л)°.
а) 2,5; 6)1,75; в) 1,25; г) 2,25.

336
Тесты
Алгебра. 7—9 классы
2. Упростите выражение
-з 2
771 • 771
^4 '
/71
а) т" ; б) /п" ; в) /п ; г) /п .
3. Упростите выражение
з-1
(т) •©
6\-2
а>Т; б)^; В>Т^5 г>12а-
12а'
4. Упростите выражение
(с-2 + 2а"1 + 1) • (с + I)"2.
—1 —1 —2
а)а + 1; б)(а+1) ; в) а ; г) а .
5. Порядок натурального числа а равен 3.
Сколько цифр содержит десятичная запись
этого числа?
а) 4; 6)3; в) 2; г) 10.
6. Стороны прямоугольника х = 2,8 • 10" м и
_2
у = 6,5 • 10 м. Найдите периметр
прямоугольника.
а) 9,3 • 10"3 м; в) 18,6 • 10~3 м;
б)6,9Ю_1м; г)1,82 10"2м.
7. Диагональ квадрата равна л/8 - 10 см.
Найдите сторону квадрата.
а) л/2 м; б) 2 м; в) 80 см; г) 4 м.
8. Решите неравенство
-5я< \ +2ях<2я (я «3,14).
В ответе запишите сумму целых решений,
а) 5; б) -5; в)-2; г)-3.
9. Решите уравнение
(х + З)"2 = х~2
и найдите значение выражения 2х0 + 1, где х0 —
корень этого уравнения.
а)3; б) -4; в)-2; г) 1.
10. Найдите число у$ если число х составляет
20% от произведения чисел х и у.
а) 5; 6)6; в) 8; г) 4.
Тест 10
Итоговый
1. Упростите выражение
г
У . *
\ху - X
а)
2 2 !
* У
б)
*У ~ У
1
х + 2ху + у
i + !
* У
х + у'
в)х + у; г) 1.
2. Упростите выражение
72 - 1
Л
а) 2; б)"^' в)-75;
3. Решите уравнение
г)^
*2 = -|+0,5.
а)-2;1; 6)0; в)-1;0,5; г)1;-0,5.
4. Пусть числа хгих2 — корни уравнения
2
X + 4х - 771 =* 0.
Разность между корнями равна 2. Найдите ттг.
а) /71 = 3; б) 7П = -3; в) m = 8; г) тп = -8.
5. Женя шел по лесной дорожке к станции, но,
не дойдя до нее 4 км, он сделал привал на 20 мин
для сбора грибов. Чтобы успеть вовремя на
электричку, ему после привала пришлось увеличить
скорость на 1 км/ч. С какой скоростью
первоначально шел Женя?
а) 3 км/ч; б) 4 км/ч; в) 5 км/ч; г) 6 км/ч.
6. Сравните значения выражений
А = 771 (771 - П) И В = П (Ш - П).
а)А<В; б)Л<Б; в)А>В; т)А>В.
7. Решив неравенство
-0,4 - | >2(* + 2,5),
укажите наибольшее целое число, являющееся
решением этого неравенства.
а)0; б)-3; в)-2; г)-1.
8. Найдите область допустимых значений
переменной в выражении
*
х
2
л/0,2х + 1
а) (-оо; -5) U [8; +оо); в) [-8; 5);
б) (-оо; -8) U (5; +оо); г) (-5; 8].

Тесты
Алгебра. 7—9 классы
337
9. Упростите выражение
«.--•-ve-if-i.
ч л *ч l ч 2а ч 2а
а) 0; б) Ъ - а; в) —— ; г) -—-
о -г а о — а
-1 , -2 0 -з
а + а = 2а .
10. Решите уравнение
-1 , -2
а + а -
а)0;2;-1; б)-1;2; в)-2;1; г)0;1;-2.
9 КЛАСС
Тест 1
Свойства функций.
Квадратный трехчлен
У = fix)
1. Найдите область
определения функции
У'fix).
а)[-1;3];
б) [-2; 8]
в)[-1;2]
г)[-1;1],
2. Дана функция у = -2х + 7. При каких
значениях х у > 0?
а)(-3,5;+оо); в)(3,5;+оо);
б) (-00;-?); Г) (-00; 8,6).
3. Найдите нули функции
*/ =
а) 6;
б)-6;
~3Х ~2
О Ах + 4 "
в) -10, -6;
г)-|.
4. Для функции I/ = /(*)
найдите промежутки
возрастания.
а) [t; л];
б) [р; т];
в) [с; п];
r)[t;k].
5. Укажите область определения функции
Зх + 1
1
! V с */
1 • \ 1 ж
/ i \
0 I *
л & х
Р
а) х * -^ ; х * 0; х * ^ ; в) х * 0; х *£ ;
б) х * 0; х Ф -2; г) х * 0; х * 2.
6. Решите уравнение
7х - 6х - 1
7* + 1
0.
а)1; 6)1;-^; в)1;^; г)-1;^.
7. Разложите на множители квадратный
трехчлен
13х2 -10х-8.
а)(х + 2)(Зх + 4); в)<* + 2)(*-|);
б) (х - 2) (3* + 4); г) (х + 2) (-Зх - 4).
8. Упростите выражение
2х2 - Ъх - 3
1-4*2 в
, х + 3 *ч х - 3 ч х + 3 ч * " 3
а) т:—7; б);—тг; в) -——; г)
2х - 1 ' ' 1 - 2* ' 1 - 2* ' 2х - 1
9. Упростите выражение
х2 - 4 1
2х + 7х + 5
х + 1
ч X + 1 -ч 1 v X - 1 4 11
а)27П: б)27П; в)5^; p>* + 1-
10. Д а н о: ■ тх - 3.
X + с
Найдите сити запишите произведение
(с • /п = ?).
а)-3; б)-2; в) 2; г) 3.
У =
х - 2хл
Тест 2 #
Квадратичная функция
и квадратные неравенства
1. Найдите координаты вершины параболы
у = -2х2+8х-13.
а) (2;-5); б) (-2;-9); в) (2;-7); г) (2;-5).
2
2. Найдите нули функции у = -9х + 7х .
а)0;-ф 6)0;?; в)0;ф г)0;-?.

338
Тесты
Алгебра. 7—9 классы
3. Найдите промежуток (промежутки) воз-
растания функции у = -2х + 7х - 3.
а) (-оо; 1J6]; в)[-3,5;+оо);
б)[1,75;+оо); г)(-оо;3,5].
,4. Найдите множество значений функции
у = х + Зх - 5.
а)(-оо;-5]; в) (-оо; -7,25];
б) [-5; +оо); Г) [-7,25; +оо).
5. Укажите график функции у = -х + 4х - 3.
*У
-1
а)
и
О х
6. Укажите график функции у = (х + 2) + 1.
7. При каких значениях х значения функции
у = -х2 - 2х + 8
положительны?
а) (-оо; -4) U (2; +оо); в) (-2; 4);
б) (-4; 2); г) (-оо; -2) и (4; +оо).
8. Решите неравенство Зх - Ьх + 2 > 0.
а) (-оо; -1] U [-§; +оо) ;
б) [-1;-|];
г)(-оо;|]и [1;+оо).
о
9. Решите неравенство -х + 9 > 0.
а) (-оо; -3) U (3; +оо); в) (-3; 3);
б)(-оо;3); г)(-3:+оо).
2
10. Решите неравенство < 0 и
укажите наименьшее целое решение этого
неравенства.
а)-3; б)-2; в)-1; г) 4.
Тест 3
Решение уравнений и систем
3 2
1. Решите уравнение х + х - 2х = 0.
а)-1;2; б)-2;1; в)2;0;-1; г)-2;0;1.
2. Решите уравнение х -Вх -9 = 0.
а)-1;1; в)3;-3;
б)1;3; г)3;-3;1;-1.
3. Решите уравнение
(х2 + 4х + 1)(ж2 + 4х + 5) = -4.
а) 4;-2; б)-1;-3; в) 1; 3; г)-2; 4.
4. Какие из перечисленных ниже пар чисел
являются решением системы
х + 2у = 5,
-х2 + ху = -4?
А (2; 1,5), В (-1; 3), С (1; 2), D (-2; 3,5).
a)C;D; б) A; b)B;D; г) В.
5. Решите систему уравнений
j х + 2у = 5,
\ху = 2.
а)(1;2);(4;|); в) (1; -2); (б; -\);
б) (9; -2); (б; -\ ]; г) (9; 2); (б; \ ).

6. Решите систему уравнений
г 2 2 -
\х -у = -5,
1 2*2-i/2 = -l.
а) (2; 3); (-2; -3);
б)(2;3);(-2;3);(2;-3);(-2;-3);
в)(2;-2);(-2;2);(3;-3);(-3;3);
г)(2;-2);(3;-3).
7. Сумма цифр натурального двузначного
числа равна 10, а произведение цифр этого
числа равно 24. Найдите это число, а если их
несколько, то укажите их сумму.
а) 73; 6)132; в) 110; г) 64.
8. Курьер ехал на велосипеде до станции по
грунтовой дороге 10 км с некоторой скоростью,
а возвращался обратно лесной дорогой
протяженностью 5 км с другой скоростью, затратив на
весь путь 1 ч 5 мин. Найдите скорости
велосипедиста по грунтовой и по лесной дороге, если на
обратный путь он затратил на 15 мин меньше,
чем на дорогу до станции.
а) 12 км/ч и 16 км/ч; в) 15 км/ч и 12 км/ч;
б) 16 км/ч и 10 км/ч; г) 12 км/ч и 10 км/ч.
3 2
9. Один из корней уравнения х +2х -х + а =
= 0 равен 1. Найдите (если они существуют)
другие корни этого уравнения.
а)-2;-1; б)2;1; в)-1; г)-2.
10. При каком значении параметра т система
г 2,2 а
\х +1/ =6,
| х + у = т
имеет единственное решение?
а) /п = 3; в) т = 6 или т = -6;
б)т = 2*/з или/п = -273; г)/п = з72.
Тест 4
Арифметическая
и геометрическая прогрессии
1.В арифметической прогрессии а5 = 8,7 и
а8 = 12,3. Найдите d и av
а) d = 1,6 и ах = 2,3; в) d = 1,2 и аг = 3,9;
б) d = 3,6 и аг = -5,7; г) d = 1,4 и аг = 3,1.
Тесты ООП
Алгебра. 7—9 классы OOi7
2. В арифметической прогрессии аг = -7,3 и
а2 = -6,4. На каком месте (укажите номер)
находится число 26?
а) 39; 6)38; , в) 27; г) 28.
3. В арифметической прогрессии ах = 38,1 и
а2 = 36,7. На каком месте (укажите номер) стоит
первое отрицательное число? Найдите это
число.
а)-0,5; б)-0,7; в)-1,1; г)-0,3.
4. Найдите сумму первых шестнадцати членов
арифметической прогрессии, заданной формулой
«п = 6п + 2.
а) 864; 6)848; в) 792; г) 716.
5. В геометрической прогрессии аг = 72 л/2;
а3 = 8 л/2 . Найдите знаменатель q.
а) 9; 6)3; в) g ; г) g или-g.
6. В геометрической прогрессии ах = g и а2 = «•
Найдите шестой член этой прогрессии.
а>ш; б)Ф в)ш; г)101-
7. В геометрической прогрессии Ьг = 0,4 и Ь2 =
= 1,2. Найдите сумму пяти первых членов этой
прогрессии.
а) 18,8; 6)80,2; в) 48,4; г) 39,6.
8. Найдите первый член геометрической
прогрессии, если аг + аъ = 20 и а2Н-а3 = 17.
а) 4; 6)6; в) 2; г) 8.
9. Для периодической дроби 0,41(6) найдите
несократимую обыкновенную дробь. Запишите
разность числителя и знаменателя.
а) 12; 6)7; в) 8; г) 11.
10. Дано: (Ьп) — геометрическая прогрессия,
&i = 3, q = 2. Какой цифрой оканчивается &2о?
а) 6; 6)2; в) 8; г) 4.
Тест 5
Итоговый 1
1. Решите уравнение
(Зх + 2)2 = 10 + 3(х - 2)(х + 2).
а)1;-1; б)-1; в)0;1; г)72;-72.

340
Тесты
Алгебра. 7—9 классы
2. Сократите дробь
2х2 - Ьх - 12
2х + 3
а)2(*-4); б) х- 4; в) 1; г) 4-х.
3. Укажите график функции
у = -х2 + 2х + 3.
4. Решите неравенство
-х > 0,5*.
а)(-0,5;0); в)[-0,5;0];
б) [0; +оо); г) (-оо; -0,5] U [0; +оо).
5. Решите систему уравнений
f 2* + у-1,
1 Зх2 -ху= 18.
а) (2; -3); (1,8; -4,6); в) (-2; 3); (1,8; 4,6);
б)(2;-3); г) (2;-3); (-1,8; 4,6).
в. Две бригады трактористов, работая вместе,
могут вспахать поле за Зт ч. Работая порознь,
первая бригада вспахивает поле на 4 ч быстрее
второй. За сколько часов могут вспахать поле
первая и вторая бригады, работая по
отдельности?
а) 6 ч и 10 ч; в) 4,5 ч и 8,5 ч;
б) 3 ч и 7 ч; г) 5 ч и 9 ч.
7. Решите неравенство
х - 5 2х - 1
> х-2.
а)(-оо;-7); в)(-^;+оо);
6)(-00;-i); г)(-7;+00).
8. В арифметической прогрессии а3 = 6, d =
= 1,2. Найдите сумму первых семи членов.
а) 42,6; б) 54; в) 46,8; г) 50,4.
9. В возрастающей геометрической прогрессии
Ьг = 2, сумма первых трех ее членов равна 26.
Найдите &4.
а) 32; 6)162; в) 54; г) 48.
10. Решите неравенство
х
(можно использовать графики).
а) (-оо;-1) и (0; 1); в)(-оо;-1);
б)(-1;0)и(1;+оо); г)(-1;1).
Тест 6
Четная и нечетная функции.
Корень /t-й степени
1. Что можно сказать о функции
а) Четная;
б) нечетная;
в) ни четная, ни
нечетная;
г) все первые три
высказывания неверны.
2. Какое из высказываний о функции
2
/(*) =
6-х"
3
х + 2х
верно?
A. f(x) — четная;
B. f(x) — нечетная;
C. ни четная, ни нечетная;
D. высказывания А, В, С неверны.
a)D; б) С; в) А; г) В.
1997 1998
3. Даны функции f(x) = х и g(x) - х .
Расположите значения
/(-1), /(1), g(-6) и ДО)

Тесты
Алгебра. 7—9 классы
341
в порядке убывания.
a)g(3),/(l),g(-6),/(-l);
б) А-1), /(1), g(-6), ЖЗ);
B)g(-6),f(l),g(3),f(-l);
r)*(-6),g(3),«l),/(-l).
4. Найдите значение выражения
3J^-V£0081--^.
»/Тб
а)3;
б) -5,8; в) 2;
Ч Л19
5. Решите уравнение 0,4 ух + 10 =4.
а) 16; 6)999; в) 9990; г)-9.
1 з
6. Формула объема конуса V = ^ яД , где Л —
радиус основания конуса. Выразите R через V.
а)
MW
б) *h'
в)
3
7. Упростите выражение
1/3 V
к ''
3ЩГа
T)3h-
Г)бл/С.
a) Ja; б) Va;
8. Найдите значение выражения
злЛт
(V9 - 1)(V9 + 1)'
а)|73; 6)1; в) 7з -1; г) 1,5.
9. Избавьтесь от иррациональности в
знаменателе дроби: *
1
а)
6)
3Л+Л.
а + 1 '
3J? - 3Л + 1
а + 1
3/S + 1
в)
г)
VS-1
а - 1
«/а - 1
10. Упростите выражение
Jb - 1 _як 1
а)
л/ь + 1' V& + 1
; в)
Jb - 1
ьТь - 1*
1 .1
ъ + Jb + i' г)ь'
Тест 7
Степень с рациональным показателем
1. Найдите значение выражения
2
,1,5 ft-0,5 , f 1N 5
4»-9-**+Й)
а)|; 6)27; в) 21; г)2з|.
1 1
з_з
2. Сократите дробь -у у—j
2 3 6
* - х у
1 1
6 , 6
оЛХ + У .
б б
* - у
1 1
6' 6
1 1
з з
ч х у
3 3
X - У
1 1
6 6
6
X
3. Упростите выражение
1,5 ,1,5 2,0,5 ,1,5
а -о __ а о - ао
0,5 ,0,5 1,5 0,5, •
а - Ь а ,' - а Ь
0,5,0,5
а о
0,5 ,0,5
а — о
а)——; б)а-Ь; в)а + Ь; г)
и и а + о
4. Найдите область определения функции
1
2 3
у=(2х- * ) .
а) (0; 2); в) [0; 2];
б) (-°о; 0] U [2; +оо); г) (-оо; 0) U (2; +оо).
г) 4.
5. Решите уравнение
( \)
4
X
2
= ж-2.
\ /
а) 1; 4; б) 1; в) корней нет;
6. Упростите выражение
( А
и
V J
3
4
-1,6
ху
( 0,5 ~b]
а)-; б)х у
9
В
. -3 v X
) ху ; г) -

342
Тесты
Алгебра. 7—9 классы
7. Для функции у =
график.
К8
- I / 0,5Ч2
х \ - (х ) укажите
а)
и.
h
U
в)
-1
8. При каких значениях х верно равенство
1
(х ) =-х ?
а) (-°о; 0]; в) 0;
б) (-ОО; +00); Г) [0; +00).
9. Расположите числа в порядке возрастания
liii
1Л* fl\* fl\* п\*
3 я
10. Решите уравнения х = 9 и 0,2 =5.
Запишите сумму корней этих уравнении.
JL. г)-
27' г' 27
1 26
а)80; 6)26; в)1»; г)-^.
а)_31. 6)_J_. B)J_. г)81
' 20 * ' 20 ' ' 9П ' ' 9П '
Тест 8
Тригонометрические формулы
1. Найдите значение
3 sin2 120° - 4 cos 180° + 3 tg 135°.
а)-2,5; 6)5,5; в)-4,75; г) 3,25.
2. Определите знаки
sin 169°, tgl32\ cos (-78°), ctg247°.
Выберите правильный порядок
расположения знаков:
а) + - -Ч-; в) - - + +;
б) + - + +; г) + .
3. Д а н о: sin а = ^ , « < а < п- Найдите
значение cos а - tg а.
~~ " вЧ 20 ' 1' 20
4. Упростите выражение
sin (я - oOcosfgH - ouctgfft + ex J
tg (2к - a) *
2 2
a)l; 6)-sin а; в)-1; г) sin a.
5. Упростите выражение
1 - (1 - sin a)(l + sin a)
tg a cos a
а) -cos a; 6) sin2 a; в) cos a; r) sin a.
6. Упростите выражение
cos (a + 125°)
sin (a + 35°)
а)1; в)-1;
б) tg (a + 35); r) -ctg (a + 55°).
7. Упростите выражение
cos (a - P) - cos (a + P).
2 2
а) 2cos a cos P; в) sin a sin P;
б) 2sin a sin P; r) -2sin a sin p.
sin 4 a
8. Сократите
1
cos 3a + cos a
б) 2 cos a; г) 2 sin a.

Тесты
Алгебра. 7—9 классы
343
9. Упростите выражение
2
sin 2а(1 + ctg а)
1 + соз 2а
в) tg а;
г) ctg а.
а) -
sin а соз а
б) 5 sin 2а;
10. Дано: cos а = -1. Какая из
перечисленных ниже формул верна?
а) а = 2ял; в) а = я + 2ял;
б) а = я + ял;
ч Зя ,
г) а = -о- + яп.
6. В арифметической прогрессии аг = 2, а9 = 14.
Найдите сумму всех ее членов от а5 до а9
включительно.
а) 47; 6)55; в) 56,5; г) 45,5.
7. Упростите выражение
, -1,5.3 о,5 1
_4 0,5
1 " (а 4)
а)
1 - а
в)-
1 -I- а
6) —
г)
1 - а
Тест 9
Итоговый 2
1. Найдите значение выражения
-10-3,5: [\\ -5| ).
а)8|; 6)2^; в)-9^; г)-10^(
2. Упростите выражение
Л - Л + (75 - I)2
Л (Л - i)(V7 + 1)'
а>~Т' б)—з—
3. Решите уравнение
2 4
B)f; г) 75.
= 1.
* х + 3
а)3;-2; б)-6;1; в) 2;-3; г)6;-1.
4. Решите неравенство
х х + 1
<1.
а) (-оо; -2) U (11; +оо ]; в) (-1J ; 2 );
б) (-°°;-l| ]и(2; +оо); Г) (-2; lg ).
5. Решите систему уравнений
2 2-с
х -у =15,
*-!/ = 5.
а)(4;1);
б)(-4;1);
в) (4; -1); (-4; 1);
г)(4;-1).
У = f(x)
8. Укажите формулу,
которая задает функцию
У-Пх).
а) у = х + 6л: + 8;
б) I/ = -х2 + 6* + 8;
в) у = -х2 - 6х - 8;
г) I/ = -л: + 6х - 8.
9. От города до турбазы туристы шли на
байдарке и прошли 16 км. Вернулись обратно на
автобусе по шоссе, проехав 20 км. Скорость
автобуса на 22 км/ч больше скорости байдарки.
Найдите скорость автобуса, если на обратный путь
туристы затратили на 1 ч 20 мин меньше, чем на
путь до турбазы.
а) 34 км/ч; в) 35 км/ч;.
б) 30 км/ч; г) 28 км/ч.
10. Может ли выполняться равенство
sin (а + р) = sin (а - р)?
Если может, то при каких условиях?
а) Может, при условии, что Р = 0;
б) может, при условии, что sin Р = 0;
в) может, при условии, что sin Р = 0 или cos а =
= 0;
г) нет, не может.
Тест 10
Итоговый 3
1. Найдите значение выражения
а) -50;
2 - 5/1
Ъп + 1
б)-6;
при п = -0,4.
в) 50;
г) 6.

344
Тесты
Алгебра. 7—9 классы
2. Упростите выражение
9. Решите систему
а
1(а - &)2
а + о
а — о
&
2
а -
3. Решите систему
•)(-»;-!);
»(:
-00.-1V
f 2j'
f4x +
l-i-
\ . 4а2 + 4Ь2
b2J ' а2 - 2а& + Ь
n) *
"' 4а + 4&'
г) 4а + 4Ь.
2*>0.
в)-|;-1;
г)-1.
4. Решите систему неравенств
х2 - 9<0,
х + 2х>0.
a)(-3;-2)U(0;3); в)(-2;3);
б) (-2; 0); г) (-оо; -3) U (3; +оо).
5. Решите уравнение
2х - 3
-2
1-х
л: " х + 4
а) -6;3; б) 4;-3; в) 6;-2; г) 2,5;-4,5.
6. Найдите сумму первых пяти членов
геометрической прогрессии, если Ъх = -3; Ь2 = -1,5.
a)-5j|; б)-б||; в)-8,25; г)-12.
7. Вычислите значение выражения 2sin а + 1,
если
cos ос=7о и "2"<а< 2я.
ч 011 ЛЧ 11 Ч125 ч 1
а)~213; б)"13; в)126; г)"1з-
8. 9 « А> класс сделал 54 скворечника, а 9 «Б» —
40 скворечников, причем 9 «А» класс работал
на 2 дня больше, чем 9 «Б», а 9 «Б» делал на
1 скворечник в день больше, чем 9 «А».
Сколько скворечников в день делали 9 «А» и 9 «Б»
вместе?
а) 16; 6)19; в) 18; г) 21.
2 2 2
У - х - а ,
а
при условии у + * = 18иа>0.
а)(15;3); в) (24;-6);
б) (-4; 20); г) (8; 10).
10. Графики функций у = ах иу = Ь-х
пересекаются в точке с координатами (2; 3). Найдите
координаты другой точки пересечения графиков.
а>(~8§;8§); в)(-3;8);
б)(4;1); г) (-1,5; 6,5).
ОТВЕТЫ
7 класс
т—1
Задание
Ответ
1
г
2
а
3
г
4
в
5
в
6
б
7
а
8
г
9
б
10
а
Т—2
Задание
Ответ
1
а
2
в
3
б
4
в
5
г
6
а
7
г
8
б
9
в
10
г
Т—3
Задание
Ответ
1
б
2
г
3
г
4
в
5
а
6
в
7
б
8
а
9
г
10
г
Т—4
Задание
Ответ
1
а
2
в
3
г
4
б
5
в
6
г
7
а
8
б
9
в
10
г
Т—5
Задание
Ответ
1
в
2
б
3
а
4
в
5
а
6
б
7
в
8
б
9
г
10
б
Т—6
Задание
Ответ
1
г
2
б
3
в
4
в
5
а
6
г
7
б
8
а
9
в
10
б

Тесты
Алгебра. 7—9 классы
345
8 класс
Задание
Ответ
1
а
2
г
3
б
Г—7
4
в
5
г
6
а
7
г
8
б
9
в
10 1
б
Т—8
Задание
Ответ
1
в
2
г
3
б
4
б
5
а
6
в
7
а
8
г
9
б
10
г
Т—9
Задание
Ответ
1
г
2
в
3
а
4
б
5
г
6
а
7
в
8
в
9
а
10
б
Т—10
Задание
Ответ
1
в
2
а
3
в
4
г
5
г
6
б
7
а
8
в
9
б
10
г
Т—6
Задание
Ответ
1
в
2
б
3
б
Г—]
4
г
L
5
в
6
а
7
в
8
б
9
г
10
г
Т—2
Задание
Ответ
1
г
3
а
3
б
4
г
5
б
6
а
7
б
8
в
9
б
10
г
Т—3
Задание
Ответ
1
б
2
г
3
а
4
г
5
б
6
в
7
г
8
а
9
в
10
г
Т—4
Задание
Ответ
1
а
2
в
3
а
4
б.
5
г
6
г
7
б
8
в
9
а
10
б
Т—5
Задание
Ответ
1
г
2
в
3
а
4
в
5
б
6
б
7
а
8
г
9
а
10
г
)9 класс
т—1
Задание
Ответ
1
в
2
б
3
а
4
г
5
а
6
в
7
б
8
б
9
г
10
в
Т—7
Задание
Ответ
1
б
2
б
3
в
4
г
5
в
6
а
7
г
8
б
9
б
10
б
Т—8
Задание
Ответ
1
б
2
б
3
а
4
г
5
в
6
в
7
в
8
б
9
г
10
г
Т—9
Задание
Ответ
1
б
2
г
3
в
4
г
5
а
6
б
7
б
8
г
9
в
10
а
Т—10
Задание
Ответ
1
а
2
б
3
в
4
б
5
а
6
в
7
б
8
г
9
г
10
в
Задание
Ответ
1
б
2
г
3
б
4
в
5
в
6
а
7
г
8
б
»■ ■
9
а
10
в
Т—2
Задание
Ответ
1
а
2
в
3
а
4
г
5
в
6
б
7
б
8
г
9
в
10
а
Т—3
Задание
Ответ
1
г
2
в
3
б
4
г
5
а
6
б
7
в
8
в
9
а
10
б
Т—4
Задание
Ответ
1
в
2
б
3
в
4
в
5
г
6
б
7
в
8
а
9
б
10
г

346
Тесты
Алгебра. 7—9 классы
Задание
Ответ
1
б
2
б
3
г
Т—5
4
в
5
г
6
а
7
б
8
г
9
в
10
б
Т—6
Задание
Ответ
1
а
2
г
3
г
4
б
5
в
6
б
7
а
8
г
9
б
10
в
Т—7
Задание
Ответ
1
г
2
б
3
в
4
в
5
г
6
а
7
б
8
а
9
в
10
г
Т—8
Задание
Ответ
1
г
2
б
3
б
4
б
5
г
6
в
7
б
8
г
9
а
10
в
Т—9
Задание
Ответ
1
в
2
а
3
б
4
в
5
г
6
б
7
б
8
в
9
б
10
в
Т—10
Задание
Ответ
1
б
2
в
3
г
4
а
5
в
6
а
7
б
8
б
9
г
10
а

Алгебра и начала анализа. 10—11 классы
10 КЛАСС
Тест 1
Тригонометрические тождества
7Rtt
1. Запишите cos -г- с помощью
наименьшего положительного числа:
ч . Я -v . Я v я v я
a) sin j-r ; б) sin tq ; в) cos jg ; г) cos jz •
2. Сравните с нулем выражения
sin -g- , cos 5 и tg 1,6л.
Выберите правильную серию ответов:
а)--+; 6) + + -; в)- + -; г)- + +.
3. Найдите значение выражения
5sin -т- - 3cos « + tgrc.
а) 2,5; 6)1,25; в) 1,75; г) 1,5.
4. Упростите выражение
8Ш(Я + (Х)С08(Я - а)
ГЗя
ct*(y" а)
2 2 2
a) cos а; б) -sin а; в) sin а; г) cos а.
5. Дано: cos а = -г= и « < ос < я.
Найдите sin(« -а].
а)-
5^3 + 12
26 ;
в)
б)
5УЗ - 12
26
г)-
5^3 + 8
26 ;
5л/3 - 8
26
6. Упростите выражение
. 4 4
sin а - cos а
sin а cos а
a)2tg2a; 6)-2ctg2a; в) 2ctg 2а; r)-2tg2a.
7. Оцените значение выражения
2 - 3sin2 a.
а) [-2; 4]; б)[-1;5]; в)[-1;2]; г)[-5;1].
8. Найдите значение-выражения
sin a - 3cos a
2sin a + 5cos a
, если tg a = -2.
7 2
a)-g; 6)-3; B)g; r)-5.
9. Преобразуйте sin x - cos x в выражение
вида
A • sin (x + a).
а) 72 sinfjc + «J; в)-л/2 sinfx + т);
б) 72 sin(x - j); г) ^ sin(* + i)-
10. Найдите а, если
cos 51° - cos a = 2 sin 17° • sin 68°.
a) a = 85; 6) a = -85; в) a =136; r)a = 34.
Тест 2
Свойства функций
1. Найдите область определения функции
а) [4; +оо); • в) (-оо; -4] и [4; +°о);
б) [-4; 4]; г)(-оо;4].
2. Найдите область значений функции
у = -х + Ьх - 9.
а)[-2|;+оо) B)(-oo;-8j];
б)(-оо;-2|]; r)[lb+oo).
3. Что можно сказать о функции
.. ч х - 2 sin х
fix) g :
3cos х + х
а) четная; в) ни четная, ни нечетная;
б) нечетная; г) периодическая?
4. Найдите «нули» функции
а)0;7§; б)-4; 4; в) 78 ; г)-2^2; 2^2.

348
Тесты
Алгебра и начала анализа. 10—11 классы
5. При каких значениях х f(x) < 0, если f(x) =
_3 - 2х
4х + 1
а)(-°°;|); в)(-0,25;1,5);
6)f-oo;4)ufl,5;+oo) г) g ; j] .
6. Найдите промежуток (промежутки)
убывания функции f(x) = л/9 - 6х Н- лг2.
а) [3; +оо); в) (-оо; 3];
б)(-оо;+оо); г)[-3;3].
7. Укажите график функции у =
х + 2
-1.
а)
-2
"Л
б)
2 х
-2
-1
\У
ii
-1
8. График какой
функции изображен на
рисунке? *
а) у = \х2 - 2х - 3|
6)z/ = *2-2|*|-3
в)у=ф2-2*-3|
г) у = х2 + 2|х| - 3
9. Дана функция f(x) = х - 2ах + 5.
Известно, что /(-1) = -3. Найдите /(-2).
а) 10; б)-12; в) -17; г)-5.
10. Найдите «нули» функции
/(х) = х3-х2-17х-15.
Запишите их сумму,
а) 5; б)-3; в) 8; г) 1.
Тест 3
Свойства и графики
тригонометрических функций
1. Найдите область значений функции
у = 2 - 3sin х.
а)[-1;5]; б) [-4; 2]; в)[-5;1]; г) [-2; 4].
2. Найдите «нули» функции у = gcos 2х на
промежутке Г-5 ; 2я| и запишите их сумму,
а) 1,5 тс; б) 2я; в)3,75я; г) 2,25 я.
3. Для функции у = sin [ | - g J найдите
точку минимума на промежутке [0; 4л].
ч Юте ч 5я
в)-з~; г)т.
а) у; б)^;
4. Найдите промежутки убывания для функции
y = cos(l +lx\
ч Г я , 2 тс , 2 ■] _
аН""2 3 КП; 2 3 ^J' П е ;
б) Г-| + Зпп; к + Зяд 1, л € Z;
в) Г| + Зпп; 2я + Зяп ], п е Z;
ч / я , 2 2к , 2 \ _
5. Расположите в порядке возрастания числа
sin 1, sin (-5) и cos 1.
а) sin (-5), sin 1, cos 1; в) sin (-5), cos 1, sin 1;
б) sin 1, sin (-5), cos 1; r) cos 1, sin 1, sin (-5).
6. По графику некоторой функции запишите
формулу, которой она задана.
a)i/ = sin(2x-gl;
б) 1/= sin [2* + у!; _т
в) у = sin (х + ^J;
г) i/ = sing -£).
Ь
L-1
у - sin (kx + ф)
7. Найдите значение выражения
arcsin
а) 3,5;
arctg -£-
б) -4,5 я; в) -5,5; г) -3,5.

Тесты
Алгебра и начала анализа. 10—11 классы
349
8. Вычислите cos (arcsin (-0,6)).
а)-0,36; 6)0,6; в)-0,8; г) 0,8.
9. Найдите arcsin х, если arccos х = г .
о
а) у; б) 0,3л; в) 0,8я; r)-g.
10. Найдите сумму координат точки
пересечения графиков функций
я
у — arccos х и у = ~ + х-
2» "'х' °' 2
а) 5; 6)1; в) 5+1; г)я+1.
Тест 4
Простейшие тригонометрические
уравнения и неравенства
1. Решите уравнение
cos 0,5* = -1.
а) х = Зя + 4ял, л е Z; в) х = тс + 2ял, пе Z;
б) х = 2я + 4ял, пе Z;r)x= ъ + "5" * Л € ^'
2. Решите уравнение
sin (4*-I) = i.
а) л: = (-1) • g + т ;
б) х = (-1) • 24 + 12 + Т ' п е Z;
\ / 1 \Л я ял
в)* = (-1) -ё+Т;
v я , ял „
г) х = g +Y»neZ.
3. Решите уравнение tg 2х = -J3 и найдите
сумму его корней, принадлежащих промежутку
НИ-
а)1,5я; б)у» в)*5 г) з •
4. Решите уравнение sin х = sin 3.
а) х = 3;
б) л: = (-1)71 • arcsin (я - 3) + яд, пе Z;
в) х = (-1)" • (я - 3) + ял, п € Z;
г) х = 3 + 2ял, пе Z.
5. Решите неравенство
sin х < 5 .
«hi)'
б) (g + ял; у + ял j, л € Z;
в) [g + 2ял; -т? + 2ял\пе Z;
г) (-£ + 2ял; -g^ + 2ял\пе Z.
6. Решите неравенство
cos 2х > 0.
а) (ял; 5 + тел ], л е Z;
б) [ - j + ял; т + тел j, л € Z;
в) f-g + 2ял; я + 2ял ], л g Z;
г) Г-j + 2ял; | + 2ял\ л е Z.
7. Решите неравенство
ч/'ТС.Я я . я Л «-
a)("l2+2n;4+2n>neZ;
6)("6+2n;3+2n>nGZ;
в) Г-g + ял; g + ял ], л € Z;
г)(-00;5+?л),Л€^ '
8. Решите систему
cos х - «2»
sin х > 0
и найдите сумму ее решений, принадлежащих
промежутку [0; 4я].
5я
10я
13я
а) 2,5я; 6) -s-; в) -s- ; г) -s-
3
3
6
9. Решите уравнение
sin 2х J-x2 + 2х + 3 = 0
и найдите сумму его корней
4 ' "» -> 2
а)3,5я + 2; 6)^+2; в) j + 2; г)-^-2.

350
Тесты
Алгебра и начала анализа. 10—11 классы
10. Решите неравенство
sin х > cos х.
В ответе укажите сумму натуральных чисел,
меньших 10, удовлетворяющих данному
неравенству.
а) 17; 6)30; в) 6; г) 23.
Тест 5
Тригонометрические уравнения
и неравенства
1. Решите уравнение
2cos х = 3sin х.
а) х = « + 2ял, л е Z;
б)х = (-1)п • g + ял, л е Z;
в) х = (-1) • g + яп, пе Z;
г) х = (-1)я+1 • 5 + пп> пе Z.
2. Решите уравнение
tg* + ctg* = 2.
а) х = т + ял, л е Z;
б) х = j + 2ял;
в) л: = ± j + ял, пе Z;
r)x = -j Н-ял, ле Z.
3. Решите уравнение
cos 2х = 2sinx + 1.
Запишите сумму его корней,
принадлежащих промежутку [0; 2я].
а) у; б)^; в)4,5я; г) 2я.
4. Решите уравнение
sin х + sin Ъх = 0,
найдите его наименьший положительный
корень.
а)ё; б)д; в)5; г)^
5. Решите уравнение
2 2
3sin х + sin х cos х = 2cos х.
а)
б)
х e I + ЯЛ*
л, ft е Z;
х = - arctg « = я£,
JC = ~т + ЯЛ,
х = arctg « + nk,
пу k е Z\
в)х = 2 + 2ял, лег;
г)
х - д + ял,
Lx = arctg 1,5 + nk
п, ke Z.
6. Решите уравнение
sin Зх • sin 2х = 1.
а) х = g + г ял; б) лг = ял; в) х = 2ял; г) 0 .
7. Решите уравнение
2
1 - 4sin х = 0.
Найдите сумму его корней, принадлежащих
промежутку [0; 2я].
7я
а)
6 '
б) 4я;
в) 2л;
ч 5
г) g п.
8. Решите систему уравнений
[3sin х - 2cos z/ = -2,
4cos z/ - sin x = -1
и найдите наименьшее значение произведения
*о */о» гДе *о и Уо — положительные числа,
удовлетворяющие данной системе.
г2 5 2 v 2
a) g ; б) з я ; в) я ;
9. Решите неравенство
2
r)gic.
a) I -g + ял; л + яп
3 - 4cos х> 0.
J, л е Z;
5я Л
+ ял; -g- + ял 1, л € Z;
в) [ ? + 2пп; -т- + 2пп J, п е Z;
г) (| + 2пп; у + 2кп\ ,neZ.

Тесты
Алгебра и начала анализа. 10—11 классы
351
10. Решите неравенство
cos х л/4 - х2 < 0.
а) (-2; 2); в)0;
б) (-тс; -2) U (2; тс); г) [-2; - fj U (§; г]
Тест 6
Производная.
Техника дифференцирования
1. Найдите производную функции
№=£ -0,5*2-3* + 2,
вычислите ее значение при х = -1.
а)-2,5; 6)1,5; в) -1,5; г) 2,5.
2. Найдите f (*)> если /(*) = х*/х.
a)ife; б)2-£; B)irx; г)1'5^
3. Найдите производную функции
3 + 2х
£(*) =
а)-
б)
13
(х - 5)2!
8
х - 5
в)
г)
(х - 5)2
1-х
(х - 5)2 ' (х - 5)2 '
4. Найдите значение /'(0,5), если
3
№
5 - 4х'
а)3; б)|; в) 2?; г) 2.
5. Для функции f(x) = 3sin х вычислите
п-Ь-
а) 6; б)-3; в)-1,5; г) 0,5.
6. f{x) = {2x-Z)Jx. Найдите /'(1) + /(!)•
а) 15; 6)7,5; в) 2,75; г) 0,5.
g
7. /(*) = 4х 4- - . Решите уравнение
/'(*) = о.
а)0;2; в)-72; 72;
б) 72 ; г) -2; 2.
8. £(х) = (х - 3)(х + 2) . Решите неравенство
£'(*) < 0.
a)(-l|;2); в)(-2;3);
б) (-2; l|); г)(-0,5;1).
9. При каких значениях х функция
f(x) = V*4 - 2х2 + 1 не дифференцируема?
а)1; 6)0; в)-1;1; г)0.
10. и(х) = 7х, v(x) = Зх - 2, /(*) = u(v(x)).
Решите уравнение
f'(x) = 0,375.
а) 12; 6)8,5; в) 2,5; г) 6.
Тест 7
Метод интервалов. Геометрический
и физический смысл производной
1. Точка движется по координатной прямой
по закону
s(t) = t2-6t + 3.
Найдите vcp на промежутке [4; 6].
а)3; 6)5; в) 7,5; г) 10.
2. Точка движется по координатной прямой
по закону
&(*) = -*2 + 10* - 7.
Найдите vMrH(3).
а)-5; 6)14; в) 19; г) 4.
3. Вращение точки вокруг оси совершается
по закону
<р(*) = -*3 + 12*2+7*,
где <p(f) — угол в радианах, t — время в
секундах. Известно, что ускорение а в некоторый мо-
_ рад
мент времени t равно 9 ^-g-.
с
Найдите этот момент времени t.
а) 5; 6)4; в) 2,5; г) 3,5.
4. Найдите уравнение касательной к графику
функции
f(x) = -х2 - 4* + 2
в точке с абсциссой х0 — -1.
а) у = -2х - 3; в) у = -2* + 3;
6)z/ = 2x-l; r)z/ = 2x + 3.

352
Тесты
Алгебра и начала анализа. 10—11 классы
5. К графику функции у =
проведены
х + 2
две параллельные касательные, одна из
которых проходит через точку графика с абсциссой
х0 = -1. Найдите абсциссу точки, в которой другая
касательная касается графика данной функции,
а)-2; 6)2; в) 1; г)-3.
6. Напишите уравнение касательной к
графику функции
f(x) = х2 - 4* + 5,
если эта касательная проходит через точку (0; 4)
и абсцисса точки касания положительна.
а) у = 2х + 4; в) у = -4х + 4;
б) у = -2х + 4; г) у = Ах - 3.
7. Решите неравенство
- >4-х.
х
а) (0; 1) U (3; +оо); в) (-оо; -1) и (1; 3);
б) (-оо; 0) и (1; 3); г) (-оо; 1) и (3; +оо).
8. Решите неравенство
(х2 - 9)У2 - х
2х + 3
найдите произведение целых чисел,
удовлетворяющих данному неравенству.
а)-6; 6)6; в) 12; г) 0.
9. При каких значениях а все
положительные числа являются решениями неравенства
х3 - ах + х > 0?
а)а<0; б)а>1; в)а<1; г)а>0.
10. Прямая у = х - 2 касается графика
функции у = /(*) в точке х0 = -1. Найдите /(-1).
а)1; б)-3; в)-2; г) 2.
Тест 8
'0,
Исследование функций
с помощью производной
1. Дана функция
х3 х2
/(*) = -§ +| + 2*-3.
Найдите ее критические точки.
а)2;-1; б) 1;-2; в)-3;1; г) -2; 3.
2. Найдите точки экстремума функции
/(х) = 0,5х4-2*3.
а)*,
max
= 3> *min " 0; в) xmhi - 3, xmax = 0;
= 3; г) 0.
б)*шш = 3;
3. Дан график функции у = /(*). Какие из
утверждений верные:
1) а, с — критические
точки;
2) а, с — точки
экстремума;
3) на (*; t) fix) —
дифференцируемая ;
4) [а, с] — промежуток
убывания функции;
Ь)1 — точка максимума;
6) max f(x) - л;
[k;t]
7)*шах=а?
а) 2, 3, 4, 6, 7; в) 3, 4, 5, 6, 7;
6)1,2,4,6,7; г) 1,2, 3,4, 5, 6, 7.
4. Найдите промежутки убывания функции
f(x) = х3 - 6х2 + 5.
а)[-4;0]; в)[0;4];
б) (-оо; 0]; [4; +оо); г) 0 .
5. Найдите промежутки возрастания функции
Зх + 2
«*) =
Г2
1 - 4х
а) (-оо; 0,25); (J ; +оо ); в) (-0,25; 0,25);
б) (-оо; 0,25); (0,25;+оо); г)0.
6. Укажите график функции
fix) = х - х - х.

Тесты
Алгебра и начала анализа. 10—11 классы
353
7. Укажите формулу, которой задана
функция у = f(x).
аЖ*)=-*2-2*-1;
б)Л*)--
в)Л*) =
г)/(*) =
х- Г
1
(*-1)2;
1
2 -1
8. Найдите экстремумы функции
f(x) = (6-3x)Jc.
а) 2; 6)1,5; в) \; г)4^.
9. При каком значении а функция
f(x) = xja - jc2
имеет экстремум в точках jc = -2hjc = 2?
а) 2; 6)12; в) 8; г) 4.
10. Укажите наименьшее целое число,
удовлетворяющее неравенству
2х - sin х > 0.
а)0; б)-1; в) 2; г) 1.
Тест 9
Наибольшее и наименьшее
значения функции
1. Найдите наибольшее значение функции
f(x) = xs - 2х2 + х - 3
на промежутке Г g ; 21.
1 94
a)i; 6)1; в)-1; r)-2g.
3 2
2. При каком значении х функция у = х - х
на промежутке [0,5; 1] принимает наименьшее
значение?
а) 0,5; б)|; в) 1; г)0.
о
3. Площадь прямоугольника равна 81 см .
Найдите наименьший возможный периметр
этого прямоугольника.
а) 54 см; б) 18 см; в) 72 см; г) 36 см.
4. Периметр равнобедренного треугольника
равен 20 см. При каком значении боковой
стороны площадь треугольника наибольшая?
см.
а) 7,5 см; 6) 6« см; в) 8 см; г) 6
5. Наименьшее значение функции
f(x) = х +bx + c
равно 1, а значение с на 25% больше Ь. Найдите
положительное значение Ъ.
а) Ь = 2 или Ъ = 3; в) Ъ = 1 или Ъ = 4;
б)&=1; г)& = 2.
6. Найдите область значений функции
Л*) = х2*_ г » гДе ~°»5 < х^ § '
3 2i
a)L 8;3_|;
в) [-1,5; 1];
. г б 3-1
Г>Гб;4_|-
7. Найдите наименьшее значение функции
±й ч sin Зх г4я "|
дх) = —g-r- на промежутке -д-; л .
8. Дана функция
f(x) = xjx + 3.
Найдите ab, где min /(а) = Ь.
[-3; +оо)
а) 2; б) -4; в) -2;
9. Решите уравнение
х2 - 3
х - 2
а)1; 6)3;
10. Дана функция
/(*) =
Найдите а, если
max /(*) = -2,5,
(-оо; а]
а<-1.
а)-3,5; б)-2,5; в)-3;
г)-1.
г) 4.
= 2cos (х - 3) + 4.
в) 0; г) 0.
х2 + 1
г)-2.
12-1019

354
Тесты
Алгебра и начала анализа. 10—11 классы
Тест 10
Итоговый
1. Упростите выражение
sin 2а - 2со8 а
1 + соз 2а
8. Укажите график функции f(x) = -х + Зле.
-tgec.
ч ! *ч 1 ч 1 ч 1
а) —— ; б) ; в) ; г) —:— .
' sin ос' ' cos а ' ' cos а' ' sin а
2. Решите уравнение 4cos х + 4sin х - 1 = 0.
В ответе укажите наименьший положительный
его корень.
а)у; б)ё; в)--, г) у.
х 1
3. Решите неравенство cos о > ~5 *
а) (-5 + 2лл; g + 2кп ), n е Z;
4 4
б) -= + 4яп < х < « я + 4яп, neZ;
2 2
в) -= п + 2ял < л: < « я + 2ял, пе Z;
г)-= + 4яп < х < « + 4яп, пе Z.
а ъ (* ~ 2)2л/5 - х. л _
4. Решите неравенство тг > 0. В от-
х2 - 36
вете укажите сумму наибольшего целого
отрицательного решения и наименьшего
положительного решения.
а) 2; б)-5; в)-4; г) 4.
5. Вычислите /'(s) Для Функции
f(x) = (2х - 5) sin Зх.
а) 1,5; б)-3; в)-2; г)-1,5.
2
6. К графику функции f(x) = х - 4х
проведена касательная в точке М (1; -3). Найдите
абсциссу точки пересечения касательной с осью Ох.
а)-1,5; 6)0,5; в)-0,5; г) 1,5.
7. Укажите целые числа, принадлежащие
промежутку (промежуткам) возрастания функ-
ti ч * + 1
а)-2;-1; б)-1;0; в)-1;1; г)-2;1.
а)
,
/ '
'-10
-2
L 2
* i
г "
№
X
б)\
2ГЛ
1-1
01 \
--2 '
X
в)
■ / •
1-2
\У
0
1 2/
9. Найдите наименьшее значение функции
4
Л*) = —~\ + * на промежутке [""2; 0].
а)-4; б)-3; в)-з|; г)-3,5.
10. Число 24 представьте в виде суммы двух
положительных слагаемых, таких, что
произведение их квадратов принимает наибольшее
значение.
а) 15 и 9; б) 4 и 20; в) 12 и 12; г) 8 и 16.
11 КЛАСС
Тест 1
Первообразная
1. Дана функция
/(x)=g -2х2-12х + 5.
Решите уравнение f'(x) = 0.
а) -3; 4; б) 3; -4; в) -2; 6; г) 2; -6.
2. Найдите общий вид первообразных F(x)
для функции
х2
f(x) = о "~ sin 2х.
а
X3
а) F(x) =| + cos 2х + С;
л\ г»/ ч *3 . cos 2х п
б) F(*) - ^ + —g— + С;

Тесты
Алгебра и начала анализа. 10—11 классы
355
r)F(x)=± -\cosx + C.
3. Найдите общий вид первообразных для
функции
f(x) = 72*- 1
на промежутке (0,5; +оо).
\ г./ ч (2х - 1)л/2* - 1 , _
a) F(x) = ■ ^ + С;
6)J(x)=4(2x-13)^T1+C;
*)F(x) =
t)F(x) =
3j2x - 1
4
372* - 1
4. Для функции
/(*) =
+ С;
+ С.
6
(4 - З*)2
найдите ее первообразную, если f (1,5) = 1.
a)f(*) =
б) *"(*) =
b)F(*) =
г)ад =
(Зх - 4)2
2
Зх - 4
2 ,
4 - Зх '
6
-15;
(4 - Зх)3
+ 3.
5./(x) = 3x2-|-5,f(-2) = 5.
Найдите F(-l).
а)-8,25; 6)10,75; в)-10,25; г) 7,75.
6. f{x) = cos х; Fix) + С — ее первообразная,
Решите уравнение gix) = 0.
а) 5 + кп> пе Z; в) -= + 2ял, п е Z;
б) 5 + 2тт, пе Z; г) -= + ял, n е Z.
7. Прямая z/ = 2х + а касается графика
функции
/(х) = -х2 + 6х.
Найдите значение а.
а) а = 6; б) а = 4; в) а = 2; г) а = 8.
о. дана
л/3 + X
Укажите график функции
у = Fix), если Fi-З) = 0.
,^^^ i
«) ^N
0
iy '
^2л/3 <*) 2 Д
3 х -3 0
i У
X
9. Точка движется по координатной прямой с
ускорением ait) = 2t + 1. Известно, что i>(2) = 4 и
s(3) = 2,5. Найдите s(6).
а) 29; 6)60; в) 73; г) 45.
10. fix) = -2х + 3, FiO) = 4. Решите систему
неравенств
Г F'ix) < 0,
I Fix) < 0.
а) (-4; 1,5); в) 0 ;
б)(-1; 1,5); г) (1,5; 4).
Тест 2
Интеграл.
Площадь криволинейной трапеции
2
f 2
1. Вычислите J (х - 6х + 9) dx.
-1
а) 27; 6)24; в) 18; г) 21.
2. Найдите f 5 dx.
J (2х - l)2
а) 1,5;
б)|;
в)-§;
г) интеграл не существует.

356
Тесты
Алгебра и начала анализа. 10—11 классы
371
3. Вычислите J cos 0,5* dx.
5
3*
а) -2; б) 2; в) -3;
г)3.
4. Вычислите J J2x + 1 dx.
о
а)в|; 6)9g; в) 7^;
г) 7
6
5. При каком значении а выполняется
равенство
а
а) а =
3'
d* = -3?
в) а = 2 или а = -5 »
б) а = 2 « или а = -2; г) а = -3.
6. Вычислите площадь фигуры, ограничен-
ной графиком функции у = -х + 4х - 3 и
прямой у = 0.
a)lj;
6)1,5; в)ф г)1±,
7. Вычислите площадь фигуры, ограничен-
2
ной графиком функции у = х +4*+ 10,
касательной к параболе в точке дс0 = -3и прямой х = 0.
,2
а) 9,5;
б) 9} 5
в) 9;
г) 8|
8. Найдите площадь фигуры, ограниченной
графиками функций у = sin х и z/ = cos х и
прямыми х = т и х = я.
а) 72;
6)2;
в) 2^2; г) 72 +1.
9. Найдите J f(x)dx. у = f(x)
-4а
a) 8па ;
б)яа ;
2
в)4яа ;
г) 2ка
\У
[ 2а
-4а -2а
10. График функции /(х) = Ах пересекает
график своей первообразной F(x) в двух точках,
одна из которых (-1; -4). Найдите площадь
фигуры, ограниченной графиками f(x) и F(x).
а) 21; 6)2l|; в) 21,5; r)2l|.
Тест 3
Корень и-й степени.
Иррациональные уравнения
и неравенства
1. Вычислите
474 - 273 ifi + 273
7о^
а) 8; 6)4; в) \; г) 2.
2. Расположите в порядке возрастания числа
37б , V30 и VlO .
а) Vio, Ve, 67зо; в) 67зо, Vio, V5;
б) Ve, 67зо, Vio; г) V5, Vio, 67зо.
3. Упростите
1 V5 + il
.V5- i
7S
eJP
л/а - 247а + 1
a' а2 '°' а ' В' а ,Г' а2
4. Решите уравнение
J3 - х = 1 - х.
а)-2;1; 6)2; в)2;-1; г)-1.
5. Решите уравнение
Jx + 4 - Jx - 1 = V* - 4.
а)12;-3; 6)5;-4g; в) 5;
6. Решите уравнение
г) 12.
л/1,5 sin х = cos х.
a)jc = -g + 2ял, Л€ Z;
б) х = ^ + 2ял, л € Z;
в) х = (-1)л • g + ял, л € Z;
г)х-(-1)я+1-g +nn9neZ.
7. Решите неравенство
л/3 + jc > Vx2 - 4х + 8.
а)[1;3]; в) [-3; 1] U [3; 5);
б)[-3;0) U[l;3]; г) (0; 1] U [3;5).

Тесты
Алгебра и начала анализа. 10—11 классы
357
8. Решите неравенство
Jx <х-2.
а)(2;+оо); б)(4;+оо); в) [0; 2); г)[0;4).
9. При каких значениях а решением
неравенства Jx - 2 < 3 - а является промежуток [2; 18)?
а) (-1; 7); б) -1; 7; в) -1; г) (-оо; 7).
10. При каком значении а площадь фигуры»
ограниченной графиками функций у = Jx и у =
= ах , равна 2«?
а)а = 1; б)а=^; в)а=^; г)а=^.
Тест 4
Степень с рациональным
показателем. Показательные
уравнения и неравенства
1. Вычислите 42>б-(|у1,6 + (j)3'5 (0,8)3'5.
a)33g; 6)6; в) 5,5; r)9g.
2. Дана функция /(*) = а*.
Известно, что /(-1,5) = 8. Найдите /(0,5).
а>^:
б) 0,25; в) 2;
г) 0,5.
Ы— 1
3. Укажите график функции у = 0,4W .
4. Решите уравнение: 5 • 2
1
а)-1;
6)4;
в)
х + 3-4-2х'1 = 9,5.
' г)-2.
5. Решите уравнение
1 = ±-3
9х 3х
Запишите сумму корней.
а) 2; б)-1; в) 4;
6. Решите неравенство
О.бТзР > -^
г)-2.
а) (-оо; -0,5);
2
в)(|;+оо)
г) (0,5; +оо).
б)(-оо;|);
7. Решите уравнение
7 • 49* + 5 • 14* = 2 • 4х.
а) 0,5; б)-0,5; в) 1; г)-1.
8. Решите неравенство 2* - 2 * > 2.
в) (-со; -1) и (2; +оо);
г)(-оо;-2)и(1;+оо).
а) (2; +оо);
б)(-оо;2);
9. Решите уравнения
Запишите сумму корней этих уравнений,
а) 2,08; 6)2,8; в) 4,008; г) 4,8.
10. Найдите последнюю цифру степени 99°.
а)1; 6)3; в) 7; г) 9.
г)
1
0,4
"*5
^
>У
-1!
^^*»^-_*
-1
Тест 5
Итоговый 1
1. Найдите общий вид первообразных F(x)
для функции
a)F(x)=* -х3-Зх2 + 2х + С;
6)F(x) = -±-f -3*2 + 2* + С;
b)F(x)= \-f -Зх2 + 2х + С;
г) F(x) = -j - х3 - Зх2 + 2х + С.

358
Тесты
Алгебра и начала анализа. 10—11 классы
2. Напишите первообразную F(x) для функции
«*>-(! -в) ,если*<4)-
2 1
nl 7?(\-\ — \ -
a)*W 2*-3 ' 3'
6)Р(х)=Щ-3)3 + 1;
П)Л,,-^"3) 5-
в) *(*) 6 3,
г)Д*)=-^--§.
Q _ * 6
3 2
3. Вычислите
3
4*
J 3cos 2* dx.
5
12*
-2
a)-1,75; 6)-2,75; в)-2,25; г)-3,25.
4. Найдите площадь фигуры, ограниченной
графиком функции f(x) = -2х + 4, графиком ее
первообразной F(x) (график функции f(x) —
касательная к графику фзшкции F(x)) и прямой х = 1.
a)2Jj; 6)2,5; в)з|; г) 2?.
5. Решите уравнения
ТзлГ^ =2 -* и J-2x - х2 = л/Зл: + 4.
Запишите сумму их корней.
а) 6; 6)2; в) 0; г) 7,5.
6. Решите неравенство х + 3 > л/3 - х.
а)(-1;+оо); в)(1;3];
б)(-1;3]; г)(-оо;-1).
7. Упростите выражение
(л/а - 1)(1 + Л)
V(a - 1)л/а - 1
а) -7= 7; б) Ja - 1; в) . ; г) 4а - 1
Va - 1 л/а - 1
8. Решите уравнение 16х - 4х =32.
а) 1,5; 6)2,5; в) 2; г) 2,25.
л Л\Х2 - Зх
9. Решите неравенство I « I > 9.
a)(-oo;-2)U(-l;+oo); в) (-2;-1);
б)(-оо;1)и(2;+оо); г)(1;2).
10. При каком значении а (а > 0) корнями
уравнения 0,5х ~ = а*2 ~ х являются числа 1 и -3? За-
з
пишите значение а .
а)1; б)л/2; в)2л/2; г) 8.
Тест 6
Определение логарифма
1. Найдите значение выражения
>2,5
log1255-logV2 g +log2.50»4-
а) -3,5; 6) 4,5;
.)ij;
г) -2\
2. Вычислите 9 °*3
а) 2,5;
б)
4'
в) 1,5; г)1|
3. Решите уравнения
log4 х = -1,5 и logx з = ""2 '
Запишите произведение их корней.
ч8
a)g;
б) l|; в) 9^; г) 8^.
4. Прологарифмируйте по основанию 10
выражение
х =
Vl00a*/l0a
1000 л/а
a)lg* = 0,75+^p; в) lg х = 1,25 - ^ ;
6)lg* = -l,75+^; r)lg* = -0,25-^p.
5. Найдите область определения функции
У =
Лх - X2
log^b - Зх)
з
a)[0;l|)u(l|;5]; в) [0; l|) U (l|; l|]
6)(-oo;0]u(l|;6]; r)[0;l|).

Тесты
Алгебра и начала анализа. 10—11 классы
359
6. Найдите х, если
log3b
log3 х = 2 log3 Va j 0,5.
v Га ^ч Га \ а \ *Jo>
a)*=4/-£-; б)л:=4/^-; в)х = ; г) -*— .
V3b' */9Ь' 4/^' > *M
7. Расположите в порядке убывания
значений выражения:
л ( Я\5 D , . Я ~ Л ТГЛ1^ cos2tc
А = (^cos gJ* ; В =logn sm ^ ; С = (tg gj
з
а) А, С, Б; б)Б,А, С; в) С, Л, Б; г) Б, С, Л.
8. По графику некоторой функции укажите
формулу, которой она
задана.
a)z/ = |log1(2 + x)|;
4
6)y = \logl(2-x)\;
4
B)i/ = |log1(2-Jc)|;
2
r)i/ = |log1(2 + x)|.
2
t^/
0,5
2 3 х
Л997
9. Сколько цифр содержит степень 2 , если
lg2« 0,301?
а) 602; 6)601; в) 600; г) 61.
10. По графику
функции у = logc х. Найдите с.
1
в) а 5;
1
а)*Га;
б)а&;
Тест 7
г) а"
Логарифмические уравнения
и неравенства
1. Решите уравнение
log025(x2-3x) = -l.
Запишите сумму квадратов его корней,
а) 20; 6)15; в) 17; г) 13.
2. Решите уравнение
log0>5 (Зх + 0,5) + log0>5 (х - 2) = -2.
Какие из его корней являются корнями
уравнения?
(х-1)(6х2-11х-10) = 0.
а)1;-§;2,5; б)1;-§; в)-|;2,5; г) 2,5.
\tr т. Ч
3. Решите уравнение (100х) = х .
Запишите сумму его корней.
а) 10,1; 6)11; в) 110; г) 1,1.
4. Решите уравнение
х 1
logx8 ■ log05 g = log9 ^ .
а) 272; 6) \ ; в) J; г) 4.
5. Решите неравенство logl (4- = дм > -l.
а)(|;б); в) (1,5; 6);
6)(l,6;2g); г) (-оо; 1,6).
6. Решите неравенство
log2 х + log0 5 х > 12.
а) (-оо; 1] и [16; +оо); в) [|; 1б];
б) (0; |] U [16; +оо); г) (о; i] U [8; +оо).
7. Решите неравенство
х2 + 2х
>0.
log0 f2(x + 2)
а)(-1;0); в)(-2;+оо);
6) (-2; -1) U (0; +оо); г) (-1; 0) U (0; +оо).
8. Решите неравенство
logx2 _80,8< 0.
а) (3; +оо); в) (-оо; -3) и (3; +оо);
б)(-3;3); г)(0;3).
9. Решите уравнение
cos 4х • lg (-х2 + х + 2) = 0.
Запишите сумму его корней.
а)2тс + 2; 6)1+тс; в)2тс-1; г) 2 + тс.
10. При каком значении m решением
неравенства
log2 (а - Зх) > log2 (х - Зх)
является промежуток (-3; 0)?
а)1; 6)3; в) 9; г) \.

360
Тесты
Алгебра и начала анализа. 10—11 классы
Тест 8
Производная логарифмической
и показательной функций
1. Найдите f'(-3) функции
-±* - 1
№ = е
= * з
+ In (3 - Зх).
1
ft) ю» б) 10 ; в) - 0 ; г) - 0 .
12
12
12
12
2. Найдите первообразную F(x), если J?(0) = 3,
для функции
X
f(x) = e*+ 1
2х + 1
а) ТО-}' + 1п<2* + 1>-1;
6)F(*)=^+ln(2* + 1)-H;
в) f(jc) = 2е2 + 21п (2л; + 1) + 1;
ч rv ч о 2 . 1п (2Х + 1) , -
г) F(x) = 2ez + —*—я + 1-
log32
3. Вычислите
а)
272 + 2
1пЗ '
в)
72 + 1
1пЗ '
б)(272-2)1пЗ; г) Щ^1 ■
4. Найдите уравнение касательной к графику
0 Ъх
функции f(x) = е * в точке с абсциссой х0 = In 4.
а) I/ = * - 2 + In 4; в) у = 2х + In 4;
б) z/ = * + 2 - In 4; г) у = 2х - In 4.
5. Дана функция у = In cos х.
Решите уравнение z/' = 0.
а) х = я/1, л е Z; в) х = 4ял, пе Z;
б) х = 27СП, л е Z; г) jc = и л, л € Z.
6. Найдите промежутки убываний функции
а)(0;7ё]; в) [7ё ;+«>);
б)(0;1)и[7^;+°°); г)(0; 1)11(1; 7^].
7. При каком значении а
) e2xdx=\l
0,5а
а) а = 21п 2; б) а = 7ё; в) а = 5; г) с = In 2.
8. Найдите площадь фигуры, ограниченной
g
графиками функций у= - и у = 6 - х.
а) 1 - In 2; в) 6 - 81п 2;
б) 3 - 41п 2;
г) 2 - In 2.
9. Найдите площадь фигуры, ограниченной
= 0.
Зе2 - 4
х 2
графиками функций у=е,у=е и х = 0
а) в2 + 2; б)е -1; в)е +1; г)
10. При каком значении а прямая у = ex + а
является касательной к графику функции f(x) =
= lnx?
а)а=-;
б) а = -2;
Тест 9
в) а = 2;
г) а = -е.
Итоговый 2
1. Вычислите значение выражения
log0>5472+310**16.
а)3; 6)2,5; в) 1,5; г)-2,5.
2. Укажите наименьшее целое число, при
котором определена функция
*.2 _ о-
а) 2; 6)1; в)-2; г)-1.
3. Решите уравнение
1
2\og2(x + 2)-\oglTZT-x "-1-
2
-х% - 4*0
Вычислите значение выражения g"
где х0 — корень данного уравнения.
а)-2,5; 6)1,5; в) 2,5; г) -1,5.

Тесты
Алгебра и начала анализа. 10—11 классы
361
4. Решите систему неравенств
[log! л/х - 1 >-1,
3
[log2(2x - 1)< log2(x + 5).
а)(4;6); б)й;1); в)й;6); г)(1;6)-
5. Найдите сумму * нулей» функции
/(x) = g2 -3x + 4)-log5(8-3x).
а) ф 6)2; в)4|;
6. Найдите /'(In 3), если /(х)
г) 4.
е2х
а) 1,8; 6)2,4; в) 2,8; г) 3,6.
7. Найдите координаты точки, в которой
касательная к графику функции g(x) = log4 (х - 2)
в точке х0 = 3 пересекает ось Оу.
3 ^ % Г г, з
в> (°' 5ih>
8. Найдите промежутки (промежуток)
возрастания функции
^з
У =
е°>5х'
а)(-оо;0)и(0;6]; в)[0;6];
6) (-оо; в]; г) [6; +оо).
9. Площадь S фигуры, ограниченной
графиками функций у = ех, у = а (а > 1) и х = -1,
равна 2а + - . Найдите а и запишите значение
площади S при этом значении а.
a) S = е + 2е ;
6)S=i + е2;
в) S = е + е ;
г) S = - + 2е2.
е
10. При каком значении а прямая z/ = 3 + х
является касательной к графику функции /(х) =
х- ап
= е
а)-
?
1
2;
Тест 10
Итоговый 3
1. Решите уравнение 2,5sin 2х-sin х = 2.
Укажите наибольший отрицательный его
корень.
ч х 2 -ч Зя v Я ч 37С
a)-arctgg; 6)--^-; в)-^; г)--^.
2. /(х) = sin 2х - х. Решите неравенство /'(х) <
<0.
а) f-g + 2ял; g + 2ял), л е Z;
б) Гg + ял; -£ + ял J, л е Z;
ВЧ'12;12 +™>W€ZS
г) f-g + ял; g + ял 1, л е Z.
3. Найдите область определения функции
л/5х-х2
'W lg (2х - 4)
а) (2,5; 5]; в) (2; 5];
б) [0; 2) U (2; 5]; г) (2; 2,5) U (2,5; 5].
4. Найдите промежутки (промежуток)
возрастания функции
... Зх - 5
/(*) =
х2 - Г
а)(-1;|];<1;8];
6)(-°°;-l);||;l);[3;+°°);
B)[|;l)(l;8];
r)(-°°;-l);[f ;l)(l;3].
6)2;
в)-2;
г) 0,5.
5. Найдите площадь фигуры, ограниченной
О
графиком функции /(х) = -х - 4х + 1,
касательной в точке х0 = -3 и прямой х = 0.
а) 10; б)9|; в)1о|; г) 9.
6. Решите уравнение 4^* -0,5х~3 = 0и най-
3 2
дите значение выражения -х0 -Зх0 + 2х0 -5,
где х0 — корень данного уравнения.
а)-5; б) -7; в)-9; г)-12.

362
Тесты
Алгебра и начала анализа. 10—11 классы
7. Решите систему
{2 2
21og4 а - log4 а • log4 Ь - 61og4 Ъ = 0,
log2 а + log05 b = 2.
Запишите произведение рациональных чисел
а и bt удовлетворяющих данной системе,
а) 64; 6)27; в) 36; г) 16.
8. Решите уравнение JC21og3x = 81х2.
Запишите произведение его корней.
а) 18; 6)8; в) 3; г) 1,5.
9. Найдите наибольшее значение функции
f(x) = х • е х а на промежутке [-1; 2].
а) 4 • е
б)4е
2 +а
а-2
в)е
г) е
1+а
1-а
10. При каком значении параметра а уравнение
\х - ах\ = х - а
имеет ровно три корня?
а)а<1; б)а<1; в)а<-1; г)а<-1.
ОТВЕТЫ
10 класс
Т—1
Задание
Ответ
1
б
2
в
3
в
4
г
5
а
6
б
7
в
8
г
9
б
10
а
Т—2
Задание
Ответ
1
б
2
б
3
б
4
г
5
б
6
в
7
а
8
б
9
в
10
г
Т—3
Задание
Ответ
1
а
2
в
3
в
4
б
5
г
6
б
7
в
8
г
9
б
10
а
Т—4
Задание
Ответ
1
б
2
б
3
в
4
в
5
г
6
б
7
а
8
в
9
в
10
г
Т—5
Задание
Ответ
1
б
2
а
3
в
4
в
5
а
6
г
7
б
8
в
9
б
10
г
11 класс
Задание
Ответ
1
в
2
г
3
а
Т—6
4
б
5
б
6
г
7
в
8
б
9
в
10
г
Т—7
Задание
Ответ
1
б
2
г
3
в
4
в
5
г
6
б
7
а
8
в
9
в
10
б
Т—8
Задание
Ответ
1
а
2
б
3
б
4
в
5
б
6
а
7
в
8
г
9
в
10
г
Т—9
Задание
Ответ
1
в
2
б
3
г
4
б
5
в
6
а
7
в
8
г
9
б
10
г
Т—10
Задание
Ответ
1
в
2
г
3
б
4
б
5
в
6
в
7
а
8
б
9
а
10
г
Задание
Ответ
1
в
2
б
3
а
Г—1
4
в
5
г
6
г
7
б
8
б
9
в
10
г
Т—2
Задание
Ответ
1
г
2
г
3
в
4
а
5
б
6
а
7
в
8
г
9
г
10
б
Т—3
Задание
Ответ
1
г
2
в
3
б
4
г
5
в
6
б
7
г
8
б
9
в
10
б
Т—4
Задание
Ответ
1
б
2
г
3
б
4
г
5
б
6
в
7
г
8
а
9
в
10
г

Тесты
Алгебра и начала анализа. 10—11 классы
363
Т—5
Т—8
Задание
Ответ
1
б
2
б
3
в
4
г
5
в
6
б
7
б
8
а
9
г
10 1
в
Т—6
Задание
Ответ
1
в
2
г
3
б
4
б
5
в
6
б
7
г
8
б
9
а
10
б
Т—7
Задание
Ответ
1
в
2
г
3
б
4
г
5
в
6
б
7
а
8
в
9
б
10
в
Задание
Ответ
1
б
2
г
3
г
4
б
5
б
6
г
7
г
8
в
9
в
10 1
б
Т—9
Задание
Ответ
1
в
2
г
3
б
4
г
5
в
6
г
7
б
8
б
9
г
10
в
Т—10
Задание
Ответ
1
б
2
б
3
г
4
в
5
г
6
б
7
а
8
в
9
в
10
г

Геометрия. 7—9 классы
7 КЛАСС
Тест 1
Аксиомы планиметрии
1. Точки С, D и 22 лежат на одной прямой,
причем длина отрезка DE в 2 раза меньше длины
отрезка CD у а длина CD больше длины СЕ на 4,8 см.
Найдите длину отрезка DE.
а) 2,4 см; в) 9,6 см;
б) 4,8 см; г) 3,2 см.
2. Угол между лучами а и Ъ равен 143°, а угол
между лучами а и с на 29° меньше угла между
лучами бис. Найдите Z-(bc), если луч с
проходит между лучами аиЬ.
а) 59°; в) 57е;
6)114°; г) 86е.
3. На плоскости отмечены четыре точки: М,
N,PnK. Прямая I разделила плоскость так, что
две из данных точек оказались в одной
полуплоскости, а две другие в другой полуплоскости.
Сколько раз ломаная MNPK может пересекать
прямую П
а) 1, 2 раза; в) 1, 2, 3 раза;
б) 1, 2, 3, 4 раза; г) 2, 3 раза.
4. Сколько можно начертить треугольников,
равных данному, если две вершины этих
треугольников совпадают с двумя вершинами
данного треугольника, лежащими на прямой П
I
а) 4
6)2
в)1
г)3
5. Точки В, С и D лежат на одной прямой,
причем ВС = 9 см и CD = 6,7 см. Найдите BD.
а) 2,3 см; в) 15,7 см или 2,3 см;
б) 15,7 см; г) 6,7 см.
6. Сколько всего треугольников можно
обнаружить на рисунке?
а) 9;
6)11;
в) 10;
г) 12.
7. Проведите различные прямые, каждая из
которых проходит через две из указанных
шести точек. Сколько всего таких прямых можно
провести?
а) 15; А
6)12; F. * .Б
в>6' £• .С
D
г) 30.
8. На какое наибольшее число частей могут
разбить плоскость четыре прямые?
а) 9; 6)10; в) 11; г) 12.
Тест 2
Углы
1. Углы COD и DOK — смежные. Найдите угол
DOK, если угол COD в 3,5 раза меньше угла DOK.
а) 128°; 6) 132°; в) 40е; г) 140°.
2. Прямые АВ и CD пересекаются в точке Е,
причем сумма углов ВЕС и AED равна 194°.
Найдите угол АЕС.
а) 97е; 6)83°; в) 117°; г) 73°.
3. Прямая CD разбивает плоскость на две
полуплоскости. Из точки Е, принадлежащей
прямой CD, проведены в разные полуплоскости лучи
ЕК и ЕМ, причем угол KED в 4 раза больше
угла DEM. Найдите угол DEM, если Z_ СЕК = 64°.
а) 39°; 6)151°; в) 29е; г) 16е.
4. Угол BOD в 2 раза больше угла АОМ, а
угол DOM на 30° меньше угла BOD. Найдите
угол BON.
а) 56е
б) 42е
в) 54
г) 68'
5. Углы BOD и COD — смежные. ОЕ —
биссектриса угла BOD, причем угол COD на 21е
больше угла DOE. Найдите угол ВОЕ.
а) 67е; 6) 74е; в) 46е; г) 53°.

Тесты
Геометрия. 7—9 классы
365
= 154°, ОС 1 ОК, ОМ —
6. Даног^АСЖ
биссектриса Z. АОК.
Найти: L СОМ.
а) 13°;
б) 27е;
в) 23е;
г) 35°.
7. Прямые MN и РК пересекаются в точке Е;
ЕС — биссектриса угла МЕР, /L СЕК = 137°.
Найдите угол КЕМ.
а) 108°; б) 84°; в) 94°; г) 82е.
8. Дано: /L АОВ - L АОС - 27°,
L АОВ - Z ВОС - 42°.
Найти: А АОВ. Г\^
а)134°г А ^^ в
б) 143°;
(О
в) 136°
г) 148°.
Тест 3
Равенство треугольников.
Медиана, высота и биссектриса
треугольника
1. Известно, что АО — медиана треугольника
ABC, АО = ОКиАВ = 6,3 см; ВС = 6,5 см; АС =
= 6,7 см. Найдите СК.
а) 6,4 см; в К
б) 6,7 см;
в) 6,5 см;
г) 6,3 см.
" \
2. ОН и ON — высоты углов треугольников
МОК и EOF, причем ОН = ON. Найдите длину
отрезка МК, если EN =7,8 см, ОЕ = 8,6 см, НМ =
= 6,3 см.
а) 13,9 см; АЕ
б) 14,1 см; Мк
в) 14,9 см; Y^LAN
г) 16,4 см. #\
3. Дано: ААВС - ADEF, Z. В - 73°; БС =
6,9 см, DF = 7,6 см.
Какое из высказываний верное?
а) DE = 6,9 см, АС = 7,6 см;
б) L Е - 73е, АС - 7,6 см;
в) DF - 6,9 см, LE = 73°;
г) АС - 7,6 см, Z 2> = 73е.
4. Треугольник C.D22 равен треугольнику
ClD1El. Периметр треугольника CDE равен 76 см.
Сторона ClD1 в 2,5 раза меньше i^-Ei, а СгЕг на
8 см меньше стороны DXEV Найдите большую
сторону треугольника CDE.
а) 30 см; в) 35 см;
б) 28 см; г) 28 см.
5. В треугольниках ABC и КРМ проведены
биссектрисы ВО и РЕ, причем А АВО - А КРЕ.
Найдите отрезок ЕМ, если АС = 9 см, а ЕМ > КЕ на
3,8 см.
а) 6,4 см; в) 2,6 см;
б) 5,4 см; г) 4,8 см.
6. Прямая МК разбивает плоскость на две
полуплоскости. Из точек М и К в разные
полуплоскости проведены равные отрезки МА и KB,
причем Z AMК = Z. ВКМ.
Какие из высказываний верные:
1) ААМВ - ААКВ; 3)АМКА - АКМВ;
2) £ АКМ =/L ВМК; 4) Z. АМВ = Z. КВМ?
а)1;3;4; б) 1; 2; 4; в) 1; 3; г) 2; 3.
7. Сколько пар равных треугольников на
рисунке?
а) 2;
6)6
в) 8
г) 4,
8. На какое наибольшее число равных
треугольников может разделить треугольник
ломаная, состоящая из трех звеньев?
а) 2; 6)4; в) 3; г) 6.
Тест 4
Равнобедренный треугольник
1. Периметр равнобедренного треугольника
27 см, причем основание на 4,5 см больше
боковой стороны. Найдите боковую сторону
треугольника.
а) 10,5 см; б) 9 см; в) 8,5 см; г) 7,5 см.
2. Периметр равнобедренного треугольника
ABC равен 28 см. АС — основание, BD — высота
этого треугольника, периметр треугольника
DBC равен 18 см. Найдите BD.
а) 5 см; б) 8 см; в) 4 см; г) 10 см.

366
Тесты
Геометрия. 7—9 классы
3. В треугольнике МКР угол М равен углу Р,
а биссектриса PC делит сторону МК пополам.
Найдите длину MP, если МС = 9,6 см.
а) 19,2 см; б) 4,8 см; в) 14,4 см; г) 28,8 см.
4. В треугольнике CDE проведена медиана СА,
причем СА = АЕ и L Е - 69е. Найдите угол DAC.
а) 146°; б) 138°; в) 126°; г) 124°.
5. Какие из перечисленных высказываний
верные?
1) Если одна высота треугольника делит
противоположную сторону пополам, то этот
треугольник равнобедренный.
2) Если треугольник равносторонний, то сумма
длин его высот равна сумме длин его медиан.
3) Если треугольник равнобедренный, то
любая его биссектриса является и медианой.
4) Если периметр треугольника в 3 раза
больше одной из его сторон, то он является
равносторонним.
а)1;2; б) 1; 2; 4; в) 2; 3; 4; г) 3; 4.
6. В прямоугольнике MNPK сторона NP вдвое
длиннее стороны РК. Найдите угол PON, где О —
середина стороны МК.
а) 100°; б) 90°; в) 60°; г) 45°.
7. На какое наибольшее число
равносторонних треугольников можно разделить данный
равносторонний треугольник тремя отрезками?
а) 2; 6)6; в) 4; г) 3.
8. Сколько всего равнобедренных
треугольников можно заметить на рисунке?
а) 10;
6)6;
в) 8;
г) 14.
Тест 5
Параллельные прямые
1. Прямая АВ пересекает параллельные
прямые РК и MN (А € РК, В € MN). Сумма углов
РАВ и МВА равна 116°. Какие из
высказываний верные?
1) Точк*;КиМ лежат в одной полуплоскости
относительно прямой АВ.
2) Точки Р и N лежат в разных плоскостях
относительно прямой АВ.
3) Сумма углов РАВ и NBA равна 180°.
4) Угол КАВ равен 122°.
а)1;3; б)1;3;4; в) 2; 4; г) 2; 3.
2. Прямая MN является секущей для
прямых АВ и CD (М е АВ, N е CD). Угол AMN
равен 78°. При каком значении угла CNM прямые
АВ и CD могут быть параллельны?
а) 102°; б) 12е; в) 78°; г) 78° и 102°.
3. Один из внутренних односторонних углов,
образованных параллельными прямыми а и Ь и
секущей с, равен 117°. На сколько градусов этот
угол больше другого внутреннего
одностороннего с ним угла?
а) 90°; б) 63е; в) 54е; г) 64°.
4. Разность между двумя внутренними
односторонними углами при параллельных прямых
а и b и секущей с равна 46°. Найдите больший из
этих углов.
а) 126°; 6)123°; в) 113°; г) 136°.
5. Дано: а II Ъ, с — секущая, DM и DN —
биссектрисы смежных углов, образованных
прямыми а и с, DE = 5,8 см.
Найти: MN.
*с а
а) 16,4 см; в) 8,7 см;
б) 11,6 см; г) определить нельзя.
6. Дано:АВ 1 ED и КМ 1 ED, А ABE -
= 34°, MN — биссектриса Z_ КМС.
Найти: AEMN. jy
а) ЮГ; К?
6)117°; ^OV N/
В)9Г; *£^Nv /
г) 113°. Е :V-^Z_c
в М
7. Дано:АС II BD, СК II DM, /LACK = 48°,
L CDK в 3 раза больше Z EDM.
Клйти:А KDE. А.
а) 64°;
б) 74°
в) 76°
г) 81°,
^
«А
м
8. В треугольнике CDE /L С = 39°, Z. Е = 57°.
Через вершину D проведена прямая АВ II СЕ.
Найдите угол ADK, где DK — биссектриса угла
CDE.
а) 84°; б) 81°; в) 81° или 99°; г) 99°.

Тесты
Геометрия. 7—9 классы
367
Тест 6
Сумма углов треугольника
1. В треугольнике CDE угол D в 2,5 раза
больше угла С, а угол Е на 24е меньше угла D.
Найдите угол Е.
а) 73°; 6)74°; в) 61е; г) 68°.
2. В равнобедренном треугольнике EFH /L F =
= 118°. ЕО — высота этого треугольника.
Найдите угол ОЕН.
а) 57°; 6)59°; в) 67е; г) 63°.
3. В равнобедренном треугольнике
биссектрисы углов при основании образуют при
пересечении угол, равный 64е. Найдите угол при
вершине этого треугольника.
а) 58°; 6)76°; в) 68°; г) 52е.
4. В треугольнике ABC медиана AD вдвое
меньше стороны ВС. Найдите угол А
треугольника ABC.
а) 100°; б) 80°; в) 90°; г) 75°.
5. Один из внешних углов треугольника в 4
раза больше другого внешнего угла этого
треугольника. Найдите разность между этими внешними
углами, если внутренний угол треугольника, не
смежный с указанными внешними углами,
равен 60е.
а) 132°; 6)136°; в) 144°; г) 148°.
6. Дано: А ABC — прямоугольный (Z. С =
= 90°), L А = 32°, СН — высота, СО —
биссектриса угла АС В.
Найти: /LHCO.
а) 17°;
Тест 7
Окружность
6)13°
в) 28'
г) 29е.
7. Дано: А РКЕ — прямоугольный (Z. К =
= 90°), КС — высота, КЕ - 9 дм.
Найти: СЕ.
а) определить нельзя;
б) 5,5 дм;
в) 6 дм;
г) 4,5 дм.
8. Найдите сумму внутренних углов
шестиугольника ABCDEF.
а) 720°
б) 640е
в) 700е
г) 750°.
Я
окружности в любой
1. Центр вписанной
треугольник — это ...
а) точка пересечения медиан;
б) точка пересечения серединных
перпендикуляров к сторонам треугольника;
в) точка пересечения высот треугольника;
г) точка пересечения биссектрис треугольника.
2. Диаметр окружности, описанной около
прямоугольного треугольника, равен 18 см. Найдите
длину медианы, проведенной из вершины
прямого угла этого треугольника.
а) 9 см; в) 6 см;
б) 4,5 см; г) определить нельзя.
3. К окружности с центром О из точки С
проведена касательная СЕ. Найдите радиус
окружности, если угол СОЕ равен 60е и расстояние
между точками О и С равно 18 см.
а) 4,5 см; б) 6 см; в) 9 см; г) 12 см.
4. Длины хорд АВ и АС окружности равны.
Угол между ними равен 120°. Найдите длину
ломаной ВАС, если диаметр окружности равен 24 см.
а) 12 см; б) 24 см; в) 48 см; г) 18 см.
5. Расстояние от центра О до хорды АВ равно
15 см. Угол ОАВ равен 45е. Точка С принадлежит
хорде АВ, причем АС = 4БС. Найдите длину
отрезка АС.
а) 12 см; б) 24 см; в) 20 см; г) 18 см.
6. Радиусы двух пересекающихся
окружностей равны 9,5 см и 13,2 см, а расстояние между
центрами этих окружностей равно 19 см. Найдите
длину отрезка CD.
а) 4,2 см;
б) 3,5 см;
в) 4,5 см;
г) 3,7 см.
7. Д а н о: А МКР — равнобедренный, МК =
= КР, L К = 82°, О — центр вписанной
окружности в этот треугольник. ОС и О А — радиусы
окружности (С е КР, А е MP).
Найти: ЛАОС.
а) 124°; 6)129°; в) 131е; г) 98е.
8. Диаметр окружности, вписанной в
равносторонний треугольник, равен 36 см. Найдите
радиус окружности, описанной около данного
треугольника.
а) 36 см; б) 18 см; в) 72 см; г) 24 см.

368
Тесты
Геометрия. 7—9 классы
Тест 8
Итоговый
1. Величины смежных углов
пропорциональны числам 4 и 11. Найдите разность между
этими углами.
а) 84е; б) 76е; в) 96е; г) 68е.
2. В прямоугольном треугольнике ABC L С =
- 90°, £В = 30°, ВС - 18 см, СК LAB, КМ 1 ВС.
Найдите MB.
а) 9 см; ^}
б) 13,5 см;
в) 12 см;
г) 10 см.
8. На каком из рисунков сумма расстояний
СЕ и DE является наименьшей?
в)
3. Прямые тип параллельные, с —
секущая. Разность двух углов, образованных этими
прямыми, равна 132°. Найдите отношение
большего из этих углов к меньшему.
а) 4,8; 6)5,8; в) 6,5; г) 6,2.
4. Периметр равнобедренного треугольника
равен 22 см, а одна из его сторон на 5 см меньше
другой. Найдите сумму боковых сторон этого
треугольника.
а) 115 см; в) 18 см или 11» см;
б) 18 см; г) 17 см.
5. Назовите верные высказывания:
А: Любая точка биссектрисы угла
треугольника равноудалена от его сторон.
В: Если углы равны, то они вертикальные.
С: Если сторона треугольника, к которой
проведена медиана, вдвое больше ее, то этот
треугольник прямоугольный.
D: Две высоты равнобедренного треугольника
равны,
а) В, D; б) А, С; в) А, В; г) С, D.
6. Расстояние от центра окружности О до
хорды CD равно 13 см. Угол COD равен 90°. Найдите
длину хорды CD.
а) 18 см; б) 13 см; в) 19,5 см; г) 26 см.
7. В треугольнике BDE угол В составляет 30%
угла!), а угол Е на 19е больше угла D. Найдите
угол Б.
а) 21е; б) 32°; в) 70°; г) 51°.
а)
б)
1 1 1 1 1 1 1 1 hki 1
1 1 1 1 1 1 1 1т I 1
f'i 1 1 11111
п II II II 1 1 1
1 1 1 1 1 1 1 1 hii 1
1 I 1 1 1 1 1 1 тч 1
hi
M
1 1 П II 1 И II
г)
»
8
8 КЛАСС
Тест 1
Параллелограмм.
Прямоугольник. Ромб
1. Стороны параллелограмма
пропорциональны числам 3 и 7. Найдите меньшую сторону, если
периметр параллелограмма равен 18 см.
а) 2,7 см; б) 5,4 см; в) 3,4 см; г) 4,5 см.
2. Один из углов ромба равен 120°, а его
меньшая диагональ равна 4,5 см. Найдите периметр
ромба.
а) 27 см; б) 15 см; в) 18 см; г) 21,5 см.
3. В прямоугольнике CKMN проведена
биссектриса угла С, которая пересекает сторону КМ в
точке Е, причем длина отрезка КЕ на 3 см меньше
длины ME. Найдите MN, если периметр CKMN
равен 51 см.
а) 8 см; б) 9 см; в) 12,5 см; г) 7,5 см.
4. В параллелограмме ABCD проведена высота
BE, причем угол BCD в 4 раза больше угла ABE.
Найдите угол ABC.
а) 116°; 6)112°; в) 108°; г) 96°.
5. Какие из высказываний верные?
А: Диагональ параллелограмма является
биссектрисой его углов.
В: Если диагонали четырехугольника
перпендикулярны, то он является ромбом.
С: В ромбе все высоты равны.
D: Если в четырехугольнике диагональ делит
его на два равных треугольника, то он
является параллелограммом,
а) С, D; б) С; в) В, D; г) А, С, D.
6. Длина диагонали прямоугольника равна
28 см, а один из углов, образованных при
пересечении диагоналей, равен 120°. Найдите
меньшую сторону прямоугольника.
а) 12 см; б) 21 см; в) 7 см; г) 14 см.

Тесты
Геометрия. 7—9 классы
369
7. В параллелограмме EKFM диагонали
пересекаются в точке О, причем A KOF = 138°, а
Z. FEM = 34°. Найдите угол К параллелограмма,
если КМ в 2 раза больше MF.
а) 112°; б) 104°; в) 96е; г) 108°.
8. Даны три точки Л, К, М, не лежащие на
одной прямой. Сколько параллелограммов с
вершинами в этих точках можно построить, чтобы
отрезок AM был его диагональю?
а)1; 6)2; в) 3; г) 4.
Тест 2
КгК2 = 14 см.
Теорема Фалеса.
Средняя линия треугольника.
Трапеция
1. Дано:^(а&),
МК II МгКг || М^2 II АГдЛТд II М4К4, ЕМ - ММг -
= МгМ2 = М2М3 = МгМ4, КК4
Найти: ЕК4.
а) 27,5 см;
б) 21 £ см; Е
в) 18,5 см;
r)23g см.
2. Средняя линия треугольника на 5,4 см
меньше основания треугольника. Найдите
сумму средней линии треугольника и основания.
а) 13,5 см; б) 16,2 см; в) 10,8 см; г) 21,6 см.
3. В параллелограмме ABCD периметр равен
36 см, Z.A= 120°, АС = CD. Найдите периметр
треугольника КВМ, где К — середина АВ, М —
середина ВС.
а) 12 см; б) 21 см; в) 15 см; г) 13,5 см.
4. В равнобедренной трапеции ABCD Z. А =
= 135°, ВС = 21 см, AD = 9 см. Найдите высоту
трапеции DK.
а) 8 см; б) 15 см; в) 6 см; г) 12 см.
5. CDEK — трапеция, MN — средняя линия,
СК = 26 см, DE = 19 см. Найдите ОА.
а) 4 см; D Е
б) 7 см; "
в) 3,5 см; М/-
г) 3 см.
iHk
отрезки ЕК и MN, причем точки Е и М
принадлежат стороне АВ, а К и N — стороне CD.
Найдите ЕК, если BE = ЕМ - МА.
а) 20 см; б) 21 см; в) 24 см; г) 25 см.
7. В равнобедренной трапеции один из углов
равен 120°, а меньшее основание равно 8 см.
Найдите периметр трапеции, если боковая
сторона равна меньшему основанию.
а) 40 см; б) 36 см; в) 48 см; г) 32 см.
8. Отрезок CD пересекает прямую т. О —
середина CD, точка С удалена от прямой т на
расстояние 16 см, a D на 31 см. На каком
расстоянии от прямой /п находится точка О?
а) 11,75 см; Q
б) 8 см;
в) 7,5 см;
г) 9 см. /О
Тест 3
6. В трапеции ABCD (AD II ВС) AD - 29 см,
ВС =17 см. Параллельно основаниям проведены
Теорема Пифагора
1. Один из катетов прямоугольного треуголь-
8
ника равен ^-= м, а гипотенуза равна 10 дм.
Найдите второй катет.
15 9 9-2
a) yj м; б) yf м; в) 9^ Дм; г) 6g дм.
2. Одна сторона прямоугольника на 4 см
больше другой, а сумма расстояний от точки
пересечения диагоналей прямоугольника до этих
сторон равна 14 см. Найдите диагональ
прямоугольника.
а) 24 см; б) 16 см; в) 18 см; г) 20 см.
3. Длины диагоналей ромба равны 14 см и 48 см.
Найдите периметр ромба.
а) 60 см; б) 100 см; в) 80 см; г) 120 см.
4. Гипотенуза КР прямоугольного
треугольника КМР равна 2 л/13 см, а катет MP равен 4 см.
Найдит$ медиану PC.
a) ^g- см; б) 6 см; в) -у- см; г) 5 см.
5. Сторона равностороннего треугольника
равна 14^3 см. Найдите биссектрису этого
треугольника.
а) 15 см; б) 24 см; в) 21 см; г) 18 см.
6. В треугольнике ABC АВ - 10 см, ВС - 17 см,
АС = 21 см. Найдите высоту BD.
а) 10,5 см; б) 8 см; в) 9 см; г) 12 см.

370
Тесты
Геометрия. 7—9 классы
7. Д ано: A CDE9 /LD = 90е, DM J_ СЕ, CD
= 6 см, СЕ = 9 см.
Найти: СМ. D
а) 7 см;
б) 4 см;
в) 4,5 см;
г) 5 см. С
8. На сторонах прямоугольного треугольника
ABC (Z. С = 90е) построены квадраты, причем
2 о 1ЛЛ 2
S3 + S2 = 1252 см , a Sx = 100 см
риметр треугольника ABC.
а) 57 см;
б) 48 см;
в) 52 см;
г) 60 см.
Найдите пе-
\s[
с
к,
«2
Тест 4 ,
Определение
синуса, косинуса,
тангенса, котангенса
1. В треугольнике ABC Z.C = 90°,
ВС = 7 см. Найдите АС.
7 v 7
L В = 56°,
а)
в)
tg 56°' "' sin 56°
б) 7 ■ cos 56°; г) 7 • tg 56е.
2. В равнобедренном треугольнике КСР (КС =
= СР) L С = 72°, /ГС = 14 см. Найдите КР.
а) 14 • cos 36°; в) 28 • sin 36°;
OQ
б) 7 • cos 36°; г) -т^го.
7 ' 7 sin 36
3. Периметр прямоугольника равен 70 см.
Найдите сторону а.
70
а)
б)
в)
г)
tg 39°'
35 - sin 39° .
1 + cos 39°'
35 (1 + tg39°)
tg 39° ;
35 • tg 39°
1 + tg 39°'
4. Известно, что cos a = yf • Найдите tg a.
a)l|; б)ф в) J; г) |.
5. Вычислите значение выражения
cos 45е - 5 sin 30°.
а)-2; б)-3; в)-1,5; г)-2,5.
6. Расположите в порядке убывания:
cos 73е, cos 56°, sin 26°.
а) cos 73е, cos 56е, sin 26°;
б) sin 26е, cos 56е, cos 73е;
в) cos 56°, sin 26е, cos 73е;
г) cos 73е, sin 26е, cos 56°.
7. На сколько метров АВ больше АС?
v 1 + cos а
"7 sin а •
sin а .
w/ 1 + cos а *
v cos а
Б/ 1 -since'
v 1 - sin а
г) .
7 cos а
8. Дано: MCDE -
= 16 см.
Найти: высоту
а) 16 • cos 74°;
б\ 8 -
6)sin37e'
. 16
в) cos 74°'
г) 16 • sin 74е.
Тест 5
А-
— ромб,
ромба.
^У01
г
В
С
L CDE - 148°, DM -
с
А
ы(
JVL \
\
К
\
°х
/
)
/
Е
Уравнения прямой
и окружности
1. Точки MnN имеют координаты:
М(3;-2), N(-l;3).
Найдите отрезок МN.
а) 6; б) 735 ; в) 9; г) 741.
2.ABCD — параллелограмм. Координаты
его вершин
В(-3;2), C(7;-l), D(6;-5).
Найдите координаты (х\ у) вершины А. В
ответе запишите сумму х + у.
а) 5; б)-2; в)-6; г) 3.
3. Д а но: ACDE, С(-5; 2), D(4; 3), Я(1; -4).
Найти: медиану DK.
а) 6; б)2л/13; в) 475; г) 8.

Тесты
Геометрия. 7—9 классы
371
4. Запишите уравнение окружности,
изображенной на рисунке.
16; 4
a)(*-4)2 + (i/ + 2)2
6)(*-4)2 + (z/ + 2)2 = 4;
в)(* + 4)2 + (1/-2)2 =
г)х2 + у2 = 16.
16;
5. В каких точках окружность
(* + 3)2 + (i/-2)2=18
пересекает ось Oyl В ответе запишите сумму
ординат этих точек.
а) 5; б)-5; в)-4; г) 4.
6. Запишите уравнение прямой CD, если
С(-3; 1), 1>(-5, 9).
а) у = 4х + 5; в) z/ = Зх - 5;
б) у = -4х - 11; г) z/ = -Зх + 8.
7. Даны уравнения двух прямых:
-Зх- у + 1 - О и 4* + 3i/ + 7 = 0.
Найдите координаты (х0; у0) точки пересечения
этих прямых и в ответе укажите сумму х0 + у0.
а) 5; 6)3; в)-3; г)-5.
8. Найдите радиус окружности, если ее
уравнение
а) 9;
х2 + у2-10х + 4у-3 = 0.
б) 6; в) 720 ; г) 4^2
Тест 6
Преобразования плоскости
1. Какое из высказываний верное?
А: Ромб имеет две оси симметрии, это две его
диагонали.
В: Ромб имеет две оси симметрии, это два
серединных перпендикуляра к его сторонам.
С: Ромб имеет четыре оси симметрии.
D: Высказывания А, В, С — неверные,
а) А; б) В; в) С; г) D.
2. Любой угол имеет осей симметрии:
а) 0; б) 1; в) 2; г) бесконечно много.
3. Известно, что при некоторой центральной
симметрии точка М переходит в точку К, а N в
точку Е (центр симметрии не принадлежит
отрезку МАГ). Назовите верные высказывания:
А: Отрезок МК равен отрезку NE.
В: Угол EMN равен углу NKE.
С: Фигура, составленная из отрезков MN,
NK, КЕ и ME, является прямоугольником.
D: Отрезок ME равен отрезку NK.
a) C,D; б) А, В; в) А, С; г) В, D.
4. Назовите верные высказывания:
А: При центральной симметрии два
соответственных отрезка параллельны.
В: При осевой симметрии два
соответственных луча сонаправлены.
С: Центр поворота, при котором А —► Аг, а
В —► Bv является пересечением отрезков ААг
и BBV
D: Некоторые шестиугольники имеют центр
симметрии,
а) В, С; б) C,D; в) А, В; г) A, D.
5. Сторона равностороннего треугольника
СКР равна 14 см, КЕ — высота треугольника.
При параллельном переносе на направленный
отрезок СЕ треугольник СКР отобразился на
треугольник EKXPV Найдите периметр фигуры
РМКгРг, где М — точка пересечения ЕКг и КР.
а) 49 см; 6) 28 см; в) 35 см; г) 42 см.
6. При параллельном переносе точка С(2; -3)
переходит в точку Сх(-1; 1). Найдите координаты
точки Fv в которую переходит точка F(-4; -1).
а)(3;-5); б)(-7;3); в)(-1;-5); г)(-1;3).
7. Б(5,6; -3,8), Вг — симметричная ей точка
относительно оси Оу9 а В2 — точка,
симметричная Вг относительно оси Ох. Найдите координаты
точки Б2.
а) (5,6; 3,8); в) (-5,6; 3,8);
б) (-5,6; -3,8); г) правильного ответа нет.
8. При гомотетии угол CDE, равный 56°,
переходит в угол C1D1EV Найдите величину угла
C1D1EV если коэффициент гомотетии равен 0,5.
а) 28°; в) 112°;
б) 56°; г) правильного ответа нет.
Тест 7
Векторы
1. МКРС — параллелограмм, Е — точка
пересечения диагоналей MP и КС. Найдите
МК - ЕР.
а) МК ; б) КС; в) СЕ; г)ЕК.

372
Тесты
Геометрия. 7—9 классы
2. AD — медиана треугольника ABC.
Найдите С А - DB.
а)ВА; б)АВ; b)DA; г) AD.
3. М(4; -5), К(2; -2). Найдите \МК\.
а) 7; б) УГз ; в) Jbb ; г) 5.
4. Дано: S(-6; 8), |я5| - 25.
Найти: X.
м11
а)1П;
б) 2,5;
в) 2,5 или-2,5;
М11 111
г)1п или-!^,
5. ABCD — параллелограмм, О — точка
пересечения диагоналей АС и BD, М — середина ВО.
Выразите СМ через АВ и AD .
а)\АВ -\aD\ b)\aD -\АВ\
6)~IaD-\Xb; t)\aB-\aD.
6. Дано: m(-2; 7), Я(-3; -4).
Найти: т • п.
а)-22; 6)22; в)-2; г) 2.
7. Дано: А ABC, А(-5; -2), В(-1; 4), С(2; 2).
Найти:^Б.
а) 120°; б) 80е; в) 100°; г) 90°.
8. При каком значении I векторы MP и KD
коллинеарны, если
М(-3;2), Р(-1;-2), К(2; 1), D(5; 1)1
а)-3^; б)-4,5; в)-5;
Тест 8
г)-4.
Итоговый
1. Периметр прямоугольника ABCD равен 48 см.
О — точка пересечения диагоналей
прямоугольника, причем расстояние от точки О до CD на 3 см
больше, чем от точки О до AD. Найдите
диагональ прямоугольника.
а) 17 см; в) 7285 см;
б) 7306 см; г) 10 73 см.
2. CDEF — трапеция, DE II CF, EF 1 DE,
Z. С = 60°. Найдите основание DE, если CD = 9 см
и DF J_ CD.
а) 15 см; в) 13,5 см;
б) 18 см; г) 12 см.
3. В прямоугольном треугольнике ABC /LC =
= 90°, АС — 8 см, а АВ на 2 см больше ВС.
Найдите tg jL А .
а) 2,5;
6>ТВ:
в) 1,5; г) 1,875.
4. Дано: ACDK — прямоугольный, ZC =
- 90°, Z К - Р, CD - &, CM J. JSTD.
Найти: СМ. ^
а) &tg Р;
б) bsin Р;
. JL.
в' sin р'
г) &COS р.
5. CD — диаметр окружности. Напишите
уравнение этой окружности, если С(1; -2), 1>(-5; 4).
a)(* + 2)2 + (z/-l)2 = 18;
6)(*-2)2 + (z/ + l)2 = 18;
b)(*-4)2 + (z/ + 2)2 = 16;
r)(x + 4)2 + (i/-2)2 = 16.
6. Прямая /п проходит через точки А(-3; 4) и
В(-9; -4) и пересекает ось Ох в точке С, а ось Оу в
точке D. Найдите периметр треугольника COD,
где О — начало координат.
а) 27 см; в) 24 см;
б) 20 см; г) 25 см.
7. ABCD — параллелограмм, С В = a, CD =
= b. Выразите через векторы В и Ь вектор EF,
где Е — середина АВ, a F делит BD в отношении
1 : 3, считая от точки D.
в) з & + 4 а;
ч 2г 1->
г)з&-4а'
ч 1ь^ 3^
а>4Ь+4а;
б) 5&- 5а;
8.А(-3; -2), В(1; 4), М(-5; 3), #(2; у). При
каком значении у векторы AM и BN
перпендикулярны?
а) 4,8; 6)4; в) 4,4; г) 4,5.

Тесты
Геометрия. 7—9 классы
373
9 КЛАСС
Тест 1
Подобие треугольников
1. Треугольник МКР подобен треугольнику
М1К1Р1, КЕ и КгЕг — медианы, причем ME в 4
раза больше МгЕг. Найдите отношение периметров
треугольников МКР и M1K1PV
а) 6; 6)8; в) 4; г) 2.
2. В треугольнике ABC проведены высоты АК
и СМ, О — точка пересечения высот. Какие из
высказываний верные?
1) А ABC со А АОС\ 3) А АМС со д СКА;
2) А СОК со АЛОМ; 4) ААКВ со АСМВ.
^)1;2; 6)3; 4; в) 1; 3; г) 2; 4.
3. В прямоугольном треугольнике МКЕ L К =
= 90°, /ГЯ - 8 см, ME - 16 см. ЛИ) — высота.
Найдите длину отрезка DM.
а) 4 см; б) 12 см; в) 14 см; г) 9 см.
4. Высоты параллелограмма равны 12 дм и
,16 дм. Периметр параллелограмма равен 98 дм.
Найдите разность между смежными сторонами
параллелограмма.
а) 7 дм; 6) 14 дм; в) 4 дм; г) 18 дм.
5. В треугольнике CDE ЕС = 26 см, MN \\ СЕ,
причем М е CD, N е ED. Найдите CD, если СМ =
= 8cmhMN = 20 см.
а) 24 см; в) 27 см;
б) 34 « см;
г) 30 см.
6. В трапеции ABCD (AD \\ ВС) ВС = 6 см, AD -
= 14 см, АС = 15 см. Е — точка пересечения
диагоналей АС и BD. Найдите СЕ.
а) 4 см; 6) 6 см; в) 4,5 см; г) 5,5 см.
7. Известно, что два треугольника подобны.
Стороны одного из них равны 7 см, 12 см, 16 см,
а стороны другого — 40 см, 30 см и х см.
Найдите х.
а) 18 см; в) 24 см;
б) 20 см; г) 18,5 см.
8. Дано: ААВС, Z. ВНА - А ВЕА - 90°.
Найти: верное высказывание.
а)АЛСБ со а НСЕ; В
б)АБСЛсо АНСЕ;
в)ААОВ со а ЕОН; у ф
г) А НОЕ со АНСЕ.
Тест 2
Вписанные углы.
Соотношения между хордами
и касательными
1. Угол МСК на 34° меньше угла МОК.
Найдите сумму углов МСК и МОК.
а) 112°;
б) 96°;
в) 68е;
г) 102°.
2. АС — диаметр окружности, О — ее центр.
ОС = ОВ = ОА. Найдите угол ОСВ.
а) 50е
б) 60°
в) 30е
г) 45°.
3. О — центр окружности, а = 136°. Найдите
угол р.
а) 108°
6)112°
в) 118°
г) 124°.
4. АС и BD — хорды одной окружности,
причем Е — точка их пересечения. Угол CED в 9 раз
больше угла ВЕС, а угол DAE на 61° больше угла
ВЕС. Найдите угол СВЕ.
а) 76е; б) 79°; в) 81е; г) 84°.
5. Дано: МК = 16 см, NC = 24 см, РМКЕ =
= 28 см.
NEC-
Найти:
а) 54 см;
б) 36 см;
в) 42 см;
г) 48 см.
в. BD и СЕ — хорды одной окружности, А —
точка пересечения этих хорд; АС = 6 см, АЕ =
= 12 см, АВ на 1 см меньше AD. Найдите BD.
а) 21 см; б) 20 см; в) 16 см; г) 17 см.
7. Дано: <Ж=16см, СР = 6 см, СМ = 24 см.
Найти:1)М. D^ >.
а) 20 см; С\/ \й
б) 18 см;
в) 16 см;
г) 15 см.
V7

374
Тесты
Геометрия. 7—9 классы
8. МК — касательная к окружности.
Найдите ВМ, если МК = 8 см, ВС =12 см.
а) 16 см; к^
б) 4 см;
в) 6 см; щ
г) 10 см. \ ^у£
Тест 3
Теоремы
синусов и косинусов
1. Стороны треугольника 5л/3 см и 4 см, а
угол между ними равен 30е. Найдите третью
сторону треугольника.
а) 6 см; б) 731 см; в) 729 см; г) 5 см.
2. Стороны треугольника равны 5 см, 6 см и
8 см. Найдите косинус наименьшего угла этого
треугольника.
ч 37
а' 60 ;
*ч 15
б>32;
. 25
В) 32'
ч 29
Г>бб'
3. Стороны параллелограмма 3 см и 8 см, а
один из углов 60°. Найдите большую диагональ
параллелограмма.
а) 9 см; б) 789 см; в) 797 см; г) 77§ см.
4. Найдите сторону треугольника, лежащую
против угла в 45е.
ч 7з
а) ^ Дм5
*ч 72
б) ^ Дм»
в) ъ дм;
г) Л дм'
5. Дано: А ABC, АВ = 1 см, АС = J2 см,
£С = 30°.
Найти: А В.
а) 45°; в) 60°;
б) 45° или 135°; г) решения нет.
6. В треугольнике одна из сторон равна 7 J2 см,
а противоположный угол равен 45°. Найдите
радиус описанной окружности.
а) 7 см; б) -^= см; в) 3,5 72 см; г) 3,5 см.
л/2
7. В треугольнике МКР МК = 8 см, КР = 12 см,
MP =15 см, КО — биссектриса угла К. Найдите
разность длин отрезков ОР и ОМ.
а) Зсм; б) 2 см; в) 2,5 см; г) 3,5 см.
8. ABCD — трапеция. Найдите основание AD.
а) 4 см; п2смс
6)573 см; /Ы^*
в) 5,6 см;
г) 6 см.
А* *D
Тест 4
Обобщающий
1. Известно, что МК = 7 см, КР = 5 см, NE
8 см. Найдите MN.
а) 4 см; _ _Р
б) 6,5 см; К а
в) 6 см;
г) 7,5 см.
ГЕ
М
N
2. В треугольнике CDE А С = 60°, DE в 2,5 раза
СЕ
больше CD. Найдите ^ .
а)
б)
в)
1 +
1 +
2
л.
2 '
76;
«/22.
» »
г)3.
3. АС = ВС, О — центр окружности, угол у на
75° больше угла а. Найдите угол р.
а) 160°
б) 220'
в) 150
г) 140'
4. Найдите сторону АВ треугольника ABC.
а) 7,5»/2 см;
б) 6-Уз см;
в) 5л/б см;
ч 15
г) А см-

Тесты
Геометрия. 7—9 классы
375
5. Стороны параллелограмма равны 7 см и 9 см,
а одна из его диагоналей равна 8 см. Найдите
вторую диагональ параллелограмма.
а) 14 см; в) Юл/3 см;
б) 12^2 см; г) 10,5 см.
6. О — центр окружности; О А, ОВ и ОС —
радиусы, угол АОВ на 30° больше угла АОС, а угол
ВОС на 30° больше угла АОВ. Причем сумма
всех трех углов равна 360°. Найдите хорду АВ,
если АС = 8 см.
/о
а) 6^2 см; б) 4^6 см; в) бЛ см; г) -g- см.
7. Угол МКР — вписанный в окружность, О —
центр окружности. Хорда MP = a, a Z_ МКР — ^ .
Найдите радиус окружности.
а' sinp; D' 0. р; В) 2sin2p; r'sin2p'
2sm g
8. AM и CK — высоты треугольника ABC. АС =
= 12^3 см, ВК = 724 см, ВС = $Л см.
Найдите отрезок КМ.
а) -= см; б) 8^3 см; в) 8 см; г) бЛ см.
л/2
4. Около правильного треугольника описана
окружность радиусом 10 Л см. Найдите радиус
окружности, вписанной в этот треугольник.
а) бТб см; в) 5л/3 см;
б) -= см;
Л
г) 10 см.
5. Внешний угол правильного
многоугольника на 144° меньше внутреннего угла. Найдите
сумму углов Данного многоугольника.
а) 3600°; в) 3060°;
б) 3240°; г) 3420°.
6. Меньшая диагональ правильного
шестиугольника равна 9л/3 см. Найдите его большую
диагональ.
а) 24 см; в) 18 см; i
б) 18 73 см; г) 24л/3 см.
7. В некотором многоугольнике можно
провести 14 диагоналей. Найдите число сторон
этого многоугольника.
а) 6; 6)7; в) 8; г) 9.
8. Сторона правильного восьмиугольника
равна 1 м. Найдите площадь описанного круга.
а) (1 - л/2)тс м2; в) Л* м2;
*ч п 2
б)П-у!м;
ч К 2
Г) р М .
2 - 72
Тест 5
Многоугольники
1. Один из внутренних углов правильного
n-угольника равен 156°. Найдите число сторон
многоугольника.
а) 12; 6)15; в) 18; г) 20.
2. Величины углов выпуклого пятиугольника
пропорциональны числам 4:5:6:7:8.
Найдите наибольший угол.
а) 144°; в) 148°;
6)136°; г) 152°.
3. Периметр квадрата 12^2 см. Найдите
радиус описанной окружности.
а) Зл/б см; в) 3^2 см;
6) -= см;
Л
г) 3 ар.
Тест 6
Площади фигур
1. Стороны параллелограмма равны 5 см и
4^3 см, а один из углов равен 120°. Найдите
площадь параллелограмма.
а) 20 см2; в) 30Л см2;
б) 30 см2; г) 20 Л см2.
2. Сторона ромба равна 25 см, а одна из
диагоналей равна 48 см. Найдите площадь ромба.
а) 600 см2; в) 336 см2;
б) 1200 см2; г) 336 Л см2.
3. Угол при вершине равнобедренного
треугольника равен 120°, а основание равно 14л/3 см.
Найдите площадь треугольника.
а) 49 Л см2; в) 42 см2;
б) 36 Л см2; г) 48 см2.

376
Тесты
Геометрия. 7—9 классы
4. Стороны треугольника равны 8 см, 10 см и
12 см. Найдите большую высоту треугольника.
а) Зл/б см; в) 3,5л/7 см;
б)
15V7
см;
г) 57з
см.
5. Площадь прямоугольного равнобедренного
2
треугольника равна 16 см . Найдите гипотенузу
этого треугольника.
а) 8л/2 см; в) 12 см;
б) 87з см; г) 8 см.
6. Площадь равностороннего треугольника
равна 24л/3 см . Найдите сторону этого
треугольника.
а) 4 см; в) 4л/б см;
б) Зл/б см; г) 4л/3 см.
7. В равнобедренной трапеции диагональ
перпендикулярна боковой стороне. Найдите
площадь трапеции, если боковая сторона равна 6 см,
а один из углов трапеции равен 60°.
а) 24 см ;
б) 24^2 см2;
в) 27 см ;
г) 27^3
см
8. Боковая сторона равнобедренного
треугольника равна 18 см. Найдите наибольшую
возможную площадь этого треугольника.
в) 180 см ;
г) 81^2 см2.
а) 162 см ;
б) 8173 см2;
Тест 7
Итоговый 1
1. Д а н о: окружность с центром О, Z. MEN =
- 45°, MN - 18 см.
Н а й т и: г.
ч 18
а) 7г см;
б) 9^2 см;
ч 9
в) -р см;
г) 9 см.
2. CDEK — параллелограмм, О — точка
пересечения его диагоналей. Найдите площадь
параллелограмма, если площадь треугольника КОЕ
равна 13,5 дм .
а) 40,5 дм ;
б) 27 дм2;
в) 54 дм ;
г) 27^3 дм2.
3. Стороны параллелограмма равны 20 см и
12 см, а одна из диагоналей равна 16 см.
Найдите сумму двух высот параллелограмма,
проведенных из одной его вершины.
а) 27,5 см; в) 24 см;
б) 30 см; г) 25,6 см.
4. Трапеция CDEK вписана в окружность
(DE || CK)t ЕК - 5 см, KD - 12 см, причем
KD J_ CD. Найдите длину окружности.
а)14ясм; в)17ясм;
б) 13ясм; г)8,5ясм.
5. Вычислите косинус угла правильного
шестиугольника.
Л
Л.
а) -,-; б) -s-; в) 5;
D-1
6. Стороны треугольника равны 8 см, 10 см и
12 см. Найдите радиус описанной окружности.
16
8
а) -= см; б) -= см; в) 2^7 см; г) 4л/3 см.
7. Дано: А МКР — прямоугольный, /. К =
- 90°, МК = 6 см, MP - 10 см, KD — высота.
SA
Найти:
'AMKD
^AKDP
а)^; б)|;
ч 9 ,3
B>l6; Г)5'
8. Даны уравнения двух прямых:
2х + у + 4 = 0 и -х + у-Ь = 0.
Найдите площадь треугольника CDE, где С и
D — точки пересечения данных прямых с осью
Ох, а Е — точка пересечения этих прямых.
а) 2,75; б) 3,5; в) 3; г) 3,25.
Тест 8
Итоговый 2
1. Треугольник CDE — прямоугольный, /- D -
= 90°, DK — высота. Найдите катет CD, если
Z. Е - 30°, KD - 8^3 см.
а) 16 см; в) 12 73 см;
** 16
б) лсм;
г) 12 см.

Тесты
Геометрия. 7—9 классы
377
2. MNKP — трапеция, NK \\ MP, MN - КР.
О — точка пересечения диагоналей, причем
МК INPn 8ШОР - 20 73 см2 и S^ok = 8 ^3 см2.
Найдите площадь треугольника MON.
а) 5л/15 см ;
б) вТз
см ;
в) б7§
г) 4л/30
см ;
см
3. Даны точки А(-1; 2) и Б(3; 8), точка С
лежит на оси абсцисс и равноудалена от точек А и
В. Найдите абсциссу точки С.
а) 8; 6)8,5; в) 8^; г)в|.
4. В треугольнике ABC DE II AC, S6DBE = 9 см ,
&ADEC = 7 см , АС = 20 см. Найдите DE.
а) 12,5 см;
б) 16 см;
в) 15 см;
г) 18 см.
i:
А С
5. KEDC — трапеция. ED \\ КС, DC J_ КС,
ED = 3 см, ЕС = 5 см. Найдите площадь
трапеции, если ЕС J_ КЕ.
а) 21,5 см;
б) 20,5 см;
2
в)22о см;
г) 24 см.
6. В треугольнике ABC АВ = 8 см, ВС =
= 10 см, АС = 12 см. BD — медиана
треугольника ABC. Найдите ее длину.
а) 6л/2 см; в) 7,5 см;
б) л/46 см; г) 4л/3 см.
7. ABCD — параллелограмм. СВ = т , CD =
= Я . Выразите через векторы тип вектор EF,
где Я — середина АВ и BF : FC -1 : 3.
ч 1-> 1 -
a) g л - j /п;
о) 2 n + 4 т'
,1- 1-.
в' ~2П ~~ 4т;
\ 1- 1->
г) ^ т - g п-
8. Стороны угла CED, равного 60°, касаются
двух окружностей с центрами Ох и 02, также
касающихся одна другой, причем ЕОг = 21 см.
Найдите радиус окружности с центром 02.
а) 4л/2 см;
б) 6 см;
в) 4,5 см;
г) 3,5 см.
ОТВЕТЫ
7 класс
Т—1
Задание
Ответ
1
б
2
г
3
в
4
г
5
в
6
б
7
а
8
в
Т—2
Задание
Ответ
1
г
2
б
3
в
4
б
5
г
6
а
7
в
8
б
Т—3
Задание
Ответ
1
г
2
б
3
б
4
в
5
а
6
г
7
в
8
б
Т—4
Задание
Ответ
1
г
2
в
3
а
4
б
5
а
6
б
7
в
8
г
Т—5
Задание
Ответ
1
б
2
г
3
в
4
в
5
б
6
а
7
г
8
в

Тесты
Геометрия. 7—9 классы
Т—6
Задание
Ответ
1
в
2
б
3
г
4
в
5
в
6
б
7
г
8
а
Т—7
Задание
Ответ
1
г
2
а
3
в
4
б
5
б
6
г
7
в
8
а
Т—8
1 ш
Задание
Ответ
1
а
2
б
3
в
4
в
5
б
6
г
7
а
8
б
8 класс
Т—1
Задание
Ответ
1
а
2
в
3
г
4
в
5
б
6
г
7
б
*н
а
Т—2
Задание
Ответ
1
г
2
б
3
г
4
в
5
в
6
б
7
а
8
в
Т—3
Задание
Ответ
1
а
2
г
3
б
4
г
5
в
6
б
7
б
8
г
Т—4
Задание
Ответ
1
г
2
в
3
г
4
б
5
а
6
в
7
г
8
г
Т—5
Задание
Ответ
1
г
2
в
3
б
4
в
5
г
6
б
7
в
8
г
Т—6
Задание
Ответ
1
а
2
б
3
г
4
г
5
в
6
б
7
в
8
б
Т—7
Задание
Ответ
1
г
2
в
3
б
4
в
5
б
6
а
7
г
8
в
Т—8
Задание
Ответ
1
б
2
в
3
г
4
г
5
а
6
в
7
б
8
в
9 класс
т—1
Задание
Ответ
1
в
2
г
3
б
4
а
5
б
6
в
7
г
8
а
Т—2
Задание
Ответ
1
г
2
в
3
б
4
б
5
в
6
г
7
а
8
б
Т—3
Задание
Ответ
1
б
2
в
3
в
4
г
5
б
6
а
7
а
8
в
Т—4
Задание
Ответ
1
в
2
б
3
г
4
в
5
а
6
б
7
б
8
в

Тесты
Геометрия. 7—9 классы
379
Т—5
Т—7
Задание
Ответ
1
б
2
а
3
г
4
в
5
б
6
в
7
б
в|
г
Т—6
Задание
Ответ
1
б
2
в
3
а
4
б
5
г .
6
в
7
г
8
а
Задание
Ответ
1
б
2
в
3
г
4
б
5
г
6
а
7
в
вП
в
Т—8
Задание
Ответ
1
а
2
г
3
б
4
в
5
в
6
б
7
в
8
г

Геометрия. 10—11 классы
10 КЛАСС
Тест 1
Аксиомы стереометрии.
Следствия из аксиом
1. В пространстве даны три точки: М, К и Р
такие, что МК = 13 см, MP = 14 см и КР =15 см.
Найдите площадь треугольника МКР.
а) 42 см ;
6)42-72 см2;
в) 84 см ;
г)4273
см
2. Треугольник ABC — равносторонний со
стороной, равной 8 см. Точка D лежит вне
плоскости треугольника ABC, причем DB = DC = 5 см, а
DA = 3 Л см. Найдите косинус угла между
высотами DK и АК соответственно треугольников
BDCnABC.
3. Точки С и К лежат в плоскости Р, а точка
D — вне плоскости р. Найдите расстояние от
точки D до отрезка СК9 если CD = СК = 10 см, a DK =
= 4 Jb см.
а) 8 72 см;
б) 6 Л см;
в) 6 см;
г) 8 см.
4. В пространстве отмечены шесть точек, и
через каждые две из них проведены прямые.
Рассмотрев все случаи расположения точек,
найдите наибольшее число образовавшихся
различных прямых.
а) 30; в) 12;
б) 15; г) 18.
5. Проведены четыре различные плоскости.
Каждые две из них пересекаются или не
пересекаются. Сколько всего прямых попарного
пересечения двух из этих плоскостей может оказаться?
а) 0, 1, 2, 3, 4, 6; в) 0, 1, 2, 3, 4, 5, 6;
6)0,3,4,5,6; г) 0, 1,3,4,5,6.
6. Некоторая окружность касается двух
пересекающихся прямых в пространстве. Найдите
радиус этой окружности, если угол между прямыми
60е, а расстояние от центра этой окружности до
точки пересечения прямых равно (Л - Л ) см.
, Л + 1
а) —g— см;
6)(73 -1)см;
v Л - 1
в) —т=— см;
г)(7б -1)см.
7. Четыре точки пространства М,К9РиО
образуют прямоугольник МКРО. Найдите площадь
круга, описанного около этого прямоугольника,
3 5
если ОР = - дм и ОМ = «- дм.
ч 39 2
a) JJ дм ;
*ч 61 2
б> шдм ;
, 25 2
в) 55 дм ;
ч ЗЯ 2
г) j ДМ .
8. Прямые /71, п и I пересекаются в одной
точке. Через каждые две из них проходит плоскость.
Сколько всего различных плоскостей может быть
проведено?
а) 3 или 4; в) 1 или 2;
б) 1 или 3; г) 6.
Тест 2
Параллельность
в пространстве
1. Плоскость Р пересекает стороны MP и КР
треугольника МРК соответственно в точках N и
Е, причем МК || р. Найдите NE, если МК = 12 см
nMN:NP = 3:5.
а) 85 см; б) 9 см; в) 7,5 см; г) 8,5 см.
2. Отрезок CD пересекает плоскость Р, точка
Е — середина CD. Через точки С,2)и£
проведены параллельные прямые, пересекающие
плоскость Р соответственно в точках Cv Dx и Ev
Найдите EEV если CCt = -= см и DDt = J% см.
Л
Л
а) ^- см; б) — см; в) Л см; г) 2 Л см.

Тесты
Геометрия. 10—11 классы
381
3. Плоскости аи^, параллельные стороне АВ
треугольника ABC, пересекают сторону АС
соответственно в точках N и М, а сторону ВС — в
точках Ей К. Отрезок MN в три раза больше отрезка
CN, а отрезок AM вдвое короче MN. Найдите АВ,
если ME = 12 см.
а) 64 см; б) 72 см; в) 60 см; г) 66 см.
4. ABCDA1B1C1D1 — прямоугольный
параллелепипед, АВ = AD = 12 см, ААг = 3 см.
Найдите площадь сечения АКЕС, где К — середина
АгВг иЕ — середина ВгСг.
а) 36 72 см2; в) 18 7з см2;
6)27^/6 см2;
г) 24 см
5. ABCDAlBlClDl — куб, Е — середина CCV
Определите число сторон сечения плоскостью,
которая проходит через точки А, Вг и Е.
а)3; 6)4; в) 5; г) 6.
6. CDEK — ромб, сторона которого равна 8 см,
CKMN — параллелограмм. Найдите периметр
четырехугольника DEMN, если КМ = 6 см и ZCN =
= 60°.
а) 4( л/13 + 4) см; в) 8 7з см;
б) 6( 72 + 3) см; г) (2 ЛЗ +15) см.
7. В треугольной пирамиде SMEF все ребра
равны 4 см. Найдите периметр сечения,
проведенного параллельно ребру МF и проходящего
через точки ЕиР, где Р — середина отрезка SF.
а) 3(2 + 3 72 ) см; в) 2( 1 +2 7з ) см;
б) 6(3 72+1) см; г) 6 73 см.
8. ABCDAlB1ClD1 — куб, точка Е — середина
CD, Оделит реброAD в отношении 1:3, считая от
точки D. В каком отношении делит ребро ААг
(считая от точки А) плоскость, проходящая через
точкиВ1,22и2'7
а) 1:2; 6)2:1; в) 2:3; г) 3:2.
Тест 3
Перпендикулярность
в пространстве
1. CDEK — квадрат со стороной, равной 2 см.
BD 1 (CDE). Найдите расстояние от точки В до
плоскости CDE, если ВК = 772 см.
а) 8 72 см; б) 6 см; в) 8 см; г) 6 7з см.
2. ВО — перпендикуляр к плоскости а, ВА и
ВС — наклонные, ОА и ОС — их проекции на
плоскость а, причем сумма их длин равна 24 см.
Найдите расстояние от точки В до плоскости а,
еслиАВ = 47б см и ВС =1272 см.
а) 8 см; б)б72см; в)б73см; г) 472 см.
3. В треугольнике МКС СМ 1 КМ, точка Е
не принадлежит плоскости треугольника МКС
и ЕМ J_ МК. Какие высказывания верны?
\)EML(MKC)
2) KM L (МЕС)
а)1;4; 6)2
3) КМ 1 СЕ;
4) ЕМ J_ СК.
3; в)3; г)1.
4. Треугольник ABC — прямоугольный, ZA =
= 60°, ZC = 90°. СН — высота треугольника
ABC, причем СН - 8 см. Отрезок ВК —
перпендикуляр к плоскости треугольника ABC.
Найдите отрезок ВК, если расстояние от точки К до
стороны АС равно 20 см.
а) 12 см; в) 87з см;
б) 15 см; г) 10 72 см.
5. Треугольник ACD — равносторонний. Точка
S удалена от вершин треугольника ACD на 6 см,
а от плоскости треугольника ACD на 3 см.
Найдите сторону треугольника ACD.
а) 6 72 см; в) 4 72 см;
б) 9 см; г)47з см.
6.ABCD — квадрат с периметром, равным
16 7з см. Точка Е удалена от всех сторон
квадрата на 4 см. Найдите расстояние точки Е от
плоскости ABC.
72
a)273
см;
б) ~- см; в) 272 см; г) 2 см.
7. Плоскость а перпендикулярна плоскости р.
Точка С принадлежит плоскости а. Отрезок ССг —
перпендикуляр к плоскости Р, точка D
принадлежит плоскости Р и DDt — перпендикуляр к
плоскости а. Найдите длину отрезка CXD19
который принадлежит линии пересечения плоскостей
аир, если ССг = 8 см, DDX = 12 см, CD = 15 см.
а) 672 см; в) 7l7 см;
б) 713 см; г) 3 73 см.

382
Тесты
Геометрия. 10—11 классы
8. ABCDA1B1C1D1 — куб, ребро которого равно
У32 см. Найдите расстояние между прямыми
CC1hDB1.
а) 6 см; б) 4 см; в)4л/2см; г)2л/3см.
Тест 4
Параллельность
и перпендикулярность
в пространстве
1. ABCDA1B1C1D1 — прямоугольный
параллелепипед. Найдите площадь сечения,
проведенного через точки С, D и Av если АВ = 8 см,
ААг = 6л/2 см и AD = 2 л/7 см.
а) 30^7 см2;
б) 40 л/2 см2;
в) 72 см ;
г) 80 см2.
2. Если BCDEBfi^^y^ — куб, М — середина
ВгСг и N — середина BXEV то укажите верные
высказывания:
1) ZBEXD = 90°; . 2) MN \\ СЕ.
а)1; в)1;2;
б) 2; г) верных нет.
3. Плоскости равнобедренного треугольника
ABC и квадрата ABDE перпендикулярны.
Найдите расстояние от точки С до стороны DE, если
АВ = 6 см и ZABC = 90°.
а)6л/2 см;
б) 4 л/2 см;
в) 5л/3 см;
г) Зл/б см.
4. Прямая / параллельна стороне МК
треугольника МСК. Расстояние от прямой / до
плоскости МСК равно 15 см, а расстояние от I до
стороны МК равно 17 см. Найдите расстояние от
точки С до прямой Z, если Z МСК = 90°, МС =
= 7б см, КС = 2 л/3 см.
а) 4л/б см;
б)5л/13 см или 3729 см;
в) 5л/Гз см;
г)4лУб смили2л/б см.
5. Плоскость Р проходит через сторону AD
ромба ABCD, причем Р перпендикулярна плоскости
ромба. В плоскости Р проведена прямая а,
параллельная стороне AD. Найдите расстояние между
прямыми ВС и а, если CD = 10 л/3 см, Z BCD = 60°
и расстояние между прямыми а и AD равно 5 см.
а) 6 л/2 см; в) 8 см;
б) 8л/3 см; г) 5л/1о см.
6. Ребро куба ABCDA1B1C1D1 равно 20 см.
Найдите расстояние между прямыми CD и BCV
а) Юл/2 см; в) 20 см;
б) 10 см; г) Юл/3 см.
7. Плоскости равностороннего треугольника
CDE и треугольника DEM перпендикулярны.
Найдите длину отрезка СМ, если DE = 18 см,
DM = 16 см, ЕМ = 20 см.
а) 12л/2 см; в) 7лДо см;
б) л/213 см; г)8л/3 см.
8. Точка К лежит вне плоскости
равнобедренной трапеции ABCD (ВС IIAD) и удалена от ее
сторон на 15 см. Найдите расстояние от точки К до
плоскости трапеции, если AD = 24 см, ВС = 6 см,
АВ = 15 см.
а)8л/3 см; в) 3 л/21 см;
б) 12 см; г) 12 л/2 см.
Тест 5
Координаты в пространстве
1. Б(-7; 4; -3). Найдите сумму расстояний от
точки В до оси Ох и от точки В до плоскости yOz.
а) 6; 6)12; в) 14; г) 10.
2. Известны координаты вершин
треугольника CDE: С(-3; 4; 2), D(l; -2; 5), Е(-1; -6; 4). DjRT —
медиана треугольника. Найдите DHT.
а) УП ; б) л/18 ; в) л/Гб ; г) л/10 .
3. ABCD — параллелограмм:
А(4; -1; 3), В(-2; 4; -5), С(1; 0; -4), D(x; у; г).
Найдите координаты точкиDhb ответе
запишите число, равное х + у + г.
а)-3; б)-5; в) 6; г) 4.
4. Координаты точек: Р(4; -5; 2), С(-1; 3; 1).
Найдите сумму координат точки К, лежащей на
оси О г и равноудаленной от точек Р и С.
а) 14,75; б) 13; в) 15,5; г) 17.

Тесты
Геометрия. 10—11 классы
383
5. В (-2; 5; 3). Точка С симметрична точке В
относительно плоскости xOz, а точка D
симметрична точке С относительно оси Ог. Найдите
расстояние между точками В и D.
а) 4^2; в) 4;
6)6; г) 6^2.
6. При параллельном переносе точка А(-2; 3; 5)
переходит в точку Аг(1; -1; 2). Найдите сумму
координат точки Bv в которую переходит при
этом параллельном переносе точка В(-4; -3; 1).
а)-8; б)-10; . в) 6; г) 4.
7. Треугольник CDE — равнобедренный, CD =
= DJS, С(4; -2; 3), Я(-1; 1; 2), D(x; у; г).
Запишите уравнение относительно х, у, z,
удовлетворяющее условиям задачи.
а) 8х - 4у - 2г + 7 = 0;
б) 5* + 8i/- 3z-15 = 0;
B)6x+5y + 42-15 = 0;
г) 10 х - 6z/ + 2z - 23 = 0.
8. Найдите площадь треугольника MNT, если
М(-6; 0; 0), N(0; 8; 0), Т(0; 0; 2).
а) 24; 6)36; в) 25; г) 26.
Тест 6
а) 30°;
б) arccos -р;
в) 60е;
v 1
г) arccos «
Углы между прямыми
и плоскостями
1. Треугольник CDE равнобедренный, CD =
= DE = 40 см, ZC = 60°. Плоскость а проходит
через сторону CD, причем сторона СЕ образует с
плоскостью а угол 30°. Найдите расстояние от
точки Е до плоскости а.
а) 18 см; в) 20 см;
б)10 7з см; г) 12^2 см.
2. Плоскость а проходит через сторону AD
квадрата ABCD и образует со стороной АВ угол,
синус которого равен -<г • Найдите угол,
который образует с этой плоскостью диагональ
квадрата BD.
а) 30°; б) 45е; в) 60°; г) 90е.
3. Сторона квадрата ABCD равна а. Сторона
равностороннего треугольника ВМК равна 2а.
Стороны AD и МК параллельны, и расстояние
между ними равно V2 а. Найдите угол между
плоскостями ABCD и ВМК.
4. Треугольники CDK и СКЕ —
равнобедренные, причем CD - DK = 25 см, СК = 14 см и Z Е =
= 90°. Найдите косинус угла между плоскостями
CDK и СКЕ, если длина отрезка DE — 23 см.
,5 _ 2 ч 3 ,2
a)g; 6)g; в) g ; г) ^ .
5. ABCDA1B1C1D1 — куб. Найдите угол
между прямыми DCX и CBV
а) 45°; б) 30°; в) 60°; г) 90°.
6. Угол между плоскостями равнобедренного
треугольника ABC и ромба АВМК равен 30°.
Найдите длину отрезка СНГ, если АС = ВС = 10 см,
АВ - 12 см, a Z АВМ = 120°.
а) 3 72 см; в) 4 73 см;
6)2j7 см; г) 4^2 см.
7. 22МС — равносторонний треугольник,
через сторону МС проведена плоскость Р под углом
30е к плоскости ЕМС. Отрезок ЕО —
перпендикуляр к плоскости р. Найдите сторону МС, если
2
площадь треугольника МСО равна 18 см .
а) 6 л/3 см; в) 4 JS см;
б)4л/2 см; г)б72 см.
8. Угол между плоскостями аир равен 45е.
m Л ~ 2
Точка В находится на расстоянии —«— Дм от
плоскости а и 1 дм от плоскости р. Найдите
расстояние от точки В до прямой пересечения
плоскостей а и р.
а) 4 см; в) 2 «/б см;
б) 2 см; г) (7б - 72 ) см.
Тест 7
Векторы
I.ABCDAjBjCjZ)! — куб. Найдите вектор,
равный AAj - DCl + ВС .
а)ВСх; 6)BD; в) DB ; г) СгВ .

384
Тесты
Геометрия. 10—11 классы
2. ABCDAlB1C1Dl — куб, ААг = т, AD = Я,
АВ = I. Выразите через векторы т, й и Z вектор
КР , где ИГ — середина CCV Р — середина AD.
а)-5/п- ъп-1\ ъ)-ът+ ъп + 1\
2'" 2
2"* ' 2
б) ^ тп + ^ и - Z; г) g m - ^ n ~~ '•
3. Даны координаты точек:
С(-4; -3; -1), Д-1; -2; 3), М(2; -1; -2), N(0; 1; -3).
Найдите \3CD -2MN\.
а) 7329 ; в) V397 ;
б) 7413 ; г) 7366 .
4. Даны координаты точек:
MU -1; -4), В(-3; -1; 0), С<-1; 2; 5), D(2; -3; 1).
Найдите косинус угла между векторами АВ
и CD.
а) 0,8; б)-0,5; в) -0,7; г) 0,6.
5. При каком значении (значениях) т
векторы а(4; /п - 1; /п) и Ь(-2; 4; 3 - т)
перпендикулярны?
а) 4; б) -3; в) -3; -2; г) 3; 4.
6. При каком значении а векторы CD и MN
коллинеарны, если С(-3; 2; 4), .0(1; -4; 2),
М(1; -2; а), #(-1; а + 3; -1)?
а)-2; - б)-3; в) 1; г)-1.
7. Дано: \т\ = 2, |Я| = 3, Z (т, Я) = 120°.
Найдите cos а, где а — угол между векторами т и т + Я.
ч 2 *ч 2 ч *> ч 1
а)7б; б)7т; B)I7f; Г)7Ё'
8. Найдите длину вектора а - Ь - с, если |3| = 2,
|Ь| = 3, |с| = 4, Z (а, &) = 60е, Z (&, с) = 90е, Z (а, с) =
= 120°.
а)37§; б)731; в) 729 ; г) ТЗЗ .
Тест 8
точках Cv Dx и Ег соответственно. Найдите длину
отрезка EEV если ССг = 14 см и DDX = 20 см.
а) 16,5 см; в) 18 см;
б) 17,75 см; г)18| см-
2. Плоскости треугольника ABC и ромба ABMN
перпендикулярны, причем ZACB = 90°, АС = 4 см
и ВС = 2 см, Z АВМ = 150°. Найдите расстояние
от точки С до прямой MN.
а) 2 7з см; в) 7*^2 см;
б) 2,8 см; г) JTfi см.
3. Треугольник МКР — прямоугольный, Z К =
= 90°. Точка А, лежащая вне плоскости
треугольника, равноудалена от сторон этого
треугольника на 8 см. Найдите расстояние от точки А до
плоскости МКР, если MP = 13 см и КР =12 см.
а) 6 см; в) 2 7l5 см;
б) 3 7б см; г) 4 72 см.
4. Плоскость Р проходит через сторону MN
треугольника MKN. Сторона KN образует с
плоскостью Р угол 30°. Найдите синус угла между
плоскостями Р и MKN, если МК =12 см, KN =
= 13 см, MN= 5 см.
а)0,7; 6)g§; в)|; г) \.
5. Треугольник ABC — равнобедренный,
Z ABC = 90°, ACDE — ромб, Z САЕ = 45°.
Найдите косинус угла между плоскостями
треугольника и ромба, если расстояние от точки В до
прямой DE равно 4 75 см и АВ = 8 см.
ч 2 ~ 1
а) 5 ; б) 5 ;
в)
372'
Т)Ш
Итоговый
1. Отрезок CD не пересекает плоскость а, а
точка Е делит отрезок CD в отношении 5:3, считая
от точки С. Через точки С, D и Е проведены
параллельные прямые, пересекающие плоскость а в
6. Точка В(-6; -3; 8). Точка С — основание
перпендикуляра ВС, проведенного к оси Оу. D —
основание перпендикуляра BD9 проведенного к
плоскости хОг. Найдите сумму расстояний ВС и
BD.
а) 18; 6)11; в) 13; г) 17.
7. \а\ = 1, \Ь\ = 2, \с\ = 4, Z (а, Ъ) = 120°, Z (&, с) =
= 60°, Z (а, с) = 90°. Найдите \а + & - с|.
а) 3; в) ТГЗ ;
б) 7П ; г) 715 .

Тесты
Геометрия. 10—11 классы
385
8. ABCDAlBlClDl — куб. Точка К — середина
ребра AD. Найдите площадь сечения, проходящего
через точки Bv С и К, если ребро куба равно 12 см.
в) 120^2 см2;
г)9б7з см2.
а) 162 см ;
б) 144 см2;
11 КЛАСС
Тест 1
Двугранные и линейные углы.
Многогранные углы
1. Двугранный угол, образованный
полуплоскостями а и Р, равен 30е. Точка М удалена от
граней двугранного угла на Л дм и на 1 дм.
Найдите расстояние от точки М до ребра
двугранного угла.
а) 2 7з см; в) 3 Л см;
б)2*/7 см; г) 272 см.
2. ABCD — ромб, ВЕК — равносторонний
треугольник, причем АВ = BE = a, Z BAD = 30°.
Найдите угол между плоскостями ромба и
треугольника, если ЕК II AD и расстояние между
Л
этими прямыми равно -к- а.
a) arccos т ; в) 30е;
6)120; г) 150°.
3. ABCD — равнобедренная трапеция, AD \\ ВС,
причем ВС = 2 см, AD = 5 см, Z BAD = 45е.
Плоскость треугольника ВСК образует с плоскостью
трапеции угол 60е. Найдите расстояние от точки
К до стороны трапеции AD, если ВК = Л см и
СК = 1 см.
v Л
а) -г- см;
б) J см;
, Vl2 - Зл/5
в) g см;
г) л/3 см.
4. Плоскость а проходит через сторону AD
квадрата ABCD и образует с плоскостью
квадрата угол 30°. Найдите угол, который образует с
плоскостью а диагональ BD.
а) 45е; в) 60°;
*ч . Л
6) arcsm -г-;
г) arcsm -«-.
5. Дан трехгранный угол с вершиной В.
Плоскость Р пересекает его ребра в точках С, D и
Е, так что BC = BD = BE. Найдите угол СВЕ9
если Z CBD = 90е, Z DBE = 60е, a Z CDE - 45°.
а) 30е; 6) 45е; в) 60°; г) 90°.
6. ABCDAlB1ClD1 — куб. Найдите угол
между плоскостью сечения, проходящего через
точки Av C1nD,n плоскостью основания.
а) 45е;
Л
б) arccos -g-;
v Л
в) arccos -g-;
г) arctg Л .
7. Ребра трехгранного угла с вершиной В
пересечены плоскостью Р в точках С, D и К,
причем плоские углы CBD и KBD прямые, а угол
СВК равен 30е. Найдите длину отрезка BD, если
&ACBD = ^1» ^Д DBK = ^2 и S&CBK = ^8-
а)
<S1 ' ss
2S„
в)
»Г*2,
2S,
•№ *£
8. ABCD — ромб, сторона которого равна 8 см,
a ZD = 135е. Отрезок АЕ — перпендикуляр к
плоскости ромба, причем точка Е удалена от
прямой ВС на л/128 см. Найдите угол между
плоскостью, проходящей через точки Б, С и £, и
плоскостью ромба.
а) 30е; в) 60е;
б) 45е; г) arctg 2.
Тест 2
Цараллелепипед
и призма
1. Площадь поверхности куба равна 18 Л см .
Найдите площадь диагонального сечения этого
куба.
а) 4 7б см2; в) 6 Л см2;
2 2
б) 6 см ; г) 8 см .
2. Длины диагоналей трех граней
прямоугольного параллелепипеда, имеющие общую
вершину, равны 2*/l0 см, 2*/l7 см и 10 см.
Найдите диагональ параллелепипеда.
13-1019

386
Тесты
Геометрия. 10—11 классы
а) 4 726 см;
б)4*Д0 см;
в) 2 726 см;
г) 8 72 см.
3. Стороны основания прямого
параллелепипеда равны 2 см и 4 см, а синус угла между ними
77
равен -j-. Найдите угол, который образует
меньшая диагональ параллелепипеда с
основанием, если ее длина равна 4 72 см.
72
а) arccos -j-; в) 60°;
б) 30е; г) 45е.
4. Площади двух диагональных сечений пря-
2 2
мого параллелепипеда равны 16 см и 27 см .
Основанием параллелепипеда является ромб,
2
площадь которого равна 24 см . Найдите длину
бокового ребра параллелепипеда.
а) 7б см; в) 3 72 см;
б) 2 73 см; г) 3 см.
5. Сторона основания правильной
шестиугольной призмы 6 см, а большая диагональ
призмы образует с основанием угол, равный 30°.
Найдите полную площадь поверхности призмы.
а) 252 73 см2; в) 272 72 см2;
б) 288 см2; г) 272 см2.
6. ABCAlBlCv — наклонная треугольная
призма. Двугранный угол при ребре ВВг равен
60е, а расстояния от ребра ВВг до ребер ААг и
ССг равны 1 см и 2 см. Найдите площадь
боковой поверхности призмы, если ее высота равна
0,5 см, а боковое ребро образует с основанием
угол 30°.
а) 6 см2; в) (3 + 73 ) см2;
6)373 см2; г)б7з см2.
7. МКРМ1К1Р1 — правильная треугольная
призма, сторона основания которой 4 см.
Найдите площадь сечения призмы плоскостью,
проходящей через точки P,EhF, где Е и F — середины
ребер МгРг и KXPV а боковое ребро равно 3 см.
а) 3 72 см ;
б) 3 см ;
в) 4 см ;
г) 2 73 см2.
8. ABCDA1B1C1D1 — прямоугольный
параллелепипед, причем ВС = За, CD = а, ССг = 6а.
Найдите тангенс угла между плоскостями BCXD
и ABC.
а)473; 6)2716; в)37б; г) 7з.
Тест 3
Пирамида.
Усеченная пирамида
1. Все ребра правильной треугольной
пирамиды равны между собой. Найдите косинус угла
между боковым ребром и плоскостью основания.
а)|;
*ч 7з ч 1
6>Т; в)з;
г)7з
2. Найдите высоту треугольной пирамиды,
если все ее боковые ребра по 7l0 см, а стороны
основания равны 5 см, 6 см и 5 см.
а) 0,75 см;
^ 7з
б) -г- см;
72
2
715
в) -£- см;
г) ^g- см.
3. Найдите площадь боковой поверхности
правильной четырехугольной пирамиды, если ее
диагональное сечение — равносторонний
треугольник, площадь которого 2 7з см .
а) 8 72 см ;
б) 6 75 см ;
в) 4 77 см2;
г) 12 см2.
4. Основание пирамиды — ромб, один из
углов которого 60е. Каждая боковая грань образует
с плоскостью основания угол, равный 30°.
Найдите площадь основания пирамиды, если высота
пирамиды равна 6 см.
а)25б7з см2; в)24072 см2;
б) 28873 см2;
г) 320 см
5. Основание пирамиды KABCDEF —
правильный шестиугольник ABCDEF со стороцой
18 см. Ребро ВК перпендикулярно плоскости
основания и равно 27 см. Найдите двугранный
угол, образованный плоскостями боковой грани
AKF и основания.
а) 30е; б) 45е; в) 60°; г) arctg |.

Тесты
Геометрия. 10—11 классы
387
6. Стороны оснований правильной
четырехугольной усеченной пирамиды равны 6 см и 8 см.
Найдите площадь диагонального сечения, если
боковое ребро образует с основанием угол в 60°.
a)9V3 CM2i
в) 14 72 см ;
г)147з см2.
б) 15 см ;
7. Стороны оснований правильной
треугольной усеченной пирамиды равны 4 см и 8 см.
Угол между плоскостями боковой грани и
основания равен 30°. Найдите площадь боковой
поверхности данной усеченной пирамиды.
2 2
а) 48 см ; в) 24 см ;
6)2473 см2; г)12 7з см2.
8. SABCD — правильная четырехугольная
пирамида, сторона основания которой равна 10 см,
а боковое ребро равно 2^22 см. Найдите
периметр сечения плоскостью, которая проходит
через точки В и D параллельно ребру AS.
а) 1872 см; в) 24 72 см;
6)2272 см; г) 24 см.
Тест 4
Цилиндр. Конус. Шар
1. Осевое сечение цилиндра — квадрат, длина
диагонали которого равна 36 см. Найдите радиус
основания цилиндра.
а) 9 см; в) 87з см;
б) 8 см; г) 9 72 см.
2. Площадь осевого сечения цилиндра 12 Jn дм ,
2
а площадь основания равна 64 дм . Найдите
высоту цилиндра.
a) g дм;
в) у дм;
б)0,75ядм; г) Здм.
3. Отрезок CD равен 25 см, его концы лежат
на разных окружностях оснований цилиндра.
Найдите расстояние от отрезка CD до оси
цилиндра, если его высота 7 см, а диаметр основания
26 см.
а) 6 72 см; б) 6 см; в) 5 см; г) 473 см.
4. Высота конуса равна 473 см, а угол при
вершине осевого сечения равен 120°. Найдите
площадь основания конуса.
а) 120 72 см2; в) 144я см2;
б) 136я см2; г) 24 73 я см2.
5. Радиус основания конуса равен 7 72 см.
Найдите наибольшую возможную площадь
осевого сечения данного конуса.
а) 5472 см2; в) 2172 см2;
б) 35 см2; г) 98 см2.
6. Отрезок DE — хорда основания конуса,
которая удалена от оси конуса на 9 см. КО — высота
конуса, причем КО = 3 7з см. Найдите
расстояние от точки О (центр основания конуса) до
плоскости, проходящей через точки D, Е и К.
а) 4,5 см; в) зТз см;
б) 3 72 см; г) 6 см.
7. Сфера w проходит через вершины квадрата
CDEF9 сторона которого равна 18 см. Найдите
расстояние от центра сферы — точки О до
плоскости квадрата, если радиус сферы ОЕ образует
с плоскостью квадрата угол, равный 30°.
а) 4 см; в) 3 7б см;
б)47з см; г) 6 см.
8. Стороны треугольника MKN касаются
шара. Найдите радиус шара, если МК = 9 см, MN =
= 13 см, KN = 14 см и расстояние от центра
шара О до плоскости MKN равно 7б см.
а) 4 72 см; в) 3 7з см;
б) 4 см; г) 3 72 см.
Тест 5
Объемы многогранников
1. Диагональ куба равна 15 см. Найдите объем
куба.
а) 225 73 см3; в) 625 72 см3;
6)375 73 см3;
г) 450 см
2. Стороны основания прямого
параллелепипеда равны 1 дм ti 2 7з дм, а угол между ними ра-

388
Тесты
Геометрия. 10—11 классы
вен 30°. Найдите объем параллелепипеда, если
площадь большего диагонального сечения
параллелепипеда равна V38 дм .
а) 2 72 дм ; в) 3 7з дм ;
б) 4 7з дм ; г) 7б дм .
3. Все ребра наклонного параллелепипеда
равны, причем боковое ребро образует с
плоскостью основания угол, равный 45°. Меньшая
диагональ основания равна 4 72 см, а один из углов
120°. Найдите объем параллелепипеда, если
меньшее диагональное сечение
перпендикулярно основанию.
а) 64 7з см3; в) 7272 см3;
б) 84 см3; г) 84 72 см3.
4. Диагональ боковой грани правильной
треугольной призмы образует с основанием угол,
равный 30°. Найдите объем призмы, если площадь
боковой поверхности призмы равна 72 7з см .
а) 120 73 см3; в) 10872 см3;
б)847б см3; г)9б7б см3.
5. В основании прямой призмы CDEKC1D1E1K1
лежит равнобедренная трапеция, DE \\ СК,
причем ЕК = 6 см, СК = 10 см. Диагональ призмы
СЕг образует с основанием угол 45е, а плоскости
ССгЕг и КЕЕг перпендикулярны. Найдите
объем призмы.
а)240 7з см3;
в) 272,8 см ;
б) 300 см ; г) 245,76 см*.
6. Диагональное сечение правильной
четырехугольной пирамиды является прямоугольным
треугольником, площадь которого равна 24 см .
Найдите объем пирамиды.
a)40 73 см3; в) 48 72 см3;
б)32 7б см3;
г) 54 см
з
7. В треугольной пирамиде MNKP MN J_ МК
и МК _L MP, a Z PMN = 60°. Найдите объем
пирамиды, если MN = 2 7з см, МК = 12 см и РМ =
= 4 см.
а) 28 см ;
6)1873 см3;
в) 24 см ;
г) 20 7б см3
8. Через точку В бокового ребра пирамиды
проведена плоскость, параллельная плоскости
основания, причем объем образовавшейся усе-
Q
ченной пирамиды равен 372 см . Найдите объем
пирамиды, если точка В делит ребро пирамиды
в отношении 1:4, считая от вершины.
а) 240 75 см3; в) 375 см3;
6)30073 см3;
Тест 6
г) 420 см*
Объемы тел вращения
1. Отрезок CD, концы которого лежат на
разных окружностях оснований цилиндра,
пересекает ось цилиндра под углом 60е. Найдите объем
цилиндра, если длина отрезка CD равна 8 см.
в) 36 73 л см3;
а) 84 см ;
б) 72 73 л см3;
г) 48л см .
2. Объем цилиндра равен 60л см , а площадь
2
осевого сечения 24 см . Найдите радиус основания
цилиндра.
а) 4 72 см; б) 6 см; в) 5 см; г) 8 см.
3. Плоскость, проходящая через вершину
конуса и хорду CD основания, образует с
основанием угол, равный 60е, и удалена от центра
основания на 6 см. Найдите объем конуса, если длина
хорды CD равна 4 см.
а) 172 73 л см3; в) 208л см3;
б) 180 73 п см3; г) 192тс см3.
з
4. Объем конуса равен 18я дм . Осевое сечение
конуса — прямоугольный треугольник. Найдите
высоту конуса.
а)3372 дм; в)2 7з дм;
6)272 дм; г)337з дм. .
5. Шар касается сторон треугольника МКР9
причем МК = 4 см, MP = 5 см, КР = 7 см. Центр
шара — точка О находится от плоскости тре-
1#ЕГП 7Гб
угольника МКР на расстоянии, равном -тг- см.
Найдите объем шара.
з
а) 15л см ;
б) -g- см ;
в) 12л см ;
г) 8 72 л см

Тесты
Геометрия. 10—11 классы
389
6. Равнобедренный треугольник с боковой
стороной 10 см и углом при вершине 120°
вращается вокруг оси, содержащей боковую сторону.
Найдите объем фигуры вращения.
а) 140л см ;
в) 136 73 п см3;
б) 140 72 п см3; г) 250я см3.
7. Алюминиевый шар объемом 36л см
переплавили в равновеликий конус, образующая
которого равна 3 Jb см. Найдите высоту этого
конуса, если она не более 4 см.
а) 2,5 см; в) 3 см;
б) УП) см; г) 2 73 см.
8. Внутри прямоугольного параллелепипеда
лежит шар таким образом, что он касается трех
граней, имеющих общую вершину. Найдите
расстояние от центра шара до этой вершины, ес-
^ 32я з
ли объем шара равен -=- см .
а) 3 Уз см; в)3л/2см;
б) 2 73 см; г) 2 72 см.
Тест 7
Комбинации фигур
1. Куб вписан в шар. Найдите площадь
поверхности шара, если ребро куба равно л/б дм.
Г" 2 2
а) 8 л/2 п дм ; в) 16я дм ;
Г" 2 2
б) 4 л/2 к дм ; г) 18я дм .
2. Площадь поверхности правильного
тетраэдра равна 30 л/3 см . Найдите площадь
поверхности конуса, вписанного в этот тетраэдр.
а) 8 7з п см2; в) 10я см ;
б) 12,5л; см2; г) 8 J2 к см2.
3. Основанием прямого параллелепипеда
является ромб, один из углов которого р. Найдите
объем цилиндра, вписанного в этот
параллелепипед, если объем параллелепипеда равен V.
а)
б)
nVain р
nVain р
в)
г)
nVain р (
nVain р
4. Около правильной треугольной пирамиды
со стороной основания 9 см и высотой 10 см
описан шар. Найдите радиус шара.
а) 6 см; в) 5,6 см;
б) 6,35 см; г) 7,25 см.
4 з
5. В конус вписан шар объемом « я см .
Найдите объем конуса, если его высота 3 см.
/~" 3 3
а) 2 л/3 я см ; в) Зя см ;
3 г~ 3
б) 4я см ; г) 3 л/2 п см .
6. В полушар вписан цилиндр, причем одно
из оснований цилиндра лежит в плоскости
диаметрального круга полушара, а высота
цилиндра втрое меньше радиуса полушара. Найдите
отношение объема цилиндра к объему полушара.
ч 6 _ 4 ч 5 ч 273
а)£Т§; б)9; В)9; Г)"9"'
7. Прямоугольная трапеция MKPN (MN II КР
и Z N = 90°) вращается вокруг оси, содержащей
сторону КР. Найдите объем фигуры вращения,
если КР = 2 см, диагональ MP = 6 см и Z МРК =
= 60°.
з
а) 36я см ;
з
з
в) 54я см ;
г) 72я см .
б)42ясм ;
8. В правильную четырехугольную
пирамиду вписан куб. Найдите ребро куба, если высота
пирамиды 6 л/2 дм, сторона основания
пирамиды 4 л/2 дм.
а) 1,8 л/2 дм; в) 2,4^2 дм;
б) 2 л/2 дм; г) Зл/2 дм.
Тест 8
Итоговый 1
1. Найдите косинус угла между плоскостями
ромба ABCD и равностороннего треугольника
ADK, если AD = 8 см, Z BAD = 30е и расстояние
от точки К до прямой ВС равно 4 л/2 см.
ч 1 *ч */3 , л/3 ч л/3
a)i^; б)^; в)т* г>т-
2. Основание пирамиды — трапеция с
боковыми сторонами 6 см и 9 см. Найдите объем
пирамиды, если все ее боковые грани составляют с

390
Тесты
Геометрия. 10—11 классы
основанием равные двугранные углы по 60°, а
высота пирамиды равна 2 7з см.
3 г~ 3
а) 24 см ; в) 1873 см ;
6)2073 см3; г) 24 72 см3.
3. Около куба описан цилиндр, полная
площадь поверхности которого равна S. Найдите
площадь поверхности куба.
4S
а) 4 72 Sk;
6)2^2 Sn;
в)
г)
я(72 - 1)'
71(1 + 72)'
4. В конусе проведено сечение, проходящее
через его вершину и две образующие. Найдите
радиус основания конуса, если образующая
составляет с плоскостью основания угол Р,
плоскость сечения образует с плоскостью основания
угол а и удалена от центра основания на а.
а sin а
а)
б)
tgP '
а
в) a cos a tg (J;
г)
а cos а
coscctgp' ' tgP '
5. Стороны основания наклонного
параллелепипеда 2 дм и 7з дм, а угол между ними 30°.
Меньшее диагональное сечение, являющееся
ромбом, перпендикулярно основанию. Найдите
объем параллелепипеда, если боковое ребро
наклонено к плоскости основания под углом,
равным 60°.
в) 1,5 73 дм3;
а) 1,5 дм ;
б) 73 дм ;
ч 273 з
г) -g- дм .
6. Д а н о: \а\ = 2, \Ъ\ = 2^2, \с\ = 3, Z (а, Ъ) = 90е,
Z (Ь, с) = 45е, Z (а, £) - 120°. Найдите косинус
угла между векторами а-Ъ + с и а.
а) —р ; б) -= ; в) —т= 5
'3V2 7з 2V3
*f
7. На поверхности шара лежат три точки С, D
и Е такие, что CD = 7 см, D22 = 8 см, СЕ = 9 см.
Расстояние от центра шара до плоскости
треугольника CDE равно 1 см. Найдите площадь
поверхности шара.
ч 383я 2
а) -g— см ;
б) 84я см2;
ч 484я 2
в) —г— к см ;
г)92,2ясм2.
8. ABCDA1B1C1D1 — прямоугольный
параллелепипед, причем ABCD — квадрат со стороной
78 см, а ребро АЛх равно 278 см. Найдите
площадь сечения, проходящего через точки С, ИГ и
М, где К и М — середины ребер AD и BBV
а) 1272 см2; в) 12 см2;
б) 9 см2; г) 9 72 см2.
Тест 9
Итоговый 2
1. В основании четырехугольной пирамиды
лежит ромб, причем один из его углов равен Р, а
его сторона равна т. Плоскости двух боковых
граней перпендикулярны плоскости основания,
а две другие образуют с основанием угол а.
Найдите высоту пирамиды.
а)
т 8inp
tgcc '
б) msin Р tgoc;
в)
г)
/ntgoc я
sinP '
т
призмы
sin р tg ос *
2. В основании наклонной
CDEFClD1E1F1 лежит трапеция CDEF, причем
DE || CF и CF = 41 см, EF = 13 см, CD = DE =
= 20 см. Плоскость диагонального сечения,
проходящего через точку С, перпендикулярна
основанию и равна 30 720 см2. Найдите объем
призмы.
а) 640 7б см3; в) 720 7з см3;
б) 980 см ;
г) 915 72 см2
3. Ребро правильного тетраэдра равно 6 см.
Через середину ребра проведена плоскость,
параллельная одной из граней тетраэдра. Найдите
объем образовавшейся усеченной пирамиды.
1)2473
см
ч 6372 з
в) , см ;
ЛЧ 5872 з
б) —g— см ;
г)487з
см
4. ABCDA1BlC1D1 — прямоугольный
параллелепипед, причем АВ = 6 см, AD = 15 см и ААг =
= 9 см. Найдите длину отрезка РК, где точки Р и
К принадлежат соответственно отрезкам ВгСг и
ЛХС, причем ВгР :РСг =2:3 иАгК : КС =1:2.
а) 721 см; в) 2 7б см;
б)47з см; г) 726 см.

Тесты
Геометрия. 10—11 классы
391
5. Сфера с центром в точке М(3; -2; 1)
пересекает ось Оу в точках К (0; у; 0) и D(0; у2\ 0).
Найдите у2, если уг - 1.
а)-3; б)-4; в)-5; г) 4.
6. В шар вписан равносторонний конус.
Найдите отношение объема шара к объему конуса.
Т—5
. 973 . ^ 32 .
а) Т"; б) ¥;
ч 28
в) у;
г)
873
7.ABCDA1BlC1Dl — куб, диагональ которого
равнаЪ. Через точкиAv СиМ(точкаМ —
середина ВгСг) проведена плоскость. Найдите
площадь сечения плоскостью, параллельной
плоскости АгСМ и проходящей через вершину Вг.
.Ь2Л. ^Ь2Л. „.J к. .Ь2Л
а) —£— ; о) —£— ; в) Ь V3 ; г) -утр- .
8. Объем цилиндра равен 9л см . При каком
значении высоты цилиндра его полная площадь
поверхности наименьшая?
а) 2 7б см;
6)373 см;
ОТВЕТЫ
10 класс
в) 3736 см;
г) 37б см.
Т—1
Задание
Ответ
1
в
2
а
3
г
4
б
5
г
6
в
7
б
8 1
б
Т—2
Задание
Ответ
1
в
2
б
3
г
4
б
5
б
6
а
7
в
8
г
Т—3
Задание
Ответ
1
в
2
г
3
б
4
а
5
б
6
г
7
в
8
б
Т—4
Задание
Ответ
1
г
2
б
3
а
4
б
5
г
6
а
7
в
8
в
11 класс
Т-1
Задание
Ответ
1
б
2
а
3
в
4
г
5
в
6
б
7
г
8
г
Т—6
Задание
Ответ
1
в
2
в
3
б
4
г
5
в
6
б
7
в
8
б
Т—7
Задание
Ответ
1
б
2
а
3
г
4
в
5
г
6
а
7
в
8
б
Т—8
Задание
Ответ
1
б
2
в
3
в
4
б
5
г
6
в
7
б
8
а
Задание
Ответ
1
б
2
г
3
в
4
б
5
в
6
г
7
г
~8~]
в
Т—2
Задание
Ответ
1
б
2
в
3
в
4
г
5
а
6
в
7
г
8
б
Т—3
Задание
Ответ
1
б
2
г
3
в
4
б
5
в
6
г
7
в
8
б
Т—4
Задание
Ответ
1
г
2
б
3
в
4
в
5
г
6
а
7
в
8
б
Т—5
Задание
Ответ
1
б
2
г
3
а
4
в
5
г
6
б
7
в
8
в

392
Тесты
Геометрия. 10—11 классы
Т—6
Т—8
Задание
Ответ
1
г
2
в
3
в
4
а
5
б
6
г
7
< в
"~*И
б
Т—7
Задание
Ответ
1
г
2
в
3
в
4
б
5
в
6
б
7
г
8
в
Задание
Ответ
1
в
2
б
3
г
4
б
5
а
6
в
7
г
8|
б
Т—9
Задание
Ответ
1
б
2
г
3
в
4
г
5
в
6
б
7
г
8
в

Справочные
материалы
помогут более глубоко овладеть
теоретическим материалом

«Краткий справочник
по математике»
освещает понятия,
которые входят в круг
повседневного школьного
изучения,
знакомит с теоретическими
сведениями, расширяющими
математический
кругозор учащихся.
Справочный комплект
«Алгебра в таблицах»,
«Геометрия в таблицах»,
«Математика в формулах»
содержит все основные сведения
школьного курса
математики, изложенные
предельно кратко.

Краткий справочник по математике
Введение
МНОЖЕСТВО. Множество — это
совокупность, собрание, набор некоторых объектов
произвольной природы, объединенных по какому-
либо общему для них признаку (множество
учащихся данного класса, множество цветных
телевизоров в данной аудитории, множество чисел
первого десятка, множество точек на прямой и
т. д.). Объекты, из которых состоит множество,
называются его элементами. Если элементами
множества являются числа, то оно называется
числовым множеством. Множества
обозначают большими латинскими буквами (А, Б, С, ...),
а их элементы — малыми буквами этого
алфавита. Если элемент х принадлежит множеству А,
то пишут % € А; если же х не принадлежит А, то
пишут х g А. Множество, не имеющее
элементов, называют пустым и обозначают 0
(например, множество прямых углов равностороннего
треугольника, множество людей на Солнце и
т.д.). Запись {1; 2; 3; 4; 5} означает множество,
состоящее из элементов 1, 2, 3, 4, 5; запись
{х\х2 = 4} читается «множество таких х, для
которых х2 = 4*.
Два множества равны, если они состоят из
одних и тех же элементов, например: {х\х2 = 4} =
= {-2; 2}.
Объединением (или суммой) множествАиВ
(обозначение: Л и Б или А + В) называется
множество, составленное из всех элементов,
принадлежащих хотя бы одному из этих множеств.
Знак и называется знаком объединения.
Заметим, что А иА = А.
П р и м е р 1. {1; 2; 3} и {2; 3; 4} = {1; 2; 3; 4}.
Пересечением (или произведением)
множеств А и В (обозначение: An В или АВ)
называется множество, состоящее из всех тех
элементов, которые принадлежат и множеству А, и
множеству В. Знак п называется знаком
пересечения. Заметим, что A n А = А.
П р и м е р 2. {1; 2; 3} п {2; 3; 4} = {2; 3}.
Множество В называется подмножеством
данного множества А (обозначение: В С А), если
каждый элемент множества В является
одновременно элементом множества Л. Знак С
называется знаком включения. В частности, В может
совпадать с А. Пустое множество является
подмножеством любого множества.
П р и м е р 3. Множество четных чисел есть
подмножество множества целых чисел.
Если каждому элементу множества А можно
поставить в соответствие один и только один
элемент множества В и, наоборот, каждому
элементу множества В можно поставить в
соответствие один и только один элемент множества А,
то такое соответствие между множествами АиВ
называется взаимно однозначным.
Например, между множеством нечетных
чисел (А) и множеством четных чисел (В) можно
установить взаимно однозначное соответствие;
для этого следует только расположить эти
множества в виде таблицы:
А
В
1
2
3
4
5
6
7
8
9
10
...
...
и считать взаимно соответствующими числа,
расположенные в каждом ее столбце.
ВАЖНЕЙШИЕ ПОСТОЯННЫЕ.
я = 3,14159, я-1 = 0,31831,
к2 = 9,86960, тГ2 - 0,10132,
е = 2,71828, е-1 = 0,36788,
е2 = 7,38906, е"2 = 0,13534,
М - lg е - 0,43429, М~г = In 10 = 2,30259.
АРИФМЕТИКА, АЛГЕБРА
И НАЧАЛА АНАЛИЗА
Числа и алгебраические
выражения
Натуральные числа
ДЕЙСТВИЯ НАД НАТУРАЛЬНЫМИ ЧИСЛАМИ.
Числа 1, 2, 3, 4, 5, ... называют натуральными.
Множество натуральных чисел обозначают симво-

396
Справочные материалы
Краткий справочник по математике
лом N. В этом множестве определены операции
сложения и умножения; обратные операции
(вычитание и деление) применимы не ко всем
натуральным числам.
Справедливы следующие свойства сложения
и умножения натуральных чисел:
a + b = b + а (переместительное
свойство сложения);
(a + b) + с = а + (Ь + с) (сочетательное свой-
ство сложения);
аЬ = Ъа (переместительное
свойство умножения);
(аЪ)с = а (Ъс) (сочетательное свой-
ство умножения);
a (b + с) = ab + ас (распределительное
свойство умножения
относительно
сложения)*.
ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА. Говорят, что
натуральное число т делится на натуральное
число л, если существует натуральное число /
такое, что т = nl. Например, 12 делится на 3, но
не делится на 5. Любое натуральное число
делится на 1 и на само это число. Натуральные
числа, на которые делится данное число,
называются делителями этого числа. Например,
числа 1, 2, 3, 6 — делители числа 6; 1 и 5 —
делители 5. Натуральное число т (отличное от
единицы), которое имеет только два делителя: 1
и само /п, называется простым. Например, 2, 3,
5, 7, 11, 13, 17, ... Простых чисел бесконечно
много. Натуральное число, имеющее более двух
делителей, называется составным. Так, все
четные числа, кроме 2, — составные.
Основная теорема арифметики. Каждое
составное число может быть единственным
образом (с точностью до порядка сомножителей)
представлено в виде произведения простых
чисел.
Такое представление называется
разложением на простые множители. Оно производится
с использованием признаков делимости.
Приведем некоторые из них.
Натуральное число делится на:
а) 2, если его последняя цифра — четное
число или нуль;
* Переместительное, сочетательное и распределительное
свойства кратко называются еще соответственно
коммутативностью, ассоциативностью и дистрибутивностью.
б) 4, если две его последние цифры — нули
или образуют число, делящееся на 4;
в) 3, если сумма его цифр делится на 3;
г) 9, если сумма его цифр делится на 9;
д) 5, если его последняя цифра — нуль или 5.
ДЕЛЕНИЕ С ОСТАТКОМ. Если натуральное
число /п не делится на натуральное число п, т.е.
не существует такого натурального числа I, что
т = nl, то рассматривают деление с остатком.
Например, при делении числа 41 на число 19
получаем 41 = 19 • 2 + 3. Число 2 называется
неполным частным, а число 3, т.е. разность между
данным числом 41 и произведением 19 • 2, —
остатком. В общем случае т = hi + г, где /иг —
натуральные числа (исключение составляет
случай, когда /п делится на п без остатка и г = 0),
причем т> п, г < п. Результат деления с
остатком записывают в виде
п п
Например, у = 3 + g .
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. Общим
делителем нескольких натуральных чисел
называют натуральное число, на которое делится
каждое из данных чисел. Например, общим
делителем чисел 2, 4, 6, 12 является 2.
Наибольшим общим делителем (НОД)
нескольких натуральных чисел называют
наибольшее натуральное число, на которое делится
каждое из данных чисел. Для отыскания НОД
нескольких натуральных чисел необходимо
разложить их на простые множители, а затем
составить произведение всех простых множителей,
общих для данных чисел. Например, 12 = 2 • 2 • 3,
18 = 2 • 3 • 3. Следовательно, НОД чисел 12 и 18
есть 2-3 = 6.
Обычно при отыскании НОД двух чисел
применяется другой способ (алгоритм Евклида).
Большее из них делят на меньшее, затем
меньшее — на первый остаток, далее первый
остаток — на второй, второй — на третий и так до
тех пор, пока в остатке не получится нуль; тогда
последний делитель является НОД данных чисел.
Пример. Найдем НОД
чисел 357 и 273:
Отсюда следует, что НОД
чисел 357 и 273 равен 21.
84
84
273
252
21
357 1 273
273 | Г
84
3

Справочные материалы
Краткий справочник по математике
397
Два натуральных числа тип называются
взаимно простыми, если их НОД равен 1.
Понятие НОД используют при сокращении
обыкновенных дробей.
Наименьшее общее кратное. Наименьшим
общим кратным (НОК) нескольких
натуральных чисел называют наименьшее натуральное
число, которое делится на каждое из данных
чисел. Для отыскания НОК нескольких
натуральных чисел надо разложить их на простые
множители, выписать все множители
какого-нибудь одного из чисел, дописать все недостающие
множители из других чисел и все их
перемножить.
Пример. Найдем НОК чисел 10, 15 и 20.
Имеем 10 = 2 • 5, 15 - 3 • 5, 20 = 2 • 2 • 5.
Следовательно, НОК чисел 10, 15 и 20 есть 2 • 2 • 5 • 3 = 60.
НОК двух взаимно простых чисел равно
произведению этих чисел.
Понятие НОК используют при сложении и
вычитании обыкновенных дробей.
Целые числа и обыкновенные дроби
ОПРЕДЕЛЕНИЯ. Основное свойство дроби.
Числа 0, ±1, ±2, ±3, ±4, ±5, ... называют
целыми. Множество целых чисел обозначают
символом Z. Натуральные числа — это целые
положительные числа.
Обыкновенная (или простая) дробь* — это
771
выражение вида —, где тип — целые числа
(пф 0); черту можно воспринимать как знак
деления и писать т:п (или т/п). Число т
называют числителем, п — знаменателем
дроби. При п - 1 дробь имеет вид у (чаще пишут
просто т). Это означает, что всякое целое число
можно представить в виде обыкновенной дроби
со знаменателем 1. Если \т\ < \п\, то дробь —
правильная, если \т\ > \п\, то дробь —
неправильная. Неправильную дробь можно
представить в виде суммы целого числа и правильной
дроби.
Например, -«- = 3 + « • Для краткости вместо
3+ - принято писать 3 о (смешанное число).
Основное свойство дроби. При умножении
числителя и знаменателя на одно и то же число
(не равное нулю) значение дроби не меняется:
т
п
тЬ
пЪ '
Это свойство используется, в частности, при со-
93 3 31 3
кращении дробей. Например, ^ТБ в о~ГоТ = 8 *
ДЕЙСТВИЯ С ДРОБЯМИ. При сложении
(вычитании) дробей с одинаковыми знаменателями
складывают (вычитают) их числители и
оставляют тот же знаменатель. При этом полученный
результат необходимо сократить, если это
возможно. Если же знаменатели дробей различны,
то эти дроби сначала приводят к общему
знаменателю (обычно удобно находить наименьший
общий знаменатель, т.е. НОК знаменателей),
затем применяют предыдущее правило.
Пример 1.
2_
15
5
2 3
5-5-2-2
2 3 5
2
3 5
21
30
5 5
2 3 5
7 3
10 3
2 2
2 3 5
7_
= 10*
При умножении дробей перемножают
отдельно числители и отдельно знаменатели; при
делении делимое умножают на дробь, обратную
(♦перевернутую») делителю. При этом полученные
результаты необходимо сократить, если это
возможно.
Пример 2.
4 |= 4 3 = 6_.
5 " 10 5 10 25 ;
JL = § 12 = 3 10 =
.10 5 *
9
5 9
Числа, представимые обыкновенными
дробями, называют рациональными. Множество
рациональных чисел обозначается символом Q.
Очевидно, N С Z С Q.
ПРОПОРЦИИ. Пропорцией называют
равенство двух отношений:
а
Ъ
с
d
(1)
* Обыкновенную дробь еще называют отношением.
(and — крайние члены, Ьис — средние члены
пропорции, причем a,b,c,d отличны от нуля).

qqq Справочные материалы
*«**70 Краткий справочник по математике
Свойства пропорции.
1. Произведение крайних членов равно
произведению средних (основное свойство
пропорции), т. е. ad = be.
2. Крайние члены пропорции можно
поменять местами, т. е.
d = с
Ь а'
3. Средние члены пропорции можно поменять
местами, т. е.
а Ь
с d'
4. Производные пропорции:
а + Ъ _ с + d а - Ъ _ с - d
Ь " d ' b " d '
а + Ь с + d
г - 3 ит-Д-
а - о с - d
Десятичные дроби
ОПРЕДЕЛЕНИЕ. Свойства десятичных
дробей. Конечной десятичной дробью называют
дробь, знаменатель которой является
натуральной степенью числа 10. В этом случае дробь
принято записывать без знаменателя, отделяя в
числителе запятой (справа налево) столько
знаков, сколько нулей в знаменателе. Например,
33
Yqq = 0,33 (читается: «нуль целых тридцать три
сотых»), Tqqq =2,019 («две целых девятнадцать
тысячных»).
Отметим, что если в разложении знаменателя
(после сокращений) обыкновенной дроби на
простые множители содержатся только двойки и
пятерки, то эту дробь можно записать в виде
конечной десятичной дроби.
Приписывание или отбрасывание нулей
справа не меняет значения дроби. Например,
4,15 = 4,1500 = 4,150.
Умножение (деление) на 10 сводится к
переносу запятой на один разряд вправо (влево).
Примеры.
1)3,817 • 10 = 38,17; 0,05 • 100 = 0,5 • 10 = 5,0 = 5;
2) 18,11:10 = 1,811; 605:100 = 60,5:10 - 6,05.
ДЕЙСТВИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ.
Сложение положительных десятичных дробей и
вычитание меньшей дроби из большей производят
♦столбиком», записывая числа одно под другим
таким образом, чтобы запятые оказались одна
под другой.
Пр имер 1.
314,06 314,06
+ 0,423 " 0,324
314,483 313,736
При умножении десятичных дробей сначала
умножают их как целые числа, не обращая
внимания на запятые, затем в произведении
отделяют справа запятой дробную часть, число
разрядов которой равно сумме числа разрядов
дробных частей сомножителей.
П р и м е р 2. 31,07 • 0,12 = 3,7284.
При делении десятичных дробей сначала у
делимого и делителя переводят запятую вправо
на число разрядов, равное числу разрядов
дробной части делителя, затем выполняют деление
♦углом*, сохраняя нужное количество разрядов.
Число разрядов целой части определяется в
процессе деления целой части делимого на
делитель.
ПримерЗ. 7,55 : 0,2 = 75,5 : 2 = 37,75.
ПЕРИОДИЧЕСКИЕ ДРОБИ. В некоторых
случаях процесс деления «углом» натуральных
чисел, как и десятичных дробей, оказывается
бесконечным; в результате получается так
называемая бесконечная десятичная дробь, в
которой бесконечно повторяется одна и та же группа
цифр. Такая бесконечная десятичная дробь
называется периодической, а повторяющаяся
группа цифр (минимальная) — периодом дроби,
который при записи периодических дробей
указывают в круглых скобках. Например, 1,01 : 0,33 =
= 3,06060606... - 3,(06). Здесь период
начинается сразу после запятой. Такие дроби
называются чистыми периодическими. Если же период
начинается не сразу после запятой, то дробь
называется смешанной периодической. Например,
0,28 : 0,9 = 0,31111... = 0,3(1).
Каждую периодическую дробь можно
обратить в обыкновенную: в сдучае чистой
периодической дроби к целой части прибавляют
обыкновенную дробь, в числителе которой записывают
период, а в знаменателе — цифру 9 столько раз,
сколько цифр в периоде; в случае же смешанной

Справочные материалы
Краткий справочник по математике
399
периодической дроби предварительно
переносят запятую к началу периодической части,
затем обращают полученную чистую
периодическую дробь б обыкновенную и делят последнюю
на 10*, где k — число разрядов, на которые
перенесена запятая вправо.
Примеры.
1)3,(06) = 3+А=3+;|=32
2) 0,3(1) = ^ • 3,(1) = Y6
33'
°9 10 ^ 90
= 28 = 14
90 45 е
Конечную десятичную дробь можно считать
периодической с периодом нуль или девять.
Например, 1,29 = 1,29(0) = 1,28(9).
Можно доказать, что всякое рациональное
число представимо либо в виде конечной, либо
бесконечной периодической десятичной дроби.
о
Например, тт = 0,(27).
НЕПЕРИОДИЧЕСКИЕ ДРОБИ.
Иррациональные числа. Если бесконечная десятичная дробь
не содержит периода, то ее называют
непериодической. Например, 0,1010010001... —
непериодическая дробь, так как число нулей между
единицами возрастает. Непериодическую дробь
невозможно записать в виде обыкновенной
дроби.
Числа, представимые бесконечными
непериодическими десятичными дробями, называют
иррациональными.
Следовательно, дробь 0,1010010001... —
иррациональное число. Числа 72 = 1,4142..., 7з =
= 1,73205..., к = 3,14159... также служат
примерами иррациональных чисел.
ПРОЦЕНТЫ. Процентом (обозначение: %)
называют сотую часть числа. Например, 40% от
40
числа 35 составляют -tttz его частей и,
следовательно, равны
о. 40 вег 2 ЛА
35 # 100 =35# 5=14'
Если р% некоторого числа а равны Ь, то
Ъ ЮО тт
само число а = . Например, если 20%
некоторого числа а равны 15, то само число а -
15 100
20
= 75.
Выражение величины а в процентах другой ве-
а
личины Ь, т. е. г • 100%, называется
процентным отношением чисел аиЬ.
Сложные проценты — это проценты,
начисляемые в определенные сроки как на основной
вклад, так и на наращенные за предыдущий
срок проценты.
Пусть в Сбербанк внесен вклад в а руб. на р%
годовых (т. е. проценты начисляются один раз в
год). Какая сумма окажется на сберегательной
книжке вкладчика через п лет?
Через год на сберегательной книжке будет
(>♦
iooJ
руб.
через два года
K1 + ioo))(1 + ioo)=a(1 + ioo)2py6"
через п лет сумма составит
Это — формула сложных процентов.
ОКРУГЛЕНИЕ ЧИСЕЛ. При округлении
десятичной дроби крайнюю правую цифру
отбрасывают, при этом предыдущую цифру либо
сохраняют, если отбрасывается одна из цифр 1, 2, 3, 4
(округление с недостатком), либо
увеличивают на единицу, если отбрасывается одна из
цифр 5, 6, 7, 8, 9 (округление с избытком).
Например, 52,33 « 52,3; 52,36 * 52,4; 52,35 « 52,4
(знак = читается: «приближенно равно»).
Значение 52,3 называют приближенным значением
числа 52,33, а значение 52,4 — приближенным
значением чисел 52,36 и 52,35.
Округление целых чисел выполняют
аналогично, но на месте отбрасываемой цифры
записывают цифру 0. Например, 8084 « 8080, 8100 *
« 8000.
Действительные числа
МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.
Объединение множества рациональных чисел и

Справочные материалы
Краткий справочник по математике
множества иррациональных чисел называется
множеством действительных (или веществен-
ных) чисел. Множество действительных чисел
обозначается символом R. Очевидно, NcZcQcR.
Действительные числа изображаются на числовой
оси Ох точками (рис. 1). При этом каждому
действительному числу соответствует определенная
точка числовой оси и каждой точке оси
соответствует определенное действительное число.
Поэтому вместо слов «действительное число»
можно говорить «точка». Точки, изображающие
действительные числа, расположены «всюду
плотно» на оси: между любыми двумя
действительными числами найдется бесконечно много
действительных чисел. Свойством плотности
обладают также множества рациональных и
иррациональных чисел. Любое иррациональное
число можно как угодно точно приближать
рациональными числами, в частности конечными
десятичными дробями, имеющими все более
длинные дробные части; например,
Л ~ 1,4; Л - 1,41; Л - 1,414; Л » 1,4142;
Л -1,41421;...
При практических вычислениях с
ограниченной точностью различие между рациональными
и иррациональными числами не проявляется.
Действия сложения и умножения
действительных чисел обладают свойствами:
коммутативности: a + b = b + a, ab = Ьа;
ассоциативности: (а + Ь) + с = а + (Ь + с),
(ab)c = а(Ьс);
дистрибутивности: а(Ъ + с) = ab + ас.
СТЕПЕНИ И КОРНИ. Если п — натуральное
число, то п-я степень (ап) некоторого
действительного (в частности, целого) числа а,
называемого основанием степени, определяется как
произведение п сомножителей, равных а (ап =
= а • а...а). При этом число п называют
показателем степени.
По определению, при любом а Ф 0 считают
а0 = 1, а1 = а, а~п = 1 : ап. Например,
23 = 2 • 2 • 2 = 8, 2"3 = 1 : 23 = 1/8.
~5 0,5 1,4 Л к
—i 1 п—I 1—•—Г"1—н—г 1—■"
-4-3-2-10 1 2 3 4 J
Рис.1
При любых натуральных показателях тип
справедливы следующие равенства:
ат-ап = ат+п; ат :an = am~n(a*0); (ат)п = ат'п;
(а-Ь)п = ап -Ьп; (g J" = ~п (&*0).
Приведенные соотношения верны и для
любых действительных показателей при а > 0, Ъ > 0.
Если а > 0 и п — натуральное число, то
арифметическим корнем п-й степени из а называют
единственное положительное число х такое, что
хп = а. Обозначение корня: а1^п или nJa .
Корень второй степени из а (квадратный
корень) принято обозначать Ja.
Если а = 0, то nJa = 0.
Если a < 0, то корень n-й степени из а
определяется лишь для нечетных п. В этом случае nJa
есть единственное отрицательное число х такое,
что хп = а.
Например, \fl6 = 2, так как 24 = 16 и 2 > 0;
V27 = 3; Учи = -4.
Если а > 0, /п и п — натуральные числа, то,
по определению, считают
ат/п = (а1/Л)т. а-т/п = j . ат/п (а ф 0)
При этом имеют место следующие равенства:
ат/п = (пЛ)т = л7о^; mftJa = тпЛ;
пЛ* = пЛпЛ; л11=Щ(ь*о).
В тех случаях, когда подкоренное число
является целым, бывает полезно разложить его на
простые множители. Например,
ЛТбб = V4 • 289 = л/22172 = 2 • 17 = 34.
Равенства (аЪ)п - ап • Ьп, nJab - nJa пЛ
распространяются на любое конечное число
сомножителей.
ЛОГАРИФМЫ. Логарифмом loga N числа N
(N > 0) по основанию а (а > 0, а Ф 1) называют

Справочные материалы
Краткий справочник по математике
401
показатель степени, в которую нужно возвести
основание а, чтобы получить N.
Например, log2 32 = 5, так как 25 = 32.
Свойства логарифмов. При любых а >
> 0, а * 1, & > 0, & * 1, любых N > 0, Nx > 0, N2 > 0
и любом а имеют место следующие равенства:
l.logal =0;logaa = 1.
2.al0'«"=*.
3. loge (JVjATa) = loge ATj + loga N2.
4. loga (j^-J = log0 Nx - loga N2.
5. loga (№) = a • loge N.
1
6.1ogaN =
7.1ogaAT =
log^a
logbN
logbc
(ЛГ*1).
Логарифмы по основанию 10 называют
десятичными (обозначение: \g N).
Число е (см. введение, п. 2) принимается за
основание системы логарифмов, называемых
натуральными. Для обозначения натурального
логарифма числа N пользуются символом In N.
Связь между натуральным и десятичным
логарифмами числа N выражается формулой
\nN =
IgN
lg е
(if,-2-
30258 \ .
МОДУЛЬ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА.
Абсолютной величиной (или модулем)
действительного числа х называется неотрицательное
число \х\9 определяемое соотношением
w-
ху если х > 0;
-х, если х < 0.
Свойства модуля.
1.Н-Н.
2.-\х\<х<\х\.
3. Неравенства \х\ ^ а и -а < х < а равносильны.
4. Модуль суммы двух действительных чисел
меньше или равен сумме модулей этих чисел:
Это свойство справедливо для любого
конечного числа слагаемых.
5. Модуль разности двух действительных
чисел больше или равен разности модулей этих
чисел: \х-у\> \х\ - \у\.
6. Модуль произведения чисел равен
произведению модулей этих чисел: \ху\ = \х\ \у\.
Это свойство справедливо для любого
конечного числа сомножителей.
7. Модуль частного двух чисел (если
делитель отличен от нуля) равен частному
модулей этих чисел:
w
\у\'
ПРОМЕЖУТКИ. Окрестность точки.
Различают следующие виды промежутков:
1) замкнутый промежуток (отрезок,
сегмент):
[а, Ь] = {хе R\a<xKb};
2) открытый промежуток (интервал):
(а, Ь) - {х е R\a < х < Ь}
(иногда для интервала используют обозначение
]а, Ь[);
3) полуоткрытые промежутки:
(a,&] = {xe R\a<x<b}9 [a, b) = {xe R\a<:X<b}
(в других обозначениях ]a, Ь] и [a, b[
соответственно);
4) бесконечные промежутки (лучи,
полупрямые):
(-оо, а) = {хе R\x < а}, (-оо9 а] = {хе R\x<a}9
(a, -\-оо) = {хе R\x>a), [a, +<*>) = {хе R\x>a}9
(-оо, +оо) = R (числовая прямая).
Окрестностью точки х0 называют любой
интервал, содержащий эту точку; г-окрестно-
стью (е > 0) точки х0 называется интервал
(Xq - е, Xq + е), т. е. множество чисел х,
удовлетворяющих условию \х - х0\ < е.
ПОГРЕШНОСТИ ВЫЧИСЛЕНИЯ. Пусть
некоторая величина имеет точное значение а. В
результате измерения этой величины получено ее
приближенное значение х. Абсолютной
погрешностью До приближенного значения х называется
модуль разности между числом х и точным
значением a: Aq = \х - а\.
Если число а неизвестно (что бывает в
большинстве измерений), то абсолютную
погрешность вычислить нельзя. В этом случае
используется предельная абсолютная погрешность —

А(\су Справочные материалы
^*"^ Краткий справочник по математике
такое положительное число А, что А0 < А.
Очевидно, что х-А<а<:Х + А. Кратко последнее
неравенство записывают так: а = х ± А.
Точность измерения характеризуется с
помощью относительной погрешности.
Относительной погрешностью 50 приближенного значения
х называется отношение абсолютной
погрешности этого значения к модулю точного значения а:
Если точное значение а неизвестно, то
используют предельную относительную погрет-
ность — такое положительное число 8, что 8q < 8.
Для вычисления относительных
погрешностей часто используются приближенные
формулы
я А° я А
0 1*1 1*1
Эти формулы тем точнее, чем ближе значение
х к точному значению а, т. е. чем меньше
погрешность Ао или А.
Пример. Каковы предельные абсолютная и
относительная погрешности числа 1,41 —
приближенного значения числа J2 ?
Так как 1,410 < JU < 1,415, то А0 = Л - 1,410 <
< 0,005. Следовательно, можно положить А = 0,005.
Далее,
50=^<°1^< 0,0036,
откуда 5 = 0,0036 или 5 = 0,36%.
Говорят, что приближенное значение х
(записанное в виде десятичной дроби) имеет п верных
знаков, если абсолютная погрешность этого числа
меньше или равна половине единицы его n-го
разряда. Например, если 9,263 имеет три верных
знака (9, 2 и 6), то абсолютная погрешность этого
числа Aq< 0,005.
Комплексные числа
ОПРЕДЕЛЕНИЯ. Основные операции над
комплексными числами. Под комплексным
числом понимается выражение
z = x + iy, (1)
где х и у — действительные числа, a i —
мнимая единица.
Запись (1) называется алгебраической
формой комплексного числа. Числа х + i0 = х
отождествляются с действительными числами, в
частности, 0 + i0 = 0. Числа 0 + iy = iy называются
чисто мнимыми.
Множество комплексных чисел обозначают
символом С. Очевидно, N С Z С Q С Я С С.
Действительные числа хиу называются
соответственно действительной и мнимой частями
числа z и обозначаются следующим образом:
х = Re z, y = Imz.
Под модулем комплексного числа z
понимается неотрицательное число \z\ = V* + У •
Сопряженным числом z по отношению к
числу (1) называется комплексное число z = x-iy.
Два комплексных числа Zi = xi + iyi и z2 =
= х2 + iy2 равны тогда и только тогда, когда
*1 = *2 и У\ " У2-
Сложение, вычитание и умножение комплекс-
, ных чисел определяются следующим образом:
гх ± z2 = (*! ± х2) + i(yx ± у2);
г\г2 = (*i*2 - У1У2) + *(*iJ/2 + х2Уг)-
Отсюда, в частности, вытекает, что:
i2 = (0 + il)(0 + il) = (0 - 1) + i(0 + 0) = -1;
zz = x2 + y2 = \z\2.
Таким образом, введенные операции
сложения и умножения обладают свойствами:
коммутативности:
г\ + 22 = г2 + гЪ г\г2 = z2z\'y
ассоциативности:
(гг + z2) + z3 = zx + (z2 + 23),
(z1z2)z3 = z1(z2z3);
дистрибутивности:
Zi (Z2 + 23) = ZiZ2 + Z1Z3.
Деление комплексных чисел определяется так:
fl = г* *2 = (xix2 + У1У2) + 1(х2Уг - х\Уг)
г2 гг *г хЪ + у\
(г2*0).
ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ
КОМПЛЕКСНЫХ ЧИСЕЛ. Рассмотрим плоскость, в которой
задана прямоугольная система координат хОу

Справочные материалы
Краткий справочник по математике
403
(рис. 2). Так как комплексное число г = х + iy
является парой (х; у) действительных чисел, а
каждой паре (х; у) действительных чисел
соответствует одна точка плоскости и наоборот, то
каждую точку М (х; у) плоскости можно принять
за изображение комплексного числа г = х + iy.
Рассматриваемая плоскость называется
комплексной плоскостью, а г — точкой этой
плоскости.
На оси Ох расположены действительные числа:
z - х + Ю = х; поэтому она называется
действительной осью. На оси Оу расположены чисто
мнимые числа: г = 0 + iy = iy9 она называется
мнимой осью.
Заметим, что число г = \г\ представляет собой
расстояние от точки г до начала координат.
Положение точки г на плоскости, кроме ее
прямоугольных координат х9 у, может быть
определено также и полярными координатами г,
(р; при этом
х = г cos ф, у = г sin ф. (2)
Число ф будем называть аргументом
комплексного числа г. Аргумент считается
положительным или отрицательным в зависимости от
того, ведется ли его отсчет от положительного
направления действительной оси против или по
часовой стрелке соответственно.
Для заданного числа г его модуль
определяется единственным образом, а аргумент — с
точностью до слагаемого 2йтс, k= О, ±1, ±2, ... .
Значение аргумента ф, удовлетворяющее
условию -тс < ф < тс, называется главным и
обозначается arg z. При этом г = О является единственной
точкой комплексной плоскости, для которой
аргумент не определен.
УМНОЖЕНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ
ЧИСЕЛ, ЗАПИСАННЫХ В
ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ. Из формулы (2) получается
тригонометрическая форма записи комплексного
числа:
z = г (cos ф + i sin ф). (3)
Пользуясь записью (3) для комплексных чисел
Zi = гх (cos ф! + i sin <pi)f ^2 = г2 (cos ф2 + i sin ф2),
имеем:
2lz2 = г1г2 ((cos Ф1 cos Ф2 ~ s*n Ф1 sin Ф2) +
+ i (sin Ф1 cos ф2 + cos ф! sin ф2)) =
= ггг2 (cos (фх + ф2) + i sin (фх + ф2)), (4)
гг гг cos фх + i sin фх
z2 r2 cos ф2 + i sin ф2
гг (cos фх + i sin ф1)(сов (-ф2) + i sin (-ф2))
r2 (cos ф2 + i sin ф2)(сов ф2 - i sin ф2)
= - (cos (фх - ф2) + i sin (фх - ф2)) (г2 * 0).
г2
Следовательно, при умножении
комплексных чисел их модули перемножаются, а
аргументы складываются; при делении
комплексных чисел их модули делятся, а аргументы
вычитаются.
ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ
КОРНЯ. Следствием формулы (4) является
формула
zn = Iя (cos щ + i sin пф),
где п — натуральное число.
Справедлива и формула
(5)
nJz = nJr (cos ф + i sin ф) =
пГ ( ф 4- 2*тс . . Ф + 2kn\
= n*Jr cos х + i sin x ,
(, n n )
A = 0, 1,2, ..., /1-1. (6)
Пример. Найдем ш — «f-1.
Так как -1 = cos тс + i sin тс, то на основании
формулы (6) имеем
г-г тс + 2Дгтс , . . тс + 2Дгтс , л i
J-1 - cos о + i sin n , л = 0, 1.
Отсюда
тс ... тс Зтс , . . Зтс
w0 = cos 2 + 1 sin г = i, u>i - cos -5- + 1 sin -5- - -i.
ФОРМУЛА МУАВРА. ФОРМУЛА ЭЙЛЕРА.
Формулу (5) можно переписать в виде
г* (cos ф + i sin ф)л = г* (cos пф + i sin пф).
У1
У
О
1
/4
л
z = х + iy
М (х;у)
С X
Рис. 2

Справочные материалы
Краткий справочник по математике
Полагая здесь г = 1, получим формулу
(cos ф + i sin <р)Л = cos Лф + i sin шр,
называемую формулой Муавра.
Справедлива и следующая формула:
cos ф + i sin ф = е1(р,
называемая формулой Эйлера.
Часто также используются формулы
е - е е ^ + е ^
sin ф = 21 , cos ф = g »
позволяющие выразить тригонометрические
функции через показательную.
ЛОГАРИФМЫ КОМПЛЕКСНЫХ ЧИСЕЛ.
Логарифм (натуральный) комплексного числа г Ф О
имеет бесконечное множество значений:
Ln2 = lnr+i (ф + 2л£), А = 0, ±1,±2, ...
Здесь In г — обычный логарифм по
основанию е.
Главное значение логарифма:
In г = In г + мр,
где -п< ф < тс.
Примеры.
1) Ln 1 = In 1 + 2ink = 2ink;
2) Ln(-l) = ln 1 + i(n + 2nk) = in (2k + 1);
3)Ln(l + iV3) = ln 2 + i[\ + 2nk).
Алгебраические выражения
ОСНОВНЫЕ ПОНЯТИЯ. Высмотрим вьфажения
\аЧ* (1); 4^-|^+1 (2); *±» (3);
з з ? ?
*-±-J- (4); V^Tft (5); х2 - у1 (6).
Здесь буквам а,Ь, хиу можно придавать
различные числовые значения, поэтому их
называют переменными. В выражениях (1) и (2)
отсутствуют деление на переменные (или на
выражения, содержащие переменные) и извлечение
корня из переменных (или из выражений,
содержащих переменные), включая и возведение в
степень с дробным показателем; такие
выражения называются целыми. В выражениях (3) и
(4) указанное деление присутствует; такие
выражения называют дробными. Наконец, в
выражениях (5) и (6) есть указанные извлечение корня
и возведение в степень с дробным показателем;
такие выражения называют иррациональными.
Целые и дробные выражения называются
рациональными.
Характерной особенностью дробных
выражений является то, *гго они теряют смысл при
значениях переменных, обращающих знаменатель
в нуль. Так, выражение (3) не имеет смысла при
а = О, а выражение (4) теряет смысл при х = у.
Целые выражения имеют смысл при любых
значениях переменных. Иррациональное
выражение не имеет смысла при тех значениях
переменных, которые обращают в отрицательное число
выражение, содержащееся под знаком корня
четной степени или под знаком возведения в
дробную степень. Например, выражение (5)
имеет смысл только при тех а и ft, при которых
а+ Ь > 0, а выражение (6) имеет смысл только
при х>0иу>0. Значения переменных, при
которых выражение имеет смысл, называются
допустимыми значениями переменных. Множество
всех допустимых значений переменных называют
областью определения алгебраического
выражения.
Рассмотрим выражения /х (х, у) = х2 + Зху и
1г (х9 у) = х (х + Зу). Если вычислять значения
этих выражений при произвольных значениях
переменных х и у, то каждой паре значений хиу
соответствуют одинаковые значения fi(x, у) и
/2 (*>*/)•
Два выражения называются тождественно
равными, если их соответственные значения
равны между собой; равенство, в котором левая
и правая части — тождественно равные
выражения, называется тождеством.
Если равенство fi (х, у) = f2 (х, у) —
тождество, то замена выражения fi(x, у) выражением
/2 С*» У) называется тождественным
преобразованием.
Примерами тождеств могут служить
следующие равенства:
х + у = у + х (переместительный закон
сложения);
(х + у) + г = х + (у + г) (сочетательный закон
сложения);
ху = ух (переместительный закон
умножения);
(ху)г = х(уг) (сочетательный закон
умножения);
х(у + г) = ху + Х2 (распределительный закон
умножения относительно сложения).

Рассмотренные ранее правила действий над
обыкновенными дробями (сложение, вычитание,
умножение, деление, возведение в натуральную
степень) и основное свойство обыкновенной
дроби распространяются и на дроби, содержащие
переменные.
ОДНОЧЛЕНЫ И МНОГОЧЛЕНЫ. Одночленом
называется произведение нескольких
сомножителей, один из которых числовой (коэффициент),
а другие — натуральные степени с буквенными
2 Q 9
основаниями. Например, ъаЬ — одночлен.
Любой одночлен можно привести к стан-
дартному виду, т. е. представить в виде
произведения числового множителя, стоящего на
первом месте, и степеней различных переменных,
сумма показателей которых называется степе-
нью одночлена.
Многочленом называется сумма нескольких
одночленов (например, 4ху - 2ху2 + 1), а его
степенью — наибольшая из степеней входящих
в него одночленов.
Два одночлена, приведенные к стандартному
виду, называются подобными, если они
одинаковы или отличаются только коэффициентами.
Так, в многочлене Зах2 + Ъах2 + ах первые два
слагаемых подобны. В соответствии с
распределительным законом умножения имеем:
Зах2 + Ъах2 + ах = ах2 (3 + 5) + ах = 8ах2 + ах.
Тождественное преобразование, состоящее в
объединении нескольких подобных членов в
один, называется приведением подобных
членов. Если все члены многочлена записать в
стандартном виде и выполнить приведение
подобных членов, то получится многочлен
стандартного вида.
Ограничимся рассмотрением многочленов от
одной переменной.
Многочлены от одной переменной
ОПРЕДЕЛЕНИЯ. Действия над
многочленами. Многочленом (полиномом) степени п от
одной переменной х называется многочлен вида
Р (х) = а0хп + аххп~1 + ... + ап.хх + ап, (1)
где а0, ai,..., ап^\, ап (а0 * 0) — действительные
числа (коэффициенты), п — целое неотрицатель-
Справочные материалы AfkfZ
Краткий справочник по математике ^*"*J
ное число. Многочлен нулевой степени (п - 0)
совпадает с постоянной.
Два многочлена считаются равными, если
они имеют равные коэффициенты при
одинаковых степенях х.
Многочлены можно складывать, вычитать и
перемножать.
Примеры.
1) (х + 2) + (х2 - 2х) = х2 - х + 2;
2) (х + 2)(х2 - 2х) = (х + 2) х2 - (х + 2) • 2х =
- х3 + 2х2 - 2х2 - 4х = х3 - 4х.
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ.
(х ± а)2 = х2 ± 2ах + а2,
(х + а)(х - а) = х2 - а2,
(х + а)3 - Xs + Зах2 + За2х + а3,
(х - а)3 = хг - Зах2 + За2х - а3,
(х + а)(х2 -ах + а2) = х3 + а3,
(х - а)(х2 + ах + а2) - х3 - а3.
ДЕЛЕНИЕ МНОГОЧЛЕНОВ. Теорема Безу.
Разделить многочлен Р(х) на многочлен Q(x) —
значит найти многочлены М(х) (частное) и N(x)
(остаток) такие, что при всех х выполняется
равенство
Р(х) = Q(x)M(x) + N(x),
причем степень многочлена N(x) меньше
степени многочлена Q(x).
Пример. Разделим многочлен 2х3 + Зх2 + х - 1
на многочлен х2 + 2:
_ 2х3 + Зх2 + х - 1 I х2 + 2
"2*3 + 4* I 2х + з
_ Зх2 - Зх - 1
3х2 + 6
-3*-7
Здесь
Р(х) = 2х3 + Зх2 + х - 1, Q(x) = х2 + 2,
М(х) = 2х + 3, N(x) = -Зх - 7.
Если остаток от деления многочлена Р(х) на
многочлен Q(x) тождественно равен нулю, т. е.
Р(х) = Q(x)M(x), то говорят, что Р(х) делится
нацело на Q(x).
Теорема Безу. Остаток при делении
многочлена (1) на разность х-а (двучлен) равен Р(а),
т. е. равен значению многочлена (1) в точке а.

406
Справочные материалы
Краткий справочник по математике
Число а (действительное или комплексное)
такое, что Р(ос) = 0, называется корнем много-
члена (I).
Если Р(ос) = 0, т. е. число а — корень
многочлена (1), то многочлен (1) делится нацело на х - а,
что следует из теоремы Безу. Справедливо и
обратное утверждение.
РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА
МНОЖИТЕЛИ. Если многочлен (1) удается представить в
виде произведения других многочленов, то
говорят, что данный многочлен разложен на
множители.
Каждый многочлен (1) степени п можно
разложить на п линейных множителей:
Р(х) = а0 (х - аг)(х - сс2)... (х - ап), (2)
где с*!, ос2, ..., осл — корни многочлена Р(х).
Среди чисел alf ос2, ..., осл могут оказаться
одинаковые; тогда разложение (2) примет вид
Р(х) = а0 (х - 04) 1 (х - а2) 2 ... (х - ат) т.
Здесь все числа о^, ос2, ..., ат — различные;
показатели fti, &2, ..., km называются крат-
ностями соответствующих корней, причем
fc1 + fc2 + ... + fcm = n.
Если многочлен с действительными
коэффициентами Ъ качестве корня кратности k имеет
комплексное число a = р + гу, то корнем той же
кратности этого многочлена обязательно будет и число
a = Р - гу, комплексно сопряженное с первым.
При этом
(х-а)(х-а) = (х-(Р + *у))(*-(р-гу)) =
= ((*-Р)-гу)((х-р)-Му) =
= х2 - 2рх 4- р2 + у2 = х2 +рх + q,
2
гдер = -2р, <? = Р2 + у2, причем ^ - q < О (т. е.
произведение линейных множителей (х - ос)(х - ос)
можно заменить квадратным трехчленом х2 +
+ px + q).
Отсюда вытекает, что каждый многочлен (1)
с действительными коэффициентами можно
представить в следующей форме:
1 2 г
Р(х) = ос0 (х - ах) (х - а2) ... (х - аг) х
х (х +p1x + q1)l(x + р2* + ?2) -
2 ls
... (х + p.х + q.) .
Здесь линейные двучлены соответствуют
действительным корням (А,1? Х2, ..., Хг — их
кратности), а квадратные трехчлены — комплексным
корням (Zlf Z2, •••» h — их кратности)
многочлена. При этом
Хг + Х2 + ... + Xr + 2lx + 2Z2 + ... + 2ls = n,
2
p.
"4 -Qj<0> 7 = 1,2, ...,s.
Пример. Многочлен P(x) — x3 + x2 + 2x + 2
делится нацело на (x + 1), так как J?(-l) — 0. Проведя это
деление «углом», получимР(х) — (х + 1Хх2 + 2).
Укажем некоторые приемы разложения
многочлена на множители.
1) Вынесение общего множителя за скобки;
например,
28х3-35х4 = 7х3(4-5х).
2) Использование формул сокращенного
умножения; например,
х4 - 1 = (х2 - 1)(х2 + 1) = (х - 1)(х + 1)(х2 + 1).
3) Способ группировки; например,
х3 - Зх2 + Ъх - 15 = (х3 - Зх2) + (5х - 15) =
- х2 (х - 3) + 5 (х - 3) = (х - 3)(х2 + 5).
4) Иногда бывает полезно внести
вспомогательные члены или разложить какой-либо член
на подобные слагаемые; например,
х2 + 5х + 6 - х2 + 2х + Зх + 6 -
- х (х + 2) + 3 (х + 2) = (х + 2)(х + 3).
ФУНКЦИИ И ГРАФИКИ
Определение функции.
Основные свойства функций
ОПРЕДЕЛЕНИЕ ФУНКЦИИ. Пусть X —
некоторое числовое множество (например,
промежуток). Если каяедому числу х из X по некоторому
определенному правилу или закону ставится в
соответствие одно число у, то говорят, что на X
задана функция, которую записывают в виде у =
= / (х) или у = у (х) (используются и другие
обозначения функции: у = ф (х), у = у (х) и т. п.).
Запись у = f (х) читается: «игрек равно эф от икс».
Переменная х называется независимой
переменной (или аргументом). Множество X назы-

Справочные материалы
Краткий справочник по математике
407
вается областью определения функции / (х)
(обозначение: D (/)). Множество чисел вида / (х),
где х е D (/), называется областью значений
функции (обозначение: Е (/)).
Например, область определения функции
у = л/4 - х есть отрезок [-2, 2], а область ее
значений — отрезок [0, 2].
Данное определение функции относится к од-
позначным функциям; иногда рассматривают и
многозначные функции, в которых каждому
значению аргумента х сопоставляются
несколько значений у; такова, например,
функция у = ± Jx.
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ.
Аналитический способ — это способ задания функции с
помощью формул (например, у = 2х, у = х + 1,
у = х - 1, у = х2). Если уравнение, с помощью
которого задается функция, не разрешено
относительно у у то функция называется неявной.
Когда такое выражение у через х возможно,
неявная функция может быть приведена к явной
форме, т. е. к виду у = f (х). Например,
уравнение 2х + Ъу - 5 = 0 можно рассматривать как
задающее функцию неявно. Решив его
относительно 2/, мы получаем ту же функцию, но уже в
5 — 2х
явном виде: у = —«— .
Табличный способ — это способ задания
функции с помощью таблицы.
Графический способ — это способ задания
функции с помощью графика. Графиком
функции у = f (х) называется множество точек (х; у)
плоскости хОу, координаты которых связаны
соотношением у = f (х). Само равенство у = f (х)
называется уравнением этого графика.
Например, графиком функции у = х является
множество точек вида (х; х), т. е. точек,
имеющих одинаковые координаты. Это множество
точек есть биссектриса I и III координатных
углов (рис. 3).
СЛОЖНАЯ ФУНКЦИЯ. Пусть переменная у
зависит от переменной и, которая в свою очередь
зависит от переменной х, т. е. у = / (и), и = <р (х).
Тогда при изменении х будет меняться и, а
потому будет меняться и у. Значит, у является
функцией х: у = f (ф (х)). Эта функция называется
сложной функцией (или функцией от
функции), переменная и называется
промежуточной переменной. Указанную сложную функцию
называют также суперпозицией функций f и <р.
Например, функцию у = (1 + х)2 можно
рассматривать как сложную функцию: у = и2,
и = 1 + х9 определенную на всей числовой оси.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ.
Монотонность. Функция / (х)
называется возрастающей (убывающей) в интервале (а,
&), принадлежащем ее области определения,
если, каковы бы ни были значения х\ и х2 из этого
интервала, из неравенства х2 > Xi вытекает
неравенство / (х2) > / (*i) (соответственно / (х2) <
< f (*i)). Если же для таких Xi и х2 из неравенства
х2 > xi следует неравенство / (х2) > f (*i)(/ (х2) <
^ / (*i))> то функция / (х) называется
неубывающей (невозрастающей) в интервале (а, Ь).
Функции всех этих типов носят общее
название: монотонные.
Возрастающие и убывающие функции
называются строго монотонными; неубывающие и
невозрастающие функции — монотонными в
широком смысле.
Пример. Функция
У = х (1)
возрастает на всей числовой оси, а функция
У-1*1 (2)
убывает на промежутке (-°°, 0) и возрастает на
промежутке (0, +оо).
Четность, нечетность. Функция / (х)
называется четной, если для любых х из ее
области определения выполняется равенство
f(-x) = f(x).
Функция / (х) называется нечетной, если
/(-*) = -/(*).
График четной функции у = f(x) симметричен
относительно оси Оу, нечетной — относительно
начала координат. На рис. 3 изображен график не-
Рис. 3

408
Справочные материалы
Краткий справочник по математике
четной функции (1), а на рис. 4 — график четной
функции (2).
Периодичность. Функция / (х)
называется периодической с периодом Т (Т > 0), если
для всех х выполняется равенство / (х + Т) =
= f (х). Чтобы изобразить график
периодической функции, нужно построить часть его на
отрезке [0, Т], а затем продолжить ее
периодически на всю действительную ось (рис. 5).
Ограниченность. Функция / (х)
называется ограниченной, если при всех х из ее
области определения выполняется неравенство
|/(jc)| < М или неравенство Mi < f(x) < М2, где
М, Mj, М2 — какие-либо постоянные числа. В
противном случае функция называется
неограниченной.
Например, функция е"'*' является
ограниченной (поскольку 0 < е~'*' < 1), а функция - —
неограниченной.
Обратная функция. Если функция /
задает взаимно однозначное соответствие между
своей областью определения X и своей областью
значений У, то говорят, что функция / имеет
обратную функцию или что функция /
обратима. Обратная функция, по определению, — это
правило, которое каждому числу ysY
сопоставляет число х е X, причем у = / (х). Область
определения обратной функции есть множество У,
область значений — множество X.
Исходную функцию и ее обратную вместе
называют взаимно обратными. Все строго
монотонные функции — как возрастающие, так и
убывающие — имеют обратные; при этом
обратные функции также строго монотонные.
Графики исходной и обратной функций
симметричны относительно биссектрисы I—III
координатных углов, поэтому график обратной
функции можно получить отражением
относительно этой биссектрисы графика исходной
функции (рис. 6).
Линейная, квадратичная,
степенная, целая рациональная,
дробно-рациональная, показательная
и логарифмическая функции
ЛИНЕЙНАЯ ФУНКЦИЯ. Это функция вида
y = kx + Ь, где k и b — действительные числа.
Область определения: (-°°, +°°); область значений:
(-оо, +оо). Функция не является ни четной, ни
нечетной; при k > 0 она возрастает, при k < 0
убывает. Ее график (рис. 7) — прямая, k = tg а —
угловой коэффициент. При k = 0 получаем
постоянную функцию; ее график (рис. 8) —
прямая, параллельная оси Ох. Если Ъ = 0, то имеем
прямую пропорциональность у = kx; ее график
(рис. 9, а и б) — прямая, проходящая через
начало координат.
КВАДРАТИЧНАЯ ФУНКЦИЯ. 1) Функция
у = ах2 (а — действительное число, не равное
нулю) определена на всей числовой оси; область
ее значений (0, +оо) при а > 0 и (-оо, 0) при а < 0;
функция четная, возрастающая при а > 0,
убывающая при а < 0; ее графиком является
парабола. График функции при а = 1 изображен на
рис. 10.
2) Функция у = ах2 + Ьх + с (а, Ь9 с —
действительные числа, причем а Ф 0) — квадратичная
функция общего вида. Область ее определения —
вся числовая ось. Для построения ее графика
нужно выполнить следующие преобразования
у\
у = 14
О х
Рис. 4
У\
у = Ь
О х
Рис.8

Справочные материалы
Краткий справочник по математике
409
(называемые выделением полного квадрата)
квадратного трехчлена ах2 + Ьх + с:
2 , ( 2 Ь \
ах* + Ьх + с = а\ х + -х\ +с =
= а
\\
f\
4о
+ с =
+ с =
(( + ь f *
f if 6*
^ 2а) 4а
( Ь \2 lac -
= а(* + Га) +—^
Аас - Ь
Итак,
у = ах2 + &х + с = а[л: + 2~] +
4ас - b
4а
(1)
Теперь для построения графика функции
(1) нужно выполнить параллельный перенос
плоскости, поместив начало новой системы ко-
2
/Л/ / Л/ ( Ь 4ас - Ъ \
ординат х О у в точку О I -«Г"; —4 I» и в
плоскости х'О'у' построить параболу у' =
= а(*')2.
Пример. Построим график функции
у = | х2 + 4* + 5.
Имеем
у = ^ х2 + 4* + 5 - | (х2 + 8х) + 5 =
= \ ((х2 + 8х + 16) - 16) + 5 - \ (х + 4)2 - 3.
Выполним параллельный перенос плоскости,
поместив начало новой системы координат х'О'у' в
точку 0'(-4; -3), и в координатной плоскости х'О'у' по-
I'- „2
строим параболу у' = п (*')
Это и есть график функции у = « х2 + 4х + 5
(рис. 11).
СТЕПЕННАЯ ФУНКЦИЯ. Это функция вида
у = ха9 где а (показатель степени) — любое
действительное число. Область определения: (0, +о°),
область значений: (0, +оо). При а > 0 она
возрастает, при а < 0 — убывает. Для целых значений
показателя степени (а е Z) степенную функцию
рассматривают при а > 0 на всей числовой оси;
при а < 0 — на всей оси, кроме точки х = 0. При
а = -1 зависимость у = - (или у = - ) называется
обратной пропорциональностью. На рис. 10,12,
13 изображены графики функций у = х2
(парабола), y=Jx (верхняя ветвь параболы у2 = х)9 у =
= - (равнобочная гипербола).
ЦЕЛАЯ РАЦИОНАЛЬНАЯ ФУНКЦИЯ. Это
многочлен вида
у.лг-1
у - а0х™ + агхт +... + ат.гх + ат.
Она определена на всей числовой оси. Ее
частные случаи (линейная, квадратичная
функции) были рассмотрены ранее.
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ. Эта
функция определяется как отношение двух
многочленов:
т , т-1
а0х + а^
У =
+ ... + ат Лх + ат
Ь0х + Ьхх +
+ Ьп лх + Ь„
Л—1 Л
Она определена при всех значениях х9 кроме
тех, при которых знаменатель обращается в
Рис. 9
Рис. 10
1 2,. , с
Рис. 11
У1
о
1
О
\
у = Jx
7Л
1
4
i х
\\ 1
->0 1 X
Рис. 12
Рис. 13

410
Справочные материалы
Краткий справочник по математике
нуль. Дробно-рациональной функцией является,
например, функция у = - .
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ. Эта функция
имеет вид у = а*, где основание а > О, а * 1.
Область определения: х е Я, область значений:
0_
,1 =
у е (О, +°°), причем ох>0иаи=1,а-о.
Функция не является ни четной, ни нечетной (а~х * а* и
а~х Ф -а*); она возрастает при а > 1 и убывает при
О < а < 1; ее график изображен на рис. 14, а и б.
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ. Так как
показательная функция у = ах является строго
монотонной, то для нее существует обратная
функция, называемая логарифмической функцией
(обозначение: у = loga x)f ее областью
определения является промежуток (0, +°°), а областью
значений — промежуток (-°°, +°°), причем
logal = 0, loga а = 1. Функция не является ни
четной, ни нечетной: она возрастает при а > 1 и
убывает при 0 < а < 1; ее график изображен на
рис. 15, а и б.
Тригонометрические и обратные
тригонометрические функции.
Тригонометрические формулы
Тригонометрические функции острого угла.
Отношение длины катета ВС к длине
гипотенузы АВ (рис. 16) называется синусом угла а:
ВС а
sin a = тъ или sin ot = - ,
где длины сторон прямоугольного треугольника
обозначены a, Ь, с. Отношение АС/АВ называется
косинусом угла а:
Ь
cos a = - .
Отношение длин катетов ВС и АС называется
тангенсом, обратное отношение —
котангенсом угла а:
tga =
ctga =
b9 ---" a
Из этих равенств следует, что
sin a 1 cos a
tga =
cos a
ctga =
tga
sin a
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ПРОИЗВОЛЬНЫХ ЗНАЧЕНИЙ АРГУМЕНТА. Возьмем на
плоскости луч OMq и будем поворачивать его
вокруг точки О против часовой стрелки (рис. 17, а).
При повороте на угол а луч OMq отобразится
на луч ОМа; точка М0, пробежав часть
окружности с центром в точке О, попадет в точку Ма.
Если угол поворота — прямой (а = я/2), то дуга
МцМа — четверть окружности; если угол
поворота — развернутый (а = я), то дуга М$Ма —
полуокружность; если угол поворота — полный
(а = 2я), то дуга М^Ма — полная окружность,
в этом случае Ма = М0.
При дальнейшем повороте луча против
часовой стрелки точка М0 снова будет пробегать
окружность, при этом угол поворота а будет
больше полного. На рис. 17, б изображен угол
a = 2я + £ . Направление поворотов против
часовой стрелки считается положительным (а > 0),
направление по часовой стрелке —
отрицательным (а < 0).
Рассмотрим прямоугольную систему
координат хОу на плоскости и круг единичного
радиуса с центром в начале координат (рис. 18). Такой
круг называется единичным кругом. Точка Ма
на его окружности получается из точки М0 (1; 0)
в результате поворота луча OMq на угол а. Отме-
о) ук
П х
1У = \ogax (а > 1) у = \ogax (0 < а < 1)
Рис. 15

Справочные материалы
Краткий справочник по математике
411
тим, что если два угла поворота а и Р
отличаются на целое число полных оборотов, т. е. на
360е • т (т е Z), то соответствующие точки Ма
и Мр совпадают.
Координаты точки Ма обозначим х иу.
Тригонометрические функции определяются
следующим образом:
sin а х cos а
sin а = у, cos а = х, tg а = лм п , ctg а =
cos а
sin а
Для положительных острых углов эти
определения совпадают с приведенными ранее.
Значения тригонометрических функций
для наиболее часто встречающихся углов

Функция
sin а
cos а
tga
ctg а
Аргумент а
0°
0
1
0
—
30°
1
2
Л
2
Л
3
Л
45'
Л
2
Л
2
1
1
60°
7з
2
1
2
Л
л
3
90°
1
0
—
0
180°
0
-1
0
—
270°
-1
0
—
0
Из определений следует, что не существует
тангенс углов, косинус которых равен нулю, и
котангенс углов, синус которых равен нулю.
Квадранты (или четверти круга)
нумеруются в положительном направлении от I до IV
(рис. 18). Знаки тригонометрических функций в
различных квадрантах приведены в следующей
таблице.
Знаки тригонометрических функций
Квадрант
I
II
ш
IV
Функция
sin а
+
+
-
-
cos а
+
-
-
+
tga
+
-
+
-
ctg а
+
-
+
-
ГРАФИКИ И СВОЙСТВА
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ. Здесь, как обычно, аргумент
обозначаем через х9 а значение функции —
через!/.
1) у = sin х. График — синусоида (рис. 19).
Область определения: х е (-оо, +оо); область
значений: у е [-1, 1]. Функция периодическая
(период 2я), нечетная, ограниченная.
Промежутки монотонности
= (-!
+ ЯП, р + кп
)' п
е Z.
Синусоида пересекает ось Ох в точках хп = кп,
т. е. в этих точках значения функции у = sin х
равны нулю,
2) у = cos х. График — косинусоида (рис. 19).
Область определения: х е (-°°, +°°); область
значений: у е [-1, 1]. Функция периодическая
(период 2я), четная, ограниченная. Промежутки
монотонности: (тт, к 4- кп), п е Z. Косинусоида
^ 71
пересекает ось Ох в точках хп = « + кп, т. е. в
этих точках значения функции у = cos х равны
нулю.
3) у = tg х. График — тангенсоида (рис. 20).
Область определения — вся числовая ось, кроме
у = COS X
Рис. 17
Рис. 18
Рис. 19

412
Справочные материалы
Краткий справочник по математике
точек хп = 5 + ли; область значений — вся
числовая ось. Функция периодическая (период я),
нечетная, неограниченная; возрастает на
промежутках
в
+ ЯИ> о + ЯЛ
J >п
eZ.
4) у = ctg #. График — котангенсоида (рис. 20).
Область определения — вся числовая ось, кроме
точек хп = пп; область значений — вся числовая
ось. Функция периодическая (период тс),
нечетная, неограниченная; убывает на промежутках
(ял, 71 + ял), пе Z.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ.
1) Так как синус — немонотонная функция, то
для введения обратной функции следует
выбрать какой-либо промежуток монотонности
синуса. Принято следующее определение.
Арксинус числа х е [-1, 1] — это угол у е ~о' 2 г си"
нус которого равен х:
у = arcsin х9 sin у = х.
График функции у = arcsin х приведен на
рис. 21. Область ее определения: х е [-1, 1];
область значении: у е
[-1
7П
2
Функция
возрастающая, нечетная, ограниченная.
2) Арккосинус — обратная функция для
косинуса:
у = arccos jc, cos у = х; хе [-1,1], у е [0, тс].
График этой функции приведен на рис. 22.
Область ее определения: х е [-1, 1]; область
значений: у е [0, я]. Функция убывающая,
ограниченная, свойствами четности и нечетности не
обладает.
3) Арктангенс — обратная функция для
тангенса:
f п п\
y = arctgx, tgy = x; хе (-оо, +оо),ye l-g, ^ I.
График этой функции приведен на рис. 23.
Область ее определения: х е (-°°, +°°); область
значений: у е (-5» о ]" ФУНК1*ИЯ возрастающая,
ограниченная, нечетная.
4) Арккотангенс — обратная функция для
котангенса:
i/ = arcctgjc, ctgy = x; х е (-оо, +оо), у е (0, п).
График этой функции приведен на рис. 24.
Область ее определения — вся числовая ось;
область значений: (0, тс). Функция убывающая,
ограниченная, свойствами четности и нечетности
не обладает.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Степенная,
показательная, логарифмическая,
тригонометрические и обратные тригонометрические
функции, постоянная (константа) у = С — называются
основными элементарными функциями.
Всякая функция, которая получается из
основных элементарных функций с помощью
конечного числа суперпозиций и четырех
арифметических действий (сложения, вычитания,
умножения и деления), называется элементарной
функцией.
Например, элементарными функциями
являются рассмотренные выше целая рациональная
и дробно-рациональная функции.
ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ.
Основные соотношения между
тригонометрическими функциями одного и того же
аргумента:
у\
-Зтг
2
-п
-я
2
О
1 /У - tg х
к
2
п
Зтг
2
2л
X
^У = ctg X
Рис
.20
у = arcsin х
У1
тс
2
:у7
1
О 1
к
2
Рис
5.21
^
X
у = arccos х
У1
1 X
1
1
-1 О
1
я
тс
2
1 х
Рис
.22
у - arctg х
У{
О
1
тс
2^.
. к
2
Рис. \
23
X
у - arcctg х
У\
п
О
1
Ри
с. 24

Справочные материалы
Краткий справочник по математике
413
sin2ct + cos2ct= 1,
sin а х cos а
cos а
sm а
l + tg2ct=—V", l + ctg2ct = l
cos a
Формулы приведения
. 2
sin a

Функция
sin t
bos t
tg*
ctg*
Аргумент t
n
2 "°
cos a
sin a
ctga
tga
2 +0t
cos a
-sin a
-ctga
-tga
к - a
sin a
-cos a
-tga
-ctg a
к + a
-sin a
-cos a
tga
ctg a
Зя
T "a
-cos a
-sin a
ctga
tga
T+a
-cos a
sin a
-ctga
-tga
2k -a
-sin a
cos a
-tga
-ctg a
Формулы сложения и вычитания аргументов
sin (а ± Р) = sin a cos Р ± cos a sin р,
cos (а ± Р) = cos a cos Р + sin a sin Р>
Формулы двойных и половинных углов
sin 2а = 2 sin a cos a, cos 2а = cos2 а - sin2 а,
sma =
»»1
cosa =
i ,2а
^^ 2
1 + tg 2
а , /l - cos а а , /l 4- cos а
sin2=±*/ 2 'С082=±а/ 2 '
. а , /l - cos а , ot , /l 4- cos а
tg « = ± — , ctg 5 = ± ]- •
z V1 + cos а * V 1 - cos а
Знаки перед радикалами берутся в соответст-
a
вии с тем, в какой четверти лежит угол
2'
Формулы суммы и разности
тригонометрических функций
• n . a + В a-p
sm a 4- sm p = 2 sm —•^-JL cos —5-^ ,
sin a - sin P = 2 sin —«
a -_B a + P
COS
2 '
a 4- p a-p
«- nnc '
COS
cos a + cos P = 2 cos —«
cos a - cos p = -2 sin —~- sm —5— ,
. sin (a ± p)
tg a ± tg P = ^ .
& ь K cos a cos P
Формулы преобразования произведения
тригонометрических функций
в алгебраическую сумму
sm
sm
cos
acosp= sin (a - p) + sin (a + ft) ^
. n cos (a - P) - cos (a + P)
asmp= c—g - ^ ,
n cos (a - p) + cos (a + P)
a cos P = - ^~~2 "
Некоторые формулы для обратных
тригонометрических функций
sin(arcsin х) = х9 cos(arccos х) = jc,
arcsin(sin х) = jc, arccos4cos х) = х9
х е [-я/2, я/2], jc е [0, я],
arcsin(-jc) = -arcsin jc, arccos(-jc) = я - arccos jc,
arctg(-jc) = -arctg jc, arcctg(-jc) = я - arcctg jc,
arcsin jc 4- arccos jc = я/2, arctg jc 4- arcctg jc = я/2,
arcsin jc = arccos >Jl-x , arccos jc = arcsinvl - jc ,
*e[0, 1],
arctg jc = arcctg(l/jc), jc e (0, 4-oo).
Уравнения с одним неизвестным
Основные понятия
УРАВНЕНИЕ И ЕГО РЕШЕНИЯ. Уравнением с
одним неизвестным х называется соотношение
вида
/(*) = 0, (1)
где / (jc) — какая-либо заданная функция
действительного или комплексного переменного jc.
Встречаются также уравнения вида
/<*)-*<*), (2)
где f (х) и g (jc) — две заданные функции
(/ (jc) — левая часть, g (jc) — правая часть
уравнения). Перенося g(x) в левую часть, получаем
/ (jc) - g (jc) = 0 — уравнение вида (1).
Уравнение следует рассматривать в области
допустимых значений (ОДЗ), т. е. на
множестве чисел jc, на котором определены все входящие
в уравнение функции. Для уравнения (1) ОДЗ
совпадает с областью определения функции
/ (jc); для уравнения (2) ОДЗ есть пересечение
областей определения левой и правой частей.
Решить уравнение (1) — значит найти его
корни (или решения), т. е. значения jc, при
подстановке которых в уравнение получается ис-

414
Справочные материалы
Краткий справочник по математике
тинное (верное) равенство. Другими словами,
решить уравнение — значит найти нули (или
корни) функции / (х)9 т. е. значения аргумента х9
при которых значения этой функции равны
нулю. Говорят, что корни уравнения
удовлетворяют этому уравнению. Если корней уравнения
несколько, то их обычно нумеруют: jcj, х2у хЗ
и т. д.
РАВНОСИЛЬНОСТЬ УРАВНЕНИЙ. Два
уравнения
fi(x) = g1(x)9 f2(x) = g2(x)
называются равносильными
(эквивалентными), если все корни первого уравнения
являются корнями второго, а все корни второго
уравнения — корнями первого. Другими словами,
множества корней равносильных уравнений
совпадают. Например, уравнения Зх - 6 = 0 и
х = 2 равносильны (имеют один корень х = 2);
уравнения х2 = 4 и х = 2 не равносильны (корни
первого уравнения Xj = 2 и х2 = -2, корень
второго уравнения один, х = 2). Равносильность
уравнений обозначают символом <=>; например,
3jc-6 = 0<=»jc-2 = 0.
Равносильные преобразования уравнения —
это преобразования, приводящие к
равносильному уравнению:
1) прибавление одновременно к обеим частям
уравнения любого числа (в частности, перенос
слагаемых из одной части уравнения в другую с
изменением знака);
2) умножение (и деление) обеих частей
уравнения одновременно на любое число, отличное от
нуля (в частности, на -1);
кроме того, для уравнений в области
действительных чисел:
3) возведение обеих частей уравнения в
любую нечетную натуральную степень (например,
в куб);
4) возведение обеих частей уравнения при
условии, что они неотрицательны, в любую четную
натуральную степень (например, в квадрат).
Пример неравносильного преобразования —
возведение обеих частей уравнения вида
f (х) = g (х) в четную степень без учета знаков
этих частей.
Так, уравнение х2 = -1, не имеющее
действительных корней, после возведения в квадрат
превращается в уравнение х4 = 1, имеющее два
действительных корня х = ±1; это посторонние
корни для исходного уравнения (они являются
корнями уравнения х2 = 1).
Если все корни уравнения fi (х) = #х (х)
удовлетворяют уравнению f2 (х) = g2 (х), то говорят,
что уравнение f2(x) =g2(x) есть следствие
уравнения fi (х) = g\ (х), и пишут
/l (*) = ё\ (х) => f2 (х) - g2 (х).
Алгебраические уравнения
ЛИНЕЙНОЕ УРАВНЕНИЕ. Общий вид:
ах + b = О,
где а и Ь — заданные действительные числа,
называемые коэффициентами, причем а Ф 0. Оно
Ъ
имеет единственное решение х = - - .
КВАДРАТНОЕ УРАВНЕНИЕ. Общий вид:
ах2 + Ьх + с = 0,
(где a, ft, с — коэффициенты (действительные
числа, причем а Ф 0). Делением обеих частей на а
это уравнение приводится к виду
х2 + рх + q = 0
(приведенное квадратное уравнение).
Квадратное уравнение всегда имеет корни
(действительные или комплексные), которые
находят следующим образом. Вычисляют
дискриминант D = Ь2 - 4ас. Тогда:
1) если D = 0, то корень один (двукратный):
х 2а;
2) если D > 0, то имеются два
действительных корня:
-ь + 4Ъ -ъ- Jd п.
*1= Та ' *2= 2^~; (1)
3) если D < 0, то действительных корней нет,
а имеются два комплексных сопряженных корня:
_ -6 + ij1!) _ -Ь - iJ^D
Xl~ 2а > х2- 2а
где i — мнимая единица.
Для приведенного квадратного уравнения
формула (1) имеет вид
*1.2-~2 ±
г-

Справочные материалы
Краткий справочник по математике
415
Теорема Виета. Для корней приведенного
квадратного уравнения х2 + рх + q = 0
справедливы равенства
хгх2 * q, хг + х2 = -р,
т. е. произведение корней равно свободному
члену, а сумма корней равна коэффициенту при х>
взятому с противоположным знаком.
БИКВАДРАТНОЕ УРАВНЕНИЕ. Общий вид:
ах4 + Ьх2 + с = О
(коэффициенты а, Ь9 с — действительные числа,
причем а Ф 0).
Заменой t = х2 это уравнение сводится к
квадратному уравнению at2 + bt + с = 0.
При D = Ь2 - 4ас < 0 действительных корней
нет; при D > 0 получаются два действительных
-b± J5
значения t: *lt 2 = —5 ' при -^ = 0 — одно
действительное значение t: ^ = -г- . Корни
биквадратного уравнения действительны или
комплексны в зависимости от знаков ^ и t2.
ДВУЧЛЕННОЕ УРАВНЕНИЕ. Общий вид:
ахп + Ъ = 0
(а, 6 — действительные числа, причем а Ф 0).
Оно решается в явном виде: хп = с, где с = -Ъ/а.
Если & * 0, то во множестве комплексных чисел
имеется п различных корней*:
,fc = H^exp[^t^],9 = argc,
где k = 0,1,..., п - 1; если Ь = 0, то корень один:
* = 0.
ЦЕЛОЕ АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ п-й
СТЕПЕНИ. Общий вид:
апхп + an-iXn~l +... 4- а^х + а0 = 0,
где а0, а^, ..., an_j, ад — действительные числа,
причем ап Ф 0.
Основная теорема алгебры. Любое целое
алгебраическое уравнение степени п > 0 имеет во
множестве комплексных чисел ровно п корней
{каждый корень кратности т учитывается
траз).
Доказано, что ни для какого п > 5 не могут
существовать формулы, выражающие корни
произвольного уравнения степени п через его
коэффициенты с помощью, конечного числа
операций сложения, вычитания, умножения,
деления, возведения в целую или дробную
степень.
ДРОБНОЕ АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ.
Общий вид:
Р(х)
= 0,
(2)
где Р (х) и Q (х) — многочлены. Здесь
допустимые значения х — вся действительная ось, за
исключением корней знаменателя. В области
допустимых значений уравнение (2)
равносильно уравнению Р (х) = 0.
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. Такие
уравнения содержат выражения вида mJP (х), где
Р (х) — некоторый многочлен (например, урав-
■=Л2
нение х = *Jbx - 1).
Областью допустимых значений является
множество значений х е R, при которых
определены все входящие в уравнение функции. Так, в
данном примере ОДЗ представляет собой
объединение двух лучей: (-°°, -1/Уб ] и [1/ Jb , +оо).
В некоторых случаях иррациональные
уравнения удается привести к целым
алгебраическим уравнениям. Таково, например, уравнение
* Под записью ехр А понимается еА.
mJFJ7) = Q(x), (3)
где Р (х) и Q (х) — многочлены. При нечетном т
ОДЗ — вся действительная ось R, при четном —
множество х таких, что Р (х) > 0. Возводя обе
части уравнения (3) в степень т9 получаем
алгебраическое уравнение
Р (х) = Qm (х). (4)
Если т — нечетное, то уравнение (4)
равносильно уравнению (3). Если же т — четное,
то (4) есть следствие (3): вместе с корнями
уравнения (3) уравнению (4) удовлетворяют
также посторонние корни — корни уравнения
mJPW = "Q (*)•
При четном /п, найдя все корни уравнения (4),
следует произвести проверку каждого корня
подстановкой в (3).

416
Справочные материалы
Краткий справочник по математике
Пример. Решим уравнение Лх2 - 1 =х.
Имеем v5x - 1 = х => Ьх2 - 1 - х2 <=> х2 - т . Корни
*1 = о ' х2 = ~ о * °^а К°РНЯ лежат в ОДЗ; корень х2 —
посторонний, так как х% < 0. О т в е т: х = ^ .
Трансцендентные уравнения
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ.
Показательным уравнением называют уравнение, в котором
неизвестное входит только в показатели степеней
при постоянных основаниях. Показательное
уравнение вида
а/<*>_„*<*>, (1)
где а > 0, а Ф 1, равносильно уравнению
f(x) = g(x). (2)
Имеются два основных метода решения
показательных уравнений: 1) приведение уравнения
к виду (1), а затем к виду (2); 2) введение новой
переменной. ^
П р и м е р 1. Решим уравнение 3* • 9х = 81.
Имеем: 3х • З2* - З4 или З3* = З4 <=> 3* = 4, откуда
4
x-g.
П р и м е р 2. Решим уравнение 4х + 2*+1 - 24 = 0.
Переписав уравнение в виде (2х)2 + 2 • 2х - 24 = 0,
введем новую переменную, для чего положим 2х = у.
Тогда получим уравнение у2 + 2у - 24 = 0, откуда
i/j = 4, у2 = ~6. Теперь задача сводится к решению
уравнений 2х = 22 и 2* = -6. Из первого находим х = 2,
второе не имеет решений, так как 2х > 0 при всех х.
Ответ: х — 2.
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ.
Логарифмическим уравнением называется уравнение,
в котором неизвестное находится под знаком
логарифма. Логарифмическое уравнение вида
logaf(x) = logag(x), (3)
где а > 0, а Ф 1, равносильно уравнению
f(x)-g(x), (4)
рассматриваемому в области допустимых
значений х, задаваемой системой неравенств
/(х)>0, g(x)>0.
Имеются два основных метода решения
логарифмических уравнений: 1) приведение
уравнения к виду (3), а затем к виду (4); 2) введение
новой переменной.
П р и м е р 1. Решим уравнение
lg (х + 4) + lg (2х + 3) - lg (1 - 2х).
Имеем
lg((* + 4)(2x + 3)) = lg(i-2jt).
Это уравнение равносильно уравнению
(х + 4)(2х + 3) = 1 - 2х, (5)
рассматриваемому на множестве допустимых
значений х, которое задается системой неравенств х + 4 > 0,
2х + 3 > 0, 1 - 2х > 0.
Решив уравнение (5), находим хх = -1, х2 = -5,5.
Значение -5,5 не удовлетворяет, например, первому
неравенству. Значит, -5,5 — посторонний корень
данного уравнения. Значение же -1 удовлетворяет
всем неравенствам системы. О т в е т: -1.
П р и м е р 2. Решим уравнение
log2 х - 51og2 х + 6 = 0.
Полагая log2 х — у, получаем уравнение у2 - Ъу + 6 —
= 0, корни которого yi — 2, у2 — 3. Таким образом,
исходное уравнение эквивалентно двум уравнениям
log2 = 2, log2 х = 3, решения которых Xi = 4, х2 — 8.
О т в ет: 4; 8.
Тригонометрические уравнения
Простейшие тригонометрические
уравнения и их решения:
sin х = 0, х = тел; tg х = 0, х = теп;
ТС ТС
cos л: — 0, х = 5 + теп; ctg х = 0, л: = 5 + ял»
тс тс
sin х = 1, х = - + 2тсл; sin х = -1, л: = -5 + 2ял;
cos х = 1, л: - 2тсл; cos х = -1, х = тс(2л + 1);
sin х = а, х = (-1)л arcsin а + тел, а е [-1, 1];
cos х = а, л: = ±arccos а + 2тсл, а е [-1, 1];
tg х = а, л: = arctg а + ял;
ctg л: — а, л: = arcctg а + тел.
В этих формулах л — любое целое число
(л е Z).
Для решения уравнений вида / (<р (х)) = 0,
содержащих какую-либо одну
тригонометрическую функцию ф(х), вводят обозначение t =
= ф (х) и находят корни tlf *2» •••» *т полученного
уравнения / (t) = 0. Затем для каждого из этих
корней составляют и решают уравнения
ф(*) = *1> Ф(*) = *2> •••> Ф(*) = '/п- (6>
Ответ получается объединением множеств
решений каждого из уравнений (6).

Справочные материалы
Краткий справочник по математике
417
П р и м е р 1. Решим уравнение
2 sin2 2х - 9 sin 2х + 4 - 0.
Полагая t - sin 2х, где t е [-1,1], получаем
квадратное уравнение 2t2 - 9t + 4 = 0, корни которого tx = 4,
*2 в 1/2. Корень *х не дает решений
тригонометрического уравнения (так как |sin 2х\ < 1). Корню t2
соответствует уравнение sin 2х — « » откуда
2хв(-1)пагс8ш о +ял, или х = (-1)Лт2 + « л, л€ Z.
В некоторых случаях тригонометрические
уравнения приводятся к виду
a sin х + Ъ cos л: = с, где а Ф 0, Ь Ф 0. (7)
Выражение в левой части (7) можно
преобразовать к виду синуса (или косинуса) смещенного
аргумента. Имеем
a sin х + Ь cos х
= Dgsi
sin jc + ~ qos jc
>
где
D = ± *Ja + ft , знак перед корнем
совпадает со знаком а. Теперь коэффициенты в скобке
при sin х и cos х можно рассматривать как
косинус и синус некоторого вспомогательного угла у:
a/D = cos у, b/D = sin у.
Угол у находится по формуле
у = arctg (ft/a), у е (-тс/2, я/2).
Итак,
a sin х + ft cos jc = D sin (я + у),
и уравнение (7) приведено к простейшему виду:
sin (х + у) = d, где d = c/D.
П р и м е р 2. Решим уравнение
cos х + sin х + 2 cos 2х — 0.
Так как
cos 2х = cos2 х - sin2 х = (cos х - sin x)(cos х + sin х),
то уравнение равносильно следующему:
(cos х + sin х)[1 + 2(cos x - sin x)] — 0.
Получаем совокупность двух уравнений:
а) cos х + sin х — 0 <^ tg х — -1, х — -т + ял, пе Z;
б) sin х - cos х — -z , или 72 (-т= sin х—т= cos х J —
— о ; здесь у = arctg (-1) — - j , и уравнение приводится
к виду sin
1пМ)=й'
откуда
я 1
х - 2 + arcsin —— + кп, Л € Z.
Другой способ решения уравнения (7) состоит
в использовании подстановки t = tg (х/2).
Определители и системы
линейных уравнений
Определители второго
и третьего порядков
ОПРЕДЕЛИТЕЛИ ВТОРОГО ПОРЯДКА. Пусть
дана таблица (называемая матрицей),
состоящая из четырех чисел:
( \
а11 аЛ9
• (1)
а21 а22 1
Она имеет две строки и два столбца. Числа,
составляющие эту матрицу, обозначены буквами
с двумя индексами. Первый индекс указывает
номер строки, второй — номер столбца, в
которых стоит данное число.
Определителем второго порядка,
соответствующим матрице (1), называется число
alla22 ~ а12а21° Этот определитель обозначается
символом
*11 tt12
*21 tt22
Таким образом,
un u12
a21 a22
= alla22 " a12a21-
(2)
Числа ацу a12, a2i, a22 называются
элементами определителя. Диагональ, на которой
находятся элементы au и а22, называется главной,
а диагональ, на которой находятся элементы а12
и а21, — побочной.
Из равенства (2) видно, что для вычисления
определителя второго порядка нужно из
произведения элементов, стоящих на главной диагонали,
вычесть произведение элементов, стоящих на
побочной диагонали.
Пример 1.
2 4
3 7
= 14-12 = 2.
Свойства определителей.
Величина определителя:
1) не меняется, если заменить его строки
соответствующими столбцами;
14-1019

418
Справочные материалы
Краткий справочник по математике
2) не меняется, если к элементам какой-либо
его строки или столбца прибавить
соответствующие элементы другой строки или столбца,
умноженные на одно и то же число;
3) меняет знак, если поменять местами его
строки или столбцы;
4) увеличивается в k раз, если элементы
какой-либо его строки или столбца увеличить в
к раз;
5) равна нулю, если элементы какой-либо его
строки или столбца равны нулю;
6) равна нулю, если элементы двух строк
или столбцов соответственно равны.
Эти свойства используют при вычислении
определителей.
Пример 2.
25 13 -132
25 7 -60
= 25
325 -132
175 -60
13 (-12) 11
7 (-12).
5
13 11
7 5
= -300
6 6
7 5
- -300•6
= 25-(-12)
- -1800 (5 - 7) - 3600.
1 1
7 5
ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА.
Рассмотрим таблицу (матрицу), составленную из
девяти чисел:
а11 а12 а13
а21 а22 а23
а31 а32 а33
(2)
Определителем третьего порядка,
соответствующим матрице (3), называется число,
определяемое равенством
41 а12 а13
а31 а32 аа
= ana22^33 + <*l2a23a31 + a13a21a32 ""
- a13a22^3i - ац^зЛзг ~
- a12a2ia33. (4)
Для запоминания выражения, стоящего в
правой части равенства (4), полезно следующее
правило, называемое правилом треугольника:
Пример
12 3
2 3 4
3 4 5
= 15 + 24 + 24 - 27 - 16 - 20 - 0.
Все свойства определителей второго порядка
(1—6) остаются справедливыми и для
определителей третьего порядка.
Системы линейных уравнений
СИСТЕМА ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С
ДВУМЯ НЕИЗВЕСТНЫМИ. Эта система имеет вид
агх + Ьгу - сг,
а2х + Ъ2у - с2.
(1)
Здесь коэффициенты a^, а2, &i, Ь2 и правые
части Ci, с2 — заданные числа (действительные или
комплексные). Решить систему — значит найти
все ее решения, т. е. пары чисел (х; у), при
подстановке которых в оба уравнения получаются
верные равенства.
Две системы уравнений называются
равносильными, если все решения одной системы
являются решениями другой системы, и наоборот,
все решения второй системы удовлетворяют
первой системе. Перестановка уравнений местами,
умножение обеих частей какого-либо уравнения
на ненулевое число, прибавление к какому-либо
уравнению другого уравнения, умноженного на
число, — это равносильные преобразования
системы: при таких преобразованиях система
преобразуется в равносильную.
Для решения системы (1) составим
определитель системы:
А =
ai bi
а2 ь2
Если А Ф 0, то решение существует и
единственно, причем имеют место формулы Крамера:
,(1)
.(2)
Х =
У =
(2)
где
A(D =
^2 Ъ2
Д<2> =
а2 с2
Если А = 0, то решений либо нет, либо их
бесконечно много.

Справочные материалы
Краткий справочник по математике
419
На практике обычно удобнее решать системы
методом подстановки: одно из уравнений
«решаем» относительно х или г/, например
с1 - а^х
у = —г , и подставляем это выражение в
другое уравнение вместо у; тогда получим
линейное уравнение относительно х. При этом
может получиться уравнение вида 0 • х = у. Если
уФ О, то система не имеет решений; если же
у=0, то х произвольно, решений бесконечно
много, у выражается через х по формуле
подстановки.
Метод исключения (метод Гаусса), по
существу, не отличается от метода подстановки:
умножая первое уравнение на &2> второе — на &i
и вычитая второе уравнение из первого,
получаем линейное уравнение относительно одного
неизвестного х. Для нахождения у можно
поступить аналогично (умножить уравнения на а2
и ах), либо выразить у через уже известное х
с помощью первого или второго уравнения
системы (1).
Пример 1. Рассмотрим систему
х + у - 1,
х - у - 2.
Ее определитель
' 1 1
Д-
1 -1
= -2*0,
и потому система имеет единственное решение,
которое можно найти по формулам (2):
,(1)
ч(2)
X —
где
д<«-
т. е. х — ■
1 1
2 -1
-3 3
А ' * А •
= -1-2 = -3, Д<2> =
1 1
1 2
-2-1-1,
-2
-2 2'
Пример 2. Система
\х + у - 1,
[2х + 2z/ - 1
(для нее А = 0) не имеет решений, так как ее
уравнения противоречат друг другу.
Пример 3. Система
(х + у - 1,
[2х + 2z/ = 2
(для нее А — 0) имеет бесконечно много решений, так
как она сводится к одному уравнению х + у — 1.
СИСТЕМА ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ С
ТРЕМЯ НЕИЗВЕСТНЫМИ. Эта система имеет вид
са^х + Ьгу + c^z = dlf
а2х + 62i/ + с2г - d2,
[а3* + Ь^у + с32 = ^з*
Бе решение находится аналогично решению
системы (1). Заметим, что если определитель
этой системы
А =
а1 Ь1 с1
а2 Ь2 с2
Н ьз с3
*0,
то она имеет единственное решение; если же
А = 0, то решений либо нет, либо их бесконечно
много.
Неравенства
Основные понятия
ОПРЕДЕЛЕНИЕ НЕРАВЕНСТВ, ИХ
РАВНОСИЛЬНОСТЬ. Неравенствами называются
соотношения вида
А<В, А>В9 А<Б, А>В9 А*В
(читается: «А меньше Б, А больше Б, А меньше
или равно Б, А больше или равно Б, А не равно
Б>). Здесь А и Б — действительные числа или
функции, принимающие действительные
значения. Неравенство состоит из левой и правой
частей, соединенных знаком неравенства. В случае
знаков > или < неравенство называют строгим,
в случае знаков > или < — нестрогим.
Неравенство может быть истинным
(верным, справедливым) или ложным (неверным,
несправедливым). Например, 7 > -2 и 1 - */2 <0 —
истинные неравенства; 7 < -2 — ложное
неравенство; х2 - 1 < 0 истинно при х е (-1, 1) и
ложно при х ё (-1, 1); неравенство х2 + 1 > 0
истинно при всех х е R. .
Пусть имеются два неравенства. Если из
истинности первого неравенства следует
истинность второго, то второе неравенство называют
следствием первого и используют символ =>.
Например, х > 1 ^ х > 0. Если второе неравенство
есть следствие первого, а первое неравенство —
следствие второго, то такие неравенства
называют равносильными (эквивалентными) и
используют символ <=>. Например, 2а < 2Ь <=> а < Ъ при
любых a, b е R.

420
Справочные материалы
Краткий справочник по математике
ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ.
1. К обеим частям неравенства можно
прибавить одно и то же число:
А<В<=>А + у<В + у.
2. Обе части неравенства можно умножить
(или разделить) на одно и то же
положительное чцсло:
А < В <=> уА < уВ, если у > 0.
3. Обе части неравенства можно умножить
(или разделить) на одно и то же
отрицательное число (при этом необходимо изменить знак
неравенства на противоположный):
А < В <=> уА > уВ, если у < 0.
Аналогичные свойства имеют нестрогие
неравенства.
СИСТЕМА НЕРАВЕНСТВ. ДВОЙНЫЕ
НЕРАВЕНСТВА. Система неравенств (два или более
неравенств) считается выполненной (истинной),
если истинны все составляющие ее неравенства.
Например, система
Г 7>2,
{-3<1
выполнена; систе-
|7>2,
ма < Л „ не выполнена.
|3<1
Два истинных неравенства, знаки которых
одинаковы, можно почленно сложить —
получим истинное неравенство:
А<В,
C<D
► А + С<В + £>.
Два истинных неравенства, левые и правые
части которых положительны, а знаки
неравенств одинаковы, можно перемножить:
[А>В,
>AC>BD9
[C>D
если А > 0, В > 0, С > 0, D > 0.
Неравенство, обе части которого
положительны, можно возвести в любую натуральную
степень:
А < В <=> Ат < Вт, если А > 0 и В > 0.
Любое неравенство можно возвести в
нечетную натуральную степень:
Двойные неравенства — это неравенства
вида
А<В<С,А<В<Сит. д.
Такая запись означает систему
соответствующих неравенств:
JA<B,
|В<С,
[А<В,
\в*с ит'д-
А<В<=>А
2п+1
<В
2/1+1
НЕКОТОРЫЕ ПОЛЕЗНЫЕ НЕРАВЕНСТВА.
1) \а + Ъ\ < \а\ +1&|; \а - Ь\ > \ \а\ - |Ь| | — неравен-
ства треугольника;
I— а 4- Ь
2) Jab < —5— ПРИ а * 0, Ь > 0, т. е. среднее
геометрическое двух неотрицательных чисел не
больше их среднего арифметического;
3) |sin х\ < |*| при х € R; 0 < sin х < х при
х е (0, я). (Здесь угол х выражен в радианах.)
Решение неравенств с одной переменной
НЕРАВЕНСТВО С ОДНОЙ ПЕРЕМЕННОЙ И ЕГО
РЕШЕНИЕ. Пусть дано неравенство
f(x)<g (х) (или f(x)<g (х)).
Всякое значение переменной, при котором
данное неравенство с переменной обращается в
верное числовое неравенство, называется
решением неравенства. Решить неравенство с
переменной — значит найти все его решения или
доказать, что их нет.
Решение неравенств вида (1) следует
начинать с нахождения области допустимых
значений переменной х9 т. е. множества, на котором
определены все входящие в неравенство
функции. С помощью равносильных преобразований
иногда удается упростить неравенства и решить
их. Обычно решение неравенства записывается
в виде промежутка или объединения
нескольких промежутков.
ЦЕЛЫЕ АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА.
1) Неравенство Р (х) > 0 или Р (х) < 0, где
Р (х) — многочлен. Если известно разложение
Р (х) на действительные множители:
Х1 хг
Р (х) = а0(х - ах) ... (х - ar) х
2 'l
х (х + рхх + qx) х
о 2 9 *
х (х + р2х + q2) ... (х + рвх + qt) ,

то промежутки, в которых Р (х) > 0, легко
найти, пользуясь методом интервалов. Согласно
методу интервалов следует нанести на числовую
ось точки о^, а2, ..., аг, т. е. действительные
корни многочлена Р (х). Эти точки разбивают
числовую ось на интервалы, в каждом из
которых знак Р (х) сохраняется. При переходе от
одного интервала к другому через какую-либо из
этих точек (например, через а{) знак Р (х)
меняется, если Xi нечетно, и сохраняется, если А,}
четно. Квадратичные множители всегда
положительны. Теперь достаточно определить знак
Р(х) внутри одного какого-либо интервала*,
чтобы расставить знаки Р (х) на всех интервалах.
Тем самым решение неравенства получено.
Пример. Пусть Р (х) - -5(х -I- 1)х(х - 1)2(х2 + х +1).
На рис. 25 дугами показаны интервалы знакопосто-
янства многочлена Р (х). Решением неравенства Р(х)>0
является промежуток (-1, 0); решением неравенства
Р (х) < 0 — объединение трех промежутков: (-°о, -1) и
и(0,1)и(1,+оо).
2) Нестрогие неравенства Р (х) > О или Р (х) < О
решаются так же, как и строгие, при этом
концы промежутков включаются в ответ.
3) Неравенство Р (х) < Q (х)9 где Р (х) и
Q (х) — многочлены, решается переносом Q (х)
в левую часть.
ДРОБНЫЕ АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА.
1) Неравенство Р (x)/Q (х) < 0, где Р (х) и
Q (х) — многочлены. Область допустимых
значений неравенства — вся действительная ось,
за исключением корней знаменателя дроби.
Умножением обеих частей неравенства на
множитель Q2(x) (положительный в ОДЗ) сводим
данное неравенство к равносильному (в ОДЗ):
Р (х) Q (х) < 0.
Рг(х) Р2(х)
2) Яг (х) < Q2 (х) **
Рг (x)Q2 (х) - Qx (х)Р2 (х)
~ Qx(x)Q2{x) <0-
ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА.
Иррациональные неравенства содержат выражения
вида mJp (х)9 где Р (х) — многочлен. Основные
* Обычно сначала берут х в интервале, лежащем справа
от самого правого корня, где знак Р (х) совпадает со
знаком а0.
Справочные материалы ЛОЛ
Краткий справочник по математике ^*^ ■*■
приемы преобразования иррациональных
неравенств к алгебраическим те же, что и для
соответствующих уравнений, но здесь есть и
существенные отличия, связанные с возведением
неравенства в четную степень.
Например, при решении неравенства *JP (х) <
< Q (х) необходимо предусмотреть два случая:
1) Q (х) > 0, при этом неравенство Р (х) < Q2 (х)
будет равносильно исходному (в ОДЗ);
2) Q (х) < 0, здесь нельзя возводить
неравенство в квадрат (в данном случае оно не имеет
решений).
Неравенство *]р (х) > Q (х) в случае Q (х) > 0
можно возводить в квадрат: Р (х) > Q2 (х), а при
Q (х) < 0 неравенство выполняется при любом х,
принадлежащем ОДЗ.
Пример. Решим неравенство J3x >\+ J2x - 1.
Находим ОДЗ: [0,5, +°о). Так как обе части
неравенства неотрицательны, то их можно возвести в
квадрат:
Зх > 1 + 2х - 1 + 2л/2х - 1 <=> 2j2x - 1 < х <=>
<^4(2х-1)<х2 <^х2-8х + 4>0 <=>
<=* (х - хг)(х - х2) > 0,
где хг =Л - 2^3 и х2 — 4 + 2л/3 — корни уравнения
х2 - 8х + 4 = 0. Последнее неравенство выполняется
вне интервала (хх, х2). Учитывая ОДЗ, получаем
ответ:
х € [0,5, 4-273]и[4 + 27з, +оо) (рИс. 26).
ТРАНСЦЕНДЕНТНЫЕ НЕРАВЕНСТВА.
Трансцендентные неравенства содержат
показательные, логарифмические и тригонометрические
функции (соответственно показательные,
логарифмические и тригонометрические
неравенства). В некоторых случаях такие неравенства
удается решить, используя свойства входящих в
них функций или сведя эти неравенства к
простейшим. .
П р и м е р 1. Решим неравенство ах>Ь.
Если Ъ < 0, то х е R; если Ь>0, а>1, тохе (loga Ь,
+°о);еслиЬ > 0,0 < а < 1, то * € (-оо, logaЪ).
Рис. 25 Рис. 26

422
Справочные материалы
Краткий справочник по математике
П р и м е р 2. Решим неравенство 4х - 5 • 2х + 6 > 0.
Положим 2х - t (t > 0). Тогда неравенство примет
вид t2 - Ы + 6 > 0, откуда * € (0, 2] и [3, +оо).
Следовательно, х € (-со, 1] и [log2 3, +оо).
Пример 3. Решим неравенство -3 log0>7 (* + !)< 6.
Находим ОДЗ: х > -1. Разделив обе части
неравенства на -3, получаем равносильное неравенство:
bg0,7 (х + 1) > - 2 <=> log0,7 (* + !)> l°So,7 (0,7)"2 <=>
<=> х + К (0,7)"2 <=> х < -1 + (0,7)"2.
Ответ:-1<х< 51/49.
П р и м е р 4. Решим неравенство cos х < « .
Искомые значения аргумента х соответствуют
точкам графика функции у — cos х, лежащим ниже
прямой у — 5 (рис. 27). Одним из нужных промежутков
является интервал (о> "о~ 1 • Воспользовавшись
периодичностью функции у — cos х, запишем ответ:
5 + 2nk < х < у + 2я&, k € Z.
НЕРАВЕНСТВА, СОДЕРЖАЩИЕ МОДУЛИ. Для
решения таких неравенств рекомендуется
разбить числовую ось на отдельные промежутки
так, чтобы на каждом из них можно было
записать неравенство, не используя знака модуля.
В результате получается совокупность
неравенств обычного вида на соответствующих
промежутках, а множество решений неравенства
является объединением соответствующих
множеств.
Пример. Решим неравенство
|х - 1| + |х + 1| < 4.
Разобьем числовую ось на три промежутка (-°°, -1),
[-1, 1] и (1, +оо). На интервале (-со, -1) данное
неравенство равносильно неравенству -2х < 4, которое
справедливо при х > -2. Таким образом, в множество
решений входит интервал (-2, -1). На отрезке [-1, 1]
исходное неравенство равносильно верному
неравенству 2 < 4. Поэтому все значения переменной,
принадлежащие этому отрезку, входят в множество
решений. На интервале (1, +°о) получаем неравенство
2х < 4, справедливое при х < 2. Поэтому интервал
(1,2) также входит в множество решений. В
результате получаем ответ: (-2, 2).
^5
у = cos х у = 2
О я\ЁХ5я X. х
Ъп
3
Комбинаторика и бином Ньютона
Размещения, перестановки, сочетания
Комбинаторикой называется раздел
математики, изучающий вопрос о том, сколько
комбинаций определенного типа можно составить
из данных предметов (элементов).
Размещениями из п различных элементов по
т элементов (т < п) называются комбинации,
составленные из данных п элементов по т
элементов и отличающиеся либо самими
элементами, либо порядком элементов.
Например, из трех элементов а, Ь9 с можно
составить следующие размещения по два
элемента: ab9 ас, be, ba9 са, cb.
Число различных размещений из п элементов
по т элементов (обозначение: Ап ) определяется
по формуле
А™ = п(п - 1)(п - 2)... (л - т + 1).
Перестановками из п различных элементов
называются размещения их этих п элементов по п.
Как видно из определений, перестановки
можно считать частным случаем размещений
при т = п. Следовательно, число всех
перестановок из п элементов (обозначение: Рп) находится
по формуле
Рп = п(п - 1)(п - 2)...3 • 2 • 1 = п\.
Сочетаниями из п различных элементов по т
элементов называются комбинации, составленные
из данных п элементов по т элементов и
отличающиеся хотя бы одним элементом.
Отметим разницу между сочетаниями и
размещениями: в сочетаниях не учитывается порядок
элементов, а в размещениях — учитывается.
Число сочетаний из п элементов по т
элементов (обозначение: С , иногда
I) находится
по формуле
ст =
П\
Рис. 27
п т\(п - т)!
Свойства сочетаний.
i.ci-n;c;-c^-i.
2. С™=Спп~т(т = 0, 1,2, ...,п).
3. С°„ + С\ + С2п + ... + С" = 2п.
п п п л

Справочные материалы
Краткий справочник по математике
423
t-cl-cl + cl-
+ (-1)пС^ = 0.
Пример.
„12
'15
.,15-12
'15
°15
15 14 13
12 3
= 5 • 7 • 13 = 455.
Бином Ньютона
При любых действительных а и & и любом
натуральном п справедливо равенство
(a + b)n = an+C1nan-1b+... + Cknan-ty + ... + bn9(l)
называемое формулой бинома Ньютона. Числа
С„ , Сп , ..., С„ , ..., С" называются биномиаль-
п9 п9 9 п9 9 п
ными коэффициентами.
Схему вычисления биномиальных
коэффициентов удобно изобразить в виде
треугольника Паскаля:
1
1 1
12 1
13 3 1
14 6 4 1
1 5 10 10 5 1
Здесь в каждой строке выписаны
коэффициенты бинома Ньютона, имеющего
соответственно нулевую, первую, вторую и т. д. степень.
Каждый коэффициент (кроме крайних)
получается как сумма двух ближайших к нему чисел в
строке, лежащей над ним. Например, 5 = 1 + 4,
10 = 4 +бит. д.
Подставив в равенство (1) -ft вместо &, получим
(а - Ь)п = ап-с\ ап_1& + ... + (-1)*С* an"kbk +
+ ... + (-1)Л&п. (2)
Примеры.
1) (а + ft)4 - а4 + 4a3ft + 6a2ft2 + 4aft3 + ft4;
2) (a - ft)5 = a5 - 5a4ft + I0a3ft2 - 10a2ft3 + 5aft4 - ft5.
Элементы математической логики
Высказывания и операции над ними
ВЫСКАЗЫВАНИЯ. Предложение, о котором
имеет смысл говорить, что оно истинно или
ложно, называется высказыванием.
Например, высказываниями являются
следующие предложения: «3 • 3 = 9», «7 — простое
число», «Волга впадает в Черное море». Первые
два предложения истинны, а третье — ложно.
Обычно высказывания обозначают
строчными буквами латинского алфавита: р, q и т. д.
Не всякое предложение является
высказыванием. Так, предложение «Который час?»,
«Да здравствуют музы!» (как и всякие
вопросительные или восклицательные предложения) не
являются высказываниями.
В логике высказываний интересуются не
содержанием, а истинностью или ложностью
высказываний (т. е. их истинностным значе-
нием). Истинностные значения — истина и
ложь — будем обозначать И и Л (или 1 и 0)
соответственно.
ОПЕРАЦИИ НАД ВЫСКАЗЫВАНИЯМИ.
Отрицанием высказывания р называется
высказывание, истинное тогда и только тогда, когда
высказывание р ложно.
Отрицание р обозначается через р и читается
как «нер». Отрицание высказывания
определяется также следующей таблицей истинности:
или
Конъюнкцией двух высказываний р и q
называется высказывание, истинное тогда и только
тогда, когда истинны оба высказывания.
Конъюнкция высказываний р и q
обозначается через р a q и читается как «р и д».
Конъюнкция определяется также с помощью таблицы
истинности:
р
и
л
р
л
и
р
1
0
р
0
1
р
1
1
0
0
я
1
0
1
0
pAq
1
0
0
0
В разговорной речи конъюнкция
соответствует соединению высказываний союзом «и».
Дизъюнкцией двух высказываний р и q
называется высказывание, ложное тогда и только
тогда, когда оба высказывания ложны.

Справочные материалы
Краткий справочник по математике
Дизъюнкция высказываний р и q
обозначается через pvq и читается как «р или д».
Дизъюнкция определяется также таблицей
истинности:
р
1
1
0
0
я
1
0
1
0
pvq
1
1
1
0
В разговорной речи дизъюнкция
соответствует соединению высказываний союзом «или» в
неразделительном смысле.
Импликацией двух высказываний р и q
называется высказывание, ложное тогда и только
тогда, когда р истинно, a q ложно.
Импликация высказываний р и q
обозначается через р => q и читается как «р влечет д» (или
иначе, «еслир, то ?», «изр следует q>).
Высказывание р называется посылкой импликации,
а высказывание q — заключением импликации.
Импликация определяется также таблицей
истинности:
р
1
1
0
0
я
1
0
1
0
р=>?
1
0
1
1
Эквиваленцией (или эквивалентностью)
двух высказываний р и q называется
высказывание, истинное тогда и только тогда, когда
истинностные значения р и q совпадают.
Эквиваленция высказываний р и q
обозначается через р <=> q и читается как «р
эквивалентно ф». Эквиваленция определяется также
таблицей истинности:
р
1
1,
0
0
я
1
0
1
0
род
1
0
0
1
О математических доказательствах
ПРЯМАЯ И ОБРАТНАЯ ТЕОРЕМЫ. В каждой
теореме должно быть указано:
1) при каких условиях рассматривается в ней
тот или иной математический факт (условие
теоремы);
2) что об этом факте утверждается
(заключение теоремы).
Рассмотрим, например, следующую теорему.
Теорема!.. Если четырехугольник —
параллелограмм, то его диагонали, пересекаясь,
делятся пополам.
Здесь условие теоремы (р):
четырехугольник — параллелограмм; заключение теоремы
(q): точка пересечения диагоналей делит
каждую из них пополам.
Чтобы легче выделить условие и заключение
теоремы, ее часто формулируют в виде
импликации, применяя логический союз «если..., то...».
Поэтому в общем виде теорему можно записать
так: p=*q.
Доказательство теоремы состоит в том, чтобы
показать, что если выполняется условие, то из
него логически следует заключение, т. е.
приняв, что р истинно, в соответствии с
определенными правилами логики показать, что q
истинно.
Если имеется некоторая теорема р => q, то из
нее можно образовать новую теорему q => р,
называемую обратной к исходной. В этом
случае исходная теорема называется прямой
теоремой.
Например, обратной по отношению к
приведенной выше теореме 1 является следующая
теорема:
Теорема 2. Если в четырехугольнике
диагонали, пересекаясь, делятся пополам, то этот
четырехугольник — параллелограмм.
В данном случае теоремы 1 и 2 истинны, в чем
легко убедиться, проведя доказательство каждой
из них.
Однако из справедливости теоремы р => q не
всегда следует справедливость теоремы q => р.
Так, справедливо предложение «если углы
вертикальные, то они равны» (р => q), но
неверно, что «если углы равны, то они
вертикальные» (q => р). Например, прямые углы
равны, но они не обязательно являются
вертикальными.

НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЯ.
Рассмотрим следующие высказывания:
1) Если данное натуральное число четное, то
оно делится на 6.
2) Если данное натуральное число делится
на 6, то оно четное.
3) Если данное натуральное число четное, то
оно делится на 2.
4) Если данное натуральное число делится
на 2, то оно четное.
Каждое из этих высказываний можно
выразить на языке математической логики: l)pi => q\\
2) q\ =>Pi; 3)p2 => 02; 4> 02 =*P2-
Первое высказывание не является истинным,
второе, третье и четвертое высказывания
истинны.
Формулируя теорему, часто используют
термины «достаточно», «необходимо», «необходимо
и достаточно».
Условие р называется достаточным для
заключения q9 если из р логически следует д, т. е.
истинна теорема р => q.
Условие р называется необходимым для
заключения д, если из q логически следует р, т. е.
истинна теорема q^p.
Условие р называется необходимым и
достаточным для заключения q9 если из q
логически следует р, а из р логически следует д, т. е.
истинны обе теоремы — прямая и ей обратная.
В рассмотренном выше примере рг не является
условием, достаточным для glf так как из pi
логически не следует glf т. е. из истинности pi не
вытекает истинность qi; р2 является достаточным
условием для q2> так как изр2 логически следует q2.
Вместе с темрх является условием,
необходимым для glf поскольку из gj логически следует
Р\\ Рг есть условие, необходимое и достаточное
для q2, так как одновременно истинны обе
теоремы q2 =>р2 ИР2 =* 92» т* е« имеет местор2 <=» д2.
Возможны следующие случаи:
(а) условие р является достаточным для
заключения д, но не является необходимым;
(б) условие р является необходимым для
заключения д, но не является достаточным.
В случае (а) из истинности р вытекает
истинность д, но истинность д может вытекать и из
другого условия. Например, чтобы число было
четным, достаточно не только того, что оно
делится на 6, но и того, что оно делится на 4.
Справочные материалы A*)tL
Краткий справочник по математике ^***J
В случае (б) из истинности g вытекает
истинность р, однако если р является истинным, то g
все же может оказаться ложным. Например,
чтобы число делилось на 6, необходимо, но
недостаточно, чтобы оно было четным; так, число
4 — четное, однако оно не делится на 6.
При употреблении терминов «достаточно»,
«необходимо», «необходимо и достаточно»
вместо слова «условие» часто употребляют слово
«признак».
Вместо слов «необходимо и достаточно» часто
употребляют также слова: «если и только если»,
«тогда и только тогда», «в том и только в том
случае», «те и только те». Полезно иметь в виду,
что рассматриваемые отдельно части этих
связок также имеют определенный смысл:
например, слова «только в том случае», «только тогда»
и т. п. заменяют слова «необходимое условие»,
а слова «тогда», «в том случае» и т. п. заменяют
слова «достаточное условие».
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ.
Этот метод доказательства основан на так
называемом принципе математической индукции,
который заключается в следующем.
Если какое-либо утверждение,
сформулированное для натурального числа л, истинно для п — 1 и
из допущения его истинности для некоторого
значения п = k вытекает (т. е. может быть логически
выведена) его истинность для значения п — k + 1
(т. е. следующего за числом ft), то утверждение
верно для любого натурального п.
Иногда при использовании метода
математической индукции истинность утверждения
сначала устанавливается не для п = 1, а для
П = Пц>1.
Пример. Используя метод математической
индукции, докажем справедливость равенства
1 • 1! + 2 • 2! + ... + п • n!-(n + l)!-l,fi--l,2,3,.... (1)
1. При п — 1 равенство (1) очевидно.
2. Предположим, что равенство (1) справедливо
при п — k, т. е.
1 • 1! + 2 • 2! + ... + * • М - (* + 1)! - 1.
3. Составим выражение
1 • 1! + 2 • 2! + ...+*•« + (ft + 1) • (ft + 1)!
и заменим в нем сумму первых k слагаемых на
(k + 1)! - 1. Тогда получим
(k + 1)! - 1+ (k + 1) • (k + 1)! - (k + 1)! (k + 2) - 1.
Отсюда следует, что формула (1) верна для всех
натуральных п.

426
Справочные материалы
Краткий справочник по математике
Предел, непрерывность
Числовые последовательности
ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.
Числовой последовательностью (или просто
последовательностью) называется функция ап =
= f (п), определенная на множестве всех
натуральных чисел 1, 2, ..., п, ... . Значения
последовательности <*}, а2, ..., ап называются ее
членами.
Последовательность ап = f (п) иногда
обозначают так: {ап}. Это означает, что задана
последовательность с общим членом ап. По данному
общему члену всегда можно найти любой член
последовательности ak, подставив в ап вместо п
число k.
Для последовательности, как и для любой
функции, можно построить график. Он не
является линией, а состоит из отдельных точек,
расположенных справа от оси Оу. На рис. 28
изображен график последовательности {(-1)пп); он
состоит из следующих точек: (1; -1), (2; 2), (3; -3),
(4; 4),....
Последовательность {ап} называется невозрас-
тающей (неубывающей), если для любого номера
п справедливо неравенство ап > ап+1 (ап ^ ад+1).
Если ап > ап+г (ап < ад+1), то
последовательность {ап} — убывающая (возрастающая).
Последовательности всех этих типов носят
общее название — монотонные. Убывающие и
возрастающие последовательности называются
строго монотонными, невозрастающие и
неубывающие — монотонными в широком
смысле.
Последовательность {ап} называется ограни-
ченной сверху (снизу), если существует такое
число М, что для любого номера п выполняется
неравенство ап^М (соответственно ап > М).
Последовательности, ограниченные одновременно
сверху и снизу, называются ограниченными.
Число а называется пределом
последовательности {ап}, если для любого числа е > 0
существует такой номер N = N (г), зависящий от е, что для
всех п> N выполняется неравенство \ап - а\ < е.
Это обозначают так:
lim а = а или ап-> а при п -» оо.
п->оо
Пример. Докажем, что lim - = 0.
л_>оо п
Пусть е > 0 — произвольное число. Тогда
II
- 0
1 1
- < е, если п > - ,
п г
Из последнего неравенства следует, что в качестве
номера N можно взять целую часть числа - , т. е. N —
-й-
Итак, lim - = 0.
П->оо п
ТЕОРЕМЫ О ПРЕДЕЛАХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ.
1. Последовательность, имеющая предел,
ограничена.
2. Последовательность может иметь только
один предел.
3. Любая неубывающая (невозрастающая) и
ограниченная сверху (снизу) последовательность
имеет предел.
4. Предел постоянной равен этой
постоянной:
lim с =с.
п-»оо
5. Предел суммы равен сумме пределов:
lim (ап + bn) = lim ап + lim Ьп.
п—> оо п—» оо п—> оо
\\
4
3-
о.
1-
-2
-3
1
О
_J \
i '
i
*х
Рис. 28
6. Постоянный множитель можно
выносить за знак предела:
lim (сап) = с lim ап.
п—> оо п —> оо
7. Предел произведения равен произведению
пределов:
lim (ап • bn) = lim ап • lim Ьп.
п —> оо п—> оо п—> оо

Справочные материалы
Краткий справочник по математике
427
8. Предел частного равен частному
пределов, если предел делителя отличен от нуля:
lim а„
Q оо
lim т- = т т— , если lim Ьп Ф 0.
vqo о„ lim о„ п->оо
Л->00
9. Если Ьп<^ап^спи обе последовательности
{Ьп} и {сп} имеют один и тот же предел а, то
lim ап = а.
д-»оо
В теоремах 5—8 предполагается, что все
пределы в правой части равенств существуют.
Пример. Найдем предел lim -—— .
п _> оо4п + 5
Имеем
lim = lim
Д->00 4/1 + 5 П —> ОО
пЫ - -) lim Гз - -1
nU + -) lim (4+^
I, П) „_>«Л П)
lim 3 - lim -
Л —> оо л-»» Л 3 — О 3
lim 4 + 5 lim -
П->оо п->оо л
БЕСКОНЕЧНО МАЛАЯ И БЕСКОНЕЧНО
БОЛЬШАЯ ВЕЛИЧИНЫ. Последовательность {ап}
называется бесконечно малой, если ее предел
равен нулю: lim ап = 0.
л->оо
Теорема 1. Произведение бесконечно
малой последовательности на ограниченную
последовательность есть бесконечно малая
последовательность.
Например, последовательность {sin п) —
ограниченная
••й-
бесконечно малая; следова-
sm п
тельно, последовательность \ } является бес-
.. sin п
конечно малой, т. е. lim = 0.
д_>оо П
Последовательность {ап} называется
бесконечно большой, если для любого
положительного числа М найдется такое натуральное
число N, что для любого п> N выполняется
неравенство \ап\ > М. В этом случае пишут: lim ап = оо.
Теорема 2.
Если lim а = 0, то lim — = оо;
л->оо п->оо Ад
если lim ап = со, то lim — =0.
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ.
Арифметическая прогрессия — это последовательность
{ап}, каждый член которой, начиная со второго,
равен предыдущему, сложенному с одним и тем
же числом d, называемым разностью прогрессии:
ап+1 = ад + d, п = 1, 2, 3, ... .
Например, последовательность 1, 3, 5, 7,... —
арифметическая прогрессия, у которой aj = 1,
d = 2.
Иногда рассматривают не всю
последовательность, являющуюся арифметической
прогрессией, а лишь ее первые несколько членов. В этом
случае говорят о конечной арифметической
прогрессии.
Формула общего члена арифметической
прогрессии:
ап = ai + d(n - 1).
Формулы суммы п первых членов
арифметической прогрессии:
2аг + d(n - 1)
2 Пу S* = 2 * п'
Характеристическое свойство
арифметической прогрессии:
ап_х + ад+1
Sn =
а1 + ад
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.
Геометрическая прогрессия — это последовательность
{Ьп}, первый член которой отличен от нуля, а
каждый член, начиная со второго, равен
предыдущему, умноженному на одно и то же отличное от
нуля число q, называемое знаменателем
прогрессии:
&л+1 = bnq, п = 1, 2, 3, ... .
Например, последовательность 1, 2, 4, 8,
16, ... — геометрическая прогрессия, у которой
&i = i,g = 2.
Иногда рассматривают не всю
последовательность, являющуюся геометрической
прогрессией, а лишь ее цервые несколько членов. В этом

Справочные материалы
Краткий справочник по математике
случае говорят о конечной геометрической
прогрессии.
Формула общего члена геометрической
прогрессии:
bn = b1qn~1.
Формулы суммы п первых членов
геометрической прогрессии:
1 - q 1 - q
Характеристическое свойство
геометрической прогрессии:
Ъп = Ъп-1Ьп+1-
Бесконечно убывающая геометрическая
прогрессия — это геометрическая прогрессия,
знаменатель которой по модулю меньше
единицы: |д| < 1. В этом случае справедливы
приведенные выше формулы, а также существует предел
суммы п первых членов прогрессии при п —> оо
(называемый суммой этой прогрессии и
обозначаемый через S):
ь1
S = lim S„ = .
n->oo п 1 - q
Предел функции
ОПРЕДЕЛЕНИЕ ПРЕДЕЛА «&УНКЦИИ. Пусть
функция / (х) определена в некоторой
окрестности точки х = а, кроме, может быть, самой
точки а.
Число А называется пределом функции f (х)
при стремлении хка (или в точке а), если для
любого числа е > 0 существует такое число
8 = 8(e) > 0, что для всех х, удовлетворяющих
условию 0 < \х - а\ < 8, имеет место неравенство
|/ (х) - А\ < г. Это обозначают так: lim f (х) =А
х->а
или f (х) -»А при х -» а.
Другими словами, число А есть предел
функции / (х) в точке х = а, если для всех х9
достаточно близких к числу а и отличных от него,
соответствующие им значения функции / (х)
оказываются сколь угодно близкими к числу А
(естественно, в тех точках х, в которых функция
f(x) определена).
Пример. Покажем, что lim х «■ 1.
Пусть е — произвольное положительное число.
Выбрав 8 = е, получим, что \х - 1| < е, как только
О < \х - 1| < 8. Следовательно, согласно определению
предела функции lim х — 1.
При изучении свойств функций приходится
рассматривать также предел функции при
стремлении аргумента х к бесконечности.
Число А называется пределом функции f (х)
при стремлении х к бесконечности (или в
бесконечности), если для любого числа е > 0
существует такое положительное число N = Щг), что
для всех х9 удовлетворяющих условию \х\ > N,
имеет место неравенство |/ (х) - А\ < е. При этом
пишут: lim f(x)=A.
х->°°
Рассматривают также пределы функции при
х -> +оо их-» -оо. Предел функции / (х) при
х —» +оо (я _» -оо) определяется аналогично
пределу / (х) при х —» оо, только в самой
формулировке определения условие \х\ > N следует
заменить на х > N (соответственно на х < -N).
БЕСКОНЕЧНО МАЛЫЕ И ИХ СВОЙСТВА.
Функция а (х) называется бесконечно малой при
х -> а, если lim а(л:) = О, т. е. для любого числа
х —>а
е > 0 существует такое число 6 > 0, что для всех х,
удовлетворяющих неравенству 0 < \х - а\ < 8,
выполняется неравенство |ос (х)\ < е.
Бесконечно малую функцию а(х) называют
бесконечно малой величиной или просто
бесконечно малой.
Функция f(x) называется ограниченной при
х -> а у если существуют положительные числа
М и 8, такие, что при условии 0 < \х - а\ < 8
выполняется неравенство |/ (х)\ < М. Например,
любая бесконечно малая а (х) является
ограниченной функцией при х —»а.
В дальнейшем будем рассматривать
бесконечно малые при х —» а.
Свойства бесконечно малых.
1. Если функции ах (х) и а2 (х) являются
бесконечно малыми, то функция а^ (х) + а2 (х) также
есть бесконечно малая.
Это свойство распространяется на случай
алгебраической суммы любого конечного числа
бесконечно малых.
2. Произведение ограниченной при х -» а
функции на бесконечно малую есть функция
бесконечно малая.
3. Произведение постоянной на бесконечно
малую есть бесконечно малая.

Справочные материалы
Краткий справочник по математике
429
4. Произведение двух бесконечно малых есть
бесконечно малая.
Это свойство распространяется на любое
конечное число бесконечно малых.
БЕСКОНЕЧНО БОЛЬШИЕ. Функция / (х)
называется бесконечно большой при х —» а, если
для любого числа М > 0 существует такое число
8 > 0, что |/ (х)\ > М для всех х9
удовлетворяющих неравенству 0 < \х - а\ < 8. Это обозначается
так: lim fix) — оо.
х->а
Если при этом / (х) положительна
(отрицательна) при 0 < \х - а\ < 8, то пишут: lim / (х) =
х->а
= +оо ( lim / (х) = -оо).
х->а
Бесконечность (оо) не число, а символ,
который употребляется, например, для того, чтобы
указать, что соответствующая функция есть
бесконечно большая.
Бесконечно большая функция / (х) при х -> а
не имеет предела, так как предел переменной
(если он существует) — некоторое число. То же
относится и к бесконечно большой
последовательности.
В дальнейшем всегда под пределом
последовательности (функции) будем понимать
конечный предел, т. е. число, если не оговорено
противное.
Ниже рассматриваются бесконечно большие
функции при х —> а.
Связь между бесконечно большими
и бесконечно малыми.
1. Если функция f (х) бесконечно большая,
1
то
fix)
— бесконечно малая.
2. Если функция а (х) бесконечно малая и не
обращается в нуль, то
а(х)
— бесконечно
большая.
ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ.
1. Для того чтобы число А было пределом
функции f (х) при х —» а, необходимо и
достаточно, чтобы эта функция была представима
в виде f (х) = А + а (х)9 где а (х) — бесконечно
малая.
2. Функция не может иметь в одной точке
два различных предела.
3. Предел постоянной величины равен самой
постоянной.
4. Если функция f (х) положительна
(отрицательна) при всех х в некоторой
окрестности точки а, кроме, быть может, самой точки а,
и в точке а имеет предел, то lim fix) > О
х-> а
( lim f(x) < 0).
х->а
5. Если функции fi ix) и f2 (*) имеют пределы
при х —» а, то при х —» а имеют пределы также
их сумма /х ix) + f2 (*)» произведение fi ix) • f2 ix)
/iW
и при условии lim f2 ix) * 0 частное / ( .,
х->а /2 '*'
причем
lim (/х ix) + f2 ix)) = lim /x ix) + lim f2 ix), (1)
x->a x->a x->a
lim (fx (x) • f2 (x)) = lim' U (x) • lim f2 (x), (2)
x-*a x->a x->a
/, (x) lim h {x)
x™af2(x) " lim f2(x)-
x->a
Формула (1) распространяется на случай
алгебраической суммы любого конечного числа
слагаемых, а формула (2) — на случай любого
конечного числа сомножителей.
6. Если функция f (х) имеет предел при
х ->а, то
lim (/(*))" = ( lim/(*))*,
х->а х->а
где п — натуральное число.
7. Постоянный множитель можно
выносить за знак предела:
lim Cf ix) = С lim / ix), С = const.
x->a x->a
8. Если для функций fix), fiix) и f2ix) в
некоторой окрестности точки а выполняется
неравенство fiix) < fix) < f2ix) и lim f\ix) =
x->a
= lim f2 ix) =A, mo lim / ix) =A.
x->a x->a
Все предложения, сформулированные ранее,
остаются в силе и для случая, когда х —» оо.
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. Справедливо
равенство
_. sin х
lim = 1,
*->0 х

430
Справочные материалы
Краткий справочник по математике
называемое первым замечательным преде-
лом, и равенство
1\х
lim (1 + - ) = е,
называемое вторым замечательным пределом.
Число е является иррациональным и
приближенно равно 2,71828.
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ.
Рассмотрим отношение двух бесконечно малых а (х) и
Р (х) при х -> а (для простоты будем обозначать
их а и (J). Выделим три случая.
1. lim « = 0. В этом случае говорят, что а —
х-*аг
бесконечно малая более высокого порядка,
чем р.
П р и м е р 1. При х -> 2 функция (х - 2)3 —
бесконечно малая более высокого порядка, чем х - 2, так
г (* " 2)3 п
как lim — = 0.
х->2 х - 2
2. lim X = А * 0. В этом случае функции а
и Р называются бесконечно малыми одного
порядка.
П р и м е р 2. При х -> 0 функции 5х2 и х2
являются бесконечно малыми одного порядка, так как
с 2
1- 5х
lim —г- — 5.
« т. « ~
3. lim тд = оо. в этом случае говорят, что а —
х->а к
бесконечно малая более низкого порядка, чем р.
Можно сказать также, что Р — бесконечно
малая более высокого порядка, чем а.
Пример 3. При х -> -1 функция х + 1 есть
бесконечно малая более низкого порядка, чем (х- 1) х
Y 4- 1
х (х + I)2, так как lim 5 = °°-
*->-* (X - 1)(Х + 1)
Если функции а и Р — бесконечно малые
одного порядка, причем lim х = 1, то они назы-
х->а Р
ваются эквивалентными бесконечно малыми.
Символически это записывается так: а - р.
Из приведенного определения, в частности,
следует, что если lim « = А Ф 0, т. 'е. если а
х->а Р
и Р — бесконечно малые одного порядка, то а
и Ар являются эквивалентными бесконечно
малыми: а - Ар.
«• л ,. ^ 1. sin х
Пример 4. Как было отмечено ранее, lim =
*->о *
= 1, т. е. sin х и х при х -»0 являются
эквивалентными бесконечно малыми.
Теорема. Если существует предел
отношения двух бесконечно малых а и Р, то он
равен пределу отношения соответствующих
им эквивалентных бесконечно малых.
Эта теорема позволяет во многих случаях
упрощать отыскание предела.
„ _ .. sin 5х .. 5х
Пример 5. lim —5 = lim «-
* х->0 6Х х->0 ах
sin 5х ~ 5х при х -> 0.
о , так как
Непрерывность функции
ПОНЯТИЕ НЕПРЕРЫВНОСТИ. Пусть функция
у = f (х) определена в некотором интервале, а х0
их — два произвольных значения аргумента из
этого интервала. Положим х - Xq = Ajc, откуда
х = Xq + Ах. Говорят, что для перехода от
значения аргумента х0 к значению х первоначальному
значению придано приращение Ах.
Приращением Ау функции у = f (х),
соответствующим приращению Ах аргумента х в
точке Xq, называется разность
Ay = f(x0 + Ax)-f(x0).
Функция y = f(x) называется непрерывной в
точке Xq, если бесконечно малому приращению
Ах аргумента х в точке х0 соответствует
бесконечно малое приращение функции Ау, т. е.
lim Ay = lim (/ (х0 + Ах) - / (х0)) = 0.
Ах -> 0 Ах -> 0
Другими словами, функция у = f(x)
непрерывна в точке х0, если lim f (х) = f (xq), т. е.
х->х0
предел функции в точке х0 равен значению
функции в этой точке.
Функция, непрерывная в каждой точке
интервала, называется непрерывной на этом
интервале.

Справочные материалы
Краткий справочник по математике
431
Пример 1. Функция у = х непрерывна при
любом значении х — х0. В самом деле, Ay = Xq + Ах - х0 =
= Ах, и значит, lim Ay — lim Ах — 0.
Аж->0 Д*->0
Пример 2. Функция у — sin х непрерывна при
любом значении х — х0. В самом деле,
/ Ах\ Ах
Д# = sin (х0 + Ах) - sin х0 = 2 cos I х0 + -«- J sin -jr .
Отсюда lim Ay — 0, так как cos
Дх->0 I
Ах
А sin тг а
,. Ах ,. 2 Ах
lim sin тг e lim —т • -«- — 1
Дх->0 * Дх^О Д* *
n lim Дх = 0.
* Д*->0
а точка х0 называется точкой разрыва
функции / (х).
Пределом функции f (х) в точке xq слева
(справа) называется предел, вычисляемый в
предположении, что х стремится к Xq, оставаясь
все время меньше (больше) значения х0.
Пределы слева и справа, называемые
односторонними пределами, соответственно обозначают
lim / (х) и lim f(x).
х-> х0 - 0 х->х0 + 0
Точка х0 разрыва функции / (х) называется
точкой разрыва первого рода, если
существуют односторонние пределы lim / (х),
СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ.
1. Если функции f\(x) и f2(x) непрерывны в
точке х0, то в этой точке непрерывны также
их алгебраическая сумма /х (х) ± /2 (*)»
произведение fi (х) /2 (*) и при условии /2 (*о) ф 0 частное
Для алгебраической суммы и произведения
это свойство распространяется на любое
конечное число функций.
2. Если функция и = <р(х) непрерывна в
точке xq, а функция у = f(u) непрерывна в
точке uq = (р (х0), то сложная функция у = f (ф(#))
непрерывна в точке х0.
Таким образом, сложная функция y = f(<f> (х)),
образованная из двух непрерывных функций
/ (и) и ф (х), является непрерывной.
3. Если f (х) — непрерывная функция,
имеющая однозначную обратную функцию, то
обратная функция также непрерывна.
4. Функция f (х), непрерывная в точке xq, не
равная нулю в этой точке, сохраняет знак в
некоторой окрестности точки х0.
5. Все основные элементарные функции не-
прерывны там, где они определены.
Отсюда следует, что всякая элементарная
функция непрерывна во всех точках,
принадлежащих ее области определения.
ТОЧКИ РАЗРЫВА ФУНКЦИИ. Если функция
/ (х) не является непрерывной в точке х0, то
говорят, что в этой точке функция разрывна,
lim / (х) (при этом функция / (х) не обяза-
х -> х0+ о
тельно должна быть определена в точке х0).
Разность lim / (х) - lim / (х) называют
х->*0+0
х -> х0 - 0
скачком функции / (х) в точке х0.
Все прочие точки разрыва функции / (х)
называются ее точками разрыва второго рода.
Пример 1. Рассмотрим функцию у = f (х),
определенную на отрезке [0, 4] следующим образом:
/<*)-
х - 1, если 0 < х<3;
3-х, если 3 < х < 4.
Эта функция (рис. 29) определена во всех точках
отрезка [0, 4], и ее значение при х = 3 равно нулю. Однако
в точке х = 3 функция претерпевает разрыв первого
рода, так как при х -» 3 имеем: lim / (х) = 2,
*-»з-о
lim / (х) = 0.
*->3+0
Скачок функции в этой точке равен 2.
Точка х0 разрыва первого рода, в которой
lim f(x) — lim /(х), называется точкой уст-
х-*х0+0 Х-¥Х0-0
ранимого разрыва.
Рис. 29

432
Справочные материалы
Краткий справочник по математике
«• Л ^ sin х
Пример 2. Функция в точке х — 0 имеет
устранимый разрыв, так как
lim
*->о+о
sin х
= lim
х ->0-0
sin л:
= 1.
О,
Пример 3. Так как lim |х| — lim х
х->0+0 х->0+0
lim |х| — - lim х = 0, то функция у = \х\ непрерыв-
*->о-о *->о-о
на в точке х — 0.
Функция / (х) называется непрерывной в
точке xq слева (справа), если lim f (х) = f (xq)
jc->jc0-0
( lim /<*)-/(*<,»•
x->x0+0
ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА ОТРЕЗКЕ.
Функция / (х) называется непрерывной на от-
резке [а, ft], если она непрерывна в интервале
(а, ft) и, кроме того, в точке а непрерывна
справа, а в точке ft — слева.
Теоремы о функциях, непрерывных
наотрезке.
1. Если функция f(x) непрерывна на отрезке
[а, ft], то она ограничена на нем, т. е.
существует такое положительное число М, что
\f (х)\ < М при а<х<:Ь.
2. Теорема Вейерштрасса. Функция f (х),
непрерывная на отрезке [а, ft], достигает на
этом отрезке своих наибольшего и наименьшего
значений, т. е. существуют такие точки xi и
*2 отрезка [а, ft], что для всех х из [а, ft]
выполняются неравенства f (х{) > f (x)uf (х)> f (*2).
3. Если функция f (х) непрерывна на отрезке
[а, Ь]и на концах его принимает значения
разных знаков, то между точками а и b найдется
такая точка с,- что f (с) = 0.
Эта теорема имеет простой геометрический
смысл (рис. 30): если непрерывная кривая
переходит с одной стороны оси Ох на другую, то она
пересекает ось Ох.
У\
у = М
а\ Ус Ь х
Рис. 30
У1
В-
С-
А-
0
1
~7fA
a i
У
г
№
г 1
= /(
№
°) х
Рис. 31
4. Теорема Больцано—Коши. Пусть
функция f (х) непрерывна на отрезке [a, b]u f (а) =А,
f (ft) = В. Тогда для любого числа С, заключенного
между А и В, внутри этого отрезка найдется
такая точка с, что f (с) — С.
Эта теорема геометрически очевидна.
Рассмотрим график функции y = f(x) (рис. 31). Так
как / (a) =A,f (b) = В, то прямая у = С, где С —
любое число, заключенное между А и В,
пересечет его по крайней мере в одной точке.
1 Таким образом, непрерывная функция,
переходя от одного значения к другому, обязательно
проходит через все промежуточные значения.
Производная и ее применение
Понятие производной, ее механический
и геометрический смысл
ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ
ПРОИЗВОДНОЙ.
Задача о скорости движущейся
точки. Пусть s = s (t) представляет закон
прямолинейного движения материальной точки. Это
уравнение выражает путь s, пройденный
точкой, как функцию времени t. Обозначим через
As путь, пройденный за промежуток времени At
от момента t до t + At, т. е. As = s(t + At) - s (t).
Отношение — называется средней скоростью
точки за время от t до t + At. Чем меньше At, т. е.
чем короче промежуток времени от t до t + А*,
тем лучше средняя скорость характеризует
движение точки в момент времени t. Поэтому
естественно ввести понятие скорости v в данный
момент t, определив ее как предел средней
скорости за промежуток от t до t + At, когда At -> 0:
v = lim тт .
At ^ 0 At
Величина v называется мгновенной
скоростью точки в данный момент t.
Задача о касательной к данной
кривой. Пусть на плоскости хОу дана кривая
уравнением у = f (х). Требуется провести
касательную к данной кривой в данной точке
^о(хО^ / (*()))• Так как точка касания М0 дана,
то для решения задачи потребуется найти только
угловой коэффициент искомой касательной, т. е.

Справочные материалы
Краткий справочник по математике
433
tg ф — тангенс угла наклона касательной к
положительному направлению оси Ох (рис. 32).
Через точки М0 (х0; f (х0)) и Mi (х0 + Ах;
f (х0 + Ax)) проведем секущую MqMv Из рис. 32
видно, что угловой коэффициент tgoc секущей
Ау
MqMi равен отношению — , где Ay = f (х0 + Ах) -
-/(*о).
Угловой коэффициент касательной MqT к
данной кривой в точке М0 можно найти на
основании следующего определения: касательной к
кривой в точке М0 называется прямая М0Т,
угловой коэффициент которой равен пределу углового
коэффициента секущей MqMi, когда Але —» 0.
Отсюда следует, что tg <р = lim tg а = lim ~ .
Ах -> о Ах -+ о ах
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ.
Математическая операция, требуемая для решения
рассмотренных выше задач, одна и та же. Выясним
аналитическую сущность этой операции.
Пусть функция y = f(x) определена в интервале
(а, Ь). Возьмем какое-нибудь значение х из (а, Ь).
Затем возьмем новое значение аргумента х + Ах
из этого промежутка, придав первоначальному
значению х приращение Ах (положительное или
отрицательное). Этому новому значению
аргумента соответствует новое значение функции у + Ау =
= / (х + Ах), где
Ay = f(x + Ax)-f(x).
Составим отношение
Ay = / (х + Ах) - / (х)
Ах Ах
которое является функцией от Ах.
^
Если существует предел отношения т*1-
приращения функции Ау к вызвавшему его
приращению аргумента Ах, когда Ах стремится к
нулю, то этот предел называется производной
функции у = / (х) в данной точке х и
обозначается через у' или f'(x) (читается: «игрек штрих»
или «эф штрих от икс»):
у'= /'(*) =
lim f{X
— lim
lim
Дх->0
+ Ах)
Ах
Ах
-fix)
Для обозначения производной принят также
и следующий символ: -р (читается: «дэ игрек
по дэ икс»). Этот символ надо рассматривать как
целый символ, а не как частное.
Если существует предел справа lim -г*
Ау
(или предел слева lim т*- ), то он называется
дх-^о-оД*
правой (или левой) производной функции / (х) в
точке х.
Действие нахождения производной функции
называется ее дифференцированием, а
функцию, имеющую производную в точке х,
называют дифференцируемой в этой точке. Функция,
дифференцируемая в каждой точке
промежутка, называется дифференцируемой в этом
промежутке. При этом если промежуток от а до Ъ
есть отрезок [a, ft], то в точке а речь идет о
правой производной, а в точке ft — о левой
производной.
Функция, имеющая непрерывную
производную, называется непрерывно
дифференцируемой.
Пример 1. Найдем производную функции у =
— С, где С — постоянная.
Имеем у + Ау - С, Ау - 0, т^ - 0, lim т^ - 0,
т. е. у' = 0. Следовательно, производная постоянной
равна нулю: (С)' — 0.
Пример 2. Найдем производную функции у = х.
Имеем у + Ау = х+Ах, Ау = Ах9 т^ = 1, lim 7""—li
шС Дх —»0 А*
т. е. у' = 1. Итак, (х)' = 1.
Из рассмотренных выше задач следует:
1. Скорость v прямолинейного движения есть
производная пути s по времени t: v = -тт . В этом
Xq Xq + Ах X
Рис. 32

434
Справочные материалы
Краткий справочник по математике
состоит механический смысл
производной. По аналогии с этим производную любой
функции часто называют скоростью изменения
этой функции.
2. Угловой коэффициент касательной к
кривой у = f (х) в точке с абсциссой Xq есть
производная f'(x0). В этом состоит геометрический
смысл производной.
Поэтому уравнение касательной к кривой у =
= / (х) в точке М0 (лг0; у о) примет вид
у-Уо = Г(хо)(х~хо)-
Нормалью к кривой в некоторой ее точке
называется перпендикуляр к касательной к этой
кривой в той же точке. Следовательно, если
/4*0) * 0» то> используя условие
перпендикулярности двух прямых, уравнение нормали к
кривой у = f(x) в точке Mq(xq; yQ) можно
записать так:
У~Уо =
П*п)
(X - Xq).
Теорема. Если функция y = f(x)
дифференцируема в некоторой точке х, то она
непрерывна в этой точке.
Обратное утверждение не имеет места, что
видно из следующего примера.
Пример 3. Функция у = \х\, график которой
изображен на рис. 4, непрерывна в точке х = 0.
Вместе с тем ясно, что в этой точке в соответствии с
геометрическим смыслом производной функция £/ = |jc|
не дифференцируема, так как в ней нет определенной
касательной.
Формулы дифференцирования
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ. Пусть
y = f(u), где и = ф (я), причем / (и) имеет
производную по и у а ф (х) — по х. Тогда
di£ _ dy du
dx ~ du dx'
ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ. Пусть
у = / (х) и х = ф (у) — взаимно обратные
функции. Тогда если функция y = f(x) имеет не
равную нулю производную f'(x), то обратная
функция имеет производную ф'(г/), причем
1
фЧу) = Г00'
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ И
ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ
ФУНКЦИЙ.
I. (С)' = 0.
П. (u + u)' = m' + u'.
III. (uv)' = u'v + uvf.
IV.(Cu)'=Cu'.
w - y2 •
VI. (ua)' = <xua_V.
VII. (au)' = auu'In a.
VIII. {eu)'= euu'.
IX. (loga u)' = —у— .
v b0 ' ulna
X.(lnu)' = —.
XI. (sin u)' = u'cos u.
XII. (cos u)'= -u'sin u.
ХШ.
XIV.
XV. i
XVI.
xvn
V47TT
(tgu)'=-
и'
2 *
cos и
(ctgu)' = -
(arcsin u)'-
(arccos u)
. (arctg u)'
T /AWW%+*1> ,.
и'
. 2 *
sm и
и'
УГТ2'
и'
JT^?
и'
2 *
1 + и
и'
или, короче,
ху у:
1 + и
Здесь и = и(х) и v = v(x) —
дифференцируемые функции, С — произвольная постоянная,
а — действительное число.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ.
Производная у' = f'(x) данной дифференцируемой
функции у = f (х)> называемая производной
первого порядка, представляет собой некоторую
новую функцию. Возможно, что эта функция
сама имеет производную. Тогда производная от
производной первого порядка называется про-
изводной второго порядка (или второй
производной) и обозначается так: у" = (уУ или /" (х).
Аналогично, если существует производная от
производной второго порядка, то она называет-

Справочные материалы
Краткий справочник по математике
435
ся производной третьего порядка (или
третьей производной) и обозначается так: у'" = (у"У
или /'" (х) и т. д.
Вообще производная от производной порядка
п-1 называется производной порядка п и
обозначается у{п) = (у^'^У-
Производные четвертого, пятого и более
высоких порядков обозначаются также с помощью
римских цифр: i/IV, i/v, i/VI и т. д. В таком случае
порядок производной можно писать без скобок.
Примеры.
= *.*
,' = ь-*-1
Jfe-2
1) У = х\ у' - kx*-\ у" - k(k - 1)х"
у{п) = k(k - l)(k - 2) ...(fe - n + 1)х*_л; если k —
натуральное число, то y{k) = Л! и у**+1) - у(*+2) = ... = 0.
2)у = ekx, у' - *е**, у" - Л**, ..., уМ - *»«**.
3) у = а*, у'- а* In а, у" = ах In2 а,..., у(п) - а* In11 а.
4) у = In х, у' =
У -
V
,(п) =
(-1)-(-2)...(-д + 1)
= (-1)
n-i(n-l)!
5) у = sin х, у' = cos х — sin (* + о J» #" = ~s*n х в
= sin (х + тс) = sin [ х + 2 • 5 j,..., j/n* = sin (x + n • 5) •
Свойства дифференцируемых функций
ТЕОРЕМА ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И
КОШИ.
Теорема Ферма. Если функция у = f (х)9
определенная в интервале (a, ft), достигает в
некоторой точке с этого интервала наибольшего
(или наименьшего) значения и существует
производная Г (с), то f'(c) = 0.
Геометрический смысл этой теоремы состоит
в том, что касательная к графику функции у =
= f(x) в точке с абсциссой с параллельна оси
абсцисс (рис. 33).
Теорема Рояля. Если функция у = f (х),
непрерывная на отрезке [а, ft] и
дифференцируемая в интервале (а, ft), принимает на концах
этого отрезка равные значения f (а) = / (ft), то в
интервале (а, ft) существует такая точка с, что
Г(с) = 0.
Геометрически эта теорема означает
следующее: если крайние ординаты кривой у = f (х)
равны, то на кривой найдется точка, в которой
касательная параллельна оси абсцисс (рис. 34).
Теорема Лагранжа. Если функция у = f (х)
непрерывна на отрезке [а, ft] и
дифференцируема в интервале (а, ft), то в этом интервале
найдется такая точка с, что
Ь — а
Эта теорема имеет простой геометрический
смысл (рис. 35): на графике функции y = f(x)
между точками А и В найдется такая внутренняя
точка С, что касательная к графику в точке С
параллельна хорде АВ.
Следствие. Если f'(x) = 0 в интервале (a, ft),
то в этом интервале функция f (х) постоянна.
Теорема Коши. Если функции f (х) и g (х):
1) непрерывны на отрезке [а, ft]; 2)
дифференцируемы в интервале (а, ft); 3) g'(x) Ф 0 в этом
интервале, то в интервале (а, ft) существует
такая точка с, что имеет место равенство
fib)-f(a)
g{b)-g (а)
Г (с)
ё'{с)
ПРАВИЛО ЛОПИТАЛЯ. Ранее мы
познакомились с некоторыми приемами нахождения
пределов отношения двух бесконечно малых или
бесконечно больших, т. е. раскрытия неопреде-
ленности соответственно вида -z или — . Теперь
рассмотрим новый простой прием для раскры-
yk
т
0\ с
Рис. 33

436
Справочные материалы
Краткий справочник по математике
тия этих неопределенностей, называемый
правилом Лопиталя:
Предел отношения двух бесконечно малых
или бесконечно больших функций равен пределу
отношения их производных, если последний
существует, т. е.
lim —:—- = lim —77—\ •
*->аФ(*) хчаФ (X)
Здесь предполагается, что функции f(x) и
Ф (х) определены и дифференцируемы в
некоторой окрестности точки а, исключая, быть
может, саму точку а.
Примеры. 1) lim
х _> о Sin X
«l^i = lim i£zJ$.
х^0 (Sill X)
= lim — In 2; 2) lim — lim -r = 1.
x _> 0 cos x x _> 0 x x -> 0 *
ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ.
Теорема. Если функция f (х),
дифференцируемая в интервале (a, ft), удовлетворяет в нем
условию f'(x) > О (соответственно f'(x) < 0),
то эта функция возрастает (убывает) в
интервале (а, Ь).
Пример. Функция у = х2 убывает в промежутке
(-оо, 0), так как в этом промежутке у' = 2х < 0. Эта
же функция в промежутке (0, +оо) возрастает, так
как в указанном промежутке у' — 2х > 0.
МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИЙ.
Говорят, что функция / (х) имеет в точке х0
максимум (минимум), если существует такая
окрестность (Xq - 8, Xq + 8) ТОЧКИ Xq, ЧТО ДЛЯ ВСвХ X
из этой окрестности, отличных от х0,
выполняется неравенство f (х) < f (х0) (соответственно
f(x)>f(x0)).
Иначе говоря, функция / (х) имеет в точке xq
максимум (минимум), если для достаточно ма-
У%
У ^f(x)
хх х2 х
Рис. 36
лого приращения Ах (любого знака)
выполняется неравенство
/ (х0 + Ах) < f (х0) (f (х0 + Дх) > / (х0)).
Максимум и минимум функции называются
экстремумом функции.
По определению, максимум и минимум
функции могут достигаться лишь внутри
области определения, а концы отрезков области
определения, не могут служить точками, в которых
функция принимает экстремум.
На рис. 36 изображен график функции,
которая имеет в точке х± максимум, а в точке х2 —
минимум.
Теорема1 (необходимое условие
существования экстремума). Если функция f (х),
дифференцируемая в интервале (а, Ь), имеет в
точке xq, а< х0<Ь, экстремум, то ее производная
в этой точке равна нулю:
Г(х0) = 0. (1)
Условие (1), будучи необходимым условием
экстремума, не является достаточным условием
экстремума, что показывает следующий
пример.
П р и м е р 1. Функция / (х) = х3 не имеет
экстремума в точке xq - 0 (разность f (x)-f (0) меняет знак
при изменении знака аргумента х), хотя ее
производная у' - Зх2 обращается в этой точке в нуль.
Теорема2 (первое достаточное условие
существования экстремума). Если
производная функции f (х) обращается в точке х0 в нуль
(такие точки называются критическими) и при
переходе через эту точку в направлении
возрастания х меняет знак с 4 плюса* (♦ минуса*) на
* минус* (« плюс*), то в точке х0 функция имеет
максимум (минимум). Если же при переходе через
точку Xq производная функции f (х) не меняет
знака, то в этой точке функция f (х)
экстремума не имеет.
Отсюда следует правило исследования
функции на экстремум с помощью первой
производной. Пусть в интервале (а, Ь) дана
дифференцируемая функция / (х). Тогда для исследования
ее на экстремум:
1) находят производную f'(x);
2) находят корни уравнения f'(x) = 0;
3) выясняют знак f'(x) слева и справа от
каждого из этих корней и согласно теореме 2 делают
заключение об экстремуме;

Справочные материалы
Краткий справочник по математике
437
4) вычисляют значения функций в точках
экстремума.
П р и м е р 2. Исследуем на экстремум функцию
/(х) = х3-Зх + 2.
Вычисляем производную f'(x) - Зх2 - 3 - 3(х2 - 1) -
= 3(х + 1)(х - 1) и находим корни уравнения /'(*) = 0.
Имеем Xi — -1, х2 — 1. Затем согласно полученному
правилу последовательно заполняем строки таблицы:
*
/'(*)
Я*)
х<-1
+
x1--li
0
Максимум
-К * < 1
-
*2-1
0
Минимум
«*2> - 0
Х> 1
+
ИССЛЕДОВАНИЕ ФУНКЦИЙ НА ЭКСТРЕМУМ
С ПОМОЩЬЮ ВТОРОЙ ПРОИЗВОДНОЙ.
Теорема (второе достаточное условие
существования экстремума). Пусть функция
f (х) имеет в точке х0 и ее окрестности
непрерывные первую и вторую производные, причем
/'(*о) = 0, f" (xq) * 0. Тогда функция f (х)
достигает в точке xq минимума (максимума), если
f"(xo) > 0 (соответственно f"(x$) < 0).
Эта теорема позволяет сформулировать
правило исследования функции на экстремум
с помощью второй производной. По сравнению
с предыдущим правилом меняется лишь п. 3,
который заменяется на следующий: находят
вторую производную f"(x), вычисляют ее
значения для каждого из корней уравнения f'(x) = 0
и согласно теореме делают заключение об
экстремуме.
Заметим, что пользоваться вторым правилом
обычно проще, чем первым. Однако если вторая
производная при значении, равном корню
первой производной, обращается в нуль, то
используют первое правило отыскания экстремума.
Пример. Исследуем на экстремум функцию
/ (х) = х3 - Зх + 2.
Имеем f'(x) = Зх2 - 3, f"(x) - 6х. В примере 2
предыдущего пункта мы нашли корни уравнения f'(x) =
= 0; Xi — -1, х2 — 1. В точке хг = -1 функция f (х) имеет
максимум, так как /"(-1) — -6 < 0, а в точке х2 — 1 —
минимум, так как /"(1) = 6 > 0.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
ФУНКЦИИ НА ОТРЕЗКЕ. Чтобы найти
наибольшее значение функции / (х) на отрезке [а, Ь], надо
найти все максимумы этой функции на
интервале (а, Ь), затем вычислить значения функции f(x)
на концах* отрезка [а, Ь], т. е. / (а) и / (ft).
Наибольшее из всех этих чисел и будет наибольшим
значением функции / (х) на отрезке [a, ft].
Очевидно, если непрерывная на отрезке [a, ft]
функция имеет в интервале (а, Ь) только один
экстремум, то в точке экстремума (т. е. в точке
интервала (a, ft), где функция имеет экстремум)
она принимает наибольшее значение в случае
максимума и наименьшее в случае минимума.
Пример. Пусть из квадратного листа жести со
стороной а необходимо сделать прямоугольную
коробку наибольшего объема, вырезая по углам равные
квадраты и сгибая края (рис. 37).
Обозначим сторону вырезаемого квадрата через
х. Тогда объем коробки выразится равенством
V — х(а - 2х) , где х изменяется в интервале
н>
В этом интервале производная V" — (а - 2х) (а - 6х)
обращается в нуль в единственной точке х = ^ . Так как
V" = -4а < 0 при х = ^ , то при этом значении х объем
V достигает максимума, а значит, согласно
сделанному замечанию, и наибольшего значения. Таким
образом, объем коробки будет наибольшим, если сторона
а
вырезаемого квадрата равна ~ .
ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКА
ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА. На рис. 38
изображен график дифференцируемой функции
у = / (х). В точках А, В и С построим
касательные к графику. Видно, что все точки графика,
достаточно близкие к точке А и лежащие по обе
стороны от нее, расположены ниже касательной.
В этом случае график функции у = f (х)
называется выпуклым в точке А. Все точки графика,
достаточно близкие к точке С и лежащие по обе
У*
X
X X
а-2х
X
Рис. 37
Рис. 38
* Функция может достигать своего наибольшего
значения не только во внутренних точках отрезка [а, ft], но и на
его концах (см. рис. 30).

Справочные материалы
Краткий справочник по математике
стороны от нее, расположены выше
касательной. В таком случае график функции у = f (х)
называется вогнутым в точке С.
График дифференцируемой функции y = f(x)
называется выпуклым (вогнутым) в
интервале (а, Ь), если он является выпуклым (вогнутым)
в каждой точке, абсцисса которой принадлежит
(а, Ь). График, изображенный на рис. 38, между
точками А и В является выпуклым, а между
точками В и С — вогнутым.
Касательная к графику в точке В пересекает
график. При этом во всех точках графика,
близких к точке В и лежащих слева от нее, график
является выпуклым, а во всех точках графика,
лежащих справа от точки В и близких к ней, —
вогнутым. Точка графика дифференцируемой
функции у = f (х)у при переходе через которую
график меняет выпуклость на вогнутость и
наоборот, называется точкой перегиба. Значит,
В — точка перегиба.
Теорема 1. Если вторая производная
f" (х) функции у = f(x) положительна
(отрицательна) в интервале (а, Ь), то график этой
функции является вогнутым (выпуклым) в этом
интервале.
Теорема 2. Если вторая производная
f" (х) функции у = f (х) обращается в точке Xq в
нуль и при переходе через эту точку меняет
знак, то точка (х0; f (х0)) графика данной
функции является точкой перегиба.
Пример. Кривая у - х3 выпукла в промежутке
(-оо, 0), так как в этом промежутке у" - 6х < О, и
вогнута в промежутке (0, +°°), так как в нем у" — 6х > 0;
при х — 0 имеем у" =0, следовательно, точка (0; 0) —
точка перегиба (рис. 39).
Кривая у = хг называется кубической параболой.
АСИМПТОТЫ. Многие линии имеют
асимптоты, т. е. прямые, к которым неограниченно
приближается данная линия, когда ее точка
неограниченно удаляется от начала координат.
Рис. 39
Различают асимптоты вертикальные (т. е.
параллельные оси ординат) и наклонные (т. е.
непараллельные оси ординат).
Прямая х = а называется вертикальной
асимптотой графика функции у = f (х), если
хотя бы одно из предельных значений
lim / (х)9 lim f(x) является бесконечным,
х->а+0 х->а-0
т. е. равно +оо или -оо.
П р и м е р 1. Прямая х = 0 является вертикальной
асимптотой графика функции у — - (см. рис. 13), так
1 . ,.1
как lim - — +°о, цщ - — -оо.
*->о+о х ж->0-0 х
Предположим, что функция у = f (х)
определена при сколь угодно больших (по модулю)
значениях аргумента.
Прямая у = kx + Ь называется наклонной
асимптотой графика функции у = f (х) при
х —»+ оо, если эта функция представима в виде
/ (х) - kx + b + а (х),
где lim а (х) = 0.
*->+оо
Аналогично определяется наклонная
асимптота для случая х —» -со.
Пример 2. ПрямаярО является
горизонтальной асимптотой графика функции у — - при х -> +оо
и при х -> -оо.
Построение графиков функций
Наиболее наглядное представление о ходе
изменения функции дает ее график. Поэтому
построение графика является заключительным
этапом исследования функции, в котором
используются все результаты ее исследования.
П р и м е р 1. Построим график функции у = ——- .
Функция определена и непрерывна для всех
значений х, кроме х = 1. Она не является ни четной, ни
нечетной. Ее график не имеет точек пересечения с осью
Ох, так как х2 + 1 > 0 для всех вещественных х. При х =
— О имеем у — -1. Далее,
х2+ 1 ,. х2+ 1 _^
lim - --оо, hm - = +оо,
ж_>1-0 х - 1 *->1+о х - 1

Справочные материалы
Краткий справочник по математике
439
т. е. прямая х = 1 является вертикальной асимптотой.
Если х -> +оо, то у -> +°о, а если х -> -со, то z/ ~> -со.
х2 - 2х - 1
Производная у = 5— обращается в нуль
(*- If
в точках х1 = 1-Л/2,х2=!=1 + 72. Эти точки
разбивают всю числовую ось на три промежутка (-°°,
1 - 72 ), (1 - 72 ,1 + 72 ), (1 + 72 , + со), внутри каждого
из которых производная у' сохраняет знак. Очевидно,
что в первом и третьем промежутках у' > 0, и,
следовательно, здесь функция возрастает, во втором промежутке
у' < 0, и, значит, в этом промежутке функция убывает.
Вторая производная у" —
~з всюду отлична
(х- 1)
от нуля (поэтому точек перегиба график функции не
имеет); в промежутке (-°°, 1) выполняется
неравенство у" < 0, и, следовательно, здесь график функции
является выпуклым и в точке хг функция имеет
максимум; в промежутке (1, +со) выполняется
неравенство у" > О, т. е. в этом промежутке график вогнутый и
в точке х2 функция имеет минимум. Наконец, по-
х + 1 . - .
скольку — — х + 1 +
2 2
и lim = О,
х — 1 х->±оо х — 1
х - 1
график имеет наклонную асимптоту у — х + 1 как при
х-> +оо, Так и при х -» -со. График функции у =
х2+1
х- 1
изображен на рис. 40.
Пример 2. Построим график функции у=е
Эта функция определена, непрерывна,
положительна на всей числовой оси и является четной.
Поэтому достаточно построить ее график в I квадранте.
При х = 0 имеем у = 1. Если х -» +со, то у -> 0, значит,
прямая у = 0 является горизонтальной асимптотой.
_ 2
Производная у' = -2хе х обращается в нуль только в
Рис. 40
Рис. 41
точке х0 — 0; если х > 0, то у' < 0, т. е. при х > 0 функ-
-х2
ция убывает. Вторая производная у" =2(2х-1)е
в точке Xi = —=. обращается в нуль; в промежутке
(-р, +со J имеем у" > 0, и, следовательно, здесь
график вогнутый, а в промежутке (х0, хг) имеем у" < 0,
т. е. здесь график выпуклый. Таким образом, хг —
абсцисса точки перегиба графика, и, наконец, в точке х0
2
функция имеет максимум. График функции у = е
изображен на рис. 41. Это так называемая кривая
Гаусса.
Неопределенный интеграл.
Понятие о дифференциальном
уравнении
Первообразная функция
и неопределенный интеграл
ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И
НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА. Функция F (х)
называется первообразной функцией для
данной функции / (х) (или, короче, первообразной
данной функции / (х)) на данном промежутке,
если на этом промежутке F'(x) = / (х).
Пример. Функция F (х) — х3 является
первообразной функции / (х) = Зх2 на всей числовой оси, так как
(х3)' = Зх2 при любом х. Отметим, что вместе с
функцией F (х) - х3 первообразной для / (х) = Зх2 является
любая функция вида Ф (х) — х3 + С, где С —
произвольное постоянное число (это следует из того, что
производная постоянной равна нулю). Это свойство
имеет место и в общем случае.
Теорема 1. Если Fi (х) и F2 (х) — две
первообразные для функции f (х) в некотором
промежутке у то разность между ними в этом
промежутке равна постоянному числу.
Из этой теоремы следует, что если известна
какая-нибудь первообразная F (х) данной
функции / (х), то все множество первообразных для
/ (х) исчерпывается функциями F (х) + С.
Выражение F (х) + С, где F (х) —
первообразная функции / (х) и С — произвольная
постоянная, называется неопределенным интегралом
от функции / (х) и обозначается символом
J / (х) dx, причем / (х) называется
подынтегральной функцией у f (х) dx — подынтеграль-

440
Справочные материалы
Краткий справочник по математике
ным выражением, х — переменной
интегрирования; J — знак неопределенного интеграла.
Таким образом, по определению
jf(x)dx = F(x) + C9
если *"(*) = /(*).
Возникает вопрос: для всякой ли функции
/ (х) существует первообразная, а значит, и
неопределенный интеграл?
Теорема 2. Если функция f (х) непрерывна
на [a, ft], то на этом отрезке для функции f (х)
существует первообразная.
Ниже мы будем говорить о первообразных
лишь для непрерывных функций. Поэтому
рассматриваемые нами далее в этом параграфе
интегралы существуют.
СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
l.£cif(x)dx = f(x).
2.JF'(x)dx = F(x) + C.
3. Постоянный множитель можно вынести
за знак интеграла:
\kf(x)dx = k\f(x)dx. (1)
4. Интеграл от суммы двух функций равен
сумме интегралов от этих функций:
\ (fi (х) + h (*)) «to - J /i (x) dx + \f2 (x) dx. (2)
Равенства (1) и (2) следует понимать с
точностью до постоянного слагаемого.
Свойство 4 распространяется на случай
алгебраической суммы любого конечного числа
функций.
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ. Таблица
содержит формулы, легко проверяемые
непосредственным дифференцированием:
П. J — = In \х\ + С.
III. J ах dx = т^— + С.
In а
kx
IV.jekx dx= ~- + С.
V. J sinaxdx = -- cos ax + С.
a
VI. J cos ax dx — - sin ax + С
vn.|
dx 1 . , _
—r- =-tg a* + C.
cos ax
2
sin ax
= — ctgax + C.
Ji
IX. f-f^- -llnl^ + al + C.
J x + a
x f dx = 1
A' 2 ^ 2 a
J x + a
J
arctg - + C.
a
XI.
XII.
, = arcsin - + С
ГЪ 2 a
л/а - x
[f== =ln|jc+7^T^| + C.
J ых + a
""•br?-^
x - a
x + a
+ C.
НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ.
Метод непосредственного интегрирования связан с
приведением подынтегрального выражения к
табличной форме путем преобразований и
применения свойств неопределенного интеграла.
Пример l.\(Jfo*-to? + l)dx-b\&dx-b\ #dx +
+ Jdx = x5-x3 + x + C.
Пример 2
I
6 5 . -
х - X + 1
dx = j(x*-x? + x-2)dx =
5 4 -
XXI
+ С.
5 4
Пример 3. Нл/х - \[х)24х =
- J<*- 2х5/6 + х2/3) dx = ^ - }| х11^ + | х5/з + с =
ЗАМЕНА ПЕРЕМЕННОЙ ИНТЕГРИРОВАНИЯ.
Этот способ часто бывает полезным в тех случаях,
когда интеграл J / (х) dx (f (х) непрерывна) не
может быть непосредственно преобразован к
виду табличного. Если х = <р (*), где <р (t) —
функция, имеющая непрерывную производную, то
JHx)dx = jf(q>(t))q>'(t)dt. (3)

Справочные материалы
Краткий справочник по математике
441
i л
Пример. Найдем I -р dx,
Воспользуемся подстановкой х - t2. Тогда х'= 2*,
е - ef, -7= = т . Значит,
J
-Л
.«£
V dx - 2 Ь< dt - 2е< + С - 2ецх + С.
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ. Пусть и = и (х)
и у = v (х) — непрерывно дифференцируемые
функции. Тогда справедлива формула
J uv' dx = uv-\ vu' dx. (4)
Пример. Найдем J xex dx.
Положим и — x, v'= ex; тогда u'= 1, v = ex. Теперь,
используя формулу (4), получим
\хе* dx - ди?* -je*dx = xex -ex + C.
Понятие о дифференциальном
уравнении
ЗАДАЧИ, ПРИВОДЯЩИЕ К
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ. В различных областях
науки и техники весьма часто встречаются задачи,
для решения которых требуется решить одно
или несколько уравнений, содержащих
производные некоторых функций. Такие уравнения
называются дифференциальными.
Задача 1. На плоскости хОу требуется найти
кривую, проходящую через точку О(0; 0) и
обладающую тем свойством, что угловой коэффициент
касательной, проведенной в любой точке кривой,
равен удвоенной абсциссе точки касания.
Пусть у т8 / (х) — уравнение искомой кривой.
По условию, в каждой точке М(х; f (х)) имеется
касательная к этой кривой, угловой
коэффициент которой, т. е. f'(x), равен 2х. Таким образом,
У' = 2х. (1)
Это дифференциальное уравнение, так как
оно содержит производную искомой функции.
Из уравнения (1) следует, что функция у есть
первообразная функции 2х. Поэтому
у — J 2х dx
или
У = х2 + С,
где С — произвольная постоянная.
(2)
Из формулы (2) видно, что
дифференциальное уравнение (1) имеет бесконечное множество
решений. Чтобы из этого множества решений
выбрать искомое, надо воспользоваться тем, что
искомая кривая проходит через точку О (0; 0).
Следовательно, координаты этой точки должны
удовлетворять уравнению (2), т. е. 0 = 0 + С,
откуда С = 0. Итак, искомая кривая — это
парабола у = х2.
Задача 2. Требуется найти закон
движения свободно падающего в пустоте тела, если
пройденный путь начинает отсчитываться от
момента времени t = 0 и начальная скорость
падения равна нулю. В этом случае, как известно,
скорость выражается формулой и — gt.
Так как скорость прямолинейного движения
есть производная пути по времени, то
v = s' = gt. (3)
Из этого уравнения следует, что функция s
есть первообразная функции gt. Поэтому
s = \gtdt
или
2 +ь.
(4)
Для нахождения произвольной постоянной С
воспользуемся тем, что начало отсчета пути
совпадает с началом отсчета времени, т. е. s = 0 при
t = 0. Подставляя эти значения в равенство (4),
имеем 0 = 0 + С, откуда С = 0 и, следовательно,
2 '
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ И ЕГО
РЕШЕНИЕ. В рассмотренных двух задачах мы
пришли к дифференциальному уравнению вида
у'= ф(х). Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и другие
процессы описываются гораздо более общими и
сложными дифференциальными уравнениями.
Дифференциальным уравнением называется
соотношение, связывающее независимую
переменную ху искомую функцию у = / (х) и ее
производные.
Всякая функция у = f (х), которая, будучи
подставлена в это уравнение, обращает его в

Справочные материалы
Краткий справочник по математике
тождество, называется решением уравнения.
9 St
Например, функции у = лг и s = -5- являются
решениями соответственно уравнений (1) и (3),
поскольку функция у = х2 обращает в тождество
gt2
уравнение (1), а функция s = -г- — уравнение (3).
В функции (2) и (4), также являющиеся
решениями соответственно уравнений (1) и (3),
входит произвольная постоянная С. Такие
решения называются общими решениями этих
уравнений.
Решение, которое получается из общего
решения при некотором фиксированном значении
произвольной постоянной С, называется частным
2
2 St
решением. Например, функции у = х и s = -5- —
частные решения соответственно уравнений (1)
и(3).
Условие, состоящее в том, что при х = jcq
значение функции у должно быть равно заданному
числу z/o> называется начальным условием.
Начальное условие дает возможность выделить из
общего решения какое-либо частное решение.
Порядок старшей производной, входящей в
дифференциальное уравнение, называется
порядком данного уравнения. Например,
уравнения у' - у = 0иу" + у = 0 имеют соответственно
первый и второй порядок. Заметим, что в общее
решение уравнения первого порядка, как это
было видно на примере уравнений (1) и (3),
входит одна произвольная постоянная, в общее же
решение уравнения второго порядка — две
произвольные постоянные и т. д.
ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ.
1) у' = 0. Общее решение: у = С, где С —
произвольная постоянная;
2) у' = f (х)9 где / (х) — заданная функция.
Общее решение: у = J / (х) dx + С, где С —
произвольная постоянная;
3) у' — ш/, где а — заданное постоянное число.
Общее решение: у = Сеах9 где С — произвольная
постоянная. Уравнение у' = ау при а > 0
называется дифференциальным уравнением показа-
тельного роста, при а < 0 —
дифференциальным уравнением показательного убывания.
К этим уравнениям сводится решение многих
задач из физики, техники, биологии и
социальных наук;
4) у" + o)2i/ = 0, где со — постоянное число.
Общее решение: у = С\ cos (djc + С% sin (djc, где С\ и
С2 — произвольные постоянные. Это уравнение
называется уравнением гармонических
колебаний.
Определенный интеграл
и его применения
Понятие определенного интеграла
ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Задача о пройденном пути.
Требуется найти путь, пройденный движущейся по
прямой точкой за отрезок времени [f0, Т]9 если
известен закон изменения мгновенной скорости
v = v (t).
Разобьем отрезок [*0, Т] моментами времени
(точками) tQ < ti < t2 < ... < tn = Т на. п отрезков
времени (частичных отрезков) и положим Atk =
= tk - tk_i, k = 1, 2,..., п. Наибольшую из этих
разностей обозначим через А,: А, = max Atk. Если эти
отрезки достаточно малы, то без большой
ошибки движение на каждом из них можно считать
равномерным, что дает для пути приближенное
выражение
s « v (хг) Мг + v (т2) Д*2 + ••• + v (тд) л*д>
где xk — одна из точек сегмента [fy_i, tk]. Эта сум-
п
ма (ее будем кратко обозначать V и (тл) А*а)
k = 1
тем точнее выражает искомый путь s, чем
меньше каждый из временных отрезков [f&_i, tk],
k= 1, 2, ..., п. Поэтому за путь s, пройденный
точкой в течение промежутка времени Т - 10 со
скоростью v = v (t), естественно принять предел
указанной суммы при А, —> 0:
п
8= lim ^ v(xk)Atk. (1)
k — 1
Задача о площади криволинейной
трапеции. Пусть требуется найти площадь

Справочные материалы
Краткий справочник по математике
443
плоской фигуры аЛВЪ (рис. 42), ограниченной
графиком функции у = f (х)9 непрерывной и
неотрицательной на отрезке [а, ft], и отрезками
прямых у = О, х = а, х = Ь. Эта фигура
называется криволинейной трапецией. Разобьем [а, ft]
точками а = х0 < xi < я2 < ... < хп = ft на п
частичных отрезков и положим Ах^ = х^ - *k-l>
fc = 1, 2, ..., п. Наибольшую из этих разностей
обозначим через X: X = тахАлс^. На каждом
частичном отрезке [Jfy-i, xk]f fc = l,2, ...,п,
выберем произвольную точку тЛ (#fc-l < т^ < xk).
Произведение / (xk) Axk даст площадь
прямоугольника, имеющего основание Axk и высоту
п
f (тЛ), а сумма V / (т^) АхЛ — приближенно
k = 1
площадь S криволинейной трапеции аАВЬ.
Отсюда, как и в предыдущей задаче,
S =
lim
X f(xk)**k-
(2)
ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. Из
решения приведенных задач видно, что хотя
они имеют различный смысл, но математический
аппарат для их решения один и тот же. В этих
задачах получается выражение одного и того же
вида:
lim
Х->0
X fbk)b*k.
(3)
Если существует предел (3), не зависящий от
способа разбиения отрезка [а, ft] и выбора точек
тл, то этот предел будем называть
определенным интегралом функции / (х) на отрезке [а, ft]
ь
и обозначать символом Г / (х) dx, т. е.
дел, ft — верхний предел), а сумма V /(тл) Axk —
л- 1
интегральной суммой.
Теорема. Если функция f (х) непрерывна
на отрезке [a, ft], то она интегрируема на этом
отрезке.
В условиях рассмотренных выше задач,
приведших к понятию определенного интеграла,
выражения вида (1), (2) (пределы сумм) являются
определенными интегралами. Рассмотрим это
подробнее.
1) Путь s, пройденный точкой по прямой за
время Т -t0co скоростью v = v(t)(v (t)непрерыв-
т
на на [*о> Т]), есть \v (^^(механический
'о
смысл определенного интеграла). /
2) Если функция f(x) непрерывна и неотрица-
ь
тельна на отрезке [а, 6], то | / (х) dx представ-
а
ляет собой площадь криволинейной трапеции,
ограниченной сверху графиком функции y = f (х),
снизу отрезком [а, ft] оси Ох и с боков отрезками
прямых х = а, л: = ft (геометрический
смысл определенного интеграла).
Основные свойства
определенного интеграла
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Ниже рассматриваются функции, непрерывные
на отрезке [a, ft]. По определению полагают, что
определенный интеграл от функции с равными
верхним и нижним пределами интегрирования
равен нулю:
Ь
f (х) dx = 0.
г
J / (x) dx = lim £ / (tfc) Axk.
a k = 1
Функция / (x) в этом случае называется
интегрируемой на отрезке [a, ft]. При этом / (х)
называется подынтегральной функцией, f (х) dx —
подынтегральным выражением, числа а и ft —
пределами интегрирования (а — нижний
преем*i xk-i xk . х
Рис. 42

444
Справочные материалы
Краткий справочник по математике
1. Постоянный множитель можно выносить
за знак определенного интеграла:
ь ъ
[Af(x)dx=A[f(x)dx.
а а
2. Определенный интеграл от суммы двух
функций равен сумме определенных интегралов
от этих функций:
ь ъ ъ
$ (fi (х) + f2 (х)) dx = jfx (х) dx + J f2 (x) dx.
a a a
Это свойство распространяется на случай
алгебраической суммы любого конечного числа
функций.
3. При перестановке пределов
интегрирования определенный интеграл меняет знак на
противоположный:
ь ь
jf(x)dx = -jf(x)dx.
а а
4. Интеграл по отрезку равен сумме
интегралов по его частям:
Ь с Ъ
[ f(x)dx= f / (х) dx + f / (х) dx, где а < с < Ь.
а а с
ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА.
Если функция f (х) непрерывна на отрезке
[а, Ь] и F (х) — первообразная функции f (х) на
этом отрезке, то
Ъ
jf(x)dx = F(b)-F(a). (1)
а
Формула (1) называется формулой
Ньютона—Лейбница.
Г 2I1
П р и м е р 1. I 2х dx - х |0 =1.
о
тс
2 -
Г 2 Я
П р и м е р 2. I cos х dx — sin x\Q — sin « - sin 0 = 1.
о
ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ
ИНТЕГРАЛЕ. Предположим, что функция / (х)
непрерывна на отрезке [a, ft], функция х = <р (t)
имеет на отрезке [а, (3] непрерывную
производную, при этом а ^ ф (t) < ft и ф (а) = а, ф (Р) = ft.
Тогда
ь Р
lf(x)dx = jf(<f>(t))<f>'(t)dt. (2)
а а
Пример. Найдем (*]l - х dx.
Воспользуемся подстановкой х = sin t; тогда
х' = cos t. Найдем новые пределы интегрирования:
я
если х — 0, то t -— 0, если х = 1, то t = 5 • Применив
формулу (2), получим
1 ( я/2
я/2
J л/1 - х dx = J л/1 - sin t cos t dt - J cos21 dt -
о 0
*/2 /9
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ. Пусть и =
= и (x)f v = v (х) — непрерывно
дифференцируемые на [a, ft] функции. Тогда справедлива формула
ь
Г и (х) v'(x) dx =
а
Ь
= [и (X) V (х) ]\ - J V (х) и'(х) dx. (3)
а
я
Пример. Найдем (х cos х dx.
о
Положим и — х9 i/ - cos х, откуда и' - 1, у =
= sin я. Согласно формуле (3) находим
я я
Jjc cos х dx = [x sin jc ]J - Jsin jc dx =
о 0
= cos x|0 = —2.
Несобственные интегралы,
их сходимость
При введении понятия определенного
интеграла мы предполагали, что подынтегральная
функция является ограниченной, а пределы
интегрирования — конечными. Такой интеграл
называется собственным (слово
«собственный » обычно опускается). Если хотя бы одно из
этих двух условий не выполнено, то интеграл
называется несобственным.
ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
ИНТЕГРИРОВАНИЯ. Пусть функция / (х) непре-

Справочные материалы
Краткий справочник по математике
445
рывна при а < х < +oof т. е. при х > а. Тогда по
определению полагают
+ оо Ъ
f / (х) dx = lim [f (x) dx.
J b -> oo J
a a
Если этот предел существует, то говорят, что
интеграл
+ оо
jf(x)dx (1)
а
сходится, а если предел не существует, то
интеграл называют расходящимся. Такому
интегралу не приписывают никакого значения.
Геометрически для неотрицательной при х > а
функции / (х) несобственный интеграл (1) по
аналогии с собственным интегралом
представляет собой площадь фигуры, ограниченной
сверху графиком функции у = f (х), слева отрезком
прямой х = аи снизу осью Ох (рис. 43).
+оо Ь
Пример 1. f е~хdx — lim [е~хdx =
J &_>+ooJ
о о
= lim (1-е~ь) = 1,
6->+oo
т. е. данный несобственный интеграл сходится.
Пример 2. f — = lim f— = lim lnb = +°o,
J X &_>+ooJ X &_»+oo
1 1
т. е. данный интеграл расходится.
П р и м е р 3. Установим, при каких значениях а
+?dx
интеграл — сходится.
J х
1
Случай а — 1 был рассмотрен в примере 2. Если
ос*1,то
Значит, данный интеграл сходится при а > 1 и
расходится при а < 1.
Все изложенное непосредственно переносится
а
на интеграл вида Г / (х) dx, который
определяется так:
f / (x)dx= lim [f (x)dx.
Наконец, по определению,
+ oo
J / (x)dx= J / (x)dx+ J / (x)dx,
-oo -oo с
где с — какое-нибудь число (выбор его
безразличен). Последнее равенство следует понимать так:
если каждый из интегралов, стоящих справа,
сходится, то сходится и интеграл, стоящий слева.
Если же расходится хотя бы один из интегралов,
стоящих справа, то расходится и интеграл,
стоящий слева.
ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ
ФУНКЦИЙ. Пусть функция / (х) непрерывна при
а < х < Ь. Пусть эта функция стремится к
бесконечности, когда х -» Ь (т. е. на отрезке [а, Ь]
функция / (х) не ограничена). Положим
Ь Ъ-г
[f (x)dx= lim f / (x)dx.
J e->0+0 J
a a
Если этот предел существует, то говорят, что
интеграл
\f (x)dx
(2)
'dx
Ьг~а - 1
р ax .. о — 1
—- = lim — -
J ха ь->+оо 1 - a
+оо при а<1,
1
при а > 1.
а - 1
уЧ(х)
сходится, а если предел не существует, то
интеграл называют расходящимся.
Подобным же образом равенство
ь ъ
U (x)dx= lim f / (x)dx
J e->0+0 J
a о + e
дает определение интеграла от функции / (х),
стремящейся к бесконечности при х -» а.
Наконец, если функция / (х) стремится к
бесконечности при приближении аргумента к обеим
концам промежутка (а, Ь), то полагают
Ь с Ь
[f (х)dx = f/ (х)dx + U (x)dx,a<c<b.

446
Справочные материалы
Краткий справочник по математике
Если при этом сходятся оба интеграла в
правой части последнего равенства, то сходится и
интеграл слева.
Геометрические приложения
определенного интеграла
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР.
Пусть функция / (х) непрерывна на отрезке
[а, 6]. Если при этом f (х) > О на [а, 6], то
площадь S криволинейной трапеции, ограниченной
линиями у = f (х)9 у = 0, х = а, х = Ь9 выразится с
помощью интеграла:
S =
= jf (х)
dx.
(1)
Если же / (х) < 0 на [a, ft], то -/ (х) > О на
[а, 6]. Поэтому площадь S соответствующей
криволинейной трапеции находится по формуле
ь
S = -J/ (x)dx9
или а
S = \jf (x)dx\.
(2)
Наконец, если линия у = f (х) пересекает ось
Ох9 то отрезок [а, Ь] надо разбить на части, в
пределах которых / (х) не меняет знака, и к каждой
части применить ту из формул (1) или (2),
которая ей соответствует.
Пример 1. Найдем площадь плоской фигуры,
ограниченной графиком функции у = sin х и осью
абсцисс при условии 0 < х < 2я (рис. 44).
Разобьем отрезок [0, 2 л] на два отрезка: [0, тс] и [к,
2я]. На первом из них sin х > О, на втором sin х<0.
Тогда, используя формулы (1) и (2), находим искомую
площадь:
S = Г sin х dx +
о
2*
Г sin х dx\
2 тс,
= -cos х|0 +|[-совх]я 1 = 4
Vi
1
О
-1
1
2я
^ЩЩГ х
Рис. 44
Площадь криволинейного сектора ОАВ
(рис. 45), ограниченного лучами <р = а, <р = Р и
кривой АВ, заданной в полярной системе
координат уравнением г= г (<р), где г (<р) — функция,
непрерывная на отрезке [а, Р], выражается
формулой
S=\ Jr*(q>)*p.
(3)
П р и м е р 2. Найдем площадь круга радиуса R.
В полярных координатах г, (р уравнение
окружности с центром в начале координат и радиусом R имеет
вид г — R, причем 0 ^ ф < 2я. Тогда, используя
формулу (3), получим
о
ВЫЧИСЛЕНИЕ ДЛИН ДУГ И ПЛОЩАДЕЙ
ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ. Длиной дуги
называется предел, к которому стремится длина
ломаной линии, вписанной в эту дугу, когда длина
наибольшего звена ломаной стремится к нулю.
Длина I дуги АВ, заданной уравнением
у = / (х)9 х е [a, b] (f (х) — функция, имеющая
на [а, Ь] непрерывную производную),
выражается формулой
1= Ml + у'2 dx9
(4)
а площадь S поверхности вращения этой дуги
вокруг оси Ох — формулой
S = 27t f i/ а/1 + У'1 dx.
(5)
Если кривая АВ задана параметрическими
уравнениями х = х (t)9 у = у (t) (а < t < Р),
причем функции x(t) и y(t) имеют непрерывные
производные x'(t) и y'(t) на [а, Р], то формулы (4)
и (5) примут вид
Р
I = f Jx'2 + у'2 dt,
а
0 ,
S = 2nfj/ 4х'2 + у'2 dt.

Справочные материалы
Краткий справочник по математике
447
Если же кривая АВ задана в полярных
координатах уравнением г = г (<р) (ос < <р < Р), то
формулы (4) и (5) примут вид
Р
1= f л/г + г' dip,
а
Р - -
S = 2n f г sin ф л/г + г' dip.
а
П р и м е р 1. Найдем длину дуги цепной линии
У = | (ех + <ГХ), (К х < 1 (рис. 46).
Имеем у' = -z (ех - е"ж). По формуле (4) находим
J- jjl +J(e2x-(2 + e"2x))dx =
о
= |}(e* + e-*)d*=l(e*-e-*)|;-f(e-i).
о
Пример 2. Найдем площадь боковой
поверхности шарового пояса (рис. 47), образованного вращением
вокруг оси Ох дуги окружности х2 + у2 «■ R2,
соответствующей изменению х от а до 6 (-Л < а < Ь, О < Ь < Л).
Здесь z/ - 7я2 - *2, у' - -*;, 1 + у'2 2 й
у У
формуле (5) находим
по
S - 2яД J dx - 2яД (Ь - а).
В частности, при 6 — Я получаем площадь боковой
поверхности шарового сегмента с радиусом R и
высотой h = Я - а:
S - 2яДЛ,
а при а = -Д, Ь — Л — площадь сферы радиуса R:
S = 4тсД2.
ВЫЧИСЛЕНИЕ ОБЪЕМОВ. Объем V тела Б,
заключенного между плоскостями х = а и х = Ь
(рис. 48), у которого площадь
перпендикулярного оси Ох сечения для каждого х из отрезка [а, Ь]
есть функция Q (х) (Q (х) непрерывна на [а, &]),
находится по формуле
V =
-J«<*>
dx.
(6)
В частности, если тело образовано вращением
вокруг оси Ох криволинейной трапеции,
ограниченной непрерывной кривой у = / (х) (f (х) > 0),
осью Ох и прямыми х = а, л: = Ь (а < ft), то
Q (х) = я/2 (я), а значит,
ь ь
V = п f f2 (х) dx или V= к [у2 dx. (7)
а а
П р и м е р 1. Найдем объем пирамиды, высота
которой равна Я, а площадь основания равна S.
Пусть Р — плоскость, в которой лежит основание
пирамиды. Проведем через вершину пирамиды
плоскость а, параллельную р (рис. 49). Выберем ось Ох
так, чтобы она была перпендикулярна плоскостям а
и р. Точку пересечения плоскости а с осью Ох
примем за начало координат; тогда абсцисса вершины
пирамиды равна нулю, а абсцисса точки В
пересечения плоскости Р с осью Ох равна Я. Рассмотрим
поперечное сечение пирамиды плоскостью у,
перпендикулярной оси Ох и отстоящей от вершины О на
расстояние х. Площадь этого сечения обозначим через
Q(x).
Как известно, в пирамиде площадь основания и
площадь сечения, параллельного основанию,
относятся как квадраты их расстояний от вершины,
поэтому
Q (х) х2 _ / ч S о
^-^ 5 ' т. е. Q (х) 5 х •
s Я2 Я2
1,
V1
V
о
+ £ )
I /
J
Л .
1 х
Рис. 46
Рис. 47
Рис. 48
Рис. 49

448
Справочные материалы
Краткий справочник по математике
Для вычисления объема пирамиды воспользуемся
формулой (6):
я
F =
I Я2
So. S х
Я2 3
н
= -3SH.
П р и м е р 2. Найдем объем прямого кругового
цилиндра с высотой Н и радиусом основания R.
Рассматривая данный цилиндр как тело,
полученное вращением прямоугольной плоской фигуры с
вершинами в точках О (0; 0), А (0; Л), В (Я; Л), С (Я; 0)
вокруг оси Ох (рис. 50), по формуле (7) находим
я
V=k JR2dx = nR2H.
о
Рассуждая аналогично, можно получить
формулы для объемов других пространственных тел.
ГЕОМЕТРИЯ
Геометрические фигуры
на плоскости
Основные геометрические фигуры
на плоскости. Углы
ПРЯМАЯ, ЛУЧ, ОТРЕЗОК. Основными
геометрическими фигурами на плоскости являются
точка и прямая. Точки обозначаются
прописными (заглавными) латинскими буквами: А, Б,
С, ...; прямые — строчными латинскими
буквами: а, Ь, с, ... .
Через любые две точки на плоскости можно
провести прямую, и притом только одну.
Прямая, лежащая на плоскости, делит
(разбивает) эту плоскость на две полуплоскости.
Произвольная точка О, лежащая на прямой,
делит эту прямую на два луча (или полупрямые).
Точка О — начало обоих лучей; говорят, что
лучи исходят из начала. Лучи обозначаются двумя
буквами, первая из которых обозначает начало,
вторая — какую-нибудь другую точку луча
(например, лучи ОА и ОВ на рис. 51).
Две точки А и Б на прямой ограничивают от-
резок, обозначаемый АВ или ВА; точки А и Б —
концы отрезка; длина отрезка АВ обозначается
\АВ\ или АВ. Два отрезка считаются равными,
если равны их длины.
Если точка О лежит на отрезке АВ между
точками А и Б, то |АБ| = |АО| + \ОВ\ (рис. 51).
УГЛЫ, ИХ КЛАССИФИКАЦИЯ. Пара лучей,
исходящих из общего начала, называется углом.
Стороны угла — это лучи, его образующие;
вершина угла — общее начало его сторон. Угол,
образованный лучами OAi и ОА2> обозначается
/-AiOA2 или /LA2OAi (рис. 52, а). В
практических задачах целесообразно рассматривать угол
как меру поворота луча вокруг его начала до
заданного положения (рис. 52, б). В геометрии
углы считаются положительными.
Два угла считаются равными, если при
наложении они могут совместиться.
Биссектриса угла — это луч, исходящий из
вершины угла и делящий угол пополам (рис. 53).
Если при повороте вокруг начала луч совершил
один полный оборот до совпадения с
первоначальным положением (А2 = А{)9 то соответствующий
угол называется полным (рис. 54, а). Половина
полного угла называется развернутым углом
А
(
k
[ y = R В
\ (
11
cV
)•
Рис. 50
BOA
-О • 0-
Рис. 51
а)
О
б)
А2 А2 О А\ О
Рис. 54

Справочные материалы
Краткий справочник по математике
449
(рис. 54, б). Стороны развернутого угла лежат на
одной прямой. Половина развернутого угла
называется прямым (рис. 54, в).
Градус (обозначается «°>) — это 1/360 часть
полного угла. Прямой угол содержит 90°,
развернутый — 180°, полный — 360°. Углы, меньшие 90°,
называются острыми (см. рис. 52, а); большие
90°, но меньшие 180° — тупыми (см. рис. 52, б).
Угловая минута — это 1/60 часть градуса,
угловая секунда — это 1/60 часть минуты. Запись
57°17'45" читается: «57 градусов 17 минут 45
секунд». Углы можно измерять транспортиром.
Пусть две прямые пересекаются, при этом
образуются четыре угла (рис. 55). Углы 1 и 2 (а также 2
иЗ, Зи4,4и 1) — смежные; углы 1 и 3 (а также
2 i/i 4) — вертикальные. Вертикальные углы
равны; сумма смежных углов равна 180е.
При пересечении двух прямых третьей прямой
образуются восемь углов (рис. 56). Углы 4 и 5
(как и углы 3 и 6) называются внутренними
односторонними; углы 4 и 6 (как и углы 3 и 5) —
внутренними накрест лежащими.
ПАРАЛЛЕЛЬНОСТЬ И
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ. Две (различные) прямые на
плоскости либо пересекаются, т. е. имеют одну
общую точку, либо параллельны, т. е. не имеют
общих точек. Свойство параллельности прямых
обозначается символом «II»; например, а II Ь.
Через точку, не лежащую на данной прямой, можно
провести одну и только одну прямую,
параллельную данной прямой.
Теорема Фалеса. Если параллельные
прямые, пересекающие стороны угла, отсекают на
одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Признаки параллельности прямых.
Две прямые параллельны, если:
1) каждая из них параллельна третьей
прямой;
2) они пересечены третьей и внутренние
накрест лежащие углы равны;
3) они пересечены третьей прямой и сумма
внутренних односторонних углов равна 180°.
Две прямые перпендикулярны
(ортогональны), если, пересекаясь, они образуют прямые
углы. Свойство перпендикулярности
обозначают символом «J_»; например, a Lb. Если обе
стороны одного острого угла параллельны сторонам
другого острого угла (либо обе стороны
соответственно перпендикулярны), то эти углы равны.
Окружность
ОКРУЖНОСТЬ И ЕЕ ЭЛЕМЕНТЫ.
Окружность — это множество точек на плоскости,
расположенных на одинаковом расстоянии от
заданной точки (центра). Радиус окружности —
отрезок, соединяющий какую-либо точку
окружности с центром.
Прямая имеет с окружностью либо две общие
точки, либо одну общую точку (точку касания),
либо ни одной общей точки (рис. 57). Прямая,
имеющая с окружностью одну общую точку,
называется касательной. Касательная
перпендикулярна радиусу, проведенному в точку
касания (рис. 58).
Хорда — это отрезок, соединяющий две
точки на окружности. Хорда, проходящая через
центр, называется диаметром. Диаметр —
самая длинная хорда; диаметр состоит из двух
радиусов.
Дуга — это часть окружности; обозначение:
kj АтВ (рис. 59).
ОКРУЖНОСТЬ И УГЛЫ. Центральный угол
образован двумя радиусами (угол а на рис. 59).
Вписанный угол образован двумя хордами,
общая точка которых — вершина угла — лежит на
окружности (угол Р на рис. 59). Центральный
Рис. 55
Рис. 56
Рис. 57
Рис. 58
Рис. 59
15-1019

450
Справочные материалы
Краткий справочник по математике
угол ос и вписанный угол Р опираются на дугу
АтВ.
Вписанный угол, опирающийся на ту же
дугу, что и центральный, равен половине
центрального угла: Р = ос/2. Вписанные углы,
опирающиеся на одну и ту же дугу, равны (рис. 60).
Вписанный угол, опирающийся на
полуокружность, — прямой.
Радиан (рад) — это центральный угол,
опирающийся на дугу, длина которой равна радиусу
окружности (рис. 61). В градусной мере 1 рад
приближенно равен 57° 17'45". Прямой угол
равен я/2 рад, развернутый — к рад, полный —
2л рад.
Если а — значение угла в градусах, Р — в
радианах, то
а =
р 180°
к
или Р =
0С71
180°
р-
Например, угол 30° имеет радианную меру
30° к _ к
180° ~ 6'
КРУГ И ЕГО ЧАСТИ. Часть плоскости,
ограниченную окружностью, называют кругом
(рис. 62, а).
Сектор — это часть круга, ограниченная
центральным углом и дугой, на которую он
опирается (рис. 62, б).
Сегмент — это часть круга, ограниченная
дугой и стягивающей ее хордой (рис. 62, б).
ДЛИНА ОКРУЖНОСТИ, ДЛИНА ДУГИ,
ПЛОЩАДЬ КРУГА, СЕКТОРА, СЕГМЕНТА. Длина
окружности и площадь круга:
I = 2кг = nd, S = яг2,
где к « 3,1415926536 « 3,14, г — радиус, d —
диаметр.
Длина дуги:
1а = ссг,
где а — центральный угол (в радианах).
Площадь сектора:
(а — в радианах).
Площадь сегмента:
S^-|r*(P-Sin р)
(Р — в радианах).
Треугольники
КЛАССИФИКАЦИЯ ТРЕУГОЛЬНИКОВ И ИХ
ОСНОВНЫЕ СВОЙСТВА. Пусть А, В, С — три
произвольные точки, не лежащие на одной прямой.
Фигура, состоящая из трех отрезков АВ, ВС, АС,
называется треугольником ABC (обозначается
А ABC). Иногда треугольником называют часть
плоскости, ограниченную отрезками АВ, ВС, АС.
Точки А, В, С — вершины, отрезки АВ, ВС, АС —
стороны треугольника (рис. 63). Углы Z.CAB,
/-АВС, /.ВСА треугольника ABC часто
обозначают одной буквой (А, В, С соответственно) или
греческими буквами а, Р, у (при этом внутри
углов рисуют дуги, см. рис. 63). Говорят, что угол
А противолежит стороне ВС или сторона ВС
противолежит углу А; так же /-В и AC, А.С и АВ
противолежат друг другу.
Сумма углов треугольника равна 180°, или
тс рад:
а+р + у= 180°.
Если один из углов треугольника прямой,
то треугольник прямоугольный (рис. 64, а);
если один из углов тупой — тупоугольный
(рис. 64, б); если все три угла острые —
остроугольный (рис. 64, в).
О А
Рис. 60 Рис. 61
Рис. 62
В
\а
А Ь С
Рис. 63
а)
б)
в)
Рис. 64

Справочные материалы
Краткий справочник по математике
451
В прямоугольном треугольнике сторона,
лежащая против прямого угла, называется
гипотенузой, две другие стороны — катетами.
Треугольник, две стороны которого равны,
называется равнобедренным (АС = ВС на рис. 65, а).
Третья сторона — основание, равные стороны —
боковые стороны.
Треугольник, три стороны которого равны
(АС = ВС = АВ на рис. 65, б), называется
равносторонним.
В любом треугольнике против большей
стороны лежит больший угол; против равных сторон —
равные углы, и обратно. В равнобедренном
треугольнике углы при основании равны; в
равностороннем треугольнике каждый угол равен 60°.
Продолжив одну из сторон треугольника (АС
на рис. 66), получаем внешний угол /-BCD.
Внешний угол равен сумме внутренних, с
ним не смежных: /LBCD = /LA + /_В.
Любая сторона треугольника меньше суммы
и больше разности двух других сторон (а<Ь + с,
а>Ь-с).
ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ И ТОЧКИ В
ТРЕУГОЛЬНИКЕ. Пусть в треугольнике ABC точка
М — середина стороны АВ, луч CS делит угол С
пополам, СИ 1 АВ, MP 1 АВ (рис. 67). Тогда
СМ — медиана стороны АВ, CS — биссектриса
угла С, СН — высота к стороне АВ, прямая
MP — серединный перпендикуляр к стороне АВ.
Две высоты тупоугольного треугольника лежат
вне его: AF _L ВС, BG LAC (рис. 68).
Свойства биссектрисы угла
треугольника:
1) точки биссектрисы равноудалены от
сторон угла;
2) биссектриса делит противолежащую
сторону на части, пропорциональные прилежащим
сторонам треугольника:
AS:BS=AC :ВС.
Четыре замечательные точки в
треугольнике:
1) три медианы пересекаются в одной точке,
являющейся центром тяжести треугольника;
2) три биссектрисы пересекаются в одной
точке (центре вписанной окружности);
3) три высоты (или их продолжения)
пересекаются в одной точке (^ортоцентре*);
4) три серединных перпендикуляра
пересекаются в одной точке (центре описанной
окружности).
Точка пересечения медиан делит каждую
медиану в отношении 2:1, считая от вершины.
Средняя линия треугольника — это отрезок,
соединяющий середины двух его сторон, —
параллельна третьей стороне и вдвое ее короче
(рис. 69).
ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ.
Треугольники называются равными, если у них
соответствующие стороны и соответствующие
углы равны.
Признаки равенства
треугольников. Два треугольника равны, если:
1) две стороны и угол между ними одного
треугольника равны соответственно двум
сторонам и углу между ними другого («по двум
сторонам и углу между ними»);
2) сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне
и прилежащим к ней углам другого («по стороне
и прилежащим к ней углам»);
3) три стороны одного треугольника равны
соответственно трем сторонам другого (*по
трем сторонам»).
Для прямоугольных треугольников, кроме
трех перечисленных признаков равенства,
имеются другие признаки:
если гипотенуза и острый угол одного
треугольника соответственно равны гипотенузе и
А С
Рис. 66
А Н S М В
Рис. 67
Рис. 68
Рис. 69

452
Справочные материалы
Краткий справочник по математике
острому углу другого («по гипотенузе и острому
углу»);
если гипотенуза и катет одного
треугольника соответственно равны гипотенузе и
катету другого («по гипотенузе и катету»).
ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ. Два
треугольника называются подобными, если
углы одного соответственно равны углам
другого, а соответствующие стороны
пропорциональны (рис. 70):
^А = ААг,
Z.B = /-Bl9
AB
ВС
AC
Признаки подобия
треугольников. Два треугольника подобны, если:
1) два угла одного треугольника
соответственно равны двум углам другого;
2) две стороны одного треугольника
пропорциональны двум сторонам другого и углы,
образованные этими сторонами, равны;
3) три стороны одного треугольника
пропорциональны трем сторонам другого.
Для прямоугольных треугольников, кроме
перечисленных признаков подобия, имеется и
другой признак: если гипотенуза и катет
одного треугольника пропорциональны гипотенузе
и катету другого, то такие треугольники
подобны.
ОСНОВНЫЕ СООТНОШЕНИЯ МЕЖДУ
ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКА. Любой элемент
треугольника можно найти по нескольким заданным
элементам. Введем обозначения: S — площадь; а, Ь,
с — стороны; ос, р, у — углы; р = (а + Ъ + с)/2 —
полупериметр; R — радиус описанной
окружности; г — радиус вписанной окружности; hc —
высота, тс — медиана, 1С — биссектриса,
проведенные из вершины С.
1) Прямоугольный треугольник (рис. 71):
с2 = а2 + Ь2 (теорема Пифагора), ос + Р = 90 °,
а =? с sin а = Ь tg ос, sin а = cos Р, tg ос = ctg Р,
аЬ
>hc= ~ >
1 аЬ
* а + b + с
1 , abj2
2) Произвольный треугольник (рис. 72):
с2 = а2 4- Ь2 - 2аЬ cos у (теорема косинусов),
п. h г
2R (теорема синусов),
sin а sin р sin у
S = 5 яЛа, S = 5 ab sin у, S = гр,
S = Jp(p - а)(р - Ь)(р - с) (формула Герона),
ha = b sin у = с sin Р,
mt
= о yb + с + 2Ьс cos а ,
2Ьс
'■"ьТ^0085' г =
а
2
2S
а + b + с
Многоугольники
1. Ломаная. Пусть на плоскости имеется
конечная последовательность отрезков; у каждого
отрезка один из концов назовем началом. Если
начало второго отрезка совпадает с концом
первого, начало третьего — с концом второго и т. д.,
то совокупность (объединение) этих отрезков
называется ломаной (при этом предполагается,
что никакие два соседних отрезка не лежат на
одной прямой). Отрезки, составляющие
ломаную, — звенья, концы отрезков — вершины
ломаной (ломаная АхАг*.-As на рис. 73, а). Ломаная
называется простой, если она не имеет самопе-
Рис. 73

ресечений; замкнутой, если конец последнего
отрезка совпадает с началом первого отрезка
(рис. 73, б).
МНОГОУГОЛЬНИК. Многоугольник — это
простая замкнутая ломаная. Звенья ломаной —
стороны, вершины ломаной — вершины
многоугольника. Многоугольник с п сторонами
называется п-угольником. Иногда многоугольником
называют часть плоскости, ограниченную
простой замкнутой ломаной. Периметр
многоугольника — сумма длин его сторон.
Многоугольник называется выпуклым (рис. 74),
если он лежит по одну сторону относительно
прямой, содержащей любую его сторону.
Углы (внутренние) выпуклого
многоугольника — это углы, образованные соседними
сторонами. Число углов многоугольника равно числу
сторон и числу вершин. Среди углов невыпуклого
многоугольника имеется хотя бы один угол,
больший 180°. Сумма углов выпуклого
многоугольника равна (п - 2) • 180°, или (п - 2)я.
Многоугольник, описанный около
окружности (окружность касается всех сторон
многоугольника), — выпуклый; его площадь S = рг,
где г — радиус окружности, р — полупериметр,
т. е. полусумма всех сторон.
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК.
Многоугольник называется правильным, если у него
все стороны равны и все углы равны. Любой
правильный многоугольник — выпуклый.
Примеры правильных многоугольников: правильный
(или равносторонний) треугольник, квадрат,
правильные пятиугольник, шестиугольник и т. д.
В любой правильный многоугольник можно
вписать Окружность и около него можно описать
окружность. Справедливы формулы
а а
2sin(7c/n)' Г~ 2tg(7t/n)'
где а — сторона, п — число сторон
многоугольника, R — радиус описанной окружности, г —
радиус вписанной окружности (апофема
правильного многоугольника). Площадь
правильного многоугольника:
S = -z паг = -: па* ctg - .
ct 4 П
ПАРАЛЛЕЛОГРАММ. РОМБ. Параллелограмм —
это четырехугольник, противоположные сторо-
Справочные материалы a ^q
Краткий справочник по математике ^**/0
ны которого попарно параллельны (рис. 75). Он
обладает следующими свойствами:
1) противоположные стороны равны;
2) противоположные углы равны;
3) сумма углов, прилежащих к одной
стороне, равна 180°;
4) диагонали точкой пересечения делятся
пополам;
5) точка пересечения диагоналей является
центром симметрии параллелограмма.
Длины сторон и диагоналей связаны
формулой
d\+d\= 2(а2 + ft2).
Площадь параллелограмма находится по
формулам
S = aha = bhb, S = ab sin a = ab sin P
(обозначения приведены на рис. 75).
Признаки параллелограмма.
Четырехугольник является параллелограммом, если:
1) его противоположные стороны попарно
равны;
2) две его противоположные стороны равны и
параллельны;
3) его диагонали, пересекаясь, делятся
пополам.
Ромб — это параллелограмм, все стороны
которого равны (рис. 76).
Кроме общих свойств параллелограмма, ромб
обладает следующими свойствами:
1) диагонали ромба перпендикулярны и
делят его углы пополам;
2) ромб симметричен относительно
диагоналей (см. § 14.2, п. 1).
Площадь ромба выражается через его
диагонали так:
5=2 ага2>
а
Рис. 74 Рис. 75 Рис. 76

Справочные материалы
Краткий справочник по математике
ПРЯМОУГОЛЬНИК. КВАДРАТ.
Прямоугольник — это параллелограмм, все углы которого
прямые (рис. 77). Кроме общих свойств
параллелограмма, прямоугольник обладает
следующими свойствами:
1) диагонали прямоугольника равны;
2) прямоугольник имеет две оси симметрии
(штриховые линии на рис. 77).
Справедливы формулы
S = ab, d= *Ja + 6 .
Квадрат — это прямоугольник, все стороны
которого равны (рис. 78). Он обладает всеми
свойствами прямоугольника и ромба.
Справедливы формулы
S = a2, d = aj2.
ТРАПЕЦИЯ. Трапеция — это
четырехугольник, две стороны которого параллельны, а две
другие не параллельны (рис. 79). Параллельные
стороны называются основаниями, две другие
стороны — боковыми сторонами. Средняя линия
трапеции — это отрезок MN, соединяющий
середины боковых сторон. Средняя линия
параллельна основаниям и равна их полусумме. Площадь
трапеции находится по формуле
где а и b — основания, h — высота.
Трапеция называется равнобедренной (или
равнобочной)t если ее боковые стороны равны.
Равнобедренная трапеция имеет ось симметрии —
серединный перпендикуляр к основаниям.
Геометрические фигуры
в пространстве
Основные геометрические фигуры
в пространстве. Углы
ПЛОСКОСТИ И ПРЯМЫЕ В ПРОСТРАНСТВЕ.
Основными геометрическими фигурами в про-
Рис. 77 Рис. 78 Рис. 79
странстве являются точка, прямая и
плоскость.
Через всякие три точки, не лежащие на
одной прямой, можно провести плоскость, и
притом только одну.
Через любую прямую и не лежащую на ней
точку можно провести плоскость, и притом
только одну.
Плоскость делит (разбивает) пространство на
два полупространства. Две плоскости в
пространстве либо параллельны (т. е. не имеют
общих точек), либо пересекаются по прямой.
Прямая либо параллельна плоскости (т. е. не имеет
с ней рбщих точек), либо пересекает ее в одной
точке, либо целиком лежит в плоскости.
Признак параллельности прямой и
плоскости. Если прямая параллельна какой-нибудь
прямой, лежащей в плоскости, то она
параллельна этой плоскости.
Две прямые в пространстве либо
пересекаются (имеют одну общую точку), либо
скрещиваются, либо параллельны (на рис. 80 прямые
а и Ь пересекаются, прямые а, с и d
параллельны, прямые bud скрещиваются).
Через две пересекающиеся прямые можно
провести плоскость, и притом только одну; то
же справедливо и для параллельных прямых.
Через две скрещивающиеся прямые
невозможно провести плоскость.
Признак параллельности прямых. Две
прямые, каждая из которых параллельна третьей
прямой, параллельны между собой.
Прямая, пересекающая плоскость,
называется перпендикулярной (ортогональной, или
нормальной) этой плоскости, если она
перпендикулярна всем прямым, лежащим в этой
плоскости (рис. 81). Если прямая перпендикулярна
двум непараллельным прямым, лежащим в
плоскости, то эта прямая перпендикулярна
плоскости. Пусть прямая пересекает плоскость
в точке А и перпендикулярна плоскости;
отрезок АВ этой прямой (рис. 82) называется
перпендикуляром, проведенным (или опущенным)
Рис. 80 Рис. 81 Рис. 82

Справочные материалы
Краткий справочник по математике
455
к этой плоскости из точки В. Длина
перпендикуляра АВ называется расстоянием от точки В
до плоскости.
Из произвольной точки вне плоскости можно
опустить на плоскость один перпендикуляр и
множество наклонных (рис. 82). Если АВ —
перпендикуляр, ВС — наклонная, то АС — проекция
наклонной на плоскость, точка С — основание
наклонной9 точка А — основание
перпендикуляра. Угол между прямой и плоскостью
определяется как угол между этой прямой и ее
проекцией на плоскость.
Теорема о трех перпендикулярах. Прямая
на плоскости перпендикулярна наклонной,
если она перпендикулярна проекции этой
наклонной (рис. 82). Верно и обратное утверждение.
УГЛЫ. По определению, угол между двумя
скрещивающимися прямыми равен углу между
двумя параллельными им пересекающимися
прямыми (так, на рис. 80 угол между
скрещивающимися прямыми Ь и d — это угол а).
Угол между двумя пересекающимися
плоскостями — это угол между прямыми, по
которым эти плоскости пересекаются с третьей
плоскостью, перпендикулярной линии пересечения
данных плоскостей (рис. 83).
Плоскость, проведенная через прямую,
перпендикулярную другой плоскости,
перпендикулярна этой плоскости.
Двугранный угол — это совокупность двух
полуплоскостей, имеющих общую границу (ребро
двугранного угла, рис. 84). Двугранные углы
измеряются соответствующими углами между
плоскостями. Многогранный угол образован
несколькими плоскими углами, имеющими общую
вершину (на рис. 85 изображен трехгранный угол В).
Многогранники
МНОГОГРАННАЯ ПОВЕРХНОСТЬ.
МНОГОГРАННИК. Многогранная поверхность — это
поверхность, образованная из плоских
многоугольников (граней поверхности) так, что
каждая сторона любого из этих многоугольников
(ребро поверхности) является стороной еще
одного многоугольника (смежного с первым), а от
каждой грани можно перейти к любой другой,
переходя последовательно по смежным граням.
Вершины многоугольников называются
вершинами многогранной поверхности. В каждой
вершине сходится не менее трех ребер.
Многогранник — тело, ограниченное
многогранной поверхностью. Выпуклый
многогранник лежит по одну сторону от плоскости,
содержащей любую его грань.
ПРИЗМА, ПАРАЛЛЕЛЕПИПЕД, КУБ.
Призма — это многогранник, две грани которого
(основания) — равные /г-угольники, лежащие
в параллельных плоскостях (рис. 86), а
остальные п граней — параллелограммы (боковые
грани). Стороны боковых граней, не лежащие
на основаниях, называются боковыми ребрами.
Призму можно рассматривать как результат
параллельного переноса основания вдоль
некоторого отрезка (ребра).
Высотой призмы называется расстояние
между ее основаниями. Объем призмы находится
по формуле
где S0CH — площадь основания, Н — высота
призмы.
Боковые ребра прямой призмы
перпендикулярны основаниям. У прямой призмы боковые
грани — прямоугольники. Площадь боковой
поверхности прямой призмы находится по формуле
* бок
= РН,
где Р — периметр основания (сумма длин сторон
основания).
Призма называется правильной, если она
прямая и ее основания — правильные
многоугольники. Боковые грани правильной призмы —
равные прямоугольники.
Рис. 83
Рис. 84
Рис. 85
Рис. 86

456
Справочные материалы
Краткий справочник по математике
Параллелепипед — это призма, у которой
основания — параллелограммы (рис. 87). У
параллелепипеда противоположные грани — равные
параллелограммы. Все четыре (внутренние)
диагонали пересекаются в одной точке (в центре
симметрии) и делятся в ней пополам.
Все грани прямоугольного
параллелепипеда — прямоугольники, все его ребра
перпендикулярны соответствующим граням (рис. 88), все
четыре (внутренние) диагонали равны, при этом
Объем и площадь поверхности
прямоугольного параллелепипеда находятся по формулам
V=abc,
= 2(аЪ + ас + be).
Куб — это прямоугольный параллелепипед,
все двенадцать ребер которого равны. Все шесть
граней куба — равные квадраты. Диагональ
куба d = а л/3 . Объем и площадь поверхности куба
выражаются так:
У-**> «полиса2.
ПИРАМИДА, УСЕЧЕННАЯ ПИРАМИДА. Пира-
мидой называется многогранник, одна из
граней которого (основание) — многоугольник
(рис. 89), остальные грани (боковые грани) —
треугольники, имеющие одну общую вершину (вер-
шину пирамиды).
Высота пирамиды — это расстояние от
вершины до плоскости основания. Объем
пирамиды находится по формуле
1
g ^осн-*
У — о Snr4 Н9
где S0CH — площадь основания, Н — высота.
Пирамида называется п-угольной, если ее
основание — /г-угольник. Пирамида
называется правильной, если ее основание —
правильный многоугольник, а вершина проецируется в
центр основания (рис. 90). Боковые грани
правильной пирамиды — равные равнобедренные
треугольники. Площадь боковой поверхности
правильной пирамиды выражается так:
1
~ 2
^бок - oPht
где Р —периметр основания, h — высота
боковой грани (апофема правильной пирамиды).
Если пирамида пересечена плоскостью
A'B'C'D\ параллельной основанию (рис. 91), то:
1) боковые ребра и высота делятся этой
плоскостью на пропорциональные части;
2) в сечении получается многоугольник
A'B'C'D\ подобный основанию;
3) площади сечения и основания относятся
как квадраты их расстояний от вершины.
Усеченная пирамида получается из пирамиды
отсечением от нее верхней части плоскостью,
параллельной основанию (фигура ABCDA'B'C'D'
на рис. 91). Основания усеченной пирамиды —
подобные многоугольники, боковые грани —
трапеции. Высота усеченной пирамиды —
расстояние между основаниями. Объем усеченной
пирамиды находится по формуле
V= 1h(S + JSS~' +S'),
где S и S' — площади оснований ABCD и
A'B'C'D\ Н — высота.
Основания правильной п-угольной усеченной
пирамиды — правильные /г-угольники.
Площадь боковой поверхности правильной
усеченной пирамиды выражается так:
£бок=|сР + ^>>
где РиР' — периметры оснований, h — высота
боковой грани (апофема правильной
усеченной пирамиды).
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.
Правильный многогранник — это выпуклый многогран-
!\- /I
i * Г
Рис. 87
Рис. 89
Рис. 90
^/
••/'
*#
Л±'
/А'
/ **•
ji
Рис.
91
1в
1в

Справочные материалы
Краткий справочник по математике
457
ник, все грани которого — равные правильные
многоугольники и все многогранные углы
которого равны. Существует всего пять правильных
многогранников (см. таблицу):
Название
Тетраэдр
Куб
/ZZA
s±/
Октаэдр
Додекаэдр
Икосаэдр
Число граней
и их форма
4
треугольника
6 квадратов
8
треугольников
12
пятиугольников
20
треугольников
Число
ребер
6
12
12
30
30
Число

вершин
20
12
Тела вращения
ПОВЕРХНОСТЬ ВРАЩЕНИЯ. ЦИЛИНДР.
Поверхность вращения — это поверхность в
пространстве, образованная вращением плоской
кривой вокруг некоторой оси, лежащей в ее
плоскости.
Цилиндр (прямой круговой) — это тело,
ограниченное поверхностью вращения
прямоугольника вокруг прямой, проходящей через
середины противоположных сторон (рис. 92).
Поверхность цилиндра состоит из двух кругов
(оснований) и боковой поверхности. Плоскости
оснований параллельны, расстояние между ними —
высота цилиндра. Ось цилиндра — это прямая,
проходящая через центры оснований.
Боковая поверхность состоит из
образующих — равных отрезков, параллельных оси.
Боковую поверхность можно развернуть на
плоскость — получится прямоугольник.
Объем, площади боковой и полной
поверхностей цилиндра выражаются формулами
^бок = 27tRff,
V = kR2H,
= 2nRH + 2яД2,
где R -
линдра.
радиус оснований, Н — высота ци-
КОНУС, УСЕЧЕННЫЙ КОНУС. Конус (прямой
круговой) — это тело, ограниченное
поверхностью вращения равнобедренного треугольника
вокруг его оси симметрии (рис. 93).
Поверхность конуса состоит из круга (основания) и
боковой поверхности. Вершину конуса можно
соединить с любой точкой окружности основания
образующей — отрезком, лежащим на боковой
поверхности. Высота конуса — расстояние от
вершины до основания. Сечение боковой
поверхности плоскостью, параллельной основанию, —
окружность.
Объем, площади боковой и полной
поверхностей конуса находятся по формулам
v = § Soch # н = § ПТ^Н>
s6ok - 2 PL * nrLy Sn0JIH = Яг(г + L)'
где г — радиус основания, Р — длина
окружности основания, L — длина образующей, Н —
высота конуса.
Усеченный конус — это часть конуса,
заключенная между его основанием и сечением,
параллельным основанию (рис. 94). Усеченный конус
можно рассматривать как результат вращения
равнобедренной трапеции вокруг ее оси
симметрии.
При вращении основания трапеции
описывают круги — основания усеченного конуса.
Высота усеченного конуса — это расстояние
между основаниями.
Объем и площадь боковой поверхности
усеченного конуса находятся по формулам
V= g nh(rx + г2 + ггг2), S6oK = n(rx + r2)U
где h — высота усеченного конуса, гх и г2 —
радиусы оснований, I — длина образующей
усеченного конуса.
i
i
1 •
н
Рис. 92
Рис. 93
Рис. 94

458
Справочные материалы
Краткий справочник по математике
Развертка боковой поверхности конуса —
сектор, радиус которого равен образующей
конуса; развертка боковой поверхности усеченного
конуса — соответствующая часть кругового
кольца (рис. 95).
СФЕРА, ШАРОВОЙ СЕГМЕНТ, ШАРОВОЙ
СЕКТОР, ШАРОВОЙ СЛОЙ. Сфера — это множество
точек в пространстве, равноудаленных от
фиксированной точки (центра сферы). Шар — это
тело, ограниченное сферой (рис. 96); его можно
рассматривать как результат вращения круга
вокруг его диаметра. Радиус сферы —
расстояние от центра до любой точки сферы, диаметр —
длина отрезка, соединяющего две точки на
сфере и проходящего через центр. Диаметр равен
двум радиусам. Иногда радиусом и диаметром
называют сами отрезки.
Плоскость в пространстве либо не имеет
общих точек со сферой, либо имеет одну общую
точку (точку касания), либо пересекается по
окружности. Плоские сечения шара
представляют собой круги, наибольший из которых
проходит через центр шара (большой круг).
Через две точки, не лежащие на концах
одного диаметра, можно провести одну и только одну
окружность большого круга. Касательная к
сфере плоскость перпендикулярна радиусу,
проведенному в точку касания.
Объем шара и площадь сферы выражаются
формулами
V= |тсД3, S = 4kR2,
где R — радиус шара.
Шаровой сегмент — эта часть шара,
отсеченная от него плоскостью (рис. 97).
Сегментная поверхность — это часть сферы,
отсекаемая плоскостью. Объем шарового сегмента и
площадь сегментной поверхности находятся по
формулам
V = | nh2 (SR - h), S = 2nRh,
где R — радиус шара, а Л — высота шарового
сегмента.
Шаровой сектор — это тело вращения
плоского кругового сектора вокруг его оси
симметрии (рис. 98). Шаровой сектор можно составить
из конуса и шарового сегмента. Полная
поверхность шарового сектора состоит из сегментной
поверхности и боковой поверхности конуса.
Объем и площадь полной поверхности шарового
сектора выражаются так:
V — дЯЯ ^> ^полн
I J~2
= 2nRh + nR>j2Rh - h ,
высота шарового сег-
где R — радиус шара, h
мента.
Шаровой слой — это часть шара, вырезаемая
из него двумя параллельными плоскостями
(рис. 99). Объем и площадь полной поверхности
шарового слоя находятся по формулам
v=\nh3 + 1яЛ(г1 + г2>'
^полн = 2nRh + л( гг + г2),
где h — высота, rj и г2 — радиусы оснований
шарового слоя.
Геометрические преобразования
Движение
ДВИЖЕНИЕ ПЛОСКОСТИ. Движение
плоскости — это взаимно однозначное преобразование
точек плоскости, при котором сохраняются рас-
Рис. 95
Рис. 96
Рис. 97
Рис. 98
б) с' В'
А/Л- г 'а
Рис. 99
Рис. 100

Справочные материалы
Краткий справочник по математике
459
стояния: если точка А переходит в А', В — в Б',
то А'В' = АВ. При движениях также
сохраняются углы. Примеры движений плоскости:
параллельный перенос (рис. 100, а), поворот
вокруг некоторой точки О — центра поворота
(рис. 100, б), отражение относительно
некоторой оси I (осевая симметрия, рис. 100, в). Любое
движение плоскости можно составить из этих
трех типов движений. Говорят также о
движениях фигур на плоскости. Две фигуры на
плоскости считаются равными, если их можно
совместить движением (таковы, например, пары
соответствующих треугольников на рис. 100, а—в).
ДВИЖЕНИЕ ПРОСТРАНСТВА. Движение
пространства определяется аналогично: это взаимно
однозначное преобразование точек
пространства, при котором сохраняются расстояния. При
этом углы также сохраняются, фигуры
переходят в равные фигуры. Примеры движений
пространства: параллельный перенос (рис. 101, а),
поворот вокруг некоторой оси I (рис. 101, б),
отражение относительно некоторой
плоскости или зеркальное отражение (рис. 101, в).
Симметрия. Подобие
СИММЕТРИЯ. Точки М и М' на плоскости
или в пространстве называются
симметричными (друг другу) относительно центра О, если
точка О — середина отрезка ММ' (рис. 102, а).
Точки М и М' называются симметричными
относительно оси I, если I — серединный
перпендикуляр отрезка ММ' (рис. 102, б).
Фигура F симметрична фигуре F'
относительно центра (относительно оси), если
все точки F симметричны точкам F'
относительно этого центра (относительно этой оси). На
рис. 102, а изображены фигуры F и F',
симметричные относительно центра О, а на рис. 102, б —
относительно оси I.
Говорят, что плоская фигура обладает
центральной симметрией (фигура центрально-
симметрична), если она симметрична сама себе
относительно центра. Такая фигура
совмещается сама с собой при повороте на 180° в плоскости
вокруг центра. Примерами
центрально-симметричных фигур служат круг, параллелограмм
(рис. 103, а).
Говорят, что плоская фигура обладает осевой
симметрией (фигура осесимметрична), если
она симметрична сама себе относительно оси,
лежащей в плоскости фигуры. Такая фигура
совмещается сама с собой при повороте плоскости
(в пространстве) вокруг оси на 180°. Примерами
осесимметричных фигур служат равнобедренная
трапеция, парабола (рис. 103, б).
Фигура может обладать обоими видами
симметрии: круг, ромб (рис. 103, в).
В пространстве рассматривается еще один вид
симметрии: точки М и М' называются
симметричными относительно плоскости, если
отрезок ММ' перпендикулярен этой плоскости
и делится пополам в точке пересечения с ней
(рис. 104). Можно сказать, что М' — зеркальное
отражение точки М в плоскости симметрии.
Фигура F симметрична фигуре F'
относительно плоскости (фигура
зеркально-симметрична), если все точки F симметричны точкам F'
относительно этой йлоскости (рис. 104). Фигура F
обладает зеркальной симметрией, если она сим-
а)
Щф *?+
Рис. 101
а) б), . в)
ОшахЦ О О
Рис. 102
М\
Рис. 103
Рис. 104

460
Справочные материалы
Краткий справочник по математике
метрична сама себе относительно плоскости.
Примеры зеркальносимметричных фигур: шар,
куб, цилиндр, прямая призма.
ПОДОБИЕ. Преобразование подобия
плоскости (пространства) — это взаимно однозначное
преобразование точек плоскости (пространства),
при котором расстояния умножаются на одно и
то же положительное число у (коэффициент
подобия):
А'В' = уАВ.
Преобразование подобия в общем случае
состоит из движения и растяжения (сжатия;
рис. 105). Фигуры F и F' называются
подобными, если F' получается из F преобразованием
подобия. Примеры подобных фигур: подобные
треугольники, любые отрезки, окружности,
квадраты, шары.
Элементы
аналитической геометрии
Векторы и линейные операции
над ними
ПОНЯТИЕ ВЕКТОРА. Вектором называется
направленный отрезок, имеющий определенную
длину, т. е. отрезок определенной длины, у
которого одна из ограничивающих его точек
принимается за начало, а вторая — за конец. Если А —
начало вектора и В — его конец, то вектор
обозначается символом АВ (или АВ). Обычно
векторы обозначают одной малой латинской буквой
с чертой (или со_стрелкой) либо выделяют
жирным шрифтом: а, а, а. Вектор изображается
отрезком со стрелкой на конце (рис. 106).
Длина вектора АВ называется его модулем и
обозначается символом \АВ\.
Вектор а, у которого |а| = 1, называется
единичным.
Вектор называется нулевым (обозначается 0
или 0), если начало и конец его совпадают.
Нулевой вектор не имеет определенного
направления и имеет длину, равную нулю.
Векторы а и ft, расположенные на одной
прямой или на параллельных прямых, называются
коллинеарными. Нулевой вектор коллинеарен
любому вектору.
Два вектора аиЬ называются равными, если
они коллинеарны, имеют одинаковую длину и
одинаковое направление. В этом случае пишут
а = Ь. Все нулевые векторы считаются равными.
Из определения равенства векторов следует,
что вектор можно переносить параллельно
самому себе, помещая его начало в любую точку
пространства (в частности, плоскости). Такой
вектор называется свободным.
Пример. Рассмотрим квадрат ABCD (см. рис. 106).
На основании определения равенства векторов можно
записать: АР = ВСиАВ = DC, но АВ Ф AD, ВС Ф ВС,
хотя \АВ\ - \AD\ = \ВС\ = \DC\.
Два коллинеарных вектора (отличные от
нулевых векторов), имеющие равные модули, но
противоположно направленные, называются
противоположными. _
Вектор, противоположный вектору а,
обозначается -а. Для вектора АВ противоположным
является вектор ВА.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
Линейными операциями называются
операции сложения и вычитания векторов и
умножения вектора на число. _ _
1) Сумма а + ft векторов а и ft находится по
правилу треугольника (рис. 107, а) или по
правилу параллелограмма (рис. 107, б) — эти
правила равносильны. Правило треугольника удобно
при сложении_нескольких векторов (рис. 107, в).
Отметим, что а + 0 = а.
Сложение векторов коммутативно и
ассоциативно:
а + ft = ft + а, а + (ft + с) = (а + ft) + с.
Рис. 105
Рис. 106

Справочные материалы
Краткий справочник по математике
461
Разность векторов а - b можно определить
как сумму а + (-Ь), т. е. вычитание заменяется
прибавлением противоположного вектора.
Удобно также правило треугольника: векторы а и Ь
откладывают от общего начала, тогда разность
а - Ъ есть вектор, начало которого совпадает с
концом Ь, а конец — с концом а (рис. 107, г)^
2) Произведением Ха (или аХ) вектора а на
действительное число X называется вектор Ь,
коллинеарный вектору а, имеющий длину,
равную |А,| \а\, и то же направление, что и вектор а,
если X > 0, и направление, противоположное
направлению вектора а, если X < 0. Так,
например, 2а есть вектор, имеющий то же надравле-
ние, что и вектор а, а длину, вдвое большую,
чем вектор а (рис. 108). В_случае, когда X = 0
или а = 0, произведение Ха представляет собой
нулевой вектор. Противоположный вектор — а
можно рассматривать как результат умножения
вектора а на X = -1 (рис. 108):
-а = (-1)а.
Очевидно, что а + (j-а) = 0.
Пусть дан вектор а. Рассмотрим единичный
вектор а0, коллинеарный вектору а и одинаково
с ним направленный. Из определения
умножения вектора на число следует, что
а = \а\ а0,
т. е. каждый вектор равен произведению его
модуля на единичный вектор того же направления.
Условие коллинеарности двух векторов.
Два вектора аиЬ коллинеарны тогда и только
тогда, когда имеет место равенство
Ь = Ха.
Умножение вектора на число обладает
распределительным свойством:
Х(а + Ь) = Ха + Kb, (Xi + Х2)а = Х<±а + Х2а
и сочетательным свойством:
Х\(Х2а) = (Х{Х2)а.
Компланарные векторы — это три или
более векторов, лежащих в одной плоскости или в
параллельных плоскостях. Любые три
компланарных вектора а9Ъ9с связаны зависимостью
oca + pfe + ус = 0,
где хотя бы один из коэффициентов а, Р, у
отличен от нуля.
ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. Проекцией
вектора на ось I называется произведение модуля
вектора на косинус угла между вектором и
положительной полуосью I:
пр^а = \а\ cos ср. (1)
Ось I — это прямая, на которой выбрано
положительное направление; каждая точка оси
делит ее на положительную и отрицательную
полуоси.
Проекция вектора положительна, если угол
ф — острый (рис. 109, а), отрицательна, если угол
тупой (рис. 109, б), и равна нулю, если угол
прямой. Очевидно, пр^а = ± PQ, где Р и Q —
основания перпендикуляров,_опущенных на ось из
начала и конца вектора а; знак «плюс» («минус»)
соответствует острому (тупому) углу <р.
Из равенства (1) следует также, что проекции
равных векторов на одну и ту же ось равны
между собой.
Системы координат
КООРДИНАТНАЯ ОСЬ. Координатной осью
называется прямая, на которой отмечена точка
О (начало отсчета или начало координат),
выбран масштаб, т.е. указан отрезок единичной
длины для измерения расстояний (единичный
или масштабный отрезок), и задано
положительное направление. Так, на рис. 110
единичный отрезок на координатной оси х обозначен
ОЕ, направление от точки О к точке Е считается
положительным (показано стрелкой). Начало
координат О делит координатную ось на два лу-
Рис. 108
Е Р
Рис. ПО

462
Справочные материалы
Краткий справочник по математике
ча: положительную полуось (которой
принадлежит точка Е) и отрицательную полуось.
Координатой точки Р, лежащей на оси х,
называется число х = ±ОР (где ОР означает
длину отрезка ОР), причем знак «плюс» («минус»)
соответствует расположению точки Р на
положительной (отрицательной) полуоси; если Р = О,
то х = 0. Расстояние между двумя точками Рх и Р2
на оси х выражается формулой Р\Р% = |*i - х2\,
т. е. оно равно модулю разности
соответствующих координат.
Орт оси х — это вектор ОЕ; длина орта равна
единице, а его направление совпадает с
положительным направлением оси.
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА
ПЛОСКОСТИ. Прямоугольная (или декартова)
система координат на плоскости задается
парой взаимно перпендикулярных координатных
осей, имеющих общее начало в точке О и
одинаковый < масштаб (рис. 111). Оси координат на
плоскости обычно обозначают Ох и Оу (оси
абсцисс и ординат соответственно). Координатную
плоскость обозначают хОу.
Координатные оси делят плоскость хОу на
четыре квадранта (или четверти): I, II, III, IV
(рис. 111). Пусть точка Р лежит на плоскости
хОу. Опустим из этой точки перпендикуляры на
координатные оси; основания перпендикуляров
обозначим Рх и Ру. Абсциссой точки Р
называется координата х точки Рх на оси Ох,
ординатой — координата у точки Ру на оси Оу.
Координаты точки обычно указывают в скобках
рядом с обозначением точки: Р(х; у). Между
точками на плоскости и парами их координат
имеется взаимно однозначное соответствие.
Расстояние между двумя точками Pi(*i; у{) и
^2(*2» У2) на плоскости определяется с помощью
теоремы Пифагора:
Орты осей х, у — это единичные векторы i, у
с началом в точке О.
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В
ПРОСТРАНСТВЕ. Прямоугольная (или
декартова) система координат в пространстве
задается тройкой попарно перпендикулярных
координатных осей, имеющих общее начало в
точке О и одинаковый масштаб. Оси координат в
пространстве обычно обозначают Ох, Оу, Ог (оси
абсцисс, ординат и аппликат соответственно).
В пространстве возможны правые (рис. 112, а) и
левые (рис. 112, б) системы координат; мы
будем использовать правую систему координат.
Орты осей Ох, Оу, Ог — это единичные
векторы i, j, k с началом в точке О; направления
ортов совпадают с направлением осей. Орты
правой системы координат образуют правую тройку
векторов.
Координатные плоскости хОу, уОг, хОг дег
лят пространство на восемь октантов.
Координаты х, у, г точки Р в пространстве
определяются аналогично координатам на
плоскости: это координаты (на соответствующих
осях) оснований Рх, Ру, Р2 перпендикуляров,
опущенных из точки Р на оси Ох, Оу, Ог, —
соответственно абсцисса, ордината и
аппликата. Координаты обычно указывают в скобках:
Р(х; у; г). Между точками в пространстве и
тройками их координат имеется взаимно
однозначное соответствие.
Расстояние между двумя точками P\(xi\ у^\
Zi) и Р2(х2; У2> 22) в пространстве определяется с
помощью теоремы Пифагора:
I 2 2 2
d = tJ(x1 - х2) + (уг - у2) + (гг - г2) .
В частности, расстояние любой точки Р(х; у; г)
до начала координат равно
■-1
(*1 " *2> + (У\ ~ 02>
, Гг. 2~2
а0 = *Jx + у +г
У1
РУ
III
1
I
„р
i
i
°IV
р* х
а) *
б)
*•
JSo
Рис. 111
Рис 112

Справочные материалы
Краткий справочник по математике
463
Координатами аХ9 ау9 аг вектора а в
прямоугольной системе координат Охуг в
пространстве называются его проекции на координатные
оси Ох, Оу9 Ог: _
ах = \а\ cos а,
ау = \а\ cos Р,
а2 = \а\ cosy.
Здесь а, р, у — углы между вектором и
соответствующимиположительными полуосями
(рис. 113). Вектор а с координатами аХ9 ау9 а2
записывают в виде а (ах; ау; аг) или а = {ах; ау\ а2}.
При сложении векторов их соответствующие
координаты складываются, при умножении
вектора на число — умножаются на это число:
а + Ъ = {ах + Ьх\ ау + Ьу\ а2 + Ьг}\
\ia = {\iax;iiay;iiaz}.
Модуль вектора а (ах; ау; а2) вычисляется по
формуле
коллинеарны тогда и только тогда, когда их
одноименные координаты пропорциональны,
т. е.
а а а
К~ъу-ъг
(1)
В равенстве (1) некоторые из знаменателей
могут оказаться равными нулю. Условимся вся-
а с
кую пропорцию г = -J понимать в смысле равен-
а а а
ства ad = bc. Например, равенства "7Г = n = Т
означают, что 2ах = 0 • а29 2ау = 0 • а29 О • ах =
= 0 • ау9 т. е. что ах = 0, ау = 0.
В случае векторов на плоскости условие (1)
принимает вид
.-. Г~2~ 2~ 2
|а|= 4ах + ау + az '
а а
х ___ у
Ь ~~ Ь
х "у
(2)
В случае векторов на плоскости хОу
справедливы те же формулы, но отсутствует третья
координата; например,
Пусть даны точки Мх(хх; уг; гг)9 М2(х2; у2; z2).
Требуется найти точку М(х; у; г), лежащую на
отрезке МХМ2 и делящую его в данном
отношении:
W= Ja2x + а
Координаты вектора АВ, заданного двумя
точками A(xi\ ух; 2\) и В(х2\ у2\ z2)9 равны
разностям соответствующих координат точек А и В:
АВ = {х2 - хг; у2 - уг; z2 - гг}9
т. е. чтобы найти координаты некоторого
вектора, достаточно из координат его конца вычесть
одноименные координаты его начала.
Любой вектор а на плоскости может быть
разложен по ортам i, j прямоугольной системы
координат хОу:
а = ахТ + ау].
Разложение по ортам i9 у, k в пространстве
имеет вид
а = axi + ayj + azk.
Векторные слагаемые axi9 ayj9 azk
называются составляющими (или компонентами)
вектора а по осям Ох9 Оу9 Ог.
Условие коллинеарности двух векторов.
Два ненулевых вектора
а = axi + ayj + a2k nb = bxi + byj + b2k
мгм
MM0
= X.
Очевидно, что МХМ = XMM2 или
(х - xjji + (у - {/х)7+ (г - z{)k =_
= Цх2 - x)i + Цу2 - y)j + Цг2 - z)k.
Значит, х - хг = Цх2 - х)9 у - уг = Цу2 - у)9
2-гг = Цг2 - г)9
откуда находим
JC =
Хл ~г i^Xn
1 + X
«/ =
1 + X '
1 + X '
(3)
Рис. 113

464
Справочные материалы
Краткий справочник по математике
Если точки Mi и М.2 принадлежат плоскости
хОу, то в формулах (3) третья координата
отсутствует.
ПОЛЯРНЫЕ КООРДИНАТЫ. Зафиксируем на
плоскости точку О и выходящую из нее
полупрямую Ор, а также выберем единицу масштаба
(рис. 114). Точка О называется полюсом,
полупрямая Ор — полкрной осью.
Произвольной точке М (отличной от О)
плоскости поставим в соответствие два числа:
полярный радиус г, равный расстоянию от
точки М до полюса О;
полярный угол <р, равный углу между
полярной осью Ор и полупрямой ОМ.
Полярный угол ф измеряется в радианах,
отсчет положительных (отрицательных) значений
ф ведется от Ор против движения (по движению)
часовой стрелки. При этом обычно полагают,
что -% < ф < к.
Полюсу О соответствует полярный радиус
г = 0, полярный угол для него не определен.
Запись М(г; ф) означает: точка М с
полярными кооординатами г и ф.
Совместим начало координат О прямоугольной
системы хОу с полюсом О, а луч Ох примем за
полярную ось Ор (рис. 115).
Из рис. 115 видно, что декартовы и полярные
координаты точки М связаны формулами
х — г cos ф, у = г sin ф (4)
и
/ 2 , 2 , У
(5)
которые верны при любом расположении точки
М на координатной плоскости.
Заметим, что соотношение tg <р = " дает два
значения ф (где -п < ф < к). Поэтому для
вычисления полярного угла ф точки М по ее
прямоугольным координатам х и у предварительно
выясняют, в каком квадранте лежит точка М.
М(х;у)
Пример. Даны прямоугольные координаты точ-
киА: х = 1, у = 1. Найдем ее полярные координаты.
По формулам (5) находим г = >Jl + 1 = J2 ,
tg ф = 1. Из двух значенийф — j и(р = -т выбираем
ф = J» так как точка А лежит в I квадранте. Итак,
г = л/2 , ф = 2 — полярные координаты данной точки.
Скалярное и векторное произведения
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. Ска-
лярное произведение а • Ь двух векторов аиЬ —
это число, равное произведению модулей
векторов на косинус угла между ними:
а • Ъ = \а\ • \b\ cos (а; 5).
Скалярное произведение обозначается также
а Ь или (а Ь), иногда (a, ft). Если угол между
векторами — острый (тупой), то скалярное
произведение положительно (отрицательно); если угол —
прямой, то оно равно нулю. _
Скалярное произведение векторов а{ах\ ау; а2) и
Ь(ЬХ; Ьу; Ь2) выражается через координаты этих
векторов по формуле
а Ъ = ахЪх + ауЪу + а2Ь2. (1)
Пример. Пусть а(1; 3; -1), 5(1; 0; 4). Тогда по
формуле (1)_находим
аЪ = \ • 1+3 • 0 + (-1) • 4 = -3.
Угол между векторами а и 5 можно найти по
формуле
а • Ь
а Ъ + a b + a ft
**xux у у 2WZ
w'w J"l + *2y + «22Jbl + b2, + b2
.(2)
'У ' ~Z ЛГХ "У
Условие перпендикулярности двух
векторов. Два вектора а и Ь перпендикулярны тогда
и только тогда, когда ab = 0 или
ах^х + ауЬу + аг^г = 0.
(3)
В случае векторов на плоскости в формулах
(1) и (3) отсутствует слагаемое а2Ь29 а формула
(2) принимает вид
cos <р =
а • Ь
а Ь 4- а Ь
**хих у у
151151 ЙЧЯ^*
(4)
Рис. 114
Рис. 115
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Векторным произведением axb двух векторов а и

Справочные материалы
Краткий справочник по математике
465
Ь называется вектор с, определяемый
следующим образом:
1) \с\ = \а\ • |b| sin (а; Ь), т. е. модуль векторного
произведения численно равен площади
параллелограмма, построенного на данных векторах;
2) с J_ а, с J_ ft, т. е. вектор с перпендикулярен
плоскости, в которой лежат сомножители;
3) векторы a, ft, с образуют правую тройку
векторов, т. е. кратчайший поворот вектора а к
вектору Ь виден из конца вектора с как поворот
против часовой стрелки (правило буравчика;
рис. 116).
Векторное произведение обозначается также
[а Ь], иногда [а, 5].
Если векторы аиЬ коллинеарны, то а х Ъ — 0.
Свойства векторного произведения:
1)аха = 0;
2) а х Ъ = -Ь х а (векторное произведение анти-
коммутативно);
3) (а + Ъ) х с = а х с + Ь х с, (ца) х & = ц(а х Ь).
Координаты векторного произведения в
прямоугольной системе координат:
а х Ъ - {aybz - az£y, az6x - axbz; ах&у - a^}.
Кратко векторное произведение записывается
в виде определителя третьего порядка:
ах& =
i j k
а а а
х **у 2
*х by Ьг
(5)
Векторные произведения ортов i, у, k:
X х I ==_ у х ] = k х ft = 0, _ 7_х / = -7 х I = ft,
Ixft = -ftxl = -/, ]xk = -kx] = 1.
Пример. Вычислим площадь треугольника с
вершинами А(1; 1; 1), Б(2; 3; 4), С(4; 3; 2).
Площадь треугольника ABC равна половине
площади параллелограмма, построенного на векторах
35(2 - 1; 3 - 1; 4- 1) - (1; 2; 3)ДС(4- 1; 3 - 1; 2 - 1) =
= (3; 2; 1). Поэтому найдем АВ хАС. Согласно
формуле (5) имеем
АВхАС =
Итак,
i j k
1 2 3
3 2 1
= -& + S] - 4ft.
Saabc=1\-U + *J-*4= 5VI6 + 64+16 -
Объем параллелепипеда, построенного на
векторах a, b, с (рис. 117), можно вычислить по
формуле
V=\a • (Ьхс)\.
Прямая на плоскости
ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ. Общее
уравнение прямой на плоскости хОу:
Ax + Bi/ + C = 0, (1)
где А, В, С — постоянные действительные числа
(коэффициенты), причем А2 + В2 > 0. Числа А, В
являются координатами вектора,
перпендикулярного этой прямой (нормального вектора
прямой).
УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ
КОЭФФИЦИЕНТОМ. Если в уравнении (1) В Ф 0, то его
можно переписать в виде
y = kx + b. (2)
Последнее уравнение называется уравнением
прямой с угловым коэффициентом ft. Здесь
ft = tg <р; ф — угол наклона прямой к оси Ох,
отсчитываемый от положительного направления
оси Ох против часовой стрелки (0 < (р < к).
УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ
ДАННУЮ ТОЧКУ В ДАННОМ НАПРАВЛЕНИИ.
Если прямая (2) проходит через точку Mq(xq; i/0)»
то
I/O - Ьх0 + Ь. (3)
Вычитая из равенства (2) равенство (3),
получаем
У - Уо = *(* - *())• (4>
Это уравнение прямой, проходящей через
данную точку в данном направлении.
НЕПОЛНЫЕ УРАВНЕНИЯ ПРЯМОЙ. Общее
уравнение (1) называется неполным, если хотя
бы один из коэффициентов А, Б и С равен нулю.
= | л/96 =724.
Рис. 116

466
Справочные материалы
Краткий справочник по математике
Рассмотрим все возможные виды неполных
уравнений.
1) С = 0; уравнение Ах + By = 0 определяет
прямую, проходящую через начало координат.
2) А = 0; уравнение By + С = 0 определяет
прямую, параллельную оси Ох.
Аналогично, уравнение Ах + С = 0 (В = 0)
определяет прямую, параллельную оси Оу.
3) А = 0, С = 0; уравнение By = 0 (или, что то
же, I/ = 0) определяет ось Ojc.
Аналогично, уравнение Ах = 0 (В = 0, С = 0)
или, что то же, х = 0 определяет ось Oi/.
УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ. Пусть в
уравнении (1) все коэффициенты отличны от
нуля. Переписав его в виде
_с Л
А В
С С
и полагая для краткости --г = а, - ~ = Ь9
получаем
х
а
У =
Ь
(5)
Уравнение (5) называется уравнением
прямой в отрезках. Это название объясняется тем,
что числа а и Ь определяются отрезками ОА и
ОВу которые прямая отсекает на осях координат
(рис. 118).
УГОЛ МЕЖДУ ПРЯМЫМИ. УСЛОВИЯ
ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМЫХ. Пусть уравнения данных прямых U и U
имеют вид
Ахх + Вгу + Сг = 0, А2х + В2у + С2 = 0.
Углом между прямыми 1\ и 12 называется
любой из двух смежных углов, образованных
этими прямыми (достаточно определить один из
этих углов, так как их сумма равна п). Один из
У
ь)
о
1
sB (0;6)
а
\А{а
X
них_равен углу_ф между нормальными
векторами ni(Ai; В{) и п2(.А2; В2) этих прямых. Поэтому
COS(p =
АхАг + ВХВ2
Ja\ + в\ \а\ + в\
(6)
Пример 1. Вычислим угол между прямыми х =
= 0их + 1/ = 0.
По формуле (6) находим
11+01 1
COS ф = , :—. = -р ,
т. е. ф = 2 • Итак, один из двух смежных углов равен т •
Условие параллельности прямых 1Х и 12.
Это условие совпадает с условием
коллинеарности векторов /ij и п2 и, следовательно, имеет
вид
ll3
^2 *2
(7)
Условие перпендикулярности прямых ^ и £2.
Это условие следует из формулы (6) и имеет вид
А1А2 + Б1В2 = 0. (8)
Пример 2. Прямые 2х-# + 2 = 0и4х-2#-1=0
параллельны, так как выполнено условие (7); прямые
3*-4z/ + 8 = 0h4x + 3z/-9 = 0 перпендикулярны,
так как выполнено условие (8).
Пусть ф1 и ф2 — углы наклона к оси Ох
(рис. 119) соответственно прямых 1Х и 12,
заданных уравнениями
у = А1х + 61, y = k2x + b2,
а ф — один из углов между этими прямыми. Из
рис. 119 видно, что ф = ф2 - Фх и, значит,
tg Ф2 - tg фх k2 - kx
т. е.
tg<p =
^2 ^1
1 т НлКп
(9)
Рис. 118
Рис. 119
(для другого угла между этими прямыми,
смежного с ф, выражение справа отличается знаком,
так как tg (тс - ф) = -tg ф).
Из формулы (9) получаем:
условие параллельности прямых 1Х и 12:
ki = k2\

Справочные материалы
Краткий справочник по математике
467
условие перпендикулярности прямых 1± и 12:
УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ
ДВЕ ДАННЫЕ ТОЧКИ. Уравнение прямой,
проходящей через две данные (различные) точки
Mi(*i; У\)и М2(*2; У2>» имеет вид
х - хЛ
У\
Х0 - X
1 У2-У1
(Ю)
Здесь обращение в нуль одного из
знаменателей означает обращение в нуль и
соответствующего числителя. Если, например, у2 - ух = 0, то
У = У1-
Пример. Составим уравнение прямой,
проходящей через точки Mj(4; -2) и М2(3; -1).
Используя уравнение (10), получим
х - 4 _ у + 2
3-4
-1 + 2
, или х + у - 2 = 0.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ.
Пусть даны уравнения прямых ^ и ^:
Ахх + Вгу + Сх = 0,
А2х + В2у + С2 = 0.
(И)
(12)
Если прямые 1± и ^ пересекаются в
некоторой точке, то ее координаты должны
удовлетворять одновременно двум уравнениям (11) и (12).
Следовательно, чтобы найти координаты точки
пересечения прямых ^ и Z2, надо решить
систему указанных уравнений. Если эта система
имеет единственное решение, то прямые
пересекаются в одной точке. Если же система не имеет
решения или имеет бесконечно много решений,
то прямые соответственно параллельны или
совпадают.
Пример. Найдем точку пересечения прямых
2х + 3#-8 = 0и*-2# + 3 = 0.
Решив систему уравнений
2х + Ъу - 8 = 0,
х - 2у + 3 - 0,
получим х = 1, у = 2. Значит, данные прямые
пересекаются в точке (1; 2).
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ.
Расстояние d от данной точки Mq(xq; у0) до прямой I
(под этим расстоянием понимается длина
перпендикуляра, опущенного из точки М0 на
прямую 0э заданной уравнением Ах + By + С = 0,
определяется по формуле
\Ах0 + Ву0 + С\
d =
№ ' "2
(13)
ил + я'
Пример. Найдем расстояние от точки Mq(-6; 3)
до прямой Зх - 4у + 15 = 0.
Согласно формуле (13) получим
, [3 (-6) -43 + 15[ 15 Q
а = = = -=- = о.
^2 5
</з2 + (-4)2
Плоскость
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ. Общее
уравнение плоскости в пространстве Oxyz
имеет вид
Ах + By + Cz + D = 0,
(1)
где х, у, z — координаты переменной точки
плоскости, А, В, С, D — постоянные
действительные числа (коэффициенты), причем
А2 + В2 + С2 > 0. Числа А, В, С являются
координатами вектора, перпендикулярного этой
плоскости (нормального вектора плоскости).
НЕПОЛНЫЕ УРАВНЕНИЯ ПЛОСКОСТИ.
Общее уравнение (1) называется неполным, если
хотя бы один из коэффициентов А, В, С, D равен
нулю.
Рассмотрим все возможные виды неполных
уравнений.
1) D = 0; уравнение Ах + By + Cz = 0
определяет плоскость, проходящую через начало
координат.
2) А = 0; уравнение Bi/ + Cz + D = 0 определяет
плоскость, параллельную оси Ох (поскольку
нормальный вектор этой плоскости п(0; В; С)
перпендикулярен оси Ох).
Аналогично, уравнение Ах + Cz + D = 0 (В = 0)
определяет плоскость, параллельную оси Oi/,
а уравнение Ar + By + D = 0 (С = 0) — плоскость,
параллельную оси Oz.
3) А = 0, В = 0; уравнение Cz + D = 0
определяет плоскость, параллельную координатной
плоскости хОу (так как плоскость параллельна
осям Ох и Oi/).
Аналогично, уравнение By + Z) = 0 (А = 0,
С = 0) определяет плоскость, параллельную
координатной плоскости xOZy а уравнение Але + D = 0
(В = 0, С = 0) — плоскость, параллельную
координатной плоскости yOz.

468
Справочные материалы
Краткий справочник по математике
4) А = О, Б = О, D = 0; уравнение Cz = 0
определяет координатную плоскость хОу
(поскольку плоскость Сг = 0 параллельна^ координатной
плоскости хОу и проходит через начало
координат).
Аналогично, уравнение By = 0 (А = 0, С = 0,
D = 0) определяет координатную плоскость #Oz,
а уравнение Ах = 0 (Б = 0, С = 0, D = 0) —
координатную плоскость уОг.
УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ. Это
уравнение имеет вид
а Ь с
где числа а, Ь, с определяются отрезками,
которые плоскость отсекает на осях координат
(рис. 120).
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ. УСЛОВИЯ
ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ
ПЛОСКОСТЕЙ. Пусть уравнения данных
плоскостей имеют вид
Агх + Вгу f Сгг + £>! = 0,
А2х + В2у + С22 + D2 = 0- (2)
Углом между плоскостями (2) называется
любой из двух смежных двугранных углов,
образованных этими плоскостями (достаточно
определить один из этих углов, так как их
сумма равна к). Один из них равен углу <р
между нормальными векторами ni(Ai; В±\ С{) и
п2(А2; Б2; С2) этих плоскостей. Поэтому
cos<p =
АХА2 + ВХВ2 + СгС2
JaJ + б? + с\ Ja22 + в22 + с
(3)
П р и м е р 1. Вычислим угол между плоскостями
Х- 2 = 0 Иу -2 = 0. _
Здесь лх(1; 0; -1), л2(0; ^5 "!)• По формуле (3)
находим
Vi
о
1 ^_М(х;у)
( R/ \
V М0 (х0;у0)1
X
coscp =
10 + 01 + (-!)(-!)
Vl2 + О2 + (-1)2 Vo2 + l2 + (-1)2
= г = Х
откуда Ф = о . Итак, один из двух смежных двугран-
к
ных углов равен
3'
Условие параллельности плоскостей (2).
Это условие совпадает с условием
коллинеарности векторов п1 и п2 и, следовательно, имеет
вид
■^2 ^2 ^2
(4)
Условие перпендикулярности плоскостей (2).
Это условие следует из формулы (3) и имеет вид
АХА2 + ВХВ2 + С^ = 0. (5)
Пример 2. Плоскости Зх + 2у - 7г + 8 = 0 и
3* + 2у - 7 г + 32 = 0 параллельны, так как
выполнено условие (4). Плоскости 2х + 3z/ - 2г - 4 = 0 и
13* - 8у + г + 44 = 0 перпендикулярны, так как
выполнено условие (5).
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ.
Расстояние d от точки Mq(x0; уо; z0) До плоскости (1)
определяется по формуле
d =
\Ах0 + Ву0 + CzQ + Д|
(6)
Пример. Найдем расстояние от точки М0(1; 0; -2)
до плоскости 2х - I/ + 2г - 4 = 0.
Согласно формуле (6) получим
d= 12 1 - 1 0 + 2 (-2)-4[ =6 =2
722 + (-1)2 + 22 3
Кривые второго порядка
Рассматриваемые ниже линии (окружность,
эллипс, гипербола, парабола) называются
кривыми второго порядка, так как в прямоугольной
системе координат они определяются
алгебраическими уравнениями второй степени
относительно х и у.
УРАВНЕНИЕ ОКРУЖНОСТИ. Окружность с
центром Mq(xq; уц) и радиусом R (рис. 121)
задается уравнением
Рис. 120
Рис. 121
2= z?2
(х-х0У + (у-у0) * = R
(1)

Справочные материалы
Краткий справочник по математике
469
Если центр окружности совпадает с началом
координат, по последнее уравнение примет вид
х2 + у2 = R2 (в полярных же координатах г и <р
уравнение этой окружности записывается в виде
г = Д((К<р<2я)).
ОПРЕДЕЛЕНИЕ И КАНОНИЧЕСКОЕ
УРАВНЕНИЕ ЭЛЛИПСА. Эллипсом называется
множество точек плоскости, сумма расстояний каждой
из которых до двух данных точек F± и F2
(называемых фокусами) есть величина постоянная,
равная 2а (рис. 122):
MFX + MF2 = 2а.
Если ось Ох провести через фокусы, а начало
координат поместить в середине отрезка FiF2
(рис. 122), то уравнение эллипса примет
канонический (простейший) вид:
2L+IL.
+
= 1,
(2)
а Ь
где а — большая у b — мал&я полуось эллипса,
7~~2 2
а -с , 2с = FiF2 — расстояние между
фокусами, с<а. Эллипс имеет две оси симметрии —
оси координат, и центр симметрии — начало
координат. Площадь, ограниченная эллипсом: S =
= nab.
ОПРЕДЕЛЕНИЕ И КАНОНИЧЕСКОЕ
УРАВНЕНИЕ ГИПЕРБОЛЫ. Гиперболой называется
множество точек плоскости, разность расстояний
каждой из которых до двух данных точек F1 и
F2 (называемых фокусами) есть величина
постоянная, равная 2а (рис. 123):
MFx-MF2 = ±2a.
Гипербола состоит из двух бесконечных
симметричных ветвей. Если ось Ох провести через
фокусы, а начало координат поместить в
середине отрезка FiF2 (рис. 123), то уравнение
гиперболы примет канонический вид:
1L -У- =
= 1,
(3)
а Ь
где а — действительная, Ъ — мнимая полуось
П 2
гиперболы, Ь = л/с - а , 2с = FiF2 — расстояние
между фокусами, с > а. Гипербола имеет две
асимптоты — прямые у = ± - х, к которым
неограниченно приближаются точки гиперболы при
\х\ —> оо. Если а = 6, то гипербола называется
равнобочной, при этом угол между
асимптотами — прямой. График обратно
пропорциональной зависимости у = - (см. рис. 13) —
равнобочная гипербола, асимптоты которой совпадают с
осями координат Ох и Оу. Для построения
асимптот гиперболы строят основной
прямоугольник гиперболы со сторонами х = а, х = -а, у = Ь,
у = -Ь. Прямые, проходящие через
противоположные вершины этого прямоугольника,
являются асимптотами гиперболы (рис. 123).
ОПРЕДЕЛЕНИЕ И КАНОНИЧЕСКОЕ
УРАВНЕНИЕ ПАРАБОЛЫ. Параболой называется
множество точек плоскости, равноудаленных от данной
точки F (называемой фокусом) и от данной
прямой I (называемой директрисой);
предполагается, что точка F не лежит на прямой I (рис. 124).
Если ось Ох провести через фокус
перпендикулярно директрисе, а начало координат
поместить на равных расстояниях от директрисы и от
фокуса (рис. 124), то уравнение параболы
примет канонический вид:
у* - 2рх,
(4)
где р — расстояние от фокуса до директрисы.
Эта парабола имеет ось симметрии — ось Ох.
Vi
ъ
-ь
Рис
1
^v
Fjax
—<S
.122
у%
м
F х
Рис. 123
Рис. 124

470
Справочные материалы
Краткий справочник по математике
Очевидно, что каждому из уравнений у2 =
= -2рх, х2 = 2ру, х2 = -2ру (р > 0) соответствует
парабола, по форме тождественная с параболой
(4), но расположенная иначе. Эти параболы
изображены на рис. 125 и 126.
НАЧАЛА ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Событие и вероятность
Основные понятия
ПОНЯТИЕ О СЛУЧАЙНОМ СОБЫТИИ. Опыт,
эксперимент, наблюдение явления называются
испытаниями. Примерами испытаний
являются: бросание монеты, извлечение шара из урны,
бросание игральной кости. Результат, исход
испытания называются событием. Событиями
являются: выпадение герба или цифры, взятие
белого или черного шара, появление того или
иного числа очков на брошенной игральной
кости. Для обозначения событий используются
заглавные буквы латинского алфавита: А, В, С
и т. д.
Два события называются совместимыми,
если появление одного из них не исключает
появление другого в одном и том же испытании.
Пример 1. Испытание: однократное бросание
игральной кости. Событие А — появление четырех
очков. Событие В — появление четного числа очков.
События А и Б — совместимые.
Два события называются несовместимыми,
если появление одного из них исключает
появление другого в одном и том же испытании.
Пример 2. Испытание: однократное бросание
игральной кости. Пусть события А±, А2, А3, А±, А5, А$ —
соответственно выпадение одного очка, двух, трех,
четырех, пяти, шести. Эти события являются
несовместимыми.
у\
у2 = -2рх
х2 = 2ру
О х
х1 - -2ру
Рис. 125
Рис. 126
Два события А и А называются
противоположными, если в данном испытании они
несовместимы и одно из них обязательно
происходит.
Пример 3. Испытание: бросание монеты.
Событие А — выпадение герба, событие А — выпадение
цифры.
Событие называется достоверным, если в
данном испытании оно является единственно
возможным его исходом, и невозможным, если
в данном испытании оно заведомо не может
произойти.
Пример 4. Испытание: извлечение шара из
урны, в которой все шары белые. Событие А — вынут
белый шар — достоверное; событие В — вынут
черный шар — невозможное.
Событие А называется случайным, если оно
объективно может наступить или не наступить в
данном испытании.
Пример 5. Событие Аб — выпадение шести
очков при бросании игральной кости — случайное. Оно
может и не наступить в данном испытании.
АЛГЕБРА СОБЫТИЙ. Суммой событийАиВ
называется событие С = А + В, состоящее в
наступлении по крайней мере одного из событий А
или В.
П р и м е р 1. Испытание: стрельба двух стрелков
(каждый делает по одному выстрелу). Событие А —
попадает в мишень первый стрелок, событие В —
попадает в мишень второй стрелок. Суммой событий А и
В является событие С = А + В — попадает в мишень
по крайней мере один стрелок.
Аналогично, суммой конечного числа
событий Ai, А2,..., Ak называется событие А = Ах +
+ А2 + ... + Ak, состоящее в наступлении хотя бы
одного из событий At (i = 1, 2, ..., k).
Из определения суммы событий
непосредственно следует, что А + В = В + А. Справедливо
также и сочетательное свойство. Однако А + А =
= А (а не 2А, как в алгебре).
Произведением событий А и В называется
событие С = АВ, состоящее в том, что в
результате испытания произошли и событие А, и
событие В.
Аналогично, произведением конечного
числа событий Ai, А2, ..., Ak называется событие
А = А^А2 ... Ak, состоящее в том, что в
результате испытания произошли все указанные
события.

В примере 1 произведением событий А и В
является событие С = АВ, состоящее в попадании в
мишень двумя стрелками.
Из определения произведения событий
непосредственно следует, что АВ = ВА.
Справедливы также сочетательный и дистри-
бутивный законы. Однако АЛ = А (а не А ).
Определения вероятности
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ. Всякое испытание влечет за собой некоторую
совокупность исходов — результатов испытания,
т. е. событий.
Говорят, что совокупность событий образует
полную группу событий для данного
испытания, если его результатом обязательно
становится хотя бы одно из них.
Пример 1. Полными группами событий
являются: выпадение герба и выпадение цифры при одном
бросании монеты; выпадение одного, двух, трех,
четырех, пяти и шести очков при одном бросании
игральной кости; попадание в цель и промах при одном
выстреле.
Рассмотрим полную группу попарно
несовместимых событий Ui> U2, ..., Un, связанную с
некоторым испытанием. Предположим, что в
этом испытании осуществление каждого из
событий Ut (i = 1, 2, ..., п) равновозможно, т. е.
условия испытания не создают преимущества в
появлении какого-либо события перед другими
возможными.
События Ulf U2, ...» Uk, образующие полную
группу попарно несовместимых и равновозмож-
ных событий, будем называть элементарными
событиями.
Пример 2. Пусть Ut — событие, состоящее в
том, что при одном бросании кости выпадает грань с
цифрой i. Тогда события £/lf U^ ..., U$ образуют
полную группу попарно несовместимых событий. Так
как кость предполагается однородной и
симметричной, то события Ui9 U2, ...i Uq являются равновоз-
можными, т. е. элементарными.
Событие А называется
благоприятствующим событию Ву если наступление события А
влечет за собой наступление события В.
Пример 3. Пусть при бросании игральной кости
события L^2» ^4 и ^6 — появление соответственно
двух, четырех и шести очков и А — событие,
состоящее в появлении четного числа очков; события {72, U±
и Uq благоприятствуют событию А.
Справочные материалы
Краткий справочник по математике
Классическое определение вероятности.
Вероятностью Р(А) события А называется
отношение числа элементарных событий,
благоприятствующих событию А, к числу всех
элементарных событий, т. е.
Пример 4. Вычислим вероятность выпадения
герба при одном бросании монеты.
Очевидно, событие А — выпадение герба и событие
В — выпадение цифры образуют полную группу
несовместимых и равновозможных событий для данного
испытания. Событию А благоприятствует лишь одно
событие — само А. Поэтому Р (А) = « .
П р и м е р 5. Очевидно, что в опыте с игральной
костью (см. пример 2) Р (Ut) = ~ , i = 1, ..., 6.
Примерб. Найдем вероятность того, что при
однократном бросании игральной кости выпадет четное
число очков (событие А).
Здесь число элементарных событий равно 6. Число
благоприятствующих элементарных событий равно 3
(выпадение двух, четырех и шести очков). Поэтому
Р(А) = | = 0,5.
Из классического определения вероятности
следует:
1) вероятность достоверного события равна
единице;
2) вероятность невозможного события равна
нулю;
3) вероятность любого события А
удовлетворяет условию 0 < Р (А) < 1;
4) элементарные события являются
равновероятными, т. е. обладают одной и той же
вероятностью.
СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ. Классическое определение вероятности не
является пригодным для изучения
произвольных случайных событий. Так, оно неприемлемо,
если результаты испытания не равновозможны.
Например, при бросании неправильной
игральной кости выпадение ее различных граней не
равновозможно.
В подобных случаях используется так
называемое статистическое определение вероятности.
Пусть произведено п испытаний, при этом
некоторое событие А наступает т раз.
Число т называется абсолютной частотой
(или просто частотой) события А, а отношение

Справочные материалы
Краткий справочник по математике
Р* (А) = — называется относительной часто-
п
той события А.
П р и м е р 1. При транспортировке из 10 000
арбузов испортилось 26. Здесь т = 26 — абсолютная часто-
26
та испорченных арбузов, а Р* (А) = 1Q ~~~ = 0,0026 —
относительная.
Результаты многочисленных опытов и
наблюдений позволяют заключить: при
проведении серий из п испытаний, когда число п
сравнительно мало, относительная частота Р* (А)
принимает значения, которые могут довольно
сильно отличаться друг от друга. Однако с
увеличением числа п испытаний в сериях относи-
771
тельная частота Р* (А) = — приближается к
некоторому числу Р(А), стабилизируясь возле него
и принимая все более устойчивые значения.
Пример 2. Было проведено 10 серий бросаний
монеты, по 1000 бросаний в каждой. Относительные
частоты выпадения герба оказались равными 0,501;
0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494;
0,484.
Эти частоты группируются около числа 0,5.
Статистическое определение вероятности.
Вероятностью события А в данном
испытании называется число Р(А), около которого
группируются значения относительной
частоты при больших п.
Так, в примере 2 вероятность в
статистическом смысле равна 0,5.
Таким образом, относительная частота
события приближенно совпадает с его вероятностью
в статистическом смысле, если число
испытаний достаточно велико.
С этой точки зрения величина т = пР(А)
представляет собой среднее значение числа
появления события А при п испытаниях.
Свойства вероятности
Теоремы сложения
и умножения вероятностей
СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
НЕСОВМЕСТИМЫХ СОБЫТИЙ.
Теорема. Вероятность суммы двух
несовместимых событий А и В равна сумме
вероятностей этих событий:
Р(А + В) = Р(А) + Р(В).
Точно так же формулируется теорема и для
любого конечного числа попарно
несовместимых событий.
Следствие. Сумма вероятностей
противоположных событий А и А равна единице:
Р(А) + Р(А) = 1.
Пример. При стрельбе в мишень вероятность
выбить десять очков равна 0,2, а вероятность выбить
девять очков равна 0,5. Чему равна вероятность
выбить не менее десяти очков?
Пусть случайное событие А означает «выбить
десять очков *, В — «выбить девять очков * иА + В —
«выбить не менее девяти очков». Так как случайные
события А и Б несовместимы, то согласно
приведенной теореме
Р(А + В) = Р(А) + Р(В) = 0,2 + 0,5 = 0,7.
УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ. Два события А
и В называются независимыми, если
вероятность появления каждого из них не зависит от
того, появилось другое событие или нет.
В противном случае событияАиВ называютза-
висимыми.
Пример!..В урне находятся 2 белых и 2 черных
шара. Пусть событие А — вынут белый шар.
Очевидно, Р(А) = о . После первого испытания вынутый шар
кладут обратно в урну, шары перемешивают и снова
вынимают шар. Рассмотрим событие В — во втором
испытании вынут белый шар. Оно также имеет
вероятность Р(В) = п , т. е. события А и Б — независимые.
Предположим теперь, что в первом испытании
вынутый шар не кладут обратно в урну. Тогда если
произошло событие А, т. е. в первом испытании вынут
белый шар, то вероятность события В уменьшается
(Р(В) = о)» если же в первом испытании был вынут
черный шар, то вероятность события В увеличивается
2
(Р(В) = о )• Здесь вероятность события В зависит от
появления или непоявления события А, т. е. события
А и Б — зависимые.
Пусть А и В — зависимые события. Условной
вероятностью РА (В) события В называется
вероятность события Б, найденная в
предположении, что событие А уже наступило.
Пример 2. Как было установлено в примере 1,
вероятность события Б при условии, что событие А
уже наступило, т. е. условная вероятность РА (Б),
равна ~ . Вероятность же события Б при условии, что

событие А не наступило (а наступило событие А), т. е.
2
условная вероятность РА (В), равна « .
Заметим, что если события А и В —
независимые, то
РА(В) = Р(В).
Теорема 1. Вероятность произведения
двух зависимых событий АиВ равна
произведению вероятности одного из них на условную
вероятность другого, найденную в
предположении, что первое событие уже наступило:
Р(АВ) = Р(А)РА(В). (1)
Пример З.В условиях примера 1 рассмотрим
случай, когда в первом испытании вынутый шар не
кладут обратно в урну. Поставим следующий вопрос:
какова вероятность вынуть первый и второй раз
белый шар?
По формуле (1) находим
р^=\ -i-g-
Теорема 2. Вероятность произведения
двух независимых событий АиВ равна
произведению вероятностей этих событий:
Р(АВ) = Р(А) Р(В). (2)
Отметим, что в случае независимых событий
эта теорема распространяется на любое
конечное их число.
Пример 4. Найдем вероятность одновременного
поражения цели двумя орудиями, если вероятность
поражения цели первым орудием (событие А) равна 0,8,
а вторым (событие В) равна 0,7.
События А и В независимы, поэтому по формуле (2)
искомая вероятность
Р{АВ) = 0,7 • 0,8 = 0,56.
СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ СОВМЕСТИМЫХ
СОБЫТИЙ.
Теорема. Вероятность суммы двух
совместимых событий АиВ равна сумме вероят-
носщей этих событий минус вероятность их
произведения:
Р(А + В) = Р(А) + Р(В) - Р(АВ).
Если события А и В несовместимы, то их
произведение АВ — невозможное событие и,
следовательно, Р{АВ) = 0, т. е.
Р(А + В) = Р(А) + Р(В).
Пример. Вероятности попадания в цель при
стрельбе из первого и второго орудий соответственно
равны Р(А) = 0,9 и Р{В) = 0,7. Найдем вероятность по-
Справочные материалы
Краткий справочник по математике
падания в цель хотя бы одним из орудий при залпе из
обоих.
Очевидно, события А и Б совместимы и
независимы. Поэтому
Р(А + В) = Р(А) + Р(В) - Р(АВ) =
= 0,9 + 0,7-0,9 • 0,7 = 0,97.
Повторные независимые испытания
ФОРМУЛА БЕРНУЛЛИ. Пусть производится п
независимых испытаний, причем вероятность
появления события А в каждом испытании
равна р9 тогда вероятность ненаступления А равна
q = l-p.
Если Рп (т) есть вероятность появления
события А т раз в п испытаниях, то
Pn(m)=C*pmqn-m
или Рп(т)= ., П- mVPmQn~m-
т\(п — ту.
Эта формула называется формулой
Берну пли.
Пример. Пусть всхожесть семян некоторого
растения составляет 90%. Найдем вероятность того, что
из четырех посеянных семян взойдут: а) три; б) не
менее трех.
а) В данном случае р = 0,9; q = 1 - р = 0,1; п = 4;
т = 3. Применяя формулу Бернулли, получим
Р4(3) = 4 • (0,9)3 • 0,1=0,2916.
б) Искомое событие состоит в том, что из четырех
семян взойдут или три, или четыре. По теореме
сложения вероятностей имеем Р(А) = Р± (3) + Р4 (4). Так
как Р4 (4) = (0,9)4 = 0,6561, то
Р(А) = 0,2916 + 0,6561 = 0,9477.
ФОРМУЛЫ ЛАПЛАСА И ПУАССОНА. При
больших п вычисления по формуле Бернулли
становятся затруднительными. В этом случае
используют приближенную формулу Лапласа
« , ч 1 (т - пр\
Рп(т)=-== ф -7=^ Ь
*jnpq V Jnpq )
где
2
X
1 "2"
При малых р более точное значение дает
формула Пуассона
т
где ц = пр.

474
Справочные материалы
Краткий справочник по математике
Пример. Завод отправил на базу 500
доброкачественных изделий. Вероятность того, что в пути
изделие будет повреждено, равна 0,002. Найдем
вероятность того, что на базу поступят 3 негодных изделия.
По условию, п = 500, р = 0,002, т = 3. Тогда ц =
= 500 • 0,002 = 1 и искомая вероятность
500
(3) = || в'1 « 0,06.
ЗАКОН БОЛЬШИХ ЧИСЕЛ.
Теорема Бернулли. Пусть т — число
наступлений события А в п независимых
испытаниях up — вероятность наступления
события А в каждом из испытаний. Тогда, каково
бы ни было положительное число е,
lim Р
п-»оо
(|пЧ<£)
= 1.
Это утверждение называется также законом
больших чисел.
Практический смысл теоремы Бернулли
состоит в следующем: если вероятность
случайного события А во всех испытаниях постоянна, а
число испытаний неограниченно возрастает, то
с вероятностью, как угодно близкой к единице
(т. е. как угодно близкой к достоверности),
можно утверждать, что наблюдаемая относительная
частота случайного события будет как угодно
мало отклоняться от его вероятности.

Алгебра в таблицах
1. Действительные числа
Множество натуральных чисел
N
Натуральные числа 1; 2; 3...
Множество целых чисел
Z
N
0
N.
Целые числа состоят из натуральных, нуля и чисел, противоположных
натуральным.
JVcZ
Множество рациональных чисел
Q
Z
Дроби
Р
Рациональные числа представимы как —, гдер —целое, ад — натуральное.
Nt^ZczQ
Множество действительных чисел
R
Q
Q
Зе#,
Действительные числа — это бесконечные десятичные дроби.
NczZczQ^R
Рациональные числа — бесконечные периодические дроби. Период не может
состоять из одних девяток. Если период состоит из одних нулей, дробь может
считаться конечной десятичной дробью.
Множество иррациональных чисел.
Иррациональные числа — бесконечные непериодические десятичные дроби.
3eZ, -6^N, -6eZ, 0,25 e N, 0,25 e Z, 0,25 e Q, 0,25 e R.
Делимость целых неотрицательных чисел
Число а делится на число 6, если существует с такое, что а = Ьс.
а • Ъ; Ь — делитель а; а — кратное Ь.
Свойства делимости
Нуль делится на любое натуральное число.
Любое число делится на единицу.
Любое число делится само на себя.

476
Справочные материалы
Алгебра в таблицах
1. Действительные числа
Свойства делимости (продолжение)
Если а > 0 и а ' Ь9 то а > Ь.
Если а • Ъ и Ь '- с, то а '- с.
Если а ; с и Ъ \ с, то (а + Ъ) \ с.
Если а • (6с), то а • Ь, а • с и (а : 6) • с.
Если а ; Ь и 6 ^ а, то а = 6.
Если а '• b и k Ф 0, то ak '• bk.
Если а ^ с и Ь i с, то (am + Ьп) '• с.
Если а '• с и (а + Ь)" с, то & '• с.
Деление с остатком
Для любых двух натуральных чисел а и & найдутся такие целые
неотрицательные диг, что а = Ъ - q + г, 0<г<6.
Если г = 0, то а • 6. Число г называется остатком от деления а на &.
Признаки делимости
Число делится на два, если его последняя цифра делится на два.
на 2
Число делится на пять, если его последняя цифра делится на пять.
на 5
Число делится на четыре, если число, составленное из двух его последних цифр, делится
на четыре.
на 4
Число делится на двадцать пять, если число, составленное из двух его последних цифр,
делится на двадцать пять.
на 25
Число делится на три, если сумма его цифр делится на три.
наЗ
Число делится на девять, если сумма его цифр делится на девять.
на 9
Число делится на одиннадцать, если алгебраическая сумма его цифр
ч/1-l
ао "" а1 + а2 "" аз + ••• + (""!) ап -1 делится на одиннадцать.
на 11
Десятичная запись п-значного натурального числа:
'ап-1ап-2-а2а1ао' = ап-1 • Ю71"1 + вц-2 ' 10""2 + - + а2 • Ю2 +
+ аг • 101 + a0; at — цифры числа, an_x Ф 0, п е N.
НОК (а; Ь)
Наименьшее положительное из общих кратных чисел а и
Ь называется наименьшим общим кратным этих чисел.
НОК (15; 10) = 30
НОД (а; Ъ)
Наибольший из общих делителей чисел аиЬ называется
наибольшим общим делителем этих чисел.
НОД (15; 10) = 5
НОК (а; Ь) • НОД (а; Ь) = а • Ь
Числа а и Ь называются взаимно про-
сть1миу если НОД (а; Ъ) = 1.
Натуральное числор называется простым, если оно имеет
ровно два различных делителя (единицу и само это число).
2; 3; 5; 7; 11; 13; 17; 19; 23... — простые числа

Справочные материалы
Алгебра в таблицах
477
1. Действительные числа
Свойства простых чисел
Любое натуральное число либо делится
на простое, либо взаимно просто с ним.
Произведение натуральных чисел
делится на простое число тогда и только
тогда, когда хотя бы одно из них
делится на это простое число.
Простых чисел бесконечно много (нет самого большого
простого числа). '
Если натуральное число не делится ни на одно простое,
квадрат которого не превосходит это натуральное
число, то оно само простое.
Любое простое число р (р > 3) представимо в виде
p = 6k±l,ke N.
Каноническое разложение натурального числа п(п> 1):
Pi1 Р22' Рз3 ••• Pkk» T№Pi — простое, pi <Pj + i и 0 <atG N. 120 = 23 • З1 • 51
2. Модуль
|ак
а, а>0
-а, а< 0
Основные свойства модуля
\а\ > 0 |-а| = \а\ \а - Ь\ = \Ь - а\
|а|-|Ь|<|а±Ь|<|а| + |Ь|
Геометрическая интерпретация модуля
Если точка А на числовой оси имеет
координату а, то расстояние от А до 0 равно \а\.
Расстояние между точками А (а) и В (Ь) на прямой равно \а - b\.
Уравнения с модулем
\х\ = а
\х - b\ = а
|/<*)| = |*<*)|
I/<*)!-*<*)
а<0
решений нет
а<0
решений нет
а = 0 х=0
а = 0 х = b
а>0
х = а
х = -а
а>0
равносильно
объединению уравнений
f(x) - g(x)
f(x) = -g(x)
x = b - a
x = b + a
равносильно
системе уравнений
fix) = g(x)
f(x) = -g(x)
g(x) > 0
Неравенства с модулем
\x-b\<a
\x-b\>a
\f(x)\< g(x)
\f(x)\>g(x)
a<0
решений нет
a<0
XG R
a>0
b-a<x < b + a
a>0
х<:Ь-аилях> b + a
равносильно
системе:
f(x)<g(x)
f(x)>-g(x)
равносильно
объединению:
f(x)>g(x)
f(x)<-g(x)
Неравенство |/ (x)\ > \g (x)\ равносильно неравенству f\x) > g2(x)
или неравенству (/ (x) - g (x)) (f (x) + g (x)) > 0.

478
Справочные материалы
Алгебра в таблицах
2. Модуль
Примеры
Раскрытие модулей
«по промежуткам»
уН* + 2| + 3|х|-2|*-1|
-2 0 1 х
х<-2,
у - -(х + 2) - 3* + 2 (х - 1) - -2х - 4
-2 <*^0,
у = х + 2-Зх + 2(х- 1) = 0
0<*<1,
у = * + 2 + Зх 4- 2 (* - 1) = 6*
*> 1,
у = л: + 2 + 3* - 2 (х - 1) = 2х + 4
У
6
у - -2х - 4
\
V2
1 у - 2х + 4
/|
1 '
/' '
I у =6х
1 ' '
/ ' '
!V-°F ' ' .
-3-2 0| 1 2 х
Решить уравнение
З*2 - 5|х| -8 = 0.
Заметим, что \х\2 = #2;
введем обозначение |*| = t.
3t2-5t-8 = 0.
8
|jc| = -1, решений нет.
, | 8 8 8
1*1 — § » xi " ~§ » *2 ~~ § •
8 8
Ответ: хх = -g ; х2 = g .
Построить график функции
I/ = tg jc • |cos jc|.
Данная функция
периодическая, период Т = 2я.
Построим график на каждом
промежутке знакопостоянства
косинуса.
При cos х > 0 х <=^2> g 1 >
I/ = sin х;
при cos х < 0 * е 1 5» "5" ]»
1/ = -sin jc.
i
\у
о 2 X Зя х
^Х 2
3. Действия с многочленами
Сложение многочленов: (а2 4- аЬ - Ь) 4- (За2 - 2аЬ 4- Ь) = 4а2 - аб.
j Вычитание многочленов: (2а - Ь) - (За + Ь) = (2а - Ь) 4- (-За - 6) = -а - 26.
Умножение многочленов: (а + 36)(а - 6) = а2 - аб 4- ЗаЬ - ЗЬ2 = а2 4- 2ab - 3&2.
Формулы сокращенного умножения
квадрат суммы
(а + Ь)2 = а2 + 2аЬ + Ь2
квадрат разности
(а - Ь)2 = а2 - 2а6 4- б2
куб суммы
(а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ъ3
куб разности
(а - Ъ)3 = а3 - За2Ь + ЗаЬ2 - Ъ3
разность квадратов
а2 - Ь2 = (а + Ь) (а - Ь)
разность кубов
а3 - Ь3 = (а - Ь) (а2 + аб + б2)
сумма кубов
а3 + б3 = (а + ft) (а2 - аб + б2)

Справочные материалы
Алгебра в таблицах
479
3. Действия с многочленами
Бином Ньютона: (а + 6)л = ап + Сп ап х b +
+ с\ап~2Ъ2 + ... + Скпап~ кЪк+ ... + Ъп
1 2 tt(tt - 1)
с* =
Л!
• ск = сп ~ k •
п (п - k)\ k\' п п
neNtn>l (01 - 1; 1! - 1; и! - 1 - 2 •... • л).
Треугольник Паскаля
1
1 1
12 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
(а + Ь)4 = а4 + 4а36 + 6а2&2 + 4а63 + б4
(а - б)7 = а7 - 7а6Ь + 21а562 - 35а463 + 35а364 - 21а2Ь5 + 7аЬ6 - Ь7
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобку
2аЬ + 14а2 + 2а = 2а (Ь + 1а + 1);
За263 - 15а3Ь = За2Ь (Ь2 - 5а).
Метод группировки
аЪ + ас-Ъ-с = а(Ь + с)- (Ь + с) = (Ь + с) (а - 1).
Использование формул
сокращенного умножения
а2 + 4аЬ + 462 = (а + 2Ь)2;
а4 + 4 = а4 + 4а2 + 4 - 4а2 =
= (а2 - 2а + 2) (а2 + 2а + 2).
(а2 + 2)2 - (2а)2 -
Дополнительные формулы
(аЛ-1)= (а-1)(а/1-1 + а/1-^ + ... + а+1);
(а2т + 1 + 1) = (а+1)(а2т-а2т~1 + ...-а+1).
Многочлены от одной переменной
Общий вид: / (х) = апхп + ап _ х^л ~ 1+ ... 4- агхг + а0,
/г — степень многочлена, ai — коэффициенты,
ап — старший коэффициент, ап Ф 0.
Если ап = 1, то многочлен называется приведенным.
Зх4 - х3 + 2х2 - 5 — многочлен 4-й степени с
коэффициентами: а4 = 3; а3 = -1; а2 = 2; а1 = 0; а0 = -5.
Квадратный трехчлен — многочлен
второй степери
ajc2 + bx + c(a* 0),
а — первый коэффициент, Ь — второй
коэффициент, с — свободный член.
Деление многочленов
Теорема о делении с остатком
Р(х) = М(х) • Q(x) + R(x), где Р(х) — делимое, М(х) —
делитель, Q(x) — частное, R(x) — остаток. Если
остаток не равен нулю, то его степень меньше степени
делителя.
Зх3 - х2 - Зх - 2 =
Р(х)
= (х2 + х- 1) (Зх - 4) + (4* - 6)
М(х)
QW
Щх)
Деление «уголком»
_3x3-x2-3x-2 1*2 + *-1
Зх3 + З*2 - Зх Зх - 4
-4*2 -2
-4*2-4х + 4
4*-6
Р(х) = Зх3 - х2 - Зх - 2
М(х) = х2 + х - 1
Q(x) = Зх - 4
R(x) = 4* - 6

480
Справочные материалы
Алгебра в таблицах
3. Действия с многочленами
Деление многочлена f(x) на двучлен х - а
Теорема Безу.
Остаток от деления многочлена на двучлен х-а равен:
значению этого многочлена при х = а, т. е. R = /(а).
f(x) = (x-a)Q(x) + f(a)
Схема Горнера.
Разделить многочлен
/(х) = х3 + 5х2-Зна(л:-5)
а = 5
Ь2 = а3
&о = &i • 5 + а±
R - &0 • 5 + а0
Д = /(5) = 247
а3 а2 ах а0
pi
1 1
5
10
0
50
^Н
247
Корнем многочлена называется такое число х0, при
котором значение многочлена равно нулю (/ (х0) = 0).
Целые корни многочлена с целыми
коэффициентами являются делителями его свободного члена.
Пример
х3 + 5х2 + 2х - 8 = 0
Целые корни можно искать только среди
чисел -1; 1; 2; -2; 4; -4; 8; -8.
Ответ: х = 1; х = -2; я = -4 — корни.
4. Квадратные корни
Определение арифметического
корня
Ja = 6 <=><
b>09
,2
6 = a
Тождества
(Та) = а, а ^ 0
7а = И» а ^ R
л/Тб = 4, так как 4 > 0, 42 = 16;
725 Ф 7, так как 72 Ф 25;
725 * -5, так как -5 < 0;
7-8 не определен.
ТоГЗб = 0,6;
74900 = 70;
70,0001 =0,01;
2 < 78 < 3;
0,8 < 7678 <0,9.
Основные свойства
Ja • Jb = 7а • 6
Та /а
7& чъ
Jri = M'J\b\
fa J\a\
7? = (7W)'
Сравнения, связанные с квадратными корнями
Если a>b>0,ToJa>Jb. Ja + Jb > Ja + b.
Если a > 1, то a > Ja и Ja > 1. Если 0<a<l9Toa<JanO<Ja<l.

Справочные материалы
Алгебра в таблицах
481
4. Квадратные корни
Вынесение из-под корня
л/а2& = |а| • Jb, Ь > О
Внесение под корень
b>0
-л/а Ь, если о<0,
а Ь, если а > О
ТбЗ = 79~7 = з77;
77а5 -»|а| • 77;
ToV + 7& =Ь75 + Л',
7з? + л/^С = -Сл/3 + Т^с
5- 73 = л/з • 52 = 775;
-2^/7 =-728;
(75 - 2) • 79 + 475 - л/(75 - 2)2 • (9 + 475) - 1;
(73 -2)-77 + 473 =-7(73 - 2)2(7 + 473) =-1.
2 273
7з з
Иррациональность в знаменателе
5 5(73 + 1) _ 5(л/з + 1) = 5(УЗ 4- 1)
3-1 2
л/з - 1 (л/з - 1)(7з + 1)
Сравнение среднего геометрического
(пропорционального) двух чисел и их среднего
арифметического
а + Ь г—
—7г— > */аЬ,а>0;Ь>0.
Построение Jn (п ^N) на числовой прямой
1 Л л/3 2
з М
(Vn+T)2 = (Vn)2 + i2
Примеры
Найти л: и упростить выражение
х = 73 - 272 - л/3 + 2л/2.
Заметим, что л: < 0, т. к. 3 - 2л/2 < 3 + 2^2 .
х2 = 3- 272 -2л/9 - 8 + 3+272 =6-2 = 4.
Значит, л: = -2.
Ответ: х2 = 4; 7з - 2л/2 - л/з + 272 = -2.
Тзз — 1
Сравнить числа 72 + 1 и « .
Запишем:
72 +1
Тзз - 1
2
272+2 ? ТЗЗ -1
Те +з ? Тзз
Так как сравниваемые числа положительны, то
можно сравнить их квадраты:
17 + 678 ? 33
б7§ ? 16
7288 > 7256
Следовательно, 72 + 1 >
Тзз - 1
16-1019

482
Справочные материалы
Алгебра в таблицах
5. Корни натуральной степени
Определение арифметического корня
натуральной степени из
неотрицательного числа а
Извлечение корня нечетной степени
из отрицательного числа
Корень четной степени
Тождества
Если nJa существует, то(nJa)n = а.
2nJ7~n = |а|, а € R
2л - l/ 2л - 1
*Ja = а, а е R
Сравнения, связанные с корнями
Вынесение из-под корня
Внесение под корень
V27 =3;
5Л024 =4;
У§ =3;
V0, 008 - 0,2;
V0, 0000001 =0,1;
2 < V9 < 3;
0,2 < V0, 00036 < 0,3.
Если а < 0, то 2/l" Va = -2п~\Ра .
3/Is =-V8 = -
5л/^24з = -№;
37(7з-2)3=-
2;
*=-3;
3V(2 - 7з)3
= -(2-7з)=7з
из отрицательного числа не определен.
-2.
Основные свойства
nfija = nm7o;
V5 "^
•j/s = п*л£*
»
.
Еслиа>Ъ>0,то nJa > nJb.
nJa + Vb > "л/а + Ь •
Если а > 1, то 1/а > 1 и Ve < а.
Если 0 < а < 1, то 0 < nJa < 1 и nJa > а.
V24 = Уз~8 = 2 • V3 ;
4л/(1 -л/2)4-5 =(72 -D-V5;
3л/(1 - 72)3-6=(1-72> V6.
3 • V2 = 4л/з4 • 2 = VT62 ;
-2 • 673 = -6л/26 • 3 = -V192 ;
(1-73)-472 =-4л/(1 -73)4-2;
(l-75)-V2 =3л/(1 -75)3-2.

Справочные материалы
Алгебра в таблицах
483
5. Корни натуральной степени
Тождества (продолжение)
Иррациональность в знаменателе
Действия с корнями различных
показателей
Среднее геометрическое
и среднее арифметическое
неотрицательных чисел
Основные свойства (продолжение)
3 3-V25 3-V8
V2 2 2 ;
2 2 (V9-V3 + 1) я~ я/-
VS + 1 3 -х
^ л/i - "VP • ^ - "\&
№:7в-5№;^-^-М;
72 • 372 • V2 = V23 • 22 • 2 = 6л/26 = 2.
Сравнить Vs и 37з.
Vs-12^ = 4/125,
VS - "Тз1 = 12л/81.
Так как 125 > 81, то 12Vl25 > 12781 и i/b > З/З .
_ . (1. + я, + ... + о.,
Пл/°1 ' a2 • • • • an < ^
Равенство достигается при a^ = a2 = ... = a„.
6. Степени. Степенная функция. Функция у = nJx
Степень с натуральным
показателем
Степень
с рациональным показателем
для неотрицательного числа а
а1 = а
ап = (х • а -... • д, , п ^Nfa ^R
v
праз
т
а = л/а
m^Z9n^N
Если т < 0, то а > 0.
Если т > 0, то а ^ 0.
2 3
3§ -8/§. о5 =0;
3
252 = л/255 = 125;
1
(0,04)2 = 70,04 =0,2;
1
3
(-27) не определена.

484
Справочные материалы
Алгебра в таблицах
6. Степени. Степенная функция. Функция у = nJx
Степень с целым показателем
а°=1,
лелг
п9
3"2=Ь (-1,2)° = !;
(Г-(1)'-
125
8
Понятие о степени
с иррациональным
показателем
З3 < 3я < З4
Зз,1 < 3* < з3»2
33,14 <3к <33»15
(я = 3,1415...)
(0,3)2 <(0,3)^ <(0,3)г
(0.8)1'5 <(0,3)^ <(0,3)м
(0,3)м2 <(0,3)^ <(0,3)М1
(72 =1,4142...)
Степень с
действительным показателем
ar9r<=R
г<0, | г>0,
и
а>0
а>0
Свойства степеней
аР-аг = аР + г
аР:аг = аР-г
агЬг = (аЬ)г
(аР)г = аРг
(«Г
Свойства степеней,
связанные
с неравенствами
а>Ь>0
г>0
а>&>0
г<0
а >Ь
а <Ь
р>г
а>\
р>г
0<а<1
р г
р г
=>а <а
Графики
степенной
| функции
У = хг9
Ire R
vl
0<р<г<1
D(y) = [0;+оо);
Е(у) = [0;+оо);
v^£ возрастает на
^[0; +оо).
1 <р<г
D(y) = [0;+оо);
Я(*/) = [0;+оо);
возрастает на
[0; +оо).
р<г<0
D(y) = (0;+оо);
Е(у) = (0;+оо);
убывает на
(0; +оо).
у= Jx\ у =
У Jx
у- х
Ч у- х
ггП т
y=2nJx\ у=2п+\/х; neN
2nSx yk

Справочные материалы
Алгебра в таблицах
485
7. Элементарные функции школьного курса
Линейная функция у = ах + Ь
D(y) = R.
При а = О Е(у) = {Ь} (постоянная), все точки — точки
экстремума. При а * О Е(у) — Л.
При а > О возрастает на Л. При а < 0 убывает на R.
Экстремумов нет.
График — прямая
у - ах + Ь(а <
"Ау-М
Функция y = kx — пряная пропорциональность (k>0).
Нечетная функция.
hx = tg а А2 = tg р
0-А2х
Квадратичная функция у = ах2 + 6* + с (а * 0)
D(y) = R
При а > 0 убывает на (-оо; х0] и возрастает на [х0; +оо),
&
*о = ~о~ точка минимума,
У о = */(*о) минимум.
Е(у) - 0/0; +°°).
При а < 0 возрастает на (-оо; #0] и убывает на [л:0; +оо),
b i ч
х0 = - 5~ — точка максимума, у0 = i/(jc0) — макси-
и а
Мум. £([/) = (-оо; у0].
Вид графика — парабола.
Координаты вершины параболы:
хо = -2^Уо = У(хо)-
Ось симметрии х = дс0.
При а < 0 1/0 — наибольшее значение.
При а > О i/o — наименьшее значение.
у = ах2
у k
Четная функция
D = Ъ2 - 4ас> О
D = &2 - 4ас = О
D = б2 - 4ас < О
Два корня хх и я2;
график пересекает ось Ох
в двух точках.
Один корень х0;
график касается оси Ох.
Нет корней;
график лежит по одну
сторону от оси Ох.
а>0
и
$у
О х0 х
а <0
п
*о
Г\

486
Справочные материалы
Алгебра в таблицах
7. Элементарные функции школьного курса
Дробно-рациональная функция
ах + b
У =
сх + d
(ad -ЬсфО)
Вид графика — гипербола
у - - , где k = (be - ad)/c2.
k
Функцияy = - (fc * 0).
D(i/) = (-oo;0)u(0;+oo),
Д(у) = (-°°;0)и(0;+оо).
Два промежутка монотонности (-°°; 0)
и (0; +оо); при k < 0 функция
на каждом из них возрастает,
при k > 0 на каждом убывает.
Экстремумов нет.
Нечетная функция.
Вертикальная асимптота х = 0, горизонтальная у = 0.
*<о
h
обратная пропорциональность
Примеры дробно-рациональных функций
У = г =3 +
х - 1
хф\\ уФЗ; у =
х - 1
JL
ortu х
2*- 1 0 3
У = —— =2-
х + 1
х + 1
хФ-1;уФ2;у = -~
j
• f
'UW
6 - 2х Л , 3
2х - 3
2х - 3
3/2
* *3/2; 1/*ч-1; у = —
"*
1
3/2V3 х
-т_
Функция у = Jx
Функция у = ^с
D(y) = [0;+oo) = E(y).
Возрастает на D(y). Экстремумов нет.
Четностью и нечетностью не обладает.
1
У -
2</х'
*<
2
1
0
1
f i
1
У- л/*
1
1
4
X
D(y) = (-00;+00) = £(!/).
Возрастает на D(y). Экстремумов нет.
Нечетная функция.
*J?

Справочные материалы
Алгебра в таблицах
487
7. Элементарные функции школьного курса
Степенная функция у = хп
у' =пхп~1
п - 0; у = 1; D(y) - (-оо; 0) и (0; +оо); Е(у) = {1}.
п > 0, натуральное
п < 0, целое
л — четное
п — нечетное
п — четное
п — нечетное
D(y) = R
Е(у) = [0;+оо)
D(y) = R
E(y) = R
Я0/) = (-°°;0)и(0;+оо)
Е(у) = (0; +оо)
^0/) = (-оо;0)и(0;+оо)
Четная функция
Нечетная функция
Четная функция
Нечетная функция
п — не целое число
п > 1
0<п < 1
п <0
D(y) = [0;+oo) = E(y)
D(y) = (0;+oo) = E(y)
Сравнение графиков
степенных функций
W<0<V<U<l<t<8

488
Справочные материалы
Алгебра в таблицах
7. Элементарные функции школьного курса
Показательная функция
у = ах (а > 0; а * 1)
у' = ах • In а
Логарифмическая функция
1
У = logaJC (a > 0; а * 1) yf =
х- lna
Я0/) = (0;+°о);
один промежуток монотонности;
экстремумов нет.
D(y) = (0; +оо);
E(y) = R;
один промежуток монотонности;
экстремумов нет.
а > 1
возрастает на Л
а >1
возрастает на D(y)
У1
а
0
1 1
м
1
1
X
0 < a < 1 убывает на R
0<а <1
\1
a
0
1
Ч-
1
— ^
X
убывает на D(y)
yi
0
i
1
v .
V;
е = 2,718281828459045... = 2,7 — основание натурального логарифма (loge* = In х).
(ехУ = ех
ОпхУ--
bg0x
d<c<1<a<ft
a<&< Kc<d
Тригонометрические функции
j/ =sin X
у = COS ЛГ
у =tg*
л
[-1; 1]
(-£ +я*;5 +7ift)fteZ
[-1; 1]
R

Справочные материалы
Алгебра в таблицах
489
7. Элементарные
функции школьного курса
Тригонометрические функции (продолжение)
Бесконечное
множество
промежутков
монотонности
Точки
минимума
Точки
максимума
Минимумы
Максимумы
Нули
Промежутки
знакопостоян-
ства (у > 0)
Промежутки
знакопостоян-
ства (у < 0)
Период
Четность
Асимптоты
Производная
Графики
Убывает на
[?+2лА;^ +2тгё];
возрастает на
х=-\ + 2л&
х = \ + 2nk
-1
1
х - nk
(2nk; п + 2nk)
(-я + 2nk\ 2nk)
2n
Нечетная
sin (-x) = -sin x
нет
cos X
у = sin x
^Щ
Ojc/2 X- x
Убывает на [2nk; к + 2я&];
возрастает на
[-n + 2nk;2nk].
х = п + 2яА
jc = 2nk
-1
1
х = \ + 7tft
(~| -4-27Л; \+2nk)
(?+2тй;у+2ЛЙ)
2л
Четная
cos (-х) = COS JC
нет
-sin х
у = COS X
У\
к
^-1
I
1 5
оЛЦЛ
Возрастает на каждом
промежутке
непрерывности
нет
нет
нет
нет
х = nk
(nk; \ + nk)
(\ + я£;я + я£)
п
Нечетная
tg(-x) = -tgx
Вертикальные
x=l +nk
l/cos2x
У =tgx
J ft i
[-24
1 '■
1
III
# Iя /
/7.
0 J / ■

490
Справочные материалы
Алгебра в таблицах
7.
Элементарные функции школьного курса
Обратные тригонометрические функции
1КУ)
\Е(у)
Монотонность
Четность
Производная
Графики
у = arcsin х
[-1; 1]
1 2' 2J
Возрастает на Щу)
Нечетная
1
к
2
-1
1 /
1 _
У 1
0 1 тх
я
2
1/ — arccos х
[-1; 1]
[0;тс]
Убывает на D(y)
—
1
л/1-*'
(хф±\)
h
-1 0
л
2
1 ж
у = arctg ж
Л
1 2'2;
Возрастает на D(y)
Нечетная
1
1 + х2
Я
2
1 -^
Я'
~2
1
0
8. Основные приемы преобразования графиков
f(x + а)
/(^) + ь
-fix)
Перенос графика у = f(x) на вектор р (-а; 0).
Перенос графика у = f(x) на вектор р (0; Ъ).
Симметрия относительно оси абсцисс.
1
0
-1
\у - Ух + 2 _
/oil . i 1
-2-1
1 1 2 4 х
р(-2;0)
1
> ъ^^^ ^
^1 *
Р(0;-1)
lh
t
°г
У - Jx
si " '
У - -Jx

Справочные материалы
Алгебра в таблицах
491
8. Основные приемы преобразования графиков
/<-*>
Симметрия относительно оси ординат.
1Л*)1
Часть графика в верхней полуплоскости и
на оси абсцисс без изменения, а вместо
части графика в нижней полуплоскости
строим симметричную ей относительно оси Ох.
У1 х
Часть графика в правой полуплоскости и на
f(\x\) | оси ординат без изменения, а вместо части в
левой полуплоскости строим симметричную
правой относительно оси Оу.
{/-(0,5)
f{kx) I При k > 1 сжатие к точке (0; 0) вдоль оси абс-
{k > 0) | цисс в k раз; при 0 < k < 1 растяжение от
точки (0; 0) вдоль оси абсцисс в 1/k раз.
kf(x)
(k>0)
При k > 1 растяжение от точки (0; 0) вдоль оси
ординат в k раз; при 0 < k < 1 сжатие к точке
(0; 0) вдоль оси ординат в 1/k раз.
У ■■ 2С08Х
у — COSX

492
Справочные материалы
Алгебра в таблицах
9. График уравнения с двумя переменными
ах + Ьу = с
Прямая линия.
(х-а)2 + (у-Ь)2 = В?
Окружность с центром (а; Ь) радиуса Д.
\Jjy—'
у = Ja2-:
Полуокружность с центром (0; 0) радиуса а.
у = ах2 + Ьх + с
Парабола вида у = ах2;
при а > 0 ветви вверх,
при а < 0 ветви вниз;
вершина
Ъ i ч
х = ay2 + by + с
Парабола вида х = ау2;
при а > 0 ветви вправо,
при а < 0 ветви влево;
вершина
(х - а)(у -b) = k
кФО
Гипербола вида у = - ;
асимптоты х = а; у =Ь.
ко *
V *>0

Справочные материалы
Алгебра в таблицах
493
9. График уравнения с двумя переменными
W + M-i
Квадрат
l*-fl| + \у-ь\ в г
т п
т > О, п > О
Ромб
Н-М-1
« Перекресток »
Если дан график зависимости F(x; у) = 09то график зависимости F(x - а; у - Ь) = 0 можно получить
переносом всех точек на вектор р (a; ft);
график F (\х\; у) = 0 можно получить, оставив часть графика в правой полуплоскости и на оси
ординат без изменения, а вместо части в левой полуплоскости построить линию, симметричную
правой относительно оси Оу; график F (х; \у\) = 0 можно получить, оставив часть графика в верхней
полуплоскости и на оси абсцисс без изменения, а вместо части в нижней полуплоскости построить
линию, симметричную верхней части графика относительно оси Ох.
10. Квадратный трехчлен
Квадратный трехчлен ах2 + Ьх + с — это
многочлен второй степени; а Ф 0 — первый
коэффициент; Ь — второй коэффициент; с —
свободный член.
График функции F(x) = ах2 + Ъх + с — парабола;
Ъ
координаты вершины х0 = - 5— »
Lid
Уо = Р(хо) = -
Ъ -4ас
4а
2Э
'4а'
Выделение полного квадрата:
ах
+ Ьх + с=а(х + £] -
b -4ас
4а
D = Ь2 - 4ас
трехчлена.
дискриминант квадратного

494
Справочные материалы
Алгебра в таблицах
10. Квадратный трехчлен
Корни квадратного трехчлена
D<0
Квадратный трехчлен не имеет корней и
сохраняет знак первого коэффициента при
всех значениях х:
а • F(x) > 0.
а<0 ук
-Sl—
I I
а>0
\У
х0
D=0
Квадратный трехчлен имеет один корень
(два равных корня) х = х0 = - «—"
У функции F(x) два промежутка знакопо-
стоянства, на каждом из которых она
сохраняет знак первого коэффициента:
aF(x) >0(хф х0).
Парабола касается оси абсцисс в своей
вершине.
о<0 ук
а>0
Л
Т
\
и
D>0
Квадратный трехчлен имеет два корня:
-ъ-Jd -& + Ур
2а ; *2 2а
У функции F(x) три промежутка знакопо-
стоянства.
а<0 ук
*1-
*о
хх>х2
*1<*2V
Теорема Виета
Если квадратный трехчлен ах2 + Ъх + с
(квадратное уравнение ах2 + Ъх + с = 0) имеет корни
Xi и х2 (т.е. D > 0), то
*1 + *2---;
*l-*2-S
Для приведенного (а — 1) квадратного
уравнения х2 + рх + q = 0
х1 + х2 = ~~Р» *1 " *2 = 9*
Обратная теорема: Если числа *х и t2 таковы,
что ti + *2 = """ и *1 " *2 = ""» то они являются
корнями квадратного трехчлена ах2 + Ьдг + с
(квадратного уравнения ая2 + &х + с = 0).
Пример. Квадратное уравнение я2-(5+ *Jl)x + bjl = 0 имеет корни л: = 5; л: = Jl.
Разложение квадратного трехчлена на линейные множители
D<0
Квадратный трехчлен на линейные множители не раскладывается.
£>>0
D = 0
ах2 + Ъх + с = а(х - хг)(х - х2)
ахг + Ъх + с
= а(д
А12
2aJ

Справочные материалы
Алгебра в таблицах
495
10. Квадратный трехчлен
Составление квадратного трехчлена с корнями tl
Существует бесконечно много квадратных
трехчленов с корнями ti и t2; они имеют вид
а(х2 - (*! + t2)x + *! • t2),
среди них один приведенный:
х2 - (tx + t2)x + tx • t2.
И *2
Призер. Приведенный квадратный трехчлен с
корнями 2 и 8.
*2~
так как 2 + 8 = 10,,
Юл:+ 16,
2 а= 16.
Корни квадратного трехчлена ах2 + Ьх + с
положительны, если
*
с
хл • х9 = — > 0
1 г а
хл +х9 = >0
1 2 а
D - &2-4ас£0
отрицательны, если
«
*1 *2 - 7 > 0
*1+*2= ""J <0
1> = &2-4ас>0
одного знака, если
,
*1 Х2 = "|>0
D - 62-4ас^0
разных знаков, если
хл • х9 — — <0
1 z a
11. Прогрессии
Последовательность — функция натурального аргумента.
Задание последовательности формулой общего
члена
Задание последовательности рекуррентным
соотношением
an = /(л), п е ЛГ
an = л2 + л + 41
а^ = 43; а2 = 47; аз — 53; ...
Дано: ах; а2;...; ап _х
Числа Фибоначчи: 1; 1; 2; 3; 5; 8; 13; 21; 34; ... . (аг = а2 = 1; ап +2 = ап + ал + 1)
Формула общего члена: ап = -y=[f * ) ~( ~2 ) )•
Свойства: аг + а3 + а$ + ... + а2п + 1 = а2п + 2; а2 + а± + а6 + ... + а2п = а2п +1 - 1.
Арифметической прогрессией называется
последовательность, заданная рекуррентным
соотношением: ап + i = ап + d, п е jv
(ax — первый член прогрессии, d — разность
прогрессии).
Геометрической прогрессией называется
последовательность, заданная рекуррентным
соотношением: Ьп +1 = Ьп • g
(Ьх * 0 — первый член прогрессии; q Ф 0 — зна-
менатель прогрессии).

496
Справочные материалы
Алгебра в таблицах
11. Прогрессии
Допустимые значения
Формула общего члена
Характеристическое
свойство
Формула суммы
п первых членов
Другие формулы
Арифметическая (-*-)
a1nd любые
/ал = ^ + (71 - \)-d
2 =а*
, а1+ал 2a1+(n-l)d
* Sn= 2 " п = 2 "п
ап~ат
— а, (Д 4- /71)
ал +1 = sn +1 - Sn
ах + ал = а2 + ад >! = ... = ал
+ ад-* + 1
Геометрическая (-н-)
&! и q не равны нулю
ft.-fti-ff""1
К +1 • &п -1 = ъп
ьп*о
-1 с b*~b»q fc i-<?"
g = l,S„=n-&1
&n + 1 = Sn + 1 ~ &n
bl'bn=b2'bn-l = — = bk'bn-k + l
Бесконечно убывающая геометрическая прогрессия (0 < \q\ < 1)
п Ь1
lim q = 0, S = lim S = .
7l-»00 Л-»00 1 —q
Формула суммы:
1-g
Примеры
0 37 37
0,(37) = 0,37 + 0,0037 + ... = г _'Q Q1 = ^
(&! = 0,37; q = 0,01)
0,5(2) = 0,5 + 0,02 + 0,002 + „.. = \ + ,0,°2. =
* 1—0,1
Суммирование
l + 2 + 8 + 4 + ... + n-*^; 1^2^32-f4^ + ... + n^n(ra + 1)6(2ra + 1)
l3 + 23 + 33 + 43 + ... + n3=n2(7l/<+1)2
4
Примеры
Если аЛ арифметическая прогрессия, то
1 1 , 1 f 1 . 1
ага2 а2аг <
в1-в»+Г
*За4 ап'ап + 1
Все натуральные числа, дающие при делении
на 7 в остатке 5, имеют вид
ап = 7(л - 1) + 5 = In - 2, п е JV.

Справочные материалы
Алгебра в таблицах
497
12. Тригонометрическая окружность
Тригонометрической (единичной) окружностью называется
окружность с центром в начале координат, радиуса 1. Точки
единичной окружности можно поставить в соответствие
действительным числам. Числу 0 ставится в соответствие точка
Р0(1; 0), а каждому числу t ставится в соответствие точка Pt,
полученная поворотом точки Pq(1; 0) на угол t вокруг начала
координат (если t > 0, то поворот осуществляется против
часовой стрелки, если t < 0 — по часовой стрелке).
Таким образом, каждому действительному числу t
соответствует единственная тоЧка на единичной окружности Pt,
а каждой точке Pt — бесконечное множество
действительных чисел вида t + 2nk9 k ^ Z.
Длина дуги P^Pt = * (0 < * < 2я).
I четверть: о + 2nk < t < г + 2nk .
II четверть: ^ + 2nk<t<n + 2nk .
Ill четверть: n + 2nk < t < -z- + 2nk
Зя
IV четверть: -=- + 2nk <t <2n + 2nk.
Связь градусной и радианной мер: а = к • I ттгг0) (радиан); х (радиан) = I - • 180 1 .
Две точки, симметричные относительно
оси абсцисс
оси ординат
начала координат
а = ±* + 2пт, т GZ
а = (-l)nt + nn,n^Z
а = t + nk9 k ^ Z
Вершины правильного n-угольника,
вписанного в единичную окружность
(одна из вершин Pt).
1
P-t "* Pln-t
Pt(a;b)
P^(-b;a)
t+2
Pn+t(-a;-b) Р^;-а)
>-t
(b;a)
Pn.t(-a;b) P3*_/ b; a) P.t(a;-b)

498
Справочные материалы
Алгебра в таблицах
13. Тригонометрические функции
Косинусом числа * называется абсцисса точки Pt
единичной окружности, а синусом — ордината
этой точки.
t(cost; sin О
1 х
Тангенсом числа * называется отношение sin * к
cos * (cos t Ф 0).
sin*
cos*
Ось тангенсов — прямая x = 1.
Котангенсом числа * называется отношение
cos * к sin *.
tg* =
cost
ctg * = -г-:
ь sin*
(sin t * 0)
Ось котангенсов — прямая у = 1.
N(ctgf;l) '
7\
4
fi 1
Ы
1*" l
y-i
1 ^
Основные формулы
sin21 + COS2 * = 1, t € R.
j. . sin* л
tg * = , t * « + лЛ, ft e Z
& COS* 2
COS*
ctg * = -^— ,t*Kl,l<=Z
& sin*
Дополнительные формулы
1 + tg2* = g" » * * \ + лт, m e Z
COS *
9 1
1 + Ctg t = 2" »^^,ftGZ
sin *
Я/
tg*'Ctg* = 1,^T,/GZ
Формулы приведения
преобразуют
тригонометрические функции чисел « - ос,
я Зя
2 + а, я - а, я + а, у - а,
Зя
-р- + а в
тригонометрические функции числа ос ^ JR.
(Удобно считать а углом
первой четверти.)
cos *
sin *
tg*
я- а
я + а
-cos а
-cos а
sin а
-sin а
-tgoc
tgoc
я
2"а
sin а
cos а
ctg а
+ а
-since
cos а
-ctg а
Зя
-а
-sin а
-cos а
ctg а
Зя
у+а
sin а
-cos а
-ctg а
Периодичность
Четность
cos (* + 2я) = cos *
tg (* 4- Я) = tg *
cos (-а) = cos а
sin (* + 2я) = sin *
^sin = 2л
ctg (* + я) = ctg *
Tctg = K
sin (-a) = -sin a
tg (-a) = -tg a

Справочные материалы
Алгебра в таблицах
499
13. Тригонометрические функции
Значения тригонометрических функций некоторых углов
а, рад
О
я/6
я/4
я/3
я/2
Зя/2
а
0°
30°
45°
60°
90°
180
270
sin а
1
2
72
7з
2
-1
cos а
7з
2
_1_
72
1
2
-1
tga
7з
7з
не опр.
не опр.
ctg а
не опр.
7з
7з
не опр.
Тригонометрические функции в прямоугольном треугольнике
а
sin а = -
с
tga- g
cos а — -
с
ctg а =
Приближеные значения тригонометрических функций некоторых углов
a
5°
10°
20°
30°
40°
50°
60°
70°
80°
85°
sin a »
0,09
0,17
0,34
0,50
0,64
0,77
0,87
0,94
0,98
1,00
= cosa
tga =
0,09
0,18
0,36
0,58
0,84
1,19
1,73
2,75
5,67
11,43
= ctga
85°
80°
70°
60°
50°
40°
30°
20°
10°
a
Для малых положительных чисел sin a = а и tg a = a.
Знаки тригонометрических функций по четвертям
sin a
cos a
tg a и ctg a

500
Справочные материалы
Алгебра в таблицах
13. Тригонометрические функции
Способы нахождения значений тригонометрических функций числа (угла) а
по формулам
cos а в -0,6; II четверть
||sina|=» Vl-cos2a = Vl-0,36 =0,8
sin а > 0 ^ sin а = 0,8
sina 4
tga= —— -- =
cos a 3
1 3
ctg a = - jn ; IV четверть
1 л , . 2 169
—— = 1 + ctg'a - rjl
sin a x**
i • i 12
|sin a| = jg
Л 12
sin a < 0 => sin a = - j-3
■ | Г. ~Г /7~T44 5
|cosa|=Vl-sin a-Jl-jgg = ^
cos a > 0 ^ cos a = 75
1 12
tga-ctrs=-y
no вспомогательному треугольнику
tg a - 3; III четверть
l
3
sin a < 0 => sin a = - -7=
Л6
|9ччч^ /7q cos a < 0 =» cos a = - -7=
1 ^^ cf.ff (7 > 0 —> rtrr nr = —
sin a = 0,1; I четверть
l
«/99
v cos a > 0 => cos a = -rjr
^4" 1
>^ tga>0^tga=^
л/99 ctg a > 0 =» ctg a = л/99
Формулы сложения
f cos (x + i/) = cos л: cos у - sin x sin i/
] cos (л: - у) = cos # cos i/ + sin x sin i/
*\ sin (л: + у) = sin jc cos i/ 4- cos x sin i/
1 sin (л: - у) = sin л: cos i/ - cos x sin j/
"tg(x+„)-^^-..*5+»s
1-tgxtgp 2
у±\+ъп\х + уФ\л-кп,п^2
1 + tgxtgy 2
у * | + ran; x -у ф\+ nn, n GZ
Формулы двойного угла
(£cos 2л: = сов2л: - вт2л:
cos 2л: = 2 cos2* - 1
cos 2л: = 1 - 2 вт2л:
v\/)sin 2л: = 2 sin л: • cos х
^g2*=-^-;
1-tg л:

Справочные материалы
Алгебра в таблицах
501
13. Тригонометрические функции
Формулы понижения степени
Дополнительные формулы
£№os2* = 2 (1 + cos 2*)
sin2* = «(I -cos 2*)
(sin * + cos x)2 = 1 + sin 2x
1 + cos 2x = 2 cos2*
1 - cos 2x = 2 sin2*
sin x • COS x = о sin 2*
Формулы половинного угла
Универсальная подстановка
Icosfl-J!
N.fl-£
+ COS*
COS X
-COS*
x _ sin* _ 1 -cosjc
g 2 ~ 1 +cos* " sin* !
* * nky k e Z
sin* =
'Ml)
* ф к + 2яА, Л <= Z
Формулы преобразования
суммы в произведение
произведения в сумму
cos
cos
* + cos у = 2 cos —о
— • ППб
COS
* - cos 1/ = -2 sin —о
* + l/ . *-l/
sin
sin * + sin у = 2 sin о r • cos —2
cos * • cos у = о (cos (*-i/) + cos (* + y))
sin * • sin у = 2 (cos (* - 1/) - cos (* + y))
sin * • cos у = 2 (sin (* + z/) + sin (* - y))
sin
* - sin у = 2 sin —r
*-y * + £/
COS
, A sm(x + u) x x sin(*-i/)
tg * + tg 1/ = *•*- tgx-tgy = * SLJ-
& * cos * • cos у cos * • cos у
, , , sin(y + *) sin(i/-*)
ctg * + ctg у = -i—y . ctg * - ctg 1/ = -—y .
& & * sin * • sin у e 6 * sin * • sin у
Формула дополнительного угла
= л/Я
2 2
a cos * + Ъ sin * = л/л + & ' cos (* - а), где cos а:
л/а2+Ь
, sin а =
/ 2 , , 2
л/а + ft
,а2 + 62*0

502
Справочные материалы
Алгебра в таблицах
14. Логарифмы
Логарифмом положительного числа а по
положительному и не равному единице основанию Ь
называется показатель степени, в который надо
возвести число Ь, чтобы получить а.
log& а = с (а > 0; Ь > 0; Ь * 1) тогда и только
тогда, когда Ьс = а
Основное логарифмическое тождество:
Ъ = а.
Примеры
log с 7
5 5 = 7
logo 0» 7
2 2 =0,7
logo 3 я 1о*2 3 logo 3 3 Q
8 2 =(23) = (2 ) = 33 = 27
log2 8 = 3, так как 2* = 8
log9 27 =1,5, так как 9 =27
log0>25 16 = -2, так как 0,25 2 = 16
log25 J$ = 0,25, так как 250'25 = Jb
logg (-7) не определен, так как -7 < 0;
log(_2) (-8) не определен, так как -2 < 0, -8 < 0;
logx 27 не определен, так как не выполнено условие Ъ Ф 1.
Логарифмы по основанию 10 называются десятичными логарифмами: log10 а = lg а.
Лрцжеры
lgl00 = 2; lg 0,0001 = -4; lg 100000000 = 8;
3 < lg 2156 < 4; -К lg 0,56 < 0.
6
8
lga «
0,30
0,48
0,60
0,70
0,78
0,85
0,90
0,95
Логарифмы по основанию е называются натуральными логарифмами: loge а = In a.
е = 2,718281828459045... иррациональное число; е = 2,7.
6
8
9
10
100
1000
In a ~
0,69
1,10
1,39
1,61
1,79
1,95
2,08
2,20
2,30
4,61
6,91
Свойства логарифмов
Основные соотношения
Дополнительные соотношения
loga 1 = 0
tofcj—1
loga a = 1
log m a = -
a m
loga am =m
log m a = -
a m
Логарифм произведения:
logc (ab) = logc a + logc b.
Логарифм частного:
logc (a/b) = logc a - logc ft.
Логарифм степени:
logc ak = k logc a.
Переход к новому основанию:
logc a
loga & =
log6a
log mbn = Jlogaft
7П
logn ft logm ft
= logc ft
lognc logmc xv&c
log„ ft • log^ с = log^ b • log„ с
log„ b logn a
a = b

Справочные материалы
Алгебра в таблицах
503
14. Логарифмы
Примеры
1
log65
= 510*5в=6.
/yiog549 1og725 = 7log749 1og525
= V2~2 =2.
Сравнить: 4 и 6
logo 4 logo 6
Так как 6 = 4 и log3 7 > log3 6,
л10**7 ^ л1о*3*
то 4 > о
Сравнение логарифмов
Если 0 < а < 1 и 0 < хг < jc2, то loga jcx > loga jc2.
(знак неравенства меняется)
Если а > 1 и 0 < jcx < jc2, то loga хг < loga jc2.
(знак неравенства не меняется)
Если 1<а<Ь hjc>1,
Если 0<а<Ь<1и:
— - -» «=>а --с»с/ —
Если 0<a<fr<lnjc>l, тоlogaх>logbх.
Если \<а<Ь h0<jc<1, тоlogaх<log6jc.
Если 0<a<b<ln0<jc<l, тоlogajc<logbjc.
to loga x > log6 *.
log6.
log*.
logb*.
logb a > 0 тогда и только тогда, когда
положительные числа а и Ь лежат «по одну сторону от едини-
цы>: а>0;Ь>0и(а- 1)(Ь - 1) > 0.
log& а < 0 тогда и только тогда, когда
положительные числа а и ft лежат «по разные стороны от
единицы»: а>0;Ь>0и(а- 1)(Ь - 1) < 0.
Примеры
log0,7 0,2 <log0>7 0,11
logo,2 7 > log0>8 7
log62<log6ll
log5 7 > log8 7
log4 5 < log3 5 < log3 6 =
=> log4 5 < log3 6
Сравнить log4 15 и Vl7 .
Так как log4 15 < 4, a Vl7 > 4, то log4 15 < Jll .
Сравнить log3 4 и log4 5.
/ способ. log3 4 ? log4 5
log3 4-1 ? log4 5 - 1
, 4
log35
, 5
l°g4 7
4 5,4,5,^5
Так как g > j , то log3 g > log3 ^ > log4 ^ ,
т. e. log3 4 > log4 5.
IT способ. Рассмотрим функцию
In (x + 1)
In JC
/(*) = logx (*+!) =
при JC> 1.
In JC
JC+ 1
ln(* + 1)
JC
<0
(Injcr
_ jc-lnjc - (jc + 1) ln(jc + 1)
JC(JC + 1) (In jc)2
npnjc> 1.
Значит, log3 4 > log4 5, так как функция
/(jc) убывает.

504
Справочные материалы
Алгебра в таблицах
15. Уравнения
Корнем уравнения называется значение
переменной, при подстановке которого в уравнение
получается верное равенство.
Два уравнения называются равносильными,
если множества их корней совпадают.
Примеры
jc3 + х = 0 — один корень: х = 0.
(jc2 + х - 12) • л/х + 3 = 0 —- два корня:
jc = -3, х = 3.
sin (пх) = 0«— бесконечное число корней jc ^ Z.
jc2 + 2л: + 1 = (jc + I)2 — верно при всех х ^ R.
х2 = х2 + 1 — нет корней (пустое множество
корней 0).
Примеры
х2 = х + 2 и jc2 — jc — 2 = 0 равносильны.
х4 + 2 = -16 и sin 3jc = 2 равносильны.
Jx = 2jc - 6 и jc = (2jc - б)2 неравносильны.
Неравносильные преобразования могут привести к:
потере корня
появлению «посторонних» корней
х(х + 5) = 2л:
х + 5 = 2
JC--3
Потерян корень х
правильное решение:
х2 + 5л: - 2х = 0
л:2 + Зх = 0
jc(jc + 3) = 0
х = 0; л: - -3
jc +JC-1 4jc-3
jc-1 jc-1
л^ + л:-1 = 4г-3
л:2 - 3jc + 2 = 0
х = 1 ил: = 2
«Посторонний* корень jc = 1.
правильное решение:
л;2+л:-1 - 4jc-3
л;*1
х2-Ъх + 2 - 0
jc*1
Ответ: х = 2.
Методы решения уравнений
Разложение на множители
Произведение нескольких множителей равно
нулю, если хотя бы один из них нуль, а
остальные при этом существуют.
(х - IX*2 - 4) • Jx = 0 »
Ответ: 0; 1;2.
л: - 1
jc = ±2
л: = 0
л:^0
х - 1
л: - 2
л: = 0
Замена переменной
(х + 1 )4 + jc2 = 1 - 2л: <=> (х + 1 )4 + С*2 + 2л: +1) = 2 <=>
* - (jc + 1) ^0
.r + f-2 - 0
л: = -2
л: - 0
* - 1
f^0
Сравнение обеих частей по величине
sin7 л: - cos22 * = 1 <=> sin7 л: = 1 + cos22 jc,
sin JC < 1
1 + COS JC > 1
cos jc = 0 Icosjc = 0

Справочные материалы
Алгебра в таблицах
505
15. Уравнения
Использование монотонности
2х + Ъх = 29. Функция f(x) = 2х + 5х возрастает; /(2) = 29 => х = 2 — единственный корень.
Использование однородности
3(х + 8)2 - 4(х + 8)(х2 + 2х + 2) + (х2 + 2х + 2)2 - 0. Пусть х + 8 = а; х2 + 2х + 2 - Ь.
Тогда За2 - 4аЬ + Ь2 = 0,
х + 8 = х2 + 2х + 2
х2 + л: - 6 = 0
Xi = -3; х2 = 2
2Ь±Ь L Ь
а1,2 " "",о""; а или а = 3 "
Зх + 24 = х2 + 2х + 2
jc2 - х - 22 = 0;
1±J89
^3,4-—2~
Ответ: -3; 2;
1-789 1+789
Линейные уравнения (приводимые к виду ах = Ь)
а*0
один корень х = -
а
а =Ь = 0
бесконечное множество корней х е Д
а = 0, Ь*0
решений нет
Квадратные уравнения (приводимые к виду ах2 + Ьх + с = 0 (а * 0))
Ь\2 Ь-4ас
(0 Vе
х + «"J =
Наличие корней зависит от знака выражения: D = Ъ2 - 4ас (дискриминант квадратного уравнения).
4а'
D<0
корней нет
D = 0
один корень х = -=-
2) > 0 два корня
х" 2а ,Х" 2а
а>0 \ку
и
а>0
*У
а>0
kz
*о *
Частные формулы для решения квадратных уравнений.
Приведенное квадратное уравнение
х2+рх +д = 0 (а = 1)
Квадратное уравнение с четным вторым коэффициентом
ах2 + 2Ах + с = 0 (Ь = 2k)
Если D > 0, xlt 2 = "2 ;
если!) =0, х =2*
Z>* = A2-ac CD*=jD)
Г"*
Если 2)* > 0, х12 = ; если2)* = 0, х=

506
Справочные материалы
Алгебра в таблицах
15. Уравнения
Неполное квадратное уравнение
ах2 + с = 0 (& = 0)
ах2 + Ъх=0 (с = 0)
ах2 = 0
Если ас > О, решений нет;
если ас < О, х = ± / - - .
х(ах + fr) = О два корня:
b
jc =0, jc = -- .
а
один корень
jc=0
Алгебраические уравнения высших степеней
(приводимые к виду fix) = 0, где fix) — многочлен степени выше 2)
Разложение на множители
^з
- 2х2 - jc + 2 = О
х\х - 2) - (х - 2) - О
(jc - 2)(jc2 - 1) = 0 => х = 2; jc = ±1
Подстановка (биквадратное уравнение)
jc4 - 3jc2 + 2 = 0; jc2 = t
t2-3t + 2 = 0
t = 1; t = 2=>x =±1; jc=±72
Применение схемы Горнера
x3 - 4jc2 + jc + 6 = 0
-1
2
3
1
1
1
1
-4
-5
-3
0
1
6
0
6
0
=>x = -l
=>x = 2
=> x = 3
Использование монотонности
х3 + х-6л/5 =0
х3 + х = 6л/б
Функция Fix) = jc3 + jc возрастает на R;
*Хл/5) = 6л/5 =>
jc — л/б — единственный корень.
Возвратное уравнение
2jc4 - 5х3 + 6х2 - Ьх + 2 = О
Так как jc = 0 не является корнем, можно делить
Hajc2.
2jc2 - 5jc + 6 - - + 4 = О,
* jc2
2(x» + ;i)-6(x + i)+e-0.
Подстановка: i/ = x + - ; у2 - 2 = x2 + -5.
* x
2(i/2 - 2) - 5y + 6 = 0
2y2 - by + 2 = 0
Использование однородности
Зх2 + 4x(x2 + Зх + 4) + (x2 + Зх + 4)2 = О
Пусть у = х2 + Зх + 4.
Тогда Зх2 + 4ху + у2 = 0.
Решаем относительно х: х = -у; х = —z у.
Следовательно,
х - -х -Зх-4
2
Зх - -х -Зх-4
Ответ: -2; -3 ±Уб .
Уравнение <//(*) = Six) равносильно системе:
/(х) = g\x)
g(x)Z0
Уравнение JKx) = Jg(x) равносильно системе:
fix) = g(x)
/(х)^0(или£(х)^0)
Неравенства в системах, как правило, проверяют, а не решают.

Справочные материалы
Алгебра в таблицах
507
15. Уравнения
Иррациональные уравнения
Простейшие
V3* + l =2
Зх + 1 = 4
JC = 1
Vl-2* =-5
корней нет
Возведение обеих частей уравнения в степень
[5х + 6^0; 3* + О0
л/5х + 6 + л/Зх + 4=2» j 5*+ 6 + 3*+ 4 + <=>
1+2«/(5* + 6)(Зл; + 4) - 4
Г5х + 6£0
U(5* + 6)(3x + 4) = -4*-3
[5* + 6£0;-4*-3>0
1(5х + 6)(Зх + 4) - (-4*-3)2
<=> х = -1
Замена переменной
л/2 -х = 3* + 8
Пусть у = л/2-д: ^ 0.
Тогда х = 2 - у2 и i/ = 3(2 - у2) + 8 <=>
2 ^
3i/ Н-1/-14 - О
<=> I/ = 2 <=> V2-* = 2 <=> х = -2
<=>
Уравнения, связанные со степенной функцией
Гс 2/3 , 1/3 с л
15* + * -6 = 0
I х>0
5i/2 + i/-6 = 0=>i/ = 1;i/ =
х1/3 = 1 =* х = 1
<0
53л£* +tyx -6 = 0
5у2 + I/ - 6 = О
i/ = \fx = 1, у = У* =-g
х UJ 125
n i 216
Ответ: x = 1; jc = -777^ .
1 2 4
3 3
J JC • X
[ jc>0
3 + 3
X =
*2 = 4
л: =±2
Ответ:
=
4
л: =
4
=2
Показательные уравнения
Решение простейших показательных уравнений
основано на монотонности показательной функ-
ции у = ах (а > 0, а Ф 1, Z)(i/) = Я, £(i/) = (0; +00)).
Простейшее показательное уравнение ах = Ь
при Ь > 0 имеет единственное решение, записы-*
вающееся в общем виде х = loga b.
При Ь < 0 решений нет.
6* = 36
jc = log6 36
х = 2
J 8
* =log2(1/8)
* = -3
100* =10
* = logioo Ю
х =0,5
10* = 3
* = lg3
ех = 2
х =1п2
625х = -25
решений нет
Уравнения вида af^ = а**** равносильны уравнению f(x) = £(*).

508
Справочные материалы
Алгебра в таблицах
15. Уравнения
Методы решения показательных уравнений
Приведение к одному основанию
X
5х -0,2= 1252 л/5"
Зх 1
5* • 5"1 = 5 2 • 52
3* + 1
5* " х = 5 2
Зх + 1
ж - 1 = —5— =^ дс = -3
Вынесение за скобку
7* + 7* + 2 = 350
7*(1 + 72) = 350
пх 350
7х = : = 7
1 + 72
х = 1
Логарифмирование обеих частей уравнения
61/*.2* = 12
Логарифмируем по основанию 2:
-log26 + x=log212<=>
<=> 1 + log2 3 + jc2 = (2 + log2 3)jc
x2 - (2 + log2 3)x + (1 + log2 3) = 0
Ответ: x = 1; л; = 1 + log2 3.
Составление отношения
4х + з*-1 = 4*-1 + 3* + 2
4х -4х~1 = Зх + 2-Зх~1
4*_1(4-1) = 3*_1(33-1)
4*-1-3 = 3*~1-26
4х"1 26 (4Л*-1 26 26 ,
«Завуалированное» обратное число
(75 -2)х+(7б +2)*= 18
(75 -2)(75 +2) = 5-4 = 1
Пусть(75 -2)х =у >0
«/ +- = 18=>1/=9±475
(75 -2)* =9-475 =
= (75 -2)2=>*=2
(75 -2)х = 9 + 475 =
= (75 +2)2 = (75 -2)_2=>х = -2
Ответ: 2; -2.
Замена переменной
25* + 5* + г - 6 = 0
5* = i/ > 0
i/2 + 5i/ - 6 = 0
i/ = l;i/=-6<0
5* = 1 => x = 0
Использование однородности
3 16*-12*=4-9*
Делим на 9х > 0:
з(1Г-(1Т-4-°
IlycTbfgJ =у>0^
=>3y2-y-4 = 0=>
4 , л
=>у-д;у=-ко=>
Использование
монотонности
2х + 5* = 29
/(jc) = 2* + 5х возрастает
наЯ./(2) = 29=>* = 2 —
единственный корень.
Логарифмические уравнения
Решение простейших логарифмических уравнений основано
на монотонности логарифмической функции
y=\ogax(a>0;a*l;D(y) = (0;+°o); E(y) = R).

Справочные материалы
Алгебра в таблицах
509
15. Уравнения
Типы простейших логарифмических уравнений
1) 1°£а х = Ь при всех допустимых а имеет единственное решение х = а*.
2) loga (f(x)) = b равносильно уравнению f(x) = a6.
3) loga (/(*)) = £(*) равносильно уравнению f(x) = a****.
4) loga (f(x)) = loga (g(x)) равносильно системе:
/(*) - *(*)
/(*)>0
g(x)>0
Причем любую из двух последних строк можно (и, как правило,
нужно) опустить.
В логарифмических
уравнениях, как правило,
совершенно не обязательно
находить области
существования функций,
входящих в уравнение.
Достаточно проверить, какие
из полученных корней
уравнения системы
удовлетворяют неравенствам
в системе.
Уравнения, сводящиеся к типу 4
log2 (я2.+ х - 2) - 1 + log2 х »log2 (х2 + х - 2) - log2 (2х) <^>
2 , «л Г 2
\х +х-2 = 2х
<=> < <=>
2*>0
дг-2 = 0
х>0
х = -1
<=> <\ х = 2 <=>* = 2
I *>0
Замена переменной
*■(£) +Ifx-Т
(lg 10 - lg xf + lg x = 7
J/ = lg*=>(l-l/)2 + J/ = 7:
lgx = 3
L lg x = -2
Ответ: x = 1000; * = 0,01.
Потенцирование уравнений, сводящихся к типу 4
logj (х +1) + log3 (!) - 2" 21°Si (*2)<=> loSi (* +1)" logj \ - lo8i §
-logx(*2)<=>j
з
x>0
w 2(* + l) _ J_ « 2(* + l) 1 »
lOgl lOgx —k - —5
9x'
x>0
9*
<=> x =
Vll-3
Уравнение с неизвестным в основании логарифма
log
<=><
On
*5=3«
*>0
** 1 <
3 к
jc = 5
teem: \[b.
<=>*
= зу
log 2 * =0,5<=>
х2*1
*>0
. 2 0.5
(* ) - X
<=* i
х>0
**-1
лс>0
**1
Ответ: х е (0; 1) и (1; +оо).
log(_x) 25 = -2
дс<0
**-1
(-х)-2
25
*<0
**-1
* " 25
Ответ: х = - г .
о

510
Справочные материалы
Алгебра в таблицах
15. Уравнения
Тригонометрические уравнения
sin х = а
cos х = а
Н>1
Н<1
H>i
H<i
л-arcsin а,
arcsin а
решении нет
решений нет
х = (-l)*arcsin а + яд, n^Z
-arccos а
х = ± arccos а + 2яд, д ^ Z
При |о| < 1:
- 5 ^ arcsin а < ~
sin(arcsin а) = а
arcsin (-а) = -arcsin а
arcsin а
arccos а
0
Л
2
7з
2
arcsin а + arccos а =
При |а|< 1:
0 < arccos а < я
cos(arccos а) = а
arccos (-а) = я - arccos а
tg х = а
ctg jc = а
х = arctgа + яп, д е Z
х = arcctg а + яд, д
Z
arcctg а
я+arcctg
При любом а:
я х я
«2 < arctg а < -
tg (arctg а) = а
arctg (-а) = -arctg а
arctg а + arcctg а = ^
При любом а:
О < arcctg а < я
ctg (arcctg а) = а
arcctg (-а) = я - arcctg а
Частные решения
х = яд. п ^ Z
х — р + 2яд, д
х = р + яд, мд ^ Z
2яд, д е Z

Справочные материалы
Алгебра в таблицах
511
15. Уравнения
sin (/(*)) = а
при \а\ < 1:
/(x) = arcsin a + 2nn
_ /(x) = к -arcsin a + 2nn
n^Z
cos (/(x)) = a
при \a\ < 1:
/(x) = ±arccos а + 2ял
л GZ
tg (/(*)) = a
при всех a:
f(x) = arctg a + теп
л GZ
Методы решения тригонометрических уравнений
Тригонометрические уравнения, приводимые к уравнениям от одной
тригонометрической функции одной переменной, решаются (как
правило) подстановкой.
sin2 х + 4cos х = 2,75
1 - cos2 х + 4cos x = 2,75
COS X = t\ \t\ ^ 1
t2- 4*+ 1,75 = 0
1 7 л
к
x =±Z + 2яп, n ^ Z
tg x + 3ctg x = 4
tg x + i = 4
* tgx
tgx = t
t2 - 4* + 3 = 0
* = 1; t = 3
4 n,k<^Z
x = arctg 3 + rcfc
cos2 x + cos 4x = 0,25
0,5(1 + cos 2x) + 2cos2 2x
cos 2x = u; \u\ ^ 1
4u2 + u - 1,5 = 0
1 3
u = 2;"=~4
1 3
x = ±p arccos(-j ) + nn;
x =±~ + яя, n^Z
о
-1 = 0,25
Однородные тригонометрические уравнения и уравнения, сводящиеся к ним
2sin х • cos х - cos2 х = 0
cos x(2sin x - cos x) = 0 (
cos x = 0 =* x = 5 + ли, n ^Z
2sin x - cos x = 0
Корни уравнения cos x = 0 не удовлетворяют
этому уравнению.
Делим на cos х ф 0:
2tg х - 1 = 0;
1
tgx = 2
х = arctgo + яп, n^Z
5sin2 x + sin x • cos x - 2cos2 x = 2
5sin2 x 4- sin x • cos x - 2cos2 x = 2cos2 x
3sin2 x + sin x • cos x - 4cos2 x = 0
cos x * 0. Делим на cos2 x:
3tg2 x + tgx-4 = 0=*tgx = l; tgx =
к 4
x = T + ял; x = -arctgo + nk;
n,k^Z
+ 2sin2x
4
3
Разложение на множители
л/2 sin х • cos х - 2 = cos х -2 л/2 sin х
л/2 sin х • cos х - cos х - 2 + 2 л/2 sin x = 0
cos x( 72 sin x - 1) - 2(1 - л/2 sin x) - 0
(л/2sin x - l)(cos x + 2) = 0
л/2втх-1 = 0
, cosx + 2 = 0
1
sin x = -=
V2
x = (-l)n • j +nn;nGZ
cos x = -2, корней нет.

512
Справочные материалы
Алгебра в таблицах
15. Уравнения
Уравнения, решаемые на основе условия равенства тригонометрических функций
sin f(x) = sin <p(jt)
f(x) - ф(*) + 2яА
f(x) = я-<р(д:) + 2яп
n^Z.k^Z
cos f(x) = cos <p(jt)
Г /(*) = ф(дг) + 2тт
1 /(*) = -<p(x) + 2яА
tg /(*) = tg <p(x)
/(*) = ф(х)+Я71
<р(*)*2+я*
Уравнения с обратными тригонометрическими функциями
arcsm х = а
arccos х = а
arctg х = а
arcctg х = а
к к
"2<а<2
х = sin а
О < а < п
х = cos а
п п
"2<а<2
х =tga
О < а < я
jc = ctg а
а < -г или а > о
решений нет
а < 0 или а > к
решений нет
. п п
а < -о или а ^ о
решений нет
а < 0 или а ^ я
решений нет
Уравнения с параметрами
2* + 3 л
Решить уравнение = 0 для каждого зна-
х - а
чения а.
Данное уравнение равносильно системе
\2х + 3 - О
\х - а*0
X - -:
**а.
3 3
Ответ: при a * -г * = -5 ,
при Д = ~~2 решении нет.
Найти все такие значения р, для которых один
из корней уравнения х2 - Зрх + 2р2 = О равен
1, и для каждого такого значения р найти
остальные корни.
Для того чтобы один из корней уравнения был
равен 1, необходимо и достаточно, чтобы
I2 - Зр • 1 + 2р2 = 0, т. е. 2р2 - Зр + 1 = О,
- 1
Pl = l, Р2=2'
Прир = 1 х2 - 3* + 2 = 0, хг = 1, х2 = 2;
1 2 3 1 л , 1
прир = g х - 2^+ 2 = °» *i = lf *2= 2"
Ответ: прир = 1 и прир = «. Прир =1 х2 = 2;
1 1
прир =2 *2=2'
При каких значениях а уравнение 4х - (а + 2) 2х + 2а = 0 имеет а) хотя бы одно решение; б) ровно
одно решение; в) более одного решения?
Сделаем замену 2х = t, t2 - (a + 2) • t + 2a = 0, tx = a, *2 = 2.
2* = 2, x = 1 при любом a.
2* = a, при a ^ 0 решений нет; при a > 0 jc = log2 a.
Заметим, что при a = 2 jc = 1 совпадает с первым корнем.
Ответ: а) при всех значениях а; б) при а < 0 и а = 2; в) при 0<а<2иа>2.

Справочные материалы
Алгебра в таблицах
513
15. Уравнения
При каких значениях Ь уравнения sin2 х - (3 + b) sin х + ЗЬ = 0 и х2 = Ъ равносильны?
Если первое уравнение имеет решение х0, то оно имеет и бесконечно много решений вида х0 + 2яЛ,
т. е. не может быть равносильно уравнению х2 = fr, имеющему не более двух решений.
Уравнения равносильны, если они оба не имеют решений.
Уравнение х2 = Ъ при Ъ < О не имеет решений, второе уравнение равносильно объединению
[~ Q не имеющему решений при Ь < -1 или Ъ > 1. Таким образом, оба уравнения не имеют
Sin X — о,
решений, т. е. равносильны при Ь < -1.
Ответ: при Ъ < -1.
Найти все значения р, при которых сумма действительных корней уравнения х2 -рх + 3 = 0
меньше пяти.
\р<Ъ
ПриЛ^О хг + х2=р. in^n»i_2
fp<5
[D^ О
Ответ:ре (-оо; -273]и[2л/3 ; 5)
«i «(-оо;-2л/3]и[273;5).
[р - 12 > О
При каких значениях m уравнения л^ + 3х-т = 0и /их2 + х + 3 = 0 имеют общий корень? Для каждого
такого значения т найти этот корень.
Пусть t — общий корень уравнений. Составим систему двух уравнений с двумя неизвестными (t и т):
t2 + 3f - т = О
2 **
mt + t + 3 = О
- т [t(t + 3) = т
т = — mt • t
шг + 3) =
U + з = -
\х2 + Зх = О
При/71 = 0< общий корень х = -3; при t = -1 /я = (-1)(-1 + 3) = -2
U + з = о
t(t + 3) = т
Г/п = О
х + Зх + 2 = О
общий корень х = -1.
-2х2 + х + 3 - О
Ответ: при m = -2 х = -1;прит = 0 х = -3.
Найти все пары действительных чисел а и Ь, при
которых уравнение |х - 1| + |х + 3| = адг + Ъ имеет
бесконечное множество решений.
|х-1| + |х + 3| =
-2х - 2
4
2х + 2
при х<-3
при -3 ^ х < 1
при х > 1
Уравнение имеет бесконечное множество
решений, если ах + Ъ тождественно равно -2х - 2,
т. е. а = -2; Ь = -2.
Аналогично ах + Ъ тождественно равно 4,
т. е. а = 0; Ь = 4.
Аналогично а = 2; b = 2. Ответ: (-2; -2); (0; 4);
(2; 2).
При каких значениях m уравнение
х2 - тх +1=0 имеет два корня, расстояние
между которыми на числовой оси равно 2?
Уравнение имеет два различных корня, если
D > 0, т. е. т2 - 4 > 0. Расстояние между
корнями на числовой оси равно
, , \т - Jd т + V5
l*i-*2l= J 2 2 1
т2-4>0
•*Jm2 - 4 = 2
Ответ: т = -ijl, m = 2л/2 .
Имеем систему:
\т = -
= 272
272
17-1019

514
Справочные материалы
Алгебра в таблицах
16. Методы решения систем уравнений
Метод подстановки
[ж + Ъу = 6
[х2 + Зу = 4
6 - х
У =
ж2 + д.6^ = 4
I/ "
Ьх2-
6-х
Зх - 2 = О
У =
6 - х
х°-ъ
х = 1
2 <=>
2
32
у = 25
*= 1
У = 1
2 32
Ответ: (-g; jjjjMl; 1)-
2* + I/ = я
cos(3* - 2у) = 0,5
«=>
у = я - 2х
cos(3jc - 2я + Ах) = 0,5
соэ7л: = 0,5
у = я - 2х
_ п_ 2%k
х~ 21 + 7
19я
У =
4яй
7
я
21
23л
21
2яп
7
4яге
7
n,*GZ
Л . .. 2rcft 19я 4яЛЛ
Ome^/nrigi + — ;^-~ — J;
"21 + 7 ; 21 7 J* Д*
Метод алгебраического сложения
сложим
|5х + 2у = 9 умножим на 3 J15jc + 6у = 27 уравнения [29jc = 29
[7х - Зу = 1 умножим на 3 [l4x - 6у = 2
Ответ: (1; 2).
<=>
х = 1
7х - Зу = 1 [у - 2
[cos х cos i/ = 0,75 сложим уравнения системы f cos xcos у + sinx sin у — 1
[sin х sin у - 0,25 вычтем уравнения системы [cos xcos у - sin* sin у - 0,5
cos(x - у) = 1
cos(x + i/) = 0,5
x - у = 2nk
к
3
x + у = ±5 4- 2кп
x - у = 2rcft
х + у = о + *ял
х - у = 2rcft
х + у = -г + ^яд
Ответ: (~ + я(п + ft); « 4- я(п - ft)]; (~g + я(п + ft); -г + я(п - ft) j, л, ft ^Z.

Справочные материалы
Алгебра в таблицах
515
16. Методы решения систем уравнений
Дополнительные методы
Применение теоремы Виета
х + у = 5
х-у - 4
х,у — корни уравнения:
а2 - 5а + 4 = 0.
а = 1;а =4.
Ответ: (1; 4); (4; 1).
Симметрические системы
2 2 Л
* + 1/ - Ъху =
х + у - ху - 1
-1
замена
X + 1/ =р
*У - 3
(р' - 2q) -3q-
р - q = i
-i
Сведение к объединению более простых систем
х-у = 0
| х- - бху + 4у2 = О ((х-у)(х-4у) = 0
с - бху + 4
[Зх2-2у = 8
Зх*-2у = 8
<=»
2 (1>
Зх -2у - 8
*-4у = О
Зх2-2у = 8
(2)
(2; 2)
I* -У
(1)1зх2-2х-8 = 0^(-4/3;-4/3)
(2)
Г* = 4j/
-у-4 = 0 ^
1+7385 1+«/385\ А-7385. 1-7385^
.24у--»-4-П V 12 ' « Д 12 ' 48 j
!)(
Использование однородности
| Зх хуЛ-у 5 Умножим первое уравнение на (-3),
lx2 + 2i/2 = 3
второе — на 5 и сложим.
[-9x2 + 3xi/-3i/ = -15 f-4xz + 3xi/ + 7i/ = 0 Г(У + *)(7у-4х) = О
[б*2 + 10i/2 = 15 U2 + 2у2 = 3 U2 + 2у2 = 3
\у + х = О
[jc2 + 2i/2 = 3
\1y-4x = О
l*2 + 2i/2 = 3
r(i;-D
Ц-1; 1)
'ПЛ 4j3\
У 9 ' 9 )
\(_7j3 _4j3\
[{ 9 ; 9 )
Ответ: Ц; -1); (-!; 1); (if, 4-^ ); (-Z£ -*£ ).
17*

516
Справочные материалы
Алгебра в таблицах
17. Неравенства
Строгие неравенства
Число а > Ъ (а больше ft), если разность (д - ft) положительное число.
Если а < ft, то Ь > а. В этом случае разность (а - ft) отрицательное число.
Нестрогие неравенства
g^ft
c>d
Свойства числовых неравенств
д, ft — любые числа
Если д > ft и ft > с, то а > с (свойство
транзитивности).
Если д > ft, то а + с > Ь + с (с ^ R).
Если а > Ь и с положительное число, то ас >Ьс.
Если д > ft и с отрицательное число, то ас < be.
Если д > ft и о d, тод+oft+d.
а,Ь — положительные числа
Если g > ft > 0, то - < т •
а Ь
Если а > b > 0 и с > d > 0, то ас > bd.
Если а>Ь>0и mEJV,Toam>b'n.
Если g > ft > 0 и m^N9 то mJa > mJb,
Двойное неравенство (д < b < с)
Сложение двойных неравенств
g<ft<c, p<:m<q =$a+p<:b + m<c+q
Умножение двойных неравенств с
положительными членами
0 <а <Ь <с; 0 <р < т <q => ар <bm <cq
Методы доказательства неравенств
Составление разности (если разность двух чисел
положительна, то уменьшаемое больше
вычитаемого).
Метод использования известных неравенств.
Метод усиления (использование транзитивности).
Использование монотонности функции,
применение производной.
Пример. Доказать неравенство: ех > 1 + х при х > 0.
Рассмотрим функцию f(x) = ех - 1 - х. f'(x) =
= ех - 1 > 0 при х > 0. Следовательно, f(x)
возрастает на [0; +оо). Но /(0) = 0. Значит, f(x) > 0 при
х > 0. При х = 0 неравенство обращается в
равенство. Итак, ех - 1 - х > 0, то есть ех > 1 + х\
при х > 0.
Сравнение средних величин положительных чисел (а > b > 0, at > 0, п ^ N)
Среднее арифметическое
Среднее геометрическое
Среднее гармоническое
двух чисел
g + ft
2
двух чисел
Jab
двух чисел
2аЬ 2
а+Ъ 1+1
а ft
п чисел
а1+а2 + ...^ап
п
п чисел
фг-а2-...-ап
п чисел
п
а\ °2 ап

Справочные материалы
Алгебра в таблицах
517
17. Неравенства
Сравнение средних величин положительных чисел (а > Ь > О, ai > О, п ^ N) (продолжение)
Среднее квадратичное
двух чисел
I
l 2 . l 2
д чисел
/22 2
l^+aj + .-.+a,,
д
а >J__>— » Tab >i—J >&
+ 7
a о
(верно и для д чисел)
Линейные неравенства (приводимые к виду ах > Ь; ах > Ь; ах <Ь; ах < Ь)
3 • х > -6
х>-2
jc е (-2; +оо)
-5 • х > 1
*^_5
xe(-oo;-g]
0-х <2
Я
0-х >8
jc^{0}
(75 -Jl)x>{Jl-*tf)
д: < 1, так как л/б - л/7 < О
* €= (-оо; 1)
Квадратные неравенства
(приводимые к виду ах2 + Ъх + с > 0, a#2 + frx + с < 0, a > 0)
Для решения квадратного неравенства вычислим дискриминант
D = Ъ2 - 4ас и определим корни квадратного трехчлена.
Неравенство
D<0
\^у
D = 0
Х_-/
D>0
\^А
ах2 + Ьх + с > О
Я
xe(-OO;x0)U
u (х0; +оо)
X
е (-°°; *i) и
и(х2;+°°)
ад:2 + &х + с < О
решении нет
решении нет
х е (jq; д:2)
Простейшие иррациональные неравенства
Л/Х <!
Jx > а
а <0
решении нет
д: > 0 <=> д: е [0; +оо)
а = 0
решений нет
* > 0 <=> х е (0; +оо)
а >0
„2
О < х < аГ, х е [0; а*)
д: > а2 <=> д: е (а2; +оо)

518
Справочные материалы
Алгебра в таблицах
17. Неравенства
Простейшие иррациональные неравенства (продолжение)
Жх) < gix)
JKx) >g(x)
JfW) > ЛЦГ)
равносильно системе
[g(x) > О
2
fix) > О
равносильно объединению систем
g(x)<0
fix) > О
*(*) > О
f(x)>g\x)
равносильно системе
fix) > gix)
g(x) > О
Простейшие показательные неравенства
а**> < т
jf(x)
> т
тп ^0; а >0, а * 1
нет решении
R
нет решении
D(f)
т >0; а > 1
х < \ogam
х > logam
f(x) < \ogam
f(x) > logam
fix) > \ogam
m>0;0<a<l
x > \ogam
x < \ogam
при a > 1 равносильно неравенству fix) > gix)
при 0 < a < 1 равносильно неравенству fix) < gix)
fix) < \ogam
a«*> > a*(*>
Простейшие логарифмические неравенства
m^R
logax < m
logax > m
logjix) < m
logjix) > m
a>l
x<a
x>0
x>an
fix)<a
f(x)>0
fix) > aP
0<a < 1
x>a"
x<a
x>0
fix) > a"
fix)<a
f(x)>0
logjix) < logagix)
l°eH{x)fix) < ^OgH{x)gix)i
при a > 1
равносильно системе
f(x)<g(x)
f(x)>0
при 0 < a < 1
равносильно системе
f{x)>g{x)
g(x)>0
равносильно объединению систем неравенств:
Н(х)>1
f(x)<g(x) и
f(x)>0
H(x)>0
Н(х)<1
f(x)>g(x)
gix)>0
Примеры простейших тригонометрических неравенств
sin х <-1,3
sin х >-1,3
sin х
<УПз
sin X >
ЛТз
решении нет,
-1 < sin х < 1
х ^ Л, так как
sin х < 1 < ТПЗ
решении нет

Справочные материалы
Алгебра в таблицах
519
17. Неравенства
sin х < -0,5
sin х > -0,5
sin х <
Я
2я
7
^
yJ
*?
0
гт
ь>
X
(2*/i-y;2*n-jj)
X ^ (2лп-^;-т-+2ял j
nGZ
я 7я
i; 6
nGZ
х^(2лл + у;у+2ял)
пег
cos * < -З0'7
cos х < In 3
COS JC > - g
COS JC > в
0,2
решении нет
так как cos х < 1 < In 3
хей,
так как cos х ? -1 > -г
решении нет,
так как в0,2 > 1
sin х >
л
cos х < - -5-
cos jc < 0,5
xe (2яп + |;у+2яд)
л ez
jc S [2ял + -г; -т-+2ял)
n ^Z
jc S (2лл + о; -тг+2ял)
П GZ
cos jc > 0
cos jc > 0,7
tgx< 73
*l
V °
1
^^N. arccos 0,7
Л
0,7|Jl x
^^/^-arccos 0,7
jc e [гяд-о; 2 + 2яд j
x e (2яп - arccos 0,7;
arccos 0,7 + 2яп) n^Z
n GZ
я я 1 _ „
Лп""5»5+яп » n^Z

520
Справочные материалы
Алгебра в таблицах
17. Неравенства
tg х < -2
-1
**»-£
ctg X > 1
К-I)
»]
/ ч
f ч
1 0
1
"*>
ч
^Г '
г^^ п
1 6
1 *х
\_Л
3
Ч 1
/ 0
* —V
у 4Л
i /г л
,\ /
X
lltn--Z> KJl-SLTCtg о j, n^Z
[Я Я \ „
jc ^ (яд; т + яп J, n^Z
Более сложные примеры решения тригонометрических неравенств
cos (2x--g- j <0
sin х > cos x
tglx < 3
sin X « COS X
2ЯП + ;
;; у+2яп1
Л я . 5я Л
2яп + j < jc < -т- + 2яп,
neZ
2яя + о<2х~~1Г<1Г + Л
7я 15я
ЯД + Тд < X < -Т7Г + ЯП, П ^ Z
|tg*|< V3 „
Ugx ^-7з
^ Г я я 1 ^ _
XG ЯД-«J q+Я71 , n^Z
6cos2jc - cos jc - 1 < О
Пусть i/ = cos jc. Тогда
[б/-у- КО
[\y\ < 1
-8<^<2
1 1
-g <cosjc < 2
iOi+'y
I 2яп - arccos (-« ); 2яп - arccos 5" Ju (^яп + arccos 5 5 2яп + arccos f -5 j j
[ 2яп - arccos [-0 ); 2яп - 5 j u ( 3 + 2яп; arccos [-- j + 2яп j, n ^ Z

Справочные материалы
Алгебра в таблицах
521
17. Неравенства
sin х - sin 2х < О
sin* (1-2 cosx)< О
Используем метод интервалов на тригонометрической окружности,
считая х е [0; 2я).
F(x) = sinx (1 - 2 cos х); F(x) = 0 => х
5я
х е 2яп + 5; я + 2яп u 27cn + -«-; 2п + 2пп , п ^Z
/©JL4j-^
Ч|Я
\©Н
^Ч^
°у*
J^
У з
Примеры неравенств с обратными тригонометрическими функциями
arccos х < -5
решений нет, так как
0 ^ arccos х^п
arrcos х > -4
х<Е[-1;1]
arccos х < 5
^(0,5;1]
arccos х > 1
х e[-l;cos 1)
arcsm х < к
*^[-i;i]
arcsin х <-1,7
решений нет, так как
—z ^ arcsin х < г
arcsin х < —z
о
хе[-1;-0,5]
arcsin х > 0
х^(0;1]
arctg jc < 2
х ^ Л, так как
я х тс
-g < arctg х < g
arctg х > 5
решений нет
arctg х < ^
c«=(-00;tg5]
arctg х < 0
х е (-оо; 0]
Метод интервалов (промежутков)
Методом интервалов решают неравенства,
приведенные к виду F(x) > 0 или F(x) < 0, F(x) > 0
или F(х) < 0.
Метод основан на том, что непрерывная на
промежутке функция может менять знак только в
тех точках, где ее значение равно нулю (но
может и не менять).
Алгоритм применения метода
Найдем D(F(x)) и промежутки, на которых F(x)
непрерывна.
Найдем нули функции F(x) — значения х, при
которых F(x) = 0.
Нанесем на числовую ось найденные
промежутки и нули.
Определим интервалы знакопостоянства и в
каждом из них поставим найденный подсчетом
или рассуждением знак.
Выпишем ответ.
Примеры
х(х - 4)(х + 5)2 >0
Рассмотрим функцию F(x) = х(х - 4)(х + 5)2.
D(F) = Л, функция непрерывна на R. F(x) = 0 в точках х = 0; х = 4; х = -5.
F(-6) > 0; Ft-1) > 0; F(l) < 0; F(5) > 0.
Ответ: (-оо; -5) и (-5; 0) и (4; оо). х(х - 4)(х + 5)2 < 0 при х е {-5} и [0; 4].

522
Справочные материалы
Алгебра в таблицах
17. Неравенства
Примеры (продолжение)
F(x) =
х-5
Рассмотрим функцию
х(х + 2)
х-5 '
D (F) = (-оо; 5) и (5; оо). F(x) = 0 в
точках х = 0; х = -2. F(-3) < 0;
F(-l) > 0; F(l) < 0; F(6) > 0.
Ответ: (-oo; -2] u [0; 5).
-2 0 5
л/Зх + l > 2x. Приведем неравенство к виду: Jbx + l - 2х> 0.
F(x) = л/Зх + 1 - 2х.
D^) = [-г 5 +°°). Найдем нули этой функции.
*/Зх + 1-2х = 0<=> < .
l8x + l - 4ж2
F(x) = 0 при х - 1. F(0) > 0; F(5) < 0.
Ответ:
[-И
18. Неравенства с двумя переменными
ах + {и/ + с>0иах + &1/+с<0-
полуплоскости (а2 + Ь2 * 0)
ах2 + Ьх + с > у
и ах2 + Ьх + с < у
оу2 + Ьу +с> х
и ay2 + Ъу +с <х
граница — прямая
ах + by + с = 0
граница — парабола
ах2 + Ъх 4- с = 0
& \ах + Ьу + с > О /
/
V7.
ад: + Ьу + с < О
Z
граница — парабола
ay2 + by + с = х
Ч
| ^ ay2 + Ьу + с<х
ajf + by + cfxy
(х - х0)(у -y0)>k
и (х - х0)(у -y0)<k(k* 0)
(х - x0)(i/ - Уо) > О
и (х-х0Ху-Уо)<0(*-0)
(x-x0)2 + (i/-i/o)2^
и (x-x0)2 + (i/-i/o) <^;(^>0)
граница — гипербола
(х - x0)(i/ - 1/0) = k (две ветви)
граница — две прямые
х = х0 и I/ = 1/0
t &У/У/,
(x-x0)(y-y0)<k\
О
(x-x0)(y-y0)>i
х-х0)(у-у0)>к,
граница — окружность
(х - х0)2 + (у - у0)2 = т
Jm — радиус окружности
,(х-х0)2 + (у-у0)2>т

Справочные материалы
Алгебра в таблицах
523
19. Дифференцирование
Производной функции / в точке х0 называется
предел отношения приращения функции
Af = f(x0 + Ах) - f(x0) к приращению аргумента Ах
при стремлении Ах к нулю.
/(х0+Ах)-/(х0)
f(x0) = lim
Дх-»0
Ах
Операция нахождения производной функции
называется дифференцированием.
Необходимое условие
дифференцируемости функции
Для того чтобы функция / была
дифференцируема (имела производную) в точке х0,
необходимо (но недостаточно), чтобы она была
непрерывна в этой точке (т. е. Af(x) = f(x) - f(x0) -> 0).
Примеры нахождения производной функции / по определению
fix) = х2
ч2 Л2
А2)= lira (2+Af} ~2 = lira 4Д* + Д* = lira (4 + Д*) =4
Дх-»0 АХ Д*->0 АХ Ах->0
f(x)=3Jc
х0*0
3Jxn + Ах - \fx~n
f(x0) = lim 4-!L_ 1-9= lim
Ах -> 0 АХ Дх
(х0+Ах)-х0
°(*1(х0+Ах)2 + 8/(х0 + Ах)х0 + зД )Дх З.з/^
/(х) = sin х
х0^Д
0 . Ах f Ах\
„ ч r sin(x0+Ax)-sinx0 2BinT-coB^0 + TJ
f(x0) = hm — = hm
Лх-»о Ax лх->о Ax
= cos x0
f(-2) = lim
Ax-»0
|-2+Ax|-(-2 + Ax)2-8 _ r (2 - Ax)(-2 + Ax)2 -8 _
Ax
= lim
Ax
= -12
Пример непрерывной, не дифференцируемой в точке х0 функции
Л*)Ч*-2|
х0 = 2
f(2) = lim -г ' = lim Ц—* предел не существует, /'(2) не существует.
Ах д* -> о Ах
Дх->0
Дх) = V^i
Х0=1
./n ,. V(l+Ax)-l-0 ,. VAx ,. 1 ^ ,,/1Ч
f(l) = hm — —* = hm -*-— = hm = оо,/'(1) не существует.
Дх-»0
Ах
Дх->0 Ах Дх-»0 з/д 2
Вторая производная
Производные высших порядков
Г(х) = (Пх)У
f(n){x) = {f(n-l)ix)y
(cos х)'"= (-sin х)' = -cos х
( Ку _ Г -±- Y - ( ir"3/2Y - ^"5/2 - -JL.

524
Справочные материалы
Алгебра в таблицах
19. Дифференцирование
Таблица производных
(с)' = 0, с ^ Д (константа)
(х)' = 1, IGB
(хпУ = пхп " х, л ^ ЛГ, х <= Д; или -л <= iV, х * 0;
или n ^ Z, х > 0 •
(cos хУ = -sin х, х ^ Д
(sin хУ = cos х, х ^ Д
(tg х)' = —— , X * \ + 7lft, ft <= Z
COS X
(ctg X)' = — , X * rtft, ft €E Z
sin x
(In*)'-j, xe(0;+oo)
(iogax) x lnfl , x с: (o, +oo)
(г)'вг, x ^ Д
(ахУ = ах1па, х€ЕД
Производная сложной функции
(f(u(x)))' = f(u)-u'(x)
(u")' = rtun-1-u'*
(cos и)' = -sin ы • u'
(sin и)' = cos u • и'
(tg u)' = -\- • u'
cos u
(ctgu)' = ~'u'
sin u
1 *"
(In ")'="•"' •
/lr»rr тЛ' .if'
dogeu) -u.lna и
(eu)' = eu • a'
(au)' = a" • In a • u'
* u = u(*)
Производная обратной функции
Функции у = /(х) и у = ф(х) взаимообратны.
fflTV»ci"n v\f — ———— V £^ (—1 • 1 ^
VI -х2
(ягссоя х)' = —^=^=. х £— f—1: 1Ъ
л/1-л:2
(arctg *)' = ;, xeR
1
(arcctg xj — - «, х {— it
1+x^
Правила дифференцирования
(u + v)' = u' + l>'
(u • u)' = и' • и + и • l>'
/"uV u' - v-uv'
W - u2
(arcsin
(arccos
(arctg i
(arcctg
/(о) = & « a = <p(&) 1
1Г(а)-фЧЬ) = 1|
uV - • и'
Гл 2 U
и\' . и'
-/TV
Л' . u'
1 + U
1
u\' .11'
"'- 1x2 »
1 +Ц
Следствия из основных формул
(и - v)' = и' -v'
(с-и)' = с- и'
Примеры
(cos Jx)' = -sin л/х • (л/х)' = 7=- ;
2V*
((2*2 - ж + I)10)' = 10 • (2*2 - х + I)9 • (2Ж2 - х +
+ 1)' = 10 • (2*2 - х + I)9 • (4* - 1).

Справочные материалы
Алгебра в таблицах
525
19. Дифференцирование
Физический смысл производной
Геометрический смысл производной
Пусть s = s(t) — зависимость пути от времени,
тогда:
v = v(t) = s'(t)
Скорость — производная пути по времени.
a=a(t) = v'(t) = s"(t)
Ускорение — производная скорости по времени
(вторая производная пути по времени).
Касательной к графику функции f(x) в точке
х0 называется прямая, задаваемая
уравнением:
У = Л*о) + /'(*<))' (* "" *о)
/'(*о) = *£ «кас = *кас
Значение производной функции в точке равно
угловому коэффициенту касательной к
графику функции в этой точке.
Касательная к графику функции
Уравнение касательной (не вертикальной) к графику функции у = f(x) в точке графика с
абсциссой х0:
У = Л*о) + f'(x0)' (* - *о)
Если функция f(x) не имеет производной в точке х0, но непрерывна в этой точке, то у графика
функции в этой точке либо вообще нет касательной, либо есть вертикальная касательная.
у = |*| не имеет касательной в точке графика с абсциссой х = 0.
у = V* имеет в точке графика с абсциссой х = 0 вертикальную касательную х = 0.
Примеры решения задач на составление уравнения касательной
Составить уравнение касательной к кривой у = дс3 - х2 в точке графика с абсциссой х0 = 1.
Координаты точки касания x0 = l;i/0=l3-l2 = 0.
у'=3х2-2х => kK8iC = y'(l)=l.
Уравнение касательной: i/=0 + l#(jt-l) => [у = х - 1
Составить уравнение касательной к кривой f(x) = (х2 + 6х + 3)/2,
не пересекающей прямую у = 2х + 5.
Так как касательная не пересекает прямую у = 2х + 5, значит, она параллельна касательной.
Следовательно, f'(x0) = 2. Но /'(*) = * + 3.
Отсюда х0 + 3 = 2ид:0 = -1. Ордината точки касания у0 равна
((-I)2 + 6 • (-1) + 3)/2 = -1. Координаты точки касания (-1; -1).
Уравнение касательной i/=-1 + 2(jc + 1) или \у = 2х+ 1
Составить уравнение касательной к кривой у = *3, проходящей через точку («; -1 )• Пусть (х0; у0) —
3 2 3 2
точка касания. Тогда у0 = *0; Акас = Зх0. Уравнение касательной jy = jc0 -h 3jc0(jc — x0). Точка
I «; -1J лежит на касательной. Поэтому -1 = х0 + 3*0 (« -х0 ) => 2х0 - jc0 - 1 = 0 => jc0 = 1 =>
Уравнение касательной i/ = 1 + 3(х - 1) или | у = Здс -2

526
Справочные материалы
Алгебра в таблицах
19. Дифференцирование
Исследование функции при помощи производной
Монотонность функции
Теорема Лагранжа ,
Если f(x) непрерывна на [а; Ь] и дифференцируема
на (а; Ь), то существует с е (а; Ь) такое, что
f(a)-f(b)=f'(c)-(a-b).
(Заметим, что таких точек с на (а; Ь) может быть и более одной.)
f
I i ii
i ii
—I—i 1—■-».
О а с Ь
Для исследования функции f(x) на монотонность можно
исследовать ее производную на знакопостоянство.
Если f'(x) > 0 на (а; Ь), то f(x) возрастает на (а; Ь).
Если f(x) непрерывна на [а; Ь], то f(x) возрастает
на [а; Ь].
Если f\x) < 0 на (а; fr), то f(x) убывает на (а; Ь).
Если f(x) непрерывна на [а; Ь], то f(x) убывает
на [а; Ь].
f(x) - х2 - 6х + 1; f\x) = 2х - 6 > 0 при х > 3 =>
f(x) возрастает на [3; +оо).
f(x)= J=i;f'(x) =
убывает на (-°°; 0].
-1
2*/=х
< 0 при х < 0 => f(x)
Если f(x) возрастает и дифференцируема на [а; &],
то /'(*) > 0.
Если f(x) убывает и дифференцируема на [а; Ь],
то/'(х)<0.
Критические точки функции
Внутренние точки области определения функции, в которых производная равна нулю
или не существует, называются критическими точками функции.
Г(*о) = 0;
х0 — крит. точка;
f(xo) = /max*
и
Г(*о) = 0;
х0 — крит. точка;
Д^о) = /min*
*о|0 | х
Пх0) = 0;
х0 — крит. точка;
Дх0) не является экстремумом.
Критические точки (примеры)
f'(x0) не существует;
х0 — крит. точка;
f(x0) не является экстремумом.
f'(x0) не существует;
х0 — крит. точка;
Л^о) = /min-
Нет критических точек;
х0 = 0 не является внутренней
точкой области определения.

Справочные материалы
Алгебра в таблицах
527
19. Дифференцирование
V*
?
Нет критических точек;
х0 — точка разрыва.
v
ч
У
f'(x) = 0 при всех х ^ (-3; 4);
f'(-3), /'(4) не существуют; все
х ^ [-3; 4] критические точки.
\\j
*о
f'(x0) не существует;
х0 — крит. точка;
Л*о) = /min-
Экстремумы
х0 ^ D(f) — точка максимума f(x), если существует
5 > 0 такое, что при х ^(х0- 8, х0 + 8)
f(x0)>f(x)
х0 ^ D(f) — точка минимума f(x), если существует
8 > 0 такое, что при х е (х0 - 8, х0 + 8)
fooXftx)
Точки максимума и минимума функции называются ее точками экстремума, а
значения в них — экстремумами (максимумами или минимумами).
f(xo)= О ПРИ х<хо f(x)> °J ПРИ х>хо f(x) < О
Хо \ х
Г(х0) = 0 при х < х0 /'(*)< 0; при *>*0 /'(*)> О
Примеры критических точек различных функций
1) у = |*|; х0 = 0; у'(0) не существует;
1/(0) = 0 — минимум.
2) у = *2; дг0 = 0; у'(0) = 0; у(0) = 0 — минимум.
3) у = лг; jc0 = 0; у'(0) = 0; экстремумов нет.
4) у = 2* - |*|; Jt0 = 0; у'(0) — не существует;
экстремумов нет.
Примеры исследования функций на монотонность
f(x) = х6 + х* + х - 5;
/'(*) = Зх2 + 2* + 1 > О
при хЕЙ;
f(x) возрастает на R.
©
Л*)
f(x) = x*-3x;
f'(x) = S(x - l)(x + 1) = 0
при x = -1 и jc = 1;
/(*) возрастает на (-°°; -1]
ина[1;+оо);
f(x) убывает на [-1; 1].
Нх) © -i Q i © ^
max min
f(x) = 2x+\;f'(x) = 2--3;
X X
Г(х) = 0прих= 1;
f(x) возрастает на (-°°; 0)
ина[1;+оо);
f(x) убывает на (0; 1].
ж © о ©i ©
fix)
разрыв min
f(x) = x4- x3; f'(x) = 4x3 - 3jc2 = x2(Ax - 3);
f(x) возрастает на т; +oo J;
Ддг) убывает на f-oo; -J. /(x) © о © ! ©
' min *
f{x) = x + l;f'(x) = l-\;
* x
f{x) возрастает на (-oo; -l] и на [1; +°o);
f(x) убывает на [-1; 0) и на (0; 1].
r'w 0-iG oG i ©
max раз- mm
рыв

528
Справочные материалы
Алгебра в таблицах
20. Исследование функций
Область определения функции D(f) — множество значений jc, при которых функция определена.
X +1
D(f) = R
D{f)-{x\x*l)
f(x) = MT^x
ЩП-{х\х<1)
f(x) = J2x-x2-l
£(/) = {!}
f(x) = lgx + lg(-x)
D(/) = 0
Область значений функции E(f) — множество значений, которые
может принимать f(x) при х е D{f).
(Все значения а, при которых уравнение f(x) = а имеет решения.)
f(x) = x3-3x
E(f) = R
f(x) = 1 + -3
JC
E(f)-{y\y*l)
fix) = V2x-x2
E(f) = {y\y<l}
f(x) = 1 + л/4х-х2-4
E(/) = {1}
/(jc) = sin x + cos jc
Четность
Нечетность
ft-x) = /W,xGD(/)
я-х)—я*),*бдл
График четной функции симметричен
относительно оси ординат.
-х О
График нечетной функции симметричен
относительно начала координат.
Примеры четных функций
/(*) = jc4-21jc2; g(x) = bx + 5-
if(x) = \/l-x + Vl+*
Примеры нечетных функций
h(x) = х3- 20jc; и(х) = 5* - 5~х
v(x) = Jl-x - JT+x
f(x) = sin x - cos jc не обладает четностью или нечетностью.
Периодичность
f(x -t) = f(x + t) = fix), X €= D(/), t * 0
Число t называется периодом функции, а наименьшее
положительное значение t основным периодом функции (!Г).
fix) = sin 4jc
1 4 2
/(jc) = cos 2rtjc
т= — =
Г = 1/3=3*
/(jc) = 17
f ^ (0; +oo) основного периода нет
/(jc) = jc + sin jc; /(jc) = cos(jc2) — непериодические функции.
График периодической функции состоит из
повторяющихся фрагментов на отрезке длины Т;
на любом таком отрезке периодическая функция
принимает все свои значения.
V 1
Л'
\ °
-Л
I /(лг)-ашх-
F!4'
4
-cos*, Г-2л
Л-
/ U7C *

Справочные материалы
Алгебра в таблицах
529
20. Исследование функций
Корень (нуль) функции —
значение аргумента, при котором значение функции равно нулю.
/(*) = 4*--
корни: х =±р
f(x) = x • VT^
корни: х = 0;
JC = 1
f(x) = (l + x)-Ji
корень: х = 0
f(x) = sin х + cos x
корни: x = --: + яп, п ^ Z
/(*) =
sin X
корней нет
Промежуток знакопостоянства —
промежуток, на котором все значения функции положительны
(или отрицательны), а на любом его расширении нет.
Примеры
f(x) = Зх2 + Ъх - 8; f(x) < 0 при х е f-g; ll; /(*) > 0 при я е f-oo; -|^ и (1; +оо)
fix) =х~2; два промежутка знакопостоянства (-со; 0) и (0; +°°), на обоих функция положительна.
Монотонность
Функция f(x) называется возрастающей на
промежутке J, если для любых хг и х2 из этого
промежутка
*1>*2 => /(*l)>/(*2)-
Промежуток J называется промежутком
возрастания функции fix), если на этом
промежутке функция возрастает, а на любом его
расширении нет.
Функция fix) называется убывающей на
промежутке J, если для любых хг и х2 из этого
промежутка
*1>*2 => /(*l)</(*2>-
Промежуток I называется промежутком
убывания функции fix), если на этом промежутке
функция убывает, а на любом его расширении
нет.
Промежутки возрастания и убывания называются промежутками монотонности функции.
Критерий монотонности функции
fix) возрастает на промежутке, если fix) > 0.
fix) убывает на промежутке, если f'(x) < 0.
Примеры
fix) = Зх2 + Ъх - 8;
5
Г(*)>0при* >-g-,
5
fix) < 0 при х <-g;
/'(*) = 6*+ 5;
/(jc) возрастает на промежутке -^; +сю ) ;
/(jc) убывает на промежутке (-°°; -g .
/(jc) = —5; два промежутка монотонности (-°°; 0) и (0; +°°); на обоих функция возрастает.
fix) — 3jc + 4 возрастает на Я, один промежуток монотонности (-°°; +°о).

530
Справочные материалы
Алгебра в таблицах
20. Исследование функций
Критерий монотонности функции (продолжение)
f(x) = Зх2 + 6* - 8;f'(x) = 6(х + 1) = 0 при х = -1;
/'(-2) < 0 => f(x) убывает на (-оо; -1];
/'(0) > 0 => f(x) возрастает на [-1; +°°);
х0 = -1 — точка минимума; /(~1) = -11 — минимум.
f(x) = х3 — экстремумов нет.
Исследование функции при помощи производной. Построение графика
Найдите D(f).
Найдите производную, критические точки,
исследуйте знаки производной.
Найдите промежутки монотонности, точки
экстремума, определите вид точек экстремума.
Найдите экстремумы функции.
Исследуйте функцию на четность, нечетность,
периодичность (периодическую функцию
лучше исследовать на промежутке длины Г).
«Набросайте* эскиз графика.
Найдите E(f).
Найдите несколько значений функции (по
крайней мере по одному в каждом промежутке
монотонности).
По возможности
Исследуйте поведение функции на концах
области определения и в точках разрывов.
Найдите горизонтальные и вертикальные
асимптоты.
Найдите корни и промежутки знакопостоянства
функции.
Постройте график функции.
Пример
х
У =
х2 + 1
D(y) = R.
Функция нечетная: у(-х) = -у(х).
,. х ,.1
lim —
*-*°°х +1
= lim
1-(х +1)-х-2х
2 2
1£
-х
2 2;
(1+Х )
1
Х + -
X
= 0.
у' существует при х е R; „'© -1 © 1 ©
у =0при*=±1. „*-^ —^ —*
min max
Утт = yi-V = -2' Утах * У^ = 2 '
у = 0 — горизонтальная асимптота;
вертикальных асимптот нет.
у = 0 при х = 0 (корень),
у > 0 при х > 0;
у < 0 при х < 0.

Справочные материалы
Алгебра в таблицах
531
21. Нахождение наибольшего и наименьшего
значений функции на промежутке
Наибольшим (наименьшим) значением функции f(x) на I называется
такое число М (т)9 что существует х0 ^ I такое, что f(x0) = М
(Л*о) = т), М > f(x) (m < f(x)) для всех х из J.
"V"
_Щ
Y^
Наибольшее и наименьшее значения непрерывная на I функция может принимать либо на
концах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.
Алгоритм нахождения наибольшего и наименьшего на [а; Ь] значений функции, непрерывной на [а; Ь].
1) Найдите f(a) и f(b) — значения функции на 3) Найдите значения функции в критических точ-
концах промежутка. ках.
2) Найдите критические точки функции внутри 4) Из всех найденных значений выберите наиболь-
промежутка (т.е. на (а; &)). шее и наименьшее; они и будут наибольшим и
наименьшим значением функции на [а; 6].
Пример
f(x) = 8х2 -х\х<= [-1; 3]. /(-1) = 7; /(3) = -9;
f\x) = 16* - 4*3 = 4*(4 - х2) = О => х = 0; х = 2; х - -2 §£ [-1; 3]. /(0) = 0; /(2) = 16.
max {7; -9; 0; 16} = 16 => max f(x) = 16; min {7; -9; 0; 16} = -9 => min f(x) = -9.
[-U4 t-i;8]
Пример
Если непрерывная функция имеет на промежутке / единственную точку экстремума и этот
экстремум максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение
функции.
f(x) = sin х + а/З • cos х, х ^ [0; я]. /(0) = 7з ; /(я) = - 7з ; /'(*) = cos х - 7з sin *;
г- 1 я
/'(я) = 0 при cos х = д/3 sin jc ^ tg х = -р => jc = 5 + яЛ е [0; я] при k = 0. , ^ ~
л/3 b ч Мх) 0 СР^ U Я ^
max /(х) = /(g) = sin g + л/Зсов g - 2; min /(*) = /(я) = -^3
Пх)
Задача
В полукруг радиуса Д вписать прямоугольник наибольшей площади так,
чтобы одна его сторона лежала на диаметре полукруга, а две вершины —
на дуге полукруга.
Обозначим стороны прямоугольника АВ = х,
/2 2
AD = 2у. Тогда его площадь S = 2 ху. Заметив, что у = л/Д - х , получим
S = 2х • л/л2 - *2 = 2 • л/Я V - х4 , * €= (0; Д).
Исследуем на максимум функцию f(x) = Д2*2 - *4 при х ^ (0; Д).
f'(x) = 2 Д2* - 4х3 = 2*(Д2 - 2*2).

532
Справочные материалы
Алгебра в таблицах
21. Нахождение наибольшего и наименьшего значения функции на промежутке
Задача (продолжение)
R
f'(x) = 0 при х = -= (так как х е (0; В)).
Следовательно, при х = -т= площадь прямоугольника наибольшая.
Ответ. Прямоугольник имеет наибольшую площадь, если его стороны х =
*
/и © 0
в • в
Л
= ^,2у = л72.
22. Первообразная и неопределенный интеграл
Функция F(x) называется первообразной
функции f(x) на промежутке /, если для всех х из
этого промежутка F'(x) = f(x).
Множество всех первообразных функции f(x)
называется неопределенным интегралом и
обозначается
jf(x)dx.
Если F(x) одна из первообразных функции f(x)
на /, то любая первообразная функции f(x) на
этом промежутке имеет вид F(x) + С, где Сей.
[f(x)dx = F(jc) + С, где F(x) — любая первообразная
/(*), аСей.
Свойства первообразных
Первообразная f(x) равна /(*) + С.
Если первообразная f{x) равна F(x), то
первообразная f(t) равна F(t).
Если первообразная /(#) равна F(x), то
первообразная АД*) равна kF(x).
Пусть первообразная fi(x) равна Fi(x),
первообразная f2(x) равна F2(x), тогда
первообразная fx(x) + /2(*) равна 2ri(Jc) + .F^*)*
Пусть первообразная /(#) равна F(x), тогда
первообразная f(kx + р) равна т F(kx + р).
Для того чтобы доказать, что функция F(x)
является первообразной функции f(x) на промежутке J,
нужно показать, что для всех х из этого
промежутка F'(x) = f(x) (т.е. воспользоваться определением).
Задачи
Доказать, что функция F(x) = 5 sin 2* + jc является первообразной для функции f(x) = 1 + cos 2* на R.
F'(x) = 5 cos 2х • 2 + 1 = 1 + cos 2х - /(*).
Полученное равенство верно для всех действительных значений х.
Найти первообразную функции f(x) = 3jc2 - 1, график которой проходит через точку М(1; -1).
Любая первообразная функции f(x) = 3jc2 - 1 имеет вид F(x) = *3 - х + С.
График искомой первообразной пройдет через точку М(1; -1), если F(l) = -1, т. е. I3 - 1 + С =
= -1 => С--1.
Ответ. F(x) - х3 - х - 1.

Справочные материалы
Алгебра в таблицах
533
22. Первообразная и неопределенный интеграл
Задачи (продолжение)
Найти первообразную функции f(x) = cos2 5 •
v 1 1 1
Преобразуем f(x) = cos2 5 = 5 (* + cos х)= Ъ + 2 cos Хл
Первообразная суммы равна сумме первообразных. Следовательно, первообразная F(x) = 5 х +
+ 5 sin jc + С, где С — произвольная постоянная.
Найти неопределенный интеграл [sin 3jc • cos х dx.
fsin3jc -cosxdx= 5 [ (sin 4jc + sin 2jc) djc = 5 " ("7 *cos4jc + (-5 J-cos2jc ] = -::cos4jc- tcos2jc + C.
Найти первообразную для функции f(x)
1 .
4jc - 1
1 ^
Преобразуем f(x) ^2 _ ^ 2 U jc - 1 2.
F{x) = | (| ln|2x - 1| - | ln|2x + 1|) = \ In
r + 1 У
2* - 1
2x + 1
.
Следовательно, первообразная
+ C.
Таблица первообразных
/(*)
к
xa
<a*-l)
1
X
ex
ax
COS JC
sin jc
1
2
COS JC
1
. 2
sin JC
F(x)
kx+C
a + l
a + l
In И + С
ex+C
In a
sin jc + С
4 -cos jc + С
tgx +C
-ctg jc + С
Промежуток I
R
aEJV,jcEfi;-aGJV,xE (-00; 0) u (0; +00);
a m Z, jc e (0; +00)
(-00; 0) или (0; +oo) 1
R
R
R
R
(-£+яА; 5+я*1 k^Z
(nk; к + яЛ)> JGZ

534
Справочные материалы
Алгебра в таблицах
23. Определенный интеграл и его приложения
Если функция f(x) непрерывна на промежутке J
числовой оси, содержащем точки х = а и х = Ь,
то разность значений F(b) - F(a) (где F(x) —
первообразная f(x) на /) называется
определенным интегралом от функции f(x) от а до Ь:
jf(x)dx=F(b)-F(a).
Определенйый интеграл есть число.
Основные свойства
\f(x)dx = jf(t)dt = jf(z)dz
\f(x)dx = О
jf(x)dx =-jf(x)dx
b с b
\f(x)dx = (f(x)dx + \f(x)dx, если a, b и с —
а а с
любые точки промежутка I непрерывности f(x)
b b
jkf(x)dx = k • jf(x)dx
a a
b b b
j(fiix) + f2(x))dx = jf1(x)dx + jf2(x)dx
Дополнительные свойства
b pb + q
ff(px + q)dx = l j f(t)dt
pa + q
Если f(x) четная, то J f(x)dx = 2 • f f(x)dx,
Если f(x) нечетная, то J f(x)dx = 0.
(x v
jf(t)dt
'Я*)
Примеры
4 4
* + l
3/2 1/2,
f X + l _, f/ 1/2, -1/2, , (X ' t X \\
|(43/2-l)-f2(41/2-l)=|.7-f2.1 = f
3 2 + 4
dt
f dx __ 1 л dt _
J.(3* + 4)2~ 5 "J ,»
;i(8* + 4)
1 1
"3 7
10
3 (-D + 4
3U0 3) 90
3* + 4 = *
25* + 5* + 1 , = f^5V
10
x-l
"* - jfej10,i*+
/(fo)"
50d* =
= 10j2,5*da: + 50j0,5xdje =
= 10
2,5
In 2,5
+ 50'
0,5
In 0,5
15 _25_
In 2,5 In 2

Справочные материалы
Алгебра в таблицах
535
23. Определенный интеграл и его приложения
Площадь криволинейной трапеции
Фигура, ограниченная прямыми у =0; х =а; х = Ь и графиком
непрерывной и неотрицательной на [а; Ь] функции f(x), называется криволинейной-
ь
трапецией. Площадь криволинейной трапеции S = \f{x)dx
yk
b х
Вычисление площадей
S = jf{x)dx-jg(x)dx
ас b
S = -jf(x)dx
fix) > g(x)
на [a, b]
S = j(f(x)-g(x))dx
S = j(f1(x)-g(x))dx +
a
b
+ j(f2(x)-g(x))dx
g(x)
• • / (x) i«.
S = \(Kx)-g(x))dx +
a
b
+ \(g{x)-f{x))dx
Вычисление объемов тел вращения
Криволинейная
трапеция
(вокруг оси Ох)
V0x=njf\x)dx
Конус
я
rfRxy. nR
2 3
X
н
= \nR2H

536
Справочные материалы
Алгебра в таблицах
23.
Определенный
интеграл и его приложения
Вычисление объемов тел вращения (продолжение)
Шар
-Г
0
1
к:
X
Путь, пройденный материальной точкой за время
*2 " *i (*2 > *i) ПРИ прямолинейном движении со
скоростью v(t), равен:
R R
Vm = n [ (*JR2-x2)*dx = 2n[(R2-x2)dx =
-R
0
R
= Ue*
0 d
S = jv{t)dt.
h

Геометрия в таблицах
1. Элементы теории доказательств
♦А => В» — данная теорема; «В => А> —
обратная теорема;
«не А => не В> — противоположная теорема;
«не В => не А» — теорема, обратная
противоположной.
Если из А следует В, то А достаточно для В,
а В необходимо для А.
Если из А следует В, а из В следует А, то А
необходимо и достаточно для В.
Для того чтобы четырехугольник был
параллелограммом, необходимо у чтобы диагональ
делила его на два равных треугольника (но
недостаточно).
Для того чтобы четырехугольник был
параллелограммом, достаточно, чтобы все его
стороны были равны (но не необходимо).
Для того чтобы целое число делилось на 3,
необходимо и достаточно, чтобы сумма его
цифр делилась на 3.
Для того чтобы треугольник был
прямоугольным, необходимо и достаточно, чтобы
квадрат одной из его сторон был равен сумме
квадратов двух других.
«Необходимо и достаточно» заменяется на
«тогда и только тогда, когда».
Четырехугольник тогда и только тогда
является параллелограммом, когда его
диагонали, пересекаясь, делятся пополам.
Диагонали четырехугольника, пересекаясь,
делятся пополам тогда и только тогда,
когда четырехугольник является
параллелограммом.
Отношение обладает свойством симметрии,
если из того, что А находится в данном
отношении к В следует, что и В находится в
данном отношении к А.
Примеры симметричных отношений:
параллельность прямых,
перпендикулярность прямых, параллельность плоскостей,
перпендикулярность плоскостей, равенство
чисел, равенство фигур.
Отношение обладает свойством
транзитивности, если из того, что А находится в
данном отношении с В, а В с С следует, что А и С
находятся в данном отношении.
Примеры транзитивных отношений:
равенство чисел, подобие фигур, отношения
«меньше» и «больше» (<; >), параллельность
несовпадающих прямых и плоскостей.

Справочные материалы
Геометрия в таблицах
ПЛАНИМЕТРИЯ
2. Углы и параллельность
Углом называется фигура, образованная
двумя лучами, выходящими из одной
точки (вершины).
Луч, выходящий из вершины угла и
делящий его пополам, называется
биссектрисой угла.
Угол называется развернутым, если его
стороны лежат на одной прямой.
Градус — величина (градусная мера) угла,
1
равного rgg части развернутого угла.
Радиан — величина угла, градусная мера
которого равна 1 — 1.
Центральный угол в 1 радиан стягивает
дугу, длина которой равна радиусу
окружности. Центральный угол, стягивающий
а
дугу длины а, равен р = а радиан.
Угол, равный половине развернутого,
называется прямым (90°).
Угол меньше прямого называется острым.
Угол больше прямого, но меньше
развернутого называется тупым.
Смежные углы
Два угла, у которых одна сторона общая, а
две другие являются дополнительными
лучами, называются смежными.
Сумма смежных углов равна 180°.
Угол, смежный с прямым, — прямой.
Вертикальные углы
Два угла, стороны одного из которых
являются дополнительными лучами сторон
другого, называются вертикальными.
Вертикальные углы равны.
в^^*-*^^С AM — биссектриса =>
вершина ■ ^ Л ш „ *" л ш,
угла ^^^ => £ВАМ = £САМ
А^^^ /- ВАС — развернутый
В^*^ Ае(ВС)
^^ L ВАС = 180°
f J^£^jaH дл.АВ = Д
\ а \ У дл. CmD
\. J/ ~—^- = а радиан
т* J) R
VJ
А
Р Су^ Z BAD = 90° — прямой
■р^\ £- CAB < 90° — острый
В 90° < А ВАН < 180° — тупой
5?А £- ВАС и 4- CAD — смежные
^В <LBAC + /LCAD=180°
4я-
чИ Z. ВАС, Z. HAD — вертикальные
\|\л) /L ВАН, Z. DAC — вертикальные
с\ LBAC-LHAD

Справочные материалы
Геометрия в таблицах
2. Углы и параллельность
Угол между прямыми
Углом между двумя пересекающимися
прямыми называется меньший из
вертикальных углов, образовавшихся при
пересечении.
Прямые, образующие прямой угол,
называются перпендикулярными.
Две прямые плоскости, не имеющие общих
точек, называются параллельными.
При пересечении двух прямых третьей
(секущей) образуются пары углов:
(1; 2); (3; 4); (5; 6); (7; 8) накрест лежащие,
(1; 8); (5; 3); (4; 6); (7; 2)соответственные,
(1; 3); (2; 4); (5; 8); (7; 6) односторонние.
А^Д*" A (a, b) = ^LAFB<^LBFC
Y^^. (Z.AFB = A BFC) =>
\ ^ =>(Z(a,b) = 90°)=>(alb)
а
——-• ь al|fr<=>anft = 0
\^з °
.—*^ ' \ аг\с Ъпс
Пересечение параллельных прямых секущей
Накрест лежащие углы равны
(Z. 1 = Z. 2; Z. 3 = Z. 4; L 5 = Z. 6; 1. 7 = L 8).
Соответственные углы равны
(Z. 3 = L 5; L 1 = А. 8; А. 2 = ^ 7; L 4 = /. 6).
Сумма односторонних углов 180°
(^l+^3 = Z5 + z!8=^2+Z4 =
= Z 6 + ^ 7 = 180°).
Аксиома параллельности
Через точку, не лежащую на данной прямой, проходит только одна
прямая, параллельная данной.
Признаки параллельности прямых
Если две различные прямые параллельны
третьей, то они параллельны между собой
(транзитивность параллельности).
Если при пересечении двух прямых
третьей накрест лежащие углы равны, то
прямые параллельны.
Если при пересечении двух прямых
третьей соответственные углы равны, то
прямые параллельны.
Если при пересечении двух прямых
третьей сумма односторонних углов равна 180°,
прямые параллельны.
a
/ Ь
/ / с
/ (а || Ь; Ь II с) => (а II с)
р

540
Справочные материалы
Геометрия в таблицах
2. Углы и параллельность
Сумма углов треугольника равна 180°
mil АС
£А + £В + £С = 180°
Теорема Фалеса
Если на одной из двух
прямых отложены несколько
равных отрезков и через их
концы проведены
параллельные прямые, пересекающие
вторую прямую, то и на ней
отложатся равные отрезки.
А1А2=А2Аз=АзА4
АгВг || А2В2 || А3В3 IIА4В4 =>
=> В^В2 = В2В$ = В$В4
Деление отрезка
на равные части
ACi — С\С2 — С2С$ — ... —
= С4С5 — произвольные
равные отрезки
ВСЪ II С4М4 || СгМг || С2М2 II
II СгМг=> АМ1 = М1М2 =
= М2Мг = МгМ4 = М4В
«Расширенная» теорема Фалеса
Если на одной из двух прямых
отложены несколько отрезков
и через их концы проведены
параллельные прямые,
пересекающие вторую прямую, то
на ней отложатся отрезки,
пропорциональные данным.
сг II с2 || с3 II с4 => АгА2 : А2А3 :
: А3А4 = Вф2 : В2В$ : BSB4
3. Множества (геометрические места) точек на плоскости
Множество точек, равноудаленных от двух дан-
| ных точек, есть серединный перпендикуляр
отрезка, соединяющего эти точки (на нем лежат
центры окружностей, проходящих через
данные две точки).
Множество точек, равноудаленных от сторон
данного угла (меньшего, чем развернутый),
есть биссектриса угла (на ней лежат центры
окружностей, касающихся сторон угла).
А
^
с
О/ в
AO = OB\cLAB
\х (Xec)<=>(vlX = XB)
"^Л*..Я- ' АЮ = / нлг
^-^У (X е ОС) о (р(Х, ОА) =
В"-- = р(Х,ОВ))*
* р(Х, а) и р(Х, ОА) — обозначение расстояния от точки до прямой.

Справочные материалы
Геометрия в таблицах
541
3. Множества (геометрические места) точек на плоскости
Множество точек, равноудаленных от двух
параллельных прямых, есть параллельная им
прямая, проходящая через середину отрезка их
общего перпендикуляра (на ней лежат центры
окружностей, касающихся данных прямых).
а\\Ь9с\\а
(р(Х,а) = р(Х,Ь))<=>(Хбс)
Множество точек, равноудаленных от двух
пересекающихся прямых, есть две взаимно
перпендикулярные прямые, на которых лежат
биссектрисы вертикальных углов, образовавшихся при
пересечении данных прямых (на них лежат центры
окружностей, касающихся данных прямых).
аг\Ъ
" (р(Х,а) = р(Х,&))«
X е т
или
Хе п
Множество точек, удаленных на данное
расстояние от точки, есть окружность с центром в
данной точке.
р(Х,0) = а
Множество точек, удаленных на данное
расстояние от прямой, есть две параллельные ей
прямые.
X
т
1
1 т
ш *
р(Х, а) - р(У, а) - т
Ь\\а;с\\а
Множество вершин прямоугольных
треугольников с данной гипотенузой есть окружность,
построенная на гипотенузе как на диаметре
(исключая концы гипотенузы).
^АХВ = 90°
Множество точек, из которых данный отрезок
виден под данным углом, есть две
симметричные, опирающиеся на данный отрезок, дуги
(исключая концы этих дуг).
LAXB = LAYB
Окружность Аполлония
Множество точек М, таких что AM = kMB, есть
окружность с диаметром NiN2 на прямбй АВ
такая, 4toANi: iV^B = k и AN2 ". N2B = k (k Ф 1).

542
Справочные материалы
Геометрия в таблицах
4. Треугольник
Неравенство треугольника
В любом треугольнике каждая сторона меньше
суммы двух других сторон.
а-b < с < а + ft, где а, ft, с — длины сторон
треугольника, причем а > ft.
Внешний угол треугольника равен сумме двух
внутренних, не смежных с ним углов.
L ВАМ = £В + £С
Сумма углов треугольника 180°
В треугольнике против большей стороны лежит больший угол, против
большего угла — большая сторона.
а2 + ft2 > с2
а2 + Ь2 = с2
а2 + Ь2<с2
остроугольный
прямоугольный
тупоугольный
Признаки равенства треугольников
По двум сторонам и углу
между ними (СУ С).
По стороне и двум
прилежащим к ней углам (УС У).
По трем сторонам (С С С).
^\^\
^У^\
\^\^
Сходственные (соответствующие) элементы равных треугольников
равны.
Признаки подобия треугольников
По двум углам (У У).
*н A /n А
По двум сторонам и углу
между ними (СУ С).
2^ 2^У
По трем сторонам (С С С).
Ж 24
kb
kc

Справочные материалы
Геометрия в таблицах
543
4. Треугольник
Прямая, параллельная стороне треугольника,
отсекает от него треугольник, подобный данному.
Сходственные линейные элементы подобных
треугольников пропорциональны сходственным
сторонам.
Периметры подобных треугольников
относятся как сходственные стороны.
Площади подобных треугольников относятся
как квадраты сходственных сторон.
\ac=*aabc™apbq.
АВ ^АС =ВС . _
^ РВ PQ BQ К
коэффициент подобия
АА
РРХ || ААг => —^ = k
РР,
АВ + АС + ВС
РВ + PQ + BQ
= k;
*АВС __ь2
= k<
'PBQ
Примеры подобных треугольников
в
МЛ
N
А ABC ™ д NBM
k= АВ _ АС ВС
BN MN ВМ
A ABC ™ д АВгВ
АВ ^АС _ ВС_
Н АВ* АВ ВВЛ
Медиана
Медианой треугольника называется отрезок,
который соединяет вершину треугольника с
серединой противолежащей стороны.
Медианы треугольника пересекаются в одной
точке {центре тяжести треугольника) и
делятся этой точкой в отношении 2:1, считая от
вершины.
Медиана делит треугольник на два
равновеликих треугольника. Три медианы делят
треугольник на шесть равновеликих треугольников.
AM : МАг = ВМ : МВХ =
- СМ : МСХ = 2:1
Л А2 2
ААг = та
2Ъ2 + 2с2
Биссектриса
Биссектрисой треугольника называется отрезок
биссектрисы внутреннего угла треугольника.
Все биссектрисы треугольника пересекаются в
одной точке — центре вписанной в
треугольник окружности.
Биссектриса делит противолежащую сторону
на отрезки, пропорциональные прилежащим
сторонам треугольника.
АС ПА аЬ
ТЪ => САл = -
АВ 1 ь + с
ас АО
Ъ + с; ОАл
Ь + с
АА\ =АВ • АС-АХВ • АХС
2 АВ АС А
^1 = АВ+АСС°*2

544
Справочные материалы
Геометрия в таблицах
4. Треугольник
Биссектрисы внутреннего и смежного с ним
внешнего углов треугольника перпендикулярны.
Биссектриса внешнего угла неравнобедренного
треугольника пересекает продолжение
противолежащей стороны в точке, отстоящей от концов
этой стороны на расстояния,
пропорциональные длинам двух других сторон.
/LLAM = 90°
LB АВ
LC "АС
Высота
Высотой треугольника называется отрезок
перпендикуляра, опущенного из вершины
треугольника на прямую, содержащую
противолежащую сторону.
Все высоты треугольника пересекаются в одной
точке — ортоцентре треугольника.
AAV BBV ССХ — высоты A ABC
ААг = ha; ВВ1 = hb; CCi = hc; H — ортоцентр
ha hb hc r
r — радиус вписанной окружности
Средняя линия
Средней линией треугольника называется
отрезок, соединяющий середины двух сторон
треугольника.
Средняя линия параллельна третьей стороне и
равна ее половине.
PQWAB
pq=\ab
Серединный перпендикуляр
Серединным перпендикуляром называется
прямая, перпендикулярная стороне треугольника
и делящая ее пополам.
Все серединные перпендикуляры сторон
треугольника пересекаются в одной точке —
центре описанной около треугольника
окружности. Около каждого треугольника можно
описать окружность и притом только одну.
Точка пересечения серединных
перпендикуляров треугольника является точкой пересечения
высот треугольника, образованного средними
линиями данного.
с АО = ВО = СО = 1

Справочные материалы
Геометрия в таблицах
545
4. Треугольник
Площадь треугольника
5д = g а^а = 2 ЬЬъ = 2 с^с
SA= -zab sin С= -zac sin В = 5 be sinA
SA = Vp(jP - d)ip - b)(p - с) (формула Герона)
gfrc
4Д
p = «(a + fr + с) — полупериметр
г — радиус вписанной окружности
R — радиус описанной окружности
5Д =
Теорема косинусов
Теорема синусов
а2 = Ь2 + с2 - 2&с cosA
Квадрат стороны треугольника равен сумме
квадратов двух других сторон без удвоенного
произведения этих сторон на косинус угла
между ними.
= 2Д
sin A sin В sin С
Стороны треугольника пропорциональны
синусам противолежащих им углов.
Вписанная окружность
В каждый треугольник можно вписать
окружность и притом только одну.
_Ее_аешр-^=^ш>ч1са_Д€р£Свчежхя биссектрис.
Радиус (г) вычисляется по формулам:*
SN
г= -
Р
г=(р-а) • tgg =(p-ft) • tgg =(р-с)
/(Р - а)(Р - &)(Р - с) _ g
Ч Р Р
р — полупериметр
*п
ОПАС;
OF1AB.OW1BC
А7=АГ=р-о
BV = BW = p-b
CW = CT = p-c
Описанная окружность
Около каждого треугольника можно описать
окружность и притом только одну.
Бе центр — точка пересечения серединных
перпендикуляров к сторонам треугольника.
Радиус (R) вычисляется по формулам:
а Ь с
R
R =
2 sin А
abc
4S
2sin В 2sinC
АВ1 = ВХС; АСх = СХВ;
ВА1=А1С
ОАх 1 ВС; ОВх 1 АС; ОС1=АВ
OA = OB = OC = R
IX 1019

546
Справочные материалы
Геометрия в таблицах
4. Треугольник
Прямоугольный треугольник
Сторона прямоугольного треугольника,
противолежащая прямому углу, называется
гипотенузой, две другие стороны называются катетами.
Теорема Пифагора
Квадрат длины гипотенузы равен сумме
квадратов длин катетов.
с2 = а2 + Ь2
Ь катет
Свойства прямоугольного треугольника
Медиана, проведенная к гипотенузе
прямоугольного треугольника, равна половине гипотенузы.
Только в прямоугольном треугольнике центр
описанной окружности лежит на стороне
треугольника (совпадает с серединой гипотенузы).
А OA = OB = OC = R=2c
Площадь прямоугольного треугольника
S= 5а&; *S= ос^' *'
высота, проведенная к гипотенузе
Тригонометрические функции острых углов прямоугольного треугольника
Синусом острого угла в прямоугольном
треугольнике называется отношение
противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном
треугольнике называется отношение прилежащего
катета к гипотенузе.
Тангенсом острого угла в прямоугольном
треугольнике называется отношение
противолежащего катета к прилежащему.
Котангенсом острого угла в прямоугольном
треугольнике называется отношение
прилежащего катета к противолежащему.
а Ь , а
sin а = -; cos а = -; tg а = g
Р = 90°-а
sin Р - sin(90° - а) = - = cos а
cos Р = cos(90° - а) = - = sin а
tgP = tg(90°-a)=£ =ctga
Пример.
sin 54° = cos 36°; tg 89° = ctg 1G
Значения тригонометрических функций некоторых углов
sin
cos
tg
30°
~T~
2
ТЕ
2
~Т~
Л
45°
~"Т~
Л
л
60°
ТЕ
2
~Г
2
Л
90°
180°
-1
не опр.

Справочные материалы
Геометрия в таблицах
547
4. Треугольник
Признаки прямоугольных треугольников
Если квадрат одной из сторон треугольника равен сумме квадратов двух
других сторон, то такой треугольник прямоугольный.
Если медиана треугольника равна половине соответствующей ей
стороны, то треугольник прямоугольный.
Решение прямоугольных треугольников
Дано: гипотенуза и острый угол
х = a cos а
у = a sin а
Р = 90° - а
Дано: катет и острый угол
х - a tg а
а
У в
* cos а
Дано: высота, опущенная на гипотенузу, и
острый угол.
Л_ Л_
" cos а ™ sin а
г = h ctg а t = h tg а
Катет, лежащий против угла 30°, равен
половине гипотенузы.
А
Соотношения в прямоугольном треугольнике
ВС2 = ВСгАВ; а2 = аг-с
АС2=АСгАВ; Ъ2 - Ьг • с
СС\ = ВСг • СгА; h2 = a1- Ъг
. аЬ
ti= —
с
Вычисление радиусов вписанной и описанной окружности
2R=AB
=>2R = a + b-2r
2(R + г) = а + Ь
с = (Ь- г) + (а- г)=>
а + b - с
-р-с
Ъ-г
IX*

Справочные материалы
Геометрия в таблицах
4. Треугольник
Треугольники классифицируют по сторонам: разносторонние,
равнобедренные, равносторонние; а также по углам: остроугольные,
тупоугольные и прямоугольные.
Треугольники
остроугольные
тупоугольные
прямоугольные
разносторонние
^
4
^\
п ^Чч>^
равнобедренные
Л
л^ч
■ 1
-, fK
равносторонние
Л
Равнобедренный треугольник
Равнобедренным треугольником называется
треугольник с двумя равными сторонами.
Общая вершина равных (боковых) сторон
называется вершиной равнобедренного треугольника,
а третья сторона основанием.
Свойства равнобедренного треугольника
Углы при основании равны.
Высота, проведенная из вершины
равнобедренного треугольника, является медианой и
биссектрисой (осью симметрии).
Высоты (биссектрисы, медианы), проведенные к
боковым сторонам, равны.
%
вершина равнобедренного
треугольника
$/ \ \
// W
основание
3
АЛЯ II—гт ^ 4>^j^
1 ВС «=> ААл = ССл
LAB
Все эти свойства равнобедренного треугольника обратимы и могут
быть использованы для получения признаков равнобедренного
треугольника. [
Правильный треугольник
Правильным (равносторонним) называется
треугольник, все стороны которого равны.
*
Л |

Справочные материалы
Геометрия в таблицах
549
4. Треугольник
Правильный треугольник (продолжение)
Свойства правильного треугольника
Все углы равностороннего треугольника
равны 60°.
Только в правильном треугольнике совпадают
точки пересечения медиан, биссектрис, высот,
серединных перпендикуляров. Эта точка
называется центром правильного треугольника и
является центром вписанной и описанной
окружностей.
Центр правильного треугольника делит его
высоты в отношении 2:1, считая от вершины.
Только в правильном треугольнике:
п « 2L а
R = 2r= „h= -p.
3 V3
Площадь равностороннего треугольника
S =
г2Л
АВ = ВС=АС = а
AA1 = BB1 = CC1 = h
h=Ya
Дополнительные теоремы о треугольнике
Теорема Чевы
Отрезки ААХ, ВВ^ CCi тогда и только тогда
пересекаются в одной точке, когда:
АВЛ САЛ
ВгС
АгВ
ВСг
С^А
= 1.
Теорема Менелая
Точки Aif Bi, Сi тогда и только тогда лежат на
одной прямой, когда:
АВЛ ВС,
ВгС
СгА
САг
А^В
= 1.
Теорема Стюарта
AAi = U тогда
Ь ах + с а2
Р =
аг + а2
«1^2-

550
Справочные материалы
Геометрия в таблицах
4. Треугольник
Дополнительные теоремы о треугольнике (продолжение)
Центры вневписанных окружностей лежат в
точках пересечения биссектрисы внутреннего
и двух биссектрис внешних углов
треугольника.
АТг = АТ2 = ^ (АВ + ВС + СА) =р
ВК = р-с;СК = р-Ь
i
5. Параллелограмм
Параллелограммом называется четырехугольник,
противоположные стороны которого попарно параллельны.
Свойства параллелограмма
Диагональ делит параллелограмм на два равных
треугольника.
Противоположные стороны параллелограмма
равны.
Сумма соседних углов параллелограмма 180°.
Диагонали параллелограмма, пересекаясь,
делятся пополам.
Дополнительные свойства параллелограмма
Биссектриса угла параллелограмма отсекает от
него равнобедренный треугольник.
Биссектрисы соседних углов параллелограмма
перпендикулярны, а биссектрисы
противоположных углов параллельны или лежат на
одной прямой.
Диагонали параллелограмма делят его на
четыре равновеликих треугольника.
Высоты параллелограмма обратно
пропорциональны соответственным сторонам
параллелограмма.
Высоты параллелограмма, опущенные из одной
вершины, образуют угол, равный углу
параллелограмма при соседней вершине.
Середина любого отрезка с концами на
противоположных сторонах параллелограмма лежит на
прямой, проходящей через середины двух
других сторон.
и и _<°
Ъ< , тет /Л+/В^180°
^Э^* -& ' "\ AB = BF
\Х\Л BMLAF
А и
В
а С
/ и 1 1
-Л / (К ! КЛ = / А
А";—* U к а* и*
В /Е С
&
Afc^ D

Справочные материалы
Геометрия в таблицах
551
5. Параллелограмм
Признаки параллелограмма
Если в четырехугольнике две противоположные стороны равны и
параллельны, то это параллелограмм.
Если в четырехугольнике противоположные стороны попарно
равны, то это параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, делятся пополам,
то это параллелограмм.
Периметр параллелограмма Р = 2а + 2Ь
Площадь параллелограмма
S = aha = bhfj
S = ab sin ф
S= 2«l«2sina
Сумма квадратов диагоналей параллелограмма
равна сумме квадратов его четырех сторон.
d\ + d\ = 2a2 + 2b2
Квадрат
Квадратом называется прямоугольник, у
которого все стороны равны (ромб с прямыми углами).
Квадрат обладает всеми свойствами ромба и
прямоугольника.
Квадрат — правильный четырехугольник.
d = aj2
г-J.
Площадь квадрата
S = a2=\d2
Ромб
Ромбом называется параллелограмм, все стороны которого равны.
Свойства ромба
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба лежат на биссектрисах его
углов.
Высоты ромба равны.
В ромб можно вписать окружность
г = 5 А = оа sin А*
Ромб обладает всеми свойствами
параллелограмма.
h = a sin А = a sin В = 2г

552
Справочные материалы
Геометрия в таблицах
5. Параллелограмм
Ромб (продолжение)
Признаки ромба
Бели в параллелограмме диагонали взаимно перпендикулярны, то это ромб.
Если диагональ параллелограмма лежит на биссектрисе его угла, то это ромб.
Если стороны четырехугольника равны, то это ромб.
Площадь ромба
S = ha = a2 sin А = « dxd2
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника
Диагонали прямоугольника равны.
Около прямоугольника можно описать
окружность
R= о^= 2^а + * "
Прямоугольник обладает всеми свойствами
параллелограмма.
А
а
■■III н^ни |f- -
"V%4W* лг
\ ^*Фх
D
JIT O^K*
J
^J
AC = BD = d
OA = OB = OC = OD
= R=\d
d2 = a2 + b2
Признаки прямоугольника
Если в параллелограмме диагонали равны, то это прямоугольник.
Если в параллелограмме один угол прямой, то это прямоугольник.
Если в четырехугольнике три угла прямые, то это прямоугольник.
Площадь прямоугольника
S = ab
S = 5 ^2 sin а
6. Трапеция
Трапецией называется четырехугольник, две стороны которого
параллельны, а две другие не параллельны.
Элементы трапеции
ВС и AD — верхнее и нижнее основания,
АВ и CD — боковые стороны,
АС и BD — диагонали,
MN — средняя линия,
MN= 1(BC+AD).
Высота трапеции BBi — расстояние между
прямыми оснований.
я
/
м/
t
С ВГ^^—*с
\iV h
: Y
лА -^АГ
лА
АВ[ » В, А D\
BBxLAD,BBx = h

Справочные материалы
Геометрия в таблицах
553
6. Трапеция
Площадь трапеции
S = h- MN= |a(BC+AD) = ^ACBDx
х sin /.(AC, BD)
Неравенство для сторон трапеции
AB + CD>AD-BC
CDX || BD
Неравенство для диагоналей трапеции
AC + BD>AD + BC
J^^x
2S
h =
ACD.
AD.
di + d2>b + a
Разбиение трапеции на параллелограмм и треугольник
ВА а Vе ВВХ || CD;
ii/ V2 V2 bcdbi—
Л \ \ ВС = а = 1
/ b -а\ а \_
— параллелограмм;
BXD
AD = b=>AB1 = b-a.
ССХ\\АВ;
ABCCi — параллелограмм.
Если известны стороны трапеции, можно вычислить по формуле Герона площадь отсеченного
треугольника (SA), высоту трапеции (А = Х5~ или А = g—^) и площадь трапеции.
Построение трапеции по основаниям и боковым сторонам
Пусть заданы отрезки а, 6, Zlf Z2> причем ^ +
+ 12 > Ь - а (Ь > а): неравенство для сторон
трапеции.
1. Строим AABBi по трем сторонам: Ь - а, 1±, 12.
2. Проводим через точку В прямую ВХ \\ ABi.
3. На лучах ВХ и B{Y строим отрезки ВС =
= BXD = а.
Трапеция ABCD — искомая.
с X
Ъ-а
В а С
Ь-e Вх D Y
Теорема о четырех точках трапеции
Середины оснований, точка пересечения
диагоналей и точка пересечения продолжений
боковых сторон трапеции лежат на одной прямой.
BL = LC
А* * £ *-^*D АТ = TD
Свойства треугольников в трапеции.
ABOC^ADOA
ВО= СО
OD ОА
а
V s
вое
DOA
(if
>АОВ
= Si
COD

554
Справочные материалы
Геометрия в таблицах
6. Трапеция
Построение трапеции по основаниям и боковым сторонам (продолжение)
Отрезок, параллельный основаниям,
проходящий через точку пересечения диагоналей.
аЬ 2аЬ
OQ = OP= -=2- ; PQ =
а + Ь
а + Ь
Отрезок, параллельный основаниям и
делящий трапецию на две равновеликие части.
FP
4
2 + Ь2
£з
D &AFPD ~ SfBCP* ЯР II ВС
В трапецию можно вписать окружность тогда
и только тогда, когда сумма оснований равна
сумме боковых сторон.
BC+AD=AB + CD
в т—+
Равнобедренная трапеция
Равнобокой (равнобедренной) называется
трапеция с равными боковыми сторонами.
Свойства равнобедренной трапеции
Диагонали равнобедренной трапеции равны
(dx = d2).
Углы при одном основании равнобедренной
трапеции равны.
Только около равнобедренной трапеции можно
описать окружность; она совпадает с
окружностью, описанной около любого
треугольника с вершинами в вершинах трапеции. Бе
центр лежит на серединном перпендикуляре к
основаниям трапеции.
Если центр описанной окружности лежит на
основании трапеции, то ее диагональ
перпендикулярна боковой стороне.
AO = BO = CO = DO = R
В равнобедренную трапецию можно вписать
окружность, если боковая сторона равна
средней линии.
АВ =
ВС + AD
2r = h

Справочные материалы
Геометрия в таблицах
555
7. Окружность
Окружностью называется множество точек плоскости, находящихся
на одинаковом расстоянии от данной точки (центра окружности).
Отрезки в окружности
Для любой точки М окружности с центром О
выполняется равенство: ОМ = R (отрезок ОМ —
радиус окружности).
Отрезок, соединяющий две точки окружности,
называется хордой.
Хорда, проходящая через центр окружности,
называется диаметром окружности (D).
D = 2R
Длина окружности
С = 2яД.
Дуга окружности
Часть окружности, заключенная между ее
двумя точками, называется дугой.
Две любые точки М и N окружности
определяют на ней две дуги: MkN и МIN. Любую из этих
дуг стягивает хорда MN.
Равные дуги стягиваются равными хордами.
Длина дуги
АСВ - Да, где а — величина угла АОВ в
радианах;
АСВ = ВТогГ*» где ф — величина угла АОВ в
градусах.
Круг
Кругом называется часть
плоскости, ограниченная
окружностью.
Для всех точек N круга
выполняется неравенство: ON < R.
Часть круга, ограниченная
дугой и двумя радиусами,
называется сектором круга.
Любые два радиуса задают
два сектора.
Часть круга, ограниченная
дугой и стягивающей ее хордой,
называется сегментом.
Любая хорда делит круг на два
сегмента.
Сегмент, задаваемый
диаметром, называется полукругом.

556
Справочные материалы
Геометрия в таблицах
7. Окружность
Круг (продолжение)
Диаметр, перпендикулярный хорде, делит эту
хорду и стягиваемые ею дуги пополам.
Если диаметр делит хорду, не являющуюся
диаметром, пополам, то он ей перпендикулярен.
MN1AB=>AT = BT
Если две хорды АВ и CD имеют общую точку М,
то
AM • МВ=СМ • MB.
Для данной точки М внутри окружности
произведение отрезков хорды, на которые делит ее
данная точка, есть величина постоянная и
равная:
(Д + ОМ)(Д-ОМ).
AM-MB = (R + OM)(R-OM)=R*-OM2
Центры всех окружностей, проходящих через
две данные точки, лежат на серединном
перпендикуляре к отрезку с концами в данных
точках.
Прямая и окружность
Прямая, имеющая с окружностью одну общую
точку, называется касательной к окружности;
прямая, имеющая с окружностью две общие
точки, — секущей.
Прямая касается окружности тогда и только
тогда, когда диаметр, проходящий через общую
точку прямой и окружности, перпендикулярен
этой прямой.
секущая
касательная* ОМ _L а
Если расстояние ОМ от центра окружности до
прямой
больше радиуса — прямая не имеет с
окружностью общих точек;
равно радиусу — прямая касается окружности;
меньше радиуса — окружность высекает на
прямой хорду длиной 2
яг-
OM>R OM = R
OM<R
ОМй
Если окружность касается сторон данного угла,
то:
центр окружности лежит на биссектрисе угла,
отрезки касательных равны между собой.
биссектриса
AM=AN

Справочные материалы
Геометрия в таблицах
557
7. Окружность
V Свойство хорд, секущей и касательных
Если из точки вне окружности к ней проведены
касательная и секущая, то квадрат длины
отрезка касательной равен произведению всего
отрезка секущей на его внешнюю часть.
Произведения длин отрезков секущих,
проведенных из одной точки, равны.
АТ2=АВ-АС =
= AY-AY =
= (ОА-Д)(ОА + Д) =
= ОА2-Д2
Две окружности
Если расстояние d между центрами двух окружностей больше
суммы (Ri + Д2 < d) или меньше разности (Дх - Д2 > d) их радиусов, то
окружности не имеют общих точек.
Дт + До < d
Rx-R2>d
Если Ri + Д2 = d или Ri - Д2 = d, то окружности касаются (внешним
или внутренним образом).
внешнее касание
Rl + R2 = d
внутреннее касание
Ri -~ До — d
Если Ri - Д2 < d < Ri + Д2, то окружности имеют общую хорду.
MiV = Д2 - Дх + d
MN = fi! + fi2-d
4S,
АВ =
ОхА02
Две окружности, имеющие общий центр,
называются концентрическими.
MN = Ri-R2
d = 0

Справочные материалы
Геометрия в таблицах
7. Окружность
Углы в окружности/
Центральным углом в окружности называется
угол между двумя ее радиусами.
Градусная мера центрального угла равна
градусной мере дуги, на которую он опирается
(измеряется дугой, на которую он опирается).
Угол, вершина которого лежит на окружности,
а стороны содержат хорды, называется
вписанным углом.
Вписанный угол измеряется половиной дуги,
на которую он опирается.
Вписанный угол, опирающийся на диаметр,
прямой.
Вписанные углы, опирающиеся на одну и ту же
дугу, равны.
Вписанные углы, опирающиеся на одну и ту же
хорду, либо равны, либо их сумма 180°.
J/Угол между хордой и касательной измеряется
1 половиной содержащейся в этом угле дуги
окружности.
Угол с вершиной внутри окружности (угол
между двумя хордами).
Угол с вершиной вне окружности (угол между
двумя секущими).
Р £АОВ=АРВ = а° \
А
/^^ /С~^\ £ВАС = £ВРС =
1 \У\ \Х\° 11-
P^^L/ x4te23*c /_ ВАС = 90°
В А
\\^^У £ВРС = £ВАС
в^ L ВАС + АВТС = 180°
( </ \ \м
Ч^ ^,/ъ АВАС=\ВМА
сЛ/\ J /LBAC = £CC1B +
^ ^ = \ (ВМС + BiLCx)
И/С^ч z. вас = /.с1вв1 -
^1т--~ \ -^ссгв =
А Л ;с1 1 w
\. У = ^(BiMCt- BLC)

Справочные материалы
Геометрия в таблицах
559
7. Окружность
Общие касательные двух окружностей
Если одна окружность лежит вне другой, то у
них четыре общие касательные.
Если одна окружность касается другой
снаружи, то у них три общие касательные.
две внутренние касательные
одна внутренняя касательная
d = Ог02 > Ri + R2
1 с
ю2 = 5ППГ d; NlN* + (Ri+ R2)2 = d2
d = Дх + R2
МХМ2 = 27^^
МгВ = BA = BM2
Если одна окружность
касается другой изнутри, то у них
одна общая касательная.
Если окружности
пересекаются, то у них две общие
касательные (две внешние
касательные, внутренних
касательных нет).
Если одна окружность лежит
внутри другой, то общих
касательных нет.
Mi
Если Oi02 = d, то
2 = ^2
МХМ\ + (Rx - Д2) = d
Вписанная окружность
Окружность называется вписанной в
многоугольник, если она касается всех его сторон.
Ее центр должен принадлежать всем
биссектрисам внутренних углов этого многоугольника. Ее
радиус можно вычислить по формуле г = -, где
S — площадь, а р — полупериметр
многоугольника.
Не во всякий многоугольник можно вписать
окружность.

560
Справочные материалы
Геометрия в таблицах
7. Окружность
Вписанная окружность (продолжение)
В любой треугольник можно вписать
окружность и притом только одну. Бе центр лежит в
точке пересечения биссектрис внутренних углов,
а радиус может быть вычислен по формулам:
S
г= -
Р
ABC
r = (p-a)tg ■£ = (p-&)tg g =(P~c)tg 2>
где S — площадь треугольника, ар — его
полупериметр.
ABi=ACi=p-a
ВС1=ВА1=р-Ь
СА^СВ^р-с
р=2<а + & + с) —
полупериметр
В выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда суммы
длин его противоположных сторон равны.
AB + CD = BC+AD
С
Описанная окружность
Окружность называется описанной около
многоугольника, если она проходит через все его
вершины. Бе центр лежит на всех серединных
перпендикулярах сторон (и диагоналей) этого
многоугольника. Радиус вычисляется как
радиус окружности, описанной около треугольника,
определенного любыми тремя вершинами
данного многоугольника.
ОА = ОВ = ОС =
= OD = OE = R
Около любого треугольника можно описать
окружность и притом только одну. Ее центр
лежит в точке пересечения серединных
перпендикуляров сторон треугольника, а радиус
вычисляется по формулам:
п_ Д Ь с
2 sin А 2 sin В 2 sin С
аЬс '"
AS
a, b, с — длины сторон треугольника, S — его
площадь.
Д =
АВ^90°=>ААОС<2В
zLB> 90° =>
Z.AOC = 180° -2В

Справочные материалы
Геометрия в таблицах
561
7. Окружность
Описанная окружность (продолжение)
Около четырехугольника можно описать
окружность тогда и только тогда, когда сумма его
противоположных углов равна 180°.
L А + Z. С = А В + Z. D = 180 °
Теорема Птолемея
Во вписанном четырехугольнике произведение
диагоналей равно сумме произведений его
противоположных сторон.
АС • BD - АВ • CD + ВС • AD
8. Площади
Площади равных фигур равны.
Если фигура составлена из нескольких фигур, не имеющих общих
внутренних точек, то ее площадь равна сумме площадей этих фигур.
Фигуры, имеющие равные площади, называются равновеликими.
Площадь квадрата
\s = a2
Площадь параллелограмма
\ S = а • ha = Ь • h^
S = ab sin а
Площадь треугольника
Основные формулы
5=2 а^* = 2 *** = 2 с^с
S = 5 л& sin С = 5 лс sin Б = 5 &^ sin А
Формула Герона
, 1
S- JpiP - а)(Р - Ь)(р - с),гдер= ^(а + Ь +
+ с) — полупериметр
Площадь прямоугольника
S = ab
в
1
La
л LL-
fi в
^^ / /
Лв / /
/ /«/
-1 /_ . Л /
с
А.
п
А
vv
TV° >ч
\$йг °
в

562
Справочные материалы
Геометрия в таблицах
8. Площади
Дополнительные формулы
S = гр, где г — радиус вписанной окружности
о аЬс D
S = "jp , где R — радиус описанной окружности
S = 2Д2 sin A sin Б sin С
Некоторые соотношения площадей
треугольников
Площади подобных треугольников (фигур)
относятся как квадраты сходственных элементов
(сторон, медиан, высот и т. п.), их отношение
равно квадрату коэффициента подобия.
AABC^AMNC
CCi = А; СХ = х; АВ = с
MNC
'авс
MN
= k2
Площади треугольников, имеющих равные
высоты (общую высоту), относятся как стороны,
соответствующие этим высотам.
&АВС : &BFG —АС : FG
Площади треугольников, имеющих равные
стороны, относятся как соответствующие этим
сторонам высоты.
&АВС : &АЕС ~" BBl : EEl
с
Площади треугольников, имеющих равный угол
(или общий угол), относятся как произведения
сторон, содержащих этот угол.
ЪАВС АВ АС
AF АЕ
DAFE
Медиана делит треугольник на два
равновеликих треугольника.
Три медианы треугольника делят его на шесть
равновеликих треугольников.
*АВВЛ
= S
вгвс
^ACCi - SdCB
8АСА, = SAtAB
SAGBi *" ^GC e SCGAl " SAiGB "
" SBGCl " ScfiA

Справочные материалы
Геометрия в таблицах
563
8. Площади
Некоторые соотношения площадей треугольников
(продолжение)
Площадь прямоугольного треугольника.
S=2ab=2ch
с
Площадь правильного треугольника.
S =
г2Л
Примеры решения задач
на нахождение площадей
Пример 1.
Дано: СМ = 2MB; CN = NA; SABC = S
Найти: SMBAN.
Решение:
scmn СМ • CN 2
3
ЭАВС
СВ СА
1
2
1
3
SCMN = § S :
> SMBAN - SABC " SCMN ~~S~ 3S~~ $S'
Пример 2.
Дано: 3CAi = АгВ; АО = ОАг; SABC = S.
Найти: Sr
>ОВА
Решение:
AABAi и ААВС имеют общую высоту,
проведенную из вершины А:
ЭАВАЛ
*АВС
АгВ
СБ
3
4
*АВАЛ
!«•
ВО — медиана AABAi =* ^ова
8s.

564
Справочные материалы
Геометрия в таблицах
8. Площади
Примеры решения задач на нахождение площадей (продолжение)
Пример 3.
Дано: AU = \ BU; ВТ =\сТ; АХ = XY = YC;
&АВС = S-
Найти: SXuTY'
Решение:
&АТВ = 5 &АВС = о «S (общая высота).
Snrr/ — 5 SiinT =
В7Т/ ~ 5 °авг = о S (общая высота).
2
91
Аналогично, STYC = - S;
SAXU~ gs=> s
XUTY=gS-
Пример 4.
Дано: YX \\ AC; XZ \\ AB; SBXY = Sx; Scxz = S2.
Найти: SAYXZ.
Решение:
AXYB™ACZX=* ^ = \^.
SAYXZ - 2 * SAXZ - 2 # ^r # SCXZ :
AZ
zc
vy
^-S2-2JS^
Площадь трапеции
S = ^^ • A - MW • A,
а и ft — длины оснований,
A — высота, MN — средняя линия.
в а
M<S
>S / h
Sa / b - a
С
h
V xr
;^^_^^
E Cx
Пусть заданы основания a, & и боковые
стороны АВ = Zlf CD = Z2- Проведем СЕ || АВ.
Тогда А£ = a,ED = b-a,CE = lv
2St
ССЛ = А =
*ECD
b - а
, S^Cjrj вычисляется по
формуле Герона.
Соотношение площадей фигур, связанных с трапецией
£i =(вс\2
s2 [ad) ;
SAOB - SCOD
=7^
DOC = ^ sl = ft ^2
Snnn — " Si — г S:
P. *^
CP II BZ) => S^c^ - SACP

Справочные материалы
Геометрия в таблицах
565
8. Площади
Соотношение площадей фигур, связанных с трапецией (продолжение)
Площадь произвольного
четырехугольника
S= -zAC • BD • sin а
Площадь ромбоида
S = | AC • BD
Площадь произвольного
многоугольника (триангуляция)
&ABCD = Si + ^2 + S3 + S4,
где Е — произвольная точка
внутри многоугольника.
в
Площадь правильного п-угольника
S=|rP
0 nR . 2я
S = —=— • sin —
2 п
~ 9. я л па к
п
S = 5 Л-Р» * — апофема.
Площади правильных многоугольников
0 6Д2 . 2я ЗТЗД2
S6 = — smy = -^—
2
_ &R 2тс rt_2 /^
S8 = —sin-g- = 21TV2
12Д2 . 2я оп2
-5>i2 = 2 sm 12 =
Ал.
А1А2 = ...А/гА1 = а
Р = ап — периметр
R — радиус описанной
окружности
г — радиус вписанной
окружности
Площадь круга
S = 7C*2 = j2)2=!*C
С — длина окружности,
D = 2R — диаметр.
С = 2яД
Площадь сектора
* 2п 180°
S=!*2cc
(-
радиан
сектор
Площадь сегмента
S = 5 Д2(а - sin а),
а — радианная мера дуги
АтВ или АпВ (соответственно
для сегментов АтВ или АпВ).
^сегмАтВ ~~ &секАтВ &АОВ
&сегмАпВ = SCeKAnB + SaOB

566
Справочные материалы
Геометрия в таблицах
8. Площади
Соотношение площадей фигур, связанных с трапецией (продолжение)
Пример 1.
Площадь большого полукруга
kR2 „
-о- • Площадь каждого из ма-
<!/
лых полукругов
Площадь заштрихованной
фигуры S :
яД'
2
Л/Г
8
3nR*
Пример 2.
АО = 2R; АС = Д 73 (по т.
Пифагора).
Площадь АСОВ = 2SACO =
= д27з.
Площадь сектора
Площадь заштрихованной
фигуры S = Д 73 - -д- =
-Ыл-9-
Пример 3.
СТЕРЕОМЕТРИЯ
9. Основные аксиомы и определения
Через любые три точки, не лежащие на одной
прямой, проходит одна и только одна
плоскость.
Если две точки прямой лежат в плоскости, то и
вся прямая лежит в этой плоскости.
М е a, L е а
М е а, L е а
аса
Если две плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту
точку.
В любой плоскости выполняются аксиомы
планиметрии.
М е а, М € Р =
а n Р - а
\М е а
1а ЭМ
Две прямые, имеющие только одну общую
точку, называются пересекающимися.
м
a nb = М

Две прямые, лежащие в одной плоскости и не
имеющие общих точек, называются
параллельными.
Две прямые, не лежащие в одной плоскости,
называются скрещивающимися.
Прямая, все точки которой принадлежат
плоскости, называется прямой, лежащей в этой
плоскости.
Прямая пересекает плоскость, если у них есть
только одна общая точка.
Прямая называется параллельной плоскости,
а плоскость — параллельной прямой, если они
не имеют общих точек.
Две плоскости, не имеющие общих точек,
называются параллельными.
Два луча называются сонаправленными, если
' один из них является частью другого, или если
они лежат на параллельных прямых в одной
полуплоскости относительно прямой,
проходящей через начала лучей.
Прямая называется перпендикулярной
плоскости (а плоскость прямой), если прямая
перпендикулярна любой прямой, лежащей в этой
плоскости.
Справочные материалы
Геометрия в таблицах
9. Основные аксиомы и определения
NM и NK сонаправ- АХ и BY сонаправлены
лены. АХ || BY
.
а
(с " ° \
^ | Zs
1
а _1_ а => (а _1_ с, а _1_ Ь)

568
Справочные материалы
Геометрия в таблицах
10. Теоремы стереометрии
Через прямую и не лежащую на ней точку
проходит одна и только одна плоскость.
М ё а
{аса
Месс
Через две пересекающиеся прямые проходит
одна и только одна плоскость.
anb = M-.
{аса
Ьса
Через две параллельные прямые проходит одна
и только одна плоскость.
a lib:
аса
Ьса
Если точки А, В, С, D не лежат в одной
плоскости, то прямые АВ и CD (АС и BD, AD и ВС)
скрещиваются.
Если прямая АВ лежит в некоторой плоскости,
а прямая CD пересекает эту плоскость в точке,
не лежащей на АВ, то прямые АВ и CD
скрещиваются.
А, В, С е а
D т а
AB^-CD
AC^BD
AD^-BC
Если одна из параллельных прямых пересекает
плоскость, то и другая прямая пересекает эту
плоскость.
a lib
ana
bna
Признак параллельности прямых
Если две прямые параллельны третьей, то они
параллельны между собой.
ь с
а и с
Ъ\\с
=>а\\Ъ
Признак параллельности
прямой и плоскости
Если прямая, не лежащая в плоскости,
параллельна какой-либо прямой, лежащей в
плоскости, то она параллельна этой плоскости.
a lib
Ьса
► а II а

Справочные материалы
Геометрия в таблицах
569
10. Теоремы стереометрии
Если одна из пересекающихся плоскостей
проходит через прямую, параллельную другой
плоскости, то линия пересечения плоскостей
параллельна этой прямой.
а п Р = ft
аса
а ИР
=>а II Ь
Если каждая из пересекающихся плоскостей
проходит через одну из двух параллельных
прямых, то прямая пересечения плоскостей
параллельна этим прямым.
a n Р
Г?*-
аса
ftcp
а lib
а || с
ft II с
Если две пересекающиеся плоскости
пересечены третьей плоскостью по параллельным
прямым, то линия их пересечения параллельна
этим прямым.
а n р = с
уп а = а
уп р = ft
а II ft
с II а
с II ft
Если две пересекающиеся плоскости
пересечены третьей плоскостью по пересекающимся
прямым, то точка их пересечения лежит на
линии пересечения плоскостей.
Углы с соответственно сонаправленными
сторонами равны.
L ВХАХСХ = /- ВАС
Признаки параллельности плоскостей
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
пересекающимся прямым другой плоскости, то эти
плоскости параллельны.
a n ft - М
а С a; ft с а
а || аг; Ь || Ьх
аг с р; Ьх С р
►а||р
Если две плоскости параллельны третьей, то
они параллельны между собой.
а II у
My
►а||р

570
Справочные материалы
Геометрия в таблицах
10. Теоремы стереометрии
Свойства параллельных плоскостей
Если плоскость пересекает две параллельные
плоскости, то прямые пересечения
параллельны.
yn а = а
уп Р - Ь
а ИР
■a\\b
Если прямая пересекает одну из параллельных
плоскостей, то она пересекает и другую
плоскость.
ana
а ||р
anp
Если плоскость пересекает одну из
параллельных плоскостей, то она пересекает и другую
плоскость.
a ИР
yn a
Y^P
Через точку, не лежащую на плоскости, можно
провести одну и только одну плоскость,
параллельную данной плоскости.
М t a
а с a
& с a
существует
ах || а
Ьх || Ь
ainbi= М

существует единственная плоскость р || а, М е р
Признак перпендикулярности прямой и
плоскости
Если прямая перпендикулярна двум
пересекающимся прямым плоскости, то она
перпендикулярна самой плоскости.
a nb
а с а;
с L а
с Lb
]
& с а
► с _1_а

Справочные материалы
Геометрия в таблицах
571
10. Теоремы стереометрии
Признак перпендикулярности прямой и плоскости (продолжение)
а) Если прямая перпендикулярна одной из
параллельных плоскостей, то она
перпендикулярна и другой.
б) Если две плоскости перпендикулярны одной
и той же прямой, то эти плоскости
параллельны.
в) Через точку проходит единственная
плоскость, перпендикулярная данной прямой.
а)
б)
a lip
а _1_ а
а _L а
Р±а
а±р
>а||р
в)
М е а
М е а
существует единственная плос-
костьсс±а<=|^* а
\М е а
а) Если одна из параллельных прямых
перпендикулярна плоскости, то и другая прямая
перпендикулярна этой плоскости.
б) Если две прямые перпендикулярны одной
плоскости, то эти прямые параллельны.
в) Через точку проходит единственная прямая,
перпендикулярная данной плоскости.
b_Lcc
>a\\b
в) М е а ^ существует единственная прямая
a_Lct,М е a <= Af g a
Теорема о трех перпендикулярах
Если (ортогональная) проекция наклонной
перпендикулярна прямой на плоскости, то и сама
наклонная перпендикулярна этой прямой.
Если наклонная перпендикулярна некоторой
прямой плоскости, то и (ортогональная)
проекция наклонной на эту плоскость
перпендикулярна этой прямой.
(с 1 т) <=>
о(И/п)
Если плоскость проходит через перпендикуляр
к другой плоскости, то она перпендикулярна
этой плоскости.
Га
1—
а
)
у
аса
al Р
alp

572
Справочные материалы
Геометрия в таблицах
10. Теоремы стереометрии
Перпендикуляр к одной из двух
перпендикулярных плоскостей либо лежит в другой
плоскости, либо ей параллелен.
alp
alp
• а С а или а II a
Если две пересекающиеся плоскости
перпендикулярны третьей плоскости, то и линия их
пересечения перпендикулярна этой плоскости.
a n Р — а)
a 1 у ^=>aly
Ply
Угол, образованный наклонной и плоскостью,
не больше угла между этой наклонной и любой
прямой плоскости.
Углом между наклонной и плоскостью
называется угол между наклонной и ее ортогональной
проекцией на эту плоскость.
ply
any b = пр а
a<ty
тсу
А (а, у) = а = А (а, Ъ) < Р = Z. (а, т)
Отрезки параллельных прямых, заключенные
между параллельными плоскостями, равны.
a ,Ъ
а II Ь
Теорема Фалеса
Параллельные плоскости, пересекающие
прямые и отсекающие на одной из них равные
отрезки, отсекают равные отрезки и на других
прямых.
«1 Ai/ \Bi <y^)
a! II a2 II a3,
А1А2=А2Аз=>
=ф BiB2 = -82-83,
C1C2 = C2C3

Справочные материалы
Геометрия в таблицах
11. Расстояния в пространстве
Расстояние между точками А и В равно длине
отрезка АВ.
Расстояние есть неотрицательное число.
Расстояние между точкой и фигурой
(множеством точек) равно нулю, если точка
принадлежит фигуре, или длине наименьшего отрезка,
одним из концов которого является данная
точка, а другим — ближайшая точка фигуры (если
такой отрезок существует).
Расстояние между двумя фигурами
(множествами точек) равно нулю, если фигуры имеют
общую точку, и расстоянию между ближайшими
точками этих фигур, если такие точки
существуют.
Расстояние от точки до прямой, не
содержащей эту точку, есть длина отрезка перпендику-
Расстояние от точки до плоскости^ не
содержащей эту точку, есть длина отрезка
перпендикуляра, опущенного из этой точки на
плоскость.
Расстояние* между двумя пересекающимися
прямыми равно нулю.
Расстояние между двумя параллельными
прямыми равно длине отрезка их общего
перпендикуляра.
Расстояние между двумя параллельными
прямыми равно расстоянию от любой точки одной
из этих прямых до другой прямой.
Расстояние между двумя скрещивающимися
прямыми равно длине отрезка их общего
перпендикуляра (такой отрезок единственный).
А В
p(A,B)=AB>0
/^^Л м XeF9AeF
(f F A]Z7* p(M,F) = MA
V xJ^ P(K,F) = 0
4 ^ MX>MA
Р(*Ъ f2) = o
P(^l,^2)=^l^2
Ax e FlfA2e F2
M \
\ ^^ Mt a
\^"^ P(M, a) = MA
Z^^a Aea.MALa
( J$/^~ J M* a
V ^/^^ P(M*a) = MA
V L^^ A e a, MA ± a
—*^*^ ^s ar\b=A, p(a, b) = 0
a^0^^ \^ all b, p(a, b)=A1B1=A2B2
V^^Bg ^I e a*A2e a;Bie b;B2e b
b<^% AXBX _L a, A2B2 J. a
b^^^ a || b, A e a => p(a, b) - p(A; b) |
j
В
a^-b
p(a,b)=AB,
^■^— As a,B<= b,AB_La,AB_Lb

574
Справочные материалы
Геометрия в таблицах
11. Расстояния в пространстве
Расстояние между двумя скрещивающимися
прямыми равно расстоянию от любой точки
одной из этих прямых до плоскости, проходящей
через вторую прямую параллельно первой, или
расстоянию между двумя параллельными
плоскостями, содержащими эти прямые.
(а — Ь => а || 6,
аСа)=> р(а, Ь) = р(Ь, а)
а — fr, а с а,
Ь С р => р(а, Ь) = р(а, Р)
Расстояние от прямой до непараллельной ей
плоскости равно нулю.
а # ос => р(а; а) = О
ЬСа^ р(Ь; а) = О
Расстояние между прямой и параллельной ей
плоскостью равно длине отрезка их общего
перпендикуляра.
Расстояние от прямой до параллельной ей
плоскости равно расстоянию от любой точки
этой прямой до плоскости.
а || а, А е а, В е а|
АВ _L а; АВ 1 а [ »
р(а, а) - АВ I
<_j> \М е а, а || а
I р(а, а) - р(М, а)
Расстояние между двумя параллельными
плоскостями равно длине отрезка их общего
перпендикуляра.
а || р, А е а, В е р,
AB_Lcc,AB-LP
р(а,Р)=АВ
Расстояние между двумя параллельными
плоскостями равно расстоянию между точкой
одной из этих плоскостей и другой плоскостью.
ос II (3, А е ос
р(а,Р) = р(А;р)
Расстояние между двумя параллельными
плоскостями равно расстоянию между любой парой
скрещивающихся прямых, лежащих в этих
плоскостях.
а || р, а С а; Ъ С Р; а - Ъ
р(а, р) = р(а, Ь)
Расстояние от точки до сферы равно модулю
разности расстояния от этой точки до центра
сферы и радиуса сферы.
p(M,S) = MA = MO-R, Ае S
p(Mlf S) = MXAX = R - МгО;
AxeS
г p(M9S) = \MO-Hi

Справочные материалы
Геометрия в таблицах
575
11. Расстояния в пространстве
Расстояние между двумя шарами, не
имеющими общих точек, равно разности расстояния
между их центрами и суммы их радиусов.
Qx, Q2 не имеют общих точек
p(Ql,Q2) = 0102-(R1 + R2)
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства, удаленных от
данной точки на данное расстояние R, есть
сфера с центром в данной точке радиуса R (R > 0).
Множество точек пространства, удаленных от
данной прямой на данное расстояние R, есть
цилиндрическая поверхность (R > 0).
Множество точек пространства, удаленных от
данной плоскости на данное расстояние а, есть
две параллельные ей плоскости (а > 0).
а II Рх,а II р2; АМх=АМ2 = а
MiM2 -L а, А е а, А е MiM2
Множество точек пространства,
равноудаленных от двух точек, есть плоскость,
проходящая через середину отрезка с концами в этих
точках перпендикулярно прямой, проходящей
через эти точки. В этой плоскости лежат центры
всех сфер, проходящих через данные точки.
АМ = МВ;АК
АВ±а
KB
Множество точек пространства,
равноудаленных от трех точек, не лежащих на одной
прямой, есть перпендикуляр к плоскости этих
точек, проходящий через центр окружности,
описанной около треугольника с вершинами в этих
точках. На этом перпендикуляре лежат центры
всех сфер, проходящих через данные точки.
ОА = ОВ = ОС\
МО la I
^>МА = МВ = МС
Множество точек пространства, равноудаленных
от четырех точек, не лежащих в одной
плоскости, есть единственная точка — центр сферы,
проходящей через данные четыре точки.

576
Справочные материалы
Геометрия в таблицах
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства,
равноудаленных от двух параллельных прямых, есть
плоскость, проходящая через середину отрезка
общего перпендикуляра этих прямых и ему
перпендикулярная .
В этой плоскости лежат центры сфер,
касающихся этих прямых.
а || Ь, X е а, У е Ь, М е а 1
ХУ1а, XYLa, XY 1 b
XZ = ZY J
=>МХ = МУ
Множество точек пространства,
равноудаленных от двух пересекающихся прямых, есть две
плоскости, перпендикулярные плоскости этих
прямых и проходящие через биссектрисы
углов, образованных этими прямыми.
Pi 1 а, р2 -L а
Множество точек пространства,
равноудаленных от прямых, содержащих стороны
треугольника, есть четыре прямые,
перпендикулярные плоскости треугольника, проходящие
соответственно через центр вписанной и
каждый из трех центров вне вписанных для этого
треугольника окружностей.
та J_ a, mb _L а
тс -L а, m0 -L а
Множество точек пространства,
равноудаленных от сторон данного треугольника, есть
перпендикуляр к плоскости треугольника,
проходящий через центр вписанной в него
окружности. На этом перпендикуляре лежат центры
всех шаров, касающихся сторон треугольника.
ХО _L (ABC) 1
ОСг = ОАх = ОВх >=>
ОСг 1АВ, ОАг .L ВС, ОВг LAC \
X => ХСг LAB, ХВг LAC,
ХАг 1 ВС; ХА1=ХВ1 = ХС1
а) Множество точек пространства,
равноудаленных от двух параллельных плоскостей, есть
параллельная им плоскость, проходящая через
середину отрезка их общего перпендикуляра.
В ней лежат центры всех шаров, касающихся
обеих плоскостей.
б) Множество точек двугранного угла,
равноудаленных от граней этого угла, есть биссек-
торная полуплоскость этого угла. В ней лежат
центры всех шаров, вписанных в этот угол.
S?X
^d
^7
\жу
а II Р, у II а, АВ1 а, АС = СВ
Хеу=>р(Х,а) = р(Х,р)
Z (М, АВ, X) = /. (X, АВ, N)
Хеу=>р(Х,а) = р(Х,Р)

Справочные материалы
Геометрия в таблицах
577
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства, равноудаленных
от двух пересекающихся плоскостей, есть две
биссекторные плоскости, проходящие через
прямую пересечения этих плоскостей и
делящие образованные двугранные углы пополам.
В них лежат центры всех шаров, касающихся
обеих плоскостей.
JZT zl(a,Y) = ^(P,Y)
Xey=>P(X,a) = p(X,P)
zl(a,8) = ^(P,8)
Ye8=>p(Y,a) = p(Y,p)
13. Углы в пространстве
Угол между прямыми
Угол между параллельными или
совпадающими прямыми считается равным нулю.
а ||Ь
(a, b) = A (a, b) = 0
Углом между пересекающимися прямыми
называется наименьший из углов, образованных
при пересечении прямых.
anb = M;<L(a,b) = Z. РМТ
Углом между скрещивающимися прямыми
называется угол между пересекающимися
прямыми, соответственно параллельными данным
скрещивающимся.
a — b; ах II а; &i II b; ainbi = M\
А (а, Ь) = /. (av Ъг)
Две прямые называются перпендикулярными (ортогональными), если угол между ними прямой.
Угол между двумя прямыми находится в пределах от 0° до 90°. 0° < z. (a, b) < 90°
Примеры нахождения углов между двумя прямыми в многогранниках
Пример 1. Дан куб.
1) /L(AB, DiCi) = 0°
2) Z.(AD, ВСг) = £(ВС, ВСг) = 45°
3) £(DC, ВСХ) = ^(DXCV ВСг) - 90°
4) ЦРхВ19 ВСг) - /.(DB, ВСг) = 60°
(A DBCi — правильный)
5) ДАхД ВСг) = /-(ВгС, ВСг) = 90°
6) /-(ABV ВСг) = <L(DCV ВСг) = 60°
7) /.(AiC, ВС{) = 90° (теорема о трех перпендикулярах)
19-1019

578
Справочные материалы
Геометрия в таблицах
13. Углы в пространстве
Примеры нахождения углов между двумя прямыми в многогранниках (продолжение)
Пример 2. Дан правильный тетраэдр
1) L(DO, АВ) = 90° (DO _L (ABC))
2) Z_(AD, ВС) = 90° (теорема о трех перпендику
лярах) А*
3) L.(DO, KZ) = /.(DO, BD), так как KZ || BD
4) А(АК, BZ) = Z.(AK, Кгг)9 где KZX II BZ.
Рассмотрим AAKZi.
2
Дано:
AB = BC = CA=AD = BD =
= CD = a
BK = KC,KeBC
DZ = ZC,ZeDC
AK = ^;KZX
2 , «.« x 15Z = | ^p ; AZ? = a2 + f jY - 2a • | cos /L ACD (теорема косинусов в A AZXC).
AZ\ = ^ . AZ\ = АЙГ2 + KZ\ - 2ART • HTZx cos ф, где ф = L(AK, KZX) (теорема косинусов в A AKZ{).
Следовательно, /~(АК, KZX) = ф = arccos ~ ,
Угол между прямой и плоскостью
Прямая называется перпендикулярной данной
плоскости, а плоскость — перпендикулярной
прямой, если прямая перпендикулярна любой
прямой, лежащей в этой плоскости.
Прямая, пересекающая плоскость и не
перпендикулярная ей, называется наклонной к этой
плоскости.
Угол между прямой, параллельной данной
плоскости (или лежащей в плоскости), и
данной плоскостью считается равным нулю.
тСа=> /~(т, а) = 0°
а _1_ а => /.(а, а) = 90°
Z.(AB, a) = /L AqBA = ф;
в1Пф
= Р(А, а)
АВ
Если прямая и плоскость взаимно
перпендикулярны, то угол между ними считается равным
90°.
Синус угла между наклонной АВ и
плоскостью, в которой лежит точка В, равен
отношению расстояния от точки А до этой
плоскости к длине отрезка АВ.
Угол между наклонной и плоскостью равен
углу между наклонной и ее проекцией на эту
плоскость (ортогональной проекцией).
Угол между прямой и плоскостью находится
в пределах от 0° до 90а.
0° < /.(а, а) < 90°
Примеры нахождения углов между прямой и плоскостью
Найти: ф = /-(BDV (ВВгСг)).
Пример 1.
Дано: ABCDA^CiDi — куб.
Решение:
1. DXCX 1 (ВВХС{) => ВСХ — проекция BDX => ф = Z. DXBCV
2. В A EDiCi sin ф = -=?-=• = —F = "7=
1 г ПХВ aj3 73
=> ф = arcsin -= = arctg -=.
л/з Л
D\c\ а 1 а 1
= —р = -р (или tg ф = —7= = —) =>
ajl 72

Справочные материалы
Геометрия в таблицах
579
13. Углы в пространстве
Примеры нахождения углов между прямой и плоскостью (продолжение)
Пример 2.
Дано: ABCDA^xCiDx — куб.
Найти: фх = £(ADV {DAxBj))\ ф2 = ^(CDV (DA&)).
Решение:
1. ADX ±AXD; AXBX 1 (AA^) => АгВг _L ADV
2. ADX 1 (DA&) =><?! = 90°.
3. ADX _L (2)A1B1); ADX n (DAxBi) = F=>FC — проекция CDX на (DA^) => ф2 = ADXCF.
FDX i
4.ВД2)12?С81пф2=£-£ =2 =>Ф2 = 30°.
Пример 3.
Дано: ABCD — правильный тетраэдр, AM = MD, М е AD.
Найти: ф = Z.(BM, (BDC)).
Решение: К — середина ВС.
1. (DAK) 1 (BDC), так как ВС 1 (DAK).
2. (DAK) п (2)БС) = DK, МТ 1 DK, Т е DK => МТ 1 (БХ)С)
ВМ на (В2)С) =* ф = Z.MB77.
3. МТ = 5 Р (A, (BDC)) = = 5 a*/q» гДе а — стоРона тетраэдра; ВМ = -5-
МГ 72 . 72
=> sin ф = дТ^ = — =* ф = arcsin -5-.
ВТ — проекция
Двугранный угол
Двугранным углом называется пересечение двух
полупространств, образованных
непараллельными плоскостями. (Фигура, образованная двумя
непараллельными полуплоскостями,
имеющими общую границу.)
Общая прямая полуплоскостей называется
ребром двугранного угла, а полуплоскости —
гранями двугранного угла.
Z(X,(AB),Y)-
двугранный угол
аса а±АВ;
ЬсР ЫАВ
ar\b = 0; /-{а, Ъ)
линейный угол
£_(ХЛАВ),Г) =
= Ш, b)
\ Линейным углом двугранного угла называется
пересечение этого двугранного угла и
плоскости, перпендикулярной его ребру. (Угол между
двумя перпендикулярами к ребру двугранного
угла, лежащими в гранях двугранного угла и
имеющими на ребре общее начало.)
a_LAB; ах 1АВ;
ЫАВ;Ъг±АВ
/_(M,(AB),N) = A(a,b)-
= Z(a1,b1)= £MON =
= Z. M^Ny
P(M; P)
P(M; AB)
в1Пф:
Величина двугранного угла считается равной
величине его линейного угла.
Все линейные углы данного Двугранного угла
равны между собой.
Величина двугранного угла находится в
пределах от 0° до 180°. 0° < Z(M, (AB), N) < 180°
Синус линейного угла двугранного угла
равен отношению расстояния от любой точки
одной из граней двугранного угла до
плоскости другой грани к расстоянию от этой точки
до ребра этого двугранного угла.
19*

580
Справочные материалы
Геометрия в таблицах
13. Углы в пространстве
Примеры нахождения двугранных углов в кубе
Пример 1.
Дано: ABCDA1B1C1D1 — куб.
Найти: ос = Z. (Av (ВС), D).
Решение:
1. АгВ ±ВС;АВ±ВС=>а = ААгВА.
2. Z. АгВА = 45° => а = 45°.
Пример 2.
Дано: ABCDA^CyDi — куб.
Найти: ф = Z. (Аъ (BDx)y Сх).
Решение:
1. BDX 1 (A^tD); BDX n (A^D) = О; АгО = ОСг = OD; ОАг 1 BDX;
ОСг 1 BDX => Z. A1OC1 = ф.
2. A A1DC1 — равносторонний => Z. A1OC1 = 120° => ф = 120°.
Угол между плоскостями
Плоскости называются перпендикулярными,
если они образуют прямой двугранный угол*
a_Lp=>Z.(a, р) = 90°
Угол между параллельными или
совпадающими плоскостями считается равным нулю.
a||p=>zl(a,P) = 0o
Угол между пересекающимися плоскостями
равен меньшему из двугранных углов, ими
образованных (т. е. каждый из трех остальных не
меньше данного).
Угол между двумя плоскостями равен углу
между перпендикулярными им прямыми.
^(а,Р) = фб(0°,90°)
а 1 а, Ь _1_ Р
^(а,Р) = ^(а,Ь)
Угол между двумя плоскостями находится в пределах от 0° до 90°.
0° < ^(сс, Р) < 90°

Справочные материалы
Геометрия в таблицах
581
13. Углы в пространстве
Трехгранный угол МАВС
М — вершина;
MA, MB, МС — ребра.
А АМВ, ААМС, Z. ВМС -
гранного угла.
плоские углы трех-
Неравенство трехгранного угла:
сумма двух плоских углов трехгранного угла
больше третьего плоского угла.
— вершина
плоскищ
угол
/-АМВ = С
/.АМС = В
А ВМС = А
А + В>С,А + С>В
В + ОА
А + В + С< 360°
Теорема синусов трехгранного угла
sin А _ sin В _ sin С
sin A sin В sin С
Теорема косинусов трехгранного угла
cos С = cos А • cos В + sin А • sin В • cos С,
где А, В, С — величины двугранных углов
при ребрах MA, MB, МС соответственно;
С, В, А — величины плоских углов,
противолежащих соответственно АВ, АС, ВС.
Многогранный угол MA\А2..Лп
М — вершина;
МАг, МА2,..., МАп — ребра;
LA\MA2, ..., An_iMAn — плоские углы
многогранного угла.
плоский
угол
Сумма плоских углов выпуклого многогранного
угла меньше 360°.
вершина
А АХМА2 + Z. А2МАг + ,
+ ^АД_1МАД< 360°
14. Основные задачи на построение в пространстве
В любой плоскости выполняются все
построения планиметрии.
Через три точки, не лежащие на одной
прямой, через прямую и точку вне ее, через две
пересекающиеся прямые, через две параллельные
прямые можно провести плоскость и притом
только одну.
Через точку, не лежащую на данной прямой,
можно провести только одну прямую,
параллельную данной прямой.
Через точку, не лежащую в данной плоскости,
можно провести бесконечное множество
прямых, параллельных этой плоскости.
Me а
а^ п а2 гл а$ = М
аг II а, а2 II а, а3 II а

582
Справочные материалы
Геометрия в таблицах
14. Основные задачи на построение в пространстве
Через точку, не лежащую на данной прямой,
можно провести бесконечное множество
плоскостей^ параллельных этой прямой.
М е a, m II а
аг II а, а2 II а, сс3 II а
а^ n GC2 о а3 = т
Через точку, не лежащую на данной плоскости,
можно провести плоскость, параллельную
данной, и притом только одну.
Me а
а II а; Ь II а; а п & = М
а С р; b С р; => Р || а
Через точку можно провести плоскость,
перпендикулярную данной прямой, и притом
только одну.
Me а, а С а
Хе Р;аср;
МГ1 а; ГХ1 а =
=*(МТХ) = у±а
Через точку можно провести прямую,
перпендикулярную данной плоскости, и притом
только одну.
Мй а,аСа=>
=^ существует
плоскость Р в М, Р J_ а =
MX 1 с => МАГ 1 а
Через точку можно провести бесконечно много
плоскостей, перпендикулярных данной
плоскости.
МК 1а
аг п а2 п а3 = ЛОТ
ах 1 а; а2 1 а; а3 1 а
Через одну из скрещивающихся прямых можно
провести единственную плоскость,
параллельную другой прямой.
а — Ь; т II Ъ => а II Ь

Справочные материалы
Геометрия в таблицах
583
15. Построение сечения куба
Построить сечение куба, проходящее через точки М, N, L.
В,
N
м
м
А
/\
»
/
/
т
6
^1
/
В
Bi
N
ч*1
М
А
/\
Ai 1
/в х
г
6
^1
/
В
N
к/5^~^
м
А
Al \
/в X
т
^
1>\
/
в
(MNL) - а
L ~ L " L
а n (AijDiZ)) = ML ML п (AiB^By) = ML п A^ = Хх an (AjBjCiDx) = ХЛГ
м
А
*1
кУ^-^^^
Л ^Чг-
• 'в х
1 ъ
N
1
1^-
М
А
*i 1
.Ах ,
/В N
•
1
z\[
a n (АА^В) - MX MLn (ВВ&С) = MLn ВВХ - Х2 ХЛГ n (DD^jC) = XN n Я^ = Х3 an (Di^CjC) = TP
kZ*^~~
i^~
M
A
^l i
'B
/
I
\b[
jSJI
*x2
anCBBjCjO-NT
L D
a n (АВСЯ) - LP LMKNTP — искомое сечение MX II TP, ХЛГII LP, NT \\ ML
16. Ортогональное проектирование
Ортогональной проекцией (мы будем говорить
просто проекцией) точки на плоскость
называется точка пересечения перпендикуляра,
проведенного через данную точку к плоскости, и
самой плоскости.
Мы будем обозначать: npa А = В
С np^CC^D пр^АА1 = ВВ1
Свойства ортогонального проектирования
Если точка лежит на плоскости, то пра К = К.
Проекция прямой есть прямая (или точка).
Проекция отрезка есть отрезок (или точка).

584
Справочные материалы
Геометрия в таблицах
16. Ортогональное проектирование
Проекции наклонных
Если из одной точки на плоскость проведены
несколько наклонных, то: равные наклонные
имеют равные проекции, равным проекциям
соответствуют равные наклонные, большая
наклонная имеет большую проекцию, большей
проекции соответствует большая наклонная.
М0 = праМ
<=> (MqA = MqB)
(МОМА)<=>
<=> (M0C>MqA)
Длины проекций отрезков, лежащих на
параллельных прямых (или на одной прямой)
пропорциональны длинам самих отрезков.
а||&;а1 = праа;
b! = np^&=>
=> аг II Ьг;
А1Д1 АВ
вгсг в вс;
*!<?! ВС
EXFX EF
Длина проекции отрезка равна произведению
длины этого отрезка на косинус угла между
плоскостью проектирования и прямой этого
отрезка.
Афх = пр^АВ=АВ cos ф
ф = /. (АВ, а)
Площадь проекции многоугольника равна
произведению площади этого многоугольника и
косинуса угла между плоскостью проектирования
и плоскостью многоугольника.
ww5=
= ПР^(Р1Р2Р3^4^5)
S'= S • cos ф
q> = /.((P1P2Ps),a)
Параллельное проектирование
Параллельной проекцией точки на плоскость в
направлении прямой I, не параллельной
плоскости, называется пересечение проходящей
через точку прямой, параллельной или
совпадающей с U и плоскости проектирования. Мы будем
обозначать: праА = Б.
Ортогональное проектирование есть частный
случай параллельного.
Параллельное проектирование обладает всеми
отмеченными свойствами ортогонального
проектирования.
АВ || I, В е а
В = пР^А

Справочные материалы
Геометрия в таблицах
585
17. Призма
п-уголъной призмой называется многогранник,
две грани которого — равные n-угольники с
соответственно параллельными сторонами
(основания), а остальные п граней —
параллелограммы (боковые грани).
л-угольная призма имеет: п + 2 грани, Зд ребр^,
2д вершины.
Высотой призмы называется расстояние между
плоскостями ее оснований. (Отрезок
перпендикуляра к плоскостям оснований, заключенный
между ними.)
Диагональ призмы — отрезок, соединяющий
две вершины, не лежащие в одной грани.
У д-угольной призмы п(п - 3) диагонали.
all р; А, Б, С, 2) е Р;
Alt Bv Cv Dx e a
верхнее
основаниеL
нижнее
основание
,~JAB\\AXBX\
Г вс II вхсх\
Iя CDWC^
К DA II D^
f J
AAX || BBX || CCX II DDX
AAX -I — боковое ребро
BDX — диагональ
Призматической поверхностью называется
поверхность, состоящая из прямых, содержащих
боковые ребра призмы и частей плоскостей
боковых граней, заключенных между этими
прямыми.
аг II а2 II а3 II а4
Четырехгранная
призматическая
поверхность
Перпендикулярным сечением призмы называется
сечение призматической поверхности
плоскостью, перпендикулярной боковому ребру.
Угол между плоскостью перпендикулярного
сечения призмы и плоскостью ее основания равен
углу между боковым ребром и высотой призмы.
MN±AAX\.
NP ± ВВ1 | "
(MNP) 1 ВВг
A MNP — перпендикулярное
с сечение
AG ± ABC
A (AAVAG) = Z. ((MNP), (ABC))
Площади боковой и полной поверхности
призмы
5бок = ^±- I
Зполн = 250 + ^1- *
Объем призмы
V=SQ- Н
V=S± • I
где Р± — периметр
перпендикулярного сечения, I — длина
бокового ребра, S0 — площадь
основания, Н — высота
призмы, Sj_ — площадь
перпендикулярного сечения.

586
Справочные материалы
Геометрия в таблицах
17. Призма
Прямая призма
Прямой называется призма, боковое ребро которой
перпендикулярно плоскости основания.
Все боковые грани прямой призмы
прямоугольники.
Все двугранные углы при ребрах основания
прямой призмы прямые.
Линейные углы двугранных углов при боковых
ребрах прямой призмы равны
соответствующим углам основания.
Высота прямой призмы равна ее боковому реб-
ру.
Я=*
ААХ1 (ABC),
£ABC = £(A,BBVC)
Pq — периметр основания
Sq — площадь основания:
Объем прямой призмы
v=s0- н
Площади боковой и полной поверхностей
прямой призмы
S6ok = Р0 ' Н
^полн = ^бок + 2 • S0
Правильной называется прямая призма, в основании которой лежит
правильный многоугольник.
Около призмы можно описать шар тогда и
только тогда, когда она прямая и около ее
основания можно описать окружность.
Я2 = г2 + 0,25Я2,
R — радиус описанного шара,
г — радиус описанной окружности.
5,
Н=1
ОА = ОВ = ОС = ОАг =
в - ОВг = ОСг
^У OFx = OF2 = \Н;АА1JL (ABC)
В призму можно вписать шар тогда и только
тогда, когда в ее перпендикулярное сечение
можно вписать окружность и диаметр этой
окружности равен высоте призмы.
2S
Д=г = 0,5Я;Д= -=^,
R — радиус вписанного шара, г
санной окружности.
радиус впи-
(MNP)±AA1
с FOx = FT = R
ОгО = Н
В прямую призму можно вписать цилиндр,
если в ее основание можно вписать окружность.

Справочные материалы
Геометрия в таблицах
587
17. Призма
Прямая призма (продолжение)
Около прямой призмы можно описать
цилиндр, если около ее основания можно описать
окружность.
Пример призмы, одна грань которой
перпендикулярна основанию
Ш\
\\W
А В
(АВВг) _L (ABC)
Пример призмы, внутри которой нельзя
провести перпендикулярного сечения
В' этом случае при вычислении объема
рассматривается перпендикулярное сечение
призматической поверхности (все формулы верны).
N ^ / Бх
(NKL)1AA1
Параллелепипед
Параллелепипедом называется призма, в основании которой лежит
параллелограмм. Все грани параллелепипеда — параллелограммы.
Противоположные грани параллелепипеда равны и параллельны.
У параллелепипедов и только у них любую пару
параллельных граней можно принять за
основания.
В зависимости от выбора оснований можно
рассмотреть три высоты.
Объем параллелепипеда
V = Hi$ i = H2S2 — H^Ss
Свойства диагоналей параллелепипеда
Диагонали параллелепипеда пересекаются в
одной точке и делятся ею пополам.
Сумма квадратов, диагоналей параллелепипеда
равна сумме квадратов всех его ребер.
dj + d2 + d3
+ d\ = 4a2 + 4ft2 + 4c2
АгС = dx\ BXD = d2;
ACi = d3;
BDX = d4

588
Справочные материалы
Геометрия в таблицах
17. Призма
Параллелепипед (продолжение)
В параллелепипед можно вписать тетраэдр.
Объем такого тетраэдра равен « части объема
параллелепипеда.
v = б did2 Р (dl5 d2> sin ^-(^i; d2>
AD = d1;SC = d2
Прямым называется параллелепипед, у
которого боковое ребро перпендикулярно плоскости
основания.
Диагонали прямого параллелепипеда
вычисляются по формулам:
d\ = а2 + Ь2 + с2 + lab cos а
d\ = а2 + Ь2 + с2 - 2аЬ cos а
ABCD —
параллелограмм (а * 90°)
ААг _L (ABC)
АСх = АХС = dx;
Б2)! = BXD = d2; dx * d2
Прямоугольным называется прямой
параллелепипед, в основании которого — прямоугольник.
Все диагонали прямоугольного
параллелепипеда равны.
ABCD — прямоугольник
AA1±(ABC),AB±AD
Куб
Кубом называется
прямоугольный параллелепипед с равными
ребрами.
Диагонали куба пересекаются в
точке, являющейся центром
вписанной и описанной сфер.
АВ = а
OA = OB = OC = OD = OAl = OB1 =
Кубу вписанный в сферу
R — радиус описанной
сферы, а — ребро куба.
Сфера, вписанная в куб
1
г=2а'
г — радиус вписанной
сферы,
а — ребро куба.
Ио
Центр сферы — точка О —
равноудаленная от всех
граней куба.

Справочные материалы
Геометрия в таблицах
589
18. Пирамида
Пирамидой называется многогранник, одна
грань которого — произвольный
многоугольник, а остальные грани — треугольники,
имеющие общую вершину.
М — вершина пирамиды, Ai,A2, ...,АЛ —
вершины основания. Всего д + 1 вершина.
MAi — боковое ребро, А±А2 — ребро основания.
Всего 2п ребер.
Многоугольник AiA2-. Лп — основание
пирамиды.
Треугольник МА±А2 — боковая грань. У
пирамиды п + 1 грань, из них п боковых.
Сечение, параллельное основанию пирамиды,
представляет собой многоугольник, подобный
основанию.
Плоскость этого сечения разбивает боковые
ребра и высоту пирамиды на
пропорциональные отрезки.
Площади сечения и основания относятся как
квадраты их расстояний до вершины
пирамиды.
Сечение отсекает от пирамиды пирамиду,
подобную данной.
Площадь боковой
поверхности пирамиды
S6ok = Sl + S2 + ••• + Sn>
S\9 S2, •••» Sn — площади
боковых граней пирамиды.
Угол AiMA2 — плоский угол при вершине
пирамиды.
Двугранный угол M(AiA2)Ak — угол при
ребре АуА2 основания (угол наклона боковой
грани к основанию).
Двугранный угол А1(МА2)Аз — угол при
боковом ребре МА2.
Высотой пирамиды называется расстояние
от вершины пирамиды до плоскости ее
основания. МК = Н — высота пирамиды.
Al X 1 \ \ /A* + 1
А2 А3
(AxAaAg) II (AiAjAi)
р(М,(А1А2А3)) = Я
p(M,(AiA£A£) = tf'
АхА2..Лп со А{А'2...А'п
МАг МА2 МАп н
МА\ " МА2 " "" " МА'п = Я'
SAxA2...An _ (н\*
Sa 'А' А'
А1А2"Ап
MAlA2..A.n
Площадь полной
поверхности пирамиды
S0 — площадь основания.
™МА{А'2..Л'п
Объем пирамиды
v=\hs0

590
Справочные материалы
Геометрия в таблицах
18. Пирамида
Тетраэдр
Тетраэдр — это треугольная пирамида. Все четыре грани — треугольники и любая из них
может быть принята за основание этой пирамиды (можно рассмотреть четыре высоты).
Площади боковых граней тетраэдра обратно пропорциональны опущенным на них высотам.
Отрезки, соединяющие середины
скрещивающихся ребер тетраэдра (бимедианы тетраэдра),
пересекаются в одной точке и делятся ею
пополам.
Отрезки, соединяющие вершины тетраэдра с
точками пересечения медиан противолежащих
граней (медианы тетраэдра), пересекаются в
одной точке и делятся этой точкой в отношении
3:1, считая от вершины.
э1 С
Если два тетраэдра имеют общий трехгранный
угол (два равных трехгранных угла), то их
объемы относятся как произведения ребер,
образующих этот угол.
уABCD
/AB1ClD1
АВ АС АР
АВг АСг ADj
Правильный тетраэдр
Правильным называется тетраэдр, все грани
которого — правильные треугольники.
Основные формулы
r.\h
Н = а
R + г = Н
R — радиус описанного шара,
г — радиус вписанного шара.
Площадь поверхности правильного тетраэдра
^полн - О л/3
Объем правильного тетраэдра
а Л
V =
12
AB=AC = BC*=AD = BD = CD = a
DO = tf = aJ;FO = r=itf;
г = p(F, (ABC)) = p(F, (ABD)) = p{F, (ACD)) -
= p(F,(BCD))
FD = R=\h;
FA = FB = FC = FD = R
S = SABC + SABD + SACD + SBCD

Справочные материалы
Геометрия в таблицах
591
18. Пирамида
Правильная пирамида
Правильной называется пирамида, основание
которой — правильный многоугольник, а
вершина проектируется в центр основания.
Все ребра равны.
Все боковые грани — равные равнобедренные
треугольники.
Все двугранные углы при ребрах основания
равны (боковые грани одинаково наклонены к
основанию).
Все плоские углы при вершине равны.
Все двугранные углы при боковых ребрах равны.
Все высоты боковых граней, опущенные на
ребра основания (апофемы), равны.
MFKAxAaAg)
FA1=FA2 = ...=FAq
МТ — апофема пира
МИДЫ
Площадь боковой поверхности правильной пирамиды
S = kp, где k — апофема,
р — полупериметр основания.
S =
cos а
, где S0
площадь основания,
а — двугранный угол при ребре основания.
Пирамида, все боковые ребра которой равны
между собой
Около основания можно описать окружность и
вершина пирамиды проектируется в центр этой
окружности.
Все ребра одинаково наклонены к основанию.
Около такой пирамиды можно описать шар.
Центр описанного шара лежит на прямой,
содержащей высоту пирамиды.
MA = MB = MC = MD=>FA = FB = FC = FD,
MF±(ABC)
МТ = ТС, ОТ±МС=*ОА = ОВ = ОС =
= OD = OM = R,
R — радиус описанного шара
(H-R)2 + FC2 = R2
Пирамида, одна из боковых граней
которой перпендикулярна
основанию
Высота лежит в грани,
перпендикулярной основанию пирамиды.
F е a, MF1 (ABC)
MF С (AMD)

592
Справочные материалы
Геометрия в таблицах
18. Пирамида
Пирамида, все двугранные углы при ребрах
основания которой равны между собой
В основание можно вписать окружность и
вершина пирамиды проектируется в центр этой
окружности.
Площадь боковой поверхности вычисляется по
тем же формулам, что и для правильной
пирамиды.
Высота вычисляется по формуле:
Н = г tg р, где г — радиус вписанной в
основание окружности, а Р — двугранный угол при
ребре основания.
В такую пирамиду можно вписать шар, центр
которого лежит на высоте.
В
R = г • tg 5 i где R — радиус вписанного шара,
г — радиус вписанной в основание окружности.
Fea, MF1(ABC)=>FA11AD, FBX±AB,
FCX _L ВС, FDX 1 CD,
FAi = FDi = FCi = FBi = г — радиус вписанной
в основание окружности
OF = R — радиус вписанного в пирамиду шара
BiO — биссектриса Z. MBiF
Пирамида, две соседние боковые
грани которой перпендикулярны
основанию
Высотой служит общее боковое
ребро этих граней.
(МАВ) .L а I
(МАЕ) 1 а I
MALa
Пирамида, две несоседние грани
которой перпендикулярны основанию
Высота лежит вне пирамиды на
прямой пересечения плоскостей,
содержащих грани, перпендикулярные
основанию.
F е a, MF _L а
(МАВ) 1 а, (MDC) 1 а
(ABM) n (DCM) = MF
Пирамида, два двугранных угла при
соседних ребрах основания которой
равны
Высота проектируется на
биссектрису угла между данными ребрами.
А (М, (АВ), С) = £ (М, (AD), С)
F е а, МF1 а
AF — биссектриса Z. BAD

Справочные материалы
Геометрия в таблицах
593
18. Пирамида
Пирамида, в основании которой
прямоугольный треугольник и все
боковые ребра равны
Fea, MF _L а,
(МАЕ) 1 (ABC)
FA = FB = FC
О — центр
описанного шара
MT=TB,OeMF
ОМ = OA = OB = OC = R
19. Усеченная пирамида
Усеченной пирамидой называется часть
полной пирамиды, заключенная между
основанием и параллельным ему
сечением.
Сечение называют верхним основанием
усеченной пирамиды, а основание
полной пирамиды — нижним основанием
усеченной пирамиды. (Основания
подобны.)
Боковые грани усеченной пирамиды —
трапеции.
В усеченной пирамиде Зп ребер, 2д
вершин, п + 2 грани, п(п - 3) диагонали.
Расстояние между верхним и нижним
основаниями — высота усеченной
пирамиды (отрезок, отсеченный от
высоты полной пирамиды).
Объем усеченной пирамиды
V= lH(S + JS~s + s),
Shs — площади оснований, Н — высота
Правильной усеченной пирамидой
называется часть правильной пирамиды.
Часть апофемы правильной пирамиды
называется апофемой правильной
усеченной пирамиды.
F
'It* S
/ „ W N
А' Ф^ЪЛ* Лер^нее p*. вершина
/ «' Xa ' *Л 3 X*fcu
/ Si Г2 *\ ХЦ,
/ °l 1 X \ ^vA» ~~"-\
f I •! 1 ^ An \~*r**-•* n. \
/ / i U \ боковая - - ^ \ \
/ / ^ + \ \ грань /
1 1 * H \ \ X 1
\ ^ч. 1 нижнее \/ //y
\ ребро\^ 1 основание \y J
\ нижнего ^ a4 /
\ основания д2 J
N. плоскость нижнего /
\v^^ ^ "^^^ основания У
Площадь полной поверхности усеченной пирамиды
равна сумме площадей ее граней.

594
Справочные материалы
Геометрия в таблицах
19. Усеченная пирамида
Правильная усеченная пирамида (продолжение)
Для правильной усеченной пирамиды
(а также для усеченной пирамиды, все
двугранные углы при ребрах нижнего
основания которой равны) верны
формулы:
S60K = b(P+P)>
Р ир — полупериметры оснований,
к — апофема;
s6ok - (S - в): cos а,
а — двугранный угол при ребре
нижнего основания, S и s — площади
оснований.
/
/Я
1
/ I
/ в1
/ *
/ *
L * — ~~
F
Ш
- V- 4-
апофема
ABCDA'B'C'D'— правильная усеченная
четырехугольная пирамида.
ABCD, A'B'C'D'— квадраты
Если в усеченную пирамиду можно вписать шар, то его радиус равен
половине высоты пирамиды.
20. Правильные многоугольники и многогранники
Многоугольник называется выпуклым, если он
лежит в одной полуплоскости относительно
любой прямой, содержащей его сторону.
Правильным многоугольником называется
выпуклый многоугольник, у которого все стороны
равны между собой и все углы равны между собой.
Любой правильный многоугольник
является вписанным и описанным, центры
вписанной и описанной окружностей совпадают с
центром многоугольника (точкой
пересечения серединных перпендикуляров сторон,
биссектрисе углов).
ап — сторона,
гл — радиус вписанной окружности,
Rn — радиус описанной окружности,
kn — апофема,
Рп — периметр,
Sn — площадь.
Ап-
Общие формулы
180°(д - 2)
<Хц=
п П
. ап . 180° _ 180°
г„-*д-у d«— -l^coe —
Rn-
COS
180°
2 - sin
180°
n „2 . 360° n 2 A 180° 1 „
Sn= 2 Rn em — = j an ctg — = ynPn

Справочные материалы
Геометрия в таблицах
595
20. Правильные многоугольники и многогранники
Формулы для многоугольников с числом сторон п = 3, 4, 6, 8, 12
а
Связь между г и Л
12
60°
90°
120°
135°
150°
аЛ
6
а
2
аЛ
2
а(1 + Л)
2
а(2 + Л)
2
Ол/3
3
аЛ
2
а27з
а^4 + 2V2
а- J2 + Л
За2Л
2
2а2(1 + 72)
За2(2 + 73)
Д=2г
И = гЛ
НЛ =2г
г
г __
тс
COSg
к
спя -—
72 +
2
_ 72 +
72
_^з
Многогранник называется выпуклым, если он
расположен по одну сторону плоскости каждого
плоского многоугольника на его поверхности.
Выпуклый многогранник называется
правильным, если все его грани — равные
правильные многоугольники и в каждой
вершине сходится одинаковое количество ребер
(все многогранные углы при вершинах одно-
имен иы).
Грани — правильные
треугольники
Правильный треугольник
Три ребра в одной вершине
3 • 60° < 360° — тетраэдр.
Четыре ребра в одной вершине
4 • 60° < 360° — октаэдр.
Пять ребер в одной вершине
5 • 60° < 360° — икосаэдр.
Шесть (и более) ребер в одной
вершине сходиться не могут:
6 • 60° = 360°.
Грани — правильные
четырехугольники
Квадрат
Три ребра в одной вершине
3 • 90° < 360° — куб
(гексаэдр).
Четыре (и более) ребер в одной
вершине сходиться не могут:
4 • 90° = 360°.
Грани — правильные
пятиугольники
Правильный пятиугольник
Три ребра в одной вершине
3 • 108° < 360° — додекаэдр.
Четыре (и более) ребер в одной
вершине сходиться не могут:
4 • 108° > 360°.
Правильные многоугольники, имеющие более пяти сторон, не могут
быть гранями правильного многогранника (уже для
шестиугольника^ • 120° > 360°).

596
Справочные материалы
Геометрия в таблицах
20. Правильные многоугольники и многогранники
Общий вид
11/. в,
Икосаэдр
Куб
Додекаэдр
Тип многогранника
Число
ребер
граней
вершин
Площадь
поверхности
Объем
Тетраэдр
Октаэдр
Икосаэдр
Куб (гексаэдр)
Додекаэдр
6
12
30
12
30
8
20
6
12
6
12
8
20
г2Л
2а2 Л
Ъа2Л
Ьа2
За27б(5 + 2 Л)
аГЛ
12
а3Л
^а\Ъ~Л)
j(15 + 7V5)
Для всех выпуклых многогранников
выполняется формула (теорема) Эйлера:
Р + 2 = В + Г,
где Р — число ребер, В — вершин, Г — граней.
Примеры разверток
ДА <Ш>
Тетраэдр
Октаэдр
Икосаэдр
Куб
Додекаэдр
Вписанные и описанные многогранники
Куб и октаэдр
Куб и тетраэдр
А1В1 = аЛ; АВ = а
Додекаэдр и икосаэдр

Справочные материалы
Геометрия в таблицах
597
20. Правильные многоугольники и многогранники
Вписанные и описанные многогранники (продолжение)
Икосаэдр и додекаэдр
АВ
Шар и октаэдр
aj2
FO + OM = FM=AC =
= BD = aj2
Октаэдр и шар
АВ = а
л/6
21. Цилиндр
Цилиндром (прямым, круговым) называется
тело, полученное при вращении
прямоугольника вокруг прямой, содержащей его сторону.
Круги с центрами Oj и 0% — основания
цилиндра, отрезок АВ — образующая (АВ = 1),
отрезок О^А = 0±В — радиус основания,
отрезок Oi02 (расстояние между плоскостями
оснований) — высота цилиндра (Н = 1),
прямоугольник ABCD — осевое сечение, отрезок АС —
диагональ осевого сечения, прямая O1O2 — ось
вращения, точка F (середина отрезка O1O2) —
центр симметрии.
Развертка цилиндра — прямоугольник и два
круга.
Площадь боковой поверхности цилиндра
S6oK = 2kRH = 2nRl
Площадь полной поверхности цилиндра
(площадь его развертки)
Зполн - 2яД2 + S6oK = 2n(R + H)R
D
i
А
В
А
1
^4 '
i
1
с
I
D
0
v 2nR
0
В
H
A
Объем цилиндра
V=S0- H = kR2H

598
Справочные материалы
Геометрия в таблицах
21. Цилиндр
Около цилиндра всегда можно описать шар.
Его центр лежит на середине высоты.
R2 = г2 + 0,25#2,
R — радиус шара, г — радиус основания
цилиндра.
AO = BO = CO = DO = R
В цилиндр можно вписать шар, если диаметр
основания цилиндра равен его высоте.
Д = г = 0,5#,
R — радиус шара, г — радиус основания
цилиндра.
Призма, вписанная Призма, описанная Цилиндр, вписанный
в цилиндр около цилиндра в конус
А02 = 02В = R
CD = GL = Н; OxG = г
R - г _ _R_ = г
Я f 02 F02 - Н
г Нк-Я
ffк — высота конуса,
Н — высота цилиндра
Сечения цилиндра плоскостями
Сечение цилиндра
плоскостью, паралелльной
оси цилиндра, —
прямоугольник.

прямоугольник
Сечение цилиндра плоскостью,
перпендикулярной оси цилиндра, — круг.
часть часть
эллипса
Сечение, проходящее через
середину 0\02, делит
цилиндр на два равных тела.
1 верх
ОО^ООз^Т^р^Г,
верх Л нижн

Справочные материалы
Геометрия в таблицах
599
22. Конус
Конусом (прямым, круговым) называется тело,
полученное при вращении прямоугольного
треугольника вокруг прямой, содержащей катет.
Точка М — вершина конуса,
круг с центром О — основание конуса,
отрезок МА = I — образующая,
отрезок МО = Н — высота конуса,
отрезок ОА = R — радиус основания,
отрезок ВС = 2R — диаметр основания,
треугольник МВС — осевое сечение,
Z. ВМС = Р — угол при вершине осевого сечения,
Z. МВО = ф — угол наклона образующей к
плоскости основания.
Л
Развертка конуса — сектор круга и круг.
/. BMBi = а — угол развертки.
Длина дуги развертки ВСВ^ = 2nR = la (а радиан)
Площадь боковой поверхности
^бок = nRl
Площадь полной поверхности (площадь развертки)
^полн = nRV + R)
Объем конуса
V= |яД2#
Связь между углом а развертки и углом ($ при вер-
В
шине осевого сечения а = 2я sin ^
Сечения конуса плоскостями

треугольник
Сечение конуса плоскостью,
проходящей через вершину конуса, —
равнобедренный треугольник

параболическое
сечение К

гиперболическое
q сечение
Сечение конуса плоскостью,
перпендикулярной оси
конуса, — круг
(ABC) || МО (KPL) ||
МО — высота конуса,
МТ — образующая
МТ

600
Справочные материалы
Геометрия в таблицах
22. Конус
В конус всегда можно вписать шар. Его центр
лежит на оси конуса и совпадает с центром
окружности, вписанной в треугольник, являющийся осевым
сечением конуса.
$.
HR
*к + *
Лобщ = Дш sin Ф
Около конуса всегда можно описать шар. Его
центр лежит на оси конуса и совпадает с центром
окружности, описанной около треугольника,
являющегося осевым сечением конуса.
^ "~ sinp ; Лш в (я " лш) + Rk
23. Усеченный конус
Усеченным конусом называется часть конуса,
заключенная между основанием и параллельным
основанию сечением конуса.
Круги с центрами Oj и 0% — верхнее и нижнее
основания усеченного конуса, г и R — радиусы
оснований, отрезок АВ = I — образующая, а — угол наклона
образующей к плоскости нижнего основания,
отрезок 0^2 — высота (расстояние между плоскостями
оснований), трапеция ABCD — осевое сечение.
Н = I sin а
H2 + (R-rf = l2
В усеченный конус можно вписать шар тогда и
только тогда, когда образующая равна сумме
радиусов оснований.
Дш = 0,5Я
I = R + г <=> существует вписанный шар

Справочные материалы
Геометрия в таблицах
23. Усеченный конус
Развертка усеченного конуса — часть кругового
кольца и два круга.
Площадь боковой поверхности усеченного конуса
\S6oK = Kl(r + R)
Площадь полной поверхности усеченного конуса
«полн - Si + S2 + 5бок = я*(г + *) + KR2 + 7СГ2
Объем усеченного конуса
F=| • nH(R2 + гЯ + г2)
Около усеченного конуса всегда можно описать
шар. Его центр лежит на прямой Oi02.
м
1 U^ У
2tlR х. \
/" "\ , мъгг 2я(Д - г)
V "• У
Х^_^/ Ф — угол развертки
CF = FD; OF 1 CD => О —- центр описанного
шара, Д — радиус описанного шара,
равный радиусу окружности, описанной
около A ACD
24. Сфера и шар
Сферой называется множество точек пространства, удаленных от данной точки (центра
сферы) на данное расстояние R > 0 (радиус сферы).
(Сферой называют фигуру вращения полуокружности вокруг ее диаметра.)
Шаром называется множество точек
пространства, находящихся от данной точки (центра
шара) на расстоянии, не большем данного (R > 0 —
радиус шара).
(Шаром называют часть пространства,
ограниченную сферой. Шаром называют фигуру
вращения полукруга вокруг его диаметра.)
Диаметр, проходящий через середину хорды,
не являющейся диаметром, перпендикулярен
этой хорде.
Площадь поверхности сферы
S = 4tlR2
с
CD — диаметр сферы; A,BeS
АМ = МВ=>ОМ±АВ
Объем шара
3

Справочные материалы
Геометрия в таблицах
24. Сфера и шар
Шар (сфера) и плоскость
Плоскость, имеющая со сферой (шаром) одну общую точку, называется касательной
плоскостью, более одной общей точки — секущей плоскостью.
Прямая, имеющая со сферой одну общую точку, называется касательной прямой, две
общие точки — секущей прямой.
Пусть р(0; а) — расстояние от центра шара
(сферы) с центром О и радиусом R до плоскости а.
Если р > R, то шар (сфера) и плоскость общих
точек не имеют.
Если р < R, то пересечение шара (сферы) и
плоскости есть круг (окружность) радиуса г.
/г>2 2
r= *JR - р
Всякое сечение шара (сферы) плоскостью есть
Сечение шара плоскостью, проходящей через
центр шара (р = 0), называется большим кругом
шара.
Эта плоскость является плоскостью симметрии
шара и делит его на две равные части (два
полушария).
Признак касательной плоскости
Если плоскость проходит через конец диаметра
сферы и перпендикулярна ему, то эта плоскость
касательная к сфере.
Если р = R, плоскость и шар (сфера) имеют одну
общую точку. Плоскость касается шара (сферы).
Свойство касательной плоскости
Плоскость, касательная к сфере,
перпендикулярна диаметру (радиусу), проходящему через
точку касания.
Признак касательной прямой
Если прямая проходит через конец диаметра
сферы и перпендикулярна ему, то эта прямая
касательная к сфере.
V у ОМ 1а;
^ *</ ОМ = р (О; а); р > R
р < R (^^^>ш^_
[ а \ большой круг / i
Ч^/
t/\S%°) OMnt = M;
V_^/ ОМ It =*t — касательная

Справочные материалы
Геометрия в таблицах
603
24. Сфера и шар
Шар (сфера) и плоскость (продолжение)
Все касательные прямые, проходящие через
одну точку сферы, лежат в одной плоскости,
касательной к этой сфере.
*! 1 ОМ; t21 ОМ, *3 J- ОМ =
=* *1» *2» *3 с а> а J- ОМ
Отрезки касательных, проведенных из одной
точки (лежащей вне сферы) к сфере, равны.
А, В, С — точки касания =
=>МА = МВ = МС
Шаровой сегмент
Секущая плоскость разбивает шар на два
шаровых сегмента.
Н — высота сегмента, 0 < Н < 2R,
г — радиус основания сегмента,
г= V#(2Д - Н).
Объем шарового сегмента
V = kH2(r- |я]
Площадь сферической поверхности шарового
сегмента
S = 2kRH
Шаровой слой
Шаровым слоем называется часть шара,
заключенная между двумя параллельными сечениями.
Расстояние (Н) между сечениями называется
высотой слоя, а сами сечения — основаниями слоя.
Площадь сферической поверхности (объем)
шарового слоя может быть найдена как разность
площадей сферических поверхностей (объемов)
шаровых сегментов.
Шаровой сектор
Шаровым сектором называется фигура вращения кругового сектора
вокруг не имеющего с ним общих внутренних точек диаметра круга*.
* В школьном курсе обычно рассматривается вращение кругового сектора вокруг прямой, содержащей
радиус, который ограничивает сектор.

604
Справочные материалы
Геометрия в таблицах
24. Сфера и шар
Шаровой сектор (продолжение)
Объем шарового сектора
2 О
Площадь сферической поверхности шарового
сектора равна площади сферической
поверхности соответствующего шарового сегмента.
Площадь полной поверхности шарового сектора
S = nR(2H + hRH - Я2)
::у?
Две сферы
Две сферы, имеющие общий центр, называются
концентрическими.
Две сферы, имеющие одну общую точку,
касаются друг друга.
Oi02 = R + г (внешнее касание)
O1O2 = \R-r\ (внутреннее касание)
Если \R - r\ < О^О^ < R + г, то сферы
пересекаются по окружности, радиус которой может
быть найден, например, как высота
треугольника со сторонами R, г и Oi02> проведенная к
стороне Oi02>
Через две точки пространства можно провести
бесконечное множество сфер. Их центры лежат
на плоскости, проходящей через середину
отрезка, перпендикулярно прямой, содержащей
этот отрезок.
Д2 - р2 + 0,25а2
MN = a
р = р (О, MN)

Справочные материалы
Геометрия в таблицах
605
24. Сфера и шар
Две сферы (продолжение)
Через три вершины треугольника можно
провести бесконечное множество сфер. Их центры
лежат на прямой, перпендикулярной
плоскости треугольника и проходящей через центр
описанной около треугольника окружности.
Д2 = р2+г2
p = p(O,(MLA0)
Через четыре не лежащие в одной плоскости точки можно провести
сферу и притом только одну.
Описанная сфера
Сфера называется описанной около
многогранника, если она проходит через все его вершины.
Для того чтобы около многогранника можно
было описать сферу, необходимо (но
недостаточно), чтобы около любой его грани можно
было описать окружность.
Центр описанной сферы (если таковая есть)
лежит в плоскостях, перпендикулярных ребрам
многогранника, проходящих через их
середины; а также на прямых, перпендикулярных
граням многогранника, проходящих через
центры описанных около граней окружностей.
Радиус описанной сферы равен радиусу
сферы, проходящей через любые четыре, не
лежащие в одной плоскости вершины
многогранника.
Около любой треугольной пирамиды можно
описать сферу.
Около /i-угольной пирамиды можно описать
сферу тогда и только тогда, когда около ее
основания можно описать окружность.
Около призмы можно описать сферу тогда и
только тогда, когда призма прямая и около ее
основания можно описать окружность.
Сфера называется описанной около цилиндра,
если на ней лежат окружности оснований
цилиндра.
Около цилиндра всегда можно описать сферу.
R2 = 0,25#2 + г2

Справочные материалы
Геометрия в таблицах
24. Сфера и шар
Описанная сфера (продолжение)
Сфера называется описанной около конуса,
если на ней лежат вершина и окружность
основания конуса.
Около конуса всегда можно описать сферу; ее
радиус равен радиусу окружности, описанной
около осевого сечения конуса.
Если сфера касается граней двугранного угла,
то ее центр лежит на полуплоскости, делящей
этот двугранный угол на два равных
двугранных угла.
R = ОМ sin ф = ML • tg ф = /п, где 2ф —
величина двугранного угла, ОМ — расстояние от
центра сферы до ребра, т — расстояние от центра
сферы до грани.
\ i
с
Т\
* )
_\ у
/ [ Ф° ) J
^-^Ji^ J МК LUMLLl
^"^--Jj OK 1 a; OLA. ^
Вписанная сфера
Сфера называется вписанной в многогранник,
если она касается всех плоскостей, содержащих
грани многогранника во внутренних точках
граней.
В прямую призму можно вписать сферу тогда и
только тогда, когда высота призмы равна
диаметру окружности, вписанной в основание.
Если в многогранник можно вписать сферу, то:
V— - PC
3 полн'
V — объем многогранника,
^полн — полная поверхность многогранника.
Сфера называется вписанной в цилиндр, если
она касается оснований цилиндра и
цилиндрической поверхности.
В треугольную пирамиду всегда можно
вписать сферу.
В л-угольную пирамиду можно вписать
сферу ^огда и только тогда, когда биссекторные
плоскости всех двугранных углов пирамиды
имеют общую точку.
В призму можно вписать сферу тогда и
только тогда, когда ее высота равна диаметру
окружности, вписанной в ее перпендикулярное
сечение.
в
В цилиндр можно вписать сферу тогда и
только тогда, когда его высота (образующая)
равна диаметру основания.
Д = 0,5# = Дсф

Справочные материалы
Геометрия в таблицах
607
24. Сфера и шар
Вписанная сфера (продолжение)
Сфера называется вписанной в конус, если она
касается основания конуса и конической
поверхности.
В конус всегда можно вписать сферу.
Д = г • t%\ -Sjucilr + l)
А
В
/\
1 \ \
/ ' \
l/Ri \l
\Г 7 ^
7С
25. Поверхности и объемы
Площадь полной поверхности многогранника равна сумме
площадей его граней.
Площадь боковой поверхности призмы можно
вычислить как: сумму площадей боковых
граней; произведение периметра
перпендикулярного боковому ребру сечения призматической
поверхности на длину бокового ребра.
Площадь полной поверхности призмы:
^полн = 2S0 + ^бок
(МЬМ)±ААг
Площадь боковой поверхности пирамиды равна сумме площадей ее
боковых граней.
Для правильной пирамиды:
^бок = ^ ^*
Р — периметр основания
k — апофема
Sfinv — SAT\r. + S
эбок
ADC
*ADB
+ S
BDC
Для пирамиды, все двугранные углы при
основании которой равны между собой (все высоты
боковых граней, проведенные к ребрам
основания, равны):
s --^
^бок
s0 = s
COS ф
]ABCD
z(f,ab,c) = zfjr:o = 9

608
Справочные материалы
Геометрия в таблицах
25. Поверхности и объемы
Площадь полной поверхности пирамиды SnojIH = SQ + S6oK
Площадь боковой поверхности цилиндра
^бок = 2nRH
Площадь полной поверхности цилиндра
^полн = 2nR(R + Н) = 2S0 + S^k
Я
Площадь боковой поверхности конуса
Площадь полной поверхности конуса
^полн = яД(Я + 0 = S0 + SfoK
Площадь боковой поверхности усеченного
конуса
S6oK = n(R + r)l
Площадь полной поверхности усеченного
конуса
SnojlH = Kr2 + nR2 + K(R+r)l
Площадь поверхности сферы
S = 4яД2
Площадь сферической поверхности
сферического сегмента
^бок = 2яДН
Площадь полной поверхности сферического
сегмента
^полн = 5бок + лт2 = 2лД# + яг2
r2 = B?-(R-H)2 = (2R-H) • Я
Поверхность вращения отрезка АВ, не
имеющего с осью I общих внутренних точек, равна
произведению проекции этого отрезка на ось и
длины окружности, радиусом которой служит
отрезок серединного перпендикуляра отрезка с
концами на оси и на отрезке.
S =А1В1 • 2кМО = 2nRH
Отношение поверхностей подобных тел равно
квадрату коэффициента подобия.
Объемы равных тел равны.
Если тело разбито на несколько тел, не имеющих общих внутренних
точек, то его объем равен сумме объемов этих тел.

Справочные материалы
Геометрия в таблицах
609
25. Поверхности и объемы
Объемы тел (продолжение)
Объем призмы равен:
произведению площади ее основания на высоту
V-SJB;
произведению площади ее перпендикулярного
сечения на боковое ребро
V=S±L
Vl = S0-H
V2 = SQ-h
V0
H
h
Объем пирамиды равен одной трети
произведения площади ее основания на высоту.
v=\sqh
У2 = о ^2^>
Объемы призм (пирамид), имеющих равновеликие основания,
относятся как их высоты. Объемы призм (пирамид), имеющих равные
высоты, относятся как площади их оснований.
Объемы тетраэдров, имеющих общий
трехгранный угол, относятся как произведения
ребер, содержащих этот угол.
YABCD
АВ AC AD
vab1c1d1 AB1'AC1-AD1
Объем тетраэдра может быть найден по
формуле:
V = g abc sin ф,
где а и Ь — длины скрещивающихся ребер,
с — расстояние между ними, <р — угол между
ними.
Объем усеченной пирамиды
F=iH(S! + S2+,/S^)
Объем многогранника можно получить, разбив
его на не имеющие общих внутренних точек
тетраэдры (триангуляция) и суммировав их
объемы.
Если в многогранник можно вписать шар,
то объем многогранника равен: V = ~ Я5П0ЛН,
R — радиус вписанного шара, Sn0JIH —
площадь полной поверхности многогранника.
20-1019

610
Справочные материалы
Геометрия в таблицах
25. Поверхности и объемы
Объемы тел (продолжение)
Объем цилиндра
V=nR2H
Объем конуса
У=|яД2Я
Объем усеченного конуса
7=^Я(Л2 + Дг+г2)
Объем шара
Объем шарового сегмента
V = nH2 • (r- |tfl
Объем шарового сектора
V=^kR2H
Вычисление объема тела вращения с помощью
интегралов.
ъ
,2.
Vox = n\f Wdx
y = f{*)
Отношение объемов подобных тел равно кубу коэффициента подобия.
26. Метод координат
Координаты точки на прямой
Координаты середины отрезка:
*1 + *2
Длина отрезка в координатах (расстояние между
двумя точками): MN = \xi - х% \
M(*l) Щх2)
С(хс)
Точка М прямой АВ делит отрезок АВ в
отношении X (считая от А), если AM = ХМВ
(X *-1).
Координаты точки, делящей отрезок АВ в
отношении X:
ха + Ххъ
Мха)
9
1 + X
В(*ь)
М(хт)
Координаты точки на плоскости. Прямоугольная система координат
Координаты середины отрезка:
,ха + хь уа + уь
(-
АС = СВ^>СУ 2 , 2
Длина отрезка в координатах:
АВ = J(xa - xbf + (уа - уь)2
Координаты точки, делящей отрезок АВ в
отношении X (Х*-1):
(Ха + teg. Уа + хУь^
AM = ХМВ =» М
+ х
1 + X

Справочные материалы
Геометрия в таблицах
en
26. Метод координат
Уравнение прямой
Общее уравнение прямой I: ах + by + с = О (а2 + Ь2Ф 0)
abc*0
а = 0
1\\Ох
ь = о
1\\Оу
с = 0
0^1
э
0
\L
ax+by + c = 0
by + с = О
ах + с = О
ах + by = О
Уравнение прямой с угловым коэффициентом
(Ь*0):
г/ = kx + р
Л = tg а
Уравнение прямой в отрезках (с * 0):
- + * =1
/71 Л
^4
Уравнение прямой, проходящей через точку
•МХ*0' Уо) с угловым коэффициентом к.
У = «/о + * # (* - *о)
Условие параллельности двух прямых.
k-% = к*}
Условие перпендикулярности двух прямых.
*9 = -1
Угол между двумя (неперпендикулярными)
прямыми.
tgq> =
«j я2
1 + k1k2\
Расстояние от точки М (х$; у$) до прямой
ах + by + с = 0.
а*о + &J/0 + с
777
= Р(М, Z)
Уравнение пучка прямых (всех прямых,
проходящих через точку М (х0; Уо) перпендикулярно
вектору Я (а; Ь)).
а(х - х0) + Ь(у -у0) = 0
Уравнение окружности
с центром в начале координат
х2 + у2 - г2, г > 0
с центром в точке М(х0, i/o)
(х - х0)2 + (у - j/o)2 = г2, г > 0
Любое уравнение вида х2 + у2 + ах 4- fri/ + с = 0 задает на плоскости
либо окружность, либо точку, либо пустое множество.
(* + 2а) + [» + 2bJ 4 С
20*

612
Справочные материалы
Геометрия в таблицах
26. Метод координат
Координаты точки в пространстве. Прямоугольная система координат в пространстве
Координаты точек на кубе:
О (0; 0; 0) А (0; а; 0)
В (а; а; 0) С (а; 0; 0)
О' (0; 0; а) А' (0; а; а)
В' (а; а; а) С (а; 0; а)
о'
УГ и
в'
; /у
VI
Координаты середины отрезка: АС = СВ
(ха + ХЬ Уа + УЬ га + гЬЛ
("
ч
Длина отрезка в координатах:
АВ = J(xb - ха)2 + (уь - уа)2 + (гь - zj
г (аппликата)
%. А
ix.
i
/Уь
у (ордината)
х (абсцисса)
Координаты точки М, делящей отрезок АВ в отношении Х9\*-1:
Гха + ХхЬ У а + ХУЬ га + ХгЪ
АМ=Х-МВ => м(-* г-5; ^ Р; ^ r^l
li + x l + х i + х ;
Уравнение плоскости
Общее уравнение плоскости:
ах + by + cz + d = 0 (а2 + Ь2 * 0)
Уравнения координатных плоскостей.
х = 0 — плоскость yOz
i/ = 0 — плоскость xOz
2 = 0 — плоскость хОу
п (а; Ь; с)
ах + by + сг + d = 0
у Я (а, Ь, с) ± 8 (нормальный
вектор)
Частные уравнения плоскости
а = 0
8 II Ох
ь = о
81|Оу
с = 0
81102
d = 0
O^Z
&у + cz + d = 0
ах + сг + d = 0
ах + fti/ + с = 0
ах + &i/ + сг = 0
Уравнение плоскости, проходящей через
точку М0 (х0, Уо> 2о)» перпендикулярно вектору
Я (а; &; с).
а(х - х0) + Ь(у - у0) + ф - г0) = О

Справочные материалы
Геометрия в таблицах
613
26. Метод координат
Уравнение плоскости (продолжение)
Уравнение плоскости в отрезках (d * 0).
Угол между двумя плоскостями
а^х 4- biy 4- ciz + di = 0 и
а>2х + ^2У + ctf + с?2 = 0.
cos<p =
\ага2 + ЬгЬ2 4- c2c2|
Г~2 Г2 2 Г~2 Г*2
^аг + Ьг + сг- Ja2 + Ь2 + с
Условие параллельности двух плоскостей.
с9 d0
Условие перпендикулярности двух плоскостей.
ага2 + ЬгЬ2 + с^ = 0
Расстояние от точки М(х0, Уо* 2о) Д° плоскости
ах + bi/ 4- С2 4- d = 0.
Р =
|я*о + Ь^о + с*о + d\
/ 2 l . 2 , 2
л/а 4- & + с
Параметрическое уравнение прямой
(проходящей через точку М0 параллельно вектору 5).
х « дс0 4- а*
У - */о + Р*
z = z0 + yt
ell 2
s — направляющий
вектор прямой
Мо (*о» */о> *о) е *
s(a; Р; у) II2
Уравнение прямой, проходящей через две точки
М(хг, ylf гг) и Щх2, У2> *2)
х - хл
У-У\
2 - 2Л
х2 Хг У г У\ 22 zi
Угол между двумя прямыми, заданными в
параметрической форме.
coscp =
l«la2 + PlP2 + Y1Y2I
Й + Pi+Yi K + P2+Y2
Условие параллельности прямых, заданных
параметрически.
a1:a2 = p1:p2 = Y1:Y2
Угол между прямой
и плоскостью.
sinq> =
jaa 4- ЬР 4- ryj
/ 2 , , 2 , 2 / 2 , Q2 , 2
л/a 4-Ь 4-с-л/а 4-р 4-у

614
Справочные материалы
Геометрия в таблицах
26. Метод координат
Уравнение сферы
с центром в начале координат
с центром в точке М(х0, Уо, г0)
х2 + у2 + z2 = г2; г > 0
(д^-х0)2 + (1/-уо)2 + (2-2о)2 = г2,г>0
Уравнение х2 + у2 + г2 + ах + by + сг + d = 0 задает в пространстве
либо сферу, либо точку, либо пустое множество.
(* + 2aJ +^ + 2bJ +l2 + 2cJ = 4 d
27. Векторы и координаты
Вектором называется направленный отрезок.
Вектор характеризуется направлением и длиной.
Направление — множество сонаправленных
лучей.
Длина вектора \а\ — расстояние от начала
вектора до его конца.
Коллинеарные векторы.
Сонаправленные и противоположно направленные
| векторы.
Равенство векторов.
Угол между векторами.
в
А/ АВ^\а\ = \АВ\
аг, а2, а3, а4 —
У а* коллинеарные векторы
//у*1 у**а («1 II а2 II а3 II 34)
jr yS'у аг || 22 — сонаправлен-
^ ные векторы
у*ъ a3 it 24 —
противоположно направленные векторы
а у'
у^ у^ a = S<=>
[и-w
А(ВС,СЛ) = А(ВС9ВА) = 108°
Bl *7° £(AB,BC) = £(AB,AD) = 72°
/79о 1 AD =ВС;АВ ФСГ>
АЬ™ fD _^ _^ _^
Z. (АВ , AD) = Z. (СВ , CD) = 72°

Справочные материалы
Геометрия в таблицах
615
27. Векторы и координаты
Ортогональные векторы.
а 1 Ь <=> z (а, Ь) = 90°
ъм a Lb — ортогональные векторы
Компланарные векторы — это векторы,
лежащие в одной плоскости или в параллельных
плоскостях
С,
£>__L
ААг, АВ ,ВгВ — компланарные
AD, D^AX, CjBj — компланарные
DDV DC, DA — некомпланарные
Пример 1 (нахождение угла между двумя
векторами на плоскости)
Пример 2 (нахождение угла между двумя
векторами в пространстве)
/-(АВ, CD) = 135°; £(AD, CD) = 45°
Если|1в| = 2;|5с| = 1,то
£(AC,GD) = arctg 2; Z (BD ,DC) = n-£ BDC.
По теореме косинусов:
ВС2 = BD2 + DC2 - 2BD • DC • cos Z BDC.
1 = 13 + 8 - 2Vl3 • 272 • cos Z BJDC.
5726
Z BDC = arccos
26
£(BD,DC) =
■• к - arccos
5726
26
Z (АгВ ; DCX) = 90°; Z (CA; jDBx ) = 90°
/-(Dc[; CA) = A(DC19 СгАг ) = 120°, так как
A JDCjA! — равносторонний
£(Db[;DC) = £DbADB1C =»
=> Z (DBX; DC) = arctg 72
L4-.-A
Dy
D
Сложение векторов
Правило ломаной.
a + S + c=OA+ABH-BC=OC,
где ОА =а;АВ =Ь; ВС =с
Правило параллелограмма.
а + Ь=ОА + OB =OF
?А
Правило параллелепипеда.
ОА =а,ОВ= Ь;
OBFA — параллелограмм
=>OF =а + Ь
OF=а+Ь+с

616
Справочные материалы
Геометрия в таблицах
27. Векторы и координаты
Сложение векторов (продолжение)
Законы сложения.
а + bj= Ъ + а
(а + Ь) + с = а + (Ь + с)
а+ 0 =а
Противоположные векторы.
Вычитание векторов
/ jtiA d-b = a + (-b)
М-Щ ^U = -b;b = -a;a + b = 0
AG = -b\ OG = BA
OA+AG = OG,
a-b = OA -OB =BA
Умножение вектора на число
Законы умножения вектора на число (скаляр).
а • (ка) = (аХ) • а
1 • а = а
-1 • а = -а
(а + Х)а = оса + Ы
Ца + Ь) = Ха + lb
ОА = а; ОА' = X • а (X > 0)
А' |OA'| = ?t- \а\
ов = Ь\ ов' = ц • b, (\i < 0)
|ОВ'[=-ц-|Ь|
0 • а = 0
Разложение вектора с на плоскости по двум не-
коллинеарным векторам а и Ъ (а И Ь).
с = ОА + ОБ = ха + у&
разложение вектора с
в по векторам
а и &, где а Ц 6
Разложение вектора г пространства по трем
некомпланарным векторам a, bis. с.
f=OR =ОА +ОВ +ОС =
= хa + yb + zc —
^ ^ \ разложение вектора г
ь *^_i* по векторам а, Ь, с,
в где а,Ь,с некомпланарны
Примеры разложения вектора
Пример 1.
АВ = a; Ai
DG =DC +CG =а + Г-|1& = а - | S; RD=AD-A5=S-a
АВ = a; AD = ft; BG : GC =*= 2; AF = \аС =\(a + b)=\a+\b

Справочные материалы
Геометрия в таблицах
617
27. Векторы и координаты
Примеры разложения вектора (продолжение)
Пример 2.
АВ =а;ВС =b;AD = 4BC=>AD = 4&; AF = |(а + Ь) = |а + |b
В Ь
MAT = 2*W = 2 •
и»)-!*-
3+|»
Пример 3.
ААг = а; АВ = b; AD = с; AXG = GDX; CXF = FC
GF = Ga[ + ApL +AC+CF = f-|cl 4- (-a) + (b + с) + (|al =
Пример 4.
АВ = a; AC =b; AD = с; DG = \cD\ DF = FB
4—» —> —> / 1 1^\ - 1- -> 1-
FC =JPA +AC =f-2« - 25) +Ь=-2а4'&"2С-
GF=GD+5F=JcS + ~5B=J(c--&)+|(a
- 1 - Ь 1 -
c>=2a"4&"4C
Условие коллинеарности двух векторов.
a||&«
ха + yb = О,
х2 + у2*0
а || & <=> a = Xft или & = |ia, если
a*0;b*0
Условие компланарности трех векторов.
а9Ь9с — компланарные векторы <=>
ха + yb + zc = О,
2 2 2
* + у + г *0
а, Ь, с — ненулевые компланарные векторы,
то а = осЬ + рс
Скалярное произведение векторов
а • b = |a| • |&| • cos Z. (a, &)
Свойства скалярного произведения.
a-b = b • a
a • a>0; a • a = |a|2
-|a| Jft|<2 • S<|a| • |S|
ae(& + c) = ae& + a*c
a • S = 0<=>a _L &
a • Ь = |a| • npa Ь = |b| • пр& a

618
Справочные материалы
Геометрия в таблицах
27. Векторы и координаты
Скалярное произведение векторов (продолжение)
Формулы применения скалярного умножения
к решению задач.
со8А(йГь)=\аПВ\ пРьВ=Ж
Пример 1.
Определить угол между BD и DC. Введем систему координат. Тогда В (0; 2); У
i
С (1; 2); D (3; 0), BD (3; -2), DC (-2; 2). в1
BD DC 3(-2) + (-2)-2 -5 2
cos Z(BD; DC) =
5726
\bd\\dc\ 7з2 + (-2)2-7(-2)2 + 22 ^6
5^26
A 1 Cx 2 D
26 Z(BD; DC) = rc-arccos 2Q .
Пример 2.
Определить Z(DCi; CA) = a. Введем систему координат. Тогда А (0; 0; 0);
С (а; а; 0); D (а; 0; 0); Сг (а; а; а); Dc[ (0; а; а); СА (-а; -а; 0).
* —* 2
LS
cosa =
DCt CA
0(-q) + a (-a) + a 0
-a -1
И'|са| Vo2 + a2 + a2-7(-a)2 + (-a)2 + 02 2a2 2
Следовательно, a = Z(DCX; CA) = 120°.
У
с]
Координаты вектора на плоскости. Основные формулы
Если вектор а плоскости имеет координаты
(*Г> £/i)> а вектор Ъ имеет координаты (х2; у2) то:
a - b = (Xi - х2; уг - у2)
ka = (kxi\ ky{), ke R
oca + pS = (ax! + px2; ayx + py2)> a, P e Л
a S = xxx2 + 1/ху2
Длина вектора в координатах на плоскости.
|3| = Jx\ + у\ , где а(хг; уг)
Угол между двумя векторами на плоскости.
Z. (а, 6) = arccos
хгх2 + г/ху2
Г~2~~1 2 Г~2~~ 2 '
л/*1 + Уг' л/х2 + ^2
где a(Xi; г/х), &(х2; у2)
Условие коллинеарности векторов a(xi; у{)
и Ь(х2; у2) на плоскости.
*1 = *2 = Ух '• Уг
ИЛИ\ или
I У\ = *-У2
rajCj + Pjc2 = 0,
aj/i + РУ2 = °»
la2 + |J2*0

Справочные материалы
Геометрия в таблицах
619
27. Векторы и координаты
Координаты вектора на плоскости. Основные формулы (продолжение)
Условие ортогональности векторов
а(х1*> Уг) и Нх2; у2) н* плоскости.
*1*2 + угу2 = 0
Координаты вектора в пространстве. Основные формулы
Если вектор а пространства имеет координаты
(*iJ У\\ ^i), а вектор Ъ имеет координаты (х2; у2\
z2), то:
Длина вектора в координатах
в пространстве.
Угол между двумя векторами в пространстве.
Условие коллинеарности векторов а (х^ j/^; z{)
и b (х2\ у2; г2) в пространстве.
Условие ортогональности векторов a(xi\ у±\ Zi)
и b(x2; у2\ z2) в пространстве.
а + Ь = (хх + х2; уг + у2; zx + z2)
а-Ь = (х1- х2; уг -у2\ zx - z2)
ka = (kxi; kyi\ kzi), ke R
oca + pS = (ахг + $x2\ ayx + $y2; azx +
аЛРе R
ab = xxx2 + 1/1У2 + *l*2
|5| = \x\ + i/i + 2i, a^; yx; 2X)
^(a, b) =
*i*2 + yji/2 + гггъ
cLL LtKsUb , ,
/2 2 2 /2 2 2
^ + i/a + гл • Jx2 + y2 + z2
a(xx; уг; zx), b(x2; y2\ z2)
a II b <=> Xi
или
xi ~ ьх2
Уг - ^2
2j = KZ2
:*2 =
> или <
P*2),
У1-У2 = 21: z2
ахг + p#2 = 0
ayx + pi/2 = 0
a*! 4- pz2 = 0
a2 + p2^0
*1*2 + i/li/2 + *1*2 = °

Математика в формулах
АРИФМЕТИКА
Законы арифметических действий
переместительный:
а + b = b + а
a- b = b- а
сочетательный:
(а + Ъ) + с = а + (Ь + с)
(а* Ь)* с = а* (Ь- с)
распределительный:
(a + b)'C = a-c + b'C
Правила знаков при умножении (делении)
чисел
сумма п первых членов:
Множители
(делимое и делитель)
+ .
+
—
+
—
—
Результат
+
—
+ ■
Правила действий с рациональными числами
(дробями)
а с ad + be ас ас
b d bd b d bd
а с ad - be а с ad
b d~ bd b : d " be
Арифметическая прогрессия
формула л-го члена:
ап = аг + (п - 1) d
сумма п первых членов:
аг + ап 2аг + d(n -
Sn 2 п 2
свойство:
1)
а1 + ап = а2 + ап-1 " — = ак + ап-к
Геометрическая прогрессия
формула п-го члена:
К = ЬГ Я
71 I" 9
свойство:
ЬГ &л = b2 * bn-i = — = h ' K-k
сумма n первых членов бесконечно убывающей
геометрической прогрессии (0 < \q\ < 1):
1 -q
Некоторые числовые ряды (конечные)
1 + 2 + 3 + ... + (/i-l) + n = д(д2+ 1}
1 + 3 + 5 + ... + (2л - 3) + (2л - 1) = л2
2 + 4 + 6 4-... + (2п-2) + 2п = л (д + 1)
12 + 22 + 32 + ... + (71-1)2 + л2 =
= д(д + 1)(2д + 1)
6
12 + 32 + 52Ч-...-К2д-1)2=Д(4%"1)
1Ч2ЧзЧ... + (д-1)Чп3=^
13 + З3 + 53 + ... + (2п - I)3 = л2(2/i2 - 1)
Пропорция
л-1
а с
Ъ d
равносильна следующим равенствам:
. , a b d с b
ad = bc; - = -j; г = - ;
Среднее арифметическое
двух величин:
а + Ь
2
л величин:
«1 + в2_^^+ ап
с

Справочные материалы
Математика в формулах
621
Среднее квадратичное
двух величин:
i 2 _l ь2
fa + b
п величин:
/1,2,2~ Г 2ч
^-(ах +а2 + ... +ап)
Среднее геометрическое (среднее
пропорциональное)
двух величин:
Jab
п величин:
(7а)т = ыат Jam = (л/И)"
(^)m=nJa^ ^="*лй*
Формулы сокращенного умножения
квадрат суммы:
(а + Ь)2 = а2 + 2ab + Ь2
квадрат разности:
(а-b) = а - 2ab + b
Vai •a
2 * ••• * un
Золотое сечение
Величина а делится на части хиа-х так,
чтобы
куб суммы:
(а
куб разности:
(а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3
(а - Ь)3 = а3 - За2Ь + ЗаЬ2 - Ь3
разность квадратов:
а2 - Ъ2 = (а - b) (а 4- Ь)
сумма кубов:
х = Ja(a -
АЛГЕБРА
Свойства степени
a° = l
у 1_\771 771 «771
(a • Ь) = a • b
771 71 771-71
a : a = a
l
an = *ifc
-n 1
л = —
*) =
VD " L a 0 6
a ~ u,o.
771 71 771 + 71
a • a = a
($Г-$Г
(аЛп am
, TTlvTl 77171
(a ) = a
m
a = *Ja
a + b3 = (a + ft) (a2 - a& + ft2)
разность кубов:
a3-b3 = (a-b)(a2 + a& + b2)
Бином Ньютона
(a + ft)" = ап+С1пап-1Ь+ c\anS2 + ... +
+ С* a"" V+ + ... + &"
Ч -»• Ч 2 * С» (n-ft)!fe!
п
a
Свойства квадратного (арифметического) корня
4а • 7b = Tab Tab = 7[a] • J\b\
•J-a-Jb-JTl $ -ft
Выделение квадрата двучлена из квадратного
трехчлена
2 ( 2 Ь С \
ах + Ьх + с = а\ х + -# + - 1 =
( Ь\2 , Аас - Ь2
Теорема Виета (свойство корней)
2 , л
квадратного уравнения ах + ох + с = 0:

622
Справочные материалы
Математика в формулах
приведенного квадратного уравнения
х +px + g = 0:
х1 + *2 = -Р'> Х1'Х2 = Я
приведенного кубического уравнения
х3+рх + gx + r=0:
хг + х2 + хз = ~Р
х^х2 + х2х3 + хгх3 = q
Х\Х2ХЪ = ~г
Формула корней квадратного уравнения
ах + Ьх + с = 0:
Х1,2 ~~
Л1
2а
-Ь ± л/Ь - 4ас
приведенного квадратного уравнения
2
х 4- рх + g = 0:
Х1.2 2
^4
квадратного уравнения с четным вторым коэф-
2
фициентом ах + 2kx + с = 0:
Х1, 2 ~~
-k ± >Jk - ас
Формула Кардано — формула корней неполно-
о
го кубического уравнения у + ру + q = 0:
у= а/_2 + I?2 + 2- + з _£ _ /g2 + L.
У V 2 + А/4 + 27 + V 2 <Н 27
2
Координаты вершины параболы ах + Ьх + с:
_ Ь _ 4ас - Ь
Х°"~2^; Уо~ 4а
Определение логарифма
Логарифмом числа Ь по основанию а называется
показатель степени, в которую нужно возвести а,
чтобы получить Ь.
loga b = с<*ас = b
Свойства логарифма
h°*ba - п
о = а
loga а = 1
loga 1 = 0
1 т
loga а =т
Правила логарифмирования
логарифм произведения:
logc (ab) = logc a + logc b
логарифм частного:
logc(J) = logca-logcb
логарифм степени:
logca =Alogca
логарифм корня:
\ogcnJa - -logca
переход к новому основанию:
logc a
Дополнительные формулы
loga Ь =
Факториал
ьа ~ \ogb а
logn Ь • logm с = logm Ь • logn с
l°Snb = lo*mb = . .
lognc logmc 10g<D
logn Ь logn a
a =o
1 • 2 • S •... • л = л!
Основное свойство факториала
п\ = /I • (л- 1)!
Формула Стирлинга (факториалы больших
чисел)
In (л!) = (п + g J In п - л 4- In J2n
Соединения
Размещения из д по m элементов — соединения,
отличающиеся самими элементами или их
порядком.
л!
Ат -
п (л - *1)!
= л (л - 1) (л - 2)... (л - /п + 1)

Справочные материалы
Математика в формулах
623
Перестановки — соединения, отличающиеся
только порядком элементов.
Р = л! = 1 -2-3-... -п
Модуль комплексного числа
1*1
| = Г = Jx2 + у2
Р =Ап
Сочетания из п по т элементов — соединения,
отличающиеся только самими элементами.
П\ АП
Ст =
п т\ (п - т)\ Рт
= п (га - 1)(71 - 2)...(га - т + 1)
1 2 3 ... т
Свойства сочетаний:
f^m л/t — м fjti + 1 fjn , f^m + 1
СЛ " Cn Cn + l " Cn + Cn
Неравенства
|a + ft|<|a| + |&|
|а-Ы>||а|-|Ы|
а2 + Ь2>2|аЬ|
l+l>2 (ab>0)
Аргумент комплексного числа
Arg 2 = arg г + 2яЛ (те = 0, 1, 2, ...),
где arg г = ф — главное значение аргумента.
Показательная форма записи комплексных
чисел
г = ге1ф
Формула Эйлера
ещ = cos ф 4- i sin ф
Произведение и частное комплексных чисел
*(<Pi + ф2)
= /^[cos (фх + ф2) + i sin (фх + ф2)]
fi _ ^l i(<Pi " ^2) _
*2 " Г2 *
= — [cos (фх - ф2) + i sin (фх - ф2)] (г2 * 0)
'о
а + 6
^ Jab (а>09Ъ>0)
Комплексное число
2
2 = x + iy (i =-1)
Re 2 = х — действительная часть
комплексного числа,
Im 2 = у — мнимая часть комплексного
числа.
Комплексно-сопряженные числа
г = а + ib и 2 = a-ib
Действия с комплексными числами
2Х + 22 = (Хг + Х2) + i(yt + у2)
2г-22 = (хг - х2) + i(yt - у2)
г\'гг = (*i*2 - У\У2> + *(*l!/2 + *2»1>
г1 *i*2 + У\У2 ,хгУ\ ■ xi^2
2^2
*2 + ^2
+ i
Хо +
2 + *>2
— (*2*<»
Тригонометрическая форма записи
комплексных чисел
г = г (cos ф + i sin ф)
ТРИГОНОМЕТРИЯ
Тригонометрические функции в
прямоугольном треугольнике
sin ос =
tgoc =
COS сс =
ctgcc=-
Тригонометрические тождества
tga =
sin a
cos a
2 2
cos a + sin a = 1
, cos a
ctg a = ——
Б sm a
tg a • ctg a = 1
cos
a= VT~^
. 2
sm a
tga =
ctg a
l+ctg2a = *
. 2
sin a
a= Jl-
1
tg a
l + tg2a= *
sin
ctga =
2
cos a
2
cos a
Формулы сложения тригонометрических
функций
sin (a ± (J) = sin a cos (J ± cos a sin P
cos (a ± p) = cos a cos p + sin a sin P

624
Справочные материалы
Математика в формулах
tg(a±ft- »tt±»P
1 + tg a tg р
ctg(a±P)=c_^il±l
ctg p + ctg a
Тригонометрические функции кратных углов
о
sin 2a — 2sin a cos a cos 2a= 1 - 2 sin a
2 2 2
cos 2a = cos a-sin a cos 2a = 2 cos a-1
о
sin 3a = 3sina-4sin a
з
cos3a = 4cos a-3cosa
з
sin 4a = 8 cos a sin a - 4 cos a sin a
A 2
cos 4a = 8cos a - 8cos a + 1
x о 2tg a
tg 2a = 2-«-
1 - tg a
ctg 2a
= ctg a - 1
2ctg a
1g8a-'*"-*"
1 - 3tg a
ctg3a=cJgVL^tga
3ctg a - 1
tg4a = 4tga:4tg3a4
1 - 6tg a + tg a
ctg4a=ctga:6ctga + 1
4ctg a - 4ctga
Тригонометрические функции половинного угла
sin
COS
2 fj
- cos a
oc = /l + cos a
2 V 2
, a sin a 1 - cos a
2 . 1 + cos a
sm a
a _ sin a _ 1 + cos a
C e 2 " l - cos a " sin a
Сумма и разность тригонометрических функций
sin а± sin р = 2sin —g2- cos —^~
qo а + Р а-Р
cos а + cos р = 2cos —^ cos —^
д 0 . а + р . а - р
cos а - cos р = -2sm —•£-*- sm —=|
, , , q sin (a ± P)
tg a ± tg В = z ^
6 ь r cos a cos p
x . j. о , sin (a±p)
ctg a ± ctg p = ±-:—-—r-^
Б ь r sin a sin p
cos a + sin a = J2 cos (45° - a)
cos a - sin a = Jl sin (45° - a)
x , x q cos (a - P)
tga-ctgp = -c08(a + pft)
6 ь v cos a sm p
tg a - ctg a = -2 ctg 2a
2 ct
1 + cos a = 2 cos к
1 0.2a
1 - cos a — 2 sm «
l+sina = 2cos2(45e - |]
1 - sin a = 2 sin'
1 («•-!)
Понижение степени тригонометрических
функций
.2 1 - cos 2а
sm а — 5
з 1
sin а = j (3sin а - sin За)
2 1 + cos 2а
cos а = «
з 1
cos a = 2 (cos 3a + 3cos a)
sin4 a = g (cos 4a - 4 cos 2a + 3)
cos4 a — g (cos 4a 4- 4cos 2a + 3)
Произведение тригонометрических функций
o4« nr. ™* ft - sin (a + P) + sin (a - p)
sin a • cos p = p
Q cos (a + p) + cos (a - p)
cos a • cos P = * ги~2 * —
c4« /v . cb, ft - cos (a - P) - cos (a + P)
sm a • sm p = 5

Справочные материалы
Математика в формулах
625
sin
COS
Формулы приведения тригонометрических
функций
sin (±а + кп) = ±(-1)л sin а
cos (±а + кп) = (-l)n cos а
(±а + ^ + кп) = (-l)ncosoc
(±а + ^ + кп) = T(-l)n sin а
tg [а + о + кп) =-ctga
ctg а + ; + о =-tga
Соотношения между обратными
тригонометрическими функциями
arcsm х = -arcsm (-х) = 5 "~ arccos х =
= arctg
arccos х = л: - arccos (-х) = о ~ arcsin х =
х
= arcctg
7ГТ2
arctg х = -arctg (-х) = « ~ arcctg * =
= arcsin
л/l + х2
arcctg х = я - arcctg (-х) = « ~ arc*S х''
х
= arccos
Vl + х2
НАЧАЛА АНАЛИЗА
Предел функции. Свойства
lim с = с
х->а
lim (f(x) + g(x)) = lim f(x) + lim g(x)
lim (/(*)•*(*))= lim /(x)- lim *(*)
„ ч lim f(x)
x^aS(x) lim^(x)
lim (A • f(x)) - ft • lim /(x)
Пределы некоторых последовательностей
a>0, Ь > 1, a > 0, p — натуральное число:
f. ♦ IT -
lim
,. lp + 2P + ... + np 1
lim — —
„p + г
p + 1
lim —: =e lim -7=0
п~^ооГ1/п\ n-*<*> n-
. lp + 3P + ... + (2n - l)p _ 2P
lim
J> + x
P + 1
limf—J-r + -J-; + ... + ^-1 =ln2
л-»Лп + 1 я + 2 2nJ
a
Urn \ = 0
lim Va = 1
Шп -£-=0
. 1
sin -
lim —:— = 1
«1
lim nJn =\
lim
= 1
lim /i(Va - 1) =lna.
Производная
вторая производная:
г<*>-(П*»'
производные высших порядков:
/(")W = (/(n"1)W)'
Таблица производных
(С)' = 0 (С — константа)
(х)' = 1 (cos х)' = -sin х
(х2)' = 2х (sin х)' = cos х

626
Справочные материалы
Математика в формулах
(X ) = ПХ
п V*
i\gx)'=\\ge
х 1 + х
{tgx)'=-^-
COS X
(ctgx)' = -
(arccos л:)'
(arcsin x)'
(arctgx)' =
^Qrn/»tff -v\'
1
. 2
sin X
1
h-x2
1
Vi-*2
1
1 + *2
1
Л (Л) (л-Л)
(а*)' = а* In а
(вя)'-«*
Правила дифференцирования
(и = и(х), v = vix))
iu + v)' = и' + и' (и - у)' = н' - v'
(и • и)' = u'v + hi/ (са)' = си'
fu\' u'v - dv' "'v »'
ej-
Ш - 7
Производная сложной функции
(u(uW))' = u>W)'^W
iuny = n-un~1'uf
(cos u)' = -sin и • и' (sin и)' = cos и • и'
(tgM)'--^- 'И' (ctg !/)'=-
2
COS U
. 2
sin u
(a) =a -lna-u ie ) = e - и
Производная обратной функции
fix) и gix) — взаимообратные функции;
если существует f\xQ) и g'(*o)» то
Свойства производных высшего порядка
(и + V) = U + V
Л = О
Первообразная F(x) функции fix)
F'ix) = fix)
Неопределенный интеграл — это общее
выражение Fix) + С для всех первообразных
функций от данной функции fix):
Fix) + C = ]fix)dx
Основное свойство
(J/(x)dx)' = /(*)
Таблица интегралов
j k dx = kx + С
n + 1
f xn dx - - - 4- С
J и + 1
' J ^dx = ln|x| + C
• J ex dx = e* + С
f a* dx = т^- + С
J In a
J cos x dx = sin x + С
J sin x dx = -cos x + С
J —^- dx = tg x + С
cos X
\ j- dx = ~ct£ X + C
sin x
J tg x dx = -In | cos x | + С
J ctg x dx = In | sin x | + С
Основные правила интегрирования
\k-fix)dx = k-\fix)dx
J (/(x) + gix)) dx = J /(x) dx + J £(x) dx
Формула Ньютона—Лейбница
ь
\ fix)dx = Fib)-Fia) = Fix)

Справочные материалы
Математика в формулах
627
Свойства определенного интеграла
а
\ f(x)dx = 0
а
Ь а
\ f(x)dx = -j f(x)dx
а Ь
Ь с Ь
\ f(x)dx=\ f(x)dx + \ f(x)dx
а а с
Ъ Ъ
\ k -f(x)dx = k-j f(x)dx
а а
Ь Ъ Ъ
j (f(x) + g(x))dx=\ f(x)dx + \ g(x)dx
b pb + q
j f(px + q)dx=± j f(t)dt
a pa + q
a a
Если f(x) четная, то J f(x)dx - 2 J f(x)dx
-a 0
Если f(x) нечетная, то j f(x)dx = 0
S - j |/(*)| dx
S = J (f(x)-g(x))dx
a
Длина кривой
Z= J Vl + (f'(x))2 dx
Площадь поверхности вращения
yk
\/
1 1
0
a
f(x)
\
1
b x
S=2nj f(x)*J(l + f'(x))2 dx
m(b - a) < j f(x)dx< M(b - а), где M и m — Объем тела вращения
наибольшее и наименьшее значения f(x) на [а; Ь].
Площадь криволинейной трапеции
V = nj (f(x))2dx
S = j f(x) dx
1/i
0
1
с
fix) /\
\ x X X \
i г
> X
yi
0
1 /(x)
Г1
k/
/l\
1b I'*
Несобственные интегралы — интегралы с
бесконечными пределами и интегралы от
разрывных функций.
S - -J /(x)djc
lim
&-► +
f/(je)dx = lim j f(x)dx
Ь —► + <*>
a a
& &
J f(x)dx= lim J /(x)dx

628
Справочные материалы
Математика в формулах
( f(x)dx= lim f f(x)dx+ lim f f(x)dx
-oo a с
Таблица несобственных интегралов
2 +°°
f В1ПХ , я
J "Г" dx = 2
x dx я
e - 1
x dx я
t + 1
+ oo 2
f sin x , я
0 *
+ oo oo
J sin(x ) dx = J cos(x ) dx = /5
Медиана, биссектриса, высота
2 2Ь2 + 2с2 - а
та = 1
2 _ Ьс((Ь + с) - а )
1а 2
(Ь + с)
2 4р(р - а)(р - Ь)(р - с)
Ла = 2
а
Высоты и стороны треугольника
. - - 111
ha:hb:hc=a:b:c
Теорема косинусов
2 2 2
а =Ь + с - 2bc cos А
2 2 2
b = а + с - 2ас cos В
c2 = a2 + b2-2abcosC
f In X , я
J 7 dx = "a
J x - 1 6
ГЕОМЕТРИЯ
Многоульники
Треугольник
Обозначения:
А, В, С — вершины, а также углы
при этих вершинах;
a, bf с — стороны, противолежащие
углам А, В, С соответственно;
ha, hb, hc — высоты, опущенные на
стороны a, Ь, с соответственно;
та,ть,тс — медианы;
laflb,lc — биссектрисы;
R — радиус описанной окружности;
г — радиус вписанной окружности.
Площадь треугольника
S= 2 ah" = 2 bhb = 2 chc
S = 5 оЬ sin С = g ас sin В= ^bc sin А
S=Jp(P ~ а)(Р ~ b)(p - с)
(р = \(а + Ъ + с))
S = rp
S =
abc
4R
Теорема синусов
а
sin А
__Ь
sin В £
Теорема тангенсов
a + Ь
a - b
a + с _
a - с
b + с
Ь - с
«ч*
*ч*
«ч-т
«V
..EJU
с
tin
=
— 97?
с ^Л
ctg|
ctg|
ctg^
ft^J
Прямоугольный треугольник
S=\ab=\hc (ZC = 90°)
Теорема Пифагора:
' с2 = а2 + Ь2 (ZC = 90°)
R = g = mc
Ьс : Ь = Ь : с bc : h = h : ac
Равносторонний треугольник
ал
S =
R =
a273 t _ a73
4
аТз
ft =
г =
2
ал/3
6
R = 2r

Справочные материалы
Математика в формулах
629
Квадрат
S = a2=\d2
Р = 4а
d = aj2
R~2d- —
1
Прямоугольник
S = ab= к d sin ф
R=\d=\Ja2 + b2
P - 2 (a + b)
Параллелограмм
S = aha — bhb
S = ab sin a
S= «d^sincp
P = 2 (a + b)
d* + d\ = 2 (a2 4- b2)
Ромб
2 1
S = ah = a sin a = -Rdxd2
dx = 2acos 5
a
d2 = 2asin ~
dx + d2 = 4a
1, 1 .
Г= 2 oasina
P = 4a
Трапеция
0 a + b , l»j.
о = —p— • Л = о "i ^2 sin '
средняя линияMN = ъ(а> + Ъ)
Произвольный выпуклый четырехугольник
ос + Р + у+8 = 360о
(сх, р, у, 8 — внутренние углы
четырехугольника)
a2 + b2 + c2 + d2=d\+d\ + 4m2
(т — отрезок, соединяющий
середины диагоналей)
S= od1d2sin ф
Правильный многоугольник (п сторон)
центральный угол a = 360° : п
внешний угол р = 360° : п
внутренний угол у = 180° - Р
ап = 2 Jr2 - г2 = 2J?sin | =
-2rtgJ
«л
/\ 1
/ А /
V
г
\_
\>
\
/
R =
о • a
2 sin о
г =
2t*2
0 1 2, a 1 „2 . 1 2 ,_ a
S = « nanr= nr tg к = о иД sin a = т лаЛ ctg §
Окружность и круг
Длина окружности
С = 2лг
длина дуги у соответствующая центральному
углу в п°:
Ь 180° Л
Свойства хорд, секущих и касательной
BS-ES = CS- DS
MBMC = MDME А
MA2 = МВ-МС = MD • ME
Углы в окружности
ZBAC = | ZBOC
ZBAC = 180° - ^ ZBOC

630
Справочные материалы
Математика в формулах
Площадь круга
0 2 6Г Cd
Сегмент и сектор
_ _ . а
а = 2R sin 5
площадь сектора:
soabc = 2 R а
площадь сегмента:
&АВС = &ОАВС " &ОАС
Пирамида
v=ls0.h
правильная пирамида:
^бок = 2 ^о" *
(Р0 — периметр основания,
А — апофема)
правильный тетраэдр:
= а27з
Г^
a J2 . а^/2
4
(Я-
(г-
- радиус описанной сферы)
радиус вписанной сферы)
Многогранники
Обозначения:
V — объем;
Sn0JIH — площадь полной поверхности;
^бок — площадь боковой поверхности;
SQ — площадь основания;
Р0 — периметр основания;
Р±—периметр перпендикулярного сечения;
I — длина ребра;
h — высота.
Призма
^бок = Р±1
V=S0-h
^полн - 2S0 + S6oK
прямая призма:
Параллелепипед
«полн = 2 (ab + be + ас)
F=abc
J2 2 , ,2 . 2
d =а +Ь + с
Куб
5полн = 6а
F= а
d2 = 3a2
^—^1
1 ' /'
1 sd
Jfc — —
а
^*~
а
с
^Ь
*<Л
X
1/
а> —
Г
—
усеченная пирамида:
V=\h(Sx+ JS^~2 +S2)2
где Sx и S2 — площади
оснований.
S6ok = (si - s2): cos a (a —
двугранный угол при ребре
нижнего основания)
Формула Эйлера
N — число вершин, L — число ребер, F
число граней выпуклого многогранника.
Правильные многогранники
Обозначения:
а~ — ребро;
V — объем;
S — площадь боковой поверхности;
R — радиус описанной сферы;
г — радиус вписанной сферы;
Н — высота.
Куб
V = a
S = 6a2
R =
r =
аЛ
2
H = a
j. J

Справочные материалы
Математика в формулах
631
Тетраэдр
<Л/2
V 12
аЛ
R =
r =
4
аЛ
12
аЛ
H =
Октаэдр
V =
г3Л
3
2
S = 2aj3
аЛ
R =
r =
2
аЛ
6
Тела вращения
Цилиндр
S6ok = 2лЛй
SnojIH = 2лД2 + 2nRh
V=nR2h
Конус
ЯП0ЛН = *Д(Д + /)
V=±nR?h
усеченный конус:
S^-nHR + r)
8„олн = 8бок + я(Д2 + г2)
V= |лй(Д2 + Дг + г2),
где Лиг — радиусы оснований.
Додекаэдр
а3(15 + 7^5)
4
S = 3a2V5(5 + 2л/5)
_ аТза+Тб)
Д 4
aVlO(25 + 1175)
Г= 20
Икосаэдр
5a3(3 + Л)
V =
12
S = 5a273
„_ал/2(б + ТЕ)
* 4
г =
а73(3 + VE)
Шар
^сферы = 47СД2 = лс?2
3
Y-ivf-Ц
Шаровой сектор
S = nR (2ft + a)
F =
2яД2&
3
Шаровой сегмент
a2 = ft(2i*-ft)
S^ = 2nRh = к(а2 + ft2)
«полн = я; (2Rh + a2) = тс (ft2 + 2a2)
12
r-*?(a-i)

632
Справочные материалы
Математика в формулах
Декартовы координаты на плоскости
Расстояние между точками A(xv уг) и В(х2, у2)
АВ'Я J(xi " *2>2 + (^1 " У г)2
Деление отрезка в заданном отношении
Уг + Ьу2
х =
хг + Хх2
У =
1 + X ' * 1 + X '
гдеА(хг, ух) и В(х2, у2) — концы отрезка, точка
АС
С(х, у) делит АВ в отношении пЪ =^
Координаты середины отрезка
х =
*1 + *2
У =
Уг + Уг
2 ' * 2
где А^, ух) и В(х2, у2) — концы отрезка.
Уравнение прямой на плоскости
общее уравнение: ах 4- by + с = 0;
если а = 0, прямая параллельна Ох;
если Ъ = О, прямая параллельна Оу;
если с = 0, прямая проходит через начало
координат;
с угловым коэффициентом: у = kx 4- b,
k — тангенс угла наклона прямой к оси Ох;
проходящей через заданную точку А (х0, у0):
У - У о
х - хп
= k,
k — угловой коэффициент;
X V
уравнение прямой в отрезках: - 4- | = 1,
a, b — отрезки, отсекаемые прямой на осях;
проходящей через две заданные точки A(xv уг)
и Б(х2, у2):
У " Уг х - хг
Уг ~ Уг хг~ хг
Расстояние от точки (х0; у0) до прямой
ax-\-by 4- с = 0:
\ах0 4- Ъу0 4- с\
/ 2 , . 2
Взаимное расположение прямых
агх 4- Ьгу 4- сг = 0 и а2х 4- Ь2у 4- с2 = О
условие параллельности:
a1b2-a2b1 = 0
условие перпендикулярности:
axa2 4- Ь^ = О
координаты точки пересечения
Уо =
хЛ =
Ьгс2 - Ь2сх
агъг ~ агъг
агъг " агъг
угол а между прямыми:
\a1b2-a2b1\
sin ос =
cos ос =
vai + ь\ hi + ь
\агаг + ьгьг\
ia\ + bi ^а2 +ь
Взаимное расположение прямых
у = кгх 4- Ьх и у = fc2x 4- b2
условие параллельности:
#1 = "2
условие перпендикулярности:
^1^2 = _1
координаты точки пересечения:
хп =
ьг ' ъг ,
Л1 " Л2
Уо =
fetb2 - btk2
кг - k2
угол а между прямыми:
tgoc =
«j k2
1 4- ЛХЛ2
Уравнения кривых на плоскости
парабола:
у = ах 4- Ъх 4- с
У2 - 2рх
гипербола:
2 2
*.-«- =1
2.2 х
a &
окружность с центром в начале координат:
2,2 D2
х 4-у =Д
окружность с центром в точке (а; Ь):
(х-а)2 + (1/-&)2 = Д2
эллипс:
2 2
^ 4- ^ = 1 (а, & — полуоси эллипса)
а Ь

Справочные материалы
Математика в формулах
633
Формулы преобразования декартовых
координат
при паралл
носе:
х = х' + а
или
х' = х- а
ном пере-
у=у' + Ъ
у' = у-ъ
У '
0
ъ
1
у\
0'
а
X
х'
при повороте вокруг начала координат на угол а:
х = х' cos а-у' sin а
у = х' sin а + у' cos а у
или
х' = х cos а + у sin а
у' = -х sin а + у cos а
Полярные координаты
х = р cos ф
у = р sin ф
Р= л/л
У'
у1
У
^0
1
А
1 \ ^
\ х
s^x'
X
, 2 , 2
IX + у
у\
У
0
1
А (р, ф)
* р = X
4,-1
Декартовы координаты
в пространстве
Уравнение плоскости
общее уравнение:
ах + by + сг + d = 0;
а = 0, плоскость параллельна прямой Ох;
Ъ = 0, плоскость параллельна прямой Оу;
с = 0, плоскость параллельна прямой Oz;
d = 0, плоскость проходит через начало
координат;
а = b = 0, плоскость параллельна плоскости хОу;
а = с = 0, плоскость параллельна плоскости xOz;
Ь = с = 0, плоскость параллельна плоскости yOz;
уравнение плоскости в отрезках (а, ft, с —
отрезки, отсекаемые плоскостью на осях):
а & с
проходящей через точку А(х0, у0, z0)
перпендикулярно вектору п (а, &, с):
а (х - х0) + Ь (у - у0) + с (2 - 20) = 0
Угол между плоскостями
агх + Ьху + сгг + dx = 0
и а2# + &2у + c2z + d2 = 0:
cos<p =
lglg2 + bl&2 + с1с2|
/~2~Т2~ 2 / 2 , . 2 ,
^ах + Ьх + сх ^а2 + Ь2 + с
Условие параллельности двух плоскостей
аА = ^1 = СА
а2 Ь2 с2
Условие перпендикулярности двух плоскостей
а^а2 + Ъ^Ь2 + CjC2 = 0
Расстояние от точки М0 (х0$ у0; г0) до
плоскости ах + by + cz + d = 0:
| <**o + bi/o + c*0 + d\
P =
П , L2 , 2
л/а
+ ft + с
Уравнение прямой в пространстве
канонические уравнения прямой, проходящей
через точку М0(х0; у0; z0) параллельно вектору
s (Z; т; п):
х - х0 у - у0
г - гГ
I т п
Уравнение прямой, проходящей через две
точки Мг (хг; уг; гг)иМ2 (х2; у2; z2):
х - хг у - уг
г - гл
х0 -
2 " х1 Уг- Уг г2 - 21
уравнение прямой — линии пересечения
плоскостей:
агх + Ьгу + сгг + dt = 0,
а2х + Ь2у + c2z + d2 = 0
Угол между прямыми
х - хг у - уг г - гг
и
U
х -х2 у - у2
г - 2«
12 т2 п2

634
Справочные материалы
Математика в формулах
cos ф =
|*1*2 + т\т2 + п\п^
/ПГ" 2~~ 2 ПГ[ 2~~ :
Условие параллельности двух прямых
In ТП0 Псу
Условие перпендикулярности двух прямых
12 ~^~ "^1^2 ~^* ^"1^2 = ^
X - Хп
У - Уо
2 - 2п
m
Угол между прямой —г-
и плоскостью ах + by + сг + d = О
|aZ + Ьуп + сга|
8Шф:
Г~2 Г2 2 /Гг 2 2
Условие параллельности прямой и плоскости
al + bm + сп = О
Условие перпендикулярности прямой и
плоскости
а _ Ъ_ с
I m п
Условие принадлежности прямой плоскости
{al + bm + сп = О,
ах0 + Ъу0 + сг0 + d - О
Уравнения поверхностей
второго порядка
Эллипсоид
2^2 2
2^,2^2 Х
а о с
Сфера
2 . 2 . 2 „2
X + 1/ + Z = Л
Однополостный гиперболоид
2 2 2
г л 2 г
а о с
Двуполостный гиперболоид
2 2 2
2 "*" ,2 2
а Ь с
Конус
2 2 2
2^,2 2 U
а Ь с
Эллиптический параболоид
2 2
а Ь
у Гиперболический параболоид
2 2
— - й- =22
2 ,2 *

Справочные материалы
Математика в формулах
635
Эллиптический цилиндр
2 2
*- + «- =1
а Ь
Гиперболический цилиндр
2 2
2L-IL =i
2,2 х
а Ь
Параболический цилиндр
I/ = 2рх
Векторы
Координаты вектора с началом в точке A(xv yv,zx)
и концом в точке Б(х2, у2, 2г):
AB(x2-xvy2-yv г2-гг)
Сумма векторов a (xv yv zx) и & (х2, у%> г2):
а 4- Ъ = с (хг 4- х2, уг + у2> *i + *г)
Свойства сложения векторов:
а 4- b = 5 4- а
(а 4- Ь) 4- с = а 4- (& 4- с)
а 4- 0 = а
а 4- (-а) = О
Умножение вектора на число
Х- а(х,у, z) = с(Хх, Ху, Xz)
Свойства умножения:
(X\i)a = X(\ia)
(X 4- |i) • а = Ха 4- |ia
X (a 4- b) = Xd +'X5
0 • a = XO = 0
Свойства проекций вектора на ось
npxa = \а\ • совф
прх (а 4- Ь) = прх a 4- прх b
пр (Ха) = knp a
yf
0
a ^
1 -'** ~
npxa
-
X
Скалярное произведение векторов
a(*l»tfl»2l)nft(X2»i/2'22):
_ _ - -/^-
a • & = xxx2 4- i/2i/2 4- zxz2 = \a\ • |&| • cos (a, &)
Свойства скалярного произведения
a-b = b-a
a • a>0 a • a = |a|
a(5 + c) = a-6 + a,c
(Xa)& = Ma&)
Длина вектора a (*, у, z):
\a\-J:
2 2 2
X 4- у 4- z
Угол между векторами
a (xlf ylf zx) и 5 (x2, i/2, z2):
cos (a, b) = p.
a b
Ia| • |b|
*1*2 + У1У2 + 21*2
/ 2 , Г 2 / 2 , 2~ i
^ 4- уг 4- гх ^2 4- y2 4- г
Условие коллинеарности векторов
а || b <=> хх: x2 = уг: y2 = гг : z2 или
xi ~ ^*2
У1 - ^2
2^ = Xz0
Условие ортогональности векторов
a±b<=>a'& = 0 или л:хх2 4- УхУ2 + з^г = О
Векторное произведение векторов
с = [а &]
|с| = |а| • |&| sin ф

636
Справочные материалы
Математика в формулах
Свойства векторного произведения
[аЪ] - -[Ьа]
[(а + Ь)с] = [ас] + [Ьс]
[(Ха)Ь] = \[аЪ]
[аЬ] = 0 <=> а || Ъ
Смешанное произведение векторов
(векторно-скалярное произведение}:
а-Ь- c = [ab]c
Определители
Определитель второго порядка
ai h
а2 Ь2
= алЪп — а9Ь
Пи2
2и\
Определитель третьего порядка
= агЬ2с3 + Ьгс2а3 + а2Ь3сг - сгЬ2а3 -
ai bi сг
Н Ь2 С2
а3 Ь3 с3
- Ьга2с3 - агс2Ь3
Основные свойства определителей
замена строк на столбцы:
ai bi ci
а2 Ъ2 С2
аз ьз сз
Ьг Ь2 Ь3
перестановка двух строк:
аг Ъг сг
а2 Ъ2 с2
аз ьз сг
а2 Ь2 С2
а1 Ъ\ с1
аз ьз сз
вынесение общего множителя элементов
строки:
ai bi ci
а, Ь, сг
Ха2 Xb2 Хс2
аз ьз сз
= Х
нулевая строка (столбец):
аг Ьг сг
0 0 0
аз ьз сз
= .
0 Ь1с1\
0 Ь2 с2
0 Ь3 с3
а2 Ь2 с2
а3 Ь3 с3
= 0
пропорциональные строки:
гг Ъг
Ха3 ХЬ3 Хс3
аз ьз сз
= 0
сумма элементов столбца (строки):
ai bi~^ ^i с\
а2 b2 + b2 с2
а3 Ъ3+ Ь3 с3
суммирование строк:
ai bi с1
а2 Ъ2 С2
а3 Ь3 с3
а1
а2
а3
h
h
h
ci
c2
c3
+
al bl
a2 b2
a3 bZ
a2 b2 c2 + \a2
a3 b3 c3 + Xa3
сумма произведений элементов строки
(столбца) на их алгебраические дополнения:
ai bi ci
а2 Ь2 с2
а3 Ь3 с3
= аГ
Ь2 с2
Ъ3 с3
-*г
а2 с2
а3 с3
+ с,
а2Ь2
аЗЬ3
сумма произведений элементов строки
(столбца) определителя на алгебраические
дополнения соответствующих элементов другой
строки (столбца):
= 0
Решение систем двух линейных уравнений с
двумя неизвестными
Ь1с1
ьзсз
-Ьг'
aici
a3C3
+ <v
aibi
a3b3
axx + bxy ='c1
a2* + b2y - c2
A =
a1b1
a2 b2
*0
X —
clbl
c2 b2
агЪг
a2 b2
У
агсг\
a2 C2 1
al bl
a2 b2

Подготовка
к экзаменам
поможет успешно преодолеть
все трудности

Задания письменных экзаменов
по математике
помогут эффективно
подготовиться к сдаче
выпускного экзамена за курс
средней школы
и вступительного
экзамена в вуз.
Примерные билеты и ответы
содержат минимальную
учебную информацию,
необходимую для успешной
сдачи устных
выпускных экзаменов
по геометрии
в 9 и 11 классах у
по алгебре и началам анализа
в 11 классе.

9 класс
Примерные билеты и ответы
к устному экзамену по геометрии
Билет 1
1. Признаки параллельности прямых
(формулировки и примеры).
2. Решение треугольника по стороне и двум
углам.
3. Задача по теме «Углы, вписанные в
окружность» (типа № 79—81).
4. Задача по теме «Длина окружности* (типа
№ 48, 49).
I. Две прямые, параллельные третьей,
параллельны.
П. Если внутренние накрест лежащие
углы равны, то прямые параллельны.
III. Если сумма внутренних односторонних
углов равна 180°, то прямые параллельны.
IV. Если соответственные углы равны,
то прямые параллельны.
Примеры.
I. Дано: d \\ f; f II h. Определите, параллельны
ли прямые d и h (рис. 1).
Прямые d и h параллельны, так как каждая
из них параллельная прямой /.
П. Дано: Z 1 = Z 2, Z 3 * Z 4. Определите
пару параллельных прямых (рис. 2).
Прямые end параллельны, так как
внутренние накрест лежащие углы Z 1 и Z 2 равны.
III. Дано: Zl + Z2 = 180°, Z 3 > Z 4.
Определите пару параллельных прямых (рис. 3).
Прямые е и с параллельны, так как сумма
внутренних односторонних углов (Z 1 и Z 2)
равна 180°.
IV. Дано: Z1=Z2, Z 3 * Z 4. Определите
пару параллельных прямых (рис. 4).
Прямые end параллельны, так как
соответственные углы (Z 1 и Z 2) равны.
2.
Решить треугольник по стороне и двум
прилежащим к ней углам — это значит при
заданных стороне и двум прилежащим к ней
углам найти третий угол и две другие
стороны.
Будем использовать следующие обозначения
для сторон треугольника ABC: АВ = с, ВС = а,
СА = Ьи его углов: Z А = ос, Z Б = р, ZC = у (рис 5).
Дано: а, р, у.
Найти: с, Ь, ос.
Решение:
ос=180°-(р + 7).
„ , sin В sin у
По теореме синусов Ъ = а-г-*- и с = а -т—j-.
v J sin a sin а
Единственность решения вытекает из
признака равенства треугольников:
Рис. 1
Рис. 2
ь/
/1
J2
f
е
J^
с
4
Рис. 4
Рис.3

640
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Если сторона и два прилежащих к ней
угла одного треугольника соответственно
равны стороне и двум прилежащим к ней углам
другого треугольника, то такие
треугольники равны.
3.
Углы ADC и ABC вписаны в окружность,
ZABC = 74°. Найдите градусную меру Z ADC.
Решение. Вписанные в
окружность углы,
опирающиеся на одну дугу, вершины
которых лежат по одну сторону
от хорды, стягивающей эту
ДУГУ» равны, поэтому ZADC =
= ZABC = 74°.
4.
Дуги АгВг и А2В2 равной длины I
принадлежат разным окружностям с радиусами Rx и R2.
Найдите отношение градусных мер
центральных углов, соответствующих этим дугам.
Решение. Длина дуги
окружности радиуса R,
соответствующей центральному углу в /г
на/ =
kR
kR
' 180
hAjB2 =
180 'Л1 =
•Л;А1Б1=180
nR,
рав-
= 1
ее
'2
180
180
п
2 — ^»
R,
п
отсюда
В,
*2' д0
Билет 2
1. Свойство углов, образованных при
пересечении двух параллельных прямых третьей
прямой (формулировки и примеры).
2. Решение треугольника по двум сторонам
и углу между ними.
3. Задача по теме: «Средняя линия
треугольника» (типа № 46—48).
4. Задача по теме «Неравенство
треугольника» (типа № 44).
1.
I. Если две параллельные прямые
пересечены третьей прямой, то внутренние накрест
лежащие углы равны.
II. Если две параллельные прямые
пересечены секущей, то сумма внутренних
односторонних углов равна 180°.
III. Если две параллельные прямые
пересечены секущей, то соответственные углы
равны.
Примеры.
Две параллельные KD и CG пересечены
третьей прямой AL (рис. 6).
I. Найдите градусную меру угла DAB, если
Z ABC =122°.
Решение. Угол DAB образует пару
внутренних накрест лежащих углов с углом ABC при
пересечении параллельных прямых KD и CG
третьей прямой AL. Поэтому Z DAB + Z ABC =
= 180°, откуда Z DAB - 180° - 122° = 58°.
П. Найдите градусную меру угла КАВ, если
Z ABC =122°.
Решение. Угол КАВ образует пару
внутренних односторонних углов с углом ABC при
пересечении параллельных прямых KD и CG третьей
прямой AL. Поэтому Z КАВ + Z ABC = 180°,
откуда Z КАВ = 180° - 58° = 122°.
III. Найдите градусную меру угла Z LBC,
если Z КАВ = 122°.
Решение. Угол LBC образует пару
соответственных углов с углом КАВ при пересечении
параллельных прямых KD и CG третьей прямой
AL. Поэтому Z КАВ = Z LBC = 122°.
2.
Решить треугольник по двум сторонам и
углу между ними — это значит при
заданных двух сторонах и углу между ними
найти третью сторону и два других угла.
Буде;м использовать следующие обозначения
для сторон треугольника ABC: АВ = с, ВС — а,
СА = Ъ и его углов: ZА = а, Z В = р, ZC = у
(рис. 7).
Рис.6

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
641
Дано: а, Ь, у.
Найти: с, а, р.
2 '
Решение. По теореме косинусов с = а
+ ь2-
7 2 2
а + b - 2afrcosy.
Рассмотрим угол у:
1)еслиZ у> 90°, то/аи/ Р — острые;
2) если у < 90° и а < 6, то Z а — острый.
тт ас.
По теореме синусов ^г^ = ^г^, откуда sin a =
sin a
siny
a sina
. Градусную меру угла a находим с
помощью таблиц; затем находим угол р:
p=180°-(a + Y).
3) если у < 90° и a > 6, то для нахождения
sin Р применим теорему синусов. Имеем -т—g =
= -^—. Находим градусную меру угла р, после
sin у
чего находим угол а: а — 180° - (Р + у).
Единственность решения задачи вытекает из
признака равенства треугольников:
если две стороны и угол между ними
одного треугольника соответственно равны двум
сторонам и углу между ними другого
треугольника, то такие треугольники равны.
3.
В треугольнике ABC отмечены точки D иЕ,
которые являются серединами сторон АВ и ВС
соответственно. Найдите периметр
четырехугольника ADEC, если АВ = 24 см, ВС = 32 см и
АС = 44 см.
Дано: AD = DB, BE =
= ЕС,АВ = 24 см, ВС =
= 32 см, АС = 44 см.
Найти: Р^ес-
Решение. Так как
AD = DB; BE = ЕС, то
DE — средняя линия ААВС; по свойству
средней линии DE равно половине основания АС.
Поэтому
padec = ad + DE + ЕС +АС =
= 12 + 22 + 16 + 44 = 94 (см).
4.
Расстояния от точки А до точек Б и С равны
3 см и 14 см соответственно, а расстояния от
точки D до точек В и С равны 5 см и 6 см
соответственно. Докажите, что точки А, В, С и D
лежат на одной прямой.
В
Дано: АВ = 3 см, АС = 14 см,
DB = 5 см, DC = 6 см.
Доказать: точки А, В, С и D лежат на одной
прямой.
Доказательство!. Пред- А d
положим, что точки А, В, С
и D не лежат на одной
прямой. Возможны два случая:
точки А и D лежат в одной
полуплоскости относитель- а)
но прямой ВС, точки А и D
(рис. а) лежат в разных
полуплоскостях (рис. б).
Доказательство для обоих
случаев аналогично.
Из треугольника ABC в
силу неравенства
треугольника следует, что АС < АВ +
+ ВС; 14 < 3 + ВС; т. е. ВС >
> 11. Из треугольника ABD следует неравенство
ВС < BD + DC = 5 + 6, т. е. ВС < 11. Пришли к
противоречию, следовательно, точки А, В, Си!)
лежат на одной прямой.
Доказательство 2. Воспользуемся
неравенством треугольника, которое состоит в
следующем: для любых трех точек Р, Q и R PR < PQ +
+ QPf причем PR = PQ + QR в том и только в том
случае, когда точка Q лежит между Р и R.
Тогда ВС < BD + DC, т. е. ВС < 11, АС < АВ +
4- ВС, т. е. 14 < 3 + ВС, откуда ВС = 11. Поэтому
ВС = BD 4- DC, так что точка D лежит между В
и С на прямой ВС.
Кроме того, АС =АВ + ВС = 14, так что точка
В лежит между А и С на прямой ВС. Но тогда
и А лежит на прямой ВС.
Таким образом, все четыре точки лежат на
прямой ВС, что и требовалось доказать.
Билет 3
1. Третий признак равенства треугольников
(формулировка и пример).
2. Теорема об углах, вписанных в окружность.
3. Задача по теме «Площадь» (типа № 107,108).
4. Задача по теме «Трапеция» (типа № 28, 29).
1.
Если три стороны одного треугольника
соответственно равны трем сторонам другого
треугольника, то такие треугольники равны.
21 1019

642
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Пример.
По рисунку докажите равенство
треугольников ВАС и DAC, если АВ = AD, ВС = DC (рис. 8).
В треугольниках ВАС и DAC АВ = AD, ВС =
= DC по условию, АС — общая сторона.
Следовательно, ABAC = A DAC по трем сторонам.
2.
Угол, вершина которого лежит на
окружности, а стороны пересекают окружность,
называется вписанным углом.
[П]* Угол, вписанный в окружность, равен
половине соответствующего центрального
угла.
Дано: Z ABC — вписанный, О — центр
окружности.
Доказать: ZABC = ^ZAOC.
Доказательство. Рассмотрим сначала
частный случай, когда одна из сторон угла проходит
через центр окружности (рис. 9, а).
Треугольник АОВ равнобедренный, так как у
него стороны ОА и ОВ равны как радиусы.
Поэтому углы А и В треугольника равны. А так как
их сумма равна внешнему углу треугольника
при вершине О, то угол В треугольника равен
половине угла АОС, что и требовалось доказать.
Общий случай сводится к рассмотренному
частному случаю проведением вспомогательного
диаметра BD (рис. 9,6, в).
В случае, представленном на рисунке 9, б,
Z ABC = Z CBD + Z ABD =
= \z СОВ + \zAOB = \ZA0C.
В случае, представленном на рисунке 9, в,
Z ABC = Z CBD - ZABD =
= \ZC0B- \zAOB= \zAOC.
[А]** Вписанный угол измеряется
половиной дуги, на которую он опирается.
Дано: Z ABC — вписанный, О — центр
окружности, ^АС — соответствует Z ABC (рис. 10).
Доказать: ZABC= « ^АС.
Доказательство. Рассмотрим три
возможных случая расположения луча ВО
относительно угла ABC.
1)Луч ВО совпадает с одной из сторон угла
ABC, например со стороной ВС (рис. 10, а).
В этом случае дуга АС меньше полуокружности,
поэтому Z АОС = о w ^' ^ак как угол ^^ ""
* [П] — здесь и далее ответ дается в соответствии с учебником А. В. Погорелова.
** [А] — здесь и далее ответ дается в соответствии с учебником Л. С. Атанасяна.
Рис.8
а)

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
643
внешний угол равнобедренного треугольника
АВО, а углы 1 и 2 при основании
равнобедренного треугольника равны, то Z АОС = Z 1 + Z 2 =
= 2 Z 1. Отсюда следует, что 2 Z 1 = ^ АС или
ZBC = Z1 = \ ^АС.
2) Луч ВО делит угол ABC на два угла.
В этом случае луч ВО пересекает дугу АС в нето-
котой точке D (рис. 10,6). Точка D разделяет
дугу АС на две дуги: ^ AD и ^ DC. По доказанному
ZABD= \
'ADnZDBC
CD. Складывая
эти равенства почленно, получаем:
ZABD + ZDBC= \
AD +
ср,
или Z ABC = g ^АС.
3) Луч ВО не делит угол ABC на два угла и
не совпадает со сторонами этого угла. В этом
случае луч ВО пересекает дугу АС в нетокотой
точке D (рис. 10, в). Точка С разделяет дугу AD на
две дуги: ^ АС и ^ DC. По доказанному Z ABD =
AD и Z CBD - ^
CD. Вычитая из
ZABD-ZCBD =
3.
AD-\ ^CD.ZABC=\ ^АС.
первого равенства второе, получаем
Найдите площадь ромба, если
его диагонали равны 6 см и 8 см.
Решение. Диагонали ромба
взаимно перпендикулярны, поэтому
они делят ромб на четыре равных
прямоугольных треугольника. Так
как диагонали ромба точкой
пересечения делятся пополам, то
катеты каждого из этих
треугольников равны 3 см и 4 см;
SABCD - 4
i<»
4) = 4 • 6 = 24 (сы%
4.
Диагонали трапеции делят ее среднюю
линию на три равные части. Как относятся
основания этой трапеции?
Дано: ABCD —
трапеция, ML — средняя линия,
MP = PQ = QL.
Найти: ВС : AD.
Решение. Пусть MP =
= a; MP — средняя линия А'
треугольника ABC, так что ВС = 2а. Так как
PL = 2а — средняя линия треугольника ACD9 то
AD = 4а, так что ВС : AD = 2а : 4а = 1 : 2.
Билет 4
1. Теорема о сумме углов треугольника
(формулировка и пример).
2. Решение треугольника по "трем сторонам.
3. Задача по теме: «Средняя линия трапеции»
(типа № 51).
4. Задача по теме «Окружность» (типа № 6, 7).
1.
Примеры.
1. В треугольнике один из углов равен 29°,
другой 91°. Найдите его третий угол.
Решение. Третий угол треугольника равен
180° - (29° + 91°) = 180° - 120° = 60°.
2. Найдите острые углы равнобедренного
прямоугольного треугольника.
Решение. Из теоремы о сумме углов
треугольника следует, что сумма острых углов
прямоугольного треугольника равна 180° - 90° = 90°.
Так как острые углы в равнобедренном
прямоугольном треугольнике равны, то каждый из
них равен 90° : 2 = 45°.
3. Найдите утлы равностороннего
треугольника.
Решение. Из теоремы о сумме углов
треугольника следует, что сумма углов равностороннего
треугольника равна 180°. Так как в
равностороннем треугольнике все углы равны, то
каждый из них равен 180° : 3 = 60°.
2.
Решить треугольник по трем сторонам —
это значит по трем заданным сторонам
треугольника найти его углы.
Будем использовать следующие обозначения
для сторон треугольника ABC: АВ = с, ВС =
- а, СА = в и его углов: ZA=a, ZB = P, ZC = y
(рис. 11).
Дано: а, Ь, с.
Найти: у, а, р.
Решение. Пусть а — наибольшая сторона, а <
<Ь + с. По теореме косинусов находим
наибольший угол а:
2 , 1.2 2
2 2,,2Л с + о - а
а = с + о - 2ас cos a, cos а = «-g •

644
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
С помощью теоремы синусов вычисляем sin р:
= -^—5 , sin В =
snip к
bsina
sin a sinp' *~ a
С помощью таблиц находим градусную меру
углов.
у=180°-(ос + р).
Единственность решения задачи вытекает из
признака равенства треугольников:
Если три стороны одного треугольника
соответственно равны трем, сторонам, другого
треугольника, то такие треугольника равны.
3.
В трапеции ABCD с основаниями AD = 12 см и
ВС = 8 см проведена средняя линия ML, которая
пересекает диагональ АС в точке К. Чему равны
отрезки МК и KL1
Дано: ABCD — трапеция,
ML — средняя линия, АС —
диагональ трапеции ABCD,
К — точка пересечения ML
иАС, AD = 12 см и ВС =
= 8 см.
Найти: МК и KL.
Решение. Так как ML — средняя линия
трапеции ABCD, то
AM = MBhCL = LD\ ML \\ AD и ML II ВС.
Следовательно, МК — средняя линия
треугольника ABC, а KL — средняя линия
треугольника ACD. Значит, МК = 4 см, KL = 6 см.
4.
Из одной точки к двум касающимся внешним
образом окружностям проведены три
касательные, причем одна из них проходит через точку
касания окружностей. Докажите, что
касательные равны.
Решение. Точку А, из
которой проведены касательные к
данным окружностям, и точки
касания В, С и D соединим с
центрами окружностей О и Ov
Рассмотрим треугольники
АВОх и ACOv Угол АВОг
равен углу ACOv так как эти углы прямые,
поскольку ВОг и СОг — радиусы, проведенные в точки
касания В и С; ВОг = СОг как радиусы одной
окружности; АОг — общая сторона. Следовательно,
прямоугольные треугольники АВОг и АСОг равны по
гипотенузе и катету. Значит, АВ = АС.
Аналогично доказывается, что АС = AD.
Отсюда АВ = АС = AD.
Билет 5
1. Определение синуса острого угла
прямоугольного треугольника. Пример его применения
для решения прямоугольных треугольников.
2. Свойство углов равнобедренного
треугольника.
3. Задачи по теме «Подобие треугольников»
(типа № 71, 72).
4. Задача по теме «Параллелограмм» (типа
№ 20, 21).
1.
Синусом острого угла прямоугольного
треугольника называется отношение противолежа-
а
щего катета к гипотенузе: sin a = - .
Примеры.
1. Дан прямоугольный треугольник. Найдите:
а) гипотенузу с и катет Ь, если даны катет а
и противолежащий ему угол а;
б) катеты треугольника а и Ъ, если даны
гипотенуза с и один из острых углов а (рис. 12).
h
]
к
к
\
п \
а
Рис. 12
Дано: а, ос.
Найти: Ъ, с.
Решение:
_ а
~~ sina'
,2 2 2
b =с -а .
Дано: с, ос.
Найти: а, Ь.
Решение:
а = с • sin a;
,2 2 2
b =с -а .
2. На вершину горы идет канатная дорога
длиной 1,2 км, составляющая угол 60° с
высотой горы. Чему равна высота горы?
Решение. Обозначим длину канатной дороги
через с, высоту горы через h, а угол между
канатной дорогой и высотой горы через Р (рис. 13).
Дано: с = 1,2 км, р = 60°.
Найти: h.

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
645
Решение. Из теоремы о сумме углов
треугольника следует, что сумма острых углов
прямоугольного треугольника равна 90°. Поэтому
а = 30°. Отсюда
h = с • sin а = 1,2 • sin 30° = 1,2 • ^ = 0,6 (км).
2.
Треугольник называется равнобедренным,
если у него две стороны равны. Эти равные
стороны называются боковыми сторонами, а третья
сторона называется основанием треугольника.
[П] В равнобедренном треугольнике углы
при основании равны.
Дано: ABC — равнобедренный треугольник,
АВ — основание (рис. 14).
Доказать: ZA = ZB.
Доказательство. Треугольник CAB равен
треугольнику СВА по первому признаку
равенства треугольников. Действительно, СА = СВ,
СВ = СА, Z С = Z С. Из равенства треугольников
следует, что ZA = ZB. Теорема доказана.
[А] Дано: ABC — равнобедренный
треугольник, ВС — основание (рис. 15).
Доказать: ZB = Z С.
Доказательство. Пусть AD — биссектриса
треугольника ABC (см. рис. 15). Треугольники
ABD и ACD равны по первому признаку
равенства треугольников (АВ = АС по условию, AD —
общая сторона, Z 1 = Z 2, так как AD —
биссектриса). Из равенства треугольников следует,
что ZB = Z С. Теорема доказана.
3.
Один из углов одного
прямоугольного
треугольника равен 30°, а один из
углов другого
прямоугольного треугольника
60°. Установите, подобны
ли данные треугольники.
Дано: А ABC и AFDG — прямоугольные, ZBn
ZD — прямые, Z F = 60°, Z С = 30°.
Доказать: A ABC ™ AFDG.
Доказательство. Треугольник ABC —
прямоугольный и Z С — 30°, по теореме о сумме
углов треугольника Z А = 60°. В треугольниках
ABC и FDG: ZBn ZD — прямые и ZA = Z F,
следовательно, A ABC ™ AFDG, что и
требовалось доказать.
4.
В равнобедренный треугольник вписан
параллелограмм так, что угол параллелограмма
совпадает с углом при вершине треугольника,
а вершина противолежащего угла лежит на
основании. Докажите, что периметр
параллелограмма есть величина постоянная для данного
треугольника.
Дано: ААВС —
равнобедренный (АВ = ВС), BFED —
параллелограмм.
Доказать: Pbfed = ^В + ВС.
Решение. Углы DAE и ВСА
равны как соответственные при
параллельных прямых DE и ВС,
пересеченных прямой АС. Так как треугольник ABC —
равнобедренный, то Z ВСА = Z ВАС, т. е. Z DEA =
= Z ВАС = Z DAE. Следовательно, треугольник
ADE — равнобедренный, откуда AD = ED.
Аналогично доказывается, что EF = FC.
Поэтому
pbdef = BD + DE + EF + FB =
= BD + DA + CF + FB =AB + ВС,
что и требовалось доказать.
Билет 6
1. Определение косинуса острого угла
прямоугольного треугольника. Пример его
применения для решения прямоугольных
треугольников.
Рис. 13
Рис. 14

646
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
2. Признак равнобедренного треугольника.
3. Задача по теме «Подобие треугольников»
(типа № 73, 74).
4. Задача по теме «Прямоугольник» (типа
№ 22—24).
1.
Косинусом острого угла прямоугольного
треугольника называется отношение прилежащего
Ь
катета к гипотенузе: cos а = - .
Примеры.
1. Дан прямоугольный треугольник. Найдите:
а) гипотенузу с и катет а, если даны катет b и
прилежащий к нему угол а;
б) катеты треугольника аиЬ, если даны
гипотенуза^ и один из острых углов а (рис. 16).
ъ
\
и р\
а
Г
Рис. 16
Дано: Ьиа.
Найти: с, а.
Решение:
= Ь
cosa'
2 2.2
а = с -Ъ ,
/2 «2
а = л/с - b .
Дано: с, ос.
Найти: а, Ь.
Решение:
Ь = с • cos а;
2 2.2
а =с -Ь ,
1 2 ,2
а= *Jc - Ъ .
2. Угол между лестницей эскалатора и полом
зала равен 150°. Какова длина лестницы
эскалатора, если подошва лестницы равна 117 м?
Обозначим длину лестницы эскалатора через с,
длину подошвы лестницы — через Ъ, а угол
между лестницей эскалатора и полом зала —
через 8 (рис. 17).
Дано: Ь = 117 м, 8 = 150°.
Найти: с.
Решение. Из теоремы о смежных углах
следует, что р = 30°. Находим
Ъ = 117 = 2-117
cosp 7з 7з
2
с =
= 89 73 (м).
2.
Треугольник называется равнобедренным,
если у него две стороны равны. Эти равные
стороны называются боковыми сторонами,
а третья сторона называется основанием
треугольника.
[П] Если в треугольнике два угла равны,
то он равнобедренный.
Дано: А ABC — треугольник, ZA = ZB
(рис. 18).
Доказать: ААВС — равнобедренный.
Доказательство. Треугольник ABC равен
треугольнику ВАС по второму признаку
равенства треугольников. Действительно, АВ = ВА,
Z В = Z A, Z А = Z В. Из равенства
треугольников следует, что АС = ВС.
Значит, по определению треугольник ABC —
равнобедренный.
[А] Дано: ААВС — треугольник, Z А = Z В
(рис. 19).
Доказать: ААВС — равнобедренный.
Доказательство. Так как в треугольнике два
угла равны, то равны и стороны, лежащие
против этих углов. Действительно, если
предположить, что одна из указанных сторон больше
другой, то угол, лежащий против нее, будет больше
угла, лежащего против другой стороны, а это
противоречит условию (тому, что данные углы
равны). Итак, в треугольнике две стороны
равны, т. е. треугольник — равнобедренный.
3.
Из точки D, лежащей на
катете АС прямоугольного
треугольника ABC, опущен на
гипотенузу СВ перпендикуляр DE.
Найдите отрезок CD, если СВ =
= 15 см, АВ = 9 см и СЕ = 4 см.
Дано: ААВС —
прямоугольный, Z А — прямой, DE _1_ СВ,
СВ = 15 см, АВ = 9 см, СЕ = 4 см.
Найти: CD.
Рис. 17
Рис. 18
Рис. 19

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
647
Решение. По теореме Пифагора
АС=.РГ_:Г2
15 - 9 = 12 (см).
В треугольниках ABC и EDC Z ВАС = Z DEC
как прямые, ZC — общий, следовательно,
AEDC со дABC. Поэтому
СВ_АС 15 _ 12 rn_I5li_K/ ч
CD " ЕС9 CD " 4 ;LV 12 ~~ & (СМ)'
Стороны прямоугольника равны 5 см и 4 см.
Биссектрисы углов, прилежащих к большей
стороне, делят противолежащую сторону на три
части. Найдите длины этих частей.
Дано: ABCD — прямоугольник, AD = 5 см,
АВ = 4 см, DE — биссектриса Z CDA9 AF —
биссектриса Z BAD.
Найти: BE, EF, FC.
Решение. Так как DE —
биссектриса Z CDAt то
Z CDE = Z ADE; Z ADE =
= Z CED как накрест
лежащие углы при
параллельных прямых AD и ВС,
пересеченных прямой DE,
следовательно, Z CDE = Z CED и треугольник ECD —
прямоугольный и равнобедренный. Отсюда
ЕС= CD = 4 см.
Аналогично доказывается, что AABF —
прямоугольный и равнобедренный. Поэтому
CD = СЕ = 4 см.
Так как BF + FC = ВС = 5 см, то FC = 1 см,
значит, EF = EC-FC = 3 см, ВЕ = ВС-ЕС = 1 см.
Билет 7
1. Определение тангенса острого угла
прямоугольного треугольника. Пример его
применения для решения прямоугольных
треугольников.
2. Свойство медианы равнобедренного
треугольника.
3. Задача по теме «Подобие треугольников»
(типа № 75—78).
4. Задача по теме «Ромб. Квадрат» (типа
№ 25, 26).
1.
Тангенсом острого угла прямоугольного
треугольника называется отношение противолежа-
щего катета к прилежащему: tg ос = т .
Примеры.
1. Дан прямоугольный треугольник. Найдите:
а) гипотенузу с и катет Ь, если даны катет а и
противолежащий ему угол а;
б) гипотенузу с и катет а, если даны катет Ь и
прилежащий к нему угол а (рис. 20).
ъ
\
а
Рис. 20
Дано: а, а.
Найти: Ьу с.
Решение:
2,2,2
с =Ь + а ,
L2 . 2
с = *Jb + а
Дано: Ь, а.
Найти: с, а.
Решение:
а = Ь • tg а,
2 ,2.2
/L2 , 2
с= л/Ь 4- а
2. Под каким углом падает на землю луч
солнца, если вертикально воткнутый в землю
шест возвышается над землей на 18 м и
отбрасывает тень, равную 6 V§ (рис. 21)?
Обозначим длину шеста через а, длину тени
шеста через 6, а угол, под которым на землю
падает луч солнца, через а.
Дано: а = 18 м; Ь = 6 Jb м.
Найти: а.
то
Решение. Так как tg а = г = —р = л/3,
ь 6л/3
а = 60°.
2.
В равнобедренном треугольнике медиана,
проведенная к основанию, является
биссектрисой и высотой.

648
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Дано: ААВС — равнобедренный
треугольник, ДВ — основание, AD — медиана (рис. 22).
Доказать: AD — биссектриса и высота.
Доказательство. Треугольники CAD и CBD
равны по второму признаку равенства
треугольников (стороны АС и ВС равны, так как ААВС —
равнобедренный. Углы CAD и CBD равны как
углы при основании равнобедренного
треугольника. Стороны AD и BD равны, поскольку D —
середина отрезка АВ).
Из равенства треугольников ABD и ACD
следует равенство углов:
ZACD = Z BCD nZADC = Z BDC.
Так как углы ACD и BCD равны, то CD —
биссектриса. Поскольку углы ADC и BDC
смежные и равны друг другу, они прямые.
Следовательно, отрезок AD является также высотой
треугольника ABC. Теорема доказана.
Таким образом, установлено, что
биссектриса, медиана и высота равнобедренного
треугольника, проведенные к основанию, совпадают.
Поэтому справедливы также следующие
утверждения:
1. Биссектриса равнобедренного
треугольника, проведенная к основанию, является
медианой и биссектрисой.
2. Высота равнобедренного треугольника,
проведенная к основанию, является
медианой и биссектрисой.
3.
В трапеции ABCD проведены диагонали АС
и BD. Докажите, что АСОВ ™ AAOD.
Дано: ABCD — трапеция. . *
Доказать: АСОВ со AAOD.
Доказательство.
Углы ВСА и CAD —
внутренние йакрест лежа- / ^/'СГ
щие, образованные при
пересечении параллель- А **
ных прямых ВС и AD прямой АС, поэтому они
равны: Z ВСА = Z CAD. Аналогично, Z BDA =
= Z DBC. В треугольниках СОВ и AOD Z ВСА =
= Z CAD и Z BDA = Z DBC, следовательно,
АСОВ™ AAOD.
4.
Докажите, что в ромб можно вписать
окружность.
Дано: ABCD — ромб, О — точка пересечения
диагоналей ромба.
В
Доказать: О — центр вписанной окружности.
Решение. Треугольники АВО,
ADO, СВО и CDO —
прямоугольные (так как ABCD —
ромб) и равны по гипотенузе и
катету. Следовательно и
высоты OF и ОЕ, проведенные из
вершин прямых углов, равны.
Значит, основания высот лежат
на окружности с центром О.
Так как высоты, проведенные
из вершин прямых углов,
перпендикулярны сторонам ромба,
то окружность с центром О — точкой
пересечения диагоналей ромба и радиусом, равным
расстоянию от точки О до сторон ромба, касается
сторон ромба. Следовательно, в ромб можно
вписать окружность.
Билет 8
1. Теорема косинусов. Пример ее применения
для решения треугольников.
2. Окружность, вписанная в треугольник.
3. Задача по теме «Параллельные прямые»
(типа № 1, 2).
4. Задача по теме «Теорема Пифагора» (типа
№ 30—32).
Квадрат любой стороны треугольника
равен сумме квадратов катетов двух других
сторон без удвоенного произведения этих
сторон на косинус угла между ними.
Примеры.
1. Дан треугольник со сторонами а, Ъ и с.
Против стороны с лежит угол у. Найдите сторону
с в каждом из следующих случаев (рис. 23—25).
у — острый
Рис. 23
у — прямой
Рис. 24

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
649
1) См. рисунок 23;
2 2 2
с = b + а - 2ab cos у,
2 2
а + b - 2abcosY;
2) См. рисунок 24;
2 ,2,2
с = b + а ,
/ 2 , , 2
3) См. рисунок 25;
2 2 2
с = & + а - 2ab cos y>
2 2 2
с = & + а + 2ab cos (я - у),
= л/я
2 + &2 - 2abcos(7C - у)
2. Боковые стороны равнобедренного
треугольника имеют длину 8 см и образуют угол в 135°.
Найдите длину третьей стороны (рис. 26).
Дано: АВ = ВС = 8 см, Z ABC = 135°.
Найти: АС.
Решение. Обозначим Z ABC через а. Так как
А ABC — тупой, то по теореме косинусов
АС2=АВ2 + ВС2 + 2АВ • ВС • cosa =
- АВ2 + ВС2 + 2ЛВ • ВС cos (тс - a) =
= 64 + 64 + 128 cos 45° = 128 + 128 • ^ =
= 64 (2 + J2);
AC = 8^2 + Jl (см).
2.
Окружность называется вписанной в
треугольник, если она касается всех его сторон.
[П] Теорема о центре окружности,
вписанной в треугольник.
Центр окружности, вписанной в
треугольник, является точкой пересечения его
биссектрис.
Дано: ААВС — данный треугольник; О —
центр вписанной окружности; D, EnF — точки
касания окружности со сторонами треугольника
(рис. 27).
Доказать: О — точка пересечения
биссектрис.
Доказательство. Прямоугольные
треугольники AOD и АОЕ равны по гипотенузе и катету.
У них гипотенуза О А — общая, а катеты OD
иОЕ равны как радиусы. Из равенства
треугольников следует равенство углов OAD и ОАЕ.
А это значит, что точка О лежит на биссектрисе
треугольника, проведенной из вершины А.
Точно так же доказывается, что точка О лежит
на двух биссектрисах треугольника.
[А] Теорема об окружности, вписанной в
треугольник.
В любой треугольник можно вписать
окружность.
Дано: А ABC — данный треугольник, О —
точка пересечения биссектрис, М, L и К —
точки касания окружности со сторонами
треугольника (рис. 28).
Доказать: О — центр окружности,
вписанной в ААВС.
Доказательство. Проведем из.точки О
перпендикуляры OK, OL и ОМ соответственно
к сторонам АВ, ВС и СА (см. рис. 28). Так как
точка О равноудалена от сторон треугольника
ABC, то OK = OL = ОМ. Поэтому окружность с
центром О радиуса ОК проходит через точки К,
L и М. Стороны треугольника ABC касаются
этой окружности в точках К, L, М, так как они
перпендикулярны к радиусам OK, OL и ОМ.
Значит, окружность с центром О радиуса ОК
является вписанной в треугольник ABC. Теорема
доказана.
Замечание. Отметим, что в треугольник
можно вписать только одну окружность. В самом
деле, допустим, что в треугольник можно
вписать две окружности, тогда центр каждой ок-
у — тупой
Рис. 25
Рис. 26
Рис. 27

650
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
ружности равноудален от сторон треугольника
и, значит, совпадает с точкой О пересечения
биссектрис треугольника, а радиус равен
расстоянию от точки О до сторон треугольника.
Следовательно, эти окружности совпадают.
3.
Дано: Z1 = Z 2, Z 3 *Z 4. Определите, какие
из трех прямых с, d, е параллельны.
Решение. Прямые е и
d параллельны, так как
углы /1и/2 являются
внутренними накрест
лежащими и равны друг
другу.
Прямые с и d не
параллельны, так как углы
Z 3 и Z 4 являются соответственными, но не
равны друг другу.
4.
Докажите, что если диагонали
четырехугольника ABCD взаимно перпендикулярны, то
AB2 + CD2 = BC2+AD2.
Дано: ABCD — четырехугольник, АС 1 BD.
Доказать: АВ2 + CD2 = ВС2 + AD2.
Доказательство. Так как
AC _L BD, то треугольники
АОВ, AOD, ВОС и DOC —
прямоугольные. По теореме
Пифагора: АВ2 = АО2 + ВО2,
ВС2 = СО2 + ВО2, CD2 = СО2 +
+ DO2, AD2 = АО2 + DO2.
Отсюда АВ2 + CD2 = АО2 + ВО2 + СО2 -h DO2 и ВС2 +
+ AD2 - ВО2 + СО2 4- АО2 + DO2, т. е. АВ2 + CD2 =
2 2
= ВС + AD , что и требовалось доказать.
1.
Стороны треугольника пропорциональны
синусам противолежащих углов (рис. 29):
sin а
Ь
sinp
с
siny*
Пример. Основание треугольника равно 10 см,
один из углов при основании равен 45°, а
противолежащий основанию угол равен 60°. Найдите
сторону, противолежащую углу в 45°.
Решение. Обозначим искомую сторону
буквой х. По теореме синусов
10
sin45° sin 60
Л
2
,* =
10 ■ sin45°
sin60° '
х=*
10'^ 10-72
7з
2
7з
- 10 ./jj (см).
Окружность называется описанной около
треугольника, если она проходит через все его
вершины.
[П] Теорема о центре окружности,
описанной около треугольника.
, Центр окружности, описанной около
треугольника, является точкой пересечения
перпендикуляров к серединам сторон.
Дано: ААВС — данный треугольник; О —
центр описанной около него окружности (рис. 30).
Доказать: О — точка пересечения
серединных перпендикуляров.
Доказательство. Треугольник АОС
равнобедренный: у него стороны О А и ОС равны как
радиусы. Медиана OD этого треугольника
одновременно является его высотой. Поэтому центр
окружности лежит на прямой, перпендикуляр-
Билет 9
1. Теорема синусов. Пример ее применения для
решения треугольников.
2. Окружность, описанная около треугольника.
3. Задача по теме «Сумма углов
треугольника» (типа № 15—21).
4. Задача по теме «Трапеция» (типа № 28, 29).
Рис. 30

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
651
ной стороне АС и проходящей через ее середину.
Точно так Же доказывается, что центр
окружности лежит на перпендикулярах к двум другим
сторонам треугольника.
Замечание. Прямую, проходящую через
середину отрезка перпендикулярно к нему, часто
называют серединным перпендикуляром. В связи
с этим иногда говорят, что центр окружности,
описанной около треугольника, лежит на
пересечении серединных перпендикуляров к
сторонам треугольника.
[А] Теорема об окружности, описанной
около треугольника.
Около любого треугольника можно
описать окружность.
Дано: ААВС — данный треугольник; О —
точка пересечения серединных
перпендикуляров (рис. 31).
Доказать: О — центр окружности,
вписанной в ААВС.
Доказательство. Обозначим буквой О точку
пересечения серединных перпендикуляров к его
сторонам и проведем отрезки ОА, ОВ и ОС. Так
как точка О равноудалена от вершин
треугольника ABC, то ОА = ОВ = ОС. Поэтому
окружность с центром О радиуса ОА проходит через
все три вершины треугольника и, значит,
является описанной около треугольника ABC.
Замечание. Отметим, что около треугольника
можно описать только одну окружность. В
самом деле, допустим, что около треугольника
можно описать две окружности. Тогда центр
каждой окружности равноудален от вершин
треугольника и, значит, совпадает с точкой О
пересечения серединных перпендикуляров к
сторонам треугольника, а радиус равен расстоянию от
точки О до вершин треугольника.
Следовательно, эти окружности совпадают.
3.
Найдите углы равнобедренного треугольника,
если внешний угол при основании равен 112°.
Дано: ARST — равнобедренный (RS = TS),
ZSTR = 112°.
Найти: Z STR, Z RST,
ZSRT.
Решение: Углы Z STR и
Z STP — смежные; по
теореме о смежных углах Z STR +
+ Z STP = 180°. Отсюда
ZSTR = 180° - Z STP =
= 180° -112° = 68°.
По свойству углов равнобедренного
треугольника Z SRT = Z STR = 68°, по теореме о сумме
углов треугольника Z RST = 180° - 2 • 68° = 44°.
4.
Докажите, что отрезок, соединяющий
середины диагоналей трапеции, параллелен
основаниям трапеции и равен полуразности
оснований.
Дано: ABCD — трапеция, Ох — середина АС,
02 — середина BD.
Доказать: Ог02 II AD и Ог02 II ВС,
ОП -АР-вс
Доказательство.
Проведем в трапеции ABCD
среднюю линию ML. По
свойству средней линии
трапеции ML \\ AD и ML \\
II Т>П TliJT AD + вс
II ВС, LM = g .
Так как в ABCD через середину стороны CD
проведена прямая, параллельная основанию ВС,
то она является средней линией ABCD,
проходит через середину стороны BD (точку 02) и
02L = о -ВС. Значит, средняя линия трапеции
проходит через точку 02. Аналогично
доказывается, что ОхМ = к ВС и что средняя линия
трапеции проходит через точку Ov Отсюда ОгОг II AD и
ОА
ВС и
Ог02 = LM- ОгМ - OzL = AD * ВС -\ ВС-
Рис. 31
-\*°-а-ч
ВС
, что и требовалось доказать.

652
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Билет 10
1. Построение с помощью циркуля и линейки
треугольника по трем сторонам.
2. Сложение векторов. Свойства сложения
векторов.
3. Задача по теме «Многоугольники» (типа
№ 89—93).
4. Задача по теме «Свойство прямоугольного
треугольника, у которого один угол равен
30°» (типа № 13).
Для любых векторов а (аг; а2), Ъ (Ьг; Ь2),
с (сг; с2) выполняются равенства:
а + Ь = Ъ + а, а + (Ъ + с) = (а 4- Ь) + с.
Для доказательства достаточно сравнить
соответствующие координаты векторов, стоящих
в правой и левой частях равенства. Они равны,
а векторы с соответственно равными
координатами равны.
Каковы бы ни были точки А, В, С, имеет
место векторное равенство
АВ +ВС = А€.
Дано: А (хг; уг), В (х2; у2), и С (х3; уг) —
данные точки (рис. 33).
Доказать: АВ + ВС = АС.
Доказательство. Вектор АВ имеет коорди-
1.
Построение (рис. 32). Пусть а — большая из
трех сторон. Возьмем произвольный луч с
началом С и проведем окружность радиуса а с
центром в точке С. Точку пересечения луча и
окружности обозначим В (постр. 1). Проведем еще од- Наты х2 - хг; у2 - уг, вектор ВС имеет координа-
ну окружность радиуса Ъ с центром в точке С —>
(постр. 2) и окружность радиуса С с центром в ты хв — х2> Уз ~~ У2- Следовательно, вектор АВ +
точке В (постр. 3).
Если а А Ь + с, то эти две окружности
пересекаются в двух точках. Пусть А — одна из этих
точек. Тогда по построению треугольник ABC
имеет стороны заданной длины а, Ь, с.
Если а > Ъ + с, то эти две окружности не
пересекаются, и задача решения не имеет.
2.
[П] Суммой векторов а и & с координатами
+ ВС имеет координаты х3 - хг; у3 - уг. А это
и есть координаты вектора АС. Значит, векторы
АВ + ВС и АС равны.
Доказанная теорема дает следующий способ
построения суммы произвольных векторов аиЬ.
Надо от конца вектора а отложить вектор &',
равный вектору Ь.
Тогда вектор, начало которого совпадает с на-
av а2 и bv Ь2 называется вектор с с координата- чалом вектора а, а конец — с концом вектора Ь',
ми аг + Ьг и а2 + &2, т. е. бУДет сУммой векторов а и & (рис. 34). Такой спо-
а(аг; а2) + Ь (Ьг; Ъ2) = с (аг 4- Ьг; а2 + Ь2).
соб получения суммы двух векторов называется
«правилом треугольника» сложения векторов.
Дано:
с
ъ
1 а •
Построить
треугольник
•—
с
Тв
•—
С
Построение.
s- х
•в с ^в
(2) (3)
С
А
а 'В
(4)
В(х2\ у2)
Рис. 32

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
653
Для векторов с общим началом их сумма
изображается диагональю параллелограмма,
построенного на этих векторах (правило паралле-
и АгВг четырехугольника АВВгАг равны и
параллельны, поэтому этот четырехугольник —
лограмма) (рис. 35). Действительно, АВ + ВС = параллелограмм. Следовательно, ААг = ВВг
= АС, а ВС = AD. Значит, АВ + AD = АС .
Разностью векторов а (аг; а2) и Ъ (Ьг; Ь2)
называется такой вектор с (сг; с2), который в
сумме с вектором Ъ дает вектор а:Ь + с = а. Отсюда
находим координаты вектора с = а - Ь; сг =
= аг - Ьг; с2 = а2- Ъ2.
[А] Пусть а и Ъ — два вектора. Отметим
произвольную точку А и отложим от этой точки
вектор АВ , равный а (рис. 36). Затем от точки В
отложим вектор ВС, равный Ъ. Вектор АС
называется суммой векторов аиЬ.
Такой способ получения суммы двух
векторов называется правилом треугольника.
Докажем, что если при сложении векторов а
и Ь точку А, от которой откладывается вектор
АВ= а, заменить другой точкой Лх> то вектор
Аналогично из равенства ВС = ВгСг следует,
что четырехугольник ВСС1В1 —
параллелограмм. Поэтому ВВг = ССг. На основании
полученных равенств заключаем, что ААг = ССг.
Поэтому АА1СС1 — параллелограмм, и, значит,
АС заменится равным ему вектором А1С1
Иными словами, докажем, что если АВ = АгВг
и ВС = ВгСг, то АС = АгСг (рис. 37).
Допустим, что точки А, В, Av точки В, С, Вх
и точки А, С, Ах не лежат на одной прямой. Из
равенства АВ = АгВг следует, что стороны АВ
АС = АгСг, что и требовалось доказать.
Сумма векторов аиЬ обозначается так: а + Ь.
Складывая по правилу треугольника
произвольный вектор а с нулевым вектором,
приходим к выводу, что для любого вектора а спра-
-> * ■>
ведливо равенство а + 0 = а.
Правило треугольника можно
сформулировать следующим образом: если А, В и С —
произвольные точки, то А В + ВС = АС. Это
равенство справедливо для произвольных точек
А, В и С, в частности в том случае, когда две из
них или даже все три совпадают.
Для любых векторов а, Ъ и с справедливы
равенства:
1°. а + Ъ = Ь + а (переместительный
закон).
2°. а + (Ь + с) = (а + Ъ) + с
(сочетательный закон).
а + Ь
Рис» 34
Рис. 36
АС =Л1С1 = 5 + Ь
Рис. 37

654
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Доказательство.
1°. Пусть векторы аиЬне коллинеарны. От
произвольной точки А отложим векторы АВ = а
и AD = Ь и на этих векторах построим
параллелограмм ABCD (рис. 38). По правилу
треугольника АС = АВ + ВС= а + Ь. Аналогично АС =
= AD + DC = Ь + а. Отсюда следует, что
а + 6 = Ъ + а.
2°. От произвольной точки А отложим вектор
АВ = а, от точки В — вектор ВС = Ь, а от точки
С — вектор CD = с (рис. 39). Применяя правило
треугольника, получим:
(а + Ь) + с = (АВ + BC)+CD=AC+CD=ADt
а + (Ъ + с) = АВ+(ВС + CD)-AB +BD =AD.
Отсюда следует, что
(а + Ь) + с = а + (Ь + с).
Теорема доказана.
При доказательстве свойства 1° мы
обосновали правило параллелограмма сложения некол-
линеарных векторов: чтобы сложить неколлине-
арные векторы а и Ь, нужно отложить от
произвольной точки А векторы АВ = а и AD —Ьи
построить параллелограмм^АВСО (см. рис. 38).
Тогда вектор АС равен а + Ь.
Разностью векторов а и Ь называется такой
вектор с, сумма которого с вектором Ь равна
вектору а. ^ ^
Разность векторов 2 и & обозначается а - Ь.
3.
Сколько сторон имеет выпуклый
многоугольник, если все его внешние углы тупые?
Решение. Обозначим внешний угол
многоугольника через а. По условию все внешние уг-
Д ьш_р
Рис. 39
лы тупые, т. е. а > 90°. Так как сумма внешних
углов выпуклого многоугольника равна 360°, то
a • п = 3б0°. Отсюда следует, что п не более
трех. А так как п — целое, то п = 3.#
4.
В прямоугольном треугольнике ABC (ZC —
прямой) проведена высота CD. Докажите, что,
если Z СВА = 30°, то АВ : BD = 4 : 1.
Дано: ААВС —
прямоугольный, Z С — прямой, CD —
высота, Z CAB = 30°.
Доказать: АВ : BD = 4:1.
Доказательство. По свойству
прямоугольного треугольника,
у которого один угол равен 30°,
АВ = 2СВ. В прямоугольном
треугольнике BCD угол ABC равен
60°, поэтому угол DCB равен 30°, значит, СВ =
= 2BD. Отсюда АВ = 2СВ = 4BD, T.e.AB:BD =
= 4:1, что и требовалось доказать.
Билет 11
1. Построение с помощью циркуля и линейки
угла, равного данному.
2. Умножение вектора на число. Свойство
произведения вектора на число.
3. Задача по теме: «Многоугольники» (типа
№ 94—98).
4. Задачи по теме «Свойства прямоугольного
треугольника, у которого один угол равен
30°» (типа № 14).
1.
Построение (рис. 40). Построим окружность
произвольного радиуса с центром в вершине
данного угла А. Пусть Б и С — точки пересечения
этой окружности со сторонами угла (постр. 1).
Радиусом АС проведем окружность с центром
в точке Аг — начальной точке луча I и точку
пересечения луча и окружности обозначим Сх
(постр. 2). Радиусом ВС проведем окружность с
центром в точке Сх и точку пересечения двух
окружностей обозначим Вг (постр. 3).
Проведя луч AXBV получим ZB1A1CV
равный данному. Равенство углов следует из
равенства треугольников ABC иА1В1С1 (постр. 4).

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
655
[П] Произведением вектора (аг; а2) на число X
называется вектором (Хаг\ Ха2), т. е.
(а^\ а2) Х = (Ха^\ Ха2).
По определению (аа; а2) X = Х(аг; а2) .
Из определения операции умножения
вектора на число следует, что для любого вектора а
и чисел X, ц
(Л + ц) а =Ха + ца.
Для любых векторов а и Ъ и числа X
Х(а + Ъ) = Ха + ЛЬ.
Абсолютная величина вектора равна
\Х\ | а |. Направление вектора Ха при а * О
совпадает с направлением вектора а, есци
X > О, и противоположно направлению
вектора а, если X < О.
Доказательство. Построим векторы ОА и
ОВ, равные а иКа соответственно (О — начало
координат). Пусть аг и а2 — координаты
вектора а. Тогда координатами точки А будут числа
аг и а2, а координатами точки В будут Хаг и Ха2
(рис. 41). Уравнение прямой ОА имеет вид
ах + ру = 0.
Так как уравнению удовлетворяют
координаты точки А (аг; а2), то ему удовлетворяют и
координаты точки В (Хаг; Ха2). Отсюда следует,
что точка В лежит на прямой ОА. Координаты сг
и с2 любой точки С, лежащей на полупрямой
ОА, имеют те же знаки, что и координаты а1иа2
точки А, а координаты любой точки, которая
лежит на полупрямой, дополнительной к ОА,
имеют противоположные знаки.
Поэтому, если X > 0, то точка В лежит на
полупрямой ОА, а следовательно, векторы а и Ха
одинаково направлены. Если X < 0, то точка В
лежит на дополнительной полупрямой, векторы
аиХа противоположно направлены.
Абсолютная величина вектора Ха равна:
М = JiXarf + (Ха2)2 = \Х\ Jaf + а\ = \Х\ \а\.
Теорема доказана.
[А] Произведением ненулевого вектора а на
число k называется такой вектор Ь, длина
которого равна \k\ • |5|, причем векторы а и Ъ сона-
правлены при ^>0и противоположно
направлены при k < 0. Произведением нулевого
вектора на любое число считается нулевой вектор.
Произведение вектора а на число k
обозначается так: ka.
Из определения произведения вектора на
число следует, что:
1) произведение любого вектора на число
нуль есть нулевой вектор;
2) для любого числа ft и любого вектора а,
векторы а и ka коллинеарны.
Для любых чисел k и I и любых векторов
а и Ъ справедливы равенства:
1°.(Ы) t =k(la) (сочетательный закон).
2°. (ft + I) а = ka + la (первый
распределительный закон).
3°. fe(a + Ъ) = ka + ft а (второй
распределительный закон).
Рисунок 42 иллюстрирует сочетательный
закон (равенство 1°) при k = 2,1 = 3.
Дано:
Построить
угол, равный
(1)
Построение.
С Ах % А\Ч\ Ах
(2)
(3)
Ха<
F
(Х>0) в
у\
а2
Хдх
В
1
/
/
О
Ал2 |
А
<*1 X
Л<0)
Рис. 40
Рис. 41

656
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Рисунок 43 иллюстрирует первый
распределительный закон (равенство 2°) — при k = 3,1 = 2.
Рисунок 44 иллюстрирует второй
распределительный закон (равенство 3°). На этом
рисунке треугольники ОАВ и ОАгВг подобны с
коэффициентом поДобия Л, поэтому ОА= ka; АВ =
= kb; OB = k (а + b). С другой стороны, ОВ =
= О А + АВ = ka + kb. Таким образом,
k(a + b) = ka + kb.
3.
Сторона квадрата равна 7 см. Определите
диаметр окружности, описанной около этого
квадрата.
Решение. Квадрат
называется вписанным в окружность,
если все его вершины лежат на
окружности. Из определения
следует, что точка пересечения
диагоналей квадрата совпадает
с центром описанной около
него окружности. Отсюда диаметр окружности
совпадает с диагональю квадрата. Диагональ
квадрата 7 «/2 см. Следовательно, и диаметр
окружности равен 7 л/2 см.
4.
Докажите, что в равностороннем
треугольнике расстояние от точки пересечения двух
биссектрис до стороны в два раза меньше
расстояния от этой же точки до вершины.
Дано: ААВС —
равносторонний треугольник, DC и BF —
биссектрисы, О — точка
пересечения биссектрис DC и BF.
Доказать: ВО = 2DO.
Доказательство.
Биссектриса угла равностороннего
треугольника является
одновременно его медианой и
высотой. Отсюда следует, что в треугольнике BDO
ZBDO = 90°, a ZDBO =30°. Следовательно,
треугольник BDO — прямоугольный, и один из
его углов равен 30°. Отсюда ВО = 2DO (по
свойству прямоугольного треугольника, у которого
один угол равен 30°).
Билет 12
1. Построение с помощью циркуля и линейки
биссектрисы угла.
2. Неравенство треугольника.
3. Задача по теме «Параллелограмм» (типа
№ 30—37).
4. Задача по теме «Углы, вписанные в
окружность» (типа № 39).
1.
Построить биссектрису Z А.
Построение (рис. 45). Проведем окружность
произвольного радиуса с центром в вершине
данного угла А. Пусть Б и С — точки пересечения
этой окружности со сторонами угла (постр. 1). Из
точек Б и С тем же радиусом проведем
окружность. Точку пересечения этих окружностей
О а
« i *
В
ОВ - 20А = 2(35)
ОВ = 63 = (2 -35)
Рис. 42
ОА= ka; АВ = la;
ОВ - (k + l)a = ka + la
Рис. 43
о^г + ь
ОВ - k(a + Ь) - ka + kb
Рис. 44

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
657
обозначим D (постр. 2). Проведем луч AD; этот
луч является биссектрисой Z А, что следует из
равенства треугольников CAD и BAD (постр. 3).
2.
Если точки А и Б различны, то расстоянием
между ними называется длина отрезка АВ. Если
точки А и В совпадают, то расстояние между
ними принимается равным нулю.
[П] Каковы бы ни были трц точки,
расстояние между любыми двумя из этих
точек больше суммы расстояний от них до
третьей точки.
Дано: А, Б и С — данные точки.
Доказать: АВ < АС + ВС; АС < АВ + ВС;
ВС<АВ+АС.
Доказательство. Если две точки из трех или
все три точки совпадают, то утверждение
теоремы очевидно. Если все точки различны и лежат
на одной прямой, то одна из них лежит между
двумя другими, например Б. В этом случае АВ +
+ ВС — АС. Отсюда видно, что каждое из трех
расстояний не больше суммы расстояний до
двух других.
Допустим, что все точки различны и не
лежат на одной прямой (рис. 46). Докажем, что
АВ < АС + ВС. Опустим перпендикуляр CD на
прямую АВ. По доказанному АВ < AD + BD. Так
как AD < АС и BD < ВС, то АВ < АС + ВС.
Теорема доказана.
Заметим, что в случае, когда точки не лежат
на одной прямой, в неравенстве треугольника
строгое неравенство. Отсюда следует, что в
любом треугольнике каждая сторона меньше
суммы двух других сторон.
[А] Каждая сторона треугольника меньше
суммы двух других сторон.
Дано: А ABC — данный треугольник.
Доказать: АВ < АС + ВС, АС < АВ + ВС,
ВС<АВ+АС.
Доказательство. Отложим на продолжении
стороны АС отрезок CD, равный стороне ВС
(рис. 47). В равнобедренном треугольнике BCD
Z 1 = Z2, а в треугольнике ABD Z ABD < Z 1,
значит, Z ABD > Z 2. Так как в треугольнике
против большего угла лежит большая сторона,
то АВ < AD. Но AD =АС +CD=AC + СВ,
поэтому АВ < АС + CD. Теорема доказана.
Следствие. Для любых трех точек А, В,
и С, не лежащих на одной прямой, справедливы
неравенства: АВ < АС + СВ, АС < АВ + ВС,
ВС < ВА + АС. Каждое из этих неравенств
называется неравенством треугольника.
з.
Даны две окружности с общим центром в
точке О, АС и BD — диаметры этих окружностей.
Докажите, что четырехугольник ABCD —
параллелограмм .
Дано: О — центр концентрических
окружностей, АС — диаметр большей окружности, BD —
диаметр меньшей окружности.
Доказать: ABCD — параллелограмм.
Доказательство. Так
как О — центр
концентрических окружностей,
то диаметры АС и CD
пересекаются и точкой
пересечения делятся
пополам, значит, в силу
признака параллелограмма
ABCD —
параллелограмм.
4.
Найдите градусную меру угла, обозначенного
буквой р.
Дано:
/
*■&
Построить
биссектрису
А*
Y
А
1в
(1)
А*
Построение.
¥ ^
/уЪ
(2)
с/
IF
(3)
sAD
Рис. 45

658
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Решение. Так как
угол, опирающийся на
диаметр, равен 90°, то
ZDOF = 90°. Для
окружности с центром в
точке О угол DOF
является центральным и
соответствующим
вписанному углу ABC. Так как
угол, вписанный в
окружность, равен половине соответствующего
центрального угла, то Z ABC = « ZAOC = 45°.
Билет 13
1. Построение с помощью циркуля и линейки
перпендикулярной прямой.
2. Признаки подобия треугольников (доказа-
, тельство одного из них).
3. Задача по теме «Прямоугольник» (типа
№ 38—41).
4. Задача по теме «Углы, вписанные в
окружность» (типа № 38, 39).
1.
Дано: С € п.
Построить прямую, перпендикулярную
прямой п и проходящую через данную точку С.
Построение (рис. 48).
Проведем окружность произвольного радиуса
с центром в точке С. Пусть ВиА — точки
пересечения этой окружности с прямой п (постр. 2). Из
точек ВиА радиусом АВ проведем окружность,
точку пересечения этих двух окружностей
обозначим через О (постр. 3), проведем прямую СО
(постр. 4). Перпендикулярность прямых СО и п
следует из равенства треугольников АОС и ВОС.
Дано: С in.
Построить прямую, перпендикулярную
прямой п и проходящую через данную точку С.
Построение (рис. 49).
Проведем окружность произвольного радиуса
с центром в точке С. Пусть ВиА — точки
пересечения этой окружности с прямой п (постр. 2). Из
Дано:
с € л
Построить
прямую,

перпендикулярную
прямой п
(1)
Построение.
*
¥ AJr
¥> \
(2)
Рис. 48
(3)
*
(4)
{В
Построить прямую,
перпендикулярную
прямой п и
проходящую через данную
точку С
Рис. 49

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
659
точек В и А тем же радиусом проведем
окружности и точки пересечения этих двух окружностей
обозначим через Сг и С (постр. 3). Проведем
прямую СгС (постр. 4).
Докажем перпендикулярность прямых СгС и
п. Точку пересечения прямых СгС и п
обозначим через О. Треугольники АСВ и АСгВ равны
по третьему признаку равенства треугольников.
Поэтому Z СОВ = Z СгАО. Тогда треугольники
САО и СгАО равны по первому признаку
равенства треугольников. Отсюда следует, что углы
СОА и СгОА равны. А так как они смежные, то
они прямые. Следовательно, СО —
перпендикуляр, опущенный из точки С на прямую п.
2.
[П] Первый признак подобия
треугольников:
Если два угла одного треугольника равны
двум углам другого треугольника, то такие
треугольники подобны.
Второй признак подобия треугольников:
Если две стороны одного треугольника
пропорциональны двум сторонам другого
треугольника и углы, образованные этими
сторонами, равны, то такие треугольники
подобны.
Третий признак подобия треугольников:
Если стороны одного треугольника
пропорциональны сторонам другого
треугольника, то такие треугольники подобны.
Докажем первый признак подобия
треугольников.
Дано: ABC иА1В1С1 — данные треугольники,
ZA = ZAV ZB = ZBV
Доказать: ААВС ™ Л А1В1С1.
АВ
Доказательство. Пусть k = А р .
Подвергла
нем треугольник ABC преобразованию подобия с
коэффициентом подобия А, например гомотетии
(рис. 50). При этом получим некоторый
треугольник А2В2С2- Действительно, так как
преобразование подобия сохраняет углы, то Z А2 = Z Аг;
Z В2 = Z Bv Значит, у треугольников ABC и
А2В2С2 Z А = Z А2; Z В = Z В2. Далее, А2В2 =
= kAxBx = АВ. Следовательно, треугольники
ABC и А2В2С2 равны по второму признаку
(по стороне и прилежащим к ней углам).
Так.как треугольники А1В1С1 иА2В2С2
гомотетичны и, значит, подобны, а треугольники
А2В2С2 и ABC равны и поэтому тоже подобны, то
и треугольники А1В1С1 и ABC подобны.
[А] Если три стороны одного
треугольника пропорциональны трем сторонам
другого, то такие треугольники подобны.
Дано: АВСиА1В1С1 — данные треугольники,
АВ
АгВг
ВС
вгсг
СА
СгАг
Доказать: ААВС ™ АА1В1С1.
Доказательство. По условию стороны
треугольников ABC и А1В1С1 пропорциональны:
АВ В€ СА
АгВг
ВгСг
СгАг
(1)
Докажем, что ААВС •<*> АА1В1С1. Для этого,
учитывая второй признак^подобия
треугольников, достаточно доказать, что Z А = Z Аг.
Рассмотрим треугольник АВС2, у которого Z 1 = Z Аг,
Z 2 = Z Вг (рис. 51). Треугольники АВС2 иА1В1С1
Рис. 50
Рис. 51

660
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
подобны по первому признаку подобия тре-
АВ
угольников, поэтому А р
вс2
В^[
С2А
С^А[
Сравнивая эти равенства с равенствами (1),
получаем: ВС = ВС2, СА = С^А. Треугольники
ABC и ABC2 равны по трем сторонам. Отсюда
следует, что ZA = Z 1, а так как Z 1 = Z Аг, то
Z А = Z Av Теорема доказана.
3.
Прямоугольник вписан в окружность
радиуса 5 см. Одна из его сторон равна 8 см. Найдите
другие стороны прямоугольника.
Дано: ABCD — прямоугольник, Докр = 5 см,
АВ = 8 см.
Найти: ВС, CD и AD.
Решение. Проведем в
прямоугольнике ABCD
диагональ DB. Она является
одновременно диаметром
описанной окружности,
поскольку опирающийся на
нее угол BCD прямой.
Треугольник ABD —
прямоугольный, поэтому по
теореме Пифагора:
AD2 = DB2 - АВ2 = 100 - 64 = 36, AD = 6 см.
Так как прямоугольник является
параллелограммом по определению, то АВ = CD и ВС =
= AD как противолежащие стороны, так что CD =
= АВ = 8 см, ВС = AD = 6 см.
4.
На диаметре окружности построен
равносторонний треугольник'. Определите градусную
меру дуг, на которые стороны треугольника делят
полуокружность.
Дано: ABC — равносторонний треугольник,
ВС — диаметр окружности.
Найти градусную меру дуг СК, KL и LB.
Решение. Так как ЛАВС —
равносторонний, то Z АСВ =
= ZACB = Z ВАС = 60°.
В треугольнике КОС ОС =
= ОК как радиусы одной
окружности, и, значит, Z АСО =
= Z СКО = 60°, следовательно,
Z СОК = 60°.
Поскольку градусная мера дуги окружности
равна градусной мере соответствующего
центрального угла, то ^>СК = 60°: Аналогично ^LB =
= 60°. Поэтому ^KL = 180° - 60° - 60° = 60°.
Билет 14
1. Деление отрезка пополам с помощью
циркуля и линейки.
2. Теорема о средней линии треугольника.
3. Задача по теме «Ромб. Квадрат» (типа
№ 42—45).
4. Задача по теме «Равнобедренный
треугольник» (типа № 8—10).
Дано: отрезок АВ.
Построить точку О так, что АО = ОВ.
Построение (рис. 52).
Из точек ВиА радиусом АВ проведем
окружности и точки пересечения этих двух окружнос-
Дано:
отрезок АВ
Построить
точку О так,
что АО = ОВ
В
(1)
Построение.
С
X
X
(2)
В
в
X
(3)
В
—I
Рис. 52

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
661
тей обозначим через Сг и С (постр. 2). Проведем
прямую СгС и обозначим точку пересечения
прямых СгС и п через О (постр. 3).
Докажем, что точка О является серединой
отрезка АВ. Треугольники СгАС и СгВС равны по
третьему признаку равенства треугольников.
Поэтому Z АСО = Z ВСО. Тогда треугольники
АСО и ВСО равны по первому признаку
равенства треугольников. Отсюда следует, что стороны
АО и ВО равны. Следовательно, точка О
является серединой отрезка АВ.
2.
[П] Средней линией треугольника*
называется отрезок, соединяющий середины двух его
сторон.
Средняя линия треугольника,
соединяющая середины двух данных сторон,
параллельна третьей стороне и равна ее половине.
Дано: DE — средняя линия треугольника
ABC. г
Доказать: DE II АВ, DE = ^АВ.
Доказательство. Проведем через точку D
прямую, параллельную стороне АВ. По теореме
Фалеса она пересекает отрезок АС в его середине,
т. е. содержит среднюю линию DE. Значит,
средняя линия DE параллельна стороне АВ (рис. 53).
Проведем теперь среднюю линию DF. Она
параллельна стороне АС. Четырехугольник AEDF —
параллелограмм. По свойству параллелограмма
ED = AF, а так как AF = FB по теореме Фалеса,
то ED — о^^' Теорема доказана.
[А]
Дано: MN — средняя линия треугольника
ABC.
Доказать: MN II AC, MN = ^АС.
Доказательство. Треугольники BMN и ВАС
(рис. 54) подобны по второму признаку подобия
В А
Рис. 54
,, D л „ ВМ BN 1 ч
треугольников (Z В — общий, -gj = -^ = «)>
У Л у 0 MN 1 тх /л
поэтому Z 1 = Z 2 и -jg- = 5 . Из равенства Z 1 =
= Z 2 в силу признака параллельности прямых
следует, что MN \\ АС, а из второго равенства,
что MN= \аС.
3.
Диагональ ромба равна его стороне, ее длина
равна 10 см. Найдите вторую диагональ и углы
ромба.
Решение. Так как
треугольники, на которые делит ромб
каждая из его диагоналей,
равнобедренные и BD = ВС, то
треугольник BCD —
равносторонний. Следовательно, Z BCD =
= 60°. Диагонали ромба
перпендикулярны и точкой
пересечения делятся пополам,
поэтому треугольник ВОС —
прямоугольный и по теореме
Пифагора ОС2 = ВС2 - ВО2 = 100 - 25 = 75; ОС = л/75 =
= 5^3 см,АС = 20С = 1073 см.
По определению ромб является
параллелограммом, значит, его противолежащие углы
равны, а сумма углов, прилежащих к одной
стороне, равна 180°. Поэтому Z ADC = Z ABC = 120°
nZBAD = ZBCD = 60°.
4.
На боковых сторонах равнобедренного
треугольника во внешнюю сторону построены
равносторонние треугольники. Докажите, что
отрезки, соединяющие вершины равносторонних
треугольников (отличные от вершин
равнобедренных треугольников) с серединой основания
равнобедренного треугольника, равны.
Дано: ААВС — равнобедренный (АВ = ВС),
AABD и A BCF — равносторонние, АО = ОС.
Доказать: DO = OF.
Доказательство. АВ = g
= ВС, так как ЛАВС — D^
равнобедренный; значит,
ААВС = ABCF по трем
сторонам. Отсюда AD =
= CF, АО = ОС по
условию.

662
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Z ВАС = Z ВСА по свойству углов
равнобедренного треугольника,
Z DAB = Z BCF как углы равносторонних
треугольников, следовательно, Z ВАС + Z DAB =
- Z ВСА + Z BCF = Z DAC = Z FCA. Отсюда
A ADO = ACFO. Из равенства треугольников
следует равенство соответственных сторон:
DO = OF.
Билет 15
1. Свойство параллелограмма (формулировки
и примеры).
2. Теорема о внешнем угле треугольника.
3. Задача по теме «Признаки равенства
треугольников» (типа № 3—5).
4. Задача по теме «Площадь» (типа № 50, 51).
1.
I. Диагонали параллелограмма
пересекаются и точкой пересечения делятся пополам.
II. В параллелограмме противолежащие
стороны равны и противолежащие углы
равны.
Примеры.
1. В параллелограмме ABCD диагональ BD
равна 12 см, О — точка пересечения диагоналей
параллелограмма. Чему равен отрезок DO (рис. 55)?
Решение. По свойству диагоналей
параллелограмма
DO= |в2) = 6 (см).
2. В параллелограмме ABCD постройте
медиану АБС2), проходящую через вершину С.
Построение. Проведем диагональ АС. Она
пересекает диагональ BD в точке О. Так как
диагонали параллелограмма в точке пересечения
делятся пополам, то ВО — OD, значит, СО —
медиана A BCD.
3. В параллелограмме сумма двух углов
равна 132°. Найдите градусную меру каждого из
этих углов.
Решение. Два данных угла не могут быть
прилежащими к одной стороне, так как в этом
случае их сумма была бы равна 180°. Значит,
эти углы противолежащие. По свойству
противолежащих углов параллелограмма они равны и
каждый из них равен 66°.
4. На рисунке 56 приведен фрагмент
страницы тетради в косую линейку. Отрезок АВ равен
3 см, а наклонные линии образуют с
горизонтальными угол, равный 60°. Найдите стороны
KL и NM и углы ячейки KLMN.
Решение. По определению параллелограмма
все ячейки страницы тетради в косую линейку
являются параллелограммами, так как все
горизонтальные линии параллельны и все
наклонные линии параллельны.
По свойству сторон параллелограмма АВ =
= DC (из параллелограмма ABCD), DC = KL (из
параллелограмма DCLK), KL — NM (из
параллелограмма KLMN).
Отсюда АВ = DC = KL = NM = 3 см. Углы
KNM и KLM параллелограмма KLMN равны по
свойству противолежащих углов
параллелограмма и равны 60° по условию. Так как углы
NKL и KNM — прилежащие к одной стороне
параллелограмма, то Z NKL = 180° - Z KNM,
откуда Z NKL = Z NML = 120°.
2.
Внешним углом треугольника при данной
вершине называется угол, смежный с углом
треугольника при этой вершине.
Рис. 56

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
663
Чтобы не путать угол треугольника при
данной вершине с внешним углом треугольника
при этой же вершине, его иногда называют
внутренним углом.
Внешний угол треугольника равен сумме
двух внутренних углов треугольника, не
смежных с ним.
Доказательство. Пусть ABC — данный
треугольник (рис. 57). Внешний угол при вершине
С равен 180° - Z С. По теореме о сумме углов
треугольника
ZA + ZB + ZC = 180°.
Отсюда следует, что ZA+ZB= 180° -ZC,
т. е. внешний угол при вершине равен сумме
углов А и В, что и требовалось доказать.
Отсюда следует, что внешний угол
треугольника больше любого внутреннего угла,
не смежного с ним.
3.
На сторонах угла ВАС отложены равные
отрезки АВ и АС и проведена биссектриса AD.
Докажите равенство треугольников BAD и CAD.
Дано: AD — биссектриса Z ВАС, АВ = АС.
Доказать: A BAD = ACAD.
Доказательство.
В треугольниках BAD
и CADAD — общая
сторона; АВ = АС по
условию; Z BAD = Z DAC,
так как AD —
биссектриса.
Следовательно, A BAD = ACAD по двум
сторонам и углу между ними, что и требовалось
доказать.
Как разделить данный треугольник на два
треугольника, площади которых относятся как
1:2?
Дано: AD = DE = ЕС.
Доказать: SAABD : SADBC = 1 : 2.
Доказательство.
Пусть АС = За, ВК =
= ft — высота
треугольника ABC.
Тогда 2SAABD = aft,
^adbc = 2aft, и
следовательно, SAABD : SADBC =
= 1:2, что и
требовалось доказать.
Билет 16
Рис. 57
Рис. 58
1. Теорема о средней линии трапеции
(формулировка и пример).
2. Теорема о сумме углов выпуклого
многоугольника.
3. Задача по теме «Признаки равенства
треугольников» (типа № 6, 7).
4. Задача по теме «Решение прямоугольных
треугольников» (типа № 15).
1.
Средняя линия трапеции параллельна
основаниям трапеции и равна их полусумме.
Пример.
Основания трапеции равны 13 см и 19 см,
боковые стороны равны 8 см и 10 см. Через
середины боковых сторон проведена прямая. Найдите
периметр четырехугольника, примыкающего к
большему основанию трапеции (рис. 58).
Решение. Так как FhG- середины боковых
сторон трапеции, то FG — ее средняя линия.
Она равна полусумме оснований:
FG = \ (AD + ВС) = 16 (см).
Поэтому периметр четырехугольника AFGD
равен AF + FG + GD + DA = \ АВ 4- FG 4- | CD +
+ DA = 4 + 16 4- 5 + 20 = 45 (см).
2.
Многоугольник называется выпуклым, если
он лежит в одной полуплоскости относительно
любой прямой, содержащей его сторону.
Сумма углов выпуклого п-угольника равна
180° - (п - 2).
Доказательство. Рассмотрим выпуклый
многоугольник АгА2... Ап. Соединим диагоналя-

664
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
ми вершину Аг с другими вершинами
многоугольника. Так как многоугольник выпуклый,
то в результате получим п - 2 треугольника
(рис. 59): A^AgAg, ААХА^АА, ..., AAn.1AnAv
сумма углов которых равна сумме углов л-уголь-
ника. Сумма углов каждого треугольника равна
180°, поэтому сумма углов выпуклого
многоугольника АгА2..Лп равна 180° • (п - 2). Теоре- _
ма доказана.
3.
Даны две
концентрические окружности; АС и
BD — диаметры этих
окружностей. Докажите,
что ААВО = A CDO.
Дано: АС и BD —
диаметры данных
окружностей.
Доказать: ААВО = ACDO.
Доказательство. АО = СО и OB = OD как
радиусы одной окружности; Z DOC = Z BOA —
как вертикальные. Значит, ААВО = ACDO по
первому признаку равенства треугольников.
4.
Один из углов равнобедренного треугольника
равен 120°. Найдите отношение сторон этого
треугольника.
Дано: ACDB — равнобедренный, CD = DB,
Z CDB = 120°.
Найти: CD : DB : ВС.
Решение. Проведем медиану DA. Медиана
равнобедренного треугольника является
биссектрисой и высотой, значит, ACAD —
прямоугольный, a Z CDA = 60° и Z ACD = 30°.
Обозначим DA через х.
По свойству
прямоугольного треугольника, у
которого один угол равен
30°, CD = 2DA = 2х. По
определению синуса
острого угла прямоугольного треугольника АС =
/о
Y - 2х = л/3 . Так как CD = DB, то DB = 2х.
Отсюда
CD : DB : ВС = 2х : 2х : л/3 = 2 : 2 : л/3 .
Билет 17
1. Формулы для радиусов вписанных и
описанных окружностей правильного
га-угольника (формулы и примеры).
2. Свойство диагоналей ромба.
3. Задача по теме «Равнобедренный
треугольник» (типа № 8—10).
4. Задача по теме «Подобие треугольников»
(типа № 33—36).
1.
Обозначим сторону л-угольника АВ = ап,
половину центрального угла, опирающегося на
дугу, стягиваемую стороной л-угольника, через р
1ЯО°
(рис. 60). Тогда р = ^-,
СВ ап
Rn = OB= ^-*
п sinp
2 sin
180°
Рис. 59
Рис. 60

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
665
■-.-ос-ш-
2tg
180°
Пример.
Радиус окружности, описанной около
правильного восьмиугольника равен 2 см. Найдите
радиус вписанной окружности.
Решение.
р.1^.цо:.яя#в.;
д* =
*8
8
8
* " 2sin22,5° ; 2 " 2sin22,5° ; а* ~ 4 sin 22>5°;
гл =
4sin22,5° 2sin22,5°
8 2tg22,5° 2tg22,5°
= 2 cos 22,5° (см).
sin22,5°
cos22,5°
2.
Ромб — это параллелограмм, у которого все
стороны равны (рис. 61).
Диагонали ромба пересекаются под
прямым углом. Диагонали ромба являются
биссектрисами его углов.
Дано: ABCD — ромб, АС и BD —диагонали,
О — точка пересечения диагоналей.
Доказать: AC ± BD, АС и BD — биссектрисы
углов ромба.
Доказательство. Рассмотрим ромб ABCD
(см. рис. 61). По свойству параллелограмма АО =
= ОС. Значит, в треугольнике ABC отрезок ВО
является медианой. Так как ABCD — ромб, то
АВ = ВС и треугольник ABC — равнобедренный.
По свойству параллелограмма медиана,
проведенная к его основанию, является биссектрисой
и высотой. А это значит, что диагональ BD
является биссектрисой угла В и перпендикулярна
диагонали АС. Теорема доказана.
3.
В равнобедренном треугольнике ABC (АВ = ВС)
проведена медиана BD. Найдите ее длину, если
периметр ААВС равен 50 см, а периметр AABD
равен 30 см.
Дано: ААВС — равнобедренный, АВ = ВС,
BD — медиана ААВС, РААВС = &0 см, PAABD =
= 30 см.
Найти: BD.
Решение. АВ = ВС по
условию; AD = DC, поскольку
BD — медиана ААВС. Так
как РААВС =АВ + ВС + СА =
= 2 (АВ + AD) = 50 (см), то
АВ + AD = 25 (см); PAABD =
= (АВ + AD) + BD = 30 (см).
Отсюда
BD = 30 -254 5 (см).
4.
В треугольнике из всех вершин проведены
высоты, каждая из которых разбивает его на два
треугольника. Докажите, что любые два из этих
треугольников, имеющие общую вершину с
данным, подобны.
Дано: AL ± ВС,
ВК ± АС, СМ 1 АВ. м^
Доказать: A ALC ™
™АВКС, АСМВ со AALB,
АСМА^АВКА.
Доказательство. Пря-
моугольные
треугольники ALC и ВКС подобны, так как А С —
общий, ZALC = Z ВКС как прямые, поскольку
АЫВС;ВК±АС.
Аналогично доказывается подобие и двух
других пар треугольников.
Билет 18
1. Формулы для радиусов вписанных и
описанных окружностей правильного
треугольника, правильного четырехугольника,
правильного шестиугольника (формулы и примеры).
2. Свойство диагоналей прямоугольника.
3. Задача по теме «Равнобедренный
треугольник» (типа № 11, 12).
В

666
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
4. Задача по теме «Параллельные прямые»
(типа № 1).
1.
Число
сторон п
3
4
6
Выражение радиусов вписанной гп
и описанной Rn окружностей через
сторону ап многоугольника
я»
а3
*3 = Тз
а4
R6 = a
г
а3
Гз~27з
а4
Г4=Т
а673
Примеры.
1. Найдите радиус окружности, вписанной
в правильный треугольник, если сторона
треугольника равна 5 см.
Решение:
гз =
Н 5 5л/3 , ,
i^=i^="6-(CM)-
2. Радиус окружности, вписанной в квадрат,
равен 1 см. Найдите радиус описанной
окружности.
Решение:
г4=1Г=1, *4 = 2; R*=i=T2 = 'f2
3. Радиус окружности, описанной около
правильного шестиугольника, равен 7 см. Найдите
сторону правильного шестиугольника.
Решение:
^6 = аб> ав = 7 СМв
2.
Прямоугольник — это параллелограмм, у
которого все углы прямые (рис. 62).
Диагонали прямоугольника равны.
Дано: ABCD — прямоугольник, АС и BD —
диагонали.
' Доказать: АС = BD.
Доказательство. Прямоугольные
треугольники ACD и DBA равны (рис. 62), так как углы
BAD и CD А — прямые, катет AD — общий, а
катеты CD и ВА равны как противолежащие
стороны параллелограмма. Из равенства
треугольников следует, что их гипотенузы равны, т. е. АС =
= BD, что и требовалось доказать.
з.
На сторонах угла Q отложены равные
отрезки QR и QP. Через точки R и Р проведена
прямая. Определите Z QRP, если Z RPQ = 67°.
Дано: QR = QP, Z RPQ = 67°.
Найти: Z QRP.
Решение. Так как QR =
= QP, то треугольник QRP —
равнобедренный с
основанием RP. По свойству углов
при основании
равнобедренного треугольника Z RPQ =
= Z PRQ = 67°.
4.
Докажите, что биссектриса внешнего угла
при вершине равнобедренного треугольника
параллельна его основанию.
Дано: АВ = AC, BF — биссектриса Z DBC.
Доказать: BF II АС.
Доказательство. Пусть
ZABC = а. По свойству углов
при основании
равнобедренного треугольника
Z ВАС = Z ВСА = \ (180°- а).
По теореме о внешнем
угле треугольника
Z CBD = Z ВАС + Z ВСА =
= 180° - а.
Так как BF — биссектриса Z DBC, то
Z DBF = Z FBC = \ (180° - а).
Углы ВСА и FBC — внутренние накрест
лежащие при прямых АС и FB и секущей ВС. Из
Рис. 62

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
667
доказанного выше следует
A FBC = Z ВСА = \ (180° - а).
Отсюда в силу признака параллельности
прямых BF || АС.
Билет 19
1. Формула длины окружности (формула и
пример).
2. Первый признак равенства треугольников.
3. Задача по теме «Площадь» (типа № 102—
108).
4. Задача по теме «Многоугольники» (типц
№ 45—47).
1.
Длина окружности вычисляется по формуле
I = 2nR, где I — длина окружности, R — радиус
окружности.
Примеры.
1. Как изменится длина окружности, если ее
радиус увеличить на k см?
Решение. Пусть R — радиус данной
окружности, I — ее длина. Радиус новой окружности
равен R + k (см), а длина новой окружности
равна 2я (R + k) (см). Следовательно, длина данной
окружности увеличится на
2л: (R + k) - 2kR = 2nR + 2nk - 2nR = 2nk (см).
2. Как изменится длина окружности, если ее
радиус увеличить в k раз?
Решение. Пусть R — радиус данной
окружности, I = 2kR — ее длина. Радиус новой окружности
равен kR (см), а длина новой окружности равна
1г = 2nkR = k • 2лД = hi.
Следовательно, длина окружности
увеличится в к раз.
2.
[П] Если две стороны^ и угол между ними
одного треугольника равны соответственно
двум сторонам и углу между ними другого
треугольника, то такие треугольники равны.
Дано: А ВАС = А ВгАгС19 АВ = АгВ19 АС =
= АгСг (рис. 63).
Доказать: А ABC = АА1В1С1.
Доказательство. По аксиоме существования
треугольника, равного данному, существует
треугольник АгВ2С29 равный треугольнику ABC с
вершиной В2 на луче АгВг и вершиной в той же
полуплоскости относительно прямой А1Б1, где и
лежит вершина Сг (рис. 64, а).
Так как АгВг = АгВ2, то по аксиоме
откладывания отрезков вершина В2 совпадает с
вершиной Вг (рис. 64, б).
Так как A BlAlC1 = Z Б2А1С2, то по аксиоме
откладывания углов луч АгС2 совпадает с лучом
АгСг (рис. 64, в).
Так как АгСг = АгС2, то по аксиоме
откладывания отрезков вершина С2 совпадает с
вершиной Сг (рис. 64, г).
Итак, треугольник А1В1С1 совпадает с
треугольником АгВ2С2, значит, равен треугольнику
ABC. Теорема доказана.
[А]
Дано: Z ВАС = Z B1A1CV АВ = AXBV
АС = АгСг (рис. 65).
Доказать: А ABC = ААгВгСг.
fi(C2)
ВХ(В2)
Рис. 64

668
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Доказательство. Так как Z ВАС = Z B1A1CV
то треугольник ABC можно наложить на
треугольник В1А1С1 так, что вершина А
совместится с вершиной Аг, а стороны АВ и АС наложатся
соответственно на лучи АгВг и АгСг. Поскольку
АВ =АгВг, АС=АгСг, сторона АВ совместится со
стороной AXBV а сторона АС — со стороной А1С1;
в частности, совместятся точки В и Bv С и Cv
Следовательно, совместятся стороны ВС и Б1С1.
Итак, треугольники ABC и А1В1С1 полностью
совместятся, значит, они равны. Теорема доказана.
3.
ABCD — трапеция. Докажите, что
треугольники ABD nACD имеют равные площади.
Дано: ABCD — трапеция.
Доказать: SAABD = SAACD.
Доказательство.
Площадь
треугольника равна половине
произведения его
основания на проведенную к
В
А К
нему высоту. Треугольники ABC и ACD имеют
общее основание AD. Противоположные
стороны четырехугольника KBCL параллельны, так
что этот четырехугольник — параллелограмм.
Поэтому противоположные стороны KB и CL
равны, т. е. треугольники ABD и ACD имеют
равные высоты, проведенные к основанию AD.
Следовательно, SAABD = SAACD, что и
требовалось доказать.
4.
Около окружности описан многоугольник,
все углы которого равны. Является ли данный
многоугольник правильным?
Дано: О — центр вписанной окружности,
ZB = ZC = ... = ZA.
Доказать: многоугольник ВС .... А —
правильный.
Доказательство. Соединим
точки касания К и L и
вершины многоугольника Б и С с
центром вписанной
окружности О. Прямоугольные
треугольники ОКВ и OLB равны,
так как имеют общую
гипотенузу ОВ и OK = OLy как
радиусы одной окружности.
Поэтому ВК = BL и Z КВО = Z LBO,
т. е. ВО — биссектриса Z В.
Высота OL равнобедренного треугольника
ВОС является его медианой, т. е. LB = LC, и
аналогично из треугольника АОВ получаем КА =
= КВ. Поэтому АВ = 2KB = 2LB = ВС.
Следовательно, смежные стороны
многоугольника равны, а значит, и все его стороны равны.
Поскольку все его углы равны по условию, то он
является правильным по определению
правильного многоугольника, что и требовалось
доказать.
Билет 20
1. Формулы площади треугольника (формулы
и примеры).
2. Признак параллелограмма.
3. Задача по теме «Равнобедренный
треугольник» (типа № 13, 14).
4. Задача по теме «Углы, вписанные в
окружность» (типа № 40, 41).
1.
I. Площадь треугольника равна половине
произведения его основания на проведенную к
нему высоту (рис. 66, a): S = -^ah.
Рис. 65
Рис. 66

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
669
II. Площадь треугольника равна половине
произведения любых двух его сторон на
синус угла между ними (рис. 66, б):
S = 5 аЪ s*n У-
III. Формула Герона (рис. 66, в):
S = Jp(p - а)(р - Ъ)(р - с),
где а, Ь, с — стороны треугольника, р =
а + Ь + с
= г его полу периметр.
Примеры.
1. В треугольнике ABC проведена медиана BD.
Докажите, что S^p = SCBD (рис. 67).
Решение. Так как по формуле площади
SABD=^AD- BF; S{
CBD ~ 2 DC
BF
и по условию AD = DC, то S^d = ^cbd» что и
требовалось доказать.
2. Сторона равностороннего треугольника
равна 6 см. Найдите площадь треугольника.
Решение. Так как каждая сторона
равностороннего треугольника равна 6 см, а угол между
любыми двумя сторонами равен 60°, то по
формуле площади
S = ~ • 6 • 6 • sin60° = 18 • ^у = 9л/3 (см2).
3. Найдите площадь равностороннего
треугольника, сторона которого равна а.
а + Пс = За
2 2 '
Решение: р =
S = Jp{p - а)(р - Ь){р - с) = л/р(р - а) =
г7з
2.
Параллелограмм — это четырехугольник,
у которого противолежащие стороны
параллельны, т. е. лежат на параллельных прямых.
Если диагонали четырехугольника
пересекаются и точкой пересечения делятся
пополам, то этот четырехугольник —
параллелограмм.
Дано: ABCD — четырехугольник, АС и BD —
диагонали, OD = ОВ, ОА = ОС, О — точка
пересечения BD и АС.
Доказать: ABCD — параллелограмм.
Доказательство. Треугольники AOD и COD
равны (рис. 68). У них углы при вершине О
равны как вертикальные, a OD = ОВ и ОА = ОС по
условию теоремы.
Значит, углы ОВС и ODA равны. А они
являются внутренними накрест лежащими для
прямых AD и ВС и секущей BD. По признаку
параллельности прямых прямые АВ и CD
параллельны. Так же доказывается
параллельность прямых АВ и СВ с помощью равенства
треугольников АОВ и COD.
Так как противолежащие стороны
четырехугольника параллельны, то по определению этот
четырехугольник — параллелограмм. Теорема
доказана.
3.
В треугольнике FBG сторона FG равна стороне
BG; Z BFG = Z ВАС. Докажите, что ДАВС —
равнобедренный.
Дано: Z BFG = Z ВАС, FG = BG.
Доказать: А ABC — равнобедренный.
Доказательство. Тре- ру
угольник FBG —
равнобедренный по условию.
Следовательно, углы при
основании FB равны:
Z BFG = Z BFG. Но по
условию Z BFG = Z ВАС, значит, Z FBG = Z ВАС,
т. е. ДАВС имеет два равныхугла и,
следовательно, он равнобедренный, что и требовалось
доказать.
4.
Докажите, что градусная мера угла, вершина
которого лежит вне окружности, равна
полуразности градусных мер дуг, заключенных между
его сторонами.
Дано: О — центр окружности, точка В лежит
вне окружности.

670
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Доказать: ZABC = ^ (^АС - ^DE).
Доказательство. А
Угол АЕС является
внешним углом ААВЕ при
вершине Е и по теореме о
внешнем угле
треугольника Z АЕС = Z ЕВА +
+ ZBAE, тогда Z ЕВА =
= Z АЕС - Z ВАЕ. Вписанные углы АЕС и ВАЕ
равны половинам соответствующих
центральных углов, т. е. Z ЕВА =
Z АОС - \
Z DOE.
В свою очередь, градусная мера дуги АС равна
градусной мере угла АОС, а градусная мера дуги
DE равна градусной мере угла EOD.
Следовательно, градусная мера угла ABC равна
полуразности градусных мер дуг, заключенных между
его сторонами, т
и требовалось доказать.
Билет 21
е. Z ABC = £ (^АС - ^>DE), что
па-
1. Формулы площади прямоугольника и
раллелограмма (формулы и примеры).
2. Второй признак равенства треугольников.
3. Задача по теме «Длина окружности» (типа
№ 99, 101).
4. Задача по теме «Средняя линия
треугольника» (типа № 27).
1.
I. Площадь прямоугольника со сторонами
а иЪ равна произведению их сторон S = аЪ.
II. Площадь параллелограмма равна
произведению его стороны на проведенную к ней
высоту: S = aha.
Примеры.
1. Найдите сторону квадрата, площадь
которого равна площади прямоугольника со
сторонами 8 см и 18 см.
Решение. Пусть х - искомая сторона
квадрата. Площадь прямоугольника равна: S = ab =
«8-18-144 (см2). Так как S - х2, то х = 144,
откуда х = 12 (см).
2. Стороны параллелограмма 4 см и 6 см.
Меньшая его высота равна 3 см. Вычислите
вторую высоту параллелограмма.
Решение. Площадь параллелограмма равна
aha или bhb. Так как произведения aha и bha
равны, то меньшая высота соответствует большей
стороне. Следовательно, меньшая высота
опущена на сторону длиной 6 см. Поэтому
S = aha = 6
h -S -
18
3 = 18 (см');
= 4,5 (см).
2.
[П] Если сторона и прилежащие к ней углы
одного треугольника соответственно равны
стороне и прилежащим к ней углам другого
треугольника, то такие треугольники равны.
Дано: Z ВАС = Z B1A1CV Z ABC = Z AxBtCv
АВ=А1Б1(рис. 69).
Доказать: A ABC = АА1В1С1.
Доказательство. По аксиоме существования
треугольника, равного данному, существует
треугольник АгВ2С2, равный треугольнику ABC с
вершиной В2 на луче АгВг и вершиной С2 в той
же полуплоскости относительно прямой AXBV
где лежит вершина Сг (рис. 70, а).
Так как АХВ2 =AXBV то по аксиоме
откладывания отрезков вершина В2 совпадает с
вершиной Вх (рис. 70, б). Так как Z ВгАгС2 = Z В1А1С1
Вг(В2)
?i(C2)
Вг(В2)

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
671
и Z А1В1С2 = Z АгВгС19 то по аксиоме
откладывания углов луч АгС2 совпадает с лучом А1С1, а
луч ВгС2 совпадает с лучом В1С1. Отсюда
следует, что вершина С2 совпадает с вершиной Сг
(рис. 70, в).
Итак, треугольник А1В1С1 совпадает с
треугольником А1В2С2, а значит, равен
треугольнику ABC. Теорема доказана.
[А]
Дано: Z ВАС = Z B1A1CV Z ABC = Z A1B1CV
АВ=А1В1(рис. 71).
Доказать: A ABC = ААгВгСг.
Доказательство. Наложим треугольник ABC
на треугольник АА1В1С1 так, чтобы вершина А
совместилась с вершиной Av сторона АВ — с
равной ей стороной А1Б1, а вершины С иСг
оказались по одну сторону от прямой АгВг.
Так как ZA = ZAtnZB = Z Bv то сторона
АС наложится на луч AtCv а сторона ВС — на
луч BXCV Поэтому вершина С — общая точка
сторон АС и ВС — окажется лежащей как на
луче AXCV так и на луче ВгСг и, следовательно,
совместится с общей точкой этих лучей —
вершиной Cv Значит, совместятся стороны АС и
АгСг, ВС и ВгСг. Итак, треугольники ABC и
А1В1С1 полностью совместятся, следовательно,
они равны. Теорема доказана.
3.
На сколько увеличится или уменьшится длина
окружности, если ее радиус увеличить на 10 см?
Решение. Пусть R — радиус данной
окружности, I — ее длина. Радиус новой окружности
равен R Л- 10, а длина новой окружности равна
2n(R +10). Следовательно, длина данной
окружности увеличится на
2л(Д+10)-2лД =
2яД + 2л • 10 - 2kR = 20л (см).
Рис. 71
4.
Докажите, что середины сторон равнобокой
трапеции являются вершинами ромба.
Дано: ABCD — равнобокая трапеция, G, Н, F
is.E — середины сторон трапеции.
Доказать: GHFE — ромб.
Доказательство. От- В Н с
резок GH — средняя
линия ААВС (так как
он проходит через
середины сторон АВ и ВС), Лд
значит, GH II АС и GH = Е
= о АС. Аналогично доказывается, что FE —
средняя линия AACD; FE II АС и FE = «АС.
Таким образом, GH = FE. Точно так же
доказывается, что HF = GE = - BD. Так как трапеция
ABCD — равнобокая, то ее диагонали АС и BD
равны, следовательно, GH = FE = HF — GE,
значит, GHFE — ромб.
Билет 22
1. Формула площади трапеции (формула и
пример).
2. Признак равенства прямоугольных
треугольников.
3. Задача по теме «Векторы» (типа № 64—70).
4. Задача по теме «Окружность, вписанная
в треугольник» (типа № 18, 19).
Площадь трапеции равна произведению
полусуммы ее оснований на высоту:
Пример.
2
Площадь трапеции равна 18 см , а ее высота
равна 3 см. Найдите одно из оснований
трапеции, если другое равно 5 см.
Решение:
0 а + Ь . а + Ь S 18 ai ч
S="2- 'ft; ^-=Л=У =6(СМ);
а + Ь = 12(см); а = 12 - 5 = 7 (см).

672
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
Так как в прямоугольном треугольнике угол
между двумя катетами — прямой, а любые два
прямых угла равны, то из первого признака
равенства треугольников следует, что:
если катеты одного прямоугольного
треугольника соответственно равны катетам
другого прямоугольного треугольника, то
такие треугольники равны.
Из второго признака равенства
треугольников следует, что:
если катет и прилежащий к нему острый
угол одного прямоугольного треугольника
соответственно равны катету и
прилежащему к нему острому углу другого
прямоугольного треугольника, то такие треугольники
равны.
Рассмотрим еще два признака равенства
прямоугольных треугольников:
если гипотенуза и острый угол одного
прямоугольного треугольника соответственно
равны гипотенузе и острому другого
прямоугольного треугольника, то такие
треугольники равны.
Доказательство. Из теоремы о сумме углов
треугольника следует, что в этих треугольниках
два других острых угла также равны, поэтому
они равны по второму признаку равенства
треугольников, т. е. по стороне (гипотенузе) и двум
прилежащим к ней углам.
[П] Если гипотенуза и катет одного
прямоугольного треугольника равны гипотенузе
и катету другого прямоугольного
треугольника, то такие треугольники равны.
Дано: Z С и Z Сг — прямые, АВ = AXBV
АС = АгСг.
Доказать: А ABC = АА1В1С1.
Доказательство. Пусть ABC и А1В1С1 —
данные треугольники. Построим треугольник CBD,
равный треугольнику СЕЛ, и треугольник
C1B1DV равный треугольнику C1B1AV как
показано на рисунке 72.
Треугольники ABD и AlB1D1 равны по
третьему признаку. У них АВ = АгВг по условию
задачи; AD = AxDl9 так как АС = АхСг; BD. =
= B1DV так как Б!) = АВ, B1D1 =АгВг. Из
равенства треугольников ABD и A1B1D1 следует
равенство углов: ZA = ZAV Так как по условию АВ =
= АгВ19 АС = АгСг, a Z А = Z Аг по доказанному,
то треугольники ABC и А1В1С1 равны по
первому признаку.
[А]
Дано: Z С и Z Сг — прямые, АВ - AXBV
ВС = ВгСг (рис. 73).
Доказать: А ABC = АА1В1С1.
Доказательство. Так как Z С и Z Cv то
треугольник ABC можно наложить на треугольник
АгВгСг так, что вершина С совместится с
вершиной Cv а стороны С А и СВ наложатся
соответственно на лучи СгАг и СгВг. Поскольку СВ =
= CXBV то вершина В совместится с вершиной Bv
Но тогда вершины А и Ах также совместятся. В
самом деле, если предположить, точка А
совместится с некоторой другой точкой А2 луча CXAV то
получим равнобедренный треугольник АгВгА2, в
котором углы при основании АгА2 не равны (Z А2 —
острый, a Z Аг — тупой как смежный с острым
углом fi^Cj). Но это противоречит теореме о
сумме углов треугольника, значит, вершины А и
Аг совместятся. Следовательно, треугольники
ABC и А1В1С1 полностью совместятся, значит,
они равны. Теорема доказана.
D А
Рис. 72
Рис. 73

Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
673
3.
Даны векторы СВ (3; 7) и DA (4; -1).
Определите координаты их суммы.
Решение. Суммой векторов с координатами
(аг; а2) и (Ьх; Ь2) называется вектор с
координатами (аг + Ьг) и (а2 + Ь2). Поэтому
СВ + DA = (3 + 4; 7 - 1) = (7; 6).
Определите вид треугольника, если центр
вписанной в него окружности совпадает с
центром описанной около него окружности.
Решение. Точка пересечения биссектрис
треугольника является центром окружности,
вписанной в этот треугольник, а точка пересечения
его серединных перпендикуляров — центром
окружности, описанной около этого треугольника.
Из теоремы о медиане равнобедренного
треугольника следует, что только в равностороннем
треугольнике биссектрисы углов треугольника
совпадают с серединными перпендикулярами.
Значит, центр окружности, вписанной в
треугольник, совпадает с центром описанной около
него окружности только для равностороннего
треугольника.
Билет 23
1. Формула площади круга (формула и пример).
2. Теорема Пифагора.
3. Задача по теме «Окружность, описанная
около треугольника» (типа № 26).
4. Задача по теме «Геометрическое место
точек» (типа № 16, 17).
1.
Площадь круга вычисляется по формуле
S = пЕ2,
где Е — радиус круга.
Пример.
Найдите площадь заштрихованной фигуры,
используя данные рисунка (рис. 74).
Решение. Радиус большого круга равен
диаметру меньшего круга: Ег = 2Е2 = 2 (см),
поэтому радиус меньшего круга Е2 = 1 см.
Площадь большего круга Sx = пЕ\ = 4я (см );
площадь меньшего круга S2 = яД| —п (см ).
Площадь заштрихованной фигуры равна
S = S1-S2 = 4n-n = 3n (см2).
[П] В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов ка-
тетов.
Дано: ААВС — прямоугольный, Z С —
прямой (рис. 75).
2 2 2
Доказать: АВ =АС + ВС .
Доказательство. Проведем высоту CD из
вершины прямого угла С (см. рис. 75). По опре-
А AD АС л
делению косинуса угла cos А = j-~ = jb •
Отсюда АВ • AD = АС . Аналогично cos В = ^ =
ВС 2
= jg . Отсюда АВ • BD = ВС . Складывая полу-
Рис. 74
Рис. 75
22 1019

674
Подготовка к экзаменам. 9 класс
Примерные билеты и ответы к устному экзамену по геометрии
ченные равенства почленно и замечая, что АВ +
+ DB =АВ, получим:
АС2 + ВС2 = АВ (AD + DB) =АВ2.
Теорема доказана.
[А]
Дано: ABC — прямоугольный треугольник, а,
b — катеты, с — гипотенуза (рис. 76, а).
2 2 2
Доказать: с = а + Ъ .
Доказательство. Достроим треугольник до
квадрата со стороной а + b так, как показано на
2
рис. 76, б. Его площадь S равна (а + Ь) . С
другой стороны, этот квадрат составлен из четырех
равных прямоугольных треугольников, пло-
1 .
щадь каждого из которых равна « а • Ь, и
квадрата со стороной с, поэтому
S = 4 • \аЪ + с2.
2 2
Таким образом, (а + b) = 2ab + с , откуда
2 2 , , 2
с = а + b .
Теорема доказана.
3.
Докажите, что центр окружности, описанной
около равнобедренного треугольника, лежи^ на
медиане, проведенной к основанию.
Доказательство. Точка пересечения
серединных перпендикуляров треугольника
является центром окружности, описанной около этого
треугольника. Так как данный треугольник —
равнобедренный, то по теореме о медиане
равнобедренного треугольника медиана, биссектриса
и высота треугольника, проведенные к
основанию, совпадают. Значит, высота совпадает с
серединным перпендикуляром, проведенным к
основанию треугольника. Следовательно, центр
окружности, описанной около равнобедренного
треугольника, лежит на медиане, проведенной
к основанию.
Докажите, что если три окружности имеют
общую хорду, то их центры расположены на
одной прямой.
Доказательство. Так
как общая хорда двух
пересекающихся
окружностей перпендикулярна
линии, соединяющей
центры этих
окружностей и делится ею
пополам, то прямая Ог02 перпендикулярна АВ и
проходит через точку С — середину отрезка АВ.
Аналогично прямая Ог03 перпендикулярна АВ и
проходит через точку С — середину отрезка АВ.
Так как через каждую точку прямой можно
провести перпендикулярную ей прямую и
только одну, то прямые Ог02 и Ох03 совпадают, т. е.
точки Ov О2 и Оа лежат на одной прямой, что и
требовалось доказать.

11 класс
Задачи и решения письменного экзамена
по алгебре и началам анализа
ВАРИАНТЫ ЗАДАНИЙ
Вариант 1
1. Решите .неравенство х2(2х + 1)(х - 3) > 0.
2. Упростите выражение
cos(27C - 3x)cos х + sin Зх cosf-g- + x).
Укажите множество значений x, при которых
значение данного выражения равно -1/2.
3. Решите систему уравнений
log3* + bg3y = 1,
_ Ш"2/3
- \21) '
3
х-у
4. Решите уравнение (х2 - 9)( j6-5x - х) = 0.
5. Составьте уравнение касательной,
проведенной к графику функции / (х) = -х2 + 4
параллельно прямой у = -2х + 6. Вычислите площадь
фигуры, ограниченной графиком данной
функции, этой касательной и осью ординат.
6. Исследуйте функцию у = х4 - 2х2 + 3 с
помощью производной. Определите, при каких
значениях а уравнение х4 - 2х2 + 3 = а имеет три
корня.
Вариант 2
х2(х- 2)
7. Решите неравенство -jr—j2 < 0.
,3я
8. Упростите выражение
-sin(7i; + 3x)cos х + cos Зх cos(~: - х).
Укажите множество значений х, при которых
значение данного выражения равно -Js /2.
9. Решите систему уравнений
-3/2
«•- ■ (!) ■
log2x + log2y = 2.
10. Решите уравнение (х2 - 4)( j4-3x -х) = 0.
11. Составьте уравнение касательной,
проведенной к графику функции / (х) = -х2 + 4х
параллельно прямой у = 2х + 3. Вычислите
площадь фигуры, ограниченной графиком данной
функции, этой касательной и осью ординат.
12. Исследуйте функцию у = -х4 + 2х2 -I- 8 с
помощью производной. Определите, при каких
значениях а уравнение -х4 + 2х2 + 8 = а не
имеет корней.
Вариант 3
13. Решите неравенство (0,25)2'5~°'5х2 > ^ .
14. Упростите выражение
sin а - 0,5 sin 2а cos а
. 2
sin а
и найдите его значение при а = -я/6 .
15. Вычислите площадь фигуры,
ограниченной линиями y=Jx,y = 0,5*.
16. Решите систему уравнений
log812
Зх + у = 8 8 ,
х2 + у2 - 2ху = log2144-|log281.
17. Найдите длины сторон прямоугольника с
периметром 20 см, имеющего наименьшую
диагональ.
18. Сколько корней имеет уравнение х3 - Зх2 =
= а при -4 < а < 0?
Вариант 4
19. Решите неравенство
S)
^27.
1^3-0,5*
sin 2а + cos а
20. Упростите выражение 2 2
cos а + sin а + 2 sin а
и найдите его значение при а = -я/3 .
21. Вычислите площадь фигуры,
ограниченной линиями у = 2«/х 9у = 3-х, х = 0.
22*

676
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
22. Решите систему уравнений
2 2 0 oclog53
х + у + 2ху = 25 ,
2х-у = log3135-2bg325.
23. Найдите высоту равнобедренного
треугольника с боковой стороной 12 см, имеющего
наибольшую площадь.
24. Сколько корней имеет уравнение -х3 +
+ Зх2 - 2 = а при а < - 2 ?
Вариант 5
25. Решите уравнение 72*- 1 = х-2.
26. Решите неравенство log0 25(5х -1)^-0,5.
27. Первообразная функции f(x) = Зх2 + 2х
при х = 1 принимает значение 81. Найдите ее
значение при х = -1.
28. Укажите все точки графика функции
2
у = хе х , в которых касательная параллельна
оси абсцисс.
29. Сколько корней имеет уравнение
sin2* + cos22x + cos2( ^ + 2х) + cos х tg х = 1
в промежутке (0; 2л:)? Укажите их.
30. Исследуйте функцию / (х) = х3 - Зх с
помощью производной и выясните, при каких
значениях а уравнение х3 -Зх = а имеет одно
решение.
Вариант 6
31. Решите уравнение J2x+ 1 = х - 1.
1
32. Решите неравенство log27 (8 - Зх) < т:
33. Первообразная функции / (х) = 4х3 + 2х
при х = 1 принимает значение 25. Найдите ее
значение при х = 2.
34. Укажите все точки графика функции
у = х2е~х, в которых касательная параллельна
оси абсцисс.
35. Сколько корней имеет уравнение
2cos2 х - sin (х - 5) + tg х tg(x + ^) = 0
в промежутке (0; 2л)? Укажите их.
36. Исследуйте функцию f (х) = Зх - х с
помощью производной и выясните, при каких
значениях а уравнение Зх-х3 = а имеет три решения.
Вариант 7
37. Решите уравнение
1 4- log7(x + 4) = log7(x2 + 9х + 20).
38. Найдите наибольшее целое число,
удовлетворяющее неравенству 2х + (0,5)3~х < 9.
39. Найдите площадь фигуры, ограниченной
линиями у = 2х29 у = 4х.
40. Какими должны быть стороны
прямоугольного участка площадью 1600 м2, чтобы на
его ограждение было израсходовано
наименьшее количество материала?
41. Дана функция f (х) = a sin 4х + Ъ cos 2х.
Найдите а и Ь, если известно, что f(7n/12) = 4
иГ(Зл/4) =2.
42. В задаче 39 найдите длину наибольшего
отрезка, параллельного оси Оу и заключенного
внутри фигуры.
Вариант 8
43. Решите уравнение
1+ log5 (х2 + 4х - 5) = log5 (х + 5).
44. Найдите наименьшее целое число, удов-
П\2-х
летворяющее неравенству 3 4-1^1 > 10.
45. Найдите площадь фигуры, ограниченной
линиями у = х2,у = -2х.
46. Периметр окна прямоугольной формы
равен 6 м. Какими должны быть размеры окна,
чтобы площадь его была наибольшей?
47. Дана функция f(x) = a sin 2х + Ъ cos х.
Найдите а и Ь, если известно, что f(6n/6) = 2 и
f(9n/2) =-4.
48. В задаче 45 найдите длину наибольшего
отрезка, параллельного оси Оу и заключенного
внутри фигуры.
Вариант 9
49. Решите неравенство 0,6х ~5х > 1.
50. Вычислите log1/2 16 • log5 -^ : 91о*з2.
П/2
5 25

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
677
51. Найдите площадь фигуры, ограниченной
линиями у = 9х2 - 6х + 1, у = О, х = 0.
52. Решите уравнение 16 sin2 х + 2 cos х = 11
и укажите его корни, удовлетворяющие
условию sin х < 0.
53. При каком значении а функция у = a In х +
+ х2 - х имеет экстремум в точке х = 1?
Определите вид экстремума в точке х = 1 при
найденном значении а.
54. Исследуйте функцию у = x*j4x+ 1 с
помощью производной и, используя результаты
исследования, укажите множество значений
этой функции.
Вариант 10
2
55. Решите неравенство 8 > 1.
3/2 2 1о*492
56. Вычислите log1/3 9 • log2 -g- : 7
57. Найдите площадь фигуры, ограниченной
линиями у = 4х2 4- 12х + 9, г/ = 0, х = 0.
58. Решите уравнение 36 cos2x + 4 sin х = 25 и
укажите корни уравнения, удовлетворяющие
условию cos х <: 0.
59. При каком значении а функция у = a In х -
- х2 4- Зх имеет экстремум в точке х = 2?
Определите вид экстремума в точке х = 2 при
найденном значении а.
60. Исследуйте функцию у = xVl-2x с
помощью производной и, используя результаты
исследования, укажите множество значений этой
функции.
Вариант 11
61. Решите уравнение 2х + 4 - Jx + 2 = 15.
62. Найдите все значения х, при которых
функция г/ = log2 (х2 + х) -1 принимает
положительные значения.
63. Решите систему уравнений
2
= 5°
64. Найдите наибольшее и наименьшее
значения функции у = 2 cos 2х - cos 4х на отрезке
[0;я/2].
65. Вычислите площадь фигуры,
ограниченной графиком функции у = -^х2-\-Зи двумя
касательными к этому графику, проходящими
через точку на оси Оу и образующими между
собой угол 90°.
66. Какие целые значения принимает
функция у = -9х • */2х+ 1 в промежутке [-0,5; 0]?
Вариант 12
67. Решите уравнение Jx+1 + х + 1 = 6.
68. Найдите все значения х, при которых
функция у = log3 (х2 - 2х) - 1 принимает
отрицательные значения.
69. Решите систему уравнений
9*у.3*2 + у2 = 3,
л/252х + у =
70. Найдите наибольшее и наименьшее
значения функции у = 2 sin Зх + cos 6х на отрезке
[0;л/6].
71. Вычислите площадь фигуры, ограничен-
1 2
ной графиком функции у = ^х +2,5и двумя
касательными к этому графику, проходящими
через точку на оси Оу и образующими между
собой угол 90°.
72. Какие целые отрицательные значения
принимает функция у = 2х - Jl6x-4b в
промежутке [1/4; +оо)?
Вариант 13
73. Сравните значения выражений
1+ cos 40° + cos 80°
и
Г1уЛху-2у _ к9_х.
IW
sin 80° + sin 40°
cos 105° cos 5° + sin 105° cos 85°
sin 95° cos 5° - cos 95° sin 185°

678
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
74. Найдите промежутки возрастания
функции у = « х3 - 2х2 - 8х + 4.
75. Решите уравнение х + 4 + V* + 4 = 12.
76. Найдите натуральные значения х,
удовлетворяющие системе неравенств
-2х+1
в)"
>32,
[1о*4(х-6Г<1.
77. Вычислите площадь фигуры,
ограниченными, проведенными к этому графику в точках
пересечения его с осью абсцисс.
78. Сколько корней имеет уравнение Зх2 - х3 =
= а при 0 < а < 4?
Вариант 14
79. Сравните значения выражений
sin 50° -sin 25°
1-cos 25° +cos 50° И
sin 25° cos 5° - cos 25° cos 85°
cos 375° cos 5° - sin 15° sin 5° '
80. Найдите промежутки убывания функции
у = -|х3-|х2 + 12х + 1.
81. Решите уравнение 2х - 2 - Jx- 1 =15.
82. Найдите целые решения системы
неравенств
q2x-6
О < 07»
27'
log8(l-*) «.
83. Вычислите площадь фигуры,
ограниченной графиком функции у = -х2 + 4х и
касательными, проведенными к этому графику в точках
пересечения его с осью абсцисс.
84. Сколько корней имеет уравнение *3 - Зх2 +
Вариант 15
85. Вычислите
>*я*
V5(log212-log23+31083)0'51^.
86. Решите уравнение 7з sin х cos х = sin2* и
укажите два корня, которые меньше я.
87. Найдите область определения функции
У =
2 л
х -4
ной графиком функции у = -тх +1и касатель- х + 1
88. Найдите координаты точек касания, в
которых касательные к графику функции у =
2х- 2
имеют угловой коэффициент, равный 4.
89. Найдите площадь фигуры, ограниченной
графиком функции / (х) = 2х - 2 и графиком ее
первообразной -F(jc), зная, что F(0) = 1.
90. Определите промежутки возрастания
функции у=\х- Зх\.
Вариант 16
91. Вычислите | (log6 2 + log6 3 + 2 lo*24)2 lo*s7.
92. Решите уравнение 8 sin2 х + 6 cos х - 3 = 0
и укажите два корня, которые больше я.
93. Найдите область определения функции
*/ =
1(*-2Г
+ 2 = а при а > 2?
х -25
94. Покажите, что касательные, проведенные к
х-4
графику функции у = —5 в точках пересечения
X — Ct
его с осями координат, параллельны между собой.
95. Функция F является первообразной для
функции f (х) = 2х - 4. Найдите площадь
фигуры, ограниченной графиками функций f и F>
зная, что график функции F проходит через
точку А (0; 4).
96. Определите промежутки убывания
функции у= \х-х I.
Вариант 17
97. Найдите точки пересечения графиков
функций у = х + 1иу= л/1 -х.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
679
98. Решите уравнение
2 sin2(| + х) - 5 сов(я - х) + 2 = 0.
Укажите те значения х> при которых sin х> 0.
99. Решите систему неравенств
Г24х+2
,х+1
>1,
l + log3(*-4)<log3(:e + 21).
100. Постройте график функции у = х3 - Зх2 +
+ 2 на отрезке [-0,5; 3]. Укажите множество
значений функции на этом отрезке.
101. Вычислите площадь фигуры,
ограниченной параболой у = 4х - х2 и прямой,
проходящей через точки (4; 0) и (0; 4).
102. На графике функции у = х2 найдите
точку М с положительной абсциссой, ближайшую
кточкеА(0; 3/2).
Вариант 18
103. Найдите точки пересечения графиков
функций у = V2x + 4 и у = х - 2.
104. Решите уравнение
2 sin2 2х - 5 cos 2х + 1 = 0.
Укажите те значения *, при которых cos х < 0.
105. Решите систему неравенств
-^1>9
[log0 5(х+16) < log05(x + 2)-l.
106. Постройте график функции у = - х4 +
+ 2х2 + 5 на отрезке [0; 2]. Укажите множество
значений функции на этом отрезке.
107. Вычислите площадь фигуры,
ограниченной параболой у = З*2 (х < 0), прямой у = 0 и
прямой, проходящей через точки (-3; 0) и (0; 4,5).
108. На графике функции у = Jx найдите
точку М, ближайшую к точке А (9/2; 0).
2 1
110. Решите уравнение sin х - pSin 2х = 0.
Укажите корни, принадлежащие промежутку
(я/2; 2я).
111. Решите систему уравнений
f2x~y = 4*,
6 1 - . ,
- + г- = 1.
х Ъу
112. Решите уравнение log5 (6 - 5х) = 1 - х.
113. Составьте уравнение касательной к
графику функции у = -З*2 4- 6х + 1 в точке пересечения
этого графика с осью ординат. Вычислите
площадь фигуры, ограниченной графиком данной
функции, найденной касательной и прямой х = 2.
114. Найдите множество значений функции
у = 2 cos х - sin 2х на отрезке [-я/2 ; я/2 ].
Вариант 20
115. Найдите область определения функции
У =
_ lg(~* +3* + 4)
Jx^2
116. Решите уравнение 6 sin2 х + 2 sin2 2х = 5
и укажите корни, принадлежащие отрезку
[я; 2я].
117. Решите систему уравнений
27х = 37Л
* У
118. Решите уравнение
log3(4-3x-1-l) = 2x-l.
119. Составьте уравнение касательной к
графику функции у = -2х2 4- 4'х + 1 в точке пересечения
этого графика с осью ординат. Вычислите
площадь фигуры, ограниченной графиком данной
функции, найденной касательной и прямой х = 2.
120. Найдите множество значений функции
у = 2 sin х + cos 2х на отрезке [0; я].
Вариант 19
109. Найдите область определения функции
Вариант 21
121. Решите уравнение

680
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Зх + 2
122. Решите неравенство 41 ~х < I « 1
123. Найдите произведение корней уравнения
(Зх2 - 4х - 7) log3 (2 - х) = 0.
124. Является ли прямая у = 1 - х
касательной к графику функции у = х + е ~2х? Ответ
обоснуйте.
125. Найдите площадь фигуры, ограниченной
х2 + 1
графиком функции у = J t dt и прямой у = 1,5.
126. Решите систему уравнений
2j3y + х- J6y-x = х,
л/Зг/ + л: + */6у-х = Зу.
Вариант 22
127. Решите уравнение cos х + sin [ ~ + 2х ] — 0.
128. Решите неравенство I g I > 9
2х-1
129. Найдите сумму корней уравнения
(х2 - Зх - 4) log5 (Зх - 8) = 0.
130. Является ли прямая у = Зх - 3
касательной к графику функции у = х - х £ ? Ответ
х
обоснуйте.
131. Найдите площадь фигуры, ограниченной
графиком функции у = J 3* Л и прямой у = 1.
132. Решите систему уравнений
' Jx + y- J2y- Ъх = х,
,V* + */ + J2y-5x = i/.
Вариант 23
133. Решите неравенство log1/7 (2х - 1) > -1.
134. Вычислите ординату точки пересечения
графиков функций у = 0,32х"3 и у = [ 3g) .
135. Найдите критические точки функции
у = sin Ъх cos Зх - cos Ъх sin Зх.
136. При каких значениях а число 2 является
корнем уравнения 4х-а =3а-х?
137. Найдите площадь фигуры, ограничен-
2
ной графиком функции у = — и прямыми у = 0,
х = -5, х = -2,5. Не пользуясь
микрокалькулятором, сравните полученное значение площади с
числом 2.
138. Является ли прямая у = 2 - х
касательной к графику функции у = х + 2е~х1 Ответ
обоснуйте.
Вариант 24
139. Решите неравенство 0,5х - 3 • 21 ~х < -80.
140. Вычислите абсциссу точки пересечения
графиков функций
У = 1о£о,з <*2 " х ~ 5> и У = 1о*о,з (|) •
141. Найдите критические точки функции
у = cos 2х cos 7х - sin 2х sin 7х.
142. При каких значениях Ь число (-2)
является корнем уравнения 3 4Ъ-х = 2Ь - х7
143. Найдите площадь фигуры,
ограниченной графиком функции у = ех + * и прямыми
х = -2, х = -1, у = 0. Не пользуясь
микрокалькулятором, сравните полученное значение
площади с числом 0,5.
144. Является ли прямая у = х + 2
касательной к графику функции у = 2х - In х? Ответ
обоснуйте.
Вариант 25
Зх- 1
5 х +1
145. Решите уравнение (0,4) =(2,5)
146. Вычислите ординату точки пересечения
графиков функций у = log2 (х +1,5) и у = - log2 х.
147. Найдите область определения функции
У =
х + 2х +1
х-1
148. Найдите критические точки функции
у = sin 2х + 2cos х - 2х.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
681
149. Для каждого а > О найдите площадь
фигуры, ограниченной графиком функции у = -х3 +
+ ах2 и осью абсцисс. При каких значениях а
эта площадь равна 4/3?
150. Найдите абсциссы всех общих точек гра-
4
фика функции у = х - ди касательной,
проведенной к графику этой функции в точке с
абсциссой х0 = ~2.
2х-3
v2-jc
Вариант 26
151. Решите уравнение (0,7) = 11 ^ I
152. Вычислите ординату точки
пересечения графиков функций
У = log1/3(*-g) и у = 1 - log1/3[* + !).
153. Найдите область определения функции
V* -6*+
9
154. Найдите критические точки функции
у = 2 sin х - sin 2х - 2х.
155. Для каждого а < 0 найдите площадь
фигуры, ограниченной прямыми х = 2а, х = а, i/ = О
и графиком функции у = -3/х. Сравните
полученное значение площади с числом 3.
156. Найдите все общие точки графика
функции у = \х\ (х - 3) + Зл: и касательной,
проведенной к графику этой функции в точке с абсциссой
х0 = 3.
Вариант 27
157. Решите неравенство
log0 5 (4 - х) Z 2 log0 5 3 + log0 5 1.
158. Найдите промежутки убывания
функции у = х (3 - х2).
159. Решите систему уравнений
8-2у = 41'5х + 0'5,
5 " 25 5 '
160. Решите уравнение (sin 2х) • v4 - х = 0.
161. В каком отношении делится площадь
четырехугольника ABCD, где А (-4; 0), В (-2; 4),
С (2; 4), D (4; 0), параболой у = | х2 + 2?
162. На графике функции i/ = |3х - 2|
найдите точку, ближайшую к точке А (3; 0).
Вариант 28
163. Решите неравенство
log2 (3-х)-log2 3^|log2 25.
164. Найдите промежутки возрастания
функции у = х2 (х + 3).
165. Решите систему уравнений
Г з^ _/Т|0*5-*
27 " {9)
166. Решите уравнение
:-1)л/бТ
Ьх-х = 0.
(cos Зх ■
167. В каком отношении делится площадь
четырехугольника OBCD, где О(0; 0), Б(1; 2),
С(4; 2), D(4; 0), параболой у = (2 - х)2 + 1?
168. На графике функции у = 2\х\ - 3
найдите точку, ближайшую к точке Б(2; -3).
Вариант 29
169. Вычислите
(3 log7 2 - log7 24): (log7 3 + log7 9).
170. Решите уравнение J3x + 1 = х - 1.
171. Решите неравенство 4х - 3 • 2х - 4 < 0.
172. При каком значении а прямая i/ = Зх + а
является касательной к графику функции
у = 2х2-Ьх+П
173. Найдите площадь фигуры,
ограниченной линиями у = « л:3, у = 3 - х, у = -4х.
174. Найдите критические точки функции
у = 2 73 sin х - cos 2х и укажите среди них одну
из точек максимума.

682
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Вариант 30 191. Решите уравнение
175. Вычислите (lg 2 + 3 lg 0,25): (lg 14 - lg 7). 32*2-1 _ 3(*-iX* + 5) _ 2 . 38(x-1) = Q
176. Решите уравнение J2x + 9 = x - 3. 192. Найдите площадь фигуры, ограничен-
,-- п о , о ох Лх Л ной линиями х \у\ =3, X=l, Х = 2.
177. Решите неравенство 3 + 2 • 3 - 9 > 0. * ,г"
178. При каком значении а прямая у = - 10х +
+ а является касательной к графику функции Вариант 33
у = Зх2 - 4х - 2? 193. Решите уравнение log2 (х - 3) = 2 - log2 х.
179. Найдите площадь фигуры, ограничен- /i\-*
1 о 194. Решите неравенство [ ^ ] + 23 + х < 9.
ной линиями у = -jx% у = х + 4, у = 5х. w
-Qn „ « , 195. Вычислите абсциссы и ординаты точек
180. Найдите критические точки функции ^ *"
у = 2 л/3 cos х + cos 2х и укажите среди них одну пересечения графиков функций у = 2 sin \х + gj
из точек минимума. /5
J и у = л/3 cos X.
р. «^ 196. Найдите расстояние от начала координат
Р до касательной к графику функции у = х In х, па-
181. Вычислите координаты точки пересече- раллельной оси абсцисс.
ния графиков функций м л^ „ ,
3 197. При каких значениях а график функции
у = *]2х2 - 4х - 5 и у = х - 2. г/ = Зх - 4х3 и прямая у = а имеют одну общую
182. Составьте уравнение касательной к гра- точку/
фику функции у = 2х2 - 5х + 1 в точке с абсцис- 198. Докажите, что площадь фигуры, ограни-
сои *о = 2- ченной графиком функции у = —р и прямыми
3-х
Jx
хцх
183. Решите неравенство log5 ^ >1. р = 0,х = 4,*=р(прир > 4), меньше 1.
184. Сколько корней имеет уравнение cos 2х -
- cos х = 2 - sin2 х на отрезке [-100л; 100л]? Вариант 34
185. Решите уравнение 199- Решите УРавнение
52^-1_з.5(х + 1Кх + 2)-2.5б(х + 1) = 0 log4(x + 4) = 2-log4(x-2).
186. Найдите площадь фигуры, ограничен- 2QQ решите неравенство 3х"2 - (±Г + 8 > 0.
ной линиями х \у\ = 2, х = 1 , х = 3. W
201. Вычислите абсциссы и ординаты точек
Вариант 32 пересечения графиков функций
187. Вычислите координаты точки пересече- = _sin хиу= J2 cos fх + -1.
ния графиков функций v 4/
/—g 202. Найдите расстояние от оси абсцисс до ка-
у = V2* - 10* + 9 и I/ - х - 3. сательной к графику функции у = 4 In (х - 1) - х2,
188. Составьте уравнение касательной к гра- параллельной оси абсцисс.
фику функции у = Зх2 - Ах - 2 в точке с абсцис- 203. При каких значениях Ъ прямая у = Ъ пе-
сой х0 = -1. ресекает график функции у = х3 + Зх2 более чем
5 - х в двух различных точках?
189. Решите неравенство log4 —5 > *•
х " z 204. Докажите, что площадь фигуры, ограни-
190. Сколько корней имеет уравнение cos2 х + ченной графиком функции у = 2е х и прямыми
+ sin х = cos 2х + 2 на отрезке [-50л:; 50л;]? у = 0, х = -0,5, х = * (при t < -0,5), меньше 1.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
683
Вариант 35
205. Решите уравнение
206. Решите систему уравнений
\гх-у-2ху = ъ,
9У = 34"х.
207. Найдите площадь фигуры, ограниченной
линиямиу = 1-х, у = 0 и у = (х + I)2, гдех>-1.
208. Найдите область определения функции
y = logMlog4|5f.
209. Исследуйте функцию f (х) = cos 2х -
- 2 • cos х на возрастание и убывание в
промежутке [я/3; я].
210. При каких значениях а прямая у = ах - 5
касается кривой у = Зх2 - 4х - 2?
Вариант 36
тг;
211. Решите уравнение 4Ч-2х-хл = х-
212. Решите систему уравнений
х-У
»*У
1
3'
2х-2У = 32.
213. Найдите площадь фигуры, ограниченной
линиями у=х-1,1/ = 0и1/ = (х- З)2, где х ^ 3.
214. Найдите область определения функции
у = log5 log0 5 ^|.
219. Решите неравенство log0 5 (х2 -1)>-2.
220. Найдите критические точки функции
f (х) = cos х + -=- х. Укажите одну из точек
минимума.
221. Найдите ту первообразную функции
f (х) = 2х + 4, график которой касается прямой
i/ = 6х + 3. Вычислите площадь фигуры,
ограниченной графиком найденной первообразной и
прямыми у = 6х + 3иу = 0.
222. Решите уравнение J\2xTT\ = 1 - 2\х\.
Вариант 38
2
223. Решите неравенство > 0.
2х-4
224. Найдите значение производной функции
у = In (2-х) ^— в точке х0 = -1.
х +1
225. Решите неравенство log0 5 (х2 + х)< -1.
226. Найдите критические точки функции
/ (х) = 2 sin х + л/2 х. Укажите одну из точек
максимума.
227. Найдите ту первообразную функции
f (х) = 2х - 2, график которой касается прямой
у = -4х. Вычислите площадь фигуры,
ограниченной графиком найденной первообразной и
прямыми у = -4х, у = 0.
215. Исследуйте функцию f (х) = sin2 х - sin х 228. Решите уравнение V|l-3x| = 1 - 3 |х|.
на возрастание и убывание в промежутке
[-тс/2; 5я/6].
216. При каких значениях а прямая у = ах - 7
касается кривой у = 2х2 - 5х + 1?
Вариант 37
01ГУП 0,2х-0,008 ^л
217. Решите неравенство -« < 0.
х -10х + 25
218. Найдите значение производной функции
2 + х i X п
у = е + —— в точке х0 = -2.
х -1
Вариант 39
229. Решите уравнение = 0.
3-27
log05(x2-3)
230. Решите неравенство т—« < 0.
231. Составьте уравнение касательной к
графику функции у = х2 - Зх - 4 в точке с абсциссой
х0 = 1. Напишите уравнение одной из прямых,
параллельных этой касательной.

684
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
232. Найдите все значения х, при которых
выражение *J6-x-x etg (тх ) имеет смысл и
не обращается в нуль.
1 2
233. Фигура ограничена линиями у — т х и
у = х. Отрезок наибольшей длины,
заключенный внутри этой фигуры и принадлежащий
прямой х = а, делит фигуру на две части.
Докажите, что площади этих частей равны.
4
234. При каких значениях а уравнение х + - =
= а не имеет корней?
Вариант 40
Оу" , С у. __ О
235. Решите уравнение = 0.
2х-0,25
236. Решите неравенство log (х2 - 1)•lg 0,5 < 0.
237. Составьте уравнение касательной к
графику функции у = х2-2х-3в точке с абсциссой
х0 = 2. Напишите уравнение одной из прямых,
параллельных этой касательной.
238. Найдите все значения х, при которых
выражение л/3 - 2х - х • ctg ( « х }
и не обращается в нуль.
имеет смысл
12
239. Фигура ограничена линиями у = ^ х и
у = -Зх. Отрезок наибольшей длины,
заключенный внутри этой фигуры и принадлежащий
прямой х = а, делит фигуру на две части.
Докажите, что площади этих частей равны.
240. При каких значениях а уравнение
- + 4х = а имеет одно решение?
Вариант 41
241. Решите уравнение 3 cos 2х - 5 cos х = 1.
242. Решите неравенство log1/3 (2х + 1)> -1.
243. Составьте уравнение касательной к
графику функции у = х3 - Зх2 в точке графика с
абсциссой х0 = -1.
244. Найдите площадь фигуры,
ограниченной графиком функции у = -х2 + 4х - 4 и осями
координат.
245. Какие целые значения принимает
функция у = 5 (х - 1) Jx в промежутке [0; 1]?
246. Решите уравнение
3/
1л/4* + 4-;
,х + 2
Х+1 е%2х
= 3-2х + 1-2**-2
Вариант 42
247. Решите уравнение
5cos2x + 21sinx = 13.
248. Решите неравенство logx 7 (1 - Зх) < 0.
249. Составьте уравнение касательной к
графику функции у = -х3 + х - 1 в точке графика
с абсциссой х0 = -2.
250. Найдите площадь фигуры,
ограниченной графиком функции у = х2 + 6х + 9 и осями
координат.
251. Какие целые положительные значения
принимает функция у = 2jx- 1 - 0,5х в
промежутке [1; +<»]?
252. Решите уравнение
Vl -2 • 3* + 9х = 32дс + 1 + 3-3*-2/3.
Вариант 43
253. Решите неравенство
log2(x-l)<log2(2x + 3).
254. Решите уравнение sin 2х - sin х = 0.
255. Найдите область определения функции
y=j32x-2-3x-3.
4
256. Исследуйте функцию / (х) = х + -j на
х
монотонность.
257. Найдите площадь фигуры,
ограниченной графиком функции у = х2 - 2х + 3,
касательной к графику в его точке с абсциссой 2 и
прямой х=-1.
258. Рассматриваются всевозможные
правильные треугольные призмы, каждая боковая
грань каждой из которых имеет периметр, рав-

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
685
ный а (а > 0). Найдите среди них призму с
наибольшим объемом (в ответе укажите боковое
ребро такой призмы).
Вариант 44
259. Решите неравенство
log5(2x+l)Mog5(x-3).
260. Решите уравнение sin 2х = л/3 cos х.
261. Найдите область определения функции
у=л/2-52*-5*-1.
2 16
262. Исследуйте функцию f (х) = х - — на
монотонность.
263. Найдите площадь фигуры, ограниченной
графиком функции у = 3 + 2х - х2, касательной к
графику в его точке с абсциссой 3 и прямой х = 0.
264. Рассматриваются всевозможные
правильные четырехугольные призмы, сумма всех ребер
каждой из которых равна Ьф> 0). Найдите среди
них призму с наибольшим объемом (в ответе
укажите сторону основания такой призмы).
Вариант 45
265. Найдите абсциссы всех точек
пересечения графиков функций у=хиу=1+ Jx + 5 .
266. Вычислите
3«/106^(231П§) + 10ЫС08^'
267. Решите неравенство 23/х > 0,5х ~4.
,268. Найдите площадь фигуры,
ограниченной линиями
у = (х-2)(2х-3)иу = 0.
—О 5 т
269. Исследуйте функцию g(x) = хе ' в
промежутке [-2; 2] и постройте ее график.
270. Найдите все а, при которых уравнения
х ~
sin X + COS X = 1 И COS о = а имеют хотя бы один
общий корень.
Вариант 46
271. Найдите абсциссы всех точек
пересечения графиков функций у = 2 - 2 Jx + b иу = -х.
272. Вычислите
1оЫс°8 5 + 8in I)+Iog72(cos § - 8in S)
о •
273. Решите неравенство 52/х < 0,2х"3.
274. Найдите площадь фигуры,
ограниченной линиями у = (Зх + 2)(х - 1) и у = 0.
275. Исследуйте функцию / (х) = х2е~х в
промежутке [-1; 3] и постройте ее график.
276. Найдите все Ь, при которых уравнения
cos х - sin х = 1 и sin -z = b имеют хотя бы один
общий корень.
Вариант 47
277. Решите уравнение cos (к/2 + Зх) = sin х.
278. Вычислите значение производной
функции у = е2х г + J4x + 7 в точке х0 = 0,5.
279. Найдите площадь фигуры,
ограниченной графиком функции у = х2 - 4х - 4 и прямой
У = -х.
280. Решите неравенство (х - 3) log1/3 х ^ 0 и
укажите какое-либо целое значение х,
удовлетворяющее данному неравенству.
281. Определите координаты всех точек
графика функции y=Jx - 2х + 2 + х - 1,
равноудаленных от осей координат.
282. Найдите все значения t такие, что
функция у = 2х3 - Зх2 + 7 возрастает в интервале
(*-1;* + 1).
Вариант 48
283. Решите уравнение cos Зх — sin ( х - ^ 1.
284. Вычислите значение производной
функции у = In (Зх + 1) + 7бх + 5 в точке х0 = 2/3.
285. Найдите площадь фигуры, ограниченной
графиком функции у = 3 - х2 и прямой у = 2х.
Зх-1 -
€ — 1
286. Решите неравенство ——«— > 0 и
укажите какое-либо целое значение х, не
удовлетворяющее данному неравенству.

686
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
287. Определите координаты всех точек
графика функции у = V* + 4х + 8 - х - 2,
равноудаленных от осей координат.
288. Найдите все значения р такие, что
функция у = -Jt3 + 3jc + 5 убывает в интервале
(Р\Р+ 1/2).
Вариант 49
289. Решите уравнение
log3 (1 - х) = log3 (17 - х - х2).
290. Найдите площадь фигуры,
ограниченной линиями у = х2 - 4х 4- 4, j/ = 0 и х = 0.
291. Найдите все решения уравнения
3tg2*-4cos2* = 8.
292. Решите неравенство (0,5)'" 3 ^ 4,
293. При каких положительных значениях а
наименьшее значение функции у = х*/х + а
равно-6^3?
294. Диагональ боковой грани правильной
четырехугольной призмы равна d. Найдите
длину бокового ребра, при которой объем призмы
наибольший.
Вариант 50
295. Решите уравнение
log2 (х + 2) = log2 (х2 + х - 7).
296. Найдите площадь фигуры,
ограниченной линиями у — х2 + 6* + 9, у = 0 и х = 0.
297. Найдите все решения уравнения
4 sin2 х + 9 tg2 х = 4.
*-7
298. Решите неравенство 25*х 2 ^ (0,2) ' .
299. Прч каких положительных k
наибольшее значение функции у = (k - x)Jx равно
lOVB?
300. Апофема правильной четырехугольной
пирамиды равна р. Найдите длину высоты
пирамиды, при которой ее объем наибольший.
Вариант 51
301. Решите уравнение sin 2х + cos (я - х) = 0.
302. Решите неравенство
Ы >Ы •
303. Найдите критические точки функции
4
/ (х) — х + - и среди них укажите точку
максимума.
304. Найдите площадь фигуры, ограничен-
Г 1
НОИ ЛИНИЯМИ у=4ХИу=ъХ*
305. Найдите точку пересечения касательных,
проведенных к графику функции у = х2 -\Ьх + 9|
через точки графика с абсциссами 4 и -4.
306. Решите систему уравнений
0,5+ log х г
х = Jy,
logx + 1^ = l + logx + 1(3 + 4*2).
Вариант 52
307. Решите уравнение sin (я + х) - sin 2х = 0.
308. Решите неравенство
UJ > 127J '
309. Найдите критические точки функции
f (х) = 9х + - и среди них укажите точку
минимума.
310. Найдите площадь фигуры,
ограниченной линиями у = х2 и у = Jx.
311. Найдите точку пересечения
касательных, проведенных к графику функции у = х2 +
+ |7 - 4х| через точки графика с абсциссами 3 и
-3.
312. Решите систему уравнений
l-0,21ogxy 4/5
2 +log,
V
= X
1 2
log*4-

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
687
Вариант 53
313. Найдите абсциссы общих точек графи-
ков функций у = 1 - cos хи|/ = sin 2 .
314. Решите неравенство
log1/3(3x-l)>log1/3(2x + 3).
315. Решите уравнение 2 - х + 3 J2-X = 4.
316. Найдите площадь фигуры, ограничен-
1
ной линиями у = - , у = хих = е.
317. Найдите все корни уравнения
2 + дс
5х- 2 х =40.
318. При каких значениях а точка х0 = а
является точкой минимума функции
у = 2х3 - 3(а + 1)х2 + бах - 1?
Вариант 54
319. Найдите абсциссы общих точек
графила
ков функций у = 1 4- cos хиу = cos g .
320. Решите неравенство
log1/7(* + 3)<log1/7(4x-3).
321. Решите уравнение х + 3 4- bj¥+~x = 6.
322. Найдите площадь фигуры,
ограниченной линиями у = Ъ/х и у = 6 - х.
323. Найдите все корни уравнения
1 + х
2х* 5 х =50.
324. При каких значениях Ь точка х0 = Ъ
является точкой максимума функции у = ^ х3 - (Ь -
- 2)*2 - 4Ьх + 3?
Вариант 55
325. Решите неравенство log2 (х2 - 8,5) > -1.
326. Решите уравнение
соз х + 3 sin х _ - 1
2 cos дс + sin х 3 '
327. Составьте уравнение касательной к
графику функции у = Ъх ~2/5 4- 27 в точке графика с
ординатой 32.
328. Найдите площадь фигуры, ограниченной
параболой у = Ах - х2 и прямой, проходящей
через вершину параболы и начало координат.
329. Найдите точки экстремума функции у =
= е2х + ех-Зх + 2.
330. Для каждого а найдите все решения
неравенства (х - a) *]х-2 > 0.
Вариант 56
331. Решите неравенство log1/3( "Т - * )< *• •
000 _> 2 cos х + sin х 1
332. Решите уравнение тг—. = -« •
J* 3sinx + cosx 2
333. Составьте уравнение касательной к
графику функции у = 11 - 3* ~4/3 в точке графика с
ординатой 8.
334. Найдите площадь фигуры, ограниченной
параболой у = х2 - 6* и прямой, проходящей
через вершину параболы и начало координат.
335. Найдите точки экстремума функции у =
= 4х-2ех-е2*-5.
336. Для каждого Ь найдите все решения
неравенства (5-x)<Jx-b ^ 0.
Вариант 57
337. Найдите все числа Ь, удовлетворяющие
условию
log2 (Ь + 1) = 1 + log2 3 - log2 b.
338. Решите уравнение sin 2х + sin 4х = cos *.
339. Решите неравенство
3i + x.2i-* + 3*.2-*<10j5
340. Найдите наибольшее и наименьшее зна-
2 х
чения функции i/ = —^ + ^
на промежутке [0; 2,5].
341. Найдите площадь фигуры,
ограниченной графиком функции у = -х3 -2х2 -х + Зъ
касательной к нему, проведенной в точке графика
с абсциссой -1.
342. Решите неравенство
I
х -5£-4£+26
1-х
>2.

688
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Вариант 58
343. Найдите все числа а, удовлетворяющие
условию
logg (а + 5) - 1 = 3 logg 2 - log3 а.
344. Решите уравнение cos 5х - cos Зх = sin х.
345. Решите неравенство
2х-51-х + 2х + 1-5_х>2,8.
346. Найдите наибольшее и наименьшее значе-
4
ния функции у = х+ ——г на промежутке [-2; 0].
347. Найдите площадь фигуры,
ограниченной графиком функции у = хд- 4х2 + Ах - 5 и
касательной к нему, проведенной в точке графика
с абсциссой 2.
357. Найдите площадь фигуры, ограниченной
параболами у = 4х - х2 и у = « х2.
358. Найдите наибольшее и наименьшее
значения функции / (х) = 6,75л:4 - х + 2 на
промежутке [0; 2].
359. При каких а касательная, проведенная к
графику функции у = х3 + ах2 в точке графика с
абсциссой х0 = -1, проходит через точку N (3; 2)?
360. Решите систему уравнений
2 lOgg X + lOgg X • lOgg У - logg I/ = 0 ,
ух-— = 28.
y У
348. Решите неравенство
/ 2 с . „ Вариант 61
ух + 5х-4х + 6 . 0
х-2
Вариант 59
349. Найдите область определения функции
у = л/3-х + log2(2x-l).
350. Решите уравнение (л/3)
tg х
Qtg х
351. Найдите площадь фигуры, ограниченной
параболами у = х2 - 2х и у = т х2.
352. Найдите наибольшее и наименьшее
значения функции f (х) = 0,25х4 - 2х2 + 1 на
промежутке [-1;3].
353. При каких р касательная, проведенная к
графику функции у = х3 - рх в точке графика с
абсциссой х0 = 1, проходит через точку М (2; 3)?
354. Решите систему уравнений
log| У + 1о^2 х # 1о^2 У - 21о&2 * = 0,
9х у-ху =1.
Вариант 60
355. Найдите область определения функции
= log05(x + 3)- Vl-2x.
356. Решите уравнение (л/2)
2 cosx
2-2^
361. Решите уравнение (cos х + sin х)2 = sin -g-.
362. Решите неравенство log j^ (1 - Зх) < 2.
363. Найдите координаты общих точек
графика функции у = Jx + 7 и прямой у - х - 1 = 0.
364. Найдите площадь фигуры,
ограниченной графиками функций у = 2/х и у = 3 - х.
365. Найдите наибольшее и наименьшее
значения функции у = х + 1п(-х) на отрезке
[-4;-0,5].
366. Укажите все первообразные функции
g (х) = Зх2 + 2х - 2, графики которых имеют
ровно две общие точки с графиком функции g (х).
Вариант 62
367. Решите уравнение (cos х - sin х) = cos -g-.
368. Решите неравенство log ig (2х - 1) > 2.
369. Найдите общие точки прямой у - 2х + 9 =
= 0 и графика функции у = *Jx-4 .
370. Найдите площадь фигуры,
ограниченной графиками функций у = х2 и у = 2х - х2.
371. Определите наибольшее и наименьшее
значения функции i/ = х + е~* на отрезке
[-In 4; In 2].
372. Укажите все первообразные функции
/(х) = 5 + 2х - Зх2, графики которых имеют с
графиком функции / (х) ровно две общие точки.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
689
РЕШЕНИЯ, КОММЕНТАРИИ
И СОВЕТЫ
Вариант 1
1. Решите неравенство х2 (2х + 1) (х - 3) > 0.
Решим неравенство методом интервалов.
Рассмотрим функцию f (х) = х2 (2х + 1) (х - 3).
Она непрерывна при всех действительных х и
обращается в нуль в точках 0, -0,5 и 3. Эти
точки разбивают числовую ось на четыре
промежутка. Определим знак функции в каждом из
них: / (5) > 0, f (1) < 0, / (-0,1) < 0, f (-2) > 0
(рис.1).
Ответ: (-*»; -0,5] и {0} и [3; +«>}.
2. Упростите выражение cos (2л: - Зл:) cos х +
(¥•♦*)•■
ний х, при которых значение данного
выражения равно (-1/2).
Используя формулы приведения, перепишем
данное выражение в виде cos Зх cos х + sin 3jc sin х,
что по формуле косинуса разности равно cos 2х.
Решив уравнение cos х = —z , находим х = ±« +
+ л;&, keZ.
Ответ: cos 2х; {±r +nk \ keZ}.
+ sin Зх cos
Укажите множество значе-
3. Решите систему уравнений
log3x + log3y = 1,
-2/3
гх~У
■И"
Преобразуем первое уравнение к виду
log3 (ху) = 1. При этом необходимо учесть, что
х > 0 и у > 0. (На самом деле достаточно одного
условия, например х> 0. В этом случае если
определено выражение log3 (ху), то определен и
log3 у, и приобрести посторонние решения
невозможно.) Из уравнения log3 (ху) = 1 получим
ху = 3.
Логарифмируя обе части второго уравнения
системы по основанию 3, придем к уравнению
\ху = 3,
[х-у = 2.
Выразив х через у из второго уравнения и
подставив это выражение в первое, получим
х - у = 2. Решим систему
у(у + 2) = 3,
х = у + 2.
Корнями квадратного уравнения
у + 2у - 3 = 0 являются числа 1 и -3. Получаем
две пары: у= 1, х = 3иу = -3, х = -1. Для чисел
второй пары условие х > 0 не выполняется,
поэтому пара (-1; -3) решением исходной системы
не является.
Ответ: (3; 1).
4. Решите уравнение (х2 - 9) (J6- Ъх - х) = 0.
Произведение двух сомножителей равно
нулю, когда один из них равен нулю, а другой при
этом определен.
Выражение х2 - 9 обращается в нуль при х = -3
и при х = 3. Если х = -3, то л/6- Ъх определен;
если же х = 3, то не определен. Таким образом,
х = -3 является корнем исходного уравнения.
Далее решим уравнение J6 -Ьх = х.
Возведем в квадрат обе его части при условии х > 0.
Получим 6 - Ьх — х2, откуда хг = 1, х2 = -6.
Значение х2 не удовлетворяет условию х > 0 и не
является корнем иррационального уравнения
V6-5x =х.
Итак, решениями исходного уравнения
являются числа 1 и-3.
Ответ: 1;-3.
5. Составьте уравнение касательной,
проведенной к графику функции / (у) = -х2 + 4
параллельно прямой у = -2х + 6. Вычислите площадь
фигуры, ограниченной графиком данной
функции, этой касательной и осью ординат.
Составим уравнение касательной. Так как
касательная параллельна прямой у = -2х 4- 6, то
ее угловой коэффициент равен -2. С другой
стороны, угловой коэффициент касательной равец
значению производной функции в точке
касания. Абсциссу точки касания х0 определим из*
условия f'(x0) = -2. Поскольку f'(x) = -2xf
находим х0 = 1. Уравнение касательной к графику
функции / (х) в его точке с абсциссой х0 имеет
-0,5
0
Рис. 1

690
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
вид у = f(x0) (х ~ *о) + f (*о)" Подставляя
конкретные значения в эту формулу, получим
уравнение у = 5 - 2х.
Для вычисления площади заданной фигуры
отметим, что любая касательная к параболе у =
= -х2 + 4 лежит не ниже самой параболы.
Пределами интегрирования являются числа 1
(абсцисса точки касания) и 0 (поскольку фигура
ограничена осью ординат). Имеем
1 1
S = J((5-2x)-(-jc2 + 4)) dx = j(x-l)2dx =
о о
чЗ
(*-1)
3
С - о-С-4) - S-
О т в е т: у = 5 - 2х; S = 1/3.
6. Исследуйте функцию у = х4 - 2х2 + 3 с
помощью производной. Определите, прц каких
значениях а уравнение х4 - 2*2 + 3 = а имеет три
корня.
Функция у = х4 - 2л:2 4- 3 определена и
дифференцируема при всех действительных х; у' = 4х3 -
- 4х = 4х(х - 1)(л: + 1). Критическими точками
функции являются нули ее производной, т. е.
точки -1, 0 и 1. Исследование функции на
монотонность представим в виде таблицы:
1 (1; +~)
+
71
Анализируя эту таблицу, отметим, что в
точках -1 и 1 функция имеет минимумы, равные 2,
а в точке 0 — максимум, равный 3.
Из особенностей функции отметим ее,
четность: действительно, у (-х) = (-х)4 - 2(-*)2 -I- 3 =
X
У'
У
(—;-D
—
^
Ы}
0
2
(-1; 0)
+
71
{0}
0
3
(0;1)
—
^
{1}
0
2
= х4 - 2х2 + 3 = у (х), а также отсутствие у
функции нулей.
Для определения значений а, при которых
уравнение х4 - 2х2 + 3 = а имеет три корня,
воспользуемся четностью функции. Если число х0
является корнем уравнения, то число -х0 также
является его корнем. Таким образом, для
каждого положительного корня уравнения найдется
пара — противоположное ему число,
отрицательный корень. Посколько согласно условию
уравнение должно иметь ровно три корня,
одним из корней будет число, противоположное
которому совпадает с ним самим, т. е. 0. Число 0
является корнем при а = 3. Отметим, что только
при этом значении параметра а заданное
уравнение имеет нечетное количество корней.
Убедимся, что их ровно три.
В самом деле, справедлива цепочка
соотношений: х4 - 2*2 4- 3 = 3; х2 (х2 - 2) = 0; хг = 0;
x23 = ±j2,
Ответ: при а = 3.
Рис. 2
Вариант 3
13. Решите неравенство (0,25)2'5"0'5*' > jg .
Запишем неравенство в виде (0,25)2'5 " °'5х >
> (0,25)2. Так как у = (0,25)' — убывающая
функция, то полученное неравенство эквивалентно
неравенству 2,5 - 0,5х2 < 2, или х2 > 1. Решения
последнего таковы: х < -1 и х> 1.
Ответ: (-°°; -1) и (1; +<»).
„ л -г sin а - 0,5 sin 2а cos а
14. Упростите выражение g
sin а
и найдите его значение при а = -я/6 .
Разложив sin 2а по формуле двойного угла,
запишем числитель дроби как sin а - sin а cos а =
= sin а(1 - cos2 а) = sin3 а. Тогда исходное
выражение будет равно sin а. При а = -я/6 имеем
sin а = -1/2.
Ответ: sin а;- 1/2.
15. Вычислите площадь фигуры,
ограниченной линиями у = Jx, у = 0,5 х.
Изобразим заданную фигуру (рис. 2).
Абсциссами точек пересечения графиков у
и у = 0,5* являются 0 и 4. Искомую площадь

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
691
вычислим как разность площадей
криволинейной трапеции ОВАР и треугольника АОР.
Находим
о = I г\р. лр = I • 4 • 2 = 4*
S0BAP=№d* = |*3/2|
16
3
Площадь заданной фигуры равна -=- - 4 = ~ .
Ответ: 4/3.
16. Решите систему уравнений
logo 12
Зх + у = 8 8 ,
х2 + у2 -2ху = log2144-2loS281-
Используя основное логарифмическое
тождество, перепишем первое уравнение системы в виде
Зх + у = 12. Левую часть второго уравнения
преобразуем по формуле квадрата разности, а правую
часть преобразуем так: log2 144 - 2^2 81 =
= log2 144 - log2 9 = log2 16 = 4.
Тогда исходная система примет вид
(Зх + у = 12,
< 9 , что в свою очередь равносильно
1(*-У) =4
совокупности
" Зх + у = 12,
х-1/ = 2,
Зх + у = 12,
х-1/ = -2.
Решением первой системы этой совокупности
является пара от = 3,5, у — 1,5, а решением
второй системы — пара х = 2,5, i/ = 4,5.
Ответ: (3,5; 1,5), (2,5;4,5).
17. Найдите длины сторон прямоугольника с
периметром 20 см, имеющего наименьшую
диагональ.
Пусть а и Ь — длины соседних сторон
прямоугольника, ad — его диагональ. Тогда из
условия следует, что а + Ъ = 10. По теореме
Пифагора d2 = а2 + Ъ2. Так как d положительно, то свое
наименьшее значение d принимает при тех же а
и Ъ, при которых минимально d , причем по
смыслу задачи а и Ь также положительны.
Теперь условие задачи можно
сформулировать так: требуется найти положительные числа
а и Ъ, удовлетворяющие условию а + Ь — 10, при
которых выражение а2 + Ь2 принимает
наименьшее значение.
Выразив из известного соотношения Ь
через а, запишем: d2 = а2 + Ъ2 = а2 + (10 - а)2 = 2а2 -
- 20а + 10.
Поскольку а и Ь положительны, из
неравенства Ъ > 0 получим 10 - а > 0, т. е. а < 10.
Найдем а, при котором выражение 2а2 - 20а + 10 на
промежутке (0; 10) принимает наименьшее
значение.
Исследуемое выражение — квадратный
трехчлен. Его наименьшее значение достигается при
20
а = 57о = *• Так как * е № Ю)> то наименьшее
значение выражения 2а2 - 20а + 10 в
промежутке (0; 10) также достигается при а = 5.
В результате получаем, что d2 минимально
при а = Ъ = 5, т. е. прямоугольник с периметром
20 см имеет наименьшую диагональ, когда
каждая из его сторон имеет длину 5 см.
Ответ: все стороны равны 5 см.
18. Сколько корней имеет уравнание х3 - Зх2 =
= а при - 4 < а < 0?
Для ответа на вопрос задачи исследуем
функцию f (х) = х3 - З*2 с помощью производной.
Находим f (х) = Зх2 - 6х = Здг(х - 2).
Критическими точками функции являются 0 и 2. При
х < 0 и при х> 2 имеем f (х) > 0 и функция / (х)
возрастает; при 0 < х < 2 имеем f(x) < 0 и
функция f (х) убывает. Составим таблицу
монотонности функции:
X
г
f
(-~; 0)
+
71
{0}
0
0
(0;2)
—
^
{2}
0
-4
(2; +оо)
+
а
Учитывая, что / (-1) = -4, f (3) = 0, а также
характер монотонности функции, отраженный в
таблице, делаем вывод: в промежутках (-<»; 0),
(0; 2) и (2; +°°) функция по одному разу
принимает каждое значение от -4 до 0. Следовательно, при
всех а е (-4; 0) уравнение х3 - Зх2 = а имеет три
корня — по одному на каждом из указанных про-

692
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
межутков. Для большей наглядности приведем
эскиз графика функции / (х) = х3 - Зх2 (рис. 3).
некоторая константа. Найдем С из условия
F(l) = 81. Имеем 81 = I3 + I2 + С; С = 79. Тогда
Ответ: три корня. F(-l) = (-1) + (~1)2 + 79 = 79.
Вариант 5
25. Решите уравнение J2x- 1 — х - 2.
Произведем замену переменной: t = *]2х- 1.
Тогда л: = —5—, а уравнение примет вид t =
2 х
= —5 2, или t2 - 2* - 3 = 0, откуда *х = -1,
t2 = 3. Теперь вычислим #. Уравнение -1 =
= л/2х- 1 не имеет решений, а из уравнения 3 =
= л/2х- 1 находим х = 5.
Ответ: 5.
26. Решите неравенство log0 25 (5* - 1) ^ -0,5.
Представим -0,5 как log0 25 (0,25)~°*5, что
равно log0 25 2. Функция у = log0 25 * является
убывающей в области своего определения.
Учитывая это, а также условие существования
логарифма, от исходного неравенства перейдем к
двойному неравенству 0 < Ъх - 1 < 2. Решениями
этого неравенства являются все х из
промежутка (0,2; 0,6].
Ответ: (0,2; 0,6].
27. Первообразная функции / (х) = Зх2 + 2х
при х = 1 принимает значение 81. Найдите ее
значение при х = -1.
Любая первообразная функции / (х) может
быть записана в виде F(x) = х3 + х2 + С, где С —
Vi
0
1 -4.
i
2
_ bJ/
" ^>-
Ответ: 79.
28. Укажите все точки на графике функции
у = хе~х , в которых касательная параллельна
оси абсцисс.
Касательная к графику функции
параллельна оси абсцисс, если ее угловой коэффициент
равен нулю. Так как угловой коэффициент
касательной равен значению производной функции в
точке касания, то для определения абсцисс
искомых точек необходимо решить уравнение \f= 0.
Продифференцируем заданную функцию:
у'=(хе-х2)'=е-
+ х(-2хе'х ) = е~х (1
2х2).
Очевидно, что у'= 0, если 1 — 2л: = 0, т. е. ес-
ЛИ Х = ±-7Г.
Определим ординаты каждой из найденных
72 Л -1/2
Y находим у = -£• е ' =
точек. При х =
Л 1
при х = -ту- получим у = рг .
^ J2e
1
Ответ:(.т;-^);(Т,^=).
29. Сколько корней имеет уравнение sin2 х +
+ cos2 2х + cos2 [| + 2х J + cos х tg х = 1 в
промежутке (0; 2л:)? Укажите их.
По формуле приведения получаем
+ 2 х ] = -sin 2х. Заменим третье слагаемое
cos
Рис. 3
в левой части на sin 2х и, используя основное
тригонометрическое тождество, преобразуем
исходное уравнение к виду sin2 х + cos х tg х = 0.
При условии cos х Ф 0 выражение cos х tg х равно
sin х, и уравнение примет вид sin2 х + sin х = 0,
или sin х (sin х + 1) = 0, что выполняется либо
когда sin х = 0, либо когда sin х = -1.
В первом случае имеем х = кп, где п е Z; при
этом cos jc * 0, а среди найденных значений х в
промежуток (0; 2я) попадет только х = я. Во
втором случае те значения неизвестного, при
которых sin х = -1, не являются корнями исходного
уравнения, поскольку при этом cos х = 0. Таким

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
693
образом, исходное уравнение имеет
единственный корень на промежутке (0; 2л), и он равен я.
Ответ: один корень: х = к.
30. Исследуйте функцию f (х) = х3 - Зх с
помощью производной и выясните, при каких
значениях а уравнение х3 - Зх = а имеет одно решение.
Функция / (х) определена и
дифференцируема при всех действительных х. Находим f (х) =
= Зх2 -3=3(х-1)(х+1). Критическими
точками функции являются точки -1 и 1. В них / (х)
принимает значения 2 и -2 соответственно.
Функция / (х) — нечетная, так как / (-х) =
= (-х)3 - 3(-х) = - х3 + Зх = -/ (х). Нулями
функции являются числа 0, - 7з и */3 .
Составим таблицу монотонности функции f (х):
X
fix)
(-~;-D
+
71
{-1}
ч 0
2
(-1; 1)
—
^
{1}
0
-2
(1; +~)
+
71
Функция f (х) — многочлен. Учитывая его
непрерывность, а также характер поведения
многочлена на бесконечности, заключаем, что
при х < -1 функция возрастает, принимая по
одному разу каждое свое значение от -«» до 2
включительно; при -1 < х < 1 она убывает,
причем принимает по разу все значения из
промежутка (-2; 2); наконец, при х ^ 1 она
возрастает от -2 до +°°. Таким образом, ровно один раз
принимаются значения, меньшие -2, а также
значения, большие 2. Последнее означает, что
уравнение х3 - Зх = а имеет единственное
решение при а < -2 и при а > 2.
Ответ: при всех а е (-о°; -2) и (2; +°°).
Вариант 7
37. Решите уравнение
1 + log7 (х 4- 4) = log7 (х2 + 9х + 20).
Преобразуем леэую часть уравнения: 1 +
+ log7 (х + 4) = log7 7 (х + 4). Тогда уравнение
примет вид log7 7 (х + 4) = log7 (х2 + 9х + 20).
Из условия равенства логарифмов по одному
основанию следует, что 7 (х + 4) = х2 + 9х + 20
при выполнении неравенства х + 4 > 0. Решив
последнее уравнение, находим хг =-4, х2 = 2,
причем неравенству х + 4 > 0 удовлетворяет
38. Найдите наибольшее целое число,
удовлетворяющее неравенству 2х + (0,5)3~х < 9.
Решим данное неравенство, переписав его в
виде 2х + 2х ~ 3 < 9. Далее имеем 2х (1 + g J < 9;
9-2х"3 <9; 2х"3 < 1; х-3 < 0; х < 3.
Наибольшим целым числом, удовлетворяющим
неравенству х < 3, является число 2.
Ответ: 2.
39. Найдите площадь фигуры, ограниченной
линиями у = 2х2, у = 4х.
Изобразим заданную фигуру (рис. 4). Ее
площадь будем вычислять как разность
площадей треугольника ОМА и криволинейной
трапеции ОВМА. Абсцисса точки М находится из
уравнения 2х2 = 4х, и она равна 2, ордината
точки М равна 8. Площадь треугольника О AM равна
2 О А *АМ = 8. Площадь криволинейной трапеции
16
ОВМА вычислим так: J 2х dx = gx |0 = -g-.
1 fi я
Значит, площадь фигуры ОВМС равна 8 - -«- = « .
Ответ: 8/3.
только х«
Ответ: 2.
Рис. 4

694
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
40. Какими должны быть стороны
прямоугольного участка площадью 1600 м2, чтобы на
его ограждение было израсходовано
наименьшее количество материала?
Обозначим через а и Ь соседние стороны
прямоугольника. Из условия следует, что аЪ = 1600.
Общее количество материала, необходимое для
ограждения прямоугольного участка со
сторонами аиЬ, определяется выражением 2а + 2Ь.
Понятно, что минимум выражения 2а + 2Ъ
достигается при тех же условиях, что и минимум
выражения а + Ь. Процедуру нахождения таких
значений аиЬ выполним двумя способами.
I способ. Выразим Ъ через а : Ъ = .
Будем искать положительное а, при котором
, // ч . 1600
функция f(a) = а+ принимает наименьшее
1600
1600
значение. Находим f(a) = 1 -
а" а"
Положительным корнем уравнения f (а) = 0
является число 40. При всех положительных а < 40
имеем f(a) < 0, и функция / (а) убывает; при всех
а > 40 имеем f(a) > 0, и функция f (а) возрастает.
При а = 40 производная функции меняет знак с
минуса на плюс и, следовательно, а = 40 — точка
минимума функции f (а). Если а = 40, то Ь = 40,
т.е. участок имеет форму квадрата.
II с п о с о б. Воспользуемся неравенством
между средним арифметическим и средним
геометрическим для положительных величин а и Ь =
= Ш.Имеем |(« + Ц*) > Р^ = ЛбОО =
АГк , 1600 . ол
= 40, или а + > 80, причем равенство, а
_,_ 1600
значит, и минимум выражения а +
достигается при равенстве слагаемых, т. е. при усло-
1600 тж АГк
вии а = . Итак, а = 40.
а
Ответ: все стороны равны 40 м.
41. Дана функция f (х) = a sin 4х + Ь cos 2х.
Найдите аиЬ, если известно, что f'(7n/12) = 4 и
ДЗтс/4) = 2.
Найдем производную функции / (х): f(x) =
= 4а cos 4х - 2Ъ х sin 2х. При х = тт имеем f(x) =
получим систему уравнении
= 4а cos -т- - 2Ъ sin -g- = 4а • т - 2b • (-т) = 2а + Ъ.
При х = -т- имеем f (х) = 4а cos Зтс - 2Ъ sin -5- =
= 4а • (-1) - 2Ъ • (-1) = -4а + 2Ъ.
Используя данные в условии значения
производной функции / (х) в точках 7я/12 и Зл/4,
2а + Ь = 4, „
Ее
[-4а+ 26 = 2.
решением является пара чисел а = 0,75, Ь = 2,5.
Ответ: а = 0,75, Ь = 2,5.
42. Фигура ограничена линиями у = 2#2 и
I/ = 4х. Найдите длину наибольшего отрезка,
параллельного оси Оу и заключенного внутри
фигуры.
Отрезок, о котором говорится в условии
задачи, параллелен оси Оу, поэтому все точки этого
отрезка имеют одинаковые абсциссы.
Обозначим абсциссу каждой точки отрезка СВ через р
(см. рис. 4); тогда ордината точки С равна 4р, а
ордината точки В равна 2р2. Длина отрезка ВС
равна \4p-2p I, или 4р - 2р2 (поскольку для точек
заданной фигуры ордината точки С больше
ординаты точки В). Заметим также, что для точек
этой фигуры выполнено неравенство 0 < р < 2.
Задача сводится к отысканию наибольшего
значения квадратного трехчлена Ар - 2р2 в
интервале (0; 2). Наибольшее значение на R
выражение 4р - 2р2 принимает при р = 2/ g)' т# е*
при р = 1. Так как 1 е (0; 2), то максимальное
значение квадратного трехчлена 4р - 2р2 в
промежутке (0; 2) также достигается прир = 1. Оно
равно 2 и равно длине наибольшего отрезка,
параллельного оси Оу и заключенного внутри
фигуры.
Ответ: 2.
Вариант 9
49. Решите неравенство 0,6х ~5х>1.
Функция у = 0,6* является убывающей при
всех действительных t. Используя это, заменим
исходное неравенство равносильным ему
неравенством х2 - Ъх < 0, решениями которого
являются все х из промежутка [0; 5].
Ответ: [0; 5].

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
695
50. Вычислите log1/2 16 • log5 -fjfjr : 9log*2.
Используя свойства логарифмов, имеем:
log1/2 16 = -4; log5 Щ = | log5 5 - log5 25 = \ - 2 =
3
= _|; 9i°s, 2 = 32ioga 2 = з ioga 4 = 4 окончательно
получаем -4 • f-g j : 4 = ~ ,
Ответ: 5/3.
51. Найдите площадь фигуры, ограниченной
линиями у = 9х2 - 6х + 1, у = О, х = 0.
Квадратичную функцию у = 9х2 - 6х + 1
удобно записать в виде у = (Зх - I)2. Ее график
касается оси абсцисс в точке (1/3; 0). Площадь
искомой фигуры (рис. 5) вычислим так:
1/3
Итак, условию sin х < 0 удовлетворяют следу-
5 ,
ющие корни исходного уравнения: -arccosг +
+ 2nk и —о- + 2кт; k, те Z.
5 2%
Ответ: ±arccosr + 2nk9 и±-о- + 2кт; kfmeZ;
из них условию sin х < 0 удовлетворяют
5 2я
-arccosg + 2nk и —=- + 2ятп; k9me Z.
53. При каком значении а функция у — а In л: +
+ х2 - х имеет экстремум в точке х = 1?
Определите вид экстремума в точке х = 1 при
найденном значении а.
Функция у = а\пх + х2-х определена и
дифференцируема при всех положительных х.
Необходимым условием экстремума
дифференцируемой функции в некоторой точке является
равенство нулю ее производной в этой точке.
1П UUWUUV1UV U J«*1U \S\S 111ПГ111Г1У—I Г^ "ТГИ Л* %* Л UU * >^ 4b4tvw .
31 /
J (Зх -1)2 dx = | • ^Зх"^ = 0 - [-g J = i . Производная данной функции равна | + 2х -
Ответ: 1/9.
52. Решите уравнение 16 sin2x + 2 cos х = 11 и
укажите его корни, удовлетворяющие условию
sin х < 0.
Воспользовавшись основным
тригонометрическим тождеством, приведем данное уравнение
к виду -16 cos2x + 2 cos х 4- 5 = 0, т. е. к
квадратному уравнению относительно cos х. Решив его,
5 1
находим cos х = g или cos х — -^ откуда х =
5 2%
= ± arccos g + 2яА, А е Z, или х = ±-s- + 2ят,
me Z.
Среди найденных решений отберем все,
удовлетворяющие неравенству sin х < 0. Числам
5
arccos g + 2яЛ соответствует точка I четверти
единичной окружности, а для таких точек sin х > 0.
5
Числам - arccos g + 2nk соответствует точка IV
четверти, и для всех таких точек sin х ^ 0.
_ 2я , 0 2я ,
Точки, отвечающие числам -g- + 2ят и —=- +
4- 2л:/71, лежат соответственно во II и в III
четвертях, и неравенству sin х ^ 0 удовлетворяют
числа второй из этих серий.
- 1. Из условия равенства ее нулю при х =р 1
находим а = -1. Таким образом, у' = 2х - 1 - - =
_ 2х -х-1 _ 2(х-1)(х + 0,5)
. Если 0 < х < 1, то
х х
у'< 0 и функция убывает; если же х > 1, то у'> 0
и функция возрастает. При х = 1 производная
меняет знак с минуса на плюс, следовательно, в
точке х = 1 функция имеет минимум.
Ответ: при а = -1; в точке х = 1 — минимум
функции.
Рис. 5

696
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
54. Исследуйте функцию у = xj4x + 1 с
помощью производной и, используя результаты
исследования, укажите множество значений
этой функции.
Область определения функции задается
неравенством 4х + 1 > О, т. е. она представляет собой
множество [-0,25; +«>). Нулями функции
являются числа -0,25 и 0. При - 0,25 < х < 0
функция отрицательна, при х> 0 — положительна.
Исследуем функцию на монотонность, для
чего вычислим ее производную. При х > 0,25
2х 6х + 1
имеем у' = дДх+Т +
ЛхП 74*+ 1
; у'= 0,
если х = -g . Составим таблицу монотонности
функции:
X
У'
У
{-0,25}
не опр.
0
(-0,25; -1/6)
—
^
Н/6}
0
-73/18
(-1/6; +оо)
+
71
Из таблицы видно, что -1/6 является точкой
минимума функции, а значение в этой точке —
минимальным значением функции в области
определения. При изменении х от -1/6 до
бесконечности у возрастает от -л/3/18 до
бесконечности. Таким образом, множество значений
заданной функции — промежуток [-V3/18 ; +«>).
Отв ет: Е (у) = [-73/18 ; +«>).
Вариант 11
61. Решите уравнение 2х + 4 - V* + 2 =15.
Сделаем замену переменной: t = JxV2 .
Тогда относительно новой неизвестной t получим
уравнение 2t2 - t - 15 = 0. Его корнями
являются числа tr = 3, t2 = -2,5.
Возвращаясь к исходной переменной х,
получим два уравнения: */х + 2 = 3 и *Jx + 2 = -2,5.
Из первого имеем х + 2 = 9, т. е. х — 7, а второе
не имеет решений.
Ответ: 7.
Замечание. Приведенный способ решения является
наиболее эффективным применительно к данному
примеру, хотя уравнение можно решить и другим способом,
например переписав его в виде Jx + 2 = 2х - 11,
возвести его обе части в квадрат при условии 2х -11 > 0, и т. д.
62. Найдите все значения х, при которых
функция у = log2 (х2 + х) - 1 принимает
положительные значения.
Задача сводится к решению неравенства
log2 (х2 + х) - 1 > 0, или log2 (х2 + х) > 1.
Учитывая характер монотонности логарифмической
функции по основанию, большему 1, сведем
неравенство к квадратному: х2 + х > 2, или (jc — 1)
(х + 2) > 0. Решение последнего — объединение
промежутков (-<»; -2) и (1; +«>).
Ответ: (-«>; -2) и (1; +«>).
Замечание. Мы совершенно сознательно обошлись
без упоминания об условии существования
логарифма — неравенства х2 + х > 0, поскольку оно
непосредственно следует из неравенства х2 + х > 2.
63. Решите систему уравнений
J42x+y = 2Х"У+3,
(*)
2ху-2у
= 5
9-х
Левую часть первого уравнения преобразуем
к виду 22х + у, откуда, используя условия
равенства степеней с одинаковыми основаниями,
получим уравнение 2х + у = х-у + 3, или х + 2у = 3.
Левую часть второго уравнения представим
как степень с основанием 5: 5г2^2ху~2у \ После
этого аналогично перейдем к уравнению -4ху + 4у =
= 9 - х2, или х2 - 4ху + 4у2 = 9, или (х - 2у)2 = 9.
Последнее уравнение равносильно совокупности
уравнений
~ х-2у = 3,
\x-2y = -3.
Таким образом, для решения исходной
системы достаточно решить каждую из двух систем:
\х + 2у = 3, \ х + 2у = 3,
x-2i/4= 3 \x-2y = -3.
Первой удовлетворяет пара чисел х = 3, у = 0,
второй — пара х = 0, у = 1,5 .
Ответ: (3; 0), (0; 1,5).
64. Найдите наибольшее и наименьшее
значения функции у = 2 cos 2х - cos 4jc на отрезке
[0; п/2].
Заданная функция непрерывна и
дифференцируема в каждой точке отрезка [0; я/2].
Наибольшее и наименьшее значения непрерывной на от-

Задачи и решения письменного экзамена по алгебре и началам анализа
резке функции могут достигаться либо на
концах этого отрезка, либо в критических точках,
ему принадлежащих. Для определения
критических точек функции найдем ее
производную: у' = -4 sin 2х + 4 sin 4х. Имеем у' = О, если
sin 4х = sin 2х.
Воспользуемся условием равенства синусов:
sin а = sin р, если а = |$ + 2nk или а = я - Р + 2тт,
где А, п — целые. Следовательно, Ах = 2х + 2яА,
т. е. х = nk, или 4х = к - 2х + 2л:л, т. е. х = g + ~*г»
k9ne Z. Среди чисел первой серии отрезку [0; я/2]
принадлежит число 0. Среди чисел второй серии
заданному отрезку принадлежат два числа: я/6
при п = 0 и я/2 при п = 1. (Заметим, что 0 и я/2
являются также концами заданного отрезка.)
Вычисляем значения функции в каждой из
трех найденных точек: у(0) = 1; у(я/6) = 1,5;
у(к/2) = -3. Наибольшим из этих значений
функции является 1,5, наименьшим — число (-3).
Ответ: 1,5 и-3.
Замечание. Для получения конечного результата
совсем не обязательно проводить исследование
функции на монотонность, а достаточно определить
значения функции в ее критических точках и на концах
заданного отрезка (как мы и поступили).
65. Вычислите площадь фигуры, ограничен-
1 2
ной графиком функции у = -^х-\-Зи двумя
касательными к этому графику, проходящими
через точку на оси Оу и образующими между
собой угол 90°.
Прежде всего покажем, что ось Оу является
осью симметрии двух касательных к заданному
графику, проходящих через точку этой оси.
Пусть прямая у = ах + b является касательной к
1 2
графику функции у = -= х +3. Эта прямая
проходит через точку (0; Ь). Через точку (0; Ь)
должна (по условию) проходить и другая
касательная к заданному графику, а значит, ее
уравнение можно записать как у = агх + Ь. Выразим
коэффициент аг через а.
Прямая у = ах + Ь, будучи касательной,
имеет с параболой у = -р*2 + ^ единственную
общую точку, а это означает, что уравнение ах + b =
= —z х2 + 3, или х2 + 2ах + 2Ъ - 6 = 0 имеет
единственный корень. Условием этого является ра-
Подготовка к экзаменам. 11 класс
венство нулю выражения а2 - 2Ь + 6 — четверти
дискриминанта квадратного уравнения. Если
равенство а2 = 2Ъ - 6 достигается при некотором
значении а = а0, то при постоянном Ь оно
достигается еще только в одном случае — при а = - а0.
Таким образом, ах = -а, и уравнение второй
касательной к графику функции у = —z х2 + 3
имеет вид у = -ах + Ь. Прямые у = ах + Ьиу = -ах + Ь
симметричны относительно оси Оу:
действительно, они содержат соответственно точки
— ;0] и (-;01, симметричные относительно
оси Оу> а также пересекаются в точке,
принадлежащей этой оси; этого достаточно для
симметрии двух прямых. Итак, из симметрии
заключаем, что ось ординат делит пополам один из углов,
образованных прямыми у = ах + Ьиу = -ах + Ь;
так как по условию он равен 90°, то каждая из
прямых образует с осью Оу угол 45°. Тогда и с
прямой у — 0 каждая из рассматриваемых
прямых образует угол 45°. Одна из них образует с
положительным направлением оси Ох угол 45°
и имеет угловой коэффициент 1, а другая
образует с положительным направлением оси Ох
угол 135° и имеет угловой коэффициент -1.
Уравнения касательных имеют вид у = х + Ъ
и у = -х + Ъ. Из вышеупомянутого условия а2 =
= 2Ъ - 6 найдем Ь = 3,5; уравнения касательных
таковы: у = х + 3,5 иу = -х + 3,5.
Рис. 6

Задачи и решения письменного экзамена по алгебре и началам анализа
Подготовка к экзаменам. 11 класс
Заданная фигура АВСМ симметрична
относительно оси ординат (рис. 6). Вычислим ее
площадь как удвоенную площадь фигуры ВСМ
(абсцисса точки С равна 1). Имеем
1 /
S = 2^(3,5 -*)-(-!*2 + з)) dx =
о
-liScx-i»'*- ^f-°-(-IH-
о °
Ответ: 1/3.
66. Какие целые значения принимает
функция у = -9х J2x + 1 в промежутке [-0,5; 0]?
I способ. Заданная функция непрерывна в
промежутке (0,5; 0]. Найдя наибольшее и
наименьшее значение функции в этом промежутке
(рассмотрев при этом и точку -0,5), можно будет
ответить на поставленный вопрос. Заданная
функция дифференцируема при -0,5 < х < 0 и
у'=-$Д^-1==.
V2X + 1
Производная равна нулю, если J2x +1 +
4- . х = 0, т. е. 2х + 1+ х = 0, х = -1/3. Тогда
л/2х + 1
х0 = -1/3 — единственная критическая точка в
рассматриваемом промежутке. Так как
у'(-6/12) > 0, а у'(0) < 0, то х0 — точка
максимума.
Наибольшее значение функции у(х)
достигается в точке -1/3 и равно -9 • f-g j • /2 • I -g J + 1 =
= 7з. Наименьшее значение функции у (х) в
промежутке (-0,5; 0] равно нулю.
Действительно, у(0) = 0, а для всех х из
рассматриваемого промежутка х ^ 0; «ДяТТ > 0, следовательно,
-9х</2х+ 1 > 0. Поскольку и у(-0,5) = 0,
наименьшее значение заданной функции на всем
промежутке [-0,5; 0] равно нулю.
Таким образом, на рассматриваемом
промежутке функция принимает все действительные
значения от 0 до л/3 включительно; среди них —
два целых: Ои 1.
Ответ: 0 и 1.
Замечание. Некоторым учащимся такое решение
наверняка покажется «корявым». Здесь необходимо
сделать ряд пояснений.
1. Использовать стандартный алгоритм
нахождения наибольшего и наименьшего
значений функции, непрерывной на отрезке, здесь
нельзя (функция не является непрерывной в
точке х =-0,5).
2. Учащиеся, знакомые со свойством
односторонней непрерывности в точке (этот материал
отсутствует в учебнике), смогут привести задачу к
виду, когда использование вышеупомянутого
алгоритма допустимо (функция непрерывна на
(-0,5; 0] и непрерывна справа в точке -0,5).
3. Можно использовать стандартный
алгоритм для функции у =-9xV|2x+ 1|,
непрерывной, но недифференцируемой в точке -0,5 и
совпадающей с исходной при -0,5 ^ х < 0.
II способ. По условию, должно выполняться
равенство -9х J2x + 1 = п, где п — целое, а х е
е [0,5; 0]. Пусть j2xT\ = t, откудах = (t2-1)/2.
Если -0,5 < х < 0, то t может принимать любые
значения из промежутка [0; 1]. Задача сводится
к определению всех целых значений, которые
9 9
может принимать функция (p(f) = -о^ -1НВ
промежутке [0; 1].
Функция ф(*) непрерывна и
дифференцируема во всех точках промежутка [0; 1]; <р(0) = 0;
ср(1) = 0, <р'(*) = -«(З*2 - 1). Единственная
критическая точка функции ф(0 на [0; 1] определяется
из условия ф'(*) = 0, т. е. Ы2 - 1 = 0, или t = l/Jb
(0 < t < 1). Так как наибольшее и наименьшее
значения на отрезке непрерывная функция
может принимать либо на концах отрезка, либо в
своих критических точках, лежащих на
отрезке, то
min<p(t) =Ф(0) =ф(1) =0,
Ю;1]
Отсюда следует, что ф(*) в промежутке [0; 1]
принимает два целых значения: 0 и 1. Таким
образом, функция у = -9х*/2х+ 1 в промежутке
[-0,5; 0] принимает два целых значения: 0 и 1.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
699
И
Вариант 13
73. Сравните значения выражений
1ч- cos 40° +cos 80°
sin 80° +sin 40°
cos 105° cos 5° + sinl05° cos 85°
sin 95° cos5°- cos 95° sin 185° *
Преобразуем первое выражение, разложив
cos 80° и sin 80° по формуле двойного угла:
1 + cos 40° + cos 80°
1 + cos40° + 2cos 40°-1
sin 80° + sin 40° 2sin 40° cos 40° + sin 40°
cos40o(l + 2co8 40°) = 4no
sin 40°(1 + 2cos 40°) Ctg 4U #
°(l + 2cos40°)
Числитель и знаменатель второй дроби
преобразуем отдельно, используя формулы
приведения и формулу синуса суммы:
cos 105° cos 5° + sin 105° cos 85° =
= -sin 15° cos 5° + cos 15° sin 5° =
= sin (5°-15°) =-sin 10°;
sin 95° cos 5° - cos 95° sin 185° =
= cos25° - (-sin 5°)2 = cos 10°.
_ -sin 10° , 1ЛО
Второе выражение равно гтг? = -tg 10° .
Поскольку ctg 40° > 0, a -tg 10° < 0,
значение первого выражения больше.
Ответ: значение первого выражения больше.
74. Найдите промежутки возрастания
функции у = | х3 - 2х2 - 8х + 4.
Заданная функция дифференцируема на R.
Находим у' = х2 - 4х - 8. Для определения
промежутков возрастания функции решим неравенство
у'>0. Имеемх2-4х-8>0, если* < 2-2 */3 или
х > 2 + 2 V§ . При этих значениях функция
является возрастающей; поскольку функция
непрерывна при всех действительных х9 числа 2 - 2 л/3
и 2 4- 2 7з также включаются в промежутки
возрастания.
Итак, (-«о; 2-273]и[2 + 2л/3; +«>) —
промежутки возрастания данной функции.
Ответ: (-«о; 2-2^3] и [2+ 2 л/3 ; +°°).
75. Решите уравнение х + 4 + V* + 4 =12.
Решим данное уравнение с помощью замены
переменной t = Jx + 4 . Относительно новой
переменной t уравнение примет вид t2 +1 - 12 = 0,
откуда tx = -4, t2 = 3. Вернемся к переменной х:
= уравнение *Jx + 4 = -4 не имеет корней, а из
уравнения Jx + 4 = 3 получаем х + 4 = 9, т. е. х = 5.
Ответ: 5.
76. Найдите натуральные значения х,
удовлетворяющие системе неравенств
-2х+1
>32,
1(»г
log4(*-6r ^ 1.
Решим каждое неравенство в отдельности.
Для первого из них справедливы равносиль-
ные преобразования:
в)"
> 32; 2
2дс-1
> 2°;
I
4 6 8
Рис. 7
2л:-1 > 5; х> 3.
Второе неравенство выполняется при
одновременном осуществлении двух условий: (х - б)2 > 0
и (х - б)2 < 4, первое из которых выражает
условие существования логарифма, а второе следует
из свойств логарифмической функции по
основанию, большему 1.
Неравенство (х - б)2 > 0 выполняется при всех
х, не равных 6. Неравенство (х - б)2 < 4
перепишем в виде (х - б)2 - 22 < 0, или (х - 8) (х - 4) ** 0,
откуда 4 < х < 8. Таким образом, решениями
неравенства log4(x - б)2 < 1 являются все значения
х из промежутков [4; 6) и (6; 8].
Изобразим решения каждого из двух
неравенств исходной системы на общей оси (рис. 7).
Решение системы — множество [4; 6) и (6; 8].
Элементами этого множества являются четыре
натуральных числа: 4, 5, 7 и 8.
Ответ: 4, 5, 7,8.
77. Вычислите площадь фигуры, ограничен-
1 2
ной графиком функции у = —^х + 1 и касатель-

700
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
ными, проведенными к этому графику в точках
пересечения его с осью абсцисс.
Абсциссы тбчек касания определим из урав-
1 2
нения -т* +1 = 0; они равны 2 и -2. График
функции i/ = -tjc2 + 1 симметричен
относительно оси Оу, касательные к графику проведены
через точки, симметричные относительно этой
оси, а значит, касательная, проведенная к
графику в его точке с абсциссой 2, симметрична
касательной, проведенной к графику в его точке с
абсциссой -2. Таким образом, фигура,
ограниченная параболой и двумя касательными к ней,
симметрична относительно оси ординат.
Воспользуемся этим свойством фигуры для
вычисления ее площади. Искомая площадь в 2 раза
больше площади фигуры, ограниченной парабо-
1 2
лой у = - т х +1, касательной к ней в ее точке с
абсциссой 2 и осью Оу.
Запишем уравнение касательной. Имеем у'(х) =
= -0,5*; у\2) = -1. Так как угловой
коэффициент касательной равен -1 и касательная
проходит через точку (2; 0), то ее уравнение имеет вид
У = 2 - х.
Вычислим искомую площадь:
2 2
2J ((2-x)-(--ix2 + l))dx = 2J (\x2-x + l)dx =
о о
-и<
х - 2Г dx =
_(*-2Г
6
=°-(-!Н
Ответ: 4/3.
78. Сколько корней имеет уравнение Зх2 - х3 =
= а при 0 < а < 4?
После замены а на -а получается задача, в
точности совпадающая с задачей 18. Поэтому
решение данной задачи мы не приводим.
Ответ: три корня.
Вариант 15
85. Вычислите Л (log212 - log23 + 3log*8)0'5 lg 5.
Преобразуем выражение, стоящее в скобках:
log212 - log23 + 31о*з8 = log2y + 8 = 10.
Далее имеем: 10°'51g5 = Л ; Л • Л = 5.
Ответ: 5.
86. Решите уравнение Л sin х cos х = sin2x и
укажите два корня, которые меньше п.
Перепишем уравнение в виде sin х(Л cos х-
- sin х) = 0, откуда либо sin х = 0, либо Л cos х =
= sin х. Из первого уравнения получаем х = кп,
п е Z; из второго находим tgx=V3,x=g+ nk,
k е Z. Среди корней, меньших я, укажем, нап-
ример, 0 и о •
к
Ответ: ял, « + nk; k,neZ;
0 и я/3 — два корня, меньшие я.
87. Найдите область определения функции
У =
2 А '
х -4
ли
I с п о с о б. Заданная функция определена, ес-
> 0. Для решения этого неравенства
2 .
х -4
применим метод интервалов. Областью определе-
2
ния функции f (х) =
х2-4
является вся числовая
прямая за исключением нулей знаменателя, т. е.
точек -2 и 2. Функция f (х) непрерывна в
каждой точке области определения и обращается в
нуль при х = 0. Точки -2, 0 и 2 разбивают
числовую ось на четыре интервала, в каждом из
которых'функция знакопостоянна. Учитывая, что
/ (3) = / (-3) > 0, a f (1) = / (-1) < 0, расставляем
знаки (рис. 8). Поскольку неравенство
нестрогое, значение х = 0 ему также удовлетворяет.
О т в е т: D (у) - (-~; -2) и {0} и (2;+~).
II способ. При х = 0 функция определена.
При х * 0 числитель дроби, стоящей под знаком
корня, положителен, и корень определен при
х2 - 4 > 0. Этому квадратному неравенству
удовлетворяют все значения из промежутков (-«>; -2)
и (2; +°°). Учитывая значение х = 0, получаем
приведенный выше ответ.
-2
0
Рис. 8

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
701
88. Найдите координаты точек касания, в
которых касательные к графику функции у =
2х- 2
= г- имеют угловой коэффициент, равный 4.
Угловой коэффициент касательной к
графику функции в точке графика с абсциссой t равен
значению производной функции в точке t.
2х- 2
Функцию у = ——т- перепишем в виде у = 2 -
4 4
- —г . Находим у'= г
х + 1 (* + 1)
Тогда у'= 4, если
4 2
5 = 4, т. е. (х + 1) — 1» откуда х = 0 или х =
(* + 1)2
= -2. Если х = 0, то у = -2; если х = -2, то у = 6.
Таким образом, имеются две точки касания,
удовлетворяющие условию задачи: (0; -2) и (-2; 6).
Ответ: (0;-2) и (-2; 6).
89. Найдите площадь фигуры, ограниченной
графиком функции f(x) = 2х - 2 и графиком ее
первообразной F (х), зная, что F (0) = 1.
Каждая первообразная функции / (х) может
быть записана в виде х2 - 2х + С, где С —
константа. Используя условие F (0) = 1, для функции
F (х) имеем: F (0) = С; С = 1; F (х) = х2 - 2х + 1,
или2?(х) = (х--1)2.
Найдем абсциссы общих точек графиков
функций /(х) иF(x): (х- I)2 = 2(х- 1); хг - 1; х2 - 3.
При 1 < х < 3 разность / (х) - F(x) = 2(х - 1) -
- (х - I)2 = (х - 1)(3 - х) положительна, поэтому
искомую площадь можно вычислить так:
з
J(2(x-l)-(x-l)2) dx =
i
3 3
= 2j(x-l) dx-J(x-l)2 dx =
l l
-(*-l)V
3
(*-l)
* 3 3
Ответ: 4/3.
90. Определите промежутки возрастания
функции у = |х -3*|.
Запишем данную функцию, раскрыв знак
модуля. Для этого найдем те значения х, при
которых х3 - Зх > 0. Решим это неравенство методом
интервалов. Корнями уравнения х3 - Зх = 0, или
х(х2 - 3) = 0, являются числа 0, -7з и Jb .
Рассмотрим функцию / (х) = х(х - </3 )(х + 7з).
Имеем / (3) > 0. Функция f (х) меняет знак при
переходе через каждую из точек - 7з, 0 и 7з .
Расстановка знаков приведена на рис. 9. Таким
образом, исходную функцию можно записать в
виде
х3-3х прихе [-73;0]и[73;+оо),
У =
-х3 + 3х прихе (-°o;-V3)u(0;V3).
В промежутках своего знакопостоянства
функция у дифференцируема, причем
Г Зх2-3 при х е (-73;0)и(*/3 ;+«>),
1-Зх2 + 3 прихе (-оо;-73)и(0;73).
Функция непрерывна при любом
действительном х, однако вопрос о ее дифференциру-
емости в точках 0 и ±л/3 мы обсуждать не
будем, поскольку на дальнейшем исследовании
это никак не отразится.
Нулями производной функции у являются
числа -1 и 1. Составим таблицу
монотонности функции, для чего определим знак
производной функции в каждом из шести интервалов:
У,(-3)<0; irt-1,6) >0; i/'(-0,5) < 0; j/'(0,5) > 0;
у\1,Ь) < 0; i/'(3) > 0. Тогда получим
(73;+~)
+
71
Учитывая непрерывность исходной функции,
заключаем, что имеются три промежутка ее
возрастания, а именно: [-*/3 ; -1], [0; 1] и [ 7з ; +°°).
Ответ: [-Л ; -1], [0; 1] и [Л ;+~).
Вариант 17
97. Найдите точки пересечения графиков
ФУНКЦИЙ I/ = X + 1 И I/ = Jl-x.
X
У'
У
(-~ ;-7з)
—
*
(-л/3;-1)
+
71
(-1; 0)
—
а
(0;1)
+
71
(1; л/3)
—
*
-зг
о
Рис. 9
7з

702
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Задача сводится к решению уравнения х + 1 =
- л/Г^Х.
Возведем обе его части в квадрат, учитывая
при этом условие х + 1 > 0 (*). Имеем: х2 + 2х + 1 =
= 1 - х; х2 + 3* = 0; хг = 0, х2 = -3. Из
найденных значений х условию (*) удовлетворяет
только х = 0. Координаты единственной общей
точки двух графиков таковы: х = 0, у = 1.
Ответ: (0; 1).
98. Решите уравнение 2 sin2 ( ^ + х ] - 5 cos (тс -
- х) + 2 = 0. Укажите те значения х, при
которых sin х > 0.
Используя формулы приведения, перепишем
исходное уравнение в виде 2 cos2* -I- 5 cos х + 2 =
= 0. Решив его как квадратное относительно cos х,
получим либо cos х = -2, что не выполняется ни
при каких х, либо cos х = -0,5, что имеет место
при х = ±-«- -I- 2тсА, А е Z.
Отберем корни уравнения, удовлетворяющие
неравенству sin х> 0, с помощью
тригонометрической окружности (на рис. 10 штриховкой
отмечена область, для точек которой sin х > 0).
Указанному неравенству удовлетворяют значения
х = "з" + ^я*' * G ^'
2я
Ответ: =ь-тг + 2яЛ, k е Z; условию sin х> 0
2я
удовлетворяют -=- + 2nkt ke Z.
99. Решите систему неравенств
4
l + log3(*-4) < log3(x + 21).
Преобразуем первое неравенство. Умножив обе
части этого неравенства на положительное
выражение 4* + \ получим 24х + 2>4* + 1. Далее имеем:
42* + i >4* + 1;2х+1>х + 1;х>0.
Для решения второго неравенства
преобразуем его к виду log33(x - 4) < log3(x +21).
Функция у = log3t возрастает на всей своей области
определения, т. е. при t > 0. Учитывая это
свойство, от логарифмического неравенства
перейдем к равносильному ему двойному неравенству
0 < 3(х - 4) < х + 21. Из его левой части получаем
х > 4, из правой Зх - 12 < х + 21; х < 16,5.
Решением исходного логарифмического неравенства
является промежуток (4; 16,5]. Все числа из
этого промежутка удовлетворяют неравенству х > 0,
т. е. являются также решениями первого
неравенства данной системы, а значит, решение
исходной системы неравенств представляет собой
указанный промежуток.
Ответ: (4; 16,5].
100. Постройте график функции y = xs- Зх2 +
+ 2 на отрезке [-0,5; 3]. Укажите множество
значений функции на этом отрезке.
Исследуем непрерывную и
дифференцируемую на R функцию у = х3 - Зх2 + 2 с помощью
производной. Имеем у' = Зх2 - 6х = Зх(х - 2);
у'= 0 при х = 0 и при х = 2. Учитывая, что
-0,5< х < 3, построим таблицу монотонности
для этого промежутка:
X
У'
У
[-0,5; 0)
+
Я
{0}
0
2
(0; 2)
—
*1
{2}
0
-2
(2;3]
+
71
Рис. 10
Для нахождения абсцисс точек пересечения
графика функции с осью Ох разложим
многочлен х3 - Зх2 + 2 на множители следующим
образом: х3 - Зх2 + 2 = х3 - х2 - (2х2 - 2) = х2(х - 1) -
- (2х + 2)(х - 1) = (х - 1) (х2 - 2х - 2). Нулями
многочлена х3 - Зх2 + 2 являются числа 1 и 1 ± V3 , из
которых отрезку [-0,5; 3] принадлежат 1 и 1 + J3 .

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
703
Для более точного построения графика
возьмем еще несколько контрольных точек:
-0,5
1,125
0,5
1,375
2,5
-1,125
3
2
Строим график (рис. 11) и с его помощью
определяем, что множеством значений функций
является отрезок [-2; 2].
Ответ:Я(у) = [-2;2].
101. Вычислите площадь фигуры,
ограниченной параболой у = 4я - х2 и прямой, проходящей
через точки (4; 0) и (0; 4).
Запишем уравнение прямой, проходящей
через точки (4; 0) и (0; 4). Подставив в уравнение
прямой у = ах + Ъ координаты заданных точек,
получим систему уравнений 4 = а-0 + ЬиО = 4а +
+ Ь, откуда найдем а = -1, Ь = 4. Следовательно,
уравнение прямой имеет вид у = 4 - х.
Абсциссы общих точек прямой и параболы
определим из уравнения 4* - х2 = 4 - х, или
(4 - х)(х - 1) = 0. Искомую площадь вычислим
как разность площадей криволинейной
трапеции AM ВС и треугольника ABC (рис. 12).
Ордината точки А равна 3, и площадь треугольника
ABC равна ^АС*СВ = 4,5. Далее найдем
площадь криволинейной трапеции AM ВС:
4 2 2 Л!'
SAh/n*n = \{±х-х2) dx = f2x2-yj =
°АМВС
-(„-¥)-(,-$)-..
Итак, площадь искомой фигуры равна 9 - 4,5 =
= 4,5.
Ответ: 4,5.
102. На графике функции у = х2 найдите
точку М с положительной абсциссой, ближайшую
кточкеА(0;3/2).
Пусть t — абсцисса точки М. Так как М
принадлежит графику функции у = х2, то ее
ордината равна t2. Квадрат расстояния между точками
А (0; 3/2) и М (t; t2) по известной формуле равен
(t - О)2 + (t2 - 1,5)2 = t4 - 2t2 + 2,25.
Расстояние между точками есть величина
неотрицательная, поэтому минимум расстояния
достигается при таком же t, при котором
достигается минимум квадрата расстояния.
Учитывая данное в условии ограничение t > 0,
сформулируем условие задачи следующим образом: при
каком положительном значении t функция / (t) —
= t4 - 2t2 + 2,25 принимает наименьшее значение?
Для ответа на этот вопрос исследуем
функцию f(t) с помощью производной. Находим f (t) =
= 4*3 - 4t = 4t(t + 1) (t - 1). Если 0 < t < 1, то f (t) <
< 0, и функция / (t) убывает; если же t > 1, то
f(t) > 0, и функция / (t) возрастает. При t = 1
производная меняет знак с минуса на плюс,
поэтому t = 1 — точка минимума. Таким образом,
минимум функции / (t), а значит, и минимум
расстояния между точками АиМ при t > 0
достигается, если t = 1. Итак, точка М имеет
координаты (1; 1).
Ответ: М(1; 1).
Замечание. Значение t, при котором достигается
минимум функции / (0 = tA - 2t2 + 2,25, можно было
найти и без использования производной. При поло-
Рис. 11
Рис. 12

704
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
жительных t функция и — t принимает все
положительные значения. Сделав подстановку ust2,
получим квадратичную функцию от и вида и2 - 2и + 2,25,
минимум которой достигается при и = 1. Этому
значению и соответствует t = 1. Отсюда следует, что
функция f (t) принимает наименьшее значение при
t = 1.
Вариант 19
109. Найдите область определения функции у =
J:
_ 35-2x-jc
Функций существует при одновременном
выполнении двух условий: 35 - 2х - X2 > 0 и lg х Ф 0.
Решениями квадратного неравенства 35 - 2х - х2 >
> 0, или (х - Ъ)(х + 7) < 0 являются все значения,
принадлежащие отрезку [-7; 5]. Далее, lg х Ф 0,
если х> 0 (условие существования логарифма) и
хф 1.
Оба указанных условия выполняются
одновременно при х е (0; 1) и (1; 5] (рис. 13).
Ответ: D(y) = (0; 1)и(1;5].
110. Решите уравнение sin2* - ^sin2jc = 0.
Укажите корни, принадлежащие промежутку
(я/2; 2я).
Используя формулу синуса двойной) угла,
преобразуем исходное уравнение к виду sin2* - sin х х
х cos х = 0, или sin х • (sin х - cos х) = 0.
Последнее равенство выполняется, если sin х = 0 или
sin х = cos х.
Если sin х = 0, то л: = яп, где пе Z.
Уравнение sin х = cos х равносильно
уравнению tg х = 1, откуда следует, что х = т + яЛ, где
fce Z.
Отберем корни, принадлежащие интервалу
(тс/2 ; 2л). Для первой серии решений имеем
неравенство я/2 < ял < 2я, откуда 1/2 < п < 2.
Единственному целому числу л = 1,
удовлетворяющему этому неравенству, соответствует
корень х = тс. Для второй серии решений получим
тг тг 17
2 < т + яй < 2тс, откуда т < ft < т. Последнему
неравенству удовлетворяет целое k = 1, которому
соответствует jc = 5тс/4. Итак, интервалу (я/2; 2я)
принадлежат два корня исходного уравнения: я
и 5я/4.
я
Ответ: ял, т + яЛ; ktne Z.
4
5я
принадлежат ли-т.
Промежутку ( «; 2я 1
111. Решите систему уравнений
2Х~У = 4*,
6 1 -
- + г- = 1.
х Ъу
В результате несложных выкладок из первого
уравнения имеем: 2х " у = 22у; х - у = 2у; х = Зу.
Подставив последнее соотношение во второе
2,1 - 11 1
уравнение, получим - + т- = 1, или г- = 1, или
у = -г-; у = 2,2. Отсюда находим л: = 6,6.
Ответ: (6,6; 2,2).
112. Решите уравнение log5(6 - 5х) = 1 - х.
Представим правую часть исходного
уравнения как log55x " х. Используя условие равенства
логарифмов по одинаковым основаниям,
заменим уравнение равносильной ему системой
6-5х = 51 *,
1-х
-7
0 1
Рис. 13
Выражение 5 при всех х
6-5л>0.
положительно, поэтому и равное ему выражение
6 - 5* также положительно: следовательно,
условие 6 - 5х > 0 будет выполнено для всех х,
удовлетворяющих уравнению 6 - 6х = 51 "*. Для
решения этого уравнения умножим обе его
части на 5х. После очевидных преобразований
придем к уравнению 52х " б • 5* + 5 = 0, т. е. к
квадратному уравнению относительно t = 5х. Решив
его, находим tx = 1, t2 = 5, откуда хг = 0, х2 =1.
Ответ: 0; 1.
113. Составьте уравнение касательной к
графику функции у = -Зх2 + 6х + 1 в точке пересе-

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
705
чения этого графика с осью ординат. Вычислите
площадь фигуры, ограниченной графиком
данной функции, найденной касательной и прямой
х = 2.
Угловой коэффициент касательной,
проведенной к заданной параболе в точке ее пересечения с
осью ординат, т. е. в точке с абсциссой х0 = 0,
равен значению производной квадратичной
функции в точке 0. Так как / (х)= -Зх2 + 6х + 1, то
f (х) = -6х + 6, откуда у'(0) = 6. Уравнение
касательной имеет вид у - / (0) = f(0) • х, или у =
= 6х+1.
При(Кх<2имеем -Зх2 + 6х+ 1 <6х+
1,поэтому площадь заданной фигуры можно
вычислить так:
[-тс/2; тс/2] принадлежит одно число из этой
серии: х = я/2, совпадающее с одним из концов
отрезка.
Из уравнения sin х = -0,5 находим х = (-1)л§ +
+ яя, пе Z. Для определения тех целых значений
д, при которых указанные х попадут на отрезок
[-я/2; я/2], рентам неравенство -« <(-l)ng +
+ яя < g » и™ ~"о п1 (5 ) 2 ' ри четных
я неравенство преобразуется так: ~о ^ б71 ^ 2'
3 3
или -= < я < = . Ему удовлетворяет только я = 0.
J«6*+l)-<-8*4e* + l)) <fa- 1Цш»«тшж|.шягпш-$<»(1-£)<§, ни
J»
- |3х* dx =х°|0 =8.
Ответ: у = 6х+1; 8.
114. Найдите множество значений функции
у = 2cos х - sin 2х на отрезке [-я/2; я/2].
I с п о с о б. Функция у = 2 cos х - sin 2х
непрерывна при всех действительных значениях х, а
значит, непрерывна и во всех точках
рассматриваемого отрезка. Для определения множества
значений данной функции на отрезке
достаточно найти ее наибольшее и наименьшее значения
на этом отрезке. В свою очередь, для их
нахождения необходимо вычислить значения
функции на концах отрезка и в критических точках
функции, принадлежащих заданному отрезку, а
затем выбрать из полученных значений
наименьшее и наибольшее. Эти два числа будут
являться границами отрезка, задающего искомое
множество значений.
Найдем критические точки функции. Имеем
у' = -2sin х - 2cos 2х = -2(sin х -I- cos 2х) =
= -2(sin х + 1 - 2 sin2x) = 2(2sin2x - sin x - 1) =
= 2(sin x - 1) (2sin x + 1).
Производная обращается в нуль, если sin х = 1
или sin х =-0,5.
Из уравнения sin х = 1 находим х = ^ + 2я*,
fe е Z. Нетрудно установить, что отрезку
3 3
-г < я < г. Нечетных я, удовлетворяющих
последнему неравенству, нет. Таким образом,
единственным корнем уравнения sin х = -0,5,
принадлежащим заданному отрезку, является я/6.
Вычислим значения исходной функции в
точках -я/2, я/6 и я/2: у(-|) = 0; у(|) = 2 • ^ -
~~ (~т) = 2 ; у{ъ) = °' сУчетом Указанных
выше замечаний заключаем, что множество
значений функции у = 2 cos х - sin 2х представляет
собой отрезок [0; 3 7з /2].
Ответ:Д(у) = [0;373/2].
II с п о с о б. Определим, при каких а уравнение
2 cos х - sin 2х = а, или 2 cos х(1 - sin х) = а (*)
имеет решение в промежутке [-я/2; я/2].
Множество таких а будет совпадать с множеством
значений заданной функции. В указанном
промежутке и cos х, и 1 - sin х принимают
неотрицательные значения, поэтому а > 0. Возведя в
квадрат обе части уравнения (*), получим 4 cos х х
x(l-sinx)2 = a2.
Далее преобразуем левую часть последнего
уравнения и оценим ее, используя неравенство
между средним арифметическим и средним
геометрическим четырех чисел:
4 cos2 х(1 - sin х)2 =
= 4(1 + sin х) (1 - sin х) (1 - sin х)(1 - sin х) =
23-1019

706
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
= о (3 + 3 sin х) (1 - sin х) (1 - sin х) (1 - sin х) <
^ 4/3 + 3 sin х + 1 - sin х + 1 - sin х + 1 - sin jc\4
и во втором случаях, дают одно и то же множество
значений.
*е
] = 122. Решите неравенство 4* х < [«)
1\Здг + 2
4 6^ = 27
3'44 4
Здг + 2
Перепишем неравенство в виде 4 < 4
Равенство достигается, если 3-1-3 sin jc = 1 -
- sin jc, т. e. sin х = -0,5. Последнее равенство
выполняется при х = -тс/6.
Из неравенств а2 < 27/4 и а > 0 получаем 0 <
< а < 3 7з /2. Учитывая, что функция у = 2 cos jc -
- sin 2jc непрерывна, а также то, что она
принимает значения 0 (например, при jc = я/2) и 3*/3 /2,
устанавливаем, что множеством значений
заданной функции на промежутке [-тс/2; тс/2]
является отрезок [0; 3 7з /2].
Так как у = 4* — монотонно возрастающая
функция, то можно перейти к равносильному
нерезв* 2
венству: 1 - jc< —
; 2 - 2jc < -3jc - 2; jc < -4.
Вариант 21
121. Решите уравнение
cos 2jc + sin
(-¥)=<>.
Пользуясь формулами приведения
тригонометрических функций, получим уравнение cos 2jc -
- cos jc = 0.
Приведем два способа решения этого
уравнения.
I с п о с о б. Используя формулу двойного
аргумента для косинуса, приведем уравнение к виду
2cos2jc - 1 - cos jc = 0, или (2 cos jc + 1) (cos jc -
- 1) = 0. Отсюда cos jc = -0,5, jc = ±-5- -I- 2nn, n e Z,
или cos jc = 1, jc = 2nk, k g Z.
2nk - „
О т в e т: jc = -5- , k e Z.
II с п о с о б. Используя формулу
преобразования суммы косинусов в произведение, получим
-2 sin 5 sin -5- =0, откуда sin 5 = 0, jc = 2кп, пе Z
. Зх Л 2nk . „
или sin -£- = 0, jc = -5- , л g Z.
Заметим, что первая серия ответов (jc = 2nk)
полностью включается во вторую.
Замечание. Решив уравнение двумя способами,
мы получили разные по форме ответы. Нетрудно
убедиться (например, используя тригонометрический
круг), что формулы для ответа, полученные в первом
Ответ: (-<»: -4].
123. Найдите произведение корней
уравнения (3jc2 - 4jc - 7) • log3 (2 - jc) = 0.
Произведение двух множителей равно нулю,
если хотя бы один из них равен нулю, а другой
при этом определен. Заменим данное уравнение
равносильной ему совокупностью:
3jc -4jc-7 = 0,
2-jc>0, <=>
log3(2-*) = 0
124. Является ли прямая у = 1 - jc
касательной к графику функции у = jc + е~2х1 Ответ
обоснуйте.
Для того чтобы прямая у = ах + Ъ являлась
касательной к графику функции у = / (jc),
необходимо и достаточно существование такой
точки графика функции у = / (jc) с абсциссой jc0,
чтобы выполнялись следующие требования:
|-ах0 + Ь = f(x0),
[а = Г(х0).
В данном случае
-2хп f _ -2хп
\х =
X =
х<
1-х
-1,
7
3'
2,
= 1
ч
Ответ:
"JC =
. JC =
хгх2
-1,
1.
= -1
1 - *о = *о + е
-1 = 1-2е
-2х0
1-2jc0 = е
-2хп
<=> jc0 = 0.
= 1
Поскольку такая точка существует, данная
прямая является касательной к графику данной
функции.
Ответ: да, является.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
707
125. Найдите площадь фигуры, ограниченной
графиком функции у = J tdt и прямой у = 1,5.
Вычислим интеграл:
*2 + i
J tdt = 0,5t4
,*2 + i
= 0,5((х2 + l)2 - jc4) = х2 + 0,5.
Таким образом, задача сводится к
нахождению площади фигуры, ограниченной параболой
у = х2 + 0,5 и прямой у = 1,5. Найдем пределы
интегрирования: х2 + 0,5 = 1,5, откуда х12 = ±1.
Следовательно, площадь фигуры равна значе-
1
нию интеграла J (1,5 - х2 - 0,5) dx. Окончатель-
-1
но получим
3i/ + jc = 0, \х = -3,
бу-х = 9 ^1 у = 1;
Зу + jc = 9, (х = 6,
6i/-x = 0 ^[у = 1;
3i/ + jc = 9, Jjc = 3,
бу-х = 9 **\у = 2.
Ответ:(0;0);(-3;1);(6;1);(3;2).
II способ (замена переменных). Пусть
' 2
и = Зу + jc,
и ^ 0,
2
u = V3y + jc,
J (1 - jc2) djc = 2 J (1 - jc2) dx = 2hc-|-J
У = л/бу-JC
Следовательно, jc =
система примет вид
у = 6j/-jc,
у ^ 0.
о 2 2
2ы -У
У.=
2 2
И + У
, И
Ответ: 4/3.
126. Решите систему уравнений
\2j3y + x- J6y-x = jc,
2u-v =
и > 0,
у £ 0,
м + у =
о 2 2
2ы - у
\6u-3v = 2и2-у2,
~< 2 2**
Зц + Зу = и + у
2 , 2
IX +У
1*/Зу + jc + *Jby-x = Зу.
I способ (способ алгебраического
сложения). Складывая уравнения, получим 3 V3 у + jc =
= Зу + jc. Вычитая из удвоенного второго
уравнения первое, получим 3 */6у-х = 6у - jc. Имеем
[3V3i/ + jc = Зу + jc,
[3V6i/-jc = 6у-х
[V3i/ + jc(3- J3y + x) = 0,
J6y-x(3-j6y-x) = 0
гЗу + JC = 0,
|_3у + х = 9;
Гбы-Зу = 2и -v,
<=>^ 2 <=>
9и = Зи
и = 0,
у = 0,
гбу-х = 0,
L6y-JC = 9.
Данная система сводится к четырем
системам линейных уравнений:
Зу + х = 0, Jjc = О,
бу-х = 0 **\у = 0;
и = О,
у = 3,
и = 3,
у = О,
ц = 3,
у = 3,
и = О,
о 2
Зу = у ,
и = 3,
18-Зу = 18-у
jc = О,
у = о,
х = -3,
у = 1,
2
откуда получим
\х = 6,
[У = 1.
jc = 3,
У = 2.
23*

708
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Вариант 23
133, Решите неравенство log1/7 (2х - 1) > -1.
Перепишем неравенство в виде \ogl/7(2x - 1) >
> log1/77. Учитывая область определения
логарифмической функции и монотонное убывание
функции у = log1/7t на всей области
определения, перейдем к равносильной системе:
2х-1<7, Гх<4,
2*-1>0 <^>[х>09Ъ.
Ответ: (0,5; 4).
134. Вычислите ординату точки пересечения
графиков функций
у = 0,32*-3:
"-(4Г
Сначала найдем абсциссу точки пересечения
графиков данных функций:
о,з— -(si)* .($■- -(f)' «3-*-,
Таким образом, абсцисса точки пересечения
х0 = 1. Ордината точки пересечения у0 = I 3g) ,
т. е. У0 = Зз '
Ответ: 10/3.
135. Найдите критические точки функции
у = sin Ъх cos 3* - cos Ъх sin 3*.
Согласно формуле синуса разности двух
аргументов получим sin Ъх cos 3* - cos Ъх sin Zx =
= sin 2x. Функция у = sin 2x дифференцируема
на Я. Имеем у' = 2 cos 2х. Чтобы найти
критические точки функции, решим уравнение у' = О,
или 2 cos 2х = 0, откуда * = т + « Л» Л е ^*
Л ПК „
Ответ: х=т + £ л, n € Z.
136. При каких значениях а число 2 является
корнем уравнения Jx-a = За - лг?
Так как х = 2 является корнем данного
уравнения, то необходимо и достаточно, чтобы
выполнялось условие л/2-а = За - 2. Будем
рассматривать это равенство как уравнение
относительно а. Перейдем к равносильной системе
f2-a = (3a-2)2,
[3a-2 > 0.
Решив уравнение 2 - a = 9a - 12a + 4, или
9a2 - 11a -I- 2 = 0, найдем ax = 1, a2 = 2/9.
При at = 1 имеем 3 • 1 - 2 > О, т. е. это
значение а удовлетворяет системе; при а2 = 2/9 имеем
3 • 2/9 - 2 < 0 — это значение а не удовлетворяет
системе, а значит, не является корнем
уравнения.
Ответ: приа = 1.
137. Найдите площадь фигуры,
ограниченной графиком функции у = — и прямыми у = О,
х = -5, х = -2,5. Не пользуясь
микрокалькулятором, сравните полученное значение площади с
числом 2.
Данная фигура — криволинейная трапеция,
ограниченная графиком функции у = --,
отрезком [-5; -2,5] оси Ох и прямыми х = -5 и х — -2,5
2
(рис. 14). Так как у = — > 0 при jc е [-5; -2,5],
то площадь криволинейной трапеции S
находится следующим образом:
-2,5
-' В)
dx = 21п |*|
-2,5
-5
- -2(1п 2,5 - In 5) - - 21п 0,5 = In 4.
Так как 4 < в2, то 1п4 < 2.
Ответ:5 = 1п4;5<2.
Замечание. Сравнение числового значения
площади криволинейной трапеции с числом 2 можно
провести, пользуясь рис. 14:
S<SiUCJ)-CD.iU)-|.|-2.
А-5

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
709
138. Является ли прямая у = 2 - х
касательной к графику функции у = х +2е~*? Ответ
обоснуйте.
Для того чтобы прямая у = 2 - х была
касательной к графику функции у — х + 2е~х,
необходимо и достаточно существование такой точки,
для абсциссы х0 которой выполняются условия
\f(x0) = 2-*0,
Пх0) = -1,
где / (х) = х + 2е~х, т. е.
2-х0 = х0 + 2е
\-2е и = -1
1-*о = е
= 1
<=>х0 = 0.
Следовательно, такая точка существует.
О т в е т: да, является.
Вариант 25
Зх-1
145. Решите уравнение (0,4) = (2,5)* +х.
Перепишем уравнение так, чтобы правая и
левая его части представляли собой степени с
одним и тем же основанием (так как 0,4 = (2,5)-1).
Имеем
откуда
(2,5)
Зх-1
Зж-1
5
чДГ+1
= (2,5)л
= х+1,* = -0,5.
Ответ: -0,5.
146. Вычислите ординату точки пересечения
графиков функций у = log2(x + 1,5) и у = -log2*.
Сначала найдем абсциссу точки пересечения
графиков данных функций:
log2(x + 1,5)= -log2x, или log2(x + 1,5) = log2- ,
откуда
х+1,5 = -, [2х2 + 3*-2 = 0,
х+1,5 >0
х>-1,5
гх = 0,5 ,
1х = -2,
х>-1,5 .
Следовательно, х = 0,5 — абсцисса точки
пересечения графиков. Найдем ординату этой
точки: у = log2(0,5 + 1,5) = 1.
Ответ: 1.
147. Найдите область определения функции
У =
/2
ух +
2х+1
х-1
Область определения функции найдем,
решив неравенство
fL±^±l>0o(£ll)!>0
х-1 *~1,
Воспользуемся методом интервалов. Для это-
( l\2 {
го рассмотрим функцию f(x) = -——г— • ^на не
определена при х = 1, непрерывна в каждой
точке области определения и обращается в нуль при
х = -1. Отметим указанные точки на оси Ох; они
разбивают область определения на три
промежутка (рис. 15). Определим знак функции в
каждом из них: / (2) > 0, / (0) <0, / (-2) < 0.
Ответ: {-1}и(1; +«>).
Замечание. Если от записи у
|*+и
/*2 + 2х + 1
4 х-1
Jx~^\'
перей-
то при этом возможна потеря
ти к записи у -
точки х = -1.
148. Найдите критические точки функции
у = sin 2х -I- 2 cos х - 2х.
Так как данная функция дифференцируема
на Ry то ее критические точки определяются из
условия у' = 0. Имеем
2 cos 2х - 2 sin х - 2 = 0; cos 2х - sin х - 1 = 0;
1-2 sin2* - sin х - 1 = 0; sin х (2 sin х + 1) = 0 ;
г sin х = 0, rsin х = 0,
|_2 sin х + 1 = 0 Lsin х = -0,5
х = теп, пе Z,
X = (-1)
6
+ яА, ke Z.
Ответ: яп, (-1) g + nfc; n9keZ.
-1 1
Рис. 15

710
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
149. Для каждого а > 0 найдите площадь
фигуры, ограниченной графиком функции у = -х3 +
+ ах2 и осью абсцисс. При каких значениях а
эта площадь равна 4/<&
Найдем точки пересечения графика функции
у = -х3 + ах2 с осью Ох: -х3 + ах2 = 0, х2(а -- х) = О,
хг = 0, х2 = а.
Изобразим схематически график функции
f(x) = -х3 + ах2 при а > О (рис. 16). Для этого
найдем производную у' = -Эх2 + 2ах и
определим промежутки возрастания и убывания
функции (рис. 17). Имеем / (jc) > 0 при 0 < х < а,
поэтому искомая площадь S выражается
следующим образом:
S-J(-*» + «,»)cte-(-£- + 2§-)
а
12 е
Но S = 4/3, или а4/12 = 4/3, откуда а4 = 16.
Учитывая, что а > О, находим а = 2.
О т в е т: S = а4/12; S - 4/3 при а - 2.
150. Найдите абсциссы всех общих точек гра-
4
х - г-? и касательной, прове-
фика функции у
денной к графику этой функции в точке с аб
сциссойх0 = -2.
Запишем данную функцию так:
У =
4
4
х + -
при х > О,
при х < 0.
Уравнение касательной к графику этой
функции в точке с абсциссой х0 = -2 имеет вид
у- у (-2) = у'{-2){х + 2), где i/(-2) = -4.
Вычислим ^(-2). Так как -2 < 0, то
jrtx)-(* + £)'- l-±;y'(-2) = 0.
У -
+ -
3
Значит, уравнение касательной есть у = -4.
Абсциссы общих точек графика функции и
касательной должны удовлетворять следующим
условиям:
х + - = -4,
х или
1х<0
Отсюда находим
х2 + 4х + 4 = 0,
х<0
или
х-- = -4,
х>0.
х + 4х-4 = 0,
х>0,
т. е. х = -2 или
Рис. 16
Рис. 17
Гх = -2 + 2«/2,
[х = -2-272,
1х>0.
Итак, х = -2 или х = -2 + 2 72 .
Ответ: -2, -2 + 2«/2.
Замечание. Возможная ошибка: неверное
рассуждение о том, что касательная имеет с графиком
функции только одну общую точку, т. е. точку касания.
При этом дается один ответ х = -2, и ученик
удивляется простоте задания. В этом случае задание
считается невыполненным.
Вариант 27
157. Решите неравенство
log06(4-х) > 21og053 + log05l.
Перепишем данное неравенство в виде
log0 5(4 - х) > log0 5 9. Так как у = log0 bt —
монотонно убывающая функция на всей области
определения, то (с учетом области определения)
переходим к системе неравенств
4-х < 9, \х > -5,
Л <=>1 л <=>-5<х<4.
4-х>0 [х<4
Ответ: [-5; 4).
158. Найдите промежутки убывания
функции у = х(3 - х2).
Для нахождения промежутков убывания
данной функции решим неравенство у' < 0:
у = х(3 - х2) = Зх - х3; у' = 3 - Зх2,
3 - Зх2 < 0, х2 - 1 > 0, х2 > 1, |х| > 1.
Следовательно, у' < 0 при х < -1 и х > 1 . Так
как данная функция непрерывна, то точки -1 и

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
711
1 включаются в промежутки монотонности,
поэтому у убывает при х<-1их>1.
Ответ: функция убывает
в промежутках (-«>; -1] и [1; +<*>).
159. Решите систему уравнений
8-2* = 41'5**0'5,
5 " 25 5 '
В каждом уравнении системы представим
левые и правые части уравнений как степени с
одинаковыми основаниями и далее используем
свойство монотонности показательной функции: *
\2У*3 = 23* + 1
трапеция, а парабола проходит через ее
вершины Б и С (рис. 18). Для вычисления искомого
отношения найдем площадь S трапеции ABCD,
площадь ее заштрихованной части Sx и затем
площадь незаштрихованной части трапеции S2 =
= S-Sv Имеем
S = \{AD + BC)h = | (8 + 4)-4 = 24.
Так как ^ х2 + 2 < 4 при -2 < х < 2, то
sx= J(4-(i*2+2)) dW(2-T) d*=
i/ + 3 = Здс + 1, Где = 4,
U2x = б""2
Ответ: (4; 10).
160. Решите уравнение (sin 2х) • л/TV =0.
Произведение двух множителей равно нулю,
если хотя бы один из них равен нулю, а другой
при этом определен:
fsin 2х = 0,
=*/И)
dx
(использовали правило интегрирования четной
функции), откуда
4-х > 0
,2 =
или 4 - х2 = 0.
/(«-т)*"-(«—х)
•S,-2-2§ -5|;S2
-<-|-Ф
24
4
Имеем: 4 - х = 0 при х = ±2;
sin 2* = 0 при х = у , ft е Z;
4- х2£0,х2-4<0,х2<4, |х| <2,-2<х<2.
Среди чисел вида у выберем такие, которые
принадлежат отрезку [-2; 2].
Если к = 0, то х = 0; если А = 1, то х =
= 2 f - < 2 J j если ft > 1, то х> у =тс>2; если А =
= -1,то* = -| [-2>-2];еслиЛ<-1,то х<—g- =
= -тс<2.
Неравенству 4 - #2 > 0 удовлетворяют числа
вида nk/2 при Л = -1, 0, 1.
О т в е т: {2; -2; к/2; -я/2; 0}.
161. В каком отношении делится площадь
четырехугольника ABCD, где А (-4; 0), В(-2; 4),
С(2; 4), D(4; 0), параболой i/ = | *2 + 2?
Изобразив четырехугольник и параболу на
координатной плоскости, убедимся, что ABCD —
100» О Q • О П«
'3' So
3 # 3
Ответ: 2:7 (или 3,5; возможен ответ: 7:2).
162. На графике функции у = |3х - 2|
найдите точку, ближайшую к точке А(3; 0).
Запишем данную функцию следующим
образом:
У =
3*-2 при х > 2/3,
2-3* при* < 2/3
Рис. 18

712
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
и изобразим ее график на координатной
плоскости (рис. 19).
I способ. Пусть В(х0; |3jc0 — 2|) —
ближайшая к А точка графика. Тогда
АВ2 = (х0-3)2 + (|Зх0-2|-0)2;
АВ2 = х20 - 6*0 + 9 + 9*о - 12х0 + 4 =
= 10*о -18х0+13.
Расстояние АВ минимально при том же
значении х0, при котором минимально значение АВ2.
Исследуем квадратный трехчлен 10*2 - 18jc +
+ 13. Его наименьшее значение достигается при
1 л
х = оТТл = ^»9- Таким образом, АВ2 принимает
минимальное значение при х0 = 0,9; тогда
В (0,9; |3 • 0,9 - 2|), т. е. 5(0,9; 0,7).
Ответ: ближайшая точка В (0,9; 0,7).
II способ (геометрический). Искомая
точка В является основанием перпендикуляра, про-
2
веденного из точки А к прямой MF; AM = 3 - « =
= 2|т; tg Z. ВМА = 3 (угловой коэффициент
прямой).
Из АМВА и АМВВг (рис. 20) имеем MB =
\ 14 14
= AM cos а; МВг = MB cos а = « cos2a = « х
1 +tg а
Абсцисса точки В равна 0,9, а ее ордината
равна |3* 0,9 -2| =0,7.
Итак, (0,9; 0,7) — координаты искомой точки.
III способ. Уравнение прямой, проведенной
через точку А перпендикулярно прямой у = 3* - 2,
имеет вид у = -= х + 1.
Найдем точку пересечения этих прямых:
У = Зх-2, гж = 0,9,
«*•_!_ 1 I
1 ^
у = -о*+1 U = 0,7.
Вариант 29
169. Вычислите
(3 log72 - log724): (log73 +log79).
Чтобы найти числовое значение данного
выражения, проведем ряд преобразований,
связанных со свойствами логарифмов:
(3 log72 - log724): (log73 + log79) =
-log73 i
= (log78 - log724): log727 = j-^j-j = -g.
Ответ: -1/3.
170. Решите уравнение J3x+ 1 = x - 1.
I способ. Возведя обе части уравнения в
квадрат и учитывая при этом, что х - 1 > 0,
получим
Зх + 1 = (*-1)2, <=Jx2-5* = 0, ^
х-1 > 0
х >1
<=>
-х = 0,
Г* = U,
[Ьс = 5, <=> jc = 5.
х > 1
II способ. Сделаем замену J3x+ 1 = и. Тог-
да и > 0 и jc =
ц2-1
Исходное уравнение примет
2 ,
вид м = ^-= 1, или и2 - Зи - 4 = 0, откуда иг =
= -1, и2 = 4. Значение иг не удовлетворяет
условию и > 0; при м = 4 получим jc =
42-1
= 5.
Ответ: 5.
Рис. 20
171. Решите неравенство 4х - 3 • 2х - 4 < 0.
I способ. Обозначим 2х через t (t > 0); тогда
данное неравенство примет вид t2 - 3t - 4 < 0.
Решив его, находим -1 < t < 4. Так как t > 0, то
0 < * < 4, или 0 < 2х < 4. Для любых значений х

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
713
имеем 2х > 0; остается решить неравенство 2х <
4, откуда х < 2.
II способ. Преобразуем заданное
неравенство так:
4*-3-2*-4<0;4*-4-2* + 2х-4<0;
2Х(2* - 4) + (2х - 4) < 0; (2х - 4) (2х + 1) < 0.
Так как 2х + 1 > 0 при всех значениях jc, то
2х-4<0, 2х <22, х<2.
Ответ: (-«>; 2).
172. При каком значении а прямая у = 3* + а
является касательной к графику функции у =
= 2jc2-5jc+1?
Так как прямая у =3jc + а является
касательной к графику функции у = 2х2 - Ъх + 1, то в
точке касания угловой коэффициент
касательной равен 3. Но угловой коэффициент
касательной равен производной функции в этой точке,
т. е. у' = 4jc - 5 = 3, откуда х = 2. Следовательно,
х = 2 — абсцисса точки касания.
Найдем теперь а из условия равенства
значений функций у = 3х + аиу = 2х2 - Ъх + 1 при
х = 2. Имеем 3*2 + а = 2*4-5*2 + 1;а = -7.
Ответ: при а = -7.
173. Найдите площадь фигуры, ограничен-
1 з
ной линиями у=т;х,у = 3-х,у = -4х.
Изобразив схематически графики трех
функций (рис. 21), найдем абсциссы точек А и С.
1 з
Для А: 3 - х = -4х9 х = -1; для С: g х = 3 - jc,
х = 2.
Решение последнего уравнения находится с
помощью рисунка и проверяется
непосредственной подстановкой. Можно также решить
уравнение следующим образом: ~ jc3 = 3 - х; jc3 + 8jc -
-24 = 0; jc3-8 + 8jc-16 = (jc-2)(x2 + 2jc + 4) +
+ 8(jc - 2) = (л:- 2) • (jc2 + 2х + 12), откудаjc3 + 8jc-
- 24 = 0 при х = 2.
Искомую площадь S найдем как сумму
площадей треугольника АОВ и криволинейной
трапеции ВОС:
о о
SA0B= J (3-х-(-4*)) dx = J (3 + 3jc) dx =
-l -l
-(•«♦tX
s«>c-J(»-*-t)<<*-(**-?-is)
S — S.n„ + So™ - 1,5 + 3,5 - 5.
= 3,5;
"AOB
JBOC
Ответ: 5.
174. Найдите критические точки функции у =
= 2 л/3 sin х - cos 2х и укажите среди них одну из
точек максимума.
Для нахождения критических точек
функции необходимо найти ее производную:
у' = 2 73 cos х + 2 sin 2*.
Производная у' определена при всех
действительных х. Решим уравнение у' = 0. Имеем
2 73 cos х + 2 sin 2jc = 0; l
л/3 cos x + 2 sin jc cos jc = 0;
rcos jc = 0,
cos jc (л/3 +2sinjc) = 0<=> r- <=>
Lsin jc = -V3/2
JC = o + 7Cn»
ne Z,
JC = (-1) 5 + яА,
*eZ.
Для нахождения точки максимума выберем
среди критических точек такую, в которой у'
меняет знак с плюса на минус.
Рассмотрим функцию в промежутке (0; 2тс)
(рис. 22). Если jc = тс/3, то у' > 0; если jc = к , то
у' < 0. Таким образом, jc = тс/2 — точка
максимума.
Ответ: критические точки: -z + яп, (-1) g -I- яя,
л, Л е Z; о — одна из точек максимума.
Замечание. Для нахождения точки максимума
можно использовать и такой прием. Производная у' —
= 1,5;
Рис. 21

714
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
= 2 cos х( л/3 -I- 2 sin х) меняет знак в каждой
критической точке. Выбрав две соседние критические
точки, например х - -я/2 и х — -л/3, определим знак
производной в промежутке (-к/2; -л/3). Для точек
этого промежутка cos х > О, */3 4-2 sin х < 0,
следовательно, производная отрицательна, а исследуемая
функция убывает, т. е. х — —я/2 — точка максимума.
Вариант 31
181. Вычислите координаты точки пересече-
га у = Л
ния графиков функций у = v2x -4х- 5 иу =
= х-2.
Абсциссу точки пересечения графиков
найдем из уравнения
л
/2х -4х-5 =х-2. (*)
После возведения обеих частей уравнения в
квадрат получим 2х2 - 4х - 5 = х2 - 4х + 4, т. е.
J -
х* = 9. Тогда хг = -3, х2 = 3.
Проверка: при х = -3 получаем
л/2-(-3)2-4-(-3)-5 *-3-2,
при х2 = 3 имеем л/2 • 3 -4*3-5=3-2.
Корнем уравнения (*), а следовательно, и
абсциссой точки пересечения графиков является
чисЛо 3. Ордината точки пересечения у = 3 - 2 = 1.
Ответ: (3; 1).
182. Составьте уравнение касательной к
графику функции у = 2х2 - Ъх + 1 в точке с
абсциссой х0 = 2.
Запишем уравнение касательной к графику
функции у = у (х) в точке с абсциссой х0:
у-у{х0) = у'(Хъ){х-Хъ).
Поскольку у\х) = Ах - 5, у'(х0) = у'(2) = 4*2-
-5 = 3, y(jc0) = i/(2) = 2-22-5-2 +1 =
-^уравнение касательной имеет вид у - (-1) = 3(х - 2),
или у = Зх - 7.
О т в е т: у - Зх - 7.
3-х
183. Решите неравенство log6—т > !•
3-х
Перепишем неравенство так: logs-—5 > l°£s 5-
Функция I/ = log6* монотонно возрастает, а ее
область определения задается неравенством t > О,
3-х
т. е. —о > 0. В силу указанных условий исход-
X + £
ное неравенство равносильно системе неравенств
(3-х
х + 2
3-х
х + 2
>5,
>0,
которая, в свою очередь, равносильна одному
3-х
неравенству —~ > 5- Преобразовав последнее,
получим
6х + 7
х + 2
<0.
Решим это неравенство методом интервалов.
Для этого рассмотрим функцию f(x) = х + 2 •
При х — -2 функция не определена, а при х = -7/6
принимает нулевое значение. Отметим числа -2
и -7/6 точками на координатной прямой. Они
разбивают координатную прямую на три
интервала. В каждом из них функция / (х)
непрерывна и не обращается в нуль. Определим знаки
функции в какой-либо произвольной
внутренней точке каждого интервала: ДО) > 0, /(-1,5) < 0,
/(-3) > 0. Поэтому в каждом из интервалов
функция f(x) имеет знаки, указанные на рис. 23.
Итак, в интервале (-2; -7/6) функция /(х)
принимает отрицательные значения. Все точки
этого интервала и являются решениями исходного
неравенства.
Ответ: (-2;-7/6).
184. Сколько корней имеет уравнение cos 2х -
- cos х= 2 - sin2x на отрезке [-ЮОтс; ЮОтс]?
Преобразовав исходное уравнение, получим:
2 cos2x - 1 - cos х = 2 - (1 - cos2x), или cos2x -
- cos x - 2 = 0, или (cos х + 1) (cos x - 2) = 0. Из
+ -
0 / *\4n Зп 5тс
2Х~3 Т Т
Рис. 22
271
-2 -7
6
Рис. 23

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
715
последнего уравнения видно, что исходное
уравнение равносильно совокупности уравнений
[cos х = -1,
cos х = 2.
Второе уравнение совокупности не имеет
решений, а решения первого имеют вид х = к + 2пп,
где п е Z.
На каждом отрезке длины 2л, т. е. длины,
равной периоду функции у = cos *, уравнение
cos х = -1 имеет только один корень. Заданный
отрезок состоит из 100 интервалов длины 2л. Ни
одно из чисел 100я и -ЮОя, служащих
границами заданного отрезка, не является решением
уравнения, поэтому исходное уравнение на
отрезке [-100я; 100л] имеет 100 корней.
Ответ: 100 корней.
185. Решите уравнение
' Преобразуем данное уравнение следующим
образом:
5 -3*5 -2*5 =0,
а затем вынесем за скобку 56* + 6. Получим
56x + 6(52x2-6x-7^3#5x2-3x-4^2) =Q
Так как 56* + б > 0 при всех значениях х, то
52х2-6х-7 3#5х2-Зх-4 2 =()
Введем вспомогательную переменную t:
2 2
сдг -Здг-4 . . . Л m .2 с2* -вдр-8
5 = t, причем t > 0. Тогда t = 5
г^2 ег2х2-6х-7 ~ е.2
и, следовательно, 5* = 5 . Отсюда 5* -
-3*-2 = 0.
Решив квадратное уравнение относительно t,
получим tx < 0, t2 =? 1. Значение tv очевидно, не
*• _ Ч ** — 4
подходит. Остается t2 = 1. Тогда 5 =1,
или 5х =5°. Итак, получаем уравнение
х2 - Зх - 4 = 0, которое имеет два корня: jcx = -1,
*2 = 4-
Ответ: {-1; 4}.
186. Найдите площадь фигуры,
ограниченной линиями х\у\ = 2, х = 1, х = 3.
Перепишем уравнение *|г/| =2, раскрыв знак
модуля: ху = 2, если у>0;ху = -2, если у < 0.
Изобразим рассматриваемую фигуру
штриховкой на рис. 24. Эта область ограничена
графиками л: = 1, х = 3, у = 2/ху у = -2/х. Площадь
S искомой фигуры можно/ вычислить
следующим образом:
з з
1 1
= 4(ln3-lnl) = 41n3.
Ответ: 4 In 3.
Вариант 33
193. Решите уравнение log2(* - 3) = 2 - log2*.
I способ. Правая и левая части исходного
Гх-3>0,
уравнения определены при < т. е. при
\х > и,
х > 3. Для таких значений х имеем
log2(x-3) + log2x = 2,
или
log2*(x-3) = 2.
Отсюда по определению логарифма получаем
х(х - 3) = 4, т. е. х2 - 3* - 4 = 0. Это уравнение
имеет два корня: хх = -1, х2 = 4. Условию х > 3
удовлетворяет только х = 4.
Ответ: лг = 4.
II способ. Данное уравнение равносильно
уравнению
log2(x-3) = log2-.
Воспользовавшись свойствами
логарифмической функции, получим равносильную
уравнению систему
jc>3.
У1
1
0
i
1
Шшл
Ш
Г"
— *
Рис. 24

716
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Решим уравнение системы и проверим,
удовлетворяют ли его корни неравенству х> 3. Име-
ем х2 - Зх - 4 = 0, откуда хг — -1, х2 = 4. Второй
корень удовлетворяет исходному уравнению.
194. Решите неравенство (~ J +23 + х<9.
Записав
8Г
как 2х, получим неравенство
2х + 23 + ДЧ 9, или 2х + 8 • 2х < 9, или 2*< 1.
Отсюда 2х < 2°; так как функция у = 2f монотонно
возрастает, то jc < 0.
Ответ: (-«>; 0].
195. Вычислите абсциссы и ординаты точек
пересечения графиков функций у = 2 sinf jc + « J
и у = 7з COS *.
Для вычисления абсцисс точек пересечения
графиков решим уравнение
2 sin (х + $) = 73 cos *. (*)
Воспользовавшись равенствами
2 sin [jc + ^] = 2 [sinjc* 5 + cosx* -g-J = sin jc -f-
+ cos x • J3 , перепишем уравнение (*) в виде
sin х + 7з cos jc = 7з cos х, или sin jc = 0.
Следовательно, jc = теп, где п е Z, — абсциссы точек
пересечения графиков.
Для вычисления ординат точек пересечения
подставим найденные значения абсцисс в
выражение для функции у = 7з cos х: у = л/3 cos яп.
Возможны два случая: если п четное, то cos пп = 1 и
у = 7з ; если л нечетное, то cos яп = -1 и у = -л/3 .
Ответ: абсциссы равны кп, пе Z,
ординаты равны 7з или - 7з .
+ -
2 2
Рис. 26
196. Найдите расстояние от начала координат
до касательной к графику фзшкции у = х\пх,
параллельной оси абсцисс.
Заметим, что если касательная имеет вид у = а,
то расстояние от нее до начала координат равно
N.
Поскольку касательная параллельна оси
абсцисс, ее угловой коэффициент равен нулю. Но
угловой коэффициент касательной равен
значению производной функции в точке касания.
Таким образом, необходимо найти те значения х,
для которых у' = 0: у' = (х In х)' = In х + 1, In х +
+ 1 = 0, In х = -1, х = 1/е. В точке х = 1/е
значение производной у' равно нулю, поэтому
уравнение касательной имеет вид
или у =
= т!п [ - J, или у = — . Искомое расстояние есть
Ответ: 1/е.
197. При каких значениях а график функции
у = Зх - 4х3 и прямая у = а имеют одну общую
точку?
Исследуем функцию у = Зх - 4л:8. Найдем ее
производную у' = -12х2 + 3 и те значения лг, при
которых производная равна нулю. Отметим эти
значения х точками на координатной прямой и
определим промежутки знакопостоянства
производной (они отмечены знаками «+» и «-» на
рис. 25). В интервале (-<»; -1/2] функция у (х)
убывает и принимает значения, заполняющие
промежуток [- 1; +°°). На отрезке [-1/2; 1/2]
функция возрастает и принимает значения [-1; 1].
На [1/2; +°о) функция убывает и принимает
значения (-©о; 1].
График функции у = -4х8 -I- Зх схематически
изображен на рис. 26.
Таким образом, прямая у = а имеет с
графиком данной функции одну общую точку при а <
< -1 или а > 1.
Ответ: при а < -1 и а > 1.
198. Докажите, что площадь фигуры,
ограниченной графиком функции у = —р и прямыми
x*Jx
у = 0, х = 4, х = р (при р > 4), меньше 1.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
717
По условию, х > 4, т. е. —р > 0. Значит, ис-
xjx
комую площадь можно вычислить следующим
образом:
р Р
xjx
S=jAx=jx-Z/2dx=X
-1/2
-1/2
= (-2*
л"1 -
-_2р-"2-,-2-4-1',,)-1-2
2 2
Поскольку -р > 0, имеем 1 - -р < 1. Итак, S <
л/Р л/Р
< 1, что и требовалось доказать.
Вариант 35
205. Решите уравнение Jb + 2x-x2 =х + 1.
Учитывая, что правая часть уравнения
должна быть неотрицательна, возведем обе части
уравнения в квадрат. Исходное уравнение
равносильно системе
+ 2х-х2 = (*+1)2, Г
+ 1 > 0 1
2х -4 = 0,
<=>
х > -1
(x-j2)(x + j2) = 0,
ж > -1.
Решив последнюю систему, получим ж = *]2 .
Ответ:х= J2.
206. Решите систему уравнений
l2*-y.2X!f = 8,
9" = 34"х.
Данная система равносильна системе
2*-у+ху = 23
з2у = з4-*.
. Используя свойства показательной функции,
заключаем, что первое уравнение системы
равносильно уравнению х - у + ху = 3, а второе —
уравнению 2у = 4 - х, или х — 4 - 2у. Подставив это
выражение для х в уравнение х - у + ху = 3, полу-
чим4-2у-у + (4-21/)1/ =3, или2у2-1/-1 = 0.
Итак, исходная система равносильна
следующей:
К
-у-1 = о,
4-2у
ГУ = 1.
х = 4-2у
<=>
"Г* = 2,
Гх = 5,
[У = -0,£
Ответ: (2; 1), (5;-0,5).
207. Найдите площадь фигуры, ограниченной
линиями у=1-х, у = 0иу = (х + I)2, где х > -1.
Заданная фигура выделена штриховкой на
рис. 27. Она состоит из треугольника ВОС и
криволинейной трапеции АОВ. Вычислим
сначала площадь треугольника: SABOC = 0,5*ОС*ВО,
причем ВО - ОС *= 1, так как В(0; 1), С(1; 0).
Значит, Здаде = 0,5. Площадь криволинейной
трапеции определим следующим образом:
8АОВ=1(х+1)><1х = Щр
-1
1 1
Искомая площадь равна SABOC + SAOB = о + 3 =
5
6*
Ответ: 5/6.
208. Найдите область определения функции
y = log04log4|5f •
Используя свойства логарифмической
функции, запишем неравенства, задающие область
определения исходной функции:
1о*4772>0'
5-х л
о>0.

718
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
Второе неравенство системы является
следствием первого, поэтому достаточно решить
первое неравенство. При основании, большем 1,
логарифмическая функция монотонно возрастает
и, значит,
1о^4^Г2>0^
5-х
х-2
Ъ-х
х-2
>0,
>1.
Первое неравенство полученной системы
является следствием второго. Поэтому достаточно
решить неравенство —« > 1. Приведем его к ви-
X — Ct
ДУ
2(3,5 -х)
х-2
> 0 и решим методом интервалов.
На координатной прямой (рис. 28) отмечены
точка разрыва и нуль функции f (х) =
2(3,5 -х)
х-2
и
указан знак функции в каждом из полученных
промежутков. Функция / принимает
положительные значения при 2 < х < 3,5.
Ответ: (2; 3,5).
209. Исследуйте функцию /(*) = cos 2х - 2 cos х
на возрастание и убывание в промежутке [-тс/3; тс].
Найдем производную данной функции и те
значения х, при которых она равна нулю: f (х) =
= -2 sin 2х +2 sin х; f(x) = 0, если -sin 2х -Н sin jc =
= 0, т. е. sin х(1 - 2 cos х) = 0. Последнее
уравнение, очевидно, равносильно совокупности
уравнений: sin х = 0, cos х = 0,5. Из первого
уравнения получаем х = nk> где k е Z, из второго х =
= ±о +2тш, где пе Z.
На отрезке [-тс/3; тс] расположены следующие
критические точки: -тс/3; 0; тс/3; тс,
разбивающие рассматриваемый отрезок на три части.
Определим знаки производной f(x) в каждом из
образовавшихся промежутков (рис. 29):
r-(-!)-2si„(-:)+2ata(-5)-4-i>°.
'r-[fl«>-l{f\>o.
Ответ: функция возрастает в промежутках
[-тс/3; 0] и [тс/3; тс]; убывает в промежутке [0; тс/3].
2 3,5
Рис. 28
/'
+ -
f-\S° Ч \S*
Замечание. Обратим внимание на следующее:
функция f(x) определена и дифференцируема на Я,
поэтому точки -тс/3 и тс нужно рассматривать как
критические точки из промежутка [-тс/3; тс]. Если бы
функция была задана только на промежутке [-тс/3; тс], то
-тс/3 и тс не могли бы рассматриваться как
критические точки, поскольку не являлись бы внутренними
точками области определения. В этом случае вопрос о
включении концов в промежутки монотонности был
бы более сложным.
210. При каких значениях а прямая у = ах - 5
касается кривой у = Зх2 - 4х - 2?
Для того чтобы прямая у = ах - 5 касалась
кривой у = Зх2 - 4х - 2 в точке с абсциссой х0,
необходимо и достаточно, чтобы значения обеих
функций при х = х0 совпадали и значение а
(угловой коэффициент прямой) было равно значению
производной функции у = Зх2 - 4х - 2 при х = х0.
Производная этой функции равна у' = 6* - 4.
Значит, искомые значения а должны
удовлетворять системе
\ах0-Ь = 3*о-4х0-2,
[а = 6jc0-4.
Подставив выражение для а в первое
уравнение системы, получим
3*0-3 = 0,
а = 6хп-4
<=>
х0 = 1, <=>
а = 6jc0-4
а = -10,
*о = !»
а = 2.
Итак, искомые значения а равны -10 и 2.
Ответ: при а — -10 и а = 2.
Вариант 37
0,2*-0,008 .Л
217. Решите неравенство -= ^ 0.
х -10*+ 25
I способ. Перепишем данное неравенство в
0,2*-0,008 ^ л „
виде — -^— < 0. При всех х * 5 выполняет-
(*-5)2
ся условие (х - 5)2 > 0. Поэтому исходное
неравенство равносильно системе
[0,2х < 0,23,
Рис. 29
0,2-0,008 ^ 0,
х*Ь,
или
х*5.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
719
Поскольку функция у = 0,2* монотонно
убывает, неравенство 0,2х < 0,23 равносильно
неравенству х > 3. Отсюда и из условия х Ф 5
получаем множество решений исходного неравенства:
[3; 5) и (5; +«>).
Ответ:[3;5)и(5;+оо).
II способ. Решим исходное неравенство
методом интервалов. Для этого найдем корни
числителя и знаменателя. Имеем 0,2х - 0,008 — 0
при х = 3; х2 - 10* + 25 = 0 при х = 5.
Итак, 3 и 5 — точки возможной перемены
знака функции / (jc), заданной дробью, стоящей
в левой части исходного неравенства.
Определим знаки функции в промежутках, на которые
точки 3 и 5 разделяют координатную прямую.
Подстановкой какого-либо произвольного
значения из данного промежутка устанавливаем,
что знаки функции распределяются по
промежуткам так, как показано на рис. 30. В самом
деле, подсчет или прикидка по знаку дают
следующие результаты: /(0) > 0, Д4) < 0, /(6) < 0.
218. Найдите значение производной функции
2 + х i X Л
у = е + —g— в точке х0= -2.
х -1
Вычислим производную данной функции:
•-(«* + х)'+[ -/Ч'-
= е
2 + х . (х)'-(х2-1)-(х2-1)'-х =
2 - 2
(* -1)
2 i о 2
- „2 + х , X -\-2х
= е
2 2
(* -1)
= е
2 + х
1+х
2 2
(* -1)
Подставив значение х = -2 в выражение для \/>
находим у' (-2) = 4/9.
Ответ: 4/9.
219. Решите неравенство log0 5(х2 -1)> -2.
Область определения функции уг = log0b(x2 -
- 1) задается условием х2 - 1 > 0. Графиком фун^
кции у = х2 - 1 является парабола с ветвями,
направленными вверх (рис. 31). Она пересекает
ось абсцисс в точках -1 и 1. Значит, функция у —
= х2 - 1 принимает положительные значения при
х < -1 или при х> 1.
Функция у = log0 5t убывает в области
определения, поэтому для всех значений х из области
определения уг справедливо неравенство х2 - 1 <
^ 0,5"2, или х2 <: 5. Отсюда -Jb < х ^ 75. На
рис. 32 штриховкой изображено пересечение
отрезка [-Jb\ л/5] с промежутками (-°°; -1) и
(1;+°о), задающими область определения
функции yv Это пересечение состоит из двух
промежутков [-4b ; -1) и (1; Jb ].
Ответ: [-Уб;-1)и(1; Уб].
220. Найдите критические точки функции
л/3
f(x) = cos х + V х- Укажите одну из точек
минимума.
Заданная функция дифференцируема на
множестве всех действительных чисел, поэтому ее
критические точки являются корнями уравнения
л/3
f(x) = 0, т. е. уравнения -sin х + -у =0. Отсюда
/о п
заключаем, что sin х = -^ их = (-l)"* + пп> где
пе Z.
Рассмотрим какой-либо промежуток, в
котором находится единственная критическая
точка. Например, в промежутке [к/2; тс] лежит одна
критическая точка — это 2я/3. В ней знак
производной меняется с минуса на плюс, так как
Г (|) =-1+|<0и Пк) = 0 + ^ > 0. Значит,
271
х = -=- — точка минимума.
Ответ: критические точки (-1)" « + яи, пе Z;
2л
— — точка минимума.
Рис. 30
Рис. 31
\шщ
\ %ЩЩ-
-Л -i 1
Рис. 32
Л

720
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
221. Найдите ту первообразную функции / (х) =
= 2х + 4, график которой касается прямой у =
= 6х + 3. Вычислите площадь фигуры,
ограниченной графиком найденной первообразной и
прямыми у = 6х + 3иу = 0.
Первообразные функции /(х) определяются
так:
J/(x) dx = J(2x + 4) dx = x2 + 4x + С.
Поскольку прямая у = 6х + 3 является
касательной к параболе у = х2 + 4х -I- С, уравнение х2 +
+ 4х + С = 6х -I- 3 должно иметь единственный
корень. Приведем это уравнение к стандартному
виду: х2 - 2х + С - 3 = 0. Квадратное уравнение
имеет единственный корень, когда его
дискриминант D равен нулю. В данном случае D = 16 -
- 4С. Очевидно, что D = 0, если С = 4. Таким
образом, искомая первообразная имеет вид у =
= х2 + 4х + 4.
Вычислим площадь фигуры, ограниченной
линиями у = х2 -I- 4х + 4, у = 6х -I- 3, у = 0.
Площадь заданной фигуры удобнее всего вычислять
как разность площадей криволинейной
трапеции ABE и треугольника DBE (рис. 33).
Найдем координаты точек В и D. В точке В парабола
у = х2 + 4х + 4 касается прямой у = 6х + 3, т. е.
х2 + 4х -I- 4 = 6х + 3. Отсюда х = 1; тогда у = 9.
Значит, точка В имеет координаты (1; 9). Первую
координату точки D найдем из условия, что
прямая BD пересекает ось абсцисс в точке 2), т. е.
6х+3 = 0их = -0,5; тогда у = 0 и D (-0,5; 0).
Следовательно,
JADBE
= 0,5-Б£-1Ж = 0,5-9-1,5 = 6,75;
sabe= J(x2 + 4x + 4)dx - J(x + 2)2 dx =
-(* + 2)*
3
-2
= 9.
Искомая площадь SABE - SADBC = 9 - 6,75 =
= 2,25. 2
Ответ: первообразная у ex + 4x + 4;
площадь 2,25.
222. Решите уравнение V|2x+l| = 1 - 2|х|.
Функция у = 2х + 1 меняет знак в точке х =
= -0,5.
1) Рассмотрим случай, когда х < -0,5. Тогда
2х + 1 ^ 0 и |2х + 1| = -1 -2х. Если х < -0,5, то
х < 0 и |х| = -х. Следовательно, 1 - 2|х| = 1 + 2х.
При данных значениях х выражение 1 + 2х
принимает неположительные значения, в то время
как выражение V|2x+ 1| при любых х равно
неотрицательному числу. Итак, при х < -0,5
равенство левой и правой частей исходного уравнения
возможно только при 1 + 2х = 0, т. е. при х = -0,5.
2) Рассмотрим случай, когда -0,5 < х < 0.
Тогда |2х + 1| = 2х + 1, а |х| = -х. Исходное
уравнение примет вид 72х + 1 = 1 + 2х. Введем
обозначение: 72х+ 1 = t. Тогда исходное уравнение
можно переписать как t — t2. Отсюда tx = 0, t2 = 1.
Если t = 0, то х = -0,5; если t = 1, то х = 0. Ни
один из полученных корней не удовлетворяет
условию -0,5 < х < 0.
3) Пусть х > 0. Тогда исходное уравнение
примет вид «/2х+1 = 1 - 2х. При х > 0 имеем
72х+1 > л/2-0 + 1 =1, а1-2х<1-2-0 = 1.
Равенство 72х + 1 = 1 - 2х возможно только при
одновременном выполнении условий */2х + 1 = 1
и 1 - 2х = 1, т. е. при х = 0.
Ответ: {-0,5; 0}.
Вариант 39
229. Решите уравнение = 0.
3х-27
Дробь принимает нулевое значение, когда ее
числитель равен нулю, а знаменатель отличен
от нуля.

Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
721
Приравняв нулю числитель данной дроби,
получим квадратное уравнение 2х2 - 5х - 3 = О,
которое имеет два корня: хг = 3, х2 = -0,5.
Значит, корнями исходного уравнения могут быть
только числа 3 и -0,5. Проверим, не обращают
ли эти числа в нуль знаменатель дроби. При х = 3
знаменатель 3х - 27 равен З8 - 27 = 0. Поэтому
число 3 не является корнем исходного
уравнения. При х = -0,5 имеем З"0,5 * 27, т.е.
знаменатель не равен нулю. Значит, число -0,5 - корень
исходного уравнения.
Ответ: х = -0,5.
Замечание. Обратим внимание на то, что нет
необходимости решать уравнение, которое получается,
когда приравнивается нулю знаменатель
алгебраической дроби. Это не нужно, так как служит только
корректировке результата, а кроме того,
нерационально, да и не всегда возможно. Гораздо лучше
непосредственной подстановкой в знаменатель
проверить корни числителя.
230. Решите неравенство ^ < 0.
Знаменатель дроби, стоящей в левой части
неравенства, положителен, поэтому исходное
неравенство равносильно такому: log0 5(х2 - 3) < 0. Его
можно переписать в виде log0 5(х2 - 3) < log0 51.
Логарифмическая функция с основанием,
меньшим 1, является монотонно убывающей,
следовательно, от последнего неравенства можно
перейти к равносильному неравенству х2 - 3 > 1.
При тех значениях х, которые удовлетворяют
последнему неравенству, справедливо и
неравенство х2 - 3 > 0, которое задает область
определения функции log0 5(х2 - 3).
Таким образом, решение сводится к решению
неравенства х2 - 3 > 1, или х2 - 4 > 0. В
результате получим х <-2 или х > 2.
Ответ: (-~;-2]и[2;-Ь»).
231. Составьте уравнение касательной к
графику функции у — х2 - Зх - 4 в точке с абсциссой
х0 = 1. Напишите уравнение одной из прямых,
параллельных этой касательной.
Уравнение касательной в точке графика
функции с абсциссой х0 имеет вид у - у (х0) —
= У\х0)(х - х0). Здесь i/'= 2х - 3, у(х0) = -6,
у'(х0) = -1. Подставив эти значения в уравнение
касательной, получим у - (-6) = -(х - 1), т. е. у —
= -х - 5.
Параллельные прямые имеют один и тот же
угловой коэффициент, в данном случае он равен
-1. Тогда в качестве прямой, параллельной
касательной, можно взять, например, прямую у =
= -х+1.
Ответ: касательная у = -х - 5;
прямая, ец параллельная, у =-х + 1.
232. Найдите все значения х, при которых
выражение v6 - х - х • tgf -gx ) имеет смысл и
не обращается в нуль.
Выражение имеет смысл при одновременном
существовании обоих множителей, что
обеспечивается следующими условиями:
6-х-х > 0,
Я 2 Я , , „
jx *£ + 7ifc, ke Z,
или
х +х-6 < 0,
lx2*2 + 4fc, keZ.
Решив первое неравенство, найдем, что оно
справедливо при всех х е [-3, 2].
Определим все значения х из [-3; 2], для
которых найдется такое целое число ft, что
выполняется равенство х2 = 2 4- 4fe.
При * < 0 таких значений х нет.
При ft = 0 получаем хг= -л/2; х2 = л/2. Оба
эти значения принадлежат отрезку [-3; 2].
При ft = 1 имеем хг = -л/б, х2 = л/§. Число-л/б
принадлежит промежутку [-3; 2], а число л/б —
нет.
При k > 2 выполняется условие х2 > 10, при
котором ни одно значение х не принадлежит
отрезку [-3; 2].
Таким образом, выражение имеет смысл при
х € [-3; 2], за исключением точек -л/б, -л/2 , л/2 .
Выясним, при каких значениях х данное
выражение обращается в нуль. Это происходит
тогда, когда хотя бы один из множителей равен
нулю, а другой при этом имеет смысл:
л/6 - х - х2 =0 при х = -3, х = 2;
tgf тх2 ] = 0, если х2 = 4л, л € Z.
При п < 0 таких значений х нет. При п = 0
имеем х = 0.

722
Подготовка к экзаменам. 11 класс
Задачи и решения письменного экзамена по алгебре и началам анализа
При п = 1 получаем два значения х: хг = 2, х2 =
= -2. Оба эти числа принадлежат отрезку [-3; 2].
При п = 2 получаем два значения х: xx = -2j2
принадлежит отрезку [-3; 2], х2 = 2 72 - не
принадлежит этому отрезку.
При п > 3 решения уравнения х2 = 4п не
принадлежат отрезку [-3; 2].
При всех остальных значениях х из
числового промежутка [-3; 2] выражение не обращается
в нуль.
Ответ: (-3;-2л/2 ) и (-2л/2 ;-7б) и (-ТВ ;-2) и
и (-2; -72 ) и (-72 ; 0) и (0; 72) и (72 ; 2).
1 «
233. Фигура ограничена линиями у = т лг и
у = jc. Отрезок наибольшей длины, заключенный
внутри этой фигуры и принадлежащий прямой
х = а, делит фигуру на две части. Докажите, что
площади этих частей равны.
Найдем значение а, при котором отрезок
прямой х = а, заключенный внутри фигуры, имеет
наибольшую длину. Поскольку для абсцисс точек
12
Si" J(*-J*8) dx9 S2= J(*-J*2) dx.
0 2
Докажем, что Sx = S2. Действительно,
2 4
si - S2 = j(* ^ i*2) dx - j(* - i*2J dx =
0 2
,2 3J2 , 2 3J4
-(т-к)\Лт-Ы[-°-
Таким образом, Sx = S2, что и требовалось
доказать.
4
234. При каких значениях а уравнение х 4- - =
= а не имеет корней?
I способ. Прежде всего заметим, что х = 0
не является корнем уравнения. Умножив обе
части уравнения на х, получим квадратное
уравнение х2 - ах + 4 = 0, которое не имеет корней,
если его дискриминант D = а2 - 16 отрицателен.
Таким образом, задача сводится к решению не-
этой фигуры выполняется условие х > т х , длина равенства а - 16 < 0, которое выполняется при
1 2
отрезка задается формулой а - т я • Рассмотрим
1 2
квадратичную функцию /(*) = х - -gx . Ее
наибольшее значение достигается в вершине
соответствующей параболы, т. е. при х = о .(-1/4) =
= 2. Итак, при а = 2 отрезок имеет наибольшую
длину.
Точки пересечения прямой у = х и параболы
у = jx2 имеют абсциссы 0 и 4, что устанавлива-
-4 < а < 4.
Ответ: при -4 < а < 4.
{i-i*)=o.
1 2
ется из уравнения х = т х , или jc
Площади частей, на которые делит фигуру
заданный отрезок, вычисляются следующим
образом:
У' +
^ max ^
Ч
S
Рис. 34
II способ. Исследуем функцию у = х + -.
4
Найдем ее производную у' = 1 —^ и определим
х
знаки производной в промежутках знакопостоян-
ства (рис. 34). В точке х = -2 функция достигает
максимального значения, а в точке х = 2 —
минимального, у(-2) = -4, 1/(2) = 4. В то же время
ясно, что если х -> -<», то у -» -<», а если х -» +«>,
то у -» +оо. Значит, множество значений
функции представляет собой объединение
промежутков: (-«о; -4] и [4; +«>).
Итак, уравнение х + т = а не имеет решений
при всех а е (-4; 4).
Замечание. В данном случае II способ более
громоздкий и требует тонких пояснений, по которым
можно было бы судить, что учащийся хорошо
представляет себе расположение графика функции.
Однако за приведенное решение (даже при отсутствии
более подробных пояснений) оценка не может быть
снижена. По существу, второе решение богаче, так как в
нем предложен общий метод ответа на аналогичные
вопросы.

Примерные билеты и ответы к устному
экзамену по алгебре и началам анализа
КУРСА
Билет № 1
1. Изобразить график функции синуса и
описать свойства функции.
2. Вычислить log2 0,5.
3. Решить, применяя метод интервалов:
2.
-1
(х - 2Х2х + 3)
4-х
>0.
1.
График функции у = sin х приведен на
рисунке 1.
Свойства функции у = sin х
1. Область определения: D(y) = R.
2. Область значений: Е(у) = [-1; 1].
3. Функция у = sin х нечетная (график
симметричен относительно точки О (0; 0).
4. Нули функции: у = 0, если х = теп, где п е Z;
5. Наименьший положительный период
функции Т = 2я.
Периодом функции являются числа вида
2яп, где п — целое число, кроме 0.
6. Промежутки знакопостоянства:
у > 0, если 2пп < х < п + 2пп, где п е Z.
I/ < 0, если тс + 2тсп < х < 2тс 4- 2тш, где п е Z.
7. Функция возрастает на промежутках
Г-s + 2яи; 5 + 2яп |, где п е Z;
функция убывает на промежутках
Г 5 + 2тш, -у + 2яп 1, где п е Z.
8. Точки максимума: л: = ~ + 2яп, где п е Z;
максимум равен 1.
Точки минимума: х = - ^ + 2яп, где п е Z,
минимум равен -1.
log2 0,5 = log2 2 = -1
3.
(х - 2)(2х + 3)
4-х
>0<=>
(jc - 2)(2х + 3)(4 - х) > 0,
[х *4.
1) Решим неравенство (х - 2)(2* + 3)(4 - х)>0.
Введем функцию у = (х - 2)(2х -I- 3)(4 - х);
D(i/) = *.
Найдем нули функции: у = 0, если л: = 2, или
х = -1,5, или х =4.
Так как функция непрерывна на всей области
определения, то на промежутках между своими
нулями функция сохраняет постоянный знак:
/(5) < 0,/(3) > 0, + _ + -
/(0) < 0, П-3) > 0. —•- • *—
(-оо;-1,5] U.[2; 4]. 1>5 г 4
2) Так как х Ф 4, решением данного
неравенства является промежуток (-°°; -1,5] U [2; 4).
Ответ: (-оо;-1,5] U [2; 4).
Билет № 2
1. Изобразить график функции косинуса и
описать свойства функции.
2. Вычислить 5/—.
3. Решить уравнение log2 (2х - х ) = 0.
1.
График функции у — cos х изображен на
рисунке 2.
у = cos х
Зкх
Рис.1

724
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Свойства функции у = cos х
1. Область определения: Щу) = Л.
2. Область значений: Е(у) = [-1; 1].
3. Функция у = cos х — четная (график
симметричен относительно оси Оу).
4. Нули функции у = 0, если х = ^ +пп> гДе
п € Z.
5. Наименьший положительный период
функции Т = 2я.
Периодом функции являются числа вида 2ял,
где л — целое, кроме 0.
6. Промежутки знакопостоянства:
у > 0, если -s + 2ял < х < « + 2ял, где л € Z;
у < 0, если я + 2ял < х < -тг + 2ял, где л € Z.
7. Функция возрастает на промежутках
[-л + 2ял; 2ял], п е Z;
убывает на промежутках
[2ял, я + 2ял], где л € Z.
8. Точки максимума: х = 2ял, где л € Z,
максимум равен 1.
Точки минимума: х = я + 2ял, где л € Z,
минимум равен -1.
2.
fi'wH'
3.
log2 (2х - х ) - 0.
Из определения логарифма следует:
2х-х'
2°;
2
2х-х -1;
х - 2х + 1 = 0;
(х-1)2=0;
х = 1.
Проверка.
Левая часть уравнения log2 (2-1-1 ) = log21 ~
= 0; 0 = 0 — истинно.
Ответ: 1.
Билет № 3
1. Изобразить график функции тангенса и
описать свойства функции.
2
2. Вычислить [07]
3. Решить неравенство log3 х > log3 5.
1.
График функции у — tg х изображен на
рисунке 3.
Свойства функции у = tg х
1. Область определения:
D(j/) = [~\ + ял; | + ял J, где л € Z.
2. Область значений: Е(у) = (-<»; +<»).
3. Функция I/ = tg х нечетная.
4. Нули функции: у = 0, если х = ял, где пе Z.
5. Наименьший положительный период
функции Т =я.
Периодом функции являются числа вида ял,
где л — целое, кроме 0.
6. Промежутки знакопостоянства:
у > 0, если ял < х < о + ял, где л е Z;
I/ < 0, если -г + ял < х < ял, где л € Z.
7. Функция возрастает на промежутках
(-| + ял; | + ял J, где л € Z.
8. Функция у = tg х не имеет экстремумов
(максимумов и минимумов).
2.
ЗУ¥
(ft) -GF) -((!)) -8Г-5
m
"2
у*
о ж
2
У,Г *в *
г2язд
2
Рис.3

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
725
з.
log3 х > log3 5. Так как основание логарифма
больше единицы, то функция у = log3 х —
возрастающая, следовательно,
| * > 5, ,
1 х> 0.
Огпвет: [5; +<х>).
Билет № 4
1. Изобразить график показательной функции
с основанием, большим единицы, и описать
свойства функции.
2. Вычислить sin 5*
3. Решить неравенство log0 4 х < 1.
1.
График функции у—а изображен на рисунке 4.
Свойства функции у = а*, где а > 1
1. Область определения: D(y) = R.
2. Область значений: Е(у) = (0; +оо).
3. Функция возрастает на всей числовой
прямой.
4. График пересекает ось Оу в точке (0; 1).
5. При любых действительных х и у
справедливы следующие равенства:
х у х +у
?-=ах-у;
ау
(abf = а V;
(а\х а*
2.
. 2 Л -2 -
SU1 к = 1 = 1-
3.
lo&0,4* <]L
Функция у = log0 4 х — убывающая, значит,
х >0,4,
х>0.
Ответ: (0,4; +оо).
Билет № 5
1. Изобразить график показательной функции
с основанием, меньшим единицы, и описать
свойства функции.
1
2. Вычислить 4 .
3. Решить уравнение sin х = 5 и указать
любые два корня.
1.
График функции изображен на рисунке 5.
Свойства функции
у = а*, где О < а < 1
1. Область определения: D{y) = R.
2. Область значений: Е(у) = (0; +оо).
3. Функция убывает на всей числовой прямой.
4. График пересекает ось Оу в точке (0; 1).
5. При любых действительных х ту
справедливы следующие равенства:
х у х +у
а ау = а у;
-у-а''У;
аг
{аЪ)х = аЬх\
(а\х а_
W ъ*;
(ах)у = аху.
2.
1 1 1
42 = л/4 = 2 или 42 - (22)2 = 2* 2 - 21 = 2.
2-;
sin х = g ;
лг = (-1)л arcsin g + теп, где п е Z;
Рис.4

726
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
х = (-1)Л£ + яп, где п е Z;
*i " б * *2 6 #
Ответ: (-1)* g + теп, где п € Z; g , -g-.
Билет № 6
1. Изобразить график логарифмической
функции с основанием, большим единицы, и
описать свойства функции.
2. Вычислить cos (-"о")-
3. Решить неравенство [о) < 27.
1.
График функции приведен на рисунке 6.
Свойства функции у = loga ж, где а > 1
1. Область определения:
D(y) = (0; +оо).
2. Область значений:
£(У) = Л.
3. Функция возрастает на всей области
определения.
4. Нули функции:
loga х = 0, если х = 1.
5. При любом положительном а (а Ф 1)
выполняются следующие равенства:
logfl (ху) = logfl х + logfl у при х > 0, у > 0;
logfl jj = logfl х - logfl у при х > 0, у > 0;
loga л^ = р • loga jc при jc > 0 и любом р.
2.
cos
(-¥)-»•
3.
6Г<№
Основание степени меньше 1, следовательно,
функция у = (о ] — убывающая, значит, jc > -3.
Ответ: (-3; +оо).
Билет № 7
1. Изобразить график логарифмической
функции с основанием, меньшим единицы, и
описать свойства функции.
2. Вычислить Vl25.
3. Решить уравнение cos х = —sr и указать
любые два корня.
1.
График функции изображен на рисунке 7.
Свойства функции
у = loga х9 где 0 < а < 1
1. Область определения:
D{y) - (0; +оо).
2. Область значений:
Я(У) = Я.
3. Функция убывает на всей области
определения.
4. Нули функции:
loga х — 0, если л: = 1.
5. При любом положительном а (а Ф 1)
выполняются следующие равенства:
logfl (ху) = logfl х + logfl у при х > 0, у > 0;
logfl - = logfl х - loga у при jc> 0, у > 0;
foga ** = Р ' 1°&а * ПРИ Х > О и ЛЮбоМ р.
2.
Vl25 = 5.
3.
COS JC
— ^.
2 •
jc = ±arccos (-^ J + 2тсп, где n e Z;
jc = ±( тс - 5 J + 2лп, где neZ;
loge&
у - logex
а > 1
У)
0
Ь»
i . У = bge
I 0 < a <
3C
1
у1 & x
Рис.6
Рис. 7

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
727
х = ±-т- + 2тсп, где п е Z;
*1 ± > х2 4 #
Ответ: ±-т- -I- 2яп, где п € Z; -т-; - -т-.
Билет № 8
1. Изобразить график степенной функции с
показателем, большим единицы, и описать
свойства функции.
2. Вычислить lg 0,001.
3. Решить уравнение tg 2х = 0 и указать
любые два корня.
1.
Графики функции для а е N изображены на
рисунках 8, а, б.
График функции у = ха, а — дробное число,
большее 1, изображен на рисунке 8, е.
Свойства функции
у = ха, а — целое число, а > 1
1. Область определения: D(y) = R, если а —
целое число.
2. Область значений: если а — четное число,
то Е{у) = [0; +оо]; если а — нечетное число, то
E(y) = R.
3. Графики функций пересекают оси Ох и Оу
в точке О (0; 0).
4. Функция является четной, если а —
четное число; нечетной, если а — нечетное число.
5. Промежутки знакопостоянства:
а) если а — четное число, то у > 0 при любом
значении х, кроме х = 0;
б) если а — нечетное число, то у > 0, если х > 0;
у < 0 при х < 0.
6. Функция возрастает на всей числовой
прямой, если а — нечетное число. Если а — четное
число, то функция возрастает на промежутке
[0; +°о) и убывает на промежутке (-°°; 0].
Свойства функции у = ха, a — дробное число,
большее единицы (рис. 8, в), приведены в билете
№9.
2.
3.
2.
3.
lg 0,001 = lg 10 =-3.
tg 2х = 0;
2х = теп, где п е Z;
х = у , где п е Z;
— п _
Ответ: -s-, где п е Z; ^ ; я.
Билет № 9
Изобразить график степенной функции с
положительным показателем, меньшим
единицы, и описать свойства функции.
Вычислить cos -г.
Определить, какие из чисел —1; 0; 1; 2; 4; 8
являются корнями уравнения log2 х = х — 2.
1.
График функции изображен на рисунке 9.
Свойства функции
= *а, 0 < a < 1
У -х
а> 1
а —
четное целое
число
а)
У = *
а> 1
а —
нечетное целое
число
У1
1
0
1
7\
1
/а> 1
/ ^
1 ж
в)
У;
1
0
i
1
У = ха
0<а < 1
L х
Рис.8
Рис.9

728
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
1. Область определения: D(y) = [0; +оо].
2. Область значений: Е(у) = [0; +оо].
3. Графики функций пересекают ось Ох и ось
Оу в точке О (0; 0).
4. Функция не является ни четной, ни нечетной.
5. Функция принимает положительные
значения при любом х, кроме х = 0.
6. Функция возрастает на всей области
определения.
2.
5л
cos -т- = COS
(„♦!)--
я
COS т —
4
л
2
3.
Из определения логарифма следует, что х > 0,
следовательно, числа -1 и 0 не являются
корнями уравнения. (Корнем уравнения называется
число, обращающее данное уравнение в
истинное равенство.) Проверим заданные числа:
1)х = 1
левая часть log2 1 = 0, правая часть 1 - 2 = -1;
0 = -1 — ложно.
2)х = 2
левая часть log2 2 = 1, правая часть 2-2 = 0;
1 = 0 — ложно.
3)х = 4
левая часть log2 4 = 2, правая часть 4-2 = 2;
2 = 2 — истинно, следовательно, число 4 —
корень уравнения.
4)х = 8
левая часть log2 8 = 3, правая часть 8-2 = 6;
3 = 6 — ложно.
Ответ: из предложенных чисел корнем
уравнения является только число 4.
Билет № 10
1. Показать на тригонометрическом круге или
графике функции решения уравнения sin х =
= 5 (или любое из значений 1; 0; -5-; -о" J
и записать их.
2. Вычислить logil.
2
3. Исследовать на возрастание и убывание
2
функцию f(x) = 2х - х + 1.
1.
Ответ: х = g 4- 2тсп, где п е Z или х = -g- +
+ 2яп, где neZ (рис. 10, а, б).
2.
logxl =0.
2
3.
1)Л(/) = Я.
2) Функция является возрастающей на
некотором промежутке, если f'{x) > 0 на этом
промежутке (убывающей, если f'(x) < 0).
Найдем производную функции у = f(x):
/'(*) = 4*-1.
а) /'(*) > 0» если
4х - 1 > 0,
4*>1,
* 4*
б) /'(*) < 0, если
4лг-1<0,
4х<1,
Х<4'
Функция возрастает на промежутке I j '* +°° )
и убывает на промежутке [-°°; j I-
Концы промежутков включены в
промежутки возрастания и убывания функции, так как
функция непрерывна в точке т .
у = sin х
а)
б)
Рис. 10

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
729
Билет № 11
1. Показать на тригонометрическом круге или
графике функции решения уравнения cos х =
= -5" (или любое из значений 1; О; «J "о" )
и записать их.
2. Найти значение выражения V5 • VI25 .
3. Найти экстремумы функции f(x) = 2х +
+ З*2 + 5.
2. Найти значение выражения loge 3 + loge 2.
3. Найти производную функции f(x) = 2х -
-*5 + 1.
1.
2.
Ответ: х = т + теп, где neZ (рис. 12, а, б).
log6 3 + log6 2 = log6 (3 • 2) = log6 6 = 1.
1.
Ответ: x = ±g 4- 2тт, где n € Z (рис. 11, а, б).
2.
V5 • Vl25 = V5 • 125 = 4л/б • 53 = \[ГА = 5.
3.
1) Экстремумами функции являются
значения функции в точках экстремума. Точка
является точкой экстремума у если производная в
этой точке меняет свой знак с + на - или с - на +.
2) Найдем производную функции:
Г(х) = 6х2 + 6х; D(f') = R.
3) f(x) = 0, если 6х(х +1) = 0;
х = 0 или* = -1;
/'(1) > 0, /4-0,5) < 0, /'(-2) > 0.
-1 и 0 — точки экстремума; + - +
/(-1) = -2 + 3 + 5 = 6, ' ' *"
/(0) = 5. Х
Ответ: 5 и 6 — экстремумы функции,
0
Билет № 12
1. Показать на линии тангенсов или графике
функции решения уравнения tg х = 1 (или
любое из значений 0; -=т; 7з) и записать их.
+2Лл
а)
б)
f\x) = 6х2 - 5х4.
Билет № 13
1. Описать, в чем состоит механический смысл
производной.
2. Упростить выражение
sin (тс - х) + cos [5 + * )•
3. Решить уравнение log^x + 2) = 1.
о
1.
Пусть материальная точка движется по
координатной прямой по закону х = x(t)> т. е.
координата этой точки х — известная функция
времени t.
Механический смысл производной состоит
в том, что производная от координаты по
времени есть скорость:
,^ = ***.,
+ 2Я/1
а)
б)
Рис. 11
Рис. 12

730
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
sin (я - х) + cos (| + х j = sin х - sin х = 0.
3.
logi(x + 2) =1.
з
По определению логарифма
х + 2 > 0;
<=> i
х >-2,
Ответ: х = -lg .
Билет № 14
1. Описать, в чем состоит геометрический
смысл производной.
_1
2. Упростить выражение (* + 2) (х + 2) .
3. Решить уравнение 2
Зж-1
8#
1.
Пусть задана дифференцируемая функция
у = f(x) (рис. 13).
Геометрический смысл производной
состоит в том, что значение производной функции в
точке х0 равно угловому коэффициенту
касательной, проведенной к графику функции в
точке с абсциссой х0; f'(x0) = k, где k — угловой
коэффициент касательной.
2.
-1 -1 + 3
(х + 2) 2 (*+2)3=(* + 2) 2 =(* + 2)2'5.
3.
Зх - 1 1
8;
з-1 = 2-з.
у|
М(*0;/(*о)^
лб/\
"" *о
i
0
^У=Пх)
V *
Функция I/ = 2 является монотонной, поэтому
3* - 1 = -3,
Зх = -3 + 1,
3* = -2,
2
Ответ: -=.
Билет № 15
1. Сформулировать теоремы о производных
суммы и произведения двух функций.
2. Упростить выражение sJx • \fx.
3. Решить неравенство lg (х — 4) > 0.
1.
Если функции иии дифференцируемы в
точке х0У то их сумма дифференцируема в этой
точке и (и + и)' = и' + у',
т. е. производная суммы равна сумме
производных.
Если функции и ни дифференцируемы в
точке х0, то их произведение дифференцируемо в
этой точке и (uvY = u'v + uv'.
Следствие. Если функция и
дифференцируема в точке х0, а С — постоянная, то функция Си
дифференцируема в этой точке и (Си)' = Си',
т.е. постоянный множитель можно
выносить за знак производной.
2.
*J?-*Ji= 3J^~x = *J? -X.
3.
Из определения логарифма следует, что х - 4 >
> 0, т. е. х > 4. Функция у = lg t монотонно
возрастает, значит, х — 4 > 1, т. е. х > 5. Таким
образом, данное неравенство верно, если
выполняется система неравенств
| х > 4,
\х>69
Ответ: [5; +°о).
т. е. х > 5.
Рис. 13
Билет № 16
1. Записать формулы производных степенной
и тригонометрических функций.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
731
2. Найти значение выражения 4J21 • 64.
3. Решить уравнение log16 х = 2.
1.
Функция

Производная
у(х) = хп
(степенная)
у\х) =
= пхп'1
У(х) =
■= sin лг
у\х) =
«cos X
У(х) =
в COS*
*/'(*) =
— -sin х
-tgx
1
COS X
2.
\jrm = Уз3 • 43 = з • 4 =
12.
3.
По определению логарифма
log16 х = 2;
* = 162;
* = 256.
Ответ-. 256.
тельной и положительным направлением оси
Ох (рис. 14).
По условию tg а > О, значит, касательные,
проведенные к графику функции в любой точке
этого интервала, образуют острые углы с
положительным направлением оси Ох; говорят, что
касательные «направлены вверх». В этом случае
график функции «поднимается» на заданном
промежутке, т. е. функция возрастает. Если
производная функции отрицательна (f'(x) < 0) в
каждой точке интервала J, то функция у = f(x)
убывает на этом интервале (рис. 15).
Пусть f{x) < 0 на некотором промежутке;
f(x) = tg а, где а — угол между касательной и
положительным направлением оси Ох.
По условию tg а < 0, значит, касательные,
проведенные к графику функции в любой точке
этого интервала, образуют тупые углы с
положительным направлением оси Оху говорят, что
касательные «направлены вниз». В этом случае
график функции «опускается» на заданном
промежутке, т. е. функция убывает.
Билет № 17
1. Сформулировать достаточный признак
возрастания (убывания) функции, дать его
наглядную иллюстрацию.
2. Найти значение выражения 3 • 3 .
3. Решить уравнение log3 (* — !) = log3 (2х + 1).
1.
Если производная функции положительна
(f(x) > 0) в каждой точке интервала J, то
функция у = f(x) возрастает на этом интервале.
Пусть f(x) > 0 на некотором промежутке. В
соответствии с геометрическим смыслом
производной f(x) = tg а, где а — угол между каса-
-0,5
32'5=32 = 9.
3.
log3 (х - 1) = log3 (2х + 1);
х> 1,
jc > - -, Решений нет.
х =-2.
|*-1>0,
2х + 1 > 0, <=> i
[jc-1 = 2jc+1;
Ответ: решений нет.
Билет № 18
Сформулировать достаточный признак
максимума (минимума) функции, дать его
наглядную иллюстрацию.
^^К^
^j/
У,
ЛГ 1
tf«i !
*1*2 0
1 1
1 1
1 1
хъ Ь
Z^y = f(*)
\ X
У=Нх)
Рис. 14
Рис. 15

732
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
2. Упростить выражение tg (тс + *)cos (тс - х).
3. Решить уравнение 3
X + X
= 1.
1.
Если функция у — f(x) непрерывна в точке
х0 (рис. 16), а /'(*) > 0 на интервале (а; лг0) и
f'(x) < 0 на интервале (jc0; Ь), то точка х0
является точкой максимума функции у = f(x).
График функции в окрестности точек максимума,
как правило, имеет вид «холма»; х0 — точка
максимума.
Если функция у = f(x) непрерывна в точке х0
(рис. 17), а /'(*) < 0 на интервале (а; х0) и
f'(x) > 0 на интервале (jc0; Ь), то х0 — точка
минимума функции у = /(*). График функции в
окрестности точек минимума, как правило, имеет
вид «впадины»; х0 и хг — точки минимума.
2.
tg (тс + jc)cos (тс - х) = tg (тс + *)(-cos х) =
sin*
COS*
cos х — -sin X.
3.
3х2 + x = 1;
з*2 + *=з°.
Функция у = 3 является монотонной, значит,
каждое свое значение она принимает один раз.
х + х = 0;
х(х + 1) = 0;
х = Оилих — -1.
Ответ: -1; 0.
Билет № 19
1. Сформулировать правило нахождения
наибольшего (наименьшего) значения функции
на отрезке.
2. Вычислить sin -g-.
3. Решить неравенство 5
ж+ 2
<25
1.
Для того чтобы найти наибольшее
(наименьшее) значения функции у = f(x) на отрезке [а; Ь],
надо:
1) найти критические точки,
принадлежащие отрезку*;
2) найти значения функции в критических
точках, принадлежащих данному отрезку;
3) найти значения функции на концах
промежутка;
4) из полученных чисел выбрать наибольшее
(наименьшее).
2.
11Я (л Я "\ .71 1
sin -g- =sin (2тс- ъ J = -sm g = -g-
з.
5 <25:
5* + 2<5"2.
Функция у = 5 — возрастающая,
следовательно,
* Для нахождения критических точек нужно:
а) решить уравнение f'(x) — 0;
б) найти те значения аргумента из области
определения функции, при которых /' не существует.
Ук У-fix)
у*
У=Нх)
Л 7
aV/ о
1
*о
i
Ь
Рис. 17

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
733
х + 2<-2;
х <-4.
Ответ: (-°°; -4).
Билет № 20
1. Сформулировать основное свойство
первообразных, дать его графическую
иллюстрацию.
2. Вычислить log3 9.
3. Определить» какие из чисел —3; 0; 1; 2
являются корнями уравнения 2* = х + 2.
1.
Любая первообразная для функции у = f(x)
на промежутке I может быть записана в виде
F(x) + С,
где у = F(x) — одна из первообразных функции
У = /(*) на промежутке /, С — произвольная
постоянная.
Геометрический смысл основного свойства
первообразной: графики любых двух
первообразных функции у = f(x) получаются друг из
друга параллельным переносом вдоль оси Оу
(рис. 18).
2.
log3 9 = log3 З2 = 2.
2)х = 1
левая часть 2=2, правая часть 1 + 2 = 3;
2 = 3 — ложно.
3)х = 2
левая часть 2=4, правая часть 2 + 2 = 4;
4 = 4 — истинно, следовательно, 2 — корень
уравнения.
Ответ: корнем уравнения является число 2.
Билет № 21
1. Записать формулы первообразных
степенной функции, синуса и косинуса.
2. Найти значение выражения lg 200 - lg 2.
3. Решить неравенство 5'
х + 2
<25
1.
Функция f
/(*) = хд, л *-1
f(x) = sin х
f(x) - COS X
Общий вид первообразной
Л + 1
X
7 +С,С — постоянная
п + 1 I
-cos х + С, С — постоянная
sin х + С, С — постоянная
lg 200 - lg 2 = lg ^ = lg 100 = 2.
Область значений функции i/ = 2 составляют
все положительные числа Е(у) = (0; +°°), поэто-
му х + 2 > 0, т. е. х > -2. Значит, -3 не является
решением уравнения. Корнем уравнения
является число, обращающее данное уравнение в
истинное равенство.
1)х = 0
левая часть 2 =1, правая часть 0 + 2 = 2;
1 = 2 — ложно.
.х + 2 1 .
5 <25'
5х + 2<5-2.
Функция у = 5
тельно,
х + 2 < -2;
х <-4.
Ответ: (-оо; -4).
— возрастающая, с ледова-
У|
,1 f-+
0
i /У=Р(х)
У y=F(x) + Cl
y/.y=F(x) + C2
У • х
Билет № 22
1. Сформулировать теоремы о первообразных
суммы двух функций / и g и произведения
вида kf.
2. Вычислить tg 71.
, 3* Решить неравенство log04 х < 1.
Рис. 18

734
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Если F — первообразная функции /, a G —
первообразная функции g, то F + G —
первообразная функции f + g.
Если F — первообразная для функции /, а
k — постоянная, то функция kF —
первообразная для функции kf.
2.
tg п = 0.
1ов0,4* <]L
Функция у = log0 4 х — убывающая, значит,
х > 0,4,
х >0,
Ответ: (0,4; +оо).
3.
т. е. х > 0,4.
2.
log2 х + log2 5jc - log2 5 = log2 (x • 5x) - log2 5 =
2
5
= 21og2 x
или
bx • x
= log2 (bx2) - log2 5 = log2 -|- = log2 x2 =
log2 x + log2 bx - log2 5 = log2
2
= log2 # = 21og2 x.
3.
2*^16;
2*>24.
Функция i/ = 2х — возрастающая, значит, x > 4.
Ответ: [4; +oo).
Билет № 23
1. Описать, в чем состоит геометрический
смысл интеграла.
2. Упростить выражение log2 х + log2 5* ~ log2 5.
3. Решить неравенство 2* > 16.
1.
Пусть функция у = f(x) непрерывна и не
изменяет на отрезке [а; Ь] свой знак.
Фигуру, ограниченную графиком функции f,
отрезком [а; Ь] оси Ох и перпендикулярами к
оси Ох в точках а и & называют криволинейной
трапецией.
Если / — непрерывная, неотрицательная на
отрезке [а; Ь] функция, S — площадь
соответствующей криволинейной трапеции, slF —
первообразная функции / на интервале [а; &], то
S = F(b) - F(a).
Для вычисления интегралов используют
формулу Ньютона—Лейбница:
ъ
jf(x)dx = F(b)-F(a).
а
Ъ
Таким образом, J f(x) Ах = S, т. е.
геометрией
ческий смысл интеграла заключается в том, что
интеграл от непрерывной и
неотрицательной функции есть площадь
соответствующей криволинейной трапеции.
Билет № 24
1. Сформулировать теоремы о свойствах
степеней с рациональным показателем.
2. Решить уравнение JSx - 2 = х.
3. Вычислить площадь фигуры, ограниченной
линиями у = 4 — х , у = 0.
1.
Степенью числа а > 0 с рациональным
покати
зателем г = —, где т — целое число, ал — на-
туральное (п > 1), называется число *]а
Для любых рациональных чисел г и s и
любых положительных а и Ь справедливы
следующие равенства:
- Г 8 Г + 8
1. а -а =а
0 г s г-в
2. а : а =а
3. (а ) = а .
4. (аЬ)г = а • &г.
6. Если 0 < а < &, г — рациональное число,
то:
а < Ьг при г > 0;
аг > Ьг при г < 0.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
735
то:
2.
7. Если г и s — рациональные числа и г < s,
а < а при а > 1;
а > а1 при 0 < а < 1.
Первый способ
[ 3* - 2 = х2,
V3*-2 = * <=> < х > о, **
I 3* - 2 > О,
[ х2 - Зх + 2 = О,
J * > О,
|х>§.
Решим квадратное уравнение
х - Зх + 2 = 0;
jc = 1 или jc = 2.
* = о,
i * > 0» или <
х = 2,
х = 1 или х = 2.
Второй способ
J3x - 2 =х;
3* - 2 = *2;
*2 - Зх + 2 = 0;
X} = 1, #2 = 2.
Проверка:
1)* = 1
левая часть л/2
•1-2
1 = 1 — истинно.
2)х = 2
= лД -1;
левая часть л/3 • 2 - 2 = л/4 = 2;
2 = 2 — истинно.
Ответ: 1; 2.
3.
о
1) I/ = 4 - х . Графиком этой функции
является парабола, вершина которой находится в
точке (0; 4), ветви направлены вниз.
2) у = 0. Графиком этой функции является
прямая, совпадающая с осью Ох.
3) Построим графики в одной системе
координат (рис. 19).
Найдем площадь криволинейной трапеции
по формуле Ньютона—Лейбница:
S = ] f(x)dx = F(x)\ba =
= F(b)-F(a).
Найдем пределы интегрирования:
4 - х2 = 0,
2 А
х =4,
х = 2 или jc =-2.
-2
S= j (4-*2)d*=(4*-^-)
-8-i-(4-C-2)-i)-8-S+8-S-
1 2
= 16 - 5g = 10g (кв. ед.).
2
Ответ: Юг (кв. ед.).
Билет № 25
1. Сформулировать теоремы о свойствах
корней it-й степени.
2. Решить уравнение sin х = s и указать
любые два корня.
3. Найти наибольшее и наименьшее значения
функции f(x) = jc3 - 12* на отрезке [0; 3].
1.
Арифметическим корнем п-й степени из
числа а называют неотрицательное число, п-я
степень которого равна а:
п*]а = Ь, если Ъ > 0 и Ьп = а.

736
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Для любого натурального л, целого k и
любых неотрицательных чисел а и Ъ справедливы
следующие равенства:
1. nJab =пЛ 'пЛ.
3. nJ\ja - nkJa, k > 0.
4. Va = nkJak, ft > 0.
5. ЛЛ* = (nJa)h (если ft < 0, то а Ф 0).
6. Для любых чисел аъЪ таких, что 0 < а < 6,
выполняется неравенство nJa < nJb.
2.
sin X = 5 •
х = (-1)д arcsin о + яд, где п е Z;
vn Я
х = (-1) g -I- тел, где л € Z;
я 5я
Ответ: (-l)n g -I- лл, где n е Z; т , -г.
3.
1) f{x) = Эх"2 - 12;
2) f{x) - 0, если 3(х2 - 4) = 0,
х = 2 или х = -2; -2 ё [0; 3].
3)«0) = 0;
f(2) - 23 - 12 • 2 = 8 - 24 = -16;
/(3) - З3 - 12 • 3 = 27 - 36 = -9;
4)тах/(х) = «0) = 0;
[0;3]
min /(х) = /(2) - -16.
[0;3]
Ответ: 0, -16.
1.
Логарифмом числа Ь по основанию а
называется показатель степени, в которую надо
возвести основание а, чтобы получить число 6:
loge6
а = 0.
При любом а > 0, а Ф 1 и любых
положительных х и у выполняются следующие равенства:
l.logfll = 0.
2. logea = l.
3. logfl (ху) - logfl х + logfl у.
4. loga- =logax-logai/.
5. logflxp=plogflx.
2.
2 ^
x - 4
x + 5
2
<0;
(хЛ - 4)(x + 5) < 0,
x*-5.
1) Введем функцию fix) = (x - 4) (x + 5),
D(f) = R.
2) Найдем нули функции у = f(x):
f(x) = 0, если х = -2, или х = -5, или х = 2.
Функция у = fix) — непрерывная, значит, на
промежутках между нулями не обращается в
нуль и сохраняет постоянный знак.
/(3) > 0, /(0) < 0, /(-3) > 0, /(-б) < 0.
+ +
-5 -2 2
(-оо; -5) U (-2; 2)
Ответ: (-оо; -5) U (-2; 2).
3.
3 „2
F(x) = it + "1Г + х + со» гДе со — некоторое
число.
Билет № 26
1. Сформулировать теоремы о свойствах лога-,
рифмов.
2. Решить, применяя метод интервалов, нера-
х - 4 ^ Л
венство — < 0.
х + 5
о 2
о. Найти первообразную функции fix) = х +
+ Зх + 1.
ОБЩЕОБРАЗОВАТЕЛЬНЫЙ КУРС
И КУРС В
Билет № 1
1. Понятие периодической функции, пример,
иллюстрация на графике.
2. Свойства степеней с рациональным
показателем. Доказательство одной из теорем (по
выбору учащегося).

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
737
3. а) Решить систему
3
* + У = 2'
sin х = О
и записать одно решение, удовлетворяющее
условию
х <0,
У<0;
б) решить систему
lg х + lg у = 3,
jt^^IOO.
1.
Функция у = /(*) называется периодической,
если существует такое число Г, не равное нулю,
что для любых значений аргумента из области
определения функции выполняются равенства
f(x-T) = f(x) = f(x + T).
Число Т называется периодом функции.
Например, у = sin х — периодическая
функция (рис. 20).
Периодом функции являются любые числа
вида Т = 2nky где k — целое, кроме 0.
Наименьшим положительным периодом является число
Г = 2я.
Для построения графика периодической
функции достаточно построить часть графика на
одном из промежутков длиной Г, а затем
выполнить параллельный перенос этой части графика
вдоль оси абсцисс на ±Г, ±2Г, ±ЗГ, ...
2.
Степенью числа а, большего нуля, с рацио-
т ,
нальным показателем г = — (т — целое число;
п — натуральное, большее 1) называется число
пГ~гп
уа , т. е.
п п т
a =nJa .
у = sin х
Степень числа 0 определена только для
положительных показателей;
0Г = 0 для любого г > 0.
Свойства степеней с рациональным
показателем
Для любых рациональных чисел г и s и
любых положительных а и 6 справедливы
следующие свойства.
1. Произведение степеней с одинаковыми
основаниями равно степени с тем же
основанием и показателем, равным сумме показателей
множителей:
Г S Г+ 8
а • а = а
2. Частное степеней с одинаковыми
основаниями равно степени с тем же основанием и
показателем, равным разности показателей
делимого и делителя:
Г 8 Г -8
а : а =а
3. При возведении степени в степень
основание оставляют прежним, а показатели
перемножают:
t TvS Г8
(а) =а .
4. Степень произведения равна
произведению степеней:
(аЪ)г = аг-Ьг.
5. Степень частного равна частному
степеней:
№-?■
Рис. 20
6. Пусть г — рациональное число и число а
больше нуля, но меньше числа Ь, 0 < а < Ь, тогда:
а < 6Г, если г — положительное число;
а > bry если г — отрицательное число.
7. Для любых рациональных чисел г и s из
неравенства г <s следует, что:
а < а при а > 1;
а > а8 при 0 <а < 1.
Докажем свойство 2. Пусть г = —и
s = - , где п ид — натуральные числа, а т ир —
целые числа. По определению степени с
рациональным показателем имеем:
т £
ап :ai=nJa!k :%&.
24-1019

738
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Приведем корни к одному показателю. Для
этого воспользуемся свойством корней n-й
степени:
nJa = nkJah, k > 0.
Имеем:
ЧЙ* : Я& = ПЛ^ : пя[аГ = ^£2.
Используя свойство частного корней, получим:
nql™Q I та /
УД _ \а ч _ па\пmq - рп
i г па\ tyO •
Применим определение степени с
рациональным показателем:
п%Га
mq - рп __
тд - рп тд _ £л
па пд пд
m _ £
= а = а
Свойства 1, 3, 4 и 5 доказываются аналогично.
Пусть г = — и s
где п и q —
натуральные числа , а т и р — целые. Имеем:
а • а8 = "Л* ' ^ = п<№Гч ' п*[а?~п =
тд + рп
а
= п^ат* • арп = п^ат* + рп =
пд пд п д r + s
*? _
= а
= а
Е
= а (свойство 1);
(aY = fa"T = la"l -lldff-
тр т j)
= №"* = "Л"** = anq = с" '« = с"
(свойство 3);
Докажем свойство 6.
т
1. Пусть г > 0, г = — , где тип —
натуральные числа. Из неравенства 0 < а < Ь и свойств
степени с целым показателем следует, что ат <
< Ът. Согласно свойству корней (для любых
чисел а и Ь таких, что 0 < а <Ъ> выполняется
неравенство nJa < nJb) из неравенства ат < Ьт
получаем неравенство n>Jam <
п№
или а <Ъ
т. е. а < Ьг.
т
2. Пусть г < 0, г = — , где т — целое
отрицательное число, an — натуральное число. Из
неравенства 0 < а < Ь и свойств степени с целым
показателем следует, что ат > Ьт. Согласно
свойству корней получаем: п*}ат > пыЬт. Это
неравенство по определению степени с рациональ-
т т
ным показателем можно записать в виде а > Ь ,
т. е. а > Ьг.
Для доказательства свойства 7 приведем рацио-
т
нальные числа г и s к одному знаменателю: г = —
и s = - , где п — натуральное число, а т и р —
целые числа.
По условию г > s, следовательно, т > р.
1 1
1. Пусть а > 1, тогда ап = nJa > 1, т. е. ап > 1.
Согласно свойству степени с целым показателем
1\т / 1\р т £
f !V
а
Отсюда а > а , т. е. а > а .
(ab)J
2 . i
/ 1_\Я 711/ l\W П/ Л1 и"1
= (ab) =л/(а&) =л/а -Ь =
7П /П
= Va ' ыЬ = а • Ь = а • Ь (свойство 4);
/л
ft Vft
т
п г
= — — — (свойство 5).
ь» ь
2. Если 0 < а < 1, то 0 < а < 1. По свойству
степени с целым показателем
т £
Отсюда а < а , т. е. а < а .
3.
' V
а
3
а) \Х + У= 2>
[ sin х = 0;
IJC = пп,
(1\р
а
v J

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
739
,--х+|, I"™
<=> { 3 п е Z.
у = g " кп>
<=>у 2
I X = кп,
Решений, для которых
п нет, так как если х < О, то
у = -х + | > 0.
v 3
Ответ: (пп; ~ "~ яп), п е Z.
б) Данная система равносильна следующей
системе:
ig(*y) = 3,
х >0,
у >о,
lgx^'-lglOO,
<=>s
лгу = 1000,
*>0,
У>0,
lg2jc = 2,
<=>
<=> S
ху - 1000,
jc>0,
У>0, ~
|lg х| = 72 ,
lg х = л/2 ,
ху =1000,
jc>0,
У >0;
^х = -л/2,
лгу = 1000,
jc>0,
У >0,
<=>
х= 10
72
3-72
х = 10
х-КГ*.
* = 103 + 7i
Ответ: (10^ ; 103 " Л); (\ЬЛ ; 103 + ^).
Билет № 2
1. Понятие о точках максимума (минимума)
функции, пример, графическая
иллюстрация.
2. Вывод общей формулы корней уравнения
sin х = а.
31oge2 + loge27
3. а) Вычислить
3
21о£з4
б) Упростить выражение
^ylogzJx + 1 - 0,51og3(*2 ~ 1)
W
1.
Точка х0 называется точкой максимума
функции Д если для всех х из некоторой
окрестности точки х0 выполнено неравенство f(x) < f(x0)
(рис. 21).
Окрестностью точки х0 называется любой
интервал, содержащий эту точку.
2
Например, функция у = -х +3 имеет точку
максимума х0 = 0 (рис. 22).
Точка х0 называется точкой минимума
функции /, если для всех х из некоторой
окрестности х0 выполнено неравенство f(x) > f(x0)
(рис. 23).
Например, функция у = х +2 имеет точку
минимума х0 = 0 (рис. 24).
2.
1) Если \а\ > 1, то уравнение sin jc = а корней
не имеет, так как |sin х\<1 для любого х.
2)Пусть|а|< 1.
| окрестность
точки х0
У\
0
■fir \i
Т\х0у
i
Ч y=f(x)
\ 1° ^
\ 1
г^г^Х^
/ *
;У
У\
у = * + 2
Рис. 21
Рис. 22
Рис. 23
Рис. 24

740
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
а) На промежутке I-g ; 5 I функция у = sin х
возрастает, следовательно, по теореме о корне,
уравнение sin х — а имеет один корень х = arcsin а.
б) На промежутке I о » "5" J Функция!/ = sin х
убывает, значит, по теореме о корне, уравнение
sin х = а имеет одно решение х = п - arcsin а
(рис. 25).
в) Учитывая периодичность функции у = sin х
(период функции равен 2тш, п — целое, кроме
0), решения уравнения можно записать так:
х = arcsin а + 2кп или х = п - arcsin а + 2тсп,
где п е Z.
Решения данного уравнения можно записать
в виде следующей формулы:
х = (-l)n arcsin а + теп, где п е Z.
При четных п {п =* 2Л) мы получим все
решения, записанные первой формулор, а при
нечетных п(п = 2fe + 1) — все решения, записанные
второй формулой.
3.
а)
31oge2 + loge27 31og62 + 31oge3
21og34
3
3(log62 + log63)
16
Ответ: -г* •
log34
3
31oge6
16
16
/1\l0g8V* + 1 - log3V(*2 - 1) /1\
Ч1) -6
log3
Jx + 1
h^
1)
*°g3 1 -21og3-
= (3-2) «^=3 -
= 3logs(-D=^_1
Ответ: x - 1.
Билет № 3
1. Понятие арксинуса числа, пример.
2. Основное свойство первообразной, его
геометрическая иллюстрация.
3. а) Исследовать функцию у = хех и
построить ее график.
б) Найти угловой коэффициент и угол
наклона касательной, проведенной к графику
функции у = 1 + sin х в точке с абсциссой
Хп = ТС.
1.
Арксинусом числа а называется число, для
которого выполнены следующие два условия:
1)-о < arcsin а < « ;
2) sin (arcsin а) = а.
Из второго условия следует, что \а\ < 1.
Пример 1. (Рис. 26.)
. 7з к
arcsin V = 3 • так как:
1)-1<§<л
2*
2)8Шд =Т.
У;
"it-arcein а/с!
V °
1
^s£ arcsin а
«2/4
/ х
Рис. 25
Рис. 26

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
741
Пример 2. arcsin -5- не имеет смысла, так
Л
как -=- > 1, a arcsin а определен при -1 < а < 1.
2.
Если функция F — первообразная функции
/ на промежутке /, то функция у = F(x) + С
(С — const) также является первообразной
функции / на промежутке J. Любая первообразная
функции / на промежутке / может быть
записана в виде F(x) + С.
Доказательство.
1) Воспользуемся определением
первообразной:
(*■(*) +С)'= *"(*) +Г -Л*),
следовательно, у = F(x) + С — первообразная
функции / на промежутке J.
2) Пусть Ф и F — первообразные функции / на
промежутке J. Покажем, что разность Ф - F равна
постоянной. Имеем (Ф(х) - F(x))' = Ф'(*) - F'(x) =
-Л*)-Л*)-О,
следовательно, по признаку постоянства
функции на интервале Ф(х) - F(x) = С. Значит, любую
первообразную можно записать в виде F(x) + С.
Графики любых двух первообразных для
функции у = f(x) получаются друг из друга
параллельным переносом вдоль оси Оу (см.
рис. 18).
3.
a) l)D(i/) = B.
2) Найдем точки пересечения графика
функции с осями координат.
Если х = 0, то у = 0; О (0; 0).
Если у = 0, то хех = 0, х = 0; О (0; 0).
3) Найдем промежутки знакопостоянства:
у < 0, если х < 0,
у > 0, если х > 0.
4) Выясним, является ли функция четной
или нечетной. Имеем
у{-х) = -хе~х = -—х Фу(х), у(-х) Ф -у(х),
е
следовательно, функция не является ни четной,
ни нечетной.
5) Найдем производную функции:
у' = х'е* + (е*)'* = ех + ехх = е*(1 + х).
6) Найдем критические точки:
D{y') = R;
е*(1 +jc) = 0<=>1 + jc = 0<=>x=-1.
7) Найдем промежутки возрастания и
убывания функции, точки максимума и минимума:
у'ф) = ер(1 + 0) >0, у'(-2) = е"2(1 - 2) < 0.
На промежутке (-°°; -1) функция у = хех
убывает, так как у' < 0; на промежутке (-1; +°°)
функция у — хех возрастает, так как у' > 0; х =
j= -1 — точка минимума, так как, проходя через
эту точку, производная меняет знак с - на +.
Найдем минимум функции:
iK-D-'-l-e"1--!.
У'
У
(-~; -1)
-
■——
-1
0
1
е
"(-1;+-)
+'
---*
Дополнительные точки: у{-2) = -2е = —g »
е
1/(1) = е.
График функции у = хех изображен на
рисунке 27.
б) k = tg а = у'(х0),
где k — угловой коэффициент касательной,
проведенной к графику функции у = f{x) в точке с
абсциссой х0; а — угол между касательной и
положительным направлением оси Ох. Имеем:
у' = cos х;
у'(тс) = costc = -1.
Следовательно, k = -1 и tg а = -1. Отсюда
Зтс
Ответ: 1, -т-.
L « _ J У = хе
-1
Рис. 27

742
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Билет № 4
1. Понятие арккосинуса числа, пример.
2. Показательная функция, ее свойства и
график. Доказательство одного из свойств (по
выбору учащегося).
3. а) Найти кинетическую энергию тела массой
т кг, движущегося прямолинейно по зако-
ну x(t) = 4t - t (м) в момент времени t = 2 с.
б) В каких точках касательная к кривой
1 3 2
у = о # — х — х + 1 параллельная прямой
у = 2* - 1?
1.
Арккосинусом числа а называется такое
число, для которого выполнены следующие два
условия:
1)0^ arccos а < тс; 2) cos (arccos а) — а.
Из условия 2) следует, что \а\ < 1.
Пример 1. (Рис. 28.) arccos о = 3 * так как:
1)0<5 <тс;
2)со8з =2'
Пример 2. arccos тс не имеет смысла, так как
тс« 3,14 > 1; arccos а определен при \а\ < 1.
2.
Показательной функцией называется
функция вида у = а*, где а — заданное число, а > 0,
а *1.
Свойства показательной функции
1. Областью определения показательной
функции являются все действительные числа:
^(у) = (-00;-ь°0).
Это следует из того, что любого х е R
определено значение степени а (при а > 0).
2. Множеством значений показательной
функции являются все положительные
действительные числа: Е(у) = (0; °о).
Это следует из свойства степени: аР > 0 при
а >0.
3. а) Показательная функция у = а*
возрастает на всей области определения, если а > 1.
б) Показательная функция у = ах убывает
на всей области определения, если 0 < а < 1.
Докажем, что если а > 1, то большему
значению аргумента (х2 > хг) соответствует большее
значение функции (а > а ). Из свойств
степени известно, если г > s и а > 1, то а > а8.
Пусть х2 > хг и а > 1, тогда а 2 > а (по
свойству степени). А это означает, что функция у =
= ах при а > 1 возрастает на всей области
определения .
Докажем, что если 0 < а < 1, то большему
значению аргумента (х2 > хг) соответствует
меньшее значение функции (а < а ). Из
свойств степени известно, если г>8и0<а<1,
то а < а8. Пусть х2 > хг и 0 < а < 1, тогда а 2 <
< а (по свойству степени). А это означает, что
функция у = ах при 0 < а < 1 убывает на всей
области определения.
4. Нет таких значений аргумента, при
которых значения показательной функции
равны нулю, т. е. у показательной функции нет
нулей.
5. Показательная функция непрерывна на
всей области определения.
6. Показательная функция
дифференцируема в каждой точке области определения,
производная вычисляется по формуле
(ах)' = ах In а.
(Вывод этой формулы см. в билете 22.)
График показательной функции изображен
на рисунке 29.
Рис.28 '
* Доказательство приведено для рациональных
значений.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
743
з.
а) а) Ек = —;
у(0 = s'(t) = 2 • At - 1 = 8t - 1;
EK(t) -=J«fi£;
б)£к(2)^(8-22-1)2=^(Дж).
б) 1) Касательная к кривой параллельна прямой
I/ = 2х - 1, следовательно, угловой коэффициент
касательной k = 2;
^ = !/'(*о)>
у'=х -2х- 1, значит,
х2 - 2х - 1 = 2,
х2 - 2х - 3 = О,
#i = —1, Х^ = 3.
2) Найдем координаты точек, в которых ка-
1 з 2 , ,
сательная к кривой у = =х - х -jc + 1
параллельна прямой у*2х-1:
i/(-l)=i(-l)3-(-l)2-(-l) + l = |;
М (-1; | )
i/(3) = | -33-32-3 + 1 = -2;
N (3; -2).
Ответ: в точках М (-1; g ) и N (3; 2)
касательные к кривой параллельны прямой у - 2 л: - 1.
Билет № 5
1. Понятие арктангенса числа» пример.
2. Логарифмическая функция, ее свойства и
график.
Доказательство одного из свойств (по
выбору учащегося).
3. а) Найти точки, в которых тангенс угла
наклона касательной к графику функции у =
= хех равен нулю.
б) Вычислить площадь фигуры, ограничен-
ной линиями у = х - 2, у = 2х - 2.
1.
Арктангенсом числа а называется такое
число, для которого выполняются два условия:
1)-| <arctga < |;
2) tg(arctg а) = а.
Например (рис. 30), arctg 7з = « , так как:
»-i<i<'
2'
2) tg | = 7з.
2.
Логарифмической функцией называется
функция вида у = loga х, где a — заданное
число, а > 0, а * 1.
Свойства логарифмической функции
1. Областью определения логарифмической
функции являются все положительные
действительные числа: D(y) = (0; оо).
Это следует из определения логарифма числа
Ь по основанию а:
loga Ъ имеет смысл, если Ъ > 0.
а)
Vi
1
0
1
X
у - a
0< a < 1
JC
б)
Рис. 29
Рис. 30

744
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
2. Множеством значений логарифмической
функции являются все действительные числа:
Е(у) = (-оо; оо).
Пусть у0 — произвольное действительное
число. Покажем, что найдется такое
положительное значение аргумента х0, что
выполняется равенство у0 = loga х0. По определению лога-
^ уо Уо л ,,
рифма числа имеем: х0 * а , a > 0. Мы
показали, что нашлось значение х0 > 0, при котором
значение логарифмической функции равно у0
(у0 — произвольное действительное число).
3. Логарифмическая функция обращается в
нуль при х = 1.
Решим уравнение loga х = 0. По определению
логарифма получаем:
а = х, т. е. х = 1.
4. а) Логарифмическая функция у = loga х
возрастает на всей области определения, если
а>\.
Докажем, что большему значению аргумента
(х2 > хг) соответствует большее значение
функции (loga х2 > loga хх), если a > 1. Пусть х2 > хх >
> 0; тогда, используя основное логарифмическое
тождество, запишем это неравенство в виде
а > а . (1)
В неравенстве (1) сравниваются два значения
показательной функции. Поскольку при а > \
показательная функция возрастает, большее
значение функции может быть только при
большем значении аргумента, т. е. loga х2 > loga xv
б) Логарифмическая функция у = loga х
убывает на всей области определения, если 0 < а < 1.
Свойство б) доказывается аналогично.
5. Логарифмическая функция у = loga х:
а) при а > 1 принимает положительные
значения, если х > 1; отрицательные значения,
если 0<х < 1.
б) при 0 < a < 1 принимает положительные
значения, если 0 < х < 1, и отрицательные
значения, если х > 1.
Пусть a > 1, тогда функция у = loga х
возрастает на всей области определения (рис. 31);
причем loga 1 = 0.
Из этого следует, что:
для х > 1
logfl х > loga 1, т. е. logfl х > 0;
для 0 < х < 1
logfl х < logfl 1, т. е. logfl х < 0.
Пусть 0 < а < 1; тогда функция у = loga х
убывает на всей области определения (рис. 32);
причем loga 1 = 0.
Из этого следует, что:
для х > 1
logfl х < logfl 1, т. е. logfl х < 0;
для 0 < х < 1
logfl х > logfl 1, т. е. logfl х > 0.
6. Логарифмическая функция непрерывна на
всей области определения.
3.
а) у = хе*;
/ х , X
у = е + хе ;
tga = i/,(^0)= е ° +х0е °;
у'(хо) = 0» если е + х0е = 0 <=>
Xq
<=> е (1 + х0) = 0 <=> х0 = -1.
Ответ: в точке х0 = -1 тангенс угла наклона
касательной к графику функции у = хе* равен
нулю.
б) 1. Изобразим схематично графики функций
у =х2 -2иу = 2х-2.
Как видно из рисунка (рис. 33), часть
заштрихованной фигуры расположена под осью
абсцисс.
2) Чтобы применить теорему о вычислении
площади криволинейной трапеции, выполним
параллельный перенос фигуры на вектор а (0; 2).
В этом случае линии будут заданы уравнениями
у = х2 и у = 2х (рис. 34). Вычислим площадь
фигуры ОтА.
Рис. 31
Рис. 32

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
745
3) sOmA " saoak ~ SkP. тр. ОтАК- Найдем
пределы интегрирования:
2
х = 2х, х = 0 или х = 2;
*W=| -2-4 = 4;
_2 2 _хз,2
^кр. тр. ОшДЛГ = J х &х = у
О
sOmA = 4-2I -1|(кв.ад.).
-I-2I.
Ответ: 1~ (кв. ед.).
Билет № 6
1. Понятие производной, ее механический
смысл.
2. Вывод общей формулы корней уравнения
cos х = а.
3. Упростить выражение:
3 3W 3
а)
i _ йр + й 1
л - Л
(
б)
(7i + n/&)
-2
Jab;
Ja - Jb
3 3
l 2 ,2
1.
. Пусть на некотором промежутке задана
функция у = /(*); х0 — точка этого промежутка;
Ах — приращение аргумента х; х0 + Ах также
принадлежит этому промежутку; Ау—
приращение функции.
Предел отношения (если он существует)
приращения функции к приращению аргумента при
стремлении приращения аргумента к нулю
называется производной функции в точке, т. е.
Пусть материальная точка движется по
координатной прямой по закону х = x(t)> т. е.
координата этой точки х — известная функция
времени t.
Механический смысл производной состоит
в том, что производная от координаты по
времени есть скорость:
2.
1) Если \а\ > 1, то уравнение cos х = а
решений не имеет, так как |cos х\ < 1 для любого х.
2) Рассмотрим случай \а\ < 1 (рис. 35).
а) На промежутке [0; тс] функция у = cos х
убывает, значит, уравнение cos х = а имеет один
корень х = arccos а.
Учитывая, что функция у = cos х —
периодическая с периодом 2ял, запишем все решения
уравнения cos х = а на промежутках [2кп; я +
+ 2кп]у п е Z, в виде
х = arccos а + 2кп, где п е Z.
б) На промежутке [-тс; 0] функция у = cos х
возрастает, следовательно, уравнение cos х = а
имеет один корень, а именно, х = -arccos а.
Учитывая периодичность функции у = cos х>
делаем вывод, что решением уравнения cos х = а
на промежутках [-тс + 2тсл; 2тсл], где п € Z,
являются числа вида
х = -arccos а + 2тсп, где п е Z.
Таким образом, все решения уравнения
могут быть записаны так:
х = ±arccos а + 2тсп, где п е Z.
Рис. 34
Рис. 35

746
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
з.
(1 «Y » »ч
Ja - Jb
Jab =
3.2
I
3.2
4|
Ja - Jb
з з
2 Л
- Jab =
_ a - b _ r^ _ (Ja) - (Jb) __ rfi =
Ja - Jb Ja - Jb
= (J5 - Jb)(a + Ja~b + b) _ г^ =
= a + Jab +b-Jab = a + b.
Ответ: a + 6.
6)
1
(Ja 4- Jb)"
Ja - Jb
2 «2 i
-l
Ja - Jb
= a -I- 2л/аЬ + Ь -a - Tab -b = Tab.
Ответ: Jab.
Билет № 7
1. Понятие производной, ее геометрический
смысл.
2. Вывод общей формулы корней уравнения
tgjc = a.
3. а) Вычислить в"*8* " 1 : (81овв2в + 1).
б) Упростить выражение
lg(x3 + 8)-0,51g(x2 + 4jc + 4)-lg(x2-2jc + 4).
1.
Пусть на некотором промежутке задана
функция у = f(x); х0 — точка этого промежутка;
Ajc — приращение аргумента х; точка х0 + Ах
принадлежит этому промежутку; Ау—
приращение функции.
Предел отношения (если он существует)
приращения функции к приращению аргумента при
стремлении приращения аргумента к нулю
называется производной функции в точке, т. е.
Пусть задана дифференцируемая функция
У - /(*) (Рис. 36).
Геометрический смысл производной
состоит в том, что значение производной функции в
точке х0 равно угловому коэффициенту
касательной, проведенной к графику функции в
точке с абсциссой х0:
f'(xo) = *» гДе * ~~ угловой коэффициент
касательной.
2.
1) На промежутке f-g » 2 ) ФУНК1*ИЯ У = *£*
возрастает, значит, на этом промежутке, по
теореме о корне, уравнение tgjc = а имеет один
корень, а именно, х = arctg а (рис. 37).
2) Учитывая, что период тангенса равен яп,
все решения определяются формулой
х = arctg а + ппу п е Z.
3.
а) 8
log82
1 : (810*826 + 1) -
= 81°**2 • 8 l: (26 + 1) = 2 • I : 27 -
= I J_ = _L
4 " 27 108 #
Ответ: ^кб •
Рис. 36
Рис. 37

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
747
б) lg(x8+8)-0,51g(x2+4x + 4)-lg(x2-2x + 4) =
= lg (xZ + 8) - lg ((х + 2)2)0'5 - lg (x2 - 2x + 4) =
= lg
xS + 8
, x + 8 , - Л
= lg-5 =lgl=0.
(x + 2)(x2 - 2* + 4) *& x3 + 8
Ответ: 0.
Билет № 8
1. Понятие о непрерывности функции, пример,
графическая иллюстрация.
2. Свойства корней rt-й степени.
Доказательство одной из теорем (по выбору учащегося).
3. Решить уравнение:
a) 4sin х + 3cos х = 5;
б)2*~1 + 2*~2+2*~3 = 448.
1.
Пусть функция у = f(x) задана на некотором
промежутке, а — точка этого промежутка. Если
для функции выполняется приближенное
равенство f(x) « f(a) с любой, наперед заданной
точностью, для всех х, близких к а, то говорят, что
функция непрерывна в точке а. Иными словами,
функция / непрерывна в точке а, если f(x) -» f(a)
при* -> а.
Функция, непрерывная в каждой точке
промежутка, называется непрерывной на
промежутке.
График непрерывной на промежутке
функции представляет собой непрерывную линию.
Иными словами, график можно нарисовать, не
отрывая карандаша от бумаги.
Например, функция f(x) = 3х непрерывна в
х 2
точке х0 = 2. Действительно, 3 —► 3 при х -> 2.
Функция f(x) = 3х непрерывна на множестве
всех действительных чисел, а ее график можно
нарисовать, не отрывая карандаша от бумаги
(рис. 38).
2.
Арифметическим корнем п-й степени из
числа а называется неотрицательное число, п-я
степень которого равна а.
Свойства корней
Для любых натуральных п, целого k и любых
неотрицательных чисел а иЬ выполняются
следующие свойства:
1. Корень п-й степени из произведения равен
произведению корней п-й степени:
п4аЪ = nJa • nJb.
2. Корень п-й степени из дроби равен
частному корней п-й степени из числителя и
знаменателя:
3. Корень п-й степени из корня k-й степени
из а равен корню nk-й степени из а:
nJhja = nhja, k > 0.
4/ Если показатель корня и показатель
степени подкоренного выражения умножить
на одно и то же положительное число, то
значение корня не изменится:
nJa = nkJak, k > 0.
5. Чтобы извлечь корень п-й степени из а в
степени k, нужно корень п-й степени из а
возвести в степень k:
Ti/а = (nJa) (если k < 0, то а Ф 0).
6. Для любых неотрицательных чисел а и Ь
таких, что а меньше Ь, выполняется
неравенство: корень п-й степени из а меньше корня
п-й степени из Ь:
nJa <nJby если 0 < а < Ь.
Докажем свойство 1. По
определению nJab — это такое неотрицательное число,
п-я степень которого равна ab> т. е.
{nJab)n = ab.
Рассмотрим правую часть данного равенства
(nJa • nJb). По определению корня п-й степени
nJa > 0 и nJb > 0, следовательно, nJa • nJb > 0.

748
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
По свойству степени произведения
((аЬ)п = ап • Ьпу где а > О, Ь > 0) имеем
(nfa • ф)п »(|5/а)я • (nJb)n.
Вновь применим определение корня n-й
степени: (nJa)n = a, (Vb)П = Ь- Таким образом,
(nJa)n • (пЛ)п = аЪ.
Следовательно,
nJab = nJa • nJb,
что и требовалось доказать.
Аналогично доказываются свойства 2, 3 и 4:
n/e = Ji£ (свойство 2);
"TVS > 0 и (V^)"* - ((пШ)П)к = (VS)* = а;
(nVa)n = а, т. е. n4hJa = nVa (свойство 3);
V^ >0и (П75)П* = anJa)*)h-ak9 (nk№)nk=a,
т.е. n*fa = nMa (свойство 4).
Докажем свойство 5.
пГк п
По определению корня n-й степени (*1а ) =
= ak\(nJa)k> 0, так как nJa>0. Найдем n-ю сте-
пень выражения С7а) • По свойству возведения
степени в степень
«пЛ)к)п=(пЛ)пк = ((пЛ)п)к;
по определению корня n-й степени
((пЛ)п)к = а\
Следовательно,
Доказательство свойства 6
проводится методом от противного. Допустим, что
nJa > nJb. Тогда по свойству степеней с
натуральным показателем имеем (nJa )n>(nJb )Л, т. е.
а>Ь. Это противоречит условию а <Ь.
Следовательно, для любых чисел а и Ъ таких, что 0 < а < Ь,
выполняется неравенство nJa < nJb.
3.
a) 4sin х + 3cos х - 5 = 0;
8sm g cos о + 3cos « "" Ssin « " Ssin о ""
-5cos о = 0;
8sin | cos | - 8sin | - 2cos | = 0.
m * x
Так как sin « и cos о не могУТ одновременно
обращаться в нуль, разделим левую и правую
2 X 2 X
части уравнения на cos 5 (cos о * ^* Получаем:
8tg2 | - 8tg \ + 2 = 0;
4tg2 § - 4tg I + 1 = 0;
(2tgf-1)2=0;
2tg \ - 1 = 0;
j. * 1
^2=2;
x 1
2 = arctg g + яп, где BeZ;
x = 2arctg 5 + 2яп, где n e Z.
Ответ: 2 arctg 5 + 2яп, где n e Z.
6) 2*_1 + 2*~2+2*~8 = 448;
2*~3(22 + 2 + l) = 448;
9х-з_448.
2*~3 = 64;
2*"3 = 26.
Функция i/ = 2 является монотонной,
значит, каждое свое значение принимает один раз.
Следовательно,
х -3 = 6;
х = 9.
Ответ: 9.
Билет № 9
1. Теоремы о непрерывности рациональных и
дробно-рациональных функций на области
их определения.
2. Свойства логарифмов. Доказательство
одной из теорем (по выбору учащегося).
3. Вычислить площадь фигуры, ограниченной:

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
749
а) линиями у = 2л/х, Зу + 2х = 8 и осью
абсцисс;
б) линиями у = х — 29 у = 2х — 2.
1.
Все рациональные и дробно-рациональные
функции непрерывны на всей своей области
определения. Этот факт следует из того, что
рациональные и дробно-рациональные функции
дифференцируемы во всех точках своих областей
определения.
3 2
Например, функция f(x) = х - 7х + 24х
непрерывна на множестве действительных чисел;
а функция g(x) = —^~Т непрерывна на проме-
жутке (-°°; 2) и на промежутке (2; +°°).
2.
Логарифмом числа b по основанию а
называется показатель степени, в которую нужно
возвести основание а, чтобы получить число Ь.
Из определения имеем:
а в = Ъ (основное логарифмическое
тождество).
Свойства логарифмов
При любом а > 0 (а * 1) и любых
положительных х и у выполняются следующие свойства:
1. Логарифм единицы по основанию а равен
нулю:
logfll = 0.
2. Логарифм а по основанию а равен 1:
logfla = l.
3. Логарифм произведения равен сумме
логарифмов:
logfl (ху) = logfl х + logfl у.
4. Логарифм частного равен разности
логарифмов:
loga ^ = logfl х - logfl у.
5. Логарифм степени равен произведению
показателя степени на логарифм основания
этой степени:
log,**" =plogfl*
для любого действительного числа р.
6. Формула перехода от одного основания
логарифма к другому основанию:
log*»*
loga х = , (х > 0, а >0 и a * 1, Ь >0 и & * 1).
log {, а
Первое и второе свойства логарифмов
следуют из определения логарифма и свойства
степени с показателем 0 и 1:
а = 1, значит, loga 1=0;
а =а, значит, loga a = 1.
Докажем свойство 3. Воспользуемся
основным логарифмическим тождеством (а =
= х) и свойством показательной функции (а* у =
= aY).
Имеем
loga{xy) logex foggy \ogax + logaV
a = xy — a a =a
Отсюда следует, что
logfl (*!/) = logfl x + logfl y.
Докажем свойство 4. Вновь
воспользуемся основным логарифмическим тождеством
logax log^
х = a , у = a
lo*ew x a ° e* logeJC - logo?
a — — = —i = a »
у logey
следовательно,
logfl ^ = logfl x - logfl y.
Докажем свойство 5. Воспользуемся
logo* D ,J°*a*.P
тождеством x = a , откуда x = (a ) =
p logex
= a (использовано свойство возведения в
степень). Логарифмируя полученное равенство,
имеем
bgflxp=plogax.
Докажем формулу перехода к
другому основанию. Воспользуемся
основным логарифмическим тожеством-(х = а ):
\ogax
log&x=log&(a );
применяя свойство логарифмирования
степени (loga Xя =ploga х), получим
log& х = logfl xlog& а.
Разделив обе части равенства на logft а, имеем
log&x
log&a
logflx.

750
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
а) 1) Графиком функции у = 2 Jx является
кривая, проходящая через следующие точки:
X
У
0
0
1
2
4
4
16
8
Графиком уравнения Зу + 2х = 8 является
прямая, проходящая через следующие точки:
х 14 1
У 0 2
Построим графики в одной системе
координат (рис. 39).
2) Найдем абсциссы точек пересечения
графиков:
2jx =
8 - 2х
;6V* = 8-2х;б7* + 2л:-8 = 0;
3jx +jc-4 = 0;jc + 37^-4 = 0.
Пусть Jx = t; тогда
*2 +3f-4 = 0;f = -4,t = 1;
J~x =-4
(решений нет)
3) SQAB = SQAC + SABC>
SABC =\АС' вс>АС - ^D - 25
ВС = \хв - хс| = 4 - 1 = 3;
или
JC = 1.
Sabc = о " 2 • 3 = 3;
4
3
-I
soac = J 2V*dx= з л:2|
о
soab = 1з+3 = 43 (кв* ед,)#
Omeemi 4« (кв. ед.).
б) Решение показано в билете № 5 (вопрос 3, б)).
У1
21
lj
о
1
ш
]
y = 2jx^
mJiy + 2* = 8
L 2 3 4N. *
Рис. 39
Билет № 10
1. Понятие о первообразной функции.
2. Функция тангенс, ее свойства и график.
Доказательство одного из свойств (по выбору
учащегося).
3. Решить уравнение:
a) log2 (9* ~ г + 7) = 21og2 (3х " * + 1);
6М10*9*2 +2 = 41°*9* + 1-410*9*.
1.
Функция F называется первообразной
функции / на промежутке /, если для всех значений
аргумента из этого промежутка F'(x) = f(x).
2
Например, функция F(x) = 4х + 3* - 1 явля-
ется первообразной функции f(x) — 12х + 3 на
множестве всех действительных чисел.
Действительно, F'(x) = 12х2 + 3, т. е. F\x) = /(*).
Функция F(x) = 2 sin jc - 8 cos x не является
первообразной для функций f(x) = 2cosjc-
- 8sin*. Действительно, F\x) = 2cos x + 8sin x,
но *"(*) * /(*)•
2.
Если каждому действительному числу
поставлен в соответствие его тангенс, то говорят,
что задана функция тангенс. Обозначается это
так: у = tg х.
Свойства функции тангенс
1. Областью определения функции являются
все действительные числа, кроме чисел вида
х = о + тс*, где k е Z.
Это следует из определения тангенса (tg х =
= 2!££ \ Нужно исключить числа, при которых
знаменатель cos х = 0, т. е. х = « + яй, где k е Z.
2. Множеством значений функции
являются все действительные числа: Е(у) = (-°°; °°).
Пусть у0 — произвольное действительное
число. Уравнение tg х = у0 имеет решение,
следовательно, найдется такое значение jc0, при
котором tg х0 - у0.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
751
3. Функция является нечетной функцией,
т. е. для любого х е D(y) выполняется равенство
tg(-*) = -tgx.
Покажем это. Имеем:
х , v sin(-x) -sin* ,
**(-*) = ;^) = "^="tg*-
4. Функция является периодической с
периодом тсй, где k — целое, кроме 0. Наименьшим
положительным периодом тангенса является
число п.
Каждому действительному числу вида х + nk>
где k е Z, соответствует единственная точка оси
тангенсов Тх + Л, которая имеет ординату,
равную tg х или tg (х + nk). Таким образом,
tg х = tg (х + nk).
Этим показано, что числа вида тсЛ, где k —
целое, кроме 0, являются периодом функции
тангенс.
При k = 1 имеем tg (х + тс) = tg jc,
следовательно, число п является периодом функции
тангенс.
Покажем, что тс — наименьшее
положительное число, являющееся периодом. Пусть Т —
положительный период тангенса, тогда tg (Т +
+ х) = tg х при любом х е D(y). Это равенство
должно быть верно и при х = 0, т. е. tg Т = tg 0 =
= 0, или tg Т = 0. Уравнение tg Т = 0 имеет
решение Т = тсй, где k € Z, значит, наименьшее
положительное значение равно тс.
5. Функция тангенс принимает значение
нуль при х =nk> где k € Z. Решением уравнения
tg х = 0 являются числа х = тсЛ, где k е Z.
6. Функция тангенс принимает
положительные значения при nk < х < « + тс*, где ft € Z.
Функция тангенс принимает
отрицательные значения при -= + я* < * < тс*» где k е Z.
Промежутки знакопостоянства (рис. 40) сле-
а а , sin*
дуют из определения тангенса: tg х = .
^ COSJC
7. Функция тангенс возрастает на всей
области определения, т. е. на промежутках
(-| + nk; ^ + тс*), где * € Z.
Докажем это свойство для промежутка
("55 5 )ПУСТЬ*1 € (~5; 5 }*2 € (~55 5 )х» >
> хг. Сравним два значения функции:
tgoc2-tgx1 =
cos* 2 COS* j
SlllXgCOSXj - 3111X2008X2
cos x 2 cos x x
sin(x2 - xx)
На данном промежутке cos x2 > 0, cos лгх > 0;
0 < x2 - xx < тс, следовательно, sin (x2 - xx) > 0.
Значит, tg x2 > tg xv т. е. большему значению
аргумента соответствует большее значение
функции. Тем самым показано, что на
промежутке (-д ; о ) функция тангенс возрастает.
В силу периодичности функции тангенс
можно утверждать, что функция возрастает на
промежутках Г-s + nk; 5 + nk J, где k е Z.
8. Функция тангенс не имеет экстремумов.
9. Функция тангенс непрерывна на области
определения.
График функции тангенс приведен на
рисунке 41.
+ У»о(1; 0)
Знаки значений Знаки значений Знаки значений
у = sin х у = cos х y = tgx
-t
а)
б)
в)
У*
°|
У - tg *
Рис. 40
Рис. 41

752
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
з.
а) log2 (9* "х + 7) = 21og2 (3х " 1 + 1).
Функции у = 9*, у = 3^ — показательные,
значит, принимают только положительные значе-
X — 1 X — 1
ния. Следовательно, 9 +7>0;3 +1>0
при любом значении х. Данное уравнение
равносильно уравнению
9х~1+7 = (Зх~1+1)2;
(32)* "47 = 32(х "1} + 2 • 3х "г + 1;
32(х-1)-32(х-1)+2.3х-1=7_1;
2-Зх"1 = 6;Зж"1 = 3.
Функция у = 3 — монотонная,
следовательно, х - 1 = 1, х = 2.
Ответ: 2.
б) 4l°*9*2 +2 = 4lo|?9X + 1-4log9X.
», AoggX
Пусть 4 = t; тогда
f2 + 2 = 4* - *, f2 - 3* + 2 = 0;
t\ = 1, ^2 = 2.
>g9X Jog 9X
4 =1 или 4 =2,
>g9x о O21og9x
4 =4 или 2 =2.
Функции у = 4 и у = 2 — монотонные,
следовательно:
a) log9 х = 0,
х«1;
6)21og9x = 1,
log9 * = g >
х = 3.
Ответ: 1; 3.
Билет № 11
1. Понятие об интеграле.
2. Функция синус, ее свойства и график.
Доказательство одного из свойств (по выбору
учащегося).
3. Решить неравенство:
1.
Пусть на отрезке [а; ft] задана непрерывная и
не отрицательная функция у = f(x); S —
площадь соответствующей криволинейной
трапеции (рис. 42).
Для вычисления площади S разобьем
отрезок [а; ft] на п равных отрезков, длина каждого
г 1 b - а
отрезка [xt; xt + х] равна ; на каждом из
отрезков построим прямоугольник, высота
которого равна значению функции f(xt); площадь
такого прямоугольника равна
/(*,)• А* = /(*,)-Ц^.
При увеличении числа промежутков, на
которые разбивается отрезок [a; ft], ступенчатая
фигура, состоящая из прямоугольников, будет
«мало отличаться» от криволинейной трапеции,
и если Sn — сумма площадей всех
прямоугольников, то Sn ~ S.
В курсе математического анализа
показывается, что для любой непрерывной на отрезке [a; ft]
функции у = f(x) существует число, к которому
стремится сумма площадей прямоугольников
при неограниченном увеличении п (п -> °°).
Это число называют интегралом, т. е.
Sn -> J f(x) dx при n -> °o.
2.
Если каждому действительному числу
поставлен в соответствие его синус, то говорят, что
задана функция синус (обозначение у = sin х).
Свойства функции синус
1. Областью определения функции синус
является множество всех действительных
чисел, т. е. D(y) = R.
y=f(x)
»(1И?Г'^
б) 51**- 3 Ъ*-1< з1***1- 51в*"\
Рис. 42

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
753
Каждому действительному числу х
соответствует единственная точка единичной
окружности Рх> получаемая поворотом точки Р0 (1; 0) на
угол, равный х радиан. Точка Рх имеет
ординату, равную sin х. Следовательно, для любого х
определено значение функции синус.
2. Множеством значений функции синус
является промежуток [-1; 1], т. е. Е(у) = [-1; 1].
Это следует из определения синуса: ордината
любой точки единичной окружности
удовлетворяет условию -1 < ур < 1, т. е. -1 < sin х < 1.
3. Функция синус является нечетной, т. е.
для любого х е R выполняется равенство
sin (-х) = -sin х.
Пусть точка Рх получена при повороте точки
Р0 на х радиан, а точка Р_х получена при
повороте точки Р0 на -х радиан (рис. 43).
Треугольник OPfP^ является равнобедренным;' ON —
биссектриса угла РхОР_х, значит, ON является
медианой и высотой, проведенной к стороне
РхР-х- Следовательно, Р^ = P-xN, т. е.
ординаты точек Рх и Р_х одинаковы по модулю и
противоположны по знаку. Это означает, что sin (-jc) =
= -sin х.
4. Функция синус является периодической с
периодом 2nk, где k — целое, кроме 0.
Наименьшим положительным периодом синуса
является число 2л.
Каждому действительному числу вида х + 2яА,
где k е Z, соответствует единственная то^ка
единичной окружности Рх + 2яА, получаемая
поворотом точки Р0 (1; 0) на угол х + 2nk радиан.
Точка Рх + 2nk имеет ординату, равную sin х
или sin (х + 2nk). Таким образом,
sin (х + 2nk) = sin х.
Этим показано, что числа вида 2яЛ, где k —
целое, кроме 0, являются периодом функции.
При k = 1 имеем sin (х + 2я) = sin jc,
следовательно, число 2л также является периодом
функции синус.
Покажем, что 2тс — наименьшее
положительное число, являющееся периодом функции
синус. Пусть Т — положительный период
функции синус; тогда sin (х + Т) = sin х при любом х.
Это равенство верно и при х = « » т. е. sin I 5 +
+ Т J = sin 5 = 1. Но sin х = 1, если х = « -I- 2тш,
где п е Z.
Наименьшее положительное число вида 2кп
есть 2тс.
5. Функция синус принимает значение нуль
при x=nk, где k е Z. Решением уравнения sin х =
= 0 являются числа х = яА, где k е Z.
6. Функция синус принимает
положительные значения при 2nk < х <п + 2nk, гдеk е Z.
Функция синус принимает отрицательные
значения при п + 2nk < х < 2% + 2тсА, где k е Z.
Промежутки знакопостоянства (рис. 44)
следуют из определения синуса.
7. Функция синус возрастает на
промежутках I -= + 2тсА; 5 + 2nk\, где k е Z, и убывает
на промежутках I « + 2я£; -«г + яй L где k е Z.
Докажем, что функция синус возрастает
на промежутке [-|; |J. Пусть jcx е |-g; gj»
*2 G ""о ' 2 и *2 > xv Сравним два значения
функции:
sin*
*i + *2
2 - sin хг = 2cos —g
sin
0<
Х2 Х1 ^ К К Х1 + Х2 П
^ -.-- < - < g»
2 ^2' 2 ^ 2
поэтому, учитывая промежутки
знакопостоянства синуса и косинуса, имеем
sin
> 0, cos
*i + *2
>0.
2 v* wo 2
Таким образом, sin х2 - sin *х > 0, значит,
большему значению аргумента соответствует
большее значение функции, т. е. функция синус
возрастает на промежутке I -« ; «J- ** силу
периодичности синуса можно утверждать, что
синус возрастает на промежутках I -= + 2яЛ; « +
+ 2nk , где k е Z.
+ Vo(i;Q)
Рис. 43
Рис. 44

754
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Аналогично доказывается утверждение о
промежутках убывания.
8. Функция синус имеет максимумы,
равные 1, в точках « + 2лЛ, где k е Z.
Функция синус имеет минимумы, равные -1,
в точках -=- + 2nk> где k е Z.
Покажем, что точка х0 — ~ является точкой
максимума. Функция синус возрастает на
промежутке I -« ; 5 L т. е. sin х < sin 5 для любого
х е I-« ; 5 J. Функция синус убывает на
промежутке Ig; -о" , т. е. sin jc < sin 5 для любого
хе |=; -5-1. Следовательно, х0 = « является
точкой максимума (по определению), а значение
sin х = 1 является максимумом. В силу
периодичности функции синус можно утверждать,
что в точках « + 2лЛ, где k е Zy функция имеет
максимум, равный 1.
Аналогично доказывается утверждение о
точках минимума.
9. Функция синус непрерывна на всей
области определения.
10. Функция синус дифференцируема в
каждой точке области определения; производная
вычисляется по формуле (sin х)' = cos х.
(Доказательство см. в билете № 21).
График функции синус приведен на рисунке 45.
г*2
•>(1Г(1Г">1^
3V2х {3\3х - 8 ^ 2
г\х - з /зу1
(Г • (I)1 >
(ГЧГ
у = sm х
Функция у = [оj является возрастающей
(основание степени больше 1), следовательно,
х - 1 > 1, х > -1 + 3, х > 2.
Ответ: (2; +оо).
б) 5lex + 5,gx"1x3,ex + 1 + 8lgx"1;
5lgx'1-(5 + l)<3l|JX'1-(32 + l);
6-51в*~
3,-51в*-
5lgx-l
5
^ю-з1**
^б-З1**"
„lg* -1
5lg*-2<3I^-2
-1#
1#
>
Функция у = 3 является показательной,
значит, при любом значении аргумента принимает
положительные значения. Следовательно,
5lgx " 2 ^ t (бЛ1** " 2 ^ (Ь\°
^! < 15 Ы < UJ •
Функция у = [о] является возрастающей,
так как основание степени больше 1. Отсюда
lg х - 2 < 0, lg х < 2.
Функция I/ = lg х — возрастающая, значит,
[х < 100,
[х >0.
Ответ: (0; 100).
Билет № 12
1. Формула Ньютона—Лейбница. Пример
применения формулы для вычисления
интегралов.
2. Функция косинус, ее свойства и график.
Доказательство одного из свойств (по выбору
учащегося).
3. Решить уравнение:
а) л/136 - х2 = х + 4;
б) J2 - 1 " V4 " 2 =-л/ГТ~2.
1.
Пусть функция I/ = /(х) непрерывна на отрезке
[а; &]; F — первообразная функции. В этом случае
ь
\ f(x)dx = F(b)-F(a).
Рис. 45

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
755
Пример. Вычислить
п .я
Jcoe(2x-j)d*-gein(2x- Ц =
= |sin(27c-5)-|smf-5) =
1 . ( п\ t 1 . (п\ 72^л/2 Л
2.
Если каждому действительному числу
поставить в соответствие его косинус, то говорят, что
задана функция косинус (обозначение: у = cos х).
Свойства функции косинус
1. Областью определения функции косинус
является множество всех действительных
чисел, т. е. D(y) = R.
Каждому действительному числу х
соответствует единственная точка единичной
окружности РХУ получаемая поворотом точки Р0 (1; 0) на
угол х радиан. Точка Рх имеет абсциссу, равную
cos х. Следовательно, для любого х определено
значение функции у = cos х.
2. Множеством значений функции косинус
является промежуток [-1; 1], т. е. Е(у) = [-1; 1].
Это следует из определения косинуса:
абсцисса любой точки единичной окружности
удовлетворяет условию -1 < хп < 1, т. е. -1 < cos х < 1.
3. Функция косинус является четной, т. е. для
любого х е R выполняется равенство cos (-лг) =
= cos х.
Пусть точка Рх получена при повороте точки
Р0 на х радиан, а точка Р_х получена при
повороте точки Р0 на -х радиан (рис. 46).
Треугольник ОР^Р^ является равнобедренным; ON —
биссектриса угла РхОР_х, значит, является и
высотой, проведенной к стороне РхР-х. Из этого
следует, что точки Рх и Р_х имеют одну и ту же
абсциссу ON у т. е. cos (-х) — cos х.
4. Функция косинус является периодической
с периодом 2nk, где k — целое, кроме 0.
Наименьшим положительным периодом косинуса
является число 2л.
Каждому действительному числу вида х + 2лЛ,
где k е Z, соответствует единственная точка
единичной окружности Рх + 2я*» получаемая
поворотом точки Р0 (1; 0) на угол (х + 2nk) радиан.
Точка Рх + 2nk имеет абсциссу, равную cos х или
cos (х + 2л£)» где k е Z. Таким образом,
cos х = cos (х + 2nk).
При k = 1 имеем cos х = cos (х + 2 л),
следовательно, число 2л является периодом функции
косинус.
Покажем, что 2 л — наименьший
положительный период. Пусть Т — положительный
период косинуса; тогда cos (х + Т) = cos х при
любом значении х. Это равенство должно быть верно
и при х = 0, т. е. cos Т = cos 0 = 0,
следовательно, cos Т = 0.
Но cos Т = 0, если Т = 2лЛ, где k е Z.
Наименьшее положительное число вида 2лЛ есть 2л.
5. Функция косинус принимает значение
нуль при х = к + я*» где k е Z.
Решением уравнения cos х = 0 являются
числа х = 5 + л*, где k е Z.
6. Функция косинус принимает
положительные значения при -« + 2я* < * < ъ + 2л*>
где k е Z.
Функция косинус принимает отрицательные
значения при х + 2л* < х < у + 2лЛ, где k е Z.
Промежутки знакопостоянства (рис. 47)
следуют из определения косинуса.
7. Функция косинус возрастает на
промежутках [-л + 2nk; 2nk], где k € Z, и убывает
на промежутках [2л/г; л + 2л£], где k е Z.
Чтобы доказать утверждение о
промежутках возрастания функции косинус, заметим, что
cos лг = sin ( 5 + х ]. Функция у = sin f о + х J
возрастает, если -«J + 2nkK 5 + х * 5 + 2л*'Где * € ^;
т. е. если -л + 2лй < х < 2л&, где k е Z.
У)
\ °
1
"^Х*
/ |МР0(1;0)
\ ! ) х
-^Р-ж
Рис. 46
Рис. 47

756
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Поскольку sin Г 5 + х J = cos х» функция у —
= cos х возрастает, если -тс + 2nk < х < 2nk9 где * € Z.
Аналогично обосновывается утверждение о
промежутках убывания функции.
8. Функция косинус имеет максимумы,
равные 1, в точках 2nk, где k е Z.
Функция косинус имеет минимумы, равные
-1, в точках к + 2nk, где k е Z.
Покажем, что функция у = cos х имеет
максимумы в точках 2nk9 где k е Z.
Замечая, что cos х = sin (5 + х ], найдем точки
максимума функции г/ = sin ( 5 + х ]. Ее точки
максимума о + х
о + 2лЛ, где ft е Z, т. е. х
= 2лЛ, где ft € Z. Максимум функции косинус
равен 1.
Аналогично проводятся рассуждения о
точках минимума.
9. Функция косинус непрерывна на всей
области определения.
10. Функция косинус дифференцируема в
каждой точке области определения; производная
функции косинус вычисляется по формуле
(cos х)' = -sin х.
(Доказательство см. в билете № 21.)
График функции косинус приведен на
рисунке 48.
3.
i)V:
136 - хс - х + 4 <=>
136 - х - (х + 4)2,
х + 4>0,
136-х = х"+8х + 16,
х>-4,
<=>
2х' + 8х-120 =
х>-4,
0, ^ х'+4х-60 = 0, ^
х >-4,
х = -10,
х>-4,
х = 6,
х>-4,
Ответ: 6.
<=>х=6.
б) 4г - 1 - V4 - 2 - -л/Г+~2;
л/г - 1 + ТТЛ - л/4 - г;
2-1 + 2л/(2 - 1)(2 + 2) +2+2 = 4-г;
|У,
2а/2 + г - 2 =3-32;
4г2 + 4г - 8 = 9 - 18г + 9г2;
5г*-
*i.i'
*i"
Яро!
1)2
-J5
- 222 + 17
11±736
5
1 или г2 ■
верка.
-1;70-
—Л-
= 0;
»
в3?
7з =
-л/3;
ИСТИННО.
2>*=Ф<ЯМ=-Я-
ложно.
Ответ: 1.
Рис. 48
Билет № 13
1. Правило нахождения наибольшего
(наименьшего) значения функции. Пример.
*
2. Формулы суммы и разности синусов
(косинусов). Доказательство одной из формул (по
указанию учителя).
3. Решить неравенство:
а) -1 + log05(4 - х) < log0>5<* + 5);
6)log2(9-2*)<3-x.
1.
Для того чтобы найти наибольшее
(наименьшее) значение функции у = /(х), имеющей на
отрезке [а; Ь] конечное число критических точек,
нужно:
1) найти критические точки,
принадлежащие отрезку [а; &];
2) найти значения функции в критических
точках, принадлежащих отрезку [а; Ь];
3) найти значение функции на концах отрезка;

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
757
4) из полученных чисел (значения функции
в критических точках и на концах промежутка)
выбрать наибольшее (наименьшее).
Пример. Найти наибольшее и наименьшее
значения функции у = х - Зх на отрезке [-1,5; 3].
1)Л({,) = Я.
2) Найдем критические точки. Имеем:
у' = Зх2 - 3;
а) у' = 0, если Зх -3 = 0,
3{х2 - 1) = 0,
х2 - 1 - 0,
х = - 1 или* = 1.
б) точек, в которых производная не
существует, нет.
3) у(-1) = -1 + 3 = 2;
у(1) = 1 - 3 = -2;
у(-1,5) = (-1,5)3-3-(-1,5) = (-1,5)3+2 1,52 =
= 1,52(-1,5 + 2) = 2,25 • 0,5 = 1,125;
у(3) = 27 - 9 = 18;
-2<1,125<2<18;
у(1)<у(-1,5)<у(-1)<у(3).
min у(х) = у(\) = -2;
[-1,5; 3]
max у(х) = {/(3) = 18.
[-1.5; 3] *
2*.
sin а + sin р = 2 sin —g-^ cos —^ ,
0 . а - р а + р
= 9 от J- РАС г •
in а - sin Р = 2 sin —«
sin
cos
do « + p а - p
cos а + cos p = 2 cos —^~ cos —д-*1 ,
а + P . а - p
- sin —s-^
(1)
(2)
(3)
cos а - cos P = -2 sin ** ' K sin —«H* • (4)
1) Пусть а = х +i/ иР = х -у;из этих
pace + p а - p
венств находим: x = —^- иу = —д-*-.
2) Выведем формулы для суммы и разности
синусов.
Докажем формулу (1). Воспользовавшись
формулами синуса суммы и синуса разности,
имеем
sin а + sin р = sin (х + у) + sin (х - у) =
= sin х cos у + sin у cos х + sin х cos у -
- sin у cos х = 2sin x cos i/ =
0 . а + p а - p
= 2 sin —g-^ cos —5~^ .
Таким образом,
n л.а + В а— В
sin а + sin р = 2sin —y^ cos —«-^.
Докажем формулу (2). Имеем
sin а - sin Р = sin (х + у) - sin (х - у) =
= sin х cos у + sin у cos х - sin x cos у +
+ sin у cos я = 2sin у cos x =
0 . а - P а 4- p
= 2sm —g-E cos —^- .
Таким образом,
. a O.oc-p oc + P
sin a - sin p = 2sin —y~ cos —-^ .
3) Выведем формулы для суммы и разности
косинусов.
Докажем формулу (3). Воспользовавшись
формулами косинуса суммы и косинуса
разности углов, получаем:
cos a -I- cos P = cos (x + y) + cos (x - y) =
= cos x cos у - sin x sin у + cos x cos у +
+ sin x sin у = 2cos x cos у =
= 2cos —о-*- cos —5~^.
Таким образом,
a + p a - p
- cos -
cos a -I- cos P = 2cos „ wa 2
Докажем формулу (4):
cos a - cos p = cos (x + y) - cos (x - y) —
= cos x cos i/ - sin x sin i/ - cos x cos i/ -
- sin x sin у — -2sin x sin i/ =
n . a + P . a - P
= -2sin —^ sin —5~^ .
Таким образом,
cos a - cos P = -2sin
a + p . a -p
sm
3.
a) 1 + log0>5 (4 - x) < log0f5 (x + 5) <=> log0>5 (4 - x) -
- log0,5 (* + 5) < 1 <=>
4-х >0,
x + 5 > 0,
4-х
x + 5
log0,5
<1,
x <4,
x >-5,
4-х
<=>
Ix + 5
>0,5,
-5 < x < 4,
4-х
x + 5
-0,5>0.
(1)
Решим неравенство ——- - « > 0- Получим
x + Бк *
8 - 2x - x - 5
x 4- 5
>0<=>
(3 - 3x)(x + 5) > 0,
хФ-Ь.

758
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Введем функцию у = (3 - Зх)(х + 5). Найдем
нули функции у — 0, если (3 - Зх)(х + 5) — 0.
Имеем
3 - Зх = 0 или х + 5 = 0;
х = 1 или х = -5.
Функция у = fix) является непрерывной, а
значит, на промежутках между нулями
сохраняет постоянный знак.
Л2)<0;/(0)>0;
Л-6)<0.
+
• ' mm
-5 1
Решением неравенства (3 - 3jc)(jc -I- 5) > 0
будут числа из промежутка (-5; 1). Таким
образом, система (1) равносильна системе
|-5<х <4,
|-5<х<1 »(-*<*< 1).
Ответ: (-5; 1).
б) log2 (9 - 2х) < 3 - х, log2 (9 - 2х) < log2 28 " х.
Функция у = log2 * — возрастающая,
следовательно,
X
(1)
1) Решим первое неравенство системы (1).
Пусть 2х = t; тогда
9-f<g;^-;2-8<0
(2х > 0, значит, t > 0); *2 - 9* + 8 > О,
it - 1)(* - 8) > 0.
Введем функцию fit) = (* - 1)(* - 8); /(f) = 0,
если t = 1 или * =3.
Функция у = fit) — непрерывная, значит, на
промежутках между нулями она сохраняет
постоянный знак.
Так как кратных корней нет, то знаки
чередуются:
+
1 8
t < 1 или t > 8.
Вернемся к переменной х:
2х < 1 или 2х > 8;
х < 0 или х > 3.
2) Решим второе неравенство системы (1):
[9-
[9-
[э-
2х
-2х
-2х
-2х
<9
<23"
>0;
2х
2х < 9 « 2х < 21°*29 <=> х < log2 9.
3) Заметим, что log2 8 < log2 9, т. е. 3 < log2 9.
Таким образом, система (1) равносильна
совокупности систем
х <0,
х < log2 9;
х >3,
х < log2 9,
Ответ: (-оо; 0) U (3; log2 9).
х <0,
3 < х < log2 9.
Билет № 14
1. Понятие экстремума функции. Пример.
*
2. Формулы сложения тригонометрических
функций и следствия из них.
Доказательство одной из формул и следствия из нее (по
указанию учителя).
2
3. а) Вычислить J fix) dx, если график функ-
-3
ции / изображен на рисунке 52.
б) Решить неравенство л/49* + 2 >72х + 1.
Л
1.
Пусть задана функция у = fix), ее график
изображен на рисунке 49.
Точка хг является точкой максимума, точка
х2 является точкой минимума, т. е. точки хг и
х2 — точки экстремума.
Значения функции в точках экстремума
называются экстремумами функции.
Например, значения функции у = cos х в
точках х = 2я/г, где k € Z, являются экстремумами
(максимумами) функции, т. е. утах = 1.
У-fix)
Рис. 49

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
759
2*.
cos (а - Р) = cos а cos Р -I- sin а sin Р; (1)
cos (а + Р) = cos а cos Р - sin а sin Р; (2)
sin (а - Р) — sin а sin Р - sin р cos а; (3)
sin (а + Р) — sin а cos Р + sin Р cos а. (4)
Докажем формулу (1).
1. Повернем радиус ОА> равный R, вокруг
точки О на угол а и Р (рис. 50). Получим радиус
ОВ и радиус ОС.
2. Пусть В(хг\ уг), С(х2; у2).
3. Введем векторы ОВ (хх; ух), ОС(х2; у2}>
4. По определению скалярного произведения
ОВ ОС = хгх2 + !/х1/2.(*)
5. По определению синуса и косинуса
хг = R cos а, уг = R sin а, х2 = R cos Р, у2 =
= R sin р.
6. Заменяя в равенстве (*) xv х2> уг и у2»
получим
ОВ ОС = R2 cos a cos Р + Д2 sin а sin р. (**)
7. По теореме о скалярном произведении
векторов
ОВ ОС = \ОВ\\ОС\-cos Z ВОС =
= Д2 cos Z ВОС,
Z ВОС = а - Р (см. рис. 50)
или
Z ВОС = 2тс - (а - Р) (рис. 51),
cos (2тс - (а - р)) = cos (а - Р).
Следовательно,
ОВ ОС = R2 cos (а - Р).(***)
8. Из равенств (**) и (***) получим:
R cos (а - Р) = R cos а cos Р -I- R sin а sin р.
2
Разделив левую и правую части на R * 0,
получим формулу (1) косинуса разности:
cos (а - Р) = cos а cos Р -I- sin а sin р.
Рис. 50
С помощью этой формулы легко вывести
формулу (2) косинуса суммы и формулу (4) синуса
суммы:
cos (а + Р) = cos (а - (~Р)) =
= cos а cos(-P) + sin а sin (-Р) =
= cos а cos Р - sin а sin p.
Значит,
cos (a -I- Р) = cos а cos Р - sin а sin p.
Докажем формулу (4).
sin (а + р) = cos (g - (а + рЛ -
= cos ((| -а]- р) = cos (| -а jcos Р +
+ sin(| - а ) sin Р = sin а cos Р -h cos а sin р.
Значит,
sin (а + р) = sin а cos Р + cos а sin р.
Докажем формулу (3). Применяя
последнюю формулу, имеем
sin (а - Р) = sin (а + (-р)) =
= sin а cos (~Р) + sin (~Р) cos а =
= sin а cos Р - sin Р cos а.
Значит,
sin (а - Р) = sin а cos Р - sin Р cos а.
При доказательстве формул (1)—(4) были
использованы следующие факты:
1) формулы приведения;
2) функция у = sin х — нечетная,
функция у = cos х — четная.
Из формул сложения, полагая Р = -g-, где пе N,
можно вывести формулы приведения для
преобразований выражений вида
cos I -s- ± а J, sin I -^ ± а I.
Например,
cos I о - а ] = cos 5 cos а -I- sin 5 sin а =
= 0 + sin а = sin а.
Аналогично выводятся следующие формулы:
sin (тс - а) = sin а;
sin (тс -I- а) = -sin а;
. ГЗп \
sin [ -5— а I = -cos а и т. п.
Из формул сложения следуют формулы
двойного аргумента:
2 2
sin 2а = 2 sin а cos а и cos 2а = cos а - sin а.

760
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
з.
2
a) J f{x) Ах = Эдво + Sbqc =
-3
-I-8-4+J-2-4-
= 6 + 4 = 10.
Ответ: 10.
б)^9х + 2>72х'г
<=>
» 7х + 2> 72х + 1« х + 2 > 2х + 1»(х < 1).
Ответ: (-оо; 1].
Билет № 15
1. Признак постоянства функции на
промежутке. Пример» графическая иллюстрация.
2. Теорема о вычислении площади
криволинейной трапеции.
3. а) Решить уравнение
log2 (9* " г + 7) - 21og2 (3х ~ г + 1).
б) решить неравенство log0 8 х • log0 8 (х + 9)>
>0.
1.
Если производная функции равна нулю на
некотором промежутке, то эта функция
постоянная на этом промежутке.
Если g'(x) = 0 на некотором промежутке, то
касательная к графику функции у = g(x)y
например g(x) = 6 (рис. 53), в каждой точке
данного промежутка параллельна оси Ох.
2.
Если / — непрерывная и неотрицательная
функция на отрезке [а; 6], slF — первообразная
f на отрезке [а; Ь], то площадь соответствующей
криволинейной трапеции можно вычислить по
формуле S - F(b) - F(a).
Доказательство.
1) Пусть у = S(x) — площадь криволинейной
трапеции, имеющей основание [а; х], где х е [а; Ь].
Заметим, что S(a) = 0, S(6) = S.
2) Покажем» что у = S(x) — первообразная
функции у = Дх), т. е. S'(x) = /(х).
Чтобы найти производную функции у = S(x)
воспользуемся определением производной:
а) зададим приращение Ах (пусть Ах > 0);
б) найдем приращение функции:
AS = S(x + Ax)-S(x);
в) составим отношение
AS = S(x + Ах) - S(x),
Ах Ах ;
г) выясним, чему равен предел отношения
при Ах т» 0.
Разность S(x + Ах) - S(x) равна площади
криволинейной трапеции с основанием [х; х + Ах]
(на рисунке 54 это площадь заштрихованной
полосы).
Если Ах —> 0, то эта площадь
приблизительно равна площади прямоугольника /(х) - Ах, т. е.
S(x + Ах) - S(x)« f(x) • Ах.
Имеем
S(x + Ах) - S(x) ,, ч А Л
— д^ — « /(х) при Ах -* 0.
Этим показано, что S'(*)= /(*)•
3) Равенство S'(x) — f(x) означает, что S —
первообразная функции / на заданном
промежутке.
4) По основному свойству первообразной имеем
F(x) - S(x) + С,
где F — какая-либо первообразная для f.
При х = а получим, что F(a) = S(a) + С, т. е.
C=F(a).
При х = Ъ имеем F(b) = S(b) + F(a),
следовательно»
S=S(6) = F(6)-F(a).
6
tf(*) = 6
х х+Ах Ь х
Рис. 52
Рис. 53
Рис. 54

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
761
з.
а) Решение показано в билете № 10 (вопрос 3, а)).
б) log0i8 х • log0,8 (ж + 9) > 0 <=>
х<1,
х >0,
х+9<1,
[х + 9 > 0;
х>1,
х>0,
* + 9>1,
х + 9>0
log0,8* >0,
log08(* + 9)>0; ^
log08x<0,
log0,8(* + 9)<0
0<*<1,
ж > -9: ^ ,
'' «* ж > 1.
*>1,
х>-8,
х >-9
Ответ: [1; +оо).
Билет № 16
1. Теорема Лагранжа, ее геометрический
смысл.
2. Степенная функция, ее свойства и график.
Доказательство одного из свойств (по
выбору учащегося).
3. Вычислить:
8inl,2n
а)
sinl,37Ctgl,87c'
б) cos а и cos 2а, если tg а = -J2,5 < а < тс.
1.
Пусть задана функция у = /(х),
дифференцируемая в каждой точке промежутка J, точки а и
Ъ принадлежат этому промежутку. На интерва-
У>
0
1 В (Ь; Щ1
A(a\№y/j)f
а с Ъ х
/'<*>'
ле (а; Ь) найдется такая точка с, для которой
выполняется равенство
КЬ) - Па)
Ъ- а #
Геометрически этот факт можно истолковать
следующим образом.
Пусть функция у = /(х) дифференцируема
на некотором промежутке, точки а и b
принадлежат этому промежутку; через точки А(а; f(a))
и B(b; /(b)) проведена секущая. Тогда на
интервале (а; Ь) найдется такая точка с, что угловой
коэффициент касательной, проведенной через
точку (с; /(c)), будет равен угловому
коэффициенту секущей АВ (рис, 55).
2.
Функция, заданная формулой /(х) = ха,
называется степенной (с показателем а).
Свойства степенной функции при а > 1
1) 2)(/) - [0; +°о), если а не является
натуральным числом.
Это следует из определения степени с
рациональным показателем.
Если а — натуральное число, то D(f) = (-00; +°°)
по определению степени с натуральным
показателем.
2) E(f) - [0; +00) для всех а > 1, кроме а = 2k +
+ 1, где* е ЛГ.
Это следует из определения степени с
рациональным показателем.
E(f)= (~°°; +°°) Для нечетных а, т. е. а = 2k +1,
где k € ЛГ.
3) Если а — четное натуральное число, то
данная функция является четной, так как
«-*) = (-х)2* = ((-х)V - (хV = *2* - /(*)•
Ясли а — нечетное натуральное число, то
данная функция является нечетной, так как
Л-х) = (-х)2* +1 = (-х)2*(-х) - x2k • (-х) =
4) При х = 0 функция f(x) — 0, /пак: icaic 0а = 0
при а > 0.
5) При х > 0 функция f(x) > 0.
Это следует из определения степени с
рациональным показателем. При нечетных a (a = 2k +1,
k e ЛГ)» если x < 0, функция принимает отрица-
2k + 1 2k 2k . n
тельные значения, так как х = х х, х > 0,
Рис. 55
* Доказательства приведены для рациональных а.

762
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
2k
но х < О, следовательно, произведение х х < О,
т. е. f(x) < О при х < 0.
6) Функция является возрастающей на
промежутке [0; +со) для любого а > 1.
Пусть а > 1 и 0 < хг < хг. Из свойства степени
с рациональным показателем (г —
рациональное число и 0 < а < Ьу тогда а < Ъг при г > 0)
следует, что хг < JCg. Таким образом, меньшему
значению аргумента соответствует меньшее
значение функции, т. е. функция у = f(x) возрастает
на промежутке [0; °о).
Докажем, что если а — нечетное число, то
функция возрастает и на промежутке (-°°; 0]
(рис. 56, б). Пусть хг < х2 < 0, тогда х* < х\ по
определению степени с целым отрицательным
показателем, т. е. данная функция возрастает
по определению возрастающей на промежутке
функции.
Аналогично можно доказать, что функция у =
= f(x) на промежутке (-°°; 0] убывает, если а —
четное целое (рис. 56, а).
Свойства функции f(x) = ха для 0 < а < 1 см.
в билете № 9. Доказательства проводятся
аналогично.
з.
а)
8т1,2я
sin 1,3 71 • tgl,8n
sin(rc -I- 0,2л:)
sin(7i + 0,3я) -tg(2n - 0,2л)
У = х
f(x) = xa У\ УТХ
cc> 1
a — четное
целое число
a)
a> 1
a — нечетное
целое число
б)
Рис. 56
a > 1
a — дробное
число
в)
_ -зш0,2я _ sin0,2ft- cos0,2n =
-sin0,3n • (-tg0,2n) sin0,3n • sin0,2n
_ cos0,2л _ со8(0,5я - 0,3ft) _ sin0,3я _ -
~~ sin0,3ft "" sin0,3ft "" sin0,3ft
Ответ: -1.
x\ i . x 2 1 2 1
6) 1 + tg a = —jp '* cos a = 2~ *
cos a 1 + tg a
Так как « < a < тс, то cos a < 0.
cos a = -
73.
sm
Vl + tg2a Jl+~* & 3 '
a = tg a • cos a = -72 ■ f —g- J = -g-;
2 2
cos 2a = cos a - sin a;
cos 2a =
= (_^h2 - (&\2 = !-?=-!
(-f)-m
3 3
Ответ: cos a = —5-; cos 2a = -5 .
Билет № 17
1 .Формула для' вычисления производной
сложной функции.
2. Нахождение первообразных.
Доказательство одного из правил (по указанию учителя).
3. а) Определить, имеет ли смысл выражение
log42 (sin = — cos g J (ответ обосновать).
б) Упростить выражение
+ 4).
lg (х* + 8) - 0,5 lg (ж2 + Ах + 4) - lg (ж2 - 2* +
1*.
Пусть задана сложная функция g(x) = f(kx + b).
Если функция / имеет производную в точке
kx0 + Ь, то производную функции g можно найти
по формуле g'(x0) = kf'{kx0 + Ь).
Например, найдем производную функции
g(x) = (7x-9)19:
g\x) = 7 • 19(7* - 9)18 = 133(7* - 9)18.
2.
Правило 1. Если F — первообразная
функции f,aG — первообразная функции g,mo F + G
является первообразной функции f + g.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
763
Доказательство. Воспользуемся
определением первообразной, т. е. найдем
производную функции F + G. Имеем:
(F + G)'-F' +G' = /+£.
Правило 2. Если F — первообразная
функции f, a k — постоянная, то kF —
первообразная функции kf.
Доказательство. Воспользуемся
определением первообразной, т. е. найдем
производную функции kF. Имеем:
{kF)' = kF' = kf.
Правило 3. Если у = F(x) — первообразная
функции у = /(#), a k и Ь — постоянные,
причем k Ф О, то функция у = г^(** + Ь) является
первообразной функции у = f(kx + b).
Доказательство. Воспользуемся
определением первообразной, т. е. найдем
производную функции у = г F(kx + b). Имеем
(\F(kx + b)\ = \F\kx + b) • k = F'(kx + b) =
= f(kx + b).
3.
а) Выражение log42 [sin = - cos g J имеет
смысл, если sin = - cos g > 0. Имеем
я я я
sin = - COS g = sin = - COS
я Зя
= sin = - sm -g-.
U 8 J
Таким образом, данное выражение имеет
. я . Зя ^ Л
смысл, если sin = - sin -g- > 0.
Так как функция у = sin х является возрастаю-
ГЛ я1 я ^. Зя я Зя ^.Л
щей на I 0; g I и = < -g-, то sm = - sin -g- < 0,
следовательно, данное выражение не имеет смысла.
б) Решение показано в билете № 7 (вопрос 3,6)).
Билет № 18
1 .Нахождение скорости при неравномерном
движении. Пример.
2. Таблица первообразных элементарных
функций.
3. Решить уравнение
а) 2*
1 + 2*~2+2x~i
= 448;
б) х
з*2 - 5* - 2 _ -
"■" j..
1*.
Пусть материальная точка движется по
координатной прямой по закону х = x(t), т. е.
координата точки — известная функция времени. За
промежуток времени А* перемещение точки рав-
но Ах, а средняя скорость *>Ср = 77 • Если
движение таково, что при А* -» 0 значение средней
скорости стремится к некоторому
определенному числу, то это число называют мгновенной
<Ах
пооп-
скоростью ( дт -» ^мгн ПРИ At -» 0 J. Но
ределению производной jr -» х' при Ы -» 0.
Мгновенная скорость определена для любой
дифференцируемой функции, описывающей
перемещение точки по прямой. Чтобы найти
скорость движения и, нужно определить
производную от координаты по времени, т. е. v(t) = x'(t).
Пример. Координата точки, движущейся по
прямой, задана формулой x(t) = 2t - 3f + 1
(x(t) — перемещение в метрах, t — время в
секундах). Найти скорость точки в момент времени
* = 2с.
Имеем:
v(t) = x\t) = 4* - 3;
1*2) = 4-2-3 = 5 (м/с).
2.
Таблица первообразных элементарных
функций
Функция
Общий вид
первообразных
Функция
Общий вид
первообразных
у -*\
Пф\
п + 1
у-е*
е' + С
у =• sin х
-coax +С
у=ах
X
та
у e cos X
sin х + С
1
У = 'х
In х + С

764
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Для доказательства воспользуемся
определением первообразной.
1)
п + 1 , ,
+ С\ =—г-г • * + С = х ;
п + 1
п + 1
2) (-cos ж + С)' = sin х + С = sin ж;
3) (sin х + С)' = cos ж + С = cos х;
4)(е* + С)' = е* + С =е*;
6) (In * + С)' = i + С = |.
3.
а) 2*"3(22 + 2 + 1) = 448;
„*-з 448
2 =—;
2*"3=64;
2*-3=26.
Функция у = 2 является монотонной,
следовательно, каждое свое значение принимает один
раз. Отсюда
х -3 = 6,
х = 9.
Ответ: 9.
б) 1) Проверим, является ли число 1 корнем
Зх2 - Ъх - 2 -
уравнения х =1.
-4
Подставив х = 1, получим 1 =1 (верное
равенство). Значит, х = 1 — корень уравнения.
2) Положим х > О, тогда
2
Зх
5х - 2 О
= х ;
х >0, х *1,.
Зх2 - Ьх - 2 = 0.
2
Решим уравнение Зх - Ьх - 2 = 0. Имеем:
JD = 25 + 24 = 49,
5 4-7
Х9 =
6
5-7
= 2,
1
3
*2 ~ 6
Принимая во внимание, что х > 0, делаем
вывод, что решением уравнения является х = 2.
Ответ: 1; 2.
Билет № 19
1. Понятие арксинуса числа. Пример.
2. Теорема о производной суммы двух функций.
3. а) Упростить выражение
1
1 +
JJ^
с* -1).
l + JJ^l
б) Упростить выражение
( VI
Ja — Jb
-2|3 3
(л/S + Jb)
\a — Ъ. J
1.
Ответ приведен в билете № 1 (вопрос 1).
2.
Если функция и и v дифференцируемы в
некоторой точке, то их сумма дифференцируема в
этой же точке и производная суммы равна
сумме производных слагаемых:
(и + v)' = и' + v'.
Доказательство. Найдем
производную суммы по определению производной.
1) Пусть задана точка х0, Ах — приращение
аргумента.
2) Вычислим приращение функции:
А(и +и) = и(х0 + Ах) + v(x0 + Ах) - (и(х0) +
+ v(x0)) - и(х0 + А*) - и(х0) + и(х0 + Ах) -
- и(х0) = Аи + Ау.
3) Найдем отношение приращения функции
к приращению аргумента:
А(ц + у) _ Ац + At; _ Ац Ар
Ах ~~ Ах ""Ах Ах#
4) Выясним, к чему стремится разностное
отношение при Ах -» 0:
^ + ^ -> и' + у' при Ах -> 0.
£^
1 + 1
v л/х-1 /2-v
а) , rt (х - 1) -
1 +
J7T

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
765
J7^
1 + 1
7х2 - 1 • (л/*2 - 1 + 1)
•(*-!>■
*2-1
-Jf-i.
Ответ: *Jx - 1.
б) Решение показано в билете Ms 6 (вопрос 3,6)).
Билет № 20
1 .Число е. Натуральный логарифм.
2. Достаточные условия возрастания
(убывания) функции.
3. а) Решить систему
А*
15х "•б" = 0,2.
б) Решить уравнение х * * = 100*.
1*.
Изобразим в прямоугольной системе
координат графики следующих показательных
функций:
у = (|)*, у - 2*, у = (§)*, у = 3х (рис. 57).
Все графики проходят через точку М(0; 1).
Проведем касательные к графикам в этой
точке.
Измерим углы наклона касательных к оси
абсцисс.
У1
д,
' 0
1*\\ф
tilth2'
#(IJ
X
У касательных к графикам функции у =
= (2) » У = 2х, У = (о) углы с положительным
направлением оси Ох меньше 45°. У касательной
к графику функции у = 3* этот угол больше 45е.
В курсе высшей математики доказано, что
существует такая показательная функция, у
которой касательная к графику в точке М(0; 1)
образует с положительным направлением оси
абсцисс угол 45*. Основание этой показательной
функции обозначают буквой е, 2 < е < 3.
Доказано также, что число е —
иррациональное число, поэтому оно записывается в виде
бесконечной десятичной непериодической дроби.
С помощью вычислительной техники найдено
более двух тысяч десятичных знаков в записи
числа, е = 2,71828... .
Наличие у показательной функции у = ех
касательной, проведенной в точке М(0; 1) и
образующей с положительным направлением оси
абсцисс угол в 45°, означает, что производная в
точке х0 — 0 равна 1.
Натуральным логарифмом называется
логарифм по основанию е. Натуральный логарифм
обозначается знаком In, т. е. loge х = In х.
2.
Если производная функции положительна в
каждой точке интервала, то функция
возрастает на этом интервале.
Если производная функции отрицательна в
каждой точке интервала, то функция
убывает на этом интервале.
Доказательство. Функция у = f(x)
называется возрастающей, если большему
значению аргумента соответствует большее значение
функции.
Известно, что значения дифференцируемой
на интервале функции, значения аргумента и
значение производной связываются формулой
Лагранжа: если функция у = f(x)
дифференцируема на некотором промежутке, точки хх и х2
принадлежат промежутку (хх < jc2), то на
интервале (хг; х2) найдется такая точка с, для которой
выполняется равенство
Нх2) - f(xx)
Г(с)
х2 - хг
Рис. 57
Пусть производная функции принимает
положительные значения на интервале J, т. е. f'(x) > 0.

766
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Возьмем два значения аргумента хг и х2,
принадлежащие этому интервалу, причем хг < х2.
Сравним значения этой функции в точках хг и х2.
По формуле Лагранжа найдется такое значение
с е (хх; х2)У для которого выполняется равенство
f(x2) - f(xx)
Г(с) =
Хл X*
Из этого условия следует, что
rt*2)-/(*i) = /'(<0-(*2-*i)-
Заметим, что /(с) > 0 (по условию), х2 - хг > О
(по предположению), значит, /'(с) • (х2 - хг) > О,
т. е. разность значений функций /(х2) - f(xx) > 0.
Таким образом, показано, что большему
значению аргумента соответствует большее значение
функции, т. е. функция у = f(x) является
возрастающей.
Аналогично показывается достаточное
условие убывания функции.
3.
= 72,
а) < 4у - *
[5*-у-5-у = 0,2;
4х-0/-х)= 22
(22)2Х~У=2
ьх~2у = ь-\
ьх-2у = ь~\
Функции у = 2* и у = 5* монотонные,
следовательно,
4х-2у-\,
х-2у =--1;
Зле- 1,5,
х-2у = -1;
Ux-2y=\,
1-х + 2у = 1;
f 1
12у = де + 1;
х =0,5,
У = 0,75.
Ответ: (0,5; 0,75).
б) lg(xlg*) = lg(100x);
lg2 х = lg х + IglOO;
lg2 x - lg x - 2 = 0.
Пусть lg x = ty тогда
f2 - * - 2 = 0;
fx = -1 или t2 = 2.
lg x = -1 или lg x = 2;
[x-10 \
|x>0 или
1
X = r^j ИЛИ X
Ответ: -tr 5 100.
|x = 102;
x >0.
= 100
Билет № 21
1. Понятие арктангенса числа. Пример.
*
2 .Таблица производных элементарных
функций (степенной, синуса, косинуса).
Доказательство одной из формул (по указанию
учителя).
3. Решить уравнения:
/ х - л/з ч* + Л
а) [5 J = 1;
б)*1** =100*.
1.
Ответ приведен в билете № 5 (вопрос 1).
2*.
Функция
Производная
(степенная)
у'-р*?'1
у - sin х
у' =cosx
у — COS X
у' = -sin х
Выведем формулу для производной
степенной функции. Пусть р — натуральное число.
Найдем производную для р = 1,р=2,р=3 (по
определению).
Если р = 3, то у = х .
1) Зададим приращение аргумента Ах.
2) Найдем приращение функции Ау:
3 3 3
Ау = У(* + А*) ~ У(*) = (х + Ах) - х = х +
+ Зх2Ах + Зх(Ах)2 + (Ах)3 - х3 = Зх2Ах +
+ Зх(Ах)2 + (Дх)3.
3) Найдем разностное отношение:
^ = Зх2 + ЗхАх + (Ах)2.
Ai/
4) Выясним, к чему стремится отношение ^
при Ах -> 0.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
767
Так как ЗхАх -» 0 при Ах -» 0 и (Але) -» 0 при
Ах -> 0, то Зх2 + ЗхАх + (Ах)2 -> Зх2 при Ах -> 0.
Имеем (xV = 3x2.
Аналогично показывается, что
(х)' = 1, (х2)' = 2х, (х4)' = 4х3 и т. д.*
Если у = х?9 где р е JV, то
(д^-рх-1. (1)
Докажем, что эта формула верна для любого
натурального р.
1) Для р = 1 утверждение верно, так как
(х)' = 1х°.
2) Допустим, что формула верна при р = fe,
т.е.(хУ = *х*~\ (2)
3) Докажем, что формула (1) верна прир = k +
+ 1,т.е.(х* + 1)' = (* + 1)х\
Найдем производную у = х . Имеем:
(х* +У - (х*х)' - (xVx + (*)'** -
= ftxfe"1x+xfe = x*(fe + l).
Таким образом,
(x* + 1)' = (fe + l)x\
Показано, что формула (1) верна при р = 1;
доказано, что из предположения верности
утверждения при р = ft следует истинность
утверждения прир = = k + 1, следовательно, формула
(1) верна при любом натуральном р.
Докажем, что формула (1) верна, если р —
целое отрицательное число (при х Ф 0). Пусть у =
= хр, гдер — целое отрицательное число и х * 0.
Найдем производную у = хр, учитывая, что -р € ЛГ:
-2/>
р- х р р-1
- -—-^^^Р -г .
Показано, что формула (1) верна и при
отрицательных показателях.
Пусть р = 0 и х * 0, тогда у = х . Найдем
производную (xV = (С)' = 0 (где С — const).
Итак, формула (х*У = рхр ~ справедлива при
целых значениях р .
* Если учащиеся знакомы с методом
математической индукции, то его можно использовать при
выводе формулы производной.
** Для неположительных значений р имеем хФО.
Выведем формулу производной функции
у = sin х,
воспользуемся определением производной.
1) Зададим приращение Ах.
2) Найдем приращение Ау:
sin (х + Ах) - sin х = 2sin -=- cos (х + -у).
3) Найдем разностное отношение:
г-*-("+т)
. Ах
Ах
*У
4) Выясним, к чему стремится д| при Ах -> 0.
Далее будем использовать два утверждения,
принимаемые без доказательства.
1. Функция косинус непрерывна на всей
области определения, т. е. cos (х + Ах) -» cos х
при Ах -» 0.
. Ах
81Пу
2. > -» 1 при Ах -» 0.
Т
Применим к полученному разностному отно-
Ау
шению т^ = cos
Ах
(-т)-
. Ах
8ШТ
Ах
2
приведенные
утверждения.
Действительно, в соответствии с
утверждениями, cos (х + y) ~* cos х ПРИ А* -* °» а
1 при Ах -» 0. В результате получаем
. Ах
81ПТ
Ах
2
д| -> cos х при А х -» 0.
Таким образом, (sin х)' = cos х.
Выведем формулу производной функции
у = cos х:
(cos хУ - (sin (| - х))' = (| - х)' • cos (\ - х) =
= -sin х.
3.
г - Дх + J
») (5х Л = 1;
Ъ'2 ~ 8 = 5°.

768
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Функция у = 5 монотонная, значит, каждое
свое значение принимает один раз.
х - 3 = 0;
х2 =3;
*=±7з.
Ответ: ±73.
б) Решение показано в билете № 20 (вопрос 3, б)).
Билет № 22
1. Понятие периодической функции, пример,
иллюстрация на графике.
*
2 .Производная показательной функции.
. а) Вычислить 0,5
б) Упростить выражение
1.
Ответ приведен в билете № 1 (вопрос 1).
2*.
При любом положительном а функция у = а
дифференцируема в каждой точке. Производная
находится по формуле
(а*)' = ах1па.
Доказательство. Известно, что
(е*)' = е*. (1)
Представим функцию у = а как
показательную функцию с основанием е:
х t Incur xlna
а = (е ) = е
Найдем, учитывая формулу (1) и правило
дифференцирования сложной функции,
производную показательной функции
xln ач / Jcln а
(ах)' = (е в)' = ехшо(*1па)' =
х\па ! х «
= е • In а = а -та.
3.
1о*25 - log215 ,Q-1 *°*2 15 ~1°** з
а) 0,5 = (2 ) =2
Ответ: 3.
б) Решение показано в билете № 2 (вопрос 3, б)).
Билет № 23
1. Понятие арккосинуса числа. Пример.
2. Касательная. Вывод уравнения касательной
к графику дифференцируемой функции в
данной точке.
3. Решить неравенство:
а) 2 • 4** - 17 • 4* + 8 < 0;
б) 51** - З1** " * < З1** + * - 51** " \
Ответ приведен в билете № 4 (вопрос 1).
2.
Касательной к графику функции,
дифференцируемой в точке х0у называется прямая,
проходящая через точку (jc0; f(x0)) и имеющая
угловой коэффициент, равный f'(x0).
Вывод уравнения касательной.
Касательная является прямой, поэтому
задается уравнением у = hx + Ь. По определению
касательной k = f'(x0). Уравнение принимает вид
y=f'(x0)x + b. (1)
Касательная проходит через точку (х0; f(x0))9
следовательно, координаты точки
удовлетворяют уравнению (1). Имеем:
f(x0) = f'(x0)-x0+b.
Найдем Ъ:
Ъ = f(x0) - Г(*0)' *о-
Уравнение (1) принимает вид
У = Г(х0) • х + /(*0) - f'(x0) • х0
или
У = f(x0) + /'(*о)' .(* - *о)-
3.
а) 2-42*-17-4* + 8<0.
1) Пусть 4* = *, тогда 2t2 - 17* + 8 < 0. Введем
. функцию у = 2t2 - Ш + 8. Имеем:
i/ = 0, если 2*2 - 17* + 8 = 0;
D = 289 - 64 = 225, + - +

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
769
h
ч
=
=
17 +
4
1
2'
\Ъ
= 8,
Функция у = 2t - 17* + 8 непрерывна,
значит, на промежутках между нулями сохраняет
постоянный знак.
y(9)>0,i/(l)<0,y(0)>0.
\<t <8.
2) Вернемся к переменной х. Имеем:
|<4*<8,
2"1 < 22х < 23.
Функция у = 2 — возрастающая,
следовательно,
-К 2х < 3,
Ответ: (-g5 2 }
б) Решение показано в билете № 11 (вопрос 3, б)).
Приближенное равенство (1) показывает, что
значения дифференцируемой в точке функции в
окрестности этой точки мало отличаются от
значений линейной функции, графиком которой
служит касательная, проходящая через точку
Таким образом, если точка такова, что
значения f(x0) и f'(x0) легко вычисляются, то по
формуле (1) можно находить значения функции f(x)
при х, достаточно близких к х0> вычисляя
значения линейной функции.
Вычислим, например, значение е ' . Имеем:
е°'03 = е° • 0,03 - 1 + 0,03 = 1,03.
3.
a) 2cos2 х + 5cos х - 3 < 0.
2
Пусть cos х = ty тогда неравенство 2cos х +
+ 5cos х - 3 < 0 принимает вид 2t + 5* - 3 < 0.
Решим его.
D = 25 + 24 = 49 > 0, следовательно,
уравнение имеет два действительных и различных
корня: *! = g; *2 = ~"3'
Билет № 24
1 . Число е. Натуральный логарифм.
*
2 . Приближенное вычисление значений
функции с помощью производной.
3. а) Решить неравенство 2cos х + 5cos х — 3 <
<0.
б) Решить уравнение log^ _ г (х - 5х + 10) = 2.
1*.
Ответ приведен в билете № 20 (вопрос 1).
2*.
Пусть задана дифференцируемая в точке х0
функция у = f(x). По определению производной
д£ в /Ч*о) с любой наперед заданной точностью
для jc, достаточно близких к х0. Из этого
приближенного равенства следует, что А/ = f'(x0)Ax
или
f(x) = f(x0) + f'(x0)Ax. (1)
-3 < t < g ,
-3 < cos t < о
-3
Учитывая, что |cos х\ < 1, имеем неравенство
cos х < к • Решим его (рис. 58):
я + 2кп < х < -=- + 2яп, где п е Z.
Ответ: ( о + 2яп; -я- + 2тсп J, где п е Z.
Рис. 58
25-1019

770
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
б) lofc.^x -5х+10) = 2;
ч2 х2 - Ъх + 10,
<
<=>i
(х - 1)
х2 - Ъх + 10 > 0,
х - 1 > 0,
х-1*1
jc2 - 2х + 1 - х2 + 5х - 10,
(х-2,5)2+3,75>0,
х > 1,
х *2
Зх = 9,
*>1, «=>(х = 3).
х*2
Ответ\ 3.
Билет № 25
1. Понятие об интеграле.
2. Достаточные условия максимума
(минимума) функции.
о. а) Вычислить log8 4+0,5
б) Упростить выражение
lg(x3 + 8) - 0,51g(*2 + 4* + 4) - lg (jc2 - 2* + 4).
1.
растания) функция у = /(*) возрастает на
промежутке (a; jc0]. Из этого следует, что f(x) < f(x0)
для любого х е (а; *0].
Если /'(*) < 0 на интервале (х0; Ь) и в точке х0
функция у = f(x) непрерывна, то (в силу
достаточного признака убывания) функция у = f(x)
убывает на промежутке [х0; b). Из этого следует,
что f(x0) > f(x) для любого х е (х0; Ь).
Таким образом, для любого значения
аргумента из промежутка (a; b) f(x) < f(x0). Это
значит, что х0 является точкой максимума.
Достаточные условия минимума функции
Если функция непрерывна в точке х0У а
производная отрицательна на интервале (а; х0) и
производная положительна на интервале (х0; Ь),
то точка х0 является точкой минимума.
Доказательство проводится аналогично
доказательству достаточных условий максимума.
3.
-logo 3 2-1 ~1°*2 3
a)log84+0,5 *2 =log9a22 + (2 1)
log2o
Ответ приведен в билете №11 (вопрос 1).
= ilog222+2-lo|?23=?log22 + 2
Ответ: 1.
б) Решение показано в билете № 7 (вопрос 3,6)).
Если функция / непрерывна в точке х0, а
производная положительна на интервале (а; х0) и
производная отрицательна на интервале (х0; Ь),
то точка х0 является точкой максимума (рис. 59).
Краткая формулировка: если в точке х0
производная меняет свой знак с + на -, то х0
является точкой максимума.
Доказательство. Если f\x) > 0 на
интервале (а; х0) и в точке х0 функция у = f(x)
непрерывна, то (в силу достаточного признака воз-
Vi
So
1
/ ! \v-f(x)
a Xq Ь \^ х
Билет № 26
1. Понятие о первообразной функции.
*
2 . Дифференциальное уравнение
гармонических колебаний.
3. Упростить выражение:
a) *L^± . (4х + 2х + 1) - 8х;
2х + 1
б)
(Л + Л)
-2
{ \-1
л - л
2 ,2 .
а - Ъ )
1.
Рис. 59
Ответ содержится в билете № 10 (вопрос 1).
2*.
В физике, в технике часто встречаются
процессы, которые периодически повторяются.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
771
Примерами таких процессов служат
колебательные движения маятника, груза, подвешенного
на пружине, и т. п. Эти процессы описываются с
помощью уравнения вида
Г(') = -<о2/(*). (1)
Говорят, что физическая величина,
изменяющаяся во времени в соответствии с уравнением
(1), совершает гармонические колебания.
Уравнение вида
Г(0 = -<о2/(*)
называется дифференциальным уравнением
гармонических колебаний.
Функция f(t) = Acos (со* + ф), где А, со и ф —
постоянные величины, является решением
уравнения (1).
Докажем это утверждение. Найдем
производную функции f(t) = Acos ((ut + ф):
/'(*) = -Asm (со* + ф).
Найдем производную функции
f'{t) = -Acosin (со* + ф):
/"(*) = -Асо2 cos (со* + ф).
Очевидно, что f"(t) = -со fit).
Постоянную А называют амплитудой
гармонических колебаний, постоянную со — угловой
частотой, ф — начальной фазой колебаний.
Графики гармонических колебаний —
синусоиды. Например, f(t) = 3sin 2t (рис. 60).
= (2х - 1)(2Z* + 2х + 1) - 8х = (2Т - 1 - 8х =
Зх
3.
а)
(4* + 2х + 1) - 8х;
4х - 1
2х + 1
2х
2у ~ * (22x + 2*+l)-8* =
2+1
,<2'-1>(2* + 1>.(2* + 2'+1)-8я-
2х + 1
f(t) = 3 sin 2t
1-8* = 8*~1-8* = -1.
= 2
Ответ: -1.
б) Решение показано в билете № 6 (вопрос 3,6)).
Билет № 27
1. Правило нахождения наибольшего
(наименьшего) значения функции. Пример.
*
2. Дифференциальное уравнение
показательного роста и показательного убывания.
3. а) Решить уравнение 4sin х + 3cos х = 5.
б) Вычислить sin (arccos = J.
1.
Ответ приведен в билете №13 (вопрос 1).
2*.
В физике, в технике, в биологии и других
науках решение многих задач сводится к
нахождению функций, удовлетворяющих уравнению
/'(#) = kf(x), где k — постоянная, определяемая
условиями задачи.
Вспоминая таблицу производных
элементарных функций, можно утверждать, что показа-
kx
тельная функция f(x) = Се является решением
этого дифференциального уравнения. Проверим
это. Имеем:
f{x) = (С • ekxY = Ck-ekx = k-Cekx = kf(x),
f'(x) = kf(x).
В курсах математического анализа
показывается, что других решений это
дифференциальное уравнение не имеет. Смысл
дифференциального уравнения f'(x) = kf(x) состоит в том, что
скорость изменения функции f в точке х
пропорциональна значению самой функции в этой
точке.
Такие дифференциальные уравнения часто
встречаются при описании процессов реальной
действительности.
Пример. Скорость размножения бактерий
m\t) связана с массой m(t) бактерий в момент
времени t уравнением m'(t) = km(t), где k —
положительное число, зависящее от вида бактерий
25*

772
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
и внешних условий. Решениями такого
дифференциального уравнения являются функции вида
m(f) = С • ekt. (1)
Постоянная С определяется из условия:
известно, что при t = 0 масса бактерий равна т0.
Найдем С:
тп(О) = С • е , тп0 = С.
Уравнение (1) принимает вид
771(f) = 7710£ •
3.
a) 4sin х + 3cos х = 5;
о . X X , 0 2* 0 . 2 X с . 2 X
8sm о cos о + 3cos о ~" 3sin 2 ~ Ssin о ""
- ocos о = 0.
Так как sin 5 и cos 5 не могут одновременно
обращаться в нуль, разделим левую и правую
2 X 2 X
части уравнения на cos „ (cos о * ^' Получаем:
8tg|+3-3tg2| - 5tg2 I -5 = 0;
8tg25 -8tg| +2 = 0;
ВЕЧЕРНЯЯ (СМЕННАЯ)
ОБЩЕОБРАЗОВАТЕЛЬНАЯ
ШКОЛА
Билет № 1
1. Определение логарифма числа, пример.
2. Формула косинуса двойного аргумента
(вывод).
1.
Логарифмом числа Ь по основанию а
называется показатель степени, в которую нужно
возвести основание а, чтобы получить число Ь:
а°Ша = 6, где Ъ > 0, а > 0 и а * 1.
о
Например, log2 8 = 3, так как 2 =8.
Формула косинуса двойного аргумента следует
из формулы сложения
cos (а + р) = cos а • cos Р - sin а • sin р.
Пусть р = а, тогда получим
cos 2а = cos (а + а) =
2 2
= cos а • cos а - sin а • sin а = cos а - sin а.
Таким образом,
2 2
cos 2а = cos а - sin а.
4tg2| -4tg| +1 = 0;
(2tg|-l)2=0;
2tg \ - 1 = 0;
. x 1
^2=2;
jc 1
2 - arctg g + кп, где n e Z;
x = 2arctg 5 + 2тш, где n e Z.
Ответ: 2arctg 5 + 2яп, где n e Z.
Билет № 2
1. Основное логарифмическое тождество,
пример.
2. Формула синуса двойного аргумента (вывод).
1.
Формулу
lo&nb
а = 6, где Ъ > 0, а > 0, а * 1,
называют основным логарифмическим
тождеством.
log3 5
Например, 3 =5.
б) Обозначим arccos g = Р, следовательно, 0 < р < я
и cos Р = g . Найдем sin р. Известно, что sin Р > 0, и
Ответ: sin(arccos g) = g .
* В данном издании приведены только первые два
вопроса билетов. Полные формулировки билетов,
включающие три вопроса (последний вопрос содержит
практическое задание), можно найти в книге: Примерные
экзаменационные билеты для проведения устной
итоговой аттестации выпускников 11 классов
общеобразовательных учреждений в 1997/1998 учебном
году. — М: Дрофа, 1998.

Подготовка к экзаменам. 11 класс
773
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
2. 2.
Формула синуса двойного аргумента следует Ответ приведен в разделе «Общеобразова-
из формулы сложения тельный курс и курс В», билет № 12 (вопрос 2).
sin (а + Р) = sin а • cos р + sin а • cos а.
Пусть а = Р, тогда
sin 2а — sin (а + а) = sin а • cos а -I- sin а • cos а =
= 2sin а • cos а = 2sin а cos а.
Таким образом,
sin 2а = 2sin а - cos а.
Билет № 5
1. Производная функции у = е*.
2. Свойства и график функции у = tg х.
Билет J№ о Функция у = ех дифференцируема в каждой
1. Производная произведения двух функций, точке области определения, (е*)' = е*.
пример. о
2. Свойства и график функции у = sin х. Л „ л
ft- т* -* у Ответ приведен в разделе «Общеобразова-
тельный курс и курс В», билет № 10 (вопрос 2).
1.
Ответ приведен в разделе «Курс А», билет
№ 15 (вопрос 1). Билет № 6
2. 1. Определение первообразной, пример.
Ответ приведен в разделе «Общеобразова- 2. Свойства и график функции у = а для слу-
тельный курс и курс В», билет № 11 (вопрос 2). чаев а>1и0<а<1.
1.
Ответ приведен в разделе «Общеобразова-
1. Производная частного, пример. тельный курс и курс В», билет № 10 (вопрос 1).
Билет № 4
Производная
2. Свойства и график функции у = cos х. ^
Ответ приведен в разделе «Общеобразова-
1. тельный курс и курс В», билет № 4 (вопрос 2).
Если функции и и v дифференцируемы в
точке х0 и значение функции v не равно нулю в
этой точке, то частное - также дифференцируе-
v
Билет № 7
1. Формула Ньютона—Лейбница, пример.
0 2. Свойства и график логарифмической функ-
(и\ _ u'v " uv' ЦИИ У = 1°£* Х ДЛЯ слУчаев Л>1и0<О<1.
UJ J--
Например, 1*
х , х , х , Ответ приведен в разделе «Общеобразова-
(—5—"1 = (в )'*(* + 1) - е (х + 1) = тельный курс и курс В», билет № 12 (вопрос 1).
U + 1) (х + I)2
2-
= ——£~ # Ответ приведен в разделе «Общеобразова-
(х + 1) тельный курс и курс В», билет № 5 (вопрос 2).

774
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Билет № 8
1. Геометрический смысл производной.
2. Формула для решения тригонометрического
уравнения cos х = а.
Ответ приведен в разделе «Курс А», билет
№ 23 (вопрос 1).
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 6 (вопрос 2).
Билет № 9
1. Механический смысл производной.
2. Формула для решения тригонометрического
уравнения sin х = а.
1.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 6 (вопрос 1).
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 2 (вопрос 2).
Билет № 10
1. Правило нахождения наибольшего и
наименьшего значений функции на отрезке,
пример.
2. Формула для решения тригонометрического
уравнения tg х = а.
1.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 13 (вопрос 1).
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 7 (вопрос 2).
Билет № 11
1. Формула перехода от одного основания
логарифма к другому основанию, пример.
2. Правило вычисления производной суммы
двух функций.
1.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 9 (вопрос 2).
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 19 (вопрос 2).
Билет № 12
1. Определение синуса числа t, иллюстрация
на единичной окружности.
2. Формула для вычисления производной
степенной функции.
1.
В системе координат хОу построим
окружность радиуса 1 с центром в точке О(0; 0)
(рис. 61). Точка Р0 лежит на окружности и
соответствует углу 0 радиан.
Синусом числа t называется ордината точки
Pv полученной при повороте точки единичной
окружности Р0 на угол t радиан.
2.
Докажем, что для любого х из области
определения производная степенной функции
находится так:
, ач / а - 1
(х ) =a*
Доказательство. По основному
логарифмическому тождеству представим х
следующим образом: х = е пх. Используя правило
возведения степени в степень, имеем:
a , lnXvOt alnx
х =(е ) -е
Рис. 61

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
775
По правилу вычисления производной
сложной функции получаем:
(ху = (еа1п*)' = еа,пх • «xln х)' = еаЫх • а • \ =
а 1 X а-1
= jc -а-- = а- — =а-х
х х
Билет № 13
1. Определение косинуса числа t, иллюстрация
на единичной окружности.
2. Формула производной показательной
функции.
1.
В системе координат хОу построим
окружность радиусом 1 и центром в точке О(0; 0)
(рис. 62). Точка Р0, лежащая на пересечении
окружности и оси Ох у соответствует углу 0 радиан.
Косинусом числа t называется абсцисса
точки Pt полученной при повороте точки Р0 на угол
t радиан.
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет 22 (вопрос 2).
Билет № 14
1. Определение тангенса числа t, иллюстрация
на единичной окружности.
2. Формула производной логарифмической
функции.
1.
В системе координат хОу построим
окружность радиуса 1 и центром в точке 0(0; 0) (рис.
63). Точка Р0, лежащая на пересечении
окружности и оси Ох, соответствует углу 0 радиан.
Точка Ра получена при повороте точки Р0 на
угол а радиан.
Тангенсом числа t называется отношение
ординаты точки Ра к ее абсциссе, т. е.
, У a since
ь *„ cos а
Прямую, параллельную оси Оу и
проходящую через точку (1; 0), называют линией
тангенсов.
Для того чтобы найти тангенс любого угла а,
поступают следующим образом:
1) через точку Ра единичной окружности и
точку 0(0; 0) проводят прямую до пересечения с
линией тангенсов; i
2) находят значение ординаты полученной
точки пересечения. Это и есть значение тангенса
числа а.
2.
Для того чтобы вывести формулу
производной логарифмической функции, покажем, что она
дифференцируема (имеет производную) в
каждой точке. Графики функций у = loga х и у = ах
симметричны относительно прямой у = х.
Показательная функция имеет производную в
каждой точке (не равную нулю), значит, график
показательной функции имеет негоризонтальную
касательную в каждой точке. Поэтому и график
логарифмической функции имеет
невертикальную касательную в любой точке. Следовательно,
логарифмическая функция имеет производную
в ее области определения.
Докажем, что производная
логарифмической функции для любого х из области
определения находится по формуле
In' х = - .
X
По основному логарифмическому тождеству
In Т
х = е при всех положительных х. Значит,
*' =(eln*)\
Производная х равна 1 (х' = 1).
Рис. 62
Рис. 63

776
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по алгебре и началам анализа
Найдем производную (е п *)' по правилу
нахождения производной сложной функции:
(elnY = eln*-(ln*)' = x-ln'x.
Подставив найденные производные в равен-
In т
ство х' = (е ), получим 1 = х • In' х, т. е.
In' х - i .
х
Билет № 15
1. Косинус суммы (разности) двух аргументов.
2. Основное свойство первообразных.
1.
Косинус суммы двух углов (аргументов)
равен разности произведений косинусов этих
углов и синусов этих углов:
cos (а + Р) = cos а cos Р - sin а sin р.
Косинус разности двух углов (аргументов)
равен сумме произведений косинусов этих углов и
синусов этих углов:
cos (а - Р) = cos а cos р + sin а sin р.
2.
Ответ приведен в разделе
«Общеобразовательный курс и курс В>, билет № 17 (вопрос 2).
Билет № 17
1. Определение криволинейной трапеции,
пример, формула площади.
2. Основные свойства логарифмов.
Пусть на отрезке [а; Ь] оси Ох задана
непрерывная функция /, не меняющая на нем знака.
Фигуру, ограниченную графиком этой
функции, отрезком [а; Ь] и прямыми х = а и х = Ь,
называют криволинейной трапецией.
Примеры криволинейных трапеций
приведены на рисунках 64, а—г.
Если / — непрерывная и неотрицательная на
отрезке [а; Ь] функция, a F — ее первообразная
на этом отрезке, то площадь S соответствующей
криволинейной трапеции равна приращению
первообразной на отрезке [а; 6], т. е.
S = F(b) - F(a).
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 3 (вопрос 2).
Ответ приведен в разделе
«Общеобразовательный курс и курс В», билет № 9 (вопрос 2).
Билет № 16
1. Синус суммы (разности) двух аргументов.
2. Правила нахождения первообразных.
Синус суммы двух углов (аргументов) равен
сумме произведений синуса первого угла на
косинус второго угла и косинуса первого угла на
синус второго:
sin (а + Р) = sin а cos Р + cos а sin р.
Синус разности двух углов (аргументов)
равен разности произведений синуса первого угла
на косинус второго и косинуса первого угла на
синус второго:
sin (а - Р) = sin а cos р - cos а sin р.
у\ y-f(x)
у1 у-fix)
Vi
\ °
1
v-f(x)
а Ь /
мШш/ х
в)
\
0
1
V-fM
dWyiWb*x
г)
Рис. 64

Примерные билеты и ответы к устному
экзамену по геометрии
КУРСА
Билет №1
1. Взаимное расположение двух прямых в
пространстве (формулировки и примеры).
2. Задача по теме «Объем тел вращения».
Шар с центром в точке О касается
плоскости в точке А. Точка В лежит в плоскости
касания. Найдите объем шара, если АВ =
= 21 см, а ВО = 29 см.
3. Задача по теме «Призма».
В правильной треугольной призме АВСАХВ1С1
проведено сечение через вершину Сг и ребро
АВ. Найдите периметр сечения, если
сторона основания равна 24 см, а боковое ребро —
10 см.
Определение. Две прямые в пространстве
называются параллельными, если они лежат в
одной плоскости и не пересекаются.
Определение. Прямые, которые не
пересекаются и не лежат в одной плоскости, называются
скрещивающимися.
Две прямые в пространстве
лежат
в одной плоскости
пересекаются
не пересекаются
параллельны
не лежат
в одной плоскости
скрещиваются
Примеры.
1) Горизонтальная прямая, начерченная на
одной стене комнаты, и вертикальная прямая,
начерченная на противоположной стене,
являются скрещивающимися.
2) На изображении прямоугольного
параллелепипеда (рис. 1) прямые АгМ и DDX являются
скрещивающимися, прямые АгМ и ВВг — пере-
29 см
секающимися, а прямые ААг и ССг —
параллельными.
3) Образующая конуса SM и диаметр
основания АВ (рис. 2) лежат на скрещивающихся
прямых.
2.
Дано: шар с центром О,
а — касательная плоскость,
А — точка касания, В € а,
АВ = 21 см, ВО = 29 см.
Найти: Ушлрл.
Решение. Радиус АО,
проведенный в точку касания, перпендикулярен
касательной плоскости а. Из А АВО по теореме Пи-
2 2
29-21 = 20 (см).
Поэтому объем шара
лт 4 оЛз 32 000 1ЛЛЛЛ2 , зч
^шара=37С#2° з~ 7С=1066637С(СМ )#
2 з
Ответ: 10 666^71 (см ).
3.
Дано: АВСА1В1С1 — правильная призма, ААг —
= 10см,АВ = 24см.
Найти: Р^всг
Решение. Сечение
представляет собой
равнобедренный треугольник АВСг.
Основание АВ = 24 см,
боковая сторона АСх
является диагональю боковой
грани АССгАг. Из прямоугольного треугольника
АССг по теореме Пифагора
24 см

778
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
АСг = л/ю2 + 242 - 26 (см).
Периметр сечения Pj^q = 2 • 26 -I- 24 = 76 (см).
Ответ: 76 (см).
Билет № 2
1. Взаимное расположение двух плоскостей
(формулировки и примеры).
2. Задача по теме «Поверхности тел
вращения*.
Прямоугольник, стороны которого равны 6 см
и 4 см, вращается около меньшей стороны.
Найдите площадь поверхности тела
вращения.
3. Задача по теме «Прямоугольный
параллелепипед*.
В прямоугольном параллелепипеде стороны
основания равны 5 см и 12 см, а диагональ
параллелепипеда наклонена к плоскости
основания под углом 45°. Найдите высоту
параллелепипеда.
1.
Определение. Две плоскости называются
параллельными^ если они не пересекаются.
Аксиома. Если две различные плоскости
имеют общую точку, то они пересекаются по
прямой.
Из этой аксиомы следует, что любые две
плоскости в пространстве либо не имеют общих
точек, т. е. параллельны, либо пересекаются по
прямой.
Две плоскости в пространстве
пересекаются по прямой
не пересекаются
параллельны
Примеры.
1) Плоскости противоположных стен в
комнате являются параллельными.
2) Плоскости любых двух граней пирамиды
(рис. 3) пересекаются по прямой.
3) Основания цилиндра (рис. 4) лежат в
параллельных плоскостях.
2.
Дано: ABCD —
прямоугольник, АВ = 6 см, ВС =
= 4 см, ВС — ось вращения.
#aumu:Sn0B телавращ
Решение. Данное тело
вращения — прямой
круговой цилиндр с высотой ВС = 4 см и радиусом
основания АВ = 6 см.
Площадь боковой поверхности
5бок.пов. = 2^-6-4 = 48л(См2)-
2 2
Площадь основания S0CH = тс • 6 = Збтс (см ).
Площадь полной поверхности
Яш*, дил. = 48тс + 2 • Збтс = 120тс (см2).
Ответ: 120л (см ).
3.
Дано: ABCDA1B1C1D1 — прямоугольный
параллелепипед, АВ = 5 см, ВС = 12 см, угол
между BDt и плоскостью ABC равен 45°.
Найти: высоту параллелепипеда.
Решение. Так как DXD — перпендикуляр
к плоскости ABCD, то
A DBDX является углом
между диагональю BDt
и плоскостью
основания прямоугольного
параллелепипеда, т. е.
A DBDr = 45°.
Из прямоугольного AABD по теореме
Пифагора BD = л/52 + 122 =13 (см). Треугольник
BDDX — прямоугольный и равнобедренный с
острым углом 45°. Следовательно, высота
параллелепипеда DDX = BD = 13 см.
Ответ: 13 см.
Сг
i
Dx
•45*'
Ч\-
5 см В
С
12 см
Рис.3
Рис.4

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
779
Билет № 3
1. Взаимное расположение прямой и плоскости
в пространстве (формулировки и примеры).
2. Задача по теме «Объемы тел вращения*.
Образующая конуса равна 25 см, а радиус
основания — 7 см. Найдите его объем.
3. Задача по теме «Пирамида*.
В правильной четырехугольной пирамиде
высота равна 12 см, а апофема — 15 см.
Найдите боковое ребро пирамиды.
1.
Определение. Прямая и плоскость
называются параллельными у если они не пересекаются.
Прямая может принадлежать плоскости
(если она имеет с ней по крайней мере две общие
точки) или не принадлежать этой плоскости. Во
втором случае она может иметь с ней либо одну
общую точку (тогда прямая и плоскость
пересекаются), либо не иметь общих точек (тогда
прямая и плоскость параллельны).
Прямая и плоскость в пространстве
пересекаются в одной точке
не пересекаются
прямая параллельна плоскости
Примеры.
1) Любая прямая, начерченная на одной
стене комнаты, и плоскость противоположной
стены являются параллельными, а любая прямая
на стене комнаты, кроме вертикальных
прямых, пересекается с плоскостью смежной стены.
N
у^\ ^\
IS"
.dW-
М i
Рис. 5
Bl
В
Q
2) Прямая АгМ параллельна плоскости грани
ClCDDl прямоугольного параллелепипеда (рис. 5)
и пересекает плоскость грани ВВгСхС.
3) Любая образующая цилиндра (рис. 6)
пересекает его основание, а любая прямая в
плоскости основания параллельна второму основанию.
2.
Дано: конус, AS = 25 см,
АО = 7 см.
Найти: VKOHyCA.
Решение. Из
прямоугольного AAOS по теореме
Пифагора высота конуса SO =
25 см
А
По-
Рис. 6
= л/252 - 72 =24 (см),
этому объем конуса
^конус*=!*-72.24 = 392я(см3).
Ответ: 392тс (см ).
3.
Дано: SABCD — правильная пирамида, SO —
высота, SO =12 см, SM — апофема, SM =15 см.
Найти: боковое ребро.
Решение. Треугольник SOM —
прямоугольный с прямым углом О. По теореме Пифагора
ОМ = л/152^ 12 =9 (см). По теореме о трех
перпендикулярах ОМ _L ВС. Точка О —
середина АС, следовательно, ОМ — средняя линия
треугольника ABC иАВ = 2 • 9 = 18 (см).
Высота SM
равнобедренного треугольника
SBC является и
медианой, поэтому
вм = \вс = \ав =
= 9 (см).
Из прямоугольного
треугольника SMB по
теореме Пифагора находим боковое ребро:
SB = Vl52 + 92 = 3734 (см).
Ответ: Зл/34 см.
Билет № 4
1* Призма. Боковая поверхность прямой
призмы. Прямая и правильная призмы
(формулировки и примеры).

780
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
2. Задача по теме «Шар».
Найдите площадь сечения шара радиуса
41 см, проведенного на расстоянии 9 см от
центра.
3. Задача по теме «Объем пирамиды».
В правильной четырехугольной пирамиде
высота равна 7 см, а боковое ребро
наклонено к плоскости основания под углом 45°.
Найдите объем пирамиды.
1.
Определение. Призмой называется
многогранник, который состоит из двух плоских
многоугольников, совмещаемых параллельным
переносом, и всех отрезков, соединяющих
соответствующие точки этих многоугольников.
Эти два плоских многоугольника называются >
основаниями призмы. Если основания призмы
имеют п сторон, то призма называется п-угольной.
Примеры.
1) Параллелепипед является
четырехугольной призмой.
2) Пятиугольная призма (рис. 7) является
выпуклым многогранником. Бе поверхность
состоит из двух оснований — пятиугольников и
боковой поверхности, состоящей из пяти
параллелограммов. Она имеет пятнадцать ребер и
десять вершин. Можно провести пять
диагональных сечений пятиугольной призмы.
3) Если в основание цилиндра вписать
многоугольник и через его стороны провести
плоскости, параллельные оси цилиндра, то получится
прямая призма: ее основания —
многоугольники, лежащие в основаниях цилиндра, а боковые
грани — сечения цилиндра плоскостями,
проходящими через соответствующие стороны этих
многоугольников.
Определение. Призма называется прямой,
если ее боковые ребра перпендикулярны
основаниям.
Боковая поверхность прямой призмы
состоит из прямоугольников, две стороны которых
являются сторонами оснований, а две другие —
соседними боковыми ребрами.
Теорема. Боковая поверхность прямой
призмы равна произведению периметра основания
на высоту призмы, т. е. на длину бокового ребра.
Пример. Дана прямая призма (рис. 8). Ее
основанием является прямоугольный треугольник
ABC у у которого катет ВС = 5 см, катет АС = 12 см,
а боковая поверхность равновелика основанию.
Найдем высоту ААг этой призмы.
5*12 2
Площади основания S = 9 = 30 (см ). По
V2 2
12 + 5 =
= 13 (см). Периметр основания Р = 5 + 12 +
+ 13 = 30 (см). Боковая поверхность S^ пов =
= 30 ААг (см2). Поэтому 30 = 30 ААг и высота
призмы ААг = 1 см.
Определение. Призма называется прямой,
если ее боковые ребра перпендикулярны
основаниям. В противном случае призма называется
наклонной.
Прямая призма называется правильной, если
ее основания являются правильными
многоугольниками.
Примеры.
1) Прямоугольный параллелепипед есть
прямая четырехугольная призма, так как его
боковые ребра перпендикулярны основанию.
2) Куб есть правильная четырехугольная
призма, так как его боковые ребра
перпендикулярны основанию и основанием является
правильный четырехугольник.
3) Граненый карандаш имеет форму
правильной шестиугольной призмы (рис. 9).
1
1
J- ■
- — — ■** ,
>
Рис.8
Рис.9

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
781
4) Гайка имеет форму правильной
шестиугольной призмы, из которой удален цилиндр.
2.
Дано: шар с центром О,
а — секущая плоскость,
Д
шара
р(0, а) = 9 см,
= 15 см.
Найти: Sce4.
Решение. Данное
сечение — круг с центром А,
причем АО _L а. Пусть В — точка на окружности
этого круга. Из прямоугольного ДАВО по теореме
Пифагора находим радиус сечения: АВ =
7 2 2
41-9 =40 (см). Поэтому площадь сечения
Sce4 = п • 402 = 1600я (см2).
Ответ: 1600я (см ).
3.
Дано: SABCD —
правильная пирамида, SO —
высота, SO = 7 см, угол
между SA и плоскостью ABC
равен 45°.
Найти: Упир.
Решение. Так как SO —
перпендикуляр к
плоскости основания, то A OAS есть угол между ребром
SA пирамиды и плоскостью ABC, т. е. A OAS =
= 45°.
Треугольник SAO — прямоугольный и
равнобедренный с острым углом А = 45°. Поэтому
АО = 7 см и диагональ основания АС = 14 см.
Площадь основания
&ABCD ~~ 2&ААВС
= 2-\ -14-7 = 98 (см2).
Таким образом, объем пирамиды
V =
пир.
98-7 = 228
(см3).
2 з
Ответ: 228« (см ).
2. Задача по теме «Цилиндр».
Радиус основания цилиндра равен 5 см, а его
образующая — 9 см. Найдите площадь осевого
сечения.
3. Задача по теме «Площадь поверхности
пирамиды».
В правильной четырехугольной пирамиде
сторона основания равна 10 см, а высота —
12 см. Найдите площадь полной
поверхности пирамиды.
1.
Определение. Параллелепипедом называется
призма, основания которой являются
параллелограммами.
Пример.
Параллелепипед (рис. 10) имеет шесть граней,
и все они являются параллелограммами. На
шарнирной модели параллелепипеда можно
показать, что существуют различные
параллелепипеды, имеющие соответственно равные ребра.
Определение. Параллелепипед называется
прямоугольным, если он прямой и его оснрва-
ния — прямоугольники.
Примеры.
1) Обычная комната представляет собой
прямоугольный параллелепипед.
2) Из всех параллелепипедов с заданными
длинами ребер наибольший объем имеет
прямоугольный параллелепипед (рис. 10), так как он
имеет наибольшую площадь основания и
наибольшую высоту.
Прямоугольный параллелепипед имеет
также наибольшую полную поверхность из всех
параллелепипедов с заданными длинами ребер,
так как он имеет наибольшие высоты всех
граней.
3) Прямоугольный параллелепипед, все
грани которого — квадраты, называется кубом.
Форму куба имеют кристаллы поваренной соли.
Теорема. Противолежащие грани
параллелепипеда равны и параллельны.
Билет № 5
1. Параллелепипед. Прямоугольный
параллелепипед. Теорема о диагонали
прямоугольного параллелепипеда. Свойство
противолежащих граней параллелепипеда
(формулировки и примеры).
Рис. 10

782
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Примеры.
1) На изображении параллелепипеда
противолежащие грани изображаются равными
параллелограммами (рис. 10,11). На изображении
куба (рис. 12) равные, но не параллельные
грани (например, передняя и верхняя)
изображаются различными параллелограммами.
2) Развертка боковой поверхности
прямоугольного параллелепипеда есть прямоугольник со
сторонами 16 см и 12 см. Может ли площадь
одной из боковых граней этого параллелепипеда
2
быть равной 100 см ?
По условию вся боковая поверхность равна
16*12 = 192 (см ). Так как противолежащие
грани параллелепипеда равны, то сумма площадей
смежных боковых граней не может быть больше
192 : 2 = 96 (см ). Поэтому и площадь любой из
2
боковых граней меньше 96 см .
Теорема. В прямоугольном параллелепипеде
квадрат любой диагонали равен сумме
квадратов трех его линейных размеров.
Примеры.
1) Для нахождения наибольшего расстояния
между двумя точками обычной комнаты,
имеющей форму параллелепипеда, надо заметить,
что это расстояние — длина диагонали
параллелепипеда, измерить длину, ширину и высоту
комнаты и воспользоваться формулой.
2) Около куба с ребром а (рис. 12) описан
шар. Так как диагональ куба d является диа-
2 2
метром шара, то d = (2Д) , где R — радиус
шара, так что За =4Д и радиус шара R = -д- .
Дано: цилиндр, ABCD —
осевое сечение, АО = 5 см,
АВ = 9 см.
Найти: S^ca-
Решение. Данное осевое
сечение есть прямоугольник
ABCD. Сторона
прямоугольника AD = 2 • 5 = 10 (см). Поэтому площадь сечения
sabcd = Ю • 9 = 90 (см2).
Ответ: 90 (см ).
Дано: SABCD — правильная пирамида, АВ =
= 10 см, SO = 12 см.
Найти: Sn(WIH.n0B.
Решение. Диагонали
квадрата ABCD в точке
пересечения делятся пополам,
поэтому АО = СО. В
равнобедренном треугольнике SBC
высота SM является и
медианой, поэтому ВМ = СМ.
Следовательно, МО — средняя линия А ABC и
МО = 5 см.
Из прямоугольного A SMO по теореме Пифаго-
V2 2
12 + 5 = 13 (см).
Боковая поверхность пирамиды
10-
4 -13 = 260 (см2).
°бок. пов. 2
2
Площадь основания S^. = 10*10 = 100 (см ).
Площадь полной поверхности
'ПОЛИ. пов.
= 100 + 260 = 360 (см").
Ответ: 360 (см ).
Билет № 6
1. Пирамида. Правильная пирамида. Боковая
поверхность правильной пирамиды
(формулировка и пример).
2. Задача по теме «Конус».
Радиус основания конуса равен 14 см.
Найдите площадь сечения, проведенного
перпендикулярно его оси через ее середину.
3. Задача по теме «Площадь поверхности
прямоугольного параллелепипеда ♦.
В основании прямого параллелепипеда
лежит ромб, диагонали которого равны 12 см
и 16 см. Высота параллелепипеда — 8 см.
Найдите площадь его полной поверхности.
Определение. Пирамидой называется
многогранник, который состоит из плоского
многоугольника — основания пирамиды, точки, не ле-
У~-7\
| Л
I
/>- 1
Рис. 11
Рис. 12

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
783
жащеи в плоскости основания, — вершины
пирамиды и всех отрезков, соединяющих вершину
с точками основания.
Пирамида, в основании которой лежит п-уголь-
ник, называется п-угольной; n-угольная
пирамида имеет п + 1 грань — основание и п боковых
граней.
Примеры.
1) Треугольная пирамида (рис. 13) является
выпуклым четырехгранником (тетраэдром).
Отрезки SA, SB и SC — боковые ребра.
Поверхность состоит из основания ABC и боковых
граней SAB, SBC и SAC.
2) Египетские пирамиды имеют форму,
близкую к правильной четырехугольной пирамиде.
Определение. Пирамида называется
правильной, если ее основанием является правильный
многоугольник, а основание высоты совпадает с
центром этого многоугольника.
Следовательно, в правильной пирамиде
(рис. 14) все боковые ребра равны и все боковые
грани — равные равнобедренные треугольники.
Боковые ребра и боковые грани правильной
пирамиды имеют один и тот же угол наклона к
плоскости основания.
Примеры.
1) Если две правильные четырехугольные
пирамиды, у которых боковое ребро равно стороне
основания, приложить друг к другу так, чтобы
их основания совпали, то получится
правильный многогранник — октаэдр. Форму октаэдра
имеет кристалл алмаза.
Четыре атома водорода (Н), входящие в
молекулу метана (СН4), расположены в вершинах
правильной пирамиды (тетраэдра). Атом
углерода (С) находится внутри этой пирамиды на
равном расстоянии от ее вершин.
Определение. Высота боковой грани
правильной пирамиды, проведенная из ее вершины,
называется апофемой.
Ъ
Теорема: Боковая
поверхность правильной
пирамиды равна
произведению полупериметра
основания на апофему.
Пример.
Сторона основания
правильной четырехугольной
пирамиды равна 6 см, а
боковое ребро равно 5 см. По свойству
равнобедренного треугольника ВМ = 3 см. По теореме
Пифагора апофема SM равна 4 см. Поэтому боко-
2
вая поверхность пирамиды равна 12 • 4 = 48 (см ).
2.
Дано: конус, ОА = 14 см, а — секущая
плоскость, a_L OS, М е OS, SM = МО, Меа.
Найти: Sce4.
Решение. Данное
сечение подобно основанию
конуса с коэффициентом
подобия о -
Площади подобных
фигур относятся как
квадраты линейных размеров.
2 2
Площадь основания S^,, = п • 14 = 196тс (см ).
Поэтому площадь сечения
\2
S_ =196тс-
■(|) =49тс(см2).
Ответ: 49тс (см ).
3-
Дано: ABCDA1B1C1D1 — прямой
параллелепипед, ААг = 8 см, АВ = ВС, АС = 16 см, BD =
= 12 см.
Найти: S„
"ПОЛИ. пов.#
Решение. Диагонали
ромба
перпендикулярны и делятся точкой
пересечения пополам. По
теореме Пифагора
сторона основания
А
8 см
J-
i
А
16 см
Г^г
Вл
В
12 см
АВ = л/б2 + 82 = 10 (см),
поэтому периметр ромба равен 40 см.
2
Боковая поверхность равна 4*10*8 = 320 (см ).
Площадь ромба S^^ = 2SAABC = 2 • —^- =
= 96 (см2).

Примерные билеты и ответы к устному экзамену по геометрии
Подготовка к экзаменам. 11 класс
Площадь полной поверхности
5„олн.по». = 320 + 2.96 = 512(см2).
2
Ответ: 512 (см ).
Билет № 7
1. Цилиндр. Сечения цилиндра плоскостями.
Площадь боковой поверхности цилиндра
(формулировки и примеры).
2. Задача по теме «Взаимное расположение
прямых и плоскостей в пространстве».
Прямая п параллельна прямой т, прямая т
параллельна плоскости а. Следует ли из
этого, что прямая п параллельна
плоскости а?
3. Задача по теме «Площадь сферы».
Сферу на расстоянии 8 см от центра
пересекает плоскость. Радиус сечения равен
15 см. Найдите площадь сферы.
1.
Определение. Цилиндром называется тело,
которое состоит из двух кругов, совмещаемых
параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих
кругов.
Цилиндр называется прямым, если его
образующие перпендикулярны плоскостям
основания.
Примеры.
1) Прямой цилиндр можно рассматривать
как тело, полученное при вращении
прямоугольника вокруг его стороны как оси.
Например, при вращении прямоугольника со
сторонами 3 см и 4 см вокруг большей стороны получится
цилиндр с высотой 4 см и радиусом основания
3 см, а вокруг меньшей стороны — с высотой
3 см и радиусом основания 4 см.
2) Прямой цилиндр можно также
рассматривать как тело, полученное при вращении
прямоугольника вокруг одной из его осей симметрии.
Например, при вращении прямоугольника со
сторонами 3 см и 4 см вокруг прямой,
перпендикулярной стороне 3 см и проходящей через ее
середину, получится цилиндр с высотой 4 см и ра-
3
диусом основания « см» а вокруг прямой,
перпендикулярной стороне 4 см и проходящей
через ее середину, — цилиндр с высотой 3 см и
радиусом основания 2 см.
3) Если склеить противоположные стороны
бумажного прямоугольника, то получится боковая
поверхность цилиндра. Высота этого цилиндра
равна длине склеенных сторон, радиус
основания равен длине другой стороны, деленной на 2л.
4) Сквозное отверстие в стене, сделанное
дрелью, является цилиндром: его основание — круг
с диаметром, равным диаметру сверла, высота —
толщина стены.
Определение. Осью цилиндра называется
прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, проходящей
через ось цилиндра, называется осевым сечением.
Теорема. Плоскость, перпендикулярная оси
цилиндра, пересекает его боковую поверхность
по окружности, равной окружности основания.
Сечение цилиндра любой плоскостью,
параллельной оси, является прямоугольником, две
противоположные стороны которого
параллельны и равны высоте цилиндра. Две другие
противоположные стороны являются хордами в
окружностях соответствующих оснований. Если
сечение является осевым, эти хорды являются
диаметрами.
Площадь боковой поверхности цилиндра
вычисляется по формуле
S = 2тсДЯ,
где R — радиус основания конуса, Н — высота.
Примеры.
1) Длина окружности основания прямого
цилиндра С = 10 м, длина образующей I = 7 м. Чему
равна площадь боковой поверхности цилиндра?
Площадь боковой поверхности цилиндра
равна произведению длины окружности его
основания на высоту: S = СН. Высота цилиндра равна
его образующей: Н = 10 м. Поэтому S = 10 • 7 =
= 70(м2).
2) Цилиндр получен при вращении
прямоугольника со сторонами 10 см и 15 см вокруг оси
симметрии. Определить площадь его боковой
поверхности.
Площадь боковой поверхности цилиндра
равна площади осевого сечения, умноженной на тс,
и поэтому не зависит от того, вокруг какой из
осей вращается прямоугольник.
2
Так как площадь осевого сечения равна 150 см ,
2
то площадь боковой поверхности S = 150л (см ).

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
785
Ах
А
/\.
г>1.
/
/
/
*1
/
/
В
2.
Ответ. Данное
утверждение неверно, так
как прямая п может
принадлежать плоскости а.
Например, ребро АВ
куба ABCDAlBlClDl
параллельно ребру AXBV ребро
АхВг параллельно
плоскости а нижнего основания, однако АВ не
является параллельным плоскости а, потому что
принадлежит ей.
Таким образом, АВ II А1Б1, АгВх II а, но АВ не
параллельна а.
3.
Дано: сфера с центром О, а — секущая
плоскость, р(0, а) = 8 см, Лсеч =15 см.
Найти: SC(J)epbI.
Решение. Данное
сечение — окружность с
центром А, АО _1_ а.
Пусть В — точка на
этой окружности. Из
прямоугольного ААВО
по теореме Пифагора
радиус сферы ВО = Jib2
му площадь сферы
Сг 1.
+ 8 = 17 (см). Поэто-
Sc<frePbi = 4п
172 = 1156л (см2).
Ответ: 1156л (см ).
Билет № 8
1. Конус. Сечения конуса плоскостями.
Площадь боковой поверхности конуса
(формулировки и примеры).
2. Задача по теме «Взаимное расположение
прямых и плоскостей в пространстве*.
Каждая из плоскостей а и р параллельна
плоскости у. Могут ли плоскости аир
пересекаться?
3. Задача по теме «Площадь поверхности
цилиндра».
Осевым сечением цилиндра является
квадрат, диагональ которого равна 3*/2 см.
Найдите площадь поверхности цилиндра.
Определение. Конусом называется тело,
которое состоит из круга — основания конуса,
точки, не лежащей в плоскости этого круга, —
вершины конуса, и всех отрезков, соединяющих
вершину с точками основания.
Конус называется прямым, если прямая,
соединяющая вершину конуса с центром
основания, перпендикулярна плоскости основания.
Примеры.
1) Прямой конус можно рассматривать как
тело, полученное при вращении прямоугольного
треугольника вокруг его катета как оси.
Например, при вращении прямоугольного
треугольника с катетами 3 см и 4 см вокруг большего
катета получится конус с высотой 4 см и радиусом
основания 3 см, а вокруг меньшей стороны — с
высотой 3 см и радиусом основания 4 см.
2) Прямой конус можно рассматривать как
тело, полученное при вращении
равнобедренного треугольника вокруг его высоты как оси.
3) Если склеить круговой сектор по двум
ограничивающим его радиусам, то получится
боковая поверхность конуса, вершиной которого
является центр круга, из которого вырезан
сектор, а образующая равна радиусу этого круга.
4) Чум и яранга у северных народов, вигвам у
индейцев Северной Америки имеют форму,
близкую к форме конуса.
Определение. Осью прямого конуса
называется прямая, содержащая его высоту. Сечение
конуса плоскостью, проходящей через его ось,
называется осевым сечением.
Теорема. Плоскость, перпендикулярная
оси конуса, пересекает конус по кругу, а
боковую поверхность — по окружности с центром
на оси конуса.
Сечение конуса плоскостью, проходящей
через его вершину, является равнобедренным
треугольником, боковые стороны которого —
образующие конуса, а основание — хорда круга,
лежащего в основании конуса. Для осевого сечения
эта хорда является диаметром основания конуса.
Сечение конуса плоскостью, параллельной
основанию, отсекает от него конус, подобный
данному.
Площадь боковой поверхности конуса
вычисляется по формуле
S = nRl,
где R — радиус основания конуса, I — длина
образующей.

786
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Примеры.
2
1) Площадь боковой поверхности конуса 30 м ,
а длина окружности его основания равна 15 м.
Чему равна образующая конуса?
Длина окружности находится по формуле
С = 2лД. Поэтому боковая поверхность S = « С1.
Отсюда образующая Z = 2 • 30 : 15 = 4 (м).
2) Могут ли разные конусы иметь равные
площади боковых поверхностей?
Если радиус данного конуса увеличить в два
раза, а его образующую уменьшить в два раза,
то площадь боковой поверхности нового конуса
будет такой же, как у данного.
2.
Ответ: нет.
Положим, что
плоскости а и Р пересекаются по
некоторой прямой с.
Возьмем в плоскости
у прямую U не
параллельную прямой с, и точку С на прямой с.
Проведем плоскость 5 через прямую I и точку С. Эта
плоскость пересекает плоскости а и (3 по прямым
аиЬ.
Прямые а и I параллельны как линии
пересечения параллельных плоскостей а и у
плоскостью 5, и точно так же параллельны прямые Ь и
I. Тем самым мы получили в плоскости 5 две
различные пересекающиеся прямые аиб,
параллельные прямой I, что противоречит аксиоме
параллельных прямых. Полученное противоречие
доказывает, что плоскости ос и Р не могут
пересекаться.
3.
Дано: цилиндр, ABCD —
осевое сечение, AB=AD,
BD = 3*/2 см.
Найти: 8П0ВЦ11Л.-
Решение. Из
прямоугольного AABD по теореме Пифа-
2 2
гора BD = 2АВ , откуда сторона квадрата АВ =
BD За/2
= —=г = —=- — 3 (см). Поэтому высота цилиндра
АВ = 3 см, радиус цилиндра О А = 1,5 см.
Площадь боковой поверхности
5боклюв. = 2л-1,5-3 = 9л(СМ2).
2 2
Площадь основания S^ = я • 1,5 = 2,25л (см ).
Площадь полной поверхности
^пов. цил.
= 9л + 2 • 2,25л = 13,5л (см ).
Ответ: 13,5л (см ).
Билет № 9
1. Сфера и шар. Сечения шара плоскостями.
Площадь сферы (формулировки и примеры).
2. Задача по теме «Взаимное расположение
прямых и плоскостей в пространстве*.
Плоскость у пересекает плоскости а и Р по
параллельным прямым. Могут ли
плоскости аир пересекаться?
3. Задача по теме «Пирамида*.
В основании пирамиды лежит
прямоугольный треугольник, гипотенуза которого
равна 15 см, а один из катетов — 9 см.
Найдите площадь сечения, проведенного через
середину высоты пирамиды параллельно ее
основанию.
1.
Определение. Шаром называется тело,
которое состоит из всех точек пространства,
находящихся на расстоянии, не большем данного от
данной точки. Эта точка называется центром
шара, а данное расстояние — радиусом шара.
Граница шара называется шаровой
поверхностью или сферой. Все точки сферы равноудалены
от центра шара на расстояние, равное радиусу
шара.
Шар является телом вращения. Он
получается при вращении полукруга вокруг его диаметра
как оси. Например, при вращении полукруга с
радиусом 3 см вокруг его диаметра получится
шар, радиус которого также равен 3 см.
Примеры.
1) Купол здания может иметь форму части
сферы, отсеченной плоскостью.
2) Земля имеет форму, близкую к шару.
3) Мячи для игры в футбол, волейбол,
баскетбол, теннис имеют форму шара.
Плоскость, проходящая через центр шара,
называется диаметральной плоскостью.
Сечение шара диаметральной плоскостью
называется большим кругом, а сечение сферы — большой
окружностью.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
787
Теорема. Всякое сечение шара плоскостью
есть круг. Центр этого круга есть основание
перпендикуляра, опущенного из центра шара
на секущую плоскость.
Следствие. Плоскости, равноудаленные от
центра, пересекают шар по равным кругам.
Площадь сферы радиуса R вычисляется по
формуле
S = 4тсД2.
Примеры.
1) Радиус сферы увеличили в три раза. Во
сколько раз увеличится площадь сферы?
Площадь сферы пропорциональна квадрату ее
радиуса. Поэтому при увеличении радиуса в три
2
раза площадь сферы увеличивается в 3 = 9 (раз).
2) Два шара радиуса г имеют в сумме такую же
площадь поверхности, что и один шар радиуса R.
Что больше: суммарный объем двух маленьких
шаров или объем большого шара?
По условию задачи 2 • 4тсг = 4кН , откуда R =
= rj2 . Общий объем двух маленьких шаров
равен:
П = 2-|*г3.
Объем большого шара равен:
^2=|тсД3=|тс-2г372.
Следовательно, Vt < V2, т. е. объем большого
шара больше суммарного объема маленьких
шаров.
2.
Ответ. Да. Например, в
правильной
четырехугольной пирамиде SABCD
плоскость основания пересекает
плоскости боковых граней
SAD и SBC по
параллельным прямым AD и ВС. При
этом боковые грани SAD и
SBC имеют общую точку S, следовательно,
пересекаются по прямой.
3.
Дано: SABC — пирамида, А ЛВС — основание,
А С = 90°, АВ = 15 см, ВС = 9 см, SO — высота,
М — середина OS, АгВгСг — сечение, (Av Bv Сх) _L
10S,Me(AvBvCx).
Найти: Sraxi.
Решение. Данное сечение подобно основанию
пирамиды с коэффициентом подобия к •
Площади подобных фигур относятся как квадраты
линейных размеров.
Из А ABC по теореме Пифагора
АС = Vl52 - 92 = 12 (см).
Площадь основания
Soch. = —2~ = 54 (см2)-
Поэтому площадь
сечения
ал2
«сеч. = 54
©-
= 13,5 (of).
2
Ответ: 13,5 (см ).
15 см
Билет № 10
1. Формула объема многогранников:
прямоугольного параллелепипеда, наклонного
параллелепипеда, призмы и пирамиды
(формулы и примеры).
2. Задача по теме «Взаимное расположение
прямых и плоскостей в пространстве».
Каждая из плоскостей а и Р параллельна
прямой т. Могут ли плоскости аир
пересекаться?
3. Задача по теме «Площади поверхностей тел
вращения».
Прямоугольный треугольник, гипотенуза
которого равна 17 см, а один из катетов —
8 см, вращается около этого катета.
Найдите площадь поверхности тела вращения.
Объем прямоугольного параллелепипеда
вычисляется по формуле
V=abc,
где а, Ь и с — ребра прямоугольного
параллелепипеда.
Пример.
Аквариум имеет форму прямоугольного
параллелепипеда. Его длина 45 см, ширина 30 см
и высота 40 см. Масса пустого аквариума 8 кг.
Объем аквариума V = 30 • 40 • 45 = 54 000 (см3).

788
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Так как плотность воды равна 1 г/см , то масса
т аквариума, наполненного водой, равна
т = 54 000 • 1 + 8000 = 62 000 (г) = 62 (кг).
Объем любого параллелепипеда вычисляется
по формуле
V=SH,
где S — площадь основания, Н — высота
параллелепипеда .
Пример.
Площадь основания па-
2
раллелепипеда S = 20 см .
Боковое ребро ААг = 8 см
и наклонено к плоскости
основания под углом
30°. В прямоугольном
треугольнике ААгН с углом А = 30° катет АгН =
= 9^1 = 4 (см).
Отрезок АгН — высота параллелепипеда. По-
з
этому объем параллелепипеда V = 20 • 4 = 80 (см ).
Объем любой призмы равен произведению
площади ее основания на высоту:
V=SH.
Примеры.
1) Если применить к одному из оснований
призмы параллельный перенос в плоскости,
которой оно принадлежит, и соединить вершины
другого основания с вершинами «нового»
основания, то ♦новая» призма будет иметь тот же
объем, что и исходная.
2) Две призмы, одна из которых прямая, а
другая наклонная, имеют равные основания и
длины боковых ребер. Какая из призм имеет
больший объем?
Основания призмы имеют равные площади.
Высота наклонной призмы короче ее ребра,
поскольку длина перпендикуляра к плоскости
всегда меньше длины наклонной, а высота
прямой призмы равна ее ребру. Поэтому прямая
призма имеет большую высоту, следовательно,
и больший объем.
Объем любой пирамиды равен одной трети
произведения площади ее основания на высоту:
v-\sh.
Примеры.
1) Если треугольник ABC лежит в некоторой
плоскости а, а плоскость Р параллельна
плоскости а, то все пирамиды с основанием ABC,
вершины которых принадлежат плоскости (3,
имеют равный объем.
2) В треугольной пирамиде проведено
сечение через вершину и медиану основания. Так
как медиана делит основание на два
равновеликих треугольника, а высоты полученных
пирамид равны, то и объемы их тоже равны.
Сг
Da--U
В
Ответ. Да. Например,
в кубе ABCDA^C^
ребро DDX параллельно ребру
ВВг. Следовательно, по
признаку параллельности
прямой и плоскости каждая из
пересекающихся
плоскостей ADD^ и CDDXCX
параллельна ребру ВВг.
3.
Дано: AAOS, /. О = 90°, SA = 17 см, SO = 8 см,
SO — ось вращения.
Найти: Sn0JIH пов.
Решение. Данное тело
вращения есть прямой
круговой конус. Высота конуса
SO = 8 см, образующая SA =
= 17 см.
Из прямоугольного A AOS по теореме Пифа-
17 см
гора радиус основания конуса ОА
= 15 (см).
Площадь боковой поверхности
S6ok. = тс-15-17 = 225я (см2).
Площадь основания
S^ =тс-152 = 255тс(см2).
Площадь полной поверхности
= 7Й^8"2 =
'ПОЛИ. ПОВ.
= 255я + 225тс = 480тс (см ).
Ответ: 480тс (см ).
Билет № 11
1. Формулы объема тел вращения: цилиндра,
конуса и шара (формулы и примеры).
2. Задача по теме «Сечения многогранников».
Высота прямой призмы равна 10 см, а ее
основанием является прямоугольник, стороны
которого равны 6 см и 8 см. Найдите
площадь диагонального сечения.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
789
3. Задача по теме «Площади поверхностей тел
вращения».
Образующая конуса наклонена к
плоскости основания под углом 30°, а его высота
равна 12 см. Найдите площадь его боковой
поверхности.
1.
Объем цилиндра вычисляется по формуле
V=nR?H,
г$е R — радиус основания цилиндра, Н —
высота цилиндра.
Примеры.
1) Труба длиной 6 м имеет толщину стенок
20 мм и внешний диаметр 440 мм. В этом
случае внешний радиус R = 220 мм, внутренний
радиус г = 200 мм. Найдем объем материала,
необходимого для изготовления такой трубы:
F = 7C(2202 - 2002)-600 =50 400 000л (мм3) =
= 50,4л (дм ).
2) Тетрадный лист бумаги свернули в
цилиндр двумя способами. Какой из цилиндров
имеет больший объем?
Если а и Ь — длины сторон листа (а < &), то
один цилиндр имеет окружность основания
длины а, т. е. радиус его основания равен kz »а объем
равен Vt = я( 5-) Ъ = х~ • Аналогично объем
,2
второго цилиндра равен V2 = -т— • Так как а < 6,
toVx<V2.
Объем конуса вычисляется по формуле
К=|тсД2#,
где R — радиус основания конуса, Н —
высота.
Примеры.
1) Так как объем конуса прямо
пропорционален его высоте, то, для того чтобы увеличить
объем конуса в два раза, не меняя его
основания, надо увеличить его высоту в два раза.
2) Даны цилиндр и конус с равными
объемами. Радиусы оснований цилиндра и конуса
равны. Так как объем цилиндра вычисляется по
формуле V = яД2#, где R — радиус основания,
Н — высота, то высота конуса в 3 раза больше
высоты цилиндра.
3) Могут ли два разных конуса иметь равные
объемы?
Если радиус данного конуса уменьшить в два
раза, а высоту увеличить в четыре раза, то новый
конус будет иметь тот же объем, что и данный.
Объем шара вычисляется по формуле
V=±nR\
где R — радиус шара.
Примеры.
1) Объем шара пропорционален кубу его
радиуса: при увеличении или уменьшении
радиуса шара в k раз его объем соответственно увели-
чивается или уменьшается в k раз.
2) Два шара радиуса г имеют в сумме такой
же объем, что и один шар радиуса R. Что
больше: суммарная площадь поверхностей двух
маленьких шаров или площадь поверхности
большого шара?
4 з 4 з
По условию задачи 2 • ^ яг = о nR » откуда
2г3 = Д3. Суммарная площадь двух маленьких
сфер равна: Sx = 8кг , площадь большой сферы
равна: S2 = 4яД . Тогда
S\ = 83тс3г6 = 128тс3(2г3)2 - 128тс3Д6,
S3 = 4 Уд6 = 64тс3Д6.
3 3
Следовательно, S2 < St, так что S2< Sv
3) Шаровой подшипник радиуса 15 мм, изго-
, з
товленныи из металла плотностью р г/см ,
имеет внутри две шаровые полости (раковины)
радиусов 1 мм и 2 мм. Какова масса подшипника?
(Массу вещества, заполняющего полости,
можно не учитывать.)
4 з
Объем шара радиуса 15мм V= =я • 15 =
= 4500л (мм ), суммарный объем полостей равен
vi + v2 = |п # !3 + \ п # 23 = 12п (мм3)-
Поэтому масса подшипника равна:
p(F- Vx - V2) = 4488 рте (г).
2.
Дано: ABCDA1BlC1D1 — прямая призма, ААг =
= 10 см, АВ = 6 см, ВС = 8 см.

790
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Найти: SA
10 см
6 см
'8 см
Б
*ААХСХС :
Решение. Диагональные
сечения данной призмы
равны, так как равны
диагонали основания и боковые
ребра.
Диагональное сечение
ААгСгС — прямоугольник.
Сторона АС — диагональ основания ABCD. Из
прямоугольного А ABC по теореме Пифагора
АС = л/б2 + 82 = 10 (см). Поэтому S^ с с =
= 10 -10 = 100 (см2).
Ответ: 100 (см ).
3.
Дано: конус, угол между
SA и плоскостью основания
равен 30°, SO = 12 см.
Найти: S6oK.
Решение. Так как SO —
перпендикуляр к
плоскости основания, то /. SAO — угол между
образующей конуса SA и плоскостью основания.
Треугольник AOS — прямоугольный. Поэтому
sin30° = 5fHtg30° = ||.
12 см
Образующая конуса AS = -—oqS
= 24 (см), радиус основания АО = . 3QO
= 12*/3 (см).
Площадь боковой поверхности
S^ =тс-127з • 24 = 288я (см2).
Ответ: 288я7з (см2).
-12:1
-»■■$
КУРС В
Билет № 1
1. Взаимное расположение двух прямых в
пространстве (формулировки и примеры).
2. Касательная плоскость к шару.
3. В правильной четырехугольной пирамиде
сторона основания равна 12 см, а апофема —
15 см. Найдите боковое ребро пирамиды.
4. Ребро куба равно а. Найдите расстояние от
вершины куба до его диагонали,
соединяющей две другие вершины.
1.
Определение. Две прямые в пространстве
называются параллельными, если они лежат в
одной плоскости и не пересекаются.
Определение. Прямые, которые не
пересекаются и не лежат в одной плоскости, называются
скрещивающимися.
Две прямые в пространстве
лежат
в одной плоскости
пересекаются
не пересекаются
параллельны
не лежат
в одной плоскости
скрещиваются
Примеры.
1) Горизонтальная прямая, начерченная на
одной стене комнаты, и вертикальная прямая,
начерченная на противоположной стене,
являются скрещивающимися.
2) На изображении прямоугольного
параллелепипеда (рис. 15) прямые АгМ и DDX являются
скрещивающимися, прямые АгМ и ВВг —
пересекающимися, а прямые ААг и ССг —
параллельными.
3) Образующая конуса SM и диаметр основания
АВ (рис. 16) лежат на скрещивающихся прямых.
2.
Плоскость, проходящая через точку А
поверхности шара и перпендикулярная радиусу,
проведенному в точку А, называется касатель-

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
791
ной плоскостью. Точка А называется точкой
касания (рис. 17).
Теорема. Касательная плоскость имеет с
шаром только одну общую точку — точку
касания.
Доказательство. Пусть плоскость а
касается шара в точке А (рис. 18). Возьмем
произвольную точку X плоскости а, отличную от А.
Так как О А — перпендикуляр, а ОХ —
наклонная, то ОХ > ОА, т. е. ОХ > R> следовательно,
точка X не принадлежит шару.
Теорема доказана.
15 см
Дано: SABCD —
правильная пирамида, АВ = 12 см,
SM — апофема, SM =15 см.
Найти: SA.
Решение. В
равнобедренном треугольнике ABS
высота SM является и
медианой. Поэтому
AM = 12: 12 = 6 (см).
Из прямоугольного Л SAM по теореме Пифа-
/ 2 2
гора боковое ребро пирамиды SA = v 15 +6 =
= 3^29 (см).
Ответ: 3*/29 см.
4.
Дано: ABCDAlBlClD1 — куб, АВ = а.
Найти: расстояние р от А до ребра BDV
Решение. Так как расстояние от точки до
прямой — длина перпендикуляра, опущенного
из данной точки на прямую, то искомое
расстояние р есть высота А треугольника ABDV
опущенная на сторону BDV
Так как АВ 1 AD и АВ _L AAV то по признаку
перпендикулярности прямой и плоскости АВ Л
_L пл. ADDV Поэтому АВ _L ADX и Л ABDX —
прямоугольный.
Из прямоугольного
треугольника ADDX по
теореме Пифагора ADX = aj2 .
Поэтому площадь
треугольника ABDX равна
S=\AB'AD1 = ^fi.
С другой стороны, пло-
^1
А
Di
/
*1
В
с
А
щадь треугольника ABDX равна S = т> BDt • А.
Так как в прямоугольном параллелепипеде
квадрат любой диагонали равен сумме квадра-
2 2
тов трех его линейных размеров, то BDX = За ,
откуда BDX = а 7з . Поэтому площадь
треугольника ABDt равна S = 2 .
Сравнивая два выражения для нахождения
площади рассматриваемого треугольника,
получаем:
р = А=—.
Ответ:
аЛ
Рис. 17
Рис. 18
Билет № 2
1. Взаимное расположение двух плоскостей
(формулировки и примеры).
2. Признак перпендикулярности прямой и
плоскости.
3. Прямоугольный треугольник, гипотенуза
которого равна 17 см, а один из катетов — 8 см,
вращается около этого катета. Найдите
площадь поверхности тела вращения.
4. Найдите боковую поверхность пирамиды,
если площадь основания равна S, а
двугранные углы при основании равны а.
1.
Определение. Две плоскости называются
параллельными, если они не пересекаются.
Аксиома. Если две различные плоскости
имеют общую точку, то они пересекаются по
прямой.
Из этой аксиомы следует, что любые две
плоскости в пространстве либо не имеют общих

792
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
точек, т. е. параллельны, либо пересекаются по
прямой.
Две плоскости в пространстве
пересекаются по прямой
не пересекаются
параллельны
Примеры.
1) Плоскости противоположных стен в
комнате являются параллельными.
2) Плоскости любых двух граней пирамиды
(рис. 19) пересекаются по прямой.
3) Основания цилиндра (рис. 20) лежат в
параллельных плоскостях.
2.
Прямая а называется перпендикулярной
плоскости а, если она перпендикулярна всякой
прямой, лежащей в плоскости а и проходящей
через точку пересечения а и а.
Теорема. Если прямая перпендикулярна
двум пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна данной
плоскости.
Доказательство 1. Пусть прямая а
перпендикулярна прямым & и с, лежащим в
плоскости а и пересекающимся в точке А. Тогда а
проходит через точку А (рис. 21). Докажем, что а А. а.
Через точку А проведем в плоскости а
произвольную прямую х и покажем, что х La.
Проведем в плоскости а еще одну прямую, не
проходящую через точку А и пересекающую прямые &, с
и х в точках В, С и X соответственно.
Отложим на прямой а от точки А в разные
стороны от а равные отрезки ААг и АА2.
Треугольник АгСА2 — равнобедренный, так как отрезок
АС является одновременно его высотой (по
условию теоремы) и медианой (по построению).
Аналогично получаем, что ААгВА2 также
равнобедренный. По третьему признаку равенства
треугольников А АгВС = Л А2ВС.
Следовательно, А АгВХ = Z. А2ВХ> поэтому
ААгВХ = А А2ВХ по первому признаку
равенства треугольников. Отсюда АХХ = A2Xf так что
ААгХА2 равнобедренный. Поэтому его медиана
ХА является и его высотой, т. е. х L а. По
определению прямая а перпендикулярна плоскости а.
Теорема доказана.
Доказательство 2. Иногда
скрещивающиеся прямые, угол между которыми равен
90°, также называют перпендикулярными. В этом
случае имеет место и более общее определение
прямой, перпендикулярной плоскости: прямая
называется перпендикулярной плоскости, если
она перпендикулярна всякой прямой, лежащей
в этой плоскости.
Пусть прямая а перпендикулярна
пересекающимся прямым р и д, лежащим в плоскости а
(рис. 22). Докажем, что a La.
Рассмотрим сначала случай, когда прямая а
проходит через точку О пересечения прямых р и
q. Пусть теперь т — произвольная прямая
плоскости а; докажем, что a Lm.
Если т не проходит через точку О, то в
плоскости а проведем через эту точку еще одну
прямую 11| т. Если же т проходит через точку О, то
в качестве I берем ту же прямую /п.
Отложим на прямой а от точки О в разные
стороны от а равные отрезки ОА и ОВ. Наконец,
проведем в плоскости а прямую, пересекающую
прямые р, q и I в точках Р, Q и L соответственно.
Прямые р и q — серединные
перпендикуляры отрезка АВ, поэтому АР = ВР, AQ = BQ. Сле-
Рис. 19
Рис. 20
Рис. 21
Рис. 22

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
793
довательно, треугольники APQ и BPQ равны по
трем сторонам. Отсюда следует, что AAPQ =
= A BPQ.
Треугольники APL и BPL равны по двум
сторонам и углу между ними, откуда AL = BL, т. е.
AABL равнобедренный, и медиана LO является
одновременно его высотой, т.е. 11. а. Таким
образом, прямая а перпендикулярна одной из
параллельных прямых I и гпу значит, она
перпендикулярна и другой, т.е. а ± т.
Если же прямая не проходит через точку О,
то проведем через эту точку прямую аг \\ а. Так
как прямая а перпендикулярная прямым р и q9
то и параллельная ей прямая аг
перпендикулярна прямым р и q. По доказанному ах _L тп,
следовательно, прямая а, параллельная av также
перпендикулярна т.
Итак, прямая а перпендикулярна любой
прямой, лежащей в плоскости а, а это по определению
и означает, что а перпендикулярна плоскости а.
Теорема доказана.
Доказательство 3. Прямая
называется перпендикулярной плоскости, если она
перпендикулярна любой прямой, лежащей в этой
плоскости.
Пусть прямая а перпендикулярна
пересекающимся прямым р и д, лежащим в плоскости а
(рис. 23). Докажем, что а ± а.
Пусть т — произвольная прямая плоскости а;
докажем, что а ±т.
Выберем на каждой из этих прямых векторы
а, р, q и т. Так как прямые аир
перпендикулярны, то скалярное произведение а*р = 0 и
аналогично а • q = 0.
Вектор т компланарен с векторами р и д, и
поскольку прямые р и q пересекаются, векторы
рид неколлинеарны. Поэтому т можно
разложить по векторам р и q9 т. е. представить его в
виде т = хр + yq> где х и у — некоторые числа.
Так как
а • т = а(хр + yq) = х(а • р) + у(а • q) = 0,
то векторы аит перпендикулярны, значит, a _1_
Л т.
а | Р q
Итак, прямая а перпендикулярна любой
прямой, лежащей в плоскости а, а это по
определению и означает, что прямая а перпендикулярна
плоскости а.
Теорема доказана.
3.
Дано: AAOS, ZO = 90°, SA = 17см, SO = 8см,
SO — ось вращения.
Найти: Sn0JIH.n0Bi.
Решение. Данное тело
вращения есть прямой
круговой конус. Высота
конуса SO = 8 см, образующая
SA= 17 см.
Из прямоугольного AAOS по теореме
Пифагора радиус основания конуса
17 см
ОА = Vl72 - 82 = 15 (см).
Площадь боковой поверхности
S6oK = к • 15 • 17 = 225тс (см2).
2 2
Площадь основания S^,, = я • 15 =25 5я (см ).
Площадь полной поверхности
• 5полн. пов. = 255* + 225* - 480* (см2>-
2
Ответ: 480я (см ).
4.
Дано: пирамида, двугранные углы при
основании равны а, площадь основания равна S.
Найти: S6oK пов.
Решение. Проекции
боковых ребер на плоскость
основания пирамиды разбивают
многоугольник основания на
треугольники, являющиеся
проекциями боковых
граней. В сумме проекции всех
боковых граней, т. е.
проекция боковой поверхности
пирамиды, составляют многоугольник основания.
Так как площадь ортогональной проекции
каждой боковой грани на плоскость равна
произведению ее площади на косинус а, то площадь
ортогональной проекции всей боковой поверхности,
равная площади основания, S = S6oK пов • cos а,
откуда
°бок. пов.
Рис. 23
Ответ:
cos а
S
cos а*

794
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Билет № 3
1. Взаимное расположение прямой и плоскости
в пространстве (формулировки и примеры).
2. Объем цилиндра.
3. В правильной треугольной пирамиде
боковое ребро равно 4 см, а сторона основания —
в см. Найдите объем пирамиды.
4. Два равных шара радиуса R расположены
так, что центр одного лежит на поверхности
другого. Найдите длину линии, по которой
пересекаются поверхности.
1.
Определение. Прямая и плоскость
называются параллельными, если они не пересекаются.
Прямая может принадлежать плоскости (если
она имеет с ней по крайней мере две общие точки)
или не принадлежать этой плоскости. Во втором
случае она может иметь с ней либо одну общую
точку (тогда прямая и плоскость пересекаются),
либо не иметь общих точек (тогда прямая и
плоскость параллельны).
Прямая и плоскость в пространстве
пересекаются в одной точке
не пересекаются
прямая параллельна плоскости
Примеры.
1) Любая прямая, начерченная на одной
стене комнаты, и плоскость противоположной
стены являются параллельными, а любая прямая
на стене комнаты, кроме вертикальных
прямых, пересекается с плоскостью смежной стены.
2) Прямая АгМ и плоскость грани CjCDJDj
прямоугольного параллелепипеда (рис. 24)
параллельны, а прямая АгМ пересекает плоскость
грани ВВгСгС.
3) Любая образующая цилиндра (рис. 25)
пересекает его основание, а любая прямая в
плоскости основания параллельна второму основанию.
2.
Геометрическое тело имеет
объем V, если существуют
содержащие его простые тела и
содержащиеся в нем простые
тела с объемами, сколь угодно
мало отличающимися от V.
Тело называется простым,
если оно может быть разбито на конечное число
треугольных пирамид. В частности, призма
является простым телом.
Теорема. Объем цилиндра равен
произведению площади основания на высоту.
Построим в основании цилиндра п-угольни-
ки Рп, содержащие основание, и Рп,
содержащиеся в основании, такие, что при
неограниченном увеличении п их площади неограниченно
приближались к площади основания.
Построим две прямые призмы с основаниями
Рп и Рп и высотой Н, равной высоте цилиндра.
Первая призма содержит цилиндр, а вторая
содержится в цилиндре. Так как при
неограниченном увеличении п площади оснований призм
неограниченно приближаются к площади
основания цилиндра S, то их объемы неограниченно
приближаются к SH. Согласно определению
объем цилиндра V = SH.
3.
Дано: SABC —
правильная пирамида, SA =
= 4 см, АВ = 6 см.
Найти: VSABC.
Решение. Радиус ОА
окружности, описанной около правильного
треугольника ABC со стороной 6 см, равен
Из прямоугольного AAOS по теореме
Пифагора высота пирамиды OS = v4 - (27з) = 2(см).

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
795
Площадь правильного треугольника
а\Д
4
6 -л/3
= 9л/3 (см2).
°ААВС~ 4 ~ 4
Поэтому объем пирамиды
* ЭТЗ -2 = 673 (см3).
VSABC ~ 3 ^ДАВС OS ~~ 3
Aff = Я
Ответ: б7з (см ).
4.
Дано: шар (О, Д), шар
(Ох, Д), ООх = Д.
Найти: длину Z линии
пересечения поверхностей.
Решение. Рассмотрим
сечение, проходящее через центры шаров. Линия, о
которой идет речь в задаче, является
окружностью (как линия пересечения двух сфер).
Треугольник ОАОг — равносторонний. Высота
Л ОАОг равна радиусу ркружности пересечения
данных шаров.
В равнобедренном треугольнике ОАОг
высота АН является медианой. Из прямоугольного
треугольника АН О по теореме Пифагора
Поэтому I = тсДл/З .
Ответ: пН*/3.
Билет № 4
1. Свойства параллельных плоскостей
(формулировка и примеры).
2. Теорема о боковой поверхности призмы.
3. Образующая конуса наклонена к плоскости
основания под углом 30°, а его высота
равна 12 см. Найдите площадь его боковой
поверхности.
4. Через основание трапеции проведена
плоскость, отстоящая от другого основания на
расстояние а. Найдите расстояние от точки
пересечения диагоналей трапеции до этой
плоскости, если основания трапеции
относятся как т : п.
1.
Определение. Две плоскости называются
параллельными, если они не пересекаются.
Свойство 1. Если две параллельные
плоскости пересекаются третьей, то прямые
пересечения параллельны.
Свойство 2. Отрезки параллельных прямых,
заключенные между двумя параллельными
плоскостями, равны.
Пример.
ABCDA1B1C1D1 — параллелепипед, AtMNP —
сечение (рис. 26). У параллелепипеда
противолежащие грани параллельны.
По первому свойству АгМ II PN и АгР II MN.
По второму свойству АгМ = PN иАгР = MN.
2.
Призма называется прямой, если ее боковые
ребра перпендикулярны основаниям.
Площадью боковой поверхности (или
боковой поверхностью) призмы называется сумма
площадей ее боковых граней.
Теорема. Боковая поверхность прямой
призмы равна произведению периметра основания на
высоту призмы, т. е. на длину бокового ребра.
Доказательство.
Боковые грани прямой призмы —
прямоугольники. Основания этих
прямоугольников являются
сторонами основания призмы, а высоты
равны длине боковых ребер, т. е.
высоте А призмы. Поэтому
боковая поверхность призмы равна
S = axh + a2h + ... + anh = (ах + а2 + ... + Q>n)h,
где av ..., ап — длины ребер основания. Но сумма
аг + а2 + ... + ап = р — это периметр основания
призмы, a h — высота и одновременно длина
боковых ребер, так что S=ph. Теорема доказана.
3.
Дано: конус, угол между SA и плоскостью
основания равен 30°, SO = 12 см.
Найти: St
бок. пов. * <
Решение. Так как SO — перпендикуляр к
плоскости основания, то Z. SAO есть угол между
образующей конуса SA и плоскостью основания.
D, М СЛ
■XJC
j^T^
^ч---
Р 1
Рис. 26
*Г\
v N\
В

796
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Треугольник AOS —
прямоугольный. Поэтому sin 30° =
12 см
OS , ОЛО OS
щая конуса AS =
1
= 12:

Образуюсь
sin 30°
= 24 (см), а радиус
основания АО =
t^ =12= f=1273 (см).
Площадь боковой поверхности
-'бок. пов.
= тс-12л/3 -24 = 288тсл/3 (см2).
Ответ: 288я*/3 (см ).
4.
Дано: ABCD — трапеция, АС П BD = О,
AD : ВС = т : п, AD с а, расстояние от ВС до а
равно а.
Найти: расстояние от
точки О до плоскости а.
Решение. Расстояние
от прямой до
параллельной ей плоскости есть
длина перпендикуляра,
опущенного из любой
точки этой прямой на плоскость. Расстояние от
точки до плоскости есть длина перпендикуляра,
опущенного из этой точки на плоскость.
Проведем перпендикуляры ВВг и ООг к
плоскости а. Тогда по условию ВВг = а, а ООг —
искомое расстояние. Отрезки ВВг и ООг
параллельны и поэтому лежат в одной плоскости, в
которой лежит и точка D — точка пересечения
прямых ВО и ВгОг.
Из подобия треугольников BDBX и ODOx имеем:
ВВг: ООг = BD:OD = (ВО + OD): OD =
= l+BO:OD.
Из подобия треугольников ВОС и DOA имеем:
BO:OD = BC:AD = m:n,
и поэтому ВВг: ООг = 1 + т : п, откуда
an
ООг = а : (1 + т : п) =
Билет № 5
т + п
1. Перпендикуляр и наклонные к плоскости
(формулировки и примеры).
2. Свойство противолежащих граней
параллелепипеда.
3. Найдите площадь сечения шара радиуса 41 см,
проведенного на расстоянии 9 см от центра.
4. Через концы отрезка АВ, пересекающего
плоскость а, и его середину М проведены
параллельные прямые» пересекающие
плоскость а в точках Av Вг и Mv Найдите
длину отрезка MMV если ААг = a, ВВг = Ъ.
1.
Прямая называется перпендикулярной к
плоскости, если она пересекается с этой плоскостью
и перпендикулярна любой прямой, которая
лежит в этой плоскости и проходит через точку
пересечения.
Определение. Перпендикуляром, опущенным
из данной точки на данную плоскость, называется
отрезок, соединяющий данную точку с точкой
плоскости и лежащий на прямой,
перпендикулярной плоскости. Конец отрезка, лежащий в
плоскости, называется основанием перпендикуляра.
Определение. Наклонной, проведенной из
данной точки к данной плоскости, называется
любой отрезок, соединяющий данную точку с
точкой плоскости и не являющийся
перпендикуляром. Конец отрезка, лежащий в плоскости,
называется основанием наклонной.
Перпендикуляр всегда меньше наклонной,
проведенной к плоскости из той же точки.
Поэтому перпендикуляр есть наименьший из всех
отрезков, соединяющих данную точку с любой
точкой плоскости, и его принимают за меру
расстояния от точки до плоскости.
Примеры.
1) Высота конуса (рис. 27) является
перпендикуляром к плоскости основания. Основанием
высоты прямого кругового конуса является
центр окружности основания. Образующие
конуса являются наклонными к плоскости
основания. Основаниями этих наклонных являются
точки окружности основания.
2) Высота пирамиды (рис. 28) является
перпендикуляром к плоскости основания. Боковые
ребра являются наклонными к плоскости
основания. Основаниями этих наклонных являются
вершины многоугольника основания.
3) Основанием высоты правильной пирамиды
является центр описанной (вписанной)
окружности основания.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
797
2.
Параллелепипедом называется призма,
основание которой является параллелограммом. Все
грани параллелепипеда — параллелограммы.
Грани параллелепипеда, не имеющие общих
вершин, называются противолежащими.
Теорема. Противолежащие грани
параллелепипеда параллельны и равны.
Доказательство. ПустьABCDA1B1C1D1 —
параллелепипед. Рассмотрим противолежащие
грани параллелепипеда АВВгАг и CDDlCl (рис. 29).
Так как все грани параллелепипеда
параллелограммы, то прямая АВ параллельна прямой DC, а
прямая ААг параллельна прямой DDV Отсюда
следует, что плоскости рассматриваемых граней
параллельны.
Из того, что грани параллелепипеда —
параллелограммы, следует также, что отрезки AD,
AXDX, ВС и ВгСг параллельны и равны. Поэтому
грань АВВХАХ совмещается с гранью DCClDl
параллельным переносом вдоль ребра ВС, так что
эти грани равны.
Теорема доказана.
3.
Дано: шар с центром О, а — секущая
плоскость, р(0, а) = 9 см, Дшара = 41 см.
Найти: Sce4.
Решение. Данное
сечение есть круг с
центром А, причем АО _L а.
Пусть В — точка на
окружности круга. Из
ААВО по теореме
Пифагора радиус сечения
АВ = л/412 - 92 = 40 (см).
Поэтому площадь сечения
= 1600л (см2).
5сеч. = 7С'
40' =
Ответ: 1600л (см ).
4.
Дано: АВ П d, М е АВ, AM = MB,
ААг || ВВг || MMVAV Bv Мх е а, ААг = а, ВВг = Ъ.
Найти: ММг.
Решение. Проведем плоскость р через
прямую ААг и точку М. Так как Me р, то прямая
ММг, параллельная ААг, лежит в плоскости р и
аналогично ВВг с р. Таким образом, все точки
А, В, М, Аг, Вг и Мг лежат в одной плоскости,
причем точки Аг, Вг и Мх лежат на одной
прямой (рис. 30, а).
Соединим точку А с Вх, точку В с Аг и
обозначим через К и L точки пересечения прямой ММг
с полученными отрезками. Рассмотрим 3
случая: Ъ > а (рис. 30, б), Ъ < а (рис. 30, в) и Ъ = а
(рис. 30, г).
v^
Рис. 29
±.-л-л
А1 м,
а)
б)
Рис. 30
в)
г)

Примерные билеты и ответы к устному экзамену по геометрии
Подготовка к экзаменам. 11 класс
В первом случае имеем: точка М — середина
АВ и ММг || ААг || BBV так что: КМ — средняя
линия треугольника АгДА, КМ = т>;
МгЬ — средняя линия треугольника АгВгА,
МгЬ=1;
KL — средняя линия трапеции АХВВХА,
0?сю№ММг=КЬ-КМ-МгЬ= Ц-2.
Аналогично во втором случае ММг = —~— •
Наконец, при Ь = а точки Ми Мг совпадают,
т. е. ММг = 0.
Ответ, общий для трех случаев, можно
записать в следующем виде: ММг = —~—•
Ответ: ММг = 1^=—' •
Билет № 6
1. Расстояние между скрещивающимися
прямыми (формулировки и примеры).
2. Площадь боковой поверхности конуса.
3. В основании пирамиды лежит
прямоугольный треугольник, гипотенуза которого
равна 15 см, а один из катетов — 9 см. Найдите
площадь сечения, проведенного через
середину высоты пирамиды, параллельно ее
основанию.
4. Плоскости аир пересекаются по прямой с
и перпендикулярны плоскости у. Докажите,
что прямая с перпендикулярна плоскости у.
1.
Определение. Общим перпендикуляром двух
скрещивающихся прямых называется отрезок с
концами на этих прямых, являющийся
перпендикуляром к каждой из них.
Определение. Расстоянием между
скрещивающимися прямыми называется длина их
общего перпендикуляра. Оно равно расстоянию
между параллельными плоскостями,
проходящими через эти прямые.
Примеры.
1) Дорога и плоский мост над дорогой не
пересекаются и имеют различное направление.
Все точки моста находятся на различных
расстояниях от дороги (расстояние от точки до
прямой измеряется по перпендикуляру). Высота
моста над дорогой равна расстоянию между
плоскостью дороги и плоскостью моста.
2) Расстояние между диагоналями верхней и
нижней граней параллелепипеда (рис. 31)
равно высоте ВгН параллелепипеда.
2.
Впишем в конус правильную n-угольную
пирамиду (рис. 32). Площадь ее боковой
поверхности Sn = 5 Рп!п> гДе ?п ~ периметр основания
пирамиды, 1п — апофема.
При неограниченном увеличении п периметр
Рп неограниченно приближается к длине С
окружности основания конуса, а апофема 1п — к
длине I образующей. Следовательно, боковая
поверхность пирамиды неограниченно
приближается к о С1. Поэтому величину « С1 принимают за
площадь боковой поверхности конуса.
Таким образом, за площадь S боковой
поверхности конуса принимают половину
произведения длины С окружности
основания-конуса на длину I его образующей:
s=\ci.
Так как С = 2nR9 где R — радиус основания
конуса, то площадь боковой поверхности конуса
можно вычислять по формуле
S= \ci = nRl.
3.
Дано: SABC — пирамида, А ABC —
основание, Z. С = 90°, АВ = 15 см, ВС = 9 см, SO — вы-
Рис. 31 Рис. 32

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
799
сота, М — середина OS,
АгВгСг —сечение,
(Alf Bv Сг) 1 OS,
Ме(А1,В1,С1).
Найти: Sce4.
Решение. Данное
сечение цодобно основанию
пирамиды с
коэффициентом подобия «• Площади
подобных фигур относятся как квадраты
линейных размеров.
Из А ABC йо теореме Пифагора
АС = Jib2 - 92 = 12 (см).
Площадь основания S^ = 2 = ^4 (см )•
Поэтому площадь сечения
5сеч. = 54 ч2
g) =13,5 (см2).
Ответ: 13,5 (см ).
4.
Дано: а П р = с, а _L у, Р _1_ у.
Доказать: с _1_ у.
Доказательство 1.
Возьмем на прямой с
точку С и опустим из этой точки
перпендикуляр СМ на
плоскость у. Предположим, что СМ не лежит в
плоскости а. '
В плоскости а проведем прямую СА,
перпендикулярную линии пересечения а плоскостей а
и у, и рассмотрим треугольник АСМ.
Так как CM J. у, то Z. AM С — прямой.
Так как прямая СА лежит в плоскости а,
перпендикулярной плоскости у, и перпендикулярна
их линии пересечения, то она перпендикулярна
и плоскости у. Поэтому Z. САМ также прямой,
т. е. в треугольнике АСМ два прямых угла.
Полученное противоречие показывает, что
СМ с а.
Аналогично можно доказать, что прямая
СМ с р.
Таким образом, прямая СМ = с, поэтому с _L у.
Доказательство 2.
Пусть I — линия пересечения плоскостей р и
у, точка О — точка пересечения всех трех
данных плоскостей. Проведем в плоскости Р
прямую т ± I. Тогда т _L у, и, проведя в плоскости у
прямую п _L I, мы получим три попарно
перпендикулярных прямых п, I
и т, которые примем за
оси координат в
пространстве — оси Ох, Оу и Ог
соответственно.
Тогда плоскость Р имеет
уравнение х = О, плоскость
у— уравнение г = 0, а
плоскость а — уравнение ах + by + сг + d = 0. Так
как О(0, 0, 0) е а, то d = 0.
Так как a _L у, то векторы (а, Ь, с) и (0, 0, 1),
перпендикулярные этим плоскостям,
перпендикулярны друг другу, т. е. их скалярное
произведение равно нулю. а»0 + Ь#0 + с»1 = 0, т. е. с = 0.
Поэтому координаты точек, лежащих на
прямой а = а П Р, являются решениями системы
уравнений
ах + by = 0,
х = 0.
Отсюда следует, что by = 0. Если b = 0, то
плоскость а имеет уравнение а* = 0, и
поскольку а * 0 (в уравнении плоскости хотя бы один из
коэффициентов отличен от нуля), х = 0, т. е. р
совпадает с а, что противоречит условию.
Поэтому b * 0, следовательно, у = 0.
Таким образом, точки, лежащие на прямой
а, имеют координаты дс = 0иу = 0, а это
означает, что прямая а — это ось Ог, т. е. а _1_ у, что и
требовалось доказать.
Билет № 7
1. Угол между скрещивающимися прямыми
(формулировка и пример).
2. Объем призмы.
3. В правильной четырехугольной пирамиде
сторона основания равна 10 см, а высота —
12 см. Найдите площадь полной
поверхности пирамиды.
4. В цилиндр вписана правильная
шестиугольная призма. Найдите угол между диагональю
ее боковой грани и осью цилиндра, если
радиус основания равен высоте цилиндра.
Углом между пересекающимися прямыми
называется угловая мера меньшего из
образуемых ими четырех углов. Угол между перпенди-

800
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
кулярными прямыми по определению равен 90°.
Угол между параллельными прямыми
считается равным нулю.
Определение. Углом между
скрещивающимися прямыми называется угол между
пересекающимися параллельными им прямыми.
Если угол между скрещивающимися
прямыми равен 90°, то их иногда, как и прямые,
пересекающиеся под прямым углом, называют
перпендикулярными .
Примеры.
1) Угол между диагоналями оснований куба,
лежащими на скрещивающихся прямых АгСг и
DB куба (рис. 33), равен 90°, так как АС II АгСг и
АС 1 DB.
2) Угол между боковым ребром SA
правильной пирамиды и противолежащим ребром
основания ВС (рис. 34) равен углу между ребром SA и
прямой Ь, параллельной ребру ВС и проходящей
через точку А.
Прямая SO — перпендикуляр к плоскости
ABC, АО — проекция ребра SA на эту плоскость,
Ь _L АО, поэтому по теореме о трех
перпендикулярах Ъ _L AS.
Следовательно, угол между SA и ВС равен 90°.
2.
Теорема. Объем любой призмы равен
произведению площади ее основания на высоту.
Доказательство. Рассмотрим сначала
треугольную призму (рис. 35, а) с площадью
основания S и высотой А, и пусть V — ее объем.
Дополним призму до параллелепипеда, как
указано на рисунке. Точка О является центром
симметрии полученного параллелепипеда. Поэтому
достроенная призма симметрична данной
относительно точки О, следовательно, также имеет
объем V. Следовательно, объем построенного
параллелепипеда равен 2V.
Объем параллелепипеда равен произведению
площади его основания на высоту. Площадь
основания равна удвоенной площади
треугольника ABC у т. е. 2S, а высота параллелепипеда
равна высоте А исходной призмы. Следовательно,
2F=2SA, откуда
V=Sh.
Мы доказали, что объем любой треугольной
призмы равен произведению площади ее
основания на высоту.
Рассмотрим теперь произвольную призму
(рис. 35, б); разобьем ее основание на
треугольники диагоналями, выходящими из одной
вершины, и проведем плоскости через каждую
диагональ и соединяемые ею боковые ребра
призмы. В результате призма будет разбита на
несколько треугольных призм. Все эти призмы
имеют одну и ту же высоту, равную высоте
данной призмы.
Объем данной призмы равен сумме объемов
треугольных призм, ее составляющих. По
доказанному объем треугольной призмы равен
произведению площади ее основания на высоту.
Отсюда следует, что объем исходной призмы равен
V = SXH + S2H + ... + SnH =
= (Sx + S2 + ... + Sn)H,
где Sv S2, ..., Sn — площади треугольников, на
которые разбито основание призмы, Н —
высота призмы. Сумма площадей треугольников
равна площади основания данной призмы. Поэтому
V = SH.
Теорема доказана.
3.
Дано: SABCD — правильная пирамида, АВ =
10 см, SO = 12 см.
Найти: S„on„ „ЛВ.
^^
б)
Рис. 33
Рис. 34
Рис. 35

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
801
12 см
Решение. Диагонали
квадрата ABCD в точке
пересечения делятся
пополам, поэтому АО = СО.
В равнобедренном
треугольнике SBC высота
SM является и
медианой, поэтому ВМ = СМ.
Следовательно, МО — средняя линия А ABC и
МО = 5 см.
Из прямоугольного A SMO по теореме
Пифагора апофема пирамиды
SM = Vl22 + 52 = 13 (см).
Боковая поверхность пирамиды
5^.^.= ^'13 = 260 (см2).
Площадь основания S^ = 10 • 10 = 100 (см ).
Площадь полной поверхности
«полн. нов. - ЮО + 260 = 360 (см2).
Ответ: 360 (см2).
4.
Дано: цилиндр, R — А, ООг — ось цилиндра,
вписанная правильная шестиугольная призма,
АВХ — диагональ боковой грани.
Найти: угол между АВг и
OOv
Решение. Так квкААг II (ОД
и ААХ пересекает АБХ, то угол
между АВг и ООх равен углу
ААХВ.
Поскольку сторона
правильного шестиугольника,
вписанного в окружность, равна радиусу, АВ = R. По
условию ААХ = R. Поэтому боковые грани
призмы — квадраты и искомый Z. ААгВ = 45°.
Ответ: 45°.
4. Тело ограничено двумя концентрическими
шаровыми поверхностями. Докажите, что
его сечение плоскостью, проходящей через
центр, равновелико сечению, касательному
к внутренней шаровой поверхности.
1.
При определении угла между прямой и
плоскостью используются определения проекции и
угла между прямыми.
Проекцией точки А на плоскость а
называется основание В перпендикуляра АВ,
опущенного из точки А на плоскость а. Проекция
произвольной фигуры на плоскость а есть фигура,
состоящая из проекций всех точек этой фигуры на
плоскость а (рис. 36).
В частности, проекция прямой на плоскость
ос, не перпендикулярную этой прямой, есть
прямая. Если прямая перпендикулярна плоскости,
то ее проекцией на эту плоскость является точка
пересечения этой прямой с плоскостью.
Углом между пересекающимися прямыми
называется угловая мера меньшего из
образуемых ими четырех углов. Угол между параллель-
ними прямыми считается равным нулю.
Определение. Углом между прямой и
плоскостью, не перпендикулярной этой прямой,
называется угол между этой прямой и ее
проекцией на плоскость. Если прямая перпендикулярна
к плоскости, то угол считается равным 90°.
Угол между прямой и плоскостью является
наименьшим из углов, образуемых данной
прямой с прямыми на плоскости, проходящими
через точку пересечения этой прямой с
плоскостью.
Примеры.
1) Угол между диагональю АСг
прямоугольного параллелепипеда и плоскостью основания
(рис. 37) равен углу САСг.
Билет № 8
1. Угол между прямой и плоскостью
(формулировка и пример).
2. Объем пирамиды.
3. Высота прямой призмы равна 10 см, а ее
основанием является прямоугольник,
стороны которого равны в см и 8 см. Найдите
площадь диагонального сечения.
Рис. 36
26-1019

802
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
2) Угол между боковым ребром SC пирамиды
и плоскостью основания (рис. 38) равен углу
SCO, где О — основание высоты, а ОС —
проекция ребра SC на плоскость основания.
2.
Два тела называются равновеликими, если
они имеют равные объемы.
Лемма. Две треугольные пирамиды с
равными площадями оснований и равными
высотами равновелики.
Теорема. Объем любой пирамиды равен
одной трети произведения площади основания
на высоту:
v-\sn.
Доказательство. Рассмотрим сначала
треугольную пирамиду с вершиной S и
основанием ABC (рис. 39). Дополним эту пирамиду до
треугольной призмы с тем же основанием и
высотой так, как показано на рисунке. Эта призма
составлена из трех пирамид: данной пирамиды
SABC и еще двух треугольных пирамид SCCXBX
nSCBBv
У второй и третьей пирамид равные
основания — А ССгВг и А ВгВС — и общая высота,
проведенная из вершины S. Поэтому по лемме о
равновеликих пирамидах они имеют равные
объемы. У первой и третьей пирамид также равные
основания — A SAB и A BBXS — и совпадающие
высоты, проведенные из вершины С. Поэтому
их объемы также равны.
Таким образом, все три пирамиды имеют
один и тот же объем. Так как сумма этих
объемов равна объему призмы SH, то объемы пира-
Si/
мид равны -д-.
Пусть теперь имеем любую, не обязательно
треугольную, пирамиду. Разобьем ее основание
на треугольники произвольным способом. Пира-
Рис. 38
миды, у которых основаниями являются эти
треугольники, а вершинами — вершина данной
пирамиды, составляют данную пирамиду. Так
как объем данной пирамиды равен сумме
объемов составляющих ее пирамид, а все они имеют
ту же высоту Я, что и данная пирамида, то
объем ее равен
F = | (SXH + S2H + ... + SnH) =
= l(sx + s2 +... + sn)H = Ish.
Теорема доказана.
3.
Дано: ABCDAlB1ClDl — прямая призма, ААХ =
= 10 см, АВ = 6 см, ВС = 8 см.
Найти: S
"ААХСХС •
~1 С,
10 см
Решение.
Диагональные сечения данной
призмы равны, так как равны
диагонали основания и
боковые ребра.
Диагональное
сечение ААхСгС —
прямоугольник. Сторона АС есть диагональ основания
ABCD. Из прямоугольного А ABC по теореме
Пифагора АС = л/62 + 82 = 10 (см). Поэтому
2
Ответ: 100 (см ).
4.
Дано: внешняя граница тела — сфера (О, Я),
внутренняя — сфера (О, г), сечение 1 проходит
через центр, сечение 2 — касательная к сфере
(О, г).
Доказать: Sce4 г = Sce4. 2.
Доказательство.
Сечение 1 — круговое
кольцо, площадь которого
«сеч.1 = *(Я2"'-2)-
Сечение 2 — круг, радиус
которого по следствию из
теоремы о сечении шара
плоскостью равен Jr2 - г2. Поэтому площадь Sa
= 71(Д2-г2).
Таким образом, площади данных сечений
равны.
Ответ: площади сечений равны.
*сеч. 2

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
803
Билет № 9
1. Угол между плоскостями (формулировка и
пример).
2. Площадь сферы.
3. В правильной четырехугольной пирамиде
высота равна 7 см, а боковое ребро
наклонено к плоскости основания под углом 45°.
Найдите объем пирамиды.
4. Докажите, что площадь полйой поверхности
2
куба равна 2d , где d — диагональ куба.
Определение. Угол между параллельными
плоскостями считается равным нулю.
Пусть данные плоскости пересекаются.
Проведем плоскость, перпендикулярную прямой их
пересечения. Она пересекает данные плоскости по
двум прямым. Угол между этими прямыми
называется углом между данными плоскостями.
Угол между плоскостями, как и угол между
прямыми в планиметрии, имеет градусную меру
от 0° до 90°.
Примеры.
1) Если плоскость симметрии судна
составляет с вертикальной плоскостью угол в 30°, то
говорят, что судно имеет крен в 30°.
2) Плоскость у (рис. 40) перпендикулярна
линии пересечения плоскостей а и р. Углом между
плоскостями а и Р будет меньший из углов,
образованных прямыми АВ и CD.
2.
Опишем около сферы выпуклый
многогранник с малыми гранями (рис. 41). Пусть S' —
площадь, т. е. сумма площадей его граней.
Найдем приближенное значение площади
поверхности многогранника, предполагая, что
линейные размеры граней, т. е. расстояние между
любыми двумя точками любой грани, меньше £,
где £— некоторое положительное число. Тогда
расстояние от центра шара О до любой точки
поверхности многогранника меньше R + г:
ОК<ОА + АК.
Объем многогранника равен сумме объемов
пирамид, имеющих своими основаниями грани
многогранника, а вершиной — центр сферы О
(рис. 42). Так как все пирамиды имеют одну и ту
же высоту, равную радиусу R сферы, то объем
многогранника
V=±S'R.
Объем многогранника больше объема шара
радиуса Д, но меньше объема шара с тем же
центром и радиусом R + £, т. е.
IkR3<Is'R<Ik(R + e)\
откуда
4ЛД2 < S' < 4я(Д + £)2fl + ~\.
Отсюда видно, что при неограниченном
уменьшении размеров граней описанного
многогранника, т. е. при неограниченном
уменьшении £, его площадь стремится к 4nR . Поэтому ве-
личина 4яД принимается за площадь сферы.
Таким образом, по определению за площадь S
сферы радиуса R принимается произведение
Итак, площадь S сферы радиуса R
вычисляется по формуле
S = 4яД2.
3.
Дано: SABCD — правильная пирамида, SO —
высота, SO = 7 см, угол между SA и пл.АВС
равен 45°.
Найти: УЛ
пир.
Рис. 40
Рис. 41
Рис. 42
26*

804
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Решение. Так как SO —
перпендикуляр к
плоскости основания, то Z. OAS
есть угол между ребром SA
пирамиды и плоскостью
ABC, т. е. L OAS = 45°.
Треугольник SAO —
прямоугольный и
равнобедренный с острым углом Z. А = 45°. Следовательно,
АО = 7 см и диагональ основания АС = 14 см.
Площадь основания
Sabcd= 2Saabc = 2- \ • 14- 7 = 98 (см2).
Следовательно, объем пирамиды
^пир.= г98-7 = 228| (см3).
2 з
Ответ: 228« (см ).
4.
Дано: куб, а — ребро куба,
d — диагональ куба.
Доказать: площадь S по-
верхности куба равна 2d .
Доказательство. В
любом прямоугольном
параллелепипеде квадрат любой диагонали равен сумме 0
S^~
1 ' х
1 \
1 \
1 у
~/Л
2 2
квадратов трех его линейных размеров: d = За .
Поэтому площадь полной поверхности куба
2 2
S = 6а = 2d , что и требовалось доказать.
Билет № 10
1. Двугранный угол. Линейный угол
двугранного угла (формулировки и примеры).
2. Теорема о боковой поверхности правильной
пирамиды.
3. Прямоугольник, стороны которого равны
в см и 4 см, вращается около меньшей
стороны. Найдите площадь поверхности тела
вращения.
4. Докажите, что если данная прямая
параллельна двум пересекающимся плоскостям,
то она параллельна линии их пересечения.
1.
Определение. Двугранным углом
называется фигура, образованная двумя
полуплоскостями с общей ограничивающей их прямой. Эта
прямая называется ребром двугранного угла.
Определение. Плоскость у,
перпендикулярная ребру CD двугранного угла (рис. 43),
пересекает его грани по двум полупрямым О А и ОВ.
Угол АОВ9 образованный этими полупрямыми,
называется линейным углом двугранного угла.
За меру двугранного угла принимается мера
соответствующего ему линейного угла.
Примеры.
1) Представление о двугранном угле дает
частично раскрытая тетрадь или согнутый пополам
(по оси симметрии) прямоугольный лист
бумаги. Края листа, перпендикулярные оси
симметрии, образуют линейный угол этого двугранного
угла. Если поворачивать одну из половин листа
вокруг ребра двугранного угла, то его мера
изменяется от 0°, когда две половины совмещаются,
до 180°, когда лист разворачивается полностью.
2) Двугранный угол образуют полуплоскости,
содержащие грани пирамиды SAB и ABC, с общей
ограничивающей их прямой АВ (рис. 44). Эти
полуплоскости являются гранями, а
ограничивающая их прямая — ребром двугранного угла.
Двугранный угол при ребре АВ пирамиды
SABC равен углу SKO, где SO — высота
пирамиды, SK — высота грани SAB9 КО — ее проекция.
Площадью боковой поверхности (или
боковой поверхностью) пирамиды называется сумма
площадей ее боковых граней.
Высота боковой грани правильной
пирамиды, проведенная из ее вершины, называется
апофемой.
Теорема. Боковая поверхность правильной
пирамиды равна произведению полупериметра
основания на апофему.
Доказательство. Если сторона
основания пирамиды равна а, число сторон п, то
боковая поверхность пирамиды равна
al __ anl __ pi
2 Л" 2 ~~ 2 '
Рис. 43
Рис. 44

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
805
где I — апофема, р — периметр основания
пирамиды.
Теорема доказана.
3.
Дано: ABCD — прямоугольник, АВ = 6 см,
ВС = 4 см, ВС — ось вращения.
Найти: S„
'пов. телавращ.*
Решение. Данное тело
вращения — прямой
круговой цилиндр с высотой
ВС = 4 см и радиусом
основания АВ = 6 см.
Площадь боковой поверхности
Ябок.пов. = 2я-6-4 = 48я(см2).
2 2
Площадь основания S^ = к • 6 = 36я (см ).
Площадь полной поверхности
«пов. тела вращ. = 48* + 2• 36я - 120* (СМ2).
Ответ: 120я(см2).
4.
Дано: а П р = с, 1\\ а, Л1 р.
Доказать: 1\\ с.
Доказательство 1. Через произвольную
точку С прямой с и прямую I проведем
плоскость у (рис. 45, б).
Плоскости а и у имеют общую точку С,
поэтому они пересекаются по прямой а, проходящей
через точку С. Так как I не пересекает плоскость
а, то JII а.
Аналогично l\\ b — линии пересечения
плоскостей Р и у, проходящей через точку С.
Но через точку, не лежащую на данной
прямой, можно провести не более одной прямой,
параллельной данной. Поэтому а = Ь.
Так как асоси&ср, то а = Ь = с,
следовательно, III с, что и требовалось доказать.
Доказательство 2. Введем в
пространстве декартову систему координат, приняв за
начало произвольную точку О на прямой с, за ось
Ох — прямую с, за ось Оу — прямую OG с а
(OG J_ с), за ось Ог — прямую ОН,
перпендикулярную плоскости а (рис. 45, в).
Тогда плоскость а имеет уравнение г = 0,
плоскость Р — уравнение ах + by + сг + d = 0, и
поскольку проходит через точки О(0, 0, 0) и F(l, 0, 0),
то d = 0, а = 0. Поэтому векторы а и 6,
перпендикулярные плоскостям аир, имеют
соответственно координаты 3(0, 0, 1) и Ь(0, Ь, с).
Возьмем произвольный вектор u(pt q9 г) на
прямой I. Так как I \\ а и I || р, то вектор и
перпендикулярен векторам, перпендикулярным этим
плоскостям, и следовательно, равны нулю
соответствующие скалярные произведения:
v • а =р • 0 + q• 0 + г* 0 = г = 0, и • Ь = qb + гс = 0.
Отсюда следует, что г = 0, qb = 0. Если 6 = 0,
то плоскость р имеет уравнение сг = 0, и
поскольку с * 0 (в уравнении плоскости хотя бы один
из коэффициентов отличен от нуля), то г = 0, т. е.
Р совпадает с а, что противоречит условию.
Поэтому b * 0, следовательно, q = 0.
Таким образом, вектор v прямой I имеет
координаты (р, 0,0), т. е. коллинеарен вектору (1,0,0),
лежащему на прямой с. Поэтому I II с, что и
требовалось доказать.
Билет № 11
1. Трехгранный и многогранный углы
(формулировки и примеры).
2. Площадь боковой поверхности цилиндра.
3. Основание четырехугольной призмы —
квадрат со стороной 10 см. Высота призмы
12 см. Диагональное сечение разбивает
данную призму на две треугольные призмы.
Найдите площади боковых поверхностей
треугольных призм.
4. В правильной треугольной пирамиде высота
равна стороне основания. Найдите угол
между боковым ребром и плоскостью
основания.
1.
Определение. Трехгранным углом (abc)
называется фигура, составленная из трех плоских
углов: (ab), (be) и (ас). Эти углы называются
гранями трехгранного угла, а их стороны —
ребрами. Общая вершина плоских углов называется

806
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
вершиной трехгранного угла. Двугранные углы,
образованные гранями трехгранного угла,
называются двугранными углами трехгранного угла.
Определение. Многогранным углом (ага2а3...ап)
называется фигура, составленная из п плоских
углов (ага2)9 (а2аг)9 (ага4)9 ..., (апаг). Эти углы
называются гранями многогранного угла, а их
стороны — ребрами. Общая вершина плоских
углов называется вершиной многогранного угла.
Двугранные углы, образованные гранями
многогранного угла, называются двугранными углами
многогранного угла.
Примеры.
1) Наименьшее число граней многогранного
угла— три. Трехгранными углами являются,
например, угол (АА19 АЕ9 АВ) при вершине А
призмы (рис. 46).
2) Примером пятигранного угла может
служить угол при вершине S пятиугольной
пирамиды (рис. 47).
2.
Впишем в цилиндр правильную /i-угольную
призму (рис. 48). Площадь боковой поверхности
этой призмы Sn = РпН9 где Рп — периметр
основания призмы, Н — ее высота.
Как мы знаем, при неограниченном
увеличении п периметр Рп неограниченно
приближается к длине С окружности основания цилиндра.
Следовательно, площадь боковой поверхности
призмы неограниченно приближается к СН.
Поэтому величина СН принимается за площадь
боковой поверхности цилиндра.
Таким образом, по определению за площадь
боковой поверхности цилиндра принимается
произведение длины окружности его основания на
его высоту.
Так как длина окружности основания С =
= 2nR9 где R — радиус основания, то площадь
боковой поверхности цилиндра можно
вычислять по формуле
S = 2nRH9
где R — радиус цилиндра, Н — его высота.
3.
Дано: ABCDAlBlClDl — прямая призма,
АССХАХ — диаг. сечение — квадрат, ААг = 12 см,
АВ = 10 см.
Найти: SABCA^B^C и SACDA^C^D.
Решение.
Треугольные призмы ABCAlBlCl
и ACDA1ClDl имеют
одинаковую боковую
поверхность, так как их
основания и высоты равны.
Диагональное сечение
ААгСгС —
прямоугольник. Сторона АС — диагональ основания. Из
прямоугольного А ABC по теореме Пифагора
АС= Л
10 см
(102 +
10" = Юл/2 (см). Поэтому
периметр основания призмы
/"осн. = 10 + 10 + 10 Л = 10(2 + Л) (см).
Боковая поверхность призмы равна:
S^noB. призмы = 10(2 + 72)-12 = 120(2 +
+ л/2) (см2).
Ответ: 120(2 + Л) (см2).
4.
Дано: АВСМ —
правильная пирамида, МО —
высота, МО = АВ.
Найти: угол между AM
и плоскостью ABC.
Решение. Все боковые
ребра правильной пирами-
Ел D,
Рис. 46
Рис. 47
Рис. 48

Примерные билеты и ответы к устному экзамену по геометрии
ды наклонены к плоскости основания под одним
и тем же углом.
Так как МО — перпендикуляр к плоскости
основания, то углом между ребром пирамиды
AM и плоскостью основания является угол МАО.
Обозначим Z. МАО = а, а МО = АВ = а.
Из прямоугольного треугольника МАО
Так как МАВС — правильная пирамида, то
О — центр равностороннего треугольника ABC;
АО является радиусом описанной окружности и
АО = ^г-. Поэтому tg а = а : -=- = 7з, и так
как искомый угол а — острый, то а = 60°.
Ответ: 60°.
Билет № 12
1. Призма (формулировки и примеры).
2. Признак перпендикулярности плоскостей.
3. Радиус основания конуса равен 14 см.
Найдите площадь сечения, проведенного
перпендикулярно его оси через ее середину.
4. В цилиндр наклонно вписан квадрат так,
что все его вершины лежат на окружностях
основания. Найдите сторону квадрата, если
высота цилиндра равна 2 см, а радиус
основания равен 7 см.
1.
Определение. Призмой называется
многогранник, который состоит из двух плоских
многоугольников, лежащих в разных плоскостях и
совмещаемых параллельным переносом, и всех
отрезков, соединяющих соответствующие точки
этих многоугольников.
Многоугольники называются основаниями
призмы, а отрезки, соединяющие
соответствующие вершины, — боковыми ребрами.
Высотой призмы называется расстояние
между плоскостями ее оснований.
Если основания призмы имеют п сторон, то
призма называется л-угольной; /i-угольная
призма имеет п + 2 грани — два основания и п
боковых граней. Боковые грани призмы есть
параллелограммы, у каждого из которых две
стороны образованы соответствующими сторонами ос-
Подготовка к экзаменам. 11 класс
нований, а две другие — соседними боковыми
ребрами.
Примеры.
1) Параллелепипед является
четырехугольной призмой.
2) Пятиугольная призма (рис. 49) является
выпуклым многогранником. Бе поверхность
состоит из двух оснований — пятиугольников и
пяти боковых граней, являющихся
параллелограммами. Она имеет пятнадцать ребер и десять
вершин.
3) Если в основание цилиндра вписать
многоугольник и через его стороны провести
плоскости, параллельные оси цилиндра, то получится
призма: ее основания — многоугольники,
лежащие в основаниях цилиндра, а боковые грани —
сечения цилиндра плоскостями, проходящими
через соответствующие стороны этих
многоугольников. Высота полученной призмы равна
ее боковому ребру.
2.
Теорема. Если плоскость проходит через
прямую, перпендикулярную другой плоскости,
то эти плоскости перпендикулярны.
Доказательство. Пусть а — плоскость,
b _L а, р — плоскость, проходящая через прямую
6, и с — прямая, по которой пересекаются
плоскости а и Р (рис. 50). Докажем, что плоскости а
и Р перпендикулярны.
Проведем в плоскости а через точку
пересечения прямой Ъ с плоскостью а прямую а,
перпендикулярную прямой с. Проведем через прямые
a sib плоскости у. Она перпендикулярна прямой
с, так как прямая с перпендикулярна прямым а
и Ъ. Так как прямые аиЬ перпендикулярны, то
плоскости аир перпендикулярны. Теорема
доказана.
Рис. 49 Рис. 50

808
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
3.
Дано: конус, ОА = 14 см, а — секущая
плоскость, а _L OS, М € OS, SM = МО, М е а.
Найти: Sce4.
Решение. Данное
сечение подобно
основанию конуса с
коэффициентом подобия £ ■

Площади подобных фигур
относятся как
квадраты линейных размеров.
Площадь основания SOCH
Поэтому площадь сечения
ах2
14 см
= я-142 = 196я(см2).
Sce4. = 196*.Q) =49я (см2).
2
Ответ: 49я (см ).
4.
Дано: цилиндр, h = 2 см, R = 7 см, ABCD —
наклонно вписанный квадрат.
Найти: АВ.
Решение. Достроим
квадрат ABCD до
вписанного
прямоугольного параллелепипеда
ABC^^B^D с
диагональным
сечением ABCD.
По построению Z.ABCX = 90°
санный в окружность угол, стороны которого
проходят через две данные точки окружности,
равен половине угла между радиусами,
проведенными в эти точки, или дополняет половину
этого угла до 180°, то АСг есть диаметр
окружности верхнего основания цилиндра.
Рассмотрим прямоугольный треугольник
ССХА: катет ССг есть образующая цилиндра и
ССг = 2; катет АСг есть диаметр цилиндра и АСХ =
Так как впи-
-Л
г* +
142 =
= 14. По теореме Пифагора АС
= 10л/2 (см).
Из прямоугольного равнобедренного
треугольника ABC по теореме Пифагора сторона
квадрата
АВ
4
(10 J2) =
Ответ: 10 (см)
= 10 см.
Билет № 13
1. Прямая и правильная призмы
(формулировки и примеры).
2. Свойства перпендикулярных прямой и
плоскости (доказательство одного из них).
3. Шар с центром в точке О касается плоскости
в точке А. Точка В лежит в плоскости
касания. Найдите объем шара, если АВ = 21 см,
а ВО = 29 см.
4. Определите, на каком расстоянии от
вершины надо провести плоскость, параллельную
основанию, чтобы площадь сечения была
равна половине площади основания, если
высота конуса равна h.
1.
Призмой называется многогранник,
который состоит из двух плоских многоугольников,
лежащих в разных плоскостях и совмещаемых
параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих
многоугольников. Многоугольники называются
основаниями призмы, а отрезки, соединяющие
соответствующие вершины, — боковыми ребрами.
Высотой призмы называется расстояние между
плоскостями ее оснований.
Боковые грани призмы являются
параллелограммами.
Определение. Призма называется прямой,
если ее боковые ребра перпендикулярны
основаниям. В противном случае призма называется
наклонной. Высота прямой призмы равна ее
боковому ребру.
Боковые грани прямой призмы являются
прямоугольниками.
Прямая призма называется правильной, если
ее основания являются правильными
многоугольниками.
Все боковые грани правильной призмы
являются равными прямоугольниками.
Примеры.
1) Прямоугольный параллелепипед есть
прямая четырехугольная призма, так как его
боковые ребра перпендикулярны основанию.
2) Куб есть правильная четырехугольная
призма, так как его боковые ребра
перпендикулярны основанию и основанием является
правильный четырехугольник.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
809
3) Граненый карандаш имеет форму
правильной шестиугольной призмы (рис. 51).
4) Гайка имеет форму правильной
шестиугольной призмы, из которой удален цилиндр.
2.
Прямая называется перпендикулярной
плоскости, если она перпендикулярна всякой
прямой, лежащей в этой плоскости и проходящей
через точку пересечения данной прямой с этой
плоскостью.
Теорема. Если плоскость перпендикулярна
одной из двух параллельных прямых, то она
перпендикулярна и другой.
Доказательство. Пусть а и Ъ — две
параллельные прямые и а — плоскость,
перпендикулярная прямой а (рис. 52). Докажем, что а ± Ь.
Проведем в плоскости а через точку А
пересечения прямой аса произвольную прямую I, a
через точку В пересечения прямой Ъ с
плоскостью а — прямую т II I. Так как а ± а, то
прямые а и I перпендикулярны. Поэтому
параллельные им пересекающиеся прямые Ъ и т тоже
перпендикулярны. Таким образом, прямая Ъ
перпендикулярна любой прямой т в плоскости
а. А это значит, что прямая Ъ перпендикулярна
плоскости а. Теорема доказана.
Теорема. Две прямые, перпендикулярные
одной и той же плоскости, параллельны.
Доказательство. Пусть а и Ъ — две
прямые, перпендикулярные плоскости а
(рис. 53). Допустим, что прямые а и Ъ не
параллельны.
Выберем на прямой Ъ точку С, не лежащую в
плоскости а. Проведем через точку С прямую Ь',
параллельную прямой а. Прямая Ъ'
перпендикулярна плоскости а по только что доказанной
теореме.
Пусть Б и В' — точки пересечения прямых Ь и
Ъ' с плоскостью а. Тогда прямая ВВ'
перпендикулярна пересекающимся прямым ЬиЬ', что
невозможно.
(пЗ\
/Ж7 Г$
Таким образом, предположение, что прямые
аиЬне параллельны, привело к противоречию.
Следовательно, эти прямые параллельны.
Теорема доказана.
з.
Дано: шар с центром О,
а — касательная
плоскость, А — точка касания,
В € а, АВ = 21 см, ВО =
= 29 см.
Найти: V,
шара*
29 см
Решение. Радиус АО, проведенный в точку
касания, перпендикулярен касательной
плоскости а. Из ААВО по теореме Пифагора радиус
7 2 2
29 -21 = 20 (см). Поэтому объем
шара
4 ОЛз 32 000 1ЛЛЛЛ2 , зч
= sя* 20 =—^—к= 10 6665 я (см ).
■шара 3 3
2 з
Ответ: 10 666 ^ к (см )
4.
Дано: конус, SO — высота, SO = h, а —
секущая плоскость, a _L SO, Ot = SOn а, 2Sce4 = S^
Найти: SOv
Решение. Сечение есть
круг.
Построим осевое
сечение конуса SAB.
Из подобия
треугольников SOA и 80гАг (по трем
углам) следует, что
SO,
АгОг
SO АО '
Площади подобных фигур относятся как
квадраты их соответствующих линейных разме-
АгОг
ров и 2Sce4. = S^, поэтому -^- = -j=
SO
*и1 1 л/2
Таким образом, -т— = -j=, SOx = Л-5-
л
л
Ответ: h-к-.
Билет № 14
Рис. 51
Рис. 52
Рис. 53
1. Параллелепипед. Прямоугольный
параллелепипед (формулировки и примеры).
2. Признак параллельности плоскостей.

810
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
3. Сферу на расстоянии 8 см от центра
пересекает плоскость. Радиус сечения равен 15 см.
Найдите площадь сферы.
4. Через сторону нижнего основания
правильной треугольной призмы проведена
плоскость, пересекающая боковые грани по
отрезкам, угол между которыми равен у.
Найдите угол наклона этой плоскости к
основанию призмы.
1.
Призмой называется многогранник, который
состоит их двух плоских многоугольников,
лежащих в разных плоскостях и совмещаемых
параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих
многоугольников. Многоугольники называются основаниями
призмы, а отрезки, соединяющие
соответствующие вершины, — боковыми ребрами.
Боковые грани призмы есть
параллелограммы, у каждого из которых две стороны
образованы соответствующими сторонами оснований, а
две другие — соседними боковыми ребрами.
Определение. Параллелепипедом
называется призма, основания которой являются
параллелограммами.
Параллелепипед (рис. 54) имеет шесть
граней, и все они являются параллелограммами.
Пример.
На шарнирной модели параллелепипеда
можно показать, что существуют различные
параллелепипеды, имеющие соответственно
равные ребра.
Призма называется прямой, если ее боковые
ребра перпендикулярны основаниям. У прямого
параллелепипеда два основания —
параллелограммы, а четыре боковые грани —
прямоугольники.
Определение. Параллелепипед называется
прямоугольным, если он прямой и его
основания — прямоугольники.
У прямоугольного параллелепипеда все шесть
граней — прямоугольники.
Три ребра прямоугольного параллелепипеда,
сходящиеся в одной вершине, называются его
измерениями (длина, ширина и высота).
Примеры.
1) Обычная комната представляет собой
прямоугольный параллелепипед.
2) Из всех параллелепипедов с заданными
длинами ребер наибольший объем имеет
прямоугольный параллелепипед (рис. 55), так как он
имеет наибольшую площадь основания и
наибольшую высоту.
Прямоугольный параллелепипед имеет
также наибольшую полную поверхность из всех
параллелепипедов с заданными длинами ребер,
так как он имеет наибольшие высоты всех
граней.
3) Прямоугольный параллелепипед, все
грани которого — квадраты, называется кубом.
Форму куба имеют кристаллы поваренной соли.
2.
Теорема. Если две пересекающиеся прямые
одной плоскости соответственно
параллельны двум прямым другой плоскости, то эти
плоскости параллельны.
Доказательство. Пусть а и Р —
данные плоскости, I и т — прямые в плоскости а,
пересекающиеся в точке А, р и q —
соответственно параллельные им прямые в плоскости р
(рис. 56).
Допустим, что плоскости ос и Р не
параллельны, т. е. пересекаются по некоторой прямой с.
Тогда прямые I и /п, как параллельные прямым
р и д, параллельны плоскости Р, и поэтому они не
пересекают лежащую в этой плоскости прямую с.
Таким образом, в плоскости а через точку А
проходят две прямые I и /п, параллельные прямой с,
что невозможно по аксиоме параллельных. Мы
пришли к противоречию, откуда и следует, что
плоскости а и Р параллельны.
Теорема доказана.
X!
Г 1
1
1
>
Y\
у
''Ж
^ Cj
т
кХ.
Рис. 54
Рис. 55
Рис. 56

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
811
3.
Дано: сфера с
центром О, ос — секущая
плоскость, р(0, а) = 8 см,
Дсеч. = 15см-
Найти: Sc4)epbI.
Решение. Данное
сечение — окружность с
центром А, АО J_ а.
Пусть В — точка на этой окружности. Из
прямоугольного ААВО по теореме Пифагора
радиус сферы
ВО = Vl52 + 82 = 17(см).
Поэтому площадь сферы
5СфеРы = 4я-172 = 1156я (см2).
2
Ответ: 1156я(см ).
4.
Дано: АВСА1В1С1 — правильная призма,
Me CCv£AMB = y.
Найти: угол между
плоскостями АВМ и ABC.
Решение. Пусть Н —
середина отрезка АВ. В
правильном треугольнике ABC
медиана СН является
высотой, так что СН _1_ АВ.
Так как боковое ребро
правильной призмы перпендикулярно ее
основанию, т. е. СгС _1_ пл. ABC, то СН является
проекцией наклонной МН на плоскость ABC. По
теореме о трех перпендикулярах АВ _1_ МН.
Так как СН _1_ АВ и МН _L АВ, то согласно
признаку перпендикулярности прямой и
плоскости, АВ _L пл. СНМ9 т. е. пл. СНМ
перпендикулярна линии пересечения плоскости сечения
и плоскости основания. Поэтому Z. СНМ —
искомый угол.
Обозначим сторону основания призмы через а;
СН — высота правильного треугольника ABCf
г*тт «л/3
откуда СН = -g- .
Треугольники АСМ и ВСМ —
прямоугольные (так как отрезок ССг перпендикулярен
плоскости ABC), имеют общий катет СМ и
равные катеты АС и ВС. Поэтому эти треугольники
равны.
Из равенства треугольников АСМ и ВСМ
следует, что AM = ВМ, т. е. ААМВ —
равнобедренный, следовательно, его медиана МН является
биссектрисой, так что Z АМН = Z ВМН = |.
Из треугольника АМН отрезок МН =
2tg|
из треугольника СНМ cos Я = т™ = 7з tg |, и
поскольку Z. СНМ острый,
А СНМ = arccos Гл/З tg |).
Ответ: arccos (л/3 tg | J.
Билет № 15
1. Пирамида (формулировки и примеры).
2. Объем конуса.
3. В правильной треугольной призме АВСА^^
проведено сечение через вершину Сг и ребро
АВ. Найдите периметр сечения, если
сторона основания равна 24 см, а боковое
ребро — 10 см.
4. Докажите, что если точка X равноудалена
от концов данного отрезка АВ9 то она лежит
в плоскости, проходящей через середину
отрезка АВ и перпендикулярной прямой АВ.
1.
Определение. Пирамидой называется
многогранник, который состоит из плоского
многоугольника — основания пирамиды, точки, не
лежащей в плоскости основания, — вершины
пирамиды и всех отрезков, соединяющих
вершину с точками основания.
Отрезки, соединяющие вершину пирамиды с
вершинами основания, называются боковыми
ребрами.
Пирамида может быть получена при
пересечении многогранного угла произвольной
плоскостью. Бе вершиной будет служить вершина
многогранного угла, основанием — сечение
многогранного угла данной плоскостью, боковыми
ребрами — отсеченные части ребер
многогранного угла.
Высотой пирамиды называется
перпендикуляр, опущенный из вершины пирамиды на
плоскость основания.

812
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Пирамида, в основании которой лежит
л-угольник, называется л-угольной, тг-угольная
пирамида имеет п + 1 грань — основание и п
боковых граней.
Примеры.
1) Треугольная пирамида (рис. 57) является
выпуклым четырехгранником (тетраэдром).
Отрезки SA, SB и SC — боковые ребра.
Поверхность состоит из основания ABC и боковых
граней SAB, SBC и SAC.
2) Египетские пирамиды имеют форму,
близкую к правильной четырехугольной пирамиде.
2.
Геометрическое тело имеет объем V, если
существуют содержащие его простые тела и
содержащиеся в нем простые тела с объемами, сколь
угодно мало отличающимися от V.
Тело называется простым, если оно может
быть разбито на конечное число треугольных
пирамид. В частности, призма является
простым телом.
Теорема. Объем конуса равен одной трети
произведения площади основания на высоту.
Существуют такие многоугольники Р и Р'
(рис. 58), площади которых при
неограниченном увеличении числа их сторон п
неограниченно приближаются к площади круга, лежащего в
основании конуса. Для таких многоугольников
объемы построенных пирамид неограниченно
приближаются к « SH, где S — площадь
основания конуса, Ц — его высота. Согласно
определению объема, отсюда следует, что объем конуса
v=\sh=\kf?h.
3.
Дано: ABCAlBlCl — правильная призма, ААг =
= 10 см, АВ = 24 см.
Найти: PABq .
Решение. Сечение
представляет собой
равнобедренный А ABCV
Основание АВ = 24 см, боковая
сторона АС1 является
диагональю боковой грани
ACC^AV Из прямоуголь-
10 см
А 24 см
ного треугольника АССг по теореме Пифагора
Рис. 58
АСг = л/lO2 + 242 = 26 (см).
Периметр сечения РАВС = 2 • 26 + 24 = 76 (см).
Ответ: 76 см.
4.
Дано: АХ = ВХ, М —
середина АВ, Me ос, а J_
.LAB.
Доказать: X е а.
Доказательство.
Предположим противное:
X е а. Так как точки Am В
лежат по разные стороны от плоскости а, то
точка X и одна из точек Am В также лежат по
разные стороны от а. Будем сначала считать, что
это точки X иА. Тогда отрезок АХ пересекает а
в некоторой точке У.
Соединим точку У с точкой В. В
треугольнике AYB отрезок YM является по условию
медианой. Так как АВ _L а, то АВ перпендикулярен
всякой прямой, лежащей в плоскости а и
проходящей через точку М, и в частности АВ _1_ УМ.
Поэтому прямоугольные треугольники AYM
и BYM равны по двум катетам, откуда AY = BY.
Из треугольника BXY имеем ВХ < BY + XY =
=AY + XY = АХ9 следовательно, ВХ < АХ, что
противоречит условию.
Случай, когда точка X и точка В лежат по
разные стороны от плоскости а,
рассматривается аналогично.
Таким образом, предположение X е а
приводит к противоречию, следовательно, X € а, что и
требовалось доказать.
Билет № 16
1. Правильная пирамида (формулировки и
примеры).
2. Свойства изображения пространственных
фигур на плоскости.

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
813
3. Осевым сечением цилиндра является
квадрат, диагональ которого равна 3 J2 см.
Найдите площадь поверхности цилиндра.
4. Плоскость, параллельная основанию
конуса, делит его боковую поверхность на две
части, площади которых равны. В каком
отношении (считая от вершины) эта плоскость
делит высоту конуса?
Пирамидой называется многогранник,
который состоит из плоского многоугольника —
основания пирамиды, точки, не лежащей в
плоскости основания, — вершины пирамиды и всех
отрезков, соединяющих вершину с точками
основания. Отрезки, соединяющие вершину
пирамиды с вершинами основания, называются
боковыми ребрами. Высотой пирамиды называется
перпендикуляр, опущенный лз вершины
пирамиды на плоскость основания.
Определение. Пирамида называется
правильной, если ее основанием является правильный
многоугольник, а основание высоты совпадает с
центром этого многоугольника.
Следовательно, в правильной пирамиде
(рис. 59) все боковые ребра равны (как
наклонные с равными проекциями) и все боковые
грани — равные равнобедренные треугольники.
Высота каждого из этих треугольников
называется апофемой. Все апофемы правильной
пирамиды равны.
Боковые ребра и боковые грани правильной
пирамиды имеют один и тот же угол наклона к
плоскости основания.
Примеры.
1) Если две правильные четырехугольные
пирамиды, у которых боковое ребро равно стороне
основания, приложить друг к другу так, чтобы
их основания совпали, то получится
правильный многогранник — октаэдр. Форму октаэдра
имеет кристалл алмаза.
2) Четыре атома водорода (Н), входящие в
молекулу метана (СН4), расположены в вершинах
правильной пирамиды (тетраэдра). Атом
углерода (С) находится внутри этой пирамиды на
равном расстоянии от ее вершин.
2.
Во всех следующих утверждениях считается,
что рассматриваемые проектируемые отрезки не
параллельны направлению проектирования.
1. Прямолинейные отрезки фигуры
изображаются на плоскости чертежа отрезками.
Действительно, все прямые, проектирующие
точки отрезка АС (рис. 60), лежат в одной
плоскости, пересекающей плоскость чертежа а по
прямой АгСг. Произвольная точка В отрезка АС
изображается точкой Вг отрезка А1С1.
2. Параллельные отрезки изображаются
на плоскости чертежа параллельными
отрезками.
Действительно, пусть АС иА'С —
параллельные отрезки (рйс. 61). Прямые АгСг и А[С[
параллельны, так как они получаются при
пересечении параллельных плоскостей с плоскостью
а. Первая из этих плоскостей проходит через
прямые АС и AAV а вторая — через прямые А'С
иА'а;.
3. Отношение отрезков одной прямой или
параллельных прямых сохраняется при
параллельном проектировании.
Покажем, например, что (рис. 62)
АВ
ВС
•вгсг
Рис. 60
Рис. 61
Рис. 62

814
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
Проведем через точку В прямую А2С2,
параллельную АгСг. Треугольники ВАА2 и ВСС2
подобны. Из подобия треугольников и равенств
АгВг = А2В и ВгСг = ВС2 следует доказываемая
пропорция.
3.
Дано: цилиндр, ABCD —
осевое сечение, АВ = AD,
BD = 3^2 см.
Найти: Sn0B цил.
Решение. Из
прямоугольного AABD по теоре-
2 2
ме Пифагора BD = 2АВ ,
откуда сторона квадрата
АВ = -тг- = —р- = 3 (см). Поэтому высота
цилиндра АВ = 3 см, радиус цилиндра О А = 1,5 см.
Площадь боковой поверхности
2Ч
S6oK.noB. = 2^-l»5-3 = 9n(CMA).
Площадь основания
Soch. = я • 1,52 = 2,25я (см2).
Площадь полной поверхности
^пов. цил.
= 9я + 2 • 2,25л = 13,5я (см ).
Ответ: 13,5я(см ).
4.
Дано: конус, а — секущая плоскость, a _L SO,
Ох = SO П а, S — площадь боковой поверхности
большего конуса, Sx — площадь боковой
поверхности меньшего конуса, 2SX = S.
Найти: SOx: ОгО.
Решение. Сечение есть
круг.
Площади подобных
фигур относятся как
квадраты их соответствующих
линейных размеров. По усло-
SO.
вию 2St = S. Поэтому -^тг = -= .
SO.
Так как ООг = SO - SOv то тгтг- =
л- г
или
SOt
ool
Ответ:
J2 + 1
3 '
72 + 1
Билет № 17
1. Цилиндр (формулировки и примеры).
2. Признак параллельности прямой и
плоскости.
3. В основании прямого параллелепипеда
лежит ромб, диагонали которого равны 12 см
и 16 см. Высота параллелепипеда — 8 см.
Найдите площадь его полной поверхности.
4. Найдите боковую поверхность правильной
четырехугольной пирамиды, диагональное
сечение которой равновелико основанию,
если сторона основания равна а.
1.
Определение. Цилиндром (точнее, круговым
цилиндром) называется тело, которое состоит из
двух кругов, не лежащих в одной плоскости и
совмещаемых параллельным переносом, и всех
отрезков, соединяющих соответствующие
точки этих кругов. Круги называются основаниями
цилиндра, а отрезки, соединяющие
соответствующие точки окружностей кругов, —
образующими цилиндра.
Цилиндр называется прямым, если его
образующие перпендикулярны плоскостям
основания.
Радиусом цилиндра называется радиус его
основания. Высотой цилиндра называется
расстояние между плоскостями его оснований.
Осью цилиндра называется прямая,
проходящая через центры оснований.
Прямой цилиндр можно рассматривать как
тело, полученное при вращении прямоугольника
вокруг его стороны как оси. Например, при
вращении прямоугольника со сторонами 3 см и 4 см
вокруг большей стороны получится цилиндр с
высотой 4 см и радиусом основания 3 см, а вокруг
меньшей стороны — с высотой 3 см и радиусом
основания 4 см.
Примеры,
1) Прямой цилиндр можно также
рассматривать как тело, полученное при вращении
прямоугольника вокруг одной из его осей симметрии.
Например, при вращении прямоугольника со
сторонами 3 см и 4 см вокруг прямой,
перпендикулярной стороне 3 см и проходящей через ее
середину, получится цилиндр с высотой 4 см и
3
радиусом основания g см, а вокруг прямой, пер-

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
815
пендикулярной стороне 4 см и проходящей
через ее середину, — цилиндр с высотой 3 см и
радиусом основания 2 см.
2) Если склеить противоположные стороны
бумажного прямоугольника, то получится боковая
поверхность цилиндра. Высота этого цилиндра
равна длине склеенных сторон, радиус основания
равен длине другой стороны, деленной на 2л.
3) Сквозное отверстие в стене, сделанное
дрелью, является цилиндром: его основание — круг
с диаметром, равным диаметру сверла, высота
равна толщине стены.
2.
Теорема. Если прямая, не принадлежащая
плоскости, параллельна какой-нибудь прямой в
этой плоскости, то она параллельна и самой
плоскости.
Доказательство. Пусть а — плоскость,
прямая а не лежит в плоскости а, Ъ — прямая в
плоскости а, параллельная прямой а (рис. 63).
Проведем через прямые а и Ъ плоскость \Ъ.
Плоскости а и Р пересекаются по прямой Ъ.
Если бы прямая а пересекала плоскость а, то
точка пересечения принадлежала бы прямой Ъ.
Но это невозможно, так как прямые аиЬ
параллельны. Итак, прямая а не пересекает плоскость
а, значит, параллельна ей. Теорема доказана.
Дано:
ABCDA^B^D —
прямой параллелепипед,
ААг = 8 см, АВ = ВС,
АС = 16 см, BD= 12 см.
Найти: S„
ь
8 см
t^Tft
16 см
12 см
'ПОЛИ, пов.*
Решение. Диагонали ромба перпендикулярны
и делятся точкой пересечения пополам. По теоре-
7 2 2
6 + 8 =
= 10 (см), поэтому периметр ромба равен 40 см.
Боковая поверхность S6oK пов
2ч
= 4-10-8 =
= 320 (см").
Площадь ромба
Тромба = 2S[д ABC = ^
16 • 6 л- t 2Ч
—5— = 96 (CM ).
Площадь полной поверхности
'ПОЛИ. пов.
= 320 + 2-96 = 512 (W).
Рис. 63
Ответ: 512 (см ).
4.
Дано: ABCDS — правильная пирамида, АВ = а,
ACS — диагональное сечение, S0CH = SAaar сеч
Найти: 8ЫЖаШЯа.
Решение. Основание
высоты SO правильной
четырехугольной пирамиды
есть точка пересечения
диагоналей АС и BD
основания. Так как SO —
перпендикуляр к плоскости
основания, то SO _L AC.
Поэтому SO — высота треугольника SAC. Пло-
SO-AC
щадь диагонального сечения S^^ сеч = —«— •
DB — диагональ квадрата, поэтому DB _1_ АС.
Значит, DO — высота треугольника ACD. Пло-
0 ое пРО-АС
щадь основания S^ = 2SAACD = 2 —g— .
_, SO* AC nDO-AC „
По условию —о— = 2 —5— , откуда SO =
= 2DO.
Из прямоугольного треугольника BCD по
теореме Пифагора диагональ основания BD = a J2 .
Так как 2DO = BD, то SO = ajl.
В равнобедренном треугольнике OMS высота
SM является медианой, т.е. М — середина АВ.
По свойству диагоналей квадрата О — середина
BD. Поэтому ОМ — средняя линия
треугольника ABD и ОМ = |.
Из прямоугольного треугольника MOS по
теореме Пифагора SM2 = SO2 + ОМ2. Поэтому
апофема пирамиды SM = у.
Так как боковая поверхность правильной
пирамиды равна произведению полупериметра
cert 4а За 0 2
нования на апофему, то S6oK пов = у • у = За •
Ответ: За .

Примерные билеты и ответы к устному экзамену по геометрии
Подготовка к экзаменам. 11 класс
Билет № 18
1. Конус (формулировки и примеры).
2. Признак параллельности прямых.
3. В прямоугольном параллелепипеде
стороны основания равны 5 см и 12 см, а
диагональ параллелепипеда наклонена к
плоскости основания под углом 45°. Найдите
высоту параллелепипеда.
4. Площадь боковой поверхности цилиндра
равна Q. Найдите площадь осевого сечения.
1.
Определение. Конусом (точнее, круговым
конусом) называется тело, которое состоит из
круга — основания конуса, точки, не лежащей в
плоскости этого круга, — вершины конуса и всех
отрезков, соединяющих вершину с точками
основания. Отрезки, соединяющие вершину конуса с
точками окружности основания, называются
образующими конуса.
Конус называется прямым, если прямая,
соединяющая вершину конуса с центром
основания, перпендикулярна плоскости основания.
Высотой конуса называется
перпендикуляр, опущенный из его вершины на плоскость
основания. У прямого конуса основание высоты
совпадает с центром основания. Осью прямого
конуса называется прямая, содержащая его
высоту. Ось цилиндра параллельна образующим.
Прямой конус является телом вращения. Он
получается при вращении прямоугольного
треугольника вокруг его катета как оси. Например,
при вращении прямоугольного треугольника с
катетами 3 см и 4 см вокруг большего катета
получится конус с высотой 4 см и радиусом основания
3 см, а вокруг меньшей стороны — с высотой 3 см
и радиусом основания 4 см.
Примеры.
1) Прямой конус можно рассматривать как
тело, полученное при вращении
равнобедренного треугольника вокруг его высоты как оси.
2) Если склеить круговой сектор по двум
ограничивающим его радиусам, то получится
боковая поверхность конуса, вершиной которого
является центр круга, из которого вырезан
сектор. А образующая равна радиусу этого круга.
3) Чум и яранга у северных народов, вигвам у
индейцев Северной Америки имеют форму,
близкую к форме конуса.
2.
Теорема. Две прямые, параллельные
третьей прямой, параллельны.
Доказательство. Пусть прямые Ь и с
параллельны прямой а. Докажем, что прямые Ъ
и с параллельны.
Случай, когда прямые а, Ь, с лежат в одной
плоскости, был рассмотрен в планиметрии.
Поэтому будем считать, что рассматриваемые
прямые не лежат в одной плоскости. Пусть Р —
плоскость, в которой лежат прямые а и Ъ, а у —
плоскость, в которой лежат прямые а и с.
Плоскости Р и у различны (рис. 64). Отметим на
прямой Ъ какую-нибудь точку В и проведем
плоскость уг через прямую с и точку В. Она пересечет
плоскость р по прямой Ьх.
Прямая Ьг не пересекает плоскость у.
Действительно, точка пересечения должна
принадлежать прямой а, так как прямая Ьг лежит в
плоскости р. С другой стороны, она должна
лежать и на прямой с, так как прямая Ьг лежит в
плоскости уг. Но прямые а и с как параллельные
не пересекаются.
Так как прямая Ьг лежит в плоскости Р и не
пересекает прямую а, то она параллельна а,
значит, совпадает с 6 по аксиоме параллельных.
Таким образом, прямая Ь, совпадая с прямой bv
лежит в одной плоскости с прямой с (в
плоскости У}) и не пересекает ее. Значит, прямые Ьис
параллельны.
Теорема доказана.
3.
Дано: ABCDAlBlClDl — прямоуг.
параллелепипед, АВ = 5 см, ВС = 12 см, угол между BDX и
пл. ABC равен 45°.
Найти: высоту параллелепипеда.
.64

Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
817
Решение. Так как DXD —
^
Pi
' Art Г
5 см В
С
12 см
перпендикуляр к
плоскости ABCD, то Z DBDX
является угол между
диагональю BDX и плоскостью
основания прямоугольного
параллелепипеда, т. е. Z. DBDX = 45°.
Из прямоугольного треугольника ABD по тео
реме Пифагора BD = л/52 + 122 = 13 (см).
Треугольник BDDX — прямоугольный и
равнобедренный с острым углом 45°. Следовательно,
высота параллелепипеда DDX = BD = 13 см.
Ответ: 13 см.
4.
Дано: цилиндр, S^*. ПОв. " Q-
Найти: 8^ Жи.
Решение. Площадь боковой
поверхности цилиндра
определяется по формуле S = 2itRH9
где R — радиус цилиндра, Н —
высота.
Площадь осевого сечения цилиндра SOCu сеч# =
= 2RH в к раз меньше площади боковой поверх-
Q
НОСТИ. ПОЭТОМУ S^ сеЧ. = - .
Ответ:*.
к
Билет № 19
1. Сфера и шар (формулировки и примеры).
2. Теорема о трех перпендикулярах.
3. В правильной четырехугольной пирамиде
высота равна 12 см, а апофема — 15 см.
Найдите боковое ребро пирамиды.
4. Дан прямоугольный параллелепипед. Угол
между диагональю основания и одной из его
сторон равен а. Угол между этой стороной и
диагональю параллелепипеда равен р.
Найдите площадь боковой поверхности
параллелепипеда, если диагональ основания равна k.
1.
Шаром называется тело, которое состоит из
всех точек пространства, находящихся на
расстоянии, не большем данного от данной точки.
Эта точка называется центром шара, а данное
расстояние — радиусом шара.
Граница шара называется шаровой
поверхностью или сферой. Все точки сферы
равноудалены от центра шара на расстояние, равное
радиусу шара.
Шар является телом вращения. Он
получается при вращении полукруга вокруг его диаметра
как оси. Например, при вращении полукруга с
радиусом 3 см вокруг его диаметра получится
шар, радиус которого также равен 3 см.
Примеры.
1) Купол здания может иметь форму части
сферы, отсеченной плоскостью.
2) Земля имеет форму, близкую к шару.
3) Мячи для игры в футбол, волейбол,
баскетбол, теннис имеют форму шара.
2.
Перпендикуляром к плоскости называется
отрезок, соединяющий точку вне плоскости с
точкой плоскости и лежащий на прямой,
перпендикулярной к плоскости. Конец отрезка,
лежащий в плоскости, называется основанием
перпендикуляра.
Наклонной к плоскости называется любой
отрезок, соединяющий точку вне плоскости с
точкой плоскости, не являющийся
перпендикуляром к плоскости. Конец отрезка, лежащий в
плоскости, называется основанием наклонной.
Отрезок, соединяющий основания
перпендикуляра и наклонной, проведенных из одной и той
же точки, называется проекцией наклонной на
плоскость.
Теорема. 1) Если прямая, проведенная на
плоскости через основание наклонной,
перпендикулярна ее проекции, то она
перпендикулярна наклонной.
2) Если прямая на плоскости
перпендикулярна наклонной, то она перпендикулярна и
проекции наклонной.
Доказательство. Пусть АВ и АС —
перпендикуляр и наклонная к плоскости а, АС —
наклонная, с — прямая в плоскости а,
проходящая через основание С наклонной (рис. 65).
Проведем прямую САг \\ АВ. Она
перпендикулярна плоскости а. Проведем через АВ и АгС
плоскость р.
1) Прямая с перпендикулярна прямой САг.
Если она перпендикулярна прямой СВ9 то она

818
Подготовка к экзаменам. 11 класс
Примерные билеты и ответы к устному экзамену по геометрии
перпендикулярна плоскости Р, значит, и
прямой АС.
2) Аналогично, если прямая с
перпендикулярна наклонной СА, то она, будучи
перпендикулярна и прямой САг, перпендикулярна
плоскости Р, значит, и проекции наклонной ВС.
Теорема доказана.
3.
Дано: SABCD —
правильная пирамида, SO —
высота, SO = 12 см,
SM — апофема, SM =
= 15 см.
Найти: боковое ребро.
Решение. Треугольник
SOM — прямоугольный а
с прямым углом О. По теореме Пифагора ОМ =
а/15* - 12* = =9 (см). По теореме о трех
перпендикулярах ОМ _1_ ВС. Точка О — середина АС,
следовательно, ОМ — средняя линия
треугольника ABC и АВ = 2-9 = 18 (см).
Высота SM равнобедренного треугольника
SBC является и медианой, и поэтому ВМ = ~ ВС =
= о АВ = 9 (см). Из прямоугольного треугольника
SMB по теореме Пифагора боковое ребро
SB = Vl52 + 92 = Зл/34 (см).
Ответ: 3*/34 см.
4.
Дано: ABCDA^C^ — А±
прямоугольный
параллелепипед, Z. ВАС = a, Z. ВАСг =
= р,АС = А.
Найти: StoK.no*..
Решение. Заметим, что
углы между стороной АВ и диагоналями
параллелепипеда равны, поэтому мы имеем право
рассматривать, например, Z ВАСг как данный в
условии угол между стороной основания и
диагональю параллелепипеда.
Из прямоугольного треугольника ABC. имеем
АВ = ftcos а, ВС = fcsin а. Периметр основания
равен 2ft(cos а + sin а).
Прямая АВ перпендикулярна плоскости
грани ВССгВг, так как она перпендикулярна
пересекающимся прямым ВС и ВВХ этой плоскости.
Поэтому АВ _L BCV т. е. A BACj —
прямоугольный, и ВСг = АВ tg р = ftcos a tg р.
Из прямоугольного треугольника ВССг
СС\ = ВС\ - ВС2 = (k cos a tg р)2 - (k sin а)2 =
2 2 2 2
— k (cos a tg p - sin a).
Следовательно,
«бок.пов.-ЗСАВ + ЯОСС!»
Рис. 65
2 / о 2 2
= 2k (cos a + sin a) vcos a tg p - sin a.

Для поступающих в вузы
Задачи и решения письменных экзаменов
по математике
ЗАДАЧИ
Вариант I1
1. Решить уравнение 2 7х + 5 = х + 2.
2*. Указать промежутки возрастания и
убывания, а также точки максимума и минимума
функции f(x) = хе
3. Решить уравнение |sin х\ = sin х + 2cos х.
4. Основание АВ трапеции ABCD вдвое
длиннее основания CD и вдвое длиннее боковой
стороны AD. Длина диагонали АС равна а, а длина
боковой стороны ВС равна Ь. Найти площадь
трапеции.
5. Рота солдат прибыла на парад в полном
составе прямоугольным строем по 24 человека в
ряд. По прибытии оказалось, что не все солдаты
могут участвовать в параде. Оставшийся для
парада состав роты перестроили так, что число
рядов стало на 2 меньше прежнего, а число солдат
в каждом ряду стало на 26 больше числа новых
рядов. Известно, что если бы все солдаты
участвовали в параде, то роту можно было бы
выстроить так, чтобы число солдат в каждом ряду
равнялось числу рядов. Сколько солдат было в
роте?
-+ 2. Решить уравнение
21g(*+|)-le(x-l)-ta(x+|) + le2.
Вариант 2
1. Решить уравнение *Jx + 8 = 2х + 1.
2*. Указать промежутки возрастания и
убывания, а также точки максимума и минимума
функции f(x) = (х + 1)е .
3. Решить уравнение |tg x\ = tg х- 1/cos х.
4. Длины основания CD, диагонали BD и
боковой стороны AD трапеции ABCD равны р.
Длина боковой стороны ВС равна q. Найти
длину диагонали АС.
Задачи, отмеченные значком *, могут быть
заменены на задачи с теми же номерами.
5. Бригады, состоящие из одинакового числа
рабочих, получили на складе спецодежду.
Каждый рабочий получил по два комплекта
спецодежды, а каждой бригаде выдали на 20
комплектов больше, чем было бригад. Если бы бригад
было на 4 больше и каждой бригаде выдавали
бы по 12 комплектов, то спецодежды на складе
не хватило бы. Сколько комплектов
спецодежды было на складе?
-► 2. Решить уравнение
lg(x+g)-lg(x-J)-glg(x + e)-glgx.
Вариант 3
1. Решить систему уравнений
\х-у = 6,
\xS-yS = 126.
2*. Найти все значения х, при каждом из
которых производная функции
у(х) = 4* - sin 2х + 4 7з sin х
равна нулю.
3. Хорды АВ и АС имеют одинаковую длину.
Величина образованного ими вписанного в
окружность угла равна я/6. Найти отношение
площади той части круга, которая заключена в этом
угле, к площади всего круга.
4. Решить неравенство
(4х2 - 16х + 7) log2 (х - 3) > 0.
-► 2. Решить уравнение
2 - cos 2х + 2 72 cos (х + я/2) = 0.
Вариант 4
1. Решить систему уравнений
[* + у = 7,
\(х2-у2)(х-у) = П5.
2*. Найти все значения л;, при каждом из
которых производная функции
у(х) = 5х + sin 2х - 4л/3 sin х
равна нулю.

820
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
3. На основании равностороннего
треугольника как на диаметре построена полуокружность,
рассекающая треугольник на две части. Длина
стороны треугольника равна а см. Найти
площадь той части треугольника, которая лежит
вне полукруга.
4. Решить неравенство
(2х - 4)(х2 - 2х - 3) > 0.
-► 2. Решить уравнение
5 + 2cos 2х - 4 7з sin (х + я/2) = 0.
Вариант 5
1. Поле разделено на три участка. За день
были вспаханы половина первого участка и 3/4
второго участка, а третий участок, который
составляет четвертую часть всего поля, был
вспахан полностью. Вспаханная за день площадь
поля в дца раза больше площади второго участка.
Какую часть площади поля составляет площадь,
вспаханная за день?
2. Решить уравнение
cos (х + 5 J + sin (х + g J - cos 2x = 1.
3. Решить систему уравнений
|* + 2* + 1 = 3,
14* + 4у-32.
4. В треугольнике ABC биссектриса угла ABC
пересекает сторону АС в точке К. Известно, что
\ВС\ = 2, \КС\ = 1, \ВК\ = Зд/2 /2. Найти площадь
треугольника ABC.
5. Найти все значения параметра а из
интервала (2; 5), при каждом из которых существует
хотя бы одно число х из отрезка [2; 3],
удовлетворяющее уравнению
log2 № ~ lsin ах^ = cos (пх ~ б )•
Вариант 6
1. Три тракторные бригады вместе
вспахивают поле за 4 дня. Это же поле первая и вторая
бригады вместе вспахивают за 6 дней, а первая и
третья вместе — за 8 дней. Во сколько раз
больше площадь, вспахиваемая за день второй
бригадой, по сравнению с площадью, вспахиваемой
за день третьей бригадой?
2. Решить уравнение
cos [ х - g J 4- sin (х - g j 4- cos 2x = 1.
3. Решить систему уравнений
I V£+lgx2 = 2,
I у + 41g x = 28.
4. В прямоугольной трапеции ABCD длина
основания АВ в 1,5 раза больше длины
диагонали АС. Углы BAD и ADC прямые. Величина угла
DCA равна величине угла ВСА. Длина боковой
стороны AD равна 4. Найти площадь трапеции
ABCD.
5. Найти все значения параметра а из
интервала (5; 16), при каждом из которых существует
хотя бы одно число х из отрезка [1; 2],
удовлетворяющее уравнению
i их - sin кх\
л . 2 (ах , 37С Л (1 >osi
1+cos (_ + _^_^
Вариант 7
1. Решить неравенство
1
11 -3
- 31
4 -9х - 11 -3*
>Ь.
- 5
2. Два бегуна стартовали один за другим с
интервалом в две минуты. Второй бегун догнал
первого на расстоянии 1 км от точки старта, а
пробежав от точки старта 5 км, он повернул
обратно и встретился с первым бегуном. Эта
встреча произошла через 20 минут после старта
первого бегуна. Найти скорость второго бегуна.
3. Решить уравнение
sin 1,5* + sin It -2,5*1 =
= sin 5,5* + sin (т -6,5* J.
4. В прямоугольном треугольнике ABC
биссектриса BE прямого угла В делится центром О
вписанной окружности в отношении \ВО\: \ОЕ\ =
= 73 : 72 . Найти острые углы треугольника.
5*. Найти все значения параметра а (а > 0),
при каждом из которых площадь фигуры, огра-
3/ 2
41 + а
4- 3 и
ничейной параболой у = х - 2хг.
41 + с
прямой у = -Злг3/——5 + 3, будет наибольшей
VI + а

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
821
-+ 5. Найти радиус шара, описанного около
правильной треугольной пирамиды, у которой
сторона основания равна Ь, а угол между боковыми
ребрами равен а.
Вариант 8
1. Решить неравенство
4 - 7 • 5х
Ь2х + г - 12-5х + 4
2. Два лыжника стартовали на дистанции
10 км друг за другом с интервалом в 6 минут.
Второй лыжник догнал первого в двух
километрах от точки старта. Дойдя до поворота на
отметке 5 км, второй лыжник повернул обратно и
встретил первого на расстоянии 1 км от точки
поворота. Найти скорость первого лыжника.
3. Решить уравнение
cos Зх + sin 7х = 2sin (I + "5" J ~ ^cos
2 9х
2 '
4. В прямоугольном треугольнике ABC
биссектриса АР острого угла А делится центром О
вписанной окружности в отношении \АО\: \ОР\ =
= (7з +1):(7з - 1). .Найти острые углы
треугольника.
5*. Найти все значения параметра а (а > 0),
при каждом из которых площадь фигуры, огра-
2 2 2
ничейной параболой у = (1 + а)х и прямой у =
= а, будет наибольшей.
-► б. В шар радиуса R вписана правильная
четырехугольная пирамида. Угол между боковым
ребром пирамиды и стороной основания равен а.
Найти площадь боковой поверхности
пирамиды.
Вариант 9
1. Решить уравнение sin 2х = 2 7з cos х.
2. Найти периметр правильного
треугольника, вписанного в окружность, если известно, что
хорда длиной 2 см этой окружности удалена от
ее центра на 3 см.
3. Решить систему уравнений
Jlog2(*2 + i/2) = 5,
i 21og4 х + log2 у = 4.
4. Магазин радиотоваров продал в первый
рабочий день месяца 105 телевизоров. Каждый
следующий рабочий день дневная продажа
возрастала на 10 телевизоров, и месячный план —
4000 телевизрров — был выполнен досрочно,
причем в целое число рабочих дней. После этого
ежедневно продавалось на 13 телевизоров
меньше, чем в день выполнения месячного плана.
На сколько процентов был перевыполнен
месячный план продажи телевизоров, если в
месяце 26 рабочих дней?
n 5. Найти площадь фигуры, которая задается
на координатной плоскости следующими
условиями:
l||*-If|-|y-l|-*-2if+lf
|(*-D2 + (i,-1)2< 1.
Вариант 10
2
1. Решить уравнение sin 2х + 2sin х = 0.
2. Найти площадь правильного
шестиугольника, описанного около окружности, если
известно, что хорда длиной 4 см этой окружности
удалена от ее центра на 5 см.
3. Решить систему уравнений
|зх2 + у2 = 81,
I log2 х + 21og4 у = 1.
4. Кулинария, перейдя на изготовление
нового торта «Лакомка», продала в первый рабочий
день месяца 100 тортов. Каждый следующий
рабочий день продажа возрастала на 5 тортов,
пока не был досрочно, причем в целое число
рабочих дней, выполнен месячный план продажи
тортов, составляющий 3150 штук. После этого
ежедневно продавалось на 11 тортов меньше,
чем в день выполнения месячного плана.
На сколько процентов был перевыполнен
месячный план, если в месяце 24 рабочих дня?
б. Найти площадь фигуры, которая задается
на координатной плоскости следующими
условиями:
\\х-у\-\у + Ц = 2у-х + 1,
Вариант 11
1. Решить уравнение
3 • 2*+1 + 5 • 2*-2* + 2 = 21.
2 2
2. Решить уравнение 3sin х - cos х - 1 = 0.
3. Расстояние между двумя городами скорый
поезд проходит на 4 часа быстрее товарного и на

822
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
1 час быстрее пассажирского. Найти скорости
товарного и скорого поездов, если известно, что
скорость товарного составляет 5/8 от скорости
пассажирского и на 50 км/ч меньше скорости
скорого.
4. Найти площадь фигуры, которая задается
на координатной плоскости условием |д:| + \у - 1| <
<4.
5. Выпуклый четырехугольник ABCD вписан
в окружность. Диагональ АС является
биссектрисой угла BAD и пересекается с диагональю BD
в точке К. Найти длину отрезка КС, если длина
отрезка АК равна 6, а длина отрезка ВС равна 4.
6. Показать, что функция
у(х) = sin2 х - 12sin х cos х + 3cos х - 2 V66
может принимать неотрицательные значения.
Вариант 12
1. Решить уравнение log2 * ~ 1°&1б х = 3-
2 2
2. Решить уравнение 5sin х = 2 - cos х.
3. Строительство туннеля велось в 3 смены с
одинаковым планом проходки на каждую
смену. Скорость проходки во вторую смену была в
1,2 раза больше, чем в первую, а в третью смену
возросла на 0,6 м/ч по сравнению со второй.
Вторая смена выполнила план проходки на 1 час
быстрее, чем первая, а третья смена выполнила
половину плана на 3 часа быстрее, чем вторая
смена весь план. Определить скорость проходки
туннеля в первую смену.
4. Найти площадь фигуры, которая задается
на координатной плоскости условием
|* + 2| + Ы<2.
5. В выпуклом четырехугольнике MNPQ
диагональ NQ является биссектрисой угла PNM и
пересекается с диагональю РМ в точке S. Найти
длину отрезка NS, если известно, что вокруг
четырехугольника MNPQ можно описать
окружность и что длина отрезка PQ равна 12, а длина
отрезка SQ равна 9.
6. Показать, что функция
y(x) = sin х - 14sin х cos х - 5cos х + Зл/ЗЗ
принимает только положительные значения.
Вариант 13
1. Для разгрузки парохода было выделено две
бригады грузчиков. Если ко времени, за которое
может самостоятельно разгрузить пароход
первая бригада, прибавить время, за которое может
самостоятельно разгрузить пароход вторая
бригада, то получится 12 часов. Определить эти
времена, если их разность составляет 45% времени,
за которое обе бригады могут разгрузить
пароход совместно.
2. Решить уравнение 8sin х + 13cos 2х = 7.
3*. Найти наименьшее из расстояний от
точки М с координатами (0; -2) до точек (х; у) та-
16
ких, что у = з " 3, х > 0.
JSx
4. В выпуклом четырехугольнике ABCD
точки Е, F, Я, G являются соответственно
серединами отрезков АВ, ВС, CD, AD; О — точка
пересечения отрезков ЕН и FG. Известно, что \ЕН\ = а,
\FG\ = b, /L FOH = л/3. Найти длины диагоналей
четырехугольника ABCD.
5*. Найти все значения параметра а, при
каждом из которых неравенство
25у2 +щ > х - аху + у - 2Ъх
выполняется для любых пар чисел (х; у) таких,
что \х\ = \у\.
3. Найти все положительные числа х, у,
удовлетворяющие системе уравнений
[ jy + ^x _ 5(у-х/3)
I 3 -1
1 х =у .
-* б. Найти все значения параметра а, при
каждом из которых неравенство
3 - \х - а\ > х
имеет хотя бы одно отрицательное решение.
Вариант 14
1. Из двух пунктов A si В навстречу друг
другу одновременно выезжают велосипедист и
автобус. Время, затрачиваемое велосипедистом на
проезд из А в Б, на 2 часа 40 минут больше
времени, которое тратит автобус на проезд из Б в А,
а сумма этих времен в5« раза больше времени,
/ 6
прошедшего от начала движения велосипедиста
и автобуса до момента их встречи. Определить,
какое время велосипедист затрачивает на проезд
из А в Б, а автобус на проезд из Б в А.
2. Решить уравнение 2cos х + 1 = 3cos 2х.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
823
3*. Найти наименьшее из расстояний от
точки М с координатами (2; 0) до точек графика
функции у(х) = л/2 /J27(x - 2).
4. В выпуклом четырехугольнике ABCD
длины диагоналей АС и BD равны соответственно а
и Ъ. Точки Е, F,Gn Н являются соответственно
серединами сторон АВ, BCf CD, DA. Площадь
четырехугольника EFGH равна S. Найти длины
диагоналей EG и HF четырехугольника EFGH.
5*. Найти все значения параметра а, при
каждом из которых неравенство
2 2 1
16* + аху - у > х - 16у + g^
выполняется для любых пар чисел (х; у) таких,
что |*| = \у\.
-+ 3. Найти все положительные числа х, у,
удовлетворяющие системе уравнений
1/2 -1
У =х ,
(хуГ
28х - Ту
-У 2
х у=у
-► 5. Найти все значения параметра а, при
каждом из которых неравенство
2 > \х + а\ + х
имеет хотя бы одно положительное решение.
Вариант 15
1. Решить уравнение
V37 - 48ctgjc = 8ctg х - 5.
2*. В равнобедренном треугольнике ABC (|АВ| =
= \ВС\ = 8) точка Е делит боковую сторону АВ в
отношении 3 : 1 (считая от вершины В). Найти
угол между векторами СЕ и С А, если \СА\ =12.
3. Из сосуда, до краев наполненного чистым
глицерином, отлили 2 литра глицерина, а к
оставшемуся глицерину долили 2 литра воды.
После переливания снова отлили 2 литра смеси
и долили 2 литра воды. Наконец, опять
перемешали, отлили 2 литра смеси и долили 2 литра
воды. В результате этих операций объем воды в
сосуде стал на 3 литра больше объема
оставшегося в нем глицерина. Сколько литров
глицерина и воды оказалось в сосуде в результате
проделанных операций?
4*. Найти наибольшее и наименьшее
значения функции
у(х) = \х2 + 2х - 3| + | In х
на отрезке [1/2; 4].
5. Решить уравнение
log3x + 7(9 + 12x + 4x2) +
+ 1о^2х + з (6*2 + 23* + 21) = 4-
-* 2. В треугольнике ABC высота BD равна 11,2,
а высота АЕ равна 12. Точка Е лежит на стороне
ВС и BE : ЕС = 5:9. Найти длину стороны АС.
4. Решить систему уравнений
Зх2 + 2у2 - Зх + Ъу = 3,
4,5*2 + Зу2 - Зх + 8у = 7.
Вариант 16
1. Решить уравнение
л/Ю - 18cosjc = 6cos х - 2.
2*. В прямоугольном треугольнике с
катетами АВ и ВС (|АВ| = 8, \ВС\ = 6) проведена прямая
AD, делящая ВС в отношении \BD\ : \DC\ = 4:5.
Найти угол между векторами АВ и AD .
3. Имеется два бака: первый бак наполнен
чистым глицерином, второй — водой. Взяли два
трехлитровых ковша, зачерпнули первым
полным ковшом глицерин из первого бака, а
вторым полным ковшом — воду из второго бака,
после чего первый ковш влили по второй бак, а
второй ковш вылили в первый бак. Затем после
перемешивания снова зачерпнули первым
полным ковшом смесь из первого бака, вторым
полным ковшом — смесь из второго бака, и влили
первый ковш во второй бак, а второй ковш в
первый бак. В результате половину объема
первого бака занял чистый глицерин. Найти
объемы баков, если известно, что их суммарный
объем в 10 раз больше объема первого бака.
4*. Найти наибольшее и наименьшее
значения функции
i/(*) = |*2 + *-2|-ln±
на отрезке [1/2; 2].
5. Решить уравнение
logx-2*(б*2-5*+1)-
-logl_3x(4x2-4x+l) = 2.
-* 2. Найти площадь равнобедренного
треугольника, если высота, опущенная на основание,

824
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
равна 10, а высота, опущенная на боковую
сторону, равна 12.
4. Решить систему уравнений
2х2 + у2 + х-2у=19
5х2 + 2,5у2 + 3х-4у = 4.
Вариант 17
1. Решить уравнение log2 (j— ■ J = 1.
2*. Вычислить площадь фигуры,
ограниченной линиями
2
у = -х +ЛГ + 2; у = 0; х = 0; х = 1.
3. На плоскости даны две окружности
радиусов 12 см и 7 см с центрами в точках Ог и 02,
касающиеся некоторой прямой в точках Мг и М2 и
лежащие по одну сторону от этой прямой.
Отношение длины отрезка МгМ2 к длине отрезка 0102
равно 2 л/5 /5. Вычислить длину отрезка МгМ2.
4. Имеются два сплава, состоящие из цинка,
меди и олова. Известно, что первый сплав
содержит 40% олова, а второй — 26% меди.
Процентное содержание цинка в первом и втором
сплавах одинаково. Сплавив 150 кг первого сплава и
250 кг второго, получили новый сплав, в котором
оказалось 30% цинка. Определить, сколько
килограммов олова содержится в получившемся
новом сплаве.
5. Найти все целые значения параметра к,
при каждом из которых уравнение
5 - 4sin2 х + 8cos | = ЗА
имеет решения. Найти все эти решения.
-► 2. Решить неравенство
34х2-Зх + 1/2<(1/3)-40х2в
Вариант 18
1. Решить уравнение log2 (I* + 1| - 2) = -2.
2*. Вычислить площадь фигуры,
ограниченной линиями
у = -х2-4х + 5; у = 0; х = 0; х = 2.
3. На плоскости даны две окружности
радиусов 4 см и 3 см с центрами в точках Ох и 02,
касающиеся некоторой прямой в точках Мг и М2 и
лежащие по разные стороны от этой прямой.
Отношение длины отрезка Ог02 к длине отрезка
МХМ2 равно 2/ 7з. Вычислить длину отрезка
ого2.
4. Команда школьников, состоящая из
мальчиков и девочек, участвовала в командных
соревнованиях по шахматам. Мальчики из этой
команды сыграли в совокупности 60 партий, а
девочки — 40. Из всех сыгранных мальчиками
партий мальчики выиграли 45% партий, а из
всех сыгранных девочками партий девочки
проиграли 50% партий. Мальчики проиграли на
7 партий больше, чем девочки сыграли вничью.
За победу в одной партии дается 1 очко, за
ничью — 0,5 очка, за поражение — 0 очков,
школьники одной и той же команды друг с
другом не играют. Определить, сколько очков
завоевано мальчиками этой команды, если вся
команда набрала 52 очка.
5. Найти все целые значения параметра А,
при каждом из которых уравнение
2-2 cos 2х = 3k +4sin х
имеет решение. Найти все эти решения.
-+ 2. Решить неравенство (1/7) < 7
Вариант 19
1. Даны две непересекающиеся окружности.
К ним проведены две касательные, которые
пересекаются в точке А отрезка, соединяющего
центры окружностей. Радиус меньшей
окружности равен R. Расстояние от точки А до центра
окружности большего радиуса равно 6R. Точка
А делит длину отрезка касательной,
заключенного между точками касания, в отношении 1:3.
Найти площадь фигуры, ограниченной
отрезками касательных и большими дугами
окружностей, соединяющими точки касания.
2. Решить уравнение
sin (2х + о л: J - 3cos (х- ^nj=l -\- 2sin х.
3. Решить неравенство
lQgi/2 (4 " *) > 1о^1/2 2 " loSi/2 (* - !>•
4. Три автоматические линии выпускают
одинаковую продукцию, но имеют разную
производительность. Производительность всех трех
одновременно действующих линий в 1,5 раза
выше производительности первой и второй линий,
работающих одновременно. Сменное задание

1одготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
825
для первой линии вторая и третья линии,
работая одновременно, могут выполнить на 4 часа
48 минут быстрее, чем его выполняет первая
линия; это же задание вторая линия выполняет на
2 часа быстрее первой по сравнению с первой
линией. Найти время выполнения первой линией
своего сменного задания.
5. Пусть тип — натуральные числа, причем
правильная несократимая дробь. На какие
натуральные числа можно сократить дробь
Зп — т
Ъп + 2/п
, если известно, что она сократима?
Вариант 20
1. Даны две непересекающиеся окружности
радиусов R и 2R. К ним проведены общие
касательные, которые пересекаются в точке А
отрезка, соединяющего центры окружностей.
Расстояние между центрами окружностей равно
2Д73. Найти площадь фигуры, ограниченной
отрезками касательных, заключенными между
точками касания и большими дугами
окружностей, соединяющими точки касания.
2. Решить уравнение
о
sin х + sin Зх + 4cos х = 0.
2
3. Решить неравенство 2 - log2 (х + Зх) > 0.
4. Двум токарям и ученику поручили
выполнение срочной работы. Первый токарь может
один выполнить всю работу за время на 3 часа
большее, чем время, за которое второй токарь и
ученик, работая одновременно, выполнят ту же
работу. Второй токарь, работая один, может
выполнить всю работу за то же время, за которое ее
выполняет первый токарь и ученик, работая
одновременно. Время, затрачиваемое вторым
токарем на самостоятельное выполнение всей
работы, на 8 часов меньше удвоенного времени,
затрачиваемого первым токарем на
самостоятельное выполнение всей работы. За какое время
будет выполнена вся работа двумя токарями и
учеником, работающими одновременно?
б. Пусть тип — натуральные числа, причем
правильная несократимая дробь. На какие
натуральные числа можно сократить дробь
2/1 — тп о
— , если известно, ч^о она сократима?
on + 2пг
Вариант 21
1. Решить уравнение
sin (2х - -я- J + sin (-«— 8х J + cos 6х = 1.
2. Решить неравенство
log*(2-*)-81og1/4(2-*)>5.
3. В параллелограмме ABCD сторона АВ
равна 6 см, а высота, проведенная к основанию AD,
равна 3 см. Биссектриса угла BAD пересекает
сторону ВС в точке М так, что \МС\ = 4 см. N —
точка пересечения биссектрисы AM и диагонали
BD. Вычислить площадь треугольника BNM.
4. Каждый из рабочих должен был
изготовить 36 одинаковых деталей. Первый рабочий
приступил к выполнению своего задания на
4 минуты позже второго, но 1/3 задания они
выполнили одновременно. Полностью выполнив
свое задание, первый рабочий после
двухминутного перерыва снова приступил к работе и к
моменту выполнения задания вторым рабочим
изготовил еще две детали. Сколько деталей в час
изготавливал каждый рабочий?
б*. Найти высоту и радиус основания
прямого кругового конуса наибольшего объема,
вписанного в шар радиуса R.
-► б. Объем правильной треугольной призмы
равен V. Угол между диагоналями двух боковых
граней, проведенными из одной вершины, равен
а. Определить сторону основания призмы.
Вариант 22
1. Решить уравнение -
sin (х + у 1 + 2sin (2х + | ) = cos (3* + к).
2. Решить неравенство
logs (в - х) + 21og1/7g (6 - х) + log3 27 > 0.
3. В параллелограмме ABCD на стороне АВ
взята точка М так, что \АВ\ = 3|Aftf|. N — точка
пересечения прямых АС и DM. Найти
отношение площади треугольника AMN к площади
всего параллелограмма.
4. В водохранилище (скоростью течения в
котором можно пренебречь) из пункта А в пункт В
отправляется теплоход. Через 4 минуты вслед за
ним отправляется «Ракета» на подводных
крыльях, которая догоняет теплоход на расстоя-

826
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
нии двух километров от пункта А. Дойдя до
пункта В, находящегося на расстоянии 19,5 км
от пункта А, и простояв там 15 мин, «Ракета»
отправляется в обратном направлении и
встречает теплоход в 5 км от пункта В. Определить
скорости теплохода и «Ракеты».
5*. Найти высоту и радиус основания
прямого кругового конуса наибольшего объема,
вписанного в шар радиуса R.
-► 5. В правильной четырехугольной пирамиде
боковое ребро, равное Ь, образует с плоскостью
основания угол а. Через диагональ основания
проведена плоскость параллельно боковому
ребру. Определить площадь сечения.
Вариант 23
1. Решить уравнение log5 (х - 1) = log5- .
2. Решить систему уравнений
/ = 4х + 8,
2х+1 + у+1 = 0.
3*. Найти наибольшее и наименьшее
значения функции
f(x) = 24* - cos 12jc - 3sin Sx
на отрезке [-я/6; я/6].
4. В трапеции ABCD сторона AD является
большим основанием. Известно, что \AD\ = \CD\ =
= 4g , Z BAD = 90° и /L BCD = 150°. На
основании AD построен треугольник AED так, что
точки В и Е лежат по одну сторону от прямой AD,
причем \АЕ\ = |ДЕ|. Длина высоты этого
треугольника, проведенной из вершины Е, рав-
2
на Ь. Найти площадь общей части трапеции
ABCD и треугольника AED.
5. Найти все значения параметра а, при
каждом из которых уравнение
|1 - ах\ = 1 + (1 - 2а)х + ах2
имеет только один корень.
-► 3. Найти все корни уравнения
2 + sin 12* - 2cos Sx = 0,
принадлежащие отрезку [-я/6; я/6].
Вариант 24
1. Решить уравнение log3 = log
2-х
2. Решить систему уравнений
у2 = 4х + 2,
2х + 2 + 2у+1 = 0.
3*. Найти наибольшее и наименьшее
значения функции
f(x) = 18* - sin 9jc + 3sin 6x
на отрезке [-7я/18; я/18].
4. В треугольнике KLM длины сторон KL и
LM равны. Длина высоты, проведенной из
вершины L, равна 7/10, а длина стороны КМ равна
2 о . Сторона КМ является большим основанием
трапеции KNPM, причем точки L и N лежат по
одну сторону от прямой КМ. Известно, что \КМ\ =
= \KN\, ZL NPM = 90° и /L KNP = 150°. Найти
площадь общей части треугольника KLM и
трапеции KNPM.
5. Найти все значения параметра Ь, при
каждом из которых уравнение
|(Ь + 1)х - 2| = (1 + Ь)х2 -2Ъх + 2
имеет только один корень.
-► 3. Найти все корни уравнения
2 - cos 9* + 2cos 6х = 0,
принадлежащие отрезку [-7я/18; я/18].
ОТВЕТЫ И РЕШЕНИЯ
Вариант 1
1. Возведя обе части уравнения в квадрат,
получим уравнение
4(х + 5) = х2 + 4х + 4. (1)
Все корни исходного уравнения являются
корнями уравнения (1), но не обязательно все
корни уравнения (1) будут корнями исходного
уравнения. Поэтому после нахождения корней
уравнения (1) из них надо отобрать те, которые
будут корнями исходного уравнения.
Квадратное уравнение (1) имеет два корня: хг = 4 и х2 =
= -4. Проверка показывает, что хг = 4 является
корнем исходного уравнения, а хг = -4 не
является корнем исходного уравнения.
Ответ: 4.
—Зх
2*. Поскольку функции у(х) = х и у(х) = е
имеют производную в любой точке х из
промежутка (-°°; +°°), то данная функция дифферен-

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
827
цируема в каждой точке и по правилу
нахождения производной произведения
/'(*) = (хе-3У = We'3* + х{е~3х)' =
= е'3х - Зхе~3х = е~3х (1 - 3*).
—Зх
Так как е > О для любого действительного
числа х9 то f'(x) положительна при х < 1/3,
отрицательна при х > 1/3 и равна нулю при х = 1/3.
Следовательно, на интервале (-°°; 1/3) функция
f(x) возрастает, на интервале (1/3; +оо) убывает,
и так как она непрерывна в точке х = 1/3, то
точка х = 1/3 является точкой максимума.
Ответ: точка х = 1/3 — точка максимума;
на промежутке (-°°; 1/3) функция возрастает,
на промежутке <1/3; +°о) убывает.
3. Первое решение. Для освобождения от
знака абсолютной величины разобьем числовую ось
на две области; первую, в которой sin х > О, и
вторую, в которой sin х < 0. В первой области
|sin х\ = sin xf и исходное уравнение
переписывается так: sin х = sin х + 2cos х, или cos х = 0. Ре-
шения последнего уравнения есть х = ^ + ™я>
т е Z. Из этих значений х надо выбрать те,
которые лежат в рассматриваемой области, т. е.
там, где sin х > 0. Легко видеть, что такими
значениями х будут ЛИШЬ X = 5 + 27Ш, 71 € Z. Во
второй области |sin х| = -sin х, и исходное
уравнение перепишется так: -sin х = sin х + 2cos х,
или sin jc + cos x = 0. Переписав это уравнение в
виде V2sin (х + т J = 0, находим его решение:
х = -т + я/, Z € Z. Из этих значений в
рассматриваемой области лежат лишь х = -т 4- 2яА, ke Z.
Следовательно, решениями исходного уравнения
будут jc = -т 4- 2яА, А € Z; jc = о + 2тт, пе Z.
Второе решение. Возведя в квадрат обе части
уравнения, получим уравнение
2 2 2
sin jc = sin х + 4sin х cos # + 4cos x,
или
cos x (sin x + cos jc) = 0.
Это уравнение равносильно совокупности
двух уравнений
cos х = 0 и sin jc + cos х = 0.
Первое уравнение имеет решения jc = « + я£>
А € Z, второе уравнение имеет решения х = -т +
+ к19 le Z. Поскольку при возведении в квадрат
могли появиться лишние корни, необходимо
сделать проверку. Непосредственная
подстановка показывает, что решениями исходного
уравнения будут лишь
ТС ТС
х = 5 + 2тт, пе Zhx = -j + 2ятп, те Z.
тс тс
Ответ: « + 2тш, пе Z;-j + 2ятп, те Z.
4. Продолжим боковые стороны БС и AD
(рис. 1) до пересечения их в точке Е. Получим
треугольник ВАЕ. Так как \CD\ = 5 |АВ|, то из
подобия треугольников CED и ВЕА получаем, что
|С£| = \\ВЕ\ = |БС| = & и |DE| = \\АЕ\ = \AD\ =
= 5 |АВ|, откуда |АВ| = |АЕ|. Следовательно,
треугольник ВАЕ равнобедренный и АС — его
медиана. Но в равнобедренном треугольнике
медиана, проведенная к основанию, является
высотой, поэтому площадь треугольника ВАЕ можно
вычислить так:
S^=\\AC\\BE\=\-a-2b = ab.
Так как CD является медианой в
треугольнике АСЕ и так как длины высот треугольников
ECD и DCA равны, то их площади равны. Далее,
так как площадь треугольника ЕСА равна
площади треугольника ABE, то площадь
треугольника CDE равна т ab. Площадь трапеции ABCD
равна разности площадей треугольников ABE и
Рис. 1

828
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
DCE, т. е. площадь трапеции равна ab - jab =
3 и
= Zab-
Замечание. Площадь треугольника CDE
можно было бы вычислить с помощью теоремы об
отношении площадей подобных многоугольников:
так как коэффициент подобия треугольников
CDE и ВАЕ равен 1/2, то
&CDE = 4 ^ВЛЕ = Т И **ABCD = а* "~ \ab = J а*)'
Ответ: j ab.
5. Обозначим через х число рядов в роте при
прибытии роты на парад. Численность роты
24* солдат. После перестройки роты рядов стало
х - 2, а число солдат в новом ряду стало 26 + (х -
- 2). Для парада осталось (х - 2)(24 + х) солдат.
Число солдат, не участвующих в параде:
24* - (х - 2)(24 + х) = -х2 + 2х + 48.
Корни квадратного трехчлена -х + 2х + 48
есть хг = -6 и х2 = 8. Значит, выражение (2)
положительно при -6 < х < 8. Так как х — число
рядов, то х — число натуральное, и потому Кх<
< 7. Нам надо из промежутка 1 < х < 7 выбрать
такие натуральные х9 чтобы выражение А = 24х
являлось полным квадратом. Имеем
соответственно: А = 24, при х = 1, А = 48 при х = 2, А =
= 72 при х = 3, А = 96 при х = 4, А = 120 при х = 5,
А = 144 при х = 6, А = 168 при х = 7. Среди этих
чисел А только число 144 является полным
квадратом: 144 = 12 . Следовательно, х = 6и
численность роты равна 24 • 6 = 144 человека.
Ответ: 144 человека.
-+ 2. Область допустимых значений уравнения
состоит из всех значений х, удовлетворяющих
1 5
условиям х + о > 0, х - 1 > 0, х + о > 0, т. е.
ОДЗ есть промежуток 1 < х < +°о. На этой
области исходное уравнение равносильно уравнению
Потенцируя его, получаем уравнение (х +
+ 2 ) =2[x+2j[x-l], равносильное
исходному на области 1 < х < +оо. Последнее уравнение
имеет два корня: хг = 3/2 и х2 = -7/2. Из них в
область 1 < х < +оо входит только хг = 3/2.
Значит, исходное уравнение имеет единственный
корень хг = 3/2.
Ответ: 3/2.
Вариант 2
1. 1. 2*. х = -3/2 — точка минимума; на
промежутке (-°°; -3/2) функция убывает, на про-
межутке (-3/2; +<х>) функция возрастает. 3. -g- +
I.J4
+ 2nk9 k € Z. 4. л/4р2 - g2 . б. 44. 2. 2.
Вариант 3
1. Из первого уравнения у = х - 6.
Подставляя х - 6 вместо у во второе уравнение, получим
уравнение
х3-(х-б)3 = 126,
которое можно переписать в виде
х2 - 6х + 5 = 0.
Последнее уравнение имеет два корня: хг = 1
и х2 = 5. Следовательно, система имеет два
решения: хх = 19ух = -5; х2 = 5» ^2 = ■"*!•
Ответ: (1; -5), (5; -1).
2*. Найдем производную данной функции:
у\х) = (4х - sin 2х + 472 cos х)' =
= 4 - 2cos 2х - 4^2 sin х = 2(2 - cos 2х - 272 sin х).
Для решения задачи надо найти все значения
х9 удовлетворяющие уравнению
2 - cos 2х - 2 72 sin х = 0. (1)
Применив формулу косинуса двойного угла,
уравнение (1) перепишем в виде
2 - (1 - 2sin2 х) - 272 sin х = 0,
или в виде
(72sinx-l)2 = 0.
Отсюда очевидно, что уравнение (1)
равносильно уравнению sin х = 72/2, которое имеет
решения
х = (-1)ят + пп9 пе Z.
Эти значения х и дают ответ в данной задаче.
Ответ:(-1)пт +тсл,пе Z.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
829
3. Пусть точка О — центр окружности иг —
ее радиус. Соединим точки Я и С с центром О и
проведем диаметр АК (рис. 2). Так как
вписанный угол ВАС опирается на дугу ВКС и его
величина равна я/6, то центральный угол ВОС9
опирающийся на ту же дугу, имеет величину я/3.
Так как хорды АВ и АС имеют одинаковые
длины, то Z. BOA = /-АОС. Поскольку
£ВОА + ЛАОС = 2к-^9
то отсюда получаем, что Z. BOA = ААОС = 5я/6.
Теперь подсчитаем площадь той части круга,
которая заключена в угле ВАС. Она равна сумме
площадей сектора ОВКС и треугольников АОВ и
АОС:
*АОВ ~ 2 г
5я _ г 0
rsin "а Т » ьАОС
. 5я
rsin-g-
г
4
5ОВЛГС
г_
2
я
3
яг
6
яг
Следовательно, Sj^KC = -т + -j- 4- -~- =
г2(я + 3) m 0 2
= 6 . Так как S = яг , то искомое
соотношение есть
ъавкс _ г (я + 3) _ я + 3
Ответ.
я + 3
6я
бяг
6я
4. Исходное неравенство равносильно
совокупности двух систем неравенств
и
4х - 16* + 7 > О,
log2(x-3)>0
4х2-16х+7<0,
log2 (х - 3) < 0.
(2)
(3)
(4)
Система неравенств (2) равносильна системе
|И)ИЬ
I х-3>1.
Множество решений первого неравенства
составляют два промежутка: -оо <х<1/2и 7/2 <
< х < +оо. Множество решений второго
неравенства есть промежуток 4 < х < +оо. Поэтому
множество решений системы (4), а значит, и
системы (2), есть общая часть решений первого и
второго неравенств, т. е. множество 4 < х < +°о.
Система неравенств (3) равносильна системе
|И)(*-1)<0' (5)
I 0<х-3<1.
Поскольку решение первого неравенства
системы (5) есть промежуток 1/2 < х < 7/2, а
решение второго неравенства — промежуток 3 < х <
< 4, то решение системы (5) есть промежуток
3 < х < 7/2.
Следовательно, множество решений
исходного неравенства есть два промежутка: 3 < х < 7/2,
4<х<+оо.
Ответ: 3<лг<7/2и4<лг< +оо.
-* 2. Поскольку cos (х + ~) = -sin х9 то исходное
уравнение можно переписать в виде
2 - cos 2х - 2 72 sin х = 0.
Это уравнение решено в задаче 2* настоящего
варианта.
Ответ: (-1)ят + я/i, це Z.
Вариант 4
1. (6; 1), (1; 6). 2*." ±g + 2йя, k е Z.
а2(37з - я)
3
ke Z,
24 . 4. -К х < 2, х > 3. 2. ±g + 2Ая,
Вариант 5
1. Обозначим через S площадь всего поля, а
через у — площадь поля, вспаханного за один
день. Пусть х — площадь первого участка; тогда
из условия задачи следует, что площадь второго
участка равна у/2, а площадь третьего участка

830
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
равна S/4. Поскольку все поле разбито на три
участка, то
7/ Q
(1)
*+| + !=s-
За один день было вспахано ~ + 7 '% + I'
что составляет у9 откуда получаем уравнение
, i+ii+i-* <2»
В задаче требуется определить, какую часть
составляет площадь вспаханного за день поля от
площади всего поля, т. е. надо определить
отношение g. Из уравнения (1) находим, что х = j S -
- |. Подставляя j & ~ | вмест0 х в уравнение
(4) равносильно совокупности уравнений 2У — -2
и2у=10.
Первое уравнение этой совокупности корней
не имеет, поскольку 2У > 0 при любом у. Второе
уравнение имеет единственный корень у = log2 Ю.
Подставляя у = log2 Ю в выражение (3), нахо-
дим, что * = 3 - 2й**10*1 = 3 - 2-21о'<10 = 3 -
-2'10 = -17. Легко проверить, что пара чисел
х = -17 и у = log2 Ю удовлетворяет исходной
системе и потому является ее решением.
Ответ: (-17; log2 10).
4. Пусть ABC — треугольник,
удовлетворяющий условию задачи (рис. 3). Из треугольника
ВСК по теореме косинусов имеем
\КС\2 - \ВК\2 + \ВС\2 - 2|8£||£С| cos ZL КВС,
(2), получаем уравнение js-J+f.g+f-i,, W = l«f + |ВС|2 - 2|^C||SC| cos Z if СБ,
откуда ! = у •
Ответ: площадь поля, вспаханного за день,
составляет 5/7 от площади всего поля.
2. Применяя формулы косинуса и синуса
суммы двух углов и косинуса двойного угла,
перепишем уравнение в виде
к к , к ,
cos х cos g - sin JC sin 5 + sin JC COS g +
+ cos x sin g - 2cos x + 1 = 1,
или в виде
cos x (1 - 2cos x) = 0.
Это уравнение (а значит, и исходное)
равносильно совокупности двух уравнений cos х = 0 и
cosjc= 1/2.
Первое уравнение имеет решения х = ~ + ял,
пе Z. Второе уравнение имеет решения х = ± « +
+ 2ятп, те Z.
Ответ: « + тт, пе Z;±z + 2ятп, те Z.
3. Из первого уравнения системы находим,
откуда cos Z #ВС = (3^/2)
+ 4-1
2-3-2л/2/2
5^/2
8
cos /L КСВ
= 1 + 4 - (3^/2/2) = 1

Следовательно, sin
Z КВС = 7l - cosV #ВС = Jl-§ =
= ^ , sin ZL iiTCB = Jl - gg = 8 ' По теоРеме
. Din sin zl ВАС
синусов из треугольника ABC имеем -—/aqb =
ВС
, откуда \АВ\ =
sin Z АСВ
sin Z. ВАС
\BC\.
\АВ\
Так как
sin Z ВАС = sin (я - 2 Z ДГВС - Z АСВ) =
= sin (2 Z. КВС + ^ АСВ) =
= 2sin L КВС • cos /L КВС • cos L АСВ +
+ (cos2 ZL #ВС - sin2 Z КВС) sin Z АСВ =
50 _ 14>у377 = 77
64 64J 8 4 '
то |АВ| = 3.
что
,У + 1
х = 3-2у . (3)
Подставляя 3 - 2У вместо х во второе
уравнение системы, получаем уравнение 4(3 - 2У ) +
+ 4\у = 32, которое можно переписать в виде
22у-8-2у-20 = 0. (4)
Поскольку квадратное уравнение г - 82 - 20 =
= 0 имеем корни гг = 10 и г2 = -2, то уравнение

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
831
Площадь треугольника S найдем по формуле
S = \ \АВ\\ВС\ sin (2 /L КВС) = \ • 3 • 2 х
x2sm/.KBCcos/LKBC = 6'^ -5728 = Щ^.
Ответ: 15 Jl /16.
5. Для любых a six справедливы неравенства
cos (их - я/6) < 1 и |sin алг| < 1. (5)
Из последнего неравенства следует, что для
любых аил:
log2(3-|sinax|)>l. (6)
Сравнивая неравенства (5) и (6), заключаем,
что данное в условии задачи уравнение
равносильно системе уравнений
COS Ых-ц )=1»
|sinax|= 1.
(7)
(8)
Уравнение (7) имеет решения х = ~ + 2/п,
т € Z, из которых отрезку 2 < х < 3 принадле-
1 13
жат лишь Jt1 = 2el + g=-g-. Таким образом,
данное в условии задачи уравнение имеет
решение на отрезке 2 < х < 3 в том и только в том
случае, когда выполнено условие
i • 13 i 1
|sinTa| = l.
(9)
Следовательно, нам надо найти все решения
уравнения (9), принадлежащие промежутку 2 <
< a < 5. Уравнение (9) равносильно уравнению
. 2 13 1
sin -g-a=l.
13
13 1 - cos-g-a
Используя тождество sin -g- a = « ,
это уравнение можно переписать так:
13 л
cos -=-a = -l.
(Ю)
Решение уравнения (10) имеют вид
a = То к{2п + 1), п е Z.
Найдем теперь все целые числа я,
удовлетворяющие неравенствам
2<^Ж2П + 1)<||.
(12)
__ ^ 26 л — 65 т,
Легко проверить, что 1<о-<Зи5<5" < 7.
оТС о ТС
Поэтому неравенству (12) удовлетворяют целые
числа пг и /i2> для которых
2/i! + 1 = 3, 2л2 + 1 = 5,
т. е. пг = 1, /i2 = 2. С помощью формулы (11)
находим теперь а, удовлетворяющие условию
задачи:
3 0 9я 3 с 15я
а1=Та 'Я-3- То» а2=То ^•5=1Т-
13 ,v " 13' "2 13
Ответ: 9я/13, 15я/13
чя7С
Вариант 6
1. В полтора раза. 2. Ая, k е Z; (-1)"£ + лл,
л € Z. 3. (щ ; 36). 4.1172 . б. 9я/5, 17л/5, 5я.
Вариант 7
1. Перенесем правую часть данного
неравенства влево и приведем все члены неравенства к
общему знаменателю. В результате получим
неравенство
11-3* *- 31 - 20-9* + 55-3* * + 25
4 • 9х - 11- 3х" Х - 5
> 0, (1)
равносильное исходному. Обозначив 3 через у9
неравенство (1) можно переписать в виде
60у2 - 66у + 18 <п
^ и,
« 12/ - Ну - 15
или
(»- 1Ху -1)
(2)
Множество решений неравенства (2) есть
объединение множества решений уравнения
(11) [у + \){у - |)
= 0 и неравенства
<0.

832
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
Уравнение имеет решение уг = « и у2 = н.
Пользуясь методом интервалов (рис. 4),
находим, что множество решений последнего
неравенства есть два промежутка: -3/4 < у < 1/2 и
3/5 < у < 5/3. Следовательно, множество
решений неравенства (2) есть два промежутка
-3/4 < у < 1/2 и 3/5 < у < 5/3.
Таким образом, исходное неравенство
равносильно совокупности двух двойных неравенств
-3/4 <3Х< 1/2 и 3/5 < 3х < 5/3.
Множество решений первого неравенства
есть промежуток -оо < х < log3 « » множество ре-
3 5
шений второго — промежуток log3 н ^ х < 1°£з § *
Значит, множество решений исходного
неравенства есть два промежутка: -оо < % < log3 5»
3 5
lOgg g <*<10g3g.
13 5
Ответ: x < log3 5 »log3 g < x < log3 5 .
2. Обозначим через x км/ч скорость первого
бегуна, а через у км/ч скорость второго бегуна.
Первый бегун пробежал 1 км за - ч, а второй —
за - ч. По условию задачи второй бегун
затратил на 1 км на 2 мин меньше времени, чем
первый, следовательно
1 _ 1 = J_
х у 30'
К моменту второй встречи первый бегун, нахо-
Из уравнения (4)
(3)
дясь в пути 20 мин, пробежал 5 х км. Значит,
второй бегун к этому моменту пробежал (10 - « *) км.
Так как он бежал 18 мин, то
1П 1 18
1°-§ЛС=60^
+ \ Г+\ Г +
зч—=—'\ з^-^ь
4 25 3
(4)
Подставляя [30 - тку) вместо х в уравнение
(3), получаем уравнение
Рис.4
которое имеет корни уг = 20 и у2 = -50. Так как
скорость бегуна положительна, то у = 20.
Ответ: скорость второго бегуна равна 20 км/ч.
3. Применяя формулу косинуса двойного уг-
2
ла sin а = 5 » данное уравнение можно
переписать в виде
-cos Зх- cos Г 5 - Ъх j = -cos Их-cos f 5 - 13дм,
или
cos IIjc - cos Зх = sin 5jc - sin 13jc.
Применяя формулы для разности синусов и
косинусов, приводим уравнение к виду
-2sin 7х sin 4х = - 2sin 4х cos 9jc.
Полученное уравнение равносильно
совокупности двух уравнений sin 4х = 0 и sin 7х = cos 9х.
Первое уравнение имеет серию решений х =
= яй/4, k е Z. Второе уравнение можно
переписать в виде
sin 7х - sin Г | - 9х J = 0,
или
2sin (8х - j J cos (j - x J = 0.
Следовательно, второе уравнение
равносильно совокупности двух уравнений
sin (8*-т 1 = 0 и cosf|-x] = 0,
первое из которых имеет серию решений * = оо +
+ -g-, п е Z, а второе — серию решений х = -у +
+ ят, т е Z. Таким образом, исходное
уравнение имеет три серии решений:
Я& - -_ ТС , 7С71 „
х= -£,ke Z; jc=g2+-g-,/i€Z;
Зя , „
х = -г- + я#п, те Z.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
833
Легко видеть, что третья серия решений
содержится в первой.
Ответ: -j-, к е Z; «о +jiW€Z.
4. Данный треугольник и вписанная в него
окружность изображены на рис. 5. Обозначим
через D и F точки касания окружности со
сторонами АВ и АС соответственно. Так как BE —
биссектриса угла В, то Z. OBD = я/4 и из
треугольника ВЕС находим, что Z. OEF = я - Z. С -
о.
- Z. ОВС = -т- - ZL С. Из прямоугольных
треугольников OBD и OEF находим
\OD\ = \В0\ sin I, \OF] = \ОЕ\ sin (^ - А С).
Следовательно, |ВО| sin j = \ОЕ\ sin f -j- - Z. С J,
откуда получаем
7з . тс
-р Sin т = Sin
sin
(?-^)-f
или
Так как 0 < Z. С <^ , то или -j— Z. С = 5 » или
z 4 о
Зтс 2 тс
-т— Z.C = -7г . Отсюда либо Z. С = 5я/12, либо
Z. С = я/12. Значит, возможны два случая: либо
LC = 5я/12, и тогда £А = к/12, либо ^ С = я/12,
и тогда Z. А = 5я/12. В обоих случаях острые
углы треугольника равны я/12 и 5я/12.
Ответ: я/12, 5я/12.
б*. Пусть а — некоторое фиксированное
положительное число. Вычислим площадь S(a),
ограниченную параболой
у = х -2х
Vl + а2
+ 3
и прямой
У = -Зх3
уГГа2
+ 3.
Координаты точек, в которых пересекаются
парабола и прямая, являются решениями
системы уравнений
у = х2-2х3р!~+3,
У = -Ъх
ЪТ?
+ 3.
Приравнивая правые части уравнений этой
системы, получаем квадратное уравнение
X + X,
П + а
Отсюда вытекает, что парабола и прямая
пересекаются в точках с абсциссами хг = -8/—^—« и
Vl + а
х2 = 0. При этом хх < х2- Легко видеть (рис. 6),
что фигура, площадь S(a) которой надо найти,
лежит под прямой у = - 3xJ——-
VI + а
и над параболой
+ 3
у = х - 2х
(lla*
+ 3
на промежутке от хх до х2, поэтому
-В
6(1 + а )
Для того чтобы найти положительное а, при
котором площадь фигуры принимает
наибольшее значение, исследуем функцию S(a). В
каждой точке области 0 < а < +°о функция S(a)
имеет производную
S'(a) =
1«(1 + q ) - q«2a
2 2
6(1 + а )
1 - а
2 2 '
6(1 + а )
(5)
Рис. 5
Рис.6
27-1019

834
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
Из (5) следует, что на интервале 0 < а < 1
производная S'(a) положительна, а на интервале
1 < а < +оо производная S'(a) отрицательна.
Значит, функция S(a) монотонно возрастает на
интервале 0 < а < 1 и монотонно убывает на
интервале 1 < а < +о°; так как, кроме того, S(a)
непрерывна в точке а = 1, то ее наибольшее
значение достигается при а = 1.
Ответ: а = 1.
-► 5. Обозначим через А9 В9 С вершины
треугольника, лежащего в основании пирамиды,
через D — вершину пирамиды и через О —
центр шара, описанного вокруг пирамиды
(рис. 7). Тогда АВ = ВС = АС = Ъ9 A ADC = а.
Обозначим через Е ортогональную проекцию
центра шара на плоскость ABC. Так как
наклонные А09 ВО, СО равны по величине и равны
радиусу шара, то равны и их проекции на
плоскость ABC. Следовательно, АЕ = BE = СЕ. Это
означает, что точка Е является центром
окружности, описанной вокруг треугольника ABC. По
условию треугольник ABC правильный, поэтому
точка Е является его центром. Из условия, что
пирамида правильная, следует, что точка D
также проецируется в центр треугольника АВС9
т. е. в точку Е. Значит, точки О, Е9 D лежат на
одной прямой.
Из равностороннего треугольника ABC и
равнобедренного треугольника ADC находим
соответственно
rw-2 .ъЛ _ЪЛ гп_ 2АС _ Ь
СЕ~3 "2 3~' CD~—а~-—а'
81П 7
2sin2
Треугольник DEC прямоугольный, поэтому
а
'2
2sin-
СЕ
sin A CDE = 7Пг = _
В равнобедренном треугольнике DOC
стороны DO и ОС равны радиусу сферы. Значит,
искомая величина DO равна
CD d
DO =
2cos Z. CDE
4 sin
а Г 4 . га
5V1 " 3sm 2
На рис. 7 центр сферы изображен внутри
пирамиды. При некоторых значениях а точка О
может находиться и вне пирамиды.
Приведенное решение не использует тот факт, что точка О
лежит на отрезке DE.
d
Ответ:
а Г 4 . га
2 J1 - 38Ш 2
Рис.7
Рис.8
4sin
Вариант 8
2 4
1. х > log5 2, log5 g < х < log5g . 2. 10 км/ч.
3. ^ + у , к е Z; g + у , п е Z. 4. ё , § . 5*. а =
= 73 . 5, S = - 4i?2sin 4a.
Вариант 9
1. Используя формулу синуса двойного угла,
перепишем исходное уравнение в виде
2sin х cos х = 2 7з cos х9
или
(sin х - л/3 cos jc)cos х = 0.
Следовательно, исходное уравнение
равносильно совокупности двух уравнений
cos х = 0 и sin jc - л/3 cos л: = 0.
Первое уравнение этой совокупности имеет
решения х = л/2 + лА,. ft е Z. Очевидно, что
решения второго уравнения удовлетворяют
условию cos х Ф 0. Поэтому второе уравнение
равносильно уравнению
tgx= 7з
и, следовательно, имеет решения jc = « +nl9le Z.
Ответ: « + лА, А € Z; « + я/, Z е Z.
2. Обозначим центр данной окружности через
О и хорду длиной 2 через АВ (рис. 8). Опустим
из точки О перпендикуляр ОС на прямую АВ.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
835
Тогда \ОС\ = 3. Так как в равнобедренном
треугольнике АОВ высота ОС является и медианой,
то \АС\ = «\АВ\ = 1. По теореме Пифагора
находим теперь \ОА\ = J\OC\2 + \АС\2 = 79 + 1 =
= УП) . Длина стороны правильного
треугольника, вписанного в окружность, равна 2sin «\ОА\,
т. е. равна */30, следовательно, периметр этого
треугольника равен Зл/30.
Ответ: Зл/30 см.
3. Так как 21og4 х = log2 * и log2 х + log2 у =
= log2 л:у, то все решения данной системы
уравнений содержатся среди решений системы
х2 + у2 = 32,
(1)
ху= 16.
Умножив второе уравнение на 2 и вычитая
результат из первого уравнения, найдем, что
2
(х- у) =0, или х = у. Подставив х вместо у во
второе уравнение системы (1), получим, что х =
= 16, и теперь легко найдем два решения этой
системы: хг = 4, уг = 4 и дг2 = -4, у2 = -4.
Проверкой убеждаемся, что пара чисел хг = 4, ух = 4
есть решение исходной системы, а пара чисел
jc2 = -4, z/2 = -4 не есть ее решение, поскольку
область определения функции log2 х состоит из
положительных чисел.
Ответ: (4; 4).
4. Обозначим через п номер рабочего дня,
когда был выполнен месячный план продажи
телевизоров. По условию количество
телевизоров, проданных в первый, во второй и так далее
дни, составляет арифметическую прогрессию с
первым числом 105 и разностью 10. Пользуясь
формулой для суммы п первых членов
арифметической прогрессии, получаем уравнение
2-105 +2Ю(Я-1)п=4000>
которое после упрощений приводится к виду
п + 20л - 800 = 0.
Полученное квадратное уравнение имеет
единственный положительный корень п = 20.
Это означает, что сверхплановая продажа
телевизоров производилась в течение 26 - 20 = 6
дней. В день выполнения месячного плана было
продано 105 + 10(20 - 1) = 295 телевизоров, а в
каждый из последующих дней по условию задачи
продавалось 295 - 13 = 282 телевизора.
Следовательно, всего сверх плана было продано 6 • 282 =
1 RQ9
= 1692 телевизора, что составляет Tqqq ' 100% =
= 42,3% от плана.
Ответ: месячный план был перевыполнен на
42,3%.
5. Обозначим х - у через а и 1 - у через Ь.
Тогда данное в условии задачи равенство запишется
в виде
||а|-М| = а + 6. (2)
Найдем все пары чисел а и Ь,
удовлетворяющие этому равенству. Рассмотрим два случая.
1) Предположим, что а > 0. Тогда равенство
(2) примет вид
\а-\Ь\\ = а + Ь. (3)
Если Ь > 0, то равенство (3) перепишется в ви-
де \а - Ь\ = а + Ь и, очевидно, не может
выполняться. Следовательно, КОиравенство
принимает вид
\а -I- Ъ\ = а + Ь,
откуда находим, что а + Ъ > 0. Итак, все пары
чисел (а; Ь), удовлетворяющие равенству (2) и
условию а > 0, лежат в области, задаваемой
неравенствами
lb < 0, (4)
\ а + Ь>0.
Легко видеть, что и обратно, любая пара
чисел, удовлетворяющая неравенствам (4),
удовлетворяет также равенству (2).
2) Рассмотрим теперь пары (а; Ь),
удовлетворяющие равенству (2) и условию а < 0. Если Ъ <
< 0, то правая часть равенства (2) будет
отрицательной, что, конечно, не может выполняться.
Значит, Ъ > 0 и равенство (2) принимает вид
\-а - Ъ\ = а + Ь,
откуда следует, что а + Ь > 0. Поэтому все пары
чисел (а; Ь)9 удовлетворяющие равенству (2) и
условию а < 0, лежат в области, задаваемой
неравенствами
[ а<0,
[ а + 6>0.
Любая пара чисел, удовлетворяющая этим
неравенствам, будет, как легко видеть,
удовлетворять и равенству (2). Следовательно, пары чи-

836
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
сел (х; у), удовлетворяющие данному в условии
равенству, есть те и только те пары чисел,
которые удовлетворяют одной из следующих двух
систем неравенств:
[ х-у<0,
1-у>о,
\ х - 2i/ + 1 > 0;
[ х~У<0,
{ 1-у>о,
I х - 2у + 1 > 0.
Проведем на координатной плоскости (рис. 9)
прямые 1 - i/ = 0, х-у = 0их-2у+1 = 0. Они
пересекаются в точке К(1; 1). Тогда все точки,
координаты которых удовлетворяют первой
системе неравенств, будут лежать внутри и на
сторонах угла, обозначенного на рис. 9 цифрой J, а
все точки, координаты которых удовлетворяют
второй системе неравенств, будут лежать внутри
и на сторонах угла, обозначенного на рис. 9
цифрой II. Неравенству, данному в условии задачи,
удовлетворяют точки круга, т. е. точки,
лежащие внутри и на окружности радиуса 1 с
центром в точке К(1; 1). Следовательно, фигура,
площадь которой надо найти, состоит из двух
секторов АКБ и CKD. Очевидно, что в силу
симметрии площадь сектора CKD равна площади
сектора ЕКВ, и поэтому искомая площадь равна
площади сектора ЕКА. Сектор ЕКА образуется
прямыми х - у = 0и1 - у = 0. Прямые х - у = 0
и 1 - у = 0 проходит через центр окружности и
угол между ними равен 45° = 360°/8, поэтому
площадь сектора ЕКА равна 1/8 части площади
круга с радиусом 1 и с центром в точке К(1; 1),
т. е. равна я/8.
Ответ: я/8.
i
1
*<
-'1 /
^—^р/
/ ^^\ i
' ^^ \А
Y'J
0 1 х
Вариант 10
1. яА, k € Z;--
72). 4.18%. 5.я/4
1. яА, k € Z; -| + я*, I е Z. 2. 58 7з см. 3. (72 ;
Вариант 11
1. Поскольку 2х + 1 = 2 • 2х, 2х + 2 = 4 • 2х, то
уравнение можно записать в виде
6-2* + 5-2х-4-2х = 21,
или в виде
2х = 3.
Рис.9
Единственное решение последнего уравнения
х = log2 3 и является решением исходного
уравнения.
Ответ: log23.
2
2. Воспользовавшись формулой cos х = 1 -
. 2
- sin х, данное уравнение можно переписать в
виде sin* = 1/2, откуда следует, что исходное
уравнение равносильно совокупности уравнений
sin х = 72 /2 и sin х = -72 /2.
Решения первого уравнения: (-1)ят + ял,
пе Z. Решения второго уравнения: (-1) j + яА,
k е Z. Объединяя обе полученные серии
решений в одну серию, получаем, что решения полу-
ченного уравнения есть х= т + ^т9те Z.
Ответ: 1+lm, meZ.
3. Обозначим через и км/ч скорость
товарного поезда. Тогда из условия задачи следует, что
8
скорость пассажирского поезда равна g и км/ч,
а скорость пассажирского поезда равна (v +
+ 50) км/ч.
Обозначим через t ч время, за которое
товарный поезд проходит расстояние между
городами. Тогда скорый поезд пройдет это же
расстояние за (t - 4) ч, а пассажирский за (t - 3) ч.
Значит,
|i*-!i**-3)f
I vt = (и + 50)(* - 4).

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
837
Из первого уравнения системы находим t =
Подставляя это значение t во
= |(*-3)и t = 8.
второе уравнение, получаем
8v = 4(i> + 50),
откуда и = 50. Следовательно, скорость
товарного поезда равна 50 км/ч, а скорость скорого
поезда равна 100 км/ч.
Ответ: скорость товарного поезда равна
50 км/ч, а скорость скорого поезда равна
100 км/ч.
4. Каждая точка плоскости лежит в какой-то
из четырех областей, задаваемых неравенствами
х>0,
у-1>09
х>0,
<0,
\х>0, \x<Q
U-ко, \у-1
х<0,
у-1>0,
х<0,
<0.
Упростим теперь в каждой из этих областей
неравенство, данное в условии задачи. В первой
области оно примет вид
х + (у - 1) < 4, или х + у < 5,
во второй
х + (1 - у) < 4, илих-у> -3,
в третьей
-х + (у - 1) < 4, или у - х < 5
и в четвертой
-х + (1 - у) < 4, или х + у > -3.
Следовательно, данная в условии задачи
фигура является объединением четырех множеств,
задаваемых неравенствами:
х>0,
///
IV
х<0,
У>1,
у-х<5;
х<0,
У<1,
х + у>-3.
Изобразим теперь каждое из множеств на
плоскости хОу (рис. 10). Первое множество есть
прямоугольный треугольник, ограниченный
прямыми х = 09 у = 1их + у = б; катеты этого
треугольника лежат на прямых х = 0иу=1и
имеют длины, равные 4. Следовательно, его
площадь равна 5 • 4 • 4 = 8. Остальные три
множества также являются прямоугольными
треугольниками, полученными симметричным
отображением первого треугольника:
а) второй относительно прямой у = 1; б)
третий относительно прямой х = 0; в) четвертый
относительно точки (0; 1) — точки пересечения
прямых х - 0 и у = 1. Данная в условии задачи
фигура складывается из этих четырех
треугольников, и поэтому ее площадь S = 4 • 8 = 32.
Ответ: 32.
5. Докажем, что треугольники ABC и К ВС
(рис. 11) подобны. Они имеют общий угол АСВ.
Кроме того, по условию Z. ВАС = Z. CAD. Но
углы CAD и CBD опираются на одну и ту же дугу,
поэтому Z. ВАС = Z. CAD = Z. CBD. Итак, в
треугольниках ABC и КВС есть по два равных угла.
Следовательно, эти треугольники подобны, и
поэтому
\ВС\ _ \АС\
или
\КС\\АС\ = \ВС\2.
Обозначив \КС\ через х и учитывая, что \АС\ =
= \АК\ + \КС\ = 6 + л;, получаем квадратное
уравнение
х(6 + х) = 16.
Оно имеет единственный положительный
корень х = 2. Следовательно, \КС\ = 2.
Ответ: 2.
6. Воспользовавшись формулами
.2 1 - cos2x
sin х = g »
2 1 + cos2x 0 . . 0
cos х = 5 » 2sin х cos jc = sin 2x,
исходную функцию можно переписать в виде
у(х) = cos 2х - 6sin 2х + 2 - 237б6 ,
или в виде
у(х) =737 f у= cos 2* - -yL sin 2x1 + 2 - 237б6 .
Рис. 10
Рис. 11

838
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
Обозначив ф = arcsin -= и учитывая, что
sin ф = -= , cos ф = -=, функцию у(х) можно
записать в виде
у(х) = 737 sin (ф - 2х) + 2 - 237б6 .
Теперь очевидно, что функция у(х)
принимает наибольшее значение в тех точках х, в
которых sin (ф - 2х) = 1. Это наибольшее значение
равно 737 + 2 - 2 V66 . Предположим, что
справедливо неравенство
737 +2-2V66 <0.
Тогда справедливо неравенство л/37 + 2 -
Первая бригада делает за один час 1/х часть
всей работы, а вторая — 1/у часть всей работы.
Поэтому, работая вместе, они за один час делают
- + - часть всей работы. Значит, работая
вместе, они затратят на всю работу
1 + 1
х у
часов.
Пусть для определенности первая бригада
работает медленнее, т. е. пусть х > у. Тогда х - у
часов есть 45% от
х у
часов, или
- 2 у 66. После возведения обеих частей этого
неравенства в куб и упрощения получаем, что
49л/37 < 298. Это неравенство можно
переписать так:
737<6+.±.
Возведя обе части в квадрат, получим
37<36+^+^=37--^.
49 492 492
Получили неверное неравенство. Оно
означает, что неверно наше предположение о том, что
справедливо неравенство
V37 +2-2V66 >0,
но оно означает, что в тех точках, в которых
sin (ф - 2х) = 1, исходная функция у(х)
принимает неотрицательные значения. Например, она
принимает неотрицательное значение в точке х =
= | - j • Итак, требуемое в задаче утверждение
доказано.
Вариант 12
1. 16. 2. ± J + тсА, k е Z. 3. 2 м/ч. 4. 8. 5. 7.
Вариант 13
1. Пусть первая бригада может
самостоятельно разгрузить пароход за х часов, а вторая — за
у часов. Тогда
* + У=12. (1)
(2)
— — 45 ху
Х У~100'х + у-
Из уравнения (1) находим, что у = 12 - х.
Подставляя 12 - х вместо у в уравнение (2),
получаем уравнение относительно х
9_ х(12 - х)
х iz + х 20 • 12 ,
которое можно переписать так:
Зх2 + 124х- 960 = 0.
Это уравнение имеет два корня: хх = -48 и
х2 = 20/3. По условию задачи х > 0. Значит, х =
= 20/3, а тогда у = 16/3. Значит, первая бригада
*2
может разгрузить пароход за 65 часов, а
л
вторая — за 5« часа.
2 1
Ответ: 6« ч, 5« ч.
2
2. Применив формулу cos 2х = 1 - 2sin х,
перепишем исходное уравнение в виде
8sin4 х - 26sin2 х + 6 = 0.
Поскольку квадратное уравнение Ау - \Ъу +
+ 3 = 0 имеет корни уг = 3 и у2 = 1/4, то
исходное уравнение равносильно совокупности
уравнений
2 2
sin х = 3 и sin х = 1/4.
2
Уравнение sin х = 3 решении не имеет, так
как числа л/3 и -л/3 не входят в область значе-
ний функции у(х) = sin х. Уравнение sin = 1/4 в
свою очередь равносильно совокупности
уравнений sin х = 1/2 и sin х = -1/2. Значит, множество
решений исходного уравнения есть объединение

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
839
множеств решений уравнений sin х — 1/2 и sin х =
= -1/2. Решения первого уравнения: х = (-1)л ~ +
+ тел, п е Z. Решения второго: х = (-l)m g +
+ кт9 т е Z. Эти решения можно объединить,
к
записав их так: х = ±~ 4- nk9 k е Z. Итак,
решения исходного уравнения: Jt = ±g + nk9 k е Z.
тс
Ответ: ±g + л&, k е Z.
3*. Квадрат расстояния от точки М с
координатами (0; -2) до точки А с координатами (х; у)
вычисляется так: \АМ\ = (я - 0) + (у + 2) . Так
как по условию координаты точки А(х; у) связа-
16
ны равенством у =
JSxS
-2, то
1>ш#|2 2^ f 16 Л2 2 , 256
Теперь ясно, что квадрат искомой величины
равен наименьшему значению функции
// ч 2 , 256
f(x) = лг + —J
3*
на множестве 0 < х < +оо. Функция f(x) в
каждой точке этой области имеет производную.
Найдем ее:
Г(х) = [х2 + Щ у = 2х - 512дГ7 =
2(х8 - 256) = 2(jc8 - 28)
7 7
Отсюда следует, что на промежутке 0 < х < 2
производная f'(x) отрицательна, а на
промежутке 2 < х < +оо производная f'(x) положительна.
Значит, функция f(x) убывает на промежутке
0 < х < 2 и возрастает на промежутке 2 < х < +оо;
кроме того, функция f(x) непрерывна в точке.
х = 2. Следовательно, наименьшее значение f(x)
на множестве 0 < х < +оо равно /(2), т. е. равно
5 5 . Значит, искомое расстояние есть 4/ л/3 .
Ответ: 4/^3.
4. Так как точки F и Н являются серединами
сторон ВС и CD (рис. 12), то FH есть средняя
линия треугольника BCD, и потому FH II BD и \FH\ =
= 5 |AD|. Аналогично EG — средняя линия
треугольника ABD, и потому EG II BD. Из этих
условий получаем, что EG \\ FH. Аналогично
получаем, что EF || GH и \EF\ = ^ |АС|. Значит,
четырехугольник EFHG — параллелограмм, у
которого угол между диагоналями равен тс/3 и
длины диагоналей равны аиЬ.
Рассмотрим треугольник OFH (рис. 12). По
теореме косинусов
\FH\2 = \OF\2 + \ОН\2 - 2\OF\ \ОН\ cos Z_ FOH.
Так как |Ftf| = \ |ВЯ|, то ^Z)|2 = {§ )2 + (| )2 -
-2^т- cos gf откуда |2Ш| = л/а + b - ab.
Теперь рассмотрим треугольник EOF. Учитывая,
9тг 1
что Z. EOF=-=-, |&F| = 5 [АС|, и применяя теорему
6 + а + ab.
Ответ: длины диагоналей четырехугольни-
/ £ 2 / 2 2
ка равны л/а +6 - аЬ и *Jb + а + ab.
5*. Пусть а — некоторое число,
удовлетворяющее условию задачи. Это значит, что если в
данном неравенстве заменить всюду у на х или у
на -jc, то получившиеся относительно х
неравенства будут выполняться при любом х. Итак, при
любом х справедливы неравенства
(a + 50)jc2-2jc+IJ6 >0,
(50 -а)х2+ ^ >0.
(3)
(4)
Очевидно, что при а = - 50 множество
решений неравенства (3) не совпадает со всей
числовой прямой. Значит, а Ф -50. Поскольку
множество решений неравенства (3) совпадает со всей

840
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
числовой прямой, то дискриминант трехчлена,
стоящего в его левой части, не может быть
положительным. Следовательно,
4-щ(50 + а)<0,
откуда > 50. Так как множество решений
неравенства (4) также совпадает со всей числовой
прямой, то а < 50. Итак, если а — число,
удовлетворяющее условию задачи, то а = 50. При а =
= 50 исходное неравенство имеет вид
25у2 + щ > х - 50*у + у - 25*2.
Его можно переписать так:
(5* + Ъу)2 - 2(5* + 5у)± + jig > 0,
или
(5*+5у-^)2>0.
(5)
Неравенство (5) выполняется при любых
значениях х и у. Следовательно, а = 50 является
единственным решением задачи.
Ответ: 50.
-► 3. Из второго уравнения находим, что у = х .
Подставляя * вместо у в первое уравнение,
получаем уравнение
*te+*W1BC**-i>. (в)
Очевидно, что хг = 1 есть решение этого
уравнения. В множестве * > 0 и * Ф 1 уравнение (6)
равносильно уравнению 4х + *~ =-15[*~ _ « )
или уравнению * =16, имеющему корни х2 = 2
и *3 = ~2. В множестве * > 0 и * Ф 1 содержится
только один из них, а именно: х2 = 2. Поэтому
на множестве * > 0 уравнение (6) имеет только
два корня: хг = 1 и х2 = 2. Значит, исходная
система имеет на множестве * > 0 и у > 0 два
решения: хг = 1,уг = 1; х2 = 2,у2 = 1/8.
Ответ: (1;1), (2; 1/8).
-► 5. Пусть а — некоторое фиксированное
число. Данное неравенство можно переписать в ви-
де |* - а\ < 3 - * . Отсюда следует, что оно равно-
сильно двойному неравенству -(3 - х )< х- а<
< 3 - * или равносильно системе неравенств
х-а<3-х ,
-(3 - х2) < х - а.
Следовательно, задача может быть
переформулирована так: определить те а, при каждом из
которых множество решении системы
неравенств
' *2 + *-3-а<0,
х2 - х - 3 + а < 0, W
х<0
содержит хотя бы одно число. Дискриминанты
квадратных трехчленов
2 2
* + х-3-а и * - х - 3 + а
равны соответственно 13 + 4а и 13 - 4а.
Поэтому, для того чтобы первое и второе неравенства
системы (7) имели решения, надо, чтобы были
выполнены неравенства 13 + 4а > 0 и 13 - 4а > 0,
13 ^ ^ 13 та „ л
т. е. --г- <а< -г- .В дальнейшем будем считать,
что а удовлетворяет этим неравенствам.
Обозначим через xv х2 и *3> *4 К0РНИ
квадратных трехчленов
х + х-3-а
и х -х-3+а
соответственно. При этом будем считать, что
х1<х2их3< х4. Так как множества решений
первого и второго неравенств системы (7) имеют
вид хх < х < х2 и х3 < х < х4, причем хг < х4 и
хг< х2, то система будет иметь решение тогда и
только тогда, когда хг < 0 и х3 < 0 или когда
-1 - Vl3 + 4
If <0и^-^|3^<0.
2 ^ v " 2
Первое неравенство выполнено для всех а из
13 13 „
множества --j- < а < -j-. Второе неравенство
равносильно на этом множестве неравенству 1 <
< 7l3 - 4а или неравенству 1 < 13 - 4а.
Множество решений последнего неравенства есть
промежуток -оо < а < 3.
Итак, система (7) имеет хотя бы одно
решение, если параметр а принадлежит
множеству -13/4 <а<3.
Ответ: -13/4 < а < 3.
Вариант 14
1. 4 ч, | ч. 2. кк, к е Z. 3*. j=.
±.\ia2 + Ь2 - 2VaV - 16S2;
У а2 + Ь2 + 2,/aV - 16S2. б.* 32. 3. (J; | ),
(1; 1). 5. -| <а<:

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
841
Вариант 15
1. Обозначим ctg х через г; тогда данное
уравнение можно переписать так:
л/37 - 482 =82-5.
Возводя обе части уравнения (1) в квадрат,
получим уравнение
1622 - 82 - 3 = О,
которое имеет два корня: гх = 3/4 и 22 = -1/4.,
Поскольку при возведении в квадрат могли
появиться лишние корни, то необходимо
проверить, будут ли корни гг и 22 корнями уравнения
(1). Проверка показывает, что уравнение (1)
имеет единственный корень гх = 3/4. Отсюда
следует, что исходное уравнение равносильно
уравнению ctg х = 3/4, а потому имеет решения:
х = arcctg j + я/i, пе Z.
Ответ:arcctg т + пп9 пе Z.
2*. Поскольку
cos ZL АСЕ =
(СЕ, СА)
(\СЕ\\СА\)
то для получения ответа надо найти \СЕ\ и
скалярное произведение (СЕ, СА). Легко видеть
(рис. 13), что СЕ = СА + АЕ и что АЕ = ^АВ .
Поэтому, пользуясь свойствами скалярного
произведения, имеем
(СЕ, СА)=(СА + АЕ,СА) =
= (СА + \аВ, СА) =
= (СА, СА) + J|AB||CA|cos (АВ, СА).
Опуская высоту Б!) в треугольнике ABC,
получаем прямоугольный треугольник ABD, в
котором cos zi BAD = \AD\ : |AB| = 6/8 = 3/4.
Поскольку величина угла между векторами АВ и
СА равна п - Z. BAD, то cos (АВ, СА) = -3/4.
Значит, (СЕ , СА) = 144 + \ 12 • 8 • (-3/4) = 126.
Далее по теореме косинусов имеем: \ЕС\ = \АС\ +
+ |А£|2 - 2|АС| \АЕ\ cos Z. САЕ = 144 + 4 -
- 2 • 12 • 2 • j =112. Теперь получаем, что
cos (СА, СЕ) =
126
зЛ
(Л12-12) 8
зЛ
Значит, (СА, СЕ) = arccos -g- ,
зЛ
Ответ: arccos
8
3. Обозначим через V л объем сосуда. После
отливания 2 л глицерина и доливания 2 л воды
глицерин занимает —~— часть сосуда. После
того как отлили 2 л смеси, глицерина стало (V -
F — 2
-2)—^т— л и после доливания воды глицерин
(У - 2) тт
занимает * 5~^ часть сосуда. После третьей
V2
(V - 2Л3
операции глицерин займет I —рг— I . Таким
образом, количество глицерина в сосуде станет рав-
(V - 2Л3 (V - 2Л3
ным Г F ] , а воды VI у I + 3. Поэтому
v(^)'tv(^)' + 3.y.
Поскольку W 0, то получившееся уравнение
относительно V равносильно уравнению v - 9 к +
+ 24F- 16 = 0, или (V- 1)(V- 4)2 = 0, откуда
ясно, что либо V = 1, либо V = 4. Так как по
условию V > 2, то V = 4. Следовательно, в результате
проделанных операций глицерина оказалось в
(V — 2Л3 1
сосуде VI —у— 1 = 5 л, а воды 3,5 л.
Ответ: глицерина 0,5 л, воды 3,5 л.

842
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
4*. Квадратный трехчлен х + 2х - 3 имеет
корни хг = -3, х2 = 1. Из них только х2 = 1
лежит на отрезке [1/2; 4]. Найдем наибольшие и
наименьшие значения у(х) на отрезках [1/2; 1] и
[1; 4]. На множестве 1/2 < х < 1 справедливо не-
2
равенство х 4- 2х - 3 < 0. Значит,
.|*2 + 2jt-3| = -*2-2x + 3
у(лг) = -jc2 - 2* + 3 + | lp jc.
Функция f(x) = -х - 2л; 4- 3 4- ~ In л;
определена на множестве х > 0 и имеет производную в
каждой точке этого множества, причем
Г(*)--2*-2+|;=-4*2+24*-3* =
= (2х - 1)(2* 4- 3)
2 *•
Отсюда следует, что на множестве х > 1/2
справедливо неравенство /'(*) < 0, т. е. на этом
множестве f(x) монотонно убывает. Так как f(x)
непрерывна при * = 1/2ид; = 1,то она убывает
на отрезке [1/2; 1]. Поскольку на этом отрезке
функции у(х) и f(x) совпадают, то данная
функция у(х) монотонно убывает на отрезке [1/2; 1].
Поэтому
min у(х) = у(1) = 0, min у{х) =
хб[1/2;1] лее [1/2; 1]
= ^(1) = I - lln2-
На множестве х > 1 справедливо неравенство
х + 2х - 3 > 0. Значит,
\х2 4- 2х - 3| = х2 4- 2х - 3
и
у{х) = х 4- 2х - 3 4- | In *.
о Q
Функция #(лг) = jc 4- 2х - 3 + £ hi л:
определена на множестве jc > 0 и имеет производную в
каждой точке этого множества, причем
g'(x) = 2x + 2+£c =
= 4х2 4- 4х 4- 3 = (2х 4- I)2 4- 2
2х 2х
Отсюда следует, что на множестве х > 0
справедливо неравенство g'(x) > 0. Следовательно,
функция g(x) возрастает на множестве х > 0 и, в
частности, на отрезке [1; 4]. Так как на этом
отрезке функции g(x) и у(х) совпадают, то данная
функция у(х) монотонно возрастает на отрезке
[1; 4]. Поэтому
min у(х) = у{1) = 0,
хе[1;4]
max у(х) « z/(4) = 21 4- 31п 2.
*€[1;4]
Итак, наибольшее значение функции у(х) на
отрезке [1; 4] равно большему из чисел у(1/2) и
у(4), т. е. у(4) = 214- 31п 2. Наименьшее значение
функции у(х) на отрезке [1/2; 4] равно у(1) = 0.
Ответ: max у(х) = у(1) = 0, min i/(x) = 0.
*е[1/2;4] хе[1/2;4]
5. Поскольку 9 + 12* 4- 4х2 = (2х + З)2, а бд:2 4-
4- 23* 4- 21 = (3jc 4- 7)(2* 4- 3), то область
допустимых значений исходного уравнения состоит из
всех значений х, одновременно
удовлетворяющих условиям
2х4-3>0, 2*4-3*1, Зх4-7>0, 3*4-7*1,
т. е. ОДЗ состоит из двух промежутков
-3/2 <х<-1 и -1<лг< +оо.
На ОДЗ исходное уравнение равносильно
уравнению
21og3x + 7 (2jc 4- 3) + log2x + з (Зх + 7) + 1 = 4. (2)
Обозначим log3x + 7 (2л: + 3) через z. Тогда
уравнение (2) можно переписать в виде
22+ - =3.
2
(3)
Уравнение (3) равносильно уравнению 2г -
- Ьг 4-1 = 0 и потому имеет корни г1 = 1/2иг2 =
= 1. Следовательно, исходное уравнение на
своей ОДЗ равносильно совокупности уравнений
log3y + 7(2*4-3) = l/2 и log3x + 7(2* + 3) = l.
Первое уравнение равносильно на ОДЗ
уравнению (2х 4- З)2 = Зл; 4- 7. Это уравнение имеет
два корня: хх = -1/4 и х2 = -2, из которых
только хх = -1/4 лежит в ОДЗ исходного уравнения.
Второе уравнение равносильно на ОДЗ
уравнению 2х 4- 3 = 2х 4- 7. Последнее уравнение
совокупности имеет корень х3 = -4, не лежащий в
ОДЗ исходного уровня. Следовательно, исходное
уравнение имеет единственный корень хх = -1/4.
Ответ: -1/4.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
843
-+ 2. Обозначим длину АС отрезка через х
(рис. 14). Из прямоугольного треугольника АЕС
по теореме Пифагора находим
ЕС = JAC2 - АЕ2
По условию BE : ЕС ••
= Jx2 - 144,
5:9, значит,
ВС = ВЕ + ЕС=^ЕС= Ц1х2 - 144.
Площадь треугольника ABC равна ^BD'AC
и одновременно « АЕ • ВС, так что
BD-AC=AE-BC,
или
11,2* =12-у л/*2 - 144.
Последнее уравнение можно переписать в виде
Зх
= 5л/*
144.
(4)
Возведя уравнение (4) в квадрат, получим,
что х = 225, откуда либо х = 15, либо х = -15.
Так как х — длина стороны треугольника, то
х = 15. Следовательно, длина стороны АС равна
15.
Ответ: 15.
-► 4. Заменяя второе уравнение системы суммой
первого уравнения, умноженного на 3, и
второго, умноженного на -2, получим, что исходная
система равносильна системе
Зх2 + 2у2 - 3* + 5х = 3,
у = 5 - Зх,
или системе
Зх2 + 2(5 - Зх)2 - Зх + 5(5 - Зх) = 3,
(5)
у = 5 - Зх.
Первое уравнение системы (5) имеет два
корня: хх = 2 и х2 = 12/7. Поэтому система (5) имеет
два решения: хг = 2, i/x = -1 и х2 = 12/7, i/2 = ""1/7.
Ответ: (2; -1), (12/7; -1/7).
Вариант 16
1. ±« + 2лА, k е Z. 2*. arccos -=. 3. Юл.
4*. min /(х) = 0, max f(x) = 4 + In 2. 5. 1/4. 2. 75.
4. (-1; 2), (7/9; 10/9).
Вариант 17
1. Область допустимых значений уравнения
состоит из всех значений х, удовлетворяющих
условию
|х-1|-1>0. (1)
Из этой области исходное уравнение
равносильно уравнению
1 -2
I* " И " 1 '
или |х - 1| = 3/2. Это уравнение имеет два корня:
хх = 5/2 и х2 = -1/2. Оба эти числа
удовлетворяют условию (1) и, следовательно, являются
решением исходного уравнения.
Ответ: -1/2,5/2.
2
2*. Решая квадратное уравнение х + х 4- 2 = 0,
находим точки х1 = -1их2 = 2,в которых пара-
бола у = -х + х + 2 пересекает ось Ох. Ветви па-
раболы у = -х + х + 2 направлены вниз.
Следовательно, фигура, площадь которой надо
найти, расположена над осью Ох и под параболой
у = -х + х + 2 на промежутке 0 < х < 1 (рис. 15).
Поэтому ее площадь S вычисляется по формуле
1
S= $ (-х2 + х) + 2) dx =
о
= Hr + T+2*)o=-I + s+2 = 2e-
Ответ: 2 ~ .
о
3. Пусть Sx и S2 — две окружности,
удовлетворяющие условию задачи (рис. 16). Поскольку
точки Мг и М2 являются точками касания
окружностей Sx и S2 с прямой М1М2, то ОгМг _1_
_L МгМ2 и 02М2 _1_ МгМ2- Соединим центры Ог и
02 этих окружностей и проведем через точку Ох
Рис. 15

844
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
прямую, параллельную прямой МгМ2. Пусть
точка К будет точкой пересечения прямых 02М2
и прямой, проведенной параллельно прямой
МгМ2 через точку Ov Получим прямоугольный
треугольник Ог02К. Применяя к
прямоугольному треугольнику ОгК02 теорему Пифагора,
имеем
p&f-prf + lKOf. (2)
ПОСКОЛЬКУ |МХМ2 | = Y » ТО l°l°2l = Y ^1М2\'
Поскольку \КМ2\ = \ОгМг\ и |ЛГОа| = |М202|, то
|-йГ02| = 5. Наконец, \ОгК\ = |МХМ2|. Теперь из
равенства (2) следует, что т |МХМ2| = |МХМ2| + 25,
откуда
\МХМ2\ =
25
= 10.
- 1
Ответ: 10.
4. Обозначим через х кг количество олова,
содержащегося в получившемся новом сплаве, а
через у кг — количество цинка, содержащегося
в первом сплаве. Так как получившийся новый
сплав весит 400 кг и в нем 30% цинка, то он со-
400 ОЛ - ОЛ
держит цинка г^ • 30 = 120 кг, а тогда во
втором сплаве цинка (120 - у) кг. По условию
задачи процентное содержание цинка в первом и во
втором сплавах одинаково, поэтому имеем
JL . юо = 120~у • 100
150 1ии 250 1ии'
Из этого уравнения находим, что у = 45.
Поскольку первый сплав содержит 40% олова, то в
40
150 кг первого сплава олова будет т^ • 150 =
Рис. 16
= 60 кг, а во втором сплаве олова будет (х - 60) кг.
Поскольку второй сплав содержит 26% меди, то
250
во втором сплаве меди будет tqq * 26 = 65 кг. Во
втором сплаве олова содержится (х - 60) кг,
цинка 120 - 45 = 75 кг, меди 65 кг, так как все
это весит 250 кг, то имеем х - 60 + 75 + 65 =
= 250, откуда х = 170 кг.
Ответ: 170 кг.
2 2
б. Применяя формулы sin х = 1 - cos х и
2 X 1 + COS*
cos о = о ' исходное уравнение запишем
в виде
* а,л 2 ч Qfl + cos* Л 0,
5 - 4(1 - cos х) - 81 g I= 3*»
или в виде
4cos2 х - 4cos х - 3 - 3k = 0. (3)
Рассмотрим квадратное уравнение
422-42-3-ЗА = 0. (4)
Его дискриминант равен D = 16(4 + 3k). Бели
D < 0, то уравнение (4) не имеет действительных
корней. Следовательно, при целых значениях ft,
при которых 4 + ЗА < 0, т. е. при целых k < -1,
уравнение (4), а значит, и уравнение (3)
решений не имеют.
Отметим, что не существует целых значений
ft, при которых D = 0. Следовательно, при целых
ft > -1 уравнение (4) имеет два корня
_ 1 + л/4 + 3ft _ 1 - л/4 + 3ft
гг g и *2 2 г ' •
Это означает, что уравнение (3) равносильно
совокупности уравнений
cosjc = jc1 и cosx = x2. (5)
Очевидно, что при любом целом ft > 2
справедливы неравенства
гг > 1 и г2< -1,
и поэтому ни одно из уравнений совокупности
(5) не имеет решений. Следовательно, ни при
каком целом ft > 2 исходное уравнение решений не
имеет. Остается рассмотреть случаи ft = -1, ft = 0
nft = l.
Если ft = -1, то гг = -1 и г2 = 0, и уравнения
совокупности имеют решения х = 2кп9 пе Z9x =
= я/2 + кт9 т е Z. Следовательно, ft = -1
удовлетворяет условию задачи.
Если ft = 0, то гг = 3/2 и 22 = -1/2, и
совокупность уравнений (5) перепишется в виде
cos х = 3/2 и cos х = -1/2.

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
845
Первое из этих уравнений решений не имеет,
а второе уравнение имеет решение х = ±^п +
s о
+ 2л/, I е Z. Следовательно, к = О также
удовлетворяет условию задачи.
Вариант 18
,1 Л
ил 1+V7 1-Л
Если к = 1, то гг = —о— и 22 = —2—
1. -3 J; 1J . 2*. 14/3.3. |01Os| = 14. 4. 36
очков. 5. При к = 0 х = я/1, /I е Z, х = 5 + 2лтп,
, и
ч/ + 1
.,. Л - 1
+ 7lZ,
уравнение (3) равносильно совокупности
уравнении cos х =
1 + Л 1 - л/7 „
2 и cos * = —2~ " Первое
из этих уравнении решении не имеет, поскольку
1 + Jl ^ t
—2— > 1, а второе уравнение имеет решения
1 - Л
х = ±arccos —«— + 2яр, р е Z, поскольку
1 - л/7
|—о—I < *• Следовательно, А = 1 также
удовлетворяет условию задачи. Итак, исходное
уравнение имеет решение при целых значениях А,
только если к равно -1,0 или 1.
Ответ: при к = 1 х = 2тт, л € Z, а: = « + Кт>
2
т е Z; при ft = 0x = ±gn + 2jrf, J € Z; при k = 1
1 - л/7
jc = ±arccos —о— + 2яр,ре Z.
2 2
-► 2. Так как (1/3)" =3 , то данное
неравенство перепишется в виде
Поскольку 3 > 1, то это неравенство
равносильно неравенству
4х2 - Зх + \ < 40х2
или
те Z, при А = 1 х = (-1) arcsin 2
leZ.2. -3/4 < х < 1/4.
Вариант 19
1. Пусть Ох— центр меньшей окружности,
02 — центр большей окружности. Обозначим
через В, D, £, С точки, в которых данные прямые
касаются окружностей (рис. 17). Так как
радиус, проведенный в точку касания,
перпендикулярен касательной, то ОгВ J_ ВС, 02С _1_ ВС и,
значит, треугольники ОгВА и 02СА
прямоугольные. Они подобны (вертикальные углы ОгАВ и
0%АС равновелики), причем из условия следует,
что коэффициент подобия равен 1/3. Поэтому
1°2С1 1
\02С\ = 3R. Но тогда sin 4. О^АС = i^-^i = g , т. е.
Z. О^АС = я/6. Кроме того, имеем
\АС\ = \А02\ cos g , \АВ\ = \ОгА\ cosg , \ОгА\ = -^ .
Легко видеть, что
Sq^c =1\02А\\АС\ sin АОгАС-
= | -6i*-6iteos g sin g = |л/ЗД2,
S0iba = g KM \AB\ sin Z OxAB =
1 R R . я л/3 ю2
= 2—S.— Sln6=TA-
sin- tgg
81П;
36x2 + 3x- I >0.
(6)
2 1
Корни квадратного трехчлена 36x + Зх - «
есть Xj = -1/6 и х2 = 1/12. Поэтому множество
решений неравенства (6), а следовательно, и
исходного неравенства есть -оо <дг<-1/6и1/12<
< лг<+°о.
Ответ: -<*><*< -1/6, 1/12 < х < +оо.
Рис. 17

846
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
Аналогично доказывается, что треугольники
02ЕА и OxDA прямоугольные, причем /L О^АЕ =
= Z. OxAD = л/6, и, значит,
&02АЕ = &02АС = 2^ ^ 9 ^OxAD = ^ОгВА = ~2~ ^ '
Искомая площадь является суммой
площадей четырех треугольников ОгВА, OxDA9 02СА9
02ЕА и двух секторов, опирающихся на дуги
ENC и BMD. Так как
£Е02С = £Е02А + £С02А = 2№ - jH= *2!
и
. £BOxD = АВОгА + £00^-2(1 -g)-^.
то центральные углы, опирающиеся на дуги
ENC и BMD, равны 4я/3 и, значит, площади
большего и меньшего секторов равны соответ-
1 4я 2 1 4я 2
ственно о • -g- (3jR) и = " -з- Л • Таким образом,
искомая площадь равна
Ответ: 10R
= 10Я
,2/^.2
(7з+|я).
!(^ + И
2. Используя формулы приведения,
перепишем уравнение в виде
cos 2х + 3sin jc = 1 + 2sin х.
Используя формулу косинуса двойного угла
cos 2х = 1 - sin л;, получим, что исходное
уравнение можно записать в виде
2sin Jtfsin х- S ) = О,
3. Область допустимых значений неравенства
состоит из всех значений х> удовлетворяющих
условиям 4-лг>0илг-1>0, т. е. ОДЗ
является интервалом 1 < х < 4. На этом интервале
исходное неравенство равносильно неравенству
(4 - х)(х - 1) < 2. Решения последнего
неравенства есть два промежутка: -сх> <х<2иЗ<дг< +оо.
Из этих решений в интервале 1 < х < 4
содержатся лишь х из двух промежутков: 1 < х < 2,
3 < х < 4. Значит, множество решений
исходного неравенства состоит из двух промежутков:
1<лг<2иЗ<л:<4.
Ответ: 1 < х < 2, 3 < х < 4.
4. Обозначим через х ч, у ч, z ч время, за
которое соответственно первая, вторая и третья
линии могут выполнить сменное задание первой
линии. Тогда за 1 ч они могут выполнить соот-
1 1 1
ветственно - , - , - часть сменного задания для
х у г
первой линии. Производительность всех трех
одновременно действующих линий в 1,5 раза
больше производительности первой и второй
линий, работающих одновременно, поэтому
х у г \х у J
(1)
За один час вторая и третья линии, работая
одновременно, выполнят - + - часть сменного
У 2
задания для первой линии. Значит, для того
чтобы выполнить все задание для первой линии,
им потребуется т г ч, причем по условию за-
У 2
дачи
которое равносильно совокупности двух
уравнений
sin х = О и sin х= 1/2.
Решения этих уравнений есть соответственно
х = nk, k g Z, и x = (~1)Л£ + ли, п е Z.
Следовательно, множество всех решений исходного Подставляя
У. г
24
Из условия задачи также следует, что
У = х = 2. (3)
Из уравнения (2) находим: - 4- - = ^ •
уравнения есть х = nk9 k е Z; х = (-1)я~ + кп9
пе Z.
Ответ: nkt k е Z; ("1)Пг + ля, пе Z.
5 1,1
; вместо —I- - в левую часть
Ьх - 24 У z
уравнения (1), а также х - 2 вместо у в правую
часть уравнения (1), получаем уравнение
+
Ьх - 24
2{х *-2/
(4)

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
847
После преобразований уравнение (4) можно
переписать в виде
Ьх - 43* + 24
= 0,
х(х - 2)(5х - 24)
откуда получаем, что уравнение (4) имеет два
корня: хх = 8 и х2 = 3/5. Из условия задачи
следует, что х > 2. Значит, условию задачи
удовлетворяет лишь х2 = 8.
Ответ: 8 ч.
5. Так как т/п — правильная дробь, то т < п
и потому (Зл - т) — натуральное число. Пусть р
(р > 1) — натуральное число, на которое можно
3/1 — /71
сократить дробь
Это значит, что нату-
5п + 2т
ральные числа Зл - т и 5л 4- 2/л делятся на р,
т. е. существуют натуральные числа N и М
такие, что
Зл - т = pN и 5л + 2/л *= рМ.
Отсюда следует, что
l^=p(2iV + M), llm=p(3M-5N),
т.е. числа 11л и 11/л делятся на р. Так как
дробь /л/л несократимая, т. е. числа л и /л не
имеют общих делителей, то 11 делится нар.
Поскольку р > 1 и 11 — простое число, то отсюда
следует, чтор = 11.
Ответ: 11.
Вариант 20
1. IR2 (2 73 + 5я). 2. g + Tift, ft g Z; -| + лл,
л e Z. 3. -4 < x < -3, 0 < x < 1. 4. 2 ч. 5. 7.
Вариант 21
1. Используя формулы приведения,
перепишем уравнение в виде cos 2х - cos 8х + cos 6jc = 1.
Применяя формулу суммы косинусбв к
первому и третьему слагаемым и формулу косинуса
двойного угла ко второму слагаемому,
перепишем уравнение в виде
2cos 4л: cos 2х - 2cos 4* = 0,
или
2cos 4x(cos 2х - cos 4дг) = 0.
Применяя формулу разности косинусов,
получим, что исходное уравнение равносильно
уравнению cos 4х sin Зх sin х = 0.
Последнее уравнение равносильно
совокупности уравнений
cos 4* = 0, sin Зх = 0 и sin х = 0.
Первое уравнение этой совокупности имеет
решения х = « + j,neZ, второе уравнение
8
Tift
имеет решения х = -«-, ft е Z, третье уравнение
имеет решения x = nl, le Z. _
Ответ: = + т > пе Z, -=-, k е Z9nl, le Z.
о 4 о
2. Область допустимых значений неравенства
состоит из всех значений л;, удовлетворяющих
условию 2 - х > 0, т. е. ОДЗ является
промежутком -со < х < 2. Поскольку на ОДЗ
1о$1/4 (2 - *> ■
log2(2 - х)
log2l/4
= -5log2(2-x),
то исходное неравенство на промежутке -со <х<
< 2 равносильно неравенству
(log2 (2 - х))2 + 41og2 (2 - *) - 5 > 0.
2
Квадратное неравенство t + 4* - 5 > 0 имеет
решения t < -5 и * > 1. Поэтому исходное
неравенство на промежутке -со < х < 2 равносильно
совокупности неравенств
log2 (2 - х) < -5 и log2 (2 - jc) > 1. (1)
Решим эти неравенства. На промежутке х < 2
первое неравенство равносильно неравенству
2 - х < 2 , решения которого есть jc > 1 ^ . Из
этих л; в промежуток х < 2 попадают лишь х из
31
промежутка 1«« ^ х <2. Они и являются
решениями второго неравенства совокупности (1).
Решим второе неравенство совокупности (1).
На промежутке х < 2 второе неравенство (1)
равносильно неравенству 2 - х > 2, решение
которого есть х < 0. Все эти х входят в промежуток х < 2.
Они и являются решениями второго неравенства
совокупности (1).
Итак, решением совокупности (1), а значит,
и исходного неравенства являются все х из двух
31
промежутков: -со < # < о, 1 on < х < 2.
31
Ответ: -со < х < 0, 1 — < * < 2.
3. Пусть ABCD (рис. 18) — данный в условии
задачи параллелограмм. Проведем через точку

848
Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
N высоту параллелограмма QR. Обозначим
через а величину угла ВАМ; тогда величина угла
АМВ равна а, так как ВС || AD и AM —
секущая. Следовательно, треугольник АВМ
равнобедренный и \ВМ\ = |АВ| = 6, откуда заключаем,
что \DC\ = |AD| = 10. Поскольку Л ВМА = /L MAD
и Z. MBN = Z. AND как накрест лежащие углы
при параллельных ВС и ADf то треугольник
BMN и AND подобны по двум углам. Так как в
подобных треугольниках сходственные стороны
пропорциональны сходственным высотам, то из
\QN\
подобия треугольников AND и BNM имеем nrfA =
\МВ\ \QN\ 6 {ГкхП 0/ft
= ]Щ • т-е- Гч^Г| - Го • откУда lQNl = 9/8'
Площадь S треугольника BNM равна
S=l\QN\\BM\-
27 2
Ответ: -g- см.
2 8°
27 / 2Ч
у (см ).
4. Пусть первый рабочий изготовляет в час х
деталей, а второй рабочий — у деталей. Так как
1/3 сменного задания составляет 12 деталей, то
а - 12
первый рабочий изготовил их за — часов, а
12
второй — за — часов. Первый рабочий
приступил к выполнению своего задания на 4 минуты
позже второго, но 1/3 задания они выполнили
одновременно, поэтому
12 _4_ = 12
х + 60 у '
После того, как каждый из рабочих
изготовил по 12 деталей, им осталось изготовить еще
по 24 детали. Второй рабочий эти детали изгото-
вил за — часов, а первый, отдохнув 2 минуты,
изготовил 26 деталей к моменту окончания ра-
В Q М С
боты вторым рабочим. Следовательно, получаем
второе уравнение
2 24
У '
Итак, для нахождения х и у получили
систему уравнений
26 +
х * 60
12
х
26
х
♦А
+ 30
12
У '
24
У '
(2)
Умножив первое уравнение системы на 2, а
второе на (-1) и сложив полученные уравнения,
найдем, что система (2) равносильна системе
2 = JL
х 10'
12 J_ = 12
х 15 у
(3)
Рис. 19
Из первого уравнения системы (3) находим
х = 20, а тогда из второго уравнения у = 18.
Ответ: первый рабочий изготовлял в час 20
деталей, второй — 18 деталей.
б*. Пусть дан шар радиуса R с центром в
точке О и в него вписан конус, высота которого х, а
радиус основания у (рис. 19). Объем этого
конуса вычисляется по формуле
тг 1 2
V= ^пу х.
Обозначим через Ог центр основания конуса
и через А его вершину. Прямая ОгА
перпендикулярна плоскости основания конуса и проходит
через центр круга, являющегося сечением шара
плоскостью основания конуса. Поэтому центр
шара лежит на ней. Проведем плоскость через
прямую ОгА. Тогда она высечет из шара круг
радиуса R с центром в точке О, а из конуса
треугольник ABC, где АС иАВ — образующие
конуса, а ВС — диаметр основания конуса (рис. 20).
Высота ОхА треугольника ВАС равна х9
поэтому длина отрезка ООх равна \х - Д|.
Поскольку радиус основания равен у, то \ОгВ\ == у.
Расстояние от точки О до точки В равно R: OB = R.
Тогда из прямоугольного треугольника ОгОВ
имеем
|ов|2 = looj2 + lo^l2
(заметим, что если х = Л, т. е. \ОгО\ = 0, то это
равенство все равно будет выполняться), т. е.
R2 = \x-R\2 + y\

Подготовка к экзаменам. Для поступающих в вузы
Задачи и решения письменных экзаменов по математике
849
2 2 1
откуда у = 2Rx - х . Следовательно, V = « n(2Rx -
2 71 2 3
- х )х = 5 (2Rx - х ). Задача свелась к тому,
чтобы найти значения х, для которых функция
Я 2 3
V(x) = g (2ito - х ) принимает наибольшее
значение на промежутке 0 < х < 2R. Найдем
производную функции V(x):
V\x) - ^ (2Дх2 - х3)' = g (4Дх - Зх2) =
-► 5. Пусть АВСА'В'С — данная в условии
задачи правильная призма (рис. 21); ее основаниями
являются равносторонние треугольники ABC и
А'В'С, боковые грани АА'В'В, АА'С'С ВВ'С'С
являются прямоугольниками. Обозначим через
а длину стороны основания призмы; тогда SABC =
1 2^3 Л 2 т - Т7
=2а Т" = ~4~а " ак как °"ъем призмы V =
= SabcH, то отсюда находим, что
Н =
SABC Л 2 а273
= gx(4R-3x).
4Д
Очевидно, что на интервале 0 < х < -=-
производная F'(x) положительна, и потому функция
F(x) на этом интервале возрастает. На интервале
in
-о- < х < 2Я производная V'(x) отрицательна,
следовательно, на этом интервале функция V(x)
убывает. Так как функция V(x) непрерывна в
точке х — 4R/3, то из сказанного следует, что
она в точке х = ^R принимает наибольшее
значение на промежутке 0 < х < 2R. Итак,
наибольший объем имеет тот конус, высота которого
4
равна g R. Радиус основания этого конуса равен
Ответ: высота -=- , радиус основания —g-R •
Рассмотрим треугольник АВ'С. Так как
АА'В'В и АС равны, т. е. АВ' = АС = л/я2 + а2 .
Следовательно, треугольник АВ'С
равнобедренный. Проведем в этом треугольнике высоту АК.
Так как треугольник АКС прямоугольный и дли-
I 2 2
на 1ГС' равна а/2, длина АС равна *JH + а ,
угол КАС = а/2, то
. а КС а
sin о =
2 АС' 2(/^Т72'
или
. 2 а
sin g =
4(Я2 + а2) (щ^ ^ 2^
4 г + а |
Из этого равенства находим, что
4sin2^-16F2
б
а =
4(1 - 4sin2f)
, или а =
-V
8Vsin(a/2)
л/3(2сова - 1)
Ответ; / В™°<«/»>
VV3(2cosa - 1)
Рис. 20
Рис. 21
Вариант 22
1. т +?ik>keZ'>n + 2пп> пе Z.2.-oo <х<
< -119, К х < 6. 3.1/24. 4. Скорость теплохода
20 км/ч, скорость «Ракеты» 60 км/ч. б*. Высота
2 /2 1 2
-т= Л, радиус основания RJ-.5. ъЬ cos a.

Предметно-тематический указатель
К РАЗДЕЛУ «КРАТКОЕ ИЗЛОЖЕНИЕ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ»
МАТЕМАТИКА. 5—6 КЛАССЫ
Вынесение общего множителя за скобки 29
Вычитание десятичных дробей 18
— натуральных чисел 7
— обыкновенных дробей 16
— положительных и отрицательных чисел 26
Деление десятичных дробей 19
— натуральных чисел 8
— обыкновенных дробей 17
— положительных и отрицательных чисел 27
Делимость чисел 10
Делители числа 10
Десятичные дроби 14
Длина окружности 34
Дроби 13
Единицы измерения времени 21
длины 20
массы 21
объема 21
площади 21
скорости 22
Задачи на все действия 27
« движение по реке» 33
деление числа на части, пропорциональные
данным числам 37
масштаб 38
нахождение дроби от числа и числа по его
дроби 36
проценты 23, 24
прямую и обратную пропорциональные
зависимости 37
сравнение величин 35
Изображение чисел на координатном луче 14
Измерение углов 40
Координатная плоскость 42
Координатная прямая 24
Координатный луч 14
Коэффициент 29
Кратные числа 12
Луч 39
Масштаб 38
Модуль числа 25
Наибольший общий делитель 11
Наименьшее общее кратное 12
Натуральные числа 7
Нахождение дроби от числа 36
— числа по его дроби 36
Обратная пропорциональная зависимость 37
Обыкновенные дроби 13
Объем прямоугольного параллелепипеда 34
Округление чисел 20
Отрезок 39
Отрицательные числа 24
Основное свойство дроби 15
Параллелепипед (прямоугольный) 34
Параллельные прямые 41
Переместительное свойство 9
Периметр 33
Перпендикулярные прямые 41
Площадь круга 34
— поверхности прямоугольного параллелепипеда 34
— прямоугольника 33
Подобные слагаемые 29
Положительные числа 24
Порядок выполнения действий 27
Преобразование буквенных выражений 29, 30
Приближенные значения чисел 20
Признаки делимости на 10, 2, 3, 4, 5, 6, 9 10
Пропорции 31
Простые числа 11
Противоположные числа 25
Проценты 23
Прямая 39
Прямая пропорциональная зависимость 37
Раскрытие скобок 29
Распределительное свойство 10
Решение уравнений 30, 31
Сложение десятичных дробей 18
— натуральных чисел 7
— обыкновенных дробей 16
— положительных и отрицательных чисел 26
— чисел с помощью координатной прямой 26
Смешанные числа 16
Сокращение дробей 15
Составные числа 11
Сочетательное свойство 9
Сравнение десятичных дробей 17
— обыкновенных дробей 15
— положительных и отрицательных чисел 25
— чисел на координатном луче 14
Среднее арифметическое 33
Степень 28
Угол 39
Умножение десятичных дробей 18
— натуральных чисел 8
— обыкновенных дробей 16
— положительных и отрицательных чисел 27
Уравнение 30
Формула длины окружности 34
— пути, скорости, времени 32
— объема прямоугольного параллелепипеда 34

Предметно-тематический указатель
К разделу «Краткое изложение школьного курса математики»
851
— периметра прямоугольника 33
— площади круга 34
прямоугольника 33
Целые числа 25
АЛГЕБРА. 7—11 КЛАССЫ
Алгебраические выражения 73, 74
Алгебраические дроби 74, 76
Аналитический способ задания функции 55
Арифметическая прогрессия 105
Арифметический квадратный корень 44
— корень п-й степени 45
Бесконечные десятичные дроби 48
Вычитание алгебраических дробей 75
— многочленов 69
Геометрическая прогрессия 107
Градус 97
Графический способ задания функции 57
решения систем уравнений 78
Действительные числа 48
Деление алгебраических дробей 75
— многочленов 72
Доказательство неравенств 96
— тригонометрических тождеств 102
Значения тригонометрических функций некоторых
углов 99
Измерение углов 97
Иррациональные числа 47
Исследование функции 118
Касательная к графику функции 117
Корень нечетной степени из отрицательного числа 45
Корни уравнения 48
Логарифм 109
Максимум функции 117
Метод интервалов 93
Методы решения рациональных уравнений 52
Минимум функции 117
Многочлен 69
Наибольшее и наименьшее значения функции 118
Непрерывность функции 116
Неравенства 90
Неравенство дробно-рациональное 93
—квадратное 92
— линейное 91
— логарифмическое 111
— показательное 108
— содержащее модуль 94
Область значений функции 55
Область определения функции 55
Одночлен 69
Основное тригонометрическое тождество 98
Переменные величины 54
Предел функции 116
Преобразования графиков 59
Приведение подобных слагаемых 69
Производная 116, 117
Промежутки знакопостоянства 58
Равенства 48
Равносильные преобразования 49
— уравнения 49
Радиан 97
Разложение квадратного трехчлена на множители 52
— многочленов на множители 71
Рациональные уравнения 48
— числа 47
Свойства арифметического квадратного корня 44
— арифметического корня п-й степени 45
— логарифмов 1 09, 110
— последовательностей 105
— степеней 43
— функций 58
— числовых неравенств 90
Симметрическое уравнение 53
Системы линейных неравенств 91
— уравнений 78—83
Сложение алгебраических дробей 75
— многочленов 69
Способы задания функции 55
Степень с натуральным показателем 43
— с рациональным показателем 46
— с целым показателем 44
Табличный способ задания функции 56
Теорема Безу 72
— Виета 50
— Ферма 117
Точки минимума и максимума функции 59
Тригонометрическая окружность 98
Тригонометрические уравнения 99, 115
— формулы 100\ 101
— функции в прямоугольном треугольнике 98
Умножение алгебраических дробей 75
— многочленов 69
Уравнение 48
— биквадратное 51
— дробно-рациональное 77
— иррациональное 85
— квадратное 50
— линейное 49
— логарифмическое 110
— показательное 108
— равносильное 49
— с параметром 88
— содержащее модуль 83
Формулы сокращенного умножения 70
— приведения 100
Функция дробно-рациональная 66
— квадратичная 62
— линейная 61
— логарифмическая 109
— монотонная 58
— непрерывная 116
— нечетная 58
*— обратная пропорциональность 62
— показательная 108
— прямая пропорциональность 60
— степенная 65
— четная 58

852
Предметно-тематический указатель
К разделу «Краткое изложение школьного курса математики»
— у = arccos х
— у = arcctg х
— у = arcsm х
— у - arctg х
223
124
122
223
— i/ = cos x 222
— y^ctgx 114
— y = s\nx 111
— y=tgx 113
Функции 54
Числовые последовательности 104
ГЕОМЕТРИЯ. 7—9 КЛАССЫ
Векторы 156
Вертикальные углы 123
Вписанная окружнбсть 167
Вписанный угол 166
Вычитание векторов 157
Длина дуги окружности 2 75
— окружности 2 74
Зависимости между сторонами и углами
прямоугольного треугольника 152
Задачи на построение 132
Значения тригонометрических функций некоторых
углов 151
Измерение отрезков 121
— углов 122
Касательная к окружности 165
Квадрат 142
Координатная ось 154
Координаты вектора 160
— середины отрезка 155
Косинус 150
Луч 120
Ломаная 172
Многоугольник 172
Неравенство треугольника 137
Окружность 131, 165
Описанная окружность 167
Осевая симметрия 147
Отрезок 119
Параллелограмм 141
Параллельные прямые 2 34
Перпендикулярные прямые 123
Площадь 2 76*
— круга 180
— кругового сектора 180
— параллелограмма 2 77
— правильного многоугольника 2 79
— прямоугольника 2 76
— ромба 2 78
— трапеции 2 79
— треугольника 2 78
Подобие 162, 164
Подобные треугольники 26*2
Полуплоскость 120
Правильный многоугольник 2 73
Преобразование фигур 164
Признаки параллельности прямых 134—135
— подобия треугольников 162
— равенства треугольников 127—129
прямоугольных треугольников 2 39
Пропорциональность отрезков хорд и секущих
окружности 168
Пропорциональные отрезки 147
Прямоугольная система координат 154
Прямоугольник 142
Радианная мера угла 2 75
Расстояние между параллельными прямыми 141
точками 154
— от точки до прямой 138
Решение прямоугольных треугольников 152
— треугольников 2 70, 171
Ромб 142
Свойства параллельных прямых 134
— равнобедренного треугольника 129
Синус 150
Скалярное произведение векторов 160
Сложение векторов 157
Смежные углы 123
Соотношения между сторонами и углами
треугольника 137
Средняя линия треугольника 144
Сумма углов треугольника 236*
Тангенс 150
Теорема косинусов 170
— Пифагора 150
— синусов 2 70
— Фалеса 144
Трапеция 146
Треугольник 126
Тригонометрические тождества 151
— функции любого угла от 0° до 180° 155
острого угла 150
Угол 120
Умножение вектора на число 157
Центральная симметрия 147
Центральный угол 166
Четырехугольник 140
ГЕОМЕТРИЯ. 10—11 КЛАССЫ
Двугранный угол 194
Векторы в пространстве 225
Изображение пространственных фигур на
плоскости 188
Конус 208
Куб 199
Многогранник 196
— вписанный 214
— описанный 214
— правильный 204
Наклонная 188
Объем 217
— конуса 220
— пирамиды 219
— призмы 218
— прямоугольного параллелепипеда 217

Предметно-тематический указатель
К разделам «Задачи» и «Контрольные и проверочные работы. Тесты»
853
— цилиндра 220
— шара 220
Параллелепипед 199
Параллельность плоскостей 185
— прямой и плоскости 185
— прямых 184
Перпендикуляр 188
Перпендикулярность плоскостей 191
— прямой и плоскости 185
— прямых 184
Пирамида 201
-г- вписанная 211
— описанная 211
Площадь поверхности конуса 208
пирамиды 201
призмы 197
цилиндра 206
шара 212
Преобразования фигур в пространстве 224
Призма 197
— вписанная 211
— описанная 211
Прямоугольная система координат
в пространстве 223
Скрещивающиеся прямые 193
Трехгранный угол 194
Тела вращения 206
Угол между плоскостями 194
прямой и плоскостью 193
скрещивающимися прямыми 193
Цилиндр 206
Шар 212
К РАЗДЕЛАМ «ЗАДАЧИ» И «КОНТРОЛЬНЫЕ И ПРОВЕРОЧНЫЕ РАБОТЫ.
ТЕСТЫ»
МАТЕМАТИКА. 5—в КЛАССЫ
Буквенные выражения 231
Вычитание десятичных дробей 233
— натуральных чисел 231
— обыкновенных дробей с одинаковыми
знаменателями 233
— с разными знаменателями 235, 317
— положительных и отрицательных чисел 237, 320
Деление десятичных дробей 233
— натуральных чисел 231
— обыкновенных дробей 236*, 318
— положительных и отрицательных чисел 238, 320
Делимость натуральных чисел 232
Десятичные дроби 315
Доли и дроби 232, 315
Единицы измерений 313
Измерение углов 234
Координатная плоскость 238
Масштаб 234
Модуль числа 237, 320
Наибольший общий делитель 235, 316
Наименьшее общее кратное 235, 316
Натуральные числа 312
Нахождение части от числа 235, 318
Обыкновенные дроби 314
Объем 315
Окружность и круг 237
Отрезок, прямая, луч 231
Отрицательные числа 237, 320
Пересечение прямых 238
Периметр 313, 315
Площадь 313, 315
Признаки делимости 316
Пропорция 236, 319
Проценты 234, 319
Прямая и обратная пропорциональности 236
Разложение на простые множители 235
Раскрытие скобок 238
Решение задач с помощью уравнений 238, 316
— уравнений 314, 316, 321
Сложение десятичных дробей 233
— натуральных чисел 231
— обыкновенных дробей с одинаковыми
знаменателями 233
разными знаменателями 235, 317
— положительных и отрицательных чисел 23 7, 320
Смешанные числа 233, 318
Сравнение натуральных чисел 313
— обыкновенных дробей 317
Среднее арифметическое 234
Умножение десятичных дробей 233
— натуральных чисел 231
— обыкновенных дробей 235, 318
— положительных и отрицательных чисел 238, 320
Формулы 232
Числовой луч 231
Повторение 285—288
АЛГЕБРА. 7—9 КЛАССЫ
Алгебраические дроби 291
Арифметическая прогрессия 250, 339
Арифметический квадратный корень 332
Выражения с переменными 323
Вычитание алгебраических дробей 244
График квадратичной функции 249
Геометрическая прогрессия 250, 339
Деление алгебраических дробей 245
Квадратные корни 245, 291
Квадратный трехчлен 248, 294, 337
Корни п-й степени 251, 340
Метод интервалов 250
Многочлены 242, 243, 289, 325
Неравенства 294, 334
— квадратные 249, 337

854
Предметно-тематический указатель
К разделам «Задачи» и «Контрольные и проверочные работы. Тесты»
— линейные 247, 292
Преобразование выражений 294, 328, 331
Прогрессии 293
Разложение на множители 289
Свойства квадратных корней 245, 332
— степени 324
— функций 249, 337
— числовых неравенств 246, 334
Системы неравенств 247, 249, 292, 335
— уравнений 244, 250, 294, 329, 338
Сложение алгебраических дробей 244
Стандартный вид числа 335
Степень с натуральным показателем 242, 324
— с рациональным показателем 251, 341
— с целым показателем 247, 335
Текстовые задачи 246, 292
Теоремы Виета 246, 333
Тригонометрические тождества 251
— формулы 252, 342
— функции 251
Умножение алгебраических дробей 245
— одночленов 242
Упражнения, содержащие параметры 244, 248, 252
Уравнения 289, 294, 338
— дробно-рациональные 246, 333
— квадратные 246, 292, 333
— линейные 241
Формулы сокращенного умножения 243, 326, 327
Функции 294
Функция квадратичная 242, 249, 337
— линейная 242, 323
— нечетная 340
— четная 340
Числовые выражения 241
— неравенства 246
Повторение 290—293, 325, 329, 336, 343
АЛГЕБРА И НАЧАЛА АНАЛИЗА.
10—11 КЛАССЫ
Дифференцирование 257, 351
Интеграл 259, 355
Исследование функции и построение графика 258,
261
с помощью производной 258, 298, 352
Касательная 257
Корень n-й степени 356
Логарифмы 260, 358
Метод интервалов 257, 351
Наибольшее и наименьшее значения функции 258,
353
Неравенства 298
— иррациональные 260, 356
— логарифмические 260, 359
— показательные 260, 357
— тригонометрические 256, 297, 349, 350
Первообразная 259, 354
Площадь криволинейной трапеции 259, 355
Производная 257, 258, 298, 351, 360
Свойства функций 255, 347
Системы тригонометрических уравнений 256
Степень 260, 357
Тригонометрические тождества 347
— функции 255, 348
Упражнения, содержащие параметры 259, 261
Уравнения 298
— иррациональные 260, 356
— логарифмические 260, 359
— показательные 260, 357
— тригонометрические 256*, 297, 349, 350
Функция логарифмическая 260
— показательная 260
Повторение 297—299, 354, 357, 360, 361
ГЕОМЕТРИЯ. 7—9 КЛАССЫ
Аксиомы планиметрии 263, 364
Биссектриса треугольника 264, 365
Векторы 269, 304, 371
Высота треугольника 26*4, 365
Движение 304
Декартовы координаты на плоскости 303
Доказательство от противного 301
Задачи на построение 302
Измерение отрезков 301
— углов 301
Квадрат 303
Координаты середины отрезка 303
Косинус 268, 370
Котангенс 268, 370
Медиана треугольника 264, 365
Многоугольники 272, 305, 375
Неравенство треугольника 303
Окружность 266, 367
Параллелограмм 267, 368
Параллельные прямые 265, 366
Параллельный перенос 304
Площади фигур 273, 305, 375
Площадь треугольника 305
Подобие треугольников 270, 272, 304, 373
— фигур 305
Правильные многоугольники 305
Преобразования плоскости 269, 371
Признаки параллельности прямых 302
— равенства треугольников 301,302
Прямоугольник 26*7, 368
Равенство векторов 304
— треугольников 264, 301, 302, 365
Расстояние между точками 303
Решение треугольников 305
Ромб 267, 368
Симметрия 304
Синус 268, 370
Смежные углы 301
Соотношения между хордами и касательными 271,
373
Средняя линия треугольника 267, 369
Сумма углов треугольника 265, 302, 367
Тангенс 268, 370

Предметно-тематический указатель
К разделу «Справочные материалы»
855
Теорема косинусов 271, 272, 374
— Пифагора 268, 303, 369
— синусов 271, 272,374
— Фалеса 267, 369
Трапеция 267, 369
Треугольник равнобедренный 264, 365
Углы 263, 301, 364
— вписанные 271, 272, 373
— вписанные в окружность 305
Уравнение окружности 269, 370
— прямой 269, 370
Четырехугольники 303
Повторение 266, 270, 273, 302, 304, 305, 368, 372,
374, 376
ГЕОМЕТРИЯ. 10—11 КЛАССЫ
Аксиомы стереометрии 275, 307, 380
Векторы 277, 309, 383
Двугранные углы 278, 385
Декартовы координаты 309
Конус 279, 387
Координаты в пространстве 276, 382
Многогранники 310
Многогранный угол 278, 385
Наклонная 308
Объем наклонного параллелепипеда 310
Объемы многогранников 280, 310, 387
— тел вращения 280, 310, 388
Параллелепипед 278, 309, 385
Параллельность в пространстве 275, 276, 308, 380,
382
Перпендикуляр 308
Перпендикулярность в пространстве 276*, 308, 381,
382
Пирамида 279, 309, 386
Площадь ортогональной проекции 308
Поверхности тел вращения 310
Призма 278, 385
Расстояние между скрещивающимися
прямыми 308
Свойства параллельного проектирования 307
Сечения многогранников 309
Скрещивающиеся прямые 307
Сфера 310
Тела вращения 310
Углы между прямыми и плоскостями 277, 383
Цилиндр 279, 387
Шар 279, 310, 387
Повторение 278, 281, 309, 311, 384, 389, 390
К РАЗДЕЛУ «СПРАВОЧНЫЕ МАТЕРИАЛЫ»
Абсолютная величина 401
— погрешность 401
— частота события 471
Абсцисса 462
Аксиома параллельности 539
Алгебраическая форма комплексного числа 402
Алгебраическое выражение
— дробное 404
— иррациональное 404
— рациональное 404
— целое 404
Алгебраические неравенства 420, 421
— уравнения 414, 415
Алгоритм Евклида 396
Аналитический способ задания функции 407
Апофема правильного многоугольника 453, 565, 594
— правильной пирамиды 456, 591
усеченной пирамиды 456, 594
Аппликата 462
Аргумент 406
— комплексного числа 403, 623
Арккосинус 412
Арккотангенс 412
Арксинус 412
Арктангенс 412
Асимптота 438
— вертикальная 438
— наклонная 438
Бином Ньютона 423, 479, 621
Биномиальные коэффициенты 423
Биссектриса треугольника 451, 543, 628
— угла 448, 538, 540
Боковая грань пирамиды 456
призмы 455
— поверхность конуса 457
цилиндра 457
— сторона равнобедренного треугольника 451
трапеции 454
Боковое ребро призмы 455
Большой круг шара 458, 602
Важнейшие постоянные 395
Вектор 460, 614
— единичный 460
— нулевой 460
— противоположный 460, 616
— свободный 460
Векторы коллинеарные 460, 614
— компланарные 461, 615
— ортогональные 615
— равные 460
Верные знаки числа 402
Вероятность 471,472
— условная 472
Вершина ломаной 452
— многогранной поверхности 455
— многоугольника 453
— параболы 485
— пирамиды 456*, 589

856
Предметно-тематический указатель
К разделу «Справочные материалы»
— треугольника 450
— угла 448, 538
Взаимно обратные функции 408
— однозначное соответствие 395
— простые числа 397, 476
Взаимное расположение прямых 467
Вогнутость графика 438
Выделение полного квадрата 409, 493, 621
Выпуклость графика 437
Высказывание 423
— истинное 423
— ложное 423
Высота конуса 457, 599
— пирамиды 456, 589
— призмы 455, 585
— треугольника 451, 544, 628
— усеченного конуса 457, 600
— усеченной пирамиды 456*, 593
— цилиндра 457, 597
Вычитание векторов 461,616
— многочленов 405, 478
— чисел 397, 398, 402, 623
Геометрический смысл определенного интеграла 443
производной 434, 525
Гипербола 469, 486, 632
— равнобочная 469
Гипотенуза 451
Главная диагональ матрицы 417
Главное значение аргумента 403
логарифма 404
Градус (градусная мера) 449, 538
Грань многогранной поверхности 455
График функции 407
Графический способ задания функции 407
Движение плоскости 458
— пространства 459
Действительная часть комплексного числа 402
Деление многочленов 405, 479, 480
— отрезка в заданном отношении 610, 612, 632
— с остатком 396, 476
— чисел 396—398, 402, 623
Делитель 396, 475
Десятичная запись натурального числа 476
Диаметр окружности 449, 555
— сферы 458, 601
Дизъюнкция высказываний 423
Директриса параболы 469
Дискриминант 414, 493
Дифференцирование 433, 523
Длина вектора 614, 635
— дуги 450, 555, 629
— кривой 627
— окружности 450, 555, 629
— отрезка 448, 610, 612
Додекаэдр 457, 596, 631
Допустимые значения переменных 404
Дробь 397
— бесконечная десятичная 398
непериодическая 399
периодическая 398
смешанная 398
чистая 398
— конечная десятичная 398
— неправильная 397
— обыкновенная 397
— правильная 397
Дуга окружности 449, 555
е-окрестность 401
Задача о касательной к кривой 432
площади криволинейной трапеции 442, 443
пройденном пути 442
скорости движения точки 432
Задачи на построение 581 —583
Задание последовательностей 495
Заключение импликации 424
— теоремы 424
Закон больших чисел 474
Законы арифметических действий 620
Замечательные линии и точки в треугольнике 451
— пределы 429, 430
Звено ломаной 452
Знаки корней квадратного трехчлена 495
— тригонометрических функций по четвертям 411,
499
Знаменатель геометрической прогрессии 427, 495
— дроби 397
Значения тригонометрических функций некоторых
углов 411, 499, 546
Золотое сечение 621
Икосаэдр 457, 596, 631
Импликация высказываний 424
Интеграл неопределенный 439, 532, 626
— несобственный 444, 627, 628
от неограниченной функции 445
с бесконечными пределами интегрирования
444—445
расходящийся 445
сходящийся 445
— определенный 443, 534
— собственный 444
Интервал 401
Испытание 470
Исследование функции с помощью производной 436,
437,526—530
Каноническое разложение натурального числа 477
Касательная 433, 449, 525, 602, 603
— к окружности 559
Касательная плоскость 602
Катет 451
Квадрант 411, 462
Квадрат 454, 551, 629
Квадрат суммы и разности 405, 478, 621
Квадратный трехчлен 493—495
Классическое определение вероятности 471
Комбинаторика 422
Конус 457, 599, 631
— усеченный 600, 631
Концентрические окружности 557

Конъюнкция высказываний 423
Координаты вектора 463, 618, 619, 635
— вершины параболы 485, 622
— середины отрезка 612, 632
— точки 462, 610, 612
Корень арифметический 400, 480
— квадратного трехчлена 494, 495
— квадратный 400, 480
— многочлена 406, 480
— нечетной степени из отрицательного числа 482
— п-й степени 482
— уравнения 413, 504
— функции 414, 529
Косинус 410, 498
Котангенс 410, 498
Коэффициент одночлена 405
— многочлена 479
Крайние члены пропорции 397
Кратное 475
Кратность корня 406
Кривая второго порядка 468 /
Круг 450, 555, 556
— единичный 410
Куб 456, 588, 596, 630
Куб суммы и разности 405, 478, 621
Левая производная 433
— система координат 462
Логарифм 400, 502, 622
— десятичный 401, 502
— комплексного числа 404
— натуральный 401, 502
Ломаная 452
— замкнутая 453
— простая 452
Луч 401, 448
Максимум 436, 527
Матрица 417
Мгновенная скорость 432
Медиана треугольника 451, 543, 628
Метод введения новой переменной 504
— замены переменной интегрирования 440, 444
— интегрирования по частям 441, 444
— интервалов 421, 521
— исключения (метод Гаусса) 419
— математической индукции 425
— непосредственного интегрирования 440
— подстановки 419, 506
— разложения на множители 504, 506
Методы решения систем уравнений 514, 515
— решения уравнений 504—513
Механический смысл определенного интеграла 443
производной 434
Минимум 436, 527
Мнимая единица 402
— часть комплексного числа 402
Многогранная поверхность 455
Многогранник 455, 595, 596, 630
— выпуклый 455, 595
— правильный 456, 457, 595, 596, 630
Предметно-тематический указатель
К разделу «Справочные материалы»
Многоугольник 453, 594
— выпуклый 453, 594
— правильный 453, 594, 595, 629
Многочлен 405, 478—480
— приведенный 479
Множество 395
— пустое 395
— числовое 395
Модуль вектора 460
— действительного числа 401, 477
— комплексного числа 402, 623
Наибольшее и наименьшее значения функции 437,
531,532
Наибольший общий делитель 396, 476
Наименьшее общее кратное 397, 476
Наклонная 455
Начало координат 461
Независимая переменная 406
Неполное частное 396
Неравенство 419, 516, 623
— двойное 420, 516
— дробное алгебраическое 421
— иррациональное 421, 517, 518
— истинное 419
— квадратное 517
— линейное 517
— логарифмическое 518
— ложное 419
— нестрогое 419, 516
— показательное 518
— с двумя переменными 522
— содержащее модули 422, 477
— строгое 419, 516
— трансцендентное 421
— треугольника 420, 542
— целое алгебраическое 420
Нормаль 434
Нормальный вектор плоскости 467
прямой 465
Нули функции 414, 529
Область допустимых значений уравнения 413
— значений функции 407, 528
— определения алгебраического выражения 404
функции 407, 528
Образующая конуса 457, 599
— цилиндра 457, 597
Обратная пропорциональность 409, 486
Обратные тригонометрические функции 412, 490,
625
Общий делитель 396
— член последовательности 426
Обыкновенная дробь, еле. Дробь 397
Объединение множеств 395
Объем (формулы)
— конуса 457, 599, 631
— куба 456, 630
— параллелепипеда 456*, 587
— пирамиды 456, 589, 590, 630
— призмы 455, 585, 586, 630

858
Предметно-тематический указатель
К разделу «Справочные материалы»
— прямоугольного параллелепипеда 456*, 630
— тел вращения 447, 535, 536, 627
— усеченного конуса 457, 601, 631
— усеченной пирамиды 456, 593, 630
— цилиндра 457, 597, 631
— шара 458, 601, 631
— шарового сегмента 458, 603, 631
сектора 458, 604, 631
слоя 458
Односторонние пределы 431
Одночлен 405
Окрестность 401
Округление с избытком 399
недостатком 399
Окружность 449, 541, 555
— Аполлония 541
— вневписанная 550
— вписанная 545, 547, 559, 560
— описанная 545, 547, 560, 561
— тригонометрическая 497
Октант 462
Октаэдр 457, 596, 631
Определитель второго порядка 417, 636
— системы уравнений 418, 636
— третьего порядка 418, 636
Ордината 462
Орт 462
Ортоцентр 451, 544
Основание конуса 457, 599
— наклонной 455
— перпендикуляра 455
— пирамиды 456, 589
— призмы 455, 585
— равнобедренного треугольника 451, 548
— степени 400
— трапеции 454, 552
— усеченного конуса 457, 600
— усеченной пирамиды 456*, 593
— цилиндра 457, 597
Основной прямоугольник гиперболы 469
Остаток 396, 476
Ось абсцисс 462
— аппликат 462
— действительная 403
— координатная 461
— котангенсов 498
— мнимая 403
— ординат 462
— тангенсов 498
— цилиндра 457
Относительная погрешность 402
— частота события 472
Отношение 397
Отражение относительно оси 459
плоскости 459
Отрезок 401, 448
— единичный 461
Отрицание высказывания 423
Парабола 469, 485, 632
— кубическая 438
Параллелепипед 456, 587, 630
— прямоугольный 456
Параллелограмм 453, 550, 629
Параллельность плоскости и прямой 454, 567
— плоскостей 454, 569
— прямых 449, 454, 538, 539, 567
Параллельный перенос 459
Первообразная 439, 532, 626
Перевод периодической дроби в обыкновенную 496
Переменная 404
— интегрирования 440
Пересечение множеств 395
— окружностей 557
— плоскостей 566
— прямой и плоскости 567
— прямых 449, 454, 566
— сфер 604
— шара (сферы) и плоскости 602
Перестановки 422, 623
Периметр многоугольника 453
Период дроби 398
— тригонометрических функций 411, 412
Перпендикуляр к плоскости 454, 570, 571
Перпендикулярность прямой и плоскости 454, 567,
570, 571
— прямых 449, 539
Пирамида 456, 589, 630
— правильная 456, 591, 630
усеченная 456, 593, 630
Плоский угол трехгранного угла 581
при вершине пирамиды 589
Плоскость 454
— комплексная 403
— координатная 462
Площадь (формулы) 561—566
— боковой поверхности конуса 457, 599, 631
правильной пирамиды 456, 591, 631
усеченной пирамиды 456, 631
прямой призмы 455, 586, 630
усеченного конуса 457, 601, 631
цилиндра 457, 597, 631
— квадрата 454, 551, 561, 629
— криволинейного сектора 446
— криволинейной трапеции 446, 535, 627
— круга 450, 565, 630
— параллелограмма 453, 551, 561, 629
— поверхности вращения 446, 447, 627
шарового сектора 458, 631
— полной поверхности конуса 457, 599, 631
куба 456, 630
параллелепипеда 456, 630
цилиндра 457, 597, 631
пирамиды 589, 630
призмы 585, 586, 630
усеченного конуса 601, 631
правильного многогранника 630, 631
— правильного многоугольника 453, 565, 629
— прямоугольника 454, 552, 561, 629

— ромба 453, 552, 629
— сегмента 450, 565, 631
— сегментной поверхности 458
— сектора 450, 565, 631
— сферы 458, 601, 631
— трапеции 454, 553, 564, 629
— треугольника 545, 546, 549, 561—563, 628
Побочная диагональ матрицы 417
Поворот вокруг точки 459
Подмножество 395
Подобие 460
Подобные одночлены 405
— треугольники 452
— фигуры 460
Подынтегральное выражение 439, 440, 443
Показатель степени 400
Полином 405
Полная группа событий 471
Полуось гиперболы действительная 469
мнимая 469
— отрицательная 462
— положительная 46*2
— эллипса большая 469
малая 469 ,
Полуплоскость 448
Полупространство 454
Полупрямая 401, 448
Полюс 464
Полярная ось 464
Полярные координаты 464, 633
Полярный радиус 464
— угол 464
Порядок бесконечно малых 430
— дифференциального уравнения 442
Последовательность 426*, 495
— бесконечно большая 427
малая 427
— возрастающая 426
— монотонная 426
в широком смысле 426
— невозрастающая 426
— неубывающая 426
— ограниченная 426
сверху 426
снизу 426
— строго монотонная 426
— убывающая 426
Посылка импликации 424
Правая производная 433
— система координат 462
Правила дифференцирования 434, 524, 626
— интегрирования 626
— логарифмирования 622
Правило буравчика 465
— Лопиталя 436
— параллелограмма 460
— треугольника для вычисления определителя 418
нахождения суммы и разности векторов 460
Предел последовательности 426, 625
Предметно-тематический указатель
К разделу «Справочные материалы»
— функции в бесконечности 428
точке 428, 625
слева, справа 431
Предельная абсолютная погрешность 401
— относительная погрешность 402
Пределы интегрирования 443
Преобразование графиков 490, 491
Приведение подобных членов 405
Призма 455, 585
— правильная 455, 586
— прямая 455, 586
Признак параллельности прямой и плоскости 454,
568
плоскостей 569
— перпендикулярности прямой и плоскости 570, 571
Признаки делимости 396,476
— параллелограмма 453, 551
— параллельности прямых 449, 539, 568
— подобия треугольников 452, 542
— прямоугольника 552
— прямоугольного треугольника 547
— равенства треугольников 451, 542
— ромба 552
Принцип математической индукции 425
Приращение аргумента 430
— функции 430
Прогрессия арифметическая 427, 495, 496, 620
— геометрическая 427, 496, 620
бесконечно убывающая 428, 496
Проекция вектора на ось 461
— наклонной 455
— ортогональная 583
— параллельная 584
Произведение вектора на число 461, 616
— векторное 464, 635
— множеств 395
— скалярное 464, 617, 618, 635
—'смешанное 636
— событий 470
Производная 433, 523, 625, 626
— высшего порядка 434, 435, 523, 625, 626
— обратной функции 434, 524, 626
— сложной функции 434, 524, 626
Производные пропорции 398
Промежуток бесконечный 401
— замкнутый 401
— знакопостоянства 529
— открытый 401
— полуоткрытый 401
Промежуточная переменная 407
Пропорция 397, 620
Процент 399
Процентное отношение 399
Прямая 448, 454
— пропорциональность 408, 485
Прямоугольник 454, 552, 629
Равенство векторов 460,614
— комплексных чисел 402
— многочленов 405

860
Предметно-тематический указатель
К разделу «Справочные материалы»
— множеств 395
— отрезков 448
— треугольников 451, 542
— углов 448
— фигур 459
Равносильные неравенства 419
— преобразования уравнения 414, 504
— системы уравнений 418
— уравнения 414
Радиан (радианная мера) 450, 497, 538
Радиус окружности 449, 555
— вписанной 628, 629
— описанной 628, 629
— сферы 458, 601
вписанной 630, 631
описанной 630, 631
Развертка конуса 599
— многогранника 596
— усеченного конуса 601
— цилиндра 597
Разложение вектора 46*3, 6*16*, 617
— квадратного трехчлена на множители 494
— многочлена на множители 406, 479
— составного числа на простые множители 396
Размещения 422, 622
Разность арифметической прогрессии 427, 495
— векторов 461
— квадратов и кубов 405, 478, 621
Расстояние между точками 632
— от точки до плоскости 455, 468, 573, 613, 633
прямой 467, 573, 611, 632
Расстояния в пространстве 573—577
Ребро двугранного угла 455, 579
— многогранной поверхности 455
Решение алгебраического уравнения 413, 504—512
— дифференциального уравнения 442
общее 442
частное 442
— неравенства 420
— прямоугольных треугольников 547
— системы уравнений 418, 514, 515
Ромб 453, 551, 629
Свойство основное дроби 397
пропорции 398
— переместительное 396
— распределительное 396
— сочетательное 396
— характеристическое арифметической
прогрессии 427, 496
геометрической прогрессии 428, 429, 496
Свойства бесконечно малых 428
— биссектрисы угла треугольника 451
— векторного произведения 465, 636
— делимости чисел 475, 476
— диагоналей параллелограмма 551
параллелепипеда 587
— квадратного корня 480; 621
— корней квадратного уравнения 494
— корня /1-й степени 482, 483
— логарифмов 401, 502, 622
— модуля 477
— интеграла 440, 627
— непрерывных функций 431
— неравенств 420
— определителей 417, 418, 636
— определенного интеграла 443, 444, 534
— параллелепипеда 587
— параллелограмма 453, 550
— первообразной 532
— проекции 583, 584, 635
— пропорции 398
— простых чисел 477
— прямоугольника 454, 552
— ромба 453, 551
— скалярного произведения 617, 635
— сочетаний 422, 623
— степеней 484, 621
— треугольника 542
прямоугольного 546
равнобедренного 548
равностороннего 549
— углов в окружности 558
— хорд, секущих и касательной 557, 629
— числовых неравенств 516
Сегмент 401, 450, 555, 630
Сегментная поверхность 458
Сектор 450, 555, 630
Серединный перпендикуляр 451, 540, 544
Сечение конуса 599
— куба 583
— цилиндра 598
— шара 602
Синус 410, 498
Симметрия относительно оси 459
плоскости 459
центра 459
Система координат полярная 464
прямоугольная в пространстве 462
на плоскости 462, 610
— линейных уравнений 418, 419, 514, 515
— неравенств 420
выполненная 420
Скачок 431
Скрещивающиеся прямые 454, 567
Следствие неравенства 419
— уравнения 414
Сложение векторов 460, 615, 635
— вероятностей 472, 473
— двойных неравенств 516
— многочленов 405, 478
— чисел 397, $98, 402, 623
Сложные проценты 399
Событие 470
— , благоприятствующее наступлению другого
события 471
— достоверное 470
— невозможное 470
— случайное 470

События зависимые 472
— независимые 472
— несовместимые 470
— противоположные 470
— совместимые 470
— элементарные 471
Соединения 622
Сочетания 422, 623
Среднее арифметическое 483, 620
— геометрическое (пропорциональное) 483, 621
— квадратичное 621
Средние члены пропорции 397
Средняя линия трапеции 454, 552
треугольника 451, 544
— скорость 1432
Стандартный вид многочлена 405
одночлена 405
Статистическое определение вероятности 472
Степень многочлена 405
— одночлена 405
— числа 400, 483, 484
Сумма бесконечно убывающей геометрической
прогрессии 428, 496
— векторов 460, 635
— интегральная 443
— кубов 405,478,621
— множеств 395
— п первых членов прогрессии 427, 428, 496
— событий 470
— углов треугольника 540
Суперпозиция функций 407
Сфера 458, 601
— вписанная 606, 607
— описанная 605, 606
Схема Горнера 480
Таблица интегралов 440, 626, 628
— первообразных 533
— производных 524, 625, 626
Табличный способ задания функции 407
Тангенс 410, 498
Тела вращения 457, 458, 597—604
Теорема Безу 405, 480
—Бернулли 474
— Больцано—Коши 432
— Вейерштрасса 432
— Виета 415, 494, 621
— косинусов 452, 545, 628
трехгранного угла 581
— Коши 435
— Лагранжа 435, 526
— Менелая 549
— обратная 424
— о монотонности функции 436
непрерывности дифференцируемой
функции 434
существовании определенного интеграла 443
первообразной 440
трех перпендикулярах 455, 571
четырех точках трапеции 55Z
Предметно-тематический указатель
К разделу «Справочные материалы»
— об эквивалентных бесконечно малых 430
— основная алгебры 415
арифметики 396
— Пифагора 452, 546
— прямая 424
— Птолемея 56*1
— Ролля 435
— синусов 452, 545, 628
трехгранного угла 581
— тангенсов 628
— Стюарта 549
— Фалеса 449, 540, 572
— Ферма 435
— Чевы 549
— Эйлера для многогранников 596
Теоремы о бесконечно малых и бесконечно
больших 427
выпуклости и вогнутости графиков 438
непрерывных функциях 432
первообразных 439
пределах последовательностей 426, 427
функций 429
— об экстремумах 436
— сложения вероятностей 472
— стереометрии 568—572
— умножения вероятностей 472
Тетраэдр 457, 590, 596, 631
— правильный 590, 630
Тождественно равные выражения 404
Тождественное преобразование 404
Тождество 404
— основное логарифмическое 502
Точка 448, 454
— касания 449, 458
— комплексной плоскости 403
— критическая 436, 526
— максимума 527
— минимума 527
— перегиба 438
— разрыва 431
второго рода 431
г первого рода 431
— устранимого разрыва 431
— экстремума 527
Трапеция 454, 552, 629
— криволинейная 443
— равнобедренная 454, 554
Треугольник 450, 542, 548, 628
— остроугольный 450, 542
— Паскаля 423, 479
— прямоугольный 450, 546, 628
— равнобедренный 451, 548
— равносторонний (правильный) 451, 548, 628
— тупоугольный 450, 542
Триангуляция 565, 609
Тригонометрическая форма комплексного числа 403,
623
Тригонометрические неравенства 518—521
— тождества 6*23

862
Предметно-тематический указатель
К разделу «Справочные материалы»
— уравнения 416, 510—512
— функции 410—412, 488—490
в прямоугольном треугольнике 499, 546, 623
Угловая минута 449
— секунда 449
Угловой коэффициент касательной 525
Углы в окружности 558, 629
— вертикальные 449, 538
— внутренние накрест лежащие 449, 539
односторонние 449, 539
— смежные 449, 538
Угол 448, 538
— вписанный 449, 558
— двугранный 455, 579
— линейный двугранного угла 579
— между векторами 464, 614, 635
плоскостями 455, 468, 580, 633
прямой и плоскостью 455, 578, 634
прямыми 466, 539, 577, 632, 633
скрещивающимися 455
— многогранный 455, 581
— многоугольника 453
— острый 449, 538
— полный 448
— прямой 449, 538
— развернутый 448, 538
— треугольника 450
внешний 451, 542
— трехгранный 581
— тупой 449, 538
— центральный 449, 558
Умножение вектора на число 461, 616
— вероятностей 472
— двойных неравенств 516
— многочленов 405, 478
— чисел 397, 398, 402, 623
Уравнение биквадратное 415
— графика 407
— двучленное 415
— дифференциальное 441
гармонических колебаний 442
показательного роста 442
убывания 442
— дробное алгебраическое 415
— иррациональное 415, 507
— каноническое гиперболы 469
параболы 469
эллипса 469
— касательной к кривой 434
— квадратное 414, 505
приведенное 414, 505
— линейное 414,505
— логарифмическое 416, 508, 509
— нормали к кривой 434
— окружности 468, 611, 632
— плоскости в отрезках 468, 633
неполное 467
общее 467, 612, 613, 633
— показательное 416, 507, 508
— прямой в отрезках 466, 632
в пространстве 633
неполное 465
общее 465, 611, 632
проходящей через данную точку в данном
направлении 465, 632
две данные точки 467, 632
с угловым коэффициентом 465, 632
— с двумя переменными 492, 493
— с модулем 477, 478
— с одной переменной 413
— с параметром 512, 513
— сферы 614
— трансцендентное 416
— тригонометрическое 416
— целое алгебраическое 415
Условие достаточное 425, 537
существования экстремума 436
— коллинеарности векторов 461, 463, 617—619, 635
— компланарности векторов 617
— начальное 442
— необходимое 425, 537
и достаточное 425, 537
существования экстремума 436
— ортогональности векторов 619, 635
— параллельности плоскостей 468, 613, 633
прямой и плоскости 634
прямых 466, 467, 611, 632, 634
— перпендикулярности векторов 464
плоскостей 468, 613, 633
прямой и плоскости 634
прямых 466, 467, 611, 632, 634
— теоремы 424
Факториал 622
Фигура зеркально-симметричная 459
— осесимметричная 459
— центрально-симметричная 459
Физический смысл производной 525
Фокус гиперболы 469
— параболы 469
— эллипса 469
Формула бинома Ньютона 423
— Вернулли 473
— Герона 452
— Кардано 622
— корней квадратного уравнения 414, 622
— Лапласа 473
— Муавра 404
— Ньютона—Лейбница 444, 626
— общего члена арифметической прогрессии 427,
496
геометрической прогрессии 428, 496
— Пуассона 473
— расстояния между двумя точками 462
от точки до плоскости 468
прямой 467
— сложных процентов 399
— Стирлинга 622
— Эйлера 404, 623

для многогранников 630
Формулы двойных и половинных углов 413, 500,
501, 624
— деления отрезка в данном отношении 610, 612,
— дифференцирования 434, 524
— интегрирования 440
— Крамера 418
— логарифмирования 6*22
— понижения степени тригонометрических
функций 501, 624
— преобразования произведения
тригонометрических функций в сумму 413, 501, 624
— приведения 413, 498, 625
— связывающие обратные тригонометрические
функции 413
тригонометрические 413, 498
— сложения и вычитания аргументов
тригонометрических функций 413, 500, 623, 624
— сокращенного умножения 405, 478, 621
— суммы и разности тригонометрических
функций 413, 501, 624
Функция 406
— бесконечно большая 428, 429
малая 428
— возрастающая 407
— дифференцируемая 433
— дробно-рациональная 409, 486
— интегрируемая 443
— квадратичная 408, 485
— линейная 408, 485
— логарифмическая 410, 488
— многозначная 407
— монотонная 407, 529
в широком смысле 407
— невозрастающая 407
— неограниченная 408
— непрерывная в точке 430
слева, справа 432
на интервале 430
отрезке 432
— непрерывно дифференцируемая 433
— неубывающая 407
— нечетная 407, 528
— неявная 407
— обратимая 408
— обратная 408
— ограниченная 408, 428
— однозначная 407
— от функции 407
Предметно-тематический указатель
К разделу «Справочные материалы»
— периодическая 408, 528
— подынтегральная 439, 443
— показательная 410, 488
— постоянная 408
— разрывная 431
— сложная 407
— степенная 409, 484, 487
— строго монотонная 407
— убывающая 407
— целая рациональная 409
— четная 407, 528
— элементарная 412
— явная 407
Хорда 449, 555
Центр окружности 449
— сферы 458
Цилиндр 457, 597, 631
Числа Фибоначчи 495
Числитель 397
Число действительное 400,475
— е 395
— иррациональное 393, 475
— комплексное 402, 623
сопряженное 402, 623
— натуральное 395, 475
— к 395
— простое 396, 476
— рациональное 397, 495
— смешанное 397
— составное 396
— целое 397, 475
— чисто мнимое 402
Четырехугольник 629
Числовая прямая 401
Член последовательности 426, 495
Шар 458, 601, 631
Шаровой сегмент 458, 603, 604, 631
— сектор 458, 603, 631
— слой 458, 603, 604
Эквивалентные бесконечно малые 430
— неравенства 419
— уравнения 414
Эквиваленция высказываний 424
Экстремум 436, 527
Элемент множества 395
— определителя 417
Элементарные функции 408—412, 485—490
Эллипс 469, 632

Учебное издание
МАТЕМАТИКА
Большой справочник
для школьников и поступающих в вузы
Авторы разделов:
Д. И. Аверьянов, П. И. Ал ты но в, И. И. Баврин и др.
Ответственный редактор М. Г. Циновская
Оформление А. В. Кузнецов
Технический редактор Н. И. Герасимова
Компьютерная верстка О. А Молочное, Т. Г. Гончарова, В. В. Комиссарова
Корректоры Г. И. Мосякина, Е. Е. Никулина
Изд. лиц. № 061622 от 07.10.97.
Подписано к печати 12.08.98. Формат 84 х 108Vie- Бумага типографская. Гарнитура «Школьная»
Печать офсетная. Усл. печ. л. 90,72. Тираж 15000 экз. Заказ № 1019.
Издательский дом «Дрофа».
127018, Москва, Сущевский вал, 49.
По вопросам приобретения продукции
Издательского дома «Дрофа» обращаться по адресу:
127018, Москва, Сущевский вал, 49.
Тел.: (095)289-03-25, 218-16-37, 289-04-85, 218-54-09.
Отпечатано в полном соответствии
с качеством предоставленных диапозитивов
в ОАО «Можайский полиграфический комбинат».
143200, г. Можайск, ул. Мира, 93.