Разбиение фигур на меньшие части - Болтянский В.Г., Гохберг И.Ц.

Автор: Болтянский В.Г. Гохберг И.Ц.

Теги: математика

Год: 1971

Похожие

Теоремы и задачи комбинаторной геометрии

Выпуклые фигуры

Гиппий меньший

Текст

ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЫПУСК 50
В. Г. БОЛТЯНСКИЙ, И. Ц. ГОХБЕРГ
РАЗБИЕНИЕ ФИГУР
НА МЕНЬШИЕ
ЧАСТИ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1971

613
Б 79
УДК 513
Болтянский В. Г., Гохберг И. Ц.
Разбиение фигур на меньшие части, М., «Наука»,
1971, 88 стр. с илл. («Популярные лекции по мате-
математике», вып. 50), 15 к.
В книге популярно излагаются некоторые теоремы, относящиеся
к недавно сформировавшемуся разделу математики — комбинаторной
геометрии.
Предназначена для учащихся 8—10 классов, интересующихся ма-
математикой, студентов и преподавателей математики.
2-2-3 513
76-71
Владимир Григорьевич Болтянский
Израиль Цудикович Гохберг
РАЗБИЕНИЕ ФИГУР НА МЕНЬШИЕ ЧАСТИ
(Серия: «Популярные лекции по математике»)
П., 1971 г., 88 стр. с илл.
Редактор Н. П. Рябенькая
Техн. редактор Л. А. Пыжсва Корректор Л. С. Сомова
Сдано в наОор 10/VII 1970 г. Подписано к печати 10/П 1971 г. Бумага 84X108'/,,
Фпз. печ. л. 2,75. Условн. печ. л. 4,62. Уч.-изд. л. 4,5.
Тираж 100000 экз. Т-02173. Цена книги 15 коп. Заказ 990.
Издательство «Наука>
Главная редакция физико-математической литературы
Москва В-71, Ленинский проспект, 15
2-я типография издательства «Наука». Москва, Шубинский пер., 10
2-2-3
75-71

ОГЛАВЛЕНИЕ
Предисловие 4
Глава I. Разбиение фигур на части меньшего диаметра 5
§ 1. Диаметр фигуры 5
§ 2. Постановка задачи 6
§ 3. Теорема Борсука . » 9
§ 4. Выпуклые фигуры 13
§ 5. Фигуры постоянной ширины 19
§ 6. Вложение в фигуру постоянной ширины .... 21
§ 7. Для каких фигур a (F) = 3? 26
Глава II. Разбиение фигур на плоскости Минковского 34
§ 8. Наглядный пример 34
§ 9. Плоскость Минковского 37
§ 10. Задача Борсука на плоскости Минковского . . 43
Глава III. Покрытие выпуклых фигур гомотетичными 50
§11. Постановка задачи 50
§ 12. Другая формулировка задачи 52
§ 13. Решение задачи о покрытии 53
§ 14. Доказательство теоремы 4 64
Глава IV. Задача освещения . , 67
§ 15. Постановка задачи 67
§ 16. Решение задачи освещения 69
§ 17. Эквивалентность двух задач 71
§ 18. Разбиение и освещение неограниченных выпук-
выпуклых фигур 76
Примечания... 80

ПРЕДИСЛОВИЕ
Эта книга посвящена нескольким связанным между собой воп-
вопросам нового интенсивно развивающегося направления в математи-
математике, которое носит название комбинаторной геометрии.
Рассматриваемые здесь вопросы объединены одной общей идеей о раз-
разрезании фигуры на несколько меньших частей. Что такое «меньшая
часть», можно понимать по-разному, в связи с чем и возникает не-
несколько различных задач, рассматриваемых в этой книге. Все дока-
доказываемые здесь теоремы являются очень «молодыми»: самая «старая»
пи них была найдена польским математиком К. Борсуком примерно
40 лет назад. Эта теорема Борсука является тем стержнем, вокруг
которого развертывается все дальнейшее изложение. Самой «моло-
«молодо?]» теореме едва исполнился год.
Вопросы, которым посвящена книга, вполне доступвы школь-
школьникам старших классов. В то же время книга подводит читателя к
ряду порешенных проблем геометрпи.
Этому же кругу вопросов была посвящена книга тех же авторов
«Теоремы п задачи комбинаторной геометрии» («Наука», 1965). Од-
Однако там основное внимание было уделено проблемам, возникающим
и трехмерном пространстве и пространствах большего числа измере-
измерений. Настоящая книга, напротив, посвящена исключительно воп-
вопросам геометрии на плоскости. Благодаря этому книга может быть
применена в работе школьных математических кружков. Книга «Тео-
«Теоремы и задачи комбинаторной геометрии», упоминавшаяся выше,
будет полезна заипторесонашнимся читателям в качестве материала
для дальнейшего чтения *).
Помещенные п конце книги примечания ('), B) и т. д. предназна-
предназначены для 6<,.'iee подготовленного читателя.
Берег Днестра, близ Тирасполя
20 августа litli!) г. _ В. Болтянский, II. Гохберг
*) Вот еше пара книг, поенншешшх вопросам комбинаторной
геометрии: X а д л и г е р и Добру и и ер, Комбинаторная
геометрия плоскости. «Наука», 1965; Дппцер, Г р к> и б а у м,
К.in. Теорема Xe.i.in и ее приложения (переводе англ,), «Мир»,
11I0S.

ГЛАВА I
РАЗБИЕНИЕ ФИГУР НА ЧАСТИ
МЕНЬШЕГО ДИАМЕТРА
§ 1. Диаметр фигуры
Рассмотрим круг диаметра d. Расстояние между любы-
любыми двумя точками М и N этого круга (рис. 1) не превос-
превосходит d. В то же время можно найти две точки А и В на-
нашего круга, удаленные друг от друга в точности на рас-
расстояние d.
Рассмотрим теперь вместо круга какую-либо другую
фигуру. Что можно назвать «диаметром» этой фигуры?
А
Рис. 1.
Рис. 2.
Сказанное выше наводит на мысль назвать диаметром фи-
фигуры наибольшее из расстояний между ее точками. Иначе
говоря, диаметром фигуры F (рис. 2) мы будем называть
такое расстояние d, что, во-первых, расстояние между
любыми двумя точками М и N фигуры F не превосходит d,
и, во-вторых, можно отыскать в фигуре F хотя бы одну

пару точек А, В, расстояние между которыми в точности
равно d (l).
Пусть, например, фигура F представляет собой полу-
полукруг (рис. 3). Обозначим через А и В концы ограничиваю-
ограничивающей его полуокружности. Тогда ясно, что диаметром фигу-
фигуры F является длина отрезка АВ. Вообще, если фигура
F представляет собой сегмент кру-
круга, ограниченный дугой I и хор-
хордой а, то в случае, когда дуга I
не превосходит полуокружности
(рис. 4, а), диаметр фигуры F ра-
равен а (т. е. длине хорды); в случае
рнс з же» когда дуга I больше полу-
полуокружности (рис. 4, б), диаметр
фигуры F совпадает с диаметром всего круга.
Легко понять, что если F представляет собой много-
многоугольник (рис. 5), то его диаметром является наибольшее
из расстояний между вершинами B). В частности, диаметр
любого треугольника (рис. 6) равен длине его наиболь-
наибольшей стороны.
Заметим, что если диаметр фигуры F равен d, то в фигу-
фигуре F может существовать и много пар точек, расстояние
между которыми равно d. Например, в случае эллипса
(рис. 7) такая пара точек только одна, в случае квадрата
(рис. 8) их две, в случае правильного треугольника (рис. 9)—
три, наконец, в случае круга таких пар точек бесконеч-
бесконечно много.
§ 2. Постановка задачи
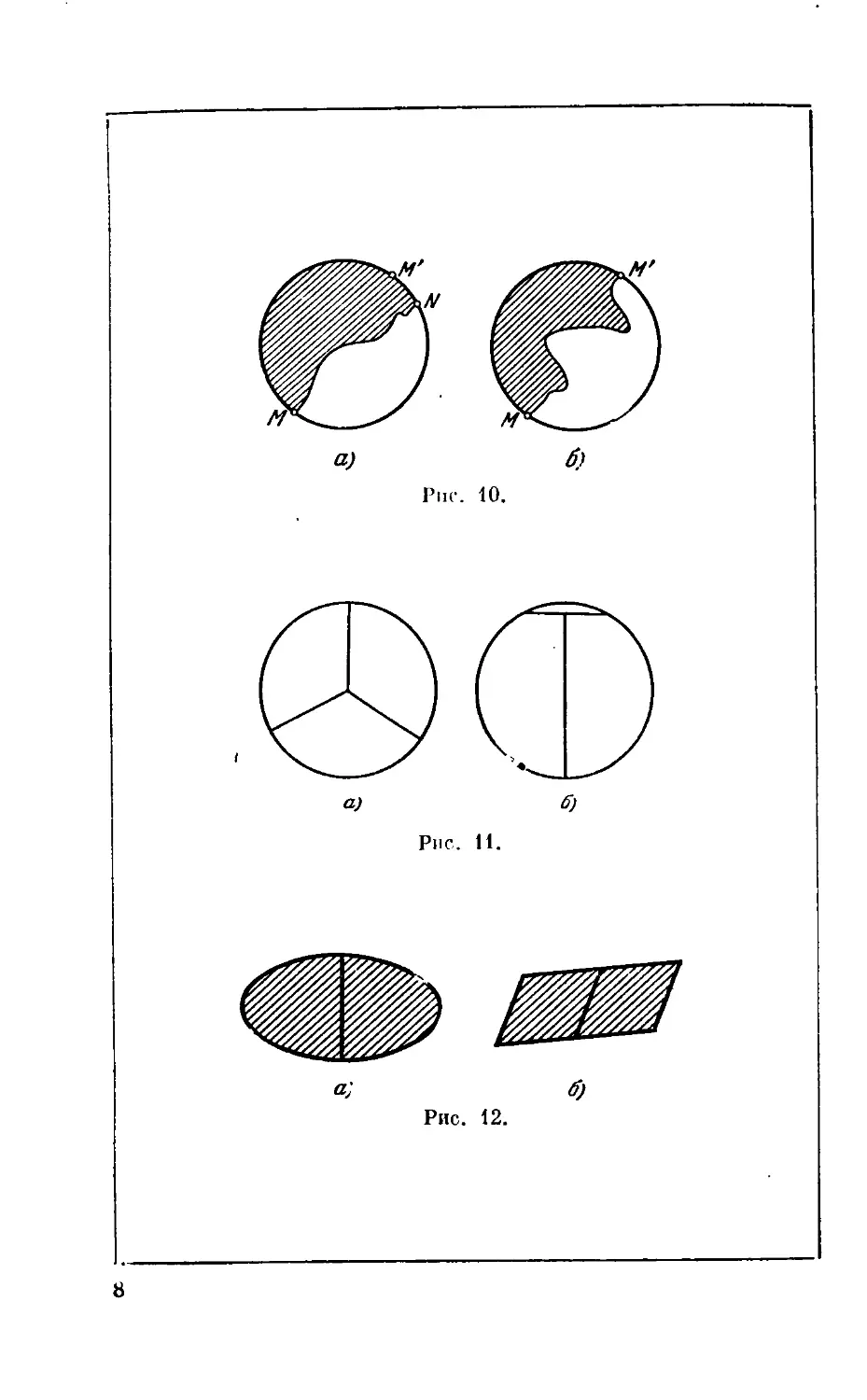
Нетрудно понять, что если круг диаметра d разрезать
некоторой линией MN на две части, то хотя бы одна из
этих частей будет иметь тот же диаметр d. В самом деле,
если М'— точка, диаметрально противоположная точке
М, то она должпа принадлежать какой-нибудь из частей,
и эта часть (содержащая точки М, М') будет иметь диаметр
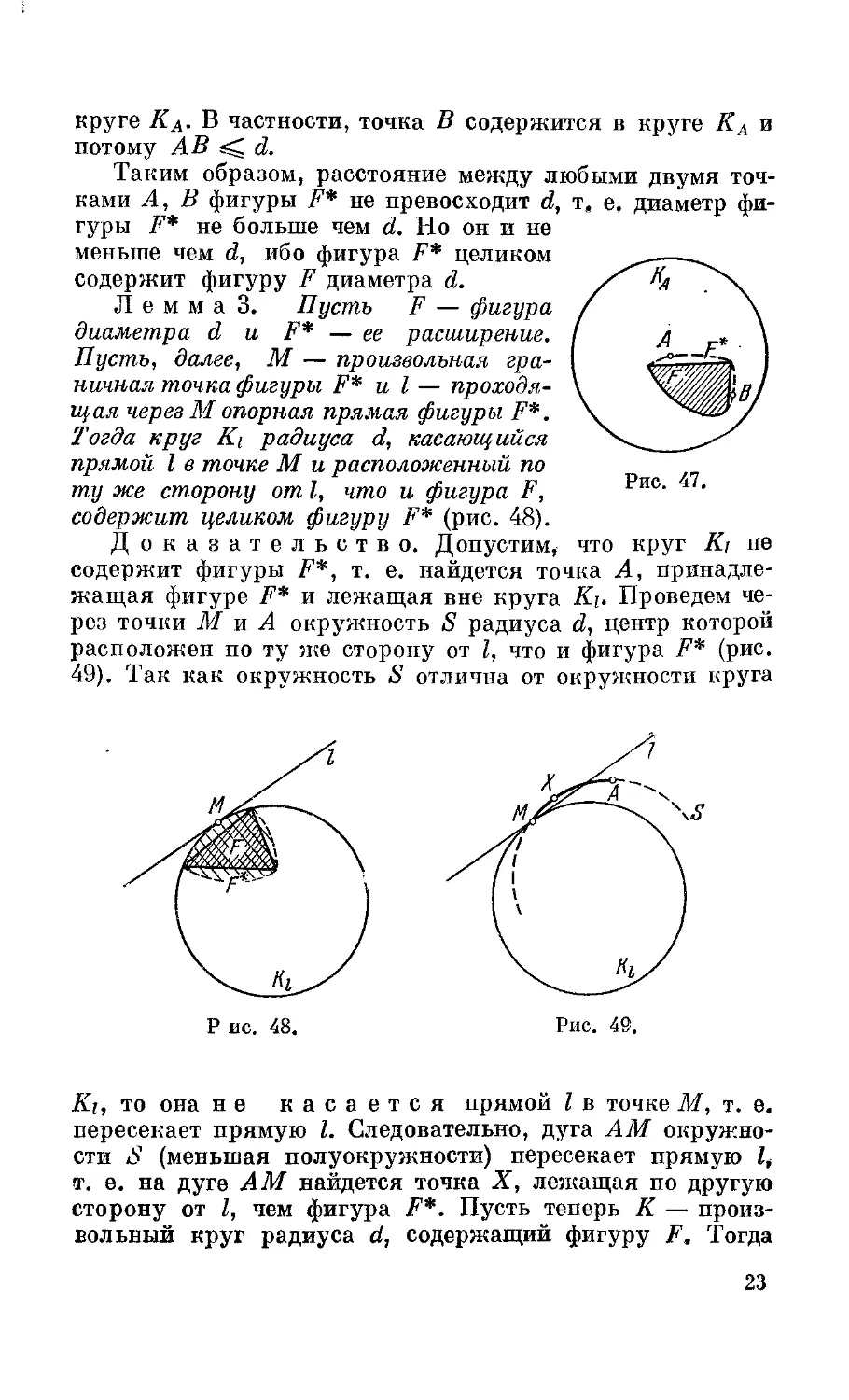
d (рис. 10, а, б) C). Вместе с тем ясно, что круг можно раз-
разрезать на три части, каждая из которых имеет диаметр,
меньший d (рис. 11, а, б).
Итак, круг диаметра d нельзя разбить на две части,
диаметр каждой из которых будет меньше d, но можно раз-
разбить на три такие части. Тем же свойством обладает рав-
равносторонний треугольник со стороной d (если он разбит

/f'
M'
а) б)
Рис. 10.
а) 6)
Рис. 11.
а:
Рис. 12.

на две части, то какая-нибудь из частей должна содержать
две вершины треугольника, и диаметр этой части будет
равен d). Но имеются фигуры, которые можно разбить
на д в е части меньшего диаметра (рис. 12, а, б).
Мы можем рассматривать для любой фигуры F задачу
о разбиении ее на части меньшего диамет-
р а (*). Наименьшее число частей, которые для этого по-
потребуются, обозначим через a(F). Таким образом, если F —
круг или равносторонний треугольник, то a(F) = 3,
а для эллипса или параллелограмма a(F) = 2.
Задачу о том, какие значения может принимать a(F),
поставил и решил (в 1933 г.) известный польский матема-
математик К. Борсук E).
§ 3. Теорема Борсука
Мы уже видели, что для одних плоских фигур a(F)
принимает значение 2, а для других — значение 3. Воз-
Возникает вопрос, нельзя ли найти плоскую фигуру, для ко-
которой a(F) > 3, т. е. такую фигуру, что для разбиения ее
на части меньшего диаметра
нельзя обойтись тремя частя-
частями, а потребуется 4 или боль-
большее число частей? Оказыва-
Оказывается, что на самом деле трех
частей всегда достаточно, т. е.
имеет место следующая теоре-
теорема, установленная Борсуком:
Теорема1. Всякая
плоская фигура F диаметра d
может быть разбита на три
части диаметра меньше d,
т. е. a(F) < 3.
Основную часть доказа-
доказательства составляет следую-
следующая лемма, которую в 1920 г. получил венгерский матема-
математик Пал:
Лемма 1. Всякая плоская фигура диаметра d может
быть заключена в правильный шестиугольник, у которого
расстояние между параллельными сторонами равно d
(рис. 13).
Доказательство. Возьмем прямую I, не пере-
пересекающую фигуры F, и начнем приближать эту прямую к
F (оставляя ее нараллельной самой себе) до тех пор, пока
перемещающаяся прямая не прикоснется к фигуре F
9
Рис. 13.

Рис. 14.
(рис. 14). Полученная прямая Zx обладает тем свойством,
что она имеет хотя бы одну общую точку с фигурой F и вся
фигура F расположена
по одну сторону от lv
Такая прямая называ-
называется опорной прямой
фигуры F(e). Проведем,
крометого,вторую опор-
опорную прямую 1г, парал-
параллельную 1Х (рис. 14). Яс-
Ясно, что вся фигура F бу-
будет находиться в поло-
полосе между прямыми 1г и 1г
и что расстояние между
этими прямыми не пре-
превосходит d (так как диа-
диаметр фигуры Нравен d).
Проведем теперь к фигуре F две параллельные опор-
опорные прямые mlt тга2, составляющие с 1Х угол 60° (рис. 15).
Прямые lv l2, mlt m2 образуют
параллелограмм ABCD с
углом 60° и высотами, не
превосходящими d, внутри
которого целиком заключает-
заключается фигура F.
Проведем теперь две опор-
опорные прямые Pi,p2 фигуры F,
составляющие с ^ угол 120°,
и обозначим через М ъ N ос-
основания перпендикуляров,
опущенных на эти прямые
из концов диагонали АС па-
параллелограмма (рис. 15). Мы
покажем, что направление
прямой I] можно выбрать та-
таким образом, чтобы . выпол-
выполнялось равенство AM=CN.
В самом деле, допустим, что
AM ф CN, и пусть, для оп-
определенности, AM<CCN. Та-
Таким образом, величина у=
=АМ — CN отрицательна. Теперь мы начнем не-
непрерывно изменять направление прямой ^ так, чтобы она
10

Рис. 16.
повернулась на 180° (фигуру F будем оставлять непод-
неподвижной). Вместе с прямой lt будут менять свое положения
и остальные прямые 12,
ff*D ль, ри р2 (так как их
положение полностью
определяется выбором
прямой lt). Поэтому при
повороте прямой I, бу-
будут непрерывно перем -
щаться и ; очки А, С, М,
N С), а значит, будет не-
непрерывно изменяться ве-
величина y=AM—CN. Но
когда прямая lt повернется на 180°, она займет положение,
которое раньше занимала прямая 12. Поэтому мы получим
тот же параллелограмм, что и на рис. 15, но в нем точки
А и С, а также М nN поменяются «ролями». Следовательно,
в этом положении величина у будет уже положитель-
положительной. Если мы теперь изобразим график изменения вели-
величины у при повороте прямой Zx от 0° до 180° (рис. 16), то
увидим, что найдется положение прямой lv при котором
величина [/обращается в нуль, т. е. AM = CN
(ибо, непрерывно изменяясь от отрицательного значения
до положительного, величина у должна в некоторый мо-
момент обратиться в нуль). Мы рассмотрим положение всех
h
ГП)
Рис. 17.
наших прямых как раз в тот момент времени, когда вели-
величина у обращается в нуль (рис. 17). Из равенства
AM = CN вытекает, что шестиугольник, образованный

прямыми 1Х, 1г, тг, т2, pv p2, центрально-симметричен. Каж-
Каждый угол этого шестиугольника равен 120°, а расстояние
между противоположными сторонами не превосходит d.
Если расстояние между рх и р2 меньше d, то мы
раздвинем эти прямые (перемещая их на одинаковое рас-
расстояние) так, чтобы расстояние между раздвинутыми пря-
прямыми было равно d. Точно так же мы поступим с прямыми
lv 1г, а затем с прямыми mv 1Щ. В результате мы получим
центрально-симметричный шестиугольник (с углами 120°),
у которого противоположные стороны удалены друг от дру-
друга на расстояние d (пунктирный шестиугольник на рис. 17).
Из сказанного ясно, что все стороны этого шестиугольника
равны между собой, т. е. этот шестиугольник—правильный,
причем фигура F расположена внутри шестиугольника.
Доказательство теоремы 1. Пусть F —
фигура диаметра d. Согласно доказанной лемме, фигура
F содержится внутри правильного шестиугольника, рас-
расстояние между противоположными сторонами которого
равно d. Покажем, что этот правильный шестиугольник
можно разрезать на три части,
каждая из которых имеет диаметр,
меньший d. При этом фигура F
также разрежется на три части,
диаметр каждой из которых и по-
подавно будет меньше d. Требуемое
разбиение правильного шести-
шестиугольника на три части показано на
рис. 18 (точки Р, Q и R являются
серединами сторон, а О — центр
шестиугольника). Чтобы убедить-
убедиться, что диаметры частей меньше
d, достаточно заметить, что в тре-
треугольнике PQL угол Q прямой, и потому PQ <. PL = d.
Таким образом, теорема 1 доказана.
Из доказательства теоремы 1 легко заключить, что
всякая плоская фигура диаметра d может быть разбита на
три части, диаметр каждой из которых не превосходит
d\f 3/ 2 ш 0,8660 d (так как из равенства PL = d легко вы-
вытекает, что PQ = d"|/r3/2; см. рис. 18). Эта оценка диа-
диаметров частей является наилучшей, ибо, как легко видеть,
круг диаметра d нельзя разбить на три части, диаметр
каждой из которых был бы меньше d ^

В самом деле, часть, имеющая диаметр меньше d У 3 / 2,
высекает на окружности множество, расположенное на
дуге, меньшей 120°, поэтому три такие части не покрыва-
покрывают всей окружности.
§ 4. Выпуклые фигуры
Теорема Борсука не дает еще полного решения вопроса
о том, чему равно число a(F) для произвольной заданной
фигуры F диаметра d. Она дает лишь оценку числа a(F)
сверху: a(F) <; 3. В то же время очевидно, что a(F) >
> 2 для любой фигуры F. Естественно возникает задача:
выяснить, для каких плоских фигур F число a{F) равно
двум и для каких оно равно трем. Решение этой задачи бу-
будет приведено в § 7. При изложении этого решения нам
потребуются некоторые сведения о выпуклых
фигурах, которые мы рассмотрим в этом и двух сле-
следующих параграфах, как правило, без доказательств,
лишь с наглядными пояснениями *).
Рис. 19. Рис. 20.
Фигура F называется выпуклой, если вместе с кажды-
каждыми двумя точками А и В она содержит и весь соединяю-
соединяющий их отрезок АВ (рис. 19). Так, например, треуголь-
треугольник, параллелограмм, трапеция, круг, сегмент круга,
эллипс являются примерами выпуклых фигур (рис. 20).
*) Более подробные сведения о выпуклых фигурах (и, в част-
частности, доказательства упоминаемых здесь свойств этих фигур) чи-
читатель может найти в книгах: Л. А. Л ю с т е р н и к, Выпуклые
фигуры и многогранники, Гостехиздат, М., 1956; И. М. Я г л о м
и В. Г. Болтянский, Выпуклые фигуры, Гостехиздат, М.,
1951. Этому же вопросу посвящена статья «Выпуклые фигуры и тела»
в V томе Энциклопедии элементарной математики (стр. 181—269).
13

На рис. 21 приведены примеры невыпуклых фигур. Фигу-
Фигуры, изображенные на рис. 20, являются ограниченными.
Существуют также неограниченные («простирающиеся в
Рис. 21.
Ряс. 22.
бесконечность») выпуклые фигуры: полуплоскость, угол,
меньший 180°, и др. (рис. 22).
Точки любой фигуры F разделяются на два класса—
внутренние точки и граничные точки. Внутренними счи-
считаются те точки, которые со всех сторон окружены точка-
точками фигуры F. Таким образом, если А — внутренняя точка
фигуры F, то круг некоторого (хотя бы очень маленького)
радиуса с центром в точке А целиком принадлежит фигуре
F (рис. 23). К граничной же точке фигуры F как угодно
близко подходят как точки, принадлежащие фигуре F,
так и точки, ей не принадлежащие (точка В на рис. 23).
Все граничные точки, вместе взятые, образуют некоторую
линию, называемую границей фигуры F. Если выпуклая
фигура F ограничена, то ее граница представляет собой
замкнутую линию (ср. рис, 19, 20),
14

Для дальнейшего важно будет заметить, что всякая пря-
прямая, проходящая через внутреннюю точку выпуклой огра-
ограниченной фигуры F, пересекает границу этой фигуры ровно
в двух точках (рис. 24), причем отрезок, соединяющий эти
Рпс. 23.
Рис. 24.
две точки, принадлежит фигуре F, а вся остальная часть
этой прямой лежит вне фигуры F.
Пусть В — некоторая граничная точка выпуклой фи-
фигуры F. Из точки В проведем всевозможные лучи, прохо-
проходящие через отличные от В точки фигуры F. Эти лучи за-
заполнят либо некоторую полуплоскость (рис. 25, а), либо
Рис. 25.
некоторый угол, меньший 180° (рис. 25, б). В первом слу-
случае прямая, ограничивающая полуплоскость, является
опорной прямой фигуры F. Любая другая прямая, про-
проходящая через точку В, будет рассекать фигуру на две
15

части (рис. 26), т. е. не будет опорной. Иначе говоря, че-
через точку В в этом случае проходит единственная опор-
Рис 26.
Рис. 27.
Рис. 28.
пая прямая фигуры F; она называется касательной к
фигуре F в точке В. Во втором случае (рис. 25, б) вся фи-
фигура F расположена внутри угла ABC,
меньшего 180°, и потому через точку В
проходит бесконечно много опорных
прямых фигуры F (рис. 27). В частно-
частности, опорными являются прямые ВА и
ВС. Лучи ВА и ВС (проведенные жир-
жирной линией на рис. 27) называются полу-
полукасательными в точке В к фигуре F.
Объединяя оба случая вместе, мы ви-
видим, что через каждую граничную точку
В выпуклой фигуры F проходит хотя бы одна опорная пря-
прямая этой фигуры. Если через точку В проходит только одна
опорная прямая фигуры F(pnc. 25, а),
то В называется обыкновенной гранич-
граничной точкой этой фигуры. Если же че-
через точку В проходит бесконечно мно-
много опорных прямых фигуры F, то В
называется угловой точкой (рис. 25, б).
Пусть теперь Ftw. F2 — две вы-
выпуклые фигуры. Тогда пересечение
этих фигур (т. е. их общая часть)
также является выпуклой фигурой
(рис. 28). На рис. 29 показаны две
выпуклые фигуры: круг Fx и угол F2 с вершиной в цент-
центре этого круга; пересечением этих двух фигур является
Рис. 29.
16

круговой сектор. На рис. 30 обе выпуклые фигуры Fv F2
неограничены (каждая из них представляет собой полосу);
пересечением этих фигур является параллелограмм. Ска-
Сказанное выше относится не только к двум, но и к большему
числу фигур: пересечение любого (даже бесконечного) числа
выпуклых фигур является выпуклой фигурой (8). Рис. 31 по-
показывает, что выпуклый многоугольник представляет со-
собой пересечение конечного числа полуплоскостей. Кру»
Рис. 30.
Рис. 31.
(рис. 32) также является пересечением полуплоскостей,
но уже бесконечного их числа. И вообще, любую выпук-
выпуклую фигуру можно представить в виде пересечения беско-
бесконечного числа полуплоскостей.
Рис. 32.
Рис. 33.
Пусть F — некоторая выпуклая фигура и А — ие при-
принадлежащая ей точка. Тогда существует прямая, разделяю-
разделяющая точку А и фигуру F, т. е. такая прямая, что вся фи-
фигура F расположена по одну сторону от нее, а точка А —
по другую (рис, 33), Это свойство выпуклых фигур

является характеристическим: если любую точку, не при-
принадлежащую фигуре F, можно отделить от нее некоторой
прямой, то фигура F выпукла. Иными словами, если фи-
фигура F невыпукла, то найдется не принадлежащая ей точ-
точка, которую нельзя отделить от фигуры F никакой пря-
прямой (рис. 34).
Рис. 34. Рис. 35.
В заключение отметим, что для любой фигуры F диа-
диаметра d существует наименьшая содержащая ее выпуклая
фигура F; эта выпуклая фигура (рис. 35), называемая
выпуклой оболочкой фигуры F, имеет тот же диаметр й.
Возможно, что фигура F н е с в я з н а, т. е. состоит из
двух или нескольких отдельных кус-
кусков — ив этом случае можно опре-
определить ее выпуклую оболочку. На-
Например, на рис. 36 показана выпуклая
оболочка фигуры F, состоящей из
двух отдельных частей Fv F2 и точ-
точки А.
Выпуклую оболочку можно себе
представлять так: на фигуру F натя-
натягивается снаружи замкнутая упругая
(«резиновая») нить; линия, по которой расположится эта
пить, и будет границей выпуклой оболочки F. Но это —
лишь наглядное описание. Точное определение выпук-
выпуклой оболочки выглядит следующим образом. Нужно рас-
рассмотреть все выпуклые фигуры, содержащие фигуру F;
тогда пересечение всех этих выпуклых фигур и будет
представлять собой выпуклую оболочку фигуры F. В са-
самом деле, согласно сказанному выше, это пересечение
будет выпуклой фигурой. Ясно также, что это пере-
пересечение содержит фигуру F и является наимень-
наименьшей выпуклой фигурой, обладающей этим свойством,
18
Рис. 36.

§ 5. Фигуры постоянной ширины
Пусть F — ограниченная выпуклая фигура и ! — не-
некоторая прямая. Проведем к фигуре F две опорные пря-
прямые, параллельные I. Расстояние h между этими двумя
опорными прямыми называется шириной фигуры F в на-
направлении I. Из рассмотрения рис. 37 нетрудно заключить,
что высота равностороннего треугольника является его
наименьшей шириной, а его сторона — наибольшей ши-
шириной. У круга ширина в любом направлении одна и та
же: она равна диаметру круга. Может показаться, что
max
Рис. 37.
Рис. 38.
круг является единственной выпуклой фигурой, обладаю-
обладающей этим свойством. Однако это не так: существует бес-
бесконечное множество фигур постоянной ширины, т. е. та-
таких выпуклых фигур, у которых во всех направлениях
ширина одинакова. Простейшим примером такой фигуры
является треугольник Релло, изображенный на рис. 38.
Он представляет собой пересечение трех кругов радиу-
радиуса h, центры которых находятся в вершинах равносторон-
равностороннего треугольника со стороной h.
Вообще, если F — правильный многоугольник с нечет-
нечетным числом вершин и h — длина наибольшей из его диа-
диагоналей, то, соединяя каждые две соседние его вершины
дугой окружности радиуса h с центром в противополож-
противоположной вершине, мы получаем фигуру постоянной ширины h
(рис. 39). Это построение проходит и в том случае, если
многоугольник диаметра h с нечетным числом сторон не
является правильным, но из каждой его вершины исхо-
исходят две диагонали длины h (рис. 40).
19

Фигуры постоянной ширины обладают рядом интерес-
интересных свойств; мы укажем лишь несколько простейших *).
Прежде всего отметим, что диаметр фигуры постоян-
постоянной ширины равен ее ширине: d — h. Через каждую гра-
граничную точку фигуры постоянной ширины d проходит
хотя бы один диаметр этой фигуры (т. е. хорда, имею-
имеющая длину d). Из этого вытекает, что для любой фигуры F
постоянной ширины справедливо равенство a(F) = 3.
Рис 39
Рис. ;0.
В
Рис. 41.
Рис. 42.
Б олее того, границу фигуры постоянной ширины d
нельзя разбить на две части меньшего диаметра. Это до-
доказывается совершенно так же, как для окружности (стр. 6
и примечание C)).
Всякие два диаметра фигуры постоянной ширины всег-
всегда пересекаются (либо внутри фигуры, либо на ее границе,
рис. 41, 42). При этом, если два диаметра АВ и АС имеют
общую граничную точку А, то дуга ВС радиуса d с
*) Доказательство этих свойств можно найти в указанной на
стр. 13 книге И. М. Яглома и В. Г. Болтянского.
20

Рис. 43.
центром в точке А целиком лежит на границе фигуры
(рис. 42).
Наконец, отметим, что если F — фигура постоянной
ширины и А В — ее диаметр, то прямые lt и 1г,
проходящие через точки А и В
и перпендикулярные к отрезку
АВ, являются опорными прямыми
фигуры F (рис. 43).
§ 6. Вложение в фигуру
постоянной ширины
Вернемся к рис. 39 и обоз-
обозначим правильный многоугольник,
изображенный на нем, через М, а
содержащую его фигуру постоян-
постоянной ширины — через F. Таким
образом, многоугольник М, име-
имеющий диаметр d, содержится
в фигуре F постоянной ширины d.
Для правильных многоугольников с четным числом
сторон аналогичное построение не проходит. Однако и
в этом случае остается вер-
верным, что правильный многоу-
многоугольник, имеющий диаметр d, мож-
можно вложить в фигуру постоянной
ширины d (рис. 44). Интересно от-
отметить, что для правильного много
угольника с нечетным чис-
числом вершин существует единст-
единственная содержащая его фигуре
постоянной ширины, имеющая тот
же диаметр. Для правильного же
многоугольника с четным числом
сторон содержащая его фигура постоянной ширины (име-
(имеющая тот же диаметр) не единственна. Напри-
Например, квадрат диаметра d содержится не только в фигуре,
изображенной на рис. 44, но и в описанном круге, кото-
который также, очевидно, является фигурой постоянной ши-
ширины d.
Сказанное выше о возможности вложения правильных
многоугольников в фигуры постоянной ширины имеет да-
далеко идущее обобщение. Имеет место следующая теорема*
Рис. 44.

Рис. 45.
Теорема 2. Всякая фигура диаметра d может быть
вложена в некоторую фигуру постоянной ширины d.
Для доказательства этой теоремы
мы предварительно введем одно по-
понятие и докажем три леммы.
Пусть F — произвольная плоская
фигура диаметра, не превосходяще-
превосходящего d. Ясно, что можно найти круг
радиуса d, целиком содержащий фи-
ГУРУ F (например, если А — произ-
произвольная точка фигуры F, то круг
радиуса d с центром А целиком со-
содержит фигуру F). Пересечение
всех кругов радиуса d, содержащих фигуру F, мы обо-
обозначим через F* и назовем d-расширением (или просто рас-
расширением) фигуры F. Например, если F есть равносторон-
равносторонний треугольник со стороной d, то F*— треугольник Рел-
ло (рис. 45).
Из определения ясно, что расширение выпуклой фигуры
^(диаметра, не превосходящего d)
само является выпуклой фигурой.
Лемма 2. Пусть F — фигура-
диаметра d. Тогда ее расширение
F* также имеет диаметр d.
Доказательство. Пусть
А и В — произвольные точки фи-
фигуры F*. Возьмем произвольную
точку М фигуры F и рассмотрим
круг Км радиуса d с центром в
точке М (рис. 46). Этот круг
содержит целиком фигуру F
и, следовательно, является одним из тех кругов, которые
дают в пересечении фигуру F*. Поэтому фигура F* также
содержится в круге Км- В частности, точка А принадле-
принадлежит кругу Км и потому
AM < d.
Итак, AM sj d для любой точки М фигуры F. Следо-
Следовательно, круг КА радиуса d с центром в точке А содер-
содержит всю фигуру F (рис. 47) и потому является одним из
тех кругов, которые дают в пересечении фигуру F*. Из
этого вытекает, что фигура F* содержится целиком в
Рис. 46.
22

круге КА. В частности, точка В содержится в круге КА и
потому А В <; d.
Таким образом, расстояние между любыми двумя точ-
точками А, В фигуры F* не превосходит d, т, е, диаметр фи-
фигуры F* не больше чем d. Но он и не
меньше чем d, ибо фигура F* целиком
содержит фигуру F диаметра d.
Л е м м а 3. Пусть F — фигура
диаметра d и F* — ее расширение.
Пусть, далее, М — произвольная гра-
граничная точка фигуры F* и I — проходя-
проходящая через М опорная прямая фигуры F*.
Тогда круг Ki радиуса d, касающийся
прямой I в точке М и расположенный по
ту же сторону от I, что и фигура F,
содержит целиком фигуру F* (рис. 48).
Доказательство. Допустим, что круг К\ не
содержит фигуры F*, т. е. найдется точка А, принадле-
принадлежащая фигуре F* и лежащая вне круга Ki. Проведем че-
через точки М и А окружность S радиуса d, центр которой
расположен по ту же сторону от I, что и фигура F* (рис.
49). Так как окружность S отлична от окружности круга
Рис. 47.
Р ис. 48.
Рис. 40.
Ki, то она не касается прямой I в точке М, т. е.
пересекает прямую I. Следовательно, дуга AM окружно-
окружности S (меньшая полуокружности) пересекает прямую lf
т. е. на дуге AM найдется точка X, лежащая по другую
сторону от I, чем фигура F*. Пусть теперь К — произ-
произвольный круг радиуса d, содержащий фигуру F, Тогда
23

круг К содержит и фигуру F* (ибо К входит в число кру-
кругов, дающих в пересечении фигуру F*), и потому точки
А и М принадлежат кругу К. Отсюда следует, что круг
К содержит целиком и дугу
AM; в частности, точка X
М ^-^^ ° принадлежит кругу К. Итак,
любой круг радиуса d, со-
содержащий фигуру F, содер-
содержит также точку X, и потому
X принадлежит фигуре F*,
вопреки тому, что I — опор-
опорная прямая фигуры F*. По-
Полученное противоречие дока-
доказывает лемму.
рис 50 Л е м м а 4. Пусть F —
выпуклая фигура диаметра d.
Если F не является фигурой постоянной ширины, то су~
ществует выпуклая фигураН диаметра d, содержащая фи-
фигуру F и отличная от нее (а следовательно, имеющая боль-
большую площадь) (9).
Доказательство. Рассмотрим расширение F*
фигуры F. Если F не совпадает с F*, то фигура
# = F*
является искомой: она содержит фигуру F, имеет диа-
диаметр d и, очевидно, имеет большую площадь, чем фи-
фигура F.
Пусть теперь исходная фигура F совпадает с F*.
Так как F не является фигурой постоянной ширины d,
то найдутся две параллельные опорные прямые Г и I"
фигуры F, расстояние между которыми меньше d. Обо-
Обозначим через М общую точку прямой Г и фигуры F, а через
К — круг радиуса d, касающийся прямой V в точке М и
расположенный по ту же сторону от прямой Г, что и фи-
фигура F (рис. 50).
Центр круга К обозначим через А. Точка А не принад-
принадлежит фигуре F (ибо AM = d, а расстояние между
прямыми Г и Г меньше d). Согласно лемме 3, круг К
целиком содержит фигуру F = F*. Следовательно, для
любой точки М фигуры F отрезок AM не превосходит d.
Иначе говоря, фигура F', состоящая из фигуры F и точки
А, имеет диаметр d. Выпуклая оболочка Н фигуры F'
(рис. 50) также имеет диаметр й.Так как площадь фигуры Н,
24

очевидно, больше площади фигуры F (напомним, что точ-
точка А не принадлежит фигуре F), то фигура # является ис-
искомой.
Доказательство теоремы 2. Пусть F —
фигура диаметра d. Если ее расширение F* является
фигурой постоянной ширины, то теорема справедлива.
Пусть теперь F* не является фигурой постоянной ши-
ширины. Будем рассматривать всевозможные фигуры диамет-
диаметра d, содержащие фигуру F*. Так как каждая фигура диа-
диаметра d содержится целиком в некотором круге радиуса d,
то площадь любой такой фигуры не превосходит ltd2.
Обозначим через ^наибольшее из таких целых чи-
чисел, что существует фигура диаметра d, содержащая F*
и имеющая площадь, большую или равную к. Выберем
одну из таких фигур и обозначим ее через Но. Ясно, что
фигура #0 обладает следующими свойствами: она имеет
диаметр d и всякая содержащая ее фигура диаметра d пре-
превосходит ее по площади не больше чем на 1 (иначе вместо
к можно было бы взять к + 1).
Обозначим теперь через кх наибольшее из таких целых
чисел, что существует выпуклая фигура диаметра d, со-
содержащая Но и имеющая площадь, большую или равную
к+ ~ . Одну из таких фигур выберем и обозначим че-
через Ну. Итак, Ну содержит фигуру Но, имеет диаметр d
и всякая выпуклая фигура диаметра d, содержащая Hv
превосходит ее по площади не больше чем на 1/10.
Таким же точно способом мы построим выпуклую фи-
фигуру Н% диаметра d, содержащую Нх и обладающую те.м
свойством, что всякая выпуклая фигура диаметра d,
содержащая Н2, превосходит ее по площади не более чем
на 1/100. Затем мы проведем такое же построение для чис-
числа 1/1000 и т. д.
При проведении этого построения могут представить-
представиться две возможности: либо па некотором шаге этого по-
построения получится фигура IIп, уже являющаяся фигурой
постоянной ширины d (и построение на этом закончится),
либо же ни одна из фигур Нп не будет фигурой по-
постоянной ширины, и мы получим бесконечную последова-
последовательность выпуклых фигур #0, Hv..., #„,..., каждая из
которых содержится в последующей. В первом случае,
когда построение заканчивается на фигуре Нп, имеющей
постоянную ширину d, эта фигура Нп, очевидно, является
25

искомой. Во втором случае обозначим через Н объедине-
объединение всех фигур Но, Нг,..., Нп,... Иначе юворя, Н состо-
состоит из всех тех точек, каждая из которых принадлежит ка-
какой-нибудь фигуре Нп A0).
Фигура Н выпукла. В самом деле, пусть А и В — две
точки этой фигуры. Тогда А принадлежит некоторой фи-
фигуре Нп, аВ — некоторой фигуре Нт. Пусть, для опре-
определенности, тг ]> т. Тогда фигура Нт целиком содержит-
содержится в Нп. Следовательно, обе точки А, В принадлежат
фигуре Нп. Вместе с ними фигуре Нп принадлежит и весь
отрезок АВ. Но тогда отрезок А В целиком принадлежит
фигуре Н, т. е. фигура Н выпукла.
Легко видеть, далее, что фигура И имеет диаметр й.
Действительно, пусть А и В — произвольные две точки
фигуры Н. Тогда, как и выше, обе эти точки принадле-
принадлежат некоторой фигуре Нп. Так как диаметр фигуры Нп ра-
равен d, то АВ <; d.
Докажем, наконец, что Н — фигура постоянной ши-
ширины d. Допустим противное. Тогда, по лемме 4, сущест-
существует выпуклая фигура //' диаметра d, содержащая фигуру
Н и имеющая большую площадь. Пусть п — такое нату-
натуральное число, что разность площадей фигур Н' и Н боль-
больше чем 1/10™. Тогда разность площадей фигур И' и Нп,
подавно, больше чем 1/10". Но это противоречит выбору
фигуры Нп. Полученное противоречие и завершает дока-
доказательство теоремы.
§ 7. Для каких фигур a(F) = 3?
Как мы уже отмечали, в некоторых случаях фигуру
диаметра d можно лишь однозначно дополнить до фигуры
постоянной ширины d (как, например, в случае правиль-
правильного многоугольника с нечетным числом сторон). В дру-
других случаях такое дополнение неоднозначно. В качестве
еще одного примера фигуры, допускающей неоднозначное
дополнение до фигуры постоянной ширины, укажем круг,
от которого отрезан сегмент с дугой, меньшей полу-
полуокружности. Диаметр d этой фигуры F равен, очевидно, диа-
диаметру исходного круга К. Поэтому круг К является од-
одной из фигур постоянной ширины d, содержащей фигуру F.
Другое дополнение до фигуры постоянной ширины по-
показано на рис. 51 (на котором AN = NB = АС =
= BD = d, а \уАВ, \jDN и <jCN—дуги радиуса d).
26

Теперь мы вернемся к сформулированной в начале § 4
задаче о нахождении всех фигур F, для которых a (F) = 3.
В этом параграфе мы дадим решение этой задачи, полу-
полученное в 1969 г. В. Г. Болтянским.
Теорема 3. Для плоской фигуры F диаметра d ра-
равенство a(F) = 3 имеет место в том и только в том слу-
случае, если фигура F однознач-
н о дополняется до фигуры
постоянной ширины d.
Так, например, для всякого
правильного многоугольника F
с нечетным числом сторон имеет
место равенство a (F) = 3, а
для всякого правильного мно-
многоугольника с четным числом
сторон имеет место равенство
a (F) = 2 (последнее, впрочем,
ясно и непосредственно; см.
рис. 52). Точно так же круге от-
отрезанным сегментом (ср.рис. 51)
удовлетворяет соотношению
a (F) — 2 (что также ясно непосредственно; см. рис. 53).
Прежде чем переходить к доказательству теоремы 3,
мы докажем ряд вспомогательных предложений.
Рис. 52.
Рис. 53.
Лемма 5. Пусть F —¦ плоская выпуклая фигура диа-
диаметра d. Если существует такой круг радиуса d, кото-
который содержит фигуру F и центр которого не принадлежит
фигуре F*, то фигура F неоднозначно дополняется до фи-
фигуры постоянной ширины d.
Доказательство. Пусть К — круг радиуса d,
содержащий фигуру F, центр А которого не принадле-
27

жит фигуре F*. Так как F* есть пересечение всех кругов
радиуса d, содержащих фигуру F, и так как F* не содер-
содержит точки А, то найдется круг К' радиуса d, содержащий
фигуру F и не содержащий точки А. Центр круга К' обо-
обозначим через В (рис. 54). Ясно, что длина отрезка АВ
больше d (ибо круг К' не содержит точки А).
Присоединяя теперь к фигуре F точку А, мы получим
несвязную фигуру F', диаметр которой, как легко видеть,
равен d. (Действительно, рас--
стояние от «новой» точки А до
любой точки фигуры F не пре-
превосходит d, так как F содер-
содержится в круге К.) Точно так же,
присоединяя к фигуре F точку
В, мы получим несвязную фигу-
фигуру F", диаметр которой равен d.
Выберем теперь какую-нибудь
фигуру Ф' постоянной ширины
d, содержащую фигуру F', и
какую-нибудь фигуру Ф" посто-
г, янной ширины d, содержащую
ис' ° ' фигуру F" (это можно сделать
по теореме 2). Ясно, что фигу-
фигуры Ф'и Ф" не могут совпадать (ибо АВ^> d, и потому ни-
никакая фигура постоянной ширины d не может содержать
обе точки А, В). В то же время каждая из фигур Ф',
Ф" содержит фигуру F. Таким образом, F неоднознач-
неоднозначно дополняется до фигуры постоянной ширины d.
Лемма 6. Пусть F — фигура диаметра d и Ф —
содержащая ее фигура постоянной ширины d. Тогда фигура
I * целиком содержится в Ф.
Доказательство. Пусть А — произвольная
точка, не принадлежащая фигуре Ф. Проведем прямую I,
отделяющую точку А от фигуры Ф. Обозначим через V и
I" опорные прямые к фигуре Ф, параллельные I, а через В
и С — общие точки этих прямых с фигурой Ф (рис. 55).
Тогда отрезок ВС перпендикулярен к прямым Г, Г и
имеет длину d. Обозначим через Kg круг радиуса d с цент-
центром в точке С. Этот круг целиком содержит фигуру Ф,
а значит, и фигуру F. Поэтому Кс является одним из кру-
кругов, дающих в пересечении фигуру F*. Следовательно,
F* содержится целиком в круге К с- Так как точка А не
принадлежит кругу Кс, то она не принадлежит и фигуре
28

I
Рис. 55.
F*. Итак, если точка А не принадлежит фигуре Ф, то она
не принадлежит и фигуре F*. Это и означает, что F* це-
целиком содержится в фигуре Ф.
Л е м м а 7. Фигура F диаметра d в том и только в
том случае однозначно дополняется до фигуры постоян-
постоянной ширины d, если ее расшире-
расширение F* является фигурой посто-
постоянной ширины d.
Доказательство. Пред-
Предположим, что F* есть фигура
постоянной ширины d, и пусть
Н — произвольная фигура по-
постоянной ширины d, содержащая
F. Тогда, согласно лемме 6, фи-
фигура Н должна содержать цели-
целиком и F*. Так как F* уже есть
фигура постоянной ширины d,
то отсюда следует, что Н совпа-
совпадает с F*. Таким образом, F од-
однозначно дополняется до фигуры постоянной ширины d.
Пусть теперь F* не есть фигура постоянной ширины
d. Тогда можно провести две параллельные опорные пря-
прямые I, /'фигуры F*, расстояние
между которыми меньше d
(рис. 56). Пусть М — точка, в
которой прямая I встречает фи-
фигуру F*. Обозначим через К{
круг радиуса d, касающийся
прямой I в точке М и располо-
расположенный по ту же сторону пря-
прямой Z, что и фигура F*. Соглас-
Согласно лемме 3, круг Kt содержит
фигуру F*. Ясно при этом, что
центр А круга Kt не принадле-
-,кит фигуре F* (ибо фигура F*
прямыми I, Г, а центр А лежит
ние этой полосы). Но тогда, согласно лемме 5, фигура F не-
неоднозначно дополняется до фигуры постоянной ширины d.
Л е м м а 8. Если при выполнении условий леммы 3 точ-
точка М не принадлежит фигуре F, то найдутся такие
две точки А, В фигуры F, лежащие на окружности
круга К[, что дуга АВ этой окружности {меньшая полу-
полуокружности) содержит точку М (рис. 57).
л ')кит в
Р"с- <г>6.
полосе между
29

Доказательство. Обозначим через N точку
круга Ki, диаметрально противоположную точке М. Для
простоты языка условимся считать прямую I «горизон-
«горизонтальной», а круг Ki — лежащим «под» прямой I (рис. 57).
'К'
Рис. 57.
Рис. 58.
Если бы левая полуокружность, определяемая точками
М и N, не содержала ни одной точки фигуры F, то круг
Kt можно было бы сдвинуть вправо, и сдвинутый круг К'
все еще содержал бы фигуру F (а значит, и фигуру F*).
Но тогда фигура F* содержалась бы в пересечении кру-
кругов Kt и 1С, и прямая I не могла бы быть опорной для
F* (рис. 58). Это рассуждение показывает, что лопая полу-
полуокружность содержит (хотя бы одну) точку А фигуры F
(рис. 57). Точно так же правая полуокружность содер-
содержит точку В фигуры F. Далее так как точки А, В, М при-
принадлежат фигуре F*, то AM <; d, BM <Si d, и потому та
из двух дуг, определяемых на окружности круга Ki точ-
точками А и В, которая содержит точку М, будет меньше
полуокружности (она даже не превосходит шестой части
окружности, ибо АВ ^ d).
Лемма 9. Если F — фигура, диаметр которой
меньше d, то ее d-расширение F* также имеет диаметр,
меньший d.
Доказательство. Обозначим диаметр фигуры F че-
через d', так что d' <z d. Далее, ^'-расширение фигуры F обо-
обозначим через Fr, a d-расширение фигуры F будем по-преж-
по-прежнему обозначать через F*. Пусть точка М плоскости не при-
принадлежит фигуре F', т. е. существует круг К' радиуса dr,
содержащий фигуру F, но не содержащий точки М. Обо-
Обозначим через А ближайшую к М точку круга К'
30

ф.
(рис. 59) и построим круг К радиуса d, содержащий круг
К' и внутренним образом касающийся его в точке А.
Ясно, что круг К также не содержит точку М (и содержит
фигуру F), откуда следует, что М не принадлежит фигуре
F*. Итак, если точка М не принад-
принадлежит фигуре F', то она не принад-
принадлежит и фигуре F*, так что фигура
F* целиком содержится в F'. Но
d'-расширение F' фигуры F диаметра
d' имеет, согласно лемме 2, диаметр
d'. Следовательно, диаметр фигуры
F* не превосходит d', т. е. меньше d.
Доказательство теоре-
теоремы 3. Пусть F — фигура диаметра рис 59
d, которая неоднозначно дополняется
до фигуры постоянной ширины d. Докажем, что a(F) = 2.
В самом деле, пусть Фх и Ф2 — две различные фигуры
постоянной ширины d, содержа-
содержащие F. Ясно, что найдется гра-
граничная точка А фигуры Фг, ле-
лежащая внутри фигуры Ф2.
Через точку А можно провести
опорную прямую 1г фигуры Фр
Пусть Z2— вторая опорная пря-
прямая фигуры Ф1? параллельная
lv а В — точка встречи этой
опорной прямой с фигурой Ф1
(рис. 60). Тогда прямая АВ пер-
перпендикулярна к прямым lv 12.
Мы докажем, что прямая АВ
рассекает фигуру F на две части, каждая из которых имеет
диаметр, меньший d.
Допустим, напротив, что какая-нибудь из этих частей
имеет диаметр d, т. е. по одну сторону прямой АВ найдут-
найдутся точки С, D фигуры F, находящиеся друг от друга на
расстоянии d. Тогда отрезки А В я CD являются диа-
диаметрами фигуры Ф2 постоянной ширины (напомним,
что фигура F содержится в Фх), и потому отрезки АВ и
CD должны либо пересекаться в точке, являющейся внут-
внутренней для обоих отрезков АВ, CD, либо должны иметь
общую концевую точку. Первое невозможно, поскольку
точки С, D расположены по одну сторону прямой А В. Сле-
Следовательно, отрезки АВ vi CD должны иметь общую кон-
Рпг. 60.
31

цевую точку. Но точка В лежит вне фигуры Фа
(ибо А лежит внутри этой фигуры и AB—d), а значит
и вне фигуры F, в то время как точки С, D принадлежат
фигуре F. Следовательно, точка В не может быть общий
концом отрезков А В и CD. Наконец, точка А, лежащая
внутри фигуры Ф2, отстоит от любой точки фигуры Ф2
менее чем на d и потому не может совпадать с концом
отрезка CD, расположенного в Ф2 и имеющего длину d.
Полученное противоречие показывает, что каждая из
частей, на которые прямая А В рассекает фигуру F, имеет
диаметр, меньший d, и потому a(F) = 2.
Пусть теперь фигура F диаметра d однозначно допол-
дополняется до фигуры постоянной ширины d. Покажем, что в
этом случае a(F) = 3. Допустим, напротив, что a(F) = 2,
т. е. F можно представить в виде объединения двух фигур
Qv Q2, каждая из которых имеет диаметр, меньший d.
Так как F однозначно дополняется до фигуры постоян-
постоянной ширины d, то F* есть фигура постоянной ширины d
(лемма 7). Обозначим й-расширение фигур Qv Q2 через Qi*,
Q2*- Согласно лемме 9, каждая из фигур Qj*, Q2* имеет
диаметр, меньший d.
Границу фигуры F* обозначим через Г. Пусть М —
произвольная точка кривой Г. Если точка М принадле-
принадлежит фигуре F, то, очевидно, М содержится в объединении
фигур Qt и (?2 и подавно содержится в объединении фигур
Qi* и Qi*- Пусть теперь точка М не принадлежит мно-
множеству F. Проведем опорную прямую I фигуры F*, про-
проходящую через точку М, и построим круг К/ радиуса d,
касающийся прямой I в точке М и расположенный по ту
же сторону от I, что и фигура F* (рис. 61). Центр N этого
круга принадлежит фигуре F* (ибо MN J_ I и MN = d,
т. е. MN есть диаметр фигуры F* постоянной ширины d).
Так как точка М не принадлежит фигуре F, то, соглас-
согласно лемме 8, найдутся такие две точки А, В фигуры F, ле-
лежащие на окружности круга Ki, что дуга АВ этой окруж-
окружности (меньшая полуокружности) содержит точку М.
Таким образом, AN = BN = d, т. е. AN и BN являются
диаметрами фигуры F* постоянной ширины d. Из зтого
следует, что N есть угловая точка линии Г и вся дуга
АВ принадлежит кривой Г, так что М есть обычная (не-
(неугловая) точка кривой Г. Но тогда ясно, что точка ./V
должна принадлежать фигуре F (ибо в противном слу-
случае, поменяв ролями М и N, мы с помощью аналогичного
32

/V
Рис. 61.
рассуждения получили бы, что М — угловая, а N — не-
неугловая точка линии Г).
Так как точка N принадлежит фигуре F, то она содер-
содержится хотя бы в одной из фигур Qv Q2. Пусть, для опре-
определенности,точка N принадлежит фигуре Qv Так как AN =
= BN = d, а множество (^имеет диаметр, меньший d,
то точки А, В не принадлежат
множеству Qt. А так как обе эти
точки принадлежат фигуре F, то
обе точки А, В содержатся в
фигуре Q2, Дуга АВ радиуса d,
содержащая точку М, очевидно,
принадлежит любому кругу ра-
радиуса d, содержащему точки А
и В. В частности, эта дуга при-
принадлежит любому кругу радиуса
d, содержащему фигуру Q2. Отсю-
Отсюда вытекает, что точка М принад-
принадлежит фигуре Q2*. Аналогично, если ^принадлежит фигуре
Q2, то М принадлежит фигуре Qx*. Таким образом, в любом
случае точка М принадлежит объединению фигур Q±* и Q2*.
Итак, любая точка М линии Г (как принадлежащая,
так и не принадлежащая фигуре F) содержится в объедине-
объединении фигур Qj* и Q2*, т. е. линия Г может быть разбита
на две части, каждая из которых имеет диаметр, меньший
d. Но это невозможно, так как Г — граница фигуры по-
постоянной ширины (ср. стр. 20). Полученное противоре-
противоречие и завершает доказательство теоремы 3 (и).
Заметим в заключение, что доказанная теорема может
быть, согласно лемме 7, сформулирована так:
Пусть F — фигура диаметра d; равенство a(F) — 3 име-
имеет место в том и только в том случае, если F* является
фигурой постоянной ширины d.
Отметим также следующий любопытный факт:
Для любой плоской фигуры F диаметра d имеет место
равенство a(F) — a(F*).
В самом деле, если a(F) = 2, то существуют две раз-
различные фигуры Ф1( Ф2 постоянной ширины d, содержа-
содержащие F. Тогда согласно лемме 6 фигура F* содержится в
каждой из фигур Ф1; ф2, т. е. F* также неоднозначно до-
дополняется до фигуры постоянной ширины d. Следователь-
Следовательно, a(F*) = 2, т. е. a(F*) = a(F). Если же a(F) = 3, то
подавно a(F*) = 3.
2 В. Г. Болтянский, И. Ц. Гохберг

ГЛАВА II
РАЗБИЕНИЕ ФИГУР НА ПЛОСКОСТИ
МИНКОВСКОГО
§ 8- Наглядный пример
Если выбран отрезок LM, принимаемый за единицу
длины, то длина произвольного отрезка АВ определяется
как число, равное отношению А В : LM. Длина отрезка АВ
зависит только от его величин ыи совсем не зависит
от направления и расположения этого отрезка.
Однако в некоторых задачах возникает необходимость в
другом определении длины отрезка, при котором длина
отрезка зависит как от его величины, так и от его
направления. Для определения длины в таком но-
новом смысле необходимо задать единицу длины для каждо-
каждого направления в отдельности. Весьма интересное опре-
определение такого рода было предложено в конце XIX в.
известным немецким математиком Г. Минковским. Это оп-
определение мы и рассмотрим в этом параграфе. Для пояс-
пояснения характера этого определения разберем сначала на-
наглядный пример.
Представим себе, что мы находимся в огромном городе
М весьма правильной планировки, на карте которого по-
половина улиц идет строго вертикально через всю террито-
территорию города, а половина строго горизонтально (рис. 62).
Некто желает пройти (или проехать в автомобиле) из точ-
точки А в точку В в этом городе. Каким будет в его представ-
представлении «расстояние» между этими точками?
Имея карту города, можно, конечно, провести по линей-
линейке отрезок АВ и измерить его длину. Однако такое расстоя-
расстояние было бы в этом городе лишь воображаемым, так как
34

Движение по отрезку АВ требовало бы умения проходить
сквозь степы домов *). Реальным расстоянием между точ-
точками А ж В следует считать длину показанной па рис. 63
ломаной АСВ. Кроме АС В существует целый ряд других
JL_
J
]
I УлАкавеми'/еснтГ
J| || || ||_
Ул
ш/<о0еная
В
1-
Рис. 62.
А
JL
С
гс
ЙС
В
Рис. 63.
реальных путей, идущих из А в В и имеющих ту же дли-
длину (рис. 64), но более коротких реальных путей не сущест-
существует.
Если ввести на карте этого города систему координат,
оси которой идут вдоль двух перпендикулярных улиц, то,
в силу сказанного, ясно, что реальное расстояние между
точками А{хи уг) и В(хг, у2) этого города М (т. е. «длина»
отрезка АВ в геометрии этого города) равно
ДЛ.м^-П -~ Х% — Xi j -р [ У2 — У\ [ (*)
(рис. 65). Умея находить «расстояние» между двумя точ-
точками в городе М, можно поставить вопрос о нахождении
'единичного круга» в этом городе, т. е. множества всех
тех точек, которые находятся на «расстоянии», не превосхо-
превосходящем единицы, от начала координат О. Так как точка О
*) Мы предполагаем, что наш Некто не обладает способностями
главного героя фильма «Человек проходит сквозь стену».
2* 35

имеет координаты @, 0), то, согласно формуле (*), рас-
расстояние от точки О до точки С(х, у) равно
дл.мОС = \х | -|- | ц |.
Следовательно, «единичный круг» в этом городе опре-
определяется неравенством
\х\ + |г/|< 1.
Теперь ясно, что на карте этого города указанный единич-
? К А
М
N
В Р F С
ал.АСВ=дл.АЕГВ=вл, ANHFB= U.AKLH&BPB^...
Рис. 64.
ный круг изображается квадратом (рис. 66). Поль-
Пользуясь этим единичным кругом, можно теперь находить
У
У,
Уг
О
@,1)
-if.
B(xz,yz)
Рис. 65.
расстояния между любыми двумя точками так, как было
указано в начале этого параграфа. Именно, если даны две
произвольные точки А и В, то мы найдем на границе «еди-
36

ничпого круга» такую точку С, что ОС || АВ, и тогда дли-
длина отрезка АВ будет равна отношению АВ:ОС.
Эта идея — считать единичным кругом некоторую вы-
выпуклую центрально-симметричную фигуру — и лежит в
основе геометрии Минковского на плоскости *).
§ 9. Плоскость Минковского
Пусть задана ограниченная плоская выпуклая фигу-
фигура G, симметричная относительно некоторой точки О
(рис. 67). Через Г обозначим кривую, ограничивающую фи-
фигуру G. Будем считать, что единицей длины, соответствую-
соответствующей направлению I, явля-
является отрезок OL луча, па-
параллельного направлению
I, от точки О до точки L
пересечения этого луча с
линией Г. Длина отрезка
АВ относительно новой
системы масштабов опреде-
определяется теперь как отпоше- рис> 67.
ние AB-.OL, где OL —
единица длины, параллель- __у
пая направлению I, определяемому вектором АВ. (В случае,
когда точка А совпадает с точкой В, естественно считать,
что длина отрезка АВ равна нулю.) В дальнейшем длину
отрезка АВ относительно системы масштабов, порождае-
порождаемой фигурой G, мы будем обозначать символом дл.е АВ.
¦ Очевидно, что дл.с ОМ = 1 в том и только в том случае,
когда точка М лежит на кривой Г. Если точка М лежит
внутри фигуры G, то дл.с ОМ <С 1, а если, наоборот, точ-
точка М лежит вне фигуры G, то дл.й ОМ ^> 1.
Заметим, что если фигура G совпадает с кругом, то мы
придем к обычному определению длины, при котором дли-
длина отрезка зависит только от его величины, но не от напра-
направления, а если G является квадратом (рис. 66), то мы при-
приходим к определению длины, рассмотренному в предыду-
предыдущем параграфе.
*) О других способах измерения расстояний (и о том, что такое
«расстояние» п самом общем математическом понимании) читатель
может прочитать в книге Ю. Л. Шрсйдера, Что такое расстоя-
расстояние? (Серия «Популярные лекции по математике», вып. 38, Фпзмат-
гиз, 1963).
37

Укажем теперь основные свойства нового определения
длины. Как мы уже знаем,
причем знак равенства в последнем соотношении имеет
место в том и только в том случае, когда точки А и В
совпадают. Кроме того, из центральной симметричности
фигуры G вытекает ра-
С_ / /Д X вепство
дл.<з АВ — дл.о В А.
Наконец,, если АВ и
CD — параллельные ог-
рэзки, причем АВ: CD =
= к, то
дл.с АВ =: А-дл.д CD.
До сих пор мы нигде
не пользовались выпук-
выпуклостью фигуры G. Ока-
Оказывается, что выпук-
выпуклость фигуры G обеспечивает справедливость следующего
очень важного свойства новой длины:
Неравенство треугольника. Во всяком
треугольнике ABC длина одной из сторон {относительно
масштабов, определяемых фигурой G) не превосходит сум-
суммы длин двух других сторон.
Доказательство. Положим
Рис. 68.
=- с.
Далее, проведем в фигуре G «радиусы» ОР и OQ, имеющие
то же направление, что и векторы ВС и СА (рис. 68). За-
Затем возьмем на отрезке ОР такую точку М, что ОМ : МР =
= а: Ъ, и проведем в треугольнике OPQ отрезок MN || OQ.
Мы имеем (учитывая подобие треугольников OPQ и
MPN)
- ОМ : ОР =
а + b '
дл.оЛ/TV = MN : OQ = МР : ОР = —~.
а -\- Ь
38

Следовательно,
ВС : ОМ =- дл.о ВС : цл.аОМ = а : -^-^ = а + Ь,
С А : MN = дл.о 6'Л : дл.о MN = Ь : ^-^ = a -f 6.
Таким образом, ВС : ОМ = С А : MN; кроме того,
/_ВСА = /JDMN. Отсюда вытекает, что треугольники
ВСА и OMN подобны, и потому АВ \\ ON и АВ: ON ==¦
= а + Ъ, т. е. дл.с АВ : дл.о ON = a +6. Итак,
пл ON - т'°АВ с
а + 0 «4-^
Но точки Р ж О принадлежат фигуре G. В силу выпук-
выпуклости этой фигуры, весь отрезок PQ принадлежит ей,
и, в частности, точка N принадлежит фигуре G. Отсюда
следует, что дл.е ON ^С 1, т. е. —цг/Г ^ ^> шш' наконец,
с scl a + 6. Это и означает, что
Плоскость, в которой масштабы длин задаются некото-
некоторой выпуклой центрально-симметричной фигурой G, на-
называется плоскостью Минковского. Сама фигура G называ-
называется единичным кругом плоскости Минковского.
Пусть г — некоторое число и С — произвольная точ-
точка плоскости Минковского. Множество всех точек А,
удаленных от точки С на расстояние, не превосходящее г,
т. е. удовлетворяющих условию дл.е СА г?С г, называется
в геометрии Минковского кругом радиуса г. Заметим, что
если две точки А, В принадлежат одному кругу радиуса
г, то расстояние между ними не превосходит 2г; в самом
деле, если С — центр этого круга, то, в силу неравенства
треугольника,
дл.о АВ < дл.с АС -|- дл.е ВС < г + г = 2г.
Для того чтобы наглядно себе представить, как выгля-
выглядит круг на плоскости Минковского, мы напомним опре-
определение гомотетии. Пусть F — некоторая плоская
фигура. Выберем на плоскости произвольную точку О и
возьмем, кроме того, положительное число к. Для любой
Точки А фигуры F мы найдем на луче О А такую точку А'
89

что ОА'\ О А = к (рис. 69). Множество всех получаемых
таким образом точек А' представляет собой новую фигуру
F'. Переход от фигуры F к фигуре F' называется гомоте-
гомотетией с центром О и коэффициентом к, а сама фигура F'
называется гомотетичной фигуре F. Если фигура F
выпукла, то и гомотетичная ей фигура F' также явля-
является выпуклой (ибо если отрезок АВ целиком принад-
принадлежит фигуре F, то от-
отрезок^ 'В' целиком при-
принадлежит фигуре F').
Заметим, что если
коэффициент гомотетии
к меньше единицы, то
фигура /"(гомотетичная
F с коэффициентом к)
представляет собой
«уменьшенную копию»
фигуры F, а если к ^> 1,.
Рис 6g_ то — «увеличенную ко-
копию».
Теперь можно сфор-
сформулировать следующее
утверждение, дающее описание всех кругов в плоскости
Минковского: некоторая фигура в том и только в том слу-
случае является кругом радиуса г =f= 1 в плоскости Минковского,
если она гомотетична единичному кругу G с коэффициентом
гомотетии, равным г. Доказательство этого утверждения
несложно, и мы его предоставляем читателю.
Пусть F — некоторая фигура на плоскости Мипков-
ского с единичным кругом G. Как и в обычной геометрии,
диаметром фигуры F (ср. стр. 5) называется наиболь-
наибольшее из расстояний между точками фигуры F, т. е. наи-
наибольшее из чисел дл.(з АВ, где А ж В — произвольные
точки фигуры F (ср. примечание {1)).
Легко понять, что если диаметр фигуры F не превос-
превосходит d, то круг КА радиуса do, центром в произвольной то-
точке А фигуры /"содержит целиком всю эту фигуру (рис. 70).
Наоборот, если каждый такой круг содержит фигуру
F, то диаметр этой фигуры не превосходит d.
Рассмотрим в качестве примера плоскость Минковско-
Минковского, в которой единичным кругом служит квадрат, изо-
изображенный на рис. 66. Легко понять, что описанный во-
вокруг него «обычный» круг (определяемый неравенством
40

з? + у1 ^ 1 и, следовательно, имеющий в обычной гео-
метрии диаметр 2) имеет в этой геометрии Минковского диа-
метр, равный 2|Л2 (рис. 71).
Пусть теперь I — некоторая прямая и А — точка, не
лежащая на ней. Рассматривая круги различного радиу-
радиуса с центром в точке Л, можно среди них выбрать лишь
Pi!с. 70.
ОА
один, для которого прямая I будет опорной. Радиус г
этого круга называется расстоянием от точки А до прямой I.
Рис. 72.
Рис. 73.
Название это объясняется тем, что если В — произ-
произвольная точка прямой I, то точка В либо лежит вне вы-
выбранного круга (рис. 72) и тогда дл.с АВ ^> г, либо лежит
на границе этого круга и тогда дл.с АВ = г. Таким обра-
образом, расстояние от точки А до прямой I — это (как и в
обычной геометрии) наименьшее из расстояний от
точки А до точек прямой I.
41

Заметим, что в геометрии Минковского расстояние от
точки А до прямой I измеряется, вообще говоря, не по
перпендикуляру, опущенному из точки А на прямую I
(ср. рис. 72). Кроме того, возможно, что на прямой I име-
имеется не одна ближайшая
к А точка, а целый
отрезок, состоящий
из ближайших точек
(рис. 73).
Легко видеть, что ес-
если / и т — две парал-
параллельные прямые, то рас-
расстояние от любой точки
А прямой I до прямой
Рис- 74. т не зависит от положе-
положения точки А на прямой
I (и равно расстоянию от произвольной точки прямой т
до прямой I). Это расстояние называется расстоянием от
прямой I до прямой т. Если, например, 1шт — две
параллельные опорные прямые единичного круга G, то
расстояние между ними равно двум (рис. 74).
Пусть F — произвольная выпуклая фигура, располо-
расположенная в плоскости Минковского с единичным кругом G,
и пусть I и т — пара параллельных опорных прямых
этой фигуры. Расстояние между прямыми I и т называет-
называется шириной фигуры F в направлении I. Диаметр произ-
произвольной фигуры F является наибольшей шириной фигуры
F П.
Пусть, например, в качестве единичного круга G при-
принимается квадрат, изображенный на рис. 66, a F — обыч-
обычный круг, описанный около квадрата G. Тогда ширина
фигуры F в направлении, параллельном стороне квадрата
G, равна 2|^2, а ширина фигуры F в направлении, парал-
параллельном диагонали квадрата G, равна 2. Таким образом,
в этой геометрии Минковского круг уже не является фи-
фигурой постоянной ширины. Вообще, если фигура F имеет
(в геометрии Минковского с единичным кругом G) во всех
направлениях одну и ту же ширину d, то она называется
в этой геометрии фигурой постоянной ширины. Если, на-
например, единичным кругом G является правильный ше-
шестиугольник, то равносторонний треугольник, изобра-
изображенный на рис. 75, является фигурой постоянной ши-
ширины.
42

Любопытно отметить, что любая ограниченная
выпуклая фигура F, содержащая внутренние точки
(т. е. не являющаяся отрезком
или точкой), является фигурой
постоянной ширины в некоторой
(и притом только в одной!) геомет-
геометрии Мииковского A3).
Из сказанного ясно, что на слу-
случай плоскости Минковского пере-
переносятся все определения, рассмот-
рассмотренные в §§ 4, 5 (диаметр выпук-
выпуклой фигуры, ширина, фигуры по- Рис. 75.
стоянной ширины). Поэтому име-
имеет смысл в плоскости Мипковско-
го рассматривать задачи, разобранные в первой главе.
К рассмотрению этих задач мы и переходим.
§ 10. Задача Борсука на плоскости Минковского
Пусть F — фигура, расположенная в плоскости Мин-
Минковского с единичным кругом G. Диаметр фигуры F в
этой геометрии обозначим через d. Мы будем рассматри-
рассматривать для фигуры F задачу о разбиении ее на части мень-
меньшего диаметра. Наименьшее число частей, которые для
этого потребуются, обозначим через uq{F). Ясно, что диа-
диаметр как всей фигуры, так и ее частей существенно зави-
зависит от того, в какой геометрии Минковского этого диаметр
рассматривается (т. е. зависит от единичного круга G).
Поэтому и число ac(F) существенно зависит от выбора еди-
единичного круга G.
Например, при обычном определении длины паралле-
параллелограмм можно разбить на две части меньшего диаметра
(рис. 12, б). Если же этот параллелограмм рассматрива-
рассматривается в плоскости Минковского, где он сам играет роль
единичного круга G, то «диаметр» всего параллелограмма
и указанных его частей, очевидно, равен двум (в плоско-
плоскости Минковского «длина» каждой стороны и каждой диа-
диагонали параллелограмма G равна двум). Поэтому в рас-
рассматриваемом случае параллелограмм G нельзя раз-
разбить на три части меньшего «диаметра». Однако четырех
частей для такого разбиения уже достаточно (рис. 76).
43

Иначе говоря, в этом случае ас (G) = 4. Это показыва-
показывает, что для некоторых фигур F и G может выполняться
неравенство aa(F)^a{F). Бывают, однако, и такие случаи,
когда ug (F) < a(F). В самом деле, если G — квадрат, а
F — круг, то легко видеть, что aG(F) = 2 (рис. 77),
в то время как a(F) — 3.
Задача нахождения величины aG (F) была рассмот-
рассмотрена в 1957 г. американским геомет-
геометром Грюнбаумом, которому при-
принадлежит теорема, близкая к фор-
формулируемой ниже теореме 4.
Теорема 4. Для любой плос-
плоской ограниченной фигуры F имеет
место соотношение
Рис 76.
причем знак равенства достигается в том и только в том
случае, если выпуклая оболочка фигуры F является парал-
параллелограммом, гомотетичным . параллелограмму G {т. е.
если фигура F содержит четыре точ-
точки, являющиеся вершинами паралле-
параллелограмма, гомотетичного G с коэф-
коэффициентом гомотетии d/2, где d— ди-
диаметр фигуры F).
Доказательство этой теоремы мы
приведем ниже (в § 14).
Результаты § 7 также допускают
интересные обобщения на случай гео-
геометрии Минковского.
Прежде всего рассмотрим случай,
когда единичным кругом плоскости
Минковского является некоторый па-
параллелограмм G. В этом случае справедлива следующая
теорема:
Т е о р е м а 5. Пусть F — некоторая фигура диамет-
диаметра d, расположенная на плоскости Минковского, единич-
единичным кругом которой служит параллелограмм G. Равенство
aG (F) = 2
имеет место в том и только в том случае, если фигура
F не содержит трех точек, являющихся вершинами равно-
равностороннего треугольника со стороной, равной d.
Рис. 77.

Разумеется, речь идет о равностороннем треуголь-
треугольнике в смысле рассматриваемой метрики Минков-
ского.
Доказательство. Допустим, что фигура F
содержит три точки А, В, С, являющиеся вершинами рав-
равностороннего треугольника со стороной d. Ясно, что ни-
никакое множество диаметра, меньшего d, не может содер-
содержать двух из этих точек. Отсюда следует, что aa(F) ^> 3.
Пусть теперь фигура F не содержит трех точек, явля-
являющихся вершинами равностороннего треугольника со
/77,
Рис 78.
стороной d. Проведем четыре опорные прямые 1Ъ 12, т1,
т2 фигуры F, параллельные сторонам параллелограмма G
(рис. 78). Эти прямые образуют параллелограмм A BCD.
содержащий фигуру F. Так как стороны этого параллело
грамма являются опорными прямыми фигуры F, то
па каждой стороне имеется хотя бы одна точка фи-
фигуры F.
Пусть К — точка фигуры F, лежащая на отрезке АВ,
и L — точка этой фигуры, лежащая на отрезке CD. Так
как обе точки К ж L принадлежат фигуре F, то дл.с- KL<Cd.
Таким образом, расстояние между некоторыми точками
прямых Zj и /2 не превосходит d, и, следовательно, рассто-
расстояние между прямыми 1Х и 12 не превосходит d. Аналогич-
Аналогично доказывается, что расстояние между прямыми m, u
т.г также не превосходит d.
Предположим, что расстояние между прямыми 1Х и L
меньше d; тогда, проведя прямую т, параллельную
45

/77,
тл и m2 и пересекающую параллелограмм ABCD (рис. 79),
мы рассечем этот параллелограмм (а следовательно, и со-
содержащуюся в нем фигуру F) па две части, диаметр каж-
каждой ил которых меньше d. Таким образом, в этом случае
ас, (F) = 2. Аналогично, если расстояние между прямыми
т1 и 1щ меньше d, то ад (F) = 2. Остается рассмотреть
случай, когда расстояние между /х
и /2> так же как и расстояние меж-
между ту и т2, равно d, т.е. /у'ABCD
является кругом радиуса d/2.
Предположим сперва, что ни
одна из точек А, С пе принадле-
принадлежит фигуре F. Тогда, как легко
видеть, прямая АС разбивает фи-
фигуру F на две части, диаметр каж-
каждой из которых меньше d. В самом
деле, в этом случае можно прове-
провести прямые nt, n2, параллельные
диагонали BD и отсекающие от
параллелограмма ABCD шести-
шестиугольник, содержащий целиком фи-
фигуру F (рис. 80). Прямая АС рассекает этот шестиуголь-
шестиугольник, а значит., и содержащуюся п нем фигуру F на две
А
Рис. 79.
Рис.
Рис. 81.
части, диаметр каждой из которых меньше d (рис. 81).
Таким образом, ая (F) = 2.
Аналогично доказывается, что если ни одна из точек В,
D не принадлежит фигуре F, то a(J (F) = 2.
46

1-0
Осталось рассмотреть случай, когда хотя бы одна из
точек А, С и, кроме того, хотя бы одна из точек В, D при-
принадлежат фигуре F. Однако этот случай реализоваться
не может. Действительно,
допустим, что хотя бы од-
одна из точек А, С (скажем,
точка А) принадлежит фигуре
F и, кроме того, хотя бы одна из
точек В, D (скажем, точка В) при-
принадлежит фигуре F. Пусть L —
точка отрезка CD, принадлежащая
фигуре F (напомним, что CD —
опорная- прямая этой фигуры).
Тогда (см. рис. 82)
дл.о АВ --= дл.о AL = дл.сЛ/, — d,
т. е. ABL — равносторонний тре- рис g2.
угольник со стороной d. Но это
противоречит предположению о
том, что фигура F не содержит трех точек, являющихся
вершинами равностороннего треугольника со стороной d.
Таким образом, теорема доказана.
Сопоставляя теоремы 4 и 5, мы можем сформулиро-
сформулировать следующее утверждение, дающее полное решение
вопроса о нахождении величины aG (F) в случае, когда G
является параллелограммом:
Если фигура F диаметра d содержит четыре точки,
являющиеся вершинами параллелограмма, гомотетич-
гомотетичного G с коэффициентом гомотетии, равным d/2 (рис. 83),
то ag (F) = 4; если это не выполняется, но фигура F со-
содержит три точки, являющиеся вершинами равносторон-
равностороннего треугольника со стороной d (рис. 84), то aG (F) = 3;
в остальных случаях а(; (F) = 2.
Таким образом, задача полного вычисления величины
uq (F) решена в двух случаях: в § 7 дано решение этой за-
задачи в обычной геометрии (т. е. когда G — круг), а здесь
было изложено решение этой задачи, когда G — парал-
параллелограмм. В остальных случаях полное решение задачи
авторам неизвестно; известно лишь (см. теорему 4), что
2 <: аа (F) <; 3. Нам кажется правдоподобной следующая
гипотеза:
Пусть F — некоторая фигура диаметра d в плоскости
Минковского с единичным кругом G, отличным от парад-
47

лелограмма. Для того чтобы имело Место равенстве»
а0 (F) = 3, необходимо и достаточно, чтобы были выполне-
выполнены следующие два условия:
1) Фигура F однозначно дополняется до фигуры по-
постоянной ширины в рассматриваемой геометрии Минков-
ского.
Рис. 83.
Рис. 84.
2) Если F* — расширение фигуры F (т. е. пересечение
всех кругов радиуса d, содержащих фигуру F), то из
каждых двух параллельных опорных
прямых фигуры F*, расстояние меж-
между которыми равно d, по крайней ме-
мере одна имеет общую точку с F.
Заметим, что если фигура G явля-
является обычным кругом, то второе ус-
условие является излишним: можно
показать, что оно вытекает из перво-
первого. В общем же случае условие 2)
необходимо. В этом можно убедить-
убедиться на следующем примере. Пусть F —
обычный круг, a G — фигура, изоб-
изображенная на рис. 85. Тогда, как лег-
легко видеть, F однозначно дополняется
до фигуры постоянной ширины (един-
(единственной фигурой постоянной шири-
ширины, содержащей F, является G), т. е.
-условию 1) выполняется. Условие же 2) не выполняется.
Н то 7це время aG (F) = 2 (см. пунктир на рис. 85). Та-
Таким образом, выполнение одного только условия 1) в
общем случае для выполнения равенства ao(F) == 3 иедо-
Рис. 85.
.48

статочно. Это, в первую очередь, связано с тем обстоя-
обстоятельством, что ад (F), вообще говоря, не совпадает с чис-
числом ад (F*) (рис. 85).
Выше у нас осталась недоказанной теорема 4, содер-
содержащая оценку величины ад (F). Из нее, в частности, сле-
следует, что для фигуры F = G имеют место следующие ут-
утверждения: ад (G) = 4, если G — параллелограмм, и
ад (G) ^3 во всех остальных случаях. Но равенство
ag(G) = 2 невозможно (это доказывается так же, как в слу-
случае, когда Gявляется кругом, стр. 6).
Таким образом, если G — не парал-
параллелограмм, то ад (G) = 3.
В случае, если G — обычный круг
или параллелограмм, разбиение на
три и соответственно на четыре части
меньшего диаметра показано на
рис. 86, 76. В этих случаях каждая
часть не только имеет меньший диа-
диаметр, но также покрывается кругом ^11С- ^-
меньшего диаметра в соответствую-
соответствующей геометрии Минковского. Естественно возникает пред-
предположение, что так же дело будет обстоять в геометрии
Минковского с люб ы м кругом G. Иными словами, воз-
возникает следующее предположение:
Всякая выпуклая центрально-симметричная фигура G,
отличная от параллелограмма, может быть разбита на
три части, каждая из которых покрывается фигурой, го-
гомотетичной G с коэффициентом гомотетии, меньшим еди-
единицы (т. е. «кругом» меньшего диаметра).
Это предположение действительно справедливо и при-
притом не только для центрально-симметричных, но и для
л ю б ы х выпуклых фигур. Доказательству этого факта
(и на его основе теоремы 4) будет посвящена следующая
глава.
3/23 В. Г. Болтянский, И. Ц. Гохберг

ГЛАВА III
ПОКРЫТИЕ ВЫПУКЛЫХ ФИГУР ГОМОТЕТИЧНЫМИ
§ 11. Постановка задачи
В этой главе мы будем рассматривать следующую за-
задачу. Дана некоторая плоская выпуклая ограниченная
фигура F. Найти мншшалыюе число гомотетичных «умень-
«уменьшенных копий» фигуры F, которыми можно покрыть всю
фигуру F. Это минимальное число обозначим через b(F).
Более точно, равенство b(F) = т означает, что существу-
существуют такие фигуры Fv F2, ..., Fm, гомотетичные фигуре F с
некоторыми центрами гомотетии и с коэффициентами го-
гомотетии, меньшими единицы, что в своей совокупности
фигуры Fv F2, ..., Fm покрывают всю фигуру F (рис. 87);
при этом число т минимально, т. е. меньшего чем т числа
гомотетичных фигур для этой цели недостаточно.
Задача о том, какие значения может принимать b(F),
была поставлена в 19G0 г. И. Ц. Гохбергом и А. С. Мар-
Маркусом. Несколько ранее эта задача (однако в иной форму-
формулировке) рассматривалась немецким математиком Ф. Леви.
Для примера рассмотрим случай, когда фигура F есть
круг. Тогда меньшими гомотетичными фигурами явля-
являются произвольные круги меньшего диаметра. Нетрудно
понять, что двумя такими кругами невозможно покрыть
исходный круг F, т. е. b(F) ~^ 3. В самом доле, пусть F1 и
F2 — два круга меньшего диаметра и Оъ О2 — их центры
(рис. 88). Проведем через центр О исходного круга F
перпендикуляр к линии центров ОхО.г. Этот перпендику-
перпендикуляр пересекает окружность круга F в двух точках А и В.
Пусть, например, точка А расположена по ту же сторону
от прямой Ofi2, что и точка О (если прямая Ofi2 прохо-
проходит через точку О, то можно взять любую из точек А,
В). Тогда АО1 > АО = г, АО2 > АО = г, где г — ради.
50

ус круга F. Так как круги Fv F2 имеют радиусы, меньшие
г, то точка А не принадлежит ни одному из них, т. е. кру-
круги Fv F% не покрывают всего круга F.
F
F,
Рис. 87.
Рис. 88.
С другой стороны, круг F легко покрыть тремя круга-
кругами несколько меньшего диаметра (рис. 89). Таким обра-
образом, в случае круга b(F) = 3.
Рис. 89.
Рис. 90.
Рассмотрим еще случай, когда F представляет собой
параллелограмм. Ясно, что никакой параллелограмм, го-
гомотетичный F с коэффициентом гомотетии, меньшим еди-
единицы, не может содержать сразу двух вершин парал-
параллелограмма F. Иначе говоря, четыре вершины параллело-
параллелограмма F должны принадлежать четырем р а з л и ч-
н ы м гомотетичным параллелограммам, т. е. b(F) !> 4.
Четырех же гомотетичных фигур явно достаточно (рис. 90).
Таким образом, в случае параллелограмма b(F) = 4.

§ 12. Другая формулировка задачи
Задаче о покрытии фигуры меньшими гомотетичными
фигурами можно придать другую форму, сближающую
ее с задачей Борсука о разбиении фигуры па части мень-
меньшего диаметра.
Пусть F — выпуклая фигура и G — некоторая ее часть.
Будем говорить, что часть G фигуры F имеет габарит, рав-
равный к, если существует фигура F', гомотетичная F
с коэффициентом к, которая содер-
содержит G, но никакая фигура, гомоте-
гомотетичная F с коэффициентом, меньшим
к, не содержит целиком G(u). Оче-
Очевидно, что если часть G совпадает со
всей фигурой F, то ее габарит ра-
веп 1. Поэтому для любой пе совпа-
совпадающей с F части G фигуры F габа-
габарит /г^ 1. Не следует, однако,
думать, что если часть G пе совпа-
Рис 91. дает со всей фигурой F, то ее габа-
габарит к непременно м е и ь ш е едини-
единицы. Если, например, F представляет собой круг, а часть
G —вписанный в него остроугольный треугольник (рис. 91),
то габарит части G равен единице (ибо никакой круг
меньшего диаметра не содержит целиком треугольника G).
Часть G фигуры F мы будем называть частью меньшего
габарита, если ее габарит /с < 1.
Пользуясь понятием габарита, мы можем придать
определению величины b(F) другую форму: b(F) есть
минимальное число частей меньшего габарита, на которые
можно разбить данную выпуклую фигуру F. Нетрудно
понять, что это определение величины b(F) эквивалентно
предыдущему. В самом деле, пусть Fx, F2, ..., Fm—мень-
Fm—меньшие гомотетичные фигуры, покрывающие F. Обозначим
через Gv G2, ..., Gm части фигуры F, высекаемые из нее
фигурами Fv F2, ..., Fm. Очевидно, что каждая из частей
Сгг, G2, ..., Gm фигуры F имеет габарит меньше единицы.
Таким образом, если фигура F может быть покрыта т
меньшими гомотетичными фигурами, то ее можно разбить
на т частей меньшего габарита. Обратно, если фигура F
может быть разбита на т частей 6^, G2, ..., Gm меньшего
габарита, то существуют фигуры Fu F2,..., Fm, содержа-
содержащие соответственно части Gv G2, ..., Gm и гомотетичные
52

фигуре F с коэффициентами, меньшими единицы. Эти фи-
фигуры Fv F2, ..., Fm и образуют покрытие фигуры F мень-
меньшими гомотетичными фигурами.
Таким образом, задачу о покрытии выпуклой фигуры
меньшими гомотетичными фигурами можно еще сформу-
сформулировать как задачу о разбиении фигуры F на части мень-
меньшего габарита. В этой форме она весьма напоминает изу-
изучавшуюся в главе I задачу Борсука.
Однако связь между этими задачами не только внеш-
внешняя. В самом деле, если фигура F имеет диаметр d, то фи-
фигура, гомотетичная F с коэффициентом к, имеет диаметр
kd. Отсюда следует, что если выпуклая фигура F имеет
диаметр d, то всякая ее часть меньшего габарита явля-
является в то же время и частью меньшего диаметра. (Обрат-
(Обратное, вообще говоря, неверно; например, равносторонний
треугольник, вписанный в круг F диаметра d, является
частью меньшего диаметра, но имеет габарит, равный еди-
единице, см. рис. 91.) Поэтому если выпуклая фигура F мо-
может быть разбита на т частей меньшего габарита, то она
подавно может быть разбита на т частей меньшего диамет-
диаметра (но, вообще говоря, не наоборот, как показывает при-
пример параллелограмма).
Таким образом, для любой выпуклой фигуры F справед-
справедливо неравенство
a(F) < b{F).
Отметим, что задача о разбиении на части меньшего га-
габарита относится лишь к выпуклым фигурам, в то
время как задача Борсука о разбиении на части меньше-
меньшего диаметра ставилась для любых (даже невыпуклых)
фигур.
§ 13. Решение задачи о покрытии
Как мы видели в § И, в задаче о покрытии выпуклой
фигуры меньшими гомотетичными фигурами (в отличие от
задачи Борсука) круг уже не является фигурой, требую-
требующей наибольшего числа покрывающих фигур: для парал-
параллелограмма число b(F) принимает большее значение, чем
для круга.
Естественно возникает вопрос, существуют ли плоские
выпуклые фигуры, для которых величина h(F) принимает
еще большее значение, чем для параллелограмма?
53

Оказывается, что таких фигур не существует; более того,
среди всех плоских выпуклых фигур только для па-
параллелограммов выполняется равенство b(F) = 4. Иными
словами, имеет место следующая теорема, установленная
в 1960 г. И. Ц. Гохбергом и А. С. Маркусом (несколько
ранее, в 1955 г., Ф. Леви был получен другой результат,
из которого также выводится эта теорема):
Теорема 6. Для любой плоской ограниченной вы-
выпуклой фигуры F, не являющейся параллелограммом, спра-
справедливо равенство b(F) = 3; если F ¦— параллелограмм, то
b(F) = 4.
Прежде чем переходить к доказательству теоремы 6,
мы введем одно определение и докажем несколько вспо-
вспомогательных предложений *).
Пусть F — некоторая выпуклая фигура и А, В — две
ее граничные точки. Условимся называть оценок АВ
АВ^-СЛ,
АВ>СЯ, %JL AB>MN
AB>MN
2?
Рис. 92. Рпс. 93.
большой хордой фигуры F, если всякая хорда этой фигуры,
параллельная АВ, имеет мельпгую длину. Например, у
круга все диаметры и только они являются большими хор-
хордами (рис. 92). У параллелограмма большими хордами
являются только его диагонали (рис. 93). Если, далее,
h> h — Две параллелытьте опорные прямые выпуклой фигу-
фигуры F, причем каждая из них имеет только одну общую точ-
точку с фигурой F, то отрезок, соединяющий эти общие точки,
является большой хордой фигуры F (рис. 94). Если одна
из двух параллельных опорных прямых lv l2 имеет с фи-
фигурой F единственную общую точку А, а другая имеет с
F обпщй отрезок ВС,то отрезок, соединяющий точку А с лю-
*) В общей сложности (вместе со вспомогательными предложе-
предложениями) доказательство теоремы G нантшает 10 страниц. Дальше
(в § 17) будет приведено еще одно доказательство этой теоремы,
54

бой точкой D отрезка ВС, является большой хордой фи-
фигуры F (рис. 95). Наконец, если каждая из двух опорных
прямых Zj и 12 имеет с фигурой F общий отрезок, то обе
диагонали трапеции, вершинами которой служат концы
этих отрезков, являются большими хордами фигуры F
ав=а'в> ел
Рис. 94.
Рпс. 95.
(рис. 96). Из сказанного следует, что если 11 и 12 — две
параллельные опорные прямые выпуклой фигуры F, то
найдется по крайней мере один отрезок с концами на
ВС=РС'> S
ВС=МВ'> MN
с
Рис. 96.
этих прямых, являющийся
большой хордой фигуры F.
Т е о р е м а .7. Всякая
выпуклая фигура F, отлич-
отличная от параллелограмма,
имеет по крайней мере
три большие хорды.
Иначе говоря, парал-
параллелограмм является е д ин-
ствепной выпуклой
фигурой, имеющей две
большие хорды. Треугольник и правильный шести-
шестиугольник являются примерами фигур, имеющих ровно
три большие хорды. Правильный 2и-угольник имеет ров-
ровно п больших хорд, а круг их имеет бесконечно шгого.
Доказательство теоремы 7. Предполо-
Предположим сначала, что граница выпуклой фигуры F не содер-
содержит ни одного прямолинейного отрезка. Проведем две
параллельные опорные прямые 1г и 12 фигуры F, и пусть
А, В — общие точки этих двух прямых с фигурой F. Тог-
Тогда АВ — большая хорда. Пусть С — произвольная гра-
граничная точка фигуры F, отличная от А и В, Проведем
55

через точку С опорную прямую тл фигуры F, и пусть
т.2 — параллельная ей опорная прямая. Общую точку
прямой т,г с фигурой F обозначим через D (не исключено,
что она совпадает с одной из точек А или В).
Отрезок CD является второй большой хордой фигу-
фигуры F (рис. 97). Возьмем, наконец, какую-либо гранич-
граничную точку Е фигуры F, отличную от А, В, С, D. Проведя
Рис. 97.
Рис. 98.
топерь опорную прямую п1 через точку Е и затем парал-
параллельную ей опорную прямую п2, мы получим еще одну
большую хорду. Таким образом, в рассматриваемом слу-
случае мы нашли три большие хорды фигуры F (впрочем, из
проведенного рассуждения ясно, что в этом случае фигура
F имеет бесконечное множество больших хорд).
Предположим теперь, что граница фигуры F содержит
хотя бы один прямолинейный отрезок, т. е. можно про-
провести опорную прямую /j фигуры F, имеющую с этой фи-
фигурой общий отрезок АВ. Обозначим через 12 опорную
прямую, параллельную lv Если /, имеет с фигурой F толь-
только одну общую точку С, то любой отрезок, соединяющий
точку С с какой-либо точкой отрезка АВ, является боль-
большой хордой, т. е. и в этом случае мы имеем бесконечное
множество больших хорд (рис. 98).
Наконец, предположим, что и прямая 12 имеет с фигу-
фигурой F общий отрезок DC. Тогда выпуклая фигура F долж-
должна содержать всю трапецию ABCD, причем обе диагонали
этой трапеции являются большими хордами фигуры F.
Если фигура F не совпадает с этой трапецией, то можно
провести опорную прямую pt фигуры F, не имеющую
56

общих точек с трапецией ABCD (рис. 99). Проведя теперь
опорную прямую р2, параллельную рг, мы получим
третью большую хорду (с концами на прямых рг и р2).
Остается рассмотреть случай, когда фигура F совпа-
совпадает с трапецией ABCD. Если АВ =J= CD, то больший из
Рис. 99.
Рис. 100.
этих двух отрезков является третьей большой хордой
трапеции ABCD (т. е. фигуры F; см. рис. 100). Если же
АВ = CD, то F — параллелограмм. Очевидно, что у па-
параллелограмма только две боль-
большие хорды.
Теорема доказана.
Лемма 10. Пусть АВ— боль-
большая хорда выпуклой фигуры F,
DE — параллельная ей хорда и О
— произвольная внутренняя точка
фигуры F. Обозначим через F1 часть
фигуры F, отсекаемую хордой DE
и не содержащую хорду АВ. Тогда
существует фигура G, гомоте-
гомотетичная фигуре F с коэффициентом
гомотетии, меньшим единицы, це-
целиком содержащая фигуру Ft и
точку О (рис. 101).
Доказательство. Пусть PQ — ^орда фигурь\
F, параллельная хордам АВ и DE и расположенная меж-
между ними. Обозначим через F' часть фигуры F, отсекаемую
хордой PQ и содержащую хорду DE. Ясно, что фигура
4 В. Г. Болтянский, И. ц. Гохберг
57

F' целиком содержит Ft (рис. 102). Так как АВ — боль-
большая хорда, то АВ ^> PQ. Обозначим через G' фигуру, го-
гомотетичную фигуре F с центром го-
гомотетии в точке Т пересечения
прямых АР и BQ и с коэффици-
коэффициентом гомотетии, равным PQ/AB
(рис. 103). Очевидно, что при этой
гомотетии хорда А В фигуры F
преобразуется в хорду PQ фигу-
фигуры G'.
Пусть М — произвольная точ-
точка фигуры F', не лежащая на хор-
хорде PQ. Проведем из точек А и В
прямые, параллельные соответст-
соответственно РМ и QM, и обозначим через
N точку их пересечения (рис.
103). Точка N принадлежит
фигуре F, так как эта точка принадлежит многоуголь-
многоугольнику ABQMP, который целиком содержится в F. При
рассматриваемой гомотетии точка N фигуры F переходит
в точку М. Отсюда следует, что точка М принадлежит
фигуре G'. Следовательно, любая точка М фигуры F'
принадлежит фигуре G', т. е. F' покрывается фигурой G'.
Рис. 102.
Рис. 103.
Итак, какова бы ни была хорда PQ, параллельная хор-
хордам АВ и DE и расположенная между ними, проведенное
построение дает нам фигуру G', которая гомотетична F
с коэффициентом гомотетии, меньшим единицы, и цели-
целиком содержит фигуру F', а следовательно и фигуру Flt

Остается доказать, что, выбрав надлежащим образом хор-
хорду PQ, можно добиться того, чтобы и точка О принад-
принадлежала фигуре С,— это и даст нам искомую фигу-
фигуру G.
Если точка О расположена по ту же сторону от АВ,
что и хорда DE, то достаточно в качестве PQ взять хорду,
отделяющую точку О от отрезка АВ. Действительно,
в а
Рис. 104.
при таком выборе хорды PQ (рис. 104) точка О принад-
принадлежит фигуре F' и, значит, содержится в G'.
Предположим теперь, что точка О находится либо на
хорде АВ, либо по другую сторону от этой хорды, чем от-
отрезок DE. Если точка О ле-
лежит на хорде АВ, то через С
мы обозначим произвольную
точку фигуры F, лежащую по
другую сторону от хорды АВ,
чем отрезок DE (рис. 105).
Если же О не лежит на от-
отрезке АВ, то из произвольной
внутренней точки Н отрез-
отрезка АВ проведем луч, прохо-
проходящий через точку О, и за
С примем точку пересечения
этого луча с границей фигу-
фигуры F (рис. 106). В обоих слу-
случаях точка О принадлежит
треугольнику ABC, но не ле-
лежит на ломаной АСВ, причем треугольник ABC лежит
по другую сторону от хорды АВ, чем отрезок DE.
Рис. 106.

Рис 107.
Проведем из точки О лучи lv /2, имеющие направле-
направления векторов СА, СВ, и обозначим через Кж Lточки пере-
пересечения этих лучей с границей фигуры F (рис. 107). Яс-
Ясно, что точки К и L лежат по ту же сторону от АВ, что и
отрезок DE. Мы выберем теперь хорду PQ \\ АВ таким об-
образом, чтобы отрезок АВ ле-
лежал по одну сторону от прямой
PQ, а все четыре точки D, К,
L, Е — по другую сторону.
Проведем теперь через точки
Р и Q прямые, соответственно
параллельные прямым А С и СВ.
Точку пересечения этих прямых
обозначим через 5. При указан-
указанной выше гомотетии с центром
У и с коэффициентом PQ/AB
треугольник ABC переходит,
очевидно, в треугольник PQS.
Остается показать, что точка О
принадлежит треугольнику
PQS. Действительно, это будет
означать, что точка, переходя-
переходящая в точку О при гомотетии, принадлежит треугольнику
ABC, а значит и фигуре F, откуда будет следовать, что
точка О принадлежит фигуре G'.
В силу выбора хорды PQ, точки К и L лежат внутри
угла PSQ, и следовательно, точка О также лежит внутри
этого угла (рис. 107). В то же время точки О и S лежат по
одну сторону от прямой PQ. Из этого следует, что О —
внутренняя точка треугольника PQS.
Лемма 11. Всякие две большие хорды выпуклой фи-
фигуры F пересекаются (внутри F или на ее границе).
Доказательство. Пусть АВ — большая хор-
хорда фигуры^ и CD — не пересекающая ее хорда. Докажем,
что CD не является большой хордой. Если хорда CD па-
параллельна АВ, то это очевидно. Предположим поэтому, что
CD не параллельна А В, ж пусть, для определенности, точ-
точка С ближе расположена к прямой АВ, чем D (рис. 108).
Проведем хорду СМ, параллельную АВ. Тогда точ-
точки В и D расположены по разные стороны прямой СМ, и
потому отрезок BD пересекается с прямой СМ в некото-
некоторой точке К. В силу выпуклости фигуры F, точка К ог-
60

Остается доказать, что, выбрав надлежащим образом хор-
хорду PQ, можно добиться того, чтобы и точка О принад-
принадлежала фигуре G',— это и даст нам искомую фигу-
фигуру G.
Если точка О расположена по ту же сторону от АВ,
что и хорда DE, то достаточно в качестве PQ взять хорду,
отделяющую точку О от отрезка АВ. Действительно,
J0
в а
Рис. 104.
при таком выборе хорды PQ (рис. 104) точка О принад-
принадлежит фигуре F' и, значит, содержится в G'.
Предположим теперь, что точка О находится либо на
хорде АВ, либо по другую сторону от этой хорды, чем от-
отрезок DE. Если точка О ле-
лежит на хорде АВ, то через С
мы обозначим произвольную
точку фигуры F, лежащую по
другую сторону от хорды АВ,
чем отрезок DE (рис. 105).
Если же О не лежит на от-
отрезке АВ, то из произвольной
внутренней точки Н отрез-
отрезка АВ проведем луч, прохо-
проходящий через точку О, и за
С примем точку пересечения
этого луча с границей фигу-
фигуры F (рис. 106). В обоих слу-
случаях точка О принадлежит
треугольнику ABC, но не ле-
лежит на ломаной АСВ, причем треугольник ABC лежит
по другую сторону от хорды АВ, чем отрезок DE.
*• 69

же вывод можно сделать и относительно части фигуры F,
отсекаемой хордой KL и не содержащей точку А. Что же
касается остающейся части фигуры F (т. е. криволиней-
криволинейного «сектора» OLD), то путем выбора точки О достаточно
близко к А эта часть может быть заключена в сколь угод-
угодно малый круг с центром в точке А. Следовательно, эта
часть фигуры F покрывается одной фигурой, гомотетич-
гомотетичной F со сколь угодно малым коэффициентом гомотетии.
Таким образом, осталось рассмотреть случай, когда
каждые две из трех больших хорд пересекаются во внут-
внутренней точке фигуры F. Обозначим шесть точек, являю-
являющихся концами этих трех хорд, обходя кривую против
часовой стрелки, буквами А, В, С, D, Е, Н, так что хор-
хорды, о которых идет речь, будут обозначены
AD, BE и СН.
Пусть MN — хорда, параллельная AD и отделяющая AD
от точек В ж С (рис. 110). Часть фигуры F, отсекаемую хор-
хордой MN и не содержащую AD, обозначим через Fu Далее,
проведем хорду PQ, параллельную BE и отделяющую BE
от точек М, А и Н (рис. 111). Часть фигуры F, отсекае-
отсекаемую этой хордой и не содержащую BE, обозначим через
F2. Наконец, проведем хорду ST, параллельную СН и
отделяющую СН от точек N и Q (рис. 112). Эта хорда от-
отсекает от F фигуру ^3 (не содержащую СН).
Пусть теперь О — произвольная внутренняя точка фигу-
фигуры F. В силу леммы 10, существует фигура G; (у = 1, 2, 3),
гомотетичная F с коэффициентом гомотетии, меньшим
единицы, и содержащая фигуру Fj и точку О. Следо-
Следовательно, G1 содержит «сектор», отсекаемый от F ломаной
M0N (рис. 113), а фигуры G2 и G3 содержат аналогичные
секторы POQ и SOT (рис. 114, 115). Эти три сектора и
тем более фигуры Gv G2, G3 покрывают всю фигуру F.
Таким образом, и в этом случае
b(F) < 3.
Покажем, наконец, что b(F) ;> 3 для любой выпуклой
фигуры F. Пусть Fx, F%— две произвольные фигуры,
гомотетичные F с коэффициентами гомотетии, меньшими
единицы, и Ог, О2— соответствующие центры гомотетии.
Проведем прямую I, проходящую через точки Ог и 0.2,
и пусть М — точка фигуры F, наиболее удаленная от
прямой I, Тогда все точки фигуры Fх расположены от I
62

Рис. 114.
Рис. 115.

на меньшем расстоянии, чем точка М (рис. 116), и то йсе
справедливо для фигуры F2. Следовательно, точка М не
покрывается ни одной из
фигур Ft и F2, откуда и
вытекает, что b(F) ^> 2.
Итак, если фигура F
не является параллело-
rpaMM0Mi то ъ (F) = 3.
Очевидно, что для па^
раллелограмма b(F)=4.
Теорема доказана.
§ 14. Доказательство
теоремы 4
Приступим теперь к
доказательству теоре-
теоремы 4.
Прежде всего рас-
рассмотрим случай, когда
фигура F выпукла. Заметим, что неравенство a{F) <J b(F)
сохраняет свою силу и в случае плоскости Минковского:
aG(F) < b(F).
Это устанавливается точно так же, как и в обычной
геометрии (стр. 53). Следовательно, если фигура F не
является параллелограммом, то, в силу теоремы
6, aG(F) < b{F) = 3.
Пусть теперь F — параллелограмм. Проведем через
центр О фигуры G две прямые, параллельные диагоналям
параллелограмма F, и обозначим через А1С1 и B2D2
отрезки, высекаемые фигурой G па этих прямых. На от-
отрезках А1С1 и 52D2, как на диагоналях, построим два па-
параллелограмма со сторонами, параллельными сторонам
параллелограмма F (рис. 117). Обозначим через F' мень-
меньший из этих двух параллелограммов; пусть это будет па-
параллелограмм A1BlC1D1 с диагональю AjCv Так как
параллелограммы F и F' гомотетичны, то ac{F) = aG(F'),
и потому в дальнейших рассуждениях мы можем вместо
F рассматривать параллелограмм F'.
Ясно, что дл-g А1С1= 2, и потому диаметр параллело-
параллелограмма F' не меньше двух. (Здесь и дальше мы имеем в
64

виду «диаметры», относительно длин, определяемых фигу-
фигурой G.) Но диаметр параллелограмма F' и не больше двух,
ибо он заключен целиком в фигуре G, имеющей диаметр 2.
Рис. 117.
Итак, диаметр параллелограмма F' равен двум.
Проведем теперь через точку О прямую р, параллель-
параллельную сторонам А1В1 и C1D1, и обозначим через М и N
Рис. 118.
Рис. 119.
точки ее пересечения с границей фигуры G. Если точки
М и N не лежат на сторонах ВгСг и A1D1 параллелограм-
параллелограмма F' (рис. 118), то весь шестиугольник AxBlMCJ)iN
содержится в фигуре G. Отсюда легко вытекает, что диа-
диаметр каждой из «половинок», на которые прямая р рассе-
рассекает параллелограмм F', меньше двух (рис. 119), так что
= 2. Если же точки М и N лежат на сторонах парал-
паралA
() р р
лелограмма F', то прямые В1С1 и AlD1 должны быть
опорными прямыми фигуры G (ибо через граничную
точку М фигуры G должна проходить опорная прямая, а
65

всякая прямая, отличная от В1С1, рассекает параллело-
параллелограмм F', а значит и фигуру G). Таким образом (рис. 120),
вся фигура G заключена в полосе между прямыми В,С.
и AXDX.
Итак, либо aG(F') == 2, либо же фигура G заключена
в полосе между прямыми В1С1 и AlD1.
Аналогично, проводя прямую q, параллельную сторо-
пам В1С1 и AXDV мы найдем, что либо aG{F')= 2, либо
же фигура G заключена в полосе между прямыми А1В1
и ClDl. Объединяя оба случая вместе, заключаем, что ли-
либо aG{F') — 2, либо же фигура G заключена внутри обеих
/
я,
Рис.
At/
Ж
Щ
л,
120.
с,
р
Рис. 121.
указанных полос, т. е. содержится в параллелограмме
F' (рис. 121). Но в последнем случае фигура G должна
совпадать с параллелограммом F' (ибо она содержит
параллелограмм F').
Итак, либо aG(F) =aG(F') = 2, либо же фигура G сов-
совпадает с параллелограммом F' (т. е. гомотетична F), и тог-
тогда, как мы уже знаем, aG{F) =aG(F') = 4. Иными слова-
словами, для выпуклых фигур F утверждение теоремы
4 справедливо.
Пусть теперь^7 — невыпуклая фигура. Если выпук-
выпуклая оболочка F фигуры F является параллелограммом,
гомотетичным параллелограмму G (рис. 83), то aG(F) — 4.
Если же фигура F не гомотетична G, то, в силу уже до-
доказанного, aG{F) ^ 3, а так как F содержится в F, то по-
подавно aG(F) < 3.
Теорема доказапа.

ГЛАВА IV
ЗАДАЧА ОСВЕЩЕНИЯ
§ 15. Постановка задачи
В этой последней главе мы рассмотрим еще одну зада-
задачу из теории выпуклых фигур. По своей постановке эта
задача весьма непохожа на предыдущие, но, как мы уви-
увидим, она тесно связана с ними.
Пусть F — плоская ограниченная выпуклая фигура
и I — произвольное направление в плоскости этой фигуры.
Будем говорить, что граничная точка А фигуры F явля-
является точкой освещенности относительно на-
направления I, если параллельный пучок лучей, имеющих
направление I, «освещает» на границе фигуры F точку А
Рис. 122.
Рис. 123.
и некоторую ее окрестность (рис. 122). Заметим, что если
прямая, параллельная направлению / и проходящая через
точку А, является опорной для фигуры F (рис. 123), то
точку А мы не считаем точкой освещенности относительно
67

направления I. Иначе говоря, точка А является точкой
освещенности, если выполнены следующие два условия:
1°. Прямая р, параллельная направлению I и прохо-
проходящая через точку А, не является опорной прямой фигу-
фигуры F {т. е. на прямой р имеются внутренние точки фигу-
фигуры F).
Рис. 124.
Рис. 125.
2°. Точка А является первой точкой фигуры F,
которую мы встречаем, двигаясь по прямой р в направ-
направлении I.
Условимся, далее, говорить, что направления lv l2,...
...,1т освещают всю границу фигуры F, если каждая гранич-
граничная точка фигуры F является точкой освещенности отно-
относительно хотя бы одного из этих направлений. Наконец,
обозначим через с (F) наименьшее из таких натураль-
натуральных чисел т, что на плоскости существуют т направ-
направлений, освещающих всю границу фигуры F. Задачу о
нахождении числа c(F) мы будем называть задачей
освещения границы фигуры F. Эта задача освещс
иия была поставлена в 1960 г. В. Г. Болтянским.
Легко доказать, что для любой плоской фигуры Ь
всегда c(F) ;> 3. В самом деле, пусть F — плоская огра-
ограниченная выпуклая фигура и lt, l2— произвольные на-
направления. Проведем две опорные прямые фигуры F,
параллельные направлению lv и пусть А и В — гранич-
граничные точки фигуры F, лежащие на этих опорных прямых
(рис. 124). Тогда ни одна из точек А, В не является точкой
63

освещенности для направления 1Ъ а направление /2 ос-
освещает не более чем одну из этих точек. Итак, двух
направлений недоста-
недостаточно для освещения
всей границы фигуры F.
В случае круга
(рис. 125) для освеще-
освещения границы достаточно
трех направлений. Для
параллелограмма (pi с.
126) трех направлений
уже недостаточно (ибо
ни одно направление не
освещает сразу двух
вершин параллелограм-
Рис. 126.
ма), а четыре направле-
направления позволяют осветить всю границу параллелограмма.
Иначе говоря, для круга c(F) = 3, а для параллелограмма
c(F) = 4.
§ 16. Решение задачи освещения
При решении задачи освещения мы используем вспо-
вспомогательные предложения, установленные в § 13, а также
следующую лемму:
Лемма 12. Пусть F —
выпуклая фигура, АВ — ее
большая хорда и D, Е — гра-
граничные точки фигуры F, лежа-
лежащие по одну сторону от хорды
АВ. Тогда всю дугу DE, лежа-
лежащую по одну сторону от хорды
АВ, можно осветить одним
направлением (рис. 127).
Доказательство. Пусть
MN — хорда, параллель-
параллельная АВ и отделяющая отре-
отрезок А В от точек D и Е. Так как
MN <С АВ, то можно взять на
отрезке АВ такие две внутренние точки PviQ, что PQ=
=^MN, и следовательно, PQNM—параллелограмм. Обозна-
Обозначим через /направление, определяемое вектором MP=NQ.
Ясно, что всякая прямая, параллельная I и проходящая
В
Рис. 127.
69

через произвольную точку С дуги MN (не содержащей
точек А и В; см. рис. 128), обладает тем свойством, что
при движении по ней из точки С в направлении I мы пере-
пересекаем отрезок MN, который состоит из внутренних то-
точек фигуры F. Иными словами, каждая точка С указан-
указанной дуги MN освещается направлением I. В частности, вся
дуга DE освещается направле-
направлением I.
Лемма доказана.
Как и в случае задачи о по-
покрытии фигуры меньшими гомо-
гомотетичными частями, в задаче
освещения параллелограмм иг-
играет особую роль. Именно, име-
имеет место следующая
Теорема 8. Для любой
плоской ограниченной выпуклой
фигуры F, не являющейся па-
параллелограммом, справедливо ра-
равенство с (F) = 3; если F— парал-
параллелограмм, то с (F) = 4,
Доказательство этой
теоремы вполне анало-
аналогично доказательству теоремы 6. Пусть фигура F не явля-
является параллелограммом. Тогда, в силу теоремы 7, фигура
F имеет три большие хорды. Как и при доказательстве
теоремы 6, рассмотрим сперва случай, когда две боль-
большие хорды фигуры F пересекаются на ее границе
(рис. 109).
Согласно лемме 12, каждая из дуг KBL и DCE может
быть освещена одним направлением. При этом точки L и
D могут быть выбраны сколь угодно близкими к А. Оче-
Очевидно, оставшуюся дугу LAD также можно осветить
одним направлением. Следовательно, в рассматривае-
рассматриваемом случае
c(F) < 3.
Перейдем ко второму случаю, когда три большие хор-
хорды AD, BE, СН фигуры F пересекаются внутри этой фи-
фигуры (рис. 110—112). Согласно лемме 12, каждую из дуг
MBN, PA Q и SD Т можно осветить одним направлением.
Следовательно, и в этом случае c{F) ^ 3,
Рис. 128.

Наконец, как уже было показано, для любой выпук-
выпуклой фигуры F справедливо неравенство
c{F) > 3.
Таким образом, если F не является параллелограммом,
то с (F) = 3.
Теорема доказана.
§ 17. Эквивалентность двух задач
Читатель, несомненно, уже обратил внимание на то, что
для любой плоской выпуклой ограниченной фигуры F
числа b(F) и c(F) совпадают (ср. теоремы 6 и 8).
Иными словами, справедлива следующая
Теорема 9. Для любой выпуклой фигуры F имеет
место равенство
b(F) = c(F).
Этот факт имеет место не только для плоских фи-
фигур, но и для выпуклых тел в пространстве (и даже в мно-
многомерном пространстве). Он был доказан в 1960 г.
В. Г. Болтянским.
Смысл доказательства теоремы 9 заключается в сле-
следующем. Из трех теорем 6, 8, 9 достаточно доказать только
две — третья, очевидно, будет их следствием. Поэтому
можно было бы доказать из этих трех теорем те две, до-
доказательства которых являются более простыми. В част-
частности, если читателю доказательство теоремы 6 (по-види-
(по-видимому, более сложное) показалось утомительным и он его
пропустил, то теперь, прочитав доказательство теоремы 9,
он получит (с помощью теоремы 8) новое доказательство
теоремы 6. Однако еще важнее то, что для пространствен-
пространственных тел, для которых решение задачи о покрытии и зада-
задачи освещения неизвестно до сих пор A5), достаточно было
бы решить лишь одну из этих задач, поскольку, в силу тео-
теоремы 9, они эквивалентны. Задача освещения, по-видимо-
по-видимому, обладает преимуществом несколько большей нагляд-
наглядности.
Доказательство теоремы 9.
Предположим, что плоскую выпуклую фигуру F можно
покрыть т меньшими гомотетичными фигурами Fv F2,...
..., Fm. Центр гомотетии, переводящей фигуру F в F-%, обоз-
обозначим через Oi, а коэффициент этой гомотетии — через
71

каждое из чисел
Рпс. 129.
ki (? = 1,2,..., т). Таким образом,
kv к%,..., кт меньше единицы.
Выберем теперь произвольную внутреннюю точку А фи-
фигуры ^, несовпадающую ни с одной из точек 0х, 02,...,0„„
и обозначим через lx, Z2,..., lm направления, определяе-
определяемые лучами ОХА, 0гА,..., 0тА. Мы докажем, что направ-
направления lv Z2,. ., lm освещают всю границу фигуры F. В са-
самом деле, пусть В —
произвольная гранич-
граничная точка фигуры F
(рис. 129). Тогда точка
В принадлежит хотя бы
одному из множеств
Fx, F\,..., Fm~ пусть,
например, множеству Fj.
Так как при гомотетии
с центром 0г и коэффи-
коэффициентом к.{ фигура F
переходит в F{, то най-
найдется такая точка С фи-
фигуры F, которая при этой гомотетии переходит в точку В.
Таким образом, 0{В : 0,С — кг. Возьмем теперь на отрезке
АС такую точку D, что AD:AC = /с,-. Из равенства
O,B:OiC = AD : АС вытекает, что BD\\O{A, т. е. прямая
BD параллельна направлению Zj. Далее, так как точка С
принадлежит фигуре F, а А — внутренняя точка
этой фигуры, то все точки отрезка АС (кроме, может
быть, точки С) являются внутренними точками фигуры F;
в частности, D — внутренняя точка этой фигуры.
Итак, прямая BD параллельна направлению 1г и про-
проходит через внутреннюю точку D фигуры F. Из этого сле-
следует, что В — точка освещенности относительно направ-
направления li. Таким образом, любая граничная точка фигуры
F освещается одним из направлений lv Z2,..., lm.
Мы доказали, что если фигура F может быть покрыта
т меньшими гомотетичными фигурами, то для освещения
ее границы достаточно т направлений. Следовательно,
справедливо неравенство
c(F) < b(F).
Установим теперь справедливость обратного неравен-
неравенства
72

Рис. 130.
Предположим, что s направлений Z/, Z2',..., Z/ осве-
освещают всю границу фигуры F. Проведем две опорные пря-
прямые фигуры F, параллельные направлению 1{ (рис. 130),
и обозначим через А и В п е р в ы е точки фигуры F, ко-
которые мы встречаем, двигаясь
по этим прямым в направле-
направлении Ц. Тогда ясно, что все
точки дуги Ai с концами А,
В (вычерченной жирно на
рис. 130), кроме концевых
точек А и В, являются точ-
точками освещенности относи-
относительно направления 1{. Та-
Таким образом, множество всех
точек освещенности относи-
относительно направления /,' пред-
представляет собой некоторую
дугу А4 без концов; это мно-
множество мы будем называть
областью освещенности отно-
относительно направления 1{. Так как направления Z/, 12',...
...,1/ освещают всю границу фигуры F, то соответствующее
области освещенности Av A2,..., А3
заполняют всю границу фигуры F.
Точка А на рис. 130 не является
точкой освещенности относительно
направления I-,', поэтому она осве-
освещается каким-либо другим из нап-
направлений Z/, Z2',..., Z/, например,
направлением Z/. Но тогда направ-
направление Z/ освещает все точки, доста-
достаточно близкие к точке А, т. е. об-
области освещенности А4 и А, п е-
рекрываются (рис. 131). Точно
так же второй конец В дуги Ai пок-
покрывается еще одной областью освещенности Ак.
Из того, что дуги Alt A2,..., As, являющиеся областями
освещенности, заходят концами одна на другую, вытека-
вытекает, что мы можем немножко уменьшить их, и эти умень-
уменьшенные дуги будут все еще заполнять всю границу фигу-
фигуры F. Иначе говоря, можно взять такие дуги AJ, А^,...
..., Л,*, заключающиеся (вместе с концами) соответствен-
соответственно внутри дуг Ах, А2,..., As (рис. 132), что вместо
А
Рис. 131.
73

Ах*, А2*,..., As* составляют всю границу фигу-
фигуры F.
Обозначим через А и В концы дуги Aj, а через Л* и
В*— концы дуги Д;*. Прямые, проведенные через точки
А* ж В* параллельно направлению I/, должны прохо-
проходить через внутренние точки фигуры F (ибо А* и В* —
точки освещенности относительно направления 1{). Дли-
Длины хорд, высекаемых фигурой F на этих прямых, обозна-
обозначим через а и Ъ и выберем отрезок hu меньший чем а и Ъ.
Тогда параллелограмм, одна сторона которого совпадает
с А*В*, а вторая параллельна 1{ и имеет длину hi, целиком
содержится в фигуре F (рис. 133). Отсюда следует,
что на любой прямой, параллельной направлению 1{
и проходящей через какую-либо точку дуги А;*, фигура
F высекает хорду длины больше }ц. Это означает, что
параллельный перенос дуги Aj* в направлении I/ на рас-
расстояние hi (рис. 134) переводит дугу А;* целиком внутрь
фигуры F. Иначе говоря, произведя параллельный пере-
перенос фигуры F в направлении, противоположном
1{, на расстояние hi, мы получим фигуру Ft*, содержа-
содержащую дугу Aj* внутри себя (рис. 135). Поэтому, выбрав
внутри Fi* произвольную точку Ог* и производя гомоте-
гомотетию фигуры Fi* с центром Ог* и коэффициентом kt* <1,
достаточно близким к единице, мы получим фигуру
Ft', гомотетичную фигуре ^j* (а значит, и фигуре F)
и содержащую дугу Aj*. Это построение мы проведем для
всех i=l,2, ...,s и получим фигуры F/, F2',..., F/,
гомотетичные фигуре F с коэффициентами гомотетии, мень-
меньшими единицы.
Пусть теперь О — некоторая внутренняя точка фигуры
F. Мы можем предполагать предыдущие построения вы-
выполненными таким образом, что каждая из фигур Fx',
F2',..., ^/содержит точку О (рис. 136); для этого лишь
нужно отрезки hi взять достаточно малыми, а коэф-
коэффициенты hi* — достаточно близкими к единице (ср.
стр. 59—60).
Обозначим, наконец, через G% «сектор» с вершиной О
и дугой А4* (этот сектор заштрихован на рис. 136). Так
как фигура F{ выпукла и, кроме того, содержит дугу
Aj и точку О, то фигура Fi содержит весь сектор (¦?{. Сле-
Следовательно, вместе взятые фигуры F/, F2',..., Fs' содер-
содержат все секторы Glt G2, ..., Gs. Но ясно, что секторы Gv
G2, ..., Gs заполняют всю фигуру F (ибо дуги Ах*, А2*,...

...,Д5* покрывают всю границу фигуры i*1). Поэтому фигуры
F/, F2',..., Fs' покрывают всю фигуру F.
Мы доказали, что если вся граница фигуры F может
быть освещена s направлениями, то фигура F может быть
покрыта s меньшими гомотетичными фигурами. Следо-
Следовательно, справедливо неравенство
b(F) < c(F).
Из доказанных неравенств с (F) ^ b(F), b(F) ^ c(F) и
вытекает справедливость равенства
h(F) = c(F),
составляющего содержание теоремы 9.
§ 18. Раабисште и освещг-пие неограниченных
выпуклых фигур
Для неограниченных выпуклых фигур (см. рис. 22)
задача Борсука теряет смысл, так как диаметр фигуры
становится бесконечным. Однако задача освещения и за-
задача покрытия фигуры меньшими гомотетичными фигура-
фигурами (т. о. фигурами, гомотетичными заданной, с коэффици-
коэффициентами гомотетии, меньшими единицы) по-прежнему сох-
сохраняют смысл. Здесь нас с самого же начала ожидает
«сюрприз»: теорема 9 о равенстве величин b(F) и c(F) пере-
перестает быть справедливой для неограниченных выпуклых
фигур.
Проще всего это увидеть па примере выпуклой фигуры,
ограниченной параболой Р. Граница Р этой выпук-
выпуклой фигуры F может быть освещена одним направле-
направлением, т. е. c(F) = 1 (рис. 137, а). В то же время, как мы
сейчас увидим, фигуру F невозможно покрыть никаким
конечны м числом меньших гомотетичных фигур, т. е.
b(F) — оо. В самом деле, пусть F' — фигура, гомотетич-
гомотетичная фигуре F с коэффициентом гомотетии k <С 1 и центром
гомотетии О, расположенным вне фигуры F (рис. 137, б).
Проведем из точки О касательные ОА и ОВ к параболе Р,
ограничивающей фигуру F. Точки А и В делят параболу Р
па три части: дугу АВ и две бесконечные дуги Ах и А2,
оканчивающиеся в точках А и В. Ясно, что фигура F' пе
содержит пи одной точки дуг А1 и Д2 (ибо если М — ка-
какая-либо точка дуги А1 или А2, то на прямой ОМ за точ-
точкой М совсем нет точек фигуры F). Таким образом, фигу-
фигура F' может содержать лишь конечный кусок параболы Р

В
Рпс. 132.
Рис. 133.

(расположенный на дуге АВ). Если же центр гомотетии О
принадлежит фигуре F, то фигура F' содержит не бо-
более одной точки параболы Р (рис. 137, в, г). Таким обра-
образом, каждая фигура, гомотетичная F с коэффициентом
б)
Рис. 137.
jfc<l, содержит лишь конечный кусок параболы Р, и
потому для покрытия всей фигуры F (содержащей пари
болу Р) необходимо бесконечно много меньших гомотети-
гомотетичных фигур, т. е. b(F) = оо.
В то же время существуют и такие неограниченны»,
выпуклые фигуры, для которых величина b(F) конечна»
Например, если F — полуполоса (заштрихован-
(заштрихованная на рис. 138, а), то b{F) = 2; заметим, что в этом слу-
случае c(F) также равно двум, т. е. b(F) = c{F).
Наконец, существуют и такие неограниченные выпук-
выпуклые фигуры, для которых обе величины b(F), c(F) конечны,
но не совпадают между собой. Например, если фигура F
77

расположена в полосе между двумя параллельными пря-
прямыми и все более приближается к краям этой полосы по
мере удаления в «бесконечность» (рис. 138, б), то, как лег-
легко показать, b(F) = 2, c{F) = 1.
В связи со сказанным возникают следующие вопросы:
Для каких неограниченных выпуклых фигур сохраняется
равенство b(F) = c(F)?
а)
Рис. 138.
Для каких неограниченных выпуклых фигур величина
b(F) принимает конечные значения?
Существуют ли неограниченные выпуклые фигуры, для
которых c(F) = оо?
Ответы на эти вопросы были найдены П. С. Солтаном и
В. Н. Визитеем A6). Мы приведем их результаты без дока-
доказательств.
Прежде всего укажем, что от теоремы 9 все же кое-что
остается и для неограниченных выпуклых фигур. Имен-
Именно, первая часть доказательства теоремы 9 полностью со-
сохраняется, и потому для любой неограниченной выпуклой
фигуры F справедливо неравенство
c(F) < b(F).
Теперь мы сформулируем теорему, дающую ответ на
второй из поставленных вопросов. Пусть F — неограни-
неограниченная выпуклая фигура. Возьмем произвольную внут-
внутреннюю точку О фигуры F и рассмотрим всевозможные лу-
лучи, исходящие из точки О и целиком содержащиеся в фи-
фигуре F. Все такие лучи, вместе взятые, образуют, как не-
нетрудно доказать, неограниченную выпуклую фигуру К',
78

она называется вписанным углом фигуры F с вершиной в
точке О. Например, для параболы (рис. 139, а) или полу-
полуполосы (рис. 139, б) вписанный угол состоит только из
одного луча, а для внутренней области одной ветви гипер-
гиперболы вписанный угол изображен на рис. 139, в). (Заметим,
а)
К
в)
Рис. 139.
что если вместо точки О взять в качестве вершины любую
другую внутреннюю точку фигуры F, то вписанный угол не
изменится, а лишь подвергнется параллельному переносу.)
Далее, неограниченную выпуклую фигуру F П. G. Сол-
тан называет почти конической, если существует такой от-
отрезок г, что все точки фигуры F находятся на расстоянии,
не большем г, от вписанного угла К. Так, например, фи-
фигуры, изображенные на рис. 139, б) и в), являются почти
коническими. В то же время фигура, изображенная на
рис. 139, а), не является почти конической, так как точки
параболы все более и более удаляются от ее оси.
Т е а р е м а 10. Величина b(F) для неограниченной
выпуклой фигуры F в том и только в том случае принима-
принимает конечное значение, если F — почти коническая фигура.
При этом для почти конической фигуры F величина
b(F) может принимать лишь значения 1 и 2. Именно, пусть
F — двумерная почти коническая фигура, не содержащая
целиком никакой прямой; если ее вписанный угол К яв-
является лучом, то b(F) = 2, а если К — угол, то b(F) = 1.
Наконец, если двумерная выпуклая фигура содержит
целиком прямую, то она может быть полосой, полупло-
полуплоскостью или плоскостью; в этих случаях величина b(F)
принимает соответственно значения 2, 1, 1. Тем самым для
плоских неограниченных выпуклых фигур вопрос о зна-
значениях величины b(F) полностью решается.

ПРИМЕЧАНИЯ
i1) (к стр. 6). Приведенное в тексте определение диаметра фи-
фигуры неявно предполагает, что каждая рассматриваемая «фигура»
представляет собой замкнутое множество (т. е. к фигуре при-
причисляются все ее граничные точки). Например, если F— откры-
открытый круг диаметра d (т. е. круг, к которому не причисляются
точки ограничивающей его окружности), то точная верхняя
грань расстояний между двумя точками фигуры F равна d; одна-
однако в этом случае не существует двух точек фигуры F, расстояние
между которыми в точности равно d. Если же мы причислим к фигуре
F все граничные точки (т. е. будем рассматривать замкнутый
круг), то эта точная верхняя грань будет достигаться: найдутся две
точки А и В, расстояние между которыми равно d.
.Вообще, если F — замкнутое ограниченное множество
(на плоскости или в евклидовом пространстве произвольного числа
измерений), то найдутся две точки А и В фигуры F, расстояние
между которыми максимально. Действительно, пусть М п N —•
две произвольные точки множества F и р(М, N) — расстояние
между ними. Функция р (М, N) непрерывна (по М, N). Но
всякая непрерывная функция (в данном случае от двух переменных
М, IV), аргументы которой меняются в замкнутом ограниченном мно-
множестве, обязательно достигает своего наибольшего (и наименьшего)
значения. Таким образом, найдутся такие две точки А и В фигуры F,
что р (А, В) ;> р (М, N) для любых точек М, N фигуры F. Расстоя-
Расстояние d = р(А, В) между такими двумя точками и представляет со-
собой диаметр множества F.
B) (к стр. 6). В самом деле, пусть А и В — две точки много-
многоугольника F. Если точка А не является вершиной этого много-
многоугольника, то найдется отрезок CD, содержащий точку А внутри себя
и целиком принадлежащий многоугольнику F (рис. 140, а, б). Бу-
Будем, для определенности, считать, что/JBAC^- /JBAD. Тогда в тре-
треугольнике ABC угол А больше или равен 90°, т. е. /JBAC~^> /_BCA,
и потому ВС > АВ. Следовательно, АВ не является диаметром фи-
фигуры F. Итак, если хотя бы одна из точек А, В не является верши-
вершиной многоугольника F, то АВ не является диаметром этого много-
многоугольника. Отсюда и вытекает, что диаметром многоугольника будет
расстояние между некоторыми двумя его вершинами, а имен-
именно, расстояние между двумя наиболее удаленными друг от друга
вершинами.
80

C) (к стр. 6). Здесь идет речь о разбиении фигуры на части и о
диаметрах этих частей. В соответствии с предыдущим примечанием,
мы будем считать, что части, на которые разбивается фигура, сами
являются замкнутыми множествами. Поэтому предложение, разъяс-
разъясненное в тексте, уточняется следующим образом: если круг F диамет-
диаметра d каким-либо образом представлен в виде объединения двух своих
замкнутых подмножеств, то хотя бы, одно из этих подмножеств
имеет тот же диаметр d. Рассуждение, приведенное на стр. 6,
с.)
Рис. 140.
конечно, не дает полного доказательства этого утверждения. Кор-
Корректное доказательство выглядит так. Обозначим через Ht и Н2 рас-
рассматриваемые замкнутые подмножества (так что ихобъедине-
и и е Я-, U Н2 дает весь круг F). Точки множества Hv лежащие на
окружности круга F, составляют некоторое множество Кг; аналогич-
аналогично определяется множество К2. Таким образом, окружность круга F
представляется в виде объединения двух своих замкнутых подмно-
подмножеств Ki и Кг. Если одно из этих множеств, например Кг,
пусто (т. е. совсем не содержит точек), то Kt совпадает со
всей окружностью; поэтому множество Къ а значит и Нь имеет
диаметр d. Если же оба множества Kt и К2 непусты, то они обязатель-
обязательно имеют общую точку А (ибо окружность связна и потому
пе может быть представлена в виде объединения двух непересекаю-
непересекающихся замкнутых подмножеств). Обозначим точку, диаметрально
противоположную точке А, через В, и пусть, для определенности,
точка В принадлежит множеству К2. Тогда К2 содержит обе точки
А, В. Следовательно, множество К2, а значит и Н2, имеет диаметр
d. Итак, в любом случае хотя бы одно из множеств Нг, Нг имеет
диаметр d.
(*) (к стр. 9). Сделаем еще одно замечание по поводу «разбие-
«разбиения» фигуры на части. Слово «разбиение» можно понимать в том смыс-
смысле, что фигура F представлена в виде объединения несколь-
нескольких своих замкнутых подмножеств:
F = Нг U #2 U • • • U Ит
(именно так было в примечании C)). В этом случае математики обычно
говорят, что множества #,, Н2 Нт составляют покрытие фигуры
F. Однако более естественно понимать термин «разбиение» в том
81

смысле, что замкнутые множества Hv Я2,..., Нт не только состав-
составляют покрытие фигуры F, но, кроме того, не перекрываются
друг с другом, т. е. попарно не имеют общих внутреппих точек.
Легко понять, что смысл задачи о разбиении фигуры на части
меньшего диаметра не меняется в зависимости от того, какое из этих
двух пониманий мы придадим термину «разбиение на части». В
самом деле, если фигура F представлена в виде объединения песколь-
ких своих замкнутых подмножеств
f = т и ih и • • • и нт
(возможно, перекрывающихся друг с другом), то мы можем, не уве-
увеличивая диаметров частей, «подправить» эти части так, чтобы они
не перекрывались друг с другом. Для этого заметим, что множества *)
Нг \ (Я, U Яз U • ¦ • U Вт),
#, \ (Я, U ... U Нт\
составляют покрытие фигуры F и попарно не имеют общих точек.
Правда, эти множества могут оказаться незамкнутыми. Однако з а-
м ы к а н и я этих множеств, т. е. множества
Нг' = Hi \ (Я2 U Я3 U • • • U
Ш = #* \ (#3 U ... U Ят) ,
уже будут замкнутыми подмножествами фигуры F, попарно не имею-
имеющими общих внутренних точек и дающими покрытие фигуры F.
Таким образом, из произвольного покрытия (Hi, Я2, ..., Нт)
фигуры F замкнутыми подмножествами мы получили покрытие (Я/,
Н, ,..., Нт), состоящее из множеств, не перекрывающихся друг с
другом. Диаметры частей при этом, конечно, не увеличились (ибо
множество Яг содержится в Hi).
F) (к стр. 9). Задачу о разбиении фигур на части меньшего
диаметра (т. е. задачу о том, какие значения может принимать
a(F) можно рассматривать не только для плоских фигур, но и для
пространственных тел или даже для тел в п-и е р н о м
евклидовом пространстве. Именно для n-мерных тел
*) Символом А \ В обозначается множество, получающееся,
если из множества А удалить все точки, принадлежащие множест-
множеству В.
82

сформулировал свою проблему К. Борсук. Полное решение проб-
проблемы было им найдено лишь для плоских фигур (теорема Борсука
излагается в § 3 этой кпиги). Борсук доказал также, что для «-мер-
«-мерного шара имеет место равенство a(F) = п + 1 (в частности, для
трехмерного, т. е. обычного, шара справедливо равенство a(F)=A). В
связи с этим он выдвинул следующую проблему: доказать, что для
любого п-мерного тела F справедливо неравенство a (F) ^ п ~\- 1.
Изящное решение проблемы, данное Борсуком для п = 2, и подку-
подкупающая простота формулировки проблемы привлекли к ней внима-
внимание многих математиков. Но для п ^> 2 проблема оказалась значи-
значительно более сложной. Лишь в 1955 г. (т. е. спустя 25 лет после пос-
постановки проблемы) английскому математику Эгглстону удалось ре-
решить проблему для п = 3; он доказал, что, как и предполагал Бор-
Борсук, для любого трехмерного тела справедливо неравенство e(F)^4.
Более простые доказательства, чем у Эгглстона, были найдены
два года спустя американским математиком Грюнбаумом и венгер-
венгерским математиком Хеппешом. Для п > 3 проблема Ворсука до сих
пор не решена. Однако все эти вопросы мы оставляем в стороне, так
как эта книжка посвящена лишь рассмотрению задач для плоских
фигур. Подробнее об этом круге вопросов интересующийся читатель
может прочитать в книге «Задачи и теоремы комбинаторной геомет-
геометрии» тех же авторов.
F) (к стр. 10). Приведенное в тексте рассуждение (связанное с
«приближением» прямой I к фигуре F) не дает, конечно, строгого дока-
Рис. 141.
зательства существования опорной прямой lv Строгое доказательст-
доказательство можно получить, например, следующим образом. Проведем пря-
прямую I, не пересекающую фигуры F, и прямую т _|_ I. Примем пря-
прямые (итза оси координат (рпс. 141) и обозначим для любой точки А
фигуры F через у (А) ее ординату (измеряемую вдоль прямой
83

т). Таким образом, на фигуре F определена функция у (А), причем
эта функция непрерывна (ибо разность у (А) — у (А') не превос-
превосходит длины отрезка АА'). Но непрерывная функция, определенная
на замкнутом ограниченном множестве F, достигает своего наиболь-
наибольшего и наименьшего значений. Иначе говоря, существуют такие точ-
точки М1 н М2 фигуры Р, что у (Мг) < у (А) < у (М2) для любой точки
А этой фигуры. Но это означа-
означает, что если мы проведем через
т очки Mi иМ2 прямые, парал-
параллельные оси абсцисс I, то вся
фигура F будет заключена в по-
полосе между этими прямыми.
Таким образом, прямые h и 13,
проходящие через точки Mi,
М% параллельно I, являются
томи двумя опорными прямыми
фигуры F, о которых идет речь
в тексте (см. рис. 14).
(') (к стр. И). Покажем,
для примера, что точка А не-
непрерывно зависит от направле-
направления прямой /,. Допустим, что
прямая 1г повернулась на неко-
некоторый угол а (рис. 142). Поло-
Положение прямых llt l2, mi, m2 в
этот момент обозначим через
h', к', т\, m2'. Через точки А
п В проведем прямые тА и тв
составляющие с т,х угол а (т. е'
параллельные прямой т\). Так_
как прямая тд рассекает фигу!
ру F, а прямая тв не имеет с F
общих точек, то опорная пря-
прямая т1 расположена между
тА и тв% Аналогично, если мы
проведем через точки А и D
прямые 1А и lD, составляющие
с 12 угол а (т. е. параллельные
прямой h'), то найдем, что
опорная прямая ti расположена между 1А и 1П> Следовательно, точка
А', в которой пересекаются опорные прямые т{ и V, расположен?»
внутри параллелограмма, образованного прямыми /яд, вд, Ia, li
Но размеры этого параллелограмма(заштрихованного на рис.142) мо-
могут быть сделаны как угодно малыми, если только угол а достаточна
мал. Таким образом, точка А' как угодно близко расположена к А,
если угол а достаточно мал. Это и означает, что точка А непрерывно
зависит от направления прямой 1г.
(8) (к стр. 17). В самом деле, пусть М — некоторая совокуп-
совокупность выпуклых фигур и Ф — пересечение всех этих фигур (т. е.
множество точек, каждая из которых принадлежит всем этим фи-
фигурам). Докажем, что фигура Ф выпукла. Пусть А и В — две точки
84

фигуры Ф. Возьмем произвольную фигуру F из совокупности М.
Тогда точки А и В принадлежат фигуре F. Так как фигура F вы-
выпукла, то отсюда следует, что весь отрезок А В принадлежит фигуре
F. Итак, каждая фигура F из совокупности М содержит отрезок
АВ, п потому фигура Ф содержит отрезок АВ. Это и означает, что
фигура Ф выпукла.
(9) (к стр. 24). В курсе геометрии средней школы понятие пло-
площади определяется лишь для простейших фигур: многоугольни-
многоугольников и круга. В действительности же понятно площади определено
для значительно более широкого класса фигур. В частности, мож-
можно говорить о площади любой выпуклой ограниченной фигуры. Мы
не приводим здесь определенно площади выпуклой фигуры (см. об
этом в статьях «Площадь и объем» п «Выпуклые фигуры и тела» в V
томе Энциклопедии яломентарпеш математики). Для пас важно лишь
то, что каждой ограниченной выпуклой фигуре F сопоставляется
некоторое положительное число s (F) — площадь этой фигуры, при-
причем если фигура F' содержит фигуру F и имеет внутренние точки,
не принадлежащие фигуре F, то s (Г") > s (F).
A0) (к стр. 26). Итак, Н определяется как объединение возрас-
возрастающей последовательности выпуклых фигур #„, Hv Hv ..., Нп, ...
(т. е. такой последовательности, что каждая фигура содержит пре-
предыдущую). В тексте доказывается, что фигура Н выпукла и имеет
диаметр d. Заметим, однако, что объединение возрастающей после-
последовательности выпуклых фигур может оказаться незамкнутой
выпуклой фигурой. Например, пусть Fv F2, ..., Fn...,-— возрастающая
последовательность кругов (замкнутых), причем все круги внутрен-
внутренним образом касаются друг друга в точке М и радиус круга Fn
равен 1 — 1/2п (рис. 143). Тогда
объединение этой возрастающей
последовательности выпуклых фи-
фигур будет представлять собой круг
радиуса 1, причем точка М причис-
причисляется к этому кругу, а остальные
граничные точки — нет. Иначе го-
говоря, указанное объединение яв-
является незамкнутой выпу-
выпуклой фигурой.
Так как мы условились рас-
рассматривать лишь зам кнутые выпук-
выпуклые фигуры, то Н, строго говоря,
следовало бы определить так:
берется объединение всех фигур
Но, Ни Но,..., II п, ... и к получен-
полученной выпуклой фигуре (которая
может оказаться незамкнутой) до-
добавляются все ее граничные точки. Однако существа дела это не ме-
меняет.
(и) (к стр.33). Заметим, что для случая пространственных (трех-
(трехмерных) тел доказанная теорема непосредственно не обобщается. Так,
например, для правильного тетраэдра F С ребром d мы имеем, очевид-
Рис. 143.
85

Рис. 144.
но, a(F)=4, т. е. a(F) принимает свое максимальное значение.
В то же время тело F неоднозначно дополняется до тела
постоянной ширины d (см. стр. 103—104 указанной на стр. 13
книги И. М. Яглома и В. Г. Болтянского). Таким образом,
равенство a (F) = 4 в случае пространственных тел диамет-
диаметра d связано с какими-то более тонкими обстоятельствами, чем
однозначность дополнения до тела постоянной ширины d.
A2) (к стр. 42). В самом деле, пусть I п Г — две параллельные
опорные прямые фигуры F (рис. 144), и пусть А, В — общие точки
этих прямых с фигурой F. Проведем в плоскости Минковского круг
КА с центром в точке А, для которого прямая Г является опорной.
Тогда радиус h этого круга равен расстоянию между прямыми I и
/', т. е. равен ширине фигуры F в
направлении I. Точка В либо ле-
лежит на границе круга КА, либо
расположена вне этого круга. По-
Поэтому дл.с АВ >feи, значит, подав-
подавно диаметр d фигуры F больше или
равен h. Итак, ширина фигуры F
в любом направлении не превос-
превосходит d, а потому и наибольшая
ширина не превосходит d.
Остается доказать, что найдет-
найдется такое направление, что ширина
фигуры F в этом направлении
р а в н a d. Пусть Мп N — две точ-
точки фигуры F, расстояние между которыми равной. Тогда круг
Кы радиуса d с центром в точке М содержит целиком фигуру F.
Точно так же круг КN радиуса d с цент-
центром N содержит F (рис. 145). Проведем
опорную прямую п к кругу Км, проходя-
проходящую через точку N. Тогда прямая т,
параллельная прямой п и проходящая
через точку М, является опорной пря-
прямой круга KN. Ясно, что вся фигура F
расположена в полосе между прямыми
тип, так что тип являются опорными
прямыми фигуры F. Из построения ясно,
что расстояние между прямыми тип
(т. е. ширина фигуры F в направлении т)
равно радиусу круга KMt т. е. равно d.
A3) (к стр. 43). Приведем дока-
доказательство этого утверждения, исполь-
используя понятие суммы выпуклых фигур (см. § 4 указанной на
стр. 13 книги И. М. Яглома и В. Г. Болтянского).
Пусть F—произвольная выпуклая фигура и F'— фигура, симмет-
симметричная ей относительно некоторой точки О. Сумму F-\~F' обозначим
через G. Тогда G есть центрально-симметричная выпуклая фигура,
которую мы и примем за единичный круг в плоскости Минковского.
Ясно, что ширина фигуры F в любом направлении I равна ширине
86
Рис. 145.

фигуры F' в том же направлении (рис. 146). Следовательно, ширина
фигуры G в произвольном направлении I вдвое больше ширины
фигуры F в том же направлении.
Но ширина фигуры G в любом направлении равна 2 (так как G —
единичный круг). Таким образом, ширина фигуры F в любом на-
направлении равна 1, т. е. F является (в геометрии Минковского, оп-
определяемой единичным кругом G) фигурой постоянной ширины 1.
Разумеется, если в качест-
качестве единичного круга вз>,ть не
фигуру G = F + F', а любую
фигуру, гомотетичную F + F',
то и в такой геометрии F будет
фигурой постоянной ширины.
С другой стороны пусть в
некоторой геометрии Минковс-
Минковского фигура Р является фигу-
фигурой постоянной ширины. Тог-
Тогда, очевидно, F' также будет
фигурой постоянной ширины,
а потому фигурой постоянной
ширины будет и F ¦+- F'. Но
фигура F-\-F' центрально-
симметрична, а, как легко
видеть, централыю-сим-
метричная выпуклая фигура
только в том случае имеет по-
постоянную ширину, если она
является кругом в рассматрива-
рассматриваемой геометрии Минковского.
Таким образом, мы доказали следующую теорему:
Теорема. Фигура F в том и только в том случае является
фигурой постоянной ширины в плоскости Минковского с единичным
кругом G, если сумма F ~\-F' фигуры F с центрально-симметричной
ей фигурой F' является в этой геометрии кругом.
Из этой теоремы и вытекает, что всякая выпуклая фигура F яв-
является фигурой постоянной ширины в геометрии Минковского с еди-
единичным кругом k (F + F') и только в этой геометрии (к — произ-
произвольное положительное число).
A4) (к стр. 52). Пусть F — выпуклая ограниченная фигура и
G — некоторая ее часть (т. е. замкнутое подмножество). Рассмотрим
всевозможные фигуры, гомотетичные Р с коэффициентами гомотетии,
но превосходящими единицы, и содержащие фигуру G. Точную ниж-
нижнюю грань всех коэффициентов гомотетии для таких гомотетичных
фигур мы обозначим через к0. Если к0 = 1, то габарит части G равен
1 (ибо не существует фигуры, гомотетичной F с коэффициентом гомо-
гомотетии, меньшим единицы, и содержащей фигуру G). Пусть к0 <[ 1.
Тогда мы можем выбрать такую последовательность F\, F2, ...,Fq,...
фигур, гомотетичных F соответственно с центрами гомотетии Оь
О2, ..., Oq, ... и коэффициентами гомотетии kv k2, ..., fc3, ..., что
каждая из этих фигур содержит G и имеет место равенство
limkq=kn. При этом мы можем считать, что справедливы неравенства
д*ос
Рис. 146.
87

Нетрудно понять, что все точки Ov O2, ..., Oq, ... расположены
на расстоянии, не большем от фигуры F (где d — диаметр фигу-
1 — /ci
ры F). В самом деле, допустим, что точка Oq расположена от F на
расстоянии, большем Тогда для произвольной точки А фигуры
1.—~'$\
F мы имеем OqA > -—— . При гомотетии с центром OQ и коэффпциен-
том kq точка А переходит в такую точку А', что OqA' = kq ¦ OqA.
Поэтому имеем ЛА' = A — kq)-OqA > A — ki)-OqA >rf. Таким
образом, каждая точка А фигуры F смещается при этот! го-
гомотетии на расстояние, большее d, т. е. переходит в точку А', не
принадлежащую фигуре F. Иначе говоря, фигура Fq,
в которую переходит F при рассматриваемой гомотетии, не имеет
общих точек с F. Но это противоречит тому, что фигура Fq содержит
часть G фигуры F.
Итак, все точки Оь О2, ..., Oq, ... расположены на коночном рас-
расстоянии от F. Поэтому последовательность О,, О2, ..., OQ, ... имеет
хотя бы одну предельную точку. Без ограничения общности можно
считать (переходя, если нужно, к подпоследовательности), что после-
последовательность Ох, О2, ..., Oq, ... имеет только одну продель-
продельную точку О0, т. е. существует предел lim Oq = О0.
Q—9-00
Легко понять, что фигура Fo, гомотетичная фигуре F с центром
гомотетии О0 и коэффициентом к0, содержит фигуру G (ибо lim kq =
q~*oo
= к0, lim Oq = O0). Таким образом, существует фигура Fo, гомоте-
q—*oo
тпчная F с коэффициентом к0, содержащая G, но никакая фигура,
гомотетичная F с коэффициентом, меньшим к0, не может целиком
содержать G (по определению точной нижней грани). Это означает,
что к0 есть габарит части G. Тем самым установлено, что понятие га-
габарита имеет смысл для любой части G фигуры F.
A6) (к стр. 71). Задача освещения становится значительно болеь
интересной и трудной для пространственных тел и тел в ге-мерном
пространстве. Более подробно имеющиеся здесь результаты и нере-
нерешенные проблемы освещены в книге В. Г. Болтянского и И. Ц. Гох-
берга, указанной во введении. Отметим лишь, что для ограниченных
трехмерных выпуклых тел (и даже для трехмерных многогранни-
многогранников) до сих пор неизвестно, всегда ли справедливо неравенство
с (F) < 8.
A6) (к стр. 78). Задачи о покрытии и освещении неограниченные
фигур становятся особенно интересными в трехмерном и многомер-
многомерном пространстве. Как доказал П. С. Солтан, теорема 10 справед-
справедлива для фигур любого числа измерений. В частности, им полностыи
решена задача о покрытии неограниченных трехмерных тел гомоте-
гомотетичными меньшими телами. Именно, в этом случае b (F) может при-
принимать лишь значения 1, 2, 3, 4, оо.