Текст
ВОПРОСЫ
ГИДРОГЕОЛОГИЧЕСКИХ
РЛСЧ ЕТОВ
ИЗДАТЕЛЬСТВО
« М И Р »
УДК 551. 491.5
ВОПРОСЫ
ГИДРОГЕОЛОГИЧЕСКИХ
РАСЧЕТОВ
Сборник статей
Перевод с английского и французского
В. С. АЛЕКСЕЕВА и В. В. ДА НИ Л О ПЛ
Под редакцией и с предисловием
Ф. М. Б ОЧ Е В Е РЛ и В. М. ШЕСТАКОВА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1964
Сборник содержит статьи американских и французских
авторов, посвященные вопросам гидрогеологических расчетов
и оценки параметров водоносных пластов в сложных природ-
ных условиях, а также проблемам моделирования на фильт-
рационных лотках и тепловых моделях. Статьи сборника
позволяют судить о современном уровне научных достижений
в области динамики подземных вод за рубежом. Сборник рас-
считан па гидрогеологов п гидротехников и в первую очередь
на специалистов, работающих в области водоснабжения и
проектирования ирригационных сооружений и плотин.
Редакция литературы по вопросам геологических наук
ПРЕДИСЛОВИЕ
За последние годы в гидрогеологии наблюдается все более широкое развитие и вне-
дрение в практику количественных методов, базирующихся па динамике подземных вод.
Весьма крупные по своим масштабам и народнохозяйственному значению мероприя-
тия, связанные с использованием подземных вод для водоснабжения городов, промышлен-
ности и сельского хозяйства, и такого же размаха мероприятия по борьбе с вредным влия-
нием подземных вод при добыче полезных ископаемых, строительном освоении терри-
торий, устройстве водохранилищ, каналов и т. д. не могут быть правильно запроектиро-
ваны без гидродинамических расчетов, т. е. количественных прогнозов.
Вполне естественно поэтому, что динамика подземных вод получила в последние годы
стимулы для бурного развития.
Достижения нашей отечественной науки в этой области, как известно, весьма зна-
чительны. Особенно существенный вклад в динамику подземных вод или в более общем
виде — в теорию фильтрации внесен советскими гидротехниками и нефтяниками.
Большие и разнообразные по своей тематической направленности и методике иссле-
дования в области динамики подземных вод и теории фильтрации проводятся также за
рубежом. Результаты многих из этих работ представляют’несомненный интерес для со-
ветских гидрогеологов-производственников и научных работников.
В свяЗи с этим и предпринято издание настоящего сборника переводов статей по
динамике подземных вод, опубликованных в зарубежных технических журналах.
Сборник открывается статьями С. Ирмей и Н. «Путинского, которые носят теорети-
ческий характер. В статье С. Ирмей рассматривается вывод общей формы основного за-
кона фильтрации, применимого за верхней границей справедливости закона Дарси. Эта
статья представляет интерес как пример современного теоретического обоснования основ-
ного закона фильтрации, имеющего серьезную гидродинамическую основу.’ Интересной
представляется статья Н. «Путинского, в которой обосновывается выражение для потен-
циалов потока, содержащего воды переменной плотности. Автор — ив этом основное зна-
чение его работы — вводит различные выражения для напоров, определяющих фильтра-
цию в горизонтальном и вертикальном направлениях. Такого рода методы должны найти
применение при изучении движения подземных вод повышенной минерализации в наклон-
ных напорных пластах, взаимодействия соленых вод с пресными и т. п.
Далее вниманию читателей предлагается серия статей М. Хантуша, посвященных
задачам неустановившегося притока подземных вод к скважинам. В этих статьях полу-
чают развитие известные работы Тейса, Джекоба, Маскета и других американских иссле-
дователей, которыми, по существу, заложены основы современной гидродинамической
теории скважин.
Весьма ценно, что в статьях М. Хантуша ясно показана последовательность и тех-
нология получения решений разнообразных задач о притоке подземных вод к скважине,
что для гидрогеологов полезно с познавательной точки зрения. Вместе с тем результаты
этих решений подробно табулированы и удобны для практического пользования. В част-
ности, они представляют большой интерес для правильной интерпретации результатов
опытных откачек и наблюдений за восстановлением уровня подземных вод при оценке
гидрогеологических параметров водоносных пластов.
5
В статье Р. Коллинса, завершающей часть сборника, посвященную вопросам при-
тока подземных вод к скважинам, выведены зависимости, с помощью которых можно опре-
делить расход жидкости в любом сечении потока при неустаповивщейся фильтрации
к скважине в напорном пласте. Эти зависимости могут быть использованы также при рас-
четах, связанных с оценкой динамики перемещения границы раздела жидкостей различ-
ного состава.
Статьи Г. Шнеебели, И. Халеви и А. Нира посвящены методике опытпо-фильтрациоп-
ных работ.
В статье Шнеебели кратко изложены основные положения способа оценки про-
ницаемости певодопасыщениых пород в естественных условиях путем закачки воздуха.
Этот способ уже получил определенную апробацию в зарубежных исследованиях (особен-
но но Франции), и, несомненно, имеются перспективы его использования в СССР, напри-
мер при изучении проницаемости пород в зонах обходной фильтрации у плотин, в районах
строительства каналов и т. п.
Статья И. Халеви и А. Нира выбрана как типовая из довольно обширной серии
публикаций по применению радиоактивных индикаторов для определения фильтрацион-
ных характеристик водоносных пластов.
Проблемы использования наблюдений за режимом подземных вод для определения
гидрогеологических параметров водоносных пластов путем решения обратных задач
касается в своей статье А. Фелнер. Автор приводит пример определения проводимости
пласта (точнее говоря, коэффициента уровнепроводности) в прибрежной зоне по анализу
связи колебаний уровней воды в реке и наблюдательной скважине в условиях неустано-
впвшейся фильтрации. Такого рода методы применяются в отечественной практике.
Однако в американских работах применяются иные приемы обработки наблюдений.
Публикуемые в последней части сборника статьи посвящены некоторым вопросам
моделирования при изучении фильтрации. Они интересны в смысле поисков новых мето-
дов моделирования. Так, в статье Д. Крайенгофф ван де Лера показана возможность при-
менения грунтовых фильтрационных лотков при использовании в качестве рабочей жид-
кости смеси спирта и воды, что позволяет регулировать ее вязкость и поверхностное на-
тяжение.
В статьях В. Ландрума и др. и Ч. Пиккеринга и др. описывается применение прин-
ципа тепловой аналогии для моделирования иеустановившейся фильтрации. Такие пред-
ложения имеются и в отечественной литературе, однако развития и практического при-
менения они не получили, хотя удобство моделирования фильтрационного потока, особен-
но при наличии систем скважин и в неоднородных пластах, побуждает к дальнейшим по-
искам в этом направлении.
Ф. Бочевер,
В. Шестаков
С. И р м е it
О ТЕОРЕТИЧЕСКИХ ОСНОВАХ ФОРМУЛ ДАРСИ И ФОРХГЕЙМЕРА1
В настоящей статье закон Дарси q -7<J (q — вектор удельного расхода; J==
=-= — grad Е — гидравлический градиент; Е — энергия потока; /< — гидравлическая
проводимость пористой среды) рассмотрен в историческом развитии.
Исходя из гидродинамического уравнения Навье-Стокса для фильтрации вязкой
жидкости и используя статистические методы, автор показал, что напор в законе Дар-
си, отличается от напора для потока вязкой жидкости.
Получена формула J=«q '-bqq-cdq/dt (а, b, с — коэффициенты изотропной сре-
ды). Обычно третьим членом можно пренебречь. Для потока с низкими значениями
числа Рейнольдса получается закон Дарси при (а— 1//0 в форме Козени-Кармана.
При больших значениях числа Рейнольдса в формуле Форхгенмера величина b зави-
сит от структурных свойств породы (диаметра зерен) и пористости; температура и вяз-
кость не учитываются. Уравнение Лапласа заменяется нелинейным уравнением типа
уравнения Пуассона с A=f (J).
ВВОДНЫЕ ЗАМЕЧАНИЯ
Установившаяся фильтрация вязкой несжимаемой и химически пассив-
ной жидкости в насыщенной гомогенной изотропной и недеформируемой
пористой среде при отсутствии сжимаемого свободного газа и низких числах
Рейнольдса, при постоянной температуре подчиняется закону Дарси [5, 14, 15]
q - Д' grad
(П
q — удельный расход (расход на единицу площади);
7 удельный вес жидкости;
v •— кинематическая вязкость;
d —диаметр зерен пористой среды;
р —давление;
g -^-ускорение силы тяжести;
7. — высота' над горизонтальной плоскостью;
/< — гидравлическая проводимость (с размерностью LT"1);
h —пьезометрический напор (комбинированное гравитационное давление и
давление силовое, потенциальное)
h Z + р/у;
J — гидравлический градиент — —grad h.
(3)
Закон Дарси применялся для неоднородных сред [1,18]; анизотропных
сред [17, 34, 1]; деформируемых сред [8, 22]; неустановившейся фильтрации
|2, 16, 29]; для сжимаемой жидкости [26]; ненасыщенных сред [30, 10,20, 3]
и для выщелачиваемых и адсорбирующих сред [6].
1 S. I г may, On the theoretical Derivation of Darcy and Forchheiiner formulas,
Trans, of Am. Geophys. Union, 39, No. 4, 702—707, 1958.
7
Детальный обзор изменения теории дан в различных учебных руко-
водствах [26, 27, 28, 29, 33].
Для больших чисел Рейнольдса Форхгеймер [9] предложил заменить
формулу (1) нелинейной зависимостью:
J = aq + bq2. (4)
См. также работу Линдквиста [25]. При параметре Рейнольдса
7?е< 1 вторым членом можно пренебречь и получить линейный закон Дарси.
Здесь а = 1//С-—гидравлическое сопротивление пористой среды. При Rc> 1
второй член будет такого же порядка, что и первый член. Этот случай
приводит к условиям нелинейной фильтрации. Ирмей [21] показал, что
неразумно в общем случае полагаться на линейное решение уравнения
Навье-Стокса, поскольку фильтрация в пористой среде происходит по кри-
волинейным путям.
При Re > 100 течение принимает турбулентный характер, как это
было показано введением индикаторов [35]. Уравнение (4) остается дейст-
вительным, но с различными величинами коэффициентов а и Ь. При очень
больших Re а — 0 (по аналогии с турбулентным движением). Смрекер
предложил иное выражение:
J - <п <2), (4а)
а П. Я. Полубаринова-Кочина [29] дает формулу:
J aq -г bq2 -5 cq3 . (45)
Далее будет показано, что только формула Форхгеймера имеет рацио-
нальную основу.
Применяя операцию дивергенции к векторному уравнению (1),
получаем
div q — div (Д' grad h) = 0. (5)
В однородной среде Д'—постоянная и
divgradh = V2 h=hxx -L 5VV -у hzz 0. (6)
Здесь hxx — d2h!dx2 и т. д. Это хорошо известное уравнение Лапласа,
В неоднородных средах с К, изменяющимся в пространстве, получим из (5)
div (^ grad й) = V2 Л+grad A - grad К 0
или
V2 h -grad h • grad In = 0, (7)
где h-~ потенциал Пуассона [18].
Шейдеггер [33] предложил заменить формулу (1) следующим выраже-
нием:
q-—grad (^/i), (В)
что приводит формулу (7) к виду:
V2 (Kh) - К V2 h -k 2 grad h grad К - r
/г ’да0. (7')
Многие авторы проверяли закон Дарси, используя различные физи-
ческие модели и аналогии, и полный обзор этих работ был дай Шейдегге-
ром [33]. Модели строились на аналогии течения в капиллярных трубках
[36, 16], теории гидравлического радиуса [37, 23, 16], теории сопротивле-
ний Эмерслебена [33], статистической теории [12, 331, термодинамической
8
теории [6], аналогии турбулентного потока по Юхара [33J и непосредст-
венном анализе уравнений Навье-Стокса [11, 13].
Недостатки перечисленных выше теорий, которые в общем сходны,
заключаются в том, что их применение не проверено или они основаны на
введении неопределенных коэффициентов, о которых будет высказано
позже несколько критических замечаний. Ни одна из них не приводит к
формуле Форхгеймера.
Покажем, что закон Дарси, а также закон Форхгеймера может быть
легко выведен из гидродинамического уравнения Навье-Стокса для условий
течения вязкой жидкости через однородную изотропную несжимаемую на-
сыщенную среду.
Уравнение Навье-Стокса для течения вязкой жидкости. Поток несжи-
маемой вязкой жидкости при ламинарной фильтрации подчиняется урав-
нению
div V - 0 (8)
и динамическому уравнению Навье-Стокса с обобщенными векторами
Vz — V X rot V X- grad (V2/2) = grad (g/z) — > rot rot V, (9)
где V — вектор скорости, Vz dV/dt; / — время, VX rot V—векторное
произведение.
Вводя энергию фильтрации на единицу веса Е (размерность L)
Е ^h + V^g-^Zyp/'i-EV^g, (10)
получим уравнение (9) в виде
grad (gE) = V X rot V — v rot rot V — Vz. (H i
Операция дивергенции даст
div grad (gE) — g y^E = div [V X rot V] = (rot V)2— V-rot rot V, (12)
где V-rot rotV — скалярное произведение.
Из уравнения (8) следует, что
div V, =- (div V)z - 0
div rot rot V = 0.
Подставляя это выражение в формулу (12), получим
2£ = g V2(/z + V2/2g) = (rotV)2 —(V-rot rotV). (13)
При очень малых значениях числа Рейнольдса (Re -= Vd/v, где d-
характеристика длины) скорость весьма мала и инерционным членом, ко-
торый имеет порядок V2 в сравнении с силой тяжести, давлением и силами
вязкости, можно пренебречь. Тогда приближенно можно записать
Х2£-0. (14)
Полагая по той же причине (rot V)2 и V• rot rot V ничтожно малыми и
аналогичным образом пренебрегая членом П2/2<7, можно записать
72/г-0. (15)
Эта формула справедлива для любой медленной фильтрации вязкой
жидкости и, следовательно, для ламинарной фильтрации в пористой среде.
Уравнение (15) идентично уравнению (6), однако аналогия здесь лишь
формальная. В формуле (15) величина h представляет собой местное дав-
ление в одной точке вязкой жидкости, текущей в порах между
зернами. В формуле (6) h представляет осредненное значение /? в
объеме, содержащем достаточно большое число зерен и пор и вместе с
тем достаточно малом, если сравнивать его со всем фильтрационным пото-
9
ком. Действительный вязкий и существенно перемешивающийся (т. е. не
потенциальный) неоднородный двухфазный поток в порах между зернами
заменяется фиктивным неперемешивающимся (т. е. потенциальным) пото-
ком однородной совокупности пористой среды. Эта среда рассматривается
так, как будто она состоит из одной фазы. Такая абстракция допустима
при осреднении достаточно большого объема. Это объясняет, почему на-
поры, отмечаемые в пьезометрических трубках, могут давать несколько
несогласующиеся результаты.
Основы формул Дарси и Форхсеймера. Рассмотрим одномерную фильт-
рацию в направлении х через пористую однородную изотропную среду со
средним диаметром зерен d и пористостью п, которая представляет собой
отношение объема пустот к общему объему грунта.
Можно легко показать, что п соответствует и средней пористости
любого поперечного сечения и пористости вдоль любого из направле-
ний [32].
Любая точка порового пространства подчиняется уравнению Навье-
Стокса (11). Вопреки гипотезе об одномерной фильтрации через пористую
среду в извилистых каналах среды имеет место трехмерное вязкое тече-
ние. В направлении х формула (11) принимает вид:
(uw)z — ut + v (мгг + и yv + иД, (16)
где х, у, z —оси плоской системы координат; и, v, w — соответствующие
компоненты вектора скорости V.
Снова рассмотрим объем, который включает в себя столь большое
число зерен, что может считаться однородным и изотропным, и в то же
время настолько малым, что в его пределах свойства потока неизменны.
Проведем осреднение уравнения (16) в пределах этого объема. Поскольку
и— главный компонент скорости V, то в однородной среде поперечные
компоненты v и w при осреднении исчезают. Следовательно,
v 0; w 0;
uv = 0; uvy -- 0; uw •• 0; uwz = 0.
Согласно уравнению (8), имеем:
И — у v — wp
11XX “ — vx\< — WXZ »
м — у — w о — 0 • 0.
.V .1 ,L V X £
Удельный расход в направлении q (фиг. 1):
q --- ип
и = q/n,
(17)
(18)
(19)
где п — средняя пористость в направлении, нормальном к х.
Если L —среднее свободное расстояние между двумя зернами, то
п = L/(L + d) или 1 ,
Ljd - - n/(l — rip /
Кроме того,
ut=--qtfn. (21)
Так как жидкость притормаживается стенками (у стенок и -0), то и
достигает максимума где-то в промежутке между зернами. Следовательно,
поверхность м(г/, z) в поровых каналах между зернами имеет выпуклость
10
в положительном направлении х, а значение «vv < 0 и uzz < 0. Осредняя
и принимая во внимание соотношения (19) и (20), мы можем записать:
»vv : — У?/, 7? - - — (1 — riflrP-q'id1,
uzz = — U7.- (1 — nyirfi-.qld-, (22)
wvy J~ uzz = — 3(1 — n'fln^-qld?,
где Зг, 32, p 3t + 3.r—численные параметры, которые зависят от формы
зерен и их структуры, но не от пористости или диаметра зерен.
Учитывая выражение (8), получим:
~ (и2)Л. = иих — uvy — uwz, или -у (и2)л. = 0. (23)
Потоки сходятся в одну точку между соседними зернами. Согласно
условию, и = 0, w = 0 в зоне' сходимости
(г^ -^)Л .у().
При больших скоростях, когда нужно учитывать наличие квадратич-
ного члена, разделение токов в зоне их расхождения сказывается в мень-
шей степени, чем в области сжатия токов. Здесь !zr-Lu>2)r=0 или отри-
цательное число. Следовательно, в обоих случаях при конвергенции и
дивергенции в среднем
+ w2)v< 0.
В уравнениях (19) и (20) мы можем оценить
(и2 -,Е-а»2)Л. - =—xj.u2jL = — 7.(1 —iv:yd-q'--d, (24)
где а — численный коэффициент формы.
Рассмотрим вектор гидравлического градиента
J = — grad Е (25)
и его компоненты Jt, Л, J;t вдоль осей х, у, г.
Учитывая (17), подставим (25) в (16):
— Ех = aq -д bq2 у cq.. (%)
11
Подобным образом
л ~~ — ё\,'0; А - — ~ d; 127)
а ;3 • [ I •— п}2/п3 vjgd", j
b -a-(l -— n\ln3A/gd, I (28)
с -A/ng. I
Подтвердил! это несколькими фактами, известными из испытаний.
В Для малых значений Re и установившейся фильтрации
Л aq; q = j
К - 1/а-------gd2/3v-n3/U --/!г J ( '
Эта эмпирическая формула Дарси (1) с выраженной по Козени вели-
чиной R: а — гидравлическое сопротивление, введенное автором [18],
которое оказывается предпочтительнее понятия проницаемости R, что
подтверждается уравнением {26).
Общее представление о гидравлической проницаемости, получаемое из
зависимости
К --- q/J
ДО)
(мы пишем здесь для упрощения J вместо </)), физически не имеет смысла.
Его можно использовать, только имея в виду соотношение
К-1/щ (31)
причем величина К, замеряемая по уравнению ДО) как универсальный
коэффициент, не используется в лабораторной практике и заменяется
величиной а.
2) Для высоких значений Re и установившейся фильтрации (26) дает
эмпирическую формулу Форхгеймера
J = aq -J- bq2.
i32)
Коэффициент b зависит от пористости п как (1 —п)/п3, среднего диа-
метра зерен d и в отличие от коэффициента а не зависит от вязкости
или температуры.
3) Член cqt, характеризующий неустановившееся движение, незначи-
телен [29] независимо от диаметра пор или температуры. Его влияние
имеет значение только в начальный период, а в последующем его вели-
чиной можно пренебречь.
4) Общие условия фильтрации в пространстве можно определить по
зависимости (26), пренебрегая незначительным членом cqt:
J aq -г bqq (а Ф bq) q,
с компонентами
Л •• -- (а Ч- bq)qt и т. д.
Из выражения (33) получаем:
J - (a Ч~ bq)q;
q - — a/2b + | (а/2b)2 -г J/b ;
q J (a -7- bq) - J/[(a/2)+(a2/4) + J/b\ = J/ (J).
Применяя операцию div к последнему уравнению, найдем:
div q div J/ (J) f (J) div J + J grad f (J) = 0;
div J + J • grad In f (J) 0.
Уравнение (25) дает:
2E gradE-gradln/ (|gradE|) - 0.
ДЗ)
(33 a)
(34)
(36)
12
Эта формула эквивалентна формуле (7), где давление h заменено
энергией Е, а гидравлическая проводимость К выражается через
F 1J) - [и 2 - ’ - ’]/ ’ а2 4 щТ/Ж4 • (37)
Уравнение (36)—это эллиптическое уравнение Пуассона. Его можно
решить методом С. А. Христиановича и П. Я. Полубариновой-Кочиной
128, 29].
Принцип минимума. Математически выражение (.6) эквивалентно ми-
нимуму интеграла по всему объему фильтрации (4)
f (grad h’\2dT minimum (38)
' (T)
или также
^^q~dT -= minimum. (38а)
Фильтрация по Дарси в пористой среде такова, что либо соответст-
вует минимуму всей кинетической энергии, либо рассеяние энергии ока-
зывается минимальным, так как оно пропорционально q-.
В этом принципе минимума содержится парадокс: должны ли мы
учитывать члены второго порядка, чтобы удовлетворить ему? Ведь здесь
поток обусловливается q2. Ответ прост: членами второго порядка можно
пренебречь, когда есть другие члены большей величины; но нельзя пре-
небрегать этими членами, когда нет других. Этот принцип действителен
также для фильтрации по закону Дарси в неоднородной и в неизотропной
среде, однако он недействителен для случая фильтрации по Форхгеймеру.
Основы закона Дарси в пористых складчатых трещиноватых средах.
Автор применил решение Пуазейля для фильтрации в пластах и трещинах
или трещиноватых породах, где трещина полагается прямой [19]. В случае
пространственной системы идентичных и равноотстоящих параллельных
трещин закон Дарси применим при гидравлической проницаемости, выра-
женной в форме Козени-Кармана. Если в трехмерной системе пласты или
трещины геометрически различны или пересекаются между собой, К ока-
зывается симметричным тензором из двух рядов, элементы которого опре-
деляются геометрией трещин. Итак, трещиноватая среда удовлетворитель-
но приводится к неизотропной пористой среде.
ЛИТЕРАТУРА
1. Boussinesq М. J., 1904а. Recherches theoriques sur I’ecoulement des nappes
d’eau infiltrees dans le sol et sur le debit des sources, Journ. Math., 10, Paris.
2. В о u s s i n e s q M. J., 1904b. Complement au memoire, Recherches theoriques sur
I’ecoulement des nappes d’eau infiltrees dans le sol et sur le debit des sources, Journ.
Math., 10, Fasc. 4, Paris.
3. Б. у д а г о в с к и й А. И., 1955. Впитывание воды в почву, Москва.
4. С о u г a n t R., Hilbert D., 1931. Methoden der Mathematischen Physik, Springer,
Berlin, 1, 469; 2, 549.
5. D a г с у H. P. G., 1856. Les fontaines publiques de la ville de Dijon, Exposition et
application des principes a suivre et des formules a employer dans les questions de
distribution d’eau, Victor Dalmont, Paris, 647.
6. E d 1 ef se n N. E., A n d er so n А. В. C., 1943. Thermodynamics of soil moisture,
Hilgardia, 15, No. 2, Agr. Exp. Sta.; Univ, of Calif., Berkeley, Calif.; 31—298.
7. Ferrandon J., 1954. Mecanique des terrains permeables, La Houille Blance, 9,
466—-480.
8. Ф л о p и н B. A., 1948. Теория уплотнения земляных масс, Стройиздат, Москва.
9. Forchheim er Ph., 1901, Z. Verein Deut. Ing., 45, 1782.
10. Gardner W., 1946. Infiltration, Trans. Am. Geophys. Union, >27, 126—128.
11. H a 1 1 W. A., 1956. An analytical derivation of the Darcy equation, Trans. Am. Geo-
phys. Union, 37, 185—188.
12. H u b b e r t M. К i n g, 1940. The theory of groundwater motion, Journ. Geol., 48,
785—944.
13
13. Hubbert M. King, 1956. Darcy's law and the field equations of the flow of
underground fluids, Publ. 104, Shell Development. Co., Houston, Texas, 18 pp.,
Journ. of Petrol. Tech., 222—239, Oct. 1956.
14. I r m a у S., 1946. On the motion of water in soil, Basic chapters in theories of soil
physics and mechanics. M. Sitz (ed.), Israel Assn. Eng. Arch; Water Section, Tel-
Aviv, 59-71 a.
15. Ir may S., 1947. Sur le mouvement des eaux dans le sol, Revue Universelie des Mines,
3, Liege, 129—139.
16. I г in a у S., 1951a. On the motion of capillary moisture in soils, Sci. Pub., 4, Hebrew
Inst. Techn., Haifa, Israel, 43—90; p. XII—XIV.
17. I r m a у S., 1951b. Darcy law for non-isotropic soils, Intern. Assn. Sci. Hydrol. IUGG;
Brussels, 2, 178.
18. Irma у S., 1953. Saturated steady flow in non-homogenotis media and its application
to earth embankments, wells, drains, 3rd Intern. Conf. Soil Meeh. Found. Eng.,
Zurich, 2, 259—263.
19. I r m a у S., 1955. Flow of liquids through cracked media, Bui. Res. Coun. Israel,
5A, No, 1, Jerusalem, 84.
20. I r m a у S., 1956a. Extension of Darcy law to unsteady unsaturated flow through
porous media, Assn. Intern. Hydrol., UGGI; Symposia Darcy, Dijon, 2, 57—66.
21. I r m a у S., 1956b. Experiments on the range of validity of Darcy’s law and the appe-
arance of turbulence in a filtering flow, La Houille Blanche, 11, 419—421.
22. J а с о b С. E., 1950. Flow of ground water Engineering Hydraulics, H. Rouse (ed.),
Wiley & Sons.
23. К о z e n у J., 1927. liber kapillare Leitung des Wassers im Boden, Sitz-Ber. Wiener
Akad., Abt. Ila, 136, 271—306.
24. Христианов ич С. A., 1940. Движение грунтовых вод, не следующее закону
Дарси, Прикл. мат. и мех., 4, вып. 1.
25. Lindquist Е., 1933. The flow of water through porous soil, 1st Congress on Large
Dams, Stockholm.
26. M u s k a t M., 1937. The flow of homogeneous fluids through porous media, McGraw-
Hill, 763.
27. Muskat M., 1949. Physical principles of oil production, McGraw-Hill, 922.
28. P о 1 u b ar i п о v a - Ko c h i ii a P. Ya., 1951. Theory of filtration of liquids in
porous media, Advanced in Applied Mechanics, Acad. Press, 2, 153—225.
29. Полу барииова - Кочипа П. Я-, 1952. Теория движения грунтовых вод,
Гос. изд. техн, и теор. лит., Москва.
30. R i с h а г d s L. А., 1931. Capillary conduction of liquids through porous mediums,
Ph. D. thesis, Cornell Univ.
31. Richards L. A., 1952. Water conducting and retaining properties of soils in rela-
tion to irrigation, Proc. Intern. Symposium on Desert Research, Jerusalem, 523—
544.
32. Rose H. E., 1943. An experimental investigation into the laws of flow of liquids
and gases through bods of granular material, Ph. D. thesis, Univ, of Manchester,
121.
33. S c h e i d e g g e r A. E., 1957. The physics of flow through porous media, Univ.
Toronto Press, 236.
34. S c h n e e b e 1 i G., 1953. Sur la theorie des ecoulements de filtration, La Houille
Blanche, 8, 186—192.
35. Schneebeli G., 1955. Experiences sur la limite de validite de la loi de Darcy et
1’apparition de la turbulence dans un ecoulement de filtration, La Houille Blanche,
9, 141 — 149.
36. Smith W. O., 1932. Capillary flow through an ideal uniform soil Physics, 3, 139—
146.
37. T e r z a g h i K., 1925. Erdbaumechanik auf bodenphysikalischer Grundlage, Franz
Deuticke, Leipzig — Wien, 399.
И. И. Л у щи нс кий
О НАПОРАХ И ФИЛЬТРАЦИИ ГРУНТОВЫХ ВОД
С ПЕРЕМЕННОЙ ПЛОТНОСТЬЮ1
Использование понятий о напорах пресной и окружающей воды предпочтитель-
но при изучении фильтрации подземных вод с переменной плотностью (система пресных,
смешанных и соленых вод). Напор пресной воды в данной точке для грунтовых вод
с переменной плотностью определяется уровнем воды в скважине, заполненной прес-
ной водой, при высоте, достаточной,- чтобы уравновесить существующее давление
в этой точке. Напоры пресной воды определяют гидравлический градиент в горизон-
тальной плоскости. Напор окружающей воды в данной точке пласта определяется как
напор пресной воды, уменьшенный в соответствии с разницей плотностей в пресных и
окружающих водах между данной точкой и свободной поверхностью подземных вод.
Напоры окружающих вод определяют гидравлический градиент в вертикальном на-
правлении. Вертикальная и горизонтальная компоненты скорости в анизотропной
среде, содержащей подземные воды переменной плотности, рассчитываются с исполь
зованием гидравлического градиента напоров пресных и окружающих вод и соответ-
ствующих компонентов тензора проницаемости. Уравнения для компонентов скорости
основаны на обобщенной форме закона Дарси. Представлены зависимости, показываю-
щие связь между напорами пресной и смешанной вод, а также формула для расчета
положения контакта пресной и смешанной воды. Уравнения основаны на концепции
о напоре окружающих вод. Найдено достаточное обоснование для установления пре-
делов применимости уравнений Гибен — Херцберга и Губберта при использовании их
для характеристики течения системы пресных, смешанных и соленых подземных вод.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Цель этой статьи: 1) введение концепции о напоре окружающих вод
и определение связи напора окружающих вод с напором воды в точке
и пресной воды; 2) вывод и иллюстрация уравнения для определения
гидравлического градиента, расхода и направления фильтрации, обуслов-
ленных изменением напоров окружающей воды вдоль вертикали и напо-
ром пресной воды по горизонтали в грунтовых водах с переменней плот-
ностью, и 3) анализ пределов применимости уравнений Гибен-Херцберга
и Губберта.
Условные обозначения и индексы пояснены там, где они впервые
употребляются, и в приложении 1.
1. НАПОРЫ В ТОЧКЕ, ПРЕСНОЙ ВОДЕ И ОКРУЖАЮЩЕЙ СОЛЕНОЙ ВОДЕ
В этом разделе даются определения понятий напора воды в точке,
пресной воде и окружающей воде, а также приводятся уравнения для
определения гидравлических градиентов и векторов скоростей с использо-
ванием напоров пресных и окружающих вод.
Назовем воду, имеющую такую же плотность, как и вода в рассмат-
риваемой точке пласта,—точечной водой. Эта вода может быть пресной,
смешанной или соленой. Напор в любой точке зависит от положения
плоскостей сравнения и плотности воды, заполняющей скважину, которая
используется для измерения напора.
1 N. J. L usczv ns k i. Head and flow of ground water of variable densitv, Journ.
<>l Geophys. Res., 66, No. 12, 4247—4256, 1961.
15
Точечный напор, или напор в точке пласта, заключающего жидкость
переменной плотности, определяется уровнем воды, отнесенным к плоско-
сти сравнения1, в скважине, наполненной водой той же плотности, что
и в данной точке, и достаточной для того, чтобы уравновесить существую-
щее давление в данной точке.
Из этого определения следует (фиг. 1а):
-I- Pi!g, (1)
где
i —любая точка в пласте с водой переменной плотности;
р,- —плотность воды в точке
Hlf) — напор воды в точке i;
Zt —ордината точки I, имеющая положительное направление вверх;
р; —давление в точке i;
g — ускорение силы тяжести.
Давление в
точке I
точечной
воды =
Piff(^ip Zu
FW
пресная вода
Давление в
точке I
пресных
вод-
DW
Смешанная вода
Ни, - напор в окружающей
воде
i
f'luuZ'ZT'
Zr Up,
[лйЛемнмг вод
----Уровень
моря
FW FW
> Для других обозначений
Давление в
точке i
окружающей
воды =
pfg(H,n- ZrgpaylZ'.-zpi
SW
Соленая вода
см. текст)
Фиг. 1. Напоры в пласте, содержащем воды с переменной плотностью.
Индекс i в буквенном обозначении Hip показывает, что напор отно-
сится к рассматриваемой точке i, а второй индекс означает, что скважину
заполняет точечная вода.
Напор пресной воды в любой точке I пласта определяется уровнем во-
ды в скважине, заполненной пресной водой от точки i до высоты, доста-
точной для уравновешивания существующего давления в точке i. Для слу-
чая, когда в скважине используется точечная вода, давление в точке i
будет № (Н 1р — Z-). Если же в скважине использовалась пресная вода
(фиг. 1, 6i, то давление получим в виде ?fg (Hif — Z{).
1 Все напоры и отметки высот отсчитываются от уровня моря.
16
Из этого равенства напор в пресных водах можно выразить через на-
пор точечной воды как
РА/ = Pi Hlp — Zt (б; — Р/), (2)
где
ру — плотность пресной воды;
nif —- давление пресной воды в точке i.
Введем понятие окружающей воды, которая в пределах от рассматри-
ваемой точки i до поверхности подземных вод имеет плотность, равную
средней по вертикали плотности подземных вод.
Напор окружающих вод определяется уровнем воды в скважине, опу-
щенной в рассматриваемую точку и наполненной окружающей водой так,
чтобы уравновесить существующее давление в данной точке.
Давление окружающей воды, исходя из равенства напоров, выражен-
ных в виде характеристик окружающей и пресной воды, определится выра-
жением
Pf^in ' Pf^if (Р/ Ре) (^i ^г)’ 0)
где
Ра — средняя плотность воды между Zr и i, причем
z
_________1 f ,
Ра ______Zi ] Р“^>
1 zi
— давление окружающей воды в i;
Zr —ордината точки г, ограничивающая участок, в пределах которого оп-
ределяется средняя плотность. Выше точки г вода считается пресной.
Координата, по которой отсчитывается высота, имеет положительное
направление вверх. Ее можно определить из равенства давлений,
выраженных через характеристики окружающей (фиг. 1 ,в) и точечной
воды (фиг. 1,а):
Pf^in 9 fl ip (Pi Pa) (Pa ’?/)• (4)
В уравнении (3) показана связь между давлением окружающих и прес-
ных вод. Соотношение напоров в окружающей и точечной воде выражается
уравнением (4).
Как установлено, ра есть средняя плотность воды между условной точ-
кой г и точкой i. Точка г должна помещаться на границе водонасыщен-
ной зоны, если верхний водоносный горизонт не содержит пресных вод.
Если же в водоносной системе верхний пласт содержит пресную воду, то
условная точка может быть выбрана в любом участке между границей на-
сыщенной зоны и первым контактом пресной и смешанной воды.
Когда условная точка совпадает с базисом (отметкой уровня моря),
7Г = 0, то (3) и (4) сводятся к
Pffln pflif ' Zi (py pa) (3t?)
II
pflin ' pflip (Pl Pa)* (^®)
В этих уравнениях pa — осредненная плотность воды между отметкой
уровня моря и точкой i.
Использование контакта пресных вод с залегающими ниже смешанными
водами в качестве такой условной точки приводит вышеупомянутые урав-
нения (3) и (4) к удобному виду, когда этот контакт представляет опреде-
ленный интерес для решения задачи (см. уравнение 9).
Гидравлический градиент. Градиент от (1) для любой точки в грун-
товой воде с переменной плотностью есть
+ Pik = V (pflip) — 2fvpi, (5a)
17
где
V — оператор градиента;
к —единичный вектор, направленный вверх по вертикали.
Аналогично из (1) и (2), исключая Hip, получим
;; b /Hif + (р,- — р/) к. О)
Итак, из (3), полагая, что (Zz— Zr) —-оа\ получим
p/ v - a - z,i |ду, =. ?/.My+(ei _ P/) k,
(5c)
где i, j — горизонтальные единичные векторы, нормальные друг к другу.
Уравнения от 5а до 5с определяют градиенты в зависимости от плот-
ности и давлений точечной воды, от плотности точечной воды и напора
точечной воды, от плотности и напора пресной воды пли от плотности
пресной воды и напора окружающей воды.
Уравнение (5с) особенно важно по следующим причинам. В вертикаль-
ной плоскости левая сторона (5с) сводится к рдс//inldz\, т. е. является
простым произведением плотности пресной воды и градиента, определяе-
мого напором окружающей воды. В любой горизонтальной плоскости пра-
вая сторона (5с) сводится к ррдНц/дх), т. е. к произведению плотности
пресной воды и градиента, определенного по напорам пресных вод.
Так как напоры окружающей воды определяют гидравлический гра-
диент по вертикали, они сопоставимы вдоль вертикали.
Поскольку давления пресных вод определяют гидравлический градиент
вдоль горизонтали в грунтовых водах с переменной плотностью, то они
сопоставимы вдоль горизонтали.
Компоненты скорости. Воспользуемся уравнением Дарси в вектор-
ной форме для описания течения в системе вод различной плотности
g\1pLJr (6)
Zi L ё j
где
q — вектор скорости в точке i;
— проницаемость среды в точке I;
Pj—динамическая вязкость в точке i.
Соответствующее значение проницаемости зависит от среды. В изо-
тропной среде проницаемость постоянна во всех направлениях.
В анизотропной среде проницаемость зависит от направления и яв-
ляется тензором. Проницаемость-тензор имеет три принципиальных на-
правления в соответствии с теорией о применении тензора к проницае-
мости, разработанной Шейдеггером [5]. Он обобщил результаты изучения
направленной проницаемости в анизотропной среде, полученные им и дру-
гими исследователями. Шейдеггер ссылается па Феррандопа и Литвшшши-
на, которые развили более или менее идентичные теории о тензоре-прони-
цаемостп и о фильтрации через анизотропные среды. Согласно этим тео-
риям, вектор скорости может рассчитываться из (6) с использованием тен-
зора симметричной проницаемости с компонентами Krs.
Для. случая произвольной ориентации координат относительно главных
осей пронипаемостей компоненты скорости можно выразить, вводя компо-
ненты тензора-проницасмостп и градиенты от напора окружающей и пресной
воды из (5с):
vy
к-. (7а>
Дккк --К» Д ?, Д4 W
18
иг = — Кз1 — Г р/ Ф7) — К-.Г Р/ z- ' — Лю —I Р/ (7с)
Z 9i L 7 (7v J t’i L 7 Щ/ J \>-i L 7 oz v '
где yv, uv, v2—-компоненты скорости вдоль координат х, у, г соответст-
венно, а7(и—компоненты, обозначенные в приложении 2.
Если х и у— горизонтальные координаты, z— вертикальная координа-
та и если эти координаты совпадают с осями основных направлений про-
ницаемостей, то
Vx = -Ки g dHif' . p/ dx .
Vy - — АД JL_ p
Д - - Кзз g ',4 Г r)f ‘ J dz
(8а)
(86)
(8с)
где Лп, /<22, /С33 в этом случае — главные значения проницасмостей в на-
правлениях х, у, г.
Итак, в анизотропной среде с горизонтальным ложем компоненты ско-
рости в двух горизонтальных направлениях, соответствующих осям двух
основных направлений проницаемости, могут рассчитываться по (8а) и (8Ь)
с использованием в каждом случае соответствующего направления прони-
цаемости, силы тяжести, вязкости воды, плотности пресной воды и гид-
равлического градиента, определяемого напором пресных вод. Вертикаль-
ная компонента скорости может рассчитываться нз (8с) с использованием
основного направления проницаемости вдоль вертикали, гравитации, вяз-
кости воды, плотности пресной воды и гидравлического градиента, опре-
деляемого по напору окружающих вод.
Так как проницаемость в анизотропной среде есть тензор, направле-
ние фильтрации обычно не параллельно гидравлическому градиенту.
Оно определяется при известных компонентах скорости по (7а —с) или
(8а—с).
Примеры. Использование данных по напорам окружающей и пресной
воды для определения гидравлического градиента и скорости в точке плас-
та, содержащего пресную, смешанную п соленую воду, иллюстрируются
на основе данных Института водоснабжения в Нидерландах. Институт
сообщил сведения об уровнях воды и концентрациях хлоридов на июль
1957 г. в скважинах, каждая из которых вскрывает различные глубины
па семи наблюдательных и одной коллекторной станции в области дюн
вблизи Гааги (фиг. 2).
Наблюдательные станции располагаются на территории с многочислен-
ными каналами и водоемами, которые предопределяют интенсивное инфильт-
рационное питание грунтовых вод. В некоторых районах рассматриваемой
области производится откачка грунтовых вод. Геологическое строение ха-
рактерно следующими особенностями: покровные комплексы, залегающие
на отметках, превышающих уровень моря, представлены дюнными отложе-
ниями, которые подстилаются песками и пластом глин. Ниже залегают
топкие пески, перемежающиеся с прослоями и линзами глин до отметки
примерно 100 м ниже уровня моря. Все описанные отложения анизотроп-
ны. Водоносный пласт горизонтален.
Данные, использованные в этой статье, лишь иллюстрируют использо-
вание данных о напорах окружающей и пресной воды для определения
гидравлических градиентов и скоростей при движении воды переменной
плотности. Действительно, величины расчетных давлений, градиентов, на-
правления и скорости не могут быть признаны точными, так как а) во вре-
мя наблюдений в июле 1957 г. одновременно не измерялись содержание
19
приблизительное расстояние от Северного моря вдоль участка, м
200 500 780 920 1050 2550 '
3800
20
чО
60
«;
&
5 80
i
^wo
I
CJ 120
I
-0,85*4”-
0,99
ОМ А
0.83, 1
1.19
-0.95
0,90
Q
N
•1.51
мм 0С
•ЗМ *0.01
Уровень моря
U
DD
•ач1
•О.Ч5 п,
•0,54 —
fnaX /ОД
6'95 ^*’.00 У У 0,59
• 1,П 1ЛС'-д°& ‘0,56
•1,06 0,50
•1.09
Пресные воды
—0,16
-0,62
*-o,ig
0,69
М>7 UJi u>3J ч.
•.58 оло ага 'х Смешанные
Щ *&s ^ды
1.55 0,35 0,10
’Л1д^3
ыог *0,86 nxi
tmmH2' “5,
г,гдао;.й ,к
Соленые воды (И400}
<0,20
J.23 -ng)
0,86 qxs
1,08 0,94
-0.60
ОБЪЯСНЕНИЕ
Р
Наблюдательная и коллекторная
станция
Наблюдательная и эксплуатационная
скважина
-----------удод-------—-------
Изохлоры, в частях на миллион частей раствора
a (12800)
Концентрация хлоридов, в частях на миллион
_________Ж[1]£щ.раствора____________
( 630) -о,оз
' ”0,05
0,32
1,21
• 1,01
0,95
Вверху- напор пресных вод в метрах
В середине-напор окружающих вод в метрах
Внизу-точечный натр в смешанной воде
в метрах
„•3,51
Напор точечной воды выше уровня моря в метрах
Без знака даны напоры выше уровня моря
Со знаком минус- напоры ниже уровня моря
’"‘•"^ччвл'П'^О
*'0,70
0,7<,
0,53
Т***-»^ 0,61
(1520Т* ом
N
шевер-
море
и
Гаага
о 1
'~idrilDD
Обзорная
карта
Ф и г. 2. Распределение напоров грунтовых вод в пласте на побережье вблизи Гааги (Нидерланды) вдоль
участка Р — DD.
хлоридов и величины напора, б) напоры определялись с точностью поряд-
ка 0,02 м и в) плотности были подсчитаны из расчета 1,025 г!мл для во-
ды при 18 000 частей хлоридов в миллионе частей раствора. Предполага-
лась двухмерная установившаяся фильтрация.
Напоры точечной, пресной и окружающей воды показаны на фиг. 2.
Напоры пресных вод были определены по (2) и окружающих — по (3) или
(За).
Точечный напор в пресной воде является также напором окружающей
воды и как таковой сравним с напором окружающей смешанной воды в
вертикальном сечении. Напоры окружающих соленых вод на семи стан-
циях характеризуются компонентами расхода, направленными вверх от не-
которой точки, а в пресной и смешанной водах — компонентами расхода,
направленными вниз.
Точечный напор в пресной воде является также напором пресной во-
ды и как таковой сравним с напором смешанной воды в горизонтальной
плоскости. Напоры пресных вод на семи станциях характеризуются ком-
понентами расхода, направленными в сторону суши в большинстве точек
как пресных, так и смешанных вод.
Рассмотрим на станции MN точку с отметкой—54 м. Гидравлический
градиент порядка 0,001 при направлении потока вниз рассчитывался как
тангенс узла наклона кривой изменения напора в окружающих водах с
глубиной в рассматриваемой точке. Таким же образом по тангенсу угла
наклона кривой изменения напора в пресной воде в рассматриваемой точ-
ке был подсчитан градиент порядка 0,0015, имеющий направление в сто-
рону суши. Для расчета использовался напор пресной воды на глубине
1,12 м (отметка—54 м, станция N)-. Он определялся по уравнению (4а) с
учетом напоров окружающей воды Путем интерполяции между их величи-
нами, равными 1,03 м на глубине с отметкой—47 м и 1,4 м— на глубине
с отметкой —56 м.
Если мы сравним направление фильтрации с результирующим гидрав-
лическим градиентом на отметке—54 м на станции MN и предположим,
что горизонтальная и вертикальная проницаемости в точке те же, что и
главные значения проницаемостей, то можем определить направление
фильтрации по компонентам горизонтальной и вертикальной скоростей рас-
четом по уравнениям (8а) и (8с) соответственно, используя горизонталь-
ные и вертикальные проницаемости и градиенты, определяемые напорами
пресных и окружающих вод. Предположив отношение горизонтальной про-
ницаемости к вертикальной равным 5, найдем, что направление фильтрации
на отметке—54 м будет в сторону суши и вниз под углом 8° к горизон-
тальной плоскости.
Если считать отношение проницаемостей равным 10, то направление
фильтрации будет к горизонтальной плоскости также в сторону суши, но
под углом 4°. Если бы это отношение было действительной величиной, то
направление фильтрации в точке должно было быть в сторону суши и су-
щественно горизонтально. Результирующий гидравлический градиент
был бы в сторону суши и вниз под углом 34° к горизонтальной плос-
кости.
Коэффициент проницаемости в горизонтальной плоскости на отметке
—54 м составляет величину порядка 25 миллидарси (1 миллидарси —
= 0,001 см/сек).
На основании этой проницаемости, горизонтального градиента 0,0015
и пористости 1/3 компонента действительной скорости на отметке — 54 м
станции MN в горизонтальной плоскости будет направлена в сторону суши и
равна 9,7 см/сутки. Принимая отношение горизонтальной скорости к вер-
тикальной от 5 до 10, вертикальный градиент 0,001 и пористость V3, най-
дем компоненту действительной скорости вдоль вертикали (она направлена
вниз и равна примерно 1,3 4-0,6 см/сутки).
21
2. УРАВНЕНИЕ (9) В СРАВНЕНИИ С УРАВНЕНИЯМИ ГИБЕН - ХЕРЦБЕРГА
И ГУББЕРТА
В этом разделе уравнение, основанное на концепции давления окру-
жающих вод, использовано для оценки ограничений уравнений Гибен—
Херцберга и Губберта в тех случаях, когда они применялись для рас-
чета пласта, содержащего пресные, смешанные и соленые воды.
Обозначим через h разность между напором окружающей воды в лю-
бой точке пласта 1 в пресной воде и в любой точке 2 в соленой воде вдоль
вертикали в водоносном горизонте, заключающем пресную, смешанную и
соленую воду (сверху вниз). Величина h представляет собой потерю напора
вследствие вертикального движения между точками 1 и 2. Из выражения
(4), написанного для точек 1 и 2, мы получим:
Pi^ip = — Z2 (р2 — р„) — Zd (оа — pj, (9)
где h --- Н 1п — Н2п~= Н1р—~Н2п и Zd — высота до контакта пресной воды со
смешанной от условно выбранной точки, в которой рассчитывается ptf. Вы-
вод (9) дан в приложении 3.
Уравнение (9) можно интерпретировать как соотношение между Н1р—
напором точечной или пресной воды в пресной воде и Zd — высо-
той до контакта пресной воды со смешанной водой. Соотношение
включает член, который учитывает различие напоров в окружающей воде
между точками 1 и 2, член, который учитывает давление точечной воды в
соленой воде, и два члена, учитывающие переменную плотность в зоне
диффузии.
Используя обозначения этой статьи, запишем уравнение Гибен — Херц-
берга [1, 2]:
--/у?,-?1). со»
где Н1р — уровень воды и Z'd—приблизительная глубина положения сме-
шанной воды. Итак, (10), очевидно, частный случай (9), в котором /1 = 0
и рв = р2. Кроме того, следует принять Zd--=Z'd. Следовательно, глубина
до смешанной воды рассчитывается по уравнению Гибен — Херцберга точ-
но или достаточно точно, когда а) перепад напоров в окружающей воде
между точками 1 . и 2 равен нулю или относительно мал, Ь) напор то-
чечной воды в соленой воде — нулевой или относительно мал и с) мощ-
ность зоны диффузии равна нулю или относительно мала. Если удов-
летворяются только условия (а) и (6), Z'a является глубиной до неопре-
деленной точки в зоне диффузии.
В обозначениях этой статьи уравнение Губберта [3] (уравнение 189)
есть
(П)
Это уравнение выражает правильную связь между Zd —высотой до кон-
такта между двумя несмешивающимися жидкостями, имеющими плотности
Pi и рз (для р2 > Pi), и Н1р и Н2р— напорами в жидкостях с соответствую-
щей плотностью в данной' точке на контакте двух жидкостей. Уравнение
(11) будет определять ординаты контакта между пресной и соленой водой
с отчетливой границей раздела. Для этого случая оно было использовано
в работе [4].
Полученная высота в пределах зоны смешанных вод в действительно-
сти характеризует пласт, содержащий пресные, смешанные и соленые воды.
Для расчетов использовались напоры, наблюдаемые в точках в одном вер-
тикальном сечении; одна точка была в пресной и другая —в соленой во-
де. Уравнение (11) действительно, когда потери напора благодаря верти-
кальным скоростям между точками наблюдения ничтожны. В этом случае
определяем приблизительную высоту теоретического контакта пресной и
соленой воды.
22
Потеря напора между любыми двумя точками по вертикали опреде-
ляется различием в напорах окружающей среды между двумя точками и
характеризуется членом рхЛг в (9). Если им нельзя пренебречь, то этот член
вводится в (11) в следующем виде:
= Pi/* + р2Н2/, — Z"' (р2 —Рх). (12)
Уравнение (12)—частный случай (9), в котором р„ — р3 и Zd = Z*.Ero
можно интерпретировать как соотношение между Н1р, напором точечной
воды в пресной воде, и Zd —действительной высотой теоретического кон-
такта между пресной и соленой водой.
Примеры. Сравним Zd— подъем, рассчитанный по (10—12) с исполь-
зованием следующих данных для двух выбранных точек на станции N
(фиг. 2) вблизи Гааги в Нидерландах:
Рх ~ 1,000 г Ли л;
р2 1,0205 г,Ойл;
== 1,09 м\
Hip — 0,21 м;
Z} = — 17 .и;
Z, - — 80 м.
В шести дополнительных точках в вертикальном сечении (фиг. 2) бы-
ли получены достаточные сведения для определения контакта между прес-
ной и смешанной водой, который оказался на отметке—37 м, и для рас-
чета h = +0,07 м между точками 1 и 2.
Z^ =—53 м был подсчитан по Гибен — Херцбергу (10), Z'd =—60 м—
по (12), Z"d = —64 м— по уравнению Губберта (11). Разницу—11 м меж-
ду Zd и Zd следует отнести за счет члена ^Н2р, разница + 4 м между Z"
и f'd обусловлена различием напоров в окружающей среде, равным +0,07 м
между точками 1 и 2. Так как поправки в этом случае очень малы, урав-
нения Гибен — Херцберга и Губберта дают отметки в пределах зоны диф-
фузии. Итак, эти отметки немногим отличаются от действительной высоты
теоретического контакта, 'Zd, между пресной и соленой водой. Теорети-
ческий контакт на 23 м ниже действительного контакта пресной воды со
смешанной водой.
на отметке—17 м была выбрана произвольно. Если вместо НУр—
= —1,41 м выбрать отметку—2 м (фиг. 2), то Z'd = — 69 м из (1), Z."d =
= — 79 м из (11) и Z.”d = —60 м из (12). В этом случае Z"d одинакова с рас-
считанной ранее. (В расчетах было использовано h = + 0,39 м.)
Сравним также глубины Zd, подсчитанные по (10 — 12) с использова-
нием следующих данных, полученных в 1958 г. по двум скважинам,
вскрывающим две различные глубины на той же вертикали у города Си-
дархерста:
рх = 0,999 + г!мл\
р2 1,020 + г'мл\
Н1р = 3,57 фута;
^2/, = —4,72 фута;
Zx ~ —167 футов;
Z2 = —520 футов.
23
Средняя плотность воды у Сидархерста в зоне диффузии между от-
метками—320 футов и —490 футов примерно равна 1,010 г/мл. На этом
основании из (9) определяется h = —0,47фута.
2'=—170 футов по уравнению Гибен — Херцберга, 2" = —339 фу-
тов по уравнению Губберта и 2" = — 421 фут по (12). Различие в
—229 футов между Z'a и 2^ вызвано членом В этом случае уравне-
ние Гибен — Херцберга дает отметку, которая соответствует даже не зоне
диффузии, а горизонту, расположенному выше ее более чем на 150 м. По
уравнению Губберта получаем глубину на 22 м меньше действительной
высоты теоретического контакта между пресной и соленой водой. Разница
в 22 м свидетельствует, что даже различие в 0,1 фута в давлении окру-
жающей воды между точками 1 и 2 дает разницу приблизительно в 5 фу-
тов между глубиной, рассчитанной по уравнению Губберта, и величиной,
рассчитанной по формуле (12).
Теоретический контакт пресной воды с соленой водой у Сидархерста
приблизительно на 101 фут ниже контакта пресной воды со смешанной во-
дой, определенного геофизическим путем равным —320 футов.
Отметки, рассчитанные по уравнениям 9 — 12. Zd в (9) — высота
контакта пресной воды со смешанной водой. Связь в (9) между напором
точечной воды в пресной воде и глубиной до этого контакта не непос-
редственная, а зависит от нескольких переменных. Однако высота контак-
та может рассчитываться, если имеются необходимые данные для оценки
h, и ра для данных 22 и р2.
2” в (12) —отметка теоретического контакта между пресной и соленой
водой. Она может быть рассчитана через точечный напор в пресной воде,
если есть необходимые данные для оценки h и Н2/, для данных 22 и р2-
Величина Z'd, рассчитанная по уравнению Гибен — Херцберга, так же
как и Zd, рассчитанная по уравнению Губберта, может не попадать в зо-
ну диффузии. Но уравнения Гибен — Херцберга и Губберта могут давать
отметки точек в зоне диффузии для условий, сформулированных при ха-
рактеристике выражений (10) и (11).
ПРИЛОЖЕНИЕ 1
Условные обозначения
g —ускорение силы тяжести;
g—вектор ускорения силы тяжести;
Hip, Hif, Н1п — напор точечной воды, пресной воды и окружающей воды в
точке i соответственно;
h — различие в напорах окружающей воды в точке 1 в пресной
воде и точке 2 в смешанной или соленой воде;
i — точка в грунтовых водах переменной плотности;
i ~ J — в пресной воде; i — 2 — в смешанной или соленой воде;
i — единичный вектор, направленный вдоль горизонтали;
kt — проницаемость среды;
к —единичный вектор, направленный вдоль вертикали;
Pz —давление;
qz— вектор скорости;
v*, t^ — компоненты скорости вдоль осей х, у, г соответственно;
Zd, Z’d, Z"d, Z"—отметки уровня смешанной воды в (9—12) соответственно;
2г—-отметка, отсчитанная по оси, имеющей положительное на-
правление вверх;
Zr — отметка условной точки г;
р! — плотность воды;
24
оа— средняя плотность воды между глубинами Zr и Zz;
Pz —плотность пресной воды;
«iz — вязкость воды;
dh-tJJdx— гидравлический градиент в точке i в направлении х (опре-
деляемый напором пресных вод);
dhifidy — гидравлический градиент в точке i в направлении у (опре-
деляемый напором пресных вод);
dhin/dz—гидравлический градиент в точке i в направлении z (опре-
деляемый напором окружающих вод);
\7 — оператор градиента.
ПРИЛОЖЕНИЕ 2
компоненты тензора коэффициента проницаемости
кг. = КМ К% 4 4 . К3 13 13 . к12 Ki It rnt j ~ i -^2 ^2 ^2 | K3l;im3) KVA - - Ktknt ) К4 4 ( 1 Кз 1-3 J
Ki 4 tni ~ Г Аз 4 /^2 . -1- К, 4 т3, ^22 /4 mt mt t К2 m2 m2 i K3m3ms Kt /771 «1 J- /С2 7772 «2 H - Кз m-3 n3.
Кз1 ^2 ^2 , Ч- Кз 4 пз ' K&t Kt nx -\~Кгтгпг П ^>3 j^3 ^3 K33 -- Kt «! «I ) -i - K2 n. n2 . -Г Аз П3 па 1
где К,, /С2, /<3 —главные значения проницаемости;
4, mv nt— направляющие косинусы между А4 и осями координат х,
У, 2;
/2, та, п.у—направляющие косинусы между /С2 и осями координат х,
у, 2;
/з, т3, п3 — направляющие косинусы между К3 и осями координат х,
у. z.
ПРИЛОЖЕНИЕ 3
Ранее проф. Р. Скалак отмечал, что возможно введение и использова-
ние понятия о напоре окружающей воды в уравнение Дарси. Произведем
обоснование введения этой характеристики, используя уже известные
работы.
Обобщенное уравнение Дарси в векторной форме:
k
Ч = — -(
(А)
Из этого уравнения можно записать выражение для вертикальной ком-
поненты скорости:
м. 1 ( d р , \
Pig \ dz j v
где
v — вертикальная составляющая скорости фильтрации;
ц — вязкость;
k — проницаемость;
g —вектор ускорения силы тяжести;
гц—плотность пресной воды;
р— давление;
25
z— вертикальная координата с положительным направлением вверх:
р(- — плотность жидкости в любой точке.
Очевидно, что правая сторона (В) есть тот же «градиент напора окру-
жающей воды», который нами определялся. Левая сторона есть градиент
потерь напора в виде скорости и градиент от h в нашем уравнении (9).
Чтобы показать эквивалентность уравнений (В) и (9), проинтегрируем (В)
от точки 2 до точки 1:
Zi
( dz --- — ( —I 4 pig (С)
J kplg J pig \ dz 1 v
z2 г.,
или
21 гг
i T^dz= —( ?idz ~(D)
J к & & J J
z2- z2 zr
Теперь определим h как потери напора, обусловленные вертикальным
перемещением; так чтобы —рг h было равно левой части (D).
Затем определяем ра, так чтобы
zr
J Pidz --= ?a(zr — z2). (Е)
Z2
Это то же самое, что и наше рй.
Далее заметим, что
Pi Pig(Hip — Zi)
и (F)
Pi = ?zg(H2p — z3).
Подставим в (D):
_Р1(Я1р —?i)-! р2(Я2/)— z2) — ptl(zr- z2) —рДг-zr). (G)
Правая сторона (G) есть (—ргН1п 4 pYH2n), где НЛп и Н2п суть давления
окружающей воды, определяемые, как мы это предложили. Уравнение (G)
можно записать как
?1Н1р = Pi^ + Р2^2Р — 4 (р2 — р„) — 4 (р„ — Pi), (НI
которое есть точное наше (9), когда Zr — Zd.
ЛИТЕРАТУРА
1. Badon Ghyben W., 1889. Nota in verband met de voorgenomen put boring nabij
Amsterdam, Koninkl. Inst. Inq. Tydschr., The Hague, 8—22.
2. Herzberg A., 1901. Die Wasserversorgung einiger Norseebader, Journ., Gasbe-
leught., 44, Munich, 815—819, 842—844.
3. Hubbert M. K-, 1940. The theory of ground-water motion, Journ. Geol., 48 (8),
864.
4. P e r 1 m u t t e r N. M., Geraghty J. J., U p s о n J. E., 1959. The relation
between fresh and salty water in southern Nassau and southeastern Queens Counties,
Long Island, New York, Econ. Geol., 54 (3), 416—435.
5. Scheidegger A. E., 1957. The Physics of Flow through Porous Media, The Mac-
millan Company, New York, 47—66.
М. С. Ха нт уш
АНАЛИЗ ДАННЫХ ОПЫТНЫХ ОТКАЧЕК ИЗ СКВАЖИН
В ВОДОНОСНЫХ ГОРИЗОНТАХ С ПЕРЕТЕКАНИЕМ1
В статье рассматриваются графические методы определения коэффициентов про-
водимости, емкости (водоотдачи) и перетекания по данным откачек из скважины. Ме-
тоды основаны на теории неустановившегося притока подземных вод в скважине, ра-
ботающей с постоянным дебитом в бесконечном неизолированном водоносном гори-
зонте. Эта теория разработана Хантушем и Джекобом. Применение предлагаемых
методов иллюстрируется расчетами параметров по данным, полученным при откачках
в артезианском бассейне Роузвел, Нью-Мексико.
ВВОДНЫЕ ЗАМЕЧАНИЯ
На основе теории Тейса [10] было предложено несколько методов оп-
ределения коэффициентов проводимости и емкости водоносного горизонта,
ограниченного водоупорными кровлей и подошвой. Наибольший интерес
представляют: графический метод Тейса, впервые описанный Джекобом [5];
метод восстановления уровня, описанный Вензелем [13]; обобщенный гра-
фический метод Джекоба [6] и графический метод Чоу [1]. Джекоб и Лох-
ман [9] дополнили теорию неустановившегося притока к скважине и дали
решение для случая, когда скважина действует с постоянным напором. На
основе этого решения ими разработан графический метод определения гид-
рогеологических параметров.
Хантушем и Джекобом [4] получено решение задачи о неустановив-
шемся движении подземных вод при откачке из скважины в бесконечном
по простиранию водоносном горизонте в условиях, когда в этот горизонт
происходит перетекание воды из соседних-—ниже и выше расположен-
ных — водоносных горизонтов через разделяющие их слабо водопроницаемые
глинистые слои, Дебит скважины считается постоянным. Это решение Хан-
туша и Джекоба выражается следующими соотношениями2:
s = (Q/4kT). j (1/г/)ехр(— у — r2/4B2y)dy; (la)
и
s = (Q/4 К Т) [2Хо (Г/В) - J (1/у) exp ( -у - г2/4ВЭ/) ] dy; (1b)
я
s^(Q/4r.T)W(ufr/B), (le)
где и ~ r2S/4Tt; q = (r2/4B2)/u = Tt/SB2; $—понижение (или восстановле-
ние) уровня; Q —дебит скважины; Т — проводимость основного горизонта
(произведение коэффициента фильтрации на мощность); S — коэффициент
1 М. S. Н a n t u s h, Analysis of Data from Pumping Tests in Leaky Aquifers, Trans.
Am. Geophys. Union, 37, No. 6, 702—714, 1956.
2 Решение основано на допущении, что в соседних (питающих) горизонтах, из ко-
торых происходит перетекание, напор в процессе откачек сохраняется неизменным.—
Прим. ред.
27
емкости (водоотдачи); К', Ь'— коэффициент фильтрации и мощность разде-
ляющего^слабопроницаемого слоя, через который происходит перетекание;
В=\/ ТЬ'/КТ —так называемый «фактор перетекания» [4]; г — расстояние от
центра скважины до любой точки; / — время с момента начала откачки или
восстановления уровня после прекращения откачки; Кп — функция Бесселя
от мнимого аргумента второго рода нулевого порядка; IF (и, г/В) — так на-
зываемая «функция скважины» в пластах при наличии перетекания.
Максимальное понижение или установившееся распределение пониже-
ния sm в районе такой скважины может быть получено из уравнения (16)
при / -> оо;
sm (Q!2r.T)K0(r/B). (2 j
В водоносных горизонтах, характеризующихся перетеканием, кроме
коэффициентов емкости и проводимости, появляется еще и третий параметр,
который характеризует способность слабопроницаемого слоя пропускать
через себя воду. Этот параметр называется коэффициентом перетекания и
выражается так:
К'/Ь' - Т/ВТ (3)
Коэффициент перетекания может быть определен как расход потока
через единицу поверхности раздела между основным водоносным горизон-
том и слабопроницаемым слоем при условии, что разница между напором
основного водоносного горизонта и слоя, из которого происходит перетека-
ние, равна единице.
Целью настоящей статьи является рассмотрение графических методов,
с помощью которых данные опытных откачек могут быть использованы для
расчета параметров водоносного горизонта: коэффициентов емкости, прово-
димости и перетекания.
УСТАНОВИВШЕЕСЯ РАСПРЕДЕЛЕНИЕ ПОНИЖЕНИЯ
Ниже рассматривается графический метод, основанный на установив-
шемся распределении понижения в районе скважины при откачке из нее
с постоянным дебитом.
Когда r/В мало (r/В Ц0,05), то уравнение (2) для практических целей
может быть апроксимировано в виде
sOT«(2,3Q/2nT)lg(0,89r/B).
(4)
Таким образом, при малых значениях r/В график изменения sm в зави-
симости от г в полулогарифмическом масштабе будет выражен прямой ли-
нией. Уклон этой прямой As/Д 1g г равен 2,3Q/2kT. По уклону прямой,
следовательно, можно определить проводимость основного водоносного го-
ризонта: Т = 2,3Q/(2k Д s/Algr). Отрезок, отсекаемый прямой на оси г, рав-
ный г0, дает возможность вычислить значение величины В 0,89 г0.
НЕУСТАНОВИВШЕЕСЯ РАСПРЕДЕЛЕНИЕ ПОНИЖЕНИЯ
Теория. Теоретический график понижения $ в зависимости от времени t
в полулогарифмическом масштабе (при t, нанесенном в логарифмическом
масштабе, см. фиг. 1) характеризуется следующими свойствами.
Уклон m в любой точке выражается в виде
m - Д s/Д lg I - (2.3Q/4 - Т) ехр (—и гЧ4ВЧТр (5)
Уравнение (5) получается в результате дифференцирования уравнения
(1) по lgТ
28
(а) Кривая s — 1gt имеет точку перегиба, в которой соблюдается сле-
дующее соотношение:
ut - r-.S 4'П; - г:'2В,
где индекс (• относится к значениям переменных в точке перегиба. Выше-
указанное соотношение получается путем приравнивания к нулю второй
производной s по 1g/ и решения для и.
^-время в точке перегиба
теплой в точке перегиба
'.Srпонижение а точке пере-\
гиба
: 2.зо .r/в i
I ЧТГГЪ
; чТ1У/?8)
j з =-------
; r |
4? = подток Т/В2 j
О
Фиг. 1. Изменение понижения во времени при работе скважины с постоянным дебитом
в неограниченном водоносном горизонте в условиях перетекания.
(Ь) Уклон кривой mt в точке перегиба
mr~y2,3Q/4mT)<rr/B (7)
или
г - 2,3В [1g (2,3Q/4 тс Т) — 1g mJ . (8)
Выражения (7) и (8) получаются путем подстановки значения щ из
уравнения (6) в уравнение (5).
(с) Понижение уровня в точке перегиба
sI = (Q/4IT)K0(r/B).= (i)s„, (9)
где sm — максимальное понижение уровня в условиях установившегося дви-
жения.
Формула (9) выводится следующим образом: в уравнение (la) вместо
и в соответствии с (6) подставляется значение г/2В. Тогда
sj(Q/4tcT)— ] (l/z/)exp(— у — r44B2y')dy (10)
(г/2В)
или
sJ(Q/4tcT) = 2К0(г/В)— [ (1/г/)ехр( — у — f44B*y)dy. (11)
(г/2В)
Уравнение (9) непосредственно вытекает из уравнений (10) и (11).
(d) Отношение между понижением и уклоном кривой в точке перегиба,
как следует из уравнений (7) и (9), выразится следующим образом:
/ (г/В) //в Ко (г В) - 2,3sz/m;. (12)
29
(е) На части кривой, где она асимптотически приближается к макси-
мальному понижению, уклон в любой точке может быть апроксимирован в
виде
m^(2,3Q/4KT)e^, (13)
где
q Tt SB". (14)
Понижение уровня в этом случае будет
s sm — (Q/4 те Т) Ei (—д),
(15)
где —Ei(—q)— интегральный экспоненциал (так называемая функция сква-
жины в изолированных водоносных горизонтах при отсутствии перетекания).
Выражения (13) и (15) представляют собой асимптотические пределы
правых частей уравнений (5) и (1а), когда и становится очень малым.
Из уравнений (13) и (15) имеем следующее соотношение:
f(q) Ei(—q)] = 2,3 (sm — s)!m. (16)
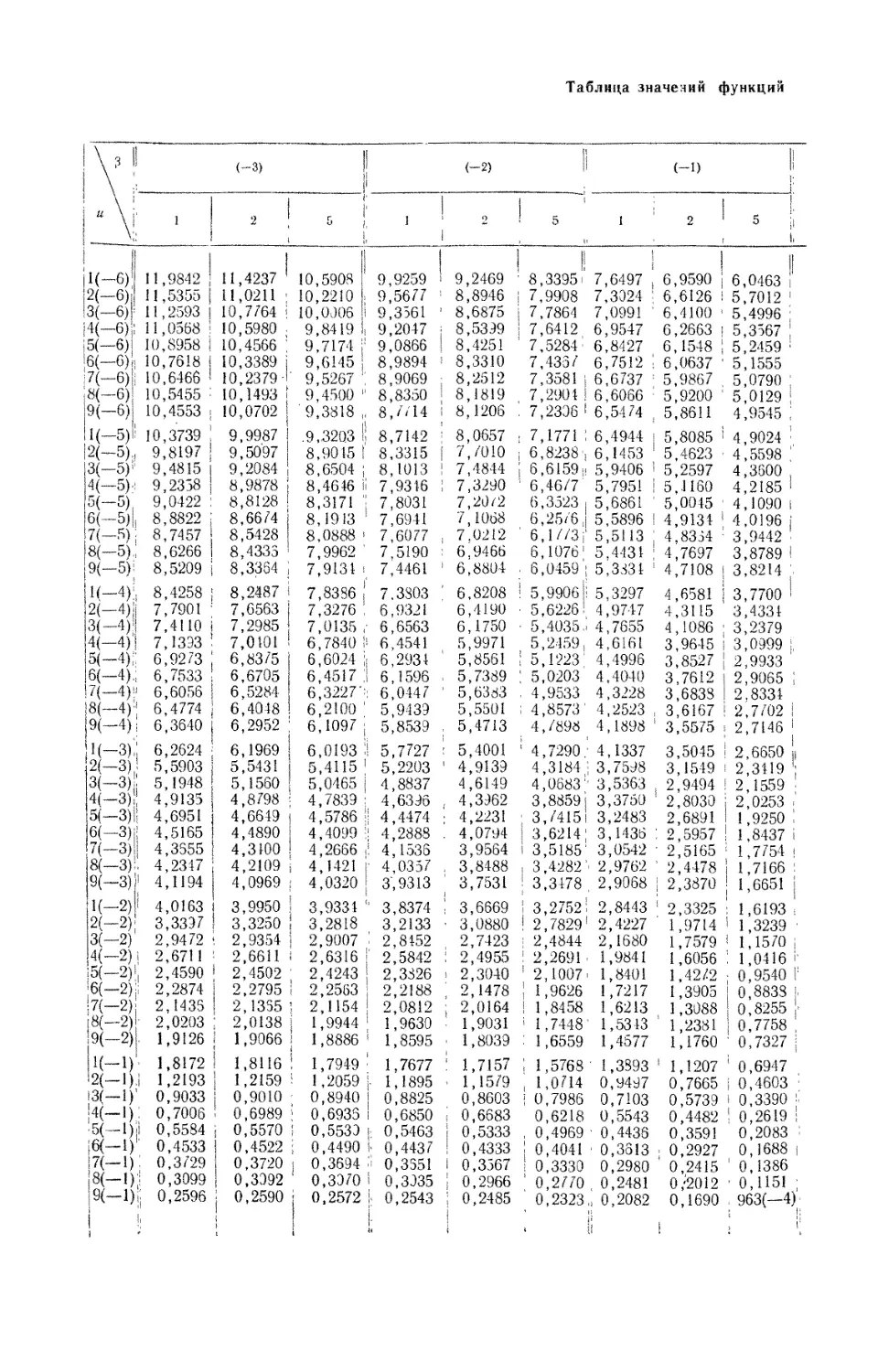
Таблицы функций. Для определения параметров водоносного горизонта
на основе указанной теории необходимы таблицы функций ех Ко (х),
e'c — Ei(—х) и W (и, r/В). Значения первых двух функций даны в табл. 1.
Для аргумента х < 0,01 эти функции могут быть апроксимированы в та-
ком виде:
ех Ко (х) Ко (х) -2,31g (0,89х);
—c,v Ei (— х) — Е1 (— х) — 2,3 1g (1,78 х).
(17)
(18)
Третья функция, W (и, r/В), дана в табл. 2.
Применение. В зависимости от характера данных, полученных в ре-
зультате опытных откачек, может быть выбрана одна из нижеследующих
процедур для расчета параметров водоносного горизонта.
При наличии одной наблюдательной скважины, если период откачек
достаточно продолжителен, для того чтобы могло быть экстраполировано
максимальное понижение, поступают следующим образом. 1) Строят кри-
вую зависимости понижения от времени по данным наблюдений в полу-
логарифмическом масштабе (время в любых удобных единицах, взятых в
логарифмическом масштабе). 2) Путем экстраполяции находят величину
максимального понижения sm. 3) Рассчитывают sz из уравнения (9)
—-sm . 4) Величина sz на кривой соответствует точке перегиба.
5) Производят отсчет времени в точке перегиба tt. 6) Определяют уклон
т, кривой в точке перегиба. Обычно он может быть довольно близко
апроксимирован уклоном прямого отрезка кривой, на котором лежит точка пе-
региба. 7) Подставляя полученные значения st и mt в уравнение (12) и
пользуясь таблицей функции ег’ь Ко (f/B) (табл. 1), находят величину г/В.
8) Зная r/В и г, рассчитывают величину В. 9) При известных Q, sir mi и
r/В по уравнениям (7) или (9) находят значение Т и по уравнению (6) —S.
10) Зная Т и В, определяют коэффициент перетекания К'/b' = Т/В~.
Теоретически рассчитанные таким образом коэффициенты при подста-
новке в уравнение (1) должны дать понижения, совпадающие с наблюдае-
мыми при откачке. Однако для раннего отрезка кривой, построенной по
фактическим данным наблюдений, такого совпадения обычно не достига-
ется. Расчет же понижений по уравнению (1) для последующих стадий
откачки близко совпадает с наблюдаемыми данными.
30
Таблица 1
Значения функций ех, Ко (х) , ех Ко (х), —Ei(—x) и — Е1(— х) ех
X ех 1 ! 1 1 1 Кв(-0 : ] Т, , 2 f! X I ех j K0(-v) • * i 5 h ! i ' « 1 ; I 1; 1 ’ 1 1 5 s i ? ® i . . l :< 1 Ш 14 t 1 '
0,010 1,0101 4,7212|4,7687 4,0379 II 4,07871> 0,051 II 1,0523 3,0945 3,2564 2,4491 2,5773
0,011 1,0111 4,6260 4,6771 3,9436 3,9874 | 0,052 1,0534 3,0752 3,2393 2,4306 2,5604
0,012 1,0121 4,5390 4,5938 3,8576 3,9044 0,053 1,0544 3,0562 3,2226 2,4126 2,5440
0,013 1,0131 4,4590 ’i 4,5173 j 3,7785 3,8282 0,054 1,0555 3,0376 3,2062 2,3948 2,5278
0,014 1,0141 4,3849 | 4,4467 3,7054 3,7578 0,055 1,0565 3,0194 3,1901 2,3775 2,5120
0,015 1,0151 4,3159j4,3812 3,6374 3,6925 0,056 1,0576 3,0015 3,1744 2,3604 2,4964
0,016 1,0161 4,2514 j 4,3200 3,5739 3,6317j 0,057 1,0587 2,9839 3,1589 2,3437 2,4811
0,017 1,0171 4,1908 j 4,2627 3,5143 3,5746, 0,058 1,0597 2,9666 3,1437 2,3273 2,4663
0,018 1,0182 4,1337 4,2088 3,4581 3,5209 1 0,059 1,0608 2,9496 3,1288 2,3111 2,4516
0,019 1,0192 4,0797 4,1580 3,4050 3,4705 0,060 1,0618 2,9329 3,1142 2,2953 2,4371
0,020 1,0202 4,0285 4,1098 3,3547 3,4225 0,061 1,0629 2,9165 3,0999 2,2797 2,4230
0,021 1,0212 3,9797 i 4,0642 3,3069 3,3771 0,062 1,0640 2,9003 3,0858 2,2645 2,4092
0,022 1,0222 3,9332 4,0207 3,2614 3,3340 0,063 1,0650 2,8844 3,0719 2,2494 2,3956
0,023 1,0233 3,8888 3,9793 3,2179 3,2927! 0,064 1,0661 2,8688 3,0584 2,2346 2,3822
0,024 1,0243 3,8463 3,9398 3,1763 3,2535 0,065 1,0672 2,8534 3,0450 2,2201 2,3691
0,025 1,0253 3,8056 i 3,9019 3,1365 3,2159'0,066 ’ 1 ’ 1,0682!2,8382 3,0319 2,2058 2,3562
0,026 1,0263 3,7664 3,8656 3,0983 3,1799 0,067 1,0693 2,8233 3,0189 2,1917 2,3434
0,027 1,0274 3,7287! 3,8307 3,0615 3,1452 10,068 1,0704 2,8086 3,0052 2,1779 2,3310
0,028 1,0284 3,6924 3,7972 3,0261 3,1119 0,069 1,0714 2,7941 2,9937 2,1643 2,3188
0,029 1,0294 3,6574 3,7650 1 2,9920 3,0800, 0,070 1,0725 2,7798 2,9814 2,1508 2,3067
0,030 1,0305 3,6235i3,7339 I 2,9591 3,0494 0,071 1,0736 2,7657 2,9693 2,1376 2,2949
0,031 1,0315 3,5908 1 3,7039 2,9273 3,0196 0,072 1,0747 2,7519 2,9573 2,1246 2,2832
0,032 1,0325' 3,5591 3,6749 2,8965 2,9908 0,073 1,0757 2,7382 2,9455 2,1118 2,2717
0,033 1,0336 3,5284 3,6468 2,8668 2,9631: 0,074 1,0768 2,7247 2,9340 2,0991 2,2603
0,034 1,0316 3,4986;3,6196 2,8379 2,9362 0,075 1,0799 2,7114 2,9226 2,0867 2,2492
0,035 1,0356 3,4697 3,5933 2,8099 2,9101 0,076 1,0790 2,6983 2,9113 2,0744 2,2381
0,036 1,0367 3,4416 3,5678 2,7827 2,8848 0,077 1,0800 2,6853 2,9002 2,0623 2,2273
0,037 1,0377 3,4143 3,5430 2,7563 2,8603 0,078 1,0811 2,6726 2,8894 2,0503 2,2165
0,038 1,0387 3,3877 3,5189 2,7306 2,8364; 0,079 1,0822 2,6599 2,8786 2,0386 2,2062
0,039 1,0398 3,3618: 3,4955 2,7056 2,8133, 0,080 1,0833 2,6175 2,8680 2,0269 2,1957
0,040 1,0408 3,3365 3,4727 2,6813 2,7907 0,081 1,0844 2,6352 2,8575 2,0155 2,1856
0,041 1,0419 3,3119 1 3,4505 2,6576 2,7688’ 0,082 1,0855 2,6231 2,8472 2,0042 2,1754
0,042 1,0429 3,2879; 3,4289 2,6344 2,7474; 0,083 1,0865 2,6111 2,8370 1,9930 2,1655
0,043 1,0439 3,2645,3,4079 2,6119 2,7267' 0,084 1,0876 2,5992 2,8270 1,9820 2,1557
0,044 1,0450 3,2415 3,3574 2,5899 2,7064f 0,085 1,0887 2,5875 2,8171 1,9711 2,1460
0,045 1,0460 3,2192 । 3,3673 2,5684 2,6866 0,086 1,0898 2,5759 2,8073 1,9604 2,1364
0,046 1,0471 3,1973 3,3478 2,5474 2,6672 0,087 1,0909 2,5645 2,7976 1 ,|9498 2,1270
0,047 1,0481 3,1758 3,3287,2,5268 2,6483। 0,088 1,0920 2,5532 2,7881 1,9393 2,1176
0,048 1,0492 3,1549 ! 3,3100 1 2,5068 2,6300j 0,089 1,0931 2,5421 2,7787 1,9290 2,1086
0,049 1,0502 3,1343,3,2918 2,4871 2,6120 0,090 1,0942 2,5310 2,7694 1,9187 2,0994
0,050 1,0513 3,1142 3,2739 2,4679 2,5945 0,091 1,09531 2,5201 I 2,7602 1,9087 2,0906
Продолжение табл. 1
1 j Л'о (Л ) 1 ех Ко (л) j -Ei (- х) ! - El (-л) ех 1 = 1 е v Л'о (л) —Ei (—.г) — Г:1 (—х) г-г
0,092 51,0964 12,5093 [ 2,7511 1,8987 2,0818 , 0,44 J 1,5527! 1,0321 * 1,6025 * 0,6397 0,9933
0,093 4,0975 [2,4986 ! 2,7421 1,8888 [2,0729 0,45 J,5683 1,0129 i 1,5886i0,6253 | 0,9807
0,094 4,0986 j 2,4881 !2,7333 1,8791 2,0643-! 0,46 1,5841 ;0,9943 ; 1,5750 '0,6114 0,9685
0,095 4,0997 ! 2,4776 ;2,7246 1,8695 ' 2,0558 [ 0,47 i 1,6000 I 0,9761 ; I,5617 0,5979 0,9566 j
0,096 4,1008 j 2,4673 2,7159 ' 1,8599 ! 2,0473 [’ 0,48 ' 1,6161'0,9584 11,5489 0,5848 ! 0,9451
0,097 1,1019 2,4571 2,7074 I 1,8505 2,0390' 0,49 1 1,6323 ; 0,9412 , 1,5363 10,5721 ! 0,9338
0,098 1,1030 2,4470 ' 2,6989 1,8412 2,0307' 0,50 '1,6437 :0,9244 1,5241 0,5598 0,9229
0,099 ,1,1041 : 2,4370 ! 2,6906 : 1,8320 ! 2,0227 0,51 [ 1,6653 0,9081 [ 1,5122 ,0,5478 0,9123
0,100 4,1052 . 2,4271 '2,6823 1 1,8229 1 2,0147 0,52 ,1,6820 0,8921 I,5006 0,5362 0,9019
о,и '!, 1163 ’ 2,3333 2,6046 2,5345 1,7371 । 1,9391 0,53 , 1,6989 [0,8766!1,4892 i 0,5250 0,8919
0,12 1,1275 2,2479 2,1695 1,6595 [1,8711 0,54 1,7160 ! 0,8614[ 1,4781 10,5140 ! 0,8820-
0,13 1,1388 2,4707 1,5889 ! 1,8094 0,55 1,7330 j 0,8466 1,4673 '0,5034 '0,4930 0,8725
0,14 4,1503 2,0972 2,4123 1,5241 1,7532,, 0,56 1,7507 0,8321 1,4567 0,8631
0,15 4,1618 2,0300 < 2,3585 1,4645 1,7015; 0,57 1 1,7683 0,8180 '1,4464 0,4830 0,8541
0,16 1,1735 1,9674 2,3088 1,4092 ' 1,6537' 0,58 ; 1,7860 j0,8042 !1,4363 0,4732 0,8451
0,17 4,1853 1,9088 2,2625 1,3578 1,6094' 0,59 1,8040 0,7907 1,4262 0,4637 0,8365-
0,18 4,1972 j 1,8537 2,2193 1,3098 1,5681 0,60 [ 1,8221 [ 0,7775 1,4167 '0,4544 0,8280
0,19 [1,2093 1,8018 2,1788 1,2649 [ 1,5295 - 0,61 1,84041 0,7646 1,4073 . 0,4454 0,8197
0,20 1,2214 1,7527 2,1408 1,2227 |1,4934 1 0,62 ! 1,8589 0,7520 1,3980 0,4366 0,8116-
0,21 1,2337 1,7062>2,1049 1,1829 ! 1,4593 - 0,63 ' 1,8776 0,7397 ।1,3889 0,4280 0,8036
0,22 1,2461 1,6620*2,0710 1 1,1454 1 1,4273 ' 0,64 1,8965 । 0,7277 ! 1,3800 0,4197 0,7960
0,23 4,2586 1,6199 2,0389 1,1099 ! 1,39691 0,65 ' 1,91551 0,7159* 1,3713'0,4115 0,7882
0,24 1,2713 1,5798 2,0084 1,0762 ’1,3681 - 0,66 i 1,9348 0,7043 11,3627 0,4036 0,7809
0,25 1,2840 1,5415 1,9793 1,0443 , 1,3409., 0,67 * 1,9542 0,6930 i 1,3543 0,3959 0,7737
0,26 1,2969 1,5048 1,9517 1,0139 1,3149. 0,68 ! 1,9739 0,6820 ,1,3461 0,3883 0,7665
0,27 1,3100 1,4697 1,9253 0,9849 ' 1,2902 ' 0,69 ' 1,9937 0,6711 ; 1,3380 0,3810 0,7596
0,28 1,3231 1,4360 1,9000 0,9573 1,2666 0,70-2,0138 0,6605 * 1,3301 |0,3738 0,7528
0,29 1,3364 1,4036 1,8758 0,9309 I 1,2441 , 0,71 ' 2,0340 j 0,6501 1,3223!0,3668 0,7461
0,30 1,3499 1,3720 1,8526 । 0,9057 1,2226 : 0,72 ; 2,0544 0,6399 1,3147 0,3599 0,7394
0,31 1,3634 1,3425 1,8304 0,8815 1,2018'! 0,73 ! 2,0751 I 0,6300 .1,3072 0,3532 0,7329
0,32 1,3771 1,3136 1,8089 0,8583 1,1820 [ 0,74 ! 2,0959 I 0,6202 ’ 1! ’ 1 1,2998 0,3467 0,7266
0,33 1,3910 1,2857 1,7883;0,8361 1,16301! 0,75 2,1170 0,6106 1,2926 0,3403 0,7204
0,34 1,4050 1,2587 1,7685 0,8147 1,1446!: 0,76 ! 2,1383!0,6012 1 1 1,2855 0,3341 0,7144
0,35 1,4191 1,2327 1,7493 0,7942 1,1270'* 0,77 [ 2,1598* 0,5920 1,2785 0,3280 0,7084
0,36 1,4333 1,2075 1,7308 0,7745 1,1101 '' 0,78 2,1815 । 0,5829 1,2716 0,3221 0,7027
0,37 1,4477 1,1832 1,7129 0,7554 1,0936' 0,79 । 2,2034 0,5740 1,2649 0,3163 0,6969
0,38 1,4623 1,1596 1,6956 0,7371 1,0779.1 0,80 I 2,2255 0,5653 1,2582 0,3106 0,6912
0,39 1,4770 1,1367 1,6789 0,7194 1,0626 1 0,81 I 2,2479 0,5568 1,2517 0,3050 0,6856
0,40 51,4918 1,1145 1,6627 0,7024 1,0478 ! 0,82 । 2,2705 1 1 0,5484 1,2452 0,2996 0,6802
0,41 1,5068 1,0930[ 1,6470- 0,6859 1,0335 * 0,83 2,2933 0,5402 1,2389 0,2943 0,6749
0,42 11,5220 1,0721 ! 1,6317 । 0,6700 1,0197 0,84 !2,3164 0,5321 1,2326 0,2891 0,6697
0,43 1,5373 1,0518; 1,6169' 0,6546 1,0063J 0,85 '2,3397 0,5242 1,2265 0,2840 0,6644
Продолжение г а б л. 1
X , ех Ко (X) о -Ei (~х) - Ei ( -х) ех * V ! 7 ; ех । ! , ) —Ei (—х) -Ei (—л) ех
0,86 2,3632 0,5165 1,2205 0,2790 0,6593 • 2,4 | 11,0232 0,0702 0,7740 0,0284 1о,3135
0,87 2,3869 0,5088 1,2145 0,2742 j 0,6545 2,5 12,1825 0,0623 0,7596 0,0249 ;0,3035
0,88 :2,4Ю9 0,5013 1,2086 0,2694 0,6495 • 2,6 ’ 13,4637 0,0554 j 0,7459 0,0219 !о,2942
0,89 2,4351 0,4940 1,2029 0,2647 0,4664: 2,7 14,8797! 0,0493'0,7329 0,0192 '0,2854
0,90 '2,4596 0,4867! 1,1972 0,2602 0,6400' 2,8 ' 16,4446!0,0438 ‘ 0,7206 0,0169 0,2773
0,91 2,4843 0,4796 1,1916 0,2557’0,6352 2,9 ; 18,17421 0,0390 0,7089 i 0,0148 0,2693
0,92 2,5093 0,4727 1,1860 0,2513 0,6306 3,0 ' 20,0855' 0,0347,0,6978 0,0131 0,2621
0,93 2,5345 0,4658 1,1806 0,2470 0,6260- 3,1 1 22,1980: 0,0310 • 0,6871 !0,0115 Ю,2551
0,94 2,5600 0,4591 1,1752 0,2429 0,6218 3,2 24,53251 0,0276 0,6770 0,0101 0,2485
0,95 12,5857 0,4524' 1,1699 0,2387 0,6172! 3,3 27,1126 0,0246• 0,6673 0,0089 0,2421
0,96 2,6117 0,4459 1,1647 0,2347 0,6130! 3,4 29,9641 0,0220 ; 0,6580 0,0079 0,2365
0,97 •2,6379 0,4396 1,1595 0,2308 0,6088! 3,5 • 33,1155 0,0196 ! 0,6490 0,0070 0,2308
0,98 2,6645 0,4333 : 1,1544 0,2269 0,6046 . 3,6 36,59821 0,0175 j0,6405 0,0062 0,2254
0,99 2,6912 0,4271 : 1,1494 0,2231 0,60041 3,7 ’ 40,4473 0,0156 0,6322 0,0055 0,2204
1,00 2,7183 0,4210 ; 1,1445 0,2194 0,5964. 3,8 ; 44.7012,0,0140 0,6243 0,0048,0,2155
1,1 13,0042 0,3656 1,0983 0,1860'0,5588 . 3,9 1 49,4025; 0,0125 0,6166 0,0043 0,2108
1,2 3,3201 0,3185 , 1,0575 0,1584'0,5259 4,0 1 54,5982 0,0112.0,699310,0038 0,2063
1,3 3,6693 0,2782 ! 1,0210 0,1355 0,4972 4,1 60,3403 0,0100 0,6022 0,0033 '0,2021
1,4 4,0552 0,2437 ' 0,9881 0,1162 0,4712 4,2 1 66,6863 0,0089 0,5953 0,0030 0,1980
1,5 4,4817 0,2138 0,9582 0,1000! 0,4482! 4)3 73,6998'0,0080 ! 0,5887 0,0026 0,1941
1,6 '4,9530 0,1880' 0,9309 0,0863; 0,5475 4,4 81,4509! 0,0071 0,5823 0,0023 :о,1903
1,7 ‘5,4739 0,1655 0,9059- 0,074710,4086 4,5 ! 90,0171 0,0064 0,5761 0,0021 0,1866
1,8 6,0496 0,1459' 0,8828 0,0647)0,3915 4,6 ' 99,4843,0,0057 0,5701 0,0018 >0,1832
1,9 :б,б859 0,1288 0,8614 0,0562.0,3758 4,7 109,94720,0051 0,5643 0,0016 0,1798
2,0 '2,3891 0,1139 0,8416 0,0489; 0,3613 , 4,8 121,5104 0,0046 ! 0,5586 0,0014 '0,1766
2,1 8,1662 0,1008 0,8230 0,0426 ; 0,3480 ! 4,9 1134,2898 0,0041 : 0,5531 0,0013 0,1734
2,2 ;9,0250! 0,0893 ’ 0,8057' 0,0372 0,3356; 5,0 148,4132'0,0037 10,5478 0,0011 [0,1704
2,3 9,9742 0,0791 0,7894 ; 0,0325 0,3242
Иногда экстраполированная величина sm оказывается меньше или
больше действительной. Это связано с тем, что прямолинейный отрезок
кривой s — lg t проводится либо положе, либо круче, чем необходимо.
В таких случаях расчетные понижения отклонятся от фактической кривой.
Поэтому необходимо уточнять значение sm и прямолинейного отрезка
кривой. Величина поправки устанавливается из сопоставления расчетных
и фактических данных. После внесения поправки вышеуказанные этапы
оценки параметров повторяются. И так до получения удовлетворительного
ответа.
Пример. На фиг. 2 показана кривая зависимости понижения от вре-
мени, полученная по данным опытной откачки, проведенной на ферме
Маутрэйз в артезианском бассейне Роузвелл, Нью-Мексико.
Расход скважины, из которой производилась откачка, составлял
3,33 фут3/сек. Ее расстояние от наблюдательной скважины — 1060 футов.
Замеренные понижения в наблюдательной скважине на ранней стадии
33
Таблица 2
оо
Значение функции IF (u, r, B) = J (1 /у) ехр (—у—г" 4В-у)(1у
п
и 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01
0 00 14.0474 12.6611 11.8502 11.2748 10.8286 10.4640 10.1557 9.8887 9.6532 9.4425
.000001 13.2383 13.0031 12.4417 11.8153 11.2711 10.8283 10.4640 10.1557 9.8887
.000002 12.5451 12.4240 12.1013 11.6716 11.2259 10.8174 10.4619 10.1554 9.8886 9.6532
.000003 12.1397 12.0581 11.8322 П.5098 11.1462 10.7849 10.4509 10.1523 9.8879 9.6530 9.4425
.000004 11.8520 11.7905 11.6168 11.3597 11.0555 10.7374 10.4291 10 1436 9.8349 9.6521 9.4422
.000005 11.6289 11.5795 11.4384 11.2248 10.9642 10.6822 10.3993 10,1290 9.8786 9.6496 9.4413
.000006 11,4465 11.4053 П.2866 11.1040 10.8764 10.6240 10.3640 10,1094 9.8686 9.6450 9.4394
.000007 11.2924 11.2570 11.1545 10.9951 10.7933 10.5652 10.3255 10.0862 9.8555 9.6382 9.4361
,000008 11,1589 11.1279 11.0377 10.8962 10.7151 10.5072 10.2854 10.0602 9.8398 9.6292 9.4313
.000009 11.0411 11.0135 10,9330 10.8059 10.6416 10.4508 10.2446 10.0324 9.8219 9.6182 9.4251
.00001 10.9357 10.9109 10.8382 10.7228 10.5725 10.3963 10.2038 10.0034 9.8024 9.6059 9.4176
.00002 10.2426 10.2301 10.1932 10.1332 10.0522 9.9530 9.8386 9.7126 9.5781 9.4383 9.2961
.00003 9.8371 9.8288 9.8041 9.7635 9.7081 9.6392 9.5583 9.4671 9.3674 9.2611 9.1499
.00004 9.5495 9.5432 9.5246 9.4940 9.4520 9.3992 9.3366 9,2653 9.1863 9.1009 9.0102
.00005 9.3263 9.3213 9.3064 9.2818 9.2480 9.2052 9.1542 9.0957 9.0304 8.9591 8.8827
.00006 9.1440 9.1398 9.1274 9.1069 9.0785 9.0426 8.9996 8.9500 8.8943 8.8332 8.7673
.00007 8.9899 8.9863 8.9756 8.9580 8.9336 8.9027 8.8654 8.8224 8.7739 8.7204 8.6625
.00008 8.8563 8,8532 8.8439 8.8284 8.8070 8.7798 8.7470 8.7090 8.6661 8.6186 8.5669
.00009 8.7386 8.7358 8.7275 8.7138 8.6947 8.6703 8.6411 8.6071 8.5686 8.5258 8.4792
.0001 8.6332 8.6308 8.6233 8,6109 8.5937 8.5717 8.5453 8.5145 8.4796 8.4407 8.3983
0002 7.9402 7.9390 7.9352 7.9290 7.9203 7.9092 7.8958 7.8800 7.8619 7.8416 7.8192
.0003 7.5348 7.5340 7.5315 7.5274 7.5216 7.5141 7.5051 7.4945 7.4823 7.4686 7.4534
.0004 7.2472 7.2466 7.2447 7.2416 7.2373 7.2317 7,2249 7.2169 7.2078 7.1974 7.1859
0005 7.0242 7.0237 7.0222 7.0197 7.0163 7.0118 7.0063 6,9999 6.9926 6.9843 6.9750
0006 6.8420 6.8416 6.8403 6.8383 6.8353 6.8316 6.8271 6,8218 6.8156 6.8086 6.8009
.0007 6.6879 6.6876 6.6865 6.6848 6.6823 6.6790 6.6752 6.6706 6.6653 6.6594 6.6527
.0008 6.5545 6.5542 6.5532 6.5517 6.5495 6.5467 6.5433 6.5393 6.5347 6.5295 6.5237
0009 6.4368 6.4365 6.4357 6.4344 6.4324 6.4299 6.4269 6.4233 6.4192 6.4146 6.4094
.001 6.3315 6.3313 6.3305 6.3293 6.3276 6.3253 6.3226 6.3194 6.3157 6.3115 6.3069
.002 5.6394 5.6393 5.6389 5.6383 5.6374 5.6363 5.6350 5.6334 5.6315 5.6294 5.6271
.003 5.2349 5.2348 5.2346 5.2342 5.2336 5.2329 5.2320 5.2310 5.2297 5.2283 5.2267
004 4.9482 4.9482 4.9480 4.9477 4.9472 4.9467 4.9460 4.9453 4.9443 4.9433 4.9421
.005 4.7261 4.7260 4.7259 4.7256 4.7253 4.7249 4.7244 4.7237 4.7230 4.7222 4.7212
.006 4.5448 4,5448 4.5447 4.5444 4.5441 4.5438 4.5433 4.5428 4,5422 4.5415 4.5407
.007 4.3916 4.3916 4.3915 4.3913 4.3910 4.3908 4,3904 4.3899 4.3894 4.3888 4.3882
008 4.2591 4.2590 4.2590 4.2588 4.2586 4.2583 4.2580 4.2576 4.2572 4.2567 4.2561
.009 4.1423 4.1423 4.1422 4.1420 4.1418 4.1416 4.1413 4,1410 4.1406 4.1401 4.1396
.01 4.0379 4.0379 4.0378 4.0377 4.0375 4.0373 4.0371 4.0368 4.0364 4.0360 4.0356
.02 3.3547 3.3547 3.3547 3.3546 3.3545 3.3544 3.3543 3.3542 3.3540 3.3538 3.3536
.03 2 9591 2.9591 2.9591 2.9590 2.9590 2.9589 2.9589 2.9588 2.9587 2.9585 2.9584
.04 2.6813 2.6812 2.6812 2.6812 2.6812 2.68Ц 2.6810 2.6810 2.6809 2.6808 2.6807
.05 2.4679 2.4679 2.4679 2.4679 2.4678 2.4678 2.4678 2.4677 2.4676 2.4676 2.4675
06 2,2953 2.2953 2.2953 2.2953 2.2952 2.2952 2.2952 2.2952 2.2951 2.2950 2.2950
.07 2.1508 2.1508 2.1508 2.1508 2.1508 2.1508 2.1507 2.1507 2.1507 2.1506 2.1506
.08 2.0269 2.0269 2.0269 2.0269 2.0269 2.0269 2.0269 2.0268 2,0268 2.0268 2.0267
.09 1.9187 1.9187 1.9187 1.9187 1.9187 1.9187 1.9187 1.9186 1.9186 1.9186 1.9185
1 1.8229 1.8229 1.8229 1.8229 1.8229 1.8229 1.8229 1.8228 1.8228 1.8228 1.8227
.2 1.2227 1.2226 1.2226 1.2226 1.2226 1.2226 1.2226 1.2226 1.2226 1.2226 1.2226
.3 0.9057 0.9057 0.9057 0.9057 0.9057 0.9057 0.9057 0.9057 0.9056 0.9056 0.9056
.4 7024 7024 7024 7024 7024 7024 7024 7024 7024 7024 7024
5 5598 5598 5598 5598 5598 5598 5598 5598 5598 5598 5598
.6 4544 4544 4544 4544 4544 4544 4544 4544 4544 4544 4544
,7 3738 3738 3738 3738 3738 3738 3738 3738 3738 3738 3738
.8 3106 3106 3106 3106 3106 Э|06 3106 3106 3106 3106 3106
9 2602 2602 2602 2602 2602 2602 2602 2602 2602 2602 2602
1.0 0.2194 0.2194 0.2194 0.2194 0.2194 0,2194 0.2194 0.2194 0.2194 0.2194 0.2194
2.0 489 489 489 489 489 489 489 489 489 489 489
3.0 130 130 130 130 130 130 130 130 130 130 130
4.0 38 38 38 38 38 38 38 38 38 38 38
5,0 11 П И 11 11 11 П И 11 И
6.0 4 4 4 4 4 4 4 4 4 4 4 1
7.0 1 1 1 1 1 1 1 1 1 1 1
80 0 0 0 0 0 0 0 0 0 0 1 0 (Continued) !
11 р о д о л ж е и и е i а б л, 2, значение г/В Д 0,01
0,01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 0.055 0.06 0.065 0.07 0.075 0.08 0.085 0.09 0.095 0.10
0 9.4425 8.6319 8.0569 7.6111 7.2471 6.9394 6.6731 6.4383 6.2285 6.0388 5.8658 5.7067 5.5596 5.4228 5.2950 5.1750 5.0620 4.9553 4.8541
.000001
.000002
.000003 9.4425
.000004 9.4422
.000005 9.4413
,000006 9,4394
.000007 9.4361 8.6319
.000008 9.4313 8.6318
.000009 9.4251 8.6316
.00001 9.4176 8.6313 8.0569
.00002 9.2961 8.6152 8.0558 7.6111 7.2471
.00003 9.1499 8.5737 8.0483 7,6101 7.2470
.00004 9.0102 8.5168 8.0320 7.6069 7.2465 6.9394 6,6731
.00005 8.8827 8.4533 8.0080 7.6000 7.2450 6.9391 6.6730
.00006 8.7673 8.3880 7.9786 7.5894 7.2419 6,9384 4.6729 6.4383
.00007 8.6625 8.3233 7.9456 7.5754 7.2371 6.9370 6.6726 6.4382 6.2285
.00008 8,5669 8.2603 7.9105 7.5589 7.2305 6.9347 6.6719 6.4381 6.2284
.00009 8.4792 8.1996 7.8743 7.5402 7.2222 6.9316 6.6709 6.4378 6.2283
.0001 8,3983 8.1414 7.8375 7.5199 7,2122 6.9273 6.6693 6.4372 6.2282 6.0388 5.8658 5.7067 5.5596 5.4228 5.2950
.0002 7.8192 7.6780 7.4972 7.2898 7.0685 6.8439 6.6242 6.4143 6.2173 6.0338 5.8637 5.7059 5,5593 5.4227 5.2949 5.1750 5.0620 4.9553
.0003 7.4534 7.3562 7.2281 7.0759 6.9068 6.7276 6.5444 6.3623 6.1848 6.0145 5.8527 5.6999 5.5562 5.4212 5.2942 5.1747 5.0619 4.9552 4.854!
.0004 7.1859 7.UI9 7.0128 6.8929 6.7567 6.6088 6.4538 6.2955 6.1373 5.9818 5.8309 5.6860 5.5476 5.4160 5.2912 5.1730 5.0610 4.9547 4.8539
.0005 6.9750 6.9152 6,8346 6.7357 6.6219 6.4964 6.3626 6.2236 6.0821 5.9406 5.8011 5.6648 5.5330 5.4062 5.2848 5.1689 5.0585 4.9532 4.8530
.0006 6.8009 6.7508 6.6828 6.5988 6.5011 6.3923 6.2748 6.1512 6.0239 5.8948 5.7658 5.6383 5.5134 5.3921 5.2749 5.1621 5.0539 4.9502 4.8510
.0007 6.6527 6.6096 6.5508 6.4777 6.3923 6.2962 6.1917 6,0807 5.9652 5.8468 5.7274 5.6081 5.4902 5.3745 5.2618 5.1526 5.0471 4.9454 4.8478
.0008 6.5237 6.4858 6.4340 6,3695 6.2935 6.2076 6.1136 6.0129 5.9073 5.7982 5.6873 5.5755 5.4642 5.3542 5.2461 5.1406 5.0381 4.9388 4.8430
.0009 6.4094 6.3757 6.3294 6.2716 6.2032 6.1256 6.0401 5.9481 5.8509 5.7500 5.6465 5,5416 5.4364 5.3317 5.2282 5.1266 5.0272 4.9306 4.8368
Продолжение табл. 2
001 002 6,3069 5.6271 6 2765 5 6118 6.2347 5.5907 6.1823 5.5638 6.1202 5 5314 6.0494 5.4939 3.9711 5.4516 5.8864 5 4047 5.7965 5.3538 5.7026 5 2991 5.605© 5.2411 5.5071 5.1803 5.4075 5.1170 5.3078 5 0517 5.2087 4 9©48 5.1 109 4.9166 5.0133 4.8475 4.9208 4.7778 4.8292 4 7079
003 5 2267 5 2166 5 2075 5 1845 5 1А?7 5 1373 5 1084 5 0762 5 0408 5 0025 4 9615 4 9!ЙО 4 872? 4 8243 4 7746 4 7234 4 6707 4 6169 4 5622
опл А 94 21 4 9Д45 4 ?24П А 9105 4 8941 4 8749 4 8530 4 8296 4,8016 4 7722 4.7406 4 7068 4 6710 4 AJ35 4 594? 4 5533 4 МН 4 4676 4.4Z30
005 4 /212 4 7152 А 706Й 4 6960 4 6829 4 6675 4 6499 4 6 30 2 4 6084 4 5846 4 5590 4 5314 4.502? 4 4ЛЗ 4 4JB9 4 4050 4 3699 4 3335 4.2960
006 4.5407 4.5357 4 5287 4.5197 4.5088 4.4960 4.4814 4.4649 4.4467 4.4267 4.4051 4.3819 4.3573 4.331! 4.3036 4.2747 4,2446 4.2134 4.1812
007 4.3882 4 3839 4.3779 4.3702 4.3609 4.3500 4.3374 4.3233 4,3077 4.2905 4.2719 4.2518 4 2305 4.2078 4.1839 - 4.1588 4.1326 4.1053 4.0771
008 4.2561 4.2524 4.2471 4.2404 4.2323 4,2228 4.2118 4.1994 4.1857 4.1707 4,1544 4.1368 4.1180 4.0980 4.0769 4.0547 4.0315 4.0073 3.9822
009 4 1396 4.1363 4.1317 4.1258 4.1186 4.1101 4.1004 4.0894 4.0772 4.0638 4.0493 4.0336 4.0169 3.9991 3.9802 3.9603 3.9395 3.9178 3.8952
01 4.0356 4.0326 4.0285 4.0231 4.0167 4.0091 4.0003 3 9905 3,9795 3.9675 3.9544 3.9403 3.9252 3.9091 3.8920 3.8741 3.8552 3.8356 3.8150
02 3.3536 3.3521 3.3502 3.3476 3.3444 3.3408 3.3365 3.3317 3.3264 3.3205 3.3141 3.3071 3.2997 3 2917 3.283 2 3.2742 3.2647 3.2547 3.2442
03 2.9584 2.9575 2.9562 2.9545 2.9523 2.9501 2.9474 2,9444 2.9409 2.9370 2.9329 2.9284 2.9235 2,9183 2.9127 2.9069 2.9007 2.8941 2.8873
04 2.6807 2.6800 2.6791 2.6779 2.6765 2.6747 2.6727 2.6705 2.6680 2.6652 2.6622 2.6589 2.6553 2.6515 2.6475 2.6432 2.6386 2.6338 2.6288
05 2.4675 2.4670 2.4662 2.4653 2.464 2 2.4628 2.4613 2.4595 2.4576 2.4554 2.453! 2.4505 2.4478 2.4448 2.4416 2.43S3 2.4347 2,4310 2.4271
06 2 2950 2.2945 2.2940 2.2932 2.2923 2.2912 2.2900 2.2885 2.2870 2 2852 2.2833 2.2812 2.2790 2.2766 2.2740 2.2713 2.2684 2.2654 2.2622
07 2 1506 2.1502 2.1497 2.1491 2.1483 2.1474 2.1464 2.1452 2.1439 2.1424 2.1408 2.1391 2.1372 2.1352 2.1331 2.1308 2.1284 2.1258 2.1232
08 2 0267 2 0264 2.0260 2.0255 2.0248 2.0240 2.0231 2.0221 2.0210 2.0198 2.0184 2.0169 2.0153 2.0136 2.0118 2.0099 2.0078 2.0056 2.0034
09 I 9185 1.9183 1.9179 1.9174 1 9169 1.9162 1.9154 1.9146 1.9136 1.9125 1.9114 1.9101 1.9087 1.9072 1.9056 1.9040 1.9022 1.9003 1.8983
1.8227 1.8225 1 8222 1.8218 1.8213 1.8207 1.8200 1.8193 1.8184 1.8175 1.8164 1.8153 1.8141 1.8128 1.8114 1.8099 1.8084 1.8067 1.8050
2 1.2226 1.2225 1.2224 1,2222 1.2220 1.2218 1.2215 1,2212 1.2209 1.2205 1.2201 1.2196 1.2192 1.2186 1.2181 1.2175 1.2168 1.2162 1.2155
з 0.9056 0 9056 0.9055 0.9054 0.9053 0.9052 0.9050 0.9049 0.9047 0.9045 0.9043 0.9040 0.9038 0.9035 0.9032 0.9029 0.9025 0.9022 0.9018
4 7024 7023 7023 7022 7022 7021 7020 7019 7018 7016 7015 7014 7012 7010 7008 7006 7004 7002 7000
5 5598 5597 5597 5597 5596 5596 5595 5594 5594 5593 5592 5591 5590 5588 5587 5586 5584 5583 5581
& 4544 4544 4543 4543 4543 4542 4542 4542 4541 4540 4540 4539 4538 4537 4536 4535 4534 4533 4532
7 3738 3738 3737 3737 3737 3737 3736 3736 3735 3735 3734 3734 3733 3733 3732 3732 3731 3730 3729
8 3106 3106 3106 3106 3105 3105 3105 3105 3104 3104 3104 3103 3103 3102 3102 3101 3101 3100 3100
9 2602 2602 2602 2602 2601 2601 2601 2601 2601 2600 2600 2600 2599 2599 2599 2598 2598 2597 2597
1 0 0 2194 0.2194 0 2194 0 2194 0 2193 0.2193 0.2193 0.2193 0.2193 0.2193 0.2192 0.2192 0.2192 0.219] 0.2191 0.2191 0 2191 0.2190 0.2190
2 0 489 489 489 489 489 489 489 439 489 489 489 489 489 439 489 489 489 488 488
3 0 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130
4 0 38 38 38 38 38 38 38 38 38 38 38 38 38 38 38 38 38 38 38
5.0 11 II II 11 II II 11 11 11 11 11 11 11 11 11 II 11 И 11
6.0 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 1 4 |
7.0 8 0 I 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0
ioMinued)
Продолжение i а б л. 2, значение г/В>0,1
Ц \ 0 .0001 .0002 .0003 .0004 .0005 .0006 .0007 .0006 .0009 .001 .002 .003 .004 .005 .006» .007 .008 .009 .01 .02 .03 .04 .05 .06 .07 .08 .09 .1 .2 .3 .4 ,5 .6 .7 .8 .9 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 0.1 4.8541 4.8541 4.8539 4.8530 4.8510 4.8478 4.8430 4.8368 4 8292 4.7079 4,5622 4.4230 4,2960 4.1812 4.0771 3.9822 3.8952 3.8150 3.2442 2.8873 2.6288 2.4271 2.2622 2.J232 2.0034 1.8983 1.6050 1.2155 0.9018 7000 5581 4532 3729 3100 2597 0.2190 488 130 38 II 4 1 0 0.15 4 0601 4,0601 4.0600 4.0599 4,0598 4 0595 4,0435 4.0092 3.9551 3.8821 3.8384 3.7529 3.6903 3.6302 3.5725 3.1158 2.8017 2.5655 2,3776 2.2218 2.0894 1.9745 1.8732 1.7829 1.2066 0.8969 6969 5561 4518 3719 3092 2591 0.2186 488 130 38 11 4 1 0 0.2 3.5054 3.5054 3.5043 3.4969 3.4806 3 4567 3 4274 3 3947 3.3598 3 3239 3.2875 2.9521 2.6896 2.4816 2.3П0 2.1673 20435 1.9351 1.8389 1.7527 1.1944 0.8902 6927 5532 4498 3704 3081 2583 0.2179 487 130 38 11 4 1 0 0 25 3 0830 3,0830 3.0821 3.0788 3,0719 3.0614 3.0476 3.0311 3.0126 2,9925 2.7658 2.5571 2.3802 2.2299 2.1002 1,9867 1.8861 1.7961 1.7149 1.1789 0.8817 6874 5496 4472 3585 3067 2572 0.2171 486 130 38 И 4 1 0 0.3 2.7449 2.7449 2.7448 2,7444 2.7428 2.7398 2.7350 2.7284 2.7202 2,7104 2.5688 2.4110 2.266! 2.1371 2.0227 1.9206 1.8290 1.7460 1.6704 1.1602 0.8713 6809 5453 4441 3663 3050 2559 0.2161 485 130 38 11 4 1 0 « 0.35 2 4654 2.4654 2.4651 2.4644 2.4630 2.4608 2 4576 2.4534 2.3713 2.2576 2.1431 2.0356 1.9369 1.8469 1.7646 1,6892 1.6198 1.1387 0.8593 6733 5402 4405 3636 3030 2544 0.2149 484 130 38 II 4 1 0 0 4 2.2291 2.2291 2.2290 2 2289 2.2286 2.2279 ’ 2.2269 2.2253 2.1809 2.1031 2.0155 1.9283 1.8452 1.7673 1.6947 1.6272 1.5644 I.II45 0.8457 6647 5344 4364 3606 3008 2527 0.2135 482 129 38 II 4 1 0 0 45 2.0258 2 0258 2.0257 2.0256 2 0253 2 0248 2.0023 1.9515 1.8869 1.8181 1.7497 1.6835 1,6206 1.5609 1.5048 1.0879 0.8306 6551 5278 4317 3572 2982 2507 0.2120 430 129 37 И 4 1 0 0.5 1.8488 1.8488 1.8487 1.8486 1,8379 1.8062 1.7603 1.7075 1.6524 1.5973 1.5436 1.4918 1.4422 1.0592 0.8142 6446 5206 4266 3534 2953 2485 0.2103 477 128 37 11 4 1 0 0.55 1.6931 1,6931 1.6883 1.6695 1.6379 1,5985 1.5551 1.5Ю! 1,4650 1.4206 1.3774 1.0286 0.7964 6332 5128 4210 3493 2922 246! 0.2005 475 128 37 II 4 1 0 0.6 1 5550 1.5550 1,5530 1.5423 1.5213 1.4927 1.4593 1.4232 1.3860 1.3486 1.3115 0.9964 7775 6209 5044 4150 3449 2889 2436 0 2065 473 127 37 !! 4 1 0 0 65 1 43(7 1.4317 1.4309 1.425! 1.4! |7 1,3914 1.3663 1.3380 1.3078 1.2766 1.2451 0.9629 7577 6080 4955 4086 3401 2853 2408 0 2043 470 127 37 И 4 1 0 0 7 1.3210 ! 3210 1.3207 1.3177 1.3094 1.2955 1.2770 1.2551 1,23(0 1.2054 1.1791 0.9284 7369 5943 4860 4018 3351 2815 2378 0.2020 467 126 37 11 4 ! 0 0 75 I 2212 1.2212 1.2210 1.2195 1 2!46 1.2052 1 1919 1.1754 1.1564 1.1358 1.1140 0.8932 7154 580! 4761 3946 3297 2774 2347 0.1995 463 !25 37 II 4 1 0 0 8 1 007 1 1307 !.!306 1 1299 ! 1270 1,1210 1.!!!6 1.0993 1.0847 1.0682 t.0505 0.8575 6932 5653 г>8 3871 3242 2732 2314 0 1970 460 125 37 И 4 1 0 0 85 1 С485 1 0485 ! 0484 ! 0481 1.0465 1.04 26 1.0362 1.0272 1.0161 1,0032 0.9890 82!6 6706 5501 4550 3793 3183 2687 2280 0.1943 456 !24 36 II 4 1 0 09 0 9735 0 9735 9733 9724 9700 9657 9593 9510 94!! 0 9297 7857 6476 5345 4440 37! 2 3123 264! 2244 0.1914 452 123 36 1! 4 1 0 0.95 0.904? 0 9049 9048 9044 9029 9001 8956 8895 68!9 0 8730 7501 6244 5186 4326 3629 3060 2592 2207 0 1885 448 123 36 11 4 t 0 1 0 0 8420 0.8420 8418 8409 8391 8360 83!6 8259 0 8(90 7148 6010 5024 4210 3543 2996 2543 2!68 0 1855 444 122 36 11 4 1 0 Continued)
Продолжение табл. 2
Время, мин
Фиг. 2. Кривая зависимости понижения от времени
при опытных откачках в Маутрэйз.
опыта (приблизительно в течение первых 40 минут после начала опыта)
нельзя использовать, так как в это время сказывается еще влияние вос-
становления уровней воды в период, предшествовавший откачке.
Из фиг. 2 величина sm составляет 19,5 фута. Следовательно, пониже-
ние уровня в точке перегиба sf - (1/2)sm = 9,75 фута. Этой точке со-
ответствует время tt = 117 мин. Уклон прямого отрезка кривой, на котором
лежит точка перегиба, равен 6,5. Тогда из уравнения (12) ertB — 2,3 X
X 9,75/6,5 — 3,45. Для этого значения функции из таблицы 1 получаем
r/В = 0,041 и ег/в = 1,042. Отсюда В = 1060/0,041 % 25 800 футов. Далее из
уравнения (7) Т = 1,3 X 3,33/4 тс X 6,5 X 1,042 0,09 фут2!сек.. Коэффи-
циент перетекания К'/Ь' — 0,09/25802 = 1,35 X Ю'10 сек~*. Наконец, из
уравнения (6) S = 0,0205 X 4 X 0,09 X 117 X 60/10602 - 0,000046.
Если имеется больше чем одна наблюдательная скважина, эта про-
цедура может быть применена к каждой из них независимо при условии,
что максимальное понижение уровня может быть экстраполировано для
каждой из рассматриваемых скважин. Коэффициенты, полученные из ана-
лиза данных по каждой скважине, усредняются с целью получения харак-
теристик исследуемого участка в целом.
Может быть использован также следующий метод, при условии, что
наблюдения ведутся не менее, чем по двум скважинам и прямой отрезок
полулогарифмической кривой зависимости понижения от времени достаточ-
но четко выражен. Последовательность операций в этом случае следующая.
1) Строят полулогарифмические кривые зависимости понижения от времени
для всех наблюдательных скважин. 2) Находят величины уклонов ш,-
прямых отрезков каждой кривой. 3) В полулогарифмическом масштабе строят
график зависимости расстояния от уклона (уклон берется в логарифми-
ческом масштабе) и проводят прямую линию через нанесенные точки
(уравнение этой прямой линии есть уравнение (8), данное выше). 4) Опре-
деляют уклон этой линии, который равен частному от деления изменения
г (Аг) на соответствующее изменение 1g m, (A lgmz). 5) Рассчитывают вели-
чину В по соотношению В = 0,434 (Ar/Algmz). 6) Определяют величину
m; =: (т,)0, когда г равно нулю. 7) Определяют величину Т из соотношения
Т =~- 2,3Q/4tc (mz)0. 8) Зная Т и В, рассчитывают коэффициент перетекания,
как и в предыдущем методе. 9) Зная Q, г, Т и В, находят значения sz в
каждой наблюдательной скважине по уравнению (8). 10) Зная sf в каждой
скважине, определяют понижение в точке перегиба и берут отсчет/z. 11) По
известным Т, г, r/В и tt для каждой скважины по уравнению (6) рассчи-
тывают величину S. 12) Средняя величина S, полученная таким образом,
рассматривается как приближенное среднее значение коэффициента ем-
кости (водоотдачи) исследуемого участка.
Пример. Полулогарифмические кривые зависимости понижения от вре-
мени для трех наблюдательных скважин были построены по данным, по-
лученным в результате опытных откачек, выполненных на ферме Бортман
в районе Орчард-Парк (артезианский бассейн Роузвелл, Нью-Мексико)
(фиг. 3). Производительность возмущающей скважины при откачке состав-
ляла 1,2 фут3/сек. Расстояние г от оси этой скважины до трех наблю-
дательных скважин равно 2420, 2800 и 4000 футов. Уклон прямолинейных
участков на кривых, построенных по наблюдениям за уровнем в этих
скважинах, соответственно равен 1,76, 1,75 и 1,69. На фиг. 4 изображена
прямая линия, построенная по точкам г, ms (в полулогарифмическом масш-
табе). Из фиг. 4 получаем A r/A 1g78 500 и (mz)0 — 1,9. Следовательно,
В = 0,434 X 78 500 = 34 100 футов; Т =2,3 X 1,2/4 тс X 1,9 = 0,116 фут^сек
и коэффициент перетекания K'/b' = 0,116/34 1002 = 1 X Ю“10 сек'1. Расчет
средней величины <8 дан в табл. 3.
В случаях, когда коэффициенты проводимости и перетекания очень
велики, максимальное понижение уровня, вызываемое откачкой из сква-
жины, достигается в сравнительно короткий промежуток времени и при
39
Фиг. 3. Кривые зависимости понижения от времени при опытных откачках
на ферме Бортман.
Фиг. 4. Кривая зависимости уклона от расстояния при
опытной откачке в Нью-Мексико.
обработке опыта большинство точек, полученных по наблюдениям за уров-
нем при откачке, ложится далеко за пределами точки перегиба. В этом
случае кривая зависимости понижения от времени образует ту ее часть,
которая асимптотически приближается к максимальному понижению в ус-
ловиях установившегося движения. При этом можно применять следующий
40
Таблица 3
Расчет величины 5
1 2420 0,071 2,766! 2,28 93 !о,0000157
2 2800 ' 0,082 2,623 [ 2,16 95 '0,0000138
3 4000 0,117 j 2,273; 7,87 92 0,0000094
Среднее значение S
0,000013
метод, с помощью которого легко получить приближенные величины па-
раметров водоносного горизонта в любой момент откачки. 1) Строят полу-
логарифмическую кривую зависимости понижения от времени на основании
наблюденных данных и оценивают значение максимального понижения sm.
2) На построенной кривой выбирают любую произвольную точку и отме-
чают ее координаты I и $. 3) Через выбранную точку проводят касатель-
ную к кривой и измеряют ее уклон т, который равен As/Algt 4) Зная
sm, s и т, рассчитывают величину функции f (q) по уравнению (16) и
подбирают соответствующие значения q, eq и Et (~—q) из табл. 1. 5) Рас-
считывают значение Т либо по уравнению (13), либо по уравнению (15).
6) Зная величину sm, рассчитывают /С0(г/В) по уравнению (9) и находят
соответствующее значение (r/В) из табл. 1 или уравнения (17). 7) Из из-
вестных г и г!В определяют величину В. 8) Зная Т и В, рассчитывают
коэффициент перетекания К'/Ь' = Т/В2. 9) Зная t, Т, В и величину q,
рассчитывают S из уравнения (14).
Фиг. 5. Зависимость понижения от времени при опыт-
ной откачке в Беррендо, Нью-Мексико.
Пример. На фиг. 5 дана кривая зависимости понижения от времени,
построенная по данным двух опытных откачек в скважинах артезианского
бассейна Роузвелл в Беррендо. Обе откачки производились при приблизи-
тельно равных дебитах —3,33 фут?!сек,. Расстояние до наблюдательной
скважины составляло 120 футов. Из фиг. 5 следует: sm = 1,26 фута; коор-
динаты выбранной точки: t = 50 минут и $ — 1,23 фута; уклон касательной
в точке Р — Д s/цикл = 0,11.
По уравнению (16) f (q) ~ 0,626. Из табл. 1ЕД—q) = 0,247, eq = 2,534
и q = 0,93. Отсюда по уравнению (13) Т = 2,3 X 3,33/4 те X 0,11 X 2,534 =
= 2,19 фупгНсгк или по уравнению (15) Т = 3,33 X 0,247/4те (1,26 — 1,23) —
= 2,18 фут?! сек. По уравнению (9) /Со ф!В} = 1,26 X 2 X X 2,19/3,33 = 5,2.
41
По уравнению (17) г/В^0,0061. Тогда В 130/0,0061 -^21,3 фута, /С/У:"=
- 2.19/213002 - 4,82 X КГ9 сек\ По уравнению (14) S = 4,82 / 1(Г5 X
X 50 X 60/0,93 - 0,0000155.
Водоносный горизонт, вскрытый скважинами, из которых производи-
лись откачки, почти целиком был сложен известняками, ангидритами и
ангидритовыми известняками. Эффективная пористость в районе выхода
этого горизонта на поверхность принималась равной 0,05.
Полученная малая величина коэффициента емкости, рассчитанная на
основании данных опытной откачки, получилась такой, как и ожидалось.
Действительно, коэффициент емкости (водоотдачи) зависит от пористости
и сжимаемости воды и пород, причем эта зависимость, по Джекобу [7],
выражается следующим образом:
S •= р у b ф + а/р) ,
где р — пористость водовмещающих пород (в рассматриваемом случае рав-
ная 0,05); 7—удельный вес воды.
Порядок величины сжимаемости водоносного горизонта определяется
следующим образом. Удельный вес воды у ^62 фунт!фут?-, Ь — средняя
мощность водоносного горизонта принимается равной 100 футам; ₽ — сжи-
маемость воды - 3,3 X Ю"6 дюймЧфунт и авертикальная сжимаемость
водовмещающйх пород.
Произведение ру&р характеризует собой часть емкости (водоотдачи),
обусловливаемой расширением воды, а произведение у 6 а — часть емкости
(водоотдачи) за счет сжатия водовмещающих пород. Таким образом, для
данных, приведенных выше, имеем: == 0,05 X 62 X 100 x 3,3 X
X 10“6/144 = 7,1 X ИГ°. Если коэффициент емкости равен 1,55 X Ю~5 (как
было получено в последнем примере), то равняется 0,84 X ИГ5, или
а = 2 X 10~7 = дюйм2!фунт.
ЛИТЕРАТУРА
1. Chow Ven Те, 1952. On the determination of transmissibility and storage coeffi-
cients from pumping tests data, Trans. Am. Geophys. Union, 33, 397—404.
2. Cooper H. H., Jr., Jacob С. E., 1946. A generalized graphical method for eva-
luating formation constants and summarizing wellfield history, Trans. Am. Geophys.
Union, 27, 526.
3. Hantush M. S., J a cob С. E., 1954. Plane potential flow of ground water with
linear leakage, Trans. Am. Geophys. Union, 35, 917—936.
4. H a n t u s h M. S., J a cob С. E., 1955. Non-steady radial flow in an infinite leaky
aquifer, Trans. Am. Geophys. Union, 36, 95—100.
5. Jacob С. E., 1940. The flow of water in an elastic artesian aquifer, Trans. Am. Geo-
phys. Union, 21, 574—586.
6. J а с о b С. E., 1946a. Drawdown test to determine effective radius of artesian well,
Proc. Am. Soc. Civ. Eng., 72, No. 5, 620—646.
7. J а с о b С. E., 1946b. Radial flow in a leaky artesian aquifer, Trans. Am. Geophys.
Union, 27, 198—205.
8. J а с о b С. E., 1950. Engineering hydraulics, chap. 5, John Wiley and Sons.
9. J а с о b С. E., Lohman S. W., 1952. Nonsteady flow to a well of constant draw-
down in an extensive aquifer, Trans. Am. Geophys. Union, 33, 559—569.
10. Theis С. V., 1935. The relation between the lowering of the piezometric surface and
the rate and duration of discharge of a well using ground water storage, Trans. Am.
Geophys. Union, 16, 519—524.
11. T h e i s С. V., 1951. Effect on artesian aquifer of storage of flood water in Hondo
Reservoir, New Mexico State Engineer.
12. Theis С. V. a n d о t h., 1942. Ground-water hydrology of areas in the Pecos valley,
N. M., Natl. Res. Planning Board, Pecos River Joint Investigation Report, Wa-
shington.
13. Wenzel L. R., 1942. Methods for determining permeability of water bearing mate-
rials, U. S. Geol. Sur. Water-supply Paper 887.
М. С. Хантуш
НОВОЕ В ТЕОРИИ ПЕРЕТЕКАНИЯ1
Получившая в настоящее время широкое распространение теория перетекания
основывается на ряде допущений. Одно из этих допущений заключается в том, что
объем воды, содержащейся в разделяющих слабопроницаемых слоях, невелик и им
поэтому можно пренебречь. Однако часто разделяющие слабопроницаемые слои, даже
и обладая очень низкой проницаемостью, могут дать значительное количество воды.
В настоящей статье рассматриваются такие системы потока, в которых учитывается
объем воды, заключенный в слабопроницаемых слоях.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Обычно слой песка ограниченной мощности перекрывается сверху
слабопроницаемым слоем глины или суглинка, который выходит на днев-
ную поверхность; через этот покровный слой происходит питание подзем-
ных вод путем инфильтрации атмосферных осадков. В иных случаях
слабопроницаемые слои, лежащие в подошве и кровле основного напорного
водоносного горизонта, в свою очередь перекрываются или подстилаются
другими водоносными пластами, водопроницаемость которых велика.
В результате понижения гидравлического напора в основном водоносном'
горизонте возникает перетекание в него воды из подстилающих и пере-
крывающих слоев.
Строго говоря, истинный поток в таких системах является трехмерным.
Однако при некоторых допущениях поток может рассматриваться как
двухмерный. Эти допущения следующие: 1) напор в слоях, обеспечиваю-
щих перетекание, является постоянным; 2) различие проницаемости слабо-
проницаемых слоев и основного напорного водоносного пласта очень
велико, в связи с чем можно считать, что поток в слабопроницаемых слоях
является вертикальным, а в основном напорном пласте — горизонтальным,
и 3) объем воды в слабопроницаемых слоях мал и им можно пренебречь.
На основе этих допущений Джекоб [12], Хантуш и Джекоб [8, 10, 11],
Хантуш [4, 5, 6, 7] проанализировали несколько схем потока в пластах,
которые могут получать или терять воду через ограничивающие их полу-
проницаемые водоупоры.
В настоящей работе анализируются случаи, когда запас воды в слабо-
проницаемых слоях принимается во внимание. При этом предполагается,
что отдача воды из этих слоев обусловливается их упругостью. Остальные
допущения остаются в силе.
ПОСТАНОВКА ЗАДАЧИ
Задача заключается в том, чтобы найти распределение понижения в
области влияния скважины, работающей с постоянным расходом в упругом
напорном водоносном горизонте, ограниченном слабопроницаемыми упру-
гими слоями. Расход скважины обеспечивается уменьшением запаса воды
1 М. S. Han tush, Modification of the Theory of Leaky Aquifers, Journ. of Geo-
phys. Res., 65, No. 11, 3713—3725, 1960.
43
данного водоносного горизонта (из которого ведется откачка) и перетека-
нием из контактирующих с ним слабопроницаемых слоев в результате
уменьшения их объема. Кроме того, учитывается поступление воды из
перекрывающих и подстилающих слабопроницаемых слоев. Гидравлические
проводимости слабопроницаемых слоев очень малы в сравнении с прово-
димостями основного водоносного горизонта, поэтому, как отмечалось выше,
принимается, что движение воды в полупроницаемом пласте является
вертикальным, а в основном водоносном горизонте — горизонтальным.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Ниже приводится список основных символов и их определений.
Ь, Ь', У'— мощность отдельных слоев, L;
В = У ТЬ'ИУ— фактор перетекания, L;
erf (х) —функция ошибок (х);
erfc (х) —дополнительная функция ошибок, или [1—erf (х)];
h — гидравлический напор в любой момент времени и в любой
точке основного пласта, L ;
р е~у ... . ______
Я (и, р) — \ erfc (р У и /У у (у — и)} dy ;
и
У —коэффициент фильтрации основного водоносного пласта, LT-1;
/С', У' —коэффициент фильтрации слабопроницаемых слоев (в верти-
кальном направлении), LT[ ;
Ко У) — функция Бесселя от мнимого аргумента второго рода
нулевого порядка ;
n = TWS,T-1;
Q —постоянный расход скважины, I3?*1;
qL —скорость перетекания в основной водоносный пласт, £3Т~1;
г — расстояние по горизонтали, измеренное от оси скважины до
любой точки, L;
s = h0—h — понижение пьезометрической поверхности в любой момент
времени в любой точке основного пласта, L ;
sn s2—понижения напора в любой момент времени в любой точке
(г, z) в слабопроницаемых слоях, L;
S^, Ss, Ss —удельная емкость основного и слабопроницаемых слоев (объем
воды в единице объема пласта, высвобождающийся при сни-
жении напора на единицу);
коэффициент емкости (водоотдачи) основного и слабопроницае-
мых слоев (безразмерные);
t0 — время начала откачки, Т;
t —время, прошедшее с момента начала откачки, Т;
Т = КЬ—коэффициент проводимости основного водоносного пласта,
РГ1;
и — ;
V = Qt — объем воды, полученный при откачке, L3;
VL — общий объем воды, полученный в процессе откачки за счет
перетекания, L3 ;
С е~у
— Ei (—и)=-- )---dy—интегральный экспоненциал — «функция скважи-
и У ны» для пластов, где перетекание отсутствует;
Sz = b' Ss
" = h” s"
44
IF(u,y) = j-----exp (— у — v2!ty) — «функция скважины» для пластов с
J У
и
перетеканием;
z — вертикальная координата, L;
а -г] КДЬГ КГГТ~,
р =(1/4)гХ;
= 1+ (S' + S")/3S ;
Г (S' + S")/S;
З3 = 1+ (5" + S'/3)/S;
v - K/Ss = T/S , 1JT ';
v' = Д'IS' = K'b'IS', ITT1;
v" - /<'7s; = K’b"IS", LC-T~l.
Дифференциальные уравнения движения. Дифференциальное уравнение
потока подземных вод в упругом водоносном пласте имеет следующий
вид:
d*hn , d2hn t d2hn = 1 dhn
дх2 ду2 "Г" дг2 >п dt
Дифференциальное уравнение движения в упругом пласте, ограничен-
ном слабопроницаемыми упругими слоями, апроксимируется следующим
выражением:
d2h , d2h , ч,(Ь") — 'ДЬ+Ь”) 1 dh
дх* ' dy2 T v dt
dhn
'4 ,x> У> t) — — Дп ,
где h (x, y, t) и h„ (x, y, z, t) — гидравлические напоры в основном водо-
носном пласте и в слабопроницаемых слоях соответственно игп — значением в
подошве и кровле горизонта (см. фиг. 1 и 2).
Если принять, что h0(x,y,t0) и h0„ (х, у, z, t0) выражают начальное
распределение гидравлических напоров в основном водоносном пласте и
полунепроницаемых пластах соответственно и s (х, у, I) и sn (х, у, z, I) —
понижения напора, вызываемые отбором воды из основного пласта, нача-
того в момент времени t6, то уравнения (1) и (2) могут быть представлены
в таком виде:
d2sn d2sn ! d2sn I dsn
дх2 1 ду2 Г dz2 dt ’ ’
d2s d2s ^z(b + Ь")—'Ц.Ь" 1 ds
~дх2~ Ду2 Д V ДГ ’ *4)
dsn
(х, у, z, t)
где s = h0 — h, sn—hOn—hn и t — время с момента начала откачки t0.
Системы потока и граничные условия. В настоящей статье рассматри-
вают три системы потока: 1) слабопроницаемые слои, контактирующие с
основным пластом, подстилают и перекрывают два других водоносных
пласта, в которых гидравлические напоры остаются постоянными; 2) слабо-
проницаемые слои подстилают и перекрывают два непроницаемых слоя;
45
3) один слабопроницаемый слой перекрывает непроницаемый пласт, а дру-
гой подстилает водоносный пласт, в котором гидравлический напор
остается постоянным.
Поток в этих системах, будучи вертикальным в слабопроницаемых
слоях и плоско радиальным в основном водоносном пласте, может быть
охарактеризован следующими граничными условиями.
Система 1.
<5% 1
dz'2 dt ’
Si (г, г, 0) = 0;
sx(г, z’, /) = 0;
S] (г, t) = s (r, 0 .
Верхний слабопроницае-
мый слой
)
(5)
(a)
(b)
(c)
Основной водо-
носный пласт
a2s i as /<' a
yp- +7 -p -p s, uo
К" d i as
_ _____ s2 /) __ __ ;
s (r, 0) = 0;
s (ТЦ 0 = 0 ;
Um d Q
n f-г- S I/, 0 = — -5-ST- .
r->0 dr ' ’ ' 2к T
Oz~ 1 as, (а) ]
(с, Z, 0) == 0 ; (6) Нижний слабопроницае-
S3 (Г, S., (г, 0, i) = 0 ; b", t) = s (г, t). (с) (7) мый слой
(7^
Система 2. То же, что и система 1, но условия (5с) и (7с) заменяются
соответственно на
2Z, 0 = 0; (5с3)
4 М/3 0, t) = Q.
(70)
Система 3. То же, что и система 1, но условие (7с) заменяется на
-^s3(r, 0, П = 0.
(JZ 4 • '
(7с3)
В указанных уравнениях = b" + Ь и z' — b" +& + Ьг.
УРАВНЕНИЯ ПОНИЖЕНИЯ И СКОРОСТИ ПЕРЕТЕКАНИЯ
Ниже приводятся результаты решения вышеприведенных уравнений
при заданных граничных условиях. Читателей, желающих ознакомиться с
деталями выводов этих решений, отсылаем к приложению.
Для случаев, представленных на фиг. 2, решения получены для двух
значений времени.
Для t меньше чем br S710/C и b’'S"i\QK”. В этом диапазоне времени
решения для трех случаев одинаковы и выражаются так:
s---Н (и, ?), (8)
46
(Jl = Q [1 — cleric (|/'nt )]; (9)
= V [1 2 / \fn-Kt-T- qc/Qnt], (10)
где: ? = (1/4)rX; и =r2S/4Tt; n = TX2/S;
) - i/Q' s' । i/ZZZZTll
V т s 1 V т s'
H (ti, 3) — неопределенный интеграл, значения которого даны в таблице.
Для больших значений времени t. В этом диапазоне времени решения
для трех рассмотренных случаев следующие.
Система 1. Нижний предел t может быть выбран как наибольшее из
двух значений bb'S'/K' и bb"S"IK"-
uMi.’):
qL =' Q[1 — (1/щ)ехр(— W7.2/r20i)], (12)
где:
Oi 1 • (S' -Г S") / 35:
7 - r ifK'ib' К'лг
' I T ! T
a W (ubi, a)—«функция скважины» для пластов с перетеканием, которая
была получена и протабулирована Хантушем [4, 5]1. Выражение для Vl
может быть легко получено путем интегрирования уравнения (12) по t от
нижнего предела диапазона времени до любого момента времени i.
Система 2. Для t больше чем lO&'s'/ZC' и 106V7/C" соответствующие
выражения будут иметь вид:
---£Ц__М)3). (13)
4т: 7 4 7 4 7
qL Q (Sr + S") / (S + S' SД, (14 )
где: о2 1 -7(S'+S")/S, а ЕЦи, о2)— экспоненциальный интеграл.
Система 3. В этом случае наибольшее из двух значений ЬЬ'Е'.'Д' и
10&"S'7/C" может быть взято как нижний предел диапазона времени и со-
ответствующие выражения будут иметь вид:
Q > "| V К' lb' \
s Д°з> г |/ --у; IЬ)
qc - Q [1 - (1 /S3) exp (- / &'П3)], (16)
где о3- 1 +(S"+S'/3)/S.
Значение Vl может быть получено путем интегрирования уравнения
(16) по t от нижнего предела диапазона времени до любого значения t.
Выражение для понижения уровня в промежуточном диапазоне време-
ни t не дается ни для одного из трех рассмотренных выше случаев. Од-
нако приближенно это может быть сделано следующим образом. Значения
s/Qi4r.T строятся в виде графических зависимостей от и или t в полуло-
гарифмическом масштабе (при и или /, взятом в логарифмическом масштабе).
После этого проводится прямая линия, соединяющая две ветви построен-
ной кривой, которая и дает значения s/Q/aT в промежуточном диапазо-
не времени. Эта процедура дает возможность рассчитать, кроме понижения
уровня s, также величины qL и Vl для промежуточных значений времени.
1 См. статью Хантуша в настоящем сборнике, стр. 34, табл. 2.
47
Пьезрметрич’е-':'-.
скии напор
нижнего _ _
~Пёрвоначаль -':
•нал пьезометри-
ческая поверхность
среднего водонос-
ного плас та з
СлабопротП
цаемый
" слой
горизонта
• Зеркало роды
Ч—' •'‘х1..."<
Слабопроницаемый слои
X И" С* х X
Пески с безна-
порными
водами
Артезианский ' ।
"горизонт
."K.S
. .•:. лу у. ну..-
Артезианский горизонт' '.-и;
’ .у::::::. y.yiv.-?
л:.-.'.-.;:: :
зеркало воды
' я
Артезианский
горизонт
Слад о проницав
мый слои
Пласт с постоянным "
напором.........
Фиг. 1. Схематическое изображение пласта в условиях
перетекания.
Поверхность
земли
Система 2
Система 1
Система 3
Фиг. 2. Схематическое изображение трех систем пото-
ков в условиях перетекания.
ТАБЛИЦЫ ФУНКЦИЙ
Функции Е1(—х) и W (х, у) уже были табулированы для широкого
диапазона рассматриваемых параметров 14, 5, 15, 16]. Функция Н (и, р) до
сих пор не была представлена в табличной форме. Ввиду этого достаточ-
ные для практических целей таблицы были составлены с помощью счетно-
вычислительной машины.
Функция И (и, 3) может быть апроксимирована в виде
Н(и, З)^Г(м) — (0,2577 4-0,6931) ехр(— и/2) (17)
для и 104^2 и
И (и, (1/2)1п0,044/р2м (18)
для и -С Ю5/32 и 10~4р2.
РЕШЕНИЯ ДЛЯ ЧАСТНЫХ СЛУЧАЕВ
Из вышерассмотренных общих решений могут быть получены реше-
ния для некоторых частных случаев.
Пласт, в котором протекание отсутствует. Если К' и К” принять
равными нулю в решениях любого из трех рассмотренных выше случаев,
то в результате получим систему потока, в которой перетекание отсутствует.
Таким образом, в пределе, когда К' и К" стремятся к нулю, уравнение
(8), как этого и следовало ожидать, переходит в формулу Тейса:
s =----Ei (—и}. (191
Пласт с перетеканием, объем воды в слабопроницаемых слоях мал и им
можно в расчетах пренебрегать. Если К", S' и S" принять равными нулю
в системах потока 1 и 3, то это будет соответствовать артезианскому пласту,
подстилаемому водоупором и перекрываемому сверху слабопроницаемым
слоем, запас воды в котором ничтожно мал. Беря предел уравнений (11)
или (15) при К7, S' и S", стремящихся к нулю, получим формулу Ханту-
ша и Джекоба [10]1:
(20)
где 1/В2-(7<76')/Т.
Другие частные случаи. Формулы для других частных случаев также
могут быть найдены путем задания параметрам, входящим в формулу,
определенных значений (см. фиг. 4, 5 и 6).
ВЫВОДЫ
Влияние объема воды, заключенной в слабопроницаемых пластах, на
понижение уровня показано на фиг. 3—8. Если отношение коэффициентов
емкости слабопроницаемого пласта и основного водоносного пласта мало
(S7S -С 0,1), то влияние объема воды в слабопроницаемых слоях на пони-
жение уровня в системах потока, подобных тем, которые показаны на фиг. 5
и 6, очень мало. В этом случае применимы формулы (19) и (20). Для от-
носительно больших значений S7S истинное понижение будет значитель-
но отклоняться от расчетного понижения по этим формулам.
Наблюдаемые изменения понижения уровня, которые показаны, напри-
мер, на фиг. 3 и 6, ранее обычно связывались с изменениями параметров
водоносного горизонта в начальный период откачки. Хотя это в некоторой
степени и справедливо, указанное явление может, как это следует из рас-
1 См. статью Хантуша в настоящем сборнике, стр. 27—42.
49
to3'o
Ф и r. 3. Типовые функции.
ч/Q/itnT
Log,0(t)
-1 0 I 2 3 * 5 6 7 8
Фиг. 4. Зависимость понижения от
времени при работе скважины, работаю-
щей с постоянным расходом в пласте,
подстилаемом слабопроницаемым плас-
том, имеющим бесконечно большую
мощность.
Log,o(t)
0
-1 0 1 2 3 « 5 6 1
7
8
9a
2
3
ч
5
6'1
Артезиан -
скии пласт
Зеркало воды^^
Песни с безнапор-'
ними водами
\\к.з ь
Л1тгтт»»»т»»)>
ti
s
Q/ЧлТ
EZ.
108'
S =~£г
rss 1 K'/b'
u°9Ti' в2 ~~
Поверхность
земли
Sb's’
к'
* в
Ф и г. 5. Зависимость понижения от
времени для скважины с постоянным
расходом в системе потока, изображен-
ной па рисунке.
I.
-2 i О I 2 ' 3 * b b I :
Фиг. 6. Зависимость понижения от
времени для скважины с постоянным
расходом в системе потока, изобра-
женной на рисунке, для различных
значений удельного объема воды.
lng,„ t.
Фиг. 7. Зависимость понижения от
времени для скважины с постоянным
расходом в системе потока, изобра-
женной на фиг. 6, в удаленной на-
блюдательной скважине.
/0
^9.о И)
Фиг. 8. Сравнение кривых зависимости по-
нижения от времени в пласте в условиях пе-
ретекания, при наличии и отсутствии объема
воды в полупроницаемых слоях.
I - перетекание отсутствует: II— перетекание при отсутствии
объема воды в слабопроницаемом слое: 111—перетекание при
наличии объема воды в бесконечном слабопроницаемом слое;
IV — перетекание ^ри наличии объема воды в конечном
слабопроницаемом слое.
Таблица значений функций
V ! (-3) 1 (-2) 1! II (-1) |]
р г 1 1 ’ 1 । 5 1'2 1 = i 1,
I1
1(- 6) 11,9842 11,4237 10,5908 9,9259 9,2469 в.ЗЗЭб!' 7,6497 । 6,9590 6,0463 1
2(—6) 11,5355 11,0211 10,2210 . 9,5677 8,8946 7,9908 7,3024 : 6,6126 5,7012 1
3(—Ь) 11,2593 10,7764 10,0906 ! 9,3561 8,6875 7,7864 7,0991 ’ 6,4100 5,4996 '
|4(-6) 11,0568 10,5980 9,8419 9,2047 8,5399 7,6412 6,9547 6,2663 5,3567 !
|5(—6) 10,8958 10,4566 9,7174 9,0866 8,4251 7,5284’ 6,8427 6,1548 5,2459 1
6(—6) . 10,7618 10,3389 9,6145 8,9894 8,3310 7,4337 6,7512 I 6,0637 5,1555
7(—6) ! 10,6466 10,2379- 9,5267 8,9069 8,2512 7,3581 ; 6,6737 ’ 5,9867 5,0790 '
8(~6) 10,5455 10,1493 9,4500 8,8350 8,1819 7,2901 ! 6,6066 : 5,9200 5'0129 ।
9(—6) 10,4553 10,0702 9,3818 8,7/14 8,1206 . 7,2306 । 6,5474 , 5,8611 4,9545 1
1(-5) ! 10,3739 9,9987 .9,3203 J 8,7142 8,0657 7,1771 : 6,4944 | 5,8085 4 9024 ।
2(—5) 9,8197 9,5097 8,9015 8,3315 7,/010 6,8238'; 6,1453 1 5,4623 4,5598
3(—Ь) 9,4815 9,2084 8,6504 8,1013 7,4844 6,6159;. 5,9406 । 5,2597 4,3600 '
4(-5) ' 9,2358 8,9878 8,4646 7,9316 7,3290 ! 6,46/7 5,7951 I 5,1160 4,2185 I
5(—5) 9,0422 8,8128 8,3171 . 7,8031 7,20/2 6,3523 1 5,6861 1 5,0045 4,1090 1
6(—5) ( 8,8822 8,6674 8,1913 1 7,6941 7,1068 6,25/б,| 5,5896 1 4,9134 4,0196 1
7 (—Ь) J 8,7457 8,5428 8,0888 7,6077 7.0212 6,1 Z/3j' 5,5113 : 4,8354 3,9442 '
8(-5) , 8,6266 8,4333 7,9962 7,5190 6,9466 6,10761 5,4431 । 4,7697 3,8789 1
9(—5) 8,5209 8,3364 7,9131 7,4461 6,8804 6,0459 ; 5,3331 1 4,7108 3,8214 ’
К-4) , 8,4258 8,2487 7,8386 7,3803 6,8208 5,990б|1 5,3297 4,6581 3,7700 ।
2(-4) ' 7,7901 7,6563 7,3276 6,9321 6,4190 5,62261 4,9747 4,3115 3,4331
3( —4) 7,4110 7,2985 7,0135 6,6563 6,1750 5,4035.. 4,7655 4,1086 3,2379
4(—4) 7,1393 7,0101 6,7840 6,4541 5,9971 5,2459; 4,6161 3,9645 3,0999 :
5( —4) 6,9273 6,8375 6,6024 6,2931 5,8561 5,1223,' 4,4996 3,8527 2,9933 '
6(—4) 6,7533 6,6705 6,4517 6,1596 5,7389 5,0203 4,4040 3 7612 2,9065 ;
7 —р j 6,6056 6,5284 6,3227' . 6,0447 5,6383 4,9533 4,3228 3,6838 2.8331
8(-4) 6,4774 6,4048 6,2100 5,9439 5,5501 . 4,8573' 4,2523 , 3 6167 2.7/02 1
У(—4) 6,3640 6,2952 6,1097 5,8539 5,4713 4,/898 4,1898 1 3,5575 2,7146 1
1(—3) 6,2624 6,1969 6,0193 5,7727 5,4001 4,7290. 4,1337 3,5045 2 6650 j
2(—3) 5,5903 5,5431 5,4115 5,2203 4,9139 4,3184 ; 3,7598 3 1549 2,3119
3(—<5^ 5,1948 5,1560 5,0465 4,8837 4,6149 4,068311 3,5363 2,9494 2’1559 ।
4(—3) 4,9135 4,8798 4,7839 4,6396 4,3962 3,88591 3,3750 1 2,8030 2^0253
5(—3)1 4,6951 4,6649 4,5786 4,4474 4,2231 , 3,7415: 3,2483 2,6891 1,9250 1
6(-3) 4,5165 4,3555 4,4890 4,4099 4,2888 4,0794 3,6214’ 3,1436 2,5957 1,8437 i
7(—3) 4,3100 4,2666 4,1536 3,9564 3,5185' 3,0542 • 2,5165 1,7754 1
S(—3) 4,2347 4,2109 4,1421 ' 4,0357 3,8488 ; 3,4282’’ 2,9762 ’ 2 4478 1’7166 :
9^—з) 1 4,1194 4,0969 4,0320 3,9313 3,7531 1 3,3478 , 2,9068 ! 2,3870 1,6651
1(-2) 4,0163 3,9950 3,9331 3,8374 3,6669 1 3,2752: 2,8443 ' 2,3325 1,6193 .
2(—2) 3,3397 3,3250 3,2818 3,2133 3,0880 ! 2,7829' 2,4227 ' 1,9714 1,3239
3(-2) 2,9472 2,9354 2,9007 2,8452 2,7423 2,4844 2,1680 1,7579 1'1570 ;
4(~— 2,6711 2,6611 2,6316 ' 2,5842 2,4955 ! 2,2691• 1,9841 1 6056 1,0416 I'
5(-2) 2,4590 2,4502 2,4243 2,3826 2,3040 1 2,1007. 1,8401 1,42/2 0/1540 1'
6(—2) 2,2874 2,2795 2,2563 2,2188 2,1478 ! 1,9626 1,7217 1,3905 0^8838 1.
7(—2) 2,1435 2,1355 2,1154 2,0812 2,0164 I 1,8458 1,6213 1,3088 O’8255 !•
8(—2) 2,0203 2,0138 1,9944 1,9630 1,9031 ' 1,7448’ 1,5343 ’ 1,2381 0'7758 '
9(—2) 1,9126 1,9066 1,8886 1,8595 1,8039 : 1,6559 1,4577 1,1760 0,7327 |
1(—“ 1j 1,8172 1,8116 1,7949 1,7677 1,7157 1 1,5768 ’ 1,3893 ' 1,1207 0,6947
2(— 1) 1,21УЗ 1,2159 1,2059 1,1895 1,1579 , 1,0714 0,9497 0,7665 0,4603 '
3( — 11 0,9033 0,9010 0,8940 0,8825 0,8603 i 0,7986 0,7103 0,5739 0,3390 :l
4(—1) 0,7006 0,6989 0,6935 0,6850 0,6683 0,6218 0,5543 0,4482 0,2619 I
5(—1) 0,5584 0,5570 0,5530 0,5463 0,5333 , 0,4969 ’ 0,4436 0*3591 0*2083 :
1 । 0,4533 0,4522 0,4490 0,4437 0,4333 1 0,4041 ' 0,3613 0,2927 0,1688 1
-1) . 0,3/29 0,3720 0,3694 0,3651 0,3567 1 0,3330 0,2980 0,2415 0,1386
8(— 1) 0,3099 0,3092 0,3970 0,3035 0,2966 ' 0,2/70 , 0,2481 0/2012 0,1151 ’
9(—1) j 0,2596 0,2590 0,2572 : 0,2543 0,2485 0,2323,, 0,2082 0J690 963(—4У
f‘e~ У Й
Н (и. — I -------- erfc -— -----—— du
J у У У (.у — и)"
и
(0) II о> 1 (2) 1
1 1 2 ' 5 ; J 2 ) 5 ' 1 1 9 5
5,3575 4,6721 3,7756 3,1110 2,4671 1,6710 1,1361 0,6879 0,2698
5,0141 4,3312 3,4412 2,7857 2,1568 1,3944 0,8995 0,5045 0,1685
4,8136 4,1327 3,2474 2,5984 1,9801 1,2409 0,7725 0,4113 0,1230
4,6716 3,9922 3,1109 : 2,4671 1,8571 1,1361 0,6879 0,3516 963(—4)
4,5617 3,8836 3,0055 2,3661 1,7633 1,0574 0,6256 0,3091 787(—4)
4,4719 3,7951 2,9199 2,2844 1,6877 0,9948 0,5770 0,2768 662(—4)
4,3962 3,7204 2,8478 ! 2,2158 1,6246 0,9432 0,5375 0,2511 568(-4)
4,3306 3,6558 2,7856 2,1568 1,5706 0,8995 0,5045 0,2302 494 (—4)
4,4728 3,5989 2,7309 ; 2,1050 1,5234 0,8617 0,4763 0,2127 436(—4)
4,2212 3,5481 2,6822 j 2,0590 1,4816 (1,8285 0,4519 0,1978 388(—4)
3,8827 3,2162 2,3660 ! 1,7632 1,2170 0,6256 0,3091 0,1166 166(—4)
3,6858 3,0241 2,1850 1 1,5965 1,0716 0,5203 0,2402 818(—4) 929(-5)
3,5468 2,8889 2,0588 1 1,4815 0,9730 0,4518 0,1978 621(—4) 590(—5)
3,4394 2,7848 1,9622 ! 1,3943 0,8994 0,4024 1,1685 4941 4) 405(—5)
3,3519 2,7002 1,8841 1,3244 0,8412 0,3645 0,1468 406(—4) 293(—5)
3,2781 2,6290 1,8189 j 1,7629 । 1,2664 0,7934 0,3341 0,1300 342(—4) 220(—5)
3,2143 2,5677 1,2169 0,7530 0,3090 0,1166 292(—4) 169(—5) 133(—5)
3,1583 2,5138 1,7139 i 1,1739 0,7182 0,2879 0,1056 253(—4)
3,1082 2,4658 1,6704 1,1359 0,6878 0,2698 963(—4) 222(—4) 107(—5)
2,7819 2,1549 1,3937 I 0,8992 0,5044 0,1684 4£М(— 4) 842(-5) 2061-6)
2,5937 I,9778 1,2401 1 0,7721 0,4111 0,1229 315(—4) 434(—5) 674(—7)
2,4617 1,8545 1,1352 | 0,6875 0,3514 963(—4) 222(—4) 260(—5) 275(-7)
2,3601 1,7604 1,0564 1 0,6252 0,3089 787(—4) И6(-4) 169(-5) 129(-7) 67/(—8)
2,2778 1,6846 0,9937 i 0,5762 0,2766 661 (—4) 1291-4) Н7(—5)
2,2087 1,6212 0,9420 1 0,5370 0,2510 7676—4) 103(-4) 834(—6) 383(-8)
2,1492 1,5670 0,8982 0,5040 0,2300 494 (—4) 841(—5) 6161—6) 2291-8)
2,0971 1,5196 0,8603 1 0,4758 0,2125 436(—4) 699(—5) 466(—6) 142(-8)
2,0506 1,4776 0,8271 1 0,4513 0,1976 388(—4) 590(—5) 361 (—6)
1,7516 1,2116 0,6238 . 0,3084 0,1164 166(—4) 169(—5) 555(—7)
1,5825 1,0652 0,5182 ) 0,2394 816(—4) 927(—5) 713(-6) 149(—7)
1,4656 0,9658 0,4496 0,1970 619(—4) 588(—5) 360(-6) 534(—8)
1,3767 0,8915 0,4001 i 0,1677 493(—4) 403(—5) 205(—6) 228(—8)
1,3054 1,2460 1,1953 1,1512 1,1122 0,8677 0,7353 0,6467 0,5812 0,5298 0,4880 0,4530 0,4230 0,3970 0,2452 0,1729 0,1296 0,1006 799(—4) 6461—4) 529 (—4) 437(—4) 0,8327 0,7843 0,7435 ' 0,7083 0,6775 0,4914 0,3965 0,3357 0,2923 0,2593 0,2332 0,2119 0,1941 0,1789 971(—4) 629(-4) 441(—4) 32Е(-4) 247(-4) 192(—4> 152(—4) 122(—4) 0,3620 0,3315 , 0,3064 < 0,2852 * 0,2670 0,1658 0,1197 ' 931 (-4) 755( 4) 6301—4) 536(—4) 464 (—4) ' 4об(—4); 359(—4) ' 143(—4) 752(—5) | 448(—5) | 2881-5) ; 195(—5) ; 137(—5) ! 9861—6) ; 728(—6) : 0,1460 0,1292 0,1158 0,1047 955(-4) 487(—4) 308(—4) 216(—4) 160(—4) 124 (—4) 982(—5) 7971—5) 658(—5) 552(—5) 149(—5) 592(—6) 283(—6) 151(—6) 87?(—7) 534(—7) 340(—7) 223(—7) 4041—4) 340(—4) 2£0(—4) 252(—4) 221 (-4) 831 (—5) 426(—5) 253(—5) 164 (—5) 112(—5) 799(—6) 587(—6) 442(—6) 340(—6) 4931—7) 126(-7) 424(—8) 171 (-8) 292(—5) 2191-5) 169(—5) 133(—5) 106(-5) 203(—6) 662(—7) 269(-7) 126<—7) 655(—8) 368(—8) 2191—8) 135(—8) 126(—6) 821 (-7) 553<—7) 384 (—7) 274(—7) 226(—8) 109(—8)
\ I3 II (-3) \ 1 „ . ... । (-2) | | (-1) 1
4 2 | 5 1 । 2 ' 5 : I ' 2 । 5 j! ! - И
1(0) 1 0,2189 1 0,2184 1 0,2169 0,2144 0,2097 ’ 0,1961 0,1758 0,1427 { 812(—4)lj
2(0) 1 488(—4) j 487(—4) ; 484(—4) 479(—4) 468(—4) ,43Э(—4) 395(—4) 322(-4)! 180(—4)1
3(0) ) 130(—4) 130(—4) i 1291-4, 128(—4) 125(—4) |И7(—4) 106(—4)' 862(—-5) 481(—5)1,
4(0) Г 377(—5) ! 376(—5) i 374(—5) 370(—5) 362(—5) 340(—5) 301 (—5)| 250(—5); 13)(—5)р
5(0) ) 115(—5) : 114(—5) Ц4(—5) 112(—5) 110(—5) Н04(—5) 934(—6)' 763(—6)1 423(—6)1
6(0) 1; 359(-6) ; 359(—6) 356(—6) 353(—6) 345(—6) ,325(—6)i 29J(—6)' 293(—6) 133(—6)i
7(0) ( 115(—6) ! 115(—6) ! 114(—6) 113(—6) 111(—6) .104(—6)| 941 (—7)' 7б9(—7) 425(—7)|
8(0) 376(-7) ' 375(—7) | 373(-7) 369(—7) 362(—7) 340(—7)' 307(—7) 251 (—7) 139(—7)'
9(0) ! 124(-7) ' 124(—7) 123(—7) 122(—7) 119(—7) 112(—7), 102(—7). 830(—8) 458(—8)
10(0) ; 415(—8) ’ 414(—8) | 411(—8) | 407(—8) 399(—8) 375(—8). 339(—8), 277(—8); 153(—8)!
1 1 1 и ' I
Примечание : числа в скобках — степени 10, на которые умножаются другие числа, например
сматриваемой теории, вызываться также перетеканием воды из перекрываю-
щих и подстилающих слабопроницаемых слоев. Такой же характер зависи-
мости понижения от времени наблюдается и в случае откачки из скважины,
которая не полностью вскрывает водоносные слои (несовершенная сква-
жина).
Фиг. 9. Зависимость (от времени) величины дебита скважины,
получаемой за счет сработки запаса воды в полунепроницае-
мых слоях.
Полулогарифмические кривые зависимости понижения от времени для
системы потока, подобной той, которая показана на фиг. 6, имеют более
или менее ту же общую тенденцию, как и кривые для системы, обладаю-
щей ничтожно малым объемом воды в слабопрэницаемом пласте [см. фор-
мулу (23)]. Кроме того, в потоках с большим запасом воды в слабопрони-
цаемом слое (фиг. 4 и 7) кривые зависимости понижения уровня от времени
в точках, отстоящих на больших расстояниях от скважины,, из которой
производится откачка, имеют тот же общий вид, что и кривые для систем,
в которых перетекание совершенно отсутствует. Таким образом, наблюден-
ный характер кривых понижения может привести к ошибочному выводу
54
Продолжение
365(—4)
ii 760(~5)
!i 196(—5)
h 558(—6)
ii 167(—6)
ii 519(—7)
993(—5) । 547( —6) ° 151(—7)
173(—5) I 551(—7) f
4О6(—-6) ; 911(—8) ’,
108(—6) ! 189(— 8)
309(—7) • |
926(—8) :
li 165(—7) : 286(—8)
' 356(—8) i
1 176(—8) j
488 (—4) = 0,0488.
о необходимости пользоваться теми или иными формулами. Для того что-
бы избежать ошибок, имеющиеся данные необходимо соответствующим
образом проанализировать (см. фиг. 8).
Величина расхода скважины и, следовательно, общий расход за дан-
ный период действия скважины, который обеспечивается за счет перетека-
ния, может быть весьма незначительным, если учесть влияние объема во-
ды в полунепроницаемых слоях. Изменение этого количества показано на
фиг. 9 для артезианского пласта, перекрываемого и (или) подстилаемого
мощными полунепроницаемыми упругими слоями.
ПРИЛОЖЕНИЕ
При решении рассмотренных задач с указанными граничными условия-
ми используется метод интегральных преобразований. Были применены
преобразования Ханкеля и Лапласа.
Преобразование Ханкеля. Преобразование Ханкеля H\f(r)], или F (а)
функции /(г), определяется следующим уравнением:
я [ f (г) ] -- F (а) - J г Jo (аг) f (г) dr.
Инверсионная формула для получения оригинала этой функции:
Д-i [F (а)] = / (г) = J' ajo (ar) F (а) da.
(21)
(22)
Интегрирование уравнения (21) по частям дает
Г 1 д I д}
Н г dr ( г дг
a2F (а) + г Jo (аг) аг/г (аг) f (г)
(23)
Преобразование Лапласа. Преобразование Лапласа L\f (t)\, или f (р(
функции f(t), определяется так:
L1/ (/)] = f (р) = f e~ptf (0 dt .
(24)
Интегрирование уравнения (24) по частям дает
а 1
L /(0 ] =Р/(Р)““/(0).
(25)
5.5
Инверсионная формула преобразования Лапласа в настоящей работе
не применяется и здесь псэтсму не приводится. Вместо нее ниже приво-
дятся только те соотношения, которые использовались при выводе реше-
ний, рассматриваемых в настоящей статье.
L“l [е~ь^ f (р)| - -- 0; 0 < I <-' b
t>b-
1 ——Д--------- — — [ 1 — eb>t erf с (h I/' Л1;
Р \b -j- j р ) Ь \ 1 и I - !
(26)
(27)
(28)
(29)
2/<о (х) -j у- ехр (—- у — к1; 4)?); (32)
'о
\ хКо (х) dx - 1. 1,32а)
о
Решение для системы 1. Граничные условия для этой системы потока
(фиг. 1) выражаются уравнениями (5), (6) и (7).
Пусть s (г, р), st (г, z, р) и s2 (г, г, р) будут преобразованиями Лап-
ласа по t от s (г, t), sA (г, z, t) и s2 (г, г, t) соответственно. Кроме этого,
пусть р}, F1 (я, z, р) и F2 (а, г, р) будут преобразованиями Ханкеля
по г от s (г, р), sx (г, 2, р) и s2 (г> р) соответственно.
Если мы сначала применим преобразование Лапласа к уравнениям (5),
(6) и (7), используя условия (25), (26), (56), (66) и (76), и далее применим
преобразование Ханкеля, используя уравнение (23) с преобразованными
условиями (6с) и (6d), мы можем привести уравнения (5), (6) и (7) соответ-
ственно к следующему виду:
(а, 2, р) = -Д-Fi (а, г, р); (а)
Ft (а, р) = 0; Ex. (а, zlt р) = F (а, р). (6) (0 (33)
а2Е(а, p)+Q/2^Tp+ у dz КДа, р) - К" д с ( ин х Ь', р)=-
= — F (а, р). (34)
^-Е2(а, z, z, р); (а)
Е2(а, 0, р) 0; (&) (35)
Е2 (а, 6", р) F (а, р). (с)
56
Решить уравнения (33) и (35) легко, поскольку
р _ р sinh (z'— z)V />''/
1 sinh b' J p/'/
p -- p. sinh ? I
sinh b" I I);'/'
Отсюда следует:
q .______ ________________
p. zlt p) J д-р coth// J /)•'/ ,
b", p) = —F | p/v" coth ft" J ph/' .
(36)
(36a)
(37)
(38)
Подставляя выражения (37) и (38) в уравнение (34) и решая относи-
тельно F, получим
F-^—^—Zp а2 /4Х + Л I • jp coth// 1/JL ж
2гЛ’ > Т I / ’ '/
+ Пк coth 5" | XL
т I ч" ? •/'
Используя уравнение
Ханкеля уравнения (39) и
(39)
(31) для получения обратного преобразования
используя уравнение (32), будем иметь
s (>, р) --- ер: Kat; О
2 к 1 р
XX ехр [^у^(-р)2/4Н
4 т: Т р J у
О
(40)
;;Д?_4-£г72 colli/)' 1/jL coth/;" I X.. Г X (41)
Из уравнения (40) может быть получено точное решение с помощью
обратного преобразования Лапласа. Решение, однако, сложно и громоздко
для выполнения численных расчетов. Вместо пего лучше применить при-
ближенные решения: одно для достаточно коротких периодов времени, а
другое для достаточно длительных периодов. Эти два решения будут ис-
пользоваться для графической интерполяции в промежуточном диапазоне
времени. Вывод этих приближенных решений заключается в следующем.
Решение для коротких периодов времени. Параметры (/ и р) в преоб-
разовании Лапласа связаны таким образом, что, когда величина t мала.,
значение р велико. В соответствии с этим решение для коротких периодов
времени соответствует решению, полученному из уравнения (40) при боль-
ших значениях р. Когда р возрастает, аргумент гиперболического котан-
генса в уравнении (41) стремится к единице. Таким образом, для Ь'^р/У/рЛО
(порядка b'~hr 10/) и b'^ph" X- Ю (порядка > 10/) гиперболические
котангенсы могут быть заменены единицей без сколько-нибудь заметного
изменения величины уравнения (40). При этом уравнение (40) может быть
переписано таким образом:
(42)
(43)
где:
g (р) ехр
С2 - IK7I' v' 4 К"IV
57
Требуемое решение дается инверсией уравнения (42):
s(r, t) =
Q С g~v £-1
4 тс T ,) у
о
Я(Р)
dy.
(44;
Применяя уравнения (29) и (27), получим
[g(?)] = 0; 0 < t < r74v у -
: erfc ( ——г с ..........-—\ t > r7'4v у.
\ 2 У t — у !
(45)
Подставляя формулу (45) в уравнение (44) и произведя сокращения,
получим окончательное решение:
s = ТРт I"ПГ erfc — ]dld = (46)
J J \ V У (У ~ У !
и
= -Др Н (и, 3), (46а)
4яГ х 1/ ' 7
которое справедливо в пределах, где величина t меньше, чем наименьшее
^/lOv' и 6"710v". Значения р и и см. в списке обозначений.
Решение для длительных периодов. Для больших значений t (малых
значений р) члены, содержащие гиперболические котангенсы, могут быть
заменены их приближенными значениями посредством связи х coth х 1 -4-
+ х2/3, когда х2<0,2. Так, для &,2р//<0,2 (порядка /У2/7 < 0,2t) и
b"2ph" < 0,2 (порядка 6"2/v"<0,2Z) уравнение (40) может быть при этом
выражено так;
оо __________________________________
S (g р) = • ехр [— у — a2/4r/] dy, (47)
*0
где
Fi (Р) ~ ехр (-------/?). (48)
Способом, аналогичным тому, который использовался при получении
уравнения (46) из уравнения (42), уравнение (47) может быть сокращено
до следующего вида:
s = -—г (' ехр [— у — я2/4у} (49)
4 я Г \ У '
ИЛИ
S 4^- wyy a). (49a)
Это уравнение справедливо при времени t, превышающем большее из
56'7v' и bb"2b".
Скорость перетекания. Величина расхода скважины, обусловленная
перетеканием, может быть получена следующим образом.
Подставляя уравнение (39) в уравнения (37) и (38) и применяя урав-
нение (31) для нахождения обратного преобразования Ханкеля результи-
рующих выражений, получим
д — , . О coth b' Ур/у' тг , ,
дГS1 Д’ Р) — 2яТ ,/—г-
У v р
58
д - Q coth b" Vp/у"
s2 (r, b", p) = 2^f j7= " h r)-
Преобразование Лапласа величины скорости перетекания qL выража-
ется так:
4L (₽) = С 2 * Г Г - К' AS1 (Г, р) + К"(', Ь", Р)1 dr.
2 я Т J L дг дг
о
(52)
Скорость перетекания в течение коротких периодов времени. Для
bnh' i>10Z и Ь//2Л"> 10/ гиперболические котангенсы в уравнениях (50) и
(51) могут, как это указывалось ранее, быть заменены единицей. При этом,
подставляя уравнения (50) и (51) в уравнение (52) и интегрируя обратное
преобразование Лапласа с помощью уравнения (28), получим
qL = Q [1 — ent erfc (У nt )].
(53)
Значение п см. в списке используемых символов.
Общий объем воды, поступившей путем перетекания за время непре-
рывной работы скважины в пределах указанного времени, получается пу-
тем интегрирования уравнения (53) по t от 0 до t. В результате получим
= + Т7 (1 —e"'erfc (]/ nt У)], (54)
где V = Qt есть общий объем воды, полученной за период t непрерыв-
ной работы скважины в пределах диапазона времени, отмеченного
выше.
Скорость перетекания в течение длительных периодов времени. Для
6'2/v' 0,2/ и Ь"'!Ч'С 0,2/ гиперболические котангенсы в уравнениях (50)
и (51) можно, как это рассматривалось выше, заменить их приближенными
значениями, используя соотношение xcthxl4~x2/3. Если повторить про-
цесс, приводящий к уравнению (53), и вместо уравнения (28) применить
уравнение (30), то в результате получим
qL = Q[1 — (1/31)ехр(—v/aV^oJ],
(55)
где все символы имеют прежнее значение (см. список).
Решения для систем потока 2 и 3, которые приведены в тексте, по-
лучены способом, аналогичным изложенному. При этом принято thx^x и
th х 1 соответственно при х2<0,10 и х2 > Ю.
ЛИТЕРАТУРА
1. Bateman Н., 1954. Tables of Integral Transforms, McGraw-Hill Book Co., New
York.
2. C a m p b e 1 1 A., Foster I?. M., 1957. Fourier Integrals for Practical Applications’
D. Van Nostrand Co., New York.
3. C h u r c h i 1 1 R. V., 1944. Modern Operational Mathematics in Engineering, McGraw-
Hill Book Co., New York.
4. H an tush M. S., Preliminary Quantitative Study of the Roswell Ground-Water
Reservoir, New Mexico Institute of Mining and Technology.
5. H an tush M. S., 1956. Analysis of data from pumping tests in leaky aquifers, Trans.
Am. Geophys. Union, 37, 702—714.
6. II a n t u s h M. S., 1957. Nonsteady flow to a well partially penetrating an infinite
leaky aquifer, Proc. Iraqi Sci. Soc., 1, 10—19.
7. H a n t u s h M. S., 1959. Nonsteady flow to flowing wells in leaky aquifers, Journ.
Geophys. Res., 64, 1043—1052.
59
8. H a n t u s h M. S., Jacob С. E., 1954. Plane potential flow of ground water with
linear leakage, Trans. Am. Geophys. Union, 35, 917—936.
9. H a n t u s h M. S., J а с о b С. E., 1955a. Steady three-dimensional flow to a well
in a two-layered aquifer, Trans. Am. Geophys. Union, 36, 286—292.
10. Hant ush M. S., J а с о b С. E., 1955b. Nonsteady radial flow in an infinite leaky
aquifer, Trans. Am. Geophys. Union, 36, 95—100.
11. Hantush M. S., Jacob С. E., 1955c. Nonsteady Green’s functions for an infi-
nite strip of leaky aquifers, Trans. Am. Geophys. Union, 36, 101—112.
12. J a cob С. E., 1946. Radial flow in a leaky artesian aquifer, Trans. Am. Geophvs.
Union, 27. 198 - 205.
13. Thei s С. V., 1935. The relation between the lowering of the piezometric surface
and the rate and duration of discharge of a well using ground-water storage, Trans.
Am. Geophys. Union, 16, 519—524.
14. Watson G. N., 1944. Theory of Bessel Functions, Macmillan, New York.
15. W e n z e I L. K-, 1942. Methods for determining permeability of water-bearing mate-
rials, U. S. Geol. Survey Water Supply Paper 887, 87—98.
16. W i s I er С. O., Brater E. F., 1951. Hydrology, John Wilev ^Sons, New York,
ch. 7.
М. С. X ан туш.
НЕУ СТАНОВИВШИЙСЯ ПРИТОК ПОДЗЕМНЫХ ВОД К СКВАЖИНЕ,
НЕСОВЕРШЕННОЙ ПО СТЕПЕНИ ВСКРЫТИЯ1
Дается решение задачи о неустановнвшемся притоке подземных вод к скважине,
несовершенной по степени вскрытия, работающей с постоянным расходом в условиях
артезианского пласта постоянной мощности. Зависимость для определения понижения
уровня получена с учетом упругих свойств пласта. Полученные результаты сопостав-
ляются с притоком к совершенной скважине. Рассматривается приложение теории
к анализу данных по опробованию пластов.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Не всегда скважины, заложенные с целью откачки, проникают в водо-
носный пласт на полную его мощность. Гидродинамический режим таких
скважин отличается от режимов скважин, полностью вскрывающих водо-
@ Возмущающая спеажина
Уравнения понижения при a-d'^O $s
IJ' in
в 'j
л ; -Etf-UpJu ydy
© I - Sln^- W 1 а, (ПРгХ1
н у nt 'jj ' п* о о ° i f ф/ Г (—5”7 1
при Ь=°° ety >u P *У *
Ф и г. 1. Схема несовершенной скважины в напорном водоносном горизонте.
носпый горизонт. Приближенные решения задачи об установившемся
потоке подземных вод к несовершенной скважине при различных гранич-
ных условиях были даны в ряде работ (Козени [9]; Маскст [IGj; Полубари-
1 М. S. Н а п t u s h, Drawdown around a Partially penetrating well, Journ. of the
Hydraulics division. Proc. Am. Soc. of Civil Eng., 87, No. 4, 5, pt. 1, 83—96, 171 — 195,
1961.
61
нова-Кочина [11]; Хантуш и Джекоб [3]). Точная теория для установившегося
притока к несовершенной скважине была разработана Доном Киркхамом [1].
Целью настоящей работы является вывод уравнений неустановивше-
гося понижения, учитывающих длину и пространственное положение фильтра
как возмущающей, так и наблюдательных скважин.
Примечание. Значения символов объясняются в тех местах, где на
них впервые даются ссылки. Для удобства список всех условных обозна-
чений приводится в конце статьи.
УРАВНЕНИЯ ПОНИЖЕНИЯ
Несовершенной по степени вскрытия скважиной называют такую сква-
жину, длина фильтра которой меньше мощности водоносного пласта.
Схема несовершенной скажины в условиях напорного пласта представлена
на фиг. 1. Движение воды к такой скважине трехмерно (в отличие от
плоскорадиального движения к скважине, полностью вскрывающей водо-
носный пласт), поэтому понижение, измеряемое в какой-либо точке пласта,
будет зависеть, кроме прочих факторов, и от пространственного положе-
ния этой точки. Точно так же понижение, измеряемое в наблюдательной
скважине, будет зависеть от длины и пространственного положения ее
фильтра.
ПОНИЖЕНИЕ В ПЬЕЗОМЕТРАХ
Пьезометрами называют трубки малого диаметра, вода в которые по-
ступает только через дно. Автором было получено [5] выражение пониже-
ния s в пьезометре, имеющем заглубление I и находящемся на расстоя-
нии г от возмущающей скважины, которая работала с постоянным расхо-
дом. При этом было принято, что длина фильтра возмущающей скважины
совпадает с глубиной вскрытия водоносного пласта, радиус скважины мал,
водоносный пласт является однородным, упругим, изотропным, бесконеч-
ным по простиранию и имеет постоянную мощность при непроницаемой
подошве и кровле и перетекание из соседних слоев отсутствует (см. фиг. 1).
Аналогичный анализ дает возможность получить более общее решение для
случая, когда фильтр несовершенной возмущающей скважины опущен
ниже кровли водоносного пласта. Если перетекание отсутствует, скважина
работает с постоянным расходом Q, причем фильтр располагается в пре-
делах между I и d (/ > d), указанное решение может быть представлено
следующими уравнениями (систему координат см. на фиг. 1).
где
ПТ.Г j
Т /
(2а)
(2Ъ)
62
оо
Таблица 1
Je~у ,
erf (ЗУ у) dy
и
u 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 o.e 1.0 1.2 1.4 1.6 1.8 2.0
0 0.1997 0.3974 0.5913 0.7801 0.0834 1.1376 1.3053 1.4653 1.6177 1.7627 2.0310 2.2759 2.4979 2.7009 2.8972
1 0.1994 0.3969 0.5907 0.7792 0.9613 1.1363 1.3037 1.4635 1.6157 1.7605 2.0292 2.2728 2.4943 2.6968 2.8827
2 0.1993 0.3967 0.5904 0.7788 0.9606 1.1357 1.3031 1.4628 1.6148 1.7595 2.0281 2.2715 2.4929 2.6951 2.8809
3 0.1993 0.3966 0.5902 0.7785 0.0805 1.1353 1.3026 1.4622 1.6142 1.7588 2.0272 2.2705 2.4917 3.0938 2.9794
« 4 0.1992 0.3965 0.5900 0.7783 0.9602 1.1349 1.3022 1.4817 1.6137 1.7582 2.0265 2.2696 2.4907 2.6927 2. 8782
16 -Q 5 0.1992 0.3964 0.5898 0.7780 0.9599 1.1346 1.3018 1.4613 1.6132 1.7577 2.0259 2. 26 89 2.4899 2.6918 2. 8772
6 0.1991 0.3963 0.5897 0.7779 0.9596 1.1343 1.3014 1.4609 1.6127 1.7572 2.0253 2.2682 2.4891 2.6909 2.8762
7 0.1991 0.3962 0.5895 0.7777 0.9594 1.1341 1.3011 1.4605 1.6123 1.7568 2.0248 2.2676 2.4884 2. 6901 2.8753
8 0.1990 0.3961 0.5894 0.7775 0.9592 1.1338 1.3009 1.4602 1.6120 1.7563 2.0243 2.2670 2.4877 2.6894 2.8745
9 0.1090 0.3060 0.5893 0.7774 0.9590 1.1336 1.3006 1.4599 1.6116 1.7560 2.0238 2.2665 2.4871 2.6887 2.8737
1 0.1989 0.3959 0.5892 0.7772 0.9588 1.1334 1.3003 1.4596 1.6113 1.7580 2.0234 3.2600 3.4805 2.6880 2.8730
2 0.1937 0.3954 0.5883 0.7780 0.9574 1.1316 1.2983 1.4572 1.6086 1.7526 2.0198 2.2618 2.4818 2.6827 2.8671
3 0. 1084 0.3949 0.5876 0.7751 0.9562 1.1302 1.2967 1.4554 1.6066 1.7504 2.0171 2.2587 2.4782 2.6786 2.8625
l5 4 0.1982 0.3945 0.5871 0.7744 0.9553 1.1291 1.2953 1.4539 1.6049 1.7485 2.0148 2.2560 2.4751 2. 6702 2.8587
10 6 0.1981 0.3942 0.5866 0.7737 0.9544 1.1281 1.2941 1.4526 1.6034 1.7468 2.0128 2.2536 2.4724 2.6721 2.8553
6 0.1979 0.3939 0. 5861 0.7731 0.9537 1. 1271 1.2931 1.4513 1.6020 1.7452 2.0110 2.2515 2.4700 2.6694 2.8523
7 0.1978 0.3936 0.5857 0.7725 0.9530 1.1263 1.2921 1.4502 1.6007 1.7438 2.0093 2.2495 2.4677 2.6669 2.8495
6 0.1976 0.3933 0.5853 0.7720 0.9523 1.1255 1.2912 1.4492 1.5996 1.7425 2.0077 2.2477 2.4657 2.6645 2.8469
9 0.1975 0.3931 0.5849 0.7715 0.0517 1.1243 1.2003 1.4482 1.5984 1.7413 2.0062 2.2460 2.4637 2.6623 2.8444
1 0.1874 0.3929 0.5846 0.7710 0.9511 1.1241 1.2895 1.4473 1.5974 1.7402 2.0049 • 2.2444 2.4619 3.0003 2.8421
2 0.1065 0.3910 0.5818 0.7673 0.9465 1.1185 1.2830 1.4398 1. 5890 1.7308 1.9936 2.2313 2.4469 2.6434 2.8234
3 0. 1953 0.3896 0.5796 0.7644 0.9429 1.1)42 1.2780 1.4341 1.5825 1.7236 1. 9850 2.2212 2.4354 2.6305 2.8001
4 4 0.1952 0.3833 0.5778 0.7620 0.9398 1.1106 1.2737 1.4292 1.5771 1.7176 1.9778 2.2128 2.4258 2.6197 2.7970
10 5 0.194x3 0.3873 0.5762 0.7599 0.9372 1.1074 1. 2700 1.4250 1.5723 1.7123 1.9714 2.2053 2.4172 2.6101 2.7864
6 ,0.1041 0.3863 0.5748 0.7580 0.9348 1« 1045 1.2636 1.4211 1.5680 1.7075 1.9656 2.1986 2.4095 2.6014 2.7768
7 0.1937 0.3854 0. 5734 0.7562 0.9326 1. 1018 1.2635 1.4170 1. 5640 1.7030 1.9603 2.1934 2.4025 2.5934 2.7679
8 0.1933 0.3846 0.5722 0.7545 0.0305 i.csm 1.2607 1.4143 1.5603 1.0080 1.9554 2.1666 2.3959 2.58J0 2.7597
0 0.1929 0.3838 0.5710 0.7530 0.9286 1.0970 1.2579 1.4112 1.5568 1.6951 1. 9507 2.1812 2. 3897 2.5791 2.7519
1 0.1925 0.3831 0.5699 0.7515 0.9267 1.0948 1.2554 1.4083 1.5535 1.6914 1.9463 2. 1761 2. .7838 2.5725 3.7440
2 0.1896 0.3772 0.5611 0.7397 0.9120 1.0771 1.2347 1.3846 1.5270 1.0010 1.9109 2.1348 2.$367 2.5195 2.6857
3 0.1873 0.3727 0.5543 0.7307 0.9007 1.0838 1.2189 1.3666 1.5066 1.6393 1. 8838 2.1032 2.3006 3.4788 3.0400
4 0.1854 0.3689 0.5486 0.7331 0. 8912 1.0521 1.2056 1.3513 1.4895 1.6203 1.8610 3.0706 2. 2702 2.4447 2.6027
10 5 0.1837 0.3655 0.5435 0.7163 0. 8828 1.0421 1.1938 1.3379 1.4744 1.6035 1.8409 2.0532 2.2434 2.4146 2. 5693
6 0.1822 0.3625 0.5390 0.7103 0.8752 1.0330 1.1832 1.3258 1.4608 1.5884 1.8228 2.0320 2.2193 2.3875 2. 5393
7 0.1808 0.3597 0.5348 0.7047 0. 8682 1.0246 1.1735 1.3147 1.4483 1.5745 1.8061 2.0126 2.1972 2. 3626 2.5117
8 0.1795 0.3671 0.5310 0.6995 0.8618 1.0169 1.1645 1.3044 1.4367 1.5616 1.7907 1.9946 2k1766 2.3395 2.4861
9 0.1763 0.3547 0.5273 0.6947 0.8557 1.0096 1.1560 1.2947 1.4258 1.5495 1.7762 1.9777 2.1573 2.3179 2.4020
1 0.1772 0.3524 0.5239 0.6901 0.8500 1.0027 1.1480 1.2855 1.4155 1. 5381 1.7625 1.9617 2.1391 2.2975 2.4394
2 0.1880 0.3340 0.4962 0.6533 0.8040 0.9476 1.0836 1.2121 1.3320 1.4464 1.6537 1. 8340 1.9935 2.1342 3.3587
3 0.1C10 0.3300 0.4753 0.6253 0.7691 0.9057 1.0349 1.1504 1. 2703 1.3770 1.5697 1.7376 1.8839 2.0116 2.1233
4 0.1551 0.3083 0.4578 0.6020 0.7400 0.8708 0.9942 1.1100 1.2183 1.3193 1.5008 1.6577 1.7932 1.9103 2.0117
10 -2 5 0.1500 0.3081 0.4425 0.5817 0.7146 0.8404 0.9588 1.0696 1.1730 1.2691 1.4410 1.5884 1.7147 1.8229 1.3150
6 0.1455 0.2890 0.4280 0.5635 0.6919 0.8132 0.9272 1.0336 1.1326 * 1.2243 1. 3877 1. 5268 1.8450 1.7454 1.8307
7 0.1413 0.2807 0.4164 0.5470 0.6713 0.7885 0.8994 1.0008 1.0958 1.1837 1. 3394 1.4711 1.5821 1.6756 1.7543
8 o.is^e 0.2731 0.4050 0.5317 0.6522 0.7658 0.3720 0.9707 1.0621 1.1484 1.2951 1.4200 1.5246 1.6120 1.6848
[0.U39
0.5176
0.7447
11.5534
0.3943
0.6346
1.2541
1.3729
1.4716
9
^0. 2660
10.8474
[0.9428
11.6210
1.0308 11.1118
110.1300 0.2503 0.3844 0.5043 0.0181 0.7249 0.8245 '0.9167 1.0016 1.0705 1.2150 1.3290 1.4223 1.4991 1.5619
2 0.1051 10.2084 0.3081 0.4030 0.4020 0.5744 0.6500 10.7186 0.7606 0.8362 0.0207 1.0029 1.0595 1.1026 1. 1352
3 | 8. 74'-2)(0.1731 0.2554 0.3331 0.4053 0.4713 0. 5309 jo. 5842 0.6313 0.6727 0.7400 0.7899 0.8261 0.8519 0.9699
, 4 ! 7.39(-2)|0. 1403 0.2153 0.2801 0.3397 0.3935 0.4415 >0.4837 0.5203 0.5510 0.0015 0.6363 0.6602 0.0700 0.0803
10 1 5.! 0.32(-2)|O. 1248 0.1835 0.2381 0.2878 0.3323 0.3714 jo.4052 0.4341 0.4584 0.4955 0.5203 0. 5362 0.5462 0.5521
0 ! 5.44(-2)l0. 1074 0. 1575 0.2038 0.2458 0.2828 0.3149 1(1.3423 0.3652 0.3842 0.4122 0.4300 0.4408 0.4471 0.4506
7 4.71(-2)!9. 29(-2) 0.1360 0.1756 0.2111 0.2421 0.2080 ’0.2C00 0. 3093 0.3242 0.3455 0.3533 0.3657 0.3698 0.3719
8 4. 1<Ц-3)’е. 06(-2) 0.1170 0.1510 0.1821 0.2082 0.2302 lO. 2484 0.2632 0.3750 0.2013 0.3007 0.3058 0. 3084 0. 3090
9 ’ 3.t>7(-2/’7.03(-2) 0.1026 0.1310 0.1576 0.1797 0.1080 {0.2130 0.2250 0.2313 0.2468 0.2537 0.2572 0.2589 0.2597
1 13.13(-2)'6.14(-2) 8. 95(-2) 0.1148 0.1300 0.1555 0.1709 |o. 1333 0.1929 0.2004 0.2101 0.2151 0.2175 O'. 2186 0.2191
2 ! 9,01(-3)|l.75(-2) 2.51(-2) 3.10(-2) 3.07(-2) 4.07(-2) 4. 35(-2)|4. 55(-2) 4.0O(-2) 4.77(-2) 4. 85(-2) 4. 88(-2) 4. 68<-2)
3 ( 2. £2(-3)j5.44(-3) 7.68(-3) 9.47(-3) 1.08(-2) 1. 17(-2) 1. 23(-2)|l. 26(-2) 1.28(-2) 1.30(-2) 1. 30(-2)
4 1 0. 20(-4)il. 78(-3) 2.44(-3):2. 0«(-3) 3.31(-3) 3.63(-3) 3.86(-3) 3-72(-3) 3.76(-3) 3.77(-3) 3.77(-3)
1 5 1 3.07(-4)l5. 80(-4) 7.90(-4 ) 0.49(-4) 1.05(>3) 1.10(-3) 1.13(-3)|1.14(-3) 1.15(-3) 1.15<-3)
6 1.04(-4)tl.95(-4) 2.64(-4) 3. Ю(-4) 3.36(-4) 3.50(-4] 3.56(-4) 13. 50(-4) 3.60(-4) 3.60(-4)
7 3.56(-5) 6.61(-5) 8.84(-5)'1.02(-4) 1.10(-4) 1.13(-4) 1.15(-4)j 1.15(-4) 1.15(-4) 1.15(-4)
8 J 1.23(-5)2.20(-5) 2.00(-5)|з.42(-5) 3.33(-5) 3.72(-5) 3.75(-5)J3.76(-5) 3.77(-5) 3.77(-5)
0 ; 4. S8(-0)l7. 70(-6) 1.03(-5)| 1.15(-5) 1.21(-5) 1.23(-5) 1.24(-5), 1.24(-5) 1.24(-5)
10 : 1.4O(-0) 2.70(-8) 3.48(-0)3.0O(-6) 4. C7(-ti) 4. 13(-0) 4.15(-6)|4.16(-6) 4.18(-0)
Values of M(u,£) are equal to W(u) for u greater than IO and all values of 3
The numbers in parenthesis are powers of 10 by which the other numbers are raised e.g,, 8.74(-2)= 0.087
« i г f а 3 < о I г i t s ! г ! z. ё s и s i. 5 г L____ V“'"« <"• MM» ora »qwl to *fo) tor u 9>.ot.r ta> 1 and oil vo<u«« o( f | s s о ?4бб.77: « co :•« co v. A ui ьз »- < s ®C0-JeCTiS-4«»biW
Й iL-HsK! glSiifBil iiiifiiii iiiiiiiii *' *. Л. Л AA A ». ГЧйГ?! i s g iiiiiiiii iiiiiiiii gsOOisf iioioii iiiiiiiii Шпон » «
Й FFFFFFFFF isiiiiSIt iiiliSfgs ifsifiiif &1=ц8\й b iiiiiiiii iiiiiiiii iiiiiiiii iiiiiiiii iiiiiiiii FFFFFFFFF OsOiiii =1 ”
Й iiiiiiiii iiiifii ********* iigsgggSi iiiiiiiii F F У F F F P У У OliiBiii 2 ж ЯРРрвр®ГГ OiSIiOi •rrPFPPPPP iOiiOO FFFFFFFFF loimo iiiiiiiii iiiiiiiii F FF F F"FF F Oliillss i2
i iiiiiiiii illilil ЙЖ5ЙЁ PPPPPFPPP sisOiHi' < • iiiiiiiii Frr.»PPFPP.: iOOsiO OiOiiO iiiiiiiii iiiiiiiii FFFFFFFFF isirOsi? g F
г 8 iiiiiiiii iiiiiiiii iiiiiiiii iiiiiiiii iiiiiiiii ioiih iiiiiiiii FFFFFFFFF OisiOss iiiifiiii iiiiiiiii Я “
i iiiiiiiii F“****.**;*;. siiiOiO iiiiiiiii iiiiiiiii iiiiiiiii iiiiiii r r:« » F F F » iOOOO F F FFF FF F F' HiOOii iiiiiiiii igisisih FFFFFFFFF isiliigif
r i r “ “ “ F F F Ilsiliiir iliiOiis iiiiiiiii iiiiiiiii 1ЙЙЙЙ г iiiiii iiiiiiiii iiiiiiiii iiiiiiiii FFFFFFFF» Oggiisai iiiisOH
8 FFFFFFFFF lOsslisI FP******* lilBIili iiiiiiiii iiiiiiiii iiiiiiiii к РРРГ1- sOis iiiiiiiii iiiiiiiii iiiiiiiii iliiiifi fiilfill! з! ”
i FFFFFFFFF “******** «iilisgg * * * F P « « P F IliilHil iiiiiiiii PP ?.•* r Г r- " “ F “ F F F sligOOi iiiiiiiii FFFFFFFFF §13181881 FFFFFFFFF ИзйгШ iiiiiiiii gl p
i FFFFFFFFF ilSsilsls iiiiiiiii * P F F « F F F F iiiisiis» iiiiiiiii iiiiifili Г- -PP*!*/ 00 iiiOiigg F F F « Р“ F lisiiiiii F F F F F F F F F SOiisili Р * p * * * * * * isiiiiiO fiiiiiiii о p
iiiiiiiii iiiiiiiii Iiiiiiiii У У У F У F У F У iilsslsi? « FFF'FFFF F ? ifiiiiBsi £ iiii iiiiiiiii iiiiiiiii iiiiiiiii .**•**.* p * • OOOiis iiiiiiiii 1
F « F F F F P F iitiiiii fffiiib iiiiiiiii iiiiiiiii ! iii aiOiggO FFFFF“FFF iflOiiii iiiiiiiii F *• p p ppp* * siiiOO! p p * p * .* * .* * 00030 £ p
issOis! iiiiiiiii iiiiiiiii FFFFFFFFF Osgliiii iiiiiiiii1 * iii iiiiiiiii iiiiiiiii • ? ,A * * ? - * * iOiOiO iiiiiiiii iiiiiiiii
iliiiifi iiiiiiiii ssiillgsg iiiiiiiii iiiiiiiii I £ iii iiiiiiiii iiiiiiiii iiiiiiiii fiiiiiiii fiiiiifii * . 1.
F F F F F P F ООО! F * • .*♦•**? iOgiOss Iiiiiiiii У РУ У.РУУУ У Isiiiiiii FPFFFFFFP ? iiiaisisg i r t.ppp “F'FFf; iiiiiiiii SiiiiiiK iifiiiiii Iiiiiiiii i:
iifiil iiiiiiiii Iiiiiiiii iiiiiiiii iiiiiiiii i S ii iOOilsi F F F F F F Л iiOilgSg iiiiiii! ********* * i »
~ « F F F F “ OOggi iiiiiiiii ««?»«'« F F »’ silOsSO «. V. w <Л V, «Л U> p, « iiiiiiiii iiiiiiiii I : .-Ж Г F Ppp.Pppp. 5 = 000» FFFFF f aigiiilgg iiiifiiii *-*>**p.**> ieiOiils P P *:* * PP* *; IliOiOi s
F F F F F F Ollis fiiiiiiii Iiiiiiiii iiiiliiir FF FF FFF <* P <• SsiSliigg i - Й FFPFFFFFF ggOiilsi FFF.F:FP-F.*P iiOiigO iiiiiii ********* iisiiiiO ********* gsgsOsgs
F F F F F « OIO! ,'fc****.**.i'*. !йй!10 liiliili У «> p. ? c-> и W v> F F F F F F F F F 80883388 s W K» W;» *»>»:»:;WW. iisliaOi iiiiiiiii iiiiiiiii **'.*.* p* .** *: siOOisT *pp***p** IsOgssli
OliO iiiiiiiii iiiiiiiii iiliiSt fSOigsl! I £ gg FFFFF.FFFF' OOOOi Iliiiifi sOg£?iO iiiiiiiii iiiiiiiii i|:
Й iffiiiiii iiiiiiiii iiiiiiiii iiiiil SiSiiii 1 I iiiiiiiii .-FFFFFFF- oosigo iliiiifi «Hisiii *p*?p*?*» вйэшр ********* iiOKOi
—
Продолжение табл.
Продолжение табл. 1
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 « 44 46 48 50
0 $.Ж4 в.3595 6.8688 6.9333 7.1684 7.3789 7.5692 7.7431 7.9030 8.0511 8.1890 8.3180 3.4392 8. 5535 8.6615 8.0616 8.9546 9.0435 9.1386 9.3102
1 fi.8738 8.3325 6.6353 8.8973 7.1279 7.3339 7.5197 7.6891 7.8445 7.9881 8.1315 8.3460 8.362? 8.4735 8. 5761 8.6741 8.7671 8.8558 8.9400 9.0306 9.0877
а 5.8845 6.3213 8.6223 6.8823 7.1111 7.3152 7.4992 7.6667 7.8203 7.9820 8,0935 8.2161 8.3309 8.4388 8.5406 6.6367 8.7279 8.8145 8.8971 8. 9758 9.0510
3 5.8573 8.3127 8.6122 6,8709 7.0982 7.8008 7.4834 7.8495' 7.8016 7.9419 8.0720 8.1932 8.3063 8.4130 8.5133 8.0081 ».««7S 8.7830 8.8641 6.9414 ».O1 S3
5.8513 8.3054 6.6038 6•8612 7.0873 7.2887 7.4701 7.8350 7.7858 7.9350 8.0539 6.1739 8.2861 8.3913 0.4904 8. 5839 8.6725 8.7565 8.8264 8. 9135 8.Ш1
1О‘в 5 5.0480 8.3990 8. 5963 6.8527 7.0777 7.3781 7.4534 7.6222 7. 7721 j.s«m 8,037® 8.1668 8. 2>3B0 8.3732 8.4702 8.5827 8.650Й 8.7331 8.8119 8.3870 8.&5S3
в 5.0418 в.2932 6.5896 6.8450 7.0691 7.3885 7.4478 7.6106 7.7596 т.вгёб 8.0235 8.1415 S. 2316 8.3549 6.4519 8.6435 e.esoo 8.7120 8.7S9® S.8540 Э.9.Ш
7 5.8357 8.2879 6.5834 6.8379 7.0611 7.3596 7.4381 7.6000 7.7481 7.8842 8.0102 8Л373 8.2366 8.3390 8.4352 8. 5258 8.6115 8.6926 8.7696 8.943® 8.8130
8 5.0338 6.2830 6.5776 6.8313 7.0537 7.2514 7.4390 7.5901 7.7374 7.8727 7. me 8.1142 8.2226 8.3242 6.4196 0.5084 8.6746 8,750? 8. 8331 8-8721
8 5.0287 8.2783 6.5722 6.8251 7.0487 7.2436 7.4305 7.5809 7.7273 7.8619 7,9863 8.1018 8.2095 8.3103 8.4049 8.4940 S.S781 8.8575 8. 73'10 8.8047 S. 8783
1 5.0251 8.2739 в.5671 6.8193 7.0402 7.2383 7.4125 7.5721 7.7178 7.8517 7.9753 8.0901 8.1971 8.2972 8. 3910 8.4794 8. 5828 8.6416 8.7163 8.7873 6. S547
Я 5.8855 8.2385 в.5257 6.7720 6.9870 7.1773 7.3476 7.5013 7.6412 7.7692 7.8871 7.9960 8.0972 8.1914 8.2795 8.3621 8.4397 S. SIM S.SSW 8.646® 8.708?
3 5.8729 8.2113 6.4940 6.7358 6.9453 7.1331 7.2978 7.4472 7.5826 7.7061 7.8195 7.9240 8.0208 8.1108 8.1S43 8.2725 8.3458 8.4145 8.4793 S.5W1 6.5»?6
5.8538 8.1884 6.4673 6.7053 6.9120 7.0940 7.2561 7.4016 7.5333 7.6531 7.762? 7.8636 7.9686 8.0428 8.1329 8.1975 8.5671 8.3322 8.3033 8.4507 8. £©<57
1О‘в S 5.8388 6.1882 8.4438 6.6785 6.8818 7.0606 7.2193 7.3615 7.4899 7.6065 7.71S9 7.8105 7.9003 7.9533 8.0602 8.1318 8.2602 8.3182 8.3735 8.4455
g 5.8217 в.1560 6.4225 6.6542 6.8546 7.0303 7.1861 7.3253 7. 4508 7.5644 7.6679 7.7626 7.8496 7.9296 8.0038 8.0725 8. ISM S.WSS S.KMB 8.2094 8.3307
7 5.8078 в.1332 6.4030 6.6319 6.8296 7.0025 7.1556 7.2921 7.4149 7.5259 7.6387 7.7188 7.8032 7.8807 7.9533 8.0183 8.0795 8.1364 8.18W 8.2384 8.2643
8 5.7848 6.1177 6.8848 6.8112 6.8063 6.9787 7.1272 7.3613 7.3815 7.4901 Т.МИ 7.6781 7.7601 7.8353 7.9044 7.9682 6.0271 8.081? 8.1323 8.1792 8. 2339
, 9 5.7828 8.1020 6.3678 6.5917 6.7844 8.9525 7.1007 7.2324 7.3503 7.4585 7.5527 1. MO! 7.7198 7.7928 7.8587 7.9314 7.9762 S.WOS 8.И»! 8.1241 8.1SSS
1 5.7710 в. 0892 в.3517 6.5734 6.7838 8.9296 7.0758 7.2051 7.3308 7.4249 7.S1SS 7.6042 7.6818 7.7527 7.8177 7.8773 7.'9321 1.S8M В.ИИ 8.0733 8.1122
Я Ь. М'4-HSi 5.9778 6.3221 6.4257 8.5982 6.7463 6.8747 6.9863 7.0856 7.1729 7.2504 7.3194 7.3811 7.4364 7 7.5307 7.5708 7.6695 7.6863
3 5.8089 5. 8928 в. 1233 6.3133 в.4725 6.6075 3.7231 6. 8227 6.9091 6.9844 7.0503 7.1080 7.1586 7.3035 7.3439 8. 2777 7.3084 1.3359 t.SWT 7.3809 7. SWT
. 4 5.5571 5.8214 в.0406 6.2194 6.3677 6.4920 6.5972 6.6868 8.7635 6.SS94 6.8363 6.9S53 6.9778 7.0148 7.0465 7.0742 7.0982 7.1Ш 7.1371 7.1528 7.1683
10** 5 5.4947 5.7589 5.9681 6.1374 8.8763 6.3915 8.4680 6.5692 3.6376 6.6981 6.7456 6.7878 8.8237 6.8544 8.8-Ю5 6.9029 6.021® 6.9880 6.9518 3.9635 8.9734
в 5.4474 5.7026 5.9031 8.0633 в.1945 6.3019 6.3808 6.4648 6.5266 6.5784 6.6218 6.6583 6.8890 6.7147 6.7363 6.7545 6.7886 6.7823 6.7929 8.8017 6. 8090
7 5.4041 5.8511 5.8487 5.9967 в. 1201 6.2305 6.302? 8.3704 6.4263 6.4736 6.5100 6. 5427 6.5800 e.sm 6.6087 6.8235 8.6357 6.6457 6.6639 «.ею» 0.Й661
в 5.3839 5.8034 5.7887 5.9348 8.0515 8.1456 6.2219 6. 2841 6.3349 6.3763 6.4103 6.4380 8.4807 6.4791 6.4942 8.5063 6.5182 6.5241 6.5306 6.5357 8 5397
8 5.3283 5.5588 5.7374 5.8771 5.9878 6.0762 6.1472 6.2044 6.2506 6. 2879 6.3181 6Г34М 8.3820 6.377? 6.3803 6.4004 6.4064 6.414? 6.4197 S.4JS5 6.4267
1 5.2008 5.5168 5.6892 5.8230 5.9281 6.0113 6.0775 6.1303 6.1724 6.2061 6.3330 6.2543 6.2713 6.2848 6.3954 6.3037 6.3102 6.J153 8;31®3 6.3222 8.3246
8 5.0095 5.1881 5.3123 5.4037 5.4701 5.5184 5.5534 5.6788 5.5970 5.6101 5.6193 5.6357 5.6302 5.6333 5.8354 5.6368 5.8377 5.8383 5.6387 5.63И) 5.6391
3 4.8008 4.8437 5.0403 5.1056 5.1498 5.1795 5.1993 5.2124 5.2208 5.2263 5.2297 5. 2318 5.2331 5.2339 5.2343 5. 2346 5.2347 5.2348 5.234» 5.234»
, 4 4.8301 4.7481 4. 8235 4.8714 4.9017 4. 8305 4.9320 4.9390 4.9430 4.9454 4.9467 4.9474 4.9478 4.9480 4.9481 4.0481
10*s 5 4.4844 4.5880 4.6426 4.6783 4.6993 4.7114 4.7183 4.7220 4.7241 4.7351 4.7856 4.7259 4.7280 4.7360 4.7860
в 4.3588 4.4398 4.4872 4.5140 4.5268 4.5387 4. 5409 4. 542» 4.5439 4.5444 4.5446 4.5447 4.544?
7 4. 3425 4.3128 4.3510 4.3714 4.3819 4.3871 4.3806 4.3908 4.3913 4.3915 4.3916 4.3916
8 4.1303 4.-4991 4.2300 4.2455 4.2530 4. 2565 4.3530 4.2587 4. 2589 4.2590 4. 2591 4.assi
8 4.0450 4.098’ 4.1212 4.1331 4.1385 4.1408 4.1417 4.1421 4. 1422 4.1423 4.1433
I 3.9583 4.0020 4.0384 4.0316 4.0355 4.0370 4.9378 4.0378 4^0378
3 3.3403 3.350? 3.353? 3.3545 3.3547 : / 3.3647
3 3.0558 3.S5&5 2.9590 2.9590
_а * 2.6304 2.8812 2.6812 2.6812
10** 6 3.487? 2.4879 < 2.4878
в 2.2953 2.295?
Values of Mlu.jS) are equal to WUJ for u greoferfhan 6 Ю гоп<1 all values ef Д
50 <82 54 56 58 60 62 64 66 68 70 72 74 78 78 80 82 84 96 88 eo
0 0.2103 9. 2838 9.3641 9.4368 9.5089 9.5747 9.6403 9.7037 9.7653 9.8249 9.6629 S.9S93 9.9940 10.0473 10.0992 10.1493 10.1902 10.2474 10.2944 18.3494 1® 3655
1 Э. 0977 9.1718 9.2426 9.3108 9.3765 9.4398. 9.5008 9. 5598 9.8168 9.6720 9.7255 8.7773 9.8378 9.8764 9. 0239 9.9700 10.0148 10.G585 10.1011 Ш1425 10.1830
а 8.0510 9.1231 9.1922 9.2585 9.3223 9.3838 9.4430 9.5001 9. 5553 9.6088 9.6602 9.7102 9.73S6 9.8056 9.8512 9.8855 9. 038S 9. 9ЮЗ 10.0210 10.0506 5 •>.<№'
3 9.0152 9.0859 9.1535 9.2185 9.2806 9.3409 0.3888 9.4543 9. GOBI S. 5600 0.6103 9.8588 9.7058 9.7513 9.7955 9.8384 9.8800 Й. 9204 9. 9597 8.997» 10.0351
« 4 8.9851 9.0545 9.1210 В. 1847 9.2459 9.3047 9.8813 a <ei4a 9.4684 9. 5191 9. 5681 9.6156 9.8613 9.7057 9.7487 9.7904 9.8308 9.8700 9.9081 9.9452 9. 0833
10 & 3.95Й 9.0369 9.0924 9. 1550 9.2152 9. 3729 9.3285 9.3819 9. 4335 9. 48S1 0.5311 0.5774 9.6322 9.6655 9.7075 9.7481 8. 7875 9.8257 9.0838 9. BBSS -9.&3&Й
в 8.9348 9.0020 0.0665 9.128® 8.18*/4 9.2442 9. 2988 9.3513 9.4019 9.4507 9. 4977 9. 5431 9.586S 8.6293 9.6703 9.7101 9.7485 9.7858 9.8220 S.8571 0.891?
7 8.9128 S. 9791 9.0427 9.1036 9.1619 9.2179 9.2716 9. 8232 9.3730 9. 4208 9.4670 9.5115 9.5545 Э.5961 9.6362 9.6751 9.7127 9.7492 9.7845 9.8187 8.8510
8 8.8821 8.9578 9.0206 9.0807 9.1382 9.1933 9, 2463 9.2971 9.3460 9.3931 9.4385 9.4322 9. 5244 9.86'52 9.6046 9.6426 9.6795 8.7151 9.7497 9.7S3! Э. Slg§
8 8.873® 8.9378 9.0000 9.0592 9.1160 9.1703 9. 2225 9.2726 9.3208 0. 3671 9.4118 9.4548 9.4962 9.5362 9. 5749 9.6122 9. 6483 9.6933 9.7171 9.7498 0Л815
1 8.8547 8.91» 8.9803 9.0389 9.0949 9. I486 9.2001 9. 2495 9.2970 9.3426 9.3885 9.4288 9.4696 9.5089 9.5469 9.5835 9.818» 9.6532 9.6863 9.7183 0ЛШ
3 8.7087 8.7873 8.8339 §. 875® 8.9263 8.9743 9.0202 9.0640 9.105» 0.1461 9.1845 Б.3213 9. 2566 9.3905 9.3230 9. 3542 9.S843 9.4132 9.4410 9.457? 9.4S3G
3 8.5976 8.6519 8.7033 8.7531 8.7983 8. 8432 8.8839 8. 9237 Я ВЛ1Й 8.9975 9.0319 9.0847 9.0960 9.1260 9.1546 0.1819 9.2081 9.2332 9.3572 9.2802 S. S0S3:
а 4 8.5047 8.5555 8.6035 8.8483 8.6918 8.7321 8.7705 8.8069 8.8414 8.8742 8.0053 8.9349 8.9630 8.9898 9.0153 9.0396 9.062.3 9.034® 9.105» 9.1260 9..1451
10*а з 8.4235 8.4713 8.5163 8.558? 8. 5986 8.0362 8.6717 8.7053 8.7370 8.7671 8.7055 8.8224 8.8479 8.8731 8.8050 8.9167 .8. 9374 8.9570 8.9758 8.993? S.0100
б §.3507 В.395» 8.4393 8.4730 8.5154 8.5505 8.5S38 8.6147 8.6440 8.6718 8.6977 8.7223 8.7455 8.7675 8.7883 3. 8078 8.8263 8.8438 8.8603 £.9760 Э. ЗЭ0®
7 8.2843 8.3271 8.3072 3.4046 8.4397 8.4720 8.5034 3.5324 8.5586 8.5851 8.6091 8.6317 8.6530 8.6730 8.6918 6.7095 8.7262 8.7419 8.7567 8.7706 8. 7838
8 8.2229 8.2836 8.3018 S.3370 8.3700 8.4009 8.4297 6.4568 8. 4821 8. 5057 8.5379 8.5487 8.5682 8.5865 8.6036 8.6197 8.6343 6.6490 8.6633 8.6747 6.6SS<J
8 8.1838 8.2045 8.2-105 8.3740 8.3052 8.3343 8.3614 8.3866 8.4103 3.4332 8,4528 8.472G 6.4899 3.5087 8.5223 8.3370 8. 5507 8.5SS5 8.57S4 8. 5058 8. sm
8.1123 8.1491 8.1833 8.2151 8. 2448 8.2720 8.2974 8.3211 8.3431 8. 3638 8. 3837 8.4005 8.4170 0.4234 8.4468 8.4601 8.4728 8.4842 8.4845 3.5050 3.5143
3 7.8982 7.7203 7.7421 7.7618 7.7767 7.7958 7.8104 7.8236 7.8355 7.8463 7.8560 7.8048 7.8727 7.8788 7.8862 7. 8920 7.0972 7.9019 7.9061 7.SOWS 7.»isa
3 7.3997 7.4163 7.4309 7.4439 7.4553 7.4654 7.4742 7.4820 7.4889 7,494® 7.5003 7.5048 7.5088 7.5124 7. 5154 7.5131 7.5204 7.5225 7.5242 7.5258 7. 53?»
7.1883 7.17®? 7.1881 7.1968 7,2043 7.3108 7.2163 7.2211 7.2251 7.4S3W 7.2315 7.2341 7.2362 7.2380 7.3395 7.2408 7.2419 7.2428 7.8438 7. S4« 7.2447
«а® 10'* 5 в.9734 6.9818 6.9888 6.9948 6.9998 7.0040 7.9075 7.0105 7.0129 7.0150 7.0167 7.0181 7.0192 7.0202 7.0209 7.0216 7.0221 7.0335 7.0233 .7.0231 7.3ЯЗЗ
6 в. 8090 6.8151 8.8201 6.8242 6.8376 8.8304 6.8227 6. 8345 6.8380 6.8373 6.838? 6.8390 6.83S6 8.8401 6.8405 6.6408 6.8411 6.6413 6.8414 6.3415 6. 8-Ш -
« 7 6.6661 6.6705 6.6741 6.9770 6.6793 8.6811 6.68®) 6.6838 6.6847 6.6854 6.6860 6.6864 6.6868 6.6871 6.8873 6. 8874 6.6375 6.6876 6.6877 6.6878 fl. 6B7S
8 8.5397 8.5430 6. 5456 8.5476 8.5492 6.5504 6.5514 6. 5521 6.S527 6.5531 8. 5535 6.5537 8. 5539 6.5541 6.5542 6. 5543 6.554Э 8. 5544 б. 5M4 6.5564 3.SS44
9 8.4287 6.4291 6.4310 6.4334 6.4335 6.4343 6.4350 6. 4354 6.4358 6.4361 6.4363 6.4364 6.4365 6.4386 6.4366 6.4367 6. 4367 6.4367 6.4368 6. «Si.
1О'3 1 8.3246 в.3363 6.3377 6.528? 8.3234 6.3300 6.3304 6.3307 8.3310 6.3311 6.3313 0.3313 6.3314 6.3314 6.3315
1U Я 5.8391 5.6392 5.0S93 5.6S93 5.8393 с.в.ш
Values ore equol vo Wiui for# qreate Ihftn 2«W’’and ан vetoes of
x z\ V л/г [ 2nb-srx-]-z\ ,, ( 2nb— x
— > — = 2j M\u, ! !— —M\u, -------------------------—
r r ] [, \ ’ r ) \ r
n=l
+ m(u, ^t, + x'~z') -M (u, 2,ll,-x + ;y ,
\ r / \ r /J
r2Ss
4Kt
(2d)
время с начала откачки, /С — коэффициент фильтрации, —удельная
емкость пласта (объем воды, высвобождающийся из единичного объ-
ма пласта при снижении напора на единицу, размерность L-1) и
V (и, у)— то, что называют функцией скважины для пластов с перете-
канием1.
- —-.-
1 Таблицы значений этой функции см. в статье Хантуша в настоящем сборнике,
65
Функция М (и, S) определяется следующим интегралом:
М (и, р) = -~У~ erf ф V у ) dy, (3ai
V У /
и
в котором erf (х)—функция ошибок. Так как erf (—х) =—erf (х), то отсюда
следует, что
М(и, -р) =— М(и, р). (ЗЬ)
Функция М (и, р) была протабулирована [12] для широкого диапазона
значений параметров, встречающихся на практике (см. табл. 1). С доста-
точной степенью точности данная функция может быть апроксимирована
следующим образом:
М {и, р) — 2 ф’г'З---т= Pl7" и ) , если и < < 0,01; (4)
\ f /
М(и, р) 2 (sh~5 р— perf (]/«)), если (5)
и
М (и, р) = —Е1 (—и), если п < -:т, (6)
где sh-1p есть обратный гиперболический синус р, а — Ei(— и) — функция
скважины для пластов, в которых перетекание отсутствует.
Уравнение понижения при относительно малых величинах времени.
Согласно уравнению 16), членом f' уравнения (2а) вполне можно прене-
бречь, если и>5[гД26 — / — г)]2. При бесконечно большом b членом Д
также можно пренебречь. Таким образом, если £<[(26— I — zVSs{(20К)]
(что соответствует относительно небольшому периоду откачки или пласту
бесконечной мощности), то из уравнения (2а) получаем
О с ( I d z \
s — "X———— £ и, ——. —. —— I (71
8г.% (l — d) \ г г ’ г / ’ v '
где функция Е выражается четырьмя членами М уравнения (2а). Уравне-
нье (7) позволяет установить, что в начальный период откачки понижение
в скважине, несовершенной по степени вскрытия, аналогично понижению
в скважине, вскрывающей пласт неограниченной мощности. Длительность
начального периода зависит от глубины вскрытия водоносного горизонта
возмущающей скважиной, глубины точки, в которой производится измере-
ние уровня, мощности водоносного горизонта и гидравлических свойств
пласта.
Уравнение понижения при относительно больших величинах времени.
Можно показать [см. табл, функции W(и, £/)], что при а< ((zr/6)2/20)
функцию W (и, nnrjb) для всех имеющих практическое значение случаев
можно заменить функцией 2K0(nr.rjb). Тогда ряд в уравнении (1) стано-
вится независимым от времени. Следовательно, при и <(1/2) (г/д)2, т. е.
при t > (&2Ss/(2/<)), уравнение (1) может быть представлено в таком виде
4г.кь [ zzl ' ( ь ’ ь ’ ь ’ ь 1 ’
причем
пг.’
nr.z
b
Здесь /(0—-символ функции Бесселя от мнимого аргумента второго
рода нулевого порядка.
66
Уравнение (8а) показывает, что в данном диапазоне времени скорость
изменения понижения такая же, как и от возмущающей скважины, пол-
ностью вскрывающей водоносный горизонт. Другими словами, влияние
несовершенства скважины на понижение уровня в пьезометрах достигает
максимальной величины.
СРЕДНЕЕ ПОНИЖЕНИЕ В НАБЛЮДАТЕЛЬНЫХ СКВАЖИНАХ
Уровень подземных вод в наблюдательной скважине отражает сред-
нее понижение на участке пласта, вскрываемом фильтром этой скважины.
Среднее понижение s в наблюдательной скважине с фильтром, находя-
щимся в промежутке глубин Г и d' (Г > d'), может быть получено путем
интегрирования уравнения понижения в пьезометрах по 2 в пределах d'
и Г и делением полученного результата на (/'— d'). Если эту операцию
выполнить для уравнения (1), то сразу можно получить
s (-«)+/(«»-ь 4> 4’ 4’ 4)]’ (9п)
в котором
у 2&2 V1 1 / . mti . nr.d \
/ = —Т77---ТГ777-7Г 2j — Sin -г- —sm х
1 т.“ (I — d) (I' — d) n- \ b b )
n=l
. nr.l' . mid' \ I Tinr \ /ril.
X j sin —-— •—sin —-— I w \u, —r— I. (96)
\ b b / \ b ]
Результаты усреднения уравнения (2a) сложны и здесь не приводятся.
Однако представляет интерес выражение для среднего понижения
при относительно малых промежутках времени, которое и дается ниже.
Уравнение среднего понижения для относительно малых величин вре-
мени. При t < [(26 —-1 —- /')25?/(20К)] членом f' для всех встречающихся
на практике случаев можно пренебречь. Результат осреднения остающих-
ся четырех членов М в уравнении (2а) выражается следующим образом:
л-fL — f(u, (Юа)
\ ’ Г ’ Г ] \ г ’ Г /О Х '
в котором
F (а, 8, а) = г (а, 3) — а/W (а, а) +
Г __ ________е-хи _ е-уи
+ 2 у erfc (Ууи ) —xerfc (|/ хи} + “—Ц ’ (106)
где х = 1 + 82 и у = 1 4- а2, erfc—дополнительная функция ошибок
(1 —erf) и М— функция, определяемая уравнением (За).
Уравнение (10а) дает среднее понижение в наблюдательных скважи-
нах в пласте бесконечной мощности для всех диапазонов продолжительно-
сти откачки.
При d = d' = 0 уравнение (7), так же как и уравнение (10а), сводится
к соответствующим особым случаям, рассмотренным в работе К. Ф. Саада
[13] по водопритоку к скважинам в мощном артезианском пласте.
Вычисления по уравнению (10а) показывают, что, если (/'//) < 2,
с достаточной для практических целей точностью можно использовать
следующее приближенное уравнение:
d Z'
г ’ г ’
8лД (I — d)
(И)
67
в котором £ —величина функции Е из уравнения (7), в котором зна-
чение z заменено на (1/2) (lf -|-dz). Другими словами, осредненное пони-
жение в наблюдательной скважине с фильтром в интервале между V и d'
можно апрокенмировать в виде среднего понижения в двух пьезометрах,
глубины которых I’ и d! соответственно при условии, что (Г/I) < 2.
Кроме этого, если (г//) > 1 и (Г//)< 1, то среднее понижение в на-
блюдательной скважине для всех имеющих практическое значение случаев
можно получить в том виде, как это выражается уравнением (7) с вели-
чиной г, произвольно выбранной между Г и нулем. Выбор обычно делает-
ся таким образом, чтобы упростить уравнение, которое в некоторых слу-
чаях может принимать следующую форму:
s (и, Р); (12)
в данном случае уравнение справедливо при t < {2b — r^)2Ss./(20K), с и
постоянные; например, если I 3d, то выбор z=d позволяет привести
уравнение (7) к виду:
s~~1е>ЕкТIм’ ~зГГ l2m
Если d = 0, то выбор г = 0 дает
4г.Д/ \ r Г
тогда как при z = I
s ~ дНдг М /z> — • (: 2с ।
Уравнение среднего понижения для относительно больших величин време-
ни. Для значительных отрезков времени, тоестьпри /> (62S5./(2/Q), функцию
\у[и, —молено, как уже отмечалось, достаточно близко апроксимиро-
вать в виде 2/(„ •
Уравнение (9а) при этом примет вид:
— Q [ р-1 х , г { r I d Г d'\\ /1~> \
s = п Дг\—-Ei(—u)~- У. ----- , (13а)
4-1\Ь ( ' 1Л \ и ’ h ’ b ’ b ’ b h, !
в котором
. , . п~Г . nr.d' /юм
X Sin—Ю-—Sin-----. \l3b)
b о J
Замечания, сделанные относительно уравнения (8а), имеют силу и зля
уравнения (13а).
Понижение в пьезометре и наблюдательных скважинах
при (г>Ь) > 1,5
Ранее было показано [5], что для относительно больших расстояний,
то есть при (г/6)>1,5, уравнение понижения в пьезометрах и наблюда-
тельных скважинах будет иметь следующий вид:
5 ю Ei (—«)]. (14)
В действительности уравнение (14) дает практически достаточно точ-
ные результаты, даже если (г/b) равно единице при условии, что
68
zz < 0,1 (г/Z?)2. Уравнение (14) то же самое, что и уравнение понижения
при откачке из совершенной скважины (формула Тейса [14]). Другими
словами, на расстоянии от скважины, равном или большем 1,5 величины
мощности пласта, трехмерное движение жидкости является плоско-ради-
альным.
Понижение уровня в возмущающей скважине. Уравнения понижения,
приведенные в предыдущих разделах, получены исходя из предпосылки,
что расход в возмущающей скважине распределяется равномерно по длине
ее водоприемной поверхности1. При этом, естественно, мы получаем пере-
менное значение величин напора вдоль этой поверхности, и в частности
на стенке фильтра скважины. Теоретически же правильнее было бы при-
нимать схему с постоянным напором вдоль фильтра. Но такое распреде-
ление напора может быть получено весьма трудоемким методом; для
этого необходимо соответствующим образом (уже неравномерно) распре-
делить расход вдоль оси скважины.
В работе [10] было показано, что максимальное понижение уровня
(или наименьший напор) на стенке скважины, определяемое приведенными
уравнениями, очень близко к тому, которое получается из более строгих
уравнений, выведенных из допущения, что вдоль поверхности скважины
напор постоянен.
Точка па стенке скважины, в которой напор является наименьшим,
зависит от пространственного положения фильтра скважины. Если скважи-
на перфорирована на всю глубину от кровли пласта, то наименьший напор
будет на кровле (г = 0). Если скважина полностью вскрывает пласт
и только в нижней части у его подошвы оборудована фильтром, наимень-
ший напор будет иметь место у подошвы пласта (г б). При расположе-
нии фильтра в интервале глубин d и / точка наименьшего напора нахо-
дится ближе к точке d, если фильтр установлен в верхней половине пласта,
и ближе к точке /, если фильтр установлен в нижней половине пласта.
Вычисления по проведенным выше уравнениям показывают вместе
с тем, что значение максимума понижения не отличается заметно от ве-
личины. полученной при z = (1 /2) (/ + d). Следовательно, уровень воды
в возмущающей скважине может быть подсчитан из уравнений понижения,
рассмотренных в предыдущих разделах при замене в них г па rw и зна-
чении г, при котором величина напора минимальная (г.г, — эффективный
радиус скважины).
СВОЙСТВА УРАВНЕНИЙ ПОНИЖЕНИЯ
Ниже будут рассмотрены некоторые характерные свойства уравнений
понижения, существенные для расчетов параметров.
1. В период времени t < [(rp)2Sv/20K] понижение уровня в несовер-
шенных скважинах может быть представлено уравнением (14), в котором
b — I. Это показывает, что в начальный период откачки течение здесь
такое же, как в том случае, если бы подошва пласта проходила через
забой скважины.
2. В течение времени t < [(2b — г ji)2S6./20/C] графики зависимости по-
нижения уровня от логарифма времени имеют точку перегиба. Положение
точки перегиба определяется соотношением
f (х) = хе*’ erf (х),
(15)
1 При этом имеется в виду, что для вывода указанных формул в качестве модели
скважины используются источники с постоянной интенсивностью.
69
logJO(l/u)
ф и г, 2. Изменение понижения во времени в несовершенных
скважинах.
1одю(1/и)
-10 12 3^56
Ф ii г. 3. Изменение понижения во времени в скважинах,
имеющих различное заглубление в напорном пласте,
в котором
— / r2St \
X = V Щ , Щ = \ ,
tt — значение времени, соответствующее точке перегиба.
Понижение st в точке перегиба выражается так:
sz=-cA4(z/., р),
а уклон /nz кривой в этой точке
т — __— 2,3 се~и'1 erf (х).
1 цикл х '
(16)
(’./'
(18)
Уравнение (15) получено из уравнения (12) приравниванием к нулю
второй производной s по log10(; зависимость (17) — из уравнения (12) путем
замены и на ut. Первая производная s по log10( [из уравнения (12)] после
замены в ней и на щ дает выражение (18).
3. Отклонение кривых понижения уровня от кривых, полученных для
пласта бесконечной мощности, происходит при следующих приблизитель-
ных значениях t или //:
__(2&-гЗ)25.? 1Ц .
td 2б7С (1ЬП)
в которых td и ud— соответственно значения t и и в точке отклонения.
4. Отклонение кривых хорошо определяется для малых значений
(г/6). В зависимости от геометрических особенностей фильтрационной
системы отклонение не выражено при
У2 (26 — г З)2"
L 5 (г»2 _
< 1,
(19)
где х и 3 —-параметры уравнения (15). Уравнение (19) получено исходя
из того обстоятельства, что отклонение имеет место, только когда
(26-гЗ)%-
20/<
(20)
5. Для относительно больших промежутков времени [(> (62Ss/2/()]
независимо от положения скважин кривые будут выражены прямой ли-
нией, имеющей один и тот же уклон т, выражаемый следующим образом:
у __ 9 q Q
цикл ’°
(21)
Это соотношение получено из уравнений (6) или (10) путем диффе-
ренцирования s по log10(; при этом принято во внимание, что для боль-
ших значений времени и становится очень мало.
УРАВНЕНИЯ ВОССТАНОВЛЕНИЯ УРОВНЯ
Можно показать, что если t и f —время, отсчитываемое соответст-
венно от начала и конца откачки, то остаточное понижение s' в пьезомет-
ре во время восстановления уровня будет иметь вид
s' — s (Л — s (/').
(22)
71
Подобно этому, среднее остаточное понижение в наблюдательной
скважине
s'8(7) — s(f), (23)
где / = и /0 — время прекращения откачки. Таким образом, уравне-
ние восстановления, соответствующее любому из рассмотренных уравне-
ний понижения, может быть сразу же получено с соблюдением тех же
критериев времени. Например, если уравнение понижения для относитель-
но короткого периода откачки сводится к уравнению (12), то уравнение
восстановления можно записать в следующем виде:
s' с [М (и, ^) — М(а', 3) + Д (ч, Ь'г, 3) — /2 (и', Ь!г, (3)], (24)
в котором и' —значение и после замены t на f и
Ф и г. 4. Зависимость остаточного понижения от 1g (///') для несовер-
шенных скважин в напорном пласте.
Для
/0 о (11_Дк!*] уравнение (24) можно апроксимпровать в виде
s' = с [Л4 (и, 3) — М (и', pl].
(26)
Для
(ДМ и г
2 к | 20 }\
уравнение (24) выражается так:
s' = j-V Г- Ei (п) - f J - сМ
4 г.Д b s
(27)
Если /0 и t' больше, чем &2SV/2K, то уравнение (24), как и общее
уравнение восстановления, сводится к следующему:
й 4 т.КЬ
— Ei — Ei (— и')
(28)
72
Предыдущие уравнения характеризуют восстановление уровня в пье-
зометрах. Аналогичным образом могут быть получены уравнения восста-
новления уровня в наблюдательных скважинах с использованием соответ-
ствующих зависимостей для осредненного понижения.
Уравнение (28) распространяется на оба случая.
СВОЙСТВА УРАВНЕНИЙ ВОССТАНОВЛЕНИЯ УРОВНЯ
Для анализа данных испытаний пластов используются некоторые осо-
бенности рассматриваемых уравнений восстановления уровня.
Уравнения восстановления для частных случаев. Большое значение
имеет уравнение восстановления уровня воды после остановки возмущаю-
щей скважины, оборудованной фильтром на всю глубину вскрытия, или
уравнение для близко расположенных скважин, которые могут рассмат-
риваться как пьезометры с глубиной вскрытия, равной нулю. В этих слу-
чаях, как и в других (см. раздел об уравнениях понижения'), уравнения
понижения при коротком периоде откачки будут иметь характер уравне-
ния (12). Следовательно, зависимости, полученные в предшествующем раз-
деле, применимы и в данном случае.
На фиг. 4 представлены графики зависимости остаточного понижения
s' (для значений параметров, показанных на фигуре) от логарифма (//С),
согласно уравнению (24).
Эти кривые имеют три главные особенности:
1. В нижней левой части кривые имеют прямолинейный участок, про-
ходящий через нуль остаточного понижения и t/t' 1.
Этот участок ясно выражен на кривых, когда (1/я0) = (4 К/0/г2 =-
= 106 и 104; нечетко он выражен для кривой при указанном соотношении,
равном 103, и совсем неясно —для кривых при этом соотношении, рав-
ном 102 и 10. Порядок времени, в течение которого прослеживается пря-
молинейный участок, зависит от продолжительности периода откачки /0 и
параметров пласта.
Прямолинейный участок выделяется при t/t' <[1 (2Д70/6255)]. Уклон
прямолинейного участка
As' 2,30
т =------= —:—
цикл 4г. 1\Ь
(29)
Это выражение получается из уравнения (28) путем дифференцирова-
ния $ по log10 (t/t') с учетом того, что значения и и и' уменьшаются при
больших значениях t.
2. Кривые имеют точку перегиба. Вблизи последней они часто апро-
ксимированы прямой линией, уклон которой практически во всех случаях
можно принять равным уклону касательной к кривой в точке перегиба.
Точка перегиба выражена на отрезке графика в период времени
t'
r(2b-nwsl
20 к J •
Таким образом, уравнение восстановления вблизи точки перегиба
дается соотношением (24), но без функции
* I f , р I
Величина и' в точке перегиба, то есть может быть выражена сле-
дующим приблизительным соотношением:
= f (х)
уТг
— хех* erf (х), (30)
в котором х — ftj/'a/".
73
Уклон кривой mt в точке перегиба может быть получен из уравнения
(24) (или другой подобной формы) дифференцированием s по logl0 (tit') и
заменой соответственно и' на и'.. Уклон т1 достаточно точно выражается
одним из следующих двух соотношений в зависимости от порядка (f/f)»
в котором имеет место точка перегиба.
а) Если точка перегиба находится в пределах (Ш') < 100, уклон
mi --= Дз'/цикл 2,3 с \ ехр (— «') erf (х) —
— (///0)ехр [—(/7/)z iiil erf (х |/ (7//),-) } ,
(31)
в котором — значение (t'ih в точке перегиба.
б) Если точка перегиба находится при (tit'} > 100, второй член урав-
нения (31) становится незначительным и его можно отбросить.
3. Если геометрические особенности фильтрационной системы таковы,
что удовлетворяется соотношение
[х2 (26 — г?)75(г?)2] < 1,
(32)
то на кривой не обнаруживается точки перегиба. Прямолинейный участок
кривой (если он имеет место) формируется в поздней стадии.
ПРИМЕНЕНИЕ ТЕОРИИ К ИСПЫТАНИЯМ ПЛАСТОВ
Прежде чем изложить методику производства расчетов, следует отме-
тить, что влияние несовершенства скважины сходно с эффектом перетека-
ния воды из мощных полупроницаемых водоупоров. Кроме того, если кри-
вая имеет перегиб, но период наблюдений недостаточно продолжителен
для установления прямолинейной зависимости s — 1g/, влияние несовер-
шенства скважины сходно с эффектом наличия контура питания (напри-
мер, реки, озера) или перетекания воды из соседних водоносных пластов
через полупроницаемые глинистые перемычки. Тот же эффект наблюдается
в совершенных скважинах в пластах с уклоном поверхности водоупорного
ложа или в пластах изменяющейся мощности. Влияние указанных условий
следует соответствующим образом исключить, прежде чем приступать к
анализу, основанному на данной теории.
Обзор методов обработки данных, испытания скважины. Полулога-
рифмические графики зависимости понижения (при откачке) и остаточного
понижения (при восстановлении уровня после остановки откачки) дают ос-
нову для анализа наблюденных данных. Следовательно, первый шаг к об-
работке результатов испытаний — построение таких кривых.
В зависимости от геометрических особенностей фильтрационного пото-
ка применяются следующие методы.
Метод точки перегиба. Если уравнение понижения для рассматрива-
емой наблюдательной скважины в течение относительно короткого периода
откачки будет иметь характер уравнения (12) или может быть апрокси-
мировано этим же уравнением и при этом графики в полулогарифмичес-
ком масштабе имеют ясно выраженную точку перегиба, в которой с дос-
таточной точностью можно провести касательную, то можно предложить
следующую методику определения параметров.
1. На графике в полулогарифмическом масштабе строится касательная
в точке перегиба и замеряется ее уклон mt = As/цикл.
2. Вычисляется f (х) = р7 | те.
3. Из зависимости (15) находят значение х и erf (х).
4. Вычисляется == (х/^)2 и ехр (—и2).
74
5. Вычисляется К по уравнению (18) с соответствующим выражением
для с,
6. Определять значение М (ult ?), следует используя табулированные
значения этой функции и рассчитанные величины ut и р, а затем вычис-
лять значение sz из уравнения (17).
7. На основе полулогарифмического графика получается значение tt,
соответствующее вычисленному значению sz. Затем вычисляется удельная
емкость = (4 К. tt щ/Р).
8. Строится прямая линия — продолжение кривой (если опытные дан-
ные позволяют сделать это) и замеряется ее уклон т = As/цикл и из
уравнения (21) определяется Т = КЬ.
9. Вычисляется значение b из подсчитанных значений К и КЬ.
Метод типовых кривых. Если на кривой, построенной в полулога-
рифмическом масштабе, наблюдается перегиб и число и распределение
наблюденных точек таково, что имеется возможность четко осветить ха-
рактер кривой до начала прямолинейного участка, то для определения
параметров пласта можно применить метод типовых кривых. Этот метод в
сущности тот же, что и графический метод Тейса. В данном случае, од-
нако, типовые кривые в соответствии с рассматриваемой фильтрационной
системой представляют собой логарифмический график функции Е (или Е)
уравнения (7) или уравнения (12) в зависимости от (1/и). Наблюденная
кривая представляется в виде логарифмического графика s (или s) от t в
том же масштабе, что и типовая кривая. Метод заключается в следую-
щем.
1. Строится типовая кривая для каждой скважины, причем исполь-
зуются табулированные значения функции М (и, р).
2. В таком же логарифмическом масштабе строится график наблюден-
ных данных.
3. Полученные кривые совмещаются, причем особое внимание обра-
щается на параллельность их координатных осей (совпадение кривых дол-
жно быть наибольшим). При совмещении наблюденной и типовой кривых
следует иметь в виду, что наблюденные точки для относительно больших
значений времени могут отклоняться вверх от типовой кривой. Это откло-
нение вызывается тем, что типовая кривая составлена по данным за сра-
внительно короткий промежуток откачки.
4. Выбирается произвольная точка в любом месте совмещенного участ-
ка с координатами
[Е (или Е), Ни] и (х(или5), /].
5. Вычисляется значение Sv по уравнению (7):
7. (33)
( — | Г2
\ И /
6. Если наблюденная кривая отклоняется от типовой кривой, записы-
вается значение (1/й) для точки отклонения. Затем рассчитывается значе-
ние b из соотношения
6^(1/2)[/ + z + гУЫиа] (34а)
для пьезометра или
b (1/2) [/ + (1/2) (/' +d') +г УЬНЦ] (346)
для наблюдательной скважины.
75
В условиях, когда Е (или Е ) сводится к М — функции уравнения
<12)’
6^(1/2) (34с)
L f ud
в котором ud — значение и для точки перегиба.
7. По вычисленным К и b рассчитывается проводимость Т = КЬ.
8. Если опытная кривая не отклоняется от типовой кривей, записы-
вают значение (1/ц) в окрестности последней наблюдательней точки. Мощ-
ность пласта будет больше, чем при расчете его по пункту 6, если исполь-
зуется истинная величина (1/zz).
Значения Т, полученные в пунктах 7 и 8, могут точно не соответ-
ствовать друг другу. Это обусловливается, например, тем, что полнее сов-
падение кривых при первой попытке наложения не было достигнуто, или
из-за .того, что прямолинейная часть графика круче или более полога, чем
это неебходимо. В этом случае процедура повторяется с необходимыми
поправками, чтобы различие между двумя величинами Т было минималь-
ным.
Метод Тейса и Джекоба. Если график в полулогарифмическом масшта-
бе по наблюденным данным, несмотря на относительно длительный пери-
од откачки, не имеет точки перегиба, то для расчета параметров пласта
можно использовать метод Тейса, а при условии, если полулогарифмичес-
кий график имеет вид строгой прямой линии,—метод Джекоба.
Метод Тейса и Джекоба с поправкой на несовершенство скважины.
В течение периода, когда образуется строго прямолинейный участок полу-
логарифмического графика, понижение выразится уравнением (8 6). Так
как вторей член этого уравнения постоянен во времени, то отсюда следу-
ет, что метод Джекоба может быть применен в том случае, если известна
численная величина этой постоянной. При этом определение параметров
производится в следующем порядке.
1. Строится график зависимости s от 1g / по наблюденным данным;
этот график выражается прямей линией, которая продолжается до пере-
сечения с осью нулевого понижения.
2. Определяется уклон т =~- As/цикл этой линии и время, соответству-
ющее пересечению с осью lg t.
3. Из уравнения (21) вычисляется Т = КЬ.
4. Вычисляется значение fs (или Д) из соответствующего выражения
(для этого обычно достаточно нескольких членов ряда).
5. С использованием соответствующих таблиц рассчитывается коэффи-
циент водоотдачи из формулы
Г2,25 Пр ехр(Ш
5 = —--------- . <35)
г2 J
Анализ данных восстановления уровня. Если уравнение пониже-
ния в наблюдательной скважине рассматривается для короткого проме-
жутка времени, оно сводится к уравнению (12) и порядок анализа сле-
дующий:
1. Строится график зависимости s' (или s') от 1g (ИТ).
2. Проводится касательная к этой кривой в точке перегиба кривой и
измеряется ее уклон гщ As'/цикл.
3. По обнаруженной точке перегиба находится значение (//Т), которое
обозначается (Z/f);. Если точка перегиба будет определена не совсем точ-
но, это, как будет показано далее, не окажет существенного влияния на
расчеты.
4. Рассчитывается значение ИДИ'), которое равно {tlT}-t—1, и (Ш(),
равное (67')z/(/0///).
76
5. Рассчитывается f (х) = (W[,A: и находятся соответствующие значе-
ния х и erf (х).
6. Определяются = (х/р)2 и величина ехр (—иф
7. Если величина {tlt')i > 100, по уравнению (31), пренебрегая вторым
членом, рассчитывают величину К.
8. Если значение {t/t')i < 100, рассчитывают величины ифф/ф и
и получают значение ехр [—zz/(/'//) J и erf (xj/ . Далее из
уравнения (31) находят К.
9. Из известных значений /0 и (Д//о) определяется величина tt.
10. Рассчитывается удельная водоотдача == (4/(Д'«//г2).
11. Если четко выделяется прямолинейная зависимость между s' и
log10 (f/Л в поздней части данных (включая начальную точку \\tit') — 1,
s' = 0], строится эта линия и замеряется ее уклон т = Дз'/цикл, по кото-
рому с помощью уравнения (29) находят величину (Кф), а затем, зная
значение К и (КЬ), величину Ь.
Следует иметь в виду, что если (?//')/> Ю, то второй член уравнения
(31) сравнительно мал. Таким образом, ошибка при определении величины
{Шф не повлияет на результаты расчета. Наибольшая ошибка будет за
счет первого члена уравнения (31), в который входит отношение фф/ф.
Однако и эта ошибка редко превосходит ±3%. Ошибка в значении <S$
приблизительно пропорциональна ошибке в определении величины Ц.
Описанный порядок действия может позволить получить приблизи-
тельное значение параметров водоносных пластов. Если прямая линия ис-
следуется по пункту (11), то значения коэффициента проводимости Т~КЬ,
поскольку они определяются по уравнению (29), являются достаточно
точными.
Примеры расчета. Для иллюстрации приложения предложенных ме-
тодов использованы опытные данные, полученные в долине Рио-Гранде
вблизи города Сокорро в Нью-Мексико. Опытные скважины вскрывают
здесь безнапорный водоносный горизонт. Однако, так как наблюдаемые
понижения малы по сравнению с глубиной возмущающей скважины, рас-
смотренную выше теорию, хотя она и разработана для артезианских на-
порных пластов, можно применять в безнапорных условиях.
Откачка на ферме Фолкнер. Обе скважины — возмущающая и наблю-
дательная—перфорированы на всю глубину вскрытия —116 и 60 футов
соответственно (фиг. 51. Наблюдательная скважина заложена на расстоянии
17 футов от возмущающей скважины. Опробование этих скважин произво-
дилось Волдроном [15] в сентябре 1952 г. Во время откачки возмущающая
скважина работала с постоянным дебитом 3,57 фут-Чсек.
Так как {141} = (69/116) < 2, то среднее понижение в наблюдательной
скважине в течение относительно короткого времени выражается уравне-
нием (7), которое при d — d' ~ 0, V 60 футов, / = 116 футов и r= 17 фу-
тов имеет вид:
s = 8’ 6) + М 5>1'3’ <36)
Анализ данных откачки. Метод типовых кривых. С помощью табл. 1
по уравнению (36) строится типовая кривая в логарифмическом масштабе.
В том же масштабе строится график наблюденных данных. Две кривые
совмещаются, как это показано на фиг. 5. Значения Е, (1/zz), s и t в сов-
падающей точке на фиг. 5 составляют: 5, 6; 500, 10 футов и 100 мин
(6000 сек) соответственно. Из уравнения (36) вычисляем Л, которое равно
, Ss. получаем равным 1,14X1 МЧрупгЧ
В период откачки опытная кривая не отклоняется от типовой кривой,
т. е. время td в точке отклонения больше, чем период наблюдения. Таким
образом, из фиг. 5 следует, что td и (1/&J больше, чем 500 и 2500 мин
2
6,86х 10 4фут/сек и S,
77
соответственно. Следовательно, мощность пласта больше, чем (1/2) [/ +
+ (1/2) Г + г у 57« ] = (1/2) [1 16 + 30+17У"5х2+00| = 1023 фута.
Метод точки перегиба. В этом случае действительнее уравнение за-
меняется приближенным уравнением в форме (12). Например, если пони-
жение в наблюдательной скважине апроксимируется уравнением для
Ф и г. 5. Кривая наблюденных данных и теоретическая типовая
кривая для наблюдательной скважины.
пьезометра с нулевым вскрытием (Г = 0), то вместо точного уравнения ; 36)
получаем
s = е 82), (371
4Ь4 7гд
для которого с --= и р=6,82 [см. формулу (12 6)].
Основываясь на уравнении (37), можно построить график по методу
точки перегиба: для этого в полулогарифмическом масштабе нанесем наблю-
денные данные (это уже сделано, см. фиг. 6). Строим касательную к кри-
вой в точке перегиба и измеряем ее уклон = 7,4 фут/цикл, f (к)
= р2/1/ к = (6,82)2/)/тс =26,2. По формуле (15) находим х = 1,666 и erf(x) =
= 0,982; = +/р>3 = 0,06 и ехр (—0,06) = 0,94. Из уравнения (18) полу-
чаем /( = 7х10~4 фут!сек. Интерполяция по таблицам функции М\и, 3)
дает М (ид 6,82) = 2,291. Из уравнения (37) получаем s = 8 футов.
Для 5^=8 футов фиг. 6 дает tt = 3,1 мин = 186 сек. Затем из 4 K^ujr'1
получаем значение 8?, равное 1,08X10+
Строго прямолинейный участок кривой плохо различим (см. пунктир-
ную линию, показанную на фиг. 6). Следовательно, проводимость
(Л70 и мощность пласта не могут быть определены из представленных
данных.
Откачка из скважины Олсон. На фиг. 7 показаны кривые изменения по-
нижения во времени, построенные в полулогарифмическом масштабе для
двух наблюдательных скважин в результате откачек. Положение этих
скважин показано на фиг. 8. Каждая из двух скважин имеет глубину
75 футов и оборудована фильтром длиной 50 футов в нижней части. Од-
на из скважин—возмущающая с дебитом 1,6 фут?!сек. Наблюдательная
78
скважина № 1 расположена в 182 футах к востоку от возмущающей сква-
жины, другая наблюдательная скважина, № 2, расположена в 384 футах к
западу от возмущающей скважины приблизительно с нулевым вскрытием
(в действительности вскрывает пласт на 1,1 фута).
Анализ данных понижения по скважине № 1 с использованием урав-
нения (И) дает осредненное понижение в этой скважине. Однако, так как
Фиг. 6. Изменение понижения во времени в наблюдательной
скважине.
(г//) = (182/75) > 1 и (Г/1) = (75/75) = 1, уравнение (11) можно апроксими-
ровать уравнением (7), в котором z произвольно выбирается между 0 и /
(см. раздел о среднем понижении в начальный период откачки). Для z =-
25 футов это условие позволяет свести уравнение (7) к уравнению (12).
Среднее понижение в этой скважине для малых порядков s в соответствии
с (1) можно будет получить из следующей формулы:
s ==..... - М (и, 0,55), (38)
которая является разновидностью уравнения (12) с с =и р=0,55.
Так как перегиб на кривой, построенной в полулогарифмическом масштабе,
проявляется четко (см. фиг. 7а), при определении параметров будет при-
меним метод точки перегиба или метод типовых кривых.
Метод типовых кривых. Из таблицы функций М (и, р) по уравнению
(38) [М [и, 0,55)] строим в логарифмическом масштабе типовую кривую.
В том же самом масштабе строим график наблюденных данных. Две кри-
вые накладываем и совмещаем в положении, показанном на фиг. 8.
Значения Е [М (и, 0,55)], (1/а), s и t в точке совмещения опытной и ти-
повой кривых соответственно равны 0,38, 10, 1 футу и 1000 мин
(6х10~4 сек). Из уравнения (38) А=4,84Х 10~4 фут/сек и 35=4Л7 (//й) г2 =
= 3,5-10~4 фут~1. В точке перегиба величина = 9. Затем из соотноше-
ния Ь = (1/2) [г, р + г |/ Ыиа ] получаем b =660 футам. Проводимость пласта
Т - КЬ -- 0,319 фут2!сек и коэффициент водоотдачи S = Ssb = 0,23.
79
Фиг. 7. о) изменение понижения во времени в наблюдательной сква-
жине, б) зависимость остаточного понижения от 1g (t/t') для скважины 1.
Метод точки перегиба. Строим полулогарифмический график, как это
показано на фиг. 7а, и проводим касательную к этой кривей на участке
точки перегиба. Замеряем ее уклон пр, который равен 1,55 фут/цикл,
f (х) = =-. (0,5517|/т 0,17. Из уравнения (15) находим х = 0,371 и
erf (х) 0,40; ut = (х/З)2 = 0,454 и ехр ( —0,454) = 0,635.
Из уравнения (18) вычисляем К = 4,78 х 10s фут/егк. Из табл, функ-
ции М {и, t3) [или типовых кривых М (и, 0,55)] определяем М [ip, 0,55) = 0,33.
Из уравнения (38) s,-== 0,88. Из фаг. 7а = 220 мин, или 13 230 сек. Сле-
довательно, Ss. ЛКфифг2 = 3,46 X ИГ1 фут~\ Строим строго прямой учас-
ток кривой 7а. Замеряем уклон 0,90 фут/цикл. Из уравнения (21) под-
считываем КЬ -= 0,326 фут/сек. Следовательно, Z? (0,323/4,78 X
\ К j
X 10 4) — 680 футов. Коэффициент водоотдачи S = 8ф = 0,235.
Время, мин
Фиг. 8. Кривая наблюденных данных и теоретическая типовая кри-
вая для скважины 1.
80
Следует отметить, что вследствие большого изменения расхода сква-
жины приблизительно в первые 100 мин с начала откачки наблюденные
точки этого периода не были приняты во внимание. Кроме этого, следует
отметить, что в начальный период откачки результат не соответствует об-
щему теоретическому уравнению в силу возможного изменения проницае-
мости пласта.
Анализ данных, по понижению уровня в наблюдательной скважине 2.
На наблюдаемой кривой в полулогарифмическом масштабе время — пони-
жение для этой скважины (см. фиг. 7) перегиба не отмечается. Известно,
что скважина имеет практически нулевое вскрытие пласта, а мощность
пласта велика. По анализу данных по скважине 1 она составляет около
700, точнее 670 футов; следовательно, г/6 = 384/670 < 1,5. Значит, оба слу-
чая, для которых применим метод Тейса и Джекоба, здесь не имеют мес-
та, хотя характер кривой время — понижение сходен с зависимостью, вы-
ражаемой формулой Тейса.
Метод Тейса и Джекоба с поправкой для несовершенной скважины.
Даже в том случае, если есть достаточное число точек на криволинейной
части наблюдаемого графика в полулогарифмическом масштабе, что гаран-
тирует удовлетворительное решение с помощью метода типовых кривых
[уравнение понижения (7) при 2=0], для расчета можно использовать ме-
тод Тейса и Джекоба, придерживаясь следующего порядка.
Замеряем уклон прямолинейной части кривой /иЛ- = 0,90 фут/цикл и
Д : 270 мин (16 200 сек) [см. фиг. 7а]. Из уравнения (21) вычисляем
Т = О = 0,326 футДсек. Из уравнения (1) рассчитываем fs, используя ве-
личину b =-. 700 футов (можно ограничиться пятью членами бесконечного
ряда) =0,81; затем ехр (0,81) = 2,25. Из S = [2,25 Ttp ехр (Д)/г2] подсчиты-
ваем коэффициент емкости — 0,18.
ЗАКЛЮЧЕНИЕ
Было получено более общее по сравнению с имеющимися уравнение
для понижения, создаваемого несовершенной по степени вскрытия сква-
жиной в артезианском пласте постоянной мощности и неограниченного
простирания. Введены дополнительные параметры, учитывающие длину и
пространственное положение фильтра возмущающей и наблюдательных
скважин. Уравнения понижения в пьезометрах и средние понижения в на-
блюдательных скважинах даны в форме, удобной для расчетов. Влияние
несовершенства скважины на создаваемое ею понижение показано на
фиг. 2 и 3.
Усредненное понижение в наблюдательной скважине, как бы близко
она ни была расположена к несовершенной возмущающей скважине, может
быть выражено формулой Тейса [см. уравнение (14)] при условии, если
фильтр наблюдательной скважины перекрывает весь пласт. Это же остает-
ся в силе, когда наблюдательная скважина расположена на расстоянии
(г/б) >1,5, независимо от пространственного положения ее фильтра. Дру-
гими словами, среднее понижение в такой скважине не зависит от несо-
вершенства вскрытия. Оно тождественно тому, как если бы возмущающая
скважина полностью пересекала пласт (см. кривую 1 фиг. 2). Независимо от
местоположения скважины и пространственного положения фильтра кривые
понижения во времени для относительно больших величин времени
(/ >62£Л/2/() имеют приблизительно одинаковый уклон—такой же, как если
бы возмущающая скважина была совершенной по степени вскрытия пласта.
Другими словами, влияние несовершенства скважины достигает своей мак-
симальной величины (см. кривые 1 и 2, фиг. 2).
Если наблюдательная скважина расположена относительно недалеко от
возмущающей скважины (г/b < 1,5), изменение среднего понижения в за-
81
висимости от логарифма времени будет иметь характер кривой 2 на фиг. 2
и кривых 1 и 2 на фиг. 3. В течение начального периода откачки и до
того момента, когда появится отклонение, кривые зависимости понижения
от времени имеют такой же общий вид, что и кривые для совершенных
скважин, которые строятся по формуле Тейса, хотя эта формула в данном
случае, конечно, неприменима. Даже на самой ранней стадии откачки, ког-
да соблазнительно допустить (чтобы получить возможность воспользовать-
ся формулой Тейса), что подсшва пласта совпадает с дном фильтра (т. е.
скважина является совершенной), эту формулу применять нельзя. Исклю-
чением являются те случаи, когда характер системы потока таков, что для
сравнительно коротких периодов откачки допустимо пользоваться форму-
лой (126). Возможность использования в данном случае формулы Тейса
определяется [см. уравнения (6) и (126)] выполнением следующего соотноше-
ния: /< (Z2Sv/20/(). Однако если уравнение понижения сводится к уравне-
нию (12), то формулу Тейса удсбнее использовать в преобразованном виде
в соответствии с уравнениями (12) и (6). Критерием применимости этого
уравнения будет соотношение t < ](r3)2S5./(20K)].
На фиг. 3 дается сопоставление понижений в наблюдательных сква-
жинах, расположенных на равных расстояниях от возбуждающей скважи-
ны. Глубина вскрытия одной из этих скважин равна нулю, другая же
скважина имеет фильтр, длина которого равна ее глубине. Понижение в
двух этих скважинах, хотя они и находятся на одинаковых расстояниях от
возбуждающей скважины, различно. Может оказаться, что при соответст-
вующем положении и длине фильтров наблюдательных скважин пони-
жения в более удаленных скважинах будут иметь большую величину.
Влияние несовершенства скважины сходно с влиянием перетекания из
мощных, полупроницаемых пластов («водоупоров») [7]. Точно так же по-
скольку имеет место перегиб кривой понижения уровня, то при малом пе-
риоде наблюдений (недостаточном для того, чтобы можно было построить
прямолинейный полулогарифмический график зависимости понижения от-
времени) влияние несовершенства скважины имеет в некотором роде сход-
ство с влиянием границы с постоянным напором [6] либо перетеканием во-
ды из соседних водоносных горизонтов через полупроницаемые слои [3].
Тот же в общем эффект наблюдается и в случае, когда совершенная сква-
жина работает в пласте с наклонным водоупором или пласт имеет изменя-
ющуюся мощность [8]. Таким образом, без достаточных сведений об ис-
следуемой фильтрационной системе характер наблюдаемого понижения мож-
но интерпретировать по-разному. Недостаточно разносторонний анализ этих
данных может дать ошибочные и в большинстве случаев нереальные резуль-
таты. Это, конечно, приводит к недоразумениям, что бывает всегда, когда
пытаются применять формулы к условиям, которым они не соответствуют.
В следующей статье будет рассмотрено применение теории неустано-
вившегсся притока к скважине, несовершенной по степени вскрытия, в
бесконечном артезианском пласте для определения параметров водоносно-
го горизонта и мощности водосодержащих пород. Приложение этих мето-
дов будет проиллюстрировано на анализе данных о подземных водах бас-
сейна в Нью-Мексико.
ПРИЛОЖЕНИЕ
Условные обозначения
Ниже приводится список основных символов, использованных в тек-
сте статьи.
С-:—-параметр функции М (и, 3); постоянная, зависящая от одной или
всех переменных (/, Г, d, d', z, г, b);
b — мощность пласта, размерность
82
с—постоянная, зависящая от расхода скважины, длины фильтра сква-
жины, гидравлических свойств пласта, размерность L;
d—расстояние от кровли пласта до верха фильтра (длина неперфо-
рированной части скважины), L;
d'— расстояние от кровли пласта до верха фильтра наблюдательной
скважины, L;
2 Х — 2
erf (х) = —f с !l dy — функция ошибок;
1 О
erfc(x) = 1 — erf (х)—дополнительная функция сшибок;
Е~ Е (a, Ur, dlr, z!r) = М [и, (I 4 г)/г] — М [и, (d 4~ г)/г] -|-
4- М [и, (I — z)/r] — М \и, (d — z)/r];
Е— Е (и, Hr, dlr, I'lr, d'/r) ~ [Е при z (I' 4- d')/2];
f = f {и, rib, lib, dib, zlb) = [26/4 (/ — d)] V (1/n) [sin (nup'6) —
H=i
— sin (n~d/b)] cos (n~z, b) W (n, n~rlb);
при 2/<0 (n~r:b), заменяющем W (it, nizr/b)];
~f rib, lib, d;b, rib, d'/b) [2d) (/'—(IM2) [sin (лк//6)-
n=l
— sin (n-d.’b)l [sin (nid'lb) — sin (nr,d'/b)] W (u, mzr/b);
fs~ [7, ПРИ 2Kn(n-nb'), заменяющем W (и, nr.r/b)\;
/' (it, b'r, xir, zir) = {M [u,, (2n6-|-x4~z)/r] — /И \u, (2nb — x — z)irj-j-
n~ i
4- M (it, (2nb 4- x — z\'r\\ — M [//, (2nb — x + z)/r]:,
К — коэффициент фильтрации пласта, LT1;
Kq (x)— преобразованная функция Бесселя нулевого порядка второго рода;
I—глубина вскрытия возмущающей скважины, L;
I'— глубина вскрытия наблюдательной скважины, L;
~у , —
Л1(«,р)== (*-— erf (ЗУ//\dy—табулированные значения этой функции
и
даны в табл. 1;
Q —постоянный расход скважины, LTT1;
г —радиальное расстояние, измеряемое от центра скважины, L;
s—понижение пьезометрической поверхности в любое время и в лю-
бой точке пласта (понижение в пьезометре);
s —среднее понижение в наблюдательной скважине, L;
s'—остаточное понижение в пьезометре, L;
s' — остаточное понижение в наблюдательной скважине, L;
S =bSs — коэффициент емкости;
S6.— удельная емкость (объем воды, освобождающейся из единичного
объема пласта при снижении напора на единицу), L*1;
t — время с начала откачки, Т;
t0 — период откачки. Т;
t'—время с момента остановки откачки, Т;
83
T==Kb—проводимость пласта, LxT \
it = (г25Д W));
и' = (r2Ss./(W));
<v> —— у
—- Ei(—u) - ^~—dy—функция скважины от («.) для пластов, в кото-
и
рых перетекания не происходит (см. табл, на стр. 31);
W(u,x) = j-у-ехр ( — х3/(4Д) — функция скважины от и и х для плас-
и
тов с перетеканием (см. табл, на стр. 34,1;
z — вертикальная координата от верха пласта с положительным на-
правлением вниз.
ЛИТЕРАТУРА
1. Don К i г k h a in, 1959. Exact theory of flow into a partially pehetrating well,
Journ. Geophys. Res., 64, 1317.
2. H a n t ush M. S., 1955. Preliminary quantitative study of the Roswell ground-water
reservoir, New Mexico Inst, of Mining and Techn.; см. также Analysis of data from
Pumping Tests in Leaky Aquifers, Trans. Am. Geophys. Union, 37, 702, 1956.
3. H a n t u s h M. S., J а с о b С. E., 1955. Nonsteady radial flow in an infinite leaky
aquifer, Trans. Am. Geophys. Union, 36, 95.
4. H a n t u s h M. S., J а с о b С. E., 1955. Steady three-demensional flow to a well
in a two-layered aquifer, Trans. Am. Geophys. Union, 36, 286.
5. H a n t u s h M. S., 1957. Nonsteady flow to a well partially penetrating an infinite
leaky aquifer, Proc., Iraq i Scientific Soc., 10—19; also reprinted by New Mexico
Inst, of Mining and Techn., Socorro, N. M,
6. H a n t u s h M. S., 1959. Analysis of data from pumping wells near a river, Journ.
Geophys. Res., 64, 1921.
7. H a n t u s h M. S., 1960. Modification-of the theory of leaky aquifers, Journ. Geo-
phys. Res., 65, 3713.
8. H a n t u s h M. S., 1962. Ground-water flow in sands of nonuriiform thickness, 66,
1961 or 1962.
9, Kozeny J., 1933. Theorie und Berechnung der Brunnen, Wasserkraft u. Wasser-
wirtschaft, 28, 101.
10. M u s k a t M., 1937. The flow of homogeneous fluids through porous media, McGraw-
Hill Book Co., Inc., New York, N. Y; or J. W. Edwards Brothers, Inc., Ann. Arbor,
Mich. 1946.
11. Polubarinova-Kochina P. Ya., 1951. Theory of filtration of liquids in
porous media, Advanced in Applied Mechanics, 2, 207.
12. Professional Paper 102, Research Div., New Mexico Inst, of Mining and Techn.,
Socorro, N. M.
13. S a a d K- F., 1960. Nonsteady flow toward wells which partially penetrate thick
artesian aquifers, thesis presented to the New Mexico Institute of Mining and Tech-
nology, at Socorro, N. M.
14. T о d d D. K-, 1959. Groundwater-Hydrology, John Wiley and Sons, Inc., New York,
90; см. также Schoeller H., «Arid zone hydrology, Recent Development, UNESCO,
Paris, France, 1959, 37.
15. W a 1 d г о n J. F., 1956. Reconnaissance geology and groundwater study of a part
of Socorro County, New Mexico, Stanford Univ, at Palo Alto, Calif.
16. Wenzel L, K-, 1942. Methods for determining permeability of water-bearing mate-
rials, U. S. Geol. Surv., Water-supply Paper No. 887, 99; см. также W i s 1 e г С. O.,
Bra ter E. F., 1951. Hydrology, John Wiley and Sons, New York, N. Y.
М. С. X ан туш
ДВИЖЕНИЕ ПОДЗЕМНЫХ ВОД В ПЛАСТАХ ПЕРЕМЕННОЙ
МОЩНОСТИ 1
ВВОДНЫЕ ЗАМЕЧАНИЯ
Движение подземных вод в пористой среде характеризуется следующим
дифференциальным уравнением [10]:
д vx/d х д vy!d у д vzid z — — Ss д ®/d t. (1)
Решение уравнения (1), удовлетворяющее определенным граничным
условиям, дает распределение напора для данной области фильтрации,
в том числе и для ее границ. В общем случае, однако, получение такого
решения оказывается чрезвычайно сложным.
В настоящей статье приводится приближенное дифференциальное урав-
нение для потока в пластах переменной мощности; характеризуются усло-
вия, при которых это уравнение является справедливым, и дается его ре-
шение для нескольких случаев, представляющих практический интерес.
ТЕОРИЯ
Приближенное уравнение движения подземных вод в пласте, имеющем
переменную мощность. На фиг. 1 показано, что водоносный пласт заключен
между поверхностями z Д (х, у) и z /3(х, у). Пласт обладает постоянным
Фиг. 1. Схема пласта переменной мощности.
коэффициентом фильтрации К и удельной емкостью S5. Подземные воды
находятся в движении, и результирующий напор в любой момент времени
меняется от точки к точке. Напор, наблюдаемый в совершенной скважине,
отражает средний напор в вертикальном сечении пласта по оси скважины
Л(х, у, t).
1 М. S. Н а п t u s h, Flow of ground water in sands of nonuniform thickness, Journ.
Gcophys. Res., 67, Nos. 2, 4, 1S62. Настоящая статья дается в сокращенном виде.
85
1 Io закону Дарси
Г v - J\ д h-д x,
V\,^ — Kdh!dy. (2i
Интегрирование уравнения (1) no z, когда мощность пласта равна
Ь(х, in fv дает
I? h h h
i (d dz | [duJdy'idz 4- 1 [dvjdz] dz — —S I (d<?/dt)dz. (3)
h ' h h ' П
Применяя правило дифференцирования под знаком интеграла и учиты-
вая, что vx и иу—•функции (х, у, z, t), а Д и Д— функции (х, у), мы можем
уравнение (3) привести к виду:
0 г , , t , д f., , , t () f;
.J | у. + У’ Л- 0 -^7
L
J Vy dz
д
д у
1 z d f} / г j d / I (
— V., IX, у, t) -Д-= -г V., (X, у, Д , /1 -Д- ч-
v ! - у у > /1 ' д у
иг1х, у, f.>, Л //, Д, /)
' л
х dt
' Д>
f ?dz
_ /1
'41
Легко вп теть, что величины в скобках уравнения (4i— это МД, bVy и bh
соответственно. Так как — поверхность тока, то общая скорость в любой
точке этой поверхности должна быть направлена по касательной. Эго же
справедливо и для Д. Следовательно, на основании геометрических построе-
ний можно показать, что
оДх, у, ft, I) ov(x, у, Д, i)df}/dx - v,(x, у, Д, hdjjdtj.
Эго выражение сохраняет справедливость, если ft заменить на Д. Та-
ким образом, используя рассмотренные выше соотношения, а также уравне-
ния (2) и (4), наконец получим:
д
<) X
1 ду
Ь (х,
Ь (х, у) dh
v д t
(5)
Если мощность пласта меняется только в направлении х, то уравнение
(4) сводится к следующему:
ash — 1 Ul
д x~ fo d x d x 1 d y3 > d t ' ' '
Приток к скважине в пласте переменной мощности.. Используем при-
ближенное диффгренцп 1льное уравнение (6) для нахождения распределения
понижения, создаваемого совершенной скважиной, работающей с постоянным
расходом или постоянным понижением в пласте, мощность которого изме-
няется по экспоненциальному закону. Площадь распространения пласта
принимается неограниченной. Расход скважины обеспечивается сработкой
упругого запаса водоносного пласта. Коэффициенты проницаемости и удель-
ной емкости считаются постоянными.
Если мощность пласта неизменна в направлении у, но1 уменьшается
в направлении х по закону (см. фиг. 2)
b - охр [—2(х—х0).'а],
(7)
86
Ф и г. 2. Схема расположения скважины
в ограниченном пласте переменной мощности.
то приближенное уравнение движения в таком пласте, выраженное через
понижение $, получается из уравнения (6) и имеет следующий вид:
д- s 2 d s , о- $ I д s
д д'2 а д х 1 д у2 ч 01
Скважина, работающая с постоянным расходом. Решение задачи о при-
токе к такой скважине может быть получено из уравнения (8) при следую-
щих начальном и граничных условиях:
s(x, у, 0) ^0, s(x, ±0О, {) - о, S(± оо, у, () - 0, (8а) (<86) (8с)
г I 0s Q Inn I г -з— а 0 . Г Л) J or J\bQ 0 (86)
Подстановка
s -Z(.r, у, t) ехр [(х ---Л'о). а| Zexp 1— - cos Н ) \ а / (9)
изменяет уравнения (8) и (8а):
и
d2Z _____________Z
д x- ' д у'1 а2 ч д t
Z>x, у, 0) - 0.
(10а)
(106)
Применяя преобразование Лапласа по t к уравнению (10а) и используя
(5/0, получим
удщуу /i.uJjz = 0. (Ня)
д х2 д у' \ ч a' j '
Гаким же образом уравнения (86) и (8с) преобразуются к виду
s (±оо , у, р) -- s(x, ± оо , р) = 0
(116)
87
II
c-Tld (1k)
(12с)
равное (Q/2k Kbop),
от (Q/2tc/(6oP) и
2-
lim
г >()
Уравнение (На) является аналогом дифференциального уравнения,
описывающего установившийся поток подземных вод в напорном пласте
в условиях перетекания [9], решение которого, выраженное через перемен-
ные уравнения (11а), имеет вид:
Z-tcK0([(x- х0)2 -Г (у-л)21!/2[(р/>) 4 1 /а211 /2)
=с/<0(г [(p/v) -4- 1/а2]’/2) (12а)
и, следовательно,
s = cexp [4-cos0) /<0(r[p/v4- 1/а2]|/2). (126)
\ О’ j 1 4 1
То, что условие (116) удовлетворяется в уравнении (126), легко увидеть,
если вспомнить, что для больших значений аргумента /(0 (х) « |/к7х"ехр (—х).
Используя условие (Нс), из уравнения (126) находим постоянную с,
равную Q/2c/C60p. В процессе нахождения значения с
дующие соотношения:
2я
2тг /0 (х) = | ехр (— х cos 0) d(4,
b
2- /г (x) — i exp (— x cos 0) • cos 8 dH,
b
lim xKt (x) 1 lim Ц (x) /Co (x) =- 0,
л -0 x >o
lim /0 (x) — 1 lim It (x) = 0.
-v->-0 x-0
Подставляя в уравнение (126) вместо с его значение,
и замечая, что обратные преобразования Лапласа
(гА'о \ (P/v)+ 1/а2) равны соответственно (Q/2 тс/(60) и (1/2/)ехр(—vAa3 —
— r-,4v(), можем, используя правило «свертки оригиналов», получить об-
ратное преобразование Лапласа уравнения (126), которое будет иметь сле-
дующий вид:
s ехр (—cos (?) IF (a, —). (13)
4 я/Cb» \ a / \ a /
Следует подчеркнуть, что уравнение (13) справедливо только в течение
периода, в конце которого влияние откачки достигает той части пласта,
где тангенсы максимальных углов наклона водоупоров становятся боль-
ше 0,2. Выражая это положение количественно, можно записать, что урав-
нение (13) справедливо в течение периода, для которого ao = ro/4v(>5,
то есть
(<ro/2Ov, (13a)
и в пределах полубескопечной плоскости, ограниченной слева (фиг. 2) ли-
нией, параллельной оси у и расположенной на расстоянии г г0 и 8 =
где г0 выражается так:
г0 = (a/2) In fa/1060). (136)
Уравнение (13a) получается из тех соображений, что понижение уровня s
при г = г0 и 0 = тс' в большинстве случаев, имеющих практический интерес,
очень мало, когда > 5. Уравнение (136) находится путем приравнивания
абсолютной величины скорости изменения мощности пласта вдоль коорди-
88
наты х [выражаемой уравнением (7)] к 0,2 и решением полученного таким
образом уравнения относительно г.
Фиг. 3 показывает распределение понижения, создаваемого скважиной,
при значениях параметров, приведенных на фигуре. Линии равных пониже-
ний имеют более или менее овальную форму в отличие от круговой, созда-
ваемой скважинами в пластах постоянной мощности. Это распределение
Фиг. 3. Распределение понижения в пласте
переменной мощности.
понижения получено вследствие наличия экспоненциального множителя пе-
ред функцией W (и, г/а). Так как ехр (/7а cos Q)^0 при значениях г/а<_ 0,01,
то кривые равных понижений в пределах этой области принимают форму
окружностей, однако распределение их, вообще говоря, отлично от распре-
деления в пласте постоянной мощности; распределение будет таким же только
при t < 2,5 ra/v.
Скважина с постоянным расходом вблизи реки. Пусть рассматриваемый
пласт будет пересекаться (фиг. 2a) достаточно протяженным и прямым
участком берега реки. Горизонт воды в реке имеет исчезающе малый уклон
и не испытывает колебаний во времени. Тогда понижение, создаваемое со-
вершенной скважиной при откачке из нее с постоянным расходом, будет
определяться решением уравнения (8), удовлетворяющим условиям (8a), (86),
(8d), а также условиям
s(°°, У, 0 = 0, (14a)
s(0, у, 0 = 0. (146)
Всем этим условиям можно удовлетворить путем добавления к реше-
нию (126) частного решения уравнения (11a), которое получается методом
разделения переменных. При этом используется соотношение
Ко [(-£ — Л'о)3 + (.У — Уо)2]^2 ) ~
J (а- 4- trip11
О
Окончательно решение принимает следующий вид:
s= ехр cos ©Hr (и, -^—\ — w{u', —U (15)
4ид&0 1 \ а ) L \ а / \ “ /j
89
Уравнение (15) справедливо для всех точек и для всех значений вре-
мени при условии, конечно, что тангенсы углов наклона водоупоров со сто-
роны реки не превосходят 0,2.
Стационарное распределение понижения можно получить из уравнения
(15), полагая в нем /->оо и и. 0. Учитывая, что W (0, z) = 2K0(z) [2],
получим
Q I r V ( г \ rr ( г'
..- ехр -—- cos Н • д0 — — д о — .
2~ /<Д} * \ а ] \ а / \ а /
(15а)
Скважина с постоянным расходом вблизи непроницаемого контура.
Если рассматриваемый пласт ограничен прямолинейным непроницаемым
барьером (фиг. 26), то формула для определения понижения уровня, вызы-
ваемого совершенной скважиной, работающей с постоянным расходом, по-
лучается из решения уравнения (8) при условиях (8а), (86), .(8), (8с), (14а)
и условия
д s (0, у, t)/dx = O,
(16)
для которого преобразование Лапласа можно записать в виде
ds(0, у, р)/дх = 0. (16а)
Как было показано ранее, члены левой части уравнения (126) с
с ~ Q/2 тг КЬ^р появились в результате выполнения условий (8а), (86), (8),
(14а). Условию (16а) можно удовлетворить, если прибавить к (126) частное
решение уравнения (На), получаемое методом разделения переменных. При
этом необходимо использовать соотношение (14 с). После преобразований
результат получаем в виде:
Q г А
s - г ——— ] ехр —- cos Н
4- КЬ0 ( 1 \ а
ехр(—2x0/a)-f((7v, Ur
F (U,, Uy, (/„) = J exp (- V- U'i) erfc (? (/, - ) *1. (17a)
J ‘
Численное интегрирование уравнения (17a) для определенных значе-
ний параметров не представляет трудности. Функцию F можно с точностью,
достаточной для практических целей, апроксимпровать следующим образом:
. erfc (Ux
ехр f — Uy\ — erfc (Uy
(176)
Уравнение (176) получено из (17a) путем замены дополнительной функ-
ции ошибок в подынтегральном выражении постоянной величиной, равной
половине ее значения в пределах интегрирования.
Поскольку пласт замкнутый, т. е. расход скважины полностью зависит
от запасов пласта, установившееся движение в данном случае не может
быть достигнуто и уровень воды в пласте будет снижаться в течение все-
го времени, пока будет работать скважина. Но по истечении относительно
продолжительного периода откачки снижение расхода в зоне, близкой к
возмущающей скважине, становится настолько малым, что движение мож-
но считать установившимся.
Из приведенных решений как частный случай могут быть получены
хорошо известные формулы для пласта постоянной мощности [10, 14].
Если пласт имеет постоянную мощность, то значение (1/а) равно нулю
[см. уравнение (7).] Так как при этой функции ехр [(r/a) cos 0] и W (и, г!а)
90
становятся равными соответственно единице и —Ei(—и), то подстановка
этих последних функций в полученные уравнения-дает решения для посто-
янной мощности. Последние решения могут быть вместе с тем использова-
ны для характеристики, притока к скважинам, вскрывающим пласты пере-
менной мощности при условии, что
(г/а)<. 0,01 (18)
и
и >г/10а
или
r<(2,5ra/v), (19)
которые получаются на основании того, что ехр [(r/a) cos 0]^ 1 при
(г!а) < 0,01 и W (и, r/a) Ei (—и) при и^>г/10а.
Скважина, работающая самоизливом с постоянным понижением. Пони-
жение, создаваемое совершенной самоизливающейся скважиной, то есть
скважиной, работающей при постоянном понижении уровня в безграничном
пласте, мощность которого изменяется по экспоненциальному закону, мо-
жет быть определено на основании решения уравнения (8), удовлетворяю-
щего условиям (8а), (86), (8с), а также условию
s(rw,f) =--sa„ (20)
или в форме преобразования Лапласа
s(rw, р) = sw/p. (21а)
Условиями (20) и (21а) заменяются условия (8d) и (Ис) в задаче с по-
стоянным расходом. В остальном они аналогичны. Следовательно, уравне-
ние (126) справедливо и в настоящем случае. Применяя условие (21а) к
уравнению (126) и решая последнее относительно с, получим
с =- sjpexp cos о) • <0(гда[(рЛ) + 1
Так как представляющие практический интерес значения rja очень
малы (обычно менее 0,01), то изменение с в зависимости от 0 незначитель-
но' и мсжно принять, что величина с является постоянной. Следователь-
но, изображение функции понижения в настсящей задаче выражается так:
с = с гхп (Г Гзд)сог0^ ^~о (4РЛ ~b l/a2)]'/») /91Ы
Переходя от изображения к оригиналу, получим ([3], уравнения (8) и (13))
s = sw ехр (г-Л-^соз e'j ~^~Jrexp[-~xrw/a2}-E(p,'z,rw/a)\, (21с)
\ а / Lz'oirwiaJ j
где
е = л. с.J- мр м «р . 2d!1. ,21„
’ .! О ы + п (?) ? + (<»/»)’ ' 1
0 1 ° О J L J
Численные значения функции Е отсутствуют. Однако если учесть, что
отношение rw/a мало (как стмечалссь выше, сно обычно <0,01), то функ-
ция Е достаточно точно мсжет быть апроксимирована следующим выра-
жением:
£(о, т, 0) = Л(р, т)— 1. (21е)
Здесь функция А (р, т) для относительно малых времен (т< 0,01) мо-
жет быть представлена в таком виде:
А (р, 0 йг;—~ Г erfc ('j 4* i erfc [ (21/1
' I'9 I \ 2V i ! 4P \ 2 A <
91
и для больших значений времен (-с > 500)
Л(о, r)~0,434£if-f-V logio(2,25т). (21^)
При подстановке выражения (2k) в уравнение (21с) будем иметь
s ~ sw ехр cos 0
[ K0(r/g)
( Уь (rw/a)
1 — А (о, т)
ехр (— тг^/а!
(22)
Уравнение (22) применимо в области, определяемой уравнением (136)»
Период, в течение которого уравнение (22) справедливо, может быть по*
лучен из значения т, д'ля которого правая часть уравнения (22) становится
< 0,01 при 0 — и и г = г0. Значение г0 выражается по (13&).
Падение расхода скважины во времени может быть получено из урав-
нения (21с):
2г.
(23)
о
Используя зависимость (12с), окончательный результат после преобра-
зований можно представить в виде
Qf = 2^Kb0swG('z, г J а).
(24)
ЗАКЛЮЧЕНИЕ
В статье дается решение задачи об определении понижения уровня
при действии совершенной скважины в пласте, мощность которого меняет-
ся по экспоненциальному закону. Результаты решения представлены в виде
функций, табличные значения которых опубликованы.
Показано, что формулы, употребляемые при расчетах скважин в пла-
стах постоянной мощности, могут быть использованы для приближенных
расчетов в пластах переменной мощности при условии, что период откачки
t < 2,5 rah и размеры исследуемой области находятся в пределах, выра-
жаемых критерием (г/а)<;0,01.
Влияние переменной мощности пласта иллюстрируется графиками на
фиг. 4. В течение периода времени t 2,5 rah график изменения понижения
log,0(1/и)
2-10123
Фиг. 4. Зависимость понижения от времени
в пласте переменной мощности.
92
в зависимости от логарифма времени в точках, для которых r/cz >0,01,
имеет ту же общую тенденцию, что и в пластах постоянной мощности, но
абсолютные понижения в том и другом случаях неодинаковы, за исклю-
чением точек, лежащих на линии, параллельной оси у и проходящей через
центр скважины.
При Z> 2,5 га/v график изменения уровня в пластах переменной мощ-
ности по форме близок к графику для пласта постоянной мощности, при
наличии источника питания (река, озеро [2], перетекание воды из соседних
горизонтов [5]). Аналогичные графики получаются для несовершенных
скважин в пластах постоянной мощности [6]. Таким образом, не распола-
гая достаточными данными сб исследуемом потоке, интерпретацию получен-
ных результатов можно производить различными путями.
ПРИЛОЖЕНИЕ
Ниже приводится список основных символов, используемых в настоя-
щей статье.
Л(р, т)— функция для скважины, работающей с постоянным понижением, в
пластах при отсутствии перетекания. Табличные значения этой функ-
ции имеются в работе [12|. Приближенные значения этой функции
приведены в тексте статьи;
а—геометрический параметр, определяющий экспоненциальное измене-
ние мощности пласта;
Ь (х) = Ьо ехр [ — 2 (х—х0)/а] — мощность пласта;
Ьо — мощность пласта в точке расположения скважины с координатами
(хо, у);
G (т, rw/a) = (rw/'a\l Ki (rja) /' Ko (rw/a) + (4/^2) exp (— тг^/ц2) X
X l -2---—2 г r---------t---функция расхода скважины, pa-
J J Ф) + Б (?•) !J-2 + (rw/a)2
Q L v U J L J
ботающей с постоянным понижением, в пласте в условиях перете-
кания; имеется в табличной форме [3];
Gi't>G(t, 0) — частный случай G(т, rw/a)— функция расхода скважины,
работающей с постоянным понижением, в пласте при отсутст-
вии перетекания; имеется в табличной форме [11, 13];
h(x,y,t) — средний пьезометрический напор в вертикальном столбике пла-
ста, расположенном в точке х, у,
ht— начальный пьезометрический напор;
Jo—функция Бесселя от действительного аргумента первого рода
нулевого порядка;
К, К — функция Бесселя от мнимого аргумента первого рода нулевого
и первого порядка;
Ко — функция Бесселя от мнимого аргумента второго рода нулевого
порядка;
Ki — то же первого порядка;
Yq — функция Бесселя от действительного аргумента второго рода
нулевого порядка;
К—коэффициент фильтрации пласта;
р—параметр преобразования Лапласа;
Q—постоянный расход скважины;
Qt—переменный расход скважины, работающей с постоянным уровнем;
г = [(х—х0)2 + (у—i/o)2r/s — расстояние, измеряемое от центра
скважины;
г' =-[(х + х0)2 + {у—уо)2]1/г-—расстояние, измеряемое отточки—х0, уо\
Га = а'21п (a/10Z?o), [см. уравнение (136)];
rw — эффективный радиус скважины;
— удельная емкссть пласта (объем воды, освобождающийся из
единичного объема пласта при снижении напора на единицу);
93
s(x, у, t) — /zz — h—понижение пьезометрического напора в любой точке
в любой момент времени х, у от начала откачки;
$(х, У, р) — изображение функции понижения уровня s(x, у, t) (преобразова-
ние Лапласа);
Sj—установившееся понижение, см. уравнение (15я);
sw—постоянное понижение на стенке скважины;
M_r2/4v^;
и' — значение и после замены г на г';
Ei (— и) = j охр (— у) ~~ — функция скважины для пластов при отсутст-
0
вии перетекания; табличные значения этой функции имеются
в работах [13, 15];
IF(<>., 8) =- ехр/ — у — ~4уI • -у- — функция скважины для пластов с пе-
0
ретеканием; табличные значения этой функции см. в статье Хан-
туша в настоящем сборнике, стр. 34.
х, у — прямоугольные координаты горизонтальной плоскости;
х0, i/o — точка, в которой расположен центр скважины;
Z(x,y,t) — значение s(x, у, f) при х = х0;
2(х,у,р)—изображение функции Z(x,y,i) (преобразование Лапласа);
v - K/Ss;
Р =- f/rw-,
- = v//r^;
Н — полярный угол с полюсом, расположенным в центре скважины
и полярной осью, параллельной оси х.
ЛИТЕРАТУРА
1. Hantush М. S., 1955. Preliminary quantitative study of the Roswell Ground-Water
Reservoir, New Mexico Institute of Mining and Technology, Socorro, N. M.
2. H a n t u s h M. S., 1956. Analysis of data from pumping tests in leaky aquifers, Trans.
Am. Geophys. Union, 37, 702—714.
3. Hantush M. S., 1959a. Nonsteadv flow to flowing wells in leaky aquifers, Journ.
Geophys. Res., 64, ’ 1043—1052.
4. H a n t u s h M. S., 1959b. Analysis of data from pumping wells near a river, Journ.
Geophis. Res., 64, 1921—1932.
5. HantushM. S., 1960. Modification of the theory of leaky aquifers, Journ. Geophys.
Res., 65, 3713—3725.
6. H a n t u s h M. S., 1961. Drawdown around a partially penetrating well, Proc. Am.
Soc. Civil Engrs., 76 (HY 4), July.
7. H a n t u s h M. S., 1962a. Flow of ground water in sands of nonuniform thickness, 1,
Flow in a wedge-shaped aquifer, Journ. Geophys. Res., 67, 703—709.
8. Hantush M. S., 1962b. Flow of ground water in sands of nonuniform thickness, 2,
Flow in a wedge-shaped aquifer, Journ. Geophys. Res., 67, 703—709.
Approximate theory, Journ. Geophys. Res., 67, 711—720.
9. H a n t u s h M. S., Jacob С. E., 1954. Plane potential flow of ground water with
linear laeakage, Trans. Am. Geophys. Union, 35, 917—936.
10. J а с о b С. E., 1950. Engineering Hydraulics, edited by H. Rouse, ch. 5, John Wiley
& Sons, New York, 1950.
11. J а с о b С. E., Lohman S. W., 1952. Nonsteady flow to a well of constant draw-
down in an extensive aquifer, Trans. Am. Geophys. Union, 33, 559—569.
12. Jaeger J. C., 1956. Numerical values for the temperature in radial heat flow, Journ.
Math. Phys., 34, 316—321.
13. P e t e r s о n D. F., 1957. Drainage of Agricultural Lands, edited by J. N. Luthin,
ch. 2, sec. 4, Am. Soc. of Agronomy, Madison, Wis., 1957.
14. Theis С. V., 1935. The relation between the lowering of the piezometric surface and
the rate and duration of sischarge of a well using ground-water storage, Trans. Am.
Geophys. Union, 16, 519—524.
15. W i s 1 e г С. О., В r a t e r E. F., 1951. Hydrology, John Wiley & Sons, New York,
ch. 7.
Л1. С. X ант у и
ЭКОНОМИЧЕСКИ РАЦИОНАЛЬНОЕ РАСПОЛОЖЕНИЕ
ВЗАИМОДЕЙСТВУЮЩИХ СКВАЖИН* 1
Использование формул, описывающих понижение уровня при откачке из сква-
жин в пласте бесконечного простирания, в сочетании с экономическими факторами
позволило получить выражения для расчета экономически наиболее выгодных рас-
стояний между взаимодействующими скважинами. Рассматриваются случаи, когда
скважины работают в условиях перетекания или же без него, когда пласты имеют
постоянную либо переменную мощность. Принимается, что затраты на эксплуатацию
водозабора могут быть уменьшены за счет расходов на дополнительную высоту подъема
воды, обусловленную интерференцией скважин; все остальные затраты выражаются
как стоимость, отнесенная к единице длины расстояний между скважинами.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Правильное расположение скважин водозабора должно учитывать эко-
номические и гидравлические факторы. Чем дальше друг от друга распо-
лагаются скважины, тем меньше их взаимное влияние, но тем выше стои-
мость соединительных трубопроводов и энергетических установок. Годовая
единичная стоимость эксплуатации водозабора межет быть уменьшена за
счет 1) снижения расходов на подъем воды на дополнительную высоту,
обусловливаемую интерференцией скважин, и 2) снижение затрат на сое-
динительные трубопроводы между скважинами и энергетической установ-
кой. Последние включают в себя стоимость монтажа, а также налоги и
прибыль на вложенный капитал и могут быть выражены величиной, соот-
ветствующей затратам на единицу длины между скважинами водозабора.
Общее понижение уровня в скважине при взаимодействии ее с други-
ми скважинами может быть рассчитано с помощью соответствующих урав-
нений. При этом дополнительное снижение уровня, возникающее в резуль-
тате взаимного влияния скважин, может быть выражено через расстояния
между скважинами, а также через параметры, характеризующие гидравли-
ческие и геометрические особенности потока.
Цель данной статьи—получение выражений, позволяющих рассчитывать
экономически наиболее выгодные расстояния между скважинами на основе
годовой стоимости эксплуатации водозабора, и формул, выражающих пони-
жение уровня.
Объяснение символов в статье приводится там, где о них впервые
упоминается. Для удобства список условных обозначений дается в прило-
жении II.
ОПТИМАЛЬНОЕ РАСПОЛОЖЕНИЕ СКВАЖИН
Исключая постоянную стоимость подъема воды из скважины в условиях,
когда она работает как одиночная, годовую стоимость эксплуатации
1 М. S. Н а п t u s h, Economical Spacing of Interfering Wells, International Asso-
ciation of Scientific Hydrology, Symposium of Athens, 1961, Ground water in Arid Zones,
1, 350—363; статья дается с сокращениями.
95
водозабора, состоящего из системы взаимодействующих скважин, можно
выразить так:
у v
С = с'о„г + с" v Qn Г Dndt, (1)
Л=1 о
где
С — общая годовая стоимость эксплуатации, которая определяется взаи-
модействием скважин;
с' — капитализированная стоимость в единицах затрат в год, приходящая-
ся на единицу длины водоводов — на монтаж, первоначальную стои-
мость трубопроводов, амортизацию и т. д.;
с" —стоимость откачки определенного объема воды на единицу длины, ко-
торая складывается главным образом из энергетических затрат и,
кроме этого, включает некоторые дополнительные затраты на обо-
рудование;
Dn—общее понижение в данной скважине, обусловленное откачкой из всех
остальных взаимодействующих с ней скважин водозабора;
Ьт — длина соединительных трубопроводов между скважинами и энергети-
ческой установкой;
П— число работающих скважин;
Q„— расход п-ой скважины;
t' — продолжительность откачки в единицах времени;
т — «параметр расстояния», который представляет собой расстояние между
двумя любыми скважинами;
о — постоянная, которая, если ее умножить на т, дает длину соединитель-
ных трубопроводов.
Минимальная стоимость будет соответствовать точке, в которой первая
производная от С по т равна нулю. Дифференцируя уравнение (1) и при-
равнивая результаты нулю, получим следующее выражение:
N V
Л=1 6
Параметр оптимального расположения скважин т0 представляет собой
величину т, которая удовлетворяет уравнению (2).
Если период непрерывной откачки \i') более года, правую часть урав-
нения (2) следует умножить на f//0, где /0 — период, равный одному году.
УРАВНЕНИЯ ПОНИЖЕНИЯ
Ниже приводятся формулы, дающие понижения в зоне влияния совер-
шенной скважины, работающей с постоянным расходом, в зависимости от
гидравлических и геометрических особенностей потока. Эти формулы верны
в той мере, в какой справедливы обычные допущения относительно упру-
гости и однородности пласта, а также неизменности параметров пласта в
пространстве и времени.
Пласты постоянной мощности.
Здесь рассматриваются два типа таких пластов.
Пласты, ограниченные водоупорными кровлей и подошвой (перетекание
из соседних пластов отсутствует).
Уравнение понижения представляет собой формулу Тейса [6]:
§ —-----Q=— Ei (— и),
(3)
96
в которой
__ г-S
— ‘ 4Т1
гг Ss
~4КГ’
s—понижение (L) в любое, время (f) с момента начала откачки на рас-
стоянии г от центра скважины, из которой ведется откачка;
Q—расход скважины
Т~КЬ—проводимость пласта (Л2/Т);
7<—коэффициент фильтрации (LlTy,
Ь—мощность пласта (L);
S—коэффициент емкости пласта (безразмерный);
Ss= (S/b)—удельная емкость пласта;
—Ei(—и)—функция скважины для пластов при отсутствии перетекания
(интегральный экспоненциал).
Используя уравнение (3), можно получить следующее соотношение:
В' = J Л = еJ£ dt = е-“' + «' £, (-«')!,
О о
в котором и' есть величина и для t = t'; г = cm, а с есть постоянная, свя-
зывающая «параметр расстояния» m с г.
Слой чистой
воды, или
грунтовые воды
Полупроницае-
мый слой
^^zzzzz^zzzzzzzzz
к „ Артезианские
г л ]; пески
/////
Артезианский пласт , из которого
происходит перетекание
а
ттяхгггпппггпггпгггт
Фиг. 1. Группа скважин в пласте, имеющем постоянную мощность.
После года непрерывной откачки (f = 1 году) величина и' обычно
оказывается меньше чем 0,02, и тогда вышенаписаннсе соотношение с боль-
шой точностью может быть апроксимирсвано в виде
Пласты с перетеканием. Для такого типа потока (см. фиг. 1а) урав-
нение понижения выражается формулой Хантуша—Джекоба [3], которая
имеет следующий вид:
Q we ( r \ Q Г 1 ( г2/в2 \ ,
—trld!J- <5)
и
Установившееся состояние выражается так:
(М
1 \ j_5 1
Здесь
ss — максимальное понижение уровня (или установившееся пони-
жение);
в = Vt7WW)~-,
К'/В'—коэффициент перетекания;
97
К'— коэффициент фильтрации слабопроницаемого разделяющего слоя
(L/T);
У—мощность слабопроницаемого слоя (!);
—ФУНКВДЯ скважины для пластов с перетеканием. Имеются таб-
- 1 личные значения этой функции [2, З]1.
Значения остальных символов уже были даны ранее.
Ф и г. 2. Группы скважин в пластах с переменной мощностью или
безнапорных пластах с наклонным водоупором.
Используя уравнение (5), можно получить следующее соотношение:
П/ Qf' (С ( Г*1^В'г\ , г wr ( г r М /с\
D exP(— У-----Щ-jdy-- и 'Щи (b)
u1
которое при относительно небольших значениях и'(и'
апроксимировано в виде
< 0,02) может быть
(6а)
Qr с „ / г )
2кТ
где —функция Бесселя от мнимого аргумента первого порядка второго
рода; ехр(х) — экспоненциальная функция х.
Пласты с переменной мощностью. Если мощность пласта непостоянна
и уменьшается в положительном направлении оси х (см. фиг. 2а), то урав-
нение понижения выразится формулой Хантуша для артезианских пластов с
непостоянной мощностью [4] при условии, что мощность пласта в пределах
относительно большой области вокруг скважины может быть апроксимиро-
вана соотношением:
b ~ Ьоехр (— — boехр f---
в котором
Ьо— мощность пласта в точке заложения скважины;
х0 — координата этой точки;
а — константа (размерность!), зависящая от относительной скорости
изменения мощности в направлении х, которая, если она зара-
1 См. табл. 2 в статье Хантуша, стр. 34.
98
нее неизвестна, может быть получена путем исследования плас-
та [4];
6 — полярный угол при полюсе, расположенном в центре скважины;
г—-расстояние, измеряемое от центра скважины, из которой ве-
дется откачка (Л).
Формула Хантуша для артезианских пластов с непостоянной мощностью
имеет вид
s “ л~Ь1Г ехР ( “ cos В W ( U, —
4тгКЬо \ а / \ а
(7)
а соответствующее выражение для условий установившегося движения
sv = 9 ехР cos© 'j 7Cof—'j > (7а)
Л 2тг f\b0 \ а ! ' а
где
и г2 Ss./4 Kt,
7<0— функция Бесселя от мнимого аргумента второго рода нулевого по-
рядка;
sv—понижение в установившихся условиях, то есть максимальное пони-
жение.
Если -^-мало (что обычно й бывает на практике), то экспоненциаль-
ная функция может быть апроксимирована единицей; если и' относитель-
но мало, то вместо уравнения (6) можно записать
D'^------LkJ-}. (8)
2 к ДО0 а 1 \ а I х '
ЭКОНОМИЧЕСКОЕ РАСПОЛОЖЕНИЕ РАЗЛИЧНЫХ ГРУПП СКВАЖИН
Выражения для расчета оптимального «параметра расстояния» для
нескольких групп скважин даются в приложении 1. С целью проиллюст-
рировать процедуру получения этих выражений рассматривается группа
из трех скважин (см. фиг. 16).
Пусть расстояние между первой и второй скважиной будет т, расстоя-
ние между первой и третьей скважинами — а'т и между второй и треть-
ей— а" т\ а' и а" постоянные, которые преобразуют истинные расстояния
в расстояния, выраженные через т. Пусть также Qlt Q2 и Q3 будут расхо-
дами данных скважин и тп— длиной соединительных трубопроводов (обыч-
но наикратчайшие расстояния, соединяющие скважины, в настоящем слу-
чае совпадающие с медианами треугольника, образованного тремя скважи-
нами, см. пунктирные линии на фиг. 1 и 2). Тогда оптимальный «пара-
метр расстояния» т0 может быть получен следующим образом.
Пласт постоянной мощности при отсутствии перетекания. Используя
уравнение (4), получим значения D'n:
= 2 г. Tin +Qs)’
°2=-~ + С») • ,9’
99
Подставляя их в уравнение (2) и решая полученное выражение относи-
тельно т, получим
то = с" <<? е (13)
Непосредственно из уравнения (10) получены следующие особые слу-
чаи.
' Три скважины имеют одинаковые расходы и расположены в верши-
нах. равностороннего треугольника со стороной т. В этом случае
= & = Qi - Q, = 1 И Й - | з'
Таким образом, из уравнения (10) т0 выразится как
с" K3Q2f
т — ' _
т0 с'~ Т
(И)
Три скважины расположены в одну линию на расстоянии т друг от
друга и имеют одинаковые расходы. В этом случае Qi = Q2 = Q3 — Q, a.'7- -
= 2, a" = 1 и 3= 2. Тогда из уравнения (10) mQ выразится как
3 с" Q2 I'
ftl -- ---------2е—
0 2 cf г. Т
Две скважины на расстоянии т друг .от друга. Если скважины рас-
положены на расстоянии т друг от друга; то т0 будет, как это следует
из уравнения (10) при Q3 0 и о = 1, выражаться как
Пласт постоянной мощности с перетеканием. Используя уравнение
(6), получим значения /У:
о; = - Дтв-(fl+>' & к (ур-)).
+ (’1б)
7~V ( Г Г\ If / \ 1 f! If / ® !
2)з . (а \7Г) а \~7Г’
при подстановке которых в уравнение (2) получим следующее выражение:
+ 1—1 + Q2Q3 f / —j = -....c„if -. (12)
Это выражение должно решаться путем подбора относительно неизвестной
величины т. Решение нетрудно получить для следующих особых слу-
чаев.
Три скважины образуют равносторонний треугольник. Если скважи-
ны расположены друг от друга на расстоянии т, то а' = а" = 1 и 5 = уз.
При этих значениях уравнение (12) дает
К (т \ —. с'-кТВУз (]2а\
ЛЧв/ c'XQ^ + QiQs + Qe&H' ’
которое легко решается с помощью таблиц TCj.
100
Три скважины расположены в одну линию на равных расстояниях
друг от друга. Если скважины работают с одинаковыми расходами
и находятся на расстоянии т друг от друга, а.' ~ 2, Т’ --- 1, 8 = 2 и =
= Qa = Q3 = Q, то в этом случае уравнение (12) дает
< т \ _ „ /2 т\ ц / т \ __ к ТВ с'
Дв) - Д1 \ Т/ сГТ(Д
(12 Ь)
которое может быть решено путем составления таблицы функции для
значений ~ в пределах 0,01 < ~ <1, редко бывает больше 1
Для -^-<0,01 случаи с перетеканием сводятся практически к случаям,
когда перетекание отсутствует. Это происходит потому, что при малых
значениях х значение хКДх)^!.
Две скважины на расстоянии т друг от друга. Для Q3 = 0, 8=1
уравнение (12) дает
- ТВс'
с" Qi QH'
(12с)
которое можно решить, используя таблицы значений Дх.
Пласты с переменной мощностью. Величина D' для данной системы
потока, выражаемая уравнением (8), аналогична по своей структуре случаю
пластов с перетеканием, выражаемого уравнением (6). В настоящем случае,
однако, мощность пласта меняется от одной скважины до другой. Если
&1, Ьч и Ь3— мощности пласта в местах расположения скважин 1, 2 и 3,
то выражение оптимального «параметра расстояния» в рассматриваемой
системе потока может быть апроксимировано уравнением (12) после заме-
ны В и Т в уравнении (12) на а и Д' соответственно и умножения первых
трех членов левой части уравнения (12) на (&х 62)/2 Ьг b2, фуb3V2 Ь3
и (Ь2 + b3)z2 b2 b3 соответственно. Результирующее выражение может быть
решено относительно т путем подбора. Используя это выражение, легко
получить решение для особых случаев.
ПРИМЕР РАСЧЕТА
Для целей иллюстрации использования рассмотренных выше выраже-
ний примем, что стоимость подъема 1 кубического фута воды на 1 фут
составляет 10"6 долларов. Пусть стоимость трубопровода и электросети
составляет 10 долларов за фут и капитализируется при 10 процентах. Ве-
личина с' будет составлять один доллар за фут в год. Примем также, что
проектируемые дебиты группы из трех скважин, образующих равносторон-
ний треугольник, составляют 20, 50 и 100 кубических футов в минуту.
Если эти скважины предполагается закладывать в пласте постоянной мощ-
ности с перетеканием и с проводимостью (Г), равной 0,0067 квадратных
футов в секунду, и коэффициентом перетекания (Д'/Ь'), равным 10“7 ку-
бических футов в минуту на квадратный фут, то оптимальный «параметр
расстояния» т0 можно получить следующим образом:
Т = 0,0067 футНсек = 0,40 футНмин-,
Д'/b' = 10~7 мин1-,
В — УТ/(К'/Ь') = у 4Х10~1/10-7 = 2000 футов;
с' = 1 дол./фут/год-,
с" = 10“ё долйфут1-,
101
i' = 1 год == 5,26-105 мин-,
Qi, Qz, Q3 равны 20, 50 и 100 фут?/мин-,
Qi (Q2 + Q3) + Q.4 Qu 8000 футУмин2.
Подставляя эти данные в уравнение (12 а), получим
Kl (2S0) (1)к (°’4) (2000) (1,732)/(1СГ6) (8-103) (5,25-105) = 1,035.
Пользуясь таблицами получим следующее:
= 0,707, или т = 1414^1410 футов.
ZvuU 1 “
Величина и' в конце года при непрерывной откачке составит
(1410)2 3/(4) (0,4) (5,26-105) = 2,36 3.
Так'как уравнение (12 а) справедливо при и' < 0,02, то величина т0, оп-
ределенная выше, применима только в том случае, если коэффициент ем-
кости пласта (3) меньше 0,01. Если перетекание в пласте отсутствует, то
оптимальный «параметр расстояния» будет, как это следует из уравнения
(10), в котором 3 равно ]/3, приблизительно равен 1940 футам.
ВЫВОДЫ
Дается вывод уравнения для расчета оптимального «параметра рассто-
яния» для нескольких групп взаимодействующих скважин. Принимается,
что группа скважин имеет определенную геометрическую форму. Рассмот-
рены следующие системы потока: пласт без перетекания и с перетеканием,
постоянной и меняющейся мощности. Скважины принимаются совершен-
ными.
В тех случаях, когда пласт имеет переменную мощность и характери-
зуется перетеканием, величины т/В, т/а и m/р меньше чем 0,01; тогда
уравнения для расчета оптимального «параметра расстояния» для скважин,
вскрывающих подобные горизонты, те же, что и для скважин, вскрываю-
щих пласты постоянней мощности и при отсутствии перетекания.
Для заданных параметров стоимости (с' и с") при условии, что вели-
чина и < 0,С2 в конце предполагаемого периода непрерывней работы, оп-
тимальный «параметр расстояния» т0 будет прямо пропорционален величи-
нам проектируемых дебитсв сквгжин и обратно пропорционален проводи-
мости пласта Т. Другими словами, т0 будет больше для пластов с мень-
шей проводимостью; для одного и того же пласта т0 будет больше при
большей интенсивности откачки, и наоборот. Величина т0 не зависит от
емкостных свойств пласта при условии, что и' < 0,02, так что . т0 будет
одинаковым для двух пластов с разными коэффициентами емкости при ус-
ловии, что они имеют одинаковую проводимость. Однакб так как общая
годовая стоимость зависит от понижения, то дешевле производить откачку
из пласта, который имеет более высокий коэффициент емкости. Это проис-
ходит потому, что понижение, образующееся в таком пласте (с высоким
коэффициентом емкости), меньше, чем в пласте с небольшим коэффициен-
том емкости.
Кривая зависимости общей годовой стоимости от «параметра расстоя-
ния» выполаживается в области минимальных значений. Таким образом,
некоторое отклонение от оптимальной величины будет небольшим, если
102
его рассчитать по выражениям, приведенным в приложении 1. Поэтому в
высокопродуктивных пластах скважины располагают, основываясь более
на удобствах эксплуатации, нежели на гидрогеологических условиях. Это
конечно, не означает, что скважины надо располагать в непосредственной
близости от насссной станции. Всегда следует проводить анализ, в кото-
ром используются соответствующие константы и уравнения оптимального
«параметра расстояния», однако при этом следует проявлять гибкость и
учитывать факторы, определяющие удобство, надежность и другие факто-
ры, которые не могут быть выражены количественно.
ПРИЛОЖЕНИЕ 1
Выражения для расчета оптимального «параметра расстояния»
Ниже даются выражения для «оптимального параметра расстояния»
для различных групп скважин. Они получены способом, который был опи-
сан в тексте настоящей статьи. Выражения даются применительно к груп-
пам скважин, изображенным на фиг. 1 и 2. Они справедливы при условии,
что величина и меньше чем 0,С2 в конце периода непрерывной откачки.
Пласты, в которых перетекание не происходит. Две взаимодейст-
вующие скважины, на расстоянии т друг от друга
Три скважины расположены в одну линию на расстоянии т друг от
друга (см. фиг. 26)
щ0
с" (Qi Q2 + QiQ8 + Q2<?3)^
2 с' пТ
Группа из трех скважин (см. фиг. 1 б)
(QiQ2 + Q1Q3 + Q2Q3)r
о Ъс'кТ
где
8 = (4 -у- 4 + /3)/7и.
Грута из четырех скважин (см. фиг. 1е)
с” t' (Q1Q2 + Q1Q3 + Q(+ Q*Qt +
где 8—(сумма двух диагоналей),'///- 8" (см. фиг. le).
Пласты с перетеканием
а) для ~ > 0,01.
D
Две взаимодействующие скважины, на расстоянии т друг от друга
„ / т\ _ с' v.TB
Три скважины, расположенные в одну линию на равных расстояниях
т друг от друга
f ( т\ / т\ _l J(, /2 т\ _ с' п ТВ
‘ (В/ Д1 (~В / 1 А1(/Г) ’Fq-7?” ’
которое решается путем построения таблицы/{—) для 0,01 <-^-<1.
\ В ) В
103
Три скважины расположены в вершинах равностороннего треугольника
со стороной т (см. фиг. 26)
Ki
т
~В
crw ТВ У~3
(QiQi + Q1Q3 4- Q2Q3)с" й
Группа из четырех скважин, образующих квадрат со стороной т
(см. фиг. 2 в)
<?,+ а а + а а+а а> к, (\ +
। (Г) О О Г) V 2 Т^2 c'tz ТВ
। V 2 ((ЛУз 1 Ч2Ч4)Л1 -g— yj ----
которое может быть решено путем подбора с помощью таблицы Кх.
Если скважины имеют одинаковые дебиты, то уравнение принимает
вид:
У2 с' пТВ
2c"Q-t'
б) Для < 0,01.
О
Когда -Д < 0,01, все приведенные выше выражения могут быть ап-
роксимированы соответствующими выражениями. Это можно сделать
потому, что величина xKt (х) стремится к единице, когда х стремится к
нулю.
Пласты с переменной мощностью. Если мощность пласта в пределах
относительно большой площади вокруг скважин может апроксимироваться
выражением
b = b0 ехр I — 2
— cos 9
а
значения символов которого даны в приложении 2, и если величина
Д-<0,1, что обычно и бывает на практике, то для расчета оптимального
«параметра расстояния» применимы следующие выражения.
1) Если глубины пласта в местах расположения взаимодействующих
скважин приблизительно одинаковы (колебания мощности пласта в преде-
лах площади расположения скважин невелики), то выражения для опти-
мального «параметра расстояния» такие же, как и те, что были даны выше,
причем в них следует заменить В и Т на а и О0 соответственно.
2) Если мощность пласта в точках расположения скважин 1,2, 3 и 4
равна Ьг, Ь2, Ь3 и 64 соответственно, то выражения для оптимального «па-
раметра расстояния» апроксимируются вышеуказанными выражениями после
замены в них Т и В на а и К соответственно и умножения каждого из
произведений QnQm там, где они появляются, на (Ьп + &т)/26я&,л. Для П0‘
лучения выражений для случаев, когда скважины имеют одинаковые
расходы, вышеупомянутые подстановки сначала нужно сделать в общем
уравнении (для различных Qs), после чего расходы берутся одинако-
выми.
104
ПРИЛОЖЕНИЕ 2
Условные обозначения
Ниже приводится список основных символов, употреблявшихся в тексте
статьи и приложении I.
а — константа, которая зависит от степени изменчивости мощности
пласта (размерность L);
a.', a", а'"— константы, которые обращают расстояния между первой и треть-
ей скважинами, второй и третьей, первой и четвертой скважи-
нами соответственно в расстояния, выраженные через «параметр
расстояния» т;
b—постоянная мощность артезианского пласта (£);
Ь' — постоянная мощность полунепроницаемого пласта в системах с
перетеканием (£);
Ьо — мощность пласта в точке расположения скважины, когда пласт
имеет переменную мощность (L);
^зи^4 — мощности пласта в точках расположения скважин 1,2, 3 и
4 соответственно;
В= VTIK'lb')—фактор перетекания (L);
с—постоянная, обращающая любое расстояние от центра скважины
в расстояния, выраженные через «параметр расстояния»;
с' — капитализированная стоимость в единицах стоимости в год монта-
жа, амортизации, первоначальной стоимости трубопровода ит. д.,
приходящаяся на длину соединительного трубопровода;
с" — цена в единицах стоимости подъема единичного объема воды на
единицу длины, которая состоит главным образом из энергетичес-
ких затрат, но также включает некоторые дополнительные затра-
ты на оборудование;
С — общая годовая стоимость эксплуатации водозабора, которая опре-
деляется взаимодействием скважин;
о — постоянная, которая обращает общую длину соединительных тру-
бопроводов между скважинами и энергетической установкой в
расстояние, выраженное через т;
V и 3"— постоянные, обращающие расстояния между второй и четвертой
скважинами и третьей и четвертой скважинами соответственно в
расстояния, выраженные через т;
Dn — общее понижение в п-й скважине, вызываемое откачкой из дру-
гих скважин (£);
D -= з— at — с -з™ at, где г -~ ст;
jam
о о
К—коэффициент фильтрации пласта (L/T);
/(' — коэффициент фильтрации слабопроницаемого слоя по вертикали
в случае пластов с перетеканием (L/T);
К'/Ь'—-коэффициент перетекания (1/Т);
7(0(х)— функция Бесселя от мнимого аргумента второго рода нулевого по-
рядка;
(х)— функция Бесселя от мнимого аргумента второго рода первого по-
рядка;
т — «параметр расстояния» данной группы скважин, который представ-
ляет собой расстояние между двумя любыми скважинами группы;
эти скважины обозначаются как 1 и 2 (размерность Л); также ин-
декс, означающий m-й пункт;
тй — оптимальный «параметр расстояния» (£);
N— число взаимодействующих скважин;
105
Q— расход скважины в единицах объема в единицу времени (1?/Т);
Qn — расход п-й скважины (ТЛТ);
г — радиальное расстояние до любой точки (г, Н), измеренное от цент-
ра работающей скважины (L);
s — понижение в любой момент времени / с начала откачки в любой
точке (г, 0) в окрестностях работающей скважины (£);
—максимальное понижение или установившееся понижение (Л);
S—коэффициент емкости пласта;
Ss. -=(5,7?) - удельная емкость пласта (1/L);
/ — время с начала откачек (Г);
Г—-время непрерывной откачки (Т);
/0 — период, равный одному году (Г);
7' КЬ— проводимость пласта (£2/Т);
r-S r*Ss
к - ------г----X •
4 Tt IKt ’
и'— значение и при i - /', то есть в конце непрерывной откачки;
X --- V
— Ei(— и) ~ ----- dy— функция скважины для пластов без перетекания;
и
W (и, -I j ~-ехр^—у—j— функция скважины для пластов с перете-
и
канием;
А'о — координата точки расположения скважины;
z — глубина воды над наклонным водоупором безнапорного горизонта
в любой точке [г, Н) в окрестностях скважины (£);
z — средняя глубина потока подземных вод (L);
z0 — начальная глубина потока подземных вод <.L>.
Л И Т Е Р А Т У Р А
1. Dwight II. В., 1958. Mathematical Tables, Dover Publ. Inc., New York.
2. Ha n tu s h M. S., 1955. Preliminary Quantitative Study of the Roswell Ground-Water
Reservoir, New Mexico Institute of Mining and Technology, Socorro, New Mexico.
U. S. A.
3. H a n t u s h M. S., 1956. Analysis of data from pumping tests in leaky aquifers, Trans.
Am. Geophys. Union, 37, 702—714.
4. H a n t u s h M. S., 1962. Ground-water flow in sands of nonuniform thickness, Part II,
Journ. Geophys. Reseasch, 1961 or 1962.
5. National Bureau of Standards, Tables of Bessel Functions, Yo, Y,, Ki, U. S.
Dept, of commerce, National Bureau of Standards, Applied Math. Series, 25, 1952.
6. T h e i s С. V., 1935. The relation between the lowering of the piezometric surface and
the rale and duration of discharge of a well using groundwater storage, Trans. Am.
Geophys. Union, 16, 519—524.
7. W e n z e 1 L. K., 1942. Methods for determining permeability of water-bearing mate-
rials, U. S. Geol. Survey, Water Supply Pap. 887.
8. W isler C. O„ Brater E. F., 1951. Hydrology, John Wiley and Sons, New York,
ch. 7.
Р. Е. Коллинс
ОПРЕДЕЛЕНИЕ РАСХОДА ФИЛЬТРУЮЩЕЙСЯ ЖИДКОСТИ В ЛЮБОМ
СЕЧЕНИИ ПЛАСТА ПРИ ОТКАЧКЕ ИЗ СКВАЖИН В УСЛОВИЯХ
УПРУГОГО РЕЖИМА1
ВВОДНЫЕ ЗАМЕЧАНИЯ
Исследование вопроса о перемещении жидкости в пласте, результаты
которого излагаются в этой работе, было направлено на получение просто-
го метода оценки размеров такого перемещения и поэтому ограничивалось
только рассмотрением простого случая, когда пласт является однородным,
имеет постоянную мощность и заключает однофазную упругую жидкость.
Очевидно, что только немногие резервуары удовлетворяют этим допущени-
ям на протяжении всей разработки. С другой стороны, упругое расширение
жидкости имеет место в большинстве пластов на начальной стадии их раз-
работки. Следовательно, результаты настоящей работы применимы к про-
ектированию разработки большинства месторождений независимо от того,
имеют ли они газовую шапку, растворенный газ или же в них поддержи-
вается водонапорный режим.
Математический анализ данной проблемы дается в приложении.
МЕТОДИКА РАСЧЕТОВ
Методика расчета перемещения жидкости основана на решении следую-
щего дифференциального уравнения в частных производных, описывающего
фильтрацию однородной упругой жидкости в однородном пласте постоян-
ной мощности:
i_ dp
дх* ' ду* k dt ’
где р — плотность жидкости; ?—-пористость; и—вязкость; с — сжимае-
мость2; k — коэффициент проницаемости; х, у— координаты, t— время. Вы-
вод этого уравнения дан в приложении.
Легко получить решение этого уравнения для одиночной скважины при
следующих допущениях: радиус скважины бесконечно мал, дебит q постоянен,
пласт имеет неограниченные в плане размеры. На основе этого решения
может быть рассчитан расход и суммарное количество жидкости, переме-
щающейся через поперечное сечение пласта длиной /, отстоящее на рас-
стоянии 3 от скважины (см. фиг. 1). В приложении показано, что все воз-
можные значения расхода жидкости q _]_, перемещающейся перпендикуляр-
но линии сечения /, могут быть представлены в виде графика зависимости
q \Jq от Величина //8 принимается как параметр. Здесь q—рас-
ход скважины. Эти кривые представлены на фиг. 2. Кроме того, было уста-
1 R. Е. Collins, Fluid Migration.Across Fixed Boundaries in Reservoirs Pro-
ducing by Fluid Expansion, Petrol. Trans., AIME, 216, 78—84, 1959.
2 Сжимаемость с зависит от сжимаемостей нефти, воды и скелета пласта. В боль-
шинстве случаев сжимаемостью скелета можно пренебречь, тогда с может быть выра-
жено как с—с0 (1 — Sw Soj , где с0 и сда — сжимаемости воды и нефти, a S® — водо-
насыщенность нефтеносных пород.
107
новлено, что суммарная добыча через линию может быть представле-
на в виде графика зависимости Q J_/Q от 4kt/^co2. Здесь Q—суммарная
добыча скважины. Эти графики представлены на фиг. 3.
Фиг. 1. Схема скважины исчезающе
малого радиуса, работающей с посто-
янным расходом.
Используя оба семейства кривых фиг. 2 и 3, путем простого вычита-
ния можно вычислить значения или Qj_ для любого отрезка линии.
Например, для отрезка ВС (см. фиг. 1) имеем
и
\. 9 )ав
/ Q±\
\ Q ]лв
Значения q Ajq и (?_]_/(? для частей сечения АС и АВ могут быть
получены из кривых фиг. 2 и 3 аналогично.
Системы скважин. Неограниченный пласт
Результаты анализа, данного в приложении, могут быть использованы
для расчета gj_ и Qj для данного отрезка сечения бесконечного пласта
при работе нескольких имеющих постоянные расходы скважин qr, q2.....
Нумерация скважин следующая: 1, 2,..., /, /+1. Будем иметь
— I
ч //
где (q A_/q)j есть значение q AJq при условии, что в пласте действует одна
только /-я скважина.
qj — дебит скважины, если она расположена ниже сечения,
’ скважины, если она расположена вы-
— qj — отрицательный дебит
ше сечения.
Значения (q AJq)j Для каждой скважины могут быть определены по
кривым на фиг. 2 и 3.
Значение q ±, полученное указанным методом, будет положительным,
если поток пересекает линию сечения сверху вниз.
Значение Q_L для систем скважин получается аналогичным образом,
а именно
108
>Ог Ю3 Ю* Ю5 10е
Безразмерное время t ttkt/<pMcS!‘
Безразмерное отношение (-&) Безразмерное отношение (
Ф и г. 2. Расход через заданное сечение.
Ф и г. 3. Суммарный расход через заданное сечение.
где Q* — суммарная добыча /-й скважины; так же как и q" она положи-
тельна, если скважина расположена ниже сечения; (Ql/Q)y-— это значение
Q±/Q, которое было бы при действии только одной /-й скважины.
Сложные сечения
С помощью описанных методов можно рассчитать приток к области,
ограниченной отрезками прямых линий а, Ь, с и т. д., в случае, когда в
бесконечном пласте работает несколько скважин, имеющих постоянные рас-
ходы. Путем простого сложения получим
Я = (7 -L )„ + (7 J.Д + (q 1 )₽ + (71 Д 4" (q 1 )е.
Аналогичным образом вычисляется Qj.. Поток, направленный внутрь
области, рассматривается как положительный. Поток через каждую линию
в отдельности рассчитывается вышеописанным методом. Особое внимание
следует обращать на знак перед q*, который будет положительным, если
/-я скважина приводит к движению потока внутрь рассматриваемой об-
ласти.
Ограниченные пласты
Для учета границ пластов можно использовать метод зеркальных ото-
бражений. На практике бывает достаточно брать отображения наиболее
близких к границам пласта скважин (фиг. 4). Для того чтобы определить,
-х Отображение.
1 Граница
Скважина
Ф п г. 4.
требуется ли производить зеркальное отображение данной скважины пли
нет, границу пласта следует принять за сечение и рассчитать для нее зна-
чение qk/q. Если значение qlJq при этом окажется пренебрежимо мало,
то отображения скважины делать не нужно.
Меняющиеся дебиты скважин
Для скважин, имеющих переменные дебиты или периоды остановок,
может быть использован следующий метод расчета.
Предположим, что дебит скважины как функция времени может быть
апроксимирован в виде ступенчатого изменения расхода q. Иначе говоря,
дебиты скважины в течение отрезков времени от tn до trliA принимаются
постоянными и равными своему среднему значению за этот период. Таким
образом, изменение расхода скважины может быть представлено следую-
щим образом: 1
q^qt, 0</</15
q^qn, \<n<N,
но
Отрезки времени, в течение которых дебит скважины постоянен, сле-
дует выбирать таким образом, чтобы действительный ее дебит оставался
близким к постоянной величине. В разделе приложения, озаглавленном
«Переменные дебиты, одно сечение», показано, что для данного случая gj_.
выражается так:
N
Vi (qt! q„~A
п I
где (g„l/g)„ есть значение q i/g в том случае, если бы дебит был постоя-
нен, а время работы скважины t— t > In,
Этот же анализ применим,и для Q | , а именно
где Qn выражается как Qn -- (qn— qn_^(t— 1п-л\ Здесь (Q ! есть значе-
ние Q±/Q для случая постоянного дебита и времени работы скважины
С помощью описанных методов может быть решено множество разно-
образных проблем миграции жидкости. Ниже приводятся примеры решения
двух таких задач.
ПРИМЕРЫ
Задача № 1
В качестве первого примера, иллюстрирующего методику расчетов ко-
личества жидкости, перемещающегося через сечение пласта, рассматривает-
ся расположение скважин, показанное на фиг. 5. Так как скважина № 2
расположена очень близко к границе пласта, рассматривается и ее зеркаль-
ное отображение — 2'.
Значение параметров в этой задаче следующее: /г ~ 25 миллидарси;
ф - -0,25; Снефти — 5>01 • 10-4 объем!объем:фунт на квадратный дюйм; сподьг-:
3-1ГГ,! объем/объем/фунт на квадратный дюйм; 5ВОДЫ - 0,20; р - - 2 сан-
типуаза (спз)-, расстояние ОА = 1600 футов.
В данном анализе расходы и суммарные значения добычи выступают
как отношения, следовательно, если члены q и Q выразить при пластовых
условиях, тогда q х и Q р также будут соответствовать пластовым усло-
виям.
Эффективная сжимаемость рассчитывается как с = сн?фТИ • (1 — 5ВОДЬ|)
оСводы-«Зводы 0,8(5,01 • 10“4) 3- 0,2(3-10“6) 4-10“4 объем/объем/фунт на
квадратный дюйм.
Теперь рассчитаем приток к рассматриваемой области для различных
значений времени: \)t - 160 сутск, в течение которых работала только од-
на первая скважина; 2)1 220 суток, когда была пущена в эксплуатацию
вторая скважина, и, наконец, 3)/- 320 суток, т. с. 100 суток спустя пос-
ле того, как вторая скважина была пущена в эксплуатацию.
Для иллюстрации метода во всех подробностях рассчитаем расход через
линию (а), вызываемый скважиной № 1 в течение / — 160 суткам. Сначала
из скважины на линию (а) опускается перпендикуляр. Таким образом по-
лучаем два отрезка сечения — один, расположенный вправо от перпендику-
ляра, равен 200 футам и второй, расположенный влево от перпендикуляра,
равен 1400 футам. Для линии, расположенной справа, //о - 2С0/50 -4,
поэтому, используя значения величин, указанных на фиг. 2, будем иметь
W __________4 25 I6Q _
фас?Л 0,25x2\4 х Ю~4 Х(50)2 .
111
Фиг. 5. Схема расположения скважин к примеру № 1.
С помощью кривых Q_L/Q на фиг. 3 было найденс), чтоQ.1/Q -0,197.
Для левой части сечения Z/3 = 1400/50 = 28 при том же самом значении
члена С помощью кривых фиг. 3 было найдено, что Q_l/Q=0,212.
Таким образом, общий объем жидкости, прошедший через линию (а), вы-
зываемый действием скважины № 1, (Q.l_/Q)t„ = 0,197 + 0,212 = 0,409.
Таблица 1
Исходные данные для первого примера
№ сква- жины X, футы и, футы (1. баррели сутки Время пуска, сутки Время работы, сутки
1 1400 50 । 150 0
2 200 200 • 100 60 /— 60
3 1400 —50 i 100 160 t — 160
4 600 —300 100 220 t — 220
2' —200 200' 100 60 t — 60
I
Суммарная добыча скважины № 1 за это же время составляет Q ==
= qyt 150-160 = 24000 баррелей, а так как скважина создает поток, на-
правленный из рассматриваемого района, toQ]*^= — —24000 баррелей.
Отсюда следует, что
(Q±)i„ — Qi
24,000X0,409
или
(Q1 _)1а — —9 816 баррелей.
112
Расчеты
Т а б л н ц а 2
линя Скважи- на № Часть ли нии (I'X I Время I работы, । сутки -W _ [ V 1 14 | <?х баррели Q - ц . барре- ли
1 часть .пиши 1 целая ! лилия '
(а) (а) I 1 ’ 28 ! 4 160 160 3,2 ;<10“ 3,2 хЮ* 0,212 । 0,197 10,409! — 2 400 1 1 ; -9816
(а) (а) , 2 2 1 7 100 100 1,25x103 1,25ХЮЯ . 0,078 1 О', 104 ' 0,182 — 10 000 - 1820
(а) (а) 2 2' ! 9 1 100 100 , 1,25хюз ' 1,25> 10я , 0.101 1 --0,078 I !0,026’ — 10 000 260
(О (О 1 1 0,25 160 160 2хЮ3 . 2x103 | - 0,030 । 0,126 ।0,096 24 000 960
(Ь) (Ь) 2 2 '0,1429 100 100 ; 2хю1 1 2X10* 0 : 0 0 10 000 0
(О 0) 2Z Г ;о,1Ш 100 100 ' 2\ К)1 2 - 10» 1 0 I 0 0 10 000 . 0
Суммарный Q _ — - 10 936 баррелей
Для расчета (Qj. )й, расхода через линию (6), вызываемого скважиной
№ 1, проводится перпендикуляр от скважины до продолжения линии (6).
Дальнейшие операции выполняются в том же порядке, что и для линии (а).
Теперь необходимо рассчитать расход через полубесконечную линию,
начинающуюся в точке А и опускающуюся вниз, и вычесть из него расход
через продленную часть линии (6). Заметьте, 4to(Q±)u здесь будет поло-
жительным, так как скважина № 1 вызывает поток, направленный внутрь
области. Результаты расчетов, выполненных для времени 160 суток, про-
шедшего с момента пуска скважины № 1, приводятся в таблице 2.
Таблица 3
Результаты расчетов
Время работы
скважины № 1,
сутки
Общий приток
к области, баррели
160
280
320
10 936
11 358
11 942
Значения Q.X для / = 220 и 320 суток, рассчитанных аналогичным об-
разом, приводятся в таблице 3. Таким образом, в рассматриваемой области
происходит убыль жидкости вследствие перехода ее в смежные области.
Задача № 2
Для иллюстрации зависимости перетока от времени достаточно рассмо-
треть не сами расчеты, а их окончательные результаты.
В данном случае сечение принимается в виде прямолинейной, имеющей
неограниченную длину линии. Схема расположения скважин показана на
фиг. 6. Расчетные данные следующие: /г 25 миллидарси, ф = 0,25; р. =
"=0,20; с=4Х1(Г| объем!объем!фунтов на квадратный дюйм (эффективная
величина). Направление потока к скважине № 1 принимается положитель-
ным.
Результаты расчетов представлены на фиг. 7 в виде графиков зависи-
мости qx. и Q L от времени. Обратите внимание на то, что после пуска
113
Фиг. 6. Схема расположения скважин к примеру
№ 2.
скважины № 2 q\_ начинает быстро уменьшаться. Очевидно, что ста-
билизировалось бы при положительном значении, и это действительно бы-
ло бы так, если бы скважина № 3 не была пущена в эксплуатацию. Од-
Таблиц а 4
Исходные данные к примеру № 2
№ сква- жины <7. баррели 1 Время пус- I ка, сутки Время работы, сутки О, футы
сутки
1 150 0 t 200
2 ! 100 100 f — 100 100
з ! 100 200 / — 200 50
нако пуск скважины № 3 снова уменьшает q _L, которое окончательно ста-
билизируется при отрицательном значении. Влияние этих изменений q | на
QX показано на фиг. 7.
114
ПРИЛОЖЕНИЕ
Математическая теория
Одиночная скважина; постоянный расход; одно сечение
Уравнение неразрывности, выражающее закон сохранения массы, имеет
следующий вид:
д , . , д , ч йр ,п
W = -т-ЭР (1)
где р —плотность жидкости; ф—пористость среды; /—время; ох и —
составляющие скорости фильтрации по осям х и у соответственно. Здесь
предполагается, что пористая среда и жидкость однородны, течение плос-
кое. Объединяя это уравнение с законом Дарси, получаем
(О\
дх у1 дх j ' ду \J ду j k dt ’
где k—проницаемость среды и [х— вязкость жидкости. Если плотность жид-
кости выразить через давление
где р — плотность жидкости при давлении р; рг — плотность при давлении
Pi и с — сжимаемость, тогда уравнение (2) можно записать как
д*Р дар = /4ч
дх* 1 ду* k д t -
Решение уравнения (4), соответствующее скважине с ничтожно малым
радиусом, работающей с постоянным расходом q (измеренном при началь-
ном давлении и температуре пласта) в пласте неограниченных размеров,
имеет вид
p(x,t/,0 1 qv-c р
?i 4nkh J е а- W
tp|ic (№ уЪ)
4kt
Заметим, что в этом решении рг в соответствии с уравнением (3) пред-
ставляет собой плотность жидкости при начальном пластовом давлении рг.
Единицы, используемые здесь и вообще в этом разделе, вполне определен-
ны и известны, за исключением случаев, которые оговариваются особо.
Это решение уравнения является основным при рассмотрении мигра-
ции жидкости в пласте через прямолинейнее сечение длиной /, находяще-
еся на расстоянии В от скважины, работающей с постоянным расходом q.
Положение сечения АВ по отношению к скважине показано на фиг. 1.
Массовая скорость потока т к скважине через линию (г/сек) выражается
так:
1 ,,
р kn , д р (х, о, i) ,
т = j — р (-t, о, /) —2 dx, (6)
6
или объемная скорость (при начальном пластовом давлении)
(7)
Уравнение (6) следует непосредственно из закона Дарси.
115
Используя уравнение (5) для о(х, у, t), получим
g~ а (х- + (/-’)/'/
ду
М-с?1
2nkh J
(8!
где для удобства введено обозначение
~4fe~ '
(9)
Затем, подставляя уравнения (8) в (7) при т, выражаемом уравнением
(6), получим
/ Л — а (х'~ с2)//
^х> (Ю)
о
что и является аналитическим выражением для расхода жидкости через
сечение, который требуется определить.
Выражение суммарного расхода через эту линию получается путем ин-
тегрирования уравнения (10) по времени:
QJ
Я.
2я/
, — о2)Д)
ое
Л-2 _1- ?,2
dx
dxdW.
(В)
Прежде чем переходить к анализу этих интегралов, их можно записать
в более удобной форме; так, делая замену переменных в интегралах, имеем
и
где
и
4kt_____
р [}. с Ъ-
7
(12)
(13)
(14)
(15)
Заметим, что размерность q, q _L, Q и не имеет значения; q SJq
безразмерно, так же как и Q J.JQ- Таким образом, расход q будет иметь
размерность в баррелях/сутки, если q будет выражено в этих же едини-
цах. Те же рассуждения верны и для Q_L и Q.
Для линии бесконечной длины, / —3 — оо, названные интегралы мож-
но выразить аналитически:
(16)
(17)
116
где а выражается по уравнению (15) и erfc — обозначение дополнительной
функции ошибок:
erfc и —Izr- (18)
Для конечного 3 решения интегралов в уравнениях (12) и (13) затруд-
нительно, поэтому необходимо использовать численное интегрирование. Ин-
теграл
в уравнении (12) имеет форму, удобную для численного интегрирования,
которое и было выполнено с помощью быстродействующей счетно-вычисли-
тельной машины для широкого диапазона значений а и р.
Прежде чем численно интегрировать уравнение (13), необходимо (по
практическим соображениям) перейти ст двойного интеграла к одному или
нескольким одиночным интегралам; это достигается соответствующей заме-
ной переменных и переменой порядка интегрирования. В результате по-
лучаем
-(г-, 1)Д. i --(г24-1)/а fl „ -(га-1)Д
f ze , > . <• ze , , 1 z-e , , ,
---7i , i , > dz — -------- .:; 7 , — CIZ — I — ..............777— d'. (19)
J (Z-S-H)2 77 .) (Z-+1)2 7L J (z-Ч- I)2 v '
0 0 0
Первый интеграл может быть определен аналитически. Имеем
— Ei I----------) — i ф.
\ ’ и. 1
v 7 1/*
(20)
(21)
Уравнение (19) с первым интегралом, выраженным уравнением
(20), имеет ферму, удобную для численного интегрирования. По-
следние два интеграла уравнения (19) численно проинтегрированы с по-
мощью вычислительной машины ,для широкого диапазона величин а и
Как указывалось выше, размерности q, q Q и Qj_ в уравнениях,
включающих отношения этих величин, произвольны. Аналогично этому,
так как = //о безразмерно, размерности I и 3 произвольны; необходимо
только, чтобы они были одинаковы. Для того чтобы выразить а в размер-
ностях нефтяного пласта (как это дано на кривых фиг. 2 и 3); имеем
/ 4kt \ а 1 со / 4й/ '
I ——^г- = 0,158 ———
I euro- I , \
\ • ‘ / нефтян. \ м
(22)
Подсчитанные путем комбинаций аналитических и численных методов
величины q Jj'q и Q _£/Q построены в виде графика зависимости от а при
3, взятой как параметр (см. фиг. 2 и 3).
Когда t и, следовательно, а стремятся к бесконечности, Q | Q в со-
ответствии с уравнением (19) стремится к
(Q- \
\ Q Е
$ С zdz । 1 f z2dz
77 J (Z2 Д- I)2 1 71 J (Z2 — Т)2’
о
(23)
1/7
Эти интегралы выражаются так:
(Qi- \
\ Q А
7-я- »
(24)
Таким образом, если QjjQ построим в виде графика зависимости от
(1ап~1Р)/2тс с а в качестве параметра, кривые для больших а будут апро-
ксимироваться прямыми линиями. Это упрощает интерполяцию. Аналогичным
образом можно показать, что
p-L X
\ У / а— по
(QJ- X
\ $ J*
(25)
Если потребуется определить 7_]_ и Qj_ через линию ВС, как это по-
казано на фиг. 1, то это делается простым суммированием интегралов в
уравнениях (12) и (13):
-(х2 — -A, а) — ^-—(^2, а, а)-—(^, S, а) (26)
ч ч ч
и аналогично для Q J_/Q. Эго означает, что величина q Ajq, соответствую-
щая линии от х — 0 до х — — х2, определяется по кривым, представлен-
ным на фиг. 2, и затем из нее вычитается значение q _J_/q, соответствую-
щее линии от х — 0 до x = li=^xk. Остаток представляет собой расход
через линию от х ~ xt до х = х2. Та же процедура применима к Q JJQ-
Системы скважин.; дебаты постоянны; одно сечение
Согласно хорошо известному правилу суперпозиции решений уравнения
фильтрации (4) для неограниченного пласта, в котором работают N точеч-
ных стоков (скважин ничтожно малого радиуса) с дебитом qn, п~ 1,2,...,А
и временем действия tn, п — 1, 2, 3, .. ., N, можно составить следующее
уравнение:
N —, £
р(*. уд) _ ис v п 7* 2_____________
Р/ 4^/l -J V» S
n=l J
(27)
где
rn2 = (x-^)2 + (£/-~t/„)2, (28)
хп и уп есть координаты n-й скважины.
Требуется рассчитать расход через линию от х ~ 0 до х = I при у — о
для этой системы скважин. Фильтрация предполагается положительной в
направлении уменьшения у. Уравнение (6)
i
т = Р ^х' ~ду (х*’
о
справедливо и в данном случае. Подстановка уравнения (27) в (6) с ис-
пользованием (7) дает
, 1 V /й ч С af(x"“x«)a + <6~у«>21//га
q JL — /1 qn (« — y„) I-------------------------------
J l(x —x„)2 +(» —yra)2]
n=l 0
dx
(29)
118
для расчета расхода через линию. Введем новый символ в следующем
значении:
<7* 7^ если 8 >Уп,
<г — 7»’ если 8 <//„. (30)
Тогда получим
q Т
(31)
и, замечая, что [о — уп\ — расстояние от zz-й скважины до линии — всегда
положительно, определим
Iй ” Уп\ (32)
и тогда имеем
Итак, видно, что q | есть алгебраическая сумма течений, вызывае-
мых каждым точечным стоком. Это означает, что для расчета расхода че-
рез линию необходимо рассматривать каждую скважину в отдельности и
вычислить q_\Jq. Затем берутся полученные (<7J_/(?)„, N = 1,2,..., N и
рассчитывается
(34)
\ 4 1 п
после чего суммируется:
N
=£<(¥) (35)
\ Ч Jn
п=1
Последнее уравнение выражает расход через линию при работе N
скважин.
Подобным же образом можно показать, что для N скважин вы-
ражается как
N
Е <?„ (36)
п=1
где
(К Q»- уп<^
(37)
. Q* == — уп >й
и (QjJ2)n есть величина Qj_/Q, которая была бы, если бы в бассейне ра-
ботала только одна скважина.
Одна неподвижная линия-, переменный расход
Уравнение (27), т. е. решение для группы скважин с постоянными де-
битами qn, п = 1,2,..., N, можно использовать для решения задачи при
одной скважине, работающей со скачкообразно меняющейся производи-
119
тельностью. Предположим, что изменение производительности скважин
будет следующим:
q = ql для 0 •'.'/< tn,
q~~qn для /„ 2,3...AZ—1.
q - qN для /л • : t.
(38)
Достаточно рассмотреть одиночную скважину с переменным расходом,
выражаемым уравнением (38). Для различных скважин, расположенных в
одной и той же точке бассейна, расходы и время их действия выражают-
ся так:
№1 : qx, 1,
№n:q„ — qn^, n - 2,3,..., N. (39)
Следуя этому приему, получим уравнение фильтрации применительно
к одной скважине с переменным расходом, выражаемым уравнением (38),
которое будет иметь вид:
Л. „ 1 _ q у , рД. Л, |40)
4 тг/г/? —i ] /•. 7
1 4[wr3
где
г2-х2--НА (41)
т. е. принимается, что скважина находится в начале координат.
Таким образом, поступая так же и при анализе для систем скважин,
можно показать, что для скважины с переменным расходом
-V
?(42)
\ 1 / п
п--\
где теперь (qJJqK есть значение q±Jq для одиночной скважины с посто-
янным расходом при 3 --- 1/8 и временем работы
Для систем скважин с переменным расходом каждая скважина обра-
батывается тем методом, как это было описано, что дает величину (q/Jf
для /-й скважины. Затем определяем:
: : C/..L);- если у}<8,
(q*l)j : - ‘ \г если ^>о.
Наконец, для системы скважин с переменными расходами имеем
q I
(41)
Этот метод может быть предложен для определения Qj_ для скважин,
имеющих переменные расходы, как это было сделано для систем скважин
в предыдущем разделе приложения.
120
В результате получаем
Л'
(45)
где (Q_L/Q)zi есть величина QJ /Q, которая имела бы место для скважины
с постоянным расходом и временем работы t—
Здесь Qn выражается как
(Qn Qn-l) (f tn-1)’
(46)
Следует отметить, что любую остановку скважины можно легко учесть,
принимая в течение времени закрытия qn равным нулю.
ЛИТЕРАТУРА
1. С а г s 1 a w Н. S., J а е g е г J. С., 1947. Conduction of Heat in Solids, Oxford U. Press.
2. H a 1 1 H. N., 1953. Compressibility of reservoir rocks, Trans. AIME, 198, 309.
Г. Шнеебели
ИСПОЛЬЗОВАНИЕ ВОЗДУХА ДЛЯ ИЗМЕРЕНИЯ ПРОНИЦАЕМОСТИ
НЕНАСЫЩЕННЫХ АЛЛЮВИАЛЬНЫХ ОТЛОЖЕНИЙ1
В работе излагаются теоретические основы использования газа для измерения
проницаемости ненасыщенных отложений.
Приводятся результаты опытов, выполненных на строительстве плотины Мете-
маль (Восточные Пиренеи, Франция).
Описанный метод не может применяться в случае, когда испытуемые породы
имеют Глинистый состав и при насыщении разбухают.
ВВОДНЫЕ замечания
Фильтрационный поток любой жидкости в пористой среде подчиняется
закону Дарси:
V =.z grad®, (1)
где
V [LT —скорость фильтрации;
g[LT-2] —ускорение силы тяжести;
/г„[£2]— коэффициент проницаемости пористой среды, характе-
ризуемый геометрией порового пространства;
v р./р [£2Г-1] —кинематическая вязкость жидкости;
гл [/Й/Д’Т4] — динамическая вязкость;
р \ML~3\ — плотность;
9 == i (р/Д[L]—-напор, выраженный через высоту столба жидкости;
о
pfML"1 Т~2] — давление;
7 ' М [МШ2Т~2] — удельный вес;
Z ---[L] — высота точки над плоскостью сравнения.
В данной форме закон Дарси выражает движение жидкости. При дви-
жении газа этот закон удобнее выражать через давление:
grad ® (1/у) grad р , gradZ.
Последний член выражает вес газа, который является незначительным,
поэтому закон Дарси для газов можно переписать следующим образом:
V =- — g(knM (grad р/у),
V =- — (Д/Дугаб р. (2)
1 G. Schneebeli, Sur 1’utilisation de Pair pur la mesure«in situ» de la permea-
bility d’un terrain alluvial non sature, La Houille Blanche, No. 1, 66—73, Janv.—Fev.,
1959.
122
При фильтрации жидкости принято вводить коэффициент фильтрации
K-=g(V0 (3)
Тогда закон Дарси примет следующий вид:
V = J< grad <р. (4)
При фильтрации газа вводится коэффициент относительной проницае-
мости по газу
К!; ~ L3T1]. (5)
Причем закон Дарси запишется как
V — — K^gradp. (6)
Для одних и тех же пород гесметричсская проницаемссть является
a priori величиной постоянней, не зависимей ст природы жидкости (далее
мы увидим, что могут быть исключения). Из этого следует, что относи-
тельная проницаемость К по жидкости с кинематической вязкостью vz и
проницаемость по газу, имеющему динамическую вязкость р связаны
соотношением
(7)
Это уравнение позволяет найти К при известном /(
Перейдем теперь к изложению принципа измерения проницаемости
in situ. Измерение проницаемости производится обычно посредством от-
качки или нагнетания воды в скважину. В случае фильтрации жидкости
поток будет характеризоваться законом Дарси, записанным в виде урав-
нения (4). К этому уравнению добавляется уравнение неразрывности, ко-
торое для несжимаемой жидкости можно записать в виде
div V = 0. (8)
Из уравнений (4) и (8) следует общее уравнение, потока
Дф = 0. (9)
Последнее, выражение представляет собой уравнение Лапласа, так что
напор <р есть гармоническая потенциальная функция, зависящая только от
условий на границах.
Легко показать, что если Q—дебит, а Н — общие потери напора, то
проницаемость будет выражаться следующим образом:
K = f[Q/(H.D)], (10)
где f— безразмерный коэффициент, зависящий от формы скважины1;
D — диаметр фильтра.
В случае газового потока уравнение неразрывности запишется следую-
щим образом:
div(pv)=^=0. (11)
Так как газы сжимаемы, то следует рассматривать дебит не объем-
ный, а весовой. Поэтому к уравнению (11) следует добавить уравнение
состояния газа, которое для потока газа в изометрических условиях бу-
дет иметь следующий вид:
(12)
1 Коэффициент f должен зависеть также от отношения длины фильтра к его ди-
аметру и от неоднородности испытуемого пласта.— Прим. ред.
12,3
Выражая закон Дарси (6) через удельный массовый дебит и принимая
во внимание уравнение (12), получим
р V = -(Ks/RT)pgrad р = — (RgfR ^)grad(p3/2). (13)
Уравнения (11) и (13) приводятся к уравнению
А(р3) = 0. (14)
В это уравнение входит давление во второй степени, которое и яв-
ляется гармонической потенциальной функцией.
Как и прежде, легко показать, что в случае газового потока, создан-
ного в пласте, проницаемость выразится следующим образом:
(15)
где Qm — объемный дебит, приведенный к среднему давлению рт;
Рт = (Л А’ Ро)/2;
pt — давление, создаваемое в скважине;
р0 — атмосферное давление;
f — коэффициент формы — тот же, что и выше;
= —
Практическое определение проницаемости путем нагнетания воздуха
Из приведенных выше теоретических рассуждений вытекает возмож-
ность определения в ненасыщенных отложениях проницаемости по воздуху
с последующим ее пересчетом по уравнению (7) в проницаемость по воде.
Последняя будет характеризовать условия после насыщения. Эта возмож-
ность представляет большой практический интерес. Например, в случае
сооружения плотины необходимо знать проницаемость пород, которые пос-
ле подтопления станут вэдонасыщенными. Определение проницаемости на-
гнетанием воздуха в этом случае обладает следующими преимуществами:
исключается необходимость учитывать тяжесть воды, капиллярные силы,
кольмотаж, который неизбежно происходит при нагнетании воды в сква-
жину и который почти полностью исключается при нагнетании воздуха.
Кроме того, исключаются трудности, связанные с необходимостью распо-
лагать источниками воды.
Первая попытка использования воздуха для исследования проницае-
мости пород принадлежит М. Ро [1], который изучал трещиноватые извест-
няки. Автор настоящей работы исследовал проницаемость аллювиальных
отложений, являющихся основанием левого примыкания плотины в Мате-
мале (Восточные Пиренеи).
ОПИСАНИЕ ОПЫТОВ ПО ОПРЕДЕЛЕНИЮ ПРОНИЦАЕМОСТИ ПУТЕМ НАГНЕТАНИЯ
ВОЗДУХА В МАТЕМАЛЕ
Матемальская плотина находится в верхнем течении реки Од. Соору-
жение располагается на аллювиальных отложениях, подстилаемых разру-
шенными гранитами (фиг. 1). Исследователи имели целью определить це-
лесообразность цементации пород в основании плотины.
Исследование проницаемости закачкой воздуха было предпринято по-
тому, что испытуемые породы располагаются выше зоны насыщения, а
также потому, что выполненные ранее определения проницаемости, путем
наливов воды показали чрезмерно низкие (учитывая характер аллювия) зна-
чения этой величины.
124
Всего было проведено около 20 опытов в 6 скважинах малого диамет-
ра, пробуренных на плато, затем опыты были продолжены на колодцах
диаметром 500 мм, оборудованных пьезометрами. С целью избежать про-
никновения воды в исследуемые породы бурение скважин осуществлялось
передвижными пневматическими установками. Скважины были обсажены
трубами и зацементированы. Цементация производилась путем задавливания
смеси бентонита, жидкого битума и небольшого количества воды (фиг. 2).
В присутствии воды бентонит превращается в плотный гель. Нижняя часть
скважин была оборудована фильтром. Для опытов использовался сжатый
воздух. Измерение расхода воздуха производилось динамическими дебито-
метрами, а давление — прецизионными манометрами.
Установка для определения проницаемости показана на фиг. 3. Воз-
дух для нагнетания в скважину брался из общей сети. Регулировка дебита
осуществлялась посредством задвижки. Редукционный клапан и дебито-
метр соединялись последовательно. Относительное положение нагнетатель-
ной скважины, диаметр фильтра которой составлял 500 мм, и пьезометров
показано на фиг. 4. Принятое расположение скважин позволило определить
степень анизотропии грунтов.
В самом деле, поток, исходящий из цилиндрического фильтра нагне-
тательной скважины диаметром 500 мм, на некотором расстоянии от него’
становится линейным. Для изотропных грунтов распределение потенциала
будет выражаться следующим образом:
Z-C + г гз + (2 + ср
р- -- Пп ——----—======== ,
Z - С + / + (Z ч- су1
где г — постоянная;
р — давление воздуха;
С — половина длины фильтра;
г — расстояние по горизонтали до рассматриваемой точки потока;
Z—ордината точки, измеряемая от середины фильтра.
Для Z “ 0, т. .е. для разделяющей плоскости тока, это уравнение при-
мет такой вид:
р2 - 2 Пп ((С/r) Ц у /(С/r)2 Ч- Е
Если отложения анизотропны, то можно показать, что предыдущее
уравнение будет иметь следующий вид:
Г 2Г1П I(С г) | (АД КД -Ь ( 1с7^Ц^СГИ7 (16)
где Kv — вертикальная проницаемость;
Kh— горизонтальная проницаемость.
Согласно уравнению (16), падение давления зависит от отношения
АД/АД, причем оно происходит тем быстрее, чем ближе отношение АД'7<0
125
•£ 'J и ф
'3 'J и ф
Фиг. 5. Опыт с воздухом. Диаметр скважины 500 мм.
Определение степени анизотропии.
к 1. Отношение Kh/Kv можно определить по степени уменьшения квадра-
та давления, измеряемого с помощью пьезометров. Это определение про-
изводится графически, путем совмещения экспериментальных точек с тео-
ретическими кривыми (фиг. 5).
Давление, создаваемое в скважинах в процессе опытов, имело величи-
ну порядка от 25 до 100 г/слЛ
Методика определения анизотропии в Матемале полностью себя оправда-
ла. Расчеты показали, что наибольшая горизонтальная проницаемость име-
ет направление в сторону оси плотины, причем величина ее в 20 раз боль-
ше вертикальной проницаемости и приблизительно в 3 раза выше прони-
цаемости в направлении, перпендикулярном оси плотины.
Причиной анизотропии является, по-видимому, общая ориентация по-
род в процессе их отложения. Аналогичное явление было установлено
нами в долине реки Роны, где анизотропия отложений совпадала с направ-
лением, параллельным реке.
Для сопоставления полученных результатов был проведен опыт по
определению проницаемости с нагнетанием воды. При этом было установ-
лено, что проницаемость пород уменьшается одновременно с увеличением
их насыщения водой, нагнетаемой в скважину, причем степень уменьше-
ния проницаемости зависит от состава пород, и тем больше, чем больше
исследуемые породы содержат глины. Для гравийно-песчаных пород ника-
кого различия между проницаемостью, определенной по воде и по воздуху,
нет.
ЗАКЛЮЧЕНИЕ
Определения проницаемости нагнетанием воздуха на строительстве в
Матемале дали вполне удовлетворительные результаты. К положительным
сторонам этого метода следует отнести простоту его осуществления по
сравнению с принятыми в настоящее время методами определения прони-
цаемости путем нагнетания воды. В случае исследования проницаемости
пород, содержащих глинистые частицы, проницаемость оказывается завы-
шенной, так как при обводнении глинистые частицы разбухают, что делает
породы менее проницаемыми.
ДИСКУССИЯ
Шоллер уточняет причины различия между водопроводимостью и воз-
духопроводимостыо. Опыты, осуществленные Международным геофизичес-
ким и геодезическим союзом, показали, что причиной отклонения является
поверхностное взаимодействие между породой и жидкостью. С другой сто-
роны, в результате опытов, проведенных в Бордо на высушенных и насы-
щенных песках, Шоллер и его сотрудники нашли соответствие между дву-
мя проницаемостями только для очень чистых кремнистых песков с ока-
танными зернами; для молласовых отложений Фронде разница может до-
стигать 5—10%.
Шнеебели указывает, что эти уточнения очень интересны в теорети-
ческом отношении, но что точность 10% практически удовлетворительна.
Феррандон отмечает, что распространение закона Дарси на газовые по-
токи поднимет некоторые сложные вопросы.
Закон Дарси, V = Д’grad 9, 'для фильтрационного потока жидкости на-
ходит свое теоретическое обоснование в статистическом распределении
уравнений потока вязкой жидкости в тонкой трубке при граничных усло-
виях, выражающих давление в трубке и скорость на ее концах.
Автор сообщения предлагает распространить это положение на фильт-
рационный поток сжимаемой жидкости. Однако это положение нуждается
128
в дополнительном обосновании, поскольку уравнение вязкой сжимаемой
жидкости _
div (pV) = 0; — grad • р + ц/З grad • div V Т(Д2 V 0
даже для изотермического режима радикально отличается от уравнений
несжимаемой жидкости содержанием члена переменной плотности.
Шнеебели признает, что применение уравнений Навье к газовой среде
поднимает ряд трудноразрешимых теоретических проблем, поскольку прак-
тически невозможно интегрировать эти уравнения.
Тем не менее Шнеебели выражает мнение, что вязкостный член 7j/3 grad
(div V) мал по сравнению с членом vt& (V) по крайней мере в обычной
используемой области давлений и градиентов. Следовательно, представ-
ляется законным распространение на газ закона Дарси в той форме, в ко-
торой он действителен для жидкости. Многочисленные лабораторные опы-
ты подтверждают эту точку зрения. Тем не менее, заключает Шнеебели,
вопросы, поднятые Феррандоном, представляют большой теоретический ин-
терес и заслуживают глубокого исследования.
В защиту опытов с воздухом выступает М. Хабиб: «Феррандон пока-
зал, что в случае газа в перистой среде нельзя говорить в полной мере о
применимости закона Дарси, так как жидкость сжимаема. Однако если дав-
ление закачки и соответственно скорости потока незначительны, то влия-
ние сжимаемости несущественно и, как доказано экспериментально, дебит
пропорционален давлению.
В 1954 г. Ро представил результаты замеров проницаемости в полевых
условиях. При закачке воздуха Давление менялось в пределах от 0,1 г/см2
до 1000 г/см2, причем зависимость между дебитом и давлением оставалась
линейной. С другой стороны, в лабораторных условиях опыты на прони-
цаемость с жидкостями или газами дают сходные коэффициенты проницае-
мости, если твердый скелет инертен по отношению к флюиду. Эти опыты
гораздо труднее проводить с песком, так как не следует менять структуру
зерен от одного опыта к другому, но соответствие будет исключительно
большим, если постараться удалить весь воздух в опытах с водой и всю
воду в опытах с воздухом».
Шнеебели уточняет, что до начала опытов в скважину примерно око-
ло часа закачивался воздух при давлении от 1 до 6 кг/см2, с тем чтобы
ликвидировать отмеченную Хабибом остаточную влажность, способную вы-
звать ошибки в расчетах.
Варле высказывает опасение, что эта продувка разрушает структуру
пор, проницаемость которых хотят измерить.
Шнеебели отмечает, что давление в 6 атм очень быстро амортизиру-
ется в породе. К тому же опыт по закачкам в глинах Матемаль показал,
что можно достичь и больших давлений, не вызывая разрушений. Естест-
венно, что допустимое давление будет тем меньше, чем меньше глубина
закачки воздуха.
Барбедет высказал следующее соображение: «В результате опытов Ро
и его сотрудников в 1955 г. была получена возможность сравнивать метод
измерения проницаемости путем закачки воздуха с классическими методами
определения проницаемости пород, поскольку в районе изысканий колеба-
ния уровня воды превышали десятки метров. При этом было установлено,
что коэффициент воздухопроницаемости оказывается отчетливо меньшим,
чем коэффициент водопроницаемости, — результат, который противоречит
соображениям Шнеебели.
Этот результат, /<воздух < /CB(M, может, без сомнения, объясняться тем
фактом, что на участке, не занятом грунтовыми водами, капиллярная вода
в грунте стремится уменьшить воздушную пористость исследуемого участка,
так как закачиваемый воздух не межет ее вытеснить, а применение боль-
шого давления грозит нарушить структуру породы.
129
Неопределенность создает также температура закачиваемого воздуха
в силу снижения давления и влияния температуры породы. Таким образом,
измерение проницаемости пород по воздуху представляет определенный
интерес, но его практическое осуществление и интерпретация результатов
сложны. Поэтому мы предпочитаем использовать для определения прони-
цаемости пород опытные закачки воды, применяя для их обработки методы
расчета фильтрации в ненасыщенных породах».
ЛИ ТЕРАТУРА
l.Raud J., 1955. Emploi de Pair pour la determination in situ des permeabilites de
terrains, Congr. Intern, des Grands Barrages, Paris.
И. Халеви и А. Нир
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА ПРИ ПОМОЩИ РАДИОАКТИВНЫХ
ИНДИКАТОРОВ1
Определялась эффективная пористость пласта доломитов прослеживанием пере-
мещения радиоактивного соединения К3Со60 (CN)6 между двумя скважинами, находя-
щимися на расстоянии 250 м друг от друга.
Экспериментальные данные были применены для расчетов пористости преобразо-
ванием координат полученной кривой активности. Опыт подтверждает пригодность
использования радиоактивных веществ в полевых экспериментах.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Общие положения. Радиоактивные вещества стали широко используе-
мым средством в гидрологических исследованиях. В последние годы были
опубликованы статьи об определении характера фильтрации, скоростей
грунтовых вод и определении параметров пласта, в которых описывалось
использование закономерностей передвижения радиоактивных веществ [1,2,
3, 5, 7, 8, 12, 14|. Обширный обзор этих работ был недавно дан в спе-
циальном выпуске Isotopes [6].
Параметры, необходимые для определения емкости подземного бас-
сейна,— мощность и эффективная пористость пласта — могут оцениваться
при введении радиоактивного индикатора в одну из опытных скважин и
откачки из второй скважины, находящейся в зоне влияния первой скважи-
ны. Известны полевые опыты этого типа [12J, где в качестве индикатора
использовался I131. .
Цель эксперимента. В Израиле при исследовании гидрологического
цикла особое внимание уделялось изучению узких водоразделов. Одним из
них является водораздел бассейна Нахаль Орен в области Кармел, южнее
Хайфы. Водораздельное пространство сложено в основном доломитами се-
номан-туронского возраста. Пласт ограниченный. Бассейн Нахаль Орен —
главный источник для водоснабжения города Хайфы. Эксперимент в оди-
ночной скважине Нахаль Орен 2 был проведен в 1959—1960 гг. для опре-
деления естественной скорости потока. Целью рассматриваемых экспери-
ментов явилось определение пористости пласта.
।
РАСЧЕТ ПАРАМЕТРОВ ПЛАСТА
Опыты проводились по схеме, представленной на фиг. 1. Радиоактив-
ный индикатор вводился в скважину 1. Затем начиналась откачка из сква-
жины 2 и непрерывно регистрировалась активность откачиваемой воды.
Во время опыта получаем кривую активности на единицу объема А (/)
в зависимости от времени. Однако для обработки удобнее составить зави-
симость активности от откачиваемого объема воды. Эту зависимость обозна-
1 Е. Н а 1 е' v у, A. N i г, The determination of aquifer parameters with the aid of ra-
dioactive tracers, Journ. Geophys. Res., B7, No. 6, 1962.
/3/
чим Л (о) и выразим в единицах активности на единицу объема (у. с/литр).
Переход от Л (0 к Л (у) получим исходя из того, что
(1)
где Q (/) —откачиваемый расход в м3/час. Это преобразование многозначно,
когда расход изменяется во время опыта.
Фиг. 1. /—скважина для
инъекции; 2 — скважина
для откачки.
Если при откачке поток считать радиальным, что справедливо для од-
нородной среды с ничтожно малым естественным градиентом и на расстоя-
нии г, большем, чем мощность пласта Ь, то
и = r.r2bs, (21
где v — объем откачанной воды в ж8;
s — эффективная пористость.
Если мы зададимся значениями b и г и предположим, что v найдено
в эксперименте с индикатором, то, согласно (2), можно рассчитать s.
Величина v определялась экспериментально по положению максимума
функции активности Л (у).
Определение положения максимума было не всегда достаточно опре-
деленным из-за присущей в большинстве случаев функции Л (у) асиммет-
ричности. В связи с этим может быть целесообразным использование за-
висимости А* (г) вместо Л (у), причем
А (у) do = Л (у (г)) -^—dr — А* (г) dr. (3;
Из уравнения (2) имеем
dv/dr = 2rurbs (4)
и
г --- |/ vibsrt. -
Следовательно,
Л* (г) = А (о) 2]/ itbsv. (6)
Максимум функции Л* (г) определялся из графика Л* (г) в зависимо-
сти от г. Значение г, соответствующее максимуму Л:(! (г), устанавливается
132
равным расстоянию между скважинами. Затем из уравнения (5) рассчиты-
ваем s.
Итак, по (2) получаем
s - v/тггЧ). (7)
Точность в определении зависит от точности измерения или оценки v
и Ь. Имея в виду формулу (7), запишем
ds/s = dv.'v — db 'b (8)
и
= [Ф.г,/у? , (9)
где и ab— ошибки в определениях s, и и b соответственно.
Как уже указывалось ранее, если b неизвестно, то из эксперименталь-
ных результатов можно рассчитать только произведение bs.
В описанном эксперименте геофизическими методами было установлено,
что мощность b равна 100 ± 15 м.
Симметрию в преобразованной кривой может нарушать гидродинами-
ческая дисперсия, и в этом случае необходимо внесение поправок. Однако,
рассматривая преобразованную кривую А* (г) (фиг. 6), в которую не вно-
сятся поправки на дисперсию, можно отметить, что влияние гидравли-
ческого рассеивания на симметрию в этом случае сказывается относитель-
но мало.
ОБОРУДОВАНИЕ, ПРИБОРЫ И РАДИАЦИОННАЯ ЗАЩИТА
Выбор индикатора. Выбор радиоактивного индикатора и его химической
формы для гидрогеологических экспериментов—проблема весьма сложная.
Критерии для выбора «идеального» индикатора для изучения грунтовых вод
были выдвинуты некоторыми авторами [7, 6]. В полевых экспериментах исполь-
зовались такие радиоактивные индикаторы, как Вг82, I131 и тритий. Пригод-
ность Со60 в виде КзСо60(СМ)в была обоснована и экспериментально оп-
робована авторами в нескольких опытах1, в частности при работах на оди-
ночной скважине [3]. Иден и Мельбурн [2] нашли, что Со (CN)^ сравни-
тельно с тритием более благоприятен для измерения периода задержки в
очистном фильтре. Принимая во внимание удовлетворительные результаты
с К3Со60 (CN)6 в экспериментах на одиночной скважине Нахаль Орен 2
[9], было решено использовать K3Co60(CN)6 в рассматриваемом опыте. Эти
эксперименты проводились при больших расстояниях и более значительных
объемах воды, чем в опытах по двум скважинам с I131 [12].
Введение индикатора. Индикатор вводился в скважину Нахаль Орен 3,
находящуюся в 250 м от возмущающей скважины Нахаль Орен 2. Обе
скважины были связаны с главной линией водоснабжения, из которой мог-
ла быть получена вода как носитель индикатора. Ранее было показано [3],
что инъекция под давлением необходима для ликвидации влияния неста-
ционарных процессов. Схема производства инъекции показана на фиг. 2.
110 тс радиоактивного индикатора, содержащегося в сосуде, растворяли в
10 л 5%-ного K3Co(CN)e в специальном баке.
До ввода индикатора производилось нагнетание в скважину от подво-
дящей линии водоснабжения с расходом 55 мЧчас. Индикатор в растворе,
тщательно перемешанном, вводился в скважину через эту же линию. Пос-
ле этого контейнер дважды прополаскивался и содержимое также вылива-
лось в скважину. В конечном итоге индикатор оказался растворенным в
13 м3 воды.
133
Индикатор и промывочная жидкость перемещаются от буровой сква-
жины в пласт при продолжающемся подтоке воды до тех пор, пока объем
поданной воды не достигнет величины, равной объему буровой скважины.
Инъекция воды на этом прекращается.
Поддерживаюшее
приспособление
Радиоантив^\
ный |
индикатор Ц
ПТЛ7Т77ТГГГМ77Т777ТПТ77. ЧТТМЬКт
Бурова*
скважина
Ф и г. 2. Схема расположения оборудования на инъекционной
скважине.
Введение 100 л 4,5%-ного раствора K3Co(CN)c производилось не-
сколькими минутами раньше начала инъекции с нагнетанием и продолжа-
лось в течение всего периода пульсации и промывки.
Выпуск ное_ __
отверстие ~
Си интилляц иипная
npoba
ЁОи-лишровый мтитот <ый
Счетчик
Счетчик Б потреби
телю
Предохрани-
тельный
клапан
Ф и г. 3. Схема расположения оборудования на скважине для от-
качки.
Откачка из возмущающей скважины продолжалась несколько дней до
инъекции. Величины времени t и объема и отсчитывались от момента окон-
чания инъекции.
Мониторная система. Часть откачиваемой воды в Нахаль Орен 2
отводилась в 600-литровый сосуд (мониторный), имеющий в центре пласт-
массовый 5-дюймовый сцинтиллятор, который записывал скорость движения
и активность воды. Детали этой системы определения будут опубликова-
ны позже Ниром, Халеви и Манделем. Оборудование обеспечивает непре-
134
рывную безупречную работу в течение нескольких месяцев в полевых ус-
ловиях. Схема устройства в скважине, из которой производится откачка,
дана на фиг. 3.
Чувствительность системы определения была произвольно выбрана рав-
ной 50% от фона и составляла 1,7 X Юр.с/л; она намного ниже максимума
допустимой концентрации Со60 в питьевой воде (Национальное бюро стан-
дартов, 1959). Стабильность в отсчетах прибора обеспечивалась закрепле-
нием источника Со60 с постоянной активностью с внешней стороны мони-
торного сосуда и наблюдением за влиянием его на изменение активности.
Предохранение от радиоактивности. Поскольку откачиваемая вода на-
гнеталась в линию водоснабжения, были приняты меры предосторожности, что-
бы исключить максимально допустимые концентрации. Если учесть нормы по-
требления этих питьевых вод на протяжении человеческой жизни, то мак-
симально допустимая концентрация Со61’ составит 10~2р с!л. Эго означает,
что для СО60 в виде Co60(CN\' максимум допустимой концентрации много вы-
ше [3]. Авторитетные представители органов здравоохранения считают, что от-
качиваемая вода может подаваться для потребления, пока активность будет
ниже 0,1 трс. При превышении этого уровня активности вода должна от-
водиться в отстойники.
При производстве инъекций и транспортировке радиоактивного мате-
риала должны быть обеспечены соответствующие меры радиологической
защиты.
РЕЗУЛЬТАТЫ И ДИСКУССИЯ
Активность как функция времени в соответствии с регистрацией в
эксперименте показана на фиг. 4, на которой также представлена реакция
наружного калиброванного источника.
Лньарь севра ль марш лгрель
Дни /961г
Ф иг. 4. Изменение активности откачиваемой воды во времени.
Остаются спорными следующие характеристики кривой: а) относитель-
но небольшие приращения активности по сравнению с фоном, которые ни-
же определенной чувствительности системы; б) выполаживание кривой при
величине, незначительно превышающей начальный фон; в) недостаточно от-
четливо выраженный максимум.
Очень низкая активность даже в точке максимума вызывает необходи-
мость проверки зависимости величины активности от изменения чувстви-
тельности системы; последняя может обусловливаться отсутствием ста-
135
бильности в напряжении или изменением фона. Такие исследования произ-
водились следующим образом: чувствительность прибора изменялась по-
степенно так, чтобы фон увеличивался до порядка предполагаемой величи-
ны активности во время эксперимента. Реакция внешнего источника опре-
делялась при различных условиях чувствительности и наносилась на график
(пунктирная линия на фиг. 5) как функция от фона. Если все пред-
полагаемые активности во время эксперимента нанести в зависимости от
чувствительности, замеры по внешнему источнику должны попасть на эту
линию. Однако, если нет изменений в чувствительности, замеры по внеш-
нему источнику должны лечь на сплошную линию фиг. 5 (прямую с укло-
ном 45°), так как внешняя активность просто добавляется к внутренней.
Общая внутренняя активность
Ф и г. 5. Данные по счетчику внешнего ис-
точника. Сплошная линия: реакция внешнего
источника на повышение активности. Пунк-
тирная линия — экспериментально получен-
ные отсчеты внешнего источника как функ-
ция изменения чувствительности приборов.
. Действительные замеры по внешнему источнику были нанесены позже
Пунктиром на фиг. 5 нанесены осредненные значения измеряемых величин
для всех экспериментальных точек и их стандартных отклонений. Они ло-
жатся довольно плотно на сплошную линию и значительно отличаются от
пунктирной линии, показывая реальное повышение активности. Так как в
экспериментах использовалось 100 тс K3Co60(CN)6, можно было исполь-
зовать и 500 тс, нс опасаясь вредных последствий радиации.
Тот факт, что уровень активности не возвращается к начальному зна-
чению в конце эксперимента, можно интерпретировать двумя путями: дли-
тельным процессом дисперсии или повышением фона благодаря адсорбции
материала в мониторном сосуде. При интерпретации результатов в соот-
ветствии со второй гипотезой повышение фона активности предполагалось
постепенным. Эго отмечено на фиг. 4 прерывистой линией. Проверяя эти
две точки зрения, можно заключить, что вторая более приемлема для по-
добного случая, так как первая, если не вносить поправку на изменение
фона, дает восстановление свыше 100%. Преобразованная кривая (фиг. 6),
которая подлежит исследованию, также показывает, что первое положение
136
неприемлемо, так как искажается форма результирующей кривой. Дейст-
вительная проверка мониторного сосуда свидетельствует о тем, что он
является достаточным источником активности для объяснения изменения в
уровне фона. Восстановление после поправки на фон составляет около
80 J 20%.
Ф и г. 6. Активность откачиваемой воды в за-
висимости от расстояния от прокачиваемой
скважины. Сплошная линия: при предпола-
гаемом постоянном фоне. Пунктирная линия
фона увеличивается в соответствии с тем,
как это показано штриховой линией фиг. 4.
Преобразование координат первоначально записанной активности А (И
фиг. 4 представлено на фиг. 6. Сплошная линия—кривая, не исправленная
с учетом фона,—является несколько асимметричной. Кривая, учитываю-
щая поправку на фон и представленная на фиг. 6 пунктирной линией, со-
вершенно симметрична. У обеих кривых имеется область максимума в от-
личие от плоской части фиг. 4.
Следует отметить, что преобразование координат дает А* (г) в зависи-
мости от г как функции параметра s. Значение vmav определялось так, что-
бы оно соответствовало середине полосы наибольшей интенсивности. Эта
величина совпадает для двух кривых фиг. 6. Теперь мы устанавливаем
известное расстояние в соответствии с vmav.
Из (5) _______
та v ~ к ^тах'^^ 250 М
и s = 0,03.
Из (9) мы можем подсчитать стандартную ошибку
5s./s гг-
Поскольку возможная погрешность величины b намного больше, чем
величины v в этом опыте, рассмотрим ошибку в определении
%/s аь!Ь = 0,15.
В результате получаем s = 0,03 + 0,0045. В- общем случае, однако,
произведение bs можно получить с точностью в пределах нескольких про-
центов.
137
РЕЗЮМЕ И ВЫВОДЫ
Определялась эффективная пористость пласта доломитов прослежива-
нием K3Cc6°(CN)6 по двум скважинам, находящимся на расстоянии 250ж
одна от другой. Преобразование полученной кривой активности было при-
менено для облегчения определения параметров, требуемых для получе-
ния пористости из экспериментальных данных.
Из экспериментов можно сделать следующие выводы:
1. Опыты свидетельствуют о возможности использования методики с
применением радиоактивных веществ для полевых опытов по определе-
нию фильтрационных свойств среды.
2. K3Co00(CN)6 представляется подходящим индикатором для доло-
митовых формаций.
3. Общая активность, используемая в опытах, была очень мала. Для
однозначной интерпретации результатов необходимо увеличить активность
индикатора примерно в 5 раз.
ЛИТЕРАТУРА
1. В а г k е г N. Т., Green J. Н., 1959. Use of radioactive isotopes in the study of
groundwater movement, Commonwealth Engr., 2—8 Feb.
2. E de n G. E., Me 1 bo u r nc К- V., 1960. Radioactive tracers for measuring the
period of retention in percolating filters, Intern. Journ. Appl. Radiation and Isoto-
pes, 8, 172—178.
3. H a 1 e v у E., N ir A., H a r p a z Y., Man de I S., 1958. Use of radioisotopes
in studies of groundwater flow, 1, Laboratory and field experiments on the suitabi-
lity of various tracers, Proc. 2nd U. N. Intern. Conf, on the Peaceful Uses of Atomic
Energy, P/1613.
4. Horton J. H., Ross D. I., 1960. Use of tritium from spent fuel elements as a gro:
undwater tracer, Soil Sci., 90, 267—271.
5. Hours R., 1955. Les traceurs radioactifs en hydrology, Comm, energie atomique,
France, Rappt. 486.
6. Isotopes, Inc,, The study of the potential applications of radioisotopes technology to
water sources investigations and utilization, contract AT (30-1) 2477, First quarterly
report, June 1, 1961.
7. К auf m an W. J., О r 1 о b G. T., 1956. Measuring groundwater movement with
radioactive and chemical tracers, Journ. Am. Water Works Assoc., 48, 559—572.
8. К n u t s s о n G., L j u n g g r e n K., 1959. Studies of groundwater flow using radio-
active isotopes, Geol. Foren. i Stockholm Forh., 81, 405—409.
9. Mandel S., 1960. Hydrological field work with radioactive tracers in Israel up to
May 1960, I. A. S. H. Commission of Subterranean Waters, Publ. 52, 497—502.
10. Mer i t W. F., 1961. Movement of radioactive wastes through soil, 2, Measurement
of direction and effective velocity of groundwater movement, AECL, 1961.
11. National Bureau of Standards Handbook 69, Maximum permissible body burdens
and maximum permissible concentrations of radionuclides in air and water for occu-
pational exposure, U. S. Dept, of Commerce, 1959.
12. N i r A., H a 1 e v у E., M a n d e 1 S., H a r p a z Y., 1957. Use of radioisotopes
in studies of groundwater flow, Water Planning for Israel Ltd., Publ., 32.
13. N i r A., H a 1 e v у E., M a n d e 1 S., 1962. Use of radioisotopes in studies of
groundwater flow, Rept. 4, Water Planning for Israel.
14. Skibitzke H. E., Cha p m a п H. T., R о b i n s о n G. M., McCullough
R. A., 1961. Radiotracer techniques for the study of flow in saturated porous mate-
rials, Intern. Journ. Appl. Radiation and Isotopes, 10, 38—46.
Э. Дж. Фслнер
ОПРЕДЕЛЕНИЕ ПРОНИЦАЕМОСТИ ДОЛИННЫХ ОТЛОЖЕНИЙ ПО
ДАННЫМ ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ РЕЧНЫХ И ГРУНТОВЫХ ВОД1
ВВОДНЫЕ ЗАМЕЧАНИЯ
Геологический комитет СШХ ведет работы по изучению ресурсов под-
земных вод округа Шампейн штата Огайо. Для решения вопроса о буду-
щем использовании водных ресурсов долины Мэц-Ривер потребовалось оп-
ределить проводимость долинных отложений. Поскольку в этом районе
имеется небольшое количество скважин, то решить эту задачу обычными
методами опытных откачек не представилось возможным. В районе Урба-
ны расположена неглубокая наблюдательная скважина, фильтр которой
установлен в отложениях речной долины. Колебания уровня воды в этой
скважине соответствуют колебаниям уровня, воды в расположенной побли-
зости реке Мэд-Ривер. Феррис [1] показал, что анализ скорости запазды-
вания и длины синусоидальной волны колебаний уровня подземных вод,
вызываемых колебаниями уровня воды в реке, позволяет определить коэф-
фициент проводимости водоносного горизонта.
Результаты, полученные методом циклических колебаний, были сопо-
ставлены с результатами опытных откачек и лабораторных определений.
Цель настоящей статьи — показать, как, пользуясь только одной на-
блюдательной скважиной, можно получить достаточно надежное значение
проводимости.
География
Река Мэд-Ривер пересекает округ Шампейн с севера на юг, протекая
приблизительно через центр его территории. К западу от реки простирается
равнина, сложенная валунными глинами. С востока к реке примыкает вы-
сокая зандровая равнина, смыкающаяся в нескольких точках с располо-
женными ниже отложениями речной долины. Разность высот долинных и
зандровых отложений составляет около 12 м.
Определение терминов
Коэффициент проводимости представляет ссбой произведение коэффи-
циента проницаемости на полную мощность водоносного горизонта в футах.
Коэффициент емкости в условиях безнапорных вод определяется как
отношение объема воды, который может выделиться при гравитационном
дренировании, к общему объему породы [2].
МЕТОДЫ ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ
Использованные в настоящем исследовании методы заимствованы из
работы Ферриса [1].
Указанные методы Феррис применял к анализу колебаний уровня воды
в наблюдательных скважинах, расположенных в долине реки Платт в штате
1 A. J. Feulner, Cyclic-fluctuation methods for determining permeability as applied
to valley-train deposits in the Mad River valley in Champaign County, Ohio, The Ohio
Journ. of Science, 61 (2), 99—106, March, 1961.
139
Небраска. В распоряжении Ферриса было три скважины. Для анализа
он использовал как подъем, так и понижение уровня воды. В настоящей
работе была использована только одна наблюдательная скважина глубиной
15 м, причем для анализа был использован только подъем уровня воды
в наблюдательной скважине. Это было сделано потому, что характер коле-
баний в исследуемом случае отличается от характера колебаний, исследо-
ванных Феррисом, и определяется быстрым подъемом и относительно мед-
ленным спадом уровней.
Фиг. 1. Обобщенный и увеличенный графики колебания
уровня воды в реке и наблюдательной скважине и метод
расчета отношения амплитуд и запаздывания максимумов
уровней.
Для анализа колебаний уровня было выбрано десять периодов, в те-
чение которых отсутствовали осадки и река не была покрыта льдом. Коле-
бания уровня воды в реке происходили вследствие выпадения осадков в се
верховьях. Рассчитывалось отношение подъема уровня воды в реке к подъему
уровня в скважине и среднее запаздывание между максимумом подъема
воды в реке и максимумом уровня в скважине. На фиг. 1 показаны в уве-
личенном масштабе графики колебания уровня воды в реке и соответствую-
щего колебания уровня воды в скважине и приведены способы получения
некоторых расчетных величин.
140
Метод отношения амплитуд
В этом методе используется отношение амплитуд колебаний уровней
подземных вод и воды в реке. Это отношение, вычисленное по данным за-
меров наблюдательного поста и наблюдательной скважины, для рассматри-
ваемого участка составляет 0,41 (см. пример на фиг. 1). Как уже упомина-
лось раньше, это отношение было определено только для периода подъема
уровня, тогда как в работе Ферриса были использованы оба периода —
подьема и снижения. Как следует из уравнения, написанного ниже, для
того чтобы определить коэффициент проводимости Т, необходимо .знать ве-
личину коэффициента водоотдачи S. Достаточно точно величину <S можно
определить, исходя из того, что пласт является безнапорным. Формула в
размерности галлон/сутки'фут, предложенная Феррисом, имеет следующий
вид:
4.4КУ
\ *0 * / L. J
Величина, стоящая под знаком логарифма (,$^/2s0), представляет собой
отношение амплитуд колебания уровня подземных вод и уровня воды в
реке. Если обозначить
1_ . 1g 2s0,%.
Ax х
ТО
Т
Ч)
где Г — коэффициент проводимости {галлон1сутки1фут)1-,
S — коэффициент емкости (водоотдачи или недостатка насыщения):
/0 — период одинакового по характеру подъема уровня (сутки);
х—расстояние в футах от скважины до реки.
Период подъема уровня воды в реке за один цикл изменяется от 9 до
18 час и в среднем составляет 12 час. Если допустить, что период сниже-
ния уровня имеет величину такого же порядка (при условии, что сток в реке
контролируется), то период колебания составит приблизительно 24 час.
Считая, что отношение положения уровня воды в реке к уровню под-
земных вод в наблюдательной скважине составляет 0,41, строим полулога-
рифмический график зависимости этого отношения от расстояния от реки
(фиг. 2). Используя величину Ах, определенную для одного цикла, и/(|
- 1 сутки, получим ,
Т --- billWls, или 970 000 S.
Отрицательная величина, показанная на фиг. 3, выражает эффективное
расстояние от берега до подводного выхода пород, которое принимается
равным половине ширины потока — 27 футов (9 м). Это допущение является
источником возможной ошибки, которая, однако, вряд ли превысит 10%.
Метод запаздывания
Средняя величина запаздываний tv между максимальным подъемом
уровня воды в реке и максимальным подъемом уровня подземных вод
составляет 4,1 час (фиг. 1). Был построен график зависимости этого запаз-
дывания от расстояния до реки (фиг. 3). Снова принимая, что эффективное
расстояние от берега до выхода водоносных пород в реке составляет 27 фу-
1 Если расстояния х измерять в м, а проводимость Т в м2/сутки, то в приведенных
зависимостях следует заменить коэффициент 4,4 на 0,59.— Прим. ред.
141
Фиг. 2. Полулогарифмический график зависимости от-
ношения подъема уровня подземных вод к уровню воды
в реке от расстояния от скважины до реки.
Фиг. 3. Зависимость запаздывания во времени от рас-
стояния от наблюдательной скважины до подводного вы-
хода пород.
тов, и пользуясь формулой Ферриса, получим величину Т (галлон/сут-
ки/фут)1'.
„ O,6Ox2/o Q
t2
Подставляя значения величин, полученных на основании фиг. 3, будем
иметь
™ 0,60 (155)2 1 с сплпппс
Т = г- или 690 000 S.
(3,5/24)“
Различие полученных двумя методами коэффициентов проводимости,
возможно, связано с неточностью определения расстояния от скважины до
подводного выхода пород или с неточностью отсчетов по графикам колеба-
ний уровней.
Осреднение результатов, полученных методами
циклических колебаний
Метод 1 Т, коэффициент проводимости ' (галлон/сутки/фут)
Принятый коэффи- циент водоотдачи 0,1 0,15 0,20 0,25
Метод отношения амплитуд : 97 000 150 000 190 000 240 000
Метод запаздыва- ния 1 69 000 100 000 140 000 170 000
Среднее (округлен- но) J 83 000 120 000 160 000' 200 000
Мощность водоносных долинных отложений в наблюдательной скважине
составляет 40 футов (13,3 ж). Используя эту величину и средние' значения
коэффициента проводимости,' приведенные выше, найдем полевой коэффи-
циент фильтрации в галлонах в сутки на квадратный фут, разделив коэф-
фициент проводимости на насыщенную мощность.
Эти значения соответственно составляют:
Коэффициент емкости 1 Коэффициент фильтрации (галл он/сутки/ф ут2)
0,10
0,15
0,20
0,25
2 900
3 000
4 000
5 000
ДАННЫЕ ОПЫТНЫХ ОТКАЧЕК
Опытные откачки в городе Урбана были проведены в 1956 г. Шифе-
ром. Откачки были проведены к северу от Урбаны, на «высоких» зандровых
отложениях в 3 милях от реки.
Полученная на основе откачек величина коэффициента проводимости Т
при одной возмущающей скважине и одной наблюдательной составила
222 000 галлон/сутки/фут (2750 мЧсутки). Величина коэффициента водо-
отдачи составила 0,14. Коэффициент проводимости, разделенный на насы-
щенную мощность в месте расположения откачек, равную 15 м, дал величину
соэффициента фильтрации, равную 44 000 галлон!сутки/фут2 (180 м/сутки).
1 Если х измерять в м, а Т в м.2/су тки, то в этой формуле коэффициент 0,6 следует
заменить на 0,08.— Прим. ред.
143
ЛАБОРАТОРНЫЕ ИССЛЕДОВАНИЯ
Лабораторные определения пористости и проницаемости были выполне-
ны на 5 образцах.
В помещенной ниже таблице приводятся результаты лабораторных
определений отобранных образцов.
i L Номер’ , .Пористость | Коэффициент ! фильтрации (галлон, сутки! ' фут?)
образца Место взятия ооразца в % ОГ объема
1 । Гравийная выработка вблизи Игл-Сити} 23,7 ! 4 500
2 . Обрыв долины к югу от Урбаны 32,6 6 000
3 Гравийная выработка на восточной
окраине Урбаны 36,3 4 500
4 ; Гравийная выработка вблизи селения
Кэйбл 26,4 3 400
5 Гравийная выработка на западной ок-।
раине Урбаны 40,3 2 000
Средняя величина пористости из вышеприведенных данных составляет
31,8%, а коэффициент фильтрации—4100 галлон!сутки/фут\
ВЫВОДЫ
Метод циклических колебаний, в котором используется только одна
наблюдательная скважина, при принятом коэффициенте емкости 0,2 дает
значение коэффициента проницаемости, которое находится в близком соот-
ветствии с результатами, полученными по данным опытной откачки и по
данным лабораторных определений.
Метод циклических колебаний уровня полезен при изучении ресурсов
подземных вод в тех случаях., когда имеется всего одна наблюдательная
скважина. Ошибка, которая при этом может иметь место, происходит из-за
того, что берег реки принимается прямолинейным. Однако если река имеет
небольшую ширину, а скважина находится на сравнительно большом от нее
удалении, то эта ошибка будет минимальной. Конечно, необходимо данный
метод испытать и для других участков, однако и без этого ясно, насколько
предлагаемый метод полезен в тех случаях, когда опытные откачки по каким-
либо соображениям оказываются нецелесообразными.
ЛИТЕРАТУРА
1. Ferris J. G., 1952. Cyclic fluctuations of water level as a basis for determining aqui-
fer transmirssibility, U. S. Geol. Surv. open-file rept.
2. Mei nzer О. E., 1923. Outline of ground-water hydrology, with definitions, U. S.
Geol. Surv. Water-Supply Paper 494, 28, 44.
3. Wenzel L. K-, 1942. Methods for determining permeability of water bearing mete-
rials, with special reference to discharging-well methods, U. S. Geol. Surv. Water-
Supply Paper 887, 7.
Д. А. Крайенгофф ван де Лер
ИССЛЕДОВАНИЕ В ФИЛЬТРАЦИОННОМ ЛОТКЕ ВЛИЯНИЯ ЗОНЫ
НЕПОЛНОГО НАСЫЩЕНИЯ НА НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ
ПОДЗЕМНЫХ ВОД СО СВОБОДНОЙ ПОВЕРХНОСТЬЮ1
Излагаются результаты исследований в фильтрационном лотке движения симмет-
ричного потока подземных вод со свободной поверхностью к дренажным каналам.
В качестве пористой среды использовался просеянный песок, в качестве фильтрую-
щейся Жидкости — смесь воды и спирта. Результаты наблюдений были сопоставлены
с результатами теоретических расчетов.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Характер потока подземных вод обычно настолько сложен, что в рас-
четах приходится вводить ряд допущений; в частности, обычно пренебрегают
фактором влияния капиллярной зоны.
Результаты полевых исследований редко позволяют оценить различие
между истинными изменениями и результатами расчетов и тем самым про-
верить справедливость положенных в основу расчетов допущений.
Исследования на моделях имеют определенное преимущество перед по-
левыми исследованиями, так как число неподдающихся учету факторов мо-
жет быть значительно уменьшено, а кроме того, меняя граничные условия,
можно определить пределы справедливости математического анализа, осно-
ванного на соответствующих допущениях.
Хорошо известно, что во многих случаях капиллярная зона сильно
влияет на общий расход потока подземных вод со свободной поверхностью,
и этим влиянием пренебрегать нельзя. Например, из данных экспериментов,
выполненных Лютином и Деем [8], которые изучали горизонтальный поток
в дюнных песках с коэффициентом фильтрации k— 1,2 см!мин, следует, что
влияние зоны капиллярной каймы эквивалентно увеличению мощности насы-
щенной зоны на 24 см. Отсюда следует, что капиллярный поток должен учиты-
ваться в тех случаях, когда мощность этой зоны соизмерима с глубиной
фреатического слоя, а в особенности в тех случаях, когда происходит ин-
фильтрация через зону аэрации при неустановившемся движении.
Из разнообразных моделей, применяемых для изучения движения под-
земных вод, только фильтрационные лотки могут быть использованы для
исследования тех сложных явлений, которые имеют место при неустановив-
шемся движении вод со свободной поверхностью.
Модель должна удовлетворять важному условию: насыщенный и не-
насыщенный потоки должны быть представлены в определенных масштабах.
Данное требование может быть выполнено при использовании в качестве
фильтрующейся жидкости спирта в смеси с водой, а в качестве пористой
среды— просеянного песка. Результаты экспериментов на указанной модели
были сопоставлены с расчетными гидрографами стока и колебаниями фреа-
тического уровня между каналами стока.
1 D. A. Kraijenhoff van de Leu г, Some Effects of the Unsaturated
Zone on Nonsteady Free-Surface Graund water Flow as Studied in a Scaled Granular Model,
Journ. Geophys. Res., 67, No. 11, 4347—-4362, Oct-., 1962.
145
Исследование движения жидкости через капиллярную среду дает урав-
нение неразрывности, относящееся одновременно к капиллярной и фреатиче-
ским зонам1. Анализ входящих в данное уравнение членов дает возможность
объяснить взаимодействие насыщенной и ненасыщенной зон.
Условные обсзначения
z — превышение любой точки над выбранной поверхностью сравнения, см;
у — высота фреатического уровня над уровнем воды в канале, см;
/ — линейный размер, см;
b — ширина лотка, см;
И — расстояние по вертикали от поверхности грунта до постоянного уровня
воды в дренажных каналах, см;
L — расстояние между дренажными каналами, см;
D — эквивалентная средняя глубина горизонтального потока по Хугхауту, см;
d — размер зерен, см;
t—время, сек;
j — резервуарный коэффициент, сек;
v — скорость фильтрации, см/сек;
k — проницаемость, см/сек;
и —скорость перемещения профиля влажности, см/сек;
£ —ускорение силы тяжести, см/сек2;
з — поверхностное натяжение, г/се№;
р — плотность, г/см3;
т( — динамическая вязкость, г/см-сек;
р — избыточное давление жидкости, г/см-сек2;
<7—расход на единицу длины дренажного канала, см3/сск-см;
/у, —расход через капилляры модели, смя/интервал;
г —питание, приходящееся на единицу площади, см3/сек-см2;
S—расход жидкости, проходящей через фреатический уровень, см3/сек-см2;
р, — объемное отношение действующих пор;
0—влажность, % от объема;
т — масштабный фактор.
Индекс т означает, что данная величина относится к модели.
Сходство сеток тока. Ламинарный поток в пористой среде описывается
законом Дарси:
Данное соотношение применимо не только к фреатическому потоку, но
также и к потоку в капиллярной зоне. Когда капиллярная зона полностью
насыщена, то она ничем не отличается от фреатической зоны, так что вся
область характеризуется одной и той же проницаемостью /г. В ненасыщен-
ной зоне, однако, капиллярная проводимость и пьезометрический градиент
изменяются в зависимости от влажности.
Даже если и не происходит сколько-нибудь значительной инфильтрации,
распределение влажности влияет на колебание верхней границы насыщенной
зоны. Например, быстрый подъем фреатического уровня, вызванный резким
повышением давления в этой зоне, приводит к сжатию насыщенного капил-
лярного слоя, если влажность в ненасыщенной зоне невелика. С другой
стороны, верхняя граница насыщенной зоны будет перемещаться более
свободно, если влажность капиллярной зоны будет относительно высока,
что обусловливает большую проницаемость капиллярной зоны.
1 Под фреатической зоной понимается область потока с положительным давлением.—
Прим. ред.
146
Отсюда следует, что при неустановившемся Движении верхняя граница
насыщенной зоны, в которой горизонтальная составляющая потока является
определяющим фактором, зависит от соответствующей влажности в. нена-
сыщенной зоне.
При использовании масштабных моделей особое внимание следуёт уде-
лять масштабным законам, которые применяются к насыщенному и ненасы-
щенному потокам. Фундаментальные исследования Ё. Миллера и Д. Миллера
[10, 11, 12] открывают новый путь к использованию грунтовых лотков.
Исследуя геометрические свойства гомогенной изотропной и постоянной
среды и потока вязкой жидкости, обладающей однородным поверхностным
натяжением, контактным углом, плотностью и вязкостью, они получили без-
размерные выражения, характеризующие все макроскопические свойства не-
насыщенного потока. Справедливость этих выражений была подтверждена
в аналогичных работах [5, 15].
При выборе подходящих комбинаций среды (в отношении величины ее
зерен) и жидкости (в отношении ее поверхностного натяжения, контактного
угла, плотности и вязкости) эти безразмерные выражения могут быть ис-
пользованы для масштабирования ненасыщенного потока.
В соответствии с анализом Миллера законы подобия для масштабной
модели ненасыщенного потока записываются следующим образом:
lm = ml-
~т d
- am
ri dm ~m
rim d a
, /2
. = d z rim
m dm zm . rj 1“
(2)
(3)
(4)
Так как масштабный фактор т представляет собой отношение любой
пары соответствующих размеров в натуре и на модели, то он применим
также и к напору: pmlf>mg — mp/og-, т~ {pmlp)(?lymY или, подставляя урав-
нение (2), получим
Данное уравнение показывает,, что выбор пористой среды и жидкости
определяет масштабный фактор модели.
Комбинация уравнений (1), (4) и (5) дает масштаб времени:
-- 7 ^21_-. ( ? \ 'т Рт ( d \ /g\
t dm zm " \ Рт/ 3 1 \ dltI/
Масштаб проницаемостей следует из комбинации уравнений (1), (3) и (5):
km __ dm ~П1 т] 1 _ ?т '1 i dm \2 /у\
k d z -г]т т р т]„г \ d / ' ’
Сходство модели и натуры требует, чтобы пьезометрические градиенты
были одинаковыми в соответствующих местах, поэтому уравнение (7) также
применимо к поверхностным скоростям и интенсивности питания:
^т ___ rm _ _ рт у I dm V zg\
U Г k р -!\т \ d ] '
Из этого уравнения можно получить масштаб расхода на единицу длины
дренажного канала:
dm_____ vmlm _ Рт С ( dm \ Л ~т dm /qx
1 I л I ' * ' 1 • \ /
q vl р Рт \ d } Рт s d
147
В вышеприведенных выводах масштабных факторов для ненасыщенного
потока степень насыщения среды не является лимитирующим фактором.
Поэтому эти масштабные соотношения справедливы также и для насыщен-
ного потока до тех пор, пока один и тот же масштабный фактор т приме-
ним ко всей модели.
Это можно пояснить' на следующем примере. Для насыщенного потока
в зернистых грунтах выражение для проницаемости имеет вид:
k — Cd2 р g/r^,
где С есть фактор формы, характеризующий геометрическое распределение
пор. Для аналогичной зернистой среды Ст — С и
/’т Рот "П ( &т __ vm ,о\
k ti У \ d / V ' '°'
к г Чт \ и 1 с
В работе о насыщенном потоке Крайенгофф [6] применил следующее
безразмерное выражение для времени: = где / = р LW2 КD, так
что tm/t = (k/km)(D/Dm) (Lm/L2) Для сходной среды р = и DJD =
Lm/L = т, поэтому tmit = (k!km)m. Подстановка уравнений (5) и (8) дает
=. Р Vm / V Р 3m __ / Р V ~т (<т / \ /д\
Prw Г1 \ dm / Рт 3 \ Рт / z У \ dm /
Таким образом, все требования моделирования могут быть соблюдены,
если использовать искусственно подобранную пористую среду и жидкость
с соответствующей плотностью, поверхностным натяжением и вязкостью
и с нулевым контактным углом. При этом следует соблюдать условие спра-
ведливости закона Дарси, который действителен для ламинарного движения
жидкости и не учитывает сил инерции. Это положение недавно особо под-
черкнули Гровер и Киркхэм [3].
В .сходной среде, имеющей одинаковое отношение пустотностей, крити-
ческий предел поверхностной скорости может быть выражен посредством
числа Рейнольдса:
Re -- vdp/ri <1 до 10.
Фиг. 3.2 в книге Тодда [14] показывает, что критическое число Рей-
нольдса Re = 1, характеризующее верхний предел применимости закона
Дарси, явно преуменьшено, и поэтому не будет большого вреда, если этот
предел повысить до Re = 10 для участков с наибольшими скоростями, рас-
положенными вблизи каналов стока.
Подстановка уравнения (8) даст
D { А \2 А , / \2 I А \3 / \2
Rem___Рт Yi / и-т I и-m Рт У __I Рт | I ат | I V |_ НО)
Rs Р Vm \ d f d р Vm \ р , \ d j \ Vm )
Уравнение (10) показывает, что увеличение зерен пористой среды может
и в самом деле привести к превышению критических скоростей потока, если
вязкость жидкости rjm мала. Таким образом, каждый раз следует проверять
значения критических скоростей для участков, где скорости оказываются
максимальными.
Постановка опытов на модели. В гидрологической лаборатории Ваге-
нингенского сельскохозяйственного института модель была изготовлена из
двух параллельных стеклянных пластин, расположенных на расстоянии
b = 1,2 см друг от друга и длиной х/3£м = 262 см и высотой 60 см. Общий вид
модели показан нафиг. 1. Пространство между стенками было частично за-
полнено просеянным речным песком с однородным размером зерен. (В настоя-
щее время сооружается модель, где в качестве пористой среды будут ис-
пользованы стеклянные бусины. Описание этой модели будет дано в сле-
дующей статье.)
148
В одну из торцовых стенок модели вмонтирована медная сетка с че-
тырьмя полукруглыми вырезами, имитирующими дренажные трубы. Медная
сетка может блокироваться металлическими пластинками, покрытыми мягкой
резиной, которые позволяют оставлять открытой одну из дрен.
В верхней части модели на равных расстояниях было установлено не-
сколько стеклянных капилляров, через которые в песок могла подаваться
жидкость. Расход жидкости через капилляры регулируется изменением вы-
соты питающего сосуда с водосливом, обеспечивающим постоянный уровень
в нем. Расход жидкости, вытекающей из модели через медную сетку, из-
меряется калиброванными стеклянными цилиндрами.
Фиг. 1. Общий вид грунтового лотка.
Модель использовалась для изучения плоского симметричного потока,
дренируемого каналами и образующегося за счет выпадения осадков. Для
соблюдения определенного масштаба модели размер зерен пористой среды
и свойства жидкости должны быть выбраны таким образом, чтобы в одно
и то же время удовлетворялись как масштаб, так и критическое число Рей-
нольдса. Низкое значение масштабного фактора lm/l ~ т = (p/pm)(^m/a)(d/dm)
требует высокого отношения размеров зерен, что вызывает необходимость
пользоваться грубозернистой средой в комбинации с жидкостью, обладающей
высокой плотностью, низким поверхностным натяжением и нулевым углом
смачивания, соответствующим воде в песке. С другой стороны, высокое
отношение dm/d может привести к нарушению закона Дарси, поэтому, чтобы
в опыте скорость потока не превышала своего критического значения, должна
быть выбрана жидкость с высокой вязкостью. Было установлено, что этому
требованию удовлетворяет 50%-ная смесь этанола и воды.
На фиг. 2 показаны изменения поверхностного натяжения и вязкости
в зависимости от процентного содержания этанола и температурых. В модели
использовалась 50%-ная смесь метилированного спирта и воды. В процессе
экспериментов концентрация смеси контролировалась ареометром.
1 Данные взяты из Handbook of Chemistry and Physics; International Critical Tab-
les, IV.
149
Температура во время проведения опытов поддерживалась в пределах
20 С. Таким образом, по сравнению с водой при 10 С имели место следую-
щие соотношения:
Поверхностные натяжения
g 74,2 ~~~
Вязкости
Лот _ . 2,90 _ 2 21 \ 1,31 ’ '
Плотности
Ддщ :•= 2^* 0,931
р 0,9997 ’
Масштаб поверхностных натяжений применим также и в случае, когда
поры частично заполнены парами спирта, так как поверхностное натяжение
этанола по сравнению с воздухом и паром отличается в незначительной
степени.
Опыт 1. Для однородного песка в естественных условиях эффективный
размер зерен по Хазену принимается d = 0,1 мм.
Так как модель заполнена просеянным песком с размером зерен от 1
до 2 мм, то отношение эффективных размеров зерен может быть принято
dm'd10. Следовательно, масштабный фактор модели
т - (1/0,931)(0,39) (1/10) - 1/23,9.
В модели половина расстояния между дренажными каналами составля-
ет 262 см, что соответствует 23,9 X 262 — 6250 см в натуре.
Нижний край модели представляет собой водоупор, подстилающий
однородный и изотропный песок, мощность которого в натуре составляет
11,5 м. Постоянный уровень воды в дренажном канале находится на 2 м
150
ниже поверхности грунта. Половина ширины и одна из наклонных боковых
сторон канала имитируются в модели 4-сантиметровым участком открытой
медной сетки ниже постоянного уровня жидкости.
Уравнение (8) показывает, что эффективная суточная интенсивность
осадков г в см в натуре должна в модели выражаться как
Г,„ - - 0.931 X 2721 > 10= X Хбб = 4’89 X 10-' г.
Так как поверхность песка равна 262 Д' 1,2 ~ 314,4 си2, то общий рас-
ход через капилляры должен составить
Fc- 314,4 х 4,89 \ КГ’г -0,154г.
В соответствии с уравнением (6) масштаб времени составляет
tm,'l 0,931“2 X 0,3 X 2,21 v 0,13 = 0,001.
Поэтому интервал времени 86 400'21 000 : 43 сек, соответствует поло-
вине суток в прототипе.
В модели расход измеряется на длину интервала, поэтому расход в
капиллярах выражается в см3 на интервал:
Fc = 43 0,154 г сма,'сек 6,6/- см3.'интервал.
В опыте норма осадков соответствовала тому их количеству, которое
выпало в районе Хельмонда (юго-восточные Нидерланды) во время ливней
исключительной силы 4 и 5 декабря 1960 г. (соответственно в эти дни вы-
пало 46,5 и 33,2 мм). В районе Хельмонда развиты песчаные почвы. Этим
дождям предшествовал довольно влажный период, в течение которого вы-
падали осадки со среднесуточной интенсивностью около 3,5 мм, так что
эксперимент был начат с кривой спада, которая была продолжена до того
момента, когда расход оттока не достиг соответствующей эквивалентной
величины. После 6 декабря в течение долгого времени дождей не было.
Следует также отметить, что эвапотрапспирация зимой 1960 г. была не-
значительна и поэтому не учитывалась.
С целью проверки точности эксперимента он быр повторен дважды,
причем оба раза начинался при соответствующем значении кривой спада.
В третьем опыте интенсивность осадков была несколько большей вследст-
вие небольшого изменения температуры жидкости—с 20,6'' до 20,8 С.
Расход измерялся через интервалы в 43 сек, соответствующие 12 час в про-
тотипе. Результаты замеров представлены в виде диаграммы на фиг. 4.
Пунктирная линия представляет собой гидрограф стока, полученный пу-
тем расчетов, разработанных в предыдущей работе автора [6, 7]. Этот рас-
чет основывается на резервуарном коэффициенте / который
включает в себя все гидрологические свойства дренажной ситуации. На
фиг. 3 показано, как этот коэффициент был получен из полулогарифмиче-
ского графика .зависимости кривых спада от стока.
Оценка результатов. Па фиг. 4 и 5 показаны гидрографы стока в па-
раллельные дрены, находящиеся на одинаковом расстоянии друг от друга,
равном 2 x 62,5 - 125 м, и графики колебаний фреатического уровня меж-
ду дренами. Фиг. 4 иллюстрирует хорошее совпадение между расчетными
и наблюденными расходами стока, если рассматривать общую форму гидро-
графа и экстремальные значения величин. Запаздывание, составляющее
около 6 час, может быть связано с временем, которое затрачивается на
продвижение фронта влажности через капиллярную зону.
Кроме того, очевидно, что допущение Дюпюи — Дарси, лежащее в ос-
нове метода расчета, не нарушается, хотя радиальный поток вблизи канала
стока значительно отличается от горизонтального направления, принимаемо-
го в этом допущении. Этот факт показывает, что заключение об эквивалент-
ной длине горизонтального потока по Хугхауту [4], которая зависит от ра-
151
диального сопротивления, также применимо и к неустановившемуся потоку
подземных вод, как это впервые предположил Маасленд [9].
В противоположность гидрографу стока фактическое изменение фреати-
ческого уровня, показанное на фиг. 5, значительно отличается от расчет-
ного. Так как в модели введен новый элемент—капиллярная зона, следу-
ет проанализировать переток из капилляров в фреатическую зону, с тем
чтобы определить, является ли указанное противоречие следствием недо-
учета влияния капиллярной зоны.
Фиг. 3. Определение резервуарного коэффициента / по кривым спада
оттока. Опыт 1, / —16 суток.
Переход от ненасыщенного к насыщенному потоку является функцией
неустановившегося движения жидкости как в насыщенной, так и в ненасы-
щенной зоне. Поэтому как форма, так и положение профиля влажности
должны изменяться во времени. Я не могу дать исчерпывающего математи-
ческого описания данного процесса, однако приближенные выражения могут
быть получены, если рассматривать порознь профили подъема и опускания,
обусловленные установившейся инфильтрацией через ненасыщенную зону,
принимая, что профиль влажности перемещается с постоянной скоростью.
Дж. Шенфельдом [13] была предложена следующая процедура, идея
которой основана нашего исследованиях по распространению волн в реках.
Данный метод, в сущности, тот же самый, что и метод, предложенный
Янгсом [16].
Основное допущение заключается в том, что профиль влажности опу-
скается вниз с постоянной скоростью и что его постоянная форма выража-
ется как z' --- z + ut, а влажность 0 ~ 0 (г'). Отсюда следует, что
эе _ а о д/
dt~ ' dz' Х dt
д®
и -г-т
дг
Это изменяет уравнение неразрывности d 0Л/1 -J- d v’d z 0 в dv/dz -
-и dB/dz', которое имеет решение:
v —- — I и 44 dz " ~ i и ^,-d z' — С — z/0 (zf). (11)
J dz dz r '
С есть произвольная постоянная, так что при любых выбранных значе-
ниях С и и между поверхностной скоростью v и влажностью 0(2') суще-
ствует линейная зависимость.
152
50
Фиг. 4. Наблюденные и расчётные гидрографы стока, вызванные дождем в декабре
1960 г. Опыт 1, /—16 суток.
и-.—......I—.... । .... ।
0 10 20 30
о v Наблюденные
—— Расчетные
°о
о
о
° с
.Ь, k I J.1, t ... Г. i I. I I... i I < . .. t.> i , ,
Cymnu в прототипе
W so 60 70 80 90
Интервалы времени на модели
Фиг. 5. Наблюденные и расчетные колебания фреатического уровня. Опыт 1, /= 16 су-
ток и !А=0,30.
Так как д^/дz - - (d&/dzr)(dz'7dz) = d0jdz', то уравнение Дарси для
вертикального движения влаги
+ г)-----^(^)(
1 др 30 .•
pg 0® dz 1
изменяется в
др ае
де dz'
(12)
15S
Из уравнений (11) и (12) следует, что
И
dz' __ k (Н) д [__________________ р \
~ /г(Н) -у v ((-)) д <-М pg г
(13)
Форму профиля влажности можно получить путем численного интегри-
рования уравнения (13), используя эмпирические зависимости для проница-
емости /г(0) и напора натяжения — p/pg(0).
влажность
Фиг. 6. Проницаемость k(B) просе-
янного песка (0,5—1,0 мм) для воды
(Чайлдс и Джордж (2J).
Ф и г. 7. Профили влажности в про-
сеянном песке (0,5—1,0 мм).
Мы не располагаем этими зависимостями для зернистой структуры
прототипа и среды модели, поэтому процедура будет продемонстрирована
на кривых k и —plpg, опубликованных Чайлдсом и Джорджем [2] для
воды в просеянном песке (d = от 0,5 до 1,0 мм). Гистерезисом между кри-
выми сорбции и десорбции пренебрегаем (фиг, 6 и профиль равновесия I
на фиг. 7).
Первый случай, который следует рассмотреть, представляет собой ко-
нечный этап периода спада, когда скорость вертикального просачивания
[Н = —v (0JJ грунтовой влаги над профилем влажности очень мала.
154
Так как профиль влажности движется вниз, то его скорость и, которая
принимается постоянной, положительна и определяет наклон прямой ли-
нии АВ на фиг. 6, выражающей уравнение (11).
В зоне просачивания над профилем влажности постоянная инфильтра-
ция /у =—ц(0х) очень мала и поддерживается только силой тяжести, так
как напорный градиент здесь не играет существенной роли, и уравнение
(12) превращается в — v (0Х) = k (00 = rv Выбор небольшой скорости про-
сачивания фиксирует точку /1 на кривой k(Q) и, следовательно, прямая
линия АВ полностью определяется данными значениями г1ии.
Очевидно, что здесь не может быть иной точки пересечения линии АВ
и кривой &(0), так как при переходе от ненасыщенного к насыщен-
ному потоку противодействующая сила напорного градиента приводит
к тому, что — у(0) будет меньше, чем /г(0). Отсюда следует, что
постоянная скорость профиля влажности постоянной формы может су-
ществовать только в том случае, если имеет место по крайней мере не-
которое просачивание при влажности 0Х. Для конца периода спада все
это представляет удовлетворительную апроксимацию.
Для численного интегрирования уравнения (13), &(0) и /?(0) + у(0)
могут быть взяты с фиг. 6, а соответствующее значение д/дЩ—p!?g) мо-
жет быть получено с профиля равновесия влажности I на фиг. 7. Резуль-
тирующий профиль влажности II также приводится на фиг. 7.
Далее рассматривается профиль просачивания после выпадения осадков.
Поверхностные скорости в этом профиле выражаются линией АС на фиг. 6;
0Х выражает остаточную влажность в зоне просачивания ниже движущего-
ся профиля влажности и 02влажность в проводящей зоне над профилем
влажности.
В самом профиле влажности—и(0) должно превосходить проводи-
мость А(0) вследствие преобладания напорного градиента.
Численное интегрирование уравнения (13) дает профиль влажности III
(гл. 7). Аналогичные профили влажности были установлены Янгсом [16J
путем теоретических и экспериментальных исследований вертикальной ин-
фильтрации.
И наконец, рассматривается поднимающийся профиль влажности после
того, как просачивание достигнет насыщенной зоны.
Прямые участки кривой на фиг. 5 дают основание считать, что ско-
рость профиля влажности и в самом деле постоянна.
В этом случае и отрицательно и линия CD фиг. 6, изображающая
—ц(0) =—С + и 0, должна иметь уклон вниз. Профиль влажности IV
на фиг. 7 был построен путем интегрирования уравнения (13).
В общем фронты влажности будут отклоняться более или менее зна-
чительно от решений уравнения (13). Практические значения этих решений
заключаются в том, что произвольный фронт влажности имеет тенденцию
стремиться со временем к форме, выраженной соответствующим решением
уравнения (13).
Оценим истинный смысл величины действующей пористости |х. При
неустановившемся движении в фреатической зоне уравнение неразрывности
имеет вид:
„ ду __ q dq
dt д дх ’
(14)
где и выражает увеличение или уменьшение жидкости в единичном объеме
фреатической зоны.
Уравнение неразрывности также показывает, что S выражает скорость
прибавления или убывания влаги через фреатический уровень независимо
от того, происходит ли это прибавление или убывание вследствие проса-
чивания или изменения фреатического уровня, когда грунтовая влага ад-
сорбируется или остается в капиллярной зоне. Поэтому следует заключить,
155
что присутствие капиллярной зоны оставляет неизменным ц, выраженное
уравнением (14), но изменит характер потока просачивания через фреати-
ческий уровень.
Чайлдс [1| показал, что истинное решение неустановившегося потока
со свободной поверхностью требует исследования грунтов в целом, как над,
так и под фреатическим уровнем. Поэтому дополнительное уравнение для
капиллярной зоны, заключенной между поверхностью грунта и фреатиче-
ским уровнем, позволяет уточнить значение S, т. е. скорость прибавления
или убывания воды через фреатический уровень.
Сначала рассмотрим идеализированный случай профиля влажности по-
стоянной формы и движущегося с постоянной скоростью, например профи-
ли II и IV на фиг. 7. .
На поверхности грунта влага входит в капиллярную зону со скоростью
г и покидает капиллярную зону со скоростью S через фреатический уро-
вень. Когда профиль влажности движется вниз с постоянной скоростью
и ^=dy/dt и когда сохраняется его постоянная форма, меняется только вы-
сота зоны просачивания с той же скоростью u - ^dyidi, поэтому в данном,
идеализированном, случае уравнение неразрывности капиллярной зоны мо-
жет быть записано как
г S— Н, dy/dt, (15)
где И, есть влажность в зоне просачивания.
Комбинация уравнений (14) и (15) дает уравнение неразрывности сов-
местно для капиллярной и фреатической зон:
([1—Ьу)ду:д1-~-г — dqldx. (16)
Данное уравнение обычно применяется к потоку фреатических подзем-
ных вод, вызываемому просачиванием через капиллярную зону при влаж-
ности Ог, но оно должно использоваться только для рассмотренного идеа-
лизированного случая, когда влажность в зоне просачивания и запас влаги
в переходной зоне, выражаемые профилем влажности, постоянны. В дан-
ном случае предполагается, что профиль влажности должен передвигаться
с постоянной скоростью. Фиг. 5 и 10 показывают, что это требование
соблюдается в течение первого интервала просачивания, когда повышение
фреатического уровня практически линейно.
Однако как только интенсивность притока г изменяется, ситуация
значительно усложняется, так как влажность в зоне просачивания и запас
влаги в переходной зоне начинают изменяться. Фактически становится
невозможным различить зону просачивания и переходную зону, так как они
сливаются, причем форма и скорость профиля влажности меняются. Оче-
видно, при таких обстоятельствах уравнения (15) п (16) уже не будут в
точности характеризовать неразрывность, и поэтому единственным способом
учета такой меняющейся ситуации является введение в уравнение нераз-
рывности члена, который характеризует изменение запаса влаги во всей
капиллярной зоне.
Если высоту капиллярной зоны выразить как Н — у, а ее среднюю
влажность как 0, то уравнение (15) примет вид:
r „ s + ^-Н (/У -!/),
где г = r((), S = S (х, t), 0 ^-= Н (х, t) и у = z/(x, t).
Отсюда следует, что
S =г -\-®dy/dt — (Н — у)дЪ.'д1. (17)
156
Подстановка в уравнение (14) дает следующее уравнение неразрывности
совместно для капиллярной и фреатической зон:
д Н д q
д ( д х ’
(18)
Рассмотрим изменение фреатического уровня между каналами стока,
где х = /, 2. Анализ фиг. 5 дает основание предположить, что в период
подъема S > г, а в течение первой части периода спада S< г — 0, что так-
же находится в соответствии с теорией. Здесь важную роль играют допол-
нительный приток и отток через фреатический уровень, выражаемые как
\&dy!dt — (Н — tf)dh)/dt\ в уравнении (18).
Очевидно, что вследствие повторения спадов и подъемов рассмотрен-
ные выше положительное и отрицательное просачивания взаимно уничтожа-
ются и общий расход просачивания в фреатическую зону будет равен ко-
личеству 'выпадающих осадков.
Из вышеприведенного мож'но заключить, что преувеличенное влияние
потока грунтовой влаги в капиллярной зоне на изменение фреатического
уровня будет наибольшим, когда происходит максимальное изменение фре-
атического уровня, что имеет место между каналами стока.
Вблизи каналов стока, однако, это изменение ограничивается влиянием
уровня воды в каналах стока. Из этого следует, что градиенты напора,
которые определяют приток к дренажным каналам, не будут подвергаться
влиянию грунтовой влаги и движущихся профилей грунтовой влажности
над фреатическим уровнем.
В заключение следует упомянуть о некоторых проблемах, которые еще
требуют количественного решения.
А. Сопоставление процесса выпадения осадков на поверхность грунта
с распределением во времени притока через статический фреатический
уровень показывает, что происходит некоторое запаздывание и деформация
графика поступления осадков, вызываемые постепенным заполнением и
опорожнением капиллярной зоны. Это запаздывание и деформация представля-
ют собой функцию как высоты, так и проводимости капиллярной зоны, а так-
же интенсивности и продолжительности выпадения осадков. Фиг. 4 показыва-
ет, что такое запаздывание соответствует инфильтрации профиля влажнос-
ти III, однако близкое совпадение между наблюденными и расчетными
гидрографами также показывает, что сколько-нибудь заметной деформации
интенсивности осадков в ненасыщенной зоне вблизи дренажных каналов
не происходит. Автор намерен исследовать вопрос, может ли отношение
между временем движения опускающегося фронта влажности и постоян-
ством интенсивности осадков являться критерием степени деформации ка-
пиллярной зоны.
В. В случаях радиального сопротивления вблизи дренажных каналов
возрастание расхода может быть связано с увеличением поверхности выса-
чивания над постоянным уровнем в канале. С одной стороны, это приво-
дит к ограничению градиентов потока, но, с другой стороны, повышение
фреатического уровня увеличивает мощность фреатической зоны. Есть ос-
нование надеяться, что это явление также может быть изучено на модели.,
С. Обращаясь к профилю III фиг. 7, можно отметить, что значитель-
ное увеличение количества осадков г вызывает незначительное увеличение
влажности 02 в зоне просачивания, так как более крупные поры становятся
активными, а это приводит к значительному увеличению проницаемости
6(0) (фиг. 6). Можно поэтому считать, что важнее изучать не дополнитель-
ное уменьшение или прибавление капиллярной зоны к фреатической, а:
скорости просачивания через капиллярную зону.
Опыт 2. Для проверки положений, упомянутых в пункте С, был
выполнен второй эксперимент при более низком уровне и при большей
157
интенсивности и продолжительности осадков. Вся боковая сторона модели
была использована в качестве поверхности стока —для того чтобы ликви-
дировать поверхность высачивания, упоминавшуюся в пункте В. Для того
чтобы продемонстрировать аккумуляцию влаги в капиллярной зоне, прове-
дение эксперимента было начато с горизонтального фреатического уровня.
Расходе модели
Фиг. 8. Определение резервуарного коэффициента. Опыт 2,
]т = 20 мин.
Результаты этого эксперимента представлены на фиг. 8, 9 и 10. Сов-
падение наблюденных й расчетных гидрографов стока также хорошее, од-
нако фиг. 9 показывает увеличивающееся запаздывание, которое может быть
связано с большей высотой капиллярной зоны. Сравнение с фиг. 10 также
показывает некоторое увеличение отклонения между наблюденными и рас-
четными фреатическими уровнями между каналами стока, но относительная
роль этого фактора меньше, чем на фиг. 5 (обратите внимание на разные
масштабы фиг. 5 и 10). Этот эффект вызывается большей^ влажностью 02 в
зоне просачивания, совпадающей с большим значением О дy/dt в уравне-
нии (18).
То, что наблюдаемые кривые спада не совпадают с расчетными, может
быть связано с более продолжительным истощением влажности сравнитель-
но высокой капиллярной зоны.
Прототипом второго эксперимента может являться грунт с относительно
малыми капиллярными силами в макропорах. Линейный масштаб в данном
эксперименте может быть найден по соотношению высоты насыщенной ка-
пиллярной зоны в натуре и на модели:
m = hcm/hc.
158
Ф и г. 9. Наблюденные и расчетные гидрографы стока. Опыт 2, jm =-20 мин.
о о наблюденные
щ п 1 1___I__I---1---1--1---1---1--1---1---1--1---1---1--1---1---1--1---1
0 50 100 150 2 00
Время, мин
Фиг. 10. Наблюденные н расчетные колебания фреатического уровня. Опыт 2, jm—
=20 мин и р.—0,30.
Масштаб поверхностных скоростей
"Опт "о г nJ г km! k,
масштаб времени
im___Pm Lm kD _ \>m k
t j y-U- kmDm ~ p-
159
Например: hcm = 2,5 см и he ---- 15 см, отсюда т ------ 2,5/15 = 1/6; km =
= 188 mi'сутки, k = 1,3 м/сутки-, поэтому vm!v --- rm/r =- 188/1,3 = 144;
= 0,30 и у = 0,05; поэтому = 1,6X0,30/0,05Х 1/144 ------ 1/144. Одни
сутки в натуре выражаются 1440/144 — 10 минутами в модели.
Скорость выпадения осадков г =10 мм1'сутки в натуре должна вы-
ражаться расходом в капиллярах Fe~ ~ (г,n!f) г = 262X 1,2X144X 1 ;
= 45 300 смЧсутки = 31,5 см3,'мин. Поэтому средние расходы во втором
эксперименте соответствуют: 21,3; 5,3 и 13,9 мм/сутки. Увеличение рас-
ходов было вызвано повышением температуры в процессе эксперимента.
Проверка чисел Рейнольдса
Опыт 1. Максимальная скорость оттока в модели равна qmax = 8,4 слС
в 43 сек. Если этот отток разделить на смоченный периметр 41,2 = 4,8 саг
канала стока, то максимальная поверхностная скорость составит t’,n:ix
= 0,0407 см!сек. Число Рейнольдса
Rc = о vd. = 0,2.
Опыт 2. ^п,ах 38,6 см3 мин.. Смоченный периметр каналов стока ра-
вен 31-1,2 = 37,2 си2. Поэтому ц11ах = 0,017 см сек и Rc = 0,08.
Хотя числа Рейнольдса могут для некоторых участков быть больше,
тем не менее можно заключить, что закон Дарси справедлив для обоих
экспериментов.
ЗАКЛЮЧЕНИЕ
Хотя эксперименты, описанные в настоящем исследовании, касаются
только двух случаев потока со свободной поверхностью, полученные ре-
зультаты тем не менее имеют значительно более широкое теоретическое
значение и позволяют сделать следующие выводы:
1. Грунтовые лотки могут использоваться для изучения взаимодействия
ненасыщенного потока в капиллярной и фреатической зонах. Масштабиро-
вание этих моделей может производиться путем подбора пористой среды
и жидкости, которая должна обладать определенной вязкостью, поверх-
ностным натяжением, плотностью и контактным углом. Есть основание
считать, что эти модели могут быть с успехом использованы для изучения
многих других проблем движения подземных вод.
2. Неустановившийся приток подземных вод в дренажные каналы мо-
жет быть рассчитан по уравнению
путем использования соответствующего значения резервуарного коэффици-
ента j — ylPl^kD, где D есть средняя глубина горизонтального потока с
поправкой, учитывающей капиллярную зону. Исходя из этого, D было оп-
ределено как «эквивалентная средняя глубина горизонтального потока по
Хугхауту».
Следует ожидать, что в тех случаях, когда дренируемая глубина у
преобладает над общей насыщенной мощностью, допущение о постоянстве
D должно приводить к отклонению расчетных гидрографов от истинных
значений расхода. Однако результаты эксперимента 2 показывают, что из-
менения у по сравнению с D должны быть значительными, прежде чем
смогут сильно повлиять на точность расчетных результатов.
3. Величина активной пористости у в уравнении неразрывности потока
со свободной поверхностью равняется величине истинной пористости зер-
160
кистой среды, если допустить отсутствие защемленного воздуха, в дрени-
руемой зоне. Рассмотренные положения приводят к концепции об измене-
нии баланса фреатической зоны, вызываемого изменением влажности в ка-
пиллярной зоне. Теоретические и экспериментальные результаты указывают,
что эффект этого изменения наиболее резко проявляется в местах с мак-
симальным колебанием уровня, причем истинные колебания фреатического
уровня будут значительно отличаться от результатов расчетов, в которых
влияние капиллярной зоны нс учитывается.
Л И Т Е Р Л т У Р Л
1. С h i 1 d s Е. С., I960. The nonsteady state of the water table in drained land, Journ
Geophys. Res., 65 (2), 780—781.
2. C h i I d s E. C., George N. C., 1948. Soil geometry and soil-water equilibria, Dis-
cussions Faraday Soc., No. 3, 78—85.
3. G г о v e r B. L., К i г k h a m D., 1961. A glassbeadglycerol model for non-steady-
state tile drainage. Soil Sci. Soc. Am., Proc., 25, 91—94.
4. H о о g h о u d t S. B., 1940. Bijdragen tot de kermis van eenige natuurkundige groot-
heden van den grond, Verslag. Landbouwk. Onderzoek., No. 46 (14), B.
5. KI u te A., W i 1 k i n s о n G. E., 1958. Some tests of the similar media concept
of capillary flow, 1, Reduced capillary conductivity and moisture characteristic
data, Soil Sci. Soc. Am., Proc., 22, 278—280.
6. Kraijenhoff van de Leur D. A., 1958. A study of non-steady groundwater
flow with special reference to a reservoir coefficient, ingenieur, Utrecht, 70 (19),
87—94.
7. Kraijenhoff van de Leur D. A., 1962. A study of non-steady ground water
flow II, Computation methods for flow to drains, Ingenieur, Utrecht, 74.
8. L u t h i n J. M., D а у P. R., 1955. Lateral flow above a sloping water table, Soil Sci.
Soc. Am., Proc., 19, 406—410.
9. Maasl and M., 1956. The relationship between permeability and the discharge,
depth and spacing of the drains, Groundwater and Drainage Ser., Water Cons. Irr.
Comm. N. S. W., Australia, Bull., 1, 35.
10. Miller E. E., M i 1 I e r R. D., 1955a. Theory of capillary flow, 1, Practical impli-
cations, Soil Sci. Soc. Am., Proc., 19 (3), 267—271.
11. M i 1 I e г E. E., M i I I e г R. D., 1955b. Theory of capillary flow, 2, Experimental
information, Soil Sci. Soc. Am., Proc., 19 271 —275.
12. Miller E. E., M i I 1 e r R. D., 1956. Physical theory for capillary flow phenomena,
Journ. Appl. Phys., 27 (4), 324—332.
13. S c h 6 n f e 1 d J. C., 1951. Distortion of long waves; equilibrium and stability, Proc.
Intern. Assoc. Sci. Hydrol. of the I. LI. G. G.. Brussels, 4, 140—157.
14. Tod d D. K-, 1959. Groundwater Hydrology, 336, John Wiley & Sons, New York.
15. W i I k i n s о n G. E., К I u t e A., 1959. Some tests of the similar media concept
of capillary flow, 2, Flow systems data, Soil Sci. Soc. Am., Proc., 23, 434—437.
16. Youngs E. G., 1957. Moisture profiles during vertical infiltration, Soil Sci., 84
(4), 283—290.
Ч. X. Пик,к,еринг, Н. Т. Котмэн, П. Крофорд
ИЗУЧЕНИЕ ДВИЖЕНИЯ ПОДЗЕМНЫХ ВОД В СЛОИСТЫХ ТОЛЩАХ С
ПОМОЩЬЮ ТЕПЛОВОЙ МОДЕЛИ1
ВВЕДЕНИЕ
Слоистость — наиболее распространенный вид неоднородности. Еще в
1927 г. Юрен [1] теоретически рассмотрел влияние слоистости на процес-
сы фильтрации жидкости. С тех пор появилось множество работ, посвя-
щенных этому вопросу.
Маскет [3] получил решения задачи о фильтрации жидкости в слоис-
тых толщах для случаев, когда изменение проницаемости происходит по
линейному и экспоненциальному законам. При этом он допускал, что в
горизонтальном направлении пласты характеризуются постоянством и не-
прерывностью свойств. Изменение пористости Маскетом не учитывалось.
В настоящей работе с помощью тепловой модели исследованы процес-
сы неустановившейся фильтрации жидкости в условиях, когда пористость
и проницаемость переменны, а также в случаях, когда имеет место меж-
пластовое перетекание.
Эти исследования основываются на сходстве уравнений, характеризую-
щих движение жидкости в пористой среде, с уравнениями распространения
тепла в твердом теле.
ЭКСПЕРИМЕНТАЛЬНОЕ ОБОРУДОВАНИЕ И ПРОВЕДЕНИЕ ОПЫТОВ
Модель слоистого пласта, примененная в настоящем исследовании,
схематически показана на фиг. 1. Для измерения температур были исполь-
зованы 16 медно-константановых термопар и регистратор температуры
системы «Leeds and Northrup Speedomax», тип G.
Эта установка позволяет регистрировать температуру каждые две
секунды.
Чтобы охарактеризовать температурное поле пластины, термопары ус-
танавливались с двух ее сторон. Изменение температуры в зависимости от
времени в различных точках линейной биметаллической пластины показано
на фиг. 2. Параметр X представляет собой отношение расстояния от ис-
следуемой точки до границы, противоположной источнику тепла, к длине
пластины. Таким образом, кривая X =0,9 характеризует изменение темпе-
ратуры в точке, расположенной вблизи источника тепла, в то время как
X = 0 характеризует температуру точки, расположенной на внешней гра-
нице пластины.
’Ch. Н. Р е с k е г i n g, N. Т. Cot man, Р. В. Crawford, A study of
flow in stratified reservoirs by use of the thermal analogy, Soc. Petrol. Engeneers Journ.,
215—222, 1961.
162
Линейные пластины представляли собой прямоугольники длиной 1 фут
и шириной 4 дюйма. Толщина пластин была различной. Термические свой-
ства металлов подбирались таким образом, чтобы иметь возможность мо-
делировать широкий диапазон изменений проницаемостей и пористостей
природных слоев.
Соединение слоев в медно-свинцовой пластине достигалось путем спай-
ки припоем из 50% олова и 50% свинца. Медная пластина сначала по-
крывалась припоем, затем на нее наносился расплавленный свинец. Соеди-
нение слоев при этом рказывалось вполне надежным. Соединение металла
I Пропеллер
Легшая :
_ванна I
Термопары
Покрытие
из алюми-
ниевой
фольги
Пласти-
на
Цилиндр
Пюсита
Регистратор
температуры
Фиг. 1. Схема модели пласта, работающего в
условиях постоянного давления.
Вуда с медными и бронзовыми пластинами осуществлялось анало гичным об.
разом, но при этом поверхность меди и бронзы обрабатывалась паяльной
Фиг. 2. Изменение температуры во времени в слоистой
линейной пластине из металла Вуда и меди.
пастой, а не припоем. Трудности возникли при соединении металла Вуда с
алюминием. Для того чтобы осуществить такое соединение, в алюминие-
вой пластине было просверлено 4 отверстия диаметром х/0 дюйма, пос-
ле чего пластина была залита расплавленным металлом Вуда. После за-
стывания металла Вуда пластины оказались прочно связанными друг с дру-
гом. Была изготовлена и трехслойная модель, состоящая из металла Ву-
да— меди—-свинца, а также четырехслойная — путем добавления к пре-
дыдущей модели со стороны свинца слоя металла Вуда. Кроме того, одна
163
трехслойная модель представляла собой слой резины, зажатый между дву-
мя металлическими пластинами стяжными болтами.
Одна сторона пластины находилась в ванне, наполненной смесью во-
ды со льдом (см. фиг. 1). Пропеллером в ванне создавался интенсивный
поток, который направлялся к охлаждаемому концу пластины, и таким
образом поддерживалось постоянство температуры на этом участке пласти-
ны. Эта модель соответствует случаю эксплуатации нефтяного пласта пу-
тем поддержания постоянства пластового давления у одной из его границ.
Пластины были помещены в цилиндр Люсита, который в свою оче-
редь— с целью избежать потерь на радиацию —был обернут алюминие-
вой фольгой. Для уменьшения конвекции в цилиндре создавался вакуум.
В начале эксперимента во всех точках пластины устанавливалась оди-
наковая температура, что фиксировалось прибором, затем очень быстро
ванна заполнялась водой со льдом, что имитировало резкое падение плас-
тового давления на одном из концов линейного пласта. Так как прибор
регистрирует температуру каждые две секунды, то измерение температуры
во всех 16 термопарах длилось 32 секунды.
Опыты были проведены на шести одгюмсталлических пластинах (ими-
тирующих однородные пласты), четырех биметаллических, одной трехслой-
ной и одной четырехслойной пластине. В многослойных системах пластины
находились в непосредственном контакте, что создавало возможность пе-
редвижения тепла из одной пластины в другую. Кроме того, была иссле-
дована одна модель, состоящая из алюминиевой и стальной пластин, раз-
деленных резиновой прокладкой, и две модели, состоящие из бронзовых
и стальных пластин, также разделенных резиновыми прокладками. Эти
последние модели соответствуют тому случаю эксплуатации пластов, ког-
да различие проницаемсстей в них составляет 500: i (см. табл. 1).
Т а б л п ц а 1
Физические свойства некоторых металлов, сплавов и резины
Материал Удельная теплоем- кость *, фунт 'фут Плотность * Теплопроводность, 1 Ь T У / ч и с! ф> у т 0 F Температуропровод- ность, ф>ут-/чаг
в 1 Hhm/ei; L ! эксперимен- тальная । вычисленная 1 1 эксперимен- тальная
Алюминий 1 0,22 1 168,5 1 117 120 1 3,15 ' 3,23
Бронза 0,094 534,4 56 61 > 1,12 * 1,22
Медь ; 0,0921 , 553 , 224 229 ‘ 4,38 ’ 4,49
Свинец 0,0316 . 587 ; 20 23 ! 0,92 : 1,08
Нержавеющая сталь ’ 0,107 ' 488 1 16 8,6 ! 0,31 ’ 0,165
Металл Вуда Резина , 0,0352 . 659,23 у у 0Д09 8,9 ! 0,334 0,0043 0,389
* Взято из [ 11 ].
** Взято из [9 п 1()|.
Поправки на потери тепла вследствие радиации и сопротивления теп-
ловому потоку, вызываемому «скин эффектом», который имеет место в об
ласти контакта пластины с ледяной ванной, рассмотрены в работе [8].
Зная температуру металлической пластины в различные моменты вре-
мени, легко рассчитать ее эффективную температуропроводность. С исполь-
зованием этого параметра оценивалась динамика потока тепла в системе
металлическах пластин, из которых были изготовлены модели, а по анало-
164
гни с этим определялся коэффициент пьезопроводности и характеризовал-
ся поток жидкости в слоистых пластах.
Для того чтобы лучше понять процессы, происходящие в многослой-
ных толщах, опыты были проведены и на однородных металлических плас-
тинах. Полученные опытные данные сопоставлялись с расчетными значе-
ниями температуропроводности (см. фиг. 3 и табл. 1). За исключением
стальной пластины, опытные значения этого параметра оказались несколь-
ко выше расчетных.
Результаты опытов с четырьмя биметаллическими пластинами пред-
ставлены на фиг. 4. Все четыре графика указывают, что в начальный пе-
риод температуропроводность уменьшается со временем. Объясняется это,
5Д|--------------------------------------
I ..о____медь_____________________:
Ф и г. 3. Сопоставление расчетных и
экспериментальных температуропровод-
ностей для пластин из различных ме-
таллов.
О 5 10 1b 20 25
Бремя, мин
Ф и г. 4. Эффективные температуро-
проводности биметаллических пластин.
возможно, тем, что в начальный период большие количества тепла, сни-
маемые с модели, образуются за счет наиболее проводящей пластины. Ме-
нее проводящая пластина также теряет тепло, но со значительно меньшей
скоростью. Суммарные потери тепла окажутся выше среднего значения
температуропроводности. Одновременно с продвижением температурной
волны к внешней границе температуропроводность уменьшается, и это про-
должается до тех пор, пока не наступит стационарное состояние. Темпе-
ратуропроводность слоистой системы зависит от температуропроводности
отдельных слагающих ее слоев, как это показано на графике для моде-
лей медь — свинец и медь — металл Вуда. Уклоны этих двух линий отли-
чаются, но незначительно, в то время как эффективная температуропро-
водность резко понижается вследствие низкой теплопроводности металла
Вуда по сравнению со свинцом.
Толщина пластин, как это видно из фиг. 5, также вызывает измене-
ние положения линий. Медно-свинцовая пластина была превращена в трех-
слойную систему путем присоединения к ее свинцовой стороне пластины
металла Вуда. В результате линия смес тилась вниз и одновременно умень-
шился ее уклон. После того как пластина металла Вуда была присоедине-
на со стороны медной пластины, было отмечено дальнейшее опускание и
выполаживание кривой. Можно считать, что данная кривая имеет незначи-
тельный уклон. Это указывает на то, что после сравнительно короткого
промежутка времени температуропроводность стабилизируется.
165
5.0
Время, мин
Ф и г. 5. Изменение температуропро-
водности во времени многослойных
линейных металлических пластин.
По полученным из экспериментов значениям температуропроводности
для нескольких слоистых моделей было решено найти удовлетворитель-
ный метод расчета этого параметра для аналогичных условий. С этой це-
лью было применено два приема осреднения параметров отдельных слоев,
которые заключаются в следующем:
п
(1)
П=1
(2)
где kn — проницаемость n-го слоя (&ф.) по данным анализа керна;
Ьп~ толщина или мощность n-го слоя, имеющего проницаемость k
по данным анализа керна;
Ст~— удельная теплоемкость;
р — плотность;
рСот — произведение плотности на удельную теплоемкость, эквивалент-
ное произведению пористости пород на сжимаемость жидкости;
k
an~~^7rJL\-температуропроводность n-го слоя (аналог пьезопроводности
при фильтрации жидкости);
т], — эффективная температуропроводность любой системы.
Величины, рассчитанные для исследованных пластин и полученные из
экспериментов, сравниваются в таблице 2. Экспериментальные значения
166
Таблица 2
Сравнение рассчитанной и экспериментальной
температуропроводности
1 Эффективная темпера- 1 туропроводность, । футЧчас с к
I п п СС
Пластина 1 Е S -nnhn ж
| я=1 п—1 О. Q <и д
/г п
! S ( Ст? )п £ 1гп 5 а
in—1 н=1 По
Алюминий — ме- талл Вуда 2,17 1,83 2,24
Бронза — металл Вуда ! 0,89 0,73 1,07
Медь — свинец 3,54 2,88 3,51
Медь — металл Ву- да 2,98 2,20 2,97
Медь — свинец — металл Вуда 3,17 2,45 3,20
Металл Вуда — медь — свинец — металл Вуда 3,11 2,37 3,08
!
О Бронза - метало Вуда ।
* Алюминий- металл Вуда j
Медь - металл Вуда |
о Медь - свинец ;
67.7 <7.2 0.6 Од 0,8
t ОЯ
' L2
Ф и г. 6. Изменение температуропроводности
во времени для биметаллических пластин.
медь металл Вуда I
А Алюминий-резина-сталь '
о Бронза-резина нержавею-
щая сталь
о металл Вуда медь сои '
нец металл Вуда ।
О 0,1 0,2 0.3 Ofi 0,5 0,6 0,7 0,8
. ад
Фиг. 7. Изменение температуропроводности
во времени для многослойных пластин.
температуропроводности были получены путем измерения площади, огра-
ниченной кривыми на фиг. 5, и последующего деления этой величины на
показатель времени. Эти значения мало отличаются от рассчитанных по
уравнению (1), за исключением лишь случая пластины бронза — металл
Вуда.
Дальнейшее подтверждение справедливости уравнения (1) было полу-
чено на основании изучения модели, состоящей из двух медных пластин
толщиной Vj. дюйма, разделенных резиновой прокладкой толщиной
0,104 дюйма. В последующих опытах толщина резины была увеличена до
0,208; 0,312; 0,392 и 0,56 дюйма. Отношение толщины резинового слоя к
суммарной толщине медных пластин при этом соответственно составляло:
0,416; 0,832; 1,248; 1,568 и 2,240. На основе опытов было установлено,
что теплоемкость резины составляет 0,6 теплоемкости меди, а ее темпе-
ратуропроводность-— 0,0С2 температуропроводности меди. Сопоставление
расчетных и эффективных значений температуропроводности, приведенное
в таблице 3, указывает на их очень хорошую сходимость.
Полученные результаты представлены в виде графиков зависимости
отношений эффективной и расчетной температуропроводностей от безраз-
мерного времени (см. фиг. 6 и 7). Эти графики могут быть использованы
для корректировки расчетной температуропроводности некоторых систем в
пределах исследованных значений безразмерного времени. Эксперименты
показывают, что двухслойная система обнаруживает значительно большее
изменение температуропроводности во времени, чем многослойные моде-
ли,— это следует из уклонов кривых.
Таблица 3
Сравнение экспериментально полученных
температуропроводностей с расчетными
по предлагаемому уравнению
t = 0,195 ! t - 0,391 1 t - 0,782
Эффективная температуро-
проводность по эксперимен-
тальным данным
0,416 1 3,52 1 1 1 3,26 1 3,19 3,14
0,832 i 2,94 , 2,92 3,02 2,95
1,248 ' 2,52 2,36 2,69 2,52
1,568 j 2,27 ' 2,24 2,24 2,30
2,240 ; 1,88 1,79 1,96
ОБСУЖДЕНИЕ
Возможность применения уравнения (1) доказывается следующим об-
разом. Пусть вместо модели имеем в соответствующем масштабе гипоте-
тический нефтяной пласт, эксплуатируемый при давлении выше давления
насыщения. Рассчитаем суммарный приток жидкости на основании уравне-
ния Херста—Ван Эвердингена [4]
Q (/„) = 2А {(Ро - Р (t,)) VГ„ [Р (Q - Р о |/Д=у} +... -г, (3)
где
Q — суммарный приток жидкости;
А — площадь поперечного сечения, перпендикулярная направлению те-
чения потока;
168
С — сжимаемость жидкости;
ф —взвешенная пористость;
Ро— начальное пластовое давление;
Р—текущее давление;
К— взвешенная проницаемость;
[л— вязкость;
tm— полный рассматриваемый период времени;
t — текущее время.
Так как данное уравнение применимо к неустановившемуся потоку в
бесконечной линейной системе, время следует выбирать так, чтобы волна
изменения давления не успевала достичь внешней границы пласта. Уравне-
ние следует упростить в соответствии с характером получаемых данных.
Внезапное соприкосновение льда с кромкой пластины аналогично мгновен-
ному снижению давления на внутренней границе линейного резервуара.
Данный метод и возможности оборудования не позволили снижать темпе-
ратуру ступенчато. Поэтому вместо ступенчатого решения было применено
единичное снижение давления в течение одного периода времени.
Вводя в уравнение аналог температуропроводности пласта k/C’^t,
получим
Q • (4)
Размеры модели будут доведены до размеров пласта путем введения
горизонтального масштаба — в 1 дюйме 1000 футов и вертикального мас-
штаба— в 1 дюйме 100 футов. Тогда площадь поперечного сечения пласта
будет в 400 000 раз больше модели. Было принято, что жидкость характе-
ризуется сжимаемостью 5,0-ИГ6 фунтов на квадратный дюйм, а ее вяз-
кость— 0,4 спз. Параметры пласта и жидкости затем были связаны с тер-
мальными свойствами путем приравнивания проводимости, выраженной в
Британских тепловых единицах: час. квадратный фут, градусы по Фарен-
гейту на фут; проницаемость k—в миллидарси, а член удельная теплоем-
кость— плотность полагали равным С[хср(10)6. Единственной переменной
величиной является в последней группе членов пористость, так как было
принято, что каждый слой заключает одну и ту же жидкость.
Время эксплуатации пласта принято равным 5000 час. Так как было
установлено, что на внешней границе пласта падения давления не проис-
ходит, то система может рассматриваться как бесконечная.
Медная пластина может рассматриваться как аналог пласта, имеющего
длину 12 000 футов, ширину 4000 футов, мощность 25 футов, пористость
25,5%, проницаемость 229 миллидарси, а свойства жидкости такие, как
об этом говорилось выше. Было принято, что начальное пластовое давле-
ние значительно превышает давление насыщения.
Свинцовая пластина представляет модель пласта тех же размеров, что
и предыдущая, полезной мощностью 22 фута, пористость которого — 10,9%,
а проницаемость — 23 маллидарси. Свойства жидкости и начальное пласто-
вое давление такие же, как и медной модели.
Расчет суммарного расхода жидкости производился при условии мгно-
венного снижения пластового давления на 100 фунтов на квадратный дюйм
на внутренней границе каждого из рассматриваемых пластов. Количество
жидкости, получаемое из пласта, имитируемого в виде медной пластины,
тогда составит
2-250-4000 (5-10-5)-255 т/' 0,33-3600-5000 1ПП спп .
-------------------- |/--------------100 =62 600 баррелей.
Аналогичным образом пласт, моделью которого является свинцовая
пластина, через 5000 час дает суммарный приток жидкости, равный 11 320 бар-
релей. Считая, что оба пласта разделены водоупором, получим, что сум-
169
Фиг. 8. Влияние слоя низкой про-
водимости на эффективную темпера-
туропроводность.
марное количество жидкости, представляющее сумму производительностей
каждого пласта в отдельности, составит 73 920 баррелей.
При расчете притока жидкости в данной системе для случая, когда
водоупор отсутствует, было использовано средневзвешенное значение по-
ристости. По уравнению (1) была рассчитана температуропроводность, в со-
ответствии с которой принято значение пьезопроводности моделируемого
пласта. При всех остальных факторах, оставшихся неизменными, приток
жидкости составил 76400 баррелей. Это составляет прирост 2480 баррелей
или 3,25% по сравнению с притоком жидкости для двух изолированных
друг от друга пластов. Это увеличение может быть объяснено тем, что по-
является переток из одного пласта в другой.
Третий слой, моделируемый метал-
лом Вуда, имеет термальные свойства,
пропорциональные проницаемости, рав-
ной 8,9 миллидарси, перистость 11,5% и
температуропроводность 0,028 футЧсек.
Мощность этого слоя 12 футов, а свой-
ства жидкости такие же, как и в двух
предыдущих моделях. Считая, что время
эксплуатации резервуара и падение дав-
ления такие же, как и раньше, полу-
чим, что приток составляет 3930 бар-
релей. Если этот пласт объединить с дву-
мя предыдущими, так чтобы получилась
трехслойная система, в которой имеет
место переток между пластами, то сум-
марный приток составит 84 200 баррелей,
в то время как сумма притоков для каж-
дого слоя в отдельности составляет все-
го 77 850 баррелей, то есть на 6350 бар-
релей, или 8,2%, меньше.
эугие гипотетические слоистые пласты, и
во всех случаях было получено, что суммарные притоки больше тогда,
Были проанализированы и
когда происходит переток жидкости в пластах.
Влияние слабопроводящего прослоя между слоями модели, характери-
зующимися относительно высокой проводимостью, показано нафиг. 8. Тем-
пературопроводность, замеренная со стороны алюминиевого слоя пластины,
вначале имеет большую величину, затем быстро падает и потом начинает
выравниваться — одновременно с тем, как наступает установившееся состо-
яние. Данные измерений, полученные со стороны пластины из нержавею-
щей стали, характеризуются в процессе опыта слабым изменением.
Крутой уклон кривой алюминиевой' пластины при небольших значениях
безразмерного времени происходит из-за меняющейся скорости перетока,
вызываемой большой разницей начальных температур между резиной и алю-
минием. Сталь по сравнению с алюминием сама характеризуется относитель-
но низкой проводимостью, и поэтому перепад температуры по ее мощности
относительно невелик.
Для определения влияния мощности слабопроницаемого прослоя на ре-
жим системы были проведены опыты на бронзовой, резиновой и стальной
пластинах. Толщина резины в первой серии опытов составляла 0,009 дюй-
ма и во второй серии опытов была увеличена до 0,106 дюйма. Полученные
результаты представлены на фиг. 9, А и Б. Данные, полученные для сис-
темы с тонким прослоем резины, аналогичны данным, полученным для
двухслойных систем. При этом отмечается только более отчетливое разли-
чие температуры в резиновом слое, то есть в резиново-бронзовой и резино-
во-стальной моделях, причем резина действует так, как если бы ее прово-
димость была выше, чем на самом деле.
170
Слой резины 0,106 дюйма вызывал большую начальную разницу тем-
пературопроводностей пластин. Эти результаты аналогичны результатам
для системы алюминий — резина— сталь.
На фиг. 10, А и Б показан безразмерный график зависимости разницы
температур по толщине пластины от времени. Максимальная разница, как
это видно, имеет место в начальный период времени вблизи источника. Пи-
ки отмечаются при значениях X ~ 0,8 — 0,6, причем на больших расстоя-
ниях от источника, чем эти, пиков не отмечается.
3.0г
2,0-
1,0;
j
Сталь
Резина
Бронза
0,116
0,106
0,250
Данные со стороны
бронзы
е>. "Q"" '" о— -.—--о
Данные со стороны
стало
02 0,3
Сталь Г7777777) 0,116
Резина 0009
'Броню еда
Время, мин
Фиг. 10. Изменение падения температуры
в слоистой системе.
Данные со стороны
Данные со стороны
стали
-
0,3
ОД
Фиг. 9. Влияние на температуропро-
водность изменения толщины слабопрово-
дящего материала между двумя металлами.
Влияние более толстого резинового слоя отчетливо проявляется в ран-
ние моменты времени. Если система рассматривается как слоистая толща,
разность давлений по краям которой составляет 200 фунтов на квадратный
дюйм, то пик, равный 0,165 безразмерного давления, будет соответствовать
разнице давлений по ширине пласта в 33 фунта на квадратный дюйм. Эта
разница будет находиться в 200 футах от депрессии давления, если счи-
тать, что длина рассматриваемой системы составляет 1000 футов. В систе-
ме с более тонким прослоем в той же самой точке и в то же самое время
разница составит 10 фунтов на квадратный дюйм. В более поздние моменты
времени это различие менее существенно.
Используя ту же аналогию для более поздних значений времени, бу-
дем иметь, что в более толстой и плотной зоне разница будет составлять
от 7 до 12 фунтов на квадратный дюйм, в то время как в тонкой плотной
зоне, максимальная разница составит 11 фунтов на квадратный дюйм вбли-
зи источника и от 2 до 6 фунтов на квадратный дюйм в остальных точках.
171
ЗАКЛЮЧЕНИЕ
В работе было получено экспериментальное подтверждение возможнос-
ти использования средних значений пористости, проницаемости и сжимае-
мости для слоистых пластов, в которых происходит межпластовое перете-
кание жидкости. Эти средние значения могут быть получены по уравнению
п
^=1------- (5)
п—1
(обозначения см. в тексте статьи).
Используя это уравнение, слоистый пласт, в котором происходит меж-
пластовый переток, можно представить как однородный и имеющий ту же
мощность и размеры, что и реальный пласт.
Особо следует подчеркнуть, что данные рекомендации применимы в том
случае, когда в пласте наступают условия квазиустановившегося движения,
так как эффективное значение проницаемости в начальный неустановивший-
ся период будет больше.
ЛИТЕРАТУРА
I. Ur е п L. С., 1927. Increasing Oil Recovery by Flooding, National Petrol. News, Aug.
3, 50.
2. L e v о r s e n A. I., 1956. Geology of Petroleum, W. H. Freeman and Co., San Francis-
co, 59.
3. M uska t M., 1950. The Effect of Permeability Stratifications in Complete Water-
Drive Systems, Trans., AIME, 189, 349.
4. Hurst W., van E ver dingen A. F., 1949. Application of the Laplace Trans-
formation to Flow Problems in Reservoirs, Trans., AIME, 186, 305.
5. Muska t M., 1937. The Flow of Homogeneous Fluids through Porous Media, McGraw-
Hill Book Co., Inc., N. Y., 139.
6. L a n d r u m B. L., С r a w f о г d P. В., 1959. A New Experimental Model for Stu-
dying Transient Phenomena, Trans., AIME, 216, 33.
7. C a r s 1 a w H. S., J a e g e r J. C., 1947. Conduction of Heat in Solids, Oxford U.
Press, 7.
8. В о w m а п С. H., C r a w f о r d P. B., A Mathematical Study of Unsteady-State,
Single-Phase Flow in Petroleum Reservoirs, Unpublished report, TPRC.
9. International Critical Tables (1929).
10. M c A d a m s W. H., 1942. Heat Transmission, Second Ed., McGraw-Hill Book Co.,
Inc., N. Y.
11. Handbook of Chemistry and Physics, 24th Ed., Chemical Rubber Publishing Co.
Б. Л. Ландрум, Д. А. Фланаган, Б, Норвуд, П. Б. Крофорд
НОВАЯ ЭКСПЕРИМЕНТАЛЬНАЯ МОДЕЛЬ ДЛЯ ИЗУЧЕНИЯ
НЕСТАЦИОНАРНЫХ ЯВЛЕНИЙ1
ВВОДНЫЕ ЗАМЕЧАНИЯ
Разработка методов изучения режима фильтрации в нефтяных коллек-
торах часто связывалась с приложением концепций об электрическом и те-
пловом движении к фильтрации жидкостей в пористых средах. Широкое
использование задач электрического и теплового движения основано на
имеющихся математических решениях, применимых ко многим проблемам,
касающимся нефтяных пластов. Относительно легкое измерение электричес-
кого тока привело к широкому применению и использованию потенциомет-
рической модели для решения фильтрационных задач.
При работе с потенциометрической моделью ограничивались изучением
условий установившегося движения, так как в этом случае имеет место
мгновенная реакция электрического тока на изменение в напряжении. Элек-
трическая аналогия — один из наших наиболее полезных методов для
изучения определенных фаз режима неустановившегося движения [1].
С другой стороны, не существует приближенных методов для опреде-
ления давлений в бассейне неправильной формы во время начального пе-
риода сработки запасов.
Течению тепла, подобно фильтрации жидкости, присуще неустановив-
шееся движение. Описываемая модель сконструирована с использованием
этих особенностей натурных неустановившихся явлений в передаче тепла,
измеримых в лабораторных условиях, для замены нестационарной фильтра-
ции жидкости в бассейне со скважиной, работающей при самоизливе.
Металлическая пластина, подобная бассейну, для изучения нагревалась
источником«скважиной». Температура в пластине увеличивается анало-
гично падению напора в полевых условиях, если в рассматриваемом пласте
производится сработка запасов или если напоры увеличиваются, когда жид-
кость нагнетается в пласт.
Цель этих исследований — изучение возможности использования естест-
венной нестационарной теплопроводности для моделирования неустановив-
шегося режима фильтрации. Следует полагать, что эта новая методика
окажет помощь в понимании одной из наиболее сложных проблем инже-
нерного изучения нестационарных явлений в коллекторах подземных вод.
АНАЛОГИЯ МЕЖДУ ПРОЦЕССАМИ ФИЛЬТРАЦИИ ЖИДКОСТИ
и передачи тепла
Тождественность уравнений, которые отражают законы фильтрации
жидкостей в пористых средах и передачу тепла в твердом теле, хорошо
известна [5]. Скорость фильтрации жидкостей определяется по закону
1 В. L. L a n d г u m, D. A. F 1 а п a g а п, В. Norwood, Р. В. Cr a w-
ford, A newexperimental model for studying transient phenomena, Petrol. Trans., AIME,
216, 33—37, 1959.
173
Дарси [3]:
-----А
и - — Ар,
fJL 1
(1)
а скорость передачи тепла по Фурье:
^== —КЛАТ. (2)
Комбинируя уравнение (1) с уравнением неразрывности для сжимаемой
жидкости (6), имеем
А • ( ргм) = — ф (3)
и в результате получаем уравнение
Д2 0 ? с Iх. .g.Р.с_ (4)
1 r k dtr ' '
Выражаем о по закону сжимаемости:
Р, =• Ро (5)
Раскрывая в формуле (5) экспоненциал и пренебрегая порядком ср вы-
ше единицы, получим
' k dtr ' ’
С другой стороны, объединяя уравнение (2) с уравнением сохранения
энергии при передаче тепла в однородном изотропном твердом теле [2],
получаем
А2Т ' 'У , (7)
a dim v 1
где а =- Кр<>тСт. Подобие уравнений (6) и (7) очевидно.
Уравнения будут в точности совпадать, если ввести следующие без-
размерные группы величин:
(8)
Pi — р® 1D
т.-т ___т . (9)
Т 'Р л и ? * / 1 w
X - V Lr D ’ У z ~ГГ ' т; " ZI> ’ (10)
L 1) ' Lm Y-=Y • Z ::Z I D ’ / D • Lm cm (H)
Лабораторная модель должна быть выдержана в надлежащем масшта-
бе, чтобы XD = XD , Yd == yD К ZD=zD. Кроме того, обозначим kt. --/Л1 02) ac\>. Lr ^>1 v ’
и X -l№ (13) Уравнения (6) и (7) запишем в виде др А2Р-дуА (14) D1
и дТ (15)
174
Приравнивая tM и 1т, найдем условие подобия тепловой модели и по-
тока в бассейне
& г а
Фс Lr L/n
ТЕПЛОВАЯ МОДЕЛЬ
Для моделирования резервуара использовалась латунная пластина
толщиной V8 дюйма (фиг. 1). Скважина моделировалась медной трубкой
диаметром % дюйма, впаянной в пластину. Пластина нагревалась цирку-
ляцией горячей воды через трубку, а предварительно на пей задавалась
постоянная температура 100°F. Потери на конвекцию и радиацию были
сведены к минимуму изоляцией пластины 2-дюймовыми слоями стеклянной
ваты. Эквипотенциали, характеризующие теплоотдачу пластины при нагре-
вании водой, имеющей температуру ISO F', и при охлаждении ее водой,
имеющей температуру 50 F, зеркально совпали. Сопоставление данных мо-
делирования при повышении и понижении температуры позволило устано-
вить, что ошибка в измерениях температуры была менее 3?о:
Температура воздушной ванны вблизи пластины поддерживалась с точ-
ностью 0,1 C'F. Колебания температуры циркулирующей воды поддержива-
лись в пределах 2,0‘F. Температура пластин замерялась медно-константа-
новой термопарой. 16-точечной самописец позволял проводить измерения в
одной точке каждые две секунды. Отклоняющееся приспособление позво-
ляет записывать температуры в 32 различных точках модели пласта. Тем-
пературы на пластине определялись с точностью в пределах 0,2rF.
МАСШТАБИРОВАНИЕ
Воображаемый резервуар, выбранный для иллюстрации использования
тепловой модели (фиг. 1), имел следующие характеристики:
Длина — 10900 футов.
Ширина 6400 футов в самой широкой части.
Площадь — 1160 акров.
Пористость — 25%.
Объем жидкости — 1950 баррели!акр-фут.
Сжимаемость жидкости — 5,3 (10-4) атм~\
Проницаемость _ дарси
Вязкость ’ спз
Пластина модели, сконструированная для замены естественного бассей-
на, имела следующие характеристики:
Длина—10,9 дюйма.
Ширина — 6,4 дюйма в самой широкой части.
Площадь — приблизительно 50,6 квадратного дюйма.
Температуропроводность — 0,333 смЧсек.
Для определения масштаба времени было использовано уравнение (16):
г ____ а
» с ч. L~ L?
‘ ' г tn
И
L2
У- j
lr -
откуда /,“ 2445 сек полевого времени/сек лабораторного времени.
175
Эквилотенциали Линии тока
Эквилотенциали Линии тока
Фиг. I и 2. Эквилотенциали и линии тока через 66 час сработки
запасов пласта.
Для определения давления в бассейне, соответствующего определенной
температуре пластин, приравниваются уравнения (8) и (9):
Pt — Р Tj~T
Pi Pw Т i T'w
или
i т__т \
Р —
\ * i * w /
Если, например, Т ; 140Т, то
р = 1700 — (1700—1000) - 1560 psi.
\ 150—100 / 7
Среднее давление бассейна (средневзвешенное давление, найденное
планиметрированием карты изобар) можно получить по выражению
-----^pd-A---------- (17)
’ общая площадь
Объем отбираемой жидкости определялся умножением величины
с^Р; — р) на объем резервуара.
ВЫВОДЫ по ИССЛЕДОВАНИЯМ БАССЕЙНА
Фиг. 1 и 2 демонстрируют эквипотенциали и линии тока при сработке
запасов жидкости для двух положений скважины примерно через 66 час
работы. В левой половине каждой фигуры даны величина и положение эк-
випотенциалей. Справа, во второй половине, показаны линии тока, постро-
енные перпендикулярно к линиям равного напора.
Форма линий равного напора для каждого положения скважины сви-
детельствует о радиальном потоке вблизи скважин, причем во втором
176
UpUMCmpb’
модели
1500
Mu -
вино тснции/1&
----1500-
Ю20-
Эквипотенциали Линии тона
"80
'гго
'520
,5О07ш
(<.60 ——
№0
№20 —~~
ноо ч
т йаГ1
шо
пго -
1300
кво
'Зю
'380
[)--10,9 дюйма
Принятые условия
в пласте
f-0,25
/5-5,3(10} ^атм-1
L ’ ID900 (рутов
дарси
сантипуаз
-
1550 —
1556'
Ф и г. 3 и 4, Эквипотенциали и линии тока через 200 час сработки
запасов пласта.
туп _
W
'220
I2M
'"/О
"80
ш
- то
то —
— ПО)
'080
!0Ю
Эквипотенциали Линии тока
Зкытотенииали Линии тока
Параметры
модели
Л -0,333 см2/сек
О-Ю,9 дюйма
Принятые условия
в пласте
f~- 0,2b
/3- 5,3 (Ю/4 атм-’
L--10900 футов
_2е дарси
’ сантипуаз
1060-
7о?<7
1260-
1300
Ф и г. 5 и 6. Эквипотенциали и линии тока через 660 час сработки
запасов пласта.
случае фильтрация остается радиальной на несколько больших расстояниях
от скважины.
Сравнение фиг. 1 с фиг. 3 и 5 и фиг. 2 с фиг. 4 и 6 показывает, что
эквипотенциали и линии тока, соответствующие им при том же положении
в бассейне, изменяют форму. В частности, при сработке запасов главным
становится приток в скважину жидкости за счет направлений из более ши-
роких частей бассейна.
Среднее давление для положения скважины 2 во всех случаях ниже
в период исследований сработки запасов. Через 100 час работы средние
напоры для положения скважин 1 и 2 около 1540 и 1440 psi соответст-
венно. Среднее давление понижается до 1290 и 1160 psi через 400 час
работы. К концу периода исследований (порядка 3000 час или 4 месяцев)
среднее давление было 1020 и 985 psi. Ясно видно, что положение сква-
жины 2 более благоприятно для достижения быстрой сработки запасов
жидкости в бассейне, поскольку оно обеспечивает более высокую совокуп-
ную производительность, чем та, которая достигается в скважине 1 на всех
этапах исследований.
РЕЗЮМЕ
Была рассмотрена аналогия между фильтрацией жидкостей в пористых
средах и передачей тепла в твердом теле. Дано аналитическое обоснование
этой аналогии.
Линии равного напора и линии тока были представлены для двух по-
ложений скважины и нескольких периодов работы. Данные показывают,
каким образом тепловую модель можно использовать для прогноза распре-
деления напоров при неустановившемся движении, среднего падения дав-
ления, совокупной производительности нефти и дебита для пласта, разра-
батываемого при режиме самоизлива.
Тепловая модель представляет новое приближение к решению одной
из многих сложных проблем, касающихся изучения добычи нефти.
Условные обозначения
рда-~ давление в скважине;
р — среднее давление в бассейне, определяемое по уравнению (17);
qh-—скорость передачи тепла;
Idi~ безразмерное время, определяемое по уравнению (12);
Д>2 — безразмерное время, определяемое по уравнению (13);
tm — лабораторное время;
tr — время в бассейне;
и — скорость фильтрации жидкости;
х, у, г — общее положение переменных;
Х/>, Ро, Zd—безразмерное положение переменных для бассейна;
Ст —удельная теплота;
К — теплопроводность;
Lm~~ длина модели;
Lr -длина бассейна;
Тр — безразмерная температура, определяемая по уравнению (9);
Тг— начальная температура пластин;
Тда — температура скважины на модели;
X, Y, Z — общее положение переменных для модели;
Хл, Yd, Zd—безразмерное положение переменных для модели;
а — температуропроводность;
р0 — первоначальная плотность жидкости;
рг - плотность жидкости;
рт—плотность модели;
Р — вязкость.
178
ЛИТЕРАТУРА
1. Bruce W. А., 1943. Electrical device for analyzing oil reservoir behavior, Trans.,
AIME, 151, 112,
2. Carsl a w H. S., J a e g e r J. C., 1947. Conduction of heat in solids, Oxford Univ.
Press., 7.
3. Darcy II., 1856. Les fontaines publiques de la Ville de Dijon, Victor Dalmont, Paris.
4. Four ier J. B. J., 1878. Theorie analytique de la chaleur, Paris (1822), Eng. Trans.
(Freeman), Cambridge.
5. Muska t M., 1937. The flow homogeneous fluids through Porous Media, McGraw-
Hill Book Co., Inc., N. Y„ 139.
6. M u s к a t M., 1949. Physical principles of oil production, McGraw-Hill Book Co.,
Inc., N. Y., 188.
СОДЕРЖАНИЕ
Предисловие ...................................... . . . . 5
С. Ирмей. О теоретических основах формул Дарси и Форхгеймера. Перевод с анг-
лийского В. С. Алексеева................................. 7
Н. И. Лущинский. О напорах и фильтрации грунтовых вод с переменной плотно-
стью. Перевод с английского В. С. Алексеева..............15
М. С. Хантуш. Анализ данных опытных откачек из скважин в водоносных горизон-
тах с перетеканием. Перевод с английского В. В. Данилова.27
М. С. Хантуш. Новое в теории перетекания. Перевод с английского В. В. Данилова 43
М. С. Хантуш. Неустановившийся приток подземных вод к скважине, несовершен-
ной по степени вскрытия. Перевод с английского В. С. Алексеева и В. В. Да-
нилова ......... . ................ 61
М. С. Хантуш. Движение подземных вод в пластах переменной мощности. Перевод
с английского В. В. Данилова и В. С. Алексеева ...............85
М. С. Хантуш. Экономически рациональное расположение взаимодействующих сква-
жин. Перевод с французского В. В. Данилова....................95
Р. Е. Коллннс. Определение расхода фильтрующейся жидкости в любом сечении
пласта при откачке из скважин в условиях упругого режима. Перевод с анг-
лийского В. С. Алексеева и В. В. Данилова ............. 107
Г. Шнеебели. Использование воздуха для измерения проницаемости ненасыщенных
аллювиальных отложений. Перевод с английского В. В. Данилова.122
И. Халеви и А. Нир. Определение параметров пласта при помощи радиоактивных
индикаторов. Перевод с английского В. С. Алексеева ......... 131
Э. Дж. Фелнер. Определение проницаемости долинных отложений по данным цик-
лических колебаний речных и грунтовых вод. Перевод с английского В. В. Да-
нилова .......................... 139
Д. А. Крайенгофф ван де. Лер. Исследование в фильтрационном лотке влияния зо-
ны неполного насыщения на неустановившееся движение подземных вод со
свободной поверхностью. Перевод с английского В. В. Данилова.145
Ч. X. Пиккеринг, Н. Т. Котмэн, П. Крофорд. Изучение движения подземных вод в
слоистых толщах с помощью тепловой модели. Перевод с английского
В. В. Данилова ........................ 162
Б. Л. Ландрум, Д. А. Фланаган, Б. Норвуд, П. Б. Крофорд. Новая эксперимен-
тальная модель для изучения нестационарных явлений. Перевод с английско-
го В. С. Алексеева......................................... 173
ВОПРОСЫ ГИДРОГЕОЛОГИЧЕСКИХ РАСЧЕТОВ
Редактор Д'. Af. Свет
Художник С. К- Милиниса
Художественный редактор Е. И. Подмарькова
Технический редактор А. Д. Хомяков
Корректор К. Г. Кривда
Сдано в производство 27/V 1964 г. Подписано к печати 23/IX 5964 г. Бумага ZOxIOSVjs --5,63 бум. л.,
15,4! печ. л. Уч.-нзд. л. 13. Изд. № 5/1755. Цена 1 р. 06 к. Зак. 368,
Издательство «МИР», Москва, 1-й Рижский пер., 2.
Ярославский полиграфкомбинат Главполиграфпрома Государственного комитета Совета Министров СССР
по печати Ярославль, ул. Свободы, 97.