Автор: Кузнецов Н.С.
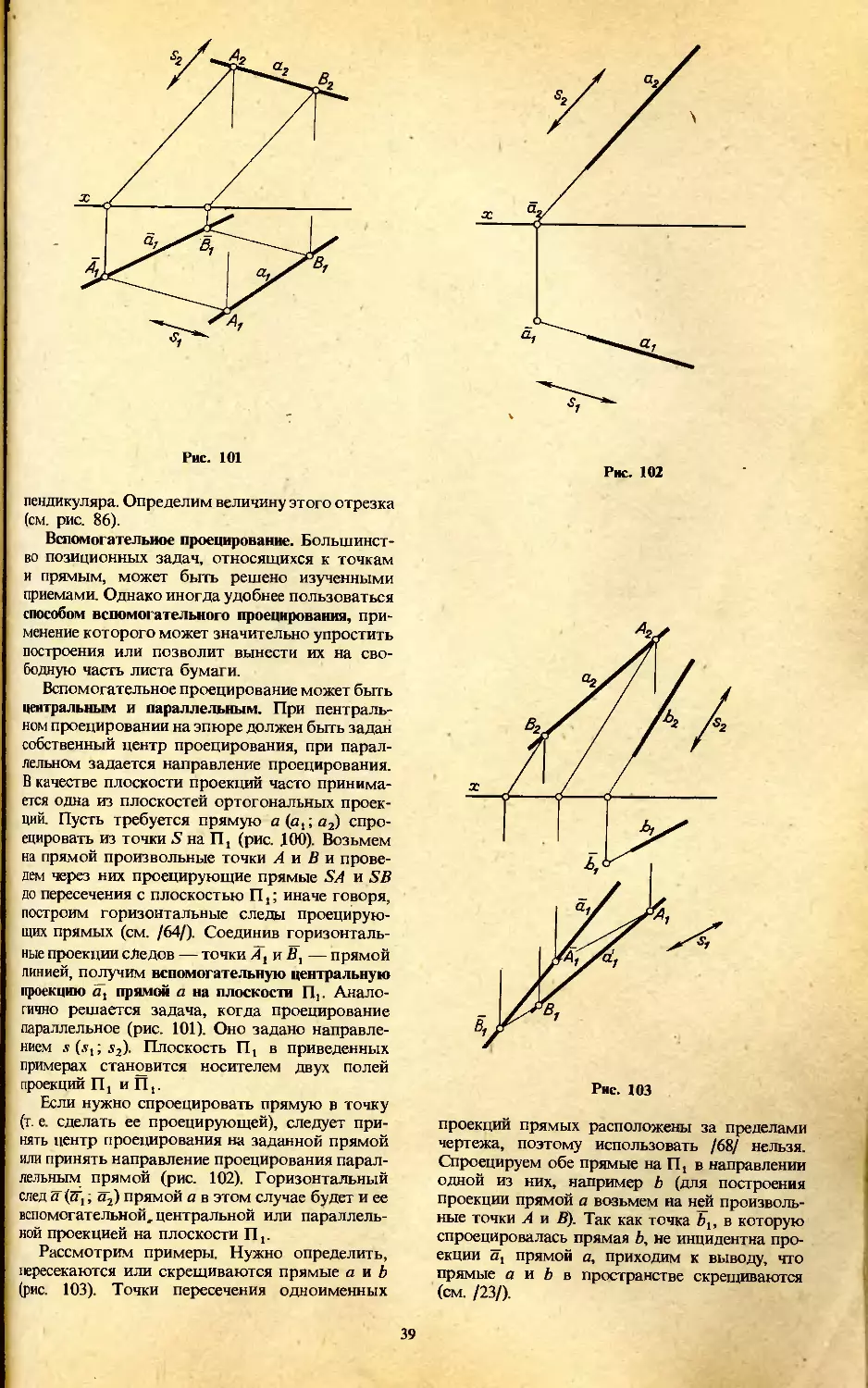
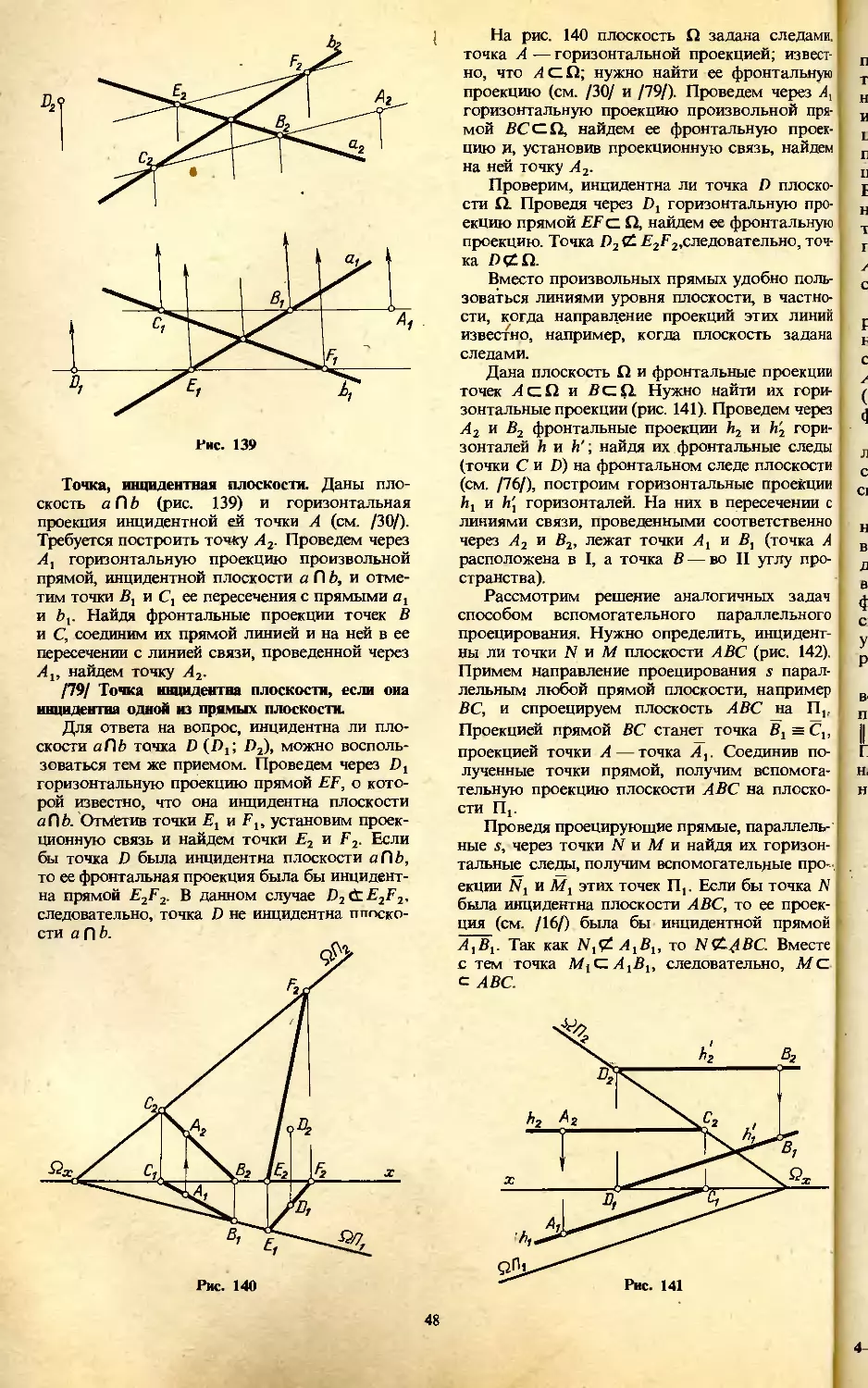
Теги: математика геометрия топология строительство инженерная графика начертательная геометрия
Год: 1981
Текст
Н.С. Кузнецов
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Н. С. Кузнецов
Н АЧ ЕРТАТЕЛЬН АЯ
ГЕОМЕТРИЯ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебника для студентов строительных
специальностей вузов
МОСКВА, «ВЫСШАЯ ШКОЛА»,
1981
ББК 22.151.3
К 89
УДК 515
Рецензент — проф. Московского архитектурного
института — Соболев Н. А.
БИБЛИОТЕКА
Ставропольского
политехнического пяетрту~а
Кузнецов Н. С.
К 89 Начертательная геометрия: Учебник
для вузов. — 2-е изд., перераб. и доп. —
М.: Высш, школа. 1981. — 262 с., ил.
1 р. ю к.
В книге изложен метод проецирования, позволяющий стро-
ить изображения пространственных фигур на плоскости. Рас-
сматриваются изображения, построенные на основе параллель-
ного и центрального проецирования (ортогональные, аксоно-
метрические проекции, проекции с числовыми отметками и
перспектива), а также тени. Даны способы решения позиционных
и метрических задач на проекционном чертеже.
Материал, приведенный в книге, соответствует программе
по начертательной геометрии для строительных специальностей
вузов, утвержденной Министерством высшего и среднего спе-
циального образования СССР.
Настоящее, второе издание книги переработано с учетом
опыта использования в учебном процессе первого издания.
Предназначается для студентов строительных специально-
стей высших учебных заведений.
20201—273
К----------76—81
001(01)—81
1702040000 515
ББК 22.151.3
© ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА». 1981
ОГЛАВЛЕНИЕ
Предисловие 4
Глава I. Введение ... .6
§ 1. Метод проецирования 6
§ 2. Проекции фигур . . . ... 9
§ 3. Некоторые свойства параллельных про-
екций ... 14
§ 4. Гомология .......................... 16
§ 5. Некоторые графические построения 20
Часть первая
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
НА ДВУХ И БОЛЬШЕМ ЧИСЛЕ
ПЛОСКОСТЕЙ
Глава II. Точка и прямая
§ 6. Точка.............. . . 26
§ 7. Прямая . . 31
§ 8. Две прямые . 35
Глава III. Плоскость
§ 9. Положение плоскости в пространстве 40
§ 10. Взаимное положение плоскостей . . 50
§11. Взаимное положение прямой и плоско-
сти общего положения 56
Глава IV. Поверхности
§ 12. Кривые линии....................... 67
§ 13. Кинематическое образование поверхно-
стей ... 72
§ 14. Линейчатые поверхности . 73
§ 15. Поверхности вращения .... 78
§ 16. Поверхности второго порядка ... 80
§ 17. Поверхности с переменной образующей 89
§ 18. Винтовые поверхности............... 90
§ 19. Поверхности, задаваемые каркасом
(каркасные поверхности) .... 93
1 лава V. Преобразования
§ 20. Плоскопараллельное перемещение . . 94
§ 21. Вращение вокруг осей, перпендикуляр-
ных плоскостям проекций ................. 96
§ 22. Вращение вокруг осей, параллельных
плоскостям проекций (совмещение с
плоскостями уровня).................. . . 99
§ 23. Вращение вокруг осей, лежащих, в пло-
скостях проекций (совмещение с пло-
скостями проекций) ... 100
§ 24. Гомологические проебразования 102
§ 25. Развертывание поверхностей . . 105
Глава VI. Пересечение поверхностей
§ 26. Пересечение поверхности и плоскости
(сечение)............................... 111
§ 27. Плоскости, касательные к поверхно-
сти ......................... . 120
3
1*
§ 28. Пересечение прямой и поверхности 122
§29. Пересечение поверхностей между собой 131
§ 30. Пересечение кривой линии с поверх-
ностью .... 146
Часть вторая
ПАРАЛЛЕЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ
ПРОЕКЦИИ НА ОДНОЙ ПЛОСКОСТИ
Глава VII. Проекции с числовыми отмет-
ками
§ 31. Точка и прямая -линия . 148
§ 32. Плоскость . . . ., ......... 151
§ 33. Поверхность 155
§ 34. Топографическая поверхность . 163
§ 35. Пересечение поверхностей ........... 167
Глава VIII. Аксонометрические проекции
§ 36. Определения и понятия .... 176
§ 37. Прямоугольная аксонометрия . . . 180
§ 38. Косоугольная аксонометрия . . 186
§ 39. Построение аксонометрии фигур . 188
§ 40. Построение аксонометрии по заданным
условиям ......................... 194
§ 41. Решение некоторых задач в аксономет-
рии ....................... .... 197
Глава IX. Перспективные проекции
§ 42. Определения и понятия............... 200
§ 43. Перспектива прямой линии частного
положения................................ 202
§ 44. Перспектива точки................... 206
§ 45. Построение отрезка заданной длины и
деление отрезка в заданном отношении 208
§ 46. Перспектива плоской фигуры ... 211
§ 47. Взаиморасположение фигур 218
§ 48. Перспектива тел..................... 219
§ 49. Выбор точки зрения и картинной пло-
скости .............................. 224
§ 50. Центральная аксонометрия............ 228
§ 51. Реконструкция перспективного изобра-
жения . . .......... ... 231
Глава X. Проекции теней
§ 52. Определения и понятия . 235
§ 53. Проекции теней при параллельном про-
ецировании ....................... 236
§ 54. Тени в проекциях с числовыми отмет-
ками ........................... . . . 249
§ 55. Проекции теней при центральном про-
ецировании . . . 251
Литература ............. . . 260
Предметный указатель . . ......... 261
ПРЕДИСЛОВИЕ
Любая математическая дисциплина, изучае-
мая в техническом вузе, призвана дать в руки
будущих инженеров аппарат, с помощью ко-
торого можно решать инженерные задачи. Аппа-
ратом начертательной геометрии является чер-
теж — графическая модель существующих или
задуманных предметов реального мира. Как и
всякая модель, чертеж позволяет изучать неко-
торые свойства моделируемого предмета и
решать задачи, относящиеся к нему. Так, про-
ведя необходимые построения, можно по черте-
жу определить внутреннюю форму какого-либо
предмета, нс прибегая к необходимости разре-
зать этот предмет пилой. Начертательная гео-
метрия устанавливает законы, по которым не
только выполняются графические модели —
чертежи, но и позволяющие получить по черте-
жу знания, которые полностью или с неко-
торыми поправками можно отнести к изобра-
женным предметам. На чертежах можно решать
различные позиционные и метрические задачи,
связанные с проектированием зданий, сооруже-
ний и машин. При этом имеется в виду, что
проведенные на плоскости чертежа построения
отражают соответствующие операции в про-
странстве.
Так как законы начертательной геометрии
позволяют изображать не только существую-
щие, но и задуманные предметы, то изучение
этой науки способствует развитию простран-
ственного воображения — умения человека мыс-
ленно представить форму, размеры, пропорции,
положение в пространстве и другие свойства
различных предметов, — без которого невоз-
можна творческая инженерная деятельность.
Как и другие отрасли математики, начер-
тательная геометрия развивает логическое мыш-
ление, способствует решению инженерных
задач.
Современное состояние науки и техники
позволяет выполнять чертежи любой сложно-
сти различными графопостроителями с по-
мощью ЭВМ — электронно-вычислительных
машин. В нашей стране существуют проектные
организации, использующие совершенную тех-
нику для этой цели. Однако чтобы научиться
составлять программы для ЭВМ, по которым
графопостроители выполняют чертежи, необ-
ходимо знать способы построения изображений
и уметь выполнять различные операции с ними
вручную с помощью чертежных инструментов.
Эти способы изложены в соответствующих раз-
делах курса начертательной геометрии.
Настоящий курс соответствует программе
по начертательной геометрии для строитель-
ных специальностей вузов. Он состоит из «Вве-
дения» и трех частей. «Введение» содержит тео-
ретические сведения, необходимые для изучения
последующего материала. Часть первая «Орто-
гональные проекции на двух и большем числе
плоскостей» является общей для всех техниче-
ских вузов; части вторая «Параллельные и
центральные проекции на одной плоскости» и
третья «Проекции теней» соответствуют спе-
цифике строительных специальностей. Необхо-
димый объем и содержание знаний по разделам
начертательной геометрии для студентов раз-
ных строительных специальностей различен.
Поэтому автор стремился так излагать ма-
териал, чтобы отдельные разделы в соответ-
ствии с рабочей программой кафедры могли
изучаться полнее за счет других разделов, ко-
торые изучать следует менее подробно.
Второе издание книги переработано с учетом
опыта ее использования в течение шести лет в
ряде вузов страны, а также рекомендаций пре-
подавателей, за которые автор приносит боль-
шую благодарность.
В книге приняты следующие условные обо-
значения фигур и их взаиморасположения.
4
Обозначение фигур
Фигура Обозначение Пример Расшифровка обозначения в примере
Точка Прописная буква латин- А, В, С, Точка А, точка В, точка С
Линия, в том числе прямая; ского алфавита или цифра Строчная буква латин- 1, 2, ... а, Ь, сл ... Точка 1, точка 2 Прямая а, ломаная Ь, кри-
при задании прямой точ- ками; отрезок, дуга Ловерхность, в том числе пло- ского алфавита Прописная буква гречес- АВ, ... АВ, АВС, ... О, X, ... вая с Прямая АВ Отрезок АВ, дуга АВС Плоскость О, поверхность S
скость; при задании плоскости точками; при задании плоскости прямыми Плоскость и поле проекций кого алфавита Прописная буква «пи» АВС, ... tl(afLb),... П, П', П,, П°, ... Плоскость АВС Плоскость £2, заданная пере- секающимися прямыми а и b Плоскость (поле) проекций
Фигура (обычно поверхность греческого алфавита Прописная буква «фи» Ф П П' — штрих, П] — один, П° — ноль Фигура Ф (например, эллип-
или тело) Угол линейный греческого алфавита Строчная буква грече- а, Р, ... соид Ф) Угол а, угол Р
Проекция фигуры обозначав ского алфавита тся той же буквой, А ] — проекция точи и А на плоскости П,
что и фигура, но с индексом плоскости (поля) проск- аг — проекция прямой а на плоскости 112,
ций или со «штрихом». Например: <23 — проекция плоскости <2 на плоскости П3
Знаки взаиморасположения фигур
Знак Смысл знака Пример Расшифровка знака в примере
л Пересечение а ПЬ Прямая а, пересекающаяся с прямой b
силиэ Инцидентность Аса Точка А инцидентна прямой а (прямая а инцидентна точке А), прямая а и точка А инцидентны
II Параллельность а || й Прямая а Параллельна плоскости Г2
X Перпендикулярность О ХЕ Плоскости £2 и Е взаимно перпендикулярны
12 Касание a Lib Прямая а касается окружности b
= 1. Результат 2. Равенство а Г\Ь = А АВ = CD Точка А есть результат пересечения прямых а и b Отрезок АВ равен отрезку CD
= Совпадение А=В Точка А совпадает с точкой В
/ Отрицание (не) Аса а ЖЬ Точка А не инцидентна прямой а Прямые а и b не параллельны
Примечание. Не приведенные в таблице обозначения и знаки разъясняются в тексте
5
ГЛАВА I
ВВЕДЕНИЕ
§ 1. МЕТОД ПРОЕЦИРОВАНИЯ
Проекцированные изображения. Чтобы по
изображению составить суждение о форме и
положении в пространстве какого-либо предме-
та, нужно, чтобы изображение обладало опре-
деленными свойствами.
Обратимость — свойство изображения, по-
зволяющее по нему однозначно восстановить
действительную форму, размеры предмета и
его положение в пространстве; это свойство
служит тому, чтобы по изображению можно
было изготовить предмет, например по проекту
построить здание. Графическое изображение,
обладающее свойством обратимости, называется
чертежом;
наглядность — свойство изображения, вызы-
вающее в мозгу зрителя пространственное пред-
ставление о предмете; высшей формой нагляд-
ности является естественность; зрительное суж-
дение о предмете по его естественному изобра-
жению близко к тому, которое возникает при
рассматривании самого предмета; естествен-
ность изображения особенно важна в архитек-
турно-строительной практике, когда по изоб-
ражению оцениваются эстетические достоинства
проектируемого объекта;
единство условностей, принятых при выпол-
нении изображения; они должны быть такими,
чтобы каждый специалист мог «прочесть» изоб-
ражение, выполненное другим лицом.
Самым естественным изображением явля-
ется перспектива (рис. 1). На перспективном
изображении наблюдаются явления, с которы-
ми мы встречаемся в жизни: параллельные ли-
нии кажутся пересекающимися, предметы по
мере их удаления от зрителя — уменьшающи-
мися и т. п. Такое изображение, однако, обла-
дает серьезным недостатком: без дополнитель-
ных, иногда довольно сложных построений по
нему нельзя установить размеры изображенного
предмета.
Изображения, выполненные с учетом неко-
торых условностей, которые будут разъяснены
позднее, даны на рис. 2 и 3. Это аксонометрии
(рис. 2) и чертеж, выполненный в ортогональных
проекциях (рис. 3).
Перспектива используется в основном в
архитектурно-строительной практике и при
проектировании автомобильных дорог, аксоно-
метрия и ортогональные проекции — во всех
областях науки и техники. Аксонометрия об-
ладает большей наглядностью, чем чертежи,
выполненные в ортогональных проекциях, но
уступает перспективе. По аксонометрическому
изображению можно выполнять некоторые из-
мерения непосредственно на чертеже Ортого-
нальные проекции менее наглядны, но удобны
для решения метрических (т. е. связанных с из-
менениями) задач.
Проецирование. Названные три вида изобра-
жений отличаются друг от друга, но построены
они по одному и тому же методу проецирования.
Рассмотрим пример, даны точка S — центр
проецирования, плоскость П — плоскость проек-
ций и точки А, В, С, Dm Е, изображения которых,
или их проекции на плоскости П, нужно по-
строить (рис. 4).
Соединив точки А и S прямой линией, на-
зываемой проецирующей прямой, отметим точ-
ку А' ее пересечения с плоскостью П Точка А’
является проекцией точки А на плоскости П,
построенной из центра проецирования S. Построе-
ния не изменятся, если центр проецирования
будет расположен между плоскостью проекций
и проецируемой точкой (точкой а).
/Г/ Чтобы построить проекцию точки, нужно
провести через нее проецирующую прямую и
определить точку ее пересечения с плоскостью
проекций.
В дальнейшем проецирующей будем назы-
вать любую прямую, проходящую через центр
проецирования.
Точка В принадлежит плоскости П или, что
одно и то же, плоскость П проходит через точ-
ку В. В этом случае говорят, что плоскость П
и точка В инцидентны* В символической записи
это выглядит так: В сП. Проекция точки В
совпадает с самой точкой. Используя знак сов-
падения =, запишем: В = В'. Точки С и D ин-
цидентны одной проецирующей прямой, по-
этому их проекции совпадают: D' = С
/2/ Любая точка, инцидентная проецирую-
щей прямой, проецируется в точку пересечения
этой прямой с плоскостью проекций.
Проекцию точки Е, если основываться на
представлениях евклидовой геометрии, постро-
ить нельзя, так как проецирующая прямая SE
параллельна П. Множество подобных точек
представляет собой плоскость £2, параллельную
П и называемую предельной плоскостью. Ниже
* Термин инцидентность удобен при изложении
материала, особенно в символической записи. Одна-
ко мы не будем отказываться и от широко принятых
выражений «прямая проходит через точку», «точка
лежит на прямой» и др
6
Рис. 1
мы узнаем, что можно строить проекции точек,
инцидентных этой йлоскости.
Через любую точку пространства можно
провести единственную проецирующую пря-
мую, которая пересекается с плоскостью про-
екций в одной точке. Исключение составляет
центр проецирования — через него проходит
бесчисленное множество проецирующих пря-
мых, что делает проекцию такой точки неопре-
деленной. Кроме того, центр проецирования
не может быть инцидентным плоскости проек-
ций, иначе проекции всех точек пространства
совпадут.
/3/ При данном центре проецирования и не
инцидентной ему плоскости проекций каждая
точка пространства (кроме центра проецирова-
ния) имеет единственную проекцию.
Множество точек пространства может спро-
ецироваться в одну точку только тогда, когда
все они принадлежат общей проецирующей
прямой.
Спроецируем на П прямую а (А; D), прямая а
задана точками А и D. Для этого через все ее
точки проведем проецирующие прямые и опре-
делим точки их пересечения с П. Множество
таких прямых представляет собой плоскость,
проходящую через центр проецирования и на-
зываемую проецирующей. Проецирующая пло-
скость пересекается с плоскостью проекций по
прямой а' (A'; D'), являющейся проекцией пря-
мой а на плоскости П, построенной из центра 5.
На этой прямой лежит и точка В'.
/4/ Чтобы построить проекцию прямой, нуж-
но провести через нее проецирующую плоскость
и определить линию ее пересечения с плоскостью
проекций.
Очевидно, что для построения проекции пря-
мой достаточно найти проекции двух ее различ-
ных точек и соединить их прямой линией.
Точка пересечения прямой с плоскостью
проекций называется следом прямой. След пря-
мой совпадает со своей проекцией, следова-
тельно, является точкой пересечения прямой и
ее проекции. В нашем случае это точка В = В'.
Кроме рассмотренного выше проецирова-
вания, называемого прямолинейным, использу-
ется криволинейное проецирование. Во втором
случае проецирующие линии — кривые. Кроме
того, проецировать можно не только на пло-
скость, но и на поверхность. В дальнейшем
мы будем изучать только прямолинейное прое-
цирование на плоскость.
Несобственные элементы пространства. Про-
ведем проецирующую прямую SF' | а. В точке F'
она пересекается с плоскостью П (рис. 4).
Рис. 3
Точка F' с позиций евклидовой геометрии не
является проекцией какой-либо точки прямой а.
так как прямые SF' и а параллельны. Предста-
вим себе, что проецирующая прямая SD сколь-
зит по прямой а (проходя все время через точ-
ку 5). По мере приближения точки D' к точке
F' точка D удаляется от точки В = В' ив пре-
деле уйдет в бесконечность. Это произойдет,
когда точки D' и F' совпадут. Следовательно,
точку F' можно рассматривать как проекцию
бесконечно удаленной точки F прямой а. Усло-
вимся, что на каждой прямой кроме обыкно-
венных (называемых собственными) точек есть
одна бесконечно удаленная, или несобственная.
7
точка, которую в дальнейшем мы ни в чем не
будем отличать от собственных точек прямой*.
В элементарной геометрии принято прямые
пространства делить на скрещивающиеся, пе-
ресекающиеся и параллельные. Пересекающиеся
прямые в отличие от скрещивающихся и парал-
лельных имеют общую точку. Что же произой-
дет, если общей для двух прямых станет несоб-
ственная точка? Оказывается, это возможно,
когда прямые параллельны. Построим из цент-
ра S (рис. 5) проекцию несобственной точки F
прямой а. Для этого проведем проецирующую
прямую SF || а и отметим точку F' ее пересече-
ния с плоскостью П. Предположим, что на пря-
мых b и d, лежащих в плоскости П и параллель-
ных а, есть свои несобственные точки S и F
Чтобы построить их проекции, нужно провести
проецирующие прямые, параллельные b и d;
но они совпадут с прямой SF'. Таким образом,
точка F' является проекцией несобственных
точек F, F и F", лежащих соответственно на
со ос со
прямых Ь и d плоскости D, что возможно
[см. (3)1, когда точки F, F и F совпадают.
1 х J СО со со
Следовательно, несобственная точка F прямых
a, b, d и других, принадлежащих плоскости Я
и параллельных им, является общей. Рассуждая
также относительно прямых ей f, параллельных
прямым а, b и d, лежащих в произвольной
плоскости L, убеждается, что и эти прямые
имеют общую несобственную точку F.
/5/ Параллельные прямые имеют общую не-
собственную точку, иначе говоря, параллельные
прямые пересекаются между собой в бесконеч-
ностя.
Прямая SF' параллельна прямым а, b и
d, , лежащим в плоскости Л, поэтому она
параллельна этой плоскости С прямыми а. b
и d, а следовательно, и с плоскостью Л прямая
SF пересекается в точке F
* При решении задач на измерение несобствен-
ные точки не всегда равноправны с собственными.
/6/ Прямая, параллельная плоскости, пере-
секается с иен в несобственной точке.
Множество несобственных точек всех пере-
секающихся прямых плоскости представляет
собой несобственную прямую этой плоскости.
Пусть даны плоскости Л, L и параллельные
прямые яСЛ и (рис. 6). В соответствии
с /5/ прямые а и b имеют общую несобственную
точку, которая является общей и для данных
плоскостей. Сказанное справедливо для любой
пары параллельных прямых, инцидентных соот-
ветственно плоскостям Л и S, следовательно,
эти плоскости имеют множество общих несоб-
ственных точек, т. е. несобственную прямую.
/7/ Параллельные плоскости пересекаются
между собой по несобственной прямой.
Множество несобственных прямых всех пе-
ресекающихся плоскостей пространства пред-
ставляет собой несобственную плоскость. В от-
личие от евклидовых прямая, плоскость и про-
странство, имеющие в своем составе несоб-
ственные соответственно точку, прямую и пло-
скость, называются проективными.
Теперь можно ответить на вопрос, где рас-
положена проекция точки Е на рис. 4. Проеци-
рующая прямая SE параллельна П, следова-
тельно, проекцией точки Е на этой плоскости
является несобственная точка Е' прямой SE.
На каждой прямой есть только одна несоб-
ственная точка. Чтобы представить себе это,
рассмотрим рис. 7. на котором проекция а’
прямой а построена на П из центра 5. Пусть
проецирующая прямая скользит по прямой а
так, что точка пересечения прямых удаляется
от следа прямой а — точки С = С вправо,
занимая последовательно положения В, D, ... .
Проекция точки пересечения (В', D', пере-
мещаясь по прямой а', удаляется от точки С = С'
вверх. Когда точка пересечения проецирующей
прямой и прямой а станет несобственной, про-
ецирующая прямая будет параллельной пря-
мой а и пересечется с П в точке F'.
Пусть теперь точка пересечения проецирую-
щей прямой и прямой а занимает последова-
8
Рис. 7
тельно положения А, Е, ... , удаляясь от точки
С=С' влево. Проекция точки пересечения (А',
Е',...) и в этом случае будет постепенно при-
ближаться к точке F'. Таким образом, в каком
бы направлении по прямой а ни удалялась точка,
принадлежащая прямой, ее проекция прибли-
жается к точке F', в конечном счете совпадая
СО
с нею. Но в соответствии с /3/ точка F' может
СО
быть проекцией единственной точки F. К ней
можно прийти, двигаясь по прямой в обе сто-
роны.
Каждая из прямых, изображенных на рис. 5
(a, b, d или t), определяет положение несобст-
венной точки F. Поэтому:
/8/, Чтобы указать положение несобствен-
ной точки, достаточно задать любую инцидент-
ную ей собственную прямую.
Введение несобственных элементов про-
странства не исключает изучения свойств про-
екций параллельных прямых и плоскостей
Любое множество точек будем называть
фигурой. К фигурам относятся точка (множест-
во, состоящее из одного элемента), прямая или
кривая линия, поверхность (в том числе пло-
скость), тело (часть пространства, ограничен-
ная замкнутой поверхностью). Плоской назо-
вем такую фигуру, все точки которой можно
совместить с плоскостью*. Пространственной
будем называть фигуру, все точки которой
с плоскостью совмещены быть не могут. Часть
плоскости, ограниченную лежащей в ней зам-
кнутой линией, назовем отсеком плоскости,
такую же часть поверхности— отсеком по-
верхности.
Множество прямых плоскости, проходящих
через общую точку, будем называть пучком
прямых, а точку их пересечения центром пучка.
Центром пучка может быть как собственная,
так и несобственная точка. Во втором случае
прямые пучка взаимно параллельны. Множест-
во пересекающихся в одной точке прямых,
* Понятие «плоская фигура» к точкам и пря-
мым линиям не относят.
не инцидентных одной плоскости, называется
связкой прямых, а общая точка — центром связ-
ки. Центр связки может быть как собственной,
так и несобственной точкой. Множество пло-
скостей, проходящих через общую прямую
(собственную или несобственную), назовем пуч-
ком плоскостей, а линию их пересечения — осью
пучка плоскостей.
Множество всех точек плоскости называется
точечным полем. Проецируя на плоскость все
точки пространства, мы получим точечное поле
проекций, или, для краткости, поле проекций.
Если заменить центр проецирования и вновь
спроецировать на ту же плоскость все точки
пространства, получим новое, отличное от пре-
дыдущего поле проекций. Таким образом, одна
плоскость проекций может нести сколько угодно
различных полей проекций. Плоскость, на ко-
торой они расположены, называется носителем
этих полей.
§ 2. ПРОЕКЦИИ ФИГУР
Проекции плоских фигур. Сказанное выше
позволяет сделать следующие выводы:
/9/ Проекцией точки является точка (см. /1/).
/10/ Проекция прямой в общем случае пред-
ставляет собой прямую (см. /4/). Исключение —
проецирующая прямая, ее проекцией является
точка (см. /2/) — след прямой.
Отрезок прямой проецируется также в от-
резок прямой (на рис. 4 отрезок АВ проецируется
в отрезок А' В'), если он не принадлежит проеци-
рующей прямой.
/11/ Проекция фигуры представляет собой
множество проекций всех ее точек, т. е. тоже
фигуру.
Прямая а (рис. 8) параллельна П, следова-
тельно, пересекается с нею и со своей проекцией
в несобственной точке (см. /5/ и /6/); отсюда
а || а'.. Исключение — проецирующая прямая, па-
раллельная плоскости проекций. Ее проекция
совпадает с несобственной точкой этой прямой.
В частном случае, когда прямая инцидентна
плоскости проекций, она совпадает со своей
проекцией.
9
/12/ Если прямая параллельна плоскости, то
ее проекция на этой плоскости параллельна самой
прямой.
/13/ Плоскость в общем случае проецируется
на всю плоскость проекций, так как множество
проецирующих прямых, проходящих через все
точки проецируемой плоскости, пересекается
с плоскостью проекпий во всех ее точках.
/14/ Проецирующая плоскость проецируется
в прямую линию ее пересечения с плоскостью
проекций (так как все прямые, проецирующие
точки плоскости, инцидентны ей).
Линия пересечения плоскости с плоскостью
проекций называется следом плоскости, поэтому
проекция проецирующей плоскости совпадает
с ее следом.
Отрезки АВ, АС и ВС треугольника АВС
(рис. 9) проецируются из центра 5 соответст-
венно в отрезки А'В', А' С и В' С. Через все
точки отсека плоскости внутри ломаной АВС А
проходят проецирующие прямые, пересекаю-
щиеся с П в точках, расположенных внутри
ломаной А'В'С'А'.
15/ Плоская фигура проецируется также в
плоскую фигуру, если она не инцидентна проеци-
рующей плоскости.
Инцидентный плоскости Я отрезок А В с
(рис. 10) проецируется в отрезок А'В', плоская и
фигура, ограниченная замкнутой кривой а, — у
в отрезок CD'. Отрезок EF проецируется в
точку Е' = F' Оба отрезка и точка Е' = F' п
инцидентны проекции Я' плоскости Я. п
/16/ Проекция фигуры, инцидентной проекци- в
рующей плоскости, инцидентна проекции пло-
скости. к
Треугольник АВС (рис. 11) параллелен П'; е
его стороны проецируются на эту плоскость в
отрезки прямых, параллельных соответствен- в
ним сторонам треугольника (см. /12/). Следо- т
вательно, треугольники А ВС и А' В' С подобны с
и подобно расположены.
/17/ Если плоская фигура параллельна пло- ,
скости, то на эту плоскость она проецируется в ь
подобную ей н подобно расположенную фигуру. t
Кривая линия может рассматриваться как
предел некоторой ломаной, что позволяет рас- 4
пространить положение /17/ и на .нее.
Проекция угла. Проецируя угол а (ВАС) из (
центра S' на П' (рис. 12), мы получим его про- (
екцию — угол а', который может быть боль-
шим или меньшим угла а в зависимости от по- j
ложения центра проецирования и плоскости ,
проекций относительно сторон угла. В частном
случае а = а' Если центр проецирования инци-
дентен плоскости угла, возможны три варианта:
при центре S" вершина угла проецируется в
точку А"; проекцией угла а становится уго л 180°.
При центре S'" проекция вершины угла пред-
10
ставляет собой точку А"', а проекцией угла а
становится угол 0е. Если центр проецирования
инцидентен одной из сторон угла, проекция
угла вырождается* в полупрямую.
/18/ Проекция угла в зависимости от его рас-
положения относительно плоскости проекций н
центра проецирования представляет собой угол,
величина которого может меняться от 0 до 180 е.
19/ Проекция угла равна углу в случае,
когда его стороны параллельны плоскости про-
екций (см. /17/ и рис. 11)**.
Проекции пространственных фигур. Множест-
во прямых, проецирующих все точки кривой
линии а (рис. 13), представляет собой кониче-
скую проецирующую поверхность. Линия ее пе-
ресечения с плоскостью проекций (след поверх-
ности) является проекцией проецируемой ли-
нии, а вместе с тем и всей проецирующей по-
верхности.
/20/ Проекция пространственной кривой пред-
ставляет собой плоскую кривую.
/21/ Проекция проецирующей поверхности
совпадает со следом этой поверхности (сравните
с /2/, /10/ и /14/).
/22/ Проекция фигуры, инцидентной проеци-
рующей поверхности, инцидентная проекции этой
поверхности (сравните с /16/).
Если точка инцидентна прямой или кривой
линии, то ее проекция инцидентна проекции
этой линии, так как след плоскости или поверх-
ности, проецирующей линию, является мно-
жеством следов прямых, проецирующих точки
этой линии. Иначе говоря:
/23/ Если фигуры в пространстве инцидент-
ны, то инцидентны н их проекции. (Но не всегда
наоборот. См. пояснения к рис. 4 и /28/.) То, что
/23/ справедливо для любых фигур, будет видно
из последующего.
/24/ Пересекающиеся прямые проецируются
также в пересекающиеся прямые, причем точка
пересечения их проекций лежит на проецирующей
прямой, проходящей через точку пересечения
самих прямых (исключение — пересекающиеся
* Вырождается — значит теряет свои основные
признаки. Основной признак угла — существование
его сторон.
** Возможны и другие случаи, когда а = а
прямые, лежащие в проецирующей плоскости.
Почему?).
Изображенные на рис. 14 прямые а и b пере-
секаются в точке К. Эта точка инцидентна как
прямой о, так и прямой бив соответствии с /23
проецируется в точку К', принадлежащую пря-
мым а' и Ь'. Сказанное относится и к случаю,
когда в одной точке пересекаются множество
прямых (пучок или связка), следовательно:
/25/ Пучок нли связка прямых проецируется
в пучок прямых, причем центр пучка нли связкя
проецируется в центр пучка проекций прямых.
Тело П (рис. 15) проецируется в плоскую
фигуру О.'. Множество проецирующих прямых,
касающихся поверхности тела (например,
S/tU П)*, представляет собой коническую про-
ецирующую поверхность. Линию а соприкосно-
вения конической поверхности и поверхности
* U —знак касания.
1!
Рис. 16
тела назовем контуром тела. Он проецируется
в кривую а', ограничивающую фигуру
Такая кривая называется проекцией контура
тела. Если в центре проецирования расположить
глаз наблюдателя, он увидит тело в пределах
его контура, иначе говоря, при названных усло-
виях контур тела является границей его види-
мости. Видимой будем считать ту часть тела,
которая обращена к центру проецирования, не-
видимой — противоположную. Если заменить
центр проецирования, почти всегда изменится и
контур тела.
/26/ Поверхность или тело проецируется в
плоскую фигуру множеством проецирующих пря-
мых, проходящих через все точки проецируемой
поверхности или тела. Границей этой фигуры
является проекция контура тела.
Виды проекций. Центр проецирования может
быть как собственной, так и несобственной точ-
кой. В первом случае проецирование называется
центральным, во втором — параллельным. Про-
екции также носят название центральных и
параллельных. При центральном проецирова-
нии должно быть известно положение плоскости
проекций и центра проецирования, при парал-
лельном — положение плоскости проекций и
направление проецирования. Это направление
задают любой проецирующей прямой (см. /8/).
Параллельное проецирование может быть
прямоугольным, когда направление проециро-
вания перпендикулярно плоскости проекций, и
косоугольным, когда угол между направлением
проецирования и плоскостью проекций отли-
чен от прямого (но также и от утла 0°, так как
в этом случае несобственный центр проециро-
вания будет инцидентным плоскости проекций
(см. /6/), что недопустимо; см. /3/.
Прямая и обратная задачи. Прямая задача
начертательной геометрии заключается в по-
строении изображений (проекций) реально су-
ществующих или воображаемых предметов
Эта задача связана с творческой проектной ра-
ботой инженеров.
Решение обратной задачи позволяет опреде-
лить по изображению форму, размеры и поло-
жение в пространстве предмета, т. е. по чертежу
воспроизвести предмет в натуре. Всякий пред-
мет (фигура) представляет собой множество
определенным образом расположенных точек,
поэтому обе задачи — прямую и обратную —
можно решить, если знать, как построить про-
екцию точки или по ее проекции определить
положение точки в пространстве.
/27/ Положение проекции точки вполне опре-
деленно, если известно положение в пространстве
проецируемой точки, центра (направления) про-
ецирования н плоскости проекций (в соответст-
вии с /3/).
Проекция D' на рис. 4 не определяет поло-
жения точки D в пространстве, так как не только
точка D, но и точка С и любая другая точка
прямой SD проецируются на плоскость П в
точку D'.
/28/ Если известны одна проекция точки я
центр (направление) проецирования, положение
в пространстве проецируемой точки не может быть
определено, гак как ею может быть любая точка,
инцидентная проецирующей прямой, проходящей
через данную проекцию.
Пусть известны точки А' и А" —проекции
точки А на плоскости П", построенные из
центров S' и 5" (рис. 16). Чтобы определить
положение точки А в пространстве, достаточно
соединить прямыми точки А и S' и точки А"
и S". В пересечении прямых расположена точ-
ка А. В приведенном примере плоскость П
является носителем двух полей проекций П
и П".
Аналогично решается задача и при двух
плоскостях проекций П' и П" (рис. 17). Через
проекции А' и А" точки А, построенные соот-
ветственно при направлении проецирования s
и из центра проецирования S, проводим проек-
цирующие прямые до взаимного пересечения
в точке А
/29/ Две проекции точки на одной или двух
плоскостях проекций при различных центрах
(направлениях) проецирования определяют поло-
жение проецируемой точки в пространстве.
О положении точки в пространстве можно
судить, когда дана одна ее проекция, центр
12
или направление проецирования и известно,
что точка инцидентна прямой линии или пло-
скости (иногда кривой линии или поверхности),
положение которых известно. Этот случай по-
казан на рис. 18. Таким образом:
/30/ Одна проекция точки определяет ее по-
ложение в пространстве, если известен центр
(направление) проецирования и прямая линия или
плоскость, которой инцидентна точка.
Положение точки в пространстве становится
известным и в том случае, когда задана одна
проекции точки, направление проецирования
и расстояние от плоскости проекций до точки
в пространстве по направлению проецирования
(рис. 19). Естественно, должно быть учтено по-
ложительное и отрицательное направление от-
счета.
'31/ Одна проекция точки определяет ее по-
ложение в пространстве, если плоскость проек-
ций служит плоскостью отсчета и известно рас-
стояние от плоскости отсчета до точки в направ-
лении проецирования.
Условимся, что во всех случаях, когда будет
идти речь о длинах отрезков (расстояниях),
то единица измерения длин раз и навсегда выб-
рана. Отступление от этого приводится в гл. VII.
Рассмотрим еще один способ задания точки
в пространстве. Даны: точка О (начало коорди-
, пат) и три выходящие из нее луча к, п и т —
' оси координат (рис. 20). Известно, что в направ-
лении к координата точки А численно равна
длине отрезка t', в направлениях и и т- соот-
ветственно t" и t’". Чтобы определить поло-
жение точки А, нужно отложить по направле-
ниям к,пит отрезки длиной соответственно г',
t" и Г'", как показано на рисунке. При этом
следует учитывать знаки + и —, проставляе-
мые перед числовым значением координаты.
В дальнейшем под словами координата точки
будем иметь в виду длину направленного от-
резка. Поэтому вместо слов отложям отрезок,
длина которого численно равна координате точ-
ки, будем говорить отложим координату точки.
Ломаная t' — t" — t'" называется коорди-
натной ломаной. Чтобы найти точку А, возмож-
но построить несколько вариантов координат-
ной ломаной.
Две несовпадающие точки определяют един-
ственную, инцидентную им прямую, поэтому
(см. /29/) при известных центрах или направ-
лениях проецирования пара проекций двух то-
чек прямой определяет ее положение в про-
странстве. Однако положение прямой в про-
странстве может быть определено и по двум ее
проекциям.
Даны проекции д' и д" прямой д (рис. 21),
построенные при направлениях проецирова-
ния s' и s" на плоскостях П' и П". Достаточно
через прямую д' провести проецирующую пло-
скость параллельно s', а через прямую д" —
I . проецирующую плоскость параллельно s". Ли-
ния пересечения плоскостей будет искомой
, прямой д.
/32/ Две различные проекции прямой на од-
ной яли двух плоскостях проекций при извест-
ных центрах (направлениях) проецирования опре-
деляют положение проецируемой прямой в про-
странстве.
13
Исключение — совпадение проецирующих
плоскостей, проходящих через прямую а па-
раллельно соответственно s' и s" (рис. 22).
Здесь мы имеем дело с одной плоскостью,
которая называется дважды проецирующей.
В этом случае по двум проекциям прямой
линии (а' =а") восстановить ее положение в
пространстве невозможно. Однако если извест-
ны проекции А’, А", В' и В" двух точек прямой,
то можно (см. /29/) определять в пространстве
положение этих точек, а следовательно, и про-
ходящей через них прямой а.
Сказанное справедливо и тогда, когда даны
проекции прямой на двух плоскостях проекций
или когда один или оба центра проецирования —
собственные точки
/33/ Если прямая инцидентна заданной пло-
скости (иногда поверхности), то одна ее проекция
определяет положение прямой в пространстве
(сравните с /30/).
Когда прямая — проецирующая, то та ее
проекция, которая определяет собой точку,
совместно с собственным или несобственным
центром проецирования определяет положение
прямой в пространстве.
/34/ Одна проекция проецирующей прямой,
представляющей собой точку, при известном
центре (направлении) проецирования определяет
положение прямой в пространстве. Она задана
двумя точками — ее следом и собственным или
несобственным центром проецирования.
§ 3. НЕКОТОРЫЕ СВОЙСТВА
ПАРАЛЛЕЛЬНЫХ ПРОЕКЦИЙ
Проекции параллельных прямых. Рассмот-
ренные выше свойства изображений присущи
им независимо от того, каково проецирование—
центральное или параллельное. Установим не-
которые свойства только параллельных про-
екций.
Построим проекции параллельных прямых
а и b (рис. 23). Проецирующие плоскости парал-
лельны между собой, следовательно, с плоско-
стью проекций пересекаются по параллельным
прямым d и Ь'.
/35/ Проекциями параллельных прямых яв-
ляются параллельные прямые.
Однако если проекции прямых параллельны,
это не значит, что и прямые в пространстве
взаимно параллельны. Проведем в проецирую-
щей плоскости a n d прямую с, не параллель-
ную а. Ее проекция с' совпадет с прямой d.
Следовательно, с' || Ь‘, но
Чтобы по проекциям параллельных прямых
(рис. 24) можно было определить их положение
в пространстве, нужно иметь не менее двух
проекций на одной или двух плоскостях
(см. /32/).
/36/ Если пара проекций прямых представ-
ляет собой соответственно параллельные прямые,
то прямые в пространстве взаимно параллельны.
Когда прямые проецируются в точки, это
значит, что они проецирующие, а следователь-
но, параллельные между собой (см. /34/).
/37/ Когда прямые проецируются в точки,
они взаимно параллельны.
Проекции отрезка. Расположим отрезок АВ
так, что точка А с П' (рис. 25), спроецируем его
на П' в направлении s'. Точки А и А' совпа-
дают (А=А'), положение точки В' зависит
от направления проецирования и угла а наклона
отрезка к плоскости П'. Если направление
проецирования (ж") параллельно АВ, отрезок
проецируется в точку (длина его проекции равна
нулю). При направлении проецирования (s'"),
приближающемся к параллельному плоско-
сти П', длина проекции отрезка неограниченно
возрастает (параллельно П' проецировать
цельзя; см. /3/).
Проекция отрезка CD, параллельного пло-
скости проекций при любом направлении про-
ецирования, равна длине проецируемого отрез-
ка. Действительно, CD\\C'D' (см. /12/), СС' ||
|| DD' — это проецирующие прямые. Следова-
тельно, фигура CDD'C’—параллелограмм и
CD = C' D'.
Если проецировать отрезок АВ в направле-
нии s'Yперпендикулярном плоскости П', длина
его проекции A' B,v = АВ-cos а.
/38/ Длина проекции отрезка прямой в зави-
симости от направления проецирования и распо-
ложения отрезка относительно плоскости проек-
ций меняется от нуля до стремящейся к беско-
нечности величины.
/39/ Если отрезок прямой параллелей плоско-
сти проекций, то его проекция при любом направ-
лении проецирования равна н параллельна самому
отрезку.
/40/ При прямоугольном проецировании дли-
на проекции отрезка прямой равна длине самого
отрезка, умноженной на косинус угла наклона
прямой к плоскости проекций. Следовательно,
при прямоугольном проецирования длина проек-
ции отрезка может меняться от нуля (отрезок
перпендикулярен плоскости проекций) до дли-
ны самого отрезка (отрезок параллелен плоско-
сти проекций).
14
Рис. 25
.в
Возьмем на отрезке АВ (рис. 26) точку С.
Она разделит отрезок в отношении АС: СВ.
Проекция С' этой точки делит проекцию отрез-
ка в том же отношении, что следует из извест-
ного положения элементарной геометрии о де-
лении сторон угла параллельными прямыми.
/41/ Проекция точки делит проекцию отрезка
в том же отношении, в каком точка делит от-
резок.
Даны отрезки АВ и CD параллельных пря-
мых и их проекции на плоскости П' (рис. 27)
Проведем АЕ\\А'В' и CF||C'D'. Тогда АЕ =
= А'В' и CF — С D'. Треугольники АВЕ и CDF
подобны, следовательно, AB:CD = AE.CF.
В силу равенства отрезков АЕ и А'В', а также
CF и CD' можем записать. AB.CD =
= A'B’.C'D'.
/42/ Отношение длин проекций отрезков па-
раллельных прямых равно отношению длин са-
мих отрезков.
Проекции плоской фигуры. Для параллель-
ных проекций формулировка положения /17/
следующая:
/43/ Если плоская фигура параллельна пло-
скости проекций, она проецируется в равную ей
и подобно расположенную фигуру.
Треугольник АВС (рис. 28) параллелен П'.
Его стороны проецируются в отрезки, соответ-
ственно равные и параллельные этим сторонам
(см. /39/). Таким образом, Д АВС = ЬА'В'С',
причем обе фигуры подобно расположены. Ска-
занное относится и к плоской фигуре, ограничен-
ной кривой линией, если эту линию рассматри-
вать как предел некоторой ломаной.
Параллельное перемещение плоскости проек-
ций. Спроецируем треугольник АВС на парал-
лельные друг другу плоскости проекций П' и П"
(рис. 29). Проекцией треугольника на П' явля-
Рис. 26
Рис. 27
Рис. 29
15
ется треугольник А' В' С, проекцией на П" —
треугольник А" В" С", который вместе с тем
можно рассматривать и как проекцию на пло-
скости П" треугольника А'В'С (почему?).
Так как П'||П", то треугольники А'В'С' и
А"В" С" равны между собой и подобно распо-
ложены (см. /43/). Отсюда:
/44/ При параллельном перемещении плоско-
сти проекций форма, величина н ориентация про-
екции фигуры не меняются.
Проекции прямого угла при направлении про-
ецирования, перпендикулярном плоскости про-
екции. Взаимно перпендикулярные прямые АВ
и CD (рис. 30) параллельны П', поэтому угол
между их проекциями А'В' и С' D' равен 90°
(см. /43/ и /19/). Плоскость, проецирующая пря-
мую CD, перпендикулярна АВ, так как в ней
лежат пересекающиеся прямые CD и DD',
перпендикулярные АВ. Пусть CD вращается
вокруг А В, —Последовательно занимая положе-
ния CD, CD, ... Множество таких прямых
представляет собой плоскость, перпендикуляр-
ную АВ. Эта плоскость совпадает с проецирую-
щей плоскостью СС' || DD', поэтому при любом
положении CD она проецируется в прямую
CD' (см. /16/).
/45/ Если одна сторона прямого угла (АВ)
параллельна плоскости проекция, проекцией пря-
мого угла является прямой угол;
Разумеется, /45/ не исключает /19/. Если
одна сторона прямого угла (CD) перпендику-
лярна плоскости проекций, проекция угла пере-
стает быть углом и вырождается в полупрямую.
Из /45/ следует
/46/ Если проекцией угла, одна сторона кото-
рого параллельна плоскости проекций, является
прямой угол, то проецируемый угол также прямой.
§ 4. ГОМОЛОГИЯ
Теорема Дезарга. Проецируя треугольник
А ВСС. О на плоскость Е из центра S, не инци-
дентного этим плоскостям, получим треуголь-
ник А'В'С' (рис. 31). Найдем след прямой АВ —
точку 1. Она лежит на прямой s — линии пересе-
чения плоскостей fi и I и совпадает со своей
проекцией (на рисунке проекция не обозначена).
Прямая АС пересекается со своей проекцией
А' С' в точке 2, а прямая ВС — со своей проек-
цией В’ С в точке 3, причем точки 2 и 3, подобно
точке 1, инцидентны прямой s.
/47/ Если два треугольника (АВС и А’ В' С')
расположены в пространстве так, что прямые
(SA, SB и SC), проходящие через их вершины,
пересекаются в одной точке (.S’), то соответствен-
ные стороны треугольников (АВ и А'В', ВС и
В' С, АС и А'С') при их продолжении пересе-
каются в точках (7, 2 и 3), инцидентных одной
прямой (.v).
Приведенная теорема называется теоремой
Дезарга для пространства. Справедлива и об-
ратная теорема.
Зададимся новой плоскостью проекций П'
и другим центром проецирования, не совпадаю-
щим с первым, например несобственным. Спро-
ецируем из нового центра на плоскость П'
треугольники АВС и А' В’С, точку S, служив-
шую нам ранее центром проецирования, и пря-
мые SA, SB, SC и s, получив треугольники
АВС и А’В'С', точку S и прямую л
Прямые АВ и А'В’ — продолженные сторо-
ны треугольников АВСи А'В' С пересекаются
между собой в точке 1-—проекции на плоско-
сти П' точки 7. Прямые АС и А' С пересека-
ются в точке 2, прямые ВС и В’ С' — в точке 3.
Все три точки инцидентны прямой s’ (см. /23/).
Сформулируем теорему Дезарга для пло-
скости": ____ _ _
/48/ Если два треугольника (АВС и А'В'С')
расположены на плоскости так, что прямые,
проходящие через их вершины_(ЛЛ', ВВ' и СС'),
пересекаются в одной точке (.S’), то соответствен-
ные стороны треугольников (АВ и А'В', ВС и
ff_C, АС и АС') пересекаются в трех точках
(7, 2иЗ), инцидентных одной прямой(s). Справед-
лива и обратная теорема.
Гомологические преобразования. При проеци-
ровании из центра S (рис. 31) каждой точке
плоскости fl соответствует в качестве ее проек-
ции определенная точка плоскости Е. В равной
мере, если плоскость Е проецировать из того
же центра на плоскость fl, то каждой точке
плоскости Е будет соответствовать определен-
ная точка плоскости fl. В этом случае говорят,
что между точечными полями плоскостей fl
и Е устанавливается взаимно-однозначное соот-
ветствие. В приведенном примере точке А соот-
ветствует точка А’ (и наоборот), точке В —
точка В’ и т. д. Точки 7, 2 и 3, в равной мере
как и другие точки прямой s, соответствуют
сами себе, поэтому их называют двойными точ-
ками, а прямую s — прямой двойных точек.
Двойные точки будем обозначать арабскими
цифрами. Вместе с тем прямой АВ соответству-
ет прямая А'В', фигуре (треугольнику) АВС —
фигура А'В'С' и т. Д.
При проецировании плоскостей fl и Е на
плоскость П' эта плоскость становится носи-
телем двух полей проекций, между которыми
устанавливается взаимно-однозначное соответ-
ствие. Точке Л соответствует точка А', точке В—
точка В', прямой АВ—прямая А'В' и т. Д.
Прямая s’ является прямой двойных точек.
Все соответственные прямые пересекаются меж-
ду собой в двойных точках на прямой &
Пусть известны точка S, прямая ^ и две
соответственные точки, например Л и Л'. Нужно
16
доказать, что при этих условиях любой точке
одного поля однозначно соответствует точка
второго поля и наоборот. Возьмем произволь-
ную точку В, принадлежащую тому же полю,
что и точка А, и найдем соответственную ей
точку В', принадлежащую второму полю. Не-
трудно видеть, что точка В' должна лежать
в пересечении прямых BS и Л'— 7; но положе-
ние точки 1 определяется пересечением прямых
АВ и s Следовательно, прямая А'—1 единст-
венно возможная, что и устанавливает одно-
значность решения задачи. Сказанное относится
к любой точке обоих полей (кроме точки 5),
поэтому можно утверждать, что любая фигура
одного поля соответствует единственно воз-
можной фигуре другого поля. Приведенное-
соответствие называется гомологией*, точка 5—
центром гомологии, прямая У— осью гомологии,
а треугольники АВС и А'В'С', в равной мере
как и любые другие фигуры, соответственные
одна другой — гомологичными фигурами. Гомо-
логичные фигуры могут быть расположены как
по обе, так и по одну сторону оси гомологии
(Почему? Как это объяснить исходя из рис. 31 ?).
При этом точке соответствует точка, прямой —
прямая Инцидентные фигуры соответствуют
инцидентным фигурам.
Из предыдущего видно, что:
/49/ Гомология задана, если известны ее
центр, ось н пара гомологичных точек (лежащих
на прямой, проходящей через центр гомологии,
но не совпадающих с центром и не инцидентных
оси) или пара гомологичных прямых. Можно и
иначе задать гомологию.
Прямые AS, BS и CS соответствуют сами
себе. Например, прямая AS соответствует пря-
мой A'S. Но эти прямые совпадают. Поэтому
следует говорить об одной — двойной — пря-
мой. Сказанное распространяется на все пря-
мые, проходящие через центр гомологии. Они
являются двойными прямыми.
Построение фигуры, гомологичной задан-
ной, называют гомологическим преобразованием
заданной фигуры.
Центр гомологии может быть как собствен-
ной, так и несобственной точкой, ось гомоло-
гии— собственной или несобственной прямой.
Кроме того, центр может быть инцидентным
оси. Если центр или ось несобственные, то го-
мологии носят название аффинных*. Каждая
из аффинных гомологий имеет свое название.
OopoZotpja — соответствие, согласие (греч.).
* affinus — родственный, соответственный
(лат.).
2—940
17
поэтому в дальнейшем гомологиями мы будем
называть только гомологии с собственным
центром и собственной осью. Это центральные
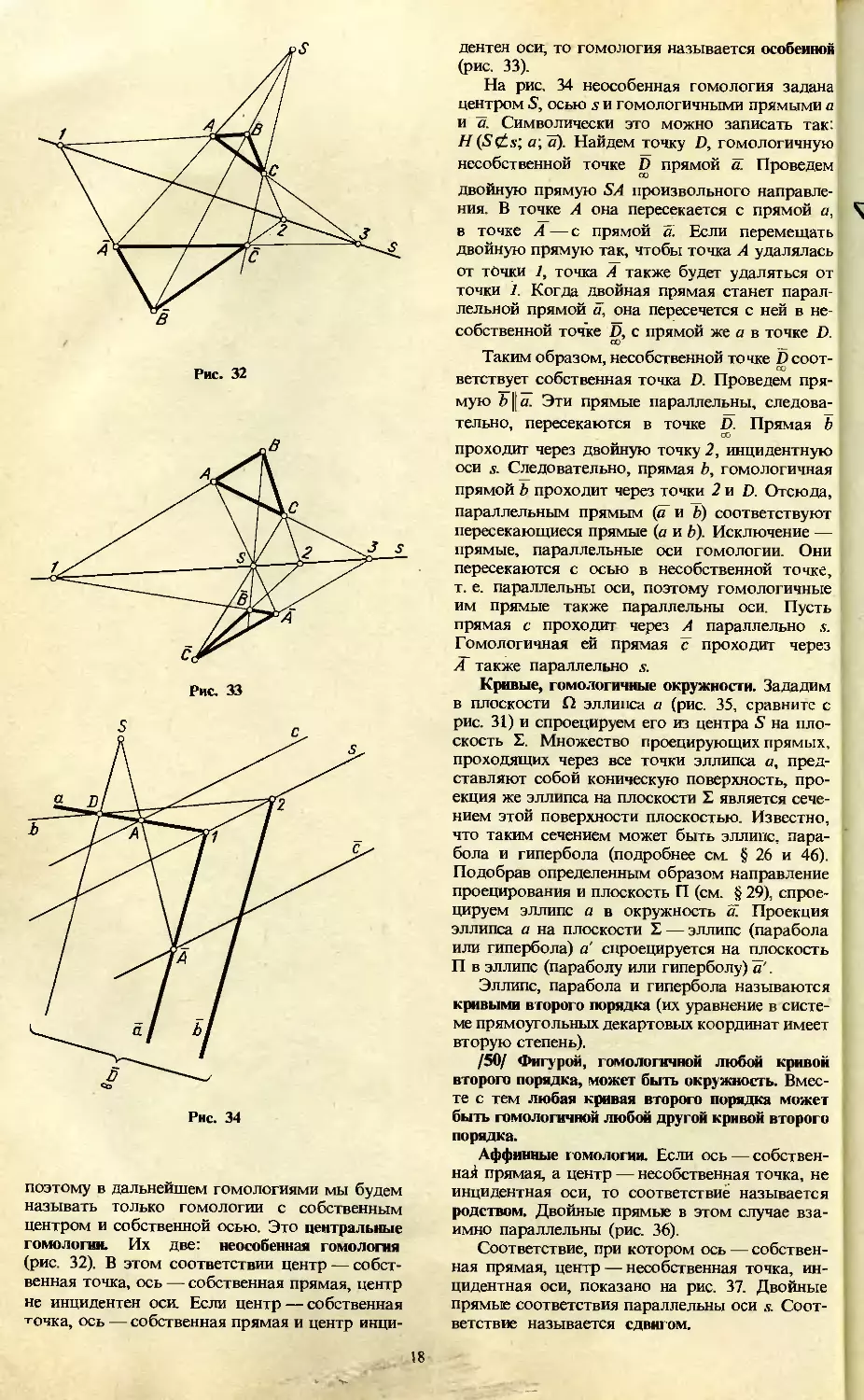
гомологии. Их две: неособенная гомология
(рис. 32). В этом соответствии центр — собст-
венная точка, ось — собственная прямая, центр
не инцидентен оси. Если центр — собственная
точка, ось — собственная прямая и центр инци-
дентен оси, то гомология называется особенной
(рис. 33).
На рис. 34 неособенная гомология задана
центром S, осью s и гомологичными прямыми а
и а. Символически это можно записать так:
H(S£s; а , "а). Найдем точку D, гомологичную
несобственной точке D прямой а. Проведем
двойную прямую SA произвольного направле-
ния. В точке А она пересекается с прямой а, \
в точке А — с прямой а Если перемещать
двойную прямую так, чтобы точка А удалялась
от точки 7, точка А также будет удаляться от
точки 1. Когда двойная прямая станет парал-
лельной прямой а, она пересечется с ней в не-
собственной точке D, с прямой же а в точке D.
Таким образом, несобственной точке D соот-
ветствует собственная точка D. Проведем пря-
мую b ||Эти прямые параллельны, следова-
тельно, пересекаются в точке D. Прямая b
ОО
проходит через двойную точку 2, инцидентную
оси .V. Следовательно, прямая Ь, гомологичная
прямой b проходит через точки 2 и D. Отсюда,
параллельным прямым (а и Ь) соответствуют
пересекающиеся прямые (а и h). Исключение —
прямые, параллельные оси гомологии. Они
пересекаются с осью в несобственной точке,
т. е. параллельны оси, поэтому гомологичные
им прямые также параллельны оси. Пусть
прямая с проходит через А параллельно s.
Гомологичная ей прямая с проходит через
А также параллельно s.
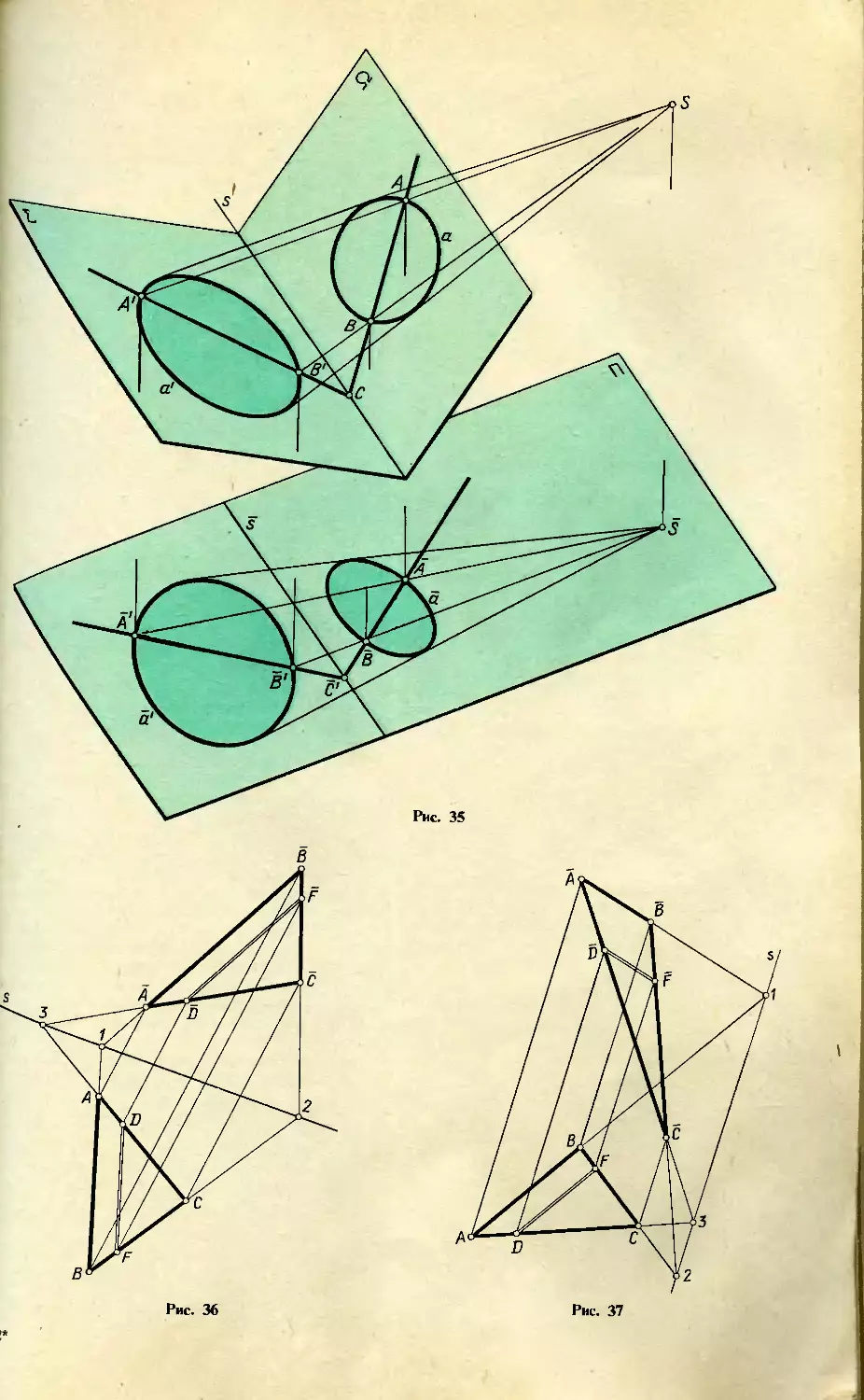
Кривые, гомологичные окружности. Зададим
в плоскости П эллипса а (рис. 35, сравните с
рис. 31) и спроецируем его из центра S на пло-
скость S. Множество проецирующих прямых,
проходящих через все точки эллипса а, пред-
ставляют собой коническую поверхность, про-
екция же эллипса на плоскости L является сече-
нием этой поверхности плоскостью. Известно,
что таким сечением может быть эллипс, пара-
бола и гипербола (подробнее см. § 26 и 46).
Подобрав определенным образом направление
проецирования и плоскость П (см. § 29), спрое-
цируем эллипс а в окружность а. Проекция
эллипса а на плоскости L — эллипс (парабола
или гипербола) а' снроецируется на плоскость
П в эллипс (параболу или гиперболу) о'.
Эллипс, парабола и гипербола называются
кривыми второго порядка (их уравнение в систе-
ме прямоугольных декартовых координат имеет
вторую степень).
/50/ Фигурой, гомологичной любой кривой
второго порядка, может быть окружность. Вмес-
те с тем любая кривая второго порядка может
быть гомологичной любой другой кривой второго
порядка.
Аффинные гомологии. Если ось — собствен-
ная прямая, а центр — несобственная точка, не
инцидентная оси, то соответствие называется
родством. Двойные прямые в этом случае вза-
имно параллельны (рис. 36).
Соответствие, при котором ось — собствен-
ная прямая, центр — несобственная точка, ин-
цидентная оси, показано на рис. 37. Двойные
прямые соответствия параллельны оси л Соот-
ветствие называется сдвигом.
18
•*
Рис. 38
Когда ось — несобственная прямая, центр
же — собственная точка (рис. 38), то соответ-
ствие называется гомотетией (преобразованием
подобия).
На рис. 39 показано параллельное перенесе-
ние. В этом соответствии и ось и центр несоб-
ственные и в силу этого инцидентные друг
другу.
Важным свойством аффинных гомологий яв-
ляется сохранение параллельности. Если прямые
параллельны (АВ и DF на рис. 36—39), то соот-
ветственные им прямые также параллельны
(прямые АВ и DF на тех же рисунках). Для дока-
зательства рассмотрим родство на рис. 40:
Н (S £ s; а; а). Несобственный центр родства
задан направлением двойной прямой Ь, назы-
ваемым направлением соответствия или направ-
лением преобразования.
Если перемещать прямую Ь так, чтобы точ-
ка А удалялась от точки 1, то и точка А будет
удаляться от этой точки. Когда прямая Ь ста-
нет несобственной, то и точка А и А станут
несобственными. Прямая с параллельна а. Ког-
да прямая b станет несобственной, то и точка В,
в которой она пересекается с прямой с, станет
несобственной — общей для прямых а и с.
Следовательно, соответственная ей точка на
прямой с"совпадет с несобственной точкой пря-
мой а. Отсюда, прямая с проходит через точку 2
параллельно прямой а.
Аффинные гомологии преобразуют кривые
второго порядка в кривые второго поряди
того же вида (т. е. эллипс в эллипс, параболу i
параболу и т. д.), кроме того, соответственны
фигуры при гомотетии подобны и подобно рас-
положены, а при параллельном перенесения
равны и подобно расположены.
Из аффинных гомологий наибольший инте-
рес для нас представляет родство. В этом слу-
чае соответственные фигуры принято называй
родственными фигурами, а ось гомологии —
осью родства.
/51/ Родство задано, если известны его ось
и пара родственных точек (так как при эти1
условиях становится известным направление
преобразования) или ось, пара родственных пря-
мых и направление преобразования (которое
определяет положение несобственного центра;
см. /8/).
Если на рис. 3) треугольник АВС проеци-
ровать из несобственного центра на плоскость I
а затем из другого несобственного центра прое-
цировать треугольники А ВС и А' В' С на пло-
скость П, то между проекциями треугольников
установится родственное соответствие с осью s
Параллельной проекцией кривой второго по-
рядка может быть только кривая второго по-
рядка того же вида, поэтому:
/52/ Фигурой, родственной эллипсу, является
эллипс, фигурой, родственной параболе — пара-
бола, родственной гиперболе — гипербола.
В частном случае /53/ фигурой, родственной
эллипсу, может быть окружность (сравните с
/50/).
§ 5. НЕКОТОРЫЕ ГРАФИЧЕСКИЕ
ПОСТРОЕНИЯ
Точность построений. Будем считать прием-
лемым в инженерных целях такое решение за-
дачи, которое найдено в результате построений,
выполненных линейкой и циркулем. Решение,
полученное с помощью лекальных кривых, бу-
дем считать недостаточно точным.
Чтобы не усложнять вопрос, станем учиты-
вать точность построений только в пределах
решения задачи, не касаясь ее исходных данных.
Например, если одним из элементов задачи
является лекальная кривая, которая дана (т. е,
проведена на чертеже), задание отнесем к точ-
н
в
т
в
т
3
г
£
п
5
к
т
к
I
3
г
т
т
г
к
3
К
(
Е
К
Г
I
I
1
1
f
(
(
20
ным. Если же ее нужно построить в ходе реше-
ния задачи, то все решение отнесем к недоста-
точно точным.
Рассмотрим построения, которые нам
встретятся при изучении дальнейшего) ма-
териала.
Задача 1.
Дана гомология Н (S с! а; А; А). Построить
гонки Ви С, гомологичные соответственно точкам
В и С (рис. 41).
Проведем прямую АВ и, отметив двойную
точку 1 ее пересечения с осью гомологии, проведем
прямую А—1. Она пересекается с двойной прямой
SB в искомой точке В.
Для определения точки С воспользуемся точ-
ками В и В. Если же их нет на чертеже, то построим
такие точки. Проведем прямую ВС и отметим точ-
ку 2 ее пересечения с осью. Соединив точки 2 и
fl, отметим точку С пересечения прямых В—2 и SA.
Задача 2. _
Дана гомология А; А). Построить
прямую а, гомологичную прямой а || г (рис. 42).
Проведем произвольную прямую А—1 и отме-
тим точку В ее пересечения с прямой а. Построим
точку В гомологичную В (см. задачу 1). Через В
проведем прямую а параллельно оси (двойная точ-
ка прямых а, а и s — несобственная).
Задача 3. _
Дано родство Н s\ А; А). Построить точ-
ки В и С, родственные соотве тственно точкам В и С
(рис. 43).
Проведем прямую АВ и, отметив Двойную точ-
ку 1 ее пересечения с осью родства, построим пря-
мую А—1. Она пересекается с двойной прямой,
проходящей через точку В параллельно АА (так как
центр преобразования — несобственная точка) в ис-
комой точке В.
Для определения точки С воспользуемся точ-
ками В и й. Если же их нет на чертеже, построим
такие точки. Проведем прямую ВС и отметим точку 2
ее пересечения с осью родства. Соединив точки 2 и
В, отметим точку С пересечения прямых АА и В—2
(сравните задачи 1 и 3).
Построить точки, родственные соответственно
точкам А, В и С, можно иначе. Воспользуемся тем,
что родство — аффинная гомология и параллель-
ные прямые преобразуются также в параллельные
прямые. Проведем через А произвольную прямую
(рис. 44) и отметим точку 1 ее пересечения с осью
1
21
родства. Соединим точки 1 и Л. Через В проведем
прямую В—2(А—7, _а через точку 2 — прямую,
параллельно прямой А —1. В пересечении этой пря-
мой с двойной прямой, проведенной через В, рас-
положена точка В. Аналогично построена и точка С.
Задача 4. _
Дано соответствие сдвига Н (S <ts, А; А). По-
строить точку В, соответственную точке В, и точку С,
соответственную точке С (рис. 45).
Проведем прямую АВ_и отметим точку 7 ее
пересечения с осью. Точка В расположена в пересе-
чении прямой А—1 и двойной прямой, проходящей
через В параллельно оси
Соединив точки С и В прямой, отметим точку 2
ее пересечения с осью. Точка С расположена в пере-
сечении прямых В—2 и АА. Не трудно попять, чт.
отрезки АС и АС равны, что можно ислользоваг
для определения точки С.
Задача 5.
Найти точки пересечения прямых а и Ъ с эллш
сом, заданным его осями, не строя эллипса (рис. 46
Для решения используем родство (см. /51/ и /53/
Проведем окружность диаметра, равного больше!
оси эллипса с центром в точке О пересечения ег
осей. Зададим родство осью s, на которой лежи
большая ось эллипса и родственными точками А
А, принадлежащими соответственно эллипсу и а
ружности и лежащими на прямой, которой приказ
лежит малая ось эллипса: Н (5 <£ з; А; А) Проведе
родственные прямые, проходящие через точки
и А параллельно оси родства. Найдя точку В пер<
сечения прямых АВ и а, проведем через нее двойку»
прямую ВВ и в пересечении ее с прямой АВ отмен®
точку В, родственную В. Прямая а, родственная i
проходит через двойную точку 1 и точку В. Отмети»
точку С пересечения прямой а с окружностью и по
строим родственную ей точку С.
Вместо прямых, параллельных оси родств:
можно воспользоваться прямыми, пересекающими:
с ней. С помощью таких прямых Н—3 и Н—3 по
строены точки К и К. Прямая Ь проходит чер:
точки К и 2 и в точке М пересекается с окружности
Родственная ей точка М расположена в пересечен»:
прямой Ь с двойной прямой ММ.
Задача 6.
На рис. 47 прямые а и Ь, точки пересечения Ы
торых с эллипсом надо построить, параллелью
осям эллипса. Как и в предыдущей задаче, эллиь
задан своими осями. Проведем окружности диаме:
ров, равных большой и малой осям эллипса с цен:
трем в точке О их пересечения. Через точку А и
рссечения прямой а -с малой окружностью пров:
дем прямую ОА и отметим точку А ее пересечен»
с большой окружностью. Проведем прямую Л
параллельно малой оси эллипса. Она пересекаете
с прямой а в искомой точке А.
Построения основаны на следующем: мала
окружность родственна эллипсу, если родство з
дано: Н (S Г; С и С1)- Родственные точки А и
принадлежат двойной прямой, совпадающей с у
данной прямой а. Вместе с тем большая окрул
ность родственна эллипсу, когда родство_зада»
77(5(z!T; £>; D). Родственные точки А и А леж-
ня двойной прямой, параллельной малой оси эллш
са. В пересечении этой прямой и прямой а находи!
искомую точку А. Аналогично построена точка
Описанный прием используется для построен!
эллипса по его осям.
Задача 7.
Даны эллипс и родственная ему окружное
(рис. 48). Касательные А А, ВВ к обеим фигур»
взаимно параллельны (что и подтверждает то, чт
эллипс и окружность родственны). Найти ось ро
ства. _ __
Касательные АА и ВВ являются двойными пр
мыми родства. Проведя произвольную хорду элли
са CD, построим двойные прямые СС и DD и сое.т
ним прямой полученные в пересечении с окружи
стью точки С и D. Эта прямая пересекается с прям:
CD в двойной точке 1. Проведя хорду ЕВ, поступи
аналогично, получив точку 2. Через точки 1 и
проходит ось родства з.
Двойные прямые пересекаются с каждой из з
данных фигур в двух точках. Поэтому вместо те
ки С может быть использована точка F, а вмес:
точки D точка Е (их нужно соответствующим обр
зом обозначить). В этом случае родственные пр
22
Рис. 48
мне CD и EF пересекутся в точке 3. Родственные
прямые F.F и DC пересекутся в точке 4. Через точки
3 и 4 проходит ось родства s', отличная от оси s.
Следовательно, задача имеет два решения.
Задача 8.
В точке А кривой второго порядка провести
касательную к этой кривой (рис. 49). Проведем
произвольную хорду АВ и параллельную ей хорду
CD. Взяв на кривой точку Е вне дуг между хордами,
соединим прямыми линиями точки А и D, В и Е,
Си F. Через точку F пересечения прямых A D и BE
проведем прямую параллельно хордам АВ и CD
до пересечения в точке G с прямой СЕ. Через точ-
ки G и А проходит искомая касательная (решение
основано на теореме Паскаля, с которой можно
познакомиться в курсе проективной геомет-
рии).
Задача 9.
1. Провести касательную к кривой второго
порядка, параллельную заданной прямой а.
1. Определить вид кривой по ее дуге (рис. 50).
1. Проведем две хорды АВ и CD, параллель-
ные прямой а, и, разделив их пополам, через полу-
ченные точки проведем прямую (диаметр кривой
второго порядка, сопряженный хордам). Через точ-
ку Е пересечения диаметра с кривой проходит каса-
тельная. Таких касательных две. Если заданная
кривая — парабола, то одна из них — несобствен-
ная прямая (в этом случае говорить о параллельно-
сти касательных нельзя).
2. Построим еще две хорды, не параллельные
хордам АВ и CD и сопряженный им диаметр. Если
оба диаметра пересекаются «внутри кривой», как
в приведенной задаче, то дуга принадлежит эллипсу.
Если они пересекаются «вне кривой», то задана дуга
гиперболы. Когда диаметры взаимно параллельны,
то изображена дуга параболы.
Задача 10.
Используя сдвиг, преобразовать несимметрич-
ную дугу 1—А—2 кривой второго порядка в сим-
метричную дугу (рис 51). Проведем через точки 1 и 2
ось соответствия и параллельно ей — касательную
к дуге (см. задачу 9). Отметим точку касания А.
Рнс. 50
23
Из середины хорды 1—2 (точки 3) восставим пер-
пендикуляр к оси и зададим на нем точку А, соответ-
ственную точке А. Теперь сдвиг задан: Н (S' Cs;
А: А"). Для построения промежуточных точек, соот-
ветственных точкам заданной дуги, проведем произ-
вольную хорду ВС, параллельную оси, и отметим
ее середину — точку D (она расположена в пересе-
чении хорды ВС с сопряженным ей диаметром А—3).
Точка D, соответственная точке D, инцидентна
прямой А—3. Отложив от нее в обе стороны в на-
правлении двойных прямых отрезки, равные поло-
вине хорды ВС, получим точки В и С, соответствен-
ные точкам В и С заданной дуги. Обратите внимание
на то, что DD = ВВ = СС. Это можно использовать
при построениях. Дуга, соответственная заданной,
проходит через двойные точки 1 и 2 (см. задачу 4).
Задача 11.
Используя гомологию, преобразовать симмет-
ричную дугу 1—А—2 кривой второго порядка в дугу
окружности (рис. 52). В точке 1 заданной дуги про-
ведем касательную к кривой (см. задачу 8) и отметим
точку ее пересечения с осью симметрии дуги. Вос-
ставим перпендикуляр 1—0 к касательной и отметим
точку О его пересечения с осью симметрии. Через
точку 1 проведем окружность с центром в точке О
(в силу симметрии аналогичные построения можно
провести используя точку 2).
Точки 1 и 2 — двойные, через них проходит ось
гомологии 5, центром гомологии является точка 5
Заданная дуга кривой второго порядка преобразу-
ется в дугу окружности 1—А—2 (или 1—А—2).
Таким образом мы получили две гомологии: Н (S
з; А; А) и Н (S; s: А; А). Точка В (или В), гомологич-
ная произвольно взятой точке В дуги кривой второго
порядка, расположена в пересечении двойной пря-
мой SB с окружностью.
Задача 12.
Построить дугу параболы по ее вершине А и
точкам В и С, симметричным друг другу относи-
тельно оси параболы (рис. 53). Построим отрезок
AD, параллельный хорде ВС, и отрезок BD, парал-
лельный оси параболы. Разделим оба отрезка на
произвольное число равных частей (на рисунке
четыре части). Соединим точки II, III, IV отрезка BD
с точкой А, а через точки II, III, IV отрезка A D про-
ведем прямые, параллельные оси. Отметим точки
Е, F, G пересечения прямых, проходящих через
точки, обозначенные одинаковой цифрой. Дуга АС
симметрична дуге АВ.
Задача 13.
Построить дугу гиперболы по ее вершине А и
асимптотам а и Ь (рис. 54). Проведем через А про-
извольную прямую и, измерив длину отрезка А—1,
в конце которого — точке I — прямая пересекаете»
с асимптотой Ь, отложим такой же отрезок от точ-
ки II пересечения прямой с асимптотой а. Получен-
ная точка С принадлежит гиперболе. Проведем через
С- произвольную прямую CD и, отложив отрезок
IV—D, равный С—III, найдем точку D. Аналогич-
но построена точка Е. Вторая вершина гипербо-
лы В симметрична точке А относительно мнимой
оси гиперболы.
24
Часть первая
ОРТОГОНАЛЬНЫЕ
ПРОЕКЦИИ
НА ДВУХ И БОЛЬШЕМ
ЧИСЛЕ ПЛОСКОСТЕЙ
ГЛАВА II
ТОЧКА И ПРЯМАЯ
§ 6. ТОЧКА
Эпюр точки. Зададим две взаимно перпенди-
кулярные плоскости проекций — вертикальную
П2 и горизонтальную П, и точку А, не инпидент-
ную этим плоскостям (рис. 55). Примем направ-
ления проецирования Sj-LIIj и $2±П2. Чтобы
построить проекцию точки А на П2, проведем
через точку проецирующую прямую, парал-
лельную s2, и отметим точку А2 ее пересечения
с этой плоскостью. Плоскость П2 назовем
фронтальной плоскостью проекций, а точку А2 —
фронтальной проекцией точки А. Плоскость ГЦ
называется горизонтальной плоскостью проек-
ций. Проведя проецирующую прямую через А
параллельно s, в ее пересечении сП), получим
горизонтальную проекцию точки А. Проекпии
точки получены в результате ортогонального
(прямоугольного) проецирования, поэтому они
называются ортогональными проекциями*.
По двум проекциям At и А2 в соответствии
с /29/ можно определить положение точки А
в пространстве.
Прямая х, по которой пересекаются плоско-
сти ГЦ и П2, называется осью проекций. Опус-
тим перпендикуляр из А2 на прямую х; он пере-
От греч. ortos — прямой, gonia угол
сечется с ней, а следовательно, и с плоскостью П
в точке Ах. Опустив перпендикуляр из At в-
прямую х, мы найдем ту же точку Ах.
Строя изображения точки, мы использовал!
два вида проецирующих прямых: перпендику
лярные П2 называются фронтально проецируй
щими, перпендикулярные ГЦ—горизонталь»
проецирующими. Таким образом, точка А прое
цируется на П2 фронтально проецирующе!
прямой, а на П) —горизонтально проецирую
щей.
Отрезок АА2 = A ,АХ представляет собой рас
стояние от точки А до плоскости П2. Отрезе-
AAt = А2АХ является расстоянием от той же
точки до плоскости П,.
Повернем плоскость П) вокруг оси х' до
совмещения с П2 (плоскостью чертежа), кат
показано стрелками на рис. 55. Вместе с плоско-
стью переместится и точка Ait а также все
другие точки поля проекций ПР В результате
(рис 56) плоскость чертежа станет носителем
двух полей проекций — nt и П2, причем так,
что каждая пара проекций любой точки про-
странства (в приведенном примере — проекции
Ai и А2 точки А) расположена на общем перпен-
дикуляре к оси проекций. Такой перпендикуляр
называется линией связи. В этом случае о точ-
ках А, и А 2, как и о любой другой парю проекций
произвольной точки пространства, говорят, что
они расположены в проекционной связи. Часто
ось проекций на чертеже не проводится, однако
ее направление всегда известно.
/54/ Чертеж, плоскость которого является
носителем двух полей ортогональных проекций,
расположенных так, что линии связи перпенди-
кулярны оси проекций, называется эпюром.
Обычно говорят об эпюре точки, эпюре
прямой, эпюре фигуры и т. д.*
/55/ Эпюром точки называется чертеж, на
котором изображены две ортогональные проек-
ции точки, расположенные в проекционной связи.
Изображение на рис. 56 представляет собой
эпюр точки А. Заметим, что на эпюре нет самой
точки, даны только ее проекции. Несмотря на
это, положение точки относительно плоскостей
* Эпюр часто называют эпюром Монжа по
имени известного французского ученого Гаспара
Монжа, внесшего большой вклад в развитие мето-
дов изображений. Ериге — по-французски очищен-
ный
26
проекций известно, так как по эпюру можно
судить о том, на каких расстояниях точка А
расположена относительно плоскостей П, и П2
(отрезки А,АХ и А,АХ)*. Следовательно, эпюр
обратим.
Рассмотрим теперь, как изображаются на
эпюре сами плоскости проекций. Предположим,
что зритель смотрит на систему плоскостей
проекций (рис. 55) спереди (в направлении s2).
Плоскость П2 перпендикулярна направлению
проецирования, плоскость П] — параллельна
ему. Таким образом, плоскость nt становится
проецирующей (см. /14/) и изображается на
плоскости П2 в виде прямой, совпадающей с
осью х. Посмотрим на систему плоскостей П,
в П2 сверху. Теперь плоскость nt перпендику-
лярна Sj, плоскость же П2 становится проеци-
рующей; ее Проекция совпадает с осью х.
Эпюр можно рассматривать как чертеж,
состоящий из двух самостоятельных изображе-
ний, выполненных при -различных направле-
ниях проецирования, но размещенных так, что
проекции одних и тех же точек располагаются в
проекционной связи.
Как видно из (54), основные элементы эпю-
ра — это поля проекций и линий связи. Положе-
ние плоскостей проекций («высота» плоско-
сти П] и «удаление» плоскости П2) не имеет
значения, так как при их параллельном переме-
щении (см. /44/) проекции фигур не меняются.
Следовательно, достаточно знать, что пло-
скость П2 расположена фронтально, а плос-
кость П, —горизонтально. В связи с этим от-
падает необходимость в проведении на чертеже
оси проекций. Однако в некоторых случаях
положение плоскостей проекций имеет значе-
ние, поэтому в дальнейшем мы будем пользо-
ваться как эпюрами с проведенной осью про-
екций, так и эпюрами без оси.
Положение точки относительно плоскостей
проекций. Точка, не инцидентная ни одной из
плоскостей проекций, называется точкой об-
щего положения (точка А на рис. 55 и 56). Рас-
смотрим некоторые случаи частного располо-
жения точек. Точка В С П2 (рис. 57); ее фрон-
тальная проекция В2 совпадает с самой точкой
(В = В2). Так как расстояние от точки В до П2
равно нулю, то горизонтальная проекция В,
лежит на оси х и совпадает с точкой Вх. Точка
С С ПР Ее горизонтальная проекция С, = С,
а фронтальная C2 = G- Наконец, точка Ьсх.
Поэтому D = Dt = D2 = Dx.
Эпюр этих точек дан на рис. 58.
Если точка равноудалена от плоскостей П,
и П2 (точка Е на рис. 59 и 60), то она лежит в
плоскости биссектора, делящей двугранный угол
между плоскостями П, и П2 пополам. В этом
случае Е2ЕХ = EtEx.
Проекции точки на трех плоскостях проекций.
Иногда нужно построить третью проекцию
Рис. 57
0^2
Разумеется, если проведена ось х.
Рис. 56
Рис. 58
27
<>
,,£ РИС. 60
фигуры. Для этого вводится еще одна плоскость
проекций П3, перпендикулярная П, и П2 и на-
зываемой профильной плоскостью проекций
(рис. 61). Линия пересечения плоскостей П, и П3
обозначается буквой у, а линия пересечения
плоскостей П2 и П3 — буквой z. Прямые у и z,
подобно прямой х, являются осями проекций.
Все три оси проекций пересекаются в точке О.
Чтобы построить проекцию А3 точки А на
плоскости П3> нужно через А провести прямую,
перпендикулярную П3 и называемую профильно
проецирующей. В пересечении этой прямой с
П3 расположена точка А3. Перпендикуляры,
опущенные из А3 и А3 на ось у, пересекаются с
нею в точке Ау; перпендикуляры, опущенные из
А2 и А3 на ось z, пересекаются с нею в точке А,.
Отметим, что отрезок АА3, равный расстоянию
от точки А до П3, равен отрезкам А3АУ, А2А-
и А-О.
Чтобы перейти к чертежу (рис. 62), на кото-
ром все три поля проекций совмещены с одной
плоскостью, повернем П3 вокруг оси z, аП, —
вокруг оси х до совмещения с П2. Одновре-
менно переместятся и точки Ау и А3
В результате на чертеже окажутся не только
три проекции точки А, но также три проекции
плоскостей П [. П 2, ПЗи осей х, у и z. При взгляде
спереди плоскость П2 будет расположена перед
зрителем, плоскости П; и П3 проецируются на
нее в прямые линии, первая — в прямую, сов-
падающую с осью х, вторая — в прямую, сов-
падающую с осью z. Проекцией оси у станет
точка О. При взгляде сверху перед зрителем
будет плоскость П1; плоскость П2 изобразится
в виде прямой, совпадающей с осью х, плос-
кость П3—в виде прямой, совпадающей с
осью у. Теперь ось z проецируется в точку 0
И наконец, при взгляде слева плоскость П;
окажется расположенной против зрителя, пло-
скости же П2 и П) изобразятся в виде прямых,
совпадающих соответственно с осями z и у
На этот раз точка О станет проекцией оси л
Обозначение приведенное на рис. 61 и 62,
значит, что эта линия — проекция оси у на
плоскости nt; обозначение у3 — проекция той
же оси на плоскости П3. В дальнейшем мы
будем опускать индексы.
Точка А3 лежит на одном перпендикуляре
(линии связи) к оси z с точкой Л2; точки А, и А3
также расположены в проекционной связи: до-
статочно опустить перпендикуляр из точки Л,
на прямую уу, полученную точку Ау, построить
на прямой у3 (ОАУ, = ОАУз) и восставить из
нее перпендикуляр к прямой у3. Он пройдет
через точку А3.
/56/ По двум ортогональным проекциям точки
можно построить ее третью ортогональную
проекцию.
Проекционную связь между точками А, и А3
удобно осуществить с помощью вспомогатель-
ной прямой ОК, проведенной через О под уг-
лом 45° к прямым yt и у3. В этом случае линия
связи имеет два звена: А2К и КА3.
Чертеж, приведенный на рис. 62, можно
рассматривать как три совмещенных эпюра:
эпюр в системе плоскостей П]/П2, в системе
Пг/Пз и, наконец, в системе П1/П3. Поля про-
екций всех трех эпюров лежат на общей пло-
скости — носителе (плоскости чертежа).
Система прямоугольных координат. Усло-
вимся, что оси проекций совпадают с осями
координат. Для осей проекций и осей коорди-
нат примем одинаковое обозначение — соот-
ветственно х, у иг. Условимся положительным
направлением оси х считать направление справа
налево, оси у — назад (от точки О к зрителю),
оси z — снизу вверх. На эпюре — положитель-
ное направление оси х справа налево, оси у
на плоскости Пл сверху вниз, на плоскости П3 —
слева направо; оси z снизу вверх
По горизонтальной проекции точки А мож-
г
28
но определить ее координаты X и Y Действи-
тельно, координата X точки А (рис. 62) равна
отрезку АХО или AtAy, координата У—от-
резкам AtAx или АуО. Фронтальная проекция
точки позволяет установить координаты X и Z:
координата X, кроме уже упоминавшегося от-
резка АХО, равна отрезку A2AZ. По профильной
проекции можно найти координаты У и Z
'.Y-A3AZ = АуО, Z = АуАу = АгО. Таким обра-
зом, по любой ортогональной проекции точки
можно узнать две ее прямоугольные коорди-
наты. Вместе с тем, чтобы определить положе-
ние точки в пространстве, нужно знать три ее
координаты. Третью, недостающую, коорди-
нату можно установить по второй ортогональ-
ной проекции точки.
/57/ По двум ортогональным проекциям точ-
ки можно определить все три ее координаты.
Построим проекции точки А по ее координа-
там X, У и Z. Отложим от точки О по осям х,
у и z соответственно отрезки X = ОАХ, У= ОАУ
и Z = О А,. Линии связи, проведенные через
полученные точки в своем пересечении, дадут
проекции точки А
/58/ По трем координатам точки можно по-
строить ее проекции.
Четыре угла пространства. Плоскости П, и
П2 делят пространство на четыре части (рис. 63).
Назовем их углами пространства. Передний
верхний угол будем считать первым, дальний
верхний — вторым, дальний нижний угол —
третьим и, наконец, нижний передний — чет-
вертым.
Ось х делит плоскости П, и П2 на полупло-
скости. Плоскость П2 состоит из верхней и
нижней полуплоскостей, а плоскость П] —
из передней и дальней полуплоскостей Усло-
вимся, что зритель всегда расположен в первом
углу пространства, плоскости же проекций не-
прозрачны. Поэтому любая фигура, принадле-
жащая первому углу, будет видимой, любому
другому углу — невидимой. В соответствии с
этим проекции точки, расположенной в первом
углу пространства, обозначим светлыми, во
всех других углах — черными кружками. В даль-
нейшем различия в обозначении точек делать
не будем
На рис. 64 показаны точки, принадлежащие
разным углам пространства, на рис. 65 дан
эпюр этих точек. Точка А расположена в I углу
Положение ее проекций нам уже известно.
Точка В принадлежит II углу пространства.
Следовательно, она расположена выше пло-
скости П] и за плоскостью П2. Ее фронтальная
проекция В2 лежит выше оси х, а горизонталь-
ная Bj — за этой осью. После поворота плоско-
сти П, горизонтальная проекция точки будет
также выше оси х. В частном случае обе проек-
ции могут совпасть, когда точка инцидентна
плоскости биссектора II угла пространства.
Точка С, принадлежащая III углу простран-
ства, расположена за П2 и под ПР Ее фронталь-
ная проекция С2 на эпюре ниже оси х, горизон-
тальная С, — выше этой оси. (В каком случае
С2СХ = С1СХЪ
Проекции точки D, расположенной в IV углу
пространства, лежат ниже оси х, так как сама
точка расположена под плоскостью П, и пе-
ред П2. Возможно совпадение проекций точки.
(Когда?)
Если точка инцидентна плоскости проекций,
то одна ее проекция инцидентна оси х Вторая
проекция может быть расположена как выше,
так и ниже оси, в зависимости от того, какой
полуплоскости принадлежит точка. Например,
точка Е лежит на дальней полуплоскости ПР
Ее горизонтальная проекция Е2 расположена
выше оси х, фронтальная проекция Е2 — на
оси х (Е2 = Ех). Определите расположение точ-
ки Е самостоятельно.
Чтобы по эпюру определить, какому утлу
пространства принадлежит точка, поступают
так: рассматривают вначале какую-либо одну
проекцию точки, например фронтальную
(рис. 66). Так как Л2 расположена ниже оси.
сама точка находится ниже плоскости П,,
т. е. в III или IV углах. Рассмотрев проекцию Л,,
определяют, что сама точка расположена за
плоскостью П2, т. е. во II или III углу. Так как
совпадает III угол, то именно ему и принад-
лежит точка А. По положению фронтальной
проекции точки В можно установить, что точка
расположена в I или во II углу. Горизонтальная
проекция точки — на оси х, следовательно,
точка может быть в любом из четырех углов
пространства. Так как совпадают I и II углы,
Рис. 64
Рис. 63
29
Рис. 67
то точка расположена на границе между ними —
верхней полуплоскости П2.
Способ замены плоскостей проекций. Плос-
кости П,,П2 иП3 относятся к основным плоско-
стям проекций. В ряде случаев, о которых будет
сказано ниже, нужно уметь проецировать точку
на вспомогательную плоскость, перпендикуляр-
ную одной из основных плоскостей, но обычно
не перпендикулярную другой плоскости. Если
новая плоскость проекции перпендикулярна П,,
она носит название замененной фронтальной
плоскости проекций и обозначает П4 Если она
перпендикулярна П2, то называется замененной
горизонтальной плоскостью проекций и обозна-
чается П5. При необходимости можно ввести
плоскости П6 , П7 и т. д. Принятые ранее наиме-
нования плоскостей «горизонтальная» и «фрон-
тальная» теряют свое буквальное значение и
остаются терминами. Действительно, всякая
плоскость, перпендикулярная П2, но не парал-
лельная П„ не может быть горизонтальной,
хотя и будет носить это название. Замененной
фронтальной плоскости проекций дадим чет-
ный индекс: П4, П6, ... ; замененной горизон-
тальной плоскости проекций нечетный индекс:
П5, П7, .. Так как на эпюре плоскости проекций
не обозначаются, введем индексацию осей про-
екций. Так, ось х при первоначальном располо-
жении плоскостей проекций обозначим х12
(следует читать икс одни, два); это значит, что
по прямой х12 пересекаются плоскости П, иП2.
Заменив плоскость П2 на П4, обозначим новую
ось проекций х14. Из этого обозначения следует,
что плоскость П| сохраняется и пересекается
с замененной плоскостью П4. Спроецируем
точку А на плоскость П4 (рис. 67). Проведем
через А проецирующую прямую, перпендику-
лярную П4 до ее пересечения с этой плоскостью
в точке Л4. Эту точку назовем замененной фрон-
тальной проекцией точки А. Горизонтальная
проекция At сохраняет свое положение. Заме-
тим, что координата Z точки А в новой системе
плоскостей П|/П4 по величине не меняется:
AAl = A2AXti = А4АХ„.
Переходя к эпюру в новой системе плоско-
стей проекций (рис. 68), совместим П4 с П,
(или П, с П4). В новом эпюре осью проекций
станет прямая х14. Проведя через At линию
связи перпендикулярно оси х14, отметим точ-
ку AXlJ и от нее по линии связи отложим коорди-
нату Z точки А—отрезок Л4ЛХ|4, равный от-
резку A2AXij.
Будем считать, что при замене фронтальной
плоскости проекций оказалась замененной и
плоскость координат xOz. Поэтому координа-
ты X и Y точки в новой системе плоскостей
изменились. Координата же Z, или, как мы ее
назвали, недостающая координата для плоско-
сти Пп сохранила свою величину. При замене
горизонтальной плоскости проекций на новую
плоскость изменятся координаты X и Z, но не
изменится координата Y, которая в этом случае
будет недостающей.
/59/ При замене одной плоскости проекций
на другую сохраняется та координата точки,
которая для иезамеиеиной плоскости проекций
является недостающей.
При решении некоторых задач нужно два,
30
Рис. 69
иногда три раза последовательно заменять
плоскости проекций. Проследим за построения-
ми по рис. 69. Вначале П2 заменена плоско-
стью П4 и построена проекция Л4 точки А.
В этой части построения аналогичны показан-
ным на рис. 68. Проделав их, мы от эпюра в
системе плоскостей П2/П, перешли к эпюру
в системе П4/П..
Заменим теперь плоскость П, и П5 (ось х45
задана). Проведем линию связи через Л4 пер-
пендикулярно оси х45 и от точки AUs отложим
координату У точки А (т. е. отрезок А,Ах14),
измеренную на эпюре в системе П4/П,. В ре-
зультате мы перейдем к эпюру в системе П4/П5.
Заменим плоскость П4 плоскостью П6 (ось х5б
задана). Из точки As проведем линию связи
перпендикулярно оси х56 и от точки А х отло-
жим координату Z точки А, измеренную в сис-
теме плоскостей Пд/Пд. Этот отрезок Л4ЛГ
В результате получим точку А6—замененную
фронтальную проекцию точки А.
Проделайте самостоятельно построения, за-
менив плоскость П; на П5, затем П2 на П4 и,
наконец П5 на П7.
§ 7. ПРЯМАЯ
Эпюр примой. Спроецировав прямую на две
плоскости ортогональных проекций и совмес-
тив плоскости с одной из них, получим эпюр
прямой линии. Проекции каждой точки прямой
расположены в проекционной связи, следова-
тельно, в проекционной связи расположены и
проекции прямой линии. Эпюр прямой линии
обратим, кроме случая, когда прямая спроеци-
руется на обе плоскости проекций одной (дваж-
ды проецирующей) плоскостью (см. /32/). Чтобы
построить эпюр прямой, достаточно построить
эпюр двух инцидентных прямой несовпадаю-
щих точек; соединив одноименные проекции
точек (т. е. фронтальную с фронтальной, гори-
зонтальную с горизонтальной) прямыми линия-
ми, получим эпюр прямой.
/60/ Эпюром прямой линии называется чер-
теж, на котором ортогональные проекции точек,
инцидентных прямой, расположены в проекцион-
ной связи (см. /55/).
Расположение прямой относительно осиоиных
плоскостей проекций. Прямая общего положении
(рис. 70 и 71) не параллельна ни одной из основ-
ных плоскостей проекций. Прямая, параллель-
ная П2, называется фроиталью (рис. 72 и 73).
31
Прямая, параллельная П] — горизонталь
(рис. 74 и 75). Прямая, параллельная П3,—
профильная прямая (рис. 76 и 77). Фронталь,
горизонталь и профильная прямая называются
линиями уровня.
Прямая, перпендикулярная П2, называется
фронтально проецирующей (рис. 78); перпенди-
кулярная II , — горизонтально проецирующей
(рис. 79), перпендикулярная П3 — профилыи
проецирующей (рис. 80). Проецирующие прямы
вместе с тем являются и линиями уровня.
Прямые могут быть инцидентными плоско
стям проекций. Это частные случаи линий уро»
ня. На рис. 81 изображены прямая Л .В СП,
(фронталь) и прямая СО СП, (горизонталь)
Рассмотрим признаки, по которым можно
судить о расположении прямой в пространств
по ее проекциям. Обратимся вначале к прямы,
частного положения.
/61/ Горизонтальная проекция фронта ли ш
раллельна оси х,
Сказанное следует из того, что координаты
всех точек прямой равны между собой (см
рис. 73). На П2 отрезок фронтали проецируете
в натуральную величину (см. /39/). Угол
наклона фронтали к П1 и угол у ее наклона к П
проецируются на плоскость П2 в равные №
утлы (см. /19/), т. е. а =а2 и у =у2.
/62/ Фронтальная проекция горизонтали ш
раллельна оси х. Действительно, координаты
всех точек прямой равны между собой (см
рис. 75). На П| отрезок горизонтали проеш
руется в натуральную величину; на эту л
плоскость проецируются углы наклона гори
зонтали к плоскостям П2 и П3 в равные »
углы (Р = Р, и у = yt).
/63/ Фронтальная и горизонтальная проект
профильной прямой перпендикулярны оси х.
Это определяется равенством координат
всех точек прямой (см. рис. 77). Отрезок пр
фильной прямой проецируется на П3 в нат
ральную величину. Углы наклона профи льне
проекции прямой к осям у и z равны соотве
ственно углам наклона самой прямой к плоек
стям П2 и П2 (а = а3 и р = р3).
Проецирующие прямые (рис. 78, 79 и 8
на перпендикулярные им плоскости проект
проецируются в точки (см. /10/), на параллел
ные плоскости — в прямые, перпендикуляры!
соответствующим осям проекций. Если прям
(рис. 81) инцидентна плоскости П, или П
то одна ее проекция совпадает с осью х (как
именно?).
32
Вернемся к прямой общего положения. По ее
проекциям (рис. 71) можно судить о том, что
прямая не параллельна какой-либо плоскости
проекций (почему?), а следовательно, и не пер-
пендикулярна ни одной из них. Длина проекции
отрезка прямой, например АВ, на любой из
основных плоскостей меньше длины отрезка
в натуре. В соответствии с /40/. AtBi =АВх
х cos а, А2В2 = АВ -cos Р, А3В2 = AB-cos у, где
а, р и у — углы наклона прямой соответственно
к плоскостям Пп П2 и П3.
Следы прямой линии. Так как следом прямой
линии является точка пересечения прямой с
плоскостью проекций, то по крайней мере,
одна координата такой точки равна нулю.
В зависимости от того, с какой плоскостью
проекций пересекается прямая, след прямой
называется фронтальным, горизонтальным или
профильным. Координата У фронтального сле-
да, координата Z горизонтального и коорди-
ната X профильного следа равны нулю.
Рассмотрим построение горизонтального
следа прямой а (рис. 82). В пересечении фрон-
тальной проекции прямой с осью х расположена
точка М2 — фронтальная проекция той точки
прямой, координата Z которой равна нулю,
т. е. ее горизонтального следа. Проведя линию
связи через точку М2 до пересечения с прямой ах,
отметим горизонтальную проекцию горизон-
тального следа — точку Xft. Наглядное изоб-
ражение проделанных построений показано на
рис. 83.
/64/ Чтобы построить горизонтальный след
прямой линии, нужно отметить точку пересече-
ния фронтальной проекции прямой с осью х и
через эту точку провести линию связи до пересе-
чения с горизонтальной проекцией прямой.
Фронтальным следом прямой является та-
кая ее точка, координата У которой равна нулю.
/65/ Чтобы построить фронтальный след пря-
мой линии, нужно отметить точку пересечении
горизонтальной проекции прямой с осью х (точка
JV, на рис. 82 и 83) и через эту точку провести
линию связи до пересечения с фронтальной про-
екцией прямой (точка N2).
3—940
33
Построение профильного следа основано на
том, что координата X этого следа равна нулю.
Строить следы прямой линии нужно, в част-
ности, для того, Чтобы решить, через какие
углы пространства проходит прямая. Прямая а
на рис. 82 проходит через II, I и IV углы. Об
этом можно судить не только по наглядному
изображению на рис. 83, но и по эпюру. Точка N
расположена на верхней полуплоскости П2,
которая разделяет I и II углы пространства.
Следовательно, в точке N прямая переходит
из II угла в I. В точке М, которая лежит на перед-
ней полуплоскости По прямая переходит из I
в IV угол пространства, так как передняя полу-
плоскость П, разделяет именно эти углы.
Выше мы условились считать видимым все
то, что расположено в I углу пространства.
В данном случае в I углу располагается отрезок
MN прямой а; поэтому его проекции вычерчены
сплошными линиями, отрезки, лежащие левее
точки М и правее точки N, — штриховыми ли-
ниями, т. е. так, как это принято в техническом
черчении.
/66/ Для определения видимости прямой ли-
нии нужно построить ее следы и найти отрезок,
расположенный в Ь углу пространства (если пря-
мая проходит через I угол).
Определение длины отрезка прямой общего
положении и углов наклона прямой к плоскост ям
проекций. Воспользуемся способом замены пло-
скостей проекций. Расположим новую плос-
кость проекций параллельно прямой. В новой
системе плоскостей проекций прямая станет
фронталью или горизонталью. Зная, что одна
из проекций фронтали и горизонтали параллель-
на оси х (см. /61/ и /62/), новую ось проекций
следует провести параллельно любой проекции
прямой общего положения.
Рассмотрим пример (рис. 84). Заменим П2
плоскостью П4 || АВ (х,4 || A ,Bt). Построим точ-
кй А4 и В4 в соответствии с описанием к рис. 68.
Отрезок A 4Bt равен отрезку А В, а ад = а, так как
в системе П4/П1 прямая АВ—фронта ль.
Выше говорилось, что ось проекций на
эпюре может быть не проведена (см. /44/)
Если отрезок изображен на «безосном» эпюре
то для определения его величины следует вна-
чале провести ось xiz (рис. 85), например, через
точку Аг (координата Z точки А будет равна
нулю). Проведем ось х14 совпадающей с At В,
на линии связи, проходящей через Bt, отложим
координату Z точки .В. Построив точку В4.
34
соединим ее с точкой А t = Л4. Одновременно
определяется и величина угла а наклона прямой
к Пь а = а4.
Для определения величины угла Р наклона
прямой к плоскости П2 (рис. 86) следует про-
вести ось х12, например, через точку Ах и за-
менить плоскость П2 на П5, пре одящую через
прямую АВ (А2В2 = х25). В системе П2/П5 пря-
мая АВ станет горизонталью, а угол Р5 = р.
/67/ Для определения величины отрезка пря-
мой общего положения и угла ее наклона к одной
из плоскостей проекций следует заменить вто-
рую плоскость проекций, расположив новую пло-
скость параллельно прямой; на этой плоскости
отрезок и угол проецируются в натуральную ве-
личину.
§ 8. ДВЕ ПРЯМЫЕ
Взаимное расположение прямых линий. Скре-
щивающиеся прямые а и b изображены на рис. 87.
Несмотря на то что прямые не имеют общей
точки, их проекции а, и Ь, пересекаются в точке
A4 = Bt, являющейся проекцией двух точек,
одна из которых (А) лежит на прямой а, другая
(В) — на прямой Ь. Следовательно, точки Ан В
инцидентны разным прямым, но проециру-
ются общей проецирующей прямой АВ (см. /2/).
Такие точки называются конкурирующими.
На эпюре скрещивающихся прямых (рис. 88)
изображены две пары конкурирующих точек:
одна пара ( А и В) конкурирует относительно П,,
вторая пара (С и D) — относительно П2. Точки,
в которых пересекаются проекции прямых
(^, = 5, и С2 -- D2), называются точками ка-
жущегося пересечения. Действительно, при взгля-
де спереди зрителю может показаться, что
прямые а и b пересекаются в точке С = D, при
Рис. 88
Рис. 89
взгляде сверху — в точке А = В. Чтобы убе-
диться в том, что прямые не пересекаются,
нужно построить фронтальные проекции то-
чек А и В и горизонтальные проекции точек
С и В.
На эпюре рис. 88 ось проекций не проведена.
В дальнейшем мы будем проводить ее только в
том случае, когда она будет нужна для решения
задачи (см. /44/).
Пересекающиеся прямые а и Ь (рис. 89)
имеют общую точку (А); на эпюре ее проекции
расположены в проекционной связи.
Следовательно, чтобы отличить на эпюре
скрещивающиеся прямые от пересекающихся,
нужно проверить; существует ли проекционная
3*
35
связь между точками пересечения одноименных
проекций прямых.
/68/ Точки пересечения одноименных проек-
ций пересекающихся прямых инцидентны общей
линии связи, такие же точки проекций скрещи-
вающихся прямых ие инцидентны общей линии
связи.
Если какие-либо одноименные проекции пря-
мых совпадают, это значит, что обе прямые
инцидентны одной проецирующей плоскости
Тогда точку пересечения прямых следует опре-
делять по тем их проекциям, которые пересе-
каются. В примере на рис. 90 можно отметить
точку К2, в которой пересекаются прямые
И
Когда обе прямые инцидентны общей про
фильной плоскости (рис. 91), совпадают не
только горизонтальные, но и фронтальные про-
екции прямых. Точку их пересечения опре-;
деляют, заменив одну из плоскостей проекций.
Построив на замененной плоскости проекции
обеих прямых, отмечают точку их пересечения
и устанавливают проекционную связь с перво
начально данными проекциями. Естественно,
что на эпюре проведена ось х, 2, если же ее нет,
то перед тем, как приступить к решению, сле-
дует провести эту ось в удобном месте.
Ранее (см. /36/ и /37/) мы установили призна-
ки, по которым можно судить о параллельно-
сти прямых по их изображениям. С учетом этих
признаков можно утверждать, что а | Ь и с || d
(рис. 92).
Однако иногда одноименные проекции пря-
мых взаимно параллельны, прямые же в про-
странстве скрещиваются. Это возможно в слу-
чае, когда скрещивающиеся прямые параллель-
ны той плоскости проекций, на которой не
дана проекция прямых. Например, прямые АВ
и CD (рис. 93) проецируются наП, иП2 в виде
параллельных прямых. О том, параллельны
ли они между собой, мы судить не можем,
так как прямые параллельны П3, проекции
на которой не даны (на рис. 93 каждая прямая
задана парой точек; почему?)
Спроецируем прямые на плоскость, не па
раллельную П, или П2. Построив замененные
36
Рис. 94
проекции прямых, убеждаемся, что прямые в
пространстве не параллельны, так как их но-
вые проекции не удовлетворяют условию /35/.
(Вместо П4 можно было использовать пло-
скость П3.)
Расстояние между двумя прямыми. При ре-
шении большинства метрических задач, отно-
сящихся к фигурам, занимающим" общее поло-
жение относительно основных плоскостей про-
екций, можно спроецировать их на новую пло-
скость так, чтобы фигуры или одна из них за-
няли частное положение относительно заме-
ненной плоскости.
Расстояние между параллельными прямыми
известно, если прямые — проецирующие. На-
пример, расстояние между горизонтально про-
ецирующими прямыми аиЬ (рис. 94 и 95) равно
расстоянию между их горизонтальными про-
екциями. Отрезки А1В1 и АВ равны, так как
прямая АВ — горизонталь (см. /162/) и она
перпендикулярна прямым а и b (см. /45/).
Если параллельные прямые лежат в плоско-
сти, параллельной одной из плоскостей проек-
ций, то расстояние между их проекциями на
этой плоскости равно расстоянию между пря-
мыми в натуре (см. /43/). Этот случай мы рас-
смотрим в гл. III.
Определим расстояние между параллель-
ными фронталямиаиЬ (рис. 96). ЗаменимП, на
П5 так, чтобы прямые стали перпендикулярны-
ми П5. Для этого ось проекций х25 проведем
перпендикулярно фронтальным проекциям пря-
мых. Расстояние между точками а5 и Ь5 искомое.
Расстояние от отрезка А2В2 до оси х25 может
быть выбрано произвольно (почему?). Уста-
новив проекционную связь, найдем точки Л,
и Bp
Определяя расстояние между параллель-
ными прямыми общего положения, нужно дваж-
ды заменить плоскости проекций. Вначале
(рис. 97) заменим П2 на П4 расположив ГЦ
параллельно прямым. Теперь задача аналогич-
на приведенной на рис. 96. Заменим П, на П5
так, чтобы прямые стали перпендикулярны-
ми замененной плоскости (см. описание к
рис. 69).
37
Рис. 98
Рис. 99
/69/ Чтобы определить расстояние между па-
раллельными прямыми общего положения, сле-
дует заменить одну из плоскостей проекций,
расположив ее параллельно прямым, затем заме-
нить вторую плоскость проекций так, чтобы пря-
мые стали проецирующими.
Кратчайшее расстояние между двумя скре-
щивающимися прямыми общего положения
может быть определено в результате двух по-
следовательных замен плоскостей проекций.
Вначале (рис. 98) заменим П2 на П4 (или П,
на П5), расположив ГЦ параллельно одной из
прямых, например EF. Теперь заменим П, на
П5, проведя П5 перпендикулярно EF. На этой
плоскости прямая EF проецируется в точку,
расстояние от которой для проекции прямой
CD равно искомому.
/70/ Кратчайшее расстояние между скрещи-
вающимися прямыми проецируется в натураль-
ную величину на той плоскости проекций, которой
перпендикулярна одна из прямых.
Чтобы показать общий перпендикуляр АВ
на первоначально заданных проекциях прямых,
воспользуемся тем, что этот отрезок на П5
проецируется в натуральную величину (так как
АВ—горизонталь), следовательно, Л4В4||х45.
Найдя точку Л4, построим точку й4, а затем,
установив проекционную связь, отметим точки
Л, и В, на горизонтальных проекциях прямых
и точки Аг и В2 на их фронтальных проек-
циях.
Описанный прием может быть использован
и для определения расстояния от точки до пря-
мой общего положения. Если же дана прямая
уровня, задача решается проще. Прямая а —
горизонталь (рис. 99). В соответствии с (45) пс
прямой угол, образованный перпендикуляром,
опущенным из А на прямую а, проецируется
на П1 также в прямой угол. Опустим из Л,
перпендикуляр на прямую at и отметим точку Bt ।
их пересечения. Установив проекционную связь
определим точку В2. Отрезки AiBi и A2B,
представляют собой проекции искомого пер-
38
Рис. 101
пендикуляра. Определим величину этого отрезка
(см. рис. 86).
Вспомогательное проецирование. Большинст-
во позиционных задач, относящихся к точкам
и прямым, может быть решено изученными
приемами. Однако иногда удобнее пользоваться
способом вспомогательного проецирования, при-
менение которого может значительно упростить
построения или позволит вынести их на сво-
бодную часть листа бумаги.
Вспомогательное проецирование может быть
центральным и параллельным. При централь-
ном проецировании на эпюре должен быть задан
собственный центр проецирования, при парал-
лельном задается направление проецирования.
В качестве плоскости проекций часто принима-
ется одна из плоскостей ортогональных проек-
ций. Пусть требуется прямую a (at; а2) спро-
ецировать из точки S на nt (рис. 100). Возьмем
на прямой произвольные точки Л и В и прове-
дем через них проецирующие прямые SA и SB
до пересечения с плоскостью П,; иначе говоря,
построим горизонтальные следы проецирую-
щих прямых (см. I6AI). Соединив горизонталь-
ные проекции следов — точки Л, и В, — прямой
линией, получим вспомогательную центральную
проекцию ах прямой а на плоскости Пр Анало-
гично решается задача, когда проецирование
параллельное (рис. 101). Оно задано направле-
нием s(s!;j2)- Плоскость П, в приведенных
примерах становится носителем двух полей
проекций П, и Пр
Если нужно спроецировать прямую в точку
(т. е. сделать ее проецирующей), следует при-
нять центр проецирования на заданной прямой
или принять направление проецирования парал-
лельным прямой (рис. 102). Горизонтальный
след а (а у, а2) прямой а в этом случае будет и ее
вспомогательной, центральной или параллель-
ной проекцией на плоскости Пр
Рассмотрим примеры. Нужно определить,
пересекаются или скрещиваются прямые а и b
(рис. 103). Точки пересечения одноименных
Рис. 102
проекций прямых расположены за пределами
чертежа, поэтому использовать /68/ нельзя.
Спроецируем обе прямые на П, в направлении
одной из них, например b (для построения
проекции прямой а возьмем на ней произволь-
ные точки А и В). Так как точка Ь2, в которую
спроецировалась прямая 6, не инцидентна про-
екции а, прямой а, приходим к выводу, что
прямые а и b в пространстве скрещиваются
(см. /23/).
39
ГЛАВА Ш
ПЛОСКОСТЬ
§ 9. ПОЛОЖЕНИЕ ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
Задание плоскости. Плоскость в простран-
стве может быть задана тремя не инцидентны-
ми одной прямой точками. Если соединить две
из них прямой линией, то плоскость будет задана
прямой и не инцидентной ей точкой. Соединив
прямой еще две точки, перейдем к заданию
плоскости двумя пересекающимися прямыми.
И наконец, можно, соединив прямой две точки,
провести через третью точку прямую, парал-
лельную первой. Плоскость будет задана двумя
параллельными прямыми. Иногда удобно за-
дать плоскость ее отсеком произвольной формы:
треугольником, кругом, частью плоскости, рас-
положенной внутри эллипса, или линиями,
определяющими границы отсека: сторонами
треугольника, окружностью, эллипсом. Эпюр
плоскости, когда она задана двумя пересекаю-
щимися прямыми, показан на рис. 104, двумя
параллельными прямыми — на рис. 105 и от-
секом (треугольником)—на рис. 106.
В некоторых случаях плоскость задается
линиями ее пересечения с плоскостями проек-
ций, т. е. следами (рис. 107). В зависимости от
того, с какой плоскостью проекций пересека-
ется данная плоскость (fl), след носит название
горизонтального, фронтального или профиль-
ного. Они обозначаются соответственно finlf
ОП2 и ОП,. Следа попарно пересекаются в
Нис. 105
точках flx, fl,- и flz на осях проекций, называе-
мых точками схода следов плоскости. Любая
пара следов задает плоскость в пространстве,
так как следы — это пересекающиеся или па-
раллельные прямые плоскости.
/71/ Плоскость в пространстве может быть
задана: тремя не инцидентными одной прямой
точками; прямой и не инцидентной ей точкой;
двумя пересекающимися прямыми; двумя парал-
лельными прямыми; отсеком; следами. На эпюре
изображаются проекции тех фигур, которые за-
дают плоскость.
Следа плоскости на эпюре (рис. 108) изоб-
ражаются так же, как и другие прямые, инци-
дентные плоскостям проекций, однако обозна-
чаются только те проекции, которые совпадают
со следами. Например, фронтальный след пло-
скости fl совпадает со своей фронтальной про-
екцией, ее мы и обозначили НП2. Горизонталь-
ная и профильная проекции этого следа не обо-
значаются. Следует помнить, что горизонталь-
ная проекция фронтального следа плоскости
совпадает с осью х (почему?), а профильная
проекция—с осью г. Определите сами, какую
проекцию горизонтального и профильного еле-
40
дов нужно обозначить и с какими осями проек-
ций совпадают необозначенные проекции сле-
дов.
Расположение плоскости относительно основ-
ных плоскостей проекций. Плоскость, не перпен-
дикулярную ни одной из основных плоскостей
проекций, будем называть плоскостью общего
положения (см. рис. 107). К занимающим част-
ное положение относятся проецирующие пло-
скости (перпендикулярные плоскостям проек-
ций). В рассматриваемых нами ортогональных
проекциях существует три вида проецирую-
щих плоскостей: перпендикулярная П j называ-
ется горизонтально проецирующей, перпендику-
лярная П2 — фронтально проецирующей, пер-
пендикулярная П3— профильно проецирующей.
Фронтально проецирующая плоскость Я
показана на рис. 109 и ПО. Так как плоскости Я
и П, перпендикулярны П2, то линия их пересе-
чения (след ЯЩ) также перпендикулярна П2,
а следовательно, и оси х. По этому признаку
можно отличить фронтально проецирующие
плоскости от других плоскостей (конечно, если
плоскости заданы следами). С фронтальным
следом фронтально проецирующей плоскости
совпадает фронтальная проекция этой плоско-
сти (см. /14/), т. е. ЯП2 = Я2. (Продумайте, как
расположен профильный след плоскости Я?)
Прямая Я2 определяет положение плоскости
в пространстве. Более того, угол ее наклона к
оси х равен углу наклона плоскости Я к Пп
а угол наклона к оси z равен углу наклона пло-
скости ж П3 (рис. 11D). Аналогичны рассужде-
ния о горизонтально- и профильно-проецирую-
щей плоскости, поэтому:
/72/ Проекция проецирующей плоскости, пред-
ставляющая собой прямую, определяет положе-
ние плоскости в пространстве (см. /14/; сравни-
те с /34/).
/73/ Угол между проецирующей плоскостью
и неперпендикулярной ей плоскостью проекций
проецируется в натуральную величину на той
плоскости проекций, которой перпендикулярна
проецирующая плоскость.
На рис. 111 и 112 изображена горизонтально
проецирующая плоскость Я. Ее фронтальный
Рис. 109
44
Рис. 116
след перпендикулярен оси х, а профильный —
оси у. Горизонтальная проекция плоскости
совпадает с ее горизонтальным следом: Я) =
= £2П1. Угол Pj наклона прямой к оси х
равен углу Р наклона плоскости к П2, а угол ее
наклона к оси у равен углу у наклона плоско-
сти к П3.
Профильно проецирующая плоскость пока-
зана на рис. 113 и 114. Ее фронтальный и гори-
зонтальный следа параллельны оси х. Про-
фильный след, совпадающий с профильной
проекцией плоскости (ЯП3 = Я3), наклонен к
оси у под углом а3 =а наклона плоскости к П,.
Угол Р3 наклона этого следа к оси z равен углу
наклона профильной проецирующей плоско-
сти к П2.
Рассмотрим эпюры проецирующих плоско-
стей при задании их точками и прямыми.
Фронтально проецирующая плоскость Я (А;
В; С) показана на рис. 115. Фронтальные про-
екции точек А, В, С лежат на прямой Я2 — фрон-
тальной Проекции плоскости.
Горизонтально проецирующая плоскость
Я (а ПЬ) изображена на рис. 116. Горизонталь
ные проекции обеих прямых совпадают с гори-
зонтальной проекцией плоскости: ах = bt = Я,.
На рис. 117 показана профильно проецирую-
щая плоскость Я (АВ || CD). По фронтальным
и горизонтальным проекциям прямых АВ и CD
нельзя судить о расположении в пространстве
определяемой ими плоскости. Профильные же
проекции прямых совпадают друг с другом и с
профильной проекцией плоскости: Л3В3 =
= СзПз = Яз, что. и указывает на проецирующее
положение плоскости. Проекционная связь меж-
ду проекциями точек А и В на плоскостях
и П3 установлена с помощью прямой, накло-
ненной к линиям связи под углом 45° (см. пояс-
нения к рис. 62), проведенной в произвольном
месте чертежа (см. /44/).
Плоскости, параллельные одной из основ-
ных плоскостей проекций, а следовательно,
перпендикулярные двум другим плоскостям,
называются плоскостями уровня. Они дважды
проецирующие.
42
. Плоскость X, параллельную П2, назовем
фронтальной плоскостью, она является горизон-
тально профильно проецирующей (рис. 118).
Параллельная плоскости Пь или горизон-
тальная, плоскость является фронтально про-
фильно проецирующей (рис. 119).
Плоскость, параллельная П3, называется
профильной. Она фронтально горизонтально про-
ецирующая (рис. 120).
Любая проецирующая плоскость может быть
задана на эпюре той ее проекцией, которая пред-
ставляет собой прямую.
Прямая, инцидентная плоскости. Построим
вторую проекцию прямой по одной ее проекции,
когда известно, что прямая инцидентна задан-
ной плоскости. Основываясь на /23/ и /30/, най-
дем точки пересечения известной проекции пря-
мой с одноименными проекциями линий, инци-
дентных плоскости. На рис. 121 даны плоскость
АВС и фронтальная проекция прямой а С АВС.
Отметим точки М2 и N2 пересечения а2 с В2С2 и
43
А2С2 и, установив проекционную связь, найдем
точки Л/j и IV,, определяющие прямую а,. I
Все прямые плоскости пересекаются с плос-1
костью проекций в точках, лежащих на следе
плоскости.
/74/ След прямой, инцидентной плоскости,
инцидентен соответствующему следу плоскости.
На рис. 122 дана плоскость X (ХЩ; ХП2)
и горизонтальная проекция а, прямой а С. 1.
Нужно найти фронтальную проекцию прямой.
Отметим точки N1 и М2 пересечения прямой я,
с горизонтальными проекциями следов плоско-
сти, затем найдем их фронтальные проекции
(точка N2 на оси х; почему? Точка М2 — нг
фронтальном следе; почему?). На рис. 123 дане
наглядное изображение построенной линии.
Плоскость, инцидентная прямой. Прямой
общего положения может быть инпидентне
множество плоскостей общего положения, прое-
цирующих же только три: фронтально проеци-
рующая Ч*, горизонтально проецирующая Q
й профильно проецирующая Е (рис. 124). Пря-
мой уровня (не перпендикулярной одной из плос-
костей проекций) могут быть инцидентны две
проецирующие плоскости и, наконец, проеци-
рующей прямой — множество плоскостей, пер-
пендикулярных той плоскости проекций, кото-
рой перпендикулярна прямая.
/75/ Прямой общего положения могут был
инцидентны три проецирующие плоскости, пря-
мой уровня — две, проецирующей прямой —. мно-
жество плоскостей, перпендикулярных той же
плоскости проекций.
Чтобы построить фронтально проецирую
щую плоскость, инцидентную прямой а общего
положения, достаточно принять фронтальнук
проекцию прямой (см. /16/) за фронтальнук
проекцию плоскости (рис. 125). Если плоскость
по условиям задачи должна быть задана следа-
ми, то ее фронтальный след совпадет с фрон-
тальными проекциями прямой и плоскости
(а2 = fl2 = Г1П2). Горизонтальный след С1П
перпендикулярен оси х. Постройте самостоя-
тельно следы горизонтально проецирующей
плоскости, инцидентной прямой а.
Построим фронтально проецирующую плос-
кость, инцидентную прямой а (а,; а2) и зададим
ее прямыми а Г) b (рис. 126). Через любую точ-
ку Ах прямой ах проведем прямую Ьх произволь-
ного направления. Прямые а2 и Ь2 в соответ-
ствии с (16) должны совпасть между собой и (
фронтальной проекцией плоскости: а2=Ь2 =
= fl2. Аналогично решается задача на проведе-
ние горизонтально проепирующей плоскости
инпидентной прямой общего положения
44
Чтобы плоскость, инцидентная прямой а,
была профильно проецирующей (рис. 127), нуж-
но через произвольную точку А прямой а про-
вести профильно проецирующую прямую Ь.
Следы плоскости. От задания плоскости
прямыми можно перейти к заданию ее следами
и наоборот (см. /74/). Дана плоскость общего
положения Я (а П Ь) (рис. 128). Найдем ее следы.
Для этого построим фронтальные проекции
фронтальных следов заданных прямых (см.
/65/) — точки В2 и D2 и соединим их прямой
линией. Вслед за этим соединим прямой гори-
зонтальные проекции горизонтальных следов
прямых — точки Л; и С, (см. /64/). Если следы
прямых, задающих плоскость, выходят за пре-
делы чертежа, следует взять в плоскости другую
пару прямых и определить ее следы. При по-
строении одного из следов плоскости может
быть использована найденная ранее точка Ях,
лежащая на оси х.
/76/ Фронтальный след плоскости инциден-
тен фронтальным следам всех прямых линий
этой плоскости.
Что можно сказать о горизонтальном и про-
фильном следах плоскости?
Угол между фронтальным и горизонталь-
ным следами плоскости в натуре (не на эпюре!)
может быть острым и тупым. Угол между теми
же следами фронтально и горизонтально про-
ецирующей плоскости всегда прямой (если это
не плоскость уровня). Соответствующие следы
профильно проецирующей плоскости парал-
лельны ОСИ X.
Особые линии плоскости. Среди множества
линий плоскости можно выделить линии, па-
раллельные плоскостям проекций: фронтали
плоскости, горизонтали плоскости и профильные
прямые плоскости. Они называются линиями
уровня плоскости. К особым относятся и линии
наклона, определяющие угол наклона плоско-
сти к соответствующей основной плоскости
проекций.
Фронталь f плоскости Я показана на рис. 129.
Все фронтали плоскости параллельны между
собой и плоскости П2. фронтальный след пло-
скости является частным случаем ее фронта-
лен, поэтому он параллелен другим фронталям
плоскости Горизонтальная проекция фрон-
тали параллельна оси х (см. /61/). Фронтальные
проекции фронталей параллельны между собой
и фронтальному следу плоскости (см. /35/).
Фронталь пересекается с ГЦ и П3 в точках М
и Р, которые являются ее горизонтальным
и профильным следами и инцидентны соответ-
ствующим следам плоскости Я.
Чтобы построить произвольную фронталь
плоскости Я, заданной на эпюре следами
(рис. 130), достаточно:
1. Провести в произвольном месте чертежа
прямую /|| х (см. /61/), найти горизонтальный
след фронтали М (М}; М2) и через точку М2
провести f2 || ЯП2.
2. Провести в произвольном месте чертежа
прямую /2 || ЯП 2; найти горизонтальный след
фронтали М (М3; М2) и через точку М3 прове-
сти прямую /, || х.
Если плоскость задана прямыми а || b
(рис. 131) и нужно провести произвольную
45
фронталь этой плоскости, воспользуемся тем,
что нам известно направление горизонтальной
проекции фронтали. Через произвольную точ-
ку А, прямой flj проведеми отметим точку В,
ее пересечения с Ь2; найдем точки А2 и В2,
которым инцидентна прямая f2.
На рис. 132, 133 изображена горизонталь h
плоскости £1 Горизонтальная проекция ht па-
раллельна горизонтальному следу £2П! пло-
скости £1 Горизонтальный след плоскости явля-
ется частным случаем горизонтали. Фронталь-1
ный след N горизонтали инцидентен фронталь-
ному следу плоскости, а профильный след Р — I
ее профильному следу. Фронтальная и профиль-
ная проекция горизонтали плоскости параллель-
ны соответственно осям х и у.
Если плоскость задана прямыми линиямв
(рис. 134), следует начать с проведения фрон-
тальной проекции h2 горизонтали, которая па-
раллельна оси х. Найдя точки А2 и В2 пересече-
ния h2 с прямыми а2 и Ь2, построим точки А, и
В, и проведем через них прямую hv
Построение проекций профильной прямой
плоскости предоставляем продумать читатели.
Используя горизонталь и фронталь, можно
построить следы плоскости. Проведем в пло-
скости £1(дп Ь) горизонталь h и фронталь /|
(рис. 135). Найдя фронтальную проекцию фрон-
тального следа горизонтали — точку Л2, про-
ведем через нее ОП2 ||/2. Отметив точку £1 пере-
сечения прямой £2П2 с осью х, проведем через
нее £2П2 | ht.
Угол наклона плоскости к плоскости проек-
ций измеряется линейным углом между прямы-
ми, инцидентными этим плоскостям и перпен-
дикулярными линии их пересечения. Это линии -
наклона и их проекции на соответствующие
плоскости. Дана плоскость £1 (рис. 136). По-
строим плоскость X З-ППр Плоскости S и £)
пересекаются между собой по прямой а, а
плоскости Е и П, —по прямой др Прямые а и
Д] перпендикулярны следу £1П 15 угол а между
ними является линейным углом двугранного
угла между плоскостями £1 и П г
Рис. 133
46
Всякая плотность имеет три вида линий
наклона, определяющих углы между этой пло-
скостью и плоскостями П1, П2 и П3. Линию
наклона к П, называют линией ската.
/77/ Угол между линией наклона плоскости
в соответствующей плоскостью проекций равен
по величине углу между этими плоскостями.
Линия наклона перпендикулярна следу пло-
скости на соответствующей плоскости проекций
(см. /45/), а следовательно, одной из линий
уровня плоскости.
/78/ Линия наклона плоскости к плоскости П2
перпендикулярна фронталям плоскости, линия
ската перпендикулярна горизонталям плоско-
сти, а линия наклона к плоскости П3 перпенди-
кулярна профильным прямым плоскости.
Угол наклона плоскости к плоскости проек-
ций. На рис. 137 дана плоскость АВС общего
положения. Определим угол ее наклона к П2.
Проведем фронталь f плоскости АВС через
произвольную точку плоскости, например А.
Фронтальная проекция линии наклона плоско-
сти Л ВС к плоскости П2 перпендикулярна фрон-
тальной проекции фронтали (см. /78/ и /45/).
Через любую точку фронтальной проекции
треугольника, например С2, проведем перпен-
дикуляр к f2 и отметим точку Р2 его пересече-
ния с/2. Установив проекционную связь, найдем
отрезок Cj Di и определим угол р наклона пря-
мой CD к П2. Этот угол равен искомому (Р = Р5;
см. рис. 86).
Аналогично решается задача, когда плос-
кость задана следами. Определим угол наклона
плоскости D к плоскости rij (рис. 138). Прове-
дем линию ската А В. Ее горизонтальная проек-
ция перпендикулярна ОПр Отметив точки At
и Bj, найдем точки Л2 и В2. Им инцидентна
фронтальная проекция линии ската. Восполь-'
зовавшись способом замены плоскостей проек-
ций (длина отрезка В1В2 равна координате z
точки В), определим угол наклона прямой АВ
к плоскости П1л равный углу между плоско-
стями О и П, (а4 = а). Тем же приемом опреде-
лим угол Р5 = р.
Если а = р,' то плоскость называется равно-
наклонной.
* ।
1
47
Рис. 139
Точка, инцидентная плоскости. Даны пло-
скость а ЛЬ (рис. 139) и горизонтальная
проекция инцидентной ей точки А (см. /30/).
Требуется построить точку Аг. Проведем через
At горизонтальную проекцию произвольной
прямой, инцидентной плоскости а Г) Ь, и отме-
тим точки Вх и Q ее пересечения с прямыми ах
и bv Найдя фронтальные проекции точек В
и С, соединим их прямой линией и на ней в ее
пересечении с линией связи, проведенной через
Ах, найдем точку А2.
/79/ Точка инцидентна плоскости, если она
инцидентна одной из прямых плоскости.
Для ответа на вопрос, инцидентна ли пло-
скости а ЛЬ точка D (Dt; D2), можно восполь-
зоваться тем же приемом. Проведем через Dt
горизонтальную проекцию прямой EF, о кото-
рой известно, что она инцидентна плоскости
а ЛЬ. Отметив точки Et и Fls установим проек-
ционную связь и найдем точки Е2 и F2. Если
бы точка D была инцидентна плоскости а ЛЬ,
то ее фронтальная проекция была бы инцидент-
на прямой E2F2. В данном случае D2<£E2F2,
следовательно, точка D не инцидентна птюско-
На рис. 140 плоскость Я задана следами,
точка А — горизонтальной проекцией; извест-
но, что Л С Я; нужно найти ее фронтальную
проекцию (см. /30/ и /79/). Проведем через А,
горизонтальную проекцию произвольной пря-
мой ВСС.С1, найдем ее фронтальную проек-
цию и, установив проекционную связь, найдем
на ней точку А2.
Проверим, инцидентна ли точка D плоско-
сти Я. Проведя через £)j горизонтальную про-
екцию прямой EFc. Я, найдем ее фронтальную
проекцию. Точка D2 ft Е2Р2,следователыю, точ-
ка ОСЯ.
Вместо произвольных прямых удобно поль-
зоваться линиями уровня плоскости, в частно-
сти, когда направление проекций этих линий
известно, например, когда плоскость задана
следами.
Дана плоскость Я и фронтальные проекции
точек Л с: Я и В С Я Нужно найти их гори-
зонтальные проекции (рис. 141). Проведем через
А2 и В2 фронтальные проекции h2 и h2 гори-
зонталей huh'; найдя их фронтальные следы
(точки Си О) на фронтальном следе плоскости
(см. /76/), построим горизонтальные проекции
/ц и h\ горизонталей. На них в пересечении с
линиями связи, проведенными соответственно
через А2 и В2, лежат точки Ах и Bt (точка А
расположена в I, а точка В — во II углу про-
странства).
Рассмотрим решение аналогичных задач
способом вспомогательного параллельного
проецирования. Нужно определить, инцидент-
ны ли точки N и М плоскости А ВС (рис. 142).
Примем направление проецирования s парал-
лельным любой прямой плоскости, например
ВС, и спроецируем плоскость АВС на П„
Проекцией прямой ВС станет точка Вх = Сь
проекцией точки А—точка At. Соединив по-
лученные точки прямой, получим вспомога-
тельную проекцию плоскости АВС на плоско-
сти ПР
Проведя проецирующие прямые, параллель-'
ные s, через точки N и М и найдя их горизон-
тальные следы, получим вспомогательные про--,
екции Nj и Mj этих точек ПР Если бы точка N
была инцидентна плоскости АВС, то ее проек-
ция (см. /16/) была бы инцидентной прямой
AtBt. Так как М^Л^!, то NGt^BC. Вместе
с тем точка Л^СА^, следовательно, Мс
с АВС.
48
На рис. 143 даны фронтальная проекция
плоского четырехугольника ABCD и горизон-
тальные проекции сторон AD и CD. Нужно
найти горизонтальные проекции сторон АВ
и ВС. Проведем диагонали фронтальной проек-
ции четырехугольника и отметим точку К2 их
пересечения. Построим горизонтальную проек-
цию диагонали АС и найдем на ней точку Kt.
Вследствие /68/ диагональ В^^ горизонталь-
ной проекции четырехугольника проходит через
точку Kt. Точка Bi с D>Ki и расположена в
проекционной связи с точкой В2. Так как
АС П BD, то определяемая ими фигура — пло-
ская.
Определение величины плоской фигуры. Для
решения задачи нужно спроецировать фигуру
на плоскость проекций, параллельную плоско-
сти фигуры (см./43/). На рис. 144 треугольник
АВС 1П2. Расположим П5 параллельно АВС
(ось х251| А 2С2) и спроецируем на нее заданную
фигуру. В результате А5В^С5 = АВС.
Если фигура лежит в плоскости общего по-
ложения, следует вначале ввести такую пло-
скость проекций, относительно которой пло-
скость фигуры станет проецирующей.
Изображенный на рис. 145 треугольник АВС
не параллелен плоскостям Hj и П2. Проведем
и нем горизонталь h и расположим П4 перпен-
дикулярно горизонтали (х14 ± h,). В результате
все горизонтали плоскости АВС становятся
фронтально проецирующими прямыми, а пло-
скость АВС фронтально проецирующей. Тре-
угольник проецируется в отрезок В4С4, кото-
рому инцидентна точка А4.
Дальнейшие построения аналогичны при-
веденным на рис. 144. Приняв плоскость П5
параллельной плоскости треугольника (ось х45[|
ЦС4В4), получим треугольник А5В5С5= АВС.
При построении проекции треугольника А ВС
на П4 мы получили угол а4
наклона его плоскости к П,.
равный углу а
Рис. 144
49
4-940
Рис. 145
Описанным приемом можно определить ве-
личину угла между двумя пересекающимися
прямыми, расстояние между Параллельными
прямыми (сравните с /69/) или расстояние от
точки до прямой.
§ 10. ВЗАИМНОЕ ПОЛОЖЕНИЕ
ПЛОСКОСТЕЙ
Линия пересечения плоскостей. Две плоско-
сти могут пересекаться, или быть взаимно па-
раллельными. В последнем случае они пересе-
каются по несобственной прямой (см./7/). Ли-
ния пересечения плоскостей представляет собой
прямую и поэтому определяется положением
двух принадлежащих ей точек.
Даны плоскости ОЛЕ (рис. 146). Чтобы
построить линию к их пересечения, возьмем
произвольные прямые ас.£1иЬс.£1я отметим
точки А и В их пересечения с плоскостью Е.
Эти точки определяют линию пересечения пло-
скостей. Очевидно, взяв произвольные прямые
ссЕ и t/cE и найдя точки С и D их пересече-
ния с £2 (рис. 147), мы получим ту же линию к.
Возможно построить эту линию, найдя точку
пересечения произвольной прямой аС О с пло-
скостью Е, а затем точку пересечения произволь-
ной прямой с с Е с плоскостью Q. Можно вос-
пользоваться прямыми, лежащими в одной из
плоскостей и параллельными второй плоско-
сти. Таковы прямые исЕ и gc£2 (рис. 148);
они параллельны линии пересечения плоско-
стей (пересекаются с нею в несобственной
точке), следовательно, достаточно найти любую
собственную точку этой линии и через нее про-
вести прямую, параллельную прямым п и g.
/80/ Чтобы построить линию пересечения двух
плоскостей, нужно найти точки пересечения двух
прямых первой плоскости со второй плоскостью
либо одной прямой первой плоскости со второй
плоскостью и прямой второй плоскости с первой
плоскостью или двух прямых второй плоскости
с первой плоскостью; прямая, соединяющая две
полученные таким образом точки, является иско-
мой.
Точка пересечения прямой линии с проецирую-
щей плоскостью. Одна проекция точки пересе-
чения прямой линии с проецирующей плоско-
стью определяется без вспомогательных по-
строений (см./16/). Это проекция на той плоско-
сти, относительно которой заданная плоскость
является проецирующей. На рис. 149 проеци-
рующая плоскость £2 в точке К пересекается с
прямой а. Построим проецирующую плоскость
Еде и определим прямую KKj пересечения
двух проецирующих плоскостей; эта прямая
является проецирующей и пересекается с П2 я
точке Kt пересечения прямых Е, = а, и £2,
/81/ Проекция точки пересечения прямой с
проецирующей плоскостью (на плоскости про-
екций, перпендикулярной проецирующей плоско-
сти) расположена в пересечении проекций прямой
и плоскости.
50
Решение задачи на эпюре не зависит от того,
чем задана проецирующая плоскость, так как
одна ее проекция всегда прямая линия. На
рис. 150 даны фронтально проецирующая пло-
скость D, заданная следами, и прямая а. Фрон-
тальная проекция К2 точки пересечения прямой
с плоскостью расположена в пересечении их
фронтальных проекций. Установив проекцион-
ную связь, найдем точку Kj на горизонтальной
проекции прямой.
Горизонтально проецирующая плоскость
АВС и прямая а изображены на рис. 151. В этом
примере известна горизонтальная проекция К,
точки пересечения прямой и плоскости. Ее
фронтальная проекция, как и в предыдущем
случае, определяется путем установления про-
екционной связи.
Линия пересечения проецирующей плоскости
с плоскостью общего положения и двух проеци-
рующих плоскостей между собой.
Если одна из двух плоскостей проецирую-
щая, одна проекция линии их пересечения опре-
деляется без вспомогательных построений
(см./16/). Она совпадает с той проекцией проеци-
рующей плоскости, которая представляет собой
линию.
На рис. 152 и 153 плоскости DOS заданы
следами. Плоскость D горизонтально проеци-
Oi
Рис. 150
51
4*
рующая, поэтому горизонтальная проекция
АаВ} линии пересечения плоскостей совпадает
с горизонтальным следом этой плоскости:
А1В1 = £1,. Чтобы найти фронтальную проек-
цию линии пересечения, будем ее рассматри-
вать как прямую, лежащую в плоскости S,
Точка Л2СЕП2, так как точка Л, Сх Точка
В2с.х, так как BjCTIlp Соединив прямой
точки А2 и В2, получим фронтальную проекцию
линии пересечения плоскостей.
Если плоскость общего положения задана
отсеком (А ВС на рис. 154), вторая (проецирую-
щая) — своей проекцией на перпендикулярной
ей плоскости проекций, задача решается в той
же последовательности. Плоскость D—фрон-
тально проецирующая, поэтому фронтальная
проекция линии пересечения плоскостей из-
вестна. Обозначим ее D2E2; точка D лежит в
пересечении прямой АС с плоскостью Q, а
точка Е — в пересечении прямой ВС с плоско-
стью П (см. /80/ и /81/). Найдя горизонтальные
проекции точек D и Е, соединим их прямой ли-
нией, представляющей собой горизонтальную
проекцию D1EJ линии пересечения плоскостей
АВС и П.
На рис. 155 изображены две горизонтально
проецирующие плоскости АВС П DEF. Линией
их пересечения может быть только горизон-
тально проецирующая прямая. На П, она про-
ецируется в точку G, = Н] пересечения гори-
зонтальных проекций плоскостей. Прямая G2H2
перпендикулярна оси х.
Если одна плоскость общего положения,
вторая — плоскость уровня (например, гори-
зонтальная), то линия их пересечения зани-
мает частное положение в пространстве
(в приведенном примере это горизонталь;
рис. 156).
/82/ Линия пересечения плоскости общего по-
ложения с горизонтальной плоскостью представ-
ляет собой горизонталь плоскости общего по-
ложения.
По аналогии:
/83/ Когда плоскость общего положения пе-
ресекается с фронтальной плоскостью, линией
их пересечения является фронталь плоскости
общего положения.
Линия пересечения плоскостей общего поло-
жения. Определим линию пересечения плоско-
стей общего положения АВС П DEF (рис. 157).
Рассечем обе плоскости вспомогательными про-
ецирующими плоскостями Й и Е Плоскость
АВС пересекается по прямой с с плоскостью I
и по прямой а с плоскостью О. В символической
записи это. выглядит так: АВСП й= а и
АВСПЕ = с.
DEF Fl Q = b и DEF Г) S = d. Отметим точ-
ку N пересечения прямых а и b (aC\b — N),
инцидентных соответственно плоскостям АВС
и DEF и, следовательно, общей для заданных
плоскостей. Точка К также общая для плоско-
стей, так как с Г) d = К.
Соединим точки N и К прямой.
/84/ Чтобы построить линию пересечения пло-
скостей общего положения, нужно рассечь их
двумя проецирующими плоскостями, определить
линии пересечения плоскостей, заданных и вело
могательных, и, отметив общие для этих линий
точки, соединить их прямой линией.
Не трудно видеть, что /84/ вытекает из /80/
Действительно, прямые а и с плоскости АВС
пересекаются в точках N и К с плоскость»
DEF или прямые bud плоскости DEF в тех же
точках пересекаются с плоскостью АБС (срав-
ните рис. 146 и 157).
Рассмотрим решение задачи на эпюре.
52
Рис. 158
(рис. 158). Рассечем заданные плоскости АВС
и DEF вспомогательной горизонтальной пло-
скостью П, проходящей, например, через точ-
ку А. Определив линии пересечения AN и GH
(см. /82/ и рис. 156) этой плоскости с заданными
плоскостями, отметим общую для них точку Т
(вначале ее горизонтальную проекцию). В дан-
ном примере мы взяли горизонтальную вспо-
могательную плоскость, однако вместо нее
можно было использовать любую другую про-
ецирующую плоскость, кроме профильной (по-
чему?). Можно упростить построения, проведя
проецирующую плоскость через одну из сторон
любого треугольника. Проведем горизонтально
проецирующую плоскость X через сторону АС
треугольника АВС. Горизонтальная проекция
стороны АС лежит на горизонтальной проекции
плоскости Z (см. сама же плоскость пере-
секается с плоскостью треугольника по прямой
стей Е и DEF, отметим точку R (АС<~1 МК = R).
Линия пересечения А ВС и DEF проходит через
точки Т и R.
Если считать, что заданы не плоскости, а их
отсеки — треугольники А ВС и DEF и они не-
прозрачны, то следует определить видимость
фигур. Для этого воспользуемся конкурирую-
щими точками скрещивающихся прямых. Возь-
мем, например, точки PCACuMCDF (рис. 159).
Их горизонтальные проекции расположены в
пересечении горизонтальных проекций назван-
ных прямых (месте кажущегося пересечения).
Найдя фронтальные проекции точек М и Р,
устанавливаем, что точка Р при направлении
проецирования, перпендикулярном П,, распо-
ложена ближе к зрителю, следовательно, она
видима. Видимой будет и прилегающая к точ-
ке Р часть отрезка АС (до точки его пересечения
с плоскостью DEF). О видимости отрезка АВ
можно судить, рассмотрев конкурирующие точ-
ки в месте кажущегося пересечения прямых DF
и АВ или EF и АВ при том же направлении
проецирования.
Для определения видимости при направле-
нии проецирования, перпендикулярном П2, рас-
смотрим конкурирующие точки L С EF и .5 С
с АВ Построив горизонтальные проекции этих
точек, устанавливаем, что_точка L с EF ближе
к зрителю, чем точка 7Г с /ГЙ.^Следовательно,
спереди виден отрезок EF от точки Е до точки
пересечения прямой с плоскостью АВС. Рассуж-
дая аналогично, устанавливаем, что отрезок DE
оказывается видимым, отрезок же DF — час-
тично закрытым треугольником АВС.
Построить линию пересечения плоскостей
можно, используя параллельное или централь-
ное вспомогательное проецирование. Спроеци-
53
54
руем плоскости АВС и DEF в направлении пря-
мой АС на плоскость П2 (рис. 160). Плоскость
DEF будет проецирующей, а задача — анало-
гичной приведенной на рис. 154. Отметив точ-
ки Kj и Gj пересечения вспомогательной про-
екции плоскости АВС с вспомогательными про-
екциями прямых EF и DF, проведем через них
проекции проецирующих прямых до пересече-
ния с соответствующими ортогональными про-
екциями тех же прямых. Направление проеци-
рования можно избрать параллельным любой
другой прямой плоскости DEF или АВС, а также
проецировать фигуры на плоскость П2. При
центральном проецировании центр проециро-
вания должен быть избран в любой собственной
точке из пересекающихся плоскостей.
Построение линии пересечения плоскостей
общего положения, заданных следами, пока-
зано на рис. 161 и 162. Точка А инцидентна сле-
дам обеих плоскостей, следовательно инцидент-
на линии их пересечения. Точно так же точка В
инцидентна этой линии. Соединим (на эпюре)
одноименные проекции точек А и В, полу-
чив проекции линии пересечения плоско-
стей.
Если какие-либо одноименные следы пло-
скостей не пересекаются в пределах чертежа
(рис. 163), можно рассечь обе заданные плоско-
сти вспомогательной горизонтальной или фрон-
тальной плоскостью (см. /82/ и /83/). Построив
линии пересечения плоскостей заданных и вспо-
могательной, определим общую для заданных
плоскостей точку. В качестве вспомогательной
плоскости на рис. 163 принята горизонтальная
плоскость Ф; Ф П й = fc и Ф Л Е = Л'. Обе гори-
зонтали (см. /82/) пересекаются между собой в
точке С; h\ =Cj; С2сЧ'2. Второй точкой
линии пересечения плоскостей й и Е является
точка D, в которой пересекаются их горизон-
тальные следы. Соединив одноименные проек-
ции точек С и D, получим проекции линии пере-
сечения плоскостей.
Ддя решения той же задачи можно восполь-
зоваться родственным преобразованием
(рис. 164). Зададим родство осью х, родствен-
ными прямыми а2 и Е2, параллельными оси, и
направлением двойных прямых, перпендику-
лярным оси родства (см. /51/). Построим точ-
ку В2, родственную В2 (пересечения прямых а2
и ХП2), и точку Е2, родственную Е2 (пересече-
ния прямых а2 и ПП2). Точкам Е2 и инци-
дентна прямая ЛП2, родственная Прямой ЛП2;
точкам В2 и —прямая ЕП2, родственная
прямой ЕП2. Эти прямые пересекаются в точ-
ке С2, родственной недоступной точке С2 пере-
сечения фронтальных следов плоскостей. По-
скольку направление двойных прямых совпадает
с направлением линий связи, горизонтальная
проекция точки С может быть найдена в пере-
сечении с осью х перпендикуляра, опущенного
из С2 на эту ось. Точкам Dj и Ct инцидентна
горизонтальная проекция линии пересечения
плоскостей, точкам D2 и С2 — линия, родствен-
ная ее фронтальной проекции. Воспользовав-
шись точками А2 и А2, построим фронтальную
проекцию D2A2 этой линии.
55
На рис. 165 изображены плоскости X и й,
горизонтальные следы которых параллельны,
фронтальные пересекаются в точке А. Точка
пересечения горизонтальных следов — несоб-
ственная; чтобы соединить ее с точкой Ах,
нужно через Ах провести прямую, параллель-
ную следам плоскостей. Такая линия является
горизонтальной проекцией горизонтали обеих
плоскостей. Ее фронтальная проекция (см. /62/)
параллельна оси х.
Положение /84/ справедливо, когда опреде-
ляется линия пересечения плоскостей, заданных
следами. Роль вспомогательных секущих пло-
скостей выполняют плоскости проекций.
Угол между плоскостями. Если заданные
плоскости — проецирующие относительно
одной и той же плоскости проекций (рис. 166),
то угол между их проекциями на этой плоскости
численно равен двугранному углу между ними
(ip =<р2).
Угол между горизонтально проецирующи-
ми плоскостями АВС и DEF на рис 155 проеци-
руется на П, в угол <р ], равный углу между пло-
скостями в натуре.
/85/ Двугранный угол между проецирующи-
ми плоскостями равен по величине линейному
углу между проекциями плоскостей на перпевди
куляриой им плоскости проекций.
Величину двугранного угла между плоско-
стями общего цоложения можно определить
если, последовательно заменяя плоскости про-
екций, расположить линию пересечения плоско-
стей перпендикулярно плоскости проекций
Определим величину двугранного угла между
плоскостями АВС и BCD, пересекающимися
между собой по прямой ВС (рис. 167). Для этого
заменим П2 на П4 || ВС, а затем П] на Щ-L ВС.
В результате обе заданные плоскости относи-
тельно П5 станут проецирующими и угол между
их проекциями на ней станет равным искомому
двухгранному углу, т е. <р5=<р (см. /85/).
Часто на заданном эпюре П^/П, нужно
показать проекции найденного линейного угла.
Для этого в произвольном месте эпюра в сис-
теме П4/П5, например через точку 04, проведем
проекцию найденного угла. Она представляет
собой прямую, параллельную оси х45 (так как
плоскость угла параллельна П5). Отметив точ-
ки F4 и Е4, установим проекционную связь и
построим точки Fx и Е], а затем F2 и Е2.
§ 11. ВЗАИМНОЕ ПОЛОЖЕНИЕ
ПРЯМОЙ И ПЛОСКОСТИ
ОБЩЕГО ПОЛОЖЕНИЯ
Пересечение прямой и плоскости. На рис. 168
даны прямая а и плоскость S; чтобы узнать
каково их взаиморасположение, проведем про-
извольную вспомогательную плоскость О э в
и найдем прямую b ее пересечения с плоско-
стью S. Прямые а и b могут пересекаться, или
быть взаимно параллельными. В первом слу-
чае точка пересечения прямых представляет
собой вместе с тем и точку пересечения прямой в
с плоскостью S. Во втором случае прямая а
параллельна этой плоскости.
/86/ Установить взаиморасположение прямой
и плоскости можно, заключив прямую во вспомо-
гательную плоскость — проецирующую и найди
линию пересечения плоскостей заданной и вспо-
могательной; если эта линия пересекается с за-
данной прямой, то заданные прямая я плоскость
56
пересекаются; если линии параллельны, то за-
данные прямая и плоскость также параллельны.
/87/ Чтобы построить точку пересечения пря-
мой с плоскостью общего положения, нужно
заключить прямую во вспомогательную плос-
кость (проецирующую), определить линию пересе-
чения плоскостей заданной и вспомогательной, а
затем точку, в которой заданная прямая пересе-
кается с построенной.
На рис. 169 даны плоскость АВС и прямая а.
Нужно найти точку К их пересечения. Проведем
горизонтально проецирующую плоскость £2эа
и построим линию DE пересечения плоскостей—
заданной и вспомогательной. Обе прямые а и
DE инцидентны плоскости £2, следовательно,
их горизонтальные проекции совпадают
(см. рис. 90), поэтому вначале нужно отметить
точку К2, а затем найти Kt. Видимость прямой
относительно треугольника АВС определена с
помощью конкурирующих точек (О и F, а
также G и Н).
На рис. 170 дано решение той же задачи,
когда плоскость S задана следами. Проведем
горизонтально проецирующую плоскость £2э«
и определим линию АВ пересечения заданной
и вспомогательной плоскостей. На ней, в ее
пересечении с прямой а, расположена искомая
точка К. Как и в предыдущем примере вначале
находим К2, а уже затем К,.
Когда с плоскостью общего положения пе-
ресекается профильная прямая, обе проекции
линии пересечения вспомогательной проецирую-
щей плоскости с заданной плоскостью совпа-
дают. Поэтому найти точку К(без дополнитель-
ных построений нельзя. На рис. 171 плоскость
АВС пересекается с профильной прямой EF.
Проведем профильную плоскость Q EF. Ли -
ния пересечения плоскостей определяется точ-
ками G и Н, в которых АС и ВС пересекаются с
П. Для нахождения точки К пересечения пря-
мых EF и GH воспользуемся способом замены
плоскостей проекций, как это было сделано на
рис. 91. (Как найти точку К2'>)
Описанные приемы позволяют решать зада-
чи, связанные со взаимным расположением
трех прямых линий. Проведем прямую а ЭЛ,
пересекающую заданные скрещивающиеся пря-
57
мые b и с (рис. 172). Возьмем точку ВаЬ и
соединим ее прямой с точкой А. Любая прямая,
инцидентная А и пересекающаяся с Ь, инци-
дентна плоскости ЬПАВ. Найдем точку К пере-
сечения прямой с с этой плоскостью. Для этого
проведем горизонтально проецирующую пло-
скость S эс и найдем линию CD пересечения
плоскостей, а на ней и точку К (см. /87/). Иско-
мая прямая проходит через точки А (по усло-
вию) и К и пересекается с b в точке М.
Прямая, параллельная плоскости. Если пря-
мая параллельна плоскости, то существует
множество прямых плоскости, параллельных
данной.
/88/ Чтобы проверить, параллельны ли пря-
мая и плоскость, нужно попытаться провести в
плоскости прямую, параллельную данной. Если
это возможно, то плоскость и прямая параллель-
ны. Естественно, что /88/ не противоречит /86/.
Проверим, параллельны ли плоскости АВС
прямые а и Ь (рис. 173). Через произвольную
точку А плоскости АВС проведем прямую AD
так, чтобы ее фронтальная проекция была па-
раллельна^- Если прямая Л! Dx параллельна
то прямая а параллельна плоскости АВС. В дан-
ном случае AiDlXai, следовательно, а Жавс.
Прямая b параллельна плоскости АВС, так как
®2 1Мг®2> а 11^1-®!-
Прямая, параллельная двум пересекаю-
щимся плоскостям, параллельна линии их пере-
сечения (почему?). Проведем прямую, инци-
дентную точке К и параллельную плоскостям
АВС и П] Она должна быть параллельной гори-
зонтальному следу плоскости АВС (т. е. линии
пересечения плоскостей АВС и П,), следова-
тельно, параллельна горизонтали плоскости
АВС. Проведем с2 || h2 и с, || h2.
На рис. 174 прямая я проведена через точку К
параллельно плоскостям АВС и ABD (а2 || А2В2
и a, HjBj).
Параллельные плоскости. Чтобы через точ-
ку D (рис. 175) провести плоскость, параллель-
ную плоскости АВС, следует построить пря-
мые, соответственно параллельные двум пере-
секающимся прямым плоскости АВС (напри-
мер, <21| Л В и £> || ВС). Плоскость а Л Ь параллель-
Рис. 173
Рис. 174
58
на заданной. Этот же прием позволяет опреде-
лить, параллельны ли заданные плоскости.
Для этого нужно в одной плоскости взять две
пересекающиеся прямые и попробовать во вто-
рой плоскости провести прямые, соответствен-
но параллельные построенным. Если это воз-
можно, то плоскости параллельны (см. рис. 173).
/89/ Плоскости параллельны, если в одной
из них возможно провести две пересекающиеся
прямые, соответственно параллельные двум пере-
секающимся прямым второй плоскости.
Параллельные плоскости пересекаются с
третьей плоскостью по параллельным прямым,
поэтому одноименные следы параллельных пло-
скостей параллельны между собой. Следова-
тельно, параллельны между собой фронтали
параллельных плоскостей и их горизонтали.
Проведем через А плоскость S || £2 (рис. 176).
Построим фронталь (или горизонталь) пло-
скости £2 и, найдя ее след — точку В, проведем
через нее ЕП] ||£2П]. След ЕП2 проходит через
точку ЕЛ параллельно следу £2П2.
Построим плоскость Е ЭЛ, параллельную
профильно проецирующей плоскости £2
(рис. 177). Проведем произвольную (кроме
профильной) прямую ВС с £2 и параллельную
ей прямую а ЭЛ. Найдя следы прямой а —
точки D и Е, построим черех них соответствую-
щие следы плоскости Е, параллельные оси х
(почему?). Плоскости £2 и Е параллельны, так
как параллельны их следы и,. кроме того, в
каждой плоскости есть прямая, параллельная
второй плоскости (но не параллельная следам;
прямые ВС и а). Существование такой прямой
необходимо, так как горизонтальные и фрон-
тальные следы всех профильно проецирующих
плоскостей параллельны друг другу (и оси х),
в то время как не все профильно проецирующие
плоскости взаимно параллельны.
Плоскость, параллельная £2, может быть
задана пересекающимися прямыми, например
прямой b || ВС и h || х.
Плоскость £2 D, параллельная данной
фронтально проецирующей плоскости АВС
(рис. 178), может быть задана одной своей про-
59
екцией fl2. При необходимости могут быть про-
ведены горизонтальные проекции произвольно
взятых прямых а с О. и b с О, проходящих
через D или другую точку плоскости Я.
В заключение построим параллельные пло-
скости, проходящие через скрещивающиеся пря-
мые а и b (рис. 179). Возьмем произвольную
точку Аса и проведем прямую с с>А, парал-
лельную Ь. Плоскость аПс параллельна Ь,
что подтверждается /88/. Взяв на b произволь-
ную точку В, проведем через нее прямую J||a.
Так как плоскости а П с и b<~id содержат по
паре взаимно параллельных прямых, то они
параллельны между собой.
Тем же приемом строится плоскость, парал-
лельная двум скрещивающимся прямым. Если
Рис. 179
Рис. 181
плоскость должна быть параллельной прямым!
а и b и проходить через заданную точку С
достаточно провести прямую е С параллель-!
но а и прямую gc>C параллельно Ь. Плоскость!
eC\f удовлетворяет условию.
Рассмотрим более общий прием, позволяю-
щий установить взаиморасположение двух пло-
скостей; если обе плоскости рассечь третье! I
плоскостью, то получим в пересечении задан-1
ных плоскостей и вспомогательной две прямые ।
линии. Они могут быть параллельными и пере-
секаться. Если эти линии пересекаются, то!
пересекаются и плоскости (почему?). Если же
прямые параллельны, это еще не значит, что
параллельны и заданные плоскости, так как в
двух пересекающихся плоскостях можно по-
строить взаимно параллельные прямые (парал-
лельные линии их пересечения). Следовательн
обе плоскости нужно рассечь еще одной пло-|
скостью, не параллельной первой (почему?):
если и теперь линии пересечения заданных пло-
скостей со вспомогательной взаимно парал-
лельны, то параллельны и плоскости.
/90/ Чтобы проверить взаиморасположенн I
двух плоскостей, следует рассечь их вспомога I
тельной плоскостью; когда линии пересечении
плоскостей, заданных в вспомогательной, пере
секаются, то пересекаются и плоскости; когда
они параллельны, нужно рассечь плоскости еще)
одной вспомогательной,. непараллельной перво!
плоскостью; если в новые линии пересечения,
будут параллельными, то параллельны н задан
ныс плоскости.
Прямая, перпендикулярная плоскости. Пря-
мая перпендикулярна плоскости, когда она
перпендикулярна двум любым пересекающимся!
Рис. 182
60
прямым этой плоскости, в частности горизон-
тали и фронтали.
В точке КС fi восставим к 12 перпендику-
ляр К (рис. 180). Проведем фронталь f и гори-
зонталь h плоскости Л. Из всех прямых, инци-
дентных точке К и перпендикулярных прямой/,
выберем ту прямую, которая перпендикулярна
и прямой h. Такая прямая удовлетворяет усло-
вию.
Дана плоскость а || b и инцидентная ей точ-
ка К (рис. 181) Проведем фронталь и горизон-
таль плоскости а || Ь, инцидентные точке К.
Фронтальная проекция к2 любой прямой, пер-
пендикулярной фронтали, перпендикулярна /2
(см. /45/). Горизонтальная проекция кг любой
прямой, перпендикулярной горизонтали, пер-
пендикулярна /1]. Две проекции к, и к2 опреде-
ляют единственную прямую, перпендикулярную
обеим линиям. Таким образом, к — искомый
перпендикуляр.
Так как фронтальные проекции всех фронта-
лен плоскости и горизонтальные проекции го-
ризонталей плоскости соответственно парал-
лельны, то фронталь и горизонталь не обяза-
тельно должны быть инцидентными точке К.
Достаточно знать направление соответствую-
щих проекций этих линий.
/91/ Фронтальная проекция прямой, перпен-
дикулярной плоскости, перпендикулярна фрон-
тальным проекциям фронтален этой плоскости.
Горизонтальная проекция такой прямой перпен-
дикулярна горизонтальным проекциям горизон-
талей плоскости.
Расстояние от точки до плоскости. Опреде-
лим расстояние от точки D до плоскости АВС
(рис. 182). Для этого построим перпендику-
ляр DK. Проведем произвольные фронталь / и
горизонталь h плоскости АВС. Фронтальная
проекция перпендикуляра инцидентна точке Р2
«перпендикулярна // Горизонтальная проекция
перпендикуляра перпендикулярна h1 и инци-
дентна точке D] (см. /91/).
Найдем точку К пересечения перпендику-
ляра с плоскостью (см. /87/) и определим вели-
чину отрезка DK, заменив П2 на П4 (см. рис. 85)
Когда плоскость задана следами (рис. 183),
роль фронтали играет фронтальный след пло
скости, которому перпендикулярна фронталь-
ная проекция лерпендикуляра. Его горизонталь-
ная проекция перпендикулярна горизонтально-
му следу плоскости. Найдем точку К пересече-
ния перпендикуляра с плоскостью и определим
величину отрезка DK (см. рис. 86).
Перпендикуляр к фронтально проецирую-
щей плоскости (рис. 184) параллелен П2, как
и любой другой плоскости, перпендикулярной
данной. Следовательно, горизонтальная про-
екция перпендикуляра параллельна оси х, фрон-
тальная же проекция перпендикулярна фрон-
тальной проекции плоскости. Аналогично рас-
положен перпендикуляр к горизонтально или
профильно проецирующей плоскости.
/92/ Перпендикуляр к проецирующей плоско-
сти параллелей той плоскости проекций, которой
перпендикулярна проецирующая плоскость.
Отрезок DK проецируется на П2 в нату-
ральную величину, так как прямая DK пред-
ставляет собой фронталь (см. /39/ и /92/).
Положение /92/ можно использовать для
определения расстояния от точки до плоскости
общего положения, применив способ замены
плоскостей проекций (рис 185). Построив фрон-
Рис. 185
61
Рис. 187
таль f плоскости АВС, проведем П5_1_/ По-
строим проекцию плоскости АВС и точки Г
на П5. Решение задачи на эпюре в системе
плоскостей П5/П2 аналогично показанному на
рис. 184. Отрезок Р5К5 равен искомому рас-
стоянию. Точки К2 и Kt найдем, установив
последовательно проекционную связь K2D2||
|| х2$, Kt —на расстоянии Ук от оси х12, изме-
ренном на эпюре в системе П5/Щ.
Перпендикуляр к профильно проецирующей
плоскости (рис. 186) является профильной пря-
мой (см. /92/), поэтому расстояние от точки D
до плоскости fl проецируется на П3 в натураль-
ную величину. Для решения задачи нужно по-
строить профильные проекции заданных точки
и плоскости.
Расстояние между параллельными плоскостя-
ми. Для его определения нужно взять произволь
ную точку, инцидентную одной из плоскостей,
опустить из нее перпендикуляр на друпую
плоскость и найти величину отрезка перпенди-
куляра, заключенного между точкой и плоско-
стью. Аналогично решается задача на прове-
дение плоскости, параллельной данной на за-
данном расстоянии от нее.
/93/ Чтобы построить плоскость, параллель-
ную данной плоскости и удаленную от нее на
определенное расстояние, следует взять произ-
вольную точку, инцидентную заданной плоско-
сти и, восставив в ней перпендикуляр к плоскости,
отложить на нем заданное расстояние. Плос-
кость, параллельная данной, инцидентна постро-
енной точке.
На рис. 187 дана плоскость а || Ь. Нужно про-
вести другую плоскость, параллельную данной
и отстоящей от нее на расстоянии п. Задача
имеет два решения (почему?), мы ограничимся
одним из них. Через произвольную точку А
прямой а проведем горизонталь А В и фрон-
таль АС плоскости а || Ь. В любой точке плоско-
сти, например С, восставим перпендикуляр к
плоскости и возьмем на нем произвольную
точку D. Определим величину отрезка CD =
= СЛГ>Л и отложим на прямой С4 D4 от точки Ct
отрезок длиной п (точка £4). Установив про-
Рис. 189
62
екционную связь, найдем точку а затем Е2.
Точка Е удалена от плоскости а || b на рас-
стояние п.
Построим плоскость, инцидентную точке Е
и параллельную плоскости а || Ь. Для этого
(см. /89/) через Е проведем прямую h, парал-
лельную горизонтали АВ плоскости а || Ь, и
прямую f, параллельную фронтали АС той же
плоскости. Плоскость hDf удовлетворяет усло-
вию
Для решения задачи можно воспользоваться
способом замены плоскостей проекций. Распо-
ложим Па перпендикулярно горизонтальному
следу заданной плоскости О (рис. 188). В систе-
ме плоскостей п,/п4 плоскость Л станет фрон-
тально проецирующей. Возьмем в плоскости
произвольную точку А (например, на ЛП2)
и построим ее проекцию А4, след ЛП4 плоско-
сти проходит через точки ЛХ14и Л4 (почему?).
Восставив из А4 перпендикуляр к ЛП4 длиной п,
получим точку В4. На П4 отрезок АВ проеци-
руется в натуральную величину (см. /39/и I92J).
Проведем Е4 э В4 параллельно Л4, а через
точку след ЁГЦЦПП,. Затем построим
фронтальный след плоскости.
Плоскость, перпендикулярная прямой. По-
строим плоскость, перпендикулярную прямой
a(at; а2) и проходящую через точку А (Л,; Л2).
Проведем /2Ла2 и Zij-Le,. Прямые /, и h2
параллельны оси х. Плоскость /10/ удовлет-
воряет условию (рис. 189).
Описанным способом нельзя решить задачу,
когда заданная прямая — профильная (рис. 190).
Горизонтали, инцидентная точке А, которой
должна быть инцидентна и плоскость, перпен-
дикулярна профильной прямой ВС, вместе с тем
представляет собой и фронталь. Чтобы решить
задачу, построим профильные проекции точки А
и прямой ВС. Плоскость, перпендикулярная ВС,
должна быть профильно проецирующей (по-
чему?). Проведем профильную проекцию Q3
плоскости, перпендикулярной ВС (О3 э А 3А и
(13±В3С3). При необходимости найденную пло-
скость можно задать двумя пересекающимися
или параллельными прямыми. На рисунке по-
строены профильно проецирующие прямые а
и Ь. Их профильными проекциями являются
точки й3 и Ь3, инцидентные прямой £13. Фрон-
тальные и горизонтальные проекции прямых а
и b параллельны оси х (почему?).
Задача 1.
Определить расстояние между параллельными
прямыми а и b (рис. 191). Возьмем на а произволь-
ную точку А и проведем через нее плоскость, пер-
пендикулярную прямым. Зададим ее фронталью /
и горизонталью h (см. /91/). Определим точку пере-
сечения прямой b с плоскостью / П h. Для этого
через b проведем фронтально проецирующую пло-
скость Q и найдем точки В и С, в которых фронталь
и горизонталь плоскости / П h пересекаются с Q.
На прямой ВС отметим точку К пересечения
прямой b с плоскостью/П й. Отрезок АК принадле-
жит плоскости а || Ь'. вместе с тем он принадлежит
и плоскости / П h, перпендикулярной прямым а и Ь.
Поэтому он перпендикулярен этим прямым. Найдем
величину (А2К2) отрезка АК (сравните эту задачу
с приведенной на рис. 97).
Задача 2.
Найти центр окружности, описанной около
треугольника АВС (рис. 192). Он расположен в точ-
ке пересечения перпендикуляров к сторонам тре-
угольника, проходящих через их середины. Разде-
Рис. 191
63
Рис* 192
лим ВС пополам (точка К). Точки К, и К2 в соответ-
ствии с /41/ делят пополам отрезки BiCi и B2C2.
Проведем через К перпендикуляр к стороне ВС.
Для этого построим плоскость f П h, перпендику-
лярную ВС. Проведя вспомогательную плоскость
Q DАС, найдем линию ее пересечения ED с плоско-
стью /э й, а на ней — точку F пересечения АС с пер-
пендикуляром. Взяв на стороне АВ точку N, деля-
щую эту сторону пополам, проделаем аналогичные
построения (на чертеже не показаны). Перпендику-
ляр к этой стороне пересекается с перпендикуляром
kF в искомой точке М.
1адачи 3»
Определить угол между плоскостями АВС и
а ||й (рис. 193).
Возьмем произвольную точку К (К,; и
опустим из нее перпендикуляры с и d на заданные
плоскости. Фронтальные проекции перпендикуля-
ров перпендикулярны фронтальным проекциям
фронталей соответствующих плоскостей, горизон-
тальные проекции — перпендикулярны горизонталь-
ным проекциям горизонталей (см. /91/). Плоскость
end перпендикулярна заданным плоскостям
(почему?), следовательно, перпендикулярна линии их
пересечения. Таким образом, линейный угод дву-
гранного угла между заданными плоскостями ле-
жит в плоскости end. Это угол у между прямыми е
и d (или дополнительный ему). Для решения задачи
остается определить величину угла у. Проделайте
построения самостоятельно и сравните их с реше-
нием такой же задачи на рис. 167.
Взаимно перпендикулярные плоскости.
/94/ Плоскости взаимно перпендикулярны,
когда одна из них инцидентна прямой, перпенди-
кулярной другой плоскости.
Проведем плоскость (рис. 194), перпендику-
лярную данной плоскости АВС и инцидентную
данной прямой а(а1; а2\ Возьмем на а произ-
вольную точку D и опустим из нее перпендику-
ляр к к плоскости АВС (для этого в плоскости
А ВС построим фронталь и горизонталь). В соот-
ветствии с /94/ плоскости а Г) к и АВС взаимно
перпендикулярны, так как плоскости а П к инци-
дентна прямая к, перпендикулярная плоскости
АВС.
Положение /94/ позволяет проверить, пер-
пендикулярны ли данные плоскости: если ока-
64
жется возможным провести прямую, инцидент-
ную одной плоскости и перпендикулярную ко
второй плоскости, то плоскости перпендику-
лярны.
На рис. 195 даны плоскости АВС и а||6.
Нужно проверить, перпендикулярны ли они.
Возьмем в плоскости а || b произвольную точ-
ку D и проведем через нее перпендикуляр к к
плоскости АВС (для чего построим горизон-
таль и фронталь плоскости АВС). Возьмем
на kj произвольную точку Ех, например, в ее
пересечении с Ьх. Приняв, что точка ЕС-Ь,
проверим, инцидентна ли она и перпендику-
ляру к. Из чертежа видно, что Е2<£к2, следова-
тельно, Е<£к, а сам перпендикуляр не инци-
дентен плоскости а || Ь. Таким образом, плоско-
сти АВС и а || b не перпендикулярны друг другу.
/95/ Проецирующие плоскости, перпендику-
лярные плоскостям общего положения, перпенди-
кулярны соответственно горизонталям или фрон-
талям плоскостей общего положения.
Чтобы через А провести горизонтально
проецирующую плоскость Я, перпендикуляр-
ную плоскости а Л Ь, нужно построить горизон-
таль плоскости а Л b и перпендикулярно ей
плоскость Л (рис. 196). Так как горизонтали
плоскости а Л b перпендикулярны Я, то перпен-
дикулярны и сами плоскости (см. /94/).
Угол между прямой н плоскостью. Угол ср
между прямой АВ и плоскостью Я измеряется
линейным углом между прямой и ее прямоуголь-
ной проекцией АВ на этой плоскости (рис. 197).
В прямоугольном треугольнике АВВ' угол 8
между АВ и проецирующей прямой ВВ явля-
ется дополнительным к искомому углу ср. На
этом основано решение задачи на рис. 198.
65
5-940
Определим величину угла между прямой а и
плоскостью АВС. Проведя перпендикуляр к
АВС, проходящий через произвольную точку D
прямой а (разумеется, использовав горизон-
таль и фронталь плоскости АВС), получим
проекции 5j и 62 угла 5, дополнительного к иско-
мому. Величину этого угла определите само-
стоятельно с учетом пояснений к рис. 145.
Найдем величину угла между плоскостью
АВС и прямой BD другим приемом (рис. 199).
Вначале заменим П2 на П4, расположив П4
перпендикулярно плоскости АВС. Затем заме-
ним П, на П5, расположив П3 параллельно А ВС.
И наконец, ГЦ заменим плоскостью П6 (как
измерить координаты Z точек фигуры при по-
строении ее проекции на плоскости П6? См. /59/),
расположив ее параллельно прямой BD. До-
статочно найти проекции только двух точек
треугольника.
Угол <р между прямой BD и плоскостью АВС
проецируется на П6 в натуральную величину
(ф6 = ф). Найдем проекции угла <р на плоско-
стях Hj и П2. Вначале построим проекцию этого
угла на П5. Проекция представляет собой пря-
мую линию, инцидентную точке В5 (конечно, и
точке Ds) и параллельную оси х56. Найдем
точку Е5 пересечения проекции стороны угла,
лежащей в плоскости АВС со стороной А 5С5, и,
установив проекционную связь, построим вна-
чале точку Ел, а затем точки Et и Е2. На плоско-
сти П2 угол <р проецируется в угол D2B2E2,
а на плоскости П, —в угол DjBjE,.
ГЛАВА IV
ПОВЕРХНОСТИ
§ 1?. КРИВЫЕ ЛИНИИ
Определения и понятия. Линию будем рас-
сматривать кинематически — как результат не-
прерывного перемещения точки в пространстве.
Кривые линии делятся на плоские и простран-
ственные. В первом случае все точки кривой
инцидентны некоторой плоскости, во втором —
не инцидентны. Ортогональные проекции всех
точек кривой расположены в проекционной
связи, поэтому эпюром кривой является эпюр
множества ее точек. Одна или несколько точек
кривой могут быть несобственными, поэтому
ври параллельном проецировании их нельзя
изобразить. Часто на эпюре изображается не
вся кривая, а только ее дуга.
/96/ Эпюр множества инцидентных кривой
линии точек определяет положение кривой в
пространстве (см. /11/, /20/, /27/).
Если известен математический закон образо-
вания кривой линии, то любую ее точку можно
считать заданной. Более того, можно устано-
вить, принадлежит ли данная точка простран-
ства данной кривой. Такая кривая называется
закономерной. Ее проекции могут быть построе-
ны с любой практически доступной^ точностью.
Если кривая задана конечным числом точек,
она называется линией, задаваемой каркасом,
или короче каркасной, а задающие ее точки —
дискретным* каркасом кривой линии. Дуги кри-
вой между точками дискретного каркаса могут
быть построены лишь приближенно. Кривые,
заданные их проекциями и не подчиненные како-
му-либо известному математическому закону,
называются графическими.
Закономерные линии иногда задаются урав-
нением или для них может быть составлено
уравнение; линией п-го порядка называется
линия, уравнение которой в системе декарто-
вых координат имеет п-ю степень. Отсюда сле-
дует, что с прямой линией такая кривая может
пересечься не более чем в и точках. Каркасные
линии часто являются результатом данных
опыта; эти данные позволяют установить рас-
положение отдельных точек относительно не-
подвижной системы координатных осей. Осталь-
ные точки, как и сама линия, определяются ин-
терполированием; графические линии встре-
чаются в основном в процессе проектирования,
когда первоначально строятся проекции линий,
удовлетворяющих каким-нибудь, например
* discretus (лат.) — состоящий из отдельных
частей.
эстетическим, требованиям, а уже затем опре-
деляется положение самих линий в простран-
стве.
На рис. 200 изображена кривая а(а1, а2).
В точках А2 = В2 и Ci= Dt проекции кривой
самопересекаются. Если бы кривая была задана
только своими проекциями, ее положение в
пространстве установить было бы нельзя. Чтобы
понять это, возьмем точку Еса и зададим ее
фронтальной проекцией Ё2. Определить гори-
зонтальную проекцию точки невозможно, так
как это может быть точка Ех, а также Е\.
/97/ Если хотя бы одна проекция кривой
дважды пересекается с линией связи, проведен-
ной через произвольную точку кривой, то без
дополнительных данных эпюр кривой не опреде-
ляет ее формы и положения в пространстве.
Для случая, приведенного на рис. 200, поло-
жение кривой в пространстве и ее форма могут
быть определены, если станут известными не
только две ее проекции, но и по две проекции
точек, например F, Е и С, и известна последо-
вательность, в какой эти точки расположены
на кривой.
Точки А и В относительно П2 и точки С и Г>
относительно П, являются конкурирующими
Рис. 200
5*
67
Рис. 203
(см. 56), а точки Аг= В2 й С, = D, — точками
кажущегося самопересечения.
На рис. 201 изображена самопересекающаяся
кривая а (точки Л, и расположены в проек-
ционной связи). Чтобы эпюр кривой был обра-
тим, должны быть заданы, например, точки В
и С, принадлежащие кривой.
Чтобы установить, какова кривая линия —
плоская или пространственная (всегда прибли- I
женно, кроме случая, когда кривая лежит в про- I
ецирующей плоскости или когда известен закон
образования кривой), нужно провести произ-
вольную прямую, пересекающуюся с кривой I
не менее чем в двух точках, и спроецировать
кривую линию в направлении прямой на произ-
вольную плоскость. Проекцией плоской кривой
будет прямая линия (почему?), проекцией про-
странственной кривой — кривая линия.
Кривые, инцидентные плоскостям уровня,
назовем кривыми уровня по аналогии с назва- ।
нием соответствующих прямых (т. е. фрон-
талыо, горизонталью и профильной кривой).
Пример горизонтали дан на рис. 202. Фронталь-
ная проекция такой линии представляет собой
прямую (или отрезок), перпендикулярную ли-
ниям связи (почему?), горизонтальная — фигу-
ру, равную и подобно расположенную самой
кривой в пространстве (см. /43/).
Касательной а к кривой b в точке А называ-
ется прямая, занимающая предельное положе- [
ние секущей (а'), проходящей через точки А и 5.
когда В, непрерывно перемещаясь по кривой Ь.
стремится совпасть с точкой А (рис. 203).
Проекция секущей а\ проходит через точки А,
и В,, инцидентные проекции кривой. При пере-
мещении по кривой точки В точка В, переме-
щается по ее проекции и при совпадении то-
чек А и В совпадает с точкой At. Таким обра-
зом, прямая становится касательной а, к
кривой ip I
/98/ Проекция касательной к кривой явля-
ется касательной к проекции кривой.
Однако если проекция прямой касательна к
проекции кривой, это еще не значит, что прямая
. касательна к кривой в пространстве.
Пусть точка А перемещается по кривой Ь.
Если при этом непрерывно изменяется положе- [
ние касательной, то кривую называют гладкой.
В отдельных точках непрерывное изменение I
положения касательной может нарушиться, та-
кие точки называются точками излома. Так.
в точке С касательная с меняет свое направле-
ние «скачком» на направление d. То же самое
происходит и с проекцией касательной b>
точке С,.
Некоторые точки кривых называются осо-
быми точками. К ним относятся точки излома
(С на рис. 203), точки возврата (А и В на рис. 204).
в которых направление касательной не меняется
для обеих дуг кривой, двойные точки (точки С
и £ на рис. 204), тройные (точка D). В двойных,
тройных и т. д. точках можно в зависимости
от формы кривой провести одну или большее
число касательных к ней.
Окружность. Параллельной проекцией ок-
ружности в общем случае является эллипс,
в частном — также окружность радиуса данной I
(см. /43/). Если окружность инцидентна проеци-
рующей плоскости (см. /16/), ее проекция
68
(эллипс) вырождается в отрезок, равный диа-
метру окружности.
Чтобы эпюр окружности был обратим, до-
статочно задать кроме проекций окружности
проекции одной инцидентной ей точки (кроме
крайних левой и правой; рис. 205) Центр окруж-
ности проецируется в центр эллипса. Большая
ось эллипса равна диаметру окружности (это
проекция того диаметра, который параллелен
плоскости проекций), длина малой оси может
меняться от нуля (окружность в проецирующей
плоскости) до величины диаметра (окружность
параллельна плоскости проекций).
По одной проекции окружности можно по-
строить ее вторую проекцию. Горизонтальная
проекция окружности задана эллипсом с осями
A,Bt и С, Dt и известна фронтальная проекция
Аг точки А (рис. 206). Проведем в произвольном
месте ось х12 и заменим плоскость П2 на П4,
расположив ее перпендикулярно АВ — горизон-
тали плоскости окружности. А В проецируется в
точку. Отрезок CD на плоскости П4 проециру-
ется в натуральную величину, так как он па-
раллелен ей.
Проведем дугу окружности с центром в точ-
ке Л4 = Вл диаметра А ] Вх до пересечения с ли-
нией связи, инцидентной точке Dt. Получим
точку Р4, либо Р'4, что соответствует двум
вариантам расположения окружности в про-
странстве. Избрав, например, точку Da, по-
строим точку С4 на прямой Р4 — (АЛ = ВЛ).
Измерив координаты Z точек С, D на эпюре
в системе плоскостей П,/П4, отложим их на
линиях связи, проведенных соответственно че-
рез точки Сь £>!, получив точки С2, D2. Так же
построим и промежуточные точки окружности,
например Е. Для этого зададим проекцию точки
на П4, найдем ее проекцию на fij (две точки),
а затем на П2.
Спрямление кривой линии. Спрямлением кри-
вой называется построение отрезка прямой,
приближенно равного длине дуги кривой линии.
Для решения задачи разделим одну из проекций,
например горизонтальную, дуги АВ на некото-
рое число частей (рис. 207) и на горизонтальной
прямой, проходящей через точку А, (или Bt),
построим отрезок AtBt, равный длине гори-
зонтальной проекции дуги между точками /1]
и fip При этом длина каждой части дуги при-
нимается равной длине стягивающей ее хорды.
Проведя линии связи через А, и fi1; найдем
точки Л2 и В2 их пересечения с горизонтальны-
ми прямыми, проведенными через- А2 и В2.
Аналогично строятся и другие точки, напри-
мер С2. Соединив найденные точки плавной
(в данном случае) кривой, получим развертку
дуги кривой.
Разделив дугу А2 В2 на произвольное число
частей, последовательно отложим их на прямой
линии, получив при этом спрямленную дугу кри-
вой— отрезок АВ. Длина отрезка АВ прибли-
женно равна длине дуги АВ.
По развертке кривой можно приближенно
определить угол а ее наклона к плоскости П,
в заданной точке С кривой. Достаточно в С2
провести касательную к дуге А2С2В2 и изме-
рить угол ее наклона к П]: а2 = «
А1
Рис. 2(15
Рис. 2П6
69
Винтовая линия. Винтовой линией будем на-
зывать пространственную кривую, образован-
ную непрерывным поступательным движением
точки по меридиану* поверхности вращения,
в то время как меридиан с одинаковой угловой
скоростью вращается вокруг оси поверхности.
Движение точки по меридиану может иметь
постоянную и меняющуюся по определенному
закону скорость. Поверхность, по которой дви-
жется точка, называется образующей поверхно-
стью, ее ось — осью винтовой линии. Винтовые
линии на прямых цилиндрической и конической
поверхностях называются соответственно ци-
линдрической и конической -Винтовыми линиями.
Построим цилиндрическую винтовую ли-
нию. Движение точки по меридиану поверхно-
сти примем равномерным (рис. 208). Разверткой
винтовой линии будет прямая, так как отрезки,
на которые точка перемещается по меридиану,
пропорциональны длинам дуг, на которые по-
вертывается меридиан цилиндра. Если прямо-
угольник с длиной катета П£> и углом между
этим катетом и гипотенузой, равным а, навер-
нуть на образующий цилиндр, то гипотенуза
станет винтовой линией. Здесь D — диаметр
образующего цилиндра, а а — угол наклона
винтовой линии к плоскости, перпендикуляр-
ной ее оси. Второй катет треугольника — отре-
зок АВ между двумя точками винтовой линии,
расположенными на общем меридиане цилинд-
ра, называется шагом винтовой линии и обозна-j
чается h. Дуга винтовой линии между точками А |
и В называется витком этой линии. На рис. 209
показан один виток.
Если при взгляде вдоль оси винтовой линии
точка будет удаляться от зрителя, вращаясь
по часовой стрелке, то винтовая линия называ-
ется правой. Удаляющаяся от зрителя и вращаю-
щаяся против часовой стрелки точка движется
по левой винтовой линии.
Эпюр винтовой линии можно построить,
используя ее развертку. Первая точка витка
А (Л,; А2) задана и известны величины D и h
(рис. 209). Построим прямоугольный треуголь-
ник с катетами h и П£>. Разделим горизонталь-
ную проекцию цилиндра на произвольное число
равных частей и на то же число частей разделим
горизонтальный катет треугольника. Пусть точ-
ка движется по винтовой линии и перейдет из
точки А в точку С, инцидентную образующей
цилиндра, проходящей через 1-е деление. По-
строим точку С2 на развертке; для этого через
Меридиавом называется линия пересечения
1-е деление горизонтального катета треуголь-
ника проведем вертикальную прямую до пере-
сечения с гипотенузой. Точка С2 расположена
в пересечении горизонтальной прямой, прове-
денной через С2, с линией связи, проходящей
70
Полагая образующий цилиндр непрозрачным,
фронтальную проекцию невидимой половины
витка между точками F2 и Е2 начертим штрихо-
вой линией. Следующий виток начинается в
точке В и в точности повторяет построенный.
На чертеже изображена правая винтовая
линия. Если бы она была левой, то фронтальная
проекция видимой части линии, начинаясь в
точке А2, была бы направлена влево.
Построить цилиндрическую винтовую ли-
нию можно и без развертки. Нужно, разделив
горизонтальную проекцию цилиндра на неко-
торое число равных частей и установив проек-
ционную связь, провести фронтальные проек-
ции образующих. Разделив отрезок А2В2 на
то же число частей, что и горизонтальную проек-
цию основания цилиндра, следует провести
через полученные точки горизонтальные пря-
мые до пересечения с соответствующими проек-
циями образующих.
Шаг винтовой линии может быть переменным
и постоянным. Если шаг переменный, то закон,
по которому он изменяется, может быть задан
разверткой одного или нескольких витков, по
которой и строятся проекции винтовой линии
(рис. 210).
Коническая правая винтовая линия с по-
стоянным шагом показана на рис. 211. Чтобы
построить ее проекции, разделим основание
конуса на произвольное число равных частей.
На то же число равных частей разделим отрез-
ки А1В1 и А2В2 (вначале найдем точку С„
а затем, проведя через нее дугу окружности
радиуса Sj Сл, — точку В,). Проведя через точки
деления фронтальной проекции отрезка гори-
зонтальные прямые, а через точки деления его
горизонтальной проекции — дуги окружностей
с центром в Sj, отметим точки пересечения этих
линий с проекциями соответствующих образую-
щих конической поверхности. Через построен-
ные таким образом точки проходят проекции
винтовой линии.
71
§ 13. КИНЕМАТИЧЕСКОЕ
ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ
Определения и понятия. Будем рассматри-
вать поверхности кинематически — как резуль-
тат непрерывного перемещения линии в про-
странстве. Линия — образующая поверхности —
в процессе перемещения непрерывно меняет
свою форму или остается неизменной. Поверх-
ность, которая может быть образована переме-
щением прямой линии, называется линейчатой;
через любую точку такой поверхности можно
провести не менее одной прямой линии, инци-
дентной поверхности. Линейчатые поверхности
делятся на развертываемые, которые можно
путем раскатывания совместить с плоскостью
без складок и разрывов, и неразвертываемые.
Если поверхность состоит из ряда отсеков пло-
скостей — граней, ее называют гранной. Она
может быть образована движением в простран-
стве по определенному закону прямой или ло-
маной линии. Все поверхности, которые не
могут быть образованы движением прямой
линии, называются нелинейчатыми.
Иногда поверхности задаются непрерывным
перемещением других поверхностей, изменяю-
щихся или неизменяющихся в процессе переме-
щения. Эти поверхности называются образую-
щими поверхностями. Задаваемая поверхность
соприкасается с образующей поверхностью во
всех ее положениях в пространстве и называется
обертывающей.
К числу условий перемещения в простран-
стве образующей линии относятся: перемеще-
ние по неподвижным линиям, называемым
направляющими, вращательное движение вокруг
неподвижной оси, винтовое перемещение, парал-
лельное перемещение и др.
Пусть кривая а (рис. 212) перемещается в
пространстве во всех своих положениях, пере-
секаясь с каждой из множества неподвижных
кривых />, />', 6", ... , последовательно занимая
положения а, а', о", ... Очевидно, что при этом
кривая а не только перемещается в простран-
стве, но и непрерывно меняет свою форму.
Множество кривых b,b', Ь”, представ-
ляет собой поверхность. Той же поверхностью
является и множество кривых а, а', а",...,
поэтому можно представить себе, что кривая b
перемещается в пространстве во всех своих
положениях, пересекаясь с каждой из множества
неподвижных кривых а, а’, а" ...
Неподвижные кривые — направляющие
(в первом случае кривые Ь, во втором — кри-
вые й) определяют условия перемещения и из-
менения формы подвижной кривой — образую-
Рис. 212
щей. Эти условия могут быть заданы и как-либо
иначе, например аналитически.
/99/ Одна и та же поверхность может быть
образована перемещением в пространстве раз-
личных линий при разных условиях, определяю-
щих перемещение линии и изменение ее формы.
Множество Неподвижных линий, инцидент-
ных поверхности и объединенных каким-либо
общим признаком, называется ее каркасом.
Для поверхности, изображенной на рис. 207,
каркасом может быть множество кривых а,
либо множество кривых Ь. Возможен и иной
каркас. Кроме того, каркасом может быть мно-
жество точек, например, пересечения линий
множеств а и Ь.
Каркас бывает непрерывным и дискретным.
В первом случае любой точке поверхности
инцидентна линия каркаса. Это значит, что
каркас определяет единственную поверхность.
Во втором случае каркас состоит из конечного
числа линий или точек; поверхность не вполне
определена, так как могут существовать поверх-
ности с одним и тем же дискретным каркасом,
отличающиеся друг от друга.
Совокупность условий, определяющих по-
верхность, называется ее определителем*. В ка-
честве определителя мы будем рассматривать
1. Задающие поверхность геометрические фи-
гуры. 2. Отношения, между ними (взаимораспо-
ложение фигур, условие перемещения одной
фигуры относительно другой и т. п.). Инфор-
мация об отношениях может быть выражена в
словесной форме, аналитически и чертежом.
Определитель задает поверхность. Это значит
что относительно любой точки пространства
можно точно или с достаточной степенью при-
ближения решить вопрос о том, инцидентна
ли она данной поверхности. Действительно,
если точка инцидентна одной из линий поверх-
ности, она инцидентна самой поверхности. Если
поверхность задана дискретным каркасом, за
дача большей частью решается приближенно.
/100/ Точка инцидентна поверхности, если она
инцидентна одной из линий поверхности (сравни-
те с /79/).
В образовании поверхности могут участво-
вать различные геометрические фигуры при
разных отношениях между ними. Это значит,
что одна и та же поверхность имеет несколько
определителей. Выбирают тот из них, который
по каким-либо признакам удобнее в каждом
конкретном случае. Приведем в качестве при-
мера прямую, круговую цилиндрическую по-
верхность, известную читателю из школьного
курса геометрии. Она может быть образована
вращением прямой вокруг параллельной ей
оси. Но та же поверхность образуется парал-
лельным перемещением окружности неизмен-
ного радиуса при условии, что ее центр всегда
инцидентен прямой линии (оси). Могут быть
приняты и другие определители.
Часто поверхности задаются аналитически.
Поверхностью и-го порядка называется поверх-
ность, уравнение которой в системе декартовых
* См.: Котов И. И. Лекции для слушателей
факультета повышения квалификации преподавате-
лей по курсу «Начертательная геометрия». МАИ.
1971.
72
координат является уравнением п-й степени.
Отсюда следует, что с плоскостью такая поверх-
ность может пересечься по кривой порядка не
выше и, а с прямой линией — не более чем в п
точках.
Эпюр поверхности. Следует делать разли-
чие между понятиями задать поверхность и
изобразить поверхность. Задает поверхность ее
определитель, изображают же не только гео-
метрические фигуры определителя, но и неко-
торые другие, например контур поверхности и
границу ее отсека, которые нужны для большей
наглядности изображения.
/101/ Эпюром поверхности является эпюр
геометрических фигур определителя, дополнен-
ный при необходимости эпюром контура поверх-
ности или ее отсека.
§ 14. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
Зададим три направляющие — кривые Ь, с
и 4 по которым скользит прямая — образую-
щая а (рис. 213). Пусть вначале образующая
инцидентна неподвижной точке А кривой b и
перемещается в пространстве, постоянно пере-
секаясь с кривой d. Образованная прямой а
коническая поверхность при данных условиях
единственно возможна. Если изменить на кри-
вой b положение точки А и Л', то прямая, пере-
секающаяся с кривой d и инцидентная точке А',
образует новую, отличную от ранее образован-
ной, коническую поверхность. Следовательно,
движение в пространстве прямой по двум обра-
зующим (Ь и d) не определяет какой-либо строго
определенной поверхности. Пусть теперь пря-
мая а, инцидентная точке А, пересекаясь с кри-
вой d, в некоторый момент пересечет и кривую с
в точке В. Иначе говоря, кривая с пересечет в
точке В коническую поверхность с вершиной А
и направляющей d. При этих условиях положе-
ние прямой а оказывается единственно возмож-
ным. Заметим, что образующая пересекается в
точке А с направляющей Ь, в точке В — с на-
правляющей сив точке С — с направляющей d.
Следовательно, для этих точек поверхности,
в равной мере как и для любой точки D прямой а,
образующая поверхности занимает единствен-
но возможное положение в пространстве. Если
бы была дана еще и четвертая неподвижная
кривая, то образующая а могла бы с нею и не
пересечься, кроме, разумеется, случая, когда
четвертая кривая инцидентна поверхности.
Сместив по кривой b точку А на бесконечно
малую дугу, получим новые точки пересечения
образующей с кривыми си d и т. д. Таким
образом, перемещая прямую по трем непод-
вижным кривым, мы построим линейчатую по-
верхность общего вида.
В качестве непрерывного каркаса линейча-
той поверхности общего вида обычно прини-
мают множество прямых линий. Определитель
такой поверхности; 1. Три неподвижные кривые
линии — направляющие, прямая линия — обра-
зующая. 2. Прямая перемещается в пространстве,
всегда пересекаясь со всеми тремя кривыми ли-
ниями.
/102/ Линейчатая поверхность общего вида
вполне определена, если известны три ее направ-
ляющие.
Чтобы задать такую поверхность на чертеже,
достаточно построить эпюр трех ее направляю-
щих (см. /101/). Следует учесть, что не всякие
три направляющие могут служить образова-
нию линейчатой поверхности.
В некоторых случаях оказывается достаточ-
ным знать расположение двух, а иногда и одной
направляющей. Начнем рассмотрение линей-
чатых поверхностей именно с этого последнего
случая.
Линейчатые поверхности с одной направляю-
щей и вершиной. Определитель поверхности:
1. Неподвижная линия (кривая или ломаная) —
направляющая; неподвижная точка — вершина
(собственная или несобственная); образующая —
прямая линия. 2. Образующая перемещается в
пространстве, оставаясь инцидентной вершине н
пересекаясь с направляющей.
Если направляющая — кривая линия, а вер-
шина — собственная точка, то поверхность на-
зывается конической (рис. 214). Если направляю-
щая представляет собой ломаную линию, то
поверхность становится пирамидальной и будет
относиться к гранным поверхностям (рис. 215).
Образующие, инцидентные точкам А, В, С,
D, ... излома ломаной линии, называются реб-
рами поверхности. Коническая и пирамидаль-
ная поверхности имеют две полости, располо-
женные по разные стороны от вершины.
73
Когда вершина — несобственная точка,
коническая поверхность становится цилиндри-
ческой (рис. 216), а пирамидальная — призмати-
ческой (рис. 217).
Если направляющая является замкнутой кри-
вой или ломаной линией, то коническая и ци-
линдрическая или соответственно пирамидаль-
ная и призматическая поверхности становятся
замкнутыми.
Рассечем замкнутую коническую или пира-
мидальную поверхность плоскостью, не инци-
дентной вершине; часть пространства, ограни-
ченную плоскостью (основанием) и поверхно-
стью, включающей вершину, называют соот-
ветственно конусом или пирамидой. Часть про-
странства, расположенная внутри конической
или пирамидальной поверхности между двух
параллельных плоскостей, расположенных по
одну сторону от вершины, называется усечен-
ным конусом'или пирамидой. Напомним, что
пирамидой называется тело, поверхность ко-
торого состоит из некоторого числа плоских
треугольников — боковых граней и одного пло-
ского многоугольника основания, число сторон
которого равно числу треугольников. По числу
боковых граней пирамида называется трех-,
четырех- и т. д. угольной пирамидой. Вместе
с тем четырехугольную пирамиду можно на-
зывать пятигранником, так как пятой гранью
ее является основание.
На практике редко изображают коническую
или пирамидальную поверхность, значительно
чаще изображаются конус или пирамида (т. е.
тела). В качестве направляющей их боковой
поверхности используется граница, основания.
Построим эпюр направляющей и соответствую-
щие проекции контурных образующих, а для
пирамиды — и проекции всех или только ви-
димых ее ребер, получим эпюр тела. ‘
Если рассечь цилиндрическую или призма-
тическую поверхности с замкнутой образую-
щей параллельными плоскостями, не парал-
лельными образующим, то часть пространства,
расположенная внутри поверхности между се-
кущими плоскостями, будет называться соот
ветсгвенно цилиндром и призмой.
Подобно пирамиде, призма — многогран-
ник. Ее боковая поверхность состоит из парал-
лелограммов, по числу которых призма назы-
вается трех-, четырехугольной и т. д. Основания
призмы — плоские многоугольники с числом
сторон, равным числу боковых граней. Четы-
рехугольная призма может быть названа шести-
гранником, пятиугольная — семигранником и
т. д.
В практике и в этом случае обычно изобра-
жаются не поверхности, а тела. В качестве на-
правляющей боковой поверхности принимают
линию ее пересечения с плоскостью одного из
оснований. При построении эпюра поверхности
строится эпюр обоих оснований и контурных
образующих. Кроме того, при изображении
призмы строится эпюр всех или только видимых
ее ребер.
Эпюр линейчатых поверхностей с одной на-
правляющей и вершиной. На рис. 218 дан эпюр
конуса с вершиной S. Его основание — эллипс b
лежит в плоскости общего положения. Так как
геометрическими фигурами определителя бо-
ковой поверхности являются эллипс*, образую-
щая а и точка S, то эпюр этих фигур можно рас-
сматривать (см. /101/) как эпюр поверхности
(рис 218, о). Такой эпюр позволяет решать по-
зиционные и метрические задачи, однако изоб-
* На эпюре эллипса должны быть заданы про-
екции инцидентной эллипсу точки (А). См. поясне-
ния к рис. 205.
74
ражение лишено наглядности. Поэтому прове-
дены фронтальные проекции контурных отно-
сительно П2 образующих AS и BS и контурных
относительно П, образующих CSn DS. Контур-
ные относительно П, образующие не могут
быть контурными образующими относительно
П2 (кроме случая, когда контурная образую-
щая— профильная прямая; почему?). Чтобы
убедиться в этом, построим горизонтальные
проекции прямых AS и BS и фронтальные про-
екции прямых CS и DS. Прямые A2S2 и B2S2
касательны к фронтальной проекции основания,
прямые C1S1 и DiS1 — касательны к его гори-
зонтальной проекции.
Определим горизонтальную проекцию точ-
ки Е, инцидентной конической поверхности и
заданной фронтальной проекцией Е2 (см. /100/).
Проведем через Е2 фронтальную проекцию
образующей FS (предполагается известным,
что она видима и поэтому пересекается с фрон-
тальной проекцией эллипса между точками С2
и А2. В противном случае возможно проведение
двух прямых F2S2 и F'jS^. Найдя точку Fr между
точками Aj и С, на проекции эллипса, соединим
ее с S, и, установив проекционную связь, най-
дем точку £,.
Эпюр цилиндра дан на рис. 219. Для задания
его боковой поверхности было бы достаточно
дать эпюр одного из оснований цилинцра
(направляющая) и направления образующих
(см. /8/). Однако для повышения наглядности
изображены оба основания и проведены про-
екции контурных образующих. Они касательны
к соответствующим проекциям оснований ци-
линдра.
Чтобы построить горизонтальную проекцию
точки А, инцидентной боковой поверхности
цилиндра и заданной точкой А2 (имеется в
виду, что точка видима при взгляде спереди),
нужно провести через нее образующую, как 'и в
случае с конусом (см. /100/).
На рис. 220 изображена четырехугольная
пирамида. Часть ее ребер невидима при взгляде
спереди и сверху. Для определения видимости
воспользуемся конкурирующими точками, на-
пример Ни К (см. /68/). Чтобы построить фрон-
тальную проекцию точки Е, инцидентной бо-
ковой поверхности пирамиды и заданной точ-
кой Et, нужно провести через точку образую-
щую FS и, установив проекционную связь,
найти точку Е2.
Грани пирамиды — плоские фигуры,
поэтому вторую проекцию заданной точки
можно построить с помощью любой прямой,
например CG, лежащей в грани CDS (см. /79/).
Поверхности коническая, цилиндрическая,
пирамидальная и призматическая относятся к
развертываемым поверхностям (см. § 25).
Линейчатые поверхности с двумя направляю-
щими и плоскостью параллелизма.
Определитель поверхности: 1. Две неподвиж-
ные линии — направляющие, прямая линия —
образующая и плоскость параллелизма. 2. Обра-
зующая перемещается в пространстве, постоянно
пересекая обе направляющие и оставаясь парал-
лельной плоскости параллелизма.
Две направляющие не определяют линей-
чатой поверхности, поэтому введено дополни-
тельное условие: образующая перемещается в
пространстве, всегда оставаясь параллельной
плоскости параллелизма. Образующая во всех
своих положениях пересекается с плоскостью
параллелизма в несобственной точке. Так как
множество таких точек представляет собой не-
собственную прямую плоскости параллелизма
(см. /6/), то эту прямую можно рассматривать
как третью направляющую линейчатой поверх-
ности (см. /102/).
Если обе направляющие линейчатой поверх-
ности, с плоскостью параллелизма — кривые
линии, то поверхность называется цилиндрои-
дом. Пример цилиндроида приведен на рис. 221.
Направляющими служат окружности b и с.
плоскостью параллелизма — П2. Горизонталь-
ные проекции образующих параллельны оси у
(почему?).
Чтобы построить фронтальную проекцию
точки А, инцидентной поверхности и заданной
горизонтальной проекцией, следует провести
через А1: горизонтальную проекцию образую-
щей (а, || х), построить ее фронтальную проек-
цию и найти на ней точку А2. Когда задана В2 -
фронтальная проекция точки и требуется найти
ее горизонтальную проекцию, нужно посту-
пить иначе (направление фронтальной проекции
образующей, проходящей через В2, неизвестно).
Проведем через В2 фронтальную проекцию
произвольной линии, инцидентной поверхности.
Для удобства фронтальную проекцию линии
примем прямой, следовательно, линия на по-
верхности будет плоской (почему?). Отметив
точки пересечения фронтальной проекции про
веденной линии с фронтальными проекциями
образующих (точки С2, D2, Е2), построим их
горизонтальные проекции и соединим плавной
кривой. На этой кривой расположена горизон-
тальная проекция точки В (см. /23) и /100/).
В технике цилиндроида встречаются, в част-
ности, при изготовлении трубопроводов боль-
ших диаметров. Пример соединения двух ци-
линдрических труб и показан на рис. 221.
Если одна из двух направляющих линейчатой
поверхности с плоскостью параллелизма пря-
мая, а вторая кривая линия, то поверхность на-
зывается коноидом. Коноиды имеют широкое
распространение в технике, например, при изго-
товлении диффузоров систем вентиляции, при
устройстве мостовых опор (рис. 222) и т. д.
Эпюр коноида, изображенного на рис. 222, при
веден на рис. 223. Одна из направляющих —
полуокружность Ь, расположенная в горизон-
76
тальной плоскости, вторая — фронтально про-
ецирующая прямая с. Плоскость параллелиз-
ма — П2.
Коноид называется прямым, если прямая
направляющая перпендикулярна плоскости па-
раллелизма (на рис. 223 прямой коноид). При
данном расположении поверхности можно про-
вести как фронтальную, так и горизонтальную
проекции произвольной образующей, что по-
зволяет точно строить вторую проекцию точки,
инцидентной поверхности (см. /100/).
Случай, когда направляющими поверхности
служат две скрещивающиеся прямые, мы рас-
смотрим в § 17.
Линейчатые поверхности с тремя направляю-
щими — прямыми линиями. Определитель по-
верхности: 1. Три неподвижные прямые—на-
правляющие; прямая — образующая. 2. Образую-
щая перемешается в пространстве, постоянно пе-
ресекая все три направляющие. Если три направ-
ляющие Ь, с и d — прямые линии, одновременно
не параллельные никакой плоскости, то переме-
щающаяся по ним прямая а образует поверх- '
ность, называемую однополостным гиперболои-
дом. Путь образующая а пересекается с пря-
мой/; в неподвижной точке А (рис. 224). Скользя
по прямой d, она образует плоскость, которая
в точке В пересекается с прямой с. Таким обра-
зом, образующая поверхности, проходящая че-
рез неподвижную точку А, занимает единст-
венно возможное положение. При перемеще-
нии точки А по прямой b меняется образован-
ная прямой а плоскость, а вместе с тем и точка
ее пересечения с прямой с. Следовательно, для
каждой точки прямой h (в равной мере и для'
прямых с и d) существует единственная
образующая поверхности (сравните с
рис. 213).
Перемещаясь по направляющим, прямая а
создает множество прямых, инцидентных по-
верхности однополостного гиперболоида
(рис. 225). Любые три прямые этого множества
могут служить направляющими для иной, от-
личной от а образующей, например Ь, которая
в свою очередь, перемещаясь по направляю-
щим, создаст множество прямых с, d, ... , инци-
дентных поверхности. Следовательно, поверх-
ность однополостного гиперболоида представ-
ляет собой два множества прямых линий.
Для наглядности поверхность на рисунке
ограничена двумя параллельными плоско-
стями.
Однополостный гиперболоид — поверх-
ность неразвертываемая.
Линейчатые поверхности с ребром возврата.
Определитель поверхности: 1. Неподвижная про-
странственная кривая — направляющая, пря-
мая — образующая. 2. Образующая перемеща-
ется в пространстве, всегда оставаясь касатель-
ной к направляющей. Поверхность с таким опре-
делителем называется торсом, а ее кривая на-
правляющая — ребром возврата (рис. 226).
Точки касания А, А', ... , инцидентные ребру
возврата, делят касательные на полукасатель-
ные, поэтому и поверхность делится на две по-
лости с границей между ними — ребром воз-
врата. Если ребро возврата — плоская кривая,
то торс становится плоскостью или отсеком
Рис. 224
77
Рис. 226
плоскости (при выпуклой плоской кривой часть
плоскости не будет покрыта перемешаюшейся
касательной).
Торс — поверхность развертываемая.
В дополнение к /W2J'.
/103/ Линейчатая поверхность определена,
если известна одна ее направляющая и вершина;
две направляющие в плоскость параллелизма;
одна направляющая — ребро возврата. Конечно,
во всех случаях должны быть известны условия
перемещения образующей.
Построение проекций точек, инцидентных
линейчатой поверхности, мы показали на при-
мере цилиндроида. Описанный прием может
быть использован для любой линейчатой по
верхности. Некоторые другие приемы буду
приведены при изучении последующего ма
териала.
§ 15. ПОВЕРХНОСТИ ВРАЩЕНИЯ
Определитель поверхности: 1. Неподвижна:
прямая — ось вращения; образующая — пряма:
или кривая линия. 2. Образующая вращается во-
круг осн так, что каждая точка образующей со-
вершает полный оборот. Если поверхность может
быть образована вращением прямой линии, ее
называют линейчатой поверхностью вращения.
/104/ Поверхность вращения задана, если из-
вестны ее ось и образующая.
Линейчатые поверхности вращения. Образую-
щая поверхности и ось вращения — прямые ли-
нии — могут пересекаться в собственной или
несобственной точке или скрещиваться. В пер-
вом случае образуется прямая круговая кониче-
ская поверхность или прямая круговая цилин-
дрическая поверхность. Любая точка образую-
щей перемещается по окружности, поэтому ок-
ружность можно рассматривать как направ-
ляющую линейчатой поверхности, а заданную
точку — ее вершиной. Следовательно, прямая
круговая коническая и цилиндрическая поверх-
ности образованы по тем же условиям, что и
линейчатые поверхности с одной направляю-
щей и вершиной.
Когда поверхность образована вращение»!
прямой а, скрещивающейся с осью вращения i,
то образованная ею поверхность будет однопо-
лостным гиперболоидом вращения (рис. 227).1
Если взять прямую, симметричную образующей
относительно плоскости, проходящей через ось,
78
и вращать эту прямую вокруг оси, то она в силу
симметрии образует ту же поверхность. Следо-
вательно, на поверхности однополостного ги-
перболоида вращения существует два множества
прямых линий, и поверхность может быть обра-
зована движением прямой одного множества
по трем прямым второго. С такой поверхно-
стью общего вида мы уже встречались (см.
рис. 225). Приведенная на рис. 227 поверхность
является ее частным случаем.
Построение эпюра отсека поверхности на
практике сводится к следующему: окружно-
сти— сечения поверхности плоскостями, пер-
пендикулярными оси вращения, — делим на
произвольное число частей, например двенад-
цать. Соединим первую точку нижней окружно-
сти с одной из точек верхней окружности (в за-
висимости от условий задачи), в примере пятой.
Вторую точку нижней окружности соединяем
с шещой точкой верхней окружности и т., д.
Проведенные линии принадлежат одному мно-
жеству прямых — образующих поверхности.
Линии второго множества проводятся симмет-
ричнр линиям первого. Проекции контура по-
верхности относительно П2 представляют со-
бой дуги гиперболы. Если одну из них вращать
вокруг оси, получим ту же поверхность.
Нелинейчатые поверхности вращения. Возь-
мем плоскую кривую а и будем вращать ее
вокруг неподвидной оси i, лежащей в плоскости
кривой (рис. 228). Каждая точка кривой описы-
вает окружность, поэтому поверхность враще-
ния представляет собой множество окружно-
стей различных диаметров (некоторые из них
могут быть равны между собой). Эти окружно-
сти называют параллелями поверхности. Выше
говорилось, что кривая, по которой поверх-
ность вращения пересекается с плоскостью,
проходящей через ось вращения, называется
меридианом. Такая плоскость носит название
меридиональной. При данном на рис. 228 рас-
положении поверхности вращения кривые а и а'
представляют собой контур поверхности отно-
сительно П2. Такие кривые называются глав-
ными меридианами. Параллели, диаметр кото-
рых больше диаметра ближайших соседних
параллелей, называются экваторами (парал-
зель А), а диаметра, меньшего, чем диаметр
соседних параллелей, — горлами (параллели с
и d). Поверхности вращения могут иметь не-
сколько экваторов и несколько горл или не
иметь ни одного горла (например, сфера).
Эпюр поверхности вращения, когда ее ось
вертикальна, состоит из фронтальной проекции
главных меридианов (контура) и горизонталь-
ной проекции экваторов, горл и линий сечения
плоскостями, как это сделано на рис. 228. Так
гак главный меридиан является фронталью, то
его горизонтальная проекция параллельна оси х.
Она инцидентна точке it. Параллели (горизон-
тали) проепирую гея на П2 в отрезки прямых,
параллельных оси х. Их 1 оризонгальные про-
екции представляют собой окружности (см. /43/)
Чтобы построить вторую проекцию точки,
инцидентной поверхности вращения, нужно про-
вести через нее соответствующую проекцию
параллели, построить ее вторую проекцию и.
установив проекционную связь, найти вторую
79
проекцию точка Так по точке At построена
точка А2. Однако проекцией точки А на П2
может быть и точка А2. В равной мере, если
известна фронтальная проекция точки, напри-
мер А2, то горизонтальной проекцией точки
может быть как точка А1г так и точка Л'/.
Поэтому при решении задач требуется уточне-
ние задания, выраженное в словесной или какой-
либо иной форме.
Если поверхность вращения — линейчатая,
можно вместо параллели провести через точку
прямую линию, инцидентную поверхности (об-
разующую).
Сфера н тор. Сфера образуется вращением
полуокружности вокруг оси, инцидентной диа-
метру. Часть пространства, расположенная вну-
три сферы, называется шаром.
Экватором сферы является параллель, инци-
дентная плоскости, проходящей через центр.
Для и ображения сферы достаточно построить
фронтальную проекцию ее главных меридианов
и горизонтальную проекцию экватора.
Поверхность, образованная вращением ок-
ружности вокруг оси, инцидентной плоскости
окружности, но не инцидентной ее центру, на-
зывается тором. Существуют разновидности
торов, которые отличаются друг от друга отно-
шением радиуса R окружности к расстоянию а
от ее центра до оси вращения.
Когда' R меньше а (рис. 229), тор носит на-
звание открытого тора или кольца; при R.
равном а (рис. 230), или при R, большем и
(рис. 231), тор называется закрытым. В послед-
нем случае вращающаяся окружность образует
самопересекающуюся поверхность. Окруж-
ность, образованную перемещением центра об-
разующей, называют кривой осью тора. Про-
екция контура на П2 при данном расположении
тора представляет собой две полуокружности
и два-отрезка параллельных прямых, касатель-
ных к ним. Проекцией контура на П1 являются
две концентрические окружности (какова про
екция контура относительно плоскостей П] и П,
закрытых торов?).
§ 16. ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
Существует девять поверхностей второго
порядка, из них шесть линейчатых
Линейчатые поверхности второго порядка.
Если, направляющей конической поверхности
может быть одна из трех видов кривых второго
порядка, т. е. эллипс, парабола или гипербола,
то поверхность называется конической поверх-
80
костью второго порядка (для краткости часто
говорят конус второго порядка. Использовать
этот термин можно, если нет опасений, что
вместо поверхности будет иметься в виду тело).
I В качестве направляющей конуса обычно при-
нимают эллипс (см. рис. 218). Поверхность имеет
' три взаимно перпендикулярные плоскости сим-
метрии (рис. 232), линию пересечения двух из
них называют осью конической поверхности
(это ось симметрии поверхности). Третья пло-
I скость (на рисунке не показана) устанавливает
I симметрию двух полостей поверхности. Она
пересекает ее в точке S (вершине). Если сечение
I поверхности плоскостью, перпендикулярной
j оси, является окружностью, то поверхность
становится конической поверхностью враще-
ния Сечением конической поверхности второго
порядка плоскостью могут быть эллипс, пара-
бола и гипербола, почему эти линии называют
кривыми конических сечений (сведения о виде
линий пересечения поверхностей второго по-
рядка плоскостью приводятся без доказатель-
ства. Интересующимся следует обратиться к
курсу аналитической геометрии).
На рис. 233 показана плоскость fl, пересекаю-
щая все образующие поверхности (способ по-
строения линий пересечения плоскости и поверх-
ности мы изложим в § 25). Линией пересечения
является эллипс. Плоскости, параллельные £2,
пересекают конус по подобным н подобно распо-
ложенным эллипсам. По мере приближения
плоскости к вершине эллипсы уменьшаются,
после перехода плоскости на другую полость
поверхности — увеличиваются. Изменив угол
наклона плоскости к оси поверхности, но сохра-
I нив условие, что плоскость пересекает все обра-
зующие конуса, мы получим эллипсы с иным
отношением длин осей В частном случае это
отношение равно единице — сечением стано-
вится окружность. Когда плоскость пройдет
через вершину поверхности, то эллипс выро-
дится в точку.
/105/ Если плоскость пересекает все образую-
щие конической поверхности второго порядка,
то линией сечения ивлиется эллипс, его частный
случай — окружность или вырожденный случай—
точка;
Когда плоскость параллельна одной образую-
щей, линией сечения становится парабола
(рис. 234). Парабола пересекается с параллель-
Рис. 234
81
6-940
ной ей образующей в бесконечности, следо-
вательно, имеет одну несобственную точку
(см. /6/), это ее несобственная вершина.
Перемещая плоскость параллельно ее пер-
воначальному положению, мы получим другие,
отличные от ранее построенной, но подобные
ей параболы. Когда плоскость пройдет через
вершину, парабола выродится в прямую (лучше
сказать в двойную прямую).
/106/ Еслй плоскость параллельна одной об-
разующей конической поверхности второго по-
рядка, линией сечения является парабола или ее
вырожденный случай — прямая.
Сечение конической поверхности плоско-
стью, параллельной двум образующим, пред-
ставляет собой гиперболу (рис. 235); Плоскость
пересекает обе полости конической поверхно-
сти, в связи с чем гипербола имеет две ветви.
С параллельными ей образующими гипербола
пересекается в бесконечности, следовательно,
эта кривая имеет две несобственные точки.
Перемещая плоскость параллельно ее пер-
воначальному положению, получим новые ги-
перболы, отличные от ранее построенной. Когда
плоскость пройдет через вершину поверхности,
гипербола выродится в пару пересекающихся
прямых.
/107/ Если плоскость параллельна двум об-
разующим конической поверхности второго по-
рядка, то линией сечения является гипербола или
ее вырожденный случай — две пересекающиеся
прямые.
На рис. 236 показаны фронтально проеци-
рующие плоскости (12, Е и Ч*), результатом
сечения которыми конической поверхности яв-
ляется: эллипс (12), парабола (Г) и гипербола
(*Р). Горизонтальные проекции сечений не по-
казаны.
Цилиндрическая поверхность второго порядка
(цилиндр второго порядка) имеет три разновид-
ности. Если направляющая эллипс, то цилиндр
называется эллиптическим (рис. 237). Он имеет
две плоскости симметрии, линия пересечения
которых является осью симметрии цилиндра.
Если плоскость наклонена к оси, а следова-
тельно, и к образующим цилиндра, то сечением
будет эллипс, отношение длин осей которого
зависит от угла наклона секущей плоскости к
образующим. Когда сечение плоскостью, пер-
пендикулярной оси, представляет собой окруж-
ность, то поверхность называется цилиндрвче-
ской поверхностью вращения. Плоскость, парал-
лельная образующим, может рассечь пилиндр
по двум параллельным прямым или одной
(двойной) прямой.
Когда направляющая — парабола (рис. 238),
цилиндр называется параболическим. Он имеет
одну плоскость симметрии. Плоскость, накло-
ненная к образующим, рассекает такой цилиндр
по параболе, параллельная образующим — по
82
двум параллельным прямым или одной прямой.
Третьей разновидностью цилиндра является
гиперболический цилицдр (рис. 239), имеющий
две плоскости симметрии. Сечением цилиндра
плоскостью, наклоненной к образующим, явля-
ется гипербола, параллельной образующим, —
две параллельные прямые или одна прямая.
/108/ Сечением цилиндрической поверхности
второго порядка может быть кривая второго по-
рядка того же вида, что н направляющая поверх-
ности, две параллельные прямые и одна прямая.
Определитель конической и цилиндрической
поверхностей второго порядка.
Гиперболический параболоид. Выше гово-
рилось, что в качестве направляющих ли-
нейчатой поверхности с плоскостью паралле-
лизма могут быть две скрещивающиеся пря-
мые. Образованную таким образом поверх-
ность называют гиперболическим параболоидом
или «косой' плоскостью». У этой поверхности
есть две плоскости параллелизма. Если угол
между ними равен 90°, гиперболический пара-
болоид называется прямым, в противном слу-
чае — наклонным. Рассмотрим наиболее часто
встречающийся в технике прямой гиперболиче-
ский параболоид (рис. 240). Направляющие
поверхности — прямые с (С; ТУ) и b (А; F), пло-
скость параллелизма параллельна граням
A DUE и BCGF. Образующей является прямая а.
Если направляющими поверхности станут пря-
мые а и а' (рис. 241), то образующей будет пря-
мая b (или с). Грани ABFE и DCGH в этом слу-
чае параллельны второй плоскости параллелиз-
ма. Гиперболический параболоид можно рас-
сматривать как два множества прямых, каждое
из которых имеет свою плоскость паралле-
лизма.
Построим точки пересечения прямых обоих
множеств с горизонтальной плоскостью, на-
пример fl (рис. 242). При данном расположе-
нии поверхности множество таких точек явля-
ется гиперболой. Сечения поверхности плоско-
стями, параллельными плоскости BF П DH,
представляют собой параболы. Отсюда и на-
83
6‘
Рис. 242
84
в
Рис. 243
звание поверхности (рис. 243). Если горизон-
тальная плоскость инцидентна точке N, то
гипербола вырождается в пару пересекающихся
прямых. Если секущая плоскость параллельна
линии пересечения плоскостей Параллелизма, то
сечением гиперболического параболоида является
парабола (или прямая), во всех остальных слу-
чаях — гиперболу (или пара пересекающихся
прямых).
/109/ Сечением гиперболического параболои-
да плоскостью может быть парабола, гипербола,
пара пересекающихся прямых и одна прямая.,
Гиперболический параболоид имеет две пло-
скости симметрии. Определитель поверхности.
И наконец, последней линейчатой поверх-
ностью второго порядка является однополост-
ный гиперболоид, показанный ранее на рис. 225.
Эта поверхность имеет три плоскости симмет-
рии. Линия пересечения двух из них представ-
ляет собой ось симметрии поверхности. Сече-
ниями однополостного гиперболоида плоско-
стями, инцидентными оси, являются гиперболы.
Множество асимптот таких гипербол представ-
ляет собой асимптотический конус (рис. 244).
Существует множество однополостных гипер-
болоидов с общим асимптотическим конусом.
Линии сечения плоскостью однополостных
гиперболоидов н их асимптотического конуса
являются кривыми второго порядка одного вида.
Поэтому сечением гиперболоида может быть
эллипс (частный случай — окружность), пара-
бола и гипербола (и ее вырожденный случай —
две пересекающиеся прямые), причем эллипти-
ческие сечения однополостиых гиперболоидов н
их асимптотического конуса параллельными пло-
скостями подобны н подобно расположены. Одно-
полостный гиперболоид можно пересечь пло-
скостью по параллельным прямым, одна из
которых инцидентна одному множеству обра-
зующих, вторая — другому.
/110/ Сечением однополостного гиперболоида
плоскостью может быть эллипс (его частный слу-
чай — окружность), парабола, гипербола, пара
пересекающихся н пара параллельных прямых.
Если сечение поверхности плоскостью, пер-
пендикулярной оси симметрии, — окружность,
то поверхность носит название однополостного
гиперболоида вращения.
Нелниейчатые поверхности второго порядка.
В качестве определителя может быть принят
определитель поверхностей с подобно преобра-
зующейся образующей. На рис. 245 изобра-
жен трехосный эллипсоид. Эта поверхность
имеет три плоскости симметрии, каждая из
которых пересекает поверхность по эллипсу,
оси которого являются и осями эллипсоида.
Плоскости симметрии попарно пересекаются
Рис. 244
85
Рис. 245
по линиям, на которых лежат оси эллипсоида.
Сечение эллипсоида плоскостью представляет
собой эллипс или его частный случай — окруж-
ность. Сечения эллипсоида параллельными пло-
скостями подобны и подобно расположены.
Концы осей эллипсоида называются его вер-
шинами; их шесть.
Если сечением эллипсоида плоскостью, пер-
пендикулярной одной из его осей, является ок-
ружность, эллипсоид становится эллипсоидом
вращения: вытянутым, когда третья ось больше
диаметра окружности (рис. 246), и сжатым,
когда эта ось меньше диаметра (рис. 247).
Меридианом поверхности в обоих случаях яв-
ляется половина эллипса. Если все три оси эл-
липсоида равны между собой, эллипсоид ста-
новится сферой. Сечением сферы может быть
только окружность.
/111/ Сечением трехосного эллипсоида может
быть эллипс, его частный случай — окружность
и вырожденный — точка.
Эллиптический параболоид ' изображен на
рис. 248. Осью поверхности является линия пере-
сечения ее двух плоскостей симметрии. Ось пе-
ресекается с поверхностью в собственной (5) й
несобственной вершинах. Плоскости, парал-
лельные оси, пересекают параболоид по пара-
болам, наклоненные к оси, — по эллипсам.
Эллиптические сечения, образованные парал-
лельными плоскостями, подобны и подобно
расположены.
/112/ Если эллиптический параболоид и эллип- I
тический цилиндр с параллельными осями рас- I
секаются плоскостью по подобным эллипсам, то J
любая другая плоскость, рассекающая парабо-
лоид по эллипсу, пересечет цилиндр по подобному
н подобно расположенному эллипсу.
Когда сечением йоверхности плоскостью,
перпендикулярной оси, является окружность,
поверхность становится параболоидом враще-
ния; ее меридиан — парабола.
/113/ Сечением эллиптического параболоида
может быть эллипс (его частный случай — ок-
ружность н вырожденный— точка) н парабола.
Последняя поверхность второго порядка —
двуполостный гиперболоид (рис. 249). Он имеет
три плоскости симметрии, две из которых
пересекаются между собой по оси симметрии
гиперболоида. Ось симметрии пересекается с
поверхностью в двух собственных точках 5 и
S' — вершинах поверхности.
Сечением поверхности плоскостью, инци-
дентной осн, является гипербола. Множество
асимптот таких гипербол представляет собой
асимптотический-конус. Существует множество
двуполостных гиперболоидов с общим асим-
птотическим конусом.. Линии пересечения пло-
скостью двуполостных гиперболоидов и их асимп-
тотического конуса являются кривыми второго
порядка одного вида. Поэтому сечением поверх-
ности плоскостью может быть эллипс, пара-
бола и гипербола. Эллиптические сечения дву-
полостных гиперболоидов и их асимптотиче-
ского конуса параллельными плоскостями по-
добны и подобно расположены.
Если сечение поверхности плоскостью, пер-
пендикулярной ее оси. симметрии, — окруж-
ность, поверхность становится двуполостным
гиперболоидом вращения.
86
/114/ Сечением двуполостного гиперболоида
может быть эллипс (его частный случай ок-
ружность и вырожденный — точка), парабола и
гипербола.
Однополостный и двуполостный гипербо-
лоиды могут иметь общий асимптотический
конус. Поэтому (с учетом /ПО/ и /114/):
/115/ Однополостный и двуполостный гипер-
болоиды и асимптотический для обеих поверхно-
стей конус пересекаются параллельными плоско-
стями по кривым второго порядка одного вида.
Эти кривые подобны и подобно расположены
(иногда кроме гипербол). Отсюда:
/116/ Если однополостный гиперболоид пере-
секается плоскостью по эллипсу, то двуполост-
ный гиперболоид и асимптотический для обеих
поверхностей конус пересекаются параллельной
плоскостью также по эллипсу, причем все сече-
ния подобны и подобно расположены.
87
Из девяти поверхностей второго порядка
шесть имеют эллиптические сечения, что мы
используем при решении задач.
Точка, инцидентная поверхности второго по-
рядка. На рис. 250 изображена коническая по-
верхность второго порядка с осью, параллель-
ной П2, и фронтальная проекция точки А,
инцидентной поверхности. Нужно определить
точку Возьмем произвольную точку D, на
Рис. 252
горизонтальной проекции оси поверхности и,
проведем окружность, касающуюся горизон-
тальных проекций контурных образующих —
прямых й] и Ь,. Будем рассматривать эту окруж-
ность как проекцию эллипса, инцидентного ко-
нической поверхности. Найдем фронтальную
проекцию точки В на прямой с2 (или </2), а точ-
ки С — на прямой d2 (или с2). Эллипс, инцидент-
ный точкам В и С, проецируется на П2 в отре-
зок В2С2, на Hj —в окружность с центром Dt.
Проведем фронтальную проекцию образующей
S2A2 и отметим точку F2 ее пересечения с фрон-
тальной проекцией эллипса. Найдем точку Ft
(или F{) и проведем горизонтальную проекцию
образующей. В ее пересечении с линией связи,
проведенной через А2, расположена точка А,.
Если поверхность — нелинейчатая, напри-
мер трехосный эллипсоид (рис. 251) с одной
осью, параллельной П2, проведем окружность
диаметра, равного малой оси эллипса — гори-
зонтальной проекции эллипсоида. Будем рас-
сматривать такую окружность как проекцию
эллипса, инцидентного поверхности. Его фрон-
тальная проекция представляет собой отре-
зок В2С2. Так как параллельные сечения эллип-
соида подобны, проведем через А эллипс, па-
раллельный построенному. Его фронтальная
проекция — отрезок D2F2 || В2С2, горизонталь-
ная— окружность диаметра DjFp На этой
окружности лежит точка А, (или А,').
Рассмотрим другой пример. Точка А, задан-
ная своей фронтальной проекцией, инцидентна
эллиптическому параболоиду (рис. 252, а). От-
сек параболоида ограничен эллипсом а (а^, а2).
Проведем через А эллипс Ь. Его фронтальная
проекция — отрезок Ь2, горизонтальная — эл-
липс Ьг, подобный и подобно расположенный
эллипсу яР Эти эллипсы можно рассматривать
как параллельные сечения конуса с вершиной S.
Эллипс я инцидентен его нижней полости,
эллипс b — верхней. Проведя через А 2 фрон-
тальную проекцию образующей конуса, отме-
тим точку В2 ее пересечения с фронтальной
проекцией эллипса я. Построим горизонталь-
ную проекцию образующей и, установив про-
екционную связь, найдем точку Аг.
Рис. 251
88
Из чертежа видно, что горизонтальная про-
екция эллипса в построениях ие участвует, по-
этому достаточно построить только его фрон-
тальную проекцию — отрезок Ь2.
Если задана точка At (рис. 252, б), найдем
точки Сл и £>j, соединим их прямой, представ-
ляющей собой горизонтальную проекцию кон-
тура параболоида относительно П2. Разделив
отрезок Q Di пополам, отметим точку —
горизонтальную проекцию вершины вспомога-
тельного конуса. Проведем прямую A1S1 и
отметим точку В2 ее пересечения с эллипсом а2.
Проведем прямую B1Di и параллельную ей
прямую А1Е1, пересекающуюся в точке Et с
прямой CjDj. Установив проекционную связь,
найдем точку Ег Через нее проходит фронталь-
ная проекция эллипса Ь. Точка Аг инцидентная
этой линии. Построения основаны на том, что
эллипсы а и b подобны.
§ 17. ПОВЕРХНОСТИ
С ПЕРЕМЕННОЙ ОБРАЗУЮЩЕЙ
Задав условия изменения формы образую-
щей в процессе ее перемещения в пространстве,
можно образовать любые поверхности. Выде-
лим те из них, которые могут встретиться в
строительной практике.
Поверхность с родственно преобразующейся
образующей. Определитель поверхности: 1. Не-
подвижная линия — направляющая; плоская кри-
вая — образующая; плоскость параллелизма.
2. Образующая, перемещаясь в пространстве и
непрерывно изменяя свою форму, остается па-
раллельной плоскости параллелизма; условия
изменения формы образующей и ее перемещения
На рис. 253 заданы направляющая Ь, распо-
ложенная в вертикальной плоскости, плоскость
параллелизма О и образующая — дуга эллипса
а. Хорда АВ эллипса в точке А постоянно
пересекается с направляющей Ь, причем хорда
всегда остается параллельной своему первона-
чальному положению и не меняет длины. Дуга
эллипса перемещается в пространстве так, что
ее плоскость остается параллельной плоско-
сти fl, а вершина С скользит по кривой с, пло-
скость которой параллельна плоскости направ-
ляющей Ь. При таком перемещении эллипса
он непрерывно преобразуется. Это родствен-
ное преобразование. Например, когда точка А
переместится в точку А, то точка С переместится
в точку С. Совместим мысленно хорды АВ и АВ,
тогда станет очевидно, что родство задано
осью, инцидентной хорде и парой родственных
точек С и С.
Частным случаем такой поверхности явля-
ется поверхность переноса (рис. 254). Образую-
щая при перемещении в пространстве не меняет
своей формы. Эпюр поверхности переноса и
пример ее использования в строительной прак-
тике показаны на рис. 255.
/117/ Поверхность переноса может быть за-
дана образующей и направляющей — плоскими
кривыми и плоскостью параллелизма.
Поверхность с подобно преобразующейся об-
разующей. К таким поверхностям можно от-
нести большинство поверхностей второго по-
рядка. Например, если рассечь трехосный эллип-
соид, изображенный на рис. 245, рядом парал-
лельных плоскостей, то сечения эллипсоида —
эллипсы будут подобными и подобно располо-
женными. Их можно рассматривать как обра-
зующую поверхности в ее различном положе-
пространстве.
Рис. 253
89
Рис. 254
нии в процессе перемещения в пространстве.
Плоскость, которой инцидентна образующая,
всегда параллельна некоторой плоскости па-
раллелизма. В качестве направляющей в при-
веденном примере удобно использовать линию,
по которой перемещается центр эллипса.
В общем случае образующая не является
кривой второго порядка, поэтому и образован-
ная ею поверхность не будет поверхностью того
же порядка. Образующая в ее любом положе-
нии не только подобна первоначально заданной
линии, но и подобно расположена.
/118/ Поверхность с подобно преобразующей-
ся образующей может быть задана направляю-
щей — прямой нли плоской кривой, плоскостью
параллелизма, образующей и условием ее пре-
образования.
Циклические поверхности. Циклическими на-
зываются поверхности, образованные переме-
щением по определенному условию окружности
переменного или постоянного радиуса.
Определитель поверхности: 1. Направляющая
прямая или кривая линия; образующая — окруж-
ность переменного или постоянного радиуса.
2. Окружность перемещается в пространстве так,
что ее центр скользит по направляющей, а пло-
скость окружности наклонена к направляющей
под постоянным или меняющимся по определен-
ному условию углом.
Любая поверхность вращения может рас-
сматриваться как циклическая с направляю-
щей — прямой линией и образующей — окруж-
ностью постоянного или переменного радиуса.
Поверхности второго порядка, обладающие
эллиптическими сечениями, также являются
циклическими, так как на них можно найти
круговые параллельные сечения.
На рис. 256 приведена циклическая поверх-
ность с направляющей — кривой линией.
Частным видом циклической является труб-
чатая поверхность. Она образуется при движе-
нии окружности постоянного радиуса так, что
ее центр скользит по кривой линии — направ-
ляющей, а плоскость окружности всегда пер-
пендикулярна ей Пример такой поверхности —
открытый тор (см. рис. 229).
/119/ Циклическая поверхность задана, если
известны направляющая я условия изменения
радиуса образующей н утла наклона плоскости
окружности к направляющей.
Циклическую поверхность иногда можно
рассматривать как обертывающую множество
сфер, центры которых инцидентны направляю-
щей линии, а радиус изменяется по определен-
ному условию. Этим свойством пользуются
для изображения циклических поверхностей:
построив проекции некоторого числа сфер, про-
водят огибающие, представляющие собой про-
екции контура поверхности (см рис 261, 484.
485).
§ 18. ВИНТОВЫЕ ПОВЕРХНОСТИ
Определитель поверхности: 1. Неподвижная
прямая — ось; направляющая — винтовая линия
с постоянным или меняющимся шагом; образую-
щая — прямая нли кривая лнння. 2. Все точки
образующей совершают винтовое перемещение;
условие изменения шага винтовой линии.
Винтовые поверхности линейчатые (гелико-
иды). Они образуются винтовым движением
прямой линии (образующей). Каждая точка
образующей перемещается по своей винтовой
линии, причем все винтовые линии имеют
общую ось, называемую осью винтовой поверх-
ности. Образующая может пересекаться с осью
Рис. 255
Рис. 256
on
и скрещиваться с ней; в первом случае геликои-
ды называются закрытыми, во втором — от-
крытыми. При изображении геликоида его обыч-
но рассекают прямой круговой цилиндрической
поверхностью, соосной с ним.
Закрытые геликоиды. Если образующая пере-
секается с осью винтовой поверхности под
углом, отличным от прямого, то геликоид на-
зывается косым. При перемещением образую-
щей угол ее наклона к оси может меняться или
оставаться постоянным.
/120/ Закрытый косой геликоид можно за-
дать перемещением прямой линии, пересекаю-
щейся с неподвижной прямой (осью поверхности)
под постоянным нли меняющимся по определен-
ному условию углом и скользящей по неподвиж-
ной винтовой линии (направляющей) переменного
или постоянного шага.
В технике чаще всего’ встречаются закрытые
косые геликоиды с постоянным углом наклона
образующей к оси и с постоянным шагом на-
правляющей винтовой линии. Такой геликоид
показан на рис. 257. Он задан правой винтовой
линией а с шагом h и диаметром D, осью вин-
товой поверхности i и образующей Ь, наклонен-
ной к оси под углом а. Построим один виток
винтовой линии, начиная от точки А, как пока-
зано на рис. 209. Для этого разделим окружность
на 8 частей. Когда точка А, перемещаясь по
винтовой линии, перейдет в положение А',
т. е. повернется на '/в оборота вокруг оси и
поднимется в направлении, параллельном оси
на ’/в шага, то точка В пересечения образую-
щей с осью переместится по оси в том же на-
правлении, что и точка А, также на ’/в шага.
Последовательно перемещая точку А по вин-
товой линии и В — по оси и соединяя их в каж-
дом новом положении прямыми линиями, полу-
чим дискретный каркас винтовой поверхности.
Соединим фронтальные проекции точки А во
всех ее положениях и построим проекцию кон-
тура поверхности .относительно П2. В резуль-
тате получим фронтальную проекцию отсека
косого геликоида. Вся поверхность (образован-
ная движением не отрезка, а прямой) делится
осью на две полости; на чертеже изображен
отсек только одной из них.
Если угол между образующей и осью равен
90°, то геликоид называется прямым (рис. 258).
При этих условиях образующая всегда парал-
лельна плоскости, перпендикулярной оси по-
верхности, а сама поверхность может быть от-
несена к коноидам.
Открытые геликоиды. Угол между осью и
образующей может меняться или оставаться
постоянным. Открытый геликоид, как и всякая
Рис. 257
Рис. 258
91
Рис. 260
линейчатая поверхность, может быть задан
тремя направляющими — винтовыми линиями
(см. /102/). Если угол постоянен, то достаточно
двух направляющих, так как условие постоян-
ства угла заменяет третью направляющую.
Вместо угла между образующей и осью иногда
задают дополнительный к нему угол между
образующей и плоскостью, перпендикулярной
оси.
Косой открытый геликоид (рис. 259). В пер-
воначальном положении образующая а парал-
лельна П2 и в точке А пересекается с направ-
ляющей Ь. Угол а ее наклона к оси i на П2 про-
ецируется без искажения. Через какую бы точку
образующей ни проходила вторая направляю-
щая, расстояние между образующей и осью
остается постоянным, поэтому при винтовом
движении образующая будет касаться цилиндра
радиуса R, равного этому расстоянию. Точка В
касания образующей и цилиндра описывает
винтовую линию радиуса R того же шага,
что и винтовая линия Ь. Ее можно принять за
вторую направляющую.
Для построения эпюра геликоида окруж-
ность Ь, разделена на 8 частей, начиная от
точки На то же число частей разделена ок-
ружность с1( начиная от точки Bt. Описанным
ранее приемом строим фронтальные проекции
обеих винтовых линий и, отметив фронтальные
проекции точек А, А', .. , В, В', ... , соединяем
их попарно прямыми линиями. На эпюре изоб-
ражен отсек одной полости поверхности, огра-
ниченной винтовыми линиями b и с; вторая
полость расположена на противоположной от-
носительно линии с стороне.
Если угол наклона образующей к плоскости,
перпендикулярной оси, равен углу наклона вин-
товой линии к той же плоскости, то образую-
щая будет касательной к винтовой линии, а
винтовая поверхность — торсом.
Эпюр открытого прямого геликоида изоб-
ражен на рис. 260. Его построение выполнено
тем же приемом, что и косого открытого гели-
коида. Образующая всегда параллельна пло-
скости, перпендикулярной оси поверхности. От-
крытый прямой геликоид может быть отнесен
к цилиндроидам.
Винтовые поверхности нелинейчатые. В ка-
честве образующей принимают или плоскую
кривую линию, в плоскости которой располо-
жена ось поверхности, или плоскую кривую
большей частью окружность, плоскость кото-
рой перпендикулярна винтовой линии (направ-
ляющей). Во втором случае (рис. 261) образу-
ется трубчатая винтовая поверхность.
92
§ 19. ПОВЕРХНОСТИ,
ЗАДАВАЕМЫЕ КАРКАСОМ
(КАРКАСНЫЕ ПОВЕРХНОСТИ)
В технике встречаются поверхности, форма
которых хотя и подчинена каким1-либо законам,
например аэро- или гидродинамики или эсте-
тическим требованиям, но не может быть за-
дана аналитически. Такую поверхность задают
конечным числом линий, т. е. ее дискретным
каркасом.
В строительной практике большое значение
имеет земная, или топографическая поверх-
ность*. Для ее изображения должен быть опре-
делен дискретный каркас, изображение кото-
рого и принимается за изображение поверхно-
сти. На рис. 262 показан отсек топографической
поверхности. Инцидентные ей горизонтальные
линии — горизонтали поверхности проецируются
на горизонтальную плоскость проекций. При
определенных условиях (см. гл. VII) такое
изображение обладает обратимостью. Если рас-
сечь поверхность вертикальными плоскостями,
получим линии, называемые профилями (напри-
мер, кривая ABCDEFGH"). Как горизонтали,
гак и профили могут рассматриваться как дис-
кретный каркас поверхности. К дискретному
каркасу могут быть отнесены и некоторые точки
(например, точка К).
/121/ Дискретным каркасом топографической
поверхности могут служить ее горизонтали или
профили или и те, и другие, а также отдельные
точки.
* Топография — (греч. topos место, местность +
•Tgrapho — пишу) наука, изучающая методы изоб-
93
ГЛАВА V
ПРЕОБРАЗОВАНИЯ
В предыдущих главах мы рассматривали
пространство как множество точек, линий, по-
верхностей или тел. Из этого множества мы
выделяли те фигуры, которые нужно было изу-
чить. Так как фигуры были элементами непод-
вижного пространства, то и они были непод-
вижными.
Однако пространство может так или иначе
преобразовываться; вместе с ним преобразовы-
ваются и принадлежащие пространству фигуры,
причем так, что каждой точке первоначально
данной фигуры будет соответствовать одна и
только одна точка фигуры преобразованной.
Напомним, что такое преобразование называ-
ется взаимно однозначным.
§ 20. ПЛОСКОПАРАЛЛЕЛЬНОЕ
ПЕРЕМЕЩЕНИЕ
Под перемещением будем понимать такое
преобразование фигур, когда все их точки, не
меняя взаимного расположения, изменяют его
относительно неподвижных плоскостей проек-
ций. При плоскопараллельном перемещении все
точки фигуры перемещаются в параллельных
плоскостях. Обычно это плоскости уровня или
проецирующие плоскости. Линии, по которым
перемещаются точки, называются их траекто-
риями, это плоские кривые.
Перемещение точки. Пусть точка А переме-
щается по кривой t, инцидентной горизонталь-
ной плоскости П, занимая последовательно по-
ложения А, А', А", ... (рис. 263). В соответствии
с/43/ горизонтальная проекция траектории
точки А равна и подобно расположена самой
траектории, фронтальная же ее проекция t2
представляет собой отрезок прямой линии,
параллельной оси х, или, что одно и то же,
перпендикулярной линиям связи (см. /16/
и /62/).
Если известна горизонтальная проекция точ-
ки в ее новом положении, например А'/'
(рис. 264), то можно найти ее фронтальную про-
екцию А'/', проведя через А2 прямую, перпен-
дикулярную линиям связи, до пересечения с
линией связи, проведенной через А. При этом
нас может не интересовать форма траектории
точки А.
/122/ При перемещении точки в горизонталь-
ной плоскости фронтальной проекцией траекто-
рии является прямая (отрезок), перпендикуляр-
ная линиям связи.
По аналогии:
/123/ При перемещении точки во фронтальной
плоскости горизонтальная проекция траектории
представляет собой.прямую (отрезок),' перпенди-
кулярную линиям связи.
Перемещение отрезка. При плоскопараллель-
ном перемещении отрезка его длина остаето
постоянной; поэтому произвольной может был
траектория только одной точки отрезка. Сохра-
няются длина проекции отрезка на плоскости
параллельной плоскостям траекторий, и угол
наклона отрезка к этой плоскости
/\2А/ При плоскопараллельном перемещении
отрезка его проекции в старом и новом положе-
нии на плоскости, параллельной плоскостям тра-
екторий, равны между собой.
/125/ При плоскопараллельном перемещении
прямой линии угол ее наклона к тон плоскости
Проекции, параллельно которой производилось
перемещение, не меняется.
Определим величину отрезка АВ и угол его
наклона к Щ (рис. 265). В произвольном месте
чертежа перпендикулярно линиям связи рас-
положим новую горизонтальную проекцию
отрезка (А^В^ = А1В1; см. /124/) и найдем
его фронтальную проекцию (см. /122/). Прямая
А'В' стала фронталью, поэтому (см. /39/)
А'2В'2 - АВ, а а'2 = а.
Переместим прямую так, чтобы она стала
проецирующей. Для этого фронтальную про-
94
екцию А2В2 (А'г В'г = А2В2) расположим па
раллельно линиям связи. Горизонтальные про-
екции траекторий точек А и В — прямые, пер-
пендикулярные линиям связи (см. /123/). Новой
горизонтальной проекцией отрезка А В станет
точка А\' = B'i .
Определим расстояние между прямыми
АВ || CD (рис. 266). Для этого, не меняя взаимо-
расположения фронтальных проекций прямых,
расположим их перпендикулярно линиям связи.
После этого горизонтальные проекции прямых
переместим так, чтобы они стали параллель-
ными линиям связи (также не меняя их взаимо-
расположения). Расстояние между точками —
проекциями прямых — искомое (сравните с/69/).
Покажем найденный отрезок на первоначально
заданных проекциях прямых: зададимся точка-
ми N" и К” на прямых А”В" и CD”. Точки
Н2 и К2 совпадают с фронтальными проекция-
ми соответствующих прямых. Поскольку отре-
зок N” К” проецируется на П2 в натуральную
величину, его проекция на П] перпендикулярна
линиям связи. Найдя точки N\ и К\ на горизон-
тальных проекциях прямых после их первого
перемещения (на соответствующих расстояниях
от точек A J и С\), проведем через них горизон-
тальные проекции траекторий (перпендикуляр-
но линиям связи) и отметим точки К, и N,.
Затем построим точки К2 и N2.
Перемещение плоской фигуры. Определим
величину угла <р, образованного прямыми anb
(рис. 267) Проведем в плоскости угла фрон-
таль f (В; С). Переместим угол так, чтобы фрон-
таль стала перпендикулярной ПР Для этого
расположим/^ параллельно линиям связи. Так
как соответственные стороны треугольников
Л2В2С2 и А2В2С2 в соответствии с /124/ равны,
то равны между собой и эти треугольники.
Сказанное можно распространить на любую
фигуру:
/126/ Величина и форма проекции фигуры на
плоскости, параллельной плоскостям, в которых
происходит перемещение точек фигуры, в резуль-
тате перемещения не изменяются.
А2 Аг А2 А2 Q2-t2 I
с——0=0—-
95
Переместим теперь угол так, чтобы его го-
ризонтальная проекция стала перпендикуляр-
ной линиям связи. Так как стороны угла теперь
параллельны П2 (см. /19/), то <р2 = Ф (сравните
рис. 267 и 145).
§ 21. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ,
ПЕРПЕНДИКУЛЯРНЫХ
ПЛОСКОСТЯМ ПРОЕКЦИЙ
Вращение фигур вокруг прямой — оси вра-
щения— представляет собой частный случай
плоскопараллельного перемещения: все точки
фигуры перемещаются по окружностям, распо-
ложенным в плоскостях, перпендикулярных оси
вращения и, следовательно, параллельных меж-
ду собой. Ось вращения обычно занимает част-
ное положение относительно плоскостей про-
екций.
Вращение точки. Если точка вращается во-
круг оси i, перпендикулярной П]; то ее траекто-
рия (окружность) инцидентна плоскости, па-
раллельной П, (рис. 268). Горизонтальная про-
екция траектории — окружность с' центром в
точке ij, фронтальная проекция — отрезок пря-
мой, перпендикулярной линиям связи, длиной
2R (R — радиус вращения точки).
Последовательные положения точки А по-
казаны на риб. 268 и 269. На эпюре дана только
та проекция оси, которая представляет собой
точку (почему?).
/127/ Если ось вращения перпендикулярна
плоскости П,, то горизонтальная проекция тра-
ектории точки представляет собой окружность
радиуса R (расстояние от точки до оси), а фрон-
тальная проекция— отрезок прямой длиной 2R,
перпендикулярной линиям связи.
Вращение отрезка. Определим величину от-
резка АВ прямой общего положения (рис. 270)
и угол а его наклона к ПР Примем ось враще-
ния i пересекающейся с прямой АВ и перпенди-
кулярной ПР Проведем прямую, инцидентную
точке ij и перпендикулярную линиям связи,
и совместим с ней точки А, и В}, вращая их
вокруг ij. Меняя направление вращения, полу-
чим точки А\ и А, а также В\ и В\'. При этом
А\В\—А\'В\' =А1В1 (см. /124/).
Горизонтальными проекциями траекторий
точек будут дуги t(A)l и f(B)i , их фронтальными
проекциями — отрезки - и . Проведя
линии связи через точки А\, В\ и А\' и В'/
до пересечения с фронтальными проекциями-
траекторий соответственно точек А и В, полу-
чим новые фронтальные проекции отрезка:
/12В2 = Л2 В2 = АВ и угла а2 = а2 = а (сравни-
те с /67/). Для решения задачи нужно построить
любую из них.
96
Часто нужно вращать отрезок вокруг оси,
не пересекающейся с его продолжением. При-
мер показан на рис. 271. Для решения предыду-
щей задачи повернем отрезок так, чтобы он стал
параллельным П2. Опустив перпендикуляр из it
на отметим точку К, их пересечения.
Повернув отрезок так, чтобы он стал па-
раллельным линиям связи, вместе с ним повер-
нем и отрезок A tBt. Точки А\ и В\ расположены
в пересечении горизонтальных проекций тра-
екторий с прямой, проходящей через К, перпен-
дикулярно линиям связи (достаточно на этой
прямой отложить от К1 в разные стороны отрез-
ки A'tK't и B'tK't).'
Построив точки Л 2 и В2, получим фронталь-
ную проекцию отрезка, проецирующегося на П,
в натуральную величину, и узнаем угол его на-
клона к П, (о 2 = <х).
Вращение плоской фигуры. Определим вели-
чину фигуры АВС, инцидентной фронтально
проецирующей плоскости (рис. 272). Возьмем
ось i (i2), перпендикулярную П2 и лежащую в
плоскости фигуры. Проведя фронтальные про-
екции траекторий точек А, В и С (окружности),
расположим фронтальную проекцию треуголь-
ника перпендикулярно линиям связи. Плоскость
А 'В' С параллельна Пь поэтому (см. /43/) на
П] треугольник проецируется в натуральную
величину.
Для решения той же задачи, когда фигура
инцидентна плоскости общего положения
(рис. 273), следует выполнить два вращения:
вначале сделать плоскость фигуры проецирую-
щей, затем параллельной плоскости проекций.
Возьмем в плоскости треугольника горизон-
таль h, а ось у, перпендикулярную ПР Повер-
нув треугольник так, чтобы горизонталь стала
перпендикулярной П2, получим фронтальную
проекцию треугольника — отрезок С В2. Взяв
вторую ось вращения i", перпендикулярную П2,
повернем треугольник так, чтобы он стал па-
раллельным Пр На этой плоскости после вто-
рого в'рагцения треугольник проецируется в
натуральную величину.
Определим величину угла между прямой и
плоскостью. Мерой такого угла является ли-
нейный угол между прямой и ее прямоугольной
7—940
97
Рис. 274
проекцией на плоскости. Угол проецируется на
плоскости проекций в натуральную величину,
«ли данная плоскость перпендикулярна пло-
скости проекций, а прямая параллельна ей.
Даны плоскость А ВС (рис. 274) и прямая A D;
определим угол между ними. Проведем гори-
зонталь А К плоскости АВС и повернем тре-
угольник вокруг оси i' так, чтобы его плоскость
стала фронтально проецирующей. На тот же
угол, на который повернуты точки треуголь-
ника, повернем и точку D (взаиморасположение
горизонтальных проекций треугольника и от-
резка не изменится). Затем повернем плоскость
и отрезок вокруг оси Г', перпендикулярной П2,
чтобы плоскость АВС стала горизонтальной.
Теперь повернем вокруг оси Г", перпенди-
кулярной П], отрезок AD так, чтобы он стал
параллельным П2. Угол б наклона АВ к пло-
скости АВС равен углу 62'. Чтобы показать
проекции угла 5 на первоначально заданных
проекциях фигур, отметим точку Е" (£['), в ко-
нтрой прямоугольная проекция отрезка А" D"
а плоскости А"В"С" пересекается со сторо-
юй В" С". Построив последовательно точки Е\,
Е, и Е2, соединим Е1 и Е2 соответственно с А ,
г А2 прямыми линиями. Фронтальной проек-
цией б2 угла б является угЪл E2A2D2, горизон-
тальной проекцией — угол EjAfDj. Сравните
фешенне с приведенным на рис. 199.
9адача 1.
Повернуть точку А (А,; А2) вокруг оси i, пер-
пендикулярной П2, до совмещения с плоскостью
BCD (рис. 275). Траектория t точки А представляет
собой окружность, плоскость которой П параллель-
. ia П2 Нужно найти точку пересечения траектории
плоскостью BCD. Для этого найдем линию EF
'вначале FjF,) пересечения плоскостей BCD и П.
Пинии EF и t пересекаются дважды —в точках А'
I А" (задача имеет два решения).
1адача 2.
Совместить с плоскостью Ь ||с прямую а, вра-
цая ее вокруг оси, перпендикулярной П] (рис. 276).
Построим точку К пересечения прямой а и
шоскости Ь || с (с помощью горизонтально проеци-
Г
рующей плоскости X) и проводим инцидентную ей
ось i (1\), перпендикулярную П,. Взяв на прямой а
произвольную точку М, совместим ее с плоско-
тью Ь || с, вращая вокруг оси i (см. предыдущую
задачу). Плоскость £2, в которой расположена тра-
ектория точки, параллельна ПР Она пересекается с
плоскостью Ь || с по прямой CD. В результате совме-
щения точка М может занять два различных поло-
жения ЛГ и М", Любой из этих точек и точке К
инцидентна совмещенная с плоскостью b || с прямая а
(а' или а").
§ 22. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ,
ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ
ПРОЕКЦИЙ (СОВМЕЩЕНИЕ
С ПЛОСКОСТЯМИ УРОВНЯ)
На рис. 277 осью вращения i является гори-
зонталь. Точка А, не инцидентная оси, описыва-
ет окружность в плоскости, перпендикулярной
оси, т. е. горизонтально проецирующей. Радиус
99
вращения — перпендикуляр, опущенный из А
на ось и пересекающийся с ней в точке К—
центре вращения. Горизонтальная проекция тра-
ектории точки (окружности) отрезок А\А" пер-
пендикулярен горизонтальной проекции оси
вращения. Его длина равна 2R. Фронтальная
проекция траектории при данном расположе-
нии оси вращения представляег собой эллипс,
который на чертеже не показан, так как для по-
строений он не требуется.
/128/ Проекция трек гории точки на тон плос-
кости, которой параллельна ось вращения, пред-
ставляет собой отрезок прямой, перпендикуляр-
Рис. 279
ной проекции оси. Длина отрезка равна 2R (где
R — радиус вращения точки).
Вращение точки и прямой. Повернем точку А
до совмещения с горизонтальной плоскостью П.
инцидентной оси вращения i (рис. 278). Опустим
перпендикуляр из А на ось — радиус враще-
ния АК. Отрезок AiK-t перпендикулярен гори-
зонтальной проекции оси '(см. /45/). С ним
совпадает горизонтальная проекция q траек-
тории точки А. Определим величину радиуса
(отрезок А^'К,), вращая его вокруг оси i',
перпендикулярной П2. Отложив в обе стороны
от К| по прямой tj длину радиуса вращения,
получим точки А у и А" (два решения за-
дачи).
/129/ Чтобы построить горизонтальную про-
екцию точки, совмещенной с горизонтальной
плоскостью, инцидентной оси вращения, нужно
провести горизонтальную проекцию траектории
точки и отложит ь по ней от проекции оси длину
радиуса вращения точки.
Фронтальная проекция точки, если ее нужно
построить, расположена в пересечении линии
связи, проведенной через новую горизонталь-
ную проекцию точки, с фронтальной проекцией
плоскости fl (почему?).
Повернем прямую АВ, в точке В пересекаю-
щуюся с осью г Точка В при вращении не меняет
своего положения. Соединим ее прямой с точ-
кой А\ (или Л)'). Отрезок А\В, = АВ.
Вращение плоской фигуры. Определим рас-
стояние между прямыми а || b (рис. 279). Про-
ведем горизонталь i плоскости а || b и, рассмат-
ривая ее как ось вращения, повернем вокруг
нее прямую а до совмещения с горизонтальной
плоскостью, инцидентной оси. Возьмем на пря-
мой а произвольную точку С, построим радиус
ее вращения СК. Вращая отрезок СК вокру!
оси f (i2), определим его величину С"К,. На
горизонтальной проекции траектории точки С
построим точку CJ. Через нее и точку А{ про-
ходит новая горизонтальная проекция а\ пря-
мой а (см. рис 278), а через точку В} параллель-
но «, — новая горизонтальная проекция Ь\ пря
мой b (прямые а и b после вращения остаются
параллельными. Почему?).
Проведя в произвольном месте чертежа от-
резок C\Dt. перпендикулярный новым проек-
циям прямых а и Ь, получим искомое расстоя-
ние. Чтобы показать проекции отрезка на перво-
начально заданных проекциях прямых, прове-
дем траекторию цр)1 точки D до пересечения
с прямой в точке I), и т. д.
§ 23. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ,
ЛЕЖАЩИХ В ПЛОСКОСТЯХ
(СОВМЕЩЕНИЕ С ПЛОСКОСТЯМИ
ПРОЕКЦИЙ)
Вращение, рассматриваемое в настоящем
параграфе, представляет собой частный случай
вращения вокруг осей, параллельных плоско-
стям проекций.
Вращение плоскости вокруг ее следа. Совмес-
тим плоскость Q с П,, вращая ее вокруг гори-
зонтального следа (рис. 280). Возьмем произ-
вольную точку А. инцидентную фронтальному
100
Рис. 280
следу. Ее радиус вращения Вл - перпендику-
ляр АВ, опущенный из А на горизонтальный
след плоскости. Траектория точки А — окруж-
ность tA расположена в горизонтально про-
ецирующей плоскости, перпендикулярной гори-
зонтальному следу заданной плоскости, по-
этому ее горизонтальная проекция перпенди-
кулярна ему. Определим величину , напри-
мер, способом замены плоскостей проекций
(рис. 281) и отложим полученный отрезок от
точки В, по прямой ft4) . С этими построения-
ми мы познакомились в предыдущем пара-
графе.
Отрезок A2Q, равен отрезку Л[£2А, так как
они являются проекциями одного и того же
отрезка AQX в первоначальном и повернутом
положении и инцидентны плоскостям проекций
соответственно П2 и П,. Поэтому достаточно
через А. провести прямую /(А) . перпендикуляр-
ную горизонтальному следу плоскости, и от-
метить точку А\ ее пересечения с дугой окруж-
ности радиуса А2£1 с центром в точке £2t.
Соединив эту точку с точкой £2.г, получим со-
вмещенный с П] фронтальный след плоско-
сти £2. Он обозначен (£2n2)j. Окружность ра-
диуса A2Qt пересекается с еще в одной
точке А'1 . Поэтому возможны два решения
задачи: в первом случае плоскость вращается
«на зрителя», во вт*бром — «от зрителя» (со-
вмещенный след во втором варианте обозна-
чен (£2П2)/.
Совмещение особых линий плоскости. Про-
ведем через точку А плоскость £2 горизонталь h
и фронталь/(рис. 282). Воспользовавшись точ-
кой В (фронтальным следом горизонтали),
совместим плоскость £2 с П,. Так как горизон-
таль параллельна горизонтальному следу плос-
кости, то (см. /35/) ее проекция h[ после совме-
щения плоскости параллельна прямой £2ПГ
Кроме того, она инцидентна точке В\. Прове-
дем совмещенный след (£2П2), и проекцию со-
вмещенной фронтали. Она проходит через свой
горизонтальный след С] параллельно совме-
щенному фронтальному следу Так как гори-
зонталь и фронталь в приведенном примере
проходят через точку А, то совместить ее с
плоскостью Г/ можно с помощью одной из
этих линий: достаточно провести горизонталь-
ную проекцию траектории точки А до пересе-
чения с проекцией совмещенной горизонтали
или фронтали или отметить точку пересечения
совмещенных проекций этих линий.
Задача.
В плоскости £2, заданной следами, построить
окружность радиуса R с центром С, инцидентным
биссектрисе угла между следами плоскости на рас-
стоянии л от точки £2х(рис. 283).
Взяв произвольную точку А. инцидентную фрон-
тальному следу, совместим плоскость £2 с П,.
Проведя биссектрису угла между прямыми £2П, и
(£2П2)',, построим на ней точку CJ на расстоянии и
от точки £2V. Используя точку С, как центр, прове-
дем окружность радиуса R. Чтобы построить гори-
зонтальную, а затем фронтальную проекцию окруж-
ности, проведем через точку С\ совмещенную фрон-
таль/, найдем проекцию ее горизонтального сле-
да— точку £>], через которую проходит горизон-
тальная проекция фронтали. В пересечении прямой
/i с проекцией траектории точки С расположена
горизонтальная проекция этой точки, фронтальная
Рис 282
101
проекция — в пересечении линии связи, проходящей
через точку С,, с фронтальной проекцией фронталн.
Аналогично построены проекции точек окруж-
ности, например В.
§ 24. ГОМОЛОГИЧЕСКИЕ
ПРЕОБРАЗОВАНИЯ
В гл. I мы рассмотрели гомологические пре-
образования на плоскости. Теперь остановимся
на преобразованиях пространственных фигур.
Вместо оси гомологии мы будем использовать
плоскость гомологии. Это плоскость двойных
точек. При заданных центре и плоскости гомо-
логии пары гомологичных точек, прямых или
плоскостей определяют гомологию.
Пусть S — плоскость гомологии, 5 — центр
гомологии, точки А и А гомологичны, т. е.. Н
(5; 1; А; А) (рис. 284). Нужно найти точку В,
гомологичную точке В. Соединим точки А и В
прямой и, найдя точку 1 (двойную точку) ее
пересечения с плоскостью гомологии S, соеди-
ним эту точку прямой линией с точкой А.
Прямые А—1 и А—1 гомологичны. Остается
провести двойную прямую через точки В и .S'.
Она пересекается с прямой А—1 в искомой
точке В.
Аналогично может быть построена точка,
гомологичная любой другой точке простран-
ства (кроме S), и соответственно линия или по-
верхность, гомологичные другой линии или
поверхности.
Примем без доказательства, что:
/130/ Фигурой, гомологичной любой нели-
нейчатой поверхности вращения второго порядка,
может быть сфера (сравните с /50/)*.
Родственное преобразование поверхностей
второго порядка.
/131/ Родство преобразует поверхность вто-
рого порядка в другую поверхность второго по-
рядка того же вида. В частности, фигурой, род-
ственной эллипсоиду вращения, может быть сфе-
ра (вытекает из /52/, /53/ и /130/),
Преобразуем вытянутый эллипсоид враще-
ния в сферу (рис. 285). Плоскость родства
(понятие, аналогичное понятию плоскость го-
мологии) S примем параллельной П, и прохо
дящей через центр эллипсоида. Направление
двойных прямых преобразования- примем пер-
пендикулярным плоскости родства.
Пусть вершина эллипсоида К (К2) соответ-
ствует точке К (К2) сферы. Тогда родство за-
дано плоскостью родства S (S2) и парой род-
ственных точек К (К2) и К (К2), т. е. Н (Qis, I;
К; К). Сравните с /51/. Окружность, по которой
эллипсоид пересекается с плоскостью родства
(экватор эллипсоида), соответствует сам ’ себе
(все точки окружности — двойные).
Найдем точку А, соответственную данной
точке А, не инцидентной эллипсоиду. Проведем
горизонтальные родственные плоскости й и.й,
проходящие соответственно через К и К. Взяв
* Интересующиеся найдут доказательство в
трудах по проективной геометрии.
io:
точку 1 С X, соединим ее прямой с точкой А
и отметим точку В пересечения этой прямой
с плоскостью £1 Проведем через В двойную
прямую ВВ || КК до ее пересечения в точке В
с плоскостью £1 Через точки 1 и В проходит
прямая, родственная прямой 1—В. На ней в ее
пересечении с двойной прямой, проведенной
через А, расположена искомая точка А (М2).
При данных условиях родственное преобра-
зование эллипсоида приводит к родственному
преобразованию его фронтальной проекции:
эллипс преобразуется в окружность, точка А2,
лежащая вне эллипса, преобразуется в точ-
ку А2, лежащую вне окружности. Горизонталь-
ная проекция не изменяется. Поэтому все по-
строения проводятся на фронтальной плоско-
сти проекций.
Родственное преобразование отсека эллип-
тического параболоида в отсек параболоида
вращения показано на рис. 286. При данном
расположении фигуры ее горизонтальной про-
екцией является эллипс. Расположим окруж-
ность диаметром АХВ} = А2В2 так, чтобы она
была в проекционной связи с фронтальной про-
екцией параболоида. Возьмем на эллипсе про-
извольную точку D, и, проведя линию связи,
отметим родственную ей точку D1 на окруж-
ности. Аналогично построим точки С\, Et и Ft.
родственные соответственно точкам С1; Ех и F,.
Проведя прямые EiFi и EiFl, отметим точку 7,
их пересечения. Найдем точку 2, пересечения
прямых Г>, С, и Через точки 7, и 2,
проходит прямая X! -горизонтальная проек-
ция плоскости родства X. Теперь родство зада-
но плоскостью родства X и парой родственных
точек, например D и D, т. е. Н (SX; D; D).
Направление преобразования перпендикуляр-
но П2 и совпадает с направлением проецирова-
ния, поэтому фронтальные проекции парабо-
лоидов данного и преобразованного совпадают.
Горизонтальной проекцией отсека преобразо-
ванного параболоида является круг диамет-
ра Л, .
Если вместо точки Dt взять точку Dt, род-
ственную точке D,, получим родственное соот-
ветствие, отличное от ранее установленного.
Хотя эллипс будет соответствовать окружности,
направление двойных прямых совпадет, но
плоскость родства займет другое положение.
Найдите эту плоскость самостоятельно (см.
рис. 48).
©А,
Рис. 285
Рис. 286
103
Построим фронтальную проекцию точки К,
инцидентной эллиптическому параболоиду и
заданной своей горизонтальной проекцией К{.
Проведем через К, прямую KiFl до пересече-
ния с в точке 5; и родственную ей пря-
мую В пересечении этой прямой с двой-
ной прямой, проходящей через Kt, располо-
жена точка Фронтальную проекцию точки К
найдем известным приемом, с помощью кото-
рого строятся проекции точки на поверхностях
вращения. Сравните рис. 286 и 252.
Два последовательных родственных преоб-
разования. Преобразуем трехосный эллипсоид
в сферу (рис. 287). При первом преобразовании
родство зададим плоскостью родства Е, род-
ственными плоскостями Si и fl и направлением
преобразования, перпендикулярным ПР В ре-
зультате трехосный эллипсоид преобразуется
в вытянутый эллипсоид вращения, фронталь-
ной проекцией которого будет круг. Фронталь-
ная проекция Сг точки С, инцидентной эллип-
соиду, преобразуется в точку С2. Вторым пре-
образованием с плоскостью родства Ч', родст-
венными плоскостями 0 и 0 и направлением
преобразования, перпендикулярным П2, эллип-
соид преобразуется в сферу. При этом эллипс
с большой осью, проходящей через точку В.
преобразуется в окружность диаметра, равного
малой оси того же эллипса. Точка С, преобра-
зуется в точку Cj. Чтобы ее найти, достаточно
провести родственные прямые, параллельные
Ч*, и проходящие соответственно через точки Dx
и Dp
Преобразование нелннейчатых поверхностен
второго порядка в сферу.
На рис. 288 изображен отсек двуполостного
гиперболоида (решение не изменится, если это
будет эллиптический параболоид или трехос-
ный эллипсоид). Нужно преобразовать его в
отсек сферы произвольного диаметра. Вначале
преобразуем поверхность в двуполостный ги-
перболоид вращения. Для этого воспользуемся
родственным преобразованием, задав родство
плоскостью родства £ (Si)|| П2 и родственными
точками А и А. В результате преобразования
горизонтальной проекцией отсека станет круг,
фронтальная проекция отсека не изменится
(почему?).
Теперь произведем гомологическое преоб-
разование отсека двуполостного гиперболоида
вращения в отсек сферы. Проведем касатель-
ную к фронтальной проекции контура поверх-
ности в точке Вг (см- Рис- 52) и отметим точку S2
ее пересечения с проекцией оси поверхности.
Будем рассматривать точку S как пентр гомо-
логии. В качестве плоскости гомологии примем
горизонтальную плоскость fl (Q),, а двух го-
мологичных точек — полюс сферы Н и (Н2)
104
и вершину гиперболоида Н (Н2). Отсек сферы,
юмологичный отсеку гиперболоида, соприка-
сается с гиперболоидом по окружности, про-
ходящей через точки В и А Центр сферы D (D2)
расположен в пересечении с осью поверхности
перпендикуляра к прямой BS, проходящего че-
рез В в плоскости главного меридиана. После
преобразования фронтальной проекцией отсека
поверхности стал сегмент круга радиуса B2D2
с центром 1)2. Горизонтальной проекцией отсе-
ка остается круг радиуса B1Si с центром в S,.
Найдем горизонтальную проекцию точки С,
инцидентной первоначально данному гипер-
болоиду и заданной ее фронтальной проек-
цией С2. При первом преобразовании направле-
ние двойных прямых было перпендикуляр-
ным П2. поэтому фронтальная проекция пре-
образованной поверхности не изменилась. Про-
ведя через С окружность с центром на оси
преобразованной поверхности, построим гори-
зонтальную проекцию окружности. Установив
проекционную связь, найдем точку С(. Прове-
дем через С (Cj) произвольную прямую и,
отметив точку 1 ее пересечения с плоскостью
родства L, построим родственную ей прямую,
а на ней — точку С (Cj).
На рис. 289 изображен отсек эллиптического
параболоида, ось симметрии которого парал-
лельна П2 и наклонена к П, под углом, отлич-
ным от прямого. Преобразуем поверхность в
параболоид, ось которого вертикальна, а сече-
ние плоскостью S совпадает с сечением этой же
плоскостью заданного параболоида. Примем X
за плоскость гомологии, направление двойных
прямых — параллельным оси х При этих усло-
виях центр гомологии будет несобственным и
инцидентным плоскости X. Как было установ-
лено ранее (см. § 4, рис. 37 и 51), такое преоб-
разование называется сдвигом. Сдвиг, подобно
родству, преобразует поверхность второго по-
рядка в поверхность второго порядка того же
вида.
Возьмем на заданном параболоиде точ-
ку A (At; А2), через которую проходи г плос-
кость, параллельная X и касательная к пара-
болоиду. Гомологичной ей точкой является
точка A (At; А2) — вершина преобразованной
поверхности. Соединим прямыми точками А
и А с точкой В — центром эллипса. Прямые А В
и АВ гомологичны. Построение проекции кон-
тура поверхности основано на том, что все
хорды, параллельные прямой Х2, преобразу-
ются в равные хорды преобразованной фигуры
(например, хорда Н2К2 преобразуется в хор-
ду N2K2, причем N2K2 — N2K2).
Построим горизонтальную проекцию точ-
ки Т, инцидентной заданному параболоиду, если
известна ее фронтальная проекция Т2. Прове-
дем через точку Т (Т2) прямую а (а2), параллель-
ную АВ, а через тонку С ее пересения с!—
прямую а (сГ2), параллельную ЛВ. Прямые а и а
гомологичны, следовательно, точка Т гомоло-
гична точке Т, расположенной в пересечении
прямой а с двойной прямой, проходящей че-
через Т. Преобразовав эллиптический парабо-
лоид Q в параболоид вращения (фигуры, за-
дающие родство, на рисунке не показаны; см.
рис. 288), найдем горизонтальную проекцию 7~t
точки Г, инцидентной параболоиду вращения.
Преобразуя параболоид вращения в эллипти-
ческий параболоид (построения не показаны,
проделайте их самостоятельно), найдем точ-
ку
Остается через 7} провести горизонталь-
ную проекцию двойной прямой (перпендику-
лярно линиям связи) и отметить точку ее пере-
сечения с линией связи, проходящей через Т2.
Если не известно, видима или невидима точ-
ка Т при взгляде спереди, задача имеет два
решения (каково второе решение?)
§ 25. РАЗВЕРТЫВАНИЕ
ПОВЕРХНОСТЕЙ
Развертыванием называется такое преобра-
зование поверхности, в результате которого она
совмещается с плоскостью. Выше мы делили
поверхности на развертываемые и неразверты-
ваемые. Первые могут быть совмещены с пло-
скостью без складок и разрывов, вторые со-
вмещаются с плоскостью приближенно в ре-
зультате некоторой деформации или условной
замены отсеков неразвертываемых поверхно-
стей отсеками поверхностей развертываемых.
Замена одной фигуры другой более простой
105
называется аппроксимацией*. С похожим пре-
образованием мы уже встречались (см. § 12
«Спрямление кривой линии»),
/132/ Развертываемой может быть только
линейчатая поверхность, причем именно такая,
две смежные образующие которой — прямые ли-
нии — пересекаются (в собственной или несоб-
ственной точке). Плоская фигура, полученная
в результате развертывания поверхности или ее
отсека, называется разверткой. Напомним, что
к развертываемым относятся все гранные. ко-
нические и цилиндрические поверхности и
торсы.
/133/ Прямая линия на поверхности преобра-
зуется в прямую на развертке; параллельные
прямые поверхности преобразуются в параллель-
ные прямые на развертке.
/134/ На развертке сохраняются длины дуг
кривых (отрезки прямых) линий, инцидентных
поверхности, величины углов между линиями и
площади фигур, ограниченных замкнутыми ли-
ниями.
Развертка гранных поверхностей. Каждая
грань гранной поверхности представляет; собой
плоскую фигуру; определив одним из рассмот-
ренных выше способов величины всех граней,
следует построить их на чертеже в той или иной
композиции. Построим развертку полной по-
верхности пирамиды (рис. 290). При данном
расположении пирамиды ее основание на П)
проецируется в натуральную величину. Опре-
делим величину каждого бокового ребра. Для
этого воспользуемся вращением вокруг оси i,
прохолящей через вершину пирамиды перпен-
дикулярно П,. Построим в произвольном месте
чертежа треугольник АВС = АВС. Зная длины
ребер, пристроим к нему треугольник BCS,
затем треугольник CAS и, наконец, треуголь-
ник BAS.
Если развертку вырезать из листового ма-
териала и согнуть по прямым BS, CS и ВС так.
чтобы А, А и А совпали, мы получим пирамиду,
изображенную на рис. 290. (Нужно учитывать
направление сгиба, чтобы не получить фигуру,
симметричную заданной.)
На пирамиде даны точки G и D. Нужно
определить кратчайшее расстояние между ними
по поверхности пирамиды. Построим точки G
и D на развертке. Так как точка G расположена
на ребре AS, следует при определении его ве-
личины повернуть и точку G. Тогда S2G2 = SG.
Отложив полученный отрезок по прямой TS
от точки S, получим искомую точку Q. Точку D
можно перенести на развертку с помощью про-
веденных через нее прямых, например FS и BE.
В их пересечении на развертке найдем точку D.
Линия поверхности, определяющая кратчай-
шее расстояние между двумя точками поверх-
ности, называется геодезической линией. На
развертке она преобразуется в отрезок прямой.
Соединив точки G и D прямой, отметим точ-
ку Н ее пересечения с ребром BS. Проделав
построения, обратные тем, что были выпол-
нены при определении точки G на развертке,
получим фронтальную, а затем горизонталь-
ную проекцию точки Ни соединим их с соот-
ветствующими проекциями точек G и D.
Каждая точка поверхности пирамиды соот-
ветствует строго опведеленной точке развертки.
(Сказанное не относится к точкам линий, по
которым поверхность разрезана. В данном слу-
чае это прямые /1S, АС и АВ. Этим объясняется,
что точка А как бы соответствует трем точкам
развертки —А, А и А. ребро AS — отрезкам
AS, AS и т. д.) Таким образом, между поверх-
ностью пирамиды и ее разверткой устанавли-
вется взаимно однозначное соответствие.
Для построения развертки боковой поверх-
ности призмы используем последовательный
поворот граней вокруг ребер (рис. 291). Вначале
спроецируем призму на плоскость ГЦ, парал-
лельную боковым ребрам. Затем повернем
грань ACFD вокруг ребра AD (фронтали в си-
стеме ГЦ/ГЦ) до совмещения с плоскостью.
* От лат approximate — приближаться.
Рис. 290
106
параллельной П4 (сМ. § 22). Так как длина ребра
известна (почему?), проведем проекцию' t4 тра-
ектории точки С и на ней от А4 отложим длину
ребра АС, получив при этом точку С. Ребро CF
на развертке равно и параллельно отрезку Л4 Л4.
Вслед за этим построим проекцию траектории
точки В и на ней от точки С отложим длину
отрезка СВ (она также известна) и т. д. Соеди-
ним точки на развертке так, как они соединены
на фигуре.
Построим на развертке точку G, инцидент-
ную поверхности призмы Проведем через нее
произвольную прямую, например образую-
щую GH. Построив проекции точек G и Н на
плоскости П4, проведем проекции их траек-
торий. Получив точку Н, проведем через нее
образующую параллельно ребрам до пересе-
чения с проекцией траектории точки G. Анало-
гично решается и обратная задача.
Развертка конических и цилиндрических по-
верхностей н торсов. Построим развертку боко-
вой поверхности конуса (рис. 292). Аппрокси-
мируем коническую поверхность пирамидаль-
ной с ребрами, проходящими соответственно
через точки А, В, С, ..., взятые на равных или
различных расстояниях друг от друга на осно-
вании. Определив величину ребер (на чертеже
найдена величина ?1S) и заменив дуги АВ,
ВС, ... хордами (их величина известна), постро-
им треугольники ABS, BCS и т. д. Ломаную
АВС ... А заменим кривой, проходящей через
те же точки. Построение на развертке точки,
инцидентной поверхности конуса (и решение
обратной задачи), а также геодезической линии
проводится аналогично тому, как это было сде-
лано на пирамиде. Проекции геодезической
линии обычно кривые линии.
Развертка цилиндра показана на рис. 293.
Если сравнить рис. 291 и 293, то построения ста-
нут ясными без пояснений. Геодезическая ли-
ния EF является кратчайшим расстоянием меж-
ду точками Е и F на поверхности цилиндра.
Чтобы развернуть торс, его аппроксими-
руют гранной поверхностью. Торс на рис. 294
задан ребром возврата а; отсек поверхности
ограничен по одну сторону ребром возврата,
по другую — плоской кривой Ь. Возьмем на
ребре возврата произвольные точки А, В, С, ...,
проведем через них образующие AF, ВG, СН,...
и отметим точки F, G, Н, ... их пересечения с
кривой Ь. Соединив эти точки попарно прямы-
ми линиями, получим треугольники ABF,
Рис. 292
Рис. 293
107
FBG, ... Совместим с плоскостью эти тре-
угольники.
Развернем в пределах одного витка гели-
коид заданный ребром возврата а и ограни-
ченный цилиндрической поверхностью (что это
за геликоид, который можно развернуть?).
Разделим горизонтальную проекцию ци-
линдра (рис. 295) на восемь частей и через
каждую точку проведем горизонтальную про-
екцию образующей геликоида, а затем по-
строим ее фронтальную проекцию. Для удоб-
ства одну из образующих {АВ) проведем парал-
лельно П2. Соединим прямыми точки А и В,
А и С, В и Сит. д., получив при этом треуголь-
ники ABC, BDC, ... Так как ребро возврата
торса (геликоида) - цилиндрическая винтовая
линия с постоянным шагом, то другие треуголь-
ники, построенные описанным способом, соот-
ветственно равны треугольникам АВС и BDC
Определим величину сторон треугольников
(величина отрезка АВ известна) и построим
треугольник АВС (рис. 296) по трем сторонам
К этому треугольнику пристроим треуголь-
ник f 9С так, чтобы точки В и С обоих треуголь-
ников совпали.
Проведем через точки А, С,..., К дугу окруж-
ности. Ее длина равна длине дуги винтовой ли-
нии на поверхности цилиндра между точка-
ми А и К. Вторая окружность проходит через
точки В и N. Ее дуга между точками BuN равна
длине дуги ребра возврата между точка-
ми В и N.
Развертки конической и цилиндрической по-
верхностей и торсов строятся приближенно,
гак как эти поверхности условно заменяются
гранями, однако они называются точными,
так как любая точка поверхности может быть
точно построена на ее развертке.
108
Рис. 298
Приближенная развертка неразвертываемых
поверхностей. Для построения приближенных
разверток неразвертываемых поверхностей их
аппроксимируют сочетанием отсеков развер-
тываемых поверхностей. Развернем поверх-
ность вращения с криволинейной образующей
(рис. 297). Для этого рассечем поверхность не-
сколькими (восемью) меридиональными плос-
костями. В результате поверхность разделена
на несколько (по числу плоскостей) отсеков —
«лепестков». Длина каждого лепестка по сред-
ней линии ABCD .. равна меридиану. Если
рассечь поверхность рядом горизонтальных
плоскостей, получим окружности, радиусы кото-
рых равны расстоянию от фронтальной проек-
ции оси поверхности до фронтальной проекции
главного меридиана. Построив дуги окружно-
стей между границами лепестка и заменив их
хордами, можем определить ширину лепестка
в его пересечении с соответствующей горизон-
тальной плоскостью. На П, хорды проециру-
ются в натуральную величину. Расстояние меж-
ду двумя смежными горизонтальными сече-
ниями может быть определено по проекции
главного меридиана, например сечение, сосед-
нее проходящему через точку D, расположено
на расстоянии НК = Н2К2. Определив необхо-
димые величины, строим развертку.
Второй прием заключается в следующем
(рис. 298): рассечем поверхность рядом плоско-
костей, перпендикулярных оси, и часть поверх-
ности между двумя смежными плоскостями
заменим отсеком цилиндрической или кониче-
ской поверхности. Построение развертки по-
верхности вращения сведется к построению
разверток боковых поверхностей цилиндров и
усеченных конусов.
Проекции и развертка цилиндроида показа-
на на рис. 299. Направляющими цилиндроида
Рис. 299
109
Одна деталь
в приведенном примере являются окружность
и эллипс, расположенные соответственно в го-
ризонтальной и фронтально проецирующей
плоскостях. Плоскостью параллелизма слу-
жит П2. Аппроксимируем цилиндроид гранной
поверхностью, состоящей из треугольников
ABC, BCD,... Определив величину отрезков ВС
и АС (построения не показаны), построим по
трем сторонам треугольник АВС (отрезок АВ
на П2 проецируется в натуральную величину).
Пристроим к нему треугольник BCD и т. д.;
точки А, С, ..., а также В, D, ... соединим плав-
ными кривыми.
Чтобы развернуть открытый тор, можно
заменить эту поверхность отсеками нескольких
конических и цилиндрических поверхностей и
плоскостей. На рис. 300 половина тора замене-
на двумя полуцилиндрами высотой h (внутрен-
ним и внешним), половинами конусов с верши-
нами в точках А и В (таких конусов по два)
и двумя отсеками плоскостей, ограниченных
полуокружностями радиусов R' и R". При-
ближенная развертка половины тора показана
на рис. 301.
Второй прием развертки тора заключается
в том, что его рассекают плоскостями, прохо-
дящими через ось тора. Отсеки поверхности
между плоскостями развертываются, как пока-
зано на рис. 297.
ГЛАВА VI
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
§ 26. ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТИ И ПЛОСКОСТИ
(СЕЧЕНИЕ)
Пересечение гранной поверхности н плоско-
сти. Каждая грань поверхности — это отсек
плоскости, поэтому можно воспользоваться
приемами, рассмотренными выше (см. /80/
и/84/). На рис. 302 точка М пересечения ребра AS
пирамиды ABCS с плоскостью DBF найдена с
помощью горизонтально проецирующей пло-
скости Q Аналогично построены точки К и Н
пересечения с плоскостью двух других ребер
(построения не показаны). Линией пересечения
является замкнутая ломаная • (треуголь-
ник КМН).
/135/ Чтобы построить линию пересечения
плоскости с трапной поверхностью, нужно опре-
делить точки пересечения ребер поверхности с
плоскостью н последовательно соединить их
между собой.
Если плоскость, пересекающаяся с поверх-
ностью, — проецирующая, построения упроща-
ются, так как одна проекция линии пересечения
становится известной. На рис. 3()3 известна
фронтальная проекция А2В2С2 (см. /16/ и /81/)
линии пересечения боковой поверхности приз-
мы и фронтально проецирующей плоскости О.
Установив проекционную связь, найдем ее го-
ризонтальную проекцию.
Можно строить сечения некоторых гранных
поверхностей так, чтобы фигура сечения была
подобна некоторой наперед заданной. Найдем
сечение боковой поверхности треугольной пи-
рамиды HEFS (рис. 304) плоскостью, подобное
заданному треугольнику АВС (рис. 305, а). Для
этого построим развертку боковой поверхно-
сти пирамиды (рис. 305, о) и, взяв на ребре,
например, FS произвольную точку А. отложим
отрезок -АВ, равный стороне АВ треугольни-
ка А ВС и пересекающийся в точке В с ребром ES.
От точки В отложим оз резок ВС = ВС так,
чтобы в точке С он пересекся с ребром HS, и,
наконец, от точки С отложим отрезок С А = СА.
Он пересекается с ребром FC в течке А. Если
точки А и А оказались на одном расстоянии от
вершины, что может быть только случайно, то
ломаная АВСА окажется разверткой линии се-
чения боковой поверхности пирамиды, равного
заданному. В данном случае Л расположена
ближе к S, чем точка А.
Уменьшим треугольник АВС до разме-
ров А В' С' (рис. 305, а) и повторим пост роения
на развертке, затем, построив треугольник
АВ" С", вновь проделаем построения и т. д.
Проведем произвольную прямую а (рис. 305, в)
и, взяв на ней точку У, отложим оз нее озрез-
ки SA, SA' и SA" по этой прямой, измеренные
на развертке. Через полученные точки прове-
дем параллельные прямые под произвольным
углом к а и отложим на них отрезки АС, А”С”
и А ’С'. Соединим концы отрезков плавной
кривой (кривой ошибок). Отложив от S отре-
зок SA'", равный SA. измеренный на развертке
по ребру F5, проведем через полученную точку
прямую, параллельную АС до пересечения с
кривой ошибок в точке С . Полученный отре-
зок построим на рис. 305, а и вновь проделаем
Рис. 302
111
построения’ на развертке, получив при этом
точки В'" и С’". Найдем точки йи Сна про-
екциях пирамиды (см. рис. 304). Треугольник
АВ”'С” на рис. 305, а является искомым сече-
нием пирамидальной поверхности плоскостью,
проходящей через точку А Возможны другие
варианты решения.
Призматическая поверхность представляет
собой частный случай пирамидальной, поэтому
найти ее сечение, подобное заданному, можно
аналогичным приемом.
/136/ Сечением треугольной пирамидальной или
призматической поверхности может быть тре-
угольник любой наперед заданной формы.
Пересечение нелинейчатой поверхности и пло-
скости. На рис. 306 нелинейчатая поверхность <1
пересекается плоскостью X по кривой а. Про-
извольная точка А этой кривой может быть'
найдена, если рассечь заданные фигуры пло-
скостью Ч', которая с X пересекаетбя по пря-
мой с, а с поверхностью — по кривой Ь. Точка А
пересечения этих линий инцидентна линии пере-
сечения заданных фигур. Построив несколько
вспомогательных секущих плоскостей, получим
точки, которые нужно последовательно соеди-
нить между собой.
/137/ Чтобы построить линию пересечения
плоскости и поверхности, следует рассечь их
рядом плоскостей, построить линии пересечения
заданных фигур и вспомогательных плоскостей
и, отметив общие для соответствующих линий
точки, последовательно соединить нх между
собой.
/138/ При решении задач, в которых исполь-
зуются вспомогательные секущие плоскости, сле-
дует выбирать, когда это возможно, такие пло-
скости, проекции линии пересечения которых с
заданными фигурами являются простейшими
(прямыми нли окружностями).
При решении задач необходимо найти точки
особого расположения, называемые опорными.
Обычно это точки, в которых линия пересечения
переходит от видимой части к невидимой, точки
наиболее близко и далеко расположенные от-
носительно плоскостей проекций и др.
Сечение поверхности вращения. Даны поверх-
ность вращения с вертикальной осью и плос-
кость АВС общего положения (рис. 307).
Рассечем заданные фигуры рядом плоско-
стей, параллельных П15 они пересекут поверх
ность по окружности (см. /138/), а плоскость —
по прямым. Пересечение окружностей и пря-
мых, инцидентных общим вспомогательным
плоскостям, определит точки, инцидентные ли-
нии пересечения заданных фигур. На рисунке
показана плоскость О, пересекающая цлос
кость А ВС по горизонтали h, а поверхность по
окружности диаметра D2EV Построив гори-
зонтальные проекции этих линий, найдем точ-
ки F, и Gj, а затем F2 и G2. Аналогично найдем
и другие точки линии пересечения.
К числу опорных относятся точки Н и К.
в которых линия пересечения при взгляде спе-
реди переходит от видимой части к невидимой.
Чтобы найти их, рассечем заданные плоскость
и поверхность плоскостью Е, проходящей че-
рез главный меридиан поверхности. Плоско-
сти S и АВС пересекаются по прямой NM,
которая пересекает главный меридиан в точ-
ках Н и К. Главный меридиан (контур поверх-
ности) делит поверхность на две части: перед-
нюю — видимую и дальнюю — невидимую.
Линия пересечения пересекла контур, следова-
тельно, перешла с видимой части поверхности
на невидимую.
/139/ Чтобы найти точки, в которых линия
поверхности переходит от видимой части к не-
видимой, следует определить пересечение этой
линии с контуром поверхности.
Положение этих точек зависит от того, в ка-
ком направлении зритель смотрит на поверх-
ность, иначе говоря, от направления проециро-
вания. Поэтому границы видимости линии,
изображенные на П2, большей частью не со-
впадают с границами видимости, изображен-
ными на П,, П3 или какой-либо иной плоско-
сти проекций.
Построить линию пересечения поверхности
вращения и плоскости можно, заменив П2 на П4
так, чтобы плоскость АВС стала проецирую-
щей. Фронтальная проекция линии пересечения
станет известной, ее горизонтальная проекция
строится с помощью дополнительных сечений,
как на рис. 307. Этот прием можно использо-
вать для определения высшей L и низшей Т
112
11b lb lb lib
8—940
Рис. 305
т
точек линии пересечения. Неудобство приема
в том, что нужно строить новую проекцию по-
верхности. Чтобы этого избежать, можно вос-
пользоваться вращением. Приняв ось враще-
ния совпадающей с осью поверхности, следует
повернуть вокруг нее плоскость АВС так, чтобы
она стала фронтально проецирующей (см. пояс-
нения к рис. 273). Проекция поверхности не
изменится (почему?). Решите такую задачу
самостоятельно.
Сечение линейчатых поверхностей. На рис. 308
даны плоскость 12 и коноид, заданные направ-
ляющими — прямой а н кривой b и плоско-
стью параллелизма Т. Рассечем как плоскость,
так и поверхность рядом горизонтально про-
ецирующих плоскостей, параллельных Т. По-
строив линии их пересечения с заданными фигу-
рами, отметим общие точки. На чертеже пока-
зана плоскость Е, пересекающая коноид по
прямой АВ (почему по прямой?) и по пря-
мой CD — плоскость 12. Линии, пересечения
пересекаются в общей для обеих заданных фи-
гур точке Е. Аналогично построены и другие
точки линии пересечения.
Сечение поверхности переноса. Поверхность
задана направляющей — параболой а, образую-
щей — параболой с и горизонтально проеци-
рующей плоскостью параллелизма 12 (рис. 309).
Рассечем поверхность и плоскость рядом вспо-
могательных плоскостей, параллельных 12.
С поверхностью они пересекутся по параболам,
равным и подобно расположенным параболе с,
с плоскостью — по параллельным прямым. На-
пример, плоскость Т пересекается с поверхно-
стью переноса по параболе d, а с заданной
плоскостью — по прямой CD. Общая для этих
линий точка Е инцидентна линии пересечения
заданных фигур. Построения параболы d мож-
но избежать, если учесть, что параболы с и d
проецируются на плоскость П2 в виде равных
и подобно расположенных парабол с2 и <72;
дуга параболы с2 между точками F2, G2 равна
дуге параболы d2 между точками А2 и В2.
Соединим точки А2 и F2 прямой и в ее направ-
лении переместим как параболу d2, так и пря-
мую C2D2 на величину отрезка F2A2. Пара-
болы с2 и d2 совместятся, а прямая пройдет
через точку С2 параллельно C2D2. В точке Е'2
она пересечется с параболой с2. Нетрудно ви-
деть, что, построив точку А2 и прямую C2D2,
можно сместить эту прямую в направлении
и на длину отрезка A2F2 и найти точку Е'2.
Смещая точку Е2 в обратном направлении до
совпадения с прямой C2D2, найдем точку Е2.
Установив проекционную связь, построим точ-
ку Ev Тем же приемом построим другие точки
линии пересечения.
Конические сечения. Как было сказано (см.
/105/, /106/ и /107Д сечениями конической по-
верхности второго порядка могут быть эллипс,
парабола и гипербола, называемые кривыми
конических сечений, или их вырожденные ва-
Рис. 308
114
Когда плоскость проецирующая, можно ус-
тановить вид линии сечения конической поверх-
ности без вспомогательных построений; на
рис. 310 показано эллиптическое сечение конуса
вращения плоскостью О. Чтобы построить
горизонтальную проекцию сечения, восполь-
зуемся тем, что фронтальная проекция — отре-
зок В2С2—известна. Точки Вх и Ct—гори-
зонтальные проекции концов большой оси эл-
липса — инцидентны горизонтальной проек-
ции главного меридиана — прямой, проходя-
щей через \ перпендикулярно линиям связи.
Чтобы найти горизонтальные проекции концов
малой оси, разделим отрезок В2С2 пополам и
через полученную точку D2 = Е2 проведем пря-
мые A 2S2 и A'2S2. Найдя их горизонтальные про-
екции, построим на них соответственно точ-
ки Dx и Ej. Если пользоваться образующими не-
удобно, можно провести через точки D и Е
окружность, инцидентную конической поверх-
ности; ее фронтальная проекция — отрезок, пер-
пендикулярный линиям связи. Отметив точ-
ку К2 пересечения фронтальной проекции ок-
ружности с контурной относительно П2 обра-
зующей, определим радиус окружности; он
равен расстоянию от К2 до фронтальной про-
екции оси конуса. Для построения точек D, и Е,
остается провести окружность с центром в точ-
ке S’] найденного радиуса до пересечения с пря-
мыми или линией связи, проведен-
ной через точку D2 = Е2.
Эллипс — горизонтальную проекцию сече-
ния — можно построить по его осям или, уста-
новив проекционную связь, найти промежуточ-
ные точки. На чертеже построена точка Н с по-
мощью образующей FS. (Можно воспользо-
ваться и окружностью, как при построении то-
чек D и Е.) Одновременно с точкой Е/2 строится
симметричная ей относительно оси EjC; точ-
ка Н\.
На чертеже способом замены плоскостей,
проекций (какая плоскость заменена?) опреде-
лена фигура B5EsCsD5 сечения.
Если рассечь коническую поверхность пло-
скостью Е, параллельной О, то фигурой сече-
ния будет эллипс, подобный эллипсу BECD.
Напомним, что коническая поверхность имеет
две полости; если провести плоскость, парал-
лельную плоскостям Я и Е, но пересекающую
другую полость поверхности, то мы вновь
получим эллипс, подобный построенным.
Если секущую плоскость поворачивать так,
чтобы менялся угол ее наклона к оси поверх-
ности (но так, чтобы она не стала параллельной
какой-либо образующей), мы вновь получим
эллипс, но уже с иным отношением длин oceij.
Частным случаем эллипса — сечения кониче-
ской поверхности — является окружность (эл-
липс с равными осями). Такое сечение кониче-
ской поверхности вращения всегда перпенди-
кулярно ее оси.
Однако возможно так расположить плос-
кость, что она не будет параллельной ее перво-
начальному расположению, но сечение окажет-
ся эллипсом, равным или подобным тому, ко-
торый был получен при ранее принятом поло-
жении плоскости. Сечением конической поверх-
ности плоскостью £1 (рис. 311) является эллипс с
большой осью C2D2. Плоскость Е, симметрич-
115
8*
по-
по-
по-
ная плоскости fl относительно фронтально
проецирующей плоскости, проходящей через
ось поверхности, рассечет конус по эллипсу с
большой осью А2В2. Оба сечения в силу сим-
метрии равны между собой и наклонены соот-
ветственно к образующим SD и SB под одина-
ковыми углами: <р = <р'. Такие сечения назы-
ваются антипараллельными. Сказанное отно-
сится и к параболическим и гиперболическим
сечениям конической поверхности.
Антипараллельные сечения могут быть
строены и на других поверхностях второго
рядка.
Сечение конической поверхности второго
рядка. Решение показано на рис. 312. Заменим
П2 на П4 так, чтобы плоскость АВС стала про-
ецирующей. Теперь построения стали анало-
гичными приведенным на рис. 310 с той разни-
цей, что нельзя воспользоваться окружностями
для построения проекций точек. Вначале найдем
опорные точки D и Е, лежащие на контурных
относительно П4 образующих. Это высшая и
низшая точки сечения. Затем найдем точки G
и F, определяющие границу видимости' кривой
при ее изображении на Пр Для этого построим
замененные проекции контурных относитель-
но 7?! образующих HS и К5 и, отметив точки
G4 и F4, построим горизонтальные проекции
этих точек. Найдем точки, определяющие ви-
димость кривой при взгляде спереди. Для этого
контурные относительно П2 образующие по-
верхности спроецируем на П1э а затем на Hi.
Отметив проекпии точек пересечения проекций
образующих на плоскости П4 с проекцией пло-
скости АВС, построим
а затем на П2.
Пъ
их проекпии
на
* См.: Сухина И. А. О некоторых приемах
построения проекций сечений конуса и примечания
посредников — линейчатых поверхностей. Труды
КПИ, Вып. 31.
Рис. 311
После этого определим участки, в которых
линия пересечения недостаточно выявлена. Про-
ведя образующие поверхности на этих участ-
ках, найдем недостающие точки. Проведем че-
рез построенные точки плавную кривую, в дан-
ном случае эллипс.
Аналогично можно строить линию пересе-
чения с плоскостью цилиндрической поверх-
ности.
Определение вида кривой конического сече-
ния. Еще до построения линии пересечения ко-
нической поверхности второго порядка и пло-
скости можно определить вид .кривой сечения*.
Установим, по какой линии плоскость а Г) b пе-
ресекает коническую поверхность (рис. 313).
Построим плоскость с f)d, параллельную пло-
скости аПЬ (см. пояснения к рис. 175) и прохо-
дящую через вершину поверхности. Определим
прямую АВ пересечения этой плоскости с пло-
скостью fl, в которой лежит направляющая по-
верхности (см. пояснения к рис. 154). В приве-
денном примере прямая АВ не пересекается с
направляющей, следовательно, плоскость с Cid
пересекает коническую поверхность в точке
(вершине). Таким образом, плоскость аГ1Ь,
параллельная плоскости с ("Id, пересекает по-
верхность по эллипсу (см. /105/).
На рис. 314 прямая АВ касается направляю-
. щей, следовательно, плоскость cdd пересека-
ется с поверхностью по одной прямой, а парал-
лельная ей плоскость аПЬ — по параболе
Рис. 312
116
(см. /106/) и, наконец, на рис. 315 прямая АВ
пересекает основание конуса в двух точках.
Плоскость с (Id пересекается с поверхностью
по двум прямым, а параллельная ей плос-
кость а Г) b — по гиперболе (см. /107/).
/140/ Чтобы определить вид кривой второго
порядка, по которой плоскость общего положе-
ния пересекает коническую поверхность, нужно
провести через вершину поверхности плоскость,
параллельную заданной, и определить вид вы-
рожденного сечения.
Эллиптические сечения поверхностей второго
порядка, подобные заданным. Пусть отношение
осей заданного эллиптического сечения рав-
но а : b (а < Ь), а поверхность *— трехосный эл-
липсоид (рис 316). Пропорционально увеличим
или уменьшим отрезки а и Ь так, чтобы отре-
Рис. 314
Рис. 316
Рис. 317
Рис. 318
зок а был равен меньшей из трех осей эллипсои-
да. Проведем дугу радиуса R = Ь/2 с центром А2
до пересечения в точке В2 с проекцией контура
поверхности относительно П2. Через В и центр
эллипсоида проходит фронтально проецирую-
щая плоскость fl, сечение которой поверхности
представляет собой эллипс с заданным отноше-
нием осей. Таковы же сечения эллипсоида пло-
скостями, параллельными fl и антипаралЛель-
ные им (ось Ь не должна быть длиннее большей
оси эллипсоида).
Сечение эллиптического параболоида, по-
добное заданному, показано на рис. 317. По-
строим эллиптический цилиндр, для которого
эллипс—горизонтальная проекция границы от-
сека параболоида является направляющей; оси
поверхностей совпадают. Эллиптические сече-
ния таких поверхностей (см. /112/) подобны и
подобно расположены. Пропорционально уве-
личив или уменьшив отрезки а и b так, чтобы
отрезок а стал равным малой оси эллипса —
сечения обеих поверхностей, проведем окруж-
ность радиуса R = Ь/2 с центром в произволь-
ной точке А2 фронтальной проекции общей оси
поверхностей до пересечения в точке В2 с про-
екцией контурной относительно П2 образую-
щей цилиндра Фронтально проецирующая пло-
скость fl, проходящая через точки А и В, рассе-
кает как цилиндр, так и параболоид по эллип-
сам, подобным заданному. Все параллельные
' плоскости fl сечения поверхностей подобны в
равной мере, как подобны им и антипараллель
ные сечения.
Решение задачи, когда поверхность —• одно-
полостный гиперболоид, приводится на рис. 318.
Пропорционально увеличив или уменьшив от-
резки а и b так, чтобы отрезок а стал равным
малой оси горла гиперболоида, проведем ок-
ружность с центром в А2. Отметим точку В2
‘пересечения окружности с проекцией контурной
о гносительно П2 образующей поверхности. Точ-
ки А и В определяют положение фронтально
проецирующей плоскости fl, удовлетворяющей
условию.
Эллиптическое сечение конической поверх-
ности второго порядка, подобное заданному,
приведено на рис. 319. Уменьшим или увели-
чим отрезки а и b так, чтобы отрезок а стал
равным малой оси эллипса — горизонтальной
проекции конуса. Проведем через точку S2
горизонтальную прямую, а через — линию
связи. В пересечении прямых отметим точку А2.
Приняв ее за вершину гиперболы, а проекции
контурных относительно П2 образующих ко-
нуса — за асимптоты, построим дугу гипер-
болы (см. рис. 54). Гиперболу будем рассмат-
ривать как проекцию контура однополостного
гиперболоида, для которого заданный конус
является асимптотическим. Построим точку В2
в соответствии с описанием к рнс. 318, про-
ведем фронтально проецирующую плоскость,
проходящую через точки S и В. Сечения кони-
ческой поверхности плоскостями, параллель-
ными fl, и антипараллельные им, удовлетво-
ряют условию (см. /115/ и /116/).
Круговые сечения поверхностей второго по-
рядка. Описанный прием можно применить для
построения круговых сечений поверхностей вто-
рого порядка (рис. 320). Для этого нужно по-
118
Рис. 320
Рис. 319
строить профильную проекцию поверхности
(ср. с рис. 317). Секущую плоскость Q можно
задать параллельными прямыми cad.
/141/ Если сечением поверхности второго по-
рядка может быть эллипс, то можно построить
сечение такой поверхности с заданным отноше-
нием длин осей эллипсов (кроме приведенного
случая, относящегося к эллипсоиду).
Пересечение поверхности второго порядка й
плоскости. Если поверхность второго порядка —
линейчатая, построения можно выполнить в
соответствии с описанием к рис. 308, если по-
верхность вращения, то в соответствии с рис. 307.
Нелинейчатая поверхность второго порядка —
трехосный эллипсоид и пересекающаяся с ним
плоскость АВС даны на рис. 321. Используя
родство, преобразуем трехосный эллипсоид в
эллипсоид вращения (см. пояснения к рис. 287).
Зададим родство плоскостью родства Е и род-
ственными точками Н(НХ) и Н^Н^. Горизон-
тальная проекция эллипсоида — эллипс преоб-
разуется в круг, треугольник А1В1С1 —в тре-
угольник А1В1С1 (нужно учесть, что преобра-
зованная проекция как бы «перевернута» по
сравнению с проекцией, не преобразованной).
После преобразования трехосный эллипсоид
становится вытянутым эллипсоидом вращения.
Рассекая поверхность и плоскость плоскостями,
параллельными П; (см. /138/), найдем точки,
инцидентные линии пересечения (на рис. 321
с помощью плоскости О. найдены точки D и Е).
Точки G и F (перехода линии пересечения от
видимой части к невидимой) построены с по-
мощью плоскости Т, инцидентной главному
меридйану.
Построим линию пересечения трехосного
эллипсоида и плоскости АВС (рис. 322). Вос-
пользовавшись приемом, показанным на
рис. 251, найдем сечение эллипсоида, проеци-
рующееся на nj в окружность. Фронтальной
проекцией сечения является отрезок D2E2. За-
ключим сечение во фронтально проецирующую
Рис. 321
119
плоскость S2 (см. /137/). Она пересечет эллипсоид
по построенному сечению, плоскость — по пря-
мой F G. Отметим общие точки N и К (вначале
их горизонтальные проекции). Взяв ряд парал-
лельных сечений, подобно тому, как это было
сделано на рис. 251, найдем необходимое число
точек линии пересечения. Точки перехода от
видимой части линии к невидимой найдем с
помощью плоскости X, проведенной через го-
ризонтальную проекцию очерка эллипсоида от-
носительно П2 (X || П2) и плоскости Ф2 ± П2.
Вспомогательные секущие плоскости рас-
секают эллипсоид по эллипсам, проекциями
которых на П2 являются окружности. Это не
только упростило решение, но и сделало его
более точным (см. /138/).
в точке А, а плоскость с П d — плоскостью, ка-
сательной к поверхности в точке А.
/142/ Две пересекающиеся прямые, касатель-
ные к двум линиям поверхности, проходящим
через данную точку поверхности, определяют
плоскость, касательную к поверхности в той же
точке.
Одной или обеими линиями поверхности,
инцидентными точке, могут быть прямые, если
поверхность линейчатая и имеет соответственно
одно или два множества прямых линий. Во вто-
ром случае прямые определяют касательную
плоскость, инцидентную точке поверхности.
/143/ Если плоскость касается линейчатой
Поверхности в одной ее точке, то она касается
нли пересекается с линейчатой поверхностью ве
менее чем по одной прямой.
Положение /143/ относится к «обыкновен-
ным» точкам поверхности, но несправедливо
в отношении «особых» точек, в которых каса-
тельная плоскость или неопределенная, или
не единственная (например, вершина кониче-
ской поверхности, точка ребра возврата тора
и др.).
Построение касательной плоскости. Постро-
им плоскость, касательную к конической по-
верхности S1 и проходящую через точку А<££1
(рис. 326). В соответствии с /143/ плоскость ка-
сается поверхности по прямой, следовательно,
проходит через вершину. Проведем прямую AS
и определим точку В eg пересечения с плоско-
стью направляющей йоверхности. Проведем
прямые ВС и BD, касательные к эллипсу. Эти
прямые совместно с прямой AS определяют две
плоскости, касательные к поверхности. Через
точки С и D и вершину проходят линии касания.
Построим плоскость, касательную к пара-
болоиду вращения в точке А (рис. 327). Прове-
дем через А параллель поверхности и к ней ка-
сательн ю а. Прямая а, перпендикулярна ра-
диусу At Bt (см. /98/), прямая а2 перпендику-
лярна линиям связи (почему?). В качестве вто-
рой линии поверхности (см. /142/) возьмем
меридиан, проходящий через точку А. Мери-
диан расположен в горизонтально проецирую-
§ 27. ПЛОСКОСТИ,
КАСАТЕЛЬНЫЕ К ПОВЕРХНОСТИ
Фигуры касания. Плоскость и поверхность
могут касаться в точке, по прямой, по плоской
кривой или по комбинациям этих фигур. Не
исключено, что плоскость в одном месте каса-
ется поверхности, в другом — пересекает ее и
что линия касания может быть одновременно
и линией пересечения. Пример приведен на
рис. 323 (плоскость X касается цилиндрической
поверхности ф по прямой а). Плоскость ф
(рис. 324) касается однополостного гипербо-
лоида X в точке А и пересекает поверхность по
двум прямым аиЬ. Фигурой касания открытого
тора и плоскости может быть или точка, или
окружность (приведите другие примеры касания
плоскости и поверхности).
Пусть через точку А поверхности S2 прохо-
дя! инцидентные поверхности линии а и. b
(рис. 325). Проведем прямые с И а и b Lid.
Они называются касательными к поверхности
120
щей плоскости, поэтому его горизонтальная
проекция проходит через точки Ах и Вх. Не строя
фронтальной проекции меридиана, повернем
его вокруг оси поверхности до совпадения с
главным меридианом. Одновременно повер-
нем и точку А, которая займет положение А'
(см. /127/). Проведем прямую Ь', касательную
к меридиану в точке А (см. /98/ и рис. 49 и 203)
и отметим точку В ее пересечения с осью по-
верхности. Повернем точку А в первоначальное
положение, а вместе с ней и касательную; она
проходит через точки В и А. Плоскость а Г) b
касается поверхности в точке А.
Аналогично строятся плоскости, касатель-
ные к любой поверхности вращения с криволи-
нейной образующей. Исключение — точка пе-
ресечения меридиана с осью вращения, если они
пересекаются под углом, отличным от прямого
(почему?).
Если поверхностью является сфера, то через
данную ее точку целесообразно провести фрон-
тальную и горизонтальную окружности, лежа-
щие на сфере, а затем прямые, касательные к ним
s.
121
(рис. 328). Это фронталь и горизонталь каса-
тельной плоскости. Если точка (В) лежит на
очерке сферы, то касательная к поверхности
плоскость (Я) — проецирующая.
§ 28. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ
И ПОВЕРХНОСТИ
Прямая и поверхность могут пересекаться
между собой в одной или нескольких точках.
Частным случаем пересечения может быть ка-
сание.
Способ сечения поверхности вспомогательной
плоскостью, проходящей через прямую. Постро-
им точку (точки) пересечения прямой а и по-
верхности Я (рис. 329). Заключим прямую во
вспомогательную плоскость £ и построим ли-
нию b пересечения плоскости и поверхности,
в общем случае кривую. Линии а и b могут пе-
ресекаться между собой (точка Л), но могут и
не пересекаться. В первом случае точка (точки)
пересечения будет общей для прямой и поверх-
ности, т. е. точкой их пересечения. Во втором
случае прямая и поверхность не пересекаются.
/14V Чтобы построить точку (точке) пере-
сечения прямой с поверхностью, нужно заклю-
чить прямую во вспомогательную плоскость,
определить линию пересечения плоскости и по-
верхности, а затем точку (точки), в которой
заданная прямая пересекается с линией пересе-
чения; (Сравните с /87/).
Вспомогательную плоскость следует выби-
рать в соответствии с /138/.
Пересечение прямой с гранной поверхностью.
Построим точки пересечения прямой d с по-
верхностью треугольной призмы (рис. 330).
Заключим прямую d во фронтально проеци-
рующую плоскость Я и построим треуголь-
ник АВС пересечения плоскости и поверхности.
В точках К и М треугольник и прямая d пере-
секаются между собой, следовательно, в этих
же точках прямая d пересекается с поверхностью
(см. /144/ и /87/).
Пересечение прямой с конической н цилиндри-
ческой поверхностями. Заключив заданную пря-
мую а (рис. 331) в плоскость, проходящую через
вершину конической поверхности (см. /138/.
/106/, /107/), построим прямые AS и BS пере-
сечения плоскости и поверхности. Для этого
возьмем на прямой а произвольную точку I)
и соединим ее с вершиной, после чего перейдем
от задания плоскости прямой и точкой (а; 5)
к заданию ее двумя прямыми (aDSD). По-
строим точки С и £ пересечения прямых а и SD
Рис. 330
122
с плоскостью £2, в которой лежит направляю-
щая поверхности — кривая Ь. По прямой СЕ
секущая плоскость пересекается с плоскостью £2.
Отметив точки А и В пересечения прямой СЕ
и кривой Ь, соединим их с вершиной. Найдем
точки К и М, в которых образующие AS и BS
пересекаются с прямой а.
Рассмотрим решение задачи на эпюре.
Направляющая b конической поверхности
расположена в горизонтальной, следовательно,
проецирующей плоскости (рис. 332), поэтому
точка С пересечения прямой а с плоскостью на-
правляющей определяется в соответствии с /81/.
Также находим точку Е пересечения с плоско-
стью £2 прямой SD, проходящей через вершину
поверхности, и произвольную точку D прямой а.
Соединив прямой точки Ей С, получим линию
пересечения вспомогательной плоскости с пло-
скостью направляющей, а отметив точки А и В
пересечения этой линии с направляющей (по-
строены только их горизонтальные проекции),
проведем образующие поверхности AS и BS.
по которым поверхность пересекается со вспо-
могательной плоскостью. Остается отметить
точки К и М пересечения образующих с пря-
мой а (фронтальные проекции этих точек рас-
положены в пересечении линий связи, проведен-
ных через их горизонтальные проекпии, с пря-
мой а2).
Если точка С за пределами чертежа, можно
провести через вершину горизонтальную пря-
мую, пересекающуюся в точке Н с прямой а.
Прямые HS п а определяют секущую плоскость,
причем прямая HS — горизонталь. Так как пло-
скость £2 — горизонтальная, то линия ее пере-
сечения с плоскостью HSna представляет со-
бой горизонталь секущей плоскости. Следова-
тельно, HS || ЕС. Построив вначале фронталь-
ную, а затем горизонтальную проекцию пря-
мой HS, найдем точку Et и через нее проведем
прямую параллельно Далее — по изло-
женному.
В практических задачах вершина конуса
иногда недоступна. Покажем, как решить задачу
в этом случае (рис. 333). Зададим родство гори-
зонтальной плоскостью родства £2, горизон-
тальными родственными плоскостями Е и X
и направлением преобразования, перпендику-
лярным к ним. Преобразуем конус с верхним
основанием, которому инцидентны точки А и В,
в конус с верхним основанием, проходящим че-
рез точки А и В. Все точки нижнего основания
двойные. Построим вершину преобразованно-
го конуса S и преобразуем прямую аъа (точка
двойная, С преобразуется в С). Теперь располо-
жение фигур аналогично приведенному на
рис. 332. Проведя необходимые построения,
найдем точки и Фронтальные проекции
точек могут быть найдены без промежуточного
построения родственных им. (Почему в резуль-
тате преобразования не изменилась горизон-
тальная проекция фигур?)
Точки пересечения прямой а с цилиндриче-
ской поверхностью построены на рис. 334.
Рис. 333
123
Вершина поверхности несобственная точка, по-
этому секущую плоскость можно задать пря-
мой а и пересекающейся с ней в произвольной
точке А прямой АВ, параллельной образую-
щим цилиндра (см. /8/). Построив точки В и С
пересечения соответственно прямых АВ и а
с плоскостью направляющей (эллипса), соеди-
ним их прямой. Она в точках D и Е пересекает
направляющую. Через эти точки проходят об-
разующие цилиндра — линии пересечения его
боковой поверхности со вспомогательной пло-
скостью. Отметим точки К и М пересечения
образующих с заданной прямой.
Построим точки пересечения прямой с ко-
нической поверхностью, когда прямая занимает
частное положение-в пространстве. На рис. 335
прямая а — горизонтально проецирующая, а
прямая b — фронтально проецирующая. В пер-
вом случае горизонтальная, во втором — фрон-
тальная проекции точек пересечения известны
(см. /2/). Проведя через них образующие (соот-
ветственно SB и SE), найдем их вторые проек-
ции, а на них проекции искомых точек. Прямая а
пересекается с конической поверхностью в одной
точке А, прямая b — в двух точках С и D. Кроме
образующих, можно через точки пересечения
прямых с поверхностью провести окружности,
инцидентные поверхности (придумайте, почему
описанное решение не противоречит /144/).
/145/ Чтобы построить точки пересечения
прямой с конической или цилиндрической поверх-
ностью, следует заключить прямую в плоскость,
инцидентную вершине поверхности (собственную
или несобственную), найти линии пересечения
плоскости и поверхности, а затем точки, в кото-
рых эти линии пересекаются с заданной прямой.
Пересечение прямой со сферой. Заключим пря-
мую (рис. 336) в горизонтально проецирующую
плоскость 12 (см. /144/). Линия пересечения
сферы и плоскости на П] проецируется в отре-
зок С] Dp Заменим П2 на П4 || а (см. /59/ и /43/)
и спроецируем на П4 окружность диаметра С, D,
и прямую а. В результате найдем проекции Л4
и В4 точек пересечения прямой й сферы. Устано-
вив проекционную связь, найдем точки Аг и В},
а затем А2 и В2.
Пересечение прямой с поверхностью враще-
ния. Даны поверхность вращения и прямая а
(рис. 337). Заключим прямую в горизонтально
проецирующую плоскость 12 и в соответствии
с /137/ построим кривую с пересечения плоско-
сти и поверхности. На рисунке показана одна
из вспомогательных плоскостей (Е), с помощью
которых построена линия пересечения. Прямая а
пересекается с кривой с в точках Л и В. Из чер-
тежа видно, что нет необходимости строить всю
кривую с, поэтому перед тем, как искать эту
линию, следует определить область возможного
пересечения линии и поверхности. Она располо-
жена между горизонтальными плоскостями,
проходящими через точки С и D. Между ними
и нужно строить кривую с.
Определение видимости линии, пересекаю-
щейся с поверхностью. Для решения вопроса
используются конкурирующие точки, одна из
которых принадлежит прямой, вторая — кон-
туру поверхности, например точки Е и F на
рис. 336. Точка Е принадлежит прямой а, точ-
ка F — главному меридиану сферы, который
на П] проецируется в отрезок прямой, проходя-
щей через О] перпендикулярно линиям связи.
При взгляде спереди видна точка Е, следова-
тельно, прямая вплоть до точки А видима.
Часто достаточно установить на видимой
или невидимой стороне поверхности располо-
жение точки пересечения с прямой линией.
Если она видима, то видима и прилегающая
часть прямой, и наоборот.
Стереографическая проекция. Прежде чем
перейти к построению точек пересечения прямой
с поверхностями второго порядка, рассмотрим
проекцию, которая называется стере ографиче-
124
ской. На рис. 338 дана фронтальная проекция
сферы (достаточно одной проекции). Возьмем
на сфере произвольную точку, например по-
люс S' (S2). Проведем через 5 диаметр сферы и
построим перпендикулярную ему плоскость Я
(Я2). Отметим точки А (А2) и С (С2) пересе-
чения плоскости с главными меридианами.
Через А проведем плоскость £ (£2) под произ-
вольным углом к Я. Сечением сферы плоско-
стью X является окружность диаметра АВ.
Спроецируем эту окружность из центра 5 на
плоскость Я. Проекция точки А совпадает с
самой точкой, проекцией точки В является точ-
ка В (В2). Окружность диаметра АВ представ-
ляет собой направляющую, а точка S — вер-
шину проецирующей конической поверхности
второго порядка. Плоскость Я пересекает эту
поверхность по эллипсу.
Угол SAC равен углу SBA (построения про-
изводятся в плоскости главных меридианов,
поэтому проекции углов, о которых идет речь
(см. /43/), равны углам в натуре), так как оба
угла опираются на равные дуги. Это возможно
лишь в том случае, когда сечения конической
поверхности плоскостями £ и Я антипараллель-
ны (см. рис. 311), а следовательно, подобны.
Так как сечение конуса плоскостью £ окруж-
ность, то и сечение конуса плоскостью Я также
окружность (диаметра А В).
Если параллельно перемещать плоскость Я,
проецируя на нее сечение сферы АВ, мы будем
получать окружности различных диаметров.
Плоскость Я может пересекать сферу или не
пересекать (рис. 339). Произвольная точка К
сечения сферы проецируется в точку К' про-
екции сечения на плоскости Я. Точка Р, распо-
ложенная внутри или вне сферы, проецируется
в точку Р', не инцидентную проекции сечения.
125
Сечение проецирующего конуса плоско-
стью 12 мы рассматриваем как центральную
проекцию на этой плоскости сечения сферы
плоскостью X. Следовательно:
/146/ Если центр проецирования инцидентен
сфере, а плоскость проекций перпендикулярна
диаметру, проходящему через цент р, то проекцией
любой окружности, расположенной на сфере,
будет также окружность (кроме, разумеется,
случая, когда окружность проходит через центр
проецирования). В этом заключается основное
свойство стереографической проекции.
Дан эллипсоид вращения (рис. 340). Распо-
ложим центр проецирования S (S2) в одной из
его вершин, а плоскость проекции 12 (122) пер-
пендикулярно оси и проходящей через центр
эллипсоида. Рассечем эллипсоид фронтально
проецирующей плоскостью X, получив эллипс,
одна ось которого проецируется на П2 в отре-
зок а2в2.
Приняв плоскость 12 в качестве плоскости
родства, а направление преобразования перпен-
дикулярным. П], родственно преобразуем эл-
липсоид в сферу (см. рис. 285) Одновременно
преобразуем и конус, проецирующий сечение А В
на плоскость О. В результате сечение АВ_(AjBj 1
эллипсоида преобразуется в сечение АВ(А2В2*
сферы, а вершина S эллипсоида — в полюс
сферы S'. Сечение АВ сферы проецируется из
точки S на плоскость 12 в окружность диамет-
ра А2В2 (см. /146/), которая в результате род-
ственного преобразования не изменилась, так
как инцидентна плоскости родства. Следова-
тельно, эта окружность является сечением двух
конусов: с вершиной S(S2) и с вершиной S(S2).
Таким образом, проекцией на плоскости 12 из
вершины S(S2) сечения АВ(А2В2) эллипсоида
вращения является окружность.
Рассмотрим аналогичную задачу, восполь-
зовавшись гомологическим преобразованием.
Дана нелинейчатая поверхность вращения вто-
рого порядка, рассеченная плоскостью Е
(рис. 341). Преобразуем эту поверхность в
сферу (см. рис. 288), задавшись плоскостью
гомологии 12 и центром гомологии К. Спрое-
цируем сечение Л В из вершины S поверхности
на плоскость 12, а гомологичное ему сечение,
лежащее на сфере, спроецируем на ту же плос-
кость из центра S. ’O6a проецирующих конуса
(с вершинами S и S) пересекаются с плоскостью
гомологии по кривой АВ, которая в соответст-
ствии с /146/ представляет собой окружность.
Таким образом:
/147/ Если центр проецирования — вершина
нелинейчатой поверхности вращения второго по-
рядка, а плоскость проекций перпендикулярна
126
Рис. 342
Рис. 343
оси вращения, то проекцией любого сечения по-
верхности будет окружность.
В зависимости" от условий задачи можно
использовать обе вершины эллипсоида и дву-
полостного гиперболоида врашения. Если же
дан параболоид вращения, целесообразно вос-
пользоваться его несобственной вершиной.
В этом случае (рис. 342) проецирующие прямые
параллельны оси параболоида. Поэтому любое
сечение параболоида проецируется на плоско-
сти, перпендикулярной его оси, в окружность.
/148/ Ортогональной проекцией любого сече-
ния параболоида вращения на плоскости, .перпен-
дикулярной его оси, является окружность.
На рис. 343 изображен отсек нелинейчатой
поверхности второго порядка, ось которой па-
раллельна П2 и наклонена к П, под углом,
отличным от прямого. Поверхность рассечена
горизонтальной плоскостью 12 по эллипсу,
проецирующемуся на П2 в отрезок C2D2 и
фронтально проецирующей плоскостью S, на-
клоненной к ПР Сечение этой плоскостью про-
ецируется на П2 в отрезок А2В2. Приняв 12
в качестве плоскости гомологии, а направление
двойных прямых параллельным оси х, произ-
ведем преобразование сдвига (см. рис. 289),
преобразовав поверхность Т в поверхность Т
с вертикальной осью. (Прямую SE не следует
смешивать с осью поверхности, которая на чер-
теже не показана. На прямой SE расположен
диаметр поверхности, сопряженный ее сечению
плоскостью 12). Сечение АВ при этом преобра-
зуется в сечение АВ, сечение же CD остается
общим для обеих поверхностей (оно лежит в
плоскости гомологии).
Спроецируем сечение АВ и АВ соответствен-
но из центров S’ и S’ на плоскость 12. Обе проек-
ции совпадут и будут представлять собой эл-
липс с осью А'В'. Если родственно преобра- ,
зовать поверхность Ч* в поверхность вращения,
то эллипс с осью CD преобразуется в окруж-
ность. В окружность преобразуется и эллипс
с осью А' В'. Следовательно, оба эллипса по-
добны. (Сказанное следует из того, что после
родственного преобразования вступает в си-
лу /147/.)
/149/ Если плоскость проекций (12) пересекает
нелинейчатую поверхность второго порядка об-
щего вида, а центр проецирования (точка S)
совпадает с одним из концов диаметра поверх-
ности, сопряженного сечению, то проекция любо-
го другого сечения представляет собой фигуру,
подобную сечению поверхности плоскостью про-
екций.
Положения /146/, /147/ и /148/ являются
частными случаями /149/.
Построение точек пересечения прямой с ие-
линейчатыми поверхностями второго порядка,
с использованием вспомогательного 'проециро-
вания из вершины поверхности. Даны отсек не-
линейчатой поверхности второго порядка и
прямая а (рис. 344, а). Заключим прямую во
фронтально проецирующую плоскость 12
(см. /144/). Сечение поверхности проецируется
на П2 в отрезок А2В2. Спроецируем из верши-
ны 5 поверхности как сечение, так и прямую а
на плоскость Е, перпендикулярную оси поверх-
ности. В соответствии с /147/ проекцией сечения
будет окружность диаметра. А ’В' (А^В,; А2В2).
Сечение АВ (А2В2) плоскостью 12, на котором
расположены искомые точки N~n К, инцидент-
но как заданной поверхности, так и проецирую-
щему конусу с вершиной S’ и основанием —
окружностью диаметра AtBt, поэтому задачу
можно свести к определению точек пересече-
ния прямой а с поверхностью конуса (рис. 344, б)
и решить ее в соответствии с описанием к
рис. 332. Раздельные рис. 344, аиб выполнены
для удобства пояснений. Задачу решать нужно
на одном чертеже. Выполните его самостоя-
тельно, руководствуясь рис. 344, в.
Строя точки пересечения прямой с эллипти-
ческим параболоидом, воспользуемся родст-
венным преобразованием (рис. 345). Зададим
родство плоскостью родства 121| П2 и родст-
127
Рис. 344
венными точками С (CJ и С (С]), инцидентны-
ми горизонтальной плоскости. В результате
преобразования эллиптический параболоид ста-
новится параболоидом вращения, прямая а
(см. рис. 46) преобразуется в прямую а (а2; аД
Заключим прямую а во фронтально проеци-
рующую плоскость X (см. /144/) и ортогонально
спроецируем на П] сечение параболоида вра-
щения. Проекцией сечения станет окружность
диаметра (см. /148/). Отметив точки N,
и К] пересечения ортогональных проекций пря-
мой a (а]; а2) и сечения, проведем через них
линии связи (они параллельны двойным пря-
мым родственного преобразования) и отметим
точки их пересечения с первоначально данными
проекциями прямой а.
Если не преобразовывать параболоид, то его
сечение плоскостью Е проецируется на П] в
эллипс, подобный эллипсу — горизонтальной
проекции отсека поверхности. Через сечение и
его проекцию проходит проецирующий ци-
линдр, занимающий относительно параболоида
положение, описанное в связи с рис. 317, что
доказывает /112/.
Построение точек пересечения прямой с по-
верхностями второго порядка с использованием
вспомогательного параллельного проецирования.
Для решения используем эллиптические сечения
поверхностей, (Если сечение — парабола или
128
гипербола, построения усложняются. Мы их
приводить не будем.) Вначале рассмотрим два
приема, позволяющие параллельно проециро-
вать эллипс в окружность, т. е. обеспечить /138/.
Первый прием. На рис. 346 изображен эл-
липс A BCD с осями, соответственно параллель-
ными П] и П2. Проведем через А2 окружность
радиуса R = CD и будем рассматривать ее как
фронтальную проекцию закрытого тора (см.
рис. 230). Проведем через В2 касательную В2Е2
к проекции контура тора. Сечение тора фрон-
тально проецирующей плоскостью, проходя-
щей через точки А и Е, представляет собой ок-
ружность диаметра, равного CD — малой оси
эллипса. Спроецируем это сечение на плос-
кость П5, параллельную ему. Эллипс ABCD
станет сечением прямого кругового цилиндра,
проецирующего окружность диаметра АЕ на
плоскость П5. Следовательно, и эллипс проеци-
руется в ту же окружность A5B5C5D5. Все эл-
липсы, подобные и подобно расположенные
эллипсу ABCD, проецируются на П5 также в
окружности. Если большая ось заданного эл-
липса перпендикулярна П2, прием использо-
вать нельзя.
Второй прием. Проведя через Сх и Dx пря-
мые, перпендикулярные линиям связи, постро-
им окружность A\B\C\D\, касающуюся этих
линий (рис. 347). Проведем через А2, В2, С2 и D2
прямые, параллельные проведенным линиям,
и отметим точки их пересечения с линиями свя-
зи, проходящими соответственно через точ-
ки А\, В\, Ср В пересечении линий отметим
точки A i , В2 и С2 = D2 . Проведем через них
фронтально проецирующую плоскость £2, ко-
торую будем рассматривать как вспомогатель-
ную плоскость проекций. Не трудно убедиться,
что, если эллипс ABCD проецировать в направ-
лении А А" (А2А2 ) на плоскость Q, а затем
полученную фигуру — эллипс А" В" С" D" про-
ецировать ортогонально на П,, то проекцией
эллипса станет окружность AjB'tCjDj. В ре-
зультате таких двух последовательных проеци-
рований все эллипсы, подобные и подобно рас-
положенные эллипсу ABCD, будут проециро-
ваться в окружности.
Второй прием можно использовать и в том
случае, когда большая ось заданного эллипса
перпендикулярна плоскости П2.
Найдем точки пересечения прямой а с отсе-
ком нелинейчатой поверхности второго поряд-
ка, ограниченным эллипсом b (рис. 348). За-
ключим прямую а во фронтально проецирую-
щую плоскость Е. Сечение этой плоскостью
поверхности представляет собой эллипс с боль-
шой осью АВ (А2В2). Малая ось перпендикуляр-
на П2 и проецируется в точку С2 = D2, 'распо-
ложенную в середине отрезка А2В2. Спроеци-
руем эллипс ABCD в окружность, для чего вос-
пользуемся приемом, показанным на рис 347.
В связи с тем, что малая ось не известна, а опре-
деление ее достаточно трудоемко, поступим
так: построим сечение поверхности плоско-
стью параллельной Е. Разделим фронталь-
ную проекцию сечения пополам и проведем
прямую через полученную точку и точку
С2 = D2. В точке Е2 = F2 эта прямая пересека-
ется с фронтальной проекцией эллипса Ь. Будем
Рис. 346
9—940
129
Рис. 348
рассматривать проведенную прямую как фрон-
тальную проекцию плоскости, в которой лежат
малые оси эллипсов, параллельных X. В ней
лежит и диаметр поверхности, сопряженный
сеЧениям. Через точки Е и F проведем пло-
скость, параллельную X, которая пересечет от-
сек поверхности по половине эллипса EF G
(£2 = F2 С2)- Построим окружность диамет-
Рис. 349
pa EF в соответствии с описанием к рис. 347
(второй конец большой оси эллипса для по-
строений не нужен, так как известна малая ось
эллипса и положение его центра Т) и найдем
плоскость П.
Построим окружность, в которую проеци-
руется эллипс A BCD (достаточно найти точ-
ки А\ и В\), проведя через А2 и В2 горизонталь-
ные прямые до пересечения с В2, а из получен-
ных точек A i' и В2 —вертикальные прямые.
Построим проекцию прямой а (возьмем на
прямой точки Н и Ли проделаем построения,
диалогичные выполненным при определении
проекций точек эллипса Вспомогательной про-
екцией прямой станет прямая Н\ L\). Отметив
точки К\ и N\ ее пересечения с окружностью,
проведем построения в обратном порядке (вна-
чале найдем точки N, и К,, а затем N2 и К2).
' /150/ Если при построении точек пересечения
прямой с поверхностью второго порядка прямая
может быть заключена в проецирующую плос-
кость, пересекающую поверхность по эллипсу,
следует этот эллипс спроецировать в окружность
и построить точки, в которых окружность пере-
секается со вспомогательной проекцией прямой.
Пересечение прямой линии и линейчатой по-
верхности с плоскостью параллелизма. Коноид
задан направляющими а и Ь и плоскостью парал-
лелизма О (рис. 349). Определим его пересече-
ние с прямой с. Заключим эту прямую в гори-
зонтально проецирующую плоскость X и по-
строим кривую d пересечения плоскости и ко-
130
ноида (см. /137/ и рис. 308). В точках К и N эта
кривая пересекается с заданной прямой.
Построение точек пересечения прямой с по-
верхностью, задаваемой каркасом, мы рассмот-
рим в гл. VII.
§ 29. ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТЕЙ МЕЖДУ СОБОЙ
Линия' пересечения поверхностей. Такой ли-
нией может быть прямая, плоская и простран-
ственная кривая или любое сочетание из этих
линий.
Построим одну из точек линии пересечения
поверхностей В и 1 (рис. 350). Для этого про-
ведем поверхность 'Р, которая пересекается с О
по кривой а, а с 1 — по кривой Ь. Точка А пере-
сечения кривых а и b принадлежит обеим задан-
ным поверхностям, следовательно, и линии их
пересечения с. Аналогично может быть найдено
любое число точек линии пересечения.
/151/ Чтобы построить линию пересечения
двух поверхностей, следует рассечь их рядом
вспомогательных поверхностей; построив линии
пересечения поверхностей данных н вспомога-
тельных, нужно отметить общие для них точки;
эти точки должны быть последовательно соеди-
нены между собой.
В большинстве случаев в качестве вспомога-
тельных поверхностей используются плоскости,
в частности при определении линии пересечения
плоскостей (см. /84/) и плоскости и поверхности
(см. /137/)
Пересечение между собой линейчатых по-
верхностей, задаваемых одной направляющей и
вершиной. Плоскость, инцидентная вершинам
обеих поверхностей, пересекает каждую из них
по двум (одной) прямым или в точке (см. /105/,
/106/, /107/ и/108/). Сечения по прямым удовле-
творяют рекомендации /138/, поэтому:
/152/ Чтобы построить линию пересечения
двух линейчатых поверхностей, каждая из кото-
рых задана одной направляющей н вершиной,
следует рассечь обе поверхности пучком пло-
скостей с осью, инцидентной вершинам поверх-
ностей. Далее—в соответствии с /151/.
Рис. 350
Пересечение двух конических поверхностей
показано на рис. 351. Соединив точки S и Т
прямой, проведем через нее произвольную пло-
скость *Р, пересекающую обе поверхности. Она
пересекается с плоскостями, которым инци-
дентны направляющие поверхностей (в данном
случае — эллипсы) по прямым NK и МК, а с на-
правляющими — в точках 1 и 2, а также 3 и 4.
Через эти точки проходят образующие задан-
ных поверхностей, по которым их пересекает
плоскость'Р. Остается отметить общие для об-
разующих точки А, В, С и D. В общем случае
их четыре. Выполняя /152/, нужно провести
столько вспомогательных секущих плоскостей,
чтобы обеспечить достаточную точность по-
строений. Среди этих плоскостей должны быть
выбраны такие, которые пересекают одну из
поверхностей по одной образующей (т. е. каса-
ются ее), а вторую по двум образующим Тако-
ва плоскость NME. В точке 5 она пересекает
направляющую поверхности с вершиной Т и
в точках б и 7 — направляющую поверхности с
вершиной 5. В этом случае будут найдены две
точки, принадлежащие линии пересечения по-
верхностей. В приведенном примере можно про-
вести еще одну плоскость, касающуюся поверх-
131
132
ности с вершиной Т и пересекающую поверх-
ность с вершиной 5. Это значит, что все обра-
зующие поверхности с вершиной Т пересека-
ются с поверхностью с вершиной 5. Такое пере-
сечение называется полным. Оно характерно
тем, что линия пересечения распадается на две
ветви. Если не все образующие каждой из по-
верхностей пересекаются с другой поверхно-
стью, линия пересечения не распадается, и пере-
сечение относится к частичным.
Представим себе, что плоскость STONE ка-
сается обеих поверхностей. В этом случае будет
найдена одна точка линии пересечения поверх-
ностей. Если же две плоскости (STONE и
STONF) касаются обеих поверхностей, то ли-
ния пересечения поверхностей распадается на
две ветви, имеющие две общие (двойные) точ-
ки; пересечение относится к полным. Возможен
случай, когда только одна плоскость пучка пе-
ресекается (касается) с обеими поверхностями.
Это значит, что обе поверхности соприкасаются
друг с Другом по прямой или в точке. И наконец,
когда ни одна плоскость, пересекающая одну
из поверхностей, не пересекается (и не касается)
с другой, то поверхности не пересекаются.
На практике направляющие поверхностей
обычно совпадают с основанием тел, ограни-
ченных этими поверхностями. Такие линии
большей частью лежат в проецирующих пло-
скостях. Именно в этом варианте рассмотрим
ряд примеров.
Направляющие двух конических поверхно-
стей расположены во фронтально проецирую-
щих плоскостях В и X, пересекающихся по
прямой а (рис. 352). Проведя прямую ST, по-
строим точки А и В пересечения этой линии с
плоскостями направляющих. Произвольная
плоскость, проходящая через прямую ST и
пересекающая обе поверхности, может быть
задана этой прямой и, например, прямой АС,
лежащей в плоскости II. С плоскостью S она
пересекается по прямой ВС. Отметим точки D,
Е, F и G пересечения прямых АС и ВС с направ-
ляющими поверхностей, проведем через них
образующие и отметим общие точки.
Часто направляющие обеих поверхностей
инцидентны одной плоскости Я (рис. 353).
Прямая ST пересекается с ней в точке М. Все
вспомогательные плоскости, проходящие через
прямую ST, пересекаются с плоскостью Я по
прямым, проходящим через М. Поэтому про-
извольную плоскость пучка вспомогательных
плоскостей можно задать прямой ST и прямой,
инцидентной плоскости Я и точке М. Проведем
прямую MR (M1R1), касательную к направляю-
щей поверхности с вершиной Т. Плоскость
ST О MR пересечет поверхность с вершиной Т
по одной прямой, поверхность с вершиной 5 —
по двум прямым. В результате будут построены
две точки линии пересечения поверхностей.
Проведя вторую касательную, убедимся, что
пересечение частичное (эта касательная не пере-
секает направляющую поверхности е верши-
ной S). Вслед за этим построим необходимое
число плоскостей, пересекающих каждую по-
верхность по двум образующим (например,
плоскость ST О МН)- Прямая МН (М1Н1) пе-
ресекает направляющую поверхности с верши-
Рис. 354
ной Т в точках F (Ft) и Е (Et), направляющую
поверхности с вершиной 5 в точках G (G,) и
Н (Ht). Через эти точки проходят образующие
поверхностей, пересекающиеся между собой в
четырех точках (А, В, Си D), инцидентных ли-
нии пересечения поверхностей.
Для определения точек линии пересечения,
инцидентных контурным образующим поверх-
ностей, нужно провести вспомогательные пло-
скости через эти образующие. На рисунке по-
казаны две из них (всего их восемь): STOMT
и ST О MU. Построенные точки относятся к
опорным.
Если вершины равно удалены от плоскости
направляющих (рис. 354), прямая ST парал-
лельна этой плоскости, следовательно, прохо-
дящие через нее вспомогательные плоскости
пересекутся с плоскостью направляющих по
взаимно параллельным и параллельным пря-
мой ST прямым.
При решении технических задач проекпии
вершин конических поверхностей могут быть
расположены за пределами чертежа. Для по-
строения линии пересечения таких поверхно-
стей воспользуемся родством (рис. 355). Зада-
дим родство плоскостью родства П, проходя-
щей через нижние основания усеченных конусов,
родственными плоскостями S (проходящей
через верхние основания конусов) и Е и на-
правлением преобразования, перпендикуляр-
133
ним nt (см. рис. 333). В результате преобра-
зования горизонтальная проекция фигур не
изменится (почему?). Построим точки S2 и Т2,
а также 5, и Т\ (продлив очерковце относи-
тельно nj образующие поверхностей до их
пересечения). Дальнейшие построения выпол-
ним по изложенному выше.
Пусть направляющие поверхностей лежат в
параллельных плоскостях (рис. 356). Построим
точки М и N пересечения прямой ST с плоско-
стями направляющих. Проведем через N пря-
мую GH, пересекающую направляющую по-
верхности с вершиной Т. Эта прямая (горизон-
таль) совместно с прямой ST определяет одну
из вспомогательных плоскостей, проходящих
через вершины поверхностей. Плоскость
ST П G// пересекается с плоскостью направ-
ляющей поверхности с вершиной 5 по пря-
мой EF, проходящей через М параллельно GH
Дальнейшие построения ясны из чертежа.
Пример, когда направляющие поверхностей
расположены соответственно во фронтальной
и горизонтальной плоскостях, приведен на
рис. 357. Построив точки N н М пересечения
прямой ST с плоскостями направляющих, про-
Рис. 356
134
ведем через точку N прямую 7/G; отметив
точку К ее пересечения с плоскостью J2, по-
строим прямую КМ. В точках Е и F она пере-
секает направляющую поверхности с верши-
ной 5. Строим общие для обеих поверхностей
точки А, В, С, D и т. д.
Характер построений не изменится, если в
качестве одной из поверхностей будет цилинд-
рическая (рис. 358). Прямая, соединяющая вер-
шины поверхностей, пройдет через собствен-
ную точку 5 и несобственную точку Т, т. е.
параллельно образующим цилиндрической по-
верхности.
Когда обе поверхности — цилиндрические
(рис. 359), то все плоскости, проходящие через
их вершины, параллельны между собой; по-
строить одну из них можно так: возьмем произ-
вольную точку А и проведем через нее две
прямые, соответственно параллельные обра-
зующим поверхностей (т. е. проходящие через
их несобственные вершины). Эти прямые опре-
деляют плоскость (см. рис. 179). Построив
точки В и С пересечения прямых с плоскостью
направляющих, соединим их прямой. Любая
плоскость, проходящая через вершины поверх-
ностей, пересечется с плоскостью направляю-
щих по прямой, параллельной ВС (почему?).
Проведя такую прямую а, отметим точки D,
Е, F и G ее пересечения с направляющими по-
верхностей; построив образующие, отметим
общие для них точки.
Описанный способ построения линии пере-
сечения поверхностей называется способом вспо-
могательных секущих плоскостей и может при-
меняться для построения линии пересечения в
любых сочетаниях конических, цилиндрических,
пирамидальных и призматических поверхно-
стей.
Отметим некоторые особенности построе-
ния линии пересечения грайных поверхностей
с конической и цилиндрической и гранных по-
Рис. 358
Рис. 359
верхностей между собой. Если пересекается
гранная поверхность н коническая поверхность
второго порядка, то линия пересечения может
состоять из линий (или отрезков, дуг), указан-
ных в /105/, /106/, /107/при пересечении гран-
ной и цилиндрической поверхности второго по-
рядка она может состоять из линий, приведен-
ных в /108/. Построим точки, в которых ребра
гранной поверхности пересекаются с кониче-
ской или цилиндрической поверхностью. До-
статочно провести через соответствующие реб-
ра вспомогательные плоскости. В приведенном
на рис. 360 (сравните с рис. 353) примере пло-
скость проведена через ребро АТ. В точках D
и Е ребро пересекается с конической поверх-
ностью.
Рис. 360
135
Линия пересечения двух гранных поверх-
ностей, каждая из которых задается одной на-
правляющей вершиной, в общем случае — про-
странственная ломаная. Достаточно найти точ-
ки, в которых ребра одной поверхности пересе-
каются с гранями второй, и наоборот. Если на-
правляющие поверхностей (основания тел) рас-
положены в проецирующих плоскостях, можно
воспользоваться построениями, приведенными
на рис. 351—359, в противном случае в соот-
ветствии с рис. 330.
Построим линию пересечения поверхностей
призмы с боковыми ребрами а, Ь, с и пирами-
ды ABCS (рис. 361). Последовательно заклю-
чив ребра пирамиды в горизонтально или фрон-
тально проецирующие плоскости (например, £2),
устанавливаем, что с гранями призмы пересе-
каются все ребра пирамиды. Вслед за этим най-
дем, что с гранями пирамиды пересекается реб-
ро призмы с. Определив точки пересечения
ребер и граней, выясним, какие из них принад-
лежат одним и тем же граням одной из поверх-
ностей и последовательно соединим их прямы-
ми линиями.
/153/ Чтобы построить линию пересечения
гранных поверхностей, следует найти точки пе-
ресечения ребер первой поверхности с гранями
второй и ребер второй — с гранями первой, по-
лученные точки соединяются путем «обхода»
по граням одной из поверхностей.
Если одна из поверхностей — проецирую-
щая, то построение линии ее пересечения с дру-
гой поверхностью упрощается — одна проек-
ция линии пересечения становится известной
(см. /22/). На рис. 362 дана проецирующая приз-
матическая поверхность, ее грани перпендику-
лярны Пр Опорными являются точки А и В,—
крайние правая и левая точки линии пересече-
ния, С и D, в которых линия пересечения пере-
ходит от видимой к невидимой части, а также
Е и F пересечения ребра призматической по-
верхности с цилиндрической. Фронтальные про-
екции этих точек, в равной мере как и промежу-
точных, можно построить, проведя через них
вертикальные вспомогательные плоскости
(см. /151/). Проведем горизонтально проеци-
рующую плоскость £1; с цилиндрической по-
верхностью она пересекается по образующим а
и Ь, с призматической — по образующей с.
Чтобы провести фронтальные проекции обра-
зующих цилиндрической поверхности, постро-
им половину нормального сечения поверхности
(проекцию на плоскость П4) и отметим на нем
образующую («4 или />4). Расстояние е от нее
до оси сечения равно расстоянию от фронталь-
ной проекции оси цилиндра до фронтальных
проекций образующих а и Ь. В пересечении
фронтальных проекций образующих обеих по-
Рис. 361
136
верхностей отметим точки М2 и К2, принадле-
жащие фронтальной проекции линии их пере-
сечения.
На рис. 363 проецирующей является цилинд-
рическая поверхность. Известна фронтальная
проекция линии пересечения; для построения
горизонтальной проекции целесообразно рас-
сечь поверхности горизонтальными плоскостя-
ми — с цилиндрической поверхностью они пе-
ресекутся по. образующим, с конической — по
окружностям. Например, плоскость П рассе-
кает коническую поверхность по окружности а,
цилиндрическую — по прямым Ьи с. Прямая b
с окружностью пересекается в точках А и В,
прямая с не пересекается. Точки А и В принад-
лежат линии пересечения поверхностей. В точ-
ках Си D линия пересечения при взгляде сверху
переходит от видимой части к невидимой; они
построены с помощью плоскости S. Высшая и
низшая точки (F и £) линии пересечения опре-
деляются по их фронтальной проекции, которая
известна.
Определение видимой части пересекающихся
поверхностей. Для этого нужно использовать
конкурирующие точки, принадлежащие конту-
рам обеих поверхностей. Определим видимость
конусов, изображенных на рис. 357. Рассмотрим
проекции контурных относительно П2 обра-
зующих SA и ТВ (рис. 364). Точка кажущегося
пересечения С2 = D2, конкурирующие точки С
и D принадлежат соответственно прямым ТВ
и SA. При взгляде спереди точка С видаа, сле-
довательно, видна и прямая ТВ. Исследовав
другие точки кажущегося пересечения, найдем
видимые части поверхностей.
При определении видимости самой линии
пересечения поверхностей следует взять на од-
ном из ее участков точку (Е в приведенном при-
мере) и определить, какой стороне каждой по-
верхности она принадлежит. Если она распо-
ложена на видимой стороне обеих поверхно-
стей, то видима и точка, если она расположена
на невидимой части хотя бы одной поверхно-
сти, то точка не видна. Переход от видимой
части линии пересечения к невидимой располо-
жен в точке, лежащей на контурной образую-
щей поверхности (точка F; см.
/154/ Чтобы определить видимые части пере-
секающихся поверхностей, следует рассмотреть
конкурирующие точки, принадлежащие конту-
рам обеих поверхностей.
/155/ Точка, принадлежащая видимой части
линии пересечения, расположена на видимой ча-
сти как одной, так и другой поверхности.
Пересечение поверхностей вращения между
собой и с другими поверхностями. Если оси по-
верхностей вращения совпадают, они называ-
ются соосными (вытянутый эллипсоид, кониче-
ская поверхность и сфера на рис. 365). Точки А
и В расположены в плоскости главных меридиа-
нов двух пересекающихся поверхностей. Вра-
щаясь вокруг оси, точки образуют общие для
смежных поверхностей окружности — линии их
пересечения.
/156/ Соосные поверхности вращения пере-
секаются по окружностям.
За ось вращения сферы может быть принят
любой ее диаметр, поэтому /156/ для сферы
следует формулировать так:
/157/ Если центр сферы расположен на оси
поверхности вращения, то эта поверхность и
сфера пересекаются по окружности (или по ок-
ружностям).
137
Рис. 365
На этом основан один из способов построе-
ния линии пересечения двух поверхностей, на-
зываемый способом вспомогательных секущих
сфер.
/158/ Если две поверхности второго порядка
пересекаются по одной плоской кривой, то они
пересекаются и еще по одной, также плоской
кривой*.
/159/ Две поверхности второго порядка, имею-
щие общую плоскость симметрии, пересекаются
по кривой, которая проецируется на эту плос-
кость или параллельную ей в кривую второго
порядка или в ее вырожденные варианты.
Построим линию пересечения двух поверх-
ностей вращения — вытянутого эллипсоида и
цилиндра, оси которых пересекаются в точке О
и параллельны П2 (рис. 366). Для решения до-
статочно фронтальных проекций поверхностей.
Построим сферу с центром О и найдем линии
* Доказательства /158/ и /159/ см. в кн.: Ч е т-
верухинаН. Ф и др. Начертательная геомет-
рия. М., 1963.
пересечения сферы с эллипсоидом и цилинд-
ром. В соответствии с /157/ это окружности,
которые на П2 проецируются в отрезки прямых
соответственно А2В2, C2D2, E2F2 и G2H2. От-
метим общие точки К2 и М2, представляющие
собой фронтальные проекции в каждом случае
двух (почему?) точек, принадлежащих обеим
поверхностям. Изменив диаметр сферы, но
оставив ее центр в точке О, получим другие
точки линии пересечения поверхностей и т. д
К ним следует присоединить точки, в которых
пересекаются главные меридианы. Проекцией
линии пересечения являются дуги гиперболы
(см. /159/).
Построим линию пересечения открытого
тора и конической поверхности вращения
(рис. 367). Ось конической поверхности и кривая
ось тора расположены в плоскости, параллель-
ной П2. Построим сечение тора плоскостью Q,
проходящей через его прямую ось; оно пред-
ставляет собой окружность, которая проециру-
ется в отрезок Л2В2 Из центра С сечения про-
ведем перпендикуляр к его плоскости до пере-
сечения с осью конической поверхности в точ-
ке О (докажите, что перпендикуляр и ось пере-
секаются). Построим сферу с центром в О
. радиуса АО = О В. Окружность диаметра АВ —
сечение тора — расположена на сфере, следо-
вательно, эту линию можно рассматривать как
линию пересечения тора и сферы. С конической
поверхностью сфера пересекается по окружно-
сти, проецирующейся в отрезок E2D2. Оба
сечения имеют две общие точки, проекции кото-
рых совпадают (F2). Взяв другое сечение тора,
найдем новые точки и т. д. Линия пересечения
поверхностей проходит через точки, в которых
пересекаются главные меридианы.
Иногда описанный прием можно использо-
вать, когда только одна из пересекающихся
поверхностей образована вращением. На
рис. 368 показаны пересекающиеся прямая кру-
говая цилиндрическая поверхность и кониче-
ская поверхность второго порядка. Возьмем
произвольное круговое сечение конической по-
верхности, проецирующееся на П2 в отрезок
А2В2. Из его центра С восстановим перпен-
дикуляр к плоскости сечения до встречи с осью
138
Рис. 368
цилиндрической поверхности в точке О. Прове-
дя сферу с центром О радиуса АО = ВО, по-
строим вторую линию пересечения сферы и
конической поверхности, также окружность
(см /158/), проецирующуюся в отрезок D2E2
и линию пересечения сферы и цилиндрической
поверхности; она проецируется в отрезок E2G2.
Отметим общие точки К и М. Возьмем другое
сечение, параллельное АВ- повторим построе-
ния и т. д. Линия пересечения проходит через
точки пересечения контурных образующих. Для
приведенного примера справедливо /159/. Сече-
ния конической поверхности, проецирующиеся
в отрезки А2В2 и E2D2, являются антипарал-
лельными. Если же известно расположение кру-
гового сечения, следует вначале поступить в
соответствии с /141/.
Построим линию пересечения открытого
тора с цилиндрической и призматической по-
верхностями (рнс. 369). Рассечем поверхности
фронтальными плоскостями. Например, пло-
скость fl пересекает тор по окружностям а и d,
призматическую поверхность — по образую-
щим b и с, а цилиндрическую поверхность —
по окружности е. Отметим точки пересечения
соответствующих линий (точки А, В, Си Л).
Поступая аналогично, получим необходимое
число точек линии пересечения. Среди них
должны быть точки, в которых линия пересече-
ния переходит от видимой части к невидимой
(точки А, В, С, Е, F; см. /154/ и /155/), точки
пересечения ребер призматической поверхно-
сти с тором (точки К, G, Н, М) и двойная точ-
ка D.
При построении линии пересечения поверх-
ности вращения с конической поверхностью об-
щего вида (в том числе и с конической поверх-
ностью второго порядка) удобно рассекать
поверхности вспомогательными коническими
поверхностями (см. /151/). На рис. 370 заданы
сфера и коническая поверхность с вершиной 5.
Рассечем сферу горизонтальной плоскостью £1.
Рассматривая полученную окружность с как на-
правляющую, а точку 5 — как вершину вспомо-
гательной конической поверхности, построим
линию пересечения этой поверхности (окруж-
ность) с плоскостью L (достаточно найти точ-
ку О' в пересечении прямой SO с плоскостью L
и точку С пересечения контурной относитель-
но П2 образующей вспомогательной поверх-
ности с той же плоскостью). Отметим точки A t
и В, пересечения окружности с центром О\ и
эллипса йр Через них проходят прямые /IpS)
и BlS1 — проекции образующих обеих кониче-
ских поверхностей, по которым Ьни пересека-
ются между собой. Проведя эти прямые, отме-
тим точки N и К их пересечения с окружностью с
< Рис. 369
139
t
(находим точки N2 и К2, а затем, не строя гори-
зонтальной проекции окружности с, точки Nx
и К,). Аналогично найдем другие точки линии
пересечения заданных поверхностей.
Если поверхность вращения пересекается с
цилиндрической поверхностью, то вспомога-
тельной поверхностью должна быть цилиндри-
ческая. Исследуйте такой пример самостоя-
тельно.
Построим линию пересечения однополост-
ного гиперболоида с призматической поверх-
/
ностью (рис. 371). Зададим родство плоскостью
родства £2 и родственными точками С (CJ и
С (СД т. е. Н (S(^ £1; С; С), и преобразуем
однополостный гиперболоид общего вида в
однополостный гиперболоид вращения; одно-
временно преобразуем и призматическую по-
верхность. Подобные преобразования выпол-
нялись ранее (см. рис. 285, 287; 321; 345 и др.),
поэтому ограничимся описанием второй части
задачи. Рассечем преобразованные поверхности
горизонтальной плоскостью S, которая с одно-
полостным гиперболоидом вращения пересе-
кается по окружности, с призматической по-
верхностью — по ее образующим. В пересече-
нии этих линий расположены точки А (А2; Аг)
и В (В2, В,). Найдем точки At и Blt соответст-
венно родственные точкам At и В2. Аналогично
строятся другие точки линии пересечения, среди
которых должны быть опорные, лежащие на
ребрах призматической поверхности и контуре
поверхности второго порядка.
Особые случаи пересечения поверхностей вто-
рого порядка.
/160/ Если две поверхности второго порядка
соприкасаются друг с другом в двух точках,
то линия их пересечения распадается на две
кривые второго порядка, плоскости которых
проходят через точки соприкосновения.
Это положение носит название теоремы о
двойном прикосновении. Из нее вытекает теоре-
ма Г. Монжа:
/161/ Две поверхности второго порядка, опи-
санные или вписанные в третью, пересекаются
по линии, распадающейся на две кривые второго
порядка или их вырожденные варианты. Плоско-
сти кривых проходят через точки пересечения
линий*.
Изображенная на рис. 372 цилиндрическая
поверхность соприкасается в точках А и В с
конической. В соответствии с /160/ линия пере-
сечения поверхностей распадается на две пло-
* Доказательства /160/ и /161/ см. в кн.: Ч е т-
верухинаН. Ф. и др. Начертательная геомет-
рия. М., 1963.
140
ские кривые (эллипсы), плоскости которых
перпендикулярны П2. Фронтальные проекции
эллипсов проходят через точки пересечения
проекций контура поверхностей и через проек-
цию точек соприкосновения А2 = В2. Горизон-
тальные проекции эллипсов могут быть по-
строены как плоские сечения цилиндрической
или конической поверхности.
Иллюстрацию /161/ ограничим поверхно-
стями второго порядка, описанными вокруг
общей сферы, т. е. поверхностями вращения.
Конические поверхности с вершинами S и Г
описаны вокруг сферы с центром О (рис. 373);
пересекающиеся в точке О оси поверхностей
параллельны П2. Построим проекции А2В2 и
C2D2 линий пересечения сферы, вписанной в
конические поверхности, с этими поверхностя-
ми (см. /157/) и найдем точку Е, инцидентную
линии пересечения конических поверхностей.
Построим другую сферу с центром в точке О
радиуса большего, чем радиус вписанной сфе-
ры. С коническими поверхностями она пересе-
кается по окружностям, которые проецируются
в отрезки F2G2 и Н2К2, отметим точку М,
инцидентную линии пересечения конических по-
верхностей. Соединим прямыми точками А2
и С2, а также F2 и К2 и рассмотрим треугольни-
ки А2С2Е2 и F2K2M2. Они гомологичны; центр
гомологии точка R2, ось — несобственная пря-
мая плоскости главных меридианов поверх-
ностей. Следовательно, точки Е2 и М2 лежат
на прямой, проходящей через точку R2. Если бы
мы взяли еще одну сферу произвольного диа-
метра, то построенная с ее помощью проекция
точки вновь оказалась бы на прямой, проходя-
щей через R2 и Е2. Следовательно, проекцией
линии пересечения конических поверхностей
является прямая (или отрезок прямой), а это
возможно лишь в случае, когда линия пересе-
чения инцидентна проецирующей плоскости.
Отсюда — линия пересечения конических по-
верхностей — плоская кривая. В соответствии
с /158/ есть еще одна плоская кривая, принад-
лежащая обеим поверхностям (ее проекция
проходит через точки Ь2 и N2). Обе конические
поверхности имеют общую плоскость симмет-
рии, параллельную П2; проекция линии их
пересечения на этой плоскости представляет
собой вырожденную гиперболу (см. /159/).
/162/ Если две поверхности второго порядка
описаны вокруг одной сферы в общая плоскость
симметрии поверхностей параллельна плоскости
проекций, то на эту плоскость линия их пересе-
чения проецируется в виде двух прямых (отрез-
ков), проходящих через проекции точек пересе-
чения контурных образующих пересекающихся
поверхностей.
Две конические поверхности, описанные во-
круг общей сферы и пересекающиеся между со-
бой по двум эллипсам, показаны на рис. 373,
по эллипсу и параболе — на рис. 374. Пересе-
чение таких поверхностей по эллипсу и гипер-
боле изображено на рис. 375. В варианте
(рис. 376) конические поверхности пересекаются
по эллипсу и прямой (это двойная прямая —
вырожденная парабола).
Пересечение поверхностей второго порядка с
линейчатыми поверхностями. Построим линию
пересечения нелинейчатой поверхности второго
порядка с линейчатой поверхностью. Для при-
мера возьмем трехосный эллипсоид с двумя
осями, параллельными соответственно П, и П2,
и третьей осью, параллельной П2 и наклонен-
ной к П1 под некоторым углом (рис. 377).
Пусть сечение эллипсоида горизонтальной пло-
скостью П представляет собой окружность
Рис.. 375
141
(если бы это был эллипс, следовало бы родст-
венно преобразовать его в окружность). С эл-
липсоидом пересекается гиперболический пара-
болоид ABCD с плоскостью параллелизма S.
Проведем на гиперболическом параболоиде
прямые, параллельные S,. и построим точки
пересечения каждой прямой с эллипсоидом.
Для этого конец диаметра, сопряженного сече-
нию поверхности плоскостью £1, точку S будем
рассматривать как центр проецирования (см.
/149/). Заключим прямые гиперболического па-
раболоида во фронтально проецирующие пло-
скости и отметим сечения этими плоскостями
эллипсоида. Посмотрим проекции как прямых,
так и сечений из центра S на, плоскости ПР
На рис. 377 показано построение точек N и К
пересечения прямой а с эллипсоидом. Она за-
ключена во вспомогательную плоскость S',
пересекающую эллипсоид по эллипсу, проеци-
рующемуся на П2 в отрезок E2F2. Построения
выполнены в соответствии с описанием к
рис. 344. Взяв ряд других прямых гиперболи-
ческого параболоида, повторим построения.
Найденные точки соединим плавной кривой.
Если позволяет место на чертеже, можно
воспользоваться приемом, иллюстрированном
на рис. 348. Построим линию пересечения
(рис. 378) нелинейчатой поверхности второго
порядка с цилиндрической поверхностью. В со-
ответствии с /138/, 1\А41 и /151/ рассечем обе
поверхности вспомогательной плоскостью У,
параллельной образующим цилиндрической по-
верхности. С цилиндрической поверхностью
эта плоскость пересекается по прямым а и Ь,
с поверхностью второго порядка — по эллипсу,
проецирующемуся на П2 в отрезок А2В2. По-
строив плоскость £2 (см. рис.348) или приме-
нив построения, показанные на рис. 346, спро-
ецируем эллипс АВ в окружность диаметраЛ, В[.
Одновременно найдем, проекции прямых а и Ь.
Для этого на прямой а возьмеМ точки С и Е.
В результате двух последовательных проеци-
рований их проекциями станут точки С, и Е\.
Через них проходит прямая а\. Построив про-
екцию £>i точки £>, проведем через нее пря-
мую Ь\ параллельно а\ (почему параллельно?).
Прямая а\ пересекается с окружностью ра-
диуса A^B'l в точках N\ и К[, прямая b не пе-
ресекается. Проделав построения в обратной
последовательности, найдем точки и Kt,
а также N2 и К2. Построив ряд плоскостей,
параллельных S, найдем необходимое число
точек, инцидентных линии пересечения поверх-
ностей, и соединим их плавной кривой.
Приведенный на рис. 378 способ целесооб-
разно применять, когда линейчатой является
Рис. 377
Рис. 376
142
Рис. 378
\
цилиндрическая или призматическая поверх-
ность, поэтому нет нужды для каждого сечения
поверхности второго порядка искать плос-
кость, подобную плоскости fl.
На рис. 379, а изображены две поверхности
вращения второго порядка со скрещивающими-
ся осями, параллельными П2: параболоид и
конус. Найдем на обеих поверхностях подобные
эллиптические сечения. Для этого впишем в па-
раболоид сферу произвольного диаметра и па-
раллельно перенесем конус так, чтобы сфера
была вписана и в него. Построения проводим
только на фронтальной проекции- фигур. Они
сводятся к проведению касательных к окруж-
ности— проекции сферы, параллельных про-
екциям контурных относительно П2 образую-
щих конуса. Вершина конуса S переместится в
точку S'. Заданный параболоид и перемещенный
конус пересекаются по двум эллипсам, проеци-
рующимся на П2 в отрезки прямых А2В2 и
C2D2 (см. /161/ и /162/). Сечения обеих поверх-
ностей плоскостями, параллельными сече-
нию АВ (или CD), представляют собой эллип-
сы, подобные эллипсу АВ (или CD). Сказанное
относится и к заданному конусу с вершиной S,
так как при параллельном перемещении по-
верхности фигура сечения не меняется.
Рассуждаем аналогично относительно лю-
бых поверхностей вращения второго порядка,
поэтому:
/163/ На двух поверхностях вращения вто-
рого порядка, оси которых скрещиваются, могут
быть найдены взаимно параллельные подобные
эллиптические сечения.
Дальнейшие построения вынесем на отдель-
ный чертеж (рис. 379, б). Рассечем обе заданные
поверхности плоскостью fl, параллельной пло-
скости сечения АВ. Используя прием, показан-
ный на рис. 346 (или на рис. 347), построим на
плоскости П5 проекции сечений обеих поверх-
ностей, представляющие собой окружности
(в данной задаче нужно учитывать /148/). Они
пересекаются в точках N5 и К5. Построим точ-
ки ЛГ2 и К2, а затем N, и К2. Взяв несколько
плоскостей, параллельных сечению АВ, найдем
необходимое число точек линии пересечения
поверхностей.
Описанный способ удобен в случае, когда
проекция контура одной из поверхностей пред-
ставляет собой две пересекающиеся (конус) или
параллельные (цилиндр) прямые. Когда пере-
секаются поверхности, контур которых про-
ецируется в кривую второго порядка, Следует
поступить иначе. На рис. 380 изображены эл-
липсоид и параболоид вращения со скрещиваю-
щимися осями, параллельными П2. Восполь-
зуемся /112/ и, вписав в эллипсоид сферу, по-
строим цилиндр вращения, описывающий сфе-
ру. Ось цилиндра параллельна оси параболои-
да. Построим линии пересечения эллипсоида и
цилиндра — эллипсы, проецирующиеся на П2
в отрезки А2В2 и C2D2. Проведем плоскость fl,
параллельную, например, эллипсу АВ. Она рас-
сечет заданные поверхности по эллипсам, про-
143
144
5)
10—940
145
ецирующимся в отрезки E2F2 и G2H2. Постро-
им окружности — проекции эллипсов на пло-
скости П5, перпендикулярной оси цилиндра.
Найдя общие для окружностей точки N5 и К5,
установим проекционную связь и построим
фронтальные, а затем горизонтальные проек-
ции точек N и К.
И наконец, покажем, как можно построить
точки, инцидентные линии пересечения двух
гиперболоидов вращения — однополостного и
двуполостного; их асимптотические конусы за-
даны (рис. 381’, а). Решение выполним с уче-
том /115/. На свободном месте чертежа прове-
дем окружность — проекцию сферы произволь-
ного диаметра (рис. 381, б). Параллельно пере-
местим конус с вершиной 5 так, чтобы он описал
сферу. Также поступим с конусом с вершиной Т.
Построим линии пересечения конусов — эллип-
сы, проецирующиеся на П2 в отрезки Л2В2
и C'2D2. Проведем плоскость О, параллельную
сечению C'2D2, она пересечет заданные поверх-
ности по эллипсам, подобным эллипсу C'2D2.
Проекциями эллипсов являются отрезки Е2Н2
и G2F2. Далее поступим в соответствии с описа-
нием к рис. 379 (построения не показаны. Предо-
ставляем выполнить их читателю).
§ 30. ПЕРЕСЕЧЕНИЕ КРИВОЙ
ЛИНИИ С ПОВЕРХНОСТЬЮ
/164/ Чтобы построить точки (точку) пере-
сечения кривой линии с поверхностью, нужно за-
ключить кривую во вспомогательную поверх-
ность, найти линию пересечения данной поверх-
ности и вспомогательной и отметить точки (точ-
ку), в которых линия пересекается с заданной
кривой.
(Сравнйте /164/ с /87/ и /144/. Какое положе-
ние является более общим?)
Перед тем как искать точки пересечения кри-
вой с поверхностью, нужно установить область
возможного пересечения. При взгляде спереди
на кривую а и коническую поверхность (рис. 382)
можно установить, что кривая не может пере-
сечься с поверхностью левее точки А и правее
точки В, принадлежащих кривой. При взгляде
сверху область возможного пересечения рас-
положена в пределах между точками С и D.
Выделим ту часть кривой, в которой она может
пересечься с поверхностью; это дуга A D.
На П2 кривая а проецируется цилиндриче-
ской поверхностью £1, для которой кривая слу-
жит направляющей, образующая перпендику-
лярна, Пг Будем рассматривать эту поверх-
ность как вспомогательную. Так как она —
проецирующая, то одна (горизонтальная) про-
екция линии пересечения известна. Построив
ее фронтальную проекцию (см. /100/; точка Е
инцидентна образующей SE), найдем точки К
и М, в которых пересекаются фронтальные про-
екции данной кривой и линии пересечения по-
верхностей конуса и цилиндра. Построим точ-
ки К, и ЛГр
Часть вторая
ПАРАЛЛЕЛЬНЫЕ
И
ЦЕНТРАЛЬНЫЕ
| ПРОЕКЦИИ
НА ОДНОЙ ПЛОСКОСТИ
ГЛАВА VII
ПРОЕКЦИЯ С ЧИСЛОВЫМИ ОТМЕТКАМИ
§ 31. ТОЧКА И ПРЯМАЯ ЛИНИЯ
Проекции точки и прямой. В строительном
деле проекции с числовыми отметками исполь-
зуются для изображения больших пространств,
например участков земной поверхности, с рас-
положенными на них сооружениями. Этот вид
проекций отличается тем, что позволяет с до-
статочной для практики точностью и нагляд-
ностью изображать предметы, горизонтальные
размеры которых относительно больше верти-
кальных. Проекции с числовыми отметками
выполняются на основе прямоугольного про-
ецирования на одну плоскость, в качестве кото-
рой обычно принимается П,. В отличие от ил-
люстраций в первой части книги чертежи в
проекциях с числовыми отметками выполня-
ются в масштабе уменьшения.
На рис. 383 дано наглядное изображение
точки А, прямых CD, ап плоскости проекций П,.
Расстояния от точек до плоскости П, обозначе-
ны буквой h с правым нижним индексом, соот-
ветствующим наименованию точки.
Известно (см /28/), что одна проекция не
определяет положения точки в пространстве.
Поэтому одновременно с обозначением проек-
ции точки указывается в скобках расстояние от
точки до плоскости проекций, называемое от-
меткой (рис. 384). В ортогональных проекциях
"мы это расстояние именовали координатой Z
(см. /31/). ----
Если точки расположены над плоскостью
проекций (точки А и D на рис. 383), то их от-
метки считаются положительными, если под
плоскостью проекций — отрицательными. От-
метки точек, инцидентных плоскости проекций,
называются нулевыми.
Вместо буквенного обозначения отметок в
скобках проставляются числа (рис. 385) или,
когда это не мешает правильному чтению чер-
тежа, сами точки и их проекции обозначаются
числами, выражающими отметки. Индекс пло-
скости проекций не ставится (рис. 386). Поло-
жительные отметки проставляются без всякого
знака, отрицательные со знаком «—» (минус),
а нулевые иногда снабжаются двумя знака-
ми «+» (плюс — минус)*. Такова отметка точ-
ки В на рис. 383, 384, 385. Чертеж, на котором
даны проекции точек и указаны их отметки,
является обратимым /см. /31/).
ГТрямая общего положения задается проек-
циями двух инцидентных ей точек с указанием
их отметок. Она может быть названа С (—7)
D (5) (на рис. 385) или (—7) (5), если такое обо-
значение не приведет к неправильному проч-
тению чертежа (рис. 386)**. В приведенных
иллюстрациях точка С расположена ниже, чем
точка D. В таких случаях говорят, что пря-
мая CD имеет спуск. от точки D к точке С
Направление спуска, когда это необходимо,
указывается стрелкой, острие которой обра-
щено от точек с большими отметками к точкам
с меньшими отметками.
Прямую общего положения можно обозна-
чить, так же как и в ортогональных проекциях,
строчной буквой латинского алфавита (напри-
мер, прямая b на рис. 387). Чтобы сделать
чертеж обратимым, нужно задать хотя бы одну
точку прямой, угол наклона прямой к плоско-
* На чертежах зданий и сооружений в соответ-
ствии с. ГОСТ 2.307—68 положительная отметка
снабжается знаком «+» (плюс) у нулевой отметки
знак не ставится.
** Скобки проставляются только в тексте,
но не на чертеже.
148
сти Пх и направление спуска Вместо угла часто
задается^укион ппямрй. обозначаемый буквой i
(рис. 388). Он равен тангенсу угла наклона пря-
мой к горизонтальной плоскости. Обозначение
уклона должно быть дополнено стрелкой, ука-
зывающей направление спуска прямой. Гори-
зонталь будем обозначать буквой h с указани-
ем в скобках соответствующей отметки, на-
пример h (5), или только отметкой (5) Верти-
кальная прямая проецируется на плоскость в
точку, ’ поэтому ее положение в пространстве
становится определенным, если дана ее про-
екция (прямая а на рис. 383, 384 и 385). Отрезок
вертикальной прямой задается концевыми точ-
ками с указанием их отметок.
Чертеж, выполненный в проекциях с число-
выми отметками, снабжается линейным масшта-
бом (см. рис. 384, 385 и др.) или числовым мас-
штабом.
Градуирование прямой. Проекция отрезка
прямой называется его заложением. Например,
отрезок £>j (см. рис. 383) представляет собой
заложение отрезка BD. Уклон i прямой BD
равен отношению длин отрезков DDr к B1D1,
или, иначе, уклон прямой равен отношению раз-
ности отметок концевых точек любого отрезка
прямой к его заложению. Если разность отметок
концевых точек отрезка равна единипе длины
(рис. 389), то заложение отрезка называется
интервалом прямой линии. Интервал обознача-
ется буквой I; i = 1/1.
/165/ Уклон прямой линии обратно пропор-
ционален ее интервалу.
Зная две из трех величин (угол, интервал
или уклон прямой линии), можно найти третью.
От изображения фигур в проекциях с чис-
ловыми отметками можно перейти к эпюру.
Ось проекций проводится в любом месте чер-
тежа. Совместив П2 с П1; получим эпюр. Роль
горизонтальной проекции фигуры в нем играет
ее проекция с числовыми отметками.
Нужно определить угол наклона прямой
А (4, 6) В (—2, 7) (рис. 390). Примем ось х совпа-
дающей с проекцией прямой и, проведя линии
связи, отложим от оси отметки точек координа-
ты Z). Положительное направление отсчета мо-
жет быть принято в любую сторону от оси х,
противоположное ему "будет отрицательным.
Отложив на перпендикуляре к отрезку АВ в
точке А отметку этой точ|И, равную 4,6 еди-
ницам, а в точке В ее отметку —2,7 единицы
(в противоположном направлении), соединим
полученные точки А2 и В2 прямой линией.
Так как отрезок АВ лежит во фронтальной
149
плоскости, его фронтальная проекция равна
отрезку в натуре, а угол между ней и осью
проекций равен искомому (см. /39/).
Построим на горизонтальной проекции пря-
мой проекции точек, отметки которых выра-
жаются целыми числами и отличаются на еди-
ницу. Для этого на линии связи А2А (4,6) от
точки А (4,6) последовательно отложим от-
резки, равные единице длины, и через получен-
ные точки проведем прямые, параллельные
оси х, до пересечения с прямой А2В2. Через
полученные точки проведем линии связи до
пересечения с горизонтальной проекцией пря-
мой в точках, отметки которых соответственно
равны 1, 2 и т. д. единицам длины. Очевидно,
что отрезки (0) (1), (1) (2), (2) (3) и другие равны
между собой. Это интервал линии. Отрезок
' А (4,6) (4) равен 0,6 интервала.
Когда уклон линии небольшой, построения
недостаточно точны. Увеличим вертикальный
масштаб по сравнению с горизонтальным. На
рис. 390 он увеличен в три раза. Отложив на
линиях связи отметки точек А и Вс учетом этого
масштаба, получим точки А 2 и В2. Отрезок А 2В2
не равен натуральной величине отрезка АВ.
Угол между прямыми А2В2 и АВ также не ра-
вен углу наклона прямой к плоскости П2.
Однако точки А и А, В и В, а также все осталь-
ные проекции точек прямой расположены в
проекционной связи. Такой чертеж называется
родствеино преобразованным эпюром прямой АВ.
" Родственно преобразованный эпюр пбзво-
ляет точнее строить проекции точки с отметкой,
выраженной дробным числом. Построим точ-
ку с отметкой 2,3. Отложим на прямой А (4,6) —
А2 заданную отметку точки с учетом масштаба.
Через полученную точку проведем прямую па-
раллельно оси х до пересечения с преобразован-
ной фронтальной проекцией прямой. Проведя
через полученную точку линию связи, в ее пере-
сечении с горизонтальной проекцией прямой от-
метим искомую точку 2,3.
Определение точек прямой с отметками,
выраженными целыми числами и отличающи-
мися друг от друга на единицу длины (или на
величину, кратную целому числу), называется
градуированием прямой линии, Графический при-
ем градуирования прямой показан на рис. 390.
Если отметки концевых точек отрезка, которым
задана прямая, целые числа, достаточно раз-
делить проекцию отрезка на число, равное раз-
ности отметок концевых точек (интервал пря-
мой — постоянная величина). Если отметки
концевых точек — дробные числа, можно раз-
делить проекцию отрезка на разность отметок,
увеличенную в десять раз. Разность отметок
точек А и В составляет 7,3 линейной единицы.
Проекцию отрезка нужно разделить на 73 ча-
сти. Отложив от А (4,6) шесть частей, получим
точку с отметкой 4, затем, отложив 10 частей, —
точку с отметкой 3. Отрезок 4—3— это интер-
вал прямой. Его следует откладывать вплоть
до точки с отметкой —2.
Взаиморасположение прямых. Чтобы опре-
делить взаиморасположение прямых А В и CD
(рис. 391), нужно решить, кажущимся или дей-
ствительным является пересечение прямых в
точке E = F. Предположим, что точки Е и F,
инцидентные соответственно прямым АВ и CD,
являются конкурирующими. Приняв П2, про-
ходящей через АВ, и П4, проходящей через CD,
построим фронтальные проекции отрезков. От-
метка точки Е равна длине отрезка Е2Е, точ-
ки F — отрезка F^F. Отметка точки Е меньше,
чем точки F, следовательно, точки Е и F —-
конкурирующие, а изображенные прямые —
скрещивающиеся. В точке кажущегося пересе-
чения видна прямая CD.
Пересекающиеся прямые изображены на
рис. 392. В этом легко убедиться, построив их
фронтальные проекции и определив отметку
точки их пересечения.
Когда нужно определить точку пересечения
прямых, инцидентных вертикальной плоскости,
эту плоскость используют в качестве плоскости
проекций и совмещают ее с Пх. Построение
точки Е пересечения прямых АВ и CD показано
на рис. 393.
Параллельные прямые в соответствии с /35/
изображаются в виде параллельных прямых.
Однако признака параллельности проекций не-
достаточно, чтобы судить о том, что и сами
прямые в пространстве параллельны (см. /36/).
Кроме параллельных проекций у параллельных
прямых должно быть одинаковое направление
спуска и один и тот же интервал, а следователь-
но, и уклон. Например, прямые АВ и CD
(рис. 394) параллельны между собой, так как у
них одинаковый интервал, одно и то же направ-
ление спуска (от £к /1 и от fi к С) и их проекции
взаимно параллельны. Прямая а также парал-
лельна прямым АВ и CD. Ее уклон равен уклону
этих прямых; в этом нетрудно убедиться, так
как единица длины укладывается в интервале
прямых АВ и CD три раза, что соответствует
уклону прямой а, равной 1:3. Направление
спуска у прямых АВ, CD и а одно и то же, а
проекции параллельны.
§ 32. ПЛОСКОСТЬ
Проекции и градуирование плоскости. Изоб-
раженная на рис. 395 плоскость задана тре-
угольником АВС, вершины которого имеют
соответственно отметки 4, 6 и 9. Такое задание
неудобно для решения большинства задач, луч-
ше, когда плоскость задана горизонталями. Для
этого нужно градуировать плоскость, т. е. по-
строить ее горизонтали с отметками, выражен-
ными целыми числами и отличающимися друг
от друга на единицу длины. Градуируем сто-
рону треугольника, расположенную между вер-
шинами, имеющими наибольшую разность от-
меток (отрезок ВС). Соединим прямой линией
точку А (6) с точкой 6, расположенной на сто-
роне ВС. Эта линия горизонтальна, так как две
ее точки имеют одну и ту же отметку. Проведя
через точки 4, 5, ... прямые параллельно пря-
мой 6 (см. /35/), получим горизонтали плоско-
сти АВС.
Проведем через произвольную точку В тре-
угольника прямую, инцидентную плоскости и
перпендикулярную горизонталям. Такая линия,
как было установлено в гл. III, называется ли-
нией ската плоскости. В данном случае линия
ската градуирована, так как точки ее пересече-
ния с горизонталями плоскости имеют те же
отметки, что и горизонтали, и различаются
между собой на единицу длины. Градуирован-
ная проекция линии ската называется масшта-
бом уклона плоскости. На чертеже масштаб
уклона условно обозначается двумя параллель-
ными линиями, из которых одна проводится
более толстой.
Угол наклона плоскости к горизонтальной
плоскости проекций определяется углом на-
клона линии ската этой плоскости. Чтобы его
найти, нужно построить проекцию линии ската
на плоскости П2, параллельной этой линии.
Уклон можно подсчитать по приведенной выше
формуле.
Плоскость имеет спуск в направлении линии
ската от горизонталей с большими отметками
к горизонталям с меньшими отметками. На-
правления спуска плоскости и принадлежащей
ей линии ската совпадают. Если известен уклон
плоскости (или угол ее наклона к П,), направ-
ление спуска и хотя бы одна горизонталь, то
положение плоскости в пространстве становит-
ся определенным. Все эти данные можно уста-
новить, если известен масштаб уклона.
/166/ Масштаб уклона определяет положение
плоскости в пространстве.
На рис. 396 плоскость задана горизон-
талью 5, уклоном i =f 1 :3 и направлением спус-
ка, которое обозначено штрихом в сторону
спуска (бергштрихом). Чтобы градуировать пло-
скость, нужно провести масштаб уклона пер-
пендикулярно горизонтали и через точки мас-
штаба уклона, имеющие целые отметки, про-
вести горизонтали плоскости параллельно за-
данной горизонтали 5. Точки, градуирующие
линию ската, можно построить, определив
интервал этой линии графически или путем
подсчета.
151
/167/ Горизонталь с бергштрихом и уклон
определяют положение плоскости в простран-
стве.
Иногда при решении инженерных задач на
местности нужно ориентировать плоскость от-
носительно меридиана Земли. Для этого введем
понятие направление простирания плоскости.
Если смотреть вдоль линии ската в сторону
спуска плоскости, то направление ее простира-
ния принимается влево. Угол 8 между северной
стороной магнитной стрелки компаса и на-
правлением простирания, измеренный против
часовой стрелки, называется углом простирания
плоскости.
/168/ Угол простирания плоскости и ее уклон
определяют положение плоскости относительно
стран света.
Точка и линия, инцидентные плоскости. Опре-
делим отметку точки А, проекция которой дана
и о которой известно, что она инцидентна пло-
скости, заданной масштабом уклона (рис. 397).
Проведем через А прямую произвольного на-
правления, инцидентную плоскости (см. /79/),
и отметим точки В и С ее пересечения с произ-
вольными горизонталями плоскости. Построив
фронтальную проекцию' прямой, определим
отметку точки А (8,7 единицы). Тот же прием
можно использовать, чтобы проверить, инци-
Рис. 398
дентна ли данной плоскости точка, заданная
проекцией и отметкой. Например, отметка
точки D равна 7.6; построив ее фронтальную
проекцию, убеждаемся, что она лежит на фрон-
тальной проекции прямой АВ, инцидентной
плоскости. Следовательно, и точка D инци-
дентна плоскости.
Отметка точки Е равна 11 единицам. Можно
без вспомогательных построений сказать, что
она не инцидентна плоскости, заданной мас-
штабом уклона (тогда ее отметка была бы боль-
ше 9, но меньше 10 единиц; почему?).
Определение величины плоской фигуры. Тре-
угольник АВС расположен в плоскости, задан-
ной масштабом уклона (рис. 398). Повернем
его вокруг, например, 7-й горизонтали до со-
вмещения с горизонтальной плоскостью. Для
этого отметим точки Е, D и F пересечения пря-
мых АВ и ВС с 7-й горизонталью плоскости и
прямой ВС — с 12-й горизонталью. Определим
величину DF2 отрезка DF (см. рис. 390). Про-
ведя проекцию траектории точки F (перпенди-
кулярно к проекциям горизонталей), построим
на ней точку F так, чтобы DF = DF2. Построив
проекции траекторий точек В и С, найдем точ-
ки В и С на прямой DF. Соединим точки ВиЕ
и построим на первой BE точку А. Для построе-
ния точки F можно определить величину ра-
диуса точки F и отложить ее от точки G по на-
правлению проекции траектории точки F.
Взаиморасположение плоскостей.
/169/ Две плоскости параллельны, если у них
одинаковые углы простирания и уклоны.
Из /169/ можно вывести и другие признаки
параллельности плоскостей. Например, если
горизонтали обеих плоскостей параллельны,
одинаков уклон плоскостей и совпадает на-
правление спуска, то плоскости параллельны.
Одного признака непараллельндсти горизонта-
лей различных плоскостей достаточно, чтобы
утверждать, что непараллельны и сами плоско-
сти. Вместе с тем, если горизонтали различных
плоскостей параллельны, это не значит, что
параллельны и плоскости (они могут иметь
различный уклон или направление спуска).
Построим линию пересечения плоскостей,
одна из которых задана треугольником
А(6)В(9)С(3), вторая — масштабом уклона
152
(рис. 399). Градуируем плоскЬсть треугольника
и проведем ее произвольные, например 4 и б,
горизонтали до пересечения соответственно в
точках Е и F с однозначными (имеющими оди-
наковую отметку) горизонталями плоскости,
заданной масштабом уклона. Однозначные го-
ризонтали различных плоскостей пересекаются,
так как инцидентны одной горизонтальной пло-
скости, поэтому описанный прием можно рас-
сматривать как сечение заданных плоскостей
двумя вспомогательными горизонтальными
(в уровне горизонталей 4 и 6) плоскостями
(см. /84/). Линией пересечения плоскостей явля-
ется прямая EF.
/170/ Чтобы построить линию пересечения
двух плоскостей, нужно отметить точки пере-
сечения двух пар однозначных горизонталей этих
плоскостей. Через них проходит искомая линия.
Для определения видимости треугольника
воспользуемся конкурирующими точками в ме-
сте кажущегося пересечения горизонталей раз-
ных плоскостей. Пусть G принадлежит плоско-
сти треугольника; тогда ее отметка равна 6.
Точка D лежит в плоскости, заданной масшта-
бом уклона, и ее отметка равна 4. Точка G
расположена выше точки D, она видима. Сле-
довательно, видима вся часть треугольника
между стороной А В и линией пересечения пло-
скостей.
Положение /170/ относится и к случаю,
когда одна из плоскостей проецирующая. Тог-
да проекция линии пересечения плоскостей
определяется без вспомогательных построений
(можно установить и отметки любого числа
точек этой линии; рис. 400). Проецирующая
плоскость 12 пересекается с плоскостью общего
положения Л(2)Д(7)С(4). Проекция линии пере-
сечения совпадает с проекцией плоскости 12.
Отметки двух точек (D и Е) этой линии можно
узнать, построив точки пересечения двух (вто-
рой и четвертой) произвольных горизонталей
плоскости треугольника с плоскостью 12.
Плоскости с параллельными масштабами
уклона пересекаются по горизонтали (рис. 401).
Чтобы ее построить, соединим прямыми ли-
ниями две пары точек с одинаковыми отметка-
ми, но расположенными на линиях ската раз-
ных плоскостей. Через точку пересечения про-
екций этих линий проходит проекция линии
пересечения плоскостей. Решение основано на
том, что расстояния от линии пересечения до
точек с одинаковыми отметками, принадлежа-
щих разным плоскостям, пропорциональны
уклонам этих плоскостей.
Пересечение прямой с плоскостью. Даны
прямая А(8)В(2) и плоскость (2)(4)(6). Заклю-
чим прямую в плоскость общего положения
(рис. 402, а), задав ее двумя горизонталями
произвольного направления, пересекающими-
ся с прямой АВ. Для этого градуируем прямую
и через две ее точки, например Е(4) и F(6),
проведем горизонтали вспомогательной пло-
скости. Направление горизонталей следует вы-
брать так, чтобы они в пределах чертежа пере-
секлись с однозначными горизонталями задан-
ной плоскости. Отметив точку N(4) пересече-
ния четвертых горизонталей плоскостей и точ-
ку М(6) пересечения шестых горизонталей, со-
единим их прямой, в пересечении которой с
заданной прямой АВ расположена искомая
точка К (см. /87/).
Второй вариант решения (рис. 402, б): за-
ключим АВ в проецирующую плоскость и по-
строим линию C(3)D(6) ее пересечения с задан-
ной плоскостью (см. описание к рис. 400).
Возьмем произвольную фронтальную плос-
кость проекций и спроецируем на нее заданную
прямую АВ и прямую CD. В пересечении их
фронтальных проекций отметим точку К2 и
с помощью линии связи цайдем точку К.
Одновременно устанавливается и отметка точ-
ки К (отрезок длиной Л).
Для определения видимости прямой исполь-
зуем конкурирующие точки G и Н. Точка Н,
инцидентная прямой (2)(4), имеет отметку, близ-
153
а)
В(2)
d=fi
точки G, принадлежащей
к
73
3; отметка
А(8)
М(6)
Рис. 402
кую
прямой АВ, больше 6 (она расположена между
точками с отметками 7и 6). Следовательно,
видна точка G и вся часть отрезка АВ от точки А
до точки К.
Прямая, перпендикулярная плоскости. Если
прямая перпендикулярна плоскости, то она пер-
пендикулярна любой прямой этой плоскости,
в том числе и линии ската (рис. 403). Следова-
тельно, угол наклона такой прямой к плоскости
проекций равен 90° —а, где а — угол наклона
плоскости к плоскости проекции. Так как уклон
плоскости равен tga, то уклон перпендикуляр-
ной ей прямой равен tg90°—а или ctga.
/171/ Уклон плоскости и уклон перпендику-
лярной к плоскости прямой обратно пропорцио-
нальны.
Отсюда вытекает: /пл = 1//пр, где /,,л— ин-
тервал линии ската плоскости, а /пр—интер-
вал прямой, перпендикулярной плоскости.
В точке К(7) плоскости, заданной масшта-
бом уклона, восставим к ней перпендикуляр
(рис. 404). Проведем.через К прямую а, перпен-
дикулярную горизонталям плоскости (см.
/91/5—проекцию перпендикуляра. Градуируем
ее: для этого или подсчитаем интервал пер-
пендикуляра по приведенной выше формуле,
или проделаем следуюшие построения: через
произвольно взятую точку А проведем отре-
зок A D, равный единице длины. Отложим отре-
зок BD, равный интервалу линии ската плоско-
сти на перпендикуляре к прямой AD; соединим
точки В и А. Проведем прямую АС, перпенди-
кулярную АВ и пересекающуюся в точке С
с прямой DB. Отрезок CD равен интервалу
перпендикуляра.
Расстояние от точки до прямой. Его можно
определить, если заключить точку в плоскость,
перпендикулярную прямой, найти точку пере-
сечения заданной прямой и вспомогательной
плоскости и определить величину отрезка меж-
ду данной точкой и построенной точкой пере-
сечения.- Задача решена на рис. 405, на котором
дана прямая В(8)С(12) и точка А(14). Построим
треугольник DGF (см. рис. 404), с помощью
которого определим интервал линии ската пло-
скости (отрезок DE) и проведем масштаб укло-
на; он параллелен проекции прямой. Заключив
прямую в произвольно выбранную плоскость
(задана 8-й и 12-й горизонталями), построим
154
линию MN пересечения заданной и вспомога-
тельной плоскостей (см. рис. 402) и отметим
точку К, в которой эта линия пересекается с
заданной прямой ВС. Определим величину
отрезка АК. Эту же задачу можно решить, со-
единив точку А с точками В и С прямыми и по-
строив натуральную величину треугольника
АВС (см. рис. 398).
§ 33. ПОВЕРХНОСТЬ
Кривая линия. В общем случае кривая зада-
ется проекциями некоторого числа ее точек
(каркасная кривая). Например, кривая (7)(4) на
рис. 406 задана проекциями точек 1, 2, 3, 4.
Это значит, что кривая градуирована; интервал
кривой всюду различен, следовательно, разли-
чен и ее уклон в разных точках. По проекции
кривой определить точно отметку какой-либо
точки невозможно (она может быть выражена
любым числом в пределах между значениями
отметок смежных точек). Для приближенного
решения используют один из следующих двух
приемов.
Первый прием заключается в том, что дуга
между двумя точками с известными отметками,
на которой расположена точка с неизвестной
отметкой, аппроксимируется отрезком прямой.
Спроецировав этот отрезок на произвольно
выбранную фронтальную плоскость, опреде-
лим отметку заданной точки (см. рис. 390).
На рис. 406 этим приемом определена отметка
точки А (отрезок длиной h).
Второй прием дает более точные результаты,
особенно при различной по направлению и зна-
чительной по величине кривизне линии. Стро-
ится развертка кривой линии. Для этого нужно
спрямить ее проекцию (см. рис. 207) и, проведя
сиетему параллельных прямых с расстоянием
между ними, равным единице длины, — сетку
горизонталей (рис. 407), построить на них точки
спрямленной кривой с учетом их отметок.
Соединим полученные точки плавной кривой.
Построив на развертке точку А, определим ее
отметку. Для большей точности решения сле-
дует родственно преобразовать развертку, т. е.
принять вертикальный масштаб большим гори-
зонтального.
Угол наклона кривой к горизонтальной пло-
скости в данной точке можно определить при-
ближенно, воспользовавшись разверткой, по-
строенной при одинаковых горизонтальном и
вертикальном масштабах (например, угол а
наклона кривой в точке А). При разных масшта-
----------------2-----------------7
бах нужно родственно преобразовать пря-
мую [Л]С (точка С — двойная).
Уклоном кривой линии в данной точке назы-
вается уклон касательной к кривой, проведен-
ной через эту точку. В общем случае уклон кри-
вой в разных точках различен, следовательно,
различно и заложение дуг кривой между точка-
ми с отметками, выраженными целыми числа-
ми и отличающимися на единицу длины. Если
уклон кривой на всем ее протяжении одинаков,
то заложения равных дуг кривой всюду равны
(рис. 408, а). Кривая может быть задана одной
точкой, направлением спуска и уклоном
(рис. 408, б). Это кривая равного уклона. Раз-
вертка кривой равного уклона представляет
собой прямую линию, угол наклона которой
к прямым сетки горизонталей равен углу на-
клона кривой в любой ее точке к горизонталь-
ной плоскости. Примером кривой равного укло-
на может служить цилиндрическая винтовая
линия с постоянным шагом и вертикальной
осью.
Поверхности. Поверхности обычно задаются
горизонталями поверхности — линиями их сече-
ния горизонтальными плоскостями. Линией ска-
та называется линия поверхности, которая в
данной точке поверхности наклонена к гори-
зонтальной плоскости под наибольшим углом;
эта линия перпендикулярна горизонтали по-
верхности, проходящей через ту же точку.
/172/ Линия ската поверхности в данной точ-
ке перпендикулярна горизонтали поверхности,
инцидентной той же точке.
Коническая поверхность. На практике чаще
всего встречается прямая круговая коническая
поверхность с вертикальной осью (рис. 409).
Сечения поверхности горизонтальными пло-
скостями (окружности) являются горизонталя-
ми поверхности. Спроецировав их на плоскость
проекций, получим ряд концентрических окруж-
ностей. Если расстояние между смежными се-
кущими плоскостями равно единице длины, то
радиус одной окружности будет отличаться от
радиуса следующей на величину интервала об-
разующей конической поверхности. Таким об-
разом, градуированная проекция любой обра-
зующей является масштабом уклона, а сама
образующая — линией ската поверхности. Пря-
мая круговая коническая поверхность с верти-
кальной осью может быть задана масштабом
уклона и вершиной. Соответственно этому по-
верхность можно задать вершиной и уклоном
образующих, как это и делают обычно на прак-
тике.
Дана проекция вершины конической поверх-
ности (2,7) и уклон образующих, равный 1 :2
(рис. 410). Проведем через проекцию вершины
проекцию образующей и градуируем ее. Через
полученные точки проведем окружности с цент-
ром в точке S — горизонтали поверхности. По-
строение горизонталей поверхности с отметка-
ми, выраженными целыми числами и отличаю-
щимися на единицу длины, называется градуиро-
ванием поверхности.
/173/ Чтобы градуировать поверхность, нуж-
но рассечь ее горизонтальными плоскостями,
имеющими отметки, выраженные целыми чис-
лами и отстояцими друг от друга на единицу
длины.
Градуированная коническая поверхность
второго порядка с горизонтальными круговыми
сечениями изображена на рис. 411. Линией ска-
та, проходящей через вершину поверхности,
является образующая, имеющая больший уклон
(прямая AS). Линия ската, проведенная через
любую точку поверхности, не инцидентной об-
разующей AS, не может быть прямой линией;
ее уклон в разных местах поверхности различен.
(Построение линий ската поверхности мы рас-
смотрим ниже). Ввиду того, что линии ската,
проходящие через различные точки поверхно-
сти, имеют разный уклон, построить единый
масштаб уклона для такой поверхности нельзя.
Чтобы градуировать поверхность конуса,
заданного, например, одной горизонталью и
Рис. 409
156
вершиной или двумя горизонталями, спроеци-
руем их на фронтальную плоскость, параллель-
ную вертикальной плоскости симметрии по-
верхности. Определив фронтальные проекции
» центров окружностей — сечений поверхности,
расположенных на отметках, отличающихся на
единицу длины, построим горизонтальные про-
екции центров и проведем окружности, радиусы
которых могут быть измерены на фронтальной
проекции поверхности.
Цилиндрическая поверхность. Боковая по-
верхность цилиндра с вертикальной образую-
щей в проекциях с числовыми отметками ста-
новится проецирующей. Проекция направляю-
щей такой поверхности совпадает с проекцией
всей поверхности. Этот случай (подробно рас-
смотренный в первой части книги) мы приво-
дить не будем. Если образующие поверхности
горизонтальны, то те из них, отметки которых
выражены целыми числами, могут служить для
градуирования поверхности.
Полуцилиндр с горизонтальной образую-
цей изображен на рис. 412. Градуируем его
боковую поверхность. Пусть известна отметка
ei о оси О. Построим фронтальную- проекцию
поверхности, расположив плоскость проекций
перпендикулярно образующей. Определим точ-
ки пересечения прямых сетки горизонталей с
фронтальной проекцией цилиндра и построим
горизонтальные проекции горизонталей. Реше-
ние не изменится, если вместо прямого круго-
вого будет цилиндр с произвольной направляю-
щей. Линия ската, инцидентная любой точке
боковой поверхности цилиндра, совпадает с
нормальным сечением такой поверхности.
В приведенном примере линия ската, инцидент-
ная точке А, представляет собой дугу окруж-
ности.
Сфера. Градуировать сферу можно тем же
приемом, что и цилиндрическую поверхность.
Проекции горизонталей сферы представляют
собой концентрические окружности, радиусы
которых определяются по фронтальной про-
екции. Линия ската, проходящая через любую
точку сферы, совпадает с ее меридианом.
Рис. 412
Поверхность равного уклона. Определитель
поверхности: 1. Примой круговой конус с вер-
тикальной осью ; направляющая — кривая ли-
ния. 2. Конус перемещается в пространстве так,
что его вершина постоянно принадлежит направ-
ляющей. Пусть по кривой линии а (рис. 413)
скользит вершина прямого кругового конуса с
вертикальной осью, занимая последовательно
положения А, В, С, D,... Поверхность, соприка-
сающаяся с конусом во всех его положениях,
называется поверхностью равного уклона. Линия
ската такой поверхности, проведенная через
любую точку кривой линии а, совпадает с той
образующей, по которой соприкасающаяся по-
верхность касается конической. Поэтому обра-
зующей поверхности равного уклона может
быть прямая линия и поверхность отнесена к
линейчатым. Направляющая поверхности —
кривая а бывает пространственной или плоской.
/174/ Поверхность равного уклона — это ли-
нейчатая поверхность, соприкасающаяся со мно-
жеством одинаковых прямых круговых конусов
с вертикальной осью и вершинами, расположен-
ными на заданной кривой — направляющей по-
верхности равного уклона.
157
На рис. 414 изображена пространственная
кривая (б)(7)(Я)(9). Уклон поверхности равного
уклона равен 1:2. Нужно [градуировать поверх-
ность.
Поскольку уклон поверхности всюду оди-
наков (он равен уклону Динии ската поверхно-
сти), то расстояние межд]у смежными горизон-
талями равно интервалу линии ската. Распола-
гаем вершины конусов в точках заданной кри-
вой и градуируем их боковую поверхность (см.
рис. 410); интервал линии ската конической по-
верхности составляет две линейные единицы.
Проведя кривые линии, соприкасающиеся с
горизонталями конических поверхностей, имею-
щих одну и ту же отметку, получим горизон-
тали поверхности равного уклона. На чертеже
построены два отсека таких поверхностей
А—(6)—(9)—Ви С—(6)—(9)—D. Линией их пе-
ресечения является заданная кривая. Расстояние
между двумя проекциями смежных горизонта-
лей в направлении общей нормали к ним всюду
одинаково. Такие кривые называются эквиди-
стантными.
Когда направляющей поверхности является
кривая, инцидентная горизонтальной плоско-
сти, она сама представляет собой одну из гори-
зонталей поверхности равного уклона. На
рис. 415 изображена кривая й(9). Построим
поверхность равного уклона с уклоном 1:1.
Взяв на кривой h произвольные точки А, В, С,...,
расположим в них вершины вспомогательных
конусов и градуируем их боковую поверхность
в соответствии с заданным уклоном. Горизон-
тали поверхности соприкасаются с горизонта-
лями конусов, это эквидистантные кривые.
Как и в предыдущем случае, заданная кри-
вая представляет собой линию пересечения двух
поверхностей равного уклона.
Если кривая линия инцидентна вертикальной
плоскости, то ее проекция представляет собой
прямую (почему?). О том, что это кривая, можно
судить по тому, что интервалы ее дуг на разных
участках различны. Построим поверхности рав-
ного уклона, проходящие через кривую
(7)(8)(9) ... (рис. 416) с уклоном 1 :1. Располо-
жив вершины вспомогательных конусов в точ-
ках с отметками 7, 8 и т. д., градуируем их и
проводим кривые, соприкасающиеся с горизон-
талями конических поверхностей — горизон-
тали поверхностей равного уклона.
Иногда направляющая поверхности равного
уклона представляет собой цилиндрическую,
реже коническую винтовую линию. В этом слу-
чае и поверхность равного уклона становится
винтовой. Рассмотрим случай, когда направ-
ляющей является цилиндрическая винтовая ли-
ния (рис. 417). Поверхность равного уклона
представляет собой косой открытый геликоид
(см. § 18). Сечением такого геликоида плоско-
стью, перпендикулярной его оси, является эволь-
вента окружности, поэтому построение гори-
зонталей связано с определением радиуса ок-
ружности, эвольвенту которой нужно постро-
ить. Не вдаваясь в подробности, отметим, что
_ ^в.л ‘ йад
1о.П
где Ro — радиус окружности; iB л — уклон вин-
товой линии; RB л — радиус винтовой линии;
io n—уклон образующих поверхности. Центр
окружности совпадает с проекцией оси винто-
вой линии.
Построим горизонтали геликоида, если ра-
диус винтовой линии равен 8 единицам длины,
ее уклон 1 :4, а уклон поверхности 1 :1,5. Под-
ставив эти данные в формулу, установим, что
радиус окружности, эвольвентой которой явля-
ется горизонталь поверхности, равен 3 едини-
цам длины. Градуируем винтовую линию и по-
строим, например, пятую горизонталь поверх-
ности. Из точки 5, инцидентной винтовой ли-
нии, проведем касательную к окружности ра-
диуса 3 единицы с центром в точке i (проекции
оси винтовой линии). Отметив точку касания А,
проведем дугу окружности радиуса А—3 до
пересечения в точке В с касательной к окружно-
сти, проходящей через точку 6. Проведем дугу
радиуса ВС. Она пересечется с касательной к
окружности, проходящей через точку 7, и г. д.
Аналогично строятся горизонтали и второго
158
геликоида, пересекающегося с первым по вин-
товой линии: проведя касательную к окружно-
сти через точку 6, строим дугу радиуса D—5 до
пересечения в точке Е с касательной к окруж-
ности, проведенной через точку 6. Радиус сле-
дующей дуги равен отрезку EG и т. д. Следует
учитывать, что построение приближенное, по-
этому, чем меньше расстояние между взятыми
на проекции винтовой линии точками, тем точ-
нее проведенная эвольвента.
Линия ската поверхности, проходящая через
произвольную точку К винтовой линии, пер-
пендикулярна горизонтали, поэтому касатель-
на к цилиндру радиуса Ai.
В частном случае, когда направляющая по-
верхности равного уклона — прямая линия, по-
верхность становится плоскостью. Чтобы по-
строить ее, достаточно в произвольной точке
прямой расположить вершину прямого круго-
вого конуса с вертикальной осью, уклон обра-
зующих которого равен заданному, и провести
плоскость, проходящую через данную прямую
касательно к конусу (рис. 418). Таких плоско-
стей две (АВС и ABD). Горизонтали плоско-
сти касательны к соответствующим горизонта-
лям боковой поверхности конуса.
A(V Рис. 418
Рис. 419
Винтовая поверхность (см. /120/). Выше мы
познакомились с изображением косого откры-
того геликоида. Косой закрытый геликоид по-
казан на рис. 419. Он задан направляющей —
винтовой линией с шагом, равным 12 единицам
длины (различие в отметках смежных точек вин-
товой линии, расположенных на общей проеци-
рующей прямой), и образующей, наклоненной
к горизонтальной плоскости; ее уклон равен 1:2.
Градуируем образующие.
Соединив плавной кривой линией точки с
одинаковыми отметками, расположенные на
образующих винтовой поверхности, проходя-
щих через точки А(12), В(11), С(10) и т. д., по-
лучим горизонтали поверхности (спирали Архи-
меда). Линия ската, проведенная, например,
через точку с отметкой 13 перпендикулярно го-
ризонталям поверхности, представляет собой
также спираль. Ее уклон резко возрастает по
мере приближения к оси винтовой поверхности.
Прямой закрытый геликоид изображен на
рис. 420. Образующая поверхности перпенди-
159
кулярна оси, а следовательно, параллельна го-
ризонтальной плоскости. Поэтому горизонтали
поверхности являются прямыми линиями. Ли-
ния ската, проходящая, например, через точ-
ку К, — винтовая линия. Ее шаг равен шагу
направляющей винтовой линии, а радиус —
расстоянию от точки К до оси поверхности.
Таким образом, уклон линии ската одинаков
на всех ее участках.
На рис. 421 дано наглядное изображение
прямого закрытого геликоида (Q) и косого
открытого геликоида (X).
Определитель винтовых поверхностей при-
веден в § 18.
Поверхность равноустойчивого откоса. Опре-
делитель поверхности: 1. Кривая образующая,
кривая направляющая. 2. Образующая переме-
щается так, что одна ее точка скользит по на-
правляющей, а ее плоскость остается перпенди-
кулярной направляющей. Это поверхность, угол
наклона которой к горизонтальной плоскости
по мере подъема откоса возрастает. Если зем-
ляной откос ограничен такой поверхностью, он
будет устойчивым. Линия ската поверхности
называется кривой нормального сечения равно-
устойчивого откоса. Ее форма определяется
опытным путем. Будем считать, что эта кривая
задана, и рассмотрим построение горизонталей
поверхности, для которой кривая является обра-
зующей.
Отсек поверхности равноустойчивого откоса
образуется перемещением дуги кривой нормаль-
ного сечения, верхняя точка которой скользит
по заданной направляющей в общем случае
пространственной кривой линии. Плоскость об-
разующей в любом ее положении вертикальна
и перпендикулярна проекции направляющей.
Образующая в одном из возможных вариантов
показана на рис. 422.
Для построения горизонталей поверхностей
представим себе, что образующая вращается
вокруг вертикальной оси, проходящей через
верхнюю точку дуги кривой. Получим поверх-
ность вращения. Пусть эта поверхность пере-
мещается в пространстве так, что ее вершина
скользит по направляющей, а ось остается вер-
тикальной. Поверхность, соприкасающаяся с
поверхностью вращения во всех ее положениях,
Рис. 421
160
7
Рис. 422
будет поверхностью равноустойчивого откоса.
Проекции горизонталей — эквидистантные кри-
вые.
На рис. 422 дана градуированная направ-
ляющая А(9)В(7). Градуируем кривую нормаль-
ного сечения равноустойчивого откоса с по-
мощью сетки горизонталей. Располагая после-
довательно вершину поверхности вращения в
точках А(9), 10 и других заданной кривой линии,
строим горизонтали поверхностей вращения,
а затем проводим соприкасающиеся с ними
кривые — горизонтали двух поверхностей рав-
ноустойчивого откоса, пересекающихся между
собой по заданной направляющей. По плоским
кривым АС и AD эти поверхности переходят в
сопрягающую их поверхность вращения. Линия
ската, проведенная через любую точку поверх-
ности равноустойчивого откоса, совпадает с
образующей поверхности вращения (например,
кривые АС и AD).
Поверхность равнодлинного откоса. Приме-
няется в основном в дорожном строительстве.
Она уменьшает опасность снежных заносов и
воздушных завихрений. Откосы, ограниченные
такой поверхностью, производят приятное зри-
тельное впечатление — хорошо вписываются в
местность. Откосы дорога с постоянной длиной
образующих можно представить себе как ленту
равной ширины, одной стороной прикреплен-
ной к бровке дороги, а другой — соприкасаю-
щейся с окружающей местностью.
Определитель поверхности: I. Отрезок пря-
мой, кривая — направляющая, поверхность.
2. Отрезок одним концом скользит по направ-
ляющей, вторым — по поверхности. Его проекция
на плоскости П, всегда перпендикулярна про-
екции направляющей.
Пусть отрезок АС скользит одним своим
концом по наклонной прямой АВ, а вторым
концом — по горизонтальной плоскости с от-
меткой 20 (рис. 423).
Поверхность, образованная движением пря-
мой АС, пересекается с горизонтальной пло-
скостью с отметкой 20 по кривой DC. Поверх-
ность равнодлинного откоса можно рассмат-
ривать как огибающую множество конических
поверхностей с вертикальной осью, вершины
которых расположены на прямой АВ, при усло-
вии, что отрезок образующей любой конической
поверхности, заключенный между вершиной и
161
11—940
। оризонтальной плоскостью, всюду одинаков,
коническая поверхность с вершиной в точке А
вырождается в вертикальную прямую, а по-
верхность с вершиной в точке В — в горизон-
тальную плоскость.
Градуируем прямую АВ и расположим в по-
лученных точках вершины конических поверх-
ностей, имеющих соответствующий уклон обра-
зующих. Градуировав эти поверхности, про-
ведем горизонтали поверхностей равнодлинно-
го откоса, соприкасающиеся с горизонталями
конических поверхностей. В проекциях с число-
выми отметками эта задача решается в той же
последовательности (рис. 424). Чтобы опреде-
лить угол наклона образующих вспомогатель-
ных конусов, построим в стороне проекцию
сферы радиуса АС. Если рассечь сферу горизон-
тальными плоскостями с расстоянием между
ними, равным высоте сечения, получим окруж-
ности, все точки которых удалены от центра
сферы на величину, равную АС. Рассматривая
эти окружности как направляющие, построим
конусы с вершиной в центре сферы. Сетку го-
ризонталей используем для градуирования ко-
нусов.
Расположив в точке 24 прямой АВ вершину
конуса, поверхность которого проходит через
4-ю относительную горизонталь сферы, в точ-
ке 23 — вершину конуса с поверхностью, про-
ходящей через 3-ю горизонталь, и т. д., прове-
дем горизонтали поверхности равнодлинного
откоса, соприкасающиеся с горизонталями ко-
нусов.
Аналогично строятся горизонтали поверх-
ности равнодлинного откоса, когда направляю-
щей поверхности является кривая линия (рис.
(рис. 425). Если окружающая местность имеет
выраженный рельеф, использовать этот прием
нельзя (см. § 35).
Цилиндроид. Когда горизонтали поверхно-
сти дороги — прямые линии, перпендикуляр-
ные ее оси, то поверхность дороги представляет
собой цилиндроид. Направляющими поверх-
ности служат две пространственные кривые
(бровки дороги), а образующей — прямая ли-
ния, в любом положении параллельная гори-
зонтальной плоскости параллелизма и обычно
перпендикулярная оси дороги (см. описание к
рис. 221 и /103/).
Если горизонтальная проекция оси доро-
ги — дуга окружности, а ось дороги имеет по-
стоянный уклон, то она становится винтовой
линией, а поверхность дорога — геликоидом
(см. рис. 421).
162
I
Циклическая поверхность. В поперечном се-
чении поверхности дороги редко бывает прямая
шния. Для стока воды и из соображений устой-
чивости дорожного полотна поверхность доро-
ги должна иметь уклон к обеим бровкам. Когда
нормальное сечение поверхности дорога пред-
ставляет собой окружность, поверхность ста-
новится циклической. Пусть поверхност ь задана
градуированной осью дороги и сечением верти-
кальной плоскостью — дугой окружности, пер-
пендикулярной горизонтальной проекции оси
(рис. 426). При незначительных уклонах дорог
различие в сечениях вертикальной плоскостью,
перпендикулярной проекции оси дороги, и пло-
скостью, перпендикулярной самой оси, незна-
чительно, им можно пренебречь. Градуируем
поверхность дороги, для чего построим сече-
ние ее поверхности вертикальной плоскостью,
перпендикулярной проекции оси. Нанеся сетку
горизонталей, найдем на сечении точки с.отно-
сительными отметками 0, —1, —2, и проек-
цию расстояний от этих точек до оси (отрезки
п, т, ...). Отложив полученные отрезки на про-
екциях сечений, проведенных соответственно
через точки 21, 20,... оси дороги, получим точки
с отметками 20, 19, ... Соединив между собой
плавной кривой точки-, имеющие одинаковые
отметки, получим горизонтали поверхности;
выделим ту часть горизонталей, которая рас-
положена между бровками полотна дороги
(например, дуга кривой A(19)F). Описанным
приемом на рис. 426 построены горизонтали
между точками оси дороги с отметками 19 и 21.
На практике нет необходимости проводить
кривые линии; их аппроксимируют ломаными.
Проведем прямую AF (нормаль к проекции оси
дороги) и отметим точку В ее пересечения с
осью; от точки 18 по оси отложим отрезок (18)D,
равный отрезку (19)В-, и проведем через D нор-
маль к проекции оси дороги; она пересечется с
проекциями бровок дороги в точках С и Е, ко-
торые соединим прямыми линиями с точкой 18.
Чтобы определить величину отрезка (18)D,
спроецируем ось дороги между точками с от-
метками, отличающимися на единицу длины на
плоскость П2 (построен родственно преобра-
зованный эпюр: вертикальный масштаб принят
в два раза большим горизонтального). Отложив
вниз от любой точки фронтальной проекции
оси (7£2) отрезок, равный е (из-за различия в
масштабах берется 2с; отрезок длиной е по-
показывает различие в высотах между точками
на оси дороги и точками, расположенными на
бровках), проведем прямую, параллельную
фронтальной проекции оси. Это фронтальная
проекция бровки дороги (допускается, что от-
резок бровки равен отрезку оси). Проведя через
точку 182 горизонтальную прямую, найдем
точку Е2 = С2, а затем, построив линию связи,
и точки Е и С; соединим их прямыми с точ-
кой 18.
Часто необходимо показать промежуточные
горизонтали. Для этого разделим, например,
на четыре части отрезки бровок дороги и оси
между двумя смежными сечениями вертикаль-
ными плоскостями. Соединив полученные точ-
ки, как показано на чертеже, между 16 к 17 точ-
ками оси получим промежуточные горизонтали
с отметками 16,25, 16,5 и 16,75.
§ 34. ТОПОГРАФИЧЕСКАЯ
ПОВЕРХНОСТЬ
Изображение топографической поверхности.
Как говорилось (см. /121/), земная (топографи-
ческая) поверхность задается ее дискретным
каркасом — горизонталями или профилями или
и тем, и другим. Они могут быть дополнены
некоторыми точками (см. рис. 262).
Участок топографической поверхности изоб-
ражен на рис. 427. Здесь он задан горизонталями
от 4-й и 11-й. По возрастанию горизонталей
(в левой части чертежа) можно судить о том,
что изображено возвышение (холм, гора — не-
ровность земли, расположенная выше Окру-
жающей местности). В правой части чертежа
обозначены не все горизонтали, но проставле-
П
163
ны бергштрихи, указывающие, в каком направ-
лении происходит понижение поверхности.
И тот, и другой способ обозначения позволяют
правильно прочитать чертеж, если он снабжен
сведениями о масштабе и принятом расстоянии
между горизонталями по высоте, называемом
высотой сечения. Высота сечения может быть
равна одному, пяти, десяти и т. д. метрам. Каж-
дая пятая горизонталь обводится более тол-
стой линией, чем остальные.
Неровность, обратная возвышению, назы-
вается котловиной. Если бы на рис. 427 возраста-
ние горизонталей происходило в обратном на-
правлении или в противоположную сторону
были бы обращены бергштрихи, то изображен-
ная неровность была бы котловиной. Высшая
точка возвышения (или горизонтальная пло-
щадка — плато), от которой местность понижа-
ется во все стороны, называется вершиной (на
рассматриваемом чертеже ртметка вершины
11,4 м), боковая поверхность — склоном. Низ-
шая часть котловины называется дном, боковые
поверхности — щеками. Неровности земной по-
верхности показаны на рис. 428. По взаиморас-
положению горизонталей можно судить о том,
где склоны возвышения или щеки котловины
имеют больший или меньший угол наклона к
горизонтальной плоскости, называемый кру-
тизной. Принято говорить о крутизне склона
или щеки в данной точке поверхности.
Отметки горизонталей подразделяются на
относительные, выражающие высоту горизон-
тали над некоторой условной плоскостью, при-
нятой за нулевую, и абсолютные, определяемые
в СССР относительно определенной точки,
расположенной в Финском заливе. Мы будем
пользоваться только относительными отмет-
ками.
При необходимости могут быть проведены
промежуточные горизонтали, расстояние между
которыми по высоте равно половине, четверти
или одной восьмой высоте сечения. Такие гори-
зонтали называются соответственно полугори-
зонталями, четвертными горизонталями, и т. д.
Дополнительные горизонтали проводятся тон-
кой штриховой линией (полугоризонталь 7,5).
При ровных скатах с мало меняющейся кру-
тизной расстояние между проекциями горизон-
талей одинаково на всем протяжении склона
или щеки. В этом случае точки полугоризонта-
лей расположенц на равных расстояниях между
двумя смежными горизонталями. При меняю-
щейся крутизне полугоризонталь сдвигается в
сторону сгущения горизонталей склона или
щеки.
Точка и линия, инцидентные топографической
поверхности. Всякая линия топографической по-
верхности градуирована точками ее пересече-
ния с соответствующими горизонталями по-
верхности. Отметка точки, расположенной меж-
164
ду горизонталями, может быть определена
приближенно. См. описание к рис. 406.
Обычно в целях упрощения дуга кривой ли-
нии, инцидентной топографической поверхно-
сти и соединяющей точки двух смежных гори-
зонталей, аппроксимируется отрезком прямой.
Установим отметку точки А, инцидентной то-
пографической поверхности (рис. 429). Прове-
дем через А прямую произвольного направле-
ния, пересекающуюся в точках Ви С с ближай-
шими горизонталями поверхности. Построим
фронтальную проекцию отрезка ВС и найдем
на ней точку А2. Измерив (с учетом принятого
вертикального масштаба*) отрезок /М2, уста-
новим отметку точки А, она равна 14,7. На том
же чертеже показано построение промежуточ-
, ных горизонталей в случае относительно спо-
койного рельефа местности. Проведя между 15
и 16 горизонталями несколько отрезков пря-
мых, разделим их на равные части (в нашем
примере четыре). Соединив точки, как показано
на чертеже, получим горизонтали с отметками
15,25, 15,5 и 15,75.
Линия ската поверхности. Крутизна поверх-
ности в данной точке равна углу наклона каса-
тельной к линии ската в этой точке. Проекция
касательной определяет направление линии ската
в данной точке. Она перпендикулярна горизон-
тали (см. /172/). Направление линии ската, про-
ходящей через точку D, на рис. 429 показано
стрелкой.
Определим направление линии ската в точ-
ке А: проведем через А (рис. 430) перпендикуляр
к 16-й горизонтали, a -через полученную точ-
ку В — перпендикуляр ВС к 17-й горизонтали
(или в обратной последовательности). Прибли-
женно направление линии ската в точке А па-
раллельно биссектрисе угла АВС. Дуга DAE
линии ската касательна к построенному на-
правлению. Точка Е расположена в пересечении
с 16-й горизонталью биссектрисы угла между
прямой АВ и направлением линии ската. Опу-
стив из А перпендикуляр на 17-ю горизонталь
и проделав описанные выше построения, най-
дем точку D. Второй прием построения направ-
ления линии ската в данной точке показан на
примере точки F. Опустив перпендикуляры из
точки F на 16-ю и 17-ю горизонтали, получим
соответственно точки Н и G. Биссектриса ост-
рого угла между прямыми FHh FG приближен-
но является искомым направлением. Точки К
и М могут быть построены так же, как точки D
и Е в предыдущем примере.
Приближенное построение линии ската, ин-
цидентной точке Е, на большом протяжении по-
казано на рис. 431. Проведем через Е перпенди-
куляр EF к 10-й горизонтали. Построенная пря-
мая может быть линией ската, если перпенди-
куляр, опущенный из точки F на 11-ю. горизон-
таль, совпадет с ней. На самом деле такой
перпендикуляр пересекается с 11-й горизон-
талью в точке G. Приближенно принимаем за
направление линии ската, проходящей через Е
на участке между 11-й и 10-й горизонталями.
* Как будет видно из последующего, ort может
отличаться от горизонтального масштаба.
Рис. 431
165
отрезок прямой EU, параллельный биссектрисе
угла EFG. Аналогично построив отрезок ЕЕ
линии ската между 10-й и 9-й горизонталями,
получим точку Н. Опустив перпендикуляр из Н
на 8-ю горизонталь, получим дочку К, перпен-
дикуляр из которой к 9-й горизонтали проходит
через ранее найденную точку К. Следовательно,
на участке между 9-й и 8-й горизонталями мест-
ности направление линии ската, проходяшей
через точку Н (или К), совпадает с перпенди-
куляром, опущенным из точки Н на смежную
(8-ю) горизонталь. Вслед за этим найдем точ-
ку L аналогично описанному выше. Опустив
из /-перпендикуляр на 6-ю горизонталь, найдем
точку М, перпендикуляр из которой к 7-й гори-
зонтали может проходить через точку N или О.
На участке между 7-й и 6-й горизонталями при-
ближенное построение линии ската заключается
в следующем: построим биссектрисы углов
NM L или LMO, соответственно прямые РМ
и RM, а затем через точку L проведем пря-
мую LS параллельно биссектрисе угла PMR;
в точке S' она пересекается с 6-й горизонталью.
С достаточной на практике точностью прово-
дим прямую LS параллельно биссектрисе уг-
ла NMO. Соединив полученные гочки Е, U,
Н, ... плавной кривой, получим проекцию ли-
нии ската
На рис. 432 построена развертка линии ската
поверхности. С помощью развертки можно
определить угол ее наклона, а следовательно,
и уклон в любой точке. Например, уклон линии
ската поверхности в точке Т равен tga (в обо-
значении проекций точек индекс опущен).
/175/ Уклон линии ската в данной точке по-
верхности определяет уклон поверхности в той же
точке.
Линия равного уклона поверхности. Такая
линия имеет одинаковый интервал на всем про-
тяжении. Построим линию равного уклона,
проходящего через точку А(12) (см. рис. 431) с
уклоном 1:4. Ее интервал равен 4 линейным
единицам. Проведя через А дугу окружности ра-
диуса, равного интервалу, получим в ее пере-
сечении с 11-й горизонталью точки В и В'.
Выбор направления линии равного уклона за-
висит большей частью от инженерных задач.
Пусть принято направление АВ. Проведя вновь
дугу окружности радиуса 4 единицы с центром
в точке В, найдем точки С и С'. Если выбрана
точка С, то линия равного уклона пройдет
через точки А, В, С. Аналогично построим и
остальные точки линии равного уклона вплоть
до точки D (или D'). Дуга с центром в точке D
(или D') не пересекается с 6-й горизонталью,
следовательно, в промежутке между 7-й и
6-й горизонталями нельзя построить линию,
уклон которой был бы равен заданному. Со-
единив плавной кривой точки А, В, С, D. полу-
чим проекцию линии, проходящей через точку А
и имеющей уклон, близкий к 1 :4. Так как длина
кривой несколько больше длины ломаной, то
уклон линии окажется меньшим заданного. Что-
бы узнать, какой он в действительности, нужно
построить развертку линии.
Иногда нужно построить линию равного
уклона, проходящую по топографической по-
верхности между двумя заданными точками
А и В (рис. 433), и уже затем определить ее
уклон. Построим линии равного уклона АС, АЕ,
AF, A D с различными интервалами. Возьмем
на произвольно выбранной прямой точку 1 и
отложим от нее интервал ломаной А С. В полу-
ченной точке восставим к прямой перпендику-
ляр и на нем отложим отрезок, равный расстоя-
нию от точки С до точки В, получив при этом
точку III. Точно так же построим точку II,
отложив интервал ломаной АЕ, а затем —
расстояние от точки Е до точки В. Так как точ-
ки F и D расположены на 4-й горизонтали с
противоположной стороны точки В, то откла-
дывать расстояние между этими точками и
точкой В на перпендикулярах к прямой нужно
в противоположную сторону При этом будут
получены точки IV и И Соединив полученные
точки, получим кривую ошибок, пересекаю-
щуюся с проведенной прямой в точке VI.
Отрезок I VI является интервалом заданной
линии. Используя найденный интервал, строим
вначале ломаную, а затем и кривую линию рав-
ного уклона, проходящую через точки А и В.
Линии водораздела и водослива поверхности.
Линия водораздела представляет собой кривую
поверхности, являющуюся границей, от кото-
рой дождевые воды стекают в разных направ-
лениях (граница двух водосборных поверхно-
стей). Это такая линия поверхности, через каж-
дую точку которой можно провести не менее
двух линий ската. Например, через М (рис. 433)
проходя? две линии ската на участке между
8-й и 7-й горизонталями (мы условно заменили
их перпендикулярами, опущенными из А на
Рис. 433
166
Хребет
Холм
7-ю горизонталь). Эта точка принадлежит ли-
нии водораздела. Через точку N на той же гори-
зонтали, что и М, можно провести только одну
линию ската NA7, так как второй перпендику-
ляр N L, опущенный на 7-ю горизонталь, пе-
ресекается с 8-й горизонталью и, следователь-
но, не может быть линией ската*.
Построив на всех горизонталях точки, по-
добные М (они расположены на выпуклостях
горизонталей), соединим их плавной кривой
линией.
Кроме линии водораздела на поверхности
существует еще одна линия, через все точки ко-
торой можно провести не меньше двух линий
ската. Это линия водослива поверхности. Линия
водослива, так же как и линия водораздела,
является границей между двумя водосборными
поверхностями и определяет направление, по
которому стекает вода, слившаяся с двух сосед-
них щек поверхности. Линии водослива и водо-
раздела показаны на рис. 434. ,
/176/ Линии водослива и водораздела поверх-
ности состоят из точек, через каждую из кото-
рых можно провести не менее двух линий ската
поверхности. •
§ 35. ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТЕЙ
Сечение поверхности проецирующей плоско-
стью. Фигура сечения поверхности вертикаль-
ной (следовательно, проецирующей) плоско-
стью называется профилем. Когда поверхность
задана горизонталями, способ построения про-
филя одинаков независимо от вида поверхно-
сти, поэтому рассмотрим пример построения
профиля топографической поверхности
(рис. 435). Секущая плоскость задана своей про-
* Существуют точки, через которые можно
провести более одной линии ската, но не принадле-
жащие линии водораздела.
167
екцией L1 Отметив точки, в которых плоскость
пересекается с горизонталями поверхности, по-
строим эпюр линии пересечения. Для этого от-
ложим отметки точек на линиях связи и через
построенные точки проведем плавную кри-
вую — профиль. На профиль наносится сетка
горизонталей. Первая горизонталь сетки на-
зывается базой профиля. База профиля может
совпадать с проекцией секущей плоскости (на-
ложенный профиль I) или быть параллельной ей
(вынесенный профиль II). Вертикальный мас-
штаб при построении профиля обычно прини-
мается большим горизонтального. На рис. 435
вынесенный профиль II выполнен в вертикаль-
ном масштабе, в два раза превышающем гори-
зонтальный (родственно преобразованный про-
филь).
Получить большую выразительность чер-
тежа можно и не прибегая к различным масшта-
бам. Для этого достаточно спроецировать точ-
ки сечения на вертикальную плоскость, распо-
ложенную под углом 60° к секущей плоскости
(профиль III также вынесенный). Все горизон-
тальные размеры профиля уменьшаются в два
раза (так как sin 30° = 0,5), вертикальные от-
кладываются в масштабе чертежа. Профили II
и III подобны.
Для построения промежуточных горизон-
талей и определения отметок точек топографи-
ческой поверхности с меняющейся крутизной
используют профили (например, отметка точ-
ки А, равная 21,5). Ряд профилей может рас-
сматриваться как дискретный каркас топогра-
фической поверхности (см. /121/).
Пересечение топографической поверхности с
проецирующей цилиндрической поверхностью.
Цилиндрическая поверхность задана своей про-
екцией Й (рис. 436). Отметим точки, в которых
она пересекается с проекциями горизонталей
участка местности, и построим развертку кри-
вой, которая называется криволинейным про-
филем (рис. 437). Вообще говоря, криволиней-
ный профиль — это развертка кривой линии,
инцидентной поверхности. С помощью такого
профиля можно определить отметки точек кри-
вой линии (например, точки А на рис. 436),
угол наклона кривой в данной точке (А) и др.
Пересечение прямой н кривой липин с поверх-
ностью. Задачи решаются с учетом /144/ и /164/.
Чтобы построить точку пересечения прямой
(2)(б) с поверхностью, заключим прямую в
плоскость общего положения (рис. 438). Для
этого градуируем прямую и через точки 5,6, ...
проводим в произвольном направлении парал-
лельные горизонтали, которыми и задаем пло-
скость. Отметив точки пересечения однознач-
ных горизонталей плоскости и поверхности,
соединим их плавной кривой, являющейся про-
екцией линии их пересечения. Эта кривая встре-
чается с заданной прямой в искомой точке К.
' Аналогично строятся точки пересечения кри-
вой линии и поверхности. На рис. 439 задана гра-
дуированная кривая (7)(4). Проведя через точ-
ки 7, б,... в произвольном направлении взаимно
параллельные горизонтали, получим цилиндри-
ческую поверхность, для которой заданная кри-
вая будет направляющей, а проведенные гори-
зонтали — образующими. Отметив точки пере-
168
сечения однозначных горизонталей цилиндриче-
ской и топографической поверхностей, соеди-
ним их плавной кривой, в пересечении которой
с заданной кривой расположена искомая точ-
ка К.
Описанный прием, конечно, может быть
использован и при нахождении точки пересе-
чения кривой линии с плоскостью.
Определение видимости прямой или кривой
производится путем рассмотрения конкури-
рующих точек. Это точки А и В на обоих черте-
жах. Отметка той из них, которая принадлежит
прямой или кривой, больше отметки точки,
расположенной на горизонтали топографиче-
ской поверхности, поэтому в месте кажущегося
пересечения видны заданные линии. Границей
видимости является точка К, в которой прямая
или кривая пересекается с поверхностью.
Если по каким-либо причинам нежелательно
проводить вспомогательные построения на чер-
теже. можно воспользоваться иным приемом
Построим точки пересечения кривой линии (76)
(27) с топографической поверхностью (рис. 440).
Заключим кривую в вертикальную цилиндри-
ческую поверхность. Так как такая поверхность
проецирующая, то ее проекция совпадает с
проекцией линии пересечения поверхностей за-
данной и вспомогательной. Приняв произволь-
ную фронтальную плоскость проекций и спро-
ецировав на нее заданную кривую и линию пере-
сечения поверхностей, отметим фронтальные
проекции точек их пересечения К и N. Между
этими точками кривая невидима, что легко
определить с помощью конкурирующих точек.
Отметки найденных точек могут быть опреде-
лены по их фронтальной проекции.
Пересечение плоских откосов сооружений.
На рис. 441 изображено пересечение плоских
откосов двух горизонтальных дорог. Отметка
одной из дорог составляет 19 м, второй — 24 м
(число, выражающее отметку горизонтальной
плоской фигуры, снабжается условным зна-
0123956789
Ml । ' । । 1 1
Рис. 441)
15 № 17 18 1920 21
169
ком — равносторонним треугольником, угол
которого обращен к небольшому заштрихован-
ному прямоугольнику). Окружающая плоская
местность горизонтальна, ее отметка 22. Уклон
откосов насыпи равен 1 :1,5, уклон откосов вы-
емки 1:1. Дорога с отметкой 24 м расположена
выше окружающей местности, т. е. на насыпи.
Дорога с отметкой 19 м — ниже окружающей
местности, т. е. в выемке.
Рассматривая бровку дороги как одну из
горизонталей откоса, строим масштаб уклона
и через соответственные точки масштаба про-
водим проекции горизонталей. Интервал пло-
скостей* откосов насыпи равен 1,5, выем-
ки—1,0.
Проведем 22-е горизонтали, по которым от-
косы обеих дорог пересекаются с окружающей
местностью, и отметим точки А, В, Си £>,
в которых горизонтали пересекаются между
собой. Затем проведем 19-е горизонтали обоих
откосов верхней дороги, по которым они пере-
секаются с полотном нижнеи дороги, и отметим
точки Е, F, G и И пересечения этих горизонта-
лей с бровками полотна нижней дороги. Соеди-
нив точки В и Е, С и F и т. д., получим линии
пересечения откосов насыпи и выемки.
Откосы искусственных сооружений обозна-
чаются условной штриховкой в направлении
линии ската 'и состоящей из попеременно про-
веденных коротких и длинных штрихов. Штри-
хи начинаются у верхней кромки откоса и в за-
висимости от сложности и величины чертежа
проводятся по всей верхней кромке или только
в свободных от различных обозначений местах
чертежа. По расположению и направлению
штрихов можно судить о направлении спуска
плоскости откоса.
Дорога, расположенная на отметке 19, про-
ходит сквозь насыпь дороги с отметкой 24.
Для этого в откосе должен быть сделан тун-
нель. Отверстие туннеля на чертеже не пока-
зано.
При решении практических задач важно
определить направление горизонталей откосов
наклонных площадок. На рис. 442 даны две
горизонтальные площадки с отметками 25 и 28
и наклонная дорога, соединяющая площадки.
Ее плоскость градуирована (отметки ее гори-
зонталей 25, 26, 27 и 28). Уклон откосов ра-
вен 1 :1.
Чтобы построить откос, соединяющий две
горизонтальные площадки, проводим масштаб
уклона (интервал равен единице) перпендику-
лярно прямой а — границе площадки с отмет-
кой 25, а также горизонталь откоса с отмет-
кой 28, являющуюся линией пересечения откоса
с верхней площадкой.
Построив окружность, диаметр которой ра-
вен трем интервалам откосов с центром в точ-
ке А (28-я горизонталь вспомогательного ко-
нуса (см. рис. 418), проведем через точку В,
имеющую отметку 28, касательную к окруж-
ности. Эта линия является 28-й горизонталью
Здесь и дальше имеется в виду интервал линии
ската плоскости.
170
откоса дороги и вместе с тем линией пересече-
ния откоса с горизонтальной площадкой, имею-
щей ту же отметку.
В точке С 28-е горизонтали откосов пересе-
каются между собой. С противоположной сто-
роны дороги откосы симметричны построен-
ным.
Рассмотрим случай, когда дорога (напри-
мер, в карьер), расположенная в выемке, не
соединяет горизонтальные площадки (рис. 443).
Дорога имеет 25, 24, 23 и 22-ю горизонтали,
следовательно, ни одна из них не может слу-
жить линией ее пересечения с горизонтальной
площадкой, имеющей отметку 28. Вершину
вспомогательного конуса расположим в точ-
ке В. Построим, например, 25-ю горизонталь
откоса, градуируем его, используя масштаб
уклона, и найдем 28-ю горизонталь, по которой
откос пересекается с горизонтальной площад-
кой. Построив откос соединяющий горизон-
тальные площадки с отметками 25 и 28, прово-
дим его 28-ю горизонталь; отмечаем точку С
пересечения 28 горизонталей откосов. Постро-
им откос, который по 22-й горизонтали дороги
пересекается с ней, а по 28-й горизонтали с го-
ризонтальной площадкой. С соседними отко-
сами он пересекается по прямой BD, и симмет-
ричной ей.
Перейдем к построению линии пересечения
откосов двух дорог в случае, когда они пере-
секают друг друга в различных уровнях, причем
одна из дорог горизонтальна и расположена на
отметке 18, другая наклонена и задана горизон-
талями 20, 21, 22 и 23 (рис. 444). Окружающая
местность плоская и расположена на отметке 22
Уклон откосов 1 :2.
Пользуясь масштабом уклона, построим
откосы дороги с отметкой 18. Эта дорога рас-
положена в выемке, следовательно, нужно стро-
ить 19-ю, 20-ю и т. д. горизонтали, вплоть до
22-й, которая представляет собой линию пере-
сечения откосов с окружающей местностью.
Вслед за этим построим откосы наклонной
дороги. Наклонная дорога идет частично в
выемке, частично на насыпи. Границей этих
частей является 22-я горизонталь (отрезок АВ),
по которой дорога пересекается с местностью.
Горизонтали откосов дороги строятся анало-
гично примеру, Приведенному на рис. 418.
Отметим точки С, D, Е и F, в которых пересе-
каются 22-е горизонтали откосов горизонталь-
ной и наклонной дорог. По этим горизонталям
откосы дорог пересекаются с окружающей мест-
ност ью. Найдя точки GwH пересечения 21-х го-
ризонталей откосов, соединим их соответствен-
но с точками С и D. Прямые CG и DH представ-
ляют собой линии пересечения откосов двух
дорог, расположенных в выемке.
Градуируя откосы наклонной дороги в той
ее части, которая располагается на насыпи,
построим 18-е горизонтали, по которым откосы
пересекаются с горизонтальной дорогой. Со-
единив точку К с точкой F и точку М с точкой Е.
получим линии пересечения откосов (вух до-
рог в том месте, гда одна дорога расположена
в выемке, другая — на насыпи. Как и в анало-
гичном примере, на рис. 441 отверстие туннеля
не,показано.
Рис. 443
Рис. 444
171
Построим линии пересечения откосов гори-
зонтальной площадки, расположенной на от-
метке 14, и дороги, соединяющей площадку с
местностью, если известно, что уклон откосов
равен 1:1, уклон дороги — 1:3, а отметка
окружающей плоской местности составляет
10 единиц. Вся площадка расположена на на-
сыпи (рис. 445).
Зная величину уклона дороги, построим ее
горизонтали. Откосы дороги строятся в соот-
ветствии с описанием к рис. 442. Построим от-
косы площадки, 14-я горизонталь которых яв-
ляется линией пересечения откоса с плоско-
стью площадки, а затем линии их пересечения.
1\П1 Проекция линии пересечения двух смеж-
ных плоских откосов, имеющих одинаковый
уклон, представляет собой биссектрису угла меж-
ду проекциями горизонталей этих откосов.
Для доказательства проведем через точку В
линии ската ВМ и BN смежных откосов A BCD
и BCEF. Так как оба откоса имеют одинаковый
уклон, то ВМ = BN, равны между собой и их
проекции. Углы BNC и ВМС прямые. Сторо-
на ВС у треугольников BNC и ВМС общая,
поэтому эти треугольники равны. Так как равны
между собой углы BCF и BCD, то прямая ВС
представляет собой биссектрису угла DCF.
Когда горизонтали откосов пересекаются под
прямым углом, проекцией линии их пересечения
является прямая (EF), проходящая под уг-
лом 45 е к проекциям горизонталей.
Используя IIT1I, посгроение проекций отко-
сов можно упростить. Проведем масштаб укло-
на перпендикулярно к любому отрезку, располо-
женному на границе площадки (например, BE).
Отложив четыре интервала, проведем через
полученную точку 10 10-ю горизонталь откоса
BEFC до пересечения с биссектрисами углов,
образованных горизонталями смежных откосов
(прямые EF и ВС). Через F проводим прямую
перпендикулярно прямой FC (10-ю горизонталь
смежного откоса), а через точку С -прямую
DC || А В. Отметив точку D пересечения этой
прямой с биссектрисой утла GAB, проведем
ЛЯ || GA.
Прямая GH представляет собой биссектрису
угла KHD (но не угла AGK). Построим пря-
мую КН, отметив точку Н ее пересечения к
прямой HD, и соединим ее с точней G
В скругленной части площадки псверхно-
ностью равного уклона будет коническая по-
верхность. Проекция ее вершины расположена
в пересечении проекций прямых ТЕ и LS. По-
строим горизонтали конической поверхности и
касательных к ней плоских откосов.
Пересечение плоских откосов с коническими.
Изображенная на рис. 446 горизонтальная пло-
щадка имеет закругление, откос которого огра-
ничен прямой круговой конической поверхно-
стью с вертикальной осью. Ее уклон равен
уклону плоского откоса (левая часть чертежа).
Тогда линией пересечения откосов будет пара-
бола (почему? см. /106/), которую построим,
отметив точки пересечения однозначных гори-
зонталей (см. § 17 и 26).
Если уклон плоского откоса меньше уклона\
конического (правая часть чертежа), то линией
пересечения будет эллипс (почему? см. /105/).
Построим эллипс тем же приемом. Для нахож-
дения крайней точки А линии пересечения (кон-
ца одной из осей эллипсов) нужно рассечь конус
и плоскость вертикальной плоскостью, перпен-
Рис. 445
Рис. 447
172
дикулярной плоскости откоса, и спроецировать
линии сечения откосов на фронтальную пло-
скость (спроецируем произвольные точки В и С
образующей конуса, расположенной в секущей
плоскости, и произвольные точки D и Е пло-
ского откоса). Отметив точку А2 пересечения
прямых В2С2 и E2D2, найдем с помощью линии
связи точку А. Если уклон плоского откоса
больше уклона конического, то в сечении ока-
жется гипербола. Гипербола будет и в том слу-
чае, если плоскость вертикальна (см. /107/).
Вернемся к рис. 445. На практике вместо
того, чтобы пересекать плоские откосы между
собой, вводят промежуточные конические по-
верхности (сопрягающие конусы) того же укло-
на, что и плоскости (рис. 447). На участках,
подобных GRT, принимается поверхность ко-
нуса второго порядка, горизонтали которого
строятся следующим образом: на биссектрисе
угла между горизонталями берем произволь-
ную точку О и, используя ее как центр, прово-
дим дугу окружности радиуса OR = ОТ. Про-
извольный выбор точки О приводит, конечно,
к различным вариантам решения задачи. Отме-
тив точку Т, проведем через нее прямую TG
и из точки V пересечения этой прямой с 11-й го-
ризонталью огкоса проведем к ней перпенди-
куляр до пересечения с прямой GO. Используя
полученную точку N как центр, проведем дугу
окружности радиуса NU и т. д. Проведенные
дуги представляют собой горизонтали кониче-
ской поверхности с вершиной в точке G.
На участке МК L вершина конической по-
верхности обращена вниз. На участке DMK LF
горизонтали строятся как дуги, сопрягающие
горизонтали смежных конусов. Уклон поверх-
ности откоса, как и на участке TGR, меньше
уклона основных откосов.
В дорожном строительстве применяются со-
оружения, часть которых ограничена гипербо-
лическим параболоидом. На рис. 222 показан
пример такого сооружения. Рассмотрим по-
строение горизонталей поверхности и пересе-
чение ее плоскими откосами в двух вариантах.
Первый вариант (рис. 448). Гиперболический
параболоид задан направляющими BE и CF и
горизонтальной плоскостью параллелизма. Че-
рез прямые BE и CF проходят плоские откосы
различного уклона, соединяющие обе горизон-
тальные площадки. В рассматриваемом ва-
рианте эти прямые представляют собой линии
пересечения плоских откосов с откосом, имею-
щим форму гиперболического параболоида.
Второй вариант (рис. 449) отличается от пер-
вого тем, что направляющими гиперболическо-
го параболоида являются прямые АВ и CD,
не лежащие в плоскостях смежных (плоских)
откосов. Для построения линии пересечения от-
косов градуируем прямые АВ и CD, что легко
сделать, так как известны отметки точек А, В,
' Ск I). Проведя через точки этих прямых, имею-
щих равные отметки, горизонтали гиперболи-
ческого параболоида, построим точки пересе-
чения однозначных горизонталей поверхности
с горизонталями смежных плоских откосов,
заданных масштабом уклона.
Пересечение поверхности инженерного соору-
жения с земной поверхностью. В качестве при-
мера рассмотрим пересечение откосов полотна
дороги с топографической (земной) поверхно-
стью. Дорога задана проекцией и горизонта-
лями. Топографическая поверхность имеет
плавный спуск от 24-й к 13-й горизонтали
(рис. 450).
Интервал оси дороги в промежутке между
23-й и 16-й горизонталями не меняется, следо-
вательно, на этом участке дорога имеет одина-
ковый уклон. Между 16-й и 11-й горизонталями
интервал меняется. Здесь дорога имеет пере-
менный уклон. Чтобы представить себе харак-
тер изменения уклона дороги, построим ее кри-
волинейный профиль по оси (рис 451). На про-
филе показано не только сечение дороги, но
и сечение топографической поверхности. Вер-
тикальный масштаб принят в два раза большим
масштаба, в котором выполнен чертеж на
рис. 450, а горизонтальный масштаб — в два
раза меньшим. Это позволило уменьшить раз-
мер чертежа По продольному профилю дороги
и местности можно судить, о том, где располо-
жена область насыпи и область выемки, какова
их высота или глубина и т. д.
В дополнение к продольному профилю обыч-
но строятся поперечные профили в направле-
нии, перпендикулярном оси дороги (про-
филь I—I на рис. 452). Продольный и необхо-
димое количество поперечных профилей дают
достаточное представление о характере земля-
Рис. 448
Рис. 449
173
ных работ, которые должны быть выполнены
при строительстве дороги. Граница земляных
работ устанавливается по плану дороги. Для
этого нужно построить откосы насыпи и вы-
емки и найти линии их пересечения с земной
поверхностью. «
Вернемся к рис. 450. Определим кривые, по
которым дорога пересекается с земной поверх-
ностью. Это две линии: на участке между 20-й и
21-й горизонталями дороги и в районе 12-й го-
ризонтали дороги. Построим пересечение на
первом участке. Для этого отметим точки А и С,
в которых 20-я и 21-я горизонтали дороги пере-
секаются с однозначными горизонталями мест-
ности. Чтобы уточнить направление кривой
пересечения, можно найти общие точки 19-х и
22-х горизонталей дороги и местности или вос-
пользоваться промежуточными горизонталями,
имеющими отметку 20,5. Они пересекаются в
точке В. Соединив точки А, Ви С кривой выде-
лим ту ее дугу которая расположена между
бровками дороги. Построив точки пересечения
11, 12 и 13-й горизонталей дороги с соответст-
вующими горизонталями местности, найдем
вторую линию пересечения дороги с местно-
стью. Из рассмотрения отметок горизонталей
дороги и местности (или по продольному про-
филю) можно определить, что между построен-
ными линиями дорога расположена на насыпи,
а за ними — в выемке.
Для построения линии пересечения откосов
дороги с местностью построим их горизонтали.
Вначале определим, в каких пределах проекция
оси дороги прямолинейна (между кривой АВС
и 19-й горизонталью), идет по дуге окружности
(имеется в виду проекция оси дороги; сама ось
в натуре представляет собой винтовую линию)
и где ось дороги является кривой линией (на
участке между 17-й и 12-й горизонталями ось
дороги — пространственная кривая).
На прямолинейном участке откосы дороги
плоские. Они построены в соответствии с опи-
санием к рис. 442—443. На участке, где проекция
оси дороги — дуга окружности, откосы по-
строены в соответствии с описанием к рис. 417.
Здесь откосы представляют собой геликоиды.
И наконец, на последнем участке откосы огра-
ничены поверхностью равного уклона (см.
рис. 414). Проекции горизонталей откосов пред-
ставляют собой плавные эквидистантные кри-
вые. Отметив точки пересечения однозначных
горизонталей откосов и местности, соединим их
плавными кривыми, представляющими собой
границу земляных работ. С бровкой дороги
граница земляных работ пересекается в той же
точке, в которой бровка пересеклась с топогра-
фической поверхностью.
Рис. 451
174
Рис. 453
Горизонтальный масштаб
0 7 2 3 4 5 6 7 8 9 10
| I !--> 1 > I I Д— к-
Вертикальный масштаб
0 12 3 4 5 6
.....................
Рис. 452
При образовании поверхности равнодлин-
ного откоса отрезок прямой одним своим кон
цом скользит по поверхности, другим концом
по пространственной кривой (см. рис. 425).
Через различные точки направляющей
(рис. 453) проведем вертикальные плоскости,
нормальные к проекции направляющей, и по-
строим сечения местности и поверхности рав-
нодлинного откоса. Там, где линии сечения по-
верхностей пересекаются, расположена точка,
принадлежащая линии пересечения откоса с
топографической поверхностью. Например, по-
строим сечение вертикальной плоскости, про-
ходящей через точку А нормально к проекции
кромки дороги, и построим наложенный про-
филь. Проведя из точки А2 дугу окружности за-
данного радиуса, отметим точку В2, в которой
дуга пересечется с проекцией сечения земной
поверхности. Установив проекционную связь,
построим точку В. Аналогично найдена точка С
на противоположной стороне дороги, где также
расположена поверхность равнодлинногр от-
коса.
Построив сечения вертикальными плоско-
стями, проходящими соответственно через точ-
ки с отметками 28, 29 и т. д., найдем линию
пересечения поверхностей равнодлинного от-
коса и топографической. Поблизости от 25-й
горизонтали дороги линия пересечения, встре-
чается с бровкой дороги. Так как в этом месте
откосы почти вертикальны, то должно быть
принято какое-либо инженерное решение, позво-
ляющее их выполнить.
ГЛАВА VIII
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
§ 36. ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
Проекция предмета и координатных осей.
Слово аксонометрия означает измерение по осям
(axon — ось, metreo — измеряю). Его смысл
отражает скорее способ построения изображе-
ний, чем само изображение, однако под аксо-
нометрией (аксонометрическими проекциями)
понимают как раздел теории изображений,
включающий способ их построения, так и
конечный результат построений — само изоб-
ражение.
Аксонометрические проекции относятся к
параллельным проекциям и, следовательно,
обладают всеми их свойствами. При изучении
последующего материала для нас особенно
важны положения /35/, /38/, /41/, /42/, изложен-
ные ранее в соответствующих местах учебника.
/178/ Аксонометрической проекцией (нли аксо-
нометрией) предмета называется его параллель-
ная проекция иа плоскости, построенная вместе
с проекцией прямоугольных координатных осей,
к которым отнесен изображаемый предмет.
На рис. 454 показана схема аксонометриче-
ского проецирования. Предмет Ф (схематизи-
рованное здание, отнесенное к координатной
системе Oxyz; координатные оси не следует
смешивать с осями проекций) вместе с осями х,
у и z спроецирован на плоскость аксонометри-
ческих проекций П°. Проекцией предмета (зда-
ния) является его изображение Ф°, проекциями
координатных осей — прямые х°, у° и z°, пере-
секающиеся в точке О ° — аксонометрической
проекции начала координат. В общем случае
прямые х и х°, у и у°, а также z и z° не парал-
лельны друг другу.
Аксонометрические оси в коэффициенты ис-
кажения. Предмет Ф в приведенном примере
так расположен относительно системы коорди-
натных осей, что АВ II у, AC || х, A D || z. В соот-
ветствии с /35/ А°В° [|у°, А°С° || х° и A°D° || z°.
Прямые х°, у° и z° называются аксонометриче-
скими осями.
/179/ Если прямая параллельна одной нз коор-
динатных осей, то ее аксонометрическая проекция
параллельна аксонометрической оси того же на-
именования.
Возьмем на координатной оси х отрезок О G;
его аксонометрией является отрезок O°G°.
Так как АСЦх, то в соответствии с /42/:
O°G° : OG = А°С° : АС.
Отношение длины аксонометрической про-
екции отрезка, лежащего на координатной оси
или параллельного ей, к длине самого отрезка
называется коэффициентом искажения по соот-
ветствующей аксонометрической оси. Следо-
вательно, отношение O°G°:OG представляет
собой коэффициент искажения по оси х°.
Чтобы построить аксонометрию А°С° от-
резка А С, если известно расположение точки А °,
достаточно провести через эту точку прямую
параллельно оси. х° и от точки А ° отложить
отрезок, длина которого равна длине отрез-
ка АС, умноженной на коэффициент искажения
по оси х° (с учетом направления отрезка).
Обозначим коэффициент искажения по оси х°
через и. Коэффициент искажения по оси у ° равен
отношению O°F°: OF, обозначим его v. Коэф-
фициент искажения по оси z° обозначается w.
Он равен О°Н° : ОН.
Зная направление аксонометрических осей и
величину коэффициентов искажения по ним,
можно найти аксонометрию любой точки про-
странства, построив для этого аксонометриче-
скую проекцию координатной ломаной (см.
рис. 20). Построение аксонометрии точки D
заключается в следующем: отложим по оси х°
отрезок О°К° — ОК-и, через точку К°, парал-
лельно оси у° проведем отрезок К°А ° = КА v
и, наконец, от точки А° отложим отрезок
A"D° — AD-w.
/180/ Чтобы найти аксонометрическую про-
екцию точки, нужно построить аксонометриче-
скую проекцию координатной ломаной, длина
каждого звена которой умножена иа соответст-
вующий коэффициент искажении.
Направление аксонометрических осей и ве-
личина коэффициентов искажения зависят от
расположения плоскости аксонометрических
проекций относительно координатных осей и
направления проецирования. В зависимости от
направления проецирования аксонометрические
проекции делятся на прямоугольные и косо-
угольные. В первом случае направление проеци-
рования перпендикулярно плоскости аксоно-
метрических проекций, во втором — составляет
с ней некоторый угол, отличный от прямого и,
естественно, от угла 0°. Коэффициенты иска-
жения в общем случае отличаются друг от
друга, тогда аксонометрия называется три-
метрней: и 4= v ф w. Если два коэффициента ис-
кажения равны друг другу, то аксонометрия
носит название диметрия. Возможны варианты:
u = v/w',u=w/v;i=k /и. И наконец, когда
все коэффициенты искажения равны между со-
бой, аксонометрия называется изометрией:
и = v=w.
176
Триметрия, диметрия и изометрия могут
быть как прямоугольными, так и косоуголь-
ными.
/181/ Аксонометрия делится на косоугольную
и прямоугольную. В зависимости от соотношения
коэффициентов искажения как косоугольная, так
и прямоугольная аксонометрия может быть три-
метрией (все коэффициенты искажения различ-
ны), диметрией (два коэффициента искажения
равны между собой, но ие равны третьему) н
изометрией (все коэффициенты искажения равны
друг другу).
/182/ Аксонометрическая проекция отрезка,
параллельного одной из координатных осей, рав-
на действительной длине отрезка, умноженной
иа коэффициент искажения по соответствующей
аксонометрической осн.
Аксонометрические масштабы. Коэффициен-
ты искажения, как правило, дробные числа, по
этому пользоваться ими при построении аксо-
нометрии неудобно. Подсчет длины аксоно-
метрии отрезков, параллельных координатным
осям, можно заменить использованием аксоно-
метрических масштабов. Плоскость аксономет-
рических проекций П° (рис. 455) пересекается с
осями координат в точках X, Y и Z. Прямые
XZ, XY и YZ представляют собой следы на
плоскости П° координатных плоскостей хПг,
х Пу и у Пг. Поэтому треугольник X YZ назы-
вается треугольником следов плоскости аксо-
нометрических проекций. Если плоскость аксо-
нометрических проекций занимает общее поло-
Рис. 455
Рис. 454
177
12—940
жение относительно координатных плоскостей,
то треугольник следов всегда остроугольный.
Построим проекции на плоскости П° осей
координат. Пусть точка О проецируется в
точку О (ее положение при заданной плоско-
сти П° зависит от направления проецирования.
Обычно она расположена внутри треугольника
следов). Ось х проецируется в прямую х°,
проходящую через точки О" и А". Прямая у°
проходит через точки О и У, а прямая z' —
через точки О° и Z. Коэффициентом искажения
по оси является отношение О°Х: ОХ, следо-
вательно, длина отрезка ОХ = ОХ- и. Анало-
гично О' У= О у- v и O°Z = OZ w.
Отложим от точки О по осям х, у и z после-
довательно отрезки, равные единице длины е,
принятой для данного чертежа, и спроецируем
их концы на соответствующие аксонометриче-
ские оси, получив при этом их проекции —
отрезки еЛ°, е’у и е°. Таким образом будут по-
строены аксонометрические масштабы для каж-
дой из аксонометрических осей. Эти масштабы
линейные; используя их, можно не производить
вычисление длины проекций отрезков с учетом
коэффициента искажения. Если известна длина
отрезка, параллельного оси х, например 5е,
достаточно по аксонометрическому масштабу
оси х° отмерить 5е, (как нужно строить аксо-
нометрические масштабы и пользоваться ими,
мы покажем позднее).
Если аксонометрия является изометрией,
то ех = ev ~ е., т. е. аксонометрические мас-
штабы по всем осям одинаковы, в случае ди-
метрии два масштаба одинаковы, но отличны
от третьего и при триметрии все масштабы
различны.
Теорема Польке—Шварца. Направление ак-
сонометрических осей и коэффициенты искаже-
ния по ним (а следовательно, и аксонометриче-
ские масштабы) могут быть выбраны произ-
вольно. Это явствует из теоремы Польке —
Шварца:
/183/ Всякий четырехугольник вместе с его
диагоналями можно рассматривать как парал-
лельную проекцию тетраэдра наперед заданной
формы.
Перед тем как доказать теорему, вспомним,
что можно построить такое сечение плоскостью
треугольной призматической поверхности, ко-
торое будет подобным заданному треугольнику
(см. /136/). Отсюда:
/184/ Параллельной проекцией треугольника
может быть другой треугольник любой наперед
заданной формы (если на треугольной призма-
тической поверхности взять два плоских сече-
ния, то одно из них можно рассматривать как
параллельную проекцию второго сечения при
направлении проецирования, параллельном реб-
рам поверхности. Форма любого из1 этих сече-
ний может быть задана)
Перейдем к доказательству теоремы. Рас-
смотрим рис. 456, на котором изображен тетра-
эдр О А ВС. Нужно доказать, что, проецируя
тетраэдр на плоскость, можно получить четы-
рехугольник вместе с его диагоналями, подоб-
ный заданному четырехугольнику О ВАС (по-
казан в нижней правой части рисунка).
Разделим ребро тетраэдра ВС в той же про-
порции, в какой точка F пересечения диагоналей
четырехугольника делит его диагональ ВС, по-
лучив при этом точку Е. Точкой D разделим
ребро тетраэдра АО в той же пропорции, в ка-
кой точка F делит диагональ четырехуголь-
ника АО. Соединив прямой линией точки £ и £>.
получим направление проецирования. Точки D
и £ конкурирующие, поэтому их проекции на
некоторой плоскости П' совпадают. Ребро
тетраэдра АО проецируется в отрезок А'О ,
а ребро ВС — в отрезок В' С. В силу /41/.
С£:В£=С'£' B E' =CF -.BF.
Рассуждаем аналогично относительно от-
резков A' D' и О' D' диагонали А'О' четырех-
угольника. Однако четырехугольник А'В'О'С'
не подобен четырехугольнику А ВОС. Найдем
такую плоскость П°, на которой проекция
тетраэдра удовлетворяла бы условию. Из /136/
мы знаем, что можно построить такой треуголь-
ник О А"С°, который будет подобен заданно-
му треугольнику ОАС и вместе с тем будет про-
екцией треугольника О'А' С'. Найдем такой
треугольник как сечение призматической по-
верхности с ребрами АА', ОО', СС и примем
его плоскость за плоскость проекций П°. Найдя
на стороне АСО° треугольника О‘/4';СС точку
£>° = £°, соединим ее прямой с точкой С° и
построим точку В пересечения прямых С°£°
и ВВ' (о том, что они пересекаются, следует из
того, что прямые СЕ и С°Е° лежат в одной про-
ецирующей плоскости). .
Остается доказать, что треугольник О'А' В
подобен треугольнику ОАВ. В соответствии
с /41/
B E : Сс£° = В'Е’ : СЕ',
следовательно,
В Е° : СЕ =BT CF.
По аналогии
A D° :О D° = AF OF.
Угол A°D°C равен углу AFC, так как треуголь-
ники AFC и А° D°C подобны (что доказано
ранее); следовательно, угол В°ЕО' равен уг-
лу BFO. Отсюда треугольнику В' Е' О' подо-
бен треугольник BFO. Подобны и треугольники
А°В°Е° и ABF.
Таким образом, четырехугольник ОВ'АС
Рис. 456
178
подобен четырехугольнику О ВАС, что и дока-
зывает теорему.
Следствие теоремы Польке—Шварца:
/185/ Расположение аксонометрических осей
и коэффициенты искажений по ним могут быть
выбраны произвольно.
Действительно, пусть вершина О тетраэд-
ра — начало координат, а ребра О А, О В и ОС —
оси координат. Тогда аксонометрическими ося-
ми будут прямые О°А°, О°В° и О°С°. Их на-
правление в соответствии с теоремой может
быть выбрано произвольно. Вследствие того,
что отношение длин отрезков О°А°, О В и
OGC° друг к другу можно принять каким угод-
но, коэффициенты искажения могут быть лю-
быми.
Зависимость коэффициентов искажения от
угла между направлением проецирования н пло-
скостью проекций. Хотя направление аксоно-
метрических осей и коэффициенты искажения
по ним могут быть выбраны произвольно, это
не значит, что они ни от чего не зависят. Дейст-
вительно, в зависимости от принятых коэффи-
циентов искажения на рис. 456 мы выбрали на-
правление проецирования. Следовательно, и
направление проецирования влияет на величину
коэффициентов искажения. Примем без дока-
зательства*, что
u2 -I- v2 + и’2 = 2 + ctg2 tp,
где tp — угол между направлением проециро-
вания и плоскостью проекций, называемый
углом проецирования.
/186/ Сумма квадратов коэффициентов иска-
жения по аксонометрическим осям равна двум
плюс квадрату котангенса угла проецирования.
Котангенс прямого угла равен нулю, следо-
вательно, для прямоугольных аксонометриче-
ских проекций
и2 + v2 -I- w2 = 2.
/187/ Сумма квадратов коэффициентов иска-
жения по аксонометрическим осям прямоуголь-
ной аксонометрии равна двум.
Приведенные коэффициенты искажения. Дана
прямоугольная триметрия с коэффициентами
искажения: и == 0,74, v « 0,82 и w « 0,88. Умно-
жим все. коэффициенты искажения на 1:0,88 =“
“ 1,136. В результате коэффициент по оси z°
станет равным единице (0,999), что упростит по-
строения, так как подсчитывать длины проек-
ций отрезков нужно только с учетом двух коэф-
фициентов искажения. Если дана диметрия, то
уже два коэффициента можно умножить на
одинаковую величину, с тем чтобы они стали
равны единице, а при изометрии — все три.
Построение аксонометрии значительно упро-
щается. Приведенными будем называть коэф-
фициенты искажения по аксонометрическим
осям, умноженные на одну и ту же величину т,
которую назовем коэффициентом приведения.
Приведенный коэффициент искажения по оси х°
U = и - т, по оси у° V = v т, и по оси z
W= wm.
Отсюда
* Доказательство приведено в первом издании
учебника.
Подставив эти значения в формулу квадра-
тов коэффициентов искажения прямоугольной
аксонометрии (см. /187/), получим
U2 + V2 + W2 = 2т2.
Аксонометрические масштабы по осям из-
меняются пропорционально коэффициенту при-
ведения. Таким образом, единица аксонометри-
ческого масштаба по оси л'с Ех=е~ит; по
оси у° Еу = е~ V т; по оси z° Е, = е- w т.
Так как е=1, то в абсолютном значении
Ех= U, Еу = V и Ez= W. Чтобы равенства
стали справедливыми, необходимо подставить
размерность, принятую для данного чертежа
(например, см, мм). Отношения величин u:v:w
справедливы и для единиц аксонометрических
масштабов по осям, в гом числе и приведен-
ных:
и : v : w = ех : е° : е° = Ех : Еу : Е,.
Задание аксонометрии. Окончательный ре-
зультат проецирования фигуры на плоскость
проекций зависит от расположения координат-
ных осей относительно фигуры, плоскости про-
екций относительно этих осей и направления
проецирования. Фигуру в пространстве можно
отнести к таким координатным осям, которые
будут соответственно параллельны ее ширине,
длине и высоте или каким-либо наиболее харак-
терным элементам (осям симметрии, ребрам
и т. д.). Практика подсказала несколько видов
косоугольных и прямоугольных аксонометри-
ческих проекций, задаваемых аксонометриче-
скими осями и коэффициентами искажения.
Такие . виды аксонометрии будут приведены
позже. Здесь же мы рассмотрим построение
аксонометрической проекции точки независимо
от того, какой вид аксонометрии принят для ее
изображения.
/188/ Аксонометрия задана, если известно
расположение аксонометрических осей, их поло-
жительное направление и коэффициенты иска-
жения по ним (в том числе приведенные) или
аксонометрические масщтабы.
Если точка определенным образом отнесена
в пространстве к координатным осям, то ее
изображение в аксонометрии с учетом /188/
становится единственно возможным.
Проводя аксонометрические оси, мы бу-
дем показывать только их положительное на-
правление. Число, указывающее коэффициент
искажения (например, 0,62), будем записывать
ря дом с осями (рис. 457). Если заданы аксоно-
метрические масштабы, будем вычерчивать их
на осях (рис. 458). Начало отсчета совпадает с
точкой О (буква), поэтому цифру 0 (ноль) из-за
одинакового начертания проставлять не будем.
Отсчет производится в положительном на-
правлении каждой оси. Аксонометрическую
ось z~ независимо от углов между аксоно-
метрическими осями будем располагать вер-
тикально.
Аксонометрия точки. Точка А, изображенная
в ортогональных проекциях, отнесена в про-
странстве к координатным осям х, у и z. Ее ко-
ординаты равны соответственно 2,2; 2,3; 3,4
линейным единицам (е), принятым для данного
179
12*
чертежа (рис. 459, а). Аксонометрия задана
аксонометрическими осями и масштабами
(рис. 459, б). Отложим от точки О в аксономет-
рии по оси х° 2,2 ej (аксонометрическую коор-
динату Х° точки А). От полученной точки А
по прямой, параллельной оси у°, отложим 2,3е£
(аксонометрическую координату У точки И).
При этом мы получим точку Л;', называемую
вторичной горизонтальной проекцией точки А.
Проводя через Л, прямую параллельно оси z°
и отложив по ней вверх от точки А^ 3,4е°
(аксонометрическую координату Z этой точки),
получим точку Л ° — искомую аксонометрию
точки Л.
Разъясним понятие «вторичная проекция».
В результате ортогонального проецирования
точки Л на плоскость П, мы получили горизон-
тальную проекцию Л; этой точки, или ее пер-
вичную горизонтальную проекцию. Точка Л,
получена в результате вторичного проецирова-
ния точки Л] на плоскость аксонометрических
проекций.
В соответствии с /28/ по одной аксонометри-
ческой проекции Л ° точки Л нельзя судить о
том, как расположена точка относительно про-
странственных координатных осей. Когда- же
известна, кроме точки Л °, и точка А,, то по
изображению можно определить все три коор-
динаты точки Л (имеется в виду, что известна
аксонометрические оси и коэффициенты иск^-
жения по ним или аксонометрические масшта-
бы, иначе говоря, что аксонометрия задана).
/189/ По аксонометрическому изображению
точки вместе с ее вторичной проекцией можно
судить о расположении точки в простран-
стве.
Прямую Л°Л°, как и в ортогональных про-
екциях, будем называть линией связи, она па-
раллельна оси z°, т. е. в данном случае верти-
кальна. Аналогично описанному можно по-
строить вторичную фронтальную проекцию Л %
ИЛИ вторичную профильную проекцию Лз точ-
ки Л. Прямые Л°Л^ и А°Аз также представля-
ют собой линии связи. Они параллельны соот-
ветственно оси у° или х°.
/190/ Аксонометрия точки н ее вторичная
проекция расположены на обшей линии связи.
Отсюда:
/191/ Чтобы построить аксонометрию точки,
нужно найти одну из ее вторичных проекций и,
проведя через нее линию связи, отложить по ней
от вторичной проекции недостающую коорди-
нату точки (вытекает из /180/).
§ 37. ПРЯМОУГОЛЬНАЯ
АКСОНОМЕТРИЯ
Форма треугольника следов прямоугольной
аксонометрии (см. рис. 455) зависит от направ-
ления проецирования относительно плоскостей
координат. Если угол проецирования 90°, то
точка О° всегда внутри треугольника следов и
совпадает с точкой пересечения его высот.
Действительно, координатная ось х перпенди-
кулярна плоскости уПг, следовательно, она
перпендикулярна любой прямой этой плоско-
сти, в том числе и прямой YZ. В соответствии
с' /45/ прямоугольная проекций х° оси х на
плоскости П° перпендикулярна проекции пря-
мой EZ на той же плоскости. По аналогии
ось у° перпендикулярна прямой XZ, а ось z° —
прямой X У Следовательно, аксонометрические
оси прямоугольной аксонометрии совпадают
с высотами' треугольника следов плоскости
аксонометрических проекций.
/19?/ Аксонометрические .оси прямоугольной
аксонометрии перпендикулярны соответствую-
щим сторонам треугольника следов плоскости
аксонометрических проекций.
Треугольник следов может оказаться в лю-
бом из восьми углов пространства, на которые
его делят три координатные плоскости. Этим
определяется взаиморасположение аксономет-
рических осей. Ось z° принято располагать
вертикально при положительном направлении
снизу вверх, оси х° и у° могут быть располо-
жены справа или слева от оси z° и направлены
вниз или вверх относительно точки О°. Изме-
нение положения аксонометрических осей, со-
ответствующее расположению плоскости аксо-
нометрических проекций относительно коор-
динатных плоскостей, позволяет варьировать
изображение и показывать предмет сверху,
снизу, слева, справа и т. д. (рис. 460, на рисунке
индекс «ноль» при обозначении аксонометри-
ческих осей опущен. В дальнейшем мы будем
вводить этот индекс лишь в тех случаях, когда
это потребуется для правильного понимания
текста).
Рис. 459
180
о
Рис. 460
181
Рис. 460. Продолжение
182
/193/ Если известно направление проецирова-
ния в прямоугольной аксонометрии, может быть
определена плоскость аксонометрических проек-
ций, направление аксонометрических осей и ко-
эффициенты искажения по ним.
Дано направление проецирования 5 (аи а2)
(рис. 461, а). Оси проекций и оси координат
совпадают. Проведем след ZX плоскости х П z
на плоскости П° перпендикулярно s2 (см. /91/),
а след X Y перпендикулярно Расстояние
между точками О и X может быть выбрано
произвольно (см. /44/). Построим след Y Z
на плоскости П°.
Зная величину отрезков X Y, XZ и YZ, по-
строим треугольник X YZ так, чтобы его сто-
рона XY была горизонтальной (рис. 461, б).
Проведя высоты треугольника 'X YZ (см. /192/),
отметим точку О° их пересечения. Отрезки
ОХ, О° У и O°Z определяют направление аксо-
нометрических осей х°, у° и z°. Найдем коэф-
фициенты искажения по ним. Отрезки, принад-
лежащие координатным осям, можно измерить
на эпюре (например, отрезок ОХ на рис. 461, а),
а их аксонометрические проекции (отрезок О°Х
на рис. 461, 6) — на чертеже, где построен тре-
угольник следов. Таким образом:
ОХ : ОСХ = и; О У: О° У = г; OZ:OGZ=w.
Коэффициенты искажения могут быть опре-
делены и в том случае, когда известны только
аксонометрические оси. Заданы оси х°, у° и z°
(рис. 461, б). Проведем прямую XY перпенди-
кулярно z° и через полученные точки X и У—
прямые XZ и YZ перпендикулярно соответ-
ственно у° и х°. Полученное изображение мож-
но рассматривать как прямоугольную проекцию
тетраэдра OX YZ, три ребра которого лежат на
осях координат, а вершина О проецируется в
точку О°. Вращая треугольник X YZ вокруг
стороны X У, совместим его с плоскостью чер-
тежа. Для этого достаточно построить на сто-
роне X У, как на диаметре, полуокружность и
отметить точку О ее пересечения с продолже-
нием отрезка O°Z (т. е с проекцией траектории
точки О, которая перпендикулярна проекции
оси вращения (см. /128/). Соединив прямыми
точку О с точками X и У, получим прямоуголь-
ный треугольник XYO — представляющий со-
бой совмещенную с плоскостью чертежа грань
тетраэдра XYO.
Так как ОХ = OX, OY=OY, можно запи-
сать ОХ:
ОХ : О°Х = и; OY:O У = г.
Для определения коэффициента искажения и
по оси z° нужно совместить с плоскостью чер-
тежа треугольник YOZ (или XOZ), вращая его
вокруг стороны YZ. Тогда OZ: O°Z = w.
Построим аксонометрические масштабы.
Отложим по прямой ОХ последовательно еди-
ничные отрезки от точки О. Через полученные
точки 1, 2, 3, ... проведем прямые, перпенди-
кулярные стороне X У, до пересечения с аксоно-
метрической осью х°. Аналогично построены
аксонометрические масштабы и на осях у ° и z°.
Если треугольник следов разносторонний,
то отрезки О°Х, О' У и OZ не равны между
собой, следовательно, коэффициенты искаже-
ния по аксонометрическим осям различны, и
аксонометрия является триметрией. При рав-
нобедренном треугольнике следов аксономет-
рия становится диметрией, при равносторон-
нем — изометрией.
Обратим внимание на два важных свойства
прямоугольных аксонометрических проекций.
Первое: сфера (шар) проецируется в виде круга
(проецирующий сферу цилиндр является пря-
мым круговым, а его нормальное сечение пло-
скостью проекций — крут). Такое изображение
сферы соответствует нашим зрительным пред-
ставлениям об этой поверхности, поэтому вос-
принимается как естественное. Диаметр круга
равен диаметру сферы. Если же используются
приведенные коэффициенты искажения, то диа-
метр круга умножается на коэффициент при-
ведения.
1194/ Прямоугольной аксонометрией сферы
(шара) является круг того же диаметра, что и
диаметр сферы.
Второе свойство: проекция окружности, ин-
цидентной горизонтальной плоскости, пред-
ставляет собой эллипс с горизонтально распо-
ложенной большой осью. Это объясняется тем,
что тот диаметр окружности, который проепи-
183
руется на П° в натуральную величину, паралле-
лен этой плоскости (см. /12/) и перпендикулярен
оси z, следовательно (см. /45/), угол между
этими линиями проецируется в прямой угол.
Вообще говоря:
/195/ Если координатная ось перпендикулярна
плоскости окружности, то аксонометрическая
ось того же наименования перпендикулярна боль-
шой оси эллипса — прямоугольной аксонометри-
ческой проекции окружности (рис. 462, а).
Большая ось эллипса равна диаметру окруж-
ности. Чтобы определить длину малой оси,
совместим треугольники OXY, OXZ и OYZ
с плоскостью чертежа, как это сделано на
рис. 461 Определим длину малой’ оси эллип-
са — аксонометрии окружности, лежащей в пло-
скости, параллельной XOZ (рис. 462, б) Вос-
пользуемся тем, что треугольники XOZ и XOZ
родственны (родство задано осью' XZ и род-
ственными точками О и О). Отложим от О в
направлении преобразования радиус окружно-
сти (отрезок ОЕ). Построим точку Е, родствен-
ную Е (прямые EF и EF родственны). Отре-
зов ОЕ равен половине малой оси эллипса.
Аналогично определены длины малых осей
двух других эллипсов.
Некоторые виды прямоугольных аксоно-
метрий рекомендует ГОСТ 2.317—69.
Прямоугольная изометрия. Аксонометриче-
ские оси наклонены друг к другу под утлом 120 .
Коэффициенты искажения по осям и = v = w =
1= 0,82. Длина малой оси эллипса — аксономет-
рической проекции окружности, лежащей в
плоскости, параллельной одной из координат-
ных плоскостей, равна 0,58. Рекомендуется
пользоваться приведенными коэффициентами
искажения: 17=Г = W= 1. Коэффициент при-
ведения т = 1,22 (единица, деленная на 0,82).
В этом случае диаметр круга — проекции сферы
равен 1,227), длина большой оси эллипса —
аксонометрической проекции окружности, пло-
скость которой параллельна одной из коорди-
натных плоскостей, составляет 1,227), а малая
ось — 0,71 D
Чаще всего используется прямоугольная
изометрия, расположение осей которой показа-
но на рис. 463. Направление проецирования
относительно •координатных плоскостей спе-
реди, сверху и справа. В этом случае ось у рас-
полагается слева на черуеже. При проецирова-
нии спереди, сверху и слева эта ось располага-
ется справа относительно оси z.
184
Все три видимые грани куба, параллельные
координатным плоскостям, наклонены под оди-
наковым углом к плоскости аксонометрических
проекций и поэтому изображаются в виде рав-
ных ромбов (рис. 464), следовательно, проек-
циями вписанных в грани окружностей будут
одинаковые эллипсы. Большие оси эллипсов
перпендикулярны соответствующим аксономет-
рическим осям (см. /195/).
На рис. 465 показана разновидность прямо-
угольной изометрии, построенной при направ-
лении проецирования спереди, справа и снизу.
В этом случае оси х° и у° обращены вверх.
Возможно изменить положительное направ-
ление оси х° или у° на противоположное, полу-
чив отличные от показанных на рис. 463 и 465
изображения (см. рис. 460).
Прямоугольная диметрия. Если треугольник
следов равнобедренный, то аксонометрия, в ча-
стности, примет вид, показанный на рис. 466.
Ось z вертикальна, одна из осей (х или у) на-
клонена к горизонтальному направлению на
чертеже под углом а = 7'310', вторая—под
углом Р=41°25'. Так как тангенс угла а равен
примерно 1/8, а тангенс угла Р— 7/8, го можно
построить оси по тангенсам углов их наклона
к горизонтальному направлению на чертеже
(рис. 467). Кроме того, ось, наклоненная под
углом р, может быть построена как биссектриса
угла между двумя другими осями.
Коэффициенты искажения составляют: по
оси z и оси, наклоненной под углом 7°10',
примерно 0,94, по оси, наклоненной под углом
41°25', примерно 0,47. Следовательно, и = к =
= 2v или v = w = 2и. Большая ось эллипсов
а, b и с (рис. 468) равна D, малая ось эллипсов
а и Ь равна 0,331), эллипса с — 0,91).. Диаметр
круга — проекции сферы равен диаметру сферы.
На практике строят прямоугольную димег-
рию, используя приведенные коэффициенты ис-
кажения:
U: W: V = 1 : Г:0.5 или К: W: V = 1:1 :0,5.
Рис. 467
185
Рис. 469
Коэффициент приведения равен примерно 1,06
(единица, деленная на 0,94). В этом случае диа-
метр круга — аксонометрии сферы должен быть
увеличен в 1,06 раза; в то же число раз должны
быть увеличены длины больших осей эллип-
сов а, b и с — проекций окружностей, располо-
женных в плоскостях, параллельных коорди-
натным. Малая ось эллипсов а и b равна 0,35 7).
эллипса с — 0,95 D.
Еще один вид прямоугольной диметрии при-
веден на рис. 469. Она внешне приближается к
перспективе и поэтому удобна для изображения
крупных предметов. Коэффициенты искажения
по осям х и у составляют примерно 0,70. Коэф-
фициент искажения по оси z примерно 0,97.
Оси хну наклонены к горизонтальному на-
правлению на чертеже под углом а к. 10°, ось z
вертикальна. Удобно пользоваться приведен-
ными коэффициентами искажения. Если
т=1,47, то [7=JZ=1, a W= 1,43
Прямоугольная триметрия. Приняв оправ-
данное для данного конкретного случая на-
правление проецирования, можно изобразить
ту или иную сторону предмета в любом ракур-
се, показать те части предмета, которые по
каким-либо соображениям важны, и т. д. Такое
построение проводится по выбранному направ-
лению проецирования. Построенное изображе-
ние бывает, как правило, триметрией (см. § 40).
§ 38. КОСОУГОЛЬНАЯ
АКСОНОМЕТРИЯ
В практике используются только изометрия
и диметрия. Плоскость аксонометрических про-
екций занимает частное положение относи-
тельно координатных плоскостей. Она или па-
раллельна одной из координатных плоскостей,
или параллельна оси z. Рассмотрим случай,
когда плоскость П° параллельна плоскости х П z
В соответствии с /12/ ось х параллельна
координатной оси х, а ось z° — координатной
оси z, т. е. х° 1 z°. Ось у' может быть под
любым углом наклонена к осям х° и z°, что
зависит от направления проецирования. Этот
угол обычно принимается равным 30, 45 или 60
(углы чертежных угольников). Расположив П
параллельно плоскости г Hz, получим аксоно-
метрию, у которой ось х наклонена к горизон-
тальному направлению на чертеже, а оси у° и z°
взаимно перпендикулярны.
Наклоненная ось может быть обращена
влево вниз, влево вверх и т. д., что соответст-
вует различному направлению проецирования
и расположению плоскости проекций относи-
тельно координатных плоскостей. Коэффици-
енты искажения по взаимно перпендикулярным
осям равны 1 (см. /39/), коэффициент искажения
по наклонной оси теоретически может меняться
от нуля до стремящейся к бесконечности вели-
чины (см. /38/). На практике его принимают
равным 1 (косоугольная изометрия; u = v =
= и’ = 1.) или 0,5 (косоугольная диметрия; и =
= w = 1; v — 0,5). Приведенные на рис. 471
и 472 аксонометрии предмета выполнены в
изометрии (а) и димегрии (б). Если наклонена
ось х, то изображение предмета в изометрии
(рис. 471) примет вид (в), а в диметрии (г)
Куб, грани которого параллельны коорди-
натным плоскостям, изображен в косоугольной
изометрии на рис. 473, а, в косоугольной ди
метрии на рис. 473, б. Окружность, вписанная
во фронтально расположенную грань, изобра-
жается в виде окружности; э<о объясняется тем,
что плоскость этой грани куба параллельна
плоскости х П z, а следовательно, и плоскости П
(см. /43/). Аксонометрии .окружностей, распо-
ложенных в других видимых гранях куба, пред-
ставляют собой эллипсы, вписанные в ромбы
(изометрия) и в параллелограммы (диметрия).
Оси эллипсов всегда наклонены к горизонталь-
ному направлению на чертеже. Когда аксоно-
метрическая ось у (или х) наклонена к горизон-
тальному направлению под углом 45 , то боль-
шая ось эллипсов а и b в косоугольной изомет-
рии равна 1,37), малая — 0,547). При том же
наклоне оси у (или х) в косоугольной диметрии
большая ось эллипсов равна 1,07 D, а малая
ось 0,337).
Если плоскость проекций расположить -па-
раллельно координатной плоскости хПу, то
угол между осями х° и у” будет прямым (по-
чему?). Аксонометрия называется горизонталь-
ной косоугольной изометрией. Расположение
186
осей показано на рис. 474. Угол а обычно при-
нимают равным 30, 45 и 60°, но он может быть
любым, вплоть до 0°. Коэффициенты искаже-
ния по осям равны 1.
На рис. 474, б в горизонтальной косоуголь-
ной изометрии построен куб. Окружность, рас-
положенная в его верхней грани, изображается
также в виде окружности. Вообше говоря, лю-
бая фигура, расположенная в горизонтальной
плоскости, изображается в виде равной и по-
добно расположенной фигуры. Это свойство
используется при изображении значительных
участков местности с застройкой. Так как гори-
зонтальная ортогональная проекция застройки
(план) не изменяется при изображении ее в
аксонометрии, то эта проекция может быть по-
ложена в основу построений. Окружности, впи-
санные в другие видимые грани куба, проеци-
руются в эллипсы.
В практике используется горизонтальная
косоугольная изометрия с осями х° и у°, обра-
щенными вверх от точки О. В этом случае
предметы изображаются при направлении про-
ецирования снизу вверх.
Пусть плоскость аксонометрических про-
екций вертикальна и наклонена под углом 45°
Рис. 472
187
Рис. 473
Рис. 476
к плоскостям х Л z и у П z, а направление проеци-
рования параллельно плоскости биссектора угла
между этими плоскостями (рис. 475). При этих
условиях коэффициент искажения по оси zc
равен 1, по осям х° и у° может меняться от 0,71
до сколь угодно большой величины (докажите
справедливость сказанного).
Вариант такой аксонометрии показан на
рис. 476. Оси х и у наклонены к горизонталь-
ному направлению под углом 30°, коэффициен-
ты искажения по ним равны 0,82, т. е. такие же,
как и в прямоугольной изометрии, но коэффи-
циент искажения по оси z равен 1. Перед пря-
моугольной изометрией такая аксонометрия
имеет преимущество при изображении значи-
тельных по величине предметов (зданий, соору-
жений), так как боковые стороны предметов
изображаются уменьшенными по сравнению с
изображенными в прямоугольной изометрии.
Поэтому изображение приближается к перспек-
тиве. Удобно пользоваться приведенными ко-
эффициентами искажения: по осям х и у рав-
ными 1, по оси z — 1,22.
§ 39. ПОСТРОЕНИЕ
АКСОНОМЕТРИИ ФИГУР
Выбор аксонометрии. Вид аксонометрии вы-
бирается в зависимости от трудоемкости ее
построения и наглядности получаемого изоб-
ражения. Нужен некоторый опыт для правиль-
ного выбора аксонометрии в каждом конкрет-
ном случае, однако существуют правила, кото-
рых следует придерживаться' если изображает-
ся сфера или ее часть, то следует применять
прямоугольную аксонометрию (см. /194/).
• При изображении предметов, имеющих зна-
чительное число окружностей, расположенных
в плоскостях, параллельных одной из коорди-
натных плоскостей, полезно использовать косо-
угольную диметрию или изометрию, выбрав
плоскость проекций, параллельную плоскостям
окружностей (см. /43/).
Для изображения крупных предметов (зда-
ний, сооружений) удобно пользоваться прямо-
угольной аксонометрией или косоугольной, по-
казанной на рис. 476.
Горизонтальную косоугольную изометрию
следует применять при изображении городской
застройки, значительных участков местности с
сооружениями на них и т. д.;
прямоугольная аксонометрия вносит мень-
шие кажущиеся искажения формы предметов,
чем косоугольная. Поэтому, когда важна есте
188
ственность изображения, предпочтительна пря-
моугольная аксонометрия (кроме косоугольной
диметрии, приведенной на рис. 476);
косоугольная аксонометрия большей частью
менее трудоемка, чем прямоугольная.
При решении особых задач следует исполь-
зовать построение аксонометрии по выбранно-
му направлению проецирования (см. § 40).
Границе тело. Для построения его аксоно-
метрии достаточно найти аксонометрические
проекции его вершин. Пирамида, изображенная
в ортогональных проекциях на рис. 477, отне-
сена к системе координатных осей х, у и z,
совпадающих с осями проекций того же наиме-
нования. Аксонометрия задана аксонометриче-
скими осями и масштабами (рис. 478). Измерив
координаты точек А, В, С, D и S на эпюре, по-
строим вторичные горизонтальные проекции
этих точек, а затем и их аксонометрические
проекции (см. /190/). Соединив аксонометриче-
ские проекции точек в том же порядке, в каком
точки соединены в натуре (об этом можно судить
по ортогональным проекциям тела), получим
аксонометрию пирамиды. В целях упрощения
на рис. 478 опущен знак ° при обозначении аксо-
нометрических осей, аксонометрических и вто-
ричных проекций точек. Такое упрощение мы
будем применять и в дальнейшем во всех случа-
ях, когда от этого не пострадает ясность чер-
тежа или пояснений к нему Соединив прямыми
точки А,, В, и др., получим вторичные горизон-
тальные проекции ребер и граней пирамиды,
а в совокупности — вторичную проекцию пира-
миды. Можно построить фронтальную и про-
фильную вторичные проекции, как это сделано
на рис. 478.
Параллелограмм AIB,C}DI подобен и по-
добно расположен параллелограмму A BCD.
В. соответствии с /44/ можно параллельно пе-
ренести аксонометрические оси в любое место
чертежа (если мы не связаны условием сохра-
нить взаиморасположение проекций коорди-
натных осей и аксонометрии фигуры), поэтому
и вторичную проекцию можно расположить на
произвольном расстоянии от аксонометрии фи-
гуры, но в проекционной связи с ней.
На практике систему координатных осей
в пространстве часто относят к изображаемой
фигуре так, что ее ребра или другие элементы
параллельны новым осям При этом меняется
аксонометрия фигуры, но значительно упро-
щаются построения. Зададим новую систему
координатных осей х', у' и z' так, чтобы точ-
ка О совпала, например, с точкой А, а оси х' и у'
соответственно с ребрами АВ и AD (см. рис. 477).
Зададим аксонометрию аксонометрическими
осями и масштабами (индекс при обозначении
осей опущен). Теперь построение аксонометрии
значительно упрощается (рис. 479): Отложим
от точки А = 0-по оси х длину ребра АВ (4 еди-
ницы), а по оси у от той же точки длину реб-
ра Л Л (4 единицы) с учетом аксонометрических
масштабов по этим осям. Через точку В про-
ведем прямую В С || у, а через D прямую DC || х
до их пересечения в точке С. Проведя диагонали
параллелограмма A BCD, найдем в их пересе-
чении точку S] и, отложив от нее вертикальный
отрезок длиной 6 единиц в масштабе оси z.
189
о
Рис. 480
построим точку 5. Соединим прямыми точку 5
с точками А, В, С и D.
Окружность. Построение аксонометрии ок-
ружности, расположенной в горизонтальной
плоскости (рис. 480, а), показано на рис. 480, 6.
Опишем около окружности квадрат со сторо-
нами, параллельными осям проекций х и у.
Отнесем окружность к системе координатных
осей х, у' иг', соответственно параллельных
осям проекций. Начало координат О' располо-
жим в одной из вершин квадрата. Взяв в про-
извольном месте точку О (или, если это необ-
ходимо, построим ее аксонометрию в систе-
ме xyz), построим параллелограмм — аксоно-
метрическую проекцию квадрата, в который
вписана окружность. Найдя аксонометрию цент-
ра окружности в пересечении диагоналей парал-
лелограмма, отметим точки, в которых прямые,
проходящие через аксонометрию центра парал-
лельно осям х и у, пересекаются со сторонами
параллелограмма. Эти точки инцидентны эл-
липсу — аксонометрии окружности. Проведем
полуокружность на одной из сторон паралле-
лограмма и ее радиусы, наклоненные к диамет-
ру под углом 45'. (Для этого достаточно описать
вокруг полуокружности половину квадрата.)
Точка А пересечения радиуса с окружностью
делит отрезок DE в том же отношении, в каком
^очка В делит отрезок DF. Проведем через В
прямую, параллельную оси у. В точке С она
пересекается с диагональю параллелограмма.
Точка С делит отрезок FG в том же отношении.
190
)
в каком точка В делит отрезок DF, а следова-
тельно, и точка А делит отрезок DE. В соответ-
ствии с /41/ точка С принадлежит эллипсу —
параллельной (аксонометрической) проекпии
окружности. Прямые, проходящие через С па-
раллельно осям х и у, пересекаются со второй
диагональю параллелограмма еще в двух точ-
ках, инцидентных эллипсу. Через одну из них
можно провести прямую, параллельную оси
(х или у), получив при этом четвертую точку.
Таким образом найдено восемь точек эллипса.
Если этого числа недостаточно, можно восполь-
зоваться вспомогательной прямой DH, про-
веденной через произвольную точку М окруж-
ности и ее центр. Построение аксонометрии
точки М ясно- из чертежа.
Когда окружность лежит в плоскости обще-
го положения (рис. 481, а), нужно, как и в пре-
дыдущем примере, описать вокруг нее квадрат.
Для этого проведем горизонтали GH и FE,
касательные к окружности соответственно в.
точках С и А. Горизонтальные проекции сторон
квадрата FG и ЕН перпендикулярны горизон-
тальным проекциям горизонталей (см. /45/).
Построив вторичные горизонтальные проек-
ции точек F, Е и И, найдем их- аксонометриче-
ские проекции (см. /191/). Соединив прямыми
точками F и Е, а также Е и Н, проведем через Н
прямую параллельно ЕЕ, а через F — прямую
параллельно ЕН (почему параллельно?) до
взаимного пересечения в точке G. Параллело-
грамм FEHG представляет собой аксономет-
рию квадрата, описанного вокруг окружности.
Проведя диагонали параллелограмма и пря-
мые, проходящие через точку их пересечения
параллельно сторонам, найдем четыре точки
эллипса А, В, С и D. Построим полуокружность
на одной из сторон параллелограмма и выпол-
ним построения, описанные в предыдущем при-
мере. В результате найдем еще четыре точки
эллипса. Если восьми точек недостаточно, мож-
но проделать построения, аналогичные тем, с
помощью которых найдена аксонометрия точ-
ми М.
Конус и цилиндр. Прямой круговой конус
изображен на рис. 482, а в ортогональных про-
екциях, а на рис. 482, б построена его аксоно-
метрия (она задана осями и коэффициентами
искажения по ним). Описав вокруг основания
конуса квадрат, построим аксонометрию впи-
санной в квадрат окружности (см. рис. 480, б).
Найдем аксонометрию вершины, как на рис. 479.
Проекции контурных образующих проходят
через точку 5 касательно к эллипсу — проекции
основания. В связи с тем, что аксонометрия за-
дана осями и коэффициентами искажения, сле-
дует длину сторон квадрата и высоту- конуса
умножать На соответствующий коэффициент
искажения.
Если координатные оси х и у не будут парал-
лельны соответствующим осям проекций, фор-
ма аксонометрической проекции конуса не из-
менится. Этого нельзя сказать об аксонометрии
цилиндра, изображенного на рис. 483, а. Она
будет меняться при повороте этих осей, так как
в зависимости от их расположения мы будем в
большем или меньшем ракурсе видеть-эллипс
BECD. Если расположить координатные оси
Рис. 482
параллельно соответствующим осям проекций,
к зрителю будет обращена та часть боковой по-
верхности цилиндра, которая закрывает эл-
липс. Если это нежелательно, нужно коорди-
натную ось у расположить параллельно оси
проекций х, а координатную ось х — парал-
лельно оси проекций у. Изображение цилиндра
в аксонометрии (она задана осями и коэффи-
циентами искажения по ним) примет вид, по-
казанный на рис. 483, б. Вначале построим аксо-
нометрию окружности нижнего основания ци-
линдра. Затем измерим в ортогональных про-
екциях координаты z точек В, С, D, Е и отло-
жим их от вторичных горизонтальных проек-
ций этих точек, предварительно умножив на
коэффициент искажения по оси z. Также по-
строим аксонометрию промежуточных точек,
например точки А. Контурные образующие ка-
сательны к обоим эллипсам.
- Поверхности, обертывающие множество сфер.
При изображении таких поверхностей следует
использовать прямоугольную аксонометрию,
так как в этом случае проекцией сферы является
круг (см. /194/).
Рис. 483
191
Рис. 484
Построим аксонометрию половины тора
(рис. 484, а). Эта поверхность огибает множе-
ство сфер радиуса R. Аксонометрию зададим
аксонометрическими осями и масштабами
(рис. 484, б). Построим аксонометрии окруж-
ностей а и Ь (см. рис. 480) и полуокружности —
кривой оси тора. Взяв на аксонометрии кривой
оси некоторое число точек и использовав их
как центры вписанных в поверхность сфер, про-
ведем окружности радиуса R. (Если использу-
ются приведенные коэффициенты искажения,
величину радиуса нужно умножить на коэффи-
циент приведения.) Эти окружности представ-
ляют собой проекции контура сфер, вписанных
в заданный тор. Остается провести огибаю-
щие — кривые линии, соприкасающиеся с ок-
ружностями и эллипсами а и Ь. Нижняя линия
контура тора в месте сгущения окружностей
переходит внутрь проекции тора, что говорит
о том, что ближайшая к зрителю' часть тора
закрывает сзади расположенную.
Описанный прием можно использовать и в
том случае, когда радиус вписанных сфер —
величина переменная. Поверхность вращения,
удовлетворяющая такому условию, изображе-
на на рис. 485, а. Центры сфер расположены на
оси вращения поверхности.
Проведем прямую параллельно аксономет-
рической оси х (рис. 485, б) и построим на ней
аксонометрии центров сфер по их ортогональ-
ной проекции (с учетом аксонометрического
масштаба по оси х). Радиусы вписанных сфер
измерим по ортогональной проекции заданной
фигуры. Построив необходимое число аксоно-
метрических проекций сфер, проведем огибаю-
щую — проекцию контура поверхности. По-
строение цилиндра ясно из чертежа.
Значительные участки местности с сооруже-
ниями на них. Для построения аксонометрии та-
ких объектов удобно использовать горизон-
тальную косоугольную изометрическую про-
екцию. Достаточно взять план застройки, на-
пример, городского квартала, повернуть его
на некоторый угол (не исключено, что план не
нужно повертывать) и, используя его как вто-
ричную горизонтальную проекцию объектов
застройки, построить их аксонометрию.
Коэффициент искажения по оси z иногда
принимают меньшим единицы (горизонтальная
косоугольная диметрия), при этом аксонометрия
становится более естественной. Пример гори-
зонтальной косоугольной изометрической про-
екции городского квартала приведен на рис. 486.
Горизонтальная косоугольная изометри-
ческая проекция может быть использована для
изображения топографической поверхности с
сооружениями на ней. Действительно, форма
проекций горизонталей, построенных в аксоно-
метрии, не отличается от их формы в проекциях
с числовыми отметками (почему?). Для постро-
ения аксонометрии топографической поверхно-
сти, изображенной на рис. 487, а, достаточно
вначале скопировать проекцию 21-й горизон-
тали с чертежа в проекциях с числовыми отмет-
ками и вычертить ее без изменения в аксономет-
рии (рис. 487, б); затем, скопировав проекцию
22-й горизонтали, следует переместить ее без
поворота в направлении оси z в аксонометрии
на величину высоты сечения. В такой же после-
довательности строятся проекции остальных
горизонталей. Когда это возможно, следует
провести проекцию контура поверхности. Что-
бы построить аксонометрию сооружения, рас-
положенного на топографической поверхности,
нужно отметить на чертеже в проекциях с чис-
ловыми отметками точки пересечения сооруже-
ния с соответствующими горизонталями по-
верхности. При построении горизонталей в
аксонометрии одновременно строятся и эти
точки, а затем соединяются плавной кривой в
той же последовательности, в какой они соеди-
нены в натуре. Верхняя часть сооружения стро-
ится в соответствии с описанием к рис. 486.
Кроме рассмотренных примеров в горизон-
тальной косоугольной изометрической проек-
ции построено изображение земляного соору-
жения на рис. 441.
192
Рис. 486
При желании изобразить предмет снизу
используется горизонтальная косоугольная изо-
метрическая проекция, оси х и у которой обра-
щены вверх, при сохранении угла между ни-
ми 90°.
Поверхности второго порядка. Эти поверх-
ности проецируются на плоскость аксономет-
рических проекций цилиндрической проеци-
рующей поверхностью, в которую вписана за-
данная поверхность. Проецирующая поверх-
ность является поверхностью второго порядка
(см. /161/) и поэтому соприкасается с данной
поверхностью по плоской кривой второго по-
рядка. Эта’ кривая является контуром изобра-
жаемой поверхности относительно плоско-
сти П°; ее проекция представляет собой кривую
второго порядка того же вида.
Если заданная поверхность — трехосный эл-
липсоид, то соприкасающаяся с ним проеци-
рующая цилиндрическая поверхность — эллип-
тическая. Линией ее пересечения с плоскостью
проекций может быть только эллипс. Поэтому
аксонометрией контура эллипсоида всегда явля-
ется эллипс. Проекцией контура параболоида
может быть только парабола, гиперболоида
как однополостного, так и двуполостного — ги-
пербола (проекцией однополостного гипербо-
лоида может быть еще эллипс, но в практике
такой случай не встречается).
Построим прямоугольную аксонометрию
отсека параболоида вращения (рис. 488,' а). За-
дадим направление проецирования s (s}; s2).
Оно перпендикулярно плоскости П°. Повернем
прямую s так, чтобы она стала параллельной П2
(прямая s'). Так как ось вращения параболоида
параллельна этой плоскости, то поворот отсека
поверхности не изменит его проекций. Это дает
возможность провести проекцию проецирую-
щей прямой, касательной к поверхности, па-
раллельно s2. Она проходит через точку А2.
Горизонтальная проекция проецирующей пря-
мой совпадает с горизонтальной осью проекции
поверхности на плоскости ПР Линия соприкос-
новения проецирующей цилиндрической по-
верхности (это параболический цилиндр) с за-
данной поверхностью представляет собой па-
раболу с вершиной А. Ее плоскость (как и всех
парабол, инцидентных параболоиду) парал-
лельна оси поверхности.
Определив точки параболы D, Е, F, G, про-
ведем фронтальную проекцию Щ плоскости П°
перпендикулярно s2. Отметим точки пересече-
ния с ней фронтальных проекций проецирую-
щих прямых, проходящих через найденные точ-
ки, а также точки В, С, Н, N и А.
' Возьмем в произвольном месте чертежа точ-
ку А (рис. 488, б) и, отложив по вертикальной
прямой, проходящей через эту точку, отрезок,
равный а (рис. 488, а), построим точку N.
Отрезок b равен малой оси эллипса — проекции
13—940
193
Рис. 488
окружности HCNB на плоскости П°. Большая
ось (СВ) равна диаметру этой окружности (по-
чему?). Спроецировав на ГГ точки Е, D, F и G,
построим их аксонометрии (расстояние между
точками Е и D, а также F и G равно расстоянию
между их горизонтальными проекциями. По-
чему?).
В результате построений получим дугу па-
раболы FEA DC — проекцию контура отсека
параболоида и эллипс CNBH — проекцию ок-
ружности, соприкасающейся с параболой
В приведенном примере координатные оси
расположены так, что ось z совпадает с осью
вращения поверхности.
§ 40. ПОСТРОЕНИЕ
АКСОНОМЕТРИИ ПО ЗАДАННЫМ
УСЛОВИЯМ
Выбор направления проецирования. Когда
аксонометрия задана (направление аксономет-
рических осей и коэффициенты искажения или
аксонометрические масштабы), нельзя гаран-
тировать, что будут видимы те части изобра-
жаемого предмета, которые представляют осо-
бую важность. Например, если предмет имеет
углубление, нельзя заранее сказать, будет ли
видно его дно; какой-либо выступ может за-
крыть ту часть предмета, которую нужно было
бы показать, и т. д. Однако возможно построить
такую аксонометрию, которая будет удовле-
творять, если не всем, то большинству из предъ-
являемых к ней требований.
Для этого нужно определенным образом за-
дать направление проецирования. Построим
аксонометрию предмета, изображенного на
рис. 489, а, при условии, что:
а) предмет должен быть виден спереди,
справа и сверху;
б) задняя левая колонна должна быть за-
крыта верхней плитой не ниже, чем до пря-
мой а;
в) расположенный справа выступ I не пол-
ностью закрывает нижнюю плиту II предмета.
Выполняя условие (а) » часть условия (б),
проведем горизонтальную проекцию проеци-
рующей прямой s спереди и справа налево через
крайнюю левую точку горизонтальной проек-
ции передней колонны и правую переднюю точ-
ку проекции дальней колонны. Проверим, вы-
полняется ли условие (в). Для этого через край-
нюю правую точку горизонтальной проекции
выступа проведем проекцию проецирующей
прямой s' параллельно s. Она пересекается с
•проекцией нижней плиты в точке А,, следова-
тельно, видимой будет та часть плиты, которая
расположена за точкой А. Отметим, что эта
часть плиты слишком мала.
Если изменить наклон проекции проецирую-
щей прямой, то задняя колонна может быть
видна полностью или, наоборот, останется ви-
димой только часть ее передней грани. Пусть
нас удовлетворит такое направление проециро-
вания, когда будет видна половина передней
грани колонны. Тогда горизонтальная проек-
ция s'i проецирующей прямой s" пройдет
через точку Bt и левый угол проекции передней
194
Рис. 489
колонны. При этом могут быть выполнены все
три условия видимости частей предмета.
Проверяя, насколько будет видна нижняя
плита, проведем горизонтальную проекцию
проецирующей прямой параллельно через
проекцию крайнего правого угла выступа. Она
пересекается с проекцией нижней плиты в точ-
ке С], т. е. дальше, чем точка А,. Можно счи-
тать, что принятая горизонтальная проекция
направления проецирования удовлетворяет всем
трем условиям, остается найти фронтальную
проекцию направления проецирования. Для это-
го построим точку В2; она в соответствии с ус-
ловием (в) должна быть расположена на пря-
мой а2. Принять произвольный наклон фрон-
тальной проекции направления проецирования
нельзя, так как по условию мы должны видеть
точку В; следовательно, проецирующая пря-
мая, проходящая через эту точку, не должна
встретить какого-либо препятствия.
Проведем через прямую s" вертикальную
плоскость и построим фронтальную проекцию
сечения этой плоскостью заданного предмета
(на чертеже она заштрихована). Если фрон-
тальная проекция проецирующей прямой, про-
ходящей через точку В, пересечет проекцию
сечения, то в пространстве проецирующая пря
мая пересечет сам предмет, и точка В будет не-
видимой. Следовательно, нужно так провести
фронтальную проекцию проецирующей пря-
мой, чтобы она не пересекалась с проекцией
сечения или касалась его. Этот последний ва-
риант удовлетворяет заданным условиям, по-
этому проведем прямую s2 через В2 и крайнюю
правую точку проекции сечения.
Теперь выполнены все условия видимости
частей предмета, поставленные в заЛаче.
Описанный порядок определения направле-
ния проецирования удовлетворяет условиям
большинства задач, поэтому:
/196/ Выбрав направление горизонтальной
(фронтальной) проекции проецирующей прямой в
соответствии с условиями задачи, нужно заклю-
чить ее в проецирующую плоскость, построить
сечение ею заданной фигуры, после чего провести
фронтальную (горизонтальную) проекцию про-
ецирующей прямой так, чтобы она не пересекала
(или пересекала в зависимости от условий) се-
чение.
Построив треугольник следов в соответствии
с описанием к рис. 461, определим направление
аксонометрических осей, и коэффициенты иска-
жения по ним (или аксонометрические масшта-
бы). Вслед за этим построим аксонометрию
(прямоугольную триметрию) заданного пред-
мета (рис. 489, б). Анализируя изображение,
убеждаемся, что все три условия, поставленные
перед нами, выполнены.
На рис. 490, а в ортогональных проекциях
изображен предмет, имеющий форму паралле-
Рнс. 490
13*
195
лепипеда с двумя углублениями; вертикальное
углубление имеет форму цилиндра, горизон-
тальное — параллелепипеда. Нужно построить
аксонометрию, так чтобы по изображению
можно было судить, что углубления не являются
сквозными отверстиями.
Поставленное условие предопределяет на-
правление проецирования сверху, чтобы было
видно дно цилиндрического углубления, и сле-
ва — для обеспечения видимости дна горизон-
тального углубления. Естественно, что дно как
того, так и другого углубления можно видеть
только частично. Проведем горизонтальную
проекцию 5] проецирующей прямой через пе-
редний к зрителю край горизонтального углуб-
ления и отметим точку В, ее пересечения с про-
екцией дна. При таком направлении проециро-
вания дно горизонтального углубления может
быть видно вплоть до точки В (будет ли в дей-
ствительности дно, зависит от того, как будет
расположена фронтальная проекция направле-
ния проецирования).
Проведем горизонтальную проекцию про-
ецирующей прямой параллельно Sj через центр
дна вертикального углубления; заключив ее в
вертикальную плоскость, построим сечение этой
плоскостью поверхности предмета (на чертеже
фронтальная проекция сечения построена не
полностью). Зададимся условием видеть на
аксонометрии предмета точку А, лежащую на
дне вертикального углубления. Для этого про-
ведем фронтальную проекцию проецирующей
прямой, проходящей через А и верхний угол
проекции сечения (см. /196/). Остается прове-
рить, будет ли видно дно горизонтального
углубления. Проведем фронтальную, проекцию
Рис. 492
проецирующей прямой, проходящей через верх-
ний край углубления, и построим проекцию
точки В пересечения этой прямой с плоскостью
дна. Убеждаемся, что точка В не вышла за пре-
делы дна, следовательно, оно будет частично
видимым (если бы этого не произошло, нужно
было бы взять вместо точки А другую точку и
вновь проделать описанное построение; не ис-
ключено, что при иных размерах одного или
обоих углублений поставленное условие види-
мости может быть невыполнимо).
Построим треугольник следов (см. рис. 461
и 488) и определим коэффициенты искажения.
Они соответственно равны 0,825, 0,875 и 0,775
(триметрия). Проверим правильность подсчета
по формуле (см. /187/: 0,8252 + 0,8752 + 0,7752
^>2,05, т. е. очень близко к 2, что можно счи-
тать достаточно точным.
Аксонометрия заданного предмета приведе-
на на рис. 490, б. По изображению можно судить
о форме и относительных размерах углублений.
Рассмотрим еще пример. На рис. 491, а
изображен в ортогональных проекциях прямой
круговой конус; его высота по сравнению с диа-
метром основания относительно мала. Если
построить аксонометрию конуса, заданную, на-
пример, такими же осями и коэффициентами
искажения, как в примере на рис. 490, то проек-
ция вершины окажется внутри проекции осно-
вания, и чертеж не будет наглядным (рис. 491, б).
Проведем через горизонтальную проекцию
вершины конуса — точку Т\ горизонтальную
проекцию проецирующей прямой, например,
под углом 45° к координатным осям (от величи-
ны этого угла не зависит изображение конуса.
Почему?). Изображение будет наглядным, если
аксонометрическая проекция вершины лежит
вне проекции основания. Для этого возьмем точ-
ку А, инцидентную плоскости основания конуса
и проецирующей прямой, проходящей через
вершину. Зададимся ее горизонтальной проек-
цией А, (чем дальше от основания точка А,
тем выше расположена аксонометрическая про-
екция вершины конуса). Положение точки А2
определяет фронтальную проекцию проецирую-
щей прямой, проходящей через точку Т.
Построив треугольник следов, определим
направление аксонометрических осей (построе-
ния на чертеже не показаны) и коэффициентов
искажения. На рис. 491, в дан окончательный
результат — аксонометрические оси и коэф-
фициенты искажения. Аксонометрия является
прямоугольной диметрией. Условия нагляд-
ности: проекция вершины расположена вне
проекции основания.
Аксонометрия, построенная прн нескольких
направлениях проецирования. Иногда для более
наглядного изображения предметов, состоящих
из разъемных частей, бывает полезно раздельно
выполнять аксонометрические изображения
каждой детали, но так, чтобы создалось впе-
чатление общности всего изделия. С этой целью
применяют параллельное перемещение коор-
динатных осей, к которым отнесен предмет
или, что приводит к тем же результатам, пере-
мещение деталей предмета относительно осей.
Например, детали узла, изображенного на
рис. 492, смещены одна относительно другой
в направлении оси х.
196
z'
Другой прием основан на том, что детали
узла изображаются в различных аксонометриях,
что соответствует разным направлениям про-
ецирования (или относятся в. пространстве к
разным координатным осям). Например, одна
деталь рассматривается сверху и справа, дру-
гая — снизу и слева и т. д. Если для каждой
детали принять свою аксонометрию, отличную
по направлению осей и показателям искажения
от аксонометрий, использованных для изобра-
жения других деталей, чертеж не будет созда-
вать впечатления общности деталей. Поэтому
следует использовать такие аксонометрии, у
которых или симметричны оси, или равные
по одноименным осям коэффициенты иска-
жения.
Общность изображения сохранится и в том
случае, если ось z расположить горизонтально
или с некоторым наклоном, сохранив углы
между осями такими же, какими они приведены
в таблице (см. рис. 460). На рис. 493 изображен
узел строительной конструкции. Детали i—6
построены в аксонометрии xyz, заданной аксо-
нометрическими осями и коэффициентами ис-
кажения. Расположение осей аналогично полу-
ченному при проецировании из первого угла
пространства (рис. 460). Детали 1и 2 соедине-
ны так, как это должно быть в натуре. Детали
3, 4 и 5 опущены, что позволило дать пред-
ставление об их форме; благодаря этому де-
таль 6 как бы растянута. Можно считать, что
построены две аксонометрии (детали I,. 2, 6
и детали 3, 4, 5) или узел в пространстве разъ-
единен и в таком виде изображен в аксономет-
рии. Направление осей и коэффициенты иска-
жения в обеих аксонометриях одинаковы.
Чтобы показать форму вырезов на детали Z
ее пришлось изобразить в другом виде аксо-
нометрии x'y'z', аналогичном построенной при
проецировании из IV угла пространстве (см.
рис. 460). Направление осей изменилось по
сравнению с аксонометрией других деталей,
но коэффициенты искажения совпадают.
Несмотря на то что узел изображен в трех
видах аксонометрии, единство чертежа сохра-
няется.
На рис. 494 изображен другой узел строи-
тельной конструкции. Группа деталей 1 по-
строена в аксонометрии xyz. Они соединены
между собой так, как это имеет место в натуре.
Деталь 2 приподнята, что позволило показать
конструкцию ее соединения с группой деталей 1.
Деталь 3 передвинута в направлении оси у,
поэтому видны соединяющий эти детали болт
и вырез в детали .2, в который входит деталь 3.
Для деталей 2 и 3 использованы аксонометрии,
направление осей которых совпадает с направ-
лением оси аксонометрии xyz, совпадают и
коэффициенты искажения. Чтобы показать ха-
рактер вырезов в детали 4, ее нужно повернуть,
что соответствует использованию другого вида
аксонометрии x'y'z'. Здесь оси у’ ||у, z'||x,
х' || z. Ось х' обращена вниз. Расположение
осей этой аксонометрии аналогично их распо-
ложению при проецировании из V угла про-
странства; кроме того, оси х и z повернуты,
что позволило показать заднюю (относительно
зрителя при построении аксонометрии xyz)
сторону детали.
•§ 41. РЕШЕНИЕ НЕКОТОРЫХ
ЗАДАЧ В АКСОНОМЕТРИИ
Большинство позиционных задач в аксоно-
метрических проекциях может быть решено,
когда оси и коэффициенты искажения или аксо-
нометрические масштабы не известны. На при-
веденных ниже чертежах оси показаны для
большей наглядности. Обычно достаточно, что-
бы положение фигур в пространстве определя-
лось их аксонометрическими и вторичными
проекциями (или двумя вторичными проек-
циями и линиями связи).
Пересечение прямой н плоскости. Плоскость
АВС и прямая DE заданы своими аксонометри-
ческими и вторичными горизонтальными про-
екциями (рис. 495). Решим задачу в соответст-
вии с /87/. Заключим прямую в вертикальную
плоскость, положение которой определяется
прямыми DD, и ЕЕПрямая DjE) представ-
ляет собой вторичную горизонтальную про-
екцию этой плоскости. Вторичная горизонталь-
ная проекция любой фигуры, расположенной
в ней, совпадает с этой линией. Отметим точки
Fj и Gj пересечения прямой DlEi соответст-
венно с прямыми А, С, и В, С, и, проведя через
эти точки линии связи, найдем в их пересече-
197
нии с аксонометрическими проекциями сторон
треугольника АС и ВС точки F и G. Соединив
их прямой, найдем искомую точку К в пересе-
чении прямых DE и FG.
Определим видимость DE относительно от-
сека плоскости АВС (треугольника). Видимость
фигур в ортогональных проекциях и аксономет-
рии может не совпадать (почему?). Для решения
задачи в аксонометрии воспользуемся конку-
рирующими точками, например Н и Т, инци-
дентными соответственно прямым DE и ВС.
Проведя линию связи через эти точки, найдем
их вторичные проекции. Вторичная горизон-
тальная проекция прямой НТ параллельна ли-
ниям связи. Ближе к зрителю расположена
точка Т, о чем можно судить по положению ее
вторичной горизонтальной проекции (см. на-
правление стрелки), следовательно, в точке
Н = Т прямая DE невидима.
Пересечение прямой с поверхностью. На
рис. 496 изображены конус и прямая; обе фигу-
ры заданы аксонометрической и вторичной
проекциями, причем известно, что плоскость
основания конуса совпадает с плоскостью х Г)у.
Заключив прямую а в плоскость, проходя-
щую через вершину конуса (см. /145/), задав ее
прямыми а и BS (В — произвольная точка пря-
мой д). Прямая а пересекается со своей вторич-
ной проекцией в точке А, прямая BS со своей
проекцией — в точке С. Соединив точки А и С
прямой, получим линию пересечения плоскости
основания конуса со вспомогательной плоско-
стью а Л BS. Эта линия встречается с основа-
нием конуса в точках D и Е; через них проходят
образующие конуса, по которым вспомогатель-
ная плоскость пересекает коническую поверх-
ность. Отметим точки N и К пересечения обра-
зующих с заданной прямой.
Для установления видимости прямой можно
воспользоваться конкурирующими точками, на-
пример F и G, инцидентными прямой а и. кон-
турной образующей конической поверхно-
сти TS. Кроме того, можно рассуждать и так:
образующая конической поверхности ES не-
видима, следовательно, невидима и принад-
лежащая ей точка К, а умеете с тем и весь отре-
зок от точки К до очерковой образующей TS.
Сечение поверхности плоскостью. Для при-
мера рассмотрим сечение плоскостью цилинд-
рической поверхности. Плоскость задана аксо-
нометрической и вторичной горизонтальной
проекциями пересекающихся прямых а и Ь, по-
верхность — аксонометрической проекцией и,
кроме того, вторичной проекцией образую-
щей с. Плоскость нижнего основания цилиндра
совпадает с плоскостью хЛу (рис. 497).
Построим аксонометрию линии пересече-
ния плоскости основания цилиндра с секущей
плоскостью. Для этого достаточно найти точ-
ки А и В пересечения аксонометрических и вто-
ричных проекций прямых а и b и соединить их
прямой. В произвольном месте проведем вер-
198
тикальндю плоскость, параллельную образую-
щим цилиндра; вторичная горизонтальная про-
екция э!гой плоскости (прямая Et DJ параллель-
на вторичной проекции сх образующей с. По
прямой CD вертикальная плоскость пересека-
ется с заданной плоскостью a Fib.
Проведем ряд вспомогательных вертикаль-
ных плоскостей, параллельных построенной и
пересекающих боковую поверхность цилиндра
по образующим, а заданную плоскость — по
прямым, параллельным CD Построения сво-
дятся к следующему: проведем, например, пря-
мую Fjff, || с, через точку F ее встречи с линией
пересечения плоскостей aClb и нижнего осно-
вания цилиндра; через ту же точку F проведем
прямую FG || CD. Обе прямые определяют пло-
скость, которая пересекается с поверхностью
цилиндра по образующей HG; точка G распо-
ложена в пересечении прямых HG и FG.
Пересечение гранных поверхностей. Рассмот-
рим пересечение гранных поверхностей на при-
мере схематизированного здания (рис. 498).
Вторичные проекции здания и пристройки за-
даны и известны высоты (координаты Z) редер
крыш и трубы (высоты откладываются с уче-
том коэффициента искажения по оси z).
Начнем построение с точки С, расположен-
ной в пересечении прямой а с плоскостью стены
здания. Так как эта плоскость вертикальна, до-
статочно определить точку С,; в пересечении
прямой а и линии связи, проходящей через С,,
найдем точку С. Линия пересечения плоскости
стены с плоскостью ската пристройки а Г) b
параллельна прямой Ь, которая параллельна
плоскости стены (по каким признакам можно
прийти к такому заключению?). Чтобы по-
строить точку А пересечения ребра с крыши
пристройки с плоскостью крыши основного
здания, нужно заключить ребро в вертикаль-
ную плоскость, которая пересечет скат крыши
по прямой ED. Прямые ED и с пересекаются в
точке А. Аналогично построены точки пересе-
чения и других горизонтальных ребер крыши
пристройки с плоскостями крыши и стены ос-
новного здания.
Линия пересечения передней правой грани
трубы с плоскостью ската крыши определяется
в результате сечения плоскостью этой грани
(вертикальной) плоскости ската. Точка В рас-
положена в пересечении левого вертикального
ребра стены здания с линией пересечения пло-
скостей крыши и стены.,
Пересечение конических и цилиндрических
поверхностей. Пересекаются два цилиндра, об-
разующие одной поверхности вертикальны, вто-
рой — горизонтальны (рис. 499); вертикальный
цилиндр задан основаниями, горизонтальный —
основанием (аксонометрическая и вторичная го-
ризонтальная проекции) и направлением обра-
зующих. Известно, что нижнее основание верти-
кального цилиндра расположено в плоскости
х пу.
Проведем вертикальную плоскость через
любую образующую, например АС, горизон-
тального цилиндра. С поверхностью горизон-
тального цилиндра она пересечется по обра-
зующим АС и BD, с плоскостью х пу — по пря-
мой y4j = В, —Q = Dj, представляющей собой
вторичную проекцию этих образующих, и, на-
конец, с вертикальным цилиндром по образую-
щей CD, проходящей через точку С, = Dt. В ре-
зультате можно отметить точки С и D, принад-
лежащие обеим поверхностям. Точка D лежит
на контурной образующей горизонтального
цилиндра и, следовательно, является границей
видимости линии пересечения поверхностей.
Проведя необходимое число плоскостей, па-
раллельных принятой секущей плоскости, полу-
чим общие для обеих поверхностей точки, кото-
рые соединим плавной кривой.
Конус и цилиндр на рис. 500 заданы аксоно-
метрическими и вторичными горизонтальными
проекциями оснований. Проведем пучок верти-
кальных плоскостей, проходящих через верши-
ну конуса. Одна из плоскостей пучка пересекает
боковую поверхность конуса по образующим
СА и DB, а поверхность цилиндра — по обра-
зующей АВ, проходящей через точку At=Bt
(это следует из того, что образующие цилиндра
вертикальны). В результате могут быть по-
строены точки А и В, принадлежащие обеим
поверхностям. Построив точки, расположенные
в других секущих плоскостях, соединим их меж-
ду, собой плавной кривой.
ГЛАВА IX
ПЕРСПЕКТИВНЫЕ ПРОЕКЦИИ
§ 42. ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
В современном русском языке слово перспек-
тива имеет много значений. Они близко связа-
ны между собой и говорят об изображениях
предметов или самих предметах, расположен-
ных в определенном порядке перед зрителем.
Примерно так это слово переводится с латин-
ского языка, на котором perspicire значит
«видеть вперед». Основное явление перспекти-
вы хорошо известно: предметы, расположенные
ближе к зрителю, кажутся бблыпими, чем оди-
наковые с ними, но удаленные предметы. В кар-
тинах художников, на фотографиях и архитек-
турных перспективных чертежах это явление
получает отражение и влечет за собой ряд дру-
гих. Например, параллельные в натуре прямые
изображаются пересекающимися.
Способы изображения формы предметов
независимо от их цвета, материала, обработки
и j. д. изучаются в разделе начертательной гео-
метрии, называемом геометрическая перспек-
тива; явления, относящиеся к влиянию расстоя-
ния от предмета до зрителя, состоянию погоды
и других факторов на воспринимаемые зрите-
лем цвет и освещенность предмета, относятся
к физической перспективе, изучаемой в курсе
рисования.
Геометрическая перспектива делится на ли-
нейную перспективу, когда изображения строят-
ся на плоскости (рис. 501), панорамную (на ци-
линдрической или конической поверхности) и
купольную (на сфере, эллипсоиде и т. д. при рас-
положении зрителя в двух последних случаях
«внутри» поверхности). Мы рассмотрим только
линейную перспективу.
В архитектурной практике перспективные
изображения используются для оценки эстети-
ческих достоинств объектов на стадии выпол-
нения проекта, так как позволяют как бы «уви-
деть» будущее сооружение задолго до его воз-
ведения. Поэтому важно, чтобы зрительное
суждение о сооружениях в натуре было близким
к зрительному суждению, вызванному их перс-
пективными изображениями.
Под понятием «перспективная проекция»,
или, короче, «перспектива», будем иметь в виду
центральную проекцию предмета с введением
некоторых ограничений:
изображаться может только та часть про-
странства, которая расположена по одну сто-
рону от зрителя (центра проецирования)*,
* Точнее, по одну сторону от предельной плос-
4 кости (см. дальше).
изображаемый предмет должен быть поме-
щен внутри конуса с вершиной в центре проеци-
рования и углом между противоположными
образующими, не превышающим определенной
величины;
плоскость проекций располагается перпен-
дикулярно горизонтальной проекции оси такого
конуса;
рассматривать изображение нужно из той
точки, из которой оно построено или, по край-
ней мере, близкой к ней.
К основным элементам перспективного ап-
парата (рис. 502) относятся плоскость перспек-
тивных проекций ГГ, называемая картинной
плоскостью или картиной, центр проецирова-
ния, или точка зрения, S и объект проецирования
(на рис. 502 точка А). Плоскость П° может быть
вертикальной, наклонной и горизонтальной.
Мы будем строить перспективу только на вер-
тикальной картинной плоскости.
Проведем горизонтальную плоскость П|
на произвольном расстоянии от точки S. Это
уже знакомая нам горизонтальная плоскость
ортогональных проекций, однако назовем мы
ее предметной плоскостью. Линия пересечения
картинной и предметной плоскостей — пря-
мая к — называется основанием картины.
Через точку S параллельно П° проходит
предельная плоскость. Она делит пространство
на две части — изображаемую и неизображае-
мую. Изображаемая часть пространства может
быть расположена как по одну, так и по другую
сторону предельной плоскости. Предметная и
предельная плоскости пересекаются между со-
бой по прямой, параллельной основанию кар-1’
тины и называемой предметным следом предель-
ной плоскости.
Опустив перпендикуляр из S на П,, отметим
точку — горизонтальную ортогональную
проекцию точки зрения, или, короче, проекцию
точки зрения. Основание перпендикуляра, опу-
щенного из точки А на П1; является горизон-
тальной проекцией А, этой точки.
Спроецируем из точки S на П° точки А и А
Проекцией точки А станет точка А° — перспек-
тива точки А, проекцией точки At —точка А\,
называемая вторичной (горизонтально^) проек-
цией точки А. С этим термином мы познако-
мились при изучении аксонометрии. Точки
А° и А ° расположены на одном перпендикуляре
к основанию картины (плоскость ASHAjS
инцидентна прямой А А ,, перпендикулярной П,,
следовательно, она вертикальна. С вертикаль-
200
। ной же плоскостью П° она пересекается по
вертикальной прямой). Прямая A°At является
линией связи.
/197/ Перспективная и вторичная (горизон-
тальная) проекции точки расположены в проек-
ционной сиязи; линия связи вертикальна (см. ана-
логичное утверждение в /190/).
В дальнейшем, для простоты, вторичную
проекцию точки будем обозначать так же, как
и горизонтальную ортогональную проекцию,
т. е. Ait Вг, ...
По аналогии с /189/:
/198/ Перспективная и вторичная проекции
точки определяют положение точки в простран-
стве.
Опустив перпендикуляр из S на П°, получим
точку Р — главную точку картины. Точку Р —
ортогональную проекцию главной точки на
основание картины — назовем основанием глав-
ной точки. Вообще говоря, ортогональную про-
екцию на основание картины любой точки,
инцидентной картинной плоскости, будем на-
зывать основанием этой точки {например, точ-
ка А °).
Прямая SP называется главной проецирую-
щей прямой, а отрезок SP — главным расстоя-
нием. Отрезок S,P — горизонтальная проекция
главного расстояния — равен и параллелен от-
резку SP, следовательно, перпендикулярен ос-
нованию картины. Горизонтальная плоскость,
проходящая через S, называется плоскостью
горизонта. Она пересекается с П° по прямой h.
проходящей через точку Р и называемой гори-
зонтом*. Горизонт и точка зрения равно удале-
* horizon — разграничивающий. Горизонт —
линия, разграничивающая на изображении небо
и землю.
ны от предметной плоскости. Отрезок =РР
называется высотой горизонта или, что одно и
то - же, высотой точки зрения.
Будем рассматривать изображения, постро-
енные на плоскости nj и П°, а также элементы
этих плоскостей раздельно. При взгляде сверху
на плоскость П, (рис. 503, а) мы увидим пря-
мую к — основание картины (но, кроме того,
горизонтальную проекцию плоскости П°)г точ-
ки S1; Р и At. Такое изображение называется
планом. При взгляде спереди (рис. 503, б) будет
видна прямая к, с которой совпадает ортого-
нальная проекция предметной плоскости на
картинной. На прямой к лежит точка Р, а на
линии связи, проведенной через эту точку, —
главная точка картины Р. Через Р проходит
горизонт h. Кроме того, будут изображены точ-
ки А' и Л]. Это изображение назовем перспек-
тивой.
В будущем мы будем пользоваться такими
разрозненными чертежами. Общим для них'
Рис. 502
201
является основание картины к с точкой Р на
нем.
По плану и перспективе можно определить
положение точки зрения относительно картин-
ной и предметной плоскостей: расстояние от
точки зрения до П° равно отрезку S,P, а ее
высота — отрезку РР.
На рис. 503, а и б плоскости П, и П° ограни-
чены прямоугольниками, чтобы их изображе-
ния можно было сопоставить с изображением
этих плоскостей на рис. 502. В дальнейшем, как
правило, такого ограничения мы делать не
будем.
§ 43. ПЕРСПЕКТИВА ПРЯМОЙ
ЛИНИИ ЧАСТНОГО ПОЛОЖЕНИЯ
Проецирующие прямые и плоскости. Извест-
но, что любая прямая или плоскость, инцидент-
ные центру проецирования, называются про-
ецирующими. По расположению в пространст-
ве (относительно плоскостей П° и П,) проеци-
рующие прямые могут быть горизонтальными
(параллельными предметной плоскости), па-
раллельными картинной плоскости (в том числе
вертикальными) и прямыми общего положения
(не параллельными ни П,, ии П°). Положение
проецирующих плоскостей в пространстве опре-
деляется тем, каким проецирующим прямым
они инцидентны.
На рис. 504 изображены проецирующие пло-
скости Д и I, инцидентные наклонной проеци-
рующей прямой NM. Точка М (или N) может
быть выбрана произвольно, положение второй
точки зависит от того, где расположена первая.
Будем рассматривать прямую NM как ось пуч-
ка проецирующих плоскостей, которому при-
надлежат плоскости 12 и S.
Прямая а плоскости 12 и прямая b плоско-
сти Е являются линиями пересечения этих пло-
скостей с П], или предметными следами этих
плоскостей. С плоскостью П° плоскости 12
и Е пересекаются соответственно по прямым а°
и Ьс, являющимся их картинными следами.
Назвав точку М предметным следом, а точ-
ку N — картинным следом оси пучка плоско-
стей, можем отметить, что:
/199/ Предметные следы пучка проецирую-
щих плоскостей пересекаются в предметном сле-
де оси этого пучка (Л/), картинные следы пло-
скостей — в картинном следе (7V) оси пучка
(см. /25/).
Вместе с тем картинный и предметный следы
проецирующей плоскости пересекаются между
собой в точке, расположенной на основании
картины. Поэтому, если известен предметный
след проецирующей плоскости, а следователь-
но, и точка его пересечения с основанием кар-
тины, а также картинный след оси пучка пло-
скостей, то картинный след плоскости всегда
может быть построен.
Пусть на предметном следе а плоскости 12
лежит точка А. Проецирующая прямая AS
инцидентна плоскости 12, следовательно, пере-
секается с П° в точке А°, лежащей на картин-
ном следе этой плоскости — прямой а°. Так как
сказанное распространяется на любую точку
прямой а (см. /16/), в том числе и на точку В,
лежащую на основании картины и совпадаю-
щую со своей перспективой (В = В), то пря-
мая а проецируется вд плоскость П° в прямую
а°, или, иначе говоря;:
/200/ Перспективой предметного следа про-
ецирующей плоскости является ее картинный
след.
Построим перспективу точки А, инцидент-
ной предметной плоскости (рис. 505). Зададим-
ся двумя проецирующими прямыми NM и ТВ
и проведем через них и точку А проецирующие
плоскости 12 и Е. Предметные следы а и b этих
плоскостей проходят через А и соответственно
точки М и Т, картинные — а° и Ь° — через точ-
ки 1 и 2 и пересечения предметных следов с осно-
ванием картины и точки N и R. Точка А инци-
дентна предметным следам проецирующих пло-
скостей, следовательно, ее перспектива А° в
202
соответствии с /23/ и /200/ расположена в пере-
сечении картинных следов плоскостей.
Для построения перспективы какой-либо
иной точки, инцидентной предметной плоско-
сти, можно воспользоваться другой парой про-
ецирующих плоскостей, проходящих через пря-
мые MN и RT. Вообще говоря, для построения
перспективы множества точек предметной пло-
скости нужно провести через прямые MN и RT
множества (пучки) проецирующих плоскостей.
Пересечение картинных следов каждой пары
плоскостей, из которых одна принадлежит од-
ному пучку, другая — второму, определит
перспективу какой-либо одной точки предмет-
ной плоскости. Так как предметная плоскость
может быть расположена на произвольной вы-
соте, то ее можно провести через любую точку
пространства. Поэтому описанным способом
можно построить перспективу какой угодно
точки.
/201/ Чтобы построить перспективу точки,
нужно провести через нее две проецирующие пло-
скости и определить точку пересечения их кар-
тинных следов.
При решении задач следует использовать
такие оси пучков проецирующих плоскостей,
применение которых упрощает графические по-
строения. Обычно это прямые частного поло-
жения.
Пучок плоскостей с осью MN || Пс изобра-
жен на рис. 506. Картинные следы плоскостей
параллельны прямой Л/N, так как пересекаются
с нею в бесконечности. Отсюда, угол а наклоца
прямой MN и картинных следов плоскостей к
плоскости IIj одинаков.
/202/ Если ось пучка проецирующих плоско-
стей параллельна картинной плоскости, то кар-
тинные следы плоскостей пучка параллельны
между' собой и оси пучка. Предметные следы
пересекаются в точке, лежащей на предметном
следе предельной плоскости.
На рис. 507, а изображены в плане предмет-
ные следы проецирующих плоскостей такого же
пучка, как и на рис. 506. Они пересекаются с
основанием картины в точках 7, 2 и 3. Чтобы
построить картинные следы этих плоскостей
(рис. 506, б), достаточно измерить в плане от-
Рис. 507
резки Р 7, Р—2, Р—3 й, отложив их от точ-
ки Р по основанию картины в перспективе,
провести через полученные точки 7, 2 и 3 кар-
тинные следы плоскостей под углом а. Этот
угол можно определить, совместив точку S с
плоскостью П„ вращая ее вокруг предметного
следа предельной плоскости. Угол а удобно
принимать равным 45 ° или 60°, что позволит
использовать при проведении картинных сле-
дов чертежные угольники.
Когда ось пучка плоскостей перпендикуляр-
на предметной плоскости (прямая SS, J_ П, на
рис. 508), пучок состоит из вертикальных пло-
скостей. Их предметные следы пересекаются в
точке Sj, картинные — перпендикулярны осно-
ванию картины. Чтобы построить (рис. 509),
например, картинный след а° плоскости S2,
когда известен ее предметный след а, нужно
отметить точку 1 пересечения прямой а с осно-
ванием картины в плане и, измерив расстояние
от нее до точки Р, отложить его от той же точки
по основанию картины в перспективе. Через
полученную точку 1 проходит прямая а° пер-
пендикулярно основанию картины.
/203/ Если ось пучка проецирующих плоско-
стей параллельна предметной плоскости, то пред-
203
метные следы плоскостей пучка параллельны
между собой и оси пучка, картинные следы пере-
секаются в точке, лежащей на горизонте
(рис. 510).
Точка F°, в которой пересекаются картин-
ные следы, называется точкой схода перспектив
параллельных прямых или, короче, точкой схода.
Чтобы ее найти, нужно из точки провести
прямую, параллельную предметным следам
проецирующих плоскостей, до пересечения с
основанием картины и через полученную точ-
ку F ° — основание точки схода — провести ли-
нию связи до пересечения с горизонтом в
точке F° (рис. 510 и 511). Для построения кар-
тинных следов проецирующих плоскостей до-
статочно найти точки пересечения предметных
следов с основанием картины и соединить их с
точкой схода.
Когда ось пучка проецирующих плоскостей
перпендикулярна картинной плоскости, точ-
ка F° и Р совпадают. Предметные следы пло-
скостей перпендикулярны основанию картины,
картинные следы пересекаются в точке Р
(рис. 512 и 513).
Если ось пучка проецирующих плоскостей
горизонтальна и наклонена к П° под углом 45°.
(рис. 514, а), то под тем же углом предметные
следы плоскостей наклонены к основанию кар-
тины. Точка схода лежит на горизонте и уда-
। лена от точки Р на величину, равную главному
расстоянию (рис. 514, 6). В этом случае точка
схода называется точкой дальности и обознача-
ется буквой D°.
/204/ Точка дальности удалена по горизонту
от главной точки картины на величину, равную
главному расстоянию.
Точек дальности для горизонтальных пря-
мых две — одна по одну, другая по другую
сторону от главной точки картины.
Когда ось пучка проецирующих плоскостей
параллельна как картинной, так и предметной
плоскостям (рис. 515 и 516), то и предмет-
ные, и картинные следы проецирующих пло-
скостей параллельны основанию картины, а сле-
довательно, и между собой (см. /202/ и /203/).
Перспективы прямых. Предметные следы
проецирующих плоскостей всегда горизонталь-
ны (лежат в предметной плоскости). Поэтому
положения, касающиеся следов, могут быть
отнесены к горизонтальным прямым.
/205/ Если горизонтальные прямые пересе-
каются в точке, лежащей на предметном следе
предельной плоскости, то нх перспективы парал-
лельны между собой (см, рис. 506, 508).
/206/ Когда горизонтальные прямые пере-
секаются в проекции точки зрения (рис. 508),
то их перспективы перпендикулярны горизонту
(основанию картины).
/207/ Перспективами параллельных горизон-
тальных прямых являются примые, пересекаю-
щиеся в точке схода, расположенной на горизонте 1
(рис. 510, 511).
/208/ Если горизонтальные прямые наклоне-
ны к картинной плоскости под углом 45е, точкой
схода их перспектив ивляется точка дальности
(рис. 514).
204
/209/ Перспективы прямых, перпендикуляр-
ных картинной плоскости, пересекаются в глав-
ной точке картины (рис. 512, 513).
/210/ Если прямые параллельны основанию
картины, то их перспективы также параллельны
основанию картины (рис. 515, 516).
На рис. 517, а в плане, а на рис. 517, б в
перспективе изображены различные горизон-
тальные прямые. Так как такими линиями мы
будем пользоваться при построении перспектив
различных объектов, то приведенный чертеж
можно рассматривать как справочный. Пря-
мая а (сплошная) проходит через проекцию
точки зрения; ее перспектива а° вертикальна
(см. /206/). Прямая b (сплошная) перпендику-
лярна основанию картины; перспектива Ь° этой
прямой проходит через главную точку картины
(см. /209/). Прямая с параллельна основанию
картины (штрихпунктирная с одной точкой);
ее перспектива с° также параллельна основа-
нию картины (см. /210/). Перспектива d° пря-
мой d (штрихпунктирной с двумя точками),
наклоненной к основанию картины под произ-
вольным углом, проходит через точку схода F°,
лежащую на горизонте (см. /207/). И наконец,
прямая е проходит через точку N, инцидентную
предметному следу предельной плоскости и
удаленную от проекции точки зрения на высоту
точки зрения (горизонта); ее перспектива е°
наклонена к основанию картины под углом 45°
(прямые е и е° проведены штрихпунктирными
с тремя точками. См. /205/). Все прямые инци-
дентны точке А, поэтому их перспективы инци-
дентны точке А° (см. /23/).
Вернемся к рис. 510 и 511. Точка F° получена
в результате пересечения с горизонтом проеци-
рующей прямой, параллельной заданным пря-
мым. Следовательно, точка схода представляет
собой перспективу несобственной точки F за-
данных прямых. Отсюда введение знака <х> при
обозначении точки. Индекс ° говорит о том,
что точка F° является перспективой точки F
оо со
(СМ. 15/).
Точку Р можно рассматривать как перспек-
тиву несобственной точки прямых, перпенди-
кулярных картинной плоскости, а точку даль-
ности — как перспективу несобственной точки
горизонтальных прямых, наклоненных к кар-
тинной плоскости под углом 45°. Точка схода
перспектив прямых, параллельных основанию
h
Рис 513
205
картины, является несобственной. Она совпада-
ет со своей перспективой.
Горизонт представляет собой перспективу
множества несобственных точек горизонталь-
ных плоскостей, или, иначе говоря, перспективу
несобственной прямой таких плоскостей
(см. /7/).
Все наклонные линии, кроме параллельных
картинной плоскости, будем делить на нисхо-
дящие, т. е. такие, точки которых по мере уда-
ления от зрителя в изображаемой части про-
странства опускаются, и восходящие, точки
которых по мере удаления от зрителя подни-
маются.
Перспективы как восходящих, так и нисхо-
дящих параллельных прямых имеют свои точки
схода. Они расположены в пересечении с кар-
тинной плоскостью проецирующих прямых, па-
раллельных заданным прямым. Как строить их
перспективы, мы рассмотрим ниже, отметим
пока, что:
/211/ Точка схода перспектив восходящих
параллельных прямых расположена выше го-
ризонта, нисходящих прямых — ниже горизонта.
Известно, что прямая, параллельная пло-
скости, проецируется в параллельную ей пря-
мую (см. /12/), поэтому:
/212/ Параллельные между собой прямые,
параллельные, кроме того, картинной плоскости,
параллельны своим перспективам (точка схода
перспектив таких прямых несобственная. См. /6/).
Отсюда:
/213/ Перспективы вертикальных прямых вер-
тикальны.
В дальнейшем понятие «точка схода» мы бу-
дем использовать, когда речь пойдет о перспек-
тиве какой-либо одной прямой. Это перспекти-
ва ее несобственной точки. С целью упрощения
обозначений во всех случаях, когда это не может
быть неверно понято, будем опускать индек-
сы ° и ». Таким образом, точки схода в пер-
спективе будут обозначены буквой F, точки
дальности — буквой D, вторичные проекции
точек, так же как и в ортогональных проекпиях,
с нижним правым индексом 1 (например, А,),
основания точек — без индексов ° и <ю (напри-
мер, Г).
§ 44. ПЕРСПЕКТИВА ТОЧКИ
Построим перспективу точки А, инцидент-
ной предметной плоскости (рис. 518). В соот-
ветствии с /201/ воспользуемся двумя проеци-
рующими плоскостями: вертикальной и пер-
пендикулярной картине. Предметные следы
этих плоскостей инцидентны точке А,
(рис. 519, а). Измерив отрезки Р— 7 и Р—2
на плане и отложив их от точки Р по основа-
нию картины в перспективе (рис. 519, б), про-
ведем картинные следы плоскостей — прямую
1—Р и прямую, проходящую через точку 2
перпендикулярно основанию картины, до их
взаимного пересечения в. точке А°:
Если точка не инцидентна предметной пло-
скости, нужно провести новую предметную
плоскость через эту точку. Точка В выше точки А
на величину п. Проведем через нее новую пред-
метную плоскость. Новое основание картины к'
в перспективе выше ранее проведенного на ве-
личину п. На нем расположено новое основание
главной точки картины Р' в пересечении пря-
мых РР и к'. В соответствии с /44/ проекции
точки В на ранее проведенной и новой предмет-
ных плоскостях совпадают, поэтому изменение
положения предметной плоскости в плане не
обнаружится.
Проведя через В аве проецирующие плоско-
сти, построим их предметные следы с и d и
отметим точки 3 и 4, в которых они пересека-
ются с основанием картины. Найдя эти точки в
перспективе на соответствующих расстояниях
от точки Р', соединим точку 4 с точкой R,
а через точку 3 проведем вертикальную прямую.
В их пересечении расположена точка В'. По-
строения не изменятся, если изображаемая точ-
ка расположена. выше точки зрения.
Предметные следы проецирующих плоско-
стей являются горизонтальными прямыми раз-
личного расположения. Картинные следы пред-
ставляют собой перспективы таких прямых.
Поэтому положение /201/ можно сформули-
ровать так:
/214/ Чтобы построить перспективы точки,
нужно провести через иее две горизонтальные
прямые и определить точку пересечения их пер-
спектив.
В большинстве случаев для построения пер-
спектив горизонтальных прямых нужно знать,
где прямая пересекается с основанием картины
и точку, в которой перспектива прямой пересе-
кается с горизонтом. Рассмотрим случай, когда
Рис. 519
206
горизонт расположен за пределами чертежа
Нужно построить перспективы точек А, В и с
(рис. 520, а). Точки Аи В инцидентны предмет-
ной плоскости, точка С выше ее на величину и
Воспользуемся /202/ и /205/. Зададимся точка-
ми М и N, инцидентными предметному следу
предельной плоскости (см. рис. 506 и 507) и
отстоящими от точки S] на расстоянии
SS) • cos 60°. Чтобы их построить, нужно со-
вместить точку S с предметной плоскостью,
вращая ее вокруг предметного следа предель-
ной плоскости. При этом угол а наклона к пло-
скости П] осей пучков плоскостей, а следова-
тельно, и перспектив прямых, проходящих че-
рез точки М и N, равен 60°.
Для построения перспективы А (рис. 520, б)
проведем через Ал прямые А}М и A,N. Они пе-
ресекаются с основанием картины соответст-
венно в точках 1 и 2. Построив их в перспективе,
проведем через них прямые под углом 60° к
основанию картины и отметим точку А° их
пересечения. Угол 60° удобен тем, что можно
не проводить перспективы вспомогательных
прямых. Достаточно из точки 1, как из центра,
провести дугу радиуса 1—2 до пересечения с
такой же дугой, проведенной из точки 2. Имен-
но так и построена перспектива точки В.
Если точка (С) расположена над предметной
плоскостью (или под ней), нужно на соответ-
ствующую величину поднять (или опустить)
основание картины в перспективе, как это сде-
лано на рис. 519, б. Такой способ называется
способом замены предметной плоскости. Эту же
задачу можно решить иначе.
Даны вторичные проекции At и В, точек
А и В в перспективе (рис. 521). Известно, что
точка А расположена над предметной плоско-
стью на высоте h, точка В — ниже предметной
плоскости на величину t. Нужно построить
перспективы этих точек. Проведем через At
горизонтальную прямую произвольного на-
правления. Точка схода F ее перспективы рас-
положена на горизонте. Отметим точку 1 пере-
сечения прямой AjF с основанием картины и
проведем через нее вертикальный отрезок 1—2,
равный h. Отрезок 1—2 инцидентен картинной
плоскости, следовательно, проецируется в на-
туральную величину. Проведем через точку 2
перспективу прямой, параллельной A,F. Она
пересекается с горизонтом в точке F (см. /20/).
Проведем через At вертикальную прямую до
пересечения с 2—F. Отрезки 1—2 а ААГ парал-
лельны (так как оба вертикальны) и равны
(так как заключены между параллельными пря-
мыми). Аналогично построена перспектива точ-
ки В, с той разницей, что отрезок 3—4 = t
отложен от основания картины вниз.
Описанный способ называется способом вы-
несения фигуры на картинную плоскость.
Построим перспективу параллельных вос-
ходящих прямых. Даны (на эпюре) прямые а || Ъ
(рис. 522, а), основание картины и точка .
Перспектива (рис. 522, б) задана горизонтом с
точкой Р на нем и основанием картины. По-
строим перспективу точки А, в которой пря-
мая а пересекается с плоскостью П] (построе-
ния не показанье Их можно выполнить в соот-
ветствии с описанием к рис. 519 или 520). Про-
ведем на эпюре проекцию Е2 плоскости гори-
зонта (расстояние от нее до оси х равно длине
отрезка РР) и отметим точку С, в которой пло-
скость S пересекает прямую а. Построим пер-
спективу точки С. Для этого проведем пря-
мую CjS) — горизонтальную проекцию верти-
кальной проецирующей плоскости (см. рис. 508)
Рис. 522
207
и, отметив точку 1 ее пересечения с основанием
картины, построим эту точку в перспективе.
Перспектива точки С расположена в пересече-
нии вертикальной прямой, проходящей через
точку 1 (картинного следа вспомогательной
плоскости), и линии горизонта.
Аналогично построим перспективу BE пря-
мой Ь. Перспективы прямых а и b пересекаются
между собой в точке F, расположенной выше
горизонта (см. /211/). Ее вторичная проекция Ft
расположена на горизонте в проекционной свя-
зи с точкой F (см. /197/). Вторичные проекции
прямых а и b (они горизонтальны) пересекаются
с горизонтом в точке Ej.
/215/ Вторичная проекция точки схода пер-
спектив параллельных наклонных прямых пред-
ставляет собой точку схода вторичных проекций
этих прямых и лежит на горизонте.
Решим некоторые задачи.
Задача 1.
Даны точки A(A.;At), В (В; ЕД С (С; С,) и
Е (Е; Et) (рис. 523). Нужно провести:
через А горизонтальную прямую а произволь-
ного направления и прямую f параллельную осно-
ванию картины;
через В прямую Ь, параллельную прямой а;
через С вертикальную прямую с и прямую d,
параллельную П° и наклоненную к Щ под углом а;
через Е прямую е, параллельную прямой d.
В последнем случае найти предметный след пря-
мой — точку М. Все прямые следует задать их пер-
спективными и вторичными проекциями.
Решение.
Через А проведем прямую а произвольного на-
правления и отметим на горизонте перспективу F
ее несобственной точки (точку схода). В соответ-
ствии с /207/ прямая а горизонтальна, ее вторичная
проекция а, проходит через точки Аг и F (так как
в натуре а и параллельны. См. /12/).
Перспективная и вторичная проекции прямой /
параллельны основанию картины, так как сама
прямая в натуре параллельна этой линии (см. /210/
и /12/). Чтобы прямая Ъ была параллельна прямой а,
достаточно провести ее перспективную проекцию
через точки В и F, а вторичную проекцию — через
точки В, и F.
Перспектива прямой с вертикальна (см. /213/).
Ее вторичная проекция — точка С, — совпадает с
точкой С (точки С и С] совпадают, следовательно,
сама точка расположена в предметной плоскости).
Прямая d параллельна картинной плоскости,
следовательно ее перспектива параллельна самой
прямой (см. /212/). Поэтому перспектива прямой
наклонена к основанию картины под углом а.
Ее вторичная проекция параллельна основанию
картины (плоскость dOd^ параллельна картинной,
следовательно, пересекается с предметной плоско-
стью по прямой г/,, параллельной основанию кар-
тины).
Прямую е строим так же, как прямую d. Перспек-
тивные и вторичные проекции прямых соответствен-
но параллельны. След М = прямой е находим
в пересечении ее перспективной и вторичной
проекций.
Задача 2.
Через точку A (A; А,) провести прямую Ь, па-
параллельную восходящей прямой а (а; а,)
(рис. 524).
Решение.
Отметив точку Ft пересечения прямой а, с гори-
зонтом, установим проекционную связь и найдем
точку F (точку схода прямой а См. /211/). Искомая
прямая b проходит через точки А и F, ее вторичная
проекция — через точки At и F, (см. /215/).
§ 45. ПОСТРОЕНИЕ ОТРЕЗКА
ЗАДАННОЙ ДЛИНЫ И ДЕЛЕНИЕ
ОТРЕЗКА В ЗАДАННОМ
ОТНОШЕНИИ
Даны перспективы вертикального отрезка
АВ и точек С и G (рис. 525), причем известно,
что точки В, С и G инцидентны предметной
плоскости. Нужно: определить длину отрезка
АВ; построить вертикальный отрезок СЕ=АВ;
построить вертикальный отрезок GH длиной п.
Проведем через В горизонтальную прямую
произвольного направления и отметим точки F
и 1 ее пересечения соответственно с горизон-
том и основанием картины. Через А проведем
прямую, параллельную 1—F. Ее картинный
след расположен в точке 2 на перпендикуляре
к предметной плоскости, восставленном в
точке 1. Отрезки АВ и /—2 в натуре равны,
причем отрезок . 1—2 инцидентен картинной
плоскости и проецируется на нее в натуральную
величину. Отсюда, длина отрезка АВ в натуре
равна длине отрезка 1—2 (см. пояснения к
рис. 521).
Проведем через С прямую, параллельную
основанию картины (см. /210/), до пересечения
Рис. 525
208
Рис. 526
равный отрезку АВ. Через точку 4 проведем
прямую, параллельную прямой 3 С, по пере-
сечения в точке Е с вертикальной прямой, про-
ходящей через точку Е. Отрезок ЕС в натуре
равен отрезку АВ
Проведем через G горизонтальную прямую
произвольного направления (можно через F)
и отметим точки 5 и F' ее пересечения соответ-
ственно с основанием картины и горизонтом.
Восставив в точке 5 перпендикуляр к предмет-
ной плоскости, отложим на нем отрезок дли-
ной п от точки 5 и через полученную точку б
проведем прямую в точку F'. Прямые 5—F'
и б—F' в натуре параллельны. Проведя через G
вертикальную прямую, отметим точку Н ее
пересечения с прямой б —F'.
Построим отрезки горизонтальных прямых
заданной длины. Даны перспективы прямых а
и Ь (рис. 526). Прямая а перпендикулярна, пря-
мая b параллельна картинной плоскости; обе
прямые инцидентны предметной плоскости.
Главное расстояние известно.
Нужно: от точки 1 (пересечения прямой а
с основанием картины) отложить по прямой а
отрезок длиной п; на прямой b от точки 4 вправо
отложить отрезок длиной т. Разделить отрезок
длиной п в отношении 2 :3.
Построив точку дальности D (см. /204/),
отложим от точки 1 по основанию картины
отрезок длиной п и через полученную точку 2
проведем прямую в точку дальности. В пере-
сечении прямых 1—Р и 2—D расположена
точка 3. Отрезок 1—3 в натуре равен отрезку
1—2 длиной п (прямая 1—Р в натуре перпенди-
кулярна основанию картины, прямая 2—D на-
клонена к нему под углом 45°; треугольник
3—1—2 равнобедренный прямоугольный).
Проведем через точку 4 произвольную гори-
зонтальную прямую 4—F (можно 4—D) и от-
метим точку 5 ее пересечения с основанием
картины. Отложив от точки 5 по основанию
картины отрезок 5—б длиной т. проведем
через полученную точку б, прямую б F. Она
пересекается с прямой b в точке 7. Отрезок 4—7
в натуре равен отрезку 5—б, длина которого
равна т (прямые 5 F и б F в натуре парал-
лельны. Прямая b параллельна основанию кар-
тины. Следовательно, фигура 5—4—7—б па-
раллелограмм).
Разделив точкой 8 отрезок 1—2 в отноше-
нии 2 :3, соединим точку 8 с точкой D. В пере-
сечении прямых 8—D и 1—Р расположена
искомая точка 9, делящая отрезок 1—3 в отно-
шении 2:3. Из приведенных пояснений следует,
что отрезки 9—3 и 8—2 в натуре равны. Отсюда:
/216/ Прямые предметной плоскости, про-
ходящие через точку дальности, отсекают иа
пересекающихся с ними прямых, перпендикуляр-
ных основанию картины, и на самом основании
картины равные отрезки.
Прямая а, инцидентная предметной плоско-
сти, не перпендикулярна и не параллельна осно-
ванию картины (рис. 527, а). Требуется: отло-
жить по прямой а от точки А пересечения пря-
мой с основанием картины отрезок длиной и,
а от точки В — отрезок длиной т. Главное
расстояние и точка Р известны.
Решим эту задачу в плане (рис. 527, б).
Отложим по основанию картины от точки А
отрезок длиной п, получив точку 1. Отложив
такой же отрезок по прямой а от точки А, по-
лучим точку 2. Соединим точки 1 и 2. Построим
основания точек схода прямых а и 1—2 соответ-
ственно точки F и F'. Треугольники А—2—1 и
FF'St равнобедренные и подобные, поэтому
F'F = StF.
Перейдем к перспективе (рис. 527, а). Отме-
тив точку схода F прямой а, построим ее осно-
14—940
209
вание — точку F. Отложив по перпендикуляру
к основанию картины, проведенному через Р,
отрезок PS', равный заданному главному рас-
стоянию, получим точку S'. Проведем дугу
радиуса S'F с центром в F и отметим точку F'
ее пересечения с основанием картины. Устано-
вив проекционную связь, определим точку F'
на горизонте. Эта точка называется точкой изме-
рения прямой а (параллельных ей прямых).
Отложив от А по основанию картины от-
резок А—1 длиной «. проведем прямую I—F',
которая пересекается с прямой а в точке 2.
Отрезки А—1 и А—2 в натуре равны. Проведем
через В прямую BF' до пересечения в точке 3
с основанием картины. Отложив от точки 3
по основанию картины отрезок 3—4 длиной т,
через полученную точку 4 проведем прямую
4—F'. Она пересекается с прямой а в точке 5.
Отрезки В—5 и 3—4 в натуре равны. Аналогич-
ные построения проделаны в плане на рис. 527, б.
/217/ Прямые предметной плоскости, про-
ходящие через точку измерения данной примой,
отсекают на ней и на основании картины равные
отрезки.
Из сравнения /216/ и /217/ видно, что точка
дальности является точкой измерения горизон-
тальных прямых, перпендикулярных основа-
нию картины.
Определим величину отрезка АВ прямой
a (A; A,; F). Точка В задана своей перспектив-
ной проекцией Кроме того, отложим по пря-
мой а отрезок АС длиной « и определим угол а
наклона прямой а к плоскости П] (рис. 528).
Главное расстояние задано.
Вначале определим вторичную проекцию
отрезка АВ. Для этого построим точку F, в
пересечении с горизонтом линии связи, прохо-
дящей через F. Соединим прямой точки А, и F1
и отметим точку Bt на ней. Построим точку
измерения F' прямой А}В} (см. рис. 527, я) и
соединим ее прямыми с точками Ах и Bt.
Прямые F'At и F'B1 пересекаются с основа-
нием картины соответственно в точках 1 и 2.
Проведем через F' прямые F'А и F' В до пере-
сечения в точках 3 и 4 с перпендикулярами к
предметной плоскости, восставленными соот-
ветственно в точках 1 и 2. Соединим прямой
точки 3 и 4. Отрезок 1—2 равен длине вторич-
ной проекции отрезка АВ, отрезок 1—3 равен
высоте точки А, а отрезок 2—4 высоте точки В
над предметной плоскостью (см. рис. 525).
Следовательно, длина отрезка АВ в натуре
равна длине отрезка 3—4.
Отложив от точки 3 по прямой 3—4 отре-
зок 3—5 длиной «, соединим полученную точку 5
с точкой F'. В пересечении прямых 5—F' и а
расположена точка С. Угол а наклона прямой
3—4 к основанию картины равен углу наклона
прямой а к предметной плоскости.
Из приведенного примера видно, что опреде-
ление длин отрезков прямой а и ее вторичной
проекции производилось с помощью одной и
той же точки измерения.
/218/ Точка измерения наклонной прямой и
ее вторичной проекции общаи.
Используя построения, приведенные на
рис. 528, можно разделить отрезок в данном
отношении. Однако если задача не связана с
определением йатуральной величины отрезков,
ее можно решить проще.
Разделим в отношении 2 :1 отрезки прямых:
АВ || к, GFirT], и АЛ/ЦП] произвольного на-
правления (рис. 529). Так как прямые АВ и EG
параллельны картинной плоскости, деление от-
210
резков производим известным из элементар-
ной геометрии способом (см. /17/). Чтобы раз-
делить отрезок NM, проведем через N (или М)
прямую, параллельную основанию картины,
и отложим на ней последовательно отрезки,
равные двум и одной произвольным единицам
длины, получив точки 5 и 6. Соединим прямой
точки 6 и М и отметим точку схода F прямой
М—6. Соединим прямой точки 5 и F, она пере-
сечется с прямой NM в точке К, делящей от-
резок NM в отношении 2:1 (прямые 6—F и
5—F в натуре параллельны, следовательно,
треугольники NM—6 и NK—5 в натуре подоб-
ны. Отсюда NK : КМ = 2:1).
Теперь разделим в отношении 2 :1 отрезок
АВ(А1В1) восходящей прямой (рис. 530). Для
этого разделим в заданном отношении отре-
зок А1В1 (см. рис. 529) и через полученную точ-
ку Cj проведем линию связи до пересечения в
точке С с заданным отрезком.
Несколько проше разделить отрезок на две,
четыре, восемь и- т. д. равных частей. Дан отре-
зок АВ горизонтальной прямой (рис. 531). Взяв
на горизонте произвольную точку F, соединим
ее прямыми с точками А и В. Проведем через
А и В прямые, параллельные основанию кар-
тины, до пересечения соответственно с прямы-
ми AF и BF в точках 2 и 1. Соединим прямой
точки 1 и 2. Фигура А—2—В-—1 в натуре
параллелограмм, диагонали АВ и J—2 кото-
рого пересекаются в точке 3, делящей каждую
диагональ пополам. Проведя через точку 3
прямую 3—5 параллельно основанию картины,
а затем прямую 5—4, получим в ее пересечении
с АВ точку 6, делящую отрезок А—3 на две
равные части, и т. д. у
Разделим наклонный отрезок на две, четыре,
восемь... равных частей (рис. 532). Построим
прямые AF и BF. Проведем через А и В верти-
кальные прямые,. получив прямоугольник
А—1—В—Аг. Диагональ прямоугольника
1—А, делит отрезок АВ в точке С пополам.
Построив прямоугольник С—2—В—3, прове-
дем его диагональ, которая разделит отрезок СВ
пополам, и т. д.
§ 46. ПЕРСПЕКТИВА
ПЛОСКОЙ ФИГУРЫ
Перспектива фигуры, инцидентной горизон-
тальной плоскости. Фигура ABCEGHK (рис. 533)
инцидентна плоскости Пр Положение картин-
ной плоскости определено ее основанием к,
положение точки зрения — точкой S) и высотой
горизонта п. Проведем горизонт и основание
картины на заданном расстоянии п (рис. 534),
определим положение точки Р в плане (рис. 533)
и отметим ее и точку Р в перспективе.
Фигура ABCEGH ограничена в основном
двумя группами параллельных линий. Направ-
ления этих линий являются доминирующими,
почему рассмотренный ниже способ построе-
ния перспективы носит название способа точек
схода перспектив параллельных линий домини-
рующих направлений. На практике его называют
короче — способом архитекторов.
Одно из доминирующих направлений опре-
деляется прямыми ВС, GE и АН, другое —
прямыми АВ, HG и СЕ. Определим для них
точки схода (см. /207/), для чего через Sx прове-
дем прямые, соответственно параллельные пря-
мым доминирующих направлений, и отметим
14*
211
точки F' и F" пересечения этих прямых с осно-
ванием картины. Построим точки F' и F"
в перспективе на соответствующих расстояниях
по горизонту от точки Р.
Начнем построение перспективы, например,
с точки Е. Через нее проходят прямые (см. /214/)
GE, СЕ. Отметим точки 1 и 2, в которых они
пересекаются с основанием картины. Перспек-
тива прямой GE проходит через точки 1 и F',
перспектива прямой ЕС — через точки 2 и F"*.
В пересечении этих прямых расположена пер-
спектива точки Е. Для построения перспективы
точки С воспользуемся тем, что эта точка лежит
на прямой ЕС, перспектива которой уже по-
строена. Поэтому проведем через С еще одну
прямую, например, перпендикулярную основа-
нию картины. Она пересекается с основанием
картины в точке 3. Перенеся точку 3 в перспек-
тиву, построим перспективу 3—Р прямой С—3.
Точка G лежит в пересечении прямых GE и GH.
Для построения ее перспективы нужно постро-
ить только перспективу прямой GH, так как
перспектива прямой GE уже найдена. Отметив
точку 4 в пересечении прямой GH с основанием
картины, проведем через эту точку и точку F"
перспективу прямой GH.
Найдем перспективу точки Н. Воспользу-
емся, например, прямой, проходящей через
эту точку и точку S,. Перспектива такой прямой
идет через точку 5 вертикально. В ее пересече-
нии с перспективой GH отметим точку Н.
Перспектива прямой Л Л проходит через точки Н
nF'. На ней лежит перспектива точки А, по-
строенная с помощью прямой, проходящей
через точку А и точку S,.
Для построения перспективы точки В до-
статочно провести перспективы прямых АВ и
ВС, которые проходят соответственно через
точки F" и F'. Перспектива точки К построена
с помощью горизонтальных прямых К—7 и
К—8, из которых первая перпендикулярна осно-
ванию картины (ее перспектива проходит через
точку Р), а вторая параллельна прямым, точ-
кой схода перспектив которых является точка F'.
Выбор прямых, с помощью которых строятся
перспективы точек фигуры, зависит от конкрет-
ных условий задачи. В настоящем примере были
использованы три типа горизонтальных пря-
мых: проходящих через точку перпендику-
лярных основанию картины и наклоненных
к нему. Для последних были построены точки
схода К' и F" (см. рис. 517).
При небольшом расстоянии между основа-
нием картины и горизонтом перспектива фигуры
сильно сжата в вертикальном направлении, что
снижает точность проводимых построений.
Чтобы повысить точность, строят так назы-
ваемый опущенный или поднятый план. Опустим
предметную плоскость так, чтобы расстояние
между нею и плоскостью горизонта равня-
лось пОснование картины к' в перспективе
опустится относительно горизонта на ту же
величину.
Произведя построение перспективы с уче-
том того, что фигура ABCEGHK лежит в новой
предметной плоскости П'1; убедимся что пер-
спективы одноименных точек расположены на
линиях связи. Фигура А'В' С'Е' G'Н'К' явля-
ется опущенным планом относительно фигуры
ABCEGHK. Опушенный план можно строить
непосредственно по ортогональным проекциям
как перспективу фигуры, лежащей в предмет-
ной плоскости, но можно построить и на уже
законченной перспективе. Например, чтобы по-
* Все размеры в перспективе увеличины в
2,5 раза.
212
строить опущенный план точки С (точку С'),
достаточно отметить на линии связи, прове-
денной через точку 3 в ее пересечении с пря-
мой К', точку 3' и, соединив ее с точкой Р,
провести линию связи через точку С до пересе-
чения с прямой 3'—Р.
Так же строится и поднятый план. Если пред-
метную плоскость расположить выше плоско-
сти горизонта на высоте п", то основание кар-
тины к" на ту же величину должно быть под-
нято над горизонтом. Поднятый план также
может быть построен как по ортогональным
проекциям, так и на перспективе.
Перспективы одноименных прямых основ-
ного, поднятого или опущенного планов на-
правлены в общие точки схода, так как эти пря-
мые в натуре параллельны.
Перспектива окружности, инцидентной пред-
метной плоскости. Перспективой окружности
может быть одна из кривых конических сечений.
Множество проецирующих прямых, проходя-
щих через все точки окружности, предст авляет
собой коническую поверхность второго порядка;
перспектива окружности является сечением этой
поверхности картинной плоскостью. На рис. 535
показана перспектива а° окружности а, инци-
дентной предметной плоскости. Все прямые,
проецирующие точки окружности, рассечены
картинной плоскостью, следовательно, перспек-
тива окружности — эллипс (см. /105/)г Когда
окружность (рис. 536) касается предельной пло-
скости. ее перспективой будет парабола (обра-
зующая .S.S'j параллельна картинной плоскости;
см. /106/). Если окружность (рис. 537) пересекает
предельную плоскость в двух точках, то пер-
спективой окружности становится гипербола
(предельная плоскость пересекает коническую
поверхность по двум образующим AS и BS,
которые параллельны картинной плоскости;
см. /107/. Если бы не было условия, что можно
проецировать только то, что расположено по
одну сторону предельной плоскости (см. пер-
вое условие отличия перспективы от централь-
ной проекции), то можно было бы по-
строить проекцию и той части окружности,
которая расположена за предельной плоско-
стью (вторую ветвь гиперболы).
Сказанное относится и к тому случаю, когда
окружность лежит в плоскости общего поло-
жения.
/219/ Если окружность не имеет общих точек
с предельной плоскостью, ее перспективой явля-
ется элЛипс, когда окружность касается предель-
ной плоскости, перспектива Окружности — пара-
бола, если окружность пересекается с предельной
плоскостью, То ее перспективой становится ги-
пербола (одна ветвь).
В практике чаще встречается эллипс.
Построим перспективу окружности, инци-
дентной предметной плоскости (рис. 538, а).
Опишем вокруг окружности квадрат А ВСЕ со
сторонами, соответственно параллельными и
перпендикулярными основанию картины. От-
метим точки 1 и 2 пересечения прямых АВ и СЕ
с основанием картины и, перенеся их на основа-
ние картины в перспективе (рис. 538, б), соеди-
ним с точкой Р (см. /209/). Проведем диагональ
квадрата АС и отметим точку 3 пересечения
Рис. 535
213
Рис. 538
прямой АС с основанием картины. Построив
точку 3 в перспективе, соединим ее с точкой
дальности D (см. /208/). В пересечении прямых
1—Р и 3—D отметим точку А. Проведя через А
прямую, параллельную основанию картины
(см. /210/), отметим точку Е ее пересечения с
прямой 2—Р. Через точку С пересечения пря-
мых 3—D и 2—Р проведем прямую, парал-
лельную основанию картины (см. /210/). Она
пересекается с прямой 1—Р в точке В. Трапеция
АВСЕ представляет собой перспективу квад-
рата АВСЕ. Проведем диагональ BE трапеции
и соединим точку пересечения диагоналей с точ-
кой Р. Эта прямая разделит в точках 5 и 4 от-
резки ВС и АЕ пополам (см. рис. 531). Прямая,
параллельная основанию картины и проходя-
щая через точку пересечения диагоналей разде-
лит в точках б и 7 стороны АВ и СЕ также по-
полам. Через точки 4,6,5 и 7 проходит эллипс —
перспектива.окружности, В этих точках стороны
трапеции касаются эллипса (см. /98/).
Если нужно построить дополнительные точ-
ки (рис. 539), проведем полуокружность на
одной из сторон трапеции, параллельных осно-
ванию картины (на стороне АЕ одной трапеции
и стороне GH другой) и опишем вокруг нее пря-
моугольник AERT. Соединим центр полуок-
ружности — точку 4 с точками Ги R и отметим
точки, в которых проведенные прямые пересе-
каются с полуокружностью. Проведем через
них прямые, параллельные Л Г до пересечения
с основанием картины. Полученные точки сое-
диним прямыми с точкой Р. Эти прямые пере-
секают диагонали трапеции в точках, принад-
лежащих эллипсу.
Если и этих точек недостаточно, проведем
214
.через центр полуокружности произвольную пря-
мую 4—7 и отметим точку 5 ее пересечения с
прямой TR. Проведем прямую 5—б параллель-
но А Т и полученную в пересечении с прямой АЕ
точку 6 соединим с точкой О. Проведем прямую
7—8 и через точку 8 прямую 8—-Р. Она пересе-
кается с прямой, проходящей через точки б и О
в точке 9, принадлежащей эллипсу. Так можно
построить любое число точек эллипса (сравните
рис. 539 и 480).
Пусть через прямую SP (рис. 535) проходит
вертикальная плоскость, а центр окружности
ей инцидентен; это единственный случай, когда
эллипс — перспектива окружности расположен
симметрично относительно прямой РР.
Эллипс, вписанный в трапецию К GHM, —
так же проекция окружности, но его оси накло-
нены к основанию картины. Наклон осей тем
больше, чем дальше от прямой РР удалена
точка О.
Перспективные сетки. При построении пер-
спективы пространственной кривой линии нужно
взять на ней необходимое число точек и, по-
строив их перспективы, соеднить их в той же
последовательности, что и на заданной фигуре.
Если же кривая — плоская, применяется дру-
гой прием. Рассмотрим его на примере.
Даны: основание картины, точка Sj и кривая
линия, инцидентная предметной плоскости
(рис. 540). Перспектива задана горизонтом и
основанием картины (рис. 541).
Построим в плане сетку, состоящую из квад-
ратов, стороны которых соответственно парал-
лельны и перпендикулярны основанию картины.
Обозначим линии сетки: перпендикулярные ос-
нованию картины буквами a, b, с, d, ... , парал-
лельные ему — римскими цифрами I, II, III, ...
Отметим точки пересечения прямых а, Ь, с ...
с основанием картины и, измерив расстояния
от них до Р, построим их на основании картины
в перспективе. Перспективы прямых а, Ь, с, ...
пересекаются в точке Р (см. /209/).
Проведем в плане диагональ квадратов,
проходящую через левую крайнюю точку сетки,
и построим ее перспективу. Она проходит через
точку D (см. /208/). Отметим точки пересечения
диагонали с прямыми b, с, d, ... Через них про-
ходят перспективы прямых сетки, параллель-
ных основанию картины (см. /210/). Обозначим
их так же, как и в плане, римскими цифрами.
Чтобы построить прямые VI и VII, проведем
через, точку пересечения прямых а и V еще одну
диагональ. Она пересекается с b и с в точках,
через которые проходят прямые VI и VII.
Перспективу заданной фигуры врисуем на
глаз в перспективу сетки. Точка 1 расположена
на I линии сетки. Она делит сторону квадрата
в том же отношении, в каком ее перспектива
делит перспективу этой стороны (см. рис. 529,
отрезок АВ). Точка 2 лежит на прямой Ь. Если
не требуется большой точности, то ее перспек-
тиву найдем на глаз с учетом перспективных со-
кращений в направлении точки Р. Точки 3 и 4
построены, как и точка 1. Точка б расположена
в пересечении линий сетки е и III.
Если для некоторых точек кривой требуется
большая точность построения их перспектив,
поступим так: проведем через точку 2 прямую
под углом 45° к основанию картины. В точке 9
она пересекается с основанием картины. По-
строив точку 9 в перспективе и проведя через
нее прямую в точку D, отметим точку 2 пересе-
чения этой прямой с прямой Ь. Строя перспек-
тиву точки 7, проведем через нее прямую,
перпендикулярную основанию картины, и от-
метим точку 8 их пересечения. Построим пер-
спективу 8—Р этой прямой до пересечения с
линией //сетки. Точка 10 не инцидентна линиям
сетки. Проведем через нее прямую 10—11 пер-
пендикулярно основанию картины и прямую
10—12, наклоненную к основанию картины под
углом 45°, и построим их перспективы (прямые
11—Р и 12—D), которые пересекаются в точ-
ке 10.
Перспектива фигуры, инцидентной вертикаль-
ной плоскости. Дана .перспектива вертикально
расположенного прямоугольника АВСЕ
215
(рис. 542). Построим окружность, инцидентную
плоскости А ВСЕ, с центром в данной точке О
радиуса г (задан на чертеже рядом с перспек-
тивой). Главное расстояние SP известно.
Построим точку измерения F" (см. рис. 527)
И с ее помощью найдем горизонтальный диа-
метр окружности. Для этого проведем прямую
OtF" и отметим точку 1 ее пересечения с осно-
ванием картины. От точки 1 по основанию кар-
тины в обе стороны отложим заданный радиус
и через полученные точки 2 и 3 проведем пря-
мые в точку F”. В точках 4 и 5 они пересекаются
с прямой АЕ. Проведя прямую OF до пересе-
чения с прямой СЕ, инцидентной картинной
плоскостью, отметим точку 6 и, используя ее
как центр, построим половину окружности за-
данного радиуса; в точках 7 и 8 она пересека-
ется с прямой СЕ. Построим трапецию — пер-
спективу квадрата, в которую впишем эллипс —
перспективу окружности. Боковые стороны тра-
пеции лежат на прямых 7—F' и 8—F', основа-
ния - на прямых, проходящих через точки 4 и 5
вертикально. Дальнейшие построения выпол-
нены в соответствии с описанием к рис. 539.
Прямая F'F' представляет собой линию
схода плоскости АВСЕ. Точки схода пересекаю-
щихся прямых этой плоскости инцидентны ли-
нии схода. Если провести диагональ трапеции,
в которую вписан эллипс, она при продолжении
пересечется с линией схода в точке D, удален-
ной от горизонта на то же расстояние, на какое
линия схода удалена от точки зрения (его можно
измерить на плане — отрезок SF'). Это точка
дальности вертикальной плоскости АВСЕ. С про-
тивоположной от горизонта стороны располо-
жена вторая точка дальности. Точки дальности
можно использовать для построения перспек-
тивы окружности. Пусть полуокружность диа-
метра 7—8 построена. Проведем через точки 7
и 8 прямые в точку F'. Они пересекутся с пря-
мой О D в точках, через которые проходят осно-
вания трапеции. Дальнейшие построения ясны
из чертежа.
/220/ Точки дальности вертикальной плоско-
сти инцидентны ее линии схода и удалены от го-
ризонта на величину, равную расстоянию от точки
зрения до линии схода плоскости.
Рис, 543
Если плоскость окружности параллельна П
то проекцией окружности станет также окруж-
ность (см. /17/). Чтобы построить ее перспек-
тиву, нужно найти перспективу центра О и про-
извольной точки бкружности, например N. При
построениях может быть использована' любая
точка схода, в том числе и точка Р.
Мелкие членения плоских фигур строятся с
помощью перспективного делительного масшта-
ба. Рассмотрим пример.
Дана перспектива стены дома АВСЕ
(рис. 543) и ее ортогональная проекция — фасад
стены (рис. 544). Нужно построить перспективу
окон. Выполним построения в соответствии с
описанием к рис. 529. Проведем через Е в пер-
спективе прямую, параллельную основанию
картины, и отложим на ней от точки Е последо-
вательно отрезки 8—7, 7—б и т. д, измеренные
на фасаде стены. Соединив точку 7 с перспек-
тивой точки Л, отметим точку F " до пересечения
прямой 1—А с горизонтом. Проведя прямые
2—F", 3—F" и т. д., отметим точки их пересе-
чения с прямой АЕ. Через эти точки проходят
вертикальные прямые, между которыми рас-
положены окна и простенки стены.
Делить можно не только отрезок АЕ, но и
параллельный ему отрезок ВС. Выбирать сле-
дует тот из них, деление которого даст более
точный результат. При необходимости можно
воспользоваться опущенным или поднятым пла-
ном (см. рис. 534).
Разделив отрезок СЕ (рис. 543) пропорцио-
нально его делению точками 9 и 10 на фасаде
стены, получим точки, через которые проходят
прямые, ограничивающие окна сверху и снизу.
Перспективы этих прямых направлены в точ-
ку F'.
Перспектива фигуры, инцидентной наклонной
плоскости. Построим перспективу прямоуголь-
ника АВСЕ, эпюр которого дан на рис. 545.
Точка зрения и расположение картинной пло-
скости относительно прямоугольника заданы.
Построим способом архитекторов (см. рис. 534)
216
Рис. 545
перспективу прямоугольника А1В1С1Е1
(рис. 546) — вторичную проекцию заданного
прямоугольника. Высоту перспективы точек А и
В определим, как на рис. 525, с помощью от-
резка 1—2.
Построим точку схода F' параллельных
прямых АЕ и ВС (см. рис. 522), для чего через
F\ проведем линию связи до пересечения с
плоскостей, парал-
схода плоскости АВСЕ и
лельных ей. Перспектива несобственной точки
любой прямой плоскости АВСЕ или параллель-
ной ей инцидентна линии схода FF'.'Ранее мы
установили, что линией схода горизонтальных
плоскостей является горизонт, вертикальных —
вертикальная прямая, проходящая через точку
схода произвольной прямой плоскости (напри-
/221/ Линия схода плоскости (параллельных
плоскостей) — это перспектива ее несобственной
прямой. Если плоскость горизонтальна, то ее лиг
иней схода явлиется горизонт, если вертикальна,
то вертикальна и линия схода. Линия схода на-
клонной плоскости наклонена к горизонту или
параллельна ему. Чтобы построить линию схода
плоскости, нужно определить точки схода двух
пересекающихся прямых этой плоскости.
Построим перспективу окружности задан-
ного радиуса с центром в точке О пересечения
диагоналей прямоугольника. Воспользуемся
способом вынесения фигур на картинную пло-
скость. Построим точку измерения F" прямой
ВС (построения выполнены на плане) и вынесем
отрезок ВС на картинную плоскость (это отре-
зок 3—5; сравните построения с приведенными
на рис. 528). Разделив отрезок 3—5 пополам и
отложив от полученной точки в обоих направ-
лениях заданный радиус, получим точки б и 7.
Соединим эти точки с F" и отметим точки, в ко-
торых прямые 6—F" и 7—F" пересекаются
с прямой ВС. Соединим их прямыми с точкой F.
Построим точку измерения F"' прямой ЕС.
Отрезок ЕС, вынесенный на картинную пло-
скость, совпадает с основанием картины. Про-
ведем прямую F O до ее пересечения с прямой
ЕС и вынесем на картину полученную точку
(точка 8). Проведем полуокружность заданного
радиуса с центром в точке 8, получив при этом
точки 9 и 10. Опишем вокруг полуокружности
прямоугольник и проделаем построения, ана-
логичные приведенным на рис. 539. Построен-
ные точки соединим прямыми с точкой F'"
и отметим точки, в которых прямые пересека-
ются с отрезком ЕС. Соединим их с точкой F'.
Теперь в плоскости АВСЕ построена перспек-
тива квадрата. Проведя ее диагонали до пере-
сечения с построенными линиями, получим 8
точек эллипса — перспективы окружности за-
данного радиуса.
§ 47. ВЗАИМОРАСПОЛОЖЕНИЕ
ФИГУР
но можем определить видимость прямых. На
рис. 547 прямая а в месте кажущегося пересече-
ния А = В расположена ближе к точке зрения,
чем прямая h (точка А, инцидентная прямой а,,
расположена дальше от горизонта, чем точ-
ка Bt, инцидентная прямой hj.
Прямые с и d на том же рисунке пересека-
ются в точке С, так как точки пересечения пер-
спективной и вторичной проекций прямых рас-
положены на линии связи (см. /68/).
Пересечение прямой и плоскости. Когда пло-
скость вертикальна (плоскость Q на рис. 548),
то вторичная проекция точки ее пересечения с
прямой а расположена в пересечении вторичных
проекций прямой и плоскости (см. /16/ и /81/).
Проведем линию связи через Кх до пересече-
ния с перспективой прямой в точке К.
/222/ Перспектива точки пересечения пря-
мой линии и вертикальной плоскости расположе-
на на линии связи с точкой пересечения их вторич-
ных горизонтальных проекций.
Если плоскость наклонена, задача выполня-
ется в соответствии с /87/. Построим точку пере-
сечения прямой а и плоскости АВС (рис. 549).
Проведем через а вертикальную плоскость.
Ее положение определяется пересекающимися
прямыми а и а,. С плоскостью а Па, прямая А С
плоскости АВС пересекается в точке Е, прямая
ВС — в точке N (см. пояснения к рис. 548).
Построив линию EN пересечения плоскостей,
Взаиморасположение прямых. Если прямые
параллельны, то их перспективы имеют общую
точку схода, расположенную в проекционной
связи с точкой схода их вторичных проекций
(точка Г на рис. 546). Когда прямые скрещи-
ваются, то точка кажущегося пересечения пред-
ставляет собой две точки, инцидентные общей
проецирующей прямой (конкурирующие). По-
строив вторичные проекции этих точек, мы не
только убеждаемся, что их действительно две.
218
отметим точку К, в которой прямая а пересека-
ется с этой линией. Для определения видимости
прямой воспользуемся конкурирующими точ-
ками G и Я, инцидентными соответственно
прямым а и ВС. Построив их вторичные проек-
ции, убеждаемся, что в месте кажущегося пере-
сечения прямых а и ВС видима прямая ВС.
Пересечение плоскостей. Все задачи могут
быть решены в соответствии с /80/ или /84/
с учетом пояснений к рис. 549. Однако иногда
удобно воспользоваться линиями схода плоско-
стей. Определим линию пересечения плоско-
стей, заданных параллелограммами АВСЕ и
GTKH (их перспективы построены; рис. 550).
Прямые АЕ и КН инцидентны предметной
плоскости и пересекаются в точке N. Нужно
построить еще одну точку. Найдем точку схо-
ца F' прямых АВ и СЕ. Линия схода плоскости
АВСЕ инцидентна точкам F и F' (см. /221/).
Построив точку F'", найдем линию схода F" F"'
плоскости GTKH. Линии схода плоскостей
пересекаются в точке F,v, представляющей
собой перспективу несобственной точки линии
пересечения плоскостей. Соединим ее с точ-
сой N.
проводится вертикальная прямая, инцидентная
картинной плоскости. Точка 3 ее пересечения с
основанием картины соединяется с произвольно
выбранной точкой схода F". На вертикальной
прямой откладывается от основания картины
высота строящейся в перспективе точки п и
через конец полученного отрезка 4 проводится
прямая в точку схода. Проводим Т1—51| к,
строим вертикальный отрезок 5—6, проводим
6—ГЦ/с до пересечения с линией связи, прохо-
дящей через точку Tt (см. рис. 525; построение
перспективы точки Е).
/223/ Способ вторичных проекций применя-
ется в случае, когда нужно построить перспекти-
вы большого числа точек, расположенных иа раз-
личной высоте.
Способ замены предметной плоскости
(см. рис. 519 и 520). Поднимем основание кар-
тины к' на высоту п над принятым ранее осно-
ванием картины к. Используя две горизонталь-
ные прямые, проходящие через точку Т, инци-
дентную замененной предметной плоскости,
построим ее перспективу, это прямая, перпен-
дикулярная основанию картины и пересекаю-
щаяся с ним в точке 7, и прямая, проходящая
через Sj. Она пересекается с основанием карти-
ны в точке 8. Горизонтальные проекции
(рис. 551) прямых Т1—2 и Тг—7, а также —1
и Г,—8 совпали, так как замена предметной
плоскости не. влияет на изображение в плане
(см. /44/).
/224/ Способ замены предметной плоскости
применяется в случае, когда нужно построить
перспективы большого числа точек, располо-
женных на одной высоте.
Способ обхода. Применяется в основном при
построении перспективы архитектурных объек-
тов. Отметим в плане точку 9, пересечения
прямой А1В1 и прямой, проведенной через
параллельно А^Е, и В1С1. Построим ее пер-
спективу. Она расположена в пересечении пря-
мых T}F и АВ. Примем, что высота точки 9
§ 48. ПЕРСПЕКТИВА ТЕЛ
Перспектива гранных тел. Гранные тела
1аще всего встречаются в строительной прак-
тике— это здания, сооружения и их детали.
Каждая грань тела является отсеком плоскости,
ограниченном ребрами тела. Именно ребра.
-. е. отрезки прямых линий, и Строятся в пер-
Построим перспективу наклонной четырех-
угольной пирамиды (рис. 551). Основание пира-
миды— квадрат построим способом архитек-
торов, определив точки схода F и F' перспек-
ив прямых АЕ, ВС и АВ, СЕ (рис. 552; перспек-
ива увеличена в два раза). Остается построить
перспективу вершины Т, т. е. точки, располо-
кенной над плоскостью П,. Задача может быть
1ыполнена разными способами.
Способ масштаба высот. Строится вторич-
,ая проекция точки Т (с помощью прямой
niSJ, пересекающейся с основанием картины в
очке 1 и Т]—2, перпендикулярной основанию
картины; см. рис. 551). Затем определяется пер-
пектива самой точки с использованием мас-
штаба высот. Для этого в произвольном месте
219
над предметной плоскостью равна высоте точ-
ки Т. Отметим точку, в которой перспектива
прямой АВ пересекается с основанием картины.
Проведем через нее вертикальную прямую и
отложим на ней от основания картины отрезок,
равный п — высоте точки 7. Через конец отрез-
ка— точку 11 проведем прямую в точку F'
до пересечения с линией связи, проведенной
через точку 9t, получив при этом перспективу
точки 9. Соединив точки F и 9 прямой линией,
отметим точку Т ее пересечения с линией связи,
проведенной через точку 1\.
В способе обхода используются точки схода
перспектив параллельных линий доминирую-
щих направлений.
/225/ Способ обхода применяется в случае,
когда перспектива объекта построена с приме-
нением точек схода перспектив параллельных
линий доминирующих направлений (архитекто-
ров).
Перспектива схематизированного здания. На
рис. 553 изображено схематизированное здание.
Построим его перспективу (рис. 554)* способом
архитекторов. Найдя точки схода F и F', по-
строим вторичную проекцию здания
(см. рис. 534). Определив с помощью масштаба
высот (точка схода его параллельных линий F")
перспективу точки А (высота точки А равна
длине отрезка 3—4), проведем через нее пря-
мые АС н АВ соответственно в точки F и F'.
В пересечении этих прямых с линиями связи,
проведенными через точки Cj и Bt, получим
перспективы точек С и В. Также построена пер-
спектива стен высотной части здания. Перспек-
тива точки Е найдена с использованием ее вто-
ричной проекции и масштаба высот, точки N —
в пересечении прямой EF со стеной высотной
части здания (см. рис. 548). Чтобы построить
перспективу прямой MN — линии пересечения
ската крыши низкой части здания со стеной
высотной части, найдем точку Т пересечения
прямой АС с плоскостью стены высотной
части. Для этого отметим точку Т\ пересечения
прямых NMt и ЛдСд, на линии связи найдем
точку Т в ее пересечении с прямой АС и соеди-
* Перспектива увеличена в 2,5 раза.
ним ее с точкой N. В пересечении прямой TN
с вертикальным ребром стены отметим точку М.
При построении перспективы точки К восполь-
зуемся тем, что эта точка расположена в пере
сечении прямой СИ (перспектива этой прямой
не показана, дана лишь ее вторичная проекция)
со стеной высотной части здания. Найдя вто-
ричную проекцию К] точки К, проведем через
нее линию связи до пересечения с прямой МГ.
Крыша высотной части здания представляет
собой правильную четырехугольную пирамиду.
Построив перспективу диагоналей ее основания,
проведем через точку их пересечения вертикаль-
ную прямую и с помощью масштаба высот най-
дем на ней перспективы точек L и G. Для боль-
шей точности построения точки пересечения
диагоналей воспользуемся поднятым планом.
Перспектива лестницы. Построим перспек-
тиву двухмаршевой лестницы (рис. 555, а), схема
которой приведена на рис. 555, б. Заключим
проекцию первого марша лестницы в прямо-
угольник АВСЕ и построим его перспективу
(построения не приводятся, они могут быть вы-
220.
7
Рис. 554
полнены любым из описанных способов). Раз-
делим отрезок ВС в перспективе на 5 (по числу
ступеней) равных частей (см. рис. 529; деление
отрезка ЕС) и соединим полученные точки с
точкой F (она была найдена при построении
перспективы прямоугольника АВСЕ). Через точ-
ки 1 и А проведем прямую и отметим точку F"
ее пересечения с линией связи, проходящей
через точку F. Отметим точки 5, 6 и 7 пересече-
ния прямых 2—F, 3—F и 4—F с прямой AF".
Через точку 5 проведем вертикальную прямую
до пересечения с прямой 1—F, через точку 6 —
также вертикальную прямую до пересечения с
прямой 2—F и т. д.
Соединим прямой точки G и F". Нисходя-
щие прямые GF" и AF" в натуре параллельны,
их перспективы пересекаются в точке F". Пер-
спективы горизонтальных ребер ступеней пере-
секаются с прямой GF". Проведем через эти
точки прямые в точку F’.
Аналогично построена перспектива второго
марша лестницы. Точкой схода восходящих
прямых 8—Н и параллельной ей является точ-
ка F'".' Вт оричные проекции точек F'" и F"
совпадают с точкой F, так как в ней пересека-
ются вторичные проекции построенных нами
нисходящих и восходящих прямых.
Рис. 555
221
Рис. 556
Перспектива тел с линейчатой поверхностью.
На рис. 556 показана перспектива прямого кру-
гового конуса и двух прямых круговых цилинд-
ров, ось одного из которых вертикальна, второ-
го горизонтальна. Ортогональные проекции
этих тел не приведены, однако по построениям,
показанным на чертеже, ясно, как была выпол-
нена перспектива. Оба цилиндра были заклю-
чены в параллелепипеды. Для горизонтального
параллелепипеда были найдены точки схода
его ребер, грани вертикального параллелепи-
педа приняты соответственно параллельными
и перпендикулярными картинной плоскости,
что позволило использовать главную точку
картины и точку дальности в качестве точек
схода ребер и диагоналей оснований. При по-
строении перспективы конуса его основание
было вписано в квадрат. Вторичная проекция Tt
вершины была найдена в пересечении перспек-
тив диагоналей квадрата^ Высота вершины, в
равной мере как и высота точки А, располо-
женной на боковом ребре параллелепипеда,
в который вписан вертикальный цилиндр, от-
ложена с помощью масштаба высот. Контур-
ные образующие цилиндра касательны к осно-
ваниям, контурные образующие конуса прохо-
дят через его вершину касательно к основанию.
Пересечение прямой с поверхностью. Прямая
а (а; а,) пересекается (рис. 557) с вертикальным
цилиндром. Построим точки А и В пересечения
прямой и поверхности. Отметим вначале точ-
ки A j и В} пересечения вторичных горизонталь-
ных проекций прямой и поверхности. Проведя
линии связи через A ) и В}, отметим точки А н В
их пересечения с перспективой прямой
а (см. /145/).
Построим точки пересечения прямой а с ле-
жащей на плоскости П) треугольной призмой
(рис. 558). Заключим прямую в вертикальную
плоскость (см. /144/) и построим сечение АВС
этой плоскостью призмы. Точки Л и С располо-
жены в пересечении прямой at с перспективами
ребер bud. Отметив точку Bs пересечения пря-
мых Од ИС), проведем линию связи до пересече-
ния с прямой с (см. /222/). В точке К прямая а
пересекается с гранью b || с и в точке Е —
с гранью b || d.
Даны конус (рис. 559), основание которого
инцидентно плоскости П,, и прямая a (a; at).
Построим точки пересечения прямой с боковой
поверхностью конуса.
Решим задачу в соответствии с /145/. Взяв
на прямой а произвольную точку А, проведем
прямую AT (AT; AtTt). Прямые а и АТ опреде-
ляют плоскость, проходящую через заданную
прямую и вершину конуса и пересекающую бо-
ковую поверхность конуса по двум пересекаю-
щимся прямым. Отметив точки В и С, в кото-
рых прямые АТ и а пересекаются с плоскостью
основания конуса (это точки пересечения пер-
Рис. 557
222
спективных и вторичных проекций прямых)?
соединим их прямой линией и отметим точки
£ и G ее пересечения с основанием конуса. Про-
ведя образующие ЕТ и GT, найдем в их пересе-
чении с заданной прямой искомые точки N и К.
Построения не отличаются от аналогичных по-
строений в аксонометрии.
Перспектива поверхностей второго порядка.
Вначале рассмотрим перспективу сферы. Когда
центр проецирования расположен вне сферы,
множество касательных к сфере проецирующих
прямых представляет собой коническую по-
верхность вращения. Со сферой она соприкаса-
ется по окружности (см. /157/), а с картинной
плоскостью пересекается по одной из кривых
конических сечений (см. /105, /106, /107/). Следо-
вательно, перспективой контура сферы (окруж-
ности) может быть эллипс (предельная пло-
скость не пересекает и не касается сферы),
парабола (предельная плоскость касается сферы)
и гипербола (предельная плоскость пересекает
сферу; см. /219/).
/226/ Перспективой сферы в зависимости от
ее расположения относительно предельной пло-
скости может быть фигура, расположенная «внут-
ри» любой кривой второго порядка.
На практике чаше всего перспективой сферы
бывает эллипс. Чтобы его построить, нужно
рассечь сферу рядом плоскостей, параллель-
ных П°, и, построив перспективы сечений (ок-
ружности; см. рис. 542), провести соприкасаю-
щийся с ними эллипс. Так как эллипс не соответ-
ствует привычным зрительным представлениям
о сфере, его обычно заменяют окружностью.
При построении перспективы других поверх-
ностей второго порядка множество проецирую-
щих прямых, касательных к поверхности, пред-
ставляет собой коническую поверхность вто-
рого порядка, соприкасающуюся с данной.
Линия соприкосновения поверхностей — кривая
второго порядка — является контуром изобра-
жаемой поверхности (рис. 560). а линия сечения
конуса картинной плоскостью — его перспек-
тивой.
/227/ Перспективой контура поверхности вто-
рого порядка может быть только кривая второго
порядка или ее вырожденные случаи — две пере-
секающиеся прямые (перспектива конуса или
цилиндра)' и две параллельные прямые (перспек-
тива цилиндра, образующие которого парал-
лельны картинной плоскости).
Построим перспективу отсека параболоида
вращения с вертикальной осью (рис. 561). По-
строим плоскость, инцидентную параболоиду
и точке S, и повернем ее вокруг оси поверхности
так, чтобы она стала параллельной П2, или за-
меним П2 на П4, расположив П4 параллельно
этой плоскости. Проведя проекцию S2A2
(или 54Л4) проецирующей прямой, касательной
к поверхности, построим через точку касания А
проекцию линии соприкосновения параболоида
и конической поверхности Эта линия в натуре
(гипербола) проецируется в прямую, проходя-
щую через А2 (или Л4) под углом к оси х, близ-
кий к прямому. Для упрощения построений за- ,
меним его прямым углом. Тогда прямая, про-
ходящая через Л2, будет проекцией параболы,
лежащей в вертикальной плоскости. Останется
построить перспективу плоских фигур: пара-
223
болы, лежащей в вертикальной плоскости и
окружности, инцидентной плоскости П,. Ре-
зультат построений показан на рис. 562.
§ 49. ВЫБОР ТОЧКИ ЗРЕНИЯ
И КАРТИННОЙ ПЛОСКОСТИ
Право выбора точки зрения, как правило,
предоставлено автору перспективы, однако он
связан рядом условий. Рассмотрим те из них,
которые относятся к построению архитектур-
ных перепустив по ортогональным проекциям
объекта — здания и сооружения, городского
квартала, поселка и т. д.
Если здание или сооружение после его воз-
ведения будет расположено среди других строе-
ний, точка зрения должна быть выбрана с уче-
том того, чтобы эти строения не закрывали изоб-
раженного в перспективе здания. В случае,
когда здание возводится на свободном участке
местности, точка зрения может быть располо-
жена с любой его стороны, однако предпочти-
тельно размещать ее там, где предполагается
наибольшее число зрителей, которые будут
видеть здание в натуре, например на тротуаре
противоположной стороны улицы. Если стро-
ится всего одна перспектива, нужно выбрать
такую, которая наиболее полно выявила бы
форму объекта.
Высота горизонта. Предметная плоскость мо-
жет быть проведена на любом расстоянии от
точки зрения, поэтому расстояние между гори-
зонтом и основанием картины — величина пере-
менная; в связи с этим мы ввели главную пред-
метную плоскость. При построении архитек-
турных перспектив принято в качестве главной
предметной плоскости принимать плоскость
земли, на которой расположено здание, а когда
участок земли неровный, то некоторую услов-
ную горизонтальную плоскость, на которой
будет расположено большинство зрителей. Та-
кой плоскостью может быть площадка перед
зданием, тротуар на противоположной стороне
улицы и т. д. Расстояние между главной пред-
метной плоскостью и плоскостью горизонта
будем называть высотой горизонта или высотой
точки зрения. В перспективе высота горизонта
равна расстоянию между горизонтом и основа-
нием картины. В зависимости от высоты гори-
зонта могут быть перспективы с высоким гори-
зонтом, перспективы с нормальным или низким
горизонтом и перспективы с горизонтом, совпа-
дающим с основанием картины.
Перспективой с высоким горизонтом будем
называть такую перспективу, когда все или
большинство точек предмета расположены ни-
224
же плоскости горизонта (рис. 563; горизонт не
поместился в пределах чертежа); перспективой
с низким горизонтом — когда все или боль-
шинство точек предмета расположены выше
плоскости горизонта (рис. 564).
В архитектурной практике для изображения
одиночных объектов чаще всего используются
перспективы с нормальным горизонтом, высота
которого равна высоте человеческого роста в
масштабе тех ортогональных проекций, по ко-
торым строится перспектива, или несколько
больше (рис. 565). К перспективам с горизон-
том, совпадающим с основанием картины
(рис. 566), прибегают очень редко. Такое изобра-
жение может быть получено, когда зритель ле-
жит на земле.
Перспективы с высоким горизонтом приме-
няются для изображений значительных про-
странств — городских кварталов, поселков, за-
водских территорий и т. д. Перспективы с низ-
ким горизонтом строятся при изображении зда-
ний, расположенных на горе, на берегу реки и
т. д., т. е. в случае, когда зритель расположен
много ниже здания.
Угол зрения. В зависимости от широты охва-
та изображаемого пространства перспективы
делятся на нормальные и широкоугольные. При
построении перспективы естественно стремить-
ся к тому, чтобы изобразить как можно больше
предметов, расположенных перед зрителем (точ-
кой зрения). Однако когда угол между крайни-
ми горизонтальными или вертикальными про-
ецирующими прямыми слишком велик, на пер-
спективном изображении возникают искажения,
Имеющие в своей основе геометрические и пси-
хологические причины. Рассмотрим некоторые
из геометрических причин перспективных иска-
жений.
На рис. 567, а построена перспектива парал-
лелепипеда из точки зрения 5 (5Д Высота гори-
зонта равна трети высоты параллелепипеда.
Перспективы горизонтальных прямых пересе-
каются соответственно в точках F и F'. Изобра-
жение создает правильное представление об
изображенном объекте. Если рассматривать
параллелепипед как схематизированное невы-
сокое здание, то принятая высота горизонта
позволяет отнести изображение к перспективам
с нормальным горизонтом.
Переместим точку зрения в направлении,
перпендикулярном картинной плоскости впе-
ред,— точка S’ (5J). Точки схода сблизятся
(F" и F'") и изображение (рис. 567, б) в меньшей
степени будет вызывать представление о парал-
лелепипеде. Такую перспективу называют «ост-
рой», так как угол между боковыми гранями
объекта зрительно воспринимается меньшим
прямого. Если переместить точку зрения назад
(точка 5'/), то точки ’схода отодвинутся соот-
ветственно налево и направо. Такое изображе-
ние (рис. 567, в) также будет создавать неверное
представление о параллелепипеде (угол между
передними гранями воспринимается бблыпим
прямого). Перспектива становится «вялой». При
еще большем удалении точки зрения она будет
напоминать аксонометрию.
Угол между горизонтальными проекциями
крайних проецирующих прямых называется
углом зрения. На рис. 567, а он принят равным
30°. Именно такой угол рекомендуют в ка-
честве нормативного при построении перспек-
тив с нормальным горизонтом. Во всяком слу-
чае он не должен превышать 45—50°. При еще
большем угле перспектива называется широко-
угольной. Ее в этой книге мы изучать не будем.
Перспектива параллелепипеда на рис. 568, а
аналогична построенной на рис. 567, а. Картин-
ная плоскость расположена перпендикулярно
биссектрисе угла зрения.
Проведем картинную плоскость под каким-
либо иным углом к биссектрисе угла зрения
(основание картины в плане К'). Тогда перспек-
тива будет выглядеть, как показано на рис. 568,6.
В изображении нарушены зрительно воспри-
нимаемые пропорции заданного параллелепи-
педа, поэтому так располагать картинную пло-
скость нельзя.
И наконец, сравним перспективу, построен-
ную при нормальном горизонте (рис. 569, а)
с перспективой при высоком горизонте
(рис. 569, б). Горизонтальная проекция точки
зрения совпадает, следовательно, угол зрения
при построении перспектив одинаков (сравните
рис. 569 с рис. 534). Перспектива прн высоком
горизонте создает неверное представление об
объекте, так как угол между боковыми гранями
воспринимается как острый. Этого не было бы,
если бы угол зрения был уменьшен.
15—940
225
226
Из сказанного вытекает:
/228/ Угол зрения для перспектив с нормаль-
ным горизонтом принимается равным или нем-
ного большим 30°.
/229/ Угол зрения для перспектив с высоким
горизонтом должен быть уменьшем по сравнению
с углом зрения для перспектив с нормальным
горизонтом.
/230/ Картинная плоскость проводится пер-
пендикулярно биссектрисе угла зрения.
При построении перспективы с высоким го-
ризонтом следует пользоваться графиком на
рис. 570. С его помощью определяется величина
угла зрения. По вертикальной шкале графика
отложена высота горизонта в метрах (с учетом
масштаба ортогональных проекций объекта,
по которым строится его перспектива), по гори-
зонтальной шкале — угол зрения. Определим
величину угла зрения для перспективы jc высо-
той горизонта 6,5 м. Проведем через соответ-
ствующую точку вертикальной шкалы горизон-
тальную прямую до пересечения с линией гра-
фика а и через полученную точку — вертикаль-
ную прямую до пересечения со шкалой углов.
Получим угол 18°. При желании построить
более острую перспективу можно воспользо-
ваться любой точкой на отрезке АВ вплоть до
точки В на линии графика Ь.
При построении перспективы с низким гори-
зонтом следует пользоваться линиями а и с
графика. В этом случае по вертикальной шкале
откладывается расстояние от верхней точки
объекта до плоскости горизонта (например,
4,5 м). Следует выбирать угол между точками С
и D на линиях графика а и с. Также следует по-
ступать при построении перспективы объекта,
высота которого значительно превышает его
ширину и длину.
Горизонтальная проекция точки зрения и осно-
вания картины в плане. Если нет особых сообра-
жений по выбору точки зрения, то для изобра-
жения здания, план которого показан на рис. 571,
ее целесообразно разместить так, чтобы был
виден выступ здания. Примем точку зрения
S' (Sj). Проведем проекции крайних проеци-
рующих прямых и измерим угол между ними.
Он должен быть близким к 30° (при нормальном
горизонте). Если измеренный угол отличен от
намеченного, проведем его биссектрису и смес-
тим по ней проекцию точки зрения так, чтобы
Рис. 570
15
227
угол между проекциями крайних проецирую-
щих прямых стал равным 30° (точка S,).
Основание картины проведем перпендику-
лярно биссектрисе угла зрения. Главное рас-
стояние выбирается в зависимости от того,
какой должна быть ширина Перспективного
изображения. На рис. 571 показаны четыре ва-
рианта расположения основания картины. Пря-
мая к проведена между горизонтальными про-
екциями точки зрения и здания. В этом случае
ширина перспективы здания равна отрезку 1—2.
Основание картины к' проведено через проек-
цию одного из углов здания. Ширина перспек-
тивного изображения — отрезок 3—4. Основа-
ние картины может пересечь план здания (к"’,
ширина перспективы равна отрезку 5—6) и,
наконец, все здание может быть расположено
между плоскостью проекций и точкой зрения
(основание картины к”'), что позволит по-
строить перспективу шириной, равной отрез-
ку 7—8.
Если потребуется построить перспективу на-
столько крупную, что основание картины не по-
мещается в пределах чертежа, следует все как
горизонтальные, так и вертикальные отрезки,
полученные в процессе построения перспективы
на картинной плоскости, увеличить в необходи-
мое число раз.
Ракурс перспективы. Перспектива зданий,
показанная на предыдущих рисунках, называ-
ется угловой в отличие от изображенной на
рис. 572 фронтальной перспективы. Основным
признаком фронтальной перспективы является
совпадение одной из точек схода перспектив
параллельных линий доминирующих направ-
лений с главной точкой картины.
Чтобы перспектива предмета была фрон-
тальной, нужно расположить картинную пло-
скость параллельно одной группе параллельных
горизонтальных прямых объекта (т. е. парал-
лельно фасаду здания).
В ряде случаев возможно построение сме-
шанной, фронтально угловой перспективы. Это
относится к объектам, имеющим несколько
групп параллельных линий.
Масштаб перспективы. Напомним, что мас-
штабом называется отношение длины проек-
ции отрезка к длине отрезка в натуре в случае,
когда отрезок параллелен плоскости проекций.
Это Определение относится к параллельным
проекциям и не может быть использовано в
центральных. Действительно, величина проек-
ции отрезка, параллельного картинной плоско-
сти, зависит от того, на каком расстоянии от
нее он расположен.
Если перспектива строится по ортогональ-
ным проекциям объекта, то имеет место по-
строение изображения не самого здания или
сооружения, а как бы его модели, уменьшенной
в соответствии с масштабом ортогональных
проекций. Все измерения фигур, лежащих в
картинной плоскости, будут выполнены с уче-
том этого масштаба.
Пусть отрезок 1—2 на рис. 571 вдвое меньше
отрезка 7—8. Перспектива, построенная на кар-
тинной плоскости с основанием к, окажется
вдвое меньше перспективы, построенной на
плоскости с основанием к'". Если масштаб ор-
тогональных проекций здания уменьшить в два
раза и в два раза уменьшить высоту горизонта
и главное расстояние, то перспектива на плос-
кости с основанием к”' будет равной перспек-
тиве, построенной на плоскости с основанием к,
когда масштаб ортогональных проекций еще
не был уменьшен. Но несмотря на то что раз-
меры перспективных изображений окажутся
одинаковыми, их масштабы будут отличаться
в два раза.
Таким образом, масштаб перспективы зави-
сит от положения точки зрения относительно
картинной и предметной плоскостей и предмета
относительно картинной плоскости.
/231/ Если точка зрения выбрана в соответ-
ствии с масштабом ортогональных проекций, по
которым строится перспектива, то масштабом
перспективы является масштаб этих ортогональ-
ных проекций.
Чтобы по перспективному изображению
установить его масштаб, нужно знать, где рас-
положены главная точка, основание картины и
горизонтальная проекция точки зрения.
§ 50. ЦЕНТРАЛЬНАЯ АКСОНОМЕТРИЯ
Графический способ построения аксономет-
рии. Взяв в произвольном месте картинной
плоскости вертикальную прямую (рис. 573),
отложим по ней от основания картины одина-
ковые отрезки, равные масштабной единице,
принятой для ортогональных проекций, по ко-
торым строится перспектива; соединим их кон-
цы с точкой Р. Отложив по основанию картины
от вертикальной прямой отрезки той же длины,
также соединим их концы с точкой Р. Исполь-
зовав точку дальности D, построим перспек-
228
тиву сетки квадратов, лежащих в предметной
плоскости, а затем и в вертикальной плоскост и.
Для этого используем точки, в которых гори-
зонтальные прямые линии сетки пересеклись с
прямой ОР. Вертикальную сетку можно по-
строить и без горизонтальной. Достаточно по
вертикальной прямой, проходящей через Р,
отложить главное расстояние и через получен-
ную точку D' провести диагонали вертикально
расположенных квадратов. Вертикальная сетка
представляет собой перспективный масштаб вы-
сот и глубин, горизонтальная — масштаб широт
и глубин. С помощью таких масштабов можно
решать различные задачи.
Дана перспектива точки А, инцидентной
предметной плоскости. Нужно построить пер-
спективу точки В, расположенной левее точки А
на 5 единиц, дальше точки Л на 3 единицы и выше
на 4 единицы.
Проведем через А прямую, параллельную
основанию картины, и отмерим по ней 5 еди-
ниц, каждая из которых равна отрезку прямой
между двумя параллельными (их перспективы
направлены в точку Р) сторонами квадратов.
Из полученной точки С проведем прямую в
точку Р и отмерим три единицы с учетом их
уменьшения по мере удаления от основания
картины, при этом получим вторичную проек-
цию Bt точки В. Высоту точки В—4 единицы —
отмерим с помощью бокового масштаба.
Приведенные построения в принципе не от-
личаются от тех, которые мы выполняли в раз-
деле «Аксонометрия». Различие в том, что пер-
спективы равных в натуре отрезков, последова-
тельно откладываемых в направлении, перпен-
дикулярном картинной плоскости, по мере при-
ближения к точке Р уменьшаются. Перспективу
точек А и В на рис. 573 можно назвать их цент-
ральной аксонометрией.
Графический перспективный масштаб мо-
жет служить и как перспективная сетка (см. § 46)
для построения перспективы различных пло-
ских фигур с криволинейными или прямолиней-
ными очертаниями, лежащих как в горизон-
тальной, так и в вертикальной плоскости. Сов-
местное применение горизонтальной и верти-
кальной сеток позволяет строить перспективу
объемных предметов.
Аналитический способ построения централь-
ной аксонометрии. При построении перспективы
(центральной аксонометрии) объектов, ограни-
ченных кривыми линиями, особенно простран-
ственными, пользуются вычислением коорди-
нат перспектив точек этих линий.
Зададимся системой осей натуральных коор-
динат (рис. 574, б). Примем ось х совпадающей
с основанием картины (к = х), ось у — с пря-
мой StP, ось z (которая, как будет видно из
последующего, для построений не требуется)
вертикальной.
В перспективе (рис. 574, а) ось х° совпадает
с основанием^картины (к = х°), ось z° совпадает
с прямой РР.
Воспользуемся построениями, приведенны-
ми на рис. 519, и определим перспективу А°
точки А,^инцидентной предметной плоскости.
Отрезок Р—2 назовем перспективной координа-
той Х° точки Л, а отрезок Л °—2 ее перспектив-
Рис. 573
ной координатой Z°. Высоту горизонта обозна-
чим и, а главное расстояние т.
Из треугольников Р—2—Sj и 2—Л j—1 опре-
делим Х°:
Из треугольников РР—1 и Л °—2—1, под-
ставив полученное значение Х°, определим Z°:
z° = и fi------Y
\ т + У J
Таким образом, при условии, что точка Л
инцидентна предметной плоскости, чтобы опре-
делить перспективные координаты Г и Z° до-
статочно знать ее натуральные координаты X
и У.
Если ось хс провести совпадающей с гори-
зонтом, а расстояние от точки пространства,
перспектива которой должна быть построена,
до плоскости горизонта обозначить через Z.
то ее перспективная координата Z° — п—Z',
т. е.
z° = z m v
т + У
229
Для построения перспективы точек можно
совместно с (1) пользоваться как (2), так и (3)
формулами.
Пример. На рис. 574, в требуется построить
перспективу точки А, инцидентной предметной пло-
скости и удаленной от основания картины на 30 еди-
ниц и от прямой StP вправо на 20 единиц. Высота
горизонта 35 единиц, главное расстояние — 50 еди-
ниц (т. е. X = 20, У= 30, Z = —35 и т = 50).
По формуле (1) подсчитаем координату Х°
точки Л °. Она равна 12,5 единицы. Координата Z°,
подсчитанная по формуле (3), равна 21,9 единицы.
Не трудно видеть, что изображения точки А, одно
из которых получено графическим путем на
рис. 574, а, другое — аналитическим на рис. 574, в,
одинаковы.
Дана точка В (—25 , 40; 20). Подсчитав ее пер-
спективные координаты по тем же формулам
(Х° = —13,8; Z? = 11,1), построим ее перспективу.
Если нужно изобразить отрезок прямой АВ, доста-
точно соединить точки А° и В” прямой линией.
При построении перспектив большого числа
точек, удобно пользоваться таблицей:
Точка X Y Z или л т т+ У х° У°
А В 20 —25 30 40 —35 20 0,625 0,555 12,5 —13,8 —21,9 И,1
Подсчитав перспективные координаты всех
опорных точек объекта, строят их перспективу.
Аналитический способ позволяет использовать
вычислительные машины для подсчета перспек-
тивных координат и в ряде случаев переходить
на автоматическое построение перспективы в
системе ЭВМ — графопостроитель.
Аналитический способ построения перспек-
тивы (центральной аксонометрии) удобен, когда
объект ограничен незакономерной поверхно-
стью и трудно выделить такие точки его поверх-
ности, которые лежат в одной плоскости. Таки-
ми объектами, в частности, могут быть авто-
мобильные дороги.
Рис. 576
/232/ Аналитический способ построения пер-
спективы (центральной аксонометрии) следует
применять, когда на поверхности объекта трудно
выделить группы точек, так, что каждая группа
инцидентна одной плоскости.
Перспектива земной (топографической) по-
верхности. Обычно земная поверхность задается
горизонталями. Строить их -перспективу целе-
сообразно только тогда, когда, рельеф поверх-
ности достаточно выражен и окажется возмож-
ным построить проекции линий контура от-
дельных участков.
На рис. 575 в проекциях с числовыми отмет-
ками изображен участок местности, основание
картины и горизонтальная проекция точки зре-
ния заданы. Построим перспективу поверхности.
Используем прием, показанный на рис. 520.
Проведем предметный след предельной пло-
скости и на нем на равных расстояниях от точ-
ки отметим точки М и N. Совместим точку
зрении с П„ вращая ее вокруг следа предельной
плоскости, и, соединив полученную точку с
точками М и N, определим угол а наклона
картинных следов проецирующих плоскостей,
проходящих через точки М и N.
Если мы хотим задаться углом а, равным 45",
то точку зрения можно не совмещать. Достаточ-
но от точки S', влево и вправо по предметному
следу, предельной плоскости отложить высоту
точки зрения. Если угол а должен быть равным
60', то, совместив точку зрения, проведем через
нее прямые под углом 60е к предметному следу
предельной плоскости до пересечения с ним в
точках М и N.
Предметную плоскость будем проводить
через каждую горизонталь; отметим основания
картины в перспективе с индексами, соответ-
ствующими отметке той горизонтали, через
которую проведена предметная плоскость
(рис. 576). Расстояние между смежными основа-
ниями картины равно высоте сечения, принятой
для изображения земной поверхности в гори-
зонталях на данном чертеже.
Отметим точки 1 и 2 пересечения горизон-
тали 25 с картинной плоскостью. Их перспек-
тивы расположены на основании картины к(25).
Точно так же отметим точки 3 и 4 на основании
картины к(26).
Возьмем точку А на горизонтали 27. Чтобы
построить ее перспективу, нужно опустить точку
зрения на величину, равную расстоянию между
горизонталями 25 и 27, т. е. две высоты сечения.
Проведя через полученную точку S'21 (см.
рис. 575) прямые под углом а к следу предель-
ной плоскости, получим в пересечении со сле-
230
дом тонки М и N. Построение перспективы точ-
ки А выполним в соответствии с описанием к
рис. 520: через точки 5 и б (рис. 576) проведем
прямые под углом а к основанию картины до
взаимного пересечения в точке А. При построе-
нии перспектив точек В, С и других, инцидент-
ных горизонтали 27, используются те же точ-
ки М и N.
Переходя от построения перспективы одной
горизонтали к построению перспективы другой,
следует переместить точки М и N в сторону
точки St всегда на одну и ту же величину.
Поэтому, определив ее один раз, можно не воз-
вращаться к начальным построениям.
Выше говорилось, что угол а нужно подби-
рать так, чтобы при построениях использовать
чертежные угольники или циркуль. Во втором
случае а = 60°.
§ 51. РЕКОНСТРУКЦИЯ
ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ
Поскольку перспектива служит оценке эсте-
тических достоинств объекта на стадии проекти-
рования, проектировщик часто вносит коррек-
тивы в проект вначале в перспективе, а затем
уже в чертежах, выполненных в ортогональных
проекциях. Поэтому нужно уметь реконструиро-
вать перспективу, т. е. выполнять чертежи пред-
метов в ортогональных проекциях по их пер-
спективным изображениям.
Перспектива фигуры обратима, если извест-
но расположение точки зрения относительно
картинной и предметной плоскостей и вторич-
ная проекция фигуры. Необходимо, чтобы точ-
ка зрения была задана или ее положение могло
бы быть определено по дополнительным к
чертежу сведениям.
Докажем теорему:
/233/ Любой выпуклый плоский четырех-
угольник можно рассматривать как перспективу
параллелограмма заданной формы и размеров
(исключение — параллелограмм, который не
может быть перспективой другого параллело-
грамма).
Даны выпуклый плоский четырехугольник
АВСЕ (рис. 577, а) и параллелограмм А'В' СЕ’
(рис. 577, б). Расположим четырехугольник так,
чтобы точки F и F' пересечения его продленных
сторон лежали на горизонтальной прямой. Бу-
дем рассматривать прямую FF' как горизонт,
а четырехугольник — как перспективу фигуры,
лежащей в предметной плоскости.
Проведем через Е прямую, параллельную
горизонту, и отметим точку 1 ее пересечения
с продленной стороной ВС. Установим пропор-
цию, в которой точка С в действительности
(а не на перспективе) делит отрезок В—1 (по-
строения вынесены на рис. 577, в; сравните их
с приведенными на рис. 529). Построим точку Г
на продолжении стороны параллелограмма
В' С' так, чтобы точка С делила отрезок В'—Г
в той же пропорции (построения на рис. 577, г).
Соединив точки Е' и Г, получим прямую,
параллельную основанию картины в плане (так
как прямая Е—1 параллельна основанию карти-
ны в перспективе; см. рис. 515 и 516).
Проведем вертикальные прямые А—3 и С—2
и будем рассматривать их как перспективы
231
прямых, проходящих через точки .А' и С и
точку St (см. рис. 509). Построим точки 2'
и 3', сохранив пропорциональность расположе-
ния их перспектив на рис. 577, а (построения
вынесены на рис. 577, д) и соединим прямыми
точки С' и 2', а также А' и 3'. В пересечении
прямых С2' и А'З' расположена точка S',.
Ширина перспективного изображения равна
длине отрезка 2—3; отложим ее от точки 3'
по прямой 3'—Г и через полученную точку 8'
проведем прямую параллельно A'St до пере-
сечения с прямой С'—2' в точке 7'. Через 7'
проходит основание картины параллельно пря-
мой 3'—Г.
Продлим сторону параллелограмма А'Е'
до пересечения с основанием картины в точке 4'.
Измерив длину отрезка 4'—7', отложим ее на
рис. 577, а от точки 2 по прямой 3—1, получив
точку 9. Через 9 проведем вертикальную пря-
мую (перспективу прямой —9') до пересече-
ния в точке 4 с продолжением стороны АЕ че-
тырехугольника. Через эту точку проходит осно-
вание картины в перспективе. Построив точку Р
в плане, определим положение точки Р в пер-
спективе.
Таким образом, все необходимые элементы
перспективы известны, а фигура АВСЕ стала
перспективой параллелограмма А'В'С'Е', что
и доказывает теорему /233/. Если рассмат-
ривать четырехугольник как вторичную про-
екцию здания, а параллелограмм (большей
часть прямоугольник) как его план, то можно
восстановить элементы перспективы, а затем
определить высоты отдельных точек, длины
отрезков и т. п.
Дан эллипс (рис. 578, а), о котором известно,
что он представляет собой перспективу окруж-
ности заданного диаметра KR (рис. 578, в),
инцидентной предметной плоскости. Горизонт
и точка Р на нем известны. Требуется построить
перспективу прямого кругового конуса высотой
NM и диаметром основания KR, считая, что
заданный эллипс является его вторичной пер-
спективной проекцией.
Проведем прямые а и Ь, параллельные гори-
зонту и касающиеся эллипса, а также прямые с
и d, касающиеся эллипса и проходящие через
точку Р. Отметив точки А, В, С и Е пересечения
прямых, получим трапецию АВСЕ, которую
в соответствии с /233/ будем рассматривать как
перспективу квадрата, описанного вокруг ок-
ружности заданного диаметра.
Построим план окружности, перспективой
которой является эллипс на рис. 578, а. Для
этого проведем диагональ BE трапеции до пере-
сечения с горизонтом в точке дальности D,
найдя при этом главное расстояние. Оно равно
длине отрезка PD.
Вначале предположим, что основание кар-
тины в плане проходит через одну из сторон
квадрата А^В^С^Е^, описанного около окруж-
ности (рис. 578, б). Перенесем на него с перспек-
тивы точки Е и С, получив при этом точки Е'} и
C't. По стороне Е\С\ построим квадрат. Изме-
рив расстояние от точки Е до линии связи,
проходящей через Р, построим на том же рас-
232
6)
стоянии от точки Е\ точку Р. Найдем точку Sj,
удаленную от основания картины на величи-
ну PD. Однако диаметр окружности оказался
меньше заданного. Проведя прямые S1E\ и
.8, С/, найдем отрезок Ej С\, параллельный осно-
ванию картины и равный заданному диаметру
окружности. Построим квадрат и впишем в
него окружность диаметра KR (или, не строя
квадрата, найдем центр окружности).
Продолжим одну из диагоналей (В}Е,) квад-
рата до пересечения с основанием картины в
точке lt и построим точку 1 в перспективе.
Она расположена на диагонали трапеции BE на
таком же расстоянии от прямой РР, как и точ-
ка 7] в плане.
Отложим на вертикальной прямой, проходя-
щей через точку 7, отрезок 1—2, равный высоте
конуса, и построим точку Т в перспективе.
На рис. 579, а изображена перспектива, а на
рис. 579, б — фасад (фронтальная проекция)
схематизированного здания. Проектировщик,
исходя из композиционных соображений, изоб-
разил в перспективе два окна — внизу прямо-
угольное, вверху арочное. Нужно построить
эти окна на фасаде здания и, кроме того, по-
строить арку в перспективе.
Если не известно положение основания кар-
тины в перспективе, но задан план здания, сле-
дует выполнить построения в соответствии с
описанием к рис. 577. Найдя основание картины
(построения не показаны), вынесем на картину
отрезок ВС (отрезок 8—11), построив предва-
рительно точку измерения F" (см. пояснения к
рис. 527). Отрезок 8—11 равен отрезку В2С2.
Отметим на В2С2 точки, соответствующие точ-
кам 9 и 10, и проведем через них вертикаль-
ные прямые. Вынесем на картину отрезок АВ
(отрезок 7—2, равный отрезку А2В2) и отметим
Рис. 580
на нем точки 3, 5, 6, ..., соответствующие деле-
нию отрезка АВ линиями, проходящими через
точку F'. Построим соответствующие точки
на отрезке А 2В2 и проведем чёрез них горизон-
тальные прямые. Проведя через центр полуок-
ружности на фасаде горизонтальную прямую,
построим ее перспективу (она проходит через
точки 4 и F'). Построим перспективу арки в
соответствии с описанием к рис. 542 (почему
ее нельзя было построить ранее?). Вместо вы-
несения отрезков АВ и ВС на картину, можно
воспользоваться пропорциональным делением
(см. рис. 543).
/234/ Чтобы реконструировать перспективу
фигуры, нужно знать положение точки зрении
относительно предметной н картинной плоское гей.
Сама фигура должна быть задана своей перспек-
тивной и вторичной проекциями (вторичная про-
екция может быть определена по данным черте-
жа или дополнительно изложенным условиям).
Найдем ортогональные проекции точки А,
заданной ее перспективой и условием, что точка
лежит в плоскости прямоугольника BCEG, пер-
спектива которого дана на рис. 580, а ортого-
нальные проекции — на рис. 581 (перспектива
увеличена в Два раза). Построим точку F'
в пересечении перспектив соответствующих сто-
233
16—940
Рис. 582
рон прямоугольника и отметим ее вторичную
проекцию. Приведем через А прямую AF' и,
отметив точку 1 ее пересечения с прямой GE,
проведем через нее вторичную проекцию пря-
мой AF' —прямую 1—F{. Вторичные проек-
ции сторон прямоугольника GB и СЕ в натуре
параллельны, поэтому их перспективы пересе-
каются в точке Fj. Следовательно, вторичная
проекция прямой AF', в натуре параллельной
отрезкам GB и СЕ, также должна пройти через
точку FJ.
С помощью линии связи отметим точку At
на прямой 1—F\ и проведем через нее прямую
AlF. Отметив точки 2 и 3 пересечения этих
прямых с основанием картины, построим их
Рис. 583
в плане. Горизонтальная проекция точки А
расположена в пересечении прямых 2—А и
3—At, соответственно параллельных прямых
StF и StF'. Фронтальную проекцию точки А
найдем, зная ее высоту над предметной пло-
скостью (отрезок 4—2) или с учетом (79).
Задача на реконструкцию перспективного
изображения обратна построению перспективы.
Поэтому во вногих случаях можно реконструи-
ровать перспективу теми же приемами, которые
применяются для ее построения.
‘Построения с недоступными точками. Дан
параллелепипед, одна грань которого располо-
жена в предметной плоскости (рис. 582). Гори-
зонт не проведен. Точки схоЛа горизонтальных
ребер недоступны (расположены за пределами
чертежа). Определить горизонт.
Переместим отрезок АЕ вправо, получив
точки А' и Е' (прямые А А' и ЕЕ' горизонталь-
ны). Проведем прямые ВА' и СЕ' и отметим
точку их пересечения, через которую проходит
горизонт.
Через точку А, инцидентную вертикально
расположенному прямоугольнику ВСЕН
(рис. 583), провести прямую, в натуре параллель-
ную горизонтальным’ сторонам ВС и НЕ. Пока-
жем два приема.
Прием первый: проведем через А верти-
кальный отрезок KR. Разделим точкой М сто-
рону СЕ в том же отношении, в каком точка Я
делит отрезок KR. Через точки А и М прове-
дем прямую.
Прием второй: соединим точку А с точками
В и Н. Построим треугольник СТЕ, подобный
треугольнику ВАН (ВА|| СТ и АН^ ТЕ). Прове-
дем прямую АТ.
ГЛАВА X
ПРОЕКЦИИ ТЕНЕЙ
§ 52. ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
Геометрические и физические основы теории
теней. Освещенность предмета зависит от его
удаления от источника света, угла, под которым
падает свет на поверхность предмета, интен-
сивность источника света и т. д. Помимо дей-
ствительной существует кажущаяся освещен-
ность: так, темный предмет кажется менее
освещенным, чем светлый. Если при этом учесть,
что светлые предметы по мере удаления их от
зрителя из-за воздушной среды кажутся более
темными, а темные — более светлыми, то ста-
нет понятным, что действительная освещен-
ность может значительно отличаться от ка-
жущейся.
Если предмет ограничен нелинейчатой по-
верхностью, то обычно нельзя установить чет-
кую границу между его освещенной и неосве-
щенной частью. Тень самого предмета и падаю-
щая от него на другие предметы никогда не
бывает одинаковой интенсивности — сказыва-
ется воздействие лучей света, отраженных от
других предметов. Если поверхность предмета
гладкая, то на определенном ее участке возни-
кает блик. Местоположение блика зависит от
того, где находятся источник света и зритель.
Описанные явления изучаются в курсах фи-
зики, рисования и других предметов. Начерта-
тельная геометрия обычно ограничивается гео-
метрическими построениями, относящимися к
определению границы тени.
Источник света. Источником света могут
быть Солнце, лампа, фонарь и др. Из-за боль-
шой удаленности Солнца от Земли принято
считать, что солнечные лучи взаимно парал-
лельны, а само Солнпе представляет собой
светящуюся, несобственную точку (см. /5/).
Лампа или фонарь рассматриваются как соб-
ственные светящиеся точки. Лучи света в этом
случае представляют собой связки пересекаю-
щихся прямых. В параллельных проекциях —
ортогональных, с числовыми отметками и ак-
сонометрии источник света принимается бес-
конечно удаленным, в перспективных проекциях
возможны оба варианта расположения источ-
ника света.
Тени тела. На рис. 584 показана тень от тела
Q на поверхности Е. Источник света располо-
жен в точке L. Множество лучей света, осве-
щающих тело, представляют собой конус с
вершиной L. Назовем его световым. По про-
тивоположную относительно источника света
сторону тела расположена неосвещенная часть
пространства — продолжение светового конуса.
Она называется теневом конусом. Световой и
теневой конусы имеют общую вершину, общую
направляющую и общую образующую. Сле-
довательно, геометрически это один конус.
Назовем его лучевым конусом. Фигура Q*
сечения лучевого конуса поверхностью S явля-
ется падающей тенью от тела Q на поверх-
ность Е. Если уменьшить тело до размеров
точки (точка А), то' лучевой конус выродится в
луч света. В точке А* луч света пересекается с
поверхностью Е; эта точка представляет собой
падающую тень от точки А на поверхность Е.
/235/ Чтобы построить тень от точки, падаю-
щую на поверхность, нужно провести через точку
луч света и построить точку его пересечения с по-
верхностью.
Если нет падающей тени от одной части тела
на другую, то каждый луч лучевого конуса
пересекается с поверхностью тела в двух точ-
ках, одна из которых расположена на освещен-
ной стороне тела, другая — на неосвещенной.
Однако некоторые лучи пересекаются с поверх-
ностью тела (касаются ее) только в одной точке.
Множество таких лучей представляет собой
обертывающую лучевую поверхность. Она со-
прикасается с телом по линии а и пересекается
поверхностью X по линии а*. По одну сторону
линии а расположена освещенная, по другую —
неосвещенная часть поверхности тела. О не-
освещенной части поверхности будем гово-
рить, что она находится в собственной тени.
Кривую а назовем границей собственной тени.
Тень В* от произвольной точки В, инцидентной
границе собственной тени, инцидентна кривой
а* — границе падающей тени.
/236/ Граница падающей тени тела является
тенью от границы собственной тени того же тела.
Геометрические построения при определе-
нии проекций аналогичны построениям при
нахождении теней. Если вместо обозначений
а*, В*, ... поставить а', В',... , а вместо точ-
ки L (источник света) взять точку S (центр прое-
цирования), то чертежом можно иллюстри-
ровать построение проекции тела J2 на поверх-
ности X из пентра 5 Поэтому при построении
теней справедливы положения, относящиеся к
построению проекций: /1/, /2/, /4/, /9/, /10/,
/14/ и др., если заменить в них слово «проекция»
словом «тень» и произвести аналогичные за-
мены. Поэтому, изучая тени, мы в соответ-
ствующих местах будем ссылаться на ранее
235
16*
доказанные положения, относящиеся к проек-
циям.
/237/ Для построения на поверхности (пло-
скости) тени от прямой линии нужно провести
через нее лучевую плоскость и построить линию
ее пересечения с поверхностью (см. /4/).
При построении тени от прямой на плоско-
сти следует учитывать, что если прямая парал-
лельна плоскости, то тень параллельна прямой
(см /12/). Когда прямая проходит через источ-
ник света, то ее тенью становится точка (см. /10/).
Когда лучи света падают на поверхность (пло-
скость), то одна сторона поверхности освеще-
на, другая — затенена (расположена в соб-
ственной тени). Затенена и такая плоскость, ко-
торая проходит через источник света.
§ 53. ПРОЕКЦИИ ТЕНЕЙ
ПРИ ПАРАЛЛЕЛЬНОМ
ПРОЕЦИРОВАНИИ
Направление лучей света в ортогональных
проекциях обычно принимают параллельным
диагонали куба, грани которого попарно па-
раллельны плоскостям проекций. При этих
условиях проекции лучей света наклонены к
оси х под углом 45°. Такое направление лучей
света назовем стандартным. В аксонометрии
принимают как стандартное, так и произволь-
ное направление лучей света.
Падающая тень от т очки и прямой. Построим
тень от точки А на плоскости П, (рис. 585).
Направление лучей света определяется прямой I
(см. /8/). Проведем через А прямую парал-
лельно I, а через At — прямую параллельно lt.
В пересечении прямых расположена точка А*
тень от точки А на плоскости П,. Построение
аналогично определению следа прямой линии,
так как тенью от точки А на плоскости nj явля-
ется горизонтальный след луча света, проходя-
щего через точку А.
Пусть кроме А дана точка В и они соединены
между собой прямой. Построим тень от от-
резка АВ на плоскостях П] и П2. Построим
точку (В*) аналогично тому, как была найдена
точка А*. Луч света, проходящий через В, вна-
чале пересекается с П2 в точке В*, а уже затем
с ПР Следовательно, тенью точки В является
точка В*; назовем ее действительной тенью точ-
ки В в отличие от (В*), называемой мнимой
тенью той же точки. Если убрать плоскость П2,
то точка (В*) станет тенью действительной
(в этом случае в ее обозначении следует снять
скобки). Вообще говоря, «мнимой» будем на-
зывать такую тень, которая могла бы быть,
если бы'на пути лучей света не было бы препят-
ствия. В соответствии с/10/ тенью от прямой А В
должна быть также прямая. Соединив точки А*
и (В*), получим тень от отрезка АВ на плоско-
сти П,. В точке 1 она пересекается с осью х
и переходит на плоскость П2. Для построения
тени на П2 достаточно соединить точки 1 и В*.
Таким образом, тенью отрезка АВ на плоско-
стях П, и П2 является ломаная А* -— 1—В*.
Чтобы построить точку В*, можно найти пере-
сечение луча света, проходящего через В с
его вторичной фронтальной проекцией, или,
найдя точку, в которой вторичная горизонталь-
ная проекция луча света, проходящего через В,
пересекается с осью х, провести через нее ли-
нию связи до пересечения с аксонометрической
проекцией луча света.
Аналогичная задача в ортогональных про-
екциях решена на рис. 586. Направление лучей
света стандартное. Проведя через проекции
точек А и В соответственно фронтальные и го-
ризонтальные проекции лучей света, построим
проекции действительных теней А* и В* и
• мнимой тени (В*). Соединив прямой А* и
(В*), отметим точку 1 ее пересечения с осью х
и соединим ее с точкой В*.
Нетрудно видеть, что построение тени фи-
гуры на плоскости проекций при ортогональ-
ном проецировании геометрически не отлича-
ется от построения вспомогательной параллель-
ной проекции фигуры на той же плоскости. >
Тени от прямых частного положении. Отрезок
АВ на рис. 587 вертикален. Точка В инцидентна
Рис. 585
Рис. 586
236
плоскости П, и совпадает со своей действи-
тельной тенью на той же плоскости (В} = В*).
Мнимой тенью точки А на П] является точка
(А*). Соединив эти точки, получим тень пря-
мой АВ на плоскости Пп которая параллельна
горизонтальной проекции лучей света.
/238/ Тень на горизонтальной плоскости от
вертикальной прямой параллельна горизонталь-
ным проекциям лучей света.
Отметив точку А* пересечения построенной
тени с осью х, соединим ее с точкой А*. Отрезок
А*—А* вертикален. Вследствие стандартного
направления лучей света отрезки А*А* и (Л*)
(А *) равны между собой.
Прямая CD перпендикулярна П2. Проведем
через С2 = С* прямую, параллельную фрон-
тальной проекции лучей света, а из точки ее
пересечения с осью х — перпендикулярную ей
прямую до пересечения с горизонтальной про-
екцией луча света, проходящей через Dt.
/239/ Тень на фронтальной плоскости от пер-
пендикулярной ей прямой параллельна фронталь-
ным проекциям лучей света.
На рис. 588 показаны аналогичные построе-
ния в аксонометрии.
Тени от АВ на плоскости П2 и от CD на пло-
скости П] параллельны самим прямым. Поло-
жение /12/ для построения теней формулиру-
ется так:
/240/ Тень от прямой линии на параллельной
ей плоскости параллельна самой прямой.
Тени от точки и прямой на плоскости общего
положения. Способы лучевых сечеинй и обратных
лучей. Даны плоская фигура АВС и отрезок DE
(рис. 589). Построим тень от АВС и DE на пло-
скостях П| и П2 и от DE на АВС. Тень от Е на
плоскости АВС найдем в соответствии с /87/.
Для этого луч света, инцидентный точке Е,
заключим во вспомогательную фронтально про-
ецирующую плоскость £2, найдем линию NK
пересечения плоскостей данной и вспомога-
тельной и на ней искомую точку Е* (Е*: Е*).
Аналогично построена тень от точки D Для
этого луч света, инцидентный точке D, заклю-
чен во фронтально проецирующую плоскость X
и найдены точки М и Т, определяющие линию
пересечения плоскостей АВС и I. В пересечении
прямой МТ с лучом расположена точка (£>*).
Это мнимая тень точки D, так как действитель-
ная тень расположена на плоскости П,. Соеди-
нив точки Е* и (D*), получим тень от отрезка DE
на плоскости АВС. Так как задана не плос-
Рис. 588
кость АВС, а ее отсек — треугольник, то дей-
ствительная тень расположена между точками
Е* и F*. Описанный способ построения тени
называется способом лучевых сечений.
При построении тени от DE на АВС можно
воспользоваться способом обратных лучей. Для
этого предварительно построим тень от АВС
на nj (или П2, или на обе плоскости проекций).
Выполним построение теней от АВ, ВС и АС
в соответствии с описанием к рис. 586. Вслед
за этим построим тень_ на плоскости П, от
отрезка DE. В точке F* она пересекается с
тенью от стороны АС. Продолжение тени от
DE пересекается с тенью от ВС в точке R*.
Проведем через точки F* и R* лучи света в об-
ратном направлении до пересечения с соответ-
ственными сторонами треугольника в точках F*
и R*. Через них проходит тень от прямой DE
на плоскости Л ВС.» Отметим пересечение этой
линии с лучом света, проведенным через точку Е
(точка Е*). •
/241/ Способ лучевых сечения применяется
в основном, когда по условиям задачи не нужно
строить падающую тень от предмета на пло-
скость проекций или какую-либо другую пло-
скость. В противном случае применяется способ
обратных лучей. Возможно одновременное ис-
пользование обоих способов.
Освещенность отсека плоскости. Определим
освещенность самого треугольника АВС. Для
этого воспользуемся конкурирующими точка-
ми N и G (точка G инцидентна лучу света, про-
ходящему через Е, а точка N — стороне А В).
При взгляде спереди точка G ближе к зрителю,
следовательно, лучи света падают на треуголь-
ник со стороны зрителя и он видит освещенную
сторону треугольника. Возьмем конкурирующие
точки на луче (17) и на стороне АВ ( L). При
взгляде сверху мы вначале видим точку L,
а затем уже точку G. Следовательно, лучи па-
дают на плоскость треугольника с противопо-
ложной относительно зрителя стороны пло-
скости, и мы видим ее неосвещенную сторону.
/242/ Чтобы проверить освещенность плос-
кой фигуры, следует провести луч света и, взив
конкурирующие точки иа луче (до его пересече-
ния с плоскостью) и одной нз линий фигуры,
установить, что ближе к зрителю — луч или
линия. Если ближе луч, то фигура освещена,
и наоборот.
Кроме того, можно пользоваться прави-
лом: .читаем обозначение проекций точек фи-
237
гуры по часовой стрелке; Л,, С,, В,. Обозна-
чение точек проекций теней фигуры (также по
часовой стрелке) читается в ином порядке —
Ait (В.), Ct. Следовательно, видна неосвещен-
ная сторона плоскости. Если бы была видна
освещенная сторона, то порядок прочтения
обозначений не изменился бы. Проверьте спра-
ведливость сказанного при рассмотрении фрон-
тальной проекции фигуры и ее тени.
Способ обратных лучей можно применять
и в аксонометрии. Треугольник АВС и отре-
зок DE на рис. 590 заданы своими аксонометри-
ческими и вторичными проекциями (направ-
ление осей и коэффициенты искажения не даны,
как и в ряде других задач, решавшихся нами в
аксонометрии). Направление лучей света за-
дано аксонометрической / и вторичной Ц про-
екциями. Так как точки А и С инцидентны П;
(А =Л]) и (C=Cj), то для построения тени
от треугольника достаточно найти тень от точ-
ки В и соединить ее с точками А и С, совпадаю-
щими со своими тенями. Точка D отрезка BE
также инцидентна плоскости Пп поэтому нужно
построить тень от £ и соединить ее с точкой D.
Тень точки Е на плоскости П, мнимая, так как
расположена внутри тени от фигуры. Построим
тень от этой точки на плоскости треугольника.
Для этого продлим тень (£*) D* до пересече-
ния в точке Г* с тенью от АВ. Проведя через F*
обратный луч, найдем точку F*, лежащую на
стороне АВ. Отметим точку 1, в которой тень
Рис. 590
238
от DE на плоскости П, пересекается с отрез-
ком АС. В этой точке тень отрезка переходит
SD. В соответствии с /236/ эти ребра являются
границей собственной тени тела. Построение
с П, на плоскость треугольника. Соединим
точки 1 и F* и отметим точку Е* пересечения
луча света, проходящего через Е, и прямой
1-F*
Если плоская фигура параллельна плоскости,
на которую падает тень, то тень равна и подоб-
но расположена самой фигуре (см. /43/). На
рис. 591 построены падающие тени от окруж-
ностей аиЬ, плоскости которых соответственно
параллельны П2 и П,. Для построения тени от
окружности на параллельную ей плоскость до-
статочно построить «тень» от ее центра Е и
провести окружность диаметра данной окруж-
ности. Тень от окружности а частично перехо-
дит на ПР Для построения этой части тени
удобно заключить окружность в квадрат,, стро-
ить точки тени подобно аксонометрическим
проекциям точек окружности.
Тени тела. Построим тень пирамиды SABCD
на П, и П2 и найдем собственную тень тела
(рис. 592). Основание пирамида расположено
на Пь поэтому тень от него совпадает с самим
основанием. Тенью точки 5 на П] является
точка (S*). Соединив ее с точками А, В, Си D,
получим тень от боковых ребер пирамиды.
Тень от граней ограничена тенью ребер SB и
теней в ортогональных проекциях и аксономет-
рии, как видно из чертежа, аналогично.
На рис. 593 показано построение падающей
и собственной тени конуса. Найдя мнимую тень
(5*) вершины на плоскости П15 проведем через
нее касательные к основанию, представляющие
собой границу падающей от конуса тени. По-
строение основано на том, что граница падаю-
щей тени определяется линией пересечения пло-
скостей, касательных к поверхности, с плоско-
стью, на которую падает тень. Эти йлоскости
заданы лучом 5 (S*) и прямыми, проходящими
через точку ($*) касательно к основанию (см.
2 27, рис. 326).
В соответствии с /236/ через вершину и тоя-
ки 1 и 2, в которых границы падающей тени
пересекаются с основанием, проходят границы
собственной тени. При обычных условиях осве-
щения границы собственной тени на конусе
не бывают четкими. Однако их строят для
того, чтобы по ним определить тень, падающую
от конуса на другие поверхности.
Тени от прямых круговых конуса и цилиндра
показаны на рис. 594. В зависимости от угла
наклона образующих конуса к П1; тень от его
вершины будет расположена вне основания.
239
Рис. 594
на его границе или внутри основания. Во втором
случае собственная тень конуса представляет
собой прямую, в третьем случае тени нет вовсе.
При стандартном направлении лучей света от-
резки и (S*) (5*)'равны между собой, что
упрощает построение точки 5*, если известна
точка (S*), и наоборот. Граница собственной
тени конуса построена в соответствии с описа-
нием к рис. 593.
Падающая на П, тень от цилиндра ограни-
чена двумя параллельными линиями, касатель-
ными к нижнему основанию цилиндра, и тени
от его верхнего основания. Тень от вер икаль
ной прямой АВ (границы собственной тени ци-
линдра) на плоскости П, параллельна I, (см.
/238/). В точке 1 она пересекается с осью х и идет
вертикально до пересечения в точке А*2 с лучом,
проходящим через точку А (см. рис. 587). От
точки Л* начинается граница тени, падающей
от верхнего основания цилиндра на плоскость
П2. Она построена в соответствии с описанием
к рис. 591.
Тени от точки и прямой на поверхности. За-
дачи решаются в соответствии с /137/ и /144/.
Построим тень от отрезков MN и EF на поверх-
ности конуса (рис. 595). Прямая MN верти-
кальна, следовательно, вертикальна и проходя-
щая через нее лучевая плоскость. Горизонталь-
ная проекция линии пересечения лучевой пло-
скости и конической поверхности известна
(см. /16/). В данном случае линией пересечения
является гипербола (почему?). Тень от прямой
общего положения EF может быть построена
путем сечения поверхности и лучевой плоско-
сти вспомогательными плоскостями. На черте-
же показаны плоскости S2 и S. С лучевой пло-
скостью они пересекаются по прямым, парал-
лельным тени от EF на плоскости П, (почему?),
с конической поверхностью — по окружностям.
Определив общие точки прямых и окружно-
стей, соединим их плавной кривой. В данном
случае это эллипс (см. /105/). Построения вы-
полнены способом лучевых сечений. При по-
строении падающей гени от прямых на по-
верхность можно не строить падающую тень
от поверхности. Если же она построена, то
удобно воспользоваться способом обратных
лучей.
На рис. 596 изображены конус и прямая EF
Предыдущего примера. Возьмем произвольную
образующую S—1 и построим ее падающую
тень (5*) — 1* на плоскости П,. В точке (N*)
она пересекается с тенью от прямой EF; про-
ведя обратный луч через эту точку до пересе-
чения с образующей 5—1, получим одну из
точек тени от EF на поверхности. Аналогично
построены остальные точки, в том числе точ-
240
ка К, в которой тень от прямой пересекает гра-
ницу собственной тени конуса.
Вернемся к построению тени от вертикаль-
ной прямой MN на рис. 595. На эпюре гори-
зонтальная проекция тени на плоскости П,
и поверхности конуса, в равной мере как и на
любой другой поверхности, параллельна гори-
зонтальной проекции лучей света. Очевидно,
что фронтальная проекция тени на любой по-
верхности от прямой, перпендикулярной пло-
скости П2, будет параллельна фронтальной
проекции лучей света.
/243/ Горизонтальная проекция тени на лю-
бой поверхности от горизонтально проецирую-
щей прямой и фронтальная проекция тени от
фронтально проецирующей прямой параллельны
соответственно горизонтальной и фронтальной
проекциям лучей света.
Положение /243/ не следует смешивать с
/238/ и /239/, так как оно относится только к
ортогональным проекциям теней, в то время
как /238/ и /239/ справедливы для всех видов
проекций.
Построение тени от прямой EF в аксоно-
метрии показано на рис. 597. Здесь, как и в не-
которых предыдущих примерах, не даны оси
и коэффициенты искажения. Направление лучей
света задано аксонометрической (/) и вторичной
горизонтальной ((,) проекциями луча. Исполь-
зован способ обратных лучей.
На рис. 598 построена тень от отрезков MN
и EF на призме. Горизонтальная проекция тени
от отрезка MN (отрезок N*M*) найдена в
соответствии с /243/. Фронтальная проекция
тени — отрезок 12—32 перпендикулярна оси х,
так как в натуре тень от прямой MN на верти-
кальной плоскости ABCD вертикальна (см.
/240/). При построении проекций тени от EF
найдем отрезок Е* (F\) (тень на плоскости П,)
и точку F* пересечения с гранью АВК. L луча
света, проходящего через F. На этой грани
тень от прямой EF (отрезок 4, — F*t) параллель-
на E*t (F*), так как грань параллельна П(.
Построив точку 42, соединим ее с точкой 22,
получив при этом фронтальную проекцию тени
отрезка EF на грани ABCD. При определении
падающей на плоскость П, тени от призмы
нужно учесть, что ^К^Ц/, (см. 1ЕЗ%1\ По-
строив точку K*j, проведем K’5L’J||K1L1 (см.
/240/). Причем К* L* = К, L, (см /39/). A* L* ||
||Л, L, и, наконец, С)Л’}||/1.
Тень от одного тела, падающая на поверх-
ность другого. Падающие и собственные тени
схематизированного здания в аксонометрии
показаны на рис. 599. Найдя тени от точек А и
С, соединим их прямой. Тень от отрезка АВ
в соответствии с /240/ параллельна А В. Тень
от вертикальной прямой, проходящей через Е,
параллельна горизонтальной проекции лучей
света (см. /238/). Тень точки D расположена в
пересечении с лучом света прямой A*D*, парал-
лельной воображаемой прямой AD. Горизон-
тальная вторичная проекция тени от вертикаль-
ной прямой, проходящей через точку F, парал-
лельна /Р Отметив точку ее пересечения с гори-
зонтальной вторичной проекцией конька крыши,
установим проекционную связь и найдем точ-
ку К, через которую проходит тень В точке F*
241
с тенью пересекается луч света, инцидентный
точке F. Найдя аналогичным приемом точку М*,
проведем через нее тень от прямой МТ парал-
лельно этой прямой (почему?). Точка Р найдена
в пересечении обратного луча, проведенного
через Р* с вертикальной прямой, проходящей
через Е.
Чтобы не ошибиться при построении гра-
ницы падающей тени, следует придерживаться
правила:
/244/ Если через точку тела проходит п ли-
ний, следует построить п теней, а затем выбрать
те нз них, которые составляют границу падающей
тени тела.
Например, через F проходят три линии:
вертикальная и две горизонтальные. Тени двух
из них входят в состав границы падающей тени
от трубы на крышу, третья (от прямой, парал-
лельной плоскости ската крыши) расположена
внутри тени от трубы. При сложной конфигура-
ции изображенного тела правило ЦАЦ имеет
большое значение.
При построении тени, падающей от конуса
на призму (рис. 600), следует вначале найти па-
дающую на П, и собственную тень (S—7, .S—2)
конуса. Эта часть задачи решается в соответ-
ствии с описанием к рис. 593 и 594. Теперь,
учитывая /236/, строим тень на призме от пря-
мой S'—7. Она начинается в точке 3, в которой
тень от конуса переходит с плоскости на
грань призмы 6||с. Затем рассечем лучевую
плоскость, проходящую через прямую S—1,
горизонтальной плоскости Г2. Линия сечения
6—4 параллельна границе тени 1Х—£$ (так как
П! || fl) и пересекается с призмой в точке 4 на
ребре Ь. Проведя плоскость S, найдем точку 5.
Соединим между собой точки 3 и 4, а также
4 и 5. Через точку 5 проходит тень 5—7 от пря-
мой S—7 параллельно S'*—lt (грань «||6 па-
раллельна П,). Так же строится тень от прямой
S—2. В приведенной задаче использовался спо-
соб лучевых сечений.
Задача на рис. 601 решена способом обрат-
ного луча. Строим падающие на П, тени от
конуса и пирамиды, предположив, что пирами-
да не имеет граней и состоит из одних ребер.
Определяем точки (7*), (2*), (4*), (5*), ... пере-
сечения границы падающей на П, тени от ко-
нуса с тенями от ребер пирамиды. Обратными
лучами находим точки -1, 2,4 и 5 на ребрах
пирамиды. В точках 6 и 7 тень от конуса пере-
секается с ребром ТЕ, лежащим в плоскости П,
и совпадающим поэтому со своей тенью. Чтобы
определить тень от вершины S на поверхности
пирамиды, проводим через точку (5*) прямую
Т, -—3* и, проведя обратный луч, найдем точку 3
на ребре АВ; соединим ее с вершиной Т. На пря-
мой Т—3 отметим тень S* от вершины S на
грани АВТ (в пересечении прямой Т—3 с лучом,
проходящим через точку S). Соединив после-
довательно точки 6, 4, 2, S*, 1, 5 и 7, получим
падающую на пирамиду тень от конуса. Для
определения освещенности граней пирамиды
воспользуемся /236/. Граница падающей тени
состоит из теней от ребер EF, FA, АВ и ВС.
Следовательно, эти ребра определяют границу
собственной тени пирамиды. Когда нужно оп-
ределить тень, падающую от одного тела на
поверхность другого, часто вначале строят соб-
ственную тень тела, от которого падает тень.
Проводя через ее границу лучевую поверх-
ность, находят линию ее пересечения с поверх-
ностью тела, на которое падает тень. Покажем
построение собственной тени некоторых тел
вращения, оси которых вертикальны.
Пристроим к фронтальной проекции конуса
(рис. 602) полуокружность. Из точки 7 проведем
прямую 1—2 параллельно проекции левой кон-
турной образующей конуса до пересечения с
горизонтальным диаметром в точке 2. Через 2
построим прямую под углом 45 к тому же
диаметру и отметим точку 3 пересечения пря-
мой с окружностью. Проведя через 3 вертикаль-
ную прямую, найдем точку 4. через которую
проходит видимая граница собственной тени
конуса. Проведя через точку 2 прямую 2—5
также под углом 45" к диаметру, а через точку 5—
вертикальную прямую, получим точку 6, через
которую проходит невидимая граница собст-
венной тени.
242
Рис. 602
Аналогично построение тени на цилиндре.
Поскольку его вершина несобственная, то точ-
ка 2 совпадает с центром полуокружности.
Проведем на проекции шара вертикальный,
горизонтальный и два наклонных под углом
45° диаметра. Через точку 1 проведем горизон-
тальную и вертикальную прямые, а также пря-
мые, наклоненные под углом 30° к диаметру
1—2. В пересечении прямых с соответствую-
щими диаметрами получим точки 3, 4, 7 и 8.
Аналогично построены точки 5 и 6. Через по-
лученные точки проходит эллипс — фронталь-
ная проекция границы собственной тени шара.
Построим тень от шара, падающую на приз-
му и плоскость rij (рис. 603). Вначале найдем
границу собственной тени шара в соответствии
с. рис. 602. Взяв на этой линии произвольную
точку К, проведем через нее луч света и, заклю-
чив его во вспомогательную горизонтально
проецирующую плоскость Й (см. /S'?7), найдем
пересечение луча с гранью призмы ABDE
Аналогично построена тень от М и других
точек.
Если, кроме того, требуется найти тень,
падающую от шара на плоскость П|; то и в
этом случае может быть использована собствен-
ная тень шара. Множество лучей, инцидентных
точкам границы собственной тени шара, пред-
ставляет собой лучевую прямую круговую ци-
линдрическую поверхность диаметра, равного
диаметру шара. Эта поверхность пересекается
плоскостью П| по эллипсу, большая ось кото-
рого — отрезок N* (М*). Малая ось располо-
жена посередине этого отрезка и равна диаметру
шара. Промежуточные точки эллипса строятся
как тени от произвольно взятых точек собствен-
ной тени шара. В точках 4 и 5 тень от шара пере-
ходит с плоскости П, на грань призмы ABDE.
При построении падающей тени от призмы
достаточно провести луч света только через
244
одну точку А (или £). Соединим ее'тень с точ-
кой Bt. Тень от равна и параллельна этому
отрезку (см. /240/). Найдя тень от точки Е,
соединим ее с точкой D,.
Примеры построения теней в строительной
практике. Тень в прямоугольной нише показана
на рис. 604, а. Найдя тень от точки А на пло-
кости стены, проведем через нее прямые, па-
раллельные соответственно прямым АВ и АС
(см. /240/).
Аналогично построение тени в нише на
рис. 604, б. Здесь тени от отрезков АВ, ВС и CD
параллельны самим отрезком.
Тень в полукруглой нише показана на
рис. 604, в. Необходимо построить «тень» точ-
ки С и провести дугу окружности с центром в
построенной точке. Тень от вертикального реб-
ра ниши касательна к тени от полуокружности.
В цилиндрической нише (рис. 604, г) падаю-
щая тень ограничена прямой линией, делящей
нишу пополам, и четвертью окружности. При
принятом направлении лучей света лучевая
плоскость (профильно проецирующая), инци-
дентная прямой АВ, пересекает цилиндрическую
поверхность по эллипсу, который на П2 проеци-
руется в окружность В этом нетрудно убе-
диться, если построить профильную проекцию
ниши и лучевой плоскости.
На рис. 605, а показана тень от полуколонны
на стене и от абака (прямоугольной плиты) на
колонне и стене, а также собственная тень ко-
лонны. Полуколонна имеет форму полуцилинд-
ра; ее собственная тень найдена в соответствии
с рис. 602. Построение падающей тени от ко-
лонны и абака на стену основано на том, что
линии, от которых падает тень, занимают част-
ное положение. Найдем тень С* от точки С на
стене. Через С проходят три линии (см. /244/)
Рис. 604
Рис. 605
I
245
поэтому построим три тени. Тень от CD вер-
тикальна (см. /240/), тень от АС горизонтальна,
тень от прямой, проходящей через С перпенди-
кулярно к стене, параллельна фронтальной
проекции луча света (см. /239/). Она нам не
нужна, так как расположена внутри тени, па-
дающей от абака. Через точку D также проходят
три линии. Тень от одной из них (CD) мы по-
строили, тень от горизонтальной прямой, па-
раллельной стене, не нужна, так как она внутри
тени от абака, тень от прямой, перпендикуляр-
ной стене, параллельна фронтальной проекции
лучей света. Тень, падающая от колонны, может
быть найдена по собственной тени колонны,
как показано на чертеже. Она вертикальна, так
как вертикальна граница собственной тени
колонны.
Через точку А, проходят три линии. Тень
от вертикальной прямой не нужна, так как эта
прямая не принадлежит границе собственной
тени абака. Тень от АС — в натуре дуга эллип-
са — проецируется на Пг в дугу окружности
(при принятом направлении лучей света); в
этом можно убедиться, как и в случае с цилин-
дрической нишей, спроепировав полуколонну и
лучевую плоскость на П3. Тень от А В параллель-
на фронтальной проекпии лучей света (см. /243/).
Если абак — полуцилиндр (рис. 605, б), нуж-
но взять на нижнем основании полуцилиндра
некоторое число точек и, проведя через них
лучи света, определить тени точек на поверх-
ности колонны. Точка С пересечения границы
собственной тени колонны с границей тени,
падающей от абака на колонну, построена
способом обратных лучей (через С* проведен
обратный луч до пересечения с границей соб-
ственной тени в точке 0. Так же с помощью
обратного луча построена точка А*, в которой
граница падающей тени пересекается с левой
контурной образующей цилиндра (колонны):
вначале построена точка Аг, затем найдена Л2.
Через А 2 проведена фронтальная проекция луча
света, которая пересекается с фронтальной про-
екцией образующей в точке А^. Граница тени,
падающей от абака на стену, представляет
собой две дуги подобных эллипсов и отрезок
прямой, касательной к ним. Построения вы-
полнены в соответствии с рис. 591.
Найдем собственную и падающую тень тела
вращения. Построив собственную тень на шаре,
конусах и цилиндре (рис. 606, а) в соответствии
с описанием к рис. 602, определим тень, падаю-
щую на цилиндр от шара и на конус от цилиндра.
Решение второй части задачи показано
на рис. 606, б. Взяв произвольную точку А
на границе собственной тени шара, строим
гень от нее А* йа поверхности цилиндра.
Так же построены и остальные точки падаю-
щей ;ечи
246
7
Рис. 608
Построим тени схематизированного соору-
жения (рис. 607). Тень от границы основания
полого полуцилиндра построена путем опреде-
ления теней от отдельных точек, например А.
Граница собственной тени полуцилиндра про-
ходит через точку В, в которой линия, парал-
лельная фронтальной проекции 12 луча света,
касается того основания полуцилиндра, кото-
рое лежит на грани параллелепипеда. Тень от
полуцилиндра на параллелепипеде параллельна
12 (см. /239/), а на земле — параллельна образую-
щей ВС (см. /240/). Построение теней в нишах
ясно из чертежа. />
Тени на лестнице. Рассмотрим пример
(рис. 608). Тень на земле от вертикальной пря-
мой а параллельна lt (См. /238/). Найдя точку 1
пересечения этой тени с вертикальной гранью
первой ступени, проведем тень на этой грани
параллельно а (см. /240/). Через точку 2 про-
ходит тень от прямой а параллельно тени от
той же прямой на земле. Проведем луч света
через А и построим тень А* от этой точки на
горизонтальной грани первой ступени. Найдем
точку В, в которой прямая b пересекается с
горизонтальной гранью первой ступени (по-
строим точку пересечения прямых b и d).
Тень от В на горизонтальной грани первой
ступени совпадает с самой точкой В = (В*).
Соединим точки А и В и отметим точку 3 ее
пересечения с вертикальной гранью второй
ступени. Построим точку С пересечения верти-
кальной грани второй ступени с прямой h
(она расположена в пересечении прямых b и е)
и соединим ее с точкой 3 (тень от прямой b на
вертикальной грани второй ступени проходит
через точку 3; тень от точки С на той же грани
совпадает с самой точкой). Тень от прямой b
на горизонтальной грани второй ступени про-
ходит через точку 4 параллельно тени А*—3,
а тень на вертикальной грани третьей ступени
параллельна прямой 3-4 (почему?). Найдя
точку 5, проведем через нее тень от прямой b
на площадке лестницы параллельно А*—3 и
отметим точку D* пересечения тени с лучом
света, инцидентным точке D. Через D* прохо-
дит тень с т прямой с, параллельная самой
прямой (см. /240/). В точке 6 она пересекается
со стеной. Прямая б—7 представляет собой тень
от прямой с на плоскости стены; она параллель-
на фронтальной проекции лучей света (почему?).
Построение тени от боковой части лестницы на
земле ясно из чертежа.
Аналогичная задача в ортогональных про-
екциях показана на рис. 609. Построим гори-
зонтальную проекцию тени от прямой а на
плоскости земли и отметим точку 1, в которой
она пересекается с вертикальной гранью пер-
вой ступени. На этой грани тень проходит через
точки 1 и 2 параллельно а. Горизонтальная
проекция тени от а на горизонтальной грани
первой ступени является продолжением гори-
зонтальной проекции тени от той же прямой
на земле (см. /243/), фронтальная проекция
совпадает с проекцией плоскости грани. По-
строим тень ( О*) от точки D на горизонтальной
грани первой ступени и соединим ее с точкой А*.
'2
Построенная прямая представляет собой тень
от прямой Ь. Отметим точку 3 пересечения
тени A* (£>*) с вертикальной гранью второй
ступени и найдем мнимую тень (D*)' точки D
на той же грани (тень построена с помощью
обратного луча). Тень от прямой b на верти-
кальной грани второй ступени проходит через
точки (£>*)' и 3. Отметим точку 4, в которой
тень пересекается с горизонтальной гранью
второй ступени. По этой грани тень от прямой Ь
проходит параллельно А*—3 вплоть до точки 8,
от которой переходит на вертикальную грань
третьей ступени. Построив точку 5, проведем
тень от прямой b на площадке, которая ограни-
чивается точкой D*. Через D* проходит тень
от прямой с параллельно самой прямой. С пло-
скостью стены она пересекается в точке б, через
которую проходит тень от прямой с на плоско-
сти стены (каково ее направление?).
Тени тел вращения. Построим собственную
и падающую тени тела вращения (рис. 610).
Рассечем его поверхность рядом горизонталь-
ных плоскостей. Построим тени построенных
окружностей, падающие на П,, — также окруж-
ности (см. рис. 591) и проведем линию, огибаю-
щую их. Эга линия представляет собой границу
падающей на П, тени тела. Отметим точки,
в которых огибающая соприкасается с окруж-
ностями (например, А*). Проводя обратные
лучи через точки соприкосновения до пересече-
ния с соответствующими линиями сечений (точ-
ка А на линии сечения плоскостью Q), найдем
точки, принадлежащие границе собственной
тени тела (см. /236/).
Если нужно построить только собственную
тень тела (например, для решения задачи на
определение его падающей на какую-либо по-
верхность тень, см. пояснения к рис. 603),
можно поступить так." рассечем поверхность
тела (рис. 611) рядом горизонтальных плоско-
стей и между ними заменим (аппроксимируем)
поверхность отсеками конических или цилин-
дрических поверхностей вращения и сфер.
Используя описанный ранее прием (рис. 602),
строим границы собственной тени на каждом
отсеке заменяющих поверхностей. Отметим
точки А, В, С, в которых границы собственной
тени заменяющих поверхностей пересекаются
с горизонтальными плоскостями. Границу соб-
ственной тени заданной поверхности вращения
проведем между точками, принадлежащими
заменяющим поверхностям (например, между
точками В и С). Чем больше заменяющих по-
верхностей, тем ближе друг к другу располо-
жены точки, подобные В и С, и тем точнее
строится граница собственной тени поверх-
ности вращения.
Тени поверхностей иторого порядка. Ранее
было установлено, что собственная тень по-
верхности строится по тем же законам, что и
контур поверхности. Следовательно, граница
собственной тени эллипсоида при освещении
параллельными лучами света представляет со-
бой эллипс, параболоида — параболу, гипер-
болоида — гиперболу.
Если будет построена граница собственной
тени, построить падающую тень не представит
трудности.
248
Определим границу собственной тени на
половине трехосного эллипсоида (рис. 612) при
заданном направлении лучей света I ; /2).
Задавшись плоскостью родства Е, парал-
лельными родственными прямыми, проходя-
щими через точки Et и £/, и направлением
преобразования, перпендикулярным П2, пре-
образуем трехосный эллипсоид в вытянутый
эллипсоид вращения (см. /51/) Одновременно
преобразуем и направление лучей света. После
преобразования оно станет (//; /2). Приняв в
качестве плоскости родства О и задав родство
направлением преобразования, перпендикуляр-
ным Пь и параллельными родственными пря-
мыми, проходящими через S2 и S2, преобразуем
эллипсоид вращения в сферу. В результате пре-
образования направление лучей света станет,
I' 10-
Заменим плоскость П2 на П4, параллельную
преобразованным лучам света (ось х14 парал-
лельна прямой //), и спроецируем на замененную
плоскость сферу — результат двойного преоб-
разования эллипсоида. Проекция лучей света
на П4 станет параллельной прямой /4 (ее по-
строение ясно из чертежа).
Границей собственной тени сферы является
окружность, лежащая в плоскости, проходя-
щей через центр перпендикулярно направлению
лучей света. На П4 эта плоскость проецируется
в прямую, перпендикулярную /4 (почему?).
Построим фронтальную и горизонтальную про-
екции тени: проведем плоскость © (©4), парал-
лельную Пр Она рассечет сферу по окружности
а (а4). Найдем проекции этой линии —а/ и а2.
Точка F, расположенная в пересечении окруж-
ности а с границей собственной тени, проеци-
руется в точки Fj и F2. Преобразуя точку F{,
Рис. 612
получим точку Ff. Аналогично построены и
другие точки границы собственной тени эллип-
соида. Высшей точкой тени оказалась точка G.
Построение ее проекций ясно из чертежа.
В приведенном примере направление лучей
света взято произвольным. Построения не изме-
нятся, если его проекции будут наклонены под
углом 45° к оси х.
§ 54. ТЕНИ В ПРОЕКЦИЯХ
С ЧИСЛОВЫМИ ОТМЕТКАМИ
Тень точки. Построим тень от точки А (9)
на плоскости общего положения, заданной
масштабом уклона. Направление лучей света
задано проекцией луча, проходящего через А,
и углом а его наклона к горизонтальной пло-
скости (рис. 613). Градуируем луч света и про-
ведем через него плоскость общего положения
(см. /87/), задав ее, например, 5-й и 8-й горизон-
талями произвольного направления. Построив
точки пересечения однозначных горизонталей
плоскостей заданной и вспомогательной, соеди-
ним их прямой, в пересечении которой с лучом
света расположена тень точки А на плоскости
(см. /170/).
В приведенном примере луч света направлен
под произвольным углом к горизонтальной
плоскости, произвольно же задана и его проек-
ция. Однако часто направление лучей света
ориентируется относительно стран света, угол
же их наклона к горизонтальной плоскости уста-
навливается в зависимости от высоты Солнца.
Угол между земным меридианом и горизон-
тальной проекцией прямой линии, измеренный
от северного конца магнитной стрелки по часо-
вой стрелке, называется азимутом. Азимут и
угол наклона лучей света к горизонтальной
плоскости определяют направление лучей света.
В данном случае азимут равен 35°.
Если луч света параллелен диагонали куба,
две грани которого параллельны горизонталь-
ной плоскости, то градуирование луча упроща-
ется (рис. 614). Достаточно из проекции произ-
17—940
249
вольной точки луча, например А (9), отметка
которой известна и выражена целым числом,
провести прямую под углом 45° к проекции
луча, отложить на ней линейную единицу и
через полученную точку провести прямую, пер-
пендикулярную ранее проведенной, до ее пере-
сечения с проекцией луча. Точка пересечения
прямой и проекции луча света имеет отмет-
ку, отличающуюся на единицу от отметки
точки А.
Построение тени точки, падающей на по-
верхность, заключается в определении точки
пересечения луча света с поверхностью (см. /144/
и рис. 438). Заключим луч в вертикальную пло-
скость (рис. 615) и построим фронтальную про-
екцию луча и линию пересечения плоскости и
заданной поверхности. Поскольку положение
луча света в пространстве определяется в част-
ности, углом его наклона к горизонтальной
плоскости, фронтальную плоскость проекций
следует располагать параллельно лучу. Этот
угол на фронтальную плоскость проецируется
в натуральную величину. Построим фронталь-
ную проекцию А* точки А* в пересечении фрон-
тальной проекции луча света, проведенного
через А, с проекцией линии пересечения поверх-
ности и вспомогательной плоскости. Установив
проекционную связь, найдем точку А*.
При решении можно использовать плоскость
общего положения, проходящую через луч света
(тень точки В). Градуируем луч света, проходя-
щий через В, и через инцидентные ему точки с
отметками 9, 8, 7 проводим горизонтали вспо-
могательной плоскости. Строим линию пере-
сечения плоскости и поверхности; она пересекает
луч'в точке В*.
Тень прямой. Если отрезок прямой вертика-
лен (см. /243/), то задача сводится к построению
тени от его концов.
Построим тень от отрезка АВ горизонталь-
ной прямой на топографической поверхности
(рис. 616). Направление лучей света задано
проекцией луча, проходящего через В, и углом
наклона лучей к горизонтальной плоскости.
Градуируем лучевую плоскость, инцидентную
прямой АВ. Для этого градуируем луч света,
как было сделано на рис. 613, и, проведя гори-
зонтали лучевой плоскости параллельно АВ,
определим точки их пересечения с однозначны-
ми горизонталями поверхности. Через постро-
енные точки проходит тень от прямой Л В на
поверхности. Найдем точки, в которых лучи
света, инцидентные точкам А и В, пересекаются
с построенной кривой.
Построим тень от отрезка наклонной прямой
(рис. 617) на топографической поверхности.
Соединив прямыми линиями точки с одинако-
выми отметками на луче света, проходящем
через В, и прямой АВ, получим горизонтали лу-
чевой плоскости, инцидентной АВ. Отметив
точки пересечения однозначных горизонталей
плоскости и поверхности, соединим их плавной
кривой, являющейся падающей тенью от пря-
мой АВ на поверхности. В точке С тень пере-
секается с самой прямой (С = С*), следова-
тельно, прямая в точке С пересекается с по-
верхностью (сравните решение с приведенным
на рис. 438).
I
250
§ 55. ПРОЕКЦИИ ТЕНЕЙ
ПРИ ЦЕНТРАЛЬНОМ ПРОЕЦИРОВАНИИ
При построении теней в перспективных про-
екциях величиной Солнца пренебрегают и рас-
сматривают его как несобственную светящуюся
точку. Если источник света искусственный, он
представляет собой собственную светящуюся
точку.
Расположение источника света. Относитель-
но зрителя (центра проецирования) Солнце
может быть расположено спереди, сзади и сбоку.
Если Солнце (точка L) спереди (рис. 618), то
его перспектива выше горизонта. Она же явля-
ется точкой схода солнечных лучей (см. /211/).
Вторичная проекция этой точки расположена
на горизонте. Луч света, инцидентный любой
собственной точке пространства, представляет
собой восходящую прямую.
Чтобы построить тень от точки А на. пред-
метной плоскости, проведем через А луч света
LA до его пересечения со вторичной проекцией
луча EjAj в точке А*.
Если Солнце за зрителем (рис. 619), то его
лучи становятся нисходящими прямыми. Их
точка схода расположена под горизонтом, а ее
вторичная проекция — на горизонте. Для удоб-
ства точку схода солнечных лучей обозначим,
как и Солнце, буквой L. Построим тень точки А
на предметной плоскости. Для этого через А
проведем луч света LA, а через ее вторичную
проекцию — вторичную проекцию луча LiAi
до их взаимного пересечения в точке А*.
Когда Солнце расположено сбоку (слева или
справа), его лучи параллельны картинной пло-
скости (рис. 620). При построении тени проведем
через А луч света под заданным углом его на-
клона к предметной плоскости. Вторичная про-
екция луча параллельна основанию картины
(почему?). В пересечении луча с его вторичной
проекцией найдем точку А*.
Автор перспективы вправе выбрать любое
расположение Солнца, однако следует избегать
случая, когда отрезок LLt на перспективе
(но, конечно, не в натуре!) равен отрезку ААг
или меньше его, а также расположения Солнца
в зените.
Если окажется необходимым построить тени
от предметов при строго определенном распо-
ложении Солнца на небосклоне, следует опре-
делить положение перспективы одного луча по
заданному углу его наклона к горизонтальной
плоскости и расположению горизонтальной
проекции луча.
/245/ Возможны три случая расположения
бесконечно удаленного источника света (Солн-
ца) — перед зрителем, за зрителем н сбоку от
него.
Фонарь, изображенный на рис. 621, освещает
три точки: А, Ви С. Лампа фонаря (светящаяся
точка) задана перспективной L и вторичной
проекцией Lj. Проведя перспективные и вторич-
ные проекции лучей света через заданные точки,
в пересечении соответствующей перспективной
проекции со вторичной получим тень от точки
на предметной плоскости. Обратим внимание
на то, что тень точки А ближе к картинной пло-
скости, чем точка А, тень точки С дальше, чем
17*
251
сама точка, а тень точки В удалена от картинной
плоскости на то же расстояние, что и точка В.
Иначе говоря, луч LA является восходящей
прямой, луч LC — нисходящей, а луч LB —
прямой, параллельной картинной плоскости.
Если искусственный источник света распо-
ложен за зрителем (рис. 622), нужно задать его
мнимые перспективную и вторичную проекции.
Пусть это точки (Z.) и (L;). Проведя луч света
через точку Л и построив его вторичную проек-
цию найдем тень этой точки. Случай, когда
источник света расположен в предельной пло-
скости, мы рассматривать не будем.
/246/ Искусственный источник света может
быть расположен в изображаемом пространстве
(перед зрителем) и в неизображаемом пространст-
ве (за зрителем).
Тень, падающая от прямой и плоской фигуры
на плоскость. Построим тень на предметной
плоскости от фигуры АВСМ (рис. 623). Извест-
но, что отрезок АВ в натуре вертикален, от-
к предметной плоскости. Источник света —
Солнце — расположен за зрителем. Тень от
точки В совпадает с самой точкой, поэтому в
соответствии с /238/, построив тень (А*) от
точки А, соединим ее с точкой В = Вх.
Для центральных проекций /238/ формули-
руется так:
/247/ Теш от вертикальных прямых на гори-
зонтальной плоскости пересекаются между' собой
во вторичной проекции источника света.
Так как AM параллельна предметной пло-
скости, то в натуре тень от нее на этой плоскости
параллельна самой прямой. Следовательно,
тень (Л*) М* направлена в точку F. Чтобы
найти тень от точки М, достаточно провести
через нее луч света до пересечения с прямой
(Л‘) F.
/248/ Тень на плоскости от прямой, парал-
лельной плоскости, проходит через точку схода
этой прямой.
Тень от отрезка АС проходит через точки
(Л*) и С = С,. Тень от фигуры EG НК на пред-
метной плоскости построена в соответствии с
ранее рассмотренными примерами: найдены
тени от точек К и Н", так как прямые GH и ЕК
параллельны AM, их тени направлены в точку F.
В пересечении теней с лучами, проведенными
соответственно через точку Ей G, расположены
тени этих точек.
Построим тень от точки Л на плоскости
EG НК. Лучевая плоскость, проходящая через
Л В, вертикальна, следовательно, ее предметный
след совпадает со вторичной проекцией луча
света. Отметив точки I и 2 пересечения лучевой
плоскости с ребрами прямоугольника, построим
линию пересечения плоскостей. В ее пересечении
с лучом расположена точка Л*. Тень отрезка АВ
на плоскости прямоугольника представляет со-
Рис. 623
252
Воспользовавшись обратным лучом, по-
строим точку 3; соединив ее с точкой А*, полу-
чим тень от отрезка АС на плоскости EG НК.
Отрезок AM параллелен плоскости EGHK',
тень на ней в натуре параллельна отрезку и про-
ходит через найденную ранее точку А* Тень
на предметной плоскости также параллельна
отрезку и проходит через точку (А*). Следова-
тельно, перспективы обеих теней направлены в
точку F. Точка 4 пересечения тени с ребром EG
лежит на одном луче света с точкой 4* пересе-
чения теней от отрезков AM и- EG на предмет-
ной плоскости. Поэтому, если известна одна
из точек А* или (А*), можно построить вторую.
Перспектива прямой 1—2 имеет точку схода
F", расположенную на линии связи, проходя-
щей через L (на линии схода вертикальной лу-
чевой плоскости).
Так как в натуре тени на плоскости от парал-
лельных прямых параллельны между собой,
то для построения теней от других вертикаль-
ных прямых достаточно найти одну точку тени
и через нее провести тень прямой в точку схода.
Именно так построена тень от вертикального
отрезка NT, пересекающегося в точке Т с пло-
скостью EG НК.
/249/ Точка схода перспектив теней от вер-
тикальных прямых на плоскости общего поло-
жения расположена на линии связи, проходящей
через точку схода солнечных лучей.
Тени на лестнице. Тени на лестнице от пря-
мых линий показаны на рис. 624. Отрезок А В
горизонтален и параллелен ребрам ступеней,
отрезок АС вертикален. Тень отрезка АС на
плоскости rij направлена в точку (см. /247/).
Отметив точку 1 ее пересечения с нижним реб-
ром первой ступени, проведем тень 1—2 вер-
тикально (см. /240/). Тень 2—3 на горизонталь-
ной грани первой ступени направлена в точку L,
и так далее, вплоть до точки А*. Тень А*В*
направлена в точку схода F прямой АВ
(см. /248/).
Продлим отрезок А*—б до пересечения с А С
в точке 7. Через точку 7 проведем прямую в
точку F до пересечения с ВС в точке 8. Точка 8
расположена относительно плоскости П] на
той же высоте, что и площадка лестницы.
Поэтому на плоскости площадки тень от точ-
ки 8 совпадает с самой точкой. Соединим ее с
точкой В* и отметим точку 9 пересечения пря-
мой 8—В* с ребром площадки и точку F'"
пересечения с горизонтом. Построив точку F'
схода прямой ВС, проведем через точку 9
прямую 9—F' до пересечения с горизонтальной
гранью следующей ступени в точке 10. Через
точку 10 проведем прямую 10—Fи отметим
точку 13 ее пересечения с ребром ступени.
Аналогично строим тени на остальных сту-
пенях и на плоскости Пр Если точки F' и F"
найти трудно (они могут быть далеко за преде-
лами чертежа), построим точку 12 на отрезке ВС
так же, как была найдена точка 8. Последующие
построения ясны из чертежа.
Рассмотрим случай, когда отрезок, не парал-
лелен вертикальным граням ступеней (рис. 625).
Источник света задан перспективной и вторич-
ной проекциями луча, проходящего через точ-
ку А- Проведем через прямую AAt лучевую
плоскость и определим линию 1—2 ее пересе-
чения с вертикальной гранью верхней ступени.
Через точку 3, в которой прямая 1—2 пересе-
кается с верхним ребром ступени, проведем
прямую 3— L1. В ее пересечении с лучом света,
проходящим через А, получим тень от этой
<---------- ------------>
в F Рис. 624
253
в F
254
точки на лестничной площадке. Соединим точ-
ки Ви А у прямой линией и отметим точку F
ее пересечения с горизонтом. Проведя прямую
F—4, отметим точку 5 ее пересечения с пря-
мой АВ. Точка 5 расположена на той же высоте,
что и площадка лестницы (прямые А* — 4 и
4—5 горизонтальны), следовательно, ее тень
на этой плоскости совпадает с самой точкой.
Таким образом, тень от АВ на площадке лежит
на прямой 5—А*. Соединим точки 2иб прямой,
представляющей собой линию пересечения лу-
чевой плоскости, проходящей через АВ с плос-
костью вертикальной грани верхней ступени.
Отметим точки 10 (пересечения с нижним реб-
ром верхней ступени) и 14 (пересечения с пред-
метным следом плоскости вертикальной грани
этой ступени). Разделив отрезки 5—В и 6—14
на три (по числу ступеней) равные части (как
это сделать?), попарно соединим полученные
точки между собой. Тень от АВ проходит через
точки А*, б, 10, 9 и т. д.
Построения могут быть упрощены, что осо-
бенно существенно при большом числе ступе-
ней, если определить точку схода теней на гори-
зонтальных гранях F' и точку схода F" теней
на вертикальных гранях. Чтобы определить
точку F', достаточно найти точку пересечения
одной из построенных прямых (б—А* или
В*—14) с горизонтом. Точка схода F" располо-
жена в пересечении линии связи, проведенной
через точку схода горизонтальных ребер сту-
пеней с прямой 2—14.
Освещенность плоской фигуры. В зависимо-
сти от положения зрителя и источника света
относительно плоской фигуры будет видна ее
освещенная или неосвещенная сторона. Для
решения вопроса используем конкурирующие
точки.
Треугольник АВС освещен лучами Солнца,
расположенного за зрителем (рис. 626). Прове-
дем луч света через произвольную точку тре-
угольника, например С, и рассмотрим конкури-
рующие точки 1 и 2, лежащие соответственно
на луче и прямой АВ (см. /242/). Чтобы опреде-
лить, которая из них расположена ближе к зри-
телю, построим вторичные проекции этих точек.
Точка дальше от горизонта, чем точка 2];
следовательно, точка 1 ближе к зрителю. Так
как она принадлежит лучу, то треугольник об-
ращен к зрителю освещенной стороной.
/250/ О взаимном положении конкурирую-
щих точек в перспективе можно судить по их
вторичным горизонтальным проекциям. Та точка
ближе к зрителю, вторичная проекция которой
дальше от горизонта.
Тени от тел на плоскости. Тень от вертикаль-
но расположенного параллелепипеда на на-
клонной плоскости (например, тень от трубы
на крыше) показана на рис. 627. Источник света
задан точками £и L,. Точки F и F' известны.
Предполагается, что на рис. 627 дан фрагмент
перспективы, на всем же изображении точки F
и L доступны. В противном случае надо исполь-
зовать прием, показанный на рис. 583. По-
строим тень от А на плоскости. ’Для этого
продлим отрезок BE до пересечения с горизон-
тальной прямой 1—6 и через полученную точ-
ку 4 проведем (в точку F') вторичную проек-
цию прямой BE, на которой отметим точку В,.
Заключим прямую АВ в лучевую плоскость
(она определяется,прямыми АВ и Bt Lt) и по-
строим линию пересечения лучевой и заданной
плоскостей (прямая В—3), на которой найдена
тень точки А.
Тень отрезка АС принадлежит линии пере-
сечения лучевой плоскости, проходящей через
прямую АС, с заданной плоскостью. Чтобы
ее построить, найдем точку 5 пересечения пря-
мых АС и BE и соединим ее с точкой А*. Точ-
ка 5 принадлежит трем плоскостям: АВЕС,
лучевой плоскости и плоскости, на которую
строится тень; поэтому линия пересечения двух
последних плоскостей проходит через эту точку.
Найдя тень от точки С в пересечении луча света,
проходящего через С, с прямой А*—5, прове-
дем тень от отрезка С С параллельно этому
отрезку (в точку F; см. /240/). Найдя точку G,
соединим ее с точкой Н.
На рис. 628 построена тень от параллелепи-
педа на вертикальной плоскости (от балкона на
стене). Проведя лучевую плоскость LALiAi
через ребро АВ, построим линию ее пересече-
ния с заданной плоскостью 1—А*. На прямой
1—А* расположены тени точек А и В. Тень от-
резка АН параллельна самому отрезку и на-
правлена поэтому в точку схода F прямой АН
(см. /240/). Найдя точку Н* в пересечении тени
А*Н* с лучом, инцидентным точке Н, соеди-
ним ее с точкой Е = Е*. Точку В* соединим с
точкой С С*.
Тень от абака. Если колонна представляет
собой параллелепипед (рис. 629, а), то ребра
абака параллельны или перпендикулярны его
граням. Построим тень от А на колонне. Луч
света, инцидентный А, задан его перспективной
и вторичной проекциями. Вторичная проекция
построена на нижней горизонтальной плоско-
сти абака, ее направление определяется поло-
жением точки L,. Тень от АВ параллельна
этой прямой, следовательно, направлена в ее
точку схода F (см. /240/). Чтобы построить
тень от горизонтального ребра абака, проходя-
щего через А перпендикулярно АВ, отметим
точку 1, в которой это ребро пересекается с
плоскостью передней грани колонны. Тень точ-
255
Рис. 630
ки 1 на этой плоскости совпадает с самой точ-
кой. Соединим ее с А*.
Также решается задача, когда колонна пред-
ставляет собой восьмигранную призму
(рис. 629, б). Построим тень от А, соединим ее
с точкой 1. в которой ребро АВ пересекается с
плоскостью той грани колонны, на которой
лежит тень от А. На этой грани тень от АВ про-
ходит через точки 1 и А*. Точка 3 построена так
же, как точка /, а точка 4, как точка 2. Через
точку 4 тень от АС проходит по грани, парал-
лельной АС, следовательно, она параллель-
на АС. Найдя точки 5 и б, построим тень от АС
на крайней левой грани.
При построении тени на круглой колонне
нужно на ребрах абака взять несколько точек
и, построив их тени, соединить их плавной кри-
вой (рис. 629, в). На этой линии будет излом
в точке, где тень от одного ребра абака перей-
дет к тени другого ребра (точка А*). Необходи-
мо найти тень от ребра абака на контуре ко-
лонны в ее освещенной части (точка В*). Прове-
дем через точку 1 пересечения контура колонны
с нижней гранью абака вторичную проекцию
луча света до пересечения с ребром в точке В.
Луч света, инцидентный В, пересекается с кон-
туром в точке В*. Точка С расположена в пере-
сечении с ребром абака вторичной проекции
лучей, касательных к колонне. Она касается
линии пересечения поверхности колонны с ниж-
ней гранью абака в точке 2. Проведем через
точку 2 границу собственной тени колонны и
найдем на ней точку С*.
Тень в нише. Линия, от которой падает тень
на стену ниши (рис. 630), параллельна плоско-
сти стены, поэтому граница тени в натуре по-
добна этой линии. От вертикального отрезка
ААг тень вначале идет по плоскости П; в на-
правлении /,, затем от точки 1 — вертикально
по стене вплоть до точки А*. Далее граница
тени — в натуре окружность, а ее перспектива —
эллипс. Чтобы его построить, нужно взять не-
сколько точек на линии полукруга ниши (на-
пример, В) и построить их тени. Если в плоско-
сти стены провести горизонтальную прямую,
касательную к полукругу ниши (точка каса-
ния С), то тень этой прямой будет касательной
к границе тени (и линия, и ее тень направлены
в общую точку схода на горизонте). Тень от
прямой АА1 касательна к эллиптической части
тени.
Тени здания. Рассмотренные приемы по-
зволяют строить тени на сложных по форме
объектах. На рис. 631 изображено схемати-
зированное здание. Из-за низкого горизонта
для построения теней использован опущенный
план, который, кроме того, позволяет многие
построения вынести за пределы основного изоб-
ражения. После построения теней опущенный
план можно убрать. Так как большинство по-
строений разъяснено в приведенных ранее при-
мерах, рассмотрим только некоторые из них.
Тень от вертикального шеста АВ является
линией сечения лучевой плоскостью поверхно-
сти земли, стен и крыши здания, а также по-
верхности трубы. Предметный след лучевой
плоскости в точках 3t, 4t и т. д. (на опущен-
ном плане) пересекается со вторичными проек-
256
Рис. 631
Рис. 633
циями соответствующих частей здания. По-
строив перспективные проекции этих точек,
построим тень. Тень от наклонного шеста СЕ
построена аналогично тому, как была найдена
тень на ступенях лестницы (рис. 625), по прямым
11—12, 5—13, б—14 лучевая плоскость пересе-
кается с соответствующими плоскостями зда-
ния. Тень от ребра крыши 8—9 на стене парал-
лельна в натуре самому ребру.
Вариант построения тени от горизонталь-
ного ребра крыши, проходящего через точку 9
показан на рис. 631, а. Точка 10 расположена в
пересечении этого ребра с плоскостью стены.
Тени на земной поверхности. Построение
тени, падающей на топографическую поверх-
ность от наклонного отрезка АВ, показано на
рис. 632. Используя пропорциональное деление,
градуируем отрезок и через полученные точки
проведем горизонтали лучевой плоскости. Луче-
вую плоскость зададим прямой АВ и тенью
от АВ на плоскости П] (в уровне нулевой гори-
зонтали поверхности). Построив тень (В*) точ-
ки В на плоскости П]5 определим точку схода F
прямой А (В*) и соединим с ней точки 1, 2,...
отрезка АВ. Отметив точки I, II, III, ... пере-
сечения однозначных горизонталей лучевой
плоскости и топографической поверхности, сое-
диним их плавной кривой, которая представляет
собой сечение лучевой плоскостью поверхно-
сти, т. е. тень от прямой на поверхности. Най-
дем на ней точки А* и В*.
Аналогично строятся тени от вертикальных
отрезков.
Тени при искусственном источнике света.
На рис. 633 показано построение теней в слу-
чае, когда источником света является лампа,
расположенная за зрителем. Ее положение опре-
делено мнимыми перспективной и вторичной
проекциями ( £) и ( L,). Построим тень точки А,
проведя через нее вертикальную лучевую пло-
скость, которая с плоскостью пола пересека-
ется по прямой А1 ( L1), а с плоскостью стены —
по вертикальной прямой 1—А*. В пересечении
этой прямой р лучом света, инцидентным точ-
ке А, расположена тень А* на стене. Тени от
остальных точек стола построены с учетом
того, что тень, например, отрезка АВ параллель-
на в натуре самому отрезку (см. /240/)., следо-
вательно, у них общая точка схода. Тень от
вертикального отрезка СЕ на полу направлена
в точку (Lj), а на стене — вертикальна. Для
построения тени от вертикального отрезка КН
проводим лучевую плоскость, которая с плос-
костью пола пересекается по прямой Kt—2,
с плоскостью стены — по прямой 2—3, с плос-
костью потолка — по прямой Н—3. Тень от-
резка — ломаная К*—3—Н. При построении
тени от картины, достаточно найти тень точ-
ки М, так как тень отрезка ТМ в натуре парал-
лельна отрезку, а тень от точки N совпадает
с ней.
ЛИТЕРАТУРА
Бубенников А. В., Громов М. Я. Начерта-
тельная геометрия. М., 1973.
Винницкий И. Г. Начертательная геометрия.
М., 1975.
Добряков А. И. Курс начертательной гео-
метрии. М., 1952.
Климу хин А. Г. Начертательная геометрия.
М., 1973.
Колотов С. М., Евстифеев М. Ф., Михай-
ленко В. Е., Подгорный А. Л., Пономарев А. М.
Начертательная геометрия с элементами про-
граммирования. Киев, 1975.
Колотов С. М., Дольский Е. Е., Михай-
ленко В. Е., Гусев Н. А., Горленко Б. С., Коло-
това О. А. Курс начертательной геометрии. М ,
1961.
Короев Ю И, Федоров М. В. Архитектура
и особенности зрительного восприятия. М.:
1954.
Ланюк А. В. Аксонометрические проекпии.
М., 1956.
Михайленко В. Е., Обухова В. С., Подгор-
ный А. Л. Формообразование оболочек в архи-
тектуре. Киев., 1972.
Русскенич Н. Л. Начертательная геометрия.
Киев, 1971.
Федоров М. В. Рисунок и перспектива. М.,
1960.
Фролов С. А. Методы преобразования ор-
тогональных проекций. М., 1963.
Симонин С. И., Котов Ю. В., Срулевич А. А.
Наглядные изображения при проектировании
автомобильных дорог. М., 1975.
Симонин С. И. Инженерно-топографиче-
ское черчение и наглядные изображения. М.,
1969.
Четверухин Н. Ф. Проективная геометрия.
М.; 1969.
Четверухин Н. Ф., Левицкий В. С., Пря-
нишникова -3. И., Тевлин А. М., Федотов Г. И.
Начертательная геометрия. М., 1963.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксонометрия 6
— косоугольная 186
— прямоугольная 180
Аппроксимация 106
Бергштрих 151
Вершина 73
— несобственная 82
Виток винтовой линии 70
Вращание 96
Высота
— горизонта 201
— точки зрения 201
— сечения 164
Геликоид 91
Гиперболический параболоид 83
Гиперболоид 77, 85
Гомология 16
— аффинная 17
— особенная 18
— неособенная 18
— центральная 18
Гомотетия 20
Горизонт 201
Горизонталь 32
— однозначная 153
— плоскости 45, 52
— поверхности 156
Горло поверхности вращения 79
Градуирование 149
Граница
— видимости 12
Грань 74
Диметрия 185
Дуга кривой спрямленная 70
Заложение отрезка прямой линии 149
Изометрия 184
Интервал прямой линии 149
Инцидентность б
Каркас
— дискретный 67, 72
— непрерывный 72
Картина 200
Коноид 76
Контур 12
Конус 191
— асимптотический 85
Координата 13
— аксонометрическая 180
— прямоугольная 28
— недостающая 29
Координатная ломаная 13
Кривая
— второго порядка 18
— гомологичной окружности 18
— ошибок 111
Коэффициент
— искажения 176
— приведения 179
Линия
— винтовая 70
— водослива 167
— водораздела 167
— геодезическая 106
— графическая 67
— закономерная 67
— каркасная 67
— кривая 67
— кривая гладкая 68
— кривая самопересекающаяся 68
— кривая уровня 68
— наклона 45.
— направляющая поверхности 73
— образующая поверхности 72
— равного уклона поверхности 166
— связи 26
— ската 47
— схода плоскости 216
— уровня 45
Масштаб 149
— аксонометрический 177
— высот 219
— перспективный делительный 216
— уклона плоскости 151
Меридиан 70
Метод проецирования 6
Направление
— линии ската поверхности 165
— преобразования 20
— проецирования 12
— простирания 152
— соответствия 20
— спуска 148
Носитель поля проекций 9
Область возможного пересечения 124
Обратимость 6
Объект проецирования 200
Окружность 68
Основание
— картины 200
— точки 201
Определитель поверхности 72
Ось
— аксонометрическая 176
— винтовой линии 70
— вращения 78
— гомологии 17
261
Ось
— конической поверхности 81
— координат 176
— кривой тора 80
— поверхности вращения 80
— проекций 26
— пучка плоскостей 9
— родства 20
Отметка 148
Отсек 9
Параболоид 151
Параллель поверхности вращения 79
Перемещение 16
— плоскопараллельное 94
Перенесение параллельное 20
Пересечение
— полное 133
— частичное 133
Перпендикуляр 60
Перспектива 6
План 201
Плоскость 40
— аксонометрических проекций 176
— биссектора 27
— дважды проецирующая 14
— гомологии 102
— горизонтальная 43
— двойных точек 102
— картинная 200
— касательная 120
— меридиональная 79
— общего положения 41
— отсчета 13
— параллелизма 76
— перспективных проекций 200
— предельная 6
— предметная 200
— проективная 8
— проекций 6, 26, 29
— проекций замененная 30
— проецирующая И
— профильная 43
— равнонаклонная 47
— родства 102
— уровня 42
Поверхность 67
— винтовая 90
— вращения 78
— второго порядка 80
— гранная 72
— задаваемая каркасом 90
— замкнутая 74
— коническая 73, 78
— линейчатая 72
— линейчатая с одной направляющей и верши-
ной 74
— линейчатая с плоскостью параллелизма 76
— нелинейчатая 72
— неразвертываемая 72
— обертывающая 72
— образующая 70, 72
— переноса 89
— призматическая 74
— проецирующая .11
— равнодлинного откоса 161
— равного уклона 157
— равноустойчивого откоса 160
— развертываемая 72
— топографическая 93
— трубчатая 90
— цилиндрическая 74
— циклическая 90
Поле
— проекций 9
— точечное 9
Полость поверхности 73
Полуплоскость 29
Преобразование 94
— гомологическое 16
— подобия 20
— родственное 102 .
Проекция 6, 7, 9
— аксонометрическая 176
— вспомогательная 39
— вторичная 200
— замененная 30
— ортогональная 6, 26
— перспективная 200
— параллельная 124
— отрезка 14
— стереографическая 124
— точки зрения 200
— угла 10
— центральная 12
Проецирование 6
— вспомогательное 39
— косоугольное 12
— криволинейное 7
— параллельное 12
— прямоугольное 12
— прямолинейное 7
— центральное 12
Пространство
— проективное 8
— евклидово 8
Профиль 93, 167
— вынесенный 168
— криволинейный 168
— наложенный 168
— родственно преобразованный 168
Профиля база 168
Прямая 26
— восходящая 206
— горизонтально проецирующая 26, 32
— двойная 17
— двойных точек 16
— касательная 68
— нисходящая 206
— общего положения 31
— проективная 8 /,
— проецирующая 6, 7, 26
— профильная 32
Пучок
— прямых 9, И
Развертка
— 1 дуги кривой линии 69
— приближенная 109
— поверхности 105
— точная 108
Развертывание поверхности 105
Расстояние главное 201
Ребро 73
— возврата 77
Родство 18
Связка прямых 9
Сдвиг 18
Сетка
— перспективная 215
— горизонталей 155
Сечение
— антипараллельное 116
— коническое 114
— круговое 118
След
— прямой 10
— плоскости 10
— поверхности 11
Совмещение 99
Соответствие взаимно однозначное 16
262
Способ аналитический построения перспективы
—- архитекторов 211
— вспомогательного проецирования 39
— вспомогательных секущих плоскостей 122
— вторичных проекций 219
— вынесения фигуры на картинную плоскость 207
— замены плоскостей проекций 30
— замены предметной плоскости 207
— обхода 219
— точек схода перспектив параллельных линий до-
минирующих направлений 211
Спрямление кривой линии 69
Спуск
— прямой 152
— плоскости 151
Сфера 80
Теорема
— Дезарга для пространства 16
-------- плоскости 16
— Польке—Шварца 178
— Монжа 140
Тор 80
Торс 77
Точка 26
— возврата 68
— дальности 204
— двойная 16, 68
— зрения 200
— излома 68
— измерения 210
— кажущегося пересечения 35
— картины главная 201
— конкурирующая 35
— несобственная 7
— общего положения 27
— опорная 112
— особая 68
— собственная 7
— схода 204
— схода следов плоскости 40
Траектория точки 94
Треугольник следов 177
Триметрия 176
Точность построений 20
Угол
— между плоскостями 56
— наклона плоскости 47
— проецирования 179
— простирания 152
— пространства 29
Уклон
— кривой линии 156
— прямой линии 149
Фронталь 31
— плоскости 45
Фигура 9
— плоская 9
— пространственная 9
— гомологичная 17
— родственная 20
Центр
— вращения 100
— гомологии 17
— проецирования 6
— связки прямых 9
— пучка прямых 9
Цилиндр 191
— гиперболический 83
— параболический 82
— эллиптический 82
Цилиндроид 76
Чертеж 6
Шаг винтовой линии 70
Экватор поверхности вращения 79
Эллипсоид 85
Эпюр 26
— кривой линии 67
— Монжа 26
— поверхности 73
— тела 74
— точки 26
— родственно преобразованный 150
Николай Сергеевич Кузнецов
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Зав. редакцией К И. Аношина. Редактор Л Н. Чу-
пеева. Младший редактор Н. М.' Иванова. Художе-
ственный редактор Н. К. Гуторов. Переплет худож
ннка В. М. Аладьева. Иллюстрации художника-
графика Д. С. Котлова. Технический редактор
3. А. Муслимова. Корректор Р. К. Косинова.
ИБ № 2929
Изд. № От-301. Сдано в набор 17.11.80. Подп. в пе-
чать 09.07.81. Формат 70х108]/16. Бум. тип. № 3.
Гарнитура тайме. Печать офсетная. Объем 23,10 усл
печ. л. 46,55 усл. кр.-отт. 29 уч.-изд. л. Тираж 85 000 экз
Зак. № 940. Цена 1 р. 10 к.
Издательство «Высшая школа»,
Москва, К-51, Неглинная ул., д. *29/14.
Ярославский полиграфкомбинат Союзполиграфпрома
при Государственном комитете СССР по делам изда-
тельств, полиграфии и книжной торговли, 150014,
Ярославль, ул. Свободы, 97.