Труды по аэродинамике - Голубев В.В.

Автор: Голубев В.В.

Теги: механика авиация аэродинамика

Год: 1957

Похожие

Аэродинамика птиц - парителей

Аэродинамика птиц-парителей

Аэродинамика. Несжимаемая жидкость

Основы авиационной техники

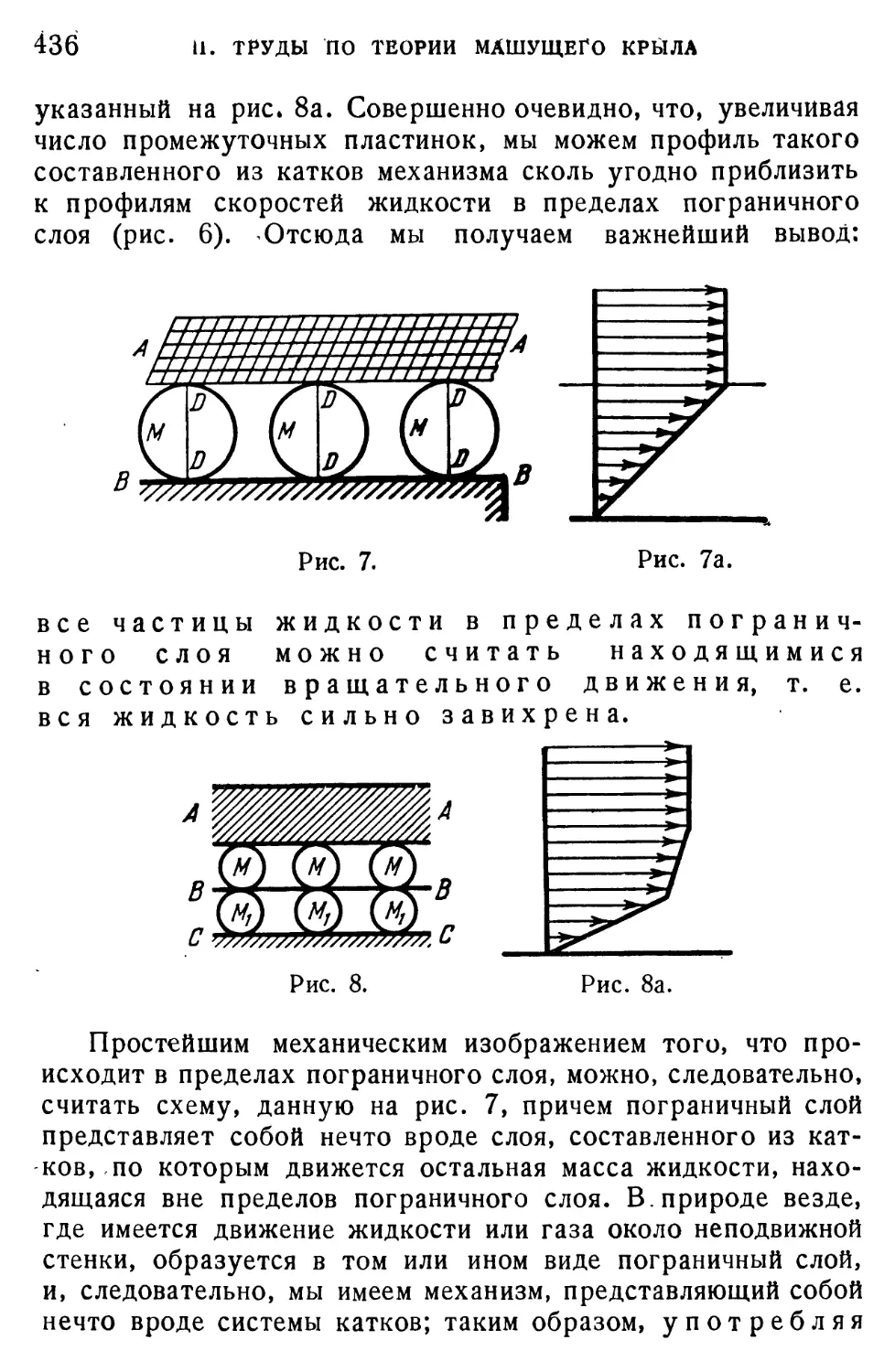
Текст

БИБЛИОТЕКА.
РУССКОЙ
НАУКИ
БИБЛИОТЕКА РУССКОЙ НАУКИ
ж аигежатиксь
at еханик а
CLcvcbjjOHoatusi
ч
.ЗЪсцдарст&енное издатеЛбсгво
ТЕХН И КО-ТЕОРЕТИЧЕСКОЙ Л ИТЕРАТУРЫ
«Л€о ел ва -Лен ин град
1957
/л
I
В.В. ГОЛУБЕВ
ТРУДЫ
по
АЭРОДИНАМИКЕ
С приложением очерка
JUL Космодемьянского
о Жизни и деятельности
Л. Л. Золцдева
Зосцдарственное издательство
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
ъЛЬосква -Лен it нград
1957
12-5-4
ИЗДАНИЕ ОСУЩЕСТВЛЕНО
ПОД НАБЛЮДЕНИЕМ Н. А. СЛЕЗКИНА.
В. В. ГОЛУБЕВ
(1881—1954)

ОТ ИЗДАТЕЛЬСТВА
Перу выдающегося ученого, педагога и общественного
деятеля Владимира Васильевича Голубева принадлежат мно-
гочисленные исследования в области математики и механики.
Широко известны его монографии: «Лекции по аналитиче-
ской теории дифференциальных уравнений» (1941 и 1950 гг.),
«Лекции по интегрированию уравнений движения твердого
тела около неподвижной точки» (1953 г.), «Теория крыла
аэроплана в плоскопараллельном потоке» (1927 и 1938 гг.),
«Теория крыла аэроплана конечного размаха» (1931 г.) и
«Лекции по теории крыла» (1949 г.). На более ранних из
этих книг приобщилось к научной работе целое поколение
научных работников и инженеров, более же поздние про-
должают служить и поныне пособиями для учащихся и науч-
ных работников.
Менее известны- широким кругам научных работников и
инженеров отдельные исследования В. В. Голубева по аэро-
динамике, печатавшиеся в свое время в журналах и ведом-
ственных изданиях. В настоящей книге собраны эти труды,
и сейчас представляющие интерес для всех изучающих тео-
ретическую и прикладную аэродинамику. Все помещенные
в книге работы сгруппированы в четыре раздела (труды по
теории предкрыла, закрылка и щитков; труды по теории
машущего крыла; труды по теории крыла малого удлине-
ния; труды по разным вопросам аэродинамики). Кроме того,
в отдельный раздел выделены биографические очерки, соста-
вленные В. В. Голубевым.
В конце книги помещен очерк о жизни и деятельности
В. В. Голубева, составленный А. А. Космодемьянским.
Издание осуществлено под наблюдением Н. А. Слезкина.
В проверке выкладок принимал участие также А. А. Зайцев,
Замеченные при проверке опечатки выправлены,
- i I.J л. л..' . XL wy

В.В. ГОЛУБЕВ
ТРУДЫ
по
АЭРОДИНАМИКЕ
ТРУДЫ ПО ТЕОРИИ
ПРЕДКРЫЛКА
ЗАКРЫЛКА И ЩИТКОВ

О РАЗРЕЗНЫХ КРЫЛЬЯХ1)
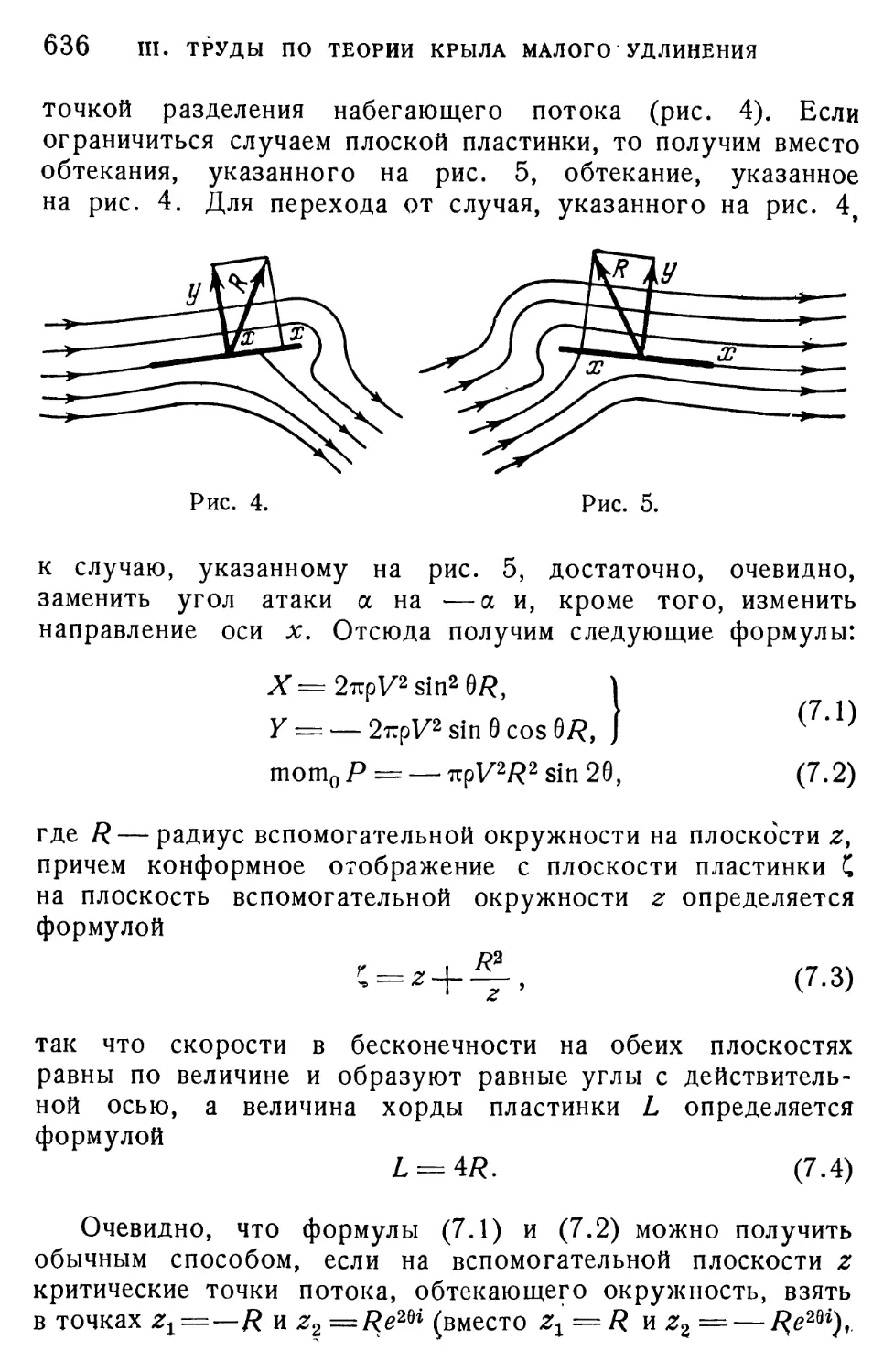
В 1921 г. Лахманом в Германии и Хэндли-Пэджем
в Англии было предложено ставить на аэропланах вместо
крыльев сплошных — так называемые разрезные крылья, со-
стоящие из ряда отдельных несущих поверхностей, разделен-
ных друг от друга щелями, идущими вдоль всего размаха
крыла.
Несмотря на то что разрезные крылья получили значи-
тельное распространение, теория их действия почти совер-
шенно отсутствует. Настоящее сообщение является попыткой
дать гидродинамическую теорию работы простейшего раз-
резного крыла, состоящего из основной несущей поверхно-
сти и относительно небольшого добавочного крыла, т. е.
предкрылка, поставленного перед основной частью крыла
на некотором расстоянии от передней его кромки.
Разбор экспериментальных данных показывает, что при-
сутствие предкрылка сказывается в том, что основная несу-
щая поверхность плавно обтекается потоком при углах
атаки, значительно превосходящих те углы, при которых
плавно обтекается потоком сплошное крыло. Следовательно,
действие предкрылка проявляется, в сущности, не в увеличе-
нии подъемной Силы, а в увеличении тех углов атаки, при
которых к крылу приложима теория Н. Е. Жуковского и
С. А. Чаплыгина. Так, если крыло без предкрылка плавно
обтекается при углах, не превосходящих обычно 15—20°,
х) Доклад 21 мая 1931 г. на секции аэродинамического расчета
и динамики полета первой Всесоюзной конференции по аэродина-
мике. Опубликован в сборнике «Первая Всесоюзная конференция
по аэродинамике», Москва, 1932. (Прим, ред.)
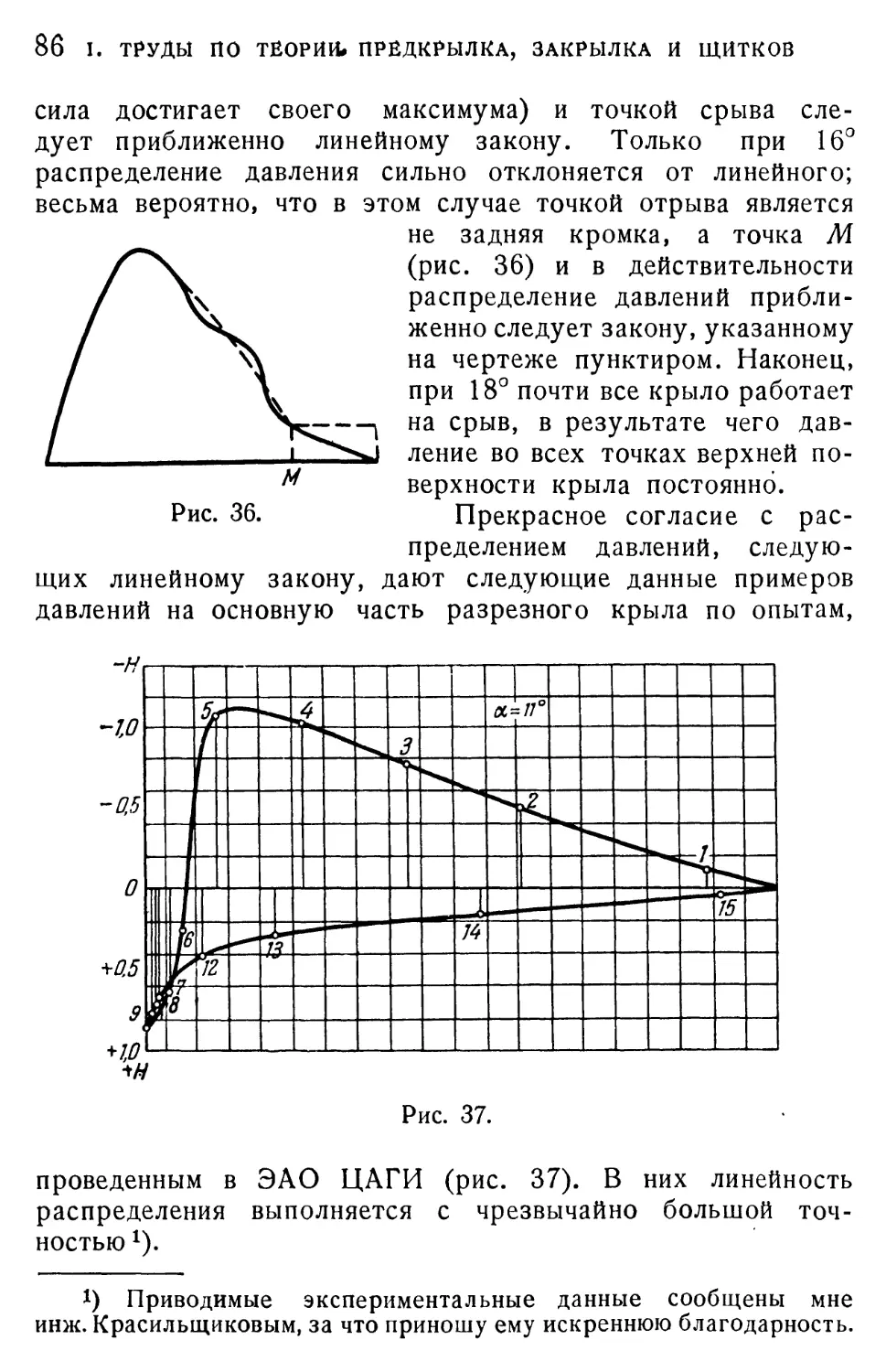
12 ь ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
то крыло с предкрылком работает, как показывает анализ
диаграмм Лилиенталя, до 25 и даже до 30°.
Из теоретических исследований в этой области надо
прежде всего указать фундаментальную работу акад.
С. А. Чаплыгина, в которой изучается влияние прорезов
в дуговом крыле в условиях полного обтекания1). Кроме
того, можно привести ряд замечаний Бетца, Прандтля и др.,
в которых указываются следующие причины изменения усло-
вий обтекания крыла:
а) образование благодаря предкрылку турбулентности
в потоке, обтекающем верхнюю поверхность крыла;
б) передача через щель крыла кинетической энергии
в поток, обтекающий верхнюю поверхность крыла (это сообра-
жение принадлежит Прандтлю);
в) влияние сбегающйх с предкрылка вихрей, размываю-
щих образующиеся на верхней поверхности крыла вихревые
сгустки (это замечание принадлежит акад. С. А. Чаплыгину).
Мы попытаемся объяснить- работу крыла в присутствии
предкрылка, исходя из теоретических соображений об отрыве
струй с верхней поверхности крыла, сущность которых
мною доложена конференции в докладе «О пограничном слое».
Рис. 1.
Если отобразить плоскость ($), на которой находится
крыло А (рис. 1) с предкрылком В, на плоскость (z) так,
чтобы крыло перешло в окружность Д' радиуса 1 с цен-
тром в z = 0 и точка т перешла в точку т', где z==l,
то, заменяя предкрылок вихрем интенсивности-—/, получим
*) С. А. Чаплыгин, Схематическая теория разрезного крыла
аэроплана, Научно-технич. вестник НТО ВСНХ, 1921, № 4—5; Собр.
соя., т. 2, 1948.
О РАЗРЕЗНЫХ КРЫЛЬЯХ
13
следующее выражение для производной характеристической
функции течения на плоскости (z):
1
dw_V —
dZ Vc°V ^2
1 1 г
~T[~2Tz
2nZ ' z Н
1
dw п ,
так как ~г~ = 0 в точке z — 1, то
dz
0 = Voa{e^-e^-±
1
J_ 2пГ
Г (2)
Исключая Г (циркуляция вокруг основного крыла), имеем:
d_w_v g-lK-ai । +______________J (?-!)(//-!) 1
dz z z> 2п/^о(1 + „)(г + Я)(г + _!_у’
(3)
Если принимать крыло А за крыло типа инверсии, то из (3)
и формул преобразования плоскости (£) в плоскость (z) найдем
скорость в любой точке поверхности крыла в форме
J H — 1
2к V ‘/7+1
= K
cos
, * п
sin 2
2 cos X + Я4- ~
Г1 _
(1 — e)3 cos3- ~ — 4 (1 — e) cos ~ sin ~ sin --------------+ 4 sin2
£ \ £ J 4
(4)
где X — угол, определяющий положение точки z на поверх-
ности цилиндра, соответствующей точке £ крыла; 2а—цен-
тральный угол скелета крыла, е характеризует утолщение
крыла, 6_—угол атаки. Полагая приближенно cos-^-=l и
откидывая по малости е2, получим наибольшую скорость
на поверхности крыла при X = тс
Vmax = ^OO |j5in 0 _ +~ . (5)
14 I. ТРУДЫ ПО ТЕОРИЙ ПРЕДКРЫЛЙА, ЗАКРЫЛКА и щитков
и скорость на задней кромке при Х=0
Vo = V’oocos0(l —е).
(6)
Отсюда, так как по результатам моего доклада «О по-
граничном слое» срыв начинается, если =
и (6) получаем для определения наибольшего
1,2, то из (5)
угла атаки,
при котором нет отрыва струй, уравнение
tg 0
J Н 1,2е
2к (Н 4- 1) (Н— 1) cos 0 ~ 1 + Зе •
(7)
Так как при отсутствии предкрылка (т. е. когда J=0)
соответствующий угол 0О будет по (7) определяться урав-
нением
'88» = ПРГ., Р)
то, принимая приближенно cos 0=1 из (7) и (8), имеем:
tg б — tg 0О
J н
2^ 7/2—1
или, приближенно,
п 0 _ J Н
° °0 2лИт №—\
(9)
Формула (9) и дает увеличение предельного угла атаки,
при котором крыло работает на обтекание для разрезного
крыла 0, сравнительно со сплошным крылом 0О. Чтобы опре-
делить угол 0 — 0О, надо найти J.
Если назвать хорду предкрылка через Ь, скорость в точ-
ках предкрылка потока, обтекающего крыло, через Vr и
угол атаки предкрылка (относительно направления скоро-
сти Vh) через р, то, как известно,
7=7Гу-я^; (Ю)
из (3) приближенно получим:
Vs = К» ]/"1 + jj2 -jj cos 20
или, полагая cos20 = l,
H+2s H~X
Уя— Уооя_1+2б н .
(И)
(12)
О РАЗРЕЗНЫХ КРЫЛЬЯХ
15
Угол, образуемый скоростью Vh с действительной осью пло-
скости (£), найдется по формуле
tg^ = tg9g±l. (13)
Отсюда имеем:
J= тсУсо fj- (14)
и
А А _ 1 A W+2e 1 й
9 9°— 2 ЬН— 1 -}-2еZ/+ 1 Р'
Если заметить, что хорда основного крыла в наших вы-
числениях приближенно равна 4, то окончательно, обозначая
через L хорду крыла, получим:
А А ___О 7/4“ 3 /1 г\
О —. (15)
Например, если а = 0,2, 4“==4', Н=2, то
L о
е-9о = 2.1.^|=ода
Заметим, что для предкрылка до известной степени ту же
роль играет само крыло. Так как при этом Ь и L меняются
местами, то увеличение предельного угла атаки для пред-
крылка может дойти до 100% сравнительно с полученными
выше 23% для крыла. Так, если предельный угол для крыла
равен 20°, то для предкрылка он может дойти до 40°, и
тогда 6 —> 90 = 10°.
Из изложенного следуют выводы, представляющие непо-
средственный конструктивный интерес:
а) предкрылок надо ставить в той области крыла, где
скорость обтекающего потока — наибольшая (на основании
формулы (10)), т. е. около передней кромки крыла;
б) предкрылок надо ставить возможно ближе к крылу
(т. е. так, чтобы Н—1 было мало), при этом, однако, про-
странство между крылом и предкрылком не должно стеснять
поток воздуха;
в) предкрылок надо ставить под наибольшим относитель-
ным ; углом, атаки р, при котором предкрылок работает
на обтекание (так как иначе отсутствует циркуляция J).
16 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ1)
Представление об идеальной жидкости, лежащее в основе
современной гидродинамики, как показали работы Н. Е. Жу-
ковского и С. А. Чаплыгина, а также работы ряда иностран-
ных ученых, приводит к возможности построить основания
гидродинамической теории крыла. Но целый ряд существен-
ных факторов, влияющих на работу крыла, не может быть
учтен на основах теории идеальной жидкости. Самообразо-
вание вихрей, играющих основную роль во всей теории
крыла и пропеллера, не может быть выяснено на основе
Соображений теории идеальной жидкости; равным образом
не могут, по-видимому, быть объяснены на основе этой
теории и такие явления, как двойной режим, трение крыла
об обтекающую его жидкость и т. д.
Все это приводит к необходимости учитывать вязкость
жидкости даже в случае обтекания преград воздухом, где
силы вязкости малы. Это приводит к необходимости при
теоретическом изучении аэродинамических вопросов исходить
не из уравнений идеальной жидкости, а из гораздо более
сложных уравнений вязкой жидкости.
Интегрировать при данных граничных условиях уравне-
ния вязкой жидкости при современном состоянии математики
мы не умеем; поэтому в решении задач аэродинамики, свя-
занных с теорией вязкой жидкости, приходится прибегать
к различного рода приближенным решениям. Таких методов,
пригодных к решению аэродинамических задач, в настоящее
время имеется два: метод Озеена (Oseen) и метод, предло-
женный Прандтлем и носящий название теории пограничного
слоя.
Теория Озеена, хотя и вносит существенные упрощения
в уравнения вязкой жидкости, но сама по себе настолько
сложна, что нельзя указать ни одной технической задачи,
которая была решена этим методом, наоборот, теория
Прандтля, несмотря на значительные трудности, которые
она представляет, позволяет во многих случаях дойти до
*) Доклад на первой Всесоюзной конференции по аэродинамике
18-го мая 1931 г. опубликован в сборнике «Первая Всесоюзная кон-
ференция по аэродинамике», 1932. (Прим, ред,)
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
17
полного решения вопроса. В сегодняшнем докладе я и поста-
раюсь изложить метод решения одной важной технической
задачи, исходя из теории Прандтля.
В основе теории Прандтля лежит весьма простое физи-
ческое представление о поведении жидкости, обтекающей
погруженное в нее тело. Опыт показывает, что вдали от тела
жидкость вязкая, подобная воде или воздуху, в своем тече-
нии следует почти в точности уравнениям идеальной жидко-
сти; только в тонком слое около тела резко проявляются
силы вязкости. В пределах этого слоя, так называемого
пограничного слоя Прандтля, скорость изменяется очень
быстро от нуля на поверхности тела до скорости обтекаю-
щего потока на внешней поверхности слоя. Сама по себе
идея пограничного слоя не нова и многократно высказыва-
лась чуть ли не всеми гидродинамиками, начиная с Эйлера
и братьев Бернулли; но заслуга Прандтля в том, что он
придал скорее качественным представлениям о погранич-
ном слое точную количественную оценку и, основываясь на
ней, дал метод приближенного интегрирования уравнений
движения вязкой жидкости.
Общие уравнения вязкой, несжимаемой жидкости в слу-
чае двумерного течения имеют вид
ди . ди ______ 1 др ! / д2и । д2и \
U дх ' V ду р дх ”* V \дх2 ' ду2) ’
ди . ди 1 др . (д2и . д2и\
дх 1 ду рду \дх2 1 ду2)
ди ! ди п
дх ' ду
С точки зрения пограничного слоя эти уравнения надо
применять только внутри тонкого поверхностного слоя, а вне
слоя применять уравнения идеальной
жидкости, т. е. положить в урав-
нении (1) \ = 0.
В пределах слоя скорость и из-
меняется от нуля до скорости обте-
кающего потока, при этом мы рис. j
предполагаем, что координата х
дает расстояние от некоторой точки по твердой стенке ц
координата у перпендикулярна к стенке (рис. 1).
18 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
слоя, а потому и
Отсюда следует, что выражение велико в пределах
д2и *
величину можно считать большой.
Следовательно, в сумме
д2и , д2и
дх2 ’ ду2
второй член ^2 значительно превосходит первый. Чтобы
оценить порядок этих величин, изменим координаты в пре-
делах слоя так, чтобы в пределах слоя изменение обеих
координат было одного порядка.
Для этого введем малую величину е, которая характе-
ризует размеры того слоя, где проявляются силы вязкости,
слоя, непосредственно прилегающего к телу.
Таким образом, е — характеристика размера этого слоя,
и пусть у = еух; тогда при изменении у в пределах очень
маленьких, в пределах от нуля до толщины слоя, переменное yt
изменяется от 0 до 1. Делая такую замену в уравнении (1),
мы получим:
ди
и —
дх
dv
и —
дх е
v ди 1 др
е ду±
v dv 1 др
Р£ &У1
Р дх
9 д2и
------
дх2
( , &Н)
е2----
I дх2
А так как
ди . 1 dv _____(
дх "* е ду!
ди ___ 1 dv
дх е ду!
и нет никаких оснований считать очень большим , то
дх
1
множитель у в правой части должен быть чем-то компен-
сирован. Это достигается тем, что мы вводим замену и для.v.
б ТЕОРИИ ПОГРАНИЧНОГО слоя
19
полагая ^ = 8^. После такого изменения мы получим такую
систему уравнений:
ди , ди 1 др . w I 9 д2и . д*и\
U дх + V1 dyt ‘ р дх + е3 \ дх* + ду2 / ’
еи^+е^^=—L^ + z./£3^+e^\ .
дх 1 ду± ре ду! е2 у дх2, ду2 j
ди ^1_п
дх ' дУ1
(2)
В эту систему уравнений входит переменный малый пара-
метр е— толщина слоя. Мы имеем здесь задачу, которая
встречается в механике и в области чистой математики,
например в задаче о трех телах в небесной механике. Во всех
этих задачах чрезвычайно удобно применять разложение
интегралов по степени малого параметра е; этот параметр
в задачах небесной механики вызывает пертурбацию. Поэтому
мы упрощаем эту систему (2), или, как сказал бы Пэнлеве
(PainlevS), вводим упрощенные уравнения, рассматривая слу-
чай, когда 8 — 0. Конечно, при этом условии в уравнении
отпадают все члены, в которые входит е в первых степенях.
Переходя к прежним переменным, мы получим такую си-
стему уравнений:
ди . ди 1 др . д*и
^ = о,
ду
да . ди ____п
дх ду
(3)
Это — уравнения Прандтля. Таким образом, в качестве
первого приближения вместо системы трех уравнений (1)
мы получим гораздо более простую систему (3), правда,
тоже.сложную, но значительно более простую, чем система (1).
Для первоначальных уравнений уравнения (3) играют
такую же роль, как, скажем, уравнения двух тел небесной
механики для задачи о трех телах.
Хотя уравнения ,и упрощаются, но для интеграции также
представляют большие трудности. В первоначальном виде
эти уравнения были использованы сначала самим Прандтлем
26 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
в задаче об обтекании пластинки. Методы,, которые приме-
нялись для решения этой задачи, были разработаны одним
из сотрудников Прандтля, его учеником Блазиусом. Суще-
ственный прогресс в эту теорию был внесен благодаря
некоторому интегральному соотношению, полученному Кар-
маном (Karman), которое может быть получено интегриро-
ванием первого уравнения Прандтля, а также непосредственно
из соображений, относящихся к механике; в целом ряде
конкретных задач это уравнение оказывается достаточным
для решения задач, точно так же как в динамике оказы-
вается иногда достаточно для решения задачи пользоваться
одним интегралом живых сил. Это интегральное соотношение
Кармана иногда позволяет получить решение задачи без урав-
нений Прандтля. Такое соотношение выгодно тем, что по-
зволяет перейти от системы уравнений с частными произ-
водными к обыкновенному дифференциальному уравнению.
Форма этого интегрального соотношения такова:
h h
j-^dy-U^?udy = -h^.-R, (4)
О о
где h — толщина слоя, U — скорость на внешней границе
R — величина силы трения на границе.
Метод, который позволяет проводить интегрирование
уравнения Кармана, принадлежит Польгаузену и состоит
в следующем. Пусть U есть скорость потока, параллельного
границе тела. Мы будем предполагать, что имеем тело, может
быть, и искривленное, со столь малой кривизной, что ею
будем пренебрегать и будем рассматривать такого рода коор-
динаты: х по направлению стенки тела и у перпендикулярно
к стенке (см. рис. 1).
Где-нибудь на этом теле находится начало координат.
Берем одну координату х и затем в качестве координаты у
берем отрезок нормали в пределах пограничного слоя. Вся
теория, подлежащая нашему рассмотрению, относится к очень
тонкому слою Прандтля, который окружает тело. В области,
далекой от поверхности тела, мы можем применить уравне-
ния гидродинамики идеальной жидкости.
Таким образом, с точки зрения Прандтля, мы всю зону
течения разделим на отдельные части: зона, близкая к по-
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
21
др
ду - -
одной и той же нор-
верхности тела, где приходится применять уравнения вязкой
жидкости и где имеют место уравнения Прандтля, и зона
всего остального течения, где вязкость потока не проявляется
и где можно применить уравнения идеальной жидкости.
В зоне слоя Прандтля, который мы считаем малым, мы
назовем через и скорость по направлению, параллельному
стенке, и считаем, что а удовлетворяет интегральному соот-
ношению Кармана и граничным условиям.
На самой поверхности стенки жидкость прилипает к стен-
кам и и = 0. Затем, изменяясь в пределах слоя, скорость
достигает на внешней границе слоя того значения, которое
имеет окружающий поток. Значит, мы в пределе этого тон-
кого слоя имеем резкое изменение скорости по направлению,
нормальному к поверхности тела.
По второму уравнению Прандтля —у = 0, а потому р
в пределах слоя не меняется вдоль
мали к поверхности тела.
Так как на поверхности тела и = 0 и v = 0, то из пер-
г-г м д2и
вого уравнения Прандтля найдем значение на поверхно-
сти тела.
На поверхности тела, т. е. при у = Ъ, имеем:
l){t = 0, © —0, 2)^ = - —.
7 7 ду2 v
На наружной границе слоя u — Ut т. е. равно скорости
окружающего потока. За пределом слоя мы имеем гидро-
динамику идеальной жидкости. Таким образом, мы имеем
при y = h, где h — толщина слоя:
3) ц = и, и в силу отсутствия вязкости 4) ^- = 0.
Кроме того, несколько условно Польгаузеном вводится
еще условие:
^ = 0
ду2 и
Мы имеем теперь пять условий и можем подобрать и
в. виде многочлена, расположенного по степеням у:
и = ay + by2 + су3 + dy4-
22 I. ТРУДЫ ПО ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
По данным граничных условий найдем:
О_^(12 + Х),
, UU’ и\
2v “ 2Л2’
с~ 2ЛЙ<4
где
Z = — .
Подставляя это значение и в уравнение Кармана, полу-
чим для z такое уравнение:
^ = 0,8Х
дх
9072 + 1670,4л — ^47,4 + 4,8
. (5)
74 U [— 213 4-5,76X4- Х2]
Это уравнение Польгаузена и есть то уравнение, кото-
рым заменяется уравнение Прандтля. Из него найдем тол-
щину слоя, а через толщину слоя мы можем выразить все
коэффициенты, через которые можно выразить и силу тре-
ния и все другие величины,' представляющие Механический
интерес для слоя Прандтля. Пусть, например, мы имеем пла-
стинку, поставленную по потоку; тогда на наружной поверх-
ности слоя скорость U везде будет постоянна, а раз так,
которые вхо-
1 U'№ п ,
то л =-----= 0 и, стало быть, все члены, в
дит X, исчезают.
Теперь уравнение (5) интегрируется, и
уравнение, из которого определяется толщина
толщину слоя, находим выражение силы вязкости.
Так как она равна > т. е* то оказывается,
что сила вязкости на некоторой пластинке длины I по напра-
мы получаем
слоя А, а зная
О ТЕОРИИ ПОГРАНИЧНОГО слоя
23
влению потока и ширины Ь, обтекаемой с двух сторон, выра-
жается такой формулой:
/?= ЬЗ/деЦз/ .
Эта формула впервые получена Прандтлем, а потом более
точно Блазиусом. Можно было бы таким же образом пы-
таться получить решение задачи для других тел. Пытались,
например, из этих уравнений определить, где находятся
точки отрыва струй от шара. Вопрос нахождения точек отрыва
является вопросом, основным для теории крыла. В самом
деле, когда мы рассматриваем крыло в обтекающем его
потоке, то положение точки отрыва на этом крыле
вполне определяет тот режим, на котором крыло работает.
Можно сказать, что если в какой-нибудь точке Л4 проис-
ходит отрыв, то крыло работает в двух совершенно раз-
личных по характеру течений
областях (рис. 2).
В передней части имеется плав- /г"*4
ное обтекание, которое и лежит
в основе теории Н. Е. Жуков-
ского, а в остальной части—
отрыв струи.
Таким образом, чтобы опре- Рис-
делить, как работает крыло и
какие силы на него действуют, надо выяснить, где нахо-
дится дочка отрыва струй. Эта задача чрезвычайно сложна,
но для всех прикладных задач аэродинамики является основ-
ной. Замечу, что основная теория крыла Жуковского и
Чаплыгина совершенно не касается этого вопроса. Там мы
рассматриваем течение такое, что поток обтекает тело, по-
груженное, в него, струей, отходящей плавно с кромки, и
все крыло работает на обтекание. Наоборот, при отрыве
струй получается более или менее широкий хвост, который
с точки зрения идеальной жидкости надо было бы считать
спокойной жидкостью, на самом же деле он сильно завихрен
и тянется за крылом. Вопросы об образовании этого хвоста,
о его толщине, о том, при каких углах атаки он полу-
чается,— являются основными в теории, и первое, что можно
сделать для решения этих вопросов — это пытаться решить
аналогичные задачи для круглого цилиндра.
24 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Но оказывается, что задачи для круглого цилиндра более
трудны, чем для крыла. Попытка разрешить эту задачу
натыкается на следующие затруднения. На цилиндр набегает
поток, который где-то от него отрывается. Мы можем при-
менить наши уравнения, но для этого надо знать скорость
окружающего потока, того потока, который получается при
отрыве струй. Если же мы хотим знать ту скорость, которая
наступит после отрыва, то необходимо знать, где начинается
отрыв. Таким образом, задача становится на первый взгляд
теоретически неразрешимой. Опытным путем можно опреде-
лить давления в различных точках цилиндра и по ним найти
скорость U. Попытки в этом направлении приводят к чрез-
вычайно сложным экспериментальным формулам для U, и,
подставляя их в уравнение (5), получаем уравнение, которое
можно интегрировать. Оказалось, что точка отрыва на
цилиндре находится примерно в 80° от точки разделения
струи. Как показал опыт, этот результат близко подходит
к тому, что наблюдается в действительности. Такой результат
оставляет очень мало надежды для решения этим методом
какой-нибудь конкретной задачи, связанной уже не с цилинд-
ром, а с крылом. Конечно, без дополнительных эксперимен-
тальных данных в этой области невозможно что-либо получить.
Просматривая целый ряд результатов измерений лаборатории
в Геттингене и в Торонто и пользуясь экспериментальными
Рис. 3.
данными, которые получены в на-
шей лаборатории в ЭАО, я под-
метил одно важное обстоятельство:
оказывается, если рассматривать
распределение давления на верх-
ней поверхности крыла, то оно
примерно получается такое, как
показано на рис. 3.
Здесь Л4 — точка, где наибо-
лее сильно действует та подса-
образует на верхней поверхности
крыла силу, тянущую крыло кверху. Таким образом, близко
около передней кромки крыла имеется точка, где давление
наименьшее. А затем давление линейно изменяется и посте-
пенно доходит до давления, которое наблюдается в точке
отрыва> Я приведу несколько примеров, которые показывают,
сывающая сила
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
25
что линейный закон изменения давления в достаточной мере
оправдывается. Если ввести это дополнительное условие, то
всю задачу можно довести до конца, не делая никаких других
предположений. Будем считать, что р изменяется линейно от
той точки, где скорость достигает максимальной величины на
верхней поверхности, до точки отрыва струй. Тогда ^ = С
будет величиной постоянной. Стало быть, UU' есть тоже
величина постоянная. Подставляя это выражение в уравне-
ние (5), мы получаем более простое уравнение, именно урав-
нение с разделяющимися переменными. Это уравнение никаких
затруднений не представляет и после интеграции дает такой
результат:
^Апах • tA точке отрыва = 1 >2,
т. е. отношение максимальной скорости к скорости в точке
отрыва равно 1,2 — результат несколько неожиданный.
Оказывается, что если мы имеем линейное распределение
давлений на верхней поверхности крыла, то получается вполне
определенное отношение максимальной скорости к скорости
в точке отрыва, примерно на 20% первая больше второй.
Это сейчас же позволяет решить конкретнее задачи о режиме
работы крыла.
Пусть дано некоторое крыло. Определим, при каком
угле атаки точка отрыва струй начинает отходить от задней
кромки. При очень малом угле атаки точка отрыва струй
помещается на задней кромке крыла. При увеличении угла
атаки некоторое время точка отрыва струй держится на
Задней кромке крыла, но при значительном увеличении угла
атаки точка отрыва начинает смещаться с задней кромки
крыла по направлению к передней, и по мере того как она
смещается к передней кромке крыла, мы получаем падение
подъемной силы и увеличение лобового сопротивления, что
является ухудшением свойств крыла. Мы можем проследить
это по поляре Лилиенталя.
Если взять крыло, представляющее собой инверсию пара-
болы с малым изгибом, то, оказывается, можно считать, что
максимальная скорость на таком крыле выражается формулой
Г т V • д 1 -j*- 2е
^max — Ко ЯП 0 ,
26 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
где е есть величина, характеризующая утолщение крыла,
а 0^—угол атаки. Скорость в точке отрыва на задней кромке
равна
Ц) = ^оо cos 0 (1 —е).
Отсюда, деля одно на другое, получаем:
^max j—. g 1 Ц- Зе
а для того чтобы точка отрыва струй помещалась на задней
кромке, это отношение* должно быть равно 1,2,
Отсюда
= (6)
Стало быть, до угла, определяемого формулой (6), можно
рассматривать дело так, как будто никакого отрыва струй
нет и крыло работает вполне на обтекание.
Рассмотрим примеры..
Если, взять е = 0,05, то оказывается, что, 0 = 3°20'. Если
взять поправку на конечность крыла, то получим 0 около 6°.
Далее, если 8 = 0,1, то 0 = 5°2О', а с поправкой равна 8°.
Наконец, если е = 0,2, то 0 = 8°, а с поправкой, равна
около 11°, т. е. для последнего крыла перемещение точки
отрыва хтруй от задней кромки начинается около, 11°, До 11°
точка отрыва струй, все, время, помещается на задней кромке.
Когда после увеличения угла атаки точка отрыва отходит
от задней кромки, то можно думать, что вначале, это,мало
заметно. Когда точка отрыва струй переместилась от задней
кромки очень мало, то падение соответствующих . летных
свойств крыла очень мало заметно..
Подсчитаем, при каких углах атаки точка отрыва струй
переходит на середину верхней поверхности крыла. Эту
задачу тоже нетрудно было, решить. Оказывается, что для
перехода на середину крыла при очень тонком крыле_.полу-
чается совершенно ничтожное увеличение угла/ атаки, т. е.
для тонкого крыла струя, оторвавшаяся от задней кромки,
очень быстро смещается вперед, для крыла же.более толстого
угол атаки увеличивается с 5 до 8° и, наконец, для крыла
еще более толстого угол увеличивается от 8 до 14°, т. е.
увеличение угла атаки значительно.
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
27
Сказать точно, насколько уменьшится изменение подъем-*
ной силы и насколько увеличится лобовое сопротивление,—
трудно. Можно сказать одно, что, оперируя уравнениями
теории Прандтля, можно решить чисто теоретически задачу,
представляющую большой технический интерес.
Теперь посмотрим рисунки, иллюстрирующие изложенное.
На рис. 4 представлены данные Геттингенской лаборато-
рии, которые показывают изменения давлений.
При увеличении угла атаки приближение к прямой увели-
чивается, но образование впадины показывает, что начинается
срыв струи около задней кромки.
Рис. 5 дает распределение давлений на верхней поверх-
ности крыла при больших углах атаки. Здесь уже нет ничего
похожего на прямую; это указывает только на то, что обра-
зовался отрыв струи. До образования отрыва струи мы имеем
приближенно прямолинейное распределение.
На рис. 6 приведены данные, полученные в нашей лабо-
ратории ЦАГИ. Распределение давления на верхней поверх-
ности крыла почти в точности прямолинейно.
На рис. 7 дана дужка крыла с е, равным 0,2. У этого
крыла по предшествующей теории точка отрыва струй отхо-
дит от задней кромки при 11° и доходит до середины крыла
при 16°.
Все предыдущее приводит к вопросу, нельзя ли каким?
Нибудь образом улучшить крыдо в том отношении, чтобы
28 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА., ЗАКРЫЛКА и щитков
О ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
29
избавиться от отрыва струй и тем самым заставить крыло
работать на обтекание так» как этого требует теория Жуков-
ского и Чаплыгина. Для этого нужно каким-нибудь способом
изменить отношение (Jmax : потому что это отношение,
чтобы не- было отрыва, должно быть равно 1,2. Следова-
тельно, при уклонении этого отношения от указанной вели-
чины надо либо увеличить скорость на задней кромке крыла,
либо уменьшить максимальную скорость и тем добиться,
чтобы распределение давлений на верхней поверхности крыла
не резко менялось, а было более или менее равномерным.
Рис. 7.
Отсюда вытекает задача, нельзя ли выработать какое-нибудь
приспособление, какую-нибудь форму крыла такую, которая
улучшила бы крыло так, чтобы оно могло работать при
углах атаки, при каких обычные крылья не работают на
обтекание благодаря тому, что изменение давлений стано-
вится слишком резким.
Каким образом можно было бы этого достичь, я изложу
в другом докладе на заседании крыловой секции, и лишь
некоторые соображения я позволю, себе здесь привести.
Известен факт, что если на круглый цилиндр набегает
поток, то сзади него образуется область, где начинается
отрыв струй и образуется широкий завихренный хвост. И вот
оказывается, что можно этот завихренный хвост значительно
убавить, поставив на цилиндре под углом приблизительно 45°
маленькую заслонку: тогда набегающий поток образует хвост
и отрыв струй доходит до угла. 120° вместо угла 80°. Для
объяснения этого явления можно привести соображения,
основанные на турбулентности потока. Известно, что* турбу-
лентный поток. да.ет лучшее обтекание. Но можно стать и
на иную точку зрения. Когда мы ставим на цилиндре заслонки,
то уменьшаем максимальную скорость, а если скорость
уменьшается, то, с нашей точки зрения, обтекание должно
быть более полное. Стало быть, уменьшение скорости в той
точке» где скорость близка к максимальной, должно вести
30 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
к тому, что точка отрыва струи перемещается назад. Возни-
кает вопрос, нельзя ли это обстоятельство использовать и
в крыле. Нельзя ли добиться того, чтобы максимальная ско-
рость не была слишком большой Около передней кромки
крыла? Нельзя ли для этого поставить такие же заслонки
около передней кромки крыла, т. е. там, где развиваются
большие скорости?
Ответы на вопросы по докладу
С точки зрения теории Прандтля, точка отрыва струй
образуется следующим образом.
На рис. 8 представлено распределение скоростей в погра-
ничном слое. Тогда, если скорость на наружной поверхности
падает, получается изменение скоростей согласно диаграмме
(рис. 8).
Присутствие точки М указывает, что за этой точкой
скорость меняет свое направление. Такая точка и является,
по теории Прандтля, тем местом, где начинается отрыв струй.
Таким образом, отрыв струй начинается
там, гДе поток начинает идти в обратную
/д ---В сторону.
Аккерет показал, что точка отрыва
Рис. 9. струй перемещается дальше, если за точ-
кой Л4 подсасывать поток. Спрашивается,
нельзя ли это сделать у крыла. Если мы имеем крыло и
у этого крыла поставим заслонку АВ (рис. 9), тогда в точке А
скорость будет очень большая, в точке В— малая. Таким
образом, эта заслонка должна вызвать образование потока
подсасывающего воздуха из В в А, Можно ожидать, что
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 3'1:
это подсасывание улучшит крыло в данном отношении и
позволит выдерживать большие углы атаки. Может быть,
можно было бы сконструировать приспособление, которое
могло бы выдерживать большие углы атаки. Задача улучше-
ния летных свойств крыла сводится к тому, чтобы заставить
крыло работать на больших углах атаки. Для этой задачи
есть более удовлетворительные решения, с которыми я надеюсь
познакомить вас в докладе, который буду читать по разрез-
ным крыльям в крыловой секции.
Упрощения в уравнении Польгаузена получаются, если
. UU" п .
вообще принять, что —g- — С (в случае, разобранном в до-
кладе, С = — 1).
При изменении С распределение скоростей будет, конечно,
довольно разнообразным. Если при этом С меняется в пре-
делах от —10 до +5, то коэффициенты уравнения (5)
сравнительно мало меняются и результат, изложенный в до-
кладе, остается приблизительно правильным.
Слабым местом теории Прандтля является то, что она
не связана с числом Рейнольдса. Попытки Польгаузена и Кар-
мана ввести в уравнение пограничного слоя число Рейнольдса
вместо е, которое туда входит, не привели ни к чему.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ
РАЗРЕЗНОГО КРЫЛА1)
ЧАСТЬ I
Теория предкрылка в плоскопараллельном
потоке
Краткое содержание
Настоящая работа ставит целью изучение влияния предкрылка
На подъемную силу основной части крыла в плоскопараллельном
потоке. Разбор экспериментальных данных показывает, что влияние
Предкрылка сказывается в увеличении тех углов атаки, до которых
*) Опубликованы в Трудах ЦАГИ, вып. 147, 1933. (Прим, ред.)
32 I. ТРУДЫ ПО ТЕОРИИ ПРЁДКГЫЛКА, закрылка и щитков
крыло может работать в условиях полного обтекания. В настоящей
работе изучается влияние предкрылка на отрыв струй от поверх-
ности крыла.
Решение этой задачи в общем случае представляет большие
трудности. В работе дается приближенное решение, причем пред-
крылок заменяется одним вихрем, но форма основной части крыла
сохраняется. Для определения точки отрыва струй от поверхности
крыла применяется теория отрыва струй Прандтля, основанная на
теории пограничного слоя.
В первой главе изучаются экспериментальные данные и даются
общие формулы, позволяющие учесть влияние вихрей, близки^
к крылу, на величину подъемной силы и лобового сопротивленш
Во второй главе для определения точки отрыва от поверхности
крыла применяется метод Прандтля — Кармана в форме, данной
Польгаузеном. Решить задачу оказывается возможным благодаря
тому, что распределение давлений на верхней поверхности крыла,
как показывают экспериментальные данные и теория, следует доста-
точно точно линейному закону от точки, где давление наименьшее,
до точки отрыва струй. Это соображение позволяет проинтегриро-
вать уравнение Польгаузена и найти положение точки отрыва струй
в зависимости от угла атаки. Далее изучается вопрос о влиянии
толщины крыла на точку отрыва и определяется наивыгоднейшая
величина утолщения крыла и характер кривой Лилиенталя для
толстых крыльев.
В главе третьей дается формула, позволяющая учесть влияние
предкрылка на отрыв струй, приводятся конструктивные выводы,
вытекающие из предыдущей теории, и влияние основной части крыла
на предкрылок.
Предисловие
Предложенные еще 10 лет назад Лахманом и Хэндли-
Пэджем разрезные крылья до настоящего времени не изучены
сколько-нибудь подробно с точки зрения аэродинамики.
Кроме фундаментальной работы С. А. Чаплыгина, посвящен-
ной теории частного типа разрезного крыла, которое рабо-
тает в условиях, полного обтекания, можно указать только
ряд мелких замечаний, весьма мало выясняющих аэродинами-
ческую сущность их работы. Настоящее исследование пред-
ставляет собой попытку дать аэродинамическую теорию
разрезного крыла, состоящего из основной части и из доба-
вочного маленького крыла, поставленного у передней кромки
основной части, так называемого предкрылка.
Основой всей предлагаемой теории является теория по-
граничного слоя Прандтля и вытекающая из нее возможность
теоретического определения точки отрыва струй от поверх
ности крыла. Влиянием предкрылка на положение точки
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 33
отрыва струй и объясняется вся работа разрезного крыла и
предкрылка. Исследование ведется для крыла в плоскопа-
раллельном потоке. В дальнейшем мы надеемся вернуться
к учету влияния концов предкрылка, т. е. к аэродинами-
ческой теории разрезного крыла конечного размаха.
Изложенная ниже теория, по-видимому, полностью не
переносится на случай разрезного крыла, поставленного
около задней кромки основной части, так называемого за-
крылка. Для этого случая основы аэродинамической теории
,$адо искать в идеях, изложенных в работе С. А. Чаплыгина.
Глава I
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ; ПОСТАНОВКА ЗАДАЧ;
ОСНОВНЫЕ УРАВНЕНИЯ
§ 1. Современное положение; литература. § 2. Экспериментальные
данные; поляры Лилиенталя. §3. Экспериментальные данные; спектры
обтекания. § 4. Об отрыве струй; постановка задачи. § 5. Общая
формула о действии вихрей. § 6. Механическое истолкование пре-
дыдущих результатов; круглый цилиндр. § 7. Приложение общей
теоремы к разрезному крылу; подъемная сила. § 8. Приложение
общей теоремы к крылу; лобовое сопротивление. § 9. Лобовое со-
противление по поляре Лилиенталя.
§ 1. Теория дужек в настоящее время изучена настолько,
что в этой области едва ли возможно ждать какого-нибудь
существенного улучшения их аэродинамических свойств;
по-видимому, теоретическим пределом аэродинамических
свойств являются формы дужек, мало отличающихся от инвер-
сии параболы. Значительного прогресса в этом направлении
можно ожидать только от применения ряда дополнительных
приспособлений, сильно влияющих на аэродинамические свой-
ства потока, обтекающего крыло; сюда относятся такие при-
способления, как подсасывание пограничного слоя крылах),
помещение дополнительных насадков на крыло* 2) и т. п.
Однако в настоящее время до технического осуществления,
1) О. Schrenk, Versuche mit einem Absaugefliigel, Zeitschr.
fur Flugtechnik und Motorluftschiffart, № 9, стр. 259, 1931.
2) См., например, О. Kreil, Druckverteilung an der Luftumstrom
den Kugel, Zeitschr. f. F. и M. Jahrgang 22, Heft 4, стр. 97, 1931.
34 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
применяемого довольно широко в современном самолетострое-
нии, доведена только одна из самых первых попыток в этом
направлении, связанная с применением разрезных крыльев.
Как известно, разрезные крылья были почти одновременно
предложены в Германии Лахманом и в Англии Хэндли-Пэд-
жем еще в 1921 г. Сущность изобретения сводится к тому,
что к основному крылу добавляется или маленькое добавоч-
ное крыло около передней кромки основного крыла (пред-
крылок), или добавочное крыло около задней кромки основ-
ного крыла (закрылок). В более общем случае к основному
крылу добавляются одновременно и предкрылок и закрылок;
кроме того, делались попытки и основное крыло заменять
рядом более мелких крыльев, расположенных друг за другом.
Несмотря на то, что разрезные крылья известны уже
более 10 лет и получили достаточно широкое распростране-
ние в технике, теория их до настоящего времени находится
в зачаточном состоянии. Среди довольно значительной лите-
ратуры, содержащей экспериментальный материал по раз-
резным крыльям, можно указать очень мало работ, посвя-
щенных теории разрезных крыльев, а именно, только одну
фундаментальную теоретическую работу С. А. Чаплыгина1),
в которой дана весьма подробная теория одного частного
типа разрезных крыльев, исходя из предположения, что
крыло работает в условиях полного обтекания идеальной
жидкостью. Кроме того, можно указать ряд работ в ино-
странной литературе, где имеются некоторые теоретические
соображения о работе разрезных крыльев; сюда надо отнести
прежде всего работу Лахмана 2), в которой рассматривается
структура потока, обтекающего разрезное крыло; далее
работу Бетца3), в которой крыло с предкрылком рассматри-
вается как частный случай биплана. Кроме того, можно ука-
зать ряд теоретических замечаний Прандтля, Бетца, Клем-
х) С. А. Чаплыгин, Схематическая теория разрезного крыла
аэроплана, Научно-технич. вестник, № 4—5, стр. 21, 1921. [Собр.
соч., т. 2, 1948.]
2) G. L а с 11 m a n n, Die Stromungsvorgange an einen Profil mit
Vorgelagerten Hilfsflugel, z. F. u. M. Jahrgang, 14, 1923.
3) A. Betz, Die Wirkungsweise von unterteilten Flugprofilen,
Berichte und Abh. der Wissenschafte Gesellschaft fur Luftfahrt, 1922,
Januar.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 35
перера и др. Но во всех перечисленных работах нет никакой
законченной теории с точки зрения учета вязкости воздуха,
которая, по-видимому, во всех явлениях, связанных с улуч-
шением работы крыла, играет существенную роль.
Отсутствие законченных теоретических представлений
о работе разрезного крыла ведет к тому, что и обильный
экспериментальный материал недостаточно использован для
получения общих выводов о целесообразности того или иного
положения отдельных частей, что иногда приводит к совер-
шенно неправильному представлению о работе крылах);
точно так же из-за отсутствия теоретических соображений
и дальнейшее усовершенствование разрезных крыльев ведется
путем экспериментальных исследований в значительной сте-
пени вслепую. Все это показывает, что при настоящем по-
ложении дел теоретические изыскания в области разрезных
крыльев являются одной из актуальных задач теории крыла
и аэродинамической теории самолета.
Настоящая работа и ставит своей задачей дать возможно
полную теорию в простейшем случае, когда мы имеем крыло
с предкрылком; при этом учитывается влияние вязкости
воздуха путем систематического применения теории погра-
ничного слоя Прандтля.
§ 2. Основной вопрос, который возникает при построе-
нии теории разрезного крыла, —это вопрос о том, в чем
сказывается влияние предкрылка на работе всего крыла.
В основном экспериментальные данные приводят к следую-
щему.
Весьма чувствительным мерилом работы крыла является
его полярная диаграмма Лилиенталя. Рассмотрим данные
некоторых экспериментов, проведенных для разрезных
крыльев в лаборатории Прандтля в Геттингене2).
На рис. 1 даны диаграммы Лилиенталя для крыла сплош-
ного (пунктиром) и для разрезного крыла с предкрылком
т) См., например, W. Klemperer, Ein Beitrag zum Spaltflu-
gelprofil, Abh. aus Aerodyn. Inst. a. d. technischen Hochschule zu
Aachen, H. 2, S. 1—8, также его замечания по докладу Betz’a;
yil ordentliches Versammlung der Wissenschaftlichen Gesellschaft
fur Luftfahrt 4—8/IX 1921.
n 2) Ergebnisse d. Aerodynamischen Versuchsanstalt zu Gottingen,
11 Lieferung, стр. 56, H. 59, 1923.
36 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Рис. 1.

Рис. 2.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I- 37
(сплошной линией). На рис. 2 даны диаграммы Лилиенталя
для крыла с вращающимся предкрылком; пунктиром дана
полярная диаграмма, когда предкрылок задней кромкой при-
жат к крылу и, следовательно, крыло работает как сплош-
ное, сплошной же линией дана полярная диаграмма для
крыла с открытой щелью и, следовательно, крыло работает
здесь как разрезное. Из рассмотрения полученных диаграмм
мы заключаем, что у разрезного крыла при малых углах ата-
ки лобовое сопротивление значительно больше, чем у сплош-
ного; при этом при очень малых углах атаки сопротивле-
ние разрезного крыла весьма мало превосходит сопротивле-
ние соответствующего неразрезного. Если построить для
рассматриваемого случая график коэффициента подъемной
силы, пользуясь данными Геттингенской лаборатории, в зави-
симости от угла атаки, tq получим следующие графики
38 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Аналогичные результаты получим и из рассмотрения
следующих данных Хэндли-Пэджа(рис. 5,6).. Здесь мы
также замечаем увеличение
лобового сопротивления.
Если рассматривать гра-
фики подъемной силы в за-
висимости от угла атаки,
то увидим, что подъемная
сила у разрезного крыла
при малых углах атаки, при
которых работают крылья
сплошные, меньше, чем
у сплошного крыла. Но
подъемная сила возрастает
для разрезного крыла, сле-
дуя приблизительно линей-
ному закону, до углов зна-
чительно больших, чем для
крыла сплошного (для
крыла Хэндли-Пэджа с 10
до 20—22°, в крыле Прандтля с 16 до 20°). Так как
резкое уклонение изменения подъемной силы в зависи-
мости от линейного закона, или, что то же, резкое
уклонение кривой Лилиенталя от линии, эквидистантной
1) Handley Page, Neuere Forschungen am «Handley Page»
Spaltflugel, Fortschritte der Luftf^hrt, Jahrbuch, 1929—1930.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 39
параболе индуктивного сопротивления, указывает на то, что
крыло работает не на обтекание, а на срыв, то отсюда сле-
дует, что разрезное крыло работает на обтекание до боль-
ших углов атаки, чем сплошное.
Таким образом, экспериментальные данные приводят
к следующим выводам.
1. При тех углах, при которых крыло разрезное и
сплошное, полученное из раздвижного крыла закрытием
щели, оба работают в условиях более или менее полного
обтекания, разрезное крыло с предкрылком не дает уве-
личения подъемной силы, наоборот, оно дает некоторое
(незначительное) ее уменьшение.
2. В присутствии предкрылка крыло работает на обте-
кание при углах, значительно превосходящих соответствую-
щие углы для сплошного крыла, следовательно, присут-
ствие предкрылка увеличивает угол атаки, при котором
начинается срыв струй,
3. При очень малых углах атаки лобовое сопротивление
разрезного крыла незначительно превосходит лобовое сопро-
тивление сплошного крыла; при углах атаки более зна-
чительных лобовое сопротивление разрезного крыла
40 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
значительно больше, чем сплошного, и это отношение со-
храняется до углов, при которых начинается отрыв струй от
сплошного крыла, что влечет за собой резкое увеличение
лобового сопротивления.
Интересно отметить, что экспериментальные данные ука-
зывают на очень сильную зависимость формы кривой Лилиен-
таля, в частности, положения точки, где начинается резкое
увеличение лобового сопротивления, от положения предкрылка
относительно основного крыла. Рис. 7а и 76 показывают,
как изменяется форма кривой Лилиенталя при изменении
положения предкрылка.
Из рис. 7а и 76 видно, что приближение предкрылка
в передней кромке крыла смягчает скачок изменения лобо-
вого сопротивления и отодвигает его на большие углы атаки.
Отсюда, в частности, возникает вопрос, нельзя ли рацио-
нальным помещением предкрылка добиться перемещения
резкого увеличения лобового сопротивления на такие углы
атаки, которые превосходят углы, обычно применяемые во
время полета, так как при такой конструкции и неподвиж-
ном предкрылке разрезное крыло при обычных летных уг-
лах работает как крыло сплошное, а при больших углах
атаки получается значительно большая подъемная сила, чем
для крыла сплошного. Как известно, этот результат дости-
гается в современных конструкциях раздвижным предкрыл-
ком, который при малых углах плотно придвигается к крылу
и крыло .работает как сплошное, а при больших углах
системой рычагов отодвигается от основного крыла и крыло
работает как разрезное.
§ 3. Кроме поляр Лилиенталя, можно использовать для
экспериментальной оценки работы разрезного крыла снимки
спектров течения потока вокруг разрезного и неразрезного
крыла. Такого рода снимки дают чрезвычайно поучительный
материал, но, к сожалению, в этом направлении еще очень
мало сделано.
Мы приведем ряд снимков для иллюстрации обтекания тон-
ких и толстых крыльев разрезных и для сравнения соответ-
ствующих сплошных, приведенных в работе Хэндли-Пэджах).
1) Hendley Page, Neuere Forschungen am «Handley Pago
Spaltflugel, Fortschritte der Luftfahrt, Jahrbuch, 1929—1930.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 41
Рис. 7а.
Рис. 76.
42 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
На рис. 8—12 приведены спектры обтекания двух крыльев
с соответствующими предкрылками и обтекания сплошных
крыльев при различных углах атаки.
Первая серия снимков относится к крылу толстого про-
филя.
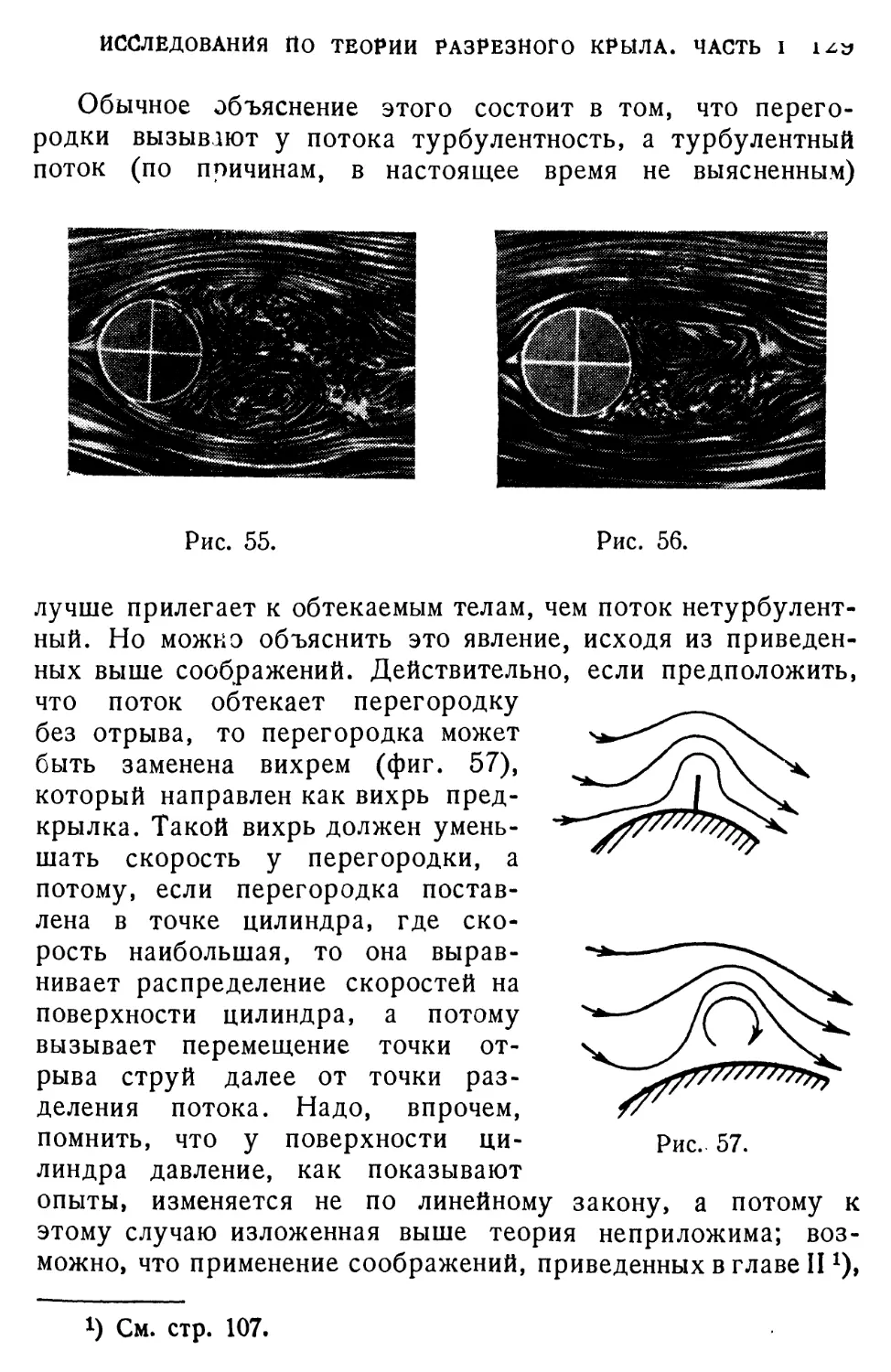
На этих снимках мы видим следующее:
1. При угле атаки 0° присутствие предкрылка не улучшает
обтекания крыла; наоборот, в присутствии предкрылка
за крылом образуется больше вихрей, чем за крылом
сплошным.
2. При больших углах атаки в присутствии предкрылка
получается плавное обтекание на таких углах атаки, при
которых крыло сплошное работает на срыв. На снимках
это сказывается в образовании сильных вихрей у передней
кромки (рис. 10) в случае отрыва струй; при том же
угле атаки крыло с предкрылком работает на обтекание,
так что за крылом почти не образуется вихрей.
Такие же выводы можно получить из рассмотрения спек-
тров более тонких крыльев.
На рис. 12а видна сильно развитая система вихрей за
верхней поверхностью крыла сплошного, а на рис. 126
заметно весьма плавное обтекание у такого же разрезного
крыла; заметим, что и у этого крыла при малом угле атаки (9°)
разрезное крыло не вносит никакого заметного изменения
в обтекание.
§ 4. Из экспериментальных данных предшествующего
параграфа следует, что работа предкрылка сводится к уве-
личению предельных углов, при которых крыло работает
на обтекание.
Следовательно, теоретическое изучение работы предкрылка
должно сводиться к решению следующих двух основных
задач:
а) выяснить, при каких условиях начинается отрыв струй
на поверхности крыла;
б) выяснить, каким образом предкрылок влияет на усло-
вия, вызывающие отрыв струй.
Вопрос об отрыве струй в современной аэродинамике
решается с двух различных точек зрения. Попытки реше-
ния, основанные на применении теории идеальной жидкости,
привели к методу, разработанному для простейших случаев
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 43
Рис. 8а.
Рис. 86.
44 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Рис. 9а.
Рис. 96.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 45
Рис. 10а.
Рис. 106.
46 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Рис. 11а.
Рис. 116.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 47
Рис. 12а.
Рис. 126.
48 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
в работах Кирхгоффа, Рэлея, Митчеля, Жуковского1),
а позднее в значительно усовершенствованном виде в мето-
дах Леви-Чивита и Билля2), и до настоящего времени для
случаев криволинейных обтекаемых контуров удалось про-
вести в очень ограниченном числе случаев; здесь необходимо
отметить работы об обтекании дуги круга А. И. Некра-
сова3) и об обтекании дуги параболы Н. С. Аржаникова 4 *).
К сожалению, этот метод, представляя очень большие ана-
литические трудности, до сих пор не получил приложения
к определению точек отрыва у контуров типа контура
крыльев.
Другой метод, основанный на применении теории погра-
ничного слоя, развитый в работах Прандтля, Блазиуса, Кар-
мана, Польгаузена и др.б), также представляет большие
аналитические затруднения и до сих пор с успехом был
применен только к случаю пластинки и к случаю круглого
цилиндра. В дальнейшем мы увидим, как этим методом
может быть приближенно решен вопрос об отрыве струи
от поверхности крыла.
Второй основной вопрос о влиянии предкрылка на усло-
вия обтекания потоком крыла аэроплана также можно ре-
шать различными методами. В общем виде эта задача пред-
ставляет собой частный случай теории биплана и приводит,
по-видимому, к эллиптическим функциям.
Частный случай, когда предкрылок и основное крыло
представляют собой дуги одной и той же окружности, был
до конца решен в работе С. А. Чаплыгина6). Однако
в рассматриваемом случае дело упрощается тем, что раз-
меры предкрылка малы сравнительно с размерами крыла;
9 Например Н. Е. Жуковский. Видоизменение метода Кирх-
гоффа [Собр. соч., т. II, 194Й]; также В. В. Голубев, Теория крыла
аэроплана в плоскопараллельном потоке, гл. V, Труды ЦАГИ, вып. 21,
1927.
2) См., например, V i 11 a t, Apersu theoriques sur la Resistance
des fluides, 1920.
3) «Известия Ив.-Возн. политехнического института», № 5, 1922.
4) Математический сборник, 1928.
б) Prandtl, Vier Abhandlungen f. Hydrodynamik, 1927.
6) С. А. Чаплыгин, Схематическая теория разрезного крыла
аэроплана, Научно-технич. вестник, № 4—5, стр. 21, 1921. [Собр.
соч., т. II, 1948.]
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 49
поэтому, как первое приближение, можно заменить пред-
крылок одним вихрем, неподвижно закрепленным и вхо-
дящим, следовательно, в систему присоединенных вихрей
разрезного крыла. На первый взгляд может показаться,
что такая схема дает результат чрезвычайно грубый и по-
тому мало полезный; но не нужно забывать, что в основе
всей теории Прандтля лежит еще более грубое допущение,
состоящее в том, что вся вихревая несущая система крыла
заменяется одним вихрем переменной циркуляции; тем не
менее интегральные результаты, касающиеся величины подъем-
ной силы, величины лобового сопротивления, скоса потока
и т. п., оказываются вполне удовлетворительными; только
в таких вопросах, как определение точки приложения сил
давления, распределение скоростей около крыла и т. д.,
теория Прандтля оказывается совершенно недостаточной и
ее приходится дополнять, применяя, например, теорию пло-
скопараллельного потока к отдельным элементам крыла.
Таким образом, мы будем рассматривать обтекание
крыла в присутствии неподвижного вихря, неразрывно
связанного с крылом,
§ 5. Мы начнем с рассмотрения общей задачи о работе
крыла, обтекаемого потоком в случае, если около крыла
имеется система неподвижно связанных с крылом вихрей.
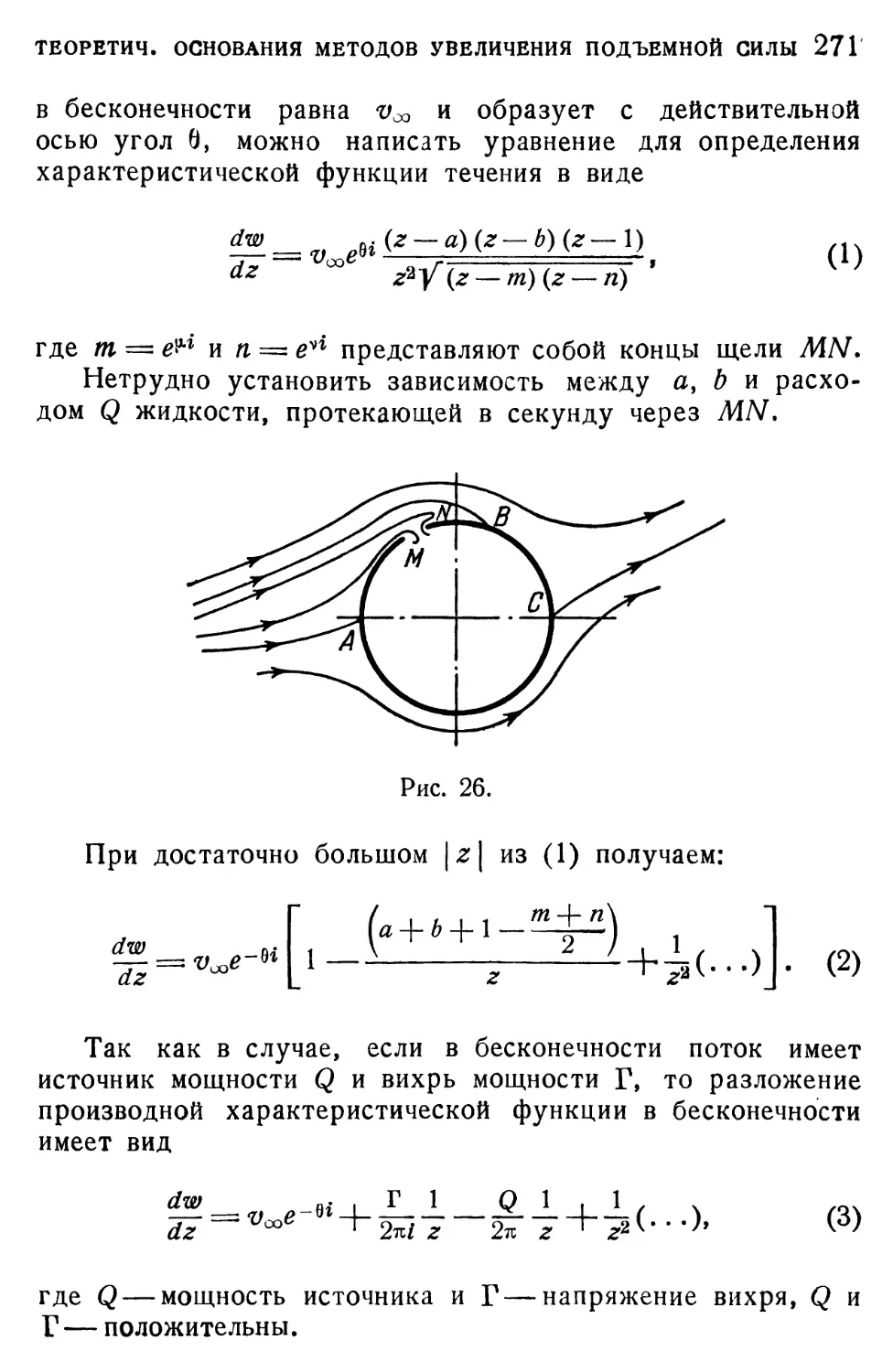
Пусть на плоскости С = имеется крыло (рис. 13),
около которого имеется система вихрей Jk, оси которых
--------------------£
Рис. 13.
находятся в точках Отобразим плоскость С на плоскость
z~x-\-iy таким образом, чтобы внешняя область крыла
перешла во внешнюю часть окружности |z|=l (рис. 14).
50 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Тогда вихри перейдут в некоторые точки Ьк плоскости z и
задняя острая кромка М перейдет в точку z—1, а точка
С — оо перейдет в точку z — схэ (рис. 13). Тогда производ-
ная характеристической функции обтекания цилиндра полу-
чится в виде
dz 00 \ г3 / * 2tcZ z ‘
। V 1 V 1 4
‘ Jj2tcZz— bk Zd z— ак'
где Voo и 0 — скорость потока, обтекающего цилиндр, и
угол, образованный ею с осью х, Г — основная циркуляция
вокруг крыла, Ьк и ак — оси добавочных вихрей, причем
__ 1 -
ак—(Ьк—сопряженное с Ьк), так что точки Ьк и ак
Ок
лежат на одной прямой, проходящей через начало.
Пусть С = — функция, дающая конформное отобра-
жение плоскости z\ как известно, вне окружности | z | = 1
для 7 (z) имеем разложение
Тогда, называя через X и Y компоненты подъемной силы
крыла, получим по формуле Чаплыгина — Блазиуса:
Y-\~iX=
где С — любой контур, охватывающий окружность L и не
заключающий точек Ьк,
Отсюда, подставляя (1), имеем:
(1 -5) + 2-Ll +
а
। 1 у Jk__________1_У I2 dz
' 2kZ Z4 z — bk 2iti Z^ 2 — akl yd (z) ‘
Для вычисления интеграла применим теорию вычетов.
Так как на контуре и вне контура у' (z) везде конечно, то
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I. 51
полюсами подынтегральной функции внутри С будут точки
z = 0 и z = ak. Найдем вычеты всех этих полюсов:
v i /X —_- f (v2 e 23i( 1 1—) -—1-4
2 J Г oo V г2/'(2<г2^
c
_l 1 V
(* —*fc)2
r2
к
1 (2ш)2 jL (z — a^2
z — ak
2 Г у 4 _J________________________2 у 44
(2л/)2 Zj z (г — ak) "T" (2nZ)2 U. (z — bk) (z — be)
2 JkJe____________
(2tcZ)2 jL (z — ak) (z — ae)
2 V Jkh 1 dz
(2kZ)2 (z - bk) (z - ae)l y' (z) ’
Вычисление всех интегралов формулы (2) представляет
ту трудность, что поведение функции хСО внутри окруж-
ности |^| = 1 неизвестно, а потому нельзя применять непо-
средственно теорему Коши к внутренней части кривой С.
Что касается поведения y(z) вне окружности |.г|=1, то
там х'СЮ нигде не обращается в нуль, так как вне окруж-
ности функция yr (z) дает везде конформное отображение;
следовательно, —вне окружности (z | = 1 везде голо-
морфно.
Отсюда следует, что интегралы, у которых в подынте-
гральной функции в знаменатель не входит разность (z — bk)t
можно брать вместо окружности |^| = 1 по любой кривой,
содержащей внутри себя эту окружность; мы будем брать
эти интегралы по окружности Ci бесконечно большого ра-
диуса с центром в начале:
f fl _^\2_^_ = о- f - = 0;
J V *2/ х'(О ’ Jj-YW ’
Г______ о- f_____________—---------- 0;
J — «л)2х'(г) ’ J (г — ак)(г— ae)xz(*)
tA Ci
52 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА -и щитков
Для вычисления интегралов, в которых в знаменатель
входит выражение z— bk, поступим следующим образом.
Окружим точку Ьк окружностью Ск столь малого радиуса,
так
чтобы Ск вся помещалась вне С; тогда J +
J J
ск С С1
как между окружностями С, Ск и С± подынтегральные функ-
ции голоморфны.
Но, применяя те же преобразования, как и выше, най-
дем, что интегралы, которые в знаменателе имеют произве-
дения (z — — Ьк) или (z— bk)z, или (z — bk)2 на
окружности Ср равны нулю, следовательно, для всех этих
интегралов имеем:
dz
J ~А-)2/'(*)
с
Ск
1
с Ск
______dz Г dz ___________
(z — Ьк)2к' (z) J (г — Ьк)2 У (г) —
ск
f dz I_!__________Г(М (z_b ч , ) 2к, z'W.
J (Z - brf (у/ (bk) (Ьк) *)+•••) 2 >
ск
dz
(г — bk) if (г)
_______dz
— ьк) if (г)
dz
(г — bk) If (г)
= 2к/:- —2та (1 —
а bJ
1
7/ (Ьк)5
f_____dz______ _____ Г dz ___________ f______dz_________
J г (г — bk) if (z) J z(z — bk) if (z) J z(z — bk) if (z) ~
c c, ck
— 7—L-r;
ь1Л'{ЬкУ
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 53
_________dz______________Г___________dz___________
(г — bk) (z — be) х' (г) ~ J (z — Ьк) (г — be) х' (z)
Gk
__ f__________dz_______________2 .________1_________
J (г — bk) (z — be) i' (z) ~ ™ (bk — be) x' (bk)
— 2kZ----------------*
(be-bk)x'(be) ’
_________dz____________
(z — bk) (z — ae)x'(z)~
+ p 2uZ 2 bkif\bk) + P 2r.i L {(bk - be) x' (bk) +
^~(be-bk)x'(be)} ?2^^iJe^i(bk-ae)x'(bk)~2X
1 ,
2nlZi 7#(bk) •
В случае, если вихрей Jk нет, то получаем формулу
Н. Е. Жуковского
y_|_ZX = —(Г)
В случае, если есть только одна пара вихрей J, то полу-
чим:
И, + 1Х1 = - Pv^-«[г 1 - J(1 - уЬ] +
I г 7__________р 1 р J*
’ 2tcZ byf (Ь) 2 2^1 Qjy 2ъ1 (Ь — a) yf (by '
Отсюда влияние вихрей скажется в добавочной силе,
определяемой уравнением
л/ДХ= rx + IX.—(Г + IX) = рJ[Гоое-64(1 — X
V_J_____l-L-J____ г J I
л x' {by “f" 2kZ Ы' (b) T 2л (6 — a) x' (b) "r' 4k ^2 (6) J'
54 i. труды по теории предкрылка, закрылка и щитков
у e~oi Л___
°°е V b^J^2nl b~ \dz)z-b’
где w0 есть характеристическая функция при отсутствии
вихрей, а потому
AV I А V J I IJ2 1 , ZJ2 у/ (Ь)
1 Р \ dz )z=b т! Ф) Р 2тс (b — а) (Ь) Р 4л~ %'2 ’
Совершенно иной результат получится, если все вихри
войдут в несущую систему присоединенных вихрей; тогда
для определения силы давления потока надо брать интеграл
по контуру, охватывающему все вихри.
Следовательно, в этом случае за контур интеграции
можно взять окружность бесконечного радиуса С1ОО. При-
меняя к этому случаю выведенные выше формулы и поль-
зуясь равенством (I"), получим:
r + iX = —
1 2 1 тс/ а 1 Ы и а
1 \ .1
(11)
Таким образом, в этом случае сила выражается совер-
шенно такой же формулой, как и в отсутствие вихрей Jk.
Однако не следует думать, что в этом случае подъем-
ная сила не зависит от добавочных вихрей. Легко показать,
что в случае крыла циркуляция Г зависит от величин доба-
вочных вихрей Jk.
В самом деле, если острой задней кромке крыла соот-
ветствует точка z~l, то по основной гипотезе Н. Е. Жу-
ковского
=0.
\ (iz)z=l
Следовательно, имеем уравнение
у ______yA_L_ = 0
°°е J )-t-2nl ф Л42-Л 1 — bk ~Zi2nil—ak
Отсюда
Г = -2^V jt -f-L-),
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 55
Легко видеть, что из этого уравнения значение Г полу-
чается действительное. В самом деле, пусть ак — ?кеак\ тогда
Ьъ = — еакг. Следовательно,
1________1 == 1________________1 =
l-aft i—bk i_p^V
1—e k -f-e k 2pfc cos ak (pk -f-1)
?h i 2
!~Pfc
l-2pfccosafc+p^ ’
Следовательно,
г = -^Vm sin 9 + У jk '~Pk . (Ill)
Так как в отсутствие вихрей
Го = —4^00 sin О,
то
ДГ=г—Го = У Jk —-—^-—2. (ПГ)
2Pj-cosaft+p*
i— pl
Так как < 1, то выражение ----------------- всегда
1—2pfc cos <x* Ч- Р*
положительно. Отсюда имеем следующий результат: если
около крыла есть вихри, то циркуляция крыла меняется,
причем каждый добавленный вихрь того же направления,
как основная циркуляция (направление взято для вихря
в точке вне крыла), увеличивает циркуляцию вокруг крыла;
каждый добавленный вихрь, направленный в обратную
сторону относительно основной циркуляции, уменьшает
Циркуляцию.
Отсюда, объединяя этот результат с предшествующим
выводом, мы видим, что если около крыла есть вихрь с цир-
куляцией, направленной в ту же сторону, как циркуляция
крыла, то общая подъемная сила, действующая на вихрь и
на крыло, больше, чем для изолированного крыла; если же
56 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
добавочный вихрь имеет циркуляцию, противоположную на-
правлению циркуляции крыла, то подъемная сила системы
меньше, чем для изолированного крыла.
§ 6. Для выяснения механического смысла выведенной
выше формулы рассмотрим частный случай, когда поток
обтекает цилиндр, имеющий циркуляцию, и вихри помещены
вдали от цилиндра. В этом случае С = 2, 1 иа=1.
Тогда формула (I) примет вид
y+,х _ - Р1/„е »[г - V _ pzr J Д+
+ Р‘ 2 '‘i 2х
Но | | = Vko суть скорости, которые создаются в центре
круга вихрем Jk\ называя Ьк = имеем:
или
откуда Рк = рГУ\.о, vk = аА-|-к; эти равенства выражают
теорему Н. Е. Жуковского, примененную к вихрю Г, поме-
щенному на оси цилиндра, в предположении, что на него
действует скорость, вызываемая присутствием вихря Jk
(рис. 15 и 16). Совершенно подобным же образом можно
истолковать смысл выражения piJk к-7^-------г.
\Dq dk)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I . 57
Действительно, | | есть величина скорости, ко-
торую создает вихрь Je в точке, где помещается вихрь
Пусть Ьв — а,к — rkee*ke%> тогда, называя все выражение че-
рез Yke~\~iXkei имеем:
Тогда
= рЛ 2^- ;
кв
отсюда
Рке = РА 2кгке ’ VkG ~ аке'
Следовательно, рассматриваемое выражение дает теорему
Н. Е. Жуковского в применении к вихрю, помещенному
в точке ак под действием скорости, вызываемой вихрем Je.
Выражение представляет собой силу, вызывае-
мую согласно теореме Н. Е. Жуковского у присоединенного
вихря цилиндра потоком, обтекающим цилиндр, и аналогично
выражение рУ^-Ч/^ представляет собой соответствующие
силы для вихрей Jk, являющихся изображениями вихрей Jk.
Отсюда получаем для настоящего случая теорему, кото-
рую можно рассматривать как обобщение теоремы Н. Е. Жу-
ковского: если круглый цилиндр находится в жидкости,
у которой в бесконечности помещается диполь, на конечном
расстоянии конечное число неподвижных вихрей, то действие
потока на цилиндр сводится к равнодействующей сил, вызы-
ваемых скоростью потока от диполя и от всех отдельных
вихрей у присоединенного вихря цилиндра и у вихрей,
являющихся изображениями вихрей окружающего потока
внутри цилиндра. Каждая из отдельных сил равна произве-
дению плотности потока на интенсивность вихря и на ту
скорость, которую поток имел бы в оси вихря от диполя
или от отдельного вихря окружающего потока; направление
силы получается из направления скорости на оси вихря по-
воротом на прямой угол против направления циркуляции
отдельного вихря. Иначе, равнодействующая слагается
из сил, определяемых по теореме Н. Е. Жуковского,
58 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
вызываемых у присоединенного вихря и у изображений окружаю -
щих вихрей всеми скоростями от диполя и вихрей вне крыла.
В общем случае любого обтекаемого тела, по-видимому,
нельзя получить подобной простой формулировки вследствие
искажений расстояний и направлений • потока в силу кон-
формного отображения, что и вызывает в формуле появле-
ние членов, зависящих от у/ и у".
§ 7. Из предыдущего следует, что подъемная сила
крыла без вихрей выражается формулой
Y-\-iX=—рУсое-е^Г,
в присутствии вихрей подъемная сила на всю систему, вклю-
чая и вихри:
Г1 + iX1 = - р Vooe-и 1 (Г + ДГ).
Следовательно, увеличение силы дается формулой
д rx+1 дл;=—pVeoe 1 дг,
ИЛИ
Д Yt +1 ДХ, = — рИсое-к - У
а
A(l-pj)
1—2pft cos ай + р*'
Рассмотрим простейший случай. Пусть около крыла
имеется добавочное малое крылышко, поставленное таким
образом, что оно работает
на обтекание (это достигает-
Jf /7 ся выбором соответствующего
\^( Q^******^ч^ угла атаки крылышка в по-
\ токе, который его обтекает)
(рис. 17).
Рис. 17. Тогда, если размеры кры-
лышка малы сравнительно с его
расстоянием от крыла, то приближенно его можно заменить
одним вихрем интенсивности, которая определяется по раз-
меру крылышка, его углу атаки и скорости потока в точ-
ках, занимаемых крылышком.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I. 59
Так как при рассматриваемом расположении J отрица-
тельно, то
лг1+ ,
где р и а — координаты оси изображения вихря в конформ-
ном изображении внешней части крыла на внешнюю часть
круглого цилиндра радиуса 1. Отсюда имеем:
др = рует 1 / . -1~~р2 . .
r I а | 1 — 2р cos а р2
Что касается направления этой силы, то она определяется
по теореме Н. Е. Жуковского, так как формула остается
та же.
Отсюда видим, что для увеличения подъемной силы всего
выгоднее брать добавочное крылышко в точках, чтобы
cosa=l, т. е. у задней кромки крыла. Тогда
Итак, наиболее заметное увеличение подъемной силы
получается для закрылка.
Если же поместить добавочное крылышко у передней
кромки, то a = к и, следовательно,
ГТУ 1111
Тогда
ДР1_Л+Р\2
ДР2~\1-р/ ‘
Например, если то ^^ = 25.
гр Р 2 Д/^2
1аким образом, при одинаковых прочих условиях увели-
чение подъемной силы от предкрылка менее заметно, чем
от закрылка,'
Так как основная сила крыла равна Р —
отношение
ДР _ J 1 — р2
Р Г 1 — 2р cos -a -|- рЗ
ру“йг’ то
60 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
дс„
Таково же отношение , если брать крылья с одинако-
вой полной поверхностью.
Для крыла циркуляция выражается приближенно фор-
мулой
где р—угол атаки, V — скорость, Z — хорда и 2а — цен-
тральный угол дужки крыла. Обозначая через Pi угол атаки,
L—хорду и 2аг— центральный угол дужки добавочного
крылышка, имеем:
VI (^-+ ₽1)
Ср
1 — р2
1 — 2р cos а + р2
Отсюда видим, что для увеличения подъемной силы надо:
1) ставить крылышко в точках, где скорость наибольшая
(что имеет место около передней кромки); 2) дать возможно
большую хорду L; 3) брать наибольший возможный угол
атаки рх; 4) а = 0 (что про-
______________М' тиворечит п. 1).
Нетрудно выяснить и
УТл ~~~~' ~ механический смысл этого
результата. В самом деле,
Рис. 18. в присутствии вихря J и
его изображения f и при
основной циркуляции Г точка схода струй благодаря
вихрю J' при той же основной циркуляции смещается
в некоторую новую точку М' (рис. 18). Так как по
основному принципу Н. Е. Жуковского точка схода должна
быть 7И, то циркуляция Г должна увеличиться настолько,
чтобы точка схода сместилась в 7И. Это и дает то увеличе-
ние циркуляции, которое подсчитано выше. Аналогичный
эффект получается, если направление циркуляции J обратно
направлению циркуляции Г; тогда точка схода сместится
в М", а потому, чтобы удовлетворить требованию Н. Е. Жу-
ковского, необходимо циркуляцию Г уменьшить, Этот резудь*
тат и был выше указан,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I. 61
§ 8. В предыдущем параграфе мы учитывали влияние
вихрей, принадлежащих крылу (предкрылка или закрылка).
Перейдем теперь к учету влияния вихрей, не связанных
с крылом. Такие вихри могут образоваться в тех зонах
около поверхности крыла, где создаются условия, вызываю-
щие образование отрыва струй. Известно, что в вершинах
выступающих углов скорость потока равна бесконечности;
благодаря этому около таких вершин или образуются вихре-
вые насадки, округляющие крыло, или происходит срыв струй.
Если крыло имеет острую переднюю кромку, то, как
указал Н. Е. Жуковский х), около передней кромки обра-
зуется вихревой насадок, вызывающий образование добавоч-
ного вихревого сопротивления. Аналогичный эффект полу-
чается при достаточном угле атаки и для округленного
крыла; в настоящее время это явление можно считать в до-
статочной степени изученным * 2).
Подобное же явление должно наблюдаться и в точках,
где крыло имеет впадины. Пусть в поверхности крыла имеем
углубление. Тогда может —
получиться отрыв струй и ~~ ______ у
в полости углубления мы _ ____
получим слой неподвижной WZOflx—
жидкости, который по не- А
которой поверхности отде- е / V
ляется от текущей жидко- A
сти. Вследствие наличия А.
трения образуется вихрь J
в полости Л, направленный, . рис 19
как указано на рис. 19.
Такие вихри, назовем их паразитическими вихрями, являются
вихрями, не принадлежащими крылу; их действие мы те-
перь и изучим.
г) Н. Е. Жуковский, О поддерживающих планах типа Антуа-
нет, Труды Физ. отд. о-ва люб. естеств., т. XV, вып. 11, 1911
[Собр. соч., т. IV, 1949]; также В. В. Голубев, Теория крыла
аэроплана в плоскопараллельном потоке, стр. 136, 1927.
2) См., например, Ф. Г. Шмидт, К теории сил лобового сопро-
тивления плоского потока, Изв. Гос. гидрол. ин-та, Xs 18, 1917;
С. Н. М и ч у р и н, К вихревой теории лобового сопротивления аэро-
плана, Уч. зап. Сарат. ин-та с. х., 1929; см. также В. В. Голу-
бев, Теория крыла аэроплана конечного размаха, гл. V, 1931,
62 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
1
Мы видели, что добавочная сила, получающаяся от при-
сутствия одного паразитического вихря, выражается фор-
мулой
ДГ+/ДХ=р(^9) ——hp—---------------
\^Л= 6//(*) 2л (ft —а)х'(*) 4л х' (*)’
гр [dWa 11 Т7
Так как -z---4 =Vh — скорости потока в точке оси
\.dz 1'(z)Jz=b b н
вихря, то
Дr+ i?VbJ+ р —----------------н р — .
^*2u(ft-a)x'(*) 4лХ'2(*)
1
Вихри могут образоваться только весьма близко к по-
верхности крыла, а потому (Ь — а) очень мало. Поэтому
приблизительно можно заменить всю вторую часть выраже-
ZJ2
нием тг-77--------------------------, так как осталь-
2тЦ& — а)ч' (Ь)
ные слагаемые можно считать ма-
лыми сравнительно с ним.
С другой стороны, приближенно
(Ь — а) х' Ю = х Ю—X (°)-
Следовательно,
ДУ+/ дх= 2TO[Z(/)LZ(a)] •
Точки у (Ь) и у (а) суть оси вихрей паразитического и
его изображения на плоскости крыла (рис. 20). Тогда
дг-j-iьх= i„ ?|71 ,| /|.
2л[х(6) —х(а)]1 1
Пусть
х(&)—х(й) = ^е“;
тогда
ДК4-гДЛ,= р^е_(“_г)*|/|>
где = есть скорость, сообщаемая вихрю в точке у (а)
его изображением в точке у(Ь). Пусть
ДГ-j-Z A?C= ДР (sin 9cos 6) = ДРе'* ' .
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 63
Следовательно,
2 ) г — рф | J | е( 2 *) г .
Отсюда
ДР=р<у| J\ и 6 = а.
Эти уравнения показывают, что паразитический вихрь
вызывает силу, направленную по прямой, соединяющей ось
изображения паразитического вихря внутри крыла с осью
самого паразитического вихря. Можно иначе сказать, что
добавочная сила равна $\J\v и ее направление получается
из скорости поворотом ее на прямой угол против напра-
вления циркуляции вихря, т. е. получаем теорему Н. Е. Жу-
ковского.
Легко видеть, что полученный результат приводит к сле-
дующему практически важному выводу. Всякие впадины на
крыле, где могут образоваться паразитические вихри,
вызывают увеличение лобового сопротивления.
Действительно, для образования паразитических вихрей
необходимо, чтобы поток отрывался от передней стенки
впадины; при этом образуются вихри, находящиеся в поло-
жении, указанном на рис. 20, и образуется добавочная сила,
направленная назад, т. е. сила, увеличивающая лобовое
сопротивление.
Применим это соображение к разрезному крылу. Если
угол атаки таков, что на отрезках АВ и А'В' (рис. 21)
СКЛППГТИ ПГГГПТ/Я ПЙРММ я пп-
жидкость, заключенную внутри щели, то продувания потока
в щели нет и крыло работает как крыло неразрезное.
Следовательно, мы можем применить к этому случаю
предыдущие соображения. На краях щели образуются вихри
(рис. 22) 4 и J2, на которые действуют скорости и т>2,
64 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
вызываемые их изображениями и J2. Следовательно, со-
гласно предыдущему, развиваются силы Р± и Р2, вызываю-
щие лобовое сопротивление. Так как интенсивность вихрей
«4 и 4 незначительна, то и соответствующее увеличение
лобового сопротивления невелико.
Отсюда же, между прочим, видно, что если мы имеем
подвижной предкрылок, то закрытие щели с одной сто-
роны должно уменьшать силу
) /Л лобового сопротивления, так как
I при этом будут образовываться
/ вихри только с одной стороны
с ' щели (рис. 23).
Рис. 23. Как окончательной итог имеем,
что лобовое сопротивление разрез-
ного крыла, работающего как крыло сплошное, всегда
больше сопротивления сплошного крыла.
Замечание. Все предыдущее имеет место, если ско-
ростью всего остального потока можно пренебречь сравни-
тельно со скоростью от изображающего вихря внутри
крыла. Положение совершенно меняется, если вихрь
образуется в точках, где скорость окружающего потока
очень велика; тогда, наоборот, можно пренебречь влиянием
изображения вихря и взять только скорость обтекающего
потока. В этом случае по
предыдущему образуется си- u
ла Р, так же направленная ... -__
по направлению потока, т. е. (F
сила лобового сопротивления.
Сила Р направлена в обрат- Рис. 24.
ную сторону (рис. 24) отно-
сительно силы потока, действующего на вихрь по теореме
Н. Е. Жуковского; это объясняется тем, что мы ищем
силу, действующую не на вихрь, а на крыло.
Экспериментальные данные в достаточной мере подтвер-
ждают это заключение, но показывают, что соответствую-
щее увеличение лобового сопротивления весьма мало.
§ 9. В работе разрезного крыла (крыло с предкрылком)
надо различать три различных режима.
1. При подходящем расположении крыла и предкрылка
при малых углах атаки крыло может работать как крыло
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 65
сплошное. При этом предкрылок работает на срыв, но сор-
вавшиеся с него струи примыкают к основной части крыла и
плавно обтекают ее (рис. 25). Для возможности такого
режима необходимо, чтобы скорость на АВ и CD была одна
и та же; тогда и давления
будут равны и не будет про-
текания потока через щель.
В этом случае разрезное крыло
раоотает как неразрезное; не-
которое отличие получается
только в том, что благодаря
вязкости воздуха в точках А
и с образуются вихри, вы-
зывающие увеличение лобового сопротивления. Так как
интенсивность этих вихрей невелика, то и соответствующее
увеличение лобового сопротивления незначительно. На диа-
грамме Лилиенталя, в соответствующей части ее, получим
небольшое смещение поляры сплошного крыла параллельно
оси лобового сопротивления. сме
Этот режим возможен, по-видимому, только при доста-
точной узости щели, так как иначе едва ли возможно по-
стоянство давлений на АВ и CD, Во всяком случае, этот
режим невозможен, если предкрылок помещен высоко над
основным крылом, подобно расположению крыльев в биплане,
или когда он помещен впереди крыла и угол атаки пред-
крылка мало отличается от угла атаки основного крыла,
т. е. когда имеем расположение, близкое к тандему; оба эти
случая указаны на рис. 26.
Рис. 26.
2. При увеличении угла атаки возможен тако’1 режим,
когда предкрылок работает на срыв, основное крыло — на
обтекание и поток протекает через щель (рис. 27). Этот
режим характеризуется резким увеличением лобового сопро-
тивления и уменьшением подъемной силы сравнительно со
сплошным крылом.
66 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Причиной увеличения лобового сопротивления является
образование вихревого хвоста (вихревой дорожки Кармана)
за предкрылком, что должно резко увеличить лобовое со-
противление.
Уменьшение подъемной силы вызывается уменьшением
хорды части крыла, работающей на обтекание (вместо / для
сплошного крыла получается /J (см. рис. 27).
Рис. 27.
На диаграмме Лилиенталя соответствующий режим ска-
жется в резком сдвижении соответствующей части поляры
по оси лобового сопротивления и в уменьшении значе-
ний Ср (коэффициента подъемной силы) сравнительно с моно-
планом. Начало этого режима на поляре характеризуется,
таким образом, более или менее резкой ступенькой в поляре.
3. При дальнейшем увеличении угла атаки вихревой
хвост за предкрылком становится ^же, что вызывает умень-
шение лобового сопротивления, следовательно, поляра раз-
резного крыла должна постепенно приближаться к поляре
крыла сплошного. Наконец, при значительном увеличении
угла атаки предкрылок начинает работать без срыва на
обтекание. В этом случае предкрылок начинает работать
как вихрь, что вызывает, как было показано, увеличение
подъемной силы основной части крыла.
Соответствующий режим скажется на поляре в увеличе-
нии значений Ср и приближении поляры к поляре сплош-
ного крыла. Собирая все эти результаты и изображая их
на диаграмме Лилиенталя, получим следующее.
Пусть AW—поляра сплошного крыла при условии, что
оно при всех углах работает без срыва струй (рис. 28).
Тогда часть поляры I соответствует первому из указанных
выше режимов, часть II — второму, характеризующемуся
увеличением лобового сопротивления и уменьшением подъем-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 67
ной силы, часть III характеризует третий режим, причем
нет резкого перехода из режима II в III.
Так как при больших углах атаки сплошное крыло, как
показывают экспериментальные данные, начинает работать
на срыв при меньших углах
работа сплошного крыла ха-
рактеризуется не полярой
AW, а полярой
Как выше было указано,
надлежащим размещением
крыла и предкрылка можно
достигнуть того, что часть
II поляры отсутствует.
Работа разрезного кры-
ла представляет интерес
главным образом при боль-
ших углах атаки. Отсюда
следует, что при больших
атаки, то в действительности
Рис. 28.
углах атаки предкрылок работает как вихрь, помещенный
вблизи крыла. Такой эффект действия предкрылка мы
в дальнейшем и изучим.
При малых углах атаки (часть II на поляре Лилиенталя)
предкрылок ухудшает крыло. Чтобы избежать этого ухуд-
шения, возможны два пути.
Во-первых, можно крыло сделать раздвижным, причем
при малых углах атаки (часть I и II поляры) предкрылок
плотно прижимается к крылу и крыло с предкрылком рабо-
тает как одно сплошное крыло. При значительных углах
атаки (примерно с точки Т поляры) предкрылок при по-
мощи соответствующего механизма отодвигается и крыло
далее работает как разрезное. В этом случае поляра будет
иметь приблизительно вид кривой MTN. Этот путь обычно
и применяется в конструктивном осуществлении разрезного
крыла, например в крыльях Хэндли-Пэджа.
Можно, во-вторых, попытаться соответствующим распо-
ложением крыла и предкрылка отодвинуть часть II на такие
углы атаки, чтобы до минимума сократить интервал углов
атаки, при которых крыло работает при режиме II. Воз-
можно, что этим путем можно добиться некоторых поло-
жительных результатов, В этом случае не понадобятся
68 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
более или менее сложные механизмы для раздвигания
крыльев.
Подведем итоги полученным в этой главе результатам.
1. В работе предкрылка надо различать три разных ре-
жима; при больших углах атаки предкрылок работает на
обтекание и приближенно может быть заменен одним вих-
рем, связанным с крылом, помещенным у передней кромки
основной части крыла.
2. Вихрь, заменяющий предкрылок, не вызывает значи-
тельного увеличения подъемной силы; следовательно, эффект,
вызываемый работой предкрылка, надо искать не в непосред-
ственном увеличении подъемной силы, а в изменении харак-
тера обтекающего потока, благодаря чему крыло работает
на обтекание при углах атаки, значительно превосходящих
соответствующие углы крыла без предкрылка.
3. При малых углах атаки предкрылок работает на срыв;
вихри, образующиеся за предкрылком, вызывают увеличение
лобового сопротивления.
Отсюда следует, что для построения теории работы
предкрылка нужно выяснить, при каких условиях начинается
отрыв струй от поверхности крыла и как влияет присут-
ствие предкрылка на условия отрыва струй. Эти две задачи
и решаются приближенно в двух следующих главах.
Глава И
ОПРЕДЕЛЕНИЕ ТОЧКИ ОТРЫВА СТРУЙ
ОТ ПОВЕРХНОСТИ КРЫЛА
§ 1. Теория пограничного слоя. Уравнения Прандтля, Кармана,
Польгаузена. § 2. Распределение скоростей на поверхности крыла.
§ 3. Распределение давлений на поверхности крыла. § 4. Случай
плоской пластинки. § 5. Экспериментальные данные. § 6. Интегри-
рование уравнения Польгаузена для случая крыла. § 7. Предель-
ные углы атаки. § 8. Перемещение точки отрыва на поверхности
крыла. § 9. Обобщение предшествующих результатов.
§ 1. В настоящем параграфе мы приведем исходные со-
ображения теории пограничного слоя, которые послужат
нам для определения точки отрыва струй.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 69
Известно!), что в пределах толщины слоя вместо основ-
ных уравнений гидродинамики имеют место уравнения
Прандтля:
ди . ди 1 др । д2и
Ох 1 ду р дх ’ ду2
^ = 0,
ду
да . dv____п
дх ' ду ’
(1)
где течение принимается плоскопараллельным, кривизной
стенки пренебрегаем и считаем ее плоской, причем и — ком-
понента скорости, параллельная стенке, и v—ей перпен-
дикулярная.
Первое из уравнений (1) после интеграций и некоторых
преобразований дает следующее интегральное соотношение:
h h
A J ?u2dy_U^^?udy = ^^fi_^^^ (2)
о о
— уравнение Кармана; где h — толщина слоя, U — скорость
на границе слоя.
Сравнительно с системой уравнений Прандтля интеграль-
ное уравнение Кармана имеет следующие два преимущества.
1. Уравнение Кармана содержит одну неизвестную функ-
цию а, кроме того, h зависит от положения точки на поверх-
ности стенки (от х).
2. Порядок дифференциального соотношения (2) пони-
жен путем интеграции сравнительно с уравнением (1).
Если известно U (х), т. е. распределение скоростей на
др
наружной поверхности слоя, то известно и так как из
уравнения Бернулли следует, что
£=-W- (3)
х) См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, гл. II, Труды ЦАГИ, вып. 108, 1931.
70 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Для приближенного решения уравнения Кармана сравни-
тельно простой метод дан Польгаузеном1); этот метод со-
стоит в следующем.
Представляем искомую функцию в виде
и = ay + by2 -|~ су3 -|- dy4
и для определения a, b, с, d, неизвестных функций пере-
менного х, применяем следующие граничные условия:
1. На внутренней границе слоя при у = 0 по свойству
Прандтля имеем:
и = 0; v = 0. (4)
Отсюда по первому из уравнений (1) имеем
— — т. е. по (3)
р дх к '
д*и_____UU'
ду2 v
2. При y — h на внешней границе слоя
u — U.
д2и
(5)
(6)
Далее, так как на внешней границе слоя не проявляется
сила вязкости, то
?=о. (7)
ду v 7
Кроме того, так как скорость и асимптотически прибли-
жается к U, то Польгаузен увеличивает порядок соприкос-
новения, полагая
^ = 0- (8)
Уравнения (5), (6), (7) и (8) позволяют определить коэф-
фициенты а, Ь, с, d.
!) К. Pohlhausen, Znr naherungsweisen integration der Dif-
ferentialgleichung der laminaren Grenzschicht, Z. M. M., 1, стр. 252—255,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 71
Получаются следующие значения:

_ UU' _ 1Л-
~~ ' 2> ~ 2ЛЗ’
С ~~ —6Л4^
(9)
где
U'h2
Подставляя эти значения в уравнение (2) и заменяя
А2
z = — так, что \ = U'z, получим для определения z урав-
нение х)
dz 0,8 [- 9072 + 1670,4k - (47,4 + 4,8 — (1 кз]
dx = (7[—213,12+ 5,76Х + Х2] — •
(Ю)
Это уравнение мы приложим к определению точки отрыва
струй. Чтобы получить точку отрыва, надо найти такое х,
чтобы Q == 0, т. е. для этого должно быть а = 0, откуда
У~ Х = —12. (11)
С другой стороны, так как \ = U'z, то Х = 0 в той
точке, где U достигает максимума; помещая в этой точке
начало координат, получим U' — Q или у = 0, х = 0.
Приведем уравнение (10) к другому виду, сделав замену
Z=zu7i откУда
(fk
dz___ dx . U"
K IF
Получаем:
dl I/___ UU" _
dx U' K U'2 —
0,8 9072 + 1670,4k — (47,4 + 4,8 — (i +
’ —213,12 + 5,76k 4-k2 •
______ (12)
и. В- в« Голубев, Теория крыла конечного размаха, Труды
НАГИ, вып. 108, стр. 108, 1931.
7е! I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Отсюда надо найти интеграл к такой, что Х = 0 при
х = 0; пусть этот интеграл есть U-F(x). Тогда, решая
уравнение
F(x)= 12,
(13)
найдем точку отрыва.
Из предшествующего видно, что для определения точки
отрыва надо знать функцию LJ (х), т. е. надо знать ско-
рость на внешней границе слоя при наличии отрыва;
определение этой скорости в свою очередь требует знания
положения точки отрыва. Следовательно, теория Прандтля
в ее современном положении не дает возможности опре-
делить точку отрыва без некоторых дополнительных
данных, например данных о распределении скоростей или
давлений на поверхности крыла.
Рассмотрим теперь два случая распределения скоростей
и давлений на верхней поверхности крыла: 1) случай, когда
положение точки отрыва известно; 2) случай, когда поло-
жение точки отрыва неизвестно.
§ 2. В случае, если крыло работает в условиях полного
обтекания, точкой отрыва струй является задняя кромка
крыла; в дальнейшем мы будем предполагать, что крыло имеет
форму инверсии параболы, следо-
вательно, задняя кромка его —
острая, что вполне определяет
место отрыва струй.
Чтобы получить крыло формы
инверсии параболы, поступим сле-
дующим образом.
Отобразим окружность С при
помощи подстановки:
1 Г = —
Рис. 29. —
Называя угол ОАО' через у (рис. 29), получим:
AJ2 cos2
С = *Н-------
(1)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 73
Пусть г = тогда из треугольника ОВО' имеем:
R2 = p2-|-R2sin2y----2/? Sin у р sin ср.
Отсюда
р = R sin ~ sin ср ± j/"R2 sin2 sin2 ср 4~ R2 cos2 у.
Пусть_____________________________________________
рх = R ^sin ~ sin ср -]- |/ sin2 у sin2 ср cos2 ~ j . (2)
Из равенства
Р1Р2 = — Я2 cos2 -|
имеем:
1 _ , Р2
Р1 R2 COS2 ~
R2 cos2
= “р2= ________________________
= R siп2 sin2 ср cos2 — sin у sin ср^ . (3)
Подставим (2) и (3) в уравнение (1) и, полагая
имеем:
£ iri = R (sin — sin ср —yf sin2 sin2 cp cos2 X
X (cos cp 4~ i sin cp) R (sin2 ~ sin2 cp -|- cos2 —
— sin у sin cp^ (cos cp — i sin cp).
Отсюда
£ = 2R 1/ sin2 ~ sin2cp -|- cos2 • cos cp,
(4)
= 2R sin у sin2 cp.
I. 74 ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Из последнего уравнения видим, что 0 при всяком ср.
Из уравнений (4) имеем далее:
£2 7]2 = 4/^2 | Sjn2 Sjn2 cos2 cos2 ,
£2 ^2 4/J2 J cos2 ----CQS а sjn2 у | ,
и, подставляя sin2 ср =--------- из (4), получим:
2R sin
4 4- + 2 ~ -со? ° 7] = 4/?2 cos2 ,
sinT
иначе:
4+
R cos а\2
sin
(5)
п а
Итак, при конформном отображении при помощи урав-
нения (1) внешняя часть окружности С переходит в часть
окружности (5), лежащую выше оси Найдем ее положе-
ние, радиус и центральный угол.
Для этого найдем отрезки т и п
(рис. 30).
Из (5) имеем:
m = 2R cos ~ , п = 2/?sin ~.
Так как из (5) видим, что радиус
о R
окружности Rt =------- , то от-
сюда имеем: sin ~2
. п т о . а а
sin р = = 2 sin у cos-у = sin а.
Рис. 30. 2 2
Следовательно, р = а.
Окончательно имеем результат: преобразование (1) пре-
образует конформно внешнюю часть окружности С на внеш-
о
нюю часть дуги С± радиуса ------- с центральным углом 2а.
slny
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 75
Отсюда легко получить и формулу для отображения ин-
версии параболы.
Преобразуем при помощи формулы (1) окружность С
радиуса (1—е) (рис. 31) и возьмем поток, обтекающий
цилиндр Cv радиуса 1, тогда, очевидно, получим на пре-
образованной плоскости по-
ток, обтекающий инвер-
сию параболы со скелетом,
являющимся изображением
окружности С.
На плоскости (хх, и
^i) (рис. 31) изображе-
ние, как показано, дается
формулой
cos2-^- (1 — е)2
= ------—--------. (6)
Рис. 31.
Перенося на плоскости z начало в —(1—e)cos-^
и на плоскости в точку ^ = 2(1—e)cos~| , что соответ-
ствует задней кромке крыла, получим формулы перехода
С1 = С + 2 (1 — е) cos у; zr = z2 -j- (1 — е) cos у.
Отсюда, вставляя эти выражения в (6), получим:
cos2 %? (1 — е)2
С=г2 —(1 — e)cosy-|--------(7)
гг + О-Осоз-у
Повернем около точки Л на плоскости z2 оси на угол-}--^»
тогда = 2 *. Из (7) получим:
„ --i „ COSa-^-(l — е)2
Z = z3e * _(1_e)cos|_|--------_J------------(8)
z3e 2 + О — £) cos 2
76 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Наконец, перенесем на плоскости z3 начало в центр
окружности Cf, тогда г3 = z—1 и из (8) получим:
С = 1) —(1—s)cosy +
COS2 ~ (1 — е)2
+-------------------------• <9)
(z—l)e 2 * + (1 — e)cos у
Это и есть искомое преобразование, переводящее внеш-
нюю часть окружности Сх во внешнюю часть инверсии па-
раболы, построенной на дуге радиуса -1 .
sin|
Заметим еще, что отношение радиуса меньшей окруж-
ности к большей в формуле (9) равно 1—е; часто берут,
обратно, отношение радиуса большей окружности к мень-
шей в виде l-j-ер Легко е выразить через Называя
соответственно через г и R радиусы малой и большой окруж-
ности, имеем:
£=1 + ^.
откуда
(1_£)(1 + £1)=1 И £=_А_=£1_£2+ ...
При малых е и ер порядка 0,1, можно приближенно
считать е = ех; но при больших г разница уже весьма чув-
ствительна; так, гх = 0,25 при г = 0,2; ех = 0,43 при г = 0,3,
и т. д.
Из уравнения (9) имеем:
dr (1 — e)2cos2y
-т1 = е 2 1----------------------------,
dz Г «I2
L |(г— 1) е 2 +(1 —e)cosyj J
или
rfC _ е - « (г “ ~~ 1>е 2 1 + 2 ~ Е) C0S -j]
[(г — 1) е 2 * + (1 — е) cos у J2
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 77
Характеристическая функция обтекания круглого ци-
линдра при наличии циркуляции имеет вид
. / Л’ЗЪ'Х Г
--------------) + х—- In г,
00 \ 1 z / * 2к/
откуда
duo - / р 1
— * ) + ^-7- . (10)
dz \ г2 / ’ 2тЛ z v 7
Если расположить оси таким образом, чтобы точка от-
рыва соответствовала значению г=1, то в этой точке со-
гласно исходному положению Н. Е. Жуковского = 0.
Итак,
— -}-^ = 0. (11)
Исключая Г из (10). и (И), получим уравнение
S=^'-,‘4r!(l+'-?)• (12>
Из (12) имеем:
dw___
~dZ ~~
dw dz
dz d£

Г -ТГ * a 12
I (г— 1)«? 2 +(1— e)cos-jj
[a .
(z—})e 2 1 4-2(1 — e) cos y
Так как равно модулю скорости
точке Z то
потока в данной
e-6i
I --i a 12
ew | |(г-1)е 2 +(l-e)cos 4
(г — l)e 2 4-2(1 — e) cos 2 |
•|14 (l3>
^=4

78 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Точке на поверхности крыла соответствует точка на
поверхности цилиндра; пусть z — exit тогда
I г сс |2
2 + (1 __ £) COS -
Vr = + ------------—---------------(14)
| (eli — \ )e 2 г + 2 (1 — e) cos ~ |
Ho
I £(0-X) г | | g ( 2) 2 ) г| . 2 COS ^6-^;(15)
|(^xi—l)e 2 *__|_(1—£)cos-^-|2 =
I 1 /1 \ « I2
= e\2 2/ 2zsin -g-—|—(1—e)cos-£- =
= [(1 — e) cos — 2 sin у sin 0- — +
4- 4 cos2 (y — -j) sin2 4 ’’ (16)
(gXi — i) e 2 г_^_2(1 —e)cos~|2 =
= j 2 2 г2/ sin 4 + ^ (1 — s) cos 12 =
= 4 I (1 — e)2cos2y — 2(1 — s) cos ~ sin 4 sin (4 —1*) +
+ sin24}« (И)
Подставляя эти значения в (14), имеем:
y(. = Vcocos (б—4) X
(1 — е)2 cos3 — 4 (1 — е) cos sin j sin + 4 sin3 * 18
(1 — £)2 cos2 J — 2 O—e) cos -g- sin 4 sin (4 ~ y) + sin2 4
(18)
Эта формула дает возможность подсчитать величину ско-
рости в любой точке поверхности крыла типа инверсии
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 79
параболы при условии точного обтекания крыла, т. е.
когда точкой отрыва является задняя кромка крыла.
§ 3. Зная распределение скоростей, легко рассчитать и
распределение давлений в различных точках крыла. Приме-
няя формулу Бернулли, получим:
А = С—= С—tV^cos2(0— 4) х
[(1—e)2cos2 у — 4 (i — e) cos у sin A sin (A — +4 sin2 Aj2
(1 — e)2 cos2 у — 2 (1 — s) cos у sin у sin (A — y^ + sin2 A
Полученную точную формулу заменим приближенной при
следующих предположениях: 1) е мало (порядка до 0,3),
2) 9 мало (до 15°), 3) а мало (порядка 20°). Тогда, так как
cos ^9 — = cos 6 cos у + sin 9 sin ,
считая 9 и X малым, имеем
cos (9----2 )= cos О cos ~2
и приближенно можно положить:
е2 = 0; cos 9=1; sin 9 = 0; cos ^9---^ = cos~;
. /X а\ . X
Sin \2 — 2>Sltl 2’
получим
Г1— 2e — 4(1 — e) sin2 X- + 4 sin2 A?
Pt. = C — 4 V2m cos24 cos2 0 L-------------*-------_£1
1— 2e — 2(1— e) sin2 A4-sin24
ИЛИ
, Г1 — 2e -j- 4e sin2 A
Pl = c—4 vL COS2 4 cos2 01----------------------------±_
(1 - 2e) (1 - Sin2 A)
t. e.
P'—C—4-VA(l — 4e-+8ssin2 A] cos2 0,
80 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
ИЛИ
= С — ~У1 2О {1—4s cosX} cos2 9.
Но на крыле 2 cos X приближенно равно расстоянию от
середины крыла s, так что
р^ = С—£ vL{ 1 — 2ss} cos2 9 = (с—+ pVlscos2 9 -s.
Для задней кромки 5 = 2 и
ро = с— 4s)cos29.
Следовательно,
Др = р0 — = V^cos2 9 {4s — 2ss} = pV^scos29(2— s).
Отсюда мы видим, что давление линейно возрастает вдоль
верхней поверхности.
Рис. 32.
Данное выше доказательство применимо только при не-
большом ~ и при небольшом 9; таким образом, линейность
распределения давления исчезает вблизи передней кромки
(где Х= 180°).
Дадим график распределения давлений (рис. 32), полу-
ченных теоретическим путем х).
1) W. G. А Р е г г i n g, The theoretical pressure Distribution
around Joukowsky aerofoil, Technical Report of the Aerodynamical
Rescerches, 1927.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 81
На приведенных изображениях (рис. 32) видно, что ли-
нейность изменения давления в достаточной мере выполняется
в весьма широких размерах: можно считать, что давление
меняется линейно для толстых крыльев на всем протя-
жении от точки, где давление наименьшее (т. е. где V?
принимает максимальное значение), и до точки схода струй
(т. е. до задней кромки).
Для тонких крыльев (при малых е) это не выполняется;
причиной этого является очень большое значение скорости
около передней кромки и соответственно этому чрезвычайно
резкое уменьшение силы давления. Но из общей теории
крыла известно, что образование очень больших скоростей
около передней кромки невозможно с точки зрения теоремы
С. А. Чаплыгина1)- Благодаря этому около передней кромки
образуются вихревые воздушные насадки, которые действуют
на крыло так, как если бы увеличилось соответствующее
значение е; в результате этого надо ожидать и для тонких
крыльев распределения давления, ближе подходящего к ли-
нейному на всем интервале от наименьшего значения давле-
ния до точки схода струй.
Отсюда получаем любопытный результат, который экспе-
риментально хорошо известен. Точка, где скорость наиболь-
шая, находится около передней кромки. Таким образом,
можно считать, что давление распределено линейно и на
верхней и на нижней поверхностях крыла. Отсюда легко
показать, что центр приложения силы давления находится
на х/3 хорды, считая от передней кромки, — результат, часто
применяемый в приложениях.
Действительно, если принять, что увеличение давления
на нижнюю поверхность крыла и уменьшение давления на
верхнюю поверхность крыла следуют линейному закону
на всей поверхности крыла, то центр давления будет
находиться на линии, соединяющей точку О, центр тяжести
треугольника АВС (подсасывающая сила на верхнюю поверх-
ность), и точку Ох, центр тяжести треугольника АВС± (избы-
ток давления на нижнюю поверхность крыла), т. е. направление
Ч См., например, В. В. Голубев, Теория крыла аэроплана
в плоскопараллельном потоке, Труды ЦАГИ, вып. 29, Москва,
стр. 32, 1927.
82 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
силы отсекает от хорды крыла третью часть от передней
кромки (рис. 33).
Из предшествующего видно, что это предположение
только приближенное. В действительности точка приложения
Для величины давления
стинки получим выражение
определяется построением па-
раболы метацентров.
§ 4. Рассмотрим одно со-
вершенно элементарное прило-
жение полученных формул к
теории крыла.
В случае плоской пластин-
ки формулы для скорости по-
тока, обтекающего ее, полу-
чим из формулы § 2, положив
в ней а = 0; е = 0. Отсюда
— А)—L-. (1)
7 cos ng-
потока в некоторой точке пла-
— С — |vLcos2(9— 4)—Цу. (2)
' z cos2 -?
Возьмем две точки пластинки: одну, на верхней по-
верхности пластинки (т. е. X > 0) и находящуюся под ней
точку С2 нижней поверхности пластинки (X < 0). По (2)
соответствующие давления выразятся так:
cos2
cos 2
Отсюда давление на крыло всего потока равно
—Аг = Ар = 4 Vi —Ly (cos2 (б- 4) - cos2 (е+4)},
COS2 7г
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ 1 83
или
Др = 2pV^ —J—cos 6 cos sin 6 sin -^ = 2pV^sin0cosOtg^-.
c°sI 2 -j (3)
Чтобы получить все давление потока на пластинку, надо
взять сумму давлений на все элементы пластинки.
Так как из § 2 (9)
а (1 — e)2cos2-^-
r=(z— Y)e 2 —(1—e)cos-2-H-------------—---------------,
(г—l)e 2 +(1 —e)cosy
в рассматриваемом случае имеем:
; = (2_l)_l + _JrT__2+±„2, (4)
откуда
1—1
dz z*
и на поверхности пластинки, где z =
| А| = | i_e-2H| = |exi_e-xi|==2sink.
Называя через $ расстояние точки пластинки от задней
кромки, имеем по свойству модуля
I dz I d\ ’
а потому
ds = 2 sin 1 d\t
следовательно, сила давления потока на крыло равна
7С
Р== J kpds = 4pV^sin 0cos 9 J tg-lsinXdX =
о
%
= 4pVlsin 9 cos 9 | 2 sin2 1 d\ — 4крУ^> sin 9 cos 9.
о
84 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Между тем известно, что если рассчитать величину силы
давления потока на крыло по теореме Н. Е. Жуковского
или по формуле Чаплыгина — Блазиуса, то получим:
Р1==4крV^sin6 !).
Кроме того, Р направлено перпендикулярно к пластинке,
а РА— перпендикулярно к скорости потока (рис. 34).
Отсюда видно, что Р± представляет собой равнодействую-
щую силы Р и перпендикулярной к ней и, следовательно,
р направленной по направлению
7 А "1Р пластинки силы Q, причем
/ I /
/ \J Q = Рх sin 9 == 4крV^sin 0.
7 Отсюда мы видим, что в
4'*ч***^_ случае пластинки теорема Ча-
плыгина —Блазиуса или тео-
---------—------1--—рема Жуковского дает невер-
Рис. 34. ное выражение силы давления
потока на пластинку. Это
обстоятельство было впервые отмечено Кутта, который дал
и объяснение его* 2); более подробное изучение этого явле-
ния принадлежит Н. Е. Жуковскому3).
Причиной этого служит то, что у передней кромки обра-
зуется вихрь, и теорема Чаплыгина—Блазиуса дает силу
давления потока не только на крыло, но и на вихрь, так
как входящий в теорему Чаплыгина интеграл берется по
кругу столь большого радиуса, что он охватывает и крыло
и образующийся у передней кромки вихрь. Применяя к вихрю
теорему Н. Е. Жуковского, получим силу давления потока
на вихрь; она по величине равна силе Q, но направлена
в противоположную сторону.
Вычитая из Р± эту силу, получим действительную силу
давления потока на пластинку Р, которую мы и нашли
иным путем выше.
Э См., например, В. В. Голубев, Теория крыла аэроплана
в плоскопараллельном потоке, стр. 80. При этом нужно помнить,
что хорда пластинки в рассматриваемом случае равна 4, как видно,
например, из выражения (4).
2) Там же, стр. 137.
3) Там же, стр. 143.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 85
Такое явление будет наблюдаться во всех случаях, когда
передняя кромка крыла острая или вообще когда у перед-
ней кромки скорость потока превосходит скорость звука х).
В главе I мы рассматривали аналогичные явления, вызы-
ваемые образованием вихрей как у выходящих углов крыла,
так и во входящих углах* 2).
Примененный выше метод расчета давления потока на
крыло можно применять в случае любого крыла, но, как
легко видеть, в более сложных случаях вычисления стано-
вятся чрезвычайно сложными. Теорема Чаплыгина — Блазиуса
дает возможность решить эту
задачу гораздо более простым
способом.
§ 5. Полученные выше тео-
Рис. 35.
ретические результаты, даю-
щие распределение давлений
на крыле, в достаточной мере
подтверждаются эксперимен-
тальными данными. При этом
обнаруживается весьма инте-
ресный факт: приближенно ли-
нейность выполняется и тогда,
когда точка отрыва отходит
от задней кромки. В этом
случае приближенно линейное
распределение давления выпол-
няется в промежутке от точки,
где давление минимальное, до
точки, где наступает срыв.
Как пример рассмотрим следующие данные о распреде-
лении давления на середину крыла (Геттинген, № 387) при
углах атаки от —4° до 18°, по данным лаборатории в То-
ронто 3) (рис. 35). Во всех этих графиках распределение давле-
ния между минимальным значением (т. е. где подсасывающая
Ч См., например, В. В. Голубев, Теория крыла конечного
размаха, стр. 221.
2) Там же, стр. 12.
3) University of Toronto, Faculty of applied science and enginee-
ring school of engineering [research, Bulletin № 10, Aeronautical Pa-
pers of Parnin, 1927.
86 I. ТРУДЫ ПО ТЕОРИИ# ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
сила достигает своего максимума) и точкой срыва сле-
дует приближенно линейному закону. Только при 16°
распределение давления сильно отклоняется от линейного;
весьма вероятно, что в этом случае точкой отрыва является
не задняя кромка, а точка /И
(рис. 36) и в действительности
распределение давлений прибли-
женно следует закону, указанному
на чертеже пунктиром. Наконец,
при 18° почти все крыло работает
на срыв, в результате чего дав-
ление во всех точках верхней по-
верхности крыла постоянно.
Рис. 36. Прекрасное согласие с рас-
пределением давлений, следую-
щих линейному закону, дают следующие данные примеров
давлений на основную часть разрезного крыла по опытам,
Рис. 37.
проведенным в ЭАО ЦАГИ (рис. 37). В них линейность
распределения выполняется с чрезвычайно большой точ-
ностью х).
*) Приводимые экспериментальные данные сообщены мне
инж. Красилыциковым, за что приношу ему искреннюю благодарность.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 87
Совершенно аналогичные результаты дают следующие
измерения в Геттингенской лаборатории Прандтля (рис. 38,
39 и 40) 9.
На рис. 39 и 40 при углах 11,5° и 14,6° видно, что
часть крыла (отрезки ОА на рис. 39, ОА на рис. 40) ра-
ботает на срыв. Интересно отметить, что для наиболее тол-
стого крыла отрыв струй начинается раньше, чем для более
тонкого. Причину этого мы увидим ниже, в § 7.
§ 6. Результаты, разработанные в двух предыдущих
параграфах, позволяют высказать следующее положение:
давление на верхней поверхности крыла изменяется по
линейному закону в интервале от точки, где давление
наименьшее, до точки срыва.
9 «Ergebnisse d. Аег. Versuchanst zu Gottingen», И, стр. 45—46.
88 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
В случае схода струй с задней кромки крыла этот ре-
зультат приближенно выражает зависимость, получаемую
теоретическим путем; в случае отрыва струй ранее задней
кромки этот результат приходится рассматривать как факт,
даваемый экспериментом.
Пользуясь этим результатом, можно легко разрешить
задачу о нахождении точки отрыва струй от верхней по-
верхности крыла, поставленную в § 1 настоящей главы.
Возьмем уравнение (10) § 1:
4 0,8 ^—9072+1670,41— ^47,4+4,8 Ха— (1 +
dx~ 77 [—213,12+ 5,76X4-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 89
По свойству пограничного слоя Прандтля давление на
поверхность крыла равно давлению на наружную поверх-
ность слоя, а на наружной поверхности слоя по предыду
Рис. 40.
тему давление изменяется по линейному закону. Отсюда
следует, что
dx
(2)
Но по теореме Бернулли имеем:

(3)
90 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Отсюда
dp rr dU
-f- = —p(7 .
dx r dx
Так как -^-^- = 0, то имеем:
у^+("у_о,
dx2 1 \dx)
а потому
UU"
Ufi
(4)
(5)
Подставляя выражение (5) в уравнение (1), имеем:
dz _ 0,8 [— 9072 + 1670,4k — 42,6X2]
dx ~ U{— 213,12 + 5,76ХН-Х2] •
Но
d'K
К dz dx . U"
Z =— и —=----------------A—о.
U' dx U' U'2
Подставляя это в уравнение (5') и используя (5), получим:
dK и _ 0,8 [— 9072 + 1670,4k — 42,6X2] .
dx U'~ —213,12+ 5,761+ Х2
или
dK U _ — 7257,6 + 1549,4k — 39,8k2 _ _ 1
dx U' ~~ — 213,12 + 5,76k + k2 R(K)'
Отсюда
(6)
Проинтегрируем обе части (6) в следующих пределах.
Будем измерять х от той точки поверхности, где скорость
максимальная (т. е. где давление наименьшее); так как
\ = U'z=U'—, где h — толщина слоя, то в этой точке
Х = 0. В точке срыва, как было показано в § 1, Х =— 12;
называя расстояние от х = 0 до точки срыва через х0, получим
из (6)
—12
| J R(K)dK.
о о
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 91
Отсюда
о
ln7W = -
—*12
(7)
где U (х0)—скорость в точке отрыва струй и U (0) — наи-
большая скорость в точке верхней поверхности крыла; будем
ее называть t/max, скорость в точке отрыва — UQ.
Найдем величину интеграла (7). График кривой у — R (X)
имеет вид, указанный на рис. 41.
Искомый интеграл представляет площадь, заштрихован-
ную на фигуре. Применяя способ трапеций и замечая, что
/?(0) = 0,03 и /?(—12) = 0,0045,
имеем:
о
J R (X) d\ = ^3 + °4)(>45 12 = 0,20 »).
-12
Приближенно будем считать его равным 0,2. Тогда из (7)
имеем:
^0 р-0,2
^7 щах
И
г) Точнее см. § 9 гл. Ц,
92 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Отсюда получаем следующий основной результат: в слу-
чае, если в интервале от точки, где скорость потока
наибольшая (и, следовательно, давление наименьшее), до
точки срыва давление изменяется по линейному закону,
отношение наибольшей скорости потока к скорости
в точке срыва равно 1,2.
Заметим, что линейность распределения давления является
основным условием для получения этого результата. При
обтекании тел, сильно уклоняющихся по форме от крыла,
линейный закон распределения давления совершенно не вы-
полняется; потому и полученный вывод будет совершенно
неприложим к случаю обтека-
ния цилиндра.
Следующий график (рис. 42)
дает распределение скоро-
стей у цилиндра, по данным
Хименца — Польгаузена х); так
как {/гаах = 30,5 и точка срыва
получается при х = 6,94, где
[/0 = 29,5, то приближенно
= 1.04,
б'о
что совершенно не согласует-
ся с полученным выше резуль-
татом. По-видимому, в настоящем случае сильно сказывается
кривизна цилиндра, в то время как у крыла кривизна в пре-
делах рассматриваемой части верхней поверхности крыла
незначительна.
Этот пример показывает, что для очень толстых крыльев
(большое е) или для крыльев с сильно изогнутым скелетом
(большое а) полученный результат не имеет места.
§ 7. Полученный вывод позволяет сейчас же решить
вопрос об определении тех углов атаки, до которых данное
крыло работает в условиях полного обтекания. Будем назы-
вать такие углы предельными углами атаки. При решении
1) К. Pohlhausen, Zur naherungsweisen Integration der Dif-
ferentialgleichungen der laminaren Grenzschicht, Zeits. f. Math. u. Meeh,
1, 1921. '
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 93
поставленной задачи ограничимся, как и выше, крылом типа
инверсии параболы.
При условии полного обтекания при предельном угле
точкой срыва является задняя кромка, которой соответствует
значение Х = 0. В этом случае по формуле
V, = Уюсоз(б--у) X
(1 — e)2cos2y — 4(1 — е) cos у sin у sin (у — у) + 4 sin2y
лГ(1—е)2 cos2 у — 2 (1—г) cos у sin у sin (у — у) + sin2 у
т м £ £ у £ £ / £
(1)
скорость 1/0 получится в виде
Vo = VqqCosS (1 —e)cos-^-. (2)
Так как наибольшая скорость получается около передней
кромки, которая при малых ~ получается приблизительно
при Х = то по формуле (1) имеем:
[(1 — е)2 __ 4 (1 _ е)] cos2 + 4
^гаах ^L=: Vсо Sin 9 _ -----
]/ [(1_£)3 — 2(1-s)]cos2| + 1
(1 -|- £)2 cos2 4- + 4 sin2
= Voo sin 9-- 2 -=4-. (2х)
J/ e2 cos2 ~ + sin2
При малом а можно считать cos-|~=l. Тогда
^max = ^sin9(li<1). (3)
Из (2) и (3) имеем:
Kina* — tg 9 +-еУ- (4)
Ио S е(1-е)- < '
!) Заметим, что полученный результат близко подходит к при-
олиженной формуле, данной у В. В. Голубева в «Теории крыла
аэроплана в плоскопараллельном потоке», Труды ЦАГИ, вып, 29,
СТР- 135, 1927,
94 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
По результатам предшествующего параграфа в случае,
если точка отрыва находится на задней кромке, имеем:
-^- = 1,2.
Подставляя это значение в (4), получим следующую
формулу для определения предельного угла атаки:
tg0^1.2 *^#- (5)
Рассмотрим несколько примеров.
Пусть е = 0,5; тогда 9 = 2°50'.
При 8 = 0,1
tg9= 1,2 °’}29,9 =0.09; 9 = 5°9'.
При е = 0,2
tg 0 = 1,2 0’^'9,8 =0,14; 9 = 8°.
ь 1,44
При в = 0,3
tg 9 = 1,2 —|^’7- =0,15; 9 = 8°30'1).
Если рассматривать крылья конечного размаха, то, так
как поправка на скос потока получается в рассматриваемых
случаях около 3°, кажущиеся предельные углы атаки 60
в рассматриваемых случаях получим в виде
е = 0,1 8=0,2; е = 0,3;
9О = 8°; 0о=110; 9о=11°ЗО/.
Заметим, что данный результат в точности справедлив
для симметричного крыла (а=0; руль Н. Е. Жуковского2)),
но приближенно он верен при всяком малом а.
Из формулы (5) видно, что при очень малом е и 0 также
весьма мало; так, если е = 0,05, то по (5) найдем 0 = 3°20'
и кажущийся угол атаки будет около 5°.
*) Необходимо помнить, что при больших е точка с Vmax уже
значительно удалена от передней кромки и формула (5) дает при-
ближение весьма неточное.
2) См., например, В. В. Голубев, Теория крыла в плоско-
параллельном потоке, стр. 124.
ИССЛЕДОВАНИЯ НО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 95
Нетрудно найти крыло, которое работает на обтекание
при наибольшем угле атаки.
Из (2) и (2') имеем:
1/ е2 COS2 — + sin3-^- (1 — е) cos —
tg 6=1,23 ~-------------------------------,
(1 е)2 cos2 ~ + 4 sin2 ~
или
(1 —£)1/" e2 + tg2y
{g 0 = 1,23-------'-------4-, (6)
(l + e)3 + 4tg27
причем (6) .справедливо только при малом а, так как иначе
предположение, что Vmax получается при X =-зт, не имеет
места.
Найдем максимум выражения (6) в зависимости от s и
tgy . Полагая tg — =t и дифференцируя по е и /, получим
для определения в и t уравнения
(в _ 2е2 — /2) [(1 _4_ s)2 4^2j __ 2 (в2 + /2) (1 _ е2) = 0, 1
7 (12е —7г2 —4/2) = 0. )
Отсюда получаем первое решение
7 = 0, г = у,
а для второго
4/2= 1-|“2е —7е2
и, подставляя в первое из уравнений уравнение (7), имеем:
(е—1)(1-4-2е —Зв2)=0,
откуда в — 1, в =----. Второй ответ в = — ~ не годится,
а при первом — t мнимое.
Итак, единственным годным решением является в = -^-,
tg= 0, т. е. а= 0.
96 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Следовательно, выгоднейшим крылом, которое рабо-
тает на обтекание при наибольшем угле атаки, является
руль Н. Е. Жуковского (симметричная инверсия параболы),
1
для которого 8 = у .
В этом случае, как было показано, предельный угол
атаки (с поправкой на скос потока) равен 11°30'.
Рис. 43.
На рис. 43 дано построение Трефтца для случая выгод-
нейшего крыла = у^.
То обстоятельство, что увеличение е сверх известной
границы влечет за собой ухудшение свойств крыла ввиду
уменьшения предельного угла атаки, ясно хотя бы из того,
что при безграничном увеличении е получается в пределе
круглый цилиндр, который обтекается с отрывом струй при
любых углах атаки.
Для сравнения приведена диаграмма Лилиенталя весьма
толстого крыла (рис. 44).
§ 8. Предельные углы атаки, получаемые при помощи
формулы (5) или (6) предшествующего параграфа, оказы-
ваются слишком малыми. Изучение экспериментальных дан-
ных показывает, что в действительности крылья работают
на обтекание при углах атаки, значительно превосходящих
границу, даваемую этими формулами. Особенно значитель-
ное расхождение получается при очень малых е, т. е. для
крыльев очень тонких.
Для выяснения причин этого расхождения разберем
отдельно случай тонких и толстых крыльев.
ИССЛЕДОВАНИЯ ПО ТЕОРИЙ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I
В случае тонкого крыла, как показали исследования
Н. Е. Жуковского, Ф. В. Шмидта и С. Н. Мичурина,
образуется у передней кромки крыла вихревой насадок;
действие этого насадка сводится к тому, что за счет насадка
увеличивается величина е, т. е. крыло становится как бы
толще. В результате этого предельный угол атаки увели-
чивается. Возможно, что этим и объясняется главным обра-
зом расхождение между теоретической и экспериментальной
величинами предельного угла атаки у тонких крыльев.
&S I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Сложнее обстоит дело для крыльев толстых. Для реше-
ния этого вопроса найдем предварительно, при каком угле
атаки точка отрыва струй переходит в данную точку верх-
ней поверхности крыла.
По выведенным выше формулам
V^VooCOS^—4)х
(1 — е)2 cos2 — 4 (1 — е) cos ~ sin у sin (4 ~ У) + 4 Sin2 Т
]/"(1 — е)2 COS2 j — 2(1 — е) cos jSin-^-sin^ — |) + sin2|
(!)
= V„sin 6 . (2)
HldX V-A*' g \ /
Так как для точки отрыва
= 1,2 или -Ео-^0,82,
то, полагая приближенно а=0, имеем:
е)2 — 4(1 — е) sin2 4 sin2
............ /X
— е)2 — 2 (1 — е) sin2 J- sin2
е
X 0 _|L е)2 =0,82. (1 )
Отсюда
(ctgScos --I- sin у) X
(1 — е)2Ц-4е Sin2^
x-z—.................. 2 {
у (1 — e)2 + 2esin2y — sin2 у
А
7, 2Ч = 0,82.
(1 +е2)
Ограничиваясь первыми степенями е, отсюда получим:
(ctg 6 cos 4 4- sin —Ц— = 0,82,
\ Z 2, ] к
cos 2
или
ctg 0
0,82 х X
—-------fg 2*
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 99
и
Отсюда
П I / °>82
9 = arcctg (——
^6 Е3
4/А 1 О 9
1,3 COS^Y
(3)
Таким образом, скорость изменения угла атаки при
перемещении точки отрыва прямо пропорциональна ква-
драту е и обратно пропорциональна cos2 ~ . Следовательно,
скорость изменения угла атаки возрастает при увеличении е
и медленнее всего меняется угол атаки в начале отхода от
задней кромки (т. е. когда Х=0).
Отсюда следует практически важный результат. У тол-
стых крыльев (е большое) при перемещении точки отрыва
угол атаки изменяется сильнее, чем у тонких. Следовательно,
изменения угла атаки сильнее сказываются у тонких крыльев.
Предыдущий вывод сделан в предположении, что е
весьма мало, так что членами выше первой степени относи-
тельно е можно пренебречь. Для больших е более надежна
следующая оценка. Найдем, при каком значении угла атаки
точка отрыва дойдет до середины крыла.
Так как середине крыла соответствует значение
то формула (Iх) примет вид
или
(ctg е + 1) L+A г ... . * = о,82,
У1 — 2е +2еЗ (1 + е)3
откуда
0)
По формуле (4) можно рассчитать соответствующий угол
атаки. Вычислим по ней 6 при различных значениях е.
100 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Получаем:
при 8 = 0,05 ctg 6 = 16,4, 9 = 3°30':
» 8=0,1 ctg 9 = 7,99, 9 = 7°50л
» 8 = 0,2 ctg 0 = 3,54, 9= 18°10';
» 8 = 0,3 ctg 9 = 2,18, ’ 9 = 24°25'.
Сравним эти данные с углами, при которых начинается
отход отрыва струй от задней кромки. Называя предельный
угол атаки 90 и углы, найденные сейчас через 0, имеем:
£=0,05, 9о = 2°5О/, 6= 3°30', Д9 = 9 —90 = 0о40л,
е=0,1, 9О = 5°9', 9= ^бО', Д9 = 2°41';
£ = 0,2, 9О = 8°, 9=18°10/, Д9 = 10°10';
8=0,3, 6о = 8°30', 6 = 24°25', ДО = 15°55'.
Отсюда получается следующий практически важный
результат: у крыльев тонких (8 = 0,05) точка отрыва
струй очень быстро перемещается по крылу после от-
хода от задней кромки, так что при очень малом уве-
личении угла атаки за предельный угол крыло начинает
работать все целиком на срыв, что должно вызвать
резкое уменьшение подъемной силы и увеличение лобового
сопротивления. При увеличении толщины крыла переме-
щение точки отрыва в зависимости от увеличения угла
атаки за предельный угол становится все более медлен-
ным, а следовательно, ухудшение летных свойств крыла
происходит сравнительно медленно в зависимости от
увеличения угла атаки.
Если изобразить этот результат на диаграмме Лилиен-
таля, то получим следующие теоретические схемы поляр
Лилиенталя для тонких и толстых крыльев (рис. 45).
У тонкого крыла поляра Лилиенталя на малых углах
идет эквидистантно параболе индуктивного сопротивления
(благодаря сопротивлению поверхности); затем в искомой
точке А, которая соответствует предельному углу атаки,
она отходит от эквидистантной кривой MN, и очень близко
к А получаем точку, соответствующую тому углу атаки,
при котором крыло целиком начинает работать на срыв.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 101
Для толстых крыльев за предельным углом атаки, кото-
рому соответствует точка Alf кривая медленно отходит от
эквидистантной кривой и режим полного отрыва струй
наступает при углах, значительно больших предельного
угла атаки.
Как было указано выше, образование воздушных вихре-
вых насадков у передней кромки крыльев смягчает переход
от режима полного обтекания к режиму полного отрыва
струй. Благодаря этому поляры тонких крыльев не так
резко отличаются от поляр для крыльев толстых. Сравни-
тельно медленный отход поляры для тонких крыльев от
кривой MN, по-видимому, и указывает на образование
воздушных вихрей насадков, так как отход благодаря сме-
щению точки отрыва по предыдущему привел бы очень
быстро тонкое крыло к режиму полного срыва струй.
Весьма вероятно, что незначительное смещение точки
отрыва от задней кромки почти не отражается на летных
свойствах крыла, а следовательно, и на его поляре» Поэтому
на поляре Лилиенталя точка А (или AJ, соответствующая
началу отхода точки отрыва струй от задней кромки, в дей-
ствительности отмечает такой режим, когда точка отрыва
уже настолько отошла от задней кромки, что это перемеще-
ние делается заметным благодаря значительному уменьшению
подъемной силы и соответствующему увеличению лобового
сопротивления. Этим, возможно, и объясняется значительная
102 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
разница между предельными углами, которые дает теория,
и теми предельными углами, которые дает, например, изу-
чение поляр Лилиенталя; на полярах соответствующие углы
атаки для толстых крыльев (s от 0,2 до 0,3) получаются
в среднем градусов на 5 больше тех, которые дает теория.
В среднем можно считать, по данным Геттингенской
лаборатории, соответствующие углы атаки такими:
£ = 0,1, 0о= 12°х) вместо 60= 8°;
е = о,2, 9о=15° » о0=и°;
е = 0,3, 00=17° » 9о=11°ЗО',
где 90 вычислена по формуле (5) § 7.
§ 9. Все предшествующие выводы получаются из пред-
положения о линейности изменения давления вдоль верхней
поверхности крыла от точки, где давление минимальное, до
точки отрыва струй. Естественно поставить вопрос о том,
нельзя ли все сделанные выводы сохранить и при более
широких предположениях о законе изменения давления.
Легко видеть, что все выводы можно с такой же лег-
костью проделать и при более широком предположении.
Основное уравнение Польгаузена имеет вид
0,8 Г— 9072 + 1670.4Х — (47,4 + 4,8— (1 + X3]
ds _ L . \ U'2 J \ U'2J ]
dx~ U\— 213,12 + 5,76Х + X2]
где X — U'z, откуда z =
Л U , U"U
dx U' цЛ
0,8 9072+1670,4Х—^47,4+4,8— (1 + ^^)х8
— 213,12 + 5,76Х + Х2
Очевидно, что уравнение приведется к разделению пере-
менных, если
UU" п
U'2
1) 0о с поправкой на конечное удлинение.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 103
Вся предшествующая теория получена в предположении,
что С =—1. Выясним, какие получатся результаты при
любом С.
Из уравнения (2) имеем:
и' = AUC. (3)
Так как по условию задачи в рассматриваемом инте-
грале U' <0, то А надо считать отрицательным, а потому
будем (3) писать в виде
U' = — AU°.
Из (3) окончательно
1
U = [B — Л(1— фр-с . (4)
Уравнение (2) не содержит х; поэтому можно считать х
от произвольной точки поверхности крыла. Будем считать х
от той точки, где скорость наибольшая, и пусть расстояние
от нее до точки отрыва есть I. Тогда при х = 0 U = Vmax;
при х = I U = Ио.
Тогда из (4) имеем:
и = [Vma? — (ViTaf — , (5)
или, полагая
имеем:
= (7)
L I т ° | Z J
Формула (7) годится при С < 1; при С > 1 подобным же
образом получим:
или, обозначая I — х = у, получим:
104 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Наконец, при С = 1 получим:
и = v —
v max х
т 1
(9)
Выясним характер кривых, даваемых формулами (7), (8), (9).
Для этого найдем, как изменяется т в зависимости от С.
UU"
Подставляя ---— = С в уравнение Польгаузена, приведем
его к виду 2 —— D J UDUVIUIV X 1VHV1 CAJf О V/1 A CI. , 11 ^7 XI и ATI "° + =«(>-)". <‘«>
где
/(X) = \2_|_ 5j76x — 213,12, ।
т(X) = — 0,8k3 — 37,92k2-|- 1336,32k— 7257,6, I (И)
ф(к) = -f- 0,2k3 -f- 1,92k2 — 213,12k. J
Из (10) имеем: 0
Для вычисления интеграла составим таблицы значений
функций /(к), ср (к), ф(к) для целых к от нуля до—12.
Значения функций /, ср, Ф
/ (к) = к2 4 5,76 к — 213,12
к 0 — 1 — 2 — 3 — 4
213,12 — 217,88 — 220,40 — 221,40 — 220,16

к — 5 — 6 — 7 — 8
/(*) — 216,92 — 211,68 — 204,44 — 195,20

к — 9 — 10 — 11 — 12
/(Ч — 183,96 — 170,72 — 155,48 — 138,24
ИССЛЕДОВАНИЯ ПО ТЕЭРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 105
Ч>(Х) = — 0,8 ХЗ — 37,92X2 4- 1336,32k — 7257,6
X 0 — 1 — 2 — 3 — 4
<р(М — 7257,6 — 8631,04 — 10075,52 — 11586,24 — 13158,40
X — 5 — 6 — 7 — 8
<р(М — 14787,20 — 16467,84 — 18195,52 — 19965,44

X — 9 — 10 — 11 — 12
— 21772,80 — 23612,80 — 25479,64 — 27371,52
’ИМ = — 0,2 X3 + 1,92X2 —213,12 X
X 0 — 1 — 2 — 3 — 4
0 214,84 432,32 651,24 870,40

X — 5 — 6 — 7 — 8
1088,60 1304,64 1517,32 1725,44

X — 9 — 10 — 11 — 12
-ИМ 1927,80 2123,20 2310,44 2488,32
По этим данным легко рассчитать приближенно значения
интеграла; мы применим для этого приближенную формулу
106 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
трапеций
о
s= /кМд='»0)-+«<^> +
+ «(—l) + R(-2)+-.. + R(-ll).
Следующая таблица дает значения S для различных зна-
чений С:
С 3 С 3 С 3
— 60 0,046 — 6 0,127 3 0,204
— 50 0,050 — 5 0,132 4 0,224
— 40 0,060 — 4 0,137 5 0,242
— 30 0,070 — 3 0,144 6 0,271
— 20 0,086 — 2 0,152 7 0,306
— 10 0,109 — 1 0,160 8 0,366
— 9 0,115 0 0,170 9 0,458
— 8 0,118 1 0,179 10 0,662
— 7 0,123 2 0,191 11
Из (6) и (12)
уи — x .— g
т- уд -е .
Подставляя значение т в формулы (7), (8) и (9), получим
соответствующее изменение скорости вдоль верхней поверх-
ности крыла.
Рассмотрим несколько примеров.
Пусть С = — 60, тогда m = 1,047, а 4.
ГТ Z
При х = у получим:
1
^ = ^[1-1^ = ^11-0,006],
т. е. U почти в точности равно Игаах.
При С = —1 m = 1,2. Полагая х = -^, получим:
и = Vmax [ 1 - (1 - щ) т]2~ °-72у.
ИССЛЕДОВАНИЯ ПО ТЕОРИЙ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 107
Такйм образом, в рассматриваемых случаях кривая имеет
бйд, приближенно, указанный на рис. 46. Такой же вид
для кривой распределения давлений получается при С <—1.
В этом случае и распределение давлений следует такому же
типу; его можно назвать
вогнутым типом' рас-
пределения давлений; ему
соответствует значение
т <1,2 (точнее, 1,17).
При т=1,2 получаем
линейное распределение дав-
лений; этот случай для кры-
ла можно назвать нор-
мальным типом рас-
пределения давлений.
Рис. 46.
Наконец, при т > 1,2 (С > — 1) имеем распределение
давлений, изображаемое
выпуклой кривой; этот тип можно
назвать выпуклым тйпом
распределения давлений.
Все эти три типа схемати-
чески изображены на рис. 47:
/—вогнутый тип, II—нормаль-
ный тип, III—выпуклый тип.
Отсюда получаем следующий
приближенный метод для опреде-
ления точки отрыва струй.
Среди кривых распределения
скоростей (или давлений), давае-
мых формулам (7), (8), (9), надо
найти наиболее подходящую к эмпирическому распределе-
нию и по ней определить С и т. По найденным значе-
ниям С и т можно так же определить точку отрыва, как
это сделано в настоящей главе для случая нормального рас-
пределения давлений.
Заметим, что для случая круглого цилиндра по этой
схеме надо взять С около —60.
Заканчивая настоящую главу, считаем нужным отметить,
что создание теории отрыва струй от поверхности крыла,
по-видимому, является при настоящем развитии аэродинами-
ческой теории основной задачей, полное решение которой
108 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закРылка И Щитков
чрезвычайно важно для решения технических вопросов, свя-
занных с улучшением конструкции крыла. Приведенное выше
приближенное решение представляет только первый шаг
к полному аэродинамическому решению поставленной
задачи.
Все приближенное решение, приведенное в настоящей
главе, основывается на предположении о линейности распре-
деления давления на верхней поверхности крыла. Возни-
кает вопрос, нельзя ли обойтись без этого предполо-
жения.
Следующий прием естественно намечается для решения
этой задачи. Предположим сначала, что при данном угле
атаки отрыв начинается в задней кромке крыла. Тогда,
применяя общие теоремы, получим распределение скоро-
стей на верхней поверхности слоя, а по уравнению
Польгаузена—и соответствующее положение точки отрыва
Это дает первое приближение положения точки отрыва. Имея
точку отрыва, строим соответствующее обтекание и новое рас-
пределение скоростей на наружной поверхности слоя (72(х) и
по нему, применяя уравнение Польгаузена, найдем более
точное положение точки отрыва х2. Применяя несколько раз
такое построение, найдем последовательно xv х2, .. ., хп, . ..
и, предполагая, что существует limxw, что весьма вероятно,
найдем действительное положение точки отрыва x = limxw.
Но такой метод определения точки отрыва, представляющий
собой метод последовательных приближений, фактически
невыполним при настоящем состоянии теории по следующим
причинам.
Во-первых, задав точку отрыва струй от поверхности
крыла, весьма трудно определить характеристическую функ-
цию течения и распределение скоростей на поверхности
обтекаемого тела ввиду чрезвычайной сложности теории
струй для случая кривых поверхностей.
Во-вторых, определение точки отрыва при заданном U
на внешней поверхности слоя требует интеграции уравне-
ния Польгаузена, что представляет большие вычислительные
трудности.
С точки зрения изложенных выше соображений разра-
ботка двух вышеуказанных частных задач и является в на-
стоящее время очередным вопросом теории крыла.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 1б§
Глава III
ТЕОРИЯ РАБОТЫ ПРЕДКРЫЛКА
§ 1. Общие соображения. § 2. Основная формула. § 3. Опреде-
ление скорости у предкрылка. § 4. Окончательные формулы
для предкрылка; приближенное решение. § 5. Точная формула.
§ 6. Конструктивные выводы. § 7. Экспериментальные данные.
§ 8. Действие крыла на предкрылок. § 9. Распределение скоростей
у поверхности предкрылка. § 10. Замечания о распределении дав-
лений у крыла.
§ 1. Результаты предшествующей главы показывают,
что отрыв струй имеет место в случае, если падение ско-
рости достигает известной величины. Отсюда следует, что
всякие методы, позволяющие выравнивать распределение
скоростей на верхней поверхности крыла, увеличи-
вают предельный угол обтекания крыла и, следовательно,
улучшают его работу. Таких методов можно указать
несколько, но наиболее простой и практически применимый
состоит в добавлении вихря у поверхности крыла, позво-
ляющего выравнивать распределение скоростей. Конструк-
тивно такой вихрь осуществляется добавлением к крылу
дополнительного крылышка, работающего на обтекание и,
следовательно, вызывающего в потоке, обтекающем крыло,
такой же эффект, как вихрь, помещенный около поверхности
крыла. Отсюда намечается следующая основная задача:
определить влияние вихря, помещенного около поверх-
ности крыла, на распределение скоростей у верхней
поверхности крыла. С решения этой задачи мы и начнем.
Характеристическая функция обтекания цилиндра при
наличии вихря интенсивности Г в точке а == ре^ (р > 1) и
при основной циркуляции К вокруг цилиндра удовлетворяет
уравнению
— уе / j ___ g291 \____L -L J— (----1-------------- ]
dz \ z2 / 2л/ z ' 2л/ < z — ре^г 1 > ’
г Z----\
I р f
(1)
Предполагая, как это мы делали и раньше, что точка
схода помещается в точке цилиндра z=l, имеем:
г |----1---------1---1 0 (2)
v i_fe« 1_1 «
I P '
110 к Труды ПО ТЁОРЙИ ПРЕДКЁЫЛКА, ЗАКРЫЛКА И ЩЙТЁОВ
Исключая К из уравнений (1) и (2), найдем:
Функция, отображающая
на внешнюю часть крыла имеет
внешнюю часть цилиндра
на плоскости С вид1)
(1 —E)2COS2-^
_(l„s)cos|4--------------------.
(? — 1)е 2 +(1— e)cos-g
(3)
Отсюда
а .
,г (г— 1) (z—\)e 2 + 2(1—е) cos
А — z. - «»___L
dz -е Г
(z—l)e 2 +(1 —e)cos-|
И
р£?г"
(1 — ре^) (г — ре^)
_ а_ • I2
(z—l)e 2 +(1 —e)cos-|
р * CL
z (г— 1)е 2 +2(1 —е) COS-|
(4)
О См. § 2 гл. II.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 111
у — 1^.1
V° I U
Г
2ш
= V2cos94
Отсюда получим скорость Уо для точки схода, положив
z= 1:
Lefi
Р________
1—1 е'И')2
Р /
ре?< , (1—0COS 2
(1—р^)21 2
или
2ycos0 + —
1 к
sin ?
1 I2
-----2 cos ? I
р----J
- к Я
(1 — е) COS -у
--------9-----" • (5)
Для определения наибольшей скорости заметим, что она
получается около передней кромки крыла; приближенно
можно принять, что наибольшая скорость Утах получится
при z~—1.
Тогда из (4)
V
v max

________р£^________
(1 — (1 4- ре?*)
а . 2
;—2е 2 +(1 — e)cos^
а
— 2е 2* 4-2(1 — e)cos-|
или, подставляя
а . 2
-уг а
—2е 2 +(1—е) COS-?y
а а а
—2 cos у + (1—е) cos у + 2z sin у
= (l+£)3 cos3 у 4-4 sin3-^- =( 1—e)3 cos3 у — 4 (1— e) cos3 у + 4;
|—2e 2 -{—2(1—e)cos|-| = [ — 2cosy-(-2(l—e)cosy4-
-{-2isiny |=j/~4e2 cos2 y-{-4 sin2 y=2j/~e2cos2y -{-sin2y=
= 21Л(1—s)2cos24 —2(1—s)cos24-H -
Г 2 2
112 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
имеем:
(1-]- е)2 cos2-^-4~4sin2-^-
2|/~e2cos2-^ 4"sin3 77
(6)
Для оценки формул (5) и (6) заметим, что у крыльев
угол а весьма мал; поэтому, заменяя приближенно
а
cos2
через 1 и sin у через 0, имеем:
2Vcos9 +
(6')
Vmax= 2Vsin9
Для выравнивания скоростей на верхней поверхности
крыла нужно увеличить VQ и уменьшить Vmax; этого мы
достигнем, если
Г sin ср > 0 и Г cos ср >0. (7)
Чтобы удовлетворить неравенствам (7), надо
при Г > 0 взять ср в первой четверти,
при Г < 0 взять ср в третьей четверти.
Соответствующее расположение крыла и вихря в том и
другом случае ясно из рис. 48 и 49.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 113
Чтобы осуществить конструктивно первый случай, надо
было бы поместить у задней кромки крыла над его верхней
поверхностью перевернутое крыло (рис. 50); при этом,
однако, заметим, что такая конструкция мало выгодна
по следующим причинам. д
1. Скорость около задней
кромки сравнительно мала,
а потому и интенсивность <***^^^
вихря Г получится незна- f ___
чительная, а следовательно, —
выравнивание скоростей бу- Рис. 50.
дет слабее.
2. Сила, действующая на крыло В, направлена вниз, а по-
тому она уменьшает подъемную силу всего разрезного крыла.
Заметим, что второе соображение отпадает, если вихрь В
не принадлежит к несущей системе крыла; по-видимому,
это имеет место при наличии вихрей, отходящих от пред-
крылка. К разбору этого вопроса мы вернемся в другой работе.
Удовлетворить второму случаю мы можем, поместив доба-
вочное крыло у передней кромки под крылом (тс<а<"2“)
или перед крылом (а = тс). Выгоднее помещение перед кры-
лом, так как около передней кромки крыла скорость наиболь-
шая, а потому можно достигнуть наибольшего значения Г.
Это и приводит, очевидно, к применению для улучшения
летных качеств крыла так называемого предкрылка.
§ 2. Из результатов предшествующего параграфа легко
получить окончательные формулы для случая предкрылка.
Полагая ср = тс и ср = 0, получим для скорости максималь-
ной и для скорости в задней кромке выражения
г(р-----(1+е)2 cos2 ~ -|-4sin2 у
COS2-J--]-Sin2“
\ г / -1 г Z Z
Vmax= 2VsinH
г (l + e)acos2-^- + 4sin2-^-
= 2Vsin9 + —-2^-J------------r .....................(1)
I ' ' к p2—1J / a a
2y e2 cos3-£- + si°2 -%
Vo = Vcos 9 (1 — s) cos-x-. (2)
4
114 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Так как по
с задней кромки
результатам главы II для случая срыва
1,2, то имеем уравнение
-м 1,2(1—s) cos 2-1/ е2 cos2-2- —|—sin2-2-
to-9-к—___________Р___= __________-_____VL____________L1______?
Ь (р2—1) cos 6 „ 9 а 9 а
vr 7 (1 + £)2 cos2 -у + 4 sin2 -у
Ввиду малости угла а можно положить приближенно
cos -2=1 и sin у == 0; получаем:
fo- 9 ______Р — 1,2 е (1 е)
^ ^2кУ(р2—1)cosO“- (1 + s)2 ’ к 7
а замечая, что у предкрылка Г < 0, и полагая | Г | = J,
окончательно имеем:
to 0 = 1,2 £ Q.T £) -I_I____Р___ (4)
g (1 + £)2 (р2—1) cos 6 * k 7
Соответствующий предельный угол атаки без пред-
крылка 90 получится из (4) при J=0. Итак,
А _ 1,2е(1 — е)
(1 е)2 ‘ (5)
Отсюда получаем для приращения угла 9 от действия
предкрылка формулу
tg 9 tо- 90 = р2_ у —Q,
или
sin (9 — 90) = + +jCos90. (6)
Приближенно
^ = 0-00 = ^^005 90. (6')
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 115
Следовательно, для нахождения угла ДО надо определить
величину J.
Предположим, что предкрылок представляет собой неболь-
шую плоскую пластинку, поставленную у передней кромки
крыла (рис. 51); тогда, называя ширину предкрылка через Ь,
имеем по известной формуле теории крыла

где Va — скорость потока около предкрылка и 8— угол
атаки предкрылка относительно направления скорости
Рис. 51.
(относительный угол атаки). Следовательно, определение J
приводится к нахождению величины и направления скорости
потока около предкрылка; эти две задачи мы теперь и
разрешим.
§ 3. Для нахождения скорости у предкрылка мы имеем
формулу (4) § 1; кроме того, надо помнить, что вихрь сам
себе не создает скорости. Таким образом, для определения
скорости возьмем формулу
dw
Ж
X еi) 2
i) См., например, В. В. Голубев, Теория крыла конечного
размаха, стр. 161.
116 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закРылка и 1ЦЙТКОЙ
Следовательно, полагая z = = — р, т. е. ср = имеем:
а . 2
~ 'о" г а
— (р + 1)г +(1 —e)cosy
Р — (р + 0* 2 + 2 (1 — е) COS —
I L-Oi _ _|_ _1_______р______I х
1\ р ;-f-27^ (р + 1)(Р2-1) I А
а . 2
~ ~2 г Ct
— (P + D* +(1 — Ocosy
р - (р+1)/2 + 2(1 — е) cos2-^-
Рассмотрим член ъ ,гг-гъ—ггт—г~гг; взяв его модуль, по-
г (pJ—1)(р + 1)
лучим:
|_г________р_____| =
|2wV (р + 1) (р2- 1) I
_ 1 |Г| р 1 2^(р-у)р _ v j
“ 2" V (р2-1)(р+1) 2л У(р2-1)(р+1) Fp+1’
где v — скорость, создаваемая присутствием вихря Г в точках
предкрылка. Во всех аналогичных случаях предполагаем,
что скорость, создаваемая добавочными вихрями, мала срав-
нительно со скоростью потока; поэтому в сумме выделенным
членом мы можем пренебречь и получим приближенную
формулу
р
а . 2
9 г CL
— (Р + 1)<? +(1 — e)C0S-^
а .
а
— (р + 1)е +2(1 —е) cos
ИССЛЕДОВАНИЯ 110 ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАЙТЕ I 117
Так как
I I -> Г ( (A cos 6 \2 . / . ь , Sin 6 \2
|е-0г_.—1 = -|/ (COSO---) +(S1n6 + —) =
= /
— (р+0* 2 г4-(1 —e)cos у =
==[ —(p + s)cosy + i(p4- l)sin^-|2 =
= (Р + е)2 cos21 + (р + I)2 sin2 ~ .
По малости а можно положить приближенно, что рас-
сматриваемое выражение равно (р-[-е)2.
_(р+1)Г2< + 2(1-е)со5|| =
= j/~ (р— l + 2£)2cos2-J + (p+l)2sin2|;
и при малом а это выражение приближенно равно р— 1 2е;
следовательно,
1 +4—-cos26 "7 (ltE)a n • (2)
a r 1 p2 p p (p + — 1) v
При увеличении p стремится к Vt чего и нужно ожи-
дать; при уменьшении р и приближении его к 1 выражение
стремится к
V /2(1—cos 20) = V sin 0 (1.+/>3 ,
что и получено выше *).
Нетрудно найти и направление скорости Va. По общим
формулам имеем, называя через рь угол, образуемый ско-
ростью Va с действительной осью,
а Л ~ dz Л
х) См. гл. II, стр. 98.
118 I. ТРУДЫ ПО ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОЙ
и при малом а имеем приблизительно:
откуда
• / \
“ \ Р )
(р + Ю2
р (р- 1 +2е)
Va (cos [i — i sin p.) =
= V [cos 0 (1----) — i sin 0 (1 -j- —? о \
L \ Р/ \ ' p/Jp(p — 14-20
Следовательно,
cos= V (1-----? o~\ cos
‘ a \ Р / P(P —1 +2e)
sin = V (1 + —) —z о \'sin
r a \ г P J P (P — 1 + 2e)
откуда
tgp- = tgo^hl (3)
г
Из формулы (3) видим, что при увеличении р угол р
стремится к 0 и при уменьшении р до 1 угол р стремится к .
Так, при 0 = 20° имеем:
при р 1,25
р, 66°
1,5 I 2
61° I 47° *
Формулы (2) и (3) и решают вполне задачу, поставлен-
ную в предыдущем параграфе.
§ 4. Мы можем теперь легко получить окончательные
формулы, определяющие работу предкрылка.
Так как J=TtVab$, то, подставляя значение Va, получим:
j=k1z_(p + 42 t/~ 1+4 — 4 cos 29^, (1)
р (р — 1 + 2е) V 1 Р2 Р r V
где р — угол атаки предкрылка относительно набегающего
на него потока.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 119
Если назвать наклон предкрылка к действительной оси
через у, то из рис. 52 видим:
(2)
и по предыдущему
И
Подставляя найденное значение в формулу (6') § 2, по-
лучаем следующую величину для увеличения предельного
угла атаки:
= 2 (рЗ—1)J—1 4-2е) 1 7 COS 29 b$ COS 9°‘
Мы получим нижний предел соответствующего увеличения
Рис. 52.
предельного угла атаки, положив 9 = 0; тогда
Лб = 2р (Р + 1)(р — 1 4- 2е) C0S 9°’
или приближенно
дэ = 9 , , , 9 х ь$. (з")
2р (р + 1) (р — 1 + 2е) r V 7
Заметив, что хорда основной части крыла при сделан-
ных построениях равна 4, мы можем написать формулу (3")>
откидывая член е2, в виде
Д9=х2± p+j\------L (4)
Ар — 1 + 2е р + 1 v 7
Рассмотрим числовой пример. Пусть = 0,2, е = 0,2,
р 1,5, тогда
W=_2.0,2.^.^ = °.33f.
120 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Например, при р = 20° соответствующее- Д9 равно 7°.
При увеличении р выражение Д9 убывает. Так, если
в предшествующем примере взять р = 2, то получим
Д9 = 0,23р
и при р = 20° получим для Д9 около 5°. Этот результат
совершенно ясен, так как при увеличении расстояния оси
предкрылка до крыла быстро уменьшается Vai а вместе
с тем падает и интенсивность присоединенного вихря пред-
крылка.
Формула (4) или (3) показывает, что при увеличении е
величина Д9 убывает. Следовательно, предкрылок испра-
вляет тонкие крылья лучше, чем толстые. Наибольшее зна-‘
чение для Д9 получается при е = 0; тогда
Д9 = 2-^-Ц-4п-.
£ р — 1 р -р I
Полагая, как выше, -^- = 0,2, р == 1,5, получим:
Д9 = 0,41р.
При р = 20° получим Д9 = 8°; этот результат можно
применять для очень тонких крыльев.
В предыдущем мы приближенно заменяли в выражении (3)
0=0. Между тем угол 9 есть угол атаки при работе пред-
крылка, а потому в случае, когда 90 около 15° и соответ-
ствующая поправка около 5°, угол 9 будет около 20°;
в этом случае
cos 29 = cos 40° = 0,766.
Если подставить это значение в выражение для Д9, то
вместо
Д9 = 2р (р + 1) 1 +2е)
получим:
2(р2_ 1)(р_ 1 +2е) Г 1 ^р* р
Следовательно,
ДО' _ Ур2+1 —1,53р _ | о,47р
ДО ~ Р—1 — Г 1 (Р — 1)2’
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 121
В общем случае любого 9 аналогично получим:
, ДО' Г. , 1 — cos 20 _Г. , 4 sin2 0
= V ! + (p_f)2 Р = У i-b^ZTTjaP-
Так как 0, как показывают опыты, колеблется от 20
до 30°, то выражение k заключается в пределах
/14

0,47р
(Р-1)2
k
Р
(Р — 1)а *
Подсчитаем эти границы для различных р:
р 1 К ^(р-1)2
1,5 1,9
2 1,4
2,5 1,2
1/~ 1 Я-----—
У? = 2,6
Уз = 1,7
УУГ = 1,4
среднее
2,2
1,5
1,3
Так как Д9'= АД9 и в
личение угла атаки ДО', то
действительности мы имеем уве-
окончательно имеем формулу
ДО' = 2
Ь р + 2е ₽
L р-1+2е р+1
или
ДО' = до&,
где для k можно брать значения, даваемые таблицей.
Например, при р = 1,5, А —о,2 и е = 0,2 мы видели,
что Д0 = О,ЗЗр; следовательно, ДО'= 0,72,3; так, ДО'=10,8°
при 0О=15°, т. е. предельный угол атаки равен 26°.
При р = 2, ~ = 0,2 и е = 0,2 мы имели ДО = 0,23,3; так
как k = 1,5, то ДО'= 0,34,3; так, ДО' = 5° при 9О=15° и
предельнй угол атаки равен 20°.
Если взять среднее значение для множителя при ,3, кото-
рый, как видно, для интервала р от 1,5 до 2 и для 9 между
20 и 30° равен около 0,5, то получаем из всего предыду-
щего такой результат: ДО' 0,59о при = 0,2, т. е. от
действия предкрылка предельный угол атаки возрастает
приблизительно в 1,5 раза.
122 i. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Резюмируя все содержание настоящего параграфа, полу-
чим такой результат: от действия предкрылка предельный
угол атаки, при котором крыло работает на обтекание,
возрастает на величину
Д9 = 2 44 • ~ГТk?’
L р — 1 4- 2е р + 1 ‘
где коэффициент k дается таблицей и в среднем его
можно считать равным 1,8.
§ 5. Из формул (6) § 2 и (1) § 3 легко получить точ-
ную формулу для определения ДО, заменяющую приближен-
ную формулу (7) § 4, но менее удобную по своей слож-
ности для вычисления.
По формуле (6) § 2, подставляя туда значение J из § 4,
имеем:
sin де = ~ cos 60 V P2+l-2pcos26, (1)
НО
cos 20 = 1 — 2 sin2 9=1—2 sin2 (90 + ДО).
Полагая
b q (P 4- е)2 cos 0o - о g .... (P + £)2 . cqsq _ Л
2 Pp(p-l + 2£)(p2-l) ~ 2 L Hp(p-l + 2e)(P2-l) 0 ’
из (1) имеем:
sin2 ДО = A2 [(p — I)2 4- 4p sin2 (0o 4- ДО)], (2)
или
sin2 ДО = Л2 (p — 1 )2 (sin2 Д9 4- cos2 Д9) 4- 4рЛ2 (sin2 90 cos2 Д9 4-
4~ 2 sin 90 cos 90 sin Д9 cos Д9 4“ cos2 ^0 sin2
откуда
tg2 ДО {Д2 (p — 1 )2 4- 4Л2р cos2 0o — 1} + 4рЛ2 sin 20o tg Д9 4-
+ A2 [(p — 1 )2 4- 4p sin2 0o] = 0,
io- Afi - А 2Лр sin20o± У(р~ l)24-4p sin2 0o — (p2 — I)2 A2 _
tgau — А 1_Л2{(р_ 1)2 4-4p cos2 60} • W
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 123
Для выбора знака в формуле (3) заметим, что при 9о = О
из (3) имеем:
,вм-±л. (4)
1 —(р + 1)2^3 /1 — (р+1)2Л2 v
Отсюда видим, что для положительного tg ДО, что соот-
ветствует условиям задачи, надо взять знак плюс. Таким
образом, имеем окончательно следующую формулу для опре-
деления ДО:
Afi _ л 2Лр sin 20о + У(р - 1)2 + 4р Sin2 0О - (р2 - 1)2 Л2
tgAW — А 1_Л2{(р_1)2 + 4рСОз2 0о} ’ W
где
А = 2 ~ р —-----g—р- cos 90.
гР(Р — 1 + 2е)(р2 — 1) и
Рассмотрим пример. Пусть = 0,2, е = 0,2, р = 1,5,
9О=15° и 3=15°.
Тогда
Л-2 1 . 1 ^'О-97 -о и
5 4 1,5-0,9-1,25 — ’
1,5 • 2 • 0,17 • i + У 0,25+4 • 1,5 - 0,07—0,25 • 6,25 • 0,0289
tgA9 = 0,17
или
1 — 0,0289 (0,25 + 4 • 1,5 • 0,972)
приращения угла ДО величину 10,8°,
tg ДО = 0,20, Д0 = 11,5°.
Следовательно, предкрылок увеличивает угол, при кото-
ром крыло работает на обтекание, с 15° (без предкрылка)
до 31,5° (с предкрылком). Выше при помощи приближенной
формулы мы имели для
близкую к найденной.
Пусть еще ~ = 0,2,
Тогда
е = 0,2, р = 2, 90 = 15° и 3 = 15°.
1.1.А81=012
5 4 1,4-3 ’ ’
2 • 2 • 0,12 • 4 + /1 + 4-1 -0,07—9-0,014
tgA9==0,12
или
Д = 2 .
1 —0,014(1 + 4-2-0,972)
tgA9 = O,16, Д9 = 9°.
124 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Следовательно, в этом случае предкрылок увеличивает
предельный угол атаки с 15 до 24°. Выше по приближен-
ной формуле мы нашли ДО = 5, т. е. выведенная выше фор-
мула дает сильно уменьшенный ответ.
В предшествующих примерах мы брали угол 90 произ-
вольно. Но в главе II была дана следующая формула для
вычисления предельного угла атаки без действия пред-
крылка:
(1 _|_ е)2 » (6)
причем необходимо помнить, что надо взять поправку на
конечность крыла и, может быть, на то, что передняя часть
работает на обтекание при углах, значительно превосходя-
щих угол, определяемый по формуле (6). В § 8 главы II
дана формула, по которой можно вычислить угол, при кото-
ром точка отрыва струй доходит до средины крыла.
Заметим, что в формулу (5) входят углы, определяющие
интенсивность вихря; если отрыв происходит вдали от перед-
ней кромки, то под углом 9 в предыдущих формулах можно
брать угол атаки, при котором отрыв начинается около сре-
дины крыла.
Приведенные в этом параграфе данные дают увеличение
предельного угла атаки от действия предкрылка, согласное
с опытными данными, но формула (6) дает для 90 слишком
малые углы атаки; если их подставлять в формулу (5), то
также получим слишком малые, не согласные с опытом зна-
чения для ДО. Причину этого можно видеть в соображениях
этого параграфа и в данных § 8 главы II.
Если положить р = 1,5, 9=10°, р=15°, г = 0,2 и
~ = 0,2, то, произведя подобные же вычисления, получим
Д9 = 9° х).
Вообще при уменьшении 9 поправка Д9 уменьшается,
как видно из формулы (5); при -^-=0,2, е = 0,2, р = 1,5,
9 = 0, р=15° имеем по (4) Д9 = 6°.
9 Благодаря влиянию величины хорды предкрылка формула (3)
имеет место в гораздо более широких границах, чем (6). Ср. прим,
на стр. 94.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 125
§ 6. Полученные результаты приводят к следующим
конструктивным выводам.
Работа предкрылка сводится к выравниванию скоростей
потока на верхней поверхности крыла; это выравнивание
тем сильнее, чем больше интенсивность присоединенного
вихря, который определяется по формулам
(1)
или
J = ~V . (р + е,)а9 . 1/" 1 + 4 — - cos 20^. (2)
р (р — 1 + 2е) У 1 р3 р ‘ v 7
Из (1) имеем следующий результат:
1. Для усиления действия предкрылка надо помещать
его около передней кромки крыла, в точке, где скорость
обтекающего крыла потока наибольшая.
Из (2) следует, что при увеличении р уменьшается J.
Следовательно,
2. Предкрылок нужно помещать возможно ближе
к крылу, но таким образом, чтобы между предкрылком
и крылом оставалось такое пространство, которое
давало бы предкрылку возможность работать с образо-
ванием циркуляции вокруг него.
Далее по (2) следует, что J увеличивается с увеличением
угла р. Следовательно,
3. Предкрылок надо ставить под наибольшим отно-
сительным углом атаки, при котором предкрылок рабо-
тает на обтекание.
Если поставить предкрылок под таким углом атаки р,
что он будет находиться в условиях, при которых проис-
ходит срыв, то вся предыдущая теория неприложима. Можно
думать, что большие относительные углы атаки, при кото-
рых образуются срыв потока с предкрылка и завихренная
область за предкрылком, вызывают образование турбулент-
ного течения у верхней поверхности крыла. Таким образом,
если бы улучшение свойств крыла от действия предкрылка
вызывалось образованием турбулентности в обтекающем
потоке, то, по-видимому, выгоднее было бы ставить пред-
крылок под столь большими относительными углами атаки,
при которых поток срывался бы с предкрылка с образова-
нием отрыва струй.
126 I. ТРУДЫ . ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Опыт показывает, что относительные углы атаки пред-
крылка берутся такой величины, что предкрылок работает
в условиях более или менее полного обтекания; по-види-
мому, это обстоятельство может служить подтверждением
того, что причину, вызывающую при наличии предкрылка
улучшение летных свойств крыла, надо искать не в обра-
зовании турбулентности в обтекающем крыло потоке,а в дей-
ствии присоединенных вихрей предкрылка.
Вся предшествующая приближенная теория работы пред-
крылка основывалась на замене предкрылка одййм присоеди-
ненным вихрем; отсюда следует, что хорда предкрылка b
не может быть взята во всех предыдущих формулах боль-
шей сравнительно с Л, т. е. отношение ~ есть небольшая
дробь.
Но по формуле (2) видно, что интенсивность вихря воз-
растает с увеличением Ъ. Отсюда следует:
4. Хорда предкрылка не должна быть очень мала
сравнительно с хордой основной части крыла.
Из формулы (2) и из формулы (5) § 5 видно, что ДО
возрастает с увеличением угла 90. Следовательно,
5. Основная часть крыла должна быть взята такого
вида, чтобы она выдерживала без отрыва возможно боль-
шие углы атаки.
Мы видели в главе II, что для этого выгодно брать
крылья достаточно толстые, т. е. что наиболее выгодной
величиной г, как показывает теория, является 0,3.
§ 7. Можно привести экспериментальные данные, кото-
рые могут служить для оценки предшествующих выводов.
Мы рассмотрим один интересный пример, приведенный
в трудах Геттингенской лаборатории1).
На рис. 53 даны поляры Лилиенталя для разрезного
крыла при различных положениях предкрылка.
Расположение За. Предкрылок расположен далеко
от крыла и относительный угол атаки мал. По предыдущим
выводам и то и другое невыгодно и не может дать значи-
тельного улучшения свойств крыла.
- 1) «Ergebnisse d. Aerodynamischen Versuchsanstalt zu Gottingen»,
II Lieferung, стр. 57, 1923.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 127
Расположение ЗЬ. Предкрылок поставлен далеко
от передней кромки, в области, где скорость потока отно-
сительно невелика; кроме того, велико и расстояние пред-
крылка вообще от поверхности крыла. Предыдущее показы-
вает, что это расположение невыгодно: предкрылок не может
дать значительного улучшения.
Расположение Зс. Предкрылок поставлен близко
к крылу, в области, где скорость наибольшая; относитель-
ный угол атаки значительный. Расположение теоретически
выгодно»
Расположение 3d (с закрытой щелью между крылом
и предкрылком)* Крыло работает как сплошное; полость
между крылом и предкрылком, заполненная воздухом, спо-
собствует образованию в ней вихрей, увеличивающих лобо-
вое сопротивление.
Общий вывод тот, что наиболее выгодно расположе-
ние Зс. Это и подтверждается видом кривых Лилиенталя;
128 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
кривая Зс дальше всего идет эквидистантно параболе индук-
тивного сопротивления и работает в условиях обтекания
потоком. Следовательно, экспериментальные данные под-
тверждают полученные выше теоретические выводы.
Остановимся еще на одном приложении предшествующих
выводов. Известно, что у крыльев очень тонких или с острой
передней кромкой отрыв потока от крыла и образование
струй должны начинаться при малых углах атаки; однако
практически этого обычно не наблюдается. Наоборот, такие
крылья часто работают очень
хорошо, причем они работают
в условиях более или менее
полного обтекания. Причину
этого надо искать в образова-
нии вихрей у передней кромки
рис 54. крыла *) (рис. 54); но такой
вихрь впереди крыла играет
роль предкрылка, а потому он вызывает по предыдущему
увеличение углов атаки, при которых возможно обтекание
без срывов; отличие от предкрылка будет только в меньшей
устойчивости этого вихря сравнительно с предкрылком,
а потому и в более слабом действии вихря на выравнивание
скоростей на верхней поверхности крыла.
Возможно, что подобным же образом можно объяснить
и действие щитка, поставленного у цилиндра, на обтекание
цилиндра. Проф. Креллю (О. Kreil) принадлежат интересные
опыты о влиянии заслонок, поставленных у цилиндра, на
обтекание цилиндра * 2).
На рис. 55 изображено течение вокруг круглого глад-
кого цилиндра, точки отрыва начинаются приблизительно
при удалении на 45° от точки разделения струй. На рис. 56
имеем обтекание такого же цилиндра, у которого под
углом 45° от точки разделения потока поставлены перпен-
дикулярно к поверхности цилиндра тонкие перегородки.
В этом случае отрыв струй начинается значительно дальше
от точки разделения потока (приблизительно под углом 120°).
1) См., например, В. В. Г о л у б е в, Теория крыла аэроплана
конечного размаха, стр. 239.
2) Druckverteilnng an def luftumstromten Kugel, Zeitschrift f.
Flugtechnik und Motorluftschiffart, Jahrbuch 22, № 4, стр. 97, 1931.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I
Обычное объяснение этого состоит в том, что перего-
родки вызывают у потока турбулентность, а турбулентный
поток (по причинам, в настоящее время не выясненным)
лучше прилегает к обтекаемым телам, чем поток нетурбулент-
ный. Но можно объяснить это явление, исходя из приведен-
ных выше соображений. Действительно, если предположить,
что поток обтекает перегородку
без отрыва, то перегородка может
быть заменена вихрем (фиг. 57),
который направлен как вихрь пред-
крылка. Такой вихрь должен умень-
шать скорость у перегородки, а
потому, если перегородка постав-
лена в точке цилиндра, где ско-
рость наибольшая, то она вырав-
нивает распределение скоростей на
поверхности цилиндра, а потому
вызывает перемещение точки от-
рыва струй далее от точки раз-
деления потока. Надо, впрочем,
помнить, что у поверхности ци-
линдра давление, как показывают
опыты, изменяется не по линейному закону, а потому к
этому случаю изложенная выше теория неприложима; воз-
можно, что применение соображений, приведенных в главе II *),
х) См. стр. 107.
130 i. труды ilo Теорий предкрылка, закрылка и щитков
позволит перенести и на случай цилиндра соображения, ана-
логичные изложенным выше. Случай цилиндра оказывается
здесь гораздо более сложным,
л /z*****~**^'^ чем слУчай крыла.
U С——§ 8. Все предыдущие сооб-
ражения можно применить к дей-
Рис. 58. ствию крыла на предкрылок. Для
вывода соответствующей фор-,
мулы возьмем уравнение (5) § 1 настоящей главы. Если
считать, что хорда предкрылка перпендикулярна к дей-
ствительной оси, по которой направлена хорда основного
крыла (рис. 58),7 то ср = — и формулы (6') имеют вид
и
= О')
Отсюда
^0 _ Гн_ о _ Г(рЗ-1)р 1 е(1-е)
L S ‘ 2я (Р2 4- 1 )2 Sin ₽ V J (1 + ер ’
ТО
Так как для срыва-должно выполняться условие
max
Vo
Г(р2-1)р _ (1+е)3
ё 1 2хV(р2 4- I)2 sin р ~ 1,2 (1 — е) е •
1,2,
(2)
Так как для срыва при отсутствии добавочного вихря
выполняется условие
_ (1 + е)8
°~" 1,2(1 — е)е ’
то из (2)
ctg р ctg Ро == 27LV(p3 -4- 1)2 sin р
или
sin (^ р0) 2^ sin ро.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 131
Так как циркуляция Г отрицательна для рассматриваемого
случая, то, полагая Г = —J, получим:
sin(^ —po) = 2^^4^Ssin?o- (3)
Здесь J есть величина циркуляции основной части крыла;
по известной формуле
J = V’oqTc/ sin О,
где I — хорда основной части и 6 — угол атаки. Следова-
тельно,
V I sin 0 sin ₽ор (р2 — 1)
sin (Р - р0) = - 2lz(P4 ^------ ’ (4)
где V — скорость потока, которую он имел бы в отсутствие
предкрылка около его оси, р0— угол атаки, выдерживаемый
без отрыва струй предкрылком, взятым для крыла, 9 — угол
атаки крыла.
Пусть расстояние от средины крыла до оси предкрылка
равно R ; тогда для определения скорости на оси
предкрылка можно применить формулу
/ 1+^_2cos29 ^'+2.) <4 5>
где, однако, нужно ввести поправку на изменение масштаба.
Хорда крыла равна /; следовательно, радиус круга, изобра-
жающего сечение основного крыла, когда оно преобразуется
в окружность, равен . В формуле (5) соответствующий
радиус принимается равным 1; поэтому, чтобы применить
формулу (5) к настоящему случаю, нужно вместо р поста-
вить отношение
4
где pt — величина, характеризующая удаление предкрылка
от основной части крыла. Приближенно можно принять,
132 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
что расстояние до средины крыла, назовем его выра-
жается по формуле /? = р-|--|-, так как, если считать
малыми а и е, переход от круглого цилиндра к крылу
дается формулой t = z-\~ — и z = — р и t = — R. При
этих условиях получим:
________-__________ (±1 + е Y
^а = ^со1/ 1 +(-Л-У — COS 2 9 (6)
V ^\4Pi/ 2Р1 4£1/^1_1+2\ 4
Так как приближенно можно считать, что несущий вихрь,
« I
заменяющий основное крыло, находится на расстоянии -д-
Рис. 59.
от его передней кромки, то расстояние от оси вихря до оси
предкрылка получится по формуле
Окончательно получим:
sltl ZQ _ о s = VeoZslnBsin^^-l)
sin(P Ро2 2У(р2-}-I)2

Формулы (7) и решают задачу о величине изменения
предельного угла предкрылка под действием основного
крыла. На рис. 59 даны геометрические значения Z, pf
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ I 133
Рассмотрим пример: I = 10, -у! = 1,5, pt == 3,75, 9 = 25°,
30—15°,
р = 3,75 +1,66— 1,66 = 3,75,
11,0 • 1
. /0 10-0,42-0,26-3,75.13,06 п ло
sm (? — р0) =---------------= 0,08,
Р-р0=4,5°.
Таким образом, приращение угла получается меньше,
чем для основного крыла. Это объясняется неблагоприят-
ным расположением вихря относительно предкрылка.
Нужно, конечно, смотреть на приведенные здесь вычисле-
ния только как на определение порядка поправки, так как
все расчеты приближенные.
§ 9. Выведем общую формулу, дающую распределение
скоростей у поверхности предкрылка. В § 1 настоящей
главы дана формула (4)
— Q^i
Р
2 ОС 1
аг (г—1)е + (1 — е) cos -75-I
,2 __L_______________________
Г а .
2~ i сс
2 (г— 1)е * 2 +2(1 —E)cos-|
ре^
(1 — ре&) (г — ре^)
Пусть z — exi, тогда
134 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Г
2тс/
р#И
— ре&) (г — ре^)
—
_______Р__________
1---— (г-------—
Р /\ Р
__IWp |________1__________________1 |__
2тс/ 1(р — е^) (гр — е^) (1 — ре^)(г—ре^)1
х .
/> х
ГР(Р2
к(Р3+1—2р cos ср) [(р21—2р cos (ср — X)] * (1)
Следовательно,
— 2V cos
2_ e4>i
_Р____________________
(г —— <
Гр(рЗ
ре^
— ре^) (г— ре?*)
тс (р2 + 1 — 2р cos ср) [р2 + 1 — 2р cos(cp — л)]
При малом а, полагая cosy=l, sin у = 0, имеем:
Г
2
2
= 1 е2 — 2е cos X,
{z—1)е 2*-|-(1—e)cos4
(z—1)е —f—2(1—e)cos-^-
= V1 +(1 — 2е)2 +2(1— 2е)cosX .
Из (1) при замене Г через — J окончательно имеем:
^Х =
тс (р2 + 1 — 2р cos ср) [р2 + 1 — 2р cos (ср — X)]
14-е2 — 2е cos X
/1 + (1—2e)3 + 2(l—2e)cosX '
ИССЛЕДОВАНИЯ ИО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ 1 135
Рассмотрим скорости на задней половине верхней поверх-
ности крыла, т. е. когда Так как 9 < , то
cos ^9---^г) > 0* Если sin (у — ср^>0, то второй член
в скобках формулы (2) показывает, что в рассматриваемой
области поверхности крыла скорость увеличивается от при-
сутствия вихря J, а следовательно, давление уменьшается.
Таким образом, присутствие около крыла добавочного
вихря может вести к выравниванию давления около верхней
поверхности крыла; такой эффект вызывает присутствие
крыла у предкрылка. Для определения величины выравнива-
ния рассмотрим следующий числовой пример.
Пусть угол атаки предкрылка 9= 15°> угол атаки основ-
ной части крыла ^ = 20°, ср = — 60°, р = 4, е = 0 и хорда
основной части крыла равна Z. Тогда J = nVl sin (3 = tzVI< 0,34.
Подставляя в формулу (2), получим:
2lZcos(15° —^4-
4-15 sin(4+60°)
I V7 . п Q4.4 10 ___\ z____/_1_
-t-VL 13 17_8cos(60o_|_X)
ИЛИ
1
п * ’
2 cos -g-
[17—8 cos (60°4-Х)] cos А
Вычисляя по этой формуле при значении К, равном 0°,
45, 90 и 135°, получим следующие значения:
К = 0°, Ух = V (0,97 +10,052);
X = 45, Vx = V (1,08 +10,044);
К = 90, = V (1,22 +10,044);
k= 135, Их = 17(1,60 + Z0,065).
Рассматривая полученные выражения, видим, что можно
подобрать такое Z, при котором от К = 0 до К == 90° (т. е.
на задней половине верхней поверхности крыла) скорость
постоянна.
136 I. ТГУДЫ ЙО ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Для этого, очевидно, должно быть:
1,22 + /- 0,44 = 0,97 + /- 0,052,
откуда / = 31,25.
Так как при сделанном предположении (е = 0) пред-
крылок представляет
собой плоскую пластинку длины 4,.
то хорда крыла приблизительно в
восемь раз длиннее хорды пред-
крылка.
Отрезок хорды крыла, на ко-
тором скорость и давление постоян-
ные, равен ^=2+1,41=3,41,
т. е. составляет ^-=0,85 всей
верхней поверхности крыла.
Таким образом, распределение скоростей и давлений на
верхней поверхности крыла принимает совершенно необыч-
ный для крыла вид. Схематически
распределение давлений указано
на рис. 60 вместо обычного рас-
пределения, указанного сплош-
ной линией.
Экспериментальные данные
вполне подтверждают приведен-
ные выше выводы.
Приводим график рис. 61
распределения давлений на пред-
крылках, по данным измерений
ЦАГИ1) (угол атаки крыла 15°).
Подобным же образом можно
подсчитать давление и на ниж-
ный поверхности крыла, но опре-
деление величины давления на ней
едва ли можно надежно выпол-
нить предыдущим способом. Бли-
зость основной части крыла и
сравнительно узкий проход, который остается между задней
кромкой предкрылка и основной частью крыла, значительно
1) За сообщение материалов приношу мою глубокую благодар-
ность инж. П. П. Красильщикову.
К ТЕОРИИ РАЗРЕЗНОГО КРЫЛА
137
уменьшают скорость предкрылка; этого обстоятельства нельзя
учесть, если влияние основной части заменяется, вихрем.
§ 10. Результаты предыдущего параграфа указывают
на возможность распределения давлений на верхней поверх-
ности крыла, приближающегося к прямэугольному, т. е.
замены действительного распре-
деления давлений вида АВС рас- 4
пределением давлений вида AB'C I
(рис. 62). Такое равномерное рас- R {
пределение подсасывающей силы |\ у
на верхней поверхности крыла I4’-----
во многих отношениях представ- \ В'
ляет значительные выгоды; от-
сюда намечается задача, какими рис. 52.
техническими приспособлениями
можно добиться в значительном интервале углов атаки рав-
номерного распределения скоростей и давлений на верхней
поверхности крыла.
Вероятно» этого можно достигнуть подсасыванием потока
у задней кромки крыла, благодаря чему увеличивается ско-
рость у задней кромки крыла. Такого же эффекта можно
добиться размещением вихрей вблизи поверхности крыл&,
частный случай чего как раз и представляет разобранное
выше разрезное крыло х).
К ТЕОРИИ РАЗРЕЗНОГО КРЫЛА * 2)
В работе по теории разрезного крыла3) было изучено
влияние предкрылка на выравнивание скоростей на верхней
поверхности крыла и на проистекающее отсюда увеличение
предельного угла атаки.
В настоящей заметке изучается влияние предкрылка на
смещение критической точки на крыле; это смещение также
х) Вторую часть этого исследования см. на стр. 291. {Прим. ред.).
2) Опубликовано в сборнике общетеоретической группы
НАГИ III, Труды НАГИ, вып. 240, 1935. {Прим, ред.)
3) В. В. Голубев, Исследования по теории разрезного крыла,
ч. I, Труды ЦАГИ, вып. 147, 1933, [см. настоящее издание, стр. 31—
137].
138 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
ведет к увеличению предельного угла атаки, причем подъем-
ная сила не уменьшается.
При помощи конформного отображения можно область
течения отобразить на внешнюю часть круглого цилиндра.
Предполагая, что хорда предкрылка мала, заменим пред-
крылок одним вихрем, расположенным в точке z = а вне
цилиндра |z|=l, изображающего крыло.
Пусть скорость потока в бесконечности равна Voo и
образует с осью х угол 0; пусть циркуляция вокруг цилиндра
равна Г и циркуляция вокруг предкрылка равна J. Тогда
характеристическая функция течения имеет вид
w
Г , . J . z— а
--InzH---In---—
2uZ 2rcZ z — a
где
a = p^ и a = у e'^
отсюда
- si (i _ , _L 1 , f _L_ _
dz Vc°e I.1 z> )' z 2nZ U — a
Предполагая, что одной из критических
схода) является точка z=l, имеем:
(1)
z — a f
точек (точкой
г2^)- &
Исключая из (1) и (2) Г, приведем выражение производ-
ной характеристической функции к виду
<3>
aZ Z \ \ Z / (г-- д) (г-др
где
А =----£(я —«) __ , (4)
2к (1 — а) (1 — а)
Отсюда для скорости на поверхности цилиндра получим
выражение
A [cos (i-A+< ‘'"(Р11) 1 5)
dz 2 L \ 2/ 1 г— cos(? — |x)J
где
W^K и г=4(р + 7)’ г =
К ТЕОРИИ РАЗРЕЗНОГО КРЫЛА
139
- В случае, если интенсивность вихря J достаточно велика,
на цилиндре получатся четыре критические точки, одной
из которых является точка z=\\ ей соответствует значе-
ние ср = 0.
Для нахождения остальных трех точек надо решить
уравнение
cos fo — -|)k— cos(<p — p.)] + Ksin — h) = 0. (6)
Решение этого уравнения можно свести к решению кубич-
ср
ного уравнения с неизвестным tgy.
Называя корни этого уравнения через а, р, у, можно
свести уравнение (5) к виду
dz — zv^e
sin sin g- sin У-2-- sin -
Г— COS (ср — р.)
(7)
Можно доказать, что между углами а, {3, у и р. суще-
ствует соотношение
« + ? + l = 29 + 2tx + K. (8)
Если через а называть угол, соответствующий смещен-
ной точке разделения струй, то угол
2о = а — к — 29
можно назвать смещением критической точки. Точно так же
назовем смещениями критических' точек, образованных от
действия вихря J, углы р — р и у — р-. При этих обозначе-
ниях уравнение (8) выражается следующим образом.
Сумма смещений критических точек под
действием добавочного вихря J равна нулю.
Это свойство обобщается на случай произвольного числа
добавочных вихрей. Предполагая, что смещение критической
точки разделения потока невелико, можно из уравнения (6)
приближенно определить величину 5. Получим:
* =________К cos (6 — р)______
r+ cos (26 — р.) 4- /<sin(6 —р) ’ w
140 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Так как обычно предкрылок помещается вблизи перед-
ней кромки, то приближенно можно написать:
* __ К COS (6 — у,) rqZ.
г + cos (26 — у)’ У '
или, заменяя К его значением:
*______________Р COS (6 у.) ✓ <
cosy г 4~ cos (26 — у) ’ v '
Отсюда
а = 20-4-23. (И)
Из формулы (10) видим, что, так как J< 0 и при обыч-
ном расположении предкрылка у близко к к и 0 мало, то
8 < 0, т. е. присутствие добавочного вихря уменьшает угол а,
что равносильно кажущемуся уменьшению угла атаки, так
как по (11) вместо угла атаки 0 имеем кажущийся угол
^аки fr-pS < 0.
Из результатов, полученных для разрезного крыла х),
оказывается, что при этом подъемная сила не уменьшается,
но слегка увеличивается сравнительно с подъемной силой,
соответствующей углу атаки 0.
При небольшой величине циркуляции J добавочного вихря
критические точки потока, возникающие от этого вихря,
будут вне цилиндра, а потому углы р и у будут мнимые.
При этом формула (7) примет вид
SIn3L^zzl) + sh32.
. ср ср —а 2 ' 2
Sln 2 Sin 2
dW QI7
Г — COS (ср — у)
(12)
2
где
, = щ , S = (г+ 8 {1 +3 tg(9-А)}
и Д = у — к.
Если положить
Г— COS (ср — у)
1) В. В. Голубев, Исследования по теории разрезного крыла,
ч. I, Труды ЦАГИ, вып. 147, 1933, стр. 17 [см. настоящее издание,
стр. 56].
К ТЕОРИИ РАЗРЕЗНОГО КРЫЛА
141
то формулу (12) можно написать в виде
^ = 8V„s-<’+-J)‘sln|sln’^i. (13)
Так как для обтекания цилиндра без добавочного вихря
имеем аналогичную формулу
= sin-2sin“T~’ (14)
то присутствие добавочного вихря сводится:
1) к изменению положения критической точки разветвле-
ния потока (а =^4-28);
2) к изменению величины скорости на поверхности ци-
линдра благодаря присутствию множителя L в формуле (13).
Как было указано выше, изменение положения критиче-
ской точки влечет за собой кажущееся уменьшение угла
атаки при небольшом увеличении подъемной силы. Можно
показать, что присутствие множителя L влечет за собой
выравнивание скорости на верхней поверхности цилиндра,
так что скорость обтекания уменьшается вблизи предкрылка
и увеличивается вдали от него. Эффект действия этого
выравнивания и был изучен в первой части работы «Иссле-
дования по теории разрезного крыла».
Таким образом, увеличение предельного угла атаки про-
исходит за счет двух факторов:
1) не ухудшая характера обтекания, можно увеличить
в присутствии предкрылка предельный угол атаки на вели-
чину (8), определяемую по формуле (10);
2) можно еще увеличить предельный угол атаки за счет
выравнивания скорости, происходящей от присутствия мно-
жителя L\ расчет соответствующего увеличения указан
в «Исследованиях по теории разрезного крыла».
Необходимо отметить, что увеличение предельного угла
атаки на (8) совершенно не зависит от характера обтекания
и структуры пограничного слоя.
Все предыдущие соображения целиком переносятся на
случай крыла любой формы, причем величина интенсивности
добавочного вихря J, заменяющего предкрылок, определяется
методом, указанным в «Исследованиях по теории разрезного
крыла».
142 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
О РАБОТЕ КРЫЛА
С ОТСАСЫВАНИЕМ ПОГРАНИЧНОГО СЛОЯ1)
Настоящая заметка представляет собой попытку дать
аэродинамическую теорию влияния отсасывания на работу
крыла.
В случае обтекания цилиндра с отсасыванием погранич-
ного слоя можно определить характеристическую функцию
течения в области z — оо уравнением вида
dz 00 ’ 2kZ z 2u г ' г2 * ” ''
где Г—циркуляция скорости, Q — мощность источника
в бесконечности.
Применяя в этом случае уравнение Чаплыгина—Блазиуса,
получим силу давления потока при помощи формул
Г = — pVoo(rcos6 — Qsin 0), I
Х= — pVco(Гsin0 — Qcos9). J (2)
Разлагая силу по направлению скорости потока в бес-
конечности и по направлению, к нему перпендикулярному,
идя чего достаточно положить в (2) 9 = 0, получим:
= —рУооГ, (3)
X^UZ^pVooQ. (4)
Формула (3) дает подъемную силу Жуковского, а (4)
дает силу импульсивную, возникающую от отсасывания.
Для обтекания цилиндра с отсасыванием пограничного
слоя рассматриваем течение, определяемое характеристиче-
ской функцией, заданной уравнением
где k= 1, = р2 = eia*, причем точки и являются
концами щели на поверхности обтекаемого цилиндра. Се-
1) Опубликовано в Технических записках ЦАГИ, № 45, 1935.
(Прим, ред.)
О РАБОТЕ КРЫЛА С ОТСАСЫВАНИЕМ ПОГРАНИЧНОГО СЛОЯ 143
кундное количество втекающей через щель жидкости опре-
деляется уравнением
Обозначая через / интеграл, входящий в предшествую-
щую формулу, имеем:
и (5) принимает вид
^*1 + %
dw qle 4 С — 1
1 —*M)G —*
Разлагая (7) в области С = оо, имеем:
cos 1-Т-- - . q sin 7?- - • 1 -
dw . 4 1 ч 4 1 f 1
~dT~~iq I T I C 'T'caV • )•
(8)
Из (6) и (8) можно определить значение /:
——- , = 2тс sin а*-у-аз = 2тс sin а. (9)
, Ф — он , а2 — ср 4
у sin -^-2 sin -^-2.
Для определения сил давления потока на круглый ци-
линдр применим формулы (2), получим:
X = pV^o cos 9 — 4tcV’oo sin2 0 — q ctg у sin 9J,
Y = pVoo [4тсУоо sin 9 cos 9 q ctg ~ cos 9 -|- q sin 9
144 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Добавочные компоненты сил от влияния отсасывания вы-
ражаются формулами

cos (4 ~ 6
ду=рую9__Ц_
sin Т
Из (10) следуют формулы
ДР = рУсо? ctg, 1
ДГ = pVmq. J
(10)
(И)
Отсюда имеем вывод: от действия отсасывания
увеличиваются и подъемная сила и лобовое
сопротивление; увеличение не зависит от угла
атаки и прямо пропорционально количеству
отсасываемой жидкости и скорости потока
в бесконечности.
Переходя к случаю крыла, получим те же формулы (10).
Скорость потока на поверхности крыла дается формулой
Vp = 4Vm {cos (б—1) +
I q 1________ ______1 — 2 cos уе + &__ . J
4lV sin / l+2cosy(l-2e) + (l-2e2) • 1 '
Подсчет распределения скоростей на поверхности ци-
линдра по формуле (12) приводит к выводу, что меняется
распределение скоростей на поверхности крыла в резуль-
тате отсасывания и вместе с тем изменяется предельный
угол атаки, при котором крыло работает в условиях обте-
кания. При этом получаются следующие выводы:
1) увеличение предельного угла атаки имеет место только
для крыльев достаточно толстых (е^>0,1);
2) щель невыгодно помещать близко к задней кромке;
при этом чем толще крыло, тем ближе к задней кромке
надо помещать щель.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
145
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА1)
§ 1. Постановка задачи
Среди различных приспособлений, применяемых для улуч-
шения аэродинамических свойств крыла, самым старым и
лучше всего разработанным* конструктивно является так на-
зываемое разрезное крыло. В простейшем случае разрезное
крыло представляет собой основное крыло, у которого на
некотором расстоянии от передней кромки добавляется
маленькое добавочное крыло, предкрылок, или добавляется
добавочное крыло около задней кромки, закрылок. Такие
крылья были введены еще в 1921 г. одновременно Хэндли-
Пэджем (Handley-Page) в Англии и Лахманом (Lachmann)
в Германии и получили довольно широкое применение в со-
временном авиастроении. В 1921 г. одновременно с экспе-
риментальными работами Хэндли-Пэджа и Лахмана было
напечатано обширное теоретическое исследование С. А. Ча-
плыгина, в котором было подробно изучено разрезное
крыло, состоящее из двух или нескольких отдельных перьев,
представляющих собой в сечении отрезки одной и той же
прямой или окружности; исследование было проведено
в предположении полного обтекания без образования струй
в условиях плоскопараллельного течения.
С иной точки зрения изучалась теория разрезного крыла
в работе В. В. Голубева2); в ней автор ставил себе зада-
чей изучить влияние предкрылка на образование отрыва
струй от поверхности крыла, причем предкрылок заменялся
одним присоединенным вихрем предкрылка и, следовательно,
не учитывалось влияние размера (хорды) предкрылка.
Настоящая работа посвящена теории крыла с предкрыл-
ком или закрылком в первом из указанных выше направле-
ний: в ней изучается плоскопараллельное течение, обтекаю-
щее без срыва крыло, состоящее из основной части и
предкрылка или закрылка, причем и основная часть крыла
Ч Работа написана совместно с академиком С. А. Чаплыги-
ным. Впервые опубликована в Трудах ЦАГИ, вып. 171, 1935.
(Прим, ред.)
2) В. В. Голубев, Исследования по теории разрезного крыла,
ч. 1, Труды ЦАГИ, вып. 147, 1933 [см. настоящее издание, стр. 31].
146 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
и добавочное крыло принимаются в виде плоских пласти-
нок, наклоненных друг к другу под малым углом. Поста-
вленная задача, очевидно, представляет собой частный слу-
чай задачи о работе биплана и, как все задачи о биплане,
приводит к применению эллиптических функций. Предпо-
ложение о малости угла наклона добавочного крыла к основ-
ной части крыла значительно упрощает задачу.
Метод исследования состоит в том, что двусвязная
область течения, ограниченная сечениями основной части
крыла и добавочного крылышка, отображается на внутрен-
ность прямоугольника во вспомогательной плоскости; внутри
построенного вспомогательного прямоугольника и строится
течение, изображающее течение несжимаемой жидкости, обте-
кающей разрезное крыло.
§ 2. Отображение плоскости с двумя вырезами
Построим на вспомогательной плоскости комплексного
переменного (и) прямоугольник A'B'C'D' со сторонами
А'В' — (« и A'D' = у и рассмотрим эллиптическую функ-
цию с периодами 2w и 2 а/ (рис. 1).
Легко показать, что функция
7
Рис. 1.
z = а
фи — фаГ
(1)
где а — действительное положительное
число и 0<а<р<у, дает отобра-
жение внутренности прямоугольника
A'B'C'D' плоскости (и) на нижнюю полуплоскость. Известно,
что при изменении и вдоль сторон прямоугольника A'B'C'D'
переменное z действительно, и мы получаем следующее
соответствие между точками плоскостей (и) я (z):
и 0 со со coz al
2 а e2 — ?ai es — $al 0 оо
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
147
Так как при р> а
то из равенства (1),
получим:
Отсюда мы видим,
прямоугольника
№ > рои,
положив
dt — ‘
что z при изменении и вдоль сторон
О, со, а) -|~ а/, со'
уменьшается, так что
е2-^1 е3-^1 0
e1 — ^ai е2 — pal —
Следовательно, изображения вершин прямоугольника 0, <о,
ci)-j-u/, а/ на плоскости (и) будут действительные числа,
Рис. 2.
изображаемые точками Л, В, С, D плоскости (г), как пока-
зано на рис. 2, и прямоугольник A'B'C'D' конформно ото-
бражается на нижнюю полуплоскость (г).
Если взять на плоскости (и) прямоугольник A' A"D”DJ
со сторонами и о/, то по принципу симметрии он пред-
ставляет собой конформное изображение двусвязной области
плоскости (г), ограниченной отрезками DC и ВА (рис. 3);
148 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
стороны A'D' и Л"/У' соответствуют разрезу на плоскости (г),
идущему от точки А через оо к D по действительной оси,
стороны А'А" и D'D" соответствуют двум сторонам разре-
зов АВ и CD, причем А'В' и D'C' соответствуют нижним
краям разрезов АВ и DC, а В'А" и С'/У'— верхним краям
тех же разрезов. Так как
^z —p«Z
du (фи— (PaZ)2

то в точках и — 0, w, (d4-w\ о/мы получим — =0 вслед-
ствие того, что в этих точках ф'и = 0, а потому конформ-
ность отображения нарушается, как это и видно непосред-
ственно из рис. 3.
В разобранном случае разрезы DC и ВА лежат справа
от точки 2 = 0; изменив несколько вид функции, можно
поместить точку z = 0 или между разрезами, или на раз-
резе. Для этого достаточно взять вместо р/ другую точку
Уд (z)
D СО В A О С В J
—о—<*|> и > £ "°-0
Рис. 5.
на сторонах прямоугольника A'B'C'D'. Так, если взять
функцию

(2)
то на плоскости (г) точка z = 0 окажется между разрезами
АВ и CD (рис. 4). Точно так же, если взять функцию

(3)
где 0 < b < (о, то точка z==0 окажется на разрезе CD
(рис. 5), при этом на стороне /У/У' (рис. 3) точке z = 0
соответствуют точки их~ d -\-Ь и и2 2 св— причем
первая точка изображает точку О на нижнем краю разреза,
а вторая — на верхнем краю разреза.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
149
§ 3. Определение постоянных отображения
их следующим образом.
(Z)
Л ,

Для отображения двусвязной области плоскости (г) надо
по данным точкам А, В, С, D на плоскости (z) определить
коэффициенты a, Ь, а, р и периоды w и а/. Предыдущие
формулы позволяют определить
Рассмотрим отображение на
прямоугольник в случае располо-
жения разрезов, указанном на
рис. 6. В этом случае отобра-
жение дается функцией
фи —
z = а %------------.
фи — фа1
6—
XI
С В
В
Рис. 6.
Назвав
ственно
что
длины разрезов и расстояние между ними
через Л, g, /, как указано на рис. 6, и
соответ-
заметив,
za = а;

имеем:
h-zA—
h — zA zB — a ei_^a[ ,
hA_,Zt Zn~a^l~^ai
h + l~zA-zG-a e^_^ai ,
h + l + g^z^ — zD = a-^—^r,
________
& ° D — j?aZ) G?3 — Jf'aZ) ’
n ^l-e2)(^i-lpal)
B G~
+ £ в d a{ei_pal){e3_pai).
отсюда
е2 g3 _ gh — ^2 _
^1 — ^3 + W + O ^1 — ^3 U + W + /)*
Как известно, модули k2 и k2 функций Якоби выра-
жаются через е2, е3 в виде
£2 ^2 ^3 ^2 —_. ^2
— ^3 ’ 1 е1 — е3 *
150 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Следовательно, в рассматриваемохм случае имеем:
Ь2 _ _ &
и
/(A + ff + Z)
1 U + 0(A + Z) ’
(4)

(Z.)
Рис. 7.
D С В
Как легко увидеть, все предшествующие результаты
останутся в силе и в случае отображений, даваемых функ-
циями (2) и (3). Незначитель-
ная разница получится только
в том, что вместо выражения
^Z— ficd войдут в формулы
соответственно ft (со -|- $1) — paZ
в случае (2) и $ (Ь 4~
в случае (3). Таким образом,
например, в случае (3) получим (рис. 7):
П~а в1-ра1 ’
(ei-pal)(e2-pal) ’
~=а (g2-g3) W +
S (e2 — — pal) ’
откуда
. — в2 __ I #2 — ^3 ___ S
e2 — h>* e2~^al I + h + g
и равенства (4) останутся без изменения.
Добавив к равенствам (6) соотношение
ei + е2 Ч” ез = 0»
А
(5)
(6)
(7)
найдем отношение величин
£2 £з_ £«£
ei ’ ei * ei 1
и так как во все предшествующие формулы входит только
отношение величин elf е2, е3, paZ, (jp(£—}— cdz), то можно по-
ложить, например, е1=1, и тогда найдем е2, е3, fiai. При
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
151
определении всех этих величин можно идти следующим пу-
тем. Определив по формулам (4) k2 и k2 и воспользовавшись
формулой
£2 = ^2 — ^3
21 — ^3
или
2*2 + *1 = <2 =
2*i + *2 “ (g + l)(h + l)
и положив
^=1. (8)
найдем
__ 2А>2 — 1
е2— 2 —
И
1 + 1 /О\
*3 1 2__#2 • (9)
Найдя е2 и е3, определим периоды по формулам1)
1 -к', «/ = r..L^-K', (Ю)
V <?! — es У ^ — e3
где
тс
1 ¥
к _ Г___________dx________= f dy
J У (1 — х*)(1 — №х*) J У1 — sin* ? ’
0 \ (11)
1 2
Д-/ = f_________dX________— f __ _____
J ]/(l — x2)(l — Л2х2) У ]/1 — k\ sin2 <P
Рассмотрим числовой пример. Пусть
Тогда
/г=Ю, Z=l, g=2.
,2 2-10 20
k ==зйГ= зз’
,2_ 1 • 13 _ 13
Л1 ~ 3-11 — 33
(й2+^= 1).
9 См., например, L. Bianchi, Lezioni sulla teoria delle funzioni
di variabile complessa e delle funzioni ellitiche, Pisa, стр. 352, 1901.
152 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Отсюда по формулам (9) на основании равенств (8) и (7)
мы получим:
— Л — _ 53
*2 ~ 46 ’ *3 “ 46 '
Зная ev е2, е3 и k* 2 и найдем по формулам (11) К и К'.
Положив k — sin 6 и kx = sin 0V найдем в настоящем случае
0 = 51°7' и 01 = 38°52' и по таблицам1) имеем:
К= 1,9561, К' = 1,7733.
Отсюда по формулам (10) найдем:
ш= 1,333, (1)'= 1,208/.
Для нахождения а определим по формулам (6) ^aZ; из
первого равенства (6) найдем:
««'-4Ы1 +*)-‘I-
В рассматриваемом примере имеем

383
— 46 ‘
Отсюда можно определить а. Для этого можно воспользо-
ваться уравнением2)
1 + &? 1 1
^aZ = ~зхз уз /а ’ 02)
где
х == .
Подставив в уравнение (12) найденные значения paZ, fe? и
найдя л2 = — , получим из этого уравнения
sn(y, ^==0,4804.
9 См., например, С. П. Г л а з е н а п, Математические и астро-
номические таблицы, Таблица XIV, стр. 79.
2) См., например, Appell et Lacour, Principes de la theorie
des fonctions elliptique, стр. 158.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
153
Отсюда, помня, что = 38°52', найдем1) по таблицам
V = 0,5085 и а = 0,3466.
А
В дальнейшем нам будут нужны еще значения ^'а/, Са/
и %]. Покажем, как можно их определить. Перемножив
равенства (5), получим:
h (/ + h) (g4-/ + Л) =
= а3 IP(t> + а/)^г), (13)
p/2ai = 4 (pai — ej (j?al — e2) (j?ai — e3),
следовательно, из уравнения (13) имеем:
- 4„. |Н> + *') ~ 1W „ „ +t) +, + (14)
Но из уравнений (5) мы находим:
a [j? {b + a)') — paZ] = (/ + Л) (е2 — fpai);
подставив сюда е2— JpaZ из равенства (6), имеем:
a IP (Ь + «') — paZ] = (е, — ег) (/ + Л) |.
Следовательно, по формуле (14) имеем:
5 ai l4s + i + h) •
Отсюда, заметив, что
Г«‘ = -2' [i+
т. е. при малых положительных значениях a
p'a/== —2ZN,
!) См., например, С. П. Г л а з е н а п, Математические и астро-
номические таблицы, Таблица XV, стр. 80.
154 I. ТРУДЫ Ito теории ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
где N— положительное число, мы из равенства (15) окон-
чательно получим:
= 21 ,2)1 (16)
В разобранном выше примере
^'а/ = — 47,63/.
Для вычисления т] можно воспользоваться формулойх)
тс
т
Tj = ег — е3 j* У1 — k2 sin2 ср dy — ^о).
о
В рассматриваемом примере k = sin 0 и 6—5Г7'. Отсюда
по таблицам2) мы находим:
тс
f у 1 — Jfe2 sin2 <р d<? = 1,2955
О
и
т] = 0,5687.
Наконец, для нахождения Са/ всего проще воспользо-
ваться формулой
Га/ = -___а3/3______а6/6
w al 60 140 * ’ ”
т. е.
где
g2 = — 4 (ere2 + е±е3 -f- е2г3), g3 = 4e1e2e3.
Подставив найденное выше значение а = 0,3466, найдем
в рассматриваемом примере С = — 2,894/.
Приведенный расчет относится к случаю отображения,
даваемого функцией (3); весь расчет можно повторить с не-
существенными изменениями и в случае функций (1) и (2).
1) См., например, L. Bianchi, стр. 385.
а) С. П. Г л а з е н а п, Математические и астрономические
таблицы, Таблица XIV, стр. 79.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
155
Выше мы видели, что а заключается между нулем
и у, а b — между нулем и w. Если а мало, то замечаем,
что можно приближенно написать:
h а, )
I — г2) а2, } (17)
gva^- е3)а2. )
В этом случае I и g весьма малы Рис. 8.
сравнительно с /г, следовательно, мы
получаем расположение, схематически указанное на рис. 8.
Пусть, обратно, а близко к ; тогда близко к е3,
и, положив aZ = w' — v, найдем приближенно
paz==(?34--^v2p"(a/).
Но из уравнения
г2 = 4 . ej Щи — ег) Щи — е3)
получим:
о 7 [ 1 1 1 I 1
р'« I fiu — er ~ Р« — е2 “И фи—-е3
Отсюда, подставив и — <о', имеем:
= 2 (е3 — ej (е3 — е2).
Следовательно,
— е3 = (е3 — q) (е3 — е2) (о/ — at)2.
В этом случае
g _ (<?2 —<?3) (£i — ________________(ег — <?з) (*t — gs)______
I (e,—e2)(e3 — %>at) ~ / ш' \2 ’
’ (ei — e2)(e3 — e1)(e3 — e2){— — a)
t. e.
£_____________!_________
I ~ . . / o>' \2 •
(^i — ег) ----“J
Таким образом, в этом случае g велико сравнительно ,с /;
подобным же образом найдем, что g велико и сравнительно
156 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
с h. На рис. 9 указано схематически расположение разре-
зов в этом случае.
В дальнейшем мы будем рассматривать случаи, когда h
представляет собой сечение основной части разрезного крыла
и g—его предкрылка или закрылка. Очевидно, что в этом
случае надо считать а величиной малой.
Переходим к определению роли величины Ь. В случае
отображения, даваемого функцией (3), имеем:
__ е2^^(^ + Ь)
Ш zc — a e2-$)al ’
откуда при малом а приближенно
находим:
Рис. 9. _ е2~ $(<*'+Ь)
Zd~ — S? <<*' + ь) *
Так как b изменяется
величина ^((о'4~^) близка
от нуля до (о, то при малом b
к е3, а потому отношение
гя
велико, и мы имеем расположение, указанное на рис. 10.
Если же b близко к w, то + близко к е2 и отноше-
ние (18) мало; в этом случае имеем расположение, указан-
ное на рис. И.
Рис. 10. Рис. 11.
Наконец, относительные величины I и g при малом а
определяются значением е2. Действительно, если Z > g, то
по формулам (17) мы находим:
откуда
е2 > е2
ег < С
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
157
Следовательно, если / > g, то е2 < 0; обратно, если I < g,
то е2 > 0. Так как из равенства (17) мы получаем
g—I — Заа2е2 = 3/га2е2
и из них же при ех — 1 находим
1 1 1
а2 Д — 1 ^2>
ТО
a2=^3H- <19>
Эта формула дает приближенный способ определить а; она
приближенно верна при малом а. В разобранном выше при-
мере (h— 10, g = 2, /=1) мы по формуле (19) получим:
а2=4- и а= 0,361,
что довольно близко к найденному выше более точному зна-
чению 0,3466.
Подобным же образом можно рассмотреть случай, когда а/
близко к а/. Так как в этом случае приближенно имеем
Ы = е3 + (aZ — u>') (е3 — ej (е3 — е2),
то получим следующие приближенные формулы:
е1 — ^3
l + ^a HU-')-».,
' ^2 — ^3
Б • и 1 »
-(aZ—
/ ~ a gi — g2 + «>') — «я .
^~es |(a/_e')8|)V
Отсюда
___________j______ ^2 п______р 4~— g3________
S е2 — еъ ( w'\2/
2 V-------Г/ (*3 —^)G?3 —*2)
158 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Из этого выражения мы видим, что Z > g при е2 > 0 и / < g
при е2 < 0. Таким образом, и здесь знак е2 определяет
относительные размеры / и g,
§ 4. Отображение плоскости с двумя разрезами.
Общий случай
От разобранного в предшествующих параграфах ото-
бражения на прямоугольник плоскости с разрезами АВ и CD,
лежащими на действительной оси (или вообще на одной
прямой), можно перейти к общему случаю отображения пло-
скости с двумя прямолинейными разрезами, уже не лежащими
на одной прямой. Очевидно, что для этого достаточно
построить функцию z = у (и), определенную внутри прямо-
угольника с вершинами О, о), <о —со', о/ плоскости (и) и
обладающую следующими свойствами:
1) функция cp(zz) на противоположных сторонах прямо-
угольника A'D' и A"D" в соответствующих точках прини-
мает равные значения, т. е. cp(zz) имеет период 2со (рис. 3);
2) на стороне AfА" функция cp(zz) действительна;
3) на стороне D'D” значения функции расположены вдоль
прямой, которую далее будем предполагать проходящей
через точку z = 0;
4) внутри прямоугольника A'A"D”D' функция cp(zz) одно-
листная, т. е. всякое значение принимает один раз;
5) функция cp(zz) внутри и на сторонах прямоугольника
принимает значения, покрывающие всю плоскость комплекс-
ного переменного.
Для построения таких
ные выше отображающие
писать иначе, выразив их
применяя формулу
функций заметим, что разобран-
функции (1), (2), (3) можно на-
через функции о. Действительно,
ст (и — а) а (и, -f- а)
можем переписать формулу (1) в виде
_______________________ о (и — р/) ст (rz -f~ РО g2gZ
% а (и — al) ст (и al) ст3^/ *
или, так как а2а/ и о2р/ действительны, то, положив
ст3а/
e> = ai’
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
159
где ах— действительное, можно написать:
_ g (zz — ftZ) cj (а + $1)
1 а (и — aZ) а (и -|- aZ)
(20)
Подобным же образом можно преобразовать и функции (2)
и (3); получим соответственно:
__ g (zz — ю — р Z) ст (zz -|— со —$1)
Z a (^ — aZ) a (и 4* aZ) a2 (co 4- ^Z) *
__ a (u — <oz — b) a (zz 4~ <*>z 4~ b) 1
Z ’ a (u, — al) g (u -|- a0 °2 (oj/ + b) ’
(21)
(22)
причем a± — действительное число.
Введя в выражения (20) и (21) действительный пара-
метр b и в выражение (22) действительный параметр с,
построим функции
a(u — b — $i)a(u, — b-\-$l) *4 ~ *
а (и — al) <з (иal) *
g(u — b — о — ftZ) g (zz — 4~ щ 4~ PO u
g (zz — al) g (u -|- al) g2 (<o 4" 0Z) 1
(23)
(24)
g (a — — <DZ) g (a 4- Z> 4- a)z) 1 ~ ™
1 g (и 4- c — aZ) g (w 4"c 4~ a0 a2(<oz4-^)
Покажем, что функции, определяемые уравнениями (23),
(24) и (25), удовлетворяют условиям 1)—5) и, следовательно,
дают отображение прямоугольника A'A"Dr'Dr на плоскость
с двумя прямолинейными разрезами.
1) Покажем, что функции (23), (24) и (25) имеют
период 2о). Для этого рассмотрим функцию
СО Г/А = с (а — 6 — m) g (zz — 6 4- ю) (&+С) ~
YW а(^4-с —n)g(zz4-c4-n)
Положив в <p(zz) соответственно т — р/, n = az, с = 0, или
т — а) 4~ РЛ п = az, с = 0, или т = о/, п — al, мы получим
переменные части функций, определяемых уравнениями (23),
(24), (25). Таким образом, достаточно доказать, что функ-
ция cp(zz) имеет период 2<о. Так как
а (и — b — т-\- 2(d) — — е2г^ (.и-ь-тл-ш) a
160 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
И т. д., то
? (и + 2ш) =
X
_ ^^е2^{-2Ь-2с}-F4TJ (6+с) = ср (ц),
что и требовалось доказать.
2) При действительном и и действительном а± функции,
определяемые уравнениями (23), (24) и (25), действительны;
таким образом, выполняется и второе условие.
3) Покажем, что функции (23), (24) и (25) удовлетво-
ряют и третьему условию. Для этого найдем <р («—|—ш').
Так как
о (и — b — т + о/) = — (и-ъ-т) а3(ц — Ь — т) аи/
и т. д., то

g3(u — b — т) <з3(и — bт) (&+<>)
°з (и + с — п) с3 (и 4- с + п)
где
{(w-6-w»)+(u--b + w»)-(u+c-n)-(u+e+n)}^273 + ш
= e2{b+c)(.r>
Ь+с .
---- г
ш
Применив полученное соотношение в случае функции, опре-
деляемой уравнением (23), получим:
z (и 4~ <*>') =
g3(g — 6 — ftp g3 (ц — 6 + $1)
с3 (и — al) а3 (и -|- al)
п ь ь
2т — и тс —
е ш е ш
i
Отсюда следует, что при изменении и вдоль прямой А' А"
(рис. 3) функция zt определяемая уравнением (23), изме-
няется вдоль прямой, наклоненной к действительной оси под
углом
b
и == тс — .
Г СО
Функция
03(а — — $i) a3(u — b + $t)
с3 (и — al) а3 (и 4" «О ’
К ТЁОЙИИ ПЁЕДКЁЫЛКА и ЗАКРЫЛКА
161
как произведение двух комплексных сопряженных чисел,
при действительном и есть число положительное. Отсюда
следует, что при изменении и вдоль стороны D'D" функция,
определяемая уравнением (23), принимает значения, лежащие
на отрезке CD, направление которого проходит через
точку z = 0 под углом
b ук и
и —тс — к действительной оси н ь
<о я т /Г “
(рис. 12). Беря различные b г ?
в интервале от нуля до 2со, од Л
мы получим различные углы рис 12.
наклона от нуля до 2тс.
Перейдем к функции, определяемой уравнением (24).
В этом случае, положив по предыдущему
ю ЛА — ° — Ь — ш W ° — b + 03 + U
а (и — az) а (и + ai)
мы получим:
/и I (У) а8(и ——<0 —^)»8(ц —6 4-ш + РО
Ч4 ' ~ cj3(zz — а/) сг3 (zz-f-а/)
Но
<j3 (и — b -|- <*> -j- ро = е ~ v ~6 ь ш+р*)
и
о (zz — b —о) —pz* —о) ) == о (и — Ъ — со —|— р/ —|— со —|— 2со) -—;
=— (и-Ъ+№+<»')q — ь — со —р/—со) =
_ _ (и-&--<о + Зг)аз ш +
Таким образом,
аз (и — b + w + РО =
_______(и-Ъ + ш + {и-Ь-w + pi)^2iQ (и-Ь + fii-ha»') х
X о3 (и — Ь — и)-|~р/) = — <»+2’1<»'e2r) (и-b)+2rfi
X в3(«—ь — °> + Р0
и
"ГС .
2 — I
2т^(о -- 2 --------- |
162 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Следовательно,
о3 (и — b + а) + р/) = е2^и (~6)+2^а3 (и — b — ш 4" р/).
Итак,
ср = q3 — & — <*> — РО °3 + РО
а3 (и — al) (J3(zz4-aZ)
о Ь Ь .
2*у) • - - эд тс %
g2vj (u—b) + 2vfiig * ш g <»
С другой стороны,
о (о) —|— pz) == ^^р/аа).
Отсюда имеем:
Z (ll —j— (D ) =
а c3(u-b-<*-$l)a3(u-b-<* + W {u^b)e2ri
1 а3 (и — al) а3 (и al) з2р/а2со
Так как
а3 (и — b — со — ₽/) а3 (и — Ь — со
а3 {и — al) а3 (и 4- al)
есть количество положительное, как произведение двух ком-
плексных сопряженных количеств, и — число мнимое, то
тс — i
г (и 4-о/) — Re* ш \
___ где R—число положительное.
<^с В Следовательно, в рассматривае-
мом случае изображением точек,
лежащих на стороне A'D" (рис. 3)
Рис- 13- на плоскости (zz), служат точки
отрезка CD, как указано на рис. 13.
Рассмотрим, наконец, случай функции, определяемой
уравнением (25). Из выражения
— n ф-Ь-^(и + Ь + »') e2ri^u
' * 1 а (и -j- С — al) а (и Ц- с а0 а2 С*0' +
имеем:
2tj — и 2т]
, __ a(u — b)a(u + b + 2^)e ш е ш
Z W а (и -|- С — al 4- <^z) а (zz с 4" + wZ) q2 4"
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
163
Но
o(zz b -|- 2а/) = — е2^ (w+&+«/)0 (ji
о (и -|- с — а/ + о)') = — (м+саг43 (и-\-с — ш) <зо/,
а(и 4“ с + а/-|- <*/) — — е4 <м+с+а%з с 4~ а/) оа/,
о (а/ Ь) = — 6.
Следовательно,
2:(zz4-(d,) = — X
у__________^(и — Ь)а(и + Ь) е2^ (и+ь + ш')_____е2^и
а3 {и С — а/)а3 (и -|- С 4~ а/) а4а>43 Ье2^Ье2^’ (и+с)
ИЛИ
2(M+<o')=-fllH-----------а(М-6),(ы + 6) >
а3 (и С — al) а3 (и 4" С-\-аГ) а4 со
где
rt <ОГ п , 2с , , . СТС .
2тс-----2т/с ----(гш'-г/w) - I
Н — е ш = е ш = е ш .
Так как в рассматриваемом случае прямоугольника перио-
дов т/ и и/ — чисто мнимые, то —действительное.
Таким образом, можно написать:
с .
z (u-]-^) = Re^
где
п = _ п ^(u — b)a(u + b) 2V ш, =
1 °з (и 4“с — «0 <?з (и 4~с + а0
= а a(b-u)a(b-\~u) с^ш,
1 сз (и ~Ьс — а0 аз (и 4"с 4" а0
Так как знаменатель R — число положительное, как произ-
ведение двух комплексных сопряженных количеств, то R
меняет знак при проходе и через значение b и при
u — b R = 0.
Следовательно, в рассматриваемом случае изображением точек,
лежащих на стороне DfDrf, являются точки отрезка CD
164 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
(рис. 14). Таким образом, во всех трех случаях выполняется
и условие 3).
Переходим к доказательству того, что функции вида (23),
(24), (25) удовлетворяют и условию 4). Действительно, пусть
k — некоторое число, отличное от тех значений, которые z(u)
принимает на сторонах прямоугольника A'A”D"D' (рис. 15).
Покажем, что внутри этого прямоугольника найдется один
корень уравнения
z(u)— k = Q.
Для этого
Так как
то
а потому
найдем величину интеграла
Г zf (и) du
I z (и) — k ’
A'A"D"Df
z (и + 2(о) == z (и),
Г zf (и) du Г zr (и) du
J z (и) — k J z (и) — k ’
A"D" A'D'
Г Z' dtL I [ Z ________________i
J z(u) — £ ' J z(u) — k '
A”D" A'D'
Следовательно,
f zf (u) du Г zr (u) du x f zr (u) du
J z (u) — k J z(u) — k ' J z (u) — k '
A'A"D’'D' A'A1' D"Dr
Покажем, что оба интеграла правой части равны нулю.
Достаточно это доказать, например, для первого интеграла.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
165
Сделав в нем замену z (и) — t, получим:
где правые интегралы берутся по действительной оси между
А и В, Так как k не лежит между А и В, то интегралы
взаимно уничтожаются. Следовательно,
А,А"Ъ"П'
J z(u) — k
Отсюда, назвав через М и N соответственно число нулей
и полюсов функции z (ц) — k внутри прямоугольника A'A”D"D',
имеем, что
M = N.
Но функция z(u) имеет внутри A'A"D"D' один полюс пер-
вого порядка в точке и = 2о>— с-|-а/ (или, при отрица-
тельном с, в точке —с—|— а£), а потому
N= 1,
что и требовалось доказать.
Из предыдущего рассуждения следует, что z^u) внутри
и на сторонах прямоугольника A'A"D"Dr принимает значе-
ния, соответствующие всем точкам плоскости (г); при этом
всякое значение, соответствующее точкам сторон прямоуголь-
никач<г(и) принимает два раза, что соответствует двум сто-
ронам разреза, в которые переходит на плоскости (г) пери-
метр прямоугольника. Таким образом, для функций, опре-
деляемых уравнениями (23), (24), (25), выполняются все ука-
занные выше условия.
Подводя итоги этого параграфа, укажем:
1) функция
дает отображение прямоугольника A'A"D"D' на плоскость (z)
с разрезами АВ и CD, как указано на рис. 12;
166 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
2) функция
g (tt — 6 — Z|3 —• 0)) СТ (tt — 6 + ^ + 272 4 и ((27\
а (и — ai) а (иal) $1) ' '
дает отображение прямоугольника на плоскость (z) с раз-
резами АВ и CD, как указано на рис. 13;
3) функция
Z (и — b — Z (и ~ b + о/) Ъ и
z~~ а а (и — al) а (и + а/) (<>' + b) k >
дает отображение прямоугольника на плоскость (z) с раз-
резами АВ и CD, как указано на рис. 14.
§ 5. Отображение плоскости с двумя разрезами, случай
малого угла наклона
В случае, когда АВ и CD лежат на одной прямой, точ-
кам А, В, С, D на плоскости (z) соответствуют точки О,
со, (D-|-ca,, со' на плоскости (и). Найдем, какие точки на пло-
скости (и) соответствуют концам разрезов в случае, когда
АВ и CD образуют друг с другом некоторый угол, кото-
рый мы в дальнейшем будем считать малым, для чего доста-
b / с \
точно считать, что — или — есть величина малая или
(О \ (О /
что Ь (или с) мало, так как, очевидно, можно считать u> = 1.
В случае отображения, даваемого формулой (26), заме-
тим, что в точках А, В, С, D конформность отображения
нарушается, а потому имеет место уравнение
dz 1 dz
-— = 0 или —=0.
du z du
(29)
При b = 0 это уравнение принимает вид
du ($и — (paz)2 °
оно имеет корни
и = 0, и = со,
и соответствующие им точки на плоскости (z) суть
et— (?8Z е2—^1
хл = а> хв^а±-^, Хс=а£_П_,
и = СП ,
(30)
D е3-фаГ
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
167
Следовательно, при малом b корни уравнения (29) мало от-
личаются от значений (30), а потому имеют вид
ZZq, (О—О) —|— U)Z —ZZ2,
где
1«о1> 1«1|> 1«2|> 1«з1
— величины малые.
В случае отображения, даваемого функцией (26), при
b #= 0 уравнение (29) имеет вид
7£ = r’(“-&—+
— С(м — at) — С(«4-а0 + 271^- = 0. (31)
Разложив выражение (31) по степеням и и Ь, считая их
малыми и ограничившись первыми степенями, получим:
« {— Н— — Р (^) + Р (— to) + Р (to)) +
+ z>{H_zp)+m)+2_i j = 0.
Отсюда
P^+v
“° Р^ — $>lab' (32)
Точно так же мы найдем и корни и±, и2, заменив в урав-
нении (31) и соответственно через о> —|—4/, или а) -|- а/ и,
или и разложив выражение по степеням и и Ь. Мы
получим:
P(“+W+-J-
“1 = + Ь’
Р (<> + <"'+ ^)+“-
“2 = + + (М-Ь<о' + /а) Ь'
Р (“'+ОД+ -}
“3 р (о/ zfl) — (р (о/ la)
Заметим, что
Р («+»>+<»')=—(«+(Ь+О = е2+;
168 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
отсюда, проинтегрировав в пределах от нуля до 2со, найдем:
— С (2в) + оз 4- со') 4-: (и) 4- o)z) =
2ш
= 2ше2 -J- (е2 — ех) (е2 — е3) | 4=4, ’
О
или
2ш
2*1 = ~ 2ше2 4- (ег — е2) (е2 — е3) J ^4 е,
6
и
2<о
Л । р _ (gi — ga) (ei ~ f du п
<о ' 2 2«> J — е2
О
Точно так же из уравнения
Р (« + «>') = е3 4- (<?3~4
получим:
2ш
+ е3 = — (4 — е3) (е2 — е3) J ^4 < °'
б
Так как
W < е3,
то
^ + |<4 + ^<0;
точно так же
p(u>4-u>,4-Zp) > е2,
а потому
P(a)4_tt)'+zp)+i>o,
+ «₽) < ?3
И
Ки/ + <-р)4_|< о.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
169
С другой стороны, при р > а мы получаем:
J’zp > pZa, #» (<» + /р) < Н0) + Za),
р (w -f- ц/ _|_ Zp) = jja (о) и/ — /р) > Р (ш -j- ш' — la) =
= F (“> + о)/ + Za),
F (о/ 4- Zp) = $ (и)' — Zp) < <Ц> (о/ — fa) = $ (и/ + Za).
Следовательно, при положительном b имеем:
«о
О,
«1
О,
«2
zz3
0.
Точки, изображающие концы разрезов на плоскости (zz),
при положительном b расположатся, как указано на рис. 16.
При этом сторонам прямоуголь-
ника, соединяющим вершины со
7
(U)
А'
Uo
________в'
CU+U;
Рис. 16.
(t)+(i)+U2
Рис. 17.
с (n-|-(j/ и о/ с 0, соответствуют на плоскости (z) некото-
рые линии /t и /2’ расположенные, как указано на рис. 17.
Зная значения zz, легко найти соответствующие значения z.
Действительно, разложив выражение ~ по степеням и и Ь,
мы получим, ограничиваясь вторыми степенями малых величин:
In у = {: (- Zp) + (Z?) — : (- Za) - : (Za)) и +
+ {- с (- zp) -: (/р)} ь+1 {[- р (_ zp) - ^zp +
+ Н— Za) + $?Za] + 2 [j? (— Zp) + j?Zp +
+ l-pzp—^Zpj*2}’
или
ln-|- = у {—2 (jazp — ^Za) и2 4-4 ^zp +-^^«/7 —2^zpz>2 ).
170 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Подставив сюда значение и0 по выражению (32), имеем:
отсюда, перейдя от логарифма к «числу» и ограничившись
второй степенью Ь, имеем:

(33)
Точно так же найдем:
z, _____ю/й J (j? (w + z’₽) + —)
Zb = а I 1 + [ + (<o + Za)— ®
e^ZG^ae-^=^\
e2 — %>ia (
2
’ L (“ + 0)/ + Zf') — jp (ш /a)
$ ((0-|-(JO,-|-/p) Ь2 j ,
2
+ b2 ,
(36)
где Za> Zb, Zq, z^ — значения z в концах разрезов. Совер-
шенно тот же прием можно применить и в других разобран-
ных случаях. Так, в случае отображения, даваемого функ-
цией (27), вместо уравнения (31) получим:
— id — b — z₽)-H(zz + (o — b-\-i$) —
— г (и — ai) — С (и -|- a/) -|- 2tq = 0,
откуда аналогично предыдущему найдем:
(Р(о, + ед + А
“° = IP (» + /₽) — $»(«> +1«)Ь'
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
171
Подобным же образом, если заменить и через (d-|-zz, или
о) —|—g)7 —zz, или и/ -\-и, получим приближенные значения uv
из'
M1 pz₽ - Р (® 4~ «Г ’
Р (“' + *₽)+ ^-
j? (и' -}- $ (® -|- ш' -f- la)
P (<-> + <»'+ 40 +-J
M3 IP (ш 4- ш' 4- zp) — (P (u>' 4- ia) b’
Подставив найденные значения в выражение для z, анало-
гично предыдущему получим:
zA= а
Р(“ + 40+4
_ Р (“ + 40 — Vla
_ _ *1-P(“ + 4O
в~ ^1—pi® I
1 +
P(o>+i₽)
р/р — Р (<> + «)
— pip №{,
е~^гс = а
12 —Р(о> —<[3)
<?2— (р/а
1 +
(р (<>' +40+ ^У
IP (О)' + i₽) - IP (ш 4- о/ 4-/а)
— Р(ш' + /Р) />2
^з—Р««
(р(“ + «'4-/3)4-А)2
.P(“4-«'4-if>)-P («' + «)
Перейдя к случаю функций вида (28), получим уравнение
С (и — b — и/) —{— С (it -j- b —и/) — С (# —j— с — (хГ) —
— С (и -|- с «0 + 2?]с = О,
172 I. ТРУДЫ ПО ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА и Щитков
из которого аналогично предыдущему имеем:
“° —+ pal С' (37)
Р (« + /«) +
“1 = p(<o + <o' + *)-S?(<o + aZ) С’ (38)
(р (<В4_м'_|-а/)_|_Л
“2 = Н" + *) - !Р (“ + “' + “О С’ (39)
Р (“' + «0 + 77
м3 = уЬ __ (о/ aZ) С • <4°)
По найденным значениям и найдем соответствующие значе-
ния z\
2
__ a {
ZA - o3 (<>'+*) I
a
jZ((0' + 6)-Spaz + ^a4J c2j’
гл~~ a* («'+/,)
(41)
ex — jpaZ
7) Д
^(w + aZ) С2
(42)
e -*iz„ = a g2 — 8?(“Z + »)
G ay (a/ b) e2 —
(w 4- a>' 4- az)
+ P (“' + «0
1
c21. (44)
Формулы (33)—(36) дают следующий важный результат.
Если оставить периоды постоянными и заменить угол на-
клона, т. е. изменить b или с, то, как показывают эти фор-
к ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
173
мулы, при этом изменяются и Za, Zb, Zq, z^, t. e. не только
отрезок CD поворачивается вокруг точки z = 0, но и изме-
няются длины и расстояния концов отрезков от точки z = 0.
Но, если считать b (или с) величиной настолько малой, что
можно пренебречь членами с квадратом этих величин, то фор-
мулы (33)—(36) принимают более простой вид. Если назвать
через z*A, z*B, z*c, z*B значения z для концов разрезов при b
(или с = 0), когда оба разреза лежат на одной прямой, то,
например, формулы (41) — (44) можно написать в виде
zG = е^г*с
/ Т)\2
Н+^)
(<">' + Ь) — ^а.1
(а(‘+ “)
IP (<» + *)-&>(<-> + <>' +“О
•+ Р («> + «>'+a0
p-PK+a/) + (">' +az)_
отсюда, откинув члены с с2, мы получим:
ZB ZB,
zc=^iz*C’
ZD==e^ZD-
(45)
Уравнения (45) показывают, что при малых с с точностью
до членов, содержащих с2, можно считать, что точки А и В
неподвижны и отрезок CD постоянной длины при измене-
нии с вращается вокруг начала. Таким образом, в этих
условиях мы имеем формулы, дающие вращение предкрылка
постоянной длины при сохранен’/и постоянной длины
174 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
и положения основного крыла. Отсюда следует важный вывод:
мы можем считать при малых углах наклона
предкрылка к основной части, что при пово-
роте предкрылка величины (о и о/ постоянны,
т> е. прямоугольник периодов не изменяется при изменении
угла наклона CD и АВ.
§ 6. Общие замечания об отображении
Если дана двусвязная область, образуемая частью пло-
скости, лежащей вне двух отрезков АВ и CD, то, про-
ведя оси, как показано на рис. 18, мы видим, что эта об-
ласть вполне определяется положе-
/ А нием четырех точек:
с/ А(Х1’ В('Хг'
С(Х3’ Уз)’ D(X4’ л).
—т. е. восемью действительными чис-
лами:
Рис. 18.
х1> Л! х2, у2; х3, у3-, х4, yv (46)
При данном выборе осей имеют место соотношения
х± х2, х3
У1~ У? Уз —у?
В частности, можно считать ух = 0, у2 = 0, так что в ря-
ду (46) остается пять произвольных величин.
Задача конформного отображения двусвязной области
на прямоугольник будет решена функцией вида (26) или,
при другом расположении разрезов, функцией вида (27)
или (28), если мы по данным пяти постоянным определим
постоянные, входящие в функцию (26); эти постоянные суть
а, Ь, а, р, о), у;
но очевидно, что величина периодов не имеет значения,
а потому важны только отношения
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
175
так что мы можем, например, считать со = 1. Величина b
определяется по углу наклона
и при <о=1 мы получаем:
и
a = z\.
Таким образом, считая, что со= 1, надо найти следующие
величины: а (из условия а = ^), b ^из условия & =,
о/
далее, а, р и т. е. всего пять неизвестных.
Определение этих постоянных в общем случае предста-
вляет очень большие трудности. Заметим, прежде всего,
что для нахождения значений zz, соответствующих точкам Л,
Bt С, Z), в которых нарушается конформность отображения,
надо решать уравнение
~ = 0. (47)
du v 7
Корни этого уравнения, как выше было указано, нам не из-
вестны, так как изображения точек Л, В, С, D смещаются
из вершин прямоугольника
и — 0, zz = со, zz = (Оzz ~ со'.
Уравнение (47) должно иметь два действительных корня
и $2, соответствующих точкам Л и В, и два комплексных
корня $3-|-(о7 и ^-I'-co', соответствующих точкам Си/).
Величины £2, £3, мы найдем из уравнения (47) как
функции пяти величин a, b, а, р, у. Найдя величины
^2’ и подставив их в уравнения z = /(zz), получим
систему уравнений
xi + 1У1 = /1 (Bl) = ?1 (a, b, а, р, 1, «/),
х2 ~Н (У 2 == /г Сг) == 9г (&’ <*’ Р> 1> Oj/)>
•*"3 Н-(Уз ~/з (£з) ~ ?з (а> а> Р> 1> w/)>
х*+г'Л = = Ь’ •»').
176 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Разбив правые части этих уравнений на действительную
и мнимую части, мы получим уравнения
= а, р, 1, (o'), У1~7.1(а> 1, <*>')>
х2 = ФгС0» а, 1, а/), У2 = 7.2 (а> Ь, а> 1, о/),
х3 = ф3(а, а, р, 1, coz), Уз~Хз(а’ а’ Ь <*/)’
х4 = ф4(я, Ь, а, р, 1, со'), У± = 7л(а, b, а, р, 1, со').
В силу выбора функций f должны выполняться условия
л = °> y2 = G
и
£з„*4
Уз У4*
Из оставшихся пяти уравнений мы и должны определить
пять величин: а, Ь, а, р, и/.
В том случае, который разобран в предшествующем
параграфе, мы видим, что при малом b величины а, а, (3, а/
не зависят от b и могут быть найдены по формулам (9)—(16)
§ 3, а величина b найдется по углу наклона р. из уравнения
§ 7. Построение характеристической функции;
случай предкрылка
Мы переходим теперь к решению второй задачи: к по-
строению характеристической функции потока, обтекающего
составной контур АВ и CD (рис. 12); в зависимости от от-
носительных размеров частей кон-
(рис. 19), где точки
разрезов Л, В, С, D,
тура и от направления потока в
бесконечности мы получим случай
или крыла с предкрылком, или
крыла с закрылком. В настоящем
параграфе мы разберем случай кры-
ла с предкрылком.
Производная характеристиче-
ской функции на плоскости и
Л', В', Cr, D' соответствуют концам
имеет период 2со (в силу результатов
§ 5 эти точки Л, В, С, D сдвинуты из углов прямоуголь-
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
177
ника OPQSy, кроме того, на ОР и SQ производная действи-
тельна, так как ОР и SQ суть линии тока, а потому в силу
принципа симметрии в точках, симметричных относительно
ОР и SQ производная характеристической функции прини-
мает сопряженные значения. Следовательно, она имеет и пе-
риод 2о) и есть эллиптическая функция с периодами 2<о и 2(1/.
В точке и = — с-|-а/, соответствующей на плоскости (г)
точке z = oo, характеристическая функция имеет полюс пер-
вого порядка (диполь) и логарифмическую точку (вихрь).
Следовательно, производная будет иметь полюс второго по-
рядка в точке и = -—и в ей сопряженной точке
и = — с — al. Применив обычную формулу разложения эл-
липтической функции по главным частям и дав постоянным
форму, удобную для дальнейшего, мы можем написать про-
изводную характеристической функции в виде
1 dw___
aVodu
= —А^ (и + с —az) + ^| —Л ^(и + с + а/) + ^ +
_|_/с[С(« + с —ai) —С(я4-с+ а/) + ^4-В, (48)
откуда
i = x[c(«+c-«i)-K] + A[:<« + c + s«-)-^ +
! ic In 4~ц-;-с--г- +Bzz^F(/z). (49)
Механическое значение постоянных определяется из сле-
дующих соображений. Интеграл по замкнутому контуру
вокруг точки —c-\-ai даст циркуляцию вокруг составного
крыла. Заметив, что направление циркуляции на плоскости (г)
обратно направлению циркуляции на плоскости (и), мы, обо-
значив циркуляцию через J, из уравнения (48) получим:
J=2uCW0. (50)
Интеграл от функции (48) по линии LY соответствует на
плоскости (z) интегралу вдоль линии т. е. циркуляции
178 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
вокруг АВ, хорды основной части крыла (рис. 20);
назвав эту циркуляцию через и заметив, что на плос-
Рис. 20.
кости (z) направление циркуляции обратно направлению
циркуляции на плоскости (и), мы найдем:
= — aV{В (и + 2(d) — В (и)};
но согласно равенству (49)
F (г/-j-2(d) — F (г/) = 2В(о;
следовательно,
= — 2B(d^ Vo.
Циркуляция вокруг CD (предкрылка) J2 найдется по
формуле
J2 = J— = 2а VQ (кС + B(d).
Мнимая часть выражения
aV0 {F(m+ <»') — F (и)}
дает секундное количество жидкости, протекающей между
крылом и предкрылком. Назвав его через Q и введя для
обозначения мнимой части выражения символ Jm, мы получим:
Q = JTOaV0{F (« + «/) — В (и)}.
На основании равенства (49) мы найдем:
f (о + Ц>') = и [с (о + с — + 1 у +J 7п-е. -
__-yt__чИ ।
(и С — al) т\и 7]С0'
О) со
‘i
-/-Г ч -г 2 jp(„ + c_a/)_es
аз(м + с_а/) _2r/ai+W
Ч е е “ + Btt + Вы',
(и -f- С + al) 1 1 ’
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
179
откуда
F („ + _ F („) = к А _ л (, £ - -
-2С" (ч “•>>')}=«• I - " (с“+^4— )| •
где Re есть символ реальной части выражения. Следова-
тельно, учитывая направление обхода, имеем:
Q = aVQ (Са
i л + л\ к
“Т" 2 ) ‘
По теореме Н. Е. Жуковского для подъемной силы ЗА полу-
чим выражение

или, подставив значение J,
Р = 2лраУоС-
(51)
Следовательно, для нахождения подъемной силы надо по
условиям задачи определить величину С,
Для определения постоянной С заметим, что в случае
предкрылка точки А и С являются точками схода струй
dw л z ч
и в этих точках — = 0 на плоскости (и), так как скорость
на плоскости (z) в этих точках конечна. Так как точки А
и С соответствуют значениям и() и а2 <*> + то согласно
равенству (48) мы получим:
— д^(ио —с —аг)Ч--^] —A [р(«0_|_c + az)_|_-lJ_|_
-НС[С(«о + с — а/) — Ч«о4- +
— + w + —+ —
— А («2 4~ ш + ш/4~с 4~ а0++
4~ (^2 4- ю —[— о)/ —|— с — си)—(#2 4“ 4- 4- 4- 4*
+ 2^] + В_0.
180 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА Й ЩИТКОВ
Отсюда мы найдем:
[р (^2 А А0)/ Ас — а0 — (^о Ас — а01 а
A A IF (^2 AQ) А 0)/т с А а0 — F (^о Ас А а01 =
= — iC [С (^д ~{— с — ос/) — С Ч~ Ч- ^2 Ч- £ — ^0 —
— (woA с A ai) А £ (и2 A w А 0)/ А с 4“ <*01 • (52)
В случае малости величин с, uQ, и2 мы, разложив функ-
ции по их степеням, ограничившись первыми их степенями
и заметив, что
(и2 А ш A ojZ Ас — <*0 =
= (in Ч~ 0)/ — а0 4“ (w2 А с) (а)/ A 0)Z — са)-\- . . . ,
и получим из уравнения (52):
— iC [С (— а/) + (wo А с) Р (— а0 — A A 0)Z — а/) —
— (“2 А ЧА (ш А 0)7 — <*0 — £ (а/) — («о А с) № +
А С (<*> А 0)/ А а0 А (и2 Ас) F (ш А03 z Ч- а01=
= А (а) + а)' — а/) + (и2 + с) (аз а/ — а/) —
F (— а0 (wo Ч- f) Fz (— а0] Ч- A IF (^ +0)/ 4“ а0 Ч~
Ч- (tt2 + с) %) (аз + а/ + а/) — ^а/ — (w0 + с) а/]
или
— iC {— 2£оа — Ц«) ц)' — ai) -|- С (а> Ч” 0)/ Ч” а0 4“
Ч-С^Ч-^ИН^Ч- <о'Ч-а/) — Hw + a)/ — а01} =
= (Д + А) [— (О) 4- О)' + а/)] —
(Д Дг) [—(ЯоЧ- с) F/ai’4~ (и2 А с) ((o-t«)z + а/)] •
Но
цш 4-_ а/) = _ Саг + + _ _±2£_;
с (о, 4- о/ аг) = Саг 4^444 al
у at — ^2
И
р (W4 о/ -±Z аг) = е2 + {ei~ ^з) .
Подставив эти значения, получим:
-гС^'аг [- 4^4 ] = <Л + A) l~ + Р («> + «>' + а )]—
— {А — 4) [— («о + О ^'аг 4 (Й2 4. с) (Ю 4. «>' 4 а0). (53)
к ТЕОРИЙ ПРЕДКРЫЛКА Й ЗАКРЫЛКА
181
Эта формула позволяет найти С через А и Xf, остается
найти А и А±. Для этого нам послужит уравнение, даю-
dW ТЛ м
щее — при z= оо. Из уравнений
1 ^ = _лк(м + с_а0 + л1
a VqcIu L 7 1 со J
_д1[р(в + с+.аг-)+^] +
-|- /сГс (« —|— с — аг) — £ (гг —|— с —|— аг) —аг'1-4- В
И
а (и — Ь — со7) а (и -|- Ь + со7) а2а/ 2г^ и
аа(и-\-С — zi) а (иС А~ а1) а3 (со7 4" е
а также вытекающего из него уравнения
7 S С (и — b — О + С(м + b + О ~
— с — al) — £ (и Ц- с -j- а/) -4 2т] ~
UCV ГГ> I
мы найдем при z = оо. Так как z = оо при и = — с-{-си,
то, считая VQ скоростью в бесконечности, имеем:
loVorfu’ a du JM=„c+ai — V0\dz)g=m = е U =
_ А °2 (о/ + b) “ 2,1 “ с+ai> । im + с—а.1) о (гг 4- c—ai)
и^-с + м Hu-Yc-al) А
•у __________________g2c(f_______________
а (— с — b 4~ а1 — “Э а (— С -р + ь -|- с°/) ’
т. е.
. л -2^-(саг-С2)
е -^ = А —k 9Т е ш X
a2az
\/ ___________________g^gZ*_______________ /54л
а (— с — b <*i — “Э а (— с 4~ az 4~ 4~ oj/) ’ J
где X есть угол, образуемый скоростью в бесконечности
с действительною осью плоскости (z). При расположении
182 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и Щитков
крыла и предкрылка, указанном на рис. 21, X есть угол
атаки. Так как
о (-— с — b —|— ос/ 0)Z) о (— с —{— ос/ —b —(DZ) =
= о [(— с -|- а/) — (Ь -р <*>')] <з [(— с а/) -J- (Ь оз)] —
= (Р + — $ (а/ — f)} °2 (Р + <*>') °2 (а/ — с),
то равенство (54) можно написать в виде
о2я/
= Ae2ri^(c~ai}____________________—______________________ Г553
abl<fl-(al — C)[P (b+ «>') — j? (aZ —c)]* k '
Так как — действительно на действительной оси, то,
Рис. 21.
заменив —с-|-а/ на —с — ai, получим аналогичное уравне-
ние для Дх:
и А ~ (с + ____________a2aZ_________________
±е a2aZa2 (— al — с) [(Р (b + “z) + (°^ + с)] ’
ИЛИ
U л (c + ai) °2aZ
е ~ А1& aaaZa2(aZ + c)[H* + H + H^ + 0]‘
Уравнения (55) и (56) можно написать в виде
е ’(х 2^',) = Л^?(С); (57)
e^^2^a)= —с)> (58)
где
-21 С-
е “
Т = с2 (az - С) [j? (6 + “')-!? + О] ’ (59)
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
183
Уравнения (57) и (58) позволяют найти А и А± и затем
по .уравнению (53) найти С. Величины A, Alf С определяются
через с, а, со, со' и через угол атаки X.
§ 8. Случай плоского предкрылка
Для вычисления циркуляции при малых с разложим вы-
ражение С по степеням малой величины с и ограничимся
членом с первой степенью с. Уравнение (53) дает:
iC = И + А) [р (№-+-«/ — «0 - +
+ (Л — Л) [ (и0 + с) + («2 + с) Г (<» + <»' + а/)]. (60)
По уравнениям (37) и (39) мы находим:
Hu/ + 6) + 2l
“° + с = р (0/ + 6) _ paZ с>
р((о + 6) + _1
^((в + 6)_р(<й + о/ + а/)С-
+ С(Л — АГ
Следовательно,
iC № (<" + <"'- “0 — +
>(<>'+*)+£
f («>' + *) - S?aZ ^aJ +
Р(«>+*) + ^ I
+ ^(п> + 6)_у>((а + <й> —а7) Г (" +и/- «0|.
Из уравнения (59), ограничившись первыми степенями с,
получим:
1
?(С)
o2az (b + а/) — ] 4~
+ с [ — 2oafoza/ (b + со') — fiai} -|- ^zaZo2aZ]
или
Д^ = о2а/ W (£ + <"') — Г«1 +
+ с [Г— 2^4 (^ (b + со') — f>az)J}. (61)
184 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Подставив это выражение в равенства (57) и (58), мы
получим:
- i (х-2а -С) a4af
л== е “
X IP (Ь 4- ш') — раг + с {p'az — 2С сЩр (b + «>') — paz]) ]
И
г (х- 2a
,47х
X [р (Ь 4-«')— paz — с {P'az — 24./[р (Z>4-(o')— paz]}]-
Отсюда, заметив, что
Г « =----7- >
J сг4(/
мы найдем:
А 4- А = 2z sin (к - 2a ]р (Ь 4- «>') - Р<А -
— 2cosk^|p'az— 2£az|p(7>4-(o')— paz]} с 4- с2 {. ..}(62)
И
A — A = -2cosk^[p(*4-(»') — paz]4"с {• • •}• (63)
Подставив выражения (62) и (63)’ в уравнение (60), имеем:
с =------—-A- sin X х
P'2“z
X [р (Ь 4- a>') — paz] [р (о> 4- (О' — az) — paz] —
— Cl 2A^at~ eA cos x Г { p'az — 2Caz [p (b 4-0,/) — Pat]} X
P' al L
X {P («> + «>' — at) — paz} 4- ta ~ IP (^ 4-0)/) — Pa»] X
(P («' 4 b) 4-
x IP («>4- (o'—az)—paz]4-{p 04(o')—paz} | __ 4
P(® +*) + ^
+ Пм + 6)_Км + ^^а-7) P' (« + «>'- «0
(64)
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
185
Полученное выражение позволяет определить по формуле (50)
циркуляцию и по (51) — величину подъемной силы. Рассмот-
рим сначала случай с = 0, т. е. когда АВ и CD лежат
на одной прямой. В этом случае из уравнения (64) имеем:
с=— sin х Н-о/—“0—^1;
НО
^/2aZ = 4 (paZ — ej (J»aZ — e2) (paZ — e3),
и по формулам (5)
joaz — e1== — £ —pa/],
№ — e2 = — —j [j? (b + (o') — £>aZ],
PaZ — e3 = — hJ[_^+g IP(P-J-(o') — £>aZ];
следовательно,
<0,2 ,__W[p(b+ *')-№¥
’ ai hyh + l)(h-Yl + g) •
Так как
p(a)H-a)'4-a/)= e2-\
(g2 — ^1) (^2 — g3)
jpaZ —
то окончательно
2C = — sinX[(S’aZ—e2)2+(ei—e2)(«2—e3)].
a [J3 (o 4- “ ) — jpaZ]2 40 " 141 i K * 6
Но по формулам (5) мы находим:
a IIP (Z> + a>')-jM = , e2-gM h
e2 — V'ti I" ’ ei — h-\-l ’
e2 — ^ai _ й +Z + g
^3—Z4-A
и по формулам (6) получаем:
^1 — ^2 _ ± e2 — e3 _ g
e3 — ^al h ’ e2— !H«Z ^b-\-g’
<g( — g2) (^2 — ea) _ Ig
(e2 — pal)* h. (i 4- g 4- h)
186 I. ТРУДЫ ПО ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА Й щитков
Следовательно,
2С = — sin X
/z(/z + Z) (/i + Z + g)r
азде(/> + со/)_(?а/]2[
е2>2—
= — sin X
h(h + l) (h + l + g)(h + g) = . h + g
ah (h 4~ I) (h +1 + g) a
и по формуле (51) мы получаем:
р = кру2 _|_ g.) sink,
т. e. в этом случае подъемная сила оказывается такой же,
как если бы предкрылок был плотно придвинут к основной
части крыла. Этот результат был ранее найден другим пу-
тем С. А. Чаплыгиным1).
§ 9. Случай малого предкрылка
Изучим теперь, пользуясь формулой (64), как влияет
предкрылок на подъемную силу или циркуляцию всего
составного крыла. Так как множитель
[Р (ft + а/) — ] [р (а) + ц/ — al) — рад],
очевидно, положителен, то для этого достаточно определить
знак выражения
I I — 2CaZ (b + а/) — ^aZ]) де (<о -f- о/ — aZ) — paZ) +
+ Za [p (b + <»') — J?aZ] [£> (<« + «/ — aZ) — tf>aZ] +
S?(<o' + 6) + ^
-W+ «/) — paZ} --^^«z +
H“+ft)1
"I- if* (<*> + ft) — J3 (<*> + — aZ) (Ш + 0)
(65)
Мы рассмотрим здесь случай, когда предкрылок мал сравни-
тельно с основной частью крыла. В этом случае, как было
*) С. А. Чаплыгин, Схематическая теория разрезного крыла
аэроплана, Собр. соч., т. II, 1948.
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
187
показано в § 3, надо считать а величиной малой. Подста-
вив в выражение (65) разложения
а2 (. . .),
° (az)2 1 4 7
= —^з+аС...),
ГТ 1
мы получим следующее. Члены с получающиеся
из —р'ои • ра/— 2Caf-j/2aZ, как легко увидеть, уничто-
жаются. Собрав члены с мы получим из уравнения (65):
г 9 9 9
z[~ F((й + о/)+(Ь + 0,0 + «wр (a) + u,/)+
+2vaZ(^-W3^("'+6)-W3v] = ^[^“+(B')-
— 4?(ш' + Ь) — Р(<о + Ш') — 2^ + p(«/ + Z>) + 2 Д = о.
Коэффициент при ~ имеет вид
- i I4 — 4) -2F у+ю'> +о ~ (6+ш/)+
Г (» + “') {?(<-> + *) + -£}
+ (ш + Ю')1 Н j? (М + *) — J3 (<0 + ш') •
Заметим, что
F' (ш + <»') = 2 (е2 + et) (е2 — е3),
(Ш' + Ь) = е3 + (g8 ’
p(<» + U)/)=e2.
188 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
После подстановки получим:
- f - 2 (А + е2) (Ь + «/) - - J е2+2 (е2 - ej (е2 — е3) X
Х b + $(>> + «>) —е2 . = -~Т — 2(J + ^)X
х/ L । (ея — е^(ея — е2) ( „ л , (е2 — е3) (е3 — <?,))
А |*з Ч fb^73 Н г2 — *1Ч &b=7s J'
+ 2(^—6!) (г2 — е3) — ^-е2= — — 4^е2 — 2г2 —
— 2(^1 — е2)(е2 — г3).
Заметим, что
g*2 ----(^2 4“ ^1^3 Ч~ ^з) = ---------[^1^2 + в3 (е1 Ч-' е2)1 —
е3 — е3
= — 4 [^е2 — (ег + е2)2] = 4 (е2 -|- е е2 + г2) = 4 -1--2- > 0.
е2
(66)
Так как при малом а мы получаем
-(Р°г2 /г) де {b + (О') — paz] №(ш + ш' — aZ) - ^1\ =
__2(pafr + ^(co + co'-aZ) ]_ 1,
^aZ Л № 2*Q
то окончательно по формуле (64) при малом a имеем:
X [if Ч~ ^2 Ч~ 2^2 + 2 (^i — £2) (^2 — ^з) j • (67)
Выражению
-у- Ч~ 4 £2 + 24 + 2 (#i — £2) (^2 — ^з) (68)
можно дать весьма простую форму. Для этого заметим, что,
как было показано выше,
^ = -е24
2 со
(gi — е2) (е2 — е3) I* du.
2<о J фи — е2 ‘
(69)
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
189
Подставив значение (66) для g2 и значение (69) для ~ в выра-
жение (68), мы получим:
2 00
4 и+«-а+«а - -ч+2 et ‘ j J
_2
3
__2
“ 3

4- 2^2 4- 2р^2 — 2е2 — 2e1e:i 4- 2г/3 =
2 00
к ( du
’в).)
О
>#1#2 З^з #2)! '
^2-6^ + 3V24-3^_-3^ +
2 00
+ 3-?(et~ ^)(е2—^з) j
О
2оо
+ 3?(е1”~е2)(^ — *з) J
О
du

du
— е2
2
(^1 ^2) (^2
Но в интеграле от 0 до
вательно,
2(о мы
2<о
4-L3^ f du
о> J фи-е2
О
получаем ех^.^и. Следо-
• (70)
2 00
о < f ———
J ^u-ez
о
при е2 > 0 мы получаем:
2 00
О < 4 + 3 -2 | ' . du - <
1 <0 J $>и— е2
о
2 00
du
2(0
е1 — е2 е1 — е2 ’
3#2 \ О^1—
е1 — е2/ е1—е2 е1—в2
о
и при е2 < 0 мы получаем:
2 00
4 4-3- ,т--— >2(2
о
। 3g2 \ __ 2 ei —
-т" et — е2 J ej — е2
190 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Итак, и в том и в другом случаях выражение (70) поло-
жительно. Отсюда по формуле (67) мы видим, что при с > 0
абсолютная величина С меньше, чем при с = 0, а при с<0
абсолютная величина С больше, чем при с = 0.
В силу уравнения (51) мы видим, что при = 0
подъемная сила меньше, чем при р. = 0, а при р < 0 подъем-
ная сила крыла больше, чем при р = 0. Итак, е с л и пред-
крылок мал, то при обычном расположении
(р>0) предкрылок уменьшает подъемную силу
крыла.
Заметим, что в рассматриваемом случае а мало, и по фор-
муле (67) уменьшение подъемной силы пропорционально а3,
т. е. весьма мало.
§ 10. Случай закрылка
Перейдем к изучению влияния закрылка. В этом случае
во все предшествующее исследование надо внести следую-
щие изменения:
1) угол атаки X надо заменить на к — X;
2) точками схода струй вместо А и С надо сделать
точки В и D. На рис. 22а указано расположение скорости
Рис. 22а.
Рис. 226.
в бесконечности в случае предкрылка и на рис. 22б —в слу-
чае закрылка. В результате замены X на к — X вместо урав-
нений (57) и (58) мы получим для определения коэффициен-
тов А и А1 следующие уравнения:
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
191
ИЛИ
4 [х+2а^£] 02aZ . .
в = —
- i [х+2<Л£] аЧа1
е 1 0,1 = — А± -s-т ср (— с).
1 aJaz т v 7
(71)
(72)
В силу того, что точками схода струй являются точки В
и О, корнями уравнения = 0 должны быть -|- оз (соот-
ветствующее точке В) и ZZ3 4-037 (соответствующее точке D).
Отсюда вместо уравнений (52) получим:
— А («i —|— <о —|— 6? — az) + “] — Al ^(«i4-<o+^+a/)4~-j-H
A-iC [c (H1-]-w + c—aZ)-C (at -f- «j-f-c + ai) + 2 -|- В == 0,
—a [if3 (“з + u)/+c—a0+4 (мз+0)/+с+аг’)+^+
4~ z’C^C — az) — £ (zz34-o),4-f 4”a0 -j- 2 4“ В = 0,
откуда
a (w3 4-0)7 Ч- c Ч- a0 — (P (4i 4~ w 4“c—az)j 4“
4~ At (zz3 4- из7 4- c 4~ za) — (zZj 4“ 4“ c 4“ az)] =
== — IC (zz^ —j— 0) —j— c — city — C (zz3 —|— (137 —|— c — cu) —
— (^i 4- w 4- 4~ az*) 4- £ (^з 4~0)7 4- c 4~ az*)]. (73)
Разложив обе части по степеням малых величин uv и3, с,
получим:
С (% 4~ 03 + с — ш) = С (оз — az) — (zzt 4“ с) (оз — az) 4~ • • •
С (^i 4- 4~ 4“ az)=== 4~ az)—(^i + с) (оз 4“ ^0 4- • • •
С (zz3 4~ 4~с — az) = (оз' — az) — (zz3 + с) (оз' — az) 4~ . • •
С (zz3 4- ез' 4- с 4~az) = С (^х 4“ az) — (й3 4~ с) (оз7 4~ az) 4“ • • •
и
(zz^ 4- (13 4~ с—&Г)—(zz3 4~ 4“ — az) — С (zZj 4“ ^4_^4~az)4“
4~ (из 4“ a)Z4-c 4“ az) = С (оз — az) — С (из 4~ az) — (из7 — az) 4~
4~ (u3,4~az) = 2Z (из — az) — 2tq — 2^ (из7 — az) 4~ 2tq7 ==
= 2 Г-1 ____I-1 ^аг 1 = -&'ai
L 2 Ipai — 2 !Pai ~-e3J 5 (jpa/—A)(jM—г3)
192 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Точно так же мы найдем:
(^3 4~ 0)7 + с — а0 = —а0 + (^з + 0^' i0)/ — «04~ •• •
^(iZi + o) 4-с — а/) = ^((о — а0 + (г/14-с)^,(со —aZ) 4- .. .
Р (^з 4~о)/ 4~с 4~ а0 — (с/ 4- а/) 4~ (^з 4-с) (0)/ 4~ а0 4~ • • •
Р (^i Ч~11) 4“с 4~ а0 = (0) 4- а0 4- (Й14~с) (ш 4- а0 4 • • •
Так как
р' (оз 4~ а0 = (—(,) — а0 = — (ш — а0
и также
(о/ 4- az) == — (а/ — aZ),
то, подставив все полученные выражения в уравнение (73),
мы получим:
iCfi'ai_______________________=
® (S?aZ — ex)(^ai — е$)
= А (о/ — aZ) — (оз — aZ) 4- (и3 4- с) ft' (о/ — aZ) —
— (их + с) (оз — aZ)] 4- (о)' — aZ) — (a) — az) —
— (zz3 4- с) (о/ — az) 4- (zzt + c) $>' (a) — aZ)],
или
= ('4+-« IS’ +
+ (4 — А) [(и3 + c) (a)' — at) — («, + c) (w — ai)J. (74)
Подставив значение (61) для в
ср (с)
мы найдем:
уравнения (71) и (72),
4 =— 4Х+2“ ^at-1-сХ
X [р'а/ — 2:at (b + «/) — ^az] ]},
41==e l2a “) {?(£ + “') — ^ai — CX
X l^'at — 2'a.i [£> (/> + a/) — ^az] J),
откуда
4 + 4г =+ 2/ sin (k + 2a J) [£> (b 4- «/) — fai] +
4-2cos(k+2a-^-l^ 2Гаг[Н^ + «>') — } c
\ M Y al '
к ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
193
и точно так же
Л —4x = 2coS (х + 2а ^)-^]р (& + <) —Р*Л + Н-..].
Подставив найденные значения Д4~А и — А в равен-
ство (74), мы получим:
Ср'*/ 77ГТ—; = 2г sin (х4-2а [р (h 4- ш') —
’ (tfal — ei)(fpal — е3) \ 1 <0 ) Q'al 1(1 4 ’
— Рог] IP (“' — аг) — Р («>—аг)] + 2с cos ^Х + 2а X
X №'ai—2Cai [р (“>' — а0 —
— р (ш — аг)] + 2 cos (х + 2а [р (Ь + <»') — Р*Л X
X К«з + с) ф' (<»' — аг) — (ггх + с) р' (а> — аг)];
отсюда
С = 2 sin (х + 2а 2!£\ (Р°* ~ *1) (Р°* ~ 3>) де (Ь «/> _ ра1] х
X IP (<»' — а/) — Р (<» — *0] — 2г cos (х 4~ 2а j X
х f ^'ai—+ш,)—ра/])Х
P'^aZ (Cj — CS)
X {Р(о>' —аг) —p(«> — aZ)}]с+ {р (& + «>') —Ра/)} X
X {(«з + с) Р' («>'—ai)—(«i + с) Р' (<«—*0} ; (75)
разложив выражения
sin^X-|-2a-^ и cos^X-]-2a^-j
и подставив при помощи формул (40) и (38)
р (О/ + aZ) + а Р* + |
“з + С — рг, _ р (o' _ aZ) с + С — pz> _ р (о/ _ aZ) С’
P(“ + «O + -J
М1 + С = |р (<о 6) — Р (<о + aZ) с + с =
р (<о <>' + Ь) 4- —
~ Р (<о + »' + *) — р (<О — al) с>
194 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
мы окончательно приведем выражение (75) к виду
с = 2 ^at~e^aL-.?^ f Sin X ]р (b + ш')-р (at)] [j? (ш'-аг)-
—p(a>—at)] — ic cosX[(p'at—2Cai[p(Z>-|-')—paZ]} {Р(ш/—at)—
—P (w—at)} +2 aZ (b + ш')—paZ] (<»'—at)—p(w—aZ)] 4-
+ {P (^ + <»') — pat} j p' (w' — at) —
P (<> + <»' + *) +-J 11
“ P (<o + <o'Ц-6) — p (a> — aZ) F (<» — at) j J J .
Рассмотрим сначала случай, когда с = 0, т. е. когда обе
пластинки лежат в одной плоскости. В этом случае
С = 2 Sin X [P (b+Ш') -
^ai (е1 — е3)
— paZ] де («' — az’) — Р («> — at)] =
=4 ls’ <4+“'>-м №
(76)
По формулам (5) имеем:
p(Z> + c/)-P(az) h-\-l
^>al — е2 а ’
h ___ e2—$al _ e2 — er .
Л-f-Z — $al —$ai z~ ’
h + l + g = e2 — ^al e2 — e3 , .
h + l й3-раг ee-^al-T-l‘
Кроме того,
p (a/ — at) — p (o> — at) = e3 + (g3 ~
__ (gl ~ e3) (el + e2) / _ Ji । ^3 — ^2 | ^2 — ^1 1 ,
^al — e±________________________________________________3 ~r jpa/_^8 I ра;__е1]

К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
195
Подставив эти выражения в формулу (76) для С, мы найдем:
C==^sink(A + g)
и по формуле (51)
Р = TtpVo(A Ц-g),
как и должно быть в силу исследований С. А. Чаплыгина1).
Перейдя к исследованию общего случая, когда с #= О,
так же как и выше, предположим, что а — величина малая;
это соответствует предположению, что закрылок мал сравни-
тельно с основной частью крыла. В этом случае произведение
[? (Ь 4- o') — ^az ] [р (о/ — az) — — *01 =
= — фа! fl — И I?’ (<»' — «О — Р (ш — “01
L о J
приближенно равно выражению
и для оценки влияния закрылка надо найти приближенную
величину выражения
{Р'аг — + — ^aZ]} {Р(о/— а/) — ^(<о— аг)} -|-
+ 2 -J aZ [р (b + со) — ^aZ 1 [р (а/ — aZ) — (а> — а0] +
№ + ~“
+ (Ь + ш') — pai} Г (<*>' — «•) —
~ I
р (a, о'4- &) _ (р (ш —az) Мq • (77>
Для этого мы найдем разложения отдельных слагаемых пред-
шествующего выражения. Найдем сначала разложение
Sx = {P'at — 2CaZ [j? (b + w') — J?aZ]} {(«>' — aZ)—(o> — at)}.
*) С. А. Чаплыгин, Схематическая теория разрезного крыла
аэроплана, Собр. соч. т. II, 1948.
196 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Так как
— m = + + ....
to [р (ft + шЭ—p(ai)] = 4- ^(г, + Ю,)
p'(ai)—2to[p(^ + “')—P(a0]=— + • ••
" Si=2У(»+-;><«1-«.)ai[й (ei_ej)+3f (4+...
Точно так же, положив
S2 = 2 Л al [р (b 4- <о') — pai] [Р (to' — ai) — p (a> — ai)]
и заметив, что
p(ft-f-(o')-par = p(^<o')4-±4-§-a2+ ....
P(®'— ai)— p(<o — ai) =— (et — e3)— j (ei—e3)e2a2-^- ..
имеем:
S2 = - 2-^=^ 4 — 2 A Zp {b + «>') (ei _ e3) a 4. ...
Положив, наконец,
f P64--^-
S3 = {P (b 4- <o') — pai} j рЬ_р(ш,_а1) Г («>' — ai) —
P (“ + <>' +*)+ -J
~ p(a>4-a>'-j-6)-P(a>-ai) — f ’
мы найдем:
^+4 ,_Г»“+^ ..г«(н+4 '
рь-ф (u'-aiy м>—\уь-е2 2 (Р6-г8)3
Р6 4-77
X [—aip"to'4- ...] =-^-ai 4~a3[. • •]•
К ТЕОРИИ ПРЕДКРЫЛКА И ЗАКРЫЛКА
197
Точно так же мы получим:
н*+<>'+*)+!
(со + ф' + 6) — ja — а/) (<й—аг) =
(р(ю + ^ + 6) + Л
= — al —,- > . 4- а3 [... 1.
Отсюда мы получим:
*. = ~41 тт;- -ро+. + и-.Л"») + «’[!.
Подставив все найденные разложения в выражение (77),
найдем:
„ к 'i Г/> _1_(Й8 — ei) (5з — g2) ।
Ч «ъ) [ез уЬ-е-л
(gg — gi)(g8 — gg) 1
^-gg J
„ ч L | Ч | («1 —g2) (g2 —gg) 1
'3'p i 4' $Ь-еъ J ’
и так как
2 оо
(^2 —^з) f dll
2(0 J фи — ё?2 ’
О
то
•$1 -J- *$2 + 5з а (^1 ^2) (^1 ^з) (^2 ^3) X
2ш
1 Г du
2(0 J фи — ^2
о
1
^Ь-е3
-----7И,
а
где
м = (ех — е2) (ег — g3) (е2—g3)
1
2со
du
фи — е2
фЬ-е3
о
198 I. ТРУДЫ ПО ТЕОРИИ .ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОЕ
Подставив все найденные значения в выражение (76) для
найдем:
х7и--------sin X — ic cos X (— — =
2(jp<xZ — *2)G?i — t «a \ « /J
a2
2(*1~^з)
1 —<?3
a3
sinX-|-
4Л4 , ) 1 . , . 244
— cosXc >=-^sinX-k-ca--------cosX.,
a j 2 1
Отсюда видим, что при с > 0 закрылок увеличивает
подъемную силу, а при с < 0 ее уменьшает. На рис. 23а
мы имеем случай, соответствующий увеличению подъемной
Рис. 23а.
силы (с > 0), на рис. 236— случай, соответствующий умень-
шению подъемной силы.
Результаты, полученные в § 9 и здесь, можно объединить
следующим образом: пусть имеется крыло с предкрылком
(рис. 24), причем и основная часть крыла АВ и предкры-
лок CD лежат в одной пло-
скости. Если предкрылок
_______вывести поворотом около
точки О из плоскости кры-
ла, то при и > 0 (с > 0)
___________ _ Угол атаки предкрылка
уменьшается и при ji <
рис 24._______________________< 0 (с < 0) этот угол увели-
чивается. Аналогично для
случая закрылка при р. > 0 (с > 0) угол атаки закрылка увели-
чивается и при < 0 (с < 0) уменьшается. Сопоставив все
предшествующие выводы, мы получаем: если, вращая
предкрылок или закрылок, мы увеличиваем
его угол атаки, то подъемная сила всего раз-
Теоретич. основания методов увеличения подъемной силы 199
резного крыла увеличивается; если угол
атаки предкрылка или закрылка уменьшается,
то уменьшается и п о д ъ е м н а я с и л а всего раз-
резного крыла.
ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ МЕТОДОВ
УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ КРЫЛА
РАЗРЕЗНЫЕ КРЫЛЬЯ, ЩИТКИ, ОТСАСЫВАНИЕ 1)
Введение
Одной из важнейших задач, выдвигаемых современным
развитием авиации, есть задача максимально возможного
увеличения скорости полета. При современном развитии
авиационной техники эта задача обычно решается путем
колоссального увеличения мощности моторов и возможного
уменьшения несущих поверхностей, трение которых о воздух
создает основную, при больших скоростях, часть лобового
сопротивления. Однако уменьшение несущих поверхностей
влечет за собой уменьшение подъемной силы, несущественное
при больших скоростях полета, но приводящее к большим
величинам посадочных скоростей, крайне нежелательных по
ряду соображений.
Отсюда возникает ряд более частных технических задач,
одной из которых является разработка крыла с максималь-
ной подъемной силой. Экспериментальные данные и теорети-
ческие исследования приводят к тому выводу, что решение
этой задачи надо искать не в подборе новых форм дужек,
где возможный предел достигнут современными конструк-
циями, а в разработке ряда приспособлений, улучшающих
работу крыла. Сюда относятся крылья с предкрылками и
закрылками, разрезные крылья с системой щелей, щитки,
отсасывание и сдувание воздуха с поверхности крыла и т. д.
В области конструкции крыла современная авиационная
техника переживает интересную эволюцию. Еще совсем
недавно крыло представляло собой неизменную и негибкую
1) Опубликовано в Трудах ВВА РККА им. Жуковского, № 46,
1939. (Прим: ред.)
200 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и ЩИТКОВ -
поддерживающую поверхность, несомненно, весьма далекую
конструктивно от гибкого, меняющегося по размерам и по
форме крыла птицы.
Постепенное введение элеронов, раздвижных крыльев,
щитков и т. п. все более и более превращает крыло в слож-
ный и гибкий механизм, приближающийся по своей под-
вижности к тому, что конструктивно представляет собой,
с точки зрения аэродинамики, птичье крыло. Возможно, что
такие приспособления, как отсасывание и сдувание воздуха,
неосуществимые на крыльях птиц, позволят со временем
крыло самолета превратить в механизм даже более совер-
шенный, чем крыло птицы, но, по-видимому, современная
техника еще весьма далека от этого.
Разработка таких конструкций представляет большой
интерес и с другой точки зрения. Несмотря на поразитель-
ные успехи, достигнутые за последнее десятилетие авиацией,
несомненно, что современная техника позволяет летать очень
хорошо с точки зрения скорости, продолжительности полета
и т. д., но полет остается крайне неэкономным с точки
зрения энергии, расходуемой на полет.
Едва ли можно сомневаться в том, что рациональная
конструкция самолета позволит значительно понизить мощ-
ность моторов, не уменьшая скорости и других качеств
самолета. В решении задачи о более экономичном полете
также достигнуты в настоящее время некоторые результаты:
выяснена роль «зализывания» конструкции, тщательности
отделки крыльев и фюзеляжа и т. п., но, вероятно, и в этом
направлении разработка конструкции различных приспособле-
ний у крыла будет иметь существенное значение.
В области различных приспособлений, улучшающих работу
крыла, в настоящее время имеется огромный эксперименталь-
ный материал. Гораздо хуже обстоит дело с теоретическим
освещением относящихся сюда вопросов: здесь многое неясно
и требует дальнейшей разработки. Между тем отсутствие
ясных теоретических представлений сильно снижает эффек-
тивность экспериментальных работ, толкая иногда экспери-
ментаторов в направлении исследований, бесплодность кото-
рых можно было бы предвидеть из теоретических соображе-
ний, и, с другой стороны, теория может подсказать такое
направление исследований, которое невозможно было бы
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 201
предвидеть без теоретических соображений. Настоящая
работа и посвящена теоретическому освещению работы раз-
личных приспособлений, повышающих подъемную силу крыла.
В конце концов все аэродинамические соображения, даю-
щие теорию таких приспособлений, основаны на идее регу-
лирования скоростей потока в различных точках крыла и
на связанном с этим регулировании так называемого погра-
ничного слоя РгапсИГя. В этих двух направлениях и ведется
все теоретическое исследование, составляющее содержание
настоящей работы.
Глава I
ОБЗОР ТЕОРЕТИЧЕСКИХ РАБОТ; МЕТОДЫ, ОСНОВАННЫЕ
НА УВЕЛИЧЕНИИ ПРЕДЕЛЬНОГО УГЛА АТАКИ
§ 1. Общие соображения о методах увеличения
подъемной силы крыла
Одной из основных задач современного самолетостроения
является задача увеличения подъемной силы крыла и вместе
с тем уменьшения посадочной скорости. Попытки решения
этой задачи представляют собой ряд интересных исследо-
ваний по общей аэродинамике крыла.
Исследования по определению подъемной силы крыла
в плоскопараллельном потоке показывают, что в случае
крыла произвольной дужки, не сильно отличающейся от
дужки типа инверсии параболы, какими и являются боль-
шинство практически применяемых дужек, подъемная сила
единицы размаха крыла определяется по формуле
р = d sin (у + Р-) .
где d — хорда дужки, 2а—центральный угол скелета,
представляющий собой меру изогнутости дужки, ир— угол
атаки. Отсюда мы видим, что увеличение подъемной силы
теоретически возможно тремя способами:
1) увеличением угла атаки р.;
2) увеличением изогнутости дужки, т. е. увеличением
угла а;
3) увеличением хорды дужки d.
202 Г. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
В А

Рис. 1.
Все эти методы увеличения подъемной силы и приме-
няются в современном самолетостроении или представляют
собой предмет теоретического исследования аэродинамиче-
ских лабораторий.
Ввиду неустановившейся терминологии, касающейся частей
крыла, в дальнейшем будем пользоваться следующими обо-
значениями. Будем называть предкрыл-
ком добавочное малое крыло, которое
ставится на некотором расстоянии от
основной части крыла у передней
кромки.
На рис. 1 имеем: А — основная
часть крыла и В—предкрылок. Если
рассматривается подвижная часть крыла, плотно приле-
гающая к передней кромке, то мы будем
открылком; на рис. 2 часть А представляет
основную часть крыла и В — открылок.
Аналогично добавочное крыло, поме-
щенное около задней кромки на некотором
расстоянии от основного крыла, будем на-
зывать закрылком; если же у крыла имеется
подвижная часть у задней кромки, плотно
к основной части крыла, то ее будем называть элероном.
§ 2. Методы увеличения подъемной силы, основанные на
увеличении угла атаки. Исследования С. А. Чаплыгина
ее называть
В____А

Рис. 2.
прилегающая
Наиболее старым
является введение так
методом увеличения подъемной силы
называемых разрезных крыльев. Такие
дужки представляют собой в про-
стейшем случае основную дужку А
с добавленным небольшим крылом
В у передней кромки (предкрылок)
или у задней кромки С (закрылок)
(рис. 1 и 3); применяются и более
сложные конструкции, когда и
основная часть крыла разрезается на отдельные части,
между которыми остаются щели (рис. 4).
Такие крылья были предложены еще. в 1921 г. одно-
временно Лахманом и Хэндли-Пэджем и в последующем полу-
чили достаточно широкое применение в авиастроении.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 203
В теории разрезных крыльев можно указать две основ-
ные точки зрения. Первая точка зрения была высказана
и теоретически обоснована в работах С. А. Чаплыгина и
состоит в том, что приспособления, представляющие собой
предкрылок или закрылок,
действительно дают уве- _____
личение подъемной силы.
Вторая точка зрения, вое-
ходящая к отдельным заме-
чаниям Прандтля, Бетца и Рис. 4.
других, более подробно
была развита В. В. Голубевым; она состоит в том, что
предкрылок не дает, в сущности, увеличения подъемной
силы, но создает условия, при которых плавное обтекание
крыла потоком оказывается возможным при углах, значи-
тельно превышающих те углы, на которых начинается срыв
струй у крыла без предкрылка. В настоящем параграфе
мы изложим основы тео-
рии разрезных крыльев,
разработанной С. А. Чап-
лыгиным. Основные идеи
этой теории находятся еще
Рис. 5. в работе С. А. Чаплы-
гина от 1910 г. Пусть мы
имеем дужку с впадиной на нижней поверхности (рис. 5).
Так как в точке А скорость потока равна нулю, то в 4
давление потока на обтекаемое тело будет максимальное
и оно направлено вверх, т. е. дает подъемную силу; сле-
довательно, такая впадина дает увеличение подъемной силы,
и С. А. Чаплыгин получает формулу, позволяющую под-
считать это увеличение. Эта идея более подробно была
разработана в более поздней работе 1931 г. С. А. Чаплы-
гина и Н. С. Аржаникова.
В этой работе рассматривается полное обтекание пото-
ком профилей, указанных на рис. 6 (случай открылка;
открылок АВ) и на рис. 7 (случай элерона; элерон CD)t
причем подробно изучен только случай элерона. При этом
авторы указывают, что «характер течения в области угло-
вых точек на крыле существенно с качественной стороны
отличается от того, который имел бы место в присутствии
204 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щиткой
щели. Но если щель узкая, то распределение давлений
в соседстве с нею на прилегающих частях крыльев в общем
количественно мало будет разниться от того, которое было бы
при закрытии щели».
В этом случае, применяя то же соображение, как и выше,
увидим, что в области точки В внизу крыла сила давления
..потока максимальная; в области той же точки на верхней
Рис. 6.
Рис. 7.
поверхности крыла скорость очень большая (математически
она, очевидно, равна бесконечности) и, следовательно, около
точки В развивается очень большая подъемная сила; то же
рассуждение приложимо и к точке С. К более подробному
разбору случая элерона мы вернемся в дальнейшем; в слу-
чае открылка в работе не проведены вычисления до конца;
заметим, однако, что в случае закрылка при расположении,
указанном на рис. 3, закрылок работает при угле атаки
большем, чем основная часть крыла, а в случае открылка
при расположении, указанном на рис. 2, открылок работает
при меньшем угле атаки, чем основное крыло, а потому
закрылок может дать увеличение подъемной силы потому,
что часть крыла работает под большим углом атаки, но
в таком случае можно ожидать уменьшения подъемной силы
от открылка сравнительно с тем расположением, когда
открылок и основная часть крыла лежат на одной прямой.
Какой из факторов оказывается преобладающим в случае
открылка, из предыдущего рассуждения не ясно, и требуется
дополнительный подсчет этого случая.
Подробное исследование частного случая разрезного
крыла дано в фундаментальной работе С. А. Чаплыгина
«Схематическая теория разрезного крыла аэроплана»1).
В этой работе исследуются дужки, указанные на рис. 8
(случай плоского крыла) и рис. 10 (случай дугового раз-
!) С. А. Чаплыгин, Собр. соч., т. II, стр. 431, 1948.
ТЁОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 205
резного крыла), в предположении, что все* отдельные части
разрезного крыла плавно обтекаются потоком.
В случае плоской дужки, состоящей из частей ОА, ВС,
DE, назовем через a, b, с, d, е длины отрезков ОА, АВ,
ВС, CD, DE\ тогда характеристическая функция течения
определяется при помощи уравнения
1 dw
Voo dz
cos □ + iR sin a,
(1)
где a — угол атаки, R определяется формулой
и знак R определяется условием, что R = -1- 1 при z = oo.
Очевидно, что на отрезках действительной оси вне отдель-
ных перьев крыла R есть вели- у^
чина действительная, а на перьях {
крыла (т. е. на О А, ВС, DE)— (£_А 3___с D Е
чисто мнимая; кроме того, в 32
точках А, С, Е R = оо и в точ- рис. 8.
ках О, В, D /? = 0 и при
изменении z в плоскости с разрезами по ОА, ВС и DE
ветви функции R однозначны.
Как показывает уравнение (1), при z=oo
1 dw
Voo dz
cos a sin a — ei<s,
откуда, называя через 0 угол с действительной осью
и замечая, что при z — оо
_L_^ = £>-ei
Voo dz ’
имеем:
— = eai,
откуда
а = к — 9,
206 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
как это и указано на рис. 9. На перьях крыла R— чисто
dw
мнимое, а потому --------действительное, и скорость направ-
лена по действительной оси, т. е, по перу; в точках О,
В, £), как выше указано, R = 0, а потому
1 dw
----— = cos о
Voo dz
и, следовательно, поток сходит с задних кромок перьев
с одинаковой для всех перьев конечной скоростью. Наконец,
Рис. 9.
в точках Л, С, В скорость обтекания бесконечна, так как
в них R = oo. Следовательно, характеристическая функция,
определяемая (1), дает поток, указанный на рис. 9, т. е.
поток, обтекающий без срыва разрезное крыло.
Отсюда легко найти подъемную силу. Разлагая правую
часть уравнения (1) в области z = со, получим:
1 иии . . . / <
------— — COS <3 -4- I Sin О 1
Voo dz 1 \
или
. . I . . CL —I— С -4- & . 1 f \
= cos а 4-1 sin a -4- i sin a —4—!-—И . . . ),
1 2г 1 г2 \ /
откуда получим циркуляцию J вокруг разрезного крыла
J = f dz — тШоо sin а (а с + е) = sin а,
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 207
где I есть общая длина хорды всех перьев разрезного
крыла. Отсюда по теореме Жуковского подъемная сила
определится по формуле
Р = qv J'гср-и2/ sin а,
‘ ОО г оо
подъемная сила
изменяется,
они с д в и-
что о б р а -
сплошное
плоского разрезного
раздвинуты ли перья
т. е. получим следующую важную теорему С. А. Чаплы-
гина:
крыла не
крыла или
нуты так,
зуют одно
крыло.
Таким образом, в слу-
чае плоского крыла разрез-
ное крыло не дает выигры-
ша в величине подъемной
силы сравнительно с кры-
лом сплошным.
Аналогичный метод при-
ложен С. А. Чаплыгиным
и для изучения другого
разрезного крыла. Ограни-
чиваясь случаем разрезного
кругового крыла, состоящего из двух перьев, рассмотрим
дужку, составленную из двух дуг AD и СВ одного и того
же радиуса (рис. 10), который будем считать равным еди-
нице. Пусть точкам Л, В и С соответствуют комплексные
числа
а = eai, b = с = £<а+Р+т)*
и пусть
«+т
d = e 4 \
Называя через w характеристическую функцию течения,
л, 1 dw
обтекающего разрезное крыло, рассмотрим функцию —-т~.
Voo dz
Эта функция должна удовлетворять следующим условиям:
1) вне перьев крыла она однозначна и конечна;
2) на передних кромках перьев, т. е. в точках С и Л,
она обращается в бесконечность;
208 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
3) на перьях дужки выражение должно быть чисто
мнимое, так как dw действительно на перьях в силу того,
dz
что перо является линией тока, а ~------чисто мнимое, так
как на пере
z = е&.
Можно показать, что при подходящем выборе действитель-
ных постоянных Д, В, Д', B't G ъ Н можно положить:
1 dw
Voo dz
где
(Д + Bi) _(Д_В1-)_ + ^- +
4- Г(Д' 4- B'i) e - 4- (Д' — B'i)

и 0o есть угол с действительной осью.
Очевидно, что правая часть удовлетворяет условиям 1)
и 2).
Полагая на перьях дужки z = eui, имеем, что
1---L — 1 — e-ui _ е 2 *2/sin ,
z 2 ’
1---— = 1 -— е 2 2i sin U Q ° ,
г 2 ’
1 -у = 1 ^-(м-а-р)г . е 2 2l Sin— g----— ,
1 —у = 1 — ₽-T)i = e~U в2₽ 141 sin ц~а^Р~1
откуда имеем на окружности | z | = 1
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 209
И радикал L на перьях крыла имеет чисто мнимое значе-
ние, так как угол и заключен соответственно в пределах 0
и а для дуги AD и а-|-(3 и а4-Р4~Т для ДУГИ 5С; на
остальной части окружности L везде действительно.
Так как на окружности |з| = 1
J- z= (Д + Bi) е1 — (A — Bi) е~г + Ш +
-4- [(Д' 4- B'i) е1 -1 + (A' — B'i) е~г d + о] L, (2)
то очевидно, что при чисто мнимом L правая часть равен-
ства (2) также чисто мнимая. Таким образом, условие 3)
выполняется.
Остается подобрать коэффициенты А, Д', В, В' так,
чтобы выполнилось условие 1). Для этого нужно подобрать
эти коэффициенты так, чтобы в области z = 0 правая часть
не содержала членов с отрицательными степенями.
Так как в области z — 0
R_ f (z-\)(z-b) у ° 4‘ ») f _b_
к~ V (г-а)(г-с) |/ а’с
где
то, собирая в правой части равенства (2) члены с -% и при-
. . 1
равнивая коэффициент при нулю, получим:
откуда
А — Bi —A' — B'i,
А = А', В — В'.
С другой стороны, при z = оо правая часть должна дать
а потому
(Д 4- Bi) e-iQo 4-(Д' 4- B'i) e~iQ° ==
210 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Следовательно,
Л + 1,
В + =
а потому
Л = =
в = В' = 0.
Таким образом, уравнение (2) принимает вид
_L^ = le-(W_______. «I
dz 2 е 2z*e г
। / 1 jQ । jO I Gd\ п
Подставляя теперь разложение R в области нуля, находя
жж 1
коэффициент при — и приравнивая его нулю, получим урав-
нение
AzA п
^- + -^ + №•==0, (3)
откуда и находим два действительных коэффициента G и Н,
По найденным коэффициентам легко определить цирку-
ляцию, для чего надо найти коэффициент при в области
бесконечности для правой части уравнения (2). Так как
в области z = со
где
2/zt = а + с — b — 1,
то
J = j* dz = 2Tziv^ е~^ -|- Gd -|- Hl},
но, заменяя I на —i в (3), имеем:
H-Gd —/Л = 0, (4)
так как hr и h — сопряженные. Отсюда
J= 2^00 • 2Hi = —4z//-Uoo.
ТЕОРЁТИЧ. основания методов увеличения подъёмной силы 211
Из (3) и (4) имеем, исключая О:
С. А. Чаплыгин вводит, далее, обозначения
а-|- Т — 4д\
а — у = 4#'.
Тогда из
2/zx = а + с — b — 1
получим
~ == е 2 * p«4cos (у 4“ q— (у 4~ #4-/)]»
и так как
1±£±1_ 0 —Л_G
2 ио ~ 2
где а — угол атаки, то еще можно написать:
2 °) г£sin sin q + sin у sin (2q' — q) 4~
-|- i sin -|- 2g^ cos q — i sin cos (2^' — 7) J ,
и, меняя i на —Z, найдем аналогичное уравнение для опре-
деления h. Подставляя эти значения, окончательно найдем:
j = — 2^00 [81ПС(° + q} (sin (у + 2ч) — sin 4 cos 2/( +
+ C°Sc(6ft?) SinISitl2q'l= —2кг’°°А'1
и подъемная сила по теореме Жуковского определится
в виде
Р = 2крг>^;
если же считать радиус дужки не равным единице, а неко-
торому г, то аналогично получим:
Рг = 2терг^/С.
212 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
В работе С. А. Чаплыгина приведены расчеты подъемной силы
при различных предположениях относительно углов а. р, *[.
Например, при а = 24°, [3 = 9°, у = 3° подсчет показы-
вает, что в разрезном крыле получается выигрыш подъем-
ной силы сравнительно с неразрезным, которое получится,
если сомкнуть перья разрезного крыла. Этот выигрыш ра-
стет с уменьшением угла атаки: при а =10° он составляет
20%, при а = 3°45' он равен 32% и повышается до 52%
при с — 0, когда при полете хорда крыла горизонтальна.
В обстоятельном мемуаре С. А. Чаплыгина, далее, изу-
чен случай плоского и дугового разрезного крыла с произ-
вольным числом перьев и дана для общего случая теория
момента подъемной силы. При этом оказывается, что в слу-
чае плоского разрезного крыла точка приложения силы
остается неподвижной так же, как и в случае пластинки,
т. е. вместо параболы метацентров имеем точку; в случае
разрезного дугового крыла имеем параболу метацентров.
Окончательный результат, полученный С. А. Чаплыги-
ным, состоит в том, что разрезное крыло увеличивает
подъемную силу более значительно при малых углах атаки.
Этот вывод не оправдывается при экспериментальном иссле-
довании обычно применяемых разрезных крыльев. Причиной
этого расхождения, по-видимому, является следующее:
1) разрезные крылья (Хэндли-Пэдж и др.) весьма сильно
отличаются от крыльев, рассматриваемых С. А. Чаплыги-
ным; они представляют собой толстые крылья, причем ске-
лет предкрылка образует со скелетом основной части крыла
значительный угол;
2) в теории, выше изложенной, предполагается, что все
отдельные перья обтекаются потоком без отрыва струй.
§ 3. Случай плоского крыла и предкрылка,
образующих малый угол
В более поздней работе С. А. Чаплыгина и В. В. Голу-
бева х), представляющей собой дальнейшее развитие идей
работы С. А. Чаплыгина и Н. С. Аржаникова по теории
Э С. А. Ч а п л ы г и н и В. В. Г о л у б е в, К теории предкрылка
и закрылка, Труды ЦАГИ, вып. 171, 1935 [см. настоящее издание,
стр. 145—199].
ТЁОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 213
крыла с открылком и работы С. А. Чаплыгина о разрезных
крыльях, рассматривается случай плоской основной части
крыла и плоского предкрылка или закрылка, образующих
между собой малый угол. В этой ра-
боте рассматривается обтекание конту- aZ
ров в случаях, указанных на рис. 11, с// М 4
где АВ—основная часть крыла, CD— 1 --ч
предкрылок и угол рь предполагается D
малым. Задача построения характеристи- Рис. 11.
ческой функции в рассматриваемом слу-
чае представляет собой частный случай задачи об обтека-
нии биплана и решается при помо-
щи теории эллиптических функций.
О С В А Предполагая, что точка пересе-
чения прямых, на которых лежат
Рис. 12. отрезки АВ и CD, находится в точке
z — 0 плоскости (z) и что основная
часть крыла АВ лежит на действительной оси, рассмотрим
сначала случай, когда рь = О(рис. 12). В этом случае не-
трудно отобразить всю область течения на прямоугольник
вспомогательной плоскости (и). Дейст- (и)
вительно, рассмотрим на вспомогатель-
ной плоскости (и) прямоугольник D'—————if'
A'B'C'D' со сторонами шиш' (рис. 13).
Эллиптическая функция вида L—_________1—
5) *
z — w Рис. 13.
позволяет отобразить область течения на прямоугольник
плоскости (и) следующим образом. Если 0 < а < р < —
(рис. 13), то
Рр/ >
и функция
есть возрастающая функция /, так как
Г(П_ ^-РЧ>0.
7 (/—j?aZ)2
214 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щиткой
Следовательно, замечая, что при изменении и вдоль сторон
прямоугольника A'B'C'D' функция $>и, оставаясь действи-
тельной, все время убывает от -|-оо до —• оо, мы получаем,
что при а > 0 функция убывает, причем z принимает после-
довательно значения:
и = 0 и = <0 и = (О <о' U = о/ u = $i u = al u = 0
z = a II °© °© Я 'СО II Б to to U Р "UD е«— фаг z = 0 Z=QO z = a
Следовательно, z пробегает всю действительную ось. Под-
бирая а = О А (рис. 14) и выбирая отношения w : о/ : р : а
таким образом, чтобы
— = О В
ei — а ’
е2 — ^1 ОС
e2 — $ai а ’
= ОР
а 1
мы получим отображение нижней полуплоскости (г) на пря-
моугольник A'B'C'D' плоскости (и), причем отрезкам АВ
(Z)
\о О с в А
Рис. 14.
и CD соответствуют стороны пря-
моугольника А'В' и C'D' и от-
резкам CBnDA — стороны С'В'
и A'D'. Так как на стороне В'С'
z действительно, то в точках,
симметричных с С'В', z прини-
мает комплексные сопряженные
значения по принципу симметрии.
Следовательно, прямоуголь-
ник A'A"D"D' (рис. 14) пред-
ставляет собой отображение всей плоскости (г) (рис. 14),
причем нижней полуплоскости соответствует прямоуголь-
ник A'B'C'D', а верхней — прямоугольник B'A"D"C'; отре-
зок А'В'А" представляет собой изображение двух сторон
разреза АВ, и таким же образом отрезок D'C'D" есть изо-
бражение двух сторон разреза DC; наконец, стороны A'D'
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 215
и A"D" представляют собой изображение всей части дей-
ствительной оси, лежащей вне DA.
Подобным же образом в других случаях положения
точки О соответствующие изображения даются функциями
фи-$а1
и
а фи-фы ’
Заменяя в (5)—(7) функции через а, получим еще:
g(tt--PZ) +
1 з (и — al) з (и -|- at) ’
___ з (и — со— pZ) з (и -|- «о -J- ₽Z)
% а (и — al) а (и al) а2 (со -|- $1) ’
___ а (и — Ь — со') з (и b а/) 1
Z________________________________а (и — al) а (и-}-al) а2 (Ь 4“ со') * ,
(6)
(7)
(8)
Для того чтобы получить функции, дающие отображение
на прямоугольник A'A"D"D' плоскости с разрезами, указан-
ными на рис. 11, вводим следующее изменение в формулы (8).
Предполагая, что b и с — некоторые действительные числа,
построим функции
z = fl («) = «1
g (а — с — pZ) я (ц — с + рг) и
а (и — al) а (и -|“ а0 1
г /,л __ п а (Ц — С — Ц — PZ) з (Ц — С + со 4- ftZ) 2TJ £ и
2' ' 1 а {и — а/) а (и 4“ aZ) а2 4~ ₽Z) ’
Г /,а __ „ (Ц—Z>—a>z) з (^4-6 4- а/) 1 £ и
3 ' ' 1 3 (w-|-c—al) а (^4~с 4" “Z) з2(а/ 4" Ь)
(9)
Можно показать, что все три функции дают отображение
прямоугольника A'A"D"D' плоскости (zz) на плоскость (г)
с разрезами АВ и CD (рис. И), причем разрез АВ лежит
на действительной оси1, а разрез CD — на прямой, образую-
щей с действительной осью соответственно углы
с
и = 77 —,
1 со
I с
Ц = 77 -4- 77 — .
k ' (О
(10)
216 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Предполагая, что с мало, и откидывая члены с с2, полу-
чим следующие приближенные формулы для положения точек
Л, В, С, D на плоскости (г):
ZA~ ZA'i ZB~ ZB> ZC~ ZI)~ZDe'1' Cl)
где Za, Zb, Zq, Zd дают положение точек Л, В, С, D при
с Ф 0 и z*A, z*B, z*0, z*D— положение их при с = 0, т. е.
когда оба отрезка лежат на действительной оси (рис. 12).
Отсюда видно, что при изменении с с точностью до с2
можно считать, что отрезок АВ остается неподвижным на
плоскости, а отрезок CD вращается около начала, сохраняя
постоянную длину.
Построим характеристическую функцию течения, обте-
кающего пластинки АВ и CD без срыва, и пусть точки А
и С являются точками схода струй. Для этого построим
характеристическую функцию течения, обтекающего стороны
прямоугольника Л,Л"£)',D, на плоскости («), при условии,
что в точках, являющихся изображениями концов А и С,
скорость равна нулю, причем в дальнейшем ограничимся
только случаем, когда точка О лежит на отрезке CD (рис. 11).
Характеристическая функция течения определяется уравне-
нием
1 dw „ Г/л / । । 1
= ^(a + c-aO + ^j-
+ + + +
—«О —+ с + + + (12)
rz гл ». dw
причем для определения К и найдем выражение при
z = оо.
Называя через К угол атаки, т. е. угол, образованный
скоростью в бесконечности с действительной осью, и под-
/л\ /«о\ dw dz
ставляя из (9) и (12) значения — и —, получим уравнение
.. 1 dw. dz
о—гл —______ — ----=
av^ du 'a du
b) Л-2^.(С««-С5) a2aZ
q2a/ e a (— c — b aZ — <•>') a (c -|~ a^"(“ 4~ “O *
ТЕОРЁТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 217
Так как — действительно на действительной оси, то,
az
меняя —с-}-al на —с — aZ, получим аналогичное уравнение
для После некоторых преобразований окончательно по-
лучим для определения К и следующие два уравнения:
К - ср (с) = е ' ш Л
„ a(2aZ) , ч {(х-2^“)
где
-2^
е ш
Ч ~ a2 (al — с) (Ь + о/) — Р (aZ — с)] *
Найдя К и К19 можно определить L и Л4 из условия, что
точки А и С являются точками схода, а потому в соответ-
ствующих точках на плоскости (и) скорость равна нулю.
Это дает уравнения
(13)
(14)
- К [р («0 - с - az) + - К. [р («о + с + «0 ++
4-ZL С(и04-с—az) — С(ао4-с4-аО + 2т]У 4-Л1 = 0, (15)
— К (<о + а/ и2 + с — аг) 4- —К [р («> 4~ 4~ «г +
4- с 4- az) -f- -J- ZL (w 4~ ш/ 4~ мг 4-c—й1) —
— С(ш + <в' + гг2 + г + а0 + 271/£1 + Л1 = 0, (16)
причем Uq и tt2+(0 + (0, представляют собой корни уравнения
— = 0, близкие к нулю и к , так как при с Ф О
изображения концов отрезков АВ и CD смещаются из точек
О, (о, о) —а)х и о/ на плоскости (и). Можно показать, что
(.аг+1
“° РК4-₽)-С
и
Р (“ + “' + “0 4- -j-
“2 = Р (" + *) — Р (" + “' + «О
(17)
218 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Из уравнений (15) и (16) получим:
/С [р (о> —<&' —1~ и2 -|- с — со) — р (Uq -|- с — aZ)] -|~
“4“ [р (ш + + и2 +с + а0-----------Р (й0 + С + а0] =
== — Li [С (^о *4~ с—ocZ) — С (w “J-’ + ^2 *4~ —
— £ (^о "4~с *4~ а0 "4~ £ (ю *4~0)/ *4~ ^2 “4”с + а0] • (18)
Вычислив интеграл от (12) вокруг точки —c-|-aZ, найдем
циркуляцию скорости вокруг крыла J:
J —ZkLVoqCi, (19)
и по теореме Жуковского получим подъемную силу в виде
р s= 2т:ру^аЬ.
Таким образом, определение подъемной силы сводится
к определению £, которое может быть выполнено по урав-
нениям (18) и (19). Окончательно получим для определе-
ния L уравнение
L = — 2(^2 g2) sin X (F (b + o>') — №\ IF (<o + (O' — at) —
IP' al
— Fai] — cl 2(Р“,2~*2) cos X [ {F'cu — 2Cai (F (b + (o') — Fat]} X
jP' al
x {F(<o + (o' —aZ) —Fa/} + i^a[F(ft + <o') —F«nx
X [F (ш + a/ — ai) — Fai] + IF (* + «>') — F^] X
lF(“'+*) + ^
X | f («>' + /’) — ^ai
F(“ + *) + -J
+ + P' (<» + (o' — ai) f .
(20)
Полученная формула в общем виде представляет боль-
шие затруднения для исследования; только в частном случае,
когда с = 0, т. е. когда пластинки лежат в одной плоско-
сти, нетрудно до конца исследовать полученное выражение.
В этом случае получаются результаты, совпадающие с выво-
дами предшествующего параграфа.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 219
В случае, когда предкрылок CD мал сравнительно с основ-
ной частью крыла АВ, полученную формулу можно значи-
тельно упростить. Можно показать, что в этом случае а
мало. Разлагая выражение (20) по степеням а и ограничи-
о
Рис. 15.
с в
ваясь членом с наименьшей степенью а, получим приближен-
ное выражение для L в виде
L = — Ф + С-^ [1Г + 4 е2+2е22+2(е1-е2)(е2~е3)],
и после некоторых упрощений можно еще написать:
L
2
sin К . с cos X . . . . .
у- а (б1 — «2> (е2 — *з) X
г- 2 со
у 4 _|_ 3 Г ______________
Х ^ <0 J фи—-е2
L о
. (21)
Отсюда видим, что при X > О и с>0 присутствие вто-
рого члена уменьшает абсолютную величину L, а потому
уменьшается и величина Р\ обратно, при с < 0 абсолютная
величина L и Р увеличивается при X > 0.
(1)
(2)
^5
Рис. 16.
Итак, в положении (/) (рис. 16) предкрылок уменьшает
подъемную силу крыла; в положении (2) он увеличивает
подъемную силу крыла.
Так как обычному расположению соответствует случай (/),
то можно сказать, что предкрылок уменьшает
подъемную силу крыла; в случае, если мы считаем,
220 i; труды по теории предкрылка, закрылка и щитков
что с и а малы, то это уменьшение незначительно, так как
по формуле (2) видно, что оно пропорционально произведе-
нию са4. Можно подобным же образом исследовать случай
закрылка. При этом оказывается, что в положении (2)
(рис. 16а) закрылок уменьшает подъемную силу и в поло-
жении (1) он увеличивает подъемную силу.
Так как обычному положению закрылка соответствует
случай (/) (рис. 16а), то окончательно получаем следующий
важный результат: при обычном расположении
предкрылка и закрылка предкрылок умень-
шает подъемную силу, а закрылок ее увели-
чивает.
§ 4. Влияние предкрылка на предельный угол атаки;
исследования В. В. Голубева
Результаты предшествующих параграфов показывают,
что эффект действия предкрылка надо искать не в увели-
чении подъемной силы, а в улучшении условий обтекания
потоком крыла. Исследованию действия предкрылка в этом
направлении посвящена работа В. В. Голубева1). Разбор
эмпирического материала по разрезным крыльям приводит
автора к выводу, что в работе предкрылка надо рассматри-
вать три различных случая.
1. При подходящем расположении крыла и предкрылка,
при малых углах атаки, разрезное крыло может работать,
как крыло сплошное; при этом предкрылок работает на срыв,
*) См. В. В. Голубев, Исследования по теории разрезного
крыла, ч. I; Труды ЦАГИ, вып. 147, 1933, [см. настоящее издание,
стр. 31—137]; см. также V. V. Golubev, Theory of the Slat in a
two-dimensial Flow, The Journ. of the R. Aeron. Soc., № 309, 1936.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 221
но сорвавшиеся с него струи примыкают к основной (рис. 17)
части крыла. Эффект действия предкрылка здесь скажется
только в некотором увеличении лобового сопротивления за
счет вихрей, образующихся в промежутке между предкрыл-
ком и основной частью крыла.
Рис. 17.
2. При увеличении угла атаки возможен такой режим,
что предкрылок работает в условиях срыва струй и основ-
ная часть крыла — в условиях полного обтекания. Этот слу-
чай скажется в резком увеличении лобового сопротивления
и некотором уменьшении подъемной силы (рис. 18).
3. При дальнейшем увеличении угла атаки вихревой хвост
за предкрылком становится уже, что вызывает уменьшение
лобового сопротивления и предкрылок начинает работать
в условиях полного обтекания.
Этот последний случай и соответ-
ствует нормальному расположению

предкрылка.
Если предкрылок работает в Рис. 19.
условиях полного обтекания, то,
пренебрегая хордой предкрылка, можно его заменить
одним вихрем, расположенным близко к передней кромке
крыла (рис. 19). Направление вращения этого вихря таково,
222 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
что он уменьшает скорость около передней кромки крыла,
т. е. в точках крыла, где скорость наибольшая. Таким обра-
зом, присутствие предкрылка, уменьшая наибольшую ско-
рость в точках крыла, выравнивает распределение скоростей
на верхней поверхности крыла, в результате чего крыло
может работать без срыва струй на больших углах атаки,
чем без предкрылка. Таким образом, чтобы изучить влияние
предкрылка, нужно изучать: 1) влияние распределения ско-
ростей на верхней поверхности крыла на положение точки
отрыва; 2) влияние предкрылка на распределение скоростей.
Эти две задачи и рассматриваются в работе В. В. Голубева.
Для решения первой задачи применим теорию пограничного
слоя Прандтля. Называя через h толщину пограничного
слоя, определяя положение
Р точки А в пределах слоя
координатами х и у, при-
чем у есть расстояние
f''7 данной точки A rq твер-
рис 20. дой стенки, обтекаемой
жидкостью, а х есть рас-
стояние от некоторой точки О стенки до подошвы перпен-
дикуляра АВ к стенке (рис. 20), и пренебрегая действием
кривизны стенки, Польгаузен дал следующее дифференциаль-
ное уравнение для определения толщины слоя:
0,8 — 9072— 1670,4k — I 47,4 + 4,8 р — | 1 + | кз
dz _ L \ и'2 ) \ и'2 ) \,
dx~ и (—213,12 + 5,76k + k2)
(22)
Л2 ' u'h? z ч
где z = — , л = —, и (X) есть скорость обтекающего
тело потока на внешней поверхности слоя и \—кинематиче-
ский коэффициент вязкости; кроме того, из теории погра-
ничного слоя Прандтля в форме, данной ей Польгаузеном,
вытекает, что в точке отрыва струй Х = —12.
Применение уравнения (22) для определения точки отрыва
струй представляет то затруднение, что определение и(х)
невозможно без знания положения точки отрыва, так как,
очевидно, распределение скоростей в потоке, обтекающем
тело, зависит от положения точки отрыва.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 223
Замечая, что из экспериментальных данных следует, что
на верхней поверхности крыла давление изменяется по ли-
нейному закону в интервале от точки, где давление наимень-
шее, до точки отрыва струй, В. В. Голубев полагает для
этого интервала, что
а так как по теореме Бернулли
Т
то
d?u
U
= 0,
а потому
UU"
-^2- = —!.
Точное решение вопроса о распределении давлений на
крыло Жуковского дает Перринг (Perring)1).
Подставляя это выражение в уравнение (22) и замечая, что
— = — = 21 _х
dx dx \и' J и' и'2
приведем уравнение (22) к виду
Я (k) d\ = —, (23)
где
n m а\ = — 213,12 + 5,76X2 + X2
a VV _ 7257,6 + 1549,4Х — 39,8X2 _ кз •
В точке, где скорость наибольшая и, следовательно,
давление наименьшее, и = 0, а потому и = 0. Так
как в точке отрыва Х = — 12, то для интервала от точки
*) W. Per ring, The theoretical Pressura. Distribution around Jou*
kowsky aerofoil. Technical Repout of the aerodynamical Recherches, 1927.
224 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И (ЦйТКОЙ
наибольшей скорости до точки отрыва получим:
х -12
J^= J
О о
откуда, выполняя приближенно интеграцию в правой части,
получим:
-^=1,2, (24)
и0
где uQ есть скорость в точке отрыва и «тах — наибольшая
скорость на верхней поверхности крыла.
Отсюда, предполагая, что точкой, где скорость наиболь-
шая, является передняя кромка крыла, получается для опре-
деления величины критического угла 9 атаки следующее
уравнение:
= (25)
где е — параметр, характеризующий утолщение крыла.
По поводу этой формулы необходимо отметить, что вся
теория Прандтля — Польгаузена опирается на предположе-
ние, что поток ламинарный. При тех скоростях, которые имеем
у крыла при обычных условиях полета, поток, несомненно,
турбулентный; тем не менее есть некоторые основания счи-
тать, что полученный вывод приложим и к этому случаю,
так как в силу замедления скорости при подходе к поверх-
ности крыла можно считать, следуя Карману, что в преде-
лах слоев, очень близких к поверхности обтекаемого тела,
где и начинается отрыв струй, течение ламинарное.
Другое основное допущение, что скорость максимальная
у передней кромки крыла, выполняется теоретически при
малых 8, т. е. у очень тонких крыльев; но эксперименталь-
ные данные указывают, что при наступлении отрыва точка
максимальной скорости перемещается к передней кромке и
у толстых крыльев. Впрочем, это предположение может быть
откинуто.
Полученная формула (25) позволяет определить то уве-
личение предельного угла, которое дает предкрылок. Заме-
няя, как выше было указано, предкрылок одним вихрем,
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ Силы 225
помещенным в точке z — pe?*, получим для характеристиче-
ской функции течения вокруг круглого цилиндра, на кото-
рый отображается крыло, уравнение
(1-р^)(г-р^)
причем точкой схода считаем точку z — 1; переходя на пло-
скость дужки, получим для случая дужки типа инверсии
параболы соответствующее уравнение:
dw rfw0 t
dz dz
а . "12
(z—\)e 2 +(1 —e)cosy
(z-l)
а .
(Z— 1)«? 2 +2(1 —е) cos
где 2а—центральный угол скелета крыла и е—параметр,
характеризующий толщину крыла. Отсюда, подставляя
z =—1 и ^ = +1» найдем скорость у передней и задней
кромок и, считая, что в момент отрыва струй в первом слу-
чае получим максимальную, а во втором случае—скорость
в точке отрыва, имеем уравнение при малом а:
2^ sin 9
(1 + 02
2е
= 2-Uqo cos 6
причем pe^ дает положение оси вихря, заменяющего пред-
крылок на плоскости круглого цилиндра, а Г—его интен-
сивность. Помещая предкрылок у передней кромки, мы
226 i. труды rid теории предкрылка, закрылка и щи1ко£
должны положить ср = тс, тогда
V
vmax
^0 = ^00^08 0(1 —е)
и, подставляя в уравнение (24), имеем для предельного угла
атаки уравнение
tg6+^_________р
ё 2wgo(p2—l)cos6 (1 + е)2 •
Так как без предкрылка, т. е. когда Г = 0,
_ 1,2е(1 —е)
°~ (1 _|_ е)2 >
то для увеличения угла атаки ДО имеем уравнение
sin ДО = —cos 90,
1 о,
или по малости ДО
Д9=75-^—5х-г cos 0О. (26)
2kVoo р2 — 1 0 4
Задача, таким образом, сводится к нахождению величины
циркуляции предкрылка Г. Применяя известную формулу
для плоской обтекаемой потоком пластинки ширины Ь, полу-
чим в предположении, что предкрылок плоский,
Г = тс^р, (27)
где —скорость потока в точке, занимаемой вихрем пред-
крылка, и р — относительный угол атаки для предкрылка.
Применяя формулу
“Т г а
(г~1)е 4-(i —ejcos-y
V
г {Z— 1)е 2 *4-2(1 —е) cos у
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 227
получим, полагая z = — р, ср —тс, следующее приближенное
выражение скорости у предкрылка:
, , 1 2 (р + £)2
®i = Vco ]/ 1 + — J COS 29 - (р _т + 2е) ’ <28'
и угол |л, образованный скоростью vv найдем по формуле
tg[i = tg9 (29)
Г 1
Если через у называть угол наклона предкрылка к действи-
тельной оси, то угол атаки р предкрылка найдем в виде
₽ = — I- (30)
Подставляя (27), (28), (29) в (26), получим окончательно,
откидывая член е2 и полагая cos0o=l:
Д0
_____(₽ + !?___ж.
2р(р+1)(р_1+2е)°Р-
Так как при сделанном построении хорда крыла L равна 4,
то еще можно написать:
Дб==2-7-----PtlV'-jn- (31)
Л р — 1 -|-2е р4- 1 4 7
Из формул (31) и (28) получаем следующие практические
выводы.
1. Для усиления действия предкрылка надо его помещать
около передней кромки в точке, где скорость обтекающего
дужку потока наибольшая, так как Г пропорционально vv
2. Предкрылок нужно помещать возможно ближе к крылу,
но так, чтобы между предкрылком и крылом оставалось
такое пространство, которое позволяло бы предкрылку ра-
ботать с образованием циркуляции; это следует из (31),
так как при приближении предкрылка к крылу р стремится
к 1 и Д0 увеличивается.
3. Предкрылок надо ставить под наибольшим относитель-
ным углом атаки, при котором предкрылок работает в усло-
виях обтекания, т. е. р нужно брать возможно большим.
4. Хорда предкрылка не должна быть очень мала сравни-
тельно с хордой основной части крыла, так как Д0 про-
порционально ~.
228 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
5. Основная часть крыла должна быть взята такого
вида, чтобы она выдерживала без отрыва возможно большие
углы атаки, так как по (28) видим, что v1 возрастает при
увеличении 6.
По исследованию крыльев с предкрылком имеется огром-
ный экспериментальный материал; данные опыта, по-види-
мому, подтверждают предыдущие теоретические выводы.
Из всех теоретических результатов, приведенных выше,
можно сделать следующий вывод: разрезные крылья не уве-
личивают непосредственно величины подъемной силы, но
увеличивают те предельные углы, при которых крыло может
работать в условиях более или менее полного обтекания,
когда к нему приложима вышеизложенная циркуляционная
теория.
Глава II
ПРИБЛИЖЕННАЯ ТЕОРИЯ РАБОТЫ ПРЕДКРЫЛКА
И ЗАКРЫЛКА; ОБЩИЕ ФОРМУЛЫ
§ 1. Метод исследования
Точное решение задач, выдвигаемых современной техни-
кой, по большей части недоступно средствам современной
теоретической механики и математики. Поэтому приходится
прибегать к различным способам приближенного решения;
при этом намечается два возможных пути:
1) или изучаемое явление записывается точно дифферен-
циальными (или интегральными) уравнениями и задача сво-
дится к точному, если это возможно, или к приближенному
решению найденных уравнений при помощи введения малых
параметров,, разложения функций в ряды, откидывания в урав-
нении малых по величине членов и т. п.,
2) или изучаемое явление с самого начала заменяется
другим, близким к данному, но более доступным для иссле-
дования, так что изучается, в сущности, не явление, поста-
вленное техникой, но некоторое другое явление, мало отли-
чающееся от данного и представляющее его упрощенную
стилизацию.
И тот и другой метод с большим успехом прилагается
к решению задач в области точного естествознания (астро-
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 229
номии, физики и т. д.), механики и техники; каждый из
этих методов имеет свои преимущества и недостатки. Пер-
вый метод, вводя приближения в решение чисто математи-
ческой задачи, позволяет иногда оценить степень прибли-
жения, а при дальнейшем развитии средств математики найти
точное решение, но зато он отличается по большей части
необычайной громоздкостью, которая при делаемых далее
упрощениях оказывается совершенно ненужной и бесполез-
ной. Второй метод, по сути дела, обладает большой про-
стотой, но не позволяет обычно дать оценку получаемой
степени приближения и принужден здесь опираться на экспе-
римент.
В области теории крыла все крупнейшие результаты
получены именно вторым методом. Замена конечного крыла
бесконечным, воздуха — несжимаемой идеальной жидкостью
позволили Н. Е. Жуковскому, С. А. Чаплыгину и др. раз-
работать стройную и практически чрезвычайно важную тео-
рию крыла самолета в плоскопараллельном потоке, при-
меняя весьма простые математические средства; наоборот,
попытка Озина (Oseen) и других ученых применять к
этой задаче теорию вязкой жидкости (каковой, конечно, и
является воздух), несмотря на необычайную сложность иссле-
дования, практически не дала никаких результатов. Наконец,
вся теория конечного крыла, разработанная Прандтлем
(Prandtl) и его школой, построена на замене крыла одной
несущей линией, и эта доведенная до предела схематизация
явления дала современную практически важную теорию,
лежащую в основе всей современной теоретической аэро-
механики.
В настоящей главе мы будем исключительно применять вто-
рой из указанных выше методов. Мы начнем изучение влияния
на работу крыла добавочных, небольших по размерам хорды
сравнительно с основным крылом, крыльев (предкрылков или
закрылков), помещенных вблизи основной части крыла.
В дальнейшем мы дадим приближенную теорию влияния
предкрылков и закрылков на работу крыла, основанную
на замене предкрылка и закрылка одним несущим присоеди-
ненным вихрем, причем будем рассматривать, как и выше,
задачу в плоскопараллельном потоке, т. е. для крыла беско-
нечного размаха; основную часть крыла мы при этом не будем
230 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
заменять одной несущей линией и воспользуемся обычной тео-
рией крыла в плоскопараллельном потоке. Такого рода метод
можно рассматривать как приближение, представляющее сле-
дующий шаг сравнительно с теориями биплана, данными
Бетцем (Betz) и Прандтлем (Prandtl), где оба крыла биплана
рассматриваются как несущие линии.
При исследовании, следуя обычному методу в теории
крыла, мы начнем со случая обтекания потоком круглого
цилиндра в присутствии вихря с тем, чтобы затем перейти
к случаю крыла в присутствии вихря, применяя метод кон-
формного отображения.
§ 2. Обтекание круглого цилиндра в присутствии
неподвижного вихря
Пусть мы имеем цилиндр радиуса 1, обтекаемый потоком
с образованием некоторой циркуляции Г, и пусть, кроме
того, есть некоторый вихрь интенсивности J, помещенный
вблизи цилиндра. Называя через а — ре?4 аффикс оси доба-
вочного вихря и полагая а — у е^, получим характеристи-
ческую функцию течения в виде
где Vqq — величина скорости потока в бесконечности и 9—-
угол, образованный ею с действительной осью плоскости г.
Из уравнения (1) получим:
-а;/. е*н\ , Г 1 . J / 1 1 \
dz ~Vc°e \ z+2nl\z — a z — а/
Для дальнейшего исследования важно найти критические
точки течения (1), т. е. точки с нулевой скоростью. Для
их определения мы имеем уравнение
00 \ z2 / * 2kZ z * 2kZ z — a a) ’
что еще можно переписать в виде
v^e-^ |jz2 — e2ei) (z—a) (z—a) + z (z — a) (z — а) +
jM — т
+ ^7—(а— а) =0
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 231
или, располагая левую часть по степеням z:
zi + - (« + «) ] + [ аа - е™ - (а+а) +
+ 2^<а — “ф2+[еШ<а + ^ +
+ 2^~аа] z — ewaa = 0. (3)
Если назвать корни уравнения (3) через zlt z2i z3, z4, то
уравнение (2) можно написать в виде
duo
— = ~Г<------W—=Г~ Zl)(z ~~ z*> ~ ~ z^- (4)
dz z* (z — a) (z — а)
Исследование уравнения (3) приводит к ряду интересных
следствий.
1. Так как по (3) имеем:
*1*2*з*< = — емаа, (5')
то, полагая zk = рке*к\ получим:
Р1Р2РзР4= И а1 + а2 + а3 + а4 = 26 + тг + 2р.Н-2№.
Но в случае, если Г и J стремятся к нулю, очевидно, что ах
стремится к 9, а2 стремится к тг-|-9 и а3 и а4 стремятся
к [1, потому в пределе имеем;
0 + 7г+0 4-2|х==204-7г4-2р. + 2Мтг,
откуда W = 0; так как N может изменяться, только при-
нимая целые значения, а ак, очевидно, изменяется непре-
рывно, то отсюда следует, что W тождественно равно нулю,
и мы имеем равенство
ai + а2 4" аз + а4 == 29 + гс -|- 2р., (5")
что еще можно написать в виде
(*! — 9) + К — (^ + 9)1 + («3 - рО + («4 — = 0. (5)
Уравнению (5) можно дать следующее интересное истолко-
вание. Замечая, что 9 и -гс-|~9 суть углы, определяющие на
цилиндре положение критических точек в случае, когда нет
232 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
вихрей, т. е. когда Г = 0 и О, назовем ах — 9 и
а2 — (тг —6) угловыми смещениями критических точек; точно
так же назовем и а3 — р- и —р- на том основании, что
при J=0 точки z3 и zv очевидно, стремятся к а и а, т. е.
а3 и а4 стремятся к рь. Введя такие названия, мы можем
выразить равенство (5) следующим образом: при обр азо-
ван ии у цилиндра вихрей Г и J сумма угловых
смещений критических точек равна нулю.
Очевидно, что при J=0 и Г ¥= 0 отсюда получим, что
(*! — 9) + [а2 — (тг + 0)] = О;
а это равносильно тому, что хорда, соединяющая критические
точки на цилиндре, параллельна скорости потока в беско-
нечности.
2. В дальнейшем мы обычно будем считать, что одна из
критических точек постоянно помещается в точке z=\.
Это равносильно тому, что мы будем считать, что точка
z= 1 цилиндра есть изображений острой задней кромки
крыла. При этом условии уравнение (5) можно написать,
полагая at = О, в виде
[a2 — (тс + 26)]4-(а3 — р.) + (а4 — |х)= 0. (6)
Так как в случае, если одной из критических точек
является точка z=l, то при J=0 второй точкой служит
точка z2 = — e2Qi, и уравнение (6) также можно выразить
приведенным выше образом, причем под смещением точки z2
будем понимать ее смещение, вызываемое присутствием
вихря Г.
Если сделать конформное отображение плоскости (z)
на новую плоскость (^) таким образом, чтобы окружность
[^|=1 перешла в действительную ось, то течения в верх-
ней и нижней полуплоскостях (zj будут совершенно сим-
метричны, а потому и положение критических точек отно-
сительно действительной оси плоскости (z^) также будет
симметричным. Следовательно, возможны два случая:
или все критические точки лежат на действительной оси
на плоскости (z^) и, следовательно, на плоскости (г) все
критические точки лежат на поверхности цилиндра,
или есть критическая точка, не лежащая на плоскости (z^)
на действительной оси; тогда обязательно найдется вторая
ТЕОРЕТИЧ; ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 233
критическая точка, ей симметричная относительно действи-
тельной оси. При отображении на плоскость (г) эти две точки
перейдут в точки, симметричные относительно окружности
1^1 = 1, т. е. если, например, = тог4 = —еаА
Оба эти случая возможны; если J мало, то будет иметь
место второй случай, так как при J = 0, очевидно, обе кри-
тические точки, z3 и z±, сольются с а и а; при значитель-
ных J будет иметь место первый случай.
Полученный результат можно выразить следующим обра-
зом: если уравнение (3) имеет корень seai, то он
1
имеет также и корень —еаг, причем, конечно, эти
корни будут различны только в случае, когда s #= 1. Этот
результат можно получить также и непосредственно из урав-
нения (3). Заметим, что доказанные выше два свойства
остаются верными при любом количестве добавочных вихрей,
помещенных около цилиндра1).
В дальнейшем будем предполагать, что точки z± и z2
лежат на цилиндре, причем z± есть точка схода и точка
z2 — точка разделения струй; точки z3 и z4 могут лежать
и на и вне цилиндра, причем обычно при небольших зна-
чениях J они лежат вне цилиндра.
3. Из уравнения (3), далее, мы имеем:
/ — ч
^1 + ^2+ ^3 + ^4 = [а-\-а —
2 ^г = ^-^-2^(а + «)+ (Ь)
к ф I
VI . — —
L z*ziz3 = “ e2G* (а + «) — аа- ' <с>
Из этих уравнений уравнение (с) в силу свойств (1) и (2)
является следствием (Ь). Действительно, разделив (с) на (5'),
получим:
V — — МдЕ I Ге~В£ ,
zk аа 2к^оо
*) См В. В. Голубев, Обтекание круглого цилиндра вблизи
Системы неподвижных вихрей, Уч. зап. МГУ, т. 7У 1936.
234 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Заменив здесь в обеих частях I на —i и замечая, что если
zk — set^i то — = — е~л^ и при замене i на —i отсюда
2к S
получим — е*к\ что по свойству (2) есть также корень
уравнения (3), а потому левая часть не изменится, получим:

а это есть уравнение (а).
Итак, независимыми уравнениями являются (а), (Ь) и (5)
или (5'). Разбивая уравнения (а) и (Ь) на действительную
и чисто мнимую части, получим следующие четыре уравнения:
2 sk cos ак = (р 4- 4 c°s 1* Г • A й sin 9, 2^00 (A')
sk sin а к = (р 4- j) sin р - 1 Г o -| cos 9, 2м/оо (A")
(ал4-аг) =
Г j / = cos 2р. — cos 29 1 2м/оо \ p+y)sin (Q+P')> (B')
^sftszsin(aft4-az) =
= sin 2р — sin 29 4- - J~ 2Woo (p + j)cos(9 4-tO (B")
и, кроме того, уравнение (5), которое мы возьмем в форме (5"):
а1 + а2 + а3 + а4 = 29 4“ К 4“ 2[1.
Нетрудно показать, что среди этих уравнений незави-
симых только четыре. Действительно, умножая уравнения (В')
и (В") соответственно на cos (9 4" I1) и sin (9 4-р-) и складывая,
найдем:
[ 2 skst cos (ак + аг)] cos (9 4- р) 4- 2 sksj sin (ак + аг) X
X sin (6 4-р.) = cos [2р— (9 + ^)1 — cos [2 9 — (9 + р)1 — О
или
2 Skst cos (ак 4- а{ — 9 — р) = 0.
(В'")
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 235
Но нетрудно показать, что это уравнение есть след-
ствие уравнения (5"). Действительно, пусть = s2 = 1 и
= как это следует по свойству (2). Тогда уравне-
ние (В"') можно написать в виде.
cos (а4 4- а2 — 9 — и) 4“ $зcos (а1 + аз — ® — н) Ч~
— cos (ах + а4 — 9 — у.) -|~ s3 cos (а2 + аз— Р
s3
—j---cos —Н ^4 —— И*) —Н cos (ос3 —ос4 —*- 9 j— у,) = 0 i
s3
Но в силу уравнения (5") имеем, например,
а1 + а2----------®----у, = 9 -|- уь 4" 71-а3-а4»
так что
COS (04 4“ а2-0---у) =----C0S (а3 4“ а4--0---у).
Поэтому окончательно можно написать:
s3 cos (at 4- a3 — 9 — <jl) — s3 cos (0^ 4~ a4 — 9 — yO 4“
+ cos (агa4 — 0 —и) ——0— y-) = 0,
*3 d3
что, очевидно, верно, так как в силу свойства (2) а3 = а4.
Итак, из этих пяти уравнений—независимых уравнений
четыре.
Таким образом, зная, например, положения всех четы-
рех критических точек, можно найти р, ц, Г и J; но если
задать только положение трех критических точек, то задача
становится неопределенной, так что обтекание без срыва
крыла с тремя острыми углами, вершины которых на цилин-
дре переходят в три заданные критические точки, не имеет
одного определенного решения.
4. Выведенные свойства позволяют написать следующее
выражение скорости на поверхности обтекаемого цилиндра.
Предположим сначала, что все критические точки лежат на
поверхности цилиндра. Тогда zk=ea^t и, полагая на ци-
линдре z — е"\ получим:
a, i —7-^ * —7^ » ---7^ i
z — zk= e* —е к = е 2 |_е 2 —е z J =
ф + аА: .
= 21е 2 г sin у ~а-.
236 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Поэтому уравнение (4) можно переписать в виде
dw
dz
(2<? +
e^i [е^_(а + а)е^ + е2^]
о — а< . ф — а< . ф — д3 . ср — а4
X sin-—з 1 sin т 2- - sin---2 6 SIH - g- ,
НО
e2^i — (а-\-а) е^-\-е2^ — « [^(ф-р-) « -р
+ (р+у)].
или, полагая
г=И₽ + 7) <г>»' <6>
имеем окончательно:
dw
dz
sin sin sin'^ sinL^
’ 2 [ cos (cp — pc) — r]
at + <x3+a, 4- a4 — 20 - 2a
x e-^e 2
или, пользуясь свойством 1,
dw
dz
. . cp — a2 • ? — a3 . 4> — a4
.. Sin -!—~ i Sin!—77-^ Sin T Shi -!—r =
«’2 2 2 2
• (7)
Аналогичный результат получим и в случае, если точки z3
и z± лежат не на цилиндре. В этом случае
z3 = se9i и z4=le₽* (p = a3 = a4),
что еще можно написать в виде
z3 = el <₽-« lu -), z± = el (P+i 1U6>.
Таким образом, в этом случае в (7) надо положить:
а3 = Р — i In s и a4=^4-/lns.
Отсюда
. ф — a3 . ф — д4 . /ф — 8
Sin 2' Sin ' 2 = sln(T'~2
. . lny\ . /? — 3 . In s \
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 237
и, применяя формулу
sin2 а — sin2 р — sin (а —|— р) siп (а — Р),
получим:
siny 2~--sin ? — sin2<F 2- —sin2==
= sin2'^i + sh2‘l£.
Так как
1 1 / ln s in 8\ . .
sh 1^ = 10" -« =
и
i-
то уравнение (7) можно написать в виде
л -(tP + v)i • Т— а1 • Т— а2 ч/
— =4vMe ' 27 sinx__JSin Г__2 х
t(s + tXcos
Хтт—П--------------• <8Л
t(p + 7)-cos (*-₽)
Если же, обратно, заметить, что
г = Н'‘ + 7) = 2{[у(^-7г)Г + ^ = 251,!!Т+1
И
cos (ср — |i) = 1 — 2 sin2 2 ,
то уравнение (7) можно еще написать в виде
л -G+yp . ф — . <р — а2 ч 7
v 27 sin ^-2—1 sinX
• Q ? - ₽ . io 1П S
sm 2^ + sh
238 I. ТРУДЫ rto т’ЁоЁии пёёдкёЫлкА, ЗАКЁьМКА И ЩЙТКОЙ
или в общем виде:
dw А -ГР+*5“)* . ср —. ср — а9 . /оч
-^=4^ ' 27 sin У—2 tsiny 2L, (8)
где L определяется формулой
4-(s + -|) —C0S(T —₽) Sin2 izii + sh2l^
j — ±3_____LL____________________f________£_ /-o'!
1 / I 1 \ , . . .. <p —[Л , ,„lnp • w
•y^P + yj—cos(<p —p.) sin2 X—Л у Sh2-Jl
Заметим, что в случае, если J= 9, точки zr и z2 сли-
ваются с а и а, а потому р = $, рь = 13 и £=1; в том
случае имеем:
dw А -('P+vp • Ф— а1 • Ф— а2
— = 4-Уоое 4 2 7 sin - 2 1 sin т 2 2-,
т. е. обычную формулу для скорости обтекания цилиндра
без добавочных вихрей.
§ 3. Влияние добавочного вихря на распределение
скоростей; смещение критической точки
В приложении к теории крыла одной критической-точ-
кой является изображение на цилиндре острой задней кромки;
эта точка не перемещается при изменении угла атаки, и мы
можем считать, что она находится в точке z=l. Тогда,
полагая в формуле (8) = 0, имеем:
^=4я.е-(’*Й‘8|„Лйп^рд. (10)
Если сравнить эту формулу с аналогичной формулой
для обтекания цилиндра без добавочных вихрей
^1= sin bin (10')
CLZ £
то мы видим, что присутствие вихрей сказывается:
1) в замене угла а' через а2, т. е. в смещении критиче-
ской точки разделения струй;
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 239
2) в появлении добавочного множителя L, который изме-
няет величину скорости в точках цилиндра.
В настоящем параграфе мы выведем формулы, служащие
для определения а2. В общем случае задача сводится к реше-
нию уравнения четвертой степени (3); так как один корень
рассматриваемого уравнения (zt = 1) известен в рассматри-
ваемом случае, то дело сводится к решению кубичного
уравнения х).
Мы дадим весьма простое приближенное решение поста-
вленной задачи. Можно считать, что интенсивность доба-
вочных вихрей мала и потому величина смещения критиче-
ской точки тоже мала настолько, что можно пренебречь
квадратом величины а2 — а'.
Мы возьмем уравнение для определения положения кри-
тических точек в форме
v л . _L(_1_________L\=o
°° ' г2' 2п1 г 2яДг — а г — а) ’
как это следует из уравнения (2).
Так как этому уравнению должно удовлетворять значе-
ние z — 1, то
(1 — e20i) + — + — (—!----------U^ = 0. (12)
v 2nl ~2nl \1 — a \—a) v
Исключая из (11) и (12) величину Г, получим:
где
z — аа I________q
(г — a) {z — a) J
(13)
J (а — а)
2гс(1 — а)(1 — а)
(14)
Если положить z = e*ii то получим из (13) уравнение
• <Р
sini
s,n(f- !*)
cos (ср — у.) — г
(15)
!) Окончательная форма его дана в работе В. В. Голубева,
Исследования по теории разрезного крыла, ч. II, Труды ЦАГИ,
ВЫп. 506, 1937 [см. настоящее издание, стр. 291—348J.
240 I, ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
где
К = (16)
оо
Так как при J=0, т. е. когда ^ = 0, уравнение (15)
даёт для положения критической точки, точки разделения
струй, значение
а' = ср = тс+ 26,
то, полагая, что а2 = а'-|-2&, так что а2 = тс+ 29+ 28, и
подставляя это значение в (15), получим:
/ я \ sln(r + 9 + S — н)
cos (9 — — 9 — 8) — К —? 7 Ой , о.---------= 0;
\ 2 / cos (тс 4" 20 4“ 2о — р) — г
разлагая по степеням 8 и откидывая члены с 82 и ^8,
имеем:
S ___________/С COS (6 р)______ z 1 уч
г cos (20 — р) К sin (0 — р) ’ ' '
для значения а2 имеем следующее приближенное выражение:
а =к + 29 + —-----------------<п-------------v (18)
2 1 1 г + cos (20 — р) 4- К sin (0 — р) v 7
где _
К___d (а а).__________________ dd, (19)
4^00 (1 — а) (1 — а) 4nv^ (г — cos р)
и
Так как
*______ Jd _________________cos (р — 0)_______________
4^ (г — cos р) [г 4~ cos (20 — р) — /< sin (р — 0)]
_______Jd____________________cos (р 0)__________________ /поч
4тст/т z ч Г I /on Xi Jd sin (p — 0) 11 7
~ (Г - COS p.) + COS (26 - |A) + 7---~ r _ co~ ]
то, замечая, что при обычном расположении предкрылка
J< 0, видим, что 8 < 0 во всяком случае, когда
к4.0 >р>л_^е>
что и имеет место в случае предкрылка.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 241
Итак, имеем следующий результат: предкрылок смещает
критическую точку разделения потока таким образом, что
это смещение соответствует фиктивному уменьшению угла
атаки на величину | 31.
Действительно, если мы заметим, что
а2 = тс -j- 29 + 23 = к + 2 (9 + 3),
и сравним с
а' = тс Ц- 29,
то получим, что смещение критической точки равносильно
замене угла атаки 9 на угол 9-|-3.
Обратный результат получим при jx, близком к нулю,
т. е. в случае закрылка. Действительно, в этом случае
cos(jx — 9) > 0 и 3 оказывается величиной положительной,
т. е. закрылок смещает критическую точку разделения струй
таким образом, что это смещение соответствует фиктивному
увеличению угла атаки на величину 3.
Для окончательного определения величины 3 надо найти J;
этот вопрос будет изучен далее, в § 5.
§ 4. Влияние добавочного вихря на распределение
скоростей. Величина L
Переходим теперь к исследованию влияния на обтека-
ние цилиндра величины L. По формуле (9) § 2 имеем:
у (s + у) — cos (<Р — Р) Sin2 У + sh2
1 I I 1 \ 7 Ч .9?— Р'|1_91ПР*
"2 V^7/~" C0S ? ~~ Sin Т"2~~ sh 2
Прежде всего нетрудно показать, что при обычном рас-
положении предкрылка и закрылка имеем следующий резуль-
тат: для предкрылка s < р и для закрылка s > р.
Действительно, возьмем цилиндр, обтекаемый потоком
образованием циркуляции, и два вихря: Jv схематически
изображающий предкрылок, и J21 изображающий закрылок,
(рис. 21). Тогда направление циркуляции у вихрей имеет
расположение, указанное на рис. 21. По расположению вих-
рей очевидно, что точка нулевой скорости А, где скорость
242 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
от вихря уничтожает скорость обтекания цилиндра, лежит
между осью вихря и цилиндром, т. е. s < р, точно так же
около вихря J2 точка В, где скорость вихря уничтожает
скорость от обтекания цилиндра, лежит далее оси вихря J2,
т. е. s > р.
Рис. 21.
Итак, предкрылок уменьшает скорость около передней
кромки сверху крыла и закрылок увеличивает скорость около
задней кромки крыла.
То и другое ведет к выравниванию распределения ско-
ростей и, следовательно, к улучшению условий обтекания
крыла.
Найдем тот интервал, где вихри выравнивают распре-
деление скоростей. Для этого найдем точки, в которых £=1.
Из уравнения
4(s + t)~cos = 1
4(p + 7)~“cos
находим
4 sin 2'
Но по уравнению (6) § 1, замечая, что а2 — (к-[-29)=2В
ц что в рассматриваемом случае а3 = а4 — имеем:
|3 —р = —8,
ТёоЁётйч. оййоёаИия МётоДов УвЁЛИЧЁПЙЯ ПОДЪЕМНОЙ силы 243
а потому из (1) имеем два угла, определяемые равенствами
<Р1 = + arcsin -----, (2)
4sinT
?2 = " — ?!• (3)
Для предкрылка $<ри8<0, а потому срх < .
Для закрылка, как видно из формулы (19) § 2, 8 > О
. р* + 3
и s >р, а потому и здесь cpt< —у2-*
Кроме того, как видно по формуле (9) § 1, при ср ==
Sin2 A—l_|-sh2-^
_
Sin2 + Sh2
4 ' 2
и, следовательно, для случая предкрылка меньше 1 и для
случая закрылка больше 1.
Схематически положение соответствующих точек указано
на рис. 22 для предкрылка и на рис. 23 для закрылка,
причем
К = arcsin
4sin-J
0<Х<
тс
т •
(4)
244 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Таким образом, в случае предкрылка мы имеем уменьше-
ние скоростей на дуге АС В и для случая закрылка — уве-
личение скоростей на дуге АСВ. Заметим, что и то и дру-
гое уменьшает подъемную силу.
Для действительного вычисления углов и ср2 надо
найти формулы для определения числа $. Выведем такую
формулу.
Всего проще получить это решение из уравнения (а) § 2.
Так как в рассматриваемом случае имеем ^=1 и z2 = ea*i
и, кроме того, z3 — se^ и — то уравнение прини-
мает вид
*+ у) = — (1 +^) + (р + у)е^ + г'уу
откуда имеем два уравнения, которые могут служить для
определения $,
( । 1 \ 0 п 9 а2 । п Г sin 6
^ + 7/C0S^:= — 2C0S 2 + 2rcosH-----27^"’
(I 1 \ . о л • а2 а2 I л • I Г COS 6 ( )
s + yjsin? = —2sin^cos^ + 2rsin|*+-^-(
причем р по уравнению (5") найдем в виде
₽ = 9 + н + ^~(6)
или, выражая через 8,
р = р, —8.
Очевидно, что действительные значения для s получим только
I 1 /О
при $ + у<2.
Заметим, что (4) может быть написано в следующей
симметричной форме:
х . Н-Н)
k = arcsin ---—*
4sinT
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 245
§ 5. Подъемная сила крыла
Переходим к определению влияния добавочных вихрей
на величину подъемной силы крыла.
Так как добавочные вихри входят в несущую систему
крыла, то для определения подъемной силы по теореме
Жуковского достаточно рассчитать полную циркуляцию во-
круг всей несущей системы, которая, как видно из фор-
мулы (2) § 2, равна Г + J—/ = Г. Но при данном угле
атаки Г в присутствии добавочных вихрей отлично от того
значения Го, которое имела бы циркуляция без добавочных
вихрей 9»
Действительно, считая, что критической точкой является
точка £=1, получим для определения Г уравнение
(\__е209 4- — -1__-_______________— О
00 2тс/ 2тс/ j—(а-\-а)~]-аа
откуда
г = —4wcosin9 + J-------—, (1)
00 1 Г — COS р. ’ V '
где
d==l(p-7) и г==т(р+7)-
Из формулы (1) видим, что при отрицательном J, что
как раз и имеет место для случая предкрылка и закрылка, | Г |
увеличивается от присутствия добавочного вихря.
Так как при отсутствии добавочного вихря
Го = — 4^00 sin 9,
то
ДГ = Г — Го = J--------
и Г — COS р,
и
|ДГ| = М----------. (2)
1 1 1 1 Г — COS р. 47
Отсюда видим, что увеличение | ДГ |тем большее, чем меньше р,,
т. е. чем ближе добавочный вихрь расположен к задней
9 См. В. В. Голубев, Исследования по теории разрезного
крыла, ч. I, гл. 1, 1936 [см. настоящее издание, стр. 31—137].
246 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
кромке крыла, так что увеличение циркуляции больше от за-
крылка, чем от предкрылка.
Отсюда увеличение подъемной силы от действия доба-
вочного вихря определяется по теореме Жуковского по фор-
муле
др=рг,| JI —*------. (3)
Г 1 1 Г— COS р, V 7
Для практического применения этих результатов имеет
важное значение решение вопроса о том, как распределена
подъемная сила между основной частью
Т крыла и его добавочной частью. Для ре-
шения этого вопроса применим следую-
щим образом формулу Чаплыгина — Бла-
зиуса.
Пусть мы имеем ось вихря а и пусть
L — линия тока, замкнутая и окружающая
вихрь (рис. 24). Найдем величину сил, с
Рис. 24. которыми поток действует на массу жидко-
сти, заключенную внутри цилиндра, по-
строенного на L и длиной в 1. В этом случае мы можем
применить теорему Чаплыгина-Блазиуса и получим:
где X и Y—компоненты сил давления на жидкость, заклю-
ченную внутри L, и определяется по формуле (2) § 2.
Очевидно, что (2) § 2 можно переписать в виде
dw I 1
и по известной формуле
(dw J 1 1 . z v,
\-dT—bd = =
где uQ и — компоненты скорости Vo в точке оси вихря
и 70 — угол Vo с действительной осью. Отсюда
А)= •
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 247
Подставляя разложение (4), применимое в области точки
2 = а, в формулу Чаплыгина — Блазиуса, получим:
= _ = (5)
т. е. получим обычную формулу Жуковского с заменой
скорости в бесконечности скоростью на оси вихря.
Так как в рассматриваемом случае J отрицательно,
то из формулы (5) имеем:
%= — рЦ)| J| sin То,
У = pV0| J|cosy0>
(6)
и отсюда получаем, что подъемная сила, приложенная к допол-
нительному вихрю (конструктивно осуществляемому пред-
крылком или закрылком), равна pV”01 J\cos у0.
Следовательно, между основной частью крыла и его
дополнительной частью распределение подъемной силы при
разобранных условиях совершается следующим образом:
Р2 = pV01 J| cos 70, (7)
Pi = P®oo(4^oo sin 0 Н- | J| r_%;) — Р^о | J\ cos То =
== 4кр®2 [sin 9 -|- J (-------------— cos т0Ч . (8)
r 00 L V — COS p. lU/J V 7
По поводу последних формул, впрочем, необходимо по -
мнить, что мы принимаем предкрылок или закрылок за один
вихрь; в действительности мы имеем дело с обтеканием
дополнительного профиля, имеющего форму крыла и раз-
меры, достаточно большие сравнительно с основной частью
(хорда предкрылка или закрылка составляет обычно
не ниже 10% хорды основной части крыла), а потому в пре-
дыдущих формулах нельзя в точности указать ни %, ни 70.
Приближенное их значение будет ниже указано.
Заметим, что общая сила, действующая на предкрылок
или закрылок, выражается формулой
^ = рК>14 (9)
248 Ь ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Для применения формул (7), (8), (9) необходимо найти 1^0
и у0; для их нахождения заметим, что из формулы (2) § 2
имеем:
«О — = \ —-Ь е2(0- р-)«
2л/ р 2л/ 1 ’
₽-7
откуда
Ио cos 7о = и0 =
1
—9 cos
Р* 2 *
Г . . J .
т— sinu4--T—;Sinu,
2кр г 1 4кб/ г
Ио sin То =
Г J
7Г“ COS U------Г—, COS U.
2лр г 4кб/ г
По этим формулам можно определить V% и у0.
§ 6. Сводка формул
Мы соберем в настоящем параграфе все выведенные
выше формулы, которые могут служить для вычисления
работы предкрылка и закрылка.
1. Положение смещенной критической точки, точки раз-
деления потока:
а2 = к + 29 + 28, (I)
_________________cos ({1 — 6)__________пп
4kvoo , чг . /ОА Jd sin (jx — 6) ’ ' '
00 (г — cosu) [г 4- COS (20 — u)l + 7-—--
v 1 1 4 r/J 1 4^ r — cos p-
2. Скорость на поверхности цилиндра (случай двух кри-
тических точек на поверхности цилиндра):
^=4^('?+^)isin4sin^^-Z.. (Ill)
dz z z
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 249
3. Определение величины А:
-o(S+t)~C0S (!Р — ₽)
—И--------------’ (,V)
2 Нт)-cos (ср~(х)
p = 6 + (Jb + 2._^ = [1_ 8) (V)
(s + t)cosP = — 2cos2^ + 2'’cos^— (VI)
(^ + ?)sin^= — sin“2+ + (VII)
4. Циркуляция и силы:
r = -4^sl»« + J?^;. (VIII)
др == pti । j ।-—<L—. (X)
r 1 1 r — COS [X 7
5. Силы, действующие на основную часть крыла и на
добавочные части:
P1 = 4kPv2 [sin 9 + ^- (---------cos То)1, (XI)
1 г оо [ • 4iwoo\r—COS {X |U/J V '
P2 = pVo I jI COS To, (XII)
P3 = PV0|J|, (XIII)
Vo cos To = [cos 9---p cos (9 — 2р.)] — sin p.,
(XIV)
vo sin To = foo [sin 9 + 1 sin (9 — 2p.)J -|_ (JL — 2^ cos p..
(XV)
Относительно формул (VI) и (VII) необходимо отметить
следующее. Величину $ + у можно найти по любой из этих
формул, но так как формула (II), служащая для определе-
ния величины В, приближенная, то и р, определенное по (V),
2S0 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
также приближенное. Следовательно, s —, найденное по
той или другой из формул (VI, VII), будет иметь вообще
различные величины, и вычисление по обеим форму-
лам может служить оценкой величины приближения, давае-
мого формулой (II).
Из таблицы формул ясно, что мы можем найти все вхо-
дящие в них величины, если найдем величину добавочного
вихря J. Его определение производится по размерам и по
положению добавочной части крыла; в III главе будет пока-
зано решение этой задачи.
Глава III
ПРИБЛИЖЕННАЯ ТЕОРИЯ ПРЕДКРЫЛКА,
ЗАКРЫЛКА И ЩИТКОВ
§ 1. Распределение скоростей по поверхности крыла
Для приложения выводов предшествующей главы к тео-
рии действия предкрылка и закрылка необходимо перейти
от случая обтекания цилиндра к обтеканию крыла с задан-
ной дужкой. Мы в дальнейшем ограничимся только случаем
дужек типа инверсии параболы (дужки Жуковского-Чаплы-
гина), так как эти дужки сравнительно просто получаются
при помощи конформного отображения и применяемые на прак-
тике дужки отличаются от них сравнительно мало.
Если взять на плоскости (z) цилиндр радиуса 1 и на пло-
скости (С) дужку типа инверсии параболы, то внешняя часть
цилиндра отображается на внешнюю часть дужки при по-
мощи следующей функции:
i п cos2-|(l — е)2
с = е 2 (Z—1)_(1—s)cos|H--------------/------------,
i а
(z—\)e - +(1— e):os-g-
(О
где 2а — центральный угол скелета крыла и е — коэффи-
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ подъемной сиды 251
циент, характеризующий утолщение крылах). Здесь радиус
скелета дужки равен
Из (1) имеем:
Л ~2
— = е 2
dz
откуда
а .
(г—1)е 2 +(1 —e)cos-^
Называя через v скорость движения крыла, т. е. скорость
в бесконечности течения на плоскости (С), и через к угол
атаки на плоскости (С), т. е. угол, образованный скоростью v
с хордой скелета крыла, и замечая, что
dw___dw dZ
~dz ~ dt> dz 9
получим, полагая в (3) z = сю,
, . a .
= ve / ,
откуда
v = v^; 0 = A 4- . (4)
Наконец, подставляя в (3) значение (2) и полагая z —
получим для выражения скорости в точках на поверхности
крыла
I rfC I
(1 — е)2 cos2y —4(1 — е) гоз у sinsin (у ~ y) + 4sin2y
4 Sln у 1/ (1—е)3 cos2 2 (1—e)cos у sin sin (y-y)+sitH-^
х) Вывод формулы (1) см., например, В. В. Голубев, Иссле-
дования по теории разрезного крыла, ч. 1, Труды ЦАГИ, вып. 147,
1933 [см. настоящее издание стр, 76],
252 I. ТРУДЫ ПО ТЕОРИИ предкрыпка, закрылка и щитков
Подставляя для случая крыла в присутствии вихря ф
из (10) § 3 главы II, имеем окончательно:
sin Чу— L X
а а со со — а cd
(1 — е)2 cos2-£- — 4(1 — е) cos -у sin ~~ sin —--h 4 sin2-^-
1/ (1 — е)2 cos2 ~ — 2 (1 — е) :os ~ sin -у sin Ц- sin2 X
(6)
где ф^— скорость в точке крыла, соответствующей точке
z = e'^ поверхности цилиндра.
Формула (6) показывает, что так же, как в случае ци-
линдра, присутствие добавочного вихря для крыла сказы-
вается в том, что изменяется положение критической точки
разделения потока и что изменяется величина скорости бла-
годаря появлению множителя L.
§ 2. Определение величины циркуляции добавочного
вихря J
Добавочный вихрь J возникает у крыла благодаря при-
сутствию добавочного крыла (предкрылка или закрылка).
Считая предкрылок за плоскую пластинку, мы получим для
величины циркуляции вокруг него выражение

(1)
где Фа— скорость потока в точках добавочного крыла,
b — его хорда и [3 — угол атаки относительно набегающего
на него потока. Следовательно, для определения J необхо-
димо прежде всего найти величину скорости va.
Из (2) § 1, пренебрегая величиной изогнутости крыла,
т. е. полагая а = 0, получим:
dZ _ (г-1)(^+1~2е) .
dz “ (Z— е)2 • V '
Подставляя (2) в формулу
dw dw t dt*
d\ dz ' dz
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 253
dw
и заменяя —— из
dz
dw a,/, е^’\ , Г 1 . J / 1 1 \
— = v^e( 1--------Н-------------(----------=),
dz \ z2 / 2к1 z \z — a z — а)
получим выражение J. Но для определения скорости на оси
z м J 1
вихря J надо из найденного выражения вычесть
и взять модуль полученного выражения. Итак,
е2^ \
а2 /
Г 1
2^Z а
VOi \1

J 1
2тс/ а — а
X
Так как a — то
1*-Ч2 *
\ а — 1 | | а + 1 — 2е | *
(3)
| а — 8 |2 = | р cos [1 — 6 —j— Zp sin рь j2 = р2 — 2ер cos р» е2,
\а — 11 = | р cos рь — 1 Zp sin рь | = ]Лр2 — 2р cos р» 1 ,
| а+ 1 — 2е | = /р2 + 2 (1 — 2е) р cos [1 + (1 — 2е)2
и
&М\ Г 1
a2 J 2tcZ а
J 1
2л Z а — а

Г e~v-i
2л Z р
J e~w
(1 —
_____L р2(9-[х) Л i J______L . 1
р2 * У 2л. р 2л 1
р-у
= i'Ucocos(9 — р.) —
V 1
— 1 C0S <6 - н) + Sin (6 — Iх) + 72 Sin (0 — Iх) +
Г г
_____J____1_
2л р 2л 1
Р
vco (1 + 4) sin (9 - ~ j- - 12 + (1 - Aj У cos» (9 - F).
p__|
254 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Отсюда, заменяя в левой части (3) va из (1) и заменяя во
второй части Г из (1) § 5 главы II, получим после возве-
дения в квадрат
/2 ( 9 1 / 1 \
{1 “7c°s2(8-1*)+^-+ 2(1 +—)sin(6—[х)Х
/ Г 1________J 1 \ / Г 1_______J 1 \2
2woo Р 2woo0_l К" Р 2wco0_l|
\ Р Р/ \ Р Р/
(р* I 2 — 2ер cos fi 4" s2)2
Х (р2 — 2р cos ц + 1) [р2 + 2 (1 — 2s) р cos + (1 — 2е)2]
или, деля на и на второй множитель правой части,
получим:
J2 (р2 — 2р cos р. 4" 1) [р2 4" 2 (1 — 2е) р cos (1 (1 — 2s)2]_
(р2 — 2ер cos fi 4- s2)2
2
= 1 — 4cos2(6 —
р"
2 sin 6
Р
d
2KVco r — cos fi 2-w
d 1
2
(4)
. Г 2 sin 0 . J d 1 J 1 "Г
' р 2kv^ г — cosfi р 2nv1
I р р J
Полученное уравнение определяет величину циркуляции Л
По характеру поставленной задачи надо взять отрица-
тельный корень.
Решение уравнения (4) представляет большие неудобства;
можно значительно упростить эти вычисления, исходя из
следующих соображений. Заменим ^b$v~ ~х* тогда УРав"
нение (4) примет вид
2 4 (Р2 - 2р cos fl + 1) [Р2 4- 2 (1 - 2е) cos fl + (1 - 2s)2] _
(р2 — 2ер cos fi 4" е2)2
= 1 —cos 2 (9 — |Х) + 1. + 2 sin (9 — |Л) [-4-
+ [_2sin6 /£__1______
\ L p 1 p r — cos fi 2d) J
ТЁОЁЕТЙЧ. ОСНОВАНИЙ МЕТОДОВ УВЁЛИЧЁНИЙ ПОДЪЕМНОЙ СИЛЫ
Но члены, содержащие множителем Ьф, малы, так как Ь —
хорда предкрылка — не превосходит 0,2 хорды основной
части крыла, а так как хорда основной части равна 4, то
b < 0,8; с другой стороны, угол атаки предкрылка (3 не
превосходит 15—20°, а потому В < 0,3 и ар < 0,25; с дру-
. \d 1 1 ]
гой стороны, выражение в скобках I у ^7^ —2JJ при
пригодных для практики значениях р и |л порядка у (напри-
мер, при р = 2скобка равна 13/24). Так как множитель в левой
части уравнения при х2 больше единицы, то общая ошибка
при откидывании указанных членов будет порядка 5%. Сле-
довательно, при вычислении величины циркуляции добавочного
вихря можно пренебрегать действием самого добавочного
вихря; такое предположение в аналогичном случае было
сделано Н. Е. Жуковским1).
Пользуясь упрощением Н. Е. Жуковского, получим для
определения J гораздо более простое уравнение:
уз (рз — 2р cos р.-|~ 1) [р2 4~ 2 (1 — 2е) р cos р.(1 — 2е)2] _
(р2 — 2ер COS р. £2)2
9 1
= l_^cos2(0-[x) + ±-
\ • д /1 । 1 \ 1 I 4 sin2 О
- 4 Sin (0 —(1) sin 0(1 уН----2~,
откуда
J = — X
Х)Л l-^cos2(H-6) + -l+4sin (|л-в)з1п01(1+±)+1^Х
Х ________________Р2 —2p£COSp.+ £2_____________ 5
/р2 —2р cos р, + 1 /р24-2(1— 2е) р cos рь-f- (1 — 2£)3’ V 7
Найденное выражение для J можно еще несколько упро-
стить. Нетрудно умножением убедиться в правильности
равенства:
1 —^cos2(|» —0) + -l + 4sin(|»-0)sin01(l +р-)+
। 4 sin2 6 /. . 2 cos (р. — 20) . 1 \ /. 2 cos р. , 1 \
р2 — Р "^Д р
г) См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, стр. 22, 1931.
256 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Отсюда получим для J следующую окончательную формулу:
J=-k^coj/' +
X р2~ 2p£COSp- + £2 /бч
Р У р2 + 2 (1 — 2е) р cos р- + (1 — 2е)2
Формула (6) позволяет рассчитать величину J весьма
просто по заданным конструктивным данным и по заданной
величине угла атаки крыла 9. Пользуясь найденными фор-
мулами, мы определим величину J и влияние его на харак-
тер обтекания при любом р., т. е. для случая предкрылка
(р, = я), закрылка (р. = 0), щитков со свободным протоком
воздуха и т. п,
§ 3. Теория работы предкрылка
Мы приложим выведенные выше формулы к случаю
предкрылка. Мы можем рассматривать предкрылок как неко-
торый вихрь с направлением циркуляции, определяемым
наклоном предкрылка, и расположенный около передней
кромки крыла, т. е. с углом р., близким к те. В дальнейшем
мы будем считать р, = те. В этом случае по формуле (6)
предшествующего параграфа имеем:
т ad .Л 2 cos 26 . 1 (р-|— е)3
------------------------Р—н? р(>-1+2.)--
С другой стороны, по (20) § 3 главы II имеем при р. = те
g__________________________Jd cos 6
А / | 14 / nn ! Jd Sin 0 \
4w__ (r + 0 I r COS 26 + ---j-T )
00 v 1 7 \ 1 4711/^ r + 1)
n Jd
Величина , как увидим из вычисления в конкретных
случаях, есть величина малая, а поэтому все выражение
Jd sin О
утру мало и в знаменателе его можно откинуть. Таким
образом, получаем следующую приближенную формулу для
величины смещения критической точки:
g___________Jd cos 6____
4-w^ (г Ц-1) (г — cos 26) * * '
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ Силы 257
и отсюда, подставляя значение J из уравнения (1), получим:
1/1 cos 2® I 1
g ______b$ V________р ~т~ р2 (р е)2 д? cos О
4 (г+ 1)(г — cos 26) р(р— 12е) *
(3)
Из формулы (3) видим, что при действии предкрылка 8
отрицательно. По формуле (10) § 3 главы II имеем для
скорости на поверхности цилиндра выражение
g = ?-(*+226 + 25)sin |. L>
где
£_ т(*+т)~С05(у-Е)
4(p + j)—cos(?~Iх)
так как точка разделения струй определяется в этом слу-
чае углом а2 — к + 29 -|- 28,
Переходя от случая круглого цилиндра к случаю крыла,
получим согласно (6) § 1 формулу, определяющую скорость
в точке крыла, в виде
т_(к +2в + 25)
>1П —2 ' л
(1 —е)2 —4(1 —е) sin2-^-4-4 sin2 %-
(4)
у (1 — е)2 — 2(1—е) sin2-j-4“ sir12
причем мы считаем а = 0, т. е. крыло берем симметричное.
Так как присутствие вихря, заменяющего предкрылок,
сказывается в замене угла T:-j-29, определяющего критиче-
скую точку, углом к-j-20-4-28 и в появлении множителя £,
то мы поставим следующий основной вопрос.
Мы будем считать, что отрыв струй от крыла вполне
определяется распределением скоростей у поверхности крыла
и что рассматриваемое крыло без добавочного предкрылка
работает при условиях плавного обтекания до предельного
258 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
угла атаки, равного 90, что соответствует распределению
скоростей, даваемому формулой
' _ с.п — (” + 2во) v
*1^ = Sin---------------
2 74
(1 — е)2 — 4(1 — е) sin2 X + 4 sin2 -у
X....=. (5)
|/ (1 — е)2 — 2(1 — е) sin2 -j- sin2^-
Найдем, какой надо взять угол атаки 9, чтобы распре-
деление скоростей у крыла с предкрылком было такое же,
как при 0О у крыла без предкрылка.
Полагая 0==0о-|-Л0, получим для определения ДО сле-
дующее уравнение, приравнивая и v':
у-(тс + 26о + 2А0 + 26) __ У-(ТС + 26О)
oiii —— 2 охи 2 • \^z
Замечая, что при малых ДО и 8 можно положить
sin ?-(» + 26о + 2Де + 25) = sjn р-(к + 290) (Д0
= sta ^-<’ + 28«> - (М + S) cos ?-%+28°> ,
можем переписать уравнение (6) в виде
[1 — ctg (Р-(тс + 28о). (Д9 _|_ 8)1 £ = 1,
или [l+^0+8)tg(| — 0о)]а=1. (7)
С другой уравнение стороны, полагая А=1—ДА, получим для ДА
1 Д£ _ S —cos [у — (я —5)]
г — cos (<р — тс) ’
где S=l(s+±).r=-(p+l);
отсюда
AL —S—cos(y —7t) + cos [у — (я —о)] Г — COS (<Р — тс) ’ '
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 259
Уравнение (7) принимает вид
[1 + tg (| - 0о) (Д6 + &)] [ 1 - Ail = 1 •
Раскрывая левую половину этого равенства и ограничиваясь
в ней членами первой степени относительно Д9, 8 и ДА,
получим:
tg(|— 0o)(A0 + 8) = Ai.
откуда
м=~а+ . О)
Формула (9) дает величину изменения предельного угла
атаки. Для подсчета правой части упростим выражение ДА.
Из (VI) имеем при = тс:
2S cos (тс— 8) = — 2 cos2(y 0 + 8J-f- 2r cos тс
Г sin 0
2wco
или, откидывая члены с 8 в степени выше первой,
г — S = — sin2 (0+8) —
Но по (VIII)
Г - й J d
----=----Sin 0 + ---------ГТ
4wOT г + 1
sin 0 + 8
г — cos 20
cos 0
Следовательно,
г — S = — sin2 (Q 8) —sin2 6 — 8 r ~ е. sin 0,
v 1 7 1 cos 0 ’
или
г — S — — 8 sin 29 — 8 fг tg 9 — 2flQ- sin 0 V
\ cos 0 )
Окончательно
г—S = —8tg0(r+1). (10)
Подставляя найденное выражение в (8), получим:
Л£ — — 5 ео (r + 1) — sin ?
Г— COS (<р — к)
260 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
и отсюда
Д0 = — 8 14
tg 9р (/•+!) + sin <Р
[г— COS(<P — u)]tg^ — 0О
(П)
Формула (11) показывает, что изменением угла атаки 9
нельзя добиться того, чтобы при наличии предкрылка ско-
рость на поверхности крыла во всех точках приняла те же
значения, как и без предкрылка, так как в правую часть
равенства (11) входит ср. Потребуем, чтобы скорость при-
няла прежнее значение в области передней кромки, т. е.
при ср = тг. Тогда (11) примет вид
Д0 = — 8 Г1 -|- tg2 в0^Ч~1 = I § I \ я C/gS-2e-0i\- • (12)
[ IS 0r_ 1J I I cos2 e0(r— 1) V 7
Формула (12) дает увеличение предельного угла атаки, при
котором скорость в области передней кромки имеет при
наличии предкрылка ту же величину, как и без предкрылка.
Исследование изменения скорости в других точках показы-
вает, что скорость при угле 6О4-А9 на верхней поверхности
крыла несколько выравнивается (благодаря присутствию
множителя А).
Следовательно, при наличии предкрылка при предельном
угле атаки 60-[-Д9 распределение скоростей на верхней
поверхности крыла таково, что отрыв не будет иметь места.
Итак, предельный угол атаки от присутствия предкрылка
увеличивается на величину Д9.
Подставляя для 8 найденное выше значение, получим:
АД /ра-2р cos 26 + 1 (р + е)2(рЗ_1)
8р3(г + 1) (г — 1) (р — 1 + 2е) cos 60
и, подставляя
r+i = (p + l)2 r_i = (p-Da
получим окончательную формулу увеличения предельного
угла атаки:
до — ^Vp2-2p cos 26 + 1 (р + е)а
“ 2р (р3—1) (р — 1 + 2е) cos 0q * '°'
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 261
Заметим, что из формулы (1) § 1 при а = 0 имеем:
при z= 1 = — (1 — S) +(1Z. £е)а = 0.
при Z = — 1 С2 = — 2 — (1— 8)4--2^^е) —
= —4(1 — 8)4-е2(...).
Отсюда, ограничиваясь членами сев первой степени, полу-
чим для длины крыла L выражение:
L = |C2-C1| = 4(1 — е).
Подставляя это значение в (13), получим для Д9 выражение
ле 2? A +,1 J ~ >. (14)
£ Р(Р2— 1)(Р—1 + 2е) cos 0О v 7
Формулы (13) и (14) чрезвычайно близко подходят к фор-
муле (31) главы Г, отличие только в том, что в (31) cos90
входит в числитель, а в (13) и (14) — в знаменатель. Таким
образом, формулы (13) и (14) дают для Д9 результат,
больший (31) в —Va"-
V 7 cos2 О
Важно отметить, что приведенный в этом параграфе
вывод совершенно не зависит от характера течения в погра-
ничном слое; результат останется верным как при ламинар-
ном, так и при турбулентном течении. В этом существен-
ное отличие вывода, приведенного здесь, от выводов § 4
главы I.
§ 4. Теория работы закрылка
Теория, развитая в предыдущем параграфе, почти без
всяких изменений может быть перенесена на случай закрылка.
Уравнение (6) и его следствие, уравнение (7), останутся
в этом случае без изменения, так что и здесь имеем:
м=-8+ V
Но величины 8 и Д£ имерт другие значения.
262 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
По формуле (6) при = 0, что соответствует случаю
закрылка, имеем:
7 до \ । 2 cos 20 . 1 (р —е)з
14-—------------------------<2>
Далее по формуле (II) имеем в этом случае
* ____________Jd cos 0_____ □.
4™^ (г — 1) (г 4-cos 20) ’
Так как / отрицательно При обычном расположении закрылка,
то 8 > 0; по результатам § 4 главы I это соответствует
уменьшению угла атаки. Подставляя J из (2), получим:
*__Ур2 + 2р cos 20 + 1 (Р — £)2d cos 0 ...
° — 4р2(р + 1— 2е) (г— 1) (г 4-cos 20) ’ W
Для определения возьмем формулу (IV); полагая в ней
= 0 и отбрасывая члены с 82, имеем:
2S = —2cos2(4 + 0 + ^ + 2r —,
откуда, заменяя Г из (VIII), имеем:
Г_5 = (;OS2(±+9 + 8)_ ,
и, подставляя J из (2), получим:
г —S = s[sin20 —-Ц^12151п9] = _8(г—l)tg9. (5)
Но при у. = О
д£ — cos <р + cos (? Н- 8) _
Г — COS у
— Ь (г—1) tg 0 — cos ср -j- cos (ср -|- о)
Г — COS ср
и отсюда по (9)
дд ____§ | — Ь (г — 1) tg9 — cos у + cos (у + 8)
(г — cos у) tg — в0)
Полагая здесь, как и в случае предкрылка, ср = тс, т. е.
требуя i чтобы скорость крыла с закрылком была равна
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЙ ПОДЪЕМНОЙ Силы 263
скорости крыла без закрылка в области передней кромки,
получим:
М =-8-S(r- 1)^ = -8 (;+ (6)
Так как 8 положительно, то Д0 < О, т. е. мы имеем от
действия закрылка уменьшение предельного
угла атаки.
Подставляя в (6) значение 8 из (4), получим окончатель-
ную формулу
* Л _ V Ра + 2р cos 20+1 (р - е)2 d
4Р2 (р2 + 1 _ 2е) (г + 1) (г - 1) cos 0О •
Заменяя
^4(1-.),
получим:
ДА — — 94 А Ра + 2р cos 26+1 (p-s)2(l-e) _
' L р (р2 — 1) (р + 1 — 2е) cos 0О • V'
Формула (7) весьма похожа по общему виду на аналогич-
ную формулу для предкрылка (14), но благодаря присут-
ствию в знаменателе множителя (р + 1 — 2s) вместо (р—14-2е)
в случае предкрылка дает для ДО значительно меньшую
величину, чем для закрылка.
Рассмотрим примеры вычисления изменения предельного
угла атаки для случая предкрылка и закрылка.
Пример 1. Предкрылок р = тс, р = 15°, ~ = 0,2,
Р= 1,5, е==0,2, 0О = 15° 1).
По формуле (14) § 3 получаем:
ДО = 9°44'.
Пример 2. Закрылок р = 0, р = 15, ~ = 0,3, е = 0,2,
Р = 2, О0=15°.
Д0 = —4°13'.
*) Примеры заимствованы из работы В. В. Голубева, Иссл е-
?оо7НИЯ по теоРии разрезного крыла, ч. II, Труды ЦАГИ, № 306,
1У37. Там же указан и метод вычисления [см. настоящее издание,
264 t. ТРУДЫ По ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Нетрудно рассчитать и действие предкрылка или за*
крылка на величину подъемной силы.
По формуле (VIII) имеем в случае предкрылка (у- = к)
г (9) = — 4Woo sin 9 + J (9) .
г "Г 1
Так как предкрылок увеличивает предельный угол атаки
на величину ДО, то имеем при предельном угле атаки
с предкрылком
Г (90 4- Д9) = — 4nVoo sin (90 + Д9) 4- J (90 4- ДО)
и при предельном угле атаки без предкрылка
Г (60) = — 4nVoo sin 90.
Отсюда для приращения величины циркуляции имеем фор-
мулу
ДГ = Г(9О4-Д9) — Г(90) =
= — 4WOO Д9 cos (90 4- 4- J (90 4- Д9) ,
где по малости Д9 считаем 2 sin у = ДО.
Так как J отрицательно, то
I ДГI = 4Woo Д9 cos (90 4- 4-1 J(90 4- Д9) I .
Отсюда мы можем найти по формулам (14) § 3 и (6) § 4
| ДГ | и по теореме Жуковского для приращения величины
поДъемнрй силы получим выражение
| ДР| = р^| ДГ|.
Так как для предкрылка по формуле (2) § 3 имеем
00 d cos 6
| J\ — 4^00 Д9 cos 90 + —IL t
то, подставляя в (X), стр. 249, и откидывая в соз(904~Д9)
величину Д9, получим следующую весьма простую формулу:
ДР = 4-тгртл^о Д9 cos 90r = 4-гер-и^о Д9 cos 90 р . (8)
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 2,65
Подъемная сила без действия предкрылка при предельном
угле атаки 90 определяется формулой
Р = 4кр^ sin 90.
Отсюда
^ = ctg90^ Д0. (9)
др
Если подсчитать отношение по этой формуле для при-
веденного выше примера = 0 = 15°, -^-=0,2, р=1,5,
е = 0,2, 90=15°), то получим:
^ = 0,68,
т. е. предкрылок увеличивает максимальную подъемную силу
крыла на 68%. Аналогично можно разобрать и случай за-
ДР
крылка; при этом оказывается, что для отношения
остается без изменения формула (9), где только Д9 надо
заменить | Д9 [, так что для закрылка
^==ctg0o^±l|A9|i). (10)
В случае приведенного выше примера (и = 0, 0 = 15°,
~ = 0,3, р = 3, е = 0,2, 60= 15°^ получим по (10)
^=0,34,
т. е. закрылок дает увеличение максимальной подъемной
силы на 34%.
Мы видели, что предкрылок дает значительное увели-
чение предельного угла атаки и сравнительно малое увели-*
чение циркуляции; обратно, закрылок дает небольшое умень-
шение предельного угла атаки и значительное увеличение
циркуляции. Отсюда имеем: предкрылок увеличивает подъем-
ную силу главным образом за счет увеличения предельного
угла атаки, а закрылок — за счет увеличения циркуляции.
9 См. В. В. Голубев, Исследования по теории разрезного
крыла, ч. II, 1937 [см. настоящее издание, стр. 291—-348].
266 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
§ 5. Теория работы щитков
Мы рассмотрим здесь частный случай щитков, щитки-
подкрылки, т. е. такую конструкцию, когда под основной
частью крыла А имеется добавочное крыло В (рис. 25),
поставленное таким образом, что
/I около крыла В возможно
Н1" свободное обтекание воз-
духа, т. е. что крыло В нахо-
0 дится от А на некотором рас-
стоянии и неплотно прилегает к
Рис- 25. а в отличие от обычных щитков,
которые плотно прилегают к кры-
лу, не оставляя никакого свободного промежутка для про-
текания воздуха х).
Мы будем считать, что щиток-подкрылок находится по-
средине нижней поверхности крыла так, что |i = — у.
Рассчитаем для этого случая 8. По формуле (17) § 3
главы II имеем:
Уе°»(о+-|) капв
r+cos(2,+ -)
Но
к =М Jd
^KVoo (r — cos И) 9
а потому
*__ JkZsinO
4^ (r — sin 20) ‘ '
Так как по формуле (6) § 2 главы III имеем при ji = — у
2 sin 20 । 1 _р1 2 -|- £2
Р + Р* Р УРа+(1-2е)3 ’
1) См. также О. В. Голубева и В. В. Голубев, Исследова-
ния^ по теории щитков крыльев самолета, Труды ЦАГИ, вып. 398
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 267
то окончательно имеем:
8 = _bi Ур3-2Р sin 26 + 1 Р3+е* Р3~1 s.n 0
2р р2 — 2р sin 20 4" 1 W2 + (l — 2е)2 р2-|-1
т. е.
. g^5i„8. (2)
2р рЗ _ 2р sin 20 + 1 /р2 + (1 — 2е)2 р2+ 1
Отсюда легко определить смещение предельного угла
атаки аналогично случаю предкрылка и закрылка. В этом
случае уравнение, аналогичное (6) § 3, имеет вид
?-(тс + 20 + 2В) ^~(z + 20o)
ып 2 “1 2 ,
и, полагая 0 = 9О4~Д9, получим отсюда
где
г — S — cos (
Г — COS ( <f> + у J
Полагая здесь, как и в предыдущих случаях, <р = -тг, по-
лучим:
Д9= —8
r-S + cos^ + b) = _ r-S + 8
' г ‘ г
(4)
Найдем г—S. Для этого возьмем формулу (VI")* Полагая
в ней и =— , получим:
2S sin ~ = — sin (тс 4” 20 + 28) — 2г cos
268 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
и, подставляя сюда Г из (VIII), получим:
г я—S = sin 6 cos 0 + cos 268 — cos 6 sin 0 4-- - — cos 6,
1 1 4nvoo r
и, заменяя J из (1), окончательно имеем:
r — S = cos2684-8^=^|^cos0 = 8[rctg9— 1]. (5)
Подставляя (5) в (4), получим:
Д9 = _ 8 + 8 ctg 6 = 8 (ctg 0 — 1). (6)
Отсюда, подставляя 8 из (2), имеем окончательно:
Д9=- 4= г.. ?а+Е* /
р /2 /рЗ — 2р sin 20 + 1 / р2 -|- (1 — 2е)2
(7)
предель-
рассмот-
Формула (7) показывает, что подкрылок уменьшает
ный угол атаки.
Найдем величину этого уменьшения. Для этого
рим пример:
пусть b = 1, р = 2, е = 0, 9=15°.
По формуле (6) имеем:
Д0 = —. Р . 0,11,
т. е. уменьшение угла атаки составляет х/9 угла атаки под-
крылка. Мы далее увидим, что р доходит до 50—60°; сле-
довательно, уменьшение угла атаки будет порядка 5—6°.
Впрочем, необходимо заметить, что при таких значительных
углах атаки подкрылка формулы перестают быть точными
ввиду того, что все выводы сделаны в предположении не-
больших углов атаки.
§ 6. Предельный угол атаки для щитков
Присутствие основной части крыла должно оказывать
весьма существенное влияние на условия обтекания добавоч-
ных крыльев (предкрылка, закрылка и т. д.). Мы разберем
здесь это влияние для случая щитка-подкрылка. В этом
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 269
случае основная часть крыла является для щитка предкрыл-
ком с очень большой хордой. Поэтому здесь не приложимо
исходное положение, которое принималось нами во всем
предыдущем: здесь нельзя пренебрегать хордой основной
части.
Однако полученные выше выводы можно, конечно, при-
менять и здесь в качестве некоторого приближения к реше-
нию задачи, так как на некотором расстоянии от крыла
течение весьма мало отличается от течения вокруг одиноч-
ного вихря. Дальнейшие выводы будут, таким образом, тем
ближе к действительности, чем дальше предкрылок нахо-
дится от основной части крыла.
Для- упрощения в дальнейших вычислениях мы будем
считать, что вихрь, заменяющий основную часть крыла, на-
ходится в точности на продолжении хорды щитка. Так как
формула, дающая отображение круглого цилиндра радиуса 1
на щиток с хордой, равной 4, имеет вид
Y I 1
то, предполагая, что ось вихря находится от средины щитка
на расстоянии, равном 1,5 его хорды, мы получим для этого
расстояния, выраженного в радиусах первоначального ци-
линдра, величину 6, откуда для определения р получим
уравнение
p+j = 6»
откуда рх = 5,8 ... и р2 = 0,1 ...
Таким образом, для рассматриваемой задачи р нужно
принять равным 5—6.
Рассмотрим следующий пример:
пусть b = у L, 6=15°, р = 15°, р = 5.
По формуле (2) имеем:
А0 __ 9 У 26 — 10 cos 30° • 5 __ 9 9
16-6 cos 15° ~
т. е.
ДО = 2,2 • 15°= 33°,
и предельный угол атаки щитка равен ДО-1-р = 33°-|-15о=48о.
270 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Экспериментальные данные дают для угла атаки щитка
при наивыгоднейшем его расположении величины порядка
50—60°. Заметим, что мы здесь не вводили поправку на
изменение 6 в формулу; если учесть эту поправку, то по-
лучим угол, больший 48°.
Глава IV
ОТСАСЫВАНИЕ ВОЗДУХА; ЩИТКИ
§ 1. Общие замечания
Исследования, изложенные в предыдущих главах, пока-
зывают, что теория предкрылка, закрылка и щитков-открыл-
ков послужила предметом большого числа работ и может
считаться в основном в достаточной степени выясненной;
выведенные в этой теории приближенные формулы удовле-
творительно согласуются с данными эксперимента.
В гораздо худшем положении находится теория улучше-
ния аэродинамических свойств крыльев при помощи отсасы-
вания и сдувания воздуха и при помощи собственно щит-
ков, т. е. щитков, плотно прилегающих к крылу. В этой
области мы имеем только ряд разрозненных теоретических
результатов, относящихся к частным случаям и еще далеко
не доведенных до учета всей сложной обстановки, которую
имеет течение при наличии рассматриваемых приспособле-
ний. В частности, нет никаких теоретических соображений,
касающихся влияния сдувания воздуха на обтекание крыла
и на его подъемную силу.
В настоящей главе мы изложим исходные теоретические
соображения о влиянии отсасывания на условия обтекания,
тесно связанные с соображениями, развитыми во II и III
главах настоящей работы по теории щитков и элеронов, при-
надлежащие акад. С. А. Чаплыгину, Н. С. Аржаникову и
С. М. Таргу.
Основная схема для случая обтекания цилиндра состоит
в следующем. Круглый цилиндр (рис. 26) обтекается пото-
ком, причем часть потока вливается в щель MN, поток
образует на поверхности цилиндра три критические точки
д(а = ^), В(Ь = е^\ С(с=1). Предполагая, что скорость
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 271
в бесконечности равна и образует с действительной
осью угол 6, можно написать уравнение для определения
характеристической функции течения в виде
V (г~а>(г-Ь>> Ч
az z*y(z — m)(z — п)
где т = е^г и п = е™ представляют собой концы щели MN.
Нетрудно установить зависимость между a, b и расхо-
дом Q жидкости, протекающей в секунду через MN,
При достаточно большом | z | из (1) получаем:
dw
dz
(2)
=
Так как в случае, если в бесконечности поток имеет
источник мощности Q и вихрь мощности Г, то разложение
производной характеристической функции в бесконечности
имеет вид
dw
dz
-Hi । г 1 Q 1 । 1 / ч
~Vc°e 2л/ z 2л z^~ z^"^'
(3)
где Q — мощность источника и Г — напряжение вихря, Q и
Г— положительны.
272 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Следовательно, из (2) имеем:
= е-М —
dz -
Feos (а — в) -|~ cos (р—в)-|- COS 6 COS (р—6)—^COS (* —0)1
— ^со----------------------------------------------------
Г sin (а—0) -|- sin (j3 — 6) — sin 6 .sin (р—0)-у sin (ч—0)1
— ZVoo L------------------------------------------------’+
+i(...). (4)
Отсюда
Q = t/oo2k £cos(a — 6)-|-cos(P — 9)4“ cos 9 — ycos(p,— 9) —
— у cos 0—6) J, (5)
Г = •n0O2it [sin (a — 0) —{— sin (P — 6) — sin 6 — -i- sin (p — 0) —
— sin (v — 6)j. (6)
Формулы (5) и (6) представляют собой обобщение известной
формулы для циркуляции вокруг цилиндра в случае закре-
пления одной из критических точек (точки С); действи-
тельно, полагая
р. = v = т1
и
имеем
Q = 2^00 [cos (а— 9) —|— cos 9], (5')
Г = 2^00 [sin (а—9) — sin 9]. (6')
Так как при отсутствии отсасывания a = z4~29, то
формулы (5') и (6') в этом случае дают:
9 = 0
и
Г = —4^00 sin 9. (7)
Чтобы найти положение точек а и Ь, надо найти еще.
одно уравнение, которое мы получим, определив величину
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 273
и направление скорости течения на поверхности обтекае-
мого цилиндра. На цилиндре z — е*ч9 и, замечая, что
Lili
z — а — е^ — eai = е 2
= 2te 2 sin —2~-
и аналогично для других скобок, получим на поверхности
цилиндра из (1) следующее уравнение:
dw
~dz
= Vooe~Qi
*+« . <р+3 i Ф ; о
(21)3е 2 е 2 е2 sin У ^ а- sin ? — sin
2ie^2 /sinsin 1=2
ИЛИ
dw . (-9+^-^±
- = ^4Л 2 4
sin sin l^J sin -1
- . (8)
Если взять точку на дуге ВС, то в ней ср < а; ср < £; ср>0;
ср < ср < v и скорость образует угол 6 — ~ с осью х;
отсюда имеем:
_e+l+j_t+_'±| = O. (9')
Так как при р = = v уравнение (9) должно дать а = ^4-26,
то знак перед должен быть минус и мы имеем уравне-
ние
_6 + l+₽_E±_’_.J_o. (9)
Это уравнение можно переписать в виде
(а_ (тс + 26)1 + [р — ^±2] = 0. (10)
274 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Угол а—(к-1- 26) есть смещение критической точки;
можно назвать р — также смещением критической точки,
так как при отсутствии отсасывания, как показано выше,
p = и = Таким образом, уравнение (10) выражает
тот факт, что при отсасывании сумма смещений
критических точек равна нулю. Это свойство обоб-
щает аналогичный результат, имеющий место в случае доба-
вочных вихрей у поверхности крылах).
Уравнения (5) и (10) позволяют определить по данным Q,
{х и v величины а и р.
Называя через а угол -, можем переписать (10)
в виде
[а — (к + 20)] + [р — о] = 0. (10')
Подставляя а = а — р 4-^4" 20 в уравнение (5), получим:
cos (а — р к + 6) + cos (Р — 0) -j- cos 0 — ~ cos (jx — 0) —
-lcos(v-0) = ^-
или
— 2 sin ~ sin fp — 0 — -тй = ---cos 0 4~ cos (а — 0) cos d,
2 у 2) 2м/1 4 7
где
j __ v (половина щели).
Отсюда окончательно
cos 0 — cos (а — 6) cos d — —
2sin|
и
cos 0 — cos (а — 6) cos d — ~
P = 6 + 4“' arcsin---------------------------- , (11)
__________ 2 sin -2
*) См., например, В. В. Голубев, Исследования по теории
разрезного крыла, ч. II, 1937 [см. настоящее издание стр. 291—348].
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 275
и по (10')
cos 0 — cos (а — 0) cos d — —
а = 6 4- 4 — arcsin-------------------------. (12)
2sinT
Отсюда получаем величину смещения -критической точки а
в виде
Д = а —(k + 20) = -J —6 —
cos 0 — (cos а — 0) cos d — —
— arcsin------------------------(13)
2s,n|
Выведенные формулы можно значительно сократить,
если пренебрегать шириной щели. Если считать d = 0, то
cos 9 — cos (а — 0) cos d = cos 0 — cos (а — 0) =
= 2sin ysin(| — в).
Поэтому уравнение (11) принимает вид
р == 0 _|_ 2. _j_ arcsin
Q
4я sin
(14)
Отсюда в случае отсутствия отсасывания, т. е. при Q = 0,
имеем:
? = 0 + ^+(|-в) = ».
Аналогично для остальных критических точек имеем:
а = 9 4- ~ + к — arcsin
Q
4л sin Voo
(15)
и для смещения
Д = -^-----0 — arcsin
Q
4’tsln
. (16)
276 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Формулы (И), (12), (13) или (14), (15), (16) и решают
сполна задачу об определении положения критических точек
при заданной щели и величине отсасывания.
Перемещение критической точки а на А равносильно
изменению угла атаки на Таким образом, как показы-
вает формула (16), отсасывание увеличивает кажущийся
угол атаки, а следовательно, и подъемную силу, а на диа-
грамме подъемной силы вызывает смещение кривой влево
на
Д сг
2~~"4
1
у arcsin
Q
4л sin
. (17)
§ 2. Влияние отсасывания.
Вычисление подъемной силы и силы сопротивления
Переходим теперь к вычислению сил, действующих на
цилиндр. Применяя формулу Чаплыгина — Блазиуса и под-
ставляя (3), имеем:
=—1= — рУтое-М (Г — ZQ). (18)
Называя через равнодействующую и через у ее наклон
к оси х, имеем:
X=/?cosy, Y — R sin 7
и
YIX =R (sin у + i cos у) = rS 2 \
Если оси направить по течению (т. е. под углом 0 к оси х)
и перпендикулярно к нему, то угол у', образованный силой
с новой осью х', получится из уравнения
т = т'+0«
= д/г"*’-®)* _ (19)
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 277
Подставляя в (18), получим:
Re ~ Г ) % -ei = — pV^e-9i (Г — /0),
откуда
у'4-ь¥' = — рУооСГ—IQ)
и
V = — рУооГ = — 2гсрУ^ [sin (а—6) — sin 9 4- sin (Р—9) —
— ysin(|i—9) — -i-sin^ — 9)J, (20)
X' — pvmQ = ^TtpVooQ [cos (a — 9) -|- cos 9 4- cos (P — 9) —
— ycos(ji —9)—-i-cos(v-9)J. (21)
Выражение для подъемной силы ‘можно преобразовать
следующим образом. Обычно щель весьма мала и можно
считать:
м. 4-
Тогда
sin (a— 9)— sin 9 = 2 sin (у— 6^ cos— ,
но
а = к4-264-Д,
а потому окончательно
sin (a — 9) — sin 9 = — 2 cos sin ^9 -y ).
Также
sin (P — 9) — у sin (pi — 9) — -i sin (v — 9) ==
= sin (P — 9) — sin (a — 9) = 2 sin ^-~^-g cos (- + g — 9^.
Окончательно имеем следующее выражение подъемной
силы:
У' = 4tcp^cos у sin (9-f- j^4-4irp^sin ^Ц^соз(£у^—9)‘
278 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Так как Д обычно мало, то, считая cos-y=l, получим:
V = 4терг^sin (в -|- А)_|_ 4тсрг>^sin cos — б).
Подъемная сила при отсутствии отсасывания равна
У1 = sin 9.
Отсюда получаем увеличение подъемной силы в виде
ДУ= Г— Yt — 4-тсрх»^ А4Kp^sinl^cos(^t£—б), (22)
где приближенно положено по малости углов о и у
sin (9+4) ~sin 9=4 •
Так как из (14) видно, что при увеличении Q угол (3
уменьшается, и по (17) при увеличении Q увеличивается,
то по (22) при увеличении Q имеем увеличение ДУ.
Подсчет показывает, что при увеличении угла 9 по-
правка ДУ увеличивается, что влечет за собой постепенное
увеличение подъемной силы при увеличении угла атаки,
большее при отсасывании, чем без отсасывания. В таблице
даны эти значения.
Полученные выводы показывают, что отсасывание дает
некоторое увеличение подъемной силы и вызывает лобовое
сопротивление. Далее, в обтекании получается смещение
критической точки (точки разделения струй) и образование
еще одной критической точки около щели отсасывания.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 279
Положение этой точки зависит вообще незначительно от
величины отсасывания.
От случая круглого цилиндра можно перейти к случаю
крыла, применяя метод, аналогичный методу главы III.
Соответствующие формулы позволяют рассчитать изменение
подъемной силы и предельного угла атаки. Однако, как
показывает ряд экспериментальных работ, проведенных
в этой области, влияние отсасывания сказывается главным
образом в изменении пограничного слоя. Предшествующие
исследования не учитывают этого, а потому и вся пред-
шествующая теория не дает полной картины того, что про-
исходит в действительности. Влияние отсасывания требует,
таким образом, дальнейших изысканий, главным образом
в направлении учета изменения структуры пограничного
слоя. Полученные выше выводы, вероятно, найдут примене-
ние в оценке течения на наружной границе слоя1).
Также совершенно не изучено с точки зрения гидроме-
ханики влияние сдувания. Эта задача представляет очень
большие трудности из-за отсутствия теории струй в вязкой
жидкости, так как влияние сдувания сказывается в основном
в разрушении пограничного слоя потоком выдуваемого воз-
духа. В этой области вообще нельзя указать каких-нибудь
теоретических исследований.
§ 3. Методы увеличения подъемной силы,
основанные на увеличении изогнутости дужки
Изменение изогнутости дужки может быть достигнуто
путем отклонения элеронов. Конструктивно это достигается
подвижной частью крыла, элероном, прилежащим к задней
кромке. Действие элерона можно рассматривать или как
увеличение изогнутости крыла, или как увеличение угла атаки.
Подробная теория действия элерона в случае плоского
крыла дана С. А. Чаплыгиным и Н. С. Аржаниковым2).
i) Обильный экспериментальный материал и его оценка с точки
зрения изложенной теории даны в работе Н. А. Закс, «Аэродина-
мика крыла со сдуванием и отсасыванием пограничного слоя».
2) См. С. А. Чаплыгин и И. С. Аржаников, К теории
открылка и закрылка, Собр. соч. С. А. Чаплыгина, т. II, стр. 472,
1948.
280 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Пусть имеем плоское крыло АО с элероном ОВ (рис. 27).
Для построения потока, обтекающего крыло, отобразим
область течения на верхнюю полуплоскость вспомогатель-
ного переменного U. Полагая, что угол АОВ~(\—n)ir,
можно, как показал С. А. Чаплыгин, дать отображающей
функции вид
щ-п
z = 'ak 1)2+ ^з *)• (О
'Эта функция, которую можно рассматривать как частный
случай формулы Шварц — Кристоффеля, отображает область
течения на верхнюю полуплоскость U таким образом, что
точкам А и В соответствуют точки а и (3 действительной
оси; точке О, рассматриваемой как точка, к которой можно
подойти с верхней полуплоскости (г), соответствует точка
U = 0, и той же точке, рассматриваемой как точка, к кото-
рой можно подойти с нижней полуплоскости (z)9 соответ-
ствует точка U = сю. Постоянную k можно определить из
соответствия точек А на плоскостях U и z\ получим:
(а-1)2+^2
К “ а1-п
Из (1) имеем:
dz _пЬ (1-и)[(£7-1)2 + *2]-2Щ£7-1) п
dU~aRf [(tf —1)2 + ^]2 ’
что иначе можно написать в виде
dz (^ + ₽)(«-^)(1 + и) 1Гп
dU [(U — I)2 + Z>2]2 и ’
*) См. В. В. Голубев, Теория крыла аэроплана в плоскопа-
раллельном потоке, стр. 160, 1938.
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЁМНОЙ СИЛЫ 281
где
а (1 -I- п) = + —„2) -j- п
ИЛИ
Р (1 + и) = у 1 -4-£2(1 — П2)_ гс<
Так как значения а и В соответствуют точкам А и В,
ОВ
то для а = -7=гг найдем выражения
(У А
/р\1-П (а_ 1)2 4-63
°~\J (p+l)3 + 62-
Полагая
1 4-62(1 _/г2) =
имеем:
с + и o = £ziZL 62 = ^zz2
I + П ’ Р 1+п’67 1 — и2
И
с-1 (с + п\п
1— и2\1+«/ ’
С — 1 /с + П\п
°"“с+Т\с^7г) ’
Из последней формулы легко видеть, что так как 1,
то а 1.
Для построения потока, обтекающего крыло, С. А. Чап-
лыгин и Н. С. Аржаников применяют обычный прием, раз-
работанный С. А. Чаплыгиным, и берут для характеристи-
ческой функции течения на плоскости U уравнение
откуда
<^=akv + (2)
dU _ 1)2 + d3j » W
dw___ VooN U — ^rjn
dz 1 + n a— U ’
(3)
где точка U = у соответствует точке с нулевой скоростью
на крыле и при U = а имеем бесконечную скорость у перед-
ней кромки крыла. Так как точке z = оо соответствует
точка U = 1 4- 6Z, то из уравнения
= x/oo^-9ui
282 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
найдем:
е -М = 1+^~J (1 + bi)n. (4)
1 + « «- 1 — Ь1К 1 7 47
Полагая
Ь , Ь , и l
rz^ = t£l*i’ „-rrr = tglA2. ^ = Шз>
из (4) найдем:
--00 = + ^2 + ^3»
и, называя через т угол атаки, причем
получим:
* = 9о + те>
^ = 11 —т —|Х2 —П|13.
Для определения циркуляции Г находим коэффициент
1 dw
при в разложении
получим:

откуда после ряда преобразований получим:
1+п 1 -п
о aVoo /с + п\ 2 /С — П\~2~ . / । лч
г = -2-^(1^) sin (т-]-X),
где
^Рг + Рч—иРз —у •
По найденному определим по теореме Жуковского подъ-
емную силу в виде
Р = рС’ооГ.
Для угла X находится после ряда преобразований выражение
X = arctg
nV с2 — 1
eV 1 — п2
, /“/*2___1
п arctg л/ ~_______L ,
V 1 — п2
Заметим, что для получения циркуляции и подъемной силы
в случае, если открылок лежит в плоскости крыла и мы имеем
обтекание плоской пластинки, нужно положить п = 0,
откуда
Х = 0,
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 283
При малых значениях п, т. е. когда открылок мало наклонен
к плоскости крыла, получается следующая приближенная
формула для определения величины циркуляции:
г = — itVooL (1 — 1~рз) sin
и L = АО-\-ОВ. Откидывая при малом п член с п2, полу-
чаем .для подъемной силы выражение
Р = крг£/, sin (т + 4^-);
сравнивая полученную формулу подъемной силы дугового
крыла
P = pm£/,sin(^- + T:),
видим, что действие закрылка равносильно замене плоского
крыла дуговым с центральным углом
16л V
1— а2
Закрылок дает, таким образом, увеличение подъемной
силы.
§ 4. Щитки на нижней поверхности крыла
К числу других приспособлений, позволяющих увели-
чивать подъемную силу и уменьшать посадочную скорость,
принадлежат щитки, устанавливаемые под некоторым углом
к нижней поверхности крыла. Обычно
применяемая конструкция состоит в том,
что к нижней поверхности крыла Л4 & С-м &
ставится под некоторым углом а щи-
ток АВ, причем хорда щитка АВ бе-
рется обыкновенно равной расстоянию Рис. 28.
точки А от заданной кромки (рис. 28).
Это простое приспособление дало при экспериментальном
исследовании очень хорошие результаты; увеличение
подъемной силы доходило до 60% при а =80°, когда
щиток АВ составлял 20% от хорды крыла DC. Точно так
же очень хорошие результаты дали опыты, проведенные
в ЭАО ЦАГИ»
284 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Существующая теория этого приспособления основывается
на предположении, что при наличии щитка точкой схода
струй является не острая кромка крыла С, а конец щитка В.
Это предположение, высказанное впервые, по-видимому,
В. В. Голубевым, несомненно, далеко расходится с действи-
тельным течением, так как в действительности, как показы-
вают опыты Д. С. Вилькера в гидроканале, в угле САВ обра-
зуются вихри и срыв струй начинается в точках С и В. Тем
не менее, приближенная теория явления, развитая на осно-
вании указанного выше предположения, приводит к выводам,
которые очень хорошо качественно согласуются с данными
эксперимента.
Подробная теория действия щитка, построенная на осно-
вании вышеуказанной схемы, была дана С. М. Таргом и пред-
ставляет собой удачное раз-
витие изложенного в пред-
шествующем параграфе метода
С. А. Чаплыгина и Н. С. Аржа-
никова.
Пусть в плоскости (z) имеем
прямолинейный контур СВ со
щитком ОА. Для получения
характеристической функции
течения отобразим область (z)
на верхнюю полуплоскость
переменного (0, причем точки контура на плоскости (z)
переходят в точки действительной полуоси плоскости (/),
(t)
-J3 -* у
7^777777/777777777777777777^777777777777.
Рис. 30.
как показывают соответствующие буквы на рис. 29 и 30.
Подобные отображения можно получить при помощи функции
z= kl ,n
z R (t — ap + P’ W
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ СИЛЫ 285
где I = СВ и угол СОА — 8к (1 > 8 > 0). При этом отобра-
жении точка г = оо перейдет на плоскости t в tQ =
Так как в точках А, В, С конформность отображения
нарушается, то при /, равном —а, —р, 7, функция
-^ = 0.
dt
Дифференцируя (1), получим:
аг-ЫЪ ('+D-8 dt Rl [(t — ap + &p X
X{/3 + |l2d(l — 8)H- l]/2_ (2)
причем c2 = a2 + $2.
Называя корни уравнения через —а, —р, 7, можем
написать (2) в виде
dt ~klb [(t — ap + ^p ’ W
причем
Нт+|-<2-8)Г’
° ~ 2 (1 J) [8 <“ + Р — Т)-1]'
Величины а и р можно рассматривать как параметры, харак-
теризующие обтекаемый контур. На выбор их наложены
следующие ограничения:
а>1, 1 > Р > 0,
Y > 0, с2 > а2.
Характер контура вполне определяется отношениями
41 = OA _ _ г ( q) z»-a-8)ic *
OB _OA _ 1 1 N N z-'v z-v 1 1 ft -CD 4^ ** >
ОС *(-£)
286 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Нетрудно показать, что
/а — 1 \ 1 — 8 р _|_ 2а 5ау
а + 2а +Ч₽7
/ а — 1 \1-S у — 2а-j- оар
кТ+Т/ а4-2а + 6₽Т
и, задаваясь а и р, можно найти и S2. Коэффициент k
в выражении (3) определим из соотношения'
l = Z( — р) — 2(f),
откуда получим:
= |- (1-р)1-5 (1 + т)1-8 Г1
[ ₽ + 2а 4- oaf ' 7 — 2a 4~ &а{3 j
Полученными формулами контур вполне определяется.
Применяя формулу С. А. Чаплыгина, построим характе-
ристическую функцию потока, обтекающего в области (/)
действительную ось и имеющую в = полюс пер-
вого порядка (диполь) и логарифмическую точку. В силу
симметрии те же особенности должны быть в точке /0 = а — Ы.
Отсюда имеем:
^“7Г7^ + 7Г7? + 747- + 7Аг+Р(/)' <4)
ar {с — iQ)a — Iq) t — tQ t — Iq
где P(t)—голоморфная функция. Чтобы поток плавно сходил
со щитка, в точке / =— a ~~=0. Обозначив через s дру-
dw п
гую точку, где = 0, можем написать, что
dw _ K,v k # + “)(*-О /5х
аг —К IVOR [(^ _ e)a + ft2J2 , (О),
и из (3) и (5) получим:
_________________________У £) // I 1
dz~K Ъ (^4_p)(z —7)
Так как в?=оо имеем
= яое-в<>*,
\ dZ Jz=oo ° -
где vQ—скорость в бесконечности и 60 — угол, образованный
ею с осью х, то имеем:
(.+47»)(^,+щ <°+ '+“’) <7>
ТЕОРЕТИЧ. ОСНОВАНИЯ МЕТОДОВ УВЕЛИЧЕНИЯ ПОДЪЕМНОЙ силы 287
Положим
л— е , а 4- 6 ,
—= ctg Ро. "4 = Ctg Н1>
а — 7 . а-\-1 ,
—pL = ctg|*2, —y- = ctg|i3,
ЪЬ sin |x0 ( sin |i3 \8
sin (Ijl sin |x2 \ b /
Тогда из (7) получим:
— °o = Но — Hi — Иг + 8Нз>
или, вводя угол атаки т == 60, получим:
Но = х ~Ь Hi 4“ Нг— 8Нз-
Циркуляция потока определится по формуле
Г = —2шЛ3.
Так как
то получим:
. . &v0Z/< Г. . а-^-а а — е
Аз ~ 1 4f> [ Ь
Положив
(8)
b
cos (Но —Hi)
sin pi0 sin pi4
(9)
и заметив, что
14----------------- = 1 + ctg |10 ctg [14 =
получим по (8):
г = — kl 8г> ( sin 1X3 У cos <т + Hl + Н2 — &Нз — Hi)
2 0 \ b ) sin Hi sin [i2 sin
Полагая
„ _ _________«__________/ Sin р.3 \8
2 sin |лх sin р,2 sin \ b / ’
To — Hi 4“ № ^Нз — Рч *4“ ~2~»
получим еще
Г = ртг>0/ sin (т0 + т).
Все величины, входящие в ц и т0, могут быть вполне опре-
делены через аир.
288 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
По Г найдем величину подъемной силы по теореме
Н. Е. Жуковского в виде
Р-р^о|Г|.
Подсчет по полученным формулам привел к следующим
результатам: при 8t=l и, полагая
х = (1 — 8)К, 8=100^-%,
С. М. Тарг получил:
б 10% 20% 30%
X . . . 30° 60° 90° 30° 60° 90° 30° 60° 90°
•с0 . . . 18° 31° 42° 25,5° 43° 59° 31° 52° 72,5°
Р . . . 1,06 1,05 1,02 1,05 1,06 1,05 1,06 1,08 1,08
Отсюда видно, что |х можно считать во всех случаях
равным 1. Следовательно, весь эффект увеличения подъемной
силы у крыла со щитком происходит за счет причин, эквива-
лентных увеличению вогнутости. При этом крыло со щит*
ком дает лучший эффект, чем сильно вогнутое крыло или
крыло с элероном, так как для него обтекание сохраняется
до больших углов атаки.
р
Если рассчитать величины Ро = —х- , пропорциональные
Р^о
величине подъемной силы, то получим для углов атаки
т = 0°, 5°, 10°, 15°, 20° следующие значения:
5 ' 10% 20% 30%
X т 30° . 60° 90° 30° 60° 90° 30° 60° 90°
0° 1,02 1,71 2,22 1,44 2,28 2,87 1,71 2,63 3,17
5° 1,30 1,95 2,43 1,69 2,48 2,99 1,95 2,80 3,25
10° 1,56 2,18 2,62 1,94 2,66 3,11 2,18 2,94 3,30
15° 1,81 2,39 2,74 2,16 2,83 3,20 2,39 3,07 3,33
20° 2,04 2,58 2,94 2,37 2,97 3,27 2,58 3,17 3,33
тёорМтич. основания методов увеличения подъемной Силы 289
Щитки с В, большим 30%, уже не дают увеличения подъ-
емной силы по сравнению с меньшими значениями 8.
Максимум эффективности щитков получается при В —
= 20—30%, что хорошо согласуется с экспериментальными
данными 1).
§ 5. Экспериментальные данные. Общие выводы
По исследованию крыльев с увеличенной подъемной силой
имеется огромный экспериментальный материал. Мы рассмо-
трим здесь только некоторые опытные данные, характери-
зующие с экспериментальной точки зрения приведенные
выше теоретические выводы.
В любопытной сводке МОК (Richard М. Моск) приве-
дены данные о результатах измерений крыла Кларка (Clark)
в «Reports of National Advisor committet for Aeronautique»;
при этом в крыле делались разнообразные прорезы и добав-
лялись щитки и элероны. Эти данные приведены на стр. 290.
Рассмотрение этих данных приводит к следующим выводам.
1. Предкрылок увеличивает значительно предельный угол
атаки. В крыле без разрезов это увеличение доходит до 28°
(с 15° крыла без предкрылка) и не ниже 24° при любом
положении предкрылка.
При крыльях с разрезами, или с элеронами, или с закрыл-
ками это увеличение меньше; предельный угол атаки дости-
гает 20° (вместо 16° без предкрылка).
При увеличении предельных углов атаки с 15 до 24°
подъемная сила увеличивается на 26—37%. Так как подъ-
емная сила равна нулю при угле атаки — 5°, поэтому увели-
чение с 15 до 24° должно дать при линейном законе увели-
чение подъемной силы в рассматриваемом интервале около
45%; в действительности повышение не превосходит 37%.
Отсюда следует, что
а) предкрылок увеличивает предельные углы атаки, при
которых крыло работает без срыва;
б) предкрылок немного уменьшает подъемную силу
сравнительно с крылом без предкрылка, работающего без
срыва на тех же углах атаки.
1) Другой метод решения той же задачи дан в книге В. В. Голу-
бева, Теория крыла аэроплана в плоскопараллельном потоке,
изд. 2-е, стр. 165, 1938.
Повышение подъемной силы
Сравнение приспособлений, испытывавшихся NACA на крыле с профилем Кларк У
Число Рейнольдса при всех испытаниях было 6090Q0, что соответствует примерно
одной трети числа Рейнольдса для обычного небольшого самолета на посадочн. скорости.
Угол между вспамогатель - ной повергни исход профил. Хорда закрылка в %, % от хорды исходн профиля & Максимальный коэффициент подъемной силы Диапазон j § скоростей 4/7) При максимальной подъемной силе ® Угол атаки исходного профиля при максима ль - ной подъемной силе % °4 повыше ния подъем- ной силы %%увеличен. диапазона скоростей Ссылки на репорты ПАСА
Присравн. © с исходн. профил Присравн с простым закрылком Посравн © с исходн. профил Посравн. с простым закрылком
Исходный профиль 1,291 85,0 7,6 15° T.R. 427
Простой закрылок 45° 30%, 1,950 128,2 4,0 12° 51%, 51% T.R. 427
Щелевой закрылок с дополнительн. щиткам 45° 30% 1,980 120,5 4,0 12° 53%, 15% 427. — T.R 427
Двойная щель с закрылком —гг\ 45° 30% 2,442 117,5 4,0 16° 89% 25%, 38%О — T.R. 427
Постоянная передняя щель, вырезанная в исходном профиле 1772 73,8 5.3 24° 37% — — — T.R. 427
Вспомогательный непод- вижный предкрылок НАСА в камбия, с исходя. профилем Q) 0° 1457<> 1,705 10,45 3.5 прибл 24° 32% — 23%, — T.R 428
Неподвижный предкрылок НАСА в оптимальном положении <3> Ф 1,648 76,4 24° 27% — — — T.R 400
Автоматический пред- крылок Хендяи-Пэдж @ / imm 114,2 28° 26%, — 34,5% — T.R. 400
Предкрылок и простой закрылок /Г|втв" ii^ 45° 30% 2,182 91,0 3,8 19° 697. 12% 77о — TR 427
Предкрылок и щелевой закрылок 45° 30%, 2261 93,2 3.8 19° 75%, 16%, 10°% — T.R. 427
Предкрылок и закрылок с двойной щелью 45° 30% 2600 87,3 3.8 20° 101%, 33%, 3% — T.R. 427
Щиток, отклоняющийся без сдвига назад 50° 30% 2,16 138,5 4.3 14° 70% 107% 63%> 8%, T.N. 422
Щиток Цапа, при отклонении которого задняя кромка дви- жется по вертикали вниз '|ЯИЛЬ-^ 60° 30% 235 150,8 3.7 прибл 13° 85% 205% 77%, 17,5% TN. 428
Щиток, отклоняющийся вниз с одновременным движением оси вращ. назад до 90Z хорды 54° 40% 2,222 142,2 3.8 13° 75% 14% 67% 11%, TN. 42Z
Врыло Холле с закрытой передней щелью 48° 34% 2,08 138.8 3,6 13° 64% 67%, 63% 81%, T.N. 417
Раздвижное крыло Фаулера (площ.увелич.гриблизна 31% по сравнению с исходной) © 40° 40% 2.422 155,3 4,25 15° 90% 24,3% 837О 21%, T.N. 419
1. При сравнении свойств измененных профилей с исходным профилем, применявшиеся в каждом случае коэффици-
енты были получены при одинаковых условиях испытаний. Коэффициенты лобового сопротивления были получены
при закрытом предкрылке (в случае, если он подвижной) и при нейтральном положении закрылка
2. Малое значение L/p при максимальной подъемной силе указывает на крутой угол планирования L/p,равное в,
соответствует углу планирования примерно в 7° а значение в 8,5 означает приблизительно 169
3. Коэффициенты отнесены к полной площади крыла; приспособление для увеличения подъемной силы
находится в рабочем положении и проектируется на хорду исходного профиля. В действительности
эта площадь является конструктивно необходимой и служит базисом для сравнения
с профилем с простым закрылком
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 291
Эти выводы хорошо подтверждают теоретические дан-
ные § 3.
2. Элерон резко увеличивает подъемную силу, но несколько
уменьшает предельный угол атаки.
Предельные углы атаки вместо 15° без элерона, 12° с эле-
роном, наклоненным под углом в 45°; точно так же в случае
крыла с предкрылком имеем предельный угол 24°; в случае
крыла с предкрылком и элероном предельный угол атаки
равен 19°; в этих случаях имеем соответственно увеличение
подъемной силы на 51 % и на 69%.
3. Щитки почти не меняют предельный угол атйки
(вместо 15° без щитка имеем 14° при щитке, хорда которого
равна 30% хорды крыла и который наклонен под углом 50°
к основной части крыла), но резко увеличивают подъемную
силу (увеличение на 70%).
4. Крылья с закрылками имеют те же предельные углы,
как и крылья с элеронами (12° без предкрылка и 19 с пред-
крылками), но дают несколько большее увеличение подъемной
силы (53 и 57% вместо 51 и 69%).
5. Наибольшее увеличение подъемной силы получается
у крыла с предкрылком и закрылком и с прорезом в основ-
ной части крыла (увеличение 101 % при предельном угле
атаки в 20°).
Все эти выводы вполне согласуются с результатами
предшествующих теоретических исследований. Заметим, что
теоретически не изучено в достаточной мере влияние несколь-
ких разрезов в крыле; весьма интересные опытные данные,
по-видимому, приводят к заключению, что многочисленные
прорезы в крыльях почти не влияют на подъемную силу
и на предельные углы атаки.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ
РАЗРЕЗНОГО КРЫЛА1)
ЧАСТЬ II
ПРИБЛИЖЕННАЯ ТЕОРИЯ ПРЕДКРЫЛКА И ЗАКРЫЛКА
Краткое содержание
В первой части изложена теория действия предкрылка, осно-
ванная на теории отрыва струй при ламинарном пограничном слое.
*) Опубликовано в Трудах ЦАГИ, вып. 306, 1937. (Прим. ред<)
292 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Условия обтекания крыла обычно весьма далеки от тех, при кото-
рых можно ожидать ламинарного пограничного слоя у крыла.
В настоящей работе этого предположения не делается.
Следуя методу первой части, рассматривается обтекание крыла
в присутствии вихря, заменяющего предкрылок или закрылок. Изу-
чение влияния вихря на распределение скоростей на поверхности
крыла приводит к следующему заключению: 1) вихрь смещает кри-
тическую точку потока у передней кромки; 2) изменяет величину
скорости в точках крыла.
Смещение критической точки влечет за собой в случае пред-
крылка увеличение предельного угла атаки, при ко-
тором крыло может работать в условиях полного обтекания, и
в случае закрылка уменьшение его.
Кроме того, предкрылок уменьшает скорость у передней
кромки и выравнивает ее на верхней поверхности крыла, а закры-
лок увеличивает скорость у передней кромки.
Отсюда получается возможность, оставляя крыло в
прежних условиях обтекания, увеличить пре-
дельный угол атаки на величину А^, которая
определяется формулой
ля-Q / Ра - 2р CQS 20 + 1 (Р + 8)2
1 £р (р2 — 1) (р — 1 + 2е) cos 0о
отличающейся от формулы, данной в первой части работы, множи-
телем ---.
cos2 0о
В случае закрылка получается уменьшение предельного угла
атаки на величину
* 0 = 2 /р2 + 2р cos 20 + 1(р-е)2
2 Zp(p2—1)(р+1—2e)cos00
Вихри, заменяющие предкрылок или закрылок, меняют общую
циркуляцию вокруг составного крыла и вызывают увеличение
подъемной силы более значительное в случае закрылка и меньшее
в случае предкрылка. В работе даны формулы для вычисления
увеличения подъемной силы в случае предкрылка (91) и в случае
закрылка (103).
В конце работы изучается совместное действие предкрылка и
закрылка.
Введение
В первой части этой работы *) было подробно изучено
влияние предкрылка на выравнивание скорости вдоль верхней
*) В. В. Голубев, Исследования по теории разрезного крыла,
ч. I, (Теория предкрылка в плоскопараллельном потоке), Труды
ЦАГИ, вцп, 147, 1933 [см. настоящее издание, стр. 31—137].
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 293
поверхности крыла и на связанное с этим увеличение пре-
дельных углов атаки, при которых крыло работает в усло-
виях полного обтекания. Полученные при этом выводы
предполагали ламинарность пограничного слоя; кроме того,
окончательные формулы были выведены в предположении, что
максимальная скорость достигается у передней кромки крыла.
Условия, в которых работает действительное крыло,
весьма далеки от тех, при которых можно ожидать лами-
нарности в пограничном слое; поэтому основное предпо-
ложение, при котором получены все выводы, оказывается
сомнительным. Однако соображения Кармана, касающиеся
структуры пограничного турбулентного слоя, позволяют
считать, что пограничный слой состоит из двух частей:
слоя, непосредственно примыкающего к поверхности обте-
каемого тела и представляющего собой ламинарной слой,
и слоя турбулентного. Так как можно считать, что отрыв
струй начинается на поверхности тела, т. е. в области
ламинарного слоя, то полученные выводы останутся верными
при условии, что за скорость U на наружной границе слоя
примем скорость Ur на той поверхности, которая отделяет
ламинарную часть слоя от его турбулентной части. Однако
определение Ux по U представляет некоторые трудности.
Предположение, что t/max получается у передней кромки,
несущественно для теории, оно сделано для упрощения
дальнейших расчетов. Этому предположению удовлетворяют
только очень тонкие крылья. Поэтому такое предположение
незаконно для крыльев достаточно толстых (е = 0,2; е = 0,3),
так как для них точка с максимальной скоростью удалена
от передней кромки на значительное расстояние; результа-
том этого является то, что мы сравниваем Uo не с (Jmax,
а со скоростью, которая значительно меньше. Правда,
экспериментальные данные показывают, что при начале срыва
струй с верхней поверхности крыла точка с максимальной
скоростью перемещается к передней кромке и потому это
допущение оказывается, по-видимому, ближе к действитель*
ности, чем можно было бы думать на основании теоретик
ческих соображений. В окончательном итоге мы получаем,
что теория, развитая в первой части этой работы, приложима
только к случаю очень тонкого крыла, работающего в усло-
виях, при которых создается ламинарный пограничный слойт
294 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Метод, который был применен в предыдущей работе,
основан на замене предкрылка вихрем, ось которого непо-
движно связана с основной частью крыла; в предыдущей
работе влияние этого вихря учитывалось только с точки
зрения понижения максимальной скорости потока. Целью
настоящей работы является всестороннее изучение действия
вихрей, близких к поверхности обтекаемого тела, на рас-
пределение скоростей на его поверхности.
Важнейший результат, который при этом получается,
состоит в том, что вихри влияют на положение критических
точек на поверхности обтекаемого тела. При вихрях, заме-
няющих предкрылок, смещение критических точек полу-
чается такое, которое соответствует уменьшению угла атаки.
Таким образом, действие предкрылка сводится к следующему:
1) крыло работает в условиях обтекания, которые соот-
ветствуют углу атаки, меньшему действительного;
2) при надлежащем размещении предкрылка уменьшается
максимальная скорость потока на поверхности крыла и,
следовательно, происходит некоторое выравнивание скорости
потока.
Эти оба эффекта ведут к увеличению предельных углов,
при которых крыло может работать в условиях полного
обтекания.
Кажущееся уменьшение угла атаки позволяет подсчитать
увеличение предельных углов, причем это увеличение со-
вершенно не зависит от свойств пограничного слоя; настоя-
щая работа и посвящена подробному изучению этого воз-
можного увеличения угла атаки.
Уменьшение максимальной скорости также дает некоторое
добавочное увеличение предельного угла атаки. В настоя-
щей работе эта добавочная часть прироста предельного
угла атаки получается, исходя из следующего соображения:
угол атаки увеличивается настолько, чтобы
при увеличенном угле атаки для крыла с
предкрылком скорости распределялись так
же, как они распределяются при предельном
угле атаки крыла без предкрылка. Следовательно,
и эта часть совершенно не зависит от характера пограничного
слоя и одинаково пригодна и для ламинарного и для турбу-
лентного слоев,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 295
Исходя из этих соображений, получена формула, даю-
щая увеличение предельного угла атаки; интересно отметить,
что эта формула весьма мало отличается от формулы, выве-
денной в первой части работы из совершенно иных сооб-
ражений.
Методы, применяемые для исследования влияния пред-
крылка, применены далее и для закрылка. Первая часть
работы изучает условия обтекания цилиндра при наличии
добавочных вихрей; в ней выводятся основные формулы
теории. Вторая часть дает применение этих формул к слу-
чаю предкрылка и закрылка.
Глава I
ВЛИЯНИЕ ВИХРЕЙ, БЛИЗКИХ К ПОВЕРХНОСТИ ЦИЛИНДРА
НА РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ
§ 1. Определение скорости на поверхности цилиндра
в присутствии вихрей
Пусть имеем цилиндр, сечение которого плоскостью (z)
дает окружность |z| = l. Предположим, что на цилиндр
набегает поток, имеющий в бесконечности скорость V^,
образующую с действительной осью угол 9 (угол атаки);
пусть, далее, около цилиндра имеется циркуляционный по-
ток, циркуляция которого равна Г, и в точке а около ци-
линдра (|я| > 1) помещается вихрь интенсивности J.
Тогда, полагая а = и а = ~ ^'г, получим для харак-
теристической функции течения вокруг цилиндра выражение
W = Vme-f>i\z + —)+ 2^-1пг+ 2^{1п(г—a)—ln(z—а)},
(О
откуда
dz Vco V г22«Z 2 ' 2zZ Ig — a г — а‘‘
Имея в виду в дальнейшем переход от цилиндра к слу-
чаю крыла, будем считать, что одной из критических точек
на цилиндре (точкой схода струй) является точка z = 1
296 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щиткой
Тогда, замечая, что при z=l из (2) имеем:
o_^-..(i_s«<)+5L+22r(TJ___L?[ (3)
и, исключая Г из (2) и (3), имеем:
г-1 < / __J д-д
dz г Г°° \ г / 2nZ (1 _ й)(1—^)Х
X 2~аа -Л- (4)
(г — a)(z — а) *
Так как
___________________1_
а — а ______________Р р___ ____р2— 1
(1-«)(1-«)“2с03!Х_(р + ±) Р2 —2р cosp+l
есть число действительное, то положим, что
—/(а~~д) = А, (5)
2л(1 — а)(1 — а)
где А — действительное число. Тогда уравнение (4) примет вид
= -£—IVme~9i(1 + —) + 1А-г~аа . (6)
dz г I \ z (z_a)(z — a)l V
Чтобы получить величину скорости на поверхности ци-
линдра, положим в (6) z = е*г\ тогда
5<1++
+ --7--и—:—:-------"}•
_ (р + ^*+<Р» _]_ ₽2|и j
Но
(1 _|_ e(20-<p)i) ==e_‘2‘’[e_(e_'2’)<_|_e(9~^-)i] =
= 2 cos (б — 75Л е 2 *;
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 297
также

_ (р 4- А V М+ф< 4- e2p.i
' —е '
g * .-----------------,——
2 cos (ч> — (х)—(р + —)
2 2 —e 2 ) = 2ie 2 siny.
— 1
----:— = е
е*г
Подставим все эти значения в уравнение (6), приведем
его к виду
, / . 2sin(-^- —рА
= 2ie-^ sin -у V^2 cos (б — -у)—А-----------т- >
dZ 2| V 2 7 ScosGp-h)-^)
или, полагая
(7)
А
2^

и
имеем окончательно
dw л 17 -(?—• ?
— = 4^06 4 27 sin
COS (ср — |Л)—г
(8)
Найдем теперь положение остальных критических точек.
Здесь отметим, прежде всего, один интересный и простой
частный случай.
Пусть |x = Ozty, тогда
sin —|x^ = sin (-|—^zcosfQ —
298 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Следовательно, уравнение (8) принимает вид
dW
• ? . /? — (20 + тс)
Sin у sin'1—-—!—-
2
К
> (8')
COS
и потому двумя критическими точками течения служат
точки
?1 = °> ?2==20’4-7:»
т. е. в этом ^случае положение двух критических точек
остается такое же, как если бы добавочного
вихря не было.
Но, кроме двух найденных критических точек, в этом
случае окажутся еще две, положение которых определяется
из решения уравнения
откуда
sin (ср — 0) = — К ± г
и
<Рз = 0 + х. <р4 = 6-ч-(тс — X), (9)
где
X = arcsin (± г — К). (10)
Формула (10) показывает, что критические точки ср3 и
ср4 окажутся действительными при | г z±z | 1; при
| г ± К | > 1 углы, соответствующие значениям ср3 и ср4,
окажутся комплексными.
В случае действительных ср3 и ср4 расположение крити-
ческих точек, как показывает рис. 1, оказывается симмет-
ричным относительно прямой Оа, соединяющей ось цилиндра
с осью добавочного вихря.
Разобранный частный случай показывает, что число кри-
тических точек на цилиндре в общем случае будет равно
четырем, из которых одна (ср = 0) известна. Таким обра-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЁЗНОГО КРЫЛА. ЧАСТЬ II 299
зом, нахождение трех остальных точек может быть сведено
к решению некоторого кубичного уравнения, которое легко
получить. Действительно, из (8) видим, что три критиче-
ские точки найдутся из уравнения
cos (б— [cos(ср — |х) — г] — к — и) = О-
Это уравнение может быть переписано в виде
(cos 9 cos ~ + sin 9 sin j X
X £(cos2 — sin2 cos + 2 sin — cos ~ sin —
— r (cos2 ~ + sin2 —
— К (sin у cos — cos-|-sin^(cos2-|- + sin2 = 0,
откуда, деля на cos3 у cos 9 и полагая tg~ = Z, имеем
уравнение
-Z>[lg')(cos|1 + r) + ;<|M] +
+ Z2 [—• (cos рь + г) + 2 sin [л tg 0
+ к 5П ‘s I1] + z ['S8 (c“ I* - '> + 2 sl" f - K S] +
+ [(сози-г)+/<|!И] = 0. (И)
Решения уравнения (11) и определят положение трех
критических точек на поверхности цилиндра.
Действительное решение уравнения (11) приводит
к большим вычислениям, поэтому представляется интерес-
ным обойти эти вычисления, дав подходящий приближенный
метод определения его корней. Очевидно, что если бы был
найден один из корней уравнения (11), то нахождение двух
остальных корней не представляло бы больших затрудне-
ний; в дальнейшем мы укажем весьма простой способ опре-
деления одного из корней.
300 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Пусть, таким образом, мы из каких-нибудь соображений
определили один из корней уравнения (И); назовем его а.
Тогда из (8) имеем:
/ sln(4~H
costs — 4) — К------ . ' =0. (12)
\ 2 / cos (а — |л) — г v 7
Исключая К из уравнения
=0 (13)
и из (12), имеем:
/ ч / ч sin (~ — ix) z х
cos(0 — -П-cos O-vl-V2--------H?Sj8~^=0. (14)
V 2/ 2/sin(|-p) cos('p-(x)-r
Отсюда для определения двух остальных критических
точек имеем уравнение
cos — -|) sin — р.) cos (<Р—р)—cos (о — у) sin (у — Р-)х
X cos (а—р)—г £cos (б — ^)sin(y—Iх) —
— cos ^6---^-)sin^-|-—р)] = 0- (15)
Применяя формулу
cos A sin В cos С = -i- [sin (Д -[- В -|- С) + sin (Д -|- В — Q +
+ sin (В — A -f- С) + sin (В— А — С)],
приведем уравнение (15) к виду
sin Пр [cos (0—<p)4-cos (0—a)-|~cos 0—cos(a-[-<p—0—2p)—
— 2rcos(0 —p)] = 0. (16)
ИССЛЕДОВАНИЙ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 301
Следовательно, два последних корня найдутся из урав-
нения
cos (6 — ср) + cos (9 — а) + cos 9 — cos (а -|~ ср — 9 — 2р.) —
— 2г cos (9 — |i) = 0 (16х)
или
2 sin (у — у) sin(y + <p — 9 — =
= 2г cos (9 — р) — cos (9 — а) — cos 9,
откуда
= + ----"2+ (17)
и
. __ .2г cos (6 — р,) — cos (6 — а) — cos 0
А — arcsin--------------- г *
2 sin (у —р.)
ИЛИ
г cos (0 — р) — cos ( 0-) cos
X = arcsin----------------; (18)
найденные корни назовем Р( = ср2) и у( = ?3).
Введя корни р и у в формулу (8), можно привести ее
к следующему симметричному виду.
Так как р удовлетворяет уравнению (16), то
cos (9 — 3) —|— cos (9 — а) + cos 9 —
— cos (а + р — 9 — 2р) — 2г cos (9 — р) = 0,
а потому
cos (9 — ср) -|- cos (9 — а) -|- cos 9 — cos (а + ср — 9 — 2р) —
— 2г cos (9 — рь) = cos (9 — ср) •— cos (9 — р) —
— [cos (а —ср — 9 — 2р) — cos (а -|- р — 9 — 2р.)] =
= 2 sin (9—sin +2 sin 9 — 2р.—|—а) sin^-=^ =
= 2sin -2sin^y— pjcos(у + - — 9 — р + ^. (19)
302 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Выражение (19) обращается в нуль при ср = р и при
2
0-н + | = ±у.
откуда
ср = 29 -|~ 2[л ± тс — р — а.
Подставляя сюда значение
₽ = 0 + fx—J + k,
имеем:
? = 0 + tj'—х.
Так как, очевидно, достаточно взять в этом выраже-
нии-1-и, то отсюда видим, что ср = р
’Подставляя в (19) вместо р его значение, приведем (19)
к виду
4sin-2^₽ sin-^1 sin — у). (20)
Подставляя найденные выражения в формулу (8), получим:
/ и\. 4 sin^-y^sin^-J sin —рА
1 sin -~У 2______2 ’
dz sm 2 2 sin 2
Окончательно
dw Qxr
dz ~ Wc°e
sin ~ sin -.а- sin -У- - sin --
-----------------(21)
Г — COS (ср — |1) '
Такова окончательная формула, дающая выражение ско-
рости течения на поверхности обтекаемого цилиндра.
§ 2. Расположение критических точек
Между углами, определяющими положение критических
точек, существует замечательное соотношение. При отсут-
ствии добавочных вихрей точкой разветвления струй яв-
ляется точка z = ^20+те)<. Пусть елг — соответствующая
смещенная точка при наличии добавочных вихрей. Назовем
а — (20—|—тт) = 23 смещением первой критической точки;
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 303
точно так же положим р— = и у — р. = 82 и назовем 8Х
и 82 также смещениями критических точек. Из написан-
ных равенств имеем
а = 20 -j- тг -J- 2В, ]
Р = | (22)
у = |1-|_52. J
С другой стороны, складывая равенства (17;, где <р2 = р
и ср3 = у, имеем:
Р у = 29 2рь — а -|~ гс
или
а + Р Ч~ Т = 29 -|- + гс.
Отсюда, заменяя а, р, у по (22), имеем:
25 + 51 + 52 = 0, (23)
т. е. сумма смещений критических точек под
действием добавочных вихрей равна нулю
(рис. 2).
Легко показать, что это свойство остается верным при
любом числе добавочных вихрей и при любом их располо-
жении. Для доказательства этого обобщим формулу (21)
на случай любого числа вихрей, произвольно расположенных
вне цилиндра.
304 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Характеристическая функция потока, обтекающего ци-
линдр при любом расположении вихрей вне его, в самом
общем виде может быть написана:
п
w — Voo^-0iU4
In?—(24)
г — ак
где
Отсюда
— у g—t>i (1 _|_ _L_ 1 _|_ У . Jle (_______!_________1 _ I
dz °° V г2 j' 2x1 г Zi 2x1 \г — ак г — ак>
(25)
Если привести правую часть (25) к общему знаменателю,
то, очевидно, получим в правой части рациональную дробь,
числитель которой имеет степень такую же, как знаменатель.
Разлагая числитель на множители, имеем окончательно урав-
нение вида
dw ,, oi (z — m)(z—p) -А- (г ——
dz-V^e * 11 (z-ak)(z-ak)'
(26)
Предположим, что все точки т, р, тк) рк лежат на поверх-
ности цилиндра и, следовательно, являются критическими
точками потока. Полагая /п = еаг, р = тк = е*к\
рк — е$кг, имеем для (26) следующее выражение на поверх-
ности цилиндра:
dw„ ?X-^(^-^)fr .
dz г e2'fi JJ- (gfi _ p^i)^<pi _ 1
(27)
Но из равенства
•р + а . / <р -а . <р а Д <р + а .
е^г—еаг = е 2 \е 2 *—е 2 у = 2 г sin
4-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 305
и, следовательно,
(еи — рем) — у Z*) = e2'fi — (р +1) е(ф+|1) 4 -|- е2М =
_ е(?+Р-)г ^2cos( — pfc)}
где
^ = 4(pft+T;)-
После подстановки этих выражений в уравнение (27)
имеем:
— — V е
dz ~~ Vc°e
-Oi
/ , a+P\ .
V 2 ) 1 <P — Ф — 3
— 4e 2 7 sin ——2~“ sin
п
1
t Sin У 2aft sin — ~2
rfc-cos('p-lxft)
ИЛИ
п
^- = — 2п^Уте-^е
dz
„ sinr^*sin<L^*
r_lsin -------------?-------2 (28)
2 2 ___ me ten _ fi \ x '
Гк—cos (у —рй)
306 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Рассмотрим случай, когда <р > а, ср > (3, ср > ай, ср >
(рис. 3); тогда, называя через величину скорости в рас-
сматриваемой точке цилиндра, имеем:
* = (29)
Уравнение (28) можем переписать в виде
„ siniz^*sinJLz_₽*
X sin sin - 9 ТТ------------------------г— . (30)
2 2 JLL rk— cos (<р — |а&) 4 >
Сравнивая (29) с (30), имеем:
+ = (31)
где N — некоторое целое число.
При отсутствии всех вихрей (т. е. когда Г = 0 и Jft = 0)
Oi (0+к)г
критические точки находятся в zr — е , z2 = ; назовем
смещениями критических точек величины а — (0 -|- тс) = 8'
ЙССлЁДОВАНИЯ ПО ТЕОРИИ РАЗРЁЗНОГО КРЫЛА. ЧАСТЬ II 307
и р — 9 = 8"; точно так же назовем смещениями
Ч — = = Отсюда
а = 9 -|~ к -|~ 8 , р = 9 -|~ 8 , а* = + 8Л, Р& = [** + 8&. (32)
Подставляя значения (32) в уравнение (31), имеем:
it 5-4-5 п ( 5т. -|- oZ )
0+2+-J-—2-e+Sb+JLf-J-^H27:;v
или
ь'4-5" Д ък + ч
—J—F 2 -Ч12 = 2кМ <33>
1
Чтобы определить величину N, заметим, что при очень
малых Г и 4 величины В , 8 , 8Ь 8& сколь угодно малы;
следовательно, N может быть только нулем. Итак, имеем
равенство
8Ча" + 5Ж-Н*) = 0. (34)
т. е. сумма всех смещений критических точек
при любом расположении добавочных вихрей
равна нулю1).
Воспользовавшись равенством (34), приведем уравне-
ние (30) к виду
dw ПП4-9ТГ -(<Р+4)* . ? — а • ? — ₽
— = 2п+2Усог v 2 * * 7 Sin Sin х
. sl„(«)sln(l=£.)
X Л rk — COS (<P — |J.Zc) ’ (З5)
Это уравнение является обобщением уравнения (21) на слу-
чай любого числа вихрей; уравнение (21) получается из (35)
при п = 1.
1) Можно показать, что это свойство остается верным и при
отсасывании воздуха через щель в крыле. Другое доказательство
см. В. В. Голубев, Обтекание цилиндра потоком в присутствии
системы неподвижных вихрей, Уч. зап. МГУ, 1936.
308 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щиткой
В простейшем случае цилиндра с циркуляцией, но без!
добавочных вихрей на конечном расстоянии уравнение (34)
дает:
8'-|-8/z = O.
(36)
Уравнение (36) выражает известное свойство обтекания
потоком цилиндра при наличии циркуляции. Это свойство
обычно выражается так: хорда,
соединяющая критические точки
на цилиндре, параллельна скоро-
сти потока в бесконечности.
В случае одного добавоч-
ного вихря на конечном расстоя-
нии уравнение (23) показывает,
что при 28 = 0 имеем:
814-82 = 0.
Этот случай разобран выше
(см. формулу (9)). В этом слу-~
чае хорда, соединяющая крити-
ческие точки, получающиеся от действия добавочного
вихря, также параллельна скорости потока в бесконечности
(рис. 4).
§ 3. Приближенное определение величины а
Предшествующие исследования показывают, что вопрос
о положении критических точек разрешается очень просто,
если найти положение одной из критических
точек.
Покажем прием, который позволяет найти положение
критической точки, в которой разделяется поток, набегаю-
щий на крыло. Экспериментальные данные показывают, что
смещение критической точки разделения потока под дей-
ствием дополнительных вихрей, заменяющих предкрылок,
незначительно. Пользуясь этим соображением, положим, что
а = к+ 294-28,
(37)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II ЗОЙ
где 8 — величина малая. Подставляя значение (37) в уравне-
ние (12), имеем:
cosl 0 — 4 — 9 — 8) — к-----7--------------Л- = О
\ 2 / cos (тс -j- 20 + 2Ь — р) — г
или
— sin 8 [г -Н cos (20 + 28 — |х)] + К cos (0 — + 8) = 0;
Заменяя по малости 8 выражения sin 8 и cos 8 соответственно
через 8 и 1, имеем:
— 8 [г 4~ cos (20 — р)] 4~ К [cos (0 — р) — 8 sin (0 — р)] = 0,
откуда
*___________К cos (0 — р)_______
г cos (20 — р) 4- К sin (0 — р) *
Рассмотрим два крайних случая, соответствующих пред-
крылку и закрылку. В случае предкрылка р близко к тс;
в случае закрылка р близко к нулю. Мы рассмотрим случаи
р = 0 и р — тс.
1. р = 0.
Формула (38) принимает вид
* _ /С cos О
г 4- cos 20 + к sin 0 *
Здесь угол 0 порядка 15-—25° и, следовательно, 8 может
быть величиной малой только вследствие малости К, а потому
мы можем заменить (39) следующей приближенной формулой:
*___ К cos 0
г 4- cos 2 0 *
(38)
(39)
(40)
2. р = тс.
Формула (38) принимает вид
*____________________________/Ceos 0_____
г — cos 20 — К sin 0 1
и, следовательно, 8 может быть величиной малой только
вследствие малости К, а потому и здесь мы можем заме-
нить (39') следующей приближенной формулой:
*_____ К cos О
г — cos 20
(39')
(40')
310 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩЙТКОЙ
Так как при обычном расположении предкрылка и закрылка
циркуляции J и Г одного знака, то из написанных ниже фор-
мул (41) и (41') следует, что для закрылка поло-
жительно, а для предкрылка S2 отрицательно.
Рассмотрим более подробно величину /С. Из равенств (7)
и (5) имеем:
______J (а _____
4^(1 - а) (I- а)’
или, подставляя
получим:
(40")
и
При отсутствии предкрылка циркуляция Г определяется по
формуле (3) при J=0:
Г = 2шИоо (е^ — = — 4^ sin 9.
Следовательно, по (40") имеем:
„___ d sin 6
Г г — cos {х *
и по (38) и (40"), учитывая, что К мало,
*___ J _____д? sin 0 cos (|х — 6)_
Г (г — cos |х) (г -j- cos (20 — |х)) ’
откуда при pi = 0 (закрылок)
___J sin 0 cos 0 d ...
61 —‘ Г (г—1) (г + cos 20)
и при |х = к (предкрылок)
5. _ J cos 0 sin 0 d /41^
°2 ” Г (r + 1) (г — cos 20) ’ 1 '
откуда
I Ц 1 г + 1 г — cos 20
I §2 | г — 1 г + cos 20 *
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ П 311
Эта формула показывает, что изменение угла атаки для
предкрылка меньше, чем для закрылка, при одном и том же
J
отношении у.
п J
Для предкрылка отношение -ут, как увидим далее, по-
рядка 0,5—0,8 и р заключается обычно в пределах 1,5—2;
при этих значениях для [82| получим величины порядка
3—5°. Эти подсчеты показывают, что сделанные выше пред-
положения о малости 8 действительно имеют место.
§ 4. Влияние вихря на распределение скоростей
на поверхности цилиндра
Рассмотрим теперь влияние добавочных вихрей на рас-
пределение скоростей на поверхности цилиндра.
Положение добавочных критических точек [3 и у опре-
деляется по формулам (17)
р = в+|Х_»+х,
т = О Ч- и — -|-те —X,
причем X определяется по формуле (18):
г cos (6 — |л) — cos (б — — j cos
X = arcsin-----------------г— -------.
Полагая
Г COS (0 — |Л) — COS ( 0 — -£ ) COS ~
S =/ 2)----2-, (42)
sin (y — P ]
по формуле (18) мы видим, что X принимает действитель-
ные значения только при S^l. Найдем более простое
выражение для S. Так как а = тт —|—20 4-28, то, подставляя
в выражение S, получим:
г cos (0 — р-) — sin 6 sin (0 4 &)
cos (0 — |л Ь)
312 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Пользуясь малостью 5 и откидывая члены с 82, получим:
sin 8 sin (9 4" 8) ~ 8 sin 9,
cos (9 — 8) cos (0 — рь) — 8 sin (6 — =
= cos (6 — |х) [1 — 8 tg (8 — |i)J.
Отсюда
S = r cos (ОI —р.) — 8 sin 9 t _|_ 8 t 9 _
cos (0 — |л) 11 r/J’
«ли
S = r — Sfrtg^ — 0)Н----*'п6 .1. (43)
L ь /I cos (0 р.) J \ /
При |1 = 0, что соответствует случаю закрылка,
S1 = rH-8tg6(r—1). (44)
При |» = it, что соответствует случаю предкрылка,
s2= r + Stg9(r+ 1). (44')
Заметим, что для закрылка при обычном расположении
всегда 8 > 0 и г > 1; поэтому по (44) видим, что для обыч-
ного расположения закрылка > Г, что касается пред-
крылка, то здесь 8 < 0 и по (44') S2 может быть и меньше 1,
но из физических соображений, о которых будет далее
сказано, приходится считать и в этом случае всегда S2> 1,
так что в практически важных случаях всегда X — величина
комплексная. Найдем при этих условиях р и р
По известным формулам можно написать, что
arcsinS = у In {Sf z±z]/"l — S2},
и, замечая, что в рассматриваемом случае S>1, имеем:
X = arcsin S = у In {SZ± z/S^T} = -J — Z In {S =t .
Отсюда
= zin{S4-/s*=T),
X2 = | — l In {S—]/S^T} = -J + Z In {s + V 3^1}.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 313
Полагая
In {S-+- ys2 —1} = V, (45)
имеем:
= y — iv, /.2 = |+<v,
и отсюда
р = 6 + — ^4-Х^рь — 8 — Zv, (46)
Y = о —р, — У + тг — х = (1 — 8 + /V. (47)
Замена к! на Х2 меняет только у и р. Если подставить най-
денные значения в формулу (21), то получим выражение
скорости на цилиндре.
В этом случае
• ? — ₽ . ? — т • Г? — (р-— °) । .'И • Г?—(р-—Ч .'И
sin “21 Sln = sin Г—^2 ~ 1 2J sin L—"2—~z 2J *
По известной формуле
sin (A 4- В) sin (A — B) = sin2 A — sin2 B,
а потому в paci зматриваемом случае имеем:
• ? — ₽ ’Sln 2 ИЛИ • ? —₽ Sln 2 sin — sin2 — sin2 i , sin = sin2 -—— °)sh2 2_.
В этом случае ( формула (21) принимает следующий вид:
dz , sinal-^.-5.) + sh22 sin sin - (48) sin 2 Sin 2 г — cos (? — |х) ’
Обозначив 2 г - cos (?-н) -£’ <49>
можем еще наш <сать:
dw dz ~~ = 4VcoSin-|-sin ~--L-e О1'*'2)* • (50)
314 I. ТРУДЫ nd ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Преобразуем величину L. Заменяя
2 sin1 2 -——— = 1 — cos [ср — (|л — 8)],
2sh2-J = i(^-^2)
получим:
У (^ + ^)~cos ['Р — (Iх —“)]
--ГТ - М------------• <51)
т V + 7/cos (<р ~|Л)
Формула (51) чрезвычайно симметрична; возникает вопрос,
какое физическое значение имеет величина е\ входящая
в (51) совершенно симметрично' с р. Можно показать, что
есть расстояние от центра цилиндра до критической
точки потока х).
Из (45) имеем:
6-»= S + /S2 —1,
и отсюда
<>-* = $— /S2 — 1,
а потому
и формула (51) принимает вид
S —cos [у — (р, — д)]
Г — COS (ср — |Л)
(52)
Замечая, что для закрылка (|л = 0) В > 0, имеем по (44),
что > г, и аналогично для предкрылка (ji = k) S2 < г.
Возьмем ср = (л — у; тогда
S — cos -5-
£ =-----------=-
О
г — cos
1) См., например, В. В. Голубев, Обтекание цилиндра пото-
ком в присутствии системы неподвижных вихрей, Уч. зап. МГУ, 1936.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 315
а потому имеем следующий результат: в случае пред-
крылка (S2 < г) в точке ср = (л — -% L г) £ > 1, т. е. предкрылок умень-
шает скорость на поверхности цилиндра
вблизи предкрылка и закрылок увеличивает
ее. Физическая картина этого совершенно ясна; она пока-
зана на рис. 5.
Рис. 5.
Для дальнейшего решим вопрос о том промежутке на
поверхности цилиндра, где предкрылок уменьшает, а закры-
лок увеличивает скорость. Для этого найдем точки на
поверхности цилиндра, в которых £ = 1. Из (52) для опре-
деления ср имеем уравнение
cos [ср — (|х — 8)] — cos (ср — — S — г
или
и отсюда находим два угла:
о , . г—S
?1 = I* — у + arcsin--г,
2slnT
а , . г—S
<f-? = ji —j + K—arcsin---г
(53)
316 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Отсюда по (43), заменяя 2 sin — ^8, получим:
<Pi = t* + arcsin [г tg (|л - 6) + cos -у], |
8 । . Г 1 / । sin 6 "I |
Т2 = !*— 2+я — arcsin [г tg ((л — 9) + соГ(й " • |
Рассмотрим два крайних случая.
1. Закрылок: и = 0.
?! = — у — arcsin [tg 0 (г — 1)1,
<р2 = — у + п + arcsin [tg 0 (г — 1)[.
На рис. 6 даны примерные положения точек, соответ-
о
ствующих <рх и ср2. В этом случае в точке <р = —
= — — j L больше единицы, а потому L больше еди-
ницы на дуге АСВ и, следовательно, меньше единицы на
дуге ADB. Таким образом, множитель L увеличивает ско-
рость на всей верхней поверхности цилиндра и уменьшает
ее на дуге ADB нижней , поверхности; и то, и другое уве-
личивает подъемную силу.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 317
2. Предкрылок: |х = к.
<Р1 = к——arcsin[tg0(r-|- 1)1,
<р2 = те — j + ir-f-arcsin [tgO (r-|- 1)],
что, очевидно, можно заменить углом
<р' ~ ~Ь arcsin {tg- 6 (г-+ 01-
На рис. 7 даны положения точек, соответствующих cpt
и <р2. В этом случае в точке ср = к — у (? = |х— ту!
L меньше единицы, а потому L меньше 1 на дуге АСВ и
больше единицы на дуге ADB. Таким образом, множитель L
увеличивает скорость в точках около средины верхней
поверхности крыла и уменьшает ее на верхней поверхности
около передней и задней кромки и на всей нижней поверх-
ности крыла. Отсюда следует, что L выравнивает скорость
на дуге от ср2 до к, что способствует более плав?
ному обтеканию в тех частях крыла, которые
дают наибольшую подъемную силу; необходимо
при этом заметить, что уменьшение скорости на нижней
поверхности и ее увеличение в средних частях верхней
поверхности крыла дает увеличение подъемной силы, но это
увеличение частично компенсируется уменьшением подъем-
ной силы вследствие уменьшения скорости около передней
и задней кромки на верхней поверхности крыла. Заметим еще,
что эти выводы имеют место только, если в случае закрылка
tg 0 (г—1)<1 и в случае предкрылка tg(r-|-1)0 < 1;
в противном случае множитель L увеличивает скорость
во всех точках при закрылке и уменьшает скорость во всех
случаях при предкрылке. При действительных условиях,
как легко видеть, приведенные выше неравенства выпол-
няются и все приведенные выше рассуждения имеют
место.
§ 5. Давление потока на цилиндр в присутствии вихря
Переходим к определению подъемной силы, действую-
щей на цилиндр в присутствии вихря. Так как в дальней-
шем вихрь заменяет действие предкрылка или закрылка,
318 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
твердо связанного с крылом, то нам нужно определить силу
давления потока на цилиндр вместе с добавленным
к нему вихрем. Так как в этом случае ко всей системе
можно применить теорему Н. Е. Жуковского, то прежде
всего нужно определить величину циркуляции вокруг всей
системы, т. е. вокруг цилиндра с вихрем. Для этого доста-
точно взять интеграл по какой-нибудь кривой, охватывающей
крыло с вихрем, от выражения Применяя формулу (2),
получим:
\^-dz = V+J—J=V,
J dz 1
т. е. выражается так же, как и для крыла без вихря, но
величина Г в этом случае зависит от добавочных вихрейх).
Действительно, по формуле (3) имеем:
г= — vooe-®i(1 — e20i)2та — J--,
(1-а)(1-а)
т. е.
г = — 4^ sin 0 + J--------. (54)
°° 1 Г — COS р 4 7
Так как в случае предкрылка и закрылка J<0, то еще
можно написать:
1П = 4TtVcosin9 + l Л—•
В случае цилиндра без добавочного вихря
Г = — sin 6.
Следовательно, присутствие закрылка или предкрылка дает
увеличение циркуляции и подъемной силы, равное:
|ДГ|=|/|—1—
1 1 1 1 Г — COS р
и
7^- (55)
*) См. также В. В. Голубев, Исследования по теории раз-
резного крыла, ч. I, Труды ЦАГИ, вып. 147, стр. 16, 1933 (см.
настоящее издание, стр. 31 — 137].
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 319
Рассмотрим два крайних случая.
1. Предкрылок: |х = тс.
2. Закрылок: jx = 0.
|ДГ2| = р|-41-
Отсюда имеем при одинаковом | J\
т. е. закрылок дает увеличение подъемной силы, значительно
большее, чем предкрылок.
Общий вывод из всего предыдущего тот, что и пред-
крылок и закрылок дают увеличение подъем-
ной силы, причем при одинаковой интенсив-
ности добавочного вихря предкрылок дает
незначительное увеличение и закрылок—
очень большое.
§ 6. Влияние вихря на условия обтекания
круглого цилиндра
Полученные выше выводы позволяют сделать окончатель-
ные выводы о действии добавочного вихря в случае обте-
кания цилиндра.
По формуле (50) для скорости в точке цилиндра z —
имеем выражение
Гг л»/ I • 9 • ? — (^ + 262о) I г
= 41^00 sin j sin -—V—n--2--1-L. . £. (56)
С другой стороны, при отсутствии вихря для скорости
в той же точке имеем выражение
Vcp = 4Vqo I sin sin У —(^4- 26) |. (57)
Таким образом, действие вихря сводится, во-первых,
к замене угла, определяющего положение критической точки,
точки разделения потока; вместо критического угла к 4- 20 при
320 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и Щитков
отсутствии вихря получается угол тг-|- 29 —|—28; во-вторых,
в выражении скорости (56) получается добавочный множи-
тель L.
Разберем подробно влияние обоих этих факторов.
Если в выражении скорости (57) заменить угол тг -1~ 29
углом -п:—|— 29 —J—28 = тс —|— 2 (9 —|— 8), то это равносильно тому,
что угол атаки 9 заменяется углом 9—8. Пусть при усло-
виях обтекания, выражаемых распределением скоростей (57),
цилиндр обтекается без отрыва струй до угла утаки 90;
тогда при наличии распределения скоростей, даваемых фор-
мулой
17 А 17 I ’ ? -(ТС 4“ 20 4“ 2о) I /соч
Vcp = 4 Уоо sin ~ sin ———- , (58)
тот же цилиндр выдержит без отрыва струй обтекание
до угла атаки 9Х, причем
9Х + 8 = 90 и 9Х = 9Х — 8. (59)
Следовательно, смещение критической точки влечет за собой
тот важный факт, что, не меняя характера обтекания, мы
можем изменить предельный угол атаки на величину — 8.
Так как для предкрылка 8 отрицательно и для закрылка по-
ложительно, то изменение положения точки раз-
деления струй увеличивает на |8| предельный
угол атаки при наличии предкрылка и умень-
шает на |8| предельный угол атаки при нали-
чии закрылка.
Важно отметить, что этот результат совершенно не зави-
сит от причин, вызывающих отрыв струй, и, следовательно,
не зависит от структуры пограничного слоя.
Переходим к рассмотрению влияния множителя L. Мы
видим, что в случае предкрылка появление множителя L
способствует выравниванию скоростей на большей части
верхней поверхности крыла. Следовательно, благодаря мно-
жителю L падает максимальная скорость на верхней поверх-
ности крыла, и, чтобы довести скорость до той, при кото-
рой крыло еще работает в условиях обтекания, можно еще
несколько увеличить предельный угол.
Следовательно, действие предкрылка сказы-
вается в увеличении предельного угла атаки,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 321
которое получается из двух источников:
от изменения положения критической точки
и проистекающего отсюда кажущегося изме-
нения угла атаки и от выравнивания скорости
в результате появления множителя £; кроме
того, получаем некоторое незначительное
увеличение подъемной силы, проистекающее
от действия добавочного вихря, как указано в§5.
В случае закрылка мы имеем менее ясную картину. За-
крылок увеличивает скорость на всей поверхности крыла,
но неравномерно, и здесь Т^кже получается некоторое не-
значительное выравнивание. Таким образом, в случае за-
крылка мы получаем уменьшение предельного
угла атаки, происходящее от смещения кри-
тической точки и кажущегося увеличения угла
атаки, которое отчасти компенсируется вы-
равниванием, происходящим от присутствия
множителя £; кроме того, в этом случае имеем
резкое увеличение подъемной силы, происхо-
ходящее от действия добавочного вихря, как
показано в § 5.
Для определения величины смещения критической точки
у крыла необходимо найти величину £ Кроме того, необ-
ходимо учесть влияние на обтекание крыла множителя L.
Эти две задачи и будут разобраны в главе II, после чего
весьма легко определить изменение величины подъемной
силы, даваемое наличием предкрылка или закрылка.
Глава II
ВЛИЯНИЕ ПРЕДКРЫЛКА И ЗАКРЫЛКА НА ИЗМЕНЕНИЕ
ПОДЪЕМНОЙ СИЛЫ КРЫЛА
§ L Определение интенсивности добавочного вихря
Основываясь на соображениях, развитых в первой части
этой работы х), мы будем заменять в дальнейшем предкрылок
или закрылок вихрем, неразрывно связанным с крылом. Для
1) В. В. Голубев, Исследования по теории разрезного крыла,
ч. I, стр. 11—12, Труды ЦАГИ, вып. 147, 1933 [см. настоящее изда-
ние, стр. 48 — 49].
322 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
того чтобы применить результаты предыдущей главы, необ-
ходимо определить величину циркуляции добавочного вихря,
заменяющего предкрылок или закрылок. Если рассматривать
предкрылок или закрылок как плоскую пластинку, то, при-
меняя известную формулу1), найдем для величины циркуля-
ции вокруг пластинки следующее выражение:
(60)
где Va—скорость потока в точках предкрылка, b — его
хорда и р — угол атаки относительно набегающего на пред-
крылок или закрылок потока.
Следовательно, для определения величины J необходимо
определить величину Va и угол |3.
Мы ограничимся в дальнейшем случаем дужек типа инвер-
сии параболы, как лучше всего изученных и подходящих
весьма близко к случаю обычно применяемых дужек.
Если взять на плоскости (z) цилиндр радиуса 1, а
на плоскости (С) дужку типа инверсии параболы с централь-
ным углом скелета 2а и с коэффициентом, характеризую-
щим толщину, равным е, то по результатам первой части2)
имеем:
cos2~(l —е)2
Г = е 2 (2— l)_(l_s)cos|+---------------£-------------;
(z-l)e 21_|-(1_е)сО5^
(61)
1 — е
при этом, как известно, радиус скелета дужки равен -.
sinT
Из (61) имеем:
(1 —e)2cos2-l |
(z—l)e 2 -|-(1 — е) cos -у
!) В. В. Г о л у б е в, Исследования по теории разрезного крыла,
ч. I, стр. 56, Труды ЦАГИ, вып. 147, 1933 [см. настоящее издание,
стр. 115].
2) Там же, стр. 46.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 323
и при Z = ОО
Назовем через V скорость в бесконечности на плоскости (С)
и через X угол, образованный V с действительной осью
плоскости (С); тогда из равенства
dw dw dZ
dz ~dZ dz
при z = oo получим следующее соотношение между ско-
ростями в бесконечности на плоскости (Q и (z)\
Ь 2 \
откуда
VOQ = Vf 0 = Х + -|. (63)
Полагая, с другой стороны, z==e'^9 получим скорость V7
на поверхности крыла
где —скорость в точке, лежащей на поверхности цилиндра.
Подставляя
I I
I dz I

(г—1) | (z—1)0 2 +2(1 —е) cos у
—
а
(г— 1)0 2

получим окончательноJ):
= VooSin (1^- +8)LX
. (1 — е)2 cos2— — 4(1 — е) cos ~ sin sin — - -f- 4 sin2 ~
(1 — e)a cos2-^ — 2 (1 — e) cos sln sin У g + sin2 ~
* £ £ £ £ £
(64)
!) Вычисления см В. В.Голубев, Исследования по теории
разрезного крыла, ч. I, стр. 30—31, Труды ЦАГИ, вып. 147, 1933
[см. настоящее издание, стр. 77 — 78].
324 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
где ах == тг 20 4~ 28. Если сравнить полученное выражение
с выражением для скорости без добавочного вихря, то уви-
дим, что присутствие добавочного, вихря влечет за собой
появление в (64) множителя L и угла 28. Без добавочного
вихря Л = 1 и 8 = 0.
В дальнейшем мы будем пренебрегать изогнутостью
крыла, т. е. положим а = 0; тогда
6ZC = (г-1)(г+1-2е)
dz (z — е)2
Подставляя это значение и взяв — из (2) главы I,
получим:
йК I °° V 2*1 г +
+ _______!_U_______.
^2nl\z-a г_ «/1(г-1)(г+1-2е)‘
(65)
Формула (65) позволяет определить скорость в любой
точке течения на плоскости (С); полагая z = а, получим
искомую скорость на оси добавочного вихря, если предва-
J 1
рительно вычтем в первом множителе член , так как
вихрь сам себе не создает скорости. Называя эту скорость
через Vai имеем:
, х 1____L 1 I 1 <3 — в 1а „
'2^/а а_______ана—1|-1«+1—2е | * v^o)
Так как а = ре^, то
| а — е |2 = | р cos — 8 —j— Zp sin jx |2 = р2 — 2ре cos |х + е2,
| а — 1 | — | р cos рь — 1 -|- Zp sin |х | = ]Лр2 — 2р cos |х 1,
2e|=]/p2 + 2p(l —2e)cos|x + (l—2е)2,
1 J 1 I
1 —
5 7 ‘ 2~Z а 2тс/ а______________а
1 1 2
1 —
Р2
. Ге~^{ 1 J е~^
1 2ы р 2*1 1 Р-7
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 325
IV ___L 2(9-р.)Л|_TJ__J 1 _
= VcG V Р2 М 2к р 2к “
Р Р
= | lVm cos (9 — |i) — I cos (9 — ti) + Vqo sin (0 — p) +
+ -^Vrosin(0-|x) + ^l-^—L_ =
_________________________p~7
= ]/'j (1 4-1) sin (f) — р.) + з7 у — 27~rl +
I P P J
+ ^(1—1)2cos2(9 —p.). (67)
Заменяя в (66) Va через J из (60), подставляя найденные
значения, получим после возведения в квадрат
= { 1 -|cos2(()^?)+± +
Г 1 J 1 1
2^00 Р 2^^ 1
Р Р J
Г 1 J 1 у
2кУте Р 2ziy 1
Р Р _ .
(р3 — 2ер COS Р- + £3)3
(р2 — 2р cos р. 1) [р2 4~ 2 (1 — 2е) р cos р. + (1 — 2е)3]'
Если в (68) подставить значение Г из (54) главы I, то по-
лучим для J квадратное уравнение, из которого и можно
определить циркуляцию J, Можно показать, что корни урав-
нения (68) имеют разные знаки, и по характеру задачи ясно,
что надо взять решение J отрицательное.
Хотя числовое решение этого уравнения и не предста-
вляет затруднений, но общий вид решения очень сложен,
сложно и его исследование. Можно значительно упростить
вычисления, исходя из следующих соображений. Положим
J
2к^^
X.
326 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Уравнение (68) после введения неизвестного X принимает
окончательно вид
. (р2 —2р cos 1) [рз-р 2(1 — 2е) р cos + (1 — 2е)2]
(р2 — 2е р cos р. е2)2
= l-^cos2(0-|x) + A-+2sin (0 —И)(1 + ^)Х
X Г_ 2^11 _|_ ХЬ^ (--------------±)1 +
[ р 1 ‘ \ р г — cos pi 2d) J 1
.Г 2 sin 0 . Id 1 1 \12
—J--1--------— Xbt (-------------11 •
L p \ P r — cos pi 2d) J
Члены, содержащие множитель малы, так как b*—
хорда предкрылка — не превосходит 0,2 хорды основной
части, которая имеет величину при радиусе первоначаль-
ного круга, равного единице, около 4 (4 — хорда прямой
пластинки, в которую переходит при отображении окруж-
ность). Таким образом, b < 0,8. Угол атаки предкрылка
порядка 15—20°, поэтому 3 < 0,3, а потому Ь^ < 0,25
и величина в скобках порядка ~. В общем откидывание
этих членов дает ошибку порядка 5%. Откидывание чле-
нов, содержащих X в первой степени, равносильно тому,
что мы пренебрегаем действием вихря, симметричного с вих-
рем, заменяющим предкрылок или закрылок. Такое упро-
щение в аналогичном случае было сделано Н. Е. Жуков-
ским х).
Пользуясь таким упрощением, получим для J следующее
значение:
/ о i
1— ^cos2(p. — 6) + ± +
*_______г______________г
I . . / . fl I Zi I I \ I 4 sin2 6 ч z
4-4sin(|1 —6)sin 9 — Il +-з)4----2— X
г \ г ' г
X Pa — 2pe cos p.£2 . ,69)
Vp2 — 2p cos [J. + 1 Vp2 + 2 (1 — 2e) p cos p. + (1 — 2e)2
Формула (69) позволяет по конструктивным данным опре-
делить интенсивность добавочного вихря.
*) Н. Е. Жуковский, О поддерживающих планах типа Ан-
туанет, Труды Общ. физ. наук О. Л. Е., т. XV, вып. 2, 1911 [собр.
соч„ т, IV, 1949].
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 327
Рассмотрим два частных крайних случая, соответствую-
щих предкрылку и закрылку.
1. — 0 — закрылок.
В этом случае
1 —pcos2(H —°) + ^ + 4sin ([Л — 0)sin6 Д-(1 +^) +
, 4 sin2 6 Л 1 \2 Г, 2 cos 26 ! 11
4 v— 7/ L 4 р
и, подставляя в (69), получим:
г__ ДОТ Z 1 / 1 I 2 COS 26 . 1 (р в)2 /7А\
2. = п — предкрылок.
В этом случае
1 —^-cos2([i —0) + ^ + 4sin([). —0)sin9y(l +^) +
। 4 sin2 6 /1 । 1 \2 Г1 2 cos 26 Il
P P2 J ’
Р3
и для J получаем выражение
. 2 cos 0 . 1 (р е)2
Г"“Ч2 Р7р~1+2е) •
(71)
§ 2. Теория работы предкрылка
Выведенные формулы позволяют изучить влияние пред-
крылка на подъемную силу крыла. Как видно из предыду-
щего, действие предкрылка сводится к следующему:
I) Изменяются условия обтекания, благодаря чему уве-
личивается предельный угол атаки; это увеличение является-
следствием двух следующих факторов:
а) благодаря изменению распределения скоростей полу-
чается смещение критической точки разделения струй, соот-
ветствующее уменьшению угла атаки на вели-
чину 8;
б) благодаря выравниванию скоростей на верх-
ней поверхности крыла, вызываемому появлением
множителя Л.
328 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
2) Благодаря изменению величины циркуляции получается
увеличение подъемной силы крыла.
Мы исследуем теперь влияние, каждого фактора в от-
дельности. Скорость в точке крыла при наличии пред-
крылка и соответствующая скорость без предкрылка I/J?
выражаются следующими формулами:
V __ ту <?-+ + 20 + 2Ь) j v
— и оо SIH /х
(1 — е)2 cos2 — — 4(1 — е) cos sin -у sin + 4 sin2 -~
(1 — е)2 cos2 ~ — 2(1 — е) cos sin-^- sin а- + sin2-y
т/° т/ с:п ? (тс 4" 28О) v
у: = Коо sin------2-----X
(1 — е)2 cos2-^ — 4(1 — е) cos ~ sin -у sin а + 4 sin2 -у
.. -—_________........ —_____(72)
1/ (1 — е)2 cos2 ----2(1 — е) cos -^-sin-^-sin^ < - + sin2-у
Сравнивая (7 Г) и (72), мы видим, что
Таким образом, влияние предкрылка на распределение ско-
ростей сказывается в появлении угла 3 и множителя L.
В области передней кромки, где образование больших ско-
ростей и вызывает отрыв струй, А< 1, и так как 3 отри-
цательно, то при 6 = 0О дробь
sin?-(* +2е + 2о)
Sln^ (-+W <
1;
поэтому в области передней кромки Vr < V’?. Так как L
выравнивает скорости на верхней поверхности крыла, то
можно без опасности образования отрыва струй увеличить 0
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 329
таким образом, чтобы равнялось V®, вычисленному при 90,
равном предельному углу атаки крыла без предкрылка.
Подберем угол 9 таким образом, чтобы
. —04-20 Ч-2В) _ . Ф-(^ + 20о)
ъш 2 —5111 2-----»
отсюда
0 = 0О — В. (73х)
Итак, замечая, что зависит от 0 и V®—от 90, при этом
условии можем написать:
V,(0O — 8) = V?(0O).L. (74)
Так как L < 1 в области передней кромки, то там (О0 — В) <
<У?(0О). Не опасаясь образования отрыва струй, мы мо-
жем увеличить О0 таким образом, чтобы
К(0О + Д9 — 8) = У?(0О). (75)
При изменении 90 меняются и У°(0О) и L; найдем их из-
менения. Из уравнения (2) главы I при 7=0, т. е. без
предкрылка, имеем при z = еч*
~ = Vme -« (1 — е2 <9 - ?) ’) + i е ~
dz v 7 1 2ni
откуда
=ISI=12V“sin (0° ~т)+£ I ’
и, заменяя Г из (54) (при 7=0), имеем:
У?(0О) = [sin (<р — 0О) + sin 0О]. (76)
Отсюда, между прочим, можно получить максимальную ско-
рость в точке цилиндра при наличии циркуляции вокруг,
цилиндра, полагая ср — 90 = ~ ; тогда
V?(0o)raax = 2Vco(l+sin0o)>
откуда при О0 = О получим известную формулу для макси-
мальной скорости обтекания цилиндра без циркуляции; она
равна 2V^.
330 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Из формулы (76) имеем:
ДУ? = 2Уоо [— cos (ср — 0О) + cos 0О] Д0 =
= 4У,^ sin у sin — 0О). (77)
Так как по (76)
^“(9о) = 4УЛ sin-|-cos(y — 0О) (78)
и из (77) и (78) имеем
0О)Д9; (79)
У?(во) \2 °)
окончательно имеем:
У? (0О + Д0) = У? (0О) + дV? = V? (0о) [ 1 + tg — ©о) до].
(80)
С другой стороны, по (52)
= S — cos [у — (р — о)] _
г — cos (ср — |х)
_ | __г — S - cos (? — р) -|- cos [<Р — (р — о)]
Г — COS (<f> — р) ’
или, полагая Л=1—ДА, имеем:
д£_ г — S — cos (<р — р) + cos [? — (р — о)]
г — cos (<р — jx)
Так как по (43)
г — S = 8 [ г tg (|i — 9) -|-6... 1
L г 71 cos (в — |х) J
и
cos [<р — (р — О)] — cos (<р — 1*) = — 2 sin (ср— р + -0 Sin у,
ТО
Д£ = 5 Р 6) + ^П- И)] - 2 sln (? - ^ + 4) Si" Т
Г—COS (ср — JX)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 331
Можно придать этому выражению более симметричный вид.
Для этого заметим, что по (53') имеем:
. / . sin 0 . | / о \1
Г tg (и — 6) -------77---; = S1П I <x>i — ('1 — -Q-1 .
& v‘ 71 cos (6 — р.) LT1 V 2/J
Отсюда, заменяя 2 sin у через 8, получим:
sin [91 - (ц - у)] - sin [<₽ - (|Л - |
Г — COS (ср — ц)
или
. sin^zJgiCoSy + <Pi-> + 8
Д£ = — 28-------------7---\.
Г — COS (ср — |х)
Но из (53') имеем:
<Р1 + ?2 = 21х — 3 + ~
и
<?1 — 2[14-о = л — ср2.
Следовательно,
?ln!zhcos^(y-^.
или в следующем весьма симметричном виде:
Sin sin
ДА = — 25-----------—.------4—
Г — COS (ср — |Х)
(81)
(82)
Из равенств (74), (80) и (75) имеем:
^(0О —5)=^(6О)А,
Vi (So) [ 1 + tg (I—%) дб] (1 - ДО = V? (%);
отсюда, ограничиваясь первыми степенями малых величин ДО
и ДЛ, имеем:
tg(| — 9О)Д9 — ДА = 0, (83)
332 I. ТГ^УДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
и допустимый прирост угла определится формулой
' sin sin И-2
Де = - L-------- = 28----------------——-. (84)
tg(y— «о [г—cos (<р —p.)]tg(| —60J
Уравнение (75) должно выполняться в области передней
кромки. Если поместить предкрылок в точке, где скорость
максимальная, то нужно требовать выполнения (84) в точке
<р= рь. Тогда равенство (84) примет вид
sin х— sin
Д9 = 28-------—-----, (85)
('• —l)‘g(y—0О)
НО
о I . Г X / I sin 0 1
epi = ц — тг + arcsin г tg (а — 9) Ч-; =
Т1 ‘ 2 1 L r cos (0 — p,)J
о . . r—S
= у + arcsin—т—,
о . .r — S
= — у + — arcsin —•
Подставляя в (85), получим:
sin
ДО = 28
. r — S
arcsin —s—
о
2
2 sin
Afi = 8---------
Ограничиваясь членами первого порядка относительно 8,
можем написать:
1 . г — S\ /1 . r — S
-7Г- arcsin —;— cos arcsin —;—
2 о / \ 2 о
(/ — i) tg (|-e)
или
Д9 =-------. (86)
(r-l)tg(-J-e)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 333
Возвращаясь к формуле (73'), имеем для предельного угла
атаки выражение
9 = 9О—[—Д9 —В,
и полное увеличение предельного угла атаки от действия
предкрылка выражается величиной
Д10 = Д6 — В,
или, так как В отрицательно в случае предкрылка,
Д10=Д9 + |8|. (87)
Так как в рассматриваемом случае ji близко к тг, то мы
положим в предшествующих формулах р, = к. Тогда по (44х)
Г — 5 = — 8tg60(r 4- 1)
и
де = —tg2o0^b-j = IsI r7flc°s2\ . (88)
1 ь ur—1 11 cos2 00 (r —1) v 7
Чтобы получить окончательную формулу, определяющую Дх9
через угол атаки и через конструкцию крыла, надо опре-
делить 8.
Из (39')
g__ К cos 60
г — cos 20о ’
и по (7) и (5)
„ __ А _ Jd
2 Уоо 4~ И» (г — cos |х) *
так что
* __ 7- d «cos 0о
4тгУоо(г-|- 1) (г — cos 20о)*
Но по (71)
j= - — cos 29+1 7Др-+^-__,
и, наконец, подставляя все эти значения в (88), получим:
д о = Ур2 - 2р cos 26 + 1 (р + е)2 (Р2 _ 1)
1 8р8(г + 1)(г- 1)(р- 1 + 2е) cos 0О
И
г+1_±(р+±)+1 = <+г.
334 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
поэтому окончательно имеем:
д fl = Р2~2Р cos 20 + 1 (Р + е)2 /яоч
1 2р (р2—1)(р—1 -|- 2е) cos 0О * ' '
Это и есть окончательная формула, дающая вели-
чину приращения предельного угла атаки
под действием предкрылка.
Эта формула весьма мало отличается от выведенной на
стр. 119 первой части работы, формулы, которая имеет сле-
дующий вид:
дл__bfiУ р2 — 2р cos 20 1 (р 4- е)2 cos 0q
“ 2р“(р2-1)(р-1 + 2е) •
Следовательно, найденная величина больше Д9 первой
1
части в —s-z- раз.
cos2 ©о г
Переходим к определению изменения величины подъем-
ной силы. По формуле (54)
г (fl) = - sin е + J(0) - -d- .
/ — lUo p*
Поэтому циркуляция для угла 90Ai© при и = тг опреде-
ляется формулой
Г (0О + М) = - 4«Ко sin (0О + Дх9) + j(0 + Дх9) .
С другой стороны, циркуляция при отсутствии предкрылка
при предельном угле атаки 90 есть
Г (90) = — 4^00 sin в0.
Отсюда приращение циркуляции при действии предкрылка
и при предельном угле атаки определяется формулой
ДГ = Г (90-|-Дх9) — Г (90)—
= - sin^ cos (0О + + Ж -ь<9) •
Заменяя здесь 2sin4^ = Ax9 и помня, что J<0, можем на-
писать:
| ДГ I = 4кУм Д9Х cos (0О + +1 J(0 + дх9) I ; (90)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 335
подставляя сюда Дх9 из (89) и ДЭ-^-Д^) из (71), найдем
максимальнее увеличение подъемной силы, которое может
быть достигнуто при помощи предкрылка при предельном
угле атаки, по формуле Н. Е. Жуковского
(91)
Формуле (91) можно дать весьма простой вид, выразив ДХР
через Д19. Для этого из (39')> (7) и (5) выразим J через 8;
получим:
7=4^5 (r+..1.)/-£0.s.2e.).
00 d cos О
Заменяя здесь 8 через Д^ по формуле (88), получим:
| J] = 4к^ооД19 cos 90 ,
Подставляя найденное выражение в (90), получим:
| ДГ I = 4теУ00 Дх0 [cos (б0 + + cos (90 + Дх0) (Г — 1)]. (90')
Если в (90') заменить приближенно cos и cos(0o-f-Ai0)
через cos 90, то формула (91) примет следующий весьма
простой вид:
ЬгР = 4лоУ1’Д10 cos 0ог = 4каУ^ Aj0 cos 0О * <90")
Так как подъемная сила крыла без предкрылка при пре-
дельном угле атаки равна
Р = аКо | Го (0О) | = 4яоУ^ sin 0О,
то окончательно имеем следующую весьма удобную для
вычислений формулу:
^^ctgOo^^O. (90'")
Представляет значительный интерес определение вели-
чины силы, действующей на предкрылок; естественно, что
точное решение этого вопроса невозможно методом, кото-
рый здесь применяется. Некоторое приближение можно
336 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
получить, рассчитав величину силы, действующей на заме-
няющий предкрылок вихрь. По теореме Н. Е. Жуковского
эта сила выражается формулой
Pl = aVo.J=K0^ = ^.
Полагая, что ji = к, получим по (71)
Pt = mvty (1 — + -U -а7(р4Л49-\2 -•
1 1 \ р 1 р2(р —14-2Ю2 ‘
Для очень тонких крыльев, полагая 8 = 0, имеем:
Vi т/2 » q р2 2р COS 20 —1 . т г2 1 q
Рг = яоУ^З р2122р'+Г >
§ 3. Теория работы закрылка
Теория работы закрылка во многом совершенно похожа
на изложенную выше теорию работы предкрылка. Фор-
мулы (71), (72) и (73) остаются здесь без всякого изменения,
но для закрылка В положительно и L иначе влияет на условия
обтекания.
Повторяя предшествующие рассуждения, определим
в формуле (73)
m 21+и>
= .-(-m) -L
sin ---------— •
г r —(k4-26 + 2S) . ср —(z + 20o)
и таким образом, чтобы sin 1!-------- = sin 1——,
для чего надо положить
0 = 06 —8. (92)
Отсюда (73) принимает вид
Ус(90 — 8) = У?(0О)£. (93)
Так как L > 1 для закрылка в области передней кромки,
то в области передней кромки V\(0o— ^)>Vr?(90). Чтобы
не было отрыва струй, мы уменьшим 90 таким образом, чтобы
v,(0o — Д0 — 8) = V?(9O). (94).
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ IL 337
При этом получим по (80)
V ° (00—Д0) = V? (%) [ 1 — tg - 90) де] (95)
и, полагая
L = 14-ДА,
по (93) можем написать:
vz (6О—де—5) = V? (0о) [i — tg — е0) де] (1 + да) (96)
или, заменяя левую половину по (94) через V°(0O) и огра-
ничиваясь первыми степенями малых величин Д9 и ДА,
да—tg(|—ео)де = о,
откуда
‘g(|-eo
(97)
Пусть наибольшая скорость получается в точке ср = причем
близка к к. Тогда мы потребуем, чтобы уравнение (97)
выполнялось при ср— м. Заменяя ДА из (82), причем необхо-
димо переменить знак, получим:
sinlZlilsin^
ДА = 28-----—-------
Г — COS — |х)
и
— ср. ср9 — v
sin —sin —
де = 2В-------------;
[г — cos (v — р,)] tg — 0о
Делая здесь те же преобразования, что и в предыдущем
параграфе, и замечая, что в настоящем случае ДА имеет
обратный знак, и полагая р-= О и \=к, получим анало-
гично (86):
Д9 = -—---------------. (98)
(г + 1) tg (у — 0о)
338 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Возвращаясь к формуле (92), получим для уменьшения пре-
дельного угла атаки следующее выражение:
Д29 = Д9 + 3.
Так как по формуле (44) в рассматриваемом случае
S — г = S tg 9 (г — 1),
то (98) принимает вид
Д9 = 3 tg2 9 Ц4
ь Г + 1
и
Д 9 = § Г1tg2 9 ^=-1] = В (99)
2 | I Ь r J J COS3 6 {Г + 1) V 7
Заметим, что величина tg2 । оч^нь мала; поэтому
ближенно можно положить Д29 = 8.
Применим формулы (40), (7), (5), (70)
*__ АГ cos 6 „___ А ______ Jd
~ г + cos 20 ’ Д “ 4тсУоо(г — 1)*
J= /p2 + 2pcos 29 -Ь 1 ^4~1-2Г) •
Подставляя эти значения в (99), получим:
д П ftp Vp2 + 2PcqS 26+1(р-е)а
2 2р (ра — 1) (р-J-1 — 2е) cos 6 ’
при-
(ЮО)
Это и есть окончательная формула уменьшения пре-
дельного угла атаки при действии закрылка.
Сравнивая ее с соответствующей формулой увеличения
угла атаки для предкрылка (89), получим:
М
Дх0
1 /"*Р2 + ^P cos 2Q + * (Р — £ V ( Р — 1 + 2е \
V р2 — 2р cos 20 + 1 \р -j- е / \ р 4- 1 — 2е / *
Переходим теперь к учету изменения подъемной силы
при предельном угле атаки при действии закрылка.
Проводя то же рассуждение, как в предыдущем пара-
графе, получим:
г (90 — Д29) = - sin (90 — Д29) 4- J(9 — Д29) .
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 339
Циркуляция при отсутствии закрылка при предельном угле
атаки 90 определяется формулой
Го (%) = — 4*140 sin 90.
Отсюда
ДГ = Г(90 —Д29) —Г0(90) =
= 4*Ую2 sin cos (б0 — + У(90 - Д29)
• ^2® ДоО Ап 7
или, заменяя sin-~ через и замечая, что ДГ и j отри-
цательны,
| ДГ I = I J(90 — Д29) I Lhl — 4к^Д29 COS ( 90 — , (102)
и отсюда увеличение подъемной силы от закрылка равно
Д2Р = [| J(90—Д29)| Ш. — 4к^Д29 cos (9о — . (103)
Так же как и в случае предкрылка, можно дать Д2Р
весьма простое выражение. Замечая, что из (40), (7) и (5)
1><r+c?g.2e),
a cos О
и заменяя здесь 8 через Д20 из (99), получим:
J = — 4^00^20 cos 9 ——.
Подставляя в (103), получим:
д2р = [4*КоД29 COS (9о - Д29)(r +P-<C--2)k+J)
— 4^00 Д26 cos
или
Д2Р = 4тоз1Л^ Д29 ^cos (9о — Д29) (Р +- --8-
cos (90- .
340 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Отсюда получим приближенную формулу, опуская Д29
в аргументах при cos(90— Д29) и cos ^90—4^,
A2P=4noV^A29cose02^tl (103')
и, так же как в случае предкрылка,
^=ctgeop2+U29. (юз")
§ 4. Комбинация предкрылка и закрылка
Из выведенных формул легко получить соответствующие
формулы для случая, когда крыло находится одновременно
под действием предкрылка и закрылка. Так как было пока-
зано, что можно при вычислении величины циркуляции
добавочного вихря не учитывать влияние симметричного
вихря, то циркуляции предкрылка J± и закрылка J2 могут
быть определены по формуле (69), задавая ро blf
для предкрылка и соответствующие значения р2, ри2, Ь2, р2
для закрылка. Отсюда по формулам (86) найдем Дх9 и
Д29— углы увеличения предельнного угла для пред-
крылка и уменьшения его для закрылка.
Соответствующий угол увеличения предельного угла
для совместного действия предкрылка и закрылка Д39 опре-
делится по формуле
—Д29. (104)
Если для предкрылка р близко к тс и для закрылка р близко
к нулю, как это было выше принято, то для вычисления Дг9
и Д29 можно взять формулы (89) и (100), подставив в них
соответствующие значения для р, р, b и р.
В присутствии двух вихрей характеристическая функция
обтекания цилиндра удовлетворяет уравнению
—U). (105)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 341
Считая критической точкой, точкой схода струй, как и
выше, точку z—\, получим:
Ю?-0*(1 _
J-----7-М +
— аг .1 — ар
______L
Й2 j_
причем
«1 = Р1^\ = Г > «2 = ?2е^’ = е^г
г! г
Отсюда
г = — 4^ sin 9J,---------------------kJ,-----, (106)
1 1 — COS 1 V2 — COS р<2 4
где
J2-|(P2 — }а). Г2-|(р2+^).
Из (106) получим для предельного увеличения подъем-
ной силы при действии предкрылка и закрылка:
ьр = аут I ДГ I = О к, (4nVraA39 cos (б0 + +
+ I Л (9о+ Д39) I r-dC0Sir + I (0О + Д30) I Г Ssa 1 > <107>
г2 — COS г2 — COS р<2 ’
причем, как и выше, обычно можно принять = тс и рь2 = 0.
§ 5. Сводка формул, числовые примеры
В настоящем параграфе мы соберем все формулы, которые
служат для оценки величины влияния на подъемную силу
предкрылка или закрылка.
342 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Общие формулы
I
Определение интенсивности вихря, заменяющего пред-
крылок или закрылок:
4^^VL(l-^cos2(9-1x) + l + 2sin(9-tx)(l + ^)x
___91/ sin ® I_J_____&_____i___1 I
°° Р ' 2кKn г — cos р. р 2к У 1 '
Г оо II оо р -
L р J
, Г 9IZ sin 6 ( J d 1 J 1 I2 v
P +“ 2KV/oor-cos[xp 2кУда 1 p
L p p J
v_____________(p2 —2ep COS p< + E2)2_______ zfiox
A (p ‘ — 2p cos p. + 1) [p2 + 2 (1 — 2e) p cos p. + (1 — 2e)2] *
II
Определение угла смещения 8:
Jd • cos (6 — p.)
4k (r — cos p.) r + cos (20 — p.) *
III
Предкрылок. Циркуляция вокруг предкрылка (прибли-
зительно):
/ <тЛЧ1/ 1 2 cos 20 . 1 (р 4“е)2 /71\
J=Z — 1-----р-----р(р_1+2е)- <71>
Смещение критической точки:
Jd cos 6
4- 1) (г — cos 20)*
(40х) и (40")
Увеличение предельного угла атаки:
A О — 9 /Р2~2р cos 26+1(р + £Я(1-е) ‘)
1 /р(р2—1)(р—14-2e)COs0 У'
ИЛИ
= |S| r7flc^---n, (88)
1 1 1 cos2 0 (г — 1) v 7
1) Величину Z см. далее, стр. 344.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 343
предельное увеличение подъемной силы:
== aVm ( 4^ Дх9 cos(90 + | J (9 + Дх9) | ,
(91)
Д1Р , „ р2 + 1 . а
-р- = ctg 9O^-At9.
IV
Закрылок. Циркуляция вокруг закрылка:
(р-е)2
Р2 р (р -|— 1 - 2е)
г аотл ./< । 2 cos 20 , 1
J = — ^Vooy 1 Н------------
Смещение критической точки:
*__ cos 0 f4-0^
““47^(г— 1) (гcos 26) ’ V }
Уменьшение предельного угла атаки:
д fi _ о /p2 + 2pcos 20+1(р-е)2(1-г)
2 Zp (р2 — 1) (р + 1 — 2е) COS О
И
или
л й _ s + cos 20
“ ° COS2 0 (Г -j- 1) •
Предельное увеличение подъемной силы:
Д2Р = |j J(90 — Д2Э) | — 4тгУ^ Д29 cos (9,
(70)
(40")
(100)
(99)
Д26
Ь2Р , а Р2 + I л а
->- = ctg9o4J-M-
° F/J’
(ЮЗ)
V
Комбинация предкрылка и закрылка.
Циркуляция вокруг предкрылка и закрылка вычисляется
по формулам (71) (где надо положить blt plt определяе-
мые размерами и положением предкрылка) и (72) (где надо
положить Ь2, р2, р2, определяемые закрылком).
Увеличение предельного угла атаки:
д3е = Д0! — де2,
344 J. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка, и щитков
где Ax6 вычисляется по формуле (89) с подстановкой
Pi, Pi и ^2^’ вычисляется по формуле (100) с подстанов-
кой Ь2, ?2> Р2- Предельное увеличение подъемной силы:
=. «к. | д,о cos (е„ + 4 j +
+1 J‘ <’»+м> I <e«+4>’> I } - < 107>
Обозначения.
Во всех предшествующих формулах положение изобра-
жения вихря, заменяющего предкрылок или закрылок, на
плоскости (г) (круглого цилиндра) определяется точкой
а =
В отделе V (комбинация предкрылка и закрылка) вели-
чины, относящиеся к предкрылку, отмечены значком 1 и
относящиеся к закрылку — значком 2 (например, pt, [if, р2,
|х2 и т. д.).
Хорда предкрылка или закрылка Ь. Угол атаки пред-
крылка или закрылка р; хорда крыла /.
§ 6. Числовые примеры
Переходим к приложению выведенных формул к число-
вым расчетам. В случае предкрылка
А А — /Ра~ 2Р cos 2° + 1 (Р + £)2 /опх
1 2р (р2 — 1) (р — 1 4-2е) cos 60 ’ V '
но длина хорды крыла, которую можно определить по
формуле (9) стр. 76 первой части работы, имеющей в рас-
сматриваемом случае (а = 0) вид
г: = 2—2 + г+<1=^3> (108)
подставляя z=\ и z = —1, как легко подсчитать, равна
4 • (1—е); поэтому формула (89) может быть написана
в виде
АП = 9А± /Р2~2Р COS 20 -j- 1 (Р + е)^(1 — е)
1 Р Z ” р(р2— 1)(р— l + 2e)cos6
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 345
где 0=0о-|-Д16. Разлагая правую часть по степеням и
ограничиваясь первой степенью Д/), получим:
* л _ 9Э b_ (р + е)2(1-е) 1 /р* - 2р COS 20о + 1 ,
1 I Р(Р2__ 1)(р __ 1 _|_ 2е)\ cos60 Т
Но
d Ур2— 2р cos 201_____ sin 0 (р 4-I)2
rfO cos 0 cos2 0 Ур2 — 2р cos 20 4~ 1 ’
поэтому (109) можно переписать в виде
д п _ 9о Ь_ (Р + е)Ч1-0 ( Ур2 —2р cos 280 + 1 .
1 2'5 I р(р2—1)(р—1 Н-2е) \ cos0o '
-|--------sin 90(р 4-1)2 .х 10)
cos2 0о У р2 — 2р cos 20о 4- 1 / *
Полагая
л — оо ь (р Ч~ Ю2 (1 — е)
? I р(р2-1)(р-1+2е)’
Q Ч~ 1 (111)
cos 90 * ' '
' С = —— sin 0о (р 4~ I)2
cos2 0о Ур2 — 2р cos 20о 4- 1 *
перепишем (110) в виде
Д10 = ^(В + СД^),
откуда
4>e = T=3iC' <112>
Формулы (111) и (112) и могут служить для практического
расчета величины Дх0.
346 1. ТРУДЫ По ТЕОРИЙ ПРЕДКРЫЛКА, ЗАКРЫЛКА и Щитков
Пример. Предкрылок с данными:
(3=15°, 4 = О’2’ Р=1’5> е = 0>2, 00=15°,
Л = 2^,2-0,262
в_ /0,652 с__ sin 15°-6,25
“ cos 15° ’ “ cos2 15° /6/552’
откуда
ЛВ = 0,118, АС = 0,304, Д19 = 0,169, или А/) = 9°44z.
Заметим, что формула (112) заменяет формулу (3)
стр. 119 первой части.
Зная А^, легко подсчитать увеличение подъемной силы
по формуле
AiP г а Р2 + 1 л п
~7>- = ctg
В рассматриваемом примере
—H~ = ctg 15° ^.0,169 = 0,68,
г О
т. е. увеличение составляет 68°/0.
Приведенный расчет находится в хорошем согласии
с результатами наблюдений r)f
Приведенные вычисления сейчас же переносятся и на
случай закрылка. Согласно формуле (100)
Д о- - У P2 + 2pcos20 + l(p-e)2
2 2р (р3—1) (р + 1—2е) cos 6 ’
что можно еще записать в виде
Д 9 = 2° А 2р cos 29 + 1 (р — 02 (1 — О .,.
2 *J Z 2р (р3—1)(р + 1—2е) cos 0 * ' '
Так как 9 = 0о— А29, то, замечая, что
d /р^Ч-2Р cos 20 + 1 sinO(p —I)3
d§ cos 0 cos3 0 }^p3 -j- 2p cos 20 -|- 1
9 См., например, В. В. Голубев, Исследования по теории
разрезного крыла, ч. I, стр. 8, рис. 5 и 6, Труды ЦАГИ, вып. 147,
1933 [см. настоящее издание, стр. 38 — 39].
ИССЛЕДОВАНИЯ ПО ТЕОРИИ РАЗРЕЗНОГО КРЫЛА. ЧАСТЬ II 347
и ограничиваясь первыми степенями Д20, получим:
А А - 94 А (Р~£)3(1-£) / /Р2+ 2Р cos 290+Т
2 I? (p2-l)(p+ l-2e)I cos 90
----------sln °o(P^1)2 A 0 I (114)
cos3 90 /p24-2p cos290+ 1 J
Полагая
A _ 94 ± (p-£)2(l-£)
‘ z P (P2 - 1) (P + 1 - 2e) ’
о __ V P2 4~ 2p cos 26O (115)
cos 60 ’ v 7
c=z_________sin 90(p —I)2 ,
cos2 0O Vp2 + 2p cos 290 + 1 <
перепишем (114) в виде
Д26 = А (В — СД26),
откуда
М = (И6)
Формулы (115) и (116) позволяют произвести расчет
в случае закрылка.
Пример. Закрылок:
,9=15°, 1 = 0,3, р = 2, г = 0,2, 9О=15°,
Л = 2 0,262 • 0,3
о __ У8Л64
25 “ cos 15° ’
__ sin 15°
cos2 15° УХ464
Отсюда
АВ = 0,0734, АС = 0,0025
и
Д26 = 0,0735,
т, е.
д?6 = 4°13\
348 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Заметим, что здесь влияние поправки от Д20 ничтожно и
можно найти Д20 по формуле
Д20 = АВ,
т. е.
>;~-у, ; (117)
2 1 Z р (р3—1)(р + 1—2е) cos 6о v 7
Зная Д29, легко найдем увеличение подъемной силы по
формуле
ДР , 0 Р3 + 1 л Д
-p- = ctg 90-^—Д29.
В рассматриваемом примере имеем:
ДР
-^ = 3,73 • 1,25 • 0,0735,
откуда
~ = 0,34,
т. е. увеличение подъемной силы составляет 34%.
В окончательном итоге мы видим, что предкрылок
весьма мало увеличивает циркуляцию, но зато резко уве-
личивает предельный угол атаки, а вместе с тем и подъем-
ную силу, а закрылок незначительно уменьшает предельный
угол атаки, но зато резко увеличивает циркуляцию, что
в свою очередь значительно увеличивает подъемную силу.
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
НА ОБТЕКАНИЕ ЦИЛИНДРА1)
§ 1. В различных приложениях гидромеханики к техни-
ческим вопросам приходится рассматривать задачу об обте-
кании цилиндра в присутствии системы вихрей, неподвижно
связанных с цилиндром. Такая задача, например, имеет
место при изучении в первом приближении влияния пред-
крылка или закрылка на работу крыла, если заменить
приближенно предкрылок или закрылок одним его присое-
!) Опубликовано в Уч. зап. МГУ, вып. 7, Механика, 1937г
(Прим. ред.).
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ 349
диненным вихрем х); аналогичный случай представляет также
изучение щитков и т. д. * 2).
В настоящей работе рассматривается общая теория
обтекания цилиндра в присутствии системы неподвижных
вихрей; этот вопрос гидромеханики приводит к ряду весьма
симметричных соотношений, представляющих интерес и
с точки зрения общей гидромеханики, и с точки зрения
довольно разнообразных приложений.
§ 2. Пусть имеем цилиндр радиуса 1, обтекаемый
плоскопараллельным потоком, направленным в бесконечности
под углом 9 к действительной оси комплексной плоскости
и имеющим в бесконечности скорость, равную V<x>. Если
в точках ак = рке^г (р7г > 1) имеем вихри и, кроме того,
вокруг цилиндра имеем циркуляцию, вызванную присоеди-
ненным вихрем интенсивности Г с осью z — 0, то характе-
ристическая функция течения удовлетворяет уравнению
* = V-«(i-3 + ±l+yA|J----------------------U1,
dz \ гз / ' 2л/ z ^4 I г — ак г — ак'
(О
где
ак=±е^.
?к
Деля обе части на можем еще написать:
1 dw еЗОЛ Г' 1 Л Z ( 1 1 ]
\Г dz \ z* J z 7<l2kZ ( z — ак z — ak]
(2)
где
г = J'k = ^. (3)
к оо г оо
*) См., например., В. В. Голубев, Исследования по теории
разрезного крыла, ч. I, Труды ЦАГИ, вып. 147, 1933 [см. настоящее
издание, стр. 31 — 137].
2) Г. Ф. Лаптев, К теории щитков крыла самолета, Труды
ВВА РККА им. Жуковского, 1936,
350 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
Точки нулевой скорости (критические точки течения)
получим из уравнения
. / е™ \ Г' 1 v 4 ( 1 1 )
r« 1----------1_|--------НУ о-М------------------=- =0.
\ г2 / 2л/ z 2л/ j z — ак г — а]е j
ft=1 (4)
Назовем уравнение (4) основным уравнением и докажем
ряд свойств, которыми обладают его корни.
Теорема I. Если основное уравнение имеет ко-
ci 1 яг
рень ге‘ , то оно имеет также корень — е .
Пусть z± = ге*г есть корень уравнения (4), так что
e^\ Г' 1
— +77-
ZJ / м zr
еI 1
V А а* = о.
£ 2kZ - («ft + ak) zt + akak
(5)
Если в уравнении (5) заменить i на •—Z, то преобра-
зованное уравнение будет, очевидно, иметь корень zY — ге~*\
а коэффициенты
«ft = Pk^k' и ak = у- №
Р/С
перейдут соответственно в
/ f 1 —^*7*^
«ft=pfte k и = •
Следовательно, из (5) получим:
\ / 2тс/21 *?-(«ft + «ft) *l + «ft«ft
(6)
Пусть
1
z< = — ,
1 ^2
тогда
О ВЛИЯНИЙ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
351
кроме того,
?к
и
ак
4-=р^1 = «*•
ак
Уравнение (6) можно, очевидно, переписать в виде
_1____1_
> pOi (1 z2P - 20i 1 — Z — V1 —_____________йк ak___________— 0
e V > 2ъг2 Li ы JL J__j____1 u
Z2 'ak ak Z2 akak
или, иначе,
*29i\ Г' ~ V 4 4-^)4 _n
\ SJ 2nl Й Z^ak + ak^22 + akak
откуда, деля на z\ и меняя знак, получим:
е-«ч 1
%2
*2 .
Iv 1
2kZ z2
n t
I Jk__________ak~~ak_______
2kZ zl-(ak + ak)z2 + akak
т. e. получаем, что г2 = — е^ удовлетворяет тому же урав-
нению, которому удовлетворяет zv что и нужно было до-
казать.
Заметим, что теорема может быть получена также без
всяких вычислений, если отобразить внешнюю часть ци-
линдра на верхнюю полуплоскость; в преобразованном
течении, в силу его симметрии относительно действительной
оси, критические точки, очевидно, будут лежать симмет-
рично относительно действительной оси, откуда и полу-
чается сейчас же теорема.
352 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Приведем правую часть уравнения (2) к общему зна-
менателю и, разлагая на множители числитель, приведем
уравнение (2) к виду
п
(z - г0) (г - г') Д (г - гк) (г - гк)
— у e- Gi_________________1_______________ (7)
~~ Vc°6 п . У)
II { гЗ — (ак + ак) г + акак}
1
т г
где г0, £0, zk, zk— критические точки.
Если все вихри J/f = 0, то получим только две крити-
ческие точки z$ и z0» причем в случае, если эти критиче-
ские точки лежат на поверхности цилиндра, то, как изве-
стно, хорда, соединяющая эти критические точки, парал-
лельна скорости потока в бесконечности, в силу чего, если
__ tq g' — е (-т4-тс+29) i
Рассмотрим теперь общий случай любого числа вихрей
и предположим, что все критические точки лежат на по-
верхности цилиндра; тогда положим zk= № и zk = е^1 и
назовем ак — и $к—(&;> 1) или а0 — т и
30—(—+ 20) угловыми уклонениями критических
точек; те же самые углы назовем угловыми смещениями и в
более общем случае, когда критические точки как угодно
расположены на плоскости. Уравнение (4) можно еще
написать в таком виде:
{п
z2 ТТ [z2 — (ак + аА) z + акак\ —
1
п
— егКЦ I2'2 — (ак + «*) z + а^ак\ +
1
п
+ e^z itiТТ [г2 — (ак -\-ak)z + акак] +
1
п
, е9г (ак — ак) Д г2 [г2 — (ак + ak)z + акак]
Jk ______________1______________-_____________
2nl г2 — (ак + ак) г + а^к
= 0
(8)
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
353
или
п _
*2П+2 + AiZ2n+1 + А^п + ... + Л2я+1г-^ЦаА=0. (8')
1
Отсюда следует, что
п
п п тег 4-291 + 2 2а,.г
О 1
или
п п
ao + Po+S (а&4“Рл) — тс-|-29-|- 2 2|лЛ. (9)
Л=1 Л=1
Уравнение (9) иначе можно написать в виде
п
(ао — 9)4- [ро — (тс 4- 9)] + 2 [(ад. — |iA) 4~ ($к—1хлс)]=О• (9Z)
к-1
•р 'Уравнение (9') дает следующую теорему.
^Теорема II. Сумма всех угловых смещений крити-
ческих точек равна нулю,
В частности, если имеем один присоединенный вихрь
цилиндра Г и Jk = 0, то получим уравнение
%—б4-?о—(^4-9) = 0,
откуда
Ро =.— ао 4“ 20 4~ я
геометрически выражает тот факт, что хорда, соединяющая
г
критические точки z0 и z0, параллельна скорости потока
в бесконечности, так что уравнение (9х) есть обобщение
этого известного свойства критических точек.
Пользуясь соотношением (9), легко вывести зависимость
между коэффициентами уравнения (8'). Уравнение (8х)
можно написать в виде
22П+2 4. А1г2П+1 4- А222П 4- . . . 4_ A2nZ2 + A2n+iZ +
_|_ ^(тс+2б+Е 2^) *_q
354-1. ТРУДЫ ПО ТЕОРИИ-ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
V X г
Умножая обе части на е 4 2 7 , имеем еще:
£2П+2 е-(т+ 0+S ''•л) 1 bi22»+i 4- в2г*п + .. . + B2nz2 +
+ В2п+1^ + ^т+в+Е^' = 0. (10)
Заменим в (10) 2 = 4-; тогда уравнение (10) примет вид
z
е( 2-+e+s1>+2 + в2и+1>+14-в2 -Z2n +... 4-B~zz4-
+ в^+Г^+9+Е11*)*==о.
Заменяя здесь I на —/и обозначая через z' комплексное
число, сопряженное с z, имеем:
,г.Я + 1 + + + . . .
... Ч-а,.г'!+В1.г' + Д“+‘ + 5'!‘>) ‘ = 0. (11)
Но если z = pe*\ to z = ~e~'В 9'1 и z' — ~e** и по тео-
r P P
реме (I) zr является корнем того же уравнения, как и z9
а потому коэффициенты уравнения (11) соответственно
равны коэффициентам уравнения (10), т. е. Bl = B2n^i
В2 — В2п и т. д., т. е. вообще
В к — В2п+2_к9
но
следовательно,
Аке~^+ 9+2 ' = А2п+2_к Д+9 +2 .
Отсюда имеем теорему.
Теорема III. Между коэффициентами основного
уравнения имеют место соотношения
Лп+2 к = Аке(*+*^к>\
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
355
что еще можно написать в виде
^2П+2-Л ^к * ^2п+2* (12)
Так как в уравнении (10) имеем всего 2п-|-2 коэффициен-
тов, то уравнения (12) показывают, что если корни
этого уравнения удовлетворяют условиям теорем I и II, то
остаются произвольными коэффициенты 2^ и ^2»
А3, Ап+1, причем коэффициент Ап+1 удовлетворяет
условию
Д __ Д /*+29+2 ^к) i
^п+1 •— ,
откуда следует, что
А е-(т+8+Е^)^ A e(f+o+s'‘ft)i
^п+1^ »
т. е.
(13)
где С — действительное; таким образом, остаются
5Иь А» ^2» •••, Ап
Л„+1 = Сге(9+2^^и.
Следовательно, имеем произвольные коэффициенты
2^, А, А> •••» Ап или всего 2п4-2 действительных
коэффициентов.
§ 3. Выведенные в предшествующем параграфе соотно-
шения позволяют написать в весьма симметричном виде
выражение для скорости потока на поверхности цилиндра.
Пусть точка z лежит на поверхности цилиндра; тогда
z = е*\ Предположим, что все критические точки нахо-
дятся также на поверхности цилиндра; тогда zk = еакг и
zk = е$к\ Подставляя эти значения в (7) и замечая, что
ф + а/, / <p-<x,
Z — \е 2 1 _е- 2 1) =
^*к .
= 21е 2 sin У - 9 gfe,
356 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
и подобным же образом
z — zk = 2ie~*~ гsin ?,
г2 — (ак -[- ак) z -f- акак = e2f 1 — 2S/celJ’fcVt’ -]- е2^ —
= 4 4 е-Ь-*к> * _ 2SJ =
= _ 2е^+^4 [Sft — cos (<р — >
где 25л = рА-1 , получим из (7) следующее уравнение:
Рл
1 sin sin X
п slnlz_^sln!LzL*
УП-3^со5(?_^) •• <14)
1
Абсолютная величина правой части дает величину ско-
рости течения в точке z = e'?i, лежащей на цилиндре.
Аналогичную формулу получим и в случае, когда
точка zk не лежит на окружности. Если zk — гкеаь\ то най-
дется вторая критическая точка zk = — можно напи-
г к
сать zk и zk соответственно в виде zk — е^к~г Ыгк*г и
zk = е^к+г1пг^ Следовательно, для этого случая получим
скорость на поверхности цилиндра, заменив в формуле (14)
ак и Р/с соответственно через ак — ilnrk и ак-\- i In гк. Так
как в этом случае
Sin Т 2 -- - Sin т 2
примет вид
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ 357
то, предполагая, что все критические точки, кроме г0 И2О,
лежат вне цилиндра, получим вместо (14) выражение
g = * sin sin ЦЬ X
хП-s^mv-J <15>
1
Уравнению (15) можно дать еще иной вид. Пусть
тогда
— т(р* + ^) = 1 + 2е*»
— cos (ср — [aJ= 1—cos (<р — |Aft)4-2e| =
= 2 (sin2 т
Подставляя найденные выражения в (15), получим:
g = V„e'(’+J) > sin tpsin tz&x
n sin2^=-^ + sh2!^
ХД SMs^»,.s
1 sin —2-----* k
(16)
Знаменателю формулы (16) можно дать иной вид. Дей-
ствительно,
4а& = Рд; — 2-|-= (у?к———=
Рл V V РаУ
/ In рЛ In РлЛ2
= U 2 — е г ) = 4sh2^
и
?* = sh2
4
358 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Следовательно, (16) принимает окончательно следующий вид:
dW ли -(ф + -7г) * • ф — а0 • ?-
— =^4^ v 27 sin^-^sin^-y^X
п sina5L=^ + sh3^
X ТТ---------------г— (17)
V- sin2L=^ + sh3'MA
Эту формулу полезно сравнить с формулой, дающей
скорость обтекания вокруг цилиндра при отсутствии внеш-
них вихрей, т. е. когда Jk = 0. Для этого случая получим:
^ = 4lz„e-(»T)si„t^sinb=J. (18)
Сравнивая (18) и (17), видим, что присутствие вихрей Jk
вносит следующие изменения в выражение скорости:
1) изменяются углы, определяющие положение критиче-
ских точек на поверхности цилиндра; вместо углов аир,
удовлетворяющих условию а-|- р = гс-|- 29, которое полу-
чается из (9), когда все Jk = 0, имеем условие
а0 + Ро — 4“ 294- 2 2 (Р'А:-аД
получающееся из (9), когда Jk =# 0 и критические точки
лежат не на цилиндре;
2) входит множитель
£=ТТ-----------------Д •
J-1J-sin2'Pip + sh2!^
Рассмотрим величину отдельных множителей, входящих
в L. Для этого найдем, при каких значениях эти множи-
тели равны единице.
Из уравнения
sin? 4- Sh2 = Sitl2 + sh2
имеем
sin (<р -fr+14 sin = Sh 1-1?-^±-lnpfc. sh lnpfc~lnr* ,
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
359
sin(<р — = sh In Угк?к
откуда
sh In дГ—
г Гк
sin^p’
и получаем два значения угла
shlnl/ —
V Гк
sinpp.
с?! = ак + arcsin sh In Уrk?k
m ак + Р-А:
<?2 =----------2—
тг — arcsin
sh In /rk?k
sh In 1/"—
____г Гк
sin
(19)
Так как при у = afc
. п Ф ак । i-О in к «о ак P'fc । 1 ч in Г]?
sin2 т н— + sh2 sin2 --- + sh2
_________2_________2 ____ 4'2
1 ~ smat^ + sha!^ “ sin3 + sh2 ’
то имеем:
At>l, если inrA;>lnpA., т. е. гк > рЛ,
Ах<1, если In г* < In р*, т. е. гЛ<рЛ>
и по предыдущему при гк > pfe выражение остается
больше единицы во всех точках той дуги окружности ра-
диуса единицы с конечными точками, имеющими централь-
ные углы cpt и ср2» на которой лежит точка, определяемая
углом *к ; при гк < рЛ на той же дуге во всех точках
к< 1.
Из формул (19) видим, что угол, внутри которого вы-
полняется неравенство, равен
____________________________sh In у —
л 4~ 2 arcsin sh in Уpkrk---------------
sin ~к
360 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
и, следовательно, всегда превосходит к. Может случиться,
что углы (рх и ср2 — комплексные. Это будет, если
__________sh In —
shlnV%p*———g >1.
sin
В этом случае соответствующее неравенство выполняется
вдоль всей окружности. Это последнее обстоятельство
будет, в частности, иметь место, если ак = рк.
§ 4. Полученные выше выводы приложим к решению
следующей задачи. Пусть даны критические точки потока,
обтекающего круглый цилиндр; требуется по ним опреде-
лить вих-ри Г, Jk и их положение.
Для решения этой задачи воспользуемся уравнением
22П+2 + л<г2»+1 + + . . . + A2nZ2 + A2n+lz +Л2п+2=0,
определяющим положение критических точек.
Коэффициенты этого уравнения выражаются через вели-
чины Г, Jk, p£ и pki причем, как было доказано выше, из
этих коэффициентов независимых всего 2п-|-2 действитель-
ных коэффициента, которые, очевидно, все могут быть
найдены, если даны корни основного уравнения.
Выразив А19 Д2, . . ., А2п+2 через неизвестные величины
Л» Г, рЛ, получим для определения Зм —|— 1 неизвестных
Л» Рл» Нл и Г систему 2п-\-2 уравнений. Для того чтобы
система давала определенные решения, необходимо, чтобы
3n+ 1 < 2п 4- 2,
откуда Таким образом, поставленная задача допу-
скает определенное решение только в случае, если п = 0,
когда есть только присоединенный вихрь Г, и в случае, когда
п=1, т. е. имеем около цилиндра один добавочный вихрь
Остановимся подробнее на этих двух случаях.
В случае п = 0 уравнение (4) дает:
e29i = O,
т. е.
Л^Де94, Д2 = е("+29)4.
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ 361
Уравнения (12) и (13) сведутся к одному уравнению:
A1 = Cie9i.
Отсюда
Г' = 2тг1е~9’ Д1 = — 2те-н (zt -|- z2),
где zt и z2— аффиксы критических точек потока. Так как
„20г 1
ZXZ2 = —-е29*, Z2 =-----
где
z± — reai,
то
Г' = — 2тс/ Гге<“-9) < — — .
L r J
Дальше надо различать два случая, когда г = 1 и
г > 1:
1) г — 1, Г' = 4к sin (а — 6);
2) г>1, Г' = —2«/[cos(a —+
-4-1 sin (а— 0) (г -Ь 7 )] •
Так как Г' — действительное, то
cos (а—0) = 0, a = 0z±z~
и
Г' = 2тс (г + у) sin (а — 0).
Это — хорошо известные результаты.
Более интересен случай п = 1. В этом случае уравне-
ние (8) принимает вид при 0 = 0:
г2 [г2 — (а + a)z + аа\ — lz2 — (а + a) z + аа] 4~
+ £ 21 22—(а+2+аа 1 + 2:2 (а ~ 0 •
362 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Берем отсюда коэффициенты Alt Д2, Д4:
Д4 = — аа = — е2^ = е<<*+Ы \ (20)
А = 4 + *4 = — (p + y)(cosp. + /sin р.) — У- (21)
(Аг и Аг—действительные),
л,=- £(р+7)'’‘-1~^4М <22>
Из уравнения (20) получаем значение
In Ал 21 71 2 * (23)
Из уравнений (21) имеем:
(p+-y)cosp. = — 4,
ИЛИ
р2+ъ^?+1 = 0 (24)
LUo р*
и
(p + l)sinp + ^=-4,
откуда
= 2к (4i tgji — Ai). (25)
Наконец, из уравнения (22) имеем:
= g(p + l)-4£(p-l)
ИЛИ
251П1х_|1(р + 1)_^(р_1) = Л2г^+11)1 = С, (26)
где С, как следует из общей теории,—действительное.
Уравнения (23), (24), (25), (26) позволяют определить р,
Г', р, и Z.
Интересный случай имеем при =
В этом случае уравнение (24) имеет решение для р
только в случае р = оо или в случае Д1 = 0. При р = оо
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ 363
Приходим к предшествующему случаю, когда добавочных
вихрей нет; при Дх = О задача определения вихрей ста-
новится неопределенной.
Предшествующие соображения приводят к следующему
практическому выводу, представляющему интерес. Пусть
имеем обтекаемое потоком тело,
сечение которого указано на С О
рис. 1. Если внешнюю относитель- /“
но многоугольника ABCD часть
плоскости отобразить на внеш- д
нюю часть окружности, то точки
Д, В, С, D перейдут на окружно- Рис. 1.
сти в некоторые точки Д, В, С, D.
Из теории крыла известно, что обтекание такого тела
потоком возможно только в случае, если точки Д, В, С, D
для преобразованного потока явятся критическими точками.
Следовательно, возможно обтекание, указанное на рис. 2, при
котором около тела создается вихрь J. Выведенные формулы
позволяют рассчитать его положение и интенсивность.
§ 5. Развитая выше теория прилагается с большим
успехом к изучению влияния предкрылка на обтекание крыла,
как это показано в другой работех). Мы приложим здесь
указанный метод к изучению влияния земли на работу крыла.
Эта задача может быть решена точно применением теории
эллиптических функций как частный случай биплана, однако
получающаяся при этом формула подъемной силы настолько
9 В. В. Голубев, Исследования по теории разрезного крыла,
ч. П, Труды ЦАГИ, вып. 306, 1937 [см. настоящее издание,
стр. 291—348].
364 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Л
ниже
допу-
в
в
вблизи
3).
А'
Рис. 3.
перемещается вместе с крылом,
приближения, получаемая при
сложна, что совершенно не позволяет провести исследо-
вание в общем виде, так что приходится применять те или
иные приближения. Полученные выше результаты позволяют
дать довольно простое приближен-
ное решение поставленной задачи.
В основе приведенного
решения лежит следующее
щение.
Пусть мы имеем крыло А
поверхности земли ВВ' (рис.
Как известно, можно заменить
влияние земли на крыло действием
крыла Л', расположенного симмет-
рично с А относительно поверх-
ности земли. Заменим крыло одним
вихрем той же циркуляции, какую имеет Л', тогда в получен-
ном потоке линия ВВ' уже не будет линией тока, таким обра-
зом, сделанное упрощение влечет за собой то, что под
крылом имеется уклонение линии ВВ' от прямой и при пере-
мещении крыла это уклонение
Отсюда следует, что степень
таком допущении, может
быть оценена величиной
уклонения от прямой полу-
ченных линий тока, заме-
няющих прямую ВВ'.
Решение задачи начнем
со случая, когда имеем
круглый цилиндр и вне его
вихрь с той же циркуля-
цией, которую имеет ци-
линдр. Предположим, что
цилиндр имеет радиус осно-
вания, равный 1, и применим
к рассматриваемому случаю выведенную выше формулу-(1),
положив Г = 0; а = — ip; п = 1; 0 = 0 (рис. 4). Для производ-
ной характеристической функции течения получим выражение
(27)
\ р/
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
365
Пусть критической точкой (точкой схода струй) является
точка z = e~^\ тогда для определения / имеем уравнение

J [ 1
2к/ [ е~Ы-\-1р
1
е-9« + -
Р
откуда
(р + “ ) — 2 sin 6
Jz= 4^^ sin 0 ------j------,
р“7
или, полагая
р-4- —=25, р —- = 2/,
Р r Р
г л х т • л 5 — sin 6
J— 4^00 sin 9-------.
(28)
(28')
Подставляя (28) в (27), имеем:
хт (1 1 \ п-tz • п 5 — sin 6 / 1
_ =VM(1 гл^япО —_ —
1 \
ь7/
Для нахождения скорости в различных точках на’поверх-
ности цилиндра положим z = тогда
S = Ч<> _е-М) + 2гЯ„О .
2Z/
или, иначе,
/до Гот г .*( - । • д S — sin 6\1 .
— = [2Vme-V(sin?4-sin0 s + sr„-)J
Выражение в правой части можно еще привести к виду
= 2iVme-^ (sin ? + sin 0) (1 - , (29)
или окончательно
лхг + I ? + 0 • ? — (тс+ 6)
sin 0 \
S sin ср ) ’
(29')
Из уравнения (29') мы видим,
две симметрично расположенные
что на цилиндре имеются
относительно вертикали
366 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
критические точки z1=£-0i и z2 = £(тс+0) *; для нахождения
двух других критических точек имеем уравнение
— sin ср = S — sin 6
и получаем еще две критические точки на цилиндре при
|S—sin 0 | 1 и две критические точки вне цилиндра при
условии | S — sin 6 | > 1.
Перейдем к вычислению подъемной силы.
Применяя первую формулу Чаплыгина — Блазиуса,
получим для определения компонентов подъемной силы X
и Y уравнение
Y-{-iX—
J
2nl
2
dz.
Контур L охватывает цилиндр и, следовательно, охва-
тывает особые точки характеристической функции z = 0 и
Так как интеграл по кругу достаточно большого’ радиуса
равен нулю, то, называя окружность малого радиуса с цен-
тром в /р через С, имеем:
f {...}dz = — f {...}dz.
L С
Пусть
тогда
с
т. е.
Подставляя значение J из (28), получим следующие значения
для X и Y:
Х=0,
Y = 4r:pV^ sin О S ^sin 9 (1 4
1 sin 6 (S — sin 6)
p2 J2
(30)
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ
367
Так как для случая отсутствия вихря J при той же цир-
куляции вокруг цилиндра выражение подъемной силы есть
Yq = 47трУ^ sin 9
оно получается из (30) при р = оо), то влияние земли на
подъемную силу сказывается в появлении множителя
. __ S — sin 6 (. . 1 sin 0 (S — sin 0)|
* — d 11 "I" 72 52 I
или
, __ p2 — 2 sin Op + 1 j . r 1 2p sin 0 p2 — 2p sin 0 + 11
I “t"F'“(p-i)2 (FW Г ( }
В следующей таблице даны значения k для различных Вир.
sin 0 — 0,1 Р 1,1 1,2 1,3 1.4 1,5 2 3
k — 7,2 — 7,5 — 1,8 1 2,07 1,60 1,20

sin 0 = 0,1 Р 4 5 6 7 8 9 10
k 1,08 1,04 1,02 1,00 0,996 0,995 0,996
sin 0 = 0,2 Р 1,5 2 3 4 5 10
k 0,91 1,23 1,04 0,98 0,96 .. 0,97
sin 0 — 0,3 P 2 3 4
k 0,93 0,98 0,99
Ниже приведены графики.
368 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
линия, изображающая поверхность земли,
имеем:
Перейдем к исследованию вопроса о том, насколько
искривлена
Из (27)
т r / । 1 । 7 . z —I- Zp
w = M2'+T+s3-'n—T
l г + 7.
Отсюда
уравнение линий тока есть
мним, часть -4- In г= const. (31')
1 z 1 2к/ , i I v 7
При z = oo по вышеприведенным формулам за поверх-
ность земли можно взять линию прямую, параллельную оси х
и проходящую на равном расстоянии между осями
точками —/р и---Получим для уравнения этой
уравнение
^ = -2
вихрей
прямой
(32)
Отсюда из (31'), полагая z~-—+Si-\-x и увеличивая х
до бесконечности, получим:
мним, часть (—Si) = const,
т. e. const = — S.
О ВЛИЯНИИ СИСТЕМЫ НЕПОДВИЖНЫХ ВИХРЕЙ 369
Итак, уравнение линии, изображающей поверхность земли
в случае обтекания цилиндра, есть
мним, часть [z ——S. (33)
г । I I '
I ’ + ?/
Найдем, где эта линия пересекает ось у. Полагая z =— iy
и беря у между -|-р и » как это следует из физических
соображений, получим:
(• I I J 1 \ О /П А \
— 1У Ч--г 2~7i~ I = — о • (34)
У ’ 7“'’/
Но
1П//^\=1п /
- — iy I У — — ]
\ Р / \ Р /
и так как
^->0,
а потому
— чисто мнимый.
Следовательно, из (34) имеем:
откуда
причем перед корнем взят знак плюс, так как
lim = 1,
S->oo д
370 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
как это следует из физических соображений. Отсюда сле-
дует, что под цилиндром получается понижение линии тока
от горизонтальной прямой; называя это понижение через В,
имеем из предыдущего
s=4+/(4p7_s=/(4j47-4
ИЛИ
8 =------1
о Ь
В процентах отношение получается:
2 3 4 5
21 9,8 6 5.
От разобранного случая влияния вихря на цилиндр перей-
дем к случаю влияния вихря на пластинку. Для этого
сделаем отображение плоскости (г) на плоскость (и) при
помощи функции
« = (35)
При таком отображении окружность |z|—-1 перейдет
в отрезок прямой, действительной оси, и при 0 =£ 0 точкой
схода струй будет служить не конец отрезка; но так как
угол атаки 0 мал, то приближенно можно считать течение
близким к течению со сходом струй на задней кромке.
Из (35) имеем:
На нижней мнимой полуоси радикал, как легко видеть,
надо брать со знаком минус, и в бесконечности z = u.
Поэтому вдали от и = 0 уравнение линии, изображающей
землю, то же, что и на плоскости (z), т. е.
и — — Si -|- х.
Точке пересечения мнимой оси плоскости (г) с этой
линией, т. е. точке
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 371
соответствует на плоскости (zz) точка
zZq — — Si*
или
Таким образом, под серединой пластинки нет ни пони-
жения, ни повышения этой средней линии. Однако не следует
думать, что линия, изображающая землю, перейдет в прямую;
получится некоторая кривая, симметричная относительно
мнимой оси и имеющая незначительное углубление под сере-
диной пластинки и два незначительных симметрично распо-
ложенных относительно мнимой оси подъема.
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ
К КРЫЛУ1)
§ 1. Общие замечания
Задачей настоящей работы является изучение влияния
щитков, плотно прилегающих к основной части крыла. Эта
задача была разобрана в работе С. М. Тарга2), причем пред-
полагалось, что имеется плавное об-
текание основной части крыла и
щитка, точкой схода струй является J
кромка щитка; основная часть кры- [
ла и щиток рассматриваются в виде
плоских пластинок. Таким образом,
течение имеет вид, указанный на
рис. 1, где АВ — основная часть Рис. 1.
крыла и DC — щиток. Результаты
исследований С. М. Тарга дали вполне удовлетворительное
качественное согласие с результатами эксперимента. Тем не
1) Опубликовано в Трудах ЦАГИ, вып. 398, 1939. (Прим, ред.)
2) С. М. Т а р г, К теории крыла со щитовидным закрылком,
Труды III Всесоюзн. конф, по аэродинамике, ч. II, 1935.
372 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
менее, является желательным заменить гидродинамическую
схему, которая лежит в основе исследования С. М. Тарга,
другой схемой, более близкой к экспериментальным данным.
Опыты, проводившиеся с обтеканием подобных профилей
в водяном канале, показали, что внутри угла BCD, обра-
зованного задней частью крыла и щитком, возникают интен-
сивные вихреобразования. В настоящей работе и рассматри-
вается обтекание крыла со
щитком в условиях, когда
//внутри угла BCD образу-
( г- \ ется стационарный вихрь,
J / так чт0 течение имеет вид,
С указанный на рис. 2, и изу-
чается влияние этих вихрей
на условия обтекания.
^х В настоящей работе дан
Рис. 2. новый выход формул, по-
зволяющих решить задачу
об обтекании контуров, разобранных в работах С. А. Чап-
лыгина и Н. С. Аржаникова и в работе С. М. Тарга, и
даны некоторые результаты, выясняющие влияние вихрей,
образующихся в пазухах, между крылом и закрылком, на
условия обтекания.
Настоящая работа, так же как и исследование С. М. Тарга,
ведется в условиях плоскопараллельного потока; основой
дальнейшего исследования являются метод, представляющий
некоторое видоизменение метода С. М. Тарга, и результаты,
полученные ранее об обтекании цилиндра в присутствии
вихрей х).
§ 2. Отображение углового профиля
В работе С. А. Чаплыгина и Н. С. Аржаникова* 2) разо-
брано обтекание контура вида, указанного на рис. 3. Мы
дадим здесь новый вывод формул, позволяющих найти
подъемную силу и условия обтекания.
1) В. В. Голубев, Обтекание круглого цилиндра в присут-
ствии системы вихрей, Уч. зап. МГУ, т. 7, 1937.
2) С. А. Чаплыгин, Н. С. Аржаников, К теории открылка
и закрылка, Собр. соч. С. А. Чаплыгина, т. II, стр. 472, 1948.
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 373
Применяя обычный метод, найдем, прежде всего, отобра-
жение внешней части плоскости крыла на внешнюю часть
окружности радиуса 1. Предполагая, что профиль крыла
находится на плоскости (£) и сечение вспомогательной
окружности находится на плоскости (z), можем написать
отображающую функцию в виде
г = г [ (г—1)(г ——
* * 1J г2
(1)
где точки bv ct, dt лежат на окружности |z| = l.
Интеграл ищем в форме
/(^) = (г-^)«(г-^)2-« .
Отсюда
Г а . 2—ос 11
J z [z-b{rz-dx zj
или, после упрощений,
/Ъ)~= х
X {г2 — |a</1 + {2 — a)Z'1 — — djz —
Так как один из корней трехчлена
z2 — [ad1-]-(2 — a)bl — b1 — d1]z — b1d1 = z2ArAzArB
есть 1, то
1 — [adt —J— (2 — ос) bt — dr\ — b^d^ =. О
или
1 + ДН-В = 0. (3)
374 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
Для нахождения второго корня с± имеем уравнение
^2 + Д^ + В = 0. (4)
Из уравнений (4) и (3) получим:
(^—1)(^+1+Д) = 0,
следовательно, второй корень равен
с1 = г = -(1+Л)
или, пользуясь равенством (3),
c1=B = '—b1dl. (5)
Итак, интеграл (2) может быть написан в виде
f (£) =
и
— Ь^.
Теперь найдем длины ab = ad = lr и be — de = 12-
Пусть Ь± = е^, d± = еч\ тогда cr = ^(тс+3+8) I. Точкам Ь±
и dr на плоскости (z) соответствует точка О. Поэтому для
определения Zt и /2 надо найти
1/(1) I и |Ж)|.
Но, полагая z — получим из формул
ср— 8
z — ьх = е^г — № = е 2 sin 2-•,
Ср + З .
z — d^-e.^—еч — е 2 % 2isiny~-,
[® ® 1 • Г 3 8 (2 —а) 1 . .
, _ ]’22/2sin«(^)x
X sin2-“^=^), (6)
откуда
|/(1) | = 4|sin" sin2-a,
|/(ci) I — | ) sin2-" | = 4 cosa-^-cos2-® .
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 375
Далее, из геометрических соображений яс
на окружности должна лежать между bt и
на рис. 4.
Следовательно, полагая, что + +
-{-5>2тс, имеем:
Р < -к Д- 8 — 2 тс < 8.
Заметим, что из уравнения (3) имеем:
1 + ’
откуда при b± = 1 имеем также и dx = 1
имеем dr = — 1.
Далее, из уравнения (2) имеем при = 1
/(г) г+1_2
и, полагая с1 = —1, получим отображающую функцию в
виде
с = —2,
т. е. имеем плоскую пластинку, помещенную так, как ука-
зано на рис. 5. Точно так же при br = dr=—1 получим:
C = * + | + 2,
ю, что точка сг
dv как указано
т. е. снова получим плоскую
ную, как указано на рис. 6.
пластинку, но расположен-
Рис. 5.
Рис. 6.
Так как при отображении, даваемом функцией (2), точка
г —о помещается в вершине угла (точка b или d рис. 3),
то отсюда следует, что при Ь± (а следовательно, и dj,
близком к +1, точки b и d расположены близко к а,
376 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
т. е. ~ мало; в случае же, если Ьг (а следовательно, и dt)
Z2
близко к —1, точки b и d близки к с, т. е.-^ велико.
Отсюда следует, что, изменяя р от 0 до тс или, что то же,
изменяя Ьх от 1 до —1, мы можем дать отношению длин
сторон отображаемого угла ~ любое, значение.
Z2
Мы не будем в настоящей работе исследовать до конца
случай обтекания угла и перейдем к случаю обтекания
крыла с закрылком, в котором мы применим тот же метод,
какой мы применили в настоящем параграфе.
§ 3. Отображение профиля со щитком
Рассмотрим полное, без отрывов, обтекание контура
abcdla (рис. 7), причем точка а является точкой схода струй.
Отобразим внешнюю часть
контура abcdla на внешнюю
часть единичного круга вспо-
могательной плоскости (z).
Применяя формулу Шварца —
Кристоффеля и замечая, что
точкам a, с, d соответствуют
углы 2тс, и принимая угол
при точке b равным атс и, сле-
I равным (1—а) тс, получим
довательно, угол при точке
формулу Шварца — Кристоффеля в виде
С= Сх J —61)я~Ч-г —С1)(-г —<?1)(г —/1)~и dz,
где точки 1, bv cv ..., 1± суть точки единичной окружности,
соответствующие точкам a, b, контура на плоскости (С).
Мы будем искать выражение интеграла в виде
/(г) = . (2)
Беря от выражения (2) логарифмическую производную,
получим:
(z—blY(z — l^(z — n) Г а 1—а . 1___П
J --------------z \г—Ьх'г — 1х' z—n zJ
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 377
или, после некоторых преобразований,
\ (г—^i)a“x (z — Z1)~a z ч
/ (г) =2——— ? (г),
где
<p(z) = z3 — [a (Zr-4- n)-j-(1 — а)(^4-л) —п]г24-[а/1п +
+ (1 —— lxti— b^jz-^b^n. (3)
Для того чтобы f(z) представляло интеграл выраже-
ния (1), нужно, чтобы многочлен
г3 — [a(/i-|-n) + (l — «)(^i + »)—n]z2 +
+ [aZxn —|— (1 — а) b-ji — ltn — b^] z 4- b^n (4)
имел корни 1, cv dv
Так как многочлен (4) имеет корень 1, то
1 —1« Gi + «) + (1 — «) (Pi + «) — «1 + (к — ^i) — кп] +
+ ^« = 0. (5)
Если уравнение для нахождения корней
z3 — [a Gi + ^) + (1 — а) (Ь1 -j- п) — п] z2 +
+ [а1гп — abrn — lrn] z -|- Ь^п = 0 (6)
написать короче в виде
z* + Az2 + Bz + С = 0, (6')
то условие (5) примет вид
14-Д4-В + С = 0. (7)
Из (6') и (7) имеем
(z — 1)[^2 + (14-Д)^+ 14-4 + В] = 0,
и, применяя условие (7), получим для нахождения корней сг
и d± уравнение
г2 — [a (Zt — bj + b± — 1 ] z — b^n == 0. (8)
Точки q, dr лежат на окружности; покажем, что корни
уравнения (8) удовлетворяют этому условию.
Найдем прежде всего величину п из уравнения (5)
378 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Так как Ьг и лежат на окружности |я|= 1, то поло-
жим:
= (10)
Подставляя в (9), получим:
а +
е + 3 . £ .
ае * 2 * 4 2Z sin —"2^ + £ 2 2Z sin ~
или
4i е — В В
ае sin —х-5 * * * * * 11- -j- sin
п = —у.— ---------— • (И)
ае 2 sin + sin -|-
Так как числитель и знаменатель дроби, входящей в вы-
ражение (И), — числа комплексные сопряженные, то от-
сюда следует, что |п|=1.*
Подставляя найденное выражение п в уравнение (8),
получим:
z2— 2ie2 г ^ос£2 z sin -1~sin yj z— ^Х
ае 2 sin £ + sin
X—т-----------------— = 0. (12)
ае 2 sin £- + sin
Для того чтобы по возможности упростить решение этого
уравнения, введем новое неизвестное /, положив
11
z — e2 t\ (13)
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 379
тогда получим для t уравнение
/2 2 г sin -“2^4“ sin — j —2/ (a2sin2^-g-^-|-
1П . £ ---- В . В Е , . В | ,
2a sin —~~ sin у cos -g- -f- sin2 j t —
. £ — В . .
ae2 sin—g^--|~sin
= 0.
Пусть
2 * 9 е 3
a2 sin2----
Io . E --- В s. В . . „ В A
2---H 2a sin —cos j sin -j—|- sin2 -j- = Д.
Тогда
z = _2A±VWE?L_. (14)
e —В , В
ае 2 sin —g~c -f- sin
Отсюда, замечая, что
л ( 4^-е*—₽1 • Н/ —I* • £ — 3’ I . в \
А = I ае 2 sin а--- sin I I ае 2 sin —sin ~ I ==
и умножая числитель и знаменатель в формуле (14) на
p~\-ql, получим:
. Д/± 1<Д(1 — Д) . . .. /1С-Ч
Мы будем далее считать, что
Тогда из (15) имеем:
|/|2 =
А < 1.
Д(1 — д) +дз
ДЗ
а потому корни уравнения (15) tr и /2 и соответствующие
корни уравнения (2) zx и z2 лежат нц окружности | z | == 1.
Так как
Tib^l^ =
TQ
380 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
и, следовательно, полагая = = полу-
чим:
v = л -|~ Y + § — s. (16)
Таким образом, по данным а, е легко найдем tlt t2 и п
и выражение (2).
Так как по (1)
l = Cf(z),
то, замечая, что при z = bv z — llt z = n, £ = 0, получим,
что на плоскости (С) точка Ь± (или Zt) переходит в начало
координат, а потому
^1 = |с1/(1)ь )
= 1 (17)
i3 = l<W2)| J
и, следовательно,
__ _I f (^i) I ____ _I f (z2) I zio\
-ц-Im I ’ I mr (18)
Так как для решения задачи важно только выполнить
уравнения (18), то в конце концов при заданных и р.2
мы имеем два уравнения (18), из которых мы должны найти
величины е и р и по ним, далее, tlt /2, п и функцию (2).
Для выражений можно найти очень симметричный вид.
Для этого найдем выражение
f ,_ (е^ - е“У-* (е - е*)
Но
— е^ = е 2 г 2i sin 2— и Те д-
Отсюда
| f(e^) | = | 12а | sina?~^ | 21-® | sin1 ~а | 2 | sin 1»
рли
|/(е^) | = 4 | sin«^=-& sin1-» sin |СХ|.
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 381
Следовательно,
I 7(1)1 “
2
sin-------2
sln2
. 2
sin----2-
£
siny
т + — 4
sin--------------
sin 2
(19)
и аналогичное
рез 8.
Пример.
выражение
получим для |12» заменив
у че-
1
а— 3 ,
60°, е = 300°.
1)
-—-=120°, •J=150°> 4 = 30’.
2
2) pqi = 1 (cos 150°-j-г sin 150°)sin 120° + sin 30°.
О
, . 3 + z/3"
4l== 12 •
3) Д = |р + ^|2 = 1.
з/п + /з . /зз-з
г2— 12 1 12
откуда
Т = arg — 46°, arg zx — 7 6°,
8 = arg t2 = 193°, arg z2 = 223°.
5) >= 180°+ 46°+ 193°—300°= 119°.
Отсюда
. , . . , . 4
± L
/(1) =Д(0) = 4 sin3 30°sin330°sin 59° = 4 • 0,428,
382 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
1 2
/(<z1) = 4sin3 8° sin3 112°sin 21° = 4 • 0,177,
1 2
f(z2) = 4sin3 81°sin3 39°sin59°= 4 • 0,533.
Подобным же образом произведены вычисления при ряде
Рис. 8.
других предположений. Результаты этих вычислений даны
в следующей таблице.
№ ₽ 8 7 0 arg arg г2 ^/(1)
1 30° 300° 72° 238° 190° 87° 253° 0,4014 0,5913 0,2768
2 30 330 62 223 135 77 238 0,2562 0,3085 0,6263
3 60 240 71 195 206 111 225 0,703 0,533 0,0465
4 60 300 46 193 119 76 223 0,428 0,177 0,533
5 60 330 53 195 98 83 225 0,2433 0,075 0,980
Относительные размеры отдельных частей указаны на рис, 8,
к ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛАГАЮЩИХ К КРЫЛУ 383
§ 4. Об условиях, определяющих положение вихря
Мы переходим теперь к построению формул, дающих
добавочное вихревое течение.
В случае обтекания круглого цилиндра в присутствии
одного неподвижного вихря для определения положения кри-
тических точек на поверхности цилиндра имеет место сле-
дующее уравнение:
Ге81
2к/ Vc
2nlVr
(a -j- a) z3 + аа — е2^
(а — a) z2-\- e2f}i (а + а) -|-
Геи —
------аа
2л/ Уоо
— е2Каа = О1).
z —
Называя корни этого уравнения через zlt z2, z3, zv
имеем для них следующие уравнения:
— 1>8*
Zi+^+zs+z4 = e+a----------щ-; (а)
-- г • --
ZkZl — аа — 4. __ (а 4. «) + {а - а), (Ь)
и,-называя zk = e*k\ имеем:
а1 4“ а2 4“ а3 4“ а4 = %® 4“ 71 2|Х. (d)
Разбивая на действительную и мнимую части и считая,
что все zk лежат на окружности | z | = 1, имеем из (а) и (Ь)
JJcos(afc — 0) = (p + y)cos(p. — 0), (а')
JJsin(a4—6) = (p + y)sin(p. —0)4-2^-, (а")
2cos(afc4-az — [i — 0) = 0, (b')
sin (a*4- аг — p — 9) =
= 2sl„(,x-4 + 44P + l) + 24-(P-l). (f)
!) В. В. Голубев, О влиянии системы неподвижных вихрей
на обтекание цилиндра, Уч. зап. МГУ, т. 7, стр. 12, 1937 [см. насто-
ящее издание, стр. 352].
384 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щиткой
Но уравнение (bz) есть следствие уравнения (d).
Действительно,
S со s (afc + аг — р. — 0) = со s (ах + а2 — [1 — 0) Н-
—|— COS (0С-£ —0С3-р — 0) —|— cos (otj —j— ot4-p — 0) 4*
+ cos (a2 + a3 — p — 0) 4 cos (a2 4 a4 — p — 0) +
+ cos(a3 + a4 —p —0). (1)
Но по уравнению (d)
cos (a3 4* a4 — H — 0) = cos (20 + 2p 4- — «i — a2—p — 0) =
= cos (it 4" 0 + p — «i — a2) = — cos (at 4 a2 — H — 0)»
а потому в сумме первый и последний члены взаимно со-
кращаются; точно так же взаимно сокращаются члены 2-й
и 5-й, 3-й и 4-й.
Таким образом, остаются следующие не зависимые друг
от друга уравнения:
cos (a* — 0) = (р + jjcos(p. — 0). (а')
У sin(aj — 0) = (p + l)sin(p — 0) +4“’ (а")
sin (aft + а, — р,—0) =
= 2«Ь(и-Ч+5^-(р + ±) + г^-(Р-1). (Ь")
ai 4* а2Ч“ аз 4“ а4 “ 20 4” тс 4* 2р. (d)
Из этих четырех уравнений (а") и (bzz) могут служить
для определения величин Г и J. Следовательно, для опре-
деления величин р и р могут служить уравнения (az) и (d); но
в этих уравнениях еще неизвестно а4 — критическая точка
набегания струй.
Действительно, в силу результатов § 1 имеем, что точ-
кам a, с, d профиля соответствуют углы 0, т + у, В 4 у
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 385
(рис. 9), а потому, если, например, потребовать, чтобы
вихрь имел расположение, указанное на рис. 10, то трем
критическим точкам будут соответствовать углы 0, 0,
'[ + '5' и четвертая точка имеет неопределенное положение.
§ 5. Физические выводы. Примеры
Предшествующие выводы относятся к случаю, когда
около крыла имеются связанные с ним вихри; известно, что
такие вихри, расположенные вблизи крыла, вызывают сме-
щение критических точек. В частности, благодаря присут-
ствию таких вихрей может случиться, что одной из крити-
ческих точек крыла окажется острый выходящий угол, что
уничтожит бесконечную физически невозможную скорость
обтекания в соответствующей вершине. Изучением таких
случаев мы и займемся в настоящем параграфе.
Можно показать, что вихрь, направленный в ту же сто-
рону, куда направлена циркуляция около основного крыла,
смещает критическую точку против направления циркуля-
ции, если он помещен около задней кромки, и смещает кри-
тическую точку по направлению циркуляции, если он рас-
положен около передней кромки; изменение направления
вращения вихря, естественно, вызывает изменение направле-
ния смещения критических точек1).
Приложим эти соображения к случаю обтекания контура
со щитком вида, рассматриваемого в настоящем параграфе.
г) В. В. Голубев, Исследования по теории разрезного
крыла, ч. II, стр. 20, Труды ЦАГИ, вып. 306, 1937 [см. настоящее
издание, стр. 319].
386 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
В случае обтекания контуров вида, указанного на рис. И,
в пазухе, заключенной между крылом и щитком, как пока-
зывает эксперимент, образуется вихрь. С другой стороны,
около передней кромки образуются физически невозмож-
ные бесконечные скорости, если она не является
критической точкой течения. Естественно, воз-
никает вопрос, не могут ли вихри,
образующиеся за задней кромкой,
сместить критическую точку к
передней острой кромке. Пре-
дыдущие соображения позволяют
очень просто ответить на этот
вопрос. Рассмотрим случай тече-
ния типа, разобранного в ра-
боте С. М. Тарга, но с вихрем,'
образовавшимся около задней кромки; в этом случае
течение имеет вид, указанный на рис. И, причем полу-
чается добавочный вихрь около задней кромки, напра-
вленный в ту же сторону, куда направлен циркуляционный
поток около крыла. Из предшествующих рассуждений сле-
дует, что в точку С критическая точка может быть сме-
щена таким добавочным вихрем только в том случае, если
без вихря критическая точка (точка, в которой разделяются
струи) помещается на верхней стороне линии ВС; если же
критическая точка находится на нижней стороне линии ВС,
то вихрь может только отодвинуть ее от точки С вправо.
Следующие примеры, в которых проделан весь расчет, под-
тверждают эти выводы.
Рассмотрим крыло, профиль которого дан на рис. 8
под № 5.
Пример 1. Пусть а = у, р = 60°, е = 330°.
Тогда arg zr = 83°, arg z2 = 225°, м = 98°.
- Полагая
«,_ (г — by (z — е)1-* (z — п)
получим при малом ср(г = ^)
2 2 2 ' sin** "sin1-* sin
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 387
Рис. 12.
где /?— действительное положительное число. Следовательно»
на плоскости (Q отрезок ab образует с действительной по-
ложительной осью угол
к+ уН--------2-----^2'
В настоящем случае имеем
угол
. 8а . е(1—а) .
^+у + —^"2—-~^~2 или
1Qno , 60°. 1 , 330°.2 ,
180 + ----2ТТ" +
4-49° = 349°.
Следовательно, имеем расположение, указанное на рис. 12.
Найдем в качестве примера такое течение, когда крити-
ческими точками будут:
ах = а2 = 0, а3 = 83°, а4 = 330° и 0 = 55°.
В этом случае по (d)
413°= 180°+ 110°+ 2р., р.= 62°
и по (а')
1 j 1 \_____2 cos 55° + cos 28° + cos 85° _
У \Р I- ~р) ~ 2 cos 7° —
_ 1,1472 4-0,88294-0,0872 _ 2,1173 _ . nfifi
—' 2 0,9925 — 1,9850 — 1 ,U00’
откуда р = 1,42. Ось вихря определяется данными на пло-
скости (z) р=1,42, р = 62°. Течение имеет вид, указанный
на рис. 13.
Пример 2. Рассмотрим то же крыло, но возьмем
угол 0 = 0.
Тогда из уравнения (d) р. = 64° и по уравнению (а')
имеем:
.1 2 + cos 83° — cos 45° Q QO
P —I— Z? 4 0 “ V , 4 4 j
1 1 p cos 64
откуда p = 2,87.
388 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Данными [1 и р вполне определяется положение доба-
вочного вихря. В этом случае имеем течение, указанное
на рис. 14.
Рис. 13.
Рис. 14.
Рассмотрим теперь случай, когда направление вращения
добавочного вихря — обратное по отношению к направле-
нию циркуляции вокруг крыла. В этом случае общий
характер течения указан на рис. 15.
Рис. 15.
Так как добавочный вихрь направлен против направле-
ния циркуляции вокруг крыла и находится около задней
кромки, то из предыдущего следует, что смещение крити-
ческой точки будет в ту же сторону, куда направлена
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 389
циркуляция вокруг крыла, а потому, если критическая точка
потока при отсутствии вихря помещается на нижней сто-
роне пластинки ВС, то от действия добавочного вихря она
может сместиться к передней кромке. Рассмотрим следующий
частный случай: пусть имеем профиль № 2 (стр. 382). На
рис. 16 указаны углы, соот-
ветствующие на плоскости (z)
отдельным точкам профиля.
Так как при рассматриваемом
обтекании точкой схода струй
должна быть точка С, то мы
сделаем на плоскости (z) по-
ворот осей так, чтобы точка С
лежала на действительной оси.
(161°) ,5в 1
П_____________О—_________С(0°)
(253°)E^3^
\д(283°)
Рис. 16. Рис. 17.
После такого преобразования точкам профиля соответст-
вуют углы, как показано на рис. 17.
Отображающая функция имеет вид
С = /(2) =
или после замены z — e^zf, где величина / в градусной
мере равна 77, получим:
£ = е[*х+(1-°0 x+x-xl»---------------------------£------>__________£______I
z'
Полагая zf = e^, получим:

е*ге 22 24 |sin
2
X £sin ——j sin ,
390 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА и щитков
или
c=el4^^-l*4[slnrf=2>]-X
Отсюда следует, что пластинка DC наклонена под углом
— 2 “Г" 2 ‘2 • К
плоскости (С) образует
к действительной оси на плоскости (С); так как в настоящем
случае а = ~, р = 30° и е = 330°, то & = 362°30'. Следо-
вательно, профиль расположен, как указано на рис. 18.
При больших (У) имеем
£ = eV'rf + ...» а потому угол,
образуемый направлением по-
тока в бесконечности с дей-
ствительной осью на пло-
скости (С), больше, чем на
плоскости (У), на 77°.
Рассмотрим поток на пло-
скости (У) под углом 6 = 5°;
соответствующий поток на
82° с действительной осью
или 79°30' с плоскостью CD.
Выясним, возможно ли обтекание с критическими точками
в С, D и с вихрем в углу АВС с критическими точками
в А и С.
В рассматриваемом случае ‘имеем:
а1 0, а2 = 161°, а3 = 283°, а4 = 360°.
Из уравнения (Ь") найдем = 307°. Подставляя в урав-
нение (а'), получим:
I 1 cos 5° + cos 156° + cos 278° + cos 355° Q •
p ' P — cos 302° 2,6•
Отсюда p — 1,72.
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 391
Следовательно, положение добавочного вихря опреде
ляется данными и = 307°, р= 1,72. Итак, возможно обте
кание профиля со щитком, изо-
браженное на рис. 19.
Разобранные примеры по-
казывают, что образование
вихрей в пазухах углов, обра-
зуемых щитками, весьма резко
изменяет условия обтекания.
При этом небольшие щитки,
расположенные на нижней по-
верхности крыла, вызывают
образование вихрей, смещаю-
щих критическую точку к передней кромке и благодаря
этому улучшающих условия обтекания и работу крыла; на-
оборот, большие щитки вызывают образование вихрей, уда*
ляющих критическую точку от передней кромки, что должно
ухудшить условия обтекания.
§ 6. Влияние вихрей на подъемную силу
Перейдем теперь к учету влияния образующихся между
крылом и щитком добавочных, «паразитических» вихрей
на подъемную силу крыла. Так как добавочный, паразити-
ческий вихрь не принадлежит к несущей системе крыла,
то в рассматриваемом случае нельзя применить теорему
Жуковского; мы приложим для определения величины силы
теорему Чаплыгина — Блазиуса.
Пусть J—интенсивность паразитического вихря, который
помещается в точке, переходящей при отображении внешней
части крыла на внешнюю часть круглого цилиндра в точку
a = r^(r> 1). Тогда характеристическая функция соот-
ветствующего течения вокруг цилиндра радиуса 1 удовле-
творяет уравнению
^ = ^-<(1-4)+-Ll+-L(-!---------------L), (1)
dz . \ z2 / 2л7 z 2~Z \z — a z — aJ
где
а = — е^.
г
392 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, закрылка и щитков
Предполагая, что изображением задней кромки является
точка z=l, получим соотношение
Vrae-ei(i_^)+JL+^L(—!-------------г1-) = о. (2)
2ni 2rcZ \1 — а 1 — а/ а
откуда
Г = — 2шУсо (е~м — е9*) — J--,
(1_а) (!_«)’
или, иначе,
Г = — к sln 9---------' " . (3)
2cos|x-^^ + -j
По формуле Чаплыгина — Блазиуса имеем, называя через X
и Y компоненты силы давления потока на крыло,
Zj
где крыло считается расположенным на комплексной пло-
скости (С). Переходя к переменному z, получим:
' <4>
L dz
причем контур L оставляет вихрь / вне его. Если ^ — y(z)t
то окончательно имеем:
= —JL f . (4')
1 2 J \ dz ) x (z) v ’
L
Так как по формуле (1)
Zrfm>\3 = у2 e-29i Л _ Л2 , 27^-ИГЛ \ 1' .
\ dz) те \ za / 2л/ \ г* / z ’
гз 1
(2тс/)2 гз
+ 2К^^-(1
2к/ \
/ 1
г2 / \ z — а
. 2Г/ 1 / 1_________1 \ , J2 / 1____________1 \2
(2kZ)2 z — a z — а/ (2^)2\г — a z — а)
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ 393
и члены
I/2 -26i(i 1 1
006 ' (z) 2vlz3 '/J (г)
и
Г2 1 1
(2тс/)а г» г'(г)
не имеют вычетов, то остается вычислить интегралы от
остальных слагаемых. При этом необходимо помнить, что
точка а лежит внутри контура L и точка а — вне его.
Вычисления всех этих интегралов дают следующие ре-
зультаты:
Г 2V>-0*T 1 dz
> =
-2^-ХГ^). (5)
так как контур L можно заме-
нить окружностью бесконечно
большого радиуса:
2тс/ z__a
L
Рис. 20.
вычислим следующим образом. Очевидно, что
Г 1 dz _______ fl dz . Г 1 dz
J z —a i' (*) ~ J г —a x'(^) ' J z — a / (*)
C L Lt
(рис. 20).
Если С удалить в бесконечность, то
[ —------= 2Ш
J z — a х'(г) X (°°)
С
и
f —------^ГТ = 2кг’^ТТ’
J z — a х (г) X («)
а потому
1i 7^ 7%) = /У <6>
L
394 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
3) В интеграле
f 2Vcoe-'>i — (l
J 2nl \
L
e2^ \ dz
z2 / (г—a)x'G0
контур интеграции можно заменить окружностью сколь
угодно большого радиуса, а потому
—)---------------- 2 Vme -0i
/ (z — a)x'(2) Х'(со)
217^-0* 1-
J 2rcZ \
L
л\ 1 л Г 2Г^ 1 dz
4) Интеграл -----с -т,- v вычисляется
’ v J (2л/)2 г (г —а) '//(?)
гично интегралу (2), и мы получим:
[ 2ГУ dz___________________2ГУ 1
J <2л/)2 г (г — а) /' (г) 2п1 arf (а) ’
L
5) Интеграл
(7)
анало-
(8)
f 1 I____________dz ___о /дч
J (2л/)2 z г—~а х' (г)
L
что легко получается из того замечания, что L может быть
заменен окружностью сколь угодно большого радиуса.
6) Наконец,
Г J2 / 1___________1 \2 ate _ J2 ( Г dz________________
J (2tcZ)2 \ z — a z — а/ у' (z) (2rcZ)2 ( J (z — а)2 yf (z)
L L
— 2 f 1 _ I f I —
J(2 — a)(2 — a) / (2) J (г — a) (г) J
= —12774+2—)• (10)
2л/ 11'2 a — a l' (a) )
так как в первом и во втором интеграле можно применить
тот же прием, как и в интеграле (2), и
I (2 — а)2//(г) J (z-a)2V//(a) x («) J
L
К ТЕОРИИ ЩИТКОВ, ПЛОТНО ПРИЛЕГАЮЩИХ К КРЫЛУ . 395
а в третьем интеграле контур интеграции можно заменить
окружностью сколь угодно большого радиуса.
Подставляя все найденные значения в формулу (4'),
окончательно получим:
г_|_ ZX =—4 ( 2VO0e-^ -4—л + 2Vme(-77—4—гЦ—
' 2 1“ //(оо)г \Х'(оо) Х'(а)/
1 1
— 2j — 2 V^e-^J -rr-v-
a^'(a) “ x'(°°)
2IV 1 . J2 Гх" (а) i 2
xzzW _______=____
2rcZ 1 2rcZ L Xz2 (л) a—a7f(a)J j 7
Формула (И) и позволяет рассчитать величину подъем-
ной силы при наличии вихрей между щитком и крылом.
Эту формулу можно упростить следующим образом.
Можно считать малым влияние вихрей друг на друга,
а потому можно опустить в первом приближении члены,
содержащие произведение вихрей, т. е. члены с Г/ и J2.
Тогда получим более простую приближенную формулу:
г 1 ___e-eij__!____Wi_____L ] —
e-w fn ry,(co)r1 t zm\
Подставляя сюда значение Г из формулы (3), получим
окончательно:
л—0Z
r+zx=-Pv^
J
— 4711/00 sin 9 + --------
2 cos
(13)
откуда при J—0 получается обычная формула для подъем-
ной силы крыла при отсутствии вихрей.
В этой формуле значения найдем из формулы (1) § 2.
Так как
dz —
396 I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА, ЗАКРЫЛКА И ЩИТКОВ
ТО
= Х,(°°) = С1
и
Xz (оо)
X' (л)
/?2
---------------—------------------------— . (14)
(а— 1)(а — *х)“ 1(a—cJ)(a — d1)(a — l1) а
Формулы (13) и (14) позволяют рассчитать подъемную
силу при наличии вихря у щитка.
ТРУДЫ ПО ТЕОРИИ
МАШУЩЕГО КРЫЛА

К ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ *)
Одной из причин отсутствия сколько-нибудь разработан-
ной теории тяги у машущих крыльев является следующее: если
требовать, чтобы при сходе с крыла при его взмахах вих-
рей и при сносе их потоком острая задняя кромка крыла
была точкой схода (основная гипотеза Чаплыгина — Жуков-
ского), то необходимо допустить, что циркуляция уно-
симого потоком вихря изменяется при удалении от крыла,
а это противоречит основным теоремам теории вихрей. Это
обстоятельство впервые встретилось в исследованиях Н. Е. Жу-
ковского по разрезанию вихрей, но, по-видимому, прошло
незамеченным. Возникающие при этом чисто теоретические
трудности авторы работ по теории крыла, колеблющегося
в потоке воздуха, пытались обходить, предполагая, что
за крылом при его колебании образуется волнообразный вих-
ревой слой. Такое предположение в достаточной мере согла-
суется с экспериментальными данными в случае колебаний
£ малыми амплитудами при вибрациях крыла. К вопросам
вибрации крыла главным образом и применялись получаю-
щиеся при этом результаты. Однако при резких взмахах
крыла с большой амплитудой, по-видимому, нет никаких
экспериментальных данных, указывающих на образование
ва крылом непрерывного вихревого слоя, тянущегося за кры-
лом в виде волнообразной вихревой поверхности. Наоборот,
за колеблющимся крылом можно наблюдать вихреобразова-
ния типа вихревых дорожек Кармана, образованные отдельно
т) Опубликовано в юбилейном сборнике «Двадцать лет ВВА
РККА им. Жуковского», 1942. (Прим, ред.)
400 И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
движущимися вихрями. Все указанные затруднения остаются,
например, в случае образования при резком изменении угла
атаки так называемого 1 начального вихря Прандтля; в этом
случае имеющиеся экспериментальные данные не дают также
никаких оснований к каким-либо заключениям о существова-
нии непрерывного распределения вихрей за крылом.
Настоящая статья ставит своей целью показать, что
указанное выше противоречие может быть устранено, если
учесть влияние пограничного слоя крыла. Основой дальней-
ших соображений является систематическое приложение тео-
рии пограничного слоя к объяснению процессов, происходя-
щих при колебаниях крыла в его пограничном слое. Про-
цессы образования вихрей могут быть объяснены вязкостью
воздуха, которая, как известно, с точки зрения теории погра-
ничного слоя, проявляется только в пределах пограничного
слоя. С этой точки зрения и основная гипотеза о том, что
острая задняя кромка является точкой схода струй, так назы-
ваемая гипотеза Чаплыгина—Жуковского, является только
своеобразным и удачным учетом вязкости воздуха. Часто
кинематическое выражение этой гипотезы как предположе-
ния о физической невозможности существования течений
с бесконечно большими скоростями едва ли имеет какой-
нибудь смысл в применении к идеальной жидкости; в случае
полного отсутствия сил трения в жидкости едва ли можно
ставить границы для величины скорости течения.
С точки зрения теории, развиваемой в настоящей работе,
изменения в структуре пограничного слоя и являются тем
регулятором, который позволяет, не нарушая основных тео-
рем теории вихрей в идеальной жидкости, объяснить выпол-
нение гипотезы Жуковского при отходе от крыла вихрей
с постоянной, не изменяющейся при движении циркуляцией.
Во всем дальнейшем мы рассматриваем пограничный слой
крыла как своеобразный регулятор в течении вокруг крыла.
По-видимому, с этой точки зрения, достаточно только прибли-
женной, грубо схематической теории пограничного слоя.
Оставаясь на точке зрения обычных представлений теории
пограничного слоя Прандтля, изобразим себе профиль крыла £
и охватывающий его профиль £р представляющий наружную
границу пограничного слоя (рис. 1). За пределами контура Lt
мы имеем потенциальное течение, причем ввиду малой толщины
К ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
401
пограничного слоя мы можем считать распределение скоро-
стей, а следовательно, и давлений на контуре Lv не отличаю-
щимся от распределения скоростей и давлений на контуре L.
Поэтому для циркуляции
где w есть комплексный
потенциал потока, обтекаю- рис
щего профиль.
С другой стороны, по свойствам пограничного слоя на L
скорость течения равна нулю, а потому
f dz = 0. (2')
J dz 4 7
L
Из этих уравнений следует, что
Г dw , Г dw , С dw ,
Г = — б/г — \ —dz= \ —dz, (3')
J dz J dz J dz 47
Д L L.-L
причем за границу —L мы принимаем весь контур, огра-
ничивающий внутренность пограничного слоя (рис. 2). Следо-
Рис. 2.
вательно, с кинематической
точки зрения, мы можем за-
менить вязкий пограничный
слой завихренным слоем
идеальной жидкости, причем
общая завихренность его
равна циркуляции вокруг
крыла. Такую схему погра-
ничного лоя и положим в
основу дальнейших построений. Вихри, образующие погранич-
ный слой, по своим свойствам подобны тем вихрям, которые
принимаются в теории так называемого жидкого крыла:
они являются связанными с областью пограничного слоя.
Следовательно, всякое изменение в величине циркуляции
вокруг крыла вызывает соответствующее изменение в цирку-
ляции пограничного слоя.
402
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
С точки зрения теории вихрей, система вихрей, располо-
женная около твердой границы, должна сопровождаться систе-
мой вихрей, представляющих изображение данной системы
вихрей относительно твердой стенки; эти вихри мы можем
рассматривать или как вихри чисто фиктивные, заменяющие
действие твердой границы, или, оставаясь на точке зрения
теории жидкого крыла, как действительные вихри в той массе
воздуха, которая заменяет крыло.
Таким образом, в крыле мы имели следующие две
Рис. 3.
вихревые зоны: зону пограничного слоя I (рис. 3) и зону
расположенную внутри крыла и представляющую зеркаль-
ное отображение зоны I относительно контура крыла (зона II
на рис. 3).
При изменении величины циркуляции вокруг крыла, напри-
мер при изменении угла атаки, изменяется и завихренность
внутри этих слоев. При этом возможно также, что при изме-
нении условий обтекания, например при изменении угла атаки,
часть завихренной массы воздуха, образующей пограничный
слой, отрывается и образует вихрь, отходящий от крыла;
тогда симметричный вихрь, входящий в слой //, остается
внутри крыла. При этом знак отходящей с вихрем цирку-
ляции и знак циркуляции, заменяющей влияние стенки крыла,
противоположны, а их абсолютные величины равны. Такое
положение создается, например, при образовании начального
вихря Прандтля; мы можем его рассматривать как резуль-
тат отрыва части пограничного слоях).
*) Заметим, что на снимках Прандтля очень ясно видно, как
отходящий начальный вихрь образуется за счет свертывания схо-
дящей с крыла части пограничного слоя.
К ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
403
Аналогичные обстоятельства имеют место и в других слу-
чаях, например при отходе вихрей при взмахах машущего
крыла или при неустановившемся, например, ускоренном дви-
жении крыла, которое было разобрано в работах Вагнера;
в последнем случае вихревой след, образующийся сзади равно-
ускоренного движущегося крыла, с нашей точки зрения,
представляет часть сорвавшегося с поверхности крыла погра-
ничного слоя. При таком взгляде на структуру пограничного
слоя и на происхождение циркуляции вокруг крыла естествен-
но, что вне пограничного слоя, т. е. в пределах, занятых иде-
альной жидкостью, всегда будет выполняться теорема Лагран-
жа— Томсона о неизменности циркуляции. Но в пределах по-
граничного слоя эти вихри могут зарождаться, так как в по-
граничном слое, с физической точки зрения, мы имеем область,
занятую вязкой жидкостью; замена ее вихревым слоем носит
только чисто кинематический характер. Примером такого не-
прерывного образования вихрей в пределах пограничного слоя
является образование вихревой дорожки Кармана сзади обте-
каемых жидкостью тел. Отдельные вихри дорожки Кармана,
с нашей точки зрения, представляют собой результат рас-
пада пограничного слоя, причем отдельные, оторвавшиеся
части слоя и образуют вихри дорожки Кармана.
Присутствие вихревой системы в пределах пограничного
слоя может сказываться при обтекании не только в образова-
нии вихрей, сходящих с крыла, т. е. таких вихрей, как
вихри Кармана или начальный вихрь Прандтля.
Распределение вихрей внутри пограничного слоя может
влиять, например, на положение точки отрыва.
Из теории крыла известно, что для суммарного опреде-
ления подъемной силы или ее момента не нужно знать точ-
ного распределения циркуляции у отдельных элементов
поверхности крыла; например, в теории крыла конечного
размаха для вывода основных формул достаточно заменить
систему присоединенных вихрей одним несущим вихрем пере-
менной вдоль размаха крыла циркуляции. Совершенно таким
же образом можно для дальнейшего исследования заменить
и пограничный слой некоторой приближенной схемой, доста-
точно грубой, но пригодной для оценки общего суммарного
эффекта, вызываемого действием пограничного слоя. С изло-
женной выше точки зрения, пограничный слой и его зеркальное
404 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО крыла
изображение представляют в первом приближении си-
стему вихрей, указанную на рис. 4, где L — контур крыла
и / есть область пограничного слоя, а //—область, занятая
зеркальным изображением пограничного слоя. Ввиду малости
Рис. 4.
толщины пограничного слоя расстояние между вихрями
системы I и II очень мало, а потому действие таких двух
систем вихрей можно с известным приближением заменить
действием системы диполей, оси которых расположены по
стенкам крыла. Таким образом,
систему вихрей, указанную
на рис. 4, мы заменим систе-
мой диполей (рис. 5). Так как
Рис. 5. действие такой системы дипо-
лей, непрерывно распределен-
ных по поверхности крыла, можно заменить источником и сто-
ком, помещенных в концах пограничного слоя, при условии,
что интенсивность всех непрерывно распределенных диполей
постоянна, то в первом приближении мы можем заменить
действие пограничного слоя и его зеркального изображения
источником и стоком, помещенных в двух точках поверхно-
сти крыла. Такая замена предполагает постоянное распре-
деление вихрей в пограничном слое и условно вводит «начало»
и «конец» пограничного слоя; поэтому такое упрощающее
предположение, естественно, является весьма грубым, но оно
не представляет никаких затруднений сделать эту схему более
гибкой, введя, с одной стороны, систему вихрей в погранич-
ном слое, ближе совпадающую по распределению даваемых
ими в пограничном слое скоростей с данными эксперимента,
и, с другой стороны, не заменяя их путем предельного пере-
хода диполями, источниками и стоками.
Общим выводом из предшествующих рассуждений
Является следующее положение: с кинематической точки
К ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
405
зрения можно заменить действие пограничного слоя поме-
щенными на поверхности крыла источником и стоком неко-
торой подходящей интенсивности.
Приложим эти соображения к изучению влияния на обте-
кание круглого цилиндра вихря, находящегося вблизи цилин-
дра. Предполагая, что мы имеем обтекание цилиндра с цир-
куляцией Г и в присутствии вихря интенсивности J, полу-
чим для характеристической функции обтекания следующее
выражение:
w = Ve-«(z + «^) + l;ln2 + ^ln_i5^, (1)
~7"
где R — радиус цилиндра, V— скорость потока вдали от
цилиндра, 6 — угол ее с действительной осью и —аффикс
вихря J.
Отсюда
Г-| 7 / 1\ (2)
\ Р I
Предположим, что точкой схода струй является точка
z = /?; тогда получим:
Ve-oi (1 — е™) + ——|- — Г —Ц-.--------1 = °- (3)
lnlR 2л/ R— ре** R_^.eV4
Р
Найдем такую линию, что, поместив J в какой-нибудь
ее точке, получим уравнение (3) при постоянных Г, J, V
и 0. Для этой линии из уравнения (3) получим уравнение
Г
1 1 _ 2ZVsin9—2^ __ 4лР7? + Г m
т?-р^ _L м ’ 1 '
р 2л/
Если применить это рассуждение к тому случаю, когда
вихрь отходит от цилиндра, причем интенсивность вихря и
циркуляция вокруг цилиндра постоянны и точка схода струй
не смещается, то, как показывают экспериментальные данные,
406
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
вихри уходят в бесконечность; полагая в уравнении (4)
р = со, получим:
1 _4*W + r
Я JR '
Тогда из (4)
--------г----Lz__________—_____L . (6)
№ (1 + eW) — R (р + у)
Из уравнения (5) и (6) имеем:
Г — J= — btVR,
2Ясозр, — (р-Ьу)
Из последнего уравнения (7) получим:
р cos = R или x = R.
Итак, при условиях задачи вихрь должен перемещаться
перпендикулярно к оси х по касательной к окружности LL
(рис. 6).
Этот результат явно противоречит как теоретическим
соображениям, так и эксперименту; и то и другое показы-
Попробуем удовлетворить
вает, что вихри в потоке
смещаются по линиям тока,
т. е. при условиях задачи
по линии, параллельной ли-
нии MMV Отсюда полу-
чаем вывод: нельзя подо-
брать линию, по которой
перемещается вихрь в сво-
бодном потоке, таким об-
разом, чтобы точка схо-
да оставалась неподвижной
при постоянной циркуля-
ции Г и интенсивности вих-
ря J.
постоянным условиям, введя
влияние пограничного слоя. Возьмем слой в том упрощенном
К ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
407
виде, как это было указано выше. Характеристическая функ-
ция имеет вид
до = Ve~iQ (z -J-
W0i‘\ . Г t , J f z — pe*4
-----I T о—i 111 % ~4“ n—i 111 -----
z } 1 2tcZ * 2kZ
P
К 1и z — Re^
--In ----xy
2k z — Re^
(8)
где К — мощность фиктивного источника и стока, заменяю-
щих пограничный слой, и Re™, Re^ — их аффиксы.
Отсюда
dw
dz
R№*\ . Г £ . J Г 1__________1
г2 ) 2nl z 2nl z—pe^ z R*
P
1
z — Re^
1
z — Re**
и для точки схода z = R получим уравнение
уе-м (i _ е2^
_i_JL+AF_l_________!___1 +
^2kZ/?^2kZ /?— ре^ х —
57 [/?—— /? —№₽i]= °' (1°)
Замечая, что по условию V, Г, J, 0 — постоянные, и
полагая, как и выше, р=оо и считая, что при р = оо
К = 0, получим:
г I
+ (11)
отсюда
Г — J= — 4WR.
Из уравнений (10) и (11) имеем:
2rcZ £2(1-1-^) —?Цр-|-^
L___________|_±
) К
eai — e^
2-^R 1 — (е^ + е^) + e(a+w ‘
408
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Отсюда
или
Окончательно имеем:
2 sin
2 cos —- — 2 cos —
2 /?2
Уравнение (12) показывает, что при любом изменении
величин р и рь, т. е. при любом перемещении вихря J, можно
подобрать /С, а и р так, чтобы уравнение (10) выполнялось,
т. е. регулированием пограничного слоя всегда можно до-
биться того, чтобы при перемещении вихря постоянной
интенсивности J и при постоянной циркуляции Г (или Г — J)
вокруг цилиндра точка схода струй на цилиндре оставалась
неподвижна.
Полученный вывод показывает, что в процессах, имею-
щих место при неустановившемся движении, роль погра-
ничного слоя не ограничивается только образованием сил
трения и условий, вызывающих отрыв струй от поверхности
крыла; по-видимому, учет влияния пограничного слоя является
единственным возможным путем построения теории машущего
крыла, не противоречащей основным положениям гидро-
механики.
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА 409
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ
МАШУЩЕГО КРЫЛА1)
Несмотря на большое число исследований по теории
неустановившегося движения крыла и, в частности, по тео-
рии машущего крыла, гидродинамическая картина явления
образования тяги у машущего крыла является весьма неясной.
Основной причиной этого надо считать, по нашему мнению,
сложность гидродинамической схемы, лежащей в основе всей
современной теории крыла, которое рассматривается нахо-
дящимся в условиях неустановившегося движения и непре-
рывно изменяющейся циркуляции скорости вокруг профиля
крыла.
Основная трудность, с которой приходится встречаться
при построении теории колеблющегося или машущего крыла,
заключается в следующем. При взмахах крыла, так же как
и при изменении скорости движения или при изменении угла
атаки, меняется циркуляция крыла. Выполнение одного из
основных положений теории вихрей, так называемой теоремы
Томсона, требует, чтобы при изменении циркуляции крыла Г
на некоторую величину ДГ от крыла отходил вихрь с цир-
куляцией — ДГ, который, сходя с крыла, далее уносится
потоком. С другой стороны, основное положение, на кото-
ром построена вся современная теория крыла, гипотеза
Чаплыгина — Жуковского, состоит в том, что острая задняя
кромка крыла является линией схода потока с верхней и
нижней поверхностей крыла. Но положение точки схода
потока с верхней и нижней поверхностей крыла зависит от
величины циркуляции вокруг крыла, а также от величины
и положения внешних вихрей; при изменении положения
внешних вихрей точка схода может оставаться на задней
кромке крыла только при условии непрерывного изменения
величины циркуляции, что в свою очередь по теореме Том-
сона вызывает сход вихрей с крыла. Основываясь на этом,
Прандтль предложил следующую гидродинамическую схему:
за крылом, находящимся в условиях неустановившегося дви-
жения, образуется вихревая пелена, непрерывно сходящая
Ч Опубликовано в сборнике «Научная конференция ВВА КА»,
1944. (Прим, ред.)
410 П. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
с задней кромки крыла. Такая вихревая пелена является
поверхностью разрыва скоростей. Таким образом, крыло
в условиях неустановившегося движения сопровождается по-
верхностью разрыва скоростей, сходящей с задней кромки
крыла.
Такая поверхность разрыва скоростей или, что то же,
вихревая поверхность оказывает на крыло известное воз*
действие, как и всякая система вихрей, влияя, например, на
поле скоростей, в котором находится крыло; учет этого
воздействия представляет огромные теоретические трудности.,
В теорию неустановившегося движения приходится вно-
сить различные упрощающие предположения относительно
строения поверхности разрыва. Например, обычно предпо-
лагается, что такая поверхность разрыва представляет собой
плоскость; однако такое упрощение, допустимое при взма-
хах крыла с весьма малой амплитудой, каковы, например,
вибрации крыла, оказывается совершенно непригодным в слу-
чае машущего крыла с большими амплитудами взмахов.
Эта же гидродинамическая схема явления представляет и
большие трудности для учета величины тяги машущего
крыла и для выяснения самого механизма образования тяги.
В современной теории машущего крыла возникновение
тяги обычно объясняется образованием подсасывания у пе-
редней кромки крыла. Однако такое объяснение предста-
вляется сомнительным по следующим причинам. Как известно
из исследований Н. Е. Жуковского, подсасывающие силы
образуются у острой передней кромки крыла. Но машущие
Крылья, например у птиц, так же как и аэродинамические
профили крыльев самолета, имеют округлые очертания
у передней кромки, т. е. имеют форму, как раз невыгод-
ную для образования тяги.
Между тем построение теории машущего крыла и,
в частности, выяснение механизма образования тяги пред-
ставляют несомненный технический интерес. Дело в том,
что, несмотря на громаднейшие успехи современной авиа-
ции, вопрос экономичности полета современных самолетов
остается далеко не решенным. Весьма возможно, что энер-
гия, затрачиваемая на полет при помощи машущих крыльев-
окажется значительно ниже той, что тратится в современных
самолетах, где огромные скорости полета вызывают колос-
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА
411
сальные затраты мощности моторов и расход горючего.
Но вопрос о сравнительной экономичности современных
летающих машин и аппаратов, основанных на применении
машущих крыльев, упирается в отсутствие сколько-нибудь
разработанной теории машущего крыла.
В настоящей статье сделана попытка изложить основы
тех соображений, которые, по нашему мнению, позволяют
построить гидродинамическую теорию работы машущего
крыла при любой величине амплитуды взмахов. Задачу мы
будем рассматривать в условиях плоскопараллельного течения.
Как было указано выше, основную трудность теории пред-
ставляет -учет вихреобразований, которые сходят с крыла.
По идее Прандтля, принимаемой всеми исследователями
этого вопроса, с машущего крыла сходит непрерывная
вихревая пелена. В основе предлагаемой теории лежит отказ
от такой гидродинамической схемы. Путь к согласованию
тех требований, к которым приводит постулат Чаплыгина —
Жуковского, с одной стороны, и теорема о сохранении
величины циркуляции (теорема Томсона), с другой стороны,
мы видим в учете влияния пограничного слоя крыла, т. е.
с физической точки зрения в
учете влияния вязкости.
Пограничный слой крыла с
кинематической точки зрения на-
до рассматривать как область,,
заполненную завихренной жидко-
стью. Пусть АВ — поверх-
ность обтекаемого тела и CD —
В -> С
А В
Рис. 1.
наружная поверхность слоя (рис. 1); в силу вязкости
скорость на поверхности АВ равна нулю, а на CD—равна
скорости потока, обтекающего тело; поэтому циркуляция
скорости по контуру ABCD отлична от нуля, что и служит
признаком завихренно.сти жидкости внутри пограничного
слоя. Можно представить себе следующую кинематическую
модель пограничного слоя. Возьмем несколько цилиндров
с диаметром, равным толщине пограничного слоя, которые
катятся по поверхности твердого тела таким образом, что
скорость движения их равна половине скорости потока,
текущего по наружной границе пограничного слоя (рис. 2).
Несколько осложнив эту схему, нетрудно представить себе
412
П. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
кинематическую модель, дающую в пределах пограничного
слоя и распределение скоростей, соответствующее экспери-
ментальным данным.
Для того чтобы выяснить, какой эффект оказывают вихри
пограничного слоя на условия обтекания крыла, отобразим,
как это обычно делается в теории крыла, область, занятую
текущей жидкостью, на внешнюю
часть круглого цилиндра радиу-
са таким образом, что острая
задняя кромка крыла изобразится
точкой z — R. При этом вихревой
пограничный слой крыла изобра-
зится вихревым слоем S вокруг
цилиндра (рис. 3).
Рис. 2. Рис. 3.
Пусть вихревая плотность в слое есть с; характеристи-
ческая функция обтекания цилиндра может быть записана
в виде
w = Vcoe~^ + +
+ij ^dxdy’ (1)
s z re
где Vqo — скорость потока в бесконечности, 6 — угол атаки,
Г — циркуляция вокруг цилиндра, ге^ — аффикс вихря слоя
02 z
с вихревой плотностью а и — е*—аффикс изображения
этого вихря относительно поверхности цилиндра.
Так как точка z~R есть изображение острой задней
кромки, то для выполнения постулата Чаплыгина — Жуков-
ского необходимо, чтобы
m =о,
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА
413
т. е.
140^(1 — ^) +
+ 27/ я- — 2^7 Д' J J с га —2^rcos <р + /?2 dxdy = O, (2)
S
откуда
Г - - MV. sin « + J / П г,_2;’г7.м + Д» “* d>- <3>
Я
Как показывает формула (1), вихри пограничного слоя
не дают непосредственно циркуляции, так как входят по-
ра .
парно с противоположными знаками в точках ге"г и — ечг,
но они оказывают влияние на величину циркуляции косвенно
в силу выполнения постулата Чаплыгина — Жуковского (так
как они влияют на положение точки схода потока с крыла).
В теории крыла обычно принимают
Г == — 4^00 sin в, (4)
что равносильно предположению
Ио -о—-------——г—dxdy = 0. (5)
. г2 — 2Rr cos ср + Р2 v '
S
Предположим теперь, что около цилиндра находится
вихрь J в точке r^ai. Характеристическая функция течения
примет вид
z----eoi 6
(6)
При выполнении постулата Чаплыгина — Жуковского
получим аналогично предыдущему
Г = — 4т:Р Vqo sin 0 + J
r*-R2
г2 — 2Rt\ cos a -|- R2
+ Г f a "2--oB----dx йУ* W
1 J J r2 — 2Rr cos ф 4- R2 J v 7
Я
414
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Отсюда мы видим, что при отходе вихря J, т. е. при
изменении i\ и а, меняется и величина циркуляции Г, — это,
как было указано вначале, противоречит условию сохране-
ния циркуляции (теорема Томсона). Но нетрудно показать,^
что можно построить такие условия изменения вихрей внутри
слоя (где, естественно, теорема Томсона не может быть
справедлива в силу проявления вязкости), при которых цир-
куляции Г и J не будут меняться при любом положении
вихря J. Прежде всего, если вихрь J уйдет в бесконечность,
то из (7) найдем:
Г = —4^1/00 sin О+ J J а°о Г2 _ 2Rr cos с? 4- /?2 dx dy> (8)
где Ооо — вихревая плотность слоя, когда вихрь J находится
в бесконечности и, следовательно, его изображение нахо-
дится в центре цилиндра.
Из уравнений (7) и (8) получим, что при выполнении
условия
Г f г2 — J?2
J J ~ 0°°) гЗ _ 2Rr cos dx dy +
j 2R (ft cos a — R)
r* — 2/?rx cos a 4- R2
(9)
циркуляция вокруг цилиндра (Г — J) остается при выпол-
нении постулата Чаплыгина — Жуковского постоянной при
любом положении вихря J.
Условию (9) можно удовлетворить надлежащим подбором
плотности с, причем, принимая обычное в теории крыла
условие (5), можно считать:
f f r2__ D2
°ОО -Q---------------Г~Тл» dx dy = 0.
J J г2 — 2Rr cos cp 4- RA J
(10)
Например, если ограничиться простейшей кинематической
моделью пограничного слоя, указанной на рис. 2, то вместо
поверхностного распределения вихрей в пограничном слое
надо взять линейное (по линии центров вихревых цилиндров,
катящихся по поверхности крыла); если при этом считать,
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА 415
что удаление вихревой линии от центра круглого цилиндра
равно R-\-eR, где е мало, то вместо (9) получим:
<Pi
J °
<Ро
2е + е2
2 + 2е + е2 — 2 (14-е) cos с?
^iCOSa-/?) 0>
rf — 2Rrt cos Я 4- R2
или, пренебрегая е2,
Cpl — ср0
sln 2 2/? (/j cos Я —/?)
<Ро , ?i ' J г2 — 2Rr< cos я 4- R2
sin -у sin 1 1 1
где ср0 и — углы; соответствующие началу и концу вих-
ревой линии, заменяющей пограничный слой г).
Общий итог всех предшествующих рассуждений следую-
щий: для выполнения постулата Чаплыгина — Жуковского
при отходе от крыла сорвавшихся с него вихрей нет надоб-
ности вводить непрерывно сходящую с задней кромки крыла
поверхность разрыва скоростей; влияние изменения положения
вихрей на точку схода потока с крыла компенсируется изме-
нением в структуре пограничного слоя или, что то же,
влиянием вязкости воздуха.
Приложим теперь предшествующие соображения к сле-
дующей простейшей схеме машущего крыла.
Рассмотрим плоскую пластинку ширины Ь, совершающую
в условиях плоскопараллельного течения колебания конечной
амплитуды h. Пусть скорость потока в бесконечности есть Vqo,
и будем считать, что скорость крыла при опускании и при
поднятии крыла (-j-w и — w) остается за время опускания
и поднятия постоянной, резко изменяясь в крайних точках
амплитуды колебания.
Пусть при отсутствии ‘взмахов крыла угол атаки равен 6;
тогда величина циркуляции при отсутствии взмахов Г опре-
делится по формуле
r — K&IZooSinO. (И)
1) Эта простейшая схема указана мною в статье: «К теории ,
пограничного слоя», Юбилейный сборник «Двадцать лет ВВА РККА
имени Жуковского», 1942. [см. настоящее издание, стр. 399 — 408].
416 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
При опускании крыла получается добавочная относитель-
ная скорость, направленная вверх и равная w; при этом
. w
угол атаки увеличится на величину arctgy—, а величина
''со
У скорости набегающего по-
Гтока примет видКw2.
При взмахах крыла в
крайних точках амплитуды
колебания от крыла от-
ходят вихри, которые мо-
гут вызывать изменение
циркуляции; но если учесть
Рис. 4. предшествующие сообра-
жения, то влиянием этих
отходящих вихрей на величину циркуляции можно пре-
небречь.
При этих условиях величина циркуляции за время опу-
скания Го определится по формуле
Го = ъЬ Vw2sin 0'+ arctg . (12)
Если оси расположить так, как показано на рис. 4, то
циркуляция Г будет отрицательной; поэтому для Го получим
окончательно выражение
Го = — nbV w2 sin ^0 —arctg-у-); (12')
точно так же для случая поднятия крыла циркуляция Гп
Гп = — itbVw2sinf0 — arctg-^-} . (13)
\ *^oo /
Следовательно, при переходе от опускания к поднятию
крыла, т. е. в нижней точке амплитуды колебания, цирку-
ляция изменяется на величину Гп—Го, что по теореме Том-
сона вызовет отход от крыла вихря =— (Гд — Го); из
уравнений (12) и (13) имеем:
Yi = — 2~b<w cos 9. (14)
МЬХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА
417
Точно так же в верхней точке амплитуды колебания от
крыла отойдет вихрь у = — (Го — Гп) = — Ti, т. е.
у == cos 9. (15)
Итак, при взмахах крыла в верхних и нижних точках
амплитуды колебания от крыла отходят вихри интенсивно-
сти у и ^Г> следовательно, за крылом образуется вихревая
дорожка, аналогичная дорожкам Кармана, образующимся за
преградами, но с обратным направлением вращения вихрей
(рис. 5).
Можно принять, что ширина дорожки есть h. Обозначая
период колебания крыла через Т, скорость, сообщаемую
вихрям дорожки всеми другими вихрями дорожки, через
и расстояние между двумя последовательными вихрями
через Z, получим:
/ = (^+«0)Т, |
2h = wT. J (16>
Примем, как это следует из известных формул Кар-
мана,
y h~
Uq 21^-Т *
или, подставляя из (15) значение у, получим:
«0 = Пу wcosO th (17)
Так как в дальнейшем удобнее иметь отношение
определяемое конструкцией машущего крыла, то можно еще
написать:
«o = 4'cos0 * ^[Tth т]’ U8)
418
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Исключив Т из уравнений (16), получим:
(19)
Так как, очевидно, у > 0, то для образования дорожки
необходимо выполнение условия
^>2А. (20)
V СО *
В частности, если дорожка удовлетворяет условию устой-
чивости Кармана, то -у = 0,281 и th^y = y=; тогда ра-
венство (19) примет вид
h А w ' '
0,35 cos 6 pr-
И
> 0,562. (22)
*со
Все предыдущее позволяет нам вывести и основные
уравнения движения машущего крыла. Для этого, следуя
Карману, мы напишем уравнение количества движения, при-
меняя его к массе воздуха, заключенной внутри некоторой
контрольной поверхности, за которую мы возьмем прямо-
угольный параллелепипед, построенный на квадрате с очень
большими сторонами; центр параллелепипеда пусть нахо-
дится в начале координат, а стороны параллельны осям
координат. При этом будем предполагать, что крыло со-
вершает колебания около центра квадрата, параллельно
оси у (рис. 6).
Рассчитаем импульс сил, действующих на такую массу
воздуха за период колебания Т. Пусть давление жидкости
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА
419
на крыло дает силу с компонентами X,Y\ тогда крыло дей-
ствует на жидкость силой с компонентами —X и —Y.
Далее, на заключенную в рассматриваемом объеме
жидкость действует вся жидкость, находящаяся вне контроль-
ной поверхности. Соответствующие компоненты давления:
X' = — f pdy, Yr = j* p dx. (23)
z L
Компоненты силы и давления периодически меняются при
взмахах крыла; поэтому компоненты импульса сил имеют
вид
ПО ОСИ X
по оси у
т т
— J Xdt—f dt Jpdy,
0 0 L
T T
— J* Ydt-\-^ dt J*pdx.
О O L
(24)
Подсчитаем количество движения жидкости, протекшей
через L за время Т. Обозначая через 9 угол, образованный
скоростью с внешней к L нормалью, получим выражение
420
П. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
для количества вытекшей через элемент ds жидкости за
время dt
р dsV± dt cos 9 = р dt (и dy — v dx).
Отсюда составляющие количества движения имеют вид
по оси х pdt(udy— vdx)u,
по оси у pdt(udy— vdx)v.
Следовательно, приращение количества движения за
время Т имеет составляющие по осям:
т
по оси х р j* dt j* (tidy — vdx)u,
°T L (25)
по оси у р j* dt § (tidy — vdx)v.
о L
Далее, за период Т через сторону ВС пройдут два
вихря. Уносимое ими количество движения имеет составляю-
щие по осям: по оси х pyh и нуль по оси у.
Применяя теорему количества движения, получим следую-
щие два уравнения:
т т т
— У X dt — У dt У р dy = р У dt У (и dy — v dx) и ур/г, (26)
О О L О L
Т Т Т
— У Y dt dt $ р dx = р £ dt f (a dy — vdx)v. (27)
О О L О L
Умножая обе части уравнения (26) на I и складывая
соответственные части (26) и (27), получим после некоторых
преобразований
т
j (Y-\-iX)dt =
о
т
=—pj dt J [(tidy—vdx)(al-l~v)—y-(dx—i dy/| —p^hi. (28)
о It
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ. МАШУЩЕГО КРЫЛА 421
Обозначая потенциал скорости через ср(х, y9t)t -получим
для интеграла Лагранжа выражение
P = Po(t> —-^(uz-+v2) — р^. (29)
и, так как
f Ро (О (dx ~ i dy) — О
L ;
и также
т
J dt J (dx — i dy) = О,
о L
в силу периодичности функции ср уравнение (28) примет
вид
т т .
J(F-4rZAr)rf/ =— J JZ J {р(и^у— vdx)(ul + v) +
О O L
+ (u2 + v2) (dx — i dy)} — fyhi.
Так как скорость потока в бесконечности есть то,
полагая
и = КхэЧ-г/
и принимая во внимание, что
и'2 — v2 — 2iu'v = (и' — iv)2 = »
где w — характеристическая функция того течения, которое
налагается благодаря колебаниям крыла на основное течение
со скоростью Voo, и, кроме того, что
J* u'dx~t-vdy = J* (Voo-H u')dx-\-vdy =
L L
— ^udx-]~vdy==r,
422
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
где Г — циркуляция вокруг крыла, и в силу неразрывности
течения
J* и' dy—vdx = и dy — vdx = Ot
L L
приведем уравнение (28) к виду
т
j(Y-\-lX)dt =
О
т т
= — pVooJ Ydt — j- j dt j (^)2 dz— ?1hi. (30)
О 0 L
Вводя еще среднее значение силы с компонентами Хсрк Уср
и соответственно среднее значение циркуляции Гср, приведем
уравнение (30) к виду
Гор + /Хр=-рУСЮГСр—J (^УНр (31)
L
Для вычисления интеграла
J(£)^
L
заметим, что характеристическая функция течения состоит:
1) из характеристической функции потока, набегающего
со скоростью К», т. е.
Wj = V^z,
2) из характеристической функции циркуляционного
потока, возникающего вокруг крыла,
3) из характеристической функции течения, образован-
ного вихрями дорожки сзади крыла,
Причем на стороне ВС будем считать дорожку бесконечной
в оба конца;
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ МАШУЩЕГО КРЫЛА
423
4) ко всему предыдущему надо добавить еще некоторую
поправку, вызываемую присутствием в потоке крыла (вместо
одиночного вихря) и его перемещением при взмахах, а также
тем, что вихревая дорожка слева от ВС конечна.
Если все эти поправки объединить в остаточный член 7? (z),
то характеристическая функция всего течения примет вид
w' = VoaZ + In z + <?(*) + R (Z), (32)
откуда
I/ । Г 1 . dy . dR /ппч
« ———+ ~, (33)
dR
причем порядок величины на сторонах квадрата ABCD,
а также порядок величины на сторонах ЛВ, CD и DA
1
есть ,—гй.
И2
Откидывая в полученной формуле течение со
стью Ко, получим окончательно:
dw f , Г 1 . dy । dR
~d^U —+
Из теории дорожек Кармана известно, что
sin(z —*i)-£
? = 2Ь1П—-----------------
sin (г — z2)y
скоро*
(34)
(35)
где zt и z2 — аффиксы одного вихря верхнего ряда и одного
вихря нижнего ряда.
Подставляя выражение (34) в интеграл J
..вс
покажем, что этот интеграл отличается от интеграла
f л 1
I членом грядка .-ут.
вс 2
Следовательно, увеличивая контур ABCD до бесконечно*
сти, получим:
Гор-МХор = — рУооГо,—>£- f (g)2dz — ^hl j, (36)
\ ВСх
424 if. труды по теории машущего крыла
й, применяя обычный в теории дорожек Кармана метод
вычисления интеграла правой части равенства (36), получим
окончательную формулу
Гор+= - р ОоР- z g (7 th 1) -
где
T=-----1---
^ + «0 •
Отсюда
х₽ - ё {тth т - 4 - ? < +“о). (37)
Гер = рУооГср. (38)
Так как
Гор = 4- [Гп + Го] = — Я V 4- w2b sin 9 cos arctg—,
z * оо
окончательно получим:
Гср = —nVoo^sin 9,
т. е. среднее значение циркуляции равно значению цирку-
ляции при отсутствии взмахов.
При помощи уравнения
Y XL.
Uq 21 V
уравнение (37) можно привести к виду
^₽ = |£-£r(V“ + 2zzo)- (39)
Это выражение средней величины тяги совершенно ана-
логично известной формуле для величины сопротивления,
данной Карманом, и получается из формулы Кармана, если
переменить знаки у у и uQ.
В частности, если подставить условия устойчивости
вихревой дорожки, т. е.
то получим:
ХОр = - piv^ [о,314 (^)2 4-0,794 (40)
МЕХАНИЗМ ОБРАЗОВАНИЯ ТЯГИ. МАШУЩЕГО КРЫЛА 425
Выражение силы тяги (40) также совершенно, аналогично,
известной формуле для сопротивления, данной Карманом.
Интересно отметить здесь, что задача определения силы
тяги машущего крыла значительно проще определения вели-
чины сопротивления. Как известно, в случае, когда мы
ищем величину сопротивления, нет теоретических путей для
определения интенсивности отходящих вихрей у; в случае
машущего крыла мы легко находим величину у по фор-
муле (15).
Пользуясь формулой (15), можно для силы тяги дать
следующее выражение:
Хср = - cos 6 —X
TthT
причем в общем случае мы найдем величину у по кон-
структивным и кинематическим данным из решения урав-
нения (19):
Наконец, в случае, если режим полета таков, что выпол-
няются условия устойчивости, для силы тяги получается
следующее весьма простое выражение:
Хср = — о,94рйУоода cost» [1 + 1,2^]. (42)
Весьма вероятно, что наиболее выгодным режимом по-
лета и. является тот, когда выполняются условия устойчи-
вости дорожки.
Подводя итоги, заметим, что, как показано, учет вяз-
кости воздуха путем введения пограничного слоя кры-
ла чрезвычайно упрощает теорию машущего крыла,
426
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА'
Возможность отказаться от введения непрерывных поверхно-
стей разрыва с заменой их вихревыми дорожками позволяет
решить задачу о машущем крыле при любых размерах
амплитуды взмаха. Из предыдущего ясно, что таким же
образом можно построить теорию и в случае крыла любого
профиля и при любом законе изменения скорости взмахов
крыла w.
ТЕОРИЯ МАШУЩЕГО КРЫЛА
И ОБЩАЯ ПРОБЛЕМА ТЯГИ И СОПРОТИВЛЕНИЯ 9
В одном из своих произведений, всегда несколько не-
ожиданных и загадочных по содержанию, недавно скончав-
шийся писатель А. С. Грин (всем, вероятно известный по
написанному на его сюжет балету «Алые паруса») описы-
вает следующую сцену. Дело происходит в цирке. Испол-
нителем одного из номеров программы выступает никому
не ведомый актер, который должен показать нечто необык-
новенное. На арену вышел самый обыкновенный человек и
стал посредине арены, Все смотрят и ждут . . . Вдруг ма-
ленький мальчик, сидевший в первом ряду, нагнулся и за-
кричал:
•—Он поднялся от земли!
И все стали нагибаться и смотреть; оказалось, что че-
ловек посредине арены оторвался от земли и стоял уже не
на земле, а над землей...
Примерно в таком же положении оказались зрители,
собравшиеся 36 лет назад, осенью 1908 г., на беговом,
ипподроме на Ходынке смотреть полеты Уточкина, одного
из первых русских авиаторов. Правда, чтобы увидеть, что
Уточкин поднялся в воздух, не нужно было нагибаться: он
поднимался на высоту второго этажа, метров на 6—8, и
пролетал на своем нескладном «Фармане», напоминавшем
большой коробчатый змей, метров 150 вдоль трибуны,
а затем садился опять на землю. В сущности, это был
*) Опубликовано в сборнике «Общее собрание Академии наук
СССР», 1944.
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 427
даже не полет: просто летчик делал прыжок и затем неко-
торое время двигался над землей.
Восторг зрителей не поддавался описанию. Толпа бежала
к самолету; Уточкина качали, кричали «ура». Об Уточкине
писали во всех газетах. И немудрено: на полетах Уточкина
москвичи увидели, что человек оторвался от земли и поле-
тел на громадной и тяжелой машине.
Потом пришли различные рекорды: Лятам поднялся на
300 метров над землей, кто-то обогнал в полете ласточку,
Блерио перелетел Ламанш... Важно было сделать первый
шаг — взлететь. Дальнейшее пришло само собою, пришло
в искусстве смелых летчиков, в изобретательности талант-
ливых инженеров, конструкторов, в расчетах ученых, раз-
рабатывавших научные проблемы авиации.
Еще сорок лет назад, перед первыми полетами братьев
Райт, Сантос Дюмона, Фармана, искусство летать было
задачей будущего, мечтой, фантазией ученого, над которой
смеялись, как в свое время смеялись над Жуковским, зани-
мавшимся в механическом кабинете университета «пустяками»,
собиранием бумажных заводных бабочек и различной формы
воздушных змеев.
Теперь человек научился замечательно летать; он летает
неизмеримо выше и быстрее птиц; скорость полета прибли-
жается к такой, что в самом близком будущем расстояние
от Москвы до Ленинграда можно будет покрыть на самолете
в один час; так, конечно, не летает никакая птица.
Современный самолет поднимает огромные грузы: десятки
и сотни пассажиров, десятки вооруженных солдат, тонны
грузов, бомб, бензина; поднимает артиллерийские орудия и
даже танки. Первая механическая задача — выяснить, откуда
берется подъемная сила самолета, каков механизм образо-
вания подъемной силы, — естественно, и была поставлена
перед наукой. И эта задача была полностью разрешена
в гениальных трудах ученых — основоположников совре-
менной технической аэромеханики: Н. Е. Жуковского,
академика С. А. Чаплыгина, Людвига Прандтля, Манчестера
и других. Их теории, формулы и расчеты дают возможность
современным конструкторам, инженерам .проектировать и
строить огромные стальные птицы, которые несут колос-
сальные грузы на своих распростертых крыльях. Теория
428
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
подъемной силы есть в настоящее время вполне законченный»
классический отдел механики.
Но при взгляде на современный самолет возникает, есте-
ственно, и другой вопрос. Мы научились замечательно
летать, но насколько-экономно мы летаем? И здесь сейчас
же возникает одно сравнение, весьма маловыгодное для
наших современных самолетов. С одной стороны, мы имеем
в природе замечательные примеры полета — полет птиц.
Взмахами крыльев они создают себе и подъемную силу, и
тягу; бесшумно, с большой скоростью и на очень большие
расстояния летят они, взмахивая крыльями. И рядом наши
самолеты с их дико ревущими моторами, с пропеллерами,
делающими тысячи оборотов в минуту, с распростертыми
неподвижно крыльями; самолеты, пожирающие в своих мо-
торах колоссальные запасы ценнейшего топлива — бензина.
Если мы научились прекрасно летать, то экономичность
современного способа летания стоит под большим сомнением.
А отсюда, естественно, возникает основная задача: изучить
различные методы образования тяги, тянущей силы само-
лета. Некоторыми теоретическими соображениями, относя-
щимися к проблеме образования тяги самолета, и разрешите
занять ваше внимание.
Мне придется при этом говорить о соображениях, весьма
далеких от современной авиационной техники, и, мало того,
о таких соображениях, которые, возможно, и вообще никогда
не будут использованы техникой. Но ведь уж такова задача
науки: исследовать новые, порою сомнительные и ненадеж-
ные пути. Утешением здесь служит то, что в случае удачи
эти новые пути открывают широчайшие возможности для
техники, а в случае неудачи по крайней мере получатся
надежные указания, в каком направлении не нужно идти
в попытках технического разрешения задачи.
В проблеме об условиях и о механизме образования тяги
прежде всего бросается в глаза следующее: техническое
решение задачи об. образовании тяги путем применения про-
пеллера, воздушного гребного винта, коренным образом
отличается от того решения задачи об образовании тяги,
которым идет природа, где тяга, которой пользуются при
-полете птицы, образуется совершенно иным путем, путем
взмахов ,крыльев.
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 429
Совершенно ясно, что для техники необязательно и
нетипично прямое подражание природе. Достаточно вспо-
мнить технические применения качения в форме разнообраз-
нейших колес, катков, роликов и т. п., начиная от перво-
бытной арбы и кончая самыми усовершенствованными паро-
возами, подшипниками современных машин, автомобилей,
гусеничных механизмов и т. п. Надо еще заметить, что
в природе, по крайней мере на первый взгляд, качение
почти не встречается. Наоборот, для перемещения живот-
ных применяются более или менее сложные стержневые
механизмы, каковыми являются ноги человека и животных.
Я сказал, что в природе качение «почти» не встречается;
далее мы увидим, что в природе есть механизм,, достаточно
распространенный, где мы имеем такого рода качение,
причем, по-видимому, в форме, гораздо более совершенной,
чем' это достигается в технике.
Во всяком случае, предыдущие соображения показывают,
что изучение вопроса о возникновении тяги при помощи
взмахов крыльев есть задача, заслуживающая подробного и
и внимательного изучения. Но если мы обратимся к совре-
менным научным теориям, то встретимся с тем неожиданным
фактом, что, в то время как механизм образования тяги
путем вращения винта изучен весьма подробно в ряде работ
различных ученых, и прежде всего в классических исследо-
ваниях Н. Е. Жуковского, механизм образования тяги путем
взмахов крыльев совершенно не изучен. Приведу как пример
две попытки дать решение этой задачи.
В некоторых исследованиях по теории крыла сила тяги
объясняется подсасыванием, возникающим у передней кромки
крыла. Такое подсасывание действительно может иметь
место независимо от взмахов, если передняя кромка острая.
Но, увы, у крыльев всех птиц передний край как раз
не острый, а округленный, как ему и полагается
быть по соображениям общей теории крыла, а кроме
того, такое объяснение никак не связано с взмахами
крыльев.
В одном курсе физики дается такое объяснение: «При
полете с помощью ударов крыльев птица активно создает
себе подъемную силу. При этом крыло несколько закручи-
вается, так что задняя часть его выгибается кверху.
430 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Благодаря этому стоящая косо к направлению движения по-
верхность крыла создает импульс вперед» *).
Но передняя часть также оказывается выгнутой вперед,
и при таком рассуждении от нее должна была бы образо-
ваться сила, тянущая назад.
Об этих объяснениях можно сказать, что утопающий
хватается за соломинку: раз нет объяснения, хоть сколько-
нибудь похожего на дело, то все годится. Пессимистически
заканчивается рассмотрение этого вопроса, например, в «Аэро-
динамике» Дюренда:
«Точное определение величины тяг затруднительно. Мы
не будем исследовать эту задачу»i) 2).
Впрочем, надо заметить, что в этой последней книге
авторы (Карман и Бюргерс), по нашему мнению, близко
подходят к правильному пониманию дела.
Восполнить пробел в теории крыла в этом направлении
и составляло цель исследований, проведенных мною и моими
сотрудниками в Институте механики МГУ; в настоящем
сообщении я попытаюсь дать общее представление об этих
исследованиях и постараюсь познакомить вас с выводами,
к которым эти исследования привели.
Когда дело идет о возникновении силы тяги, то прежде
всего встает вопрос, откуда эта сила может появиться.
Механика учит нас, что действие равно противодействию,
что всякая сила вызывает силы, действующие в обратном
направлении. Сила, выбрасывающая снаряд из орудия, вызы-
вает силы, образующие откат, отдачу орудия, причем эта
сила поглощается действием компрессора и сопротивлением
земли. При прыжке, отталкиваясь от земли, мы вместе с тем
отталкиваем землю; только благодаря колоссальной массе
земли тот толчок, который мы сообщаем при прыжке земле,
совершенно нечувствителен. Самолет, взлетая над землей,
передает через воздух давление на землю и отталкивает
ее в обратную сторону. Сила, толкающая вперед ракету,
создается за счёт сил, отбрасывающих газы, выбрасываемые
из ракеты горящей смесью, и т. д. В пропеллере этот отброс
назад воздуха создается лопатками пропеллера, который,
i) Э. Гримзел ь, Курс физики, т. I, вып. 1, ГТТИ, 1933.
2) Дюренд, Аэродинамика, т. II, стр. 347, 1938.
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 431
вращаясь, гонит воздух назад, в результате чего, в силу
закона действия и противодействия, и получается тянущая
сила пропеллера. И, в сущности, все теории пропеллера
сводятся к тому, что выясняется, как образуется сзади рабо-
тающего пропеллера отбрасываемая им струя воздуха. Но если
отброс воздуха работающим пропеллером механически более
или менее ясен, то отброс назад воздуха машущим крылом
совершенно неясен, так как крыло совершает взмахи в на-
правлении, перпендикулярном к направлению движения и,
следовательно, к направлению отброса воздуха.
Ответ на этот вопрос может дать другая задача, в извест-
ном смысле обратная проблеме возникновения тяги, — это
задача о возникновении сопротивления тел, обтекаемых пото-
ком. Ведь алгебраически совершенно ясно, что сопротивле-
ние есть отрицательная тяга и, обратно, тяга есть отрица-
тельное сопротивление, совершенно так же, как прибыль
есть отрицательный убыток и убыток есть отрицательная
прибыль.
Итак, представим себе, что в потоке воздуха или жидко-
сти стоит неподвижно некоторая преграда, которую поток
обтекает и которая от этого потока испытывает более или
Рис. 2.
Рис. 1.
менее значительное давление. Примером могут служить устои
моста в реке, на которые давит поток воды. Спросим себя,
что при этом происходит и откуда берется сила давления
потока. На рис. 1 и 2 мы имеем снимки того, что проис-
ходит в потоке, когда он обтекает преграду. Мы видим,
что плавно текущий поток образует за телом на первый
432
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
взгляд довольно беспорядочное течение. Нам и предстоит
сейчас осмыслить то, что происходит перед нами, понять
механический смысл этого сложного течения.
Если бы мы попытались с совершенной точностью изо-
бразить теоретически происходящий перед нами процесс,
то мы вообще не получили бы никаких научных результатов.
Но ведь в том-то и дело, что наука не есть фотограф, во
всех деталях точно передающий мимолетное и, вообще говоря,
случайное состояние изображаемого. Нет! Наука есть вели-
кий художник, и как художник она упрощает и стилизует
действительность. Как Левитан в своих пейзажах не ставит
себе задачей изобразить точно, во всех деталях, все листья
и сучки деревьев, как Репин в своих портретах не стремится
вырисовать все морщинки на изображаемых лицах, а стре-
мится, отбрасывая случайные и нехарактерные мелочи, точно
передать то характерное и общее, что выражает сущность
изображаемого, — совершенно так же и всякая научная тео-
рия принуждена откинуть случайные и несущественные де-
тали, чтобы, стилизовав, упростив явление, тем самым вы-
явить его основные черты, те механические законы, которые
им управляют. Не будем удивляться этой стилизации: куби-
ческий портрет Пикассо также передает до какой-то степени
характер и сущность изображаемого лица. Единственным
критерием ценности всякой научной теории является только
опытная проверка полученных на ее основании выводов.
Итак, каким же образом наука стилизует получаемую
из опыта картину обтекания?
Первая попытка такой стилизации принадлежит Гельм-
гольцу и Кирхгофу, а в дальнейшем была с большим успе-
хом развита в работах ряда других ученых и особенно
успешно в трудах лорда Рэлея и Н. Е. Жуковского. Это —
так называемая теория струй. Сущность этой теории мы
легко схватим из следующих, совершенно ясных из повсе-
дневной жизни наблюдений. Когда дует сильный ветер, то мы
от него прячемся за углом здания; когда на реке сильное
течение, то мы можем отстаиваться от него в лодке за остров-
ком. И за углом дует ветер, и за островком есть течение,
но только более слабое. Итак, стилизуем явление! Пусть
за преградой вместо каких-то сложных круговращательных,
но сравнительно слабых течений мы имеем совершенно спо-
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 433
койную зону, область аэро- или гидродинамической тени.
Таким образом, вместо действительной картины течения
(рис. 1 или 2) будем . рассматривать схематическую, стили-
зованную картину (рис. 3 или 4), причем зона S, находя-
щаяся сзади обтекаемой преграды, заполнена .совершенно
неподвижной средой, а на границе L, отделяющей зону тече-
ния от области, занятой неподвижной жидкостью, текущая
жидкость скользит по неподвижной совершенно так же,
как рука скользит по хорошо полированному столу.
Как показали Гельмгольц, Кирхгоф, Рэлей, Жуковский
и другие, такую схему можно подвергнуть точному матема-
тическому расчету; в частности, Рэлей дал формулу, по кото-
рой можно подсчитать давление потока на преграду. Но полу-
ченная таким образом теоретическая величина силы давления
не дает хорошего согласия с опытом; она примерно вдвое
меньше наблюдаемой в действительности. Отсюда получаем
вывод:
Лежащая в основе теории струй стилиза-
ция явления обтекания весьма далека от дей-
ствительной картины явления и не может счи-
таться удовлетворительно передающей сущ-
ность явления.
Если внимательно просмотреть все наши предшествую-
щие рассуждения, то легко усмотреть и тот пункт, в кото-
ром, как можно думать, мы слишком далеко отошли от
действительности. Это — те круговращательные, вихревые
движения жидкости, которые мы видим за преградой и
которые мы совершенно не учитывали в теории струй. В том
434
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
беспорядочном, на первый взгляд, течении, которое мы наблю-
даем за обтекаемым телом, эти вращательные, вихревые дви-
жения выступают совершенно отчетливо. Мало того, если мы
отойдем несколько от обтекаемого тела, то совершенно ясно
подметим, что эти вихри образуют за обтекаемым телом
очень стройную конфигурацию: они образуют, как говорят
механики, двойную вихревую дорожку, причем вихри той
и другой стороны этой дорожки сдвинуты друг относительно
друга на половину расстояния между вихрями, так что вихри
Рис. 5.
дорожки расположены, как
говорят, в шахматном по-
рядке (рис. 5). Такие вихре-
вые дорожки можно наблю-
дать за устоями мостов на
реках, если только течение
достаточно быстрое; напри-
мер, в Ленинграде такие
вихревые дорожки можно
прекрасно наблюдать у Туч-
кова моста.
Такая вихревая дорожка
иногда тянется довольно да-
леко, причем вихри дорожки благодаря вязкости жидкости
постепенно размываются и, наконец, исчезают. Такие устой-
чивые вихревые образования уже давно служили предметом
систематического и подробного изучения; наиболее сущест-
венные реультаты были получены Бенаром и Карманом,
поэтому такие дорожки обычно называют «дорожками Бе-
нара — Кармана».
Нам предстоит теперь механически осмыслить то, что
дает непосредственное наблюдение. Механика учит нас, что
такие вихри могут образовываться и исчезать в жидкости
только в силу вязкости жидкости и что в жидкостях мало-
вязких, т. е. не таких, как патока, варенье, масло и т. п.
действие вязкости проявляется только непосредственно у по-
верхности обтекаемого тела, в пределах некоторого, вообще
говоря, весьма тонкого, так называемого «пограничного»
слоя; за его пределами вязкость настолько незначительна,
что можно с достаточной точностью считать, что там среда
вообще лишена вязкости. К числу таких сред с весьма малой
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 435
вязкостью принадлежат и воздух, и вода. Таким образом,
из предыдущего следует, что причину образования вихрей
за телом надо искать в действии вязкости в слоях жидкости
или газа, непосредственно прилегающих к обтекаемой поверх-
ности, т. е. в пределах пограничного слоя.
Но что же происходит в пограничном слое?
Опыт показывает, что текущая жидкость прилипает
к стенке и, следовательно, неподвижна относительно нее,
а при удалении от стенки скорость постепенно увеличивается
и на некотором расстоянии она равна той скорости, которую
имел бы поток, если бы вязкости вообще не было; на рис. 6
даны графики, показывающие распределение скоростей в пре-
делах пограничного слоя при различных скоростях течения,
или, как говорят, дающие «профиль скоростей».
Представьте себе, с другой стороны, что пластинка АА
катится на катках М по неподвижной плоскости ВВ
(рис. 7). Если заметить, что точки прикосновения катков М
к неподвижной плоскости являются мгновенными центрами
вращения и, следовательно, имеют скорость, равную нулю,
то профиль скоростей в точках движущейся пластинки АА
и в точках, лежащих на диаметре катка DD, имеет вид, ука-
занный на рис. 7а. Очевидно, что если катки расположить
в два ряда, как показано на рис. 8, причем пластинка АА
движется на роликах М по пластинке В, которая в свою
очередь движется на катках М± по неподвижной плоско-
сти СС, то соответствующий профиль скоростей имеет вид,
436 il. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
указанный на рис. 8а. Совершенно очевидно, что, увеличивая
число промежуточных пластинок, мы можем профиль такого
составленного из катков механизма сколь угодно приблизить
к профилям скоростей жидкости в пределах пограничного
слоя (рис. 6). Отсюда мы получаем важнейший вывод:
Рис. 7а.
Рис. 7.
все частицы жидкости в пределах погранич-
ного слоя можно считать находящимися
в состоянии вращательного движения, т. е.
вся жидкость сильно завихрена.
Простейшим механическим изображением того, что про-
исходит в пределах пограничного слоя, можно, следовательно,
считать схему, данную на рис. 7, причем пограничный слой
представляет собой нечто вроде слоя, составленного из кат-
ков, по которым движется остальная масса жидкости, нахо-
дящаяся вне пределов пограничного слоя. В . природе везде,
где имеется движение жидкости или газа около неподвижной
стенки, образуется в том или ином виде пограничный слой,
и, следовательно, мы имеем механизм, представляющий собой
нечто вроде системы катков; таким образом, употребляя
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 437
в технике всякого рода колеса, ролики, катки
и т. п., мы только весьма несовершенно подра-
жаем неизмеримо более тонкому механизму,
имеющему чрезвычайно большое распростра-
нение в природе везде, где имеется течение
с образованием пограничного слоя.
Пользуясь такой механической схемой, мы можем теперь
очень просто ответить на вопрос о том, откуда берутся
вихри, образующие за обтекаемым телом дорожки Бенара —
Кармана. Представим себе, что неподвижная плоскость ВВ,
по которой катятся ролики М (рис. 7), оканчивается. Тогда
соскочившие с края плоскости ролики отойдут от нее, имея
вращение. Совершенно таким же образом и вихри, образу-
ющие пограничный слой, срываясь с краев обтекаемого тела,
дальще движутся за телом в жидкости. Для случая течения
жидкости или газа дело обстоит несколько сложнее только
в том отношении, что срывающиеся вихревые образования
представляют собой целые более или менее сложные системы
таких катков и, кроме того, вызываемое ими вихревое дви-
жение увлекает за собой всю массу жидкости, как находя-
щейся перед преградой, так и за нею. Этим и объясняется
весьма сложная на первый взгляд система вихревых дви-
жений, которую мы наблюдаем за обтекаемым телом
(рис. 1 или 2).
Итак, мы можем теперь сказать, что вихри, обра-
зующие дорожки Бенара — Кармана, предста-
вляют собой распад вихревого пограничного
слоя.
Нам остается выяснить, почему на некотором расстоянии
сзади обтекаемого тела вихри, на которые распадается непре-
рывный пограничный слой, образуют стройную систему,
двойную вихревую шахматную дорожку. Этот вопрос был
полностью разъяснен еще тридцать с лишком лет назад
в работах Кармана *)• Оказывается, что из всех вихревых
образований, которые могут возникнуть сзади обтекаемого
тела, единственная система, обладающая достаточною сте-
пенью устойчивости, есть система, образующая двойную
*)• Th. v. Karman, Fliissigkeits-und Luftwiderstand, Physik.
Zeitschrift, вып. XIII, 1912.
438
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
вихревую шахматную дорожку, причем расположение вих-
рей должно следовать точному закону, а именно: если на-
звать через / расстояние между двумя последовательными
вихрями дорожек, а через h ширину дорожки, то для устой-
чивости дорожки необходимо выполнение условия
ch2 ^ = 2,
откуда
у- = 0,281.
Так
только
как в природе, естественно, могут существовать
устойчивые образования,
и
h-l
то системы вихрей, наблю-
даемые сзади обтекаемых
тел, и удовлетворяют этому
условию (рис. 9).
С физической точки зре-
ния, мне кажется, чрезвы-
чайно интересен самый факт
своеобразного квантования
завихренной среды при
метод подхода к решению
Рис. 9.
распаде пограничного слоя, а
поставленной задачи весьма напоминает решения ряда во-
просов теории атома и квантовой механики, где такую
исключительную роль играют вопросы устойчивости неко-
торых дискретных состояний материи.
Подведем теперь некоторые итоги и, прежде всего,
постараемся схематически изобразить процесс образования
вихревых дорожек. Простейшая схема, как это следует- из
предыдущих соображений, следующая: пограничный слой,
образующийся на передней стороне обтекаемой преграды,
с механической точки зрения, представляет собой ряд воз-
душных катков или роликов, по которым катится обтекающая
преграду среда; эти ролики, схематически изображающие
завихренную материю пограничного слоя, скатываются с кон-
цов преграды в точках А и В (рис. 10) и далее уносятся
жидкостью, образуя в ней двойную шахматную вихревую
дорожку, удовлетворяющую условиям устойчивости.
Отличие построенной кинематической схемы от действи-
тельного течения жидкости состоит, прежде всего, в том,
ТЕОРИЯ МАШУЩЕГО КРЫЛА И 'ОБЩАЯ ПРОБЛЕМА ТЯГИ 439
что твердые ролики, скатываясь с краев обтекаемого тела,
только сами вращаются, в то время как вихри, сбегающие
с преграды, приводят в движение всю массу жидкости.
В частности, если учесть направление вращения вихрей, то
получим, что каждая вихревая цепочка дает вихрям другой
цепочки некоторую добавочную скорость, направляемую про-.
тив движения потока. Под-
счет показывает, что эта
скорость для вихрей, не
очень близких к обтекае-
мой преграде, определяется
по формуле
Г ,, hn
Uq 2Z ’
где Г — интенсивность от- Рис. 10.
дельных вихрей дорожки.
Подобным же образом получается, что от действия
вихрей вихревой дорожки Бенара—Кармана
вся масса жидкости, текущей между двумя
цепочками вихрей, приобретает скорость,
направленную против направления скорости
первоначального течения, как это показано на
рис. 10.
Мы имеем теперь все данные для того, чтобы выяснить
механизм образования силы тяги машущего крыла. Мы уви-
дим далее, что за машущим крылом образуется
также двойная шахматная вихревая дорожка,
в которой направление вихрей обратно на-
правлению вращений в дорожках Бенара—
Кармана. Мы будем называть такую дорожку обращен-
ной дорожкой Бенара — Кармана.
Причиной всего этого является следующее. В основе
современной теории крыла, созданной в основных чертах
трудами Н. Е. Жуковского и академика С. А. Чаплыгина,
лежит механическая идея, что крыло самолета можно рассма-
тривать как помещенный в поток вихрь: это — присоеди-
ненный вихрь крыла, как его называет Н. Е. Жуков-
ский. Интенсивность этого вихря зависит, с одной стороны,
от геометрических свойств разреза крыла, а с другой
440
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
стороны, от условий полета. Математически все это выра-.
жается формулой
r = 7tfv(-J+e),
где Г — интенсивность вихря, b — хорда (ширина) крыла,
V—скорость полета, а — величина, характеризующая изо-
гнутость крыла, и 0 — угол
атаки. На рис. И дано пояс-
нение всех этих величин. По
знаменитой формуле Жуков-
ского эта величина Г сейчас
же определяет и величину
подъемной силы крыла Р:
р = pVTs,
где р — плотность воздуха и
s—размах крыла. Эти фор-
мулы, полученные чисто тео-
ретическим путем, хорошо со-
гласуются с опытными дан-
ными при небольших углах
атаки, которые применяются исключительно в авиации. На
рис. 12 дан примерный опытный и теоретический график
изменения интенсивности при-
соединенного вихря крыла в
зависимости от угла атаки.
Все эти формулы мы и при-
меним теперь к случаю машу-
щего крыла, причем, чтобы не
осложнить дело, мы возьмем
простейший случай крыла —
плоскую прямоугольную длин-
ную пластинку, совершающую
резкие колебания вверх и вниз
со скоростью w. В этом слу-
Рис. 12.
чае изогнутости нет, д потому
а = 0 и график изменения Г имеет вид, указанный на рис. 13.
Рассмотрим два положения машущего крыла: одно, когда
крыло опускается вниз, и другое, когда крыло поднимается
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 441
кверху (рис. 14). Когда крыло опускается вниз, скорость
потока, набегающего на крыло, слагается из двух скорстей:
из скорости V, равной скорости полета, но направленной
в противоположную сторону, и из перпендикулярной к ней
скорости w, направленной
вверх, так как крыло опу-
скается вниз. Таким образом,
результирующая скорость
образует с крылом угол ата-
ки 01э больший того угла ата-
ки, который был бы, если бы
не было скорости опускания
крыла. Совершенно аналогично
получим для случая поднятия
крыла результирующую ско-
рость w2, составленную из
скорости V и из скорости W,
направленной вниз, так как крыло поднимается кверху; в
этом случае результирующая скорость образует угол ата-
ки 02, меньший 9.
Обращаясь теперь к графику, дающему величину Г, мы
видим, что интенсивность присоединенного вихря крыла
Рис. 14.
во время опускания больше, чем во время поднятия крыла
Г2, на некоторую величину у (рис. 13). Таким образом,
при переходе в верхней точке амплитуды колебания крыла
от поднятия к опусканию крыла интенсивность присоеди-
ненного вихря увеличивается на величину у, а при переходе
в нижней точке амплитуды колебания от опускания к под-
нятию крыла интенсивность присоединенного вихря умень?
шается на величину у. Но по основным теоремам теории
вихрей такие изменения циркуляции возможны только в том
442
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
случае, если от крыла в потоке отходит вихрь с интен-
сивностью, равной по величине изменению интенсивности
присоединенного вихря крыла и противоположной по знаку.
Таким образом, в верхних точках амплитуды колебания
от крыла отходит вихрь интенсивности у и направленный
против направления вращения присоединенного вихря,
а в нижних точках отходит вихрь также интенсивности у,
но направленный в ту же
-----------------------—£ сторону, что и присоеди-
I ненный вихрь (рис. 15). Так
—г** .______~~ -*-* как эти отходящие вихри
уносятся потоком, то за
• ------- крылом образуется двойная
вихревая дорожка с шах-
Рис. 15. матным расположением вих-
рей, но, как видно из
чертежа, направление вращения этих вихрей обратно направ-
лению вращений в дорожках Бенара — Кармана. Таким обра-
зом, мы имеем следующий основной результат: за машу-
щим крылом образуется обращенная вихре-
вая дорожка Бенара — Кармана.
Полученный нами результат сейчас же позволяет объяс-
нить возникновение тяги у машущего крыла и найти ее ве-
личину. В самом деле, направление вращения вихрей полу-
чившейся обращенной дорожки указывает, что как сами
вихри, так и вся масса жидкости, заключенная между двумя
вихревыми цепочками, получает от них добавочную ско-
рость, направленную назад от крыла, а потому по класси-
ческим законам механики на крыло должна действовать сила
отдачи, направленная вперед; это и есть сила тяги. Совер-
шенно подобным образом в случае образования обыкновен-
ной дорожки Бенара — Кармана за обтекаемым телом сооб-
щенная жидкости скорость, направленная против направления
течения, вызывает силу отдачи, направленную по течению,
т. е. силу давления потока. Резюмируя все изложенное, мы
можем сказать:
взмахами машущего крыла мы вызываем
образование за ним обращенной вихревой до-
рожки Бенара — Кармана, которая в свою оче-
редь создает силу, направленную в сторону,
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 443
противоположную той, которая возникает от
обыкновенной дорожки, т. е. силу тяги.
Такова физическая основа предлагаемой теории образо-
вания тяги машущего крыла. Остановимся теперь на иных
попытках решения этой же задачи. В основе предлагаемой
теории лежит то соображение, что в крайних точках ампли-
туды колебания от крыла отходят сорвавшиеся с него вихри.
Не входя здесь в подробности, заметим, что и эти вихри
мы также рассматриваем как результат распада погранич-
ного слоя, совершенно аналогично соображениям, приведен-
ным выше. Но на первый взгляд все эти выводы противо-
речат одному постулату, достаточно точно обоснованному
экспериментально. В 1910 г. С. А. Чаплыгиным было вве-
дено одно положение, лежащее в основе всей современной
теории крыла. Это положение—основная гипотеза теории
крыла — состоит в том, что при плавном обтекании крыла
острая кромка крыла является точкой схода струй (рис. 16).
Но нетрудно показать, что если от крыла отходит вихрь, то
его перемещение вызывает, вообще говоря, смещение точки
схода струй, и, следовательно, постулат Чаплыгина не выпол-
няется. Чтобы при таких условиях постулат Чаплыгина вы-
полнялся, необходимо было допустить, что при перемеще-
нии внешних вихрей изменяется и циркуляция крыла, что
противоречит основным теоремам теории вихрей. Итак,
чтобы принять ту схему, которая изложена выше, каза-
лось бы, или нужно отказаться от хорошо проверенного
экспериментально постулата Чаплыгина, или пожертвовать
основными теоремами теории вихрей.
444
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Авторы, работающие в этом направлении, обходили эти
затруднения таким путем: они предполагали, что при пере-
мещении внешних вихрей постулат Чаплыгина выполняется,
а изменение циркуляции происходит за счет непрерывного
схода вихрей с задней кромки крыла, результатом чего
является образование сзади машущего крыла непрерывно
сбегающей вихревой пелены. Однако, по-видимому, можно
считать экспериментально доказанным, что такой непрерыв-
ной пелены не наблюдается; опыты в гидроканале гидравли-
ческой лаборатории МГУ достаточно убедительно показали
образование за машущим крылом дискретных вихрей, обра-
зующих обращенную двойную дорожку вихрей. Таким обра-
зом, для обоснования всей предыдущей теории необходимо
было показать, что у крыла есть такой механизм, который
позволяет удовлетворить постулату Чаплыгина, одновре-
менно не нарушая основных теорем теории вихрей.
Можно показать, что таким механизмом является погра*
ничный слой крыла. Вихри, из которых состоит погранич-
ный слой, как легко видеть, не влияют на величину цирку-
ляции крыла, но влияют на положение точки схода струй.
Таким образом, если при отходе от крыла внешних вихрей
надлежащим образом изменяется пограничный слой, то легко
примиряются постулат Чаплыгина, с одной стороны, и
основные положения теории вихрей, с другой стороны.
Относящиеся сюда математические соображения были даны
мною в небольшой заметке два года назад х).
Заметим здесь, что до сих пор пограничный слой крыла
рассматривался как источник образования сопротивления
крыла и он же позволял объяснить физически явление
отрыва струй. С точки зрения развиваемых здесь теорети-
ческих соображений роль пограничного слоя в выяснении
механизма обтекания тела жидкостью оказывается значи-
тельно сложнее: сверх всего отмеченного выше, погра-
ничный слой является своеобразным регуля-
тором процесса схода струй с крыла. Весьма
вероятно, что самый процесс квантования отходящих от
1) В. В. Голубев, К теории пограничного слоя, Юбилейный
сборник «Двадцать лет ВВА РККА им. Жуковского», 1942 [см. на-
стоящее издание, стр. 399 — 408].
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 445
крыла вихрей, образующих вихревые дорожки, вполне опре-
деляется условиями равновесия пограничного слоя, которых
мы в настоящее время не знаем.
Все изложенные выше теоретические соображения сей-
час же позволяют получить и формулы, дающие величину
тяги. Прежде всего, нетрудно показать, что этот метод,
который применил Карман для решения задачи о сопроти-
влении, применяется и для вычисления тяги машущего крыла,
поэтому и окончательный результат получится почти совер-
шенно такой же. Карманом дана для величины силы сопро-
тивления такая формула:
Г = р/У2 [о,794 £ — 0,314
В настоящем случае отличие будет в том, что и — ско-
рость, образуемая действием вихрей дорожки, — изменит
знак, так как направление вращения вихрей, а следовательно,
и направление создаваемого этими вихрями течения — про-
тивоположное; точно так же изменит знак и сила W, так
как в настоящем случае сопротивление заменяется тягой.
Отсюда мы получаем для силы тяги следующее выражение:
Т = — p/V2 [о,794 4- 0,314 .
В дальнейшем, однако, оказывается, что определение
силы тяги значительно проще определения
силы сопротивления. В самом деле, скорость zz0 опре-
деляется через интенсивность вихрей дорожки Кармана у по
формуле
Т At, h*
“°-2/th I '
В случае определения величины сопротивления мы в н а-
стоящее время не имеем никаких надежных
теоретических путей для определения вели-
чины y’» эта весьма тонкая задача, несомненно, связана
с вопросом об устойчивости вихревого пограничного слоя.
А отсюда следует, что формула Кармана не дает возмож-
ности полного теоретического определения величины сопро-
тивления. Развитые выше теоретические соображения позво-
446
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
ляют очень просто определить величину у в случае машу-
щего крыла. Она определяется по формуле
у = cos 9.
Отсюда легко получить и окончательное выражение силы
тяги
т = — l,76PZ>wVcos 9 [14-0,25-^ cos 6^
Все предыдущие выводы получены в предположении, что
образовавшаяся сзади машущего крыла вихревая дорожка
удовлетворяет условиям устойчивости. В общем случае любой
дорожки получим формулу более общую:
2Лл Х1 Лл j hn hit -
—th -т--II , — th -у-1
m L I 1 i w n h I I
тгр w | V I Q hn hit
rthT I 2Tth--1
cos 9.
Как показывает самая структура формулы, сила тяги
может обратиться в нуль или даже изменить знак. Инте-
ресно отметить, что отсутствие силы тяги у машущего
крыла наступает только при режимах, далеких от выполне-
ния условий устойчивости.
Возможность обращения в нуль силы тяги при наличии
вихревой дорожки объясняет, может быть, тот трудно меха-
нически объяснимый факт, что взмахами крыльев можно дер-
жаться в воздухе без поступательной скорости, как это
можно наблюдать при полете стрекоз и, в течение весьма
непродолжительного времени, у птиц, которые, работая
крыльями, могут держаться на одном месте. Необходимостью
для образования силы тяги выполнения режима, во всяком
случае близкого к выполнению условий устойчивости, по-
видимому, объясняется тот хорошо известный всем охотни-
кам факт, когда дичь, вспугнутая выстрелом, пытаясь уйти
из-под обстрела, начинает с чрезвычайным усилием судо-
рожно махать крыльями, но этим не увеличивает скорости
полета. С рассматриваемой здесь точки зрения это объяс-
няется тем, что она выходит при этом из условий полета,
создающих тягу.
Подведем теперь некоторые итоги. Как оказалось, задача
определения силы тяги машущего крыла привела нас к двум
ТЕОРИЯ МАШУЩЕГО КРЫЛА И ОБЩАЯ ПРОБЛЕМА ТЯГИ 447
в известном смысле противоположным задачам: определения
силы тяги и определения величины сопротивления. Мы теперь
можем несколько пополнить те соображения, которые лежат
в основе струйной теории сопротивления Рэлея. Мы видели,
что эту теорию приходится отвергнуть, как не согласую-
щуюся с опытом; она дает чрезвычайно заниженную сравни-
тельно с опытными данными силу сопротивления. Нетрудно
теперь указать и физические причины этого. Мы видели,
что в этой теории принимается, что на границе раздела
движущаяся масса жидкости скользит по неподвижной, как
по какой-то совершенно гладкой и твердой стенке. Но такое
представление о поверхности раздела в применении
к жидкости или газу лишено всякого физического смысла.
В жидкости или газе поверхность разрыва
скоростей может мыслиться только как вих-
ревой слой; бенар-кармановские вихревые дорожки и
представляют собой такой вихревой слой, распавшийся
в силу неустойчивости на отдельные вихри. Но тогда,
в частности, получается тот вывод, что на образование вих-
рей, заменяющих поверхности разрыва скоростей, необхо-
дима добавочная затрата энергии, которая может быть полу-
чена только за счет увеличения сопротивления; вот этой
последней части сопротивления и не может, естественно,
учесть струйная теория.
Мы вернемся теперь к общей теории сопротивления. Во
всем предыдущем мы не рассматривали влияния концов обте-
каемого тела и концов крыла; выражаясь языком механики,
мы рассматривали задачу тяги и сопротивления в плоско-
параллельном потоке. Перейдем теперь к пространственной
задаче.
Представим себе, что мы имеем некоторое тело, обте-
каемое потоком. За этим телом также образуется зона гидро-
динамической тени, и, следовательно, сюда можно перенести
все предыдущие рассуждения. Впервые Н. Е. Жуковский попы-
тался построить вихревую теорию сопротивления для этого
случая. По всей вероятности, идеи этой теории возникли
у него в связи с его работами по вихревой теории пропел-
лера. Как известно, эта теория основана на том, что сзади
вращающегося винта образуется система вихрей, которую
упрощенно можно представить в виде вихревого цилиндра
448
и. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и вихри, расположенные
L L L
Рис. 17.
(рис. 17), причем на нем вихри расположены по образую*
щим и по окружностям L, L, ... и, кроме того, образуется
осевой вихрь Г. Мы не будем рассматривать осевой вихрь
по образующим цилиндра, так
как все они не дают тяги, а
создают только вращение среды,
заключенной сзади винта.
Рассмотрим вихри, располо-
женные на окружностях L, L, .. .
Очевидно, что они создают внутри
цилиндра добавочную скорость,
направленную от винта, т. е. соз-
дают отбрасывание воздуха прочь
от винта назад, а потому в силу
реакции винт получает тягу
вперед.
Если, с другой стороны, рассмотреть тело, например круг-
лый диск, обтекаемый потоком, то видим, что за ним обра-
зуется система вихрей, представляющих собой распад по-
граничного слоя, образующегося на обтекаемой пластинке.
За обтекаемым телом также образуется вихревая поверхность,
аналогичная поверхности за винтом, образованной вихрями
L, £,..., но направление вращений в этих вихрях обратно
направлению вращений вихрей за винтом, а потому и созда*
ваемая ими добавочная скорость течения направлена теперь
против скорости (рис. 18). Результатом этого является
образование силы по направлению течения потока, т. е.
силы сопротивления. Такова вихревая схема явления.
К сожалению, в настоящее время из этой вихревой
схемы не только не удалось получить теорети-
ческим путем величину силы, сопротивления,
но даже мы не имеем сколько-нибудь ясной
картины распределения скоростей за обте-
каемым телом. Здесь науке не удалось создать схемы,
сколько-нибудь удовлетворительно объясняющей процессы,
происходящие в природе. А между тем едва ли кому-нибудь
не ясно техническое значение этих исследований. Ведь
огромные мощности, создаваемые моторами современных
самолетов, и преодолевают в основном силы сопротивления,
образующиеся благодаря действию разнообразных вихревых
ТЕОРИЯ МАШУЩЕГО крыла и общая проблема тяги 449
систем, срывающихся с крыльев и фюзеляжа самолета. Изу-
чением всех этих вопросов мы и занимались в годы войны
в Институте механики МГУ.
В предыдущем мы неоднократно видели, что эти иссле-
дования в различных направлениях связываются с теми
идеями, которые мы находим в трудах нашего знаменитого
Рис. 18.
основоположника современной технической аэромеханики,
«отца русской авиации», Н. Е. Жуковского. И не только
в научных идеях мы пытаемся продолжать научные тради-
ции Н. Ё. Жуковского. Мы пытаемся их культивировать и
продолжать и в методе исследования. Всей своей блестящей
научной деятельностью Н. Е. Жуковский показал, какую
ведущую, основную роль играет в механике ясная физиче-
ская схема, точно поставленный эксперимент. Его научное
творчество показало, что механика есть, прежде всего,
естественная наука, задачей которой является изучение
одного из простейших явлений природы, изучение движения
материи. Этой сущностью механики, как науки естествен-
ной, науки о природе, определяются сполна и задачи, и
метод механики.
Пусть же те результаты о механизме образования тяги,
наблюдаемом везде в природе, в полете птиц и насекомых,
которые я имел честь и удовольствие в общих чертах изло-
жить здесь перед вами, послужат скромной данью глубокого
450
11. ТРУДЫ ПО ТЕОРИЙ МАШУЩЕГО КРЫЛА
уважения к деятельности нашего замечательного естество-
испытателя, президента Академии наук Союза ССР, В. Л. Ко-
марова, знаменательную дату славной деятельности которого
мы отмечаем на настоящей сессии.
ТЯГА МАШУЩЕГО КРЫЛА 9
В современной гидро- и аэромеханике исследования по
вопросам неустановившегося движения занимают, несомненно,
одно из центральных мест. Самые разнообразные и весьма
актуальные задачи современной авиации, как теория фигур-
ных полетов, влияние отдельных порывов ветра на летящий
самолет, влияние восходящего потока воздуха, учет разно-
образных колебаний крыла, начиная с теории машущего
крыла и кончая различными явлениями вибрации крыла,
работа гребных винтов, представляют частные задачи тео-
рии неустановившегося движения жидкости. Практическая
важность исследований в этой области привела к появлению
очень большого числа работ, в частности, в СССР мы имеем
за последнее десятилетие ряд превосходных работ по не-
установившемуся движению. На одной из сессий АН СССР
несколько месяцев тому назад мы слышали интересный до-
клад члена-корреспондента АН СССР А. И. Некрасова,
в котором были даны обзор и анализ многочисленных иссле-
дований по теории крыла в нестационарном потоке.
Настоящий доклад, посвященный той же области, ставит
гораздо более скромную цель — изложить здесь соображе-
ния, лежащие в основе методов решения одной частной
задачи теории периодических движений крыла.
В октябре 1944 г. я имел честь доложить на заседании
общего собрания АН СССР некоторые самые общие физи-
ческие соображения, лежащие в основе предлагаемой те-
ории; целью настоящего доклада являются обоснование
этих соображений и частные выводы, к которым они при-
водят.
1) Доклад на сессии Отделения технических наук АН СССР
11—12 января 1946 г. Опубликовано в Изв. АН СССР, Отд. техн,
наук, № 5, 1946. (Прим, ред.)
ТЯГА МАШУЩЕГО КРЫЛА
451
В современной гидромеханике теория крыла является
вполне сложившейся частью ее, изучающей плавное обтека-
ние тел с многозначным потенциалом, причем во всей теории
основную роль играет циклический период, характеризую-
щий многозначность потенциала, — величина циркуляции ско-
рости вокруг крыла. Определение величины циркуляции
основывается на экспериментальном положении, состоящем
в том, что при плавном обтекании крыла задняя острая
кромка крыла является линией схода струй. Это положение,
так называемый постулат Чаплыгина — Жуковского, является
основой всей современной теории крыла. Однако физическая
сущность этого постулата в настоящее время не является
вполне ясной; можно думать, что этот постулат есть кос-
венный учет влияния вязкости в современной теории крыла,
построенной, исходя из теории идеальной, т. е. совершенно
лишенной вязкости, среды.
Как подсказывают подсчеты, величина циркуляции, через
которую выражаются величины сил, действующих на крыло,
зависит частью от формы крыла, частью от скорости набе-
гающего на крыло потока и от ориентировки крыла отно-
сительно потока (угол атаки). Отсюда получается чрезвы-
чайно важное для всей теории крыла в нестационарном
потоке следствие: при изменении скорости потока или при
изменении угла атаки, вообще говоря, изменяется величина
циркуляции вокруг крыла, если выполняется постулат Чап-
лыгина — Жуковского.
С другой стороны, в силу одной из основных теорем
теории вихрей, теоремы Томсона, в идеальной жидкости
циркуляция по одному и тому же материальному контуру
не меняется во время течения (принцип сохранения цирку-
ляции). Примирение этих двух взаимно противоречащих по-
ложений в теории крыла достигается тем, что при измене-
нии циркуляции вокруг крыла на какую-нибудь величину
от крыла в обтекающей среде отходит вихрь с циркуляцией,
равной и по знаку противоположной величине изменения
циркуляции вокруг крыла. Таким образом, суммарная цир-
куляция по материальному контуру, охватывающему крыло
и отошедший от него вихрь, остается постоянной, как и
требует теория Томсона. Заметим здесь, что самое образо-
вание отходящего от крыла вихря физически невозможно
452
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
в идеальной жидкости, т. е. без учета сил вязкости; сле-
довательно, выполнение теоремы Томсона возможно только
при учете вязкости среды. В настоящее время наиболее
удобным средством теоретического учета сил вязкости
является так называемая теория пограничного слоя; с точки
зрения этой теории, отходящие вихри представляют собой
распад завихренного пограничного слоя. Такого рода отхо-
дящие вихри можно наблюдать чрезвычайно ясно на опыте;
есть, например, прекрасные киносъемки, показывающие
образование отходящих вихрей при начале движения крыла
(так называемый начальный вихрь).
Следствием всех приведенных выше рассуждений является
то, что в идеальной жидкости, в которой нигде не про-
является сил вязкости, современная циркуляционная теория
крыла не имеет места: в ней при плавном обтекании тела
ничего, кроме парадокса Даламбера, не получим. С точки
зрения современных физических представлений, такой идеаль-
ной жидкостью является жидкий гелий; с точки зрения раз-
виваемых здесь взглядов, в жидком гелии нет никаких сил
Жуковского, течение — бесциркуляционное и в точности
выполняется парадокс Даламбера. Вполне понятно, что
было бы весьма интересно проверить на опыте полученные
заключения.
Предыдущие соображения приводят к тому выводу, что
при непрерывном изменении скорости полета или угла атаки
с крыла непрерывно сходят вихри; эти вихри затем уносятся
потоком и образуют за крылом непрерывную вихревую
пелену р]. Так как вихри, непрерывно распределенные по
поверхности, создают увеличение скорости течения, с одной
стороны, и уменьшение—с другой, эта поверхность является
поверхностью разрыва скоростей. Такие поверхности разрыва
скоростей фигурируют во всех исследованиях по движению
крыла в нестационарном потоке с изменяющейся циркуляцией.
Присутствие вихревых поверхностей разрыва скоростей
создает исключительные трудности для всей теории крыла
в нестационарном потоке. Образующие ее вихри влияют и
на крыло, и друг на друга. Влияние этих вихрей друг на
друга ведет вообще к распаду пелены, так как можно
показать, что подобные вихревые образования неустойчивы;
распад вихревой пелены приводит к образованию некоторой
ТЯГА МАШУЩЕГО КРЫЛА
453
системы дискретных вихрей. Влияние вихрей на крыло сво-
дится к тому, что вихри изменяют скорость вокруг крыла,
что чрезвычайно осложняет вычисление действующих на
крыло сил. Поэтому в теоретических исследованиях, посвя-
щенных движению крыла в нестационарном потоке, прихо-
дится вносить те или иные упрощающие задачу предполо-
жения. Обычно эти упрощения идут в двух направлениях.
Во-первых, указанные выше трудности отпадают, если
при неустановившемся движении циркуляция благодаря под-
ходящей комбинации условий движения крыла остается по-
стоянной. Подобные случаи отметил впервые С. А. Чаплыгин
в 1926 г.; впоследствии ими занимался ряд других ученых.
Несмотря на очень большой теоретический интерес подоб-
ных изысканий, необходимо помнить, что они носят совер-
шенно частный характер; изменение циркуляции есть, конечно,
наиболее характерный факт в неустановившемся движении,
и, отказываясь от его рассмотрения, мы, по существу, в этой
задаче «выплескиваем из ванны вместе с водой и ребенка».
Во-вторых, можно сделать упрощающие предположения
относительно формы отходящей вихревой пелены; так, на-
пример, в теории вибраций крыла ввиду малости амплитуд
колебаний предполагается, что вихревая пелена есть пло-
скость. Это предположение, не очень убедительное и при
малых амплитудах, но при волнах не очень пологих уже
совершенно недопустимо в случае больших амплитуд коле-
бания, которые мы имеем в задаче о машущем крыле.
В результате всего этого в случае нестационарного течения
вокруг крыла с изменяющейся циркуляцией в теоретических
исследованиях мы имеем почти исключительно результаты,
относящиеся к случаю бесконечно малых колебаний, что
чрезвычайно ограничивает задачу.
Я хотел бы здесь подчеркнуть, что отмеченные выше
трудности носят не математический, а чисто фи-
зический характер. Дело состоит в неясности
самой физической схемы, которой можно
было бы стилизовать процесс, происходящий
при взмахах крыла, и недостаток этой физической
схемы не может быть заменен никакими дифференциальными
или интегральными уравнениями или другими математическими
средствами, как бы сложны они не были.
454
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Теория, которую я попытаюсь здесь изложить, основана
на некоторой физической схеме явления машущего крыла,
совершенно отличной от указанной выше. Мы при этом
ограничимся случаем машущего крыла, несколько искус-
ственным, но более четко передающим основную физическую
схему явления: мы предположим, что скорость поднятия
крыла w и скорость его опускания —w остаются в тече-
ние поднятия и опускания постоянными; в дальнейшем легко
убедиться, что та же схема, без всяких изменений, может
быть положена в основу теории машущего крыла и в общем
случае, когда w меняется по любому закону.
Физическая гипотеза, положенная в основу настоящей
теории, состоит в следующем: при взмахах крыла от
него не отделяется непрерывная вихревая
пелена, но в верхних и нижних точках ампли-
туды колебания от крыла отходят вихри, кото-
рые и образуют позади крыла двойную вихре-
вую дорожку типа дорожек Бенара — Кармана.
Нам нужно прежде всего показать, каким образом при
такой физической схеме можно удовлетворить и постулату
Чаплыгина — Жуковского, и теореме Томсона. Дело в том,
что отходящие от крыла вихри дорожки изменяют скорость
в точках поверхности крыла и,
следовательно, непрерывно изме-
няют при выполнении постулата
Чаплыгина—Жуковского вели-
чину циркуляции, что в свою
очередь должно было бы вызвать
yi непрерывный сход вихрей, т. е.
^4--^ мы опять возвращаемся к схеме
вихревой пелены.
/ Выход из создавшегося за-
труднения может быть найден
в учете влияния вязкости. Чрез-
вычайно удачная мысль Прандтля
свести действие вязкости к
Рис- воздействию пограничного слоя
приводит с кинетической точки
зрения к тому, что пограничный слой можно рассматривать
как завихренную зону идеальной жидкости. Таким образом,
;гяРа Машущего крыла
455
крыло находится не только под воздействием потока, но и под
воздействием непрерывно распределенных вихрей, заполняю-
щих пограничный слой. Применим теперь метод, ставший
трафаретным в теории крыла: отобразим область течения на
внешнюю часть круглого цилиндра вспомогательной пло-
скости комплексного переменного (z) (рис. 1); пусть при
этом задней кромке крыла соответствует точка z = R. При
таком отображении завихренный пограничный слой вокруг
крыла перейдет в завихренный слой S около поверхности
цилиндра.
Применяя обычный метод рассуждения, получим следую-
щее уравнение, которому в настоящем случае удовлетворяет
характеристическая функция обтекания цилиндра
w (z)-= Ve( z 4- 4- JL In z
z — re^
z-y-e’f1
dxdy, (1)
где!/ — скорость в бесконечности, 9 — образованный ею угол
с осью х, Г — циркуляция вокруг цилиндра, ге&— аффикс
точки завихренной зоны с вихревой плотностью а.
Как известно, выполнимость постулата Чаплыгина — Жу-
ковского приводит к требованию, чтобы скорость в точке
z = R на цилиндре была равна нулю, т. е. чтобы выполня-
лось уравнение
1 f Г Г2 — /?2
--° “9------------............dX dy = О,
J J г2 — 2rR cos ? + Z^2 л
s
откуда для циркуляции вокруг крыла Г получим выражение
г = -О + J Jс ЧхЛу. (2)
Эта формула отличается от обычно применяемой (без
учета вихрей пограничного слоя)
Г = — 4nRV sin 9
456
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
членом
По —2————। • dx dy. (3)
г2 — 2r R cos ср + R% v 7
Таким образом, обычный вывод величины циркуляции
требует, чтобы выражение (3) было равно нулю, что не
требует о = 0, т. е. отсутствия вихревого пограничного
слоя.
Как показывает уравнение (1), вихри пограничного слоя
сами не дают циркуляции, так как входят попарно с интен-
сивностью -|-о и —о; но они влияют на величину циркуля-
ции косвенно благодаря выполнению постулата Чаплыгина —
Жуковского, так как они влияют на положение точки схода.
Уравнение (2) показывает, что при изменении V и 9 цир-
куляция Г может оставаться постоянной, если изменение V
и 6 компенсируется соответствующим изменением о, т. е.
завихренности пограничного слоя.
Уравнение, аналогичное (2), можно написать и для слу-
чая, когда около крыла имеем один или несколько отходя-
щих вихрей. Аналогичное рассуждение приведет нас к за-
ключению, что влияние отходящего вихря на величину цир-
куляции может быть компенсировано соответствующим
изменением завихренности пограничного слоя, так что,
с одной стороны, будет выполняться постулат Чаплыгина —
Жуковского (в силу выполнения уравнения (2)), а с другой
стороны, будет выполняться теорема Томсона (в силу по-
стоянства Г). Очевидно, что такая компенсация изменения
течения изменением пограничного слоя возможна только до
тех пор, пока эти изменения не вызовут распада погранич-
ного слоя.
Таким образом, положенная в основу рассматриваемой
теории гипотеза состоит в следующем: при переходе крыла
из верхней точки амплитуды колебания в нижнюю и обратно
влияние отходящих вихрей на положение точки схода при
постоянном Г компенсируется соответствующим изменением
структуры пограничного слоя, так что выполняется посту-
лат Чаплыгина — Жуковского; при этом соответствующее
изменение пограничного слоя достаточно мало, так что не
вызывает его распада. В крайних точках амплитуды коле-
бания вследствие резкого изменения условий обтекания (угла
ТЯГА МАШУЩЕГО КРЫЛА
457
атаки) такая компенсация становится невозможной и погра-
ничный слой распадается, выделяя отходящие вихри.
С этой точки зрения пограничный слой при колебаниях
крыла не распадается непрерывно, выделяя все новые и
новые вихри, образующие вихревую пелену; распадение
пограничного слоя происходит отдельными каплями, кван-
тами, в верхней и нижней точках амплитуды; при пере-
ходе же крыла из одной крайней точки в другую в погра-
ничном слое образуется набухание этих капель, которые
при достаточной скорости взмахов отрываются в крайних
точках амплитуды колебания.
Следовательно, пограничный слой, т. е. вяз-
кость жидкости, является своеобразным регу-
лятором, позволяющим одновременно вы-
полняться и теореме Томсона и постулату
Чаплыгина — Жуковского.
Совершенно понятно, что если бы мы знали точно,
при каких условиях сохраняется равновесие пограничного
слоя, то мы могли бы точно указать, когда из него будут
выделяться вихри, и, следовательно, не понадобилось бы
делать никаких дополнительных физических гипотез, в част-
ности, не понадобился бы и постулат Чаплыгина — Жуков-
ского. К сожалению, несмотря на огромное количество работ
по пограничному слою, об условиях
его устойчивости мы почти ничего не
Принятая нами гипотеза позволяет
определить все элементы получающейся
сзади крыла вихревой дорожки. Дей-
ствительно, пусть и 02 — углы атаки V
при опускании и при поднятии крыла Рис. 2.
и 1\ и Г2 — соответственно циркуля-
ции крыла при опускании и при поднятии его. Тогда, замечая,
что при опускании крыла относительная скорость w направ-
лена вверх и дает увеличение угла атаки на arctg— (рис. 2),
по известной формуле получим выражение циркуляции в виде
1\ = — nbVV2+w2 sin + 9Х -f- arctg .
458
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Точно так же при поднятии крыла, когда относительная
скорость направлена вниз, получим уменьшение угла атаки
w
на arctg — (рис. 3) и для циркуляции получим выражение
г2 = — ~ЬУ V2 4- w2 sin (у + 62 — afctg у).
где а — изогнутость скелета крыла.
Полученные формулы справедливы, если не учитывать
влияния отходящих вихрей; но в силу принятой выше физи-
ческой гипотезы они будут справед-
ливы и при наличии вихрей, так как
по принятой гипотезе циркуляция Г
не меняется, если неограниченно про-
должать опускание или поднятие кры-
ла, когда влиянием вихрей дорожки
можно пренебречь ввиду ее удален-
ности.
Отсюда следует, что в верхней точке амплитуды коле-
бания при переходе от поднятия к опусканию циркуляция
вокруг крыла изменяется на величину (Гх — Г2). Так
как в силу теоремы Томсона циркуляция по контуру, охва-
тывающему крыло, не меняется, то в верхней*точке амплитуды
колебания от крыла отходит вихрь
Т = -(ГХ-Г2).
Полагая = и ~2~ — в> у— = 8, из на-
писанных формул найдем:
у = 2тг£ cos a [V sin 8 + w cos 8]. (4)
Совершенно подобным же образом получим, что в нижних
точках амплитуды колебания от крыла отходят вихри с цир-
куляцией -—у.
Таким образом, за машущим крылом образуется двойная
вихревая дорожка с направлением вращения вихрей, указан-
ным на рис. 4; ширину дорожки можно считать равной
амплитуде колебания крыла в силу сделанной выше гипотезы.
ТЯГА МАШУЩЕГО КРЫЛА
459
Пусть период колебания крыла Т. Пусть zz0— скорость,
сообщаемая вихрям дорожки вдали от крыла ^семи другими
I
----------------——--------------6
---------------------j---------5-------
Рис. 4.
вихрями дорожки; тогда вдали от крыла имеем (рис. 4):
1 = (У+и0)Т, (5)
2й = wT. (6)
Так как из теории вихревых дорожек известно, что
= (7)
то в настоящем случае имеем, подставляя значение у,
uQ = к — cos о (V sin 8 -j- w cos 8) th ~. (8)
Из уравнений (5) и (6) имеем:
± =, (9)
~т \~г~~г\cos а [sin & + V”cos
или, принимая значения для случая устойчивости у =0,281
и th — = —— , найдем:
I V 2
-^-0,562
4=---------4-------------; (Ю)
0,35 cos a I sin о — cos о I
Из полученных уравнений следует, что
-р-> 0,562.
460
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Предыдущее показывает, что задача о вычислении силы
тяги машущего крыла оказывается проще задачи об опре-
делении вихревого сопротивления, решенной Карманом, так
как в задаче о вычислении величины вихревого сопротивле-
ния нет теоретических путей для определения величины
циркуляции отходящих вихрей.
Предлагаемая здесь физическая схема явления имеет
следующие преимущества перед схемой непрерывной вихре-
вой пелены (поверхности разрыва скоростей).
Во-первых, достаточно разработанная теория вихревых
дорожек позволяет исследовать вопрос об устойчивости их;
многочисленные теоретические исследования приводят к тому
заключению, что условия устойчивости, данные Карманом,
соответствуют вихревым образованиям, во всяком случае
более устойчивым, чем все другие вихревые конфигурации
подобного типа; то же самое подтверждают многочисленные
экспериментальные данные (Бенара и др.), которые давали
для реально существующих вихревых систем достаточно
точное согласие с теорией Кармана. Существование вихре-
вых дорожек позади машущего крыла было экспериментально
проверено в лаборатории Московского государственного
университета.
Во-вторых, полученная здесь схема применима, очевидно,
к различным типам изменения скорости w, так что самый
закон колебания может принимать разнообразные виды.
В-третьих, этот метод позволяет дать полное исследова-
ние динамической стороны задачи: определение сил, действую-
щих на машущее крыло. К этой задаче мы теперь и перейдем.
Как известно, в теории вихревого сопротивления ана-
логичная задача была решена Карманом при помощи при-
менения ’ теоремы о количестве движения (теоремы Эйлера).
Пожалуй, не мешает несколько остановиться на вопросе
о методах, пригодных для решения динамических задач
в теорий нестационарного движения.
Есть два метода решения динамических задач в теории
крыла. Один из них основан на применении общих теорем
динамики (теоремы количества движения), второй — на под-
счете непосредственно давления на элемент поверхности
тела; этим методом, весьма удобным в простейших случаях,
систематически пользовался С. А. Чаплыгин, которому и
ТЯГА МАШУЩЕГО КРЫЛА
461
принадлежит вывод первых общих уравнений теории крыла
в случае неустановившегося движения.
Несомненно, что методу, основанному на общих теоремах
механики, надо решительно отдать предпочтение во всех
задачах, где дело идет о течениях с отходом тех или иных
вихреобразований (линий раздела, дорожек и т. п.). Наличие
движущихся около крыла вихрей делает невозможным непо-
средственное определение скоростей и давлений на поверх-
ности крыла; этим в значительной степени и объясняется
весьма слабый Прогресс в теории неустановившегося движе-
ния. Метод, основанный на теореме об изменении количества
движения, требует знания течения на некотором расстоянии
от крыла, где поток всегда принимает более регулярную
форму, выравнивая те особенности, которые в него вносит
крыло при неустановившемся движении.
Заметим, кстати, что по методу подсчета сил давления
на элементы поверхности нельзя подсчитать давление даже
на плоскую пластинку при условии ее плавного обтекания.
В случае теории машущего крыла основные динамические
уравнения приобретают следующий вид. Непосредственное
применение теоремы количества движения к массе воздуха,
заключенной в контрольном объеме, построенном на пря-
моугольнике L (рис. 5), приводит к уравнениям
— X— j pdy = -^-t j Jpudxdy,
L S
— У+ j pdx = -^-t j Jpvdxdy,
L s
462
ri. труды rid теорий машущего йрь1ла
где Ху Yкомпоненты силы, действующей на крыло, И
S—площадь, заключенная между контуром L и про-
филем крыла. При этом производная по t во второй
части является субстанциональной производной, так как
относится не к геометрическому контуру, а к массе жидкости,
в нем заключенной. Учитывая это и замечая, что через
элемент контура L протекает за время dt количество жидкости
p(tidy— vdx)dt, приведем уравнения к виду
— Xdt — J*pdydt — d§ j*pzz dx dy-\-dt J\u dy — v dx) pu,
l s L
— Y dt-\- J*pdxdt — d§ Jpv dx dy + dt J\u dy — v dx)pv,
L S L
и отсюда после обычных преобразований и интеграции по t
в пределах периода получается основное уравнение
т
(r0 + ZX0)T=_±.j^ J — idy) —
0 L L
f f dw
J J -dtdxdy
s
где ср — потенциал скоростей и Хо, Уо— средние значения
компонентов сил за период. К решению этого основного
уравнения и сводится задача об определении сил, действую-
щих на крыло при любом периодическом течении.
Задача эта послужила предметом исследования ряда
математиков. На некоторых из этих исследований следует
остановиться, хотя почти все они относятся не к случаю
машущего крыла, а к случаю вихревого сопротивления,
где дело обстоит несколько проще. Вывод у ряда авторов,
повторяющих в основном Кармана, состоит в следующем.
Если бы не было образования вихрей внутри контроль-
ного прямоугольника, то для выражения сил надо было
использовать уравнение Чаплыгина — Блазиуса. Если мы
возьмем прямоугольник достаточно больших размеров, пере-
мещающийся с вихревой дорожкой, то на его поверхности
движение можно считать установившимся и, следовательно,
ТЯГА МАШУЩЕГО КРЫЛА
463
для вычисления давления можно применить формулу Лагранжа
У"2
в виде р + р-2" = С. С другой стороны, ввиду образования
за период Т пары вихрей количество движения внутри
контрольного прямоугольника увеличивается на количе-
ство руй, направленное против течения. Поэтому к силам,
получаемым по формуле Чаплыгина — Блазиуса для состав-
ляющей по направлению течения, надо еще добавить при-
ращение количества движения за единицу времени за счет
образования вихрей, равное
С точки зрения выведенной выше формулы получаем
в настоящем случае следующее.
Если взять подвижной контур L, движущийся со ско-
ростью вихревой дорожки, а размеры контура достаточно
большими, то по отношению к этим осям средний член
формулы (И) не войдет, так как уравнение Лагранжа надо
брать в форме для установившегося течения, т. е.
вместо
p+PdF + _2=;?0’
откуда и входит член, содержащий ср.
Итак, формула принимает вид
у т
(Ео-Ь/Хо) Т= —I J ^dxdy\ .
О L L & JO
(12)
Далее, замечая, что второй интеграл представляет собой
изменение количества движения внутри контрольного объема,
которое происходит благодаря выходу двух вихрей из него
за время Г, получаем, что составляющие по оси от обоих
слагаемых оказываются — Ру^о*)^ и РТ*» причем
второй член есть просто составляющая по оси х количеству
464
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
движения, унесенного парой вихрей; так как Т =
I
v—ue
то из полученных соображений получим формулу Кармана
Р7“ол)4-рт О'—«0)7.
или
Х=рт(у_2йо)4 + ^
(13)
Примерно так выводится формула Кармана у самого
Кармана в монографии Фукса — Хопфа и у Голубева
Опасность подобного рода рассуждений, не подкреплен-
ных подробным анализом уравнения (И), ясна из следующего
ошибочного рассуждения, принадлежащего Н. Е. Жуков-
скому l2L Так как на первый взгляд кажется, что измене-
ние количества движения за период внутри контрольного
объема жидкости, неподвижно связанного с обтекаемым
телом, сводится к выходу из него двух вихрей, уносящих
с собой количество движения, равное ру/г, что соответствует
изменению количества движения, равному
то Жуковский и принимает силу сопротивления равной
полученному выражению, т. е.
X=p-f(V-«0)4
вместо формулы (13). Ошибочность такого рассуждения
состоит в том, что не учитывается влияние добавочной ско-
рости uQ в полосе дорожки, направленной против течения
и создающей добавочное вытекание жидкости на сторонах
контрольного прямоугольника, параллельных направлению
течения, с соответствующим изменением количества движения.
Весьма тщательный анализ происходящих здесь явлений
дан в курсе Н. Е. Кочина и Н. В. Розе^, где путем кро-
потливого исследования изменения количества движения
получено данное выше выражение лобового сопротивле-
ния (13); при этом авторы не пользуются какими-нибудь
Общими формулами, аналогичными уравнению (11).
ТЯГА МАШУЩЕГО КРЫЛА
465
Приведенное выше ошибочное заключение Н. Е. Жу-
ковского показывает опасность рассуждений, аналогичных
приведенному выше рассуждению Кармана. Ненадежность
получаемых выводов ясна хотя бы из того, что выходящие
из контрольного объема вихри меняют, конечно, выраже-
но/
ние а потому не ясно, нужно ли к выражению
т
(* С fdw\2
р Jt \ I — \ dz еще добавлять член ру/г, так как соответ-
0 L
ствующее количество движения могло быть учтено и в пер-
вом члене.
Приведенное выше основное уравнение в форме (11),
по-видимому, было впервые использовано Сэйнджем также
в задаче о вычислении вихревого сопротивления. Однако
метод Сэйнджа может быть применен и к случаю машущего
крыла и вообще ко всем случаям периодических движений
крыла с вихревыми образованиями за ним, в то время как
все предыдущие методы, по-видимому, не могут быть при-
ложены в случае наличия отличной от нуля основной цир-
куляции вокруг крыла, по крайней мере если их не подвер-
гнуть весьма существенной переделке.
Однако вывод Сэйнджа содержит существенную ошибку.
Сэйндж берет контрольный прямоугольник, неподвижный
относительно обтекаемого тела, так что через его границы
за период уходит пара вихрей дорожек. Сейндж считает,
что выражение
[Ш^Г
L s Jo
силу периодичности движения равно нулю. Следовательно,
т
дело сводится к вычислению выражений dt dz и
о *
L
Остановимся на вычислении второго интеграла. Путем
весьма сложного и путаного расчета Сэйндж получает для
него значение у/г. Однако легко показать без всяких вычис-
лений, что этот интеграл равен нулю.
466
II. ТРУДЫ ПО ТЕОРИИ МАШуЩЕГО КРЫЛА
Действительно, пусть
[<р],+ Т = ? <*’ У> t + n-? (X, у, t) = f(x, у, t). (14)
Отсюда
д? (х, у, t-\-T)ду (х, у, t) _df_
дх дх дх9
но в силу периодичности течения в точке (х, у) при непо-
движных координатах
и (х, у, t + Т) — и (х, у, t) = О
или
д? (*> У,*+Т)ду (х, у, 0 п
дх дх
Итак, = О и аналогично= 0. Следовательно,
дх ду
В частности,
[<р if = /(0) = const,
а потому
j Wo(dx — idy) = 0.
L
Следовательно, из рассуждений Сэйнджа вытекает, что
т
(r0 + ZX0)T = -|J dt J(2)2rf2’
О L
т. е. при периодическом движении в среднем за период коле-
бания остается справедливой теорема Чаплыгина — Блазиуса,
а потому при правильном расчете, повторяя вычисления
Сэйнджа, мы получим вместо формулы (13) ее первый член,
так что ошибочные рассуждения Сэйнджа в известном
смысле обращают ошибку Жуковского.
Весьма вероятно, что ошибка Сейнджа, помимо неправиль-
ного вычисления интеграла J [<p]^(Jx—i dy), заключается еще
L
ТЯГа Машущего крь1лА
4б?
6 неправильном предположении, что
= 0,
вследствие чего не учитывается количество движений, уно-
симое парой выходящих из контрольного прямоугольника
вихрей.
Однако при весьма малом изменении метода, применяемого
Сэйнджем, легко получить формулу для вихревого сопро-
тивления и силы в случае машущего крыла.
Чтобы избежать трудностей, связанных с учетом влияния
на величину интеграла особых точек, проходящих за период Т
через контрольную поверхность, достаточно взять контроль-
ный прямоугольник не неподвижный, а движущийся вместе
с вихревой дорожкой; при этом, как оказывается, чрезвычайно
упрощается и вычисление интеграла —idy), кото-
рый в настоящем случае не равен нулю. Таким образом,
получим прием вычисления, в известном смысле соединяющий
метод Сейнджа и метод, используемый Н. Е. Кочиным и
Н. В. Розе.
Если взять прямоугольник со сторонами 2Н2 по направ-
лению течения и 2Н перпендикулярно к нему, то подсчет
дает следующие значения для интегралов:
468
II. ТРУДЫ ПО ТЁОРИИ МАШУЩЕГО КРЫЛА
и отсюда, подставляя в основное уравнение (И), получим:
Ко + /Ло = Р«оГ-1] —
^^*4 I t ъ J
-рГ(Г+«0)-ф/ + 0Ш;
\нгГ
переходя к пределу при Н-+оо<, получим:
ro + /Xo = -pVr-i[g/j^th^-l) + ^(V + «o)]>
откуда
(16)
r0 = -pvr. J
Заметим, что при отсутствии основной циркуляции вокруг
обтекаемого тела
— idy) = Q
L
в силу уравнения
(x + l,y,t+T)_ д? (х, у, /) 7
дх — дх
выполняемого при неподвижных осях, и, следовательно,
(хь yt> /+ 7) = d? (xt, уь /)
дх дх
при подвижных осях; это и согласуется с уравнением (14).
Так как
7 xt, h™
ий — 2Z th -j-,
то уравнение (16) можно еще написать в виде
*о = ^~^ + 2«о). (18)
Эта формула отличается от формулы Кармана переменой
знака у у и zz0, как и нужно ожидать по формуле вихревой
дорожки.
ТЯГА МАШУЩЕГО КРЫЛА
469
Подставляя сюда по условиям устойчивости дорожки
у = 0,281, 7 =
получим:
X» = — р/У2 |^о,314 + 0,794 (-^-)] (19)
аналогично формуле Кармана для сопротивления
X0 = plV2 [0,794 (-р) — 0,314(-^у],
получаемой из (19) изменением знака у zz0.
Для случая тяги выгоднее написать ее величину через
конструктивные и кинематические данные. Полагая
у = 2izb cos о (V sin 3 —|— w cos 8)
и
uQ — у cos о (V sin 8 + w cos 8) th ,
при условиях устойчивости получим:
XQ = — 1,76 p#V2 cos о f sin 8 -- :osS) X
\ V f
X p -И0,25— coso (sin 8-|- -^cosS^j. (20)
Так как
то окончательно
Хо= — 0,94 pW2 cos a (sin 8+ у cos8)( 1 + 1,2 pr). (21)
Наконец, формула (15) дает подъемную силу
Уо = —pVT0,
что вполне соответствует теореме Жуковского; при этом
Г = — itbV sin о (cos 8 — у sin 8^. (22)
4?0
II. ТРУДЫ ПО ТЕОРИЙ МАШУЩЕГО КРЫЛА
Мы закончим рассмотрение этого вопроса некоторыми
замечаниями о происхождении тяги от «подсасывания» у пе-
редней кромки.
Хорошо известно, что «подсасывающие силы» представ-
ляют собой силы, необходимые для выполнения теоремы
Жуковского. Например, если не учитывать «подсасывающей
силы» у пластинки, то при обтекании действие потока
сведется к силе R, нормальной не к скорости потока вдали
от пластинки, а нормальной к пластинке: появление «под-
подъеме. Если взять
х Qi —
колебания Q = 9— -
сасывающей силы» Q ведет к тому,
что результирующая сил R и Q и
дает силу Жуковского Р. Таким
образом, «подсасывающие силы»
просто являются выполнением тео-
ремы Жуковского (рис. 6).
Так как при взмахах крыла на-
правление результирующей скорости
меняется при подъеме и опускании
крыла, то поочередно появляется тя-
нущая составляющая силы Жуков-
ского (рис. 7) при опускании и
сопротивление Q2 (рис. 8) при
среднее значение тяги за период
то получим силу тяги, выражаемую
формулой
Q = rcpftw2 COS0.
Если сравнить величину Q с ранее найденным выраже-
нием силы XQ, то окажется, что Q> Хо; это станет понятным,
ТЯГА МАШУЩЕГО КРЫЛА
471
если заметить, что отходящие вихри увеличивают скос потока
при опускании и уменьшают его при поднятии.
В заключение заметим, что углы атаки и 02 лимити-
руются величиной критического угла профиля. Так как действи-
тельные углы атаки при опускании и при поднятии крыла
соответственно равны
614-arctgy и 92 — arctgp:,
то отсюда следует, что допустимый без отрыва струй угол
атаки 0Х при опускании меньше, чем угол 02 при поднятии;
при этом получается даже, что при опускании 0Х < 0. Это
обстоятельство, возможно, и создает иллюзию отгребания
крылом потока воздуха назад.
Если учесть свободный полет крыла, то, вообще говоря,
получим, что при опускании крыла центр тяжести летящей
системы поднимается, а при подъеме крыла опускается;
отсюда легко показать, что средняя величина подъемной
силы должна быть равна весу летящей системы, если в сред-
нем полет совершается на одной и той же высоте.
Дальнейшее развитие этих соображений позволяет рас-
считать максимальную возможную силу тяги. При этом
получается следующий результат. Пусть 1% есть критический
угол атаки крыла, т. е. максимальный угол, при котором
возможно обтекание без срыва; пусть 0о есть угол атаки,
при котором при скорости полета V крыло дает подъемную
силу, достаточную для поддержания аппарата в воздухе.
Тогда оказывается, что максимальная тяга выражается фор-
мулой
^ах = -^(91-»о)2 4-
Рассмотрим разность между наибольшей возможной
подъемной силой и силой, достаточной для поддержания
летящего аппарата в воздухе,
0L + _|_»0 ) = (Р, — ,%) .
Эта величина до известной степени аналогична запасу
плавучести корабля; ее можно назвать для самолета запа-
сом подъемной-силы. Из предыдущего следует, чтр
472
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
крыло самолета может развивать тягу только в том случае,
если оно обладает запасом подъемной силы; если же запаса
подъемной силы нет, то при взмахах крыла самолет будет
терять высоту, т. е. падать вниз.
Все предыдущие выводы сделаны в предположении
существования вихревой дорожки за машущим крылом; сле-
довательно, эти выводы предполагают устойчивость вихревых
дорожек. Нетрудно показать, что условия устойчивости
налагают зависимость периода колебаний при заданных V
и w от размера хорды.
Действительно, мы видели, что
-^> 0,562.
С другой стороны,
„ у-0’562
0,35 cos с ^sin о + cos
Следовательно, по данным у , а = y-f- g-- и ° = 2—
мы можем найти по b величину амплитуды h, а затем и I
из уравнения
4=о’281-
Так как, с другой стороны,
uQ = cos □ (V sin В 4“ w cos В) th ~,
то по данным th^- = —и 4* = 0,281 найдем и, сле-
Z /2 Z
довательно, период Т (или число колебаний крыла в секунду N)
найдем по формуле
т 1 ___ I
1 N V+uQ'
В качестве примера, иллюстрирующего полученные выводы,
рассмотрим следующий частный случай. Пусть а = 0, 8 = 0,
ТЯГА МАШУЩЕГО КРЫЛА
473
о = 15° и V — 18 км!час — 5 м!сек. Тогда имеем следующие
результаты:
Т = 0’6 ь 0,5 м 0,1 м 0,01 м
т 1,8 сек 0,36 сек 0,036 сек
N 0,55 2,8 28
^ = 07 т 0,51 сек 0,1 сек 0,01 сек
N 2 10 100
II Т 0,17 сек 0,03 сек 0,003 сек
N 6 33 333
Таким образом, для крыла определенного размаха и при
заданных скоростях w и V получаем совершенно опреде-
ленное число колебаний W, которое увеличивается с умень-
шением размеров крыла; в то время как крылья большие
совершают взмахи сравнительно медленно, число колебаний
при b м-алом очень велико. Взмахи крыльев крупных птиц
сравнительно медленные, но, с другой стороны, быстрое
колебание крыльев насекомых (например стрекоз и т. п.),
по-видимому, подтверждают эти выводы.
Этими общими замечаниями о режиме полета мы и закон-
чим рассмотрение вопросов, связанных с образованием тяги
машущего крыла.
Развитые выше соображения далеко не ограничиваются
приложениями к теории машущего крыла. Создание Н. Е. Жу-
ковским и С. А. Чаплыгиным вихревой теории подъемной
силы и замечательные работы Н. Е. Жуковского по вихре-
вой теории гребных винтов показали совершенно исключи-
тельное значение вихревых движений в природе и в различных
474 И. ТРУДЫ ПО ТЕОРИЙ МАШУЩЕГО КЙЫЛА
технических приложениях. Можно думать, что разно-
образные приложения найдет и весьма частный вид вихревых
движений — более или менее устойчивые вихревые образова-
ния в форме вихревых дорожек. Счастливая мысль Кармана
подвергнуть систематическому изучению, с точки зрения их
устойчивости, двойные вихревые дорожки и приложить их
к объяснению возникновения сил сопротивления при течении
жидкости вокруг плохо обтекаемых тел открыла широкие
возможности для применения подобных же соображений
к ряду других механических явлений, среди которых нахо-
дится задача об определении тяги машущего крыла.
Заканчивая свой доклад, я хочу показать, что в природе
и в технике существует ряд явлений, механическое объяс-
нение которых и их теория, по-видимому, самым тесным
образом связаны с теорией вихревых дорожек. Я здесь оста-
новлюсь на ряде задач, связанных с образованием тяги при
плавании.
Простейшим примером является образование силы тяги
у лодки при гребле веслами. На первый взгляд механиче-
ская картина явления кажется совершенно ясной: при гребле
мы захватываем лопаткой весла некоторое количество воды и,
отбрасывая его назад, создаем, с точки зрения теоремы
количества движения, необходимое для образования силы
тяги, направленное назад количество движения. Однако более
внимательное рассмотрение явления показывает, что оно сов-
сем не так просто. Действительно, образование силы тяги
за счет отброса назад некоторого количества жидкости мы
имеем, например, в случае работы гребного винта, позади
которого образуется отбрасываемая струя жидкости. Между
тем. в случае работы весел мы не имеем никакой отбрасы-
ваемой назад непрерывной струи; наоборот, если мы построим
около лодки контрольную поверхность, то через ее границы
'будут выходить вихри жидкости, присутствие которых мы
и наблюдаем всегда позади лодки. Каждая пара таких вих-
рей уносит назад количество движения, определяемое фор-
мулой
Q~^h,
где р —плотность жидкости, у —циркуляция вихря, h — рас-
стояние между вихрями и Q—уносимое вихрями количество
ТЯГА МАШУЩЕГО КРЫЛА
475
движения. Механически совершенно ясна и самая картина
образования вихрей у конца лопасти весла благодаря обра-
зованию разрыва скоростей.
Вихревую картину, еще более приближающуюся к вихре-
вой схеме, которую имеем при образовании вихревого сопро-
тивления и по изложенной выше теории, и в случае тяги
машущего крыла, мы имеем в случае образования пропуль-
сивной силы у лодки при работе кормовым веслом, как это
часто применяется у рыбачьих лодок. Здесь в результате
действия кормового весла позади лодки образуется типичная
двойная вихревая дорожка с шахматным расположением вих-
рей и с направлением их вращения, противоположным тому,
которое имеет место в дорожках Бенара — Кармана позади
плохо обтекаемых преград. С точки зрения образования
силы тяги получаемая здесь вихревая схема полностью
совпадает с тем, что мы имеем в случае машущего
крыла.
Наконец, чрезвычайно близко к работе кормового весла
стоит механизм образования силы тяги при работе хвоста
рыб. Мы имеем в СССР исследования В. В. Шулейкина
о механизме образования пропульсивной силы у рыб, построен-
ные на совершенно иных соображениях, в которых важную
роль играют волнистые, змеевидные движения тела рыб.
С точки зрения развиваемых здесь соображений хвост рыбы
работает совершенно так же, как кормовое весло, причем
весьма сложные извилистые движения хвоста, может быть,
представляют очень тонкий механизм, заставляющий сходить
вихри только при наибольшем отклонении хвоста, что, есте-
ственно, выгодно с точки зрения вихревой природы обра-
зования пропульсивной силы. В пользу таких вихревых сооб-
ражений говорит и тот факт, что присутствие вихреобра-
зований, и притом достаточно интенсивных, позади плывущей
рыбы установлено экспериментально, например на фотогра-
фиях Грэя; причем в теории, предложенной В. В. Шулей-
киным, эти вихри рассматриваются как бесполезная трата
энергии на побочные явления, в то время как с точки зре-
ния развиваемых здесь соображений эти вихри, уносящие
с собой некоторое количество движения жидкости, и вызы-
вают образование пропульсивной силы. Может быть, в пользу
развиваемой здесь теории говорит и тот факт, что голова
476 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и корпус рыбы при работе хвоста почти не совершают
колебаний, аналогично корпусу лодки при работе кормо-
вым веслом l6L
Все предыдущее, мне кажется, в достаточной степени
показывает, какое важное значение в объяснении механиче-
ских явлений в природе и в технике имеют вихревые дви-
жения. Здесь, может быть, уместно вспомнить слова осново-
положника теории вихрей Гельмгольца, которые Н. Е. Жуков-
ский поставил эпиграфом к своим лекциям по теоретическим
основам воздухоплавания:
«Насколько я могу судить, в настоящее время нет
никаких оснований не пользоваться гидродинамическими
уравнениями для точного выражения законов, управ-
ляющих наблюдаемыми в действительности движениями
жидкости».
Среди общих гидродинамических уравнений уравнения
теории вихрей и, в частности, свойства вихревых дорожек
имеют, по-видимому, исключительное значение. Но в теории
таких явлений мы имеем еще очень много совершенно
неисследованных вопросов. Здесь, прежде всего, не вы-
яснены условия образования вихрей в результате рас-
пада пограничного слря; несомненно, что эта задача самым
тесным образом связана с другой весьма сложной и совер-
шенно неизученной задачей об устойчивости пограничного
слоя.
В связи с вопросом об условиях образования вихревых
дорожек стоит второй важный вопрос: о возможности обра-
зования дорожек, резко отличающихся от направления общего
течения позади тела. В частности, теоретически образова-
ние таких дорожек возможно, если машущее крыло совер-
шает колебания таким образом, что время поднятия крыла
отлично от времени его опускания. Если такие дорожки
физически возможны, что может быть решено только экспе-
риментально, то здесь, вероятно, кроется объяснение того
парадоксального явления, что насекомые и мелкие птицы
работой крыльев могут создавать подъемную силу, не пере-
мещаясь поступательно.
Наконец, с точки зрения приложения вихревых дорожек
к наблюдаемым в действительности явлениям представляет
большой интерес разработка теории периодических вихре-
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ МАШУЩЕГО КРЫЛА 477
вых движений с неопределенно распределенными завихре-
ниями, для которых вихревые дорожки являются только пре-
дельным и весьма схематическим случаем.
Институт механики
Академии наук СССР
ЛИТЕРАТУРА
1. Л. Прандтль, О. Титьенс, Гидро- и аэромеханика, т. I,
стр. 169 и 193, ГТТИ, 1932.
2. Н. Е. Жуковский, Поли. собр. соч., Лекции, вып. 1. Тео-
ретические основы воздухоплавания, ч. 1, стр. 315, 1938.
3* Н. Е. К о ч и н, Н. В. Розе, Теоретическая гидромеханика,
ч. 1, стр. 198, 1938.
4, Г. Билля, Теория вихрей, стр. 96, 1936.
5. В. В. Шулейкин, Физика моря, стр. 680—704, 1941.
6. В. В. Шулейкин, Физика моря, стр. 685 (начало § 3) и
стр. 682 (начало § 2), 1941.
7. Fuchs-Hopf, Aerodynamik, 1922.
8. В. В. Голубев, Теория крыла конечного размаха, 1931.
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ
МАШУЩЕГО КРЫЛА 0
Одним из самых крупных достижений Н. Е. Жуковского,
памяти которого посвящены «Ломоносовские чтения», яв-
ляется создание им основ современной технической аэро-
механики: теории крыла и теории пропеллера. Две основные
идеи были положены в основу теории крыла. Во-первых,
теория многозначного потенциала в плоскопараллельном тече-
нии, плавно обтекающем некоторый контур; использование
многозначного потенциала, как известно, привело к откры-
тию основной теоремы Жуковского, на которой основывается
расчет подъемной силы крыла, тяги пропеллера и т. п.
Во-вторых, применение схемы несущего вихря, позволяющей
с чрезвычайным успехом дать приближенное решение задачи
о работе крыла конечного размаха и построить приближен-
ную теорию гребного винта.
1) Доклад на «Ломоносовских чтениях», 1947 г., посвященных
столетнему юбилею со дня рождения Н. Е. Жуковского. Опублико*
вано в Уч. зап. МГУ, вып, 152, т, III, 1951. (Прим, ред.)
478
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Теория крыла конечного размаха есть, конечно, весьма
частный случай общей теории обтекания тела потоком, т. е.
классической задачи, привлекающей внимание ученых со
времен Эйлера и Даламбера, основоположников гидромеха-
ники. Но, несмотря на огромное число попыток разъясне-
ния вопроса о силах, с которыми поток, обтекающий тело,
действует на него, теория обтекания тела находится в совер-
шенно зачаточном состоянии. Если не рассматривать став-
шие классическими исследования Стокса об обтекании шара
вязкой жидкостью, дополненные впоследствии Озееном, и
знаменитые результаты Эйлера и Даламбера, относящиеся
к плавному обтеканию тела идеальной жидкостью и привед-
шие к знаменитому парадоксу Эйлера — Даламбера, об общем
случае обтекания тела мы почти ничего не знаем. Причиной
этого, несомненно, является тот факт, что мы не имеем
сколько-нибудь ясного представления о структуре кильва-
терной зоны, в которой проявляется влияние особенностей
потока, возникающих благодаря присутствию в нем обте-
каемого тела. Всякое построение теории обтекания тела пото-
ком начинается с построения некоторой физической схемы,
приближенно представляющей строение кильватерной зоны.
В настоящее время мы имеем, в сущности, только две попытки
представить структуру кильватерной зоны.
Во-первых, можно вообще отказаться от учета кильва-
терной зоны и считать, что ее нет и что имеется плав-
ное обтекание; это предположение приводит к ярко вы-
раженному противоречию с опытными данными, к пара-
доксу Эйлера— Даламбера. Во-вторых, можно считать, что
кильватерная зона представляет область, заполненную сре-
дой, неподвижной относительно обтекаемого тела, к кото-
рому она примыкает. Такое предположение приводит к тео-
рии струй, которая достаточно хорошо разработана для
случая плоскопараллельного течения и совершенно не раз-
работана для случая пространственного течения. Она позво-
ляет рассчитать величину сопротивления, но полученная вели-
чина сопротивления оказывается приблизительно вдвое меньше
наблюдаемого в действительности. Кроме того, такая схема,
очевидно, совершенно неприложима к случаю обтекания
крылообразных профилей при малых углах атаки. Причина
несоответствия теории струй опытным данным кроется в том,
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ маШун!его крыла 479
что положенная в основу гипотеза о строении кильватерной
зоны, по-видимому, совершенно не соответствует действи-
тельности, так как кильватерная зона, как показывают опыты,
представляет зону не неподвижной жидкости, а зону сильно
завихренной жидкости. Озееном и Бюргерсом были сделаны
попытки построить схему течений в кильватерной зоне
с учетом вихревых течений, но эту попытку нельзя считать
удачной ввиду искусственности положенных в ее основу
предположений и ввиду несогласия полученных выводов
с опытными данными.
На этом довольно безнадежном фоне замечательным
достижением является теория конечного крыла. Заме-
чательный успех этой теории обязан тому, что схема при-
соединенного вихря и связанной с ним системы свобод-
ных вихрей позволила сделать совершенно ясной, с физи-
ческой точки зрения, картину строения кильватерной зоны,
несомненно, весьма близкую к тому, что имеется в действи-
тельности. По-видимому, ярко выраженное вихревое строе-
ние кильватерной зоны в теории крыла заставляет предпо-
лагать, что дальнейший успех в теории обтекания тела
может быть достигнут только путем удачного обобщения
вихревой схемы структуры пограничного слоя и на случай'
обтекания тел произвольной формы.
Теория крыла конечного размаха является первым суще-
ственным успехом в теории обтекания тел жидкостью после
работ Стокса.
Вторым существенным успехом является идея, лежащая
в основе теории вихревых дорожек, предложенная Карма-
ном. Замечательная схема устойчивых дорожек предста-
вляет, несомненно, прогресс в изучении структуры киль-
ватерной зоны. К сожалению, до настоящего времени мы
не умеем полностью подсчитывать сопротивление, так
как неизвестной остается величина циркуляции отходя-
щих вихрей; кроме того, большие трудности представляет
перенос основной схемы вихревой дорожки на случай обте-
кания произвольного тела жидкостью.
Вероятно, дальнейший успех в решении основной задачи
гидромеханики об обтекании тела и связан с вопросом об
изучении, с одной стороны, вихревых образований типа вихре-
вой пелены за крылом и, с другой стороны, вихревых дорожек.
480
П. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
С задачей определения сопротивления тесно связана за-
дача, в известном смысле обратная, определения величины
тяги машущего крыла.
В нескольких докладах, сделанных в АН СССР, мною
было показано, как можно приложить теорию вихревых доро-
жек к расчету силы тяги. Той же задаче посвящен и печа-
таемый доклад.
Среди различных случаев полета с машущими крыльями;
совершенно исключительным с гидродинамической точки зре-
ния является полет «на месте», или, как его называют био-
логи, «трепещущий полет», когда птицы или некоторые виды
насекомых, работая крыльями, весьма устойчиво стоят наг
одном месте. Такой полет можно наблюдать, например,
у стрекоз, у некоторых видов мух и у мелких птиц: ко-
либри, стрижей и т. п.
Если объяснение возникновения тяги и подъемной силы
можно получить, исходя из схемы отходящей вихревой
дорожки, и это объяснение соответствует действительности,
то надо ожидать, что то же объяснение можно приложить
и к случаю полета на месте. Такое объяснение могло бы
существенно укрепить данное нами ранее объяснение
возникновения силы тяги на основании теории вихревых
дорожек.
Мы покажем, что такое объяснение можно получить
весьма просто, исходя из формул, данных мною для общего
случая машущего полета.
В моей работе были выведены следующие формулы для
подъемной силы и тяги машущего крыла:
подъемная сила Y — рУГ0,
тяга X = — 0,95pZ>V2 cos a (sin 8 4~ ~ cos 3^ 1 —f— 1,2 у),
где b — хорда крыла, w— скорость поднятия и опускания,
„ __ Iх I — 02
----2~’ 6------2--’
причем и 62 —соответственно угол атаки при опускании
и при поднятии крыла и —угол, характеризующий изо-
гнутость крыла.
О Некоторых вопросах теории машущего крыла 481
Из этих формул мы видим, что при отсутствии посту-
пательной скорости, т. е. при V = 0, подъемная сила
обращается в нуль (/=0), а тяга сохраняет значение,
отличное от нуля,
X = — 1,13p#w2 cos о cos 3.
(1)
Следовательно, естественно искать объяснение возник-
новения подъемной силы при отсутствии поступательной
скорости в том, что летящие птицы или насекомые при
помощи изменения расположения тела в пространстве или
при помощи изменения характера движения крыльев пре-
вращают тягу в подъемную силу.
Из теории машущего крыла мы имеем следующие выра-
жения для циркуляции при опускании и поднятии крыла:
1\ = — ~b yv2 + w2 sin 0^ -Ml + arctg
и
Г2 = — УУ2 + w2 sin ~M2 — arctg;
отсюда из предположения, что V = 0 и что крыло симмет-
ричное (т. е. и = 0), мы получим следующие выражения
для циркуляции:
pj = — Tzbw sin
(2)
Г2 — — кЬ™ sin f 0 _Л
V2 2
(3)
Углы и 02 лимитируются тем, что угол наклона крыла
к направлению скорости набегающего потока, т. е. дейст-
вительный угол атаки, не может превосходить критического
угла атаки профиля. Учитывая все это, мы получим следу-
ющее расположение крыла при опускании и при поднятии
(рис. 1).
Как видно из рис. 1, при опускании мы имеем ^<0,
а при поднятии Г2 > 0- Если назвать через а действитель-
482
it. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
ный угол атаки в том и в другом случае, то в формулах
(2) и (3) мы будем иметь:
о2 — 2 а>
а потому
Г? = — 7zbw sin а, (4)
Г2 = sin а. (5)
Отсюда для величины циркуляции вихрей отходящей
дорожки получим следующие выражения:
для вихрей верхней полосы
Yi = —(1\ — Г2) = 2it/?w sin а (6)
и для вихрей нижней полосы
у2 = -—71 = — 2k£w sin а. (6Z)
Мы можем теперь подсчитать силу тяги и все элементы,
характеризующие работу машущего крыла при рассматри-
ваемом здесь условии V = 0.
Так как из приведенных формул получаем, что
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ МАШУЩЕГО КРЫЛА 483
и, следовательно, cos8 = sina, то по формуле (1) мы полу-
чим следующее выражение для силы тяги:
X =— 1,1 ЗрЬм2 sin а.
Согласно предыдущему, для того чтобы получить для
полета на месте вместо силы тяги подъемную силу, доста-
точно повернуть на прямой угол направление взмахов, и мы
получим расположение, указанное на рис. 2.
Рис 2.
Вводя новые оси, как показано на рис. 2, мы получим
для подъемной силы Y и для тяги X следующие значения:
Х = 0, | '
Y — 1,13pZ>w2 sin a. J
Полученную формулу интересно сравнить с формулой
подъемной силы, полученной при поступательном полете
с образованием циркуляционной силы по теореме Н. Е. Жу-
ковского.
Рассмотрим величину подъемной силы, которая полу-
чается при полете со скоростью w, т. е. со скоростью,
равной скорости взмахов крыла, и при угле атаки а.
По известной формуле получим для подъемной силы при
поступательном движении выражение
Fj = sin а, (8)
а потому
-£- = -^ = 0,35, (9)
т. е. подъемная сила при полете на месте составляет 35%
от подъемной силы поступательного полета при скорости w.
484
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Таким образом, с точки зрения величины подъемной
силы, полет на месте оказывается маловыгодным.
Этому результату можно дать следующее толкование.
Так как Y есть, очевидно, та подъемная сила, которая
нужна для поддержания птицы в воздухе, т. е. та сила,
которая нужна для взлета, то, обозначая через еш1 скорость
взлета, можем написать:
Y = sin 6,
а потому из (8) и (9)
w2: w2 = 0,35,
т. е. имеем wx = 1^0,35^ или wx = 0,6w.
Таким образом, механизм взмахов при полете на месте
в рассматриваемом случае состоит в том, что крыло пере-
мещается не вверх и вниз, а вперед и назад, как указано
на рис. 3.
Рис. 3.
Для достижения такого перемещения крыльев надо или
иметь механизм, который позволяет перемещать крылья
при взмахах не вверх и вниз, а вперед и назад, или надо
перевернуть корпус летящей птицы или насекомого из
горизонтального положения в вертикальное. Заметим, что
при взмахах вперед и назад крыло необходимо поворачивать
на угол tz — 2а. Полагая, что а равен критическому углу,
который у хорошо обтекаемых крыльев имеет порядок 15°,
мы получим, что поворот крыла около горизонтальной оси
достигает величины 150°.
Зная величину у, мы найдем скорость дорожки по
известной формуле
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ МАШУЩЕГО КРЫЛА 485
В рассматриваемом случае, подставляя величину у
из уравнения (6) и предполагая, что отходящая дорожка
удовлетворяет условию устойчивости Кармана th ,
получим:
~Ь • /О/\
= r~ w sin а. (8 )
0 /2/ 4 7
Далее, называя через Т период взмаха и через h ампли-
туду взмахов, получим уравнения
I =
2/г = wT,
откуда
и
I 2nb .
—j— = —r-^ sin a —
h V21
2k h b
У2 1 h
sin a
1 — ( 1 \2 1 1
h \h ) п у 2” sin a
или, полагая согласно условиям устойчивости
-у = 0,281,
Ъ __ 1
h 0,34 sin a ’
откуда
h = 0,34# sin a, (9Z)
т. e. для выполнения условия устойчивости дорожки необ-
ходимо, чтобы амплитуда взмахов, как показывает уравне-
ние (9х), составляла, вообще говоря, малую часть хорды
крыла. Так, если считать
1
sin a = —г,
4
то
h = 0,09#.
Может быть, эта малость амплитуды взмахов оправды-
вает то название, которое употребляется в биологических
работах для характеристики полета на месте, — «трепещу-
щий полет».
486 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Далее, можно определить /, пользуясь условием устой-
чивости,
/==да = 1’246sina> (10)
и, подставляя значение / в выражение rz0, получим
= 1>8w (П)
и из уравнения
I = и(}Т
найдем продолжительность взмаха Т
т___ I ___1,246 sin a_ sina b
Uq l,8w 1,45 w
и отсюда имеем для числа колебаний в секунду выражение
V- (13)
Т sin a b
Пользуясь найденными выражениями, можно найти выра-
жение подъемной силы через число колебаний N. Действи-
тельно, из (13) имеем
w==44t-M==0«7M'sina (14)
1,45 v 7
и, подставляя найденное выражение в соотношение (7),
получим:
Y = 0,57pAW sin3a. (15)
Если обе части уравнения (15) умножить на размах
крыла L и заметить, что YL\bL = р, где р — нагрузка
на единицу площади, то получим:
р = 0,57pN2#2 sin3 a,
и отсюда
0,57р62 sin3 a ’
р
Если вес летящего тела есть Р, а площадь S, то р =
и необходимое для поддержания тела в воздухе при полете
на месте число взмахов определится из формулы
N2 = л-*? еда ---• О6)
0,57pS62 sin a. ? 7
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ МАШУЩЕГО КРЫЛА 487
Полученные выводы, конечно, было бы чрезвычайно
интересно проверить на опыте. Однако никаких опытных
данных в этом направлении нет, и единственно, чем можно
было бы воспользоваться для проверки, хотя бы грубо-
качественной,— это данными о полете птиц, которые,
также имеются в совершенно недостаточном количестве.
Конечно, надо помнить, что применение выведенных формул
для плоскопараллельного течения при несколько упрощен-
ных условиях полета (резкое изменение скорости в крайних
точках амплитуды колебания и прямолинейное движение
крыла с постоянной скоростью в первую и вторую поло-
вину взмаха) к случаю взмахов крыльев птиц, которые,
несомненно, весьма сильно отличаются от разобранной здесь
схемы, не может дать вполне надежной проверки преды-
дущей теории и может служить только в качестве первой,
достаточно грубой прикидки.
С этой точки зрения чрезвычайно большой интерес
представляют данные, приведенные о «трепещущем полете»
в диссертации Гладкова «Биологические основы полета
птиц» 9- Мы и приведем здесь некоторые данные из этой
работы, касающиеся полета
колибри (Melanotrochilus).
Вот общая характери-
стика полета; «Когда ко-
либри „висит" в воздухе / /
перед цветком, она делает /
быстрые движения крыльями \/
почти в горизонтальной I/
плоскости. Однако тулови- и
ще в это время находится
в положении, близком к вер- Рис. 4.
тикальному. Следовательно
(относительно туловища птицы), общее направление движе-
ния крыла — это сверху вниз и несколько вперед...»
(Гладков, стр. 180).
«При этом кончик крыла описывает удлиненную вось-
мерку (рис. 4). При опускании крыла вниз, а лучше сказать,
1) Докторская диссертация; защищена в феврале 1947 г. на
биологическом факультете МГУ.
488
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
при движении его вперед, крыло премирует, при обратном
движении — супирует. Нижняя сторона его оказывается при
этом сверху; и самое интересное, что это не просто
необычная ориентация крыла в пространстве, а временная
перемена функций той или другой стороны крыльев.
Верхняя сторона выполняет при этом функцию нижней
стороны, и наоборот. В общем получаются те же соотно-
шения, что у аэроплана, летящего в перевернутом состо-
янии ...».
«...Таким образом, можно сказать относительно ко-
либри, что она регулирует положение своего туловища и
движение крыла так, что возникающая отсюда сила тяги
направлена вверх и уравновешивается весом птицы. Ниже
мы увидим, что совершенно такие же силы возникают
у других птиц, когда они прибегают к трепещущему
полету».
Эта общая характеристика полностью согласуется со схе-
мой полета машущего крыла на месте, указанной выше
(рис. 3). Для количественной оценки весьма интересны дан-
ные о скорости и числе взмахов. Вот эти данные.
«Линейная скорость крыла Me anotrochilus изменяется
от 4 мм/сек ( при наиболее вытянутом вперед положении)
до 20 мм!сек на уровне туловища».
Число взмахов, по определению Штольца и Циммера
(лупа времени), составляет:
у Chlorostilbon 36—39 в сек
у Melanotrochilus 27—30 » »
Штреземан и Циммер с помощью стробоскопического
метода определили
у Eupetomen macroura 21—22 в сек
у Chlorestes coeruleus 30—33 » »
у Chrysolampis mosquites 32—33 » »
у Phaeternus ruber 50—51 » »
«При трепещущем полете чайка машет крыльями еще
чаще, чем при взлете (6 раз в секунду, при взлете 4—5
раз, при нормальном полете 3 раза)».
Большим затруднением при попытках количественно
сравнить полученные выше формулы с приведенными дан-
О НЕКОТОРЫХ ВОПРОСАХ ТЕОРИИ МАШУЩЕГО КРЫЛА 489
ными о полете птиц является отсутствие аэродинамических
характеристик для птиц и прежде всего отсутствие данных
о нагрузке. Потому приходится данные о нагрузке экстра-
полировать по имеющимся данным, что, естественно,
является не очень надежным.
Есть формула Гартинга, связывающая площадь крыльев
и вес птицы. Эта формула может быть получена из сооб-
ражений подобия, но она требует, чтобы удлинение крыльев
было также постоянным, как это сейчас же следует из
соображений подобия. Таким образом, формула Гартинга
справедлива при одинаковом удлинении крыльев, что в дей-
ствительности не соблюдается х).
Формула Гартинга имеет вид
(по определению Марея), если мерить S в см2 и Р в г.
Если брать вес в кг и площадь в м2, то получим:
= °,Э 42,
У А
откуда
р=41-=5>7Гл
•^1
т. е. нагрузка убывает пропорционально кубическому корню
из веса птиц; по-видимому, для птиц малого веса при-
веденная формула дает нагрузки, несколько завышенные.
Вес колиэри 2 г; таким образом, по формуле Гартинга,
нагрузка получится равной
р = 5,7 f 2-Ю-8 = 0,57 ]ХТ.
Мы едва ли сделаем большую ошибку, приняв нагрузку
несколько меньшей; положим р = 0,5. Это может быть
достигнуто максимальным увеличением поверхности крыла.
Э См. М. К. Тихонравов, Полет птиц и машины с машу-
щими крыльями, стр. 16, 1937.
490
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
При таком предположении имеем:
X = 2"’ -8'1 = 2РГ
Подставляя найденные значения в формулу (16), получим:
_______________________________—-______ .
0,57 (-£•) sin8 а
Называя через К удлинение крыла, получим b = ~ и
bL S-
cP = —г— = --
л к

итак,
2Р^
N2 =
п г7 1 \ е2 е. <> 0,57/^ sin8 а
0,57 I -g- I б* sin 5 а ’1
т. е.
N2 = 3
Р± sin3 а
Для колибри Р± = 2 г —- 2 • 10 3 кг, следовательно,
N
г sin8 а
Можно считать, что X заключается в пределах от 1 дс 2
и а — от 45° до 30°. Отсюда получим:
Nmax=421/’27= 168,
Mnin - 42
По-видимому, выведенные выше формулы дают довольно
завышенное число колебаний; может быть, здесь сказы-
вается влияние конечности крыла. Однако порядок вели-
чины получается достаточно близкий.
Из полученных формул следует, что при увеличении
веса Р число колебаний убывает. Если это замечание при-
ложить к чайке (чайка сизая— Larus canus, Р=0,89 /сг,
Х= 7,6), то получим для числа взмахов выражение в
т/ 490 ]о раз меньше, чем для колибри. Следовательно,
г 3,8
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
491
по приведенным выше числам имеем, что число взмахов для
чайки колеблется от 7 до 17. Выше было показано, что оно
равно 6, что уже довольно близко к теоретическому зна-
чению.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ
МАШУЩЕГО КРЫЛА1)
Введение
Целью настоящей работы является выяснение механизма
образования тяги машущего крыла. Несмотря на большое
число исследований, посвященных теории неустановившегося
движения крыла и, в частности, теории колеблющегося или
машущего крыла, вопрос о причинах, вызывающих образо-
вание тяги, остается далеко не выясненным.
Если откинуть всякого рода механически не обоснованные
и ни к чему не приводящие соображения об отгребании или
отбрасывании назад воздуха взмахами крыла, то в общем
можно указать две основные точки зрения.
В ряде работ образование тяги машущего крыла при-
писывается действию подсасывающей силы, образующейся
у передней кромки тонких крыльев. Как известно, на воз-
никновение таких сил было обращено внимание в работе
Н. Е. Жуковского Ш; в частности, Н. Е. Жуковский пы-
тался объяснить таким путем возникновение лобового сопро-
тивления. Такого рода соображения представляются весьма
сомнительными в приложении к крыльям, профили которых
имеют форму, более или менее округленную у передней
кромки, а таковыми являются все обычно применяемые
в авиации профили и профили крыльев птиц. В дальнейшем
мы увидим, что с точки зрения общих механических сооб-
ражений образование подсасывающей силы есть, в сущности,
проявление образования циркуляции вокруг профиля, а отсюда
следует, что влияние таких подсасывающих сил на образо-
вание тяги можно приписать только изменению при взмахах
крыла циркуляции и связанному с ним отходу вихрей сзади
крыла.
1) Опубликовано в Уч. зап. МГУ, вып. 154, т. IV, 1951. (Прам.
ред.)
492
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Другая точка зрения на образование тяги связана
с представлением об образовании за машущим крылом линии
разрыва скоростей с волнообразно распределенными около
нее линиями тока 1131. Причины, вызвавшие введение за кры-
лом линий разрыва скоростей, лежат в трудности в случае
машущего крыла с изменяющейся при взмахах циркуляцией
увязки теоремы Томсона о сохранении циркуляции, с одной
стороны, и постулата Чаплыгина — Жуковского о сходе
потока с острой задней кромки, с другой стороны. Однако
введение таких поверхностей разрыва в теорию машущего
крыла чрезвычайно осложняет дело; этим объясняется до
известной степени то, что в теории почти исключительно
рассматриваются малые колебания крыла. Между тем при-
нятие малости колебаний крыла, вполне достаточное в тео-
рии вибраций, совершенно непригодно для общей теории
машущего крыла. Кроме того, и самая физическая схема
является крайне сомнительной, так как такие поверхности
разрыва скоростей неустойчивы и, по-видимому, никогда
не наблюдаются в действительности. На опыте наблюдаются
за машущим крылом системы вихрей, аналогичные дорожкам
Кармана, которые, конечно, можно рассматривать как ре-
зультат распада непрерывной у самого крыла поверхности
разрыва.
В настоящей работе рассматриваются колебания крыла
с любой амплитудой в условиях плоскопараллельного потока.
Первой задачей, возникающей здесь, является нахождение
путей, позволяющих примирить теорему о сохранении вих-
рей с постулатом Чаплыгина—Жуковского в случае отказа
от образования за крылом поверхности разрыва скоростей.
Решение этого вопроса основывается на учете влияния по-
граничного слоя, который, таким образом, рассматривается
как некоторый механизм, регулирующий сход потока
с крыла.
Физическая схема, положенная в основу настоящей ра-
боты, состоит в следующем. При взмахах крыла в крайних
точках амплитуды колебания от крыла отходят вихри, обра-
зующие за крылом двойную вихревую дорожку. Подробное
рассмотрение такой дорожки показывает, что направление
вращений вихрей в ней обратно направлению вращений
вихрей в дорожках Кармана, образующихся при обтекании
Исследования по теории машушего крыла 49$
преград. Эти соображения позволяют применить для опре-
деления величины подъемной силы и тяги машущего крыла
теорему о количестве движения, которую с таким успехом
применил Н. Е. Жуковский в общей теории крыла и Кар-
ман— в задаче об определении величины сопротивления
плохо обтекаемых тел.
Некоторые результаты, полученные нами, были ранее
сообщены в заметке, напечатанной в 1942 г. М, и в докладе
на научной конференции в ВВА КА в июле 1944 г.
общие физические соображения, лежащие в основе рассма-
триваемой теории, были изложены в докладе на общем
собрании АН СССР 17 октября 1944 г. Один частный
случай задачи о машущем крыле был рассмотрен в докладе
на «Ломоносовских чтениях» в МГУ в 1947 г.
§ 1. Пограничный слой крыла
Как известно, с точки зрения теории пограничного слоя
эффект вязкости жидкости при движении тела в среде
с малым коэффициентом вязкости проявляется только в не-
посредственной близости к обтекаемому телу в пределах
так называемого погранич-
ного слоя.
Пусть АВ есть граница
тела (рис. 1) и А1В1 — на-
ружная граница погранич-
ного слоя.
За пределами погранич-
ного слоя A±BX жидкость
можно рассматривать как
идеальную. Так как на границе твердого тела жидкость
прилипает к телу и, следовательно, скорость жидкости
равна нулю, а на наружной границе слоя A±B± ско-
рость равна скорости обтекающего тело потока идеаль-
ной жидкости, то циркуляция скорости по контуру MNPQ
отлична от нуля. Следовательно, можно рассматривать
область пограничного слоя с кинематической точки зрения
как область, заполненную идеальной завихренной жидкостью.
Посмотрим, какой эффект вихри пограничного слоя ока-
зывают на условия обтекания. Так как в дальнейшем мы
494
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
будем рассматривать обтекание крыла, то, применяя обыч-
ный в теории крыла метод, отобразим конформно внешнюю
часть профиля крыла на внешнюю часть круглого цилиндра
у радиуса R (рис. 2); при этом рас-
положим оси таким образом, чтобы
Х/*-острая задняя кромка крыла на
/(______\\ плоскости круглого цилиндра изо-
[ I______И £ бражалась точкой z = R. Вихре-
\д О J I вой пограничный слой при этом
перейдет в некоторый вихревой
слой S, расположенный вокруг
цилиндра. Пусть вихревая плот-
рис 2. ность в этом слое равна а; тогда
характеристическая функция тече-
ния вокруг цилиндра, соответствующего течению вокруг
крыла, примет вид
W^Ve^iz + In 2 +
\ 1 Z ] 1 27LZ 1
+ i f I 1П °dxdy, (1)
z — — е'^
° г
где ге'^— аффикс точки пограничного слоя с вихревой
плотностью о, Г — циркуляция вокруг цилиндра, V—ско-
рость потока в бесконечности и 0 — угол, образованный ею
с действительной осью.
Потребуем, чтобы течение, определяемое характеристи-
ческой функцией (1), удовлетворяло постулату Чаплыгина—
Жуковского. Для выполнения его, как известно, необхо-
димо, чтобы скорость течения в точке z = R, соответ-
ствующей задней кромке, обращалась в нуль. Отсюда имеем
уравнение
или
уе-9г(1— е2вг)_|_ 2. 1 __
v ' 2т R
— I f ° "2—dx dy = О» (2)
2~iR J J r2 — 2Rr cos -f- R* \ /
s
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
495
откуда получим величину циркуляции
г = —Vsinе4- f , D2 dxdy. (3)
1 J J г* — 2Rr cos + R2 v 7
S
В выражении характеристической функции (1) вихри
пограничного слоя не дают непосредственно циркуляции
вокруг крыла, так как вихри эти входят попарно в точках
R2
гечг и — е'гг с одинаковой интенсивностью а, но с противо-
положным направлением вращения. Однако, как показывает
равенство (3), эти вихри влияют на величину циркуляции
косвенно, благодаря необходимости выполнения постулата
Чаплыгина — Жуковского.
В теории крыла обычно не учитывается влияние на цир-
куляцию вихрей пограничного слоя, что равносильно пред-
положению а = 0; тогда вместо уравнения (3) получим:
Г = —4^1/sine,
(4)
что равносильно предположению
r2 — R2
° га — 2Rr cos с? + R2
dx dy = 0.
(5)
Условие (5) не требует отсутствия вихрей пограничного
слоя; оно требует только, чтобы скорость течения, вызы-
ваемого этими вихрями, в точке z — R, соответствующей
на цилиндре задней кромке крыла, равнялась нулю. Воз-
можно, что условие (5) выражает то обстоятельство, что
система вихрей пограничного слоя неустойчива и что в дей-
ствительности пограничный слой может существовать только,
при условии, что выражение
Г f r2-—R2 , ,
J J ° г2 — 2Rr cos ? + Я2 dx dy
s
достаточно мало; в противном случае вихри пограничного
слоя срываются с крыла.
496
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
§ 2. Пограничный слой крыла в присутствии вихря
Применим теперь такие же соображения к случаю, когда
около крыла имеется вихрь интенсивности J. Переходя
к вспомогательной плоскости (z), мы получим для характе-
ристической функции течения, обтекающего вспомогатель-
ный круглый цилиндр, следующее выражение:
w = Ve-Bi О + + JLln z + )п
z-----е™
+ J°ln Z~^ dxdy, (1)
я z---------------е'?ъ
о r
где 1\е™— аффикс вихря J.
В этом случае выполнение постулата Чаплыгина — Жу-
ковского приводит к условию
л. г 1 J Я2— г?
+ тгЮ I о т>~,™—-----------i—dx dy = 0. (2)
2лг J J R (R2 — 2Rr cos ср -|- г2) л 47
8
Поставим следующий вопрос: нельзя ли удовлетворить
условию (2) при постоянных Г, J, V, 9 и при произволь-
ных гг и а, т. е. при постоянной циркуляции вокруг крыла,
при постоянном вихре J, при заданной по величине и по
направлению скорости в бесконечности, но при произволь-
ном положении вихря J?
Полагая, в частности, г± = сю, получим из уравнения (2)
r = -4=Rl/sl„0 + J+ [ + <3>
S*
где Oqo — плотность вихрей пограничного слоя при 1\ = сю,
т. е. когда внешнего вихря нет. При этом, очевидно, цир-
куляция вокруг крыла есть Г — J и
Г -J = — 4ir/?vsinе-Н I —v-aidxdy. (4)
1 J J г2 — 2/?r cos -|- /?2 v '
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
497
Равенство (4) для рассматриваемого случая аналогично
равенству (3) § 1. С другой стороны, из равенства (2)
имеем:
Г = _ 4K/?Vsin 9 -4- J
r\~R2
г2 — 2Rt\ cos a -|- R2
+ I [ о -x—~dx dy, (5)
J J r2 — 2Rr cos у R2 v 7
что можно еще написать следующим образом:
Г — J =—4тс/? V sin 9 Ц- | | Ооо-2——№—^^dxdy-\-
J J г2 — 2Rr cos ср -f- R2 J 1
s
J 2R (rt cos a — /?) .
r2 — 2Ri\ cos a + R2
Иг2 —R2
(<3 — Ooo) r2_2/?rcoS((>_|_^2 dx dy-
s
Отсюда имеем, что если выполняется условие
j 2R (rt cos a — R) .
г2 — 2Rrr cos a 4- R2
+ f 1(6 —<Jco)-5—(6)
I J П ОО/ r2 _ <2Rr COS cp 4- R2 Л V 7
s
то при любых r1 и a, т. e. при любом положении вихря J,
постулат Чаплыгина — Жуковского выполняется при по-
стоянных Г, Л V и 9. Но условию (6), конечно, можно
удовлетворить надлежащим подбором вихревой плотности а.
Если принять, как это обычно делается в теории крыла,
что
Г Г г2 — R2 . . п
dx dу = О,
J J г2 — 2Rr cos ср R^ s
s
то условие (6) примет вид
j 2R (rt cos a — R)
г2 — 2Rrr COS a -j- R2
—----dx dy =0. (6')
r2 — 2Rr cos cp 4- R2 4
498 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Равенство (6) или (6х) показывает, что структура по-
граничного слоя зависит от J, г\ и а, т. е. от интенсив-
ности и положения внешнего к крылу вихря. Изложенные
соображения показывают, что пограничный слой крыла
можно рассматривать как своеобразный регулятор схода
потока с крыла. Влияние пограничного слоя приводит
к тому, что при отходе от крыла вихрей нет надобности
для выполнения постулата Чаплыгина—Жуковского вводить
непрерывно сходящую с крыла поверхность разрыва ско-
ростей. Например, при взмахах крыла можно считать, что
вихри отходят от крыла только в крайних положениях
крыла; в дальнейшем же при постепенном отходе сошед-
ших с крыла вихрей выполнение постулата Чаплыгина —
Жуковского обеспечивается регулирующим влиянием погра-
ничного слоя.
В заключение заметим, что член
/ J ° г2 — 2Rr cos f -|- R?
s
в уравнении (3) § 1 представляет собой учет влияния на
величину циркуляции пограничного слоя, т. е. учет влияния
вязкости воздуха. Аналогичную роль играют соответствую-
щие члены и в уравнениях § 2. Принятие условия (5) § 1
или условия (6х) § 2 равносильно тому, что мы пренебре-
гаем влиянием вязкости на величину циркуляции.
§ 3. Экспериментальные данные
Физические соображения, изложенные в настоящем пара-
графе, лежат в основе всей дальнейшей теории, поэтому
представляла большой интерес их экспериментальная про-
верка. Такая проверка была выполнена в 1948 г. Я. Е. По-
лонским .
На рис. 3 дано схематическое изображение прибора,
который он построил для этой цели. Основную часть при-
бора представляет тележка, которая катится по рельсам
вдоль канала, заполненного водой. К тележке прикреплено
крыло, которое при движении тележки совершает колеба-
ния, перпендикулярные к направлению движения тележки;
Исследования по теории машущего крыла
499
тележка и крыло перемещаются при помощи электромотора.
Фотоаппарат, неподвижно установленный над лотком, поз-
воляет производить съемку вихреобразований, возникающих
в воде за машущим крылом, причем для их наблюдения и
фотографирования вода посыпалась смесью из порошка
ликоподиума и талька.
Набор кулачков позволял полу 1ать различные режимы
движения крыла, например менять скорость взмахов крыла
Рис. 3. Установка для эксперимента с машущим крылом.
1 — газотронный выпрямитель, 2 — мотор с радиатором, 5 —съемный редукторе
кулачком, 4 — подвижная рамка с роликом, 5 —пружина, 6 — направляющие движе-
ние рамки, 7—державка с крылом, 8 — ведущий шкив, 9 — ведомый шкив тетзж<и,
70—рама тележки, 11 — рельсы, 12— лоток с визирными линиями, 13 — фотоаппарат.
при движении в ту или другую сторону. На рис. 4, 5, 6
и 7 даны фотографии, полученные Я- Е. Полонским. При
этом рис. 4 дает «прямую» дорожку, получаемую, когда
скорости движения крыла в одну и другую сторону оди-
наковы. На рис. 5, 6 и 7 даны «косые» дорожки, т. е.
дорожки, отклоняющиеся от направления движения тележки;
§00 Й. ТРУДЫ ПО ТЕОРИИ М.фуЩЕВЙ
-ато направление на фигурах уОЙЙно направляющими Пря-
мыми линиями. «Косые» дорожки поА^чаютфа, когда ско-
рости движения йрыза в ту и другую сторону, т-. е. его
взмахов вверх и вниз, различны.
Результаты многочисленных опытов привели Я- Е. По-
лонского к следующим выводам.
«В крайних положениях крыла при переходе от опуска-
ния к поднятию и от поднятия к опусканию от крыла отде-
ляется вихрь.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
501
Получить отделение вихря в промежуточном положении
крыла не удалось. В процессе перехода крыла от одного
Рис. 6.
Рис. 7.
крайнего положения в другое происходит весьма заметное
нарастание завихренности жидкости на задней кромке крыла.
При равномерных взмахах крыла (скорость опускания
равна скорости поднятия) отходящие от него вихри обра-
502 И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО крыла
зуют дорожку шахматного вида. Ось дорожки параллельна
направлению поступательного движения крыла (оси лотка).
Относительно неподвижной жидкости дорожка перемещается
в направлении, противоположном направлению поступатель-
ного движения крыла. Направление вращения вихревой
дорожки противоположно направлению вращения вихрей
дорожки Кармана.
Величина отношения ширины дорожки h к расстоянию
между вихрями I была неодинаковой в различных экспери-
ментах и колебалась между значениями 0,287 и 0,47. Экспе-
h
риментальное значение величины р для дорожки за машу-
щим крылом и дорожки Кармана в общем одинаково».
Таким образом, эксперимент дает достаточное подтвер-
ждение физических соображений, положенных в основу раз-
виваемой в настоящей работе теории.
§ 4. Определение величины циркуляции вихрей,
отходящих при взмахах крыла
Рассмотрим крыло с хордой Ь, совершающее колебания
амплитуды h в условиях плоскопараллельного течения, и
будем считать, что скорость поднятия крыла и скорость
опускания, резко изменяясь в крайних точках амплитуды
колебания, остаются далее за время поднятия и опускания
крыла постоянными и соответственно равными <w и —
Если скорость потока в бесконечности есть V и угол
атаки 0, то при отсутствии взмахов крыла величина цирку-
ляции определяется по известной формуле
r = (1)
При опускании крыла получается добавочная относи-
тельная скорость, направленная вверх и равная w; это вы-
зовет отклонение результирующей скорости вверх и увели-
чение угла атаки на величину arctg —, и величина скорости
набегающего потока примет вид У V2w2. Кроме того,
на величину циркуляции крыла влияют отходящие от крыла
при его взмахах вихри, но если принять, как это указано
выше, что отходящие от крыла вихри образуются только
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
503
при крайних положениях крыла, то влияние отходящих вих-
рей на величину циркуляции за время опускания или за
время поднятия крыла не нужно учитывать. Действительно,
представим себе, что крыло, совершающее колебания,
с момента, когда оно начинает опускание, перестает совер-
шать взмахи вниз и вверх и в дальнейшем продолжает без
конца опускаться со скоростью w. Если опускание крыла
продолжается достаточно долго, то можно считать, что
крыло находится в установившемся движении, и его цирку-
ляция Го определится по формуле
ro = ^yV2 + w2sin(y + 9 + arctg-^. (2)
Так как мы предполагаем, что отходящие от крыла
вихри образуются только в крайних положениях крыла, то
после отхода вихря, когда крыло находилось в крайнем
верхнем положении, дальнейшего отхода вихрей при опу-
скании крыла не было и, следовательно, во все время опу-
скания крыла циркуляция сохранила величину (2). Заметим,
что, как было разъяснено выше, влияние отходящих вихрей
на положение точки схода струй уничтожается изменениями
в структуре пограничного
слоя, т. е., иными словами,
влиянием вязкости воздуха,
чем и обеспечивается вы-
полнение постулата Чаплы-
гина — Жуковского.
В дальнейшем мы рас-
положим оси, как указано
на рис. 8. При таком выбо-
ре осей циркуляция вокруг
крыла окажется отрицательной,
атаки относительно направления
скания крыла есть 615 то
время опускания крыла получим
Рис. 8.
Если еще считать, что угол
скорости V во время опу-
окончательно для циркуляции во
выражение
1\ = — + + + (3)
Совершенно таким же образом получим, что при под-
нятии крыла относительная скорость w направлена вниз и
504
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
угол атаки уменьшается на величину arctg рг; называя угол
атаки при поднятии крыла через 62, получим для величины
циркуляции Г2 за время поднятия крыла выражение
Г2 = — Tt/V2 + w2&sin (у+92— arctg™). (4)
Отсюда следует, что при переходе от поднятия крыла
к опусканию величина циркуляции изменяется на
Г!-Г2.
Называя далее ту + 0 через рь, получим:
Гг — Г2 = — 2к У V2 + b cos sin + arctg ,
где
и ^2 = -2" + 92;
пусть
Н + Р-З тл Р-1—Р-2 *
И ----— = ь,
тогда
1\ — Г2 — —2~ У V2 4- w2 b cos a siп 8 —|— arctg ,
или
1\ — Г2 = — cos о [V sin о 4- w cos В]. (5)
Так как по теореме Томсона циркуляция по контуру,
охватывающему крыло, при этом не должна изменяться, то
такое изменение циркуляции вокруг крыла должно сопрово-
ждаться отходом от крыла в окружающую жидкость вихря
такой же величины, но обратного направления; называя
такой вихрь у, имеем:
у = 2tc&cos а (V sin 8 -j-w cos 8). (6)
Совершенно подобным же образом покажем, что при
переходе от опускания к поднятию крыла от него отходит
вихрь — — у.
Таким образом, при взмахах крыла в крайних точках
амплитуды колебания от крыла отходят вихри: интенсив-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
505
ности у в верхних точках амплитуды и —у в ее нижних
точках, а потому за крылом образуется вихревая дорожка
типа дорожки Кармана с расположенными в шахматном по-
рядке вихрями интенсивности у; направление вращений вихрей
обратно направлению вращений у дорожек, образующихся
за преградами (рис. 9).
Рис. 9.
Мы примем, что ширина дорожки h равна амплитуде
колебания крыла. Такие обращенные дорожки Кармана легко
наблюдать сзади машущего крыла в водяной ванне.
Пусть период колебания крыла Т\ тогда, называя через rz0
скорость, сообщаемую вихрю дорожки вдали от машущего
крыла всеми остальными вихрями дорожки, получим для рас-
стояния между двумя последовательными вихрями каждого
ряда дорожки I и для ширины дорожки h следующие выра-
жения:
/ = (V + «0)7’) |
2A = wT. J ( '
Из теории вихревых дорожек известно, что
«o = ^th^. (8)
или, подставляя найденное выше выражение для у,
и0 = 77 ~ cos а (V sin 8 -|- w cos S) th .
Для дальнейшего более удобно иметь вместо отношения у
b
отношение-^-, определяемое, очевидно, конструкцией машущего
506
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
крыла; поэтому возьмем z/0 в следующем виде:
/т г • a I <S\ 7t/Z ,. Тс/i /л\
rz0 —~coso(V sin о —wcos o) -y th —. (J)
Исключая из уравнений (7) период колебания Т, полу-
чим следующее соотношение:
w h
L =___________ZZJZ____________. (Ю)
2 4 \~Т~т]cos а [sin + V cos
Так как у положительно, то для образования дорожки
указанного выше вида должно выполняться условие
4>24‘ <П)
Применим уравнения (9) и (10) к случаю, когда вихревая
дорожка, образующаяся за машущим крылом, удовлетворяет
условию устойчивости, данному Карманом. В этом случае,
как известно, — = 0,281, th—= —подставляя эти зна-
I I V 2
чения в (10) и (11), имеем:
(12)
у > 0,562.
(13)
При увеличении у, как видно из равенства (12), отно-
b * 1
шение -т- увеличивается, приближаясь к ;----=
h J г 0,35 cos о cos с
_ 2,86
cos a cos 6
Рассмотрим следующий простой пример. Пусть а = 0,
= 92 = 9; это — случай плоской пластинки, наклон которой
к направлению поступательного движения при поднятии и
опускании один и тот же. В этом случае 8 = 0, о = 9 и
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
507
при различных -у имеем следующие значения — (полагая,
что 9 мало и cos 9 = 1):
W V 0,7 0,8 0,9 1 2 3 4 со
£ h 1,8 1,2 0,95 0,8 0,48 0,43 0,41 0,35
§ 5. Основное уравнение теории машущего крыла
Основой всех дальнейших исследований послужит урав-
нение, определяющее силы воздействия потока на машущее
крыло; это уравнение выражает теорему количества движе-
ния для ограниченной массы воздуха, заключающей внутри
себя машущее крыло.
Рассмотрим систему координат (хп yt), относительно ко-
торой крыло совершает периодические колебания; пусть Olt
начало координат этой системы, ес?ь средина амплитуды,
которую описывает при колебаниях некоторая точка крыла.
Пусть V —скорость потока, набегающего на машущее крыло,
далеко впереди крыла; мы направим ось О±х± по направле-
нию скорости V. Согласно принятой нами физической схеме
явления от крыла отходит двойная вихревая дорожка, причем
далеко сзади крыла, где дорожку можно считать вполне
сформировавшейся, вихри дорожки движутся по направлению
оси О1х1 со скоростью У4-я0. Построим вторую систему
координат (х, у), относительно которой вихри дорожки вдали
от крыла неподвижны. Мы предположим, что в начальный
момент оси (хх, yt) и (х, у) совпадают; в дальнейшем оси (х, у)
перемещаются относительно (хр yt) по направлению оси О±х±
со скоростью V-l-zZo и за период колебания Т начало О
системы координат (х, у) переместится по оси О±х± на рас-
стояние I = (V-|- Uq) Т. Условимся называть систему коорди-
нат (хх, yj неподвижной, а (х, у) подвижной. Скорость
воздуха вдали от крыла и от вихревой дорожки равна
V— (у .— Uq и направлена по оси х.
Рассмотрим прямоугольник L, построенный на подвижной
плоскости (х, у), со сторонами, параллельными осям коор-
508
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
динат, и точку пересечения его диагоналей поместим в по-
движное начало О; пусть его стороны суть АВ = 2Н и
ВС = 2R (рис. 10).
Построим на ABCD прямоугольный параллелепипед Q
с высотой, равной единице. Предполагая, что размеры по-
строенного прямоугольника достаточно велики, так что в те-
чение одного периода колебания Т профиль крыла остается
внутри L, применим к массе воздуха, заключенной внутри Q,
теорему количества движения.
Называя через X, Y компо-
ненты силы давления воздуха
на крыло и через р давление
воздуха, напишем уравнения,
выражающие теорему коли-
чества движения, в виде
— X— I pdy=^-t I jpudxdy,
L ‘ S
— f pdx=^-t [ pvdx dy,
L *S *
где S— площадь, занятая воздухом внутри L, и производ-
ная по t понимается как субстанциальная, учитывая протека-
ние воздуха через контур L.
Переписывая уравнения в виде
— Xdt — j* р dy dt = d J J pu dx dy,
l s
— Y dt 4- j* p dxdt^d J* J pt/ dx dy
L S
и замечая, что за время dt через элемент контура L вытекает
количество жидкости, равное p(udy — vdx)dt, можем пере-
писать уравнения в виде
— X dt— j* р dy dt = д j* j* pu dxdy-\-dt f (tidy— v dx) pu,
l s L
— Y dt P p dx dt = d J* J* pv dx dy dt f (u dy — v dx) pt/,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
509
причем дифференциалы д относятся к неподвижному кон-
туру А, ограничивающему S. Умножая первое уравнение на I
и складывая со вторым, получим после незначительных пре-
образований
(Y-\-iX) dt = —dt J* p [(я dy—v dx) (ui-\-v)—p(dx—idy)]—
L
— d j* J p (v + ia) dx dy.
s
Так как по теореме Лагранжа в рассматриваемом случае
Р = Ро (0 — Р («2 -+ ^2)>
то, подставляя значение р в написанное уравнение и заме-
чая, что
р dy — v dx) (al + Ч) + у (и2 + ^2) (dx — I dy)J =
= — iv)2 (dx -+-idy) = ±- ) dz,
где \Г = ср4"4*Ф есть комплексный потенциал течения, так что
dW
—7- = и---IV,
dz
получим после интегрирования по t уравнение в виде
т
(Го + ZX0) Т = -1 J dt J (^)2 dz~
0 L
— Р | — i dy)~ Pi
L
где XQ, Yq — средние значения компонентов силы давления
потока воздуха на крыло за период колебания; они опре-
деляются формулами
т т
fXdt-=X0T, f Ydt=YaT.
О о
j , (1)
510 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Таким образом, для нахождения величин XQ, Ио надо
определить величины трех интегралов правой части равен-
ства (1).
§ 6. Определение функции W(^, Z) и контура L
Так как в дальнейшем мы можем размеры контура L не-
ограниченно увеличивать, то найдем аналитическое выражение
. dW г х
функции в области бесконечно удаленной точки.
Построим контур Lo; пусть его точка пересечения диаго-
налей находится в начале подвижной системы координат (х, у),
стороны параллельны осям и размеры сторон выберем на-
столько большими, что вихревую дорожку вне Lo можно
считать вполне сформировавшейся и образующей систему
неподвижных на плоскости (х, у) вихрей. Контур Lo мы далее
будем считать постоянным. Кроме того, будем считать раз-
меры контура L настолько большими, что Lo лежит внутри L,
Рис. 11.
и пусть Со» ^1» • • •» = + —аффиксы вихрей верх-
него ряда двойной вихревой дорожки и Со> Сь Сг»
= — аффиксы вихрей нижнего ряда вихревой
дорожки, лежащей вне Lo (рис. И).
Очевидно, всегда можно выбрать ось х (и ось хх) таким
образом, чтобы она проходила посередине вихревой дорожки.
Тогда имеем при расположении, указанном на рис. 11 и
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА 511
определяемом выбором размеров Ло,
ч—= (1)
где h—ширина и I — расстояние между двумя последова-
тельными вихрями одного ряда дорожки.
Составим выражение
О (г)
ОО
(2)
Очевидно, что ряд (2) абсолютно и вне Ск и равно-
мерно сходится; кроме того, полагая z = (nt^ty
и получим:
___ 1
*=°j/r (^-ь«+«)2+(4~'/гУ V (w+m+«+^y+(4+”)2
^4 £2/2 + m2
1
Z ^к
Отсюда следует, что при т —> оо выражение O(z) стре-
мится к нулю.
Рассмотрим разность

Функция f(z) вне Lo не имеет на конечном расстоянии
особых точек, и по предыдущему f(z) при неограниченном
512
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
увеличении т стремится к —zz0; отсюда следует, что в об-
ласти z = оо имеем разложение
---О(г)= —+ ... (4)
Заметим, что неподвижны на плоскости (z). Инте-
грируя обе части равенства (4) по контуру L и замечая, что
между L и Lq функция f(z) голоморфна и число точек
и С&, лежащих между L и Lo, в силу выбора размеров кон-
тура L одно и то же, имеем:
о • f dW . ,Лг.
— -у— dz. (4Z)
1 J dz v 7
z.
Нетрудно найти механический смысл av В каждый мо-
мент внутри Lo лежит некоторое количество М вихрей верх-
него и N — нижнего ряда вихревой дорожки. Тогда, называя
через Г(/) циркуляцию вокруг профиля крыла, получим:
= — N). (5)
Lo
По сделанным предположениям циркуляция Г меняется
скачками, пусть Г = 1\ при отходе вихря верхнего ряда, т. е.
при опускании крыла, иГ = Г2 при отходе вихря нижнего ряда,
т. е. при поднятии крыла. Кроме того, в силу теоремы
Томсона при переходе от опускания к поднятию крыла
в нижней точке амплитуды колебания, когда отходит вихрь
нижнего ряда, имеем:
r1 = r2-7. (6)
Так как средняя за период колебания величина цирку-
ляции определяется уравнением
го по (6) имеем:
Г-Г1 + у = Г2—1. (7)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
513
Рис. 12.
Если мы рассматриваем промежуток опускания крыла,
то имеем расположение вихрей, указанное на рис. 12, а по-
тому М=М и по равен-
ству (5)
= =
L
Если же рассматриваем
промежуток, соответствую-
щий поднятию крыла, то имеем расположение, указанное на
рис. 13, и, следовательно, М — N = —1, а потому
Г dW , „ ТУ 7
—-dz = r2 — т = Г—-ту.
J dz i 2
гг fdW Л
Таким образом, величина dz не зависит от времени,
L
теоремы Томсона, и, следо-
вательно, в силу выбран-
ного размера £0 имеем
по (4Z)
что, впрочем, прямо следует из
2ШЙ! = —у+Г.
Рис. 13. Подставляя это значение
в разложение (4), получаем
dW
следующее аналитическое выражение в области беско-
нечно удаленной точки:
dW 1 7 V ( 1 1 ) ,
dz - + +
г — —
+ <8>
Функция зависит от z и от времени /, а потому
коэффициенты разложения а2, а3 суть функции /.
Система осей (х, у) перемещается относительно осей
(хх, j/i), а потому расположение плоскости (z = x-\-iy)
514
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
относительно неподвижной системы координат в момент t = О
и t = Т различно, как показывает рис. 14. С другой сто-
роны, в любой точке А, неподвижно связанной с неподвиж-
ными осями (xlf j/1), в силу периодичности движения скорость
в момент t = 0 и в момент t = Т одна и та же. Отсюда
следует, что
(dW\ ( dW\
“ lV~\dz\^ \dz)t^T ’
2 = Z0 Z-Zq-1
и, применяя это условие к разложению (8), имеем уравнение
m°+2k/L{2_(^+/) 2_(C;+Z)) +
Г--~
I___2 1 ! Л2(Р !
‘ 2™ z —Z ' (z —Z)2 ' ‘ ‘ ‘ ’
откуда, произведя сокращение и разлагая по степеням
имеем равенство
г-1 1 1
+ -2^+л2(О-«2(0)] ..]+ ....
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
515
откуда
1«210Г = «2 (D - а2 (0) = [- (Г — -}) 14- т (:0- С'о)],
и так как
то окончательно
--о — —----------------2 Н-
: j'A I 17 I
о 2 г. * —2тс
(9)
Переходим к выбору прямоугольника L. В дальнейшем
мы будем неограниченно увеличивать размеры L, и при этом,
как показывает неравенство (3), на стороне CD выраже-
ние G(z) удовлетворяет неравенству
I 0(2)1 <Х Ко-(Ю)
а потому
[ G(z)dz
CD
(Ю')
При увеличении размеров L выражение (10') стремится
к нулю, если
1. Н ~
lim — = О,
а для этого достаточно положить
R = /А.
(11)
В дальнейшем мы и будем брать прямоугольник L со сто-
ронами АВ = <2Н и ВС =2Н3,\ При таком выборе размеров
С , ч , А1
сторон выражение I G(z)dz стремится к нулю, как —,
cd И
что мы запишем так:
G (z) dz
CD
(12)
Для дальнейшего мы несколько уточним выбор прямо-
угольника Ц мы будем проводить сторону АВ так, чтобы
516
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
она прошла посередине между двумя точками и С&, как,
показано на рис. 15. Так как, очевидно, можно провести
сторону А0В0 на расстоянии — от Со, то т — число точек
и лежащих между £0 и L, определится из уравнения
где 2г = В0С0.
Пусть z — х—iy и Нетрудно оценить вели-
чину | G(z)|-
Действительно, если положить 1 , то
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
517
С другой стороны, для точек, лежащих вне L, имеем:
= (х-и2 + (з/-4)2>/"
и аналогично
k—^|>]/” (*—m)2z2+(^—4)2.
а потому
Таким образом,
Наряду с функцией G(z) рассмотрим другую функ-
цию G0(z), определяемую следующим равенством:
Go (z)
1
z
(15)
Найдем некоторые свойства этой функции для z, лежа-
щего на стороне АВ или на ее продолжении, т. е. при
518
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
z = Так как при этом, очевидно,
\z—(4+zi*-OTi)2+(^—4)2
>]/"/2|Л — т\2+(у— Ау ,
(4+zia-w02+(^-4)2>
> у/~p\k — m|24-(j/ — |)2 ,
TO
т. e.
I Ш |CO-+ 1 |C0-Cil^. (16)
При тех же условиях
сю
I °(г)I < у- Ко—С121—гп—П < ~I I г- (17)
Наконец, на стороне АВ
сю
|G0(^)—G(z)| = i|co-c;|2
о
или, иначе,
______________1______________
(/73/’+г + ^)2 + (|у1-|)2
|G0(X)— G(z)\< X|r,0_c;|x
Г сю
х|гг----н Г----
\и^-г J(H%_
|0о(г)-G(^)| <^|:0 — ^о|х
х'гг-п+п—
Н 1 — Г 7 / I v I _
dx I
\2 । /, . h \2 ’
II \
1 У I — -9 I
arctgn%—К (18)
Н'* — г ।
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
519
§ 7. Нахождение величины J* [cp]o\tfx — idy)
Мы видели, чтох)
dW
dz
Следовательно,
2^'T z~^
г__L
---Linz——
2r.z z 2г2
и
+--- (D
Замечая, что С& и Г не зависят от /, имеем:
(«Pio* = ?(*> у, Т) —<Р(Х, у, 0) = —д. 4.^-+ ..
а потому по формуле (9) § 6
_ . ч1г х Г/ у
1А’=-ьг+?”ь?47"1.'-в!+- (2)
Покажем, что
д.
L
1) См. (8) § 6.
интегралы
[a*]’’(dx — I dy)
Ч-------Р-1------
при
£>2
520
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
стремятся к нулю при безграничном увеличении А. Действи-
тельно,
Г [ак]о (dx — I dy) f\ak]%ds Н*1’
,1Д-4--------------- < J -T7j^< 8•
L L
Следовательно, по (2) имеем:
х (dx — I dy)
V-2 v2
L
L
rz f у (dx — I dy)
2k J x2 4- y2
(3)
Так как
н
+ >2 d
4l arct^2
и, следовательно,
-idy)
1
стремится к нулю, как —— , и
н3/2
-2 j =
— — 4 — arctg —7—^ ,
\2
то, подставляя все эти значения в равенство (3), получим:
J [<р] ** (dx - i dy) = г/ + О (. (4)
§ 8. Вычисление выражения
"1 т
dx dy
L~S’ Jo
„ [ f dVv , 1
ность значений интеграла | -j^-dxdy, вычисленного для
момента t=T и, следовательно, для положения A1B1C1Dt
D Г f f dW
Выражение
представляет собой раз-
L
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
521
прямоугольника L относительно неподвижных осей (х1?
(рис. 16) и для положения ABCD в момент t = 0.
Заметим, что в силу периодичности течения по отноше-
нию к осям (хр у^) скорость в точке с одними и теми же
Рис. 16.
координатами в момент / = 0 и t — T одна и та же, и, сле-
довательно, | \—^dxdy в момент / = 0 и t=T имеет
одно и то же значение и взаимно сокращается в рассма-
триваемом выражении.
Таким образом,
J ^1 ~ — ivydxdy —
- S Jo A*BtBA
j J (и — iv)dxdy, (1)
причем оба интеграла правой части можно взять и для / = 0,
и для t=T.
Согласно результатам § 6 (соотношения (10) и (12))
в области DfifiD (рис. 16)

7U 1 \
2? У77з /
522
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и, следовательно,
J j G(z)dxdy
D&CD
С другой стороны, в области А^Е^ВА согласно (18) § 6
|g0(£)-g(*)I<^K-^|x
( °° 1
чг) 1 I f__________________ I
\H^-r J (//3/’-г + /х) + (|у|-|У)
т. e.
|G0(2)-G(z)|<-i|C0— r
1 7TT
1 1 \
I tf^-rE
и так как площадь A^BJSA равна 2Н/, то
I j’o0(z)dxdy— J
а'в/ва а.в.ва
T^o-4|(/+1)77#
Далее,
dx dy
н
f dy =
г2 -4- v2
А.В.ВА
lEEl -Н
А.В.ВА
, dx . Н . . Нг/‘
! — arctg — < к In -----------
J х х Н'^ — 1
I
н3/* ’
Таким образом, с точностью до членов порядка
1
при интегрировании в области D^DC можно положить:
Г — ~
dW _ . 2 1
dz ио\ 2
(3)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
523
и в А±В±ВА
оо р_7
dW I 7 V / 1 1 \ , 2 1
---= — ^о+— 71 I----------714------
dz 2ni \ z — С z — С / 2л/ z
_ ОО \ К к /
ИЛИ
^- = — «о+2ZZ I ct£(z— ’0)7 — ctg(^ — Qy} +
г-у 1
+ -ьА4- <4>
Далее заметим, что прямоугольник А±В±ВА конгруэнтен
с D^CyCD и точке (х, у) в А±В±ВА соответствует точка
(—х — Z, у) в D^CD, т. е. точке z = x-\-iy в АХВ±ВА
соответствует точка zx = — х — l-\-iyt т. е. zr — — z—I
в D^CD (z — x — iy).
Отсюда имеем:
+ ~ j — ctg(* — $ypxdy+O(^)-
Л.В.ВА
Но
1+ 1 =1+X-.L+...
z z-\-l z z z^
и
J J [7
^B.BA
A.B.BA
dx dy= 2
x dy
x2 + y2
Так как
я3/^
л f i H , . Л1 , H
— 4 arctg — dx < 4/ arctg—r-------------
J x H — I
524
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и, следовательно,
И [7
А.В.ВА
окончательно имеем:
= 277 J J [ctg(г_’о)7 ~ctg7]dx dy+0(^)(5)
АХВ,ВА
Рассмотрим на плоскости (г) вспомогательное течение
с комплексным потенциалом Wlf удовлетворяющим уравнению
= 277 [ctg - С<>) Т ~ ctg (z -'-«) т] *
Полагая
(6)
(7)

sin (z —Со)у
sin (z-Q-J-
имеем:
sin (z — Со) у sin(z —Со)у sin (z—Со)у
= оЦ,п------------— ту In •-------------------,
sin(z-C0)y| sin (z - Со) - sin (z - Co) у
ИЛИ
cos[z + z — (Co + Co)]y — cos[z — 7—(Co—C0)]y
= — -jL 1 n ---------------l-------------------- .
cos [z + z - (c; + Q] у - cos [z - z-(C'-Q] у
Так как при = С0 = £4-гу}, ^' = 5' — Ztq'
z -f- z = 2x, z — z — 2iy
и T. Д.» TO
cos 2/ (y — тр— cos 2 (x — S)-^-
<11 = — -X In--------------------------l---------------------L_
cos 2Z (у — if) — cos 2 (x — $') у
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
525
или

2(2/-^) у -2(27-7]) у
е 1 +е — 2cos2(x —6)у
(8)
2(2,'-т]')у
е L
+ е — 2 cos 2 (х — £') у
Пользуясь (6) и полагая = и± — ivv получим:
J J [ctg(z—^т~~cts(z~=
А&ВА
= J ^dxdy + i J \^dxdy.
А1В1ВА А.В.ВА
Из уравнения (7) имеем:
lF1(z+/) = IF1(z) + 2A/T,
где N—целое; отсюда следует, что
Ф1 (x + Z, у) — фх {х, у).
Но
Я
J J lx"dx dy = .1 (я/’’ — (w’/a—1> j)] dy = О
А.В.ВА -Н
И
Я3/э
f \^dxdy= I Н) — ^(х,—H)]dx, (9)
АЛВА н=/,__г
и при большом И имеем по уравнению (8)
Я)== —^-1пе 2(11 >г Ч-е = -^-('Г) — 7]')-Н.
фх(х, —//) = —^-1пе2(11 11 ’ i 4-S1 = — — O+Si
526
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и потому
н7з
[ \l>ydxdy== .1 7)')dx4-e2 =
Z-B,2?A у н^/а-г
= т 01—О 4- е2 = й+е2.
1
где е, ер е2 стремятся к нулю, как .
Отсюда имеем окончательный результат
(Ю)
§ 9. Вычисление выражения
Как было выше показано,
dW . т V /_1__________L_\ ।___
dz ° У*—z— Vk] 2ni z z*
r 7
1_____1_
2 z ^k
где
____2 2
2 я i z

/«=>+>+...
(1)
(2)
Следовательно,
oo
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
527
1 \
z~~^k)
2
— (^) +
оо р____Т
+ 2тт S (—-----------
2гЛ \2 — ^к z~^k) z
(3)
Так как в силу равенства (2)
f/(z)^ = O, j±f(z)dz = O, j* [/(z)]2 dz = 0
h l i
и также
1
z~^k
так как внутри L согласно выбору контуров LQ и L имеется
одинаковое число точек £к и Cki то для вычисления
остается вычислить интегралы
и, кроме того, интеграл
1
z ^к
2
dz.
(6)
Для вычисления интегралов (4) и (5) подсчитаем предва-
рительно интеграл
\ftf)-^dz. (7)
528
II.- ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Рассмотрим два случая:
1) когда точка С лежит внутри Ц
2) когда С лежит вне L.
В первом случае интеграл (7) равен нулю, так как кон-
тур L можно заменить окружностью С сколь угодно боль-
шого радиуса г, и так как при больших г можно выбрать
такое /п, что
1/(г)|<|,
ТО
Г г/ ч dz
т. 2пг
г—|С| ’
(8)
и при безграничном увеличении г правая часть неравен-
ства (8) стремится к нулю. Если же С лежит вне А, то,
окружив С окружностью с малого радиуса h и построив
окружность С, включающую внутри себя L и с, получим по
предыдущему
С L с
и так как
С
ТО
(8')
L
Применяя равенство (8'), получим:
f/(г) 2 (—Мdz=2та‘ 2 [/(О- /сад], о)
L О V к = т+1
причем суммирование в правой части равенства (9) распро-
странено только на точки и Сд., лежащие вне L, а потому
1^|>^3/’+(£ — т)1, |^|>№А+(£ —/п)/.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
529
Следовательно,
-4-2 I*___—______= — -I_____!__
~ J (H'^ + xl)2
О
Таким образом,
1
L й = 0 \
z~ ^к
(10)
Предыдущие преобразования можно применить и к инте-
гралу (4), и мы получим:
но
Учитывая все полученные результаты, после очевидных
преобразований имеем:
Таким образом, остается вычислить интеграл
(12)
530
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Покажем, что интеграл (12) по линии L можно заменить
интегралом по стороне АВ.* Для этого, кроме прямоуголь-
ника ABCD со сторонами АВ = 2Н и ВС = 2Н\ построим
квадрат MNPQ (рис. 17) со сторонами 2Н\ Тогда инте-
грирование вдоль L можно заменить интегрированием вдоль
квадрата MNPQ. Но согласно неравенству (14) § 6 на сто-
ронах PN и QM, где |у| =
т. е. можно подобрать такое постоянное М, что
и то же неравенство в силу неравенства (10) § 6 справед-
ливо и на PQ. Следовательно,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
531
Далее, неравенство (13) справедливо и на BAZ, и на ДМ,
а потому
и такое же неравенство справедливо и для интеграла
вдоль ДМ. Таким образом, окончательно имеем:
Далее покажем, что в интегралах равенств (16) можно
заменить функцию G(z) через GQ(z). В самом деле, по
неравенствам (18) и (17) § 6
532
ii. труды по Теории машущего крыла
Итак, окончательно имеем, подставляя найденные значе-
ния в равенство (11),
2
|ctg(^---o)--ctg(2-Co)-] = '
I* L I z J
и так как
то еще
lt sin2 (z — co) у sin2 (z — ф y
p (' / dW \2 ,
7Г —j— dz =
2 J \ dz /
L
AB
sin2 (Co Co)
sin2 (z—Со) у sin2 (z—ф у
Покажем, наконец, что интеграл по АВ в равенстве (18)
можно заменить интегралом по всей бесконечной прямой
х = н’/г.
Действительно, повторяя преобразования § 8, покажем,
что
I sin (Z —QySltl (Z — Со)у| =
= У [cos 21 (у — Т()у — cos2(x — У у] X
X [cos 21 (у — т]') у — cos 2 (х — В) у] =
1 Г 2(г/-1))у -2(г/-т])у л]
= Р +* 1—2 cos 2 (х — OyJX
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
533
Хе г-{-е 1—2 cos 2 (х— £)yl =
=ils?l«ll[/!^+(!-.,4]+0(1!l,l)==
а потому интеграл
sina^-ф^ Г
-----------------------dz < Me~is ds = ^-e-il1.
в Sin3(z-Co)yshi3(z-C;)y i
Итак, неравенство (18) мы можем переписать в виде
НО--Н)-
L
„ °°/ sin2(r _ф ”
-я ----------й+о(4 . (19)
Способ вычисления последнего интеграла хорошо изве-
стен. Его можно вычислить, например, следующим образом.
Вычислим сначала интеграл
р sin(C0 —С0)у
J -------------те--------'г—~^Z ~
-£> i sin (z — Со) у sin (г — С') у
оо i
= j ^Ctg(£ —С0)у —Ctg(z —Со) ypz =
—оо i
тс оо г
z sin (г — Со) у
= — In ---------------- =
7С р f ч 7С
sin (г — Со) -Г-
L -оог
(z-Q-y' * “(2Л)у г ' = 2(С0 — С)1.
534
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Таким образом,
оо i f
f ------------—-----------= 2Z----. (20)
-со i sm (г — Со) у sin (г — ф у sin (Со — ф у
Дифференцируя равенство (20) по параметрам £0 и Со, по-
лучим:
р cos [z — Со) у Sin (г — Со) у
---------------------------dz =
-£i 81пз(г-ф^
/ sin Ко - Ф Т - Т Ко - & cos Ко - Ф Т
= 21-----------------—----—------------—
” ^2Ко-Фт
и
ОО % . у f \ 7С у . 7С
(• cos (г — Со) у sin (г — Со) у
I ------------------------dz —
- тог Sin2 (z — Со) у Sin2 (г — Ф у
t sin (Со - ф у - у (Со - С^) cos (Со - а')
= -21----------------------------------------------1—,
" si"2Ко-Ф Г
и, вычитая второе равенство из первого и умножая на
sin (Со — Q-y> имеем:
f sin2(C0 — ф^
-------------------------dz =
sin2 (г —Со) у з!п2(г —Cq) у
= 4Z1 [1 -(Со — ф ctg(Co-С^)у].
При выбранном расположении линии Ао имеем:
Со —^ = -y+AZ,
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
535
а потому
(Со - ф у ctg (Со - ф 1 /) Ctg (-| + xj=
I к \ Ьк ,\ hn
=-(-y+Tl)tthT-
Следовательно,
f*
--------------------------dz =
_sin2 (z — Co) у sin2 (z — С') у
и, подставляя в уравнение (19), имеем:
или
+ zpf.r^th^- i]+o(-L-V
2tlZ L z i J W2 /
Но по формуле (8) § 4
Y XL
‘ “° 2/^ — »
а потому
Y2 xt, Y
PT/thT = P“° Y’
и, следовательно, окончательно имеем:
536
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
и отсюда, так как первые члены второй части равенства
(21) не зависят от времени,
Ил J (")'*—₽“»г7'+
О L •
fch — — 1] 74-о (4г)- (22)
2nl L/ I J \Н'Ч 4 7
§ 10. Подъемная сила и тяга машущего крыла
Вернемся теперь к основной формуле (1) § 4
(K0+ZX0)T = -| J dt J {^)2dz-
0 L
— P J [<?]T(dx — idy) — J ™dxdy\o . (1)
Так как мы нашли:
’> i ,fdt (Ш'- "
0 L
+‘й(ти,т-1)7'+°Ш l<22,§91'
1(4) § 71,
1(10) § 8],
то, вставляя найденные значения в (1) и замечая, что
I = (у-j- Uq) Т, получим после деления на Т
Ио + «„ = Р«„г -; 4т1,1 т — 1) -рГ (V+«„) -
<2>
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
537
и, переходя к пределу, увеличивая неограниченно размеры,
получим окончательное уравнение для определения средних
значений величин сил, действующих на машущее крыло,
Го+ 1Х0 = -рУГ—-i [g(yth 1) + ^(V+«o)]. (3)
Отсюда
^o — g2/(TthT” +
Fo = —рУГ. (5)
я»
По поводу приведенного вывода уравнения (3) заметим,
что по идее он близок к методу Сэйнджа (1), которым для
случая цилиндра со сходом с него двойной вихревой до-
рожки и дано впервые уравнение (3). Однако вывод Сэйн-
джа содержит очевидную ошибку1). Кроме того, Сэйндж
для потенциала вихревой дорожки, бесконечной в одну
сторону, использует свойства функции Г (г). Приведенный
вывод показывает, что это является совершенно излишним;
достаточно, как показано в § 6, подобрать надлежащим
образом контур А.
Уравнение (5) дает, очевидно, в рассматриваемом случае
аналог теоремы Жуковского. Так как
г = у(г1|+г2|)=4(г1+ Г2),
!) В выводе Сэйнджа L неподвижно. При этом в силу перио-
дичности течения
откуда следует, что = const и J* (dx — i dy) = 0, в то
L
время как у Сэйнджа имеем:
J [?]^(^ — ldy) = 4h.
L
538 И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО крыла
то, замечая, что по формулам (3) и (4) § 4
Гх = — ~b ]/V2 Н- w2 sin + arctg у),
Г2 = — ~b ]/V2 w2 sin (p.2 — arctg y),
получим, что
Г — — кЬ /V2 + w2 sin a cos ^3 -|- arctg j,
где
Z * Z £
Отсюда окончательно получимx):
Г — —• nbV sin о £cos 8 — sin 3 -у j. (6)
В частности, если = 02 = 9 и, следовательно,
[l1 = p.2 = 6 + y> то
Г = —K&Vsin(| + 0), (7)
т. е. Г есть та циркуляция, которую крыло имеет при
отсутствии взмахов.
Преобразуем равенство (4). Так как
Т хь к™
Uq 21 I ’
то
Xo = £-er<V+2“o)- <8>
Формула (8) полностью совпадает с формулой, данной
Карманом для вычисления лобового сопротивления, если
в ней переменить знаки у у и «0. Этого и нужно, было
ожидать, так как с точки зрения, на которой построена
настоящая работа, отличие тяги от сопротивления, вызывае-
*) Заметим, что, как показывают подсчеты, в формуле (6)
w
cos 3 — sin^-pr может бытьрбольше единицы, так что коэффициент
подъемной силы машущего крыла несколько выше, чем у стацио-
нарного крыла.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
539
мого вихрями дорожки, состоит только в изменении вра-
щения тех вихрей, которые образуют дорожку, и в пере-
мене в связи с этим знака zz0.
Если в уравнение (8) подставить условия устойчивости
вихревой дорожки
•у-=0,281 и т=//8и0>
то получим силу тяги в виде
хо = — p/V2 [о, 314 (у)2 + 0,794 у j ; (9)
уравнение (9) соответствует известной формуле Кармана
для сопротивления.
В случае рассматриваемой задачи величину силы тяги
нужно выразить через данные, определяющие форму и
движение крыла. Так как по формуле (6) § 4
у = 2кЬ cos о [sin SV + cos Sw] (10)
и по формуле (9) § 4
uQ = ~ cos о [sin SV -|- cos Sw] th , (11)
то, подставляя эти значения в формулу (4), получим:
' ЪкрЬ cos о (У sin В -|- cos Sw) X
X [у- cos о (sin SV + cos Sw) { 2 th — 1 | + y- vj,
или
Xo = —2кр^ V2 cos a (sin S + cos S p) у X
X [1+jCOsa^sin3-hcoso^X{2 TthT— ’}]' ^12)
В частности, если = 02 = 0, когда о — у-|- 9 и 8= 0,
X) = — 2крЖад cos (у + °) у X
x[1+X«s(T+e)^2TlhT- '}] <|3)
540
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
При выполнении условия устойчивости дорожек из (12)
имеем:
Хо ='— 1,76р&V2 cos о (sin 8 + cos В X
X + 0,25-^- cos о (sin 8cos 8-^^. (14)
Так как при выполнении условия устойчивости по
уравнению (12) § 4
, — 0,562
b___________V_______________
Л Л ОК Г . - I W 1 ’
0,35 cos a sin о cos о -рг
то из (14) имеем окончательно1):
Хо = —0>94Pfty2Cosa(sin8H-cos8y)[1 + 1’2 у]- (15)
Возвращаясь к общему случаю, заметим, что по урав-
нению (10) § 4
— — 2 А
Ь _______________V I_________________ (. б)
Л h \hr hn\ Г • * । . W] ’ ' '
2 — I— th — I cos a I sin о -|- cos о — J
и, подставляя это значение в выражение (12), получим:
Хо = —»крЛV2 cos a (sin 8 -j- cos 8 X
2^th —1
Лк Лк .
JW h TthT~l
’4 1
(17)
Выражению для величины силы тяги можно дать другой
вид. Во-первых, замечая, что циркуляция у вихрей, обра-
зующих дорожку, выражается по формуле
у = 2кЛ cos a (sin 8V-|- cos 8w),
!) Заметим, что в уравнении (15) -р->0,562.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
541
можем переписать равенство (17) в виде
2^th^- 1 f
Хо = — pVT ————— {
2^th j V
Лл hr. ч
h I ‘Ь i 1 I
2-7-4--7----У - О7')'
Z „ hit . Iit , I 4 7
2TthT-4
Наконец, из уравнения (16) можно получить:
t Г • S5 I ? w 1 1 Гw n hl I 1
Z'coso sin§+cos8vJ = ft^-2TJ^ -^—
2TthT
а потому равенство (17) можно еще написать в виде
Х0=-кР^/[^— 2А]Х
1гт1гт. П Ак hit .
„ - 2>.TlhT-1 2-lhT-‘ ..
/ ' 2^14-1] (
Во всех этих выражениях следует помнить о необходи-
мости выполнения соотношения (16). Последнее соотноше-
ние, положив
Ак., Ак
— th у = /И,
можно переписать в виде
хт ohirw Q h М— 1 1 2Л4 — 1 1
Xo = - ^V4 [ v - 2 T] [v - 2 T j] —ж,
и так как
Л4—i 1 М
2Л4—1 “ 1 2Л4— 1 ’
то имеем еще
[ V-21] [(V-2 т) 2-т-+4] 2Ж 7'">
Так как данными, определяющими работу машущего
крыла, являются величины bt и
откуда определяются а - у- и L о'~"> а также
542
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Ь W
величины у и -у , то для расчета величины тяги из урав-
нения (16) надо найти у и по уравнению (17) Хо. При
этом мы должны помнить, что для возможности существо-
вания течения вокруг крыла с физической точки зрения
необходимо выполнение условия
W \ 9 А
v i •
(18)
Рассмотрим выражение
7 ’ М [V I 2М — 1 J ~
(2М-1)^-2-^(М-1)
=--------Т------------<19)
Так как
(2М—1)^—2-|(М—1) = (2М—1) (^-2|)+2АМ)
то по условию (18) следует, что при 2Л4—1>0
/(Л4)>0 и, следовательно, XQ < 0, т. е. при М =
hn .. tin . 1.
= -j-th у > имеем тягу. Это условие выполняется при
у > 0,245. Итак, при у > 0,245 имеем тягу при любом
отношении у , удовлетворяющем условию (18). Из уравне-
ния (19) видим, что Ло = О при
w __ 9 h М — 1 __ 9 h 1— М
Z I 2М— 1 2 I 1— 2М ’
Так как имеет место условие (18), то это уравнение
имеет решения, удовлетворяющие условию (18), только
когда 2Л4 < 1. При этом
Так как
/(Ж)
о АА
v t \
(20)
__2М — 1 Г w п h /.
— Af L I \
1— 2MJJ
' 1 — 2М ) ’
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
543
то при
т<т<2тк1 + гаи)
(21)
/(Л4)<0, а потому по формуле (17)
Хо > О,
т. е. при Л1 < у или при у < 0,245 и при -у, удовлет-
воряющем условию (21), машущее крыло дает не тягу,
а сопротивление. Заметим, что такой случай может иметь
место только при режимах, далеких от удовлетворяющих
условию устойчивости вихревой дорожки. При выполнении
условия устойчивости (у = 0,281^ получим тягу при любом
> 0,562. При этом мы, конечно, считаем, что
sin 8 + -prCosS > 0.
В частности, при 8 = 0, когда = 62»
az /а I л\2Л1— 1 Гш п h М—11
XQ -rcpMZwcos^2 + м [у/ % I 2M—1J
§ 11. Об эффекте подсасывания
Теорема импульса сил точно указывает механизм воз-
никновения сил, действующих на погруженное в жидкость
Рис. 18.
тело. С этой точки зрения образование силы тяги машу-
щего крыла, как оно выше изложено, имеет следующий
простой механический смысл. Образующаяся за машущим
крылом обращенная двойная вихревая дорожка (рис. 18)
544
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
создает добавочную скорость, направленную в сторону на-
бегающего потока; эта скорость и связанное с ней напра-
вленное по потоку количество движения являются резуль-
татом действия приложенной к жидкости силы, направлен-
ной по направлению скорости течения и, следовательно,
равной ей по величине, но направленной в сторону, про-
тивоположную скорости набегающего потока, силы, при-
ложенной к машущему крылу. Это и есть сила тяги. Каким
бы образом мы ни пытались объяснить возникновение силы
тяги, во всяком случае эта сила по теореме импульсов
должна вызывать отброс массы жидкости назад. С этой
точки зрения мы и постараемся выяснить сущность влияния
на крыло так называемых «подсасывающих» сил.
В основу всех соображений мы положим метод учета
подсасывающих сил, принадлежащий Н. Е. Жуковскому,
причем ограничимся случаем плоской пластинки р]. Пред-
ставим себе поток, обтекающий пластинку (рис. 19) так,
Рис. 19.
что задняя кромка В является точкой схода потока с пла-
стинки. При этом около передней кромки образуется физи-
чески невозможная бесконечная скорость. Идея Жуковского
состоит в том, что очень близко к передней кромке обра-
зуется вихрь такой интенсивности J, что в самой точке А
скорость конечна и обтекающий крыло поток воздуха обте-
кает пластинку и некоторую вихревую область около перед-
ней кромки. Отсюда следует, что давление потока, обте-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
545
кающего пластинку, состоит из давления на вихревую
область, заполненную воздухом и дополняющую крыло, и
из давления на само крыло. Рассчитаем то и другое
давление.
Отобразим при помощи функции
= 0)
внешнюю часть окружности |г| = /? на внешнюю часть
пластинки; при этом радиус R окружности будет равен
где b — ширина (хорда) пластинки.
Обтекание круглого цилиндра дается комплексным по-
тенциалом
W = Ve-^(z+^\^^\aZ. (2)
Из уравнений (1) и (2) найдем для комплексной скорости
потока, обтекающего пластинку, выражение
?E = v(coS0±/'‘-^iSlne), (3)
причем для верхней поверхности пластинки квадратный
корень входит со знаком плюс и для нижней — со знаком
минус. Давление на пластинку снизу (рн) и сверху (рв)
выразится по формуле
Рв = с—| vB2,
и отсюда направленное кверху и нормальное к поверхности
пластинки давление
Др = ря —рв = | —Vh2] = | 2 Vcos 02V sin О
а потому вся сила давления потока на пластинку на-
правлена по нормали кверху и равна
+ 6/2 ____
(* /* h с) £
= 2pV2 sin 6 cos 6 J у g- dz = TtpV2b sin 6 cos 6. (4)
-b/2
546
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Нетрудно проверить, что сила Рг приложена в точке—- —.
Подсчитаем теперь силу Р2, приложенную к вихрю J,
образующемуся в точке, близкой к передней кромке крылат
Рассмотрим характеристическую функцию обтекания круг-
лого цилиндра в виде
r = lnz +
+ ^[ln(z+fl(1 + s))-In(z+I^-7)], (5)
где Г — основная циркуляция вокруг крыла и J—циркуля-
ция вихря, находящегося в точке—около перед-
ней кромки, так что е — величина малая.
Из (5) имеем:
dz \
, г 1 ,
£2 ) z "+
4-—Г_______1___—
г + Л(1 + 0
Для того чтобы скорость около передней и задней кро-
мок крыла у пластинки была конечна, необходимо, чтобы
при z — ±R обращалось в нуль. Отсюда имеем урав-
нения
Ve-«(1_e.i)+jr_+^(_l__>±2) = 0,
1,е-.<(1-в.«)_^+24(±+1±Л) = 0. (7)
откуда
sintl
2. -j- ze
или приближенно по малости е
J = — 4z V7?e sin 9. (8)
Рассчитаем теперь скорость течения на оси J. Для этого
надо найти выражение
О)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА 547
где [1 — точка плоскости С, соответствующая—/?(1—(—s).
Пусть С = /(г) — отображение, даваемое формулой (1).
Тогда, называя еще — /?(1 —Н ©) через а, имеем:
£—1х = Х(г) — Х(о):=:Сг — я)х'(а)+
и
In (С — ц) = In (z — а) + In Xх (а) +
+ £7-“7Й+(г”“),(")'
Отсюда, обозначая компоненты скорости на оси вихря
через и и v, имеем:
“ -= Tz [Ve"ei (z+ln z - iiln x' <a> -
___x г—ax" (a)
2^1 2 xz (a)
(z — a)2(.. .)—
v 7 v 7 2nl \ 1 1+е/_|г=а^С
Иначе,
«-Iv- «Т‘)+
L \ 22 /
2_J____J 1 xz/ (a)_J 1 ~| (dz\
"* 2rcZ z 2k I 2 xz 00 2rcZ । R \dt/z=a*
Z+ 1 + e Js=a
Так как a — — /?(1-|-е), то
Ve~*(\ -Ц = Ve-oi Л_______^L\______L_ _L
Z* rzvlzj^a Ve l.1 (l+e)3/ 2kZ/?1+s-
что по малости e можно еще написать в виде
и в силу уравнения (7)
ye-Bi (1 __ ^20i)
Г
2nlR
J 24-е
2nlR е
J 1
2nlR s
D2 уХ/ /2\
Далее, так как / (£) = £-+—, то * ? ^7 =
х" (а) 2/?2 Z ' 1
а потому ^-) = ^/?8(1 + t)(2e + >a)^-_.
2^3
г(гЗ —/?2) *
548
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Точно так же
/ 1 \ __ 1 + е _ 1
. Р /?(2е—£2)~ 2/?е •
\ 1 + е / z = a
Наконец,
(d2\ -- ( & \ • ___(1 + е)2^1
ULa ~ - W L -R (l+s) ~ 2е + е2 ~ 2е •
Отсюда следует, что
• Г J 1 J 1 J 1] 1 _
“ lV [ KZ/?s-|_27tZ/?2e_,_2^2ej2e —
_ J 1 _ J _ J
2nlRi 2e — 4ш7?е2 > T' e- V 4л^е2 '
Для вычисления силы P2 приложим теперь к массе
жидкости, охваченной течением около передней кромки,
теорему Жуковского, тогда для величины силы Р2 получим
выражение
P2 = P^|J| = 4^ = 4^p/?V2sin29. (10)
Направление этой силы получим по теореме Жуковского,
как показано на рис. 20.
Рис. 20.
Подводя итог всему, что было выше сказано, имеем,
что на пластинку действует сила Р, величина которой
определяется по формуле
Р = у P2-I-P2 = 4лр/?V2 sin 9 = ттр&У2 sin 9,
и эта сила направлена перпендикулярно к V, так как
tga = ^ = tg9 и а = 0 (рис. 21).
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА 549
Отсюда следует, что сила, определяемая по теореме
Жуковского (или, что то же, по формуле Чаплыгина —
Блазиуса), включает в себя и подсасывающую силу,
а потому для учета подсасывающей силы для машущего
крыла достаточно только учесть
действие силы, определяемой фор-
мулой Жуковского.
Таким образрм, если мы строим
теорию машущего крыла, исходя
из физической схемы полного об-
текания крыла без образования
струй, как и строятся все обычные
теории колеблющегося, или машу-
щего, крыла, т. е. исходя из сил,
вычисляемых на основании тео-
ремы Жуковского, то нет никаких
оснований говорить о
подсасывающих силах.
Основываясь на теореме Жуковского и не учитывая
действия отходящих вихрей, можно дать следующую весьма
грубую оценку величины силы тяги. Рассмотрим пластинку,
расположенную так, что без взмахов угол атаки равен 6.
,Тогда при опускании пластинки вниз угол атаки равен
6 +arctgу. Отсюда сила, действующая на пластинку, по
теореме Жуковского равна
кр (V2-)- w2)b sin
(0+arctg-у)
Так как эта, сила Р перпендикулярна к результирующей
скорости, то у нее имеется слагающая R19 направленная
вперед; это и есть сила тяги (рис. 22). Она определится по
формуле
#1 = Кр (V2+ w2) b sin (f) + arctg -^0 sin arctg -у.
Точно так же при поднятии крыла кверху получим
силу, направленную назад,
/?2 = — кр (V2 + w2) b sin (9 — arctg -у ) sin arctg -у.
550
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Так как силы Rx и /?2 действуют в течение одного и
Т
того же времени , то их эффект в образовании им-
Рис. 22.
пульса и связанного с ним количества движения опреде-
лится по формуле
R = у— = тгр (V2 —|— ^2)^sin arctg ^rj2cos 6,
т. е.
R = Tzpbw2cos0. (И)
Сравнивая R, вычисленную по формуле (11), с найден*
ной выше средней величиной силы тяги
az L т г о 244 — 1/w h М — 1 \
Х> = - cos 9 (у-2 т ,
где Л4 = у th у , покажем, что Хо < R при условиях,
близких к условиям устойчивости дорожки.
Действительно, составим разность
244 — 1 (w h М — 1 \ 1Z44 — 1 ( w о h\
Так как-у >2у, то эта разность положительна при
М > 1, что, как мы видели, имеет место при у >0,38,
т. е. весьма далеко от выполнения условий устойчивости,
когда—1 = 0,281, Таким образом, формула (11) дает пре-
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА 551
увеличенную силу тяги, что и понятно, так как отходящие
вихри, как легко видеть, уменьшают изменение скоса потока.
Подсчет количества движения жидкости, проходящей
через контрольную поверхность, позволяет обойти те труд-
ности, которые возникают при учете непосредственного
влияния отходящих вихрей на скорость около крыла.
§ 12. Режим полета
Рассмотрим центр тяжести самолета с машущим крылом
и выясним вопрос, при каких условиях этот центр тяжести
по истечении периода колебания Т будет возвращаться на
одну и ту же высоту над землей.
На центр тяжести- действует сила веса самолета mgt где
ш — масса самолета, направленная вниз, и, кроме того, подъ-
емная сила, вызываемая взмахами крыла, направленная вверх
и изменяющая свою величину от Рг — mj19 соответствующей
опусканию крыла вниз, до Р2 = mj2i соответствующей под-
нятию крыла вверх. Для полета в рассматриваемом нами
случае необходимо, чтобы mj\ > mg^ mj2.
Рассмотрим сначала тот режим полета, когда центр
тяжести от самой нижней точки поднимается вверх; это соот-
ветствует, во-первых, опусканию крыла вниз и, во-вторых,
некоторому промежутку времени, когда крыло уже подни-
мается вверх, но центр тяжести по инерции еще продол-
жает двигаться вверх.
Направляя вертикально вверх ось х для первого проме-
жутка времени, получим уравнение движения в виде
откуда, считая в самой нижней точке хо = 0 и скорость
г/о=0, получим для этого первого промежутка времени
/2
— g)-2 •
Пусть промежуток времени, в течение которого при таком
режиме происходит поднятие центра тяжести, 7\ (7i< у)»
552
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
тогда к концу промежутка 1\ величина поднятия центра
тяжести есть
у2
Л1 = (/1—(2)
и скорость
V1 = (J1 —g)rv
В течение того промежутка времени, когда крыло под-
нимается вверх, но центр тяжести по инерции также еще
продолжает двигаться вверх, уравнение движения центра
тяжести есть
= — (g—J2), (3)
с начальными значениями v± = (j\ — g)l\ и h± = (j\ — g)~2~
Из уравнения (3) и начальных данных долучим:
^ = -(g-A)' + C/i—g)7\.
t2 Л
х = - (g - A) 7 + Ui — g) T\t + (7i - £) -у- •
В самой верхней точке поднятия центра тяжести полу-
чим:
-(g-AK+(A—£)Л = о,
и, называя через продолжительность этого второго режима
поднятия центра тяжести, получим:
Ti = Т± (4)
1 g~J2 1 4 7
и для соответствующей
всего режима поднятия
. . л
величины поднятия Нг в течение
+ (h-g) Tl+fJ.-g) ,
т. е.
. ^2
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
553
и для общей продолжительности поднятия
Л + ч = (5)
Обозначая общую продолжительность поднятия через ах,
имеем:
2
„ (6)
J1—J2 *
Подобным же образом рассмотрим второй период, пе-
риод опускания центра тяжести. Этот период состоит
также из двух частей: во-первых, когда имеет место урав-
" нение (2) и, во-вторых, когда имеет место уравнение (1).
Из уравнения (3) и начальных условий x = Hlt v — 0
имеем за продолжительность этого режима Т2:
dx / » чz
х== —
Следовательно, в момент Т2 имеем:
Xi — — (8—J) у+ ^i-
В дальнейшем движение идет по уравнению
d?x .
~dP~^ S
с начальными данными xt и v±. Следовательно,
/2 Т\
X = 0’1 — g) -J — (g—Jz) T2t — (g—jj -у 4- Hv
Если продолжительность этого режима есть т2 и в конце
его центр тяжести возвращается в начальное состояние, то
имеем:
о = (У1—g) Т2 — (g —J2) Т2,
•с2 Т2
о = (Ух - g) — (g-Jz) T^z - (g—J2) + Ht,
554
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
откуда
(7)
Если же ввести полное время опускания центра тяжести а2,
то получим:
а2= Т2 +т2 = А=^Т2 (8)
И
2
я (g-AXA-g)^, (9)
Jl — 2
т. е. равенства, совершенно аналогичные полученным выше.
Из уравнений (5) и (9) имеем:
= °2>
т. е. время поднятия и время опускания центра тяжести равны
друг другу.
Если период колебания крыла есть Г, то по предыду-
щему
т1+7*2 =и т2-{-Т1 = ,
откуда, подставляя значения и т2 из (4) и (7), имеем:
^Л+г2=^т2+Л.
или
А + h — 2g । Ji + А — 2 g у» q
g — h 1 ' A — g 2
или, иначе,
(/1 +/2-2g) ^7 = о
Jl—J 2
и, следовательно,
J1~^J? = g ИЛИ = mg. (10)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
555
Полученный результат выражает следующее положение:
Для полета на постоянной высоте в случае
машущего крыла средняя подъемная сила
должна быть равна весу самолета.
Рассчитаем, насколько изменится положение центра тя-
жести самолета за время опускания крыла; очевидно, оно
равно разности путей, пройденных за интервалы Т± и т2.
Называя этот путь через ht получим по формуле (2)
h = (/i — g) -у- +1 (Л — g) — (g —/2) ^2 j •
или, подставляя из (7) т2,
*т»2
«=W, - Т + ((Л - | (f^)’ Tl - T^gTi],
т. е.
(л-g)2
2(h-g)
или окончательно по уравнениям (5) и (8)
/г = 0,
т. е. в начале и в конце промежутка опуска-
ния крыла центр тяжести его находится на
одной и той же высоте.
Очевидно, то же самое справедливо и для интервала под-
нятия крыла. Таким образом, в среднем дело обстоит
так, как будто центр тяжести находится на
одной и той же высоте и крыло смещается от
этого среднего положения вниз и вверх.
§ 13. Максимальная тяга крыла
Подъемная сила крыла определяется, как известно, по
формуле
р = руг/,
где I — размах крыла, или, подставляя значение Г,
P = pyWsin(y+0).
556
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Пусть профиль крыла допускает обтекание без отрыва
струй до угла 9t, так что максимально возможная подъем-
ная сила крыла равна
^ax = ^V4in(-J + 91).
Пусть, с другой стороны, для получения подъемной силы
крыла, равной весу самолета, достаточно иметь угол атаки 90,
так что
mg = nplbV2 sin (y+ 9o) •
По результатам предшествующего параграфа, если при
взмахах крыла подъемная сила колеблется от максималь-
ной Р± до минимальной силы Р2, то для полета на одина-
ковой высоте должно выполняться условие
P1 + P2 = 2mg]
отсюда, называя через 92 Угол атаки, соответствующий
в рассматриваемом случае минимальной подъемной силе Р2)
получим уравнение
sin 9^sin (у + 62) — 2 sin • 0)
Так как по малости углов можно вместо (1) написать
01Ч_ 02 = 29о, (2)
то отсюда по данному 9Х найдем 92.
Пусть углы атаки относительно направления полета при
опускании и поднятии крыла соответственно имеют вели-
чину и г)2, так что
»1 + arctgy=011
г% —arctg ^ = 02 = 29о—0J. (3)
Из этих уравнений имеем:
п2 — = 2 arctg ® — (0Х — 02) = 2 [arctg у — 61~62] .
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
557
Как мы видели, из условий устойчивости дорожки полу-
чается, что у > 0,562, так что arctg у > 30°; с другой сто-
роны, порядок величины 9Х и 92 составляет у современных
крыльев при достаточных скоростях полета соответствен-
но 15° и 5°. Следовательно, 02 > и при этом отрица-
тельно, а $2 положительно. Таким образом, получаем такой
результат:
при опускании крыла угол атаки меньше,
чем при поднятии крыла, причем при опуска-
нии крыла угол атаки отрицательный, а при
поднятии положительный.
Возможно, что этим объясняется то наблюдаемое при
полете птиц явление, когда кажется, что птица при опу-
скании как бы отгребает, гонит назад воздух.
Из найденных равенств весьма легко найти и максималь-
ную величину тяги крыла. Для этого найдем максимальную
величину циркуляции у вихрей, образующих отходящую от
крыла дорожку. Так как при опускании крыла и при его
поднятии циркуляция соответственно равна
Г\ = — тс )/V2 -|- w2 6 sin 9t,
Г2 — — тс )/V2 — w2 b sin 92,
то
у = Г2 — Г\ = 2тс J/V2 w2 6 sin — у — cos --^--2-
и по предыдущему
ei + 02 _Q 01 — 02 __ л л
- —и0 и 2 о0.
Следовательно,
7 == 2тс У V2 -j- w2 b sin (9t — 90) cos 90.
С другой стороны,
2^ th — 1
2^th^
Ao = -PVT
, — th --1
W n hl I__
V I 9 hit hn 1
2Tth--1
558
И. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
т. е. при заданном h/l средняя величина тяги пропорцио-
нальна циркуляции у. Отсюда окончательно получаем макси-
мальную величину тяги в виде
XQ = — рУ2к j/V2 + ®’2 sin (0i — 0О) cos % X
hit xl hit 1
— th ---1
w Q A 1________
v I 9 hn Alt 7
2-thT“1
2^th^-l
2TthT
Рассмотрим уравнение
£ — 9 A
b_________________V I__________________.
A o h Г/itc .,/inl Г i s ।
2 — I -j- th — I cos a I sin 6 4~ cos о — I
замечая, что
sin 8 + cos 8 у- = у У V2 + w2 sin ^8 + arctg у
и
8 = = arctg
так что
8 + arctg ® = hrA = 01-0Oi o = iL±i2=lL±!2=0O(
мы имеем:
«L__9A
b_ =_____________V I_________________
h h Г vgfl
2y M cos e0 з1п(в,-e0)y 1+рз
Определим отсюда имеем квадратное уравнение
W2 Г1 [ п Ь ,, 0 . п \ ]а1 л w । л
уз f 1 I 2 cos 90 sin (9Х 90) | J 4 -{- 4
— 4 2И2 cos2 0О sin2 (0, — 60) = О,
и так как величина 2-j Af cos 0О sin (0, — 90) значительно
меньше единицы, то отсюда приближенно имеем:
= 2 4 ± 1Л4 — 4 5 + 4 м2 cos2 60 sin2 (0j — 0О) .
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
559
m w . n h
Так как рг>2у, то окончательно
£ = 2|(144(т‘Ьт)™^1-0«)1- (4)
Г £ \ IV \ * •> / 9
Подставляя это значение в формулу (17'") § 10, мы полу-
чаем окончательное выражение максимальной тяги крыла
Хо = — круг/ {th cos 90sin(9Х — 90)).X
X {AcosO.sinte, — 9o)(2^lh£- 1) + 2‘)
2 I h I
т. е.
Хо = — y pV26 cos 90 sin (0Х — 0О) X
у cos 90----£------sin (9Х — 90) + 2
7
что еще можно приближенно написать в виде]
Хо = —J Р^> (01 — 0о) [2 + 4 У (2 т th т - 1) — Ч •
(5)
Если сюда вставить значения, соответствующие условию
устойчивости, то получим:
Хо = - у Р V2Z> (9Х — 90) [2 + 0,91 А (9Х — 90)] , (6)
Хо = — рУ2* (9Х — 90) [3,14 4- 1.43 А (9Х — 90)] , (7)
или приближенно, ввиду малости 9t — 90,
— 0О). (8)
Полученную формулу интересно сравнить с формулой
максимальной подъемной силы стационарного крыла
560
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Из уравнения (8) имеем:
*гаах=- *?v*b [(о,+- (б2+|)] 2 А =
= -{Гтах-Г0} 0,562. (9)
По аналогии с теорией корабля выражение Fmax— Ко
можно назвать запасом подъемной силы крыла и, следова-
тельно, уравнение (9) дает следующий результат:
максимальная величина тяги машущего крыла
равна его запасу подъемной силы, умножен-
о h
ному на 2у .
Отсюда, в частности, следует, что полет на постоянной
высоте возможен только в том случае, если при данной
скорости полета крыло имеет запас подъемной силы. Так
как при полете с постоянной скоростью тяга машущего
крыла идет на преодоление сопротивления, то отсюда имеем
также, что полет на постоянной высоте возможен только
в том случае, если сопротивление самолета меньше запаса
подъемной силы крыла.
Пусть коэффициент сопротивления самолета есть с^, тогда
сила сопротивления на единицу размаха крыла равна с^рУ2#, и,
следовательно, сравнивая с (9), имеем для возможности полета
на постоянной высоте неравенство
cQ < 0,562т: (01 — 90) = 1,76 (0г — 6^.
§ 14. Выгоднейшие режимы полета; примеры
Если рассматривать такие режимы полета, при которых
выполняются условия устойчивости Кармана, то предыдущие
результаты позволяют показать, что число взмахов при
заданных V и w связано с размерами хорды и с величиной
скорости полета V весьма простым соотношением.
Действительно, как показывают формулы (12) и (13)
§ 4, при полете в рассматриваемых условиях должно выпол-
няться условие
-^> 0,562.
(1)
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
561
С другой стороны, величина отношения -у позволяет
определить при заданных и 02, откуда сейчас же найдутся
сс . 0< -4- 60 $ 01 — 0о
величины а = у 4—и о = ——-, величину по
формуле
-^-0,562
* ---------V------------ (2)
П Л ОК Г : * I i W 1
0,35 cos а sin о -|- cos о -ту
откуда найдем /, пользуясь соотношением
А = 0,281.
Из соотношений (2) и (3) найдем:
1,246 cos о pin б 4“ cos & ~у
0,562
(3)
(4)
Так как
6 Г • * । wk, Ь /гя
uQ — -г cos a sin о + cos 8 V -т- th -у-,
гь L г j t ►
то, подставляя из уравнения (2) значение и замечая, что
при у = 0,281 имеем th -р- = 0,616, получим еще
«0 = 1,8 (-у — 0,562) V. (5)
Если обозначить число взмахов в секунду через JV, то
1 V+«o
Т I
откуда, подставляя значение I и и0 из уравнений (4) и (5),
получим:
—0,562)][-® _0,562]
* = ~И Т'
1,246 cos о I sin В -|- cos б — )
562
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Величины у, о и 8 характеризуют режим полета при
взмахах, поэтому величину
К
[1 + 1,8 - 0,562)] - 0,562]
1,246 cos a sin 6 4~ cos & -г? 1
(7)
можно назвать коэффициентом режима полета.
При подстановке К в уравнение (6) получим:
W = (8)
Формула (8) показывает, что при одинаковых
режимах полета (при равных К) число колеба-
ний прямо пропорционально скорости полета
и обратно пропорционально величине хорды.
Сравнивая формулы (7) и (2), получим для коэффи-
циента К выражение
К = 0,281 [1 + 1,8 (у — 0,562)] 4 > (9)
при этом, если у-у—0,562j мало, как это обычно бывает,
то приближенно имеем:
К = 0,281-^-. (10)
Очевидно, что формула (10) получается из выражения
если в нем пренебречь членом -р; таким образом, еще полу-
чаем выражение для N в виде
W =.0,281-?-, 4г = 0,281(11)
’ h, ’ b ’ h v 7
Рассмотрим следующий пример.
исследования по Теории машущего крыла 563
Критический угол машущего профиля 0тах = 16°; режим
полета определяется следующими данными:
arctg -у = ~= 0,577, а = 0;
углы атаки при опускании крыла (0t) и при поднятии
крыла (02) определяются условиями
£+01+arctg^=0max,
у4-02—arctg-y = 0,
откуда 0t =—14°, 02 = 30° и, следовательно,
а = 8°, о = — 22°;
п Ь
1) находим
Ь_ 0,577 — 0,562 — 0 97-
h — 0,35 • 0,99 [ — 0,3746 + 0,9272 • 0,577] U’2' ’
2) находим среднюю циркуляцию Г:
Г = — TzbVsina^cosB— sin8 -y-j,
т. e.
Г = nbV 0,1392 [0,9772 + 0,3746 • 0,577] = — itbV 0,165;
отсюда получаем среднюю подъемную силу:
Го = ->рУГ=-О,5рУ2&;
3) для определения числа взмахов N применим формулу (8),
отсюда
К = 0,0777,
а потому
W = 0,0777
О
4) наконец, для определения силы тяги воспользуемся
формулой (15х) § 9
Xq — — 0,94pW2 cos a (sin 8 -J- cos8 (1 -J- 1,2 ^0;
564
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
подставляя найденные значения, получим:
Хо = — 0,258 РУ* 2 3 * *&,
так что сила тяги составляет почти половину подъемной силы.
В качестве частных примеров рассмотрим следующие;
1. Нагрузка летающей машины на единицу площади
р = 20 кг/м2, Ь = 3 м', определим скорость и число взмахов
для полета на постоянной высоте1); из KoZ = O,5pV2W
(/ — размах) имеем:
р =-у-= 0,5 рУ2 и V = y/~-^- = /320 = 18 м!сек,
N = 0,0777-£ = 0,47.
и
2. Тот же самый вопрос при р = 5 кг/м2, /> = 0,1 м\
V = 1/ = 7 м/сек,
Г 0,5 р 1
М = 0,0777-£ = 5,4.
’ ь *
Данные соответствуют приблизительно полету голубя;
наблюдения дали2) для N от 4 до 10, для V от 13 до
30 м/сек.
3. Тот же вопрос8) при р = 0,66 кг/м2, b = 0,0002 м\
V = 3,2 м/сек, N = 123.
Данные приблизительно соответствуют полету мухи;
наблюдения дают N от 180 до 350.
В качестве второго примера рассмотрим работу машу-
щего крыла при следующих данных. Критический угол атаки
профиля 15°, а = 0. Режим полета определяется следую-
!) Данные близки к орнитоптеру А. Сольтау (по М. К. Тихо-
мирову, Полет птиц и машины с машущими крыльями, ОНТИ,
1937, стр. 104). Аппарат не летал (см. далее).
2) Данные по М. К. Тихомирову, стр. 19, 28, 80.
3) Данные по М. К. Тихомирову, стр. 67, 68, 70. При оценке
полученных чисел надо помнить, что механизм махания различен
в рассматриваемой работе и в данных М. К. Тихомирова.
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
565
щими данными: arctg—= 0,6 (31°) и углы атаки крыла
определяются из уравнений
0t + 31° = 15°, 9<=—16°,
„ 1 а = 10°, 8 =—26°.
02 — 31° = 5°, 02 = 36°,
По этим данным:
1) 1=1,1,
2) Г= — 0,634 bV,
3) Уо = 0,634 pV2i,
4) = 0,33,
5) JVo = O,16pV2£.
Прилагая к частным случаям при данных, принятых выше,
наши выводы, получим:
1) при р = 20 яг/л*2, b = 3 м скорость V и число взма-
хов на постоянной высоте W будут:
V = 31 м/сек, W = 3,3;
2) при р = 5 кг/м2, b = 0,1 м
V = 2,8 м/сек, N = 533;
3) при р = 0,66 кг/м2, Ь = 0,002 м
У= 16 м/сек, М = 2640.
Сравнение полученных результатов с наблюдениями, при-
веденными выше, показывает, что режим полета орнитоп-
тера Сольтау ближе ко вторым данным, так как в первом
случае имеем несообразно большое
А== 0^7 = 11 М‘
Заметим, что при N= 1,5 аппарат не взлетел (во втором
случае h = —- = 2,7 м} ; случай полета голубя и случай
полета мухи ближе к первой схеме, так как в первом слу-
чае имеем для голубя h = = 0,4 м (во второй схеме
h = 0,1 м)\ точно так же в случае полета мухи ближе под-
566
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
0,002 2
ходит первая схема, где h==-Q27~ = Q27 мм=‘>^ мм (по
второй схеме h = 2 мм). Необходимо, впрочем, помнить, что
все данные о полете птиц и насекомых весьма неопределен-
ные. Полученные выводы, относящиеся к данным, чрезвы-
чайно различным по размерам (орнитоптер, птица, насекомое),
дающие достаточное согласие с действительностью, по-види-
мому, подтверждают приложимость полученных выводов
к наблюдаемым в действительности случаям полетов с машу-
щими крыльями.
Заметим в заключение, что в обеих схемах множитель
cos В — sin 8 больше единицы, а благодаря этому коэффи-
циент подъемной силы машущего крыла выше, чем у ста-
ционарного крыла при среднем значении угла атаки; так,
в первой схеме коэффициент подъемной силы соответствует
значению угла атаки в 9°, в то время как о = 8°, во второй
схеме коэффициент подъемной силы соответствует углу
атаки 12°, в то время как а =10°.
§ 15. Некоторые дальнейшие выводы1)
Изложенная в настоящей работе теория машущего крыла
получила дальнейшее развитие. Несомненный интерес пред-
ставляет изучение вопроса об образовании и механических
свойствах «косых»» дорожек. Нами было указано, что тео-
ретически возможно образование дорожек, направление ко-
торых отклоняется от направления поступательного движения
машущего крыла. Такие «косые» дорожки могут образо-
ваться в том случае, когда скорость опускания и поднятия
крыла неодинакова. Этот случай был подробно изучен тео-
ретически и экспериментально в работе Я. Е. Полонского l10L
Полученные им экспериментальные результаты сводятся к сле-
дующему.
«При неравномерных взмахах крыла (скорости опускания
и поднятия различны) отходящие вихри образуют дорожку,
ось которой наклонена к направлению поступательного дви- Э * *
Э Ср. заключение в статье В. В. Голубева, Тяга машущего
крыла, Изв. АН СССР, № 5, ОТН, 1946. [см. настоящее издание,
стр, 450—477].
ИССЛЕДОВАНИЯ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
567
жения. Дорожка отклоняется в сторону большей скорости
взмаха и не имеет шахматного расположения вихрей. При
отклонении дорожки вверх вихри верхнего ряда сдвинуты
вправо сравнительно с шахматным расположением. При откло-
нении дорожки вниз от направления поступательного движе-
ния вихри верхнего ряда сдвинуты влево относительно шах-
матного расположения.
Эксперимент дал один неожиданный результат — это
нешахматное расположение вихрей „косой" дорожки, причем,
как оказалось, это имеет основное значение при рассмотре-
нии таких дорожек».
Последнее замечание указывает на следующее. Для обра-
зования «косой» дорожки необходимо, чтобы, помимо ско-
рости по направлению поступательного движения крыла,
дорожка имела еще скорость, направленную перпендикулярно
к направлению поступательного движения крыла; такой
«дрейф» дорожки возможен только при структуре дорожки,
промежуточной между шахматным и параллельным располо-
жением вихрей. При этом возникает вопрос об устойчивости
таких дорожек, так как во всей изложенной теории условие
устойчивости Кармана играет существенную роль. В. А. Ива-
нова показала, что в случае таких дрейфующих дорожек
имеет место следующее условие устойчивости в смысле
Кармана *):
ch2-^4-cos2 ^=2, (1)
где Ъ— смещение вихрей одной стороны дорожки относи-
тельно другой. В случае шахматного расположения Ь =
и условие (1) переходит в условие Кармана
ch2-^- = 2;
в случае Ь = 0, т. е. при параллельном расположении вихрей,
из (1) имеем:
1) В. А. Иванова, Об устойчивости «косых» вихревых доро-
жек, Дипломная работа защищена на мех.-матем. факультете МГУ
в 1949 г.
568
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
откуда Л = 0, т. е. обе стороны дорожки должны слиться,
и, следовательно, в силу противоположного направления
вращения вихрей в двух рядах дорожки устойчивая дорожка
исчезает. Это вполне согласуется с известным фактом, что
дорожки с параллельным расположением вихрей неустойчивы
в смысле Кармана.
В своей работе Я. Е. Полонский подробно изучил кине-
матику и динамику «косых» вихревых дорожек: полученные
им формулы представляют собой обобщение выведенных
выше формул, в которые они и переходят в том случае,
когда скорости опускания и пэднягия крыла равны по вели-
чине.
Другой случай, который получил подробное рассмотре-
ние,— это случай полета «на месте», который можно наблю-
дать при полете мелких птиц и насекомых. В работе В. В. Го-
лубева показано, что такой случай полета можно объяснить
на основании формул (4), (6) и (15) § 10. Действительно,
из уравнений, определяющих подъемную силу Ко и тягу XQ,
Yq = — pitbV2 sin a [cos 3 — sin 8 -yj,
Ло = — 0,94pftV2coso^sin 8-|-cos8^ [1 4~1,2 ^] =
— — 0,94p£ cos о (V sin 8 -J- w cos 8) [ V-|“ 1,2w],
видим, что при отсутствии поступательной скорости, т. е.
при V = 0, подъемная сила Уо обращается в нуль, но тяга Хо
отлична от нуля, так как при V = 0
XQ — — 1,13 cos о cos 8w2.
Таким образом, заменяя тягу подъемной силой, для чего
нужно повернуть тело птицы из горизонтального положения
в вертикальное, что и наблюдается при полете птиц «на месте»,
можно уничтожить тягой вес птицы. В указанной выше ра-
боте дано подробное исследование этого явления.
По-видимому, разбираемая здесь вихревая схема позво-
ляет определить силы, действующие не на машущее крыло,
а на вращающееся крыло. Образование вихревых дорожек
в этом случае было отмечено в работе Д. С. Вилькера и
Л. П. Смирнова 1141 в 1937 г.
О КСЗФФИЦИЕНТЕ ПОЛЕЗНОГО ДЕЙСТВИЯ МАШУЩЕГО КРЫЛА 569
ЛИТЕРАТУРА
1. Н. Е. Жуковский, О поддерживающих планах типа
Антуанетт, Поли. собр. соч., т. IV, 1949.
2. Г. Билля, Теория вихрей, 1936.
3. В. В. Голубев, Теория крыла аэроплана в плоскопарал-
лельном потоке, 1938.
4. В. В. Голубев, К теории пограничного слоя, Юбилейный
сборник ВВА КА, стр. 35, 1942.
5. В. В. Голубев, Механизм образования тяги машущего
крыла, Труды научной конференции ВВА КА, 1943.
6. В. В. Голубев, Теория машущего крыла и общая проблема
тяги и сопротивления, Общее собрание АН СССР 14—17 октября,
1944 г., стр. 193, 1945.
7. В. В. Голубев, Тяга машущего крыла, Изв. АН СССР
ОТН, № 5, 1946.
8. В. В. Голубев, Лекции по теории крыла, Гостехиздат, 1949.
9, В. В. Голубев, Некоторые вопросы теории машущего
крыла, Уч. зап. МГУ, 1950.
10. Я. Е. Полонский, Вихревые дорожки и их приложения
в теории машущего крыла, Диссертация ВВА КА имени Жуков-
ского, 1948.
11. Н. Е. К о ч и н, И. А. К и б е л ь, Н. В. Розе, Теоретическая
гидромеханика, т. I, 1939.
12. Л. И. Седов, Теория плоских движений идеальной
жидкости, 1939.
13. 0. Титьенс, Л. Прандтль, Гидро- и аэромеханика,
т. II, ОНТИ, 1935.
14 . Л. П. Смирнов, Неустановившееся движение, Механика
в СССР за XXX лет, стр. 368, 1950.
О КОЭФФИЦИЕНТЕ ПОЛЕЗНОГО ДЕЙСТВИЯ
МАШУЩЕГО КРЫЛА
§ 1. Предварительные замечания; число Струхаля
В ряде работ, посвященных теории машущего крыла,
нами были выведены основные формулы, дающие величину
подъемной силы и тяги, в предположении, что крыло совер-
шает колебания, перпендикулярные к направлению полета,
амплитуды h, причем скорость колебания в течение подня-
ния и опускания крыла постоянна и равна ±w. В основу
теории была положена физическая схема, состоящая в том,
*) Опубликовано в Уч. зап. МГУ, т. V, 1954. {Прим, ред.)
570
П. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
что сзади машущего крыла в верхних и нижних точках его
амплитуды колебаний от крыла отходят вихри, образующие
сзади крыла двойную вихревую дорожку, подобную дорожке,
образующейся сзади плохо обтекаемого тела, но с противо-
положным направлением вращения вихрей. Построенная тео-
рия предполагает, что ширина дорожки равна амплитуде
колебания крыла и дорожка удовлетворяет условию устой-
чивости, данному Карманом. Существование подобных доро-
жек было подтверждено экспериментально х).
Называя через V скорость набегающего потока, или, что
то же, скорость полета, и через uQ дополнительную ско-
рость отходящих вихрей, вызываемую влиянием вихревой
дорожки, через I расстояние между последовательными вих-
рями одного и того же ряда и через п число вихрей ряда,
отходящих в одну секунду, получим соотношение
ге/ = У-|-и0> (1)
откуда
2£=*(1+^). (2)
Отвлеченное число мы будем называть числом Стру-
халя (SH) для машущего крыла, так что
= (3)
С другой стороны, так как путь, пройденный за один пол-
ный взмах по направлению, перпендикулярному к направле-
нию полета, равен 2/г, то
2nh = w (4)
и из уравнений (1) и (4) имеем:
v-2t(1+v)' <5>
Из уравнений (3) и (5) имеем:
V = 2SH- (*)
1) См., например, В. В. Голубев, Исследования по теории
машущего крыла, Уч. зап. МГУ, Механика, т. IV, вып. 154, 1951
[см. настоящее издание, стр. 491—569].
О КОЭФФИЦИЕНТЕ ПОЛЕЗНОГО ДЕЙСТВИЯ МАШУЩЕГО КРЫЛА 571
Из уравнения (3) имеем:
и, полагая у ~ 0,281, имеем:
и по (5)
SH> 0,281
-у >0,562.
§ 2. Работа машущего крыла
Подъемная сила, приложенная к крылу, направлена всегда
Рис. 1.
вверх, но по величине различна при опускании и при под-
нятии крыла. Пусть циркуляция крыла при опускании есть 1\
и при поднятии Г2; тогда, за-
мечая, что и Г2 отрица-
тельны, имеем для выражения
силы при опускании и при
поднятии соответственно вы-
ражения — pViPj *и —рУ\Г2,
где — составляющая ско-
рости* по направлению оси х
(рис. 1) в плоскости колеба-
ния крыла. Скорость составляется из скорости потока
далеко впереди крыла, равной и противоположно направ-
ленной скорости полета, мы ее назвали через V, и из
составляющей по оси х скоростей, вызванных присутствием
вихрей дорожки, которую мы назовем а.
Найдем среднее значение составляющей а за период
взмаха крыла вдоль прямой, параллельной оси х и лежа-
щей внутри дорожки.
По формулам теории двойных вихревых дорожек с щах*
матным расположением вихрей
. 2*7
sh—~
X________I
I , 2тсу 2тсх'
ch — COS -у-
572 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО крыла
Так как за период взмаха х изменяется в пределах от нуля
до Z, то искомое среднее значение получим по формуле
, 2лу *
_1sh~r [
— J2 I
О
dx
, 2uy 2tix
ch —р —
или
r Ttl
. 2т:у
Sh-T
ch^ + 1
--
t. e. окончательно
27
“op= Kl arct£
(7)
Итак, получаем интересный результат6. zzcp не зависит
от у, т. е. одна и та же для всех прямых, парал-
лельных оси х и лежащих внутри дорЪжки.
Так как выражение (7) выведено в предположении, что
дорожка бесконечна в обе стороны, то, применяя обычное
рассуждение, получим для плоского колебания крыла, т. е.
для начала дорожки, бесконечной в одну сторону для вели-
чины средней добавочной скорости, значение вдвое мень-
шее, т. е.
Так как по формуле теории вихревых дорожек имеем
7 .. nh 7
zz = -L th — = —,
0 2Z Z 2Z V 2
где zz0—относительная скорость движения вихрей цепочек,
то отсюда имеем для величины среднего значения добавоч-
ной скорости в начале дорожки выражение
J = ’ (8)'
О КОЭФФИЦИЕНТЕ ПОЛЕЗНОГО ДЕЙСТВИЯ МАШУЩЕГО КРЫЛА 573
и, следовательно,
(9)1)
Мы можем теперь легко рассчитать работу крыла при
взмахе вверх, когда направление движения
правлением силы, и при движении вниз,
когда эти направления противоположны.
При опускании крыла направление
движения противоположно направлению
силы (рис. 2) и, следовательно, работа
подъемной силы отрицательная и выра-
жается формулой
-А(—рУ1Г1) = рУ1Г1А. (10)
совпадает с на-
Точно так же при поднятии крыла направление подъем-
ной силы и направление движения совпадают (рис. 3) и,
следовательно, работа подъемной силы по-
к-рЦГ ложительная и выражается формулой
Рис. 3.
Й(-Р^Г2) = — рУ^Л. (11)
Таким образом, в течение одного полного
взмаха подъемная сила совершает работу
ргда — — Г2)/г. (12)
Но из теории машущего крыла следует, что 2)
-Гх + Г^т,
где у—циркуляция вихря верхней цепочки дорожки. Отсюда
получаем следующее выражение работы подъемной силы за
Один полный взмах крыла:
— pVijA.
(13)
*) Заметим, что в предыдущих работах мы не учитывали вели-
чину добавочной скорости и принимали Vi = V.
а) См., например, В. В. Голубев, Лекции по теории крыла,
стр. 392.
574
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
Так как у положительна, то крыло совершает отрицатель-
ную работу и для того, чтобы крыло совершало взмах,
необходимо приложить работу, равную
PV17A. (14)
Пусть крыло за одну секунду совершает п полных
колебаний. Так как крыло движется вверх и вниз с постоян-
ной по величине скоростью w, то имеем:
= w,
а поэтому для выражения секундной работы Е, которую
нужно потратить на взмахи крыла, имеем:
E = pV1T*n = p(V+«oy2)-J. <15)
§ 3. Коэффициент полезного действия машущего крыла
Выведенные формулы позволяют найти коэффициент
полезного действия машущего крыла, который мы назо-
вем 7j. Как известно х), средняя величина тяги машущего
крыла Q выражается формулой
Q = Pp(y_1_2ao)-g) (16)
и, следовательно, секундная работа силы тяги, т. е. полез-
ная работа, совершаемая машущим крылом /?, определится
по формуле
и так как
«0 = —
0 21 / 2
то можно еще написать:
Я = Р^у[у+Ио(2-1^Ц)]. (17)
1) См., например, В, В. Голубев, Лекции по теории крыла,
стр. 390,
О КОЭФФИЦИЕНТЕ ПОЛЕЗНОГО ДЕЙСТВИЯ МАШУЩЕГО КРЫЛА 575
Из выражений (15) и (17) находим:
R иЦи+.а(г-ХЦ)]
4 е nIV+«0 /21
ИЛИ
У [1+0,397-^]
(18)
Пользуясь формулой (18), можно выразить vj или только
через отношение у, или через отношение у == 2SH.
Так как по формуле (5)
w _ О h fl I M
V — 2 I v v)’
то выражение (18) можно написать в виде
1+0,397^ 1 4-0.4 v
т, = ---------- *1----- « -------—Г------ . (19)
[1 + 1.414 [1 + 1.4^] [1+у]
_ W
Если же все выразить через отношение—, то получим:
0,339 + 0,397 у 0,34 + 0,4 у
71 = [2,516^-0,414]-^ ~ [215^—0,4]^-’
или еще
0,169 4-0.3973/7 0,17-]-0,4S/7
71 ~ [5,0323/7 — 0,414] ЗЯ~ [53/7 — 0,4] 3/7*
Выведенные формулы показывают, что vj изменяется от 1
(при zzo = 0 или у = 0,562, 5/7 = 0,281^ до 0 при У==0.
Так как при 21 = 0,45 h~^t то, если считать практи-
чески целесообразным только такие режимы полета, при
576 II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
1 На
которых 7] > , мы ВИДИМ, ЧТО для таких
полета изменяется в пределах
О < < 0,45,
ИЛИ
0,562 < у < 0,814
И
0,281 <SH< 0,407,
режимов
т. е. режимы, соответствующие экономически выгодному
полету, заключены в достаточно тесном интервале отноше-
ния скоростей, или чисел Струхаля.
ТРУДЫ ПО ТЕОРИИ
КРЫЛА
МАЛОГО УДЛИНЕНИЯ

К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ 9
В славной научной деятельности нашего знаменитого
ученого Н. Е. Жуковского, светлой памяти которого посвя-
щено настоящее заседание, в одинаковой мере замечательны
как полученные им научные результаты, так и те ориги-
нальные и своеобразные методы исследования, которыми он
с таким успехом пользовался в своих изысканиях.
Технические задачи, которые ставит перед теоретической
механикой деятельность инженера или естествоиспытателя,
за крайне редкими исключениями, исключительно сложны;
трудно сполна учесть все индивидуальные особенности рас-
сматриваемого случая скупыми схемами теоретической меха-
ники. Поэтому всякая задача в процессе своего разрешения
подвергается по необходимости тому или иному упрощению,
своеобразной стилизации и только в таком стилизованном и
упрощенном виде поступает затем уже в обработку мето-
дами теоретической механики. Естественно, что подобное
упрощение, в том или ином виде искажающее изучаемое
физическое явление, рассматривается как своего рода печаль-
ная необходимость, вызываемая ограниченностью средств
современной науки. Исследователи обычно стремятся воз-
можно полнее, с наименьшим упрощением в исходных урав-
нениях записать изучаемое явление и в дальнейшем свести
задачу к чисто математическому исследованию, которое
х) Доложено на торжественном заседании Отделения техни-
ческих наук и Института механики АН СССР, посвященном 100-летию
со дня рождения Н. Е. Жуковского (январь 1947 г.). Опубликовано
в Изв. АН СССР, ОТН, № 3, 1947. (Прим. ред).
580 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
предполагается по самому своему характеру наиболее пол-
ным и глубоко проникающим в сущность дела.
Существенной особенностью научного творчества Н. Е. Жу-
ковского является то. что стилизацию, упрощение изучае-
мого явления, которое рассматривается обычно как печаль-
ная необходимость, вызываемая недостаточным развитием
методов науки, он сделал методом исследования, система-
тически применяя его в многочисленных работах, и показал
его большую мощь.
Дело в том, что стремление возможно полнее описать
изучаемое явление при помощи соответствующих дифферен-
циальных или интегральных уравнений или иных математи-
ческих средств обычно приводит к тому, что получаемые
уравнения или вообще не решаются при современном состоя-
нии науки, или решение их в общем виде приводит к анализ
тическим выражениям, с чрезвычайным трудом поддающимся
числовым расчетам или качественной интерпретации. Поэтому
приходится для доведения решения до практически пригод-
ного результата вносить в полученные общие уравнения те
рли иные упрощения. Математика имеет большой запас средств
для такого упрощения; достаточно назвать здесь, например,
метод введения малого параметра, откидывание в уравнениях
некоторых членов, как это делается при так называемой линеа-
ризации уравнений, введение уравнений в вариациях и т. д.
При этом сплошь и рядом оказывается, что большие усилия,
потраченные на составление возможно полных уравнений или
на. их решение в общем виде, в значительной степени обесце-
ниваются необходимостью делать в дальнейшем соответствую-
щие упрощения; при откидывании, например, в уравнении
квадратичных членов законность этого часто не может быть
достаточно мотивирована, оценка точности приближения при
разложении в ряды не может быть произведена и т. п. Все
это, конечно, в значительной степени обесценивает получаемые
таким путем результаты.
Н. Е. Жуковский в своих работах часто идет совершенно
иным путем. Вместо того чтобы рассматривать данное явление,
он заменяет его некоторым другим явлением, схематически
представляющим данное явление, но гораздо более простым
и сравнительно легко поддающимся полному математическому
исследованию. Это упрощение обычно достигается на .осно-
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1947). 581
вании опытных данных или общих физических сообра-
жений.
Классический пример такого метода исследования пред-
ставляет современная приближенная теория крыла, основанная
на замене крыла несущим вихрем, спутной зоны — вихревой
пеленой и т. д. Разумеется, введением некоторой упрощающей
физической схемы пользовались ученые и ранее Жуковского;
достаточно привести в качестве примера идею Гаусса о «раз-
мазывании» массы возмущающей планеты по ее орбите; между
прочим, возможно., что эта идея Гаусса послужила прототипом
для Жуковского в его работе о воздушных винтах, где отхо-
дящие от лопастей винта свободные вихри «размазываются»
по поверхности вихревого цилиндра. Но несомненной заслу-
гой Жуковского является то, что такой метод, указанный
вскользь и между прочим другими учеными, Н. Е. Жуковский
сделал систематически применяемым, достаточно общим мето-
дом и, связав его с широким использованием лабораторных,
экспериментальных данных, создал прочную базу для его
применения.
Тот краткий доклад, который я имею честь предложить
вниманию настоящего собрания, и представляет иллюстрацию
к изложенному сейчас методу. Доклад посвящен задаче, кото-
рая за последнее время приобрела значительную актуальность.
Как известно, современная приближенная теория крыла
основана на замене крыла одним присоединенным вихрем
переменной циркуляции, от которого отходит вихревая пе-
лена свободных вихрей, образующая за крылом спутную зону.
Как показывают многочисленные экспериментальные данные,
эта теория, представляющая, несомненно, весьма грубое при-
ближение к действительности, дает достаточное для техни-
ческих целей согласие с экспериментальными данными при
крыльях с удлинением порядка 5 и выше, т. е. для крыльев
достаточно длинных, какие обычно и применяются в авиации.
Однако за самое последнее время техника выдвинула задачу
об использовании крыльев с удлинениями очень малыми, по-
рядка 1 или даже десятых долей (Х = 0,2—0,5). Такие
удлинения имеют место в элементах оперения авиабомб, летаю-
щих снарядов, а в совершенно иной области — подводная часть
-корабля — в задаче об учете влияния дрейфа. При таких малых
удлинениях приложимость обычной элементарной схемы,
582 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
применяемой в теории крыла, уже a priori представляется сомни-
тельной; и действительно, многочисленные экспериментальные
данные показывают очень резкое расхождение с теоретиче-
скими выводами, благодаря чему обычный теоретический расчет
оказывается совершенно не пригодным для крыльев малых
удлинений. Достаточно сказать, что теоретическое значениеСу
в некоторых случаях может оказаться вдвое меньше значе-
ния, полученного экспериментальным путем.
Основные пункты расхождения теории и эксперимента до-
статочно ясны из рис. 1, на котором приведены старые (1932 г*)
20 30 40
Рис. 1.
данные Флахсбарта о величине Су для прямоугольных пла-
стинок. Как видно из данных Флахсбарта, у крыльев малых
(порядка Х=1) и, особенно, очень малых (порядка Х = 0,1)
удлинений наблюдается следующее, резко выраженное рас-
хождение с теорией.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1947)
583
1. При малых удлинениях мы имеем резкое увеличение
критического угла атаки (с 10—12° при удлинении Х = 5
до 35° при k = 1 и даже до 40—45° при Х = 0,2).
Такое увеличение критического угла само по себе очень
хорошо объясняется современной приближенной теорией, так
как при малом удлинении отходящая вихревая пелена ока-
зывается весьма узкой и, следовательно, образующие ее вихри
вызывают очень большой скос. Но при этом существующая
теория совершенно не дает объяснения резкого увеличения СуУ
наблюдаемого на опыте, сравнительно с теоретическими дан-
ными. Действительно, при Х = 0,2 и при а =-30° экспери-
ментально установленное значение Су превышает теорети-
ческое на 140%. При этом при больших X экспериментально
установленные значения Су оказываются меньше теоретических
значений, а максимальное значение Су соответствует углам
большим, чем получаемые из теории (на рис. 1 при К = 5
Сутах получается при а= 15°; теоретически такое же значе-
ние Су получается при а= 11°). Наоборот, при малых.удли-
нениях экспериментальные значения Су значительно превы-
шают теоретическое и соответственно Сугм^ получается при
углах значительно меньших, чем получаемые из теории для
того же Су [на рис. 1 при ^ = 0,2Суп1ах получается при
а =40°, а такое же теоретическое значение должно полу-
читься примерно при а=80° (!)].
2. Подобным же образом получается большая неувязка
между экспериментальными и теоретическими значениями со-
противления. Оказывается, что экспериментальное значение
сопротивления значительно меньше теоретического; так, по
данным Винтера оказалось, что полное сопротивление было
ниже теоретически вычисленного индуктивного сопротивления.
Большое число позднейших экспериментальных работ
привело к аналогичным результатам.
Грубо приближенный характер современной теории крыла
и, в частности, ее непригодность для расчета крыльев малого
удлинения привели к попыткам дать более совершенную
с гидродинамической точки зрения теорию крыла конечного
размаха.
С точки зрения интересующего нас вопроса теория строи-
лась на более точном учете влияния на аэродинамику крыла
его формы в плане; очевидно, что теория крыла малого
584 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
удлинения есть частный случай этой более общей задачи.
В основном исследования шли в следующих двух напрдвле-
НИЯХ.
Во-первых, крыло заменялось не одним несущим вихрем,
а системой вихрей, непрерывно заполняющих всю поверх-
ность крыла. В этом направлении можно указать старые
работы Боллея, Бленка и других; в самое последнее время
появилась обстоятельная работа Г. Ф. Бураго. Основные
трудности, которые возникают в этом направлении, состоят
в невозможности теоретическим путем определить распреде-
ление вихрей по поверхности крыла. В работе Г. Ф. Бураго
‘сделана попытка ввести некоторое осреднение этих вихрей,
что значительно упрощает применение подобных теоретических
соображений. Однако все эти методы оставляют место для
значительного произвола в выборе распределения вихрей, не
совсем ясны с физической точки зрения и при современном
положении не дают полного теоретического разрешения
задачи.
Другой метод основан на отказе от вихревой схемы крыла.
Задача об обтекании крыла потоком решается путем построе-
ния потенциала течения по граничным условиям на крыле и
на поверхности разрыва скоростей за крылом, представляю-
щей спутную зону крыла. В этом направлении, мы имеем
работы Киннера, Н. Е. Кочина по теории круглого крыла,
которые можно, конечно, рассматривать как частный случай
крыла малого удлинения с Х=1, 2........и, наконец, более:
поздние работы по эллиптическим крыльям Кринеса.
Несмотря на огромный теоретический интерес этих работ,
в особенности работ Н. Е. Кочина и Кринеса, надо отме-
тить, что лежащие в основе их физические соображения не
вполне убедительны. Кроме того, действительный подсчет
по полученным по этому методу формулам приводит к чрез-
вычайно сложным вычислениям, вследствие чего весьма
трудно оценить качественную картину изменений, вносимых
этой теорией в существующую элементарную теорию крыла,
а вместе с тем и оценить ее согласие с экспериментальными
данными.
Предлагаемая нами теория основана на совершенно иных
физических соображениях и представляет, в сущности, по-
пытку учета влияния затекания воздуха через боковые кромки
К ТЕОРИИ КРЫЛА МАЛОГО- УДЛИНЕНИЯ (1947)
5&5
крыла. Мы будем в дальнейшем рассматривать прямоуголь-
ное крыло, хотя с некоторыми изменениями эти соображения
можно применить и к крыльям, имеющим другую форму
в плане, и, что весьма существенно, будем далее рассматри-
вать крыло цри скоростях, далеких от скорости звука, т. е.
будем оставаться в области гидромеханики.
В основе предлагаемой теории лежит следующий факт,
впервые полученный А. Н. Волоховым в продувках, которые
он, по нашему предложению, про-
делал в 1939—1940 гг. Оказалось,
что при обтекании прямоугольной
пластинки, поставленной под неко-
торым углом атаки, воздух затекает
на верхней ее грани через боковые
стенки приблизительно ДОу или
длины хорды, считая от передней
кромки, и стекает через боковые
кромки на остальной их части.
Общее распределение линий тока
показано на рис. 2. Аналогичные
результаты были получены при про-
дувках в Московском университете,
проведенных в 1941 г. группой сту-
дентов под руководством аспиранта
Кудашевах).
Какое можно дать физическое
истолкование этому полученному из
опыта факту?
Нам представляется, что наиболее естественное объяс-
нение этого наблюдаемого при продувках факта состоит
в следующем: наблюдаемое затекание есть ре-
зультат воздействия на поток вихревой пе-
лены, сходящей с крыла по линии, совпадаю-
щей с линией центров давления, которая,
как известно, удалена от передней кромки
в случае пластинки на ее хорды.
А) Погиб осенью 1941 г. в боях с немецкими захватчиками под
Москвой.
586 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Вихри пелены, засасывающие воздух через боковые
кромки в передней части крыла, создают далее увеличение
скорости течения на верхней поверхности крыла, что и
вызывает уклонения от обычных результатов современной
элементарной теории. Эти вихри действуют в условиях, при
которых верхняя поверхность крыла представляет твердую
стенку, так что вихри действуют около поверхности не-
которого экрана. Эффект засасывания и влияние экрана не
учитываются современной теорией; учет их представляет
сущность предлагаемой теории. Физически совершенно ясно,
что эффект засасывания воздуха через боковые кромки может
быть чувствителен только при крыльях очень малых удли-
нений, так как при больших удлинениях вызываемое им уве-
личение скорости на верхней поверхности крыла, распреде-
ляясь по всему размаху крыла, оказывается совершенно
ничтожным. Таким образом, необходимость учета затекания
воздуха через боковые кромки есть специфическая особен-
ность крыла малого удлинения.
Для полного представления вихревой схемы крыла мы
должны еще отметить следующее. В задних частях боко-
вых кромок воздух, перетекающий с верхней поверхности
крыла на вго нижнюю поверхность, завихряется, как при
, всяком обтекании вокруг острой кромки. Завихренные таким
образом частицы воздуха постепенно передвигаются вдоль
боковых кромок и сходят с концов боковых кромок, образуя
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1947)
587
позади два вихревых добавочных шнура, сходящих с концов
крыла с направлением вращения, противоположным направле-
нию вращения соответствующих вихрей пелены свободных
вихрей. На рис. 3 и 5 представлена физическая схема, соот-
Рис. 4.
ветствующая предлагаемой теории; для сравнения дана соот-
ветствующая схема обычной теории (рис. 4).
Рис. 5.
Мы переходим теперь к тем количественным выводам,
которые можно получить из предлагаемой физической схемы.
Прежде всего заметим, что, несмотря на чрезвычайную физи-
ческую простоту предлагаемой схемы, ее тем не менее
588 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
очень трудно подвергнуть математическому учету без су-
щественных дополнительных упрощений.
Во-первых, огромную трудность представляет опреде-
ление тех добавочных скоростей, которые возникают на
верхней поверхности крыла благодаря влиянию отходящих
вихрей. Так как мы ограничимся во всех дальнейших вы-
водах только первой, достаточно приближенной оценкой,
то будем считать, несмотря на прямоугольную форму крыла,
что циркуляция вдоль его размаха изменяется по эллипти-
ческому закону; получаемая при этом погрешность не является
слишком большой. Отсюда получаем, что, если назвать
через Го циркуляцию в среднем сечении крыла, то
r0 = rcW—?), (О
где V—скорость полета, b — хорда, &—угол атаки и
ср — угол скоса. Так как в случае эллиптического распре-
деления
<?=4W> (2>
то, подставляя (2) в уравнение (1), получим:
Го = „1/М_(3)
2/
где удлинение К — -у; из (2)
? = (4)
Отсюда видим, что при X, стремящемся к нулю, ср стремится
к углу атаки & и Го стремится к нулю.
Пелена отходящих свободных вихрей находится около
твердой стенки поверхности крыла, на которой эти вихри
вызывают добавочные скорости. Для того чтобы получить эти
добавочные скорости, мы сделаем предположение, в известном
смысле противоположное тому, которое делается в обычной
теории крыла.
В обычной теории крыла предполагается, что крыло
никакой поверхности не имеет и, следовательно,
отходящие вихри не вызывают на поверхности крыла ни-
какой добавочной скорости. ’
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1947)
589
Мы примем, что отходящие вихри вызывают
на поверхности крыла такую же добавочную
скорость около линии центров давления, как
если бы крыло представляло безграничную
во всех направлениях плоскость. Применяя обыч-
ную схему зеркальных изображений и заменяя действие по-
верхности крыла действием добавочной фиктивной вихревой
пелены, представляющей зеркальное изображение пелены
свободных вихрей, как указано на рис. 6, мы легко получим
для скорости w выражение
= = (5)
и для искомой добавочной скорости v выражение
v = 2w (S — ср) = 2wB —jprjX ’ (6)
т. е.
’=ы'да?*’ т
Наконец, для того чтобы применить обычные рассужде-
ния теории крыла к данному случаю, мы заменим течение
на верхней поверхности, указанное на рис. 2, течением, ука-
занным на рис. 7; аналогичную замену произведем и на
нижней поверхности крыла.
590 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
Таким образом, течение вокруг крыла состоит из двух
течений: 1) из обычного течения, скорость которого опре-
деляется по существующей теории и которая создает вокруг
крыла циркуляцию Го, и 2) из добавочного течения, которое
на линии центров давления дает добавочную скорость v и
добавочную циркуляцию ДГ.
11 f I 11 —
♦ ♦

——►- —
♦ 1
♦ t Г • "1
Рис. 7.
Заметим, что жидкость, вызывающая эту добавочную ско-
рость, втекает и вытекает через боковые кромки, не проте-
кает через заднюю кромку и, следовательно, не подчи-
няется основной гипотезе Чаплыгина — Жу-
ковского.
Естественно возникает вопрос, какой эффект должна
вызвать замена одного течения другим. Если внимательно
рассмотреть направление линий тока в том и другом тече-
нии, то можно ожидать, что искажение потока, которое
получается при такой замене, сводится к увеличению ско-
рости в точках верхней поверхности крыла и к ее умень-
шению на нижней поверхности крыла, т. е. в окончательном
виде — к преувеличению подъемной силы; при этом легко
усмотреть, что это преувеличение менее чувствительно при
большем удлинении.
Мы имеем теперь все, что нужно для подсчета влияния
затекания воздуха через боковые кромки крыла. Применяя
обычный в теории крыла метод, перейдем от задачи об обте-
кании крыла к задаче об обтекании круглого цилиндра
в плоскопараллельном потоке и определим добавочное
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1947)
591
течение вокруг цилиндра, исходя из того соображения1 что
оно вызывается добавочным вихрем с циркуляцией ДГ и что
известна скорость, вызываемая этим течением в точках ци-
линдра, соответствующих линии центров давления на поверх-
ности пластинки. Путем очень простых вычислений получим
для величины ДГ следующее выражение:
= (8)
и, следовательно, для общего выражения циркуляции вокруг
пластинки получим;
г=г,+дг=«т^[1+«/з^]. (9>
Так как циркуляция без учета влияния затекания через
боковые кромки при принятых условиях по (3)
то, как видно из уравнения (9), влияние затекания на вели-
чину циркуляции сказывается в появлении в выражении цир-
куляции некоторого множителя &(Х, 8), определяемого урав-
нением
Й(Х, 8)=14_к/з’7-^г. (10)
При значительных X и малых 8 величина fe(k, 8) весьма
мало отличается от единицы; таким образом, влияние зате-
кания воздуха через боковые кромки приобретает заметную
величину только при малых X и при значительных углах
атаки.
Следующая таблица дает значение выражения
8 0° 10° 20° 30° 45°
5 0,77 0,82 0,87 0,92
1 0,40 0,47 0,53 0,60 0,70
1/5 0,11 0,13 0,16 0,19 0,22
692 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Рис. 8.
чину индуктивного
тическое строение
сечения
Зная величину циркуляции, можно легко определить
применяя формулу Жуковского, как это обычно делается
в теории крыла конечного размаха, и величину подъемной
силы, и величину коэффициента Су\ в том и другом выра-
жении появится лишний множитель А(Х, 8). Таким образом,
мы можем вывести следующее общее заключение: учет влия-
ния затекания воздуха через боковые кромки крыла рас-
сматриваемым здесь методом приводит к тому выводу, что
величина циркуляции, величина подъемной силы и величина
коэффициента Су увеличива-
ются в £(Х, 0) раз.
Отсюда следует, что зави-
симость Су (&) выражается гра-
фически параболой.
Не входя в дальнейшие
подробности, остановимся еще
на влиянии затекания воздуха
через боковые кромки на вели-
ления. На рис. 8 указано схёма-
вихревой пелены позади крыла
по обычной теории и на основе развитых выше соображе-
ний о влиянии затекания воздуха. Присутствие добавочных
вихрей, образующихся благодаря перетеканию воздуха
в задних частях боковых кромок, вызывает, как легко ви-
деть, с одной стороны, расширение вихревой пелены, а с дру-
той стороны, уменьшение скоса. И то и другое ведет к умень-
шению индуктивного сопротивления. Однако здесь значительно
труднее учесть количественную сторону уменьшения сопро-
тивления вследствие трудности определения интенсивности
добавочных вихрей.
Заметим, что, по-видимому, невозможно учесть влияние
затекания воздуха через боковые кромки, если заменять
крыло системой вихрей, параллельных передней кромке крыла.
Таким образом, экспериментально установленное затекание
воздуха не может быть учтено методом, которым пользо-
вались Боллей, Бленк и другие исследователи.
В заключение я хотел бы подчеркнуть наиболее сущег
ственные положения предлагаемой теории.
1. Физическая схема, положенная в основу современной
теории крыла, в случае крыла малого удлинения нуждается
К ТЕОРИИ КРЫЛА . МАЛОГО УДЛИНЕНИЯ (1948} 593
в дополнениях, учитывающих влияние затекания воздуха
через боковые кромки; это затекание и является существен-
ным фактором теории крыла малого удлинения.
2. Дополнительное течение может быть учтено теми же
средствами, как и основное течение, но для него является
характерным невыполнение основного постулата Чаплыгина—
Жуковского.
3. Принятая физическая схема вносит изменение в наши
.представления о вихревом строении спутной зоны; в част-
ности, весь успех теории крыла конечного размаха зависит
.от понимания физической структуры спутной зоны и от уме-
ния ее достаточно удачно представить в виде удобной для
теоретического исследования вихревой схемы; это удается
сделать в случае малых углов атаки, где спутная зона схе-
матизируется ,в виде вихревой пелены, но это не удается
сделать в случае крыла в закритической области.
- Мы полагаем, что вопросы теории крыла малого удли-
нения представляют интерес и с точки зрения общей теории
крыла, и с точки зрения задачи . об обтекании потоком
жидкости тела произвольной формы, частным случаем чего
является задача о крыле. Можно надеяться, что глубокие,
чисто физические идеи теории крыла, своими корнями ухо-
дящие в методы, которые применил Н. Е. Жуковский и
.которые нашли широкое развитие в работах Чаплыгина,
Прандтля и других, могут дать решение и общей задачи
об обтекании потоком произвольного тела, задачи, которая
со времен работ Стокса не получила, по существу, никакого
продвижения.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ х)
§ 1. С точки зрения гидродинамики основная задача те-
ории крыла — определение сил, с которыми поток воз-
духа действует на обтекаемое им крыло, — есть весьма част-
ный случай более общей задачи об определении сил, дейст-
Ч Опубликовано в Уч. Зап. МГУ, вып. 122, Механика, т. II,
1948. (Прим, ред.)
594 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
вующих на помещенное в потоке тело произвольной формы.
Как известно, современная гидромеханика не имеет ника*
ких общих методов для решения этой задачи. Известны
только весьма частные случаи, когда теория позволяет сде-
лать некоторые выводы. Так, при плавном обтекании тела
идеальной жидкостью, как следует из парадокса Эйлера —
Даламбера, равнодействующая сил давления потока на тело
равна нулю.
Таким образом, в случае, если в потоке жидкости, ко-
торую можно приближенно считать идеальной, на тело
действует некоторая сила, вызываемая воздействием потока,
необходимо образование за телом области, в которой про-
являются особенности в течении; эту область мы будем на-
зывать спутной зоной. Как показывают опытные дан-
ные, эта область заполнена, вообще говоря, системой бес-
порядочно расположенных вихрей. С точки зрения теории
пограничного слоя эту зону надо считать областью, запол-
ненной вихрями, образующимися в результате распада по-
граничного слоя, т. е. образование зоны есть результат
действия сил вязкости.
Между тем для составления уравнений, дающих компо-
ненты сил, действующих на обтекаемое тело, приходится
пользоваться теоремой импульсов (формулы Эйлера) и при
этом необходимо знание состояния жидкости в спутной зоне.
Незнание характера течения в спутной зоне и представляет
основную трудность в решении задачи об обтекании тел
трехразмерным потоком.
Простейшее предположение о состоянии жидкости
в спутной зоне представляет основная предпосылка теории
струй, когда предполагается, что жидкость в спутной зоне
неподвижна относительно обтекаемого тела. В случае плоско-
параллельного течения, как известно, есть метод, позволя-
ющий рассчитать действие сил в предположении образова-
ния срыва струй, однако этот метод дает результаты, плохо
согласующиеся с экспериментальными данными, и, кроме
того, этот метод не удалось перенести на случай трехраз-
мерного потока.
Случай обтекания крыла представляет особенности, чрез-
вычайно упрощающие задачу. При малых углах атаки, при
каких исключительно и изучается крыло, можно считать
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) 595
спутную зону в виде тонкой плоской пелены, ширина кото-
рой равна размаху крыла, составленной из системы парал-
лельных вихрей, отходящих от присоединенного вихря крыла.
§ 2. В основных вопросах современной технической аэро-
механики, в аэродинамической теории крыла и винта, обычно
приходится иметь дело со случаями, когда удлинение крыла
ил1г лопасти винта не ниже 5. Для этих случаев современ-
ная приближенная теория крыла конечного размаха, осно-
ванная на замене крыла его несущей вихревой линией, дает
результаты, вполне удовлетворительно согласующиеся с имею-
щимся обильным экспериментальным материалом и при
современном положении дела не требует каких-либо сущест-
венных изменений. Многочисленные работы в этой области
или касаются техники вычислений, давая более или менее
удобные для технических расчетов методы, или касаются
исключительных случаев обтекания, например работы крыла
на закритических углах атаки, или влияния на обтекание
резких нарушений плавности очертания формы крыла в плане,
например при наличии у крыла вырезов, щелей и т. п.
Между тем уже при расчете работы оперения самолетов мы
имеем случаи, когда удлинение крыловых элементов опере-
ния по величине близко к единице; еще значительно мень-
шие удлинения имеют место при расчете оперения авиа-
бомб и других аналогичных конструкций, где удлинение
элементов оперения по своей величине уже близко к 0,1—0,2.
Подобный же случай мы имеем при обтекании потоком воды
подводной части корабля, когда набегающая жидкость вызы-
вает явления дрейфа. Отсюда возникает весьма актуальная
задача об изучении крыла при малых (порядка Х=1) или
весьма малых (порядка Х = 0,1) удлинениях.
Уже самые общие физические соображения позволяют
ожидать, что теория крыла, основанная на замене крыла
одним несущим вихрем, будет давать тем худшее прибли-
жение к действительности, чем меньше удлинение. Действи-
тельно, как показывают достаточно многочисленные экспе-
риментальные исследования при малых и весьма малых удли-
нениях, данные аэродинамического расчета уже настолько
расходятся с экспериментом, что теряют всякое значение.
Обычная теория несущей линии оказывается в этих случаях
совершенно неприложимой.
596 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
• Еще в 1932 г. Флахсбарт U1 показал, что при продувке
плоских пластинок выражение Су получается значительно
большее, чем дает теория. Так, при к=1 и при угле атаки
а = 25° ошибка получается порядка 25%, а при К = 0,2
и а = 30° ошибка доходит даже до 140% (рис. 1). При
этом, если при Х = 5 срыв
потока начинается при кри-
тическом значении угла
атаки а0 = 10°, то при X = 1
критический угол атаки до-
стигает величины а0 = 40°,
а при Х = 0,2 даже прево-
сходит эту величину. Ре-
зультаты Флахсбарта впо-
следствии были подтверж-
дены многочисленными изме-
рениями различных авторов;
так, аналогичные резуль-
таты получили Вейниг И,
Винтер I3J, Шильханзль.
Аналогичные результаты
были получены аспирантом-
Кудашевым при продувках
прямоугольных пластинок в
аэродинамической лабора-
тории Московского университета в 1940—1941 г. и при
продувках в ЦАГИ; так, Б. Я. Кузнецов при продувках
(4 \
Х = —^1,21 нашел
для критического угла атаки значение а0 порядка 35—37°.
Точно так же, как показал Винтер 131, получается весьма
сильное расхождение между теоретическим значением вели-
чины индуктивного сопротивления, рассчитанного по формуле
С2 V2
и данными, полученными из измерений; при этом оказалось,
что экспериментальное значение полного сопротивления было:
меньше полученного теоретическим путем индуктивного
сопротивления. Точно так же Винтер на основании своих
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948)
597
проду-ок высказал предположение, что при К, стремящемся
к нулю, величина коэффициента Су стремится к 2 sin2 а,
в то время как обычная теория приводит к тому результату,
что Су приближается к нулю, что видно хотя бы из урав-
нения параболы индуктивного сопротивления, которая при
Х = 0 вырождается в дважды взятую полупрямую, поло-
жительную полуось Сж; по поводу этого предположения
Винтера заметим, что из опубликованных им материалов
этот вывод не является достаточно убедительным.
Таким образом, все имеющиеся экспериментальные дан-
ные по крыльям малого и весьма малого удлинения приво-
дят к следующим выводам.
1. Приближенная теория крыла конечного размаха, осно-
ванная на замене крыла несущей линией, не приложима
к случаю крыльев малых удлинений, так как дает резко
заниженное значение для Су и преувеличенное значение
для Сх; расхождение теоретических данных с измерениями
резко возрастает при уменьшении к.
2. При малых удлинениях критический угол- атаки воз-
растает, достигая значений порядка 50—60°, в то время как
для крыльев нормальных удлинений (X 5) критический угол
атаки имеет величину порядка 10—15°.
§ 3. Недостатки существующей теории крыла конечного
размаха и, в частности, ее непригодность для расчета
крыльев малых удлинений привели к попыткам заменить
теорию крыла, основанную на введении одной несущей
линии, теориями, более точно учитывающими влияние формы
крыла в плане. Это развитие теории шло в основном по
двум различным направлениям.
1. Были сделаны попытки заменить крыло не одним не-
сущим вихрем, а системой вихрей, непрерывно распреде-
ленных по поверхности крыла.
2. Были сделаны попытки построить теорию крыла, ко-
нечного размаха, отказавшись совершенно от схемы одного
или системы подковообразных вихрей и заменив ее построе-
нием потенциала течения, в предположении существования
некоторых особенностей на поверхности крыла и в его спут-
ной струе, причем в этом случае потенциал определяется
непосредственно пограничными условиями и его особенно-,
стями. - ......
598 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА малого удлинения
К первому направлению принадлежат работы Боллея М,
БленкаН, и совсем недавно этому же вопросу было по-
священо исследование Г. Ф. Бураго I6), П1. Исследования
в этой области наталкиваются на теоретически непреодо-
лимые трудности в определении вихрей, заменяющих крыло.
Теоретическая возможность замены может быть доказана
вполне строгой, но в настоящее время гидромеханика не
дает возможности определить теоретическим путем беско-
нечную систему вихрей, распределенных внутри и на поверх-
ности крыла и заменяющих его поверхность. Это заста-
вляет делать те или иные предположения о расположении
системы вихрей, заменяющих крыло. Так, обычно предпо-
лагается, что оси вихрей расположены по размаху крыла
параллельно друг другу. Такое предположение, совершенно
невероятное у крыльев, не прямоугольных в плане, сомни-
тельно даже в случае крыла прямоугольного; действительно,
наблюдение показывает, что у прямоугольного крыла имеет-
ся весьма сильное затекание воздуха через его боковые
кромки, что совершенно необъяснимо при наличии только
вихрей, оси которых перпендикулярны к боковым кромкам.
Таким образом, такое предположение представляет само по
себе достаточно грубую схематизацию явления. Кроме того,
даже при таком упрощающем предположении самый расчет
сил, действующих на крыло, представляет очень большие
трудности Й.
Значительное упрощение в практическом проведении ме-
тода расчета, основанного на замене крыла системой парал-
лельно расположенных вихрей, предложил Г. Ф. Бураго
введя некоторое осреднение влияния всей этой системы вих-
рей; это позволило ему свести вычисления к решению урав-
нений, аналогичных тем, которые встречаются в теории не-
сущей линии, но с некоторыми добавочными коэффициен-
тами, характеризующими среднюю величину влияния всей
системы присоединенных вихрей. Таким образом, этот метод
в настоящее время не дает возможности получить полное
теоретическое решение задачи о влиянии на действующие
на крыло силы формы крыла в плане; однако, неопределен-
ность, имеющаяся в распределении вихрей, позволяет при
помощи некоторых более или менее произвольных дополни-
тельных предположений получить лучшее согласие с опытными
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) 599
данными, как это и показано, например, в работе
Г. Ф. Бураго l6L
Гораздо более многообещающим, на первый взгляд, пред-
ставляется второй метод, который использовали в своих
исследованиях Киннер 1101 и Н. Е. Кочин!11!. В самом деле,
построение по граничным условиям потенциала течения могло
бы дать полное решение задачи. Однако дело обстоит не
совсем так; приходится делать, так же как и в предыдущем
методе, достаточно сомнительные дополнительные предполо-
жения, без наличия которых невозможно получить потен-
циал течения, подходящего к тому, которое имеется в дейст-
вительности. Так, в работе Н. Е. Кочина предполагается,
что по передней кромке крыла расположен вихрь подхо-
дящей интенсивности; далее, ввиду того, что необходимо
знать границы течения, предполагается, что сзади крыла
имеется плоская поверхность разрыва, что, конечно, не
имеет места в действительности. Далее, при всех сделан-
ных предположениях метод приводит к исключительно слож-
ному математическому аппарату; поэтому для получения
возможности дальнейшего продвижения приходится огра-
ничиться частным случаем: крыло предполагается круглым
в плане и плоским; обобщение метода для случая эллиптиче-
ского крыла I12] приводит к дальнейшему осложнению и без
того уже чрезвычайно сложной математической задачи. В конце
концов, дело приводится к решению некоторого интеграль-
ного уравнения, которое решается приближенно, разложе-
нием решения по малому параметру, причем приходится
ограничиваться только первым членом разложения. Малым
параметром здесь является угол атаки, а потому этим мето-
дом даже в случае круглого плоского крыла можно опре-
делить силы только для малых углов атаки, т. е. в случае,
который для крыла малого удлинения, каковым и является
круглое крыло, представляет весьма мало интереса, так
как основная особенность, с которой мы встречаемся в слу-
чае крыла малого удлинения, состоит в том, что оно может
работать в условиях обтекания для таких больших углов,
как 40—50°,
Достаточно трудно оценить допустимость тех добавоч-
ных предположений, которые делаются в этих исследова-
ниях, т. е. существование вихря на передней кромке и плоская
600 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
поверхность разрыва. Однако косвенные соображения, по-ви-
димому, показывают, что такая схематизация явления весьма
далека от действительности. Н. Е. Кочин проделал подсчеты
подъемной силы для нескольких частных случаев, и при
этом оказалось, что вычисленная по этому методу подъем-
ная сила значительно (до 40%) ниже той, которая полу-
чается по обычным формулам. Это является резким противо-
речием с опытными данными, которые, как мы выше видели,
показывают, что действительная подъемная сила не меньше,
-а значительно больше той, которая получается по обычному
расчету; по крайней мере, это получается при значительных
углах атаки, а при малых углах получается достаточное
совпадение экспериментальных данных с результатами рас-
чета по теории несущей вихревой линии.
Таким образом, несмотря на большую чисто теоретическую
ценность этих исследований, в особенности исследований
Н. Е. Кочина, которые намечают совершенно новые пути
в решении основной аэродинамической задачи о силах,
действующих на погруженное в жидкость крылообразное
тело, в своем современном виде этот метод не дает конкрет-
ных результатов как по своей исключительной сложности,
не позволяющей его применить в практически интересных
случаях (крылья не круглые в. плане, значительные углы
атаки), так и по весьма большой спорности физической
схемы, положенной в основание расчета.
§ 4. В настоящей работе делается попытка п встроить
теорию крыла малого удлинения, исходя из совершенно иных
физических соображений, основанных на результатах наблю-
дений за характером обтекания пластинок потоком, сделан-
ных в 1939^—1940 гг. в ЦАГИ А. Н. Волоховым.
А. Н. Волохов исследовал направление течения на верхней
поверхности пластинок; при этом оказалось, что около перед-
ней кромки имеется затекание через боковые кромки прямо-
угольной пластинки, с нижней поверхности на верхнюю,
а далее, приблизительно, начиная с трети хорды, отсчиты-
ваемой от передней кромки, мы имеем обратно затекание
с верхней поверхности на нижнюю, как это отмечено на
рис. 2, где АА±—передняя кромка и ВВ±— задняя кромка.
Эти данные позволяют сделать следующий вывод: вихре-
вая пелена,, .образующаяся сзади крыла, схо-
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) . 601
дит не с задней кромки крыл а, а с некоторой
линии CClt совпадающей приблизительно с
линией, пред-
Рис. 2.
линией центров давления, т. е. с
ставляющей собой присоеди-
ненный вихрь.
Таким образом, мы можем на основании
экспериментальных данных А. Н. Во-
лохова считать, что вихревая пелена
сходит с верхней поверхности крыла
приблизительно на расстоянии одной чет-
верти хорды от передней кромки, т. е.
вдоль линии CCV
Из этого первоначального вывода
сейчас же вытекает важное следствие: от-
ходящая вихревая пелена CC^D^D (рис. 3)
находится в таких условиях, что для образующегося потока
поверхность крыла является твердой стенкой.
При современном состоянии науки едва ли можно рас-
считывать получить решение пространственной задачи об
обтекании конечной пластинки
ПРИ наличии отходящей вихревой
________________________^/пелены DCCJD^. Поэтому при-
А Уу ходится делать те или иные упро-
щения в постановке задачи. Фи-
зически более или менее очевид-
но, что при большом удлинении
влиянием этой твердой стенки на
В поток можно пренебречь; то же
рИСв з. самое можно получить и путем
подсчета, основываясь на обыч-
ном использовании формулы Био — Савара. Такое упрощение
делается в обычной теории крыла. Также очевидно, что такое
упрощение становится совершенно не пригодным для слу-
чая очень малых удлинений. Поэтому в случае малых удли-
нений мы введем предположение, в известном смысле про-
тивоположное, и мы будем рассматривать течение в предпо-
ложении,, что поверхность крыла представляет
собой плоскость,, неограниченно простираю-
щуюся во все стороны. Таким образом, получим тече-
ние, схематически представленное на рис. 4, гдеЗ — плоскость,
602 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
заменяющая крыло, a DCC^D^ по-прежнему представляет
вихревую пелену, отходящую от крыла. С физической
точки зрения можно ожидать, что такая гидродинамическая
схема ближе подойдет к случаю крыла малого удлинения,
чем обычная замена крыла несущей вихревой линией, при
которой влияние на поток по-
верхности крыла совершенно
не учитывается. Такая физиче-
ская схема и положена в основу
настоящей работы.
Для изучения характера
течения, представленного на
рис. 4, применим обычный
прием: введем в рассмотрение,
кроме вихревой пелены DCC1DV
еще симметрично с ней рас-
положенную относительно плоскости крыла, но с про-
тивоположным направлением вихревых вращений пелену
ЕСС^Е^ (рис. 5). Далее, для упрощения дальнейших рас-
четов предположим так же, как и в случае обычной теории
крыла, что отходящая вихревая пелена плоская и совпа-
дает с направлением отходящего потока; таким образом,
угол а, который образует вихревая пелена с плоскостью
крыла (рис. 4), равен действительному углу атаки.
Пусть w (рис. 6) есть скорость, вызываемая в какой-
нибудь точке М линии CClt которую будем называть несу-
щей линией; тогда w перпендикулярно к плоскости вих-
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948)
603
ревой пелены DCCtDlt Пусть точно так же есть ско-
рость, вызываемая в точке М вихревой пеленой ЕСС^Е^
Совокупность скоростей w и вызывает в точках линии
СС± добавочную скорость <i/ = 2wsin(& — ср), где & — угол
атаки и ср — скос потока. Эта скорость направлена по верх-
ней поверхности крыла в сторону направления течения.
Таким образом, влияние отходящей от крыла
пелены свободных вихрей крыла вызывает на
верхней поверхности крыла увеличение ско-
рости обтекания крыла потоком.
Мы можем теперь вывести величину этого добавочного
увеличения скорости. Пусть циркуляция по размаху рас-
сматриваемого крыла изменяется по эллиптическому закону.
Тогда циркуляция крыла выражается формулой
/ ~2
Г = Г0|/ 1—
где координата z направлена по размаху и I — полуразмах
крыла; таким образом, Го есть величина циркуляции в сред-
нем сечении крыла.
Пусть & есть угол атаки и ср — величина скоса потока;
тогда, как известно, справедливы равенства
r0 = *W—ср) (1)
и
2Z . ,
откуда, исключая ср и полагая -у = А, где А есть удлине-
ние крыла, получим:
(3'
И, следовательно,
<4>
“-’-’“Ч-Ти- <5>
Отсюда получаем для скорости опускания w выражение
(6)
604 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
и для выражения дополнительной скорости
v = 2w sin (8 — ср) = 2kV—£^—5 «2.
‘ (тс + 2X)J
(7)
Итак, от действия пелены отходящих свободных вихрей на
верхней поверхности крыла образуется добавочная скорость,
направленная по потоку; величина этой добавочной скоро-
сти на линии СС± приближенно определяется формулой (7).
Заметим, что формула (7) выведена в предположении,
что крыло имеет эллиптическое распределение циркуляции;
так как в первом приближении остается эллиптическое рас-
пределение циркуляции и в случае прямоугольного крыла,
то все предшествующие выводы в первом приближении
можно применить и в случае прямоугольного крыла.
§ 5. Физическая схема, положенная в основу крыла
малого удлинения, однако, настолько сложна, что при совре-
менном положении не может быть пол-
V l Г'.Л-и^ ностью доведена до возможности рас-
*] Г чета крыла. Поэтому мы в дальнейшем
сделаем еще одно весьма существенное
упрощение: мы предположим, что крыло
при скорости вдоль линии CClf опреде-
ляемой на основании изложенных выше со-
ображений, работает в условиях плоско-
параллельного течения.
•pUJ ЦЬк Физический смысл сделанного пред-
& положения состоит в замене течения,
Рис. 7. указанного на рис. 2, другим течением,
указанным на рис. 7.
Такое предположение, вероятно, увеличивает циркуляцию,
а вместе с тем и подъемную силу, так как увеличение ско-
рости, получаемое на верхней поверхности крыла благодаря
затеканию через боковые кромки, теперь распределяется на
всю поверхность крыла.
Аналогично на нижней поверхности крыла мы получим
уменьшение скорости благодаря вытеканию части воздуха
через боковые кромки.
Заметим, что добавочный поток, налагаемый на основное
течение вокруг крыла, не подчиняется основной
гипотезе теории крыла (гипотеза Чаплыгина — Жу-
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948). 605
ковского).: Действительно, так как он сходит через боковые
кромки крыла, то естественно, что его наличие не связано
с требованием, чтобы циркуляция крыла была такова, чтобы
острая задняя кромка была линией схода. Гипотезе Чаплы-
гина— Блазиуса подчиняется только основная часть потока и
не подчиняется часть потока, образующаяся благодаря зате-
канию через боковые кромки.
Это добавочное течение равносильно увеличению цир-
куляционного потока вокруг крыла. Таким образом, при-
ходим к следующему результату: добавочная ско-
рость на верхней поверхности пластинки,
вызываемая действием свободных вихрей,
увеличивает по абсолютной величине цирку-
ляцию вокруг пластинки.
Мы постараемся теперь определить величину увеличения
циркуляции и влияние этого на условия обтекания пластинки.
Для определения увеличения циркуляции перейдем с пло-
скости течения вокруг пластинки (плоскость С) на плоскость
вспомогательного потока, обтекающего вспомогательный
круглый цилиндр (плоскость z). Переход от одной плоско-
сти к другой дает уравнение
(1)
где b — ширина (хорда) пластинки, 7?— радиус цилиндра.
Из уравнения
dW _dW . dC _dW . b / 7?з\
dt ~ dz : dz~ dz ‘ 47? \ Z* )
получим соотношение между скоростями на плоскости С
(т0 и на плоскости z (v2)
(2)
Для точки отхода пелены свободных вихрей С =»
2тс .
— г
откуда по (1) z = Re3 .
606 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Следовательно, из уравнения (7) § 4 получим:
b .
^ = ^2^sin -3.
т. е.
b . 2тс Tib УЗ Т7 2к
Vz ~'Vr- 2R Sltl ~3 ~ ~R ~ V (л + 2Х)2 в '
Если считать, что полученная скорость ог вызывается дей-
ствием некоторого вихря ДГ, ось которого находится на
оси круглого цилиндра, то имеем уравнение
= = (3)
Эта формула и дает величину того увеличения цирку-
ляции, которое вызывается действием краев пластинки.
Итак, окончательная величина циркуляции вокруг пла-
стинки оказывается равной
r = r»+4r = «W^[l + «/3,-Jy. (4)
2k
В этой формуле множитель —учитывает
действие скоса потока на несущую линию,
а множитель
[ч-^з^
—действие скользящей по пластинке состав-
ляющей скорости опускания.
§ 6. Из формулы (4) предшествующего параграфа мы
видели, что действительный угол атаки заменяется кажу-
щимся углом атаки &, определяемым по формуле
’’ = \-Та[1 + "^54й]- <»
Так как поток набегает на пластинку под углом то
отсюда получаем следующий результат.
Пусть в плоскопараллельном потоке пластинка (или
профиль) выдерживает без отрыва обтекание до критиче-
ского угла 0?; тогда та же пластинка (или тот же профиль)
при удлинении X выдержит без отрыва обтекание до угла
(кажущегося) 0°, Найдем этот угол.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) 607
Решая уравнение (1) относительно 0, получим:
8 = ------7 81 (2)
' 1±/l + ^Lp#1
г А
Так как при Х = оо должно быть & = то в знаме-
нателе надо взять знак плюс.
Таким образом, окончательно
» = \ . (3)
1+/ 1 + ?г.О»,
Множитель
-----г 1 г- <4>
1 + / 1 + 2’У«,
больше 1, а потому при всяком К & > Таким образом,
влияние удлинения сводится к тому, что
уменьшается угол атаки, так что кажущийся
угол больше действительного угла атаки.
В частности, если применить равенство (3) к критическим
углам атаки, то получим:
= -я..± 2\---- 01 , 1 (5)
* , f 2л / 30?
'+]/ ’+—г-1
и так как действительный критический угол есть &?, то
получим, что критический угол атаки 8° (кажу-
щийся) увеличивается.
Подсчитаем для частных примеров это увеличение. Пусть
критический угол атаки профиля в плоскопараллельном
потоке есть -^=15°. Называя через /(X, выражение (4),
так что
,8)=2+»--------- 1 . (6)
1 + /1 + 2ф»1
608 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА. МАЛОГО УДЛИНЕНИЯ
получим следующие значения для /(к, г>1):
К 10 5 4 3 2 1 1/2 1/4 1/8
- / 1,1 1,2 1,3 1,3 1,4 1,8 2,3 3,9 4,6
Отсюда по формуле (5) получим для кажущегося кри-
тического угла атаки следующие значения:
X оо 10 5 4 3 2 1 1/2 1/4 1/8
ДО 15° 16° 18° 18° 19° 21° 27° 35° 58° 69°
Заметим, что если не учитывать влияние хорды пла-
стинки, то вместо равенства (5) получится:
При такой зависимости /(К) = ” ~Ь2Х- для &° при $<=£•
А. -а*
получим следующие значения:
X 10 5 4 3 2 1 Va V*
/(X) 1,15 1,3 1,4 1,5 1,8 2,5 4 7
до 16,6° 19° 21° 22,5° 27° 37,5° 60° 105°
Необходимо отметить здесь, что все расчеты по фор-
мулам (5) и (7) — приближенные, причем принимается, что
sin& = &, поэтому результаты при углах, больших 60°;
совершенно, не надежны.
Экспериментальные данные, по-видимому, более согла-
суются с данными формулы (5); формула (7) дает, видимо,
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948)
609
слишком большие углы, в особенности при Х^2. До Х = 2
по экспериментальным данным не получается заметного
увеличения угла атаки.
Та же формула (4) приводит и к другому результату.
Так как подъемная сила на единицу размаха по основной
формуле Н. Е. Жуковского равна pVT, то отношение
Г = Г04-АГ к величине циркуляции в условиях плоско-
параллельного потока =
^9>=-HMl+”r5-4d <8>
дает увеличение подъемной силы при заданном удли-
нении и угле атаки, происходящее от влияния концов
крыла. Таким же образом найдем аналогичное увеличение
подъемной силы, если не учитывать влияния хорды крыла;
называя его через срх(Х), получим:
ftW-VTS- <9>
Формулы (И) и (12) показывают, что при учете влияния
хорды получается для подъемной силы величина, несколько
большая; в таблице даны значения для <рх (X) == ср (X, 0) (пер-
вый столбец) и для ср (X, ft).
\ ft х\^ 0° 5° 10° 15° 20° 25° 30° 35° 40° .45°
10 0,87 0,89 0,90 0,92 0,94
5 0,77 0,80 0,82 0,85 0,87 0,90 — — — —
4 0,73 0,76 0,78 0,81 0,84 0,86 0,90 — — —
3 0,67 0,70 0,73 0,78 0,81 0,82 0,85 0 88 ~— —
2 0,57 0,60 0,64 0,67 0,70 0,74 0,77 0,80 0,84 —
1 0,40 0,43 0,47 0,49 0,53 0,56 0,60 0,64 0,67 0,70
v2 0,25 0,27 0,30 0,33 0,35 0,38 0,41 0,43 0,46 0,48
V4 0,14 0,16 0,17 0,19 0,21 0,22 0,24 0,27 0,28 0,29
?8 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17
Приведенные выше таблицы позволяют делать пересчет
кривых Cy = F(ft) для различных удлинений. На приведен-
ном ниже графике показаны результаты подобного пересчета,
причем предполагалось, что исходный профиль выдерживает
610 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
в условиях плоскопараллельного течения плавное обтекание
до угла 15° (критический угол в условиях плоскопараллель-
ного течения); за^величину Су берутся их отношения к Сутах
для исходного профиля (рис. 8),
Для сравнения даны пунктиром соответствующие графики
в предположении, что не учитывается хорда пластинки.
Сопоставление полученных данных приводит к следующим
заключениям.
1. Весьма малые удлинения (X < 1) сильно увеличивают
критический угол атаки.
По-видимому, экспериментальные данные дают несколько
большие углы (критические) при ~<Х< 1, чем найденные
вычислением.
2. Максимальные значения CWraQV остаются без изменения
111 cl A
при различных X.
3. Значения Су, вычисленные без учета затекания, дают
сильно заниженные значения Су\ имеющиеся эксперименталь-
ные данные, по-видимому, ближе подходят к значениям,
вычисленным по формуле (11), что подтверждает значитель-
ное влияние затекания через боковые кромки.
Вернемся к формуле (4) § 5. Так как
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) 611
то величина подъемной силы получится по известной фор-
муле для эллиптического крыла в виде
или, вводя площадь крыла S = 2Ы и коэффициент подъем-
ной силы Суу получим:
с.=л7^г['+«^].
Следовательно, зависимость Су от 0 является не линей-
ной, а параболической, причем соответствующая парабола
проходит через начало координат, вначале касается прямой,
выражающей линейную зависимость без учета затекания, и
имеет вершину в точке
[й=—c^=— 2^]-
При уменьшении К эта парабола приближается к прямой
Су = 0, а не к линии 2sin2а»2а2, как предполагал Винтер.
§ 7. Развитая выше теория основана на значительном
изменении тех основных положений, на которых основана
классическая теория крыла. Дополнительная циркуляция, не
подчиняющаяся основной гипотезе Чаплыгина — Жуковского,
дополнительные вихри, сбегающие с боковых кромок, пред-
ставляют собой физические образы, далеко выходящие за
схему обычной теории. Между тем, как известно, основные
формулы теории крыла могут быть выведены применением
общих теорем механики: теоремы количества движения и
теоремы живых сил к спутной струе вдали за крылом;
естественно, что при таком выводе совершенно исчезают,
по-видимому, все детали механической картины течения на
поверхности крыла. Отсюда возникает мысль о том, что
полученные выше выводы стоят в противоречии с основными
теоремами механики и, следовательно, являются несостоя-
тельными. Мы покажем, что все предыдущие выводы могут
быть полностью согласованы с основными теоремами ме-
ханики.
В основе выводов основных формул из общих теорем
механики лежит следующее предположение о структуре
612 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
спутной зоны: предполагается, что спутная зона есть
вихревая пелена, ширина которой равна раз-
маху крыла, а циркуляция вихрей распреде-
лена по размаху так же, как на крыле.
Оба эти предположения фактически не выполняются, так
как вихревая пелена неустойчива, распадается и очень
быстро за крылом свертывается в два вихревых цилиндра.
Теоретически, конечно, можно подобрать эти вихревые
цилиндры так, что подъемная сила и индуктивное сопро-
тивление остаются те же. что и при выполнении указанной
выше гипотезы, но такую за-
мену едва ли можно чем-нибудь
убедительно обосновать тео-
ретически х). Но легко видеть,
что в случае крыла малого
удлинения приходится учиты-
вать увеличение размаха пелены
сравнительно с размахом кры-
ла. Действительно, в части СВ
(рис. 9) воздух через боковую
кромку крыла перетекает с верхней поверхности на нижнюю;
в результате учета распада пограничного слоя получается
на каждой стороне добавочный, вихрь, и система вихрей,
отходящих от крыла, в сечении
рис. 10. Но вихри В и В'
вместе с ближайшими к ним
вихрями слоя создают конфи-
гурации вихрей, расширяющих
пелену. Заметим, что вихри, об-
разующие пелену, не создают
скоростей для вихрей в плоскости пелены, что и служит
известным доказательством первой половины постулата.
Итак, можно считать, что от вихрей, отходящих в точках В
и В', мы имеем растяжение вихревой пелены.
Но при расширении пелены подъемная сила не
меняется, а индуктивное сопротивление умень-
имеет вид, указанный на
Рис. 10.
ш а е т с я.
*) См. В. В. Голубев, Теория крыла конечного размаха,
стр. 208—217.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1948) 613
В самом деле, для подъемной силы Y и индуктивного
сопротивления X имеем формулы
y=2jwr01))
V гср р2
Q
Пусть Y постоянно, так что /Го — С или Го —-у, тогда
у кр С2
8 Z2 ’
т. е. индуктивное сопротивление при одной
и той же подъемной силе обратно пропорцио-
нально квадрату размаха.
Это положение уточняет известный факт, что при уве-
личении размаха уменьшается индуктивное сопротивление.
Отсюда
ах= — 2х-^-,
т. е. при увеличении размаха / уменьшение
индуктивного сопротивления обратно про-
порционально размаху.
Отсюда, например, при одном и том же X dX при 1=
в 50 раз больше, чем при / = 5, т. е. это уменьшение,
незаметное при нормальных удлинениях, становится весьма
заметным при малых удлинениях.
Заметим, что все эти трудности, возникающие в теории
крыла, представляют собой только отражение того факта,
что совершенно не разработана теория обтекания тела
в пространстве, а частным случаем такого обтекания и
является обтекание крыла, причем упрощением здесь является
только то, что в силу особой формы крыла (малости его
ширины по миделю) мы можем достаточно ясно схематизи-
ровать строение его спутной струи.
Э В. В. Голубев, Теория крыла конечного размаха, стр. .168,
614 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
ЛИТЕРАТУРА
1. О. Flach sb art, Messungen den ebenen und gewolbten
Platten. Ergebnisse der Aerodyn. Versuchsanstalt zu Gottingen, т. IV
стр. 96, 1932.
2. P. W e i n i g, Beitrage zur Theorie des Tragfliigels endlicher
insbesondere kleiner Spannweite, Luftfahrtforschung, № 12, стр. 405,
1936.
3. H. Winter, NACA. Techn. Mem., № 798. Forschungen
aus den Gebiete des Ingenieur-Wesens., t. 6, № 1, стр. 40—50; № 2,
67—71, 1935.
4. W. В о 11 a y, A Non-Linear Theorie and its Application to
Rectangular Wings of small Aspect Ratio, ZAMM, t. 19, № 1, 1931.
5. Blenk, Der Eindecker als tragende Wirbelflache, ZAMM, t. 5,
стр. 36, 1935.
6. Г. Ф. Б у p а г о, Расчет подъемной силы крыла конечного
размаха, Диссертация ВВА КА, 1944.
7. Г. Ф. Б у р а г о, Опыт расчета распределения подъемной
силы по размаху крыла на закритических углах атаки, Труды ВВА
В А им. Жуковского, вып. 120, 1944.
8. Н. Е. К оч ин, Н. В. Розе, Теоретическая гидромеханика,
ч. II, стр. 15—24, 1937.
9. Дюренд, Аэродинамика, т. II, стр. 165.
10. К i n n е г, Die kreisformige Tragflache auf potentialtheoretische
Grund lage, Ingenieur-Archiv, т. VIII, стр. 4780, 1937.
11. H. E. К о ч и н, Теория крыла конечного размаха круговой
формы в плане, Прикл. матем. и мех., т. 4, вып. 1, 1940.
12. Krienes, Die elliptische Tragflache auf potentialtheoretische
Grundlage, ZAMM, H. 2, 1940.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ О
§ 1. Общие замечания
Крылья малого удлинения, по-видимому, представляют
в настоящее время значительно большие интерес и актуаль-
ность, чем в момент появления первых исследований в этой
области. Причиной этого, несомненно, являются особенности
в работе этих крыльев, достаточно резко отличающие их
9 Эта работа печаталась в Прикл. матем. и мех., т. XIX, 1955
посмертно; она осталась в достаточно подготовленном виде в руко-
писях В. В. Голубева. Предварительный просмотр текста и чтение
корректур провел С, М. Белоцерковский,
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955) 615
от поведения в потоке воздуха крыльев больших удлине-
ний; в конструкциях, в которых могут быть применены
крылья малых удлинений, эти особенности могут найти свое-
образное использование.
С другой стороны, и с точки зрения общей теории
крыла как теории плавного обтекания тел потоком непре-
рывной среды, т. е. жидкости или газа, исследования в этой
области представляют несомненный интерес» Дело в том,
что исследования в этой классической задаче гидро- и аэро-
механики при настоящем состоянии науки носят характер
приближений и, помимо различных чисто математических
приближений, основываются на ряде механических прибли-
женных схем, которые, несомненно, не могут быть ни обо-
снованы, ни оправданы для случая общих течений, плавно
обтекающих твердое тело. Естественно, что с этой точки
зрения случаи, явно не укладывающиеся в рамки сущест-
вующих приближенных теорий, представляют особый инте-
рес, так как позволяют подойти к более точному понима-
нию изучаемого физического явления, а вместе с тем и
к построению более точной теории его.
Как известно, существующая в настоящее время теория
плавного обтекания крылообразных тел основана на идее
возникновения вокруг таких тел добавочных циркуляционных
потоков, находящих свое наглядное механическое выражение
в так называемых присоединенных вихрях, с поразительным
успехом введенных Жуковским в теорию крыла и гребного
винта. Дальнейшее развитие этой теории в трудах Чаплы-
гина, Прандтля и многочисленных других ученых позволило
путем расширения вихревой схемы Жуковского построить
теорию крыла конечного размаха и теорию гребного винта
с достаточной для технических приложений точностью, со-
гласующуюся с накопленным обильным экспериментальным
материалом.
Однако вся эта теория ;построена'я на ряде физических
допущений, оправдывающихся на опыте только приближенно,
но чрезвычайно упрощающих математическое исследование
явления. Так, в наиболее подробно и полно разработанной
в настоящее время теории крыла конечного размаха все
исследование строится, между прочим, на следующих двух
соображениях, восходящих к Прандтлю.
616 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Во-первых, крыло по размаху разбивается на ряд раз-
резов, так называемых элементов крыла, причем предпола-
гается, что каждый элемент крыла работает в условиях
плоскопараллельного потока.
Во-вторых, не учитывается влияние течений около боко-
вых кромок крыла и прежде всего не учитывается затека-
ние потока через боковые кромки, которое, несомненно,
имеет место благодаря разности давлений на нижней и верх-
ней поверхностях крыла и влиянию отходящих, так назы-
ваемых свободных вихрей.
Влияние обоих этих факторов проявляется заметно только
в частях крыла, прилегающих к боковым кромкам; поэтому
влиянием их можно с достаточным приближением пренебречь
в случае крыльев со значительным удлинением, так как вно-
симое ими изменение составляет незначительную часть сравни-
тельно с действием средних частей крыла. Однако картина
меняется для крыла малого удлинения, где влияние боковых
кромок резко сказывается на работе всего крыла, так как
благодаря малости размаха все точки поверхности крыла
оказываются близкими к боковым кромкам. А отсюда есте-
ственно ожидать, что обычная теория крыла окажется
в большей или меньшей степени не пригодной для крыла
малого удлинения.
§ 2. Специфические особенности крыльев малого
удлинения
Общие соображения предыдущего параграфа находят
полное подтверждение в обильном экспериментальном мате-
риале, накопленном в этой области. Давно было отмечено
различными экспериментаторами, что при малом удлинении,
начиная примерно с удлинения 1, крылья в потоке воздуха
ведут себя совершенно иначе, чем крылья обычных удлине-
ний, причем это расхождение в поведении крыльев увели-
чивается при уменьшении удлинения.
Известно, например, какую важную роль играет так
называемый критический угол атаки. Этот угол атаки харак-
теризуется тем, что при углах атаки, меньших критического,
крыло работает в условиях, приближающихся к плавному
обтеканию. При этом достаточно точно выполняется основ-
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955) 617
ная теорема Жуковского о подъемной силе крыла, и так
как для обычных крыльев критические углы малы и, как
правило, без применения каких-нибудь добавочных приспо-
соблений не превосходят углов порядка 15°, то в силу того,
что по данным теории в случае плавного обтекания подъем-
ная сила изменяется пропорционально синусу угла атаки,
а в пределах до углов порядка 15° синусы угла можно
заменить самим углом, имеем такой результат: при углах,
меньших критического, подъемная сила линейно зависит от
угла атаки, при углах, больших критического, крыло рабо-
тает в условиях отрыва струй, образования за крылом аэро-
динамической тени, и вся теория плавного обтекания оказы-
вается непригодной. Наиболее ощутимым результатом этого
перехода одного режима в другой является резкое умень-
шение подъемной силы при переходе в закритический угол
атаки.
Совершенно иное мы имеем в Случае крыльев малого удли-
нения. В случае крыльев с удлинением порядка 0,5—0,3 крити-
ческие углы атаки увеличиваются до 45—50°, т. е. получается
увеличение угла атаки более чем втрое сравнительно с крыль-
ями нормальных удлинений, т. е. удлинений порядка 5—10.
Вторая особенность крыльев малого удлинения состоит
в резком смещении при больших углах атаки центра давле-
ния к задней кромке крыла. В то время как у прямоуголь-
ного крыла центр давления при нормальных удлинениях на-
ходится на расстоянии, близком к четверти хорды, считая
от передней кромки, для крыльев с удлинением порядка
0,5—0,3 центр давления смещается к середине хорды; имеются
отдельные экспериментальные данные, показывающие, что
для крыльев с еще меньшим удлинением центр давления
смещается даже еще дальше, во вторую половину хорды,
до 0,6—0,7 хорды, считая от передней кромки.
Естественно, что обе эти особенности крыльев малого
удлинения имеют весьма существенное значение при приме-
нении их в различных конструкциях, например в рулях и
т. п. По-видимому, достаточно полного объяснения причин
этого отличия в свойствах крыльев малого удлинения в на-
стоящее время мы не имеем. Отмеченные выше особенности
в поведении крыльев малого удлинения позволяют сделать
некоторые выводы о физической картине их обтекания.
618 И!. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Известно, что начало перехода плавного обтекания крыла
в обтекание с образованием отрыва потока получается при
достаточном уменьшении скорости обтекания у задней
кромки. У крыла наибольшая скорость обтекания получается
в непосредственной близости к передней кромке; при уда-
лении от передней кромки скорость обтекания уменьшается.
Нами показано, что в случае, если образующийся на верх-
ней поверхности крыла пограничный слой можно считать
ламинарным, то отрыв потока от поверхности крыла начи-
нается в точке, удовлетворяющей условию
^тах _ । 2
^0 ’
где wraax — максимальная скорость обтекания крыла в точках
около передней кромки и v0— скорость в точке отрыва1).
Отсюда следует, что всякий механизм, способствующий вы-
равниванию скоростей потока в точках верхней поверхности
крыла, тем самым создает условия, благоприятствующие
плавности обтекания; в частности, в случае, если скорость
обтекания верхней поверхности во всех точках постоянна,
нет условия для образования отрыва струй.
Выравнивание скоростей может быть достигнуто или
уменьшением скорости ^тах в точках около передней кромки,
или увеличением скорости в точках, близких к задней кромке.
И тот и другой способы могут быть применены для улуч-
шения условий обтекания. Нами было показано, что путем
применения так называемых предкрылков может быть полу-
чено уменьшение ^тах; поэтому при надлежащем устройстве
предкрылков может быть получено увеличение критического
угла атаки2) с 15—16° до 25—28°.
Можно способствовать выравниванию скорости и другим
путем — путем увеличения скорости обтекания в точках около
задней кромки крыла; этого можно достигнуть путем выду-
вания воздуха из крыла в точках средней части поверхности
или путем отсасывания воздуха через щели в верхней по-
верхности крыла.
!) В. В. Голубев, Лекции по теории крыла, стр. 228, 1949.
?)* См., например, В. В. Голубев, Лекции по теории крыла,
ctp. 223,
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955) 619
Итак, резкое увеличение критического угла атаки у кры-
льев малых удлинений позволяет предполагать наличие усло-
вий, создающих выравнивание скоростей на верхней поверх-
ности крыла, вызываемое уменьшением удлинения. Но тот же
вывод получается и при учете смещения центра давления
к задней кромке. В самом деле, при постоянстве скорости
в точках поверхности крыла давление в различных точках
постоянно и центр давления приближается к середине хорды.
Общий вывод из всего предыдущего состоит в следую-
щем. Наблюдаемые особенности в поведении крыльев малого
удлинения приводят к тому заключению, что уменьшение
удлинения крыла способствует выравниванию скоростей
в точках верхней его поверхности.
Возникает вопрос о причинах, вызывающих такое вырав-
нивание. Так как, по-видимому, нет оснований ожидать при
уменьшении удлинения одновременного уменьшения скорости
около передней кромки крыла, т. е. падения ^тах, то по
аналогии с имеющимися данными естественно искать при-
чины, вызывающие выравнивание скоростей, в действии
эффекта отсасывания или сдувания пограничного слоя, более
эффективного при малых удлинениях. Такое отсасывание или
сдувание мало заметно при больших удлинениях и потому
не учитывается в обычной теории, но становится весьма
заметным при малом удлинении; оно и вызывает отмеченные
выше особенности в поведении крыла малого удлинения.
§ 3. Физическая схема работы крыла; влияние
боковых кромок
Если ограничиться случаем прямоугольного крыла, то
влияние удлинения крыла на характер обтекания его пото-
ком можно объяснить следующим образом.
В существующей теории крыла не учитывается в полной
мере влияние на обтекание крыла течений около боковых
кромок. В первом приближении можно считать, что само
по себе течение около боковых кромок прямоугольного
крыла происходит совершенно независимо от удлинения
крыла, но вносимый этим обтеканием эффект проявляется
более заметно у крыльев малого удлинения, где при одной
и той же величине боковой кромки влияние этого затекания
620 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
распределяется на меньшую площадь и, следовательно, более
заметно.
Все дальнейшее основывается на учете того влияния,
которое вносит течение около боковых кромок в. распреде-
ление скоростей у поверхности крыла; поэтому все даль-
нейшее представляет развитие тех идей, которые мною
раньше были указаны в теории крыла малого удлинения 9-
В основе всего дальнейшего лежит следующая физиче-
ская схема явления. Пусть ABCD — прямоугольное крыло,
задней кромкам крыла, и их
..., тп — его присо-
единенные вихри, nlf . . ., пп,
plt ..., рп — свободные
вихри, представляющие про-
должение присоединенных
вихрей (рис. 1). Мы пред-
положим, что всю вихревую
систему прямоугольного
крыла можно заменить пря-
моугольными вихрями, па-
раллельными передней и
продолжениями — свободными
вихрями, расположенными по прямым, представляющим линии
тока течения, не возмущенного присутствием крыла. Таким
образом, отличие предлагаемой вихревой схемы от схемы,
рацее данной, состоит в том, что мы не заменяем всю систему
присоединенных вихрей
крыла одним присоеди-
ненным вихрем.
Опираясь на такую
вихревую схему, рассмот-
рим скорости течения,
вызываемого действием
системы свободных вих-
рей в точках боковой
кромки крыла ВС или AD.
Пусть М — точка боковой кромки крыла ВС и MN —
сходящий в этой точке свободный вихрь (рис. 2). Угол а
есть, очевидно, при сделанных предположениях угол атаки.
1) Изв. АН СССР, ОТН, № 3, 1947.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
621
Найдем скорость, вызываемую дествием этого вйхря
в точке Л40 боковой кромки. Применяя, как обычно, тео-
рему Био-Савара, найдем для величины скорости следующее
выражение:
dv==^h^ +c°sa), (3.1)
где h — расстояние от точки Л40 до вихря, причем выраже-
ние (3.1) имеет место при ВМ$ > ВМ\ в случае, если
BMq < ВМ, вместо (3.1) имеем:
dv ~ г О —cos a)-
4 к Av '
(3.2)
В выражениях (3.1) и (3.2) dV— вихрь, сходящий с эле-
мента боковой кромки в точке Л4. Введем для стороны ВС
координату X, полагая, что
ВМ = х = — -i- b cos X,
где Ь — длина ВС. Тогда
Л4ОЛ4 = -1Ь (cos X — cos Хо),
где значение Хо соответствует точке Л40. Отсюда
h == у b (cos X — cos Хо) sin a,
и, называя через у вихревую плотность присоединенного
вихря, проходящего через точку 2И, имеем:
dV = 7 dx = у sin X d\.
Подставляя все значения в выражения (3.1) и (3.2),
имеем:
, т sin X (1 4- cos a) d'K \ \
dv = ---7—Ц-------Ц-r- (X < Xo),
4k sin a (cos A — COS Ao) v
. YSink(l — COS a) d'K . . 4
dv = ---7---?----- Y V (X > Xo).
4k Sin a (COS A — COS Ao) v u/
622 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Так как в случае прямоугольного крыла г)
у == 2V sin a ctg X,
то окончательно имеем:
dv = — cos2 -н---Д----s— dK (X < Хо), (3.3)
dv = - sin2 4 —1 + cosZ. d\ (X > Xo). (3.4)
те 2 cos X — cos Xo \ x- и/ \ /
Далее замечаем, что
f —Ц7-—-,--dK = (1 + cosXo) f------. T-------H [dK.
J cos X — cos Xo v 1 J cos X — cos Xo 1 J
Уравнения (3.3) и (3.4)
найти значение скорости v в
позволяют путем интеграции
любой точке, боковой кромки
®(Хо) =
где
ср (X) = cos2 (X < Xq),
Вычисление интеграла
TZ
j <р(Х)
о
d\
cos X — cos Хо
Хэ
J* d\ 4- sin2
о
<p(X) = sin2-|
d\
cos X — cos Хо
Хо
(X > Хо).
(3.6)
представляет некоторые затруднения, так как этот интеграл
несобственный. Мы будем его рассматривать так:
lim
8-> О
«,->0
d'K
о а
COS2 77 I ----Г--------7-
2 J cos X — cos Aq
о
d\
-L_ cin2 JL ------------------
’ 2 J cos X — cos Xq
(3.7)
О
x) См., например, В. В. Голубев, Лекции по теории крыла,
стр. 205 (уравнение (3)).
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
623
то
Так как г)
1 , sin-^
--->-----<— — .In
cos X — cos Xo sin Xo
d\
sin-^
— “7—7-In
sin Xo
. X -j- Xo
sm —
: X0 “ X
sln-V~
Хо- е
d\
---->----г— —-тХ-ln
I cos X — cos Xo sin Xo
о
о —
d\
I ------S--------S— -7--V- In
I cos X — cos Xo sin Xo
Xq + 81
e
sin2-
sin ~
sin
Следовательно,
Х-е
d'K
d\
о a I . 9 a
COS2 77 I ----г------г---k Sin2 -77
2 J COS X — COS Xo 1 2
0 >
= [cos2 7ln sin - i) — sit12 -§•ln sin H
+srr0 [-cos2 iln sin I+sin2 iln sin
cos X — cos Xo
Так как
'— cos2 ~ In sin ~ sin2 ~ In sin ~ =
О См., например, В. В. Голубев, Труды ЦАГИ, вып. 108,
стр. 342, 1931.
624 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
то, выбирая s и таким образом, чтобы 9
/ е \ctg2 V
ИЛИ 8! = 2 (-77 )
и полагая, что lims = 0, получим из уравнения (3.5)
lim —-L-fcos2— In sin f — sin2-^- In sin
. 0 sin Xo [ 2 \ 0 2 / 2
1 I-.
= -—г- cos a In sin An.
sin л0 0
Отсюда по уравнениям (3.3) и (3.4) имеем:
/\ x V 1 -4- cos Хл 1 • 'i i
V (Ao) =------—- cos a In Sin Ao -j—
v те sinX0 ° 1
+ v[\)cos2 + — ko)sin2-^],
или
V Г X sin24q
= — cos a ctg-^lnsinXo+Xo + ir-^^y- . (3.9)
Эта скорость вытекания через боковую кромку крыла
была получена без учета влияния поверхности крыла, кото-
рую мы принимаем за плоскую пластинку.
В случае, если бы мы имели течение, вызываемое рас-
сматриваемой вихревой пеленой, то вследствие действия
на поток плоского экрана-пластинки, заменяя действие
этого экрана, как обычно делается в гидродинамике, сим-
метричной относительно него системой вихрей, мы получили бы
скорость, вдвое большую, т. е.
a
sin2 -у
-----—-тг . (3.10)
COS a v 7
=-^-cosa ctg 1 n sin Хо + Хо +
1) Случаи a = 0, а также а = те при этом, очевидно, исклю-
чаются; причиной является то, что при подходе к прямолинейному
вихрю скорость вызываемого им течения неограниченно увеличи-
вается, но на самом деле скорость равна нулю.
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
625
Мы будем применять выражение (3.10), в точности при-
годное для бесконечной плоской пластинки и в рассматри-
ваемом нами случае плоского крыла, т. е. в случае края
ограниченной плоской пластинки. Законность такого пред-
положения не очень ясна; вероятно, мы получим при этом
несколько завышенную величину скорости
Как показывает выражение (3.9), ^(0) = — оо, т. е.
около передней кромки мы имеем втекание внутрь верх-
ней поверхности крыла окружающего воздуха; точно
так же
(_ а \
sin -ту j
к 4- к------- I,
1 COS а ]
т. е. около задней кромки мы имеем ]
кание наружу с верхней поверхности к]
При Хо, удовлетворяющем уравнению
а
7 sin2 -к-
Хо + ctg In sin Хо -р тс----= 0,
0 1 & 2 01 COS а 1
Рис. 3.
скорость вытекания с боковой кромки равна нулю; такай
точка при всяком а находится при угле Хо < , т. е. в пе-
редней половине крыла, так как
(„ а \
1 sin2 I
if 2 I
-О Ч-----/
2 1 COS а /
ИЛИ
»,(у)>0.
Ha рис. 3 дан общий вид изменения функции (Хо).
§ 4. Количество жидкости, протекающей внутри слоя
Рассмотрим поверхность крыла и пограничный слой,
примыкающий к верхней поверхности крыла. Скорость
течения на внешней границе пограничного слоя можно
считать такой же, как и на поверхности обтекаемого тела
при отсутствии пограничного слоя; это является следствием
626 Ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
того, что толщина слоя мала, а вне пограничного слоя сил
вязкости нет.
Рассмотрим слой жидкости, прилегающий извне к наруж-
ной границе пограничного слоя и достаточно тонкий для
того, чтобы можно было считать скорость течения внутри
этого слоя постоянной по толщине слоя; в силу того, что
скорость течения в области текущей жидкости изменяется
непрерывно, такой слой всегда можно с достаточной точ-
ностью подобрать и его толщину В можно считать постоян-
ной по всей верхней поверхности крыла. Количество жид-
кости Q, вытекающей из рассматриваемого слоя через
боковую кромку, равно
ь
Q = 8 J* v± dx,
или 0
Q = — Z>cosa8
sin21"
cos a
sin Xq d\Q.
Найдем предварительно интеграл
IC
/= | ctg-у sin Xo In sin Xo dX0 ==
о
ic IC
= J (1-|-cosX0)lnsinX0tZX0 = In sin Xo dX0, (4.2)
о 0
так как
IC
J* cos Xo In sin Xo d Xo = 0.
о
Далее
!C IC
T T
J* In sin XodXo = J* lncosX0dX0.
о о
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
627
Следовательно,
тс 2
I — j*lnsinXodXo = 2 J* In sin 2Х0 dX0 =
о о
тс
т
= 2 J" (In 2 -f- In sin Хо 4- In cos Xq) dX0 =
о
TC
T
= 7:11124-4 J* lnsinkodko = -rcln2 4~2Z.
о
Отсюда
Z = — Ttln2.
Далее
TC
I k0 sin k0 Ло = тс
и, следовательно,
Q = — b§ cos a
<TT
a
sin2 ту
— t: In 2 4~ я 4~ ----------
1 ‘ rne n
ИЛИ
Q = Vbbcosa
i»4+2
ra
sin3-2
COS a
(4-3)
Так как вытекание происходит через две боковые кромки,
то общий секундный объем жидкости, вытекающей через
две боковые кромки, определяется формулой
2Q = 2W>B cos a
ln-f-4-2
si"2 J
COS a
(4.4)
1 e
или, подставляя значение In-j-,
2Q = 2m cos a I 0,30685 4- 2
a
sin» у
COS a 4
628 ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Так как угол а ни при каких условиях не превосходит
60°, а с другой стороны, в дальнейшем выведенную формулу
мы будем применять при углах, превышающих критический,
который у обычно применяемых профилей бывает порядка
16°, то
или
е , о sin3 8
2" * 2 cos 16°
lnf+2
Sitl2y
COS a
+2
sin3 25°
cos 50° '
bin- 2
0,344 < In 4 + 2--------— < 0,825.
2 1 cos a
(4.5)
Далее, представляет интерес рассчитать, как распре-
делено количество вытекающей из рассматриваемого слоя
жидкости по хорде крыла. Некоторый ответ на это дает коли-
чество жидкости 2Qi, вытекающей через боковые кромки
в передней половине крыла, и аналогичное количество
жидкости 2Q2, вытекающей с задней половины крыла. Их
легко рассчитать. Действительно, применяя такие же расчеты,
как выше, получим:
2Qt = — bb cos а
J (1 “I- cos Xq) In sin Xq —Xq sin Xq —j—
о
а
sin3~2
-4- тс-------sin Xo
1 cos a u
или
/ . о а
1 sin3-у
2Qt = 2V7>B cos а I — -4 In 2-4-----------
1 \ 2 1 cos a ,
(4-6)
и аналогично
on A*4 f
О0 COS a
7U
(1 -p cosX0) in sin k0-f- k0 sin X0-f-
sin3y
_j_ к----£ sjn x
1 COS a u
2
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
629
ИЛИ
(а \
1 sin2 -9- |
-2.1П2+1 + —£). (4.7)
Легко видеть, что 2QX всегда отрицательно в рассмат-
риваемых пределах изменения а; в самом деле,
-11П2
sin2 8°
cos 16°
— In 2
a
Sitl2-2
cos a
<—4,n2
Sin2 25°
cos 50° ’
или a
1 sin2 -9-
— 0,328 < — 4- In 2 -I---- < — 0,085. (4.8)
2 1 COS a v 7
Отсюда мы имеем следующий результат: в передней
половине крыла внутри рассматриваемого слоя воздух заса-
сывается внутрь крыла.
Сопоставляя выражения (4.5) и (4.8), мы получаем, что
количество воздуха 2Q2, выбрасываемого из слоя наружу
в задней половине крыла, находится в границах
2Ш cos a • 0,672 < 2Q2 < 2m cos a • 0,910. (4.9)
Из сравнения выражений (4.8) и (4.9) получаем следую-
щий вывод.
При увеличении угла атаки с 16 до 50°
количество воздуха, втекающего в слой пе-
редней половины крыла, уменьшается п.очти
в четыре р а з а, а количество воздуха, выте-
кающего в задней половине крыла, несколько
(на0,38%) увеличивается.
§ 5. Влияние протекания воздуха через боковые кромки
на критический угол атаки
Как известно, распределение скоростей по хорде пла-
стинки в плоскопараллельном течении дается формулой 9
9 См., например, В. В, Г о л у б е в, Лекции по теории крыла,
стр. 203.
630 nt. ТРУДЫ ПО ТЕОРИИ КРЫЛА МА лого удлинения
и, следовательно, на задней кромке, когда X — тг, имеем:
Uq = V cos а.
Таким образом, в предположении, что прямоугольное
крыло обтекается потоком в условиях плоскопараллельного
течения, количество воздуха, вытекающего из рассматри-
ваемого нами слоя вдоль задней кромки, определялось бы
формулой
= Vcosa • ZB, (5.1)
где I — размах пластинки.
В случае ограниченной пластинки к рассматриваемому
течению добавляется еще течение, образованное воздухом,
затекающим через боковые кромки. Получающееся от нало-
жения этих двух течений результирующее течение можно
представить схематически, как указано на рис. 3. Поджа-
тие струй, вызываемое затеканием через боковые кромки,
должно вызывать резкое увеличение скорости течения
в средней части крыла, а это в свою очередь ведет к вы-
равниванию скоростей потока и, следовательно, к увеличе-
нию критического угла атаки.
Мы можем оценить увеличение скорости течения от дей-
ствия засасывания через боковые кромки следующим обра-
зом. Как мы видели, при отсутствии засасывания, т. е.
в условиях плоскопараллельного обтекания, количество воз-
духа, стекающего в рассматриваемом слое с крыла в одну
секунду, определяется формулой (5.1).
Если допустить, что в условиях засасывания через бо-
ковые кромки количество стекающего воздуха с задней
кромки остается тоже, то общее количество воздуха, стекаю-
щего в слое через заднюю и боковые кромки, определяется
выражением
2Q = IZ8cosa Z4~2Z>
е sin" 2 I
In 4 + 2 --------- , (5.2)
2 1 cos a j ’ v 7
что равносильно увеличению скорости течения в среднем
от и0 до vlt причем из уравнений (5.1) и (5.2) имеем:
+ = 1+ +(1пт+2
«О l \ Z
а
sin’y
cos a
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955) 631
Z
или, вводя удлинение крыла = получим:
= (5.3)
и0 |Л \ 2 1 cos а / v '
Это увеличение скорости приходится на основное тече-
ние, так как воздух, затекающий через боковые кромки,
полностью стекает и 2Q дает количество воздуха, вытекаю-
щего в основном течении.
Полученная формула (5.3) показывает, что при нормаль-
ных удлинениях р порядка 5—10 увеличение скорости
у задней кромки незначительно, в особенности при малых
углах атакй а. В самом деле, как было показано в преды-
дущем параграфе, выражение
j е 51113 Т I
1 '”4 1 (
изменяется от 0,344 при а =16° и до 0,825 при а = 50°;
принимая при грубой оценке среднее значение 0,56, полу-
чим, что отношение — колеблется в пределах от 1,19 при
ио
р = 5 до 1,1 при pi=10. Совершенно иная картина полу-
чается при малых удлинениях; приводим значения этих отно-
шений при некоторых малых значениях р:
р= 1 0,5 0,33 0,25 0,2 0,01
^1. =2,12 3,25 4,36 5,48 6,60 12,2
«о
Итак, при малых удлинениях мы получаем весьма резкое
увеличение скорости около задней кромки, а это в свою
очередь должно давать и сильное выравнивание скоростей и,
следовательно, перемещение центра давления по направле-
нию к задней кромке и резкое увеличение критического
угла атаки.
Применяя результаты, ранее полученные нами1), можно
рассчитать, исходя из предшествующих соображений, кри-
тический угол атаки. Считая, что прямоугольная пластинка
Э См. В. В. Голубев, Лекции по теории крыла, 1949.
632 ш. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
округлена у передней кромки по методу Жуковского и е —
коэффициент, характеризующий округление, мы получили
следующие формулы для максимальной скорости обтекания
профиля г/тах и для скорости г/0 у задней кромки:
у/ • G + 02 1
Wmax = V Sit! а-—1
е У (5.4)
Но = Vcosa(l — s). J
Предполагая, что влияние затекания сказывается только
вблизи задней кромки, и повторяя рассуждения предшест-
вующего параграфа, получим для скорости с учетом за-
текания потока через боковые кромки выражение
v' = V cos a 1 —s —j——-1 In + 2
о L P* \ 2
Sin2^-
cos a
или
= —s)cosa 1-4
(a
. * j oSin2’2
In -fz—2-
2 1 cos a
(5.5)
С другой стороны, опираясь на соображения, основан-
ные на теории пограничного слоя, мы получили следующее
условие для полного обтекания крыла:
•^=1,2. (5.6)
vo
Подставляя в (5.6) выражение (5.4) и называя через 0
критический угол атаки, получим:
<l+£)3 tg0 К
е(1-
Мы
ченные
1 2 1 е .
— j-------tin -4
р. 1 — £\ 2 1
= 1,2. (5.7)
6
2 sin2
cos О
видели, что в тех пределах, где прилагаются полу-
выводы, среднее значение
• я a
. е , о 51ПУ
П 2 2 cos a
0,56. Точно так же параметр s, характеризующий
равно
утолщение крыла, меняется обычно в пределах от 0,05 для
очень тонких профилей до 0,20 для достаточно толстых;
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955)
633
для приближенного расчета мы возьмем и здесь среднее
значение е = 0,1. Тогда получим среднее значение выра-
жения
(„ а \
е sin 2"|
ч+2^гИ’24- <5-8)
Из уравнения (5.7) получим следующее уравнение для
определения критического угла атаки:
Г / „6
1 2 I е sin I"
tg 9 = 1 2 l+-L-j-£— I In4-4- 2---=•, -и-,..
' L Р» 1 — e \ 2 1 COS 6 j J (1 e)2
или, подставляя приближенное значение (5.8),
£ \ ~ р, / (1 + е)2
е(1-е)
, (5.9)
(5.10)
Так как в случае плоскопараллельного течения крити-
ческий угол 90 представляется по формуле
а = 1 2 ____51
g°0 (14-е)2 ’
то уравнения (5.9) и (5.10) можно еще переписать в виде
1 [2 ( е sin2Т
tg 0 = tg 0О 1п4+2---------=-/ , (5.11)
& 5 0 L Р*1 — е\ 2 1 cos 6 / J v 7
tg9 = tg0o(i +-71)- <5-12)
Приводим результаты применения полученных формул к двум
примерам.
1. Крыло с е = 0,10:
tg0О = 1>2 = 0,09, 0О = 5°10':
р.= 6 1 0,5 0,33 0,25 0,20 0,10
0=О°1О' 11°20' 17°20' 23° 25°40' 32°5'У 50°4(И
2. Крыло с е = 0,15, 1g 0 = 0,116, 0О — 6°40':
р. = 6 1 0,5 0,33 0,25 0,20 0,10
0 = 8° 14°30' 22° 28°40' 34°40' 39°50' 57°10/
634 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
Эти примеры дают резкое увеличение подъемной силы при
малых удлинениях в пределах, достаточно близких к тем, которые
дают экспериментальные данные; по-видимому, только при очень
малом удлинении (р- = 0,1) формула (5.12) дает значительно завы-
шенные значения для критического угла сравнительно с экспери-
ментальными данными.
§ 6. О границах применения полученных выводов
Примеры, разобранные в предыдущем параграфе, дают,
по-видимому, достаточно удовлетворительное согласие
с имеющимися экспериментальными данными; тем не менее,
необходимо помнить, что они получены на основе некоторых
исходных соображений, которые нельзя считать бесспорными.
На уточнении этих исходных соображений мы и остановимся.
В основу всей изложенной теории положена физическая
схема, отличная от применяемой в обычных теориях крыла
конечного размаха: спутную зону крыла вместо вихревой
пелены, сбегающей с задней кромки крыла, мы предста-
вляем в виде двух, сбегающих с боковых кромок крыла.
Несомненно, что и та и другая схемы представляют теоре-
тическую стилизацию, не совпадающую точно с тем, что
мы имеем в действительности. Насколько нам известно, нет
экспериментальных данных, которые указывали бы на дей-
ствительное существование вихревой пелены, сбегающей
с задней кромки; все экспериментальные данные, показы-
вают, что с крыла сбегают два цилиндрических вихря,
которые обычно рассматриваются как результат свертывания
вихревой пелены. Принятая выше вихревая схема, пожалуй,
стоит в лучшем согласии с экспериментом.
Гораздо большее сомнение возбуждают выводы пред-
ществующего параграфа. Формулы (5.10), (5.11) и (5.12)
основаны, в конце концов, на принятии уравнения (5.6)
1,2.
v0
Но уравнение (5.6) не является выводом теоретическим;
оно является результатом того наблюдаемого эксперимен-
тального факта, что на верхней поверхности крыла в интер-
валах между точками, где давление наименьшее (и, следо-
вательно, скорость наибольшая), и точкой, где происходит
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955) 635
срыв струй, давление изменяется по линейному закону1).
Но надо помнить, что эти экспериментальные данные все
относятся к случаю обтекания без влияния боковых кромок;
совершенно неясно, остается ли линейность изменения давле-
ния приближенно верной и в случае, когда к основному
потоку добавляется еще течение через боковые кромки.
Соответствующих экспериментальных данных, по-видимому,
нет, и этот случай требует дополнительного эксперимен-
тального изучения.
Наконец, мы считаем, что затекание через боковые
кромки увеличивает скорость течения около задней кромки,
но не изменяет скорости течения около передней кромки.
Не ясно, насколько допустимо это предположение, так как
несомненно, что затекание через боковые кромки изменяет
и скорость у передней кромки. Мы считаем, что это изме-
нение пренебрежимо мало.
§ 7. Инверсия обтекания
Выравнивание скорости течения, вызываемое затеканием
через боковые кромки, должно, естественно, вести к пере-
мещению центра давления к середине крыла, но едва ли
таким затеканием можно объяснить перемещение центра
давления за середину крыла, ближе к задней кромке. Между
тем имеются некоторые экспериментальные данные, показы-
вающие перемещение центра давления в точки, удаленные
на 0,25—0,30 длины крыла, считая от задней кромки.
По-видимому, такое явление наблюдалось для случаев обте-
кания очень удлиненных тел типа фюзеляжа или корпуса
снаряда. В дальнейшем сделана попытка дать теоретическое
выяснение возможности подобного влияния.
Во всех исследованиях по теории крыла предполагается,
что обтекающий плавно поток сходит с острой задней
кромки, чем и определяются величина и направление цир-
куляции. Между тем, по-видимому, нет никаких препятствий
считать возможным такое обтекание, когда острая кромка
находится впереди и эта передняя острая кромка является
с Х22^М*’ напРимеР’ В-В, Голубев, Лекции по теории крыла,
636 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
точкой разделения набегающего потока (рис. 4). Если
ограничиться случаем плоской пластинки, то получим вместо
обтекания, указанного на рис. 5, обтекание, указанное
на рис. 4. Для перехода от случая, указанного на рис. 4,
к случаю, указанному на рис. 5, достаточно, очевидно,
заменить угол атаки а на —а и, кроме того, изменить
направление оси х. Отсюда получим следующие формулы:
X = 2крУ2 sin2 9/?, |
Y = — 2крУ2 sin 6 cos 07?, J
mom0 P = — ттр!/2/?2 sin 29,
(7-1)
(7.2)
где R— радиус вспомогательной окружности на плоскости z,
причем конформное отображение с плоскости пластинки С
на плоскость вспомогательной окружности z определяется
формулой
я»
Z ’
r^ = z-\
(7-3)
так что скорости в бесконечности на обеих плоскостях
равны по величине и образуют равные углы с действитель-
ной осью, а величина хорды пластинки L определяется
формулой
L = 4/?. (7.4)
Очевидно, что формулы (7.1) и (7.2) можно получить
обычным способом, если на вспомогательной плоскости z
критические точки потока, обтекающего окружность, взять
в точках zl =—R и z% = Rew (вместо zx—R и z2 — — Re2Bi),
К ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ (1955). 637
В случае пластинки при этом центр давления будет
находиться в точке £ = R = — L (вместо 5 = — R= — ~ а) ,
т. е. на одной четверти хорды, считая от задней кромки.
Весьма вероятно, что подобный случай будет иметь
место при движении клина острием вперед, а также тел
артиллерийских снарядов. Вероятно, случаи, когда различ-
ные наблюдатели замечали смещение точки приложения силы
во вторую половину хорды, и относятся к случаю такого
инвертированного, обращенного, потока.
§ 8. Общие выводы
Подведем итоги всем предшествующим соображениям.
Экспериментальные данные, касающиеся крыльев малого
удлинения, приводят к выводу, что скорости на верхней
поверхности крыла, где происходит отрыв потока, при
уменьшении удлинения крыла выравниваются, результатом
чего являются увеличение критического угла атаки и пере-
мещение центра давления от передней кромки. Причиной,
вызывающей выравнивание скорости на верхней поверхности
крыла, являются или уменьшение скорости обтекания вблизи
первой кромки, что достигается, например, введением пред-
крылков, или увеличение скорости обтекания вблизи задней
кромки крыла, что может быть, например, достигнуто
отсасыванием воздуха через щели в задней половине крыла.
Все предыдущее построено на том соображении, что боко-
вые кромки крыла в его задней части играют ту же роль,
что щели для отсасывания воздуха.
Так как особенности поведения крыла малого удлинения
проявляются главным образом при больших углах атаки,
то предлагаемая теория рассчитана прежде всего на случай
больших углов атаки. При этом в отличие от обычной
теории крыла мы делаем предположение, что присоединен-
ные вихри сходят не с .задней кромки крыла, а с его
боковых кромок, причем образуют вихревые пленки не
в плоскости крыла, а в плоскости, перпендикулярной к пло-
скости крыла (рис. 6).
Если ограничиться крылом, прямоугольным в плане, то
принятые предположения позволяют приближенно определить,
638 III. ТРУДЫ ПО ТЕОРИИ КРЫЛА МАЛОГО УДЛИНЕНИЯ
основываясь на выводах теории пограничного слоя,
изменение критического угла атаки в зависимости от удли-
нения, а вместе с тем показать увеличение скоростей
обтекания в задней половине крыла и, следовательно,
выравнивание скоростей на верх-
ней поверхности крыла при умень-
шении удлинения и смещение
центра давления к середине кры-
ла. В заключение показывается,
что перемещения центра давления
за середину крыла, на что, по-
видимому, указывают наблюдения
некоторых исследователей, воз-
можно при наступлении «инвер-
когда передняя кромка становится
точкой разделения набегающего потока, что физически
возможно.
По методу исследования настоящая работа примыкает
к моим исследованиям по теории разрезного крыла и по
влиянию отсасывания потока; во всех этих работах изу-
чается влияние различных факторов на структуру погра-
ничного слоя, т. е., в конце концов, влияние^ вязкости
воздуха на обтекание крыла, т. е. твердого тела хорошо
обтекаемой формы.
Рис. 6.
сии» в обтекании крыла,
ТРУДЫ
ПО РАЗНЫМ ВОПРОСАМ
АЭРОДИНАМИКИ

К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНАх)
§ 1. Как известно, Карманом и Н. Е. Жуковским были
получены различные условия устойчивости вихревых дорог
Бернара Кармана при шахматном расположении вихрей* 2).
Если назвать расстояние между двумя последовательными
вихрями одной стороны вихревой дороги через I и ширину
дороги через 7г, то условия устойчивости по Карману и
Жуковскому имеют вид
по Карману ch^- = j/2, откуда ~ = 0,281,
по Жуковскому ch-^- = j/^3, » у = 0,365.
Причину этого противоречия Н. И. Ахиезер пытался
объяснить тем, что условие Жуковского предполагает опре-
деленный закон смещения вихрей, представляющий собой
частный случай более общего закона смещения, рассматри-
ваемого Карманом, причем строго доказал, что, вопреки
указанию Н. Е. Жуковского, из рассматриваемых им сме-
щений нельзя получить смещений общего вида, рассматри-
ваемых Карманом3). Однако при этом нужно было бы
ожидать, что условие Кармана должно содержать условие
х) Опубликовано в Математическом сборнике, т. 40, № 1, 1933.
(Прим, ред.)
2) См., например, В. В. Голубев, Теория крыла конечного
размаха, гл. 1; Н. Villa t, Lemons sur la theorie des tourbillons,
ch. IV; H. E. Жуковский, Теоретические основы воздухоплава-
ния, [Собр. соч., т. IV, 1950].
3) Н. И. Ахиезер, К вопросу об устойчивости вихревых
Улиц, Математический сборник, XXXIV, 1—8, 1927.
642
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Н. Е. Жуковского как частный случай, а не противоречить
ему. В действительности причина противоречия кроется
более глубоко. С выяснения этого противоречия мы и
начнемг).
§ 2. Вопрос о движении вихрей, образующих вихревую
дорогу Кармана, приводится к интегрированию бесконечного
числа линейных уравнений с бесконечным числом неизвест-
ных функций. Задача, как показал Карман, чрезвычайно
упрощается, если искать интегралы системы, следующие
некоторому периодическому закону.
Пусть хт и ут—координаты смещения вихрей верхнего
ряда и х'т, у'т — координаты смещения вихрей нижнего
ряда. Тогда, располагая оси надлежащим образом и полагая
х = у х' = г'еп?\ у'=г'епч\
получим для функций г, г', г' в случае шахматного
расположения вихрей уравнения
2и/2 dr . _ , „ ,
Г dt Br
2я/з drr . , . _ ,
— -df = ~Ar-Cr+Brv
*) Правильная постановка вопроса дана А. А. Саткевичем
(«Аэродинамика как основа авиации», стр. 310), но данное им
объяснение расхождения результатов, как легко видеть, непра-
вильно.
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
643
Из (1) получим соответствующие уравнения для вихря
нижней системы, заменив Г на —Г, Л на —h и переместив
значок ' и т и п х):
dr'
Г dt
Alr 1 &1Г + С]/1 ,
(3)
2 л/2 dr.
— Air'+cir + Bir i,
(4)
где в суммах и 2 отсутствует слагаемое,
соответствующее т = 0 или п = 0.
Предположим теперь, что при движении вихрей, обра-
зующих дорогу Кармана, некоторые вихри остаются непо-
движными; тогда в суммах (2) и (4) не войдут слагаемые,
соответствующие номерам неподвижных вихрей, так как,
очевидно, достаточно заменить нулями г, rx, гг, г' в соот-
ветствующих слагаемых. Пусть вообще движутся только
вихри номеров М в верхнем ряде и N в нижнем, причем Л4
и N принимают некоторые из значений чисел натурального
ряда. Тогда уравнения (1) и (3) останутся, но формулы
для коэффициентов А, В, Ct Alf В19 Сг изменятся, так как
вместо тип войдут М и N и суммы будут распростра-
нены не на все числа натурального ряда; получим формулы,
т) См., например, В, В. Голубев, Теория крыла конечного
размаха, стр. 60,
644
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
в которых суммы распространены на некоторые из значений
причем в суммы и входят все числа нату-
рального ряда, кроме нуля.
§ 3. Из уравнений предыдущего параграфа получим
случай Н. Е. Жуковского, если положим, что 7И=0 и что
чисел N нет. Получим из уравнений (1)
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
645
Уравнение (1) приводится к
/2я/2\2 (Рг
(—) -w=A2r’
и для устойчивости необходимо, чтобы А — 0. Но, как
известно,
VV 1 к. V’ Н)’-’
Следовательно, имеем уравнение
7Г2 К2 ___ ~
3 ch2 for ’
откуда получаем:
ch2&Tt = 3,
это и есть условие Н. Е. Жуковского.
Остаются уравнения (3) предыдущего параграфа. В них
мы должны положить г' = 0 и г' = 0, так как во всем
нижнем ряде вихри неподвижны. Следовательно, получим
уравнения
— &ir + t = 0, |
и так как г и отличны от нуля, то для совместности
необходимо, чтобы = Но в настоящем случае
а потому условие (2) принимает вид
(2)
что противоречит условию Н. Е. Жуковского. Отсюда сле-
дует, что в случае, если все вихри в дороге Кармана могут
перемещаться, случай, рассматриваемой Ht Е. Жуковским,
6 46
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
н евозможен: невозможно такое движение, что все вихри,
кроме одного, неподвижны, а один движется. Впрочем, это
достаточно ясно и из непосредственных механических сообра-
жений.
Отсюда вывод: случаи движения вихрей, рас-
сматриваемые Карманом и Н. Е. Жуковским,
существенно различны. Карман рассматривает
условия равновесия системы вихрей в пред-
положении, что все вихри свободны и могут
перемещаться; Н. Е. Жуковский рассматривает
условия устойчивости равновесия, когда сво-
боден и может перемещаться только один
вихрь, а все остальные вихри дороги Кармана
прочно закреплены. В предыдущем показано, что
случай Н. Е. Жуковского нельзя рассматривать как частный
случай общей задачи Кармана. Таким образом, Карман и
Н. Е. Жуковский решали две совершенно различные задачи;
естественно, что условия устойчивости равновесия вихрей
при различных условиях задачи получились различные.
Из предыдущего следует, что попытка Н. Е. Жуков-
ского рассматривать любое смещение вихрей как наложение
смещений, полученных в рассматриваемом им случае, не-
возможна, так как в случае, если, кроме одного подвижного
вихря, в вихревой дороге Кармана есть и другие подвижные
вихри, уравнения (1) отпадают и мы не получим условия
Н. Е. Жуковского. Интересно отметить, что случай одной
вихревой цепочки получается как частный случай.
Действительно, этот случай получим из предыдущих
уравнений, если положим, что h = оо, т. е. k = oo. В этом
случае I II £ I 1 И й 1 1 -И од од Il II В = 0, ^ = 0, c = o, = 0
и система уравнений превращается 2it/a dr _ 2л/2 Г dt АГ1’ Г 2я/2 dr' , 2т.12 Л. Г. в dt dr't _ -— Ar, :АХГ'. ► (3)
Г dt 1’ Г dt
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
647
Обе системы совершенно не зависят друг от друга. Здесь
___У'
и в этом случае А также зависит от того, какие вихри
смещены. Впрочем, этот случай практически малоинтере-
сен, так как здесь всегда будем иметь неустойчивое равно-
весие. Действительно, из уравнений (2) видим, что для
устойчивости, вернее для безразличного равновесия, необхо-
димо, чтобы А == 0, но
-__vV 1 VV cos sin Л4<р
Л —п?~' 2i 12л м* '
и действительная часть не равна нулю, за исключением
случая <р = 0, когда все вихри цепочки смещены одинаково.
§ 4. Случай, разобранный Н. Е. Жуковским, можно
самыми разнообразными способами видоизменять, закрепив
часть вихрей и оставив остальные свободно перемещающи-
мися; при этом получим бесчисленное множество случаев,
среди которых случаи Кармана и Жуковского являются
частными случаями.
Пусть, например, все вихри нижнего ряда закреплены,
а в верхнем ряде часть вихрей свободна. Тогда уравне-
ния (1) и (2) принимают вид
(1)
dr л 2пР drr
“г“37Т = — Лг1’ = —
1 dt х 1 dt
где
Л2 ТС2
а=~3 ch^krt
(2)
есть действительное число.
648
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Из уравнений (1) имеем
/2л/2\2 (рГ
(—) и
г ) dt* ~лг^
и вихрь находится в состоянии безразличного равновесия,
если д. ч. А = 0, во всех остальных случаях вихрь нахо-
дится в неустойчивом равновесии. Взяв действительную
часть А, имеем уравнение
Уравнение (3) должно иметь место при всяком ср в пределах
от 0 до тс. Найдем, при каких значениях целых чисел М
уравнение (3) выполняется при 0 ср тс.
Умножая обе части (3) на cos пер, где п — некоторое
целое число, и интегрируя в пределах от 0 до тс, получим:
It ТС
а J cos nep Jep—-^2 J cos Мер cos nep dep == 0. (4)
о о
Так как
те
cos Мер cos пер 6?ep = у J cos(M-|-^) <р
0 0 о
г ;
cos(M — n)epdcp и j cos(Mzt ri)ydy — 0,
о 0
если Л1±п^0, и равно тс, если М±п = 0, то после
интеграции в сумме уравнения (4) останутся члены
или
(5)
(6)
где п — одно из чисел М, смотря по тому, принадлежат ли
числа ±п одновременно к числам М или к числам п при-
надлежит только одно из чисел: -|-п или —п. Так как
ни (5), ни (6) не равно нулю, то получаем, что условие (3)
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
6 49
не может выполняться тождественно при любом ср, если
в сумме 2 есть хоть одно слагаемое. Отсюда вывод:
если в нижнем ряде все вихри закреплены,
а в верхнем — некоторые свободны, то во всех
случаях, кроме разобранного выше случая
одного подвижного вихря (случай Н. Е. Жу-
ковского), система вихрей находится в состоя-
нии неустойчивого равновесия.
Несколько иные результаты получим, если наложим на
смещения вихрей некоторые добавочные условия, например
подберем смещения вихрей, как выше, по синусоидальному
закону с определенной длиной волны смещения, которая
определяется величиной ср.
Рассмотрим, например, случай, когда все вихри нижнего
ряда неподвижны, а в верхнем ряде свободны вихри, имею-
щие номер ns (s—постоянное число). Рассчитаем для этого
случая коэффициенты формул (2') и (4') § 2.
Имеем
у' _____ V1' еП8(?г_1 vV cos nsy . . 1 VV sin nsy
2a = 2a 2a n? ' 11? 2a n? ' '
Ho
2'-^=2't=°
Итак,
S' _ 1 yV cos n (scp)
m2 s2 21 n2
Известно, что
V 1 — cos mb , d>2 n o
2d---i = ---при 0<ф<2тг,
откуда
Seos /тгф к2 , I Ф2
(1)
Пусть ф = sep, и пусть sep > 2тс и sep = 2tcN-|- а, тогда
cos znep = cos tn (2tzN -j- a) = cos ma
Vi cos n
2j m2
2 ’
650 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Таким образом, в рассматриваемом случае
л те2 1 / те2 । а2 \ тс2
А~~3 "s^* 3 7ta + "2'/ "c¥fc’
Уравнения (1) в настоящем случае (все вихри нижнего ряда
неподвижны, следовательно, г' = 0 и г' = 0) принимают вид
2те/2 dr 2те/2 drr _
Г dt ~ АГ1' Г dt ~
Аг.
Мы получим безразличное положение равновесия при усло-
вии А = 0, во всех других случаях равновесие будет не-
устойчивое. Итак,
откуда
Обозначая через Е(х) целую часть числа х, из уравнения
scp = 2zN a
имеем:
и a=s^-E(S)2n-
Окончательно уравнение (2) принимает вид
1
ch2&Tt =-
3
те
4[s?-£(SH}
(3)
Если положить s = оо, то мы получим случай, разобранный
Н. Е. Жуковским (вихри нижнего ряда закреплены, в верх-
нем ряде свободен вихрь номера 0). Имеем в этом случае
ch2 = 3
(условие Н. Е. Жуковского).
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
651
Рассмотрим случай ср = 0, тогда все свободные вихри
смещаются одинаково. Условие (3) принимает вид
«9 1 3
ch2 kit =----р .
(4)
В случае, если смещены в верхнем ряде все вихри, то $= 1
и & = оо, т. е. второго ряда нет. Итак, если нижний ряд
закреплен, а верхний — весь свободен, то устойчивого равно-
весия не будет.
Если s — 2, то из (4) имеем:
ch2&Tt = 4, (5)
это — случай, когда вихри в верхнем ряде смещаются оди-
наково через один. Отсюда получим Ze = 0,41. Но при
других ср получим, как видно из (3), другие условия.
Вообще, если весь нижний ряд закреплен, а верхний
весь свободен и колеблется согласно закону § 1, то урав-
нения принимают вид
Необходимое условие устойчивости (точнее, условие для
безразличного равновесия) А = 0, откуда
ch2 kit = —------г-.
Следовательно, k зависит от ср, т. е. от длины волны сме-
щения вихрей верхнего ряда; при различных ср будут раз-
личные k, и при всяких длинах волн смещения вихрей общего
условия устойчивости не будет. Таким образом, система
таких вихрей неустойчива, что подтверждает результат
652
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
данный выше. Совершенно тот же результат получим и для
случая, когда в верхнем ряде могут перемещаться вихри
номера ns. Тогда, как показывает формула (3), условие
устойчивости зависит от ср, т. е. от длин волн смещения
(кроме разобранного выше случая s = сю), и, следовательно,
общего условия устойчивости не будет.
Итак, получили тот же результат, который получен
выше: в случае, если нижний ряд закреплен,
а в верхнем могут смещаться только вихри
номера ns, то безразличное положение равно-
весия получится только в случае Н. Е. Жуков-
ского; во всех остальных случаях при произ-
вольных смещениях вихрей равновесие будет
неустойчивое..
§ 5. Подобным же образом можно разобрать случай,
когда свободны вихри и в нижнем ряде.
Пусть по синусоидальному закону колеблются все вихри
нижнего ряда и часть вихрей верхнего ряда; тогда коэффи-
циенты определяются формулами
__ к2 и2 у'
А — ~3 ~ ch2 kit ~ 2j “Ж ’
Если в верхнем ряде подвижен только один вихрь (номера 0), то
ТЕ2 Г.2
А = т — ch^T’
В этом случае, как и в случае Кармана, В—число мнимое,
и для устойчивости необходимо, чтобы
А2 — С2<0;
так как при ср = тг коэффициент С обращается в нуль, то
н здесь получаем необходимое (но, вообще говоря, недо-
статочное) условие безразличного равновесия А = 0, т. е.
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
653
получаем условие Н. Е. Жуковского. Для нулевого вихря
нижней системы получим аналогично уравнения (3) § 2, где
__ 1 у*™0 7:2
1 т2 2^ т? ch2 kn ’
По общему условию Кармана для устойчивости необходимо,
чтобы выражение
В, = ± V Al — С?
было чисто мнимое, т. е. чтобы, в частности, В было чисто
мнимое, что при любом ср не выполняется.
Итак, если весь нижний ряд свободен, а
в верхнем свободен только вихрь номера О,
то система неустойчива.
Из предыдущих выводов естественно ожидать, что в слу-
чае, если в верхнем ряде вихри свободные при in ~ ks и
$#=1, в нижнем ряде все вихри свободны, то система также
находится в состоянии неустойчивого равновесия.
Действительно, в этом случае коэффициент
, _ \У (2М+1)£ /0*4)’
Заметим, что в уравнениях (1) при изменении знака г и гг
(или г' и г') меняется знак у В.
Пусть, разделяя в Вг действительную и мнимую части,
имеем:
654
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
тогда
к-u- V' <2^+i)fe 0“4) ’
к LI Zj г / 1 \2 12 е
Следовательно,
Для случая устойчивого равновесия, по предыдущему, необ-
ходимо, чтобы R = 0 при всяком ср в пределах от 0 до к.
Итак, подберем такие целые Л4, чтобы уравнение
(1)
выполнялось при ср к.
Умножая (1) на cos^n-j-y^cp и интегрируя в пределах
от 0 до к, получим, замечая, что
2-Л =
= yCOs(M+n+ 1) ср -1- у cos (Л4 — п)ср,
у' (2Л4 + П
_о
J cos(44 — n)cprfcp = 0. (2)
о _
Так как интегралы, стоящие в (2), отличны от нуля только
в случае, если Л4 —|—п —1 = 0 или Л4— п = 0, то после
интеграции получим:
2/2+1 , - 2(п + 1)+1
или
2п + 1 2п + 1
К ТЕОРИИ ВИХРЕВЫХ ДОРОГ КАРМАНА
655
Следовательно, условие (1) может выполняться только в том
случае, если числа пи —(п-|- 1) одновременно принадлежат
к ряду чисел 7И; в случае, если из этих двух чисел к ряду чи-
сел Л1 принадлежит только одно число, то в (2) остается только
одно слагаемое, отличное от нуля, и (2) не выполняется.
Так, например, если в нижнем ряде свободны только
вихри номера ks, где k— любое целое число, то должно
быть:
n = k1s и —(п+ 1) = k2s, откуда kiS-]~k2s = —1
и s может быть только равно 1. Следовательно, удовлетво-
рить условию (2) можно, предположив, что все вихри
верхнего ряда смещены по с инус о идальному
закону. Это — случай Кармана, когда все вихри
и верхнего и нижнего ряда подвижны.
Итак, в случае, если вихри нижнего ряда все
свободны, а в верхнем ряде свободны только
вихри номера ks и $>1, то система находится
в состоянии неустойчивого равновесия; исклю-
чением является случай Кармана, когда сво-
бодны все вихри верхнего и нижнего ряда
§ 6. С предшествующими выводами интересно сопоставить
экспериментальные данные. Первые опыты с весьма несовер-
шенными установками были произведены Карманом и Рубахом,
а также в лаборатории МВТУ Жуковским; полученные ре-
h
зультаты дали для отношения -у следующие значения:
опыты Н. Е. Жуковского (лаборатория МВТУ) х):
у = 0,320; 0,337; 0,366; 0,363;
опыты Кармана и Рубаха * 2):
для пластинки у = 0,306,
для круглого цилиндра у = 0,282.
1) Н. Е. Жуковский, Теоретические основы воздухоплава-
ния, [Собр. соч., т. VI, 1950].
2) Fuchs-Hopf, Aerodynamik, стр. 169.
656
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Большое число весьма тщательно поставленных опытов
произвел Бенар (Henri Benard). В общем, эти опыты дали
плохое согласие с теоретическими данными. Вот результаты
одной серии наблюдений. Отношение у вблизи преграды и
вдали от нее колеблется в пределах
вблизи вдали
0,09 0,21
0,15 0,26
0,17 0,41
0,38 0,49
В других опытах были случаи, когда величина отноше-
h
ния -у не меняется столь значительно при удалении от пре-
грады и остается приблизительно постоянной, причем зна-
чения k = ~ в этом случае также весьма разнообразны и
колеблются от 0,13 до 0,49. Все перечисленные данные
весьма плохо согласуются как с значением Кармана (0,282),
так и со значением Н. Е. Жуковского (0,365). В общем,
Бенар резюмирует свои работы следующими неблагоприят-
ными для теории Кармана выводами: En resume, les lois de
Karman sont tres loin de s’appliquee aux tourbillpns des li-
quides reels х).
Плохое согласие результатов опытов с теорией, по-
видимому, надо видеть в следующем. В теории Кармана
предполагается, что все вихри абсолютно свободны. Между
тем при постановке опытов надо иметь в виду, что вихри
имеют место при наличии вязкости жидкости, что на движе-
ние вихрей влияет свободная поверхность жидкости и, нако-
нец, что при опытах совершенно невозможно говорить о ви-
хревой дороге, бесконечной в обе стороны.
Предыдущие результаты показывают, что устойчивость
вихрей при закреплении отдельных вихрей дороги Кармана
является чрезвычайно редким исключением; при этом в этих
!) Н. Benard, «С. R.», т. 182, 1926, стр. 1523.
К ТЕОРИИ ВЛИЯНИЯ ЗЕМЛИ НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 657
исключительных случаях, в сущности, нельзя говорить об
устойчивости вихрей, так как даже в случае Кармана при
ср = к мы имеем случай не устойчивого, а безразличного
равновесия. Возможно, что влияние вязкости жидкости и
конечности вихревой дороги совершенно уничтожает воз-
можность устойчивости равновесия.
К ТЕОРИИ ВЛИЯНИЯ ЗЕМЛИ
НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 9
Изучение влияния земли на подъемную силу крыла послу-
жило предметом длинного ряда работ. В общем виде эта
задача представляет частный случай задачи о биплане и
решается до конца при помощи теории эллиптических функ-
ций. Однако окончательные формулы, которые при этом
получаются, оказываются достаточно сложными, и исследо-
вания характера изменения величины силы в зависимости от
расстояния до поверхности земли и от угла атаки предста-
вляются весьма затруднительными.
В настоящей заметке дается приближенное, совершенно
элементарное решение этого вопроса, основанное на сохра-
нении формы крыла и на замене влияния земли влиянием
одного добавочного вихря; при этом приходится считать
поверхность земли под крылом не совсем плоской, в чем и
сказывается влияние приближения в решении поставленной
задачи. Вся задача решается в условиях плоскопараллель-
ного потока.
Рассмотрим сначала обтекание цилиндра, пересекающего
комплексную плоскость по окружности |^|=1 в случае,
когда скорость в бесконечности направлена в положитель-
ном направлении оси х и имеет величину и, кроме того,
имеем два неподвижных вихря интенсивности J и —J, рас-
положенных в точках
Z = — zp(p > 1) и z = — !_.
г
*) Опубликовано в трудах ЦАГИ, вып. 301, Теоретический сбор-
ник ЦАГИ, IV, 1937. {Прим, ред.)
658
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Характеристическая функция обтекания определяется урав-
нением
\ р I
Предполагая, что точка схода потока на цилиндре нахо-
дится в получим для определения циркуляции J
уравнение
I I г е~ъг I--I
\ р /
откуда
J = 4тсУоо sin 9 -—- — -, (2)
где
'-|(р + 7) “ "--Ир-т)-
Подставляя значение J из (2) в (1), получим:
dz V‘
I 1 л - а г — Sin 6
1 -4„„9
v+7/(г + /р)
(3)
и для точки цилиндра z = имеем из (3)
g = +т)i 4^ sin L±6 sin У.-.(1+ 9) p
sin 6 л
r -|- sin <f J
• (4)
Уравнение (4) дает распределение скоростей на поверх-
ности цилиндра.
Применяя первую формулу Чаплыгина — Блазиуса, полу-
чим для величины подъемной силы выражение
v л Т72 ’ (х р2—2Р sin О-]-1 Г1
Y = 4KPIZQOsin9 —,2Zl - - 1
p l L
1 2p sin 0 (p2—2p sin
— P2 (P2- I)2 J ’
(5)
Так как для
подъемной силы
случая отсутствия земли выражение для
есть
Уо = 4крУ^о sin 9
(6)
К ТЕОРИИ ВЛИЯНИЯ ЗЕМЛИ НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 659
(оно получается из (5) при р = оо), то величина влияния
земли сказывается в появлении множителя
p2-2psin0 + ir , 1 2р sin 0 (р2-2р sin 0 + 1) 1
Р2 — 1 L р2 (р2- 1)2 J • V'
Следующая таблица дает величину К при различных р и 6.
sin 0 — 0,1 Р 1,1 1,2 1,3 1,4 1,5 2 3
к — 7,2 — 7,5 — 1,8 1 2,07 1,60 1,20

sin 0 = 0,1 р 4 5 6 7 8 9 10
к 1,08 1,04 1,02 1,00 0,996 0,995 0,99
sin 0 = 0,2 Р 1,5 2 3 4 5 10
к 0,91 1,23 1,04 0,98 0,96 0,97
sin 0 = 0,3 Р 2 3 4
к 0,93 0,98 0,91
Определение линии, заменяющей поверхность земли, здесь,
конечно, до известной степени условно. Можно считать за
поверхность земли, например, линию тока, на которой вблизи
точки —Zp лежит критическая точка течения, т. е. точка
нулевой скорости. Эту точку можно найти из уравнения
•in ? + 6 sin т —(” + 8) Г!
11Г1 2 ^i ri 2 j
---“!i-) = 0
г + sin J
(8)
660
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
которое получается из (4). Из уравнения (8) получим реше-
ния <р =—9 и <р = тт4-9, дающие критические точки, лежа-
щие на крыле, и, кроме того, две критические точки, полу-
чаемые из соотношения
sin ср = — (г — sin 9), (9)
которое дает или два действительных, или два комплексных
корня.
Можно показать, что уравнение (9) может быть заменено
уравнением
s + -| = 2(r — sin6), (10)
если уравнение (9) имеет два комплексных корня, причем
— si представляют собой аффиксы критических точек, не
лежащих на цилиндре.
Чтобы перейти от рассматриваемого случая к случаю
крыла, имеющего форму плоской пластинки, надо сделать
конформное отображение, переводящее окружность | z | = 1
в прямую, причем в концы прямой должны перейти точки
z—e~^ и z—-—e~ei, а так как 9 мало, то можно сделать
отображение при помощи формулы
(11)
при этом крыло перейдет в пластинку, параллельную оси х
с хордой, равной 4. Точка —р/ на плоскости z перейдет
в точку (р----i на плоскости и.
Например, если взять случай, когда sin 9 = 0,1 и р = 2,
то из (10) получим = 1,7 (s2 = 0,6), т. е. искомая крити-
ческая точка есть —4,7. Отсюда по (11) найдем и ——1,1/.
Взяв данные из приведенной выше таблицы и замечая,
что при помощи отображения (И) цилиндр переходит в пла-
стинку ширины 4, в этом случае видим, что подъемная сила
у плоского крыла, находящегося на расстоянии четверти
хорды от поверхности земли, увеличивается от присутствия
земли на 60%; точно так же можно показать, что на рас-
стоянии от земли, равном 0,6 хорды крыла (при sin 9 = 0,1),
подъемная сила увеличивается на 20%. Можно далее пока-
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО
661
зать, что увеличение подъемной силы имеет место до рас-
стояния крыла от земли, равного 1,7 величины хорды (при
угле атаки, определяемом уравнением sin 9 = 0,1); при даль-
нейшем увеличении расстояния до земли величина подъем-
ной силы в присутствии земли оказывается меньше, чем
в свободном потоке.
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО
В НЕОДНОРОДНОМ ПОТОКЕ 9
§ 1. При испытании крыла в аэродинамической трубе
мы имеем случай, когда поток,
неоднородный; в таком потоке
личных точках. Аналогичный
работающее в потоке при на-
личии пропеллеров. Настоящая
заметка дает решение мето-
дом Треффтца — Глауэрта за-
дачи о силах, действующих
на крыло в неоднородном по-
токе.
Пусть на крыло М см. рису-
нок набегает поток, распреде-
ление скоростей в котором ука-
зано на диаграмме. Мы будем
в котором находится крыло,
скорости различные в раз-
случай представляет крыло,
считать распределение скоростей симметричным относительно
середины крыла. Вводя согласно методу Глауэрта вспомо-
гательное переменное по формуле
Z = —I cos ft,
можем считать V вдоль размаха функцией ft. Пусть V — /(ft).
Разложив /(ft) в тригонометрический ряд по sin kft, полу-
чим:
^ = ^o+25resin«ft. (1)
1) Опубликовано в Трудах ЦАГИ, вып. 342, Теоретический
сборник ЦАГИ, V, 1938. (Прим, ред.)
662 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
При этом, если распределение скоростей симметричное
относительно середины крыла, то п пробегает только нечет-
ные значения, Vo есть скорость на концах крыла.
Предположим, что циркуляция Г представлена тригоно-
метрическим рядом
r = 2?lnsinnft. (2)
Тогда подъемная сила выражается формулой
г
Р =Р f ГУ dz =
-I
= pZ j* { Vo + S sin ( S An sin } sin ft ^ft»
о
или
тс
P = Л) + P^ f S AnBm sin nft sin mb sin & db, (3)
о
где
it
PQ — pZV0 J S Ai sin nft sin 0 dft = у рЛАДр (4)
о
t. e. PQ—подъемная сила, которую имело бы крыло в по-
токе со скоростью Vo.
Пусть
7U
AP = p/J 2 АпВт sin nft sin mb sin f) db. (5)
о
Так как
sin mb sin nb = у [cos (m — ti)b — cos (in 4- n) &],
TO
sin mb sin tib sin & — у [cos(m—n) 0 sin 0 —cos(/n4“n) & sin &]=
= ~ [sin (m 4~ 1 — n)b — sin (m — 1 — n)b —
— sin (m -j- 1 4~ ft) ft 4“ sin (zn — 14" ft]*»
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО
663
здесь т и п — числа нечетные; следовательно, т-\-п и
т— п—числа четные и —числа нечетные и по-
тому отличные от нуля.
Так как
получим:
J sin sin пЬ sin & =
о
_____!___________!____
2 I т— п 1 т — п — 1
_____1_____j_________1_____
т-\- п-\-\ * 1 * * * V т-\- п — 1
= ±(_______~2 _|________2_______]
2 I (т — и)2 — 1 ’ (т 4- и)2 — 1 )
1 1 — 4тп
(/П 4" «)2 — 1 (/П — Л)2 — 1 [(т + И)2 — 1] [(гп — и)2 — 1]
Отсюда
др ; X1 л О —4znn
Aflbm [(лп4- лг)2— 1] [(лп — лг)2— 1] —
=р/ { 4 4^1 — 4 2 АпВт [(m+n)2—1] [(и—п)2—1] } =
п т, п
тфп
=4р/ { 2 АпВп 4пЗ=1 ““ 2 АпВт [(от+п)2—1] [(m—n)2—1]} •
п т,п
т^п
Уравнения (4) и (6) дают окончательное выражение подъем-
ной силы.
Остановимся на частном случае формулы (6). Пусть с до-
статочным приближением можно принять, что
V = Уо+ sin ft,
так что
В3 = В5 = В7= ... =0.
664
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Тогда формула (6) примет вид
др = 4р/! Л1В1 J — Bj Ап 1)2_ 1] [(„_ 1)2 _ 1] ? ’ (7)
I 71 = 3 J
или, замечая, что
[(/2 1)2 _ 1] [(„ _ 1)2 _ 1] („2 2/2) («2 _ 2/2) = «2 („2 _ 4)>
получим еще:
др=4 piBi I а—У -/-¥-”-гч > • (8)
3 г 1 । 1 п(п2 — 4) v 7
I п=з )
Подставляя сюда числовые значения, имеем:
ДР = 4 р/ВИ1 ( 1 — °,2 + 0,03 +
+а0’01+а0,004+•••]}• (9)
Переходим к определению величины индуктивного сопро-
тивления. По общей формуле имеем
[ У
(Ю)
ИЛИ
+ £ ____
г (у) = у СУ) 4 (И)
4 Д У — У
Но
~Ь Z 7С
f dV (у) 1 f У, пАп cos /гЭ я у sin я»0
J у___7 I J COS $ — COS i% I П п sin т)0 ’
-I J 7 б
где
у — — I cos Оо.
Следовательно, уравнение (И) принимает вид
Е A Sin п&0 = | Vo + 2 вп sin nf>0) 2 пАп Sv ’
(12)
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО 665
и для индуктивного сопротивления имеем х):
+ 1
= — р j rwdy^^nAl (13)
Л
т. е. совершенно такое же выражение, как в случае потока
с постоянной скоростью.
§ 2. Решение основного интегрального уравнения. Для
решения основного интегрального уравнения перепишем урав-
нение (1) в виде
V = { 1 + S^sinraft},
где
и Bn = V£n.
Основное интегральное уравнение (12) можно переписать
в виде
Е A,Sinn» = vo[(1 + 2 sinпЪ)ъЬч\ — ^-^пАп,
ИЛИ
2 Ап sin raft = Vo (1 + sin /г») J nAn .
(1)
Назовем через bQ, т)0 соответственно хорду и выражение
а . ао ।
7+ <р в середине крыла, так что т]0 = + ПУСТЬ
а «0 I л
''l — 'По = 2- — у +? —
Заметим, что, если изогнутость и закрутка крыла не
меняются при изменении угла атаки, то Дт; от ср не зависит.
Отсюда
= ^о + = у + ?о~+-Дт. = С + <Ро>
1) См. В. В. Голубев, Теория крыла конечного размаха,
стр. 173.
666
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
где £ = у4- Дт) не зависит от угла атаки в середине крыла ср0
и, следовательно, зависит только от ft.
Деля обе части равенства (1) на 4/У0 и полагая
•Ап
^aresinn& = ( 1 + sin ) л 7) —
(2)
Для практического применения формул выгодно выделить
члены, зависящие от угла атаки, и члены, не зависящие от
него.
Для этого положим an = an4-an. Уравнению (2)
S«+an)sinrea =
= {1 + (С-ГФо)—$
очевидно, удовлетворим, подобрав и а" так, чтобы они
удовлетворяли условиям
2a»sinra& = ( 1 + p„sin | С—§ (3)
И
£a"Sinn» = {l + 2Min«»)$<Po—$24^-- (4)
Для решения уравнений (3) и (4) поступим следующим
образом: разделим уравнение (3) на £0, уравнение (4) на ср0,
получим:*
Полагая
~ — у' И — = у",
Со 'п ?о 1п
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО
667
имеем:
Sinn» = (5)
и
2 т" sin п» = (1 + 2 Min п» } — J • (6)
Здесь Со есть значение С в середине крыла, т. е. Со = -^;
уравнения (5) и (6) совпадают друг с другом, если С=С0
вдоль всего размаха крыла, что можно считать признаком
аэродинамически плоского крыла.
Для решения уравнения (5) напишем его в виде
sin Tn s*n ~
= (1 + 2 sin «& )^sin & — J]sin га&
ИЛИ
«М1+sin& £ - S nT»sJn
(5')
Разложим выражения
и ( 1 + sinn&) sin
в ряды следующего вида, годные в интервале от 0 до it:
2/ sin О V* а
—^~= 2jCncosw&-
{1 + Min «& } = Dn sin
Подставляя в (5'), получим:
2 2 Q cos 5 Ъп sin /п& = 2 Dn sin — 5 ti^'n sin
или
2 5 cos sin && — S Dn sin — 2 nTn sin (7)
m, к
Так как
2 cOs sin k$ = sin (k + rti) & + sin (fi — iri)§.
668 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
то уравнение (7) примет вид
2 sin (k 4- от) & + 5 CmYfc sin (k — m) & =
к, m к, m
= 2 Dn sin — 2 nYn sin
Если положить в первом ряде k-\-m = n, откуда т =
= п — k, иво втором ряде k — m = nlt откуда т = k — nlt
то получим:
S сп_лsin sin и,<) =
= 2 Dn sin — 2 nYn sin
Отсюда
2 (С„-Л + Yft) =Dn~ nln’
t. e.
».-«T>Si(C,J+C1 J, (8)
причем С с отрицательными индексами, очевидно, все равны
нулю.
Беря в (8) последовательно п == 1, 3, 5, ..., получим:
ъ = 2Т;с0+т;с2+т;с4+...,
Ds — 3Тз = У'1С2 + 2ЪСо+ TsC2 +•••>
ч-5т;=-г;с4+ъс2+2т;со+--- .
и т. д., или
(2С0+1)+т;с2+т;с4+ т;с6+... =
т£2+ ъ (2с0+3)+<С2+ъс4+ • • • =°з,
Ъс2+ь (2СО+ 5)+т;с2+... = о6,
или еще в виде
11^ bsCo + l^bsCo+l^baCo + l-1-’ • • 2Co + l ’
т12С’о+з + 'Гз+Т5 2сДз+Ь2Со+з+‘ "=2Со + 3'
2С0+б+V2C0+5+Т5+^ 2С0+б'+'’ ’ •=2С0 + 5’
(9)
О СИЛАХ, ДЕЙСТВУЮЩИХ НА КРЫЛО
669
Совершенно таким же образом можно решить систему урав-
нений (6). Для этого разложим:
sinft • { 1 + 2 Pnsin ^ } = 5 Gnsin О О')
После подстановки получим, очевидно, систему уравнений,
совершенно аналогичную (9), но с заменой Dn через Gn,
т. е.
" I Y" С2 I // _ I /7 С6 . _ Gt
11 -Г 7з 2С0 + 1 ‘ l52C0 + l 2С01 ' ’ ’ ' 2С0 + 1 ’
./7 С2 I 77 Д_ 77 С2 . 77 Q . _ G2
т12С0 + 3^7з । 15 2С0 + 3*7 2С0-(-3 ' ‘ ‘ 2С0 + 3’
С* I I I I ______ G3
+ + 17 2C0 + 5"r • • • 2C0 + 5'
(10)
При помощи коэффициентов и у" подъемная сила
и сила лобового сопротивления выразятся следующим
образом.
Так как
а'=т'£ и а" =
п >п 0 п *П‘О’
ТО
= и Лп = 4/^о[тХ+т>о1-
Следовательно, по (4)
^=2^о[^о+т;ч]- с11)
по (6)
др = 4Рр v* р (тХ + ТХ) -
q / 7 «z । 7/ \ ТПП
Ju Prn \7П% ' 7Л) [(zn + п)2— 1] [(тп— и)2 — 1] f
6 70 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
что можно еще написать в виде

т, п
/ »2 _____
п 4 л2— 1
п
о г ___________тп____________
I РЛ [(/п+ л)2 — 1] [(/л — л)2 — 1]
ь
П
Со —
_ V R /'________________________________
I П I n [(zn и)2 — 1] [(/л — л)2 — 1]
т, п
В частном случае, когда V = У0 + Вх sin ft,
1
То- (12)
ДР-4рРУ2Р1 Т'1 - 2 Т.
п п(п? — 4)
п=з
-4?^
То-
^0
Наконец, W напишется в виде
r=2MV2Sn(TX+T>0)2- (14>
В случае, если С вдоль размаха постоянно, т. е. £ = С0,
уравнения (5) и (6) совпадают и потому Dn=Gn и угп = у",
а при этом соответствующим образом упрощаются уравне-
ния (И), (12), (13) и (14).
Относительна приближенного решения систем (9) и (10)
заметим следующее. Если крыло близко к эллиптическому,
4Z sin ft 4/ sin ft 4Z
то —г— близко к ——к = -^, т. е. к Постоянной; поэтому
по0 sin ft iw0 J
можно считать для крыльев, близких к эллиптическим
(трапециевидных, с центропланом и т. п.), что С2, С4, . . .
очень малы, а потому из уравнений (9) и (10) получим:
ц аналогично
_ ^3
2С0+1 ’ 1з 2С0 + 3’ ’ * ’
п __ б?з
2Со + 1 ’ 2Q+3’ •”
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 671
Если при этом поток равномерный, то все рп = 0 и
из (10') имеем в случае эллиптического крыла
Gx = 1, G3 = О5 =...== 0
и Tg =Т5= • • • =0* Аналогично при постоянном С полу-
чим из (5Z) = 1 и все Dn = 0 при п^>2, а потому
Т8 = ^=-”=°-
Следовательно, в этом случае
р« = 2’«адГП (? + ’)
Но Со в этом случае определяется уравнением
Г — .2Z _ 2/2 _ 2/2
/2 -
где S — площадь крыла; иначе, Со = -, где b — средняя
Ь • 2Z
величина хорды эллиптического крыла. Следовательно,
с _ 1 —12L— х
° “ 2Ь ~~ 4 Ь 4 ’
где X—удлинение крыла. Следовательно,
1 _ 1 _ 2
2С0+1 2,1 Х + 2
2 ф
и
— известная формула эллиптического крыла1).
О ВЛИЯНИИ НАДСТРОЕК
НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 2)
§ 1. Задача и метод исследования
При современной конструкции самолетов на основной
форме крыльев приходится делать различные добавочные
части, заключающие по большей части моторы; можно и
х) См., например, В. В. Голубев, Теория крыла конечного
размаха, стр. 170, формула (10).
а) Опубликовано в Трудах ЦАГИ, вып. 342, 1938. (Прим, ред.)
672 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
самый фюзеляж рассматривать как некоторую надстройку
на крыльях. Присутствие всех этих надстроек, несомненно,
весьма сильно влияет на аэродинамические свойства крыла.
Отсюда намечается задача изучить влияние таких надстроек
на аэродинамику крыла.
Как и вся теория крыла, теория надстроек может быть
изучаема при двух различных предположениях. Можно изу-
чать влияние надстроек при условии, что воздух плавно
обтекает крыло с надстройками; можно, с другой стороны,
изучать влияние надстроек при условии, что их присутствие
вызывает отрыв струй.
Задачей настоящей работы является изучение влияния
насадков при условии, что они не вызывают образования
срывов, так что крыло с насадками плавно обтекается пото-
ком. Основанием к такой постановке задачи может служить
хотя бы то обстоятельство, что при конструктивном осу-
ществлении надстроек для помещения моторов принимаются
все меры, чтобы не создавать условий для образования
отрыва (плавные контуры, зализывание и т. п.).
Методом исследования явится изучение обтекания крыльев
с насадками в условиях плоскопараллельного потока; от
изучения условий обтекания в плоскопараллельном потоке
нетрудно уже затем перейти к обтеканию крыла конечного
размаха, применяя обычные методы Треффтца — Глауэрта и др.
Весьма существенным является для исследования вопрос о
форме насадков. Как известно, формы теоретических крыльев
определяются не аэродинамическими заданиями, а простотой
отображения внешней части профилей на внешнюю часть
окружности; так получены почти все теоретические формы
крыльев (Жуковского, Чаплыгина, Мизеса и т. д.). Тот же
самый метод мы применим и в настоящей работе; мы изучим
насадки, которые могут быть образованы добавлением ко
всей вихревой системе крыла вихрей, близких к его поверх-
ности. Этот метод был использован в работах по учету
влияния предкрылков и закрылков. Применяемый в настоя-
щей работе метод отличается от метода, применявшегося
в теории предкрылка и закрылка г), только расположением
1) В. В. Голубев, Исследование по теории разрезного крыла,
ч. II, Труды ЦАГИ, вып. 305, 1937 [см. настоящее издание,
стр. 291—348].
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 673
добавочных критических точек: в случае предкрылка и за-
крылка добавочные критические точки находятся вне крыла,
в случае же, рассматриваемом в настоящей работе, крити-
ческие точки находятся на поверхности крыла.
§ 2. Случай плоской стенки
Если надстройки невелики сравнительно с размерами
крыла и помещены не у самых кромок, то можно заменить
поверхность крыла плоской стенкой. В настоящем параграфе
мы рассматриваем случай плоской стенки, обтекаемой пото-
ком.
Рассмотрим течение, определяемое характеристической
функцией
У Г J < Z—at ...
W = О)
Так как
dw___J 2а i
dz ~Vco 2шг2 4-а2’ W
то для определения положения критических точек имеем
уравнение
^ + а2__^. = о, . (3)
откуда
оо
Мы будем далее рассматривать только тот случай, когда
критические точки находятся на действительной оси, для
чего необходимо, чтобы
(5)
Мы будем, далее, называть расстояние до критических
точек от точки z = 0 через Л, так что из (3) имеем:
A2+a2_^_ = 0. (3')
у оо
Найдем уравнение линий тока. Так как
г — al X + (у — a) f _ /~*2 + (у — а)2
Z-\-al x + (y + a)Z V Xa + (y + “)S ’
674 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
то из (1) имеем:
w = (х + iy) + { In
ха 4- (У — <х)2
' х2 + (У + а)2
-НФ
Отсюда уравнение линии тока
у v -I- — In а)2 — с
У°°У^ 4пх* + (у + «)2 ~ С*
(6)
Найдем значение произвольного постоянного, соответ-
ствующего оси х. Так как на оси х у =0, то из (6) имеем
С = 0. Так как критические точки лежат в А и В, то линии
тока рассматриваемого течения имеют вид, указанный на
Рис. 1.
рис. 1. Так как точки А и В линии тока АСВ лежат одно-
временно и на оси х и на линии АСВ, то значение постоян-
ной С на оси х и на АСВ одно и то же, а потому урав-
нение линии, состоящей из оси х и из дуги АСВ и ей сим-
метричной относительно оси х, есть
У у _!_Л ]п х2 + (У — °02 _ Q /у\
°°У ' 4л л2(у 1 «)2 ‘
Рассмотрим сначала предельный случай, соответствую-
щий а = 0, причем будем считать, что при а—>0 J->oo,
так что lim 2Ja=Q.
а->оо
При этом условии из уравнения (1) получим:
TZ j 1 Л 2а/ \
w = V^z — и— In 1----------—
или
2+aj
тг t 2Jdl , /. \ 2ai
W = Уоо2 4~ Q~i—i—7Г 'nil---------i—-1 ,
1 2it(z-|-aZ) \ z-|-aZ/ ’
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 675
откуда при а->0 получим:
*" = г”г+я|- О')
Полагая 9 = fe2, можем написать (1') в виде
’оо
™ = М* + т)-
Отсюда получим уравнение линий тока в виде
k?y
и уравнение линии, распадающейся на действительную ось
и окружность, получится при с = 0; это уравнение можно
получить предельным переходом из уравнения (7). Отсюда
следует, что линия АСВ есть искажение той окружности,
которая получается при предельном переходе.
Найдем точку пересечения линии АСВ с осью у, для
чего надо решить уравнение
tz । J 1 (у — а)2 л
In 7----------i--\9 ==
(У + а)2
или, замечая, что для искомой точки у > а, имеем уравне-
ние
<8>
Назовем корень уравнения (8) через /, тогда
= <9>
Найдем, как изменяется отношение h : / при изменении J и а.
Из уравнения (3') имеем:
J _ + «2
— а
Подставляя найденное значение —в уравнение (9), полу-
чим:
2/ = ^±^-1п£±^.
а I — а
676 IV, ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Полагая / = аХ, Л = ау, получим:
откуда
Y2+l 2Х X—Г
Так как h—величина действительная, то - * , 1,
тому имеем следующее неравенство, ограничивающее
чину X:
а по-
вели-
(10)
1ПХ—1
2Х.
Уравнение (10) дает решение при X — 1,2. При этом / = 1,2а,
h=Q и расположение линий тока указано на рис. 2.
1. При увеличении X разделяющая линия приближается
все более и более к полуокружности по мере увеличения X;
Рис. 2.
так, при Х= 10 уже имеем
расположение, весьма близкое
к полуокружности.
Отсюда следует, что ли-
нии тока, имеющие общие точ-
ки с действительной осью,
имеют или форму, приближаю-
щуюся к полуокружности,’ или
форму, приближающуюся к ли-
нии L на рис. 2. Для получе-
ния линий, ограничивающих
области, имеющие продолговатую форму, рассмотрим тече-
ния, определяемые характеристической функцией
J 4 Z 1 Cl Z
-a
+ (11)
Это течение можно рассматривать как наложение на пря-
молинейное течение ряда диполей, непрерывно расположен-
ных на отрезке действительной оси от —а до -\-а.
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 677
1
Из (И) имеем:
dw__1 г I 1 f 1 1 1__1 г । 1 2а
dz 00 lz — a z-j-al 00 г2 —а2 ’
и для получения критических точек имеем уравнение
Z2^a2_^^=sQ>
*
откуда
2 ik
чтобы критические
для этого надо k
вместо k величину
а2
Мы подберем k таким образом,
лежали вне отрезка [ — а,
отрицательным. Подставляя в (11)
получим окончательно следующую характеристическую функ-
цию искомого течения в виде
tz I L 1 z 4- а
W + k In ---------!--,
1 z — a
где k > 0 и Voo > 0. Критическими точками этого течения
являются точки
ТОЧКИ
взять
—k,
(12)
, , / 9 . 2ak
2 = «2+и~-
v оо
Назовем расстояние от начала координат до критической
точки через /, тогда
1 / 9 । %ak f -a I 2£
z = y «2 + у- = «У 1+^.
оо к оо
Найдем уравнения линий тока. Уравнение (12) можно напи-
сать в виде
(13)
или
И* Cv by

х2 -|- У2 — Д2 2y# 1
(х — а)2-{-у2 1 (х — а)2 + у21*
Если взять x2-j-y2 < а2, то отсюда можно еще написать:
х-k kIn 1/
VooX-r/ein у (x__a)2 + y2
«2 —
678
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Следовательно, уравнение линий тока имеет вид
Vooy 4- k (к 4- arctg д2_2^_ уа) = С
(14)
На действительной оси, которая является линией тока, у =0,
а потому из (14) имеем С = и уравнение этой линии
тока есть
V^y + k arctg 0. (15)
Из уравнения (15) легко получить, прежде всего, пре-
дельный случай. Пусть а стремится к нулю, но 2ak =
= ЛУоо = const. Тогда, подставляя k = , имеем,
гая еще х2 + _у2>^2,
пола-
или
откуда
18^
2ау = (х2 4- у2 — a2) tg ,
tg^
? = (х24-^-а2)-^-4,
А
и в пределе при а, стремящемся к нулю, имеем:
Ау = (х2-|- у2) у или у(х2~]-у2 — Д) = 0.
Найдем пересечение линии (15) с осью у. Полагая в (15)
х=0, получим:
Vooj/4-^arctg-^-^^O. (16)
ч> у
Мы будем искать т^чку пересечения кривой, лежащую
в верхней полуплоскости. Из уравнения (16) имеем:
Vcoj = —fe arctg
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 679
или, замечая, что
— ^ctg = к — arctg ,
имеем:
V№y =k(n — arctg - a2^ 2 ) . (17)
Называя расстояние от точки z == 0 до точки пересечения
через Л, можем из (17) написать:
=h.
пусть
тогда
k аК
V7— , 2Х *
00 It — arctg у—у2
arctg 1^ = 2 arctg X.
Следовательно,
k X X
2 arctg X о / к *
s 21 v —arctg X
т. е. 2k aV Из (13) и (18) имеем: 1 т. е. -1=1/ а у ~ = arcctg X’ <18> /~ 1 ч — f 1 arcctg X / А Н 4-. (19) arcctg —
680 IV^ ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Формулы (13), (18) и (19) позволяют, задав отношение
\ = — найти — и -Ду-. Заметим, что 2/ есть длина на-
fl а
садки и h — его толщина.
Называя = я из (19), имеем:
** - 1 I-----пгт ,
1 arcctgk’
или
к
L . к , ж к COS^-1
arcctgk = ^zn и X = ctg^т=------------,
sin -s-г
и2— 1
и если к мало, то
к = -4—, Х2 = М2_1>
т. е.
h2 = l2 — а2 и a = Vl2 — h2t (20)
т»е. а и h служат катетами прямоугольного
трехугольника с гипотенузой I.
§ 3. Случай круглой стенки
Течение, определяемое характеристической функцией
, 1 z — а
^S) =&1п ----7- ,
1 2 — Ь ’
есть течение, линиями тока которого являются окружности,
проходящие через точки а и Ь. Если взять точки а и b
на окружности z=\, то характеристическая функция
+ + + <20
дает некоторое течение, обтекающее окружность радиуса 1.
Определим Г так, чтобы точка z = l была критической
it 1 dw ~
точкой, т. е. чтобы при z=\ — = 0.
r d2
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 681
Из (21) имеем:
= у e-0ifl П I Г 1 I А а~Ь
dz 00 \ г2 / ' 2тт/ z ' к (г — a) (z — b) ’
а потому для определения Г имеем уравнение
!») +ja+t-(Г-")?.-» °0' <22>
откуда, исключая Г, имеем:
+ k (а — Ь) {г —а) (г — А)}'
Общее уравнение для нахождения критических точек имеет
вид
г* + . . . — e2Biab = 0.
Называя корни этого уравнения через zi9 z2, z3, z4, имеем:
= — e2Biab.
Если а=ел\ b — № и zk — M, то отсюда имеем:
+ ?2 + ?3 + К + a +
или, замечая, что z± = 1 и <р4 = 0, имеем:
[<?х - (к + 29)] + [<р2 — a-±fj -Ь [?3 - 5L+P] = 0, (23)
т. е. сумма уклонений критических точек
равна нулю, если считать уклонения <рх от положения
передней критической точки без действия источников в а
и b и уклонения ср2 и ср3 от середины точки
в-—♦
Для нахождения критических точек надо решить урав-
нение
1 +?)+№- «- «
(23')
682
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Полагая
а = eai, b = z = eV,
получим уравнение
0 = 4-е(29-<рН]_|_
4- k (ел{ — е₽*>____________g_(«+px-_g0____________
' к > (1 — е”) (1 — eV) (eV — е™) (eV — ё^) ’
Так как
«+Р __ О
£ai--e^i е 2 2Z Sin * ,
£(a+0)i--ец>1 = g( 2 + 2 ) г 2/ Sin ---,
1 — e*i = е 2 г(— 2Z) sin ~,
— г В
1 — е₽г = е 2 (— 2Z) sin ~,
<р4-а .
~т“ г ~ ср — а
есрг-еаг __ е 2 2/ Sin - 2 ,
г ср-В
^срг_ерг__е 2 2Z Sin,
e-»i(l е(20-<р) i) = е 2 *2 cos 6^- —9
то, подставляя, получим для нахождения критических точек
уравнение
гУсоСоз^—е)+-
' 2 а В ср —а ср — В ’
4 sin у sin у sin Y - sin Y ---
ИЛИ
COS — б) sin sin Ц^-ft 4- sin (у — = 0, (24)
где
. _ t “-2~
‘ 8V_ 8.п 8.п |
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 683
Если утолщения на крыле невелики, то можно считать,
что передняя критическая точка разделения струй смещается
мало, а потому можно положить, что передняя критическая
точка соответствует углу
к + 29 + 28 = ?1,
где 8 — величина малая, так как k мало.
Но
cos— 9 = cos -|“8^ = — sin8 = — 8
и получаем для 8 приближенное уравнение
sln (у + 9 + ^ —“ )
sin 8 ='--т--------—----г---т----—------гг. (25)
sin + в + 5 — ) sin (-J 4- в + 5 - £)
или
*icos 0 )
8 ----------V . (25')
cos(-|-0)cos(|-e)
Если мы знаем один корень уравнения, то остаются две
неизвестных корня, которые и найдем.
Рассмотрим уравнение
cos(4~ 0 ) sinsin (у —М^) = 0.
По характеру разрешаемой нами задачи это уравнение
должно иметь два корня: > а и близкий к а и у2 < р и
близкий к р (а > Р) (рис. 3).
Подставляя имеем:
Но если
то это уравнение имеет корень только при kx > 0; тот же
результат получим и для /2.
684
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Если же считать отрицательным и а и р тоже отри-
цательными, то из того же уравнения получим, что kr < 0.
Рис. 3.
Итак, kr > 0, если насадок
kr < 0, если насадок в нижней
Так как
в верхней полуплоскости, и
полуплоскости.
. а — р
sin—
Ъ — —__________£ -
^87 а В ’
00 sin у sln
то при расположении насадков, как указано на рис. 4,
имеем для случая < 0 а и р отрицательные и а тоже
отрицательное и при kt > 0 а, р положительные и k тоже
положительное. Следовательно, в обоих случаях k > 0.
§ 4. Влияние насадков на подъемную силу
Для определения величины подъемной силы достаточно,
очевидно, найти величину циркуляции Г. Из уравнения (22)
имеем:
Г = ~ (t) 2”-
Но
А а — b к е™ — е№
к (1—л)(1 —6) — к (1—^)(1—
а + Р .
• а — ₽ . а — В
е 2 2Z sin —“ sin —
_ Ъ_____________2 _ 1 2
а . 0 . 2/ а В *
-тг* а Тг а. , ₽ 1 sin —sin
е 2 2/ sin 2"е sin у 2 2
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 685
Отсюда после преобразования имеем:
sin —
Г = —4kV№ sin 9 — kit-----. (26)
. а . р
sin^ sin|
Следовательно, задача сводится к определению величины k
по заданным размерам насадка. Мы решим эту задачу при
следующих условиях:
1. Мы будем считать стенку плоской; это допустимо,
если размеры насадка считать небольшими сравнительно
с размерами радиуса кривизны в точках дуги, на который
делается насадок.
2. За скорость обтекания мы будем считать скорость
в средней точке дуги.
Для решения этой задачи мы имеем уравнения
h
а
arcctg —
(19)
(18)
Первое уравнение позволяет по данным h и I найти а, вто-
рое позволяет определить k. В случае очень вытянутых
насадков можно взять вместо
(19) уравнение (20).
Пусть дано крыло, про-
филь которого изображен на
рис. 5, и пусть на рис. 6 дано
(У
Рис. 5.
его отображение на единичную окружность. Предполагая,
что профиль есть инверсия параболы, мы можем для пере-
хода от скоростей на плоскости z к скоростям на
686 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
плоскости С применить формулу х)
V^VooSin^^x
(1 — е)2 cos2 -у — 4 (1 — е) cos -jr- sin sin а -j- 4 sin2 -5-
А 2 2 2 2
У (1 — о2 cos2 — 2 (1 — е) cos sin i sin - а + sin2—
= Vrosin^-2M(?), (27)
где
Л4(ср) =
(1 — е)2 cos2 — 4(1 — е) cos у sin ~ sin g— + 4 sin2 —•
1/ (1 — е)2 cos2 — 2(1 — е) cos sin sin У.л—- 4~ sin2-|-
И
а2 = те —р 26,
так что
sin (т)=sin(i ~ i -6)=cos (I—6)
И
Vc = VooCOs(| — б)л4(<р). (28)
Пусть положение средины дуги, на которой находится на-
садок, соответствует на окружности точке т с углом ф;
тогда соответствующая скорость
V^KoCosd — б)м(ф).
Задав на профиле крыла I и /г, найдем по (19) или по (20)
величину ли по (18) k из уравнения
2k X
arcctg X ’
*) В. В. Голубев, Исследование по теории разрезного крыла,
ч. I, Труды ЦАГИ, вып. 147, 1933, стр. 31 [см. настоящее издание,
стр. 78].
О ВЛИЯНИИ НАДСТРОЕК НА ПОДЪЕМНУЮ СИЛУ КРЫЛА 687
Следовательно,

(29)
Если это значение подставить в уравнение (26), то получим:
Г = — 4-rcVco sin 9
hn
2 arcctg к
sin —
Voo cos (I - 9) a g M (®.
V 7 Sin sin b
(30)
Так как при отсутствии выступа (т. е. при /г = 0) цирку-
ляция определяется формулой
Го = — ^VooSinQ,
то приращение циркуляции ДГ определяется по формуле
а — 8
sin
ir —7^тт««> Р‘>
6 4 7 Sin у Sin
и приращение подъемной силы по теореме Жуковского
равно
а — р
ДР = р — т: —---------------М (<b)cos (4 — 9) • (32)
r 2 arcctg X . a p \2 / v 7
6 sin sin
Здесь угол а соответствует точке/ более удаленной от
задней кромки. Отсюда видим, что
1) подъемная сила увеличивается при насадках на верх-
ней поверхности крыла (т. е. h > 0, 180°>а>р>0)
и уменьшается при углублениях в верхней поверхности крыла
(т. е. при h < 0, 180°> а> р > 0).
, 2) подъемная сила увеличивается при углублениях в ниж-
ней части крыла (т. е. h < 0, — 180° < а < р < 0) и умень-
шается при насадках на нижней поверхности крыла (т. е.
при h > 0, — 180° < а < р < 0).
688 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ
ПОВЕРХНОСТИ РИМАНА1)
Большое число гидродинамических задач, как задачи
о бипланах и полипланах, задачи об ударе пластинок о воду
и т. п., приводит к исследованию течений на многолистных
поверхностях Римана. Однако авторы обходят обычно рас-
смотрение течений на всей многолистной поверхности, огра-
ничиваясь изучением течения на одном листе рассматривае-
мой поверхности. Такой путь, по нашему мнению, отли-
чается значительной долей искусственности; формально давая
решение задач, он в то же время не позволяет ясно пред-
ставить себе всю гидродинамическую картину течения, да-
ваемого теми многозначными функциями, которые входят
в выражение комплексного потенциала, определяющего те-
чение.
Настоящая заметка ставит своей целью дать основные
соображения, связанные с течением на поверхностях Римана.
Представляя собой, естественно, иллюстрацию к гениальным
идеям Римана, позволяющим дать гидродинамическое толко-
вание всей созданной им теории алгебраических функций,
она стремится сблизить ряд прекрасных результатов, полу-
ченных за последние годы С. А. Чаплыгиным и другими
исследователями, с основными соображениями теории алге-
браических функций; с этой точки зрения настоящая работа
примыкает к тому кругу идей, которые были в свое время
развиты Ф. Клейном в его известной работе «К теории
алгебраических функций, данной Риманом».
§ 1. Течения на поверхностях Римана
Пусть дана некоторая поверхность Римана Rlf соответ-
ствующая алгебраической функции /, причем
Ф(/, ^) = 0 (1)
есть уравнение, определяющее функцию t. Рассмотрим тече-
ние на поверхности /?х, причем будем предполагать, что
*•) Опубликовано в Уч. зап. МГУ, вып. 24, Механика, книга II,
1938. (Прим, ред.)
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 689
это течение — установившееся, потенциальное и вызывается
конечным числом вихрей, источников и стоков на /?р а
жидкость — несжимаемая.
Назовем <w=f(z) характеристическую функцию этого
течения. Тогда
есть однозначная функция на Rlt так как в каждой точке
скорость имеет определенную величину и направление. Так
как на Ri функция f'(z) есть однозначная функция с конеч-
ным числом полюсов, то f'(z) есть рациональная функция t
и z, т. е.
и следовательно,
w = j* R (t, z) dz,
т. е. характеристическая функция течения на есть абе-
лев интеграл, взятый на поверхности
В случае, если поверхность двулистная, то, называя че-
рез alt Ьъ а2, Ь2, .. ., ап, Ьп критические точки, можем взять
уравнение (1) в виде
t2 * = (z — aj(z — Z?i) ... (z — an)(z — bn),
и по известному свойству двузначных алгебраических функ-
ций можем написать R(t, z) в виде
Rit, =
В этом случае абелев интеграл превращается в гипер-
эллиптический. Таким образом, характеристическая функция
течения на двулистной поверхности есть некоторый гипер-
эллиптический интеграл вида
Г 1 ____________________5(г)
11 j--->-------------------------——'1 dz, (2)
J L V(z — ai)(z — bj ... (г — an)(z — bn)\
где r(z) и s(z)—рациональные функции.
Рассмотрим функцию
r(z)^----------------
r ______________________________________= F (z).
/(•? — (z — ... (г — an) (z — bn)
(3)
690
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
F (z) есть алгебраическая функция, причем точки bit .
..., ап, bn суть алгебраические критические точки второго
порядка. Применяя для определения жанра функции р извест*
ную формулу Римана
N
р = 2^-™+1,
Л = 1
где гп—порядок критической точки и т — число листов,
получим в рассматриваемом случае (/и = 2, N = 2п, гп = 2)
2п
р = ^-2+1=»-1. (4)
1
Если на поверхности провести разрезы, соединяющие точки
с bi, а2 с Ь2 и т. д., то получим п разрезов. Таким
образом, в рассматриваемом случае двулистной поверхности
жанр на единицу меньше числа разрезов.
Подвергая риманову поверхность /?х обычным преобра-
зованиям (т. е. растяжениям и преобразованию при помощи
обратных радиусов-векторов), превратим ее в шар из двух
слоев, причем все критические точки могут быть всегда
расположены на одном меридиане I. Проведем через I пло-
скость Р и возьмем вместо 2-го листа поверхности его зер-
кальное изображение относительно плоскости Р; получим
Рис. 1.
Рис. 2.
вместо разрезов с переходами, указанными на рис. 1, пере-
ходы, указанные на рис. 2.
Таким образом, вместо первоначальной поверхности Рх
получим преобразованную поверхность /?ь представляющую
шар с толстой оболочкой с п отверстиями, причем двум
листам поверхности Рх соответствуют наружная и внутрен-
няя поверхности оболочки и разрезам соответствуют отвер-
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ
691
стия в поверхности шара. Растягивая шаровую поверхность
в плоский диск так, чтобы краем диска сделался один из
разрезов, превратим поверхность в поверхность диска с п — 1
отверстиями. На рис. 3 показан вид полученной поверх-
Рис. 3.
ности при п = 3, причем линии Llt L2f представляют
края разрезов.
Число отверстий п—1 и дает здесь жанр в его геоме-
трическом определении.
§ 2. Особые типы течений
Для приложений представляет интерес рассмотрение таких
течений на двулистной поверхности, что если рассматривать
течение на одном листе, то оно представляет обтекание
системы прямолинейных отрезков 1п, лежащих на одной пря-
мой А, причем характеристическая функция однозначна при
изменении z на рассматриваемом листе.
Чтобы получить такое течение, достаточно поместить
в двух точках, симметричных относительно прямой А, и на
различных листах два источника одинаковой мощности с на-
правлениями течений, симметричными относительно £; при
этом два листа поверхности должны быть связаны друг
с другом переходами по линиям Zw. Получающиеся течения
указаны на рис. 4.
На рис. 5 показано соответствующее течение на двух
сторонах диска, в который можно преобразовать по пре-
дыдущему двулистную поверхность в случае жанра 2. Здесь
ввиду того, что диполи расположены друг над другом
692
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 693
с симметричным направлением течения в них, наружный край
и края отверстий являются линиями тока; они являются изобра-
жениями разрезов Llt L2i L3 на рис. 4. Для получения соот-
ветствующей характеристической функции заметим, что две
Рис. 5.
ветви характеристической функции согласно уравнению (3)
удовлетворяют уравнениям
^l=r(z)+
dz к Yv\(z-ak)(z-bk)
rfw2 r ___________s(z)_____ j
dz Yn(z-ak}(z-bk) ’ .
где ak и bk—концы отрезков L, которые мы будем считать
лежащими на действительной оси. Из уравнений (5) мы имеем:
dwx । dw2
~dz ' dz
2r (z),
dwi dw2_____2_______s(£)_______
d? “ dF “ y \\(z-ak){z-bk) '
(6)
(7)
Так как на обоих листах лежит по одному источнику, то,
полагая, что источники лежат в точках z+zai, имеем, что
+ (8)
694
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
где А и А — сопряженные комплексные числа в силу тоМ
условия, что направления течений в источниках симметричнц
относительно действительной оси. Если нет других источ!
ников, кроме z+zaZ, то ф(£) должно быть голоморфно н|
всей плоскости и, следовательно, представляет собой целую
функцию; но так как нет источников и в бесконечности, то
lim (5 + 5)= Ит = (9)
z->oo\u^ ’ г->оо
а потому ф(<г) = О.
Кроме того, чтобы характеристическая функция была
однозначна на каждой плоскости (т. е. без переходов че-
рез /Д необходимо, чтобы вычеты 2г (z) относительно осо-
бых точек были равны нулю, т. е.
а = = (10)
Итак,
r = (Z — alp + (г 4-а Z)3 ' D
_ dw\ dw?
Применяя те же рассуждения к , получим, что
dwt dw2____
dz dz
__Г i _ _L ^£*1 _j_ 2v (z} 1 X
— [(г__а/)2 -Г (г + а/)2 Z — al^ Z + УЛ)
у__________1________ (12)
yx\(z-an)(z-bn)'
Рассмотрим изменения выражения (12) на отдельных
листах поверхности при выбранном способе переходов. На-
зовем
г (г) = - - 1 =-. (12')
/П(г-а„)(г-М
Тогда на действительной оси вне lk t(z) — действитель-
ное и на всех 1к— чисто мнимое. В силу этого на каждом
листе в симметричных точках относительно действительной
оси т (z) принимает комплексные сопряженные значения и на
различных сторонах разрезов1к t(z) принимает чисто мни-
мые значения, отличающиеся знаком; в частности, если
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 695
в точке ai x(ai) === р-\- b, то т(—ai) = jjl — W на первом
листе, а тогда на втором листе x(ai) =—ji — nZ и т(—aZ) =
= — 1* + ^-
Рассмотрим поведение в области z — оо. В об-
r dz dz
ласти £ = оо для t(z) имеем разложение вида
t(z)
Так как функция в бесконечности должна быть
az dz
нулем в силу того, что в бесконечности нет источников, то
iim
2-> ОО
dwx
.dz
dw2\
dz )
lim
n-> oo

Следовательно, /(г) многочлен не выше т—1-й степени;
но ввиду отсутствия в бесконечности вихрей и циркуляция
вокруг бесконечности равна нулю, поэтому у может быть
степени не выше т — 2, где т—число разрезов 1к. Итак,
$ (Z\ —__в._______51____I__О___|__01___|_
ц ‘ (г + aZ)2 ' Z — aZ^^+aZ '
+ ^«1-2 ^m-З + . . . + Ст 2
Окончательно имеем:
dw Л . А х / В . Bi .
dz ~ (z — а/)2 ‘ (г 4~ aZ)2 •” \ (г — aZ)2 ' (<гaZ)2 *
+^+ИЬ+с»г”"+-"+с"-')’<2)- <|3)
Остается определить В, Bn С, СР Для этого заметим, что
на первом листе нет полюса —ai и на втором листе нет
полюса 4*
Разложим t(z) в области z =—>ai на первом листе:
т (г) = т (— ai) + (^ 4~ а0 (— а0 4~ (z 4“ а02 (— а0-
696
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Из (12') имеем:
In т (z) = — у 2 [In (z — ап) + In (z — £„)]
и
«—4 ’ <г> 2 I-1.,., +
а потому
т' (- 00 = -1 г (- aZ) J () • (14)
Подставляя эти значения в (13), получим:
dw ___ А А . Г В .
dz (z — аГ)% ’ (z 4- aZ)2 ‘ [ (z — aZ)2 ’ (z -|- aZ)2 ‘
+ <74кг>+<7та + ‘'«2’~г+•••]><
x [T(— aZ) + (^ + az)T'(-aZ)+ . . (15)
Выделяя в (15) главную часть разложения в области
точки z = '—aZ, получим:
“F Т"'^1 -\2 т (— а0 “I-(— а0 ~Ь
dz (^^-«Z)2 1 (г-|-а02 v * + aZ 4 71
_]---г-i—.т(— a/)-4- гол. часть.
1 z + v
Для отсутствия полюса необходимо выполнение условий
А -|- (— az) = О,
(— aZ) + CjT (— aZ) = 0,„
или
д+В1([х — Zv) = O )
± (- а») 2 +С1Т (_ а° = °
И
С! = _ Т S (at + «„“*“ az + *n) =
п
= Л .... у /11_______________|_ 1 Л.
2 (fx — Z4 afcJ \ aZ + ~ aZ + bn)
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 697
Подобное же рассуждение проведем и на втором листе для
точки z = aZ.
В этом случае получим уравнения
Л-4-Вт (о/) = О,
Вт' (aZ) Ст (aZ) = О,
где x(aZ) = —— vZ — значение функции т в точке aZ на
втором листе; наконец, вместо (14) получим:
т' (aZ) =--т (aZ) У -----------1— =
2 \ al al — bn)
“ 2
ап— al ' bn — alt
Отсюда
С =
1
B = — —-—,
— p, — vZ p, Z\»
1___L. .. L_\ =
al — an 1 al — bn)
= * л у f_______1 _______
2 p, lv AJ \an—al~T~ bn — alt
Из (18) видим, что, называя через В комплексное
сопряженное с В, получим:
в = = —в1;
р — IV 1
итак,
В1== —В.
(18)
число
(20)
Точно так же
С~~ 2 (*— Ь 2 («„ + <*/+ bn+ al)— C1
И
С1== —С. (21)
Из соотношений (20) и (21) следует, что сумма
В
(г —aZ)2
Bt . С . Ct
(г 4- al)2 ’ z — ai * Z -|- al
698
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
при действительном z — чисто мнимая, как и должно быть,
так как на отрезках 1к скорость направлена нпо действи-
тельной оси, а т(г) на 1к— чисто мнимое.
Отсюда следует, что все коэфициенты с0, clt ... —также
чисто мнимые; мы их далее обозначим в виде ck = 2skl,
где sk — действительное.
Итак, в конце концов (5) принимает вид
dw
dz
А . Л । г В В .
(г —aZ)2 * + — аГр ~
+-7^7-^? + 2^”‘”2 + 2^’-з+ ...
' ‘ + 2Sm"2']
(22)
Это и есть окончательный вид искомой характеристической
функции.
Так как w, по нашему предположению, должна быть
однозначная функция на каждом листе, то циркуляция вокруг
каждого отрезка 1к равна нулю. Отсюда получим 'условия
Ъп
J [(г-«о»
а
п
в . С___________________с_
(z + aZ)2 ‘ <Z — ai z + aZ
+ 2y0Z^m 2+ . .. + 2sw-2d -
J у П(г — an)(z — bn)
(23)
Условий (23) всего m, но одно из них есть следствие
других в силу отсутствия циркуляции вокруг точки z = al.
Мы в дальнейшем будем считать все т условий (23) неза-
висимыми, но условие (17), определяющее коэффициент С,
не будем принимать в расчет и, следовательно, С будем
считать неизвестным коэффициентом, который может быть
определен через уравнения (23).
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 699
Уравнение (22) можно написать в весьма симметричном
виде:
dw
dz
л । Г В j С । . _2 ।
(Z — а/)2 + [(г—aZ)2 + Z— at + lS0Z +
г1УП(г-ап)(г-Ьп)
{Z + az)2 — ['(г+а/)2 “1“ г 4-а/ “ 2 +
1
(ts ) 2т-3 + . _|_ (is ) I t . (24)
J уп(г — ап)(г— bn)
Мы будем предполагать, что точка z = 0 лежит вне отрез-
ков 1к.
Из (24) мы можем получить формулу, представляющую
вырождение (24), положив а=0. В этом случае полюсы
правой части лежат на листах поверхности Римана друг
над другом.
При этом условии получим:
=д+i+["./ + +2iv.»-2 +
dz z* ’ [ г2 2 0
4~ 2/5!^т 3-|- . . . + 2/sw_21 _у-- . (25)
J у П (z an) (z bn)
Пусть
A = Re^t A = Re-v,
Так как т(0) равно действительному числу, то в форму-
лах (18) и (19)м = 0, В = А и с = —1 A V /J- । 1 \
Р- 2 |* ^\an Ьп) ’
так что
В = — е^, В = — е~^,
р. р.
С = С = R^-M,
где
700 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Пользуясь этими уравнениями, мы напишем (25) в виде
dw 27? cos 6 . о./7? sin 0 . D sin 0 a
+ So*”1-2 + S12M~3 +'. • . 4- S'm-г') r * • (261
1 m г/УП(г-ап)(г-Ьп) J
Можно, наконец, еще несколько упростить эту формулу,
если перенести полюс в бесконечность. Прежде всего, заме»
тим, что |1 = т (0) = • Г.1 . Сделаем, далее, преобразова-
1 у |П апЬп
ние z = -^\ тогда вместо (26) получим:
— с2 — = 2R cos 0С2 + 2г sin S’? + R{ sin К -J- sm_
1 1 \
p 4“ • • • rm-2 )_________/“ / .1\/
Vnanbn-\/ n(C--Mk-
и после сокращения
= 2R cos (k+0)4-2Zp? sin («49) sin (0-|-к) 'w*~1
__о (.Г™-2_ _A] ______I______
m-2‘ ’ ’ и, /п—пт;—г
что, очевидно, можно написать, вводя новые обозначения,
в более симметричном виде:
== 7? cos 9 +1 (R sin Oz™ + C^z™-14~
“Г T • • • T~ ... X/ ~
у П (г - an) (z — bn)
Это и есть окончательный вид характеристической функции
в случае вырождения.
Условия (23) здесь примут вид
f 7? sin 0^ + co^--i+...+cw dz = ^t
J / П (z — an) (z — bn)
an
л таких условий согласно предыдущему т.
(28)
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 701
Интересно отметить, что на поверхности Римана, взятой
в виде, указанном на рис. 5, случай вырождения принци-
пиально не отличается от общего случая, так как располо-
жение полюсов в общем случае, как указано на рис. 6 и 7,
Полюс:г-Л1
1лист
Полюс: г--ои
Илист
Рис. 6.
такое же, как и в случае вырождения, так как полюсы
помещаются друг над другом.
§ 3. Нули и полюсы производных характеристических
функций; их порядок
Правая часть уравнения (13) представляет собой некото-
рую алгебраическую функцию F (г). Таким образом,
(г — а/)* 1 2 3 • aZ)2 ' [ (г — aZ)2 * (z -f- a/)2 ' 2 — ai
(29)
Если между A, A, B, Blt С и Сг нет никаких соотноше-
ний вида (16), (17), (18), (19), то F (z) имеет на римановой
поверхности следующие полюсы:
1) при z = ai на каждом листе полюсы второго порядка,
что эквивалентно четырем простым полюсам;
2) то же в точке z = — aZ;
3) простые полюсы в точках Ък\ всего 2/п простых
полюсов.
Таким образом, F (z) имеет 8-|-2/п простых полюсов.
Следовательно, F (z) есть функция 8-|-2/п-го порядка и
принимает на поверхности Римана всякое значение 8-]-2/п раз;
в частности, она имеет 8 2/п нулей.
702
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Порядок функции F (z) понижается при выполнении
условий (16) — (19). Действительно, при выполнении эти$
условий F (z) имеет на римановой поверхности следующие
полюсы:
1) при z = ai имеем один полюс второго порядка на
первом листе поверхности, что эквивалентно двум простым
полюсам;
2) при z = — at имеем один полюс второго порядка
на втором листе поверхности, что также эквивалентно двум
простым полюсам;
3) простые полюсы в точках ак и Ьк\ всего 2/п простых
полюсов.
Итак, F (z) имеет в этом случае 4-|-2/п простых полю-
сов и есть функция порядка 4 +2/п и, следовательно, имеет
на поверхности Римана 4-|-2/п нулей. Найдем их положение.
Прежде всего, F (z) имеет на каждом листе поверхности
Римана нули второго порядка в бесконечности. Действи-
тельно, полагая z = ~ , получим из (29):
F(,)_ ЛС2 г ВСз .О,
V ’ (1—а/С)2 ' (1 + «Л) [(1—а/С)2 ' (1 + а/С)2 1—а/С “
I . Со + С1:4-...+С(В/л~21
что, очевидно, можно написать в виде
F (Z) = ;2 [Л | А Г Bt? в&
У } 41(1 — a/c)2^(i+ «/q2^L(i — ад2 Hi+ад3
а С£ п._1_Л.Г_1_ L, _Г>»-21
' 1 — aZC ' 1 + alZ
^т — 2
^ш-2
г. -----г = С2Ф(С), (30)
/п(1-ад(1-ад)
где Ф (С) голоморфно в области £ = 0 на том и на другом
листе, т. е. независимо от знака радикала ]/П(1— аЛС)(1—Ьк£).
Из (30) видим, что в точке С = 0, т. е. z = oo, F (z)
имеет на каждом листе нуль второго порядка, что равно-
сильно четырем нулям, лежащим в бесконечности. Таким
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 703
образом, должно быть 2/п нулей, лежащих на конечном
расстоянии.
Из гидродинамических соображений следует, что все
эти 2/п нулей лежат на отрезках 1к, причем т нулей имеют
место на одной и т — на другой стороне отрезка Zft, т. е.
при различных знаках радикала; на рис. 4 указаны эти
нули (точки вр а2, а3; т2, т3). Аналитически легко дока-
зать это свойство для случая вырождения.
Для этого заметим, что многочлен в формуле (27)
(30')
имеет т действительных нулей, которые все лежат на отрез-
ках /л. Действительно, из (28) следует, что между ак и Ьк
есть нуль многочлена (30'), так как иначе подынтегральная
функция в (28) сохраняла бы знак между ак и Ьк и инте-
грал (28) не мог бы равняться нулю.
Итак, на каждом отрезке 1к по крайней мере по одному
нулю, но всего нулей /п. Следовательно, на каждом отрезке
есть непременно по одному нулю.
Назовем эти нули ап а2, ...» Тогда (27) можно
написать в виде
^ = Rcos 94-t . (31)
dz УЩг-ак)(г-Ьк)
Рассмотрим изменение функции
у = R sin 9 ~ gt) а2> • • • (* - a™L (32)
/~П(х-ай) (х-Ьк)
на отрезках /й. Пусть на Zx сверху корень берется положи-
тельный; тогда снизу он отрицательный. На Z2 сверху корень
Палюс:г=а1
-±-------— —±— I
+ 13 П(МЮС: Z*-atf
Рис. 6а. Рис. 7.
отрицательный, снизу — положительный и т. д.; знаки корня
указаны на рис. 6а* Полагая R sin 6 > 0, рассмотрим знак
числителя.
704 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
Если т — четное, то получим следующее распределение
знаков числителя дроби (32), изображенное на рис. 8, и,
сопоставляя с рис. 6а, получим распределение знаков вели-
+ "7 + ~
zs ct2 z-------------------ч
lj-----1------ 12----------h— 13---------------•-----
Рис. 8.
, + fz ~ I__________I -..............t-fe
- + 1г - + v - +
Рис. 8а.
чины у (32), данное на рис. 8а. Так как на концах отрез-
ков у обращается в бесконечность, то график (32) имеет
вид рис. 9 и 10.
Рис. 9. На верхней стороне
оси х.
Рис. 10. На нижней стороне
оси х.
Пусть /?cosO положительно; отложив на рис. 9 /?cos6,
найдем точки а2, аз на верхней стороне и т15 т2, т3 на
нижней, в которых -^- = 0. Так как общее число решений
этого уравнения равно 2/п, то график функции у имеет вид,
указанный на рис. 9. Течение имеет вид, указанный на
рис. И (/?>0).
(Для направления течения sin 6 < 0 и cos9>0, т. е.
направление скорости — угол четвертой четверти.)
Если радикал взять с обратным знаком, то все течение
примет вид, указанный на рис. 12.
Разобранные течения представляют течения на двух
листах поверхности Римана.
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 705
Подобным же образом рассмотрим и другие случаи
(пг — нечетное и т. д.).
Перейдем теперь к общему случаю, когда функция имеет
вид (22).
В общем случае, когда имеем уравнение (29), чтобы
найти корни уравнения F(&) = 0, надо решить следующее
уравнение, получаемое из (29):
(Д + Д) (z2 — а2) + 2а/г (Д — Д) +
, (В - В) - а2) 4- 2а/> (В + Вг)
Г V\l^-ak)(z-bk)
I C(z-\-ai) (г*—я2)—С(г + «0(г2—а2) + c0z™+2-|- ... _ q
< П(г-а*) (z — bk)
В этом случае вместо (30) имеем выражение
(В — B)(z2 — а2) + 2а/г(В4-В1)+ . . . +сог»«+2 + . . ., (33)
степень которого /п+2; функция (33) имеет /п+2 корня,
из которых /п действительные и лежат соответственно
в интервалах 1к, как это видно из уравнений (23). Докажем,
что остальные два корня не лежат в этих интервалах. Дей-
ствительно, если бы два оставшихся корня находились
706 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
в каком-нибудь интервале 1к, то или в одном интервале
было бы три корня, или в двух интервалах было бы по два
корня. В этих интервалах график кривой, соответствую-^
щей (32), имел бы вид, указанный на рис. 13 (случай, когда
в интервале заключены 3 корня), или вид, указанный на
рис. 14 (случай, когда в двух интервалах есть по два корня),
и во всех остальных интервалах-кривая имеет вид, указан-
ный на рис. 10. С другой-стороны, линия
у = (А + Л) (х2 — а2) + 2а/х (А — А) (34)
есть парабола, и так как А и А могут быть какие угодно,
то при пересечении с кривой с одной стороны получится
три точки (точки Mlf M2i Л43)
и симметрично , с другой
стороны еще точка (или три),
т. е. в одном интервале по-
Рис. 15. Рис 16.
лучится четыре (или шесть) точек; так как в каждом из
остальных интервалов будет по два нуля, то общее число
нулей в этом случае равно или больше
2.(/п—1)+4 = 2/п + 2,
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 70?
что невозможно, так как общее число нулей равно 2/п.
Следовательно, случай, указанный на рис. 14, невозможен.
В случае рис. 14 при пересечении с параболой получим
или четыре точки ДГ2, ДГ3, N4, что по предыдущему
невозможно, или две точки, лежащие с одной стороны
(рис. 15), но в этом случае на одной стороне 1к течение
идет в одну сторону, а на другой есть две критические
точки (рис. 16); в этом случае не выполняется уравнение (23),
так как циркуляция, взятая по стороне, где нет нулей,
очевидно, отлична от нуля.
Итак, из всего предыдущего рассуждения выходит, что
. dw
в каждом интервале есть по два нуля функции , причем
один нуль — одной ветви и другой нуль — другой ветви.
Общий характер течения указан в начале работы (рис. 4).
§ 4. Инвариантность уравнения; его преобразования;
число независимых параметров
Уравнение (22) и его вырождение (27) обладают свой-
ством инвариантности по отношению к некоторым преобра-
зованиям. Этим можно воспользоваться для упрощения
уравнений.
Начнем с уравнения (27). В этом случае уравнение не
меняет своего вида, если над переменными сделать линейные
преобразования вида
z = azt + р (а, р — действительные);
w В (А— действительное, В — комплексное число).
После такой замены уравнение примет вид
4^ = 4 Я cos 9+/ Гя 4 sin 02Т + mR? sl"8 + c°
uZ'j A L А А
. , /?sin6^ + C0^^+ ... +Cm-]

1
а
• (35)
Мы можем теперь подбором надлежащих значений а, 3 и А
упростить уравнение (35).
708
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Например, можно выбрать их таким образом, чтобы
= /?sinop’»+c0p»-i4-...+cOT.= o( -^=1.
Тогда уравнение приведется к виду
-^- = cos9 4-«(sin92:’» + C0z’’»-14- .. .-\-Cm_2z) X
v -7r=====J======. (36)
Иначе можно положить
а п __ | Р | Р ____________ I
Л ’ а * а ’
тогда уравнение (35) приведется к виду
= cos 0 -1- i (sin 9гт4~ . • •
. • • + Ст-1) 1 ---. (37)
V^-l)^-^)^-^) ...
Подсчитаем в уравнениях (36) и (37) число остающихся про-
извольных параметров.
В уравнении (36) остаются параметры
С0, ..., Ст__2, аз* •••» ат> ^1» ^2» •••> ^т-
Всего I-)-(/п — 1) -р (т — 1) 4~ zn = 3/п — 1 параметров.
Но, кроме того, мы имеем т уравнений (28), связывающих
эти параметры. Таким образом, остается 2/п—1 свободных
параметров.
То же самое получим и из уравнения (37).
Перейдем теперь к общему случаю, когда уравнение
имеет вид (22). Здесь, прежде всего, при помощи преобра-
зования z = kzl можно сделать а = 1, так что уравнение(22)
примет вид
dvo _. А . А . / В В' С __
dz ~ (г — Z)2 (z + Z)2 +“ \(г — Z)2 (z + Z)2 z — i
— -^-;+2s02:«‘-2-}-2s1Z’»-3+ ... -j- г 1 ---
г + о -Г ! -Г -Г т 2) уЦ{г_ак){г_Ьк) •
(38)
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 709
Уравнение (38) инвариантно по отношению к преобразова-
ниям вида
и к дробно-линейному эллиптическому преобразованию
с неподвижными точками z±zZ, которое переводит точки
действительной оси снова в точки той же оси; такое пре-
образование имеет вид
z — I
г + 1
откуда
__ z± cos а 4“ sin а
— Zi sin а -|- cos а

Z1 + k
или Z = т г
1 —Zijz
(k = tga).
Делая эти преобразования, приведем уравнение (38) к виду
rfwj _ Л(1+#>) 1 . Л(1+#>) 1 ,
dzt ~ М (1 + Zfc)2 C?i — О2 м (1 —(г1 + О2 '
+ I ----------- Qw + 2(<t) . (39)
(г2 + 1)У П
где Qm+2(.z\) — многочлен степени /п-|-2 с действительными
коэффициентами. Здесь мы располагаем двумя параметрами,
при помощи которых можно, например, сделать
I Л(1 + ^)2 I t
|Л1(1 + ^)| 1 A + a±k
Таким образом, уравнение (39) можно привести к виду
dw _ е** . । Г В ~В . С
dz ~ (г — ' (г Y Vp ' \\z — ф (z + /)2 ' z — I
-+n-4-C0Z^-j-C1^+ • +CW_2] X
X r 1 (40)
/(г— 1)(г — 4) (z — a2) (z—b2)...
В этом уравнении коэффициенты В и С определяются по
Уравнениям (18) и (19). Таким образом, остаются свобод-
ными параметрами
£(), ^1» • • •» ^пг-2’ ^2» ^3’ • • ’’ °"гп^ ^1’ ^2’ • * •’
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 711
через Л4 число нулей и через М число полюсов w при
изменении z на верхнем листе:
М — N = ~
Z7ZI
dw
w — а*
(41)
где интеграл должен быть распространен на обе стороны
отрезков 1к и на окружность бесконечно большого радиуса.
Но интеграл по обеим сторонам 1к равен нулю в силу усло-
вий (23) и интеграл по бесконечно большой окружности
равен нулю в силу того, что в бесконечности
dw _ А-\-В . н р>2
dz " z* ' г3 * г4 ’
как это следует из (22), и w — а конечно, так как а от-
лично от w(oo). Отсюда и из (41) следует, что
и так как w имеет на первом листе один полюс первого
порядка в точке а/, то N = 1 и М = 1, что и требовалось
доказать. Отсюда следует, что и значения w на различных
разрезах также различны, так как иначе функция w при-
нимала бы значения, близкие к тем, которые она прини-
мает на 1к также по нескольку раз, что невозможно в силу
доказанного выше.
Аналогичное рассуждение можно приложить и к случаю
вырождения. Впрочем, для функции, определяемой уравне-
нием (25), предшествующее рассуждение остается без всякого
изменения, а случай уравнения (27) получается отсюда при
помощи дробно-линейного преобразования.
С точки зрения течений на поверхности Римана этот
результат имеет следующий гидродинамический смысл. На
верхнем листе поверхности Римана мы имеем течение вида,
Указанного на рис. 17.
На плоскости w, т. е. на плоскости характеристической
Функции течения w = <p4-Z<|> всем линиям тока будут соот-
ветствовать линии ф = const, т. е. прямые, параллельные
действительной оси, и, в частности, отрезки llt /2» • • •
Верейдут, как линии тока, в отрезки прямых, параллельных
действительной оси на плоскости w, причем концами этих
°трезков будут точки 7\, S2, Т2, . . ., представляющие
710
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
всего 1 —(zn—1) + (/п—1)-4-/п = 3/п—1 коэффициентов.
Но, кроме того, существует т уравнений (23), из которых
независимых только т—1, так как сумма циркуляций во-
круг всех отрезков 1к равна циркуляции на первом листе
вокруг точки Z, которая равна нулю в силу выбора коэф-
фициента С.
Итак, при сделанных условиях остается 3/п — 1 —.
— (т—V) = 2m свободных параметров.
§ 5. Приложение полученных результатов
к задаче конформного отображения
Рассмотрим поведение характеристических функций w
при изменении z на первом листе. Эта функция однозначна
при всяких изменениях z на верхнем листе римановой по-
верхности; нетрудно доказать, что эта функция однозначна
и принимает всякие комплексные значения по одному разу.
Действительно, прежде всего заметим, что w монотонно
изменяется при обходе отрезка 1к от точки тЛ до ак (рис. 17),
Рис. 17.
следовательно, на отрезках w принимает различные значе-
ния, образующие прямолинейный отрезок, который парал-
лелен действительной оси, так как на действительно.
К az
Кроме того, в бесконечности w имеет конечное значение,
dw
так как в бесконечности имеет нуль второго порядка.
Применяя обычную формулу для определения числа нулей
и полюсов функции к функции w — а, где а отлично от
значений w в бесконечности и на 1к, получим, обозначая
712
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
изображения точек и т. д. на плоскости г, как это
следует из знаков производной на различных частях отрез-
ков 1к (рис. 18).
Возникает следующий основной вопрос: если мы имеем
на плоскости w ряд отрезков Lki параллельных действи-
тельной оси и в остальном расположенных как угодно, то
Рис. 18.
можно ли найти такую функцию w^z) типа, даваемого ука-
занными выше уравнениями, которая дает отображение пло-
скости z с разрезами /1? /2, . .., /т, лежащими на действи-
тельной оси, на плоскость с разрезами Llt L2, ...»
В работе С. А. Чаплыгина «К теории триплана» дано
решение этого вопроса и показано, что ответ получается
утвердительный в случае двух
и трех отрезков Lk. Этот за-
мечательный результат следует
из приведенных ниже сообра-
жений.
Рассмотрим систему парал*
лельных отрезков, как угодно
расположенных, на плоскости
(рис. 19).
Пусть их длины — Ар
А2, . . ., Lm, расстояния между
Рис. 19.
ними — Нъ Н2, . . ., Нт__х и их сдвиги (рис. 19) друг отно-
ительно друга — Dlt D2, . .., всего получается
+ (т — 1)-|- (т — 1) -= 3m — 2 размеров, определяющих
их относительное расположение. Так как при помощи пре-
об азования подобия w = можно любой из этих раз-
меров сделать равным произвольно заданному, отличному
от нуля числу, то масштаб не имеет значения и важны только
К ТЕОРИИ ТЕЧЕНИЙ НА ДВ\ГЛИСТНОЙ ПОВЕРХНОСТИ
713
относительные размеры, т. е. отношения
* Т/2 • А3 : ... ; Lm *. Н1 : Н2 *....*. Hm_i . . D2 L)m_х,
т. е. всего 3m — 2— 1 = 3m — 3 отношения размеров. .Сле-
довательно, если мы хотим систему отрезков, лежащих
на действительной оси плоскости z, отобразить на систему
отрезков Lif L2, ..., Lm, то нам придется удовлетворить
3m — 3 уравнениям, дающим относительные размеры фигуры
на плоскости w. Задача становится возможной, если число
свободных параметров, которыми мы располагаем в ото-
бражающей функции, равно или превосходит 3m — 3.
Но выше было показано, что в случае общей формулы,
определяемой уравнением (24), число свободных параметров
равно 2m; итак, для возможности решения поставленной
выше задачи должно выполняться условие
3m — 3 < 2m,
т. е.
т < 3.
Итак, при помощи функции общего вида, определяемой
уравнением (24), задача может быть решена только в слу-
чае двух и трех отрезков.
Если взять функцию, определяемую уравнением (27), то
в нем число свободных параметров равно 2m— 1; тля реше-
ния поставленной выше задачи необходимо выполнение условия
3m — 3 ^ 2m— 1,
т. е.
m 2.
Таким образом, при помощи функции, определяемой уг ав-
нением (27), задача может быть решена только в слу г-.е
m = 2.
К-более, подробному исследованию отображений в слу ас
m = 2 мы и перейдем.
§ 6. Исследование отображения в случае т = 2
При m = 2 уравнение (37) может быть написано в виде
— = cos О — i (sin 9г2 4- CQz -|- Сх) I - .............
714 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Рассмотрим прежде всего следующий частный случай, когда
=— #2=Тогда (42) можно написать в виде
1
= cos 6 — i (sin OzI 2 * * -|- С^г -j- Cx)
Условия (28) в этом случае принимают вид
Г sin 6г2 4~ Сог 4- ~
J /(1—z2)(l—£2г2)
1
~ к
1
к
Г s*n 9^2 ~Ь С®2 dz = О
J /(1 — z2) (1 — £2z2)
1
Заменяя в (44) z = — zlt приведем (44) к виду
к
Г sin 6г2 — Cnz + Сх dz==Q
I /(1 —z2)(l —£2z2)
i
и из (45) и (46) имеем:
1
к
Г z dz j сх
C?q I —~ ~ ---- —? dZ —= 0.
J /(1— г2)(1 — kW)
1 •
Отсюда Со = 0, и (43) принимает вид
— cos 9 — I (sin Oz2 -J- Cx) ~ ..-- :
dz /(1— z2) (1 — k2z*)
. (43)
(44)
(45)
(46)
(47)
(48)
и условия (44) и (45) в этом случае совпадают.
Уравнение ^- = 0 в этом случае превращается в биква-
дратное уравнение; его корни обозначим соответственно
±t.
Уравнение (30) в этом случае имеет вид sin Gz2-^ Сх = 0,
его корни ± j/~——— . Называя их ztza, напишем урав-
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 715
нение (48)’ в виде
2*2 — «2
COS 9--I sin Qk z-j: .
/(1—^2) (1—^2)
(49)
dw
dz
Мы видим, что в этом случае все элементы, определяющие
характер течения, расположе-
ны симметрично относительно
начала координат. Этот случай
можно назвать симметричным.
На рис. 20 показано соот-
ветствующее течение.
В этом случае для опреде-
ления трех постоянных 0, k2, а2
имеем уравнения. На рис. 20
показано, во что переходят
(-S)
^2
(*t)
Рис. 21.
И,
I о,
\(*3)
точки рис. 21 на плоскости w. Отсюда имеем
уравнения
Я cos 9 — i sin 9& . a —--1 dz= Lif
V (1—z2)(l—^2z2)J
t
что еще можно переписать в виде
4
( / 5*2_ <7.2 \
(cos О — I sin 6 k ----- - | dz -I-
J \ /(1 — z2)(l —
8
+ (cos 9 -4- i sin 9& -—========) dz =
J\ /(1—г2)(1—£3?2)/
£
к
716
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
ИЛИ
Z2 — а2
У(1 — г2) (1 — £2г2).
к
— 2 sin Ok j
8
г2—а2
У"(1 — г2) (1 — k2z2)
(50)
Точно так же
-1
f 7 z2____а2 \
(cos 0 + i sin Ok dz — L2
Jk K(1 — z2)(l — k2z2))
-8
(здесь знак радикала — обратный, так как из -\-t до —$
приходится обойти по полуокружности две критические
точки -f- 1 и —1, что изменит знак радикала).
Но ту же длину получим, если возьмем интеграл
f (cos 0 4“ i sin Ok ~----- ...... dz -j-
J k /(1—z2)(l — k2z2)J
8
-t
J* / ____ CL2 \
(cos 0 4- i sin Ok —- ) dz = L2
k /(1—Z2)(l—£2Z2)/
J.
к
ИЛИ
1
к
(* / л । . . л » г2 — а2 ч
— ( cos 9 4-1 sin Ok _______ = dz —
J\ У(1— г2)(1— k2z2)J
8
i 2 2
| (cos 9 — i sin Ok ~ -r a ) dz — L2,
Jk К(1-г2)(1-^г2)/
i
к
К ТЕОРИИ ТЕЧЕНИЙ НА ДВУЛИСТНОЙ ПОВЕРХНОСТИ 717
ИЛИ
1
к
(* / Z^* - OL& \
— I (cos 0 +1 sin 0й - _ | dz -4-
J\ /(1—г2)(1—/г2г2)/
8
8
[* / 2*2_дг2 \
+ (cos6 — Z sin Qk _ . —dz-4-
J\ /(1 — z2)(l — k^)J
t
£
к
J* / л • • д, Z3 — a3 \ , ,
( cos □ — i sin vk —======== ] dz = Ao,
\ У(1 — z3)(l — £3z2)/
t. e.
Z- — a2
t
ZsinOZs ______________
/(1 — z2) (1 — &z*)J
£
к
C ^2 __ a2
— 2sin0£ —==========dz — L2. (51)
J <(1 — z2) (1 — £2z2) v
8
Z% — a3
Сравнивая (50) и (51), видим, что в рассматриваемом сим-
метричном случае
Из параметров 0,
рое здесь имеет вид
Lt = L2. (52)
а2 в силу соотношения (28), кото-
k2,
к
sin 0 -
Z2 — a2
г .. ... — .. _____dz = 0,
/ (1 —z2)(l —£2Z2)
(53)
свободных параметров остается только два; так как отно-
шения параметров, определяющих относительное положение
разрезов Ах и L2t в силу соотношения (52) имеют вид
’ Ь2 : 7/х : £)х,
то число этих отношений, остающихся произвольными, тоже
два:
Ц : Н, : Dv
718
(V. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Следовательно, подбором параметров можно всегда сделать
отношения размеров Нх и £)х произвольными.
Выпишем уравнения, определяющие эти параметры.
Чтобы найти и Dt, возьмем интеграл
( (cos9isin Bk r Z.-~. 0(2 dz,
<(1—2-2) (1 — ^2);
L
Сравнивая рис. 20 и 21, видим, что
= I fcosO-|-f sin Bk a. ~.—:=\dz. (54)
1 J \ <(1 - z2) (1 - №)) v 7
Разбиваем (54) на действительную и чисто мнимую части,
получим:
8
8
i sin Bk f —- г -.= dz +
J <(1—Z2)(l—£2Z2)
1
Z3 — a2
D1=“ J
-t
in Bk — ________ : dz,
J <(1—Z2)(l—£2Z2)
-i
— — sin
Z2 — a2
r_________________dz =
/(1— г2)(1 — kW),
a2 — Z2
= Sin Bk I dz,
J <(1—Z2).(l—£2Z2)
или
z2 — a2
D< = — (s +f) cos В — i sin Bk I —r_u ——dz,
V ' <(1—z2)(l —£2Z2)
a2 — z2
H. = 2 sin Bk —7====== dz,
J <(1 —z2)(l—£2z2)
0
(55)
(56)
и сюда надо добавить еще уравнение
8
f (cos 0 — i sin Bk dz = Lv (57)
<(1— z2)(l— k^)J 1
t
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
719
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
НА ПОМЕЩЕННОЕ В НИХ КРЫЛО САМОЛЕТА1)
§ 1. Обзор работ по теории влияния эллиптических труб.
Работы Розенхида и Лотц
Широкое применение в работе аэродинамических лабора-
торий аэродинамических труб с эллиптическим сечением,
позволяющих помещать в трубы крылья сравнительно боль-
шого размаха, поставили перед теоретической аэродинамикой
вопрос об учете влияния труб эллиптического сечения на
аэродинамические свойства помещенного в трубах крыла и
хвостового оперения. Решению этой задачи посвящен ряд
работ, важнейшие из которых принадлежат Сануки и Тани2),
Розенхиду3) и Лотц4 5), причем наиболее полное решение
дано в работе Лотц. Обычный прием, которым пользуются
при решении этой задачи большинство авторов, сводится
к построению потенциальной функции по ее пограничным
значениям для дополнительного потока, заменяющего действие
стенок трубы или свободной границы струи, причем предва-
рительно строится конформное отображение внутренности
эллипса на внутренность некоторого прямоугольника6).
Добавляя симметричные изображения вихрей, можно при-
вести задачу к построению потенциала, образованного систе-
мой вихрей.
Однако действительное выражение потенциала, дающего
влияние границы трубы, оказывается чрезвычайно сложным.
В работе Лотц потенциал добавочного течения получается
в виде ряда, расположенного по функциям Матье; действи-
тельное вычисление поправок на скос потока и на величину
*) Опубликовано в Уч. зап. МГУ, вып. 117, Механика, т. 1, 1946.
2) S а и u k i, Т a n i, The wall interference of a Windtunnel of
elliptic cross-section. Proc. Phys.-Math. Soc. Jap., Ill ser., t. 14,
стр. 592—603, 1932.
3) Rosenhead, The aerofoil in a Windtunnel of elliptic section,
Proc. Roy. Soc., London, A. 140, стр. 579—604, 1933.
4)lrmgard Lotz, Korrectur des Abwindes in Windkanalen
mit Kreisrunden Oder elliptischen Querschnitt. Luftfahforschung, t. 12,
№ 8, стр. 250—264, 1935.
5) См., например, И. И. Привалов, Введение в теорию функ-
ций комплексного переменного, изд. 4-е, стр. 323, 1935.
720
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
индуктивного сопротивления приводит к весьма сложным
вычислениям. Между тем для практического вычисления чрез-
вычайно важно получить решение в виде, удобном для вы-
числений. В практических задачах по большей части нет
надобности требовать очень большой точности, но получае-
мые формулы чрезвычайно желательно иметь в виде, не пред-
ставляющем особых осложнений для вычисления. С этой точки
зрения указанные выше работы нельзя считать удовлетворяю-
-щими практическим потребностям.
Упрощение может быть достигнуто в различных напра-
влениях. Так, можно заменить эллиптическую трубу трубой,
например, прямоугольного сечения, причем подобрать раз-
меры сторон прямоугольной трубы таким образом, чтобы
влияние ее на крыло мало отличалось от влияния на крыло
эллиптической трубы. В этом направлении в настоящее время
никаких результатов не имеется. Наконец, можно искать
упрощения и в другом направлении, рассматривая крыло
в особом, наиболее удобном для вычисления расположении
относительно трубы. Совершенно очевидно, что расположе-
ние несущей линии вдоль большой о.си сечения трубы должно
внести упрощения в вывод общих формул для расчета влия-
ния трубы на скос потока и индуктивное сопротивление.
Величины, которые естественно входят во все формулы
в теории конечного крыла, представляют коэффициенты
разложения циркуляции в известной форме тригонометри-
ческого разложения Треффтца — Глауэрта: через них выра-
.жается подъемная сила, индуктивное сопротивление, величина
скоса потока и т. д. Поэтому наиболее простой для практи-
ческих расчетов вид формулы, дающей учет влияния трубы,
представляла бы такая формула, которая давала бы неко-
торые поправочные множители для коэффициентов разложения
Треффтца — Глауэрта, выражающие зависимость поправок
от размеров эллиптической трубы. В случае круглой трубы
такие поправки можно вывести, исходя из теории Прандтля1).
Аналогичные поправки, в известном смысле даже более
простые, чем для случая круглой трубы, были даны Мала-
вардом и Пэрэ для случая трубы эллиптической.
х) См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, стр. 329.
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
721
§ 2. Метод, данный Л. Малавардом и Ж. Пэрэ 9
Метод расчета влияния эллиптических труб, предложен-
ный Л. Малавардом и Ж. Пэрэ, относится к частному слу-
чаю расположения крыла, когда крыло занимает фокальный
отрезок эллипса сечения трубы или часть этого фокального
отрезка. При этом, как и во всех других методах учета
влияния труб, крыло заменяется одной несущей линией.
Мы можем всегда предположить, что циркуляция несу-
щей линии распределена вдоль всей линии гДе и
F2—фокусы эллипса. Действительно, если крыло занимает
часть АВ фокального отрезка то можно считать, что
циркуляция Г отлична от нуля на отрезке АВ и равна нулю на
отрезках F±A и BF2. Называя расстояние FrF2 через 2г, введем
переменный угол 6, определяемый формулой z = — с cos 6,
и разложим, аналогично методу Треффтца — Глауэрта, цир-
куляцию на отрезке FrF2 в тригонометрический ряд
Г~2Лп81пп9. (1)
Если крыло занимает весь фокальный отрезок FrF2, то
разложение (1) совпадает с обычным разложением Треффтца —
Глауэрта циркуляции; если крыло симметрично относительно
его середины и помещено так, что его середина находится
в центре эллипса,, то в разложении (1) все Ап с четными п
тождественно равны нулю.
Требование, чтобы крыло не выходило своими концами за
Пределы фокального отрезка FtF2, не вносит существенного
ограничения. Действительно, обычно применяются эллипсы
с отношением полуосей 2, так что,, считая большую полуось
равной а, получим для малой полуоси у и с = а = 0,86tz,
т. е. при таком отношении полуосей размеры самолета по
размаху должны составлять це более 86% боль-
шой оси эллипса. Это требование является крайне не-
выгодным только при отношении полуосей, близком к 1,
т. е. когда эллиптическая труба близка к круглой — случай,
1) L. Malavard, J. Peres, Correction de parois dans le cas
d’un tunnel de section elliptique, C. R., t. 204, № 10 (8 Mars 1937);
C. R., t. 204, № 19 <10 Mars 1937).
722 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
который, естественно, не имеет места в действительности.
Но отсюда следует, что из дальнейших результатов нельзя
получать как частный случай формулы Прандтля для случая
круглой трубы.
Пусть полуоси эллиптического сечения трубы суть а и Ь
и фокальное расстояние 2с (с = |Ла2 — Ь2). Предполагая, что
эллипс, представляющий сечение трубы, находится на пло-
скости 24 (24 = *1+ ^i), сделаем конформное отображение
вспомогательной плоскости z на плоскость zt при помощи
формулы
~2 (z + т) '
Тогда окружность радиуса 1 на плоскости z перейдет
в отрезок действительной оси плоскости zx и окружность
радиуса R (R > 1) на плоскости z перейдет в эллипс с полу-
осями
Полагая
получим отсюда
а-[-Ь
а-[-Ь
а — b
(4)
Итак, область., заключенная между фокальным отрезком
и эллипсом на плоскости z1} переходит при конфбрмном
отображении, даваемом формулой (2), в кольцеобразную
область на плоскости z, заключенную между окружностями
1 Г» -я /“ 4“
радиуса 1 и R = у ь *
Рассмотрим плоскость S сечения трубы, в которой поме-
щается несущая линия.
Если циркуляция вдоль несущей линии выражается рядом
Г = 2 Ai sinnO,
то с каждого элемента несущей линии сходят свободные
вихри интенсивности
dV = — 5 пАп cos rfO.
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
723
Так как эти вихри идут от крыла в одну сторону в беско-
нечность, то каждый из них создает на плоскости (zt) тече-
ние, характеристическая функция которого имеет вид
-£ln(^4-c-cos 0).
Следовательно, характеристическая функция течения,
вызываемая на S всей системой свободных вихрей, имеет вид
тс
f(Zj) — — пАп j* cos n0 In -|-с • cos 0) <70,
о
и так как
тс
j cos In (zt -j- с • cos б) z/0 =
о
sin /20 . z , .
—— • ln(^i+c • COS 0) +
0
c f sin /20 sin 0 rfO
n J + c • cos 0
0
I sin тгО • sin 6
J zx + c • cos 6 *
о
то
г, v с V* д Г sin /20 • sin 0 db
J \zi) 4kZ 2^ n J г-i 4- c • cos 0
о
8kZ S An
js (n — 1)0 dft
гх 4~ c- cos 0
I cos C71 + 0 Q
J zi + c • cos °
о
или, полагая
С cos тгО
J zr 4- c • cos 0 ’
о
окончательно имеем:

8^S^{4-i-/n+1}- (5)
Можно показать x), что если zr = с • ch k лежит вне отрезка
— ct 4~f> то, полагая zY = с- ch k,
In = (— l)n—
n v 7 c • sh k
1) См. приложение.
724 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
Отсюда имеем окончательно следующее выражение для /(24):
f(zi) = 8^7 АП с . sh к Х
X {(_ X___________(_ X},
ИЛИ
= Т(6)
Перейдем теперь на плоскость z.
Так как
то
т. е.
z — е\
а потому
т
Таково выражение характеристической функции течения,
вызванного свободными вихрями на вспомогательной пло-
скости.
Заметим еще, что в наиболее важном случае, когда рас-
пределение циркуляции симметрично относительно точки
zr = 0, все Ап с четным п равны нулю, а потому можно
написать:
= (8)
Приложим формулу (7) к определению величины скоса
потока и скорости опускания в точках несущей линии в сво-
бодном потоке.
Если мы хотим подсчитать. скорость опускания потока,
то надо вычислить выражение
df (*i) _ V — пАп — (— 1 >»-1
dz± 4тс zn+ldz^ '
К ТЕОРИЙ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
725
Но из (2) имеем:
с /. 1 \ dz dz________ 2^2
2 \ z2/ dzr И dzr с (z2 — 1) ‘
Следовательно,
= * V/ Пп пАп <lz2
dzr 4т: ' zn+ic(z2—1)’
Точкам несущей линии на плоскости z соответствуют
точки окружности |г| = 1.
Кроме того, заметим, что в разложении циркуляции Г
в тригонометрический ряд точка 9 = 0 соответствует z = — 1.
Поэтому для получения скорости в точках несущей линии
положим:
г = е^~0^ = — е-°\ (10)
Подставляя выражение (10) в формулу (9), получим:
df(z^)__ . _ t уч л cos л0 + i sin тгв_
~dz^ ~U~ lV ПАп — ~~
__ 1 уч пАп (cos п0 Ц- Z sin п0)
4пс sin 0 ’
где и и v — горизонтальная и вертикальная составляющие
скорости течения.
Отсюда
I 1 \? л C0S Л0 Z1 . X
ZZ -— “j~ “j / j ; тг~ , ( I I )
1 4kc n sin 0 ’ v 7
1 уч . sinn0 /1ПЧ
v =—zr, 02)
4лс n sin 0 ’ v '
что совпадает с известными формулами Глауэрта1)’, из этих
формул непосредственно видно, что в случае, если имеем
расположение симметричное, так что п — нечетное, то
«в = —«гс_9, ^9 = ^-9
и, сверх того, 4z(+fl) =’—zz(_e), что соответ-
ствует течению на верхней и нижней поверхностях крыла.
*) См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, стр. 174.
726
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
§ 3. Построение дополнительного течения; случай
твердых стенок
Известно, что влияние твердых стенок сводится к тому,
что наряду с течением, создаваемым вихревой системой
крыла, необходимо добавить дополнительное течение таким
образом, чтобы слагающая скорости всего сложного течения,
направленная по нормали к трубе, была равна нулю. Так как
в том сечении трубы, где помещается несущая линия, сла-
гающая скорости по нормали к поверхности трубы создается
только действием свободных вихрей, то величину этой соста-
вляющей по нормали найдем из формулы (7) § 2.
Так как из (7) имеем
г, х I V4—(COS ЛФ— z sin л ср) - , .1ТГ
f{zx) = -4 --- rn ---------- = ф +lF’ z= ге^ ’
где Ф — потенциал скоростей и Ф— функция тока, то от-
сюда
а потому
Следовательно, слагающая скорости vr на границе круга
на плоскости z, изображающего эллипс сечения трубы, вы-
ражается формулой

(1>
Чтобы уничтожить эту нормальную составляющую скоро-
сти, добавим течение, не имеющее особенностей внутри эллип-
тической трубы; если назвать характеристическую функцию
такого течения через F (z^), то функция F (z^ должна быть
голоморфна внутри эллипса, представляющего сечение трубы.
* Сделав в функции F (z^ замену Zt = у (z -j- , найдем
новую функцию Ft(jzy, эта функция голоморфна в кольце
между окружностями |г[=1 и = а потому в этом
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ труб
727
кольце она может быть разложена в ряд
оо оо
F^) = 2 Amz™ + 2 Вт А . (2)
т = 0 т = 1
Рассмотрим значения Fxfz) в двух точках окружности
|z|=l, симметричных относительно действительной оси,
т. е. соответствующих значениям zr — и z" — на
плоскости zx этим точкам соответствует одна и та же точка,
лежащая на фокальном отрезке, как это видно из соотно-
шения — у (* + у) * Так как функция голоморфна
внутри всего эллипса, то ее значения при подходе к точкам
фокальной оси сверху и снизу должны быть равны друг
другу, а потому
Fx (е?*) = Fi (е~^)
при всяком ср. Отсюда из выражения (2) имеем:
со оо
2 (cos z sin + S (cos mcP-------------------z sin mc?) =
m = 0 m = 1
oo oo
= S Ara(cosmcP — Zsin?ncp)+ 5 Bm (cos m<? -|- i sin my), (3)
m = 0 m -1
и так как равенство (3) справедливо при всяком ср, то между
его коэффициентами должно существовать соотношение
т. е.
Ат ^т Ат “4“
= Вт (jn 0),
а потому по равенству (2) имеем:
(4)
1) Разложение (4) представляет следствие так называемых по-
линомиальных разложений Фабера, см., например, Е. Picard,
Traite d’analyse, 2-е изд., т. II, стр. 316, 1905 или P. М о n t е 1, Le-
mons sur les series de polynomes a une varible complexe, стр. 80,
1910.
728
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
при этом числа Ат, вообще говоря, — числа комплексные,
т. е. можно положить:
Ат = -+-1А”.
т т 1 т
Из формулы (4) найдем:
Fi 4) = 2 « + iA'^ ( cos (Rm + 74‘) +
+ isinm» —i)),
. откуда потенциал течения «Зд определяется по формуле
ф1 = У {<»cos (кт + — А"п sin wi<p (Rm — —)} (5)
и составляющая скорости по нормали к окружности | z \ -R
выражается формулой вида
— тЛ’т sin ту ^Rm 1 4- .
Для того чтобы скорость результирующего течения, со-
ставленного из течений, определяемых функциями f и Z7,
имела составляющую по нормали к окружности | z | = R,
равную нулю, необходимо выполнение условия
4г+ 4 = °-
т. е.
+ X(/lX”cosrt<f’(/?n 1 — •
— nX"sinn<p (Я’114 /^+1)} =-0, (6)
и так как равенство (6) справедливо при любом ср, то отсюда
имеем:
An=Q,
А (Rn l -4- * _(—l)w
и
Y = (^L)2_J______л
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ.
729
Следовательно, характеристическая функция дополнитель-
ного течения, вызываемого действием стенок трубы, опре-
деляется формулой
Совершенно аналогично выведем выражение характе-
ристической функции дополнительного течения и в случае,
когда имеем струю со свободной поверхностью.
§ 4. Построение дополнительного течения;
случай свободной струи
Пусть имеем свободный поток эллиптического сечения и
пусть осью соответствующего эллиптического цилиндра яв-
ляется ось г, а оси х и у расположены в плоскости сечения,
причем вихревая линия, заменяющая крыло, расположена
по оси х.
Называя в этом случае w скорость на границе потока
по направлению оси г, вызываемую действием вихрей крыла,
для учета влияния границы струи, как известнох), необхо-
димо построить такой добавочный поток, который на гра-
нице струи уничтожал бы скорость w. Так как добавочное
течение внутри струи не имеет особенностей, то оно имеет
потенциал Ф.
дФ
Из условия = —w получим:
z
Ф=— fwdz.
— оо
Легко показать, что w есть четная функция г, а потому
функция
я
Ф1 = — dz
о
1) См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, стр. 232.
730
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
есть нечетная функция z. Полагая еще
о
Фо = — ^wdz,
— оо
получим, что
Ф = Фо + Фх.
Можно показать, что Фо постоянно во всех сечениях
струи; следовательно, определение функции Ф внутри сече-
ния струи приводится к определению функции Фх по ее зна-
чениям на границе струи1).
Применяя далее формулу Био — Савара, найдем для rfw
следующее выражение:
V Ап sin тгО ds у
dw = —---------------------------77 ,
4к [(х— S)2 + у2 г2] /а
где 5 в настоящем случае изменяется от —с до и
ds = с sin 9 db 2). Отсюда для Фо имеем следующее выражение:
0 —о
Г У с f Г sin лб sin 0 db
Фо = — w dz == — —------- dz ------------------------,
J 4к J J [(x + c cos О)2 + у2 + г2]
oo —oo 0
или
тс 0
Ф „=_a^fsin„Osi„o«o f--------------------
4тс J J [(x + c cos О)2 + у2 + г2]/a
и так как
о
f___________dz ._________________1______3)
J [(x + c cos 6)2-f-У2 + ^P3 (x -|- c cosO)2 -|- y2
— oo
то окончательно имеем:
к
ф __ f sin nO sin 0 db
0 4?c J (x + c cos 0)2 -|- y2* '
0
9 См., например, В. В. Голубев, Теория крыла аэроплана
конечного размаха, стр. 336.
2) Там же, стр. 338.
3) Там же, стр. 339.
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
731
Пусть F(z^ есть характеристическая функция течения
в плоскости (х, у). Тогда
Р(г1) = Ф0+/ЦГ0,
причем на границе струи|значения Фо задаются выражением (1).
Но из выражения
1 _ х + с cos 6 — yl
+ С COS 6 (х 4" С COS 6)2 у2
видим, что значения F (zr) на границе струи могут быть
написаны в виде
с V.A f sin тгв Sin6 rf6
F(^) = 4------------:-----Й ,
v 17 1 4kz J 4- c cos 6
0
что еще можно написать, пользуясь выводами предшествую-
щего параграфа, в виде
/71(-г) = ^2<-1)И+175- (2)
Возьмем теперь характеристическую функцию дополни-
тельного течения в виде
/72^) = 2<Л«-ЬМ")(гП + ^)- <3)
Тогда при z = Re** действительные части выражений (2)
и (3) должны быть равны при всяком <р. Отсюда из равенств
Р /г> 1 у (—1 )п+1 Лп (cos /гср — z sin пч?)
' 4Z^ Rn
F2(Re^)= {^ + /X}/cosn<4/?M-|-4i) +
получим:
(—l)n+2 ' Лпз1п ny _
4 Rn ~
= A'n cos n<₽ (Rn + A)_ a" sin n<f (Rn — , (4)
732
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
и так как равенство (4) справедливо при любом ср, то имеем:
4=0,
„ _ (-!)»+! Ап
п 4 Я2п — 1 ’
а потому характеристическая функция дополнительного те-
чения имеет вид

Очевидно, что функция /4(2) предшествующего пара-
графа и F2(^) можно написать в следующем общем виде:
причем для свободной струи е = 1 и для трубы с твердыми
стенками е = —1.
Заметим, что в рассматриваемом случае характеристиче-
ские функции F^z) и F2(^) отличаются не только знаком,
"но и значением коэффициентов разложения.
§ 5. Изменение скоса потока в точках несущей линии
под действием границ
Чтобы получить изменение компоненты скорости vUi
вызываемое действием границ, найдем
Так как
dF^) (- 1)п+1пЛга / ,____1_\ 2z* =
dzx 4Z1 \ zn+1Jc(z^— 1)
= (-1)”+1пЛга / _ J_\ 1
2с“ R2n — е \ гп) г_1’
Z
то, подставляя сюда z = eBi, получим компоненты скорости
в точках несущей линии
dF(Zi) _ „ _ eZ у (- 1)п+1пЛга sin пб
dzt 1 1 2с 2^ — t sin 6
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
733
откуда
= О,
v (~^ПпАп sin пб
1 2с R2n—е sin О
Отсюда видим, что для трубы с твердыми стенками
(е = — 1)
__ 1 у (— 1)п+1пЛп sin пО
1 2с /?2п+1 sin6
и для случая струи (е = 1)
1 у (—1)п • пАп sin
V1 ~ 2с /?2п_ i sinQ ’
В частности, в случае эллиптического распределения
т?! = ~ ^2^7] (труба с твердыми стенками),
1 Л / ч
(СТРУЯ).
причем
D2 __ а~\~Ь
* ~ а — Ь'
так что окончательно можно написать:
для твердой трубы
л — Ь . 1 , Г а — b л
771 •— z-A-t - ~г~ 1/ -j—77 ,
1 4ac 1 4a r a + b 1 ’
для струи
л — b л 1 , / a — b л
77t =--tv A = ttI/ i~rA.
1 4bc 1 4b V a-{-b 1
Отсюда получим изменение угла скоса
ДТ = — v = —(твердой трубы),
= = А (свободной струи).
Иначе обстоит дело в случае, когда распределение цирку-
ляции отлично от эллиптического.
734
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Если мы в этом случае ищем такой средний скос и такуй
среднюю скорость опускания, при которой индуктивное
сопротивление получается равным действительному индуктив-j
ному сопротивлению, то отсюда следует, что такая средняя
скорость отличается от обычной средней скорости.
Индуктивное сопротивление элемента крыла определяется
по формуле
— рГг^ dz.
и, следовательно, полное индуктивное сопротивление вы*
ражается в виде
+ с
ДС?1 = — J pr^d*.
-с
В рассматриваемом случае
к
. „ f (V , л) « V (—l)mrnAm sinmfl . а ,0
ДО. =—р I 7. Ап sin /101 н- 7, -—з----------csin0d6,
t7 J Ш » J2c^U — s sine
О
или
AQ1==
т, п
о
sin „0 sin /п0 d0,
Я2и1-е
и так как
при
J*sin nQ • sin mO dO = О
о
J*sin sin М = у
о
при т = п,
то
Так как
при
п — нечетные, то
ЛЛ _ V 1)"+1”Лп
4 /?2п—е
симметричном распределении циркуляции
в этом случае
ЛП пАп
4Р-“/?2”—е"
К ТЕОРИИ ВЛИЯНИЙ ЭЛЛИПТИЧЕСКИХ ТРУБ
735
Следовательно, для случая твердых стенок
(е==—1) мы имеем уменьшение индуктивного
сопротивления, равное
лп _ ~ V пАп
ДС1 4 р Л8» + 1 ’
и в случае струи (s = 1)— увеличение индуктив-
ного сопротивления, равное
ЛП — я Л V лЛ”
д<?1— 4 Р — Г
Найдем теперь среднюю скорость опускания в указан-
ном выше смысле.
Чтобы получить индуктивное сопротивление, равное -AQa,
надо взять скорость опускания так, чтобы
Д^срРС J* (S sin s*n 9 d® = ^Ql,
о
Так как
п
/ sin s*n ® У *
о
то для определения Дт7ср имеем уравнение
СД 77сррЛ
те _ете VI ( 1)П+1 П^п
1 У = Т Р R2n — е
ИЛИ
д^ср — 2с R‘in — е А1'
Отсюда получим для изменения среднего скоса выражение
Д^рср —
tAi у
V ~~ 2Vc Jd
е
и для случая эллиптического распределения циркуляции
«А
Д?«р 2lZc(#a—е)'
736 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
что совпадает с приведенными
ного изменения скоса в случае
выше формулами для истин-
эллиптического закона рас-
пределения циркуляции.
Заметим, наконец, что при симметричном распределении
циркуляции имеем:
л - (4?
— 2VcZi
СВОДКА ФОРМУЛ
I. Случай трубы с твердыми стенками
1. Распределение циркуляции по фокальному отрезку
,Г = 5 sin (О С 9 -С я).
2. Характеристическая функция дополнительного течения
3. Дополнительная скорость от действия стенок трубы
в точках несущей линии
____ 1 yi (—l)n+1 пАп sin пб
V1~ 2с 21 А2'Ч~ 1 ‘
4. Дополнительное индуктивное сопротивление
дп_^У
4 2л А2«+1
5. Средняя скорость опускания
. (—1)п-п(ф^)2
\v — dl У__________\А1/_
ср 2с 2i
6. Средний скос
-А у( } W
?ср 2Vc£i ^+1
7. = (а и ь— полуоси эллипса).
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
737
II. Случай трубы с твердыми стенками; симметрично
расположенное крыло с эллиптическим
распределением циркуляции
1.
2.
3.
4.
5. Д^ср
Г = sin 9.
F (г) = — 4(^4-1) •
_ 1 At
V1 2c № + 1 '
т:р A2 _ vpa — b 2
4 Лз+1 — 8 a Al'
At ______ a — b
2c(/?2+l) “ 4ac A
A, ___ ___ a — b . __ 1 лГа — л
о- Д?ср— 2Ус 1)—““ 4^7 А1~~~4Уа Г а+~Ь А*'
1 —
III. Случай струи эллиптического сечения
1. Распределение циркуляции по фокальному отрезку
Г = 2 Аг sin пб (О 0 к)-
2. Характеристическая функция дополнительного течения
3. Дополнительная скорость от действия границ струи
_________________АХ1 (— П^пsin л 6
Vl ~~ 2с 24 1 "sinT •
4. Дополнительное индуктивное сопротивление
л _ (_1\п+1 пА^
4 4 ^—1 •
5. Средняя скорость опускания
Дг, -А у.________-___1AZ
2с 24
738 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
6. Средний скос
7. R2 = (в полуоси эллипса сечения струи).
IV. Случай струи эллиптического сечения;
симметрично расположенное крыло с эллиптическим
распределением циркуляции
1. r^^sinS.
ч V _ __ ^t(g-6)_ 1 /~а~Ь .
1 2с(/?2 —1) 46с 46 V а+ 6 р
. 4.
ад Л? ад а — 6 ,
д<5 = Т л2 — 1 ' "8 ~Т~
л ____ 1 _а — b \ Г а, — b .
’ ^ср~"2е R2 — 1“ 4bc Al~"TbV а + 1)1'
д ______ ___а — b . _ \ Га— b .
’ ‘ср ~ 2Vc (Я2 — 1) “ 4 Vbc Л1 “ 4bV V аГуЪ
Заметим, что экспериментальные данные дают не очень
хорошее согласие с теоретическими выводами. Причиной
этого является, по-видимому, влияние хорды х).
ПРИЛОЖЕНИЕ
к
n r f cos nO db
Для вычисления интегралов In = J cos g можно вос-
o
пользоваться тем же методом, который применяется Глау-
эртом в случае, когда z действительно и лежит вне от-
*) См., например, Н. М u 11 г а у, Ober die Grosse der Berichti-
gungsbeiwerte filr Widerstand und Anstellwinkel bei Freistrahlen von
elliptischen Querschnitt. Luftfahrt-Forschung, t. 12, № 8, 1935, стр. 265.
К ТЕОРИИ ВЛИЯНИЯ ЭЛЛИПТИЧЕСКИХ ТРУБ
739
резка —с, -|-с,
I = f _ 1
0 J z + с cos 6 У г2 — с2
и
= f cos6rf6 I p±CcosOrf9__£ f М
1 J z -f- c cos 6 c J z -f- C COS U C J Z ~P c cos 6
0 0 0
7C 7C z 7L У г2 — с2 — z
с с У г2 — с2 с У г2 — с2 ’
положим
z = с ch X.
Тогда
Уz2 — с2 = с Уch2X— 1 = с sh X,
поэтому
I =
0 с sh X ’
Л = —тт {sh X— ch X} =-------тт'^“х- (О
1 с sh X 1 ’ с sh X 4 7
С другой стороны,
тс
г | г _______ f COS (п 4- 1) 0 + cos (п—_____
'n+i“Wn-i — J г + ccosG
о
тс тс
___ cos п0 • cos 0 г/О 9 1 f cos п0 (г 4- с cos 0) fl
J z 4- c cos 0 c J z 4- c cos 0
о о
тс
o z f cos nO _____ a z r
c J z 4“ c cos 0 " c n’
о
t. e.
4+i+ 4-! = -244. (2)
Так как формулы для /0 и Д могут быть написаны
в виде
п v 7 с sh X ’ v 7
740
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
то, полагая, что (3) верно до номера п включительно, полу*
чим по (2)
4+1 = —2-(— ”Х — (— I)"1—^*“(га-1)х =
ПЬ1 с v 7 с sh л v 7 c-shX
= —(—l)n[2chke nX — e ('tl,X] ——
v 7 L J csh X
т. e. формула (3) верна для любого п.
О ПРИМЕНЕНИИ
ФОРМУЛЫ ШВАРЦА—КРИСТОФФЕЛЯ
К ПОСТРОЕНИЮ АЭРОДИНАМИЧЕСКИХ
ПРОФИЛЕЙ *)
Краткое содержание
Работа ставит своей целью развитие общего приема точного
получения аэродинамических профилей методами конформного ото-
бражения. Даны общие соображения, позволяющие получить при
помощи формулы Шварца — Кристоффеля, выражаемой в элементар-
ных функциях, некоторые серии профилей. Полученные общие
выводы применяются к случаю профилей с элеронами и профилей
с постоянным центром давления.
Введение
В настоящее время известно очень большое число аэро-
динамических профилей, получаемых теоретическим путем;
при этом, в общем, можно указать два пути, по которым
получаются такие профили. Во-первых, ряд авторов полу-
чает их, обобщая формулу, дающую отображение профиля
Н. Е. Жуковского,
г I
1 Z
более общую формулу
1) Опубликовано в Трудах ЦАГИ, вып. 493, 1940. (Прим, ред.)
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА----КРИСТОФФЕЛЯ
741
Таковы профили Мизеса; дальнейшее обобщение в том же
направлении дают профили Туссена и Карафоли х). Такие
профили можно назвать аналитическими профилями.
Другой прилагаемый здесь метод представляет построе-
ние скелетов профиля в виде дуги окружности, ломаной
линии и т. д., с последующим применением метода округле-
ния, указанного Н. Е. Жуковским. Большое число таких
профилей указано С. А. Чаплыгиным * 2). Такие профили можно
назвать геометрическими профилями. Для построения таких
профилей применяются более или менее искусственные сообра-
жения, которые обычно не дают возможности ни получить
обобщения получаемых профилей, ни выработать единого
общего приема для получения отображающих формул.
Задача настоящей работы — показать, что все известные
геометрические профили могут быть получены систематиче-
ским применением формулы Шварца — Кристоффеля. Попутно
дано исследование применения формул Шварца — Кристоффеля
для различных профилей и разобраны широкие классы случаев,
когда формула Шварца — Кристоффеля позволяет написать
окончательное выражение отображающей функции при помощи
элементарных функций. Наконец, полученные общие фор-
мулы приложены к подробному исследованию профиля с эле-
роном и к группе профилей, которые С. А. Чаплыгин назвал
составными профилями 3), в случае, когда они являются про-
филями с постоянным центром давления.
§ 1. Основные определения
В настоящей работе изучаются некоторые вопросы, свя-
занные с отображением на полуплоскость или на внешнюю
Ч См., например, В. В. Голубев, Теория крыла аэроплана
в плоскопараллельном потоке, гл. VI, 1938.
2) См., например, С. А. Чаплыгин, О давлении плоскопарал-
лельного потока на преграждающие тела, Собр. соч., т. II, стр. 184.
К общей теории крыла моноплана, Собр. соч., т. II, стр. 246. К тео-
рии открылка и закрылка, Собр. соч., т. II, стр. 472. Подъемная сила
составного крыла, Собр. соч., т. II, 488; 1948. См. также С. М. Т а р г,
К теории крыла со щитовидным закрылком, Труды 3-й конференции
по аэромеханике, ч. II, стр. 15, 1935 и В. В. Голубев, Теория
крыла аэроплана в плоскопараллельном потоке, гл. V, изд. 2-е, 1938.
3) С. А. Чаплыгин, Подъемная сила составного крыла, Собр.
соч., т. III, стр. 235, 1935.
742
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
часть единичной окружности областей, ограниченных отрез-
ками прямых, или лучами, или прямыми. Такие задачи весьма
часто встречаются при исследовании различных вопросов
плоской гидромеханики.
В дальнейшем мы будем рассматривать главным образом
односвязные области, ограниченные конечным числом прямых
или их частей; такие области мы будем называть много-
сторонниками, а прямые или их части, обозначающие
границы многосторонников, — сторонами многосто-
ронни к а, точки пересечения сторон — его вершинами;
точно так же вершинами назовем концы сторон, не примы-
кающие ни к каким другим сторонам. В частности, вершины
многосторонника могут лежать в бесконечности.
Возьмем точку стороны многосторонника, не являющуюся
его вершиной. Если из нее, как из центра, описать окруж-
ность, то сторона разделит одну окружность на две части,
причем сторона является диаметром. Может случиться, что
к стороне из многосторонника можно подойти с одной сто-
роны или же к ней можно подойти и с той и с другой
стороны; во втором случае взятую сторону считаем за две
стороны, сообразно со способами подхода.
Рис. 1.
Наконец, будем считать, что бесконечность никогда не
является точкой многосторонника; она может быть или точ-
кой его границы, или внешней точкой. В дальнейшем будем
рассматривать только многосторонники с конечным числом
сторон. Многосторонники, имеющие вершины в бесконеч-
ности, назовем звездообразными многосторон-
ни к а м и.
Примером многосторонника может служить обычный тре-
угольник, представляющий собой трехсторонний,
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
743
Внешняя часть треугольника также представляет собой
трехсторонний, но неодносвязный и имеющий, кроме трех
вершин, еще четвертую в бесконечности.
По этому поводу заметим, что в состав границ мы можем
включать и точки, изолированные и не принадлежащие много-
сторонние; их мы будем называть изолированными верши-
нами. Часть плоскости, ограниченная одной бесконечной
прямой, представляет собой односторонний; у односторон-
ние есть одна вершина в бесконечности.
Угол представляет собой двусторонний. На рис. 1 даны
примеры трехсторонников.
§ 2. Формула Шварца—Кристоффеля
Формула Шварца — Кристоффеля дает возможность по-,
строить общий вид функции, дающей отображение внутрен-
ности многоугольника, лежащей в конечной части плоскости,
на полуплоскость или на внутренность окружности. Нетрудно
Рис. 2.
применить формулу Шварца — Кристоффеля к случаю одно-
связной области, представляющей многосторонник в том
случае, когда некоторые его вершины лежат в бесконечности.
Рассмотрим, например, многосторонник ABCDEFGHA
(рис. 2); это — многосторонник с вершинами А, В, С, Z), Е, G
на конечном расстоянии и с F, Н в бесконечности.
744 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Найдем общий вид формулы, отображающей внутрен-
ность этого многосторонника на полуплоскость. Для этого
проведем две вспомогательные прямые F^Fp и построим
формулу Шварца — Кристоффеля, дающую отображение
верхней полуплоскости на внутренность многоугольника
ABCDEFJ^GHJ-^A.
Называя углы этого многоугольника через а^тс, а^тс, а^тс
и т. д. и замечая, что а^тс = 2тс, а^тс = 2тс, а#тс = 2тс, т. е.
аЛ = а^ = а^=2, напишем формулу Шварца-Кристоффеля
в виде
w = С J* (z — a) (z — Ь) в 1 (z — с) с (z — dy п 1 X
X (z — е) (г — /1)°^ —/2)а^ 1 (г — g) (z — \
XAz — h2)H* 1 dz, (1)
где a, b, . .., h2— точки действительной оси, соответствую-
щие вершинам многоугольника.
Представим себе теперь, что точки F1} F2 и Нг, Н2
уходят в бесконечность, тогда и /2, hr и h2 сольются
соответственно в некоторые точки f и /г, соответствующие
вершинам F и И, находящимся в бесконечности.
Формула (1) примет вид
w = C §(z — a)(z — b^B 1 (z — с)а° 1 (z — d)aj) 1 (z—e)X
X (z—f) Fi^F‘ 2 — g)(z— 2 dz. (2)
При переходе к пределу мы можем считать, что FrF2 и А^Н2
передвинутся параллельно самим себе.
Продолжив до пересечения прямые EF и FG, получим
точку F3; обозначим угол F1F3F2 через артс, получим, что
—|- ар2 —|- ар = 1, арх —|- ар2 — 1 — ар.
Аналогично получим точку Н3 и угол который
назовем а#тс, причем ая1Ч-аи2=1—ая-
Подставляя эти значения в формулу (2), получим:
w = C J (z—a) (z— b)*B 1 (z — с) c 1 (z — d)aj) 1 (z—e) X
X C?—J) dz. (3)
О ПРИМЕНЕНИИ ФОРМАМ ШВАРЦА------КРИСТОФФЕЛЯ
745
Формула (3) имеет вид обычной формулы Шварца — Кри-
стоффеля, причем показатели ар и а#, соответствующие
углам, вершины которых лежат в бесконечности, входят со
знаком минус. Короче: в случае, если отображаемый
м н о г о с т о р о н н и к имеет вершины в бесконеч-
ности, то в формуле Шварца — Кристоффеля
углы, вершины которых лежатв бесконечности,
надо считать отрицательными.
Заметим, что если мы имеем два прилежащих друг к другу
угла с вершинами в бесконечности, разделенные лучом L
(рис. 3), то соответствующие множители в выражении под
интегралом в формуле Шварца—Кристоффеля будут:
(z-a,) ’ 'l(z — b) (г —cj ^-1.
Представим себе теперь, что точка В уйдет в бесконечность,
так что останется один угол — а — j3; тогда точки а, Ь, с
сольются, и мы получим:
— — ay* V-1,
как и должно быть по формуле Шварца — Кристоффеля.
В частности, продолжения одной прямой образуют в бес-
конечности угол —тс. Действительно, проведем вспомога-
тельный луч Lr (рис. 4).
Тогда в формулу Шварца—Кристоффеля, дающую отобра-
жение такой добавленной фигуры, будут входить множители
(z — a) (z—a1)~a'1(z—l) (z — bty^~l (z — b).
746 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Если теперь точку I удалить в бесконечность, так чтобы
луч Ly исчез, то точки I, совпадут и мы получим:
,(г — a)(z— /)а~р 1 (г — Ь),
или, так как a—|—р = 1, то
(z — a)(z — iy2 (z — b),
так что точке I соответствует показатель —1 — 1, т. е;
в бесконечности имеем угол —к.
Нетрудно доказать, что при сделанных предположениях
сумма углов ^-сторонника удовлетворяет обычному условию
= — 2),
где — углы многосторонника, или
5«л = (« —2).
Для доказательства этого положения рассмотрим много-
сторонник (рис. 5) ABCDEFQA, в который входят углы
о с вершинами на конечном рас-
Д „ стоянии и углы с вершинами
в бесконечности (угол В). Пусть
77 '' число сторон многосторонника п
(на рис. 5 п = 7); проведем вспо-
могательную сторону В'В", тог-
да получим многосторонник с
п-\- 1 сторонами, для которого
формула (1) верна. Называя че-
рез 2 а/с сумму, отнесенную ко
всем вершинам, лежащим на конечном расстоянии, получим:
S ?i“F ?2 = (п+ О — 2,
где и р2тс — углы многосторонника с вершинами в В' и В".
Иначе, замечая, что
Р1+ ₽г+ Р = h
где р — угол между АВ и СВ, можем написать:
24+1—?=(«+!) —2,
откуда
S4+(—?) = «—2.
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ 747
Но —а потому 2'ай + (—= Следова-
тельно,
2 = n — 2,
где 2 ак относится ко всем углам, как лежащим своей вер-
шиной на конечном расстоянии, так и к тем, вершина кото-
рых лежит в бесконечности и кото-
рые считаются благодаря этому от-
рицательными.
Формула (1) отличается весьма
большой общностью; ее можно
применять, начиная с п=0.
Действительно, при п = 0 мы
имеем всю плоскость с выкинутой
бесконечно удаленной точкой. В этом
случае угол при бесконечно удаленной точке мы
— 2тс. К этому можно прийти из следующих соображе-
Если взять, например, четырехсторонник (рис. 6) и уда-
вершины в бесконечность, то получим равенство
будем счи-
тать
ний.
лять
аВ + aD + “л + аО ~ 2
(так как п — 2 — 4— 2), откуда
аз+ал = 2 — <41+ ас) = 2 — 4 = — 2-
Это равенство в пределе, когда А и С уйдут в бесконеч-
ность, и даст угол в бесконечности, равный ^в~\~ав =— 2,
что удовлетворяет формуле (1), которая при п = 0 дает:
В
Рис. 7.
При п = 1 мы имеем полуплоскость,
для которой есть один угол в бесконеч-
ности, равный —тс; следовательно, в этом
случае
S “л = — 1 >
как это и дает формула (1) при п=1.
При п = 2 мы имеем двуугольник с углами ср и —ср.
Сумма углов равна нулю, как это и выходит из выведенной
формулы (рис. 7).
?48 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Рассмотрим еще несколько примеров. Трехсторонний
(рис. 8) имеет сумму углов
2тс~Р(— а) + (—р) = 2тс —к,
как это и должно быть по формуле (1).
В случае четырехсторонника (рис. 9) сумма углов равна
2тг(верш. Л)—{—(—а)+ 2~ (верш. 0+ [—(2 — а)] = 4~—
— 2ir = 2тс, как и должно быть по формуле. Легко вывести
Рис. 8. Рис. 9. Рис. 10.
формулу для суммы углов, обобщающую формулу (1) на
случай многосвязной области.
Выведем сначала формулу для внешних углов много-
угольника. Пусть имеем многоугольник ABCDEA (рис. 10).
Проведем вспомогательную пря-
z мую в бесконечность, тогда
сумма углов фигуры MABCDEAM
с вершинами в Л, В, ..., Е и
в бесконечности удовлетворяет
равенству
2к) = к[(п + 2) —21,
где S % — сумма внешних углов
и п — число сторон многоуголь-
ника ABCDE, к которым в формуле приходится еще
добавлять две стороны луча L. Отсюда
S п (п+2)>
что и дает сумму внешних углов многоугольника.
В случае, если мы хотим найтл сумму внешних углов
ряда многоугольников ABCDE, A1B1C1Dlf ... и т. д. (рис. 11),
Ь ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ 749
то, проводя в бесконечность лучи L, Llt . .. и т. д., получим
S <?» + (— 2тс) = тс (ге + 2р — 2),
где 2 — сумма внешних углов всех
р — число лучей L, откуда =
= к(м-]-2р).
Если же бесконечность не входит
в состав границы области, т. е. она
имеет вид, указанный на рис. 12, то, *|
проводя разрезы L, L± и т. д., по- 1
лучим для суммы углов формулу
2?* = тс(« + 2р — 2).
которую и можно рассматривать как
самую общую формулу суммы углов
многосторонника, имеющего связ-
многоугольников и
Рис. 12.
ность р.
Таким образом, отсюда получим и сумму внутренних
углов многоугольника, полагая р = 0, и сумму внешних
углов, полагая р = 1 и учитывая угол в бесконечности.
§ 3. Упрощения формулы Шварца — Кристоффеля
Формула Шварца — Кристоффеля для отображения одно-
связного n-сторонника допускает упрощение в силу общей
справедливости углового соотношения = п — 2, если
изображение одной из вершин первоначальной области пере-
нести в бесконечность. Действительно, формула Шварца—*
Кристоффеля имеет вид
‘W = C^H(z— ак)*к 1 dz,
где
= — 2.
Если одну из точек ак, например а±, перенести в бес-
конечность, что может быть достигнуто преобразованием
1
г—а1==_,
750 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
то после подстановки получим выражение
w = C' f П'О1 —1 ——
J V ,ЕаЛ-Ш-2
где произведение П (t— Ьк)а^ 1 включает множители со
всеми показателями,
стоффеля имеет вид
кроме at—1, так как после подста-
новки выражение (z— а^1 1 перей-
дет в • Так как 2 ак — п-]-2=
= 0, то ч^ = С' Ji! (t— bk)k dt.
Приложим эти соображения к
отображению на полуплоскость звез-
дообразного трехсторонника, указан-
ного на рис. 13. В этом случае формула Шварца — Кри-
°0 1 — £) С?— $ 1 dz.
Если на плоскости (г) перенести вершину с в бесконеч-
ность, то получим:
Г z — b
w = --dz.
J (г —я)
Интеграл этот можно выразить в виде
w = /(z) =
(г — а?
где k — некоторое постоянное.
Действительно, из (1) имеем:
/-«=/«
откуда
г/ / \ 1 Г а — ] z 1 х
f (z) =-------— z----z----- (1 — a).
V (z — a)“+ L 1 “ a J
Так как a=^=l, то всегда можно выбрать k таким обра-
зом, чтобы
а — ak . , а — (1 — а)Ь
——— = Ь, откуда k =--------------.
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
751
Таким образом, отображение дается формулой
w = С
z — k
(z —л)а
Если сделать замену, положив w = —
J wt
то получим:
~ C
(*-Qa
z — k ’
и, переводя обратно на плоскости (г) бесконечность в конеч-
1 д.
ную точку, полагая, например, получим формулу
вида
Так как k может быть выбрано произвольно, то, взяв
k ~~ 0, получим:
w = CtXa (t— а^\
дробно-линейной подстановкой можно привести это выра-
жение к виду
w = C(t— 1)1-“(^+ 1)“.
о 1
В частном случае при а = у имеем:
w^cyt2 — 1.
§ 4. Об отображении звездообразных областей
Если многосторонник ограничен рядом лучей, продол-
жения которых все проходят через одну точку, то можно
придать другой вид задаче об отображении этой области
на внешнюю часть окружности. Предполагая, что точка
пересечения всех прямых, образующих границу области, есть
w = 0 (рис. 14), и делая преобразование , переве-
дем область в новую область, ограниченную несколькими
отрезками прямой, проходящими через начало координат
(рис. 15). Называя через как углы, образованные сторонами
многосторонника, и полагая, что точка О' изображается на
752
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
плоскости (г) точками alt а2, ап, получим отображаю-
щую функцию в виде
W1 = С J (г~Д1)°‘ 1 • • • —61) • -:(z bn\ dZt (p
где точки ak и bk— точки единичной окружности, т. е. все
Рис. 14.
Рис. 15.
имеют вид е* и, следовательно, определяются 2п действи-
тельными параметрами-углами. Так как, кроме того, имеется
Рис. 16.
дящихся к следующему,
вуют на плоскости (wj
то (рис. 16)
возможность сделать поворот
плоскости (г), то мы всегда мо-
жем считать, что один из углов,
например угол для точки av
может быть взят совершенно
произвольно. В дальнейшем мы
будем предполагать, что at = 1.
Таким образом, в формуле (1)
остается 2п—1 параметров.
Легко видеть, что среди этих
параметров независимых только
п—1, потому что между ними
существует п соотношений, сво-
Так как все точки а соответст-
одной и той же точке — началу,
Xj ха
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
753
где
= J (2 ~ ai^‘1 1 . {г—ап)Лп — Z>t)... (z — b
ит. д., в частности
/. -«
Хх+ХзЧ-... +лп
Эти уравнения дают п соотношений между числами
alt а2, . .., ап, bt, . .., bn. Таким образом, в уравнении (1)
остается п— 1 свободных параметров, за которые мы можем
выбрать п— 1 углов, соответствующих точкам а2, а3, . .., ап.
Меняя эти углы, мы получим различные значения для отно-
шений длин отрезков, проходящих через О',
,, — ^4 _/п
“ Zj ’ ~~ /j ’ ~ Zt ’ • • • ’ — Zt ’
где
— О Ль 12~ОГ... (рис. 15).
Аналогично предыдущему, ищем интеграл в виде
Wi (? — at)“‘ • • • (z — an) “п
Отсюда
дГа>1_(г — д,)*» ... (z — an)Лп Г gi . «2 , , ап _ П
dz z [z — ' z — a2 * * * ' z—an z J ’
причем во всех предшествующих формулах
а1 + а2 + • • • + ап = 2.
Преобразуя скобку, получим:
^dz
... (z~an)z-\-a2 (z—aj) а3)... г+... +(z—дг)(z—д2)... (^
Z (Z — (г — л2) ... (г — ап)
On)
754
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
и, преобразуя числитель, получим еще выражение
zn (ai а2 ап — О — zn~1 [04 (а2 -|- . . . -j-
+ а2 (а1 4“ + • • • + • • -+ап (а1+^2 + • • • 4“ ап-1) —
— (.ai 4“ а2 • • • ~Ь ап)1 “Ь • • • ~:zn zn~1 Iai ^1)~Ь
+ а2 (S — а2) . . . + ап ($п a.i) ^И~ • • • = zn
— zn~l\2S— S — агаг — а2а2— . . . —апап] 4" . . . =
= zn—zn -1 [a j (1 —ах) + а2 (1 — а2)+. . . -^ап (1 — ап)] +...,
где S = а2 + . . . + ап, и если разбить правую часть
на сомножители, то получим еще
(г — b^z — b2) , . . (z — bn).
Отсюда
= (z-a^ ..^Z-an)an\ {z_bi)(z_b2) t (z_
Таким образом, это выражение имеет вид формулы (1).
Числа blt b2i ... удовлетворяют, очевидно, условию
+А + • • • + + ai (а1 1) + ^2 (а2 — О + • • • =
что равносильно требованию
/
Xi + Х2+ •.. +Хд
В силу вида формулы (2), очевидно, выполняются и все
условия J* = 0. Остается выяснить, могут ли быть под-
Х/с
бором я2, я3, . . ., ап даны любые значения отношениям
Р-р Р-2, • • •> Р-п-
Пример. Пусть все а = -^-(т. е. атс — и
7С . 27С . ТС .
— г — г (2п-1) — г
а2^ еп ’ а3 = еп , ..., а2п = е п 9
или
а2 = е, = е2, ..., а2п = е2п Ч
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
755
Тогда формула принимает вид
_L 1 п_______
(г-е)п ...(z—e2n 1)п _У
2 Z '
иначе, в более симметричном виде,
_ zn-------------------------------!_
1 z1
Частный случай при п = 1 дает известную формулу
1
= z------.
1 2
Здесь, как легко видеть, все 1к равны между собой и
Можно показать, что в случае звездообразного много-
сторонника отображение всегда дается функцией (2). Впер-
вые эта теорема, по-видимому, была доказана Л. М. Лахти-
ным; идея его доказательства состоит в том, что если взять
отношение функции (2) к той отображающей функции, кото-
рая должна существовать по основной теореме конформного
отображения (теорема Римана), то можно доказать, что это
отношение постоянно х).
То же можно доказать, исходя из следующих соображе-
ний. Будем рассматривать отображение внешней части звездо-
образного многоугольника на верхнюю полуплоскость (t).
Пусть вершины звездообразного многоугольника отобра-
жаются в точки ак и $к действительной оси. Если точка О'
(рис. 15) на плоскости (w) находится в w = 0, то отобра-
жающая функция w = f(t) обладает следующими свойствами:
1) в области точек ак f(t) удовлетворяет условию
/(О—гДе ?(0 голоморфно в области
точки ак и
2) в области точки /(/) = ск-\- (t — $к)2 (О, где сА=^=0;
Ч Доказательство приведено в диссертации Л. М. Лахтина,
Приложения теоремы Шварца — Кристоффеля к теории крыла.
f 56 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
3) есть точка = т + (&¥=0), в которой f(f) имеет
полюс первого порядка; по принципу симметрии тогда есть
полюс первого порядка и в точке t0 = у — /8.
В остальных точках плоскости (/) функция f(t) голо-
морфна и отлична от нуля.
Рассмотрим функцию ~ ?2 (0* Так как при
изменении w вдоль любой стороны многоугольника имеем
w == pedi и изменяется только р, а 0 — угол наклона стороны
к действительной оси на плоскости (w) вдоль стороны
остается постоянным, то на отрезках действительной оси
плоскости (t)
1S)r _р'
W Р ’
а потому ф2(0 Действительно вдоль действительной оси.
По свойству (1) <р2(0 в области точек ак разлагается
в ряд
* u/t
где ф (0 голоморфно в области ак; по свойству (2) в области
/ — ф2(0 голоморфно.
В области точек /0 и f0 <р2 (/) имеет полюсы первого по-
рядка и разлагается соответственно в ряды
?2(0 = -т^ + Ф1(0.
<Р2(о=--Дг+ф2(о,
Г - lQ
причем фх (f) и ф2 (0 голоморфны в области t0 и t0. Во всех
остальных точках «2(0 голоморфно.
Отсюда сейчас же следует, что
= ф = у _______________1______L_
/(О Zlt — ак t — t0 t — t0’
и, интегрируя, получим:
f _с— — ап)^п
(3)
(t-tj (t-b)
О ПРИМЕНЕНИИ ФОРМУЛЫ шваРца----КРИСТОФФЕЛЯ
Для того чтобы перейти к случаю отображения на внеш-
нюю часть окружности радиуса 1, сделаем преобразование
/__t
t-tQ'
откуда
ак — 4)
где Яд. — —-— -----точки, в которые переходят точки на
ак — Ч)
плоскости (г); так как все ак— действительные, то
| = I а *1 = 1,
“fc — to I 1 А|
т. е. все точки ак лежат на окружности | z | = 1, и, следо-
вательно, действительная ось плоскости (/) переходит в окруж-
ность ]z|= 1, а так как точке соответствует z — оо, то
верхняя полуплоскость (f) переходит на плоскости (z)
во внешнюю часть окружности |z|=l.
Подставляя значения (4) в формулу (3), получим:
= f (z)__Сх а%У * ... (z
т. е. получаем равенство (2).
В заключение заметим, что нули bit Ь2, ..., Ьп функции
а1_____________I____а2 I I ап_________J_
z± — а± ~r z — а2 ' * "* z — ап z
обладают замечательными свойствами
(- 1Ж . . . bn - - (- 1)” а,а2 ...ап,
т. е.
Ь^2 . . . Ьп= яхя2 ... ап.
Пусть
bk = e^^t ак — е^к\
тогда имеем:
п п
2^ = 2’%+^-’ (5)
1 1
758 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОбАМ АЭРОДИНАМИКИ
• Назовем через 8Л угол, образованный прямой, идущей
из точки z 0 в точку Ьк, и биссектрисой угла ак^Оак.
Очевидно, что
= (6)
причем = 0, так как = 1 и = 2к.
Складывая равенства (6), имеем:
2= 2 {Ф* | £ ф*-IlWa+W. • •
• • • + (2^+ 8-w)l — 2 ф/с (S ^7с+ тс),
и, следовательно, согласно равенству (5)
S 5^ = 0,
т. е. сумма угловых смещений точек Ьк относительно сре-
дин соответствующих дуг ak+idk равна нулю, что еще можно
выразить так: в среднем все точки Ьк лежат посредине
между точками ак.
§ 5. Об отображении звездообразного четырехсторонника
Рассмотрим отображение звездообразного четырехсто-
ронника на полуплоскость, что можно всегда свести к ото-
бражению области, ограниченной ломаной линией, на внешнюю
£
(С,)
( Bib,)

Рис. 17.
часть единичной окружности (рис. 17). Такое отображение
дается при помощи интеграла Шварца — Кристоффеля
С = J (z — 1) (г — bty~1 (z - С0 (г — dj2=
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
759
Ищем интеграл в виде
f(z) = (г-61)а(г-^1)2~и ,
откуда
/2) 1=1 _ 11
Для нахождения критических точек имеем уравнение
а (г2 — zdx) + (2 — а) (г2 — zbj—[z2 — (br + dj z + ЬМ=0,
или
z2 [a -(-2 — a — 1] — z [adx + (2 — a) bt — br — dx\ — bxdx = 0,
t. e.
z2 — z [a (dx — b^ — — ^X)J — bxdr = 0,
иначе:
z2 — (a — 1) z — dj\ = 0.
По условию задачи мы должны потребовать, чтобы один
из корней был равен 1. Следовательно,
1 — (a— 1)(^ — ^) — dxbx = 0.
Так как произведение корней равно —dfi^ то второй
корень равен —d±bv
Итак, окончательно имеем следующий результат:
zt = \, z2 = — d1b1 (1)
И
1 — (a — 1) — dJi - 0. (2)
Рассмотрим случай
=
тогда [по (2)]
d^ = b2 = 1,
т. е.
= 1,
или
dx^by=— И
760
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
В первом случае
во втором случае
/(2)=<£±1г=2+1+2.
Таким образом, отображающие функции имеют вид
1) C+2 = z + A,
2) с —2 = ^ + 1.
В первом случае имеем на плоскости (С) расположение,
указанное на рис. 18, и, следовательно, точка В совмещается
с точкой А (рис. 17).
Во втором случае имеем расположение, указанное на
рис. 19, и, следовательно, точка В совмещается с С.
Рис. 19.
Отсюда имеем следующий результат: если Ьх стремится
к 1, то форма угла имеет вид рис. 20, т. е. сторона ВС
значительно длиннее АВ\ если же стремится к —1, то
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-—КРИСТОФФЕЛЯ 761
форма угла имеет вид рис. 21, т. е. сторона АВ значительно
длиннее ВС,
Отсюда следует, что, изменяя непрерывно Ьх от 1 до — 1,
мы получим углы, в которых отношение
АВ
ВС
изменяется от 0 до оо, т. е. формула

(3)
дает отображение на внешнюю часть окружности внешней
части углов при каком угодно отношении длин сторон.
Рис. 20.
Заметим, что, если стремится к ±1, то и стре-
мится также к ztl, так как из (2) имеем:
(а-1)^+1
1 (а-1) + ^‘
Таким образом, задача об отображении внешней части
угла на внешнюю часть окружности сполна разрешена при
помощи отображающей функции (3).
§ 6. Приложение полученных результатов
к изучению влияния элерона
на подъемную силу крыла
Полученные выше общие результаты позволяют дать
простые формулы для оценки влияния элерона на подъем-
ную силу крыла.
Рассмотрим случай, когда угол наклона элерона cpir мал
(рис. 22), так что в дальнейших формулах степенями ф,
начиная со второй, мы можем пренебрегать.
В этом случае
а = 1 + <р
762 iv. труды по Разным вопросам аэродинамики
и отображающая функция принимает вид
г^с(г — (z — ф (1)
Для определения положения на вспомогательной окруж-
ности плоскости (z) точек, изображающих кромки про-
филя А и С, имеем в настоящем случае уравнение
«5 г2—ср bjz—(2)
Z? f Bb и так как один корень его
с равен zr = 1, то имеем усло-
а" вие, связывающее Ьг и dlf
Рис. 22. 1—^i)—с?Л==0, (3)
и для изображения точки С (рис. 22) имеем уравнение
z2 = d^b^ (4)
Из уравнения (3) имеем:
+ (3-)
откуда, полагая b1 = e^i и d1 = e?>i) имеем:
ел = (1 4~ 2cpZ sin р),
откуда
Si = — pz —J— In (1 —|— 2cpZ sin Р),
или приближенно
8 =—р~|- 2<р sin р, (5)
и, ограничиваясь членами с ср в первых степенях, имеем
sin 8 = 2ср sin р cos р— sin р. (6)
Из уравнения (1), подставляя z1—l и z2 = — d1b1,
получим длины сторон
.zt = |c(i—^)1+’(1—rf,)1-’!,
к = I С (- d1b1 — bj (- — dj* | =
= I 1)1+,₽(^+1)1-’!,
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА----КРИСТОФФЕЛЯ
763
откуда, полагая
Z2
имеем:
_ + 1)1+‘ (&i + I)1 9 = 1 + ^1 + ^111 d+^i) 9
И (1ftj |(1+61)(1-61)
Но из (3Z) имеем:
а потому имеем, ограничиваясь первыми степенями ср,
I (1 + ^1)(1-^1)п, _ 2 м ’,п0 1 (1 + ^(1-60 | I1 6Х?1 г Следовательно, приближенно имеем: Но из (5) b ₽ 1 • D у = —у + «Sltl р, откуда приближенно b . Q Р . р . Р Sin у ~ ? Sin Р COS у— Sin у = sin ~ b Р , . п . Р f COS у = COS у + ср Sin р Sin у — COS-4 и , » , d+2Tsin’l Ctg 2 = ctg 2 В = Z Zl — 2<pcos2y Следовательно, из уравнения (7) имеем: |Х = (1 + 2?)ctg2| -Т’)н4-р. |clgy]. (’) ^2ср cos2 1 j , Г р + 2ср sin2yj ctgy С1 + 2ср). >
764 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
откуда
Ctgy =(1— <р)/Й
=—(! + <?) W;
(8)
найдем теперь постоянное С из уравнения
С(1 — 61)1+'р(1— =lv
Подставляя Ьг — и dY = e5i, имеем:
1)^—1) (1^1)^/,.
Но
Li ( 21 _Ё1\ Li о
bt — 1 = — 1 = e 2 \£ 2 — e 2 ) = 2ie 2 sin ~
и аналогично
— 1 = 2ie 2 1 sin ~,
следовательно,
Sin {
6
siny
Но из уравнения (8) имеем:
A = р—M sin a
V>+1\ P- + 1/’ 2
Иначе можно написать, откидывая члены с ср2,
откуда
COS ~ = у I
. ₽ 1
S1H — = ,
2 V>+1
m (1 +2 ? m)=ffH (1 ~? гЬ) ’
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-----КРИСТОФФЕЛЯ
765
а потому имеем еще следующую приближенную формулу:
2/р-
р- + 1 ’
sin р =
(9')
т. е. положение точки Ьг в первом приближе-
нии не зависит от ср и определяется форму-
лой (9')«
Так как формула для sinотличается от sin ~ знаком и
знаком перед ср, то аналогично получим:
sin В =
2
р- + 1
(9")
Так, например, при изменении от 10 до 1 угол р по
формуле (9') изменяется от 35 до 90°.
Заметим, что из (9') видно, что sin р остается один
1 • ₽
и тот жэ при и при —, а так как sin-g- при уменьшении
непрерывно возрастает, то отсюда легко заключаем, что
при и — sin р не изменяется, а угол р переходит в к — р.
Р-
Из равенств (8') приближенно имеем:
. ₽ / . о \ 1
Sltl 2 \ Б1П 2 ) — [х -h 1
и
Sin 2 /
—t = -(l+2?) 1--
s,n Т
а потому
(p \ ?
Sltl \ =(-—fl I 2y|x V =e±^ie'f"1(1+?Ti)~e±^i
6 J v 7\‘p-+l/ —
sin-2 у
Итак, окончательно имеем:
(1 __/ь\® 46^ i + —- «рг + тс-ог
! . <9>
причем знак перед тгср/ будет в дальнейшем определен,
766
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Из уравнения (9) находим С:
В+5 В-8
(1())
Так как отображающая функция определяется уравне-
нием (1), т. е.
C=Cz + (...)H-4(-••) + •••> (И)
то, называя через и соответственно скорость
в бесконечности на плоскости (г) и (С) и через 9 и углы,
образованные этими скоростями с действительными осями ‘
на плоскости (г) и (С), из (И) имеем, называя через w
характеристическую функцию течения,
dw dw dt
dz dt dz
и для бесконечно удаленной точки
Voae-^ = Vooe^C.
Подставляя значение (10), получим уравнение
= = = (12)
где L есть полная хорда профиля с элероном, и
6 = 0!+^+^-%^^. (13)
Выражение (13) преобразуем следующим образом:
тег 1 • tg|+‘g| 1 +? 1 — 1 +-Lz2 = ££_ Ур _ 2
ь 2 1 _Х н —1 ’
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА--КРИСТОФФЕЛЯ 767
Следовательно, равенство (13) принимает вид
0 = б1 -byqrp+'P arctg (13z)
Применяя формулу Чаплыгина — Блазиуса, найдем выра-
жение подъемной силы Р в виде
Р = sin 9 -Д-.
I с I
Отсюда, подставляя значения и С, имеем:
Р — pJrj sin 9 =
= npVl,Lsin {91 + ?[^р + arctgTC?}- (15)
Заметим, что при условии, принятом выше, хорда элерона Zx
расположена по действительной оси; следовательно, угол
атаки 9t взят относительно элерона.
Чтобы получить угол атаки 92 относительно основной
части крыла, заметим, что, как видно из рис. 23,
91= +
Следовательно, формула (15) принимает окончательно сле-
дующий вид:
Р = itpV^L Sin {б2+<р+ arctg. (15')
Чтобы определить знак в последнем слагаемом, заметим,
что при Zt=0 имеем рь = оо и формула (15) должна дать
выражение подъемной силы пластин- f
ки, т. е.
P1==Kpy^Lsin62. (16) Pi
хГ\0}
Но при рь = схэ имеем: “
Р = irpV^Lsin (62 + кер ± ттср). (17) I
Из сравнения равенств (16) и (17) ви- /
дим, что знак последнего члена дол- рис 23
жен быть отрицательный.
Следовательно, имеем для подъемной силы выражение
P=KpVlAsin jS-J-cp^^^ + aretg^^jj. (18)
768 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Из формулы (18) видим, что при == сю, т. е. когда О,
р = sin 6;
это подъемная сила плоской пластинки, иду-
щей по направлению /2-
При = 0, т. е. когда 12 = 0, мы должны взять для
а 2 У р^ л
arctg——у значение it, так как при уменьшении от оо до О
Р* * _
2 У □. .2
выражение у сначала положительно и угол arctg i
м П 1 х 2 У U
в первой четверти. При рь = 1 arctg = -у; при даль-
н 2У7
нейшем уменьшении ji выражение отрицательно и угол
arctg—находится во второй четверти.
Р* 1
Таким образом, при ji = 0 имеем:
Р = -rcpV^Z, sin (9 ттср) = -ярV^L sin 0t,
т. е. подъемную силу пластинки, расположен-
ной вдоль L
§ 7. Распределение скоростей на крыле с элероном
Выведенные формулы позволяют найти распределение
скоростей в точках поверхности крыла. Мы решим эту задачу
в случае профиля, представляющего округление разобран-
ного профиля методом Н. Е. Жуковского.
Преобразуем окружность, служащую изображением
профиля. В формулах
z
(О
и
Л = с (г - 1) (г - (г - сг) (г -
dz z2
(2)
положим
внешней
профиля.
г = тогда получим формулы для отображения
части окружности радиуса R на внешнюю часть
О ПРИМЕНЕНИИ ФОРМУЛЫ III ВАРЦА-КРИСТОФФЕЛЯ 7G9
Формулы (1) и (2) принимают вид
Г С (?! - w1+tp (*1 - W’ /ох
_ С - R) (Z1 - btRy (Z1 - C1R) (zt - .
dzx R z\ . < ,
Перенесем теперь начало координат в точку —е/?(рис. 24)
и назовем через z2 комплексное переменное, соответствую-
щее новому началу координат.
Тогда связь между и z2 устанавливается формулой
zi
Следовательно, с новым переменным z2 формулы (3) и (4)
принимают вид
С (z2-^R- Rb^ (г2 - еЯ-Rd^-v
R г2-е/? ’
dt, = С [г2-/?(е+1)] (Z2-^R-Rb1r(z2-zR~c1R)(z2-zR-Rd1r^
dz2 R (z2—-е/?)2
(6)
Положим, что /? подобрано таким образом, что
7?(1 Ч-е)= 1,
т. е. окружность L (рис. 24) есть окружность радиуса 1.
При этом формулы (5) и (6) принимают вид
; = с (1 + в) + V 1 + e-L
(7)
dz2
е+М7г £+C1W-- e+rfir¥
l+ej J-нД2 l+sLc(l+e). (8)
Г2 I + J
При преобразовании плоскости (z2) на плоскость (С)
окружность L перейдет в некоторый профиль Llt округлый
770
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
около передней кромки и у углов и D и с острой задней
кромкой (рис. 25), т. е. получим аэродинамический профиль,
вполне удовлетворяющий обыч-
ным требованиям конечности
скорости обтекания на по-
верхности профиля. Для то-‘
чек профиля L надо положить
z2 — и тогда формулы (7)
Рис. 25.
и (8) можно переписать, считая е малым и откидывая степени е
выше первой, в виде
: = С (1 + s) е (1 - е)]* + * [e8i - е - dt(l - < ? , (д)
Л (гМ-е)2
(Ю)
Так как
—£ — (1 —е) — ен—(Ъх — 1) =е^—(е^— 1) =
а_±₽ . Аз . р
= е 2 2г sin—e2iSin-g- =
о-Г Т* • ft— 3 I -31 /in
— e2 2г e 2 sin - • -|~£ sin 4г (H)
и
|^i_£ — ^(1— e)| =
1
n Г • 9 ft - 3 IO • 3 ft • ft - 3 . 2 • 9 3 1 2 /1
= 2 sin2-yJ-4-2esin ^-cosy Sin —4“ e2 sm2 ^-J (12)
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
771
и аналогично для других скобок
— е = cos 0 — г-\-1 sin ft
и
1
| ebi — е | = (1 — 2г cos ft -f- в2)2 ,
то, подставляя все эти значения в формулы (9) и (10),
получим:
• Л •
г = —4С(1-Н)е2 14 2 ' X
‘ & -]! + ? Г №
т* * . ft—Р . ,3
е2 sin—£ sin —-
-i i-<p
e 2 sin —£------1- e sin -2
cos Я — с 4- i sin ft
4|C| (l + e)sin|
dz% I 1 — 2e cos ft -j- e2
, (13)
1.
2
„ ft — ft ft _ p ft . Л 9 . Л
sin2 —^~L 4* 2e sin cos ~2 sin У + e2 slnJ 2
, 9 ft — ₽ ( о . ft — ’° ft . о 9 . o о
sin2 —y-2- -|- 2e sin —у— cos -jy sin 4~ £2 sirr "o'
• £ £ £ £ £
l
. . Г . 9 ft — YlO -ft — Y ft • Yr 9.9Y IT Z1 л
X I S1K2 —2г sin —’•cos y sin+s2 sir.2 yj . (14)
На поверхности цилиндра |z2 |= 1 скорость опреде-
ляется по формуле
<&> _ и (z2— 1) (г3 + e29i)
— -- Vent >
^z2
где = ^oo есть скорость в бесконечности на плоскости
вспомогательного цилиндра и 0 — угол атаки на плоскости
цилиндра.
Отсюда на поверхности цилиндра определится по
формуле
I dw | л . ft . ft — (я 4 20) _
= 15^ I = 4t,jo sin 1sin----- 2~
772
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Но связь между скоростью в бесконечности на
плоскости профиля и на плоскости вспомогательного
цилиндра найдется из соотношения
dw ___ dw . dt, I
dt, — dz dz |2=0O *
откуда по формуле (6) имеем:
(£U=c<1+!)
И
V
у —__________________________,
“ |C|(l + e)
а потому равенство (15) принимает вид
/tiz । । /1 । \ • ft . ft — 4~ 20)
ft = 4Voo | C | (1 + e) sin у sin-.
Отсюда легко найдем скорость v в точке поверхности
профиля по формуле
dw dw dt, I I dC I
— = — : — , откуда v = v. : — .
dt dz dz\z=seH J 1 1^21
Подставляя значения vr и | , получим:
лл г । i /1 । \ * • ft — —I- 20) . .
V = [ С | (1 + е) sin sin -—- X
1 — 2е cos ft + е2 v
X X
4 | Cl (1 + e) siny
ф
r ft — & ft—5 ft , ft | о , „ ИТ
sin2 —~---1- 2e sin —y— cos -y sin -П- 4- e2 sin2
V _______£_____________-___~~----------------- V
Л 9ft— ₽ , Q • ft— p ft 1 ₽ I 2 i 2 p
sin2 —4- 2e sin --- cos — sin -4- 4- e2 sin2 -4-
Л 111 1
X---------------------------------------------r.
Г sin2 - 4- 2e sin ^9-^ COS — sin ~ 4- e2 sin 4-1 2
I z z z z z j
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
773
или
.. . »— (71 4-20)
v = sin---------—L у
",2^ — 0 ft- 0 ft. 8 „ „ О -IT
sin2 —£---1- 2e sin —g— cos у sin "2" 4“ e2 sin2
sin2 + 2e sin cos v sin 4 + e2 sin2
— ii £ £ л —
4/ 1 — 2e COS s2
X -y
£ sin2 --y-^ + 2e sin —cos ~ sin ~ -|- e2 sin2 2
В этой формуле 9 — угол атаки на вспомогательной
плоскости (z). Переходя на плоскость профиля и вводя угол
атаки относительно основной части профиля, надо положить
по формуле (15) предшествующего параграфа
л n I 2? ]/*р. . . 2 V р.
e^ + ^f+Tarctg^.
Формула (16) и решает вполне вопрос о распределении
скоростей на поверхности крыла с элероном.
Для профиля неутолщенного (скелет профиля) имеем
при 8 = 0
ф
.. . ft —(тс 4-26)
f = Ко Sin------Чр-------
, о!
sin —
sin—
1
. ft — 7 ’
sin-^-l
(17)
откуда видим, что скорость обращается в бесконечность
в точках Я = у (передняя кромка), D = (точка В на
рис. 25 — вершина выходящего угла); в точках 0 = те Ц-29
(точка разделения струй) и $ = 8 (точка D на рис. 25 — вер-
шина выходящего угла) скорость равна нулю.
Из формулы (17) при ср = 0 имеем скорость для обтека-
ния пластинки
sin »
* = --------dr-• (18)
sin-g-
774 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
§ 8. Профили с округленным передним краем
Весьма интересный профиль был указан С. А. Чаплыги-
ным х); он состоит из дуги окружности большого радиуса
и ортогональной к ней в ее конце окружности малого
радиуса. Отображающая функция была получена для этого
случая С. А. Чаплыгиным при
помощи искусственных сообра-
жений; мы получим ее, исходя из
формулы Шварца-Кристоффеля.
Применяем формулы § 2 к
отображению области, ограни-
ченной прямой L и лучом Lr
(рис. 26). В этом случае область
ограничена прямосторонником с
углами 277 (с вершиной Л), —
(с вершиной в В в бесконечности), —(с вершиной в С в
бесконечности). Для отображения на верхнюю полуплоскость
возьмем отображающую функцию в виде
z = cf(t—a) (t—ЬУ^ (t — c)~2dt
и, полагая а = О, Ь=—1, с=1, получим:
t dt
(/2-1/
что можно еще написать в виде
z = C f
С другой стороны, отобразим плоскость (г) на некоторую
плоскость (Q при помощи функции
9 С. А. Чаплыгин, О давлении плоскопараллельного потока
на преграждающие тела, Собр. соч., т. П, 1948,
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРЛЗТОФФЕЛЯ
775
где k — действительное положительное число. Посмотрим,
во что переходит область плоскости (г) на плоскости (С).
Вдоль луча имеем г = 0 + а потому по формуле (2)
I и । •
у = — k 4- iy,

откуда, взяв действительные
части, получим:
? + V2 + 4 = 0
Рис. 27.
или
М’ + яН- (3)
Это — дуга окружности радиуса касающаяся дей-
ствительной оси в начале координат. Изображением точки А
будет точка Аг (рис. 27), координаты которой удовлетворяют
уравнению (3) и уравнению
(4)
т. е. лежит на пересечении окружности Lr и L2 (рис. 27).
Так как уравнения (3) и (4) можно написать в виде
е2 +
6 _ и
е2 + ^
откуда для точки имеем:
Т) k
т. е.
г *
(3')
(4')
(5)
Вдоль L z = — й + х, а потому вдоль L
5 _ 8
52 + v)2 ’ ’
или
'/12 + (^+25') =482"'
т. е. имеем окружность L (рис. 27).
776
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Для определения постоянных С1 и С2 заметим, что
точке A (z = ih) соответствует значение t = 0 и значению
z = — /8 -|- х соответствуют значения t > 0, причем при х > О
имеем в равенстве (1) радикал со знаком 4" и при х < О
радикал имеет знак —.
Итак, из (1) имеем уравнения
ih — iCY —1~ ^*2’
откуда
С2 = — /8,
C1 = _(ft + 8).
Таким образом, равенство (1) принимает вид
Отсюда видим, что точке
которые найдем из уравнения
//2-1
k соответствуют значения
(6)
А + о
откуда
Vh? + k‘* + 26 (А 4- ik)
k + Z6
Называя через величину, сопряженную с Z^, пре-
образуем конформно верхнюю полуплоскость (/) на внешнюю
часть ок{ ужности ] и | — 1 при помощи формулы
и ------------— ,
ИЛИ
kk=—
ku----k
Подставляя выражение (7) в формулу (6), получим:
h + *
(7)
и — 1 \2
Z8
t(„u — t
t — t
z
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ’
777
и по формуле (2)
, 7* (8)
И &!,(«-l)a-('oo“-Q2
Формула (8) и дает окончательное выражение для отобра-
жающей функции. Для приложений найдем разложение
функции (8) по степеням и в области и = &э.
§ 9. Приложение к определению величины подъемной силы
Как известно, для определения величины подъемной силы
необходимо разложить правую часть (8) в ряд вида
...
и определить величину коэффициента а.
Функцию (8) можно написать в виде
г _ К4^0 (“ — 1 )а — (/сои — ^)2
(Л + &) Q - (k + /5) У t2J2m(u - 1)2 - - ^)2 •
(1)
С другой стороны,
У fat (и — 1 )2 — (tMU - to)2 =
= У u2ft(tt — 1) —2«(£/!о — tJco) + fafa~ 0 =
= ut^ Уit — 1------У00".1..^ + (2)
У “
Подставляя в (1) разложение (2), имеем:
(Л + 8) tmu — (Л + 0) to — (6 н- «) ХА ''
где
- ----- Моо— 1 1
А = at 1/ г — 1 — -— ----- - t И (...),
-К - у „
778
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
следовательно,
1
(k + Z8)- - (Л + 5) tm
V £-1
так как
(Л + /8) Г = (* + /3)А±1 = Л4-8.
Иначе выражение (3) можно написать в виде
£,-1]
а так как
то еще имеем:
Г t2 — 1
Z = i --------------------- и+ . . .
'со +
Но
, у № + & + 2ЬЪ12ЬЪ
tco~~ k + Zo
и, полагая
&4-Z8 = v,
/г2 k2 2/zB 4- I2kb =- |1,
имеем:
v==/^pr/arct4
. 2кЪ
|X = У(h2 + fe2 + 2Л8)2 + 4Zs2o2 e g*s+*2+2^,
(3)
(5)
а потому
УУ J>(ft2 + fe2+2/iM2 + 4fe2o2 , (|afcte__^__aretg±)
°° * V № + a2
(6)
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
779
Отсюда
4 __________________
- = У(*24^2 + 2*б)2 + 4*2б2 *_{ (1 arctg - arctg|)
"° У *2 4 б2
(rt г о , 2/со \ .
I 2 arctg -— arctg ———-—-1 г
\ 6 к *№+№+2h6'
—tM
4 r__________________________
у (h* 4 *2 4 2*6 )2 + 4*262
У *2 4 62
_ . Г 6 1 l 2*6 1
X 2z sin [arctg*—y arctg -Аа + *2 + ш ] .
Кроме того,
4-» (*4°)2
(* 4li) У (k + /б)2 У У
______________(*+5)2 e2i arctg|-4arctg^+X2^
4 ___________________C
(k* + 62) у (h2 + F + 2Л6)2 + 4дда
Следовательно,
r = Ze(2aretgl~ar)i . (h + °)2__________________________________
(#4-62) у (/г2_(_й2+2Л6)2-|-4/г2б2
. 3 , 2Ao
— 2г arctg — -г arctg —————гт
X e 6 2 6 h2 4 Л2+2Ло
X-________________________VW?_-------------------—a+_
2<У(Л= | H*®1 "’b"'-4 7;lrtl'X/CC
t. e.
_____________________________(A + 8)2__________________________x
2 У*246'2 У(*24*2-42*6)2+4*262sin (arctg^-|arctg
X e’'2arctg/»s+*3^A6 1M . (7)
780
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Заметим, что, называя радиус основной части профиля
через R, центральный угол через 2а и радиус насадка
через г, получим по формулам § 8
h__ 1 й __ 1 а_______ctg а
k ~~ 2R ’ 8 — 2r ’ h ~ 2R •
Рассмотрим частные случаи, представляющие вырождения
общей формулы.
1. Пусть а = 0 и R конечно. Тогда имеем отображение
внешней части окружности на внешнюю часть другой
окружности, так как дуга обращается в точку.
В этом случае h —> оо и формула (7) дает:
----- и, | . . .
arctg j
Но
sin ( arctg ,
\ & k ) у & q2
а потому окончательно имеем:
г 1 I
28'“+ • •
ИЛИ
С = г и + ...,
как и следовало ожидать. Очевидно, что в этом случае из
остальных членов остается только один, указывающий на
смещение на плоскости (С) центра из начала координат.
2. Пусть насадок превращается в точку. В этом случае
имеем обыкновенный дуговой профиль.
Здесь надо положить В —оо. Тогда
• / , s 1 2£о \
sin (arctg- - - arctg )
обратится в
(к 1 . k\ . (тс а\ а
2-— 2-arct^^-) = Sln( 2^— 2-) = C0S 2"’
так как
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
/61
Следовательно, выражение (7) принимает вид
С =-------- 1 ---------е'11 и Н- ...
4 Ул2--| - Л’2 cos
Но
Л2 + kZ — 4/?2 sin3 а •
Следовательно, окончательно
«, У? sin а -у i -
С =--------е 2 и + . ..,
n a
2 cos
или
Z = R si п е 2 1 и + .. .
В частном случае отсюда
пластинки длины L. Для
и R —> оо, причем
1im/<sina= у.
можно получить случай плоской
этого надо положить, что a —> О
Тогда получим:
3. Рассмотрим, наконец, случай плоской пластинки
с цилиндрическим насадком. В этом случае R = оо и k = 0;
кроме того, lim 2R sin a = А, а потому h=~.
R + <x> L
В этом случае формула (7) дает:
или
(* + *)2 „
26 (Д2 2До) и
__ (2г 4- Z)2
“ 4(£ + г)
и 4“ • • •
с
Так как в этом случае Л-|-2г = Л1, где Lr есть общая
длина хорды профиля с насадком (рис. 28), то можно
782 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
написать:
и при малом г
т. е.
’-4(£1-г)“+ •••
:-t(1+Z7)“+
4 1
Таким образом, круглый насадок вызывает как бы фиктив-
ное увеличение длины хорды (с до
§ 10. Составные профили С. А. Чаплыгина
с постоянным центром давления
Формула Шварца-Кристоффеля может быть приложена
и к некоторым случаям профилей, составленных из дуг
окружностей. Замечательный случай такого применения
представляет профиль, составленный из
r W двух дуг, касающихся в некоторой точ-
ке и имеющих различные радиусы и
7 одинаковое или противоположное на-
У правление изогнутости. Такие профили
были впервые изучены С. А. Чаплыги-
ним, который их. назвал составными
Ф профилями1).
Мы разберем здесь вопрос об
7 ni условиях, при которых составные про-
рис> 29. фили С. А. Чаплыгина имеют по-
стоянный центр давления.'
Пусть на плоскости (Q имеем составной профиль АОВ,
составленный из дуг АО с центром в точке mi радиуса R
и с центральным углом cpt и дуги ВО с центром в — ni
радиуса и с центральным углом (р2 (рис. 29). Отображая
!) С. А. Чаплыгин, Подъемная сила составного крыла,
Собр. соч., т. II, стр. 488, 1948. Метод Шварца-Кристоффеля к рассмат-
риваемым профилям приложен впервые в работе В. В. Голубева,
Теория крыла аэроплана в плоскопараллельном потоке, изд. 2-ё,
стр. 169, 1938.
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ 783
на плоскость (ц) при помощи функции
(1)
получим на плоскости (CJ как изображения дуг АО и, ВО
прямые AtO и ВХО, параллельные действительной оси и ухо-
дящие своими концами ОГО2
в бесконечность (рис. 30).
Если С == ? + Ztq и
то из (1) получим:
= £2 Ч- Т)2 ’ 7)1 = И +^2 •
Уравнение дуги АО есть £2-|-
_[_7}2=2/?ть а потому вдоль Л1О1
711 = ~ 2Я •
о? 0, - -в’

Лт Г' «
Рис. 30.
Так как координаты точки А (£, 7]) через R и выражаются
в виде
£ = /?sin<p1, iq — /?(1—costpj),
то для точки At координаты имеют вид
= J_______s*n 91 * fo. 9i
2R 1 — cos?! 2/Л ь 2 ’
711 = — 2R'
Аналогично для точки В± получим координаты
^2== — 2^Ctg? ’
. _ 1
7,2 ~~ 2/?! *
На плоскости '(Q мы имеем четырехсторонник с углами 2к
в точках В± с углами —кв точках Ог и О2 (рис. 30).
Отсюда имеем для отображения четырехсторонника на верх-
нюю полуплоскость по формуле Шварца-Кристоффеля
Г ___Г (^1 а1) (^1 с1) л?, । р
784
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
где alt blt clf dr— точки действительной оси. Если сделать
преобразование
z< =1 ,
1 z— 1
переводящее верхнюю полуплоскость (z^) во внешнюю часть
окружности |zl = 1, то еще получим:
С = С ( ,(г dz + С}
J (z — c)2(Z — d)2 1 ;
(3)
где a, b, с, d — точки окружности | z | = 1, в которые пе-
реходят точки Л, В, Ох и 02-
Интеграл (3) может быть написан в виде
+ В - 4- С In -^4 + сг (4)
1 (г — b)(z — d) 1 z — d 1 1 v 7
Так как на плоскостях (С) и (z) желательно, чтобы
точка С=оо, т. е. ^ = 0, соответствовала точке г = оо, то
по (4) имеем Ct = 0 и за ветвь логарифма надо взять ту,
для которой In 1 = 0.
Так как конформность отображения исчезает в точках
а, Ь, то точки а и b являются нулями функции и, нако-
нец, при изменении z вдоль окружности z = ег^ должно
быть действительно.
Полагая
b =z d = euf z = е^,
откуда
z — b = 2ie 2 sin ,
<Р+ § • .
z — d ==2ie 2 sin у— >
получим:
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
785
Az-\-B
(z — b) (z — d)
Ае^ + В
— 4е*ге 2 sin sin
3+5 г
_ (А + Be' е 2
— 4 sin 2 sin ' '2 &
Пусть
_₽±_8 i . _₽±_8 i
Ае 2 = Ке^, Be 2 = Le*,
(5)
тогда
Az + B
(г-b) (z — d)
К cos |л L cos (v — ср) . К sin — L sin (cp — ч)
Ф — 8 cp — q I cp — ft cp—6
— 4 sin ••• sin T — 4 sin ------ sin
Так как выражение
/С sin |л — L sin (ср —
. . ф — 8 . Ч> — о
— 4 sin т - Sin —j—
при изменении ср должно быть постоянным (различным при
изменении ср от (3 до В и от 3 до 2ти—|— Р), то необходимо,
чтобы числитель обращался в нуль при ср = р и при ср = 8.
Следовательно,
К sin у- — L sin (р — ч) = 0, |
/Csin|i — Asin(8 — v) = 0. )
Из уравнений (6) следует:
sin (р — v) = sin (8 — v),
а потому
(p —v)4-(8 —v) = —к,
т. e.
,=щ+л. (7)
Отсюда из (6) имеем:

/С sin Asin
7t \ j P --- О
= — Acos4j—.
786
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Пусть /Ccos{x = N, тогда из уравнений (5) и (7) имеем:
А = (n — iL cos j е 2
В ~ Lie®* \
(8)
Так как при действительном С при z = выражение
п 1 z — b
С I п - изменяется вдоль прямых, параллельных действи-
тельной оси, то рассматриваемому условию удовлетворим',
полагая
(n — IL cos e 2 z + iLe^+^ г ,
r - I___________2 /_________________kCln— (9)
(z — b)(z — d) >^z-d> W
где Af, A, C — действительные числа.
Найдем теперь положение точек а и с. Для этого нахо-
d^x
дим производную -~
dz
z2 [С (b—d) — Я] — [С (Z>2—^)4-2Д] ?+ [С (6—rf)-M] bd+B(b+d)
(z — b)2 (z — d)2
и, следовательно, для а и с имеем уравнение
z2[C(b — d) — A] — z[C(b2 — d2)-\-2B]-\-
-\-[С (b — d)A] bd-{-В (b-}-d) = 0. (10)
Подставляя значения Д, В из (8) и полагая
z = te 2 ,
приведем уравнение (10) к виду
/2 sin j— — cos j ~ i^i [С 5*п (?—^)+^l ~h
[ 2Cz sin —2 ° + 12L cos 4“ — L cos 2 ° i = 0,
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
787
откуда окончательно можно написать выражение t в виде х)
I [С Sin (? — 8) — L} ± 1/ № — ДЗ Sin2 4С» sin*
t =------------------------------------------------------____
12С sin a-- — (n 4- IL cos -A\
x \ Z J
и легко показать, что |z|=|Z|==l, т. е. точки а и с ле-
жат на окружности | z | = 1.
Так как можно положить р —|—8 = 0, то окончательно
получим отображающую функцию в виде
г (11)
1 (г — b)(z — d) 1 z — d v 7
Так как
(z — b)(z — d) = z2 — 2z cos P + 1,
TO
__ 1____________________z2 — 2г cos ft -|- 1________________
n (W — IL cos ft) z 4~ IL 4~ (г2 — 2г cos ft -|- 1) £ In j—
Найдем разложение функции С (г) в оэласти г = сю.
Имеем:
«»<
I"—,-1"----------тг = -2/[^ + ‘-^ + 4 5-3+...|.
z — d е^1 I. г 1 2г2 • Зг3 * J
г
и отсюда
(г2 — 2г cos 3-4- 1)1п|—| =
п. Г • □ sin 2ft ,2 sin3 ft 1 । 1
= -2i[sin^-------_...J,
а потому, если положить L = 2C sin ft, получим:
"“"Ci —
__ г2 — 2г cos ft 4~ 1
Д.С1 Z'
[N—2Ci sin ft (1 -j- cos ft)] г2 4~ 2CZsinft(14-cosft^-5- sin3ft4- • • •
и
4 См., например, В. В. Голубев, Теория крыла аэроплана
в плоскопараллельном потоке, стр. 173 и далее, изд. 2-е, 1938.
788 iv. труды по разным вопросам аэродинамики
Если обозначить
Г — ^2г2 Н~ + С2
Xjz2 + В)? + Ci + ... ’
то, выполняя деление, получим С в виде
«* Ad
^1
I ,
, ^iC2 А2А1С1 А1В2В1 + А2В* 1 ।
z
где
Л?
Л2=1, В2 = —2cosp, С2=1,
—N — 2Ci sin р (1 -|-cos Р), В± = 2CZ sin р (1 -|-cos Р),
4С1 . „л
Сг =------— sin3 р.
□
Приложим разложение (12) к отысканию случаев, когда
составные профили имеют постоянный центр давления.
Можно показать, что для этого мнимая часть отноше-
ния р : т должна быть равна нулю, где т и р — коэффи-
циенты разложения
С = mz-}-n +у+ • • •
функции С (z) в области z = cq1).
Применяя этот результат к случаю разложения (12),
получим следующее условие:
[sin2 р + 3 cos р (1 Ц- cos Р)] • [№+ 4С2 sin2 р (1 -|-cos ?)2] —
= 12C2sin2P(l 4-cosP)3,
откуда
TV2
2 sin2 р
4С2 sin2 р (1 + cos р)2 3 — (2 sin2 р — 3 cos р) *
или
TV2
1 — COS Р
4С2 sin2 р (1 -|- cos р)2 1 . 0
r v 1 у cos р
(13)
х) См. В. В. Голубев, Теория крыла аэроплана в плоскопа-
раллельном потоке, гл. IV, § 1, 1938.
О ПРИМЕНЕНИЙ ФОРМУЛЫ Шварца-криСтоффеля
789
Для того чтобы N и С были действительны, необходимо,
чтобы
yH-cosp>0,
т. е. чтобы
D х. 1
cos р > —у
и
—120° < Р < 120°.
Для построения профиля необходимо найти координаты
концов. Так как можно считать, что на цилиндре изобра-
жением одной из точек (точка схода струй) является точка
zr=\, а другой z2 = е~2г<1, где
=_________N________
g 2С sin р (1 -|- cos ₽) *
то, как можно показать, точки А и В определяются на
плоскости формулами
=с рn 1 1 tg ^+< sm р+< р—z].
га,.»1 + =.5?>1в,-Япр,М2,
2 [_ cos 2y] — cos р * г । г ।
ein I
(14)
а с другой стороны, как показано выше,
Г 1 1 ?1 • 1
..-2яеВ2 .
Из этих формул легко найдем ср1} ср2> 7? и /?х и, следо-
вательно, определим форму профиля.
Рассмотрим ряд примеров.
Пусть
(см=4).
По формуле (13)
tg-r1 = O.
790
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Берем значение т| = 0. Тогда по уравнению (14) имеем,
полагая С = 1,
. ./271 УзЛ
= -----2~)’
и по формулам (15) получим:
=
ср2 =--п, R =
1
т-’гу’

Профиль имеет вид двух полуокружностей, касающихся
друг друга, как указано на рис. 31, причем точкой схода
является точка А.
При — у (cos р = аналогично имеем = 0,
т. е. имеем такой же профиль, но перевернутый, так что
точкой схода на рис. 31 можно взять точку В1).
Чтобы получить профили с постоянным центром давле-
ния, близкие к тем, которые применяются в действитель-
ности, надо найти профили с малой изогнутостью, т. е.
с малыми срх и Для этого преобразуем формулы (14),
предполагая, что tg^— величина очень большая. Вынося
J) См. В. В. Голубев, Теория крыла аэроплана в плоскопа-
раллельном потоке, изд. 2-е, стр. 175, 1938.
О ПРИМЕНЕНИИ ФОРМУЛЫ ШВАРЦА-КРИСТОФФЕЛЯ
791
:2-= с
ц-T] за скобку и полагая Ctgr^Cp получим:
= Сх ^sin р cig2 ------i ctg 7] (к — p — sin p) J ,
sin H1 + cos Ю - sin 3 у ।
1 — tg2 q
< — cos p
1 + tg2 7]
tg 4+tg 4
----------0- +*(₽ +Sin ₽) ctg 7] .
tg’'] —tgi-
(16.)
Но при большом tgTj приближенно имеем:
2 tg 4 = 2 ctg y]
1 + tg2 Y] 1 + Ctg2 Y)
2 ctg 7],
1 --tg2^
1 + tg2
1 -- ctg2 Y]
1 + Ctg2 Y]
---(1 ---ctg2 7j)2
1+2 ctg2 7j,
tgvHg-K- 1 + tg| ctg V)
In--------g =ln-------g----?Kln(l + 2 tg-|ctg7])«
tg — tg у 1 — tg у Ctg V)
- 2 tg ctg 7].
Подставляя найденные значения C2 в равенства (16),
получим:
:2 = Ct sin р
1 4- cos р — 2 ctgy)
— 1 — cos p + 2 ctg y|
-4-2tg4ctg'*l+i(? + sin|3)ctg'q].
Таким образом, получим окончательные равенства'
'1 = ct [sin ,3 ctg2 — i ctg -q (- — ,3 — sin 3),
C2 = cJ— sin p-4- 2 tg-|-ctg7)4- ictg 7) (,3 sin
(17)
792
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
откуда, полагая Сх=1, имеем:
, sin 3ctg2-^-tgTn
р = tg7! rt„ Il = 2
2 (тс— р — sinp)’ 2 (тс — р — sin р) ’
Sin₽tg7) — 2tg-|-
2 В 4- sin В
о
2(P + sin₽)’
Рассмотрим примеры.
1. Пусть р = 115; по формулам (18) получим:
(18)
/? = 12,505,
/?х= 0,979,
2. При р= 118°
/? = 27,74,
/?1 = 1.64,
?1= 12°25',
ф2= 110°10'.
Полученные профили указаны на приложенных чертежах
(рис. 32).
Общие выводы
Предшествующие вычисления показывают, что во всех
разобранных случаях соответствующие профили могут быть
получены применением формулы ЩварцА-Кристоффеля. Таким
о СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА плохо обтекаемым телом 793
образом, все существующие геометрические
профили получаются применением общих
формул ШварцА-Кристоффеля.
О СТРОЕНИИ СПУТНОЙ зоны
ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ1)
§ 1. Вводные замечания
Вопрос о теоретическом объяснении процессов, происхо-
дящих в жидкости или газе за плохо обтекаемым телом,
является, по-видимому, одним из самых темных вопросов
современной теоретической гидромеханики.
В этой области накоплен огромный эксперименталь-
ный материал2), есть большой ряд работ, посвященных
попыткам теоретического объяснения наблюдаемых здесь
явлений. Однако, как правило, все имеющиеся попытки
теоретически осветить вопрос построены на более или менее
произвольных предположениях и в отдельных частях плохо
увязываются с данными эксперимента. С другой стороны,
и данные эксперимента также сильно расходятся в работах
различных исследователей, а методика измерений и отсутст-
вие в имеющихся в литературе описаниях исчерпывающих
данных о всех подробностях измерений во многих случаях
заставляют относиться с известной осторожностью к выводам и,
в особенности, к сравнительной оценке часто весьма про-
тиворечивых данных измерений у различных исследователей.
Между тем более или менее законченная теоретическая
схема явления, по нашему мнению, представляет несомнен-
ный интерес. При настоящем состоянии теоретической гидро-
механики, конечно, едва ли можно надеяться построить
с исчерпывающей полнотой теоретическую картину таких
явлений. Едва ли можно сомневаться, что причиной всех
явлений, наблюдаемых в спутной зоне обтекаемого тела,
г) Опубликовано в Изв. АН СССР, ОТН, № 12, 1954.
2) См., например, обзор экспериментальных данных в книге
С. Гольдштейна PL
794
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
является вязкость среды; при полном отсутствии вязкости
едва ли можно ожидать чего-нибудь отличного от пара-
докса Даламбера. И именно отсутствие в науке методов,
позволяющих до конца справляться со всеми трудностями,
возникающими при интегрировании при различных условиях
общих уравнений движения вязкой жидкости, является при-
чиной трудностей построения общей и законченной теории
явления.
Однако история развития гидромеханики за последнее
полустолетие, вызванного актуальнейшими задачами совре-
менной техники, и прежде всего авиации, показывает
огромное значение методов, построенных на применении
некоторых приближенных схем, упрощающих физику явле-
ний. Успехи были получены не в уточнении и развитии
чисто математических методов исследования, а в применении
своеобразной физической стилизации, позволяющей с доста-
точным для практики приближением заменить рассматри-
ваемое явление его физической упрощенной схемой.
Для пояснения этой мысли достаточно привести два
примера. Хорошо известно, что вся современная теория
крыла и теория пропеллеров, вентиляторов и ряда других
средств техники основаны на применении так называемых
присоединенных вихрей, схематически заменяющих плавно
обтекаемое потоком тело. Идея присоединенного вихря
дала возможность Жуковскому построить теорию крыла
в плоскопараллельном потоке и вихревую теорию гребных
винтов. Та же физическая схема позволила Ланчестеру,
Чаплыгину й Прандтлю построить теорию крыла конечного
размаха. При этом интересно отметить, что лежащая в основе
теории крыла конечного размаха введенная Ланчестером
физическая схема вихревой пелены, сходящей с задней
кромки крыла, никогда не наблюдается в действительности,
так как вследствие неустойчивости она свертывается в два
вихревых жгута, которые и можно легко наблюдать; однако
вся теория, дающая вполне удовлетворительное согласие
с экспериментом, строится именно в предположении суще-
ствования этой никогда не наблюдаемой вихревой непре-
рывной пелены. Мало того, попытки построить теорию
крыла, отказавшись от такой грубо приближенной схемы
и заменив ее, казалось бы, более точным учетом влияния
о СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 795*
на течение поверхности обтекаемого тела, делавшиеся раз-
личными авторами, практически не дали результатов. '
Другим хорошим примером, также относящимся к обла-
сти гидродинамики, является теория пограничного слоя,
с которой в некоторых частных вопросах столкнулся еще
Жуковский и которая была разработана Прандтлем и мно-
гими другими учеными. Здесь также приближенная схема
позволяет с полным успехом решать многие задачи, совер-
шенно недоступные методам, основанным на применении точ-
ных уравнений движения вязкой жидкости.
Совершенно такой же характер приближенной физической
схемы явления носит разработанная Гельмгольцем, Кирх-
гоффом, Жуковским и др. теория струй с ее никогда не на-
блюдаемой в действительности зоной, простирающейся
в бесконечность и заполненной неподвижной жидкостью,
или разработанная Карманом теория двойных вихревых
дорожек. Все подобные схематические модели протекающих
в действительности явлений, в отдельных своих частях
весьма резко отличающиеся от того, что мы наблюдаем
в действительности, как показывает современное состояние
науки, являются весьма важным средством познания, а
в некоторых случаях дают решение, вполне удовлетворяю-
щее требованиям современной техники.
Настоящая статья ставит своей задачей построить та-
кую же грубо схематическую картину явлений, происходя-
щих в спутной зоне плохо обтекаемого тела, и попытаться
с общей точки зрения в какой-то мере объединить и увя-
зать в единую теоретическую схему тот необычайно пест-
рый экспериментальный и теоретический материал, который
мы имеем.
Мы думаем, что разумно поставленная попытка' теоре-
тического объединения результатов, несомненно, может
способствэвать дальнейшему продвижению вопроса.
§ 2. Исходные положения
Для случая плоскопараллельного обтекания плохо обте-
каемых тел в современной гидромеханике разработаны две
теоретические схемы, изображающие структуру спутной зоны.
Первая из них дается теорией струй. По этой схеме
за телом образуется область, ограниченная линией разрыва
796
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
скоростей или линией с непрерывно распределенными ви-
хрями, приближенно имеющая параболическую форму.
Внутри области, ограниченной линией разрыва скоростей,
жидкость неподвижна относительно обтекаемого тела и на
линии разрыва скорость равна скорости потока в беско-
нечности.
Если заменить обтекаемое тело системой надлежаще вы-
бранных особенностей течения (источников, стоков, вихрей
и т. д.),как это делается в гидромеханике с точки зрения теории
«жидкого крыла», то можно сказать, что в области спут-
ной зоны в этом случае течение, образованное набегающим
потоком, вихревыми поверхностями разрыва скоростей и
особенностями течения, заменяющими границу обтекаемого
тела, имеет постоянную скорость, равную нулю. Если пред-
положить, что поверхности раздела скоростей простираются
в бесконечность, как это и предполагается во всех выводах
теории струй, то вдали от тела, где влияние особенностей,
заменяющих поверхность тела, становится исчезающе малым,
можно считать, что границы, отделяющие спутную зону
от обтекающего потока, превращаются в две параллельные,
равномерно завихренные плоскости, между которыми ско-
рость, образованная первоначальным течением и влиянием
вихревых поверхностей разрыва, всюду в спутной зоне
постоянна и равна нулю. Исходя из такого представления,
нетрудно определить и плотность завихренности вихревых
поверхностей разрыва и скорость движения их.
Действительно, рассмотрим на плоскости линию, напри-
мер отрезок действительной оси, равномерно завихренную,
с вихревой плотностью у. Полагая, что линия простирается
от точки —а до +#, получим для комплексного потенциала
выражение
+&
J1п(2—t>)dt (2Л)
-а
и для составляющих скорости имеем:
+&
dW _ • _ Т ( dt
dz IV — 2kZ J (х — Z) + УI ’
-a
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 797
Отсюда
+6
ТУ Г dt
2л J (х — /)2 4- у2 *
-а
+6
т f (х — t) dt
2л J (х — /)3 4- у2 ’
-а
или
7 У („„I Ь — х , —а — хУ
— 2^TyT(acg_i7i—arctg-Г
v = т in (а + х)а + ,У2
4п (Ь — + у» •
Полагая здесь а и b большими, имеем:
“ = —о-
Итак, с двух сторон плоской вихревой пелены скорость
постоянна, с одной стороны (при у > 0) и — — -i у, ис дру-
У
Г .
?
Z

-/
Рис. 1.
гой (при у < 0)я =+ —у .
Отсюда следует, что две парал-
лельные вихревые пелены, бес-
конечные в обе стороны, с рав-
ными по интенсивности и про-
тивоположными по направле-
нию завихренностями (рис. 1)
создают в пространстве между
собой скорость течения, равную у, а вне — дают скорость,
равную нулю. Наконец, каждая вихревая пелена движется
только под влиянием второй пелены и при указанном на
рис. 1 расположении имеет скорость, равную Ч-у Т-
С этой точки зрения модель струйного течения вдали
от тела, где исключается влияние самого тела, представляет
две вихревые пелены такой завихренности 7, чтобы общая
скорость течения, составленного из основного течения со ско-
ростью V и из течения, образованного двумя вихревыми
полосами с вихревой интенсивностью у, равнялась в области
струи нулю. Таким образом,
V-4“T = 0> или 7= — К
(2.2)
798
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
Итак, вихревая схема
вдали от тела представл
струйного течения
яет собой вихревые
пелены интенсивности соответственно у и — у,
расположенные пар

V
Рис. 2.
аллельно друг другу, при
этом где V — ско-
рость набегающего по-
тока (рис. 2); в полосе,
ограниченной двумя па-,
раллельными, завихрен-
ными пеленами, скорость
потока и с к оро сти тече-
ний, вызванных вихревы-
м и
уничтожают друг друга;
пеленами, взаимно
вне полосы дейст-
вия двух вихревых пленок — взаимно уничто-
жают друг друга и остается только ско-
рость V набегающего потока.
Вторая из этих схем на первый взгляд существенно отли-
чается от изложенной схемы теории струй. Прежде всего,
экспериментально Бенаром 121 и рядом других исследова-
телей х) было показано, что при некоторых скоростях тече-
ния за плохо обтекаемыми телами образуется шахматная
вихревая дорожка. Теоретические исследования Кармана2)
•показали, что такие дорожки в общем случае не устойчивы*;
случай относительной устойчивости представляют только
дорожки, в которых отношение ширины дорожки h к рас-
стоянию между двумя последовательными вихрями одного
ряда вихрей I удовлетворяет следующему условию Кармана:
у =0,281.
Вихревые дорожки Бенара — Кармана представляют собой
течения неустановившиеся, периодические, и в каждой точке
полосы, заключенной между двумя рядами второй дорожки,
при движении вихрей скорость изменяется;, в этом мы имеем
существенное отличие от спутной зоны теории струи, где
9 Подробную литературу см. С. Гольдштейн W; т. II,
стр. 234.
2) См., например, Н. Е, К о ч и н, И, А. К и б е л ь, Н, В, Р о з е 131,
о СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 79)
скорость постоянна и .равна нулю. Однако это различие
окажется менее существенным, если рассчитать среднюю
скорость течения в произвольной точке двойной вихревой
дорожки.
В. теории вихревых дорожек доказывается, что компо-
ненты, скорости одного ряда вихревой дорожки выражаются
следующими формулами х):
. 2лу
тл sh -~
г sin —
г/ = -777--------г;-----1-------г;---
21 , 2тсу 2 т. х
ch —— cos ——
(2.4)
Отсюда следует, что внутри вихревой дорожки, где дей-
ствие вихрей того или. другого ряда противоположно на-
правленных вихрей удваивается, мы получим для средней
за период прохождения вихрей скорости течения выражения
I
2 I’
= I и dx,
о
Отсюда2)
. i
- Г к 2тгу f
«ср— р sh— J 2яу
о ch—7—
dx
v dx.
2Г
— • arctg
. 2кх
, sin—— dx
, 2тсу 2 т. х
ch —~ cos ——
(2-5)
(2.6)
1) См.? например, Ламб W.
2) Можно получить нср и ^ср из выражения комплексного потен-
циала дорожки; равенство ^ср == 0, очевидно, геометрически.
800 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
Таким образом, если в струе в каждой ее точке скорость
постоянна и равна нулю, то в полосе между вихрями вих-
ревой дорожки постоянна средняя скорость.
Причем, сравнивая выражения вызванной непрерывными
вихревыми полосами теории струй скорости (—у) со сред-
ней скоростью вихревой дорожки (—Г/Z), мы видим, что
средняя скорость равна скорости, вызванной двумя непре-
рывными вихревыми пеленами, если плотность пелены равна
равномерно распределенной по краям вихревой дорожки
плотности отдельных ее вихрей, т. е. у = Г/Z.
Отсюда естественно рассматривать двойную вихревую
дорожку как распавшуюся на отдельные вихри непрерывно
завихренную границу струи.
Но отсюда становится весьма правдоподобной следующая
основная гипотеза: средняя завихренность границы
вихревой дорожки равна завихренности вих-
ревой полосы в случае струи, т. е.
1-=т = У, или Г = И/. (2.7)
Эту гипотезу мы и положим в основу всего дальнейшего
исследования.
Выведенная формула (2.7) была получена впервые в 1911 г.
из иных соображений Карманомх). Однако в последующем
эта формула не получила распространения ввиду кажуще-
гося расхождения ее с данными эксперимента; в дальнейшем
мы покажем, что эти расхождения устранимы при более
точном учете условий эксперимента.
§ 3. Скорости движения вихревой дорожки
Из формул (2.3) и (2.4), дающих скорость течения, соз-
даваемую вихрями одной дорожки, получим скорость дви-
жения вихрей самой дорожки, подставив у = Л, где Л — ши-
рина дорожки, и х= 0 для случая параллельной дорожки я =
*) См. работу Кармана Н в более поздней статье Кар-
ман не приводит этой формулы ввиду кажущегося резкого расхо-
ждения выводов из нее с опытными данными. См. также В. В. Го-
л у б е в И.
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 801
и х = лля шахматной дорожки z/q. Получим:
, 2^
„ __ г Z Г .. nh
“= 2/ 2лЛ — 2/ cth I ’
ch —----1
Отсюда
/ Г\2
“=“О=Ы) •
Но если взять непрерывную дорожку, ограниченную двумя
непрерывными вихревыми пеленами, с вихревой плотностью
у= Г//, то скорость движения непрерывной вихревой пе-
лены uQ, как было показано, определяется по формуле
— Т____ г
«о — 2 — 21'
Следовательно, скорость движения непрерывной вихревой
пелены есть среднее геометрическое из скоростей параллель-
ной и шахматной дорожки.
Подставляя сюда условие устойчивости Кармана, получим:
«. = -J/2=-Ji = -0.70V,
Г V п
и0 =— 27-=— -2- = — 0.5К
Таким образом, вихри шахматной дорожки имеют наи-
меньшую скорость движения и вихри параллельной дорожки—
наибольшую скорость; следовательно, наименьшую скорость
движения имеет устойчивая система вихрей дорожки.
Заметим, что полученные выражения для скоростей доро-
жек предполагают, что дорожки бесконечны в оба конца.
Совершенно другая картина получится, если рассматривать
движение половины бесконечной вихревой дорожки и оста-
802
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
новиться на движении вихрей, находящихся в начале такой
полудорожки. Здесь имеет место явление, совершенно ана-
логичное тому, что дает в теории воздушных винтов теорема
Фруда — Финстервальдера.
§ 4. Скорость движения вихрей в начале полудорожки
Рассмотрим половину дорожки, образованной двумя вих-
ревыми пеленами, идущими вправо от мнимой оси, парал-
лельно оси х на расстоянии h друг от друга (рис. 3). Рас-
смотрим скорость точки М вихревой пелены АВ, находя-
щейся на оси у.
Рис. 3.
Применяя обычные формулы, получим для производной
комплексного потенциала выражение
и — iv
dW
dz
7 Г ____________ds__________। у f____________ds_________
2kz J z — (s -f- V2 hl) ’ J z — (s — 4<>lil)
AB AB
и в точке Л4
। 7 f ds । 7 f
U-----IV —) jy—: I--------------p ту—: I
1 J 5 2tzI J
AB AB
ds
hi — s'
Отсюда
y f hds
AB
____L_ f d s . 7 Г 5 d s
2^ J s 2k J № A- sa
AB AB
Полагая s = /^tgcp, имеем (рис. 4):
J M = (а=агс‘£чт)’
— a
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 803
1 D
или еще, замечая, что а = у к—р, и полагая, как выше,
Т = V, имеем:
« = 1] (₽ = arctg(4.1)
Равенство (4.1) показывает, что в точках, близких к на-
чалу непрерывной дорожки, абсолютное значение скорости и,
вызываемой влиянием второй стороны дорожки на движение
вихрей дорожки, оказывается меньше, чем для дорожки,
бесконечной в оба конца, на величину Azz, равную
Л I/ Р тг 1 I AM
ки = V = V -5— arcctg -г-.
2к 27Z ь h
Приводим изменение этого уменьшения для различных
значений отношения
•^ = 0 1 2 3 4 5 6 сю
h
-^- = 0,25 0,12 0,07 0,05 0,04 0,03 0,02 0
Таким образом, скорость изменяется от —0,251/ в самом
начале дорожки до —0,5У, что достигается практически
на расстоянии от начала дорожки, равном ушестеренной ее
ширине.
Переходим к определению скорости -у, которую можно
написать в виде
__ f/z3 Г ds
2л J s(/z3 + s3) -AM где берется главное значение интеграла. Полагая s = higy>, получим: те/2 I, f cos <Р 2к J sin ср — а Отсюда f —8 к/2 „ = __Llim [ (* 2тъ е о 1 J sin ср 1 J » cos ср dy sin ср
804
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
ИЛИ
Y .. L sine . 1 sin V9 тс)
v = — ~ lim In —-----------к In—>
2k g о ’ sin а 1 sin е J
т. е.
т , 1 т , (Л2 + ЛМ2)’А
V = ----7Г- In —--- = — 7Г- In ---------------
2тс sin а 2л
Полагая,
чательно:
как в предыдущем, у = — V, получим окон-
। v 1
n = + ^ln
(#* + ЛЫЗ)У2
МА
Выведенная формула показывает, что в самом начале
дорожки v обращается в бесконечность; этот результат
физически не имеет значения и является следствием того,
что вихревая пелена, как всегда, в теории принимается беско-
нечно тонкой.
В предыдущем мы рассматривали влияние конечности
в одном направлении двойной непрерывной вихревой пелены
на скорость ее перемещения в на-
чале.
Аналогичный результат получим
и для случая двойной вихревой
дорожки, состоящей из дискретных
вихрей.
Мы рассмотрим сначала слу-
чай дорожки с шахматным располо-
жением вихрей. Пусть J1} J2 — вихри
одного ряда дорожки и — вихрь
другого ряда (рис. 5). Определим
скорость по направлению вихревой дорожки вихря ряда^,
образуемую одним вихрем второго ряда, ближайшим
к вихрю Л- Скорость, вызываемая в точке Jt вихрем
интенсивности Г, направлена перпендикулярно к прямой
J'x и по величине равна
Г _ Г
~ 2г. +
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 805
и ее составляющая по направлению дорожки выражается
формулой
__ ГЛ
2к(Л2 4-1/4/2) •
Так как по предыдущему Г = VI, то
__ V Ih _ V hjl
2л Л2Ч-1/4/а “ 2лЛ2//2 + 1/4
и, подставляя -у = 0,281, имеем:
ах = —0,14V.
Так как скорость, вызываемая бесконечным в обе стороны
рядом вихрей, как мы видели, в случае дорожки с шахмат-
ным расположением вихрей равна — 0,351/ и, следовательно,
скорость, вызываемая вихрями одной половины ряда, соста-
вит— 0,187, то оказывается, что один, ближайший к началу
полудорожки вихрь создает скорость, которая составляет
0,14 : 0,18, т. е. 77% скорости, создаваемой всей полубеско-
нечной дорожкой.
Подобным же образом, если рассчитать скорость, созда-
ваемую двумя ближайшими вихрями, расположенными по одну
сторону, получим:
(A h
_ V j 4-
“2— 2я|А1д_ J_ ^2. 9 •>
I /2 + 4 р + 4 .
или
17 I | /2^4
zz2 = — 1 { 1 +^2----и = 0,141/х 1,4,
2 2л Л2 1 ! 'Л2 , 9 | ’ ’
/2 + 4 I /2 +"4 J
т. е.
и2= — 0,161/.
Точно так же, если рассчитать скорость, вызываемую
тремя ближайшими вихрями дорожки, получим:
и3 = — 0,16667, .
'Я ' 1
806
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
т. е. 94°/0 скорости, вызываемой бесконечной в одну сто-
рону дорожкой.
На прилагаемой фигуре (рис. 6) даны скорости вихрей
шахматной полудорожки, расположенных в ее начале.
-аз5У ^о,з5У ^о,з5у
*~аз2У *-азы *-аз5У
Рис. 6.
Таким образом, уже на расстоянии, равном
21 = 2h : = 7h,
где h — ширина дорожки и, следовательно, поперечник обте-
каемого тела, скорость движения вихрей дорожки чрезвы-
чайно близка к их скорости в бесконечности.
§ 5. Изменение скорости течения за плохо
обтекаемым телом
Для изучения движения вихревых дорожек непосредственно
за плохо обтекаемым телом, т. е. в самом начале дорожки,
необходимо изучить распределение скорости течения вблизи
плохо обтекаемого тела. Очевидно, что это распределение
зависит от формы обтекаемого цилиндра; чтобы иметь общее
представление о характере изменения скорости, мы ограни-
чимся самым простым случаем обтекания круглого цилиндра.
Производная комплексного потенциала обтекания круглого
цилиндра имеет вид
(5.1)
dz \ z2 J 47
Обозначая через и и v составляющие добавочной скорости,
вызываемой присутствием цилиндра в потоке, получим:
Отсюда
(5-Ч
6 СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 807
Из выражения (5.2) видим, что составляющая добавочной
скорости и обращается в нуль на биссектрисах коорди-
натных углов, положительна при
|| > |х| и отрицательна при
|_у| < |х|. Наибольшего значения
при данном х она достигает в точ-
ке, для которой х = ±гх]Лз, и
оно равно
Наименьшее значение получаем
при у = 0, и оно равно
Распределение скорости и вдоль
ординаты имеет вид, указанный на
рис. 7.
Рассмотрим еще изменение а вдоль
прямой у = R. При-
ведем значения изменений и вдоль прямой при различных
значениях х.
X — R”" 0 1 1,5 2 2,5 3 3,5
и V"- 1 0 — 0,13 — 0,12 — 0,10 —0,08 —0,06
V+u _ V 2 1 0,87 0,88 0,90 0,92 0,94
х 4 5 6 7 8 9 10
и —0,05 — 0,04 — 0,03 — 0,02 — 0,01 —0,01 —0,01
V-±u _ V 0,95 0,96 0,97 0,98 0,99 0,99 0,99
Подобным же образом легко исследовать изменение v по
уравнению (5.3). Наименьшее значение v при заданном у > О
получим при х = у [У3 и -Umin = — 0,22V’ (j7x)2 Значения
808 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамйкй
изменений v вдоль прямой y = R дано в следующей таб-
лице:
4=0 4= 1 2 3 4 5
4= 0 —0,65 —0,5 —0,16 —0,06 —0,03 —0,01
Мы можем теперь сопоставить изменение скорости за
обтекаемым телом и изменение скорости движения вихрей
в начале дорожки. Мы ограничимся только изменением ско-
рости в направлении потока и, следовательно, в направлении
вихревой дорожки. В таблице 1 дано это изменение в пре-
делах трех первых вихрей шахматной дорожки для случая
обтекания круглого цилиндра.
Таблица 1
Расстояние 0 l = 3,5 h = 7R 2Z = 7Л = 147?
V и 0,87 V — 0,18 V 0,69 V 0,98 V — 0,32 V 0,66 V V — 0,34 V 0,66 V
Приведенный расчет показывает, что в начале дорожки,
т. е. непосредственно за обтекаемым телом, уменьшение
скорости течения, вызываемое присутствием тела, и умень-
шение скорости движения вихрей дорожки взаимно компен-
сируют друг друга таким образом, что разность скорости
течения и скорости дорожки остается практически
величиной постоянной, такой же, как вдали за телом, т. е.
Vi — zzx = V— zz. (5.4)
При этом оказывается, что весьма близко за телом,
на расстоянии порядка 7/г, где h — поперечное сечение до-
рожки, МОЖНО СЧИТаТЬ С бОЛЬШОЙ ТОЧНОСТЬЮ, ЧТО V1 И ZZj
достигают своих значений вдали от тела, т. е. V и zz.
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 809
§ 6. Число Струхаля для двойной вихревой дорожки
Рассмотим спутную зону плохо обтекаемого тела, обра-
зованную двойной вихревой дорожкой, и пересечем ее не-
которой неподвижной прямой А, перпендикулярной к ско-
рости потока вдали перед обтекаемым телом. Пусть пря-
мую L пересекает в секунду N вихрей одного ряда вихре-
вой дорожки. Обозначая через I расстояние между двумя
последовательными вихрями ряда, получим, что в одну се-
кунду вихри ряда перемещаются на расстояние NI, и так как
скорость движения вихрей дорожки есть Vи, где и есть
скорость, вызываемая вихрями дорожки, то отсюда мы имеем
уравнение
^ = V^u. (6.1)
Наблюдения показывают, что I с достаточной точностью
сохраняет постоянное значение независимо от расстояния
вихрей до обтекаемого тела; точно так же, очевидно,
должно сохранять постоянное значение и число вихрей Д/
в ряде дорожки, начиная с момента распада сходящего
с обтекаемого тела завихренного пограничного слоя на от-
дельные вихри вихревой дорожки.
Что касается V и и, то из предыдущего видно,, что
они меняются в зависимости от расстояния до обтекаемого
тела и вблизи тела достаточно сильно отличаются от их
значений вдали от тела и, следовательно, вдали от начала
дорожки.
Мы будем в дальнейшем понимать под V и и значения
их влали от обтекаемого тела, где с достаточной степенью
точности можно считать дорожку бесконечной в оба конца;
соответствующие значения скорости потока и скорости, вы-
зываемой влиянием вихрей дорожки вблизи тела, будем на-
зывать через и иг. Из предыдущего следует, что
Nl = V+ и = V\+ иг. (6.2)
Далее мы сделаем следующее предположение: ширина
вихревой дорожки h равна поперечному к направлению по-
тока сечению обтекаемого тела и отношение h\l удовле-
творяет условию Кармана, т. е. Л//= 0,281.
810 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
При этих условиях из уравнения (6.1) имеем
+ или ^. = 0,281(1+^). (6.3)
Число NhjV мы будем называть числом Струхаля для
случая вихревой дорожки за плохо обтекаемым телом.
Уравнения (6.2) и (6.3) позволяют сравнить полученные
теоретические выводы с имеющимися экспериментальными
данными.
Эксперимент показывает, что за плохо обтекаемыми
телами образуются дорожки с шахматным расположением
вихрей; следовательно, по предыдущему, учитывая условия
Кармана, имеем и = — 0,35У вдали от начала дорожки и,
по данным § 4, u1 = ll2i и =—18IZ в начале дорожки.
Отсюда, подставляя значение и в уравнение (6.3), имеем:
-^- = 0,281 (1—0,35), или -^- = 0,18. (6.4)
Таким образом, получаем, что течения с образованием
за телом двойных вихревых
С
дорожек возможны только при
вполне определенном значении
числа Струхаля, равном 0,18.
Полученный результат,
по-видимому, хорошо согла-
суется с экспериментами Рел-
фа и Симмона 181 9 (рис. 8).
Отсюда получаем важное
следствие. Если отрезок ли-
нии NhjV> идущий параллель-
но действительной оси на рас-
стоянии приблизительно 0,18
на рис. 8, соответствует ре-
образованием двойной вихревой дорожки,
вихревыми дорожками образуются только
в интервале чисел Рейнольдса от R = 102 до R = 104.
Применим теперь равенство (6.2)
жиму течений
то течения с
V -|- и =
9 См. также С. Гольдштейн 14, т. II, стр. 96.
О Строении спутной зоны за плохо обтекаемым телом 811
к началу дорожки. В этом случае по предыдущему надо
положить = 1]2и = —0,1817; следовательно,
Vi — 0,1817 = V — 0,3517,
или
У\ = 0,8217. (6.5)
Расчеты, проделанные в § 5, показывают, что наимень-
шее значение и согласно (5.2) получается при х = rV3 и'
оно равно —0,13; следовательно, при этом
171 = 0,7717. (6.6)
Таким образом, если предположить, что дорожка имеет
ширину, равную ширине круглого цилиндра, то образова-
ние дорожки начинается на расстоянии x = R]/~3 =1,77?
от центра цилиндра; при этом расхождение между ско-
ростью потока, рассчитанной на основании соображений
настоящего параграфа и вычислений предшествующего па-
раграфа, дается выражениями (6.5) и (6.6).
Резкое расхождение между скоростью и для бесконеч-
ной в оба конца вихревой дорожки (—0,3517) и экспери-
ментальными данными послужило к тому, что Карманх) и
последующие исследователи отказались от положенной выше
в основу всего расчета первой основной гипотезы2).
Действительно, как показали непосредственные измерения,
произведенные Карманом, для случая цилиндра оказалось,
что и =— 0,1417 и для пластинки и = — 0,1817.
Из предыдущего следует, что это резкое расхождение
объясняется тем, что без всяких оснований предполагается,
что в начале дорожки скорость и — та же, что и вдали
от начала. Между тем, как показано выше, в начале до-
рожки, где, несомненно, и определялась экспериментально
скорость и, надо брать скорость zz1=1/2zz; при этом полу-
чим значение и = — 0,1817, что достаточно хорошо согла-
суется с экспериментальными данными Кармана —0,1417 и
—0,2017.
Заметим здесь, что экспериментальное значение для ци-
линдра дает точное согласие со значением скорости V,
1) См., например, С. Гольдштейн И, т. II, стр. 242.
2) См. § 2.
812 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
полученной в предыдущем параграфе. Действительно, пола-
гая [/х равным наименьшему значению И, т. е. полагая
V\ = 0,871/, и беря за экспериментальное значение Кар-
мана = — 0,141^, получим:
+ «i = 0,631/,
вв то время как по предыдущему
И+« = 0,651/.
Вопросу о теоретическом определении и посвящен ряд
работ. Так, впервые пытался определить теоретическим
путем zz, отказавшись от предположения Кармана, Гейзен-
берг 191. Для полученного им значения и = — 0,23У вели-
чина и1 = 1/2и = — 0,111/ и, как показали эксперименты
Кармана, оказалась явно заниженной.
Исходя из других соображений, Г. В. Каменков1) по-
лучил значение и = — 0,161/; отсюда = 1)2и = — 0,081/,
что также явно занижено. При этом, если значение Г. В. Ка-
менкова и принимать за и мы получим достаточное согла-
сие с опытными данными Кармана, то аналогичное предпо-
ложение для значения Гейзенберга дает явно завышенную
величину.
И вывод Гейзенберга, и вывод Г. В. Каменкова требуют
принятия некоторых физических предположений, по нашему
мнению, гораздо более искусственных, чем приведенная
выше основная гипотеза2).
§ 7. Количество завихренности
Предыдущие выводы позволяют рассчитать количество
завихренности, сходящей с обтекаемого тела. Обозначая
это' количество завихренности, сходящей в одну секунду
в одном ряду вихревой дорожки через Q, получим, оче-
видно,
Q = (7.1)
9 Об исследованиях Г. В. Каменкова см., например, Н. С. А р-
жа ников и В. И. Мальцев 1101, Аэродинамика, стр. 195, 1952.
2) Л. Прандтль подверг исходные положения Гейзенберга рез-
кой критике. См., например, С. Гольдштейн W, т. II, стр. 242.
о Отроении спутной зоны за плохо обтекаемым телом 813
где по-прежнему N—число сходящих в одну секунду вих-
рей в ряде и Г — циркуляция вихревой дорожки.
Подставляя в уравнение (7.1) значение Г = V7, получим:
Q = NVl, или Q = И(И+ и). (7.2)
Полагая еще и =—— 0,351/, получим окон-
чательно:
Q = 0,65V2. (7.3)
Можно получить количество завихренности Q, исходя
из совершенно других соображений. Так как вихри до-
рожки образуются из распада пограничного слоя, то рас-
считаем количество завихренности, проходящее через нор-
мальное сечение пограничного слоя в одну секунду.
Пусть АВ — граница обтекаемого тела (рис. 9), CD —
наружная граница пограничного слоя, Оу — нормальное
к поверхности обтекаемого тела сече-
ние пограничного слоя. '****’’"
За время dt через сечение Оу __
проходит количество завихренности, —
dr
равное д
* ШЯШт
I wa(y)dydt, (7.4)
У Рис. 9.
где со — плотность завихренности, и (у)— скорость внутри
пограничного слоя и h — толщина слоя.
Для определения плотности завихренности найдем цир-
куляцию у вокруг элементарного прямоугольника
~ u(y)dx — и(у-\- dy)dx= — ~dx dy = w dx dy.
Отсюда
w
ди
dy
и, следовательно
h h
J ош (у) dy dt*= — dt J и dy,
в о
814 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
опуская знак
_ [ ди , v2- v*
=—2—’ <7-5)
о
где Vo— скорость на поверхности обтекаемого тела и —
скорость на внешней границе пограничного слоя. Так как по
теории пограничного слоя Уо = 0, то окончательно имеем:
Q =—0,5Vt (7.6)
Сравнивая выражения (7.3) и (7.6), получим 0,5У1 =
= 0,64V2, или
Vi = 1,14V. (7.7)
Заметим, что на величину скорости V\ на внешней гра-
нице слоя, очевидно, влияют два фактора:
во-первых, геометрическая форма обтекаемого тела;
во-вторых, скорость, вызываемая вихрями дорожки, об-
разующейся сзади плохо обтекаемого тела.
Так как скорость по направлению течения от вихревой
дорожки в ее начале в точке отрыва вызывается только
половиной противоположного ряда вихревой дорожки, то,
предполагая для начала дорожку не распавшейся, получим
для этой скорости выражение
g" ^непр = 0,25V.
Отсюда предполагаем, что при обтекании без отрыва
скорость на внешней границе пограничного слоя равна ско-
рости на поверхности обтекаемого тела, и, обозначая эту
скорость через V2, из уравнения (7.7) получим:
V2 —0,25V = 1,14V, или V2=1,4V. (7.8)
Таким образом, скорость в точке отрыва значительно
(почти в полтора раза) превосходит скорость в бесконечно-
сти. Качественно этот результат оправдывается эксперимен-
том; точных экспериментальных данных о скорости в точке
отрыва, по-видимому, нет, но, вероятно, выражение (7.8)
дает 'сильно преуменьшенное значение скорости V2. Дей-
ствительно, как показывает уравнение (5.2), наибольшее
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 815
значение и при х = 0 получится в точке у — R и и = V,
а потому вся скорость обтекания в этой точке V + и = 2У\
Для величины Q имеются достаточно тщательные экспе-
риментальные данные.
§ 8. Определение величины сопротивления
В теории вихревых дорожек Кармана выводится следую-
щая формула для величины сопротивления х):
Xo=-^+^(V-2uq). (8.1)
В настоящем случае, как было показано выше,
Г = У/, =
Подставляя в формулу (8.1), имеем:
*о = ?Vh Vth Ч-\ >
что еще можно переписать в виде
•’f« = JThs-+2~2"’T-|- <8-2>
Вводя коэффициент сопротивления С по формуле
С=.. —2th2r-+-r7rl (8.3)
1/2Ри2А I h 1 тс/г// J v 7
и так как
th^.=4=, 4-=°«28i>
I /2 I
то окончательно получим:
с = 2—К2 + = 0,586 + 1,133 = 1,72. (8.4)
Если мы поставим вопрос, в какой мере полученная
выше формула согласуется с экспериментальными данными,
то прежде всего столкнемся с необычайной пестротой имею-
щихся данных. Как пример можно привести эксперименталь-
ные данные, имеющиеся у Гольдштейна W.
х) См., например, В. В. Голубев Щ],
816
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
§ 9. Оценка полученных результатов
Во всех предшествующих расчетах существенную роль
играло предположение, что так называемое условие устой-
чивости Кармана имеет место при течении реальной жидко-
сти, т. е. что вихревые дорожки, образующиеся за плохо
обтекаемыми телами, удовлетворяют условию Л//= 0,281.
Между тем это предположение ни в коем случае нельзя
считать достаточно установленным экспериментально и обще-
принятым; наоборот, скорее можно установить полный раз-
нобой во взглядах как на самую теоретическую схему вих-
ревой дорожки, так и на содержание условия Кармана.
Самые крайние утверждения в этом направлении состоят
в том, что течения, наблюдаемые за обтекаемым телом,
носят периодический, волнообразный характер и что, в сущ-
ности, нет никаких особых оснований схематизировать тече-
ние двойными вихревыми дорожками; теоретически гораздо
целесообразнее при теоретическом изучении течений за плохо
обтекаемыми телами пользоваться схемой просто волновых
течений.
Вероятно, основанием к такому скептицизму служит
то, что вихревые дорожки действительно при обычных наблю-
дениях являются, по-видимому, образованиями чрезвычайно
нестойкими. Они быстро распадаются и перестают быть
наблюдаемыми, в то время как волнообразный характер
течения за плохо обтекаемыми телами наблюдается в более
широких условиях.
Мы считаем, что дело обстоит совершенно не так.
Трудность наблюдения и изучения механизма движения вих-
ревых дорожек, по нашему мнению, объясняется тем, что
дорожки, образующиеся за плохо обтекаемыми телами,
состоят из вихрей, вообще говоря, весьма слабой интен-
сивности; отсюда—их быстрый распад вследствие диффузии
и трудность наблюдения имеющих здесь место закономер-
ностей.
Однако есть возможность получить вихревые дорожки
другим способом—при помощи машущего в жидкости кры-
лообразного тела; при этом можно получить вихревые
дорожки с вихрями практически произвольной интенсивности.
При этом получаются вихревые дорожки, весьма четко
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 817
развитые и хорошо наблюдаемые. Их ясно выраженная
структура делает совершенно нецелесообразным и ни на чем
не основанным стремление не пользоваться теоретической
схемой вихревых дорожек так же, как и другими схемами,
применяемыми в теории (струи, волны).
Вместе с тем в несколько ином свете предстает и условие
устойчивости Кармана. Имеющиеся в литературе данные
об отношении А/Z, полученные экспериментально, дают
чрезвычайно большой разброс, примерно от 0,240 до 0,5,
причем имеются указания даже и на значения порядка
0,7—0,8. По-видимому, впервые Гукер *) обратил внимание
на то, что во многих экспериментах не очень ясно, какие
точки принимаются визуально или на фотоснимках за оси
вихрей. Так как вследствие
диффузии вихри дорожки быст-
ро ослабевают, причем ядро
вихрей постепенно «размазы-
вается» по некоторой пло-
щадке, по-видимому близкой
к эллипсу, то ясно, что полу-
чим совершенно различные раз-
меры ширины дорожки Л, если
за оси вихрей брать фокусы
эллипсов или их центры
(рис. 10). Интересно отметить, что относительно величины Z
обычно не возникает сомнений в ее достаточной неизмен-
ности при движении дорожки.
В силу изложенного можно предполагать, что в дорожке,
составленной из более интенсивных вихрей, подобное смеши-
вание менее вероятно; при работе машущего крыла
образуются дорожки с более мощными вихрями, поэтому
можно ожидать, что они окажутся более устойчивыми и
условие Кармана будет выполняться. По-видимому, имею-
щиеся наблюдения подтверждают эти ожидания.
Вихревые дорожки, образующиеся за машущим крылом,
впервые систематически наблюдал Я. Е. Полонский 1121. Его
измерения дали следующее: значения hfl изменялись в
Рис. 10.
*) См., например, С. Го л ь д штейн Ш, т. II, стр. 248, Б е нар 121.
Подробную литературу см. С. Гольдштейн 14, т. II, стр. 234.
818 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ АЭРОДИНАМИКИ
интервале 0,33—0,395. Позднее подобные же наблюдения с до-
рожками, образующимися сзади машущего крыла, производил
Р. И. Виноградов 1131. Его наблюдения дали исключительно
хорошее согласие с теоретическим значением отношения Л//;
значения h/l колебались в интервале от 0,275 до 0,340
со средним по ряду наблюдений 0,296, в других сериях
наблюдений эти значения были соответственно от 0,270
до 0,324 со средним 0,285.
И тот, и другой наблюдатель констатировали наличие
хорошо развитых, точно очерченных двойных вихревых
дорожек, достаточно длинных. Применение машущих крыльев
для образования вихревых дорожек представляет, по-види-
мому, удобный метод их получения.
Заметим, впрочем, что уже тот факт, что никогда
не наблюдаются дорожки с параллельным или близким к нему
расположением вихрей и что, несмотря на очень сильную
дисперсию опытных значений h/l, эти значения все-таки
не очень удаляются от теоретического (они за редкими
исключениями лежат в интервале примерно 0,250—0,360),
показывает, что значения, близкие к теоретическому, играют
особую роль и как часто наблюдаемые, несомненно, более
устойчивы, чем другие расположения вихрей. Кроме того,
и теоретическое изучение этого вопроса позволяет, по-види-
мому, сделать вывод, что условие h/l = 0,281 для шахматной
дорожки нельзя рассматривать как критерий их полной
устойчивости. Вывод этого условия предполагает периоди-
ческий закон смещения и приводит к тому, что при выпол-
нении его равновесие получается или устойчивое или без-
различное. Как показали исследования Кармана и Н. Е. Жуков-
ского, возможны другие законы смещения, не приводимые
к характеру периодического смещения Кармана и приво-
дящие к другому условию устойчивости hjl = 0,309. Этот
результат и доказывает, в сущности, что в рассматриваемом
случае нет полной устойчивости. То же было получено
позднее из других соображений Н. Е. Кочиным.
Все изложенное служит обоснованием тех двух основных
положений, на которых основано все предшествующее иссле-
дование:
во-первых, в соответствующем диапазоне
чисел Рейнольдса сзади плохо обтекаемых
О СТРОЕНИИ СПУТНОЙ ЗОНЫ ЗА ПЛОХО ОБТЕКАЕМЫМ ТЕЛОМ 819
тел образуются двойные вихревые шахматные
дорожки;
во-вторых, наблюдаемые шахматные дорожки
удовлетворяют с допустимым приближением
условию устойчивости Кармана hjl = 0,281.
Рассматривавшиеся в настоящей работе режимы течения
за плохо обтекаемыми телами не единственные: они имеют
место только в некотором интервале чисел Рейнольдса, т. е.
возникновение их обусловлено и регулируется проявлением
сил вязкости. Как было показано, рассматриваемые режимы
течений соответствуют определенному значению числа Стру-
халя, близкому к 0,18, и подобные режимы возможны при
значениях чисел Рейнольдса в интервале от 102 до 104. Вне
этого интервала режима обтекания, достаточно точно изобра-
жаемого теоретически шахматными вихревыми дорожками,
по-видимому не существует и течение приближается к струй-
ному или носит турбулентный характер, плохо поддаю-
щийся, по-видимому, сколько-нибудь простой теоретиче-
ской схеме.
Все предыдущие соображения надо рассматривать как
попытку связать некоторой общей теоретической схемой
явления, наблюдаемые в течениях сзади плохо обтекаемых
тел. Имеющиеся экспериментальные данные не позволяют
при настоящем положении дел рассматривать ее как доста-
точно обоснованную теорию рассматриваемой группы явлений.
Надо рассматривать ее как попытку дать возможное решение
задачи, и, несомненно, этот запутанный вопрос требует
дальнейшего изучения и теоретического, и эксперименталь-
ного, которое должно дать более тщательно проверенные
наблюдаемые данные.
ЛИТЕРАТУРА
1. С. Гольдштейн, Современное состояние гидроаэроди-
намики вязкой жидкости, т. I и II, 1948.
2. Bena rd, Comptes Rendus, т. 147, стр. 839—847, 1908.
3. Н. Е. К о ч и н, И. А. К и б е л ь, Н. В. Р о з е, Теоретическая
гидромеханика, т. I, 1948.
4. Г. Л а м б, Гидродинамика, 1947.
5. Karman, Ober den Mechanismus des Widerstandes den ein
bewegter Korper in einer Fliissigkeit erfahrt. Nachr d. Gesellschaft
fur Wissenschaften zu Gottingen, H. 5, стр. 509—517, 1911.
820 IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ аэродинамики
6. Th. Karman, Н. L. Rub ас h, Ober den Mechanism us des
Fliissigkeits- und Zeitwiderstandes, Physik. Zeitschrift, №2, 1912.
7. В. В. Голубев, Теория крыла аэроплана конечного раз-
маха, 1931.
8. Relf, Simmons A. R. С. Reports and Memoranda, № 997,
1924.
9. Heisenberg, Physik. Zeitschrift, №23, 1922.
10. H. С. А ржаник OB, В. H. Ma л ьцев, Аэродинамика, 1952.
11. В. В. Голубев, Лекции по теории крыла, формула (2),
1949.
12. Я. Е. Полонский, Некоторые вопросы машущего крыла,
Инженерный сборник, т. 8, 1950.
13. Р. И. Виноградов, Физические основы теории само-
колебаний крыла в плоском потоке, Научно-технический сборник,
вып. 13, 1953.

БИОГРАФИЧЕСКИЕ
СТАТЬИ
Н. Е. ЖУКОВСКИЙ
(1847—1921)
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ»)
(Биографический очерк)
I
Н. Е. Жуковский родился 17 (по ст. ст. 5) января
1847 г. в небольшом имении Орехово, бывшей Владимирской
губернии. Его отец Егор Иванович Жуковский, по про-
фессии инженер-путеец, работал одно время на постройке
Нижегородской ж. д., затем вышел в отставку и занимался
сельским хозяйством в своем имении Орехово.
На скудные средства, которые давало хозяйство, Е. И. Жу-
ковскому и его жене Анне Николаевне (урожденной Стеч-
киной) приходилось содержать большую семью, состоявшую
из шести человек: четырех сыновей и двух дочерей.
Н. Е. Жуковский был третьим в семье. Несмотря на то,
что родители Николая Егоровича еле-еле сводили концы
с концами, они дали своим детям хорошее образование.
В качестве домашнего воспитателя был приглашен Альберт
Христианович Репман, человек исключительно разносторон-
ний, весьма образованный и увлекательный рассказчик;
впоследствии он был директором Московского политехниче-
ского музея. Мальчики после домашней подготовки посту-
пили в Четвертую московскую гимназию, которая помеща-
лась на Покровке.
Так как семья жила безвыездно в Орехове, то Н. Е. Жу-
ковский поступил в пансион при гимназии, где он и находился
1) Опубликовано в Поли. собр. соч. Н. Е. Жуковского, т. 1, 1937.
(Прим, ред.)
824
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
до окончания гимназии (1864 г.), приезжая летом в
Орехово.
В первых классах гимназии Николай Егорович учился
плохо. Не выказывал он больших успехов и в арифметике,
которую преподавал Малинин, автор широко известных
в свое время учебников и задачников. Но с четвертого
класса он стал заметно выделяться среди своих товарищей
успехами по математике.
Гимназию Николай Егорович окончил с серебряной ме-
далью в 1864 г. и поступил на математическое отделение
физико-математического факультета Московского универси-
тета. В это время он уже с увлечением занимался матема-
тикой и с восторгом слушал известных в то время профес-
соров и выдающихся ученых А. Ю. Давидова, В. Я. Цин-
гера и Ф. А. Слудского.
В студенческие годы Н. Е. Жуковский с особым интере-
сом занимался механикой, которую читали сначала В. Я. Цин-
гер, затем Ф. А. Слудский. Несомненно, что влияние их
сказалось на всей дальнейшей научной деятельности Ни-
колая Егоровича. Профессор В. Я. Цингер был геометр
по специальности. Как прекрасный преподаватель, талант-
ливый ученый, строгий и требовательный профессор, он
пользовался совершенно исключительным авторитетом среди
студенчества. Прекрасные лекции В. Я. Цингера, его гео-
метрический талант, вероятно, в значительной мере опре-
делили характер научного мышления Н. Е. Жуковского:
в его научных исследованиях геометрические методы играли
всегда совершенно исключительную роль.
Совершенно иного рода было влияние Ф. А. Слудского.
Большой знаток механики, Слудский видел идеал, к кото-
рому должна стремиться механика, в том методе изложе-
ния, который ей придал гениальный Лагранж в своей
«Аналитической механике». Все преподавание механики
у Ф. А. Слудского строилось на общих принципах, из ко-
торых затем получались как частные случаи различные изу-
чаемые до конца типы движения. Известно, что в «Анали-
тической механике» Лагранжа все изложение ведется чисто
аналитическим путем; такой же характер носило и изложе-
ние Ф. А. Слудского. Геометрическому элементу при та-
ком изложении не придавалось никакого значения, геомет-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
825
рические иллюстрации считались излишними, если были
найдены формулы, определяющие для любого момента по-
ложение движущегося тела. Контраст между живыми, гео-
метрически наглядными и блестящими по форме лекциями
В. Я. Цингера и точным строго аналитическим и абстракт-
ным изложением Ф. Я. Слудского был очень велик. И, по-
видимому, уже тогда Н. Е. Жуковский сделал выбор
между этими направлениями, и этот выбор был не в пользу
метода Ф. А. Слудского. Впоследствии Николай Егорович
любил вспоминать, как студенты, рассуждавшие хорошо
об общих принципах механики, не умели решать простей-
ших механических задач; этот пример, вероятно, впфше убе-
дил его в преимуществе конкретного, геометрически ясного
и наглядного изложения, которому он и следовал в даль-
нейшем в своей долгой и блестящей научной и педагоги-
ческой деятельности.
В 1868 г. Н. Е. Жуковский окончил университет. В на-
чале он не пошел по научному пути. Увлеченный своим то-
варищем Щукиным, впоследствии крупным специалистом
по паровозостроению, Николай Егорович решил посвятить
себя в дальнейшем деятельности в области прикладной тех-
ники и поступил в Институт инженеров путей сообщения
в Петербурге. Но здесь он пробыл недолго. Общая поста-
новка преподавания его не удовлетворяла; трудно давалось
ему также черчение; кроме того, непривычный петербург-
ский климат неблагоприятно повлиял на его здоровье.
Николай Егорович оставил институт, вернулся в Москву
и стал усердно готовиться к сдаче магистерского экзамена.
Первый год по возвращении из Петербурга он прожил
в Орехове, а затем в 1870 г. со своей матерью, Анной Ни-
колаевной, и сестрами переселился в Москву, где занял
место преподавателя физики во Второй женской гимназии.
В 1872 г. Н. Е. Жуковский был назначен преподавате-
лем Московского технического училища. Первое время он
преподавал математику, а затем осенью 1874 г. был
утвержден доцентом по кафедре аналитической механики
в том же Техническом училище, где и преподавал механику
в течение 47 лет.
В 1876 г. в VIII томе «Математического сборника» на-
печатана первая научная работа Н. Е. Жуковского, его
826
V. БЙОГРАФИЧЕСКИЕ СТАТЬИ
магистерская диссертация «Кинематика жидкого тела». Этой ра-*
ботой, которая сразу выдвинула молодого ученого, начинается
длинный ряд его работ по гидро- и аэромеханике, работ,
которые дали их творцу мировое имя. В этой первой ра-
боте Николая Егоровича совершенно ясно сказываются уже
те тенденции, которыми была проникнута его дальнейшая
исследовательская работа.
Глубокие исследования по деформациям элемента жидкости
во время ее движения, начало которых восходит к ра-
ботам Лагранжа и Коши, носили исключительно анали-
тический характер, а потому были лишены той наглядности,
которую вносят геометрические методы исследования. Вы-
ражаясь современным языком, все эти исследования носили
количественный характер, качественного исследования ха-
рактера движения произведено не было. Н. Е. Жуковский
переводит все исследование совершенно в иную плоскость.
Основная идея этой выдающейся работы точно и ясно фор-
мулирована им во введении к работе.
«Та высокая степень ясности, которая была внесена
в область динамики твердого тела геометрическими иссле-
дованиями неизменяемой системы, заставляет ожидать зна-
чительного успеха гидродинамики от сближения ее с кине-
матикой изменяемой системы. К сожалению, геометрическая
теория движения изменяемой системы находится только
на первых ступенях своего развития. Все работы по этому
предмету ограничиваются небольшим числом исследований
движения простейших изменяемых систем и общими сообра-
жениями о движении непрерывно изменяющегося тела». ..
«Предлагаемое нами сочинение имеет в виду дать краткий,
но, по возможности, наглядный очерк теории скоростей
и ускорений непрерывно изменяемого тела и может быть
рассматриваемо как вступление в гидродинамику. При со-
ставлении его мы старались поставить общие теоремы
о движении жидкости в уровень с тем развитием, которое
получили исследования изменяемых систем частного вида».
В этом введении к своей первой крупной научной ра-
боте Николай Егорович дает тот лейтмотив, который будет
звучать во всех последующих его научных работах.
Много лет спустя, в речи на собрании, посвященном
25-летнему юбилею Московского математического общества,
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
827
Н. Е. Жуковский возвращается более подробно к вопросу
о роли геометрии:
«Механика при своем первоначальном развитии опиралась
исключительно на геометрический метод. Механические иссле-
дования Архимеда, Галилея и Гюйгенса — геометрического
характера. Весь строй изложения в „Принципах натураль-
ной философии" Ньютона — чисто геометрический. В том же
направлении шли работы последующих авторов: Бернулли,
Айвори, Маклорена и др. Но после того как Декарт дал
способ выражать движение в пространстве по трем движе-
ниям на осях координат и анализ бесконечно малых, откры-
тый Ньютоном и Лейбницем, вошел во всеобщее употреб-
ление, в исследованиях по теоретической механике стал все
более и более преобладать аналитический метод, который
в творениях Лагранжа и его последователей достиг своей
высшей точки. Геометрическая постановка задачи замени-
лась составлением возможной работы, реакции связей—не-
определенными множителями, изыскание движения отожде-
ствилось с задачей об интегрировании дифференциальных
уравнений.
Поощренные успехом, выразившимся рядом блестящих
теорий в общей теории интегрирования уравнений динамики,
представители аналитического метода стремились возможно
шире ставить рассматриваемые вопросы, почти совершенно
игнорируя их геометрическую и механическую стороны.
Вследствие этого возникали аналитические трудности, иногда
нисколько не вызываемые сущностью дела. Данная механи-
ческая задача запутывалась и усложнялась вследствие отне-
сения ее к произвольной системе координат и упущения
из виду той, которая всего ближе к ней подходит»...
«Так, задача о движении твердого тела по инерции, хотя
и разрешенная аналитически Эйлером, представлялась труд-
ной и запутанной, а задачи гидродинамики, хотя и сведен-
ные Эйлером и Лагранжем к уравнениям с частными про-
изводными, оставались без решения, так как последнее не-
разрывно связывалось с отысканием общих интегралов этих
уравнений. Здесь на помощь анализу снова явилось забытое
на время геометрическое толкование. В своем изящном ме-
муаре „ThSorie nouvelle de la rotation des corps" Пуансо
поставил себе задачей ^изучить вещи сами в себе" и.
828
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
следуя этому девизу, довел геометрическую интерпретацию
рассматриваемого движения до той степени наглядности,
при которой оно со всеми подробностями рисуется перед
глазами читателя» ... «Подобным же образом геометрическое
толкование сослужило важную роль в исследованиях
по гидродинамике. В своем замечательном сочинении „Ober
Integrate der hydrodynamischen Gleichungen" Гельмгольц дает
геометрическую интерпретацию интегралов гидродинамики,
которые 20 лет раньше были найдены Коши и оставались
без применения» .. . «Таким образом, конец нашего столе-
тия ознаменовался возвращением к геометрическому толко-
ванию и соединением аналитического метода исследования
с геометрическим. Механика сознательно пошла по тому
пути, которого при своем возникновении держались по
необходимости».
«Отстаивая достоинства геометрического метода иссле-
дования, я далек от мысли об его исключительности. Ме-
ханика должна равноправно опираться на анализ и геомет-
рию, заимствуя от них то, что наиболее подходит к су-
ществу задачи. Своими новыми методами: исследованием
интегралов по дифференциальным уравнениям, изысканием
признаков, при которых существуют алгебраические инте-
гралы, и т. д. анализ дает нам могущественное орудие
для разрешения задач динамики. Но последняя обработка
решений задачи всегда будет принадлежать геомет-
рии».
«Геометр всегда будет являться художником, создающим
окончательный образ построенного здания».
Таково было научное кредо Николая Егоровича, и мы
видели, что уже в первом своем крупном исследовании
он твердо наметил путь, по которому и шел всю свою долгую
и плодотворную научную жизнь. Так пышно проросли се-
мена, которые были посеяны университетским преподава-
нием, лекциями Цингера и как контраст к ним лекциями
Ф. А. Слудского.
В 1877 г. Н. Е. Жуковский защитил магистерскую
диссертацию и вскоре был командирован за границу:
в Берлин и Париж. В Берлине он слушал лекции Гельм-
гольца, Кирхгоффа, Куммера, а в Париже главным образом
занимался у Дарбу и Резаля. За границей он завязал нц-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ 829
учные знакомства, главным образом среди тогдашней науч-
ной молодежи; в частности, в Париже он познакомился
с тогда еще совсем юным Анри Пуанкаре и близко со-
шелся с Резалем, который поместил две его работы
«Об ударе» и «О начале наименьшего действия» в «Жур-
нале Лиувилля» (1878 г.). Статья Н. Е. Жуковского
«Об ударе» была особенно отмечена Дарбу; эта его ра-
бота вместе с сочинением на ту же тему Дарбу послужила
основанием чисто геометрического исследования явления
удара, которому в дальнейшем были посвящены работы
Делоне, Занчевского, Бельтрами и др.
По возвращении из-за границы в 1879 г. Н. Е. Жу-
ковский получает назначение сверхштатным профессором
механики в Техническом училище вместо ушедшего в от-
ставку профессора А. В. Летникова.
В 1882 г. появляется в печати вторая крупная работа
Н. Е. Жуковского: его докторская диссертация «О проч-
ности движения». В этой работе, представляющей развитие
первых работ по этому вопросу Томсона и Тэта, сам Ни-
колай Егорович считал наиболее ценным определение вели-
чины, которая им названа мерой прочности. Для случая
системы с двумя степенями свободы мера прочности играет
роль, аналогичную гауссовой мере кривизны поверхности.
Устойчивость движения зависит от знака меры прочности.
Работа Н. Е. Жуковского в свое время была крупным ус-
пехом в этой сложной области механики и была посвящена
актуальнейшему вопросу механики; достаточно сказать, что
одновременно с диссертацией Николая Егоровича появилось
обширное исследование на ту же тему одного из крупней-
ших английских механиков Рауса (Routh), который разра-
ботал иной метод оценки устойчивости движения. Впослед-
ствии этим вопросом занимался один из крупнейших рус-
ских ученых А. М. Ляпунов, который в 1892 г. защитил
в Московском университете диссертацию «Общая задача
об устойчивости движения», причем Н. Е. Жуковский был
оппонентом. Ляпунов значительно продвинул этот сложный
вопрос и исправил некоторые неточности, которые были
в работе Н. Е. Жуковского.
В 1882 г. Н. Е. Жуковский защитил диссертацию
и получил Степень доктора прикладной математики.
830
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
С 1885 г. Н. Е. Жуковский начал свое преподавание
в Московском университете. В 1886 г. он был назначен
экстраординарным профессором механики (после выхода
в отставку проф. Ф. А. Слудского). В связи с работой
в университете Николай Егорович в 1885 г. оставил долж-
ность преподавателя физики во Второй женской гимназии.
Характерно, однако, что он не порывал совсем связи со
средней школой. Еще в 1873 г. он поступил преподавате-
лем в Московскую практическую академию коммерческих
наук и продолжал там преподавание непрерывно до 1920 г.
Несомненно, эта связь со средней школой сыграла -значи-
тельную роль в его педагогической и научной деятельности.
Высшая школа не учит и не может научить своих работни-
ков методам преподавания; можно было бы назвать боль-
шое число крупнейших ученых, которые в то же время яв-
лялись очень слабыми преподавателями. Как остроумно за-
метил известный русский педагог К. Д. Ушинский, вся
методика чтения лекций в университете может быть выра-
жена в двух словах: «Знай хорошо свой предмет и излагай
его ясно». Однако это второе требование, ясность изложе-
ния—‘большое и сложное искусство, которое постигается
далеко не сразу. И вот, работа в средней школе и дает
возможность овладеть этим немаловажным для профессора
искусством. Вероятно, длительная работа в средней школе
и выработала из Николая Егоровича прекрасного препода-
вателя. Эта же педагогическая работа развила у Николая
Егоровича вкус к популяризации и наглядности изложения.
В цитированной выше речи он так резюмирует свое отно-
шение к наглядности преподавания:
«Можно говорить, что математическая истина только
тогда должна считаться вполне обработанной, когда она
может быть объяснена каждому из публики, желающему ее
усвоить. Я думаю, что, если возможно приближение к этому
идеалу, то только со стороны геометрического толкования
или моделирования».
Отсюда интерес Николая Егоровича к собиранию и по-
стройке моделей. Механический кабинет Московского универ-
ситета, созданный главным образом профессором Орловым
и Н. Е. Жуковским, обязан им своими прекрасными кол-
лекциями моделей. Следующий естественный шаг — это пре-?
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ 831
Вращение кабинета механических моделей в механическую
лабораторию.
Годы преподавания физики в средней школе привели
к тому, что в руках Николая Егоровича механика была
не теоретической абстрактной наукой, целиком замыкаю-
щейся в математические методы исследования, а естествен-
ной наукой, изучающей широкий, разнообразный и живой
мир механических явлений природы.
II
Защита докторской диссертации в 1882 г. и связанное
с этим упрочение положения Николая Егоровича составляют
важную дату в его жизни. Перед ним открывалась широкая
возможность разносторонней научной работы как в Техни-
ческом училище, так и в университете, где позднее,
в 1891 г., он сделался ординарным профессором. Первые
крупные работы Н. Е. Жуковского создали ему солидный
авторитет, а общение с выдающимися представителями на-
учной и технической мысли того времени (среди которых
назовем крупнейших ученых, профессоров: Бредихина, Сто-
летова, тогда начинающего талантливого геометра, живого
и энергичного преподавателя Б. К. Млодзеевского и быв-
ших учителей, а теперь товарищей Н. Е. Жуковского
по работе в Московском университете: Ф. А. Слудского,
Н. В. Бугаева и других, а также профессоров-инженеров,
товарищей Н. Е. Жуковского по работе в Московском выс-
шем техническом училище) позволило ему быть в курсе
широких научных и технических интересов. Все это созда-
вало для Николая Егоровича исключительно благоприятные
условия для расцвета его выдающихся научных творческих
способностей. После защиты диссертации в ближайшие же
годы Н. Е. Жуковский развивает исключительно разносто-
роннюю и продуктивную научную работу. В 1883 и 1884 гг.
появляется ряд его интересных исследований; некоторые
из них в дальнейшем послужили исходными для разработки
сложных научных и технических задач. К этому же вре-
мени относится начало ряда работ Николая Егоровича
по астрономическим вопросам, по теории вычисления пла-
нетных орбит и по теории кометных хвостов; здесь сказы-
832
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
вается влияние знаменитого творца теории к ^ых хво-
стов, профессора Московского университета А. Бреди-
хина, с которым Н. Е. Жуковский в эти годы был осо-
бенно близок.
Наряду с большим числом сравнительно мелких работ
отметим появление в 1885 г. крупного исследования
Н. Е. Жуковского «О движении твердого тела, имеющего
полости, наполненные однородной капельной жидкостью»,
удостоенного Московским университетом в 1886 г. премии
имени профессора Брашмана. По поводу этой работы ее рецен-
зент, профессор Ф. А. Слудский, сказал: «Если бы сочине-
ние Н. Е. Жуковского состояло лишь из шести последних
страниц, то и тогда оно было бы вполне достойно премии
покойного профессора Брашмана». В этих последних стра-
ницах, о которых говорит Ф. А. Слудский, дано доказа-
тельство того, что трение жидкости в полости тела влияет
на асимптотическое приближение его оси вращения к оси
инерции рассматриваемых движущихся масс. Н. Е. Жуков-
ский заканчивает свое сочинение вопросом: «не этой ли тео-
ремой следует объяснить то обстоятельство, что, несмотря
на всякие случайные начальные скорости, планеты вра-
щаются около своих осей инерции?»
Впоследствии Ф. А. Слудский сделал приложение этой
теоремы к некоторым вопросам астрономии.
В 1890 г. был напечатан выдающийся труд Н. Е. Жуков-
ского «Видоизменение метода Кирхгоффа для определения
движения жидкости в двух измерениях при постоянной ско-
рости, данной на неизвестной линии тока». Работа эта, кото-
рую особенно ценил он сам, представляет собой чрезвычайно
остроумное видоизменение метода Кирхгоффа в теории струй,
позволяющее находить течения несжимаемой жидкости с любым
числом критических точек и с любым числом струй. Инте-
ресен употребляемый Николаем Егоровичем в этой работе
геометрический метод, основанный на применении двух сетей
линий. Хотя эта работа и не дает расширения метода Кирх-
гоффа, так как можно показать, что всякая задача, решаемая
его методом, разрешима и методом Кирхгоффа, но геометри-
ческая наглядность метода и огромное число частных слу-
чаев, разобранных Николаем Егоровичем этим методом, сооб-
щает этой работе исключительный интерес. Одновременно
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
833
появившаяся работа Митчела, который применяет метод,
близкий к методу Н. Е. Жуковского, далеко уступает работе
Николая Егоровича, так как в ней нет ни геометрического
приема, ни таких разнообразных и интересных приложений,
как в работе Н. Е. Жуковского.
Об интенсивности работы Николая Егоровича в этот пе-
риод достаточно ярко говорит тот факт, что за восемь лет им
написано и опубликовано в печати 36 работ. Если мы всмот-
римся в тематику его работ, как появившихся за эти годы,
так и опубликованных в последующие годы, то нетрудно
заметить, как постепенно расширяется круг тех вопросов,
которыми он занимается. К исследованиям по гидромеханике
и механике твердого тела постепенно присоединяются работы
астрономического содержания и по вопросам гидравличе-
ского характера (например, работы Н. Е. Жуковского по
теории влияния реакций втекающей и вытекающей жидкости,
по гидродинамической теории смазки), по теории упругости,
по теории подпочвенных вод, о форме судов, об артиллерий-
ских снарядах Шапеля и т. д. В этом разнообразии тем
исследования все более и более начинает проявляться одна
черта» чрезвычайно характерная для всей научной деятель-
ности Николая Егоровича, — это все большее тяготение его
научных интересов к вопросам техники.
В этом сказывается одна общая тенденция, которая посте-
пенно проникает в чисто теоретические науки. Как известно,
первые успехи механики и ее твердое обоснование связаны
с решением механических задач астрономии. Работы Нью-
тона главным образом посвящены астрономическим вопросам.
На смену им в конце XVIII столетия пришли задачи, связан-
ные с общими проблемами теоретической физики. На рабо-
тах по теории тепла, по теории волн создавались и разра-
батывались математические методы механики. В это время
задачи техники почти совершенно не влияли на развитие
механики. Можно, пожалуй, указать только одну область
технического, прикладного характера, которая привлекла
внимание теоретиков, — это теория корабля, которой Эйлер
и Бугер посвятили первые трактаты, позволяющие подвести
некоторую теоретическую базу под чисто технические задачи.
В других областях техника шла своим путем, заменяя
точное научное исследование вопроса полуэмпирическими,
834
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
приближенными и временами не достаточно научно обоснован-
ными методами. Но с дальнейшим развитием техника все чаще
и чаще обращается за помощью к точной теоретической науке.
Это стремление разрешать технические, чисто приклад*
ные задачи методами точной теоретической механики все
более и более проявляется за последние десятилетия, и
Н. Е. Жуковский был одним из первых крупных теоретиков-
механиков, которые вполне ясно осознали эту потребность
техники и пошли ей навстречу. Это тем более интересно;
что годы, когда формировалось его научное мировоззрение,
совпадают с эпохой, создавшей такие классические образцы
чисто теоретических, оторванных от всяких приложений
исследований, как общие методы интегрирования уравнений
динамики, как задача о движении твердого тела, задача
трех тел и т. п. Достаточно привести два замечательных
образца этого направления: классическая книга Якоби «Лек-
ции по динамике», по которой, несомненно, учился Нико-
лай Егорович, и работы С. В. Ковалевской по теории вра-
щения твердого тела вокруг .неподвижной точки, работы,
которые произвели глубокое впечатление на научные круги
и создали С. В, Ковалевской по справедливости мировое имя.
Этим направлениям Николай Егорович также отдал дань.
Вопросам общей динамики посвящено несколько его мелких
работ; к этому же направлению можно отнести его доктор-
скую диссертацию; случаю движения твердого тела, откры-
тому С. В. Ковалевской, посвящена одна из статей Н. Е. Жу-
ковского, в которой он по своему обыкновению дает красивую
геометрическую картину движения. Но все симпатии, все его
научные интересы все более и более склоняются совершенно
в иную область — в область научного решения механических
задач техники, а это в свою очередь наложило совершенно
своеобразный отпечаток на методы научной работы Нико-
лая Егоровича.
Технические задачи требуют немедленного решения. Если
можно утешаться тем, что со временем с развитием методов
исследования интегралов дифференциальных уравнений задача
трех тел будет во всех подробностях изучена, то в области
технических наук нужно немедленное решение конкретных
задач, выдвигаемых практикой; пусть это решение будет
не очень точное, пусть оно годится только в частных слу-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
835
чаях, но его нужно найти и найти вовремя, когда в нем
нуждается инженер, работающий на производстве. Отсюда-—
развитие приближенных методов при решении технических
задач. Но и сами приближенные методы могут быть различны.
Во-первых, можно записать изучаемое явление совершенно
точными уравнениями, например дифференциальными урав-
нениями, и затем ввиду невозможности их точного решения
искать приближенные методы решения, разлагая, например,
интегралы в ряды, вводя малые параметры и т. п.; во-вторых,
можно с самого начала изучаемое явление заменить другим,
более простым и допускающим полное исследование, но
сохраняющим основные черты изучаемого явления, иными
словами, стилизовать изучаемое явление, заменить его более
простой моделью.
Естественно, что можно воспользоваться и тем и другим
методом; в небесной механике, например, обычно применяют
первый метод; в технике, пожалуй, второй метод дал наи-
более интересные и важные результаты.
Н. Е. Жуковский обладал исключительным умением упро-
щать изучаемое явление, заменять его более простым и,
опираясь на эту упрощенную схему, доводить исследование
до конца. Он любил говорить своим ученикам, что «меха-
ника есть искусство выражать задачи о движении уравне-
ниями, которые до конца интегрируются», и этим искус-
ством Николай Егорович владел исключительно виртуозно.
Длительная работа в Техническом училище, среди специали-
стов-инженеров, а затем заседания инженерно-механического
отдела Политехнического общества, в котором Николай
Егорович с 1872 г. был одним из самых активных участников
и докладчиков и мог постоянно поддерживать самую живую
связь с инженерами, работавшими на производстве, содей-
ствовали тому, что он непрерывно и все более глубоко втяги-
вался в области чисто прикладных вопросов.
Глубокий теоретический фундамент, разносторонняя подго-
товка Николая Егоровича и постоянное общение с науч-
ными силами в университете, а затем и в Математическом
обществе (он был одним из старейших и активнейших
членов общества, с 1903 г. его вице-президентом, а с 1907 г.
президентом) — все это позволяло ему быть в курсе всех
новинок не только в области механики, но и в смежных
836
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
областях математики, астрономии, математической физики,
всех отделов точного естествознания, которое «мерою и
числом» познает природу. Неудивительно, что Николай Его-,
рович, обладавший исключительным талантом исследователя
и живо интересовавшийся практическими вопросами техники,
быстро становится тем центром, около которого группи-
руются инженеры и к которому они обращаются за советом
при решении технических вопросов. Профессор П. К. Худя-
ков, который близко наблюдал деятельность Николая Его-
ровича в Техническом училище и в Политехническом обществе,
в своих воспоминаниях о нем говорит:
«Достойно внимания то обстоятельство, что не было
никогда ни одного случая, чтобы Николай Егорович, что
называется, отмахивался от предложенной ему темы. В каж-
дый вопрос, за разъяснением которого обращались к нему
инженеры, его бывшие ученики, он вдумывался самым серь-
езным, самым добросовестным образом и отвечал на него
или тут же непосредственно, или же путем длительной
разработки, за которой следовали: или специальный доклад
на предложенную тему, или сооружение научной модели,
разъясняющей затронутый вопрос, или — это бывало не-
редко—целое экспериментальное исследование по его пла-
нам и указаниям».
Научные интересы Н. Е. Жуковского постепенно и прочно
врастали в круг чисто технических задач, а сам он в со-
знании окружающего его передового в научном отношении
инженерства перерастал в импозантную фигуру «сверхинже-
нера», к которому шли, чтобы получить совет, разъясне-
ние, поддержку, указание, инженеры, его бывшие ученики
по Техническому училищу, и другие технические работники,
которым необходимо было его авторитетное мнение по тому
или другому вопросу.
Задача науки — решать общие широкие научные проб-
лемы; удел техники — заниматься конкретными частными во-
просами, но зато доводить их до полной ясности, до пол-
ного разрешения, до возможности рассчитать и претворить
в конструкцию язык формул и геометрических построений.
Практические вопросы техники, все более и более за-
хватывавшие Николая Егоровича, естественно, влекли его
в область решения конкретных, частных задач. Поэтому
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ 837
в научном творчестве Н. Е. Жуковского подавляющее место
занимает решение конкретных задач, решение их частными,
часто виртуозно подобранными и всегда наглядными, целе-
сообразными и всегда простыми методами. Только в первый
период его деятельности, в годы, когда складывались его
научные интересы, он занимался общими теоретическими
вопросами. Его две диссертации и работы, указанные в первом
разделе нашего очерка, — результаты этих занятий. В по-
следующие годы он почти не занимался общими теорети-
ческими проблемами, не разрабатывал общих теоретических
методов исследования. Это не значит, конечно, что он не
получал общих научных результатов, позволяющих ввести
в науку широкие, принципиально новые общие идеи. Но эти
идеи получались как зрелый плод в результате разрешения
конкретных задач. К общим истинам науки с одинаковым
успехом ведет и индукция — от частных результатов к теоре-
тическим широким обобщениям — и дедукция, позволяющая
сразу охватить широкую группу однородных явлений. Ни-
колай Егорович работал методами индукции. И эта осо-
бенность его творчества наряду с геометрическим складом
его ума давала исключительную законченность, ясность и
конкретность его научным результатам.
Из многочисленных и разнообразных работ Н. Е. Жуков-
ского за этот период мы остановимся здесь только на одной
группе тем — это работы, связанные с гидродинамикой под-
земных вод и с вопросами работы водопроводов. Эти ра-
боты необходимо отметить прежде всего потому, что ими
Н. Е. Жуковский приобрел себе европейское имя крупней-
шего специалиста по гидромеханике. Около 1890 г. в связи
с быстрым ростом населения Москвы значительно увеличился
расход воды московского водопровода. Был поднят вопрос
о расширении мытищинского водопровода. В связи с этим
появилась работа Николая Егоровича «Теоретическое иссле-
дование о движении подпочвенных вод» и ряд последую-
щих статей и докладов на ту же тему. Он установил связь
между колебанием барометра и высотой стояния уровня под-
почвенных вод. По величине колебаний уровня подпочвенных
вод оказалось возможным определить емкость водовме-
стилища и предельный расход воды. В результате работ
Николая Егоровича мысль о расширении мытищинского
838
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
водопровода была оставлена и была построена новая, Руб-
левская водопроводная станция. Между прочим, эти работы
обратили на себя внимание гигиенистов на конгрессе врачей
в Вене в связи с влиянием колебания уровня подпочвенных
вод на развитие эпидемий. В дальнейшем при постройке
нового московского водопровода возник вопрос о причи-
нах частых разрывов водопроводных труб. Приглашенный,
главным городским инженером Н. П. Зиминым принять учас-
тие в разъяснении этого вопроса, Н. Е. Жуковский орга-
низовал обширное экспериментальное исследование измене-
ния гидродинамического давления в трубах и распространения
этого изменения давления вдоль трубы при прекращении
течения воды путем быстрого закрытия задвижки в конце
трубы. Полученные интересные экспериментальные резуль-
таты послужили ему материалом, на основе которого им
была разработана подробная теория гидравлического удара
в водопроводных трубах, причем попутно оказалось воз-
можным на основании теории по ударной диаграмме
отыскать место утечки воды в водопроводной трубе. Заме-
чательная, ставшая классической работа Н. Е. Жуковского
на эту тему «О гидравлическом ударе в водопроводных
трубах» была переведена на английский и французский языки
и выдвинула его на одно из первых мест среди теоретиков,
работающих в области гидродинамики. К этой же области
относятся работы Н. Е. Жуковского о гидравлическом
таране, а по методу исследования близко подходит его
любопытная статья, напечатанная много позднее (1914 г.),
«Определение скорости движения продуктов горения в за-
водской трубе по фотографии выбрасываемого ею дыма».
К вопросу о распространении волн в водопроводных тру-
бах Николай Егорович неоднократно возвращался в после-
дующих работах и докладах.
Если темы исследования Н. Е. Жуковского в период
с 1882 по 1890 г. поражают своим разнообразием, то еще
более разнообразными являются его работы в последующее
десятилетие. Помимо вопросов, связанных с гидродинамиче-
ской теорией течения жидкости в трубах, Николай Егоро-
вич в этот период продолжает заниматься вопросами гид-
родинамики идеальной и вязкой жидкости, теорией
вихрей.
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
839
Случайно заинтересовавшись задачей о вращении вере-
тена в кольцевых ватерах, он находит новую и интересную
конструкцию веретена; установленный им при этом принцип
движения немедленно нашел применение в плоских рассевах
сельскохозяйственных машин.
Исследования профессора Н. П. Петрова над трением
подшипников вызвали со стороны Н. Е. Жуковского ряд ра-
бот по гидродинамической теории смазки (последняя рабо-
та на эту тему написана Н. Е. Жуковским совместно
с проф. С. А. Чаплыгиным).
В эти же годы среди других тем начинают появляться
работы Н. Е. Жуковского по механике полета в воздухе,
области, которая полностью захватила Николая Егоровича
в последние два десятилетия его жизни и нашла отражение
в ряде исследований, поставивших его имя в числе творцов
современной теоретической и прикладной аэродинамики.
В 1890 г. появилась первая его статья в этой, области —
«К теории летания», через два года появляется вторая ра-
бота— «О парении птиц», затем идут статьи: «О летательном
аппарате Отто Лилиенталя», «О гибели Отто Лилиенталя»
(посвященная его памяти) и, наконец, статья «О наивы-
годнейшем угле наклона аэроплана». Вопросом о летании
на .приборах тяжелее воздуха Николай Егорович начал инте-
ресоваться, по-видимому, еще очень давно. Он тщательно
собирал всевозможные летающие модели, воздушные змеи,
заводные летающие бабочки и т. п. С Отто Лилиенталем
Николай Егорович был лично знаком и получил от него
в подарок один экземпляр построенных им крыльев, которые
теперь находятся в Центральном аэрохимическом музее.
Перечисленные статьи являются попытками Николая Егоро-
вича уяснить сложное явление полета, и по ним можно про-
следить, с каким трудом вырабатывались основные идеи,
которые впоследствии дали возможность создать законченную
и глубокую гидродинамическую теорию, неразрывно связан-
ную с именами Н. Е. Жуковского и С. А. Чаплыгина.
111
Начало текущего столетия ознаменовалось первыми удач-
ными попытками полета на самолетах. Братья Райт в Аме-
рике и Фарман во Франции были пионерами летного
840
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
искусства. ^Техники ставили перед наукой труднейшую; новую
задачу — дать теоретическое объяснение возникновению сил,
поддерживающих в воздухе самолет, задачу, над которой
в течение тысячелетий, начиная от Аристотеля, Леонардо
да Винчи и кончая Кирхгоффом, Гельмгольцем, Рэлеем
и другими, упорно размышляли ученые.
Вся предыдущая научная деятельность Н. Е. Жуковского
как бы специально готовила его к работе над разреше-
нием этой труднейшей задачи. Начиная с магистерской
диссертации, Николай Егорович непрерывно занимался во-
просами теоретической и прикладной гидромеханики, а ин-
терес к задачам воздухоплавания держал его постоянно
в курсе последних технических достижений в этой области.
Естественно, что известия о первых удачных полетах братьев
Райт, Фармана и других должны были именно на Николая
Егоровича произвести особенно сильное впечатление. Здесь
техника вызвала к жизни целый новый отдел теоретической
науки.
Возможно, что именно обширные и настойчивые занятия
гидромеханикой привели Н. Е. Жуковского к тому, что он,
более чем кто-либо другой из механиков-теоретиков, ощу-
щал близость механики к области опытных естественных
наук и яснее сознавал необходимость в механике лабора-
торного научно поставленного эксперимента. Конечно, вся
механика представляет собой науку, выросшую из экспери-
ментального материала, но отдельные ее части так давно
и так прочно заключены в рамки аксиоматики, что участие
опыта в них так же мало чувствуется, как участие опыта
в развитии геометрии. Так, например, теория движения
твердого тела еще Ньютоном была приведена к столь совер-
шенной и законченной форме, что все задачи в этой области
представляются, в сущности, чисто математическими зада-
чами на интегрирование дифференциальных уравнений; если
опыт и привлекается здесь, то только для иллюстрации тех
результатов, к которым приводит математическая теория.
Совсем иную картину представляет собой область гидро-
механики. Несмотря на гениальные творения Ньютона, Эйлера,
Лагранжа и длинного ряда выдающихся ученых, совре-
менная наука еще весьма далека от полного понимания
того, что происходит в движущейся массе жидкости; от
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
841
аксиоматики, столь же совершенной, как в динамике твер-
дого тела, наука в области гидро- и аэромеханики еще
чрезвычайно далека. Достаточно вспомнить вопросы, связан-
ные с явлениями турбулентности, чтобы вполне оценить
те трудности, которые в этой области предстоит преодолеть.
При таких условиях роль опыта в гидромеханике высту-
пает на первый план, и эта роль Николаем Егоровичем
была учтена совершенно ясно. В первые же годы текущего
столетия, когда интерес к авиации как за границей, так
и в России заметно оживился, он приступает к системати-
ческим опытам над движением крылообразных тел в воздухе.
Это уже не случайные опыты, а систематическое исследо-
вание явления в тех же масштабах и с теми же приемами,
как при исследованиях в физических лабораториях. В 1902 г.
Николай Егорович строит в механической лаборатории Мо-
сковского университета первую аэродинамическую трубу
в России и одну из первых в мире. Около этого же
времени по планам Николая Егоровича строится лаборатория
в Кучино на средства Д. П. Рябушинского и позднее,
в 1910 г., строятся аэродинамические трубы в Московском
техническом училище и в университете. Во всех этих лабо-
раториях ведутся систематические исследования величины
подъемной силы и зависимости ее от формы обтекаемых
тел. В частности, в Кучинской лаборатории ведутся изме-
рения подъемной силы как на воздушных змеях, так и на
моделях в аэродинамической трубе. По-видимому, здесь же
осенью 1904 г. у Николая Егоровича явилась гениальная мысль
о влиянии так называемой циркуляции на величину подъем-
ной силы. Нельзя сказать, что он первый высказал эту
идею. Еще значительно раньше она была вскользь затро-
нута Рэлеем, а в 1894 г. ее высказал в одном из докладов
англичанин Ланчестер, но в такой неопределенной и мало-
убедительной форме, что эта идея в свое время прошла
совершенно незамеченной и о ней вспомнили только много
позднее, когда вся современная теория полета была в сущест-
венных чертах разработана. Впрочем, тут было еще одно
существенное обстоятельство, которое не дало идеям Лан-
честера широкого распространения. Дело в том, что меха-
ника есть точная наука, ее выводы должны быть выражены
в форме, которая допускает точный подсчет и сравнение
842
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
теоретических выводов с экспериментальными; между тем
соображения Ланчестера были выражены в качественной форме,
которая не поддавалась никакому количественному подсчету,
и, следовательно, не могли быть подвергнуты эксперимен-
тальной проверке. Это с самого начала позволяло рассмат-
ривать соображения Ланчестера только как остроумную,
но неубедительную и нйчем не подтвержденную догадку.
Перед Николаем Егоровичем стояла сложная задача —
придать своим соображениям количественную форму и дать
им теоретическое объяснение. Трудность этой работы,
вероятно, и привела к тому, что гениальная мысль, возник-
шая интуитивно в уме Н. Е. Жуковского и представшая
ему, вероятно, сразу в полной ясности, получила четкое
оформление только через два года в опубликованном им
классическом мемуаре «О присоединенных вихрях», который
в области гидромеханики открывал совершенно новую эру
и поэтому может быть поставлен рядом с классическими
работами Бернулли, Эйлера и Лагранжа. Этой работой
в область механики жидкостей было введено представление
о течениях жидкости, принципиально отличных от тех, кото-
рые в ней рассматривались ранее.
Как известно, при настоящих условиях механика не обла-
дает ни методами интегрирования общих уравнений гидро-
механики, ни теоремами, позволяющими до конца судить
об условиях, единственным образом определяющих течение.
При таких условиях приходится ограничиваться изысканием
частных типов решений дифференциальных уравнений гидро-
механики. Простейшим типом таких решений является так
называемое потенциальное течение жидкости, на которое
обратил внимание еще Лагранж и которое было весьма
подробно изучено; простота этого типа движения объя-
сняется прежде всего тем, что все течение вполне опреде-
ляется одной функцией, которая, к тому же, в рассмотренных
в механике случаях принадлежит к классу функций,
хорошо изученных в математике (так называемые гармони-
ческие функции). В середине прошлого столетия Гельмгольц и
Кирхгофф ввели в рассмотрение другой возможный вид
течения — течение с разрывом скоростей, так называемое
струйное течение. Введение этих двух типов течения по-
зволило дать объяснение ряду гидродинамических явлений,
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
843
наблюдаемых в действительности, но оно далеко не исчер-
пало всех возможных типов течения, удовлетворяющих
гидродинамическим уравнениям и граничным условиям. Резуль-
тат, вытекающий из содержания работы Н. Е. Жуковского
«О присоединенных вихрях», состоит в том, что в гидромеха-
нику в случае, когда пространство, занятое текущей
жидкостью, неодносвязно, введен в рассмотрение еще новый
тип течения, потенциального во всей жидкости, но с не-
однозначным потенциалом, ввиду чего при обходе вокруг
погруженных в жидкость тел циркуляция скорости может
быть отлична от нуля; для этого типа течения, как показал
Николай Егорович, характерно образование сил, действую-
щих по направлению, перпендикулярному к направлению
первоначальной скорости. Для этой силы — «силы. Жуков-
ского», как ее теперь называют, — Николай Егорович дал
очень простую формулу, Позволяющую данную силу рас-
считать по величине циркуляции, скорости первоначального
потока и плотности жидкости. Этот замечательный результат
в настоящее время вошел как классическая основа во все
учебники гидромеханики наряду с самыми основными ре-
зультатами, как уравнения Эйлера, теорема Бернулли — Ла-
гранжа и т. п. Уже одно это показывает огромную ценность
полученного им результата.
Тип течений, введенных в гидромеханику Н. Е. Жуков-
ским, как оказалось впоследствии, является как р£з таким,
который объясняет все основные явления, происходящие
в воздухе в области летящего тела. Все попытки заменить
течения, введенные Н. Е. Жуковским, иными типами течений,
например попытки Витошинского, оказались неудачными и
ненужными. Естественно, что в действительности вследствие
вязкости воздуха и отчасти из-за его сжимаемости явление
протекает не вполне так, как это изображается Н. Е. Жу-
ковским, но его теория дает превосходную приближенную
модель явления, его схему, которая вполне охватывает его
основные черты и нуждается только в дополнениях и неко-
торых поправках, представляющих последовательные при-
ближения к тому явлению, которое имеет место в действи-
тельности.
Вся гениальность полученного результата не сразу стала
ясна как самому Николаю Егоровичу, так и другим ученым,
844
v. биографические Статьи
работавшим над вопросами гидромеханики и приложением
их к вопросам авиации и воздухоплавания. Нужно было
время, чтобы эта гениальная мысль дала свои плоды, и
нужны были соответствующие методы исследования, кото-
рые позволили бы применить идеи Н. Е. Жуковского, сде-
лать их, так сказать, рабочим аппаратом исследования слож-
ных вопросов гидромеханики.
Чтобы вполне оценить всю глубину и важность тех идей,
которые выросли из открытия Н. Е. Жуковского, следует
обратить внимание на учебники по гидромеханике, которые
выходят в настоящее время. Если в старых учебниках на*
первый план выдвигались такие вопросы, как теория волн,
теория форм равновесия жидкости под влиянием сил при-
тяжения, то в новых учебниках вместо этого все чаще и
чаще входит теория несущих поверхностей, прандтлевская
теория несущих поверхностей и т. п. Достаточно про-
смотреть новые французские курсы гидромеханики Билля,
Пере (Villat, J. Рёгёэ), чтобы убедиться в изменении напра-
вления научной мысли, которое нашло отражение в новом
содержании основной учебной литературы.
Как всякая новая и глубокая идея, открытие Н. Е. Жуков-
ского было, конечно, не случайно: к нему привело и раз-
витие науки и те задачи, которые к науке предъявляла тех-
ника. Естественно, что к тем же идеям с разных сторон
подходили и другие исследователи. Одного из них, Лан-
честера, мы выше упоминали; необходимо здесь отметить
и другого исследователя, который на четыре года раньше
Н. Е. Жуковского для одного частного случая крыла, имею-
щего в сечении форму дуги круга, дал формулу подъем-
ной силы, соответствующую теореме Н. Е. Жуковского, —
это был тогда начинающий германский ученый Кутта (Kutta).
В заграничной, главным образом немецкой, литературе основ-
ная формула для выражения подъемной силы обычно назы-
вается формулой Кутта — Жуковского. Не умаляя значения
прекрасной работы Кутта, написанной в 1902 г., необхо-
димо, однако, заметить, что Кутта рассматривает совер-
шенно частный случай и не делает в этой работе никакой
по пытки показать, что найденный им совершенно частный
результат в действительности имеет гораздо более общее
значение. Форма, в которой дан результат Н. Е. Жуков-
ИикОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ 84§
ского, представляет чрезвычайно общую теорему; резуль-
тат Кутта является совершенно частным выводом, принци-
пиальное и общее значение которого остается совсем
неясным. Этим замечанием достаточно ясно определяется
основное отличие работы Н. Е. Жуковского от работы
Кутта.
Первый вопрос, который возникал при дальнейшем раз-
витии теории крыла, — это вопрос об определении величины
циркуляции вокруг обтекаемого тела. Приблизительно одно-
временно Н. Е. Жуковский и С. А. Чаплыгин указали метод
определения величины циркуляции в случае контуров, имею-
щих острую заднюю кромку. Соображение, на котором осно-
вывалось определение циркуляции, состояло в том, что физи-
чески невозможно рассматривать течение, в котором в неко-
торой точке скорость равна бесконечности. Отсюда сейчас
же вытекало, что острая кромка крыла должна быть точ-
кой схода струй, т. е. одной из критических точек течения,
и это позволяло определить величину циркуляции течения.
В иностранной литературе это положение обычно называется
«основной гипотезой Н. Е. Жуковского».
Все дальнейшие успехи теории крыла были связаны
с замечательными результатами, полученными С. А. Чаплы-
гиным. Рассматривая крыло в условиях плоскопараллель-
ного течения, т. е. с физической точки зрения, не учиты-
вая влияния концов крыла и применяя метод теории функ-
ций комплексного переменного, С. А. Чаплыгин вывел две
замечательные формулы, позволяющие определить величину,
направление и точку приложения результирующей силы,
действующей на крыло; эти формулы в настоящее время
носят название «формулы С. А. Чаплыгина». Необходимо,
впрочем, заметить, что почти в том же виде эти формулы,
независимо от С. А. Чаплыгина, были найдены германским
ученым Блазиусом и в иностранной литературе иногда носят
название «формулы Блазиуса».
Таким образом, были вполне выяснены и физические
предпосылки теории, и был найден метод, позволяющий
вести расчет действующих на крыло сил. Механическая
задача для случая крыла в плоскопараллельном потоке была
полностью сведена к чисто математической задаче, задаче
конформного отображения. Оставалось пожать плоды.
846
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
В период с 1906 по 1913 г. Н. Е. Жуковский выпу-
скает ряд статей, посвященных приложению обоих этих
результатов к различным частным случаям. Первые примеры
обтекания крылообразных профилей были даны в замеча-
тельной работе С. А. Чаплыгина в 1910 г.; в этой работе,
между прочим, был разобран случай профиля, представляю-
щего собой инверсию параболы. Одновременно с этим появ-
ляется работа Н. Е. Жуковского, в которой рассматривается
аналогичный профиль,, построенный на совершенно иных
соображениях. Здесь Николаю Егоровичу принадлежит гео*
метрически совершенно ясная и весьма остроумная идея
«округления» многоугольных контуров, «скелетов крыла»;
округление отрезка прямой д^ет так называемый «руль
Жуковского», округление дуги круга дает инверсию пара-
болы, ранее разобранную С. А. Чаплыгиным. Эти профили
в иностранной литературе обычно называются «профилями
Жуковского».
Далее Н. Е. Жуковский рассматривает профили, пред-
ставляющие округление луночки, ограниченной двумя дугами
кругов; этим профилям Николай Егорович дал название
профилей типа Антуанет; в иностранной литературе они
называются профилями Треффтца — Кармана, по имени уче-
ных, которые много позднее разобрали случай таких про*
филей. Необходимо вообще отметить тот печальный для
русской науки факт, что большинство работ Н. Е. Жуков-
ского и другого творца современной прикладной аэродина-
мики, С. А. Чаплыгина, неизвестны за границей и их резуль-
таты, найденные позднее за границей, несправедливо при-
сваиваются заграничным ученым.
Работы Н. Е. Жуковского в этой области далее были
продолжены замечательными исследованиями С. А. Чаплы-
гина по общей теории крыла. В сущности, работы
Н. Е. Жуковского и С. А. Чаплыгина до конца исчерпали
теорию моноплана; дальнейшее развитие в этой области
дало только приближенную теорию тонких крыльев, вы-
званную чисто математическими затруднениями, связанными
с конформным отображением.
Естественно было в дальнейшем развивать эту теорию
в следующих направлениях: 1) развитие теории крыла конеч-
ного размаха; 2) изучение крыла, движущегося не посту-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
847
пательно, а вращательно, т. е. развитие теории гребного
винта. Из этих задач, конечно, первая значительно проще
второй; и в той, и в другой приходится учитывать влияние
на поток вихрей, сбегающих с конца крыла или с лопастей
винта, так что метод исследования совершенно одинаков,
но по степени трудности подсчета эти задачи коренным
образом отличаются; учет влияния плоской вихревой полосы,
а в простейшем случае теории подковообразного крыла,
даже учет влияния двух сбегающих с его концов вихрей
гораздо проще учета весьма сложных вихревых образова-
ний за лопастями вращающегося пропеллера. Сейчас трудно
понять, почему Н. Е. Жуковский почти совершенно не
занимался теорией крыла конечного размаха и посвятил
свои дальнейшие работы теории пропеллеров. Может быть,
здесь сказалось то обстоятельство, что теорией винта
Н. Е. Жуковский интересовался и ранее и основные идеи
теории винта, например теория так называемого идеаль-
ного пропеллера, хорошо знакомая ему, послужили для
него в дальнейшем руководящей схемой в его собствен-
ных изысканиях; может быть, здесь сказалось и то, что
после разработки теории крыла в плоскопараллельном
потоке он считал задачу крыла конечного размаха слиш-
ком простой и не заслуживающей затраты сил, а теория
винтов ему казалась более практически важной; Н. Е. Жу-
ковский любил говорить, что «мотор есть сердце са-
молета».
Теории крыла конечного размаха Н. Е. Жуковский
касался в некоторых докладах, которые им были сделаны
в период 1911 —1915 гг., а С. А. Чаплыгин вывел фор-
мулы подъемной силы и индуктивного сопротивления в до-
кладе, сделанном в 1913 г. в Московском математическом
обществе1), но эти результаты не были опубликованы
в печати и остались совершенно неизвестными для широ-
ких кругов.
Как бы то ни было, но честь создания замечательной
теории крыла конечного размаха и индуктивного сопроти-
вления принадлежит полностью Прандтлю и его школе, хотя
1) См. В. В. Голубев, Теория крыла конечного размаха,
стр. 147, Труды ЦАГИ, вып. 108, 1931.
848
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
в работах Н. Е. Жуковского по теории гребных винтов
вся вихревая схема этой теории полностью использована
в случае, значительно более сложном, и много ранее
Прандтля.
Несомненно, что работы Н. Е. Жуковского по вихре-
вой теории гребных винтов принадлежат к важнейшим резуль-
татам, найденным им; созданная им теория далеко опере-
дила работы в этой области заграничных ученых, и четыре
мемуара Н. Е. Жуковского, посвященные теории винтов,
представляют классические работы, которые будут служить
основой всех дальнейших работ в этой области.
Работы по теории крыла и по теории винтов являются
главнейшими работами Н. Е. Жуковского за последние
два десятилетия его жизни; они упрочили за Н. Е. Жуков-
ским мировую известность и поставили его в один ряд
с творцами механики жидкостей.
Но научные интересы Николая Егоровича не замыка-
лись в области этих двух основных задач, хотя они, есте-
ственно, потребовали от него огромной затраты времени
и труда, так как, помимо чисто теоретических исследова-
ний, он руководил огромной экспериментальной работой
в лабораториях Высшего технического училища и Москов-
ского университета и в лаборатории Д. П. Рябушинского
в Кучине; во всех этих лабораториях велась интенсивная
работа как по поверке теоретических выводов, так и но
чисто практическим вопросам, связанным с выработкой изме-
рительной аппаратуры, техники измерений и различных прак-
тических расчетов в применении к действительно существо-
вавшим самолетам. Несмотря на огромную работу в этом
направлении, Николай Егорович находил еще время и для
ряда других сложных и трудных вопросов. Диапазон науч-
ных интересов Николая Егоровича был поистине огромный:
он занимается и вопросами, связанными с релятивистской
механикой (которой была посвящена его речь, подготовлен-
ная к университетскому акту 25 января 1918 г.), и зада-
чами чисто математическими, посвященными геометрическому
доказательству теорем С. А. Чаплыгина по интегрирова-
нию уравнений, и методами вариационного исчисления, и
исследованиями, связанными с вихревой теорией лобового
сопротивления, и чисто прикладными артиллерийскими и
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
849
железнодорожными вопросами; все эти разнообразные области
привлекают внимание Н. Е. Жуковского, и всюду он вносит
методы точного научного исследования.
IV
Параллельно с огромной научной работой, которую вел
Николай Егорович, шла и его педагогическая работа. Он
принадлежал к тем ученым, для которых работа в ауди-
тории, чтение лекций, ведение постоянной работы со сту-
денчеством были не обузой, мешающей научной работе,
а необходимым живым и интересным делом, без которого
немыслима жизнь и научная работа. Этой живой связью
с аудиторией была наполнена вся долгая трудовая жизнь
Николая Егоровича, от первых его педагогических шагов
буквально до последних минут его жизни. Интерес к пре-
подаванию, любовь к молодежи, к широкой аудитории соз-
давали исключительную популярность Николаю Егоровичу.
Без всякого преувеличения можно сказать, что среди
профессоров Московского университета и Московского выс-
шего технического училища он был одним из самых люби-
мых молодежью и самых популярных профессоров, хотя
никогда не заискивал перед • молодежью, никогда не доби-
вался популярности.
Во время Октябрьской революции, когда в широких
кругах интеллигенции наблюдался распад и колебания, Нико-
лай Егорович один из первых твердо и решительно пошел
с советской властью, с теми, кто поставил себе задачей
построение новых форм свободной и счастливой жизни.
Николаю Егоровичу было 70 лет, когда началась револю-
ция, и надо удивляться, что он, глубокий старик, с такой
юношеской энергией руководил молодежью и вместе с ней
создал два крупнейших центра, которые в дальнейшем
сыграли исключительную роль и в научном освоении трудней-
ших задач, связанных с развитием авиации, и в организа-
ции военной мощи Советского Союза. Центральный аэро-
гидродинамический институт и Военно-воздушная акаде-
мия РККА носят имя Н. Е. Жуковского; в создание их
Николай Егорович вложил остатки той • неукротимой твор-
ческой энергии, которой была насыщена его жизнь.
850
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Плодотворная, неутомимая и разносторонняя научная и
педагогическая работа Николая Егоровича и результаты этой
деятельности говорят о том, что он был замечательным учи-
телем и исключительным научным организатором. Однако
Николай Егорович совсем не был блестящим лектором.
Поглощенный творческой научной работой, он был очень
рассеян. Его ученики любовно рассказывали самые невероят-
ные истории о его рассеянности, и хотя^ среди этих рас-
сказов много анекдотичного и преувеличенного, но дей-
ствительно бывали, например, такие случаи, что Николай
Егорович по рассеянности читал студентам II курса лекции,
предназначенные для III курса.
Та же рассеянность, а кроме того, и чрезвычайная доб-
рота Николая Егоровича иногда использовались студен-
тами. Он был очень добродушным и мягким экзаменатором,
но не это создавало ему популярность. Студенты весьма
охотно используют излишнюю доброту своих учителей, но
справедливость требует сказать, что в глазах студентов
это качество никогда не служит к славе профессора.
Необычайная популярность и огромное влияние Николая
Егоровича на его учеников обусловливались прежде всего
мощью его творческого таланта, широтой его научной фан-
тазии и его совершенно исключительной любовью к постоян-
ному, напряженному научному творчеству, к научным во-
просам, над которыми он неустанно работал. Непрерывной
творческой работой, напряженными научными исканиями
объяснялись и его рассеянность и дефекты, которые иногда
бывали в его преподавании. Его слушатели прежде всего
видели в нем настоящего ученого, для которого наука — не
отбывание служебной повинности, а единственное, основное
содержание всей его жизни. Студенты знали, что если
к Николаю Егоровичу обратиться с каким-нибудь научным
вопросом, то никогда не последует лаконический, формаль-
ный, не затрагивающий существа дела ответ, показываю-
щий, что профессор желает только поскорее отделаться
от поставленного ему вопроса; наоборот, каждый серьез-
ный вопрос всегда находил у Николая Егоровича живой
отклик и исчерпывающее разъяснение.
Когда в 1872 г. Н. Е. Жуковский начал чтение лекций
цо механике в Московском высшем техническом училище,
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
851
то там теоретические предметы стояли не на очень высо-
ком уровне; курс теоретической механики ограничивался
только самым необходимым минимумом, непосредственно
нужным при изучении и применении техники. Николай Егоро-
вич с самого начала сделал курс механики более обшир-
ным и более углубленным теоретически, так как совер-
шенно ясно понимал, что развитие техники потребует от
инженеров все большего повышения их чисто научной под-
готовки.
В течение долгой преподавательской деятельности курсы
Николая Егоровича, естественно, постепенно менялись сооб-
разно тем требованиям, которые, с одной стороны, обусло-
вливались развитием науки, применением и усовершен-
ствованием ее методов и, с другой, — требованиями, предъя-
вляемыми к механике смежными техническими дисципли-
нами. Курсы лекций, которые читал он, всегда отличались
большой продуманностью в выборе материала и в его изло-
жении.. Курсы Николая Егоровича, которые из года в год
издавались студентами в литографированном виде, по своему
построению и изложению чрезвычайно характерны для его
педагогических взглядов. В них, как и в его научных
работах, ярко сказывается геометрический' характер ума
Николая Егоровича, четко выраженная конкретность его
мышления.
В речи на юбилее Математического общества Николай
Егорович следующим образом формулирует свои педагоги-
ческие идеи:
«Если могут быть споры о самостоятельной роли гео-
метрии при решении недоступных до сих пор задач дина-
мики, то ее высокое значение в преподавании механики не
подлежит сомнению».
«Ум изучающих весьма часто склонен к формальному
пониманию. Я из своего педагогического опыта знаю, как
часто запоминаются формулы без усвоения стоящих за ними
образов... Если формулы и подстановки некоторыми из
изучающих легко запоминаются, то так же скоро они исче-
зают бесследно из памяти; но раз усвоенные геометриче-
ские образы, рисующие картину рассматриваемого явления,
надолго западают в голову и живут в воображении изу-
чающего».
852
V. БИОГРАФИЧЕСКИЕ ЙТАТЬИ
«Сравните, например, способы изложения теории при-
тяжения эллипсоидов, данные Шалем и Дирихле. Оба спо-
соба одинаково прекрасны: один в области геометрии, дру-
гой в области анализа. Который из них ближе ознакомит
изучающего с рассматриваемой задачей?»
«Из способа Дирихле он узнает остроумный искусствен-
ный прием брать многократные интегралы, ничего общего
с притяжением эллипсоидов не имеющий; способ же Шаля
проведет его через теоремы Айвори, Маклорена и Лап-
ласа, выясняющие существенные свойства рассматриваемого
явления»..
«В этом отношении геометрическое толкование, пред-
почтение геометрического доказательства аналитическому
всегда приносит пользу».
«Говоря о высоком значении геометрического толкова-
ния в преподавании теоретической механики, не скрою, что
некоторые авторы геометрией злоупотребляют. Нагромо-
ждение кинематических теорем, так же как и нагроможде-
ние формул, только запутывает дело преподавания».
«Геометрическое толкование должно быть ясно и просто
и должно всегда близко прилегать к рассматриваемой задаче,
стремясь к изучению вещей самих в себе».
Эти педагогические идеи Николая Егоровича нашли свое
полное выражение в курсах, которые он читал. Необычай-
ная простота и конкретность, геометрическая наглядность
и ясность изложения делают его курсы лекций совершенно
исключительными. Можно только пожалеть, что среди постоян-
ной научной, исследовательской работы он не нашел вре-
мени привести в порядок, до конца обработать и издать
в печатном виде читавшиеся им курсы, и мы можем о них
судить лишь по воспоминаниям его учеников и по литогра-
фированным студенческим запискам, естественно, спешно
составлявшимся и далеко не выражавшим педагогических
намерений Николая Егоровича. Тем не менее, даже издан-
ные в таком несовершенном виде, некоторые его курсы
поражают замечательным совершенством формы изложения;
особенно следует отметить здесь его лекции по аналитиче-
ской механике, читанные в Техническом училище.
Два курса из числа прочитанных Николаем Егоровичем
необходимо особенно выделить. Оба они посвящены вопро-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
853
сам гидро- и аэромеханики, но один написан еще в первые
годы, а. другой принадлежит к последним годам его про-
должительной педагогической деятельности; это — «Лекции
по гидродинамике», читанные в Московском университете
в 1886 г., и «Теоретические основы воздухоплавания» —
курс, прочитанный им в Московском техническом училище
в 1910 г.
Лекции по гидродинамике—единственный курс, кото-
рый был Николаем Егоровичем напечатан в обработанном
виде. Чрезвычайно характерна для Николая Егоровича всту-
пительная лекция (введение), где он, кратко охарактери-
зовав развитие механики, приходит к выводу, что «XIX век
можно приветствовать как век блистательного развития дина-
мики непрерывного тела».
Охарактеризовав развитие теории идеальной жидкости,
Николай Егорович далее указывает:
«Правильное употребление приемов вместе с внимательным
изучением могущих образоваться разрывов сплошности при-
водят нас к результатам, хорошо оправдываемым на опыте,
так что мы можем совершенно смело здесь повторить слова
Гельмгольца о том, что „можно считать уравнения гидро-
динамики за истинные законы, управляющие движением физи-
ческой жидкости".
«Если в старое время гидродинамика изгонялась из кур-
сов теоретической механики, как недостойная этого назва-
ния, то теперь, разумеется, она должна занять видное место,
являясь одной из блестящих глав механики».
«Вот уже 15 лет, как я с интересом занимаюсь гидро-
динамикой, я много передумал и переработал разных во-
просов за это время. Я старался отбросить все, что не заклю-
чало в себе успешных результатов, и изложить возможно
простым образом те выводы, которые к ним приво-
дили».
«Оканчивая теперь мое вступление, позволю себе, мои
будущие слушатели, выразить надежду, что вы получите
интерес и любовь к предмету, которым я сам занимался
с таким увлечением. Я думаю, что в настоящее время вели-
ких открытий в области аэронавигации и подводного пла-
вания такая надежда не должна быть тщетной. Может быть,
некоторым из вас и самим придется заниматься гидродина-
854
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
мическимй опытами, освещенными истинным пониманием тео-’
рии, и внести свою лепту в сокровищницу науки».
Это введение—целая программа научной деятельности
Николая Егоровича, и мы знаем, каким блестящим образом
были выполнены скромные надежды Николая Егоровича;
трудами его самого в первую очередь и трудами его бли-
жайших учеников именно в области гидромеханики, непо-
средственно примыкающей к чисто техническим дисципли-
нам, была внесена «не скромная лепта», а фундаментальные
вклады глубоко принципиального значения.
Николай Егорович в этом курсе собрал результаты своих
15-летних размышлений и изысканий по вопросам гидроди-
намики; несомненно, что и все его другие курсы включили
результаты его продолжительной вдумчивой работы над
самыми разнообразными вопросами механики. И вот эта насы-
щенность и глубина научной мысли Николая Егоровича заста-
вляли его слушателей видеть в его лекциях нечто чрезвы-
чайно ценное, чего порой нет в самых блестящих по форме,
но лишенных глубокого внутреннего содержания курсах и
лекциях.
Как бы ответом на пожелания, выраженные во введении
к курсу лекций по гидродинамике, является другой курс,
читанный им в 1910—1911 гг., — «Теоретические основы
воздухоплавания», изданные в 1911 г. в литографированном
виде его ближайшими учениками. Во введении Николай Его-
рович ставит задачей курса «связать богатый опытный мате-
риал, накопленный аэродинамическими лабораториями, с тео-
ретическим исследованием рассматриваемых задач с помощью
основных уравнений гидродинамики и теории вязкости
жидкостей». В этих лекциях впервые в мировой литературе
в систематически разработанном виде была дана теория
подъемной силы крыла самолета, основанная на учете влия-
ния циркуляции скорости. Эти лекции являются замечатель-
ным памятником того, насколько работы Н. Е. Жуковского
стояли впереди работ подавляющего большинства загранич-
ных ученых.
В подтверждение этого можно привести такой факт. Зна-
чительно позднее, а именно в 1916 г., в своем курсе «Общей
аэронавтики» директор Высшей аэронавтической школы
в Лозанне и бывший профессор общей аэродинамики в Выс-
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
855
шей политехнической школе Льежа Рикардо Броцци (Riccardo
Brouzzi) утверждал: «Аэродинамика бесспорно есть наука
вполне эмпирическая. Все заслуживающие доверия законы
являются и должны быть указаниями действительного опыта.
Нет ничего более опасного, как применять математический
аппарат с целью достичь построения этих законов».
Понятно, с каким глубоким интересом лекции Николая
Егоровича были встречены всеми специалистами, работаю-
щими как в области прикладной аэродинамики, так и тео-
ретиками-механиками. В 1916 г. «Теоретические основы
воздухоплавания» были переведены на французский язык
и изданы в Париже Джевецким; два французских издания
этой книги (второе в 1931 г.) достаточно характеризуют
значение и популярность ее за границей. Несомненно, что
до самого последнего времени эта книга являлась почти
единственным систематическим изложением современной тео-
рии сил, действующих на самолет.
В этих лекциях опять в полной мере проявляется черта
всех курсов Н. Е. Жуковского — это исчерпывающее зна-
ние излагаемого материала во всех деталях и глубокая про-
думанность содержания и формы изложения.
Теми же чертами, которыми отмечена педагогическая
деятельность Николая Егоровича, характеризуется и его
организационная работа. Конечно, в его руководстве лабора-
торной работой нельзя искать элементарного организационно-
го и административного таланта. Хозяйство, внешние формы
работы, ее материальную часть создавали и делали его
помощники, обладавшие административными и организатор-
скими способностями. Но Николай Егорович был душой всей
работы, своим руководством он оживлял и наполнял глубоким
содержанием деятельность всего коллектива, который имел
счастье работать вместе с ним. И здесь глубокое физическое
понимание явлений и исчерпывающее знание всех его теоре-
тических предпосылок позволяло Николаю Егоровичу в пест-
рой, часто неясной и противоречивой картине эксперимен-
тальных данных находить простую теоретическую сущность,
которая позволяла затем распутать весь сложный и запутан-
ный клубок изучаемых явлений.
Аэродинамические лаборатории Московского технического
училища и Московского университета выдвинулись под руко*
856
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
водством Николая Егоровича на одно из первых мест в мире,
а его ближайшие ученики и сотрудники, работавшие с ним
в этих лабораториях, явились теми научными кадрами, опи-
раясь на которые можно было создать такую крупнейшую
базу экспериментальных и теоретических исследований по
аэро- и гидромеханике, как ЦАГИ, и такие мощные центры
по подготовке авиационных кадров, как Военно-воздушная
академия и Московский авиационный институт.
V
В жизни Николая Егоровича, как и в жизни большинства
крупнейших ученых, очень трудно отметить какие-нибудь
внешние, заслуживающие особого внимания события. Обычно
весь интерес и все содержание жизни поглощаются научными
задачами, уходят на внутреннюю напряженную творческую
работу.
С 1886 г., когда служебное положение Николая Его-
ровича после назначения профессором Московского уни-
верситета вполне определилось, в его жизни почти не было
внешних крупных перемен. Работа в университете, в Тех-
ническом училище и в Промышленной академии шла из года
в гол по одному и тому же раз установленному плану.
Только в последние годы к этому еще прибавилась работа
сначала на Курсах для подготовки офицеров-летчиков,
а затем в Институте инженеров Красного воздушного флота
да интенсивная работа в аэродинамических лабораториях.
Николай Егорович непрерывно жил в Москве со своей
матерью Анной Николаевной и сестрами Верой и Марией
сначала на Немецкой улице (ныне ул. Баумана), в Дени-
совском переулке, а затем, с 1890 г., когда младшая сестра,
Вера Егоровна, вышла замуж за ученика Николая Егоро-
вича, инженера А. А. Микулина, и уехала из Москвы,
а старшая сестра скончалась, Николай Егорович переселился
на другую квартиру, в Гусятниковом переулке, и вскоре затем
переехал в Мыльников переулок. В доме Соколовой в Мыль-
никовом переулке (ныне улица Н. Е. Жуковского) Николай
Егорович и прожил всю дальнейшую жизнь.
Все домашнее хозяйство вела его мать, Анна Никола-
евна, женщина властная, но вместе с тем гостеприимная
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
857
хозяйка, чрезвычайно радушная, прекрасная собеседница,
всем живо интересовавшаяся и входившая во все мелочи,
касающиеся деятельности ее любимого Николеньки.
Радушный, спокойный и уравновешенный характер Ни-
колая Егоровича, его научный авторитет и широкие научные
интересы создали ему обширный круг знакомств среди
профессоров университета и Технического училища, со мно-
гими из которых он был в близких, дружеских отношениях.
Обаяние Николая Егоровича и радушие Анны Николаевны
привлекало в гостеприимный дом Жуковских друзей Николая
Егоровича, а также многочисленных его учеников, со мно-
гими из которых он поддерживал дружеские отношения.
В дни семейных торжеств за гостеприимным столом
Жуковских собирались его товарищи по работе—профес-
сора университета и Технического училища. Эти праздно-
вания всегда носили сердечный, радостный характер и отли-
чались искренним весельем.
В 1900 г. Николай Егорович был избран членом-корре-
спондентом Академии наук, а через год был выдвинут
кандидатом в действительные члены Академии наук. Ни-
колай Егорович отказался от этой кандидатуры, так как
не желал расставаться с Москвой, в которой имел разно-
образные научные связи и вел интенсивную научную и педаго-
гическую работу.
Николай Егорович часто бывал за границей на различ-
ных ученых съездах, но каникулярное время проводил всегда
в Орехове. Здесь он отдыхал от напряженной зимней работы.
Большой любитель природы, птиц и домашних животных,
садовод, страстный охотник, искусный пловец и неутомимый
ходок, Николай Егорович здесь, в Орехове, укреплял свое
здоровье, черпал физическую бодрость, ясность и свежесть
мысли.
Впрочем, и здесь научная мысль не замирала: отдых
сочетался с занятиями различными вопросами механики:
то Николай Егорович сооружал большие крылья и с ними
ездил на велосипеде, то стрелял из самодельного арбалета
стрелами с пропеллером и следил за временем полета; наблю-
дал форму струи, вытекающей из большого резервуара, и т. д.
Зимой жизнь Николая Егоровича, помимо его служебных за-
нятий в университете и Техническом училище, была заполнена
858 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
разнообразной научно-общественной работой. Он с 1907 г.
был президентом Московского математического общест-
ва, вице-президентом Общества любителей естествознания,
антропологии и этнографии, постоянным членом Бюро рус-
ских водопроводных съездов, председателем Научно-техни-
ческого отдела Московского общества воздухоплавания, чле-
ном Совета Общества содействия успехам опытных наук и
их практических применений имени X. Л. Леденцова, членом
Общества испытателей природы. Во всех этих организациях
Николай Егорович вел активную работу и часто выступал
с научными докладами. В Политехническом обществе, где
он состоял почетным членом, даже установился обычай начи-
нать серию докладов каждого академического года докладом
Николая Егоровича.
В 1911 г. научные и общественные круги торжественно
отпраздновали 40-летний юбилей профессорской деятель-
ности Н. Е. Жуковского.
Московское математическое общество ознаменовало этот
юбилей изданием собрания сочинений Николая Егоровича,
первый том которого и вышел в 1912 г. Война 1914—1918 гг.
не дала возможности закончить это издание; вышел только
первый том.
Совет Политехнического общества обратился в Совет
Московского высшего технического училища с ходатайством
о присуждении Н. Е. Жуковскому звания инженера-механика
honoris causa. Совет Технического училища единогласно
постановил удовлетворить это ходатайство, и Политехни-
ческое общество присвоило Николаю Егоровичу почетное
звание и поднесло ему большой нагрудный золотой инже-
нерный знак. Во всех торжественных случаях Николай Его-
рович надевал этот почетный знак, необычайный для профес-
соров механики, как бы желая подчеркнуть свою по-
стоянную связь с работами в технических прикладных
областях.
Жена Николая Егоровича, Надежда Сергеевна, рано
умерла, оставив ему двух детей: дочь Елену Николаевну
и сына Сергея Николаевича1).
i) С. Н. Жуковский впоследствии был студентом ВВА; скон-
чался от туберкулеза в 1924 г.
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
859
Мать Николая Егоровича дожила до глубокой старости
и умерла в возрасте 95 лет 4 апреля 1912 г. После ее
смерти место хозяйки дома заняла дочь Николая Егоровича
Елена Николаевна, окончившая в 1912 г. гимназию и посту-
пившая на математическое отделение Московских высших
женских курсов.
Дом Николая Егоровича все более наполнялся молодежью.
Подруги его дочери и его ученики оживляли движением
и молодыми голосами старый дом в Мыльниковом переулке.
Тихая, кроткая и ласковая Елена Николаевна была любима
всеми, кто ее знал. Но особенно большой популярностью
пользовалась она среди многочисленных студентов и изобре-
тателей, приходивших по делам к Николаю Егоровичу; все
находили у нее помощь и ходатайство перед ним.
Дочь свою Николай Егорович любил исключительно
горячо; она сопровождала его во всех заграничных поездках,
присутствовала с ним на ученых заседаниях, сопровождала
его при посещениях лабораторий и аэродромов.
С началом в 1914 г. империалистической войны деятель-
ность Н. Е. Жуковского еще более расширилась. Аэроди-
намическая лаборатория Московского технического училища
все время вела различные исследования на военные нужды;
при ней под руководством Николая Егоровича образовалось
Авиационное расчетно-испытательное бюро, целью которого
было производить поверочные расчеты и испытания суще-
ствующих самолетов, выяснять их аэродинамические качества
и необходимые требования со стороны прочности. Это рас-
четно-испытательное бюро затем было преобразовано в Экспе-
риментально-аэродинамический отдел Института путей сооб-
щения, а позднее в Центральный аэрогидродинамический
институт при Научно-техническом отделе ВСНХ; Николай
Егорович при всех этих преобразованиях оставался неизмен-
ным председателем коллегий указанных учреждений.
С организацией Московского военно-промышленного коми-
тета Н. Е. Жуковский вошел в Комиссию чугунных снаря-
дов; здесь он разработал формулы, определяющие устойчи-
вость полета снарядов нового типа.
Одновременно с этим он вступил в должность предсе-
дателя вновь образовавшегося Отдела изобретений при Мо-
сковском военно-промышленном комитете, куда направлялись
860
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
все военные изобретения. Здесь он, кроме того, состоял
экспертом по изобретениям механическим, авиационным, гид-
равлическим и по всем вопросам, связанным с теорией гиро-
скопов.
Еще ранее, когда в 1912 г. в Москве была организована
Военная школа авиации, где занималось в то время всего
10 офицеров — будущих летчиков; Николай Егорович начал
читать им лекции по элементарному курсу аэродинамики
и динамике полета. Лекции слушателям школы Николай
Егорович читал в университете и там же, в аэродинамиче-’
ской лаборатории, офицеры проходили лабораторные заня-
тия под руководством его учеников и сотрудников; такие же’
лабораторные занятия для них велись и в аэродинамической
лаборатории МВТУ. С началом войны курсы были преобра-
зованы в систематические четырехмесячные теоретические
курсы, на которых будущие летчики получали уже более
солидную подготовку по аэродинамике и по устойчивости
аэроплана.
Позднее, уже-после революции, в 1918 г., курсы авиации
были преобразованы в Московский авиатехникум, а затем
в Институт инженеров Красного воздушного флота имени
Н. Е. Жуковского. Еще позднее, уже после смерти Николая
Егоровича, в 1922 г., Институт инженеров Красного воздуш-
ного флота был преобразован в Военно-воздушную акаде-
мию имени проф. Н. Е. Жуковского.
Самоотверженная напряженная работа, которую, несмотря
на свой возраст, вел Николай Егорович, и тяжелые условия
жизни в Москве зимой 1919—1920 гг. в результате разрухи,
вызванной империалистической и гражданской войнами, по-
дорвали его здоровье.
В начале 1920 г. он заболел воспалением легких; его
крепкий организм, несмотря на преклонный возраст, упорно
боролся с болезнью. Весной Николай Егорович был помещен
в лучший подмосковный санаторий «Усово» и начал попра-
вляться. Но в мае его постигла тяжелая утрата; после
непродолжительной болезни скончалась его любимая дочь
Елена Николаевна. Николай Егорович переживал смерть
дочери очень тяжело. Тем не менее интенсивное лечение,
питание, прекрасный уход несколько восстановили его здо-
ровье. Явилась надежда на выздоровление.
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ 861
29 августа 1920 г. исполнялось пятидесятилетие его
научно-педагогической деятельности. Московское высшее
техническое училище и Политехническое общество готовились
торжественно отметить этот юбилей. Но отпраздновать этот
юбилей уже не пришлось. Николай Егорович внезапно забо-
лел тифом. Не удалось даже передать ему заготовленные
различными учреждениями приветствия.
В связи с пятидесятилетним юбилеем Н. Е. Жуковского
3 декабря 1920 г. Советом Народных Комиссаров за под-
писью В. И. Ленина было издано постановление об осво-
бождении Николая Егоровича от обязательного чтения лекций,
о назначении ему персональной ставки, об установлении
премии имени Н. Е. Жуковского за лучшие труды по ма-
тематике и механике и об издании его трудов.
Николай Егорович уже не мог оправиться от тяжелой
болезни. Медленное угасание продолжалось еще несколько
месяцев. Но сила научного творчества Николая Егоровича
еще не совсем иссякла: тяжело больной, лежа в постели,
в санатории он продолжал еще заниматься научной работой,
украдкой от врачей слабеющей рукой он писал на листах
бумаги последние выкладки...
17 марта 1921 г., в 5 часов утра, Николай Егорович
Жуковский скончался в «Усове».
Н. Е. Жуковский похоронен в Донском монастыре рядом
со своей дочерью. На могиле Николая Егоровича сооружен
памятник с его барельефом; в Военно-воздушной академии
и в ЦАГИ в память их основателя поставлены бюсты Н. Е. Жу-
ковского работы скульптора Н. А. Андреева.
VI
Полную картину той исключительной роли, которую
сыграл Н. Е. Жуковский в развитии современной механики,
дает изучение его научных трудов. От Н. Е. Жуковского
осталось более 180 работ, трактатов, составленных им курсов.
Все эти работы войдут в настоящее полное собрание его
сочинений. Однако далеко не все сделанное Н. Е. Жуков-
ским для науки можно в настоящее время собрать. В тече-
ние своей долгой научной и общественной деятельности
Николай Егорович сделал огромное количество докладов,
862
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
часто на общие принципиальные ц весьма важные темы;
содержание большей части докладов вошло в его научные
печатные работы, но значительная часть этих ценных мате-
риалов осталась неразработанной и ненапечатанной.
В последние годы Николай Егорович во время своих
докладов для сокращения времени вместо выводов встреча-
ющихся формул на доске обычно показывал их на экране
при помощи проекционного фонаря, для чего предварительно
выписывал их на стеклышках. После его смерти остались
коллекции таких стеклышек с формулами и чертежами,
по которым иногда можно восстановить основные черты
сделанного им доклада. Эта коллекция может служить неко-
торым дополнением к тому печатному научному наследию,
которое осталось от Н. Е. Жуковского.
Гораздо труднее воссоздать в возможной полноте его
образ, который оказывал такое исключительное влияние
на всех окружающих. Все его ученики, все встречавшие его
испытывали на себе влияние его замечательной личности,
но охарактеризовать во всей полноте, проследить источники
этого воздействия—задача исключительной трудности.
В умах большинства его учеников, ныне работающих
в разных областях науки и техники, представление о лич-
ности Николая Егоровича неразрывно связано с тем впечатле-
нием, которое он производил уже в преклонные годы.
В памяти всех встречавших Н. Е. Жуковского в эти.
годы встает образ величавого патриарха науки. Мощная
фигура, исключительное спокойствие, задумчивый, сосре-
доточенный взгляд, необычайная простота, естественность
в обращении с окружающими, поразительная скромность
и вместе с тем уверенность в себе и чувство собственного
достоинства создавали яркий образ ученого и мудреца.
С философским спокойствием взирал Николай Егорович
на окружающий мир; с живым интересом вникал он во всякие
суждения, избегая вступать в бесполезные споры и стараясь
во всяком мнении найти нечто ценное, заслуживающее вни-
мания.
Исключительная широта его научных дарований, счаст-
ливое сочетание геометрической интуиции, чувства живой
деятельности и аналитического искусства соединялись со столь
же широким и разносторонним взглядом на людей и на жизнь.
НИКОЛАЙ ЕГОРОВИЧ ЖУКОВСКИЙ
863
Чуждый всякой односторонности' и нетерпимости, Николай
Егорович умел объединить для общего дела людей различ-
ных взглядов, разнообразных темпераментов, разного таланта
и способностей, и каждый находил в работе, руководимой
им, место для приложения своих сил и дарований.
Николай Егорович в течение многих .лет был президентом
Московского математического общества; он умел объединить '
около Общества людей, интересовавшихся наукой и желав-
ших научно работать в области математики и механики;
в нем все научные работники находили постоянный живой
интерес к их работе, а молодые силы — поощрение и под-
держку. За долгие годы его работы в Обществе менялись
научные вкусы, исследовательские идеалы, на смену одних
научных перспектив приходили другие, и в этой. сложной
обстановке Николай Егорович с одинаковым интересом
и сочувствием следил за всяким новым ценным направлением,
за всяким проявлением новой оригинальной и живой мысли.
В те годы, когда Николай Егорович стоял во главе Обще-
ства, там с одинаковым успехом проходили доклады на самые
разнообразные темы, начиная от самых общих и абстрактных
отделов математики и кончая темами, стоящими на границе
с прикладными науками; доклады, посвященные теории транс-
финитных чисел, вопросам строения бесконечных множеств,
сменялись докладами по теории крыльев и винтов, а на смену
им шли доклады по изгибанию поверхностей, по теории
особых точек аналитических функций.
Те же черты Н. Е. Жуковского как талантливого орга-
низатора научной работы проявлялись и во всех других
случаях. Инженеров он вовлекал в занятия чистой теорией,
а отвлеченных, чистых математиков умел заинтересовать
работами совершенно прикладного характера.
С исключительной широтой научных взглядов, спокойст-
вием и мудростью истинного ученого гармонировал его
неизменно здоровый, и бодрый оптимизм. Он был твердо
убежден в абсолютной ценности искания научной истины,
которая стояла всегда перед его научным взором; сохранив
до конца своих дней выдающийся талант исследователя,
Николай Егорович всегда был чужд разочарований, сомнений
и неуверенности в своих силах. Он глубоко верил, что среди
его учеников есть и будут такие таланты, которые в силах
864 v. ёиографйческйе Статьи
разрешить задачи, не решенные им, и искренно радовался,
когда его ученикам удавалось в некоторых областях пойти
дальше своего учителя. Никогда он не пытался оказывать
давление на своих учеников своим авторитетом, никогда
не обескураживал их резким, безапелляционным отзывом.
Как истинный мудрец, Николай Егорович даже в ошибочных
и неверных утверждениях искал некоторую присущую им
долю истины.
Эта вера в окружающих его учеников, убеждение в глубо-
кой ценности научного знания, беспредельная бескорыстная
преданность науке—все эти черты слагаются в светлый
и трогательный облик замечательного человека, ученого
и учителя, облик, который всегда будет жить в памяти его
учеников.
Выдающийся ученый, один из творцов современной аэро-
механики, замечательный организатор научной работы, та-
лантливейший учитель, подготовивший первые научные кадры
в области авиации, Н. Е. Жуковский по справедливости
назван в постановлении СНК от 3 декабря 1920 г. «отцом
русской авиации».
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ
Н. Е. ЖУКОВСКОГО (1847—1947)х)
Сто лет назад, 17 января 1847 г., родился один из круп-
нейших русских ученых, знаменитый творец основ современ-
ной технической аэромеханики и вместе с тем один из самых
оригинальных и самобытных ученых-механиков, все направле-
ние деятельности которого, методы его работы, задачи
и цели науки, как он их понимал, весьма ярко проявляются
в деятельности современных ученых и, несомненно, оставят
глубокий след и в дальнейшем развитии науки.
л Для того чтобы ясно представить себе место, которое
занял Н. Е. Жуковский в русской и вместе с тем в мировой
науке, надо отчетливо уяснить состояние теоретической
механики в годы, когда он учился в университете и начинал
свою научную деятельность.
Как известно, самое начало прошлого столетия ознаме-
новалось появлением знаменитого трактата Лагранжа «Mecha-
nique analitique»2) и это гениальное произведение в течение
длительного периода было образцом, которому неизменно
следовали ученые. В математике, в теоретической механике
и в смежных областях науки мы часто недооцениваем влия-
ние общих философских идей, господствующих в ту или
иную эпоху; развитие научных идей представляется идущим
из задач самой науки. А между тем во всех областях челове-
1) Опубликовано в журнале «Успехи математических наук»,
т. II, вып. 3 (19), 1947. (Прим, ред.)
3) Первое издание вышло в 1786 г.
§66
v. Биографические СтатЬЙ
ческой деятельности и, конечно, прежде всего в научных
построениях это влияние чрезвычайно ощутительно. В част-
ности, едва ли можно сомневаться, что идеи эпохи Великой
французской революции с культом «разума» не нашли яркого
отражения в трактате Лагранжа. Основная идея этого сочи-
нения состоит в том, что аксиоматика механики, сделанная
еще Ньютоном в его знаменитых «Principia», в законах дви-
жения, позволяет свести всякую механическую задачу к задаче
чисто математической, а развитие математического анализа
позволяет еще более сузить задачу, сведя ее к интегриро-
ванию системы дифференциальных уравнений. При такой
постановке механика не только не нуждается ни в каком
экспериментальном исследовании, но даже может обойтись
и без геометрии, поскольку интегрирование уравнений меха-
нической задачи дает формулы, позволяющие определить
положение механической системы для любого момента вре-
мени. Таким образом, механика превратилась в часть мате-
матического анализа, которая если чем-нибудь и отличается
от всего содержания анализа, то это отличие лежит в неко-
торой специфике задач и в ограничении математического
аппарата.
Замечательная ясность концепций Лагранжа, с одной
стороны, и исключительная законченность его изложения,
с другой стороны, повели к тому, что подавляющее большин-
ство исследователей в дальнейшем шли по путям, гениально
намеченным Лагранжем. Работы Лапласа, Пуассона, Фурье,
Якоби, Гамильтона и других крупнейших исследователей
XIX столетия представляют собой блестящее развитие идей
Лагранжа; те же идеи через труды Остроградского, через
преподавание Брашмана господствовали и у нас в России;
по образцу, указанному Лагранжем, строилось универси-
тетское преподавание, писались курсы механики. Достаточно
здесь назвать такие курсы, как курсы Слудского, по кото-
рым учился Н. Е. Жуковский, Бобылева, Суслова. В раз-
витии тех же идей были достигнуты и замечательные научные
результаты в исследованиях Остроградского и, позднее,
А. М. Ляпунова, С. В. Ковалевской, В. А. Стеклова
и других.
Таковы были те научные настроения, среди которых
воспитывался в свои университетские годы Н. Е. Жуковский;
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 867
но было одно обстоятельство, которое с самого начала
наложило своеобразный отпечаток на все научное мировоз-
зрение Н. Е. Жуковского. Как известно из биографии
Н. Е. Жуковского, он стремился первоначально быть не уче-
ным, а инженером. По окончании гимназии он стремился
поступить в Институт инженеров путей сообщения в Петер-
бурге, и только недостаток средств заставил его отказаться
от этого и поступить в Московский университет. По оконча-
нии университета он, наконец, поступил в Институт инже-
неров путей сообщения, но вскоре принужден был его оста-
вить, так как оказалось, что институтская учеба мало подхо-
дила к способностям Н. Е. Жуковского. Тем не менее, даже
оставив институт, он продолжает мечтать о деятельности
инженера и изобретателя и только неудачные попытки изо-
бретательства, наконец, указывают ему настоящее его призва-
ние. Таким образом, в научную деятельность Николай Его-
рович вступает с ярко выраженными вкусами инженера
и изобретателя; это — менее всего кабинетный ученый и тео-
ретик. А если к этому еще добавить, что он вырос среди
деревенской природы, был страстным любителем русской
природы, прекрасным пловцом, садоводом и с детства увле-
кался охотой, то мы получим достаточно ясный облик Ни-
колая Егоровича в его молодые годы, и все эти черты
действительно гораздо больше подходят для активного строи-
теля, изобретателя или инженера, чем для теоретика, раз-
мышляющего в тиши кабинета над сложными математическими
следствиями из законов механики. Нет ничего удивительного,
что, сделавшись ученым, профессором теоретической меха-
ники, т. е., по существу, просто представителем одной
из ветвей математики, он и в этой области проявил свои
вкусы, которые так упорно влекли его в чисто прикладную
область деятельности. Но, в конце концов, с какими бы
идеями ни входил в науку ученый, над ним довлеет сила
известной традиции, обычаев, и только постепенно из их
преодоления возникают новые пути, а потому естественно,
что в своих первых исследованиях, в их тематике и методах
Николай Егорович не выходит заметно за круг тех интере-
сов и методов, которые были общепризнаны и господство-
вали в науке. Таков был первый период деятельности
Ц. Е. Жуковского, который заканчивается в основном появле?
868
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
нием его докторской диссертации «Об устойчивости движе-
ния» (1882).
Если в работах этого периода нельзя отметить особой
оригинальности ни в выборе тем исследования, ни в применяе-
мых методах, то два обстоятельства заметно проступают
в творчестве Н. Е. Жуковского уже с самого начала: это
необычайная геометрическая ясность, с одной стороны,
и исключительная конкретность выводов, с другой стороны.
Две крупнейшие работы этого периода — магистерская дис-
сертация «Кинематика жидкого тела» (1876) и «Об устойчи-
вости движения» (1882) — являлись в свое время фундамен-
тальными исследованиями, не потерявшими своего значения
и в настоящее время.
В предисловии к «Кинематике жидкого тела» Н. Е. Жу-
ковский так характеризует поставленную им задачу:
«Та высокая степень ясности, которая была внесена
в область динамики твердого тела геометрическими исследова-
ниями движения неизменяемой системы, заставляет ожидать
значительного успеха гидродинамики от сближения ее с кине-
матикой иаменяемой системы».
Таким образом, ставится задача придать кинематике
жидкого тела ту же полную наглядность, какую геометри-
ческие исследования Пуансо внесли в динамику твердого
тела. Эта цель в достаточной степени и была достигнута
Николаем Егоровичем в его диссертации; чисто аналитическая
форма исследования движения жидкости в работах Лагранжа
и Коши приобрела здесь полную геометрическую наглядность.
Интересно здесь отметить, что та же тенденция геометризи-
ровать механические результаты, носящие чисто аналити-
ческий характер, привела его к ряду исследований в более
поздние годы; такова, например, его работа «Геометрическая
интерпретация рассмотренного С. В. Ковалевской случая
движения тела около неподвижной точки» (1896), «Локсо-
дромический маятник Гесса» (.1898) и ряд других работ.
Но, может быть, исключительная наглядность и геометри-
ческая ясность изложения, к которой неизменно стремился
Николай Егорович, нашла свое наиболее полное выражение
в курсах механики, которые он читал в университете и в Выс-
шем техническом училище. Эти курсы, даже в той, несом-
ненно, несовершенной форме, в которой они до ндс дошли,
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 869
в виде студенческих записей, представляют собой совершенно
радикальный отход от аналитической формы изложения,
которой, следуя в основном Лагранжу, держались все соста-
вители университетских курсов механики. Едва ли можно
отрицать исключительную ценность этого направления в пре-
подавании механики и в настоящее время. Какое влияние ока-
зали идеи Н. Е. Жуковского на дальнейшее развитие меха-
ники в России, показывает следующий факт. Первые работы
такого ярко выраженного по свойству своего ума аналитика,
каким был один из первых учеников Н. Е. Жуковского,
С. А. Чаплыгин, были посвящены геометрическому истолко-
ванию движения твердого тела в жидкости (1894 и 1897).
Здесь, несомненно, сказалось влияние Н. Е. Жуковского.
Николай Егорович вообще придавал совершенно исклю-
чительное значение полной наглядности в научных результа-
тах; вот его утверждение:
«Можно говорить, что математическая истина только
тогда должна считаться вполне отработанной, когда она
может быть объяснена каждому из публики, желающему ее
усвоить», — утверждение, над которым не мешает задуматься
в очень многих случаях и в настоящее время.
Весьма интересна и вторая диссертация Н. Е. Жуковского,
егол докторская диссертация «Об устойчивости движения»
(1882).
Эта работа не принадлежит к числу наиболее выдающихся
его исследований. Впоследствии в своих классических иссле-
дованиях по устойчивости движения А. М. Ляпунов про-
двинул этот вопрос значительно дальше. Но достаточно
сравнить работы А. М. Ляпунова и исследование Н. Е. Жу->
ковского, чтобы убедиться в том, что мы имеем здесь двух
ученых чрезвычайно ярко выраженных и совершенно противо-
положных научных вкусов.
Для А. М. Ляпунова основной целью работы является
наиболее общее и наиболее строгое, с математической точки
зрения, исследование поставленного вопроса. Приложение
полученных результатов и исследование конкретных примеров
движения его совершенно не интересуют: в работе, содер-
жащей около 380 страниц, мы не найдем ни одного меха-
нического примера. В сущности, это мастерски написанное
исследование теоретика, чистого математика.
870
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Совершенно иную картину представляет работа Н. Е. Жу-
ковского. Для Николая Егоровича здесь прежде всего важен
конкретный механический результат. Вся работа наполнена
большим числом частных механических примеров, иллюст-
рирующих общие теоремы. Каждый найденный теоретический
результат автор немедленно стремится приложить к решению
конкретной механической задачи.
Такая конкретность исследования чрезвычайно характерна
для всего творчества Н. Е. Жуковского. В последующие
периоды его научной деятельности мы почти не найдем
работ, посвященных общим исселдованиям. Среди огромного
числа написанных им в последующие годы исследований
(около 200), пожалуй, можно указать только две работы,
в которых автор ставит разработку общих научных методов.
Это, во-первых, его работа, написанная вскоре после поя-
вления его докторской диссертации, «О движении твердого
тела, имеющего полости, наполненные однородной капельной
жидкостью» (1885) и написанная в 1896 г. работа «Видо-
изменение метода Кирхгоффа для определения движения
жидкости в двух измерениях при постоянной скорости,
данной на неизвестной линии тока».
Первая из этих работ связана, по-видимому, с космого-
ническими вопросами, которыми в то время весьма интересо-
вались московские ученые, а по методу исследования примы-
кает к исследованиям Кирхгоффа, которые Н. Е. Жуковский
в те годы подробно изучил и подробно изложил в своих
лекциях по гидродинамике, читанных в 1886 г.
Работа «Видоизменение метода Кирхгоффа» представляет
собой своеобразное параметрическое развитие известного
метода Кирхгоффа в теории струй, что дает большую
гибкость методу. Впрочем, необходимо заметить, что этот
метод не дает принципиального расширения метода Кирх-
гоффа; всякая задача, решаемая методом Жуковского, может
быть решена методом Кирхгоффа, хотя в некоторых случаях
это решение может оказаться более сложным. Наибольшую
ценность этой работы представляет то, что в ней дано
большое число примеров обтекания с образованием срыва
струй.
В сущности, этими двумя обширными теоретическими
работами и исчерпываются все исследования Н. Е. Жуков?
К СТОЛЕТИЮ do ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 871
ского, в которых автор ставит и решает общие принципи-
альные вопросы или разрабатывает общие методы исследова-
ния. Все другие работы в период после написания докторской
диссертации посвящены решению совершенно конкретных
задач, по большей части выдвинутых запросами техники.
Было бы совершенно неправильно думать, что благодаря
такой конкретности разбираемых Н. Е. Жуковским вопросов
он получает только весьма частные результаты. В своих
исследованиях он получил, как мы увидим из дальнейшего,
некоторые результаты весьма большой общности и принци-
пиального научного значения, которые вошли в науку как
ее совершенно классические результаты, но получены они
не из разработки общих теорий, а из разбора частных
и порой весьма узких технических задач, так что автор
при выводе их шел индуктивным методом, характерным для
естествознания и совершенно необычным для теоретической
механики.
Мы перейдем теперь ко второму периоду научной деятель-
ности Н. Е. Жуковского. Этот период характеризуется тем,
что Николай Егорович все более и более отходит от задач
чисто теоретических, его исследования приобретают ясно
выраженный технический уклон. Начав с решения задач тех-
нику методами точной науки, он постепенно переходит
от случайных и часто мелких технических вопросов; к слож-
нейшим задачам, давно привлекавшим к себе внимание круп-
нейших теоретиков. Блестящие результаты, полученные им
в этом направлении, дали ему всеобщее признание как одного
из крупнейших ученых.
Защита в 1882 г. докторской диссертации и получение
в 1886 г. профессуры в Московском университете вполне
упрочили материальное положение Николая Егоровича, .а ряд
написанных им крупных исследований обеспечил ему научный
авторитет и известность среди русских механиков. Николай
Егорович выдвигается на одно из первых мест среди ученых,
профессоров механики русских университетов. Все это создает
условия, при которых он мог вполне посвятить себя научной
работе в направлении, которое его особенно привлекало.
И здесь сразу проявились те научные интересы, которые
заставляли его в течение достаточно долгого времени упорно,
но, как мы видели, безуспешно стремиться к деятельности
872
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
не ученого-теоретика, профессора «прикладной математики»
университета, а к профессии инженера. Теперь, заняв кафедру
теоретической механики в Московском высшем техническом
училище и в Московском университете, он постепенно все
больше втягивается в решение средствами теоретической
механики чисто инженерных задач.
Здесь прежде всего необходимо отметить чрезвычайное
разнообразие тех вопросов, над решением которых он ра-
ботает. Наряду с разработкой таких чисто теоретических
вопросов, как задача о движении твердого тела вокруг
неподвижной точки в случае С. В. Ковалевской и в случае
Гесса, о чем выше было сказано, идут различные вопросы,
связанные со строением кометных хвостов (это было влияние
классических исследований Ф. Л. Бредихина), и, далее, разно-
образнейшие чисто технические задачи.
На первый взгляд очень трудно уловить какую-нибудь си-
стему в выборе тем его исследований по техническим вопросам.
Кажется, что их автор отзывается на каждый вопрос, кото- ч
рый имеет отношение к теоретической механике, и спешит
разобраться в нем, привлекая не грубые и не очень убе-
дительные соображения приближенного подхода, как часто
приходится делать инженерам, а точные методы теоретической
механики. Тематика его исследований исключительно разно-
образна: движение судов реакцией втекающей и вытекающей
жидкости, форма артиллерийских снарядов, деформации
велосипедного колеса, качка морских судов, теория гидра-
влического удара, вопросы фильтрации, работа веретена
в ткацких станках, полет птиц, работа пропеллеров, выте-
кание дыма из фабричных труб и т. д. — все это далеко
не полное перечисление вопросов, которыми занимается
Н. Е. Жуковский в течение 80-х и 90-х годов. Часть этих
работ посвящена весьма частным вопросам и не нашла
дальнейшего развития, но некоторые из этих исследований
привели его к чрезвычайно важным результатам. Здесь прежде
всего надо отметить его сделавшиеся классическими иссле-
дования по гидравлическому удару.
Начатые Николаем Егоровичем в связи с расширением
московского водопровода исследования о причинах разрыва
водопроводных труб велись в течение нескольких лет, потре-
бовали большого остроумия, большой экспериментальной
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 873
базы и привели его к разработке теории распространения
волн в трубах, которая полностью и разрешала поставлен-
ный первоначально узкотехнический вопрос. Были полностью
выяснены причины, вызывающие разрыв труб, были указаны
пути, позволяющие устранить возникновение разрывов или
обнаружить место разрыва.
Помимо чисто теоретического интереса, который предста-
вляют исследования Н. Е. Жуковского по гидравлическому
удару, они имеют и огромный практический интерес. Эти
замечательные его исследования были переведены на все
основные иностранные языки, получили чрезвычайное распро-
странение среди инженеров и теоретиков-гидравликов и гидро-
механиков во всем мире. Эти работы являются классическими
достижениями науки, и они дали Николаю Егоровичу во всем
мире славу крупнейшего ученого, теоретика-гидравлика.
Длительная работа Н. Е. Жуковского над разнообраз-
ными техническими вопросами наложила своеобразный отпе-
чаток на метод, который он применял в своих исследова-
ниях. Технические задачи представляют ту особенность,
что по большей части рассматриваемый вопрос чрезвычайно
осложняется влиянием огромного числа побочных факторов,
мало влияющих на течение изучаемого явления, но чрезвы-
чайно осложняющих его исследование. В чисто научных
исследованиях эта трудность обычно отпадает, так как
изучаемый вопрос ставится в упрощенной, схематизирован-
ной форме, где с самого начала устранены побочные,
затемняющие исследование факторы. Так как весьма часто
a priori влияние различных факторов на течение изучаемого
явления не ясно, то в технических задачах приходится
по возможности учитывать все обстоятельства, с тем чтобы
исследование возможно ближе соответствовало реальным
условиям. Это ведет к тому, что при составлении исход-
ных уравнений в приложениях механики к техническим
вопросам учет всевозможных факторов, которые могут
существенно влиять на исследуемое явление, чрезвычайно
осложняет дело.
Тем не менее обычно исследователи стараются возможно
точнее отобразить в исходных уравнениях изучаемое явле-
ние с тем, чтобы в дальнейшем подвергнуть уже чисто
математической разработке возможно полное изображение
874
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
реального процесса. Однако при этом по большей части
оказывается, что полученные уравнения не могут быть до
конца изучены средствами современной математики: или
получаются уравнения, которые при настоящем состоянии
наука не может решить во всей полноте, или, хотя общее
решение и может быть получено, оно оказывается настолько
сложным, что из него нельзя получить ни каких-нибудь
важных для практики указаний, ни качественной картины
изучаемого явления. Таким образом, оказывается, что урав-
нения, возможно полно изображающие изучаемый вопрос,
приходится подвергать тому или иному упрощению, чтобы
получить из них практически важные результаты. В мате-
матике мы имеем весьма разнообразные средства, позво-
ляющие внести соответствующие упрощения.
Например, часто оказывается, что некоторые опреде-
ляющие явление параметры меняются в весьма узких гра-
ницах; это позволяет применить метод малого параметра,
разлагая решения по его степеням и откидывая члены,
содержащие высокие степени малого параметра. Точно
так же данные уравнения иногда можно заменить так назы-
ваемыми уравнениями в вариациях, что ведет к их упро-
щению.
Другой метод, также весьма часто применяемый на
практике, состоит в выкидывании из уравнений тех или
иных членов, относительно которых можно предполагать,
что они мало влияют на решение. Таков, например, широко
применяемый метод линеаризации уравнений.
Однако применение всех этих математических упроще-
ний сопряжено обычно с целым рядом трудностей. Напри-
мер, при откидывании в уравнении тех или иных членов
обычно бывает весьма трудно достаточно убедительно
п оказать, что оно законно, т. е. что это откидывание мало
влияет на окончательный результат. Подобное затруднение
по большей части и имеет место при линеаризации уравне-
ний. Точно так же при откидывании в разложениях неко-
торых членов часто нельзя строго показать законность
этого откидывания ввиду невозможности дать надежную
оценку получаемой при этом погрешности. Кроме того,
такого рода упрощения иногда ведут за собой то, что
область приложения полученных результатов оказывается
к Столетию со дня рождения н. е. Жуковского 875
настолько ограниченной, что они теряют всякое значение
в тех технических приложениях, для которых и построена
вся теория.
Таким образом, в конце концов мы часто имеем такое
положение, что все усилия, потраченные на то, чтобы
возможно полнее записать в исходных дифференциальных
и интегральных уравнениях изучаемое явление, сполна обес-
цениваются теми упрощениями, которые вынуждают делать
математические трудности их решения.
В своих исследованиях Н. Е. Жуковский идет обычно
совершенно иным путем. Вместо того чтобы стремиться
в исходных уравнениях возможно полнее записать все осо-
бенности изучаемого явления, он с самого начала заменяет
его некоторой схемой, подобранной таким образом, чтобы,
с одной стороны, эта схема по возможности точно отобра-
жала изучаемое явление, а с другой стороны, допускала
сравнительно простое и полное математическое исследование
решения*. Эту идею Николай Егорович любил в шутку выра-
жать следующим определением механики:
«Теоретическая механика есть искусство разрешать раз-
личные вопросы движения при помощи до конца интегри-
руемых уравнений».
Таким образом, неполноту в записи исходных условий
задачи, которую обычно рассматривают как основной недо-
статок исследования, который надо всячески устранять, он
использовал как своеобразный метод исследования, систе-
матически его применял и показал его большую силу.
Однако такой прием представляет большую трудность
в том отношении, что часто неясно, можно ли те или иные
факторы, влияющие на изучаемое явление, считать второ-
степенными, которые в первом приближении можно совер-
шенно не учитывать. Совершенно ясно, что такая схема-
тизация при неудачном выборе важных и маловажных факто-
ров может совершенно исказить рассматриваеую задачу.
Какими критериями пользоваться в оценке важности отдель-
ных факторов?
Очевидно, что существенную помощь в такой оценке
может оказать надлежащим образом поставленный экспери-
мент. И здесь мы приходим ко второй особенности, кото-
рая отличает научное творчество Н. Е. Жуковского. Реше-
876 V, БИОГРАФИЧЕСКИЕ СТАТЬИ
ние технических вопросов средствами теоретической меха-
ники привело к тому, что он стал широко использовать
наряду с чисто теоретическим математическим исследованием
научно поставленный эксперимент. В механическом кабинете
Московского университета, которым заведовал Н. Е. Жу-
ковский, стали широко вестись исследования по самым
разнообразным вопросам, а самый кабинет из собрания
механических приборов, которые служили для демонстрации
на лекциях в виде пояснения различных излагаемых в курсе
теорем, постепенно все более превращался в исследователь-
скую лабораторию, в которой путем точного лабораторного
эксперимента разрешались различные механические вопросы,
совершенно так же как в физических или химических лабо-
раториях аналогичным путем разрешаются вопросы физики
или химии.
Наиболее крупные работы, проведенные за эти годы
Н. Е. Жуковским, как раз и представляли собой удачное
сочетание точного и тонкого чисто теоретического иссле-
дования и умело поставленного лабораторного исследования.
В этом отношении необходимо отметить его работы по
фильтрации: «Теоретическое исследование о движении под-
почвенных вод» и «О влиянии давления на насыщенные во-
дой пески» г). Оба эти исследования были написаны в связи
с работами по постройке нового водопровода в Москве и
носят ярко выраженный экспериментальный характер.
Особенно замечательна в этом отношении его работа
«О гидравлическом ударе в водопроводных трубах»* 2).
В этой классической работе, посвященной теории гидравли-
ческого удара в трубах, Николай Егорович с чрезвычайным
успехом использовал многочисленные опыты, проведенные
им самим и под его руководством инженерами Московского
водопровода. Была построена специальная установка на
Алексеевской водокачке в Москве, на которой многочислен-
ными систематическими опытами проверялись различные вы-
воды теории. Огромная практическая важность этой теории,
как было выше сказано, сделала ту работу фундаментальным
трактатом, которым пользуются инженеры всего мира.
х) Поли. собр. соч., т. VII, 1937, стр. 5—43.
2) Там же, стр. 53.
к СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 8?7
Таким образом, своеобразие задач, которые в своих
исследованиях разрешал Н. Е. Жуковский, привело и
к своеобразию применяемых им методов. В его творчестве
теоретическая механика из чисто математической дисци-
плины, как она сложилась в трудах ученых в первой поло-
вине XIX в., постепенно превратилась в науку естественную
и техническую, тесно связанную с запросами практической
жизни и опирающуюся наряду с математическими методами
исследования и на широко поставленный научный и точный
эксперимент. Так, стремление Николая Егоровича к инже-
нерной, практической деятельности и его любовь к природе
привели в конце концов к тому, что в его руках механика
стала естественной наукой, наукой о реальных движениях,
которые мы наблюдаем в природе и в технике, а сам Нико-
лай Егорович -в своем научном творчестве стал не абстракт-
ным, кабинетным теоретиком, а естествоиспытателем и ин-
женером.
Эти черты научной деятельности Н. Е. Жуковского
резко отличают его от большинства современных ему уче-
ных, теоретиков-механиков. Мы ничего подобного не найдем
в творчестве, например, таких крупнейших ученых, как
А. М. Ляпунов, В. А. Стеклов и другие. Мало того, это
своеобразие его научного творчества вызывало при жизни
Н. Е. Жуковского даже достаточно резко проявляющееся
критическое отношение к его научному направлению; его
упрекали за измену «чистой науке» и за превращение «тео-
ретической механики», точной университетской науки, в при-
кладную, эмпирическую, «неточную» инженерную механику.
Среди русских ученых, может быть, можно указать
только одного ученого, в творчестве которого задачи
практики нашли своеобразное отражение в его самых отвле-
ченных исследованиях. Это — великий русский математик
П. Л. Чебышев. Чисто практические, технические вопросы
теории механизмов, теория «прямил» в конструкции паро-
вых машин, привели его не только к разработке общей
теории механизмов, но и к созданию замечательной чисто
математической теории аппроксимации и функций, наименее
уклоняющихся от нуля.
С особой полнотой замечательное творчество Н. Е. Жу-
ковского и особенности его работы проявлялись в его иссле-
878 V. БИОГРАФИЧЕбКИЕ бТАТЬЙ
дованиях по технической аэромеханике, которые и дали ему
мировую славу.
Вопросами аэромеханики он начал заниматься очень рано.
Еще в начале 80-х годов, когда Николай Егорович приоб-
рел велосипед, он производил у себя в деревне опыты над
сопротивлением воздуха при помощи паруса, приспособ-
ленного к велосипеду. Позднее, сделавшись профессором
Московского университета, он систематически собирал в ме-
ханическом кабинете университета различные летающие
игрушки, воздушные змеи. Эта коллекция бережно сохра-
нялась в механическом кабинете долго после смерти Нико-
лая Егоровича и погибла от взрыва бомбы в 1942 г. Ни-
колай Егорович тщательно следил за всеми сообщениями
о работах по воздухоплаванию и авиации в России и за
границей, принимал самое деятельное участие в различных
воздухоплавательных съездах, лично был знаком с изоб-
ретателями, работавшими над вопросами авиации. Так, он
специально ездил в Германию к воздухоплавателю О. Лили-
енталю, наблюдал его полеты на изобретенном им планере
и даже получил от него в подарок один экземпляр крыльев,
на которых летал Лилиенталь; эти крылья в настоящее
время находятся в музее Н. Е. Жуковского.
Первая работа Н. Е. Жуковского по вопросам авиации
«О парении птиц» (1892) показывает, с какой тщатель-
ностью он изучил литературу вопроса; несомненно, что он
систематически занимался изучением проблем авиации уже
значительно раньше. В этой работе тщательно разобран
вопрос о причинах, позволяющих птице держаться в во-
здухе без работы крыльев, т. е. в условиях парящего
полета; разработкой этого вопроса Н. Е. Жуковский по-
ложил основание так называемой динамике полета. Между
прочим, автор разбирает в этой работе особые виды полета,
которые теперь обычно носят название «фигур высшего
пилотажа», и предсказывает теоретически возможность по-
лета с образованием «мертвой петли», которую много
позднее, в 1911 г., осуществил в действительности выдаю-
щийся русский пилот капитан Нестеров. Эта работа послу-
жила началом длинной серии исследований Н. Е. Жуков-
ского по различным вопросам летания, теории пропелле-
ров и т. п.
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 879
Попутно с разработкой теоретических вопросов шло
и экспериментальное изучение вопросов авиации. В 1902 г.
Николай Егорович построил в механическом кабинете одну
из первых в мире аэродинамических труб, и с этого вре-
мени начались систематические экспериментальные исследо-
вания над различными вопросами авиации самим Николаем
Егоровичем и его учениками, студентами, сначала в универ-
ситете, а затем и в Высшем техническом училище, где
также была построена под его руководством аэродинами-
ческая труба, а еще позднее, с 1904 г., в частной аэроди-
намической лаборатории в Кучино, под Москвой (построен-
ной на средства Д. П. Рябушинского).
Как известно, к самому началу текущего столетия отно-
сятся первые удачные полеты на самолетах, сконструиро-
ванных братьями Райт в Америке, Фарманом и Сантос-Дю-
моном во Франции. Эти полеты показали, что проблема
летания на машинах «тяжелее воздуха» являлась уже про-
блемой, доступной современной технике, а вместе с тем и
выдвигали задачу научного разрешения основных задач
в этой области. Однако наука была застигнута успехами,
полученными первыми авиаторами, совершенно врасплох.
В сущности, не было никакой научной базы, на которой
можно было бы строить теорию и расчет самолетов. Оста-
валась совершенно неясной физическая картина механизма
образования подъемной силы крыла, сопротивления движе-
нию тел в непрерывной среде, тяги пропеллера и т. п.
Здесь интересно отметить, что теоретическая база, на
которой впоследствии удалось построить теорию полета,
была в основном создана в 60-х и 70-х годах прошлого
столетия в трудах Гельмгольца, Кирхгоффа, Рэлея и других
ученых, но разработанная ими теория вихрей оставалась
совершенно абстрактной теорией и почти не имела никаких
конкретных физических или технических приложений. Раз-
витие авиации и дало блестящий случай применить общие,
до известной степени беспредметные теории к решению
совершенно конкретной и весьма актуальной технической
задачи. Н. Е. Жуковскому и принадлежит в основном за-
слуга дать совершенно ясное, полное и точное объяснение
основных явлений, имеющих место при полете, на основе
общих гидродинамических соображений,
880
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Задача теории самолета, или его несущей системы,
крыльев, на которых образуется подъемная сила, есть част-
ный случай общей гидродинамической задачи об обтекании
тела потоком. Так как вязкость воздуха незначительна, то
в первом приближении ею можно было пренебречь, и, сле-
довательно, задача состояла в определении воздействия по-
тока невязкой, так называемой идеальной среды на обте-
каемое ею тело. В гидромеханике было известно два типа
течения вокруг обтекаемого тела: 1) обтекание тела пото-
ком совершенно плавно, без образования за телом каких-
либо особенностей, т. е. поверхностей разрыва скоростей,
вихрей, образования гидродинамической тени и т. п.; 2) обте-
кание тела с образованием отрыва струй и образованием
за телом зоны с неподвижной относительно тела средой,
так называемой гидродинамической тенью. Случай плавного
обтекания приводит к тому, что равнодействующая всех
сил давления равна нулю, и, следовательно, такая схема не
может дать объяснения возникновения подъемной силы или
силы тяги. Случай обтекания с образованием отрыва струй,
достаточно подробно изученный для плоскопараллельного те-
чения в работах Гельмгольца, Кирхгоффа и самого Н. Е. Жу-
ковского, может дать объяснение возникновения сил; так,
сам Николай Егорович пытался применить его к теории
пропеллеров. Но оказалось, что величины сил, получаемых
при подсчетах на основе теории струй, совершенно не соот-
ветствуют тому, что наблюдается при полете самолетов;
теория струй дает чрезмерно малые подъемные силы.
Кроме того, наблюдения показывают, что при малых
углах наклона крыльев к направлению набегающего на них
потока воздуха (так называемый угол атаки) мы имеем слу-
чай обтекания, почти в точности соответствующий теоре-
тической схеме плавного обтекания. В общем, можно сказать,
что воздушные змеи летают в условиях образования срыва
струй и при этом развивают весьма малую подъемную
силу, а крылья самолета находятся в условиях плавного
обтекания, но при этом, вопреки существовавшей в то
время теории, развивают весьма большую подъемную силу.
Н. Е. Жуковскому и принадлежит заслуга дать полное
разъяснение этого противоречия между теорией и наблюде-
нием, В классическом мемуаре «О присоединенных вихрях»
К СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 881
(1906) Н. Е. Жуковский показал для случая плоскопарал-
лельного течения, что отсутствие подъемной силы при плав-
ном обтекании получается потому, что, помимо плавности
обтекания, вводится неявно еще одно предположение, на
которое никто не обращал должного внимания: предпола-
галось, что обтекание происходит при условии, что потен-
циал течения есть однозначная функция при обходе вокруг
обтекаемого тела. Как оказывается, дело совершенно
меняется, если потенциал течения многозначен, или, что то
же, если циркуляция воздуха вокруг обтекаемого тела отлична
от нуля. Н. Е. Жуковскому и принадлежит огромная за-
слуга ввести в науку изучение плавных обтеканий с много-
значным потенциалом; рассмотрение таких течений и дало
совершенно ясное и полное объяснение возникновения подъ-
емной силы, тяги и т. п. Несомненно, что возможность та-
ких плоскопараллельных течений отмечалась вскользь ранее
Н. Е. Жуковского другими авторами, например Бьеркнесом,
а электромагнитной аналогии — Маскаром, но никто не за-
метил огромной принципиальной важности такой физической
схемы течения. Важность такого случая течений ясна хотя бы
из того, что в настоящее время нет ни одного современного
учебника гидромеханики, в который наряду с такими клас-
сическими разделами, как теория вихрей, теория волн, тео-
рия струй, не входила бы как основная часть содержания
и созданная Н. Е. Жуковским теория плоскопараллельных
обтеканий контуров с многозначным потенциалом. В науке
установился обычай называть возникающие при этом силы
«силами Жуковского».
В мемуаре Жуковского интересно проследить, с каким
трудом вырабатывались и физическая схема такого обтека-
ния, и количественные выводы, которые из нее можно по-
лучить. В настоящее время основные идеи Н. Е. Жуков-
ского чрезвычайно легко объяснить, пользуясь, например,
замечательными по изяществу формулами для определе-
ния сил, действующих на обтекаемое тело, полученными
Н. Е. Жуковским и С. А. Чаплыгиным и основанными на
систематическом применении методов теории функций ком-
плексного переменного к задачам механики. С этой точки
зрения основной результат Н. Е. Жуковского может
быть получен следующим образом. Называя через w = f(z)
882
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
комплексный потенциал течения и замечая, что производная
комплексного потенциала
dw
—т— =и----IV,
dz
где и и v — компоненты скорости течения, есть функция
однозначная, мы можем разложить ее в ряд вида
dz Vco + 2nl z -Г гз • • • > (О
где Уж и & — скорость потока вдали от крыла и образуе-
мый ею с действительной осью угол, а Г — циркуляция,
скорости вокруг крыла.
С другой стороны, по формулам, данным в 1910 г.
С. А. Чаплыгиным, составляющие силы давления X, Y ц
момент давления относительно начала координат шот^ вы-
ражаются формулами
= (2)
и mom0(^ = действительной части у [ где —
L
контур, охватывающий крыло; мы сейчас же получим вели-
чину силы и ее направление, подставляя в выражение (2)
разложение (1). Применяя теорию вычетов и предполагая,
что вдали от крыла поток направлен по действительной
оси, так что & = 0, получим:
т. е.
Y-\~iX = — рУооГ,
Г = — р!4оГ, |
(3)
Полученные формулы дают выражение основной теоремы
Н. Е. Жуковского:
При плавном обтекании контура (или системы контуров)
результирующая сила давления по величине равна произве-
дению плотности воздуха (р) на скорость потока вдали
от крыла (Уоо) и на величину циркуляции скорости (Г); эта
сила направлена перпендикулярно к скорости потока в беско-
нечности, и ее направление получается поворотом скорости V#
на прямой угол против направления циркуляции.
к бтОЛЕТИЮ 6о ДНЯ РбЖДЕНЙЯ Н. Е» ЖУКОВСКОГО 883
Последнее заключение получается из того соображения,
что Г положительно, если циркуляция направлена по на-
правлению движения стрелки часов. Случай, который
почти исключительно и рассматривался до Жуковского,
соответствовал предположению, что Г = 0; тогда, конечно,
У = 0 и при этом w, как показывает разложение (1), есть
однозначная функция z.
Эта замечательная теорема, «теорема Жуковского», и
является в настоящее время основой вычисления сил давления
потока на крыло самолета, на пропеллеры и т. п. Это —
одна из самых замечательных теорем гидромеханики по изя-
ществу выражения и по общности и разнообразию приме-
нений; в гидромеханике ей принадлежит такое же класси-
ческое место, как теореме Бернулли — Лагранжа, основным
теоремам теории вихрей и т. п.
Приведенные формулы позволяют представить себе сущ-
ность введенного в том же мемуаре понятия о «присоеди-
ненном вихре».
Как видно из формул (1), (2) и (3), подъемная сила
крыла вполне определяется тремя первыми коэффициентами
разложения (1), которые только и входят в выражение вы-
четов в формулах (2) и (3). Следовательно, если мы имеем
обтекание двух различных профилей, подобранных таким
образом, что Г и а2 одинаковы в разложении комплексных
потенциалов обтекающих их потоков, то соответствующие
подъемные силы, при равных К» и 9 будут полностью
совпадать, так что с точки зрения расчета суммарного
давления одно из таких крыльев можно заменить другим.
С другой стороны, комплексный потенциал обтекания одного
неподвижно стоящего в потоке в точке z — а вихря имеет вид
-az г
z-|--2^1n(z — а),
откуда
= V e“az_j___Е_____L_
dz -j- 2я/ г_а ,
или, предполагая |,г| большим.и разлагая в ряд, получим:
dz — у сое "Г 2к/ г 1“ w
884
V. Биографические стаТьй
Следовательно, если выбрать а таким образом, чтобь!
Га
-2^7 = fl2, (5)
то в разложении (1) и (4) ксэффиценты первых трех чле-
нов разложения будут равны, а отсюда следует:
С точки зрения определения суммарной силы давления
потока на крыло (или даже на систему крыльев), его можно
заменить одним вихрем, помещенным в надлежащей точке,
определяемой равенством (5).
Такой вихрь Н. Е. Жуковский и называет присоединен-
ным вихрем. Необходимо помнить, что приведенные выше
соображения Николай Егорович не мог использовать при
выводе своей теоремы, так как формулы С. А. Чаплыгина были
найдены значительно позднее; поэтому и вывод самого
Н. Е. Жуковского оказывается гораздо сложнее.
Вероятно, во всей механике мы не найдем ни одного
случая, где более или менее сложное явление заменялось
бы столь же простой и наглядной схемой, как это дости-
гается в задачах на плавное обтекание введением «присо-
единенного вихря». Неудивительно, что все наиболее суще-
ственные результаты, полученные в современной технической
аэромеханике, так или иначе связаны со схемой присоеди-
ненного вихря.
Прежде всего нетрудно показать, применяя теорему
Стокса, что, заменяя присоединенным вихрем крыло конеч-
ного размаха, мы принуждены принять, что присоединен-
ный вихрь крыла продолжается вне крыла, образуя или
вихревые усы, сходящие в поток с концов крыла и уходя-
щие сзади крыла в виде двух прямолинейных вихрей, или,
что дает более гибкую схему, предположить, что от при-
соединенного вихря отходит система вихрей, образующих
вихревую пелену сзади крыла. Эти вихревые образования,
возникающие сзади крыла и продолжающие его присоеди-
ненный вихрь, образуют систему свободных вихрей крыла;
их весьма легко наблюдать в аэродинамических трубах
сзади обдуваемых потоком крыльев.
Весь успех современной' приближенной теории крыла
обязан использованию этой простой схемы. В работах
С. А. Чаплыгина, Л. Прандтля и его многочисленных уче-
к СТОЛЕТИЮ СО ДНЯ РОЖДЕНИЯ Н. Е. ЖУКОВСКОГО 885
ников в Германии и Ланчестере в Англии разработана в пе-
риод с 1910 по 1920 г. замечательная по полноте теория
крыла конечного размаха, полностью основанная на идеях
Жуковского, изложенных в его классическом мемуаре 1906 г.
Той же идеей воспользовался сам Н. Е. Жуковский в
своих классических работах по теории винтовх). Каждая
лопасть винта представляет также поверхность крыла, но
в отличие от крыла, движущегося поступательно, лопасть
винта совершает сложное поступательное и вращательное дви-
жения. Таким образом, и лопасть винта можно заменить
одним присоединенным вихрем, от которого отходят два сво-
бодных вихря: один прямолинейный от оси вращения
винта и другой от конца лопасти, образующий линию,
близкую к винтовой. Интересно отметить, что эти свобод-
ные вихри впервые получил на снимках с винтов, работающих
в воде, еще в 1908 г. Фламм; так как на оси вихря скорость
течения очень велика, то давление на оси вихря сильно па-
дает и начинается выделение воздуха или паров воды, ко-
торые в виде белых пузырьков выделяются из воды и обра-
зуют белые полоски в воде. Фламм не мог разобраться
в явлении и сделать из него какие-нибудь выводы, но в ру-
ках Н. Е. Жуковского эти снимки послужили исходным
эмпирическим материалом, на котором построена вся теория.
Чрезвычайно интересно проследить, с каким мастерством
Н. Е. Жуковский преодолевает исключительную сложность
вопроса влияния свободных вихрей на работу винтов. Пред-
полагая, что наружные отходящие вихри расположены в точ-
ности по поверхности цилиндра, построенного на круге,
ометаемом вращением винта, Николай Егорович далее «раз-
мазывает» вихри, расположенные по винтовым линиям на
поверхности цилиндра, и учитывает далее влияние такой вих-
ревой поверхности, что оказывается задачей гораздо более
простой. Это размазывание вихрей по смелости идеи вполне
напоминает знаменитое предложение Гаусса заменить воз-
мущающую планету ее массой, равномерно «размазанной»
по орбите. Может быть, идея Гаусса и послужила прото-
типом для Николая Егоровича при построении его знамени-
той теории винтов с бесконечно большим числом лопастей.
1) Поли. собр. соч., т. VII, стр. 74—347, 1937.
886
V. биОг£аФиче6кйе Статьй
Работы по теории крыльев и винтов самолета, а Такя4е
вопросы динамики полета заняли совершенно преобладающее
место в творчестве Н. Е. Жуковского за последние пол-
тора десятилетия его жизни, т.е. начиная с появления его
мемуара «О присоединенных вихрях». Этот третий период
его творчества замечателен тем, что, помимо огромной тео-
ретической, исследовательской работы, он становится руко*
водителем большого коллектива молодых ученых и инже-
неров, его учеников, которые с необычайным энтузиазмом
работали под его руководством над разработкой основ
новой авиационной науки.
Если ранее Николай Егорович являлся руководителем на-
учной работы как профессор и как президент Московского
математического общества, то теперь он является руково-
дителем и вдохновителем крупного коллектива, работавшего
необычайно дружно над разрешением актуальной слож-
нейшей научной и технической задачи. В условиях дорево-
люционной России с ее устарелой и малоразвитой техни-
кой, с ее вопиющей отсталостью в развитии авиации гением
этого человека была создана научная школа, далеко опере-
дившая в разработке вопросов технической аэромеханики и
авиации самые передовые страны.
Когда после Октябрьской революции открылись широ-
кие возможности для мощного технического прогресса, его
ученики и сотрудники в основном и явились строителями, и
организаторами молодой советской авиации; первые совет-
ские конструкторы самолетов, первые ученые, работавшие
над вопросами авиации и готовившие кадры специалистов,
были учениками Николая Егоровича. Их трудами, под его
непосредственным руководством, было положено основание
ЦАГИ, центру авиационной науки в СССР; они же были
организаторами и первыми профессорами первой высшей
авиационной школы в СССР, Военно-воздушной академии,
носящей ныне имя своего организатора и вдохновителя, про-
фессора Николая Егоровича Жуковского.
С. А. ЧАПЛЫГИН
(1869—1942)
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН *)
Его жизнь, научная и общественная деятельность
8 октября 1942 г. в Новосибирске скончался Герой Со-
циалистического Труда академик Сергей Алексеевич Чаплы-
гин, крупнейший ученый, выдающийся организатор и обще-
ственный деятель, несравненный учитель.
С. А. Чаплыгин родился 5 апреля 1869 г. в г. Раненбурге,
Рязанской губернии. Отец его, Алексей Тимофеевич Чаплы-
гин, служил по торговой, части приказчиком. В 1871г.,
когда Сереже было два года, отец его еще совсем моло-
дым (ему было 24 года) неожиданно умер от холеры. Мать
Сергея Алексеевича, Анна Петровна, перебралась в Воро-
неж и вскоре вышла второй раз замуж за С. Н. Давы-
дова. Жить было трудно. Отчим Сергея Алексеевича рабо-
тал в кожевенном производстве, добытчик был плохой,
семье помогал мало. Содержать семью и воспитывать де-
тей приходилось главным образом матери Сергея Алексее-
вича, женщине дельной и энергичной. Сережа был стар-
шим в семье; он помогал матери по хозяйству, бегал
в лавку, нянчил своих маленьких братьев и сестер.
К Сергею Алексеевичу отчим относился хорошо. Маль-
чик рос способный, не по годам серьезный, и, несмотря на
стесненные материальные условия, мать и отчим постара-
лись дать ему образование. Был приглашен какой-то воро-
нежский семинарист, который и подготовил Сергея Алек-
сеевича к поступлению в приготовительный класо гимназии.
1) Опубликовано в Вестнике АН СССР, № 3, 1944.
888
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
В Воронежскую гимназию Сергей Алексеевич поступил
в 1877 г., когда ему было 8 лет, и там быстро обнаружи-
лось, что ученик Чаплыгин Сергей обладает блестящими
способностями. Особенно замечательна была его память; все,
что говорили учителя, все, что он прочитывал в книгах, с
фотографической точностью оставалось в памяти мальчика.
Эту поразительную способность Сергей Алексеевич сохра-
нял всю свою жизнь и очень ею гордился.
Очень рано, лет с двенадцати, Сергей Алексеевич стал
серьезным помощником матери. Репетирование, позднее по-
ездки «на кондиции» позволяли ему не только содержать себя,
но и помогать своими сбережениями семье.
Из гимназических предметов Сергей Алексеевич больше
всего ценил те, где все было точно, ясно, убедительно
и закончено. Естественно, что любимыми предметами оказа-
лись математика, физика, космография. Сергей Алексеевич
впоследствии с признательностью вспоминал своего гимна-*
зического учителя математики, чеха Пляписа, который своим
преподаванием привил ему любовь и вкус к математике.
В 1886 г. С. А. Чаплыгин блестяще окончил гимназию
и с заработанными им 200 рублями отправился в Москву*
в университет, куда поступил на физико-математический
факультет. В то время в Московском университете препо-
давали крупные научные силы: математик В. Я. Цингер,
физик А. Г. Столетов и ряд других учителей Сергея Алек-
сеевича были выдающимися учеными, прекрасными препо-
давателями. В те годы еще только начинал свою блестящую
научную и преподавательскую деятельность Н. Е. Жуковский.
Вероятно, под влиянием А. Г. Столетова научные вкусы
Сергея Алексеевича склонялись первоначально в сторону
физики. Но, по-видимому, необходимость при занятиях физи-
кой вести кропотливую лабораторную, экспериментальную
работу, к которой Сергей Алексеевич не обнаруживал ника-
кого интереса, повела к тому, что он постепенно стал спе-
циализироваться в области теоретической механики. Несом-
ненно, что этому способствовало и живое, увлекательное
преподавание Н. Е. Жуковского, его умение возбуждать инте-
рес к научной работе, научный энтузиазм у своих учеников.
Под руководством знаменитого «отца русской авиации»
Н. Е. Жуковского началась самостоятельная научная работа
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 889
Сергея Алексеевича еще на университетской скамье. Н. Е. Жу-
ковским он был оставлен при университете. Естественно,
что научные интересы Жуковского, его методы работы,
задачи, которые он ставил и решал, должны были оказать
самое сильное влияние на начинающего ученого.
Выдающиеся ученики редко походят на своих учителей —
такова диалектика развития науки. Каждое поколение вно-
сит новые методы, свои новые научные вкусы, новые ори-
гинальные подходы к решению ранее поставленных задач
и идет своими путями, отличными от тех, по которым шли
учителя. Для прогресса в науке, так же как и в жизни,
необходимо, чтобы старое непрерывно оплодотворялось при-
током нового и свежего. Не избежал этого и Сергей Алек-
сеевич. Мы увидим далее, что эти два выдающихся ученых,
учитель и ученик, были совершенно непохожи друг на
друга, смотрели на вещи по-разному и в науке шли различ-
ными, далеко уклоняющимися друг от друга путями. Но
до этого тогда было еще далеко: от ученого, только начи-
нающего самостоятельную научную работу, трудно ожидать
полной самостоятельности. В первых трудах молодого уче-
ного, естественно, должно отразиться и влияние учителя
и общий дух научной эпохи.
Сергей Алексеевич окончил университет в 1890 г. За
три года до этого Жуковский выпустил в свет свои зна-
менитые «Лекции по гидродинамике», подводившие, как
указывает сам автор, итоги его 15-летним размышлениям
над вопросами гидромеханики. Задача, рассматриваемая
в 5-й лекции этого курса («О движении тела в беспредельной
жидкости»), и послужила предметом первых самостоятельных
изысканий С. А. Чаплыгина — его студенческого сочине-
ния х) и двух больших мемуаров, из которых первый, напи-
санный в 1893 г., был удостоен университетом премии
имени Брашмана* 2), а второй, написанный в 1897 г., явился
магистерской диссертацией Сергея Алексеевича 3).
1) С. А. Чаплыгин, О движении тяжелых тел в несжи-
маемой жидкости, Собр. соч., т. 1, стр. 312, 1948.
2) Его же, О некоторых случаях движения твердого тела в
жидкости, Собр. соч., т, 1, стр. 136, 1948.
3) Его же, О некоторых случаях движения твердого тела в
жидкости, Статья вторая, Собр. соч., т. 1, стр. 194, 1948.
890
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Сущность этих исследований состоит в следующей,
Общие уравнения для определения движения твердого тела
в жидкости были даны Кирхгоффом еще в 1869 г.; им же
даны три интеграла этих уравнений, которых, однако, было;
недостаточно для полного решения задачи в общем случае^
Условия последующих авторов (Клебша, Альфана, А. М. Ля-
пунова, В. А. Стеклова и др.) были направлены главным
образом к нахождению при различных условиях .четвертого
интеграла, наличие которого позволило бы довести до конца
.-аналитическое решение задачи. Крупным трудом в этой
области является магистерская диссертация выдающегося
ученого, впоследствии академика, В. А. Стеклова «О дви*
жении твердого тела в жидкости».
Все эти исследования носят чисто аналитический харак*
тер, рассматриваемые в них случаи совершенно лишены гео-
метрической наглядности. В своих работах Сергей Алексеевич
дал блестящее геометрическое истолкование движения, примы**
кающее по мысли к гениальным геометрическим идеям Пуансо.
Вот как характеризует эти работы Н. Е. Жуковский:
«Задача о движении по инерции твердого тела внутри
несжимаемой жидкости ввиду богатства форм допускаемых
движений живо заинтересовала меня, когда я в качеству
приват-доцента начал свои лекции в Московском универси-
тете чтением специального курса гидродинамики. При напе*
чатании этого курса я высказал некоторые соображения
о постановке этой задачи с геометрической точки зрения.
За разрешение этой задачи взялся тогда еще начинавший
свою ученую деятельность С. А. Чаплыгин и в двух своих
прекрасных работах показал, какой силой могут обладать
остроумно поставленные геометрические методы исследования.
Ему удалось в случае Клебша и Кирхгоффа дать такие же
простые геометрические интерпретации, какие дал Пуансо
для движения по инерции в пустоте» 9-
Несомненно, что в этих работах в полной мере сказалось
влияние Н. Е. Жуковского, ярко выраженного геометра
.по складу своего ума. Свойства научного творчества самого
'Сергея Алексеевича влекли его совершенно в иную сторону.
Ч Н. Е. Жуковский, Механика в Московском университете
за 50 лет, Поли. собр. соч., т. IX, стр. 208, 1937.
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 891
Насколько Н. Е. Жуковский был по складу своего ума
ярко выраженным геометром, настолько же С. А. Чаплыгин
был ярко выраженным аналитиком. Эта черта научного
творчества Сергея Алексеевича выразилась в необычайном
мастерстве аналитических вычислений, бросающемся в глаза
уже в его студенческой работе.
С полным блеском исключительный аналитический талант
Сергея Алексеевича проявился в двух группах работ, отно-
сящихся к периоду 1895—1903 гг. и посвященных динамике
твердого тела. В первой из них рассматривается задача
о движении тела с дифференциальными неинтегрируемыми,
так называемыми неголономными, связями. Можно указать
огромное количество примеров движений тел, обладающих
такими связями: шар, катящийся по шероховатой поверхно-
сти, серсо, велосипед, сани с направляющими полозьями,
катящиеся направляющие ролики счетных приборов, плани-
метров, интеграторов, интеграфов и т. д.
В то время теория таких движений только еще начала
разрабатываться. Основная трудность состояла в том, что
при неголономных связях нельзя применять общие уравнения
Лагранжа второго рода со всеми вытекающими следствиями,
касающимися их интеграции.
В ряде работ, посвященных этой задаче *), Сергей Алек-
сеевич впервые дал общие уравнения для неголономных
движений, напоминающие уравнения Лагранжа, но содер-
жащие ряд добавочных членов, исчезающих при выполнении
условий интегрируемости связей. Эти результаты опередили
работы таких ученых, как Больцман и Аппель, которые
несколько позднее дали общие уравнения движения для
случая неголономных связей..
Приложение уравнений Сергея Алексеевича позволило
ему -внести коренное исправление в решение задачи о ката-
нии шара, принадлежащее финскому ученому Линделефу,
а найденные им первые интегралы, аналогичные для
1) С. А. Чаплыгин, О движении тяжелого тела вращения на
горизонтальной плоскости (1897), Собр. соч., т. I, стр. 57; О некотором
возможном обобщении теоремы' площадей с применением к задаче
о катании шаров (1897), там же, стр. 26; К теории движения него-
лономных систем. Теорема д приводящем множителе (1911), там
$е, стр. 15,
892
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
рассматриваемой задачи теоремам площадей, приобрели осо*
бое значение только позднее, в свете исследований Пуанкаре
по общим проблемам динамики.
Замечательные исследования Сергея Алексеевича по теории
движения тел в жидкости и по движению неголономных
систем сразу же получили очень высокую оценку. В 1903 г. Рос-
сийская Академия наук присудила их автору золотую медаль.
Позднее, в 1911 г., Сергей Алексеевич еще развернулся
к задаче о движении неголономных систем и при помощи
остроумнейшего преобразования времени введением «приво*
дящего множителя» показал, что при некоторых условиях
данные им уравнения неголономных систем можно свести к виду
обычных канонических уравнений динамики и, следовательно,
распространить на них классическую теорию интегрирования
Г амильтона — Якоби.
Вторая группа работ С. А. Чаплыгина по динамике
твердого тела посвящена классической задаче о движении
тяжелого твердого тела, имеющего неподвижную точку.
Как известно, замечательный результат в этой классической
задаче был получен в 1889 г. нашей знаменитой соотечест-
венницей С. В. Ковалевской: ею был открыт и до конца
изучен новый случай интегрируемости (дополнение к извест-
ным ранее в науке случаям Эйлера — Пуансо и Лагранжа),
который и носит теперь название «случая Ковалевской»<
Классическая работа С. В. Ковалевской привлекла к этой
задаче внимание ученых всего мира. В частности, в Москве
один из учеников Н. Е. Жуковского, Г. Г. Аппельрод*
с большим успехом работал в области развития и уточнения
идей С. В. Ковалевской, а другой его ученик, Д. Н. Горячев,
нашел частное решение задачи о движении твердого тела
при некоторых частных условиях, налагаемых на моменты
инерции, положения центра тяжести и на начальные условия.
Этой же задаче посвящено и несколько работ Сергея
Алексеевича1)’, в них дано полное исследование задачи
х) С. А. Чаплыгин, Нов ый случай вращения тяжелого твер-
дого тела, подпертого в одной точке (1901), Собр. соч., т. I, стр. 118,
1948 ;Линейные частные интегралы задачи о движении твердого тела,
подпертого в одной точке (1898), там же, стр. 110; Новое частное
решение задачи о вращении твердого тела, подпертого в одной
уочке (1903), там же, стр. 337,
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 893
Д. Н. Горячева. Весьма вероятно, что в бумагах Сергея
Алексеевича найдутся и другие материалы, помимо напеча-
танных, касающиеся этой механической задачи; в частных
разговорах он неоднократно развивал свои соображения
по этому поводу, v
Мы не будем здесь останавливаться на других, более
мелких работах Сергея Алексеевича, относящихся к этому
периоду; в них рассматриваются или частные вопросы дина-
мики твердого тела или некоторые частные задачи гидро-
механики.
Подведем некоторые итоги.
Период до написания в 1902 г. докторской диссертации
занимает в научном творчестве С. А. Чаплыгина особое,
резко очерченное место. Характеризуется оно и выбором
тематики и методом научного исследования. Содержанием
всех этих работ является решение различных задач класси-
ческой механики, как она сложилась в трудах Лагранжа,
Пуансо, Якоби, Гамильтона, Кирхгоффа, С. В. Ковалевской.
Сущность этого направления можно характеризовать так:
ставится задача разработки методов интеграции дифферен-
циальных уравнений механики и изучаются случаи, когда
такая интеграция возможна в замкнутом виде, например
выполняется в квадратурах, или в функциях 0 Якоби, или
в функциях 0 Розенхайна, как это было в случае Ковалев-
ской. Геометрическая картина движения является при этом
не методом исследования, как это было, например, в рабо-
тах Пуансо, а только наглядной иллюстрацией полученных
аналитических соотношений.
Трактуемые задачи вытекают из развития самой механики.
Было бы чрезвычайно трудно уловить влияние на выбор их
каких-нибудь внешних условий, например потребностей
техники или соприкасающихся областей знания, таких, как
физика.
Невозможно установить и непосредственно практическое
значение разрабатываемых методов и задач: это влияние идет
далекими окольными путями, через посредство гидравлики,
прикладной механики, сопротивления материалов, где методы
«чистой» теоретической механики путехМ различных допу-
щений получают приложение к решению практических задач
часто в таком видег в котором трудно узнать их теорети-
894 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
ческий прообраз. Здесь теоретическая механика и приклад-
ные науки едва-едва связываются между собой некоторыми
принципиальными вопросами астрономии и физики.
В этих классических областях механики, методы которых
развиты корифеями науки, работы С. А. Чаплыгина пред-
ставляют собой совершенные образцы научного творчества
по ясности постановки задачи, по силе метода, по эффек-
тивности и законченности решения.
Автор в совершенстве владеет классическими методами
исследования, а остроумие, глубокое проникновение в анали-
тическую сущность вопроса позволяют ему «в лоб», так
сказать, «фронтальной атакой» преодолеть трудности
задачи.
Перейдем теперь к докторской диссертации Сергея
Алексеевича «О газовых струях» *). Она стоит на границе
двух этапов в научном творчестве С. А. Чаплыгина, не при-
мыкая ни к одному из них и выделяясь исключительно монумен-
тальностью изложенных в ней результатов, оригинальностью
методов исследования и тем значением, которое она зани-
мает в науке.
Эта работа была написана Сергеем Алексеевичем, как он
сам говорил, очень быстро, «в один присест», летом 1901 г.
и была защищена как диссертация на степень доктора при-
кладной математики в 1903 г.
Целью ее было разработать метод, которой позволял
бы решать задачи на обтекание преград с образованием
срыва струй для случая потока сжимаемого газа совершенно
так же, как метод Кирхгоффа или несколько видоизмененный
метод Жуковского позволяют решать аналогичные задачи
для случая несжимаемой жидкости. Специфическая трудность
этой задачи заключается в том, что в случае несжимаемой
жидкости исходное уравнение есть уравнение Лапласа, с кото-
рым связан классический аппарат теории гармонических
функций и теории функций комплексного переменного, в то
время как в случае газа соответствующее уравнение в частных
производных неизмеримо сложнее и аналитический аппарат,
аналогичный теории гармонических функций, отсутствует.
*) С. А. Чацлыгцц, Собр. соч,, т. II, стр. 19, 1948,
аИаДемик Сергей Алексеевич чайлыгин 895
Гениальное по простоте идеи решение этой задачи, дан-
ное Сергеем Алексеевичем, состоит в том, что если известно
решение некоторой задачи теории струй для случая несжи-
маемой жидкости и если обусловливающая это решение
функция допускает определенного вида разложение в ряд,
то решение аналогичной задачи для газа окажется в виде
совершенно такого же ряда, все члены которого получат
дополнительные множители, представляющие собой отно-
шение гауссовых гипергеометрических рядов.
Так как это решение в приложении к частным задачам
является достаточно сложным, то Сергей Алексеевич разра-
ботал приближенный, гораздо более простой метод, годный
в случае, если скорости течения не превосходят примерно
половины скорости звука, в то время как общий метод годен
при любых скоростях течения газа, меньших скорости звука,
которая, как известно, при атмосферных условиях равна
330 м в секунду.
На защите диссертации в числе других членов факультета
присутствовал знаменитый ботаник К. А. Тимирязев. Позд-
равляя С. А. Чаплыгина после защиты, он сказал: «Я не
понимаю всех деталей Вашего исследования, которое далеко
лежит от моей специальности, но я вижу, что оно предста-
вляет вклад в науку исключительной глубины и ценности».
Эти слова полностью оправдались. Время — самый бес-
пристрастный и самый строгий критик. Часто случается,
что научные результаты, которые в глазах современников
блестят, как чистейшее золото, очень быстро при проверке
временем оказываются ничего не стоящей мишурой.
С момента появления этой замечательной работы прошло
более сорока лет. Наши знания в области газовой динамики,
которой посвящена диссертация, за это время безмерно
увеличились, но ценность работы Сергея Алексеевича только
возросла. Надо отметить, что она долго не привлекала
к себе того внимания, которого заслуживает. Может быть,
отчасти причиной этого была ее сложность: Сергей Алек-
сеевич не принадлежит к числу авторов, произведения которых
легко читаются. Но возможно, что были и другие причины,
В то время в технике представляли интерес или скорости
движения, малые сравнительно со скоростью звука, где влия-
ние сжимаемости пренебрежимо мало, или, как в баллистике,
896 V. БИОГРАФИЧЕСКИЕ СТАТЕЙ
>1/
скорости, значительно превосходящие скорости звука, где
теория, развитая Сергеем Алексеевичем, ней^иложима.
Понадобилось современное развитие скоростной авиации,
когда в технику вошли скорости, близкие к звуковым, чтобы
выяснилось все колоссальное значение названной работы*.
На международном съезде механиков в Риме в 1935 г., когд$.
иностранные ученые впервые по-настоящему ознакомились
с содержанием работы С. А. Чаплыгина, она стояла в центр©
внимания и с тех пор стала общепризнанным классическим^
сочинением по газовой динамике. И не удивительно: она
содержит единственный в настоящее время метод решения
задач, чрезвычайно актуальных, над решением которых без-
успешно работали многие крупнейшие научные специалисты,.
Защиту докторской диссертации в 1903 г. надо считать
переломом и в научной деятельности и в жизни С. А. Чаплы-
гина. Прежде чем описать дальнейшее развитие его научного,
творчества, вернемся назад и проследим те житейские ц
служебные условия, на фоне которых протекала научная
работа Сергея Алексеевича.
В те годы, когда Сергей Алексеевич окончил университет,
при малом числе высших учебных заведений и чрезвычайно
ограниченном поле приложения сил работа молодого ученого,
начиналась обычно со средней школы.
С. А. Чаплыгин начал свою преподавательскую деятель-
ность учителем физики в женском Екатерининском институте;
затем последовало преподавание математики в Межевоя
институте, преподавание механики в Московском высшем
техническом училище, где Сергей Алексеевич был ассистентом^
Н. Е. Жуковского, преподавание механики, а позднее,
с 1901 г., и профессура в Московском инженерном училище,
преподавание механики на Московских высших женских
курсах.
В Московском университете Сергей Алексеевич состоял
приват-доцентом с 1894 г. Ряд работ, о которых сказано
выше, принес Сергею Алексеевичу общее признание как
одного из крупнейших ученых нашей страны, и в декабре
1903 г. он был избран профессором Московского универ-
ситета.
Вскоре обстоятельства сложились так, что выявилась еще
одна, совершенно новая и редкая среди ученых черта харак-
; АДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 897
тера Сергея Алексеевича. Он оказался замечательным орга-
низатором.
В Москве были частные Высшие женские курсы, создан-
ные известным историком профессором Герье. Первоначально
число слушательниц на них было невелико. Учредители курсов
ставили, по-видимому, несколько неопределенные, фемини-
стические задачи — содействовать общекультурному росту
женщин и приобщить их к достижениям современной науки.
Наступал революционный подъем 1905 г. Широкие демокра-
тические идеи, требование полного равноправия женщин
выдвинули перед курсами совершенно новые задачи. Дело
шло уже не о своеобразном культуртрегерстве среди женщин,
а о том, чтобы на курсах развернуть массовую подготовку
ученых и научных специалистов—женщин-педагогов, женщин-
врачей, женщин-химиков, биологов, историков, совершенно
так же как в университетах готовились специалисты-мужчины.
Старое руководство не могло удовлетворить этим требова-
ниям, й профессорская коллегия выбрала Сергея Алексеевича
руководителем, директором курсов.
Перед новым директором стояли исключительно трудные
задачи. Бурный рост курсов выдвинул необходимость расши-
рения помещений, а это могло быть достигнуто только путем
постройки специальных новых зданий, что, естественно,
требовало огромных сумм. От царского правительства курсы,
как частное учреждение, получили совершенно ничтожную
субсидию. Либеральные московские круги оказывали курсам
поддержку, но не надо забывать, что и среди правительст-
венных и среди влиятельных московских лиц было много
людей, для которых идеальным решением всего женского
вопроса было бы внедрение пресловутой немецкой программы
четырех «К» (Kinder, Kirche, Kiiche, Kleider— дети, церковь,
кухня, платья). Когда после революционного подъема 1905 г.
началась полоса реакции, то самое существование
курсов, проблема всего высшего женского образования
была «бельмом на глазу», предметом всяких подо-
зрений и нападок со стороны реакционно настроенных
кругов.
При этих условиях нужен был исключительный талант
организатора, нужен был огромный такт, чтобы вести и
расширять работу курсов.
8S8
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Благодаря большому авторитету Сергея Алексеевича и
его настойчивости постановлением Московской городской
лумы на пустынном тогда Девичьем поле был отведен без-
возмездно участок земли для постройки зданий Московских
высших женских курсов. Надо было немедленно приступить
к стройке, так как неиспользование участка могло повести
к его изъятию.
Сергей Алексеевич ухитрился, имея буквально гроши,
.построить те дворцы, которые и в настоящее время являются
одними из лучших учебных зданий Москвы.
Об этом шедевре хозяйственной деятельности С. А. Ча-
плыгина в свое время ходил по Москве анекдотический рас-
сказ. Строительство курсов будто бы шло так. Сергей Але-
ксеевич первым долгом заложил землю, пожертвованную
курсам Городской думой, и на полученные деньги построил
первый этаж первого учебного корпуса. Затем, заложив этот
.первый этаж, построил второй и т. д., пока не построил весь
первый корпус, заложив который целиком, начал строить
второй корпус.
Если это и не совсем верно, то во всяком случае близко
к истине. Московские старожилы, вероятно, вспомнят опи-
сание в тогдашних газетах бурных дебатов в Городской
думе, когда правые гласные требовали немедленного изъятия
у курсов отведенного им участка и отдачи под суд дирек-
тора курсов за незаконный залог дарственной земли.
Несомненно одно: Сергей Алексеевич был не только
великолепным организатором, но и совершенно исключитель-
ным, расчетливым, прижимистым и дотошным хозяином, ко-
торый не только руководил строительством, но и учитывал
в буквальном смысле каждую копейку, которую платил,
каждый кирпич, который получал.
Благодаря изумительной энергии С. А. Чаплыгина и его
хозяйственным и организаторским талантам, курсы скоро
получили новые прекрасные помещения, были открыты два
.новых факультета — медицинский и химико-фармацевтиче-
ский, были созданы великолепные лаборатории. К работе
на курсах были привлечены крупнейшие ученые Москвы.
Из стен Московских высших женских курсов вышли тысячи
прекрасно подготовленных педагогов, врачей, ученых — хи-
миков, ботаников, геологов, историков. Многие из них й
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 899-
сейчас работают в разных областях нашей необъятной
родины.
С. А. Чаплыгин был директором Московских высших
женских курсов непрерывно с 1905 по 1918 г. Вскоре центр
административной деятельности Сергея Алексеевича пере-
местился в другое огромное учреждение— в Центральный
аэрогидродинамический институт, всемирно известный ЦАГИ.
Московские высшие женские курсы были дороги Сергею
Алексеевичу не только как их директору. С 1911 г., тяже-
лого года в истории Московского университета, когда
С. А. Чаплыгин вместе с рядом других профессоров ушел
из Московского университета в знак протеста против реак-
ционной политики тогдашнего министра народного просве-
щения Кассо, и до 1917 г. курсы остались для Сергея Але-
ксеевича главным местом его педагогической работы.
В Московский университет он вернулся только после ре-
волюции, в 1917 г..
Работа в должности директора Московских высших жен-
ских курсов создала Сергею Алексеевичу широчайшую по-
пулярность. В 1917 г. он был выдвинут на пост москов-
ского городского головы, но не был утвержден царским
правительством.
С полным блеском хозяйственные способности и админи-
стративный талант Сергея Алексеевича проявились в его
деятельности в ЦАГИ. После смерти в 1921 г. Н. Е. Жу-
ковского он стал во главе научного руководства ЦАГИ
как председатель коллегии. Прекрасные, оборудованные
тогда по последнему слову науки лаборатории являются
замечательным памятником административной и хозяйствен-
ной деятельности их строителя С. А. Чаплыгина. С ЦАГИ
он был связан работой до последних дней своей жизни,
занимая непрерывно различные ответственные посты, руко-
водя всей научной деятельностью этого крупнейшего учре-
ждения. ,В период с 1928 по 1931 г. он. был директором
и начальником/ЦАГИ.
Так в своем лице Сергей Алексеевич сочетал теоретика-
ученого с общественным административным деятелем.
Как уже было сказано выше, появление докторской дис-
сертации было моментом перелома в научном творчестве
Сергея Алексеевича. От задач чисто теоретических, харак-
900
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
терных для научного творчества первого периода, его инте-
ресы переходят в область задач прикладных, самым тесным
образом связанных с потребностями современной техники.
Известно, что начало текущего столетия ознаменовалось
первыми удачными полетами на аппаратах «более тяжелых,
чем воздух». В период 1903—1905 гг. братья Райт в Аме-
рике и Фарман и Сантос-Дюмон во Франции построили пер-
вые аэропланы и совершили на них удачные полеты. Для
дальнейшего развития этой новой области техники нужна
была теория, которая могла бы быть положена в основу
расчета летательных машин. Сорок лет назад гидро- и аэро-
динамика почти ничего не могли дать инженеру. Только
в 1906 г. Н. Е. Жуковский в классическом мемуаре «О при-
соединенных вихрях» изложил знаменитую формулу, кото-
рая сейчас приводится во всех учебниках гидромеханики и
служит основой аэродинамического расчета самолета. Эта
формула дает величину подъемной силы. Однако от иссле-
дования Н. Е. Жуковского до практического применения
было далеко. В формулу Жуковского входила величина так
называемой «циркуляции скорости», зависящая от угла
атаки, от скорости и от геометрической формы крыла.
Для того чтобы можно было применять формулу Жуков-
ского, надо было найти способ вычисления циркуляции по
геометрической форме крыла. Можно думать, что основная
трудность этой задачи состояла в следующем. Теорема Жу-
ковского выведена в предположении, что жидкость совер-
шенно лишена вязкости, между тем влияние формы крыла
на величину циркуляции, вероятно, сказывается через посред-
ство вязкости жидкости. По-видимому, Жуковский искал
решение задачи именно в этом направлении. Преодолеть
эту весьма трудную задачу, решения которой мы не знаем
до настоящего времени, он не мог.
Сергей Алексеевич знал, конечно, о работах по аэро-
механике Н. Е. Жуковского и других ученых, но сам
лично не проявлял интереса к этой области. По-видимому,
научные интересы его были направлены в совершенно иную
область. Можно думать, что к периоду 1905—1910 гг.
относится ряд незаконченных исследований Сергея Алек-
сеевича по небесной механике, оставшихся среди его
бумаг.
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 901
В самом конце 1909 г. в Москве состоялся очередной
съезд естествоиспытателей и врачей. На одном из заседаний
секции воздухоплавания Н. Е. Жуковский делал доклад
о подъемной силе самолетов, причем, не имея возможности
применить свою собственную, найденную за несколько лет
до этого теорему о подъемной силе, пытался объяснить
возникновение подъемной силы, исходя из влияния трения;
физически такое объяснение было, вероятно, правильным,
но оно не давало никаких путей для определения величины
подъемной силы.
Среди слушателей этого доклада был С. А. Чаплыгин,
и во время доклада у него мелькнула гениальная мысль
о возможности обойти все трудности, связанные с опреде-
лением циркуляции в формуле Н. Е. Жуковского, если
принять во внимание следующий всегда экспериментально
наблюдаемый факт: при плавном обтекании крыла потоком
воздуха острая задняя кромка является линией плав-
ного схода потока с верхней и нижней поверхностей
крыла.
Нетрудно показать, что в случае, если поток плавно
обтекает острую заднюю кромку, не сходя с нее, то ско-
рость потока на задней кромке крыла равна бесконечности.
Поэтому такой экспериментальный факт можно выразить
еще следующим образом: физически возможными являются
только такие течения, при которых скорость потока во всех
точках поля течения конечна.
Это положение, как немедленно показали вычисления и
самого С. А. Чаплыгина и Н. Е. Жуковского, которому
Сергей Алексеевич тут же после заседания сообщил о своей
догадке, позволило найти величину циркуляции, а при по-
мощи теоремы Н. Е. Жуковского— и величину подъемной
силы.
Подмеченный Сергеем .Алексеевичем экспериментально
установленный факт в настоящее время широко известен
в науке как «основная гипотеза Жуковского», однако все
значение этого положения отметил С. А. Чаплыгин, и он,
а уже по его указанию и Н. Е. Жуковский, получил все
важнейшие выводы из этого постулата.
Трудности, связанные с определением величины циркуля-
ции, более чем на четыре года задержали развитие теоре-
902
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
тической аэромеханики. Зато после гениального по простоте
и остроумию обхода этого затруднения при помощи вве-
денного С. А. Чаплыгиным постулата началось бурное раз-
витие теории крыла — основы всей современной технической
аэромеханики, а в руках Н. Е. Жуковского— и развитие
теории пропеллера.
Этот постулат открывал чрезвычайно широкие перспек-
тивы для разработки вопросов, выдвигаемых бурно расту-
щей авиацией. Решению этих задач почти исключительно и была
посвящена научная деятельность последних тридцати лет
жизни Сергея Алексеевича. Действительно, кроме неболь-
шого числа его работ по случайно встретившимся вопросам
(теория гидрокона, теория смазки и т. п.), за этот период
можно указать работы только по одному вопросу, далеко
отстоящему от задач аэромеханики: это замечательные по
оригинальности идеи и по силе анализа чисто математиче-
ские исследования по приближенному интегрированию диф-
ференциальных уравненийх).
Все остальные работы Сергея Алексеевича посвящены
теории крыла, и почти каждая из них представляет клас-
сическое исследование, методы и результаты которого на-
всегда войдут в сокровищницу основных достижений
науки. К изложению этих результатов мы теперь и пе-
рейдем.
Решение задачи об определении величины подъемной
силы крыла на основе упомянутого постулата было дано
Сергеем Алексеевичем в мемуаре «О давлении плоскопарал-
лельного потока воздуха на преграждающие тела»* 2), напи-
санном тотчас же после съезда естествоиспытателей и вра-
чей, в самом начале 1910 г.
В этой классической работе впервые была до конца
решена задача об определении подъемной силы крыла. Но
ее содержание далеко не исчерпывается решением этой за-
дачи. Работа замечательна тем, что в ней разработан систе-
матический метод решения задач плоской гидромеханики
*) С. А. Чаплыгин, Новый метод приближенного интегриро-
вания дифференциальных уравнений (четыре работы, 1919-—1920),
Собр. соч., т. I, стр. 347.
2) Его же, Собр. соч., т. П, стр. 194, 1948.
академик Сергей Алексеевич чаплыгйй
963
применением теории функций комплексного переменного.
В частности, в ней выведены замечательные формулы для
определения сил давления потока, которые теперь носят
название: у нас — «формул Чаплыгина — Блазиуса», а за
границей—«формул Блазиуса»,—название совершенно неспра-
ведливое, так как германский ученый Блазиус нашел эти
формулы независимо от Сергея Алексеевича, но несколько
позднее.
Две работы — работа Н. Е. Жуковского «О присоеди-
ненных вихрях» и работа С. А. Чаплыгина «О давлении
плоскопараллельного потока воздуха на преграждающие
тела» — представляют замечательный этап в развитии гидро-
механики. Ими было положено начало совершенно новой
области исследования течения жидкости — течения вокруг
тел с плавным обтеканием их. Этот отдел, навсегда связан-
ный с именами Жуковского и Чаплыгина, вошел в настоя-
щее время во все современные трактаты по гидромеханике
как ее основная часть наряду с теорией вихрей, теорией
струй и т. п.
В истории науки, пожалуй, не легко найти другой при-
мер, когда открытие столь общих и далеко идущих истин
совершилось при помощи столь примитивных соображений,
как это было сделано Н. Е. Жуковским в мемуаре «О при-
соединенных вихрях». Замечательная концепция присоеди-
ненного вихря получена здесь при помощи самых элементар-
ных математических средств. И рядом с этим — мемуар
,С. А. Чаплыгина, написанный с классическим совершенством
строгого математического исследования.
Если здесь допустимо сравнение, то, с одной стороны,
мы имеем широкий эскиз большой картины, в которой одни
части только намечены, остальные же не увязаны друг
с другом, а с другой, — точный, законченный и четкий рису-
нок художника-академиста, где все на месте, все выполнено
технически безукоризненно.
Характером изложения определилось и отношение к этим
двум замечательным работам. Работа Н. Е. Жуковского
при ее появлении прошла почти незамеченной: колоссальное
значение ее основных идей стало ясным только позднее.
Работа С. А. Чаплыгина сразу приобрела всеобщее и без-
условное признание.
904
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Замечательный мемуар 1910 г. открыл длинный ряд ра-
бот Сергея Алексеевича по различным вопросам теории
крыла.
Прежде всего надо отметить работу «К общей теории
.крыла моноплана»1), напечатанную в 1920 г. В этой работе
введен в науку целый ряд важнейших понятий и идей, часть
которых, по-видимому, не использована и до настоящего
времени. Понятия о параболе устойчивости, о фокусе крыла
стали основой современных исследований. В понятии об
изображающих профилях, в методах получения новых про-
филей мы имеем, может быть, источники дальнейшего раз-
вития. Идеи этой работы послужили в дальнейшем исходным
пунктом для многочисленных исследований и у нас в СССР,
и за границей.
Столь же интересна и работа «Схематическая теория
разрезного крыла»2), написанная в 1922 г. и посвященная
Сергеем Алексеевичем памяти его учителя Н. Е. Жуковского.
Основная идея этой работы состоит в том, что путем при-
соединения к крылу некоторых добавочных частей можно
добиться увеличения его подъемной силы. Это замечательное
исследование явилось началом целого ряда работ и самого
С. А. Чаплыгина и других исследователей по так называе-
мой механизации крыла.
Сущность всех этих многочисленных исследований сво-
дится к тому, чтб в целях повышения его аэродинамических
свойств крыло современного аэроплана проходит любопыт-
ную эволюцию: из неизменяемого крыла, несущей поверх-
ности, путем присоединения добавочных частей — предкрыл-
ков, закрылков, различного рода щитков, элеронов, отса-
сывания, сдувания и т. д. — оно постепенно превращается
в сложный и гибкий механизм, может быть, превосходящий
по гибкости крыло птицы. Интересно отметить, что мемуар
Сергея Алексеевича написан в годы, когда конструкторы,
по существу, еще и не подходили к решению подобных
вопросов.
Таким же открывающим новые горизонты исследованием
была работа «О влиянии потока воздуха на движущееся
Э С. А. Чаплыгин, Собр. соч., т. II, стр. 246, 1948.
2) Там же, стр. 431.
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН
905
в нем цилиндрическое крыло»1), написанная в 1926 г. Эта
работа, обобщающая основные формулы Чаплыгина — Бла-
зиуса на случай неустановившегося движения крыла, и
в настоящее время, через 12 лет после ее появления, пожалуй,
не дополнена существенно ни в одном пункте, несмотря на
то, что теми же вопросами занимались после Сергея Алек-
сеевича многие первоклассные специалисты.
В заключение этого далеко не полного обзора деятель-
ности С. А. Чаплыгина остановлюсь на работе, которая
В- научном творчестве ее автора сыграла роль «лебединой
песни». Эта небольшая работа «К теории триплана» (1936 г.)2),
написанная Сергеем Алексеевичем уже в очень преклонном
возрасте, поражает остроумием метода исследования, све-
жестью и оригинальностью идеи. Здесь гидромеханика при-
влекается дважды: один раз для решения чисто математи-
ческой задачи о конформном отображении и другой — для
решения механической задачи.
В истории науки имя С. А. Чаплыгина, конечно, прежде
и больше всего остается связанным с развитием современной
технической гидромеханики, наряду с именем другого заме-
чательного русского ученого, Н. Е. Жуковского. Оба они
своими работами создали новую широкую область науки;
во многих случаях их исследования в этой области шли
параллельно, дополняя и совершенствуя друг друга.
Но если имена С. А. Чаплыгина и Н. Е. Жуковского
стоят рядом как имена двух основоположников широкой
области науки, то в творчестве, в методах работы это были
люди совершенно различных направлений. В истории науки
нелегко найти другой пример двух столь различных по своим
научным вкусам людей, столь дружно работавших в одной
области.
Все в них было различно. Различны они были и по своим
бытовым вкусам. С одной стороны — страстный любитель
природы Н. Е. Жуковский, пловец, охотник, окруженный
всегда охотничьими собаками, снаряженный охотничьими ружь-
ями. С другой стороны—С. А. Чаплыгин, типичный горо-
Ч С. А. Чаплыгин, Собр. соч., т. II, стр. 300, 1948.
9) Труды Центрального аэрогидродинамического института им.
проф. Н. Е. Жуковского, в. 206, 1936.
906
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
жанищ проводивший даже свой отдых на лоне природы —
в Кисловодске, в Узком — за игрой в шахматы. Столь же
различны они были и по своему отношению к науке. Это
различие выражалось уже в самом взгляде на меха-
нику.
Несомненно, что механика — это естественная наука
о движении в природе твердых, жидких и газообразных тел.
И однако уже гений Ньютона сумел дать ей такую аксио-
матически законченную форму, что она приобрела чисто ма-
тематический, свободный от всякого эксперимента характер.
Механика стала походить в этом отношении на другую об-
ширную область нашего знания, об экспериментальном про-
исхождении которой мы так основательно забыли в течение
тысячелетий, что только недавно вопросы современной физи-
ки напомнили нам о ней, — это, конечно, геометрия.
И вот в механике мы видим два различных направления.
Одно — из Пизанского собора, где Галилей наблюдает ка-
чание паникадила, через опыты над жидкостями Паскаля,
Бернулли, через стрельбу из пушек, которой определялась
скорость звука, через Пантеон, где наблюдалось качание
маятника Фуко, — ведет нас длинным, но прямым путем
в современные гидро- и аэродинамические лаборатории наших
институтов и университетов, в конструкторские бюро, раз-
рабатывающие конструкции современных гирокомпасов, гиро-
горизонтов и . других аппаратов, основанных на примене-
нии самых основных принципов механики. Интересно отме-
тить, что в этом направлении шло развитие мыслей не только
специалистов-механиков. Конструкция паровых машин, ме-
ханические модели, направляющие механизмы — это источ-
ник, из которого черпал свои гениальные чисто математи-
ческие идеи гордость русской математики академик П. Л. Че-
бышев. Такова же была и та механика богатой физической
индукции, широкого эксперимента, которую мы видим
в трудах Жуковского.
А рядом мы имеем другую механику, истоки которой
в знаменитых «Axiomata sive leges motus» Ньютона, — механику
как ветвь чистой математики. Это—механика Лагранжа,
Якоби, вариационных принципов, механика С. В. Ковалевской,
классических работ академика А. М. Ляпунова. Такова ме-
ханика и С. А. Чаплыгина.
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 907
Было бы безнадежно в трудах А. М. Ляпунова искать
какого-нибудь намека на экспериментальность; мы найдем
в них не физическую индукцию, не результаты экспериментов.
В его механических исследованиях мы встретим тончайшие
и сложнейшие, чисто математические результаты. Совершен-
но такого же, чисто математического, чисто аналитического
характера были исследования С. А. Чаплыгина. Мы стал-
киваемся здесь с парадоксальным обстоятельством. Работы
Сергея Алексеевича были связаны с аэродинамикой, с рас-
четом самолетов, т. е. не только с экспериментальной об-
ластью, но с областью чисто технического конструирования.
Более двадцати последних лет своей жизни С. А. Чаплыгин
отдал работе в ЦАГИ, где как научный руководитель он
самым энергичным образом развивал научную работу гро-
мадных лабораторий. Его имя с гордостью носит одна из
больших лабораторий ЦАГИ. Однако сам Сергей Алексеевич
лично никакого отношения к эксперименту не имел.
Кто помнит Жуковского, тот, несомненно, вспомнит и
его лабораторию, его аэродинамические трубы, крылышки,
которые он сам мастерил, опыты, в постановке которых он
принимал деятельное участие.
В моей памяти живо встает воспоминание об одной встрече
с Николаем Егоровичем в его лаборатории, когда я за-
стал его самого и его лаборантов на полу; сам Николай
Егорович с его грузной фигурой, стоя на четвереньках, с
интересом наблюдал за флажками под быстровращающимся
деревянным диском.
Единственным станком, у которого работал С. А. Чап-
лыгин, был его письменный стол.
Сергей Алексеевич сам как-то рассказал мне, что в своей
жизни он проделал единственный опыт в лаборатории: сту-
дентом он хотел пройти необязательный тогда физический
практикум, и в качестве первой работы ему дали взвесить
на точных весах какую-то стекляшку. Он ее взвесил, ни-
чего хорошего не получил и после этого других попыток
связаться с экспериментом не делал.
Один иностранный химик сделал попытку разделить уче-
ных на романтиков и классиков. Силу одних составляет, по
его мнению, вдохновенная интуиция, сила живого воз-
действия, живого слова. Сила других — в классической
908
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
простоте, законченности мысли, точности и ясности ее
выражения.
Едва ли все разнообразие путей научного творчества
можно без усилия втиснуть в рамки такой бинарной класси-
фикации. Может быть, не совсем удачны и сами названия.
Но несомненно одно: в этой классификации С. А. Чаплыгин
бесспорно займет место среди классиков, так же как А. М. Ля-
пунов, как Якоби, как великий Лагранж. И так же несо-
мненно, что Н. Е. Жуковский, П. Л. Чебышев займут места
среди «романтиков», как гениальный Риман, Анри Пуанкаре
и другие.
Характером точного и ясного ума Сергея Алексеевича
объясняются его научные вкусы и, как полагается классику,
известная доля научной нетерпимости. Все незаконченное,
расплывчатое, недостаточно твердое в своих основных кон-
турах казалось ему бесполезным для науки. Он, например,
весьма критически относился ко всем результатам, связанным
с так называемым пограничным слоем. Может быть, тем же
объясняется и его критический взгляд на современную не-
ньютонианскую механику относительности: известная неопре-
деленность ее исходных положений отталкивала его. Здесь
мы имеем исконный и обычный спор двух направлений. Со-
вершенно так же классик А. М. Ляпунов находил туманными
и сомнительными гениальные математические идеи романтика
Римана.
Не любил читать лекции классик Гаусс, с величайшим
усилием читал лекции Ляпунов и при первой возможности
постарался от них освободиться. И наоборот, интересней-
шие беседы со своими слушателями проводил в перерывах
между писанием формул П. Л. Чебышев. Не мог обходиться
без учеников, без аудитории Н. Е. Жуковский,
С. А. Чаплыгин не был блестящим лектором, читать
лекции не любил и чтение их прекратил без сожаления уже
давно. Нельзя указать и учеников Сергея Алексеевича, ко-
торые были бы им, его непосредственным воздействием вве-
дены в область научной . работы.
Здесь мы также имеем разительную противоположность
между С. А. Чаплыгиным и Н. Е. Жуковским, который
был всегда окружен многочисленными учениками и сотруд-
никами.
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН 909
Но едва ли только образованием непосредственной школы
можно учитывать научное влияние ученого. Так, например,
всемирно известная математическая школа в Геттингене, свя-
занная с именами Феликса Клейна и Давида Гильберта, ока-
зала непосредственное воздействие на своих учеников. Но
не следует забывать, что из 69 докторантов Гильберта едва
наберется шесть-семь, оставивших некоторый след в науке,
и не более трех-четырех, проявивших себя как крупные на-
учные исследователи. Совершенно такую же картину мы
наблюдаем и среди непосредственных учеников Клейна. Влия-
ние же научных идей таких мастеров науки, как, например,
Анри Пуанкаре, который, кажется, вообще не имел непо-
средственных учеников, испытали на себе все современные
математики.
Точно так же и влияние мощной творческой личности
С. А. Чаплыгина, методов его исследований испытывает на
себе каждый ученый-механик, и мы все являемся учениками
этого замечательного мастера науки.
С какой бы точки зрения мы ни подходили к оценке
методов работы С. А. Чаплыгина и его учителя Н. Е. Жу-
ковского, скажется глубочайшее различие между ними. Но
было нечто в их мировоззрении, что связывало их в одном
общем устремлении,—это их взгляд на цель и назначение
науки.
В интересном докладе, который академик В. А. Стеклов
сделал в 1921 г. когда отмечалось столетие со дня рождения
П. Л. Чебышева, он следующим образом охарактеризовал
научное мировоззрение Чебышева: «Взять природу такой,
какой она является как неизбежный реальный факт наблю-
дения, и извлечь из данных наблюдений возможно большую
пользу при наименьшей затрате сил согласно с требованием
практики, которое, как говорил сам Чебышев, везде ищет
самого лучшего, самого выгодного» Ч-
Итак, задачей науки является наивыгоднейшее исполь-
зование богатства природы, ее сил. Заметим, что такое по-
нимание принадлежит не инженеру, а представителю чистой
Ч В. А. Стеклов, Теория и практика в исследованиях Че-
бышева, 1921.
910 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
науки. В творчестве А. М. Ляпунова мы напрасно искали бы
какое-нибудь отражение подобной идеи.
И Жуковскому, и Чаплыгину было абсолютно чуждо
пассивное созерцание мира. Задача науки, как ее понимали
они оба, — переделать мир, использовать силы и законы
природы, чтобы, как говорил П. Л. Чебышев, «с наимень-
шей затратой сил» заставить ее служить техническому и
общему прогрессу человечества, росту его культуры, бла-
гополучию и процветанию.
Но и в области не научных, а чисто административных,
хозяйственных дел эти два так мало похожих друг на друга
человека шли своими различными путями. Жуковский не-
удачно пытался начать жизнь как инженер, как изобретатель.
Уже много позднее известный ученый, профессор, он явился
крупным научным организатором. При этом сам Ни-
колай Егорович административными и хозяйственными та-
лантами обладал в весьма малой степени, но его научный
энтузиазм, обаяние его личности позволили ему сплотить
около общего дела талантливых организаторов, хозяйствен-
ников, администраторов.
Совсем иное дело — С. А. Чаплыгин. Он сам был ра-
чительным, умелым, талантливейшим организатором, строи-
телем, сам с необычайной аккуратностью, с исключительной
добросовестностью вникал во все детали дела.
Свой,большой организаторский талант Сергей Алексеевич
проявлял во всяком деле, которое он вел. Избранный в конце
1926 г. членом-корреспондентом Академии наук СССР,
а 12 января 1929 г. действительным ее членом, он работает
председателем группы техники; позднее, с 1933 г., яв-
ляется председателем комиссии технической терминологии;
с 1937 г. — председателем комиссии по гидромеханике.
После организации при Академии наук Института механики
Сергей Алексеевич входит в состав Ученого совета Инсти-
тута и параллельно с этим продолжает интенсивную работу
в ЦАГИ.
Но этим еще далеко не исчерпывается его работа. Как
депутат Моссовета он принимает деятельное участие в об-
щественной работе, активно работает в Московском доме
ученых и, наконец, руководит Управлением домами ученых.
Среди московских научных работников найдется немало та-
АКАДЕМИК СЕРГЕЙ АЛЕКСЕЕВИЧ ЧАПЛЫГИН *911
ких, которые с благодарностью вспомнят, какую помощь
оказал им Сергей Алексеевич в устройстве их бытовых дел.
И во всех этих делах и большого и малого масштаба
С. А. Чаплыгин всегда с величайшей требовательностью
относился и к себе и к своим сотрудникам. Работать, с ним
было не легко. В своих научных оценках он был временами
беспощаден, но, как бы ни была строга эта оценка, ухо-
дивший от Сергея Алексеевича всегда чувствовал полную
его правоту.
Самый облик Сергея Алексеевича, его величественная
фигура, несколько суровый взгляд, убедительная, неторо-
пливая речь невольно внушали чувство глубокого к нему
уважения.
Я невольно вспоминаю одну вычислительницу в ЦАГИ,
опытную, старую работницу, которая так боялась Сергея
Алексеевича, что, когда несла ему на просмэтр, как началь-
нику отдела, свои вычисления, долго простаивала в полу-
темном коридоре, около кабинета, не решаясь войти и,
вероятно, поминая «царя Давида и всю кротость его».
Понадобилось много времени, чтобы за суровой внешностью
начальника, администратора увидеть доброго, отзывчивого
и сердечного человека, < от которого в тяжелые минуты
можно было получить и моральную поддержку и материаль-
ную помощь.
* Все, кому приходилось работать с Сергеем Алексеевичем,
хранят в своих, воспоминаниях о нем, наряду с* обликом
сурового, строгого учителя, начальника, руководителя,
администратора, образ гуманного, доброго, отзывчивого
человека, человека большой души, широкого человеческого
сердца.
Всю свою жизнь Сергей Алексеевич посвятил служению
Родине. Выросший и сложившийся, как все люди его поко-
ления, в совершенно иных, не похожих на современные
условиях, он в 1917 г., в великие дни Октябрьской рево-
люции, с полным сознанием своего долга перед Родиной,
перед воспитавшим его народом отдал всего себя, весь
свой исследовательский и организаторский талант строи-
тельству нашей новой России, великого Советского Союза.
Деятельность Сергея Алексеевича Чаплыгина получила
самую высокую оценку: правительство наградило его орденом
912
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Трудового Красного Знамени, орденом Ленина, при-
своило ему почетнейшее звание Героя Социалистического
Труда.
Это был замечательный гражданин нашей Советской
страны. Это был человек, для которого потребностью жизни
было выполнение гражданского долга. Это был горячий
патриот, который больше всего любил свою Родину, свой
народ. И как горячий патриот, Сергей Алексеевич видел
величайшую радость в процветании родной страны и с гор-
достью сознавал, что его талант, его научные идеи, его
труды и труды его последователей и соотрудников, научных
исследователей, инженеров, конструкторов служат укрепле-
нию мощи и славы нашей великой Родины.
Я видел его в последний раз 18 июля 1941 г, в тяжелые
дни, когда под напором фашистских полчищ наши войска
с жестокими боями принужены были отступать, оставляя
врагу цветущие города и села, обильные поля нашей Родины.
В эти тяжелые дни единственным желанием Сергея Але-
ксеевича было увидеть победу нашей страны.
Когда мы расставались, его последними словами были:
«Я хочу только одного: дожить до того дня, когда будет
разгромлена фашистская Германия».
Судьба лишила его этой радости. Он умер в те дни,
когда в Сталинградской битве под ударами наших войск
германская армия потеряла свою самоуверенность и окон-
чательно развеялся миф о ее непобедимости.
Ему не пришлось дожить до того счастливого времени,
которое мы переживаем сейчас, когда «праздник пришел
на нашу улицу», когда неудержимой лавиной движутся на
запад наши победоносные войска. И ведет их вперед не-
сокрушимая воля советского народа, беззаветный творческий
труд рабочих, колхозников, инженеров, ученых, всей ин-
теллигенции, всего многомиллионного коллектива нашей
страны, воинская доблесть его сынов, военные таланты
полководцев.
В. П. ВЕГ чинки и
(1888—1950)
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
I. Детство, гимназия.
Годы студенчества в МВТУ
Выдающийся русский ученый, один из основателей рус-
ской авиационной науки, талантливый изобретатель и инже-
нер, замечательный учитель и профессор высшей школы —
Владимир Петрович Ветчинкин родился 17 (29 по н. с.)
июня 1888 г. в г. Кутно тогдашней Варшавской губернии.
Отец Владимира Петровича был человек весьма образо-
ванный с широкими научными интересами: с большим инте-
ресом он изучал физику и астрономию, из любознательности
совершил кругосветное путешествие, любил заниматься
ремеслами.
Мать Владимира Петровича, Лидия Николаевна Бахтина,
также была женщина хорошо образованная, обладала не-
дюжинными математическими способностями.
Полк, в котором служил П. Н. Ветчинкин, часто пере-
водился из города в город, и семья Ветчинкиных переезжала
с ним: из Кутно в г. Плоцк, из Плоцка в Люблино. Здесь
Володя Ветчинкин поступил в 1899 г. в первый класс Люб-
линской классической гимназии. Подготовила его в гимназию
мать, она была его первой учительницей; она даже изучила
латынь, чтобы следить за занятиями сына.
В 1904 ’г. Ветчинкины переехали в Нижний Новгород
(ныне г. Горький), и Володя Ветчинкин был переведен в
Нижегородскую губернскую гимназию. Через год, в 1905 г.,
в связи с русско-японской войной полк был отправлен на
Дальний Восток, а Володя с матерью переехал в Курск,
где продолжал учиться в Курской классической гимназии.
914
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
В 1907 г. Володя Ветчинкин окончил с золотой медалью
Курскую классическую гимназию. Надо было избирать даль-
нейший путь. Под влиянием отца Владимир Петрович увле-
кался естественными науками, астрономией и физикой; ве-
роятно, от матери он унаследовал большие математические
способности и интересы. Но Владимир Петрович не пошел
по пути теоретической научной подготовки в университете,
куда, естественно, открывалась в то время дорога по окон-
чании гимназии, — он избрал инженерную деятельность.
В том же 1907 г. он поступил по конкурсным экзаменам
в знаменитое Московское высшее техническое училище, слав-
ный рассадник инженерных кадров в России.
Возможно, что в этом выборе сказалась практическая
направленность интересов его отца, Петра Николаевича;
можно думать, что его увлечение усвоением различных прак-
тических, ремесленных навыков не прошло бесследно и для
Владимира Петровича^ В дальнейшей его деятельности стрем-
ление не только руководить и направлять, но и принимать
личное участие в осуществлении своих планов и расчетов,
работать и в лаборатории, и в мастерской, и на заводе
является отличительной чертой Владимира Петровича. Но,
вероятно, еще большее влияние на выбор практической,
инженерной деятельности оказало то, что уже в годы учения
в гимназии Владимир Петрович увлекался авиацией, которая
в те годы как раз одерживала свои первые поразительные
победы.
В МВТУ Владимир Петрович пробыл с 1907 по начало
1915 г. Едва успев поступить в МВТУ, осенью 1907 г., он
уже стенографирует на лекциях Н. Е. Жуковского по тео-
ретической механике дополнения по графостатике, которые
в курсе читались впервые; попутно Владимир Петрович
изучил стенографию, которую в дальнейшем широко при-
менял. Эти дополнения в записи и обработке Владимира
Петровича вошли в последующие издания лекций Н. Е. Жу-
ковского по теоретической механике.
В осеннем семестре замечательного в научном развитии
Владимира Петровича 1910 г. Н. Е. Жуковский начал чтение
факультативного курса «Теоретические основы воздухо-
плавания». К этому времени исследования Н. Е. Жуковского
ц С. А. Чаплыгина позволили довести теоретические иссле-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
915
дования по авиационным вопросам механики до такого со-
стояния, что стало возможным систематическое изложение
основ аэромеханики и авиации с общей теоретической точки
зрения. Курс Н. Е. Жуковского и ставил задачею систе-
матическое изложение гидромеханических основ авиации; это
,был, по-видимому, первый опыт изложения совершенно
нового раздела механики непрерывной среды. Чтение этого
курса вызвало огромный интерес среди студентов; был орга-
низован издательский студенческий коллектив (студенты:
В. П. Ветчинкин, Я- М. Гольдберг, Г. В. Фенстер, Н. Г. Чен-
цов) по записи и изданию этих замечательных лекций.
Владимир Петрович со свойственной ему энергией быстро
стал душой работы этого коллектива; он не только вел
запись лекций Н. Е. Жуковского, но и систематически
обрабатывал их для издания.
Для молодого студента работа над изданием этого заме-
чательного, курса, которая велась под. непосредственным
наблюдением такого выдающегося ученого, каким был
Н. Е. Жуковский, была превосходной школой. Талантливый,
чрезвычайно энергичный, Владимир Петрович обратил на
•себя внимание выдающегося русского ученого, основополож-
ника современной авиационной науки; постоянное обсужде-
ние с ним отдельных частей издаваемого курса, а в связи
с этим и частые беседы на общенаучные темы как нельзя
лучше, открывали перед Владимиром Петровичем широкие
горизонты современной науки.
Лекции Н. Е. Жуковского «Теоретические основы воз-
духоплавания», записанные и подготовленные к печати
В. П. Ветчинкиным, вышли в свет в 1911 г.; впоследствии
они, переиздавались в 1925, 1939 и I960 гг.; в 1916 г.
они были переведены на французский язык и переизданы
в 1933 г. также при ближайшем участии Владимира Пет-
ровича. В течение долгого времени эта замечательная книга
оставалась основным и единственным пособием по теорети-
ческим вопросам авиации.
Совместная работа по изданию лекций необычайно сбли-
зила учителя и ученика. Для Н. Е. Жуковского его талант-
ливый ученик становится самым близким сотрудником и
продолжателем его работы. Излишне говорить, что в гла-
зах В. П. Ветчинкина его учитель и друг являлся величай-
916
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
шим и не подлежащим критике авторитетом, учителем в самом
высоком и полном значении этого слова.
Работа с Н. Е. Жуковским над изданием его лекций
была для Владимира Петровича прекрасным введением и
началом самостоятельной научной работы; она определила
все дальнейшее направление деятельности В. П. Ветчинкина.
Одновременно, осенью 1910 г., В. П. Ветчинкин работал
и в другой, важнейшей для его дальнейшего творчества области.
Профессор Е. А. Болотов читал специальный курс «Теория
упругости». И здесь Владимир Петрович был не только
внимательным слушателем: он и этот курс тщательно стено-
графировал.
В том же 1910 г. он вступил в члены Воздухоплава-
тельного кружка МВТУ, которым руководил Н. Е. Жуков-
ский; членами этого кружка были в то время студенты,
а впоследствии крупнейшие работники в области авиации:
А. Н. Туполев, Б. Н. Юрьев, Г. X. Сабинин, Н. Г. Ченцов
и др.
Участие в работах кружка, работа по изданию «Теоре-
тических основ воздухоплавания» и возникшее отсюда сбли-
жение с Н. Е. Жуковским привели к тому, что В. П. Вет-
чинкин избирает своей ближайшей специальностью воздухо-
плавание. В 1910 г. он вступает в члены Московского кружка
(впоследствии Общества любителей астрономии), в работах
которого в дальнейшем он принимает самое деятельное
участие.
Как отмечал сам Владимир Петрович, с 1910 г. он стал
самым деятельным сотрудником Н. Е. Жуковского, вел
корректуры всех научных статей его на русском и на ино-
странных языках. Естественно, что научные интересы учи-
теля должны были захватить и его талантливого ученика.
Еще с 1890 г., со времени появления первых исследований
Н. Е. Жуковского по вопросам авиации, его внимание
особенно привлекал вопрос о теории работы гребного винта,
пропеллера; в первом издании «Теоретических вопросов
воздухоплавания» изложению существовавших в то время
исследований по теории винтов посвящен большой раздел.
После появления классических исследований по теории крыла
в плоскопараллельном потоке, знаменитого мемуара Н. Е. Жу-
ковского 1906 г. «О присоединенных вихрях» и замечатель-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
917
них исследований 1911 г. С. А. Чаплыгина и Н. Е. Жу-
ковского по расчету крыльев в плоскопараллельном потоке,
стало совершенно ясно, что существовавшие в то время
теории винтов требуют решительной перестройки. Созданию
гидродинамически обоснованной теории винтов и посвящены
были основные работы Н. Е. Жуковского после 1910 г.
Основываясь на идее присоединенного вихря крыла,
Н. Е. Жуковский создает замечательную вихревую схему
работы винта, которая немедленно получила блестящее экспе-
риментальное подтверждение в имевшемся в то время
обильном экспериментальном материале, например в данных,
приведенных в книге Фламма по теории винтов. Как известно,
основой вихревой теории винтов, созданной Н. Е. Жуковским,
является представление о лопасти винта как о крыле, кото-
рое можно заменить его присоединенным вихрем, причем
продолжение его, т. е. свободные вихри лопасти, с одной
стороны, образуют осевой вихрь винта, а с другой стороны,
сбегая с концов лопастей винта, образуют вихревую поверх-
ность разрыва скоростей сзади винта, наличие которой еще
было замечено в первых исследованиях по так называемой
теории идеального пропеллера. Это была ясная и совер-
шенно наглядная вихревая схема, вытекавшая из работ
Н. Е. Жуковского по теории крыла; фотографии Фламма
дали блестящее подтверждение теоретическим выводам
Н. Е. Жуковского.
Основы вихревой теории винтов были Н. Е. Жуковским
изложены в 1912 г. в его работе «Вихревая теория греб-
ного винта», статья первая. Но в этом замечательном иссле-
довании попутно решена и другая задача: лопасть винта
с его присоединенным вихрем и сбегающими с концов лопасти
свободными вихрями, осевым и винтообразным, представляет
собой вихревую схему крыла конечного размаха, а расчет
вызываемых этими вихрями индуктивных скоростей есть не что
иное, как теория крыла конечного размаха. Таким образом,
теория крыла конечного размаха, основанная на схеме под-
ковообразного вихря, обычно приписываемой Л. Прандтлю,
по существу, находятся в мемуаре Н. Е. Жуковского, где
к тому же рассматривается более сложный случай дви-
жения— не поступательное, а винтообразное движение
крыла.
918
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
В этих исследованиях Н. Е. Жуковского, несомненно,
деятельное участие принимал В. П. Ветчинкин; вот, как
учитель сам характеризует сотрудничество своего ученика:
«Начиная с 1912 г., я и В. П. Ветчинкин занимаемся тео-
рией и опытной обработкой вихревой теории гребного винта
и напечатали по этому вопросу ряд статей. При этом
В. П. Ветчинкин дал основанный на этой теории способ
расчета гребных винтов и приложил его к конструированию
•пропеллеров, поставленных на аэропланы (винты типа НЕЖ)
и давшие результаты, согласные с теориею».
Первые работы В. П. Ветчинкина по теории винтов были
посвящены одному вопросу, не разобранному Н. Е. Жу-
ковским, но необходимому для практического расчета винта,
им была выведена формула, позволяющая определить доба-
вочную осевую скорость в зависимости от циркуляции, а
это давало возможность рассчитать радиус вихревого шнура,
сходящего с лопасти, и угол, образованный им с осью
винта. Полученный таким путем метод расчета винтов был
доложен В. П. Ветчинкиным в 1912 г. на II Всероссийском
съезде воздухоплавателей в Москве.
В дальнейшем Владимир Петрович дал замечательное
обобщение вихревой теории винтов на случай переменной
по лопасти винта циркуляции. Переводя полученные им для
случая лопасти винта результаты на теорию крыла конеч-
ного размаха, мы сейчас же получаем самую общую вихре-
вую схему крыла конечного размаха.
Таким образом, Н. Е. Жуковский и В. П. Ветчинкин
значительно раньше Ланчестера и Прандтля дали вихревую
схему теории крыла конечного размаха и указали все пред-
посылки для полного расчета; это является общепризнанной
основой как теории винта, так и крыла конечного размаха.
Все эти результаты были помещены в вышедшей в 1913 г.
первой печатной работе В. П. Ветчинкина «Расчет гребного
винта». Это был блестящий научный дебют молодого уче-
ного, еще студента МВТУ.
Летом 1912 г. В. П. Ветчинкин был командирован по
представлению Н. Е. Жуковского для осмотра аэродинами-
ческих лабораторий в Германию, Францию, Италию и
Австрию. Эта поездка, естественно, дала ему и ценные све-
дения о состоянии научной работы за границей, и раз-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
919
нообразный опыт организации аэродинамических лабора-
торий.
Теоретические и расчетные работы по теории винтов
В. П. Ветчинкин продолжал и в последующие годы. В 1914 г.
напечатана вторая его крупная работа «Об инвариантах
гребного винта». Ценность этой работы видна хотя бы из
того, что она послужила основой для расчета вентиляторов
в работе Н. Е. Жуковского. Введенные в этих работах
В. П. Ветчинкиным отвлеченные коэффициенты вошли
в инженерную практику не только в теории винта, но и
в других областях аэромеханики.
Роль В. П. Ветчинкина в распространении идей вихре-
вой теории винтов среди широких технических кругов со-
вершенно исключительна. Достаточно отметить, что в период
1913—1920 гг. он лично рассчитывал, а затем под его
руководством рассчитывались все первые проекты самолет-
ных винтов и ветряков типа НЕЖ; таким образом было
рассчитано свыше 30 проектов. Разработанные при этом
методы и приемы расчета с некоторыми добавлениями при-
менялись в течение свыше полутора десятков лет, когда на
смену им пришли другие методы, в основном разработанные
учениками В. П. Ветчинкина.
Осенью 1914 г. В. П. Ветчинкин приступил к диплом-
ному проектированию, как это требовалось по учеб-
ным планам МВТУ. Интересно отметить тему проекта,
который он выполнял под руководством Н. Е. Жуков-
ского.
В то время среди заграничных конструкторов было
широко распространено убеждение в невозможности по-
стройки самолетов с большой подъемной силой. Идея
постройки тяжелых самолетов с большой грузоподъемностью
впервые зародилась в России, где в 1912 г. группа русских
конструкторов впервые в истории авиации приступила
к проектированию и постройке первого тяжелого самолета.
В мае 1913 г. первый в мире четырехмоторный самолет-
гигант «Русский витязь» поднялся в воздух. Постройка
этого огромного по тогдашним масштабам самолета с полез-
ным весом в 4200 кг, биплана с площадью несущих поверх-
ностей в 120 м2 и со скоростью 90 км!час, была славной
победой русской технической мысли. Следом за «Русским
920 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
витязем», в конце того же года был построен еще более
мощный самолет «Илья Муромец».
В то время теоретические базы проектирования самолетов
и методы расчета были разработаны весьма мало, во многих
случаях приходилось идти ощупью; естественно, что при
постройке таких огромных и тяжелых самолетов эти труд-
ности были особенно велики.
Темой своего дипломного проекта Владимир Петрович
и взял расчет тяжелого самолета, этой сложной и весьма
мало разработанной, но актуальной конструкции.
В 1914 г. В. П. Ветчинкин избирается членом правле-
ния студенческого издательского общества при МВТУ, где
принимает деятельное участие в подготовке текста печатного
издания курса лекций по теоретической механике Н. Е. Жуков-
ского, куда вошел и раздел по графостатике» составленный
по стенограммам Владимира Петровича в 1907 г.; кроме того,
он принимал деятельное участие и в других изданиях общества,
например в издании сборника переводных статей «О про-
дувке двухтактных двигателей». С ноября 1914 г. он состоит
вторым редактором журнала «Труды Физического отделения
О-ва любителей естествознания, антропологии и этнографии
при Московском университете»; в члены этого общества он
был избран по представлению профессоров Н. Е. Жуковского
и Е. А. Болотова еще в 1910 г. В 1913 г. В. П. Ветчин-
кин участвует в качестве докладчика на III Всероссийском
съезде воздухоплавателей в Петрограде и на VIII съезде
естествоиспытателей и врачей в Тифлисе.
Если к этому добавить, что с осени 1914 г., когда
были открыты при МВТУ теоретические курсы авиации для
подготовки летчиков, В. П. Ветчинкин начал на них препо-
давание по расчету аэропланов и винтов, то мы ясно пред-
ставим себе и круг научных интересов, и ту огромную
работу, которую тогда вел В. П. Ветчинкин.
19 января 1915 г. В. П. Ветчинкин отлично защитил
проект в МВТУ; он был первым русским инженером, полу-
чившим диплом по авиационной специальности.
Еще до окончания Владимиром Петровичем МВТУ Учеб-
ный комитет, учитывая его блестящие способности и необы-
чайную трудоспособность, возбудил перед Министерством
народного образования ходатайство о назначении, ему сти-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
921
пендии для подготовки его к преподавательской деятель-
ности, причем особенно отметил огромное значение «для
России проектирования в области воздухоплавания».
В представлении об оставлении В. П. Ветчинкина в Учеб-
ный комитет МВТУ его учитель Н. Е. Жуковский дал
следующую оценку работе своего выдающегося ученика.
«В. П. Ветчинкин под моим руководством занимался воз-
духоплаванием с того самого времени, как началось его пре-
подавание в Т. У. *). Он принимал участие в качестве глав-
ного издателя моего курса «Теоретические основы воздухо-
плавания». Им были напечатаны две статьи: «Расчет гребного
винта» в Бюллетенях Политехнического Общества за 1913 г.,
№ 5 и «Об инвариантах гребного винта» в Трудах и отде-
лениях физики О.Л.Е., том XVII, вып. 1.
В этих статьях В. П. Ветчинкин проявил полное знание
дела и самостоятельность мысли и внес весьма важное при-
бавление к расчету винтов по предложенной мною теории.
В аэродинамической лаборатории В. П. Ветчинкин произ-
вел ряд опытных работ по практическому измерению гели-
коптерных винтов, построенных по вихревой теории, а также
по применению маятников в качестве амортизаторов коле-
баний измерительных приборов. Такие -маятники поставлены
им на нашем большом аппарате для измерения винтов и
дали весьма хорошие результаты.
Исследование Ветчинкина на эту тему было сообщено
им на заседании Политехнического общества при Т. У. Вет-
чинкин много занимался изучением математики, механики
и теории упругости. Его основательные знания . в послед-
ней области будут весьма полезны для ведения проектиро-
вания по конструкции аэропланов и дирижаблей. Он раз-
рабатывает специальный проект по аэроплану больших раз-
меров типа „Илья Муромец"».
Позднее, в частном письме на имя Министерства,
Н. Е. Жуковский писал: «... Я считаю В. П. Ветчинкина
моим лучшим учеником. Он уже 4 года занимается теорией
воздухоплавания и сделал ряд самостоятельных исследова-
ний».
х) Т. У. — Техническое училище — так сокращенно называлось
тогда МВТУ.
922
V. биографические Статьи
В. П. Ветчинкину была назначена министерская стипен-
дия, и он был оставлен работать в МВТУ под руководством
Н. Е. Жуковского.
II. Первые годы самостоятельной научной
и учебной работы
Годы пребывания В. П. Ветчинкина студентом МВТУ и
начала его научной и инженерной деятельности были време-
нем формирования основных направлений, постановки основ-
ных задач современной авиационной науки и техники. Пер-
вые конструкторы самолетов шли в решении основных задач
путем проб, путем большого числа неудачных попыток;
сколько-нибудь надежных методов инженерного расчета
не было, все надо было создавать с самого начала.
Если в аэродинамике, в аэродинамическом расчете крыла и
винта самолета исходные идеи расчета стали ясны благодаря
работам Н. Е. Жуковского, С. А. Чаплыгина и самого
В. П. Ветчинкина, то в области расчета авиационных конструк-
ций на прочность почти ничего не было сделано. Хорошо раз-
работанные методы обычной строительной механики были
в большинстве случаев совершенно неприложимы к тем свое-
образным ферменно-расчалочным конструкциям, какие пред-
ставляли тогдашние самолеты, где к тому же первенствую-
щую роль играла задача всемерного облегчения авиационных
конструкций.
Все эти вопросы совершенно отчетливо возникли перед
Владимиром Петровичем при работе над своим дипломным
проектом и в работе преподавателем по расчету аэропланов
и винтов на теоретических курсах авиации при МВТУ, где
он начал работу с осени 1914 г.
Дело осложнялось еще тем, что работы по расчету
самолетов приходилось вести в напряженной обстановке
начавшейся 1 августа 1914 г. первой мировой империали-
стической войны, которая с первых дней стала предъявлять
к авиации все новые и новые требования.
1 июля 1916 г. Н. Е. Жуковский и В. П. Ветчинкин
организовали при МВТУ Авиационное расчетно-испытатель-
ное бюро.
В. П. Ветчинкин составил подробную программу
работы бюро; в задачи бюро входили разработка методов
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
923
расчета самолета — аэродинамического и на прочность,—
лабораторные и летные испытания существующих самолетов,
определение нагрузок, действующих на самолет в различных
условиях полета, при взлете, при посадке и т. д., расчет
и проектирование винтов, шасси и другие вопросы самолето-
строения. Общее руководство бюро принадлежало Н. Е. Жу-
ковскому, вопросами прочности и расчета винтов руково-
дил В. П. Ветчинкин, аэродинамическим расчетом руководил
А. Н. Туполев.
Авиационное расчетно-испытательное бюро сыграло ис-
ключительную роль в развитии самолетостроения в России.
Под руководством В. П. Ветчинкина в бюро был проведен
расчет нескольких десятков самолетов, в том числе почти
всех самолетов русской конструкции.
В. П. Ветчинкин, ясно понимая всю необходимость си-
стематического изучения поведения самолета в условиях его
полета в воздухе, не довольствуется лабораторными и тео-
ретическими исследованиями, он устанавливает прочные связи
с работой летчиков на аэродроме Московской авиационной
школы. С декабря 1914 г. он начинает полеты на самолете
«Фарман-IV» с инструктором А. Докучаевым и летом 1915 г.
уже проводит систематические летные испытания винтов НЕЖ
во время полетов с талантливым молодым летчиком Гуле-
вичем, студентом МВТУ. Наблюдения были прерваны из-за
гибели Гулевича: его самолет упал и разбился, причиной
гибели был производственный дефект самолета.
Аэродинамическая лаборатория МВТУ, расчетно-испыта-
тельное бюро и летные испытания представляли уже настоящий
научно-исследовательский институт. Однако его работе ме-
шали полное безразличие, а порой и явная враждебность
бюрократического аппарата царской России, проникнутого
совершенно невежественным преклонением перед заграницей,
недоверием ко всему русскому, к русским инженерам, к рус-
ской науке. Для развертывания работ бюро не отпускалось
необходимых средств, не было возможности получить не-
обходимое оборудование для лаборатории, а работы рус-
ских конструкторов, испытанные и проверенные бюро, вся-
чески затирались. Так фактически была сорвана постройка
тяжелого самолета «Святогор» конструкции талантливого
русского инженера Слесарева, в расчетах которого деятель*
924
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
ное участие принимало бюро. При таких условиях даже то,
что делало Авиационное расчетно-испытательное бюро, часто
не приносило той пользы для русского воздушного флота,
которую оно могло бы принести. Надо было много горя-
чего патриотизма, научного энтузиазма и уверенности в важ-
ности своего дела для Родины и для науки, чтобы при
таких условиях вести работу с таким напряжением и таким
успехом, как ее вели «отец русской авиации» Н.. Е, Жу-
ковский и руководимый им коллектив молодежи его учени-
ков, в котором одно из ведущих мест занимал В. П. Вет-
чинкин.
Дело решительно изменилось после Великой Октябрь-
ской социалистической революции. Советское правительство,
Коммунистическая партия и гениальный В. И. Ленин бук-
вально в первые дни после Октябрьской революции обра-
щают особое внимание на развитие советской авиации, под-
готовку советских боевых и инженерных авиационных кадров,
на всемерное развитие советской авиационной науки.
Уже летом 1918 г. по инициативе летчика Б. И. Рос-
сийского организуется под руководством Н. Е. Жуковского
и В. П. Ветчинкина «Летучая лаборатория» для всесторон-
него изучения самолетов в полете; Владимир Петрович при-
нимает самое деятельное участие в работах этой лабора-
тории.
Первые исследования по изучению условий полета само-
летов, траекторий, описываемых летящим самочетом, воз-
действия воздуха на самолет, описывающий более или менее
сложную траекторию, принадлежат Н. Е. Жуковскому.
В работе «О парении птиц», относящейся еще к 1890 г.,
и в более поздних работах «Теоретические основы авиации»
и «Динамика аэропланов в элементарном изложении»
Н. Е. Жуковский дал основы науки о движении самолета —
динамике полета. С этими работами своего учителя В. П. Вет-
чинкин был хорошо знаком, и все огромное значение их
стало ему совершенно ясно, как только он стал системати-
чески заниматься вопросами прочности авиационных кон-
струкций.
Основой расчета самолета на прочность являются дан-
ные о тех нагрузках, которые испытывают во время полета
крылья самолета, лопасти винта, фюзеляж, различные стойки
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
925
и растяжки авиационной конструкции. Но эти нагрузки
в отдельных деталях чрезвычайно резко меняются при изме-
нении условий полета, получаются так называемые пере-
грузки. Между прочим, В. П. Ветчинкину принадлежит и
точное определение понятия перегрузки; так под перегруз-
кой в направлении подъемной силы Владимир Петрович
понимает отношение подъемной силы в криволинейном по-
лете к величине подъемной силы в Горизонтальном полете.
Очевидно, что знание величины перегрузок при различных
условиях полета чрезвычайно важно для рационального рас-
чета самолета на прочность.
Работая на аэродроме, В. П. Ветчинкин не только вел
исследовательскую работу и учился технике полетов, но и
принимал самое деятельное участие в регулировании само-
летов. В те годы самолеты имели многочисленные растяжки
и стойки; при регулировке можно было дать растяжкам
различное натяжение, а это оказывало сильное влияние на
прочность самолета.
При изучении натяжения растяжек на самолетах В. П. Вет-
чинкин с большим успехом применял хорошо известный по
курсу физики прибор «монохорд».
Одновременно с научно-исследовательской и инженерной
работой в эти годы Владимир Петрович много внимания
и сил уделял и обучению полетам.
Напряженнейшая научно-исследовательская работа в рас-
четно-испытательном бюро, в Летучей лаборатории и в Аэро-
динамической лаборатории МВТУ далеко не исчерпывала
всей деятельности Владимира Петровича в эти годы стано-
вления авиационной науки и ее инженерных и летных кадров.
Уже в декабре 1915 г. В. П. Ветчинкин избирается
членом бюро Отдела изобретений Московского военно-
промышленного комитета, где он проводит экспертизу глав-
ным образом по авиационным и механическим изобретениям.
В том же 1915 г. в течение ряда месяцев он исполняет
обязанность помощника заведующего машиностроительной
станцией Московского сельскохозяйственного института.
С 1916 г. он начинает свою преподавательскую деятель-
ность в стенах МВТУ, где ему поручается руководство
проектированием аэропланов, винтов и крыльчатых венти-
ляторов.
926
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
В 1916 и 1917 гг. во Всероссийском земском союзе он
занимался изучением трения полозьев аэросаней о снег и
состоял экспертом на конкурсе моторных саней, устроен-
ном при Отделе изобретений Московского военно-промыш-
ленного комитета. А с осени 1917 г., когда было открыто
при Отделе изобретений конструкторское бюро, занял при
нем должность консультанта.
В 1917—1918 гг. в течение двух семестров, до перехода
Института из Москвы обратно в Ригу, В. П. Ветчинкин
преподавал теоретическую механику в Рижском политехни-
ческом институте, который по обстоятельствам военного
времени был временно эвакуирован в Москву.
С мая 1918 г. Владимир Петрович состоял преподава-
телем теоретических курсов при Московской школе авиации
по предмету «Основы авиации», а 19 мая того же 1918 г.
был избран действительным членом «Общества содействия
успехам опытных наук и их практических применений
имени Христофора Семеновича Леденцова». Наконец, с 1 сен-
тября по 1 декабря 1918 г. работал в качестве помощника
заведующего аэродинамическим отделом только что откры-
того Экспериментального института путей сообщения, где,
кроме того, состоял заведующим бюро по расчету аэро-
планов и винтов на прочность и в декабре принимал самое
деятельное участие в организации под руководством
Н. Е. Жуковского знаменитого научно-исследовательского
учреждения Центрального аэрогидродинамического института
(ЦАГИ), которое сыграло совершенно исключительную роль
в развитии авиации в нашей страна; в этом замечательном
учреждении он непрерывно работал до последних дней
своей жизни. .
Ко всей, этой огромной работе надо еще добавить, что
Владимир Петрович находил время и для занятий астроно-
мией, популяризаторской работой и т. п.
В те годы исключительно напряженной и разнообразной
работой были охвачены все патриотически настроенные уче-
ные, инженеры, профессура, все. рабочие/и работники
умственного, труда. С временем и силами не считались. Уж
слишком велики были потребности й перспективы, открыв*
шиеся в строительстве новой, социалистической России.
С крайним напряжением работала не только молодежь, но
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИЙкИН .
927
и такие старики, как семидесятилетний Н. Е. Жуковский.
Не приходится удивляться, что в эти героические годы такой
патриот и энтузиаст, каким был молодой В. П. Ветчинкин,
работал с крайним напряжением сил.
Он обладал очень большой творческой фантазией, спо-
собностью быстро схватывать новые идеи и, может быть,
еще большей способностью возбуждать у молодежи твор-
ческий энтузиазм. Все это, конечно, в высокой сте-
пени способствовало тому, что он делал в эти героические
годы. Но этого было мало: высказанные им глубокие идеи
надо было доработать, оформить, сделать понятными и ясны-
ми, доступными для ознакомления с ними в печати; много-
численными с воодушевлением работающими сотрудниками
надо было упорно и настойчиво руководить, вести скучную,
не интересную для творчески работающего ученого, адми-
нистративную, работу. Между тем при такой огромной
загрузке у Владимира Петровича времени для доделки
и оформления не хватало, и в результате многое осталось
недоделанным и не известным для инженеров и конструкто-
ров; впоследствии Владимир Петрович потерял приоритет
на многие глубокие научные идеи. Не было у него и жест-
кой административной хватки, которая заставляла бы его
сотрудников неукоснительно идти в направлении, четко
указанном руководителем; мягкий по своей природе, Влади-
мир Петрович с особым интересом и сочувствием следил
и поддерживал всякую инициативу и самостоятельность мысли
своих сотрудников. Эти его черты, проявившиеся в первые
годы, его самостоятельной работы, остались его характер-
ными чертами, в течение всей жизни. Здесь он во многом
походил на своего учителя, Н. Е. Жуковского, но-учитель
настойчиво доводил свои научные идеи до классически закон-
ченного состояний в виде научных статей и не распылял
свои творческие силы так, как это делал его талантливый
ученик-»
Научные исследования В. П. Ветчинкина, относящиеся
К этому периоду, в основном посвящены вопросам проч-
ности самолета и подготовительным исследованиям по дина-
мике полета. В 1915—1918 гг. им напечатан, ряд статей по
расчету самолета на прочность; в литографированных мате-
риалах Авиационного расчетно-испытательного бюро им
928 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
напечатаны в непосредственной связи с его работами на
аэродроме статьи «О влиянии предварительной затяжки про-
волок на напряжение их в биплане» (1916 г.); «О выборе
материалов для аэроплана под условием наименьшего веса
всей конструкции» (1917 г.); «Конспект лекций по расчету
аэропланов на прочность» и «Наставление для регулировки
аэропланов на затяжку проволок» (1917 г.); «Схема расчета
аэропланов на прочность» и «Требования, которым должен
удовлетворять аэроплан с динамической и аэродинамической
стороны» (1918 г.).
Параллельно шли его предварительные исследования по
динамике полетов, в результате которых были опубликованы:
«Отчеты о деятельности Летающей лаборатории Московского
областного военного комиссариата» (1918 г.), куда вошла
статья В. П. Ветчинкина «О посадке, капотировании и пара-
шютировании аэропланов и о расчете шасси».
Но этими печатными работами далеко не исчерпываются
результаты напряженной работы В. П. Ветчинкина за
1914—1919 гг. Им за это время сделано свыше десяти
докладов на самые разнообразные темы, от «Применения
маятниковых динамометров взамен маслянных успокоителей»
(доклад 8/III 1914 г. в Политехническом обществе; идеи
этого доклада получили одобрение Н. Е. Жуковского и
нашли применение в лабораторной практике) и до «Выдер-
жек из автобиографии курского астронома-самоучки Федора
Алексеевича Семенова» (доклад 22/1 1917 г. в заседании
Московского общества любителей астрономии); Владимир
Петрович находил время для занятий астрономией и в эти
годы, насыщенные напряженной технической, авиационной
работой.
III. Организация ЦАГИ. Научная и инженерная работа
Организация в декабре 1918 г. Центрального аэрогид-
родинамического института (ЦАГИ) оказала совершенно
исключительное влияние на развитие советской авиации.
Мы видели выше, что В. П. Ветчинкину, как и, несомненно,
всем в то время весьма немногочисленным специалистам,
ученым и инженерам, успешно работавшим под руководством
Н. Е. Жуковского, еще в 1916 г. ясно представлялась
необходимость учреждения научно-авиационного центра
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
929
с целью быстрейшей подготовки к отечественному самолето-
строению. Царское правительство, с его недоверием к рус-
ской науке, к русским ученым, инженерам и изобретателям,
не смогло сделать решительный шаг в организации такого
учреждения, и дело ограничилось полумерой, организацией
расчетно-испытательного бюро при МВТУ со скудными
средствами, без перспектив существенного расширения
необходимых лабораторий и мастерских, без возможности
немедленно приступить к опытному русскому самолетострое-
нию. В этом отношении характерен факт, приводимый Вла-
димиром Петровичем в его воспоминаниях. Когда в конце
1916 г. руководство Авиационным расчетно-испытательным
бюро подало в правительство докладную записку о желании
и возможности проектировать и руководить постройкой
опытных экземпляров самолетов, то последовал отказ, моти-
вированный загруженностью заводов.
Организация ЦАГИ в 1918 г. и дала возможность пре-
вратить маленькую полудобровольную организацию, какой
было расчетно-испытательное бюро, в мощную научную
базу советской авиации.
По первоначальному проекту, составленному В. П. Вет-
чинкиным в 1916 г. , задачи расчетно-испытательного бюро
формулировались следующим образом:
1. Выработка экспериментально наилучших профилей
крыльев, пользуясь теоретическими профилями С. А. Чап-
лыгина и данной С. А. Чаплыгиным в 1913 г. теорией
индуктивного сопротивления.
2. Выработка хороших типов винтов, пользуясь вихре-
вой теорией Н. Е. Жуковского и выработанными В. П. Вет-
чинкиным методами проектирования винтов — расчета их на
прочность, подбора наилучших винтовых дужек и отыска-
ния наивыгоднейшего (вариационного) распределения нагру-
зок вдоль лопасти.
3. ' Аэродинамические расчеты существующих самолетов
с попутной разработкой методов расчета и сверка резуль-
татов расчета с полетными данными.
4. Выполнение поверочных расчетов существующих само-
летов на прочность с попутной разработкой методов рас-
чета; лабораторное испытание на прочность отдельных частей
и деталей или целых самолетов.
930
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
5. Выполнение полетных испытаний для установления тех
нагрузок, которым подвергается самолет в неспокойном
воздухе и при фигурных полетах.
Эта первоначальная программа работ к моменту основа-
ния ЦАГИ, т. е. к концу 1918 г., была выполнена, и здесь
много было сделано В. П. Ветчинкиным. Ему принадлежали
существенные дополнения к аэродинамической теории вин-
тов и даны первые методы их практического расчета-и аэро-
динамического, и на прочность, Ему принадлежали первые
методы расчета самолетов на прочность, а вместе с тем он
же, по-видимому, первым применил на практике первые
статические испытания на прочность загрузкой мешков с
песком (первые статические испытания крыльев «Фармана 27»
были проведены Владимиром Петровичем на заводе «Дуке»
в 1916 г.). В. П. Ветчинкиным впервые были проведены
летные испытания самолетов и определены перегрузки, кото-
рым подвергается самолет в неспокойном воздухе и при
фигурных полетах; при этом им проделан ряд исследова-
ний, легших в основание динамики полета.
Когда в 1918 г. основывался ЦАГИ, то, кроме дальней-
шего изучения поставленных выше вопросов, в которых
многое оставалось неясным, возникли новые задачи, среди
них основная задача — проектирование новых советских
самолетов с учетом всех достижений авиационной науки,
а также руководство и непосредственное участие в строитель-
стве опытных самолетов.
Но вместе с этой основной задачей возникли и другие
новые задачи технической аэродинамики. Разновидностью
воздушных винтов являются осевые вентиляторы; проекти-
рование и постройка их начались в связи с постройкой
аэродинамических труб, а затем мощные осевые вентиляторы
нашли широкое применение в разнообразных частях
техники.
Проектирование винтов, но уже не для самолетов, а для
морских судов поставило ряд вопросов гидродинамических,
которыми с таким успехом занимался Николай Егорович
Жуковский четверть века назад.
Наконец, обращенные воздушные винты представляют
собой ветряные двигатели, и как раз ко времени органи-
зации ЦАГИ относится начало работ В. П. Ветчинкина над
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
931
проблемой использования энергии ветра. Осенью 1918 г.
старый знакомый Владимира Петровича, известный курский
изобретатель Анатолий Георгиевич Уфимцев, пригласил
к себе в Курск В. П. Ветчинкина и познакомил с расче-
тами и схемой инерционно-кинетического аккумулятора,
позволявшего успешно решать задачу аккумулирования энер-
гии ветра. Будучи сам изобретателем, Владимир Петрович
всю свою жизнь проявлял к изобретателям самое горячее и
трогательное внимание; он изучил идеи А. Г. Уфимцева и по
возвращении в Москву познакомил с ними Н. Е. Жуков-
ского, который также дал им положительный отзыв.
В организации ЦАГИ В. П. Ветчинкин принимал самое
деятельное участие и горячо отстаивал идею создания ЦАГИ
именно как комплексного института, объединяющего весь
комплекс вопросов, связанных с техническим использованием
гидро- и аэродинамики.
Впоследствии этому направлению своей деятельности
Владимир Петрович придавал особое значение.
В конце концов идея создать институт с широким кру-
гом исследований была осуществлена, что и нашло свое от-
ражение в самом его названии «Центральный аэрогидродина-
мический институт». В ЦАГИ были организованы отделы,
и Владимир Петрович с 1919 г. возглавил Общетеорети-
ческий отдел (ОТО).
Другим организационным вопросом, который в те годы
занимал Владимира Петровича, была постановка исследова-
ний по использованию энергии ветра. При организации ЦАГИ
Владимиру Петровичу удалось заинтересовать Н. Е. Жуков-
ского идеями Уфимцева, и предполагалось даже включить
в состав ЦАГИ в качестве филиала лабораторию Уфимцева
в Курске. Впоследствии эта мысль была оставлена, но
в составе ЦАГИ был создан Отдел ветряных двигателей
(ОВД), который, однако, пошел в решении вопроса об акку-
мулировании энергии ветра другим (электротехническим)
путем. Это направление работ ОВД, одобренное руковод-
ством ЦАГИ, Владимир Петрович считал неправильным и
всячески поддерживал и развивал направление исследований
Уфимцева, в курской лаборатории которого он был постоян-
ным научным консультантом, а после смерти Уфимцева
и научным руководителем. Впоследствии, уже по окончании
932
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
.Отечественной войны, он организовал ветросиловую лабо-
раторию на территории нового ЦАГИ в г. Жуковском,
где под его руководством шли исследования в направле-
нии развития идей Уфимцева.
Мы видели, что Владимир Петрович принимал самое
.деятельное участие в преподавании на курсах летчиков при
МВТУ. На базе этих курсов, первоначально носивших вре-
менный характер, после Великой Октябрьской революции
был образован сначала Авиатехникум, преобразованный
позднее в Институт инженеров красного воздушного флота,
а еще позднее, в 1922 г., уже после смерти Н. Е. Жуков-
ского, в Военно-воздушную академию им. Жуковского
(ныне Военно-воздушная инженерная академия им. проф.
Н. Е. Жуковского, или ВВИА).
В. П. Ветчинкин принимал самое деятельное участие
и в организации и в преподавании в этих авиационных
учебных заведениях.
Владимир Петрович вместе с небольшой группой своих
товарищей по МВТУ и при содействии инженерной авиацион-
ной молодежи с необычайной энергией включается в работу.
В ВВИА он берет на себя преподавание одного из основных
разделов курса—теории воздушных винтов. Он много работал
«в этой области и, несомненно, был в ней крупнейшим специа-
листом. Уже в 1926 г. выходит в свет литографированная моно-
графия В. П. Ветчинкина «Теория гребных винтов». Эта заме-
чательная работа, выросшая из курса, читанного в ВВИА,
и ставившая своей целью служить пособием для высшей
-школы, явилась одним из учебников, создание которых
.ставил своей задачей преподавательский коллектив ВВИА.
Первоначально вышедшая в небольшом числе экземпля-
ров. «Теория гребных винтов» очень быстро разошлась и
гуже в 1931 г. была переиздана в переработанном и расши-
-ренном виде В. П. Ветчинкиным и Н. Н. Поляховым, его
.сотрудником, начинавшим в те годы свою научную деятель-
ность. В третий раз, в 1940 г., эта книга снова была
переиздана с рядом изменений и дополнений и со второй
частью^ посвященной расчету винта на прочность.
По-видимому, эта работа и до настоящего времени
^является в мировой литературе наиболее подробным и полным
низложением теории гребного винта.
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
933,
'Как известно, русским ученым принадлежит почетное
место в разработке теории винта. В первых. работах
С. К. Джевецкого, относящихся еще к 1909 г., были поло-
жены основы так называемой теории элемента лопасти винта,
представляющей приложения к винту методов расчета, при-,
меняемых в теории крыла. В последующих исследованиях
Г. X. Сабинина и Б. Н. Юрьева, которые начали работу
по теории гребных винтов, еще будучи студентами МВТУ,
эта теория получила полное развитие. В. П. Ветчинкин по-
ставил своей задачей дать полное и систематическое изло-
жение всех существующих теорий с доведением их до прак-
тических расчетов, до проектирования винтов; занимаясь
главным образом развитием вихревой теории винта, он в то
же время внес много нового и в другие направления в тео-
рии винтов, в теорию идеального пропеллера и в теорию
элемента лог.асти. Между прочим, исследования В. П. Вет-,
чинкина показали полную идентичность вихревой теории
Н. Е. Жуковского и теории Г. X. Сабинина и Б. Н. Юрьева,
а отсюда стало возможно излагать теорию Н. Е. Жуков-
ского, основываясь только на общих теоремах механики и
не прибегая к понятиям о циркуляции и q вихрях, что
в свою очередь представляет значительное удобство в.пре-
подавании.
Изданная в 1940 г. В. П. Ветчинкиным и Н. Н. Поля-
ховым в переработанном виде «Теория и расчет воздушного
гребного винта» представляет собой наиболее подробное
изложение и аэродинамической теории винта и расчета его
на прочность. В трех частях этого капитального произве-
дения (аэродинамика винта; расчет винта на прочность;
вариационные гребные винты) изложены все существенные
результаты, полученные в то время. В этой работе, в част-
ности, систематизировано изложение полученных, ранее
В. П. Ветчинкиным частных результатов, . разбросанных
в различных изданиях и докладах, часть из которых вообще
не была ранее напечатана».
К работам В. П. Ветчинкина по теории гребных винтов,
близко примыкают его исследования по теории ветряков и
по общей проблеме ветроиспользования. Этой областью
он начал интересоваться еще в студенческие годы, когда»
перенес теорию идеального пропеллера на теорию ветряков;,
934
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
позднее, в 1918 г., он работал над приложением вихрейой
теории Н. Е. Жуковского к теории ветряков. С открытием
в ЦАГИ Отдела ветряных двигателей (ОВД) В. П. Ветчин-
кин принимал в нем деятельное участие, руководя в тече-
ние 1920—1923 гг. аэродинамическим расчетом первых
ветродвигателей ЦАГИ. В связи с работами А. Г. Уфим-
цева по инерционному аккумулятору В. П. Ветчинкин по-
святил исследованию и теории такого аккумулятора ряд ста-
тей; к сожалению, эти статьи остались ненапечатанными,
напечатан был только ряд газетных заметок Владимира
Петровича о работах А. Г. Уфимцева.
В общем, В. П. Ветчинкиным написано по теории вин-
тов и задаче ветроиспользования свыше 40 работ, считая
крупные трактаты, журнальные статьи, доклады, материалы
по проектированию и т. д.; значительная часть этих работ
осталась ненапечатанной. Наиболее крупными результатами
в этой области сам В. П. Ветчинкин считал следующие:
1. Теория вихревой пелены, сбегающей с лопасти винта.
Впоследствии Л. Прандтлем и его учениками аналогич-
ная теория была разработана в приложении к крылу конеч-
ного размаха.
2. Введение в теорию винта отвлеченных коэффициентов
и понятия об инвариантах винта.
3. Метод выбора наивыгоднейших дужек винта, удовле-
творяющих условию прочности.
4. Расчет лопасти винта на изгиб в поле центробеж-
ных сил.
5. Введение вариационных винтов с учетом прочности.
6. Применение вихревой теории Н. Е. Жуковского к вет-
ряным двигателям.
7. Идея быстроходного ветряного двигателя (совместно
с Н> В. Красовским).
8. Работы по применению к ветряку авиационного акку-
мулятора (совместно с А. Г. Уфимцевым).
Пожалуй, еще большее значение имеют исследования
В. П. Ветчинкина в области динамики полетов, или, как
называл позднее Владимир Петрович, динамики самолета.
В. П. Ветчинкину принадлежит свыше 30 исследований,
посвященных самым разнообразным вопроса^м динамики по-
лета: теории разбега и послепосадочного пробега само-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
935
лета по земле, посадке, капотированию и парашютированию
самолетов, теории шасси, мертвым петлям, виражам, спи-
ралям, изысканию наивыгоднейших спиралей, выдержива-
нию самолета параллельно земле, падению и планированию
самолета в среде переменной плотности, перекручиванию
крыльев в потоке воздуха и т. д.
Начав исследования в этой области параллельно с лет-
ными наблюдениями, Владимир Петрович неизменно стре-
мится при разработке теории использовать весь имеющийся
экспериментальный материал. Он неизменный участник в ра-
боте комиссий по испытаниям планеров, ведет лабораторные
исследования, тщательнейшим образом следит за зарубежными
работами, принимает деятельное участие в переводе важ-
нейших из них и их издании в СССР и т. д.
Итогом этой огромной работы является издание им фун-
даментальных трактатов. Первое издание «Динамики поле-
тов» В. П. Ветчинкина (совместно с С. И. Каменевым) вышло
в 1927 г.; второе издание, сильно расширенное и допол-
ненное, «Проф. В. П. Ветчинкин. Динамика самолета.
Части первая и вторая» — вышло в 1933 г. Этот замеча-
тельный трактат представляет, по-видимому, и в настоящее
время наиболее подробное, систематическое изложение дина-
мики самолета в мировой технической литературе.
В. П. Ветчинкин неоднократно читал курсы лекций по
динамике полетов в МВТУ и других вузах. Его работы
в этой области с успехом продолжали другие крупные спе-
циалисты, многие из которых были учениками В. П. Вет-
чинкина (В. С. Пышнов, Я. М. Курицкес, В. С. Ведров,
М. А. Тайц и др.).
Огромная работа, проведенная в этой области В. П. Вет-
чинкиным, позволяет по праву считать его одним из основа-
телей современной динамики полетов.
Работа Владимира Петровича над дипломным проектом
и позднее его занятия в Летучей лаборатории послужили
началом его исследований по расчету самолета на проч-
ность, а вместе с тем и исследований по сопротивлению
материалов и по прикладным вопросам теории упругости.
Первоначальные исследования Владимира Петровича в этой
области связаны с его работами по его расчету гребных
винтов и получили окончательную обработку в его трактате
936 V. БИОГРАФИЧЕСКИЕ СТАТЬИ
«Теория и расчет воздушного гребного винта», где вся вто-
рая часть посвящена расчету винта на прочность.
Второй цикл исследований В. П. Ветчинкина связан
с вопросом о влиянии перегрузок при фигурных полетах,
при выходе самолета из пикирования и т. п. на напряжения
в различных частях самолету. Мы уже видели выше, что
Владимир Петрович, * летчик-наблюдатель, по-видимому,
впервые в мировой авиационной технике изучал эксперимен-
тально этот сложный вопрос. Эти вопросы постепенно при-
вели его к общей задаче расчета самолета на прочность.
Ему принадлежат в этой области работы на самые разно-
образные темы: материалы по расчету самолетов на проч-
ность и расчету на прочность двухлонжеронного крыла
планера; о жесткости стержневых ферм; влияние лобовых
сопротивлений на жесткость изгиба и кручение крыла;
устойчивость желобчатых пластинок.; о критической угловой
скорости растянутого, или сжатого вращающегося вала
и т. п. Здесь особенно надо отметить две работы, оставшиеся
ненапечатанными, по вопросам баллистики: «Расчет на проч-
ность чугунного 3" артиллерийского снаряда» (1916 г.) и
«Расчет того же снаряда на продольные колебания» (1916 г.).
Обе эти работы являются результатом исследований Влади-
мира Петровича в Комиссии чугунных снарядов при Поли-
техническом обществе, выполненных в связи с войной 1914 —
1918 гг.
В области расчета на прочность и теории упругости
В. П. Ветчинкиным написано свыше 50 работ, заметок, до-
кладов, однако значительная часть их не была .напечатана.
Из многочисленных результатов, полученных В этой области
Владимиром Петровичем, он сам считает наиболее существен-
ными следующие: испытание самолета на перегрузки при
фигурных полетах, создание научнооснованных норм за-
паса прочности частей самолета при различных условиях
его эксплуатации, перекручивание крыльев самолета и др.
Большая группа работ В. П. Ветчинкина посвящена
разработке методов приближенных вычислений. Впервые он
встретился с подобными вопросами еще при. работе над
своим дипломным проектом многомоторного самолета в 1914 г.
Впоследствии он много раз возвращался к исследованиям
в этой области; поводом всегда служила необходимость
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
937
дать решение встретившейся технической задачи, приводив-
шей к сложным вычислениям.
О работах В. П. Ветчинкина в этой области имеется
обстоятельный отзыв академика Н. Н. Лузина, дающий
также и общую оценку деятельности В. П. Ветчинкина.
Отзыв Н. Н. Лузина написан в январе 1936 г, В после-
дующие годы Владимир Петрович написал ряд исследова-
ний по теории приближенных вычислений; однако и здесь
многое осталось в виде рукописей.
В предыдущем были перечислены основные направления
научны^ работ Владимира Петровича. Однако они далеко
не исчерпывают всего разнообразия вопросов, которыми он
занимался. По-прежнему он работал над различными астро-
номическими и аэронавигационными вопросами, вопросами
составления звездного календаря, рефракции, астрономиче-
скими и аэронавигационными приборами. В 1935 г.
Владимир Петрович напечатал три статьи по вопросам дви-
жения ракет и реактивного самолета: в 1941 г. им выпол-
нен ряд работ по бомбометанию с аэроплана.
Владимиру Петровичу принадлежит ряд статей о рабо-.
тах Н. Е. Жуковского и С. А. Чаплыгина и проведена огром-
ная работа по изданию трудов Н. Е. Жуковского; в част-
ности, в 1929 г. он провел большую работу по изданию на
французском языке работ Н. Е. Жуковского по вихревой
теории гребного винта,.
В. П. Ветчинкиным написано всего свыше 150 научных
работ; из них 137 работ напечатаны. Всю свою жизнь Вла-
димир Петрович непрерывно работал над различными науч-
ными вопросами; это был ученый-исследователь с широкими
научными идеями, с большим научным кругозором, отдавав-
ший всю свою творческую энергию делу развития совет-
ской техники и науки.
IV. Черты характера. Профессорская деятельность
В. П. Ветчинкина.
Последние годы жизни
В. П. Ветчинкин был поэт в области науки и техники.
Всякая новая техническая идея, особенно е.сли она была
неожиданна по своей смелости и открывал необъятные
938
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
горизонты, увлекала его и целиком захватывала его твор-
ческое воображение.
Но это был поэт, самым тесным образом связанный
с землей, с проблемами сегодняшнего дня. В дни его юности
только что нарождавшаяся авиация, казалось, открывала
совершенно безграничные горизонты по преодолению чело-
вечеством пространства и времени, по объединению его в
единый творческий коллектив, творящий добро и красоту, —
и Владимир Петрович, увлеченный открывающимися беспре-
дельными горизонтами, избирает своей специальностью
авиацию. Позднее он также увлекается идеями К. Э. Циол-
ковского о ракетных полетах, которые могут привести
к межпланетным путешествиям, к связи не только между
планетами нашей солнечной системы, но и с удаленными
светилами окружающего нас безграничного мира. И еще
позднее его увлекают идеи А. Г. Уфимцева покрыть землю
гигантскими ветровыми плотинами и из потоков воздуха
черпать безграничные потоки энергии, несущей человечеству
свет, тепло, безграничные запасы хлеба... Все это было
творчество, направленное на создание добра и красоты. . .
Во всех этих мечтаниях было много фантазии, пока еще
невыполнимой; но все эти мечты каким-то своим краем упи-
раются в то, что уже осуществлено современной техникой.
Человечество уже летает, преодолевая пустыни, океаны, по-
лярные льды; ракеты несут на далекие расстояния колос-
сальную силу современных взрывных снарядов; ветряки на-
чинают освещать города.
Необычайный интерес ко всему новому позволял Влади-
миру Петровичу быть в курсе самых разнообразных новинок
и вообще всяких технических и научных вопросов, далеко
выходящих за границы его непосредственной специальности,
но это же, отвлекая его научные интересы в самые разно-
образные области, несомненно, способствовал тому, что
многие интересные и важные идеи Владимира Петровича
остались неразработанными.
Владимир Петрович являлся ученым, целиком преданным
науке, глубоко сознающим свой долг перед советской нау-
кой и свою ответственность как ученого за каждую выска-
занную им научную мысль. И как исключительно честный
ученый и гражданин он те же черты научной честности ви-
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
939
дел в каждом, кто к нему обращался и с полным доверием
подходил к нему, тратил на беседу с ним свои силы и время.
Владимир Петрович был человек исключительной доб-
роты и доброжелательства. Среди его сотрудников было
много людей, которым он помогал в трудную минуту со-
ветом, помощью, помогал устройством на работу, про-
движением их первых научных трудов, а иногда и просто
финансовой помощью из своего кошелька. Многие из них
впоследствии сами стали крупными работниками и с благо-
дарностью вспоминают своего учителя и друга.
Своеобразие характера Владимира Петровича ярко про-
являлось в его преподавании. Он начал свою педагогическую
деятельность еще студентом МВТУ, когда он вел препода-
вание на курсах подготовки летчиков, и не прерывал бук-
вально до последнего дня своей жизни.
Если своеобразие его характера делало его поэтом
в области науки и техники, то не меньшим поэтом он был
в своей педагогической деятельности. И прежде всего бро-
сается в глаза одна черта в деятельности В. П. Ветчинкина
как профессора высшей школы: он почти никогда не читал
и не стремился читать курсы с установившимися програм-
мами, с твердым, ставшим трафаретным содержанием.
Кажется, единственным исключением из этого общего
правила были его преподавание и руководство кафедрой
механики в МВТУ, которое он взял на себя уже в послед-
ние годы жизни, в 1947 г., после смерти профессора А. П. Ко-
тельникова. Но тут были совершенно исключительные
в глазах Владимира Петровича обстоятельства. Этой кафед-
рой в его студенческие годы руководил Н. Е. Жуковский,
и взять руководство этой кафедрой для Владимира Пет-
ровича значило продолжить славное дело своего великого
учителя. Легко понять, с каким энтузиазмом он взялся за
это дело и как он старался в преподавании этого класси-
ческого предмета сохранить ведущие идеи своего учителя,
Н. Е. Жуковского, механика-естествоиспытателя, экспери-
ментатора и инженера.
Во всех остальных случаях содержанием преподавания
Владимира Петровича, в сущности, были его собственные
работы, развитие его собственных оригинальных мыслей.
Когда он в 20-х годах читал в ВВИА или в МВТУ лекции
940
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
по теории гребных винтов, то он читал об исследованиях,
в которых он принимал самое деятельное участие. Здесь еще
не было сколько-нибудь выработанной системы изложения
и выбора материала, не было ни программы, ни учебника;
их нужно было создавать, и в процессе работы создаются
трактаты Владимира Петровича по теории винтов.
Позднее, когда Владимир Петрович читал лекции по тео-
рии реактивного движения, он также говорил о вопросах,
которые он сам разрабатывал в те годы. По приближенным
вычислениям Владимир Петрович написал и напечатал целый
ряд трактатов, но было бы совершенно неверно заключить
из этого, что он читал лекции по тем вопросам приближен-
ных вычислений, которые им до конца разработаны. На-
оборот, в своих лекциях в МВТУ, в МГУ или в ВВИА он
читал с особым удовольствием о тех вопросах теории при-
ближенных вычислений, которые он еще только разрабаты-
вал. Для неугомонной творческой мысли Владимира Петро-
вича чтение лекций было творческой разработкой новых
научных вопросов.
Естественно, что при таком подходе к преподаванию в
лекциях Владимира Петровича трудно было ожидать изло-
жения, предмета, законченного и уравновешенного во всех
своих частях. Ддя него не представлялось затруднительным,
прочитав на лекции изложение найденного им решения ка-
кой-нибудь задачи, предложить на следующей лекции своим
слушателям зачеркнуть все изложение предыдущей лекции
и написать новое, только что найденное им решение той же
задачи, если он считал, что новое решение значительно пре-
восходит первоначальное. Конечно, слушать курс у такого
необыкновенного лектора было нелегко; но зато все, кто
терпеливо и внимательно работал на лекциях Владимира
Петровича вместе с лектором, получали не только знание
предмета, но и учились самому процессу научной творче-
ской работы с преодолением встречающихся затруднений,
исканием различных путей, ведущих к поставленной цели,
с ее разочарованиями и радостью окончательной победы.
Для В. П. Ветчинкина решение научных вопросов было
главным и единственным содержанием его жизни, и эта твор-
ческая напряженность его научных исканий была особенно
привлекательна для всех, кто имел удовольствие встречаться
ВЛАДИМИР ПЕТРОВИЧ ВЕТЧИНКИН
941
с ним в жизни. Этот невысокий, необычайно живой и энер-
гичный человек, с доброй улыбкой на лице прежде всего
поражал взглядом своих ясных голубых глаз: они всегда
смотрели куда-то в одному ему видимую даль.
Напряженная научная деятельность В. П. Ветчинкина
нашла высокую оценку Советского правительства и научной
и инженерной общественности нашей великой Родины.
В. П. Ветчинкин был награжден за свои научные заслуги
двумя орденами Трудового Красного Знамени и орденом
Красной Звезды. В годы Великой Отечественной войны
Владимир Петрович был эвакуирован в Новосибирск и, как
всегда, вел там напряженную не только научную, но и общест-
венную работу — он был председателем Новосибирского
отделения Общества машиностроителей (ВНИТОМАШ).
В 1943 г. за выдающиеся заслуги в создании советской авиа-
ционной науки Владимиру Петровичу была присуждена Ста-
линская премия.
Несколько позднее, в 1947 г., В. П. Ветчинкин был
избран действительным членом Академии артиллерийских наук.
В этом нашли высокую оценку его важные труды по бал-
листике, по приближенным вычислениям.
В годы после окончания Великой Отечественной войны
он развивает огромную деятельность по решению проблемы
ветроиспользования и, в частности, по практическому при-
менению идей Уфимцева по механическому аккумулированию
энергии ветра. Благодаря его кипучей энергии на новой
территории ЦАГИ в г. Жуковском была построена спе-
циальная ветросиловая лаборатория, где под непосредствен-
ным руководством Владимира Петровича велись различные
исследования в этой области. Ветросиловая лаборатория была
последним созданием неукротимого творчества Владимира
Петровича; в ней он работал до последних лет жизни.
Между тем колоссальная нагрузка, которую в течение
долгих лет нес Владимир Петрович, начинала сказываться;
годы брали свое. 18 октября 1948 г. с Владимиром Петро-
вичем случился тяжелый сердечный припадок (инфаркт мио-
карда). К лету 1949 г. после длительного лечения он опра-
вился настолько, что вновь приступил к занятиям. Влади-
мир Петрович не умел беречь себя. Началась опять
напряженная работа в ветросиловой станции в ЦАГИ, поездки
942
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
в Курск на работу в лабораторию Уфимцева. Сильно под-
точенное здоровье Владимира Петровича уже не могло вы-
держать такой нагрузки. В конце 1949 г. сердечный
припадок повторился в более тяжелой форме. Дело ослож-
нилось еще воспалением легких. На этот раз принятые меры
лечения уже не могли помочь.
Владимир Петрович Ветчинкин скончался 6 марта 1950 г.
Он похоронен на Новодевичьем кладбище.
А.А. КОСМОДЕМЬЯНСКИМ
ЖИЗНЬ
И ДЕЯТЕЛЬНОСТЬ
В.В. ГОЛУБЕВА

ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
Его жизнь и научная деятельность
I
Окружающих поражала его энергия. Долгие годы он был
директором Научно-исследовательского института механики
и деканом механико-математического факультета А\ГУ, на-
чальником кафедры высшей математики Военно-воздушной
инженерной академии имени Н. Е. Жуковского, заведую-
щим кафедрой аэромеханики в Московском университете.
Владимир Васильевич систематически читал ряд курсов по
аэромеханике и высшей математике в Академии имени
Н. Е. Жуковского и в Московском университете. Ежегодно
он выступал с оригинальными научными докладами, публи-
ковал две-три научные статьи, рецензировал большое
количество докторских и кандидатских диссертаций. Рабо-
тая продуктивно сам, он вносил в исследовательскую и орга-
низаторскую работу вдохновение и страстность юноши,
заражая своим энтузиазмом и целеустремленностью в иска-
ниях научной истины всех сотрудников и товарищей. Когда
в 1944 г. отмечался его шестидесятилетний юбилей, его
трудоспособности завидовали тридцатилетние.
«Есть разные типы ученых. Одни бесстрастно и спо-
койно, как посторонние наблюдатели, присутствуют при
рождении научных направлений и школ, при открытии новых
методов и путей в науке; с одинаковым безразличием идут
они по всевозможным путям научных исследований, видя
идеалом для себя созерцание величия и красоты достижений
946
А. А. КОСМОДЕМЬЯНСКИЙ
науки, научного понимания мира, его гармонии, великой
общности управляемых им законов.
И есть другие ученые, которых их темперамент строи-
теля и борца заставляет быть не пассивным созерцателем
мира, не безразличным и бесстрастным участником великого
прогресса науки, а влечет их в самую гущу жизни, застав-
ляет их в найденных ими законах, в таблицах и формулах,
в сочетании математических символов искать средство воз-
действия на мир, воздействия в целях творческого
переустройства его. Такие ученые вносят в свою
творческую научную работу не аскетизм оторванного от
жизни отшельника, теоретика, а полноту сознания жизни,
ее задач, требований; они и в науке полнокровно и на-
пряженно стремятся и бьются в научных исканиях, умеют
любить и ненавидеть»х).
Ученым-строителем новой жизни России, ученым темпе-
раментным и целеустремленным, ученым, знающим великую
и противоречивую книгу реальной жизни, был Владимир
Васильевич Голубев.
Он умел напряженно работать ежедневно. Эта дис-
циплина систематического труда, чувство долга перед
страной рождали необычайную энергию и творческий опти-
мизм. Он шутил и смеялся с друзьями, а грустил только
в одиночестве. Созидание нового, научное творчество в са-
мом романтическом значении этого слова поддерживали его
в тяжелые и трудные моменты жизни.
Интересы науки, искание научной истины, как он ее
понимал, были незыблемым законом всей его жизни. Он был
строг и беспощаден к наукообразию, к сорнякам и пусто-
цветам на ниве научной. Он был честен и глубоко прин-
ципиален в науке, и даже лучшие свои научные открытия
он оценивал весьма скромно.
Отдавая должное крупным научным достижениям деятелей
науки всех наций и стран, Владимир Васильевич был все же
сдержан при оценке ряда произведений наших современников.
Он знал, будучи первоклассным историком науки, как строг
и беспощаден суд времени и как много «шумахеров» раз-
1) В. В. Голубев, Сергей Алексеевич Чаплыгин, издание
ЦАГИ, стр. 103—104, 1947.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
947
личных академий, имевших право чинить суд и расправу
над неугодными учеными, канули в Лету и их имена
вспоминаются в исторических мемуарах только в связи
с деятельностью тех подлинных ученых, которых они
преследовали.
Владимир Васильевич искренне радовался, когда его ра-
боты служили отправным пунктом новых научных изысканий.
Работы своих учеников, независимо от их научного ранга,
он популяризировал и часто излагал как на лекциях, так
и в монографиях. Зная как различны люди, он никогда
не настаивал на каких-либо канонах творчества. Так среди
его учеников я знаю людей с творческим почерком, совсем
не похожим на творческий стиль учителя.
Он был блестящим лектором и оратором, человеком
большой культуры, широких знаний и редкого остроумия.
Его глубокий аналитический ум и поразительная способность
мгновенно оценить создавшуюся ситуацию делали его
опасным полемистом и оппонентом в научных дискуссиях
и при защите диссертаций.
Он прожил трудовую содержательную жизнь, жизнь
борца, исследователя, большого Человека. Он ушел из жизни
внезапно и неожиданно — на следующий день после семи-
десятилетнего юбилея, произнеся на юбилейно^м собрании,
где присутствовало более двух тысяч ученых, инженеров,
преподавателей, студентов и служащих Университета, почти
часовую зажигательную речь, изложив в ней «кредо» своих
исканий, своего отношения к науке, к педагогической деятель-
ности, к Университету.
Наша Родина может гордиться таким сыном.
II
Владимир Васильевич Голубев родился 4 декабря 1884 г*
в Сергиевом-Посаде, ныне город Загорск Московской области.
В своей автобиографии он писал: «Мой отец Василий Сер-
геевич Голубев до 1889 года был учителем латинского языка
в ВолоколамскОхМ духовном училище, а с 1889 года — свя-
щенником церкви в Москве, у Кропоткинских ворот; он был
из духовных и в 1883 году окончил Московскую духовную
академию, которая помещалась в Сергиевом-Посаде; мать
948 а. а. Космодемьянский
Клавдия Матвеевна Голубева, урожденная Кузьмина, была
дочерью мелкого торговца (булочника), из крестьян Моло-
говского уезда Ярославской губернии».
Среднее образование Владимир Васильевич получил
в московской Первой мужской гимназии, которую окончил
в 1903 г. с золотой медалью. После окончания гимназии
поступил на математическое отделение физико-математиче-
ского факультета Московского университета, где специали-
зировался по чистой математике. Большое значение для ма-
тематического образования Владимира Васильевича имели
лекции- профессоров Б. К. Млодзеевского и Л. Н. Лахтина.
За студенческое сочинение «Обыковенные дифференциаль-
ные уравнения второго порядка с неподвижными критическими
точками» он получил от физико-математического факультета
премию имени Д. Д. Гнусина. По окончании Университета
был оставлен при Университете для приготовления к про-
фессорскому званию. Магистерские экзамены закончил
в марте 1911 г.
С осени 1908 г. В. В. Голубев начал преподавательскую
работу в средних школах Москвы. Он вел преподавание
математики и космографии в частном коммерческом училище
А. А. Плестерер и в частной женской гимназии И. Г. Брю-
хоненко. Уже тогда он проявил себя хорошим педагогом,
умеющим заставить работать весьма недисциплинированный
состав учащихся, собранный в этих частных учебных заве-
дениях.
В 1911 г. была опубликована в Математическом сбор-
нике первая научная статья В. В. Голубева «Об одном при-
ложении теоремы Пикара к теории дифференциальных урав-
нений», и в этом же году он был избран членом Моско-
вского математического общества.
Весной 1913 г. Владимир Васильевич был командирован
физико-математическим факультетом Московского университета
на один год за границу для научных занятий. С апреля 1913 г.
по февраль 1914 г. Владимир Васильевич был в Геттингене
(Германия), где слушал лекции и работал в семинарах у
профессоров Гильберта, Каратеодори, Вейля и Куранта.
Основное время он посвящал изучению аналитической теории
дифференциальных уравнений и теории функций комплексного
переменного.
В. В. ГОЛУБЕВ в 1901 г.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
949
С февраля 191^ г. по июнь 1914 г. Владимир Васильевич
был в Париже, где слушал лекции профессоров Пикара,
Аппеля, Гарнье и работал в семинаре у Адамара.
По возвращении в Москву В. В. Голубев продолжал препо-
давание в коммерческом училище и женской гимназии, а кро-
ме того, с сентября 1914 г. был зачислен сверхштатным пре-
подавателем математики в Московский институт инженеров
путей сообщения, где начал вести практические занятия по
математике.
В сентябре 1915 г. В. В. Голубев начал работать штатным
преподавателем Московского технического училища и, кроме
того, читал специальные курсы по математике в Московском
городском университете имени Шанявского и на Московских
педагогических курсах. Педагогическая работа нравилась
Владимиру Васильевичу, хотя она отнимала много времени.
Осенью 1915 г. В. В. Голубев закончил магистерскую
диссертацию «Однозначные аналитические функции с совер-
шенным множеством особых точек», которая в 1916 г. была
напечатана в Ученых записках Московского университета.
Публичная защита диссертации состоялась в мае 1917 г.,
и Владимир Васильевич получил ученую степень магистра
чистой математики. Оппонентами были Д. Ф. Егоров и
Н. Н. Лузин.
Осенью 1917 г. Владимир Васильевич был зачислен
приват-доцентом Московского университета и объявил спе-
циальный курс «Особые точки аналитических функций»,
однако он проработал в Университете всего один семестр.
В ноябре 1917 г. Владимир Васильевич был выбран орди-
нарным профессором математики Саратовского университета,
где начал чтение лекций с 1 февраля 1918 г.
В Саратовское университете В. В. Голубев провел боль-
шую научную, лекторскую, литературную и административ-
ную работу, являясь одним из подлинных организаторов
этого университета. В 1918—1922 гг. он занимает после-
довательно должности: декана физико-математического фа-
культета, проректора и ректора университета. Кроме уни-
верситета, В. В. Голубев с 1921 по 1930 г. преподавал
математику в Саратовском институте сельского хозяйства
и мелиорации, где заинтересовался приложениями математи-
ческой статистики к лесному делу. В 1929 г. он издал
950
А/ А. КОСМОДЕМЬЯНСКИЙ
книгу «Основания математической статистики в приложении
к лесному делу»; эта книга много лет с успехом применялась
в качестве учебника в сельскохозяйственных вузах.
В 1924 г. Владимир Васильевич заинтересовался работами
Н. Е. Жуковского и С. А. Чаплыгина по теории профиля
крыла. Затем он начал читать факультативный курс по этим
вопросам, и в . 1927 г. в Трудах ЦАГИ была напечатана
его монография «Теория крыла аэроплана в плоскопарал-
лельном потоке».
Следует отметить, что Владимир Васильевич всегда шел
от самостоятельных занятий по интересующей его научной
проблеме к чтению специальных и факультативных курсов,
а затем создавал или учебник, или монографию. Так были
созданы монографии по аналитической теории дифферен-
циальных уравнений, теории движения твердого тела около
неподвижной точки и теории крыла аэроплана.
Осенью 1930 г. В. В. Голубев переехал в Москву, где
с октября начал работать старшим инженером ЦАГИ,
а в ноябре был назначен профессором и действительным
членом Научно-исследовательского института математики и
механики Московского университета.
В июле 1932 г. В. В. Голубев был назначен начальником
кафедры и профессором математики Военно-воздушной
инженерной академии им. проф. Жуковского, позднее
(2 августа 1939 г.) он был зачислен в кадры Красной Армии
в звании бригинженера. В 1944 г. ему присваивается воен-
ное звание генерал-майора инженерно-авиационной службы.
В 1934 г. В. В. Голубев избирается членом-корреспон-
дентом Академии наук СССР; в 1943 г. ему Присваивается
звание Заслуженного деятеля науки и техники.
С 1934 по 1939 г. Владимир Васильевич был членом
Ленинградскогр районного Совета г. Москвы, а с 1939
по 1946 г.— депутатом того же райсовета.
- Так же как и в молодые годы в Саратове, одновременно
с преподаванием в Московском университете и Военной
академии В. В. . Голубев вел большую научно-организацйон-
ную работу. С 1936 г. он был бессменным директором
Института механики при Московском университете; с 1933
по 1934 т.,да затем с 1944 по 1952 г. он являлся деканом
механико-математического факультета.
В. В. ГОЛУБЕВ в 1948 г.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ 951
Преподавательскую работу Владимир Васильевич вел
до последних дней своей жизни.
Владимир Васильевич Голубев оставил о себе светлую
память, прожив прекрасную большую жизнь ученого, педа-
гога, военного инженера, организатора и общественного
деятеля.
Он был награжден Советским правительством орденом
Ленина, орденом Трудового Красного Знамени, четырьмя
орденами Красной Звезды и медалями.
III
1. Научная деятельность В. В. Голубева была продук-
тивной и многообразной. Он начал свои научные изыскания
в 1907—1908 гг. в области чистой математики, а именно
в аналитической теории дифференциальных уравнений. Цикл
его последних работ по аэродинамике (1942—1954 гг.) был
посвящен Созданию основ теории машущего крыла, где
указания эксперимента и проницательный взгляд на повсе-
дневные явления природы сыграли решающую роль . в. уста-
новлении механизма явления. Главное значение для форми-
рования научных интересов Владимира Васильевича в чистой
математике имели работы профессоров Университета
Д. Ф. Егорова (1869—1931) и Н. Н. Лузина (1883-Л950);
в области механики и аэромеханики он был учеником Н. Е. Жу-
ковского (1847—1921) и С. А. Чаплыгина (1869—1942).
Важную роль для русской культуры имеют блестящие
статьи Голубева по истории науки. Он дал детальный раз-
бор научного творчества Жуковского, Чаплыгина, Кова-
левской, Лузина, Ветчинкина и ряда других ученых. .Он
писал много научно-популярных статей в журналах и газе-
тах; издавал небольшие брошюры, посвященные пропаганде
тонких воиросов науки. Научные доклады В. В. Голубева
в Институте механики МГУ, перед общими собраниями
Академии наук СССР, на конференциях Военно-воздушной
академии, на Ломоносовских чтениях в Университете всегда
привлекали большую аудиторию, отличались высокой куль-
турой изложения, были насыщены глубокими мыслями,
интересными сопоставлениями, захватывали новизной' выдви-
гаемых вопросов.
952
л. а. Космодемьянский
Магистерская диссертация В. В. Голубева «Однозначные
аналитические функции с совершенным множеством особых
точек» (1916 г.) имеет важное значение для общей теории
функций комплексного переменного. «Одной из основных
проблем, которые поставлены В. В. Голубевым в названной
диссертации, явилась проблема о распространении класси-
ческих формул теории комплексного переменного (например,
интеграла Коши) на произвольные спрямляемые контуры.
Из точных результатов, достигнутых В. В. Голубевым, сле-
дует отметить в первую очередь сохранение теоремы Фату
(Fatou) об ограниченных функциях для спрямляемых замкну-
тых контуров. Здесь же В. В. Голубев высказал свою
известную гипотезу об инвариантности множеств линейной
меры нуль при конформном отображении, послужившую
предметом дальнейших работ других авторов.
В этой же диссертации В. В. Голубев, после того как
впервые установил ряд важных теорем о функциях проек-
тивно ограниченных, дал чрезвычайно ценное понятие о «мно-
жестве Пикара» и показал, что знание геометрического
строения этого множества имеет большое значение, так как
от него зависят глубокие свойства аналитических функций» *).
Следует указать также «на открытие В. В. Голубевым
функций, непрерывных всюду и имеющих совершенное мно-
жество особых точек с нулевой плоскостной хмерой. Суще-
ствование таких функций подвергалось сильным сомнениям,
и В. В. Голубеву принадлежит заслуга установления их
существования» * 2).
Общей теории функций комплексного переменного посвя-
щена и вторая большая работа В. В. Голубева «Исследо-
вания по теории особых точек однозначных функций»,
законченная в 1922 г. и опубликованная в Ученых записках
Саратовского университета в виде серии статей 1924—1929 гг.
Эта работа вначале была задумана Владимиром Васильевичем
как диссертация на соискание ученой степени доктора чистой
математики, но защищать ее не пришлось, так как в 1919 г.
ученые степени были упразднены «В. В. Голубев исследовал
1) См. Обзор научных трудов В. В. Голубева, Изв. АН СССР,
ОТН, 12, стр. 9, 1954.
2) Там же, стр. 10.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
953
применимость приемов, употребляемых в теории целых
функций, к функциям, имеющим окружность особой линией.
Для этого класса функций он получил аналоги теорем Ада-
мара, Бореля, Линделефа и др. В. В. Голубев занимался
также изучением частоты значений независимого переменного,
при котором функция принимает равные значения. При этом
он независимо получил как предельный случай знаменитую
теорему Витали относительно распределения нулей ограничен-
ной функции». «Наконец, В. В. Голубевым много было
сделано по переносу результатов, связанных с теоремой
Пикара, на функции, данные внутри окружности. Здесь же
В. В. Голубев дал впервые результаты о дескриптивном
строении множеств» х).
Известным итогом многочисленных работ Владимира Ва-
сильевича по теории дифференциальных уравнений явилась
его книга «Лекции по аналитической теории дифференциаль-
ных уравнений», первое издание которой вышло в 1941 г.,
а второе — в 1950 г. В этой книге, кроме ряда классических
методов, относящихся к теоремам существования, единствен-
ности решений и классификации особых точек функций,
основное внимание уделяется уравнениям с неподвижными
критическими точками. В этой связи подробно излагается
метод малого параметра и элементы теории алгебраических
функций.
Аналитическое изучение свойств интегралов дифферен-
циальных уравнений класса Фукса естественно связывается
с задачей конформного отображения на полуплоскость об-
ластей, ограниченных дугами окружностей. Отображающая
функция z = f(w) будет в этом случае многозначной функ-
цией, а ее критическими точками будут точки а2, %...
на действительной полуоси плоскости в которые пере-
ходят при отображении вершины многоугольника. Изучение
многозначных функций и групп подстановок приводит к поли-
эдрическим функциям, функциям Шварца и модулярным функ-
циям, Эти задачи тесно связаны с основными идеями магистер-
ской диссертации В. В. Голубева! так как представляют функ-
ции с особыми линиями. Владимир Васильевич показы-
вает далее, что можно построить функции с совершенным
9 Изв. АН СССР, ОТН, № 12, стр. 10, 1954.
954
л. а. Космодемьянский
всюду прерывным множеством особых точек, а затем
в главе VII, развивает теорию автоморфных функций, которые
тесно связаны с теорией алгебраических функций (униформи-
зацией алгебраических функций) и интегрированием линейных
дифференциальных уравнений. Эта книга В. В. Голубева
пользуется заслуженным вниманием студентов-математиков
и научных работников, сталкивающихся в своей работе с раз-
личными задачами интегрирования дифференциальных урав-
нений.
2. Весьма близко примыкает к работам по аналитической
теории дифференциальных уравнений монография В. В. Го-
лубева «Лекции по интегрированию уравнений движения
тяжелого твердого тела около неподвижной точки» (1935 г.).
Центральное место в этой монографии уделено рассмотре-
нию «случая С. В. Ковалевской». Как указывает Владимир
Васильевич, во всех ранее известных случаях интегрирования
динамических уравнений Эйлера (случаи Эйлера — Пуансо,
Лагранжа — Пуассона) интегралы, выражающие углы Эйлера
ср, ф, 6 в функциях времени, представляли собой однозначные
функции, мероморфные на всей комплексной плоскости пере-
менного Z, так как выражались через эллиптические функ-
ции. Ковалевская в своей широко известной работе поста-
вила целью найти все случаи, когда интегралы уравнений
движения тяжелого твердого тела представляют собой одно-
значные, мероморфные функции на всей плоскости перемен-
ного t. Время t рассматривается Ковалевской как комплекс-
ное переменное, что позволяет применить к исследованию
проблемы хорошо разработанный аппарат теории функций
комплексного переменного. Именно применение современного
аналитического аппарата теории функций комплексного Пе-
ременного и обусловило, по-видимому, интерес Владимира
Васильевича к этой классической задаче механики. В моно-
графии излагается метод последнего множителя Якоби;
в случае двух уравнений показывается, что всякую систему
уравнений вида
dx _dy ___dz_
можно рассматривать как уравнение траекторий установив-
шегося течения жидкости, причем компоненты скорости vx,
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ 955
vyi vz соответственно равны X, Y, Z, а плотностью жидко-
сти в таком течении является какое-нибудь значение послед-
него множителя Якоби. Гидродинамическая трактовка ана-
литических функций, рассмотрение течений на поверхностях
Римана пользовались особым вниманием Владимира Василье-
вича, и он посвятил этому вопросу специальную статью
«К теории течений на двулистной поверхности Римана»
(1938 г.).
Излагая работы Пуанкаре и Пэнлеве по обоснованию
метода малого параметра, Голубев показывает, как этим
методом можно найти условия, при которых исходная система
уравнений (три динамических уравнения Эйлера и три кине-
матических уравнения) не имеет подвижных критических
точек, т. е. критических полюсов и критических существенно
особых точек. Точная математическая формулировка этих
условий позволяет в случае, когда эллипсоид инерции для
неподвижной точки есть эллипсоид вращения, найти новый
случай интеграции—случай Ковалевской.
Главы V и VI монографии посвящаются теории алге-
браических функций, теории тэта-функций Якоби и задачам
обращения эллиптических и ультраэллиптических интегралов.
Весь этот арсенал математических методов позволяет дать
в главе VII решение задачи Ковалевской в законченном виде,
а. в главе VIII рассмотреть некоторые частные случаи инте-
грирования уравнений тяжелого твердого тела, движущегося
около неподвижной точки.
Как показывает этот краткий обзор математических
исследований В. В. Голубева, его основные достижения
в той или иной степени связаны с развитием теории функ-
ций комплексного переменного. «Уже давно отмечено, что
научная деятельность всякого отдельного математика часто
бывает в принципе проникнута только одной идеей, по-
священа, в сущности, одному только методу. Так, излю-
бленным методом знаменитого Анри Пуанкаре была оценка
коэффициентов ряда Тейлора, в которой он не знал себе
соперников и которая была источником почти всех его ре-
зультатов. Изучая все работы ; В. Д. Голубева, легко убе-
диться, что и здесь мы имеем дело с одним только мето-
дом, многообразно варьируемым1 автором в зависимости от
намечаемых богатых приложений, но который, по, существу,
956
А. а. Космодемьянский.
всегда остается тем же самым: это метод функций
комплексного переменного, причем автор то дер-
жится в границах классической теории этих функций, то
уходит в теорию модерн, смотря по характеру намеченных
им результатов» х).
3. В. В. Голубев вел интенсивную научную работу по
ряду актуальных разделов современной аэродинамики. Он
опубликовал с 1927 г. более 40 работ, относящихся к тео-
рии механизированного крыла, теории пограничного слоя,
теории вихревого сопротивления, теории крыла конечного
размаха и теории машущего крыла. Монографии В. В. Го-
лубева по теории крыла в плоскопараллельном потоке и
теории крыла конечного размаха получили высокую оценку
в нашей стране; по этим книгам учились и учатся студенты,
аспиранты и научные работники. Профессор В. В. Голу-
бев — один из создателей теоретической аэродинамики в нашей
стране.
Рассмотрим кратко методы проф. Голубева, развитые
при изучении проблемы механизированного крыла. Обще-
известно, что современные самолеты имеют весьма высокие
максимальные скорости полета. Из соотношений между аэро-
динамическими коэффициентами крыла самолета следует,
что с увеличением максимальной скорости полета вырастает
одновременно и посадочная скорость. Большие посадочные
скорости осложняют эксплуатацию самолетов, требуя высо-
кой квалификации летчиков. Если посадочная скорость само-
лета превышает 60 м!сек, то посадка становится трудной
даже для летчиков высшей квалификации. Для уменьшения
посадочной скорости инженерами были предложены так
называемые механизированные крылья. В технической прак-
тике наибольшее распространение получили: предкрылок,
закрылок, щиток и щитовидный закрылок. Для выяснения
аэродинамических характеристик крыла с предкрылком или
закрылком В. В. Голубев поступает следующим образом.
Влияние предкрылка или закрылка на поле скоростей основ-
ного крыла исследуется при помощи замены предкрылка
(или закрылка) присоединенным вихрем.
i) Н. Н. Лузин, Отзыв о работах члена-корреспондента
АН СССР В. В. Голубева. (Хранится в делах кафедры высшей
математики ВВИА им. Жуковского.)
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
957
Пусть в плоскости комплексного переменного имеется
окружность радиуса R = 1. Предположим, что на эту
окружность набегает поток, имеющий в бесконечности ско-
рость Уоо, пусть угол атаки равен 9, а циркуляция скоро-
сти по контуру окружности R = 1 равна Г. Помещая в точке
а = ре^ вихрь с циркуляцией у, мы можем написать ком-
плексный потенциал течения в виде
W (z)=Vme-(2+ 4“) + ^7ln 2 + 2b Iln (*—«)—•“ (*—«)]•
(1)
Имея в виду, что при конформном отображении внеш-
ней части окружности на внешнюю часть профиля крыла
можно потребовать, чтобы острой кромке профиля соответ-
ствовала точка z~ 1, мы получимлля комплексной скорости
следующее выражение:
^ = £=1 1А z~a'a
dz z L \ г / (z — a) (z — a)
(2)
где
A =
(1 — a) (1 — a)
Так как на контуре цилиндра z — e™?, то комплексную
скорость можно записать в виде
dw лхг т) . Ф
— = 41/^ sin У
cos(9-g)-/<cos(;i|x)JJ,(3)
где
Изучая расположение критических точек на окружности
/? = 1, Владимир Васильевич доказывает очень интересную
теорему: «сумма смещений критических точек
на окружности R = 1 под действием добавоч-
ных вихрей равна нулю». Оказывается, что это свой-
ство критических точек на окружности остается верным при
любом числе добавочных вихрей и при любом их располо-
жении около окружности.
958
А. а. Космодемьянский
Указав способ определения положения критических точек '
на окружности R = 1, можно проанализировать влияние пред-
крылка и закрылка на картину распределения скоростей по
контуру профиля крыла.
Действие добавочного вихря у сводится к изменению
положения критической точки разделения потока и к изме-
нению величины скорости. Смещение передней критической
точки позволяет, не меняя характера обтекания, изменить
предельный угол атаки на некоторый угол 8. Для пред-
крылка 3 > 0, а для закрылка 8 < 0. Изменение положения
точки разделения струй увеличивает на 8 предельный угол
атаки при наличии предкрылка и уменьшает на 18 | предель-
ный угол атаки при наличии закрылка.
Изменение картины распределения скоростей, обусловлен-
ное вихрем у, сводится к некоторому выравниванию скоростей
на большей части верхней поверхности крыла. Уменьшение
максимальной скорости позволяет также увеличить предель-
ный угол атаки, при котором профиль крыла работает в усло-
виях плавного обтекания.
Анализ кинематической картины обтекания профиля при
наличии вихрей позволил формулировать следующие основные
результаты о механизме действия предкрылка и закрылка *)•
Действие предкрылка сказывается в увеличении пре-
дельного угла атаки, которое получается от действия
двух источников: от изменения положения критической точки
и проистекающего отсюда кажущегося изменения угла атаки
и от выравнивания скорости в результате перераспределения
скоростей по контуру профиля крыла.
В случае закрылка имеет место уменьшение предельного
угла атаки, происходящее от .смещения критической точки
и кажущегося увеличения угла атаки, которое отчасти ком-
пенсируется перераспределением скоростей.
Применяя ко всей системе (окружность плюс вихрь) тео-
рему Жуковского, мы найдем, что
1) В. В. Го лу б е в, Исследования по теорий разрезного кры-
ла, ч. II, Труды ЦАГИ, вып. 306, стр. 21, 1937 (см. настоящее из-
дание стр. 291—348).
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
959
но величина циркуляции присоединенного вихря Жуков-
ского Г будет зависеть от у.
Анализ изменения Г от присутствия добавочных вихрей,
проведенный в работе В. В. Голубева, дает:
для предкрылка | АГХ | = | Т | d
для закрылка | ДГ21 = | Т | При одинаковом | у | имеем: d т— 1 •
I АГХ | _r- j
|ДГ21 г+1’
т. е. закрылок дает увеличение циркуляции, а следовательно,
и подъемной силы, значительно большее, чем предкрылок.
Весьма существенным вопросом для получения количе-
ственных результатов, характеризующих работу предкрылка
и закрылка, является определение циркуляции у присоеди-
ненных вихрей. Циркуляция у определяется В. В. Голубевым,
исходя из следующей гипотезы: циркуляция у равна цирку-
ляции скорости вокруг пластинки, хорда которой равна
хорде предкрылка или закрылка, а скорость потока равна
той скорости, которая получится в точке z =а при отсут-
ствии добавочных вихрей. Таким образом, для малых углов
атаки
T=^Vap,
где b — хорда предкрылка (или закрылка), р — угол атаки
относительно набегающего потока, Va — скорость потока
в точке, соответствующей центру добавочного вихря.
Вычисления, проведенные В. В. Голубевым для ряда кон-
кретных случаев, показали, что предкрылок весьма мало
увеличивает предельный угол атаки, а вместе с тем и подъем-
ную силу, а закрылок незначительно уменьшает предельный
угол атаки, но зато резко увеличивает циркуляцию, что в свою
очередь значительно увеличивает подъемную силу. Иначе
говоря, действие предкрылка сводится к уве-
личению критического (предельного) угла
атаки; действие закрылка эквивалентно влия-
нию изменения изогнутости основного про-
филя.
960 л. а. Космодемьянский
Для изучения работы щитка и щитовидного закрылка
(задач, решенных академиком С. А. Чаплыгиным, Н. С. Аржа-
никовым и С. М. Таргом) В. В. Голубевым была развита
общая теория обтекания внешней части многоугольника
с использованием формулы Шварца — Кристоффеля, дающей
отображение внешней части многоугольника на внешнюю
часть окружности радиуса /? = 1. Развитие этой теории
позволило получить результаты Чаплыгина, Аржаникова и
Тарга единым методом и дополнительно рассмотреть течения
около так называемых звездообразных профилей.
4. В области теории пограничного слоя профессору
В. В. Голубеву принадлежат следующие научные результаты:
интегральные соотношения Голубева, метод интегрирования
уравнения Польгаузена для «односкатного» профиля рас-
пределения скоростей и качественный анализ решения урав-
нения пограничного слоя для плоской пластинки.
Интегральные соотношения Голубева получаются следую-
щим образом (мы ограничиваемся рассмотрением стационар-
ного пограничного слоя для р = const).
Основное дифференциальное уравнение пограничного слоя
имеет вид
дм , ди ,т' . д2и /Л.
и -т--Г- v -ч— = UUx —I- v -д-q . (4)
дх ' ду 1 ду2 v 7
Умножим (4) на ик dy и проинтегрируем в пределах
от нуля до 8, где 8— толщина пограничного слоя.
Будем иметь после несложных преобразований х)
6 §
д Гм^^а д Г ,
гт dy — т-7—i 3“ udy =
дх j k-\-\ 1 л
о о
О *5
= ии'х \u*dy — ->k j a*' (g-)2 dy. (5)
0 (>
При k = 1 из (5) следует интегральное соотношение
Л. С. Лейбензона, полученное применением теоремы о кине-
1) См. Н. Е. К оч ин, И. А Кибел ь, Н. В. P о з е, Теорети-
ческая гидромеханика, т. II, 1949.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
961
тической энергии к элементу пограничного слояг). При k — О
из (5) можно получить интегральное соотношение Кармана,
обычно получаемое при помощи теоремы о количестве дви-
жения 1 2).
Советские ученые (Л. Г. Лойцянский, А. М. Файнзиль-
бер и др.) показали широкие возможности исследования
конкретных задач, вытекающих из системы интегральных
соотношений В. В. Голубева. Только при использовании
системы интегральных соотношений удалось показать, что
ранее известные интегральные соотношения Кармана и Лей-
бензона, ни каждое в отдельности, ни рассматриваемые
совместно, не эквивалентны дифференциальным уравнениям
пограничного слоя. Бесконечная совокупность интегральных
соотношений В. В. Голубева эквивалентна этим уравнениям.
При построении приближенных решений пограничного слоя,
исходя из соотношений Кармана или Лейбензона, этот ре-
зультат следует иметь в виду.
В научной литературе по теории пограничного слоя
большое распространение получил тот случай интеграции
уравнений пограничного слоя, когда распределение давлений
вне пограничного слоя изменяется по линейному закону
(односкатный профиль давлений). Следует указать, что реше-
ние уравнений пограничного слоя для этого частного слу-
чая было впервые дано В. В. Голубевым.
Рассматривая нелинейное уравнение Польгаузена для
определения толщины пограничного слоя
0,8 Г— 9072 4- 1670,4k — (47,4 4- 4,8 к»— (Я
d /52\ _ L ' U ' \ U'2 /1
ах\ч) U [—213,12 4- 5,76k 4-кЗ]
(6)
U'^
где к = —, В. В. Голубев отметил случай, когда это
уравнение может быть сведено к квадратурам.
Пусть давление р вне пограничного слоя изменяется по
линейному закону. Будем иметь тогда:
£ = ife(CP —р 7/7/'= const. (7)
1) Л. С. Л е й б е н з о н, Энергетическая форма интегрального
условия в теории пограничного слоя. Труды ЦАГИ, вып. 240, 1935
а) См., например, Шлихтинг, Теория пограничного слоя.
962
А: А, КОСМОДЕМЬЯНСКИЙ
Дифференцируя (7) еще раз по х, получим:
pt/'* 2+pt/(/" = o,
откуда
UU" =
U'2
UU"
U'2
Полагая в уравнении (6)
1, мы существенно его
упрощаем, и, как показал В. В. Голубев, в этом случае
определение закона нарастания толщины пограничного слоя
сводится к простым квадратурам *).
В известной книге В. В. Голубева2) дано качественное
исследование дифференциального уравнения пограничного
слоя, причем впервые в научной литературе по погранич-
ному слою строго доказан монотонный характер интеграль-
ной кривой этого уравнения, удовлетворяющей краевым
условиям. Кроме того, из качественного исследования выяс-
нено, что если F (z) является интегралом уравнения погра-
ничного слоя, то и функции k2F (kz), зависящие от пара-
метра kt также будут интегралами этого уравнения. Это
позволяет формулировать вспомогательную краевую задачу
с упрощенными граничными условиями, решение которой
дает возможность найти интеграл уравнения пограничного
слоя с реальными условиями на границах слоя.
5. В. В. Голубеву принадлежит разъяснение противоре-
чий в условиях устойчивости шахматных вихревых дорожек,
полученных в хорошо известных работах Кармана иН. Е. Жу-
ковского. Если обозначить через h расстояние между вих-
ревыми цепочками, а через I расстояние между двумя сосед-
ними вихрями какой-либо цепочки, то по Карману условие
устойчивости имеет вид
у = 0,281,
и по Н. Е. Жуковскому
у = 0,36.
1) В. В. Г о л у б е в, Исследования по теории разрезного крыла,
ч. I. Труды ЦАГИ, вып. 147, 1933 (см. настоящее издание, стр. 31).
2) В. В. Голубев, Теория крыла аэроплана конечного раз-
маха. Труды ЦАГИ, вып. 108, 1934.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ 963
В. В. Голубев показал, что условия устойчивости шах-
матных вихревых дорожек получаются различными при раз-
личных способах наложения возмущений. Если смещать
только один вихрь, как это делал Жуковский, тогда усло-
вие устойчивости будет у = 0,36; если смещать все вихри,
то мы получаем условие устойчивости Кармана. Налагая
возмущения на вихри только верхней цепочки или только
нижней цепочки и т. д., можно получить целую серию усло-
вий устойчивости. Так как возмущения, рассмотренные Кар-
маном, являются наиболее общими, следует считать полу-
ченное им условие устойчивости наиболее близким к геоме-
трическим конфигурациям реально наблюдаемых вихревых
дорожек, образующихся за плохо обтекаемыми телами.
6. При решении основного интегро-дифференциального
уравнения крыла конечного размаха широкое распростране-
ние получил приближенный метод Глауэрта. Этот метод
обладает одним существенным недостатком, состоящим в том,
что результаты n-го приближения нельзя использовать при
отыскании решения (п4“0“го приближения. Все вычисления
для (п-{-Г)-го приближения приходится проводить заново.
Кроме того, даже в тех случаях, когда заранее известно,
что знания, скажем, первых четырех коэффициентов разло-
жения достаточно для приближенного определения подъем-
ной силы и индуктивного сопротивления крыла, точность
все же оказывается далеко не наилучшей.
В. В. Голубев дал новый метод решения основной задачи
теории крыла конечного размаха, названный им методом
тригонометрических разложений. Вот основная идея метода
В. В. Голубева:
Если взять разложение циркуляции в тригонометриче-
ский ряд по Глауэрту в виде
Г (6) = Ar sin 6 —j— Д3 sin 39 —. —j— sin (2^ —H 0 ® “H • • •»
то для . определения коэффициентов ряда мы приходим
к уравнению ...
~ S sin 0 $in == Sin б — 2 nCnSin. (&)
где коэффициенты Ст совпадают с Ат с точностью до по-
стоянного множителя,
964
А. А. КОСМОДЕМЬЯНСКИЙ
В уравнении (8) правая часть разложена по синусам.
Проф. Голубев разлагает в тригонометрический ряд по си-
нусам кратных дуг и левую часть уравнения (8). Возьмем
функцию /п(9), определяемую следующим образом: '
при 0 9 тс fn (0) = sin 9 sin (n9),
при —тс^9^0 /п(6) =— sin 9 sin (п9).
Так как /п(9)— функция нечетная, то ее можно разло-
жить в ряд вида
fn (9) = b± sin 9 + b2 sin 29 -|- b3 sin 39 -|- . . .
По известным формулам Фурье коэффициенты blf . .bn
определяются следующим образом:
4-тс тс
Ьп = J /(9) sin п9 dG = [/(9) sin п9 ^9. (9)
-тс О
Вычисления, проведенные проф. Голубевым, показывают,
что в интервале 0^9^тс будем иметь:
sin n9 sin 9 = — V Г7——Д—г — ,---Д—Л sin (/п9), (10)
7Г 4-72)2—1 (т—72)2— 1J \ /’ X /
т
где п — нечетное и т пробегает все нечетные положитель-
ные числа.
Возвращаясь к уравнению (8) и приравнивая коэффи-
циенты при sinTn9, мы получаем следующую систему урав-
нений для определения Ст:
при т = 1 — 2СП[(л_|_ 1)2_ 1 — („—1)2 — 1] = 1 — >
при /п>1 -{т_ --,] = -^шСт.
т
Развитые впоследствии за рубежом методы последова-
тельного определения коэффициентов Ст (метод Лотц и др.)
все исходили из идеи проф. В. В. Голубева о разложении
функции /те(9) в тригонометрический ряд по синусам крат-
ных дуг.
7. В годы Отечественной войны В. В. Голубев поставил
и разрешил одну из труднейших задач нестационарного
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
965
движения крыла. До этого цикла работ Владимира Василье-
вича в теории нестационарных движений крыла рассматри-
вались задачи двух типов:
— нестационарные движения крыла с постоянной цирку-
ляцией— этот класс задач был впервые обследован
С. А. Чаплыгиным;
— нестационарные колебательные движения крыла с пе-
ременной циркуляцией и линией раздела (вихревым
слоем), отходящей от задней кромки крыла, — этот
класс задач был формулирован Л. Прандтлем и раз-
вит в большом числе работ как в нашей стране, так
и за границей (работы Бирнбаума, Вагнера, Седова,
Келдыша и др.). Весьма существенным предположе-
нием во всех этих работах является предположение
о малости амплитуды колебаний крыла и малой тол-
щине профиля крыла.
В исследованиях В. В. Голубева рассматриваются конеч-
ные колебания крыла в плоскопараллельном потоке при до-
статочно общих предположениях относительно геометриче-
ских параметров профиля и углов атаки.
Трудности постановки задачи о машущем крыле, как
неоднократно подчеркивал Владимир Васильевич, «носят не
математический, а чисто физический характер. Дело состоит
в неясности самой физической схемы, которой можно было бы
стилизовать процесс, происходящий при взмахах крыла, и
недостаток этой физической схемы не может быть заменен
никакими дифференциальными или интегральными уравне-
ниями» *).
Теория машущего крыла, развитая В. В. Голубевым,
исходит из физической гипотезы о том, что при взмахах
крыла при горизонтальном полете от него в крайних верх-
нем и нижнем положениях отходят дискретные вихри с ко-
нечной циркуляцией, которые образуют позади крыла шах-
матную вихревую дорожку типа дорожек Бенара — Кармана,
но с противоположным направлением вращения вихрей. Для
того чтобы согласовать такую структуру кильватерной зоны
за машущим крылом с теоремой Томсона и гипотезой Жу-
1) В. В. Голубев, Тяга машущего крыла, Изв. АН СССР,
ОТН, № 5, стр. 643, 1946 (см. настоящее издание стр. 450).
966
А. А. КОСМОДЕМЬЯНСКИЙ
ковского, приходится дополнительно предположить, что
влияние отходящих свободных вихрей с постоянной цирку-
ляцией на величину циркуляции присоединенного вихря крыла
компенсируется соответствующим изменением завихренности
пограничного слоя. Таким образом, В. В. Голубев считает,
что пограничный слой при колебаниях крыла не распадается
непрерывно, выделяя все новые и новые вихри, образующие
вихревую пелену; распадание пограничного слоя происхо-
дит отдельными каплями, квантами, в верхней и нижней
точках амплитуды; при переходе же крыла из одной край-
ней точки в другую в пограничном слое образуется набу-
хание этих капель, которые при достаточной скорости взма-
хов отрываются в крайних точках амплитуды колебания 1).
Отсюда видно, что согласно воззрениям Владимира Василье-
вича вязкий пограничный слой является своеобразным регу-
лятором, позволяющим одновременно выполняться и теореме
Томсона и гипотезе Жуковского о конечности скорости
потока вдоль задней кромки крыла.
Применяя к системе крыло плюс свободные вихри тео-
рему об изменении количества движения механической си-
стемы, В. В. Голубев получает следующие формулы для
подъемной силы (К) и тяги (АГ) машущего крыла:
Г = р(70Г,
X = — 0,95pWo cos a (sin 8 H-^-cos 8W1 + 1,2 ,
\ Uq / \ C/qJ
где p —плотность воздуха, b — хорда крыла, w —скорость
поднятия и опускания крыла,
----2-> 2—,
причем Oj и 62 — соответственно угол атаки при опускании
и при поднятии крыла и р.— угол, характеризующий изо-
гнутость крыла. Эти формулы дают удовлетворительное
согласие с данными экспериментов.
-«Среди различных случаев полета с машущими крыльями
совершенно исключительным с гидродинамической точки зрё-
1) В. В. Голубев, Тяга машущего крыла, Изв. АН СССР
ОТН, № 5, стр. 645, 1946 (см. настоящее издание, стр. 450).
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
967
ния является полет „на месте", или, как его называют био-
логи, „трепещущий полет", когда птицы или некоторые виды
насекомых, работая крыльями, весьма устойчиво стоят на
одном месте. Такой полет можно наблюдать, например,
у стрекоз, у некоторых видов мух и у мелких птиц — ко-
либри, стрижей и т. п.» г). Исходя из полученной формулы
для тяги (X #= 0, когда UQ = 0), В. В. Голубев дал анализ
явления трепещущего полета, и эти его исследования нашли
применение в биологических работах 1 2).
8. Ряд работ 3) В. В. Голубева посвящен теории крыла
малого удлинения. Экспериментально было выяснено, что
при малых удлинениях (Х<1) крылья имеют интегральные
аэродинамические характеристики, существенно отличные от
характеристик крыльев больших удлинений (К = 4—12). Тдк,
например, Сутах крыльев больших удлинений, имеет место
при углах атаки («критических углах атаки») 15—16°;
в случае крыльев малых удлинений (X = 0,3—0,5) коэффи-
циент подъемной силы Су растет до углов атаки 45—50°;
следовательно, критические углы атаки крыльев малых удлине-
ний в три раза больше, чем у крыльев больших удлинений.
Вторая особенность крыльев малого удлинения состоит
в резком смещении при больших углах атаки линии цен-
тров давлений к задней кромке крыла. В то время как
у прямоугольного крыла большого удлинения линия центров
давления находится на расстоянии, близком к четверти хорды,
считая от передней кромки, для крыльев с удлинением
0,3—0,5 линия центров давления смещается к средине хорды.
Размышляя много лет над этими особенностями крыльев
малых удлинений, Владимир Васильевич пришел к следую-
щей физической картине их обтекания. В существующей
теории крыла большого удлинения не учитывается в полной
мере затекание потока через боковые кромки крыла (торцы
1) В. В. Г о л у б е в, О некоторых вопросах теории машущего
крыла, Уч. зап. МГУ, вып. 152, стр. 4, 1951 (см. настоящее издание,
стр. 477).
2) Гладков, Биологические основы полета птиц, Докторская
диссертация, 1947.
3) В. В. Г о л у б е в, К теории крыла малого удлинения, Изв.
АН СССР, ОТН, № 3, 1947. К теории крыла малого удлинения,
Прикладная математика и механика, т. XIX, вып. 2, 1955 (см. на-
стоящее издание, стр. 614).
968
А. А. КОСМОДЕМЬЯНСКИЙ
крыла), которое, несомненно, имеет место благодаря раз-
ности давлений на нижней и верхней поверхностях крыла.
Владимир Васильевич считает, что эффект затекания имеет
место у крыльев любого удлинения, но проявляется более
заметно у крыльев малого удлинения. Если взять прямо-
угольное крыло малого удлинения, то вихревая схема такого
крыла состоит по Голубеву из присоединенных прямолиней-
ных вихрей, параллельных передней кромке крыла, и двух
систем прямолинейных бесконечных свободных вихрей, схо-
дящих с боковых кромок крыла. Эти системы свободных
вихрей составляют две вихревые пелены, расположенные
в параллельных плоскостях, каждая из которых перпенди-
кулярна к передней кромке крыла. Исходя из такой вихре-
вой схемы, можно количественно определить скорости в раз-
личных точках боковых кромок крыла. Принятая гипотеза
о структуре системы свободных вихрей позволяет прибли-
женно определить, ^щовываясь на выводах^теории погра-
ничного слоя, изменение критического угла атаки в зави-
симости от удлинения и выявить увеличение скоростей обте-
кания в задней поло вин е крыла.-ВыраБ“нйванйясТ<оросте1Гпо
всей верхней поверхности крыла, естественно, вызывают
смещение линии центров давления к средине крыла. Опре-
деленные теоретические значения критических углов атаки
для крыльев малых удлинений оказались в удовлетворитель-
ном согласии с данными экспериментов.
9. Параллельно с огромной научной и научно-организа-
ционной работой В. В. Голубев вел ежегодно большую педаго-
гическую работу в Московском университете и Военно-воздуш-
ной инженерной академии. Как мы указывали, для Владимира
Васильевича чтение лекций было необходимым элементом твор-
ческой научной работы. Постоянное общение со студенче-
ством «было не обузой, мешающей научной работе, а необ-
ходимым живым и интересным делом, без которого немыслима
жизнь и научная работа». Основные монографии В. В. Го-
лубева по теории крыла аэроплана х) возникли из обработки
специальных курсов, которые он в разное время читал сту-
дентам Саратовского, Свердловского и Московского уни-
9 В. В. Голубев, Теория крыла аэроплана в плоскопарал-
лельном потоке, 1-е изд., 1927, 2-е изд. 1938. Теория крыла аэро-
плана конечного размаха, 1931. Лекции по теории крыла, 1949.
ВЛАДИМИР ВАСИЛЬЕВИЧ ГОЛУБЕВ
969
верситетов. Эти монографии являлись одновременно превос-
ходными учебниками по теории крыла. В. В. Голубев умел
органически связать последовательное изложение важнейших
идей, высказанных другими авторами в области теории про-
филя крыла и теории крыла конечного размаха, со своими
собственными изысканиями в этой области. Особенно большое
значение уделяется в монографиях Владимира Васильевича
трудам основоположников теоретической аэродинамики в на-
шей стране, трудам Н. Е. Жуковского и С. А. Чаплыгина.
Тонкая и умная пропаганда идей теории крыла русской
аэродинамической школы способствовала подъему культуры
аэродинамических исследований в наших научных и учебных
заведениях. Не будет преувеличением сказать, что почти все
ныне здравствующие аэродинамики нашей страны воспиты-
вались под значительным воздействием монографий Голубева
по теории крыла. Благодаря педагогическому мастерству
Владимира Васильевича стали доступны широким слоям науч-
ных работников авиации и студенчеству глубокие идеи
С. А. Чаплыгина, изложенные, как правило, в оригинальных
статьях С. А. Чаплыгина очень кратко и трудно. Интересно
проследить, как постепенно внедрялись в монографии
новые задачи, тесно связанные с актуальными запросами
авиационной техники. Если в первом издании теории крыла
в плоскопараллельном потоке основное содержание посвя-
щено классическим работам, изложенным с широкой точки
зрения теории функций комплексного переменного, то в тео-
рии крыла конечного размаха учет влияния вязкости, явления
в пограничном слое, анализ экспериментальных данных зани-
мают добрую половину книги. Во втором издании теории
крыла в плоскопараллельном потоке значительное место уде-
лено теории механизированного крыла, в которой сущест-
венные открытия принадлежат Владимиру Васильевичу. На-
конец, в монографии «Лекции по теории крыла» (194J)
Голубев достаточно подробно излагает теорию тонких про-
филей, теорию механизированного крыла и дает общие науч-
ные основы для понимания теории крыла малого удлинения
и теории машущего крыла.
Ограничивая себя в отборе материала, Владимир Василье-
вич всегда стремился дать ясную картину основных ре-
зультатов и методов, не отвлекаясь на излишние подроб-
970
А. А. КОСМОДЕМЬЯНСКИЙ
ности, которые «при первом изучении могут только затем-
нить руководящие научные идеи».
При построении своих курсов по теории крыла аэроплана
В. В. Голубев исходил из следующих двух основных идей:
«Во-первых, автор пытался возможно полнее отметить
чисто механические, физические идеи, лежащие в основе
этого раздела механики, памятуя, что механика и ее техни-
ческие приложения суть раздел точного естествознания и
по самому своему характеру резко отличаются от того, что
принято называть прикладной математикой.
Во-вторых, весь курс построен на систематическом
использовании аппарата теории функций комплексного пе-
ременного. Предназначенный для студентов, имеющих доста-
точно основательную и разностороннюю общематематическую
подготовку, курс и ставил своей задачей показать, что тео-
рия функций комплексного переменного, помимо присущих
ей, как и всякой другой математической дисциплине, внут-
ренних, вызываемых развитием самой науки, задач, является
в то же время рабочим аппаратом важных разделов точного
естествознания и техники, также, со своей стороны, опреде-
ляющих дальнейшее развитие теории».
В созданных Голубевым курсах-монографиях видны неза-
урядный ум автора, подлинное знание актуальных задач
научного и технического прогресса, любовь к Родине и
достижениям отечественной науки.
* * *
Владимир Васильевич показал мне в 1953 г. следующие
строки из Максима Горького:
«Не жалей себя — эта самая гордая, самая красивая муд-
рость на земле. Есть только две формы жизни: гниение и
горение. Трусливые и жадные изберут первую; мужествен-
ные и щедрые — вторую. Каждому, кто любит красоту, ясно,
где величественнее».
Я думаю, что в этот момент он обозревал свою жизнь.
Москва 19/1 1957 г.
список научных Трудов в. в. голубева
1. Об одном приложении теоремы Picard’a к теории дифферен-
циальных уравнений (Сообщено Московскому математическому
обществу 21 декабря 1910 г.), Математический сборник, М., 1911, т. 27,
вып. 4, стр. 560—562.
2. К теории уравнений Painleve (Сообщено Московскому мате-
матическому обществу 17 января 1912 г.), Математический сборник,
М., 1912, т. 28, вып. 2, стр. 323—349.
3. О звезде Mittag Leffler’a, Математический сборник, М., 1914,
т. 29, вып. 1, стр. 171—181.
4. Snr les fonctions a singularites discontinues Note de M. W. Go-
loubeff, presentee par M. Emile Picard (Analyse Mathematique). Comp-
tes rendus hebdomadaires des seances de I’Academie des sciences,
Paris, 1914, t. 158, №1, стр. 1407—1408.
5. Однозначные аналитические функции с совершенным мно-
жеством особых точек, Ученые записки Московского университета,
М„ 1916, стр. 162.
6. Введение в математическую статистику (1—4 стр. — Всту-
пление В. В. Голубева, 5—12 стр. — очерк А. Ковалевского), Са-
ратов, 1920, Крайиздат, стр. 1—4, 13—94.
. 7. Теория логарифмов в курсе средней школы, Ученые за-
писки Саратовского педагогического института, 1921.
8. Исследования по теории особых точек однозначных функций,
Ученые записки Саратовского гос. университета, Саратов, 1924,
т. 1 и 2, вып. 3, стр. 1—48; 1924, т. 3, вып. 1, стр. 49—72; 1925, т. IV,
вып. 2, стр. 73—92; 1926, т. V, вып. 2, стр. 93—112; 1927, т. VI,
вып. 3, стр. 113—127.
9. Об одном обобщении теоремы Picard’a, Математический сбор-
ник, М., 1924, т. 31, стр. 557—567.
10. О соответствии границ при конформном отображении, Мате-
матический сборник, М., 1925, т. 32, стр. 55—57.
11. Sur une fonction automorphe bornee Note de M. W. Goloubeff
(Analyse Mathematique), Comptes rendus hebdomadaires des seances
de TAcademie des sciences, Paris, 1927, t. 185, стр. 694—698.
12. Теорий крыла аэроплана в плоскопараллельном потоке. Труды
ЦАГИ, М., 1927, вып. 29, стр. 207,
972
ЖИЗНЬ И ДЕЯТЕЛЬНОСТЬ В. В. ГОЛУБЕВА
13. Об элементарном вычислении некоторых сумм. Отчет о дея-
тельности и математической конференции педагогического общества
Дальневосточного университета, Владивосток, 1927.
14. Об аналитическом представлении одного класса автоморфных
функций, Труды Всероссийского съезда математиков в Москве
27 апреля — 4 мая 1927 г. под редакцией Привалова, М. — Л.,
Госиздат, 1928, стр. 198—199.
15. К теории медленно растущих автоморфных функций, Уче-
ные записки Саратовского гос. университета, Саратов, 1929, т. VII,
вып. 3, стр. 31—36.
16. О конформном отображении границ областей, Ученые за-
писки Саратовского гос. университета, Саратов, 1929, т. VII, вып. 3,
стр. 37—39.
17. О теореме Picard’a, Ученые записки Саратовского гос. уни-
верситета, Саратов, 1929, т. VII, вып. 3, стр. 41—44.
18. Элементы математической статистики в приложении к лес-
ному делу, Московское государственное сельскохоз. изд-во «Новая
деревня», 1929, стр. 247.
19. К теории лакунарных рядов, Бюллетени съезда математи-
ков, Харьков, Государственное изд-во Украины, 1930, № 1, стр. 1718.
20. Recherches sur la theorie des fonctions automorphes. Annali di
Matematica, Bologna, 1930, 4 серия, т. 8, стр. 29—52.
21. Теория крыла аэроплана конечного размаха, Труды ЦАГИ,
М., 1931, вып. 108, стр. 350.
22. О теории пограничного слоя, Первая Всесоюзная конферен-
ция по аэродинамике 16/V—21/V 1931 г., Труды ЦАГИ, М., 1932,
стр. 35—45.
23. О разрезных крыльях, Первая Всесоюзная конференция по
аэродинамике 16/V—21/V 1931 г., Труды ЦАГИ, М., 1932, стр. 166—170.
24. Об устойчивости вихревых дорог Кармана, Известия Ака-
демии наук СССР, М., 1932, стр. 1103—1108.
25. Гидро- и аэромеханика (совместно с Е. С. Кузнецовым)
в книге: Наука в СССР за пятнадцать лет (1917—1932). Механика.
Под редакцией В. В. Голубева и Л. С. Лейбензона, Гостехиздат,
1932, стр. 33—101.
26. К теории вихревых дорог Кармана, Математический сбор-
ник, М., 1933, т. 40, вып. 1, стр. 73—85.
27. Исследования по теории разрезного крыла. Часть 1. Теория
предкрылка в плоскопараллельном потоке, Труды ЦАГИ, М., 1933,
вып. 147, стр. 72.
28. К вопросу об аналитическом изображении автоморфных функ-
ций. Учекые записки Саратовского гос. университета, Саратов, 1934,
т. 12, сгр, 85—91.
29. Математика и техника, «Фронт науки и техники», М., 1934,
№ 5—6, стр. 38—42.
30. К теории продувки цилиндров двигателей внутреннего сго-
рания (совместно с С. -А. Чаплыгиным), Труды ЦАГИ, М., 1934,
вып. 175, стр. 48, или С. А. Чаплыгин, Поли. собр. соч., Л., 1935,
т. III, стр. 251—308, или С. А, Ч а п л ы г и н, Собр. соч., М, — Л., 1950,
т, III, стр. 169—242,
СПИСОК НАУЧНЫХ ТРУДОВ В. В. ГОЛУБЕВА
973
31. Аэродинамические основания методов увеличения подъемной
силы крыла, Труды 3-й Всесоюзной конференции по аэродина-
мике 23—27 декабря 1933 г., Труды ЦАГИ, М., 1935, ч. 2,
стр. 5—13.
32. К теории предкрылка и закрылка (совместно с С. А. Ч а-
плыгиным), Труды ЦАГИ, М., 1935, вып. 171, стр. 39, или С. А. Ча-
плыгин, Собр. соч., 1948, т. II, стр. 586—639.
33. К теории разрезного крыла, Труды ЦАГИ, М„ 1935, вып.
240, Сборник общетеоретич. группы ЦАГИ, III, стр. 14—17.
34. О работе крыла с отсасыванием пограничного слоя, Техни-
ческие заметки ЦАГИ, М., 1935, № 45, стр. 41—43.
35. О математических и механических проблемах, связанных
с задачей улучшения работы крыла самолета. Труды Военно-воздуш-
ной ордена Ленина академии РККА им. Жуковского, М., изда-
ние Академии, 1935, Сб. № 13, стр. 7—17. [Сборник под редакцией
В. В. Голубева содержит несколько дополненные доклады, про-
читанные авторами на конференции по научно-исследователь-
ской работе ВВА РККА в секции математики и теоретической ме-
ханики.]
36. Математика и техника, Журнал «Сорена», М., 1935, № 10,
стр. 11—17.
37. Единство теории и практики (К 15-летию со дня смерти
Н. Е. Жуковского). В газете «За индустриализацию», М„ 1936,
17 марта, стр. 3.
38. Theory of the slat in a two dimensional flow, The Journal of
the Royal Aeronautical Society, London, 1936, сентябрь, № 309,
стр. 681—708. [Text translated from the Russian and edited by Crean,
B. Sen (Eng). Transactions of the Central Aero-Hydrodynamical Insti-
tute, Moscow, № 147 (Februares, 1933), «Investigations into the theory
of the slotted Wing», Part I.]
39. К теории влияния земли на подъемную силу крыла, Труды
ЦАГИ, М., 1937, вып. 301, Теоретический сборник IV, стр. 36—38‘
40. Исследования по теории разрезного крыла. Том II. При-
ближенная теория предкрылка и закрылка, Труды ЦАГИ, М., 1937,
вып. 306, стр. 40.
41. Н. Е. Жуковский (биографический очерк). В книге: Собра-
ние сочинений Н. Е. Жуковского, М. — Л., ОНТИ, 1937, т. 1,
стр. 15—55.
42. О влиянии системы неподвижных вихрей на обтекание
цилиндра, Ученые записки Московского гос. университета, М., 1937,
вып. 7, стр. 19.
43. Вывод некоторых формул гидромеханики. В книге: В. Ф.Дю-
р е н д, Аэродинамика, т. 1. Перевод под редакцией проф. В. В.
Голубева, М. — Л., Главная редакция авиационной литературы, 1937,
стр. 421—435.
44. О подъемной силе крыла самолета. Физика в школе, М.,
Учпедгиз, 1937, № 5, стр. 36—40.
45. Работы по гидромеханике в СССР. В книге: Математика
и естествознание в СССР (очерки развития за 20 лет), М. — Л.,
Изд. АН СССР, 1938, стр. 101—120.
974
ЖИЗНЬ И ДЕЯТЕЛЬНОСТЬ В. В. ГОЛУБЕВА
46. О силах, действующих на крыло в неоднородном потоке,
Труды ЦАГИ, М., 1938, вып. 342, V теоретический сборник ЦАГИ,
стр. 16—23.
47. О влиянии надстроек на подъемную силу крыла, Труды
ЦАГИ, М., 1938, вып. 342, V теоретический сборник ЦАГИ,
стр. 24—35.
48. К теории течений на двулистной поверхности Римана, Уче-
ные записки Московского гос. университета, 1938, вып. 24, кн. 2,
стр. 3—23.
49. Теория крыла аэроплана в плоскопараллельном потоке
(2-е переработанное издание), М., 1938, стр. 259.
50. Исследования по теории щитков крыльев самолета (со-
вместно с О. В. Голубевой), Труды ЦАГИ, М., 1939, вып. 398,
стр. 54.
51. Теоретические основания методов увеличения подъемной
силы крыла. Разрезные крылья, щитки, отсасыватели, Труды ВВА
РККА им. Жуковского, М., 1939, вып. 46, стр. 72.
52. О применении формул Шварца—Кристоффеля к построению
аэродинамических профилей, Труды ЦАГИ, М., 1940, вып.. 493,
стр. 40.
53. Н. Е. Жуковский, Физика в школе, М„ 1941, №2, стр. 2—5.
54. Академик С. А. Чаплыгин (К 50-летнему юбилею научной
и общественной деятельности), Техническая книга, М., 1941, № 2,
стр. 24—26.
55. Гениальный ученый (Жизнь и деятельность Н. Е. Жуков-
ского), Самолет, Бюро новой техники НК АП, М., 1941, март, № 3,
стр. 11—12.
56. Академик Сергей Алексеевич Чаплыгин (К 50-летию науч-
ной и Общественной деятельности), Известия АН СССР, ОТН, М.,
1941, № 3, стр. 5—10.
57. Методические вопросы преподавания математики во втузах,
Вестник высшей школы, М., 1941, № 5, стр. 9—12.
58. Лекции по аналитической теории дифференциальных урав-
нений, М. — Л., Гостехиздат, 1941, стр. 398.
59. Н. Е. Жуковский (1847—1921), М., БНТ НКАП, 1941,
стр. 95.
60. К теории пограничного слоя. Юбилейный сборник Военно-
воздушной ордена Ленина академии РККА им. Жуковского, М.,
изд. ВВА, 1942, стр. 35—42.
61. Механизм образования тяги машущего крыла. В книге: Труды
Научно-технической конференции ВВА им. Жуковского, М., 1944,
т. 3, стр. 7—19.
62. Академик Сергей Алексеевич Чаплыгин (Его жизнь, науч-
ная и общественная деятельность), Вестник Академии наук СССР,
М., 1944, № 3, стр. 50—65.
63. Академик С. А. Чаплыгин (Его научная и общественная
жизнь), Наука и жизнь, М., 1944, № 4—5, стр. 31—36.
64. Роль русской механики в развитии мировой науки. В книге:
Московский государственный университет. Научная конференция:
Роль русской науки в развитии мировой науки и культуры
СПИСОК НАУЧНЫХ ТРУДОВ В. В. ГОЛУБЕВА 975
(5—12 июня 1944 г.). Программы и тезисы докладов. М., изд. МГУ,
1944, стр. 67.
65. Машущее крыло; общая проблема тяги и сопротивления.
В книге: Общее собрание Академии наук СССР 14—17 октября
1944 г., Изд. АН СССР, 1945.
66. Академик Сергей Алексеевич Чаплыгин (Его жизнь, науч-
ная и общественная деятельность). В книге: Общее собрание Ака-
демии наук СССР 14—17/П 1944 г., Изд. АН СССР, М. — Л., 1944,
стр. 57—73.
67. Исследования русских ученых в области технической аэро-
механики, Вестник АН СССР, М., 1945, №5—6, стр. 72—90.
68. К теории влияния эллиптических труб на помещенное в них
крыло самолета. Ученые записки Московского гос. университета,
М., 1946, вып. 117, стр. 3—17.
69. Влияние формы крыла в плане на его аэродинамические
характеристики; крылья малых удлинений, Ученые записки Москов-
ского гос. университета, 1946.
70. Н. Е. Жуковский — отец русской авиации. (Стенограмма
публичной лекции 5/11 1945 г. в Доме летчиков в Москве), М., Изд.
лекционного бюро ВКВШ при СНК СССР, 1945, стр. 17.
71. Работы П. Л. Чебышева по интегрированию алгебраических
функций. В книге: Научное наследие П. Л. Чебышева. 1. Матема-
тика, М., Изд. АН СССР, 1945, стр. 88—120.
72. Тяга машущего крыла, Известия АН СССР, ОТН, М., 1946,
№ 5, стр. 641—658.
73. Русские работы по механике и влияние их на развитие миро-
вой науки, Ученые записки Московского гос. университета. «Роль
русской науки в развитии мировой науки и культуры» М., 1947,
вып. 91, т. 1, книга 1, стр. 97—104.
74. К теории крыла малого удлинения. Известия АН СССР, ОТН,
М., 1947, № 3, стр. 261—270.
75. Отец русской авиации (К столетию со дня рождения Н. Е. Жу-
ковского), Московский большевик, М., 1947, 17 января, № 15,
стр. 3
76. Н. Е. Жуковский (К 100-летию со дня рождения), Физика
в школе, Л., Государственное учебно-педагогическое изд-во, 1947,
№'2, стр. 3—12.
77. Н. Е. Жуковский и современная техническая аэромеханика.
В книге: Юбилейный сборник, посвященный 30-летию Великой
Октябрьской социалистической революции, М. — Л., Изд. АН СССР,
1947, ч. II, стр. 503—523.
78. Сергей:Алексеевич Чаплыгин, М., БНТ НКАП, 1947, стр. 122.
79. П. Л. Чебышев, Об интегрировании иррациональных диф-
ференциалов. В книге: П. Л. Чебышев, Поли. собр. соч., М — Л.,
1947, т. II, стр. 485—491.
80. Н. Е. Жуковский, Успехи математических наук, М. — Л.,
1947; т. II, вып. 3 (19), стр. 17.
81. Николай Егорович Жуковский. Замечательные ученые Мо-
сковского университета, Ученые записки Московского гос. универ-
ситета, М., 1947, вып. 1, стр. 64.
976
ЖИЗНЬ И ДЕЯТЕЛЬНОСТЬ В. В. ГОЛУБЕВА
82. [Краткие комментарии к работам Чебышева] «Об интегри-
ровании с помощью логарифмов», «Вступительное слово к защите
диссертации». В книге: П. Л. Чебышев, Поли. собр. соч., т. V,
М. —Л., 1951, стр. 177—179.
83. К теории крыла малого удлинения, Ученые записки Москов-
ского гос. университета, М., 1948, т. II, Механика, вып. 122,
стр. 3—16.
84. Николай Егорович Жуковский (биографический очерк).
В книге: Н. Е. Жуковский, Избранные сочинения, М. — Л., 1948,
т. 1. стр. 7—24 (см. также Н. Е. Жуковский, Собр. соч., т. I,
М. — Л., 1948, стр. 7—24.
85. Лекции по теории крыла, М. — Л., Гостехиздат, 1949, стр.
480.
86. Научные идеи Николая Егоровича Жуковского в современ-
ной гидромеханике. Сталинский сокол, М., 1950, 1/VIII, № 155,
стр. 3.
87. Сергей Алексеевич Чаплыгин (биографический очерк).
В книге: С. А. Чаплыгин, Собр, соч., т. Ill, М.—Л., Гостех-
издат, 1950, стр. 425—<48.
88. Работы С. В. Ковалевской о движении тяжелого твердого
тела вокруг неподвижной точки, Прикладная математика и меха-
ника, М., 1950, т. XIV, вып. 3, стр. 236—244.
89. Крыло и винт самолета. В книге: Механика за XXX лет,
М., 1950, стр. 341—357.
90. Лекции по аналитической теории дифференциальных урав-
нений, М. — Л., Гостехиздат, 1950, изд. 2-е, стр. 436.
91. О некоторых вопросах теории машущего крыла (Доклад
на Ломоносовских чтениях 1947 г., посвященный 100-летию со дня
рождения Н. Е. Жуковского), Ученые записки Московского гос.
университета, М., 1951, вып. 152, Механика, т. III, стр. 3—12.
92. Работы Н. Е. Жуковского по аэродинамике, Известия
АН СССР, ОТН, М., 1951, № 8, стр. 1152—1158.
93. Биография Н. Н. Лузина (совместно с Н. К. Бари). В книге:
Н. Н. Лузин, Интеграл и тригонометрический ряд, М, — Л.,
Гостехиздат, 1951, стр. 11—31.
94. Работы Н. Е. Жуковского в области теории крыла и винта
самолета, Вестник Воздушного Флота;f М., 1951, № 3, стр. 36—40.
95. Сергей Алексеевич Чаплыгин (1869—1942). Замечательные
ученые Московского университета, Ученые записки Московского
гос. университета, М., 1951, стр. 56.
96. Исследования по теории машушего крыла, Ученые записки
Московского гос. университета, М., 1951, вып. 154, т. IV, стр. 3—55.
97. Вихревое движение, БСЭ, изд. 2-е, Л., 1951, т. 8,
стр. 209—211.
98. Гидродинамика, БСЭ, изд. 2-е, Л., 1952, т. 11, стр. 281—285.
99. Гидростатика, БСЭ, изд. 2-е, Л., 1952, т. 11, стр. 328—330.
100. Н. Е. Жуковский, БСЭ, изд. 2-е, Л., 1952, т. 16,
стр. 227—229.
101. С. А. Чаплыгин (К 10-летию со дня смерти.), Наука и жизнь,
М., 1952, № 10, стр. 37—38.
СПИСОК НАУЧНЫХ ТРУДОВ В. В. ГОЛУБЕВА
977
102. Пособия по элементарной математике, Советская книга, М.,
1952, октябрь, стр. 54—56.
103. Лекции по интегрированию уравнений движения тяжелого
твердого тела около неподвижной точки, М., Гостехиздат, 1953,
стр. 287.
104. Выдающийся советский аэродинамик (К 10-летию со дня
смерти С. А. Чаплыгина), Природа, М., 1953, январь, стр. 79—88.
105. Работы Н. Е. Жуковского по аэродинамике. В книге: Труды
по истории техники, М., Изд. АН СССР, Комиссия по истории
техники, 1954, вып. IV, стр. 26—33.
106. О коэффициенте полезного действия машущего крыла,
Ученые записки Московского гос. университета, М., 1954, т. V,
Механика, вып. 172, стр. 3—7.
107. О строении спутной зоны за плохо обтекаемым телом,
Известия АН СССР, ОТН, М„ 1954, декабрь, № 12, стр. 19—37.
108. Последнее слово профессора Московского университета
В. В. Голубева в день семидесятилетия, 3 декабря 1954 года, Вест-
ник Московского гос. университета, М., 1955, № 2, стр. 173—182.
109. К теории крыла малого удлинения, Прикладная матема-
тика и механика, М., 1955, т. XIX, вып. 2, стр. 143—158.
ПО. Ф. А. Слудский, БСЭ, изд. 2-е, М., 1956, т. 39, стр. 367.
111. Владимир Петрович Ветчинкин. Очерк жизни, научной,
инженерной и педагогической деятельности. В книге: В. П. В е т-
ч ин к ин, Избранные труды, М., Изд. АН СССР, 1956, т. 1.
стр. 7—32.
112. С. А. Чаплыгин, БСЭ, 2-е изд. (печатается).
ОГЛАВЛЕНИЕ
Стр.
Отиздательства ...................................... 5
I. ТРУДЫ ПО ТЕОРИИ ПРЕДКРЫЛКА,
ЗАКРЫЛКА И ЩИТКОВ
О разрезных крыльях................................. 11
О. теории пограничного слоя....................... . 16
Исследования по теории разрезного крыла. Часть I. (Теория
предкрылка в плоскопараллельном потоке).......... 31
К теории разрезного крыла..........................137
О работе крыла с отсасыванием пограничного слоя....142
К теории предкрылка и закрылка.....................145
Теоретические основания методов увеличения подъемной силы
крыла. Разрезные крылья, щитки, отсасывание......199
Исследования по теории разрезного крыла. Часть II. (При-
ближенная теория предкрылка и закрылка) ........ 291
О влиянии системы неподвижных вихрей на обтекание цилиндра 348
К теории щитков, плотно прилегающих к крылу.........371
II. ТРУДЫ ПО ТЕОРИИ МАШУЩЕГО КРЫЛА
К теории пограничного слоя..........................399
Механизм образования тяги машущего крыла............409
Теория машущего крыла и общая проблема тяги и сопро-
тивления ........................................426
Тяга машущего крыла.................................450
О некоторых вопросах теории машущего крыла..........477
Исследования по теории машущего крыла...............491
О коэффициенте полезного действия машущего крыла .... 569
ОГЛАВЛЕНИЕ
979
III. ТРУДЫ ПО ТЕОРИИ КРЫЛА
МАЛОГО УДЛИНЕНИЯ
К теории крыла малого удлинения (1947)............. 579
К теории крыла малого удлинения (1948)............. 593
К теории крыла малого удлинения (1955)............. 614
IV. ТРУДЫ ПО РАЗНЫМ ВОПРОСАМ
АЭРОДИНАМИКИ
К теории вихревых дорог Кармана......................641
К теории влияния Земли на подъемную силу крыла.......657
О силах, действующих на крыло в неоднородном потоке ... 661
О влиянии надстроек на подъемную силу крыла..........671
К теории течений на двулистной поверхности Римана .... 688
К теории влияния эллиптических труб на помещенное в них
крыло самолета.....................................719
О применении формулы Шварца—Кристоффеля к построению
аэродинамических профилей . . .....................740
О строении спутной зоны за плохо обтекаемым телом .... 793
V. БИОГРАФИЧЕСКИЕ СТАТЬИ
Николай Егорович Жуковский (биографический очерк) .... 823
К столетию со дня рождения Н. Е. Жуковскйго (1847—1947) 865
Академик Сергей Алексеевич Чаплыгин. Его жизнь, научная
и общественная деятельность.......................887
Владимир Петрович Ветчинкин (1888—1950). Очерк жизни, науч-
ной, инженерной и педагогической деятельности......963
А. А. Космодемьянский. Жизнь и деятельность
В. В. Голубева...............................943
Список научных трудов В. В. Голубева ...........971