у.сойЕР	ПУТЬ В
СОВРЕМЕННУЮ МАТЕМАТИКУ
W. V/. SAWYER
A PATH TO MODERN MATHEMATICS
PENGUIN BOOKS
HARMONDSWORTH, MIDDLESEX 1969
у. у. СОЙЕР
ПУТЬ
в СОВРЕМЕННУЮ МАТЕМАТИКУ
Перевод с английского
В. Н. Шапкиной
Под редакцией и с предисловием проф. И. К. Андронова
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1972
512
С58
Сойер У. У.
С58 Путь в современную математику. Пер. с англ. В. Н. Шапкиной. Под ред. и с предисл. проф. И. К. Андронова. М., «Мир», 1972.
200 с. с илл. (В мире науки и техники)
Книга «Путь в современную математику» написана в свете тех проблем, которые связаны с обновлением школьного курса математики. Рассматривая отдельные темы современной математики (отображения, матрицы, векторные пространства и др.), которые приобретают важное значение в научной и инженерной практике и поэтому должны быть, по мнению автора, включены в школьные программы, профессор Сойер показывает, как они возникают и развиваются из тем традиционной математики.
Книга найдет многочисленных читателей и среди тех, кто преподает или собирается преподавать математику, и тех, кто ее изучает.
2-2-3
173-72
512
Редакция научно-популярной и научно-фантастической литературы
предисловие редактора перевода
«Путь в современную математику» — не первая встреча советских читателей с известным английским математиком и педагогом У. У. Сойером. В Советском Союзе опубликованы две работы этого талантливого популяризатора математических идей: книга «Прелюдия к математике» (изд-во «Просвещение», 1965) и статья «Алгебра», вошедшая в сборник «Математика в современном мире» (изд-во «Мир», 1967). Перу У. У. Сойера принадлежит много интересных книг, главным образом методологического характера. Круг проблем, которые рассматриваются в них, определяется многолетним опытом автора в области преподавания математики и подготовки учителей средних школ.
У. У. Сойер выступает как горячий поборник реформы сложившегося традиционного содержания и методов преподавания математики. Однако, по его мнению, проведение этой реформы невозможно, с одной стороны, без изучения того, какие достижения математики представят ценность для науки и производства в ближайшее время, а с другой — без решения вопроса, как сделать математику достаточно понятной для учащихся, заинтересовать их и пробудить творческую активность.
В связи с последним особую роль он отводит проблеме подготовки высокообразованных и увлеченных своим делом учителей.
Предлагаемая вниманию читателей книга У. У. Сойера входит в задуманную им серию «Введение в математику» («Introducting Mathematics»). Цель этой серии — дать читателям «существо, квинтэссенцию математической грамоты», сделать
5
математические идеи интересными и понятными самой широкой аудитории. Книга написана в свете тех проблем, которые связаны с обновлением школьного курса математики. Направленность движения за об-н'бвлёние школьных программ отражает призыв «за современную математику», а суть его состоит в стремлении приблизить содержание курса математики средней школы к тенденциям современной математической науки и к запросам практики. Однако решить эту задачу оказалось не так-то просто. Какими темами современной математики, какими понятиями и идеями следует обогатить школьный курс? На какой ступени математического развития это следует сделать и в какой последовательности? С какой степенью строгости и обобщения? Все эти вопросы составляют основную трудность в решении извечной проблемы математического образования — в своем исторически дозволенном отставании не отрываться слишком далеко от достижений математической науки. Как сделать, чтобы система математического образования давала каждому новому подрастающему поколению те основы математических знаний, которые позволили бы ему, освоив математические достижения века, поставить их на службу обществу и развивать дальше, создавая потенциал для новых достижений.
В предлагаемой книге автор делает попытку выделить те ценные конструктивные элементы, которые, по его мнению, должны быть введены в школьную программу. Рассматривая отдельные темы, связанные с недавними открытиями в математике, которые, по общему мнению, могут оказаться особенно важными и приобрести особую значимость в человеческой деятельности и научной практике (отображения, матрицы, векторные пространства и др.), он показывает, что идеи и понятия этих тем возникают и развиваются из идей и понятий традиционной классической математики как их естественное продолжение или обобщение, только на более высокой ступени абстракции. Для нашей советской школы, где реконструкция образования осуществляется постепенно, прежде всего за счет повышения теоретического и логического уровней изучения традиционной математики и обнов
6
ления ее элементами современной математики (посредством факультативных курсов), такая позиция автора представляет особый интерес.
На разнообразных конкретных примерах автор иллюстрирует одну из наиболее часто повторяющихся идей современной математики — алгебра, геометрия и математический анализ охватывают значительно большую область, чем это представлялось ранее. Если прежде сферой приложения алгебры считались в конечном итоге соотношение и свойства чисел, то сейчас общепризнанно, что все виды объектов — операции, перемещения (движения) и т. п. — имеют алгебраическое выражение.
Со свойственной ему изобретательностью автор проводит читателя через векторное пространство (с базой «кошки — собаки»), матрицы, их собственные векторы и подводит его к обсуждению понятия линейности. Этот увлекательный экскурс заканчивается эскизным представлением идей Фреше по обобщению понятия дифференцирования и идей Банаха по обобщению понятия пространства.
Автор не дает систематического изложения материала, как это принято в учебниках, а сообщает лишь ключевые идеи и понятия рассматриваемых разделов математики. При этом он всегда стремится довести до сознания читателя те идеи, которые привели математика к открытию нового понятия, показать ту перспективу, которую сулит его дальнейшее развитие-Книгу выгодно отличают удачно подобранные задачи, наглядно иллюстрирующие приложение рассматриваемых разделов математики. Она адресована весьма широкому кругу читателей, среди которых могут быть и студенты математических факультетов пединститутов, и учащиеся старших классов, которые намереваются продолжить свое математическое образование в высших учебных заведениях, и учителя, размышляющие над проблемами обновления школьного курса математики, и все те, кто интересуется современной математикой.
И. Андронов
ПРЕДИСЛОВИЕ И РУССКОМУ ИЗДАНИЮ
Советским читателям, возможно, будет интересно познакомиться с теми обстоятельствами, которые привели к написанию этой книги.
Запуск первого советского спутника в 1957 году произвел в США огромное впечатление. Поскольку технический прогресс находится в непосредственной зависимости от уровня математического образования молодежи, решено было немедленно внести в систему образования ряд изменений, которые коснулись прежде всего программ по математике. Был брошен замечательный лозунг: «Модернизировать обучение математике!» Однако ошибочная интерпретация зачастую сводила роль этого лозунга к нулю. Власти, преисполненные чувства миссионерского рвения, были в восторге от всего, что проделывалось в этом направлении. Казалось, им невдомек, что Соединенные Штаты Америки были одной из тех немногих стран, которые в 900-е годы не откликнулись на международное движение за реформу математического образования. Поэтому все здание современной математики строилось там на устаревшем фундаменте. А отсюда и модернизация носила поверхностный и неосновательный характер, слов было больше, чем идей. Боюсь, что материальные средства и энтузиазм, отданные пропаганде такой модернизации, не были оправданными, особенно если учесть тот серьезный вред, который эта пропаганда нанесла системам математического образования других стран. В период моего пребывания в Гане я наблюдал пагубность американского влияния в странах Африки.
Надо было дать бой этому искажению необходимой и полезной кампании. И единственно правильную
9
и эффективную тактику этого боя я усматривал в конструктивных предложениях, которые и попытался дать в этой книге.
Особенности, которые накладывает на человека его профессия, в какой-то мере затрудняют общение людей разных специальностей. И поэтому математик, находящийся в центре математической жизни с ее открытиями и достижениями, испытывает некоторое затруднение в общении с учителем, у которого не остается времени для повышения уровня своих знаний. В США эта разобщенность ощущается особенно сильно. Математики, гордые сознанием «чистоты» своего предмета, стали считать физиков низшей кастой, а инженеров просто «неприкасаемыми». Профессора педагогики вели постоянную войну с «академической бесплодностью» и в подготовке будущих учителей насаждали пагубную методику — как передавать знания без ссылки на содержание этих знаний. Вследствие этого в большинстве американских средних школ (иногда вопреки желанию учителей) математика преподавалась в изрядно выхолощенном виде. Учителя не смели, да и не в состоянии были критически оценить указания своих университетских наставников и выступить против них.
Среди влиятельных руководителей школьного образования лишь очень немногие готовы были посмотреть в глаза реальности. Трещины в математическом образовании не устранялись, их просто прикрывали, как прикрывают новыми обоями потрескавшиеся стены. Именно поэтому, особенно на ранней стадии, в движении за реформу упор делался на введение новых терминов, но не идей, усвоение которых требовало времени. Учителя, употреблявшие при каждом удобном случае слово «множество», считали себя пионерами педагогических изысканий. Это слово приобрело такие магические и мистические обертоны, что утратило способность правильно передавать свою суть. Вот почему этот вполне пригодный специальный термин я намеренно не употреблял в данной книге, боясь быть неправильно истолкованным неравнодушными к нему читателями.
Все, что я вынес из знакомства с воображаемым переворотом в математическом образовании.
10
в США, — это сознание того, что я нахожусь в большом долгу перед более ранней революцией в этом области. Реформистское движение, о котором я уже упоминал, в Англии характеризовалось одной особенностью, о которой стоит сказать несколько слов. В движении приняли активное участие учителя, которые по уровню знаний не уступали (а иногда и превосходили) университетским профессорам математики. Это произошло вот отчего. В то время вопрос о всеобщем начальном образовании еще не ставился. Ведущую роль в обучении подрастающего поколения играли частные школы, в которых условия для педагогов были лучше, чем в государственных учебных заведениях. Многие из способных математиков после окончания университета оседали в такого рода школах, предпочитая там должность старшего преподавателя должности ассистента в университете. Эти молодые высокообразованные учителя в течение длительного времени, около 35 лет — с 1867 по 1902 год, вели борьбу за реформу математического образования против университетской оппозиции. Таким образом, ядром движения были люди, объединявшие высокую математическую подготовку с большим опытом преподавания. На встрече в 1902 году, явившейся кульминационным моментом этого реформистского движения, были представители всех специальностей, так или иначе связанных с математикой: инженеры (такие, как Перри), физики (такие, как Хевисайд), учителя, воспитатели и молодые университетские профессора. Общепризнанно, что это выросшее в стенах привилегированных школ движение несло в себе идеи, полезные и для общеобразовательной школы. Дело в том, что, как свидетельствует школьная документация, дети состоятельных родителей, обучавшиеся в пансионатах, как правило, не отличались особой одаренностью, поэтому учителям приходилось искать такие методы преподавания, которые сделали бы математику доступной и понятной учащимся с самыми разными интересами и способностями.
В решении проблемы математического образования ощущается потребность в сильном руководящем и направляющем центре, способном оценить нужды не
11
только науки и производства, но и всего общества в целом. Этот центр должен объединить людей многих специальностей, в том числе математиков, понимающих проблемы обучения, и педагогов, владеющих математикой. В заключение я хочу сказать, что меня восхищает та энергия и энтузиазм, с которыми в настоящее время разрабатываются и внедряются новые школьные программы в СССР. И я буду вполне удовлетворен, если моя книга окажется полезной советским читателям в освещении одной из сторон этой большой проблемы.
Торонто
4 мая 1971 года
У. У. Сойер
ВВЕДЕНИЕ
Очень хорошо, когда с первых страниц читатель получает некоторое представление о содержании книги, ее назначении и степени сложности.
В связи с этим сразу же следует сказать, что настоящая книга может быть полезна учителю, который хотел бы внести новое в преподавание математики ученикам в возрасте от 11 до 18 лет; она может стать пособием для учащихся выпускных классов, а также для учителей, не имеющих специального математического образования и преподающих математику в младших классах. Книга предполагает знакомство читателя с основами математического анализа. Однако это не значит, что матанализ необходим при чтении всех ее разделов. Так, в I и III главах развивается метод, вначале использованный в журнале Scientific American, который если и стоит критиковать, то, по-видимому, лишь за то, что он может показаться по-детски упрощенным. Точно так же значительная часть IX главы была апробирована в школах и оказалась понятной и занимательной для учеников, знакомых лишь с началами алгебры и теоремой Пифагора. В книге, насколько это было возможно, применялся язык элементарной математики. Но можно ли было всю книгу написать в этих рамках? Конечно нет, и вот почему.
Я встречал самые различные способы изложения современной математики, порою весьма загадочные: новое понятие вводилось без всякого пояснения, учащимся не сообщали ни того, откуда оно взялось, ни того, каж с ним обходиться. Они должны были принять на веру, что это математическое понятие очень важно, но всю жизнь так и оставались в неведении
13
почему. Но ведь в математике, как ни в какой другой области, не принимают ничего на веру, здесь всегда требуются доказательства. Вряд ли стоит начинать кампанию за реформу математического образования с «промывания мозгов», после которого учителя, потеряв всякое желание мыслить критически, примут любые изменения, не отдавая себе отчета в том, так ли уж они необходимы. Нельзя утверждать, будто вы обучаете современной математике, если вы попросту «выдернули» несколько новых математических идей и понятий и преподносите их совершенно изолированно, не показывая ни их связей с другими областями математики, ни тех проблем, которые можно с их помощью разрешить, ни тех причин, по которым математики придают им столь большое значение.
Следовательно, при изложении необходимо показать те идеи, которые приводят к новому понятию, и перспективу его дальнейшего развития. Ведь авторы всех решающих математических открытий нашего века были воспитаны на математике прошлого века. Именно она вскормила их воображение. Они стремились осветить те разделы логики, которые XIX век оставил в тени, решить те проблемы, которые XIX век не разрешил, дать строгие ответы на вопросы, которые ранее решены были лишь приблизительно, глубже проникнуть в те области, которые изучались поверхностно, объединить то, что оставалось разобщенным, обобщить то, что трактовалось как нечто частное. Открытие XX века считается тем значительнее, чем больше света оно проливает на проблемы века XIX. Рассказывать о современной математике без всякой ссылки на математику прошлого — это то же самое, что играть третий акт пьесы, не объяснив предварительно, что происходило в первых двух.
Математика XVII — XIX веков насквозь пропитана идеями математического анализа. Конечно, отдельные разделы математики, скажем проективную геометрию или некоторые вопросы теории чисел, можно рассматривать изолированно, не привлекая математический анализ. Но если бы кто-то •захотел изложить историю развития математики между 1’600 И 1900 годами, не прибегая при этом к идеям матема-14
тического анализа, его работа не была бы признана, ибо тогда в каждой цепи причинно-следственных связей неизбежно отсутствовали бы необходимые звенья.
Во многих странах до последнего времени математический анализ в средних школах либо не изучался совсем, либо изучался очень немногими и только в выпускных классах. В таких странах решение проблемы обучения современной математике весьма затруднительно, да и вряд ли возможно. К счастью, Англия в этом смысле составляет исключение. После продолжительных дискуссий и борьбы (еще в 1870— 1920 годы) в колледжах стали преподавать математический анализ. Быть может, обучая наших шестнадцатилетних школьников математическому анализу, лучше не слишком вдаваться в тонкости, хотя некоторые математики именно в них видят сущность анализа. Для наших целей это лишнее. Главное для нас—язык математического анализа. Если читатель знает, что dsfdt связано со скоростью, a dy/dx с наклоном кривой, что интегрирование имеет дело с площадями, а ех связано со сложными процентами и ростом популяции, то такое умение оперировать языком математического анализа очень поможет ему понять затронутые в этой книге вопросы. Разумеется, здесь, как в матанализе, так и в алгебре, вы не встретите каких-то сложных вычислений.
В главе VI вы найдете раздел, который называется «Эрзац математического анализа», где дается объяснение того, как электронно-вычислительная машина умудряется перевести сложные задачи математического анализа на простой язык арифметики. Я не берусь утверждать, что именно таким должно быть первое знакомство с математическим анализом, однако в этом разделе использован такой подход к нему, который должен помочь читателям, давно не сталкивавшимся с матанализом, вспомнить некоторые моменты, имеющие к нему отношение. Моя цель не в том, чтобы навязать идеи математического анализа или, наоборот, игнорировать их. Математический анализ применялся в этой книге именно там, где новое понятие было либо подсказано им, либо тесно с ним связано. Такое решение вопроса может
уменьшить число читателей настоящей книги, но это представляется мне куда меньшим злом, чем стремление порождать из ничего новые концепции, оставляющие читателя в состоянии недоумения.
Необходимость аргументации
Я надеюсь, что, прочитав эту книгу, читатели не просто познакомятся с новыми идеями, но и увидят сферу их приложения. Они смогут сами судить, насколько важны те или иные идеи. Необходимо научить читателя самостоятельно судить о важности того или иного раздела, ибо что важно в одном случае, может оказаться несущественным в другом. Так, крайняя путаница произошла с термином «современная математика», который употреблялся в самых разных, порою противоположных значениях. В частности, он мог вмещать в себя такие понятия:
а)	математические открытия XX века и более ранние работы, подготовившие их. Именно это значение, как я полагаю, имели в виду те, кто первыми употребили термин «современная математика»;
б)	математика, необходимая для науки и техники настоящего и будущего;
в)	изменения в арифметике и других разделах математики, вызванные совершенствованием электронно-вычислительных машин и т. п.;
г)	любой метод обучения математике, недавно изобретенный или популярный в настоящий момент. Кроме того, термин «современная математика» часто без достаточных оснований использовали в качестве броских^ заголовков.
Все эти значения, за исключением последнего, следует иметь в виду при разработке путей математического обучения. При составлении программы мы хотим охватить все известные разделы математики; мы стремимся, чтобы наши ученики могли справиться с достижениями математики в век научно-технического прогресса; мы не считаем нужным, чтобы они тратили время и силы на работу, которую с большим успехом может выполнить машина. Наша цель преподавать им как можно лучше. Действительно повысить уровень математического образования можно
16
лишь в том случае, если принять во внимание все эти соображения, а в нашем быстро изменяющемся мире, где не найдется ни одного человека, достаточно компетентного во всех отраслях знаний, это не так-то просто.
Любой математик должен очень много и упорно работать, чтобы овладеть хотя бы 5% современной математики. При этом вряд ли он сможет быть одинаково сведущ в науке, технике и методике преподавания. Примерно в таком же бедственном положении находятся и другие специалисты. Учителя поставлены перед труднейшей задачей — заимствовать у специалистов и объединить в одно целое разнообразнейшие знания.
Такая задача чрезвычайно сложна, и всякое пренебрежение этой сложностью может принести большой вред.
Еще в то время, когда споры о математическом образовании только начинались, в некоторых странах среди математиков был проведен опрос, что они считают в этой области наиболее важным. При этом, по-видимому, предполагалось, что ответы автоматически послужат материалом, полезным производству и в то же время достаточно привлекательным для обучения детишек. Однако трудно найти свидетельство в пользу этой призрачной гармонии. Напротив, имеются веские основания считать, что все получилось как раз наоборот. Это и понятно, потому что специалисты отличаются друг от друга не только своими знаниями, но также и своей жизненной фило: Софией и тем, что именно они считают важным. Игнорировать это — то же самое, что купить автомобиль по совету человека, который судит о нем лишь’ по окраске.
Чтобы вам не показалось, что я преувеличиваю, приведу цитату из статьи одного из ведущих математиков, который много писал по вопросам современного математического образования, профессора Дьедонне1). Дьедонне жаловался на то, что многие не
!) J. Dieudonne, L’EcoJe francaise moderne des mathema-tiques, Philosophia Mathematics 1, 2 (1964).
17
всегда правильно понимают смысл его высказываний* когда речь идет о прикладной математике или электронно-вычислительных машинах. Свою точку зрения на современную математику Дьедонне объясняет так (курсив Дьедонне):
«Изучение математических проблем постепенно приводит нас к введению понятий, значительно более абстрактных, чем идеи числа или формы,., и заканчивается полным абстрагированием от чувственного мира. Эти новые понятия естественно порождают бесчисленное множество задач, для решения которых мы должны вводить другие понятия, еще более абстрактные. Рой этих понятий неудержимо растет, уходя все дальше и дальше от начал математики в природе, и уводит математиков все более и более от решения проблем, поставленных физиками или инженерами... Поэтому можно сказать, что в принципе современная математика в основе своей не имеет какой-либо утилитарной цели, а представляет собой интеллектуальную дисциплину, практическая польза которой сводится к нулю. Однако может случиться так, что абстрактные идеи однажды найдут неожиданное «применение». Все равно математик в своих исследованиях никогда не руководствуется мыслью о степени, полезности полученных результатов в будущем (что, впрочем, и невозможно предсказать), скорее он руководствуется желанием проникнуть в понимание математического явления, как явления, заканчивающегося на себе самом.
Несомненно, еще очень многие с трудом принимают такую точку зрения. Они всегда хотят, чтобы математика «служила» чему-нибудь, их шокирует мысль, что математика — не более чем «роскошь», которую может позволить себе цивилизация... Математики просто, хотят, чтобы другие признали за ними то же право «на существование», каким обладают, например, астрофизики, палеонтологи или поэты».
№ /
Дьедонне далее утверждает, что сегодня около 80% математиков совершенно не интересуются прикладной стороной своей науки. Я не лишаю профессора Дьедонне свободы выбора и права заниматься чистой математикой. Однако необходимо указать, что технический колледж или высшее учебное заведение с техническим уклоном при выборе программы по математике должны относиться с некоторой осторожностью к советам Дьедонне, так как его оценки и цели не совпадают с их собственными. Похоже, что Дьедонне советует высшему техническому учебному заведению, связанному (как тому и следует быть) с утилитарными проблемами, отвернуться от математики XX века, сообщая учащимся более глубокое знание математики предшествующих столетий, когда представители этой науки еще не слишком оторвались от решения проблем, поставленных физиками и инженерами.
Нельзя не признать, что в словах Дьедонне о современном состоянии математических исследований немало правды. Значительная часть этих исследований не имеет отношения к нуждам ученых, инженеров, экономистов, хозяйственников, социологов и представителей других специальностей, где используется математика. И все же в картине, нарисованной Дьедонне, краски несколько сгущены. Все-таки в современной математике есть моменты, которые представляют интерес как для сугубого практика, так и для чистого математика. Вполне естественно предположить, что некоторые разделы математики XX века станут для инженеров будущего столь же необходимыми и привычными, как неотъемлем от современного инженера математический анализ XVII века.
Цель этой книги — представить те идеи современной математики, которые могут вызвать интерес как у самих математиков, так и у непрофессионалов. Идеи эти тесно связаны с наиболее распространенной в современной математике точкой зрения, которая состоит в том, что алгебра, геометрия и математический анализ находят гораздо более широкое применение, чем это представлялось ранее, когда, например, считали, что алгебра имеет дело только со свойствами чисел. Теперь уже стало общепризнанным, что
Г9
природа операций, движений и т. п. носит алгебраический характер.
Точно так же геометрические представления и процессы, используемые в математическом анализе, могут применяться гораздо шире, чем это считалось в прошлом.
В книге приведено много примеров, которые одновременно помогают понять еще один из наиболее спорных вопросов, связанный с выступлением учителей против изобилия формальных преобразований в курсе алгебры. Учителям не по душе, что дети выполняют десятки изнурительных упражнений с единственной целью — выработать механические навыки в проведении алгебраических операций. В некоторых случаях эта позиция приводит к плачевным результатам: учащиеся не усваивают основных традиционных алгебраических правил. Такие учащиеся окажутся не способными разобраться в ситуациях, возникающих в высшей алгебре, которая имеет ряд аналогий с элементарной.
После того как были написаны несколько глав этой книги, меня поразило, что их содержание имеет непосредственное отношение к данному вопросу. Читая эти главы, можно заметить, что умение с легкостью преобразовывать элементарные алгебраические выражения весьма полезно и для изучения алгебры современной.
Обращение к современной алгебре, конечно, не единственная причина изучения элементарной алгебры. До сих пор многое в науке зависит от способности хорошо и грамотно пользоваться языком простейшей алгебры. И этому должна научить не новая, а старая традиционная математика, уже достаточно хорошо разработанная. Теперь самое время упомянуть о тех проблемах, которые эта книга не рассматривает, но без которых нельзя обойтись, если мы занимаемся вопросами математического образования.
Основная часть книги посвящена математике XX века, которая представляет собой многочисленные ветви на едином стволе старой традиционной мате^ матики. Но недавно появились и новые побеги, идущие от корней этого дерева. Это те разделы математики, которые почти совсем не связаны с традицион
20
ной математикой. Например, математическая логика. Было бы очень полезно дать обзор этих новых разделов, который бы не только охватывал их математическое содержание, но и, насколько это возможно, давал оценку их распространения и влияния в будущем.
Рост автоматизации требует соответствующих изменений в образовании. Научный прогноз в этом направлении был бы также чрезвычайно полезен. Автоматизация позволяет машине заменить человека в любом виде его умственной или физической деятельности, который можно свести к стандартным действиям по строго заданным правилам. Большая часть современной человеческой деятельности поддается такому сведению, но изрядная доля ученического времени тоже уходит на эти шаблонные действия. Такое обучение, очевидно, становится устаревшим. Автоматизация все больше будет вытеснять человека в область творческих профессий, требующих качеств, свойственных исключительно человеку: понятливости, принципиальности, оригинальности, критичности, инициативности. Очевидно, что «автоматизированное общество» предъявит особый спрос на высокоразвитое творческое начало.
Вполне вероятно, что минимальный уровень знаний каждого члена общества будет неуклонно возрастать. Именно это прежде всего должны иметь в виду учителя и все те, кто несет ответственность за обучение подрастающего поколения. Человечество достигло небывалого могущества, позволяющего более чем когда-либо, вторгаться в окружающий нас мир. Хотелось бы, чтобы как можно больше людей осознали это могущество и мудро и умело им пользовались. Человеку 2000 года, несомненно, потребуется гораздо более солидный научный фундамент, чем нашему современнику. Быть может, ему понадобится знакомство с исследованием операций, чтобы принимать рациональные решения при большом разнообразии ситуаций. В его общем образовании некоторые разделы математики несомненно займут свое место. Остается надеяться, что будет проведено исследование всех этих вопросов, а результаты его опубликованы.
21
О сложности и скуке
В обучении игре на фортепьяно есть та первоначальная ступень, когда вы играете только гаммы, которые невозможно слушать. Они вам ужасно надоедают, но ничего другого пока вы исполнить не можете. Эта трудность — явление обычное. То же самое происходит и при изучении традиционной алгебры, когда человеку приходится потратить массу времени на нечто скучное и невдохновенное, пока он не обретет способности заняться какой-нибудь более или менее стоящей задачей. То же самое, конечно, относится и к современной алгебре.
Когда я писал I и II главы, они казались мне прелюдией к драме, где зритель только знакомится с действующими лицами, но они еще не успели привлечь его внимания. Возможно, что читатель прочтет эти главы довольно быстро. Однако полученные в них результаты по мере изложения будут использоваться все больше и больше.
Особо следует оговорить употребление сносок. Одни из них — это ссылки на цитируемые произведения, другие связаны с историей вопроса, третьи призваны разъяснить трудный момент. Кроме того, писать в точных выражениях краткое введение к книге всегда очень трудно. Как правило, автор начинает упрощенно объяснять сложное, прибегая к общим выражениям, а перечитывая написанное, старается уточнить его дополнительными описаниями. В результате предисловие утрачивает краткость, становится громоздким и трудным для понимания. Чтобы избежать этого, я и тут прибегал к сноскам. Я давал сноски и в тех редких случаях, когда критически настроенный читатель мог бы возразить. Некоторые из сносок IV главы выполняют функцию приложения. Они содержат вычисления, которые не имеют существенного значения для изложения основного материала, и потому читатель может себя ими не утруждать.
Обозначения
Существуют два способа обозначения функции: старое,, традиционное, и новое, современное. Если сле^ 22
довать традиционному обозначению, то можно вызвать недовольство тех, кто с большим трудом приспособился к новому. Если пользоваться только новым обозначением, то сторонники традиционности в этом вопросе должны будут не просто изучать новые идеи, а изучать их, так сказать, на иностранном языке. Попытка объединить оба способа привела к излишнему многословию, и я почувствовал, что должен придерживаться чего-нибудь одного. Я выбрал традиционный способ. Возможно, что этот рискованный шаг только подольет масла в огонь. Известный математик, профессор Хочшильд, рецензируя книгу профессора Якобсона по алгебрам Ли, резко писал: «На странице 290 введено условное обозначение, основанное на варварском принципе смешения функции с одним из ее значений». А ведь мы все были воспитаны на этом принципе. Именно это обозначение использовали Конт!) и Лебег* 2). Мы говорим, например, о функции х2 или функции f(x). Я должен предупредить читателей, воспитанных на более современной терминологии, чтобы они относились к подобным выражениям, встречающимся в этой книге, как к своего рода сокращениям. В пользу традиционного обозначения и терминологии у меня были следующие соображения:
1)	Я не верю, что в математике можно мыслить по-разному. Если попросить сторонника традиционного способа обозначений начертить график х2 и обратиться с той же просьбой, но в несколько других терминах к приверженцу нового способа, то оба они начертят одну и ту же параболу. Слова различны — понятия одинаковы.
2)	Неудобство применения традиционной терминологии проявляется только на более высоком уровне изучения математики. Поэтому вполне естественно, когда такой ученый, как Хочшильд, выступает против традиционной системы, но для школьника, изучающего дифференциальное и интегральное исчисление, она вполне приемлема. И в этой книге затруднения появляются лишь в X главе, последнем ее
’) С a u n t, Infinitesimal Calculus.
2) А. Лебег, Интегрирование и отыскание примитивных функций, М. — Л., изд-во «Техническая литература», 1934.
23
разделе. В конце этой главы обсуждается не только проблема нового обозначения, но и причина его введения.
3)	Чтобы развивать математику дальше, надо свободно владеть как старой, так и новой символикой.,
В очень интересном учебнике Симмонса !), а также в «Основах современного анализа» Дьедонне* 2), имеющих более специальный характер, используется новое обозначение. В серьезном исследовании Э. Хилле3) автор следует традиционному обозначению. Традиционные обозначения использует и Смирнов в своей многотомной работе «Курс высшей математики»4), рассчитанной главным образом на физиков.
Если Лебег, Хилле и Смирнов способны мыслить о современной математике в старой терминологии и обозначениях, что наиболее привычно для большинства читателей, то это служит мне достаточным оправданием, ибо моя книга не более чем введение в мир идей современной математики. Нельзя забывать, однако, что каждому, кто захочет более глубоко изучить современную математику, придется овладеть новой терминологией и обозначениями.
J) G. F. Simmons, Introduction to Topology and Modern Analysis, McGraw-Hill, 1963.
2) Ж. Дьедонне, Основы современного анализа, изд-во «Мир», 1964.
з) Э. Хилле, Р. С. Филлипс, Функциональный анализ и полугруппы, М., ИЛ, 1962.
4) В. И. С м и р н о в, Курс высшей математики, изд. 22-е, изд-во «Наука», 1967.
ГЛАВА I
арифметика пространства
Если мы предложим ребенку такие вопросы, как: «Сколько будет, если к 1 кошке и 2 собакам прибавить 3 кошки и 1 собаку?» или «Сколько получится, если количество из 2 кошек и 1 собаки увеличить в 3 раза?» — то вряд ли они вызовут у него затруднения. Сами по себе эти вопросы могут показаться слишком примитивными, однако на самом деле они помогают значительно облегчить понимание геометрии.
Если обозначить совокупность животных, упоминаемых в первом вопросе, через А и В, то его решение можно записать в виде
। А — 3 кошки и 1 собака ’ В = 1 кошка и 2 собаки
С = 4 кошки и 3 собаки
Третья строка получена сложением первых двух, поэтому мы пишем С = А + В. На рис. 1 это решение представлено на листке из тетради «в клеточку». Точка А с координатами (3, 1) представляет 3 кошки и 1 собаку, аналогичный смысл имеют точки В и С.
На рисунке видно, что точки О, Д, В, С являются вершинами параллелограмма. Можно проверить экспериментально, что это же произойдет при любом другом выборе чисел. (В исключительных случаях точки О, А, В могут оказаться на одной прямой, и тогда параллелограмм, как бы становясь «тонким», вырождается в отрезок.) Связь между сложением и параллелограммами известна тем, кто изучал механику: по правилу параллелограммов складываются силы и скорости.
25
Посмотрим теперь, как наш второй вопрос, связанный с умножением, выглядит на бумаге в клеточку.
^,Р — 2 кошки и 1 собака X	3
= 6 кошек и 3 собаки
Эти вычисления показывают, что R — ЗР. Графически этому решению соответствуют точки О, Р и R (рис. 2), расположенные на одной прямой таким образом, что точка R находится в три раза дальше от точки О, чем точка Р.
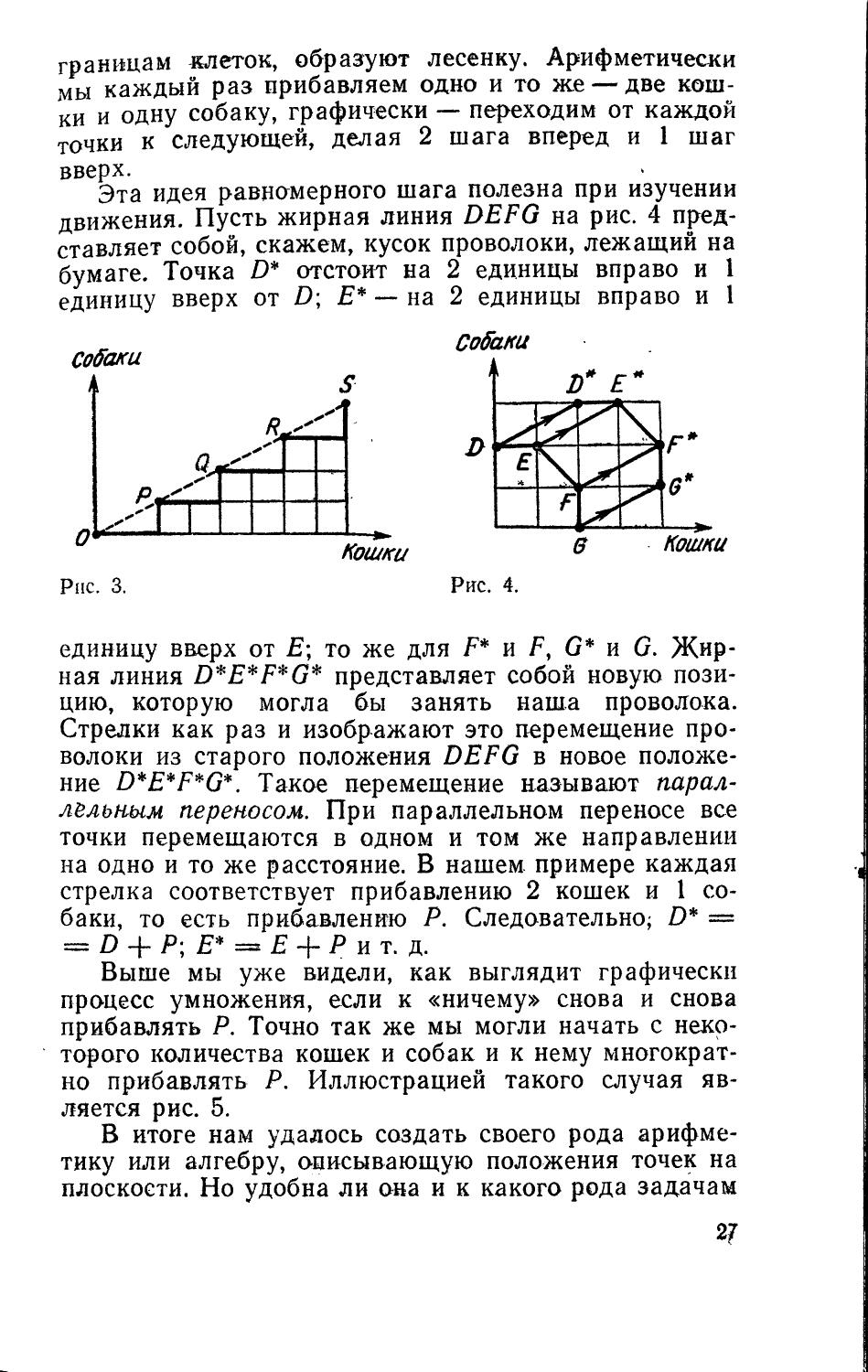
Умножение сводится к повторному сложению, и это поможет нам представить его графически. Начнем с того, что к «ничему» будем последовательно прибавлять по 2 кошки и 1 собаке. Вычисление будет выглядеть так:
I 0 кошек и 0 собак ~ О .	2 кошки и 1 собака
। 2 кошки и 1 собака — Р '2 кошки и 1 собака
। 4 кошки и 2 собаки = Q = 2Р
** 2 кошки и 1 собака
1	6 кошек и 3 собаки = R — ЗР
2	кошки и 1 собака
8	кошек и 4 собаки — S — АР
Результаты обозначим соответственно точками О, Р, Q, R, S и нанесем их на листок в клеточку (рис. 3). Отрезки, соединяющие эти точки и проходящие по 26
границам клеток, образуют лесенку. Арифметически мы каждый раз прибавляем одно и то же — две кошки и одну собаку, графически — переходим от каждой точки к следующей, делая 2 шага вперед и 1 шаг вверх.
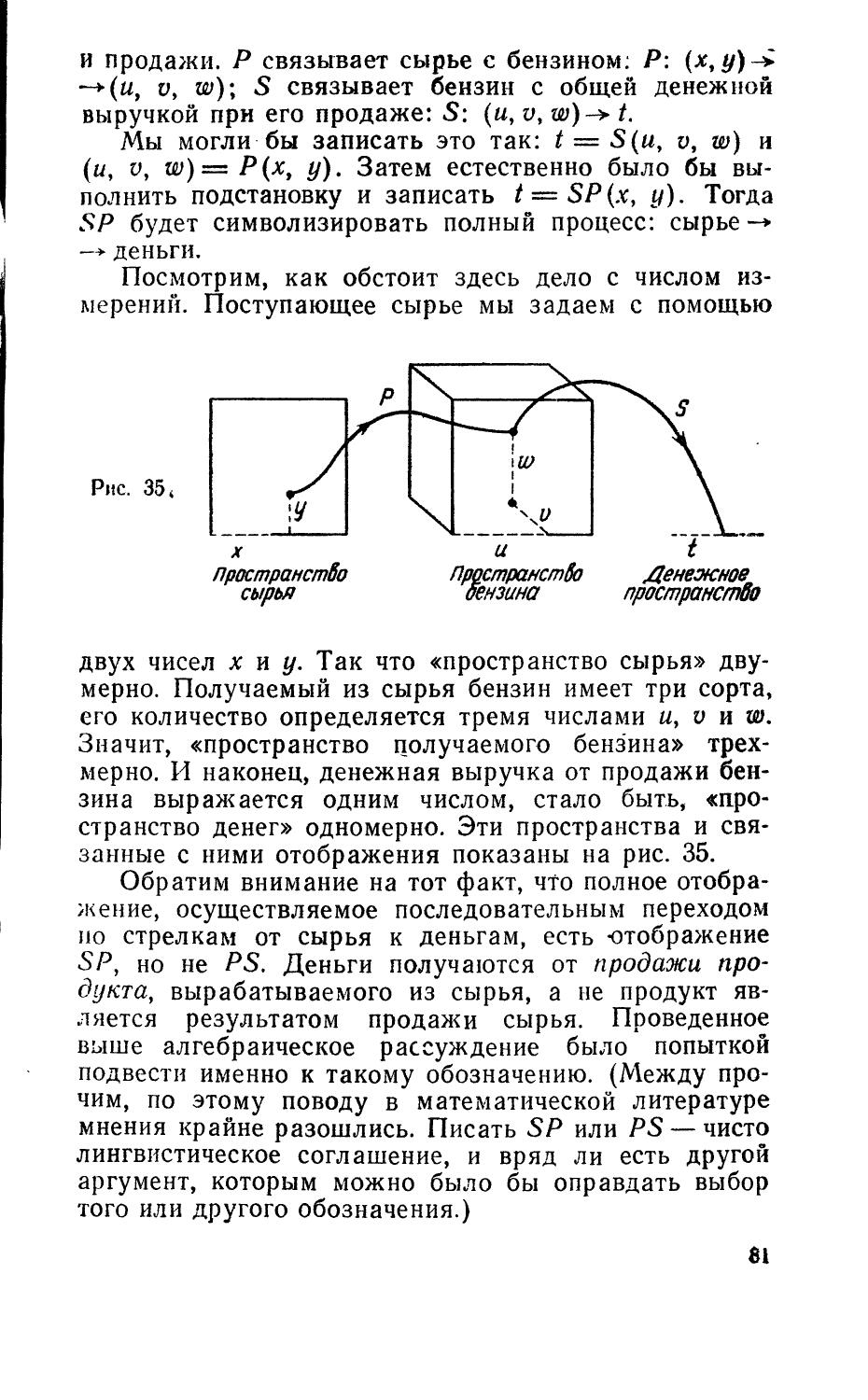
Эта идея равномерного шага полезна при изучении движения. Пусть жирная линия DEFG на рис. 4 представляет собой, скажем, кусок проволоки, лежащий на бумаге. Точка D* отстоит на 2 единицы вправо и 1 единицу вверх от £>; Е* — на 2 единицы вправо и 1
Собаки
Рис. 4.
единицу вверх от Е\ то же для F* и F, G* и G. Жирная линия d*E*F*G* представляет собой новую позицию, которую могла бы занять наша проволока. Стрелки как раз и изображают это перемещение проволоки из старого положения DEFG в новое положение D*E*F*G*. Такое перемещение называют параллельным переносом. При параллельном переносе все точки перемещаются в одном и том же направлении на одно и то же расстояние. В нашем примере каждая стрелка соответствует прибавлению 2 кошек и 1 собаки, то есть прибавлению Р. Следовательно; D* = — D + Р\ Е* = Е Р и т. д.
Выше мы уже видели, как выглядит графически процесс умножения, если к «ничему» снова и снова прибавлять Р. Точно так же мы могли начать с некоторого количества кошек и собак и к нему многократно прибавлять Р. Иллюстрацией такого случая является рис. 5.
В итоге нам удалось создать своего рода арифметику или алгебру, описывающую положения точек на плоскости. Но удобна ли она и к какого рода задачам
27
применима? На рис. 5 точки К, К. + Р, К + 2Р и т. д. напоминают следы человека, идущего равномерным шагом в одном направлении, так как они расположены на одной прямой и на одинаковом расстоянии друг от,друга. Это наводит на мысль, что нашу алгебру можно использовать в задачах, где речь идет об отрезках прямых, разделенных на равные части. До сих пор под символом Р мы понимали «2 кошки и 1 собаку». Теперь же под Р удобнее будет понимать
любое количество кошек и собак, которое подойдет для решения задачи. Наши задачи будут формулироваться так: даны две точки К и L; каким должен быть шаг Р, чтобы через определенное число таких шагов попасть из точки К в точку L?
Вот простейшая задача такого рода: найти формулу для средней точки М отрезка KL. Поскольку положение точек К и L задано в терминах числа «кошек и собак», то и положение точки М мы будем определять в этих же терминах.
Если на пути из точки К в точку L мы сделаем 2 шага, то как раз пройдем через точку М. Поэтому шаг Р выбираем так, чтобы точки К, К. + Р, К + 2Р совпали соответственно с точками К, М и L. Но где взять информацию, необходимую для того, чтобы найти Р? Мы не получим ее, глядя на первую точку (рис. 6), так как это просто даст нам К — К.. Не получим мы ее и глядя на вторую точку, так как М пока неизвестна (скорее, именно Р поможет нам найти М). А вот третья точка дает нам равенство 1 = = К + 2Р. Решив его относительно Р, имеем Р = 28
== !/2£— ЧгК. Так как М = К + Р, то после подстановки Р получим, что М = К + С/2Р — Ч2К) = V2K +
7гЬ. (Кстати, результат показывает, что М является средним арифметическим К и L.)
Пусть, например, требуется найти середину пути между точками (2, 1) и (8, 3). В принятых нами терминах К = 2 кошкам и 1 собаке; L = 8 кошкам и 3 собакам. Поэтому 1/2К — 1 кошке и V2 собаки, i/2L = 4 кошкам и - В/2 собаки. Тогда М = Х)2К -Н +	— 5 кошкам и 2 собакам. Теперь вернемся к
нашей бумаге в клеточку. Точка (5, 2) есть искомая середина М.
<•) известное
• неизбестное
Рис. 6.
Позволив себе говорить о половине собаки, мы допустили некоторую вольность, в дальнейшем мы усугубим эту вольность, используя такие понятия, как —3 кошки. Разумеется, обращение к животным не следует принимать всерьез. Животные использованы здесь с целью: 1) показать, что рассматриваемые идеи просты и вполне доступны даже детям, 2) создать ситуацию, в которой сложение и умножение овеществлены и имеют естественный смысл, и 3) запастись выражениями типа «сложение кошек и собак», которыми в дальнейшем удобно было бы оперировать.
Формула для середины отрезка позволяет доказать хорошо известный геометрический факт, что диагонали параллелограмма в точке пересечения делятся пополам. Для простоты предположим, что одна вершина параллелограмма лежит в точке О, а другие —-в точках Л, В и С, как показано на рис. 7. Из сказанного выше («сложение кошек и собак» всегда соответствует параллелограмму) следует, что С — А + В. Нам нужно показать, что середина ОС совпадает с
2»
серединой АВ. Для этого подсчитаем их по только что выведенной формуле М «= 1/2К 4- ’/гЬ.
Середина АВ определяется как ’/И 4- ’/г#; середина ОС — как V2O 4* ‘/гС, или просто ЩС, так как точка О означает нуль кошек и нуль собак. Но С — = А + В, откуда V2C == 11%А 4- i/zB, то есть середины ОС и АВ совпадают. Теорема доказана ‘)-
Деление отрезка на любое число частей
Проведенное выше рассуждение легко применить и к решению других аналогичных задач. Допустим, мы хотим получить формулу для точки 3, находящейся на отрезке KL на расстоянии 3/4 всего отрезка от точки К.
В этом случае мы достигаем L, сделав из точки К в направлении точки L 4 шага, каждый длиной Р, то есть L = К 4- 4Р (рис. 8). Отсюда P — ^^L— К). Подобным образом легко определить и точки Q, Р и 3. Так, в частности, найдем, что 3 = К 4" ЗР — К 4-+ (3/4£ — 3/tK) = '/Ji. + 3liL. Легко догадаться, каким получился бы результат, если вместо 3/4 взять другую дробь. Обратим внимание на то, что 3/4 превращаются в коэффициент при L, а у К. появляется коэффициент */*, который равен (1 — 3/4).
Упражнения
1. Догадайтесь, какими будут формулы для точек, находящихся на отрезке KL на расстоянии % и всего отрезка от точки
!) Более общий результат можно было бы точно так же доказать, рассматривая параллелограмм с вершинами в точках КУК + А,К + В}К + А + В.
30
К. Проверьте свою догадку, проведя полное рассуждение (получив и решив уравнения относительно Р).
2. Найдите общую формулу для точки, находящейся на отрезке KL на расстоянии т/п всего отрезка от точки К.
Медианы
Рассмотрим следующий случай. Даны три точки А, В и С (рис. 9); точка D — середина ВС. Найти формулу для точки G, находящейся на AD на расстоянии УзАй от точки А. Полученные выше результаты (включая и упражнения) позволяют свести все решение задачи к стандартным вычислениям. Точка G находится на расстоянии 2/зАй от точки А, следовательно, G = */3А + 2/з£>; D — середина ВС, значит, D = =	+ '/гС. Подставляя второе выражение в пер-
вое и упрощая его, находим G = 1/зА + 2/з(1/з^ L+'/2С) = 7зД+ 1/3ВН-.'/зС.
Ответ симметричен, то есть совершенно одинаков по отношению к А, В и С, несмотря на то что условие формулировалось относительно точки А. Следовательно, если бы мы отправились из В в точку, находящуюся на расстоянии 2/3 пути от В к Е (середине АС), то попали бы в ту же самую точку G. Аналогичное заключение можно сделать и относительно точки С. Фактически точка G, как показано на рис. 10, лежит на каждой из медиан AD, BE и CF и отсекает от каждой из них одну треть. Точка G, конечно, известна в механике как центр тяжести треугольника АВС, или центр тяжести равных масс, помещенных в точках А, В и С.
Только что проведенное доказательство существования общей точки отрезков AD, BE и CF проще любого из доказательств евклидовой, геометрии,
исключая разве доказательство с помощью теоремы Чевы. Но ведь она так поздно пришла в евклидову геометрию!
Мы можем заметить, что всякая работа, основанная на нашем методе, будет обязательно простой, так как операции, которыми мы пользуемся, — это исключительно сложение и умножение на число. Сколько бы мы их ни повторяли, они никогда не приведут к по-настоящему сложным алгебраическим выражениям. Мы всегда будем иметь дело с выражениями первой степени, встречающимися в начальной алгебре при выполнении упражнений вида «к 4х 4-4* 5у 4- 8г прибавить 2х + Зу — 2» или «5х 4- 4у — Зг умножить на 7». Эти алгебраические вычисления легко интерпретируются геометрически. Нашим основным инструментом служит тот факт, проиллюстрированный на рис. 5, что точки К, К 4- Р, К 4- 2Р, К 4- ЗР,... лежат на одной прямой на одинаковом расстоянии друг от друга. Таким образом, для любых трех точек U, V и W (заданных на языке «кошек и собак») можно определить, лежат ли они на одной прямой или нет. Если лежат, то можно найти отношение расстояний UV и VW.
В книге «Прелюдия к математике»4) мне пришлось прибегнуть к воображаемому существу, лишенному какого-либо физического опыта. У этого существа восприятие геометрии основывалось исключительно на знании арифметики, так как оно лишено было способности видеть и осязать. Здесь мы также введем в геометрию существо, не имеющее геометрического опыта. За основу возьмем рассматриваемый метод, согласно которому точка определяется как «х кошек и у собак», или коротко (х, у). Результаты, полученные в этой главе, мы используем как определения. Середина отрезка АВ определяется как 1/%А 4- '/гВ, точка отрезка АВ, находящаяся на расстоянии % от А, как ’ДЛ 4-4- 3/tB и, наконец, точка, делящая АВ в отношении //(1 — t), определяется как (1 — t)A 4- tB, где Р лежит между 0 и 1. (Это определение дается на основании результатов упражнений на стр. 30.)
‘) У. У. Сойер, Прелюдия к математике, М., изд-во «Просвещение», 1965.
32
Располагая этими данными, существо уже в состоянии вести исследование плоскости арифметическими методами. Если мы спросим его, что примечательного оно может сказать о точках А, В, С, D, Е, F, G, Н, /, где А = (1, 1), В = (2, 1), С = (3, 1), D = = (1, 2), Е = (2, 2), Е= (3, 2), 6= (1, 3), Н = = (2, 3), / = (3, 3), то оно сообщит нам, что точка В — середина АС, точка D — середина AG, точка Я — середина GI, точка F — середина CI, а точка Е — одновременно середина отрезков А/, DF, GC и НВ.
В справедливости сказанного можно убедиться, нанеся эти точки на листок в клеточку. Для существа эти суждения будут иметь* чисто формальный, арифметический характер, ибо оно не только не может изобразить их на бумаге, но даже не представляет себе, что такое тетрадь в клетку. Однако метод, которым располагает наше существо, позволяет ему производить расчеты и делать вполне разумные геометрические утверждения. Но сможет ли существо построить с помощью этого метода всю евклидову геометрию? Противники доказательства методами аналитической геометрии будут убеждены, что нет. Алгебра же этой главы слишком примитивна, чтобы справиться с такой задачей. Метод «кошки — собаки» даже не упоминает о таких понятиях, как «длина отрезка», «перпендикулярные прямые», которые играют большую роль в евклидовой геометрии. До сих пор на всех наших рисунках «ось собак» была перпендикулярна «оси кошек» и обе оси делились на отрезки одинаковой длины. Это не имеет никакого отношения к математике — просто мы привыкли именно к такой разновидности бумаги в клеточку и, как правило, имеем ее под рукой. Действительно, почему бы собакам и кошкам быть «перпендикулярными друг другу» или иметь «одинаковую длину»? На рис. 11 даны три различные иллюстрации
2 Зак. S1
33
расположения точек А, В, С, D, Е, F, G, Н, I, о которых нам сообщило существо. В случае а «оси собак и кошек» взаимно перпендикулярны, в.случаях бив — нет. В случае .а интервалы по «оси кошек» такие же, как и по «оси собак»; в случае б они длиннее, а в случае в короче. Однако каждый из трех рисунков одинаково хорошо иллюстрирует высказывания нашего существа. На любом из них В — середина АС, Е — середина GC и т. д.
Углы без размера
Нередко некоторые суждения, встречающиеся в математических теориях, ставят нас в затруднительное положение. Так, когда речь идет о двух прямых, мы, не смущаясь, можем спросить, как велик угол между ними. Однако ответ, что он не имеет размера, нас, естественно, озадачит. Есть два пути справиться с этой трудностью. Первый я назову аксиоматической точкой зрения, второй — подходом с позиции Эрлангенской программы.
Аксиоматическая точка зрения предполагает, что нам даются исходные положения, из которых следует вывести все следствия. Эти исходные данные вместе со следствиями составляют содержание математической теории. У нашего существа тоже есть исходные положения, позволяющие ему делать определенные геометрические суждения. Однако ни одно из этих суждений не позволяет ему различать случаи а, б и в, представленные на рис. 11, потому что им соответствуют одни и те же алгебраические уравнения. Например, в каждом из этих случаев мы имеем A A-B=F; Е = 24, В + D = 1. Любое из этих уравнений, справедливое для а, будет справедливо и для б и в, хотя соответствующие им рисунки отличаются как углом, под которым нанесена сетка, так и отношением длин АВ и AD. Дело в том, что в теории, развивающейся лишь на базе той. исходной информации, которой .располагает существо, этих углов и отношений как .бы вовсе не существует.
Прежде чем перейти ко второму методу рассуждения, полезно отметить, что в случае параллельного расположения отрезков существо может сравнивать
34
их длины. Так, уравнения Н = D + А и I = А + 2А (рис. 11) в ранее принятой нами терминологии означают, что из D в Н можно попасть, сделав шаг А, а из А в / - сделав два таких шага. Исходя из этого, существо может оценить, что путешествие из А в / вдвое длиннее путешествия из D в Н. Оно фактически располагает материалом, достаточным для доказательства имеющей здесь место теоремы Евклида: отрезок прямой DH, соединяющий середины сторон GA и G1 треугольника AGI, параллелен основанию AI и равен его половине. Однако существо не может сравнивать длины непараллельных отрезков. Так, суждение «AD составляет половину АС» для него лишено смысла. На самом деле оно верно лишь для случая ст, а в случаях б и в оно ложно.
Эрлангенская программа
Аксиоматическая точка зрения достаточно четко определяет математический предмет, но делает это до некоторой степени формально. Как уже указывалось выше, при аксиоматическом подходе нам дают набор утверждений и предлагают извлечь из него логические следствия. При этом может оказаться, что сами по себе исходные утверждения не стимулируют наше воображение и мы не знаем, как к ним подступиться: Нам бы хотелось иметь какой-то способ, позволяющий видеть, что мы делаем. Но здесь-то мы и встречаемся с затруднением. Если прибегнуть к рисункам, то появляется опасность показать на них слишком много: передать то, чего не содержала первоначальная информация.
Тот предмет, который развило наше существо, принято называть аффинной геометрией1)- В аффинной геометрии, как мы обнаружили, не существует прямых углов, а длины могут сравниваться только при
’) По аналогии с евклидовой геометрией, созданной великим математиком Евклидом, кто-нибудь может предположить, что аффинная геометрия является результатом творчества некоего математика по имени Афф. Но это не так. Слово, «аффинный» происходит от слова «аффинность», которому Эйлер в 1748 году придал значение специального технического приема, когда писал о «подобии* и аффинности» кривых.
2*
35
определенных условиях. Окружающий нас мир нашел свое очень близкое отражение в евклидовой геометрии: повсюду мы видим прямые углы и длины. И чтобы почувствовать, ощутить смысл аффинной геометрии, мы должны найти какой-то способ избавиться от части той информации, которая дается нам органами чувств.
Существенный намек на то, как это сделать, кроется в рис. 11. Вообразите, что, едва мы выполнили рисунки на бумаге в квадратную клеточку, соответствующей случаю а, как кто-то, проходя мимо, исказил бумагу так, что квадраты стали параллелограммами, как в случаях б или в. При этом одни свойства фигур нарушаются, другие сохраняются. Только те свойства, которые остаются неизменными при таком искажении, и относятся к аффинной геометрии. Можно доказать, что наше существо способно узнать любое из свойств, «выживших» при таком искажении, и выразить его на языке той алгебры, которой оно располагает. Дозволенные в данной ситуации искажения представляют собой комбинацию из следующих операций: а) изменение масштаба по «оси кошек», в) изменение масштаба по «оси собак», с) изменение направления осей. Можно определить допустимые искажения и по-другому: искажение допустимо, если точки прямой оно переводит в точки прямой и параллельные прямые — в параллельные. Фактически аффинная геометрия может быть построена из двух понятий: прямая линия и параллельность.
С аксиоматической точки зрения исходные положения, приводящие к аффинной геометрии, составляют часть тех исходных положений, которые приводят к евклидовой. Так что каждая теорема, которую можно доказать в аффинной геометрии, необходимо является и теоремой евклидовой геометрии. Но не все теоремы евклидовой геометрии справедливы в аффинной геометрии.
Аффинная геометрия много проще евклидовой, поэтому всякий раз, когда теорема принадлежит аффинной геометрии, ее стоит доказывать аффинными методами, так как они менее громоздки. Мы можем легко определить, принадлежит теорема аффинной геометрии или нет, применяя перечисленные выше искажс-36
ния; Всякая теорема, которая все еще остается верной после любого из дозволенных искажений фигуры, является теоремой аффинной геометрии. Заметим, что все теоремы этой главы выдерживают такое испытание, поскольку они доказаны средствами алгебры «кошки — собаки».
Уже в XIX веке выделились и получили самостоятельное развитие различные геометрии: евклидова, аффинная, проективная, инверсная, неевклидовы геометрии Больяи — Лобачевского и Римана. Следовательно, уже тогда был собран значительный материал1 для исследования различных геометрий. В основу классификации геометрий был положен принцип, сформулированный Феликсом Клейном в знаменитой Эрлангенской программе, изложенной им в лекции, которую он прочитал в 1872 году по случаю вступления в должность профессора Эрлангенского университета.
Согласно одной из основных идей Клейна (выраженной, правда, в его лекции в несколько иной форме!), вид вашей геометрии определяется теми преобразованиями, которые вы позволяете делать над своими рисунками. В этом смысле географию можно было бы отнести к наиболее ограничительной из всех геометрий, так как вы не можете изменять в ней ни расстояния, ни направления, если не хотите нарушить истинности ваших утверждений.
В-евклидовой геометрии вы можете быть менее придирчивы. Вас не особенно расстроит, если, например, при печатании вашего рисунка, иллюстрирующего какое-либо свойство, изменят его масштаб, поместят рисунок в-другом месте страницы, повернут его на какой-то угол или, наконец, напечатают не сам рисунок, а его отражение в зеркале. Во всех случаях рисунок будет одинаково правильно иллюстрировать рассматриваемое свойство. Заметим, что все это можно делать и в аффинной геометрии в дополнение к ранее рассмотренным искажениям1). Проективная
, ’) В нашей алгебре «кошки — собаки» точка О стоит вместо «ничего» и занимает особое положение: мы не можем изменять начало О. Поэтому можно сказать, что алгебра этой главы соответствует чуть более ограничительной аффинной геометрии, в которой не разрешены параллельные переносы,
37
геометрия допускает еще большую свободу искажения: например, вы можете заменить фигуру ее фотографией, сделанной под косым углом. И наконец, меньше всего ограничений имеется в топологии (которую во: времена Клейна называли по-латыни analysis situs — геометрия положения). Она разрешает как угодно растягивать фигуру, мять ее, не допуская лишь разрывов. Топологическое свойство при этом не нарушится. В топологии, например, вы не можете отличить треугольник, квадрат и круг, так как на достаточно эластичной пленке каждый из них может быть деформирован в любой другой.
Эрлангенская программа далеко не исчерпывается: этими замечаниями. Нашей целью было лишь показать два подхода к такому предмету, как аффинная геометрия: один логический, который строится на аксиомах, другой — иллюстративный, наглядный. При: наглядном способе аффинная геометрия получается из евклидовой, если разрешить в ней искажения, устраняющие нежелательные и не относящиеся к делу свойства рисунка. Последний прием позволяет пользоваться рисунками, не опасаясь того, что в наше мышление незаконно прокрадется информация, не оправданная аксиомами;
Изменение осей
Мы уже убедились, что условие взаимной перпендикулярности осей на бумаге в клеточку вовсе не является для них обязательным: любые две пересекающиеся прямые могут служить осями. И если двоим людям предложить, чтобы они покрыли плоскость сеткой параллелограммов, соответствующих бумаге в клеточку, то они могут выбрать совершенно различные системы. Сложно ли будет при этом перевести данные, записанные в одной системе, в форму, понятную для другой? На первый взгляд это Может показаться трудным. Однако на деле задача решается достаточно просто с помощью элементарной алгебры.
На рис. 12 изображены две системы. Оси одной системы помечены словами кошки и собаки. В этой системе любая точка определяется как «х кошек» и «у
33
€вбак», или для краткости xc + yd*). Оси другой системы помечены словами КОШКИ и СОБАКИ, и любая точка в ней будет определяться как «X КОШЕК» и «У СОБАК», или коротко ХС + YD. Строчные. буквы относятся к первой системе, прописные — ко второй. Быть может, это и не справедливо по отношению к первой системе, так как точки плоскости так-
же помечены прописными буквами F, И, Е, М, К, J, N, L, хотя их можно рассматривать в обеих системах.
Точка Ее запись в первой системе Ее запись во второй системе
С	Зс + d	С
Е	6c + 2d	2С
D	с -f- d	D
F	2с + 2d	2D
М	Зс -4" 3d	3D
11	4c + 2d	C + D
J	7c + 3d	2C + D
Сравнивая обозначения в таблице, замечаем следующее. Точка D соответствует с + d\ 2D соответствует 2с -|- 2d, то есть вдвое большему количеству; 3D соответствует Зе + 3d. Если это не случайное совпадение, то мы можем найти эквиваленты точек 4D, 5D,
*) В применении малых -букв для обозначения осей автор следует вербальной алгебре. То есть «ось кошек» и «ось собак» он обозначает соответственно начальными буквами английских слов cat (кошка) n dog (собака). — Прим. персе.

6D и т. д.» вовсе не прибегая к бумаге в клеточку. Так, 6D должно соответствовать 6с + 6d. Тот же эффект мы наблюдаем и для точек С и 2 С. Фактически дело обстоит так, как показано на рисунке. Если D обменивается на с + d, то 2D на 2с 4- 2d, 3D на Зс 4- 3d и т. д. А как используется эта идея в том случае, если мы одновременно рассмотрим С и Z)? Поскольку С обменивается на Зс d, a D на с + d, то следует ожидать, что С + D обменяется на сумму 4с 4- 2d. Так оно и есть на самом деле. Данные в таблице, относящиеся к оставшейся точке /, также полностью согласуются с установленным методом вычисления.
Эти результаты совпадают с нашей геометрической интерпретацией сложения и умножения. Рассмотрим точку 4С + 5Z), в которую мы попадаем, сделав из начала 4 шага С, а затем 5 шагов D. В первой системе точка С выражается как Зс + d, поэтому 4 шага С означают прибавление 12с + 4d; аналогично, поскольку D выражается как с + d, то 5 шагов D означают прибавление 5с + 3d. В итоге получим 17с -\-9d.
Алгебраически вычисление 4С + 5D сводится к простой подстановке: С = Зс + d\ D — с 4- d. Следовательно, 4С + 3D = 4(3с + d) +.5 (с + d) = 17с 4" 9d.
Все проделанное с 4С + 3D мы могли бы применить к любой точке ХС + YD, найдя при этом, что ХС + YD = Х(3с + d) '+ У(с + d) = (ЗХ + Y)c + + (X + Y)d. Если эта точка выражается в первой системе как хс 4“ yd, то должны выполняться равенства
x = 3X-\~Y,	(1)
У-X+Y,	(2)
которые указывают нам правило перехода от координат точки (X, У) во второй системе к ее координатам (х, у) в первой системе.
Иногда нужно сделать обратный переход: зная (х, у), найти (X, У). Для этого достаточно решить уравнения (1) и (2) относительно X и У. В итоге получим
Х = ±х-^у,	(3)
К =	(4)
40
Сейчас мы уже в состоянии переводить утверждения с языка одной системы на язык другой, что часто бывает необходимо. Нередко случается так: начав решение задачи при одном расположении осей, в процессе решения мы замечаем, что при другом их расположении все было бы гораздо проще, поэтому мы меняем оси. Такая замена используется, например, при решении задачи из механики, в начале IV главы.
Некоторые старые книги по аналитической геометрии создают впечатление, что очень трудно работать в косоугольной системе, другими словами, если оси не взаимно перпендикулярны. В этих книгах изложение всегда ведется вначале в перпендикулярных осях, а если появляется косоугольная система, то привлекается тригонометрия. Хотя на рис. 12 обе системы косоугольны, нам удалось перейти от одной системы к другой, даже не упоминая о тригонометрии. При этом мы не использовали ничего более сложного, чем линейные выражения и решение системы двух линейных уравнений, да и то в самом конце.
Обобщение
В настоящей главе мы начали с того, что рассмотрели совокупности кошек и собак. Естественно возникает вопрос, почему мы ограничились двумя видами животных? Можно ли провести вычисления с тремя, четырьмя, пятью или, наконец, с любым нужным числом видов животных?
Сначала мы совершали какие-то арифметические или алгебраические действия, а затем давали им образное истолкование.
Очевидно, увеличение числа видов животных не вызовет больших изменений в алгебре. Прибавление 5 кошек, б собак и 7 поросят к 2 кошкам, 3 собакам, 4 поросятам не приведет к новой задаче или к появлению существенно новых черт. Совсем иначе обстоит дело с геометрической, наглядной иллюстрацией. Когда мы берем три вида животных, п = 3, то еще можем наглядно представить ситуацию, перейдя к трехмерному пространству и направив «ось кошек», скажем, на восток, «ось собак» на север, «ось поросят» вверх. Однако при п = 4 все наши попытки проиллю-
41
етрировать ситуацию графически терпят неудачу. Дело в том, что физическое пространство, в котором мы живем, трехмерно и не подходит для иллюстрации сложений более чем трех видов животных. Чем должна определяться наша позиция в случаях, когда п ^4, — простотой алгебры или отсутствием физической модели? Прежде чем ответить на это, рассмотрим физическую картину для случая п — 3.
Трехмерная бумага в клеточку
Многие из нас обладают весьма бедным пространственным воображением. Возможно, именно поэтому к координатной геометрии в пространстве принято относиться с особым благоговением, отчего ее изучение отодвигается математической программой на весьма дальний срок. А жаль! В конце концов мы живем в трехмерном пространстве. Большинство вещей, которые мы производим и которыми пользуемся, будь то самолет или автомобиль, занимают пространство трех измерений, а не разостланы на плоскости, подобно узору ковра или печатной схеме. Привлечение реальной модели во многом упрощает усвоение трехмерных координат, делая их доступными пониманию совсем юных учащихся. Сделать такую модель нетрудно. То, что мы будем называть «трехмерной бумагой в клеточку», представляет собой приспособление, с помощью которого удается быстро измерить расстояние в каждом из трех направлений: на восток, на север и вверх. Такое приспособление показано на рис. 13. Оно представляет собой дощечку с отверстиями, в которые можно вертикально вставлять круглые колышки. Точка А (рис. 13) удалена от точки О на 3 см на восток, 1 см на север и 2 см вверх. Она обозначает 3 кошек, 1 собаку и 2 поросят, коротко Зс М + 2р. В координатной геометрии это было бы записано в виде точки (3, 1, 2).
Практическое использование приспособления потребует некоторой его модификации. Чтобы колышки были более устойчивыми, дощечка должна быть возможно толще. Или, наоборот, две одинаковые тонкие дощечки со сквозными отверстиями можно скрепить так, чтобы между ними был промежуток. Тогда колы
42
шек будет держаться еще устойчивее. 'Однако оставим все эти детали на усмотрение того, кто будет делать модель.
Трехмерное пространство мы будем рассматривать аналогично пространству двух измерений. Как на модели можно увидеть результат сложения? Как связаны между собой Р и R, если R = ЗВ? Каков результат повторения одного и того же шага В? На все эти
Рис. 13.
вопросы учащиеся могут ответить самостоятельно, экспериментируя со своими досками и, возможно, получая от этого удовольствие. Их ответы обнаружат большое сходство с нашими ранее полученными результатами. Ниже эти ответы выделены в маленькие разделы.
Соответствие сложения правилу параллелограмма.
На рис. 14 показано сложение: С — А 4- В, или
t А = 4с + 2d + р -г B = c + 3d + 2p
C = 5f+ 5z/4-3p ’
Точки О, Л, В, С все лежат в одной -плоскости и являются вершинами параллелограмма, хотя это и нелегко показать на чертеже. Можно вырезать из картона параллелограмм и придать ему положение, показанное на рисунке пунктиром. Дальнейшими экспериментами можно проверить, что результат не зависит от выбора А и В.
Эффект умножения. На рис. 15 показано соотношение R — ЗР при Р = Зс + 2d 4- р и R = 9с 4-’ 4- 6d 4“ Зр. Как и в случае двух измерений, замечаем, что точки О, Р и R лежат на одной прямой и точка R расположена втрое дальше от точки О, чем точка А
43
Равномерные шаги. Если на этом же рисунке дополнительно к точкам О, Р и R рассмотреть еще точку Q = 2Р = 6с + 4d + 2р, то совокупность точек О, Р,
Q и R будет иллюстрировать последовательное прибавление Р. Они расположены на одной прямой и па
одинаковом расстоянии друг от друга. Наш прежний образ деления прямой с помощью шагов еще работает. Только сейчас мы как бы поднимаемся в гору или идем по наклонной крыше.
44.
Этот результат для нас весьма важен, ибо именно с помощью шагов мы получили формулы для средней точки и для точки, делящей отрезок в любом заданном отношении. Все эти формулы без какого-либо изменения остаются в силе и для пространства трех измерений. Так, если 4, В и С — три произвольные точки в пространстве, то для точки G. пересечения медиан треугольника АВС остается в силе соотношение с==4л+1в+1с-
На рис. 16 в качестве примера изображен брусок, вершина которого лежит в точке О. Так как D и Е —
Рпс. 16.
середины ВС и СА, то AD и BE — медианы треугольника АСВ, которые пересекутся где-то внутри бруска в точке G.
Так как граница OBJC бруска есть параллелограмм (фактически прямоугольник), то J — В + С. Если из точки J мы сделаем шаг А, то попадем в точку L, поэтому L — АД-] — АА~В-\-С> Сравнивая результаты для G и L, видим, что L в точности равна трем G: L == 3G. Значит, G лежит на диагонали OL и отсекает от нее 7з* Но точка G лежит в плоскости треугольника АВС, следовательно, именно в этой точке плоскость АВС пересекается с прямой OL. В итоге имеем: плоскость АВС пересекает прямую OL в точке G, лежащей на расстоянии XUOL от точки О, и в этой же точке G пересекаются медианы треугольника АВС, Этот весьма солидный результат мы доказали средствами простой арифметики.
Я установил этот результат специально для «бруска», так как брусок — это привычный объект, который легко описать. Я не пользовался неуклюжим
45
специальным термином «прямоугольный параллелепипед». Однако все ранее сказанное о нашей алгебре и искажениях, допустимых в аффинной геометрии, остается в силе и здесь. Так, проведенное доказательство ни в малейшей степени не зависит от того, что брусок имеет прямые углы. Поэтому наше доказательство остается верным и для деформированного бруска, у которого грани представляют собой не прямоугольники, а параллелограммы.
Такое же замечание справедливо и для нашей трехмерной бумаги в клеточку. Совершенно несущественно, что оси направлены на восток, на север и вверх. Причины того, что были выбраны перпендикулярные направления, носят чисто практический характер. Нелегко достать дощечку с отверстиями, образующими параллелограммы да еще и просверленными под углом. К тому же у большинства людей представление о трехмерных фигурах легко ассоциируется с прямоугольным каркасом; возможно, это происходит потому, что в жизни нам с младенчества сопутствуют прямоугольные бруски. Но каковы бы ни были практические или психологические причины использования перпендикулярных осей, мы не должны упускать из виду, что математика этой главы не только не требует использования прямых углов, но даже не предполагает их существования.
Из только что проделанной работы возникает одно общее соображение, которое составляет предмет одного из разделов современной математики. В трехмерном пространстве, рассуждая по аналогии с двумерным пространствам, мы получаем такие же формулы. Это наводит на мысль, нельзя ли найти способ получения и развития этих результатов без упоминания о том, в пространстве какой размерности мы находимся? Тогда бы мы имели теорию, приемлемую для любого числа измерений; Она избавила бы нас от необходимости повторять доказательства для пространствам двух или трех: измерений, сократив вдвое объем работы. А .если, как мы сейчас собираемся сделать, найти возможным: рассматривать пространство четырех, пяти, шести или и измерений^ то экономия мысли в этом случае будет буквально неограниченней.
Пространство четырем и более измерений
Правомерно ли говорить о пространстве п измерений, когда п больше трех? Мы уже отмечали, что наш физический опыт знакомит нас с геометрией прямой (одно измерение), геометрией плоскости (два измерения) и геометрией пространства (три измерения), но не дает нам прямого способа наглядно представить четыре измерения. Какова сама идея четырехмерного пространства? .
Прежде всего мы договоримся рассматривать этот вопрос вне связи с физикой. Ни теории относительности, ни вопроса о том, является ли время в некотором смысле действительно четвертым измерением, мы касаться не будем. Нам все равно, в какой вселенной мы находимся: нашей или какой-то другой, где, например, могут обитать существа, имеющие опыт жизни в 6 измерениях. Нас интересует лишь математическая сущность идеи, мы хотим знать, можно ли с помощью n-мерного пространства делать корректные умозаключения, так как фактически идея n-мерного пространства имеет приложения ко вполне мирским вопросам (например, к статистике) и нам важно знать, можно ли положиться на те выводы, которые из нее вытекают.
Алгебраическая сторона вопроса, пожалуй, ясна и вряд ли вызовет затруднения. Если кто-нибудь захочет рассматривать коллекции животных, перенеся на них операции сложения и умножения, то ничто не помешает ему брать совокупности со сколько угодно большим числом разновидностей животных.
Далее мы установили некоторое соответствие между операциями с двумя или тремя видами животных, с одной стороны, и плоскими и пространственными объектами, с другой. Мы могли бы и наше существо обучить переводу алгебраических результатов (скажем, А + В = С) на геометрический язык: ОАСВ — параллелограмм. Но какую пользу это принесет ему? Совершенно никакой. Ведь оно никогда не встречалось с фигурами и не может их себе представить. Слово «параллелограмм» оно найдет бессмысленным, а само упражнение пустым и бессодержательным. Нам же такой перевод выгоден. Мы
l47
с рождения живем в физическом мире, постоянно наблюдая формы и движения объектов, наш мозг переполнен всяческими ассоциациями, которые вызывает геометрический язык. Перевод с языка алгебры на язык геометрии дает нам два преимущества. С одной стороны, он позволяет нам применять точную технику алгебры для получения геометрических результатов, которые, с точки зрения нашего наглядного воображения, не являются очевидными (например, доказанное ранее свойство бруска). С другой стороны, он позволяет наглядно, в виде рисунков и чертежей, представить формальные алгебраические результаты. Эти рисунки придают алгебраическим уравнениям как бы вторую жизнь, они делают их более яркими, значительно облегчая тем самым запоминание многих результатов, особенно если они связаны с очевидными геометрическими фактами. Кроме этого, наглядные образы, помогая осмысливать алгебру, подводят к открытию результатов, до которых без их помощи мы бы вряд ли додумались.
Геометрическая точка зрения особенно помогает при рассмотрении вопросов, включающих в себя изменение осей. Допустим, что, работая в какой-то системе координат, мы установили определенные результаты. Затем понадобилось изменить систему. Можно ли при этом все еще пользоваться полученными результатами, или их следует заново проверить? Оказывается, это зависит от природы полученных результатов. Если они выражают собой то, что мы называем геометрическими фактами, то они не изменятся и в новой системе. В противном случае этого может не случиться. Например, доказав, что какая-то точка лежит между двумя другими точками и на одинаковом от них расстоянии, можно быть уверенным, что изменение осей не повлияет на этот факт. Но когда геометрическая интерпретация того или иного уравнения отсутствует, вполне возможно, что в новой системе оно утратит свою правильность.
В качестве примера рассмотрим точки F, Н и Е на рис. 12. Допустим, что мы начали работу с бумагой в клеточку, нанесенную жирными линиями. Так как F = 2D, Н = С + D, Е = 2С, то Н = Ц2Е + + */гЛ то есть Н — середина EF. Этот геометриче
48
ский факт не пострадает, если сетку жирных линий поменять на сетку тонких. Тогда мы получим F = = 2с + 2d, Н = 4с + 2d, Е = 6с + 2d, откуда, как и следовало ожидать, Н — '/2Е + l/2F. В противоположность этому сравним в «жирной» системе координаты точки F (0, 2) с координатами точки Е (2, 0). Мы видим, что они отличаются только порядком. Перейдя в другую систему, мы уже не обнаружим такого «обращения» у координат этих точек: F{2,2), Е (6, 2). То есть подмеченное соотношение между координатами было случайным, обусловленным выбором осей, и потому не сохранилось при их изменении.
Существуют проблемы, которые подводят нас к изучению четырехмерного пространства. В элементарной алгебре график функции у = х2 помогает понять свойства самого уравнения. График, конечно, лежит в двух измерениях, поскольку его уравнение включает две переменные х и у. Однако позже, встретившись с комплексными числами, содержащими 1=У—1 , мы увидим: если w и г — комплексные числа и z = х -f- iy, w = и + iv, то уравнение w — z2 уже включает четыре числа х, у, и, v и для его графика потребуется четырехмерное пространство. Живи мы в четырехмерном пространстве и умей вычерчивать такого рода графики, изучение комплексных чисел значительно упростилось бы. Однако, не будучи в состоянии видеть такого рода графики, мы все же пытаемся найти способы их осмысления.
С этой целью и по ряду других причин мы хотим изобрести геометрический способ истолкования ситуаций, которые включают четыре числа или более. Тем самым мы ставим себя в положение нашего существа. Мы изыскиваем определенные правила для перевода алгебраических утверждений на язык геометрии, то есть в геометрические утверждения. В отличие от существа мы обладаем одним неоспоримым преимуществом — мы знаем, как выглядит пространство одного, двух и трех измерений. Таким образом, геометрический язык стимулирует наше воображение, подсказывая аналогии. Некоторые из этих аналогий, однако, могут ввести в заблуждение, поскольку соотношения между четырьмя числами могут вести себя иначе, чем соотношения между тремя.
. 49
Поэтому в сомнительных случаях мы возвращаемся: к алгебре и проверяем верность вашего воображения. Так что все вопросы логики и доказательства должны или решаться с помощью алгебры, или логически следовать из тех геометрических утверждений,: которые сами доказаны алгебраически.
При чисто логическом подходе, следовательно, та-, кие термины, как «параллельная», «на прямой», «посредине между», должны впервые появиться как перевод алгебраических ситуаций. В частных случаях' пространств одного, двух и трех измерений, если бы мы обратились к иллюстрациям алгебры с помощью бумаги в клеточку, то обнаружили бы, что они вполне согласуются с их привычным смыслом. Но это был бы экспериментальный результат. Например, в самом начале главы мы видели, что С = А В на бумаге в клеточку соответствует точкам О, А, В, С, образующим параллелограмм (в повседневном физическом смысле слова). Этот результат не доказывался, его нельзя доказать, да и нет в этом надобности. Соответствие между алгеброй «кошки — собаки» и подлинными рисунками на бумаге — явление реального мира, оно может быть установлено только через опыт, эксперимент, но не путем рассуждения.
Можно смело утверждать, что геометрия Евклида дает весьма точное описание того, как ведут себя реальные объекты, и что это (более или менее) логическая система. Можно ли доказать средствами евклидовой геометрии, что точки ОАВС должны образовать параллелограмм? Конечно, можно. Однако евклидова геометрия куда сложнее сравнительно легкой алгебры этой главы. Наша цель скорее показать, что, передавая существу содержание этой главы вместе с небольшими дополнительными инструкциями, мы в состоянии доказать все теоремы евклидовой геометрии. При этом мы не исходим из евклидовой геометрии, а стараемся подойти к ней.
Согласно этому мы избераем следующую последовательность действий: начинаем с алгебры «кошки — собаки»; обеспечиваем словарь для выражения ее результатов на языке аффинной геометрии; экспериментально проверяем, что теоремы аффинной геометрии полезны для описания реального мира; в даль-50
нейшем увеличиваем число принятых допущений (аксиом) и с их помощью конструируем евклидову геометрию.
Следовательно, когда мы говорим о пространстве четырех или большего числа измерений, мы не переходим логически в новую веру. Мы лишь вводим образный наглядный язык, который оказывается полезным при установлении аналогий между алгеброй п символов и нашим повседневным геометрическим опытом.
ГЛАВА II
ГЕОМЕТРИЧЕСКИЙ СЛОВАРЬ
Если в заключение первой главы мы говорили о принципе создания словаря для перевода геометрии на язык алгебры, тю здесь мы рассмотрим некоторые его детали, сохранив прежний подход. Из соответствий между алгеброй и геометрией, поддающихся осмысливанию в двух- и трехмерном пространствах, мы сконструируем определения, которые охватывали бы пространства любого числа измерений независимо от того, можем мы их себе представить или нет.
Прямая, проходящая через начало координат. Из рис. 3 мы установили, что точки О, Р, 2Р, ЗР, 4Р, ... лежат на одной прямой. Если в качестве сомножителей при Р взять числа дробнее, иррациональные или отрицательные, но нетрудно обнаружить, что и в этом случае точки окажутся на той же прямой; только при отрицательных сомножителях они будут лежать по другую сторону от начала. Согласно этому, мы определяем прямую ОР как множество всех точек вида fP, где t — любое действительное число.
Выбор буквы t здесь не случаен: нашу прямую можно представить как след движущейся точки. В первый момент (/ = 0) точка находится в начале координат, через 3 секунды (/==3) она окажется в положении ЗР, а 5 секунд назад (/ = —5) она была в положении —5Р. То есть прямая состоит из всех точек, в которых либо находилась, либо будет находиться движущаяся точка.
А теперь вообразите себе ученика, который плохо начал, но благодаря упорной работе сумел улучшить свои оценки необыкновенно регулярным образом, как показано ниже,
52
Недели	Арифметика '	Английский язык	- Естествознание	География	Французский язык
Первая	0	0	0	0	0
Вторая	10	3	7	9	2
Третья	20	6	14	18	4
Четвертая	30	9	2!	27	6
Поскольку успеваемость ученика за каждую неделю характеризуется пятью оценками, то для ее графического изображения потребовалось бы пятимерное пространство. И если через Р обозначить успехи ученика за первую неделю, то нетрудно сообразить, что в последующие недели они выразятся соответственно как 2Р и ЗР. Эти точки тоже окажутся на прямой, проходящей через начало, но лежащей уже в пятимерном пространстве.
Прямая общего вида. Аналогичные рассуждения в случае, представленном на рис. 5, подводят нас к определению прямой как множества всех точек вида Л + tP, где К и Р — фиксированные точки, a t — любое число.
Отрезок прямой. Под отрезком понимается часть прямой, лежащая между точками А и В. Из ранее полученной формулы для точки, лежащей между А и В и делящей расстояние АВ в отношении t к 1 — t, следует, что отрезок АВ состоит из всех точек вида (1 — t)A + tB, где t изменяется в границах от О до 1.
Это определение отрезка вполне согласуется с предыдущим определением прямой как совокупности точек вида К + tP. Действительно, переписав выражение (1—t)A -j- tB в виде A -f- t(B — А), получаем нужную форму, соответствующую перемещению из точки А шагом (В — А), который переносит нас за один раз в точку В. Таким образом, в момент t = 0 мы находимся в точке А, в момент t = 1 — в точке В, а в промежутке между 0 и 1 — где-то между А и В.
53
Упражнения
Дано пятимерное пространство. В нем,буквы cf d, е, f, g могут обозначать кошек, собак, слонов, лягушек и гусей. Точки располагаются следующим образом:
А = 5с + 3d + е 4- f + 6g; В = Зс 4- d 4- 5е + f 4- 4g;
С = с 4-	4- Зе 4- 7/ 4- 2g; D = 2с 4- 3d 4- 4е 4- 4f 4- 3g;
Е = Зс 4« 4d 4- 2е 4- 4f 4- 4£; Р = 4с 4- 24/ + Зе 4- f 4- 5g;
G = Зс +3<Z 4-Зе+ 3/4-4g.
1.	Которая из данных точек является серединой АВ?
2.	Вы отправились из точки D шагом Р, где Р = с — е — f + + g. В какие из вышеуказанных точек вы придете и через сколько шагов?
3.	Вы отправились из точки С шагом Q, где Q = с — 2d + + е — 3f + g. В какие из вышеуказанных точек вы придете и через сколько шагов?
4.	Является ли какая-либо из данных точек серединой CG?
5.	Имеется ли среди данных точек точка, лежащая на FC на расстоянии ЧзРС от F?
6.	Какой шаг надо сделать, чтобы попасть из С в Е?
7.	Если вы выйдете из С шагом, о котором идет речь в вопросе 6, то через какие из вышеуказанных точек вы будете проходить?
8.	Какую фигуру образуют точки А, В, С, D, Е, F, G?
Внутренняя область треугольника
Ранее мы нашли, что точка G пересечения медиан треугольника АВС лежит внутри треугольника и удовлетворяет равенству Q — ЧзА + Чз& + '/зС. Чем вообще характеризуются внутренние точки треугольника? Что, например, можно сказать о точке R, лежащей на Лф на расстоянии 3/tAQ от А, если сама точка Q лежит на ВС на расстоянии 2/з#С от В (рис. 17)? Чтобы ответить на поставленный вопрос, переведем эти геометрические данные на язык алгебры. То, что AR составляет 3/4 расстояния 4Q, a BQ — 2/3 расстояния МС, означает соответственно, что R = xJiA + 3/4Q и Q = Vs# 4- 2/зС. Объединяя эти результаты, получим 7? =’/И + ^(’/з# + 2/зС) = = ’/И + V4# + '/2С.
В выражениях для Q и R всякий раз получаются дроби, которые (как легко заметить) при сложении дают 1. Используя другие точки и варьируя дроби, всякий раз будем получать такой же результат, в чем нетрудно убедиться алгебраически.
54
Все это подводит нас к следующему определению понятия «внутри». Говорят, что точка /? находится внутри треугольника АВС, если /? = хА + уВ + zC, где х, у, z — положительные числа удовлетворяющие условию х + у + z — 1. Вы можете заметить здесь аналогию с ранее*данным определением отрезка как множества точек вида (1 — t)A + tB, где дроби t и 1 — t тоже в сумме дают 1. Поэтому мы могли бы при желании определить внутренность отрезка
Рис. 17.
Рис. 18.
как совокупность всех точек вида хА+ У&, где х и у — положительные числа; удовлетворяющие условию х + у = 1.
Внутренняя область тетраэдра
Дан тетраэдр ABCD (рис. 18). Точка О является точкой пересечения медиан треугольника АВС, поэтому G — Ч&А ~Ь 1[зВ 1/зС. Точка Н находится на расстоянии zltDG от D. После простых вычислений мы получим Н — 1/±А + ’ДД + V4C + 'AG.
Точка Н в тетраэдре, конечно, должна обладать теми же геометрическими свойствами, что и точка G в треугольнике АВС, хотя в данный момент эти свойства нае не интересуют. Отметим только, что Н находится внутри тетраэдра и в формуле для И дроби дают при сложении 1. Частные примеры или общие
') Каждое из этих чисел должно быть строга положительным, в противном случае мы получили бы не. внутреннюю,, а граничную точку; Аналогичное замечание верно и для внутренних точек тетраэдра. — Прим. ре9.
55
алгебраические рассуждения убеждают нас в том, что для любой внутренней точки S отрезка RD, конец которого лежит внутри грани АВС, алгебраическое выражение будет содержать дроби, дающие в сумме 1. Следовательно, точку S мы определим как внутреннюю по отношению к тетраэдру, если S = хА + + у В + zC + wD и х, у, z, w — положительные числа, удовлетворяющие равенству х+у+^+ш= 1.
Рассматриваемые точки А, В, С и D не лежат в одной плоскости, и фигуру на рис. 18 мы воспринимаем лежащей в трехмерном пространстве. Однако это определение, как и другие данные выше определения, остается в силе и тогда, когда точки А, В, С и D лежат, скажем, в пространстве 5 измерений. Например, если A = 5c--|-3d + e + f + 6g, В — Зс t+ d + 5е + f + 4g, С = с + 5d + Зе + 7f + 2g, D = *=* 7c + 7d + 7e + 7f + 4g, то мы еще можем узнать, что Н, равное 4с + 4d + 4е + 4f 4g, удовлетворяет соотношению Н == Ч*А + Ч±В +	+ ЧФ и, следо-
вательно, является внутренней точкой тетраэдра. Аналогично точку G == Зс + 3d + Зе + 3f + 4g. мы можем отождествить с точкой V3A + ЧзВ + ЧзС, лежащей внутри грани АВС. Далее можем проверить, что G лежит внутри отрезка, соединяющего.точку А с серединой ВС, которой является точка 2с	3 d + 4е' +
+ 4f + 3g.
Внутренние точки симплекса
- Рассмотренная выше фигура, определявшаяся четырьмя точками А, В, С и D, находилась самое меньшее в трехмерном пространстве.
Рассуждение, связанное с пятью точками А, В, С, D, Е, приводит нас по меньшей мере к четырехмерному пространству, которое уже не поддается чувственнонаглядному представлению.
Однако близкая аналогия с предыдущим помогает нам определить внутреннюю точку S фигуры ABCDE равенством S = хА + уВ + zC + wD + vE, где х, у, z, w и v — положительные числа и х У + 4-2+^ + D = 1.
Все точки, удовлетворяющие этому условию, заполняют некоторую область, которую мы назовем 53
четырехмерным симплексом. При желании мы могли бы внутреннюю область тетраэдра, треугольника или отрезка отнести к симплексу соответственно трех, двух или одного измерения. Аналогично можно было бы определить симплекс пяти, шести, семи или п измерений.
Есть много простых рассуждений, которые мы используем в знакомых геометрических ситуациях. Так, ёсли мы видим непрерывный график (рис. 19), который в точке А расположен, скажем, «ниже уровня моря», а в точке В — «выше», то делаем вывод о существовании на АВ промежуточной точки, в которой
график проходит как раз «на уровне моря». Таким доводом часто пользуются при численном решении уравнений.
Далее, если нам говорят, что внутренняя точка треугольника АВС, точка Р, соединена какой-то непрерывной кривой с какой-либо точкой» лежащей вне этого треугольника (рис. 20), то можно быть уверенным, что на кривой найдется точка /?, лежащая на одной из сторон этого треугольника.
Нередко современная математика занимается именно тем, что старается приспособить какие-то весьма знакомые и подчас ничем не примечательные суждения (а не получать захватывающие новые результаты) к ситуациям, котор&е с трудом поддаются воображению и в которых невозможно прибегнуть к. рисунку, чтобы сделать их более ясными, как, например, в случае с фигурой, лежащей в пространстве более чем трех измерений.
Так, при решении обычных элементарных задач может появиться симплекс. Например, смесь, которая состоит на V* из красной, па V4 из голубой и на 1/2
57
из желтой красок, мы могли бы изобразить в виде
4-	4- Ч2С. Сумма дробей с необходимостью
равна 1. Этот двумерный симплекс можно представить в виде обычного треугольника. Любой сплав из пяти металлов составил бы четырехмерный симплекс. А какой-нибудь кулинарный рецепт из 17 компонентов — шестнадцатимерный.
Конечно, мы не можем представить себе эти симплексы так же наглядно, как представляем треугольник. Но даже в этом случае геометрическое описание оказывает нам часть той услуги, которую
оказывает график. Оно наводит на мысль, что рассматриваемые области—это нечто вроде треугольника или нечто вроде тетраэдра, но гораздо большее «нечто»! Оно сообщает нам, что они ограничены в своей протяженности, а не уходят в бесконечность, что они состоят из одного куска и имеют угловые точки. При всей своей неполноте эта информация способна навести на полезные размышления.
Имея много моделей треугольников, вы могли бы путем склеивания их в различной последовательности получить большое разнообразие фигур. Так, из шести треугольников вы могли бы склеить плоскую фигуру с отверстием в середине, которая представлена на рис. 21. Вы могли бы выйти из плоскости и сделать модели фигур, поверхность которых приближается к поверхности сферы или кольца для штор. Аналогичным образом склеивая тетраэдры, мы могли бы получить более сложные пространственные фигуры. Этот способ склеивания простых объектов для получения более сложных — один из основных инструментов комбинаторной топологии. Он нашел отражение в принятой там терминологии: симплексом
58
называют простой строительный блок1), сконструированный же из симплексов более сложный объект называется комплексом. Рассматривая симплекс как обобщение треугольника для любого конечного числа измерений, математики, интересующиеся комбинаторной топологией, не ограничены рамками пространств, доступных нашему чувственно-наглядному представлению.
Снятие ограничений
Мы определили внутренность треугольника как множество точек вида хА 4- уВ + удовлетворяющих двум условиям: 1) числа х, у, z должны быть положительными и 2) х + у 4- z = 1. Естественно задать вопрос, что изменится, если снять одно из этих условий или оба одновременно?
Этот вопрос проще исследовать на простых случаях в такой последовательности: сначала представить его графически, затем дать логическое объяснение тому, что мы заметим. Естественно начать со случая хА 4- уВ, Допустим сначала, что мы соблюдаем условие х 4- У — 1, но не требуем, чтобы х и у были положительными. Тогда х может быть любым числом, а у должен удовлетворять равенству у — 1 — х. То есть мы рассматриваем все точки вида Ах 4-+ (1—х)В или В4-*И — В), Такая форма, как мы уже знаем, отвечает прямой, которая получится при движении из точки В в направлении А шагом, длина которого соответствует всевозможным множителям (положительным, отрицательным, дробным), стоящим перед (4—В),
Предположим теперь, что мы отбросили оба условия и рассматриваем все точки вида хА 4- уВ. Немедленно появляется графическая интерпретация. Точка хА лежит нУ прямой ОА, точка уВ — на прямой ОВ (рис. 22). Сумма xA-j-уВ отыщется построением параллелограмма и изобразится точкой Р. Варьируя выбор х и у, точку Р можно поместить в любом месте плоскости ОАВ, то есть ее положения могут заполнить всю плоскость.
9 Simplex (англ,) — простой.
59
Определение плоскости, проходящей через начало координат. Учитывая только что сказанное, мы определим плоскость ОАВ как совокупность точек вида хА уВ при условии, что точки О, А и В не лежат на одной прямой. Если бы мы жили в пространстве двух измерений, плоскость ОАВ для нас означала бы
«все имеющиеся точки». Но так как мы действуем в трехмерном пространстве, этого не происходит. Мы сплошь и рядом обнаруживаем точки, не принадлежащие плоскости ОАВ, то есть лежащие вне ее.
Линейные пространства
Итак, мы имеем два определения: прямая ОА — это все точки, вида хЛ; плоскость ОАВ — это все точки вида хА + уВ. Прямая, имеет одно Измерение, плоскость — два. В повседневной жизни мы на этом и останавливаемся, так как в определении пространства трех измерений у нас просто не возникает надобности. Для нас оно вселенная, в которой мы живем и движемся. Но если мы собираемся вообразить пространство п измерений, то не можем на этом остановиться. Точно так же как плоскость расположена-в трехмерном пространстве и, следовательно, сконструирована не из всех, а лишь из некоторых его точек, и трехмерное пространство можно сконструировать, используя лишь некоторые точки четырехмерного пространства и т. д. Существует очевидный путь, чтобы продолжить указанную выше конструкцию. Линейное трехмерное пространство ОАВС — это все точки вида хЛ уВ + гС; линейное четырехмерное
60
пространство OABCD — это все точки вида хА -р 4- уВ +	и т- д- д0 бесконечности.
Данное здесь определение трехмерного пространства согласуется с нашим повседневным опытом. Если мы возьмем точки О, А, В и С так (рис. 16), чтобы прямая ОА была направлена на восток, ОВ — на север и ОС — вверх, то одновременным перемещением на расстояния х, у и г в каждом из этих направлений соответственно можно достичь любой точки нашей вселенной.
Однако выйти за пределы трехмерного пространства наше восприятие, бессильно. Мы не можем вообразить нашу вселенную как некоторый плоский объект, лежащий в пространстве четырех измерений. Для большей наглядности я игнорирую теорию о возможной искривленности нашего пространства. Поэтому в такого рода вопросах мы должны полагаться на смесь алгебры с аналогиями.
Пример. Дано четырехмерпое пространство с базисными символами («животными») с, d, е, ]. Пусть А—c^-d; В = = d — е; С = е — f. Нужно показать, что точка с + d 4- е 4- f не лежит в трехмерном пространстве ОАВС,
Решение. Если бы указанная точка лежала в трехмерном пространстве, то мы имели бы c4-^4-£ + f = x'4 4-#B4~zC — = x(c-d) +y(d~~e] +г(е — f) = хс + (у — x)d 4- (z — у)е — — zf. Приравнивая сомножители при с, d, е и f в первом и последнем выражениях, получим уравнения х == 1, у — х ==* 1; z— — у= 1; —z = 1. Из первых трех уравнений найдем значения х == 1; у = faz ==• 3, которые противоречат четвертому уравнению. Следовательно, точка с + d 4- е 4- f не может выражаться в форме хЛ 4- уВ 4- zC и потому не лежит в пространстве ОАВС, что и требовалось доказать.
Линейная зависимость
Обратим внимание на один важный момент. Определяя плоскость как совокупность всех точек вида хА уВ, мы должны были оговориться, что точки О, Л, В не лежат на одной прямой. Ведь если ОА указывает на восток и ОВ тоже указывает на восток, то любая комбинация хА 4- уВ опять-таки приведет нас на восток. Иными словами, если А означает 2 кошки, а В — 3 кошки, то хА 4- уВ означает (2x4-3#) кошек. Как бы мы ни выбирали хи#, мы не можем соскочить с оси кошек, то есть мы
61
всегда будем получать точки-на прямой, а не на пло-скости.
Аналогичный эффект может получиться в пространствах любого числа измерений. Пусть в привычном нам трехмерном пространстве с, d, е представляют соответственно точки востока, севера и подъема вверх относительно начала О. При обычных условиях выражение хА -|- уВ 4- гС дало бы нам все точки нашего пространства. Но предположим, что А = с, В = = d, С = с А~ d. Прибавление А переносит нас на восток, прибавление В — на север и прибавление С — на северо-восток. Все эти путешествия проходят в горизонтальной плоскости, и при любом выборе х, у и z мы не сможем оторваться от земли. Предполагается, что мы имеем дело с тремя ингредиентами А, Ви С. Но А, В и С сами составлены из двух ингредиентов с и d:
Всякий раз, когда нас постигнет подобное разочарование, мы назовем ингредиенты линейно зависимыми. Условимся, что пространство, состоящее из всех точек хА А- уВ 4- zC, порождено точками А, В и С; пространство, состоящее из всех точек хА -ф + у В + zC 4- wD, порождено точками А, В, С и D и т. д. Следовательно, мы можем сказать, что отдельные точки линейно зависимы, когда они порождают, пространство меньшего измерения, чем то, которое могло бы определяться их числом; Другими словами, в случае линейной зависимости точек порождаемое ими пространство, могло быть порождено меньшим числом точек.
Когда пространство порождается несколькими точками А, В, С, ..., мы можем представить себе, что они даются нам по очереди. Первая точка образует прямую хА; с появлением точки В мы ожидаем, что это множество точек расширится до плоскости хА 4-, + уВ‘, с помощью точки С мьг надеемся сконструировать трехмерное пространство и т. д. Если каждая точка по мере своего появления! увеличивает размерность пространства на 1, то в конце концов мы непременно получим пространство ожидаемой размерности!.
Вели же мы получим пространство меньшей размерности, то это!значит, что по крайней-мере одна из 60
точек.при своем появлении не вносит ничего нового и попадает в пространство, порожденное ее предшественницами. Примером этого является рассмотренный случай сА — с; B = dnC = c — d. Первые две точки А и В породили поверхность земли. Точка С оказалась тоже на земле и не внесла ничего нового. Алгебраически это выражается уравнением С = А +• 4-В,.которое.показывает, что С есть комбинация уже заданных элементов. Такая неудача может случиться на любом этапе. Возьмем, скажем, А = 2с; В — Зс и С = d. Здесь С привносит нечто новое, но В уже все испортило и ничего нельзя исправить! Единственная точка С не в состоянии одна добавить двух новых измерений, чтобы поправить ляпсус точки В и спасти положение. Алгебраически неспособность В внести что-то новое выражается равенством В — = l'/г А. Можно было бы решить, что с А такого никогда не произойдет, так как у нее нет предшественников, которым можно было бы подражать. Однако представьте .себе, что А совпадаете началом .О, тогда она представляет собой полное отсутствие кошек, собак и слонов. Как ингредиент А — ничто. В алгебре это выражается равенством А — О.
Трем рассмотренным случаям соответствуют три уравнения А + В — С — О, ЗА —2В = О и А = О. Во втором уравнении коэффициент при С нуль, а в третьем.два коэффициента — при В и при С — равны нулю. Но, конечно, линейную зависимость нельзя было .бы установить, .составив уравнение, О-А +' + О-В + О-С = О, у которого все коэффициенты равны нулю. В этом случае . любые значения А, В и С удовлетворяют уравнению и между ними вообще невозможно установить какой-либо зависимости. Все это оговорено в формальном определении линейной зависимости, принятом в учебниках: А, В, С линейно зависимы, если они удовлетворяют равенству рА 4* + qB + гС — О, в котором по крайней мере одно из чисел р, q или г. отлично от нуля. Аналогичное определение можно сформулировать и для п точек.
В логическом построении формальной теории линейной зависимости есть места, в которых , нужно действовать особенно осмотрительно. В .агой теории не происходит ничего неожиданного. Тщательное
>03
обоснование просто подтверждает все то, что вы угадали по аналогии с обычной геометрией трех измерений. Однако понятие линейной зависимости важно.
Проверка на линейную зависимость
Предположим, что в пятимерном пространстве заданы три точки А, В и С:
А= с + 2d + Зе 4-4f + 5g, В = бе + 7d 4- 8е + 9/ 4- 10g, С = 11е 4 12d 4-13е 4-14/4-15g.
Спрашивается, будут ли эти точки линейно зависимы? Такая задача ставится часто, и решить ее можно с помощью следующего рассуждения. Представим себе, что точки даны в порядке А, В, С. Очевидно, что А не совпадает с О, так что А делает свое дело — порождает прямую. А что происходит с В? Для В просчет был бы в том случае, если бы она оказалась кратной А. Поскольку А начинается с с, а В с 6с, то множителем кратности при А может быть только число 6, но тогда В должна выглядеть как 6А — 6с 4- 12d 4- .., что не согласуется со вторым числом 7d в записи В. Значит,. В не кратна А, она не совпадает с А по направлению, и потому точки вида хА 4- уВ заполняют плоскость. Лежит ли точка С в этой плоскости? Мы попытаемся выразить С в форме хА 4- уВ. То есть нам нужно найти такие два значения х и у, которые удовлетворяли бы равенству хА 4- у В — С, для этого достаточно иметь два уравнения, поэтому рассмотрим только первые два члена. Так как А начинается с с 4- 2d 4- • • •, а В начинается с бс -f- 7d 4- •  • > то хА 4- уВ начинается с (х 4- бу) с 4- (2х 4- 7у) d 4- ... . Это совпадает с началом С, если х-\-бу = 11 и 2х-|-7у = 12, и приводит к х = — 1 и у = 2. Только эти числа дают верное начало для С. Если они не сделают правильным все выражение для С, тогда нужной комбинации А и В не найдется совсем. В нашем случае —А + 2В полностью совпадает с С. Таким образом, точки А, В и С 64
линейно зависимы. (Между прочим, В — середина Л С.) Стоит только изменить у С какой-то из коэффициентов, как точки Л, В, С окажутся линейно независимыми и породят трехмерное пространство.
Полезный результат
Есть одно очевидное замечание, которое только на первый взгляд может показаться не очень полезным. Пусть в двумерном пространстве с базисными символами с и d даны три точки Л, В, С, например: А — = Зс + 8d, В = 7с + 5d, С = 27с + 31d. Находясь в одной плоскости, проходящей через О, эти три точки не могут породить трехмерного пространства. Поскольку они составлены из двух ингредиентов с и d, то максимальное, что они могут породить, — это плоскость. Следовательно, они должны быть линейно за^ висимы и удовлетворять равенству рЛ + <?В''С = = О, в котором хотя бы одно из р, q или г не равно нулю. Данные конкретные точки фактически удовлетворяют равенству 2Л + ЗВ — С = О. Но сделанное выше замечание касается любых трех точек, лежащих в двумерном пространстве.
Аналогичные рассуждения верны и в трехмерном пространстве. Так, четыре точки Л, В, С, Z), лежащие в трехмерном пространстве, не могут породить четырехмерного пространства, поэтому они должны быть линейно зависимы и связаны уравнением рА + qB + 4- rC + sD = О.
Обобщая рассуждение, мы приходим к выводу, что п 4- 1 точек n-мерного пространства должны быть линейно зависимы и связаны аналогичным уравнением.
Этот факт, сам по себе вполне естественный с геометрической точки зрения, может показаться слишком обычным, чтобы обратить на себя внимание. Однако он полезен тем, что позволяет нам во многих случаях показать, что именно удовлетворяет какому-то уравнению. Ниже мы убедимся в этом на примере матриц, а пока ограничимся рассмотрением числового примера. Мы _хотим показать, что если взять / = I + 5 /2 +4/34-7/6 , то оно удовлетворяет
3 Зак. 51	$5
уравнению четвертой степени, в котором, конечно, не должны появляться иррациональные числа, такие, как У2, У 3 , ]/б . Обозначим с=1> d=y2, е=УЗ., f — Уб и запишем t в форме t = 1с + 5d + 4е + 7/, которая соответствует записи точки в четырехмерном пространстве. Далее найдем /2. Для этого следовало бы заняться малоинтересньшл арифметическими расчетами; но, к счастью, нам не нужен точный ответ, а достаточно знать, что t2 выражается через взятые нами числа 1, У 2 , ]/3 , Уб , а также целые числа, то есть представляет собой некоторую комбинацию с, d, е и f. (Действительно^перемножив, получаем /2 = 393 + + 178/2 + 148 /3 +54 /б, то есть £2 = 393с+: + 178d + 148е + 54/.) Эти конкретные числа не игра-ют никакой роли. Что для нас важно, так это то, что /2 — точка в том же самом четырехмерном пространстве. Аналогично выясняем, что t3 и /4 также принадлежат этому пространству. Получилось, что пять точек 1, /, /2, t3, ft находятся в пространстве четырех намерений. Значит, эти точки должны быть линейно зависимыми, и, следовательно, должно существовать связывающее их уравнение р\ + qt -j- rt2 +	+
kft = 0. Можно показать, что числа р, q, г, s, k рациональные, не содержат У2, Уз, Уб, которые здесь обозначены как d, е, f и выступают в той же пассивной роли, какую ранее играли собаки, слоны и лягушки.
Итак, мы показали, что существует некоторое уравнение четвертой- степени, которому удовлетворяет t Этот пример одновременно характеризует силу и границы современной алгебры. Проведенное рассуждение проще любого, используемого в традиционной алгебре для доказательства этого результата, так как избегает длинных вычислений. Однако его возможности ограничены доказательством лишь существования' уравнения. Когда же требуется знать конкретно само уравнение, мы вынуждены проводить подробные вычисления. При всем этом современная алгебра в ряде случаев предлагает такие методы реальных вычислений, которые вряд ли пришли бы нам в голову без ее помощи.
66
Модели линейных пространств
Материал первых двух глав может показаться довольно однообразным, ибо вся его математика связана с простыми выражениями вида 2с + 5d + 4е, которые, однако, получали самую разную интерпретацию. В одном случае с означало кошку, в другом — точку, в третьем — отметку по арифметике, в четвертом — число У 2 .
В каждой из рассмотренных ситуаций операция обозначалась знаком «+», но ее смысловые значения отличались друг от друга. В случаях, когда с стояло
Рис. 23.
Рис. 25.
вместо кошки или У 2 , смысл «+» соответствовал житейскому прибавлению, то есть сложение понималось в арифметическом смысле. Однако для двух точек А и В сумма А + В означала четвертую вершину, параллелограмма с тремя данными вершинами О, А и В, так что знак «+» ассоциировался с далеко не очевидной операцией. Правда, это определение сложения через построение параллелограмма давно уже используется как в механике, так и в разделах естествознания (электричество, магнетизм, аэродинамика), основанных на ее законах. Только там с и d обычно интерпретируются не как точки А и В, а как направленные отрезки О А и ОВ, соединяющие начало О с этими точками (рис. 23). Что же касается самих вычислений, связанных с с и d, то они вовсе не зависят от того, интерпретируем ли мы с как точку А или как направленный отрезок ОА. Последняя интерпретация часто бывает удобна. На рис. 4 показан результат прибавления к D, Е, F и G одной и той же величины Р, который выразился в параллельном переносе, показанном направленными отрезками DD*, ЕЕ*, FF* и GG*, идущими в одном и том же направлении и
з*	67
имеющими одну и ту же длину. По аналогии с этим прибавление d к с можно передать переносом направленного отрезка d в конец отрезка с, как показано на рис. 24. Это избавляет нас от вычерчивания параллелограмма, значительно упрощая чертеж, особенно в случае, если нам надо сложить более чем две величины, как показано на рис. 25 *).
Сама идея' сложения сил, скоростей, ускорений и других физических величин получила признание еще в XIX веке. Объекты (величины), представляемые направленными отрезками, были названы векторами, а рассмотренная операция их комбинирования — векторным сложением. Профильтрованная через математическую физику, эта идея перешла в чистую математику, вызвав определенное смещение в акценте и интерпретациях. Для физика и математика-прикладника за векторами стоял определенный, вполне признанный класс величин. Взглянув на величину, вы могли сразу определить, является ли она вектором. Скорость, например, подходила для изображения направленным отрезком, а масса нет. Следовательно, скорость в отличие от массы была вектором. Но чистого математика не интересовала физическая природа объектов, раз их можно было представить символами. Его волновала лишь математическая закономерность, которую проявляли эти объекты (величины). В результате он пришел к определению векторного пространства как некоторой совокупности объектов, с которыми можно оперировать, используя такие же формальные правила, какие применяются к векторам в физике. На языке главы I векторы суть объекты, которые можно комбинировать так, как если бы они были коллекциями животных. Под это определение подходят многие вещи, совсем не похожие на силы и скорости. Сравним вычисление
, 2х2 + 3х+ 4	к/ 2х2+ Зх+ 4
’ 5х2 + 6х4- 7	х	5
7х2 + 9х+ 11	10х2 + 15х + 20
1) Это правило сложения направленных отрезков (векторов) называется правилом многоугольника. Оно приводит к тем же результатам, что и последовательное применение правила параллелограмма. — Прим. ред.
68
и вычисление
। 2 кошки,	3	собаки	и	4	поросенка
5 кошек,	6	собак	и	7	поросят
7 кошек,	9	собак	и	11	поросят
, 2 кошки,	3	собаки	и	4	поросенка
5
10 кошек, 15 собак и 20 поросят
В обоих случаях проводятся одни и те же операции. Следовательно, мы можем сказать, что квадратные трехчлены вида ах2 4- Ьх + с образуют векторное пространство трех измерений. Сравним еще два вычисления:
। 2sin/ + 3cos/	। 2 кошки и 3 собаки
' 4 sin t + 5 cos t	’4 кошки и 5 собак
6sin/ + 8cos/ 6 кошек и 8 собак
Мы видим, что они опять идентичны, и говорим, что все выражения вида a sin / + & cos / тоже образуют векторное пространство двух измерений.
Пусть мы имеем длинную туго натянутую струну. В точках В и С, как показано на рис. 26, подвешены грузы Р и Q, под действием которых струна оттягивается соответственно на х и у дюймов. Это положение струны ABCD можно охарактеризовать двумя числами х и у, другими словами, точкой S с координатами х, у. Но тогда можно считать, что все возможные положения струны образуют пространство двух измерений. А это в свою очередь предполагает возможность говорить о сложении двух положений струны. Однако имеет ли оно смысл? На рис. 27 показаны три точки J, К, L и те положения струны, которым они
69
соответствуют. Данные об этих положениях следующие:
Положение	Р Q х	у
J	10 2	1
/С	0 112
L	113	3
Точки О, /, К и L на бумаге в клеточку образуют параллелограмм, так что L = J + К. Из приведенной
здесь таблицы видно, что это равенство имеет физический смысл. Все числа—входы в строке L можно получить сложением соответствующих чисел — входов; строк J и К. Фактически из таблицы легко получить все возможные положения струны. Если бы мы захотели узнать, что произойдет при подвешивании 5 фунтов в точке- В и 3 фунтов в точке С, мы бы рассмотрели ситуацию 5/ + ЗК, которой соответствует следующая таблица:
Ситуация	Р	Q	х	у
5J	5	0	10	5
ЗК	0	3 3	&
57 + ЗЛГ	5	3	13	11
Если бы на струне были взяты три промежуточные точки, как показано на рис. 28, то для определения такого положения струны понадобилось бы три числа 7&
x, у, z. Положение струны задавалось бы точкой трехмерного пространства. С чисто математической позиции, о которой упоминалось выше, нам нет надобности говорить, что положение струны может быть проиллюстрировано в трехмерном пространстве. Достаточно просто сказать, что возможные положения струны образуют пространство трех измерений. В случае, когда струна имеет смещения в 7 точках, то ее возможные положения образуют пространство семи измерений, в п точках — пространство п измерений
Но вернемся к чертежу и таблице, иллюстрирующим положение А = / -[- К Там смещение х точки В в положениях J и К равнялось соответственно 2 и 1 и определялось >в положении L простым сложением 2+1 = 3.
Рис. 29.
То есть смещение в точке В в положении L вполне определяется ее смещениями в положениях J и К. Нам ничего не нужно было знать о смещениях в других точках. Это остается верным при любом числе фиксированных на струне точек. На рис. 29 изображена часть струны в трех различных положениях U, V и U + V. Поскольку в положениях U и V смещение Е обозначено соответственно через s и i, то в положении U + V оно есть 5 + t. Так определяется
71
положение точек С, D, Е, lt G ;	(И) графика (7 ф V и вообще любой
Is	точки этого графика.
i __	Заметим попутно, что такой
прием сложения весьма элементарен и распространен. Пусть, —например, какая-то фирма зани-—-И?	,у) мается распродажей сапог и бо-
।	тинок, ежемесячно фиксируя реа-
. j	лизованный товар. Тогда график
U мог бы представлять ежеме->	сячную продажу сапог, а график
___	V — ботинок. Тогда график U V ।	представил бы общую реализа-
+ / aj+V) цию товаРа- Так, если бы в марте !	* было продано s пар сапог и / пар
{	ботинок, то весь реализованный
---------------j-------------- товар составил бы s + t пар обу-Рис. 30.-------вп. В годовом отчете было бы 12
входов и каждый из графиков образовывал бы двенадцатимерный вектор. Весьма сомнительно, способствовало ли бы знание всех этих тонкостей процветанию фирмы.
При очень большом числе фиксированных точек на струне наши рисунки напоминали бы гладкие кривые. Это наводит па мысль, что рассмотренный прием сложения можно применить к любым графикам, а не только в случае, когда они состоят из отрезков ломаной. Справедливость этого нетрудно доказать. Сгладив изломы на рис. 29, мы получим рис. 30. Как и прежде, s и t считаем высотами точки Е на графиках (7 и V. Складывая их, получим соответствующую точку графика U + V с высотой s + /.
Таким образом мы поступаем, если нам даны два графика, но нет ни уравнений, ни данных, по которым эти графики построены, а нам надо начертить график суммы.
Если бы графики. U и V задавались простыми формулами у — х3 и у — х2, то график U ф- V задавался бы формулой у — х3 + х2.
В общем случае, когда графики U и V задаются функциями у = f(x) и у — q?(x), графику U + У соответствует функция у = f(x) 4- ф(х).
72
Ранее мы видели, что квадратные трехчлены ях2-}--}- &%+ с и тригонометрические выражения a sin t -j-+ &cos/ можно складывать подобно выражениям «кошка — собака» и, следовательно, относить к разряду векторов. Таким образом, мы подошли к весьма широкому обобщению: такие же вычисления можно производить с любыми функциями, какими бы нерегулярными они ни были. При этом не требуется, чтобы формула, задающая функцию, была простой — ее может не быть вовсе. Функции могли бы быть заданы графиками, начерченными от руки. И тогда они все равно относились бы к векторам и мы могли бы еще складывать суммы
। 2/(х) + Зф(х) + 4f (х) + 5<р (х)
6f (х) + 8<р (х)
точно так же, как если бы f(x) означало кошку, а ф(х) — собаку.
Итак, функции можно рассматривать как векторы. Многим это покажется удивительным, ибо в нашем представлении функции и векторы — это понятия разные. Функции у нас ассоциируются с графиками вида У — х2, а векторы — со стрелками, показывающими скорость ветра, дующего, например, в северо-восточном направлении со скоростью 20 км/час. Вышеприведенные соображения показывают, что теория векторов может дать нам некоторые сведения и о функциях.
Поначалу эта мысль может вызвать восторженное удивление, но потом наступит разочарование, так как одной этой идеи, как бы нова и заманчива она ни была, недостаточно для того, чтобы получить значительный результат. Нам же хотелось бы поскорее перейти к делу и показать ценность этой идеи, получив вполне определенные результаты, относящиеся к функциям. Тогда бы мы имели право заявить: «Смотрите, мне удалось получить эти результаты потому, что я знал, что функции можно рассматривать как векторы».' Но на этой ступени наше воображение совсем не получает дальнейшего развития. Что касается векторов, то они представляют собой очень простые
73
понятия, о которых можно сказать мало интересного. Наша работа с векторами основывалась „на алгебре простых выражений вида ЗД-+-44, и мы обходились не такой уж сложной математической техникой. Чтобы получить более замечательные результаты, мы должны ввести больше идей.
В заключение заметим, что векторное пространство и линейное пространство в нашем случае— синонимы. Так о трехчлене x2-f-2x-f-3 мы можем говорить как о векторе в векторном пространстве всех квадратных трехчленов и как об элементе (или точке) линейного пространства, состоящего из всех квадратных трехчленов. В принципе можно было бы один ИЗ этих терминов объявить устаревшим. Однако оба термина еще бытуют в математической литературе и иногда удобно использовать их оба.
ГЛАВА III
ОБ ОТОБРАЖЕНИЯХ И МАТРИЦАХ
В жизни- мы часто; наблюдаем ситуации,, в которых одна совокупность предметов порождает, превращается или обменивается на какую-то другую. Тонна угля в газовых печах превращается в определенное количество кокса, аммония, серы, бензина и смолы. Монета, брошенная в автомат, «оборачивается» плиткой шоколада. Определенное количество стали, резины, меди, других материалов и человеческих усилий превращается в автомобиль.
Эти процессы нельзя обратить или возобновить, они совершаются раз и навсегда. Если вы сожгли уголь, то, вернув в газовую печь кокс, аммоний и прочие составляющие, вам не. удастся получить его вновь. Автомат, выдавший вам плитку шоколада, как правило. не может принять ее- обратно и выдать что-то взамен. Автомобильный завод не ставит свои новые машины на конвейер в надежде превратить их в более сложные.
Однако многим процессам присуща способность неоднократно возобновляться. Поместив дивиденды от денежного вклада в банк того же акционерного общества, в случае удачи получают прибыль; Выращивая животных, можно продать приплод, а можно оставить его для увеличения поголовья скота. Одни заводы можно использовать для сооружения других новых заводов.
Оба вида процессов — и те, которые совершаются раз и навсегда, и те, которые способны возобновляться, — обладают определенной математической закономерностью, которую мы рассмотрим на упрощенном языке I главы, оперируя не химическими компонентами или деталями автомашин, а животными.
75
Кстати, приложения этой результативной математической теории выходят далеко за пределы экономики или промышленного производства.
«Банковские схемы с животными»
Представим себе общество, все богатства которого выражены в форме животных. Если вы положите в банк U кошку, то через год получите овцу. Это можно записать, как U: c->s, что означает «в схеме U за кошку дают овцу». В банке V за ту же кошку вы получите через год лошадь, или V: с -> h. Банк В/

О L И N 0
О 1 2 J * С
более щедр: вы получаете там за кошку и овцу, и лошадь, то есть W: c-+s + h. Очевидно, схема W равноценна схемам U и V, взятым вместе. Обозначим это как W = U + V,
Таким образом мы можем не только складывать банковские схемы, но и умножать их на число. Если схема U такова, что с->$, то мы принимаем, что схема 3U в 3 раза лучше, то есть в ней c->3s. Таким же образом схема 51/ обозначала бы	поскольку
в схеме V: c-^h. Наконец, мы могли бы взять схему, равноценную 3U и 5V, вместе взятым. Мы записали бы ее в виде 3t/4~5V, что означало бы с 3s + 5/l
Если предположить, что банки принимают только кошек, а выплачивают наборы овец и лошадей, то по этому правилу можно было бы записать любую банковскую схему. Если в некоторой схеме кошка порождает а овец и b лошадей, то эта схема есть aU + bV. Всевозможные банковские схемы такого вида образуют' линейное пространство двух измерений, все они имеют форму aU + bV.
76
Действие банковской схемы можно представить геометрически. На рис. 31 иллюстрируется схема W: c-+s-\-h. Точками О, L, М, К на прямой слева представлены возможные вклады, выражающиеся числами 0, 1, 2, 3 кошки. Точки, изображенные справа и обозначенные теми же буквами О, L, М, N, показы^ ваюг доходы с этих вкладов. Однако на этом рисунке изображено не все. Как мы только что видели, возможные банковские схемы образуют двумерное пространство. Частная схема W была произвольно выбрана из этого пространства. Если мы хотим проиллюстрировать ситуацию полностью, то нам придется рас-
смотреть прибор, показанный на рис. 32. Имеется панель с кнопками, соответствующими (7, V, W и другим банковским схемам. Если нажать на черную кнопку, то на экране появятся точки О, L, М, N, как показано справа. Если нажать на другую кнопку, например U. то на экране появятся точки, соответствующие этой кнопке.
Введенное выше обозначение U: с -> s можно заменить другим: Uc — st означающим: «банковский процесс в приложении к с дает s». Аналогично V: с -+h можно записать как Vc = /г, a W: c-^s + h как Wc — s + h. Равенство W — U + V позволяет записать Wc = (U + V)c. Если бы мы вдруг забыли о смысле этих обозначений и по привычке продолжили бы равенство по правилам элементарной алгебры Wc = (U -Ь V)c = Uc + Vc = s + Л, то все равно пришли бы к верному результату. Дело в том, что хотя смысловые значения J7, V, W, с, s, h в данной ситуации отличаются от значений, приписываемых им элементарной алгеброй, где под символами понимаются числа, формальные операции остаются в силе.
77
Размерности
На рис. 31 мы уже видели, что, согласно схеме W7:	точкам О, L, М, N на прямой соответ-
ствуют точки, обозначенные теми же буквами на бумаге в клеточку. Мы можем сказать, что прямая отображается в листок бумаги. Операция W, следовательно, осуществляет отображение одномерного пространства («прямую кошек») в двумерное («плоскость овец и лошадей»).
Быть может, вы подумаете, что не всякое пространство можно отобразить в другое пространство. Но это не так; если даны два векторных пространства, вы всегда можете отобразить одно в другое с помощью банковской схемы.
Если, например, банковская схема переводит кошку в овцу, собаку в 2 овцы, слона в 10 овец, то эго будет отображением трехмерного пространства в одномерное. Здесь вклад определяется тремя числами: х кошек, у собак, z слонов; результат же выражается всего одним числом: п овец, фактически п — х + + 2у + 10г. При этом в трехмерном пространстве может оказаться несколько точек, отображающихся в одну и ту же точку одномерного пространства. Так, например, 20 овец может получиться от вклада либо 2 слонов, либо 10 собак, либо 20 кошек, либо комбинации из 6 кошек, 2 собак и 1 слона1).
Оплачивая счет в магазине, вы тем самым каждый раз иллюстрируете отображение пространства нескольких измерений в одномерное пространство. Пусть магазин имеет в своем ассортименте товары, скажем, 100 видов. Вы решаете, сколько вам нужно товаров, каждого вида; без сомнения, для большинства видов мерой будет «нисколько». Следовательно, чтобы охарактеризовать покупку, потребуется 100 чисел; иными словами, покупку можно отождествить с точкой стомерного пространства. Однако ваш счет, как бы велик он ни был, выражается в терминах одного объекта — денег; он измеряется всего одним числом — количеством пенсов.
!) Используя математическую терминологию, можно сказать, что в этом случае отображение не является взаимно однозначным. — Прим. ред.
78
Если бы вы вдруг надумали путешествовать самолетом, то, вероятно, вам потребовалось бы знать не только общую стоимость, но и общий вес вашей покупки. В этом случае с каждой покупкой, определяемой 100 числами, вы связали бы два числа: стои-
Рис. 33. с
мость покупки и ее вес. Тем самым осуществлялось бы отображение стомерного пространства в двумерное.
Приведенный ранее пример с оттянутой струной (рис. 26) можно рассматривать как отображение одного двумерного пространства в другое двумерное
пространство, так как мы можем выбирать грузы Р и Q, подвешенные в точках В и С. Они вызовут смещения х и у в 'В и С. Эти смещения задаются фактически уравнениями
x = 2P + Q, 1/ — P + 2Q.
Это отображение показано на рис. 33. Отображения легко иллюстрировать на схемах электрических цепей. На рис. 34, а изображена цель, в которой
79
источник тока Е определяет силу тока х в одном и силу тока у в другом проводнике, так что Е у). Это отображение одномерного пространства в двумерное, На рис. 34,6 мы имеем два источника тока Е и F и четыре проводника, в каждом из которых в зависимости от сопротивления устанавливается своя сила тока %, у, z, и. Следовательно, здесь мы имеем отображение двумерного пространства в четырехмерное.
Частный вид отображения будет зависеть от сопротивлений, выбираемых на участках цепи. Здесь у нас те же три составные части, что и в примере с вкладами. Электродвижущая сила источника тока в цепи соответствует вкладу, сопротивления на участках— банковской схеме, сила тока на этих участках — доходу с вклада.
Сложные отображения
Вообразим себе следующую ситуацию. На нефтеперерабатывающем заводе имеются два вида сырья. Галлон сырья I типа дает при переработке а галлонов бензина высшего сорта, b галлонов среднего и с галлонов низшего сорта. Галлон сырья II типа дает соответственно d, е и f галлонов бензина высшего, среднего и низшего сортов. Таким образом, х галлонов сырья типа I и у галлонов сырья типа II при совместной переработке дадут ц, v и w галлонов бензина высшего, среднего и низшего сортов, где.
и == ах + dy v ~ Ьх + еу W = CX + fy
(I)
Если бензин продавать соответственно по цене а, Р и у пенсов за галлон, то полная выручка составит t пенсов, где
t = аи + рц -4- yw.	(2)
Следовательно, мы выбираем х и у, определяем и, и и w и с их помощью находим t.
Иными словами, мы имеем здесь два отображения Р и S, соответствующие операциям производства
8G
и продажи. Р связывает сырье с бензином: Р: (х,у)^> —►(u, v, w); 8 связывает бензин с общей денежной выручкой при его продаже: 8: (и, v, w)-> t.
Мы могли бы записать это так: t = 8(и, v, w) и (и, v, w)= Р(х, у). Затем естественно было бы выполнить подстановку и записать t = SP(x, у). Тогда SP будет символизировать полный процесс: сырье -* -+ деньги.
Посмотрим, как обстоит здесь дело с числом измерений. Поступающее сырье мы задаем с помощью
двух чисел х и у. Так что «пространство сырья» двумерно. Получаемый из сырья бензин имеет три сорта, его количество определяется тремя числами и, v и w. Значит, «пространство получаемого бензина» трехмерно. И наконец, денежная выручка от продажи бензина выражается одним числом, стало быть, «пространство денег» одномерно. Эти пространства и связанные с ними отображения показаны на рис. 35.
Обратим внимание на тот факт, что полное отображение, осуществляемое последовательным переходом но стрелкам от сырья к деньгам, есть -отображение SP, но не PS. Деньги получаются от продажи продукта, вырабатываемого из сырья, а не продукт является результатом продажи сырья. Проведенное выше алгебраическое рассуждение было попыткой подвести именно к такому обозначению. (Между прочим, по этому поводу в математической литературе мнения крайне разошлись. Писать SP или PS — чисто лингвистическое соглашение, и вряд ли есть другой аргумент, которым можно было бы оправдать выбор того или другого обозначения.)
61
Умножение матриц* 1)
Отображения Р и S определялись уравнениями (1) и (2). Подстановкой и, v, w из уравнений (1) в уравнение (2) можно получить одно, уравнение, непосредственно связывающее t с х и у и определяющее отображение (х, у) -* t, которое имеет вид
t = (аа +	+ ус) х 4- (ad + ре 4- yf) у. (3)
Можно добиться некоторой экономии в записи, используя матричные обозначения. В наших дальнейших рассуждениях эти обозначения оправдают себя интересными следствиями, а пока они лишь сокращенная запись уравнений (1) и (2), которую мы получаем, опуская буквы и, v, w, х, у, г.
Преобразование Р в матричной форме упрощается до записи
(a d\
b е].	(4)
с fJ
Эта запись передает нам сущность уравнений (1), ибо шесть чисел a, b, с, d, е, f занимают здесь то же положение, что и в уравнениях (1). При желании можно легко перейти от матричной записи (4) к первоначальной записи (1).
Аналогичной записью
S = (a, 0, у)	(5)
выражается сущность уравнения (2).
Из уравнения (3) мы бы получили
SP = (aa + ₽& + YC> ad + ре 4- yf). (6)
Итак, выражение SP мы определили двумя способами: записали его непосредственно в виде равенства
*) Матрицей называется таблица чисел, расположенных в п строк и т столбцов, например:
1 2 0\
4 3 2/
1 О 0\	/17
О 101,149
0 0 1/	\ 6 I
и т. п. - Прим, ред.
за
(6) и установили, что оно есть результат комбиниро* вания отображения Р, определяемого матрицей (4), и отображения 3, определяемого матрицей (5). Значит, уравнение (6) можно полностью передать в матричной форме. Для этого достаточно в левую часть уравнения (6) вместо S и Р подставить их значения из уравнений (5) и (4). В результате получим
(а
ь
с
d\
е j — (аа + 06 + ус, ad + 0<? + yf). (7) fj
Из этого равенства мы можем получить механическое правило комбинирования матриц. Если посмотреть на первое выражение аа -j- $Ь + ус в правой части равенства, то можно заметить, что латинские буквы а, Ь, с взяты из первого столбца матрицы Р и умножены на соответствующие греческие буквы из строки матрицы S. Аналогичную закономерность можно усмотреть и во втором числе ad +	+ yf —
латинские буквы второго столбца матрицы Р умножены на греческие буквы строки матрицы 3.
Это механическое правило весьма удобно1)- Если мы знаем отображения в их матричной форме, то можем комбинировать их, не утруждая себя полной записью уравнений и соответствующей подстановкой. Заметим, что верность самого правила оправдывается лишь тем, что оно дает такой же ответ, какой бы дало полное алгебраическое рассуждение. Например, если кто-то не очень ясно представляет себе, как комбинировать
(a d\ Ь Д с l)
1) В математике такую операцию над матрицами, как это и указывает далее автор, называют умножением матриц. Она весьма отличается от соответствующей операции над числами. Так, например, если определено произведение АВ двух матриц А и В, то может быть не определено произведение ВА, или если и оно определено, то может не выполняться равенство АВ = В А. — Прим, ред.
83
то он может сам найти это правило. Первая матрица выражает существо двух уравнений:
t =з an + &v + yw j s = ди + 8V +	)
Вторая матрица передает суть уравнений
и = ах + dy | v = bx + еу |.	(9)
w ==-- сх + f У )
Если мы подставим и, v, w из (9) в (8), то получим уравнения, выражающие t и s через х и у:
t = (аа + $Ь + ус) х + (ad + 0с + yf) у,
s = (da + гЬ + &) х 4- (dd + ге +	(
Если теперь в полученных уравнениях (10) убрать х и у, то останутся четыре члена искомой матрицы. Между прочим, правило комбинирования матриц содержит ответ на вопрос, часто вызывающий затруднения: какую форму и размеры должна иметь искомая матрица? В даннОлМ случае уравнения (10) показывают, что она должна иметь две строки и два столбца, то. есть форма ее будет иной, чем форма исходных матриц.
Можно дать задачу на комбинирование матриц, не имеющую никакого смысла. В качестве примера поставим вопрос о комбинировании матриц
1а с\
<И|
Первая матрица соответствует уравнению t = аи 4--f-pv + вторая — системе уравнений:
и — ах + су, п — bx + dy.
Попытка выразить I через х и у с помощью соответствующей замены и и v из последних уравнений не удается, так как нам недостает величины w. Значит, поставленная задача бессмысленна. Примечательно, что «бессмысленность» обнаруживается и при использовании механического правила комбинирова-84
ния матриц, состоящего в составлении сумм произведений элементов строк на соответствующие элементы столбцов. Начав по этому правилу получать первый элемент искомой матрицы аа +	» мы тут же
встаем в тупик — нам не на что умножить греческую букву у, так как латинские буквы все исчерпаны. Опасно было бы в самом деле пользоваться правилом, дающим ответ на бессмысленный вопрос.
На этот вопрос можно взглянуть и с геометрической точки зрения. На рис. 35 мы смогли составить отображение SP, так как любая точка «пространства сырья» отображением Р посылалась в «пространство
Пространство Пространство Пространство Пространство Л	В	С	])
Рис. 36.
бензина», откуда она (уже преобразованная) отображением S посылалась в «денежное пространство». Такая комбинация отображений возможна лишь при наличии общего промежуточного пространства (каким здесь являлось «пространство бензина»). Это в свою очередь накладывает дополнительное требование на матрицы, представляющие комбинируемые отображения. Результат первой операции должен быть таков, чтобы к нему можно было применять вторую операцию. Это не было соблюдено в вышеприведенной бессмысленной задаче (рис. 36). Операция /а с\	. .
\d) от°бражает двумерное пространство А в двумерное пространство В, Операция (а, р, у) отображает трехмерное пространство С в одномерное пространство D. Поэтому осуществить переход от пространства А к пространству D не удается.
Линейные преобразования, пространства
Рассмотренные выше операции, не способные к повторному возобновлению, суть отображения одного пространства в другое. При этом результирующее
85"
пространство отличается от исходного. Кошки переходят в собак, уголь в каке, фунты в дюймы, нефть в деньги. Такие отображения имеют большое значение как в жизни, так и в математике. Но с точки зрения алгебры они неудобны. Для операции, которую нельзя повторить, мы не сможем говорить о РР или, коротко,; о Р2. В одних случаях мы можем комбинировать разные отображения вроде SP, а в других — нет.
Значительно большую свободу мы получаем, имея дело с возобновляющимися операциями — теми, которые отображают пространство в себя. В атом случае становится возможным комбинировать любые две операции и образовывать, как мы ниже увидим, степень любой операции. То есть мы сможем пользоваться выражениями вида SB, Р2, Р3, S2P, оперируя ими так же, как делали это выше, например образуя Р3 + 5Р2 + 7S2P + 2SP. Практически в нашем распоряжении оказывается большая часть техники, которой располагает элементарная алгебра. В настоящей главе мы познакомимся с тем, как это происходит, а еще дальше увидим, какую пользу из этой техники можно извлечь.
В отличие от уже рассмотренных нами схем типа «кошкаовца» здесь мы займемся схемами, в которых капиталовложение из кошек и собак оборачивается опять, кошками и собаками, а они в свою очередь могут снова стать капиталовложением. Рассмотрим банковскую схему /(, в которой c->c + d и rf——с1). Возможно, в банковской терминологии это и не имеет смысла, но тем не менее приводит к интересной геометрической картине. Результат этой операции показан на рис. 37. Слева показано положение точек Л, В, С ... до применения операции, справа — положение этих же точек Л*, В*, С* ... после применения операции. Заметим, что новые точки образуют сетку, очень похожую на сетку, образованную прежними точками. И это не случайно. Посмотрим, как мы получили точки Л*, В*, С*, В* и В*. Согласно схеме /(, перевод точки Л в точку Л* означает, что за кошку мы получаем кошку и собаку. Так
’) За кошку вы получаете кошку и собаку, за собаку получаете собаку и отдаете: кошку. — Прим. пере&
М
-как точка В представляет капиталовложение в 2 котки, то и прибыль от пего В* должна быть вдвое больше, то есть В* — 2Л*. На чертеже это означает, что В* лежит на одной прямой с А* и О*, но в 2 раза дальше от начала О*, чем А*. Точно так же мы можем убедиться, что капиталовложения в 3, 4 и т. д. кошки (соответствующие им точки дежат па прямой ОА) порождают равноотстоящие Точки на прямой О*А*. Точка С* означает, что, согласно схеме К,
Рис. 37.
Капиталовложение
d 4-Л-4
1 собака (точка С) переходит в d—с. Что касается точки £>, то она представляет собой капиталовложение из кошки и собаки. Соответствующий ей результат D* должен получиться от сложения результата вложения кошки (точка Л*) и собаки (точка С*), то есть D* = А* -|- С*. А это значит, что точки Л*5*С*О* образуют параллелограмм. Аналогично убеждаемся, что капиталовложению Е, представляющему на левом чертеже сумму капиталовложений В и С (ОВЕС—параллелограмм), на правом чертеже будет соответствовать результат Е* = В* 4- С*, определяющий четвертую вершину параллелограмма по трем данным О*, В*, С*.
Любопытно, что положение точек Л* и С* на бумаге в клеточку позволяет без каких-либо вычислений, путем простейшего построения определить положение всех остальных точек. Этот геометрический факт означает, что, зная результат вложения 1 кошки и 1 собаки, вы знаете тем самым и результат вложения любого другого числа кошек и собак.
На рис. 37 капиталовложения и их результаты для большей наглядности показаны на отдельных чертежах, хотя оба они представляют одно и то же
87
пространство: пространство кошек и собак. Так точка Л*, например, выражает собой то же самое, что и точка О. Поэтому вместо двух отдельных чертежей с изображением прежнего и нового положений точек мы могли бы ограничиться одним, показав стрелками, куда переходят точки. В этом случае (рис. 38) стрелка $з А в D означает, что операция К переводит точку А в тбчку D, Поскольку операция К приложима к любой точке пространства, то такие стрелки будут исходить из каждой точки плоскости, что частично н
G	О Л В
Рис. 38.
показано на рис. 38. Эти стрелки естественно объединяются в потоки. Отправившись из точки А в направлении стрелок, мы могли бы после последовательного прохождения через положения D, Н, J продолжить это движение и попасть в другие точки, не показанные на рисунке. Каждый шаг этого продвижения соответствует осуществлению операции К. Вложение А дает доход D, новое вложение D дает доход Я, в свою очередь Н даст доход / и т. д. Поэтому точки Л, D, Н, J можно связать следующими равенствами: D — — КА, Н — KD, J = КН. Отсюда получаем, что Н = — KD = К (КА) = К2А, J — КН — К3А, то есть точка /, например, есть результат троекратного применения операции К к точке А. Аналогично G === К2С.
Записать банковскую схему для К2 очень просто. Как мы видим, К2 посылает А в Н, С в G. Поскольку А представляет с, а С представляет d, то операция К2 переводит с—>2d, d-+—2с. Этой информации достаточно для того, чтобы указать, куда переходит каждая точка.
На бумаге в клеточку К2 геометрически интерпретируется как «поворот на 90° и удвоение масштаба». 88
Однако выше уже говорилось, что для представления пространства.«кошки — собаки» совсем не обязательно использовать бумагу только в квадратную клетку. Операции /(, К2 и К3 можно так же хорошо представить и на косо разлинованной бумаге, такой, как на рис. 11. В этом случае геометрическая интерпретация К2, конечно, отличалась бы от только что данной.
Следует остерегаться . неправильного представления, которое может сложиться при рассмотрении рис. 37. На этом рисунке квадраты OADC п ABED перешли соответственно в фигуры О*Д*/)*С* и A*B*E*D\ которые тоже оказываются квадратами.
G Н
Ряс. 39.
Е
О Я Б
F*.G* Н'
О" /7* В
Однако ошибочно было бы думать, что банковские схемы всегда преобразуют квадраты в квадраты.
. Во-первых, банковские схемы определяются в терминах пространств животных, в которых мы даже не знаем, что такое квадраты. Мы ничего не говорили о «перпендикулярности кошек собакам» или о том, что кошки имеют «такую же длину, как собаки». Короче говоря, на языке главы I, мы все еще имеем дело с аффинной геометрией, где углы не имеют размеров, а длины отрезков можно сравнивать только в случае, если они лежат на прямых одного направления. Во-вторых, если даже кто-нибудь из всех возможных видов бумаги в клеточку выберет именно бумагу в квадратную клеточку, то утверждение, что каждая банковская схема отображает квадраты в квадраты, все равно останется неверным. Простейшим примером схемы, не сохраняющей «квадрат-ность», является схема с —► d, d —► с + rf, результат которой представлен на рис. 39. >
В дальнейшем нам будет весьма интересно отобрать именно те банковские схемы (назовем их ортогональными преобразованиями), которые сохраняют
89
форму и размер квадрата. В связи с этим позднее мы остановимся на тех дополнительных аксиомах, которые следует ввести в нежёсткое пространство «кошка — србакаэ, чтобы оно стало евклидовым. А пока мы будем вести рассуждения в рамках аффинной геометрии, которая не знает ни квадратов, ни прямых углов. При этом время от времени исключительно для большей наглядности мы будем использовать бумагу, разграфленную на квадраты.
Тождественный оператор *)
Вероятно, простейшей будет та операция, которая оставляет все в таком виде, в каком это было до ее применения. С этой точки зрения, при отображениях одного пространства в другое, например при отображении «кошка -> овца» или «нефть -> деньги», эта простейшая операция не может иметь места, ибо никакой набор овец не является кошкой, а монета — галлоном нефти. Но когда вся наша работа протекает в одном пространстве, то совсем нетрудно оставить вещи в прежнем положении. Эту операцию называют тождественной операцией и обозначают буквой /. Ее свойства напоминают умножение на 1. Если Р обозначает некоторую операцию, то имеем IP — == PI = р. IP означает «примени операцию Р и оставь все как есть», Р1 — «оставь все как есть, а затем примени операцию Р». В любом случае результатом будет Р.
Введение символа I может показаться бесполезным, поскольку ему соответствует операция, которая оставляет все без изменений. Однако зададим себе такой вопрос: если U есть операция с—d-*c, то что собой представляет операция С/2? Оказывается, операция U заменяет кошку собакой, а собаку кошкой. Ясно, что если мы дважды применим эту операцию, то опять-таки придем к тому, из чего исходили. Иными словами, результат операции U2 будет таким же, как если бы мы ее не применяли вовсе. Следовательно, U2 — I. Без символа I мы не могли бы этого выразить.
') Тождественный оператор называют также единичным, а со-ответствующуюему матрицу — единичной матрицей. — Прим. ред. 90
Упражнение
Каков геометрический смысл операции U (применительно к обычной бумаге в клеточку)?
Вычисления с матрицами
Несколько выше мы ввели матричную стенографию и показали, как подсчитать SP. Отыскание SP по S и Р обычно называется умножением матриц. До этого на примере банковских схем мы выяснили, что понимать под U 4- V и 5U для случая линейных преобразований. Если бы U и V были определены в матричной форме, то и здесь с помощью ранее данных пояснений в каждом конкретном случае можно было бы вычислить матрицы для U 4- V и 5U. Частая надобность в таких вычислениях делает целесообразными рассуждения в общем виде, результаты которых дают в наше распоряжение стандартный способ решения подобных задач.
Пусть банковской схеме U, по которой х кошек и у собак переходят соответственно в х* кошек и у* собак, отвечают уравнения
х* = ах4~ by, у* = ex 4~ dy.
Тогда схему можно представить матрицей
По аналогии с этим банковскую схему V тоже зада-
• Схема U 4* V по результату действия должна быть эквивалентна схемам U и. V, вместе взятым. Так как х кошек и у собак в схеме U дают ах 4- by кошек и сх 4- dy собак, а в схеме V дают ах 4- $у кошек и ух 4- бу собак, то в схеме U +; 4- И они должны дать в результате соответствующие суммы кошек и собак; то есть [(а4-а)х4* (&4-₽)И кошек и [(с 4~ ?)х 4"(^ + 6)?/] собак. Следовательно, схеме U V соответствует матрица
а 4~ ci b 4~ Р \ с 4- у. d 4- 6 /.'
а b ,с d
(а р\ дим матрицей . I
\ V о /
c-t- И =
91
Обратите здесь внимание на соответствие букв а и а, 6 й 0 и т. д., объединяемых в суммы.
Правило вычитания матриц можно получить через дополнение. Так, U — V означает: «что надо прибавить к матрице V, чтобы получить матрицу I/?» Отвечая на этот вопрос, догадываемся, что
6 —
d-b '
а —а U - У = \ с — у
Что касается схемы 5t7, то, результативней схемы U: Иными словами, согласно ей, х кошек и у собак дают 5ах -f- 5Ьу кошек и 5сх + + 5dy собак. Появляющиеся здесь четыре числа определяют матрицу
очевидно, она в 5 раз
/ 5а
5[/ = с \5с
56 \
5d )'
получить, заменив пя-
Общую формулу можно терку на Hi в доказательстве, и в результате.
Матрицы U и V определяют отображения двумерного пространства в себя. Однако, как мы видели в главе I, линейные пространства вовсе не чувствительны к своей размерности. Так, для матриц, определяющих преобразования в /г-мерном пространстве и потому имеющих п строк и п столбцов, результаты весьма сходны с результатами, полученными для п — 2. Правила действия с ними можно легко угадать по аналогии с проведенными выше рассуждениями или же повторить те же доказательства применительно к трем видам животных.
Сейчас же займемся получением матрицы, соответствующей тождественному оператору I. Мы связываем с ним уравнения х* = х, у* — у. Если сравнить эти уравнения с их общей, формой х* = ах + by, у* = ck -f- dy, то нетрудно увидеть, что в нашем случае а = 1, 6 = 0, с — 0, d = 1. То есть имеем
/1 0\
/ = (о 1)'
Нам надо получить еще одну матрицу, а именно О. Нулевой оператор О можно интерпретировать как
92‘
банковскую схему, соответствующую банкротству. Сколько бы вы ни положили в банк, вы ничего не вернете, то есть х* = Ох + Оу, у* = Ох -|- Оу. В соответствии с этим
О
О
0 =
0\
О/
Этот оператор обладает свойствами, которые ассоциируются с нулем. Для любой матрицы U U + + О = О + U = U и 0U = U0 = О.
Эти утверждения можно проверить, применяя правила матричного исчисления или осмысливая результаты банковских схем. Например, U0 означает следующее. Сначала вы сделали вклад в фирму, которая неожиданно обанкротилась и ничего вам не дала; вы забираете свой нулевой доход и вкладываете его в банковскую схему U. Естественно, что в итоге вы ничего и не получите.
Для любого числа измерений нуль-матрица содержит только нули.
Единичная матрица / в трехмерном пространстве имеет вид
/ 1 ° 0\
10 1 0 1.
\0 0 1/
Мы скажем, что она составлена из единиц па главной диагонали и пулей на остальных местах.
Введение символа О для нуль-матрицы позволяет записывать соотношения между матрицами в стандартной форме элементарной алгебры. Например, встреченное нами ранее уравнение U2 — I можно записать в форме V2 —1 — 0.
Упражнения
1.	д.««,	,|-(о J. в_(( J. 0)
Найднте^Л 4- В и проверьте, справедливо ли равенство А + В -
93
2.	Найдите Л2 и А3. Догадайтесь, какую трица Ап.
3.	Какая разница между А2 4- 1 и 2Л?
4.	Упростите выражение 52 —2В4~/.
5.	Найдите W, если W == I 4- U.
6.	Покажите, что W2 = 2W.
1. Если в уравнение IF2 = 2W вместо W и применить к символам правила элементарной чим уравнение относительно U. Запишите это _ средственной подстановкой в уравнение матрицы U проверьте, удовлетворяет ли она полученному уравнению.
8.	Найдите АВ и ВА, Равны ли они?
9.	Найдите выражения Л2 4~ 2ЛВ 4- В2 и Л2 4“ ЛВ 4- ВА 4- В2 Проверьте, равно ли каждое из них (Л 4- В)2?
Найдите I 4-26 4- 62, равно ли оно (/ + 6)2?
/1 2 \
Пусть С =1 I. Вычислите С2 — 5С — 2/.
форму имеет ма-
подставить /4-17 алгебры, то полууравнение. Непо-
10.
12.
13.
G2 и 26 4- kl.
ответом на второй вопрос.) чтобы эти выражения стали
ли подобрать числа q и k
Пусть D = I ). Подсчитайте выражение В2 —3D —2/.
\ Ji о /
/ 1
Пусть Е — ( I. Покажите, что для некоторого k выполняется равенство Е2 — 8£ = kl. Найдите k.
/2 1 \
14.	Пусть F = | I. Есть ли какое-нибудь простое урав-\ 1 4 /
нение, связывающее F2 4- 7/ и В?
/ 1 2\
15.	Пусть 6 — 1 I. Найти
(Символ Л, очевидно, определится Можно ли подобрать число k так, равными?
16.	Пусть	Можно
так, чтобы выполнялось равенство Н2 «== qH 4* kl?
17.	Настоящая задача требует длительного исследования. В вышепредложеннЫх вопросах все указанные матрицы удовлетворяли квадратным уравнениям. Можно ли в связи с этим утверждать, что вообще все матрицы 2X2 удовлетворяют квадратным уравнениям. Исследуйте это на достаточно большом чис-(а ь\
ле частных примеров пли взяв матрицу в общем виде ( I.
\ с d J
18.	Р
Найдите матрицу Р 4~ 2Q + 3R 4- 4S.
19.	Найдите матрицу 2Р 4“ Q 4- 4“ 4S.
20.	Представьте матрицу G в упражнении 15 в виде комбинации матриц Р, Q, R и S, участвующих в упражнениях 18 и 19. Сделайте то же самое для матрицы /.
21.	В упражнении 1 матрицы Л и В таковы, что Л = Р 4-4- Q 4- S и В ~ Р A- R + S. Сложение этих выражений дало бы
94
2Р + Q + # + 2S. Согласуется ли это с величиной А 4- В, найденной в упражнении 1?
22.	Всякую ли матрицу 2X2 можно выразить в формуле аР -F bQ 4- cR 4- dS, где a, d ~ числа?
23.	Составляют ли Яйтрицы 2X2 линейное пространство? Если да, то какого измерения?
24.	Что можно сказать о пространстве, образованном всеми матрицами 3X3?
25.	Выполните умножение матриц
/2
\ 1
3
-1

5
3
ГЛАВА IV
СКРЫТАЯ ПРОСТОТА
Математика, по словам Пуанкаре, — это искусство давать разным вещам одно название. В результате математика приводит к экономии мысли, потому что, изучив одну математическую закономерность, мы затем узнаем ее во множестве самых различных ситуаций. На рис. 40 мы видим три совершенно очевидно различных процесса. В случае а материальная точка
Рис. 40.
совершает колебательное движение вдоль гладкой кривой вблизи ее нижней части, в случае б тело колеблется на конце пружины, а в случае в показан балансир часов. Мы знаем из опыта, что в поведении этих трех систем много общего. Математически эта общность проявляется, например, в том, что кинетическая Т и потенциальная V энергия этих процессов имеет одно и то же выражение: Т = и V = = УоЪЛ Здесь и — скорость изменения х. Формула ia же, но смысл символов различен. В случаях а и б 98
буква т выражает колеблющуюся массу, а в случае в — момент инерции. В случаях а и б буква л показывает (пусть несколько по-разному) отклонение этой массы от своего положения равновесия. В случае в х измеряет угол, на который поворачивается балансир.
В динамике имеет место следующий интересный факт: поведение той или иной системы (при условии, что она свободна от трения и удовлетворяет некоторым весьма разумным условиям) полностью определяется формулами кинетической и потенциальной 'энергии. Если в трех вышеназванных системах Лит будут иметь одно и то же числовое значение, то формулы для Т и V в этих системах будут идентичны. Это значит, что при одновременном «запуске» систем их поведение будет настолько аналогичным, что, наблюдая за одной из систем, мы сможем сказать, что происходит в другой (в каждом случае колебания предполагаются достаточно малыми).
Рассмотрим как наиболее удобную систему а. Потенциальная энергия массы, находящейся под действием силы тяжести, пропорциональна ее высоте. Так что в случае а кривая, по которой перемещается материальная точка, представляет собой график потенциальной энергии материальной точки V = x!2kx2. Вспомните, как захватывает дух на качелях или американских горках. Это происходит в момент, когда потенциальная энергия, которую вы набрали, поднявшись до наивысшей точки, на самой низкой точке уменьшается и переходит в кинетическую. Это дает нам живую картину того, что означают кинетическая и потенциальная энергии. Мы часто можем наглядно представить себе физический процесс, мысленно наблюдая за движением некоторого воображаемого тела. Так, изменение потенциальной энергии интересующей нас системы можно проследить по движению воображаемого объекта по соответственно подобранному неровному ландшафту.
Сейчас мы воспользуемся этим приемом применительно к системе колеблющейся струны (рис. 41). Выбор этой системы продиктован, с одной стороны, простотой и наглядностью ее описания, с другой — типичностью ее поведения для широкого класса
4 Зак. 51
97
задач, связанных с колебательным процессом и представляющих либо научный интерес, либо техническую ценность. На рис. 41 показана туго натянутая струна, закрепленная в точках А и D. В точках В и С на ней подвешены небольшие грузики т, колеблющиеся вверх и вниз. Натяжение струны берется равным 1.
Нетрудно показать, что потенциальная энергия струны определяется формулой V = х2 — ху + у21). Поэтому нам предстоит сконструировать ландшафт, поверхность которого соответствует этой формуле.
Вообразим себе, что на плоском столе лежит лист бумаги в клеточку. В каждой точке (х, у) вообразим колышек высотой х2 — ху + у2, равной значению потенциальной энергии в этой точке. Вершины колышков образуют некоторую поверхность. Представим теперь себе медный резервуар, который лежит как раз на вершине этих колышков, поверхность резервуара отвечает уравнению z = х2 — ху + у2, (В лучших математических традициях пренебрежем многими деталями, создающими неудобства, например толщиной медного резервуара.) Если теперь материальная точка будет катиться по внутренней поверхности резервуара, то в каждом положении (х, у) ее потенциальная энергия будет определяться формулой V = = X2 — ху + у2.
Таким образом, мы построили модель поверхности, или ландшафта, которая воспроизводит формулу по-
9 Потенциальная энергия возникает в результате натяжения струны в новом положении, из которого она стремится выйти, чтобы принять свою первоначальную длину. Длины АВ, ВС и CD можно найти по теореме Пифагора. Учитывая, что для малых k имеет место приближенное равенство V1 + fe « 1 4- получим, что АВ = 1 + ЧгХ2; ВС = 1 + i/2(x —r/)2, CD == 1 4- '/2у2. Иными словами, нить растягивается на длину Ц2х2 4* VaCx—'У)2 4-4- ЧъУ2, или в упрощенном виде на х2 — ху + у2.
98
тенциальной энергии для системы колеблющейся струны. К счастью, получилось так, что и формула кинетической энергии также оказалась воспроизведенной1). Теперь, наблюдая движение частицы по поверхности резервуара, мы будем знать, как колеблется струна AD.
Рис. 42 представляет собой контурную карту поверхности резервуара. Контурные линии суть эллипсы, заданные уравнениями х2 — ху + у2 — const.
По форме резервуар отдаленно напоминает лодку, которая более полога в направлении на северо-восток или на юго-запад и гораздо круче — на северо-запад или на юго-восток.
Материальная частица, помещенная в любой точке резервуара, будет чувствовать, что ее тянет вниз. Направления ее движения показаны стрелками, перпендикулярными контурным линиям. Движение частицы, свободно отпущенной из точки Н, будет довольно сложным, и представить его себе нелегко.
Однако на поверхности резервуара есть два положения, которые обеспечивают частице исключительно простое движение. Это движение из точки G и движение из точки М в направлении точки О. Частица, помещенная в точке G, начнет скатываться в направлении точки О, пройдет через положение О и
*) Фактически Т — ’/2 ш(хг -f-z/2), где х = dx/dt-, у = dy/dt.
4*	99
поднимется по склону в точку F. Затем она вновь возвратится в точку G и повторит это колебательное движение неограниченное число раз (если представить, что трение отсутствует!).
Аналогичным образом колебалась бы частица вдоль прямой MON. Только в этом случае ее колебания проходили бы быстрее, так как в этом направлении резервуар искривлен больше, чем в направлении GOF,
Эти два движения — движение вдоль GOF и движение вдоль MON — примечательны не только как два простых частных случая движения. Комбинируя их, можно получить все возможные движения частицы. Как это можно было бы осуществить, показано на рис. 43. Одни провод жестко прикреплен к металлическому бруску, который колеблется в направлении с северо-востока на юго-запад. Его колебания должны воспроизводить колебания частицы в резервуаре вдоль GOF. Второй провод также жестко прикрепляется к бруску, колеблющемуся в направлении с северо-запада на юго-восток. Колебания второго бруска имитируют колебания частицы в резервуаре вдоль MON. При такой конструкции точка пересечения проводов, точка /?, будет передавать движение точки, свободно скользящей в резервуаре.
100
Интересно посмотреть, как интерпретируются эти два простейших движения вдоль GOF и MON в терминах колеблющейся струны. Прямая GOF имеет уравнение у == х. Поэтому колебание вдоль нее характеризуется равенством х и у. Вспомнив смысл х и у на рис. 41, обнаружим, что струна будет последовательно проходить стадии, показанные на рис. 44.
Рис. 44.
Прямая MON имеет уравнение у = ~ х и соответствует движению, в котором смещения в точках В и С равны по абсолютной величине, но противоположно направлены, как это представлено на рис. 45.
Для того, кто знаком с теорией звука, очевидно, что эти два вида колебаний напоминают первую (основной тон) и вторую гармоники фортепьянной струны.
Если струна колеблется, чувствительное музыкальное ухо сможет уловить оба колебания: и первую и вторую гармоники. Здесь мы снова имеем пример сложения. Такой сложный звук можно было бы получить от двух- одновременно звучащих камертонов: одного — порождающего основной тон, другого —вторую гармонику. Было бы разумно говорить здесь о сложении двух звуков.
В действительности музыканты сыграли существенную роль в развитии математической теории колебаний. Математикам легко удалось найти два простых решения, соответствующих первой и второй гармоникам. Но прийти к сложению этих двух найденных решений и тем самым получать сложные решения они смогли лишь после того, как музыканты заявили, что они могут слышать обе эти ноты одновременно1).
J) См. Jahreshericht der Deutschen Mathematiker Vereinigung, t. .10, II, 1 (1901 —1903), стр. 5. Впервые эту связь установил Д. Бернулли (примерно в 1730—1750 годах). Математики того времени не приняли его точки зрения.
101
Устройство на рис. 43 представляет один из способов, который осуществляет это сложение. Изображенный на рисунке четырехугольник OSRT всегда будет параллелограммом, поэтому, согласно главе I, можно записать, что R — S -j- Т. По мере перемещения проводов точка S (точка, где первый провод пересекает GOF) «скачет» взад и вперед вдоль GOF, а точка Т — взад и вперед вдоль MON, но с более высокой частотой. Поскольку R = S -j- Т, то движение точки R
О х
Частица брезервуаре б
можно .рассматривать как комбинацию этих двух движений, то есть мы имеем пример сложения векторов, о котором говорилось в главе I.
Заметим, что, кроме сложения векторов, здесь имеют место и матричные операции. Вернемся к системе колеблющейся струны. Оттягивая струну, как это показано на рис. 46, а, мы приводим в действие силы, которые пытаются вернуть точки В и С в их первоначальное положение. Такими силами будут сила Р, стремящаяся уменьшить расстояние х, и сила Q, стремящаяся уменьшить расстояние у. Так как поведение частицы в резервуаре дает точную динамическую картину состояния струны, то появляется возможность определить силы Р и Q в терминах искусственно созданной модели с.резервуаром. В указанной
102
системе эти силы действуют так, как показано на рис. 46, б: сила Р тянет частицу на запад, а сила Q — на юг. Результирующая сила показана на рис. 42 стрелками «склонов»:
Сами силы Р и Q даются линейными уравнениями
Р = 2х — у,
Q = — х 4- 2у, которые, легко записать в матричной форме.
Изучение рис. 43 показывает, что мы неудачно выбрали оси и вот почему. На рис. 42 х измеряет расстояние в восточном направлении, а у — в северном. Однако в проведенных выше рассуждениях эти направления не играли существенной роли. Напротив, мы неоднократно слышим о направлениях вдоль прямых FOG и MON, указывающих соответственно на северо-восток и северо-запад.
При постановке задачи с колеблющейся струной мы не могли обойтись без х и у, обозначив ими смещения в точках В и С. Это были естественные переменные, в которых выражались силы Р и Q и потенциальная энергия V. Когда же мы перешли к решению задачи, оказалось желательным перейти к новым осям, направленным на северо-восток и северо-запад.
Вряд ли целесообразно приводить все решение подробно, ибо это потребовало бы рассуждения о силах, ускорениях, дифференциальных уравнениях и отвлекало бы нас от главного1)- Мы сосредоточим свое внимание на главной особенности, на линейных уравнениях, определяющих силы Р л Q в терминах хну. У нас есть основания подозревать, что эти уравнения упростятся, если мы введем новые оси FOG и NOM.
Изучение преобразования
Теперь целесообразно обозначить Р и Q через х* и у* и говорить о преобразовании (х, у) -> (х*, у*),
') Хотя в этих рассуждениях нет ничего устрашающего. Уравнения движения суть х=—2х + р, р = х-г.2р. Чтобы ввести новые оси, положим х = и 4- о, у = и — V. После подстановки в первые два уравнения получим новые уравнения й — —и, о=—За, решения которых суть м= Acos^-f- В sin/, о = = С cos (/Уз) + К sin (/ /З);
103
которому соответствуют уравнения
I	(I)
Эти уравнения сами по себе мало говорят нам о характере преобразования. Не улучшит ли дело намеченное нами изменение осей? На рис. 47 показано, что новые направления совпадают с направлением векторов С и D, тогда как прежние оси соответствуют векторам с и d.
Рис. 47.
А как поступает наше преобразование с точками С и О? В прежних осях точка С имела , координаты х — 1, у~ 1. Подставив эти значения в уравнения (1), найдем х*=1, у* — .1. То есть .преобразование оставляет точку С пеизменнрй. Капиталовложение С оборачивается той же суммой С->С. Что касается точки £>, то, подставив ее координаты х — —1, у — I в уравнения, получаем, что х* == —3 и у* = 3. А это значит, что преобразование переводит D = —с + d в £)* = —Зс + 3d. То есть D* есть то же самое, что 3D.
Следовательно, символически преобразование можно записать как С~>С, D —► 3D. Банковская схема, соответствующая этому преобразованию, капиталовложение ХС + YD переводит в ХС + 3YD. Приравнивая соответствующие количества в этих выражениях, получим
=
У* = ЗУ.
(2)
Эти уравнения проще исходных, к тому же они имеют вполне очевидный геометрический смысл: X* = X означает, что мы не меняем первую координату точки, a Y* — ЗУ — что мы растягиваем вторую координату втрое. Геометрически это отображение
104
представлено на рис, 48. Оно очень простое и напоминает концертино. Но как здорово оно было скрыто! Рассматриваемое отображение было подсказано нам уравнениями Р — 2х— у и Q = —х + 2у, которые связывали силы, приложенные к струне, и вызванные
ими смещения. Однако в самой задаче о колеблющейся струне не было ничего такого, что наводило бы па мысль, что здесь имеет место столь простое преобразование. Простота была скрыта за неудачным выбором осей.
Диагональная форма
Уравнения (1) в предшествующем разделе соот-/ 2 —1 \
ветствовали матрице I Л Изменив оси, мы получили уравнения (2), соответствующие в свою оче-/1 0\
редь матрице n Ql, в которой везде, кроме главки о у
ной диагонали, стоят пули. Такую форму матрицы называют диагональной формой.
Матрица, заданная в диагональной форме, обладает той особенностью, что она передает геометрический смысл соответствующего ей преобразования. /2 0\
Рассмотрим в качестве примера матрицу	)•
\ V О /
Она соответствует уравнениям х* — 2х и у* = Зу, которые определяют преобразование (рис. 49),
105
переводящее точку Р в точку Р*. Результат преобразования— удвоение масштаба по оси ОХ и утроение его по оси OY. Его можно уподобить деформации картинок, нарисованных на куске эластичной пленки, подвергнутой соответствующему растяжению.
Ниже предложено несколько упражнений, в которых требуется посредством изменения осей привести матрицу преобразования к диагональной форме. Все задачи можно решить методом, использованным в предыдущем разделе.
Упражнения
1.	В разделе «Изучение преобразования» мы ввели новые оси, основанные на равенствах С — с d; D = —с d. Найдите, как выглядят в новой системе осей следующие преобразования;
а)	=	у*=х,
б)	х* — Зх — у; у* = — х + Зу,
в)	х‘ = х + у, у’^х + у.
2.	Какой матрице из упражнений главы III соответствует преобразование «а» и какой — преобразование «в»?
Собственные значения и собственные векторы
Мы только что рассмотрели преобразование х* = — 2х, у* = Зу и его геометрический смысл. На рис. 50 оно воспроизведено вторично. Взяты точки А, В, С,... и показаны их новые положения после преобразования— точки А*, В*, С*, ... Из чертежа видно, что в точках В, С и D происходит излом. Точки О, В и В*, например, не лежат на одной прямой. Направление 106
О В* более северное, чем направление ОВ. То есть данное преобразование в общем случае меняет направление произвольно выбранного вектора. Так, если мы выберем произвольный вектор v и v -> и*, то векторы v и как правило, будут иметь разное направление. Однако из этого общего случая есть два исключения: переводя точку А в Д*, Е в £*, преобразование оставляет неизменным направление двух векторов ОА
и ОЕ. Такие векторы, направление которых не изменяется при преобразовании, называют собственными векторами.
Это геометрическое описание собственного вектора легко перевести на язык алгебры. Поскольку всякий вектор, имеющий направление вектора v и длину, в k раз большую длины вектора v, обозначается как k-v, то равенство v* = k-v (для некоторого k) означает, что вектор и* имеет то же направление, что и вектор V. Это представлено на рис. 50, где А* — 2А и Е* = ЗЕ.
В определении собственного вектора принято брать вместо k греческую букву X и определять’собственный вектор как вектор v, удовлетворяющий равенству и* = \v. Число X называется собственным значением вектора. Таким образом, вектор А есть собственный вектор, собственное значение которого равно 2. На
107
менее формальном языке это означает, что вектор ОА (при сохранении направления) претерпевает растяжение в 2 раза. Вектор ОЕ растягивается в 3 раза, следовательно, это собственный вектор с К = 3.
Оказывается, что отыскание осей, приводящих матрицу к диагональной форме, есть то же самое, что и отыскание собственных векторов. Это видно из сле
дующего рассуждения.
Допустим, что мы нашли оси, обеспечивающие
матрице диагональную форму. Пусть это будет ма-
Р трица К
0\
q/
Ей соответствуют уравнения х* = рх,
у* = qy, и общий вид преобразования запишется как хс + yd -> рхс -j- qyd. Положив х = 1, а у = 0, найдем с-+рс\ положив х = 0, а у = 1, получим d —►
qd. То есть с — собственный вектор с собственным значением р, a d — собственный вектор с собственным значением q.
Проведем обратное рассуждение. Пусть мы нашли два собственных вектора с и d, имеющих разные направления. Покажем, что если выбрать эти направления в качестве осей, то матрица преобразования будет иметь диагональную форму. Пусть собственные величины векторов будут соответственно р и q. Тогда с -> рс и d -> qd, а хс + yd -> хрс + yqd. Уравнения преобразования примут вид х* = рх и у* — qy, а со-
Р 0\
п , кото-О q)
рая является диагональной. Обратите внимание, что по главной диагонали стоят числа р и q, которые являются собственными значениями и показывают, во сколько раз растягиваются собственные векторы. Довольно утомительно каждый раз говорить о том, что преобразование представляется матрицей в диагональной форме. Проще говорить о преобразовании, «заданном в диагональной форме». Таковым является преобразование с-+рс и d-+qd, ибо соответствующая ему матрица, как мы видели, имеет диагональную форму.
Диагональная форма преобразования позволяет легко подсчитывать степени этого преобразования. Обозначим, например, через М преобразование
ответствующая им матрица — форму
108
2c, d —► 3d, рассмотренное выше. Двукратное применение этого преобразования /VI2 даст с ->4с, d >9d; троекратное — М3 даст с—* 8с, d —► 27с?; п-кратное — Мп даст с —► 2лс, d—►3nd. То есть всякий раз применение М удваивает с и утраивает d.
В связи с этим нетрудно вычислить и многочлен относительно М. Например, М2 -f- М соответствовал бы преобразованию с—> 6с, d-*12d, потому что «доход» от М2 + М находится сложением «доходов» М2 и М. На самом деле арифметический расчет скрывает имеющуюся здесь закономерность. Если мы запишем преобразование М2 + М подробно, то есть с —> ->(224-2)с, d —► (З2 -j- 3)d, то сможем обнаружить, как закономерность вида к2 + х проявляется в данном конкретном случае. Если же вместо конкретных чисел, таких, как 2 и 3, мы используем алгебраические символы, то закономерность обнаружится немедленно. Пусть, например, Т обозначает преобразование с pc, d —► qd. Тогда Т2 означает с р2с, d -> q2d, а Тп означает с -> рпс, d qnd. Выражение Т3 4-4- ЬТ2 •+ 7Т определяет преобразование с ->(р3 + 5р2 + -j-7p)c, d -+(q3 + bq2 + 7q)d, в котором с очевидностью проступает кубическая закономерность х3 + + 5х2 + 7х.
Результат, очевидно, не зависит от того, что мы выбрали в качестве примера кубический трехчлен. Ясно, что здесь скрывается очень общая закономерность. Если /(х) обозначает некоторый многочлен, то f(T) означает преобразование вида c-*f(p)c, d~* -+f(q)d. Однако здесь есть момент, который можно уподобить ложке дегтя в бочке меда. Как будет обстоять дело, если полином включает свободный член, например f(x)=x + 1? Что в этом случае означает f(T)? Непосредственная замена х на Т в двучлене даст Т + 1, то есть преобразование, сложенное с числом 1, а это, как известно, лишено смысла.
Дабы найти выход из этого затруднительного положения, обратимся к тому, что мы надеемся получить в общем случае. Мы хотим, чтобы f(T) дало нам преобразование вида c-+f(p)c, d-*f(q)d. А это и приводит нас прямо к цели, даже если f(x) = х + 1. Согласно сказанному выше, искомое преобразование должно иметь вид	и d->(g-|-l)d.
109
С другой стороны, поскольку f(x) = %+ 1, мы хотим его интерпретировать как «Г + что-то». Значит, чтобы получить f(T)t мы должны выполнить замену: заменить х на Г, а 1 на что-то такое, что мы пока не решили. Рассуждаем далее. Преобразование Т есть с—> -*рс, d—*qd. Те же рс и qd входят как часть в искомое преобразование с —>(р+ 1)с, d—►(</ + l)d, но не исчерпывают его. В нем присутствуют еще слагаемые end, соответствующие преобразованию с —► с, d-+d, которое является не чем иным, как тождественным преобразованием /. Следовательно, I и есть то самое «что-то», которое мы разыскиваем. Это открытие нас вполне устраивает, ибо I более всего схоже с 1, и при небольшом дополнительном соглашении нам удается сохранить наметившуюся у нас теорему. Итак, при переходе от f(x) к f(T) договоримся 1 заменять тождественным преобразованием I. Например, если f(x) = х2 + 2х + 3, то f(T) = Т2 + 2Т + 3/. С учетом этого теорему можно сформулировать так: если Т — преобразование вида с-+рс, d-+qd, то f(T) — преобразование вида c~+f(p)c, d-+f(q)d. Заметим, что с и d — собственные векторы преобразования f(T) с собственными значениями f(p) и f(q)-В матрице для f(T) мы обнаружили бы на главной диагонали члены f(p) и f(q), во всех других местах — нули.
Эта аргументация, проведенная для двумерного преобразования, столь же хорошо оправдывается и для /z-мерных преобразований. Например, для трехмерного преобразования при Т, соответствующем с —► ~+рс, d-+qd, e-+re, f(T) соответствовало бы преобразованию c-+f(p)c, d-*f(q)d, e-+f(r)e.
Преобразования, представляющие исключение
Мы видели, что если преобразование дается в диагональной форме, то его геометрический смысл легко усматривается, а алгебраические расчеты значительно упрощаются. Отсюда ясно, что если дано преобразование, то желательно найти те оси, которые позволяют записать его в диагональной форме. Возникает вопрос: всегда ли это возможно? Оказывается, обычно возможно, но не всегда.
НО
Обсуждение этого вопроса покажет, ценность гео? метрического подхода. Вопрос можно было бы сфор* мулировать и изложить в терминах алгебры, но результаты вычислений в этом случае не обладают ни простотой, ни особой ясностью. Поэтому гораздо лучше рассматривать его геометрически.
Чтобы сделать матрицу диагональной, надо, как мы видели, в качестве осей выбрать собственные век-торы, то есть такие векторы, которые под действием преобразования лишь растягиваются, но не меняют своего направления. Поэтому, если найдется преобразование, не приводимое к диагональной форме, то только потому, что нельзя найти двух таких направлений, которые бы не менялись под действием этого преобразования.
С примером такого преобразования мы уже встречались (хотя и не осознавали этого). В первом упражнении предыдущей главы оно определялось матрицей А и проиллюстрировано здесь на рис. 51. Его уравнения суть х* = х + у. у* = у. Каждая точка при этом преобразовании движется горизонтально: точки D, Я, F смещаются на 1 единицу вправо, а точки О, Я, К — на 2 единицы. Направление OG поворачивается и принимает направление O*G*, направление ОН—О*Н*. Все точки, лежащие выше оси ОВС, смещаются вправо. Все направления, исходящие из начала О, поворачиваются в направлении на восток. Если продолжить рис. 51 с целью показать точки под осью, то мы найдем их смещенными влево, а соответствующие им направления, исходящие из точки О, — повернутыми на запад. Точки О, В, С, лежащие на оси, остаются на месте, то есть преобразование не меняет направления ОВ.
Западно-восточное направление — единственное направление, не тронутое преобразованием. Все другие
-111
прямые поворачиваются в этом направлении, что по форме напоминает закрывающиеся ножницы.
Следовательно, вектор ОВ есть собственный вектор и потому является подходящим для одной из осей. Второго собственного вектора, отличного от В, не существует. Таким образом, исследование показало, что нельзя найти двух осей, в которых это преобразование выражалось бы матрицей в диагональной форме.
Когда можно привести преобразование к диагональной форме?
Теория матриц была бы очень простой, если бы каждое преобразование можно было представить в диагональной форме. Но, к сожалению, это не всегда возможно. Отсюда, естественно, возникает вопрос: как узнать, когда преобразование представимо в диагональной форме, а когда нет? В следующей главе мы обнаружим, что уравнение, которому удовлетворяет матрица, дает очень простой критерий. А пока мы приводим таблицу с уравнениями, которым удовлетворяют матрицы, взятые из упражнений главы III. В этой таблице также даны собственные значения этих матриц и указано, какая из матриц приводима к диагональной форме, а какая нет. Несмотря на скудность материала таблицы, знакомство с ним, быть может, позволит вам догадаться, как по уравнению узнать, приводится ли матрица к диагональной форме или нет.
Матрица X	Уравнение, которому удовлетворяет матрица	Собственные значения Л	Существует ли диагональная форм.-; матрицы '
и	х^-1 = 0	+ 1,-1	Да
W	X2 - 2А' = О	2,	0	»
I	Х — 1 = О	1	»
А	X2 - 2Х + I = О	1	Нет
В	Х2-2Х +1 = 0	1	»
ГЛАВА V
ПОЛЬЗА МЕТОДА УРАВНЕНИЙ
Начало этой главы на первый взгляд может показаться не относящимся к теме, но это только на первый взгляд. На рис. 52, а показан график функции у = х4 — 2х2 + 1. Он симметричен относительно оси OY: каждой точке Р(х, у) на графике соответствует другая точка Q(—х, у), ее отражение относительно OY. На рис. 52,6 представлен график функции у = = х3 — х, на котором каждой точке Р(х, у) соответствует точка Q по другую сторону от начала О с координатами (—х, —у).
В случае рис. 52, а мы называем график симметричным, в случае рис. 52, б — антисимметричным. График у = /(х) симметричен, если f(—x)—f(x), и антисимметричен, если f(—х) = — f(x). Эти понятия хорошо известны и часто используются при построении графиков от руки. Однако далеко не все графики обладают названными свойствами. Значительно большую их часть нельзя причислить ни к симметричным, ни к антисимметричным графикам. Например, график функции y — g(x) при g-(x) = х3 + 5х2 —7х + 2 не обладает свойством симметрии или антисимметрии. Однако существует теорема, утверждающая, что
113
всякую функцию можно представить в виде суммы двух частей, одна из которых является симметричной функцией, другая — антисимметричной. Для функций, подобных функции g(x), эта теорема очевидна, ибо симметричная и антисимметричная части легко обнаруживаются при отделении четных степеней х от нечетных. Менее очевидна эта теорема в случаях графиков у — = (х + 5)/(2х + 3), или у = 10х. Вероятно, можно было бы попытаться постепенно, шаг за шагом доказать эту теорему сначала для полинома, потом для дробных функций, затем для бесконечных рядов и т. д. Но такой подход был бы совершенно неправильным, так как сам факт разложения функции на симметричную и антисимметричную функции не зависит от того, будет ли функция простой или сложной. Он одинаково верен как для графика, свободно начерченного от руки, который задается без всякой формулы, так и для графика функции, имеющей конкретное аналитическое выражение, например у = х2 + х. При этом от функции не требуется ни гладкости, ни непрерывности: она может иметь острые изломы и резкие скачки. Есть только одно ограничение — она должна быть функцией, то есть каждому значению х должно соответствовать одно значение у.
Допустим, что нам дан график некоторой функции у = G(x) и мы хотим выразить G(x) в форме f(x) + ф(х), где f(x) — симметричная, а <р(х) — антисимметричная функции. Подставим вместо х произвольные числа а и —а. При х = а мы надеемся получить
G(a) = f(a) + <p(a),	(1)
при х = — a G(—a) = f(—a)+(p(—a). Используя свойства симметрии и антисимметрии функций-составляющих /(—o)=f(a) и <р(—а)=—ф(а), найдем, что
G(—a) = f(a) —ф(а).	(2)
Легко решить систему уравнений (1) и (2), в которых G(a) и G(—а) известны, a f(a) и ф(а) —неизвестные, которые мы хотим найти. Имеем
f(a) = l[G(a) + G(-a)],
<Р (a) =' j [G («) — G (— a)].
(3)
114
Следует иметь в виду, что под а здесь понимается любое число. Итак, если искомые функции f(x) и <р(х) существуют, то они вполне определяются системой (3).
Можно проверить, что эти функции удовлетворяют всем нужным требованиям. Если в первом уравнении системы вместо а взять х, то получим f (х) =1/2[G (х) 4- G{—х)]. Легко видеть, что функция симметрична, так как при замене х на —х в правой части меняется только порядок слагаемых. Аналогично убеждаемся, что функция ф(х) = 1/2[G(x) — G(—х)] антисимметрична, так как при замене х на —х знаки членов в правой части меняются на противоположные. Но сумма функций / (х) и ф(х) дает G(x), то есть нам удалось разбить функцию G(x) на две части: симметричную и антисимметричную.
Графически это решение представлено на рис. 53. График y=G{—х) получается зеркальным отражением графика у = G(x) относительно оси OY,
Функция f(x) есть среднее арифметическое G(x) и G(—х), следовательно, ее график расположен посередине между двумя графиками y=G(x) и у = = G(—х), как и показано на чертеже. Тогда <р(х) надо прибавить к f(x), чтобы получить на чертеже G(x). Мы не изобразили график у = <р(х). Вместо этого вертикальными стрелками показан результат прибавления функции <р(х). Чтобы из графика у = — f(x) получить график у = G(x), надо поднять правые точки «точечной кривой» у = f(x) и опустить левые. Антисимметричность <р(х) проявляется в направлении стрелок.
Как уже упоминалось, на природу функции G(x) не накладывается никаких ограничений. В основе доказательства лежит операция замены х на —х. Поэтому целесообразно ввести для этой операции символ,
115
пусть это будет М. MG(x), следовательно, означает G(—х).Из рис. 53 легко усматривается и графический смысл операции М\ она симметрично отражает график относительно оси OY.
Операцию М особенно легко выполнить, когда G(x) задается формулой. Так, если G(х) =х3-\- 5х2— — 1х + 2, то MG(x) = —х3 + 5х2 + 7х + 2. Она применима и к функциям, заданным в виде таблицы. Например, если бы была дана таблица
х -2—1012
G(x) 4	11 7 2 9
то после применения операции М мы бы получили х —2 —1 0	12
G(-x)	9	2 7 11 4
то есть мы бы просто переставили порядок входов во второй строке таблицы.
Ясно, что двукратное применение операции М возвращает нас к исходному, то есть М2 = /. Всякое симметричное выражение f(x) не меняется под действием М. Поэтому равенство Mf(x) — f(x) является условием симметрии.
Всякое антисимметричное выражение под действием операции М меняет свой знак па противоположный. Условие антисимметрии, следовательно, запишется равенством Л4ф(х) = —ф(х).
Свое рассуждение мы начали с некоторой функция G(x), получив из нее f(x) и ф(х). Функция f(x) симметрична и равна V2[G(x) + G(—%)], что в терминах М запишется как + Af)G(x). Можно ли убедиться, что и в этом обозначении f(x) симметрична? Симметрия f(x) означает, что она не меняется цод действием Л1, а это можно показать непосредственно, используя только одни алгебраические свойства М.
Так как если f — ’/г (/ + Af)G, то A4f = 1/2Л1 (/ -j-+ /М) G = 1,/2(Af + Л42) G — V2 (Л4 + /) G. Последний шаг сделан на основании того, что М2 = I, Получим, что Mf — f, то есть функция f(x) симметрична. Аналогичное вычисление показывает антисимметрию функции ф(х), ф = 1/2(/~-M)G, Мф= V2M(/-M)G = = */2(Л1 —AP)G =	— I)G.
116
Сравнивая результаты для ф и Л4ф, видим, что Мф = —ф, а это и есть критерий антисимметричности.
Наконец, мы должны проверить, что G — f + ф, то есть что G = V2(/+ M)G + ]/2(/— A4)G. Если переписать равенство, заменив в левой части G на /G, IG = 72 (/ + Af) G + 72(/ — M)G, то оно становится очевидным. Действительно, теперь его можно рассматривать как результат приложения тождества / = — 7г(/ + М) + 7г (/ — М), составленного для операторов, к вектору G.
Доказательство этих последних трех пунктов можно было бы провести, не выясняя, что скрывается за М и G, достаточно было знать, что М2 — I и что здесь приложимы обычные алгебраические преобразования. Приведенная выше аргументация фактически подсказывает, что здесь должна быть более общая теорема приблизительно такого типа: если М2 = /, то любое G можно представить в виде суммы f + ф, где Mf = f и Л1ф = — ф. Однако мы не можем это утверждать, не сделав каких-то предположений как относительно М и G, так и относительйо вида объектов I и Ч>-'
Отыскание нужных условий
Так как в сформулированной выше теореме упоминается сумма f + ф, то самбе малое мы должны допустить, что f и ф в каком-то смысле можно складывать. По мере проведения доказательства обнаруживается необходимость и других допущений.
Согласно доказательству, f определяется выражением 7г[^ + iW]G. Что мы понимаем под выражением (/ -}-M)G? Прежде всего, что это G-f-AlG. Следовательно, MG должно быть таким, чтобы его можно было прибавить к G. Для краткости обозначим MG через Н. Иначе говоря, мы должны придать смысл сумме G + Н, а затем перейти к f — V2(G И), то есть мы должны находиться в системе, в которой имеет смысл умножение на 7г- Только что введенные операции принадлежат к типу операций с совокупностями животных, которые встречались нам в главе I. Это операции сложения и умножения на число. Там мы неформально определили векторное пространство как
117
систему объектов, в которой можно производить вычисления по правилам, приложимым к совокупностям животных. Согласно этому, чтобы гарантировать смысл f = */2(0 + Н) и ф = 7г (G — Н) и возможность обращаться с ними так, как это делалось в главе I, достаточно будет сказать, что G и Н принадлежат к некоторому векторному пространству. Тогда рассматриваемые операции, например f + ф = G, вполне осмыслены.
Итак, G и Н должны принадлежать одному и тому же векторному пространству. Поскольку Н есть MG, то MG принадлежит тому же векторному пространству, а, значит, М должно быть операцией, отображающей это пространство в себя. Ни одно из ранее рассмотренных преобразований не подходит в качестве М. Рассуждения предшествующего раздела включали выражение Mf, где f = i/z(G + #)» и допускали действия вида М: 72(G + Н) - 72(AfG + МН).
Оказывается, все это можно проделывать с любым линейным преобразованием. Преобразование Т называют линейным, если выполняются соотношения T(u + v)=Tu + Tv и T(ku)=kTut где и и v — произвольные векторы, a k — любое число. Этими свойствами автоматически обладает всякая «банковская схема»: доходы от двух капиталовложений суммируются, и увеличение капиталовложения в k раз соответственно в k раз увеличивает прибыль. Именно поэтому банковские схемы были использованы при введении в тему линейных преобразований.
Любое преобразование, определяемое линейными уравнениями (или матрицей, что то же самое), является линейным преобразованием.
Сейчас мы уже можем сформулировать нашу общую теорему с точным описанием ситуаций, к которым она приложима.
Если задано векторное пространство и некоторое линейное преобразование М этого прост-' ранства в себя, удовлетворяющее равенству М2 5= /, то для любого вектора G можно найти такие векторы f и ф, что будет выполняться равенство G = f + ф, где Mf = f и Мф = — ф.
Это звучит довольно многословно и может отпугнуть тех, кто не знаком со специальной терминологией.
Ив
Однако эти слова, если понимать их правильно, — способ напомнить нам очень сжато о проделанной работе. Расшифруем смысл этих слов полностью. Слова «задано векторное пространство» означают все то, что говорилось в главе I о кошках, собаках и параллелограммах. Помните наш разговор о физиках, складывающих скорости, и об утверждении чистого математика, что формальные правила сложения скоростей приложимы к сложению квадратичных или любых других функций? Если вы помните его, то поймете, что эта теорема приложима к очень большому числу ситуаций, между которыми обнаруживаются известные аналогии. Далее идут слова «М — линейное преобразование этого пространства в себя». В главе Ш мы рассматривали такого рода преобразования и дальше встретим еще много примеров линейных преобразований. Выделенные нами слова определяют ситуацию или условия, в которых будет развертываться теорема. Их можно уподобить сценическим ремаркам, убрав которые, мы получим суть теоремы, промелькнувшей перед нами на стр. 117.
Эту теорему можно считать типичной теоремой современной математики в том смысле, что в ней совсем не упоминается о каком-либо конкретном случае. Она относится к большому числу ситуаций, обладающих общностью в определенном аспекте. Такая абстрактность часто беспокоит и затрудняет учащихся, потому что они не могут ясно представить себе все те ситуации, к которым эта теорема приложима.
Чтобы преодолеть эту трудность, часто бывает полезно вести изучение с двух концов, то есть рассматривая частные случаи и одновременно следя за развитием логики доказательства.
Примером простого векторного пространства может служить плоскость. В качестве М можно выбрать отражение плоскости относительно горизонтальной оси ОХ, так как при этом Af2 = 1. Этот пример проиллюстрирован на рис. 54. На плоскости выбирается произвольная точка G. Вектор G вы можете представить себе по желанию либо как эту самую точку, либо как стрелку OG. Вектор Н есть отражение вектора G относительно ОХ, поэтому Н = MG. При доказательстве теоремы мы нашли, что f — V2(G + Н). А это
119
представляет собой, согласно изложенному на стр. 29, формулу, определяющую положение средней точки между G и Н. Точка F лежит посередине между G и Н. Мы можем считать, что f представлена точкой Л, или, быть может, что более удобно, стрелкой OF. Так как G должно равняться f + Ф, то ф — это то, что следует прибавить к f, чтобы получить G. Вектор ф можно представить стрелкой FG, или, как на рисунке, стрелкой OL. В результате применения операции /И вся фигура зеркально отражается относительно оси ОХ. При этом вектор f остается неизменным, а направление вектора ф меняется на противоположное. То есть, как и ожидалось, Mf = f и Л1ф = —ф. Этот пример, давая достаточно простую и ясную иллюстрацию теоремы, помогает нам увидеть геометрические и алгебраические процессы, используемые при ее доказательстве. Еще с целым рядом примеров вы познакомитесь в следующем разделе этой главы.
’ Следует заметить, что, рассматривая частные примеры, изучающий всякий раз должен обращаться к доказательству, постигая, как одно и то же рассуждение способно охватить самые разные случаи. При таком методе всякое ощущение странности постепенно исчезает.
Еще примеры	"
Дополнительные геометрические примеры можно получить из темы, связанной с симметричными и антисимметричными функциями, которыми начиналась эта глава, и операцией М перехода от f(x) к f(—х). Поскольку мы живем только в трех измерениях и собираемся сопровождать изложение рисунками, то это вынуждает нас наложить на рассматриваемые функции некоторые ограничения.
Для начала возьмем квадратный трехчлен ах2 4-4- Ьх + с. Операция М превратит его в ах2 — Ьх -]~ с. Если через a*, fe*, с* обозначить коэффициенты второго трехчлена, то получим а* — а\ Ь* = —Ь; с* — с. Результат преобразования показан на рис. 55, где а соответствует направлению на восток, с — на север и. b — направлению вверх. Видим, что преобразование М есть простое отражение относительно горизонталь-
120
ной плоскости. Любой вектор OG можно разложить на два вектора: вектор f — OF в горизонтальной плоскости и вектор ф = OL, лежащий на вертикальной прямой, проходящей через точку О. В результате применения операции М вектор f остается неизменным, вектор ф меняется на противоположный, так что L отображается в К.
Горизонтальная плоскость и вертикальная прямая, проходящие через точку О, называются инвариантными подпространствами. Любая точка L па вертикальной прямой переходит в точку (К) той же прямой. Любая точка F горизонтальной плоскости переходит в точку той же плоскости (фактически в ту же точку F). То есть горизонтальная плоскость и вертикальная прямая представляют собой свои собственные отражения. Поэтому мы называем их инвариантными (то есть неизменными), так как операция М оставляет их в прежнем положении.
Эти инвариантные подпространства обладают весьма полезным свойством. Если мы знаем, что в них происходит, мы тем самым знаем, что происходит с любой точкой пространства, так как мы убедились, что любую точку G можно представить в виде суммы f + ф, где f лежит в горизонтальной плоскости и ф — на вертикальной прямой. Зная, что делает операция А1 с f и ф, можно узнать результат ее воздействия на G, так как MG = MfМ^. На нашем чертеже
121
G = F + L. Поскольку F-+F и £->/<, то F + L-+ -> F + Л. Ho F + К и есть на самом деле //, отражение G относительно горизонтальной плоскости.
Обратим внимание на то, что инвариантные подпространства — прямая и плоскость — суть линейные пространства. Это обусловлено не поставленной нами частной проблемой, а справедливо для всех линейных преобразований.
Заметим также, что каждый вектор в горизонтальной плоскости есть собственный вектор с X = + 1, а каждый вектор на прямой — собственный вектор с А= —1.
Упражнение
Вместо квадратного трехчлена рассмотрите выражения вида ах3 + Ьх2 + сх. Каков геометрический смысл операции М в этом случае? Что представляют собой инвариантные подпространства и какие значения Л соответствуют векторам этих подпространств?
Если мы возьмем кубическое выражение вида ах3 + Ьх2 + сх -j- d, то рассматриваемое преобразование М будет определяться равенствами а* = —а, Ь* = Ь, с* = —с, d* = d. Условие того, что вектор останется неизменным под действием операции М, выразится равенствами а — 0, с = 0. Все факторы вида (0, Ь, 0, d) образуют инвариантное подпространство, которое фактически есть плоскость, поскольку каждый вектор в ней имеет форму Ьи 4- dv, где и — (0,1,0,0), и = (0, 0, 0, 1), и является собственным вектором с	Аналогично плоскость, содержащая все
точки вида (а, 0, с, 0), есть инвариантное подпространство, каждый вектор которого есть собственный вектор с А =—1. Любой произвольный вектор четырехмерного пространства можно изобразить в виде суммы двух векторов f 4- ф с f в первой из указанных плоскостей и ф — во второй. Мы не можем отчетливо представить себе четырехмерное пространство, одна-
') Фактически пространство многочленов не выше третьего порядка является четырехмерным векторным пространством. Если в качестве -«направляющих векторов осей» (базисных векторов) взять х3, х2, х, 1, то многочлен dx3&х2сх + d -будет иметь координаты (в, b, c,d). — Прим. ред.
122
ко ясно, что здесь имеется аналогия с уже изученной нами ситуацией в трехмерном пространстве.
Рассматриваемое преобразование М, записанное равенствами а* = —a, b* = +b, с* = —с, d* = d„ уже представлено в диагональной форме, которая позволяет достаточно хорошо изучить его, не прибегая к теореме о разложении в виде G = f + <р. Однако эта теория могла бы оказаться полезной при рассмотрении графиков ломаных линий типа G, представленных на рис. 56. Операция М обращает, то есть
MG
Рис. 56.

зеркально отражает, этот график (сравните со стр. 115) и определяется уравнениями а* = d, b* = с, с* — b, d* = а. Мы знаем, что G можно представить в виде суммы двух функций f 4- <р, где f имеет симметричный график со входами р, q,q,p,a <р — антисимметричный, со входами г, s, —s, —г (как показано на рис. 56). Следовательно, a = p4-r, b — q-{-c, с = q — s и d = p — г. Введением новых переменных р, q, г и s это преобразование приводится к диагональной форме р* = р, q* = q, г* = —г, s* = —s.
График G на рис. 56 определяется четырьмя числами а, Ь, с, d. Совокупность всех таких графиков G образует векторное пространство четырех измерений. Если бы мы взяли больше точек, то, соединив их прямыми линиями, могли бы получить векторное пространство с большим числом измерений. Взяв точки достаточно густо и последовательно соединив их отрезками, мы получили бы ломаную линию с очень большим числом очень коротких звеньев, напоминающую непрерывную кривую. Это наводит на мысль, что графики непрерывных функций могут образовывать
векторное пространство с бесконечным числом измерений. Таким образом, мы здесь возвращаемся к мысли, высказанной в главе II, что имеются векторные пространства, элементы которых суть функции. Если вы помните, настоящая глава начиналась с рассмотрения симметрии и антисимметрии функций. Анализируя этот вопрос, мы пришли к теореме, начинавшейся словами: «Если задано векторное пространство...» Понятие векторного пространства, составленного из функций, вероятно, не принадлежит к числу простых. Но интересно проследить, как само изучение функций постоянно подсказывает нам эту идею. В главе VII от этих намеков мы перейдем к точной формулировке идеи и попытаемся провести ее формально по всем правилам.
Обобщение уравнения
Рассматривая преобразование Л1, мы видели, что оно могло удовлетворять разного рода уравнениям. На всем протяжении этой главы мы были заняты уравнением Л42=/. Однако, как мы видели, имеется много других уравнений, которым может удовлетворять преобразование. Нельзя ли из нашего частного случая извлечь общие принципы? Приведенное выше рассуждение мы начали с того, что из произвольного вектора G образовали *) собственный вектор f, который представили как V2 (Л1 -(-/)(?. Почему здесь оказалось выражение V2 (Л1 + О? Поскольку М удовлетворяет уравнению М2 — Z, то нетрудно догадаться, что М + / появилось потому, что оно является сомножителем в М2— 1. Находится ли это в связи с тем, что f является собственным вектором? Условие для вектора f быть собственным (с Х=+1) состоит в выполнении равенства Mf = f, которое можно переписать как (Л4 ~ — I)f = О. В таком виде, условие содержит и другой сомножитель двучлена М2 — I. Если теперь в условие (Л4 — I)f = О мы вместо f подставим 1/2(А4 + /)<?, то
9 Вектор О тоже удовлетворяет уравнению Mf = Kf, но от этого его не считают собственным вектором. Может случиться, что 1/2(Л1 + Z)C? дает О, и тогда мы имеем исключение из выше сформулированного утверждения и других аналогичных утверждений, сделанных позже относительно образования собственных векторов.
124
в полученном произведении появится сомножитель М2 — 7, равный О. Все это вычисление выглядит так: (M-I)f = (М — /)-72(Л1 + I)G = 72(М2 —7)G = — О • G = О.
Идея проясняется. Допустим, что мы имеем дело с преобразованием Т, удовлетворяющим уравнению (Т— I) • (Т — 2/) * (Г —37) — О, и ищем вектор и, который будет удовлетворять уравнению (Г — 1)и — = О. Очевидно, и можно положить равным (Т — 21) (Т — 37) G, где G — произвольный вектор, так как в этом случае (Г — 1)и = (Г — 7 ) • (Т — 27) • • (Т— 37) -G = О • G = О. Таким же образом, если нам будет нужен вектор и, удовлетворяющий условию (Т — 2I)v=^O, мы выбираем его в виде v = <Г— 7) • • (Т— 3/)G. То есть мы берем все сомножители уравнения, за исключением того, который присутствует в данном условии.
В своих рассуждениях, связанных с М2 — Ц мы выбирали для f не (M + /)G, а 72(М + ЛС. Здесь добавочный множитель 7г не портит доказательства, ибо выражение (Л1 + 7) можно умножить по желанию на любую константу (за исключением, конечно, 0). Что касается преобразования Т, рассмотренного выше, то вполне законно взять и — а(Т — 21) (Т — — 37) G и v = Ь(Т — 7) (Г — 37) G, где а и b —любые числа. Для полноты списка мы возьмем еще вектор се\ удовлетворяющий условию {Т ~3I)w = О. Согласно принципу составления искомых векторов выбираем W = с(Т — Г) • (T-2I)G.
В вычислениях с М существенным было то, что G можно было представить в виде суммы f + ср. Сейчас, следуя аналогии, мы хотим, чтобы G = и + v + то есть G^a(T-21)(T-3I)G + b(T~I)(T-— 37)G4-c(T — 1) (Г — 27) G для всякого G. Это равенство можно рассматривать так, что в правой части к произвольному вектору был применен сложный оператор, который оставил его без изменения. Значит, этот оператор есть тождественный оператор 7. Приравнивая его к 7, мы одновременно поставим задачу найти (если это возможно) числа а, b и с, удовлетворяющие получившемуся равенству
7 = а (Т - 21) (Т - 37) + b (Т - 1)(Т - 37) +
+ с (Г-7) (Г-27).
12$
Поскольку эта задача принадлежит элементарной алгебре, то мы дадим ее решение в знакомой традиционной форме. Можно ли найти такие числа а, b и су которые бы обращали уравнение
1 = а(х - 2)(х - 3) + b (х - 1)(х - 3) + с(х - 1)(х - 2)
(4) в тождество? Это можно сделать двумя путями: выполняя умножение и решая систему уравнений, или, более искусно, полагая в уравнении поочередно х=1, л=2, х==3. Эти подстановки единственным образом определят значения а = 72, & = —1 и с =72, которые дадут решение задачи.
Если теперь в качестве ау b и с взять найденные значения, то записанные ранее уравнения позволят любой вектор G представить в виде и 4- v + wy где (Г —/)п = О, (Г-2/)у = О и (Г —3/)ш = О, что эквивалентно равенствам Ти — иу Tv = 2vy Tw = 3w. Эти равенства показывают, что преобразование Т растягивает векторы иу v и w соответственно в 1, 2 и 3 раза, не меняя их направления.
Естественно, что различные векторы G приведут к различным векторам иу vy w подобно тому, как разные точки G на рис. 55 могли привести к разным точкам F. Фактически (в случае рис. 55) при изменении G возможные положения F заполнят всю горизонтальную плоскость. Аналогично и в этом примере можно показать, как возможные положения и заполнят линейное подпространство, возможные положения v — другое линейное подпространство и возможные положения w — третье. Все вычисления по существу происходят таким же образом, как и для М2 — I = О.
Если в уравнение (4) подставить найденные значения а 72, b = — 1, с = 7г и разделить его почленно на произведение (х—1) (х — 2) (х — 3), то придем к уравнению
________1____________У2______1	। Уд
(х-1)(х-2)(х-3)~х-1	х —• 2 ‘ х — 3 *
Всякий, кто хоть немного знаком с математическим анализом, узнает в этом преобразовании разложение дроби на простейшие дроби, часто используемое при интегрировании выражения, стоящего в левой части.
126

В случае операции М мы использовали тождество 1 = У2(1 -]- х)-|- '/2(1—X}. Разделив его почленно на х2—1, получим разложение на элементарные дроби:
1	. У2 '/2
Хг — 1	X — 1 X + 1 
Тому, кто хорошо владеет методом разложения на элементарные дроби, возможно, эта связь окажется полезной для того, чтобы запомнить способ представления произвольного вектора G в виде суммы собственных векторов, который сводится к следующему. Мы имеем преобразование (или матрицу) М, удовлетворяющее уравнению F(M) = О. Представим дробь 1/jF(x) в виде суммы элементарных дробей. Умножим полученное уравнение на F(x), это дает нам уравнение в форме «1 = определенное выражение». Заменим х в этом уравнении на М и полученное равенство как оператор применим к произвольному вектору G.
Однако этот способ терпит неудачу всякий раз, когда в F(x) имеются повторяющиеся сомножители. В конце главы V речь шла о матрице А, не приводимой к диагональной форме. Простейшее уравнение, которому удовлетворяет А, есть уравнение А2— 2А + + 1 = 0, которое соответствует функции F (х) — х2 — — 2х + 1. Так как х2 — 2х + 1 = (х — I)2, то нам не удается разложить дробь 1/(х — I)2 на дроби, более простые, чем она сама. Иначе говоря, в случае, когда уравнение F(x)==0 имеет кратные корни, наш способ не приводит к цели.
Можно ли сделать отсюда вывод, что наличие кратных корней в уравнении означает неприводимость матрицы к диагональной форме? Пока нет, мы лишь показали, что данным приемом решить эту задачу не удается. Но, может быть, есть другие приемы, с помощью которых мы бы с ней справились? Оказывается, нет, так как существует теорема: если матрица представима в диагональной форме, то она удовлетворяет уравнению, которое, не имеет кратных корней.
Доказательство этой теоремы несложно. На стр. ПО упоминалось о том, что когда Т представима в диагональной форме с числами р, q и г на главной диагонали, то и F(T) оказывается представимой в диагональной форме с числами F(p), F(q) и F(r) тоже на
127
главной диагонали. Аналогичный результат имеет место в случае любого числа измерений. Пусть, например, мы ведем вычисления в шестимерном пространстве, так что Т задано матрицей с шестью столбцами и шестью строками. Пусть эта матрица имеет диагональную форму с числами 1, 1, 1, 2, 3, 3. По теореме, приведенной в последнем абзаце, матрица F(T) тоже будет иметь диагональную форму с числами F({), F(l)f F(l), F(2), F(3), F(3).
Если мы сумеем подобрать функцию F так, чтобы все шесть чисел оказались равными нулю, то будем иметь равенство F(T) = О. так как F(T) имеет диагональную форму и потому у нее все числа, не стоящие на главной диагонали, нули. Но чтобы обратить эти шесть чисел в нуль, достаточно удовлетворить равенствам Е(1) =0, Е(2)=0 и F(3)=0. Это можно сделать, взяв F(x) = (x—1) • (х — 2) • (х — 3), где ни один из множителей не повторяется, то есть соответствующее уравнение не имеет кратных корней.
Формальное математическое доказательство этого результата было бы просто маленьким эссе, показывающим, что то, что было проделано для частного примера, можно сделать всегда.
Проведенные рассуждения позволили обнаружить необходимое и достаточное условие. Если преобразование удовлетворяет уравнению, которое не имеет кратных корней, то его можно представить матрицей в диагональной форме; если не удовлетворяет, то нельзя.
Отыскание уравнения
Чтобы применять сформулированную выше теорему, следует отыскать самую простую форму уравнения. В связи с этим возникают два вопроса. Первый: для всякого ли преобразования найдется уравнение, которому бы оно удовлетворяло? Второй: если да, то как при этом найти самое простое уравнение? Мы сказали «самое простое уравнение», потому что преобразование может удовлетворять многим уравнениям точно так же, как в традиционной алгебре число 3 удовлетворяет не только простейшему уравнению х — 3=0, но и уравнению (х — 3) (х — 5) =0, и в сущности любому уравнению вида (х — 3)f(x) =0, где f(x) — полином.
128
В том, что всякое линейное преобразование должно удовлетворять некоторому уравнению, нетрудно убедиться1)- Сделаем это для двумерного пространства, а на большее число измерений рассуждение легко обобщить. Прежде всего отметим (как установлено в конце главы III вопросами 18—29), что матрицы 2X2 составляют линейное пространство четырех измерений. Обратимся далее к идеям раздела «Полезный результат» на стр. 65. Пусть Т — любая матрица 2X2, рассмотрим матрицы /, Г, Г2, Г3, Г4.
Эти пять матриц тоже лежат в четырехмерполМ пространстве, следовательно, они должны быть линейно зависимыми, то есть связаны уравнением а! + ЬТ 4-+ сТ2 + dT3 + е/'4 — О, где a, ft, с, d, е — не все нули. Получили таким образом, что Т должно удовлетворять уравнению не выше 4-й степени.
В действительности дела обстоят намного лучше, чем кажется. Так, для любой 2 X 2-матрицы Т мы найдем, что матрицы'/, Г, Т2 уже линейно независимы и, следовательно, Т удовлетворяет квадратному уравнению, что и требовалось доказать.
Самое вычисление сводится к следующему. Пусть / а Ь\
Г=| dr тогда Умножением матрицы Т на себя I а2 + be ab bd\
получаем Т2=	.	, г 	• Используя маг-
\ас 4- cd be + d2 /	J
рицы P, Q, К, S, о которых говорится в упражнении 18 главы III, записываем, что
/-= Р	+ S
аР+ bQ+ сР+ dS
F = (a2 + bc)P + (ab + bd)Q + (ас + cd)R + (bc + d2) S,
!) Мы еще мыслим в терминах конечного числа измерений. Утверждение перестает быть верным, если рассматриваются бес* конечномерные пространства. Например, операция дифферент!* рования D = d/ix линейна. Она удовлетворяет определению линейности, данному на стр. 118: D(u 4- и) = Du Dv; D(ku) — «= kDu. Однако такой функции F, чтобы F(D) == 0, не суще* ствует. Остается исследовать, какому уравнению будет удовлетворять D, если сделать пространство конечномерным, например потребовать, чтобы дифференцируемые функции являлись полиномами не выше второго порядка.
5 Зек, 51
129
Можно ли найти т и п так, чтобы Т2 4*	+ п!='
= О? Оказывается, можно. Для этого достаточно прибегнуть к приему, использованному в разделе «Проверка на линейную зависимость». Умножим первые два уравнения соответственно на т и п, сложим все три уравнения почленно и потребуем, чтобы коэффициенты при Р и Q результирующего уравнения были нулями. Это даст два уравнения с двумя неизвестными тип, которые легко найти. К счастью, найденные значения тип, равные соответственно —(а 4-d) и ad — be, обращают в нули также коэффициенты при Р и S. Таким образом, Т удовлетворяет уравнению
T2-(a + d)T + (ad-bc)I = O. (5)
Уравнение (5) известно под названием характеристического уравнения матрицы Т. При его выведении мы не делали никаких допущений относительно чисел а, Ь, с, d и наш результат, следовательно, годится для любой матрицы 2X2. Однако это уравнение не обязано быть самым простым относительно Т. Если положить а=2, Ь—0, с=0 и d=2, то уравнение (5) принимает вид Т2— 4Т + 4/ = О, соответствующий уравнению (х—2)2=0 с кратным корнем. В результате появляется опасность сделать поспешный вывод о том, что Т неприводимо к диагональной форме, тогда как его матрица уже имеет, диагональную форму. Дело здесь в том, что Т удовлетворяет более простому уравнению Т — 21—0, соответствующему уравнению х— — 2=0, которое свободно от кратных корней.
Преобразования и матрицы
Всякое преобразование настолько тесно связано с матрицей, его определяющей, что многие достойные уважения математики пользуются для их обозначения одним и тем же символом: они говорят о преобразовании Т и матрице Т. Однако между двумя этими понятиями есть разница, и это следует иметь в виду. Мы уже убеждались в том, что одно и то же преобразование можно представить различными матрицами в зависимости от выбранной системы осей. И когда вы* сказывается суждение относительно какой-то матри* 130
цы, у нас нет оснований считать, что оно остается верным при замене осей. Иными словами, суждение о матрице, так сказать, субъективно, оно зависит от нашей точки зрения (от выбранных нами осей). Суждение же о преобразовании объективно; оно соответствует тому, что мы называли геометрическим фактом. Например, пусть некоторое преобразование Т удовлетворяет равенству Т2 = /, показывающему, чтэ двукратное применение преобразования Т возвращает все в первоначальное положение. От этого результата нельзя избавиться и изменением осей. При любом их выборе мы обнаружим, что Т представимо матрицей, квадрат которой есть I. Такое же рассуждение приложимо и к уравнению (5). Допустим, что некоторое преобразование удовлетворяет уравнению Т2 — Т + 1. Обе части уравнения имеют довольно простой геометрический смысл, не зависящий от выбора осей. Т* означает двукратное выполнение преобразования Т, смысл преобразования Т + I усматривается после следующего небольшого рассуждения. Пусть для любой точки Р верно равенство TP = Q. Тогда (Т + 1)Р=ТР -р 'Н~ IP — Q + P—R, где R — четвертая вершина параллелограмма OPQR, образованного точками О, Р и Q.
(Начало О, как отмечалось в примечании на стр. 37, означает ничего и является геометрическим фактом.) В итоге получается, что преобразование Т2 (так как Т2 — Т + /) должно отослать точку Р к точке R, определяемой геометрическим построением. Такого рода рассуждение применимо к любому уравнению, которому удовлетворяет преобразование Т, Поэтому уравнение (5) носит объективный характер. В каких бы осях ни было представлено Т, мы всегда придем к одному и тому же характеристическому уравнению. Остановимся на коэффициентах характеристического уравнения ввиду их особой важности. Возможно, в коэффициенте при I вы узнаете определитель ad — be матрицы Т. Коэффициент (а + d) при — Т известен под названием характера Т. Следовательно, характер равен сумме элементов матрицы Г, стоящих на главной диагонали. Он играет важную роль в изящной теории характеров групп.
Чтобы быстро получить характеристическое уравнение преобразования Т, оказывается, достаточно
5*
131
составить определитель его к нулю:
а —К
с
матрицы Т — V и приравнять
Ь
d — 7.
= 0.
(6)
Если после раскрытия определителя в уравнении (6) заменить X и 1 соответственно на Т и /, то мы получим уравнение (5). Это правило одинаково хорошо применимо для любого числа измерений. Во многих учебниках характеристическое уравнение вводится именно посредством определителя. В них, конечно, доказывается, что Т удовлетворяет полученному уравнению. Этот факт известен в математике как теорема Кейли — Гамильтона. Сам Кейли говорил, что это так Очевидно, что он просто сформулировал результат, не утруждая себя доказательством. Мы не знаем, что заставило его так думать. Однако математики почувствовали, что эта теорема должна быть доказана и притом тщательно.
ГЛАВА VI
НА ПУТИ К ПРИЛОЖЕНИЯМ
Лейтмотивом IV главы была мысль о том, что, зная диагональную форму преобразования, значительно проще увидеть результат самого Преобразования. В главе V мы рассмотрели вопрос о том, когда й как можно задать преобразованье в диагональной форме. В настоящей главе мы познакомимся с тем, где мож? по использовать все то, что составило содержание этих двух глав.
Часто в природе мы можем дать начало какому-то процессу, дальнейшее развитие которого пойдет уже согласно ейоим собственным законам. Так бывает, например, при взрыве или просто в случае,-когда в: i бросаете мяч. Изловчившись, вы можете бросить этст мяч в определенном направлении и с нужной скоро^ стью, но управлять его полетом вы уже не в состоянии. Законы движения мяча выражаются его уравнениями движения. Мы лишь задали начальные условия, а решение представит собой формулу, показывающую, как будет двигаться мяч, если он стартовал произвольным образом.
Как простую аналогию мы можем рассмотреть последовательность Фибоначчи — последовательность чисел, где каждое число есть сумма двух предшествующих. Если обозначить члены последовательности fit, «2, аз, а^ ..., то условие, ее задающее, запишется в виде ап — an-i-\- an-i. Это, конечно, не поможет нам найти первые два члена. Выбор первых двух чисел здесь можно уподобить заданию начальных условий в случае полета мяча. Если мы выберем, как это обычно и делается, в качестве первых двух чисел, например, числа 0 и 1, то вся последовательность определится автоматически: 0,1,1,2,3,5,8,13,21, ... .
133
Решение представляло бы собой формулу общего члена ап для произвольно выбранных первых двух чисел а0, Oj.
В правиле, по которому образуется последовательность Фибоначчи, скрыто линейное преобразование, которое нетрудно обнаружить. Мы закончили последовательность числами 13 и 21. Этих двух чисел достаточно, чтобы суметь ее продолжить. Следующее число должно быть 13 4-21 = 34, и сейчас «конец» последовательности будут составлять Числа 21 и 34, которые опять позволят продолжить последовательность. Иными словами, «генетический код» последовательности несут два последних числа, ибо они порождают следующую пару: (13, 2!) -> (21, 34). Обозначим первоначальную пару (0,1) через (х0, у0), вторую пару (1, 1)—через (хьу.1). Мы хотим показать с помощью уравнения, как пара (хп, уп) образует следующую пару (Xn+i, Уп+1)- В случае, когда (13,21) -> (21,34), мы замечаем, что 21, второе число на входе, повторяется первым на выходе. В общем виде xn+i = Уп> Второе число на выходе, 34, образуется как 13-4-21, то есть i/n+i = хп 4- уп. Таким образом (х„, уп) -* (уп, хп 4-4- уп)- То есть переход от одной пары (х, у) к другой (х*, у*) совершается посредством преобразования Т-. х* = у, у* = х 4- у.
Многократным повторением преобразования мы получаем все новые и новые члены последовательности: (0, !)->(!, 1)^(1, 2)->(2, 3)->(3,.5)-*- ... Начав с (х«, z/o) и применив преобразование п раз, мы достигнем (хп, уп), так что (хп, уп) = Тп (х0, уо).
Если полученные пары чисел нанести на бумагу в клеточку, как показано на рис. 57, то соответствующие им точки образуют цепочку, которая на первый взгляд кажемся нерегулярной и ничего не подсказывающей. Глава IV убедила нас в том, что характер преобразования становится более понятным, если представить Т в диагональной форме. Для интересующего нас преобразования Т имеем (на языке V главы): а = 0, Ь — с = d = 1. Его характеристическое уравнение, следовательно, Г2—Т —1 = 0. Соответствующее уравнение в элементарной алгебре имеет корни V2 (1 =*=	), или приближенно 1,62 и
—0,62. С точки зрения арифметики, эти корни неудоб-134	---
ны, но здесь важно другое — корни не повторяются. Это значит, что имеются два собственных вектора, направление которых можно рассчитать и показать пунктиром, как это и сделано на рис. 57. Относительно новых осей, совпадающих с пунктирными прямыми, преобразование должно предстать в диагональной форме, то есть как Х*=1,62Х У* = —0,62 У. Таким образом, каждый раз преобразование Т умножает координаты X на 1,62, а У на —0,62. Посмотрим, как это выглядит на рис. 57. Координата X постепенно растет. Координата У с каждым шагом сжимается, так как она всякий
раз умножается на число по абсолютной величине меньше 1. Действительно, если изобразить чуть больше точек, можно было бы видеть, как значения У становятся настолько малыми по абсолютной величине, что точки кажутся лежащими на оси X. Минус всякий раз изменяет знак У. Это видно и на рисунке. Точки перескакивают с одной стороны пунктирной оси ОХ на другую.
Детальный расчет покажет, что пунктирная ось ОХ в исходной системе координат имеет уравнение у — 1,62х. Точки (хп,уп) с каждым разом приближаются к этой прямой. А это значит, что по мере возрастания п отношение уп1хп приближается к 1,62, а точнее, к }/2 (1 + ]/5 ). То есть отношения двух соседних членов в последовательности Фибоначчи 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, ... приближаются к Ч2(1 + + }/5). Этот факт хорошо известен изучающим клас
сическую алгебру, но вовсе не очевиден для тех, кто
435
впервые видит последовательность Фибоначчи. Любопытно, что наша теория линейных преобразований подводит нас непосредственно к этому результату.
Проблема Фибоначчи
Общая проблема последовательности Фибоначчи состоит в следующем. Допустим, что в качестве 'до и Д1 выбраны любые два числа. Какой будет формула общего члена an? Fla этот вопрос 'нетрудно ответить, зная диагональную форму преобразования Т. Мы набросаем общую схему рассуждения, не вникая во все Детали. Относительно новых осей (рис. 57) мы имеем сейчас цепочку точек, начинающихся не в х — О, у = 1, а в х = о0, У = Oj. Координаты начальной точки Ро целесообразно было бы определить относительно пунктирных осей: пусть это будет (Хо, Уо). Так как при всяком применении Т координаты X и У умножаются соответственно на 1,62 и —0,62, то после л-кратного применения Т мы достигнем точки (Хп, Уп), у которой Хп — (1,62)"-Ло, Уо=(—62)”.У0. Тем самым на рис. 57 определено положение точки Рп в «пунктирной» системе координат. По известному шаблону это позволяет найти ее координаты (хп, уп) в первоначальной системе. Но хп> Уп обозначают пару ап, Дп+1 в последовательности Фибоначчи, то есть хп — ап, уп = Дп+1- Так что достаточно найти хп, чтобы определить тем самым общий член ап. Если бы мы взяли на себя труд подсчитать уп, то убедились бы только в правоте нашей формулы, не получив никакой новой информации.
Изменение осей приводит к результату вида хп — А (1,62)” 4- В(—0,62)”, где числа А и В не зависят от п, но зависят, конечно, от выбора а0 и в|.
Согласно этому, формула последовательности Фибоначчи должна иметь вид ап = Л(1,62)” + В (—0,62)". Может показаться удивительным, что формула для последовательности 0,1,1, 2,3, 5, 8, ... , состоящей исключительно из целых чисел, так сильно зависит от иррационального числа |^5.
Разностные уравнения
Мы выбрали последовательность Фибоначчи просто потому, что она интересна. Правило Фибоначчи 136
ап — On—i + ап-2 — это пример разностного уравнения *)• Разностные уравнения, будучи важны сами по себе, очень тесно связаны с дифференциальными уравнениями, которые играют огромную роль в приложениях математики. Найденный нами результат для последовательности Фибоначчи типичен для весьма широкого круга примеров.
Во многих учебниках можно найти правила для решения разностных уравнений. Учащимся не нравятся эти правила — они кажутся слишком произвольными.
Допустим, мы хотим решить разностное уравнение On — бОп—1	бОп—2*
Правило 1 гласит: «Попытайтесь найти решение в виде геометрической прогрессии, то есть в форме ап = гп». Если мы подставим это решение в разностное уравнение, то придем к уравнению г2 = 5г —6, решения которого Г] = 2 и г2 — 3. Таким образом, мы имеем два частных решения ап = 2п и ап = Зп.
Правило 2 предлагает нам скомбинировать эти частные решения, записав общее решение в виде ап = А-2п + В -Зп. К чести авторов учебников следует признать, что они доказывают верность правила 2, поэтому учащегося скорее озадачивает первое правило: почему следует искать решение в формуле г”?
Важно уяснить себе, что оба правила даются для практических целей, как самый простой и быстрый путь к решению. Мы же поведем здесь рассуждение не с целью отыскания лучшего алгоритма, а с тем, чтобы обеспечить рациональный подход и показать, как смогли прийти к этим правилам. Ибо ничто так не разрушает математические способности, как привычка принимать готовые способы решения, не задаваясь вопросами, почему следует решать именно так и как можно додуматься до этого самостоятельно.
Если бы мы изучили уравнение ап = 5an-i — 5an-z тем же приемом, что и последовательность Фибоначчи, мы бы обнаружили связь этого уравнения с преобразованием Т вида х* —у\ у* — —6х + 5у. Т имеет два собственных значения 2 и 3, соответствующие собственным векторам (1,2) и (1,3). Направив новые
') Такие уравнения носят также названия уравнений в конечных разностях или рекуррентных уравнений. — Прим. ред.
137
оси вдоль этих векторов, мы привели бы преобразование к виду X* = 2Х, У* = ЗУ. n-кратное применение этого преобразования умножило бы координаты X и У соответственно на 2п и Зп, и в результате мы пришли бы к формуле ап = хп = А -2п + В-Зп, записанной в первоначальной системе координат.
Рассмотрев один-два случая такого вычисления и увидев, почему возникает такая формула, учащиеся уже могут применить правила 1 и 2 при решении разностного уравнения.
Проделанное нами позволяет ожидать решения вида ап = Арп + Bqn, где р и q — собственные значения. Обычно именно так и происходит. Однако есть и исключения, и наш подход подсказывает это, так как не всякое преобразование можно привести к диагональной форме.
Рассмотрим последовательность чисел 0, 1, 2, 3, 4, Б, ... , удовлетворяющую уравнению an = 2an_i — ап-г-Трудно поверить (и на самом деле это неверно), чтобы члены этой последовательности можно было задать только что полученной формулой ап=Арп + Здесь преобразование Т имеет вид х* = у, у* — —х + [+ 2у и удовлетворяет уравнению (Т — 1)2=О, уравнение имеет кратный корень, и потому Т не может быть представлено в диагональной форме. Мы не намереваемся более тщательно исследовать этот особый случай.
От разностных к дифференциальным уравнениям
Эту главу мы начали с простой иллюстрации из области математической физики — полета мяча. Движение мяча происходит плавно или кажется плавным, по крайней мере мы не замечаем в нем ни толчков, ни прыжков. Если бы мы зафиксировали это движение кинокамерой, то тем самым неизбежно внесли бы скачки. Один кадр показывал бы мяч в одном месте, следующий кадр — в другом без каких-либо указаний относительно того, как он двигался между этими положениями. Если при этом занумеровать кадры чис-лами 0, 1, 2, 3, ..., то получим последовательность точек Ро, Р2, ...» где PQ показывает положение мяча в кадре 0, Pi —в кадре 1 и т. д.
138
Такая замена непрерывного процесса некоторой последовательностью промежуточных состояний довольно часто встречается как своего рода прием изучения непрерывного процесса. Так, например, зная, что всякое действительное положительное число х имеет логарифм logiox, мы не в состоянии составить таблицу, в которой были бы показаны логарифмы всех чисел между 1 и 10. Любая таблица логарифмов будет содержать лишь конечную последовательность чисел. Она может быть небольшой, давая логарифмы чисел 1; 1,01; 1,02,... или громоздкой, дающей логарифмы чисел 1; 1,0000001; 1,0000002 и т. д» Но в любом случае она дает только последователь* ность.
Вся классическая физика основана на идее непрерывности, ее характерным оружием является исчисление бесконечно малых. Уравнения движения почти неизменно выражаются дифференциальными уравнениями. В этих уравнениях делаются утверждения относительно таких величин, как скорость, ускорение, крутизна и кривизна. Все упирается в идею предела, в то, что произойдет, если какая-то величина стремится к нулю. Но допустим, что мы не собираемся переходить к пределу. Допустим, мы делаем ускоренную съемку с частотой 1000 кадров в секунду. Несомненно, из такого фильма мы можем получить хорошее представление о движении объекта. Весь вопрос в том, могли бы мы при этом дать достаточно точную оценку скорости и ускорения этого движения? Итак, если мы последуем задуманной идее, то вместо непрерывной функции получим последовательность и вместо дифференциальных уравнений — разностные уравнения (тема, с которой эта глава имеет тесную связь).
Чистые математики неодобрительно относятся к этой идее. Допустим, например, что каждый кадр фильма показывал бы объект на одном и том же месте. Мы были бы склонны считать, что объект находится в покое. Но разве нельзя предположить, что после каждого кадра он двигается и к моменту следующего кадра возвращается в свое первоначальное положение? Логически такая ситуация вполне возможна. Наша информация не доказывает, что тело находится в покое, однако она наводит на эту мысль.
139
Мы могли бы удовлетворить математика точным указанием тех допущений, которые исключили бы подобные неуклюжие возможности.
Эрзац математического анализа
Сейчас мы продолжим развитие высказанной выше идеи и посмотрим, какие формулы можно получить для скорости, ускорения и пр., находясь в мире перемещений скачками. Это рассмотрение оправдывается двумя целями. Первая цель—помочь объяснить (ско-;рее примитивным способом) смысл обыкновенных дифференциальных уравнений и дифференциальных уравнений в частных производных человеку, не совсем сведущему в математическом анализе. И вторая — показать метод, который в сущности применяется в счетно-решающих устройствах при решении задач ма; тематического анализа,'поскольку цифровая электронно-вычислительная машина имеет много общего с таблицей логарифмов. Не имея приспособления фиксировать непрерывные изменения, она может передавать i их скачками и тем самым имеет дело с последовательностями.
Наше рассуждение может пролить некоторый свет , также и на математический анализ, но при этом сле-.дует ясно понимать, что оно ни в коем случае не заменяет последнего. Парадоксально, что когда нужно !получить от электронно-вычислительной машины правильный результат, то часто приходится обращаться |К идеям самого настоящего математического анализа. Эти основные идеи математического анализа следовало бы изучать возможно большему числу людей и в возможно более раннем возрасте.
Совершенно ясно, как по фильму можно было бы определить скорость. Если на первом снимке мяч появился на высоте 7 футов, а на следующем, сделан-.ном на 0,001 секунды позже, — на высоте 7,003 фута, ,то, разделив пройденное расстояние на затраченное .время, найдем скорость 3 фута в секунду. Также и в общем случае: если бы наша камера регистрировала какие-то события через временные интервалы h и показывала последующие положения объекта на расстояниях а, Ь, с, d, е, ..., то его скорость оценивалась 140
бы следующими частными:
6 — я с — b d — с е — d
h * h * h 9 h 1 ‘ ‘ • •
Переходя к оценке ускорения, замечаем, что оно связано со скоростью так же, как последняя — с расстоянием. Так что мы просто повторим уже использованный расчет: вычесть каждый член из последующего и разделить на h.
Результаты определили бы ускорение в виде следующих частных:
с — 2Z? + д d — 2c + b e-2d-{-c
h2 >	hi	,	h2	, . . . .
В математическом анализе, если расстояние s как функция t задается уравнением s = то скорость обозначается как dsfdt или f (0, ускорение как d^sjdt^
Рис. 58.	Рис. 59.
или Анализ применяется не только к движениям, но и к графикам. Если мы имеем график у =» = f(x), то dyldx, или f'(x), измеряет его крутизну, a d2yldx\ или /'(х), показывает, как изгибается кривая. Там, где /"(х) положительна, кривая сходна с чашей, там, где f"(x) отрицательна, — с аркой.
Мы надеемся обнаружить аналогичную геометрическую интерпретацию для приближенных скорости и ускорения, найденных выше, и на самом деле мы можем это сделать. Как показано на рис. 58, (Ь — a)/h и (с — b)/h измеряют крутизну прямых АВ и ВС. Выражение (с — 2Ь -р a)lh\ оценивающее (х), геометрически интерпретируется следующим образом. На рис. 58 точка Р есть середина ..АС, следовательно, Р =» = V2^ + V2C (см. стр. 29). По координатам точек А (0, а) и С (2ft, с) и этой формуле найдем координаты
141
точки P(h, ’М + ’Ас). Если В есть (Л, Ь), то высота точки Р над точкой В равна ‘/2а 4- ‘/гс — Ь, или */2 (с — — 2& 4* й)- Поэтому величина (с — 2b-}-a)/li2 в 2/h2 раза больше высоты ВР. Когда она положительна, Р расположена выше В (как на рис. 58), когда отрицательна — ниже (как на рис. 59). В случае, когда она равна нулю, Р и В совпадают, то есть точки А, В и С Скажутся на одной прямой.
При нашем подходе мы сталкиваемся с одним затруднением, которого не возникает в настоящем математическом анализе. Частное (Ь— a)/h характеризует крутизну в любой точке прямой АВ, и мы не знаем, относить ли ее к значению f'(0) (крутизна в £бчке Л) или к значению f'(h) (крутизна в точке В). Ее можно рассматривать с одинаковым правом и так и эдак в зависимости от того, что окажется более подходящим. Меньший произвол наблюдается в отношении величины (с — 2Ь 4- а) /№. Мы уже видели, что она пропорциональна длине ВР, то есть связана с точкой В, средней из трех рассматриваемых точек. Поэтому мы скорее отнесем рассматриваемое частное к оценке f"(x) в точке В, чем в точке А или точке С.
Можно вообразить, что рис. 58 представляет часть оттянутой струны, о которой шла речь в главе IV. Натяжение струны стремится выпрямить ее так, как если бы точка В испытывала притяжение к точке Р, находящейся на одной прямой с точками Л и С. Неудивительно, что подробные вычисления, проведенные для струны с натяжением, равным 1, показывают, что сила, тянущая точку В вверх, равна (с — 2b + a)/h. Это наша оценка для	Так как рассматривае-
мые частицы находятся друг от друга на расстоянии h, то мы догадываемся, что направленная вверх сила, действующая на каждую единицу длины, и есть f" (х). Эта догадка находит истинное подтверждение в математическом анализе при рассмотрении струны, слегка выведенной из положения равновесия.
Если, как это принято в технической литературе, мы используем обозначения ао, а^, а$, а3, а4, ... вместо а, Ь, с, d, е, ..., то наши оценки примут вид
Г(пЛ)~(««+1 — «П)/Л,	1
/"(п/г)~(ая+1 - 2ап 4- «„-0/Л2. /	'
142
Знак означает «оценивается как» или «приблизительно равно». Первое равенство трактует здесь (Ь -*• — a)/h как оценку f'(x) в точке А на рис. 58. В случае если нам понадобится оценить f,z(x) в точке В, то мы должны будем взять следующие равенства:
f'(nh)~(an-an_x)lh,	V	„
f" (nh) ~ (art+1 - 2ап + a^/h?. J
Используя эти аппроксимации, мы превращаем задачу математического анализа в задачу алгебры. Дифф$ ренциальное уравнение, связывающее f(x), f'(x) й f"(x), таким образом, заменяется обычным алгебраи-ческим уравнением, связывающим ап-ь Яп и ап+ь За» дача математического анализа в конечном итоге сво-дится к задаче арифметики; решение находится вычислениями, в сущности аналогичными тем, которыми были найдены первые несколько членов 0, 1, 1, 2, 3, 5 последовательности Фибоначчи.
В качестве примера рассмотрим дифференциальное уравнение f" + З,?/7 + 3/=0. Оно могло возникнуть в системе, образованной колеблющейся массой, привязанной к струне. Движению массы препятствует вязкая жидкость (например, патока), играющая роль амортизатора. Допустим, что в качестве h мы взяли 0,1, число, соответствующее фильму с частотой 10 кадров в секунду. Используя уравнение (2) и учитывая, что 1//г2=100, 1/А= 10, перепишем дифференциальное уравнение в виде
100(а„+1 — 2а„ ara-i) + 37 (ап — an~i) + За„ = 0,
которое упрощается до
а„+1 = 1,6а„ — 0,63an-t.
Мы можем при желании справиться с этим разностным уравнением средствами одной арифметики. Задав произвольные значения а» и at подстановкой их в равенство а2=\,6а1— О,63ао, мы нашли бы а2; далее, используя а2 и соответствующей подстановкой нашли бы а3 и т. д. С другой стороны, для отыскания последовательности здесь можно было бы использовать правило решения разностных уравнений, данное ранее в этой главе. Согласно ему, мы нашли бы
143
ап — A (0,9)n + В (0,7)n. Если бы мы положили в самом начале а0 = 0, а\ = 0,2, то получили бы, что А — I, В = —1 и, следовательно, ап — (0,9)п— (0,7)п. Этим или первым арифметическим способом мы пришли бы к последовательности 0; 0,2; 0,32; 0,386; 0,416; 0,422; 0,413; 0,395; ..., в которой числа, следующие за 0,395, начали бы приближаться к нулю.
Члены последовательности изображены на рис. 60 маленькими кружочками. Тут же дана кривая, представляющая точное теоретическое решение первоначального дифференциального уравнения, которая позволяет видеть, что даже при весьма грубых приближениях, использованных нами, мы все же получили ббщую достаточно правильную картину того, каким образом колебалась масса. Взяв в качестве h значения 0,01, 0,001, мы могли получить лучшее приближение. Можно доказать (для данного дифференциального уравнения), что, взяв h достаточно малым, мы можем достичь любой требуемой точности.
Замечание относительно дифференциального уравнения
Точное решение рассмотренного выше дифференциального уравнения f" -)- 3,7f' + 3f = 0 имеет вид f(х) — Ле-1’2х + Ве~2>5х. Оно обычно получается по правилу, во многом напоминающему правило для решения разностных уравнений, только теперь правило 144
1 гласит: «Ищите решение в форме f(x) = етх. У учащихся возникает то же возражение, что и раньше: «Почему мы должны искать решение в этой форме?» Ранее приведенные объяснения вполне достаточны, цтобы показать естественность предлагаемой формы. Во-первых, это дифференциальное уравнение является предельным случаем того типа разностных уравнений, который мы изучали ранее; разумно предполагать (мы не говорим доказать), что использованные методы пригодятся и здесь. Во-вторых, рекомендуемая форма решения ничего принципиально нового собой не представляет. Если мы обозначим ет через г, то будем иметь етх = гх, но гх соответствует форме г", в которой искали решение разностного уравнения. Поэтому вполне возможно и оправданно искать решение дифференциального уравнения в форме гх. Форма етх полностью ей эквивалентна, но более удобна для использования в формулах математического анализа.
Частное дифференцирование
Частное дифференцирование — раздел на редкость запущенный. Многие из тех, кто неплохо знает основы математического анализа, совсем не осведомлены в частном дифференцировании. Однако оно находит широкое применение и для тех, кто уже встречался с математическим анализом, не содержит ничего принципиально нового. Мы попытаемся изложить идею частного дифференцирования, не привлекая при этом каких-либо результатов математического анализа.
Сначала познакомимся с нехитрым приспособлением, представленным на рис. 61. Оно состоит из диска и измеряющего устройства. Диск (он изображен внизу) может поворачиваться, его показания обозначим через х. Показания измеряющего устройства (оно изображено над диском) обозначим через г. Диск и измеряющее устройство связаны между собой механической или электрической системой, так чтб положение диска х определяет показания стрелки z.
Таким образом, z = f(x). В обычном анализе dz/dx, или f'(x), обозначает скорость, с которой изменялись бы показания стрелки при вращении диска
145
с единичной скоростью (та есть когда показания X диска каждую секунду возрастают на 1).
Далее рассмотрим новое приспособление, изображенное на рис. 62. Согласно рисунку, показания измеряющего устройства, зависят от положений двух дисков х и у, то есть z = f(x,y). Сейчас речь пойдет о том, с какой скоростью изменяется г. Из всевозможных случаев взаимосвязанного вращения дисков выберем две стандартные ситуации.
В первой ситуации диск у остается неподвижным, а диск х поворачивается с единичной скоростью. Скорость, с которой возрастают показания z, при этом принято обозначать dzjdx и называть частной производной функции z по х. Во второй ситуации наоборот: диск х остается неподвижным, а диск у вращается с единичной скоростью. Результирующая скорость изменения г обозначается dzfdy.
Теперь обратимся к другому наглядному образу. Допустим, что (х, у} обозначает координаты произвольной точки на карте, a z = f(x,p)— высоту местности над уровнем моря в точке (х,у). В первой ситуации у остается фиксированным, а х возрасгает со скоростью 1, тогда дг/дх будет измерять скорость возрастания высоты над уровнем, моря по мере продвижения на восток со скоростью 1. Она характеризует крутизну или наклон местности в восточном направлении (рис. 63). Аналогично вторая ситуация соответствует продвижению на север со скоростью 1, 146
и dzfdy измеряет наклон местности в северном направлении 1).
Величины dzldx и дг[ду можно оценить точно так же, как мы оценивали
При съемке местности невозможно нанести на карту ее высоту в каждой точке. Мы могли -бы покрыть карту прямоугольной сеткой, как показано на
Р-ис. 64.
рис. 64, и измерять высоты только в точках их попарного пересечения. Если бы решетка имела достаточно малые отверстия и ландшафт не был бы чересчур неровным, то наш прием дал бы нам достаточно хорошее представление о рельефе местности.
’) Точнее говоря, dz/dx и dz/dy равны тангенсам углов наклона (угловым коэффициентам) касательных к кривым, -получающимся в соответствующих сечениях поверхности z = f(x, у).— Прим. ped.
147
Высоту местности в точках А, В, С и т. д. договоримся обозначать соответственно через а, Ь, с и т. д. Сетку предполагаем состоящей из квадратов со стороной Л1).
Направившись в горизонтальном направлении из точки А в точку В и пройдя расстояние h, мы поднимемся на высоту b — а. Отношение (Ь— a)/h в этом направлении оценивает наклон на участке АВ, то есть dzjdx. Аналогично (Ь — e)/h измеряет наклон на участке ЕВ и дает нам представление о величине dzjdy.
Весь этот процесс можно повторить уже применительно к dzjdx и dzfdy. Так как dzjdx показывает, как быстро меняется z при движении на восток, то в свою очередь можно спросить, как быстро меняется dzjdx при движении в этом же направлении. Найдем оценки для dzjdx на участках АВ и ВС. Это будут дроби (Ь — a)/h и (с — b)/h. Разность между ними составит (с — 2Ь-\-а)/1г. Поскольку она вызвана продвижением на восток на величину /г, то, чтобы определить скорость изменения наклона, мы должны найденную разность разделить на И. В результате получим (с — 2b-\-a)/h2. Это выражение нам знакомо, оно встречалось и раньше как оценка для f/z(x). Фактически здесь мы имеем дело с одной и той же ситуацией, и если бы мы сделали вертикальное сечение какой-то местности вдоль прямой АВС, то получили бы рисунок, во многом напоминающий рис. 58. Для величины, которую мы только что определили, используется обозначение d2zjdx2. Это напоминает обозначение d2zjdx2 из начал математического анализа. Замена d на d указывает на то, что в функцию входит еще другая переменная, которая в рассматриваемом процессе остается неизменной, меняется только х.
В таком же смысле используется символ d2zjdx2, характеристика сечения местности вертикальной Плоскостью в северном направлении. Она оценивается дробью (d — 2b-{-e)lh2.
В обеих этих оценках буква b находится посередине, поэтому мы относим их к значениям d2z/dx2 и d2zjdy2 в точке В.
]) Для некоторых задач вместо квадратов удобнее использовать прямоугольники.
148
Задача из теории электричества
Довольно примечательно, что приведенные выше скудные рассуждения создают благоприятную возможность для получения уравнения
32V  д2У _ п дх2 ду2 °’
которому удовлетворяет поток электричества в сплошной медной пластине. Это знаменитое уравнение встречается в полутора десятках областей естество-знания и называется уравнением Лапласа. Выражение, стоящее в левой части уравнения, часто называют лапласианом V и коротко обозначают символами ДУ или	 
Предположим, что у нас есть кусок тонкой медной пластины, которая всюду однородна, всюду имеет одинаковую толщину и сопротивление. В пограничных точках пластины подключены батарейки, в результате чего по листу идут электрические токи. Распределение этих токов мы и собираемся исследовать.
Попробуем упростить задачу. Если мы взглянем на носовой платок, то на первый взгляд его поверхность покажется сплошной. Но при более пристальном рассмотрении обнаружится, что она состоит из переплетающихся нитей. Если бы материал платка каким-то образом превратился в медь, то электрические свойства «медного платка» очень близко напоминали бы электрические свойства медного листа. В соответствии с этим мы вместо сплошной медной пластины рассмотрим решетку из тонкой медной проволоки; нечто очень похожее на сетку, показанную на рис. 64. Мы надеемся, что это не слишком исказит нащу задачу.
Теперь мы должны рассмотреть, как по этой проволочной сетке течет электричество. Здесь действуют два довольно простых закона. Первый закон устанавливает; что электричество течет через материал так, как течет по трубам вода. То есть весь ток, входящий в какую-то точку, должен из нее выйти. Например, обозначив, как показано на рис. 65, токи, входящие в точку В, через р и q, а токи, выходящие из нее,
Н9
через г и s, согласно этому закону запишем г + s = = р + q. Общие количества токов равны.
Второй закон — закон Ома. Каждая точка проводника характеризуется числом V, называемым потенциалом. Потенциал есть нечто, напоминающее высоту для силы тяжести или температуру для тепла. Вода течет из высоких мест в низкие; тепло из мест с высокой температурой передается в места, где она ниже; электрический ток стремится из точек с высоким потенциалом в точки с низким потенциалом. Через а, Ь, с, d, е обозначим потенциалы в точках А, В,
D
s
8 { с Рис. 65.
q Е
С, D, Е. Если ток течет из А в В, как на рис. 65, то потенциал а должен быть выше (больше) потенциала Ь. Падение потенциала при переходе из Я и В равно (а — Ь) вольт. Согласно закону Ома, ток, текущий из Л в В, пропорционален этому падению потенциала. Для простоты мы предположим, что ток, текущий из Л в В, не только пропорционален, но и равен а — Ь. То есть р = а — Ь. Аналогично будем иметь q = — е — Ь, г — b — с, s = b — d. Произведя замену в уравнении р + q = г + s, определяемом первым законом, найдем, что а —- 2b + е — 2Ь — с — d.
Это уравнение можно преобразовать различными способами. Решив его относительно Ь, найдем b = = Ч4(а + с + d + е). Это интересный результат: он доказывает, что потенциал в точке В есть среднее арифметическое потенциалов в четырех соседних точках Л, С, D, Е.
Если теперь мы вернемся к полученному выше уравнению и перепишем его в виде (с — 2Ь + а)+, ,+ (d — 2b + е) = 0, то оно будет очень напоминать полученные нами ранее оценки для д2г/дх2 и д2г/ду\ 150	-
Поделив уравнение на /г2, найдем, что
с — 2Z> + а , d — 2Ь + в  п
А2 ' А2	v.	\<5)
Это уравнение подсказывает следующее уравнение:
^K. + ^L = 0.	(4)
дх2 ду2	W
А это и есть уравнение Лапласа.
Натянутые сетки и мыльные пузыри
Как упоминалось ранее, уравнение Лапласа имеет много различных приложений. Одно из них включаем что-то, напоминающее скорее всего перекошенную теннисную ракетку. На рис. 66 представлен неболь-ч шой кусок туго натянутой сетки. Вообразим себ^
что сетка сначала полностью лежит на столе, а за« тем ее пограничные точки приподнимают над столок на различную высоту и закрепляют их в этом поло* жении. Весом сетки мы пренебрегаем. Рис. 65 мы сейчас рассматриваем как часть этой сетки. Величины а, &, с, ... представляют высоту точек A, С, ... над столом. Согласно замечанию, сделанном^ на стр. 142, (с — 2b + a)/h2 пропорциональна силе натяжения, испытываемой нитью АВС в точке В и направленной вверх. (Она фактически составляет 1/Л этой силы, если сетка имеет единичное натяжение.) Аналогично (d — 2b + c)/h2 пропорциональна силе н<* тяжения, испытываемой нитью EBD в точке В и направленной вверх. Далее, если сетка установилась i положении равновесия, то общая сила натяжения В точке В должна равняться нулю. Об этом как раз и говорит уравнение (3). Значит, уравнение (3) выражает
151
условие равновесия сетки. Если вообразить последовательность сеток со все уменьшающимися отверстиями, то в пределе они будут приближаться к сплошной мембране, напоминающей барабанную перепонку или мыльный пузырь. Предположим, что уравнение (4) дает условие равновесия такого рода мембран..
Существует теорема: если V удовлетворяет в определенной области уравнению Лапласа, то V внутри этой области не может иметь ни максимума, ни минимума. В разумности этой теоремы можно убедиться двумя путями. Мы видели, что значение V в точке В было средним арифметическим его значений в четырех соседних точках, а это никак не сообразуется с существованием максимума в этой точке. Результат можно осмыслить и физически, рассматривая нашу натянутую сетку. Если В выше всех соседних точек, то все нити В А, ВС, BD потянут В вниз и она не сможет остаться в этом положении равновесия. Действительно, чтобы сетка находилась в положении равновесия, два изгиба должны иметь противоположные направления. Отсюда мы полагаем, что если нить АВС стремится поднять точку В (подобно нити на рис. 58), то нить EBD должна стремиться опустить точку В (как и представлено на рис. 59). То есть если АВС напоминает чашу, то EBD должна напоминать арку, и наоборот.
Вышеприведенные рассуждения можно использовать по-разному. Задача с натянутой сеткой или мембраной проста своей наглядностью, она помогает увидеть значение уравнения Лапласа и даже догадаться о его свойствах. Например, если мы закрепим все пограничные точки сетки в некотором положении, то наш физический опыт подскажет нам, что это одновременно определит положение всей сетки. Перекос рамки теннисной ракетки также вполне определяет новое положение нашей ракетки. Нам представляет* ся, что должна существовать теорема, согласно которой значения V внутри контура определяются значениями V на границе при условии, что V — решение уравнения Лапласа. Действительно, существует теорема, которая при определенных приемлемых условиях, накладываемых па V, утверждает то же самое, что мы только что сформулировали,
152
Далее, поскольку уравнение Лапласа имеет мно-го приложений в различных отраслях науки, то результаты, полученные в одной отрасли, можно ис-пользовать при исследовании сходных вопросов в другой. Так, например, к решению задачи из электричества можно подойти, изучая форму мыльного пузыря.
Высказанные выше мысли можно использовать также и для отыскания численных решений уравнений. Дело в том, что алгебраическое уравнение (3) так же связано с дифференциальным уравнением (4)' в частных производных, как разностное уравнение связано с дифференциальным.
Устойчивость
Всякому, кто занимается вычислениями с карандашом в руке, пользуясь настольным арифмометром или даже электронно-вычислительной машиной, полезно знать об одной западне, которую можно проиллюстрировать на примере решения простейшего дифференциального уравнения у' = —у.  Сейчас, когда его решение известно в форме у — Ае~х и имеются таблицы значений функции е~х, никому и в голову на придет решать его численными методами. Однако мы приведем здесь именно численное решение, чтобы показать ту опасность, которая подстерегает вас на каждом шагу.
Начнем с правильного изложения. В формуле (1) возьмем h = 0,1. При замене у на ап и у' на (an+i — —«п)/0,1 у нас получается разностное уравнение (an+i — «п)/0,1 = — ап, которое упрощается до равенства an+1 = 0,9an, показывающего, что каждое значение будет составлять 0,9 предыдущего значения, а все вместе они будут постепенно уменьшаться. Если нам назовут 1000 в качестве первоначального значения у, мы запишем йо = 1000. Проводя вычисления с точностью до целых, мы получили бы последовательность значений 1000, 900, 810, 729, 656, .... которые, конечно, заметно отличаются'от значений точного решения у = 1000 е~х по причине очень грубой аппроксимации, которую мы допустили. Можно было бы попытаться улучшить дело следующим образом.
153‘
На рас. 67 значение у' в точке В есть наклон касательной ВТ. Мы заменили его величиной (a»+i — —<ла)/0,1, которая сама есть наклон ВС. На рисунке видно, что для оценки наклона ВТ лучше было бы воспользоваться наклоном АС. Это подтверждается и расчетами. При значении х = 1 в точке В истинное значение у' равнялось бы приближенно —0,3679. Наклоны ВС и АС при этом равнялись бы соответственно —0,3501 и —0,3685. Для наклона ВС ошибка составила бы 0,0178, а для наклона АС всего лишь 0,0006.
Отсюда напрашивается вывод, что для получе
ния более точных результатов было бы целесообразно заменить у' наклонам АС, равным (fln+i — вп-1)/0,2. Это привело бы нас к уравнению (an+i — On_i)/0,2 = = — ап, которое упрощается до уравнения an+i = = Un—1 ““ 0,2Па.
В нижеприведенной таблице даны значения ап, подсчитанные с помощью разностного уравнения, начинающегося значениями а<> — 1000 и at — 900. В ней также указаны значения истинного решения, определяемого выражением ЮООе-*, и ошибки, вызванные заменой истинных значений значениями ап.
В поведении ап таблица показывает заметные колебания. Значения ап то увеличиваются, то уменьшаются, а ошибка отклонения неизменно возрастает по абсолютной величине, тогда как истинные значения решения монотонно уменьшаются. Наблюдаемые резкие колебания настолько неблагоприятно сказываются на оценках ап, что если действительно ©4
меньше ^6, то- и aig и а%0 оказываются больше своих предшественников.
X	п	ап	1000е - *	Ошибка
0	0	1000	1000	0
0,1	Г	900	905	—5
0,2	2‘	820	819	+ 1
0,3	3	736	741	—5
0,4	4	673	670	+3
0,5	5	601	607	—6
0,6	6	553	549	+4
0,7	7	490	497	—7
0,8	8	455	449	+6
0;9<-	9	399	407	—8
1,0	10	375	368'	+7
1,1	11	324	333	—9
1,2	12	311	301	+ 10
1,3	13	262	273	— 11
1,4	14	259	247	+ 12
1,5	15	210	223	—13
1,6	16	217	202	+ 15
1,7	17	167	183	—16
1,8	18	184	165	+ 19
1.9	19	130	150	—20
2,0	20'	158	135	+23
Если довериться этому вычислению, то мы будем введены в серьезное заблуждение относительно решения уравнения у' = —у. Заметим, что колебание в значениях ап целиком вызвано методом вычисления, а не какими-либо другими причинами.
Где здесь допущена ошибка? Что вызвало столь резкие колебания? Решая разностное уравнение ап+1 = ап-1 — 0,2ап ранее изложенным методом, найдем, что ап — Л(0,905)п 4- М(—1,105)п. Это решение может дать очень хорошее приближение к 1000 е~х, если положить К = 1000 и М = 0. В этом случае мы получим последовательность 1000, 905, 819, 741.....
значения которой при допустимой нами степени точности совпадают с истинными значениями. Это
155
самый лучший результат, который мы когда-либо имели. Он показывает, что хорда АС, как видно на рис. 67, дает значительно лучшее приближение к направлению касательной, чем хорда ВС. Это заставляет нас внимательно относиться к нашим вычислениям.
Однако вызывает беспокойство тот факт, что хороший результат получается лишь в случае, когда М берется строго равным нулю. Наша таблица, характеризующаяся резкими колебаниями, определялась первоначальными значениями ао — 1000 и fli — 900, которые получались при К = 99772 и М — 21/?- Отличие этих значений от К — 1000 и М =? 0 может показаться незначительным, особенно когда мы оперируем тысячами. Помехи вызваны коэффициентом (—1,105)” при М в формуле ап, а точнее — не самим коэффициентом, а размером члена, то есть его абсолютной величиной, которая равна Л4(1,105)". По мере возрастания п и абсолютная величина члена возрастает со скоростью, едва ли не превышающей 10%. Будучи небольшой вначале, она значительно увеличивается к концу.
Ввиду этого получается, что пока М = 0, все обстоит благополучно, но стоит допустить ошибку, в результате которой М сделается отличным от нуля (пусть на сколь угодно малую величину), как это приведет к довольно быстрому росту ошибки, постепенно все собой заполняющей.
Вполне естественно, что природа большинства вычислений предполагает некоторую ошибку как неизбежность. Правда, в случае с последовательностью Фибоначчи, все члены которой целые числа 0, 1, 1, 2, 3, 5, ..., нам удалось провести точные вычисления. Но большинство задач включает дробные числа и числа иррациональные. Ни одна счетная машина не может справиться с бесконечными десятичными дробями. Когда мы производим вычисления с бесконечными дробными числами, мы тоже прибегаем к округлению. Так, например, ведя вычисления с точностью до четырех десятичных знаков, встретившуюся нам дробь ’/з мы округлили бы до 0,3333. Возникшее, скажем, произведение чисел 0,2345 и 0,1111, равное 0,02605295, мы округлили бы до 0,0261. Ясно, что 15в
все это связано с ошибками приближения. Электронно-вычислительная машина может вести вычисление с десятью десятичными знаками, но и при этом неизбежны некоторые ошибки. А если ответ предполагает выполнение миллиона операций, то это неизбежно приводит к миллиону пусть небольших, но ошибок.
Всякое вычисление связано с осложнениями, которые не встречаются в теоретической математике. В теории все величины имеют точные значения; они растут и развиваются подобно человеку, идущему по открытой равнине. Вычисление же можно уподобить прокладыванию пути в лесной чаще. У нас есть маршрут, которому мы пытаемся следовать, но, встретив на пути дерево, мы отклоняемся влево или вправо. Весь вопрос в том, будет ли место нашего нахождения определяться нашими направляющими указаниями или тысячами тех незначительных отклонений, которые мы допускаем на своем пути.
Уравнение вида ап±\ = ап_\ — 0,2ап, в котором любая ошибка имеет тенденцию к неопределенному увеличению, называется неустойчивым уравнением.
Необходимость осторожности в выводах
Всякий, кто использует методы этой главы при решении прикладных задач, должен иметь в виду два источника появления ошибок.
Нашей основной идеей было заменить процесс непрерывного изменения процессом прерывным (допускающим скачки). Предполагая, что эти скачки становятся все меньше и меньше, а частота их появления все больше, мы рассчитываем, что наше решение для прерывной задачи будет тем самым приближаться к решению задачи непрерывной. Часто так и бывает, хотя и не всегда. Имеются случаи (внешне не вызывающие подозрений), когда решение, соответствующее скачкообразному процессу, приближается к чему-то совершенно не похожему на решение первоначальной непрерывной задачи.
Другая опасность указана в предыдущем разделе— это возможность неустойчивости.
157
Результату, полученному с помощью электронно-вычислительной машины, можно доверять лишь в случае, если величины ошибок, возникших в результате этих двух причин, внимательно оценены.
Есть рассказ (я не припомню его происхождения), в котором человек, обрабатывающий метеорологические данные, предсказал тайфун. Однако тайфун не появился. Оказалось, что это предсказание целиком было обязано неудачному численному методу,
ГЛАВА VII
НА ПУТИ К СИСТЕМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
В предшествовавших главах мы довольно свободно оперировали векторами, матрицами, линейными преобразованиями — находили Т в степени п, склады-
вали и умножали матрицы, отыскивали уравнения, которым они удовлетворяют. Во всех этих случаях использовались знакомые правила элементарной алгебры, Однако оперируя нечисловыми объектами, вы
можете столкнуться с определенными отклонениями
от обътчных правил. Например, в элементарной алгебре уравнение х2— 1 имеет два и только два реше-
ния: х=®4-1, х = — 1, тогда как соответствующее матричное уравнение М2 = /, кроме решений +/ и —I, имеет и множество других решений. Так, в упраж-
нении 1 в конце II главы мы видели, что уравнению /О П
U2 = 1 удовлетворяет матрица U = I j I и точно
такому же уравнению № = / удовлетворяет другая /1	0\
матрица К. = I q 1- Фактически уравнению М2— — I удовлетворяет бесчисленное множество матриц 2x2. Это вселяет в нас неуверенность. Очевидно, су
ществует много ситуаций, в которых элементарная алгебра приводит нас к правильным заключениям отно-
сительно матриц, но есть также случаи, когда она нас полностью дезориентирует. После того как мы закончим такое вычисление, мы не знаем, доверять ли полученному результату или нет. Ясно, что это затруднение надо преодолеть. Однако почему квадратное уравнение в случае матриц ведет себя так необычно? Посмотрим, как в элементарной алгебре можно доказать, что уравнение х2—1=0 имеет только два
159
решения: 4-1 и —1. Мы будем рассуждать следующим образом:
1)	х2- 1 = (х- 1)(хЦ-’ 1);
2)	/, (х — 1) (х 4- 1) =0, если х — решение уравнения х2— 1 = 0;
3)	произведение равно нулю только тогда, когда по крайней мере один из его сомножителей — нуль,
4)	так что х — 1 или х -|- 1 должны обращаться в нуль,
5)	то есть х должен равняться 1 или —1, что и требовалось доказать.
/0 IX
Теперь рассмотрим матрицу £7=4 Д- Убеждаем-
ся, что она удовлетворяет уравнению U2 — / = О, не будучи, однако, ни матрицей I, ни матрицей —I. На каком же этапе проведенное выше доказательство не пройдет для матриц? В пункте 2 мы не встречаем
/ —! IX
противоречия, так как £7 — 7 = I	j  1 / и U 4~ I =
/1 IX
= 1 j j I- Перемножив эти две матрицы, убеждаемся, что (U — I) (U + I) — О. Доказательство заведомо не пройдет в пункте 4, так как ни одна из найденных выше матриц £/ — 7и£74-7не равна в действительности нулю. И в самом деле, именно принцип третьего пункта доказательства неверен. Произведение (17 — — /) (U + 7) равно О, но никакой из сомножителей не равен О.
Согласно этому в матричном исчислении мы не можем положиться ни на один из результатов, полученных средствами элементарной алгебры, если его доказательство опирается на принцип пункта 3 доказательства.
Заметим, что это не единственное свойство из элементарной алгебры, которое при переходе к матрицам теряет свою силу. Рассмотрим следующее рассужде-
/0 П
ние с ранее упоминавшимися матрицами £7 = 1	I
/1 ОХ
160
6)	так как К2 = / и U2 — I, то № — U2 = О,
7)	но (Л - U) (К + U) = К2 - U2,
8)	следовательно, (Л — U) (К + U) = О,
9)	однако тогда по крайней мере либо К — U=> — О, либо К + U = О,
10)	откуда К = U и К = —U.
Совершенно очевидно, что полученный вывод неверен, и мы склонны видеть причину этого в переходе от пункта 8 к пункту 9, опирающемся на правило пункта 3, которое уже себя скомпрометировало. Однако ошибка допущена раньше, ибо уже уравнение
/ 1 ~Ц
пункта 8 неверно: поскольку /С — U — I j 1 / и / 1 1\
/(4-£7 = 1_। I, то произведение (К— U)(K +
/ 0 2\
4- U) = I___ _ I отлично от нуль-матрицы. Так как
утверждение пункта 6 не может вызывать каких-либо нареканий, то остается предположить, что ошибка допущена в равенстве 7. Действительно, мы только что убедились, что произведение (К. — U) (К + U), стоящее в левой части равенства 7, отлично от нуля, тогда как в правой части стрит выражение, равное нулю. Следовательно, формула разности квадратов применительно к матрицам неверна, во всяком случае, в качестве общего правила.
Чтобы выяснить причину ошибки, припомним, что в традиционной алгебре равенство (а — b)(a + b) = — а2 — Ь2 доказывается обычным перемножением двучленов в левой части. Выполним это умножение применительно к матрицам /Си U: (К — U) (К + U) = =	+ U)- U(K + U) = К2 + KU—UK — U2. В
элементарной алгебре мы бы вычеркнули (погасили)' KU и UK и получили бы желаемый результат. С матрицами этого делать не разрешается, ибо матрицы
/ 0 1\	/0 —1\
KU = ( । о) и £7/С = К о/ не равны.
Заметим, что приведенное выше вычисление полностью проходит в рамках элементарной алгебры, когда имеют дело с матрицами А и В, например
6 Зак. 51	161
/4 2\	/1 2\
Л— . „I, В = 1 1 I, удовлетворяющими ра-венству АВ — В А. Для этих матриц равенство (А — В) (Л + В) — А2 — В2 вполне справедливо. Когда АВ = ВА, мы говорим, что А и В коммутируют.
Любая матрица М *) коммутирует с /-матрицей и любой другой матрицей, представляющей степень Л4, то есть Мп. Действительно,	М • Мп=
— Мп • М = Mn+1. Отсюда следует, что многочлены относительно единичной матрицы умножаются по тому же правилу, как умножаются многочлены в элементарной алгебре, при этом сохраняются все известные в алгебре формулы. Например, мы без опасения принимаем, что (М — I) (М Аг I) =М2 — I. Именно поэтому утверждение пункта 1 в доказательстве вполне благополучно прошло для матрицы U.
Многие шаги, дозволенные в элементарной алгебре, неприложимы к матрицам. Еще пример: в элементарной алгебре равенство ах = ау при а 0 мы привычно отождествляем с равенством х = у. Применительно
к матрицам такое отождествление уже недопу-/-1 IX /о '•
стимо. Например, если Л = 1	.	, 1 =
/4
Нб
/ 2
НЫ1-2
IX
3/’
5Х
у J» то АХ и AY равны между собой и рав-
2Х
0 I. При этом А ¥= О, и тем не менее X и Y
JU j
не равны между собой. Это опять связано с тем, что произведение матриц может обращаться в нуль и тогда, когда каждый из сомножителей отличен от нуля. Что касается равенства АХ = AY, то оно эквивалентно равенству А (У— X) = О. Еще раньше в этой главе мы встречали две ненулевые матрицы U — I и U 4- /, дающие в произведении нуль. Только что приведенный пример и был построен подбором Л, X, У так, чтобы Л = U — I и У — Х = U + /• В случае когда АВ = О при А^О п ВфО, А и В называют дели-
телями нуля.

!) Матрица М предполагается квадратной, то есть имеющей одинаковое число строк и столбцов, это позволяет определить Мп.
16^
Классификация математических систем
Итак, мы видим, что при выполнении алгебраических операций над матрицами следует соблюдать осторожность, так как некоторые из матриц (но не все) являются делителями нуля, и часто (но опять же не всегда) две матрицы могут не коммутировать.
Чаще всего мы имеем дело с матрицами какого-то определенного типа. Так, например, мы могли бы ог-
( а — Ь \
раничиться матрицами типа ,	. Для любых
\ о а )
двух матриц Р и Q такого вида справедливы равенства PQ — QP, a PQ = О только в случае, когда Р или Q — нули. Таким образом, эта система матриц коммутативна и не содержит делителей нуля. Эти свойства выполняются в системе комплексных чисел, обладающей к тому же всеми алгебраическими свойствами действительных чисел. Последнее обстоятельство значительно упрощает механизм действий над комплексными числами. К сожалению не часто удается найти систему, обладающую такими свойствами. Обычно мы довольствуемся лишь совпадением ряда отдельных свойств. Примечательны в этом смысле матрицы 4X4 вида
У этой системы матриц единственный недостаток: она некоммутативна. Система не имеет делителей нуля. Это в сущности система кватернионов, и данная матрица представляет кватернион а + ib + jc + kd.
Вращение около начала координат (в евклидовой (а —Ь\ геометрии) представляется матрицей вида (, I, где а и b — действительные числа, удовлетворяющие равенству a2 -j- b2 = 1. При умножении двух матриц получается матрица такого же вида. Матрицы коммутируют. Деление всегда возможно: для данных
6*
163
матриц А и В всегда можно найти такую матрицу С, что С = А/В, понимая под этим, что СВ = = А. Однако если мы хотим остаться внутри взятой системы, то должны исключить сложение. Сумма двух матриц данного типа не будет в общем случае представлять вращение. (Если бы мы все-таки попытались ввести сложение, то оказались бы в системе матриц, представляющих комплексные числа.) Таким образом, мы имеем систему, в которой определена только одна базисная операция: умножение. Умножение (как и обратная ей операция — деление) ведет себя обычным образом.
В более широкой совокупности, состоящей из всех (а Ь\
матриц вида { J с определителем ad — bc=l, мы также можем умножать и делить, но не можем складывать и вычитать, так как сумма двух матриц рассматриваемого вида, как правило, не удовлетворяет условию ad — be = 1. В этой системе умножение некоммутативно, и поэтому мы должны различать два вида деления. Для любых А и В можно найти такие С и D, что будут выполняться равенства СВ *= Д, BD = Д, при этом С и D в общем случае различить
Эти четыре примера свидетельствуют о многообразии изученных математических систем, в связи с чем оказалось желательным иметь какой-то способ их классификации, для чего и были придуманы определенные названия. Система, напоминающая комплексные числа и обладающая веема алгебраическими свойствами, называется полем. Конечные арифметики, обсуждаемые в главе XIII «Прелюдии-к математике», дают другой, весьма отличающийся от первого пример поля. Система, подобная кватернионам и отвечающая всем требованиям, за исклю-. чением коммутативности умножения, называется косым полем. Рассмотренные выше вращения дают пример коммутативной группы, их часто называют абелевыми группами в честь известного норвежского fa b\
математика Абеля. Матрицы I	удовлетворяю-
щие условию ad — bc=\t образуют просто группу.
1В4
Чтобы заслужить какой-либо из этих титулов, система должна пройти определенные испытания. Узнав, что она прошла через них, мы одновременно приписываем ей те свойства, которыми обладают системы данного вида. Например, раз и навсегда доказав, что в любом поле квадратное уравнение не может иметь более двух решений, мы можем распространить это свойство на любую математическую систему, являющуюся полем. Таким образом, у нас отпадает надобность доказывать один и тот же результат или свойство при переходе от одной родственной системы к другой.
Известно, что многие отличные друг от друга математические системы представимы в матричной форме. Это может служить одним из доводов в пользу изучения матриц. Однако не следует понимать изучение матриц как самоцель. Можно рассматривать любую систему и пытаться найти ей место в нашей классификации. Например, мы можем прикинуть, куда бы нам поместить такие системы, как целые числа, рациональные числа, действительные числа, четные числа; операции, включающие в себя диффе* ренцирование или интегрирование, и т. д.
Ниже мы перечислим некоторые требования, которые можно предъявлять к системам при их классификации. Для каждой системы мы выясним, какие из нижеперечисленных утверждений в ней справедливы.
1.	Для любых двух элементов а и b системы найдется элемент этой же системы, определяемый как а + Ь.
2.	Сложение коммутативно: а + b = b + а.
3.	Сложение ассоциативно: а + (Ь + с) — (а+’ + &)+с.
4.	Система содержит такой элемент 0, что . . для любого элемента а системы а + 0 = а.
5.	В системе определено вычитание, то есть для любых элементов а и b уравнение а+, + х = b имеет единственное решение.
6.	Для любых элементов а и b системы существует элемент, определяемый как ab, тоже принадлежащий системе.
7.	Умножение коммутативно: ab — Ьа.
165
8.	Умножение ассоциативно: a(bc) = (ab)c.
9.	Система содержит такой элемент Ц что для любого элемента а системы а! = 1а — а.
10.	В системе определено деление: для любых элементов а и & каждое из уравнений ах = = b и уа = b имеет точно одно решение при условии, что а =# 0.
11.	Выполняются дистрибутивные законы: а) а(Ь + с) = ah -f- ас, б) (b + с)а — Ьа + са.
12.	Система не содержит делителей нуля: то есть ab — 0 тогда и только тогда, когда а — 0 или b = 0.
Система, удовлетворяющая всем 12 требованиям, именуется полем. Рациональные числа, действительные числа и комплексные числа — примеры таких полей. Перечисленные требования не являются полностью независимыми. Так, система, удовлетворяющая первым одиннадцати требованиям, удовлетворяет требованию 12.
Система, удовлетворяющая всем требованиям, за исключением требования 7, называется косым полем, примером косого поля служит система кватернионов.
Система, удовлетворяющая требованиям 6, 8, 9 и 10, определяется как группа. Примерами групп могут служить все вращения около начала координат; все матрицы 2X2 при условии, что ad — bc=l; положительные числа; действительные числа с выброшенным 0; пара чисел (1, —1); числа вида 10п, где п— любое целое число (положительное, отрицательное или нуль). Все эти группы иногда называются мультипликативными группами, что, может быть, и не совсем удачно. Это просто означает, что мы называем операцию «умножением». Но формальные свойства сложения и умножения одинаковы, требования 7 и 8 перекликаются с требованиями 2 и 3. Именно это сходство между сложением и умножением сделало возможным логарифмирование, изобретенное для обращения умножения в сложение.
Сходство означает, что мы имеем некоторого рода избыток в символике. Этим вызвано соглашение использовать знак «+» только для коммутативных систем. Умножение же можно использовать как для
1в6
коммутативных, так и для некоммутативных систем. Соглашение является причиной того, почему в требованиях 4, 5 и требованиях 9, 10 нельзя провести точной параллели.
Коммутативная группа, использующая знак есть тем самым система, удовлетворяющая требованиям 1—5. Примеры коммутативной группы дают целые числа; целые числа, кратные 7; любое векторное пространство. Если отдать предпочтение знаку умножения, как мы поступили, например, с матрицами, представляющими вращение, то следовало бы проверить требования 6—10.
Кольца
Рассмотрим одно очень важное понятие, которое еще не упоминалось, — это понятие кольца. Система всех четных чисел ... —4, —2, 0, 2, 4, ... классифицируется как коммутативная группа, использующая знак «4-». Из-за умножения, которое так же, как и сложение, определено в этой системе, она не заслуживает права называться полем, так как она не удовлетворяет требованию 10. В ней невозможно деление: так, результат деления 6 на 2, принадлежащих полю, не является четным числом, а 2:6 и того хуже — дробь 4/з. Системы, в которых можно выполнять сложение, вычитание и умножение без деления, именуются кольцом. Трудно объяснить, почему для такой цели выбрали это весьма своеобразное название. Из перечисленных выше требований кольцо должно удовлетворять требованиям 1—6, а также требованиям 8 и 11. Система матриц 2\2 образует кольцо. Кольцом является система всех полиномов относительно х. Имея два полинома, скажем х 4- 3 и х2 4-1, мы можем их складывать, вычитать, умножать, но не делить, ибо деление привело бы нас к дроби (х4-3)/(х24-1), которую нельзя выразить в виде полинома. Таким образом, полиномы образуют кольцо, но не поле. По той же причине целые числа также образуют не поле, а кольцо. Кольцо образует и система всех непрерывных функций, которую, однако, нельзя назвать полем. Если у = f (х) и у = ф(х) — непрерывные кривые, то непрерывными будут графики суммы, разности и произведения этих
167
функций, обозначаемых как у = f(x)-pp(x); у = = f(x) —<р(х); У — 1(*)ф(*)> чег0 нельзя сказать о графике — частном этих функций у — f(х)/ф(х). Например, функции f(x) = x и <р(х) = 2х—1 непрерывны, но частное у *= х/(2х— 1) в точке х = */г терпит разрыв.
Следует заметить, что мы применяем эти требования позитивно, а не негативно, то есть если кандидат, помимо основных требований, удовлетворяет еще каким-то другим требованиям, он не дисквалифицируется. Так, например, каждое поле одновременно является и кольцом. Это оправдано, ибо в теории колец мы доказываем теоремы, которые справедливы для любой системы, удовлетворяющей требованиям 1—6, 8 и 11, которые в поле выполнены. Они, естественно, будут справедливы также для систем, которые, кроме указанных требований, удовлетворяют еще и другим каким-то требованиям. Например, в любом кольце можно доказать, что (х3 — — х) (х8 4- х) = Xе — х2. Этот же результат справедлив и для любого поля, например для поля действительных чисел. Положение здесь напоминает геометрию, где любая теорема аффинной геометрии справедлива для евклидовой геометрии (но не наоборот) .
Часто при слове «кольцо» стоит прилагательное. Так, четные числа образуют коммутативное кольцо, ибо, кроме требований, обязательных для кольца, они удовлетворяют требованию 7. Матрицы 2 X 2 не образуют коммутативного кольца, но они содержат единичную матрицу I и удовлетворяют требованию 9, поэтому они образуют кольцо с единичным элементом, Четные числа под это название не подходят.
Можно сколько угодно много упражняться в классификации, наблюдая, какое место занимает каждая из рассматриваемых систем. Например, мы
могли бы рассматривать матрицы 2X2 типа
где а, Ъ, с, d — четные числа. Кольцо этих матриц уже не обладает упомянутыми выше дополнительными свойствами: оно некоммутативно и не имеет единичного элемента.
а Ь\ с d '
168
Вычисления в кольцах	. .. .
Доказанные нами результаты для колец, естественно, имеют большое сходство с результатами из элементарной алгебры. Так, например, в элементарной алгебре мы встречаем тождества (14-х)4== 1-}-' + 4х + 6х2 4- 4х3 + х4 и (х + </)2 = х2 + 2ху + у2 и их обобщения в виде биномиальной теоремы для (I 4 Д-х)” и (х + «/)”. Теория колец подводит нас к точно таким же результатам, но с более широким охватом.
В элементарной алгебре биномиальная теорема понимается как утверждение истинности определенной формулы для любых чисел х и у. В теории колец она устанавливает истинность этой формулы для любой системы, отвечающей определенным требованиям.
Так, поскольку в выражении (1 -f-х)" участвует 1, то система должна содержать единичный элемент. Если . х и у не перестановочны, то (x4f/)2 можно записать в форме х2 ху 4 ух 4- У2» но не в виде х2 4 2ху 4 У2 (см. ответ к упражнению 9 в конце главы III). Поэтому мы должны потребовать от системы коммутативности. Сейчас можно сформулировать биномиальг ную теорему в более широком смысле: обычные формулы для (14х)п и (х4у)п справедливы в любом коммутативном кольце с единичным элементом. (На самом деле, первая формула проходит даже то-гда,. когда кольцо некоммутативно, а вторая — даже когда нет единичного элемента.)
Доказательство биномиальной теоремы в этом широком смысле точно повторяло бы ее доказательстве в элементарной алгебре. Разница состояла бы лишь в том, что расчеты разбились бы на множество мелких шажков, каждый из которых должен был оправдываться ссылкой на соответствующее требование из числа тех требований, которым рассматриваемая система должна удовлетворять. Между прочим, в этом доказательстве нам понадобились бы и другие результаты из традиционной алгебры, если бы мы по,4 пытались показать, сколько раз член, скажем х2уп~?,' появится в результате полного умножения (или разложения) двучлена (x4-//)n.	;j
16»,.
Детали этого доказательства не так захватывающи и интересны, как сам результат, позволяющий применять биномиальную теорему ко всякого рода объектам, не являющимся числами.
Приложение
В статистике, как и в других научных исследованиях, нередко встает такая задача: подобрать подходящую простую формулу для множества данных. Пусть для некоторой функции мы получили следующую информацию: f(0) = 0; f (1) = 2, f(2) = 10, f(3) = = 30, f(4)= 68, f(5)= 130, f(6) = 222. Мы полагаем, что простой полином может удовлетворять этим данным. Так ли это? Если да, то какова его формула?
п	0	1	2	3	4	5	6
f(n)	0	2	10	30	G8	130	222
Д/ (п)	2	8	20	38	62	92	
Д7(»)	6	12	18	24	30		
Д7 («)	6	6	6	6			
А4/ («)	0	0	0				
Целесообразно составить таблицу разностей данных значений. Числа каждой последующей строки показывают шаг, с каким она возрастает по сравнению с предшествующей строкой. Сплошные нули в строке для Д4Цп) являются сигналом того, что здесь есть формула. Как ее найти? В учебниках по статистике предлагается следующий метод. Сначала мы определяем операцию Е, которая превращает f(n) в f(n + 1). то есть Ef(n) = f(n + 1). В частности, Ef(O) =f(l), Ef(l)=f(2), Ef(2)=f(3). В результате получаем, что f(0) может быть превращено в f(3) троекратным приложением операции Е. Символически это записывается как E3f(0) = /(3), а в общем виде Enf(0) = f(и). Если мы сумеем найти формулу для Enf(O), то решим поставленную задачу.
Далее, что мы можем сказать относительно Д? Рассмотрим в таблице число, например 38, равное 170
ДНЗ). Оно получается как разность двух чисел верхней строки 68—30, или f(4) — f(3). Так как [(4) — = Ef(3), то 38 есть разность Ef(3) — f(3), или (Е — __ l)f(3). Итак, мы имеем Д/(3) = (Е — l)f(3). Это наводит на мысль, что операция Д есть операция Е—1. Чем вызвана эта догадка? Тем, что число 38 из строки &f(n) было выбрано произвольно и, стало быть, проведенное рассуждение применимо к любому другому числу (входу) этой строки. Отсюда правомерно считать, что Д и £—1 представляют одну и ту же операцию, то есть Д — Е — 1 или £ = = 1 + Д.
А сейчас применим биномиальную теорему:
/(п) = £7(0) = (14-Д)пИ0) =
={ 1 + пД + Д2 +	Д3 + • • • }f (0) =
= f W+nbf (0)+^Г д2/(°)+—72(з~2) A3f (0) + • •.
В записи формулы мы ограничиваемся только первыми четырьмя членами, так как в нашей задаче А4/(0) и все остальные члены равны нулю.
Подставив в формулу f(n) соответствующие значения из первой колонки таблицы: /(0) = 0, Д/(0) = = 2, Д2/(0) = 6, Д3/(0)= 6, найдем, что
f(^) = 0 + 2n + 3n(n- 1) + п(п- 1)(п — 2),
и после упрощения получим искомую формулу f(n)=n? + n, стоящую за числовыми данными таблицы. Помнится, я познакомился с этим методом еще юношей при подготовке к первому экзамену. В то время я воспринимал биномиальную теорему только как числовую и этот метод поразил меня своим остроумием и изобретательностью как пример дерзкого формализма, пример той свободы, которую можно позволить себе в математике, получая при этом все еще правильный ответ. В действительности же этот метод вполне строг и логически оправдан, что нетрудно показать. После того как мы определили оператор £, можно пойти еще дальше и опре
171
делить любой многочлен относительно Е, например Е2 + 2Е + 3. Под (£2 + 2Е +. 3)f (п) понимается выражение E2f (n) + 2Ef (п) + 3f (п), которое есть не что иное, как f(n + 2) + 2f(n + 1) + 3f(n). Сумму двух таких полиномов легко определить. Умножение определяется как последовательное выполнение операции Е. Так, произведение (Е + 2) (£ + 3) есть операция, состоящая в последовательном выполнении сначала операции £ + 3 к исходному объекту, затем операции £+2 уже к результату выполнения первой операции. Далее в интересах лучшего уяснения нашей символики мы можем убедиться в том, что многочлены от £ действительно образуют коммутативное кольцо с единичным элементом. Сделав это (а это скорее утомительно, чем трудно), мы тем самым оправдаем приложение к нашей системе биномиальной теоремы. Так как Д = £—1, то операция А принадлежит системе и приложение биномиальной формулы к двучлену (1Д-Д)”, которое мы провели, логически оправдано.
Подобная идея используется в одном из методов решения дифференциальных уравнений. Если операцию дифференцирования обозначить буквой D, то Df(x) будет обозначать f'(x). Тогда под выражением (D2 + 2D + 3)f(x) будем понимать f"(x)+~ + 2f(x) 4-3f(x); здесь опять умножение определяется как последовательное применение операции. Обнаружено, что многочлены от D образуют кольцо с единичным элементом. Поэтому в этой системе с полным доверием можно использовать все формулы элементарной алгебры, которые включают действия сложения, вычитания и умножения. Некоторые учебники в отношении этого метода проявляют излишнюю щепетильность, утверждая, что «D-метод — это способ лишь угадывать решение дифференциального уравнения; полученные с его помощью результаты требуют обязательной проверки». Однако, к чести этого метода, даваемые им результаты неизменно оказываются правильными.
Но если начать рассматривать операции типа D + х, где (D + x)f(x) означает f'(x) + xf(x), то положение изменится. Рассмотрим это на примере, скажем, операции (D — х) (D + х). Запись (D — х) (D + 172
x)f(x) обозначает последовательное применение операций D + х и D — х к функции f(x), что можно записать в виде (D — x) и(х), где и(х) «= (D 4- x)f(x). Здесь было бы ошибочно предполагать, что (D—• —х) (£> 4- х) = D2— х2. Действительно, так как м(х) = = Г(х) + xf(x), то Он(х) = ц'(х) = f"(x) + xf'(x) +f(x). Далее (О — х)и(х) = и'(х)— хи(х) — f"(x) — x2f(x) +; .4- f(х) — Ф2— х2 + l)f(x)-. To есть мы получили, что (D — х) (D + х) = D2 — х2 + 1, — результат, непривычный для элементарной алгебры. Он вызван тем, что мы имеем дело с некоммутативной системой, в которой xD и Dx не равны. xD означает: «дифференцируй и умножай результат на х», то есть xDf(x) означает xf'(x), тогда как Dx означает: «умножь на х и продифференцируй результат». Поэтому Dxf(x) = [х/(х)]'=»: == xf'(x) 4- f(x) по правилу дифференцирования произведения. Последний результат можно записать как (х£) + 1)/(х),то есть Dx — xD 4- 1. Учитывая это, мы сможем перемнбжать (D — х) и (D 4- х) алгебраически следующим образом:
(D — х)(£) х) — D{D х) — х(Р + х), исходя из 11,6, — D2 4* Dx — xD — х2, исходя'мз 11, а, = D2 4- 1 — х2, поскольку Dx — xD — 1.
Было бы хорошо привыкнуть к такого рода вычислениям, которые зависят от порядка сомножителей в произведении, тем более что коммутативность умножения (свойство 7, ab — Ьа) — одно из тех свойств, без которого мы вынуждены будем часто обходиться. Например, система, состоящая из всех матриц 2X2, весьма напоминает систему х, D, так как она тоже представляет собой некоммутативное кольцо с единичным элементом
Одной из главных особенностей квантовой теории является то, что умножение в ней некоммутативно. Интересно отметить, что квантовую теорию удается представить и в терминах матриц, как это сделал в своих работах Гейзенберг (1925), и в терминах дифференцирования, как это сделал Шредингер (1926).
173
Упражнения
1. Найдите произведение (D + х) (D — я). Совпадает ли оно с- произведением (D — х) (Я + х) ?
2» Упростите-, выражение (D -J- х)2 — (D2 + 2xD 4- х2).
/:0	1 Ол	/ 1	0 0\
3. Пусть Х=1 0	° 1 1	,7=10	1 0
\ 0	0 0/	\ 0	0 1 /
Подсчитайте- X2 и X3.. Вычислите (/ — X)2: а) непосредственным перемножением матриц, б) по известной формуле квадрата суммы. Согласуются ли эти результаты? Можно ли было предвидеть это согласование до вычисления? Найдите (/ + %)10.
4> Что получится после полного перемножения отдельно (4+В)2 и (4 + Я)3, если А и В принадлежат некоммутативному кольцу?
5.	«Систему остаточной цифры» можно пояснить следующим образом. Используются только символы 0, 1, 2, 3, 4, 5, б, 7, 8, 9. Сложение и умножение определены так же, как и в обычной арифметике. Но в отличие от обычной арифметики в результате пишут только последнюю цифру. Например, 3 + 9 *= 2, так как 12 заканчивается на 2; 4 X 7 = 8, так как 28 заканчивается на 8. Каким требованиям удовлетворяет эта система? К какому типу она принадлежит? Справедлива ли в этой системе биномиальная теорема?
6.	«Система остаточной четной цифры» строится по аналогии с. «системой остаточной цифры» упражнения 5, только в ней используются одни четные цифры: 0, 2, 4, 6, 8. Ответьте на те же три вопроса, которые предложены в упражнении 5.
7.	Так же как в упражнении 5, рассмотрите «систему последней нечетной цифры», в которой используются только нечетные цифры: 1, 3, 5, 7, 9.
Векторные пространства
Выше было дано самое общее представление о том, что называют векторными пространствами. Сейчас мы хотим обсудить те требования, которые определяют векторное пространство.
В рассмотренных ранее задачах на плоскости мы использовали выражения вида К + 4Р, 2К + ЗР и т. д., включающие точки, или векторы, обозначенные прописными буквами К и Р, и числа. Если для обозначения чисел применим малые буквы, то рассматриваемые выражения в общем виде запишутся как. хК + уР.
Требования, определяющие векторное пространство, можно разбить на две части. В первой части 174
числа не упоминаются вовсе, здесь мы имеем дело исключительно со сложением векторов. Во второй части рассматривается умножение вектора на число.
Первая часть проста и коротка. Она состоит из 5 требований:
1.	Для любых векторов Р и Q определяется вектор — сумма Р + Q.
2.	Сложение коммутативно: Р + Q = Q + Р.
3.	Сложение ассоциативно: P-(-(Q-\-K) = = P + Q) + ^
4.	Существует нуль-вектор О такой, что Р +j + О = Р для любого Р.
5.	В системе определено вычитание: для любых двух векторов Р и Q существует только один вектор X, такой, что Р 4- X = Q.
Принято считать, что эти свойства для рассмотренных ранее систем выполняются независимо от того, интерпретируется ли вектор как точка на плоскости со сложением по правилу параллелограмма, или он интерпретируется как «х кошек и у собак».
Эти требования, между прочим, точно соответствуют требованиям 1—5, приведенным на стр. 165, которые относят систему векторов к коммутативной группе.	t
Приступая ко второй части требований, остановимся на том, как ведутся вычисления, когда одновременно имеют дело и с векторами, и с числами. От сложения 2Р и ЗР получается 5Р, то есть мы просто складываем имеющиеся числа. Алгебраически это выражается равенством аР + ЬР = (а + Ь)Р. Далее 5 раз по (Р + Q) дает 5Р + 5Q, то есть в общем виде а(Р + Q)— аР + aQ. 3 раза по 2Р дает 6Р, то есть дело сводится к перемножению имеющихся чисел, что в общем виде выглядит как а (ЬР) — — (ab)P.
В некоторых случаях нам будет удобно рассматривать Р как 1 -Р.
Ясно, что все эти понятия имеют смысл благодаря тому, что в самом начале была введена операция умножения вектора на число.
Теперь требования второй часта можно сформулировать следующим образом:
175
6.	Для любого вектора Р и любого числа а определен вектор аР.
7.	аР + ЬР = (а + Ь)Р.
8.	a{P + Q)=aP + aQ.
9.	a(bP) = (ab)P.
10.	1-Р = А
Если мы узнаем, что какая-то система удовлетворяет всем десяти требованиям, значит, она представляет собой векторное пространство, и все известные шаги, предпринимаемые нами в отношении действий над векторами этой системы, вполне оправданы. Таким образом, появляется возможность получить схему метода и связанные с ним следствия, которые приложимы к любой системе, лишь бы она удовлетворяла этим десяти требованиям.
В конце главы II мы допустили, что такие системы, как системы квадратных трехчленов, выражений вида asinx + ftcosx, непрерывных функций, следует отнести к векторным пространствам. Сейчас мы в состоянии доказать, что это действительно так. Для доказательства достаточно проверить, что каждая из упомянутых выше систем обладает всеми десятью свойствами. Сделать это нетрудно. Пусть мы имеем дело с квадратными трехчленами. Два квадратных трехчлена в сумме дают квадратный трехчлен, следовательно, требование 1 выполнено.. Если Р означает квадратный трехчлен рх2 + qx + г, то под аР мы понимаем трехчлен вида арх2 -f- aqx -|- аг, то есть аР определено и выполнено требование 6. Проверка остальных требований сводится к применению простых тождеств элементарной алгебры.
Таким же образом можно рассмотреть и систему, состоящую из всех выражений вида a sin х -J- b cos х.
Доказательство того, что непрерывные функции образуют векторное пространство, мы начнем с проверки первого требования: если f(x) и g(x)— непрерывные функции, то их сумма f(x)-j-g(x) тоже непрерывна. Это утверждение кажется вполне разумным, формальное же доказательство его сводится к несложному упражнению в математическом анализе. Если слово вектор интерпретируется в значении «непрерывная функция», то сумма двух векторов, будучи вектором, опять есть непрерывная функция.
176
Требование 1, следовательно, проверено. Условие 6 требует, чтобы умножение вектора (непрерывной функции) на число а определялось как вектор (непрерывная функция). Известно, что если f(x) непрерывна, то и a-f(x) непрерывна. Если теперь вектор Р представить как f(x), то вектор аР определится как af(x) и тем самым будет удовлетворено требование 6. Отсюда последуют и остальные требования. Нуль, о котором говорится в требовании 4, есть функция, график которой совпадает с осью Ох, то есть у = 0 для всех х.
Для непрерывных функций не имеет значения, потребуем ли мы непрерывности функции на всем множестве действительных чисел х или только на некотором интервале, скажем, между 0 и 1. В обоих случаях мы получим векторное пространство.
Система, состоящая из всех полиномов, есть векторное пространство. Сумма двух полиномов всегда полином, следовательно, требование 1 проходит; от умножения полинома на любое число а получается полином. Столь же очевидны и другие свойства. Что касается записи формального доказательства, то она может вызвать некоторые трудности как языкового, так и математического характера. Общая идея нам ясна, но вьщазйть ее не всегда просто.
Степенной ряд для функции ех обладает свойством сходимости для всех значений х, действительных или комплексных. Говорят, что ряды с таким свойством определяют целые, или, как их называют, полные функции'). Эти ряды или определяемые ими функции образуют векторное пространство.
Только что рассмотренные непрерывные функции f(x) были функциями одной переменной. Следовательно, мы исходили из одномерного пространства. Однако одно измерение не обладает какими-либо специальными преимуществами. Допустим, что функция V = f(x, у) определяет электрический потенциал в точке (х, у) куска медного листа, а функция V =
9 В русской математической литературе термин полная функция (integral function) не принят. Для функций, разлагающихся во всюду сходящийся степенной ряд, употребляется термин целые функции. — Прим. ред.
177
= g(x,y) —тоже электрический потенциал, но при каких-то других обстоятельствах. Тогда функция V = f(x,y)^-g(x, у) будет также определять потенциал. Если f(x,y) и g(x,y) — решения уравнения Лапласа, то f(x, у) + g(x) также решение уравнения Лапласа и af(x,y) тоже будет решением уравнения Лапласа для любого а. Таким образом, нам удалось для потенциалов определить операции сложения и умножения на число а при выполнении требований 1 и 6. Так же легко проверив и другие свойства, убеждаемся, что всевозможные электрические потенциалы в плоской медной пластине (при условии, что батареи соединены только с границей) образуют векторное пространство.
Мы могли бы получить другое векторное пространство, аналогичное пространству всех непрерывных функций /(х), если бы потребовали, чтобы f(x,y) определяла не потенциал, а произвольную непрерывную функцию f(x,y), заданную для всех точек какой-то части плоскости.
Векторные пространства, таким образом, не есть нечто совсем новое. Всякий, кто складывает полиномы, или сходящиеся ряды, кто рассматривает электрические потенциалы, имеет дело с векторным пространством. Новое представляет тот метод, с помощью которого мы классифицируем наш опыт.
ГЛАВА VIII
О ЛИНЕЙНОСТИ
В главе III мы рассматривали различные отображения, представимые в матричной форме. В одних случаях мы имели отображение одного пространства в другое (нефть-*деньги), в других — отображение пространства самого в себя. Но все отображения были линейными, то есть (как пояснялось на. стр. 11.8) обладающими определенными свойствами: если Р~*Р* и Q—*Q*, то Р 4- Q -> Р* + Q* и kP^r -+kP*- для любого k. Определение линейного отображения предполагает, что выражениям Р + Q и kP придается определенный смысл. Например, если Р. и Q лежат в одном векторном пространстве, а Р*, Q*— в другом (или в том же самом), то выражения' Р + Q, kP и Р* + Q*, kP* имеют вполне определенный смысл. Поэтому мы можем говорить о. линейном отображении одного векторного пространства в другое (или самого в себя). Последнее замечание, сделанное несколькими главами раньше, предполагало просто примеры вроде тех, которые рассматривались в начале III главы: отображение двумерного пространства в трехмерное и т. п. Но VII глава с ее разнообразием векторных пространств показывает нам, что линейные отображения имеют гораздо более широкий круг приложений. Они включают в себя дифференцирование, интегрирование, операторы А и Е VII главы, операции в математической физике и многое другое.
Приведем еще. некоторые примеры линейных отображений. Функции./.(х), непрерывные для 0 х
Г, образуют векторное пространство. Для каждой такой функции площадь под графиком у . = /(х)
179
задается определенным интегралом j f(x)dx. Вы на-о
зываете мне функцию f(x), я вам — число А, выражающее площадь под графиком этой функции. Иначе говоря, мы имеем отображение /(%)—► А, Исходный объект, или ввод, — непрерывная функция, выход, или результат, — число. Основные формулы математического анализа устанавливают, что это отображение линейно (сравните со сноской на стр. 129, в которой доказано, что дифференцирование ёсть линейное отображение). Так что этот определенный интеграл осуществляет линейное отображение пространства непрерывных функций в пространство действительных чисел.
Вместо площади под графиком в промежутке от О до 1 мы могли бы рассматривать площади в промежутке от 0 до х. Результат при этом уже не представляет единственное число, а зависит от х, то есть является функцией от х. Например, в случае графика функции у = х2 формула для площади в промежутке от 0ьдо х была бы А(х)— 1/Зх3. Здесь имеет место ^инейное отображение, его линейность гарантиро-’вана такими теоремами, как «интеграл от суммы равен сумме интегралов». Отображение «f(x)~*Д(х)> есть отображение «непрерывная функциянепрерывная функция». То есть мы имеем отображение векторного пространства непрерывных функций в себя. Операцию интегрирования можно повторять: мы можем рассматривать квадрат, куб и другие степени этой операции; можем комбинировать их в виде полинома, как в главе III. При этом вовсе не обязательно, чтобы непрерывные функции соответствовали Простым формулам, как в приведенном примере х2 —>1/Зх3. Исходная функция могла быть эмпирической, как, скажем, запись барометрического давления.
Известно, что не всякая непрерывная функция дифференцируема (хотя, чтобы это открыть, потребовалось около двух столетий). Поэтому оператор Дифференцирования D — d/dx применим не ко всякой непрерывной функции f(x) и, следовательно, не осуществляет отображения векторного пространства 180
непрерывных функций. В теории дифференциальных уравнений часто встречаются функции вида еж, sinx, cosx, хегх, которые принадлежат к классу целых функций, определенных в главе VII. Целую функцию всегда можно продифференцировать, получив в результате снова целую функцию. В этом случае D-. f(x)-^-f'(x) отображает пространство целых функций само в себя. Как указывалось в сноске на стр. 129, это преобразование линейное. Более того, любой полином относительно операции D будет линейным. Например, если и = «" + «, где v = (D2 -|- 1)п, то отображение и—* и линейно.
Электрическое отображение
На рис. 68 иллюстрируется простая задача из области электричества, рассмотренная на стр. 150. Внешние точки А, В, С, ..., Н подключены к батареям, потенциалы в этих точках известны и равны соответственно а, Ь, с, .... й. Потенциалы w, х, у, z внутренних точек W, X, У, Z неизвестны, но могут быть
н 6
х F
Рис. 68.
Z Е ,
С D
определены из требования, чтобы потенциал в каждой точке был средним арифметическим потенциалов в четырех соседних точках (см. стр. 150). Это требование дает четыре уравнения с четырьмя неизвестными. Решив их, найдем выражение для у
2й 7/> 4- 7с 4- 2d 4“ 2с 4- f -f- g *4“ 2h
и аналогичные выражения для w, х, z. Заметим, что выражения для w, х, у, z линейны относительно а, Ь, с, d, ..., ft; мы, следовательно, имеем линейное отображение потенциалов в граничных точках в реэулъти-
рующие потенциалы внутренних точек. Линейность отображения сохраняется и для сетки с большим числом узловых точек, только число уравнений в этом случае увеличится и сами они будут «длиннее». Более того, линейность отображения остается и тогда, когда мы перейдем к пределу и рассмотрим сплошной кусок медного листа. Так что утверждение, набранное курсивом, остается в силе и здесь.
Скрытое отображение
Линейное отображение имеет место всякий раз, когда мы осуществляем подстановку числового значения в буквенную формулу. Это отображение вида «функция —► число». Вы называете мне функцию, я вам — ее значение, полученное при подстановке в нее фиксированного числа, скажем 10. Ниже приведены результаты подстановки числа 10 в различные выражения.
Выражение
X2
X3
X3 + X2 5х2
Значение выражения при х = 10 100
ЮОО
1100
500
Отображение первой колонки во вторую линейно. Если х2-*100, х3->1000, то сумма х34-х2 получается, как и должно быть, от сложения 1000 и 100. Таким же образом при х2-*100 пять раз по 5х2 дает пять раз по 100, то есть оба условия линейности выполняются.
В этом случае для линейного отображения мы всегда составляем таблицы. Пусть, например, мы составляем таблицы значений различных функций при х = 2, х = 3, х = 4. Тогда таблица для х2 дала бы три значения; 4, 9, 16. Пишем: х2-*(4,9,16). Таким же образом х3 ->(8,27,64). Следовательно, мы имеем отображение, в котором каждое выражение порождает трехмерный вектор. Легко убедиться, что это отображение линейно.
Однако не преувеличиваем ли мы роль линейности? Стоит ли устанавливать линейно то или иное ртображение или нет? Оказывается, стоит. Задачи, №2
включающие линейные отображения, обладают тем преимуществом, что позволяют решения простых задач приспособить для получения решений значительно более сложных задач.
Рассмотрим такую задачу: какой квадратный трехчлен вида рхг 4- qx + г при х — 2 примет значение а, при х = 3— значение 6, при х = 5 — значение с?
Как можно упростить задачу такого типа? Если взять а — 1, b — 0, с — 0, то вопрос сводится к следующему: какой квадратный трехчлен принимает значения 1, 0, 0, когда х принимает значения соответственно 2, 3, 5? На этот вопрос ответить проще, чем на более общий. Чтобы квадратный трехчлен при х = 3 и х — 5 давал нули, он должен иметь вид k(x — 3) (х — 5), а чтобы при х = 2 получить 1, следует взять k = */з.
Рассматривая таким же путем случаи а — О, b = = 1, с = 0 и а — 0, 6 = 0, с = 1, мы придем к следующим трем результатам:
(х — 3)(х — 5)/3-> (1, 0, 0)
— (х — 2) (х — 5)/2-> (0, 1, 0)
(х — 2) (х — 3)/6-»(0, 0, 1)
Вернемся к первоначальной задаче. Мы ищем квадратный трехчлен, принимающий набор значений (а, 6, с), и видим, что (а, Ь., с) можно изобразить в виде комбинации трех только что полученных результатов:
(а, Ь, с) = а{\, 0, 0)4-6(0, 1, 0)4-с(0, 0, 1).
Но в линейном процессе, если хотят, умножить результат (выход) на а, то умножают на а исходные данные, и если хотят сложить результаты, то складывают исходные данные. Согласно этому, мы берем а раз первый квадратный трехчлен, 6 раз второй квадратный трехчлен, с раз третий квадратный трехчлен, складываем их и получаем искомое выра-* жение.
Такого рода задача более подробно рассматривалась. в. главе IV «Прелюдии к математике», но без ссылки на линейность.
183
Линейность имеет место в очень многих областях физики, например там, где потенциал двух электрических зарядов можно найти сложением потенциалов этих зарядов. В этом и подобных случаях говорят, что имеет место так называемый принцип суперпозиции.
Замечание о функциях
То, что мы сейчас назвали отображением, часто называется функцией. Слово «функция» имеет длинную историю, в ходе которой его значение изменялось по крайней мере дважды. Начнем с того момента, когда у =J(x) означала связь между у и х, заданную какой-то одной простой формулой. В этом
смысле график, представленный на рис. 69, состоящий частично из прямой и частично из параболы, не признавался как иллюстрация функции. К нему прибегали скорее для того, чтобы показать две различные функции. В то же самое время считалось, что всевозможные бесконечные ряды определяют функции. В процессе ожесточенных и острых споров в период 1730—1760-гг. выяснилось, что один ряд, ряд Фурье, включающий синусы и косинусы, представляет функцию, график которой соответствует рис. 69. Действительно, ряд Фурье может дать и более причудливую смесь форм, чем те, которые приходилось до этого рассматривать. После этого больше не придерживались различия между кривыми, заданными одной формулой, и кривыми, заданными несколькими формулами. Более того, под записью у = f(x} стали понимать любое правило, пусть сложное, которое бы для каждого х фиксировало свое у. Например, правило могло быть таким: у — 1, если х четное; у = —1, если х нечетное, и у = 0 для всех осталь-
184
ных значений х. Но все еще сохранялось ограничение: правило должно фиксировать число у, как только задано число х. Однако в ряде задач вариационного исчисления неизвестное уже выступает не в виде числа, а в виде кривой или поверхности. Например, какая кривая на поверхности яйца даст кратчайший путь из точки А в точку В? Далее: если мыльный пузырь «помещен» в проволочный обод, то какую поверхность он примет при оседании, стремясь занять возможно меньшую площадь. Эти задачи имеют известную аналогию с задачами на максимум и минимум в началах математического анализа. Только здесь вместо числа, обеспечивающего минимум чего-то, мы должны найти кривую или поверхность, обеспечивающие этот минимум.
Итак, для данной гладкой кривой фиксируется длина, для данной гладкой поверхности фиксируется ее площадь. То есть существенный признак функции здесь налицо, и мы можем записать s=*f(C) и А ==. — f(S), где s — длина кривой С, а А — площадь поверхности S. Функции такого рода были рассмотрены в 1889 г. Арцела и Вольтера. Статья Арцела в Rendi-conti Lincei называлась «Funzioni di linee», что лучше перевести как «Функции кривых». В 1903 г. Адамар опубликовал статью по «функциональным операциям», которые представляли собой отображения: функция-* число. Определенный интеграл, приведенный в качестве первого примера в этой главе, мог бы служить простейшим примером функционала.
В историческом развитии понятия функции это была стадия, когда аргумент не был более числом, но результат все еще являлся таковым. Оставалось сделать последний шаг и спросить: «Почему в записи y=*f(x) или х —*у не разрешить под х и у понимать любые объекты?» И он был сделан. Так, в нашем примере с мыльными пузырями при условии, что форма проволочного обода однозначно определяет форму охватываемого им мыльного пузыря, мы можем записать S = f(7?), где R обозначает форму обода и S — форму мыльного пузыря.
Вполне возможно, что в 1700 г. кто-то и вынашивал идею изучения функций, допускающих объекты любого вида. Однако вряд ли он мог добиться
135
больших результатов. Чтобы сделать значительные открытия, мало задаться хорошим вопросом, необходимо широкое разнообразие примеров, которые бы подсказала вид результата,. ожидаемого в процессе открытия. Накопленные к 1900' г. достаточно богатые знания в; вариационном исчислении^ интегральных. уравнениях и: других областях математического анализа позволили сделать, общую теорию функций весьма плодотворной.
В классическом анализе первым вопросом, которым задаются при рассмотрении функции, является вопрос о непрерывности функции: ведет ли малое изменение х в функции у = f(x) к малому же изменению у? В более общей теории, где под х и у понимаются произвольные объекты, мы тоже попытаемся определить непрерывность. Например, поставим себе вопрос: является ли функция «обод -> пузырь» непрерывной? По аналогии с вышесказанным он означает: будет ли малое изменение обода вызывать* и малое изменение формы пузыря? Мы могли бы пойти еще дальше и поинтересоваться возможностью- дальнейшего обобщения идей анализа. Если х- № у объекты, отличные от чисел:, можем ли мы получить уравнение dy = f' (x)dx и придать ему смысловое значение? Фреше в 1925 г. показал, что при определенных обстоятельствах это может быть сделано.1):.
Производная Фреше
Работа Фреше была исключительно глубокой и, как всякая глубокая работа, ее отличала способность автора увидеть и выделить довольно, простую идею. Обратив внимание на первые шаги, с которых начинается анализ, Фреше нашел такой способ их описания, который оказался весьма значительным и полезным в гораздо более общих ситуациях. На рис. 70 представлена та ситуация, которую мы обычно рассматриваем, когда впервые знакомимся с производной. Кривая y = f(x) проходит через точку Р
’) «La Notion de differentielle dans 1’analyse, generale», Annates scientifiques de I’Ecole Normale Superieure, vol. XLII, 1925, pp. 293—323, 18g
•с координатами (л,&); РТ—^касательная к кривой в этой точке. .На чертеже :можно видеть, что вблизи точки Р кривая у — f(x) и касательная РТ почти неразличимы. То .есть вблизи этой точки касательная является именно той прямой, которая дает наилучшее приближение к кривой. Теория дифференцирования позволяет ответить на два вопроса: 1) существует ли прямая, аппроксимирующая кривую, и 2) если существует, то какова она? Поскольку в элементарной части математического анализа ударение
Рис. 70.
делается на втором вопросе, мы попытаемся подсчитать угловой коэффициент касательной. Позднее, при более тонком аналитическом подходе мы поймем важность первого вопроса. Мы встретимся с такими «извивающимися» кривыми, что не сумеем подобрать прямую, аппроксимирующую их поведение.
На рис. 70 длины PQ и QT обозначены как dx и dy. Таким образом, (dx,dy)— координаты точки Т относительно точки Р, принятой за начало координат. Здесь dx и dy не предполагаются «бесконечно малыми». Например, если бы график отвечал функции у — х2, то в точке Р (1,1) мы имели бы dy— = 2dx. Правомерно было бы положить dx—З и dy — б и считать, что вновь полученная точка, расположенная на 3 единицы ’восточнее и 6 единиц севернее точки Р, окажется на касательной. Идея :ма-лости dx и dy возникает лишь в случае, если мы хотим воспользоваться касательной как аппроксимацией кривой, ибо касательная только возле точки Р приближается к кривой. Положив dx = 0,001 и dy = 0,002, мы можем считать, что точка
187
с координатами (1,001; 1,002) (относительно первоначальной системы), лежащая на касательной, выглядит приближенно лежащей на кривой.
Согласно этому, касательную в точке Р можно определить как прямую, дающую наилучшую аппроксимацию графика y = f(x) в этой точке. Задача дифференцирования и состоит в том, чтобы найти эту наилучшую линейную аппроксимацию.
Итак, в этой главе мы значительно, расширили значение и объем слова линейное. Поскольку линейная аппроксимация функции связана с ее Производ-ной, то удается расширить и саму идею дифференцирования. В любой ситуации, где имеет место сложное отображение, мы вправе спросить: существует ли линейное отображение, дающее для него в ограниченной области хорошее приближение? Если Существует, то каково оно? Теория, отвечающая на эти вопросы, и есть теория дифференцирования. В этой теории аналогия с обычным дифференциальным исчислением поможет подсказать нам как сами результаты, так и способы их приложения.
В обычном анализе линейную аппроксимацию часто можно подсчитать алгебраически. Рассмотрим уже использованный пример: поведение кривой у = х2 вблизи точки (1,1). Положив х=14-й, найдем, что у ~ 1 4- 2й + h2. При й, достаточно малом, № будет еще меньше: когда й— тысячные, й2 — миллионные доли. Если пренебречь величиной й2, то можно найти точку х — 1 + й, у — 1 + 2й, близкую к точке на кривой. Давая различные малые значения й, мы всякий раз будем получать точки, лежащие на прямой, осуществляя тем самым линейную аппроксимацию кривой в виде касательной к ней в точке Р. При этом мы можем записать, что dx = й, dy = 2й, и сделать вывод, что dy — 2dx и есть то линейное уравнение, которое определяет касательную. При описанном выше приеме пренебрегают всеми членами, кроме линейных, и, естественно, приходят к линейному отношению. Так можно поступать и в менее знакомых ситуациях. Допустим, что мы имеем дело с отображением двумерного пространства на двумерное: (х, </).—>(«, и), где п = 3х2+' ,+ уг и v = ху. Нас интересует, как обстоит дело, 188
скажем, вблизи точки (1,2). Если возьмем х = 1+ft, у = 2 + k, то найдем, что
и = 1 + 6ft + 4ft + • • •, v = 2 +2ft + ft + ... .
Точками обозначены члены, которые при измерении ft и ft в тысячных долях измерялись бы в миллионных. Этими членами мы пренебрегаем и приходим к линейной аппроксимации:
du = 6 dx + 4 dy, 1 dv = 2dxdy. J
Обозначив (du, dv) через dU и (dx, dy) через dX, запишем систему уравнений (1) в более компактной /6 4\ форме: dU~MdX, где М означает матрицу I I, которая играет здесь роль производной.
Максимум и минимум
Одной из задач, рассматриваемых в математическом анализе, является отыскание максимума или минимума. В общих чертах задача решается следующим образом. Допустим, что касательная РТ, про-
веденная к кривой у = f(x) в точке Р, как представлено на рис. 71, поднимается вверх. Следовательно, точка Р не может быть максимумом, так как для поднимающейся касательной по мере продвижения по ней слева направо всегда можно найти точку Л1, лежащую выше точки Р. Поскольку касательная дает хорошее приближение кривой, то при М, достаточно близкой к Р, на кривой найдется точка /?, очень близкая к М и к тому же лежащая выше Р.
189
Таким образом, Р не может быть наивысшей точкой кривой в этой окрестности. Также она не может быть и самой низкой точкой. Двигаясь влево, мы найдем точку L на касательной, лежащую ниже точки Р. Очень близкая к L точка Q на кривой лежит ниже, чем Рч значит, точка Р не может быть самой низкой точкой окрестности.
Это рассуждение нуждается в некотором уточнении. На рис. 71 точка Q лежит выше точки L. При более подробном доказательстве мы должны были бы аккуратно показать, что Q не может находиться слишком высоко над L, чтобы не оказаться выше Л Это вполне удается разъяснить, однако здесь мы не намерены этого делать.
Аналогично можно показать, что в точке, где касательная поката, тоже не может быть ни максимума, ни минимума. Остается сделать вывод, что единственным местом, где это возможно, является точка, где касательная горизонтальна1). Этот факт лежит в основе обычного исследования на максимум и минимум, осуществляемого путем решения уравнения f' (х) = О и некоторых последующих проверок.
Мы собираемся приспособить знакомый прием сначала к задаче в трех измерениях, а затем попытаемся показать, что он приложим и к бесконечномерной задаче. Возможно, в последнем намерении кто-то увидит призыв к радикально новому мышлению. Однако это не так. Трудность, если она здесь и появляется, обусловлена тем; что при исследовании вопроса потребуется определенное количество традиционной символики и правил исчисления. Поэтому читателю, не намеренному заниматься такой работой, советуем просто бегло просмотреть конец этой главы, довольствуясь лишь общим впечатлением от проблем, к которым приложима производная Фреше.
Итак, сначала мы рассмотрим ситуацию в трех измерениях. В качестве частного примера можно рассмотреть чашевидную поверхность z = х2 + у2.
’) Мы исключаем случаи «точек-пиков», где f*(x) не существует, а также задачи, в которых область определения ограничена. Например, найти максимум для х2 при положительных х, не превосходящих 10. Здесь максимум достигается для х = 10, где угловой коэффициент касательной не 0, а 20.
190
Можно доказать, что точка (x'-pdx, y'-^dy, z'+dz) будет лежать на плоскости, касательной к данной поверхности в точке (х, у, г), при условии, что dz =* = 2х • dx 2у • dy. В более общем случае можно рассмотреть любую поверхность z—f(x,y) с касательной плоскостью, заданной уравнением dz =» p-dx+'. ,+ q-dy в точке Р. Ясно, что при р®Ои? = О^ = О для любых значений dx и dy, то есть касательная плоскость горизонтальна. Покажем, что это единственный случай, когда может иметь место максимум или минимум. Если наклонять касательную плоскость, то одни точки на ней окажутся лежащими выше Р, другие—ниже. Геометрически это легко осмыслить, для алгебраического же доказательства нужна некоторая уловка. Если в выражении dz *= « p-dx + q-dy мы сделаем подстановку dx р и dy — q, то получим, что величина dz = р2 + q2 положительна, она характеризует точку, лежащую выше точки Р. Аналогично, прибегая к замене х — —Р и у = —q, найдем, что dz = —р2 — q2 отрицательна и потому означает, что мы имеем точку, лежащую ниже точки Р. Таким образом, мы установили, что на касательной плоскости есть направления подъемов и спусков. Пройдя небольшое расстояние в одном из этих направлений (при условии, что касательная плоскость прикреплена к поверхности), мы обнаружим на поверхности точки, лежащие кате выше, так и ниже Р.
Согласно этому, максимум или минимум может иметь место лишь в случае р = 0 и q = 0. Ни при каком другом условии этого случиться не может. В нашем частном примере г = х2 + у2 мы имеем dz = 2х • dx 2у • dy, то есть р = 2х и q = 2y. Таким образом, условие р = q = 0 означает, что х = 0> У — 0, а это фактически дает минимум в точке, являющейся «дном чаши», о чем можно было бы догадаться, не прибегая к анализу.
Бесконечномерное пространство
Непрерывные функции (см. конец VII главы) образуют бесконечномерное пространство. Рассмотрим отображение типа «непрерывная функция—► число».
191
Пусть у «= f(x) — график непрерывной функции, заданной для х в промежутке от 0 до 1. Допустим, что число а определено уравнением
1
а = j (2ху — у2) dx.	(2)
о
Тогда отображение f(x)-*a напоминает отображения, рассмотренные нами в начале этой главы: вы называете мне выбранную функцию f(x), я вам — число а, полученное в результате подстановки у — = f(x) в правую часть уравнения (2) и вычисления стоящего там определенного интеграла. Ниже приведены примеры функций, которые вы могли бы выбрать, и соответствующих им значений для а:
y = f(x) у = 0 У^Ъ
У — х у — 1 +•*
У — X2
а О 0,25 0 0,3333...
—0,6666... 0,3
Отметим прежде всего, что это нелинейное отображение. Если бы оно было линейным, то, например, число а, соответствующее функции у — 1 + х, можно было бы найти сложением чисел, соответствующих функциям у = 1 и у — х. Далее, число, соответствующее у — 1, должно быть вдвое больше числа, соответствующего у = ’/г- Из приведенных примеров, однако, видно, что ни то, ни другое не выполнено.
Можно было бы поинтересоваться функцией, которая обеспечивает для а наибольшее значение, и отыскать ее. Выше наибольшее значение а = — 0,3333... соответствует функции у = х. Действительно ли это та функция, которая обеспечивает наибольшее значение для а, или другой, непоказанный выбор у обеспечит ему еще большее значение?
Представим себе, что этот вопрос был поставлен после того, как подсчитали три первые строки. Тогда У = ’/г давало бы для а самое большое значение: 0,25. По аналогии с ранее проведенным рассужде-
192
пнем мы, вероятно, могли бы установить, есть ли какой-либо другой график, отличающийся от графика у = </2, при котором а принимало значение немножко большее, чем 0,25. Если бы нам удалось это сделать, то мы доказали бы, что существует направление подъема и мы не можем иметь дело с максимумом. С этой целью рассмотрим график у = !/2 + 4-<р(х) при условии (как это представлено на рис. 72), что для каждого х на [0,1] значение <р(х)
Рис. 72.
y-h
достаточно мало. Подстановка у — '/? -f- ф (х) в равенство (2) дает нам число
0,25 j (2х — 1) ф • dx — J ф2</х.	(2')
Мы хотим здесь провести упрощающую аппроксимацию, используя снова рассуждение, что если ф измеряется в тысячных, то ф2 — в миллионных, и потому с ней можно не считаться. То есть, чтобы получить линейную аппроксимацию, мы пренебрегаем послед
ним членом  qPdx. Так как первое слагаемое 0,25
есть число, соответствующее у == */г, то приближенное изменение числа (2') дается вторым членом. Изменение у от '/г до 7а + ф вызывает, таким образом, приближенное изменение числа а от 0,25 до 0,25 4- а, где .. .	.
а= j {2х — 1)ф • dx.
(3)
При этом заметим, что отображение ф->а уже линейное, то есть уравнение (3) аналогично ранее
7 Зак, 51
193
проведенным аппроксимациям: касательная как приближение к малому куску кривой, касательная •плоскость как приближение к малому куску поверхности.
Можем ли мы в рассматриваемом случае «подни-- мятье я в гору»? Существует ли то малое изменение Ф, которое сделает а положительным? Несомненно. Взяв <р(х) = 0,001 (2х — 1), мы найдем
1
а = 0,001 | (2х — I)2 </.г, о
которое должно быть положительным, так как содержит квадрат выражения.
Можно проверить, что взятые нами приближения вполне оправданы, что у — */2 + 0,001 (2х — 1) дает для а чуть большее значение, чем то, которое соответствует у = V2, что имеется направление подъема и что у == 72 не может дать максимума.
Мы сейчас пролили свет на то, как использованные выше рассуждения можно было бы применить не только в случае с у = 1/2, но и в случае любого уравнения z/ = f(x), которое мыслилось бы как порождающее максимум. Предположим, что замена f(x) на /(х) + ф(х) вызывает соответствующее приближенное (отбрасываем ф2) изменение числа от а до а 4- а. Следуя только что проведенному вычислению, найдем вместо уравнения (3) уравнение
I
а = J 2 (х — f) ф • dx.	(4)
о
Взяв, как и раньше, ф = 0,001 (х — f), найдем, что
а = J 0,002 (х — /)2 dx. Мы снова получили под ин-о
тегралом выражение, содержащее квадрат, которое не может быть отрицательным. На миг нам могло бы показаться, что максимума здесь вообще не может существовать. Это означало бы, что при любом выборе функции f(x) мы всегда сможем осуществить
194
в ней такое небольшое изменение, которое непременно вызовет увеличение соответствующего числа. Однако при таком утверждении упускается одна возможность. Если f(x) = x, то х — f = и уравнение (4) показывает, что а = 0 для всевозможных <р. С такой ситуацией мы встречаемся на плоской вершине горы, где каждая касательная горизонтальна и отсутствует подъем. Наше рассуждение показывает, что это может случиться только при у — х.
В началах математического анализа исследование на максимум и минимум состоит в определении положения, где касательная горизонтальна, и в последующем выяснении, является ли найденная точка
(положение) точкой максимума или точкой минимума или это просто сомнительная точка (горизонтальная точка перегиба). Очевидно, в нашем примере проделанная работа соответствует только первой части — отысканию горизонтальных касательных. И когда я сделал вывод, что условие у — х соответствует вершине горы, вы верите мне на слово, ибо я не обсуждал здесь вопроса, как мы различаем вершину горы, долину, горный перевал.
На рис. 73 показаны первоначальное предположение 4/=72, усовершенствованное предположение у == i/2	0,001 (2х — 1) и окончательное решение
у == х. Можно заметить, что именно поправка к у — * = */2 привела нас к окончательному решению. График у = ’/2 в сравнении с решением у = х слишком высок в первой половине интервала и слишком низок — во второй. В нашем случае поправка имеет тенденцию исправлять эти погрешности: она опускает начальную часть графика и поднимает конечную. Это в свою очередь подсказывает, метод, который
7*	195
можно использовать в тех практических задачах, где нет известного простого теоретического решения. Рецепт довольно прост: начните откуда-нибудь подниматься в гору. Нет гарантии, что это приведет вас на вершину высочайшего пика, но при удаче вы можете подняться на вершину какого-либо холма. Повторив подъемы из разных отправных точек, можно получить некоторое представление о том, где расположены горы.
ГЛАВА IX
ЧТО ТАКОЕ ВРАЩЕНИЕ?
Если в главе I мы объясняли воображаемому существу аффинную геометрию, то сейчас попытаемся преподать ему евклидову геометрию. Целесообразно начать с геометрии на плоскости. Вычисления здесь элементарны и сводятся к использованию теоремы Пифагора и некоторых элементов алгебры, в частности формулы (а — &)2. Поэтому многое из материала этой главы можно было бы использовать для работы с учащимися младших классов, применяя так называемый проблемный метод, когда учащимся постоянно задается вопрос: «А что будем делать сейчас?»
Выполнив эти несложные рассуждения, мы попытаемся далее обобщить их на п-мерпое пространство. Эта глава поможет нам понять, как математический объект приобретает абстрактную форму. Все, что мы говорили нашему существу, абстрактно по необходимости — в разговоре с ним мы не могли рисовать картинки. Однако обсуждая послание существу между собой, мы вполне можем ими пользоваться. Получается, что мы находимся как бы внутри предмета, а существо — вне его; это вполне оправдано различием положений обучающего и ученика. Иногда создается впечатление, что абстракция означает незнание того, о чем мы говорим. Однако это совсем не так. Математик начинает создавать абстрактную сущность с рассмотрения различных ситуаций, которые ему хорошо знакомы и о которых он точно знает, в чем они состоят. Пытаясь выделить присущие им общие черты, он стремится построить единую, охватывающую их теорию. Эта теория абстрактна лишь в том смысле, что она опускает всякое упоминание о тех моментах, которыми различаются рассматриваемые ситуации.
197
Начнем с разъяснения существу геометрии на плоскости. Опираясь на наш опыт работы с бумагой в клеточку, сообщим ему основные определения. Первым из них будет определение точки.
Определение 1. Точка Р есть то, что характеризуется парой чисел (х, у).
Далее мы. хотим определить расстояние между двумя точками P(xi,#i) и Q(x2, z/2)- Как это сделать? Учащиеся, возможно, начали бы с числовых примеров, которые подвели бы их к общему рассуждению.
Согласно рис. 74, расстояние между точками Р и Q легко определяется по теореме Пифагора: PQ2 = — РМ2 + MQ2, что приводит К PQ2 — (Х2— Х])2-|-+ (У2 — yi)2- Так что наше следующее послание к су-ществу будет выглядеть таким образом.
Определение 2. Расстояние PQ от точки P(xi,.z/1) до точки.ф(х2, Ун) есть
V (х2 — *i)2 + (//2 — Z/i)2 •
Не исключено, что эта формула вызовет у существа недоумение. Почему для расстояния из множества всевозможных, формул выбрана именно она?
Конечно, только приступив к геометрии, мы бы никогда не додумались до такого определения. За ним лежит геометрический опыт двух тысячелетий. А формальный, аксиоматический, абстрактный, дедуктивный аспекты математики представляют заключительную стадию предмета и редко — начальную. И это важно иметь в виду. Обратим внимание также на то, как изменяется порядок развития соответствующих
108
идей геометрии. Теорема Пифагора была 47-м предложением первой книги «Начал» Евклида, составляя ее кульминационный момент. Именно в этом предложении содержится определение 2, которое мы собираемся передать существу.
Как правило, мы воспринимаем понятие расстояния как нечто само собой разумеющееся, не чувствуя какой-либо надобности в его формальном определении. Однако намерение использовать абстрактный подход (то есть попытка выразить некоторые факты средствами, понятными существу) заставляет нас это само собой разумеющееся понятие осмыслить и определить. Как только мы приступаем к этому, и перед нами, и перед существом возникает многозначительный вопрос: как выглядела бы вселенная, построенная по формуле, отличной от формулы, введенной определением 2? Это в свою очередь, естественно, подводит нас к идее неевклидовой геометрии и метрических пространств в целом. (Пространство считается метрическим, когда в нем каким-то осмысленным образом определено расстояние.) Эта идея проступила бы особенно ясно, если бы указанная для расстояния формула PQ2 = (х2 — Xi)2 + {у2— у\У была заменена какой-то другой формулой, выбранной наугад. Так, например, оказавшись во вселенной, в которой расстояние определяется формулой PQ4=(x2— Лч)4+ + (#2 —*Л)4, мы скоро обнаружили бы, что не можем делать поворотов на 180°. То есть родившись обращенными лицом в какую-то сторону, мы бы вею жизнь так и остались смотрящими в эту сторону. Объяснение этому факту можно найти двумя страницами ниже. Следующее наше послание существу связано фактически с движением твердых тел. Демонстрируя гибкие (носовой платок, резиновую трубку) и негибкие тела (кирпич, стальной брусок), мы могли бы задать учащимся вопрос: в чем проявляется разница в движении этих тел? В процессе обсуждения вопроса выяснилось бы, что при перемещении негибкого, или, как принято говорить, абсолютно твердого, жесткого тела в пространстве расстояние между любыми двумя его точками остается неизменным.
Поскольку в процессе движения любая точка тела из начального положения Р переходит в^ конечное
1W
положение Р*, то имеет место отображение Р->Р*, и мы можем сформулировать следующее определение.
Определение 3. Изометрией называется движение жесткого тела, при котором расстояние между его точками сохраняется неизменным, то есть при н Q->Q* всегда PQ = P*Q*. Пример изометрии дает тождественное отображение, так*как при нем взаимное положение всех точек не меняется. При этом для существа не очевидно, что имеются и другие примеры изометрии, тем более что есть геометрии, в которых ни одно подлинное движение невозможно. Примером такого рода геометрии является геометрия на поверхности статуи. Если статую покрыть плотно прилегающими латами, то заставить скользить их по ее поверхности нам не удастся: на статуе для таких лат будет лишь одно подходящее положение — положение, которое они занимают в данный момент. Поскольку определение 2 подходит для описания приведенной ситуации, то наши ссылки на скольжение как иллюстрацию изометрии будут бессмысленными. Существование различных видов изометрии требует доказательств.
Мы уже встречались с изометрией в главе I. На рис. 4 был показан результат переноса х* = х + 2, у* ~ У + 1- Можно доказать, что это изометрия. Действительно, х*2 —х\ —х2 —х{ и у2 — у\ = у2 — Найдя PQ и P*Q* по формуле определения 2, убеждаемся, что PQ = P*Q*. Поскольку такой результат получится при любом параллельном переносе, то имеем следующие два послания существу:
Определение 4. Любое отображение вида х* — — х -J- а, у* — у + b называется параллельным переносом.
Теорема 5, Всякий параллельный перенос суть изометрия.
Движение около начала координат
Существуют ли другие виды изометрии, кроме параллельных переносов? Оказывается существуют, например вращения. Вообразим себе кусок картона, который может свободно скользить по плоскому столу. Стоит только прикрепить картон к столу в какой-то
Ж
точке, как скольжение уже станет невозможным, однако способность картона вращаться вокруг закрепленной точки еще останется. Предположив, что картон закреплен булавкой в начальной точке О, дадим следующее определение.
Определение 6. Движение около начала координат есть отображение, при котором О* = О.
Попробуем отыскать такие виды изометрии, при которых начало координат оставалось бы неподвижным: О* = О.
Начнем рассуждение с точки А (1,0), которая переходит в точку Л*. Вряд ли в нашем случае можно взять точку Л* произвольной. Требуется соблюсти условие О А = ОМ*. Можно вообразить, что точки О

Ркс, 75.
и А как бы соединены стальным стержнем, не способным ни растягиваться, ни сжиматься, как это и представлено на рис. 75. Поэтому точка Л* в результате движения точки Л должна оказаться где-то на окружности с центром О и радиусом, равным 1.
Что касается существа, то лишь сообщим ему, что поскольку при изометрии расстояния между точками жесткого тела не меняются, то должно выполняться равенство О А — ОМ*. Поскольку формулы для обоих расстояний ОА и ОМ* включают квадратный корень (определение 2), равенство удобней записать в виде (ОМ*)2 = (ОЛ)2. Договоримся в дальнейшем в случае равенства двух длин брать квадраты расстояний. В случае, если точка Л определена координатами (с, s), то условие ОЛ = ОМ* дает равенство
c2 + s2==l.
(1)
И это, пожалуй, все, что мы можем сказать о точке Л*. Если взять теперь точку S(0, 1), то в силу изометрии ОВ и АВ остаются неизменными, и точка В кажется привязанной уже двумя стержнями, как это показано на рис. 76. Если предположить, что точка S*,
'201
в которую переходит точка В, имеет координаты (р, q), то условия О*В* — ОВ и А* В* — АВ приводят к двум уравнениям
p2 + g2—I,	(2)
(р — с)2 + (? — s)2==2	(3)
относительно неизвестных р и q. Эти уравнения, как часто случается в изучении естественно возникающей проблемы, удается неожиданно упростить. Так, раскрыв скобки в уравнении (3), обнаруживаем в нем
выражения р2 + q2 и с2 + s2, которые, согласно равенствам (2) и (1), заменяем единицами. В результате уравнение упрощается и принимает вид
ср + sq ~ 0.	(4)
При s ¥= 0 !) можно найти q = —cp/s и подставить в уравнение (2), которое после освобождения от дробей принимает вид р2(с2 + $2) = s2. Следующее упрощение с2 + s2— 1 приведет нас к уравнению р2 = s2, из которого для р найдем два значения р — s и р — —s. Значение q следует из упомянутого выше равенства q = —cp/s. В результате получаем ответ на поставленную задачу в виде двух решений: а) р = —5, q = +с б) р = +<$, q = —с. На рис. 77 представлена графическая интерпретация этих решений: в случае а треугольник ОАВ просто вращали, а в случае б треугольник сначала вращали, а потом перевернули обратной стороной вверх.
Могут возразить, что слово «изометрия» не вполне точно описывает решение б, так как мы не смогли
9 При 5 — 0, с 0 получим точно такое же решение, используя равенство р = —qs/c. С помощью более сложных алгебраических преобразовании можно избежать этого разделения взаимно исключающих возможностей.
202
перевести треугольник из положения ОАВ в положение 0*4 *В*, не выводя его из плоскости листа бумаги. Однако следует помнить, что «изометрией» называют всякое отображение, сохраняющее расстояния. Сейчас рассмотрим подробно только решение а, оставив решение б читателям в качестве упражнения.
Рис. 77.
Решение а
Итак, согласно решению, а, точка А переходит в точку А* (с, s), а точка В в точку В*(—s,c).
Посмотрим теперь, что при этом произойдет с любой точкой Р(х, у). Как показано на рис. 78, точку Р можно мысленно соединить стержнями с точками О,
А и В, Длина стержней не изменяется, ив связи с этим обе координаты (х*,у*) точки Р* должны удовлетворять трем условиям: 0*Р* — ОР. А*Р* = АР. В*Р* = = ВР. В общем случае два неизвестных могут не удовлетворять трем уравнениям. Это заставляет нас доказывать существование вращений, а не считать их само собой разумеющимися, тем более что в большинстве геометрий вращений не существует вовсе. Обратимся снова к определению 2, которое из небольшого числа формул, допускающих непрерывное вращение твердого тела, использует одну. Согласно определе-
203
ъию 2, три вышеуказанных условия приводят к уравнениям (5), (6), (7):
(х‘)2 + (уТ = х2 + у2,	(5)
(x‘-c)2 + (z/*~s)2 = (x-1)2 + у2,	(6)
(.r‘ + s)2 + (z/‘-c)2 = x2 + (//-I)2,	(7)
где х, у, с, s предполагаются заданными, а х* и у* следует найти. Опять проведем упрощение. Раскрыв скобки в уравнениях (6) и (7), мы придем к уравнениям (8) и (9):
х‘с 4- y*s = х,	(8)
—	+ у*с = у.	(9)
Решив их и дем, что
использовав равенство с2 + s2 = 1, най-
х* — сх — sy, У* sx + су.
(Ю)
После этого необходимо проверить, что найденное решение (10) удовлетворяет всем трем уравнениям (5),
Рис. 79.
(6) и (7). Убедившись, что это так, мы испытываем радость, а существо удивление. Но это не все. Проверка уравнений (5), (6) и (7) доказывает, что расстояния любой точки до точек О, А и В остаются неизменными. Однако в одном месте существо нам может возразить. Предположим, что мы применили преобразование (10) к двум точкам: Р с координатами . (xi,f/i) и Q с координатами (х2, f/г) • Только что проведенное вычисление гарантирует нам неизменность, с одной стороны, расстояний ОР, АР, ВР, с другой — расстояний OQ, AQ} BQ, ничего не говоря при этом
204
о расстоянии PQ, помеченном на рис. 79 пунктирной линией. И если наш геометрический опыт не оставляет сомнений в том, что PQ окажется равным P*Q*, то у существа такого опыта нет и для него это не очевидно. Чтобы убедить его в этом, мы должны были бы подсчитать P*Q* и тем самым проверить, что оно действительно равно PQ.
Аналогично решению а решение б тоже привело бы к изометрии, определяемой уравнениями
х* = сх 4- su, 1
(11) у =- SX — су. )
Легко заметить, что (10) и (11) суть линейные преобразования. На основании всех этих алгебраических вычислений мы можем сформулировать следующие результаты:
Теорема 7. Существует бесконечное множество изометрий, оставляющих начало координат фиксированным, неизменным. Различают два типа изометрий: первый тип характеризуется уравнениями (10>, второй— уравнениями (11).
Теорема 8. Каждая изометрия относительно начала координат задается линейным преобразованием.
Вращения и отражения
Огромная разница между этими двумя видами преобразований отчетливо усматривается из рис. 77. Но существо не может увидеть этот рисунок и потому не знает, что мы имеем в виду, когда говорим о «перевертывании», происходящем при отражении. Можно ли каким-то образом передать ему это?
В IV и V главах относительно линейных преобразований был задан хороший вопрос: «Что такое собственный вектор?» Характеристическое уравнение, с помощью которого мы получили на него ответ, мо
жет оказать нам услугу и здесь.
Так как вращение, как правило, меняет направление каждого вектора, то мы не надеемся найти для него собственные векторы. Если через 7? обозначить [с —s\
матрицу!	), соответствующую уравнению (10},
у s с!
205
то характеристическое уравнение относительно R запишется в виде R* 2— 2cjR +(с2 + s2)/ = О. Этому уравнению соответствуют корни с ± is, где 1= —1 . За исключением случая $ = 0, соответствующего вращению на 0 или 180°, эти корни комплексные, и, следовательно, наша догадка, что не существует ни одного действительного вектора, не меняющего своего направления при вращении, подтвердилась. Однако рассуждая в области комплексных чисел, мы пришли бы к неожиданному результату1), что все вращения имеют одинаковые собственные векторы (/,/) и (/,—i). Далеко не так обстоит дело с преобразованием, определяемым решением б. Приняв за М мат-/с	s\
рицу I	, данную уравнением (11), найдем
\	С j
для нее характеристическое уравнение М2 = /, которое в какой-то степени было изучено нами в гл. V. Там мы нашли, что для любого вектора v преобразование М оставляет выражение V2(/ + M)v неизменным, а выражение 72(/ — M) v умножает на —1. Если в качестве v выбрать вектор (2^,0), то мы увидим, что преобразование М всякий вектор вида й(1 + с, <$) оставляет неизменным, а всякий вектор вида А(1—с,—5) умножает на —1. Векторы (возможно, их лучше было бы назвать точками) вида /г(1 + с, s) заполняют определенную прямую, проходящую через начало координат. Преобразование М фактически представляет отражение относительно этой прямой.
Таким образом, различие между вращением и отражением можно определить так: вращение оставляет неизменной единственную точку, а отражение — каждую точку некоторой прямой2). Это различие принадлежит к числу тех, которые существо способно понять.
Существо способно также понять различные способы комбинирования вращений и отражений. Вра-
!) Сравните с «Прелюдиейк математике», гл. II, раздел «Пересечение окружности с бесконечно удаленной прямой».
2) Символы R и М, выбранные для обозначения преобразований, соответствуют начальным буквам английских слов «rotation» и «mirror», которые переводятся на русский язык как «вращение» и «зеркальное отражение». — Прим, перед,
206-
[ сС — sS то R\R2 = sC + cS
. (Р в форме	к
щение, следующее за вращением, дает вращение. Практически вращения образуют группу. Отражения группы не образуют: два отражения дают вращение, но не отражение. Эти результаты мы наблюдаем геометрически, а существо может проверить их перемно-(с ~s\	(c~s\
жением матриц. Если /?i—	I и /?2 = 1 с _1,
\ S С )	\ о С j
— cS — sC\ ~ о , что можно записать сС — 50 j
где р = сС — sS и q = sC 4- cS, ко
торая отвечает вращению. Для окончательного утверждения, что есть вращение, следует доказать, что р2 -р q2 = 1. Прежде всего убеждаемся, что р2 4- q2 — = (с2 + s2) (С2 4- S2), а это означает, что р2 4- q2 = 1, поскольку из того, что и /?2 — вращения, следует, что с2 + 52 = 1 и С2 + S2 = 1. Сейчас можно понять, почему в качестве координат точки А выбраны буквы с и s, начальные буквы слов cosinus и sinus. То обстоятельство, что точка А*(с, s) есть новое положение точки 4(1,0), полученное ею в результате вращения, позволяет весьма удобно ввести определения синуса и косинуса любого угла, избежав тем самым волокиты делать это сначала для углов в интервале от 0 до 90°.
Заметим, что равенства р—сС — sS и q = sC 4- cS предыдущего абзаца выражают формулы сложения для синуса и косинуса. Весьма любопытно, что, не обмолвившись ни единым словом о тригонометрии, по крайней мере до сих пор, нам удалось значительно продвинуться в ней.
Упражнения
(а	Ь\	[Л	В \
1.	Даны отражения AL=|	I и Л1\ = (	л , где
\Ь — а/ “ \В — А /
а2 + 62=1 и Д2 + В- = 1. Проверьте, что МХМ2 есть вращение.
2.	Дано, что X = и У = M2Mlt Установите, равны ли X и У. Если не равны, то нельзя ли найти между ними какую-либо простую связь.
3.	Пусть Bi — вращение в том смысле, как определялось в тексте. Найдите вид преобразования

Обобщение
В двумерном пространстве средствами элементарной алгебры нам удалось выразить все возможные виды изометрии относительно начала координат. Ясно, что с переходом в трех-, четырех-, пятимерное пространство или пространство еще большего числа измерений,. сущность рассуждений не изменится, лишь значительно увеличится объем вычислений. Поэтому целесообразно проанализировать наш опыт в геометрии двух измерений и выделить те принципы, которыми следует руководствоваться при решении общей задачи в n-мерном пространстве.
Далее, в двух измерениях вычисления оказались более простыми, чем можно было ожидать. Все условия, которым должны были удовлетворять вращения, выражались квадратными уравнениями (1), (2), (3), (5), (6), (7). Преобразования, найденные в виде уравнений (10) и (11), оказались линейными. Как это получилось?
Первым уравнением, не включающим квадраты, которое характеризовало вращение, было уравнение (4). Левая часть уравнения (3) представляла собой (Д*В*)2 и равнялась (р — с)2 + (q— s)2. Раскрыв скобки, мы обнаружили, что результат, содержит выражение р2 + q2, уже встречавшееся в виде (ОВ*)2, и выражение c24-s2, известное как (ОД*)2. После вычитания этих частей й сокращения на множитель —2 мы пришли к уравнению (4). Такой способ получения уравнения (4) эквивалентен следующему: сложить уравнения (1) и (2), вычесть уравнение (3), полученный результат разделить на 2. Записав уравнения (1), (2) и (3) в виде (ОЛ*)2 = ОД2, (ОВ*)2 = ОВ2 и (Д*В*)2 = ДВ2, проделаем с ними вышеуказанные операции и получим уравнение (4), только в иной геометрической форме:
2 '{000 + (О В*)2 - (А'В*)2} = ±{ОА2 + О В2 - АВ2}.
Уравнение утверждает, что движение не меняет величину l/2(OA2 4- ОВ2 — АВ2). Это утверждение, геометрически более запутанное, чем уравнения (1), (2) и (3), алгебраически оказывается более простым.
а»
Распространим только что рассмотренную схему рассуждения на трехмерное пространство и выясним, что это дает. Пусть мы имеем две точки P(xbf/b2i) и Q(x2, Уъ ^2). Так как при изометрии расстояния между точками остаются неизменными, то величина у {OP2 + OQ2 — PQ2} останется прежней. Как это выражение выглядит в алгебраических терминах? Известно, что
OP2 = x2 + y2 + zl OQ2^x2 + y2 + 4,
PQ2 = (-4 - х,)2 + (//2 -	(<2 -
Следовательно,
4 (Ор2 4. OQ2 — PQ2) = Х|Х2 + IJjlJi + ztz2.
Значит, никакое жесткое движение относительно начала координат не может изменить величины XiX24-+ У№ + 2i22 ни для какой пары точек. «Обращаем» ваше рассуждение: если рассматриваемое движение не меняет величин OP, OQ и xtx2 + у^уг + ZiZ2, то, как следует из последнего уравнения, оно не меняет п величины PQ. Поначалу кажется, что получилось два вида условий: одно алгебраическое, другое геометрическое, включающее длины ОР и OQ. Однако нетрудно убедиться, что- второе условие является частным случаем первого. Действительно, ОР2 — — x'j + у\ + z\. Переписав правую часть в виде XiXi-f-4- У\У\ + 212ь мы обнаруживаем, что это есть не что иное, как XiX2 4- у\У2 + Ziz2, когда точки (xi,z/t,Z|) и (х2, t/г, х2) совпадают. Аналогичное замечание можно сделать и относительно OQ-
В итоге получается, что условие изометрии состоит лишь в том, чтобы величина Х(Х2 4- У1У2 4~ ziz2 оставалась неизменной для всех точек (хь z/t, £i) и (х2,//2, г2) независимо от того, будут они различными или совпадающими.
Скалярное произведение
Выражение XiX2 4- У1У2 4~ ztz2 настолько значительно в математике, что получило специальное название— скалярное произведение векторов Р. и Q.
209
Иногда оно записывается как Р • Q и называется «точечным произведением» *)• Договоримся записывать его как (Р, Q). Скалярное произведение встречается в механике, например как работа силы ОР на пути OQ. Существует один специальный случай, когда геометрический смысл скалярного произведения очевиден. Мы видели выше, что скалярное произведение (Р, Q) возникло из выражения 1/2(ОР2 + OQ2+ PQ2). Теорема Пифагора утверждает, что если треугольник POQ прямоугольный, то это выражение обращается в нуль, то есть (Р, Q) = 0.
Мы будем использовать этот результат как обратную теорему: определять перпендикулярность ОР и OQ через равенство (Р, Q) = 0. Почему это выражение названо «произведением?» По той простой причине, что многие из его свойств, которые легко проверяются с помощью алгебраического определения скалярного произведения, напоминают свойства умножения. Например, (Р, Q) = (Q, Р); (Р, Q + Я) = (Р, Q) + + (Р, Я); (kP, Q) = k(P, Q). Эти свойства позволяют проводить над скалярными произведениями многие привычные алгебраические операции. Например, (А + В, С -f- D) можно раскрыть как (А, С) + (А, £>) 4-+ (В, С) 4- (В, D) или получить формулу разности квадратов (А 4 В, А — В) = (А, А) — (В, В).
Учтем, однако, что эта система не удовлетворяет требованию 6 главы VII. Мы определили скалярное произведение как вполне определенное единственное число, а не как вектор (x,y,z). Поэтому здесь мы имеем дело не с кольцом. В кольце выражение вида ab 4- с имеет смысл, тогда как (Р, ф)4-Я не имеет смысла, ибо означает прибавление к числу вектора.
Изменение осей
Скалярным произведением удобно пользоваться при переходе от одной системы взаимно перпендикулярных осей к другой. Пусть даны три взаимно перпендикулярных вектора Р, Q и Я. Мы собираемся использовать их в качестве осей, то есть хотим выра-
*) В русской математической литературе этот термин не употребляется. — Прим. ред.
210
эить некоторый вектор V в виде аР + bQ + cR. Предположим, что векторы Р, Q, R и V выражаются в координатной форме (х, у, z), так что, если потребуется, мы можем подсчитать любое скалярное произведение. Для отыскания, например, числа а достаточно составить скалярное произведение (Р, V). Так как V = аР + bQ + cR, то (Р, V) = (P, аР+ bQ + cR) =
— а(Р, P) + b(P, Q) + c(P, R).
Поскольку Р и Q взаимно перпендикулярны, то (Р, Q)=0, аналогично (Р, R) = 0. Остается (?,]/) = — а (Р, Р), откуда легко находим а.
Чтобы ощутить простоту этого метода, достаточно рассмотреть любой пример. Пусть векторы Р = = (1,1,1), Q = (1,2,—3), R—(—5,4,1) взаимно перпендикулярны (что можно проверить, вычислив их скалярные произведения). Любой вектор трехмерного пространства можно разложить по осям, задаваемым этими векторами. Допустим, мы хотим это сделать с вектором V — (10,4, —8). Тогда (Р, V) = 6; (Р, Р) = = 3 и доказанное выше уравнение (Р, V) = а(Р, Р) принимает вид 6 = За, откуда а = 2. Аналогично можно установить, что (Q, ]/) = b(Q, Q) и R, V = = c(R,R). В нашей задаче это дает уравнения 42=146 и —42 = 42с, позволяющие найти 6 = 3 и с = —1. В результате получаем V = 2Р + 3Q — R. Правильность этого результата можно легко проверить.
Упражнения
1. Разложите вектор V — (7,7,7) по векторам Р =(—2,3,6), Q = (6, —2, 3) и Я = (3, 6, —2).
2. Разложите вектор V == (6, 1, 4) по векторам Р ~ (1, 0, —1), Q= (1,2, 1) и/? = (1,-1, 1).
Движения в трехмерном пространстве
Возвращаясь к способу отыскания изометрии в двумерном пространстве, вспомним, что наше рассуждение распадалось на две части. В первой части исследования нас интересовало лишь то, что происходит с точками А и В, расположенными на осях. Далее
211
О А и ОВ были взаимно перпендикулярны и имели единичную длину. Естественно, изометрия не меняла этих свойств, поэтому ОА* и О В* тоже оказывались единичными и взаимно перпендикулярными векторами. Эти условия выражались равенствами (1), (2), (4) и решения а и б охватывали все случаи их взаимного расположения.
Вторая, заключительная часть исследования не потребовала никаких дополнительных ограничений. Как только мы нашли точки Л* и В*, в которые переходят А и В, мы тем самым определили положение любой другой точки, удовлетворяя одновременно всем условиям задачи. Результирующее преобразование при этом оказалось линейным: при А-+А* и В->В* отображение хА уВ хА* у В* давало требуемую изометрию.
В трех измерениях мы, очевидно, должны были бы начать рассмотрение с точек Л, В, С, где Л = = (1,0,0), В= (0,1,0), С = (0,0,1). Векторы ОЛ, ОВ, ОС также единичные и взаимно перпендикулярные. Алгебраически это выражается условиями (Л, Л) = (В, В) = (С, С) = 1 и (Л, В) = (В, С) = == (Л,С) = 0. Так как изометрия оставляет скалярное произведение неизменным, то точки Л, В, С могут перейти только в точки Л*, В*, С*, для которых (Л*, Л*) = (В*, В*) -= (С*, С*) = 1 и (Л*, В*) —
(В*, С*) = (Л*, С*)=0. А это значит, что ОА*, ОВ*, ОС* должны быть тоже единичными, взаимно перпендикулярными векторами, как раз то, что следует из геометрических соображений.
Предположим, что мы нашли три точки Л*, В*, С*, удовлетворяющие этим условиям. Будет ли линейное преобразование хА 4- уВ 4- zC ~>хЛ* 4- уВ* 4* zC*, определяемое преобразованием Л ->Л*, В->В*, С -> изометрическим? Выше говорилось, что преобразование обязано быть изометрическим, если оно оставляет величину любого скалярного произведения неизменной. Поэтому проследим, что произойдет С (Р, Q), если P=XiA + ytB + ZiC = (xi,yi,zl) и Q = x2A + y2B -j- z2C = (x2, y2, z2). Используя алгеб-раические свойства скалярного произведения, попытаемся найти (Р*, Q*) = (л'1Л* 4-J/iB* 4~ ZiC*, ХгЛ*4" + УчВ* 4- z%C*). После выполнения умножения ска-212
лярное произведение будет содержать девять членов и начинаться с зд(4*, Д*) + Я1#2(Д*, В*) + ... Но теперь мы видим, что нам предстоит нетрудная работа, так как (Д*, Д*) = 1 и (Д*, В*)=0. Фактически шесть членов из девяти обратятся в нуль, а для оставшихся трех членов применяем свойство (Д *, Д*) = (В*, В*) — = (С*, С*) = 1. В результате все выражение упрощается до знакомой суммы произведений XiX2 + У1У2 + + Z1Z2, представляющей собой первоначальное скалярное произведение (Р, Q). Так что линейное преобразование сохраняет фактически все скалярные произведения и, следовательно, является изометрическим. Нетрудно было бы закончить все это доказательством, что изометрия является линейным преобразованием. Однако этим мы заниматься не будем.
Проведенные рассуждения приложимы к пяти и к любому конечному числу измерений. Для пяти измерений у нас бы просто добавилось работы, так как вместо трех векторов Д, В, С пришлось бы взять пять: Д, В, С, О, Е.
Скалярные произведения играют важную роль в теории гильбертова пространства, которая является обобщением евклидовой геометрии для бесконечного числа измерений.
Замечание относительно логики
Следует указать на одну логическую ловушку, которая, возможно, осталась незамеченной в этой главе. Обсудим ее для простоты в терминах двумерного пространства, что не меняет существа дела.
В этой главе точки определялись координатами (х, у) и мы свободно строили рассуждения на основании идеи I и II глав. Мы складывали векторы и умножали их на числа. В этом смысле мы могли говорить об отрезке О А прямой как о совокупности всех точек /Д, где 0 t 1. Поскольку точка А имеет координаты (1,0), то сегмент О А означает все точки с координатами (/,0).
Однако настоящая глава дает нам другой путь определения сегмента ОД. Согласно определению 2, говорящему нам, что понимается под расстоянием, мы
213
могли бы определить сегмент прямой как кратчайший путь из точки О в точку А.
Согласуются ли эти два определения? Геометрический опыт подсказывает нам утвердительный ответ. Однако он требует обсуждения и доказательства. Согласованность обязана формуле, которая используется в определении 2, при других формулах ее могло и не получиться. Например, представим себе листок бумаги в клеточку, на котором координаты точек, как и принято, обозначены буквами х и у. По определению 1 каждая точка задается парой чисел (х, у). Допустим, что на этом листке нанесена карта мира и нам следует определить расстояние между двумя точками на ней, чтобы знать подлинное расстояние между соответствующими пунктами на земной поверхности. Пусть точки L и D на карте представляют Лондон и Дели. Отрезок прямой LD, определяемый выражением (1 — t)L + tD (см. главы I и II), был бы, следовательно, «прямой дорожкой», полученной соединением точек L и D на бумаге по линейке. Но самолет, летящий из Лондона в Дели кратчайшим путем, следовал бы по другому маршруту, который на карте оказался бы кривым. Таким образом, векторный подход и подход, с позиции расстояния, привели бы к различным определениям прямой линии.
Однако если исходить из определения 2, то этого осложнения не возникает. Мы сейчас покажем, что кратчайший путь из О в Л согласуется с определением сегмента прямой, соответствующим векторному подходу.
Проблема отыскания среди всех гладких кривых, соединяющих точки О и Л, именно той, которая имеет наименьшую длину, является очень хорошей математической задачей и решается вариационным исчислением, которое не так широко известно и может вызвать затруднения. Чтобы обойти эту трудность, рассуждаем следующим образом. Если точка Р лежит не на прямом маршруте из О в Л, а точка Q на прямом, то можно ожидать, что сумма расстояний ОР и РА окажется больше, чем ОА, а сумма расстояний OQ и (?Л—равной ОА. На рис. 80 точка О — начало отсчета, алочки Л, Q и Р имеют соответственно координаты (1,0), (/,0) и Полагая, что и используя определение 2, подсчитаем расстояния 214
OA, OQ, QA, OP, PA и найдем, что OQ = t, a QA= = i — t. Поскольку О A = 1, to OQ + QA = OA, что подтверждает нашу догадку, что точка Q действительно лежит на прямом маршруте из О в Л.
Иначе обстоит дело с точкой Р. Поскольку ОР — = УР 4- /г2, то очевидно, что оно больше, чем t, а РА = У(1 — О2 + h2 больше, чем 1—t- (Мы полагаем, как это изображено на рис. 80, что h ф 0.) В результате ОР + РА больше, чем /+(1—Z), то есть больше 1. Это опять согласуется с нашим мнением, что Р не лежит на кратчайшем пути из О в Л,
и подсказывает, что определение прямого пути можно построить на идее расстояния, ибо она приводит нас к тому же самому понятию отрезка прямой, которое мы имели при векторном подходе.
Ясно, что мы не можем ограничиться этим простым частным случаем точек О и Л, а должны доказать результат для любых двух точек. Это составит небольшое, но интересное алгебраическое упражнение, которое можно сформулировать так: требуется доказать, что для двух произвольных точек Н и Я сумма расстояний HP и РК будет больше расстояния. НК, если только Р не задается в форме (1 — t)H tK, 0 t 1. Для простоты доказательства следует воспользоваться тем фактом, что переносы и вращения не меняют расстояний. Сначала покажем, как это делали для ОА, что любая часть оси ОХ — кратчайший путь. Так как кратчайший путь в результате некоторого вращения и последующего за ним переноса с необходимостью перейдет в кратчайший путь, то самое лаконичное определение прямой таково: прямая есть то, что может быть получено из оси ОХ вращениями и параллельными переносами. Легко проверить,, что это согласуется с определениями прямой, использованными в I и II главах.
ГЛАВА X
МЕТРИКА И БАНАХОВЫ ПРОСТРАНСТВА
Математика часто использует в качестве своего инструмента метафору. Какое-нибудь образное выражение повседневной жизни входит в обиход математики, приобретая вполне точный и логичный смысл. Так случилось и с метафорой расстояние. Это понятие проходит через все наше мышление. Мы говорим, что фирма близка к банкротству. Незадачливые генералы часто верят, что их стратегия и тактика близки к наполеоновской. Молва может быть далека от истины. Нас поймут, если мы скажем, что Гендель
Гайдн
Гендель	индийская
музыка
и Гайдн близки друг другу, но далеки от музыки Индии или рок-н-ролла. Было бы интересной задачей из области исследования операций определить, какие именно факты — гармония, ритм и т. д. — заставляют нас чувствовать близость или отдаленность двух музыкантов. Можно было бы составить огромную схему, своего рода геометрическую классификацию естественной группировки всех музыкантов и доказывать простые теоремы типа: Гайдн близок Генделю, Гендель далек от индийской музыки, следовательно, и Гайдн далек от индийской музыки (рис. 81).
Во всех приведенных примерах говорилось о расстояниях между достаточно сложными объектами: состояние дела, способ ведения войны, стиль композитора. Эти объекты можно представить в виде точек,
46
как это показано на рис. 81. В математической теории метрических пространств за каждой точкой пространства может стоять какой-то сложный объект. Точка может обозначать вектор, матрицу, кривую, функцию или операцию (такую, например, как интегрирование). Мы будем искать точные способы определения расстояния, скажем, между двумя матрицами, а также между объектами других классов.
Совокупность объектов, для которых можно дать приемлемое определение расстояния, носит название метрического пространства. Ниже будет дано пояснение тому, что понимать под словом «приемлемое».
Может существовать несколько способов размещения объектов в одной и той же совокупности, и все они могут быть осмыслены. Мы рассматривали расположение музыкантов по стилю их композиции. 1\ коммерсант, возможно, захочет распределить музыкантов в порядке их денежного дохода; тогда они расположатся вдоль прямой, и те, кто зарабатывает больше, соберутся на одном ее конце, а те, кто меньше, — на другом. Кого-то могло бы заинтересовать, как распределяются музыканты географически и расположить их по месту рождения, тогда он воспользовался бы поверхностью глобуса.
Эти три расположения рассматривались бы как различные метрические пространства, несмотря на то что все они фактически сконструированы из одного и того же «материала», а именно музыкантов. Дело в том, что геометрия объектов, расположенных на прямой, отличается от геометрии тех же объектов на глобусе. В математике мы интересуемся главным образом расположением объектов, то есть тем, как они соотносятся друг к другу, оставаясь более или менее безразличными к их индивидуальности. При частых ссылках на такого рода расположения можно было бы ввести сокращенные обозначения. Так, первое расположение могло быть названо S (Л4, с), где S обозначает пространство, о котором мы говорим; М — точки, представляющие музыкантов, и с — расстояние, определяемое в терминах стиля композиции. Второе расположение музыкантов на прямой в зависимости от состояния их финансов могло быть названо S(M,f), третье — как S(M,g), так как в этом случае
217
расстоянию между музыкантами придается географический смысл. Эти три расположения музыкантов соответствуют трем различным целям. Поставленные цели играют основную роль в решении вопроса, как определить расстояние между объекта ми.. В одной и той же совокупности объектов в зависимости от поставленных целей могут использоваться различные определения расстояния. На каждом из графиков а, б, в рис. 82 мы видим по две кривые у — f(x) и у = — g(x). Спрашивается, можно ли кривые каждой пары рассматривать как близкие или нельзя? Является лн у = [(х) хорошей аппроксимацией y — g(x)?

Рис. 82.
В каждом случае при: определенных условиях мы могли бы дать утвердительный ответ. Если за. условие* близости кривых принять площади, заключенные- под ними, то во всех трех случаях мы могли бы считать кривые близкими, так как различие соответствующих им площадей оказалось бы незначительным. Однако может случиться так, что мы захотим составить таблицу (например, таблицу значений функций в определенных точках), в которой мы. гарантировали бы, что каждое значение имеет ошибку, не превосходящую заданного малого числа.
Для случая а. в таблице нашлось бы пусть изолированное, но достаточно большое отклонение, и мы не могли бы считать кривые близкими» тогда как в случаях б и в они бы еще оставались таковыми. При других условиях, наоборот, кривые в случае в уже не могут считаться близкими, так. как в их поведении имеется значительное отличие; Так, в исследованиях, связанных с колебаниями или длиной кривой, мы бы рассматривали эти кривые как сильно различающиеся. Могут встретиться ситуации, в которых две гладкие кривые определяются как близкие» если они согла
218
суются как по расположению, так и-по направлению. По этому признаку кривые в случае б считались бы близкими, а в случае в — нет, так как угол между их касательными, например в точках пересечения, достаточно велик.
Ограничения, накладываемые на расстояние
Не следует думать, что всякую ситуацию можно представить геометрически, с точки зрения расстояния. Например, в жизни вполне возможно, что Браун очень дружен со Смитом и Джоном, которые ненавидят друг друга. Здесь вряд ли можно выразить дружбу через близость в рассматриваемом смысле. Если мы попытаемся это сделать, то придем к противоречию. Действительно, с позиции расстояния утверждение «если Смит близок евеему другу Брауну и Джон тоже .близок Брауну, то Смит близок Джону» вполне справедливо, хотя в жизни это не так. (Между прочим, с самого начала истории человечества такое несоответствие всегда осложняло как личные, так и дипломатические отношения.) Поэтому желательно было бы иметь какие-то признаки, позволяющие видеть, представима та или иная ситуация в терминах расстояния или нет. С этой целью, вероятно, надо проанализировать понятие расстояния: какие свойства мы имеем в виду, когда говорим или думаем в терминах расстояния? В жизненной практике мы обычно; измеряем расстояние в числах, например, расстояние от Л до В равно 3 км. Число, выражающее расстояние, никогда не бывает отрицательным; мы не говорим, что место находится в —5 км. Однако оно может быть нулем, но это особый случай, соответствующий расстоянию места от самого себя. Расстояние между двумя объектами не зависит от направления его измерения: расстояние от Кембриджа до Лондона такое же, как и от Лондона до Кембриджа. Наконец, наше путешествие не станет короче от того, что мы будем осуществлять его по частям. Если мы идем; из А, в.С, а потом из С в В, то мы должны пройти расстояние, по меньшей мере равное расстоянию от А цо В. С другой стороны, если мы прошли последовательно сначала ГО км, а потом еще 4 км, то мы
219
не могли удалиться от исходного пункта более чеЦ на 14 км.
Формально требования для расстояния состоят в следующем:
1.	Для любой пары объектов А и В расстояние от А до В определено. Обозначим его d(A,B).
2.	d(A,B)—действительное, неотрицательное число.
3.	d(A,B) равно 0 тогда и только тогда, когда А и В совпадают.
4.	d(A.B)' =d(B,A).
5.	d(A, С) + d(C. В) ^d(Af В) *)•
Теория расстояния имеет дело со следствиями из этих аксиом. Поскольку аксиомы (или свойства) достаточно просты и число их невелико, то геометрия расстояния нетрудна.
Можно убедиться, что все перечисленные свойства справедливы для расстояния в евклидовой геометрии, стоит только для этого воспользоваться формулой расстояния, данной определением 2 в главе IX. При этом свойства 1—4 проверяются очень просто, немного сложнее проверяется свойство 5.
Ясно, что эти пять свойств содержат значительно меньше информации, чем аксиомы евклидовой геометрии. Они, например, выполняются для расстояний на поверхности земного шара, которая никак не похожа на евклидову плоскость. Эти требования, как выяснилось, выполняются и гусеницей, ползущей по, поверхности статуи или неподвижного велосипеда, и человеком, обследующим лабиринт. В таких случаях расстояние всегда понимается как расстояние вдоль наиболее экономного пути. Неважно, если при этом несколько путей окажутся одинаково экономными (как, например, на Земле пути от Северного полюса к Южному).
Можно построить примеры метрических пространств, определяя расстояние d(AB) как время, ко-
’) Требование 5 называется также «неравенством треугольника», так как в евклидовой геометрии оно имеет тот простой геометрический смысл, что длина одной стороны треугольника ЛВС не превосходит суммы длин двух других сторон. — Прим, ред, 220
торое потребуется для перемещения из А в В. При этом следует особенно внимательно отнестись к условиям, при которых рассматривается ситуация. Так, если рассматривать движение в гору, то, вероятно, для подъема из точки А в точку В потребуется больше времени, чем для спуска из В в Л, и, следовательно, требование 4 уже не будет выполняться. Вряд ли будут выдержаны все требования применительно к уличному движению, где возможны заторы и скорость движения различна. Но при устранении препятствий такого рода можно было бы сконструировать геометрию, приняв, скажем, за ее точки города Великобритании, д за расстояния — время, требуемое для переезда из одного города в другой. Открытие новой автомобильной дороги вызвало бы интересную деформацию этой геометрии.
Метрическое пространство может быть определено посредством хода шахматного короля. Как известно, король может переходить на соседний квадрат в любом направлении. Мы определяем расстояние между двумя квадратами как наименьшее число ходов, которое потребуется королю, чтобы перейти с одного квадрата на другой. Белому королю, как это изображено на рис. 83, нужно сделать 4 хода, чтобы достичь квадрата черной пешки. Следовательно, расстояние между квадратами, на которых стоят король и пешка, равно 4. Обратим внимание, что пешка находится в четырех шагах вправо и в двух шагах вверх от короля и большее из этих двух чисел как раз дает расстояние. Королю нужно преодолеть только четыре квадрата вдоль шахматной доски, ибо оставшиеся два перемещения вверх он может осуществить одновременно, при подходе к пешке на любом из своих четырех ходов.
В этом пространстве шахматного короля круг есть квадрат, поскольку в любом двумерном метрическом пространстве окружность с центром А и радиусом г определяется как совокупность точек Р, находящихся на расстоянии г от точки Л, то есть таких точек, для которых справедливо равенство d[A,P)~r. На рис. 84 черные точки образуют круг, в центре которого находится белый король и радиус которого равен 2.
221
Может показаться удивительным, что только что описанная метрика шахматного короля имеет какой-то математический смысл. Однако она непосредственно подводит к одному из метрических пространств, кото* рое довольно часто используется в математике и способно к широкому обобщению. Если мы вообразим
себе шахматную доску, разделенную не на шестьдесят четыре квадрата, а, скажем, на миллион квадратов, то мы еще можем определять расстояние числом ходов, необходимых королю. Клетки на доске сейчас расположены так часто, что нам трудно их различать, и доска нам кажется сплошной. Это наводит на мысль приспособить сформулированное выше правило для отыскания расстояний в целом для непрерывной плоскости. Замысел удается осуществить, если перейти к разности соответствующих координат и за расстояние между двумя точками (%ь у\) и (х2,1/2) принять наибольшее из чисел | х2— Xi | и |у2—*/i| 9* В этом пространстве круг опять оказывается квадратом.
Банаховы пространства
. В современных математических работах часто делаются ссылки на банаховы пространства. Нематема-тик или математик с традиционной подготовкой могут
!) Символ |-^2 — Xi | в этом определении — это мера расстояния на действительной прямой. Она показывает удаление точки а*2 от точки Xj безразлично к тому, лежит ли х2 слева от Xi или справа. Этот же символ в применении к комплексным числам обозначает модуль или абсолютную величину; это снова мера расстояния [г2 — 211, которая, говорит нам, как далеко отстоит точка ?2 от ТОЧКИ 2ь
222
подумать, не открыл ли Банах какие-то особые новые пространства. Я помню, как все прояснилось для меня, когда, услышав о банаховых пространствах, я просмотрел его оригинальную работу1). Свою работу Банах начинает с рассмотрения десятка ситуаций из традиционной математики (математического анализа) и показывает, что в каждой из них фактически используется одно и то же рассуждение. Он спрашивает затем: «Почему нужно повторять одно и то же доказательство в каждой из десяти книг, описывающих эти ситуации? Почему не дать его в одной книге, а в девяти других ограничиться ссылкой?» Я приведу здесь его подлинные слова: «Настоящая работа исследует определенные теоремы, справедливые в самых различных областях математики, которые будут охарактеризованы несколько позже. Чтобы избежать доказательства этих теорем в каждой отдельной области, что было бы неоправданной тратой времени, я выбрал путь, который состоит в следующем. В общем виде я рассматриваю множество элементов; для этих множеств я постулирую определенные свойства, из которых вывожу теоремы, и затем доказываю, что для каждой отдельной области математики принятые постулаты справедливы».
Банаховы пространства, следовательно, не есть что-то новое. Все мы имели с ними дело, но, подобно мольеровскому герою, который всю свою жизнь говорил прозой, не подозревали этого. Скептически настроенным читателям, склонным сомневаться, я мог бы привести в качестве простейшего примера банахова пространства прямую линию.
Принцип «никогда-никогда» в математике
Целесообразно подойти к понятию банахова пространства, начав с обсуждения знакомой темы и показав, как, обобщая ее, можно воспроизвести в миниатюре путь рассуждений Банаха.
В классической математике есть много чисел , и функций, которые вполне определены, но которые
*) S. В a n а с h, Snr les operations dans les ensembles abstracts et leur application aux equations integrals, Fundamenta Maihe-matica, 3 (1922), pp. 131—181,
223
мы не в состоянии записать, если от нас этого по-требуют. Число л, например, можно было бы определить в евклидовой геометрии как площадь, заключенную внутри круга радиусом 1. Однако мы будем поставлены в затруднительное положение, если нас попросят назвать точное значение числа я. Мы можем указать сколько угодно приближений этого числа (22/7> 355/1П и др.), какие только могут потребоваться, однако само число мы никогда не представим в виде конечной дроби, ибо оно иррациональное.
В главе VI нам встречался другой пример. Точное значение 72 (14-У 5) невозможно выразить одним числом, хотя последовательность Фибоначчи дает приближения 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ..., из которых оно может быть подсчитано с любой степенью точности.
С таким же фактом мы встречаемся при рассмотрении бесконечных рядов. Так, например, когда число е задается бесконечным рядом 1-ф(1/1!) + + (1/2!) + (1/3!) +..., то это означает, что сумма первых п членов этого ряда дает приближение к е и что это приближение можно сделать как угодно, близким, взяв п достаточно большим.
Таким способом определяются не только числа, но и функции. Бесконечные ряды иногда используются как более подходящий способ вычисления функций, допускающих вполне точное определение в виде аналитического выражения. Так, например, в ряде случаев проще иметь дело не с точным выражением функции 1/(1 — х), а с ее разложением в виде бесконечного ряда: 1 +'Г + х24~ + • • • • Однако большинство функций, используемых в математическом анализе, нельзя задать точно; они определяются только’ как предел, к которому можно приближаться, по которого нельзя достичь. Это касается даже таких хорошо известных функций, как sin х, cos х. Функцию ех можно определить бесконечным рядом или как предел выражения {1 4- (х/п)}п. Функцию sin~j х — бесконечным рядом или интегралом х
J (1 — t2y'12 dt, который в свою очередь определяется о
224
как предел бесконечного процесса. Наконец, задание ряда само по себе уже может определять некоторую функцию. Так, мы могли бы говорить об исследовании функции, определенной рядом х4-х44-4- х9 4- х16 4- х25 4-. • •, где показатели суть квадраты натуральных чисел. Этот ряд появляется в теории эллиптических функций.
Некоторые математики и философы-математики придерживаются той крайней точки зрения, что в математике нельзя пользоваться числами, подобными числу л, так как их определения предполагают бесконечный процесс, который невозможно воспроизвести полностью. Но какой бы ни была логика этой позиции, подавляющее большинство математиков, да и нематематиков тоже, свободно пользуются определениями, включающими бесконечный процесс. Математика была бы очень стеснена запрещением этих определений. Однако примерно с 1760 года стали осознавать, что к использованию бесконечных процессов следует относиться с большей осторожностью. Поспешное допущение, что всякая последовательность определяет число, может привести к разного рода парадоксам. Поясним это примером. Установлено, что ряд 1 + х + х2 + х3 4-... приближает 1/(1—х) лишь при условии, что х лежит между — 1 и 4-1- Некоторые математики XVIII века, верившие, что математические закономерности всегда сами о себе позаботятся, смело ставили в указанный ряд значение х = 3 и строили на этом доказательства, полагая, что — ‘/г выражается рядом 1—3 4-4-9 — 274-81 —... Так, Фурье в своей работе «Аналитическая теория теплоты» (1829), составившей целую эпоху в математике, в разделе 208 строит одно из доказательств на допущении, что ряд 1 —14-+ 1 — 1 4* • • • означает ‘/г-
Великий математик Н. Г. Абель в письме, написанном в 1826 году, назвал такую практику «дьявольской»1). Это нестрогое рассуждение также
') Согласно Остену Оре, в сборнике работ Абеля употреблено более мягкое выражение «действительно фатально». Не берусь утверждать, какой из этих двух вариантов принадлежит Абелю.
*/<7 Зак, 5)
225
критиковал пражский профессор философии и религии Бернард Больцано (1781—1848). Он указывал, что если ряду 1 — 1 4- 1 — 1 4-... приписать значение 3, то посредством различной группировки членов ряда удается доказать, что 3 может быть любым числом. Действительно, записав 3 тремя различными способами, мы получаем разные результаты. Так, когда S = (1 — 1)4-(1 — 1)4-(1 — 1)4-..., то 3 = 0; когда S = 14-(-1 4- 1)4-(-1 + 1) + (-1 + !) + •••. то 3=1, когда 3=1 —(1 — 1 +1 — 1 4* • • •) = 1 — то 3 = ’/г- Ясно, насколько неосновательно строить математические доказательства на процессе, способном доказать, что 0 = 1/2 = 1. Таким образом, мы должны различать ряды хорошего поведения, или сходящиеся ряды, например 1 4-Vz +’А 4-Ve + •• • > и ряды плохого поведения, или расходящиеся ')ряды, такие, как, например, рассмотренный выше ряд 1 — —14-1------(-•••• Существуют еще более тонкие при-
знаки различения рядов очень хорошего поведения (или абсолютно сходящихся), к которым можно применять почти все разумные операции, от рядов сносного поведения (или условно сходящихся), с которыми следует обращаться с некоторой осторожностью. Мы собираемся рассмотреть довольно простой результат, связанный с рядами очень хорошего поведения, известными в XIX веке для действительных и комплексных чисел. Банах показал, что этот результат можно было бы распространить на ситуации более общего вида.
Изображение ряда в виде цепочки
Чтобы развить нашу тему дальше, удобней изображать ряд в виде цепочки, как это представлено на рис. 85 применительно к ряду 1 4- */г + ’А 4-4* */в +  • • • Пусть первое звено цепочки имеет длину 1 м, второе — 4/г м, третье — ‘Л м и т. д. Добавление новых звеньев в цепи увеличивает ее длину, однако как бы много мы их ни брали, мы никогда не
*) Очень доступный исторический очерк расходящихся рядог и способ, которым расходящийся ряд может быть иногда спасен можно найти в гл. XIII книги К. Knopp, Theory and Application of Infinite Series; N. Y., 1948.
226
перейдем за точку Р,° находящуюся в 2 м от начала О, хотя подойти к ней мы можем сколь угодно близко. В этом приближении цепи к точке Р и выражается сходимость ряда.
Сейчас мы затронем вопрос, ответ на который будет дан несколько позже. Допустим в качестве членов ряда я решил взять числа 1, 1/г, V4, Vs, ....
н-----------ж—I—।
Рис. 85.	।	 .	----1-----г--1—I
но предоставляю вам право по выбору ставить между ними знаки «+» или «—». Так, например, вы могли бы записать 1 — */г — *А + Vs + • • • • Спрашивается, можно ли преднамеренным выбором схемы расположения знаков «+» и «—» получить расходящийся ряд?
Оставив пока вопрос открытым, мы перейдем к рассмотрению ряда 1 4- х 4-х2 4- х3 . в пространстве двух измерений. Если в этом ряду положить х — VzG где i—V—1 , то получим ряд комплексных чисел
' Сейчас на координатной плоскости этот ряд изобра-। жается цепочкой, представленной на рис. 86. Це-Л почка спиралеобразно закручивается и, очевидно, I приближается к точке, соответствующей числу 1/(1—‘/гО- Вполне очевидно, что рис. 85 и 86
.	747*
227
показывают цепочку в двух различных положениях. В каждом случае цепочка приближается к точке, то есть представляет сходящийся ряд. Естественно задать вопрос: можно ли расположить звенья цепи таким образом, чтобы она уже не представляла сходящийся ряд? Другими словами, удастся ли вам, закрепив цепь в точке О, путем выбора направления звеньев заставить ее беспорядочно петлять, не приближаясь при этом ни к какой точке?
До того как вы сделаете какой-либо выбор, в состоянии ли я предсказать маршрут вашего курса или вы можете зайти куда угодно? Нетрудно догадаться, что возможности вашего продвижения ограничены. Ведь сколько бы. звеньев вы ни использовали, их общая длина никогда не достигнет 2 м! Значит, вам предопределено никогда не выйти из круга / (рис. 87) с центром О и радиусом, равным 2. Если первому звену вы решили придать положение ОА, то я могу уточнить предсказание вашего маршрута: цепь, оставшаяся в вашем распоряжении, не может увести вас от точки А на расстояние, большее 1. Сейчас вы заключены в круге II с центром А и радиусом, равным 1. Если вы выберете для второго звена положение АВ, «ваша тюрьма» отступит в круг /// с центром В и радиусом, равным У2, и так
228
без конца. Каждое принятое вами решение сокращает вдвое радиус круга, в котором лежат ваши последующие перемещения. ТакиАм образом, стены вашей тюрьмы непрерывно сближаются, как бы втискивая вас в окрестность некоторой точки. Эта точка находится под вашим контролем: вы можете так распорядиться, чтобы цепочка приближалась к любой точке внутри круга / или на его окружности. Но чего вы не можете, так это спастись от заключения, вечно где-то блуждая.
Это рассуждение, проведенное для конкретного ряда, полностью приложимо и к другим цепочкам. Существенным здесь является то, что при выборе сколь угодно большого числа звеньев длина цепи не может превзойти фиксированное число (радиус круга /). И всякий раз, когда длина цепи ограничена таким образом, цепь вынуждена приближаться к некоторой точке, В теории комплексных чисел этот результат появляется в форме теоремы, которая на первый взгляд может показаться тавтологией: если ряд абсолютно сходится, то он сходится. Однако эта теорема не столь бессмысленна. Слово «сходится» в теореме означает приближение цепи к некоторой точке, тогда как слова «абсолютно сходится» означают, что при любом как угодно большом числе звеньев длина цепи приближается к некоторому фиксированному, конечному числу. Весьма полезно знать, что второе обеспечивает первое, это и утверждает теорема. Что касается длины цепи, то она дается рядом чисел, в то время как отклонения цепи даются рядом векторов. На основании этой теоремы можно было бы придумать небольшой вопрос на сообразительность, задав сложный способ выбора направлений звеньев цепи. Например, можно было бы взять только что использованную цепь со звеньями L V2, Уъ Чз и т. д. и расположить их так, чтобы первое звено образовывало с осью х угол в 1°, второе — 4°, третье — 9°, /г-е— угол в п2 градусов. Учащийся должен решить, дает ли такое расположение звеньев сходящийся ряд векторов, то есть будет ли цепь приближаться к точке. Возможно, чтобы ответить на вопрос, учащийся попытается рассчитать положение л-го звена, чего делать как раз не следует. Надо
8 Зак. 51
229
лишь сослаться на вышеупомянутую теорему. Так как длина цеп» дается сходящимся рядом 1 + */г +; 4-*/4 + .то цепь будет приближаться к некоторой точке.
На плоском чертеже любое комплексное число изображается вектором z. Длина вектора записывается как |г| и называется его модулем или абсолютной величиной.
Сама цепочка, представленная на рис. 86, соответствует ряду комплексных чисел (или векторов), записанному в общем виде как
S — Z{ -J- z2 + z3 + ... .
Длина цепи дается рядом вещественных чисел
2^ —I Zj | +1 Zgl-f-1 г3| + ... .
Теорема утверждает, что из сходимости ряда L следует сходимость ряда S.
Обобщение результата
Полученный результат весьма полезен и допускает обобщения на пространство большего числа измерений. Если бы нам дали ту же цепь, что и в предыдущем примере, с началом, скажем, в центре большой комнаты и разрешили бы располагать звенья в этой комнате (а не в плоскости) любым способом, то мы бы опять обнаружили приближение цепи к некоторой точке. Рассуждения оставались бы такими же с одной лишь разницей, что вместо кругов I, 11 и 111 (рис. 87) мы говорили бы о шарах /, II, III. Без особого труда мы могли бы распространить результат и на пространство с большим числом измерений.
Чтобы использовать рассматриваемую теорему для возможно широкого круга приложений, остановимся на тех свойствах, которые используются при ее доказательстве. Ряд S == Zt 4- z2 + z3 + ... включает знак сложения, значит, операция сложения осмыслена, а это предполагает; что рассматриваемое пространство векторное. Далее, ряд L состоит из длин звеньев цепи. Поскольку длина звена опреде-230
ляется как расстояние между его концами, то мы тем самым допустили, что расстояние в этом пространстве определено, и пространство, следовательно, является метрическим.
К рассматриваемому пространству предъявляется еще одно, третье требование, которое не столь очевидно. Представим себе человека, назовем его Некто, знакомого с комплексными числами, но не знающего чисел иррациональных. Для него комплексная плоскость состоит из всех чисел вида х + iy. где х и у — исключительно рациональные числа. Поскольку цепочку можно расположить так, что она будет приближаться к любой интересующей нас точке внутри круга /, то выберем в качестве такой точки точку (1 4- [)/ |/2~, о существовании которой Некто не подозревает. С другой стороны, чтобы Некто признал цепочку, сходящуюся к выбранной точке, мы опишем ее только рациональными числами. В результате Некто может указать, как это только что делали мы, систему стягивающихся кругов /, //, III. .... Но так как он не знает точки (1-Н’)/У2, то несмотря на то, что круги ему кажутся стягивающимися и вполне удовлетворительно «нацеливаются» на определенное место плоскости, по его мнению, они ничего не захватывают, как вынутая из воды пустая рыболовная сеть. Неудовлетворительность этой ситуации и привела нас к понятию иррациональных чисел.
Если плоскость рассматривать как пространство, состоящее из точек с действительными координатами х и у. то можно быть уверенным, что система стягивающихся кругов обязательно «поймает» какую-то точку. Такое пространство называется полным. В противоположность ему пространство, в котором система вложенных друг в друга стягивающихся кругов не всегда захватывает точку, называется неполным.
Выходит, что рассматриваемое пространство должно удовлетворять трем требованиям: первое — быть векторным пространством, второе — метрическим и третье — полным. Пространство, отвечающее всем этим требованиям, называется банаховым. Позже мы сформулируем аксиомы банахова Пространства, а пока
8*
231
попытаемся проследить ход наших мыслей в направлении осмысливания по возможности разнообразных ситуаций, в которых мы надеемся доказать теорему об абсолютной сходимости, обеспечивающей просто сходимость.
Остановимся сначала на том, как мы предполагаем обобщить идею круга или шара. С этой целью полезно ввести немного новой терминологии. В традиционной геометрии слово «круг» часто используется в двух смыслах. Иногда оно относится к точкам, отстоящим на расстоянии г от центра О, и только к ним. В этом случае «кругом» мы называем геометрическое место точек и отождествляем его с окружностью. Когда же мы говорим о «площади круга», под словом «круг» мы понимаем вышеупомянутую кривую вместе с заключенной внутри нее областью. Чтобы быстро и точно описать любой из этих образов, были введены три следующих определения,^ имеющие смысл в любом метрическом пространстве, то есть в любой системе, где определено расстояние: сфера, открытый шар, замкнутый шар. Под сферой с центром А и радиусом г понимаются все точки Р, находящиеся от точки Л на расстоянии г, то есть точки, для которых выполнено условие d(A,P) — г. Открытый шар с центром А и радиусом г состоит из всех точек, находящихся внутри этой сферы, то есть всех точек, для которых d(A,P) <z г. Замкнутый шар состоит из всех точек, которые расположены либо на сфере, либо внутри нее, то есть всех точек, для которых d(A,P)^Zr. Сфера служит как бы оболочкой замкнутого шара; если эта оболочка сползет (как со старого крикетного мяча), то остается открытый шар.
Заметим, что в двумерном пространстве «сфера» означает окружность, а в одномерном — пару точек. Эти замечания могут показаться излишними, однако они необходимы, если мы хотим иметь единую терминологию для любого числа измерений, конечного или бесконечного.
В приведенном нами рассуждении с кругами //, III, ... результат следовало бы сформулировать в терминах замкнутых шаров. Рассмотрим в качестве простейшего примера ряд 1 4-V2 + 7з + V*+ ••• >
232
изображенный на рис. 88. Все круги I, II, III, ... касаются друг друга в точке Р, представляющей число 2, и точка Р принадлежит всем замкнутым шарам вашей системы. Однако не найдется ни одной точки,
принадлежащей всем открытым шарам нашей системы, ибо нет ни одной точки, которая бы попадала внутрь всех рассматриваемых кругов.
Интегральное уравнение
В связи с тем что в заглавии работы Банаха упоминаются «приложения к интегральным уравнениям», рассмотрим простейшее интегральное уравнение. Если мы проинтегрируем функцию ех в пределах от 0 до х, то получим выражение ех — 1. Мы будем писать просто f для ех и просто j для операции интегрирования в указанных пределах. Мы получаем уравнение
// = /-!> (1)
характеризующее функцию ех. Поскольку никакая другая функция, отличная от ех, не удовлетворяет Уравнению (1), то функцию ех можно было бы ввести учащимся как решение этого уравнения. Может,
233
это и неделесообразно,, но математически вполне законно. Что вы думаете о реакции класса, если осуществить это следующим образом.
Сначала заданное уравнение (1) переписать в форме
l=f-р.	(2)
это вряд ли вызовет возражения. Далее, от формы (2) перейти к форме (3)

(3)
При возможных здесь возражениях можно было бы сослаться на то, что уравнение (3) лишь лингвистическое изменение уравнения (2), ибо употребление в нем символов не противоречит уравнению (2). Затем, разделив обе части уравнения на (1 — Jj, записать его в виде
Ц--1	(4)
и выразить стоящую в правой части дробь как сумму членов бесконечно убывающей геометрической прогрессии со знаменателем J:
Н‘+Ж1+Ш+--)-1-	<5>
После чего выполнить указанное интегрирование. Интегрируя 1 от 0 до х, получим х. Применяя one1-рацию второй раз, получим х2/2. Третье применение дает х3/6. Следовательно,
у2	v3
f=l+x + v+ir+----	<6>
Нетрудно проверить, что общий член ряда (6) является общим членом ряда для функции ех. Таким образом, использованный прием имеет хотя бы ту заслугу, что приводит к правильному ответу.
Я проводил эти вычисления на многих встречах со старшеклассниками, и они неизменно встречали
234
их смехом. Между тем самое смешное состоит здесь в том, что эти вычисления совершенно строги и представляют собой стандартный процесс решения интегральных уравнений. Однако, чтобы не создалось впечатления, что в математике все дозволено, поспешу добавить, что решение можно признать строгим лишь в случае, если оно сопровождается ссылками на известные утверждения, оправдывающие каждый предпринятый шаг. Проведенное решение опирается фактически на три утверждения, истинность которых надо доказать: 1) что ряд (6) сходится, то есть что-то собой представляет, 2) что это «что-то» есть решение уравнения (1) и 3) что другого решения нет.
Сходимость ряда (6) можно доказать для сколь угодно больших значений х. Мы будем более умеренными в своих желаниях и ограничимся промежутком значений 0 х ’/2, ибо в этом случае мы можем опереться на знакомую нам геометрическую прогрессию 1 + */г + ’А + • • • и провести доказательство рассмотренным ранее методом. Напомним, что этот ряд был представлен в виде цепочки, звенья которой имели длину, равную членам этой геометрической прогрессии.
Составленная цепь будет лежать в пространстве, полученном следующим образом. Вообразим, что у нас есть очень большой запас ярлыков, на каждом из которых изображен график (или другое обозначение) какой-либо функции, непрерывной для значений х в промежутке от 0 до ‘/г. Вообразим далее, что имеется огромное пространство, в котором каким-то упорядоченным образом расположены эти графики. Поскольку, как было выяснено в главе VII, непрерывные функции образуют векторное пространство, то это должно найти отражение в расположении графиков. Остается теперь решить, что мы будем понимать под расстоянием между графиками, раз мы собираемся говорить о длине звеньев в цепи. Прежде всего условимся считать два графика близкими, если они представляют почти одну и ту же функцию, и далекими, если представленные ими функции значительно отличаются. На рис. 89 даны два графика у — f(x) и у = — g(x) и стрелкой показано наибольшее удаление графиков. Эта наибольшая разница меж:ду
235
соответствующими ординатами графиков, показанная на рисунке стрелкой, и принимается за расстояние между функциями f(x) и g(x), которое коротко записывается как d(f,g).
Нетрудно убедиться, что принятое определение расстояния между функциями удовлетворяет всем пяти требованиям расстояния, перечисленным выше. Действительно, d(f,g) определяется как вещественное неотрицательное число. В случае если d(f,g)=O, наибольшее расстояние между графиками равно О,
так что они совпадают, и, следовательно, выполняется требование 3. Столь же очевидно и требование 4. Проверка требования 5 показана на рис. 90. Она сводится к тому, чтобы доказать, что d(f,g) + d(g,h) не меньше d(f, h). Далее, d(f, h) — это длина отрезка PR, который можно разбить на PQ и QR. PQ не может превзойти DE, равное максимальному расстоянию между fug, аналогично QR не может превзойти ST, получается, что PQ + QR DE + ST. Но DE = d(f, g) и ST = d(g, /г), значит, d(f, g) -j- d(g, h) ^d(f, h), и требование 5 выполнено. Это доказательство нуждается еще в некоторой оговорке в связи с тем, что оно проведено для простейшего случая расположения графиков. Однако и при другом расположении графиков доказательство не вызывает больших затруднений.
Итак, наше пространство функций отвечает двум условиям банахова пространства: оно является век-236
торным пространством и в нем определено расстояние. Остается только показать, что это пространство полное, то есть что стягивающиеся сферы будут захватывать график какой-то непрерывной функции. Это тоже можно доказать, не прибегая к современной математике, а обходясь методами классического математического анализа, которыми пользовались математики XIX века. Банах показал, что в любом пространстве, удовлетворяющем трем вышеназванным условиям, сходимость цепи гарантируется, если мы знаем, что общая длина цепи ограничена. Поэтому нам нужно сейчас установить длину цепи, соответствующей ряду, входящему в уравнения (5) и (6).
Длина звена
Как уже говорилось, в случае комплексных чисел длина цепи (стр. 230) определялась рядом L — — |г11 + |z2| + |гз| + ;.., члены которого представляют длины отдельных звеньев цепи. Для комплексных чисел |.?i | измеряет расстояние от точки zi до на-
чала 0. В случае с функциями это подсказывает отождествить длину звена fi с расстоянием функции Л до нуль-функции, то есть d(fh 0). Под нуль-функцией мы понимаем функцию с графиком у = 0, так как-то нулевой вектор (см. сгр. 177). Выявляя и дальше аналогию с |zj, обозначим длину звена /ч через II fill. Все принятое для функции fi, естественно, распространяется и на функции f2, /з и т. д.
Для любой непрерывной функции, следовательно, под || f И мы понимаем d(f, 0), что и отражено на
237
рис. 91. Длина стрелки показывает наибольшее удаление графиков функций f(x) и нуль-функции друг от друга.
На алгебраическом языке ||f(x)|| определяется как максимальное значение |f(x)|. Знак абсолютной величины | | приходится здесь использовать потому, что f(x) может принимать как положительные, так и отрицательные значения. Мы интересуемся наибольшим расстоянием f(x) от 0, не заботясь о том, случится ли это над прямой у = 0 или под ней.
К величине || f II мы будем относиться как к размеру функции, введя тем самым новое понятие, не встречающееся в традиционном математическом анализе.
Влияние интегрирования
Уравнения (5) и (6) содержат ряд, в котором каждый член образован интегрированием предшествующего члена. Выясним, сказывается ли как-нибудь интегрирование на размере функций? Предположим, что у нас есть некоторая непрерывная функция <р(х), у
которой || <р || = М. Это значит, как показано на рис. 92, что на рассматриваемом интервале числовое значение <р (х) достигает числа М, но не превосходит его. (На рис. 92 для большей наглядности представлен простейший случай функции <р(х), которая всюду положительна. Без особого труда можно показать, что получающиеся при этом результаты одинаково хорошо проходят и в общем случае.) Далее, через ф обозна
238
чим. j <р — функцию, полученную интегрированием функции <р на промежутке от 0 до х. Мы хотим оценить || ф II, то есть размер ф(х), заданный максимальным значением |ф(х) |. Поскольку функция ф(х) выражается интегралом, то ее можно представить как площадь под графиком ф(х) в промежутке от 0 до х. На рис. 92 эта площадь заштрихована и полностью находится внутри прямоугольника с основанием 1/2 и высотой М. В результате ф(х) не может превзойти ‘/г Л4, а следовательно, и ||ф||, согласно определению, тоже не может превзойти ‘/2 М. Другими словами, размер функции ф(х) не превосходит половины размера функции ф(х), интегрированием которой она получена. Выходит, что интегрирование по крайней мере вдвое уменьшает размер функции. Оно даже может уменьшить его еще больше, что обычно и происходит.
Упражнение
Подсчитайте размеры членов ряда (6) (см. стр. 234). Найдите отношение каждого члена к предшествующему и проверьте, что это отношение, за одним лишь исключением, меньше Уг*
Полученный результат относительно интегрирования создает благоприятную ситуацию. Ряды в уравнениях (5) и (6) соответствуют цепи, в которой каждое звено есть половина от предшествующего звена или меньше ее. Иначе говоря, ряд, образованный длинами этих звеньев, сравним с геометрической прогрессией, имеющей знаменателем ’/г- Правда, многие звенья мы, возможно, и искажаем, но все равно длина цепи никогда не может превзойти удвоенной длины первого звена. Мы, следовательно, можем здесь применить нашу идею «сужающейся тюрьмы», то есть найти последовательность вложенных шаров, стягивающихся в точку, к которой приближается цепь. Таким образом мы убеждаемся, что ряды (5) и (6) сходятся.
При формальном изложении это доказательство не может считаться полным. Нам следовало бы показать, например, что непрерывная функция, к которой сходится ряд, есть решение уравнения (1) на стр. 233. Однако мы не собираемся заполнять этот пробел, ибо наша цель показать основную идею, силу и красоту
239
аналогии, на которую Банах обращает наше .внимание.
Как уже упоминалось в начале главы, в зависимости от цели исследования возможны различные разумные способы определения расстояния между двумя функциями. Использованное нами определение расстояния иногда называется равномерной метрикой. Оно тесно связано с немного затруднительным понятием математического анализа — равномерной сходимостью. Когда мы говорим, что цепочка fi+f2+fs+ • • • приближается к точке S (под этим мы понимаем, что расстояние конца цепи от точки стремится обратиться в пуль), классический анализ должен сказать в этом случае, что ряд /1(х) +/2(*) + /з(*) + • •. сходится равномерно к функции f (x). Намеченный выше геометрический подход к равномерной сходимости является одним из наиболее простых для обучения и широко используется вместо традиционного старого подхода.
Использованное нами пространство, в котором каждая точка представляет непрерывную функцию, иногда обозначают символом ^(7), который показывает, что мы имеем дело с непрерывными функциями на интервале 7 (знак & соответствует непрерывности). В нашем случае интервалом 7 был интервал (О, V2)‘
Ряды преобразований
Около двух веков назад, когда было обнаружено, что все элементарные свойства тригонометрических функций являются алгебраическими свойствами е20, тригонометрия стала рассматриваться как составная часть алгебры. Если в выражении eiQ положить 0=1, то оно упрощается до е\ в котором i интерпретируется как «поворот на прямой угол». Таким образом, уже в математике 1750-х годов мы встречаем это замечательное указание: «возвысить е в степень i значит осуществить поворот на прямой угол». Поскольку «поворот на прямой угол» относится к типу линейных преобразований, рассмотренных в главе III, то появляется возможность осмыслить ет, где Т стоит вместо преобразования или, если хотите, вместо матрицы, представляющей это преобразование. Так как ех про-240
ще всего задать в виде ряда, то нам предстоит иссле* довать на предмет сходимости или расходимости ряд, включающий степени преобразования. Наша теорема о сходимости цепи здесь будет очень кстати, однако, чтобы ею воспользоваться, мы должны найти удовлетворительные определения расстояния от преобразования А до преобразования В и размера преобразования Г, то есть определить d(A,B) и |j Т ||.
Прежде всего будем рассматривать вращения как частный пример преобразований. Правильно будет сказать, что вращение на 10° достаточно близко к вращению на 11°, но далеко от вращения па 60°. Вращение, как и всякое преобразование, воздействует на точки плоскости. В связи с этим мы будем называть такие два вращения А и В близкими, если результаты их воздействия на точки плоскости почти одинаковы. Предположим далее, что вращения А и В переводят некоторую точку Р соответственно в точки Q и R. На первый взгляд может показаться, что близость точек Q и R будет означать близость вращений А и В. Однако здесь играет роль выбор точки Р. Поясним это примером. Полагая, что Л и В суть вращения на 10 и 11°, возьмем точку Р в 1 млн. км от начала О. Тогда точки Q и R будут разделять 16000 км, что достаточно велико в обычном представлении, но достаточно мало в сравнении с 1 млн. км. В этом случае мы бы сказали так: результат воздействия операций Л и В считается почти одинаковым, если расстояние QR мало в сравнении с расстоянием ОР, то есть отношение QRIOP выступило бы в качестве меры разницы результатов воздействия операций Л и В на точку Р. Есть и другой подход: потребовать, чтобы расстояние ОР не превосходило единицу. Тогда расстояние QP может оказаться большим только за счет слишком разного воздействия операций на точку, а не из-за того, что Р находится очень далеко от начала О.
Воспользовавшись вторым подходом, найдем критерий отличия двух линейных преобразований. Пусть v означает вектор ОР, длина которого не должна превосходить 1. Точки Q и R даются векторами Av и Вс», расстояние QR — длиной вектора Bv—Av, Мы выбираем вектор v (при соблюдении ограничения на его длину) так, чтобы длина Bv—Av была по
241
возможности самой большой. Эту максимальную длину Bv— Ли мы и определим как расстояние между Ли В, то есть как d(A,B). Такое определение дает нам весьма эффективную меру сходства между операциями Л и В. Допустим, например, что для двух определенных операций Л и В мы установили d(Л, В) =0,001. Это значит, что применение Л и В к некоторому вектору v длиной 1 см удалило бы результирующие точки Av и Bv самое большее на 0,001 см. Если теперь допустить, что операция Л была задана сложной формулой, а операция В — простой и ошибкой в 0,001 в решаемой задаче можно пренебречь, то без ущерба для нашей задачи мы смогли бы сложную операцию Л заменить более простой операцией В.
Итак, определив расстояние (/(Л, В), мы в состоянии теперь определить размер преобразования А. В разделе «Длина звена» за размер комплексного числа было принято его расстояние от комплексного числа 0, за размер функции f — ее расстояние до нулевой функции. Естественно поэтому принять за размер преобразования Л его расстояние до преобразования О, то есть ||Л|| определить как й(Л,О) *). Заменив В в определении d(A,B) на нуль, мы получим, что || Л || означает максимальную длину, которую может иметь вектор Л при условии, что длина вектора v не превосходит 1.
Сказанное выше легко представить наглядно. Поскольку длина вектора v не превосходит 1, то v представляет точку внутри или на окружности единичного круга х2 + у2— 1. Преобразование Л каждый вектор v переводит в вектор Av. Если теперь все точки Av нанести на бумагу в клеточку, то они будут заполнять некоторую область, в действительности ограниченную эллипсом.
На рис. 93 показаны единичный круг и эллипс, в который переходит круг в результате преобразования Л, определяемого уравнениями х* = х + 2у, у* = = —2х + 2у. На эллипсе точки D* и Я* более всего удалены от начала О. Их расстояние до точки О равно 3 единицам.
’) В математической литературе число ||Л|| называют нормой преобразования Л, — Прим. ред.
242
Таким образом, если длина вектора v меньше или равна 1, то длина вектора Av меньше или равна 3; то есть операция А никогда не растягивает вектор более чем в 3 раза. Для этой операции Ц А |[ — 3.
Рис. 93 позволяет не только представить наглядно смысл размера преобразования, || А но и помогает увидеть, что собой представляет расстояние между двумя операциями А и В. Что касается d(A,B), то оно есть то же самое, что и размер разности двух
операций А и В. Действительно, сЦА,В) есть максимальная длина вектора Bv — Ло при условии, что длина вектора v не превосходит 1. Ви—Av можно записать как (S— Л)о. Но за максимальное значение {В—А) и принимается ||Д — А ||, размер разности В — А, значит, d(A,B) есть то же самое, что и размер разности В — А.
Например, мы хотим знать расстояние между ма-/ О —П /I 1Л
трицами I j ____j I и I__j г. Разность между
1 2\
п „I, проиллюстрированная £ £ /
на рис. 93. Как мы видели, ее размер 3. Следователь-но, расстояние между- матрицами равно 3<
ними есть матрица
243
Число || А || можно рассматривать как наибольшее увеличение длины любого вектора, осуществляемое операцией А. Если || А || = а и (| В || = Ь, то можно убедиться, что || АВ || не может превзойти ab. Каждая из операций А и В дает увеличение соответственно в а и Ь раз; операция В, сопровождаемая операцией 4, не может вызвать увеличение более чем в ab раз. Обычно она бывает меньше, потому что выбранный вектор лишь при первой операции получает максимальное увеличение, при второй этого уже не происходит. Сказанное верно и в случае, когда А = В, поэтому, как правило, ||42|| меньше, чем || А ||2.
Упражнение
В результате преобразования А : х* = Зу, у* = 2х, для которого ||Л|| = 3, вектор (0, 1) испытывает максимальное увеличение. Проверьте, что А2 = 6/ и, следовательно, ||Л2|| = 6, то есть меньше, чем З2.
Точно так же можно показать, что ||4П|| никогда не превосходит || А || п, а обычно меньше ее.
Этот параграф мы начали с вопроса, законно ли использовать ряд еА, когда в роли показателя А выступает преобразование или матрица. Мы только что отметили, что размер Ап никогда не превосходит а\ где а=||4||. Следовательно, каждый член ряда еА имеет размер, не превосходящий соответствующего члена ряда еа, который сходится для всех а. То есть мы снова имеем дело с цепочкой, состоящей из отрезков ограниченной длины, следовательно, можем воспользоваться нашим прежним рассуждением.
Ряд преобразований мы иллюстрировали вращениями, отображающими плоскость самое на себя. Однако такую же аргументацию можно было бы дать и применительно к другим пространствам. Например, в разделе «Влияние интегрирования» мы показали, что при определенных условиях операция J приводит к функции, размер которой составляет самое большее половину размера первоначальной функции. Это позволяет приписать операции J размер: 111|= */2-
Когда мы имеем дело с преобразованиями в конечномерном пространстве, например в плоскости, то каждое преобразование А имеет размер || А || = а. Мож* 244
но доказать при этом (после заполнения некоторых логических пропусков в нашем рассуждении), что для каждого А ряд еА абсолютно сходится. Обратите внимание, насколько это пояснение проще того проникновения во все детали числовых расчетов, которые имеют место при рассмотрении А2, А3 и т. д., связанных с умножением матриц.
При рассмотрении преобразований в бесконечномерных пространствах требуется соблюдать осторожность, ибо здесь нельзя утверждать, что каждое преобразование А обязательно имеет конечный размер IIЛ ||.
Подведенный выше краткий итог наводит на мысль, что мы располагаем методом рассуждения, имеющим весьма широкую сферу приложения. Так мы могли бы применить его для выражений вида 1Д1 “ /)» е$ или sin | , соблюдая, конечно, требуемую осторожность.
В главе VII мы убедились, что статистики страхового общества вполне законно могли применить биномиальную теорему к выражению вида (1 4-А)п. Сейчас мы приведем другой пример, относящийся к формализму статистики, пример того, как относительно свободно используется бесконечный ряд с символом А. Пусть мы имеем дело с аналитической функцией f(x), и пусть мы располагаем ее значениями, когда х — целое число, то есть мы знаем только f(0), f(l), f(2) и т. д. Мы хотим подсчитать /х(0), наклон функции в точке х = 0. Рассуждение проходит следующим образом. По формуле Тейлора имеем
f(x + a) = f(x) + af^x) + ±a2f"(x) + ...=
= (1+а£> + |й2Р2+ ...)f(x).
Ряд в скобках, для которого записаны только три первых члена, есть ряд для eaD. Следовательно, равенство можно переписать в виде
f (х + а) — eaDf (х).
Положим, что а = I. Слева получаем f(x + 1), которая есть не что иное, как Ef(x) или все равно что
245
(1 ’+ A)f(x). Опуская символ f(x) в каждой части равенства, получим
1 +А = ^.
Взяв логарифмы от обеих частей равенства, придем к новому равенству
D = loge(l+A)-A-4^2 + 4A3----.
представляющему один из стандартных рядов в теории логарифмов, который обычно применяется только к числам. Этот результат призван показать, как посредством операций конечных разностей, включающих только целые числа, можно выполнить дифференцирование.
Проведенное выше рассуждение носит формальный характер, и для изучающих функциональный анализ было бы хорошим упражнением превратить это формальное доказательство в кусок подлинной математики, показав тем самым, какие допущения следует принять, чтобы быть уверенным в правильности результата.
Аксиомы банахова пространства
Пытаясь выше представить себе метрическое пространство преобразований, мы действовали в следующем порядке. Сначала мы ввели || A |f, размер преобразования 4; затем обнаружили, что расстояние d(A,B) между А и В есть то же самое, что и размер' разности В — А. Такому порядку можно следовать не только в интересах наглядности, но и при самом определении расстояний. Мы можем начать с определе1 ния размера (или длины) вектора, затем определить' d(A,B) как длину В — А. Этот порядок наиболее часто используется в работе с банаховыми пространствами. Требования для банахова пространства можно свести к следующему:
1. Система должна быть векторным пространством, то есть удовлетворять всем 10 требованиям, перечисленным в последнем разделе главы VII;
246-
2. Для каждого вектора v его размер, II v ||, определяется так, чтобы выполнялись следующие условия:
и) II v || — действительное неотрицательное число;
б) || v || = 0 тогда и только тогда, когда v = О; в) для любого k || kv || — |fc| • || v (I;
г) || и + v || никогда не превосходит || и || Н~ + II v II.
3. Расстояние между и и v, d(u, v), определяется как || о — и ||.
4. Пространство должно быть полным; «стягивающиеся тюрьмы», или система вложенных замкнутых шаров, обязательно содержит некоторый вектор.
Этот перечень требований, охватывающий все ситуации, играющие важную роль в математике, как упоминалось ранее, был составлен Банахом. В главе IV энциклопедической работы Данфорда и Шварца1) приведен список двадцати шести банаховых пространств, то есть двадцати шести различных вопросов в математике, к каждому из которых приложим список перечисленных требований. Некоторые из этих вопросов принадлежат к довольно сложным разделам математики и будут понятны лишь профессионалам; другие, как, например, приведенные в этой главе, доступны всякому, кто хорошо знает общий курс математики. Банаховы пространства имеют множество приложений, относящихся к самым равным разделам математики. Однако банаховы пространства почти наверняка ничего не дадут тому, кто имеет дело, например, с черчением или расчетами, связанными с резанием металла на куски определенной формы и размера. Но они могли бы заинтересовать студента, изучающего инженерный курс математики, который включает математический анализ, бесконечные ряды, матрицы.
В банаховом пространстве мы имеем многое из евклидовой геометрии: прямые и плоскости, круги и
•4) И. Д а н ф ор д и Д. Ш в а рц, Линейные операторы, ИЛ, 1962.
сферы, параллелограммы и биссектрисы. Однако в нем не все так просто и надежно. Мы не можем себе ясно представить это пространство; мы не уверены, что объекты со столь знакомыми названиями, как прямая, плоскость и прочее, будут вести себя привычным для нас образом. Теория банаховых пространств и ставит целью рассеять эту неопределенность. Из четырех вышеуказанных аксиом путем логических умозаключений в ней доказываются определенные теоремы, на которые можно вполне положиться. Примером может служить теорема, выясняющая вопрос равенства противоположных сторон параллелограмма. Нетрудно показать, как аксиома 3, определяющая расстояние d(u, v), гарантирует утвердительный ответ на этот вопрос. С другой стороны, примерами типа «метрики шахматного короля», когда круги являются параллелограммами, теория предупреждает нас о весьма неожиданных вещах, которые могут встретиться в банаховых пространствах.
Одно метрическое пространство
Как вы помните, к определению расстояния между двумя преобразованиями мы подошли, рассматривая вопрос, какие два вращения можно считать близкими. Если отнестись ко всему этому более внимательно и рассмотреть в качестве движений вращения около начала О и отражения относительно прямых, проходящих через точку О (глава IX), то мы обнаружим, что имеем дело с небольшим, но весьма интересным метрическим пространством.
Допустим, что мы предложили кому-нибудь из учащихся множество ярлыков с символами для обозначения вращений около начала и попросили расположить их в каком-то порядке, который бы выявлял имеющиеся между ними связи. Естественно было бы ожидать, что учащийся расположит их в порядке: «Вращение на 0°», «Вращение на 1°», «Вращение на 2°» и т. д. Пройдя ярлык с символом «Вращение на 359°», возможно, он догадался бы, что вращение па 360° приводит к тому же результату, что и вращение на 0°, и решил соединить два конца последовательности вместе. При этом, вероятно, он разместил бы свои 248
360 ярлыков по.кругу равномерно. Такое расположение, согласно определению расстояния, сформулированному на стр. 242, дало бы нам метрическое пространство вращений при условии, что он выбрал круг радиусом 1. Для краткости вращение на угол а обозначим через М[, а на угол р— через Л42.
Только что описанное расположение ярлыков-символов представлено на рис. 94,6. За расстояние между их положениями принимается длина хорды единичного круга, стягивающая центральный угол р—- а.
Первоначальная плоскость Пространство вращений
Согласно определению расстояний между двумя вращениями, /?г) должно быть максимальным расстоянием между векторами R\V и	в которые, пере-
ходит вектор v, длина которого не превосходит 1. На рис. 94, а показаны точка Н, соответствующая вектору v, и ее новые положения S и К, полученные в результате вращений Rt и /?2- Независимо от выбора точки Н на окружности расстояние SR всегда одно и то же, и геометрически очевидно, что длина на рис. 94, а та же, что и расстояние от Ri до Rz на рис. 94,6.
Теперь перейдем к отражениям. Допустим, что, как показано на рис. 95, имеются два зеркала и Л12, которые образуют с горизонталью углы аир. Снова на окружности выбирается точка //, которая отражениями Л/i и М2 переносится соответственно в точки S и К. При любом положении точки Н на окружности расстояние SR опять остается неизменным и, таким образом, дает требуемое максимальное разделение точек. Предположим далее, что положение точки Н
249
соответствует углу 0, то есть ОН образует с осью ОХ угол 0. Можно показать, что угловое положение точек S и К определяется соответственно величинами (2а —0) и (20 — 0). Разница между ними, следовательно, составит 2(0 — а), центральный угол, стягиваемый хордой SK. В рассматриваемом метрическом пространстве отражения Mi и М2 должны разделяться расстоянием, равным SK. Этого удается достичь, расположив отражения по кругу единичного радиуса
с угловым положением, равным 2а для Mi и 20 для М2. Положение каждого отражения в метрическом пространстве, таким образом, определяется углом, в 2 раза большим угла, образуемого зеркалом (в первоначальной плоскости) с осью ОХ. Обозначения отражений заполнят единичный круг, но только для угла между зеркалом и осью ОХ в границах от 0 до 180°. Зеркало, образующее с ОХ угол 180°, определяет то же самое отражение» что и зеркало, образующее с ОХ угол 0®. Вышеупомянутый множитель удвоения поставлен, чтобы возместить этот «убыток».
Итак, вращения и отражения заполняют круг. Интересно поставить вопрос, что значит расстояние между вращением и отражением? Существует ли для данного вращения какое-то отражение, которое мы можем считать близким к нему? Возможно, уже кто-то и догадался, что ответ на второй вопрос будет отрицательным. Для любого отражения М и вращения /? всегда можно найти такой вектор v, соответствующий точке Н на единичном круге, что Mv и Rv будут 250
лежать на противоположных концах диаметра, и, следовательно, расстояние между ними составит 2 единицы. Поскольку это самое большее расстояние между Mv и Rv из всех возможных, то d(M, R) =2, иными словами любое отражение отстоит от любого вращения на 2 единицы.
Легко сделать модель этого пространства. На рис. 96 непрерывной линией на лицевой стороне бумаги изображена окружность единичного радиуса;
предполагается, что вдоль нее расположены ярлыки, соответствующие вращениям. Пунктирной линией показана вторая окружность тоже единичного радиуса, которая должна быть начерчена на оборотной стороне бумаги. Вдоль нее расположены ярлыки, соответствующие отражениям. С «лицевого круга на оборотный» можно перейти, только воспользовавшись маленьким отверстием в точке О. Следовательно, кратчайший путь от любого вращения до любого отражения помечен «дорожкой» ROM (по радиусу RO через отверстие О и на другую сторону бумаги по радиусу ОМ), которая и составит 2 единицы.
Замечание об обозначении функции
Почти во всех недавно вышедших книгах по математике функция обозначается способом, отличным от традиционного. Чем вызвана потребность в такого
251
рода изменениях? Обратимся к рис, 91, на котором-мы видим график функции, целиком лежащий-над осью. Ох. Как объяснялось ранее, размер такой функции дается максимальным значением f(x). Согласно традиционной терминологии, мы должны были бы сказать: «Размер функции f(x) дается максимальным значением Такое определение кажется бессмысленным: размер чего-то определяется через макси-, мальную величину того же самого. На самом деле дважды встречающийся здесь символ f используется в разных смыслах. В первом случае он используется для задания функции, а во втором — обозначает определенное число. Мы могли бы охарактеризовать функцию с помощью графика, тогда размер функции можно было бы определить как размер графика. Для ситуации на рис. 91 мы могли бы сказать, что «размер графика дается максимальной высотой точки этого графика над осью Ох».
Обе выделенные курсивом части этого предложения в традиционном варианте заменены одним символом f, хотя ясно, что в первом случае он выражает весь график, во втором — высоту одной его точки. -
Наши мысли далеко не всегда соответствуют значению произносимых слов, и всякий, кто воспитан на традиционном обозначении, не смутится при употреблении этого символа в двух различных смыслах. Его внимание концентрируется не на отдельных словах, или используемых символах, а на поставленной задаче в целом. Ему ясна идея, скрывающаяся за предложением, и он вовсе не видит повода для расстройства относительно формы ее выражения.
Можно зайти слишком далеко в желании добиться исключительно точного и последовательного определения. Мне известно, что в США некоторые студенты с трудом усваивали математический анализ только потому, что он преподносился в «современной» форме с пространными начальными обсуждениями функции, области определения, области изменения. С другой стороны, смешение обозначений при традиционном подходе вызывает трудности при изучении математического анализа. Всем известно, как легко учащиеся справляются с построением трафика функции у = 2х 4- 3 и затрудняются в слуцае функции у == 3.
252
Причиной затруднения, возможно, является то, что-в’ -равенстве у = 2х + 3 они узнают способ задания-функции, тогда как равенство у = 3 они воспринимают как число.
Функция заключает в себе своего рода ответно-стимулирующую ситуацию. В случае с функцией у — 2х + 3, если вы назовете для х число 1, я назову для у число 5; вы назовете +2, я отвечу +7 и т. д. При вычерчивании графика у = 3 мы исследуем ситуацию, где для любого названного вами х я всякий раз буду отвечать вам числом 3.
Один из способов условного изображения этого соответствия между х и у состоит в использовании символики для отображений. Так, с выражением у = 2х + 3 мы связываем следующее отображение: 1->5; 2->7 и т. д.; ваш стимул -> мой ответ. Мы должны бы, таким образом, говорить о функции, как об отображении х-+ 2х + 3. При таком подходе в случае с графиком функции у — 3 мы должны были бы попросить ученика проиллюстрировать отображение так: х->3. В качестве жизненного примера здесь можно было бы взять постоянство температуры. Если бы по истечении х минут с начала опыта вы спросили меня о температуре, я бы ответил: «+3°»; при любом х ответ должен быть один и тот же: «3°». В главе III мы имели пример такого тривиального отображения: отображение банкротства v~>0, когда при любом вкладе вы получали всегда одно и то же — «ничего».
При только что описанной системе обозначения нам следовало бы говорить, например, не о функции х2, а об отображении х->х2, не о функции f(x), а об отображении х-> f(x).
Другая система обозначения отправляется от идеи, что функция полностью может быть охарактеризована своим графиком: Идя дальше, можно сказать, что функция есть график. Например, график функции у — х2 состоит из точек (0,0), (1,1), (2,4), (3,9), (Vs, V4) и т. д. В записи всех пар порядок расположения чисел имеет существенное значение. Так, например, пара (9,3) в отличие от пары (3,9) имеет другой смысл, и соответствующая ей точка уже не лежит на графике у = х2, то есть пара (3, 9) есть упорядоченная
253
пара. Совокупность такого рода пар называется «множеством упорядоченных пар» и составляет график функции. Таким образом, функцию с графиком у — х2 можно было бы определить как «множество упорядоченных пар вида (х,х2)». На ранней стадии обучения математике это довольно пышный и бесполезный способ сказать, что функция и ее график — это одно и то же. На более высоком уровне такое определение имеет свою ценность. Например, как упоминалось на стр. 49, функции комплексной переменной вызывали у нас желание изобразить их в виде графиков в четырех измерениях. Сформулированное выше определение позволяет охарактеризовать такой график и вывести его свойства. То есть на этом и более высоких уровнях изучения математики этот способ выражения уже полезен. Если задать вопрос, на каком этапе следует начинать готовить мышление учащихся для такого определения, то, вероятно, мнения учителей в ответе на него разойдутся. Однако в любом случае важно, чтобы ученики понимали, с какой целью составлены эти громоздкие определения, и представляли, на какой ступени изучения математики они могут извлечь из них выгоды.
В главе III мы встречались с различными примерами отображений. Для определенности рассмотрим лист бумаги в клеточку и преобразование Т, представляющее собой отражение относительно оси Ох, которое переводит любой вектор v в вектор v*, где v*—Tv. Поскольку мы установили, что отображение и функция синонимы, то Т одновременно является функцией. Согласно традиционной системе обозначения функции символом f(x), нам следовало бы говорить об отображении Г(у). Но мы этого не делаем. Уже начиная с главы III, мы говорили просто о преобразовании, или ма/рице, Г. Через Tv мы обозначаем не функцию, а точку (или вектор), в которую переходит точка (или вектор) v в результате преобразования Г. Если говорить о Т как о функции, то в данном случае мы имеем дело с простейшей линейной функцией. Однако это никак не влияет на оговоренную систему обозначений, она приложима применительно к любой функции, и это широко практикуется. На графике рис. 91, как вы могли заметить, была 254
надпись «функция f», и там же для размера функции f мы пользовались символом || f ||. Здесь используется одна и та же буква f как для обозначения целого графика, так и для обозначения функции, определяемой этим графиком. Одна и та же буква f используется в обозначении Н'/г), представляющем вполне конкретное число — высоту графика для х=1/2, и в обозначении f(x), тоже представляющем число — высоту графика, соответствующую х. Обратите внимание, как привычное традиционное обозначение f(x) выживает в современном обозначении. Мы все еще говорим о кривой с уравнением у = f(x), что, строго говоря, означает, что кривая состоит из всех точек (х, у), для которых у = f (х).
ОТВЕТЫ К УПРАЖНЕНИЯМ .
Глава 11 (стр. 54)
1. Точка F.
2. В точки G и Л на первом й третьем шагах.
3? В точки D й В на первом и втором шагах.
4.	Нет.
5.	Да. Это точка G.
6.	2с - d - е - 3/ -t- 2g.
7.	Через точки Е и Л на первом и втором шагах.
8.	См. рис. 10.
Глава 111 (стр. 93) /2 1\
1.	I j g)- Равенство справедливо.
/1 2\ /1 3\ /1 п\
2’До 1 /’ к0 1)’ \0 1/'
3. Никакой, они равны.
4. О.
/2 2
6.	В обеих частях о о \ А Л
7.	U2 = I, матрица удовлетворяет уравнению.
/2 1\	/1 1\
8.	I । । I и I j 2/’ ЛВ ВЛ.
/6 4\	/5 4\
9.	W U 4/’ U 51' МатРица (2> Равна> но матрица (1) нет.
. 10. Да.’Ответ тот же, что и на вопрос 6.
11.	О.
256
12.	О.	.	.
13.	£2 — 8Е — 3/, следовательно, k = 3.
14.	Таким уравнением будет F2 -\-71 = 8F.
17 4\ /24-fe	4 \
\6 7/’ \ 6	2-j-k/' ®ыРажения равны
при k = 5.
16.	<7 = 3, k = 1.
17.	Смотри последний раздел главы V.
18.	Матрица С из вопроса 11.
19.	Матрица F из вопроса 14.
20.	G = Р 4- 2Q + 3R 4- S; / = Р 4- S.
21.	Да.
22.	Да.
23.	Да. Четырехмерное.
24.	Линейное пространство девяти измерений.
25.	/.
Глава IV (стр. 106)
1. а) Х* = Х; У* = — Y.
6) X* = 2Х; У* = 4У.
в) X* = 2Х- У* = 0.
2. U; W.
Глава V (стр. 122)
Преобразование вида а* ——а, Ь* = Ь; с* = —с, которое есть вращение на 180° около прямой Ь. Инвариантные подпространства суть плоскость b = 0 и прямая Ь. Каждый вектор на плоскости в результате преобразования меняется на противоположный, X = —1. Каждый вектор на прямой остается без изменений, X = 4-1.
Глава VII (стр. 174)
1.	D2— 1 — х2. Не совпадает.
2.	1.
	/0 0 1\	/121
3.	0 0 0 1, № = О. 1) и 2) ( 0 1 2
	\000/	\0 0 1
Результаты согласуются. Тождественность результатов можно было предвидеть: так, полиномы относительно одной матрицы ведут себе так же, как
257
в элементарной алгебре. По биномиальной теореме: (/ + X)10 = I + 10Х + 45Х2. X3 и все более высокие степени X — нули.
4.	А2 + АВ + ВА + В2, А3 + ААВ + АВА+ВАА+ 4- АВВ + В АВ 4- ВВА + В3, что равно Л34-Л2В4* 4- АВА 4- В А2 4- АВ2 4- В АВ 4- В2А + В3.
5.	Удовлетворяет всем требованиям, кроме 10 и 12. Требование 10 не выполняется, так как уравнение 2х = 2 имеет два решения: 1 и 6, тогда как уравнение 2х — 1 решений не имеет. Требование 12 не выполняется, так как, например, 2-5 = 0, хотя 2 #= 0 и 5 =£ 0. Эта система есть коммутативное кольцо с единичным элементом. Биномиальная теорема выполняется.
6.	Удовлетворяет всем требованиям. Поле. Роль нуля (требование 4) играет 0. Роль I (требование 9) играет 6. Биномиальная теорема выполняется.
7.	Сумма двух нечетных чисел четна, следовательно, сложение внутри этой системы не определенно. Поэтому сразу выбывают требования 1—5, И и 12. Требования 6—9 выполняются. Роль 1 играет 1. Требование 10 не выполняется: уравнение 5х = 5 имеет 5 решений. Уравнение 5х = 1 не имеет решений. В системе не выполнена ни одна из групп требований, обеспечивающая ей какое-либо название, о которых идет речь в главе. Биномиальную теорему даже нельзя сформулировать, так как не определено сложение.
Глава IX (стр. 207)
1.	Вращение с с = аА 4- ЬВ, s — ЬА — аВ, при этом, как и требуется, с2 4- s2 = 1.
2.	X Ф У, но ХУ = УХ = I. Например, ХУ = = М<М2М2М, = MJMt — Mi = I, так как Л41 = I и М, = I.
3.	Отражение.
Глава IX (стр. 211)
1. V = P+Q + R.
2. V = Р 4-2Q 4-ЗЯ.
ОГЛАВЛЕНИЕ
Предисловие редактора перевода Предисловие к русскому изданию		5 9
Введение		13
Глава	I. АРИФМЕТИКА ПРОСТРАНСТВА	25
Глава	II. ГЕОМЕТРИЧЕСКИЙ СЛОВАРЬ	52
Глава	III. ОБ ОТОБРАЖЕНИЯХ И МАТРИЦАХ	75
Глава	IV. СКРЫТАЯ ПРОСТОТА	96
Глава	V. ПОЛЬЗА МЕТОДА УРАВНЕНИЙ	113
Глава	VI. НА ПУТИ К ПРИЛОЖЕНИЯМ	133
Глава	VII. НА ПУТИ К СИСТЕМАТИЧЕСКОЙ КЛАС-	
	СИФИКАЦИИ	159
Глава	VIII. О ЛИНЕЙНОСТИ	179
Глава	IX. ЧТО ТАКОЕ ВРАЩЕНИЕ?	197
Глава	X. МЕТРИКА И БАНАХОВЫ ПРОСТРАНСТВА	216
Ответь;	[ к упражнениям	255
У. У. Сойер
ПУТЬ В СОВРЕМЕННУЮ МАТЕМАТИКУ
Редактор А. Г, Белевцева
Художник Ф. Инфантэ
Художественный редактор Ю. Л. Максимов
Технический редактор Е. Н. Лебедева
Сдано в набор 4/11 1972 г.
Подписано, к печати 14/IV 1972 г.
Бумага тип. № 1 84Х1081/з2==:4,06 бум. л. 13,65 усл.
печ. л. Уч.-изд. л. 11,93. Изд. № 12/6409
Цена 60 коп. Зак. 51
ИЗДАТЕЛЬСТВО <МИР>
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени
Ленинградская типография №2
имени Евгении Соколовой Главполиграфпрома Комитета по печати при Совете Министров
СССР, Измайловский проспект, 29,
ИЗДАТЕЛЬСТВО МИР
60 коп.
Как сделать, чтобы система математического образования давала каждому подрастающему поколению те основы математических знаний, которые позволили бы ему освоить математические достижения своего века?
Как увязать содержание курса математики средней школы с тенденциями в развитии современной математической науки и с запросами практики?
Книга профессора У. У. Сойера представляет собой одну из попыток ответить на эти насущные вопросы.
юлка к
СССР
у
Библиотека бесплатных учебников на сайте:
ussrvopros.ru
(перейти
каталогу