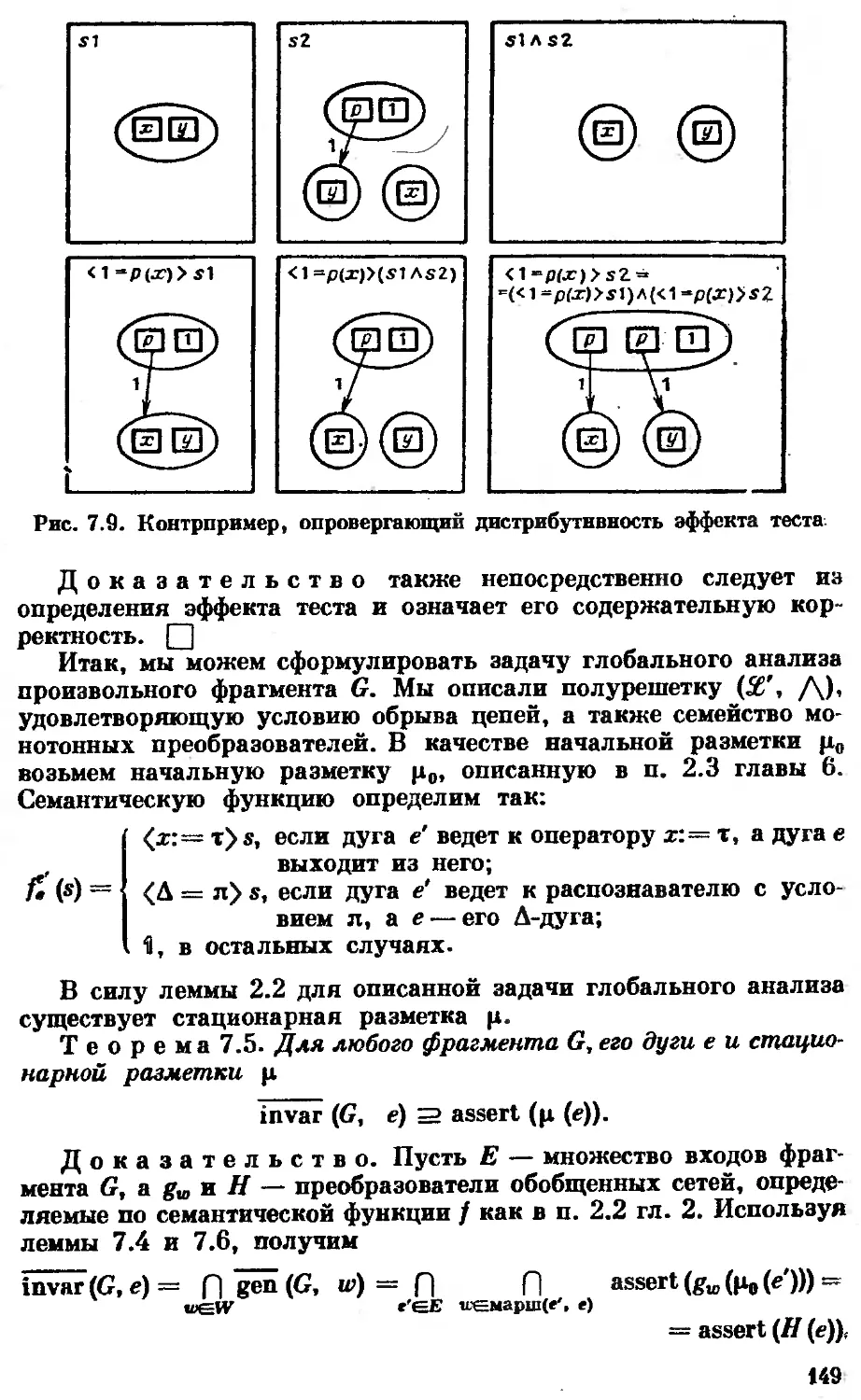
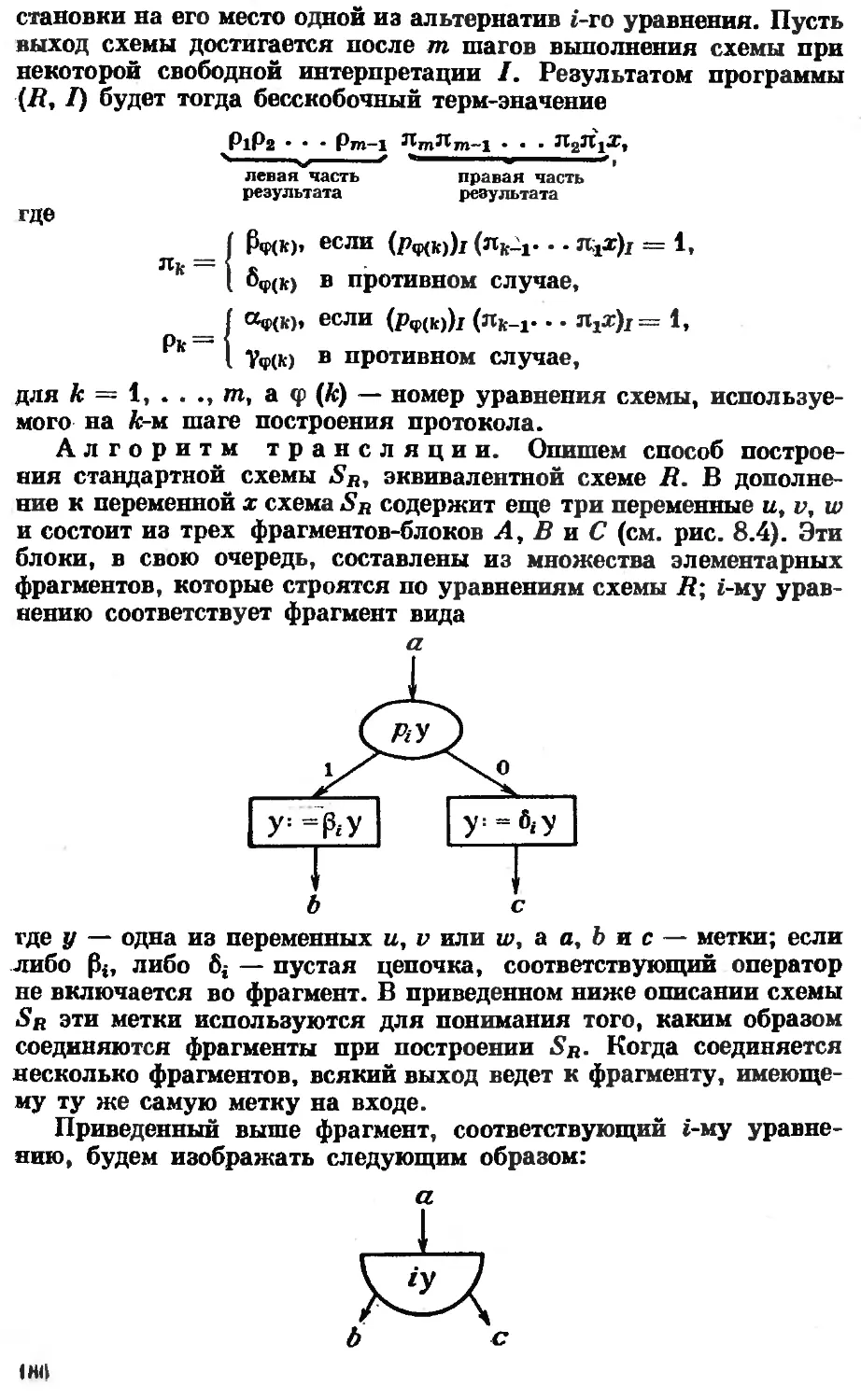
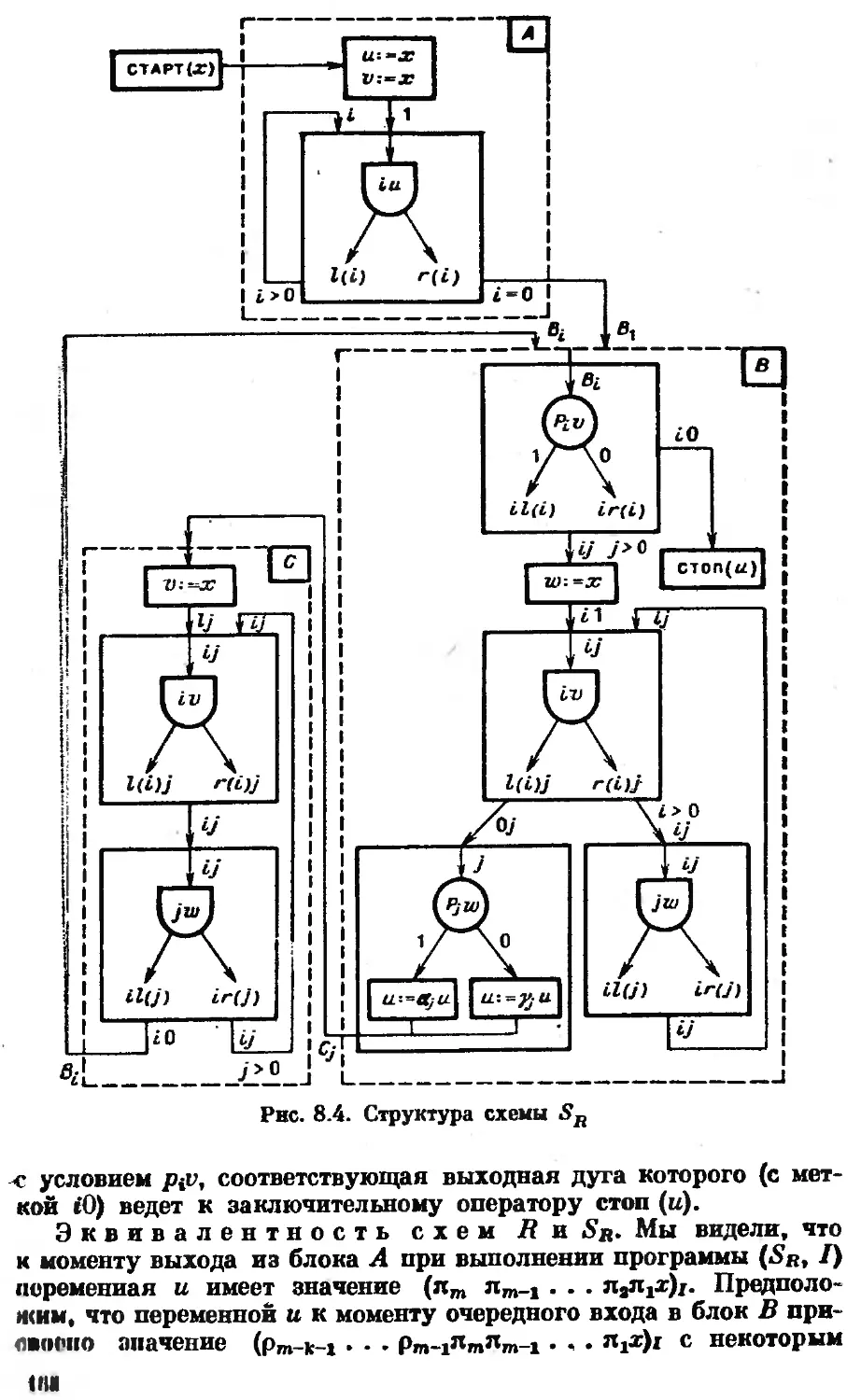
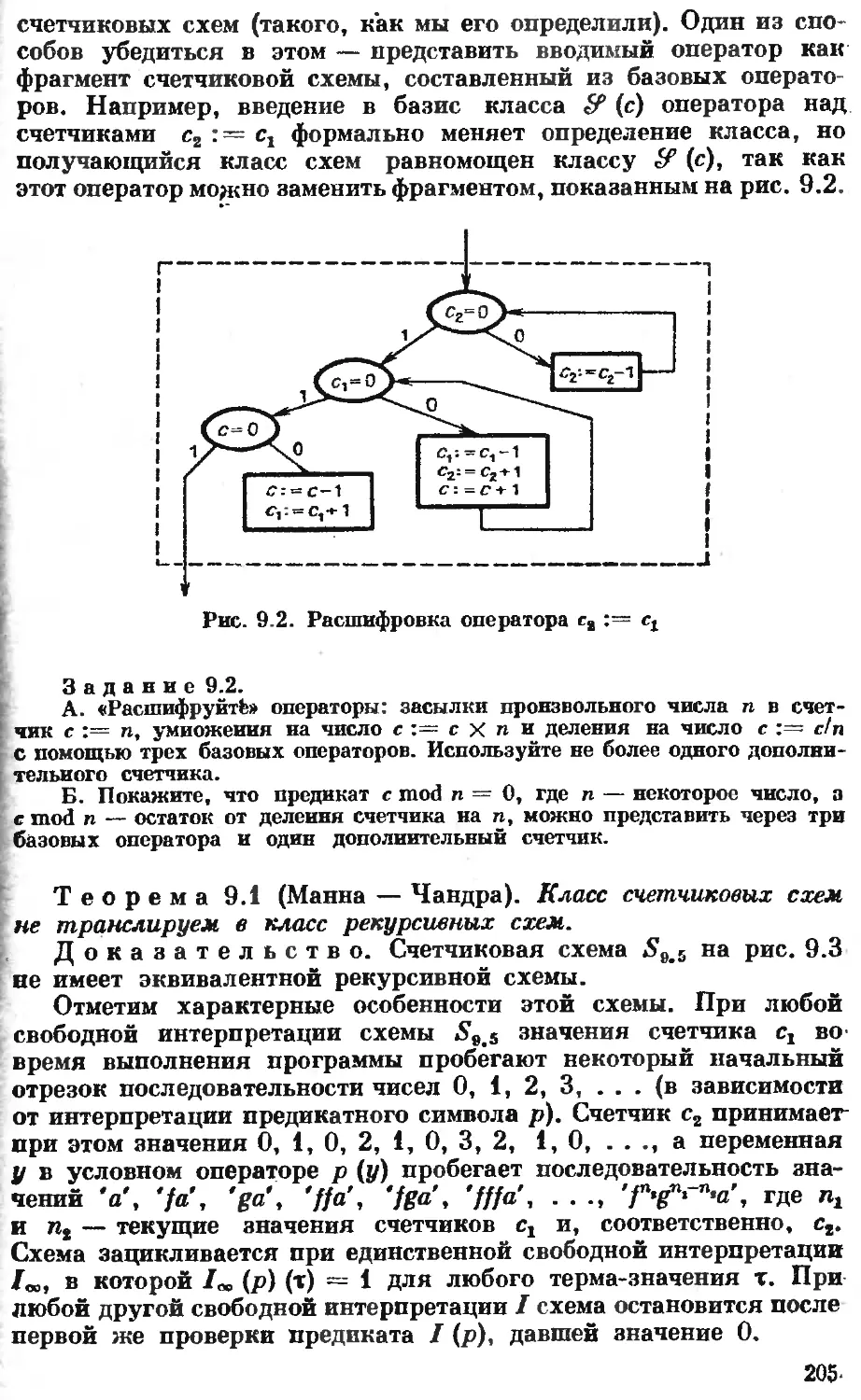
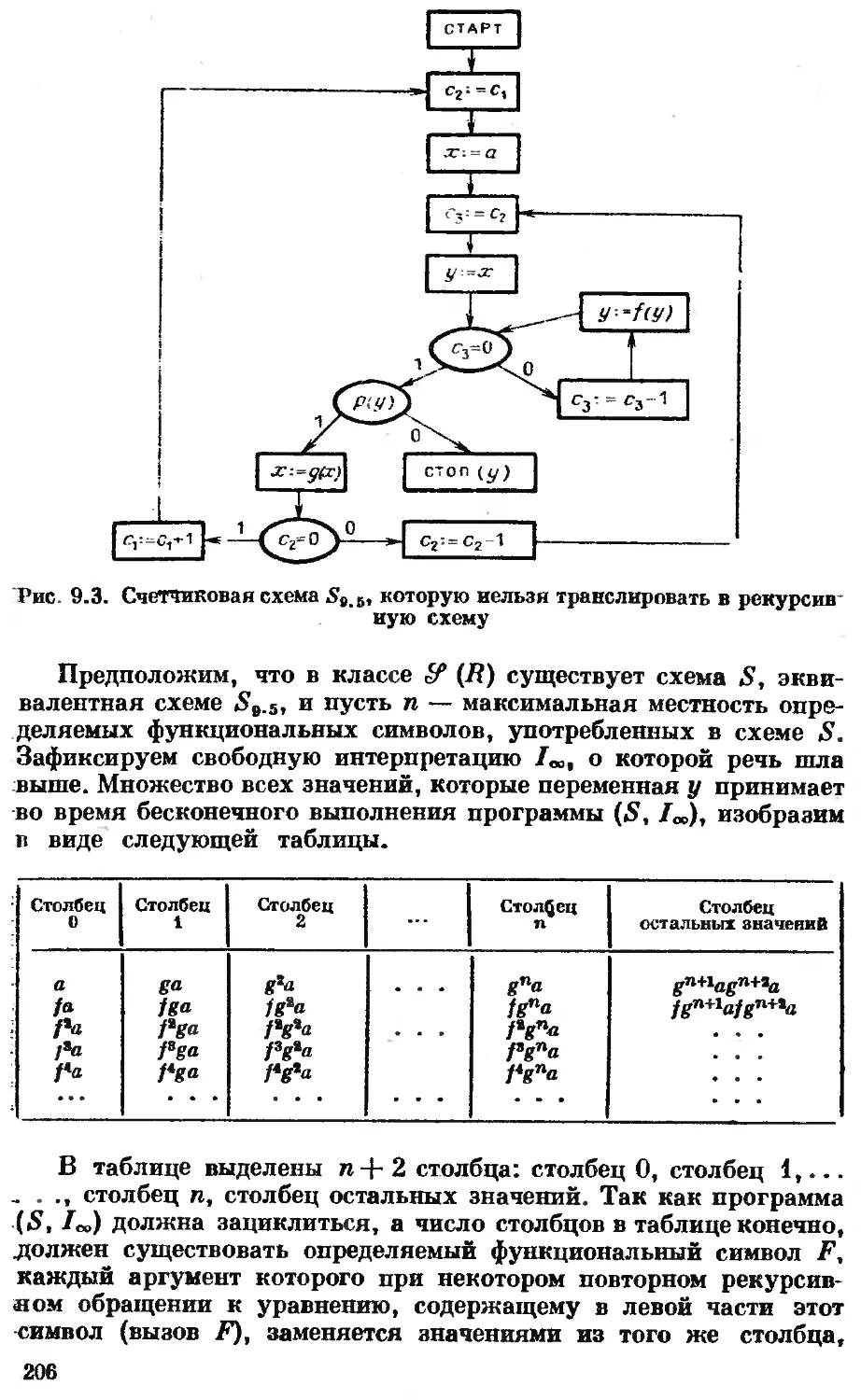
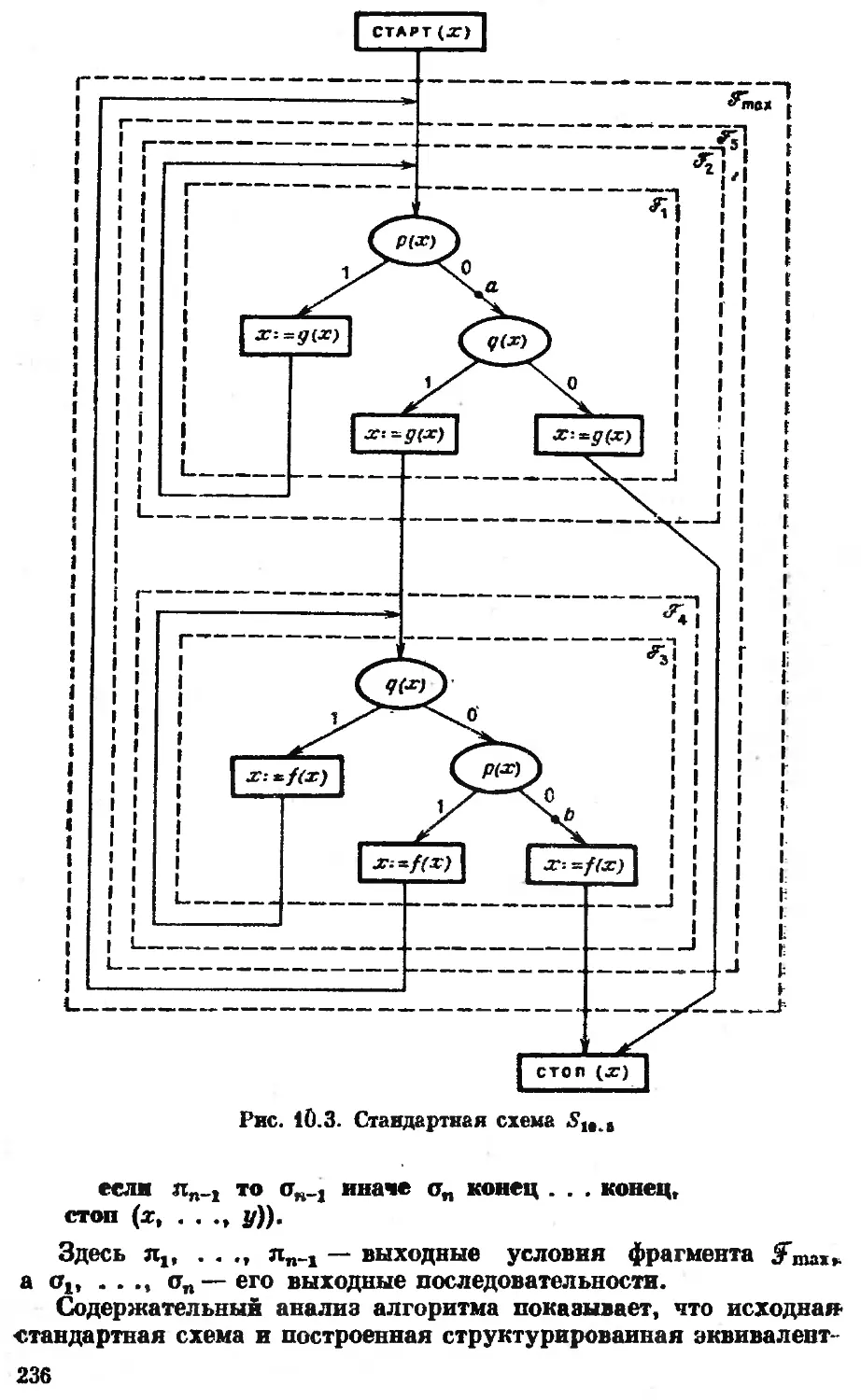
Автор: Котов В.Е. Сабельфельд В.К.
Теги: вычислительная математика численный анализ математика программирование информатика прикладная математика
ISBN: 5-02-013974-2
Год: 1991
Текст
В. Е. КОТОВ
В. К. САБЕЛЬФЕЛЬД
ТЕОРИЯ
СХЕМ ПРОГРАММ
МОСКВА «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
199 1
ББК 22.18
К73
УДК 519.681
Котов В. Е., Сабельфельд В. К. Теория схем программ.—
М.: Наука. Гл. ред. физ.-мат. лит., 1991.— 248 с.— ISBN 5-02-013974-2.
Проведено систематизированное изложение раздела теоретического про-
граммирования, изучающего неинтерпретированные модели программ — их
схемы, отражающие структурные особенности программ и в определенной
мере абстрагирующиеся от их функциональной сущности. Излагается теория
схем программ, являющаяся математической базой для развития методов
трансляции программ и создания новых конструкций в языках программи-
рования.
Для специалистов в области информатики и прикладной математики.
Ил. 61. Библиогр. 142 назв.
Научное издание
КОТОВ Вадим Евгеньевич
САБЕЛЬФЕЛЬД Виктор Карлович
ТЕОРИЯ СХЕМ ПРОГРАММ
Заведующий редакцией Е. Ю. Ходам
Редакторы: Г. А. Слепнева, Т. В. Шароватова
Художественный редактор Т. Н. Кольченко
Технический редактор Е. В. Морозова
Корректоры: Ю. В. Трушкова, Е. Б. Тихонова
ИБ № 32356
Сдано и набор 06.06.8S. Подписано к печати 20.03.91. Формат 60Х90*/№
Бумага тип. М 2. Гарнитура обыкновенная. Печать высокая.
Усл печ. л. 15,5. Усл. кр.-отт. 15,75. Уч.-ивд. л. 18,08. Тираж 7250 аиз.
Зак. 468. Цена 4 р. 80 к.
Издательско-производственное и иниготорговое объединение «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Вторая типография издательства «Наука»
121099 Москва Г-99, Шубинский пер., 6
1404000000—054
К 053(02)-91
115-91
©«Наука». Физматлит, 1991
I SBN 5-02-013974-2
Памяти нашего учителя
АНДРЕЯ ПЕТРОВИЧА ЕРШОВА
посвящается
ПРЕДИСЛОВИЕ
В развитии практики программирования для ЭВМ сложилась
парадоксальная ситуация. С одной стороны, благодаря впечат-
ляющим успехам развития вычислительной техники сегодня мы
располагаем ЭВМ, которые работают быстрее первых серийных
машин начала 50-х гг. в сотни тысяч и миллионы раз. Это озна-
чает, что мы располагаем мощным инструментом, «усиливающим»
человеческий интеллект и позволяющим автоматизировать решение
широкого круга задач. Парадокс, однако, заключается в том,
что средняя производительность труда программистов за это
время выросла всего лишь в десятки раз, а для системных про-
граммистов не выросла даже на порядок. Несмотря на появление
языков высокого уровня, мощных операционных систем и «ин-
теллектуальных» устройств общения, программисту все еще при-
ходится тратить много времени и усилий на рутинную работу
на длинном пути от математической постановки задачи до полу-
чения окончательных результатов. Не получится ли так, что
профессия программиста станет в будущем преобладающей в че-
ловеческом обществе?
Неизбежный путь преодоления возникающих проблем — это
всесторонняя автоматизация самого процесса программирования.
Многое в этом направлении уже сделано. Но для того, чтобы ра-
дикально решить проблему автоматизации любой сферы челове-
ческой деятельности, необходимо выделить ее основные компо-
ненты, понять ее структуру и фундаментальные законы. Другими
словами, нужна развитая теория, моделирующая объекты, явле-
ния и процессы этой деятельности. Необходимость и-возможность
создания математической теории программирования были про-
возглашены уже на первых этапах развития вычислительных
13
машин отчасти и потому, что первыми программистами были
высококвалифицированные математики и среди них — выдаю-
щиеся ученые нашего времени.
За последние годы выполнено много теоретических исследо-
ваний, связанных с разными аспектами и проблемами программи-
рования. Совокупность этих работ можно идентифицировать как
теорию программирования. Однако трудно дать энциклопедиче-
ское определение этого термина так, чтобы оно было методологи-
чески полезным. Слишком велико разнообразие проблем програм-
мирования (от разработки принципов построения больших систем
программирования или задач искусственного интеллекта до кон-
кретных алгоритмов синтаксического анализа или реализации
семафоров в операционных системах). Понятно, что столь разные
задачи решаются сильно отличающимися методами, привлекаю-
щими разный математический аппарат и технику рассуждений.
Легче поддается содержательной идентификации тот раздел
теории программирования, который изучает собственно програм-
мы, процесс их выполнения на машинах и результаты выполне-
ния. Однако и здесь имеются по крайней мере терминологиче-
ские трудности, связанные с тем, что программа — центральное
звено программирования, и в ней в той или иной мере отражены
все разнообразные компоненты процесса решения задач на ЭВМ.
Кроме того, и сама теория, и в особенности методы программиро-
вания продолжают развиваться, поэтому трудно дать краткое,
точное и одновременно динамичное название этой теории. Скажем,
в англоязычных странах в настоящее время используются тер-
мины «Theoretical computer science», «Mathematical theory of
computations», «Theoretical (mathematical) foundations of computer
science», «Theory of programs».
Следуя А. П. Ершову, мы употребляем термин «теоретическое
программирование» в качестве названия математической дисцип-
лины, изучающей синтаксические и семантические свойства про-
грамм, их структуру, преобразования, процесс их составления
и исполнения. Это словосочетание построено по аналогии с на-
званиями таких наук, как теоретическая физика, теоретическая
механика и т. д. В такой аналогии есть глубокий смысл: во всех
случаях теоретическая научная дисциплина изучает фундамен-
тальные понятия и законы основной науки и на основании обна-
руженных закономерностей строит более частные математические
модели исследуемых объектов, на которых ставит и решает при-
кладные задачи. В нашем случае ситуация усложняется еще тем,
4
что объект моделирования — программа — уже представляет со-
бой абстрактный объект. Раскрыть содержание теоретического
программирования на современном этапе развития помогает пе-
речисление сложившихся к настоящему времени направлений
исследований. Предлагаемая ниже рубрикация не претендует
на классификационную строгость и полноту: границы между
отдельными областями исследований размыты, подвижны и имеет-
ся глубокое взаимопроникновение как по изучаемым объектам,
так и по методам исследований.
1. Математические основы программиро-
вания. Основная цель исследований — развитие матема-
тического аппарата, ориентированного на теоретическое програм-
мирование, разработка общей теории машинных вычислений.
Эти исследования тесно соприкасаются с теорией алгоритмов
и вычислимых функций, теорией автоматов и формальных языков,
логикой, алгеброй, с теорией сложности вычислений.
2. Теория схем программ (схематология).
В этих работах внимание концентрируется на изучении структур-
ных свойств и преобразований программ, а именно тех, которые
отличают программы от других способов задания алгоритмов.
Славным объектом исследования становится схема программы —
математическая модель программы, в которой с той или иной
степенью детализации отражено строение программы, взаимо-
действие составляющих ее компонентов.
3. Семантическая теория программ. Семан-
тика программы или отдельных конструкций языков программи-
рования — это их смысл, математический смысл для програм-
миста и описание функционирования для машины. Этот раздел
теоретического программирования изучает методы формального
описания семантики программ, семантические методы преобразо-
ваний и доказательства утверждений о программах. В частности,
работы по методам проверки семантической правильности про-
грамм нацелены на автоматизацию их отладки и автоматический
синтез программ.
4. Теория вычислительных процессов и
структур (теория параллельных вычисле-
н и й). Исследования в этой области направлены на разработку
и обоснование новых методов и средств программирования, преж-
де всего методов программирования параллельных процессов.
В частности, изучаются структуры и функционирование опера-
ционных систем, методы распараллеливания алгоритмов и про-
5
грамм, ведется поиск новых архитектурных принципов конструи-
рования вычислительных машин и систем на основе результатов
и рекомендаций теоретического программирования и вычисли-
тельной математики. Многие из изучаемых здесь проблем отно-
сятся одновременно к предыдущим направлениям (например,
схемы параллельных программ изучаются схематологией).
5. Прикладные задачи теоретического
программирования. Сюда в первую очередь относятся
разработка и обоснование алгоритмов трансляции и алгоритмов
автоматической оптимизации программ, однако диапазон прак-
тических задач, решаемых методами теоретического программи-
рования, постоянно расширяется.
Вопрос о связи теоретического программирования, в особен-
ности его фундаментальных разделов, с практикой программиро-
вания неоднократно обсуждался в литературе и на научных кон-
ференциях. Легко аргументировать необходимость активного раз-
вития и изучения этой науки, указав примеры практических
идей, методов, алгоритмов, алгоритмических языков, непосредст-
венными источниками которых были теоретические работы. Од-
нако главная цель теоретического программирования — решение
фундаментальных проблем и поиск фундаментальных идей, при-
водящих к качественно новым решениям практики. Если с теку-
щими задачами помогает справиться смекалка и опыт програм-
миста, то принципиально новые решения появляются как ре-
зультат глубокого анализа основ программирования. Знакомство
с теоретическим программированием и особенно работа в этой
области стимулируют творческую активность программиста, по-
зволяют принимать обоснованные решения и служат источником
новых идей. Недаром многие ученые, внесшие значительный
вклад в развитие программирования, были зачинателями тех
или иных направлений и школ теоретического программирования
и продолжают плодотворно работать в этой области.
Эта книга посвящена только одному разделу теоретического
программирования — теории схем программ — и содержит весь
основной понятийный аппарат схематологии, постановку глав-
ных проблем и результаты, ставшие классическими в этой науч-
ной дисциплине. Правда, ряд интересных и важных для внут-
реннего развития этой теории фактов упоминается лишь в обзо-
рах. Кроме того, за рамками изложения остались исследования
параллельных схем, ряда классов структурированных схем в
почти вся неинтерпретационная теория схем.
6
Книга состоит из десяти глав. Первые три содержат элементы
теории алгоритмов, автоматов и графов в минимальном объеме,
необходимом для того, чтобы максимально замкнуть изложение
рамками книги. При этом во второй главе содержится описание
алгебраического подхода к решению задач анализа свойств гра-
фов, а в третьей главе приведено доказательство замечательного
во многих отношениях результата Берда о разрешимости проб-
лемы эквивалентности двухленточных автоматов. Четвертая глава
вводит основной объект теории — понятие схемы программы.
На базе одного из наиболее изученных классов схем — класса
стандартных схем — вводятся главные понятия, конструкции и
проблемы схематологии. В пятой главе сосредоточены «отрица-
тельные» результаты о невозможности получения алгоритмиче-
ского решения главных проблем для стандартных схем и их под-
классов. Шестая и седьмая главы посвящены разрешимым слу-
чаям проблемы эквивалентности стандартных схем: разрешимость
достигается либо за счет рассмотрения эквивалентности более
сильной, чем функциональная (отношение изоморфизма схем, ло-
гико-термальная эквивалентность), либо за счет сужения класса
рассматриваемых схем (класс сквозных схем). В восьмой главе
изучаются схемы рекурсивных программ, проблемы взаимной
трансляции рекурсивных схем и стандартных схем. Девятая и
десятая главы содержат изложение результатов сравнительной
схематологии, изучающей различные классы схем программ, от-
ношения между ними и задачи трансляции одних классов схем
в другие.
Несколько слов о том, как возникла эта книга. В 1978 г. Си-
бирское отделение издательства «Наука» издало небольшим ти-
ражом монографию «Введение в теорию схем программ», которую
первый из авторов написал на основе читавшегося им в 1973—
1976 гг. в Новосибирском университете курса лекций по теории
схем программ. Со временем материал этой монографии потребо-
вал дополнения и изменения. Так, появилась серия работ,
посвященных обоснованию алгоритмов глобального анализа
свойств программ для целей оптимизации и других преобразова-
ний. Кэм и Ульман Ц09] обнаружили, что все они допускают
единую трактовку в рамках алгебраического подхода к описанию
свойств программ. Далее, в изучении главных проблем теории
схем, и прежде всего проблемы эквивалентности, интерес смес-
тился к выделению и изучению разрешимых случаев, к построе-
нию алгоритмов распознавания с оценками их сложности. Поэтому
7
при изложении современной теории схем программ уже нельзя
ограничиваться таким игрушечным разрешимым классом схем
Янова, каким он является по сути, несмотря на важность и по-
истине историческую роль, которую схемы Янова сыграли в раз-
витии теоретического программирования. Хотя выбор разрешимых
случаев для демонстрации методов и результатов схематологии
в книге, посвященной этому предмету, не может быть случайным,
однако в известной мере этот выбор зависит от личных вкусов
авторов. Мы выбрали логико-термальную эквивалентность стан-
дартных схем и функциональную эквивалентность сквозных
схем. Эти две темы заняли значительную часть материала всей
книги, фактически стали содержанием двух ее глав.
Построение теории схем программ ие закончено, она продол-
жает развиваться. Открыты проблемы функциональной эквива-
лентности в классах схем с независимыми ячейками и свободных
стандартных схем. Главные проблемы теории рекурсивных схем
исследованы еще меньше, чем проблемы теории стандартных
схем. Например, неясен статус проблемы древесной эквивалент-
ности рекурсивных схем (см. обзор и комментарии к гл. 8).
В основном тексте ссылки на литературу приводятся не всегда,
чаще они сосредоточены в обзорах, завершающих каждую главу,
Список литературы в конце книги ни в коей мере не претендует
на библиографическую полноту; за редким исключением он со-
держит только упоминаемые в тексте публикации.
Авторы считают своим приятным долгом выразить благодар-
ность А. П. Ершову, В. А. Непомнящему, И. В. Поттосину,
А. А. Летичевскому, С. С. Лаврову и Р. И. Подловченко за пло-
дотворные дискуссии, повлиявшие на формирование взглядов
авторов па современную теорию схем программ.
ГЛАВА 1
ВЫЧИСЛИМОСТЬ И РАЗРЕШИМОСТЬ
Основу рабочего аппарата теории схем программ составляют
собственные, оригинальные понятия, являющиеся абстракциями
реальных объектов программирования. Математический инстру-
ментарий, используемый для конструирования этих понятий,
и техника исследований заимствуются из классических разделов
дискретной математики — теории алгоритмов и автоматов, логики,
алгебры, теории графов, математической лингвистики. Такое раз-
нообразие применяемых математических средств — следствие объ-
ективной сложности основного объекта исследований — програм-
мы. Отсутствие универсальной «алгебры программирования» при-
дает теории схем программ черты синтетической науки со всеми
вытекающими последствиями. Естественно, что теория схем про-
грамм наиболее тесно связана с теорией алгоритмов и автоматов,
изучающей общие законы вычислений и преобразования инфор-
мации.
В первых трех главах содержатся начальные сведения из тео-
рии алгоритмов, графов и автоматов, знакомство с которыми
необходимо для понимания постановок рассматриваемых в этой
книге проблем и методов их решения. В частности, будут приве-
дены доказательства некоторых известных теорем об алгоритмах
и автоматах, что позволит избежать частых «внешних» ссылок
на литературу и поможет лучше овладеть техникой самостоятель-
ной работы в теории схем программ.
§ 1. Вычислимые функции, алгоритмы
1.1. Функции. Все объекты и понятия в этой книге строятся
(или, при неформальных определениях, могут быть построены)
из символов (букв, цифр, математических и специальных знаков)
и целых неотрицательных чисел (будем их называть просто чис-
лами) с помощью теоретико-множественных понятий — множеств,
упорядоченных множеств (наборов), функций и отношений.
Мы полагаем, что читатель знаком с элементами теории мно-
жеств и логики, поэтому ограничимся лишь некоторыми соглаше-
ниями об обозначениях. Множества будут задаваться явным пе-
речислением (с использованием многоточия) своих элементов,
заключенным в фигурные скобки, а наборы — таким же перечис-
лением в круглых скобках. Другой способ задания множества:
9
(х | р (х)}, где х — переменная, значениями которой являются
некоторые объекты, а Р — свойство тех и только тех значений х,
которые являются элементами задаваемого множества. Например,
{(*, У) I х и у — числа, и х <z у} — множество всех пар чисел
таких, что первое число не превосходит второе. Напомним,
что Му X М2 X ... X Мп — декартово произведение мно-
жеств Му, М2, . . ., Мп, т. е. множество {(wh, т2, . . ., тп) [ mt ЕЕ
€Е Му, т2 €Е М2, . . ., тп ЕЕ Мп}, а Мп обозначает произведение
М X М X ... X М.
п раз
Приведем также общее определение функции, чтобы иметь
далее возможность сравнить это определение с определением
вычислимой функции.
Функцией, отображающей множество X во множество Y (обо-
значение F: X —► У), называется множество F С. X X Y такое,
что для любых пар (х, у) ЕЕ F и (х', у') ЕЕ F из х = х следует,
что у = у'.
Множество {х | (х, у) ЕЕ F} — область определения функции F
(или множество значений ее аргумента); множество {у | (х, у) ЕЕ
Е F) — область значений функции. Если областью определения
функции F: X -> Y служит все множество X, то F — всюду
определенная функция, в противном случае — частичная.
Конкретные функции будут задаваться не только в виде мно-
жества, как предписывает определение функции, но и менее фор-
мально, по следующей схеме: F (х) = Е, где х — переменная-
аргумент со. значениями во множестве X, a Е — выражение, свя-
зывающее значения функции (элементы из У) со значениями аргу-
мента х. Например,
F (х) = х, или F ({Ху, х2)) = Ху + х2,
или
F(x) = {
а, если х>в.
Ь в противном случае.
Функцию F: X -> У называют п-местной функцией над мно-
жеством М, если У — М и X = М\ Так, если хх и х2 в при-
мере — переменные, значениями которых являются числа, то
функцию F ((Ху, х2)) ~ Ху + х2 можно считать двухместной функ-
цией над множеством чисел (и упростить запись, убрав одну пару
скобок).
Суперпозиция двух функций сопоставляет паре функций Fyt
X —> У и F2: У —> Z третью функцию F3: X -+Z такую, что
(х, z) ЕЕ F3, если и только если х Е X, z Е 2 и существует у СЕ У,
при котором (х, у) СЕ Fy и (у, z) СЕ Fs. Запись F3 (х) = F2 (Ft (х))
задает Fs как суперпозицию функций 1'\ и F2. Определение супер-
позиции пары функций естественным образом переносится на на-
боры функций произвольной конечной длины.
Предикатом называют функцию, областью значений которой
служит множество символов-цифр {0, 1}. При этом говорят, что
10
предикат Pt X -► {0, 1} истинен для гЕ X, если Р (х) = 1,
и ложен, если Р (х) = 0. Отношение на множестве X — это двух-
местный предикат Р: X2—► {0, 1).
1.2. Словарные функции. Выделим класс словарных функций,
играющий в дальнейшем особую роль наряду с числовыми функ-
циями, т. е. функциями над множеством всех чисел.
Алфавитом называют непустое конечное множество символов.
Например, = {а, Ь}, V2 = {0, 1), Va — {а, +, 1, =} — алфа-
виты. Словом в алфавите V называется конечный объект, полу-
чаемый выписыванием одного за другим символов из V, например,
aabba — слово в алфавите Fx; 01011 — слово в алфавите V2;
а + 1 = 1 т а — слово в алфавите V3. Длина слова — число
символов в нем, пустое слово не содержит ни одного символа.
Множество всех слов в алфавите V будем обозначать V*. Если
а — символ, то ап — слово аа. ..а; множество {апЬп | п >• 1} —
п раз
это множество слов {ab, ааЪЪ, аааЪЪЪ, . . .).
поместной словарной функцией над алфавитом V называют
n-местную функцию над V*, т. е. функцию из V* X V* X . . . X V*
(и раз) в V*. Пример всюду определенной двухместной словар-
ной функции, которую называют конкатенацией: С (а, 0) = а0,
где а 6Е V*, 0 6Е Й*, а а0 — также слово из V*, полученное
приписыванием справа к слову а слова 0. Слово у — подслово слова
а, если а = 0у6; подслово у — префикс слова а, если 0 — пустое
слово; подслово у — суффикс слова а, если б — пустое слово.
Заметим, что существует взаимно однозначное соответствие
между числами и словами в произвольном алфавите V. Действи-
тельно, символы из V можно упорядочить, перенумеровав их чис-
лами 1, 2, .... п, т. е. задав функцию упорядочения К: V —►
-►{1,2,..., п}. Пустому слову ставится в соответствие 0. Слова
упорядочиваются в последовательность по' следующему правилу:
если длина слова а меньше длины слова 0 (оба из Й*), то а рас-
полагается левее 0; слова одинаковой длины упорядочиваются
в «алфавитном» порядке с учетом порядковых номеров символов
алфавита, т. е. так же, как упорядочены слова в словарях естест-
венных языков. Порядковый номер слова в полученной последо-
вательности слов и задает соответствующее ему число (числовой
код слова). Обратное кодирование осуществляется тем же спосо-
бом, т. е. с использованием некоторого упорядочения алфавита.
Имея возможность кодировать слова в произвольном алфавите
числами, а числа — словами в произвольном алфавите, можно
осуществить взаимно однозначную кодировку слов в одном алфа-
вите словами из другого алфавита.
Задание 1.1.
А. Найти аналитический вид функции, кодирующей слова в алфавите
V = {а, Ь, с) числами, если функция упорядочения Kt V —» {1, 2, 3} такова,
что К (а) = 1, К (Ь) = 2, К {с) = 3.
Б. Пусть V*n — множество всех наборов из п слов в алфавите V. По-
кажите, что между наборами из V*n и числами существует взаимно однознач-
ное соответствие. Закодировать числами пары слов в алфавите {а, Ь).
11
1.3. Вычислимые функции и машины Тьюринга. Данное нами
определение функции не содержит указаний о том, как для задан*
ных значений аргументов получить соответствующие значения
функции. Было бы практичнее переформулировать зто определение
таким образом, чтобы оно содержало конструктивную процедуру,
или алгоритм, нахождения значений функции. Однако, как будет
видно далее, такое определение уже приведенного выше, т. е.
определяет лишь некоторый подкласс функций, которые называют
вычислимыми функциями.
В середине 30-х гг. Тьюринг [141], Черч [91], Клини 1113] и
Пост [132] различным образом формализовали способы получения
значений вычислимых функций. Позднее было установлено, что
все эти независимо введенные определения вычислимости, равно
как и позднейшие формализации, например, нормальные алго-
ритмы Маркова [40], эквивалентны, т. е. задают один и тот же
класс функций. Идея Тьюринга состояла в том, чтобы определять
функцию с помощью абстрактной «математической» машины, вы-
числяющей значения функции по значениям ее аргументов. Таким
образом, конкретная машина Тьюринга задает конкретную вы-
числимую функцию, и его гипотеза (тезис) состояла в том, что
каждая функция, для которой существует алгоритм нахождения
ее значений, представима некоторой машиной Тьюринга, т. е.
является вычислимой. Тезис Тьюринга не может быть доказан,
так как наряду с формальным понятием вычислимой функции
он содержит эмпирическое понятие алгоритма. Однако интуиция,
отсутствие опровергающих примеров и равносильность разных
формализаций вычислимости убеждают в справедливости этого
тезиса.
Машина Тьюринга Т задает словарную функцию над неко-
торым алфавитом V и представляет собой описание машины —
набор (V, Q, д0, -0 — и правило функционирования, общее
для всех машин, где
V — алфавит машины;
Q — конечное непустое множество символов, называемых со-
стояниями машины (Q f] V — 0);
q0 — выделенный элемент множества Q, называемый началь-
ным состоянием;
— специальный «пустой» символ, не принадлежащий ни У,
ни ();
I — программа машины.
Программа машины — это конечное множество слов вида
qa--*-q'ad, называемых командами, где q, q ЕЕ Q, a,ar G I7 U
— вспомогательный символ-разделитель; d — элемент множест-
ва {I, г, р), содержащего три специальных символа, которых нет
ни в V, ни в Q. Предполагается также, что в программе I никакие
две команды не могут иметь одинаковую пару первых двух сим-
волов.
Правило функционирования поясним неформально на рас-
пространенной «физической» модели машины Тьюринга. Машина
12
состоит из потенциально бесконечной (в обе стороны) ленты,
управления и головки, перемещаемой вдоль ленты (рис. 1.1).
Лента разбита на клетки, которые могут содержать символы из
алфавита V или быть пустыми, т. е. содержать символ Управ-
ление на каждом шаге работы машины находится в одном из сос-
тояний из Q, расшифровывает программу, которая однозначно
определяет поведение машины и управляет головкой. Головка
в каждый момент расположена против некоторой клетки ленты
и может считывать символы с ленты, записывать их на ленту и
перемещаться в обе стороны вдоль ленты. Машина функционирует
следующим образом. В начальный момент на ленте записано
некоторое слово из V, а управление находится в начальном сос-
тоянии д0. Начальное слово, равно как и слова, появляющиеся
в процессе работы машины, ограничено с двух сторон пустыми
символами ф:. Головка обозревает крайний слева символ задан-
ного слова.
Работа машины состоит в повторении следующего цикла эле-
ментарных действий:
1) считывание символа, находящегося против головки;
2) поиск применимой команды, а именно той команды да ->
-* q'a'd, в которой q — текущее состояние управления, а — счи-
танный символ;
3) выполнение найденной команды, состоящее в переводе
управления в новое состояние q', записи в обозреваемую голов-
кой клетку символа а' (вместо стираемого символа а) и последую-
щем перемещении головки вправо, если d — г, влево, если d — I,
или сохранении ее в том же положении, если d = р.
Машина останавливается в том и только в том случае, если
на очередном шаге ни одна из команд не применима. Результат
работы остановившейся машины — заключительное слово на ленте.
Машина Тьюринга, перерабатывая начальные слова на ленте
в заключительные, задает словарную функцию, для которой на-
чальные слова — значения аргумента, заключительные — зна-
«3
чения функции. (Для представления n-местной функции началь-
ное слово на ленте имеет вид *а1 * аг * • • • # ап *, где под-
слова ах, а2, . . ап не содержат символа При интерпретации
заключительного слова на ленте как значения функции символ
* игнорируется). Если машина не останавливается, начав работу
с некоторым словом на ленте, то функция, задаваемая машиной,
считается неопределенной для этого слова. Таким образом, ма-
шина Тьюринга Т задает частичную функцию Ft и способ вычис-
ления ее значений. Хотя машины Тьюринга оперируют со сло-
вами, они могут задавать и числовые функции в силу установлен-
ной выше связи между словами и числами.
По определению, функция F является (частично) вычислимой,
если существует машина Тьюринга Т такая, что FT — F. Говорят
также, что для функции F существует (частичный) алгоритм
вычисления ее значений, задаваемый машиной Т. В следующем
параграфе мы убедимся в существовании функций, которые не
являются вычислимыми.
Для машины Тьюринга, как и для всех других формальных
способов задания алгоритмов, включая программы для ЭВМ,
характерны следующие свойства:
1) конструктивность — машина Тьюринга представляет собой
конечный объект, построенный по определенным правилам из
базовых объектов;
2) конечность — процесс нахождения значений функции для
тех значений аргументов, для которых она определена, состоит
из конечного числа шагов;
3) однозначность — результат работы машины единственным
образом определяется начальным словом;
4) массовость — машина работает с любым начальным словом
на ленте, составленным из символов ее алфавита.
1.4. Пример машины Тьюринга. Пусть алфавит V состоит из
двух символов — открывающей и закрывающей скобок: V —
= {(,)). Выделим во множестве V* подмножество М «правильных»
слов, которые определим следующим образом:
1) пустое слово е М;
2) если а принадлежит М, то слова ( ) а, а ( ) и (а) также
принадлежат М.
Построим машину Тьюринга, на ленту которой подаются слова
из V*, и машина узнает, принадлежит данное слово множеству М
или нет. Для этого машина должна остановиться с односимволь-
ным словом 1 на ленте, если начальное слово принадлежит М,
и с результатом 0 — в противном случае. Другими словами, ма-
шина Тьюринга должна задавать предикат Pz V* -> {0, 1) такой,
что
С 1, если а£М,
? ( 0, если а М.
Алфавит машины включает, кроме скобок, символы 0, 1 и *.
Искомая машина Тьюринга имеет следующий вид (для простоты
14
отождествим машину Т с ее описанием):
Т = ({(,), 0, 1, *), {д0, 91» 9а» 9з, Эд), 9о» #, Л»
где программа I содержит следующие команды (перенумерован-
ные для последующих ссылок):
1- 9о(—>9о(г*
3. 9о*~>9о*г-
5- 91(->9о*г-
7- Л#->94°^-
9- g2 *-»д2#*-
И- 9з(~*9з#^
13. д3#->9з0р.
15- 94)-* 94 Не-
2. 90)—* qi*l-
4. 9о# ->9г#1
6. 91*- *qi*l-
8. 9г Н 9з #
10. 9г*' ->д21р-
12. 9з*- >9з #
14. 94(-> 94 # г-
16. 94*- >94#>-
когда машина находится в состоянии gOl головка движется
направо в поиске первой слева закрывающей скобки. Найдя эту
скобку, она замещает ее звездочкой и возвращается назад в но-
вом состоянии в котором ищет парную открывающую скобку.
Встретив ее, вновь возвращается назад в состояние q0 и движется
направо, и т. д. Если головка достигнет левого символа #, она
записывает символ 0 (не нашлось парной открывающей скобки)
и переходит в состояние qit находясь в котором движется направо,
стирая все символы. Если же головка достигнет правого символа #,
она переходит в состояние д2 и возвращается к началу слова, сти-
рая по пути символы. Если она вернется к началу слова, не встре-
тив по пути открывающей скобки (заданное слово — правильное),
она запишет 1, и машина остановится. Если же встретится хотя
бы одна открывающая скобка (слово неправильное), машина
перейдет в состояние q3, которое заставит головку записать О
в начале слова и остановиться.
Функционирование машины Тьюринга можно описать с по-
мощью протокола работы над заданным начальным словом. Пусть
,^А1аг...а1с_1а1с...ап* — слово, возникающее на ленте в процессе
работы машины после некоторого шага, в результате которого
машина находится в состоянии q, а головка обозревает клетку,
содержащую Л-й слева символ слова. Слово #п1аг...а)с_1?ак...ап4й
называется конфигурацией машины Тьюринга. Последователь-
ность конфигураций, выписанных в том порядке, в котором
они следуют в процессе работы машины, и называется прото-
колом.
Так протокол работы рассматриваемой машины Тьюринга
над словом (( )( ) имеет следующий вид (между конфигурациями
выписаны номера выполняемых команд):
:# 9о« X )#
1 Головка перемещается направо, игнорируя
.# (9о( )( )# открывающие скобки.
15
1
#((9з)( )# 2 # (<71 (*( )#5 # (*9о*( )# 3 #' (**9о ( )# Обнаружена закрывающая скобка, которая «зачеркивается» символом «. Головка возвращается обратно и находит парную открывающую скобку, которую за- черкивает. Головка вновь движется вправо в поиске закрывающей скобки.
# (** (9о)# 2 # ’ (**91 (*# 5 # (***9о*# 3 # (****9о# 4 # (***92*# 9 Закрывающая скобка обнаружена. Обнаружена парная открывающая скобка. Снова движение направо. Головка дошла до конца слова.
# (**92*## 9 Головка движется влево в поиске лишней открывающей скобки или начала слова, стирая на пути звездочки.
# (*92*###
9
#(92*.####
9
# 9s (#####
8 Обнаружена лишняя открывающая скобка,
которая стирается.
# 9.######
13 Обнаружено начало слова, и записывается О.
#9з0####
Машина останавливается, так как ни одна из
команд ее программы не применима.
Результат работы построенной машины Тьюринга показывает,
что слово (( )() не является правильным.
Задание 1.2.
А. Постройте машину Тьюринга, которая стирает с ленты любое началь-
ное слово н записывает вместо него слово aabba в алфавите‘{а, &}.
Б. Постройте машину Тьюринга, которая любое заданное слово ai<>i.. .
... Bn в алфавите {О, 1} преобразует в «перевернутое! слово «п ...
1.5. Словарное представление машины Тьюринга. Машина
Тьюринга однозначно задается своей программой. Если упорядо-
чить ее команды произвольным образом и применить описан-
ный ниже способ кодировки последовательности команд словом
«б
в алфавите машины Тьюринга, то можно получить ее описание
в собственном алфавите.
Пусть У — алфавит машины Тьюринга Т, a Q — множество
ее состояний. Упорядочим некоторым образом множество Q,
и пусть К (q) — порядковый номер состояния q. Введем вспомо-
гательный символ *, не входящий в У, и сопоставим каждой ко-
манде qa-t-q'a'd слово в алфавите W = У U {ф, I, г, р, *} сле-
дующего вида:
*К(3)а »K(g')a'd.
Упорядоченной последовательности команд соответствует после-
довательность слов в алфавите W. Результатом конкатенации
является слово ат, однозначно описывающее машину Т (с точ-
ностью до наименований состояний). Следующий этап кодировки —
переход от представления машины в алфавите W к представлению
в алфавите У. Если алфавит У содержит п символов, то, упорядо-
чив его каким-либо образом (для кодировки слов из У* числами),
упорядочим алфавит W так, чтобы дополнительные символы, не
входящие в У, получили следующие номера: К' (ф) = n -j- 1,
К' (*) = п + 2, К' (Z) = п + 3, JT (г) = п + 4, К' (р) п + 5.
Закодировав слова из У* и W* числами описанным в разде-
ле 1.2 способом, узнав номер слова ат из W* и выбрав слово из У*
с тем же номером, найдем словарное представление машины
Тьюринга 7* в ее алфавите. По слову 0т можно однозначно (с точ-
ностью до наименования состояний) восстановить программу ма-
шины Т. Заметим, что одной и той же машине Тьюринга соответст-
вуют различные словарные представления в ее алфавите в зави-
симости от выбора упорядочений множеств Q, У, I, но по любому
из этих представлений программа машины восстанавливается
однозначно.
§ 2. Разрешимые и неразрешимые проблемы
2.1. Массовые алгоритмические проблемы. Изучая свойства
программ и их математических абстракций — схем программ, мы
имеем дело с так называемыми массовыми алгоритмическими
проблемами. Конечная цель теории схем — автоматизация про-
граммирования, в том числе автоматический анализ свойств про-
грамм и их преобразования, осуществляемые с помощью других,
специальных программ. Поэтому иас интересуют алгоритмы, ко-
торые могли бы по любой предъявленной программе установить,
завершит ли она работу или будет «циклить», дают ли две про-
граммы, исходная и оптимизированная, один и тот же результат,
является ли произвольная предъявленная Алгол-программа син-
таксически правильной и т. д.
Массовые алгоритмические проблемы формулируются следую-
щим образом. Необходимо указать алгоритм, который бы опре-
делял, обладает ли предъявленный объект из некоторого класса
объектов интересующим иас свойством; другими словами, при-
17
надлежит ли он множеству М всех объектов, обладающих этим
свойством. Если существует такой частичный алгоритм, то гово-
рят, что множество перечислимо, а поставленная массовая алго-
ритмическая проблема частично разрешима. Если этот алгоритм
к тому же всюду определен, то множество М разрешимо и постав-
ленная проблема также разрешима. В этом параграфе мы убедим-
ся в существовании неразрешимых проблем и даже проблем, ко-
торые не являются частично разрешимыми, что свидетельствует
о существовании невычислимых функций. Теоремы этого пара-
графа будут использованы в последующих главах для доказательст-
ва неразрешимости некоторых проблем теории схем программ.
Обсуждаемые понятия введем формально для множеств слов.
Пусть V — алфавит, М С V — некоторое множество слов в этом
алфавите.
Характеристической функцией множества М называется пре-
дикат V* —» {0, 1), всюду определенный на V*:
{1, если
П r-Г- ЯЛ
О, если а(£М.
Частичная характеристическая функция множества М — это
функция Нм’. V* -► {1), определенная только для слов из М и
имеющая вид Нм (а) = 1 для всех а 6= М.
Множество М называется разрешимым, если его характеристи-
ческая функция вычислима. Множество М перечислимо, если его
частичная характеристическая функция вычислима. Разрешимость
множества М означает, что существует всегда останавливающаяся
машина Тьюринга Tfm, позволяющая для любого слова в алфа-
вите V через конечное число шагов установить, принадлежит ли
это слово множеству М или нет. Перечислимость множества М
означает, что существует машина Тьюринга Тнм< которая останав-
ливается в том и только в том случае, если предъявленное слово
принадлежит множеству М. Машина Тцм не позволяет точно уста-
новить, принадлежит заданное слово множеству М или нет, так
как отсутствие ответа к некоторому времени не несет никакой
информации о том, появится он позже или нет. Однако если ма-
шина Тцм остановилась, то мы знаем, что предъявленное слово
принадлежит М.
Связь между разрешимыми и перечислимыми множествами
(и, следовательно, между разрешимыми и частично разрешимыми
проблемами) устанавливает следующая
Теорема 1.1 (Пост). Множество М с разрешимо
тогда и только тогда, когда М и его дополнение М = V* \ М
перечислимы.
Доказательство. Из разрешимости М следует его
перечислимость. Действительно, машину Тьюринга Tfm*
пякяп^ю характеристическую функцию множества М, легко пре-
образовать в машину Тцм^ Добавив к программе машины Т*м
18
команды, зацикливающие ее в том случае, когда она останавли-
вается с результатом 0. Новая машина задает частичную харак-
теристическую функцию множества М.
Пусть Тцм и Тн— — машины Тьюринга, задающие частичные
характеристические функции множеств М и соответственно М.
Алгоритм распознавания, устанавливающий, принадлежит ли сло-
во а множеству М, сводится к следующей процедуре. Выполня-
ется по одной команде каждой машины Тьюринга (с одним и тем
же начальным словом а на лентах). Если после выполнения одной
команды машина Тнм остановится, то результат работы алгорит-
ма— символ 1. Если остановится Тн—, то результат—символ 0.
м
Если ни одна из машин не остановится, то выполняется следую-
щая пара команд, и т. д. Так как а — элемент или из М, или
из М, то через конечное число шагов либо Тнм, либо Тн— остано-
вится. Таким образом, алгоритм вычисляет значения характерис-
тической функции множества М, и можно построить машину
Тьюринга ТрМг реализующую этот алгоритм, и, следовательно,
множество М разрешимо. Q
Определение разрешимых и перечислимых множеств можно
перенести на числовые множества и множества, элементами ко-
торых являются объекты более сложной структуры. Примеры
разрешимых множеств: пустое множество; множество всех слов
в некотором алфавите; множество всех словарных представлений
машин Тьюринга над алфавитом V. Теперь познакомимся с не-
разрешимыми множествами (неразрешимыми проблемами) и с не-
перечислимыми множествами (проблемами, не являющимися час-
тично разрешимыми).
Задание 1.3.
А. Покажите, что множество {апЬп | п > 1} слов в алфавите {а, 6} раз-
решимо.
Б. Пусть множества слов и М2 разрешимы, Ма и Ма — перечислимы.
Покажите справедливость следующих утверждений: V* \ Mt, М± (J Мг,
Мг П — разрешимые, а Ма (J Ма, Ма (~| Mt, Мг (J Ма, Mt П Ма —
перечислимые множества.
В. Покажите, что область определения любой вычислимой функции —
перечислимое множество.
Г. Покажите, что непустое множество перечислимо тогда и только то-
гда, когда оно является областью значений некоторой частичной вычислимой
Функции.
2.2. Проблема остановки. Машина Тьюринга, начав работу
над некоторым начальным словом на ленте, или останавливается,
или работает бесконечно. Было бы полезно иметь алгоритм, не-
который для любой машины Тьюринга Т над алфавитом V и для
любого слова а в этом алфавите выяснял, остановится ли машина,
начав работу над словом а.
Проблему остановки можно сформулировать также в терми-
нах множеств. Пусть Мя — множество всех пар слов в алфави-
те V, в каждой паре первое слово — словарное представление не-
1»
которой машины Тьюринга, второе — такое слово, что эта машина
останавливается, начав работу над ним. Является ли множество
М, неразрешимым?
Теорема 1.2 (Тьюринг). Проблема остановки машин
Тьюринга неразрешима.
Доказательство. Необходимо установить, является
ли вычислимой характеристическая функция Fms‘ V*2 {0, 1).
Предположим, что это так и TF — машина Тьюринга, вычисляю-
щая эту функцию. Из вычислимости функции FMg и разрешимости
множества Mt словарных представлений машин Тьюринга в ал-
фавите V следует вычислимость частичной одноместной функции
G: V* -► {0, 1), которая задается следующим образом: G (а) —
— Fm, (а. а) для всех а GE Mt vlGho определена для всех а Mt.
Функция G концентрирует внимание на машинах Тьюринга,
применяемых к собственным словарным представлениям.
Введем еще одну частичную одноместную функцию К: V* —>
-> {0}. Эта функция определена только для тех слов, для которых
G (а) = 0, причем для всех этих слов К (а) = G{a) — 0. Функция К
вычислима, если вычислима функция G. Действительно, машина
Тьюринга Тк совпадает с машиной Tg за исключением случая,
когда Tg останавливается: машина Тк продолжает работу, выяс-
няет, каков результат — 1 или 0, и в первом случае зацикливает-
ся, во втором — останавливается.
Пусть Рк — словарное представление машины Тк в алфавите V.
Попробуем выяснить, определено ли значение К (Рк), т. е.
попробуем решить проблему остановки для пары — машины Тк
и ее словарного представления. Допустим, что значение К (Рк)
не определено, т. е. машина Тк не останавливается, начав работу
над словом рк. Тогда FMs (Рк, Рк) = 0, G (рк) = 0 и К (Р«) = 0,
т. е. значение ЙГ(Рк) определено, что противоречит предположе-
нию. Предположим теперь, что значение К (Рк) определено, т. е.
машина Тк останавливается, начав работу над словом Рк. Тогда
Fms (Рк, Рк) = 1, G (Рк) = 1 и К (Рк) не определено, что также
противоречит предположению.
Оба допущения о функции К приводят к противоречию, что
опровергает гипотезу о вычислимости функции Fm и разреши-
мости множества Мя. Q
Теорема 1.2 устанавливает неразрешимость проблемы оста-
новки для машин Тьюринга и демонстрирует существование не-
вычислимых функций (характеристическая функция /м). Из
тезиса Тьюринга следует, что для неразрешимых проблем нельзя
построить алгоритм, который решал бы их «механически», напри-
мер, с помощью ЭВМ. Это означает, что неразрешимая проблема
представляет собой слишком общую задачу, включающую неко-
торые «вырожденные» случаи (как, например, работу машины Тк
над собственным словарным представлением). Попытки упрос-
тить неразрешимые проблемы путем исключения особых случаев
20
могут значительно обеднить их, сделать тривиальными с точки
зрения практики. В частности, теорема 1.2 не исключает возмож-
ности, что проблема остановки может оказаться разрешимой для
некоторого узкого класса машин Тьюринга.
Задание 1.4.
А. Покажите, что проблема остановки машин Тьюринга является час-
тично разрешимой.
Б. Покажите, что проблема остановки разрешима для класса машин
Тьюринга, программа которых содержит лишь одну команду.
2.3. Проблема пустой ленты и метод сведения. Попробуем
установить, разрешима ли более частная проблема остановки,
а именно остановка машин Тьюринга, применяемых к пустой лен-
те, т. е. к ленте, содержащей только символ *. Другими словами,
надо выяснить, является ли разрешимым множество МЕ словар-
ных представлений всех тех машин Тьюринга, которые останав-
ливаются, начав работу над пустой лентой.
Теорема 1.3. Проблема пустой ленты неразрешима.
Доказательство. Каждой паре (71, а), где Т — не-
которая машина Тьюринга, а а — слово в ее алфавите, сопоста-
вим машину Та, программа которой совпадает с программой ма-
шины Т, за исключением того, что, начав работу, машина Та
стирает начальное слово на ленте и вместо него записывает слово
а. Конструкция машины Та очевидна: к программе машины Т
добавляются подходящим образом команды машины из зада-
ния 1.2А.
Машина Та, начавшая работу с пустой лентой, ведет себя
после записи слова а так же, как и машина Т, примененная к а.
В частности, машина Т остановится в том и только в том случае,
если остановится машина Т. Предположим, что проблема остан вки
машин Тьюринга с пустой лентой разрешима. Тогда окажется
разрешимой проблема остановки в общем случае. Действительно,
чтобы узнать, останавливается ли некоторая машина Т, применен-
ная к слову а, следует сконструировать машину Та. Выяснив,
останавливается ли Та при пустой ленте, мы тем самым узнаем,
останавливается ли Т. Это противоречит теореме 1.2, что и опро-
вергает предположение о разрешимости проблемы пустой ленты. | |;
В только что проведенном доказательстве использована сле-
дующая схема рассуждений: выполнив некоторые вспомогатель-
ные построения, мы предполагаем разрешимость исследуемой
проблемы, что в силу проведенных построений дает нам возмож-
ность решать другую проблему, о которой, однако, известно, что
она неразрешима. Полученное противоречие доказывает нераз-
решимость исследуемой проблемы. Такой метод доказательства
называют методом сведения', известная неразрешимая проблема
сводится к исследуемой, поэтому последняя также неразрешима.
Метод сведения используется и в случае, когда доказывается,
что рассматриваемая проблема ие является частично разрешимой.
Метод сведения широко применяется и в теории схем программ.
21
Как правило, осуществляется последовательный многоступенча-
тый процесс сведения одних проблем к другим, и часто «базовой»
неразрешимой проблемой в этой цепочке оказывается проблема
остановки машин Тьюринга. (Однако метод сведения не универ-
сален, так как существуют взаимно несводимые неразрешимые
проблемы [61].)
Другая «базовая» неразрешимая проблема, часто используемая
в доказательствах методом сведения,— проблема тождества слов
Поста [132]. Она формулируется следующим образом.
Пусть X = (ах, а2, . . ., ап) и Y = (рх, р2, . . ., рп) — два рав-
ной длины набора слов в алфавите V. Пару (X, У) называют
системой Поста. Непустую конечную последовательность индек-
сов i'j, i2, . . ., ik, где все индексы >1 и называют решением
системы Поста, если . . aik — Pi,Pi, . . . Pik (слева и спра-
ва слова, полученные конкатенацией выбранных слов соответст-
венно из X и У). Существует ли алгоритм, который обнаруживает,
имеет ли система Поста решение? Пост показал неразрешимость
этой проблемы для алфавитов, содержащих более одного символа.
В то же время проблема Поста частично разрешима.
Задание 1.5.
А. Проблема тотальности для машин Тьюринга состоит в следующем:
существует ли алгоритм, который для любой машины Тьюринга Т узнает,
будет ли машина останавливаться при любом начальном слове на ленте (дру-
гими словами, является ли функция FT всюду определенной)? Покажите
{методом сведёиня) неразрешимость этой проблемы.
Б. Машины Тьюринга Т н Т' эквивалентны, если FT — FT,. Проблема
эквивалентности машин Тьюринга состоит в обнаружении алгоритма, ко-
торый для любой пары машин Тьюринга смог бы установить, эквивалентны
они илн нет. Покажите (методом сведения), что проблема эквивалентности
неразрешима.
2.4. Проблема зацикливания. Установив существование не-
разрешимых проблем и множеств, продемонстрируем существо-
вание неперечислимых множеств и проблем, которые не являются
частично разрешимыми. Проблема зацикливания состоит в сле-
дующем: существует ли алгоритм, хотя бы частичный, который
выясняет заранее для произвольной машины Тьюринга и про-
извольного начального слова а, будет ли машина работать беско-
нечно долго, т. е. надо установить, будет ли разрешимым или
перечислимым множество Мс CZ V*2 всех пар слов таких, что
первое слово — словарное представление некоторой машины Тью-
ринга, а второе — слово, на котором зта машина зацикливается.
Теорема 1.4. Проблема зацикливания машин Тьюринга
не является частично разрешимой.
До казательство. Из теоремы 1.1 иперечислимости
множества М3 (см. п. 2.2) следует, что дополнение Ms множества М,
до множества всех пар слов в алфавите V неперечислимо, так как
в противном случае оказалось бы разрешимым множество М3.
Но Ma = Мс (J Мц, где Ма — множество всех пар слов, первые
слова в которых являются словарными представлениями машин
22
Тьюринга, a Md — его дополнение. Так как множество Mt всех
словарных представлений машин Тьюринга разрешимо, множество
Md и множество Md разрешимы (см. задание 1.3Б).
Предположим, что проблема зацикливания частично разре-
шима, а множество _Л/С — перечислимо. Тогда окажется перечис-
лимым множество Ms, что неверно. 0
Обратите внимание, что разрешимые множества могут вклю-
чать (как собственные подмножества) перечислимые множества,
которые, в свою очередь, могут содержать неперечислимые под-
множества. Это означает, что разрешимые множества отличаются
не меньшей количественной мощностью, а «меньшим разнообра-
зием» своих элементов.
Задание 1.6. Покажите, что не являются частично разрешимыми
следующие проблемы:
А. Проблема зацикливания машин Тьюринга с пустой лентой.
Б. Проблема тотальности машин Тьюринга.
В. Проблема пустоты машин Тьюринга (машина пуста, если она за-
цикливается при любом начальном слове).
Г. Проблема эквивалентности машин Тьюринга.
Д. Проблема пустоты систем Поста (система Поста пуста, если она
не имеет ни одного решения).
Краткий обзор и комментарии
Понятие вычислимости основывается на двух тесно взаимо-
связанных ПОНЯТИЯХ — ПОНЯТИИ ВЫЧИСЛИМОЙ функции и понятии
алгоритма. Вычислимая функция — это функция, для которой
существует алгоритм нахождения значений вычислимой функции.
Оба понятия в интуитивной форме существуют века, но до 30-х гг.
этого столетия они играли роль методологических концепций,
а не точных математических объектов. Формализация вычисли-
мости была осуществлена двумя способами. Черч и Клини опре-
делили вычислимые функции, отождествив их с рекурсивными.
Черч [91] высказал гипотезу о тождественности класса рекурсив-
ных функций и класса всюду определенных вычислимых функций,
и эта гипотеза известна как тезис Черча. Клини [113] определил
понятие частичной вычислимой функции и обобщил тезис Черча,
постулировав тождественность этого. класса функций классу
частично рекурсивных функций. С другой стороны, Пост [131)
и Тьюринг [141] уточнили понятие алгоритма и через алгоритм*
определили класс вычислимых функций. Согласно данному уточ-
нению, алгоритм — это процесс, совершаемый некоторой гипоте-
тической машиной, конструируемой в рамках точных математи-
ческих понятий. Машины Поста и Тьюринга отличаются в несу*
щественных деталях, но общее у них то, что они с помощью
ограниченного набора средств могут имитировать все известные
интуитивные алгоритмические процессы. Класс функций, значении
которых можно находить с помощью машин Тьюринга — Поста,
был объявлен классом вычислимых функций (тезис Тьюринга),
ИГ.
я было показано, что такое определение вычислимых функций
эквивалентно определению Черча — Клини. Позднее предла-
гались другие способы формализации понятий алгоритма и вы-
числимой функции — более сложные «машины» или, наоборот,
системы с минимумом средств, как, например, нормальные алго-
ритмы Маркова [40]. Они могут быть более удобными для ка-
ких-нибудь специальных целей или классов алгоритмов, но они
эквивалентны «классическим» формализациям.
Уточнение понятий вычислимой функции и алгоритма позво-
лило формализовать понятие существования решения массовых
математических проблем, а именно, появилась возможность пере-
формулировать эту задачу как задачу о существовании (частично)
вычислимых функций, кодирующих заданную проблему. (Следует
отметить, что идеи Гильберта и работы Геделя, связанные с ис-
следованием «универсальных разрешающих процедур», обрати-
ли внимание на класс рекурсивных функций и привели к появле-
нию тезиса Черча.) Формализация понятия разрешимости дала
возможность установить существование целого ряда неразрешимых
проблем в различных областях математики. С неразрешимыми
проблемами в теории схем программ мы неоднократно встретимся
в этой книге. Факт существования таких проблем можно тракто-
вать двояко. Можно считать, что проблема неразрешима, потому
что она чересчур обща, включает «ненормальные» ситуации, и ее
нужно переформулировать так, чтобы она содержала только те
жизненные случаи, с которыми имеет дело (и успешно справля-
ется) программист. Но, как уже указывалось, редко удается клас-
сифицировать реальные факты и явления так, чтобы они были
интересными и полезными, оставаясь одновременно в рамках
разрешимых проблем. С другой стороны, можно попытаться обоб-
щить теорию вычислимости и разрешимости так, чтобы неразре-
шимые проблемы «решались» в некотором новом интуитивном
смысле. Но такое обобщение выведет нас за рамки современной
математики.
Литература по теории вычислимости и разрешимости обширна,
Мы приводим лишь классические работы и несколько известных
монографий (39, 44, 61, 71, 74, 95], которые содержат довольно
полную библиографию по этой тематике.
ГЛАВA 2
ГРАФЫ И МЕТОД РАЗМЕТКИ
Понятие графа широко используется в программировании
как средство абстракции при описании таких объектов, как про-
грамма, структура данных, а также при описании алгоритмов рас-
познавания различных свойств программ н при преобразованиях
программ. В теории схем программ ее центральное понятие — схема
программы — представляется в виде размеченного графа. Понятие
разметки вводится как отображение, сопоставляющее вершинам
или дугам графа пометки из некоторого фиксированного множест-
ва пометок. В этой главе вводится терминология, связанная с по-
нятием графа, а также описан метод разметки для решения задачи
глобального анализа свойств.
§ 1. Понятие графа
1.1. Определение графа. Ориентированным мультиграфом
(в дальнейшем просто графом, поскольку других графов мы не рас-
сматриваем). называется тройка
Г = (V, Е, Ф),
где V — множество вершин, Е — множество дуг, а Ф — функ-
ция из Е в (V (J {и})1, а> Оё V. Дуга е называется входом (графа Г),
если Ф (е) = (<а, v) для v GE V (J {<о}; выходом (графа Г), если
Ф (е) = (о, <о) для v G= V U (со); внутренней, если Ф (е) =
= (vi> yi) Для vi> vi V. Дуга е, являющаяся одновременно в
входом, и выходом графа Г, называется висячей', для нее Ф (е)=
— (со, ©). Дуги, не являющиеся внутренними, будут называться
также свободными.
Мы говорим, что дуга е ведет к вершине v, а вершина v явля-
ется концом дуги е, и записываем этот факт как v — кон (е), если
Ф (е) = (п*, v) для v GE V, v' GE V (J (со). Мы говорим, что дуга е
выходит из вершины v, а вершина v является началом дуги е,
и записываем это как v = нач (е), если Ф (е) = (v, v') для v G= У»
i?' Е F U {со}. Заметим, что в наших графах одну и ту же пару
вершин v, v' может соединять (т. е. выходить из v и вести к о')
сколько угодно различных дуг.
Говорят, что дуга е инцидентна вершине v, если е выходит
из v или ведет к v. Две дуги смежны, если существует хотя бы одна
инцидентная им обеим вершина. Множество дуг, смежных дуге е,
25
будет называться окрестностью дуги е и обозначаться окр (е).
Вершина v называется наследником, вершины v', если в графе
имеется хотя бы одна такая дуга е, что Ф (e)=(v’, v).
Изображенный на рис. 2.1 граф Г2Л содержит 4 вершины и 8
ДУГ- Дуга q — входная, дуга ев — выходная, дуга <?8 — висячая,
остальные дуги — внутренние; окр (е4) = {е4, е2, е3, е4, еЛ, ев},
окр (е8) = {е8}; вершины vt и v3 — наследники вершины vt.
Рис. 2.1. Граф Г2Л
Путем в графе Г называется всякая последовательность
...VieiVi+l... такая, что для всех i Ф (е$) — (v,, pi+1). Путь по
вершинам содержит только вхождения вершин, путь по дугам —
только вхождения дуг. Маршрутом в графе Г называется всякая
конечная непустая последовательность дуг . . еп такая, что
для всех i (1 i < п) дуги е, и ei+1 смежны. При этом говорят,
что — начало, а еп — конец маршрута, п — его длина, и что
он ведет от ех к еп. Через марш (е', е) обозначим множество всех
маршрутов графа, которые ведут от е' к е. Заметим, что
марш («', е) — либо пустое, либо бесконечное множество.
Пример: последовательность дуг еве6c3e4e2ei является маршру-
том графа Г2Л, ведущим от е6 к
Наши рассмотрения в большинстве случаев будут ограничены
конечными графами, в которых множества вершин и дуг конечны.
При этом вершины и дуги графа могут снабжаться разного рода
ломе ками. Если граф размечен, то образом пути будем называть
слово, составленное из пометок проходимых дуг или вершин.
Контур — это путь, начинающийся и заканчивающийся в одной
и той же вершине. Более подробно с основными понятиями теории
графов можно познакомиться, например, по книге Харари [75].
1.2. Связность и изоморфизм графов, деревья. Подграфом
графа (V, Е, Ф), порожденным некоторым подмножеством вершин
V' С V, называется граф (V', Е', Ф'), удовлетворяющий следую-
щим условиям:
26
a) E' С E и содержит все дуги из Е, инцидентные вершинам
из Г; >
б) для е ЕЕ Е' Ф' (е) получается заменой на ы тех элементов
нары Ф (е), которые не принадлежат V';
в) Е' не содержит висячих дуг.
На рис. 2.2 изображен подграф графа Г1Л, порожденный мно-
жеством вершин {ylt у2, и3}.
Два графа Г — (У, Е, Ф) и Г' = (V', Е', Ф') называются
изоморфными, если между их вершинами, а также между их ду-
гами можно установить взаимно однознач-
ное соответствие
Д,:У->У', 1е:Е-^Е',
сохраняющее отношение инцидентности, т. е.
V₽e Е Уу2, у2€=У
(ф (е) = (у2, ю) <-> Ф' {1Е (е))=(1с (у2), «)) &
(ф (е) = (о, у2) & Ф' (1Е (е)) = (<о, Д, (у2))) &
(ф (е) = (и, <о) Ф' (1Е (е)) = (ь>, ш)) &
(Ф (ё) = (уп у2) Ф' (ZE (е)) = (Д (yj, Д (у2))).
Две вершины у2, у2 графа Г называются
Рис. 2.2. Подграф
графа Г2Л, порож-
денный вершинами
{i'i, vt, r3}.
связанными, если у2= у2 или существует марш-
рут . . ., графа Г такой, что дуга ег
инцидентна вершине у1т а дуга еп — вер-
шине у2.
Отношение связанности вершин графа
>ефлексивно, симметрично и транзитивно,
т. е. представляет собой отношение эквивалентности на множе-
стве вершин графа. Это означает, что множество V вершин
графа Г разбивается на классы Vlt . . ., Ук попарно связанных
вершин. Подграфы Г, — (У{, Ei, Ф<), порожденные множествами
Vi, не имеют друг с другом общих вершин и дуг и называются
Компонентами связности графа Г. Компонентами связности гра-
фа Г будем называть также каждый из графов (0, {е}, Ф),
Ф (<?) = (<о, «), где е — висячая дуга графа Г.
Граф называется связным, если он содержит не более одной
змпоненты связности.
Связный граф Г без контуров называется деревом, если:
(1) в Г имеется ровно одна вершина, называемая корнем де-
ржа, к которой не ведет ни одна из внутренних дуг графа Г-;.
(2) к каждой из остальных вершин ведет ровно одна внутрен-
кя дуга графа Г;
(3) все входные дуги графа Г ведут к корню.
Вершины, из которых не выходит ни одна из внутренних дуг
;рева, называются листьями этого дерева.
27
§ 2. Метод разметки и задача глобального анализа
2.1. Неформальное введение. Под разметкой мы понимаем
отображение, сопоставляющее пометки вершинам или дугам
графа. Метод разметки используется для построения алгоритмов
распознавания различных свойств размеченных графов. Понятие
пометки формализует при этом интересующее нас свойство графа
или его частей. В качестве анализируемого размеченного графа
будет выступать обычно схема программы. Метод разметки исполь-
зует тот факт, что свойства вершины графа определяются свойст-
вами некоторых «соседей» этой вершины.
Для иллюстрации основной идеи алгоритмов разметки опи-
шем алгоритм такого типа для решения одной очень простой
задачи: определения достижимости вершин ориентированного
графа от некоторой выделенной его вершины, называемой на-
чальной. Вершина v достижима от начальной, если существует
путь, ведущий от начальной вершины к вершине v. Множеством
пометок здесь будет служить множество, составленное из двух
значений, которые мы назовем «достижима» и «неизвестно» соот-
ветственно. Начальная разметка сопоставляет пометку «дости-
жима» начальной вершине графа и «неизвестно» всем остальным
вершинам. Дальнейший процесс построения необходимой размет-
ки будет состоять в повторном применении правила разметки:
если некоторая вершина помечена пометкой «достижима»,
то
пометить пометкой «достижима» все наследники этой вершины.
Процесс завершается, когда будет достигнута стационарная раз-
метка, т. е. такая, которая не изменяется никаким применением
правила разметки.
Отметим две особенности процесса разметки. Во-первых, сразу
же возникает вопрос о том, существует ли хотя бы одна стацио-
нарная разметка. Иначе говоря, может ли завершиться процесс
разметки?
Другой вопрос связан с единственностью стационарной размет-
ки. Дело в том, что процесс разметки описан как недетермини-
рованный в том смысле, что на каждом его шаге имеется возмож-
ность выбирать, к какой из вершин применять правило разметки
Верно ли, что результирующая стационарная разметка (если она
существует) не зависит от того, в каком порядке и к каким вер-
шинам будет применяться правило разметки?
Для нашей простой задачи положительный ответ на оба воп-
роса довольно очевиден. Кроме того, легко доказать, что вершииа
достижима от начальной тогда и только тогда, когда она имеет
пометку «достижима» при стационарной разметке. На рис. 2.3
описанный процесс применяется к графу с пятью вершинами. На
этом рисунке пометка «достижима» изображена символом «*».
а пометка «неизвестно» — отсутствием какого бы то ни было сим-
вола. В дальнейшем нас будут интересовать преимущественно
28
такие процессы разметки, когда ответ на оба сформулированных
выше вопроса положителен, т. е. когда стационарная разметка
существует и единственна. Такие процессы будут называться ал-
горитмами разметки. При этом условие существования стацио-
нарной разметки достигается благодаря тому, что процесс разметки
определяется как некоторый монотонно сходящийся процесс.
Именно, на множестве пометок вводится частичный порядок,
соответствующий уменьшению «неопределепнрсти» содержащейся
в них информации, а процесс разметки организуется таким обра-
зом, что пометки одной и той же вершины в ходе этого процесса
а в в
Рис. 2.3. Иллюстрация процесса разметки
могут только уменьшаться. Тогда для существования стационар-
ной разметки достаточно потребовать, чтобы все строго убываю-
щие цепи в множестве пометок были конечными.
В нашем примере можно определить «неизвестно» > «дости-
жима» и заметить, что правило разметки может только уменьшать
неопределенность отметок вершин, но не увеличивать ее. Кроме
того, можно отказаться от некоторых «холостых» применений пра-
вила разметки, когда они не меняют ни одной из пометок вершин-
наследннков, как, например, применение правила разметки к вер-
шине с номером 1 при разметке на рис. 2.3, б. Для этой цели
вводится понятие множества активных вершин таким образом,
что на каждом шаге процесса разметки выбор вершины, к которой
применяется правило разметки, делается нз этого множества
{применение правила разметки к каждой из остальных, пассивных
вершин ничего не изменило бы). При этом правило разметки долж-
но определять теперь не только изменение разметки, нои моди-
фикацию множества активных вершин.
Новая формулировка алгоритма разметки для нахождения
вершин графа, достижимых от начальной, запишется следующим
образом.
Начальная разметка.
Начальная вершина: «достижима».
Остальные вершины: «неизвестно».
Множество активных вершин: начальная вершина.
29
Правило разметки.
Взять любую из активных вершин (с удалением ее из мно-
жества активных). Пометить пометкой «достижима» все на-
следники этой вершины. Если при этом пометка некоторой
вершины меняется (с «неизвестно» на «достижима»), то доба-
вить эту вершину к множеству активных.
В новой формулировке условие достижения стационарной раз-
метки заменяется условием пустоты множества активных вершин.
2.2. Формальная постановка задачи глобального анализа.
Полурешеткой называют множество L с заданной на нем бинар-
ной операцией пересечения Д, которая обладает следующими
свойствами:
Ух, у, z Е А х /\х — х идемпотентность
х Д у = у Д х коммутативность
х /\ (У A z) ~ (х Л У) Л z ассоциативность.
Частичный порядок на элементах полурешетки вводят, полагая
по определению
Х^у<^х/\у — X,
х<су^х/\у~х&х^=у.
Мы будем писать также хЕ> у вместо у х и х у вместо у < х.
Операцию пересечения распространим на произвольные непус-
тые конечные множества, полагая
-Д г; = х1Дх!Д...Дхп.
1^£<п
Говорят, что полурешетка L содержит нуль 0, если Ух GE L
0 Д х = О. Единицей полурешетки называют элемент “3 такой,
что Vx GE L 1! Д х = х. Всякая последовательность хя, х2, . . *.
элементов из L такая, что Vi х; xi+1, называется строго убы-
вающей цепью (с началом хх). Мы говорим, что L является полу-
решеткой с обрывающимися цепями, если все ее строго убываю-
щие цепи конечны; ограниченной, если для всякого х ЕЕ L сущест-
вует такое число Ъх, что длины всех строго убывающих цепей
с началом х ограничены числом Ъх.
Пример 1. £ь = {0, 1), ОД 1 = 1 Д 0 - 0, 1 Д 1 — 1.
L — ограниченная полурешетка.
П р и м е р 2. Lj = {®, D } (J {al | (i > 1) & (1 j i)},
Ух££1гДО = ОДх = О, X Д Я = Я Д х = х,
а* = ( аГах0' °, если i = к.
Заметим, что Lx удовлетворяет условию обрыва цепей, но ограни-
ченной не является.
В дальнейшем, если не оговорено особо, будем предполагать,
что L — полурешетка с обрывающимися цепями. Для таких
полурешеток операцию пересечения можно распространить на
30
произвольные непустые, не более чем счетные множества S следую-
щим образом. Пусть S = {х15 хг, . . .} — счетное множество эле-
ментов из L, уп = /\ xt. Тогда в силу условия обрыва цепей
последовательность р, >= у2 Е>. . . может содержать только ко-
нечное число различных элементов, т. е. Зт Уп (л > m =>
~*Уп = Ут)- Мы определим тогда Л х = Ут-
xes
Лемма 2.1. Для непустых, не более чем счетных подмно-
жеств S полурешетки с обрывающимися цепями
Ух (х Е S => х > у) ==> (Д х) > у.
xes
Доказат е л ь с т в о. Поскольку Д х{ — Д х{ для
xfeS l<i^n
некоторого л, утверждение вытекает из
( Л xi)/\y=( Л х1)Д(хпДу)= (Д ®i)Ду=-=Х1Ду=у-О
IsSisgn 1<1*<п l=gi<n
Функция /: L -+ L называется монотонной, если Ух, y<=L
(х у ==> / (х) / (у)); дистрибутивной, если Ух, у (=Lf(x/\
Д У) — / (х) Л / (У)- Условие монотонности эквивалентно, оче-
видно, следующему условию:
Ух, у Е L / (х Д у) < / (х) Д / (у),
поэтому всякая дистрибутивная функция монотонна. Заметим
также, что суперпозиция монотонных функций монотонна, а су-
перпозиция дистрибутивных функций дистрибутивна.
Окружением для анализа называется тройка (L, Д, F), где
L — полурешетка с операцией пересечения Д и обрывающимися
цепями (полурешетка свойств), F — множество монотонных функ-
ций на L (преобразователи свойств).
Сформулируем теперь, что будет пониматься под задачей гло-
бального анализа графа 'Г в заданном окружении (L, Д, F).
Пусть заданы:
(1) конечный граф Г — (У, Е, Ф),
(2) окружение (L, Д, F),
(3) разметка р0: Е -+ L (начальная разметка),
(4) частичное отображение /: Е X Е -> F (семантическая функ-
ция разметки, которая определена для всякой пары (е', е) смеж-
ных дуг из Е и сопоставляет этой паре некоторую монотонную
функцию из F). Эту функцию мы будем называть преобразователем
свойств, соответствующим переходу от е’ к е, и обозначать /f-
Построим отображение g, являющееся распространением /
на произвольные маршруты графа Г. Для шЕ марш (е', е) по-
ложим
idr., если маршрут w состоит из единственной дуги е,
fe1 ° Яши если 3 (г! ЕЕ марш (<?', el) w = wle.
Здесь idr, — тождественная функция на L, Ух Е L idt (х) = х,
а через о обозначена суперпозиция функций на L. Содержательно
31
функция gw описывает, как преобразуются свойства в результате
«прохождения) маршрута w, когда известны преобразователи
свойств, соответствующие переходам к смежным дугам.
Наконец, для дуг е £= Е определим
#(«)= Л Л (Ро («?'))•
ееЕ юемарш (е*. е)
Содержательно Н (е) можно интерпретировать как максималь,
ное из свойств, имеющих место для дуги е независимо от того-
каким маршрутом можно попасть к е.
Задача глобального анализа графа Г в заданном окружении
(L, Д, F) при заданных начальной разметке ц0 и семантической
функции / и состоит в нахождении свойств Н (е) для всех дуг е
графа Г.
§ 3. Решение задачи глобального анализа
3.1. Процесс разметки. Пусть требуется решить задачу гло-
бального анализа графа Г в заданном окружении (Z, Д, F) для
начальной разметки р0 и семантической функции /. Для этой
цели мы можем использовать недетерминированный процесс раз-
метки, основанный на применении правила разметки. Если имеет-
ся некоторая разметка графа Г, то применением правила разметки
к паре (е', е) смежных дуг этого графа называется следующая опе-
рация изменения этой разметки.
Правило разметки.
Заменить пометку у дуги е на пометку
У Л /г (х)>
где х — пометка дуги е'.
Начальную разметку, а также всякую, которая может быть
получена из нее некоторой последовательностью применений пра-
вила разметки к парам смежных дуг, назовем достижимой размет-
кой графа Г. Достижимая разметка называется стационарной,
если она не изменяется никаким применением правила разметки.
Эти определения описывают недетерминированный процесс
разметки. Наша ближайшая цель состоит в том, чтобы при сделан-
ных предположениях о задаче глобального анализа доказать
существование и единственность стационарной разметки.
Лемма 2.2. Стационарная разметка существует для любой
задачи глобального анализа.
Доказательство. Поскольку у Д (х) у, из опре-
деления правила разметки следует, что пометки одной и той же
дуги графа в ходе процесса разметки могут только уменьшаться.
Далее, поскольку все строго убывающие цепи полурешетки ко-
нечны, а дуг в графе также конечное число, процесс уменьшения
пометок не может быть бесконечным. Q
32
Замечание. Если полурешетка свойств является ограничен-
ной, то можно указать и верхнюю оценку количества применений
правила разметки, достаточного для получения стационарной
разметки. Такой оценкой будет, очевидно, число |£|-шах6цд,),
гек
где | Е | — количество дуг графа Г, а Ьх — число, ограничиваю-
щее сверху длины всех строго убывающих цепей с началом х.
3.2. Безопасность и единственность стационарной разметки.
Назовем безопасной всякую разметку р: Е -* L графа Г, прн
которой р (е) Н (е) для всех дуг е в Г. Свойство безопасности
разметки можно интерпретировать как ее корректность. Как мы
увидим позже (см. п. 3.3), точное решение задачи глобального
анализа не всегда возможно, поэтому мы заинтересованы в полу*
чении приближенных решений, когда для е ЕЕ Е определяется
какая-то «часть» свойства Н (е). Такими приближенными решения-
ми служат безопасные разметки.
Теорема 2.1. Всякая стационарная разметка безопасна.
Доказательство. Нужно доказать
рс(е)<Я(е) = Д Д gw(p0(e'))
t'e.E «емарш <е'. е)
для стационарной разметки рс и для всех дуг е графа Г. В силу
леммы 2.1 для этого достаточно показать
Ve, е' Е £ VwE марш (е‘, е) ре (е) < gw (р0 (е')).
Это утверждение докажем индукцией по длине маршрута w.
Для маршрутов w длины 1 имеем w = е' = е, поэтому
gw С1*о (И) = idr. (Но (₽)) = Но (е) > Рс (е).
Пусть рс (е) gw (Но(е')) Для всех е, е' ЕЕ Е и для всех маршру-
тов w’ ЕЕ марш (е', е), длина которых меньше к (к 1), a w —
маршрут длины к из марш (е', е). Тогда w = иЛе для некоторого
ш1 ЕЕ марш (₽', el) и el Е окр (е). Условие стационарности рс
дает
Нс (<?) = Нс (е) Л /е1 (Нс (el)),
т. е.
Нс (₽) < /? (Нс (el)).
Используя монотонность функции /е1 и индуктивное предположе-
ние для ud, получаем
Нс (е) < Л1 (Нс (el)) < fe1 (gwi (Но (е'))) = gw (Но (₽'))•□
Для доказательства единственности стационарной разметки
введем отношение частичного порядка на разметках графа Г,
полагая
Hi < Нг & Уе е Е pj (е) < р2 (е).
Теорема 2.2. Всякая стационарная разметка рс является
наибольшим среди решений системы уравнений
Уе^Е р(е) = р(е)А( А £'(н(е'))), <♦)
е'еокр(е)
2 В. Е. Котов, В. К. Сабельфельд 33
не превосходящих р0, т. е. для любого решения р этой системы
уравнений выполнено условие (ц => р цг).
Доказат е л ь с т в о. Покажем, прежде всего, что всякая
стационарная разметка рс — это решение системы (»), не прево-
сходящее ц0. В самом деле, условие стационарности рс дает
Ve е Е Уе' е окр (е) рс (е) = ре (е) Д f' (рс (е')),
откуда
р«(е) = Л (М*)Л£(М«'))) = Ме)Л( Л £ (ре (₽')))-
е'еокр(г) е'еокр(е)
Итак, рс — решение системы (*), не превосходящее р0. Пусть
р — какое-то другое решение (♦), не превосходящее р0. Покажем,
что тогда р рс. Для этого достаточно убедиться, что р р’
для всех достижимых разметок р'. Для начальной разметки это
неравенство выполнено по условию. Пусть оно верно для дости-
жимой разметки р', а разметка р" получается из р' применением
правила разметки к паре смежных дуг (е', е). Тогда
Н" («) = М' (е) Л ft (Н (е')) > I* (•?) Л fe (Н («')) = Р (*)•
Для всех остальных дуг elt отличных от е, имеем
И" (₽i) = Н' (ъ) > I4 fa)- □
Следствие. Стационарная разметка единственна.
Коклмт е л ь с т в о. Если р1т рг — две стационарные
разметки, то из теоремы 2.2 вытекает, что Pi ра и р2 Pi,
т. е. р1 = рг. □
3.3. Точное решение задачи глобального анализа. Здесь мы
покажем, что общая задача глобального анализа является, вооб-
ще говоря, алгоритмически неразрешимой. Кроме того, будут
указаны достаточные условия, при которых стационарная раз-
метка является точным решением задачи глобального анализа.
Теорема 2.3. Не существует алгоритма, который строил
бы точное решение для всякой задачи глобального анализа.
Доказат е л ь с т в о будет получено сведением проблемы
тождества слов Поста (см. п. 2.3 в гл. 1) к некоторой задаче гло-
бального анализа. Пусть (X, Y) — система Поста X — (аг, . . .
. . ., ап), Y = (Plt . . ., 0„), где а4, 0,- — слова в алфавите {0, 1}.
Зафиксируем полурешетку свойств
{х, если х — у,
A -L
®, если x=f= у.
Такая операция пересечения, очевидно, коммутативна, ассоциа-
тивна и идемпотентна, а длины всех строго убывающих цепей
в L ограничены числом 2, поскольку х < у возможно лишь при
х = О. Зафиксируем монотонные функции окружения.
Е = {id, Лх, Л2, glt . . ., j'n),
34
где
Vi (1 «С i < n) Va, p e= {0, !}♦
gi ((a. ₽)) = (a«i. ₽₽i).
gi (®) = 0, gi (S) = S; Vie Z id (x) = r,
Vx^L hj(x) = S; M®) = ®, ft(S) = S,
{0, если a — B,
S, если a^£=ft
Для доказательства монотонности функций ht и gt (i = 1, . . .
. - n) будем использовать тот факт, что x<Zy для х, у ЕЕ L
влечет х = 0. Поэтому
t>n
Рис. 2.4. Граф Гм
х < у =>Л2 (х) = Л2 (0) = 0 < Л2 (у)
и
х < У =^gi (х) = g4(0) = ® < gi (у).
Монотонность функций id и hr
очевидна — они даже дистрибу-
тивны. В качестве анализируемого
графа рассмотрим граф Г2.2, изо-
браженный на рис. 2.4. В этом
графе ровно 2n +1 дуг,, которые
мы обозначили соответственно
at, . . ., ап (входы), bt, . . ., bri (внутренние дуги), с (выход).
В качестве начальной разметки р0 возьмем
Vi (1 < i < п) р0 (а;) = (аг, ft), р0 (ft) = ц0 (с) = S-
Семантическую функцию определим следующим образом: для
всех i, j (1 < i, j «)
a. b. c b. c a. b.
fbj ~ fbf = gj, ~ faf ~ fb, == /с ~ jc —
, ( id, если i = i,
h — ld* fa\ — I если t
Для доказательства теоремы осталось заметить теперь, что
Н (с) = S для сформулированной задачи глобального анализа
выполняется тогда и только тогда, когда система Поста (X, У)
не имеет ни одного решения. Описанное сведение позволило бы
решать проблему тождества слов Поста, если бы существовал
алгоритм решения общей задачи глобального анализа. Q
Несложная модификация описанного выше сведения позволяет
доказать и более сильное утверждение: существует окружение
(L, Л, ^)» граф Г и семантическая функция / такие, что не су-
ществует алгоритма, который по всякой начальной разметке
давал бы точное решение задачи глобального анализа графа Г
в фиксированном окружении (L, Д, F) и для фиксированной
семантической функции /.
2*
/35
Условия, достаточные для того, чтобы можно было аффектив-
но находить точное решение задачи глобального анализа, дает
следующая
Теорема 2.4. Если в окружении для анализа все преобра-
зователи свойств дистрибутивны, то стационарная разметка ре
дает точное решение задачи глобального анализа, т. е.
УеЕЕ рс (е) = Я (е).
Доказательство. Учитывая безопасность стационар-
ной разметки, достаточно показать
УеС=Е рс(е)>Я(е).
Докажем для этого, что для всех достижимых разметок ц графа Г
имеет место Ve G £ р (е) >= Я (е). Для начальной разметки р№
получаем
&е<=Е р0(е) = g«(p0(e))> Л Л (Ро (*'))=# (*)•
г'еЕ ксмарш (е*. е)
Пусть это утверждение справедливо для достижимой разметки р,
а р' получается из р применением правила разметки к паре дуг
(е\ е). Тогда
р' (е) = р (е) Д Л' (Р («')) > Н (е) Д /Г (Я (е)) =
= Я(е)ДД(Д Д ^ш(р0 (₽!») =
г,&Е WGMapui (г,, е)
= Я (е) Д ( Д Д f, {gw (Ро (в!)))) >
г,&Е WGMapui (е„ е')
>Я(е)Д(Д Д £ш(Ро(«1)))-Я(е)ДЯ(е) = Я(е).
«емарш (е„ е)
Для всех остальных дуг е1г отличных от е, имеем р' (q) —
- р (ej >Я (е). □
Итак, стационарная разметка дает безопасное приближение
к точному решению в случае общей задачи глобального анализа
и точное решение в случае задачи анализа с дистрибутивными
преобразователями свойств. Для получения стационарной размет-
ки можно строить разные детерминированные алгоритмы за счет
фиксации порядка применения правила разметки к различным
парам смежных дуг, а также за счет исключения таких примене-
ний правила, которые заведомо ие изменяют разметку. Ниже
описан один из таких алгоритмов.
Алгоритм А.
Параметры алгоритма: граф Г; операция пересечения Д не-
которой полурешетки, удовлетворяющей условию обрыва цепей;
семантическая функция /; начальная разметка р0.
Инициализация. Объявить активными те дуги е’ графа Г,
для которых
Зе е окр (е') р0 (е) #= £ (Ро («'))•
38
Итерация. Пока множество активных дуг непусто, повторять
следующий
Шаг итерации: взять активную дугу е'; пусть х — ее пометка.
Удалить е из множества активных дуг. Заменить пометку у каж-
дой из дуг е, смежных с е, на пометку у /\ft (х) и объявить дугу
с активной, если оиа изменяет при этом свою пометку.
Выход алгоритма: стационарная разметка графа Г.
Задание 2.1. Задачу глобального анализа назовем прямой, если
полурешетка свойств содержит единицу, а семантическая функция та-
кова, что ft =£ fl <=> нач (е) = кок («'); обратной, если fl е L и £ ¥= fl <=>
«=> нач (е') = кои (е).
А. Сформулируйте прямую задачу глобального анализа с дистрибутив-
ными преобразователями свойств для нахождения всех вершин графа, до-
стижимых от некоторого заданного подмножества его вершин.
Б. Сформулируйте обратную задачу глобального анализа с дистрибу-
тивными преобразователями свойств для нахождения всех вершин графа,
от которых нет ни одного пути к некоторому заданному подмножеству вершин
«сходного графа.
Задан н е 2.2. Для каждой дуги графа указана ее длина — неко-
торое положительное число. Весом пути назовем сумму длин составляющих
«го дуг, а расстоянием между вершинами н vt — минимальный средн
всех путей, ведущих от к vt. Сформулируйте прямую задачу глобального
анализа с дистрибутивными преобразователями свойств для нахождения рас-
стояний от некоторой выделенной вершины до каждой из остальных вершин
графа.
Краткий обзор и комментарии
Метод разметки впервые был использован А. П. Ершовым [15]
как средство сбора нелокальной информации в схемах Янова.
Килдел [112] предложил алгебраизацию объектов-свойств и сфор-
мулировал алгоритм нахождения точного решения задачи гло-
бального анализа в случае дистрибутивности всех преобразова-
телей свойств. Кзм и Ульман [109] ввели понятие окружения для
анализа и доказали алгоритмическую неразрешимость задачи
анализа в общей постановке. Во всех этих работах рассматрива-
лись задачи одностороннего анализа, когда свойства вершины
определяются свойствами только ее предшественников (прямая
задача) или, наоборот, только свойствами ее наследников (обрат-
ная задача). Попытка рассмотрения более общей задачи, когда
свойство вершины графа может зависеть как от свойств наслед-
ников, так и от свойств предшественников, была предпринята
Касьяновым [25], предложившим алгоритм ее приближенного ре-
шения при дополнительных ограничениях на структуру свойств.
Обобщение задачи глобального анализа, описанное в настоящей
главе, было предложено Сабельфельдом [68]. Приложения метода
разметки к задачам нахождения конкретных свойств схем про-
грамм будут описаны в последующих главах книги. Что касается
графов, то литература по этой тематике весьма обширна. Назовем
здесь лишь несколько наиболее известных монографий [51, 20, 75].
ГЛАВА 3
КОНЕЧНЫЕ АВТОМАТЫ
Исследования понятия вычислимости, формализованного
в ЗО-х гг., развивались в дальнейшем в двух главных направле-
ниях. Первое связано с более глубоким изучением и анализом
самого понятия вычислимости, с установлением его связи с ос-
нованиями математики. Второе направление стимулировано появ-
лением вычислительных машин и широким практическим исполь-
зованием алгоритмов в виде программ для ЭВМ. Это направление
связано с конструированием и изучением понятий менее общих,
чем вычислимость, с тем, чтобы сконцентрировать внимание на
«более разрешимых» проблемах, решение которых могло бы дать
практический эффект. С этой целью были предложены классы
абстрактных машин, более простых, чем машины Тьюринга,
например, конечные автоматы Рабина и Скотта (133]. Эти и ана-
логичные им автоматы беднее в средствах, но обнаруживают
ряд полезных свойств, непосредственно используемых в теории
схем программ и в теории формальных языков, и имеют довольно
элегантную математическую теорию. Мы не ставим себе целью
изложить подробно эту теорию, а ограничимся лишь определени-
ем некоторых типов конечных автоматов и выделим ряд резуль-
татов, необходимых далее. Более подробно мы рассмотрим здесь
класс многоленточных автоматов и результат Берда о разреши-
мости эквивалентности двухленточных автоматов.
§ 1. Однолеиточные автоматы
1.1. Определение автомата. Конечный одноленточный (одно-
сторонний, детерминированный) автомат над алфавитом V
задается набором А = (V, Q, R, q0, #, I) и правилом функцио-
нирования, общим для всех таких автоматов. В наборе А
V — алфавит;
Q — конечное непустое множество состояний (Q р V = 0);
К С Q — множество выделенных заключительных состояний;
q3 — выделенное начальное состояние;
ф — «пустой» символ;
I — программа автомата, представляющая собой множество
команд; команда — это слово вида qa q', в котором q, q' б- Q,
а €= V, и для любой пары (q, а) существует единственная команда,
начинающаяся этими символами.
38
Неформально конечный одноленточный автомат можно пред-
ставить как абстрактную машину, похожую на машину Тьюринга,
но имеющую следующие особенности:
а) выделены заключительные состояния;
б) машина считывает символы с ленты, ничего на нее не запи-
сывая;
в) на каждом шаге головка автомата, считав символ с ленты и
перейдя согласно программе в новое состояние, обязательно пере-
двигается вправо на одну клетку;
г) автомат останавливается в том случае, когда головка до-
стигнет конца слова, т. е. символа
Говорят, что автомат допускает слово а в алфавите V, если,
начав работу с лентой, содержащей это слово, он останавливает-
ся в заключительном состоянии. Автомат А задает характеристи-
ческую функцию множества Ма допускаемых им слов в алфавите
V. Действительно, его работу можно рассматривать как процеду-
ру распознавания того, принадлежит ли заданное слово множест-
ву Ма, если связать с остановкой в заключительном состоянии
символ 1, а с остановкой в незаключительном состоянии — сим-
вол 0. Поэтому говорят также, что автомат А определяет множест-
во Ма- Однако не для всякого разрешимого множества можно
построить определяющий его автомат. Например, множество всех
правильных слов в алфавите {(,)} (см. гл. 1, § 1, п. 1.4) разреши-
мо, но не существует определяющего
его конечного одноленточного авто-
мата.
Наглядным способом задания
конечных автоматов служат графы
автоматов. Автомат А представляется
в виде графа, множество вершин кото-
рого — множество состояний Q, и из
вершины q в вершину q' ведет дуга,
помеченная символом а, тогда и толь-
ко тогда, когда программа автомата
содержит команду qa-»-q'. Легко
видеть, что граф автомата однозначно
описывает автомат. Работе автомата
над заданным словом соответствует
путь из начальной вершины q0. По-
b ь
Рве. 3.1. Автомат, допускаю-
щий множество слов {anbm I п —
= 1, 2, . . .; m = 1, 2, . . .}
следовательность проходимых вер-
шин этого пути — это последова-
тельность принимаемых автоматом
состояний, образ пути по дугам —
читаемое слово. Любой путь в графе автомата, начинающийся
в вершине q0 и заканчивающийся в вершине q ЕЕ R, порождает
слово, допускаемое автоматом.
Пример конечного одноленточного автомата, допускающего мно-
жество слов {апЬт | п = 1, 2, ; т = 1, 2, ...} в алфавите {а, 6):
А = ({а, Ь}, {д0, q2, gs), {g2}, g0, #, I).
39
Программа I
(рис. 3.1):
9о« -» ft,
9о* 9з,
9з« “* 9з,
?2^ “* ?2,
Чха 91,
91^ ~* 9з»
9за ~* 9з>
9з& 9з-
1.2. Проблемы пустоты и эквивалентности. Автомат А назы-
вают пустым, если Ма = 0. Автоматы Аг и Аг эквивалентны,
если Ма, ~ М А,. Для машин Тьюринга проблемы пустоты и
эквивалентности неразрешимы, более того, они не являются
частично разрешимыми (см. задание 1.6). Ситуация меняется для
конечных автоматов, подтверждением чему служат следующие две
теоремы.
Теорема 3.1 (Рабин—Скотт). Проблема пустоты конеч-
ных одноленточных автоматов разрешима.
Доказат е л ь с т в о. Покажем, что для обнаружения
пустоты множества Ма достаточно подать на ленту автомата над
алфавитом V некоторое конечное множество Ма слов, а именно
все те слова из У*, длина которых меньше числа состояний авто-
мата. Если автомат не допускает ни одного из них, то он пуст.
Если же автомат не пуст, то найдется допускаемое слово, длина
которого меньше числа состояний п. Предположим противное:
пусть а — минимальное допускаемое слово и его длина т больше
или равна п. Выпишем путь (хх, уг, . . ., yit . . ., xj, у}, . . .
. . ., ут, хт+1) в графе автомата, ведущий из начальной вершины
xi — 9о в вершину хт+1 = q, где ? Е Я, и соответствующий ра-
боте автомата над словом а. Число проходимых вершин этого
пути больше п. Поэтому найдется пара вхождений вершин в путь
xt и х} такая, что xt = х} ~ q', где q' СЕ Q. Очевидно, что путь,
полученный из предыдущего удалением участка (у,, . . ., х}),
также описывает работу автомата и ему соответствует слово а',
которое допускается автоматом, но имеет длину меньшую, чем
слово а. Это противоречит предположению, что а — минимальное
допускаемое слово. Г~]
Теорема 3.2 (Рабин — Скотт). Проблема эквивалентно-
сти конечных одноленточных автоматов разрешима.
Доказат е л ь с т в о. Без потери общности можем пред-
положить, что автоматы Аг и А2 имеют общий алфавит V. Пусть
At — автомат над V с тем же множеством состояний, что и авто-
мат и с определяемым множеством слов М^ = V* \ Ма,.
Такой автомат можно построить, заменив множество заключи-
тельных состояний 7?! автомата At на множество \ Rt.
Аналогично можно определить автомат Аа.
Автоматы Аг и Аг эквивалентны тогда и только тогда, когда
МА, П = 0 и МА. П = 0.
40
Таким образом, чтобы установить эквивалентность автоматов Аг
и Ая, следует проверить, пусты ли одновременно автоматы Лэ
и At такие, что
МА, = MAi П M-At * = MAt Г) м2.
Автоматы Ая и At можно построить по автоматам Alt Ая и
Аг, если допустить использование в качестве состояний не только
символы, но и пары символов состояний автоматов и At. Дей-
ствительно, автомат Ая имеет следующий вид:
Ая = (V, Q3 X Q2, Ri X R9, (?oi, <7оз)> -^a)»
где 901 — начальное состояние автомата дог — начальное со-
стояние автомата Ая, 1Я — программа автомата Ая, содержащая
команду (дъ д3) а -► (дя, д4) в том и только том случае, если
программа автомата Аг содержит команду gta -► дя и программа
автомата Аг содержит команду д^д —д4.
Аналогично строится автомат А4. Проблема пустоты конечных
одноленточных автоматов разрешима. Поэтому процедура рас-
познавания эквивалентности автоматов сводится фактически к по-
строению автоматов Ая и А4 и последующему анализу, являются
ли оба построенных автомата пустыми. Q
Задание 3.1.
А. Постройте одноленточные автоматы над алфавитом {а, Ь, с], допускаю-
щие следующие множества слов:
{апЬЬЬ|п>0}, {апсЬ”*|п>1, т > 1}, {(aaW)n| п > 1}.
Б. Покажите, что множество слов { апЬп | п > 1} в алфавите {а, 6} не
определимо никаким одноленточным автоматом.
В. Покажите, что множество правильных слов в алфавите {(,)} (см. гл. 1,
5 1, п. 1.4) не определимо никаким одноленточным автоматом.
Г. Существует лн алгоритм, который для любого автомата А распозна-
ет, является лн множество МА конечным или бесконечным?
Д. Обобщенная функция переходов 6: Q X V* —> Q конечного автомата
А — (V, Q, R, qt, /) определяется таким образом, что 6 (q, х) — это то состоя-
ние, к которому ведет путь, начинающийся состоянием q и образом которого
по дугам является слово х. Более точно,
6(?. г) =
д, если х = е,
д', если х = уа, где у Е V*,
а е V и (б (д, у) a—» q') в I.
Таким образом, МА = {х | 6 (д0, х) Е /{}. Два состояния дх и д, назовем
эквивалентными, если для всех х е У* б (qlt z) е R 6 (gs, z) е R. От-
ношение эквивалентности двух состоянии обладает следующим важным
свойством: если состояния g и д' эквивалентны, то для всех а е V состояния
б (д, в) и б (д', а) также эквивалентны. Кроме того, никакое заключительное
состояние не может быть эквивалентным незаключительному. Поэтому для
распознавания эквивалентности двух автоматов можно действовать следую-
щим образом: предположим, что автоматы эквивалентны; тогда эквивалентны
их начальные состояния, откуда можно вывести Эквивалентность для других
пар состояний, которые, в свою очередь, влекут эквивалентность новых пар
состояний, и т. д. Если в одну из таких пар попадет заключительное состояние
вместе с незаключительным, то исходные автоматы были неэквивалентными.
Если же этого не произойдет, то исходные автоматы эквивалентны.
41
Опишите подробно алгоритм, реализующий сформулированную идею.
Докажите, что он действительно распознает эквивалентность автоматов. От-
метим, что хранение пар эквивалентных состояний в таком алгоритме можно
организовать так, что время его работы будет const-n-G (п), где п — сумма
количеств состояний исходных автоматов (над фиксированным алфавитом V),
a G (п) — очень медленно растущая функция [1J:
F (0) = 1,
F (п) = 2F(”-1) для п > 0,
С (n) = min {к | F (*) > п).
Например, G (л) 5 для всех п < 2’553’.
Е. Если Л] = (V, Qlt Rlt glt /х) и Аг = (V, Q2, R2, q2,12) — два автомата
над общим алфавитом V, то автомат
Л = (V, Q2 X Q2, Ri X R2, (q2, q2), /),
где программа I содержит команду (g, д') a —» (ga, q'a) тогда и только тогда,
когда Ц содержит команду qa —» go, а программа 12 — команду q'a —» ge>
называется произведением автоматов и А2 с отождествлением входов.
Докажите, что МА — МА П мА.
§ 2. Многоленточные автоматы
2.1. Определения. Автоматы, о которых пойдет речь, возник-
ли как попытки обобщения одноленточного, одностороннего, де-
терминированного автомата за счет усложнения его поведения и
увеличения числа лент. Одноленточные обобщения, такие, как
двусторонний автомат, головка которого может перемещаться
вправо и влево, и недетерминированный автомат, очередное состоя-
ние которого выбирается произвольно из некоторого множества
состояний, оказались не более мощными, чем рассмотренный
выше автомат (133]. Это значит, что существуют алгоритмы,
которые по любому обобщенному автомату строят эквивалентный
односторонний детерминированный автомат.
Более интересными оказались многоленточные (детерминиро-
ванные, односторонние) автоматы. Формальное отличие «-лен-
точного автомата (л 2)
А = (V, Q, R, q0, #, I)
от рассмотренного в предыдущем параграфе одноленточного авто-
мата состоит лишь в том, что задано разбиение множества состоя-
ний Q на « непересекающихся подмножеств Qt, . . ., Qn. «Физи-
ческая» интерпретация «-ленточного автомата отличается тем,
что он имеет п лент и п головок, по головке на ленту. Если авто-
мат находится в состоянии q f= Qi (1 С i С в), то г-я головка
читает свою ленту точно так же, как это делает одноленточный
автомат. При переходе автомата в состояние q EzQj (/ =/= Q
t-я головка останавливается, а /-я начинает читать свою ленту.
Автомат останавливается только в том случае, когда головка на
одной из лент прочитала символ
• Мы говорим, что набор слов (ult . . ., wn) над V переводит ав-
томат в состояние q, если для некоторого т 0 существует по-
42
следовательность состояний glt q2, . . ., qm из Q, а также слово
«ja, . . . ат над V такие, что
(a) Vi (1 < i < т) -> qt) GE I,
(б) qm = q,
(в) VA (1 к п) uk — это слово, получаемое последова-
тельным выписыванием всех символов а,- слова а± . . . ат таких,
что qt Ez Q^.
Автомат А допускает набор слов (их, . . ., un), если
3i (1 < i < л) V/ (1 < у < л, у* #= i) За>, а/ такие, что и} =
= а.}а'), а набор слов (ах, . . ., а^, щ, ai+1, . . ., ап) переводит
автомат А в состояние q GE Qt, для которого (q * —* q) GE I и
q e R.
Как и раньше, Ma будет означать множество всех наборов
слов, допускаемых автоматом А. Два автомата и А2 называются
эквивалентными, если Ма, — Ма,-
Приведем пример двухленточного автомата Ag^ = (У, & (J
(J Qt, R, qe, 4#, I), который допускает множество пар лент
{(u, v) | v = ии’ для некоторого слова и}
Гд алфавитом V — {0, 1).
Здесь (Ъ = {</}, ?б), Qt
начальное состояние.
Для описания алгорит-
ма распознавания эквива-
лентности двухленточных
автоматов мы введем в рас-
смотрение упрощенную
форму многоленточного ав-
томата, понятия диаграм-
мы и полудиаграммы.
Пусть 2lt .... 2П —
конечные алфавиты, П
А 2 7 = 0 для i =5^ ]• По-
лудиаграммой (над . . .
... ,2П) называется тройка
{0. 1),
автомата показан на рис. 3.2.
= {£ ql <&}, R = Ш V =
Граф
автомат А
и 2i — функ-
где Fq = (Vq, Eq,\^q) —
размеченный ориентиро-
ванный граф без свобод-
ных дуг, Aq — выделенная Рис. 3.2. Двухленточный
выходная вершина из Vq,
из которой не выходит ни одной дуги, а Pq: Eq -*
ция разметки дуг графа Fq, обладающая следующим свойством:
если из некоторой вершины v е Vq выходит хотя бы одна дуга,
помеченная символом ст 6= 2г, то для всех ст' G имеется дуга
графа Fq, выходящая из v н помеченная символом ст'.
43
Мы будем говорить, что вершина v' является i-наследником
вершины в, если имеется дуга, выходящая из вершины V, которая
ведет к вершине v’ я помечена символом а е Коротко этот
факт будет записываться как v —* v в Q. Когда будет ясно, о ка-
кой полудиаграмме идет речь, мы будем опускать индексы у Г,
Л, р, V, Е, Ф. Полудиаграмма Q называется конечной, если Vq —
конечное множество. Вершина v €= Vq называется свободной,
если она не является выходной и не имеет наследников.
Отображение /: Vq -> Vq' называется морфизмом Q в Q‘
(обозначение /: Q —* Q’), если / (Лр) = Лр' и из v —* v’ в Q сле-
дует / (v) —♦ / (i>') в Q’. Тождественное отображение iq: Vq —» Vq,
а также композиция морфизмов ff: Vq -*• Vq>, определяемая
соотношением (//') (п) = f (f (v)), являются, очевидно, морфиз-
мами. Морфизм /: Q —> Q’ называется изоморфизмом, если сущест-
вует морфизм Q’ —> Q такой, что ff — iq и ff = Iq>. Полу-
диаграммы Q и Q’ изоморфны (обозначение Q sa Q’), если сущест-
вует изоморфизм /: Q —> Q'.
Если дан морфизм /: Q —> Q', то через Im (/) будем обозначать
полудиаграмму, определяемую следующим образом:
a) Fiintf) = {/ (») | v е Vq},
б) ЛтпКУ) = / (Aq),
В) Vi -* V2 в Im (/) <> 3i>!, f2 G Vq
такие, что vr v2 в Q и
Vi (i = l,2) f(Vi) = vi
В дальнейшем мы будем соединять несколько соотношений
таких, как vt, v1->- v3 и v2 -> v„ в Q, следующим образом:
Полудиаграмма D называется диаграммой, если она обладает
следующим свойством детерминированности: из
44
следует, что = н2. Вершина v диаграммы D называется замкну-
той, если из
|б' в D, где о eS,, o'e Sj, i&j,
следует существование такой вершины va G= Vd, что
''г
в' в D .
о
-------~vs
Диаграмма называется замкнутой, если замкнуты все ее вершины.
Схемой Берда называется пара (D, v), где v — вершина диа-
граммы D, называемая входной вершиной схемы, a D — такая
диаграмма, что для всякой вершины v, отличной от выходной,
найдется целое i (1 i п) такое, что v имеет i-наследников в
никаких других.
Заметим, что диаграмма схемы Берда является замкнутой и не
содержит свободных вершин.
С каждым путем w в полудиаграмме Q свяжем набор слов
(ut, . . ., un), определяемых следующим образом: и{ — это слово,
которое получается из последовательности пометок дуг пути ш
выбором символов, принадлежащих и выписыванием их под-
ряд. Если последовательность пометок дуг пути w не содержит
символов из 2г, то ut — пустое слово над алфавитом £ь которое
мы обозначим е{. Для произвольной полудиаграммы Q и вершины
v G= Vq через Tq (у) обозначим множество всех наборов слов,
связанных с путями в Q от вершины v к вершине Aq. Две схемы
Берда (D, v) и (Б', v') называются эквивалентными, если То(г) —
= То' («')•
Пусть Si = {я,, а2), £2 = {fcx, fc2), a D, D' и С — диаграммы
над и 22, приведенные на рис. 3.3. Понятно, что схемы Берда
(D, v} и (D', р2) эквивалентны, а С — замкнутая диаграмма. Вер-
шины этих трех диаграмм помечены для того, чтобы показать
морфизмы из Vd в Vc и из Vd' в Vc.
Теорема 3.3. Для каждого п-ленточного автомата А —
==(£, Q, R, q0, 1} существует такая схема Берда Sh (Л), что
At ~ Л2 О Sh (Лх) ~ Sh (Л2).
Доказательство состоит в построении схемы 8Ь(Л) =
—Ф, г0) по автомату Л. Если S={a1, . . ., ар}, мы возьмем п раз-
личных копий множества £ (J {#}, обозначая их = {а^, . . .
• • •» аг>\ #W), 1 i п. Пусть 5й — семейство множеств,
которое определяется следующим образом:
45
Рис. 3.3. Примеры диаграмм D,D'nC над 2а = {«у, аа), 2а = {Ьа, 6а}
a) Vi (1 < i С ») mt = {1, . . п) \ {/}, mt G 5\
б) если т S? я т 0, то m \ {min (m)} ЕЕ
в) других множеств в Ф нет.
В качестве множества вершин диаграммы D возьмем Vd =
~ Q U {vm I т €= 50 U {р«>}, Ад = v0. Дуги диаграммы D про-
водятся следующим образом:
4»
a) q —► д' в D, если (gat —► q') G= / и q Е= Qj для некоторых
q, q' ЕЕ Q, at ЕЕ 2, у ЕЕ {1, . . п);
#0)
б) д—► vmj в D, если (g# -> д') GE I, q^Qj и д' е Л для
некоторых д, д' ЕЕ Q, j е {1....«};
#0)
в) д—► у» в и, если (д#д') G/, д £ (); и д'Я для
некоторых д, д' G Q, j ЕЕ {1, •. ..«};
ор>
г) vm ► vm И Vm 121 Рт\(Д В D ДЛЯ ВСвХ И G Щ 0,
для всех i — 1, . . р и для j = min (m);
«44 #(D
д) Poo ► Poo и Рао -► Poo в D для всех i = 1, . . р.
Как нетрудно видеть, все наборы слов в Xd (р0)> р0 = 9о» имеют
вид
где ait, . . aJkn G= 2, причем
i«(1) я<1) 4L(1) /><п> Лп) 4+-<n>\ <= r x
4F , . . <if, . . . a)kn ф ) e tc (p0)
46
тогда и только тогда, когда (atl. . . a)t. . . GE MA.
Отсюда следует, что Мл полностью определяет множество Тд (v0)
и наоборот. Таким образом, проблема эквивалентности «-ленточ-
ных автоматов сводится к проблеме n-денточных схем Берда. 0
2.2. Свойства замкнутых диаграмм. Схемы Берда (D, и) в
(В', и'), приведенные в качестве примера на рис. 3.3, обладают
тем свойством, что существуют замкнутая диаграмма С и мор-
физмы /: D —» С, f: В’ С, / (п) = f (v’). Здесь будет показа-
но, что это свойство является необходимым и достаточным для
эквивалентности двух схем Берда.
Определим универсальную замкнутую диаграмму следующим
образом:
U = (Уи, Еи, Фи),
где Vu — множество всех подмножеств множества {(и,, . . .
- • ип) I Vi (1 < i < п) иг е 2j). Множество 0 имеет i-на-
следников, если 0 не содержит наборов с пустой г-й компонентой.
Если это условие выполнено, то для всех <те2| 0 —» {(uj, . . .
• • ип) | (“1, • • •, 1» CTUi, ui+l, • • •» Mn) 6 0} В U. Выходной
вершиной диаграммы U является одноэлементное множество
{(61...е„)}.
Теорема 3.4. U — замкнутая диаграмма.
Доказательство. Очевидно, что U — диаграмма.
Пусть 0 GE Vy, предположим
в
61
В U,
где ot е2(, ot GE 2/, i #= /. Тогда (ult . . ., un) GE 0j (uj, . . .
. . ., OjUi, . . ., un) G tj, поскольку у вершины 0
имеются /-наследники. Итак, 0Х имеет /-наследников, а 02 —
СТ, СГд
i-наследников. Пусть 04 —> 03 и 02 —> 04 в U. Тогда (uj, . . ., un) GE
E0S£> (их, . . ., . . ., (Uj, . . ., Ojtij,..., 02uh . . .
. . ., un) e 0 <=> (uj, . . ., о1М|, . . ., un) G0,G (Uj, . . ., un) GE 04.
Таким образом, 03 = 04, t. e. U замкнута. Q
Определим длину набора слое (их, .... ып) как сумму длин слов
ult . . ., ип. Если v — вершина полудиаграммы Q, а к 0, то
через Тд * (у) обозначим подмножество множества тд (о), состоящее
из всех наборов длины к. Через о обозначим пустое множество
наборов слов.
Лемма 3.1. Пусть С — замкнутая диаграмма. Для всех
к^ О из v v' в С следует Те+1) (v) -* тд (V) в U.
47
Доказательство проводится индукцией по к. По-
кажем сначала, что из v -* v' в С следует тс’ (у) Л тс’ (р') в U.
Предположим, а G= 2,. Если тс1 (v) не имеет i-наследников в U, то
3/ (/ ф i) («!, . - ej_t, o', е>+1, . . ., en) e t£* (p),
o'
а это означает, что v —* Ac в С. В силу замкнутости вершины v
отсюда следует, что Ас имеет i-наследников, а это противоречие.
Стало быть, Тс1 (р) имеет t-наследников. Пусть Тс’ (р) —> 0 в U.
Тогда
0 = J <(е1> • • •» еп)}« если (Ei’ • • -• ei-i> °. ei+1,..., еп) е т(с’ (р),
( со в противном случае.
Но (еп . . ., cj-i, с, ei+1, . . ., еп) СЕ тс’ (р) <Е v —> Ас в С <=?
4=> р' = Ас- Поэтому 0 — тс’ (р). Предположим теперь, что до-
называемое утверждение верно для некоторого к 0 и р —* р'
в С.. Докажем Тс+2) (р) —> т(с+1) (р') в U. Пусть Возьмем
произвольный набор (иъ . . ., ип) ЕЕ Тск+2) (р) и рассмотрим лю-
бой из путей из р к Ас, который порождает этот набор. Здесь
имеется две возможности.
1. Путь начинается /-шагом, / i, т. е. существуют рх €=
G Vc. o' ЕЕ 2; и и; СЕ 2j такие, что р—> рх в С, и} = o'uj
и (ult . . ., u}-i, u'j, и}+1, . . ., ип) (Е т?+1) (рх). В силу замкнуто-
сти С вершина vx должна иметь i-наследников. Тогда по индук-
тивному предположению Тс+1) (Pi) имеет i-наследников в U,
откуда ut =/£= в|.
2. Путь начинается i-шагом. Это сразу дает ut et.
Итак, Тс+2) (р) имеет i-наследников. Предположим, что
тЬк+1) (р) 0 в U. Тогда (ulf . . ., un) е т£+1) (р') => (и» . . .
. . ., <шъ .... un)GTc +2) (р) ..., Un)e0, т. е. т^к+1)(р') CZ 0.
Пусть теперь (itj, .. ., ип) (Е 0, тогда (их, . . ., аиь . . ., ип) СЕ
ЕЕ Тск+2) (р), т. е. существует путь от v к Ас, порождающий на-
бор (ut, . . ., (juit . . ., ип). Снова рассмотрим два возможных
случая.
1. Путь начинается /-шагом, j =/= i, т. е. существуют Pt СЕ Vc,
<т' Е Sj и uj 6 2* такие, что р Pj в С, и} — с'и, и (и,, . . .
. . ., оио . . ., u'j, . . ., ип) СЕ Tck+1) (р>). в силу замкнутости С
существует вершина vt е Vc такая, что
а »
V
о' В С .
V --------
а'
о
V,-------
48
Индуктивное предположение дает тс+1) (р,) -»• тс ’ (р2) в U,
откуда (ult . . ., иЛ1, u’j, uJ+J, . .., un) fE x^ (p2). Следователь-
но, (uv . . uw, a'u'j, uJ+1, . . un) e xc+1) (v'), t. e. (u1? . . .
...,un)GT^(v').
2. Путь начинается г-шагом v —* v'. Отсюда немедленно сле-
дует (un . . un)e x(c+1) (p').
Итак, в каждом случае (uj, . . ., ип) GE т<;+1) (р'), что дает
0 Cxg+1)(p'), т. е. 0 = тГ’ (v'). □
Если дана полудиаграмма Q, то с каждой вершиной р Е Vq
связано множество наборов tq (р) ЕЕ Vu- Таким образом, tq
задает отображение из Vq в Vu-
Теорема 3.5. Если С — замкнутая диаграмма, то ото-
бражение Тс: Vc —» Vu является морфизмом.
Доказательство. Пусть v —* v' в С, покажем Тс (и) —»
-Л тс (o') в U. Предположим для определенности о Е 2(. Тогда
(и1т . . ., ип) е ТС (v) ^Jk^Q (uj, . . ., ип) е Tc+1) (р). в силу
леммы 3.1 xg*” (р) имеет /-наследников в U, поэтому ut et.
Следовательно, Тс (v) также имеет i-наследников. Далее, (и1, . . .
. . ., ип) GE тс (р') («1, . . ., ип) GE тс’ (р') для некоторого
к > О («ц . . ., Uj.j, ouj, uJ+1, . . ., un) СЕ тс (р). Отсюда
тс (р) -> тс (р') в U. Справедливо также Тс (Ас) = {(ex, . . .
. . ., еп)} = Ли. Следовательно, тс — морфизм. Q
Таким образом, если даны две эквивалентные схемы Берда
(D, р) и [D', р'), то мы можем предъявить замкнутую диаграмму U
и морфизмы то: D -*U, тс: D' —» U такие, что то (р) = то» (р*).
Итак, осталось доказать обратное утверждение.
Теорема 3.6. Пусть f — морфизм из некоторой полудиаг-
раммы Q, не содержащей свободных вершин, в замкнутую диаграм-
му С. Тогда f ° тс = tq.
Доказательство. Если р СЕ Vq, то tq (р) С тс (/ (р)),
поскольку всякий путь от р к Aq в Q отображается морфизмом/
в путь от / (р) к Ас в С с той же последовательностью пометок
дуг. Для тс (/ (р)) С tq (р) достаточно показать, что для всякого
к 0 т?‘ (/ (р)) С tq (р) для всех рЕ Vq. Мы докажем это ин-
дукцией по к.
Заметим прежде всего, что / (р) = Ac 4=> v = Aq, поскольку
/ (р) ~ Ас => {р не имеет наследников) => р = Aq. Таким обра-
зом,
т?)(/(р)) = {
(е,,-• .,£«), если р — Aq )
Qtq(p)
<о, если p#=Aq ) '
Предположим теперь, что Тс1 (/ (р)) С tq (р) для всех р Е: Pq,
и покажем Тс'^1) (/ (р)) С tq (р) для всех р ЕЕ Vq. Если р =
— Aq, to Tck+1) (/ (v)) = co C tq (v). Если же v Ф Aq, to no
условию теоремы v имеет наследников. Пусть, для определенно-
сти, v имеет г-наследннков. Тогда / (и) имеет i-наследников, сле-
довательно, i-наследников имеет и Тс +1) (/ (v)). Поэтому (иг, . . .
• . ип) GE Тс+1) (/ (р)) => щ ф е, => щ = ouj для некоторых
о Е и uj ErS?. Пусть v -^> v‘ в Q. Тогда / (р) / (у1) в С,
а поэтому Тс+1) (/ (р)) -* Тс * (/ (р')) в U. Следовательно, (un . . .
. . ., и£_х, u'i, ui+1, . . ., un) GE Тс' (/ (у')), и в силу индуктивного
предположения (uj, . . ., u'i, . . ., ип) GE tq (р'). Отсюда следует,
что (un . . ., oui, . . ., ип) ете (р'), т. е. (их, . . ., uJetq (р'). □
Следствие 3.1. Две схемы Берда (D, р) и (D', р') экви-
валентны тогда и только тогда, когда существуют замкнутая
диаграмма С и морфизмы ft D —► С, ft D* -► С такие, что
f (v) = Г (V).
Доказательство. Необходимость уже доказана. Для
достаточности воспользуемся теоремой 3.6:
тс (р) = тс (/ (р)) = тс (/' (р')) = тр. (р'). □
2.3. Процедура распознавания. Опишем четыре операции для
конечных полудиаграмм. Первая операция — это склеивание
двух вершин полудиаграммы. Пусть Q — конечная полудиаграм-
ма и vt, v2 GE Vq. Предположим, для вершин рь р2 неверно, что
одна из них имеет наследников, а другая — это Aq. Тогда опи-
санная ниже операция склеивания дает конечную полудиаграмму
Q', а также морфизм dt Q —► Q’.
1. Пусть Vq' получается из Fq заменой вершин рх н р2 одной
новой вершиной р0.
2. Пусть d — отображение из Vq в Fq., определяемое соот-
ношением
{р0, если р — Pj или р = р2,
р в противном случае.
3. Пусть Aq' = d (Aq).
4. Определим w —> w’ в Q' тогда и только тогда, когда Зр,
v* GE Fq такие, что р —> v' в Q, d (р) = w и d (р') = w'.
Если одна из вершин vt, р2 имеет наследников, а другая —
это Aq, то мы говорим, что операция склеивания вершин рх и р2
не удается, а результат ее применения не определен. В противном
случае склеивание удается (или успешно), а морфизм d: Q-+Q*
называется результатом этого склеивания. Заметим, что d — это
морфнзм на Q’.
Лемма 3.2. Пусть р2 и р2 — вершины конечной полудиа-
граммы Q и пусть для некоторой полудиаграммы Q* существует
морфизм f: такой, что f (рх) = / (р2). Тогда склеивание
50
вершин иг и vt удается, и если d: Q -> Q' — результат склеива-
ния, то существует морфизм из Q' в Q".
Доказательство. Если, скажем, имеет наследни-
ков, то и f (vt) имеет наследников. Следовательно, / (г8) =# Aq-,
откуда vt Ф Лр. Поэтому склеивание i7t и v2 удается. Морфизм
g: Q' Q" определяется так:
_ ( / (0. если v ф v0 (у0 = d (nJ = d (г8)),
ё Г I /(fi)» если v = v0. □
Следующая операция, называемая уплотнением, пытается
применением склеиваний преобразовать конечную полудиаграм-
му в диаграмму. Исходной является полудиаграмма Qo. Если она
уже является диаграммой, то больше делать ничего не нужно.
Если нет, выбираем какую-нибудь вершину V, для которой
в полудиаграмме Q ,
где Pj =/= рг, и склеиваем рх и р8. Если склеивание удается (с ре-
зультатом d: Qo -* Qt), то с полудиаграммой Qt поступаем точно
так же, как с Qo, и т. д. Процесс, очевидно, не может продолжать-
ся бесконечно, так как каждое склеивание уменьшает число
вершин на единицу. Если какое-либо склеивание не удается, то
мы говорим, что операция уплотнения не удается. В противном
случае успешные склеивания дают последовательность морфиз-
мов
dj: Qo Qi, dt: Qt Q2, . . ., dm: —► Qm
для некоторого m 0, где Qm — конечная диаграмма. Тогда
мы будем говорить, что операция уплотнения удается (или успеш-
на), а результатом ее применения объявляем морфизм р: Qo~*
-* Qm, определяемый соотношением
f d^d^ .. dm,
Р ~ I iQ.>
если тп 1,
если т = 0.
Заметим снова, ’что р — морфизм на Qm.
Лемма 3.3. Пусть существует морфизм из конечной полу-
диаграммы Qo в диаграмму D. Тогда уплотнение Q удается, и
если его результат — это морфизм р: Qo Qm, то существует
морфизм из Qm в D.
Доказательство. Рассмотрим применение операции
уплотнения к Qo. Если Qo — не диаграмма, то выбирается
51
вершина v, для которой
В <20-
Если существует морфизм
fo' Qo Я, где ~ диаграмма, то
в D.
Следовательно, /0 (fj) — f0 (vt). В силу леммы 3.2 склеивание
вершин fj и vt удается, и если Qo — результат этого
склеивания, то существует морфизм /t: D. Теперь мы можем
повторить наши рассуждения для и т. д. В конце концов будет
получена диаграмма Qm, а также морфизм /т: Qm -► D. Q
Третья операция, называемая пополнением, просто добавляет
новые вершины и дуги в данную конечную диаграмму D следую-
щим образом:
для каждой тройки (не обязательно различных) вершин 1\,
vaE=Vi), удовлетворяющей условию
В D ,
v3
где GE <т8 GE Sy, i =/= у, в D добавляется новая вершина е
вместе с дугами
Мы говорим, что операция пополнения не удается, если существует
52
такая тропка вершин vp v„ <?s GE Vd, что
о,
в D.
где Gt GE c8G=Xy, i #= 7, и либо г2 = ЛЬ, либо t’s = Ли-
В противном случае мы получим конечную полудиаграмму D'
такую, что Vd С Vd'- В этом случае мы говорим, что операция
пополнения удается (или успешна), а результатом ее применения
объявляем морфизм включения a: D D' (это уже не морфизм
на D’).
Лемма 3.4. Пусть существует морфизм f: D -*• С из ко-
нечной диаграммы D в замкнутую диаграмму С. Тогда пополне-
ние диаграммы D удается, и если a: D -+• D' — его результат,
то существует морфизм g: D' -* С.
Доказательство будет прямым, g определяется так.
а) Если v GE Vd, то g (v) — f (v).
б) Если v GE Vd‘ \ Vd, to существуют единственная тройка-
вершин vt, va, v3 e VD, i, j G {1, . . ., и}, i #= 7, и Gt GE 2iv
a, G= S j такие, что
Поскольку С — замкнутая диаграмма, существует единственна»
вершина w GE Vc такая, что
/(^х)---
а2 Oj В С.
J °i
/(V,)--------w
В этом случае мы определяем g (и) = w. [J
Четвертая операция, называемая замыканием, пытается преоб-
разовать данную диаграмму в замкнутую диаграмму, поперемен-
но применяя операции пополнения и уплотнения. Исходной яв-
ляется конечная диаграмма Do. Если она уже замкнута, тогда и
делать больше ничего ие нужно. В противном случае применяем
пополнение Do. Если пополнение успешно (скажем, с результа-
том at: Dt —► Qo), то применяем операцию уплотнения Qe. Далее*
если и уплотнение оказалось успешным (скажем, с результатом
53.
О
Рис. 3.4. Пример диаг-
раммы над Si = {0},
£,== {1},применение опе-
раций замыкания к кото-
рой никогда не заканчи-
вается
Pi‘ Qo “*• ^i)> то повторяем тот же самый процесс с диаграммой
Dlt что и с Do, и т. д. Если применение одной из операций попол-
нения или уплотнения не удается, то мы говорим, что операция
замыкания не удается. В противном случае, если успешные по-
полнения и уплотнения дают последовательность ах: Do-*- Qo,
PT- Qo-^D^ . . am: D^-o-Q^, pm: для неко-
торого zzi 0, где Dm — конечная замкнутая диаграмма, то мы
говорим, что операция замыкания Do
удается (или успешна), а ее результатом
объявляем морфизм с: Do-»- D т, где
( а^... атрт, если т > 1,
с = < п
I iD.t если т = и.
Заметим, что для некоторых диаграмм Do
(как, например, для приведенной на
рис. 3.4) применение операции замыкания
никогда не заканчивается, так что нельзя
говорить ни о том, что операция не удает-
ся, ни о том, что она успешна.
Лемма 3.5. Пусть существует мор-
физм из конечной диаграммы Do в неко-
торую замкнутую диаграмму. Тогда если операция замыкания
диаграммы Do заканчивается, то она успешна.
Доказательство проводится аналогично доказатель-
ству леммы 3.3. □
Опишем, наконец, процедуру, называемую распознаванием
-эквивалентности, и покажем, что если эта процедура завершает-
ся, то она распознает эквивалентность двух данных схем Берда.
Исходными для процедуры являются две схемы Берда (D, v) и
(D', v'). Сначала построим диаграмму (обозначаемую D + В’),
взяв непересекающиеся копии диаграмм D и D' и склеивая их
выходные вершины. Пусть / обозначает очевидный морфизм
аналогично /' обозначает D' -* D + D'. Затем
склеим вершины j (и) и j' (i/). Если применение этой операции
оказалось успешным, а его результат — морфизм d: D + D' -*
Q, то применяем операцию уплотнения к Q. Если применение
операции уплотнения оказалось успешным, а его результат —
зто морфизм р: Q -* D, то применяем операцию замыкания к диа-
грамме D. Наконец, если и эта последняя операция оказалась
успешной, то мы говорим, что процедура распознавания успешна.
Если же хотя бы одна из упомянутых операций не удается, то мы
говорим, что процедура распознавания ломается.
Теорема 3.7. Если процедура распознавания успешна для
схем Берда (D, и) и (D', v'), то они эквивалентны; если же про-
цедура ломается, то они неэквивалентны.
Док азательство. Пусть процедура распознавания
успешна для схем(О, н) и (D', v'). Тогда успешные операции, при-
меняемые процедурой распознавания, дадут нам следующие
54
морфизмы j: D -> D + В', j': D' -+• D 4* D‘, d: D + D' Q,
p: Q-*D, c: D -»-C, где C — замкнутая диаграмма. Определим
морфизмы f: D С, D'-t- С соотношениями / = jdpc, /' =
= j'dpc. Тогда f (о) = f (у'), поскольку d (j (o)) — d (j’ (v'))*
Эквивалентность схем вытекает теперь из следствия 3.1.
С другой стороны, предположим, что процедура распознава-
ния ломается, а схемы (D, v) и (Л', v‘) эквивалентны. Тогда в силу
следствия 3.1 существует замкнутая диаграмма С и морфизмы
/: D -* С и В' -> С такие, что / (г) = /' (г')- Если применить
процедуру распознавания к этим схемам, то первый шаг даст
морфизмы у: D -> D + D' и j’-. D' -*-D + D'. Эти морфизмы
обладают тем свойством, что существует морфизм /t: D + В' С,
для которого /Д = f и i'ft = поэтому Д (у (,;)) = А О' (f'))-
Далее, применяя леммы 3.2, 3.3 и 3.5 с учетом того, что операция
замыкания заканчивается, мы получим, что все операции, при
меняемые процедурой распознавания, являются успешными.
Следовательно, успешной будет и процедура распознавания, что
противоречит нашему предположению. Q
2 А. Предельная диаграмма. Пусть операция замыкания не
заканчивается при ее применении к конечной диаграмме Do. Мы
получим тогда бесконечную последовательность морфизмов
ао: Ве “Qo, Ро- Qo Bi, Dx —>- pt: Q —► Dg, . . .
где ar: DT-*-QT — результат пополнения конечной диаграммы
DT, a pr: QT -*• Dr+l — результат уплотнения полудиаграммы QT.
Обозначим fT = arpr суперпозицию морфизмов аг и рт, fr: Dr
-> Dr+i, г 0. Последовательность морфизмов {fr} определяет
диаграмму L, называемую пределом, этой последовательности,
а также морфизмы gT‘. DT-*-L следующим образом.
Для всех г, s, г s, определим морфизм Fr.,: Вт -► D,,
полагая
а) Ег, r = ior;
б) если г < s, то FT,t = frfr+1 . . . /,_д.
Обозначим через 31 (разделительное) объединение множеств Рд,,
Vd„ • • . Тогда для всех г > 0 и v GE Vdt существует соответст-
вующий элемент множества 31, который мы будем обозначать
®г (о). Пусть = означает отношение эквивалентности на 31,
которое определяется так: (5Г1 (vt) = ®r, (о2) тогда и только тог-
да, когда существует s, s г1э s > гг, такое, что ЕГ1,, (vj =
= FTtt, (us). Тогда в качестве вершин предельной диаграммы
L возьмем классы эквивалентности множества 31 по отношению =.
Для г > 0 морфизм gT-. BT-t- L определяется как отображение,
сопоставляющее вершине v G Вг класс эквивалентности элемен-
та ®г (v). Заметим, что для s^rFti ,gt = gr. Дуги в L опре-
а ’
деляются следующим образом: —» Vi в L тогда и только тогда,
когда для некоторого г > 0 существуют г, v' GE For такие, что
5S
V v' в Dr, gT (v) = vx и gr (i/) = vi. Наконец, Лг = g0 (Ad,).
Мы изучаем свойства диаграммы L в предположении, что она
получается в результате не заканчивающейся операции замыка-
ния.
Лемма 3.6. L — замкнутая диаграмма.
Доказательство. Пусть PjG Ft и
о.
*4-----
В L
Ч
для некоторых ах GE S4, <r8G=Sy, i^=j. Тогда существуют
rt > 0 и wlt wg Vnrt такие, что wt wt в DTi,, grt (idx) =
и Sr, («>з) = vt. Кроме того, существуют г8 > 0 и w3, wt G= Kor>
такие, что ip3 —> ip4 в Drt, gTt (w3) = vt и gri (wj = v3. Поскольку
Sr, (wi) ~ Sr, (^з), существует s, rt, г8, такое, что
Pr,,s Ю — Prt, s Ю-
Это дает
Fr,.A^) ----FrvS(^A
°г в Ds .
Fr ,AWA
\ 4./
'Следовательно, существует вершина w G Vqs такая, что
as(FriAw2))
аЛргг,. ())---21—- W
Применяя морфизм pegs+1, получим
а, в L.
Ч---21—* (A^i) (w)
поскольку (Fr„ ,atp,gs+1) (w3) = (Л„ s+1gs+1) (ws) = gTl (шг) = va
и аналогично (Fri> tatpegt+1) (w4) = v3. Отсюда следует, что L —
замкнутая диаграмма. Q
56
Лемма 3.7. Диаграмма L бесконечна.
Доказательство. Предположим, что L конечна. Так
как Vc конечно, Vc — Vim(grt) для некоторого г0 > 0. Определим
тогда морфизм hT,: L -> DT, следующим образом:
a) hr, (At) = Аог>;
б) если v Ас, то выберем произвольную вершину v’ G: Vor
такую, что gr, (o') = v, и положим hr, (у) = v'.
Таким образом, hr,gr, — ic. Для г J> г0 определим отображе-
ние hr: Vc ?ог, полагая hr = hT,FT„ т. Тогда hrgT — ic, и для
всех достаточно больших s из gk (у') = v следует Fkit (v‘) —
= ha (v). Рассмотрим теперь произвольную дугу v —» vt в L.
Тогда существуют m > 0, v', v[ G^d такие, что v' —> vk в Dm,
gm (»') — V и gm (v'i) = vt. Отсюда следует, что для всех доста-
точно больших s Fm,a (i/) -> Fm>1 (щ) В Dg, Fm,a (у') = ha (v)
и t (vi) — he (yj, t. e. h, (v) —> ha (vj в Da. Поскольку в Ds
имеется конечное число дуг, то для всех достаточно больших s
v —* vt в L влечет h, (у) —> ha (yt) в Ds. Кроме того, для всех s
г0 справедливо h, (Al) — Ads. Следовательно, для всех доста-
точно больших s отображение hB является морфизмом.
Пусть v G= Vd,, v' ~ g0 (v). Тогда для всех достаточно боль-
ших s FOt, (у) = hs (у') GE Vim (fts) - Это значит, что для всех
достаточно больших s Vim<r0 8) Q Vim<hs)- Выберем s 0 так,
чтобы hg было морфизмом и Vim(F0 s) Q Vim(h8)- Пусть
К — множество неподвижных точек морфизма g8fe8, т. е.
К = {у | hs (gs (у)) = у). Для veVi, имеем hs (ga (ha (у))) =
= ha (у), следовательно, Ущцлр Q К и VIm(y0 8) Q К. Предполо-
жим теперь, что у0 GE К и у0 vx в Da. Тогда у0 Л8 (g8 (yj)
в Da, а поэтому у1 = Л8 (g8 (yj), т. е. €= К. Отсюда следует, что
если существует путь в Da от вершины у0 GE К к вершине у, то
у (= К. Очевидно, для всякой вершины у G Vdb существует путь
от некоторой вершины из Vim<r0 8) к вершине у. Поскольку
Vim(F0 8) G К, всякая вершина у GE Vds принадлежит К. Таким
образом, gahg = ipg. Но hsgs = ic, поэтому ha является изоморфиз-
мом. Итак, для некоторого s 0 имеем Ds на L, поэтому Da —
замкнутая диаграмма. Однако если одна из диаграмм Dit i 0,
замкнута, то операция замыкания, применяемая к Do, закан-
чивается. Полученное противоречие доказывает бесконечность
диаграммы L. Q
Итак, если описанная в п. 2.3 процедура распознавания за-
канчивается при ее применении к двум схемам Берда, то при
успешном завершении схемы эквивалентны, а если процедура
ломается, то схемы неэквивалентны. Однако пока процедура не
закончена, нельзя сказать, эквивалентны схемы или нет. На
Рис. 3.5. Пример двух схем Бер-
да над Si = {о0, oj}, S2 = {b„
bi}» — {с}
рис. 3.5 приведен пример двух эквивалентных (трехленточных)
схем Берда, на которых процедура распознавания будет работать
бесконечно.
2.5. Решение двухленточнон проблемы. В этом разделе мы
рассматриваем случай п = 2 (двухленточные схемы Берда). Сле-
дуя Берду, мы докажем, что в
случае п = 2 процедура распо-
знавания всегда заканчивается,
т. е. является алгоритмом рас-
познавания эквивалентности.
Путь в полудиаграмме назо-
вем 1-путем, если пара слов,
связанная с этим путем, имеет вид
(и, е), где и ЕЕ 2*. Аналогично
определяется 2-путь.
Лемма 3.8. Для каждого
i = 1, 2 и для всех вершин v опи-
санной в предыдущем разделе пре-
дельной диаграммы L существует
i-путь от некоторой вершины из
Im (g0) к вершине V.
Доказательство. До-
кажем индукцией по г, что для
v ЕЕ Vi)r существует i-путь (/ =
=1,2) в Dr от вершины из Im (Е0,г)
к вершине V. Если v G= Vd,, то са-
ма вершина v представляет собой
i-путь от вершины из Im (FOiO) к v. Пусть это верно для некоторого
г > 0. Если v G= Ког+1, то существует вершина v' G= Vqr такая,
что pr (v') = V. Мы рассмотрим два возможных случая:
a) vr = аТ (Vя) для некоторой v" GE VDr. Тогда по индуктивному
предположению существует i-путь в Dr от вершины из Im (Е0,г)
к Vя, а морфизмом /г этот путь будет отображаться в /-путь
в Dr+1 от вершины из Im (F0,r+1) к v;
б) v' Vim(ar)- Тогда существуют vt, VDr такие, что
<ЧЧ)
в ц.
aP (v2) —v'
для некоторых Oj GE 21T c2G i2. По индуктивному предполо-
жению существует w GE Vd, такая, что в Dr имеется /-путь от
Е01Г (ш) к Морфизмом ат этот путь отображается в i-путь в Qr
от вершины ат (FOtT (w)) к аг (р4). Следовательно, существует
i-путь от верщины ат (F0,r (w)) к вершине v'. Морфизмом рг этот
58
путь отображается в i-путь в диаграмме Пг+1 от вершины F0,r+1 (w)
к вершине v. [J
Теорема 3.8. Операция замыкания завершается, если она
применяется к двухленточной конечной диаграмме без свободных
вершин.
Доказательство. Пусть Do — конечная двухленточ-
ная диаграмма без свободных вершин. Как мы видели, если опе-
рация замыкания не заканчивается на Do, то существует беско-
нечная замкнутая диаграмма L, а также ее поддиаграмма Lo (Zo ~
— Im (g0)) со следующими тремя свойствами:
a) Lo конечна (в силу конечности Z)o);
б) Lo не содеряшт свободных вершин (если g0 (v) свободна
в Lo, то v свободна в По);
в) если v ЕЕ Vt, то для каждого i = 1, 2 существует i-путь от
некоторой вершины из Lo к v.
Мы придем к противоречию, показав, что всякая замкнутая
диаграмма L, содержащая поддиаграмму Lo с перечисленными
свойствами, является конечной.
Для v ЕЕ Vt и i = 1, 2 определим р, (у) как минимальное из
чисел d таких, что существует i-путь длины <2в диаграмме L от
вершины из Lo к вершине v (i-расстояние omL0Kv). Корректность
определения расстояний обеспечивается свойством б). Заметим,
что v е Vl, 4=> рг (и) = О р8 (v) = 0; кроме того, множества
{v | Pi (и) < т}
являются конечными при любых т 0, i = 1, 2.
Покажем теперь, что если v ЕЕ Vl \ и и в L для-
некоторого ст е то р8 (и) р8 (у'). Пусть у0 —> —* . . .
ст.
. . . —“ v — 2-путь минимальной длины d = р8 (v) 1 в диаграм-
ме L от некоторой вершины г?0 ЕЕ Кь. к вершине V. Очевидно, что
$= Иь,, следовательно, v0 не имеет 2-наследников в Lo. Однако
п0 =# Аь., поскольку Ль, = Ль, и вершина п0 не свободна в £0,
поэтому v0 имеет 1-наследников в £0. Пусть п0 ~* уо в Lo. В силу
замкнутости L существуют щ, . . ., v^-i ЕЕ Уь такие, что
Итак, существует 2-путь длины р8 (и) от некоторой вершины из
£0 к вершине v', т. е. р8 (v') р8 (у).
Если i/ ЕЕ Vjr, \ Иь,, то существует 1-путь
®« а. °тп-1 °т ,
п,-> пх -* . . .---------► ► V В L
59
для некоторого т > 1, G Vl, и ц, . . ., vm-i G VL \ Vc,.
Очевидно, что px (fj = 1 и pg (</) pg (vr). Пусть M —
— {f | v GE Vc & Pi (v) = 1}, da — max pa (f). Это определение
veM
корректно, поскольку множество М конечно и непусто. Следова-
тельно, pg (o') dt. Отсюда следует Vc — (v’ | pg (у') da),
а это множество конечно. Q
Следствие 3.2. Процедура распознавания эквивалент-
ности двухленточных схем Берда всегда заканчивается.
Доказательство. Пусть процедура распознавания
применяется к двухленточнь^м схемам Берда (D’, v’) и (D", v").
Если не удается одна из первых двух операций (склеивание или
уплотнение), то процедура распознавания, очевидно, заканчнвает-
-ся. Если же обе операции оказываются успешными, то приме-
няется операция замыкания к диаграмме D, которая получается
из исходных схем следующим образом (здесь d, р — морфиз-
мы):
D’ -> D’ + D”, j": D" -> D' + D”,
d: D’ +D"-+Q, р: QD.
Эти морфизмы таковы, что всякая вершина v GE Vd является
либо образом некоторой вершины из D' при морфизме j'dp, либо
образом некоторой вершины из D" при морфизме Г dp. Предполо-
жим для определенности v — (j’dp) (v')t где v’ GE Vd’. Тогда
вершина v не может быть свободной, иначе свободной была бы
вершина v'. Следовательно, в D нет свободных вершин, и опера-
ция замыкания, а тем самым процедура распознавания, заканчи-
вается. [3
Таким образом, процедура распознавания является алгорит-
мом распознавания эквивалентности двухленточных схем Берда.
Как показывает пример на рис. 3.5, это неверно для п-ленточных
•схем при п 3.
Задание 3.2. Вершину v п-ленточной диаграммы назовем квази-
полной, если 3i (1 i «5 п) V] (1 п, i ф jj вершина и имеет /-наслед-
ников. Докажите, что операция замыкания заканчивается при ее примене-
нии к таким диаграммам, в которых все вершины являются квазиполными
§ 3. Двухголовочные автоматы
3.1. Определения и пример. Двухголовочный автомат А =
— (У» Qi Ri Qoi Л имеет одну леиту и две головки, которые
могут независимо перемещаться вдоль ленты в одном направле-
нии. Множество состояний Q = Qa (J Qa разбито на два непере-
секающихся подмножества; в состояниях из активна первая
головка, а в состояниях из Qt — вторая. Как и раньше, V здесь
означает алфавит символов иа ленте, R — множество заключи-
тельных состояний, R С Q, д0 GE @ — начальное состояние,
60
— «пустой» символ, а I — программа автомата А, т. е. после-
довательность команд вида да —► д', где д, д' GE Q, а ЕЕ V, при-
чем для любой пары (д, а) существует единственная команда.
начинающаяся этими символами.
Двухголовочный автомат можно рассматривать как такой
двухленточный автомат, который работает с идентичными словами
на обеих лентах. На двухголо-
вочные автоматы естественным
образом переносятся определения
множества допускаемых слов, пу-
стоты и эквивалентности.
Несмотря на то, что двухлен-
точные и двухголовочные автома-
ты похожи друг на друга, их
свойства сильно отличаются. Так,
проблема пустоты разрешима для
многоленточных автоматов [133] и
неразрешима для многоголовочных
(135]. Более того, в последнем слу-
чае она не является даже частично
разрешимой, в чем мы вскоре убе-
димся. Проблема эквивалентности
также не является частично разре-
шимой для многоголовочных авто-
матов, что легко доказывается
сведением к ней проблемы пусто-
ты. Однако, как доказано в пре-
дыдущем параграфе, проблема
эквивалентности разрешима для
двухленточных автоматов, и оста-
ется пока открытой для многолен-
точных автоматов с тремя и более
лентами.
Приведем пример двухголовоч-
ного автомата, который прове-
ряет равенство двух последова-
тельно записанных слов в алфа-
вите V = {0, 1)*. Признаком оконч
Рис. 3.6. Двухголовочный авто-
мат А_
шя каждого из слов сделаем
вспомогательный символ *, не входящий в V. Автомат должен
допускать только слова вида а * а *, где а ЕЕ V*. Мы возь-
мем = (V и {•). Qi U Qv Я, gj, #, /), где & = {gj, gt,
gt, 9?) — множество состояний, в которых активна первая голов-
ка; Q/2 = {д3, q5l q6} — множество состоянии, в которых ак-
тивна вторая головка; И ~ {д17} — множество, содержащее един-
ственное заключительное состояние. Граф автомата показан на
рис. 3.6. На этом рисунке вместо многих «параллельных» дуг
с разными пометками нарисована одна дуга со всеми этими по-
метками.
61
Находясь в состоянии 9J, автомат передвигает первую головку
к началу второго слова и, обнаружив его, переходит в состояние
9^. Если конец ленты встречается раньше символа *, автомат
переходит в незаключительное состояние 9J. Если же автомат
приходит к состоянию 91, он считывает поочередно символы вто-
рого слова первой головкой (состояние 9>), а символы первого
слова — второй головкой (состояния 9з и 95), сравнивая эти сим-
волы. Автомат возвращается каждый раз в состояние 9*, если сим-
волы одинаковы. Если же обнаружится несовпадение символов
или первая головка встречает конец слова раньше символа *,
автомат уходит в состояние 9I. Попав в зто состояние, автомат не
может выйти из него; перемещая вторую головку к концу слова
на ленте, он достигает 41=, находясь в незаключительном состоя-
нии, так что слово на ленте отвергается. Если первая головка до-
стигнет конца второго слова, а вторая головка обнаружит, что
первое слово тоже просмотрено до конца, то автомат перейдет
в заключительное состояние 9*. В противном случае автомат
« 2
перейдет в состояние д6, отвергая слово.
Этот пример легко обобщить на случай произвольного алфави-
та V, увеличивая количество состояний множества Q.
Задание 3.3. Постройте двухголовочный автомат, который устанав-
ливает равенство пары слов в алфавите {0, 1} с точностью до перестановки
некоторой единственной пары соседних символов.
3.2. Проблемы пустоты и эквивалентности. В § 1 мы устано-
вили разрешимость проблемы эквивалентности одноленточных
автоматов, выяснив предварительно, что разрешима проблема
пустоты для этих автоматов. Точно так же поступим при иссле-
довании проблемы эквивалентности двухголовочных автоматов,
но на этот раз сначала установим, что проблема пустоты не явля-
ется частично разрешимой, а затем сведем ее к проблеме эквива-
лентности. (В конце этого параграфа обсудим еще раз связь между
этими двумя проблемами в более широком контексте). Тот факт,
что проблема пустоты двухголовочных автоматов не является
частично разрешимой, установим методом сведения, используя
проблему зацикливания машин Тьюринга.
Будем говорить, что двухголовочный автомат моделирует ра-
боту машины Тьюринга над некоторым начальным словом, если
автомат допускает единственное слово — конечный протокол ра-
боты машины над ним.
Лемма 3.9 (Розенберг). Существует алгоритм, который
для любой машины Тьюринга и для любого начального слова строит
двухголовочный автомат, моделирующий ее работу над этим словом.
Доказательство. Пусть задана машина Тьюринга
Т = (Рт, Qt, 9от, #т, It) и слово а в алфавите Vt. Преобразуем
программу 1т таким образом, чтобы на каждом шаге машина мог-
ла выполнять только одно из следующих действий: сдвинуть го-
ловку влево; сдвинуть головку вправо; записать новый символ
62
без сдвига головки. Это легко сделать, заменив каждую команду
qa -> q'a'd на две команды: qa -> q’a'p и q'a' -+ q'a'd.
Соседние конфигурация в протоколе машины, подаваемом на
ленту автомата, будут разделены вспомогательным символом ♦
Ут U Ст- Он займет место менаду символом заключающим
одну конфигурацию, и таким же символом, открывающим следую-
щую. Конец протокола будет отмечаться двумя звездочками.
Алфавит моделирующего автомата представляет собой сумму
множеств Ут, Qt н {#т, •}. Мы не будем составлять программу
автомата во всех деталях. Вместо этого опишем структуру его
программы и поведение автомата, выполняющего команды от-
дельных частей программы.
В исходном состоянии обе головки автомата обозревают, как
обычно, первый символ заданного слова (т. е. символ ф=т» начи-
нающий протокол). Первая группа команд перемещает головку 1
на одну конфигурацию вперед, проверяя, имеет ли первая конфи-
гурация вид где а — начальное слово на ленте ма-
шины Т. Если это так, то начинает работу вторая группа команд,
в противном случае — команды шестой группы, которые переме-
щают одну из головок на конец всего слова, поданного на ленту
автомата, после чего автомат останавливается в незаключитель-
ном состоянии н слово на ленте автомата отвергается.
Вторая группа команд заставляет автомат поочередно пере-
мещать головки, которые сканируют рядом стоящие конфигура-
ции и сравнивают их на совпадение (см. пример в п. 3.1). Заме-
тим, что команды первых двух и шестой групп не зависят от про-
граммы машины Т, команды первой группы зависят от слова а.
Если обе конфигурации просмотрены до конца и несовпаде-
ний не обнаружено, то это значит, что машина Тьюринга Т долж-
на зацикливаться, поэтому слово на ленте автомата не может быть
конечным протоколом и должно быть отвергнуто. В этом случае
начинают работать команды шестой (отвергающей) группы. Если
обнаружено несовпадение символов, стоящих на одинаковых по-
зициях в соседних конфигурациях, применяются команды треть-
ей или шестой группы. Команды третьей группы используются,
•если хотя бы один из несовпадающих символов — символ состоя-
ния из Qt, а команды шестой группы — в остальных случаях.
«Правильными» несовпадениями соседних конфигураций бу-
дем считать такие, которые возникают как результат применения
команд из программы машины Т. Эти несовпадения могут быть
трех типов (Р — совпадающие префиксы конфигураций, у — сов
падающие суффиксы):
D-.- *тР *|Г *т* p[/ajу#г...(команда qa-~q'afr;
2)... *т Р \aqa'} у#г * #т Р [yizaj у*г- (команда qa'+q’a'l);
3)... *гр [уа] у *т * *г *т- (команда уа—у'аг).
63
Все три «правильных» несовпадения могут быть выделены ре-
зервированием конечного числа состояний и подбором конечного
числа команд автомата, вид которых зависит от программы маши-
ны Т. Эти команды организуют поочередный просмотр несовпа-
дающих фрагментов двумя головками и выясняют, является ли
несовпадение «правильным». Для тех читателей, которые выпол-
нили задание 3.3, принцип подбора команд третьей группы по-
нятен.
Если команды третьей группы обнаружили, что несовпадения
«правильны», выполняются команды четвертой группы, проверяю-
щие совпадение суффиксов конфигураций. В противном случае
начинают работу команды шестой группы. Четвертая группа ко-
манд похожа на вторую группу.
Когда закончено сравнение двух соседних конфигураций, го-
ловка 1 смещается вперед, и начинается сравнение следующей
пары соседних конфигураций, для чего автомат переходит вновь
ко второй группе команд. Если же головка 1 обнаружит два стоя-
щих подряд символа *, предупреждающих о том, что головка
просмотрела последнюю конфигурацию, автомат активизирует
головку 2, задача которой — с помощью команд пятой группы
убедиться, что это действительно заключительная конфигурация
конечного протокола работы машины Т над словом а.
Здесь возможны два исхода. Если в программе машины Т есть
команды, которые могут продолжить протокол, то управление
передается на шестую, отвергающую группу команд. Если же
таких команд нет, то автомат переходит в заключительное состоя-
ние и активизирует головку 1, которая обозревает символ
Автомат останавливается, допуская слово-протокол на ленте.
Мы надеемся, что несмотря на неформальность доказательства
и отсутствие деталей проведенные рассуждения убеждают в том,
что построенный двухголовочный автомат допускает слово на
своей ленте только в том случае, если оно является конечны»!
протоколом работы машины Т над словом а. В любом другом слу-
чае слово на ленте отвергается (например, если оно является суф-
фиксом бесконечного протокола неостанавливающейся машины
Тьюринга, или, наоборот, конечным протоколом, надстроенным
«лишними» конфигурациями, или конечным протоколом другой
машины Тьюринга, или протоколом работы машины Т над дру-
гим словом). Q
Задание 3.4. Постройте машину Тьюринга, которая преобразует
двоичные слова в «обратные», т. е. заменяет 0 на 1 и 1 на 0. Постройте двух-
головочный автомат, моделирующий работу зтой машины над словом 101.
Теорема 3.9. Проблема пустоты, двухголовочных автома-
тов не является частично разрешимой.
Доказательство. Используем проблему зациклива-
ния машин Тьюринга и метод сведения. Предположим, что проб-
лема пустоты двухголовочных атоматов частично разрешима.
Тогда оказывается частично разрешимой проблема зацикливания
64
машин Тьюринга. Действительно, частичный алгоритм распоз-
навания зацикливания сводится к следующим действиям.
1. Для заданной машины Тьюринга Т и начального слова а
строится двухголовочный автомат А, моделирующий работу ма-
шины 7* над словом а.
2. Если частичный алгоритм, выясняющий, пуст ли автомат А,
обнаруживает, что ЛГд = 0, то это значит, что машина Т за-
цикливается, работая над словом а.
Существование частичного алгоритма распознавания зацикли-
вания противоречит теореме 1.4, что и опровергает предположе-
ние о частичной разрешимости проблемы пустоты для двухголо-
вочных автоматов. Q
Теорема 3.10. Проблема эквивалентности двухголовочных
автоматов не является частично разрешимой.
Доказательство. Предположим противное. Тогда ока-
зывается частично разрешимой проблема пустоты двухголовочных
автоматов. Действительно, пусть Ло — произвольный фиксиро-
ванный пустой двухголовочный автомат (пример такого автомата
легко построить). Частичный алгоритм распознавания пустоты
произвольного двухголовочного автомата очевиден: надо устано-
вить, эквивалентен ли этот автомат пустому автомату Ло. Получе-
но противоречие только что доказанной теореме 3.9. Q
Доказательство теоремы 3.10 демонстрирует роль понятия пус-
тоты при исследовании проблемы эквивалентности автоматов.
Аналогичную роль это понятие играет и при изучении эквивалент-
ности других объектов и формальных систем (схем программ, ак-
сиоматик, грамматик формальных языков и т. п.). Из неразре-
шимости проблемы пустоты немедленно следует неразрешимость
проблемы эквивалентности, так как пустоту можно рассматри-
вать как частный случай эквивалентности (например, эквивалент-
ность фиксированному пустому автомату, пустой машине Тью-
ринга и т. д.). Если гже проблема пустоты разрешима (частично
разрешима), то проблема эквивалентности должна исследоваться
независимо, так как в общем случае из разрешимости (частичной
разрешимости) пустоты не следует разрешимость (частичная раз-
решимость) проблемы эквивалентности. Например, проблема пус-
тоты разрешима для многоленточных автоматов, но проблема их
эквивалентности открыта (для случая трех и более лент).
Краткий обзор и комментарии
В этой главе приводится всего лишь несколько фактов из тео-
рии конечных автоматов и не включены сведения даже о тех авто-
матах, которые играют активную роль при изучении ие рассмат-
риваемых в книге проблем теоретического программирования.
В частности, не упоминались магазинные и стековые автоматы,
применявшиеся при решении ряда задач теории схем программ.
3 В. Е. Котов, В. К. Сабельфельд 65
Мы опустили также изложение основ теории формальных языков,
тесно связанной как с теорией автоматов, так и со многими раз-
делами теоретического программирования. Однако для знакомства
с основной проблематикой теории схем программ можно ограни-
читься приведенным минимумом сведений. Читателям, желающим
более подробно познакомиться с теорией автоматов и формальных
языков, будет полезна обзорная статья Ахоу и Ульмана [80].
Особое внимание в этой главе было уделено многоленточным
автоматам. Изложение в целом следует работе Берда [85]. Фак-
тически изложение пп. 2.1—2.4 получено переносом доказанных
в [85] результатов для двухленточных схем Берда на п-ленточные
схемы, а в п. 2.5 приводится результат из [85] о разрешимости
эквивалентности двухленточных автоматов. Проблема эквивалент-'
ности n-ленточных автоматов для п 3 является одной из наиболее
вызывающих открытых проблем теоретического программирова-
ния, которая почти 30 лет не поддается усилиям математиков.
Кинбер [26] доказал разрешимость проблемы эквивалентности
в классе автоматов, совершающих ограниченное число переходов
на все ленты, за исключением, быть может, двух. Другой разре-
шимый подкласс многоленточных автоматов, каждое состояние
которых содержится не более чем в одноф цикле, был выделен
Льюисом [117]. \
ГЛАВА 4
СТАНДАРТНЫЕ СХЕМЫ ПРОГРАММ
Схема программы — центральное понятие современной теории
программирования, основной инструмент исследования свойств
и преобразований программ. После обсуждения методологических
предпосылок возникновения этого понятия и неформального вве-
дения в основную проблематику схем программ определим класс
так называемых стандартных схем. На базе стандартных схем
будут введены основные понятия, связанные со схемами программ,
главное из них — отношение функциональной эквивалентности
схем.
§ 1. Схемы программ
1.1. Программы. Программа выступает как промежуточное
звено при общении человека с вычислительной машиной, связы-
вая поставленную задачу с процессом поиска ее решения на ма-
шине. Понятие задачи очень емко, и его трудно уточнить, не обед-
няя, даже на интуитивном уровне, в силу большого разнообра-
зия'целей, содержания и форм задач, которые сейчас решаются
с помощью ЭВМ. Нам достаточно представлять задачу как функ-
цию над множеством данных — объектов, кодирующих заданную
и искомую информацию. Будучи посредником между задачей и
машиной, программа* задает некоторую механическую процедуру
решения задачи, являясь одний из способов задания алгоритма.
Поэтому программа обладает всеми общими свойствами алгорит-
мов: является конструктивным объектом; работает конечное вре-
мя для тех наборов исходной информации, для которых вычисляе-
мая функция определена; для программы характерны массовость
(применимость ко множеству разных начальных данных) и од-
нозначность.
Конструктивный характер программы проявляется в том, что
она представляет собой конечный текст на некотором формали-
зованном языке, который можно изучать и преобразовывать
методами формальной лингвистики. Синтаксическая сторона про-
граммы выходит на первый план в начальной стадии программи-
рования: на этапе составления программы и в первых фазах
трансляции. Соответственно в теоретическом программировании
возникают такие задачи, как проблема распознавания синтаксиче-
ской правильности программ, нахождение оценок сложности син-
3 • 67
таксического анализа, конструирование и исследование классов
формальных языков, которые могут служить основой для разра-
ботки языков программирования с новыми синтаксическими свой-
ствами и возможностями, и т. п.
С другой стороны, программа определяет алгоритм решения
задачи (алгоритм нахождения значений функции), генерируя по-
следовательность действий машины. Каждое из этих действий
осуществляет некоторый шаг преобразования данных и вызыва-
ется соответствующими синтаксическими конструкциями языка.
Каждая отдельная конструкция и их совокупность несут опре-
деленную смысловую нагрузку. Смысл языковых конструкций и
всей программы в целом — семантическая сторона программы.
Основные проблемы как практического программирования, так и
теории схем программ связаны с семантикой программ, с изуче-
нием и использованием тех свойств и преобразований, которые
сохраняют семантику и инвариантны к синтаксису программы.
Программа универсальна в том смысле, что любой алгоритм
можно запрограммировать. Чтобы это утверждение не было по-
хоже на тезис, его можно переформулировать, используя формаль-
ное понятие вычислимой функции и фиксируя класс программ
(т. е. язык программирования, семантика которого формализова-
на). Ершов [13] построил в некотором смысле минимальный класс,
содержащий программы нахождения значений любой вычислимой
функции, заданной, например, машиной Тьюринга. Этот класс
включает программы, записанные на языке программирования,
который можно назвать микро-Алголом. Язык включает только
простые переменные, операторы присваивания, условные опера-
торы и операторы перехода на метки. При этом правые части опе-
раторов присваивания могут содержать только арифметические
выражения вида х + 1, а логические выражения в условных
операторах имеют вид отношения х = у, где хну — простые
переменные.
Воспользовавшись такой связью между программами и вы-
числимыми функциями, можно перенести на программы те свой-
ства машин Тьюринга и те результаты, о которых шла речь в гл. 1.
В частности, в терминах программ можно переформулировать
проблемы остановки, зацикливания, пустоты и другие. От боль-
шинства автоматических преобразований программ (оптимиза-
ция, трансляция и др.) требуется, чтобы они гарантировали функ-
циональную эквивалентность: исходная и преобразованная про-
граммы должны вычислять одну и ту же функцию. Так же, как и
в случае машин Тьюринга, универсальность программ делает их
мощным средством решения разнообразных задач, но имеет свои
теневые стороны в том случае, когда сами программы становятся
объектом исследования. Следствием универсальности является
невозможность построения полезной теории программ, базирую-
щейся на учете лишь их функциональной природы, так как в этой
теории нетривиальные проблемы оказываются «тривиально не-
разрешимыми».
68
Кроме того, программы являются объектами более сложной
структуры, чем традиционные системы описания алгоритмов. Сов-
ременные универсальные языки программирования предоставля-
ют в распоряжение программиста богатый набор программных
примитивов. Приведем список наиболее распространенных.
А. Средства описания структур данных.
1. Константы.
2. Простые переменные.
3. Массивы.
4. Сложные структуры данных — списки, магазины, очереди
и т. п.
5. Ссылочные структуры.
6. Блочность.
7. Типы данных.
Б. Средства описания операций.
1. Арифметические выражения.
2. Логические выражения.
3. Процедуры и функции, в том числе рекурсивные.
4. Выражения специального вида и назначения — счетчики,
операции над данными нечисловых типов и т. д.
В. Средства описания структуры программ.
1. Операторы присваивания.
2. Условные операторы.
3. Операторы перехода и именующие выражения.
4. Операторы цикла.
5. Механизмы вызова процедур.
6. Средства задания параллелизма, недетерминированности и
синхронизации выполнения операторов.
Теория, изучающая программы, должна учитывать, в отличие
от общей теории алгоритмов, структурный характер программ,
особенности различных примитивов, их взаимосвязь, возможность
замены одних другцми с тем, чтобы можно было ставить задачи
практической ориентации. >•
1.2. От программ к схемам программ. Теория схем программ
берет на вооружение обычный методологический прием теорети-
ческих разделов прикладных наук — замену сложных реальных
объектов и явлений более простыми абстрактными моделями. Ма-
тематические модели программ (заметим, что сами программы —
тоже математические объекты) должны удовлетворять обычным
для моделей требованиям, которые в этом случае звучат следую-
щим образом:
— модель позволяет изучать свойства достаточно широких
классов программ, а не отдельных конкретных программ;
— сохраняет все интересующие исследователя свойства и осо-
бенности рассматриваемого класса программ;
— позволяет игнорировать несущественные для данной проб-
лемы свойства, например, синтаксические детали;
— модель модифицируема и допускает нововведения, отсле-
живающие развитие языков программирования;
89
— дает возможность отделить разрешимые и неразрешимые
свойства программ и классов программ;
— удобно, если структура модели изобразительно подобна
структуре программ, что дает возможность привлекать на неко-
торых этапах исследований программистскую интуицию.
Схемы программ — это математические модели программ,
вполне отвечающие перечисленным требованиям. В частности,
они отвечают последнему требованию: схемы, так же как и про-
граммы, представляют собой тексты в некоторых формализован-
ных языках, а эти языки являются упрощенными репликами язы-
ков программирования. Главное отличие схем от программ со-
стоит в следующем. Арифметические, логические и другие выра-
жения программы образуются с помощью символов операций и
указателей функций, семантика которых фиксирована языком
программирования (для базовых операций) или выводима по оп-
ределенным правилам композиции из семантики базовых опера-
ций. Поэтому каждый оператор программы единственным обра-
зом задает некоторую функцию над данными, а из этих функций
образуется (вычислимая) функция, задаваемая программой в це-
лом. В схемах же индивидуальные операции н функции заменены
абстрактными символами переменных-операций и переменных-пре-
дикатов (или функциональными и предикатными символами). Если
вместо каждого такого символа подставить конкретную функ-
цию или, соответственно, предикат (как говорят, задать интер-
претацию схемы), то схема превращается в программу. Сама же
схема не задает алгоритма, в отличие от программы, и с помощью
схемы нельзя вычислять что-либо. Схема описывает строение
программы или, более точно, строение множества программ, по-
лучающихся из схемы в результате задания различных интерпре-
таций *). Следующий пример поясняет различие мещду програм-
мой и ее схемой.
Программа вычисления факториала Схема программы
начало целые х, у, начало
ввод(х); ввод (х);
У:==1; Л у:=а;
1: если х = 0 то на И; Z: если р (х) то на Z1;
yt—xXy; y--=gfo у);
х:= х — 1; х := h(x)-
на Z; на Z;
Z1: вывод (у) Z1: вывод (у)
конец конец
•) Существует разногласие, какой термин предпочтительней употреб-
лять — «схема программы» или «схема программ». Сторонники второго ва-
рианта обосновывают его тем, что одна и та же схема, будучи различным об-
разом интерпретирована, порождает множество программ. Однако авторы
предпочитают первый термин, имея в виду то, что в зтом контексте слово
«программа» имеет собирательное значение так же, как слово «функция» в
словосочетании «производная функции».
70
Слева — программа на языке Алгол-60, справа — схема програм-
мы (из некоторого класса схем, который в этой книге не рассмат-
ривается, но который близок к классу стандартных схем, опре-
деленному в следующем параграфе). Нам достаточно понимать,
что схема представляет собой текст на некотором формальном
языке, синтаксис которого подобен синтаксису языка Алгол-60,
но семантика которого не задана. Точнее, некоторый «абстракт-
ный» смысл объектов этого языка может быть указан при строгом
определении класса схем или, как в нашем случае, может быть
интуитивно понятным для тех, кто знаком с программированием
на языке Алгол-60. Для нас важно отметить, что в этом языке есть
разные группы символов: символы, которые мы будем называть
переменными (в <$4Л — х и у) и константами (а); функциональные
(в 54л — g и Л) и предикатные (р) символы и, наконец, символы-
метки и специальные символы (начало, если и т. д.). В схеме
можно выделить составленные из символов по определенным пра-
вилам объекты, называемые операторами:
— операторы присваивания (у := g (х, у));
— условные операторы (если р (х) то на Z1);
— операторы перехода (на Z);
— операторы ввода и вывода.
Сравнивая программу и схему программы из примера, заме-
тим, что схема 54л достаточно детально описывает устройство про-
граммы, а именно используемые переменные, логическую струк-
туру программы, структуру операторов. Особенно наглядным
становится схемное представление программ, если логическая
структура изображена в виде графа, вершинами которого являются
операторы, а дуги между вершинами указывают (возможные)
переходы от оператора к оператору в процессе выполнения
программы. Такая форма изображения схем близка к популяр-
ным среди программистов блок-схемам н широко используется
нами. Схема 54л в графовой форме показана на рис. 4.1.
В схеме 54л нет никакой информации о семантике перемен-
ных, функциональных и предикатных символов, на основании
которой можно было бы установить, что, собственно, вычисляет
программа, а вычисляет она факториал п!, где п — начальное зна-
чение переменной х, задаваемое оператором ввода. Проведем сле-
дующее преобразование схемы Stl. Символы-переменные х и у
превратим в переменные (в обычном смысле слова), сопоставив
им в качестве областей значений множество всех целых неотри-
цательных чисел. Константу а заменим на число 1, функциональ-
ный символ g — операцией умножения, символ h — операцией
вычитания единицы, предикатный символ р — предикатом «рав-
но 0». Другими словами, зададим интерпретацию схемы с множе-
ством всех чисел в качестве области интерпретации. В результате
получим запись алгоритма на некотором языке программирова-
ния, а именно уже выписанную выше программу вычисления
факториала. Следовательно, схема программы вместе с некоторой
интерпретацией образуют программу; одна и та же схема, интер-
71
претированиая различным образом, дает разные программы. Так,
возьмем в качестве области интерпретации множество V* всех
слов в некотором алфавите V. Константу а заменим пустым сло-
вом е. Функциональные и предикатные символы заменим опера-
циями и предикатом над словами: функциональный символ g —
двухместной функцией CONS С A R •), приписывающей первую бук-
ву первого слова ко второму слову (т. е. CON SCAR (аа, 0) — а0);
Рис. 4.1. Схема S*.i в графовой форме
функциональный символ h — одноместной функцией CDR, сти-
рающей первую букву слова (т. е. CDR (аа) = а). Предикатный
символ р заменим предикатом «равно пустому слову в». Такая
интерпретация схемы порождает программу, которая любое
слово . . ап в алфавите V, поданное в качестве начального
значения переменной х, превращает в «перевернутое» слово ап . . .
. . . а2а1 (см. гл. 1, задание 1.2Б).
Программа переворачивания слов.
начало слова х, у;
ввод (х);
у:=е;
I: если х = в то на И;
у := CONSCAR (х,у);
х:= CDR (х);
на I;
И: вывод (у)
конец
Интерпретируя по-разному переменные, функциональные
и предикатные символы, можно получить совершенно разные про-
граммы. Но все они будут устроены одинаково, имея одни и те же
•) Функция CONSCAR — суперпозиция функций CONS и CAR из язи-
ка Лисп, функция CDR — функция из зтого же языка [43].
72
переменные, одни и те же типы операторов, одну и ту же логиче-
скую структуру и т. д. Значит, все эти программы имеют одну
и ту же схему (здесь мы употребляем слово «схема» в «общем»
смысле, что лишь подчеркивает оправданность термина «схема
программы»). Анализ схемы позволяет сделать заключения, отно-
сящиеся ко всем программам, полученным из этой схемы
с помощью всех возможных интерпретаций. Пример очень прос-
того заключения: если в схеме типа схемы 54л нет ни одного ус-
ловного оператора и ни одного оператора перехода, то любая про-
грамма из множества всех программ, порождаемых этой схемой
и различными интерпретациями, будет выполняться конечное вре-
мя, после чего остановится. Более сложные утверждения о схе-
мах программ и программах неоднократно встретятся в после-
дующих разделах книги.
Между свойствами программ и свойствами схем программ ус-
танавливается «терминологическая» связь. Например, говорят,
что схема пуста, если любая программа, полученная из нее с по-
мощью интерпретации, пуста, т. е. никогда не останавливается
(зацикливается); или что две схемы эквивалентны, если програм-
мы, полученные из этих схем одинаковой интерпретацией одно-
именных функциональных и предикатных символов, эквивалент-
ны, т. е. задают одну и ту же функцию. Такая терминологическая
связь становится отражением глубокой связи — связи, по сущест-
ву, между схемами и программами, что дает возможность изучать
свойства программ, анализируя схемы — объекты более простой
природы, чем программы. Точно так же, выделив преобразования,
сохраняющие или улучшающие какие-то свойства схем, напри-
мер, преобразования, сокращающие количество операторов и од-
новременно гарантирующие эквивалентность исходной и резуль-
тирующей схем, можно непосредственно применить эти преобра-
зования для классов программ, порождаемых данными схемами.
В теории схем программ рассматривают разные классы схем,
моделирующие различные классы программ. Схемы типа 5*.! яв-
ляются абстракциями алголоподобных программ, но аналогич-
ным методом можно определить схемы программ, записываемых
с помощью более богатого или, наоборот, более бедного набора
примитивов, или даже схемы программ, конструируемых на ос-
новании совершенно других принципов. Так, в гл. 8 вводится
класс рекурсивных схем, которые моделируют программы «функ-
ционального» типа, например, программы на языке Лисп. В гл. 9
рассматриваются магазинные схемы, которые моделируют про-
граммы, использующие такие структуры данных, как стэки ма-
газинного типа. Схемы Янова (гл. 7) позволяют изучить преобра-
зования программ, которые затрагивают только их логическую
структуру. Сравнивая между собой классы схем программ, мож-
но исследовать свойства и возможности разных наборов программ-
ных примитивов, установить связь между ними, изучить пробле-
му трансляции программ, записанных на одном языке, в програм-
мы на другом языке.
73
§ 2. Класс стандартных схем
2.1. Базис. Стандартная схема программы (в линейной форме)
представляет собой текст на некотором формальном языке. Этот
язык можно рассматривать как абстрактный язык программирова-
ния, для которого не задана семантика данных и операций, т. е.
не указана область значений переменных, и символы операций
и функций не интерпретированы. Фиксация конкретной интер-
претации превращает стандартную схему, которая до этого высту-
пает как некоторая «заготовка» программы, в конкретную про-
грамму для некоторой гипотетической вычислительной машины.
Таким образом, стандартную схему программы можно рассмат-
ривать как представитель семейства «стандартных» программ *).
Из списка программных примитивов, используемых в языках
программирования (см. п. 1.1), для стандартных схем и программ
отобран небольшой набор, а именно: константы, простые перемен-
ные, выражения, операторы присваивания, условные операторы,
метки и переходы на метки. Классы схем программ, в том числе
класс стандартных схем, характеризуются базисом класса и струк-
турой схем. Базис класса фиксирует символы, из которых строят-
ся схемы, указывает их роль (переменные, функциональные сим-
волы и т. п.), задает вид выражений и операторов схемы. Наряду
с классом всех стандартных схем, характеризуемым полным ба-
зисом, будем исследовать некоторые его подклассы в базисах более
«бедных», чем полный базис. И наоборот, в гл. 9 мы рассмотрим
различные классы обогащенных схем, базис которых формирует-
ся из полного базиса (или его подбазисов) включением дополни-
тельных примитивов, например, более сложных структур данных
и операций над ними.
Полный базис класса стандартных схем состоит из четырех
непересекающихся счетных множеств символов и множества опе-
раторов — слов, построенных из этих символов. Множества сим-
волов полного базиса:
1) SC = {х, xlt . . ., у, уи . . z, Zj, . . .} — множество сим-
волов, называемых переменными;
2) & = {/<•>, /<>>, /<«>.£<»>, gv, gW, . . ., Л<°>, hW,
Л(3), . . . } — множество функциональных символов; верхний ин-
декс задает местность символа; нульместные символы {/(0),
h<°>, . . . } будем называть также константами и обозначать на-
чальными буквами латинского алфавита а, Ь, с, . . .;
3) 5й = {р(0), р(1), pw, . . ., ff(0), g*4, . . .} — множест-
во предикатных символов; верхний индекс задает местность сим-
вола; нульместные предикатные символы {р{0), </0), . . .} будем
называть также логическими константами;
4) {старт, стоп, (,),,, := } — множество специальных симво-
лов.
•) Мы вынуждены использовать этот термин несмотря на неудачное сов-
падение его с термином «стандартная программа», понимаемым как элемент
библиотеки стандартных подпрограмм.
74
Через d (s) в дальнейшем будем обозначать местность (функ-
ционального или предикатного) символа s.
Термами (функциональными выражениями) называют слова,
построенные из переменных, функциональных и специальных
символов по следующим правилам:
1) односимвольные слова, состоящие из переменных или конс-
тант, являются термами;
2) слово т вида /<п> (тп т2, . . ., т„), где тъ т8, . . ., тп — тер-
мы, является термом;
3) те и только те слова, о которых говорится в пунктах 1)
и 2), являются термами.
Примеры термов:
х, а, /W (х), f<*> (х, W3> (у, (х), о)).
Логическими выражениями, или тестами, называют логиче-
ские константы и слова вида pln> (тх, т8, . . ., тп), где р(п) — пре-
дикатный символ, а тх, . . ., т„ — термы. Примеры логических
выражений: р<°>, pw (х), (х, у, z), р№ (f№ (х, у)). Условим-
ся в функциональных и логических выражениях опускать индек-
сы местности, когда это не приводит к двусмысленности или про-
тиворечию.
Множество операторов состоит из операторов пяти типов:
1) начальный оператор — слово вида старт (хх, . . ., хк), где
к 0, а хг, . . ., хк — попарно различные переменные из базиса
33, называемые результатами этого оператора;
2) заключительный оператор — слово вида стоп (тх, . . ., тп),
где п О, а тх, . . ., — термы; вхождения переменных в тер-
мы Tlf . . ., тп называются при этом аргументами этого опера-
. тора;
3) оператор присваивания — слово вида х т, где х — пе-
ременная, ат — терм; вхощдения переменных в терм т называют-
ся аргументами, а переменная х — результатом этого опера-
тора;
4) условный оператор (или тест) — логическое выражение;
вхождения переменных в логическое выражение называются ар-
гументами этого оператора;
5) оператор петли — односимвольное слово петля.
Среди операторов присваивания выделим специальный слу-
чай, когда терм % — переменная, и назовем такие операторы пере-
сылками (например, х:= у), а также случай, когда т — констан-
та, и назовем такие операторы засылками констант (например,
х :-= о).
Базисы подклассов стандартных схем образуются выделением
подмножеств перечисленных множеств полного базиса. Напри-
мер, базис подкласса который будет рассмотрен в следующей
главе, состоит из множеств символов {хх, Xg), {a, ft1»},
(старт, етоп, ( , ),,,:=} и множества операторов {стцрт (хх, д^),
хх := / (хх), х8 := / (х2), хх := а, хг := а, р (хх), р (xt), стоп (х8,
х8)}. Другими словами, схемы из класса используют всего лишь
75
две переменные и хг, константу а, единственный одноместный
функциональный символ, единственный предикатный символ
и операторы указанного вида. Множество переменных базиса схем
Янова (см. гл. 7) состоит из единственной переменной. В дальней-
шем мы не будем каждый раз упоминать общее для всех базисов
этих подклассов множество специальных символов, а также на-
чальные операторы.
2.2. Стандартная ехема (графовая форма). Стандартную схему
мы вводим здесь как размеченный граф, т. е. граф, вершинам кото-
рого приписаны операторы из некоторого базиса 53 (полного ба-
зиса или более узкого базиса). В практике программирования ши-
роко используется так называемое блок-схемное представление
алгоритмов и программ, достоинством которого является нагляд-
ность изображения логической (или управляющей) структуры
программы. Такая форма представления оказывается удобной
и для стандартных схем программ, особенно в примерах.
Стандартной схемой в базисе 3$ называется конечный (разме-
ченный ориентированный) граф без свободных дуг и с вершинами
следующих пяти типов:
1) Начальная вершина. В схеме имеется ровно одна начальная
вершина. Она помечена начальным оператором. Из нее выходит
ровно одна дуга. В графе нет дуг, ведущих к начальной вершине.
2) Заключительная вершина. Она помечена заключительным
оператором, из нее не выходит ни одной дуги. В схеме может быть
несколько заключительных вершин.
3) Вершина-преобразователь. Она помечена оператором при-
сваивания, и из нее выходит ровно одна дуга.
4) Вершина-распознаватель. Она помечена условным опера-
тором (называемым в этом случае также условием этой вершины),
и из нее выходят ровно две дуги, одна из которых (на рисунках
обычно левая) помечена символом 1 и называется 1-дугой, а дру-
гая помечена символом 0 и называется О-дугой.
5) Вершина-петля. Она помечена оператором петли. Из нее
не выходит ни одной дуги.
Конечное множество переменных, упоминаемых в схеме *) S,
составляет ее память Xs.
Из этого определения стандартной схемы следует, что один
и тот же оператор может помечать несколько вершин схемы. В тех
случаях, когда это не приводит к двусмысленности, условимся
говорить о вершинах схемы как об ее операторах. Это позволит
нам вместо длинных выражений вроде «вершина схемы, помечен-
ная оператором х : = / (ж)» употреблять более короткие: «опера-
тор х := / (а:)».
- ; Чтобы можно было упоминать вершины схемы в рассуждениях
о них, вершины снабжаются именами. В качестве таких имен обыч-
но используются целые неотрицательные числа (мы будем назы-
•) В тех случаях, когда из контекста ясно, о каком классе схем идет
речь, мы будем кратко говорить «схема» вместо, например, «стандартная схе-
ма программ».
76
вать их метками вершин). Будем считать, что начальная вершина
схемы всегда помечена меткой 0; если в схеме п вершин, то они
помечены метками {0, . .., п — 1).
Введем обозначение арг (v) для множества переменных, яв-
ляющихся аргументами оператора р, и рез (v) — для множества
переменных, являющихся результатами оператора v в стандарт-
ной схеме.
Говорят, что переменная х задана на дуге е схемы S, если лю-
бой путь в S, начинающийся начальной вершиной и кончающийся
дугой е, содержит хотя бы один оператор с результатом х. Схема S
называется правильной, если на каждой ее дуге е заданы все пе-
ременные из множества арг(кон(е)). В дальнейшем мы будем пред-
полагать, что стандартные схемы правильны. Требование пра-
вильности схемы соответствует программистскому правилу запре-
та использования значений таких переменных, которые не за-
даны.
Задание 4.1. Сформулируем задачу глобального анализа схемы
следующим образом. Элементами полурешетки свойств будут подмножества
переменных из Х8. В качестве операции Д этой полурешетки возьмем объ-
единение подмножеств множества Х8. Начальная разметка сопоставляет
каждой дуге пустое множество переменных (т.е. единицу этой нолурешетки).
Семантическая функция определена следующим образом: для пары смежных
ДУГ (*, *') (М) — М U рез(иач (е)).
Докажите, что схема S правильна тогда и только тогда, когда при ста-
ционарной разметке р для описанной задачи включение арг (кои (е)) с р («)
выполняется для всех дуг « схемы S.
Задание 4.2. В предыдущем задании для определения свойства
правильности схемы использована разметка для решения прямой задачи
глобального анализа. Можно ли распознавать правильность схемы с помощью
алгоритма равметки, решающего обратную задачу глобального анализа
(с дистрибутивными преобразователями свойств)?
Пример (правильной) стандартной схемы в графовой форма
приведен на рус. 4.2, а. Начальная и заключительная вершины,,
а также вершины-преобразователи изображены прямоугольника-
ми, вершины-распознаватели — овалами. Операторы, метящие
вершины, выписаны внутри прямоугольников и овалов.
2.3. Стандартная схема (линейная форма). Опишем, как по
стандартной схеме S в графовой форме можно строить ее линей-
ную форму. Для этого множество специальных символов расши-
рим дополнительными новыми символами {:, на, если, то, ина-
че}. Стандартная схема в линейной форме представляет собой
последовательность инструкций, которая строится следующим
образом:
1) если выходная дуга начальной вершины с оператором старг
(z1( . . ., хп} ведет к вершине с меткой I, то начальной вершине со-
ответствует инструкция
0: старт (xlt . . ., хп) на I;
2) если вершина схемы 5 с меткой I — преобразователь с опе-
ратором присваивания х := т, выходная дуга которого ведет
77
Рис. 4.2. Схема и программы: а — схема б — программа (S4.2, IJ; « — -
программа (54.2,Ig)
к вершине с меткой It, то этому преобразователю соответствует
инструкция
Г. х := т на И;
3) если вершина схемы S с меткой I — заключительная вер-
шина с оператором стоп (тх, . .хт), то ей соответствует инструк-
ция
1-. стоп (тъ . . ., тт);
4) если вершина схемы 5 с меткой I — распознаватель с ус-
ловием р (тг, . . тк), причем 1-дуга ведет к вершине с меткой
И, а 0-дуга — к вершине с меткой Z0, то этому распознавателю
соответствует инструкция
I: если р (тг, . . тк) то It иначе 10;
f
5) если вершина схемы 5 с меткой I — петля, то ей соответст-
вует инструкция
I: петля.
Таким образом, если в схеме S имеется п вершин, то в линей-
ной форме ей соответствует последовательность из п инструкций,
помеченных метками 0, . . ., п — 1. В линейной форме схем час-
то используют следующие сокращения записи:
1. Если некоторая инструкция имеет вид I: А на It, где А —
оператор присваивания или начальный оператор, причем It =
= I 4- 1, то вместо нее пишут I: А (опускание переходов на сле-
дующую инструкцию).
78
2. Если на некоторую инструкцию нет переходов, то ее метки
можно опускать (опускание меток). В частности, первую инструк-
цию схемы можно записывать без метки 0, поскольку, в соответст-
вии с определением схемы, на нее нет переходов.
Вот полная и сокращенная линейные формы схемы S4t, при-
веденной на рис. 4.2. а:
0: старт (х) на 1, старт (х),
1: у а на 2, у а,
2: если р (х) то 5 иначе 3, 2: если р (х) то 5 иначе 3,
3: у g (х, у) на 4, 3: у := g (х, у),
4: х : = h (х) на 2, х :== h (х) на 2,
5: стоп (у). 5: стоп (у).
2.4. Итерпретация, программа. Стандартная схема не явля-
ется, как уже не раз отмечалось, записью алгоритма, и с ее по-
мощью можно исследовать только структурные свойства программ,
но но семантику вычислений. При построении «семантической»
теории схем центральными становятся такие понятия, как интер-
претация, интерпретированная схема (программа) и функциональ-
ная эквивалентность схем программ. Отметим сразу, что это не
единственная возможность построения содержательной теории
схем, существует другой подход, так называемая «формальная»
теория схем программ, которая не использует вводимое ниже по-
нятие интерпретации и, таким образом, не устанавливает явной
связи между схемами и вычислениями. С этим подходом мы по-
знакомимся в п, 3.5 настоящей главы.
Пусть задан некоторый базис S3, в котором определен класс
стандартных схем. Интерпретацией базиса S3 в области интер-
претации D называется функция I, которая сопоставляет:
1) каждой переменной х из базиса S3 — некоторый элемент
d = I (х) из области интерпретации D;
2) каждой константе а из базиса — некоторый элемент d =
= I (а) из D;
3) каждому функциональному символу /<"> (п >> 1) — всю-
ду определенную функцию F^ = / (Лп,): Dn-*~D;
4) каждой логической константе р(0) — один из символов мно-
жества {0, 1};
5) каждому предикатному символу где п 1,— всюду
определенный предикат Р(П) = I (р<">): Dn {0, 1}.
Определение интерпретации не уточняет природу объектов мно-
жества D, в конкретных примерах мы будем фиксировать в ка-
честве области интерпретации множество всех чисел или множест-
во всех слов в некотором алфавите или подмножества этих мно-
жеств. Интерпретация называется конечной, если ее область D —
конечное множество.
Пара (S, Г), где S — схема в базисе S3, л I — интерпретация
этого базиса, называется интерпретированной стандартной схе-
мой, или (стандартной) программой. Определим понятие выпол-
нения программы.
78
Состоянием памяти программы (S, Z) назовем функцию W:
Xs-*- D, которая каждой переменной х из памяти схемы S сопос-
тавляет элемент W (х) из области интерпретации D. Элемент W (х)
называется значением переменной х в состоянии W; запись W =
= W' означает, что два состояния памяти W и W' совпадают
с точностью до значений переменной х, т. е. для всех у G= Xs
у Ф х W (у) = W' (у). Если X = (хь . . хп) — некоторый
набор переменных из Xg, то W (X) = (W (х,), . . W (х„)) —
набор значений переменных . ., хп. Начальным состоянием
памяти Хв при интерпретации I назовем состояние РУ0 такое,
что 1У0 (х) = I (х) для любой переменной х из Xg.
Значение терма т при интерпретации Z и состоянии памяти W
(обозначение: Т/ (И7)) определяется следующим образом:
1) если т = х, где х — переменная, то Т/ (РУ) = W (х);
2) если т = а, где а — константа, то tj (РУ) = I (а);
3) если т = /<"> (тп . . ., тп), то т, (РУ) = I (хи (ТУ),
т,г (ТУ), TSJ (ТУ), . . ., тп, (ТУ)).
Аналогично определяется значение теста я при интерпрета-
ции I и состоянии памяти ТУ (обозначение: я^ (ТУ)): если я =
= p<n> (rlt . . ., тп), п > О, то
я, (ТУ) = Z СР<«>) (тн (ТУ), . . ., Тп/ (ТУ)).
Конфигурацией ♦) программы (5, I) назовем пару и = (I, W),
где I — метка вершины схемы S, а ТУ — состояние ее памяти. Вы-
полнение программы описывается конечной или бесконечной по-
следовательностью конфигураций, которую мы назовем протоко-
лом выполнения программы.
Протокол (u0, Uj, . . ., щ, ui+1, . . .) выполнения программы
(£, I) определим следующим образом (ниже к, означает метку
вершины, а РУ< — состояние памяти в i-й конфигурации прото-
кола, щ — (klt РУ«)):
1) «о — (О, ТУ0), где Wo — начальное состояние памяти схе-
мы S при интерпретации Z.
2) Пусть и, = (Ait WJ — i-я конфигурация протокола, а О —
оператор схемы 5 в вершине с меткой kt. Если О — заключитель-
ный оператор стоп (tlt . . ., тп), то и, — последняя конфигурация
протокола, так что протокол конечен. В этом случае говорят, что
программа (5, Z) останавливается, а последовательность зна-
чений (РУ4), Tjj (pyj, . . ., Tni (РУ4) объявляют результатом
val (8, I) выполнения программы (8, I). В противном случае, т. е.
когда О — не заключительный оператор, в протоколе имеется
следующая, (i -Ь 1)-я конфигурация uj+1 = (Ai+1, РУ4+1), причем
•) В литературе используются термины «состояние выполнения* (com-
putation state, execution state) вместо «конфигурация» и «последовательность
«полпенни» (computation sequence, execution sequence) вместо «протокол».
Наши термины заимствованы из теории машин Тьюринга для того, чтобы
подчеркнуть аналогию между соответствующими понятиями.
80
а) если О — начальный оператор, а выходящая из него дуга
ведет к вершине с меткой I, то Ai+1 = I и IFi+1 = Wt;
б) если О — оператор присваивания х := т, а выходящая из
него дуга ведет к вершине с меткой I, то &i+1 = I, IFi+1 == Wit
Wi+1 (x) = xt TO);
в) если О — условный оператор пип, (И^) = Д, где Д е
€= {0, 1), а выходящая из этого распознавателя Д-дуга ведет
к вершине с меткой Z, то Л<+1 == I и Wi+1 = Wt;
г) если О — оператор петли, то Ai+1 = и Wi+1 = Wit так
что протокол бесконечен.
Таким образом, программа останавливается тогда и только
тогда, когда протокол ее выполнения конечен. В противном слу-
чае программа зацикливается и результат ее выполнения не опре-
делен.
Заметим, что наше определение программы включает задание
начальных данных (начальное состояние памяти). Понятие ин-
терпретации иногда вводят таким образом, что интерпретируются
только функциональные и предикатные символы, а начальные
значения переменных задаются отдельно. В этом случае програм-
ма описывает алгоритм и определяет частичную функцию из Dn
в JD*, где D — область интерпретации, п — количество перемен-
ных в схеме (каким-либо образом упорядоченных), a D* — ъто-
жество последовательностей элементов нз D. Такой вариант
определения программы больше соответствует общепринятому раз-
делению на собственно программу и исходные данные. Однако для
изучения семантических свойств схем программ отделение исход-
ных данных от программы несущественно, так как основным объ-
ектом исследования остается схема, а понятие программы необ-
ходимо как промежуточный объект для определения понятий,
о которых пойдет речь в следующем параграфе. В то же время
принятое нами определение программы позволяет упростить тех-
ническую сторону дела.
2.5. Примеры программ. Вернемся к известной стандартной
схеме (см. п. 2.2 и 2.3), на примере которой поясним введен-
ные понятия (см. рис. 4.2, а). Рассмотрим две программы (<У4.а, Д)
и Л)» где Zj и Ia — интерпретации, которые сейчас будут
заданы формально, но неформально уже обсуждались в § 1 этой
главы. Интерпретация задана следующим образом:
область интерпретации ZJj — множество всех целых неотри-
цательных чисел;
h (х) = 4; А (у) = 0; Д (а) = 1;
A (s) — Gt где G: D*-*- Da — функция умножения чисел, т. е.
G (d^, da) = d4 X d^;
Л (Л) = Н, где Hz — функция вычитания единицы,
т. е. Н (d) = d — 1;
А (?) = Рц где Рг: -> {0, 1) — предикат «равно 0», т. е.
1, если d = О,
О, если dgfcO.
61
Pi(d) = {
Программа (<S4.a, Д) вычисляет 4!. Интерпретация /, задана
следующим образом:
область интерпретации D3 = У*, где V — {а, Ь, с);
/2 (х) = abc',
/2 (у) — гДе « — пустое слово;
/а (а) = е;
/2 (g) = CONSCAR, где CONSCAR: D$-+Da- функция,
приписывающая первую букву первого слова к началу второго
слова, т. е. CONSCAR (d6, у) = dy, где d GE У, б ЕЕ У*, у Е У*;
/2 (Л) — CDR, где CDR: D2-*-Dt — функция, стирающая пер-
вую букву слова, т. е. CDR (d6) = 6, где dG У, бЕ У*;
/2 (Р) — где Рг- &а {0, 1} — предикат «равно е», т. е.
^(«) = {
1, если а = е,
О, если а =/= £.
Программа (S4e2, /2) преобразует слово abc в слово сЬа. Заме-
тим, что в обеих рассмотренных программах интерпретация пере-
менной у (т. е. ее начальное значение) несущественна: можно бы-
ло бы Д (у) взять произвольным числом, а Д (у) — произвольным
словом, причем первая программа по-прежнему будет вычислять
4!, а вторая — переворачивать слово abc.
На рис. 4.2, б, в показаны обе программы в неформальной гра-
фовой форме. Неформальность этого представления программ со-
стоят в том, что программа не показана как пара — схема в гра-
фовой форме и интерпретация, а в схему вместо функциональных
и предикатных символов непосредственно подставлены общепри-
нятые обозначения функций, полученных интерпретацией этих
символов. Подобным неформальным, но наглядным представле-
нием программ мы будем пользоваться и далее в примерах.
Протокол выполнения программы (54.2, 1г) конечен, резуль-
тат программы — число 24.
Протокол выполнения программы (54.2, Д) тоже конечен, про-
грамма останавливается с результатом сЬа.
Протокол программы (S».2« Д)»
Конфигурация и, и2 иа и2 и< и5 и» и? ив ua и™ иц u12 uls u1R
Метка 01234234234 2 34 25
Значения:
х 4444333222111000
у О 1 1 4 4 4 12 12 12 24 24 24 24 24 24 24
Протокол программы (S«.z, Д).
Конфигурация ил их ut u< ub u( u, ut uj и1в ии uI2
Метка 01 234234234 2 5
Значения:
х abc abc abc abc be Ьс Ъс с с с е е е
у е е е а а а Ьа Ъа Ъа сЬа сЬа сЬа сЬа
82
§ 3. Эквивалентность и главные свойства
стандартных схем
3.1. Эквивалентность, тотальность, пустота, свобода. Гово-
рят, что стандартная схема S в базисе S3 тотальна, если для лю-
бой интерпретации I базиса S3 программа (<£, I) останавливается;
стандартная схема S пуста, если для любой интерпретации I про-
грамма (S, I) зацикливается.
Отношение эквивалентности вводится для стандартных схем
в одном базисе. Если схемы и Sa построены в двух различных
базисах 33а и S3a, то можно их «привести к одному базису», в ка-
честве которого взять объединение базисов St и S3t.
Говорят, что стандартные схемы и <£2 в базисе S3 функцио-
нально эквивалентны (51 ~ Ss), если для любой интерпретации I
базиса S3 программы (Slt I) и (Sg, I) либо обе зацикливаются,
либо обе останавливаются с одинаковым результатом, т. е.
val (5n Z) е*. val (Sa, I).
Примеры тотальных, пустых и эквивалентных схем приведены
на рис. 4.3.
Цепочкой стандартной схемы назовем:
1) конечный путь по вершинам схемы, ведущий от начальной
вершины к заключительной, или
2) бесконечный путь по вершинам, начинающийся начальной
вершиной схемы.
В случае, когда вершина v — распознаватель, условимся снаб-
жать каждое очередное вхождение v в цепочку дополнительным
верхним индексом 0 или 1, в зависимости от того, по какой из двух
исходящих из вершины v дуг продолжается построение цепочки.
Таким образом, цепочку можно записывать как последователь-
ность меток вершин, причем некоторые из этих меток имеют верх-
ний индекс 0 или 1.
Примеры цепочек схемы 2 (рис. 4.2, а):
(О, 1, 21, 5)
(О, 1, 2°, 3, 4, 2°, 3, 4, 21, 5)
(О, 1, 2°, 3, 4, 2°, .... 2°, . . .).
Цепочкой операторов назовем последовательность операторов,
метящих вершины некоторой цепочки схемы. Так, среди цепочек
операторов схемы Sa.a есть следующие:
(старт (х), у := а, р1 (х), стоп (у))
(старт (х), у := а, р° (х), у := g {х, у), х := h (х), р° (х),
У := g [х, у), х := h (х), р° (х), . . ., р° (х), . . .).
Предикатные символы в цепочке операторов помечены теми же
верхними индексами 0 или 1,< которыми помечены соответствую-
щие метки распознавателей в цепочке. (В отличие от индексов
местности, которые мы в этих случаях будем опускать, индексы О
и 1 не заключены в скобки.)
Пусть S — стандартная схема в базисе S3, I — некоторая ин-
терпретация базиса S3, (0, 1, ka, k3, . . .) — последовательность
меток инструкций схемы S, выписанных в том порядке, в котором
83
I СТАРТ (X)
a.
|ciAPI(X)|
6
Рис. 4.3. Примеры стандартных схем: а — б — St.t; в — 54.е; г — 5*.
эти метки входят в конфигурации протокола выполнения програм-
мы (5, Z). Ясно, что эта последовательность — цепочка схемы S.
Будем говорить, что интерпретация У подтверждает (или порож-
дает) эту цепочку. Цепочку стандартной схемы в базисе S3 назо-
вем допустимой, если она подтверждается хотя бы одной интер-
претацией этого базиса.
84
Не всякая цепочка стандартной схемы является допустимой.
В схеме s, изображенной на рис. 4.3, а, цепочки (0, 1, 2°, 5, 61,
7), (0, 1, 2f, 3, 4°, 7) и все другие конечные цепочки не подтверж-
даются ни одной интерпретацией. Различие между понятиями
«цепочка» и «допустимая цепочка» схемы существенно. Первое по-
нятие определено «синтаксически» без привлечения интерпрета
ций и поэтому проще второго. У нас будет возможность убедить-
ся, что свойство допустимости цепочек играет чрезвычайно важ-
ную роль в задачах, связанных с изучением введенных в этом
разделе свойств схем программ. В частности, внимание исследова-
телей привлекает класс так называемых свободных схем программ.
Стандартная схема свободна, если все ее цепочки допустимы.
Допустимая цепочка операторов — это цепочка операторов, соот-
ветствующая допустимой цепочке схемы. В тотальной схеме все
допустимые цепочки (и допустимые цепочки операторов) конечны,
в пустой схеме все допустимые цепочки (и допустимые цепочки
операторов) бесконечны.
В этом разделе мы дали формальные определения главных
свойств стандартных схем; эти же определения переносятся и на
другие классы схем программ. Названные свойства и связанные с
ними проблемы образуют опорные пункты схематологии, все они
взаимозависимы, и в то же время в каждой из них отражаются спе-
цифические задачи (и трудности) теории и практики программиро-
вания. Более частные свойства схем будут введены далее по ходу
изложения, или останутся за рамками этой книги, или составят
материал для самостоятельной работы, началом которого послу-
жит задание 4.3.
Задание 4.3.
А. На рис. 4.3 даны примеры стандартных схем. Установите, какие из
них тотальны, какие — пусты. Какие пары схем функционально эквивалент-
ны? Укажите свободные схемы.
Б. Покажите, что отношение функциональной эквивалентности стан-
дартных схем является математическим отношением эквивалентности, т. е.
оно рефлексивно, симметрично и транзитивно.
В. Скажем, что стандартная схема S тотальна (пуста) на множестве
конечных интерпретаций, если для любой конечной интерпретации I про-
грамма (У, I) останавливается (зацикливается). Постройте пример стандарт-
ной схемы, которая тотальна на множестве конечных интерпретаций, но не
тотальна на множестве всех интерпретаций.
Г. Покажите, что стандартная схема пуста тогда н только тогда, когда
она пуста на множестве всех конечных интерпретаций.
Д. Введем отношение «схемы 5t и St конечно-эквивалентны», заменив
в определении функциональной эквивалентности слова «для любой интер-
претации* на «для любой конечной интерпретации». Постройте пример пары
стандартных схем, которые конечно-эквивалентны, ио ие эквивалентны функ-
ционально.
Е. Отношение слабой эквивалентности определяют следующим образом:
схемы St и St слабо эквивалентны, если для любой интерпретации I резуль-
таты программ (5t, Z) и (St, I) совпадают в том случае, когда обе программы
останавливаются. Убедитесь, что отношение слабой эквивалентности действи-
тельно слабее отношения функциональной эквивалентности, более того, оио<
ие является отношением эквивалентности в общематематическом смысле. Ука-
жите на рис. 4.3 три схемы St, St и Sa такие, что St слабо эквивалентна
S, слабо эквивалентна 5а, ио St и Sa не являются слабо эквивалентными.
85
Ж. Стандартные схемы и St называются изоморфными, если совпадают
множества всех цепочек операторов этих схем. Покажите, что изоморфизм
схем является отношением эквивалентности в классе стандартных схем,
причем более сильным, чем функциональная эквивалентность. Укажите иа
рис. 4.3 пары изоморфных схем, а также пары не изоморфных, но функцио-
нально эквивалентных схем.
3. Стандартные схемы и St в общем базисе называют интерпретацион-
но изоморфными, если любая интерпретация базиса порождает совпадающие
цепочки операторов схем и St. Покажите, что интерпретационный изо-
морфизм является отношением эквивалентности в классе стандартных схем,
причем более сильным, чем функциональная эквивалентность, но более сла-
бым, чем изоморфизм схем (см. предыдущее задание).
3.2. Свободные интерпретации. Отношение функциональной
эквивалентности, а также свойства тотальности и пустоты стан-
дартных схем определены с использованием понятия множества
всех возможных интерпретаций базиса. Таким образом, чтобы
убедиться в том, что, например, схема S пуста, надо установить,
зацикливается ли программа (S, I) для любой интерпретации I.
Такой путь оказывается неперспективным, так как класс всех
возможных интерпретаций базиса крайне широк. Однако сущест-
вует подкласс интерпретаций, называемых свободными, или эр-
брановыми *), который образует ядро класса всех интерпретаций
в том смысле, что справедливость высказываний о семантических
свойствах стандартных схем достаточно продемонстрировать для
класса всех программ, получаемых с помощью только свободных
интерпретаций. Кроме того, свободные интерпретации дают воз-
можность установить наглядную связь между синтаксисом схемы
и ее семантикой, в чем мы убедимся в следующих разделах этого
параграфа. Читатель, знакомый с эрбрановыми интерпретациями
в логике, легко обнаружит полезные аналогии между ними и сво-
бодными интерпретациями схем программ.
Все свободные интерпретации базиса SB имеют одну и ту же
область интерпретации, которая совпадает со множеством Т всех
термов базиса SB, Все свободные интерпретации одинаково ин-
терпретируют переменные и функциональные символы, а именно:
а) для любой переменной х из базиса SB и для любой свобод-
ной интерпретации /Л этого базиса Д (х) = х;
б) для любой константы а из базиса 7Л (а) = а;
в) для любого функционального символа /(п) из базиса SB,
где и > 1, (/<n>) = F<">: З™-*- Т, где F<n> — словарная функ-
ция такая, что (rlt т2, . . ., тп) = /<п) (тц т2, . . ., тп), т. е.
функция F<n> по термам rlt т2, . . ., тп из Т строит новый терм, ис-
пользуя функциональный символ /<п>.
Что касается интерпретации предикатных символов, то она,
л отличие от интерпретации переменных и функциональных сим-
волов, полностью «свободна»: в произвольной конкретной сво-
бодной интерпретации предикатному символу сопоставлен произ-
вольный предикат, отображающий Т в {0, 1). Следовательно, раз-
•) Здесь в теории схем программ была использована идущая из матема-
тической логики идея Эрбрана о возможности построения синтаксических
моделей для непротцворечнвых теорий первого порядка.
86
ные свободные *) интерпретации различаются лишь интерпре-
тацией предикатных символов.
Таким образом, после введения свободных интерпретаций тер-
мы используются в двух разных качествах, как функциональные
выражения в схемах и как значения переменных и выражений.
Если нам потребуется различать эти два употребления термов, то
мы будем термы-значения заключать в апострофы. Так, если —
= 7 (х, а)' — терм-значение переменной х, а т2 = ’g (у)' — терм-
значение переменной у, то значение свободно интерпретированно-
го терма-выражения т3 = / (х, h (у)) равно терму-значению 7 (/ (я,
a), h (g (у)))'.
Пример. Пусть Ih — свободная интерпретация базиса,
в котором определена схема <£4.3 из раздела 2.2 этой главы, и в
этой интерпретации предикат Р = Ih (р) задан таким образом:
{1. если число функциональных символов в т больше
двух;
О, в противном случае.
Тогда протокол выполнения программы (54.2, Д) можно предста-
вить в следующем виде:
Конфигу- рация Метка Значения
X V
«0 0 *х* 'у'
W1 1 * X* *а'
и» 2 'х' *аг
Из 3 *х* 'g{x, aY
и« 4 'h (х)’ 'g aY
ив 2 'Л (г)' ’g&, aY
и« 3 'Л (х)' 'g (h (A g (г, a))
и? 4 'h(h(x)) 'g (Л (*). g (г> a))'
Из 2 •h{h(x))' 'g (h («). g (*. aYY
и( 3 •h(h(x)Y 'g(h(h(x))t g(h(x), g(x,a)))
U10 4 'Л(Л(Л(х)))' ’g(h(h[x)), g(h(x), g(x,a))Y
Иц 2 •h(h(h(x))Y ’g(h(h(x)), g{h(x), g(x,a))Y
Un 5 'Л (Л (Л («)))' 'g (Л (Л (z)), g (Л (a), g (z,a)))'
Обратим внимание на следующую особенность термов. Если
из терма удалить все скобки и запятые, то получим слово (назовем
его бесскобочным термом), по которому можно однозначно восста-
новить первоначальный вид терма (при условии, что отмечена или
известна местность функциональных символов). Например, терму
#<*> (hm (х), gW (х, у)) соответствует бесскобочный терм ghxgxy.
*) «Свободные схемы» и «свободные интерпретации» — никак ие свят,
занные между собой понятия. Совпадение первых слов в этих терминах носит
случайный характер: в первом случае допустимая цепочка может быть по-
строена «свободным блужданием» по схеме, во втором — оставлена свобода
выбора интерпретации предикатных символов. Оба термина общеприняты
в литературе.
87
Правила восстановления терма по бесскобочной записи аналогич-
ны правилам восстановления арифметических выражений по их
прямой польской записи, поэтому мы предоставляем читателю
возможность построить их самостоятельно. Бесскобочная запись
термов короче, и мы будем широко использовать ее наряду с обыч-
ной записью.
3.3. Согласованные свободные интерпретации. Так как значе-
ниями переменных и выражений в свободно интерпретированных
схемах служат термы, последние можно проинтерпретировать сле-
дующим образом. Пусть ЗВ — базис, I — произвольная интер-
претация этого базиса. Интерпретация I определена для перемен-
ных, функциональных и предикатных символов базиса Об-
ласть определения интерпретации I можно естественным образом
расширить, включая в нее множество всех функциональных и ло-
гических выражений базиса ЗВ и полагая
/(т) =
7(х), если т — переменная х,
I (а), если т — константа о,
если т — выражение вида /п)
(т15 ...,тп), где /(п>— функциональный или
предикатный символ ип>1.
Более того, мы определим интерпретацию и на последователь-
ностях термов из Т, полагая I (хх . . . тп) — I (tJ I (та) . . .
. . . I (тп) для последовательности термов хг . . . т„ (п 0).
Пусть, например, х = 'g (h (h (х)), g (h (x), g (x, а)))', а интерпре-
тация /э совпадает с интерпретацией Д из п. 2.5 этой главы за
исключением лишь того, что /3 (х) = 3. Так как la (а) = 1, Ia (g) —
-функция умножения чисел, a Ia (h) — функция вычитания еди-
ницы, получаем 1а (т) = ((3 — 1) — 1) X ((3 — 1) X (3 X 1)) —
— 1 X 2 X 3 = 6. Заметим, что если 7Л — свободная интерпре-
тация, то всякий терм из Т (а также всякая последовательность
-термов из Т) является неподвижной точкой для /Л, т. е. Ih (т) =
— т.
Будем говорить, что интерпретация I и свободная интерпрета-
ция Ih того же базиса SB согласованы, если для любого логи-
ческого выражения л справедливо Ih (л) — I (л). Например,
свободная интерпретация lh, описанная в примере п. 3.2, согласо-
вана с только что рассмотренной интерпретацией 1а и с интер-
претацией 1а из п. 2.5. Однако Ih не согласована с интерпрета-
цией Д из п. 2.5.
Лемма 4.1. Для каждой интерпретации I базиса ЗВ су-
ществует согласованная с ней свободная интерпретация этого ба-
зиса.
Доказательство. Действительно, для каждого пре-
дикатного символа из ЗВ множество наборов термов-значений
Т1 можно разбить на два непересекающнхся подмножества —
Т’р./л и Гр./.о — по следующему правилу: (тп . • хп) е Тр.г.н
если I (pW) (I (Т1), . . ., I (тп)) = 1, и (xlt . . ., тп) C
88
в противном случае. Полагая затем, что предикат Ih (р^п)) при-
нимает значение 1 на наборах из T’JJ, м и значение 0 на наборах
из Тр. i.o, получаем свободную интерпретацию 1Л, согласованную
с I. □
Очевидно, что справедливо и обратное утверждение: для любой
свободной интерпретации существует некоторая согласованная
с ней интерпретация; таковой является, в частности, сама сво-
бодная интерпретация.
Введем важное вспомогательное понятие подстановки термов,.
которым будем многократно пользоваться в дальнейшем. Если
х1э . . ., хп (п > 0) — попарно различные переменные, тх, . ..
. . ., тп — термы из Т, а п — функциональное или логическое вы-
ражение, то через л [tj/xj, . . ., тп/хп] будем обозначать выраже-
ние, получающееся из выражения л одновременной заменой каж-
дого из вхождений переменной xt на терм (» = 1, . . ., п). Более
формально, понятие подстановки термов т{ вместо переменных х,
в выражении л определяется следующим образом.
1. Для i = 1, . . ., п Xi (Tj/xj, . . ., тп/хп] = тр
2. Если n = 0 или выражение л не содержит вхождений пе-
ременных Xj, . . ., Хп, ТО Л (Tj/Xj, . . ., тп/хп1 = л.
3. Если л = g (<i, . . ., tK), где g — функциональный или пре-
дикатный символ, . . ., tk £= Т, а к > 0, то л (tj/xx, . . .
• • •» ЬАЛ = g (** ......VxJ, . . ., tR [Tj/xj, . . ., rn/xnJ).
Примеры: a (y/x] — a, / (x, y) [y/x, x/y] = f (y, x),
g (x) [g (x)/x] = g (g (x)), p (x) [a/x] = p (a).
Лемма 4.2. Пусть I — произвольная интерпретация ба-
зиса Si, W — состояние памяти такое, что для всех х W (х) £= Т.
Пусть, далее, л — произвольное выражение, х1, . . ., хп — все его
переменные, a W — состояние памяти такое, что для всех
х W' (х) = I (W (х)). Тогда
щ (W’) = T(n(W (xj/x,......W (x„)/xj).
Доказательство легко проводится индукцией по
глубине выражения и предоставляется читателю. Глубина выраже-
ния может быть определена следующим образом:
глубина (т) =
О, если т — переменная или константа,
1 -j- max (глубина (хг), —, глубина (тп)), если
* = где Tlt..., тпеГ, a g —
функциональный или предикатный символ. [П
Лемма 4.3. Пусть S — стандартная схема в базисе Si,
I — интерпретация, a Ih — согласованная с I свободная интер-
претация этого базиса. Тогда для любой пары конфигураций щ =
= (A:it Wi) и u'i — (ki, JFi) такой, что щ — i-я конфигурация про-
токола выполнения программы (S, Ih), а щ — i-я конфигурация
протокола выполнения программы (S, /), выполнено kt = ki и для
всех хЕА’8 и;' (х) = I (И7, (х)).
89
Доказательство. Очевидно,* Aj = и для всех х е=
G XSf /(Wi (х)) = W'i (х), поскольку (х) = Wo (х), W[ (х) =
— Wo (х) и 1 (РГ0 (х)) = W'o (х). Пусть для некоторого i (i > 0)
выполнено (1) ki = k'i и (2) для всех х GE Xs I (W, (х)) = Wi (х).
Докажем, что (1) и (2) будут выполняться тогда н для следую-
щего i. Рассмотрим для этого все возможные случаи (пусть О озна-
чает оператор, помеченный меткой к,).
(1) О — оператор присваивания х := т, a xlt . . хп —
все переменные терма т. Тогда Ai+1 = Aj+i и I (W\+1 (х)) =
•— (xJ/Xi, . . ., Wt (xj/xj) = Tj (Wi) = Wi+1 (x). Для пере-
менных у, отличных от х, имеем I (И\+1 (у)) = 1 (Wt (у)) =
= W- (у) = W-ii. (у).
(2) О — условный оператор л, й xlf . . ., хп — все перемен-
ные теста л. Тогда Wi+1 = Wi и W,+1 = W,, так что для всех
х е xs I (W\+1 (х)) = I (Wi (х)) = Wi (х) = Wi+1 (х). Далее, по
лемме 4.2 л/ь (И\) = Zft (л (xJ/xj, . . ., W{ (xn)/xnI) и
л/ (И7,) = I (л [И\ (Xj)/Xj, . . ., Wi (xn)/xnJ), а в силу согласован-
ности интерпретаций I и Ih правые части этих равенств совпадают,
поэтому оба вхождения распознавателя выберут одну и ту же ду-
гу, т. е. fci+1 = Ai+i.
(3) О — петля. Тогда /4+1 = к\ = kt = А,+1 и для всех х е
е Xs I (IFi+1 (х)) = I (И< (х)) = W- (X) = W-+1 (х).
Итак, в случае, когда О — заключительный оператор, имеем
I (FFf (х)) = Wi (х) для всех х G= Ха и оба протокола обрываются
яа конфигурации щ. [3
Лемма 4.4. Если интерпретация I и свободная интерпре-
тация Ih согласованы, то программы (S, Г) и (S, Ih) либо обе за-
цикливаются, либо обе останавливаются и I (val (<£, Д)) =
= val (5, I).
Доказательство. Эта лемма — очевидное следствие
леммы 4.3. □
Лемма 4.5. Если интерпретация I и свободная интерпре-
тация Ih согласованы, то они порождают одну и ту же цепочку
(цепочку операторов) схемы.
Доказательство. Непосредственное следствие лем-
мы 4.3. □
3.4. Основные теоремы о свободных интерпретациях.
Теорема 4.1 (Лакхэм — Парк — Патерсон). Стандарт-
ные схемы Sx и Sa в базисе SB функционально эквивалентны тогда
и только тогда, когда они функционально эквивалентны на мно-
жестве всех свободных интерпретаций базиса SB, т. е. когда для
любой свободной интерпретации I программы (Slt Г) и (Ss, I) либо
обе зацикливаются, либо обе останавливаются и val (<УХ, I) =
= val (St, I).
90
Доказательство. Необходимость очевидна.
Достаточность. Пусть и Sa эквивалентны на множестве всех
свободных интерпретаций, а I — произвольная интерпретация
базиса Si. По лемме 4.1 существует свободная интерпретация Д,
согласованная с I. По лемме 4.4 программы (Slt I) и (£ь Ih) либо
обе зацикливаются, либо обе останавливаются, и I (val (£n Zh)) —
= val (5t, I). Аналогично, программы (Sa, Г) и (S2, Ih) либо обе
зацикливаются, либо обе останавливаются, и I (val (5а, Zh)) =
— val (Sa, 7). Так как Sa и Sa эквивалентны на множестве свобод-
ных интерпретаций, программы (S^, Ih) и (S2, Zh) либо обе за-
цикливаются, либо обе останавливаются, и val (£n Ih) = val (Sar
Ih). Следовательно, программы (Sa, I) и (Sa, Г) либо обе зацикли-
ваются, либо обе останавливаются, и val (Slt I) = I (val (5Х,
/Л)) = I (val (£2, Ih)) = val (Sa, Г). Так как интерпретация I вы-
брана произвольно, функционально эквивалентна Sa. 0
.Теорема 4.2. Стандартная схема S в базисе Si пуста (то-
тальна) тогда и только тогда, когда она пуста (тотальна) на
множестве всех свободных интерпретаций этого базиса, т. е. ес-
ли для любой свободной интерпретации Ih программа (S, Jh) за-
цикливается (останавливается).
Доказательство. Необходимость очевидна.
Достаточность немедленно следует из лемм 4.1 и 4.4. 0
Теорема 4.3. Стандартная схема в базисе Si свободна тог
да и только тогда, когда она свободна на множестве всех свобод-
ных интерпретаций этого базиса, т. е. когда каждая цепочка схе-
мы подтверждается хотя бы одной свободной интерпретацией.
Доказат е л ь с т в о. Необходимость. Любая допустимая
цепочка схемы подтверждается некоторой свободной интерпрета-
цией, что непосредственно следует из леммы 4.1 и 4.5.
Достаточность. Очевидна. 0
Леммы 4.1—4.5 и теоремы 4.1—4.3 позволяют нам рассматри-
вать в дальнейшем только свободно интерпретированные схемы
как при исследовании проблем функциональной эквивалентности*
пустоты, тотальности и свободы, так и в других задачах, связан-
ных со стандартными схемами и схемами других классов. В по-
следнем случае нам потребуется перенос этих утверждений на но-
вые классы программ, что будет сделано без повторения всех де-
талей доказательств — лишь указанием на ход рассуждений. От-
метим, что существуют «неэрбрановы» классы схем программ, для
которых неверны утверждения, аналогичные только что доказан-
ным леммам и теоремам.
Задание 4.4.
А. Покажите, что стандартные схемы в базисе 3) интерпретационно
изоморфны (см. задание 4.3, а) тогда и только тогда, когда оин интерпрета-
ционно изоморфны на множестве свободных интерпретаций этого базиса.
Б. Покажите, что стандартные схемы в базисе 3} слабо эквивалентны
тогда н только тогда, когда они слабо эквивалентны на множестве свободных
интерпретаций этого базиса.
91
3.5. Определение логико-термальной эквивалентности и ее
корректность. Отношение эквивалентности Е, заданное на парах
стандартных схем, назовем корректным, если для любой пары
схем и 5а из ~ 5а следует, что St ~ 8а, т. е. схемы St и S,
функционально эквивалентны. Поиск разрешимых корректных
отношений эквивалентности представляет значительный интерес
с точки зрения практической оптимизации и преобразования про-
грамм, поскольку, как мы увидим в следующей главе, функцио-
нальная эквивалентность стандартных схем алгоритмически не-
разрешима. Идея построения таких (корректных и разрешимых)
отношений связана с введением понятия истории цепочки схемы.
В истории с той или иной степенью детальности фиксируются
промежуточные результаты «выполнения» операторов рассмат-
риваемой цепочки. Эквивалентными объявляются схемы, у кото-
рых совпадают множества историй всех конечных цепочек.
Одним из таких отношений эквивалентности является введен-
ная Иткиным [22] логико-термальная эквивалентность, основан-
ная на понятии логико-термальной истории.
Определим термальное значение переменной х для конечного
пути w схемы S как терм t (w, х), который строится следующим
образом.
1. Если путь w содержит только один оператор А, то
т, если А — оператор присваивания х:= т,
х, в остальных случаях.
2. Если w = w'Ae, где А — оператор, е — выходящая из него
дуга, w* — непустой путь, ведущий к A, a хп . . ., хп — все пере-
менные терма t (Ае, х), то t (w, х) = t (Ае, х) [t (и/, Xj)/xlt . . .
....tW, хп)/хп].
Понятие термального значения распространим на произволь-
ные термы т: если xlt . . ., хп — все переменные терма т, то по-
ложим
t (w, т) = т [t (w, xJ/Хц . . ., t (ш, хп)/хп].
Например, пути
старт (х); у := х; р’(х); х := / (х); р°(у); у := х; pl(x)-, х :=f (х).
в схеме на рис. 4.4, а соответствует термальное значение / (/ (х))
переменной х.
Для пути w в некоторой стандартной схеме S определим ее ло-
гико-термальную историю It (8, w) как слово, которое строится
следующим образом.
1. Если путь w не содержит распознавателей и заключитель-
ной вершины, то it (S, и>) — пустое слово.
2. Если w = w've, где v — распознаватель с тестом р (xlt . . .
. . ., тк), а е — выходящая из него Д-дуга, Д €= {0, 1), то
it (8, w) = it (5, w') p2 * * * & (t (и/, tJ, . . ., t «, -rk)).
t (w, x) =
92
5
Рис. 4.4. Две функционально эквивалентные схемы, которые логико-термаль-
но не эквивалентны
3. Если w — w'v, где v — заключительная вершина с опера-
тором стоп (тп . . Тц), то
It (5, w) = It (5, w') t (w’, xj ... t (и/, Tk).
Например, логико-термальной историей пути, упомянутого
в приведенном выше примере, будет
(/(*)).
Детерминантом (обозначение: det (£)) стандартной схемы 5
назовем множество логико-термальных историй всех ее цепочек,
завершающихся заключительным оператором. Схемы и £а на-
зываются логико-термально эквивалентными (сокращенно лт-экви-
валентными, обозначение St ~ S-J, если их детерминанты сов-
ладают.
Лемма 4.6. Логико-термальная эквивалентность коррект-
на, т. е. St~ S2 => Sx ~ S2.
Доказат е л ь с т в о. Будем говорить, что интерпрета-
ция I согласована с логико-термальной историей h некоторой ко-
нечной цепочки w схемы S, если I подтверждает цепочку w, т. е.
Для h = лх . . . nmti . . . tn (т > 0, п > 0), где nt = pf‘ (ти, . . .
• . ., Tiki), А/ GE {0, 1), t} GE Т, выполнено Af = I (pt (xtl, . . .
• • •> tiki)) для Bcex i — 1, • • •> m. Понятно, что всякая интерпре-
тация согласована не более чем с одной историей из детерминанта
схемы S. Более того, если I подтверждает некоторую бесконеч-
ную цепочку или цепочку, заканчивающуюся оператором петли,
93
то с такой интерпретацией ие согласована ни одна из логико-тер-
мальных историй схемы. Пусть ~ Sa, а I — произвольная сво-
бодная интерпретация базиса 53. Тогда возможны два случая.
1. Одна из программ (£n I) или (Sa, I) зацикливается при I.
Тогда интерпретация I не согласована ни с одной из логико-тер-
мальных историй из det (Sj) — det (S2). Это означает, что зацик-
ливаются обе программы (St, Г) и (S2, I).
2. Обе программы (S^, 7) и (Sa, Г) останавливаются. Пусть wy
и wa — цепочки схем и 8а соответственно, подтверждаемые ин-
терпретацией I. Тогда It (St, Wj) GE det (S^), а в силу det (8 J —
= det (8a) существует такая цепочка wa схемы Sa, что It (5n Wj) —
— It («$а, w2). Поскольку разные цепочки одной и той же схемы
порождают разные логико-термальные истории, отсюда следует
“’а = w2, так что It (Slt Wj) = It (Sa, wa). Для завершения дока-
зательства леммы осталось заметить теперь, что значения схем
и S2 при интерпретации I записаны в (совпадающих) логико-
термальных историях путей w4 и wa схем 34 и Sa соответственно,
т. е. если обозначить через wa и w4 пути, получающиеся из цепо-
чек w4 и w2 соответственно отбрасыванием заключительных опе-
раторов, то It (S4, Wj) = It (5lt wa) val (Slt Г) — It (S2, =
= It (Sa, w4) val (Sa, I), откуда val fo, 7) = val (Sa, Г). □
Как показывает пример на рис. 4.4, утверждение, обратное
сформулированному в лемме 4.6, неверно. Можно сказать, что
лт-эквивалентность допускает меньше сохраняющих ее преобра-
зований, чем функциональная эквивалентность. В гл. 6 будет по-
строен алгоритм распознавания лт-эквивалентности стандартных
схем, а также полная система лт-эквивалентных преобразований.
Краткий обзор и комментарии
Идея схематизации алгоритмов и программ принадлежит вы,
дающемуся советскому математику А. А. Ляпунову. В 1953 г.-
исходя из общей концепции необходимости и возможности форма-
лизации процесса программирования, он ввел понятие схемы
программы, которое в течение ряда последних лет использова-
лось в двух смыслах. Под схемой программы понималось пред-
ставление программы, использующее некоторую специальную сим-
волику, облегчающую анализ и автоматические преобразования
программ [38]. Одновременно этот термин употреблялся в том
смысле, который мы сейчас в него вкладываем. Идеи Ляпунова
были развиты в конце 50-х и в 60-е гг. его учениками и коллега-
ми — Яновым, Ершовым, Криницким, Калужниным, Подловчен-
ко. В ставшей сейчас классической работе «О логических схемах
программ» [78] Янов формализовал понятие схемы программы,
определил отношение эквивалентности схем и исследовал пробле-
му эквивалентности для класса схем, получивших впоследствии
название схем Янова (этот класс схем будет рассмотрен в гл. 7).
Ершов [13] исследовал проблему алгоритмической полноты (или
94
универсальности) систем операций в операторных алгоритмах,
предложив полную систему операций, которая упоминалась
в п. 1.1. В рамках схематологии этот результат можно трактовать
так: алгоритмически универсальными являются программы, по-
рождаемые подклассом стандартных схем с базисом, содержащим
константу, одноместный функциональный символ и двухместный
предикатный символ, и множеством интерпретаций, содержащим
единственную функцию прибавления единицы и один предикат
проверки равенства (область интерпретации — неотрицательные
числа). Криницкий [28, 29] исследовал проблему эквивалентно-
сти и эквивалентных преобразований стандартных схем, причем
для подкласса схем без циклов (т. е. схем, граф которых не содер-
жит контуров) найден алгоритм распознавания эквивалентности
и построена полная система преобразований, позволяющая любую
пару эквивалентных схем автоматически преобразовать друг
в друга. Графовая форма схем была предложена Калужни-
ным [24].
После результатов Янова следующей важной вехой в истории
схематологии стало доказательство неразрешимости проблемы
функциональной эквивалентности и других главных проблем для
стандартных схем. Этот факт был установлен почти одновременно
и независимо Лакхэмом, Парком, Патерсоном [119, 126] и Лети-
чевским [31, 32]. Доказательству неразрешимости главных про-
блем посвящена гл. 5.
Данную главу мы завершим кратким обзором работ по схема-
тологии, относящимся к периоду между «положительным» резуль-
татом Янова и «отрицательным» результатом Лакхэма — Парка —
Патерсона и Летичевского. (Более детально с историей исследо-
ваний в этот период можно познакомиться в обзорных статьях
Ершова и Ляпунова [17, 18], а в заключении гл. 7 упомянуты ра-
боты по схемам Янова.) Термин «стандартная схема программы»
предложен Иткиным и Ершовым [17, 22] по отношению к вполне
определенному классу схем, близкому к введенному нами в этой
главе. В разное время разными авторами рассматривались анало-
гичные классы схем программ, отличающихся в деталях. Для всех
стандартных схем, если употребить этот термин в широком смыс-
ле, характерны следующие особенности: схемы имеют структуру
алголоподобных (операторных) программ; в схеме 'учтена струк-
тура памяти, представляющая собой конечное множество (прос-
тых в смысле языка Алгол-60) переменных; операторы схемы име-
ют структуру, подобную структуре операторов присваивания
и условных операторов Алгола-60.
Рассмотренное нами определение эквивалентности схем
(и других главных свойств) имеет семантический характер, т. е.
вводится с использованием понятия интерпретации. Другой, «син-
таксический», подход к определению отношения эквивалентности
состоит в следующем [58]. Понятие интерпретации и интерпрети-
рованной схемы отсутствует, вместо него описывается некоторый
процесс блуждания по схеме, порождающий множество цепочек
95
схемы. Схемы считаются эквивалентными, если между порожден-
ными множествами цепочек этих схем существует некоторое вза-
имно однозначное соответствие такое, что сопоставленные друг
другу цепочки эквивалентны. Цепочки обычно считаются экви-
валентными, если им соответствует один и тот же объект, называе-
мый инвариантом цепочек. Таким инвариантом может быть неко-
торая более или менее детальная информация о свойствах це-
почки.
В частности, инвариантом может считаться сама цепочка, или
построенная по ней цепочка операторов (тогда отношение экви-
валентности становится близким к отношению изоморфизма), или
термальное значение цепочки, которое строится подобно тому,
как находится результат программы при свободных интерпрета-
циях, или информационный граф [27, 45], описывающий информа-
ционные связи между вхождениями операторов в цепочки. Не-
смотря на то, что отношение функциональной эквивалентности
и различные (корректные) неинтерпретационные эквивалентности
определяются исходя из существенно разных принципов, между
ними существует связь, о которой мы выскажем следующую гипо-
Е
тезу. Для любой пары (^”, —), где У” — некоторый класс схем,
Е
а ~ — корректная неинтерпретационная эквивалентность, су-
ществует пара (У', ~) и гомоморфизм К: & -> такие, что для
любых двух схем Su S2 ЕЕ ~ Sa тогда и только тогда, когда
ЙГ (5J ~ К (8^. Другими словами, изучение проблемы неинтер-
претационной эквивалентности для класса стандартных схем рав-
носильно изучению проблемы функциональной эквивалентности
для подходящего класса стандартных схем. Выбор того или иного
пути диктуется методологическими соображениями.
Наряду со стандартными схемами в рассматриваемый период
истории схематологии изучались «более абстрактные» классы схем,
в которых отсутствует, например, информация о структуре па-
мяти или структуре операторов. Так, Мартынюк [41, 42] ввел
и изучал класс схем, в которых операторы программы представле-
ны символами, а схемы содержат лишь сведения о возможных
последовательностях выполнения операторов. Схема Мартыню-
ка представляет собой граф (специального вида), множество вер-
шин которого — это множество символов-операторов, а дуги ука-
зывают передачи управления от оператора к оператору (такой
граф называют графом переходов или логическим графом). Эти
схемы оказались удобным инструментом для постановки и реше-
ния задач декомпозиции программы, возникающих при ее транс-
ляции и оптимизации, когда необходимо разбиение на фрагменты
с минимизацией переходов из одного фрагмента в другой. Для ис-
следования более глубоких оптимизационный преобразований
программ Лавров [30] предложил схемы, представляющие собой
схемы Мартынюка, обогащенные информацией о распределении
переменных по операторам. Каждому символу-оператору припи-
сываются два набору переменных — набор входных и набор вы.
96
ходных переменных. С помощью схем Лаврова был получен пер-
вый значительный результат теории схем программ, нашедший
практическое применение, а именно — сформулирована в терми-
нах теории графов и решена задача минимизации числа перемен-
ных в программе (задача экономии памяти) [14, 30]. Схемы Лав-
рова удобны для выделения и анализа информационных связей
в программах, а также для изучения взаимодействия этих связей
с логическими связями, описываемыми графом переходов [16].
В частности, схемы Лаврова были применены при исследовании
проблемы автоматического распараллеливания программ [27]
к для разработки алгоритмов оптимизации программ [59,81].
4 В. Е. Котов, В. К. Сабельфельд
ГЛ АВА 5
НЕРАЗРЕШИМЫЕ СВОЙСТВА СТАНДАРТНЫХ СХЕМ
В предыдущей главе были введены такие свойства стандартных
схем, как пустота, тотальность, свобода, отношение функциональ-
ной эквивалентности. Первый шаг в исследовании этих свойств
схем — установление их распознаваемости. Мы убедимся, что
проблемы пустоты, эквивалентности, свободы и тотальности для
стандартных схем неразрешимы, более того, первые три пробле-
мы не являются частично разрешимыми. При доказательстве не-
разрешимости пустоты и эквивалентности будем следовать Лакхэ-
му, Парку и Патерсону [119], использовавшим метод сведения про-
блемы пустоты двухголовочных автоматов к исследуемым про-
блемам. Причем неразрешимость будет установлена уже для
довольно частного подкласса стандартных схем, базис которых
содержит лишь две переменные, константу и по одному одномест-
ному функциональному и предикатному символу. Неразреши-
мость проблемы свободы устанавливается также методом сведе-
ния с привлечением проблемы Поста.
§ 1. Двоичный двухголовочный автомат
Для доказательства неразрешимости проблемы пустоты и эк-
вивалентности будет показано, что стандартные схемы могут мо-
делировать (в уточненном ниже смысле) двухголовочные автома-
ты, что позволит свести проблему пустоты этих автоматов к проб-
леме пустоты схем. Такое моделирование можно осуществить бо-
лее простым способом, если использовать специальный класс двух-
головочных автоматов, а именно класс двоичных автоматов, рабо-
тающих со словами над алфавитом {0, 1). Следующая лемма уста-
навливает связь между классом всех двухголовочных автоматов
н подклассом двоичных автоматов специального вида.
Лемма 5.1. Существует алгоритм преобразования двухго-
ловочных автоматов в двоичные двухголовочные автоматы, сохра-
няющий пустоту автоматов (построенный двоичный автомат Аь
пуст тогда и только тогда, когда пуст негодный автомат Л).
Доказат е л ь с т в о. Пусть двухголовочный автомат А
над алфавитом V = {а1( а2, . . ., ап} имеет множеству состояний
Qa. = tab gj*, . . ., gj*}, где верхний индекс равен 1 (активна
головка 1) или 2 (активна головка 2). Преобразование этого ав-
томата в двоичный начнем с кодировки символов и слов из V*
98
словами в алфавите {0, 1} по следующему правилу:
код (#) — 0;
код Ю = 1 1
10 (i = 1, . . ., re);
код (ащ) = код (а) код (щ).
Так как символ # кодируется нулем, любому непустому слову
на ленте автомата А соответствует двоичное слово на ленте авто
мата Abf оканчивающееся двумя нулями. Автомат останавливает-
ся, прочитав два нуля подряд (или 0, означающий пустое слово).
Автомат А преобразуется в двоичный автомат Аь (оба пред
ставлены графами) следующим образом. Каждый фрагмент графа
г
Рис. 5.1. Фрагменты двухголовочного автомата А и двоичного автомата Аь:
а — фрагмент автомата А; б — соответствующий фрагмент автомата Д(,; в —
отвергающий фрагмент; г — допускающий фрагмент
автомата А, соответствующий некоторому состоянию д' из QA w
показанный на рис. 5.1, а, заменяется фрагментом графа автома-
та Аь, показанным на рис. 5.1, б (верхние индексы у символов
состояний, указывающие номер активной головки, опущены, ког-
да эта информация несущественна; однако следует иметь в виду,
что они сохраняются при замене фрагментов). После того, как
последовательно проведена замена всех фрагментов типа фраг-
мента на рис. 5.1, а на соответствующие фрагменты типа фрагмен-
4* 99
та на рис. 5.1, б, к графу добавляются фрагменты, показанные
на рис. 5.1, в и 5.1, г.
Множество состояний автомата Л(, включает:
а) всэ старые состояния из QA\
б) для каждого старого состояния q\ п новых состояний, гдз
я — число символов в V’;
в) два новых состояния г} и г%.
Заключительными состояниями автомата Аь являются все
заключительные состояния автомата А и только они.
Вершины $а (останов допускающий) и sr (останов отвергаю
щий) носят вспомогательный характер в графе автомата Аь. Они
отмечают тот факт, что автомат прочитал два нуля подряд и оста-
новился в заключительном состоянии (случай sa) или в незаклю-
чительном состоянии (случай зг).
Сравнение фрагментов на рис. 5.1, а и 5.1, б показывает, что
если головка <(* — 1,2) автомата А, находящегося в состоя-
нии q], обозревает символ aK (1 к^п), после чего автомат перехо-
дит в состояние </т, то головка I автомата Аь, также находящегося
в состоянии д), обозревает первую единицу двоичного кода сим
вола ak, после чего сдвигается вправо к + 1 раз, переводя ав-
томат последовательно в состояния $д, sj8, . . ., s*k, Когда ав-
томат Аь перешел в состояние q™, его головка I обозревает первую
единицу кода символа, стоящего справа от ak на ленте автома-
та А. Если же группа единиц на ленте автомата Аь не является
кодом ни одного из символов из V, то автомат Аь переходит в не-
заключительные состояния г} и rj, из которых не выходит до ос-
тановки (фрагмент иа рис. 5.1, в). Если на ленте автомата Аь
после кода символа из V стоит 0, то автомат (находясь в старом
состоянии) останавливается и допускает (зс) или отвергает (s,)
двоичное слово в зависимости от того, является ли это состояние
заключительным или нет.
Индукцией по числу состояний автомата А легко убедиться,
что автомат Аь допускает двоичное слово 0 тогда и только тогда,
когда оно является двоичным кодом слова из У*, допускаемого
автоматом А. Таким образом, из пустоты автомата А следует
пустота автомата Л&, и наоборот. Ц
Пример. Двухголовочный автомат А, допускающий толь-
ко те слова в алфавите V ~ {а, Ь, с}, в которых символ а встре-
чается не меньшее число раз, чем символы b вс, вместе взятые,
показан на рис. 5.2, а (заключительное состояние — gj). На
рис. 5.2, б изображен двоичный автомат, построенный по автома-
ту А (10 — код символа а, 110 — код Ь, 1110 — код с).
Задание 5.1. Постройте двоичный автомат по двухголовочвому
автомату, изображенному на рис. 3.2.
Лемма 5.2. Проблема пустоты двоичных двухголовочных ав-
томатов не является частично разрешимой.
100
Рис. 5.2. Пример двухголовочного автомата А и построенного по нему дво-
ечного автомата Аь
Доказательство. Достаточно применить метод све-
дения с использованием теоремы 3.3 и леммы 5.1. Q
§ 2. Моделирование двоичного автомата
стандартной схемой
2.1. Класс стандартных схем. Зафиксируем класс стан-
дартных схем в следующем базисе $^1
множество переменных — {хг, х2);
множество функциональных символов — {а, /<ч);
множество предикатных символов — (p(1))l
множество операторов — {хг := / (xj, х2 := / (ха), ха а,
Ъ а, р (xj, р (х8), стоп (хп х2)).
Кроме того, предполагаем, что в каждой схеме из класса
операторы засылки констант встречаются только по одному разу
в схеме, причем в самом начале, т. е. все схемы из класса
начинаются так: (старт, хх := а, хя : = а, . . .). Отметим, что при
любой свободной интерпретации I базиса в любой программе
(5, /), где S GE переменные ха и xt могут принимать значения
только из следующего множества термов: {a, fa, ffa, . . ., /"а, . . .)
101
(термы представлены в бесскобочной форме, а /” — слово
// - • • /)•
2.2. Построение схемы, моделирующей автомат. Двоичное ело
во . . . bn согласовано со свободной интерпретацией базиса
.<Й1, если для любого i, 1 i п, 1 (р) (’fa) = bit где р —
единственный предикатный символ базиса JlBj.
Пример. Слово 101010100 согласовано с любой свобод
ной интерпретацией I такой, что для всех i 9
I(p)Cfa') = {
1, если i нечетно и меньше 9,
0, если i четно или равно 9.
Свободная интерпретация I такая, что для всех i
I (р) (’М = 0,
согласована с любым словом, не содержащим 1.
Для того чтобы свести проблему пустоты двоичных двухголо-
вочных автоматов к проблеме пустоты стандартных схем из клас-
са <5^, покажем, что для любого двоичного автомата А можно
построить схему S из которая моделирует автомат А в сле-
дующем смысле. Если на ленту автомата А подано произвольное
двоичное слово а, то программа (5, I), где I — любая свободная
интерпретация базиса согласованная с а, останавливается
в том и только в том случае, когда автомат допускает слово а.
Лемма 5.3. Двоичный двухголовочный автомат пуст в том
и только в том случае, если пуста моделирующая его стандарт-
ная схема.
Доказательство. Предположим, что автомат А пуст,
а моделирующая его схема S не пуста, т. е. существует свободная
интерпретация I такая, что (S, I) останавливается. Этого не мо-
жет быть, так как среди множества всех двоичных слов, согла-
сованных с I, нет слов, допускаемых автоматом А. С другой сто-
роны, если предположить, что схема S пуста, но существует сло-
во а, которое допускается автоматом А, то схема не моделирует
этот автомат (по определению).
Лемма 5.4. Для любого двоичного двухголовочного автомата
можно построить моделирующую его стандартную схему из клас-
са
Доказательство. Построение схемы осуществляется
в два этапа. На первом этапе заготавливаются фрагменты стан-
дартной схемы, из которых на втором этапе собирается схема.
И автомат, и схема считаются представленными в графовой фор-
ме. Фрагмент графа — это его подграф (подмножество вершин
вместе с дугами, соединяющими эти вершины). В рассматривае-
мых ниже фрагментах выделена начальная вершина (в нашем
случае — это вершина, в которую не заходит ни одна дуга, или,
в случае фрагмента с одной вершиной,— сама эта вершина).
•Фрагмент может иметь выходные дуги, не заходящие в его вер-
102
шины. У стрелок выходных дуг есть специальные пометки: в слу-
чае фрагментов графа автомата — символы состояний, в случае
фрагментов схемы — номера фрагментов. Пометки у выходных
цуг нужны для сборки схемы из фрагментов на втором этапе пре-
образования.
Пусть граф двоичного двухголовочного автомата А включает
вершины-состояния (gj, q%, . . ., qj, . . ., 7^} и две вспомо-
гательные вершины — останов допускающий и останов отвер-
гающий. В доказательстве леммы 5.1 эти вспомогательные вер-
шины обозначались s„ и $г, здесь же удобнее присвоить им «уни-
фицированные» обозначения qn+1 и qn+i соответственно.
Схема собирается из п + 4 фрагментов ^Нач. .'Fo. £1» • • •
. .. fj, .... ^п, fn+i, fn+2. Фрагмент &яач — общий для
СТАРТ-
СТОП )
6
ПЕТЛЯ
Рис. 5.3. Фрагменты стандартной схемы из класса У,: а — фрагмент <Увач-
6 — слева фрагмент графа автомата (состояние <?}), справа —фрагмент У}’,
в — фрагмент г — фрагмент ^"n+s; д — другой вариант для фрагмента
<£п+а (оператор петли)
всех схем из класса начальный фрагмент, представленный
на рис. 5.3, а. Фрагменты &j, 0 j п, соответствуют состоя-
ниям qJ и строятся по фрагментам графа автомата, связанным
с qJ так, как показано на рис. 5.3, б (обратите внимание на соот-
ветствие пометок выходных дуг фрагмента автомата и фрагмента
схемы). Фрагмент Fn+1 соответствует вершине gn+1 (см. рис. 5.3, в),
фрагмент <Гп+2 — вершине qn+t (см. рис. 5.3, г). При любой ин-
терпретации выполнение фрагмента на рис. 5.3, г сводится к бес-
конечному выполнению распознавателя, независимо от логиче-
ского выражения внутри него. Поэтому этот фрагмент эквивален-
тен оператору петля (см. рис. 5.3, д).
103
На втором этапе из фрагментов .^нач. . ., соби-
рается стандартная схема из- класса по следующему правилу:
выходная дуга с пометкой j фрагментов FBaq, Fo. • • ., Fn
заводится на начальную вершину фрагмента ф}, где 0 у
п + 2. Остается перенумеровать подходящим образом все вер-
шины полученного графа числами-метками, и стандартная схема
построена.
Работе автомата А над некоторым двоичным словом а соот-
ветствует выполнение программы ($, /), где S — построенная схе
ма, / — некоторая свободная интерпретация базиса класса <^’1,
согласованная с а. Интуитивно это соответствие состоит в следую-
щем. Команда q'jb gfc, где b — символ 0 или 1, заставляет авто-
мат выполнить очередной шаг, состоящий из двух действий —
перехода в новое состояние в зависимости от прочтенного симво-
ла Ь и сдвига головки. Шагом выполнения программы будем счи-
тать выполнение фрагмента.
Первый шаг — выполнение начального фрагмента ^нач» в ре-
зультате чего значения обеих переменных и х2 становятся рав-
ными 'а'. Каждый шаг выполнения фрагментов jFo, • -
соответствует шагу работы автомата и также состоит из двух дей-
ствий: сдвигу головки i соответствует выполнение оператора при-
сваивания Xi — I (/) (xj, переходу в новое состояние — выпол-
нение условного оператора I (р) (х;). Если автомат остановился
в заключительном состоянии, программа должна выполнить опе-
ратор стоп (xlt xs) и остановиться. Если автомат остановился в не-
заключительном состоянии, программа должна зациклиться, бес-
конечно выполняя фрагмент <Fn+s.
Покажем, что построенная схема 5 моделирует автомат А.
Мы установим индукцией по числу шагов работы автомата над
словом а, что после любого шага к имеет место следующее соот-
ветствие: если автомат А после к-ro шага перешел в состояние
gj, 0 j п + 2, а головки 1 и 2 прочитали к этому времени
префиксы bibt . . . bt и соответственно . . Ьт слова а, то
программа (S, /), где I — согласованная с а свободная интерпре-
тация, после (к + 1)-го шага выполнила фрагмент &а
Wk+1 (xi) — 'fa' и Wfc+i (*«) — 'Г"*»'» гДе ^k+i — состояние
памяти программы после (к + 1)-го шага.
Базис индукции. В начальный момент (после «нулево-
го шага») автомат находится в состоянии д£, обе головки не про-
читали еще ни одного символа. Программа сделала один шаг (вы-
полнен начальный фрагмент ^Нач) и переходит к выполнению
фрагмента Уо. (®i) — (xs) — 'а''
Шаг индукции. Пусть после Л-го шага автомата имеет
место предположенное соответствие между результатом работы
автомата и результатом (к + 1)-го шага выполнения программы.
Покажем, что такое соответствие будет иметь место и после (к +
+ 1)-го шага автомата ((к + 2)-го шага программы).
1. Пусть на (к + 1)-м шаге автомат прочитал головкой i оче-
104
Рас. 5.4. Схема, моделирующая автомат на рис. 5.2. Возле вершин-распоз-
навателей выписаны соответствующие состояния автомата
редной символ Ь на ленте и перешел из состояния gj в новое со-
стояние qlr. Для определенности положим, что i = 1. По построе-
нию схемы значение переменной после (/с + 2)-го шага програм-
мы станет равным а значение переменной ха не изменится.
Терм — значение аргумента предиката I (р) во фрагмен-
те F/. Так как слово а и свободная интерпретация / согласова-
105
яы, Г (p) ('f+ta') = b. Поэтому на следующем шаге работы про
граммы будет выполняться фрагмент ‘Г,.
2. Если после А-го шага автомат остановился и q} — заклю-
чительное состояние, то, по построению схемы, программа перей-
дет иа (А 4 2)-м шаге к выполнению фрагмента F»+i, т. е. выпол
нит оператор стоп (xlt xt) и остановится с результатом val (5, Z) —
= ('fa*, Та'), где I или т равно длине слова а.
3. Если после к-го шага автомат остановился и д} — незаклю-
чительное состояние, то программа перейдет к бесконечному вы
полнепию циклического фрагмента $-п+2-
Таким образом, для любого слова па ленте автомата и для лю-
бой свободной интерпретации I, согласованной с а, программа
(<S, I) останавливается, если автомат допускает слово а, и зацик
ливается, если автомат отвергает а. Заметим, что если програм-
ма (5, I) останавливается, то результат val (S, I) = Cf'a'. Та'),
где max {I, m) равен длине слове a. Г~1
Пример. На рис. 5.4 приведена стандартная схема, моде-
лирующая двоичный двухголовочкый автомат, изображенный на
рис. 5.2.
Задание 5.2. Постройте стандартную схему из класса У,, модели
рующую двоичный двухголовочный автомат из задания 5.1.
§ 3. Теоремы о неразрешимых свойствах
стандартных схем
3.1. Проблемы пустоты и эквивалентности.
Теорема 5.1 (Лакхэм — Парк — Патерсон). Проблема
пустоты стандартных схем не является частично разрешимой.
Доказательство. Сведением проблемы пустоты дво-
ичных двухголовочных автоматов (леммы 5.2, 5.3 и 5.4) к проб-
леме пустоты стандартных схем из класса ift на множестве всех
свободных интерпретаций устанавливаем, что последняя пробле-
ма не является частично разрешимой. Из теоремы 4.2 следует,
что проблема пустоты схем из класса if* на множестве всех ин-
терпретаций также не является частично разрешимой. Так как
— подкласс класса if всех стандартных схем, то проблема
пустоты не является частично разрешимой и в классе if, [J
Теорема 5.2 (Лакхэм — Парк — Патерсон, Летичевский)-
Проблема функциональной эквивалентности стандартных схем
не является частично разрешимой.
Доказательство. Действительно, если бы эта проб-
лема была частично разрешЕма, то существовал бы частичный ал-
горитм распознавания пустоты стандартных схем, который со-
стоял бы в установлении эквивалентности заданной схемы заведо-
мо пустой схеме, например, схеме «Уд.,, изображенной на рис. 5.5.
3.2. Проблема тотальности.
Теорема 5.3 (Лакхэм — Парк — Патерсон). Проблема
тотальности стандартных схем частично разрешима
106
СТАРТ
| ПЕТЛЯ |
Рис. 5.5. Пу-
стая схема Sit
Рис. 5.6. Дерево префиксов допустимых
цепочек схемы (см. рис. 4.3)
Доказательство. Пусть S — стандартная схема, С —
множество всех префиксов допустимых цепочек схемы 5 (допус-
тимые цепочки тоже входят в С, так как они являются префик-
сами самих себя). На множестве С введем следующее отношение
«О: Cj < с2, если Cj £ С, с2 £= ci =# сг и ci
является максимальным префиксом сг, т. е. для
любого г3 G С и с3 Ср с3 сг, не может быть,
чтобы Cj < с3 и одновременно с3 < с2. Можно оп-
ределить граф G, описывающий зто отношение.
Вершинами его являются элементы С, и из сг
ведет дуга к с2, если и только если < с2. Легко
видеть, что граф G является деревом. Его корнем
служит префикс, состоящий из единственной мет-
ки 0; из вершины с — (0, 1, . . ., к) исходит одна
дуга, если к — метка преобразователя, одна или две дуги, если
к — метка распознавателя, и эта вершина является листом, если
к— метка заключительного оператора. Таким образом, листьями
дерева G служат допусти-
мые цепочки схемы S. От-
метим также, что в С дли-
на префикса сг ровно на
единицу меньше длины
префикса с2, если сг < с2.
Для схемы (см.
рис. 4.3) дерево G показано
на рис. 5.6.
Если G — конечное де-
рево (т. е. количество его
вершин конечно), то все
допустимые цепочки конеч-
ны и схема 5 тотальна.
В противном случае, для
этого дерева выполняются
условия известной леммы
Кенига [114J, которая ут-
верждает: если G — беско-
нечное дерево, из каждой
вершины которого исходит
конечное число дуг, то в G
существует хотя бы один
бесконечный путь, начи-
нающийся в корне. Так
как длины префиксов
возрастают при удале-
нии от корня, в G сущест-
вует бесконечная допустимая цепочка, и схема S не тотальна.
Таким образом, частичный алгоритм распознавания состоит
в построении G по заданной схеме S.
Алгоритм сначала строит все префиксы длины 1 цепочек схемы
Ю7
и из них выбирает префиксы допустимых цепочек, затем префик
сы длины 2 и т. д. Для любого префикса конечной длины можно
узнать, является ли он префиксом допустимой цепочки, т. е. под
тверщдается ли он хотя бы одной свободной интерпретацией.
(Если Ci — префикс недопустимой цепочки, то все префиксы це
почек, содержащие сх в качестве префикса, также недопустимы).
Если схема 5 тотальна, то дерево G конечно и на некотором шаге
алгоритм закончит его построение, сообщив, что 5 тотальна.
В противном случае он будет работать бесконечно долго, что и под-
тверждает частичную разрешимость проблемы тотальности стан
дартных схем. Q
3.3. Проблема свободы.
Теорема 5.4 (Патерсон). Проблема свободы стандартных
схем не является частично разрешимой.
Доказательство. В гл. 1 отмечалось, что проблема
Поста не разрешима, но частично разрешима. Проблема, допол-
нительная к проблеме Поста, состоит в поиске алгоритма, кото-
рый для любой системы Поста определял бы, пуста ли эта систе-
ма, т. е. верно ли, что она не имеет решений. Дополнительная
проблема Поста не является частично разрешимой, так каи
в противном случае оказалась бы разрешимой основная проблема
Поста (в силу теоремы 1.1).
Покажем, что по заданной системе Поста можно построить
стандартную схему, которая оказывается свободной тогда и толь-
ко тогда, когда система Поста не имеет решений.
Пусть (X, Y) — система Поста над алфавитом V, где X ~
— («1» • • •» ап) и Y = (Рд, ps, . . ., рп) — наборы слов из
V*, п > 2. Стандартная схема, соответствующая системе Поста
(X, Y), показана на рис. 5.7. При построении схемы использова-
ны три переменные х, у, z, одноместный функциональный символ
/ и символы fa для каждого a G F, одноместный предикатный
символ р. Кроме того, если а ~ axaaa3 . . . ak — слово из V*,
то через та (х) обозначим терм-выражение faja, . . . fa^x‘
Схема построена таким образом, что при произвольной сво-
бодной интерпретации значения переменных х и у накапливают
термы-значения, соответствующие конкатенациям слов с одина-
ковыми индексами из X и соответственно Y. Схема не свободна
только в том случае, если в некоторой программе (S, /) к моменту
выполнения распознавателя с меткой 4 (n -j- 1) + 1 значения х
и у равны. В этом случае недопустимы цепочки, заиаичивающие-
ся последовательностью . . ., (4 (n + 1) 4- I)1, (4 (п + 1) + 2)°,
4 (п + 2). Однако такая ситуация (равенство значений х и у)
возможна только тогда, когда система Поста (X, Y) имеет реше-
ние. Следовательно, построенная схема свободна тогда и только
тогда, когда заданная система Поста ие имеет решений. Имея
возможность строить подобные схемы и предположив частичную
разрешимость проблемы свободы, получаем алгоритм частичного
ргспознавания пустоты системы Поста, что приводит к проти-
воречию. Q
108
СТАРТ (у.г)
4
Рис. 5.7 Стандартная схема 5,.а, построенная по системе Поста (X, Y)
Задание 5 3. Показать, что ие являются частично разрешимыми
следующие проблемы:
а) проблема пустоты стандартных схем на множестве конечных интер-
претаций;
б) проблема потенциальной зациклнваемости (нетотальности) стандарт-
ных схем — схема S потенциально зацикливается (не тотальна), если су*
•чествует хотя бы одна и нтерпретация I базиса схемы такая, что программа
(S, Z) зацикливается;
в) проблема натер претя циовного изоморфизма стандартных схем.
Задание 5.4. Показать, что частично разрешимы следующие проб-
лемы:
а) проблема потенциальной остановки (непустоты) стандартных схем —
схема S потенциально останавливается (ие пуста), если существует хотя бы
одна интерпретация i базнса схемы такая, что программа (5, /) останавли
вается;
б) проблема потенциальной остановки при конечной интерпретации;
в) проблема потенциальной зацикливаемости при конечной интерпре-
тации.
Краткий обзор и комментарии
Неразрешимость проблемы функциональной эквивалентности
была установлена независимо Патерссном совместно с Лакхэмом
и Парком [126, 1191 и Летичевским [31, 32J. Доказательство Па-
терсона использует неразрешимость проблемы пустоты двухголо-
вочиых автоматов (Лакхэм и Парк ранее дали косвенное доказа-
тельство неразрешимости функциональной эквивалентности).
Доказательство Летичевского опиралось на неразрешимость функ-
циональной эквивалентности дискретных преобразователей — авто-
матов, предложенных Глушковым для моделирования вычисли-
тельных процессов [6, 7]. В работах [119, 1261 показана неразре-
шимость целого ряда проблем для стандартных схем, в том числе
неразрешимость проблемы свободы и неразрешимость слабой эк-
вивалентности схем (см. задание 4.3Е). Показано, что любое отно-
шение эквивалентности схем более сильное, чем слабая эквива-
лентность, но более слабое, чем функциональная эквивалентность,
не является частично разрешимым. Иткин и Звиногродский [108]
показали, что любое нетривиальное интерпретационное отноше-
ние эквивалентности в полном классе стандартных схем не будет
разрешимым. Нетривиальность отношения эквивалентности со-
стоит в том, чю (1) из неэквивалентности схем Sr и Sa следует, что
существует интерпретация I такая, что val («Sx, 7) =# val (S2, I)
или одна из программ останавливается, а другая зацикли-
вается; (2) для того, чтобы .$! и S2 были неэквивалентными,
достаточно существования такого оператора в общем базисе,
который бы входил в цепочку схемы порождаемую некото-
рой интерпретацией 7, ио не входил бы в цепочку схемы Ss, по-
рождаемую той же интерпретацией, или наоборот. Неразреши-
мость проблемы функциональной эквивалентности стандартных
схем может быть также выведена как следствие из установленной
Карпом и Миллером [111] неразрешимости функциональной эк-
вивалентности схем параллельных программ.
ГЛАВА 6
ЛОГИКО-ТЕРМАЛЬНАЯ ЭКВИВАЛЕНТНОСТЬ
СТАНДАРТНЫХ СХЕМ
Логико-термальная эквивалентность была введена в п. 3.5
гл. 4 как неинтерпретационная эквивалентность, т. е. при ее
определении мы не использовали понятия интерпретации. Важ-
ность этой эквивалентности обусловлена обстоятельствами, имею-
щими существенное значение с практической точки зрения.
1. Лт-эквивалентность, как показано в гл. 4, корректна. Это
означает, что если мы ограничимся преобразованиями, сохра-
няющими лт-эквивалентность, то такие преобразования не будут
нарушать и функциональную эквивалентность схем.
2. Лт-эквивалентность, в отличие от функциональной экви-
валентности, является разрешимой. Более того, как будет показа-
но в этой главе, существует не слишком сложный (полиномиальный)
алгоритм распознавания лт-эквивалентности стандартных схем.
3. Класс схем, лт-эквивалентных заданной схеме, является до-
статочно «широким», чтобы допускать такие преобразования, как
перестановку преобразователей на линейных участках (т. е. фраг-
ментах, не содержащих распознавателей), расщепление операто-
ров (например, замену оператора у := g (f (х)) на последователь-
ность z / (х), у := g (z)), переименование переменных, встав-
ку и удаление неиспользуемых преобразователей. В этой главе
будет построена полная система лт-эквивалентных преобразова-
ний стандартных схем.
Из определения лт-эквивалентности вытекает, в частности, что
для подкласса стандартных схем, не содержащих распознавателей,
лт-эквивалентность совпадает с функциональной эквивалентностью.
С другой стороны, лт-эквивалентность не допускает сущест-
венной перестройки логической структуры схемы, в частности,
лт-эквивалентность нарушается уже при удалении таких, напри-
мер, инструкций, как если р (х) то т иначе т. В этом смысле
лт-эквивалентность является как бы антиподом яновской экви-
валентности (77), которая фиксирует последовательность преоб-
разователей, но позволяет осуществлять глубокие преобразова-
ния логических фрагментов.
§ 1. Фрагменты и их преобразование
1.1. Фрагменты. Для формализации понятия (правила) пре-
образования нам понадобится понятие фрагмента стандартной
схемы. Понятие фрагмента является обобщением понятия схемы.
Обобщение, по-существу, состоит в том, что снимается ограниче-
111
вне, сформулированное при определении стандартных схем: граф
фрагмента, в отличие от графа схемы, может содержать свобод-
ные дуги (входы и выходы). При этом входы и выходы фрагмента
занумерованы натуральными числами таким образом, что номер
каждого входа отличен от номеров всех остальных свободных дуг
фрагмента (заметим, что всякая висячая дуга получает при этом
два различных номера — номер входа и номер выхода). Только
такие нумерации свободных дуг, называемые правильными, и бу-
дут рассматриваться в дальнейшем. Кроме того, каждой свобод-
ной дуге фрагмента приписано некоторое конечное множество
переменных, называемых результатами входа в случае входа и
аргументами выхода в
случае выхода фрагмен-
та (отметим снова, что
висячие дуги имеют как
результаты входа, так и
аргументы выхода). При
этом выходы с одинако-
выми номерами имеют
{у}
2
Рис. 6.1. Пример фрагмента
одинаковые множества
аргументов. В приведен-
ном на рис. 6.1 при-
мере фрагмента три входа с номерами 1, 3, 4 и два выхода с од-
ним и тем же номером 2; {у} — множество аргументов каждого
из выходов с номером 2, {х, у) — множество результатов входа
с номером 1, {х} — множество результатов каждого из входов
с номерами 3 и 4. Оператор старт (xlt . . ., хп) вместе с выходя-
щей из него дугой, если только он присутствует во фрагменте,
условимся также считать входом фрагмента с номером 0 и при-
писанным ему множеством результатов (ха, . . ., хп}. Тогда по-
нятие схемы становится частным случаем понятия фрагмента.
Пусть Вх (G) означает множество номеров входов, а Вых (G) —
множество номеров выходов фрагмента G. Всякое отношение эк-
вивалентности Е, заданное для схем, можно теперь распростра-
нить на кары фрагментов Glt Gt, для которых
1) Вх (GJ = Вх (Gs);
2) Вх (GJ П Вых (Gj) = 0 (1 < i, / < 2, i^= j);
3) выходы с одинаковыми номерами имеют одинаковые мно-
жества аргументов выхода.
Для пары фрагментов Gt, Gt, удовлетворяющих этим условиям,
зафиксируем какой-нибудь линейный порядок v на объединении
множеств переменных, встречающихся в этих фрагментах, а так-
же натуральное п Вых (GJ (J Вых (Gs). Пусть G — один из
фрагментов пары Glt Gt. По всяким натуральным i ЕЕ Вх (G) и
/ ЕЕ Вых (Gt) (J Вых (Gj) U {п} построим схему £<*-Л, которая
получается из G следующим образом.
1. Из G удаляются все входы, кроме входа с номером i.
2. Все выходы с номерами, отличными от присоединяются
к оператору петля (добавляющемуся к G, если его там нет).
112
3. Если j п, то все заключительные операторы фрагмента
заменяются на операторы петля (ведущие к ним дуги остаются
без изменении).
4. Если в G есть выход с номером /, то он присоединяется к до-
бавляемому к G оператору стоп (ylt . . J/k), где ух, . . —
аргументы выхода с номером j в том порядке, который индуциру-
ется порядком V.
В дальнейшем мы ограничимся рассмотрением только пра-
вильных фрагментов G, т. е. таких, что либо Вх (G) — 0» либо
для всех i ЕЕ Вх (G) и для всех j €= Вых (G) (J (л) G^» — пра-
вильная схема.
При перечисленных условиях мы говорим, что фрагменты Ga
и G, Е-жвивалентны, если схемы Ga'11 и Е-эквивалентны
для всех i Е Вх (Gx) и для всех j ЕЕ Вых (Gx) (J Вых (<?,) (J {л}.
Заметим, что это определение объявляет эквивалентными (в лю-
бом смысле) всякие два фрагмента без входов и согласовано с оп-
ределением функциональной эквивалентности схем.
Понятия пути, цепочки, термального значения терма на пути,
а также лт-истории пути естественным образом переносятся на
фрагменты.
1.2. Информационные маршруты, зацепленность и влияние.
Информационным маршрутом переменной х во фрагменте G на-
зывается всякий путь и\ — AjAa . . . ЛП_ХЛ„ такой, что
1) Лх — вершина или вход с результатом х;
2) Л„ — вершина или выход с аргументом х;
3) путь Л, . . . Лв_х не содержит ни одной вершины с ре-
зультатом х.
При этом вершины, содержащиеся в пути Л, . . . Лп_х, назы-
ваются внутренними вершинами этого маршрута. О каждой из
дуг пути w говорят, что маршрут
проходит по этой дуге.
Опишем, как строить информа-
ционный граф заданного фрагмен-
та G. Вершинами информационного
графа являются результаты опе-
раторов и входов фрагмента G,
а также аргументы операторов и
выходов фрагмента G. Информа-
ционная дута проводится от резуль-
тата х оператора или входа Лх к
аргументу х оператора или выхода
Лп тогда и только тогда, когда в
G существует маршрут Лх . . . Лп
переменной х с началом Лх и кон-
цом Лп. Из наших определений
Рис. 6.2. Фрагмент Ge.x и его ин-
формационный граф
следует, что все аргументы и результаты, принадлежащие одной
и той же компоненте связности информационного графа фраг-
мента, должны соответствовать одной переменной.
113
Две переменные фрагмента G зацеплены, если в G имеется хо-
тя бы одна дуга, по которой проходят маршруты каждой иэ этих
переменных. В противном случае переменные не зацеплены в G.
Понятие зацепленности переменных понадобится нам для фор-
мулировки преобразования замены переменных. Например, во
фрагменте Ge,1 на рис. 6.2 переменные х и у не зацеплены, поэто-
му все вхождения переменной у можно заменить на переменную х.
Будем говорить, что вершина (или результат входа) А влияет
на вершину (или выход) В фрагмента G, если выполнено одно иэ
следующих условий:
1) А — преобразователь, и существует маршрут А ... 5 не-
которой переменной х во фрагменте G;
2) А — результат некоторого входа С, и существует марш-
рут С ... В некоторой переменной х во фрагменте G;
3) существует некоторый преобразователь С такой, что А
влияет на С, а С влияет на В.
Понятие влияния понадобится нам для формулировки преоб
разования удаления неиспользуемых преобразователей.
Задание 6.1. Сформулируем задачу глобального анализа схемы 5,
решение которой позволяет находить все вершины компоненты связности
информационного графа схемы 5, содержащей выделенный результат х вы-
деленного оператора В.
Полурешетка свойств: L — множество подмножеств двухэлементного
множества {лг f , х j }, операция полурешетки — объединение подмножеств
Преобразователи свойств: все дистрибутивные функции на L.
Семантическая функция:
fe’ (т) = {х 11 (х | е= т) & (х рез (нач («))) & (нач (е) = кон (е'))} J
и {х Т | (х | «= ш) & (х й рез (кон (с))) & (кон (е) — нач («?'))} IJ
U {х | | (х | т) & (х е рез (нач (е))) & (нач (е) — нач («')>} U
U {х | [ (х е т) & (х <= арг (кон (е))) & (кон (е) — кон (е'Н).
Начальная разметка:
[ если е — выходная дуга выделенного оператора В,
Me *.е) — | 0 в остальных случаях.
Докажите, что здесь сформулирована задача глобального анализа с ди
атрибутивными преобразователями свойств и что аргумент х (результат х)
вершины v будет относиться к искомой компоненте связности информациовь-
кого графа схемы S тогда н только тогда, когда при стационарной разметке
(е) = (х ( , х j } для хотя бы одной из дуг е, ведущих к вершине v (соот •
ветственно, выходящих из вершины v).
Как нужно изменить семантическую функцию /, чтобы можно было’
строить компоненты связности информационного графа произвольного фраг-
мента?
Задание 6.2. Постройте алгоритм разметив для нахождения отко
шеиия зацеплеииостн переменных в заданном фрагменте.
Задание 6.3. Постройте алгоритм разметки для нахождения отно-
шения влияния вершин и результатов входов на вершины и выходы в за дэв-
ном фрагменте.
1.3. Формальные преобразования. Вхождением фрагмента F
во фрагмент G называется такая часть F' фрагмента G, которая
вместе с каждой вершиной содержит и все инцидентные ей дуги
114
я для которой существует правильная нумерация свободных дуг,
а также приписываемые этим дугам множества результатов входа
и аргументов выхода, удовлетворяющие следующим требованиям:
1) при этой нумерации и расстановке множеств переменных
Л” образует фрагмент, совпадающий с F;
2) если свободная в F' дуга свободна и в G, то ее номер и при-
писываемые множества переменных совпадают с соответствующи-
ми в G;
3) все выходы в F', которые были внутренними в G, получают
номера, отличные от номеров всех выходов в С;
4) если внутренняя дуга е фрагмента G является входом в F’,
то в качестве результатов входа ей приписываются все перемен-
ные, которые заданы для е в G;
5) если внутренняя дуга е фрагмента G является выходом
в F', то в качестве аргументов выхода ей приписываются все пере-
менные, маршруты которых проходят по дуге е в G;
6) все выходы в F', которые являются внутренними в G и
имеют одинаковые номера, ведут к одной и той же вершине во
фрагменте G.
Заменой вхождения фрагмента Ft во фрагмент G фрагментом F.t
называется следующая операция: из G удаляется вхождение Fa,
и каждая свободная дуга фрагмента Fa (т. е. ее начало, если она
входная, и/или ее конец, если она выходная) присоединяется
к той вершине оставшейся части фрагмента G, к которой была
присоединена дуга вхождения Fa с тем же номером.
Системы преобразований, которые строятся в этой главе, бу-
дут описаны с помощью конечных наборов схем правил. Каждая
схема правил представляет собой описание некоторого (вообще
говоря, бесконечного) множества пар фрагментов, называемых
равносильными. Чтобы получить одну из таких пар, нужно взять
два правильных фрагмента, удовлетворяющих посылке такой схе-
мы правил. При этом фиксируется какая-нибудь правильная ну-
мерация свободных дуг так, чтобы номер каждого из входов фраг-
ментов отличался от номеров всех выходов этих фрагментов.
Правилом системы преобразований называется всякая пара
•фрагментов, которая порождается схемами правил этой системы.
Правило (Gx, G3) будет записываться также в виде Gx —> G3. При-
менением правила (Gx, G3) к фрагменту G называется замена вхож-
дения одного из фрагментов пары Gx, G3 во фрагмент G другим
фрагментом этой пары. Применение схемы правил состоит в при-
менении любого из правил, порождаемых этой схемой правил.
X
Выводом равносильности Gx ♦-* G3 в системе S называется по-
следовательность фрагментов Ft = Gx, Fa, . . ., Fn = G3 такая,
что фрагмент Fi+X получается из фрагмента Ft (i — 1, . . ., п — 1)
применением некоторой схемы правил из Е. Отношение равносиль-
ности будет записываться также в виде Gx -«-» G3, если ясно, о ка-
кой системе идет речь. Это отношение является, очевидно, реф-
лексивным, симметричным и транзитивным.
115
Система преобразований £ называется полной для отношения
^-эквивалентности в классе схем К, если всякие ^-эквивалентные
схемы класса К являются 2-равносильными.
§ 2. Инварианты и их представление в виде сетей
2.1. Функциональные сети. С каждым путем w, кончающимся
некоторой дугой е во фрагменте G, можно связать множество со-
отношений равенства термов
gen (G, w) = {х — х1 t (w, x) ~ t (ia, t)
и переменная x задана для дуги с}_
Мы будем говорить, что путь ш порождает множество gen (G, и?).
Тогда со всякой дугой е в G ассоциируется множество соот-
ношений равенства
invar (G, е) = f) gen (G, w),
wew
где пересечение берется по всем путям w, начинающимся входами
фрагмента G и кончающимся дугой е. Это множество равенств бу-
дет называться инвариантом, дуг»
е в G. Например, инвариантом
1-дуги распознавателя в схеме 5вл
на рис. 6.3 является множество
{х = X, у = у, X = у, у = .г}.
Наша ближайшая цель состоит в
построении алгоритма разметки
для нахождения инвариантов дуг
в стандартных схемах. Для этого
мы опишем полурешетку сетей
для представления инвариантов.
Функциональной сетью (или
просто сетью) будет называться
тройка s =- (У, Т, Г), содержа-
щая конечное множество вершин
V == {г}, каждая из которых, в
свою очередь, содержит конечное
множество элементов v — {с). Каждому элементу с приписан не-
который символ V (с) 3? (J от него ведет d (с)) прону-
мерованных дуг к вершинам сети; Г (с, i) означает вершину,
к которой ведет i-я дуга элемента с. Мы будем предполагать вы-
полненными три следующих условия правильности сети.
1. Каждая вершина содержит не более одного элемента, кото
рому приписан функциональный символ.
2. В сети нет элементов-дублей, т. е. таких различных эле-
ментов q, съ, для которых
T(q)=T(cs)&Vi (1 < i < d (Т (q)))
Г (^i, i) ~ Г (^s» *)•
116
3. В сети нет контуров, т. е.
Vn > О VVi........vn (== V Vq.........cn Vjlt . . Jn
(Vi (1 < i < n) q G q & (1 < h < d (*F (q)))) =>
=>(3i г (q, ii) q+1 V r (cn. 7n) ?# q)-
Ha рисунках с примерами сетей мы изображаем вершины овала-
ми, а их элементы — прямоугольниками, размещенными внутри
овалов.
Для вершины v н элементов с сети з определим множества
термов know, (и) и know, (с):
( {g}, если W (с) = g&d(g) == О,
know, (с) — {(/ (q,..тп) | Vi (1 < i < п) т.Е know, (Г (с, i))},
I если Т (с) = / и d (/) = п > О
know, (о) —- (J know, (с).
с&
Будем говорить, что элемент с (вершина v) сети s знает терм т,
если т €= know, (с) (соответственно т ЕЕ know, (г)). Например,
в сети, изображенной на рис. 6.4, вершина q знает термы z,
f(x,h) и /(у, Л).
Будем говорить, что сеть s представляет множество равенств
assert (s) = (J {х = т| (хЕ Й*)Л(х, т G= know, (о))}.
w=v
Сеть на рис. 6.4 представляет, например, множество равенств
(х = х, у = у, х = у, у == х, z = / (х, Л), z = z, z = / (у, h)}.
Назовем вершину v сети а забытой, если она не знает ни од-
ного терма, т. е. know, (v) — 0. Ранг элемента определим сле-
дующим образом:
( 0, если d(T(c)) = O,
ранг(с) = j щах шах раиг(с') 4-1. если d (V (с)) ~ п > 0.
I с'ЕГ(с, «)
Ранг вершины равен максимальному рангу содержащихся в вер-
шине элементов. В сети на рис. 6.4 ранг (q) = 1 и ранг (q) =
= ранг (q) = 0. Для уда-
ления забытых вершин будем /'г~1
использовать следующую one- qf LU L-J )
рацию.
Операция удаления забы- / X,
той вершины. Пусть вершина S
v сети s не имеет ни одного s"
элемента. Удалим тогда из t qQ [х~] [у] J f |~7~] jq
всякий элемент, от которого
хотя бы одна дуга ведет ,
после чего удалим и вер- Ряс- 6Л- n₽“*eP ФУ«кциоиальиой сетж
шину V.
Легко видеть, что если з' — результат применения к сети а
операции удаления забытой вершины, то assert (а) = assert (з*)-
117
Кроме того, из определения забытой вершины вытекает, что если
сеть содержит забытые вершины, то среди них есть хотя бы одна
ранга 0. Это означает, что последовательным .применением опе-
рации удаления забытых вершин можно удалить все забытые вер-
шины сети с сохранением представляемого множества равенств.
Пусть теперь сеть s не содержит забытых вершин. Верши-
ну v сети s назовем доступной, если в s имеется путь к v от неко-
торой вершины v' с элементом с', для которого Т (с') ЕЕ Й7. Все
остальные вершины называются недоступными. Для удаления не-
доступных вершин будет использоваться следующая операция.
Удаление недоступной вершины. Пусть к вершине и сети s не
ведет ни одной дуги и V (с) SC для всех с ЕЕ v. Удалим тогда
из s вершину v (вместе с ее элементами и выходящими из них ду-
гами).
Из определения этой операции снова непосредственно вытека-
ет, что если s' — результат применения к сети s операции удале-
ния недоступной вершины, то assert (s') ~ assert (s). Кроме того,
если сеть содержит недоступные вершины, то среди них есть
хотя бы одна, к которой нет дуг от элементов других вершин
(т. е. удовлетворяющая условиям применения операции удале-
ния недоступной вершины). Это означает, что последовательным
применением этой операции можно удалить все недоступные вер-
шины с сохранением представляемого множества равенств.
Сеть назовем приведенной, если в ней нет ни забытых, ни не-
доступных вершин. Итак, нами доказана
Лемма 6.1. По всякой сети s можно эффективно построить
приведенную сеть red (s) такую, что assert (red (s)) — assert (s).
2.2. Полурешетка приведенных сетей. Сети s и s' называются
равными (обозначение: s = s'), если существует взаимно одно-
значное отображение ID-. Vs У,-, а также взаимно однозначные
отображения id„: ID (v) для всех у Е F, такие, что
Vr Е F, Vc G г W, (id,, (с)) = V, (с) &
Vi Г,' (id, (с), i) = ID (Г. (с, 0).
Через 0 будем обозначать сеть с Уд = 0. На множестве приве-
денных сетей введем бинарную операцию произведения. Если
s >= (V, V, Г) и s' - (У', V', Г’), то s X s' - (V", V", Г"), где
F" — V X У' — декартово произведение множеств; в качестве
множества элементов вершины (р. v') возьмем {(с, е') | с ЕЕ v, с* €~
е V’, ¥ (с) = ¥' (с')}.
Далее, V" ((с, с')) = V (с) и для всех I, 1 i d (¥ (с)),
положим Г" ((с, с'), 0 = (Г (с, 0, Г' (с', 0).
Лемма 6.2. Vp ЕЕ У, Vp' ЕЕ У,- know,x,' ((р, р')) =
know, (р) f] know,' (р').
Доказательство индукцией по рангу вершин (р, р')
сети s х s'. Если ранг((р, р')) — 0, то know,x,» ((v, р')) =
- {^. (с) | Зе е р Зс' €= V ¥. (с) = ¥.' (с')} = know, (р) Г!
f] know',' (р'). Пусть это равенство справедливо для всех вершив
118
ранга не более к в сети s X s’, а ранг ((у, у*)) = к + 1. Тогда
know,x,» ((у, у’)) = U {/ (<>, . . <п) | п = d (¥, (с))> О,
(с, с8)е(е, о')
/ = Т, (с), Vi <r, е know,x,» ((Г, (у, О, Г.» (у', »)))} =
= и ({/ (<1.............<«) I « = d (Т, (с)) > 0, / = V, (с),
(с, с')е(г, с')
Vi т, е know, (Г, (у, £))} П {/ (тп . . ., т„) | п = d (V,» (с')) > О,
f =-- V,. (с'), Vi е know,» (Г,- (у', i))}) = J * (know, (с) П
П know,» (с')) = ( U know, (с)) П ( (J know,» (с')) =
сес с
— know, (у) U know,» (у'). О
На рис. 6.5 показав пример применения операции произведе
иия сетей. Заметим, что произведение двух приведенных сетей —
ие обязательно приведенная (как в этом примере) сеть.
Ряс. 6.5. Пример примеиения операции произведения сетей
Лемма 6.3. Для приведенных сетей s = s’ «4 assert (s) «
— assert (s’).
Доказательство предоставляется читателю в каче-
стве несложного упражнения. f~]
Определим операцию пересечения Д приведенных сетей,
полагая s Д s’ = red (s X s'). Таким образом, результат пересе-
чения двух сетей — по определению снова приведенная сеть.
Лемма 6.4. Для приведенных сетей
assert (s Д s’) — assert (s) Q assert (s').
11G
Доказательство. В самом деле,
assert (s Д s') = assert (s X s') =
=JJ П know,x,. ((у, у'))) X knoweXe' ((y, y')) =
- U П know, (у) [~| know,- (у')) X (know, (y) f| know,' (y')) =
= ( U ((^ Я know, (у)) X know, (y)) fl ((.2? Pl know,» (у')) X
X know,' (у'))) =
= ( U П know, (у)) x know, (y)) PI ( U (3? P)
V t>*
P) know,* (у')) X know,- (y')) =
= assert (s) P| assert (s’).
Теорема 6.1. Множество приведенных сетей вместе с опе-
рацией пересечения образуют ограниченную полурешетку.
Доказательство. Коммутативность, ассоциативность
и идемпотентность операции Д вытекают из следующих фактов.
1. В силу леммы 6.4 пересечение сетей представляет множест-
во равенств, являющееся пересечением множеств, представляе-
мых каждой из сетей.
2. Операция пересечения множеств обладает свойствами ком-
мутативности, ассоциативности и идемпотентности.
3. В силу леммы 6.3 имеется единственная приведенная сеть,
представляющая заданное множество равенств термов.
Чтобы показать ограниченность полурешетки приведенных се-
тей, введем понятие веса сети s:
вес (s) — 2k + I — — lt,
где
k — количество элементов с сети s таких, что V, (с) €Е SC',
I — количество вершин у сети s таких, что у содержит един-
ственный элемент с, причем V, (е) €= F;
1г — количество вершин сети s, содержащих хотя бы одни
элемент с, для которого V, (с) ЕЕ ЗС‘,
Z, — количество вершин у сети s таких, что Vc ЕЕ у V, (с) Е= SC.
Из определения операции пересечения сетей следует, что если
* < s', то вес (s) < вес (s'). Заметим также, что О «С вес (s) <
<3-Л, поэтому длина строго убывающей цепи с началом s огра-
ничена числом 3k.
Мы дополним множество X приведенных сетей новым, искус-
ственно добавляемым элементом 1, для которого положим по
определению VsG Ж s Д 1 = i Д s = s. Понятно, что (X, Д) —
полурешетка с условием обрыва цепей.
2.3. Нахождение инвариантов. Чтобы нспользовать алго-
ритм рааметки, сформулированный в гл. 2, для нахождения ин-
вариантов дуг фрагментов, нужно описать преобразователи се-
тей, соответствующие «выполнению» операторов присваивания и
проверке тестов в распознавателях.
120
Определим, прежде всего, операцию add, которая по сети в
и терму с дает сеть add (s, т), в которой есть элемент, знающий «.
Если 8 = 1 или в з уже есть элемент, знающий терм т, то положим
add (з, т) = s. В противном случае пусть т — f (тп . . ., тп),
л > 0, / G= «97 U Построим тогда сети s0 = s, st = add (st-i, T{)
для i = 1, . . ., n и получим add (я, т) из sn добавлением новой
вершины v с единственным элементом с, для которого мы пола-
гаем ¥ (с) = / и Vi (1 i п) Г (с, i) = pf, где v4 — вершина
из зп, знающая терм т£.
Замечание. Всякая сеть содержит не более одного элемента
и не более одной вершины, знающих заданный терм. Поиск такой
вершины и ее элемента можно делать за время, пропорциональное
размеру сети, например, используя описанный в 198] алгоритм
замыкания отношения конгруэнтности на графе.
Следующая операция эффект присваивания будет давать
приведенную сеть <а:: = т> з по заданному оператору присваива-
ния х := т и приведенной сети з. Мы положим <х := т> 1 = 1.
Для з #= 1 сеть := т> з строится следующим образом.
1. Пусть сеть si получается из сети add (з, т) добавлением но-
вого элемента с, (с) — z, к вершине, знающей терм т, где z —
новая переменная, не встречающаяся в add (з, т).
2. Сеть з2 получается из si удалением элемента с, для которо-
го (с) = х.
3. Сеть зЗ отличается от з2 только тем, что Т,3 (с) = х для
того элемента с, для которого Т,а (с) = z.
4. := т> з = red (зЗ).
Лемма 6.5. Ух «Ж* Vc G= Т Vslt s2 €= Ж
<х := т> (sj Д з2) = «ж :=т> sj Д «ж : = т> з2).
Доказат е л ь с т в о. Нетрудно показать, что простые
функции преобразов ания сетей, описанные в шагах 1 —4 при по-
строении (ж : =т> з, являются дистрибутивными. Тогда дистри-
бутивность функции <х :== т> вытекает из уже упоминавшегося
в гл. 2 факта, что суперпозиция дистрибутивных функций дис-
трибутивна. □
Лемма 6.6. Пусть s 6= Ж и gen (G, w’) = assert (з) для пу-
ти w' во фрагменте G. Тогда gen (G, w) = assert (<х := т> s)
для пути w — ю'Ае, где А — оператор присваивания х :=т.
Доказательство. Обозначим з' = : = т> з и рас-
смотрим все возможные случаи принадлежности равенства у = t
множеству gen (G, w).
1. t = у. Тогда (у = у) G gen (G, w) 44 (у = у) (Е gen (G, w') \/
\/ У ~ х <&-(у ~ у) ЕЕ assert (s').
2. у х и х не встречается в t. Тогда (у = t) (Е gen (G, w) 44
44 (у = t) е gen (G, w') 44 (у = t) €Е assert (s) 44 Эр e Va y,t&
S know, (v) 44 Bp e Vt' y, t €E know, (p) 44 (y = t) £E assert (s').
3. у x их встречается в t. Тогда (у = t) е gen (G, w) 44
44 (у = t [т/х]) e gen (G, u>') 44 Эр e V, У, t It/x] G know, (p) 44
44 Эр G V^, y, * s know,» (p) 44 (y = t) e assert (s').
121
Рис. 6.6. Стационарная разметка для схемы 5<л
4. у ~ х, t Ф х, т — переменная. Тогда (х = t) €= gen (G, w) 44
44 (т == i) G gen (G, w') <4 3t>G V, t, t G know, (r) 44 3i> €=
z, [t, « G know,- (v) 4=4 (z — t) G' assert (s’).
5. у = x и I — переменная, отличная от х. Сводится к слу-
чаю 3, поскольку (х — я) G gen (G, и) 44 (я — х) G gen (G, w).
6. у = х, а термы « и t — не переменные. Тогда (ж = t) G
~ gen (G, ip) 44 3b, . .., tn (n > 0) t — t iTi/zj, . . ., Tn/zJ & Vi
(l<i<n) (it = Tf)egen (G, w') 44 3*1, . • ., <n t ~ <s It^x^ ...
..T„/zn] & Vi (1 < i < n) 3i>f G У, xt, e know, (vt) <4 3o G
G У,- x, t G know(p) 44 (x — t) G assert (s'). □
Сформулируем теперь задачу глобального анализа фрагмента G.
В качестве окружения для анализа возьмем (Ж, Д, F), где F
содержит все функции <z:— т> s для операторов присваи-
вания х : = т из фрагмента G, функцию i (s) — s и функцию
t (s) = И. Семантику / определим следующим образом:
г: («) =
: = т> s, если дуга е ведет к оператору х: = т,
а дуга е выходит из него,
i(s). если е’ ведет к некоторому распознавателю, а
дуга е выходит из него,
И (s), в остальных случаях.
02
В качестве начальной разметки возьмем р0 (е) = se для входов е.
фрагмента G и р0 (е) = 1 для остальных дуг. Здесь для входа г
с результатами {хх, . . ., хп} через $е обозначена сеть, содержа-
щая ровно л вершин vr, .... v„, каждая из которых содержит
ровно один элемент ct €= i>f. причем V, (с,) — xt (1 i л).
Тогда непосредственным следствием теоремы 2.4 и лемм 6.6, 6.5
будет следующая
Теорема 6.2. Для стационарной разметки р сформули-
рованной задачи глобального анализа и для всех дуг е фрагмента G
invar (G, е) = assert (р (е)).
На рис. 6.6 схема Sei изображена вместе с ее стационарной
разметкой.
§ 3. Алгоритм распознавания
логико-термальной эквивалентности
3.1. Система эквивалентных преобразований 2ЛТ. Здесь мы
описываем схемы правил ЛТ1 — ЛТ8, порождающие множество
правил преобразования, которое мы обозначаем 2ЛТ.
ЛТ1 [Удаление недостижимых].
Фрагмент без входов равносилен пустому фрагменту.
ЛТ2 [Стягивание тупиков].
Фрагмент без выходов и без заключительных операто
ров, с номерами входов ах, .... ап, равносилен фрагменту
петля
ЛТЗ [Склеивание копий, или копирование].
Пусть фиксировано разбиение множества вершин фрагмента G
на непустые и непересекающиеся классы Kt, . . ., Кп такие, что
1) каждый класс содержит графически совпадающие опера-
торы;
2) если некоторая выходная дуга вершины класса Kt ведет
к вершине класса Kj, то соответствующие выходные дуги всех
других вершин класса А'г также ведут к вершинам класса Kf,
3) если некоторая выходная дуга вершины класса явля-
ется выходом фрагмента G с номером Ь, то соответствующие вы-
ходные дуги всех других вершин класса А, — также выходы
фрагмента G с номером Ь.
Пусть, далее, фрагмент G' может быть получен из G следую-
щим образом: из каждого класса Ks (i — 1, . . ., л) берется ровно
по одной вершине vt, и дуга от нее либо проводится к вершине v}
123
«(когда для этой дуги выполнено условие 2), либо объявляется
выходом фрагмента G' с номером Ъ (когда для нее выполнено ус-
ловие 3). Если в G имеется вход с номером а, ведущий к вершине
класса Кг, то к G' добавляется вход с номером а, который направ
ляется к вершине vr. При перечисленных условиях G *-* G'.
ЛТ4 [Замена переменных].
Пусть переменные х и у фрагмента G не зацеплены, причем ни
одно из вхождений переменной х в компоненту связности Г ин-
формационного графа фрагмента G — не результат входа и не ар-
гумент выхода. Тогда G <-» G', где G* — фрагмент, получающийся
из фрагмента G заменой всех вхождений переменной х в компо-
ненту Г на переменную у.
ЛТ5 [Удаление неиспользуемых преобразователей].
Пусть — такое подмножество преобразователей фраг-
мента G, что
1) к вершине vt ведет ровно одна дуга (i — 1, . . ., л);
2) вершина vt не влияет ни на один из выходов фрагмента G,
а также ни на одну из вёршиИ, отличных от nlt . . ., vn (i ~
-- 1, . . ., л).
Пусть, далее, правильный фрагмент G' получается из фраг-
мента G заменой каждого преобразователя vt (i — 1, . . ., n)
на дугу
Тогда G G'.
ЛТ6 [Удаление неиспользуемого результата входа].
Если результат х входа е фрагмента G не влияет на его вер-
шины и выходы, то G «-> G', где фрагмент G' получается из G
исключением переменной х из множества результатов входа е.
ЛТ7 [Удаление вырожденной пересылки].
Если х €= U, то
х- = х
ЛТ8 [Замена термов].
424
Пусть инварианты всех дуг, ведущих к вершине v во фрагмен-
те G, содержат равенство х — т. Тогда G ++ G', где G' получается
из G заменой аргумента х вершины о на терм т.
На рис. 6.7 приведены примеры применения каждой из схем
правил ЛТ1 — ЛТ8.
Рис. 6.7. Примеру применения схем правил ЛТ1 — ЛТ8
125
Теорема 6.3. Если +->-G2, то G1-^ G2.
Доказательство. Лт-зквивалентность фрагментов тел
пар, которые составляют правила системы 5ЛТ, проверяется не-
посредственно. Например, всякое применение схем правил ЛТ1 —
ЛТЗ оставляет неизменным множество всех конечных цепочек
операторов фрагмента. Применение схем правил ЛТ4 — ЛТ8 хо-
тя и может изменять цепочки операторов фрагмента, но оставляет
неизменной логико-термальную историю любой конечной цепоч-
ки в схеме. 0
3.2. Приведение и согласование фрагментов. Фрагмент G на-
зывается приведенным, если для него выполнены следующие ус-
ловия.
(R1) Каждая вершина фрагмента G лежит хотя бы на одном
пути, начинающемся входом фрагмента G.
(R2) От каждой вершины фрагмента G (кроме операторов пет
ли) имеется хотя бы один путь к выходу из G или к заключитель-
ному оператору.
(КЗ) К каждому преобразователю, заключительному опера
тору и оператору петли ведет ровно одна дуга фрагмента G.
(R4) В качестве функциональных подтермов в тестах и за-
ключительных операторах фрагмента G используются только пе-
ременные.
Лемма 6.7. Применением схем правил ЛТ1 — ЛТЗ, ЛТ5,
ЛТ8 всякий фрагмент можно преобразовать в приведенный.
Доказательство. Вершины, недостижимые от входов
фрагмента, можно удалить применением ЛТ1. После этого при-
менением ЛТ2 можно добиться и выполнения условия R2. Заме-
тим здесь, что нахождение вершин, недостижимых от входов, а
также вершин, от которых нет пути к выходам или заключитель-
ным операторам, можно реализовать с помощью соответствую-
щих алгоритмов разметки.
Условие R3 достигается повторным применением ЛТЗ в сто-
рону «копирования», как в примере на рис. 6.7, в. Такой процесс
закончится благодаря тому, что при условии R2 во фрагменте G
нет циклических путей, проходящих только через преобразователи.
Наконец, условие R4 достигается применением ЛТ5 и ЛТ8,
как это показано на рис. 6.7, д для случая распознавателя.
Линейным участком (коротко: лучом) называется всякий при-
веденный фрагмент без распознавателей и ровно с одним входом.
Выходным лучом приведенного фрагмента G называется вхожде-
ние в G всякого максимального луча, кончающегося выходом
фрагмента G.
Со всяким приведенным фрагментом G свяжем его логический
граф (коротко: л-граф) LG (G), который получается из G следую-
щим образом: каждый преобразователь <?-—*| V заменя-
126
ется фрагментом-дугой а •-»- Ь, после чего «стираются» аргументы
вершин и выходов, а также результаты входов.
На рис. 6.8 изображены фрагменты Gtл и его л-граф.
Рас. 6.8. Фрагмент G«.s и его л-граф
С каждой конечной цепочкой w в л-графе (т. е. путем от входа
к выходу или заключительной вершине) свяжем слово, которое
получается последовательным выписыванием номеров свободных
дуг, а также символов, приписанных вершинам цепочки ш. При
этом предикатный символ берется со знаком А (Д €= {0, 1}), если
путь продолжается по Д-дуге некоторого распознавателя. Мно-
жество слов, построенных таким образом по всем конечным це-
почкам л-графа, называется языком этого л-графа. Два л-графа
называются автоматно-эквивалентными, если их языки совпа-
дают. Два приведенных фрагмента называются подобными, если
их л-графы автоматно-эквивалентны.
Пример двух автоматно-эквивалентных л-графов изображен
на рис 6.9.
Из приведенных определений следует, что всякие лт-эквива-
лентные фрагменты являются подобными. Отношение подобия
схем в точности соответствует
эквивалентности одноленточных
односторонних автоматов, для
которой известны аффективные
алгоритмы распознавания. Ни-
же мы описываем алгоритм рас-
познавания подобия фрагмен-
тов, основанный на алгоритме
Берда распознавания эквива-
лентности двухленточных авто-
матов (см. гл. 3).
Определим для этого опера-
цию склеивания двух вершин
vt и V, некоторого размечен-
ного графа: мы говорим, что
Рис. 6.9. Пример двух автомата©-
эквивалентных л-графов
операция склеивания удается, если выполнено следующее
У ел овне 6.1: вершинам и иг приписан один и тот же
снмвол (стоп, петля или предикатный символ), всякие однотипные
127
дуги (т. е. 0-дуги или 1-дуги), выходящие из вершин и v2, яв-
ляются одновременно либо внутренними, либо выходными и име-
ют одинаковые номера.
Результатом склеивания вершин vt и о, в этом случае объяв-
ляется граф, который получается из исходного заменой вершин
v2 и о2 одной новой вершиной v. Этой вершине v приписывается
тот же символ, который был приписан вершинам vt и v2. К v при-
соединяются все дуги, которые вели к v2 или мг или выходили
из них. Если за счет этого появляется несколько однотипных дуг,
которые ведут от v к одной и той же вершине и' или являются вы-
ходами графа, то они отождествляются. Если же условие (6.1)
ложно, то мы говорим, что операция склеивания не удается,
а ее результат не определен.
Опишем теперь алгоритм распознавания автоматной эквива-
лентности двух л-графов и Я8.
1. Если в одном из л-графов имеется висячая дуга с номером
входа а и с номером выхода Ь, а в другом л-графе нет висячей
дуги с этими же номерами, то л-графы Нг и Н2 объявляются авто-
матио неэквивалентными и алгоритм заканчивается. В против-
ном случае удалим все висячие дуги в л-графах Ht и Н2.
2. Склеим попарно те вершины л-графов Ht и Н2, к которым
ведут входы этих л-графов с одинаковыми номерами.
3. Будем повторять операцию склеивания вершин пх и о2,
пока выполнено следующее
Условие 6.2: существуют вершины vlt v2, v (vt Ф v2) такие,
что из v выходят две однотипные дуги, одна из которых ведет
к вершине vu а другая к вершине v2.
При выполнении каждого склеивания будем запоминать,
какие вершины исходных л-графов склеиваются в новой вершине.
Поскольку каждое склеивание уменьшает количество вершин
в графе, описанный процесс завершится после не более чем
т + п склеиваний (тип — количества вершин в исходных
л-графах) либо из-за ложности условия (6.2), либо из-за того, что
не удается одна из операций склеивания.
Теорема 6.4 (М. Берд). Если одна из операций склеива-
ния в описанном, алгоритме не удается, то Н2 и Н2 автоматно
неэквивалентны. Если же все операции склеивания удаются и ал-
горитм завершается из-за ложности условия (6.2), то Н2 и Н2
автоматно-эквивалентны.
Пара приведенных фрагментов Gt, G2 называется согласован-
ной, если для нее выполнены следующие условия.
(С1) Множества результатов входов с одинаковыми номерами
совпадают.
(С2) Всякий выходной луч в Gx и G2 завершается так назы-
ваемым выходным вектором пересылок, т. е. лучом
~Ч ---------------Н хг: ~Уг Н*------------| */,
128
где {xlt . . arn) — множество всех аргументов выхода с номе-
ром j, и Vi (1 < i < n) yt&{xt........xn}.
(СЗ) Если некоторая переменная x встречается в каждом из
фрагментов пары, то преобразователи с результатом х имеются
только внутри выходных векторов пересылок этих фрагментов.
(С4) Логические графы фрагментов G2 и С2 совпадают.
Теорема 6-5. Применением правил из 2ЛТ всякую пару
лт-эквивалентных фрагментов можно преобразовать в согласо-
ванную пару.
Доказательство будет состоять в построении со-
гласованной пары Gi. G2, G2 G2, G2 ► G2, по заданным
лт-эквивалентным фрагментам Glt G2.
Первый шаг состоит в приведении фрагментов G2 к G2, как это
делается в доказательстве леммы 6.7. Пусть, далее, R} — мно-
жество результатов входа с номером j во фрагменте Gt (г = 1, 2).
Если R* М= то применением ЛТ6 добавим к множеству ре-
зультатов входа с номером j во фрагменте Gt каждую переменную
из \ Rj (1 h к 2, i к). Благодаря правильности фраг-
ментов Gt и G2 добавляемые результаты входов не могут влиять на
вершины фрагментов. Чтобы достичь (С2), заменим предваритель-
но всякий вход с номером j в G, на луч, состоящий из всех пере-
сылок xt:=xi с xi €Е R], а всякий выход заменим на луч, состоя-
щий из всех пересылок xr : = хТ, хт GE Z, где Z — множество ар-
гументов этого выхода. Это можно сделать повторным примене-
нием схемы правил ЛТ7. Если теперь некоторая переменная х
встречается в обоих фрагментах пары, а новые переменные у2, у2
не встречаются в G2 и G2, то применением ЛТ4 заменим на yt
в Gt и на у2 в G2 все вхождения переменной х, кроме тех вхождений,
которые относятся к компонентам связности, содержащим резуль-
таты входов или аргументы выходов. В результате будет достиг-
нуто условие согласованности (СЗ).
Добьемся, наконец, выполнения условия согласованности
(С4). Для этого применим сначала описанный выше алгоритм рас-
познавания автоматной эквивалентности к л-графам фрагментов
и G2. Из G2 — G2 следует, что Gx и G2 подобны, поэтому этот
алгоритм успешно завершится и даст результирующий граф, а
тем самым и разбиения У}, . . ., Vn и V?, . . ., Vf, множеств вер-
шин исходных л-графов на непустые и непересекающиеся клас-
сы. Здесь п — число вершин в результирующем графе, а V} в
Vi — множества всех тех вершин первого и второго л-графов со-
ответственно, которые склеиваются в i-ю вершину результирую-
щего графа.
Построим фрагмент mult (б?ь Gt) по нашим подобным фрагмен-
там Gt и G2. В качестве вершин л-графа фрагмента mult (Сп Gt)
возьмем множество (j Vj X V?. Вершине (о, v') в mult (Glt Gt)
i=l
S В. E. Котов, В. К. Сабельфельд 129
припишем тот же оператор, который был приписан вершине v
в Gt. Пусть J — луч фрагмента Glt начинающийся Д-дугой неко-
торого распознавателя ох, v2 G= Vi, и кончающийся либо дугой,
ведущей к распознавателю, оператору петли или заключитель-
ному оператору nJ, либо выходом фрагмента G^ с номером j. Тог-
да благодаря подобию Gt и G2 для всякой вершины г2 €= V/
л-графа фрагмента G2 ее соответствующая А дуга также ведет к вер-
шине оа, соответствующей распознавателю, оператору петли или
заключительному оператору, либо является выходом LG (Ga)
с тем же номером j. Во фрагменте mult (Gx, G2) в качестве луча,
начинающегося Д-дугой вершины (ох, о3), мы возьмем тогда луч
J, а его выходную дугу присоединим к вершине (щ, v2) или, соот-
ветственно, объявим выходом с номером /. Пусть, далее, J — луч
фрагмента Gx, начинающийся входом с номером к и кончающийся
либо дугой, ведущей к распознавателю, оператору петли или за-
ключительному оператору щ, либо выходом фрагмента Gx с номе-
ром /. Тогда в силу подобия Gx и G2 вход с номером к в LG (Ga)
также ведет к некоторой вершине v2 или, соответственно, явля-
ется выходом с номером /. В этом случае в качестве луча, начи-
нающегося входом с номером к в mult (Gx, G2), мы возьмем луч /,
а его выходную дугу присоединим к вершине (о{, v2) либо, соот-
ветственно, объявим выходом с номером j.
Из описанного построения следует, что фрагмент mult (Gx,
Ga) может быть получен из Gx применением схемы правил ЛТЗ
(копирование): каждый распознаватель, оператор петли и заклю-
чительный оператор о ЕЕ VJ заменяется | Vj | копиями. Столько
же копий нужно взять и для каждого из преобразователей тех
лучей, которые начинаются выходными дугами вершины у, а сое-
динение копий выполняется с использованием структуры л-гра-
фа второго фрагмента пары.
Заметим, что количество вершин фрагмента mult (Gx, G2)
не превосходит произведения количеств вершин Gx и G2. Из по-
строения следует также LG (mult (Gx, G2)) = LG (mult (G2, Gx)).
Взаимно однозначным соответствием вершин зтих л-графов будет
(г, о') <->• (o', о). Кроме того, очевидно, mult (Gx, G2) — Gx, а опе-
рация mult не нарушает свойство приведенности фрагмента.
Таким образом, фрагменты mult (Gx, G2) и mult (Ga, Gx) обра-
зуют согласованную пару. 0
На рис. 6.10 показан пример процесса согласования для двух
приведенных схем 5вл, 5в>5.
3.3. Полнота системы 2ЛТ.
Теорема 6.6. Система 2ЛТ — полная система лт-экви-
валентных преобразований фрагментов, т. е.
Gx ~ G2 4=> Gx *—► G3.
Доказательство. С учетом теорем 6.3 и 6.5 достаточ-
но показать Gx G3 для фрагментов Gx, G2, Gt — G2, составля-
130
|Рис. 6.10. Согласование двух приведенных схем и 5e.s
ющих согласованную пару. Обозначим через Jf (е) луч, начина-
ющийся Д-дугой е распознавателя или входом е во фрагменте
Gt (i = 1, 2) и заканчивающийся дугой, ведущей к распознавате-
лю, оператору петли, заключительному оператору или к первой
из пересылок выходного вектора пересылок этого фрагмента;
Id,-. Ga Ga — взаимно однозначное соответствие входов, заклю-
чительных операторов, операторов петли, распознавателей и их
5*
131
выходных дуг, которое существует благодаря совпадению л-гра-
фов Gj и G2.
Преобразуем фрагмент Gj во фрагмент Gx, заменяя в нем вся-
кое вхождение луча
Л (С)
J^e) на луч |
Jz(Id(e})
I
b ь
Это преобразование можно выполнить однократным применением
ЛТ5, поскольку в силу условия согласованности (СЗ) результаты
добавляемых преобразователей не встречаются в исходном фраг-
менте G1T а потому и не могут влиять на распознаватели, заключи-
тельные операторы и выходы в Gj.
Пусть теперь v — произвольный распознаватель, заключи-
тельный оператор или одна из пересылок выходного вектора пе-
ресылок в Gj, х — ее i-й аргумент, а у — i-й аргумент вершины
Id (v) во фрагменте G2. Покажем, что тогда инварианты всех дуг е,
ведущих к v в Gt, содержат равенство х — у. Действительно,
предположение {х = у} invar (Glt е) означает существование
такого пути w, начинающегося некоторым входом и кончающегося
дугой е в Glt что t (w, х) =/= t (w, у). Последнее, в свою очередь,
означает, что фрагменты Gt и G2 не являются логико-термально
эквивалентными, т. е. мы получили противоречие с исходным пред-
положением.
Итак, применением ЛТ8 i-й аргумент каждой из вершин-рас-
познавателей, заключительных операторов и выходных пересы-
лок v в Gt можно заменить на соответствующий (i-й) аргумент
вершины Id (v) из G2. В результате такого преобразования на каж-
дом из лучей
1г(е)^ J2(/d(e))^fc
в Gt преобразователи из 1г (е) становятся неиспользуемыми, и их
можно удалить применением схемы правил ЛТ5. После этого
преобразования фрагмент Gt окажется совпадающим с фрагмен-
том G2. □
Итак, Едт — полная система лт-эквивалентных преобразова-
ний стандартных схем и их фрагментов. Заметим, что из описан-
ного в доказательстве теоремы 6.6 процесса преобразования
лт-эквивалентных фрагментов друг в друга можно извлечь и ал-
горитм распознавания лт-эквивалентности.
132
Следствие 6.1. Существует алгоритм распознавания
лт-эквивалентности стандартных схем (фрагментов).
Доказательство состоит в описании алгоритма.
1. Преобразуем исходные фрагменты Gt и G2 в приведенные
фрагменты.
2. Распознаем подобие полученных фрагментов. Если они не
лт
подобны, то Gr Ф G2.
3. Строим согласованную пару фрагментов Gi = mult (G>,
G2) и G8 = mult (G8, GJ.
4. По Gi и Gt строим фрагмент Gt, как зто описано в доказатель-
стве теоремы 6.6, а затем его стационарную разметку.
5. Если не выполнены условия некоторых из упомянутых в до-
казательстве теоремы 6.6 применений схемы правил ЛТ8, то
ЛТ лт
Gr G„ в противном случае Gx — G8.
Задание 6.4. Докажите, что с помощью преобразований из £лт
всякую стандартную схему можно преобразовать в схему без пересылок [50],
т. е. без операторов вида х := у, где х, у е ЗС.
Задание 6.5. Покажите, что для описанного выше алгоритма рас-
познавания лт-эквивалентности стандартных схем (фрагментов) имеет место
верхняя оценка сложности 0 (п7), где п — максимум размеров исходных
схем [65].
Краткий обзор и комментарии
Логико-термальную эквивалентность ввел в рассмотрение
Иткин 122], он же построил первый весьма сложный алгоритм
ее распознавания. Буда описал [4] алгоритм распознавания
с показательной верхней оценкой сложности, сводящий пробле-
му к распознаванию эквивалентности в подклассе двухленточных
автоматов. Описанный в этой главе полиномиальный алгоритм
был построен в работе [65].
На возможность автоматического построения инвариантов
впервые указал Летичевский 134], Килдел предложил 1112] ал-
гебраизацию для объектов, которые в настоящей главе трактуются
как пометки, и описал алгоритм нахождения инвариантов. Опи-
санное здесь представление инвариантов в виде функциональных
сетей, позволяющее строить полиномиальные по сложности ал-
горитмы глобального анализа, заимствовано из работ [65, 5].
133
ГЛАВА 7
РАЗРЕШИМЫЕ ПОДКЛАССЫ СТАНДАРТНЫХ СХЕМ
Результаты гл. 5 носят «отрицательный» характер — главные
проблемы теории схем программ (проблемы эквивалентности,
пустоты, тотальности, свободы) оказываются неразрешимыми
в классе стандартных схем. В этой главе мы концентрируем вни-
мание на тех подклассах стандартных схем, для которых удалось
установить разрешимость всех или некоторых главных проблем.
Тот факт, что главные проблемы оказываются неразрешимыми
для стандартных схем, ни в коей мере не дискредитирует идею
схематизации программ, лишь устаналивает те границы, в рамках
которых следует продолжить поиск разрешимых случаев путем
сужения классов изучаемых схем и выбора отношении эквива-
лентности более сильных, чем отношение функциональной эк-
вивалентности. Неразрешимость главных проблем для стандарт-
ных схем отражает сложность взаимодействия логической и ин-
формационной структур программ, даже если для их построения
используется небольшой набор программных примитивов, пере-
численных в § 1 гл. 5. Неразрешимости в схемах проецируются
на практические программы в образе тех трудностей, которые
приходится преодолевать при создании достаточно развитых си-
стем автоматизации программирования. Поэтому особый интерес
представляет обнаружение разрешимых подклассов стандарт-
ных схем, выделение тех причин и ситуаций, которые ответствен-
ны за разрешимость или неразрешимость. Хотя сужение класса
исследуемых схем представляется естественным направлением
поиска «хороших» подклассов, само по себе оно не гарантирует
успеха, и отличие разрешимого подкласса от неразрешимого мо-
жет оказаться довольно тонким. Достаточно напомнить, что в гл. 5
была выявлена неразрешимость очень узкого подкласса стан-
дартных схем, базис которого содержит лишь две переменные,
константу, один функциональный и один предикатный символ,
а операторы присваивания имеют вид xt := а или xt / (xj,
где i = 1, 2.
Можно определить класс так, чтобы он отличался от if t
лишь тем, что он не содержит констант (и операторов засылки
констант), но содержит оператор пересылки х2 := xt. В этом
классе проблемы пустоты и эквивалентности не являются частич-
но разрешимыми. Далее, можно удалить и оператор пересылки,
считая, что каждая схема в полученном классе ifa начинается
134
фрагментом
(старт (хй),
1: а» := / (х,),
2: Xi z = / (xj),
где оператор x2 : — f (xj встречается не более одного раза в схе-
ме. Этот класс также не является частично разрешимым в отно-
шении проблем пустоты и эквивалентности.
Однако если в базис класса добавить еще одну константу
b и соответственно оператор засылки этой константы х2 : = b
и начинать все схемы одинаковым фрагментом
(старт,
1: х^ := а,
2: х2 : = Ь,
(константы нигде в схеме больше не встречаются), то получим
класс в котором проблемы пустоты и эквивалентности разре-
шимы. Легко видеть, что тогда оказывается разрешимым и под-
класс стандартных схем с базисом
= (fo, Хг}, {Р(1)}, {*1 := 1 (*i), (*2),
pfa), р(х2), стоп (xlt х2)}).
Подклассы cft, &2 и £f3 мало отличаются друг от друга: для
них характерно, что при любой интерпретации их базисов зна-
чения переменных х2 и х2 совйадают после выполнения начальных
фрагментов программ. Точно так же подклассы и имеют
общее свойство: начальные значения переменных хх и х2 в общем
случае различны и при любой свободной интерпретации символ
xt не входит ни в один терм-значение переменной х2, а х2 не вхо-
дит ни в один терм-значение переменной xt (или, как говорят,
переменные х2 и х2 разделены). Такое отличие подклассов первой
группы от подклассов и существенно влияет на разреши-
мость проблем пустоты и эквивалентности. В литературе имеются
примеры еще более простых неразрешимых подклассов стандарт-
ных схем, чем ^’1, £Р2, £f3. Так, в некотором смысле минимальным
подклассом с неразрешимой проблемой пустоты является под-
класс исследованный Непомнящим [48, 125]. Базис этого под-
класса: = ({хь х2}, {/<»}, {a^:=/(ai), ж2:=/(х2),
Xi := х2, р (х,), стоп (xlt я^)}).
Сравнивая «близкие» подклассы, одни из которых разрешимы,
другие неразрешимы, удается выделить те особенности схем этих
подклассов, которые обеспечивают характер разрешимости. На-
пример, проблема пустоты разрешима в классе <У7 с базисом S32 —
= ({*!. х2}, {fi\ Д1’}, {pW}, {х1:=/1(х1), х2:=/2(х2), х2 : =
:= Xi, р (хг), р (х2), стоп (xt, х2)}) [48, 125].
Сравнение класса <У7 с классом &2 показывает, что для раз-
решимости существен тот факт, что на разные переменные
135
«воздействуют» разные функциональные символы. Если сравнить
класс с представленным ниже классом <У8, в котором проб-
лема пустоты разрешима [48, 125], то можно заметить, что су-
щественным является использование в условных операторов,
содержащих обе переменные: ЗЭ8 = ({iq, х2}, {а^: —
:= / (*1). хг := f (*г), xi ‘= хг, хг:= х1, р (xlt х2), стоп (хи хг)}).
Выделение разрешимых и одновременно достаточно интерес-
ных с точки зрения практики программирования подклассов
стандартных схем требует внимательного изучения различных
аспектов схем, отбора и классификации тех свойств схем, которые
могут повлиять на разрешимость. Такой анализ может привести к ус-
пеху только при активном сочетании программистской интуиции
с изучением известных методов и результатов теории разрешимо-
сти в логике, теории алгоритмов, автоматов и формальных языков.
§ 1. Свободные стандартные схемы
1.1. Проблемы пустоты и тотальности. Напомним, что в сво-
бодных схемах все цепочки являются допустимыми. Переход от
общего случая к свободным схемам не кажется существенным су-
жением класса стандартных схем: программы с недопустимыми
цепочками хотелось бы считать программистским недосмотром.
Но пример в конце этого параграфа (схема 57 3, для которой не
существует эквивалентной свободной схемы) опровергает такое
рассуждение: схемы с недопустимыми цепочками дают большие
возможности при программировании. Свободные схемы представ-
ляют особый интерес в схематологии в силу того, что проблемы
распознавания некоторых свойств этих схем значительно упроща-
ются. В частности, очень просто устанавливается разрешимость
проблемы пустоты и тотальности в классе свободных схем.
Теорема 7.1. Проблема пустоты свободных стандартных
схем разрешима.
Доказательство. Действительно, из определения
стандартной схемы и определения свободной схемы следует, что
свободная схема S пуста тогда и только тогда, когда в ней не су-
ществует ни одной конечной цепочки, т. е. пути, ведущего из
начальной вершины в заключительную. Если такая цепочка су-
ществует, то она допустима и существует интерпретация /,
при которой программа (S, I) останавливается. Таким образом,
распознавание пустоты свободной схемы сводится к известной
процедуре 175] обнаружения того факта, что начальная и заклю-
чительная вершины в графе схемы не связаны ни одним путем. | )
Теорема 7.2. Проблема тотальности свободных стан-
дартных схем разрешима.
Доказательство. Свободная схема не тотальна тог-
да и только тогда, когда граф схемы содержит контур, т. е.
путь (I, llt 12, . . ., /), где I — вершина графа. Процедура распо-
знавания наличия контура в графе известна [75]. Q
136
Итак, неразрешимые в общем случае проблемы пустоты и то-
тальности становятся разрешимыми в классе свободных стандарт-
ных схем. А как обстоит дело с проблемой эквивалентности сво-
бодных схем? Эта проблема остается открытой на сегодняшний день.
Многие исследователи склонны поддержать гипотезу Патерсона
(119, 126] о разрешимости этой проблемы на том основании, что
не удалось доказать ее неразрешимость общепринятыми методами.
Но мало и результатов, поддерживающих эту гипотезу. Решение
проблемы эквивалентности свободных схем будет значительным
событием в схематологии и углубит наше знание о природе не-
разрешимости в схемах.
1.2. Проблема изоморфизма. В задании 4.3 были определены
два корректных отношения эквивалентности схем. Схемы изо-
морфны, если совпадают множества всех цепочек операторов этих
схем. Схемы и Sa в базисе ЗВ интерпретационно изоморфны,
если любая интерпретация базиса порождает совпадающие цепоч-
ки операторов в Si и 52. В задании 5.3 предлагалось доказать,
что отношение интерпретационного изоморфизма не является
частично разрешимым в классе стандартных схем. Сейчас мы убе-
димся, что ситуация меняется, если ограничиться свободными
схемами: для свободных схем интерпретационный изоморфизм
равносилен их изоморфизму, а изоморфизм схем можно распо-
знавать с помощью алгоритма, очень похожего на алгоритм рас-
познавания эквивалентности конечных одноленточных автоматов
(см. гл. 3).
Обозначим через С (S) множество всех цепочек операторов
схемы S, а через С (5, I) — цепочку операторов, порожденную
в S интерпретацией I.
Лемма 7.1. Свободные схемы St и St интерпретационно
изоморфны тогда и только тогда, когда они изоморфны, т. е.
С (Si) = С (St).
Доказательство. Достаточность. Пусть С (Sx) =
== С (St), но существует интерпретация I такая, что ct = С (Slt
I) сг == С (St, I). Тогда существует номер позиции i в обеих
цепочках, до которой (включительно) префиксы цепочек сг и с,
совпадают, а в позиции i 4- 1 стоят разные операторы (в случае
условных операторов может быть один и тот же оператор, но
с разными верхними индексами 0 и 1). Так как С (Si) — С (S2),
имеем Ci, сгЕС (Si). Это значит, что ct и с2 должны содержать
один и тот же условный оператор на некоторой позиции j, j i,
но с разными верхними индексами 0 и 1. Но это невозможно, так
как в протоколах программ (5Х, /) и (52, I) соответствующие со-
стояния памяти в любой /-й конфигурации, где / i, равны.
Необходимость. Очевидна. □
Теорема 7.3. Проблема изоморфизма стандартных схем
алгоритмически разрешима.
Доказательство. Алгоритм распознавания изоморфиз-
ма состоит из двух частей. Сначала по заданным схемам строятся
137
конечные одноленточные автоматы, моделирующие в некотором
смысле эти схемы. Затем выясняется, эквивалентны ли эти автома-
ты, и на основании результата анализа делается вывод о том,
изоморфны исходные схемы или нет.
Пусть и 5, — две стандартные схемы. Зафиксируем конеч-
ное множество {sj, . . ., sn), состоящее из всех операторов при-
сваивания обеих схем и условных операторов в двух экземпля-
рах — с верхними индексами 1 и 0. Выберем произвольный ал-
фавит V, элементы которого находятся во взаимно однозначном
соответствии К с элементами этого множества.
По каждой из заданных схем £ построим конечный однолен-
точный автомат A (S) над алфавитом У. Множество состояний
автомата A (S) включает: начальное состояние q0, состояние qc,
специальное «самозацикливающееся» состояние q^ и состояния
• • *< 9ь взаимно однозначно соответствующие дугам графа
схемы 5; обозначим это взаимно однозначное соответствие через
L. Дуги графа автомата проводятся согласно правилам, изобра-
женным на рис. 7.1, где слева показаны фрагменты графа схемы S,
а справа — соответствующие фрагменты графа автомата А (Л).
На этом рисунке
к: х := т — произвольный преобразователь схемы S;
к: если р (х, . . ., у) то иначе 12 — произвольный распозна-
ватель схемы;
К (старт (х, ..у)), K(x: = t), К(рг (х, . . ., у)), К(р° (х, ...
. . ., у)) — элементы алфавита V;
£ 0. /) — состояние автомата A (S), соответствующее дуге,
ведущей в 5 от вершины с меткой i к вершине с меткой /.
Все остальные дуги в графе автомата проводятся к «самоза-
цикливающемуся» состоянию автомата (мы не изображаем
этих дуг на рис. 7.1 и 7.2). Заключительными состояниями авто-
мата A (S) объявим состояния q0, qr, . . ., q{, qc, незаключитель-
ным — состояние q„>.
На рис. 7.2, а и 7.2, б показаны две (изоморфные) стандартные
схемы 571 и S7.2, а на рис. 7.2, в и 7.2, г — построенные по ним
в соответствии с только что описанными правилами автоматы
А (57Л) и А (57.2). Здесь V — {a, b, с, d, е}, где а = К (старт
(х)), Ь = К (р1 (х)), с = К (р° (х)), d = К (х / (х)), е =
= К (стоп (х)). (Убедитесь, что автоматы А (57Л) и А (572) эк-
вивалентны.)
Покажем, что 5Х и $2 изоморфны тогда и только тогда, когда
A (iS\) и A (S2) эквивалентны. Заметим для этого, что по построе-
нию автоматов A (S) любому префиксу произвольной цепочки
операторов в схеме S соответствует слово в алфавите V, допуска-
емое автоматом A (S). И наоборот, любому слову, допускаемому
автоматом, соответствует некоторый префикс некоторой цепочки
операторов в схеме. Обозначим через С* (S) множество всех пре-
фиксов множества цепочек С (S). Очевидно, что С (5Х) = С (S2)
тогда и только тогда, когда С* (5Х) — С* (S2). Поэтому схемы
Sj и S2 изоморфны тогда и только тогда, когда эквивалентны ав~
138
Рис. 7.1. Правила построения автомата A (S)
томаты A (Si) и A (St). Алгоритм распознавания эквивалентности
конечных одноленточных автоматов был описан в главе 3. Q
Следствие 7.1. Проблема интерпретационного изомор
физма разрешима в классе свободных стандартных схем.
Доказательство. В силу леммы 7.1 интерпретацион-
ный изоморфизм свободных схем равносилен изоморфизму, ко-
торый, как только что доказано, представляет собой разрешимое
отношение эквивалентности стандартных схем.
139
Рис. 7.2. Стандартные схемы и моделирующие их автоматы: а — схема
б — схема 5JwS; в — автомат A (SiAy, г — автомат A (5,.г)
Итак, мы установили разрешимость проблем пустоты, тоталь-
ности и интерпретационного изоморфизма в классе свободных
схем. Однако эффект этих результатов снижает тот факт, что са-
ма проблема свободы не является даже частично разрешимой
(см. теорему 5.4). Не существует и алгоритма, с помощью которого
можно было бы произвольную стандартную схему преобразовать
в эквивалентную свободную схему (88J. В частности, для следую-
щей схемы Sf.a не существует эквивалентной свободной схемы:
(старт,
х := а,
У := ь,
3: если р (х) то 4 иначе 5,
4: х : = / (х) на 3,
5: если р (у) то 6 иначе 8,
140
6: х := g (ж),
7: У := f (у) на 5;
8: стоп (ж))
Задание 7.1.
А. Докажите, что множество правил преобразования, порождаемых
описанными в п. 3.1 гл. 6 схемами ЛТ1 (удаление недостижимых) н ЛТЗ
(склеивание копий, илн копирование), представляет собой полную систему
преобразовании для отношения изоморфизма стандартных схем (а тем са-
мым и полную систему преобразований для отношения интерпретационного
изоморфизма свободных схем).
Б. Назовем схемы и 5, в базисе квазиизоморфными, если совпада
ют множества всех конечных цепочек операторов этих схем, и интерпрета-
ционно квазиизоморфными, если для любой интерпретации I базиса «Ф ре-
зультаты выполнения программ (Sn /) н (S,, Z) либо одиовременио не опре-
делены, либо определены н соответствующие интерпретации I конечные це-
почки операторов совпадают. Покажите, что отношение интерпретационного
квазиизоморфизма стандартных схем не является частично разрешимым,
квазнизоморфизм стандартных схем разрешим, а для свободных схем ин-
терпретационный квазиизоморфизм равносилен квазнизоморфизму.
В. Докажите, что множество правил преобразования, порождаемых
схемами правил ЛТ1, ЛТ2 и ЛТЗ из предыдущей главы, представляет собой
полную систему преобразований для отношения квазиизоморфизма стан-
дартных схем.
§ 2. Сквозные схемы
В этом параграфе мы выделим подкласс стандартных схем,
называемых сквозными, для которых опишем алгоритм распозна-
вания функциональной эквивалентности. Интерес к классу сквоз-
ных схем в нашем изложении обусловлен тем обстоятельством,
что он содержит несколько различных подклассов, разрешимость
эквивалентности в которых была установлена в разное время и
разными методами (см. обзор в конце главы).
2.1. Определение сквозных схем. Класс сквозных схем выде-
ляется как подкласс стандартных схем за счет двух ограничений,
накладываемых на структуру информационных связей. На базис
схем никаких ограничений при этом не накладывается.
Тот факт, что терм а является подтермом терма т, будем запи-
сывать как о -< т. Например, х -< / (ж), g (ж) -< g (ж), но (у -<
-</(*))•
Стандартная схема называется схемой со сквозными тестами,
или коротко сквозной схемой, если для нее выполнены два следую-
щих условия.
D1. Для всяких распознавателей А, В, лежащих на некотором
пути от входа к заключительному оператору, и для каждого пути
w, ведущего от А к В и содержащего только операторы присваи-
вания, справедливо
Уж е арг (Л) Зу е арг (В} ж -< t (u>, у).
D2. Для всякого распознавателя А, для всех пар ж, у различ-
ных аргументов вершины А и для всех путей, ведущих к Л от
входа схемы, выполнено t (w, ж) t (w, у).
Пример двух (эквивалентных) сквозных схем приведен на
рис. 7.3.
141
Рис. 7.3. Две эквивалентные сквозные схемы
Условие D1 означает, что в вычислениях сквозных схем не
теряется ни один из термов, на которых проверяются условия
распознавателей. Если, например, р (olt . . ., ап) и q (тг, . . .
. . ., тт) — два следующих друг за другом теста вычисления
сквозной схемы при некоторой свободной интерпретации, то
Vi 3/ Oi -< tj. Легко понять, что свойство D1 является эффек-
тивно распознаваемым.
Условие D2 означает, что в вычислениях сквозных схем при
свободных интерпретациях предикаты проверяются только на
наборах попарно различных термов. Нетрудно видеть, что пробле-
ма проверки условия D2 алгоритмически неразрешима. К ней
можно свести проблему тождества слов Поста. Действительно,
пусть (Hlt Н2) — система Поста,
= (04, .... ccn), Н2 = (Pi, • . Рп)-
Приведенная на рис. 7.4 схема 8 (Hi, Н2) удовлетворяет условию
D2 тогда и только тогда, когда система (Hlt Н2) не имеет ни одного
решения.
Отметим, что схема 8 (Hlt Н2) обладает свойством D1. Кроме
того, схема 8 (Hlt Н2) свободна тогда и только тогда, когда систе-
«42
I ctapt(x)
Рис. 7.4. Схема S (Hlt Нг)
ма Поста (Нг, Н2) не имеет решений. Это означает, что в классе
схем, удовлетворяющих условию D1, неразрешима проблема сво-
боды.
Что касается класса стандартных схем, удовлетворяющих
условию D2, то он, очевидно, содержит класс для которого,
как показано в гл. 5, проблемы пустоты и эквивалентности не
являются частично разрешимыми.
Задание 7.2. Докажите, что схемы, приведенные на рис. 7.5, функ-
ционально эквивалентны н удовлетворяют условию D1, причем схема S7.t —
сквозная, a St.B — нет.
Задание 7.3. Докажите, что для несвободной схемы на рис. 7.6,
удовлетворяющей условию D1, но ие D2, ие существует функционально эк-
вивалентной свободной схемы.
2.2. Обобщение инвариантов. Если выходная дуга распозна-
вателя ведет к распознавателю с тем же условием, что и у первого
распознавателя, то второй распознаватель избыточен, его можно
удалить с сохранением эквивалентности (см. рис. 7.7).
Чтобы сформулировать такое преобразование в более общем
виде, ниже мы обобщаем понятия инварианта и сети, введенные
в предыдущей главе. Логическое выражение л назовем ^-избыточ-
ным на пути w, если w = и\Аю2, где А — распознаватель с усло-
вием Од, л U (ш, х^/х^ . . ., t(w, xn)/xn] = a a It (^i, ..
. . t (wlf zn)/zn]; Zj, . . ., xn — все переменные, встречающиеся
в л и а а, а путь w2 начинается Д-дугой распознавателя А.
,143
Рис. 7.6. Схема $7_», для которой не существует эквивалентной свободной
схемы
Множество утверждений, порождаемое путем w во фрагменте
G, обобщается следующим образом:
gen (G, w) = gen (G, w) (J
и{Д = я|Де{0, 1}
и логическое выражение л Д-избыточно на пути п>}.
144
' Рис. 7.7. Удаление избыточного распознавателя
В качестве обобщенного инварианта дуги е фрагмента G возьмем
invar (G, е) == П gen (G, w),
wsW
где пересечение, как в п. 2.1 предыдущей главы, берется по всем
путям w, начинающимся входами фрагмента G и кончающимся
дугой е. Итак, кроме утверждений-равенств вида х — т, где х ЕЕ
ЕЕ Й7, t Е Л обобщенный инвариант может содержать также
утверждения логического типа
А = р (ть . . тп),
где А ЕЕ {0, 1), рЕ,1?, Tlt . . ., тп е Т.
Распознаватель А назовем содержательно (^-избыточным,
если его условие Од является Д-избыточным на любом пути, на-
чинающемся входом фрагмента и кончающемся дугой, ведущей
к Л, т. е. (Д — од) ЕЕ invar (G, е) для всех дуг е, ведущих к А,
Легко видеть, что если распознаватель А содержательно Д-
избыточен, то всякое вычисление, достигшее распознавателя А,
всегда будет продолжаться выбором одной и той же Д-дуги этого
распознавателя. Это значит, что распознаватель А можно удалить
из фрагмента.
В предыдущей главе был описан алгоритм разметки, который
позволял эффективно строить инварианты дуг во фрагментах
стандартных схем. Мы увидим сейчас, что совсем иначе обстоит
дело с обобщенными инвариантами дуг. Действительно, если бы
мы умели эффективно строить обобщенные инварианты дуг
в любых фрагментах, то тем самым мы решили бы и проблему до-
стижимости вершин в стандартных схемах (существует ли интер-
претация, при которой вычисление проходит через выделенную
вершину). Однако схема непуста тогда и только тогда, когда
достижимым является хотя бы один из ее заключительных опера-
торов, т. е. проблему пустоты можно свести к проблеме достижи-
мости вершин.
Таким образом, проблема нахождения обобщенных инвариан-
тов дуг в стандартных схемах является алгоритмически неразре-
шимой. Тем не менее, ниже мы опишем алгоритм разметки, с по-
мощью которого можно строить подмножества инвариантов дуг.
145
Такой алгоритм окажется достаточным для освобождения сквоз-
ных схем, т. е. для преобразования произвольной сквозной схе-
мы в эквивалентную свободную схему.
Обобщим понятие сети, введенное в п. 2.1 предыдущей главы.
Обобщенная сеть s = (V, ¥, Г) отличается от (простой) сети толь-
ко тем, что кроме прежних вершин функционального типа она
может содержать также конечное число вершин нового логиче-
ского типа. Каждая вершина логического типа также содержит
конечное число элементов, среди которых мы различаем
а) предикатные элементы с, для которых ¥ (с) GE 3°; из них
выходит ровно d (¥ (с)) пронумерованных дуг к вершинам функ-
ционального типа;
б) элементы с, соответствующие логическим константам 1 и О,
'F (c)G~ {0, 1); из них не выходит ни одной дуги (мы предполага
ем ниже {0, 1} П U Я = 0. d (0) = </(!) = 0).
Как и раньше, требуется, чтобы в обобщенной сети не было
контуров и элементов-дублей, т. е. таких различных элементов
сг и с8, для которых ¥ (сх) = ¥ (с2) & Vi (1 <1 i d (V (ех)))
Г (сх, г) = Г (с2, г). Отсюда следует, в частности, что в обобщен-
ной сети не может быть более двух элементов, соответствующих
логическим константам. Кроме того, мы потребуем, чтобы всякая
вершина логического типа содержала не более одного элемента,
соответствующего логической константе. Отметим, что в обоб-
щенной сети нет дуг, ведущих к вершинам логического типа.
Примеры обобщенных сетей приведены на рис. 7.8.
Рис. 7.8. Обобщенные сети si к s2
з2
Все понятия, введенные в предыдущей главе для сетей, есте-
ственным образом переносятся и на обобщенные сети. Мы сдела-
ем это систематически, сохраняя старые обозначения.
know (с) =
{fe), если ¥ (с) = А, Л (J U (0,1), d (h) = 0;
(/ (Tlt. •т„) | Vi (1 < i < n) Ti €= know (Г (c, i))},
если ¥ (c) =/, /GfU^. d(/) = n>0.
146
Говорят, что вершина v обобщенной сети знает множество тер-
мов know (н) = [J know (с). Обобщенная сеть s = (V, Т, Г)
ее»
представляет множество утверждений assert (s) = (J {х =
' — т | (я EE SC (J {0, 1}) & (х, тЕ know, (р))}. Каждая из приве-
денных на рис. 7.8 обобщенных сетей si, s2 представляет множе-
ство утверждений {1 = р (g (у), х), 1 = р (g (у), f (у)), х =
= / (У), 1 = 1, х = х, у = у}.
Забытые вершины сети, т. е. вершины, не знающие никаких
термов (know (р) = 0), можно удалять, как и раньше, начиная
от вершин без элементов. Ясно, что такое удаление оставляет
множество assert (s) неизменным. Вершина р обобщенной сети s
называется доступной, если в s имеется путь к v от некоторой вер-
шины р' с элементом с', для которого V (с') ЕЕ SC (J {0, 1}. Осталь-
ные вершины называются недоступными. Как и раньше, все не-
доступные вершины можно удалить, начиная с вершин р, к кото-
рым не ведет ни одной дуги и для всех элементов с которых выпол-
нено Т (с) SC U {О, !}• Такое удаление снова оставляет неиз-
менным множество утверждений, представляемое обобщенной
сетью.
Обобщенная сеть называется приведенной, если в ней нет ни
забытых, ни недоступных вершин.
Лемма 7.2. По всякой обобщенной сети s можно эффективно
построить приведенную обобщенную сеть red (s), для которой
assert ( red (s)) = assert (s).
Доказательство аналогично доказательству леммы 6.1.
Заметим, что red (si) — s2 для обобщенных сетей si, s2 на
рис. 7.8. Q
Операция пересечения Д для обобщенных сетей определяется
в точности так же, как пересечение простых сетей. Поэтому нет
ничего удивительного в том, что для обобщенных сетей справедли-
выми оказываются утверждения, сформулированные в леммах
6.2, 6.3 и 6.4 для простых сетей. Их доказательства мало чем от-
личаются от приведенных в гл. 6.
Частичный порядок для приведенных обобщенных сетей
определяется, как и раньше, соотношением
si < s2 О si Д s2 = si.
Теорема 7.4. Множество приведенных обобщенных сетей
вместе с операцией пересечения образует ограниченную полуре-
шетку.
Доказател ьство получается аналогично доказатель-
ству теоремы 6.1. Q
Множество Ж' приведенных обобщенных сетей мы дополняем,
как и раньше, элементом 1 (Vs Е X' s Д fl = 1 Д s = s)
и получаем полурешетку (55', Д), удовлетворяющую условию
обрыва цепей.
147
Определение преобразователя := т> для обобщенных се-
тей, называемого по-прежнему эффектом присваивания, ничем
не отличается от приведенного в гл. 6 определения эффекта при-
сваивания для простых сетей.
Лемма 7.3. Ух СЕ SC Ух ЕЕ Т Увх, st ЕЕ X'
<г := т> («j Д s2) = «х := т> s,) Д «г := т> s,).
Лемма 7.4. Пусть s ЕЕ X' и gen (G, w) = assert (s) для пу-
ти w во фрагменте G. Тогда gen (G, wAe) = assert «х := т> s),
где А — оператор присваивания х : — т, а е — выходящая из него
дуга.
Леммы 7.3 и 7.4 означают дистрибутивность эффекта присваи-
вания и его содержательную корректность. Доказательство этих
лемм можно получить повторением доказательств лемм 6.5 и 6.6
соответственно.
Двухместную операцию add, определенную в п. 2.3 предыду-
щей главы, можно применять и к обобщенным сетям. Если s ЕЕ
ЕЖ', а т — функциональный терм, логическое выражение или
т = Д, где Д ЕЕ (0, 1}, то применение этой операции дает обоб-
щенную сеть add (s, т), в которой есть элемент, знающий т.
Введем, наконец, еще один преобразователь обобщенных се-
тей, называемый эффектом теста л с результатом Д, <Д = л>:
Ж' -► X’, где Д б= {0, 1), а л — логическое выражение. Этот пре-
образователь произвольную обобщенную сеть SE Ж' преобра-
зует в приведенную обобщенную сеть s’ = <Д = л> s следующим
образом. Если s — И, то s' = И. Если же s=/= И, то пусть si =
= add (add (s, Д), л), а обобщенная сеть s2 получается из si объ-
единением вершин и v2, знающих Дил соответственно. Более
точно, вершины v3 и v3 заменяются одной новой вершиной, в ко-
торую переносятся все элементы вершин v3 и vt (вместе с выходя-
щими из них дугами). Если после этого окажется, что вершина
v в s2 знает обе логические константы 0 и 1, то положим s' — 11,
иначе s' = s2.
Как показывает пример на рис. 7.9, эффект теста — это, во-
обще говоря, не дистрибутивный преобразователь обобщенных
сетей. Действительно, для изображенных на этом рисунке обоб-
щенных сетей si и $2 имеем <1 = р (x)> (si Д s2) =# «1 —
= P(x)>sl)A«l=p(x)>s2).
Лемма 7.5. Эффект теста <Д ~ р (хи . . ., хп)>: Ж' -»
—►Ж' — монотонный преобразователь, т. е. Уз, s' ЕЕ X' УД ЕЕ
е (0, 1} Ур се & Ух3, ..., хп е sc
s^s’ = р (xlf . . ., хп)у s < < Д = р (гх, . . ., хп)у s'.
Доказательство непосредственно вытекает из опре-
деления эффекта теста. Q
Лемма 7.6. Пусть s е X' и gen (G, ш) = assert (s) для пу-
ти w в G, ведущего к распознавателю А с условием л. Тогда gen (G,
wAe) — assert «Д = л> s), где е — выходящая из А Ь-дуга.
148
Рис. 7.9. Контрпример, опровергающий дистрибутивность эффекта теста
Доказательство также непосредственно следует из
определения эффекта теста и означает его содержательную кор-
ректность. Q
Итак, мы можем сформулировать задачу глобального анализа
произвольного фрагмента G. Мы описали полурешетку (Ж', Д),
удовлетворяющую условию обрыва цепей, а также семейство мо-
нотонных преобразователей. В качестве начальной разметки р0
возьмем начальную разметку р0, описанную в п. 2.3 главы 6.
Семантическую функцию определим так:
<ж:= т> s, если дуга е' ведет к оператору ж:= т, а дуга е
выходит из него;
/.(«)= <Д = л>«, если дуга е' ведет к распознавателю с усло-
вием л, а е — его А-дуга;
fi, в остальных случаях.
В силу леммы 2.2 для описанной задачи глобального анализа
существует стационарная разметка р.
Теорема 7.5. Для любого фрагмента G, его дуги е и стацио-
нарной разметки р
invar (G, е) э assert (р («*)).
Доказательство. Пусть Е — множество входов фраг-
мента G, a gw и Н — преобразователи обобщенных сетей, опреде-
ляемые по семантической функции / как в п. 2.2 гл. 2. Используя
леммы 7.4 и 7.6, получим
invar (G, е) = П gen (G, w) = П П assert (gw (ро («'))) —
weW и-емарш(е', е)
= assert (Н (e))t
149
для любой дуги е фрагмента G. В силу теоремы 2.1 стационарная
разметка р фрагмента G безопасна, т. е. Vc р (е) Н (е),
поэтому
assert’(p (е)) С assert (Н (е)) = invar (G, е). Q
Будем говорить, что распознаватель А формально ^-избыто-
чен, если при стационарной разметке р <Д = ад) р (е) = р (е)
для каждой из дуг е, ведущих к Л. Из теоремы 7.5 вытекает сле-
дующее
Следствие 7.2. Всякий формально h-избыточный распо-
знаватель содержательно ^-избыточен.
Теперь мы можем сформулировать новую эффективную схему
правил преобразования фрагментов стандартных схем.
Ф1 [Удаление избыточного теста].
Пусть распознаватель А с условием од во фрагменте G фор-
мально Д-избыточен, к нему ведет ровно одна дуга е, а фрагмент
G' получается из G заменой
Тогда G «-» G'.
Теорема 7.6. Если фрагмент G' получается из фрагмента
G применением схемы правил Ф1, то G — G'.
Доказательство непосредственно вытекает из след-
ствия 7.2. □
2.3. Освобождение сквозных схем. В этом разделе мы покажем,
как с помощью эквивалентных преобразований преобразовать
произвольную сквозную схему в свободную сквозную схему.
Первый шаг преобразования состоит в приведении схемы, которое
описано в предыдущей главе. Понятно, что приведенная схема
также будет сквозной. Если на одном из последующих шагов бу-
дут нарушены условия приведенности, мы снова добиваемся их
выполнения, не оговаривая этого особо.
Луч L приведенной сквозной схемы S, который ведет от рас-
познавателя А к (другому или тому же самому) распознавателю В,
называется второстепенным, если
Vy Е арг (В) Зх Gapr (Л) t (w, у) = х,
где w — путь по всем операторам луча L. Все остальные лучи
схемы 5 называются главными. Логическим фрагментом схемы
S (короче: л-фрагментом) будем называть всякое вхождение в S
150
такого фрагмента, который не содержит ее главных лучей. До-
вольно очевидно, что для освобождения схемы S достаточно нау-
читься освобождать ее максимальные связные л-фрагменты. Все
распознаватели такого максимального связного л-фрагмента G
имеют одно и то же количество аргументов, а действия, выпол-
няемые над значениями аргументов распознавателей при любом
вычислении по G, могут состоять только в перестановках этих
значений (см. рис. 7.10).
Если X — множество переменных, а Р — множество преди-
катных символов, то через К {X, Р) будем обозначать множество
Рис. 7.10. Пример освобождения л-фрагмента
-всех сетей *), в которых для любого элемента с выполнено
Т (с) ЕЕ X (J Р LJ (0, 1). Если X, Р — конечные множества, то
(К (X, Р), Д) — конечная полурешетка.
Определим преобразователь сетей (ЗАБЫТЬ}, который про-
извольную сеть s Е 'Z' преобразует в сеть s' = (ЗАБЫТЬ} s
из К (X, Р) следующим образом:
1) если s = fl, то s' = fl;
2) если s ~/= fl, то пусть сеть si получается из s удалением всех
элементов с, для которых Ч' (с) ЕЕ s' — red (si).
Содержательно, преобразователь (ЗАБЫТЬ} удаляет из
assert (s) все утверждения, кроме равенств х = у с х, у ЕЕ <27 и
равенств Д = р(г)с Ае{0, 1), р£$, £6=Й7П. Условие распоз-
навателя А обозначается ниже оА.
Теорема 7.7. Всякую сквозную схему S можно преобразо-
вать в эквивалентную свободную сквозную схему.
Доказательство. Как уже отмечалось, для доказа-
тельства достаточно преобразовать всякий максимальный связ-
ный л-фрагмеят приведенной схемы S в свободный. Пусть G —
такой фрагмент. Если он не содержит распознавателей, то он уже
свободен н ничего делать не нужно. Пусть в G имеется k 1
распознавателей, к которым ведут входы фрагмента G. Применяя
при А > 1 правило копирования, заменим G на к его копий G4 (1
i к) так, чтобы л-фрагмент G, имел ровно один распознава-
тель А<, к которому ведут входы этого фрагмента. Еще раз приме-
няя правило копирования, преобразуем G, во фрагмент G<. При
описании фрагмента Gj будем обозначать копни вершины А из
Gi через A [s], где s ЕЕ K(Xs, Ps)- Все входы фрагмента G, напра-
вим к вершине А, [®]. Если А — распознаватель фрагмента Git
Д-дуга которого ведет к вершине В&, то Д-дугу распознавателя
A[s] в G, направим к вершине ВА [<Д = аА} s]; если А — опера-
тор присваивания х т, выходная дуга которого ведет к верши-
не В, то выходную дугу оператора присваивания A[s] направим
к вершине В [(ЗАБЫТЬ} (х т> sj.
Из построения фрагмента G, следует, что для стационарной
разметки р этого фрагмента, для всякой вершины A [s] и любой
ведущей к ней дуги е справедливо р (е) Е> s. Покажем, что если
условие аА распознавателя A [s] Д-избыточно иа некотором пути
w, ведущем к A [s], то A [s] — формально Д-избыточный распо-
знаватель. Действительно, Д-нзбыточность аА на пути w означает,
•что w = wt В [s'] wt для некоторого распознавателя В [s'], при-
чем wa начинается Д-дугой н t (ша, аА) = ад. Следовательно,
<Д = оА} s = s, т. е. распознаватель A [s] является формально
Д-избыточным. Таким образом, для освобождения фрагмента
G' достаточно удалить каждый распознаватель A [s], который яв-
ляется формально Д-избыточным с некоторым Д Е (0, 1). Пока-
•) Если ие оговорено противное, под сетью в дальнейшем будет пони-
маться произвольная обобщенная сеть (обычно приведенная).
152
жем, как это сделать. Прежде всего, можно предполагать, что
дуги такого распознавателя A [s] ведут к другим вершинам фраг-
мента, вставляя в противном случае подходящую вырожденную
пересылку х := х на эти дуги. Далее, применением правила ко-
пирования создадим копни вершины A [s] таким образом, чтобы
к каждой из копий вела ровно одна дуга. Разумеется, все копии
по-прежнему будут формально Д-нзбыточными распознавателя-
ми. Применением правила Ф1 (удаление избыточного теста) мы
сможем избавиться от всех только что созданных копий распознава-
теля А [sj. После удаления всех формально Д-избыточных с неко-
торыми Д ЕЕ {0, 1} распознавателей н последующего приведения
мы получим свободный л-фрагмент. Q
На рис. 7.10 показан пример, иллюстрирующий переход к сво-
бодному л-фрагменту.
Для описания алгоритма распознавания эквивалентности
двух приведенных свободных сквозных схем и Sa нам потребу-
ется еще, чтобы выполнялось следующее условие разделенности
переменных схем н 5а: если некоторая переменная х встре-
чается в каждой из схем Sa, Sa, то эти схемы не содержат опе-
раторов присваивания с результатом х.
Выполнение этого условия достигается совершенно аналогично
тому, как зто сделано в п. 3.2 гл. 6. Сначала применением ЛТ7 каж-
дый из начальных операторов старт (ха, ..., хп) заменяется на луч
старт (X,..х„) — =xt
*2: х2
Ха- =хп
Затем все вхождения каждой из переменных у, встречающихся
в схеме (кроме результатов начального оператора н аргументов
вставленных пересылок), применением ЛТ4 заменяются новой
переменной z, которая еще не встречается ни в 5г, ни в Sa. В ре-
зультате условие разделенности переменных схем Sj и Sa окажет-
ся выполненным.
Задание 7.4. Докажите, что для каждой стандартной схемы, удов-
летворяющей условиям D1 и приведенному ниже более слабому, чем D2,
условию D2', по-прежнему можно эффективно построить эквивалентную
свободную схему.
(D2') Для всякого распознавателя А Ух, у е арг (Л) (Vw е WA
t (w, х) = t (w, у)) V (Vu> E WA t (w, x) Ф t (w, у)), где WA — множество
всех путей, ведущих к Л от входа схемы.
Задание 7.5. Докажите, что понятия содержательной н формальной
Д-избыточностн распознавателей совпадают для фрагментов, в которых к
каждой вершине ведет ровно одна дуга.
2.4. Алгоритм распознавания эквивалентности сквозных схем.
Идея распознающего алгоритма Ш состоит в том, что по двум при-
веденным свободным сквозным схемам Sa, удовлетворяющим
условию разделенности переменных, мы строим граф О (Slt Sa),
который можно рассматривать как недетерминированную схему,,
моделирующую синхронные вычисления обеих схем.
158
Пусть Xit Pi — множества переменных и предикатных сим-
волов соответственно, встречающихся в схеме S,, i = 1, 2; X =
= Xj U Ха, Р = Л U Л. К = К (X, Р). Вершины схем Sa, Sa,
отличные от операторов присваивания, будем называть ключе-
выми. Если А, В — распознаватели схем Sa, 8а, у €= арг (В),
з Ж', s И, то положим
<р„ (Л, В, з) = {т | (у — т) GE assert (s) и терм т содержит
вхождения переменных только той из схем Sa, Sa, в которой на-
ходится вершина Л),
1е (Л, В, з) = (В — заключительный оператор или оператор
петли, а А — распознаватель) V В — распознаватели)
& (Vу GE арг (В) <р„(А, В, з) Ух е арг (А) х -<
<*в | у GE арг (В)]),
eq (А, В, s) = 1е (А, В, з) & 1е (В, А, з).
Вершинами графа О (Slt Sa) будут служить тройки [А, В, s],
где А, В — ключевые вершины схем Sa соответственно, a s G
, s =/= Я. Из каждой вершины в О (Slt Sa) будет выходить не
более четырех дуг, среди которых будут различаться Sj-дуги и
iSg-дугн, причем каждая из них может быть либо 0-, либо 1-дугой.
Вершину [А, В, s] графа О (81г Sa) можно интерпретировать как
состояние синхронных вычислений схем и которое означа-
ет, что ^-вычисление достигло вершины А, а Ха-вычисление до-
стигло вершины В, причем в этом состоянии истинны все утвер-
ждения, содержащиеся в assert (s). Истинность предиката 1е (А,
В, з) на таком состоянии означает при этом, что ^-вычисление не
опережает 52-вычисления. Точками синхронизации будут слу-
жить состояния, в которых истинно условие eq (А, В, s): 8г- и
5а-вычисления не опережают друг друга. Заметим сразу, что бла-
годаря ацикличности сетей из Ж' условие eq (А, В, з) равносиль-
но условию Ух арг (А) Зу ЕЕ арг (В) (х = у) GEE assert (s) &
& Уу ЕЕ арг (В) Зг £= арг (А) (х = у) GEE assert (s).
Для описания алгоритма 51 понадобится вспомогательная па-
мять — трехмерная таблица ТТ, в которой для всякой тройки
[А, В, s] такой, что А, В — ключевые вершины схем Sa, Sa, а
s GE К и eq (А, В, з), будет храниться некоторый элемент ТТ [А,
В, sj — сеть из Ж'.
Алгоритм 5(.
Первый этап — инициализация. Пусть (i = 1, 2) — путь
в схеме Siy начинающийся ее входом, содержащий только опера-
торы присваивания и заканчивающийся дугой, которая ведет
к ключевой вершине A,, s0 = gWt (gWl (®)). Напомним (см. п. 2.2),
что функция gw представляет собой суперпозицию преобразова-
телей сетей, соответствующих проходимым вдоль пути w верши-
нам. Граф О (Sr, Sa) будет иметь ровно один вход е0, который на-
правим к вершине v0 = 1Аа, Аа, s0J. Вершину v0 объявим дости-
жимой и необработанной.
Все элементы таблицы ТТ инициализируются значением Я.
Если eq (Alt Аа, s0), то положим ТТ [Аа, Аа, (ЗАБЫТЬ} s0] = s0.
154
Второй этап алгоритма состоит в повторении трех описанных
ниже шагов до тех пор, пока не будут исчерпаны достижимые не-
обработанные вершины графа О (Slt S2). Пусть v = [А, В, х|
какая-нибудь достижимая необработанная вершина.
Шаг 1. [Проведение 8г-дуг].
Если "“]1е (Л, В, х) & 1е (В, A, s), то никаких 5'1-дуг из v
проводнться не будет. В противном случае пусть 1уд (Д = 0, 1) —
путь в схеме Slt начинающийся Д-дугой распознавателя А,
содержащий только операторы присваивания н заканчивающий-
ся дугой, которая ведет к ключевой вершине С& в Построим
сети хд — gw& «Д = аА> х) для Д = 0, 1.
Если 8д = 1, то Д-дуга из v проводиться не будет. Если жо
хд ^f= И, то при “j eq (Сд, В, s&) проводим Д-дугу от г к вершине
уд = [Сд, В, хд[, а при eq (Сд, В, хд) построим сети хд = <ЗА-
БЫТЬу хд и Хд = ТТ [Сд, В, хд[ Д хд, положим ТТ [Сд, В, хд] =
= Хд и проведем Д-дугу вершины v к вершине Уд = [Сд, В, х'д[.
Проводимые на этом шаге дуги называются З^дугами графа
О (Зг, SJ. Вновь создаваемые на этом шаге новые вершины объ-
являются достижимыми и необработанными.
Шаг 2. [Проведение За-дуг[.
Если ~| 1е (В, А, х) & 1е (А, В, х), то никаких 38-дуг из у про-
водиться не будет. В противном случае пусть Шд (Д = 0, 1) —
путь в схеме За, начинающийся Д-дугой распознавателя В, со-
держащий только операторы присваивания и заканчивающийся
дугой, которая ведет к ключевой вершине D& в Sa. Построим сети
«л = «Л = пн> «) для Д = 0, 1.
Если Хд ~ li, то Д-дуга из у проводиться не будет. Если же
хд =#= “Я, то при eq (А, 2)д, хд) проводим Д-дугу от у к вершине
Уд = [А, Од, хд[, а при eq (А, Рд, хд) построим сети хд = <ЗА-
БЫТЬУ хд п хд = ТТ [А, Рд, хд} Д хд, положим ТТ [А, Рд,
хд] = хд и проведем Д-дугу вершины у к вершине Уд = [А, Од, Хд[.
Проводимые на этом шаге дуги называются За-дугами графа
О (Зг, S2). Создаваемые на этом шаге новые вершины объявляются
достижимыми и необработанными.
Шаг 3. [Проверка на безуспешное окончание}.
Алгоритм заканчивается без успеха, если для вершины у —
= [А, В, х[ выполнено хотя бы одно из следующих трех условий.
(За) А — заключительный оператор стоп (ха, . . ., хт), В —
заключительный оператор стоп (ylt .... уп) с некоторыми xlt . . .
. . ., хт, ух, . . ., уп ЕЕ X, причем т =£ п или Ji (1 i «С пУ
(х^ — yi) assert (х).
(36) Одна из вершин А, В — заключительный оператор,
а другая — оператор петли.
(Зв) Существует путь ylt . . ., vk в графе О (Slt Sa) такой, что
yk==y, k > 1, Vi(l i к) Vi — [Ait Bit xj & "Я eq (Ai( Bit st),
At = A,BX~ В.
Если условия (За), (36) н (Зв) ложны, то вершина у объявляет-
ся обработанной и алгоритм продолжается применением шагов
15 &
1—3 к другим достижимый необработанным вершинам графа
О (St, S2). Если все достижимые вершины оказались обработан-
ными, то алгоритм заканчивается успешно.
Теорема 7.8. Алгоритм 51 заканчивается для любой пары
приведенных свободных сквозных схем, удовлетворяющей условию
разделенности переменных.
Доказательство. Поскольку каждая достижимая
вершина обрабатывается на шагах 1—3 ровно один раз, достаточ-
но убедиться, что множество достижимых вершин конечно. Ра-
зобьем это множество на два непересекающихся подмножества
Ux и Ua
= {(Л, В, a] I eq (А, В, s)}, Ua = {[Л, В, а] | ~| eq (Л, В, а)}.
Пусть Vi = [Ль В^ а,], г > 0 — последовательность различных
достижимых вершин из О (Slt Sa), последовательно порождаемых
алгоритмом 51. Для фиксированных распознавателей Л, В схем S2
и Sa соответственно и для сети а ЕЕ К такой, что eq (Л, В, а),
рассмотрим подпоследовательность о^= [Ai;., Вц, а?р, j > О,
вершин этой последовательности, для которых
V / (Ai} = Л) & (Bi} = В) & ((ЗАБЫТЬ} si} = а).
Тогда по построению графа О (alt аа) получим V/ (ai; ai +1) &
& (si; =#= sij+i)» т- е- строго убывающую цепь полурешетки Ж'.
Поэтому конечность множества вытекает из условия обрыва
цепей для Ж', конечности множества К и множеств вершин ис-
ходных схем. Что касается конечности множества Ua, то она вы-
текает из того, что благодаря проверке условия (Зв) расстояние
каждой из вершин из Ua от вершин множества Ua или от входа е
не превосходит суммы количеств ключевых вершин исходных
схем. Q
2.5. Корректность алгоритма 51. Граф О (Slt Sa) устроен так,
что всякий путь w в нем имеет прообразы в схемах S, и Sa. Мы бу-
дем называть их проекциями пути w. Для i ~ 1, 2 положим
nPi (w) ~ пустой путь, если w — пустой путь;
пр{ (w) = wb если w = е0, где w, — путь по операторам луча,
начинающегося выходной дугой начального оператора схемы 5»
и заканчивающегося дугой, которая ведет к некоторой ключевой
вершине;
пр4 (w) ~ nPi (w')> если w = w’ve, rjjjt e — дуга, которая не
является З^-дугой в О (Sa, Sg);
пр4 (w) — пр£ (w') AiWu если w — w’ve, где e — 5гдуга вер-
шины v = LAj, Aa, s], причем если e — Д-дуга, то — путь по
операторам луча в Sit начинающегося Д-дугой распознавателя Л,
и заканчивающегося дугой, которая ведет к некоторой ключевой
вершине.
Лемма 7.7. Пусть v = [Л, В, sj — достижимая вершина
графа О (Sn S2), а w — произвольный путь от входа е0 к v. Тогда
156
•если (х = у) ЕЕ assert (s) для х ЕЕ Хаи у Xt, то I (пр, (w), х) =
-- t (пра (w), у); если (А = л) ЕЕ assert (s), то логическое выраже-
ние п ^-избыточно либо на пути пр, (w), либо на пути пр2 (w).
Доказательство. Сформулируем задачу глобального
анализа для графа О (St, Sa). В качестве полурешетки свойств
возьмем (£', Д). Начальная разметка сопоставляет сеть О входу
е0 и fl всем остальным дугам. Семантическую функцию разметки
определим следующим образом:
gnp,(e,) ° ?npi(e,)» если в = е = е0\
fg = ^npt(t>e)> если е — 5,-дуга вершины v, а дуга е' ведет к р;
fl, в остальных случаях,
где gw — преобразователь сетей, использованный в доказатель-
стве теоремы 7.5. Функцию J распространим, как в гл. 2, на про-
извольные пути wb О (5„ S2), начинающиеся входом е0 и кончаю-
щиеся некоторой дугой е.
если w = е0,
ft ° gw, если w = w ve.
Тогда для сформулированной задачи глобального анализа суще-
ствует стационарная разметка р, причем в силу теоремы 2.1 име-
ем р (е) -С Д gw (®) Для всех дуг е графа О (S„ Sa). Легко видеть’,
что граф О (S„ Sa) построен вместе с его стационарной разметкой р.
Более точно, для каждой вершины v = [А, В, s] и для всех ве-
дущих к ней дуг е справедливо р (е) = s. Поэтому если х f= Xlt
у ЕЕ Xa, w — произвольный путь от е0 к v — [Л, В, а], то из (х
~ у) GE assert (s) следует (х = у) GE assert (gw (®)).
Функция gw представляет собой в конечном счете суперпози-
цию эффектов присваивания и эффектов тестов, которые комму-
тативны, если соответствуют операторам разных схем, т. е.
»еГ »е2’ /еУ л!'
/е! ° Тег — Тег ° Tel,
если el и е2 — дуги схем 5, и Sa соответственно. Коммутативность
преобразователей является следствием условия разделенности
переменных этих схем. Более того, нетрудно видеть, что
gw, ° gw, ~ gw, ° gw,,
где Wi (i = 1, 2) — произвольный путь в схеме S,. Поэтому из
(х — у) ЕЕ assert (gw (®)) получаем t (пр, (w), х) = t (пр, (w)
пра (w), х) = t (пр, (ш) пра (w), у) = I (пр, (ш), у). Аналогично,
если (А = л) ЕЕ assert (s), то (А = л) ЕЕ assert (gw (®)) —
= assert (gnPl(W) ° gnp,(w) (®)), откуда следует, что логическое вы-
ражение л является A-избыточным либо на пути пр, (w), либо
на пути пра (ш). Q
Будем говорить, что путь w в графе О (5,, 52) согласован с ин-
терпретацией I, если пути пр, (ш) и пр2 (ш) являются начальны
157
ми отрезками цепочек схем 5, и 5а, подтверждаемых интерпре-
тацией I. Количество 5гдуг пути w назовем Si-длиной этого пути
(обозначение: 1ещ (w)).
Теорема 7.9. Если Sa, то алгоритм Ш заканчивает-
ся без успеха.
Доказат е л ь с т в о будем вести от противного. Предпо-
ложим, что 5, Sa и алгоритм 5Н заканчивается успешно. Пусть
I — интерпретация, для которой val I) val (5а, /), a
(г = 1, 2) — допустимая цепочка схемы подтверждаемая ин-
терпретацией /. Покажем, что для любых nlt пя таких, что щ
не превосходит количества распознавателей цепочки u>i (i = 1, 2),
существует согласованный с I путь w в графе О (St, 5а), для ко-
торого Vi = 1, 2 len; (w) щ. Путь w начнем входом е0 и будем
продолжать построение w добавлением вершин и дуг. Пусть на
некотором шаге уже построен согласованный с I путь w', кото-
рый кончается дугой, ведущей к вершине v = [Лп Aa, s], и для
некоторого k (1 к <1 2) lenk (w') < nk. Тогда хотя бы одна из
вершин Л,, Ая — распознаватель, н из вершины v выходит хотя
бы одна дуга. Рассмотрим два возможных случая.
Случай 1. Из вершины v выходит хотя бы одна 5к-дуга. Выбе-
рем тогда А (= (0, 1} так, чтобы путь wk в Sk был продолжением
пути прк (w’) по A-дуге распознавателя и i£{0, 1}, А =/= А.
Если бы среди 5к-дуг вершины v не было A-дуги, то по построе-
нию графа О (Slt Sa) это обозначало бы (Д=одк) G= assert (s),
а в силу леммы 7.7 и Д-избыточность теста аАк на одном из путей
пр, (и/) или пра (и/), что противоречит допустимости цепочек
ш, и wa. Таким образом, среди 5к-дуг вершины v имеется A-дуга е.
Возьмем тогда согласованный с I путь w" = w’ve и будем про-
должать построение пути w добавлением вершин и дуг к w".
Случай 2. Из вершины v не выходит ни одной 5к-дуги. Будем
считать для определенности к = 2 (симметричный случай к = 1
рассматривается совершенно аналогично). Тогда из v выходит
хотя бы одна 5,-дуга, и мы можем действовать как в случае 1,
получая согласованные с I пути добавлением новых вершин и Sa-
дуг до тех пор, пока не будет достигнута вершина, из которой вы-
ходит хотя бы одна 5а-дуга. Когда такая вершина достигнута,
выберем для продолжения £а-дугу. Если бы все согласованные
с I продолжения по 5,-дугам проходили только через такие вер-
шины, у которых нет 5а-дуг, то это означало бы существование
контура в графе О (St, Sa), проходящего по вершинам из f/a,
т. е. противоречие с предположением об успешном окончании
алгоритма Ш.
Итак, если один из результатов val (S„ I) определен, а дру-
гой — нет, то построенный описанным способом путь w ведет
к вершине, для которой истинно одно нз условий (36) нли (Зв),
так что алгоритм Ш не может заканчиваться успешно. Если же
val (Slt I) и val (5а, 7) определены, то путь w ведет к вершине
v = (Л,, Ая, з] такой, что Л, — заключительный оператор стоп
158
(xlt . . xm), Aa — заключительный оператор стоп (yt, . . ., уп).
В силу предположения об успешном окончании алгоритма 21 име-
ем т = п и Vi (1 «С i п) = у{) Er assert (s), так что по лем-
ме 7.7 Vi (1 «С i «С л) t (пр, (w), = t (npg (w), y^). Это дает
немедленное противоречие с val (5,, I) =/= val (5S, I). Q
Для доказательства успешного окончания алгоритма 21 в слу-
чае эквивалентности исходных схем введем несколько вспомога-
тельных понятий. Понятие квазисвободной интерпретации обоб-
щает понятие свободной интерпретации и отличается от него толь-
ко тем, что квазисвободная интерпретация сопоставляет перемен-
ным произвольные термы из области интерпретации. Областью
квазисвободных интерпретаций служит, как н в случае свободных
интерпретаций, множество всех функциональных термов. Будем
говорить, что квазисвободная интерпретация I согласована с сетью
s (s =/= И), если для нее истинны все утверждения нз assert (s), т. е.
(х = т) ЕЕ assert (s) ==> I (х) — I (т),
(Л = л) assert (s) => I (л) = Д.
Через CI (s) обозначим множество всех квазисвободных интерпре-
таций, согласованных с сетью s. Положим CI (И) = 0 по опреде-
лению.
Две вершины А, В (одной и той же или разных стандартных
схем) назовем s-эквивалентными (обозначение: А ~ В), если
V/ €= CI (s) val (5(A), I) ~ val (S (В), I), где через S (А) обозна-
чена схема, получающаяся из схемы, содержащей вершину А,
заменой ее начального оператора на такой оператор старт, выход-
ная дуга которого направляется к вершине А, а множество ре-
зультатов определяется требованием правильности получающейся
схемы.
Заметим, что из этих определений непосредственно вытекают
два следующих полезных свойства:
«1 sa => CI (s2) С CI (s,),
A^B & s' A ~B.
На множестве переменных 3? введем какой-нибудь полный по-
рядок и определим множество базовых переменных has (s)
для произвольной сети хЕЖ', s =/= 1: bas (s) = (х | 3v €= V»
(х S knowe (v)) & (know8 (v) <^3‘) & (Vy (E knowe (v) x y)}.
Неформально это множество всех таких переменных х, для кото-
рых правая часть всякого утверждения вида х — т из assert (s)
является переменной, которая не меньше, чем х.
Jipe квазисвободные интерпретации Ilt Ia называются согла-
сованными, если для любого логического выражения п справедли-
во 1г (л) = Ia (л). В классе квазисвободных интерпретаций
CI (s) выделим подкласс MCI (s) минимальных интерпретаций I,
(159
для которых
х, если х ЕЕ bas (s),
Z(x)==
т, если (х = т) ЕЕ assert (s) и т — терм над переменными
из bas(s).
Минимальные интерпретации, согласованные с 5, играют такую
же роль по отношению к квазисвободным, согласованным с сетью
s, какую свободные интерпретации играют по отношению ко всем
интерпретациям базиса.
Лемма 7.8. Для всякой интерпретации I ЕЕ CI (s) суще
ствует согласованная с ней интерпретация Г ЕЕ MCI (s). Для
всех минимальных интерпретаций Г, согласованных с I Е= CI (s),
VtET I (г) = I (Г (т)),
V5 val (5. I) ~ I (val (8, I')).
Лемма 7.9.
VI EE CI (s) va’ (Sjj I) val (5S, I) о
О VI' e MCI (s) val (5V I') ~ val (S2, Г).
Доказательство лемм 7.8 и 7.9 проводится аналогич-
но доказательству лемм 4.3, 4.4 и теоремы 4.1. Таким образом,
для доказательства s-эквивалентности двух вершин А, В доста-
точно убедиться, что VI ЕЕ MCI (s) val (S (Л), I) ~ Val (5 (В),
/)- □
Лемма 7.10. Пусть А — В, где А — распознаватель с ус-
ловием а а, &-дуга которого ведет к вершине Лд, вд = <Д = аАу з,
Д = 0, 1. Тогда V А Лд — В.
Доказательство. По определению результата прог-
раммы (S (Л), Z) для IE1CI ($д) имеем val (5 (Л), I) ~ val (5 (Лд),
вд *д
Z), так что УДЛд — Л. Из $д > s следует Л — В, поэтому тран-
•д
зитивность отношения зд-эквивалентности дает УД Лд — В.
Заметим, что в условии леммы не требуется, чтобы Л, В были
вершинами сквозных схем. | |
_ 8
Лемма 7.11. Пусть А — В для вершин Л, В двух разных
схем, удовлетворяющих условию разделенности переменных, при-
чем А — оператор присваивания х := t, выходная дуга которого
ведет к вершине С, a s’ — <х := ty s. Тогда С — В.
Доказательство. Возьмем произвольную интерпре-
тацию I ЕЕ MCI (s') и построим интерпретацию Z, следующим
образом:
{у, если у ЕЕ bas (s),
т, если (у— т)е assert (s) н т — терм над переменным»
из bas(s).
160
Если логическое выражение л содержит вхождения переменной х
только внутри подтермов t, то положим I, (л) — I (л [x/t]).
Если же л содержит вхождения х вне подтермов t, то при (Д =
= л) ЕЕ assert (s) положим I, (л) = Д, а в остальных случаях
определим I, (л) произвольно. Нетрудно видеть, что 7, ЕЕ MCI (s).
По интерпретации 7, построим интерпретацию Г:
1 ( если у^х'
I Л (i). если у — х.
Для произвольного логического выражения л положим Г (л) =
= 1Л (л [t/x]). По определению результата программы (S (А),
7,) имеем val (S (С), Г) cm val (S (А), 1г). Далее, поскольку А ~
~ В и 7, е MCI (s), получаем val (S (A), It) cm val (S (B), It).
С другой стороны, val (S(B), 7,) cm val (S (В), I'), поскольку
интерпретации I и Г отличаются только на выражениях, содержа-
щих переменную х, а в S (В) переменная х не встречается. Таким
образом, val (5(C), 7') val (S (В), Г). Но Г (л) = I, (л [i/xj)=
— I (л [t/x] [x/t]) = I (л) для любого логического выражения л,
т. е. интерпретации I и Г согласованы, поэтому в силу леммы 7.8
имеем val (5 (С), Г) ст Г (val (S(C), I)) и val (5 (В), Г) cm
ст Г (val (S (В), Г)). Это значит, что либо оба результата
val (S (С), I) и val (S (В), 7) не определены, либо оба определены
и Г (val (S (С), 7)) = Г (val (5 (В), 7)). Покажем теперь, что ес-
ли Г (у) — Г (т) для некоторых у е 30 и терма т над переменны-
ми из bas (s'), то I (у) — I (т). Рассмотрим для этого два возмож-
ных случая.
1) У х. Тогда I, (у) = Г (у) = Г (i) = 1а (т [i/x]) =>
=> (у — х (i/xj) е assert (s) => (у = т) ЕЕ assert (s') =» I (у) —I (т).
2) у — х. Тогда либо т = х (и I (х) = I (т)), либо терм т не
содержит вхождений переменной х. В последнем случае Г (х) =
= Г (т) => 1а (t) — 1а (т). Пусть хх, . • хп — все переменные
терма i, тогда Vi (1 «С 1 n) 3rf т = t [xjx^ , . тп/хп] и
7, (я,) — 7, (т,), откуда Vi (1 i n) (xf — т,) e assert (s) =>
=> (x = <r) e assert (s') => I (x) = I (t).
Предположим, наконец, что val (S (C), 7) =/= val (S (В), I).
Тогда найдутся такие у ЕЕ bas (s') и терм т над переменными иэ
bas (s'), что I (у) Ф I (т), но Г (у) — Г (т), а это противоречит
только что доказанному. Q
g
Лемма 7.12. Пусть А ~ В и А ~ В для двух таких сетей
slf Sj, что {ЗАВЫТЬУ sx — ^ЗАБЫТЬу s2 и (А= л) е assert (sr) <4
<=> (А = л) assert (s2) для любых А Е {0, 1} и логических выра-
жений л. Тогда А В.
Доказательство. Пусть s = sx Д Возьмем произ-
вольную интерпретацию I ЕЕ MCI (s) и построим согласованные
с ней интерпретации Д, /2, 1г ЕЕ MCI (sx), Ia ЕЕ MCI (s2). Тогда
из Vi = 1, 2 A ~B следует V/=l, 2 val (S (A), Ij) cm val (S (B), 7j),
4 В. E, Котов, В. К. Сабельфельд Д61
а лемма 7.8 дает V/ — 1,2 val (5 (Л), Ij)~It (val (S (A)t
I)) и V/ = 1, 2 val (S (B), Ij) еж Is (val (S (B), /)), откуда V/ =
= 1, 2 Ij (val (S (A), I)) at Ij (val (S (В), I)). Это значит, что
val (S (Л), I) и val (S (В), I) либо одновременно не определены,
либо определены и Vj = l, 2 Ij(yal (S(A), I)) = Ij(val (S (В),I)).
В последнем случае предположим, что val (5 (Л), I) Ф
val (S (В), Z). Тогда существуют переменная у ge bas (s) и
терм т над переменными из bas (s) такие, что V/ = 1, 2 Ij (у) —
— Ij (т), но I (у) I (т). Далее, V/ = 1,2 1} (у) = Ij (т) => V/ =
= 1, 2 (у = т) е assert (s;) => (у = Г) S assert (s) =ф I (у) =
— I (т). Полученное противоречие доказывает val (5 (Л), I) —
~ va\ (S (В), I). □
Теорема 7.10. Если S2 ~ S2 для приведенных свободных
сквозных схем S2, S2, удовлетворяющих условию разделенности пе-
ременных, то для каждой достижимой вершины v = [А, В, s]
графа О (5Х, S2) справедливо А — В.
Доказательство проведем индукцией по количеству
достижимых вершин графа О (Su S2), построенных к очередному
шагу алгоритма 3(. Для вершины v — [Л, В, s], к которой ведет
вход е0, доказательство Л — В получается повторным примене-
нием леммы 7.11. Пусть для всех вершин [Л, В, si, построенных
к некоторому шагу алгоритма 9(, уже доказано Л ~ В. Мы до-
кажем теперь, что Вг — В2 для любого из наследников v’ = [Blt
В2, s'l вершины v = [At, Л2, si, обрабатываемой на очередном шаге
алгоритма 5(. Пусть к вершине v’ на этом шаге проводится 5{-
дуга е вершины v, причем е — Д-дуга. Пусть, далее, sr == (s)
и s — (ЗАБЫТЬ} s. Применяя леммы 7.10 и 7.11, получим
~ В2. Если ПеЧ В2, Sj) или eq (Blt В2, sa) & sa = II, где
sa = ТТ [Z?lt Ва, si, то в соответствии с описанием алгоритма 9(
имеем s' = sx, так что Вх — Ва доказано. Если же eq (Въ В2, sx),
но sa Ф 3, то это означает, что среди обработанных вершин уже
имеется вершина [Въ В2, s9], так что в силу индуктивного пред-
положения Вх ~ В2. Построим в этом случае сети s* = (УДА-
ЛИТЬ} st (i = 1, 2), где операция (УДАЛИТЬ}'. £' -> X' озна-
чает преобразователь сетей, удаляющий все такие элементы с, рдя
которых ¥ (с) GE Р& 3] (1 < / d (W (с))) X П know (Г (с, /)) = 0.
Неформально, операция (УДАЛИТЬ} удаляет из assert (sf) все
утверждения Д = р (xlf . . ., тп), п 1, в которых хотя бы один
из термов Xj отличен от переменной. Легко видеть, что если
одновременные вычисления сквозных схем Sa достигли состоя-
ния [Blf Ва, s(l, для которого справедливо eq (Bn В2, s,), то ника-
кие продолжения этих вычислений не могут проверять предикаты
на таком наборе термов (отличном от проверяемого в Вг и Ва),
на котором какие-нибудь предикаты уже проверялись раньше.
8 8^
Это значит, что из В2 ~ В2 вытекает Bt — В2. Заметим теперь,
162
что для Blf Bai slf s2 выполнены все условия леммы 7.12, так что
мы можем заключить, что Bt Ва. В соответствии с описанием
алгоритма 5( в этом случае s' = sx Д sa. Но s< для г — 1, 2,
поэтому s' = Sj Д Sj > sj Д sa, откуда В2 ~ Ва. □
Следствие 7.3. Если S2 ~ S2, то алгоритм 5( заканчи-
вается успешно.
Доказательство. Если бы алгоритм 5( заканчивался
без успеха, то А — В было бы ложно по крайней мере для тех
вершин v = [4, В, s] графа О (Slt Sa), для которых одно из про-
веряемых на шагах (За)—(Зв) условий оказывается истинным.
Задание 7.6. Сформулируем новую схему правил преобразования
Ф2 (Удаление несущественного распознавателя].
Очевидно, Gi — G2, если фрагмент Gt получается из фрагмента G, при-
менением схемы правил Ф2.
Докажите, что система преобразований 2лт (J {Ф1, Ф2) является пол-
вон системой преобразований для отношения функциональной эквивалент*
кости сквозных схем.
Указание. Заметьте, что план преобразования схемы Si в схему Sa для
произвольных эквивалентных (приведенных свободных) сквозных схем со-
держится в структуре графа О (St, S2).
Краткий обзор и комментарии
Первым всесторонне исследованным классом схем программ
были схемы Янова. В работе Янова [78] впервые выделены и фор-
мализованы основные компоненты теории схем и в первую оче-
редь — понятие схемы программы и отношение эквивалентности
схем. Яновым были найдены алгоритмы распознавания эквивалент-
ности в этом классе схем, построена полная система преобразова-
ний, позволяющая трансформировать друг в друга любую пару
эквивалентных схем. Схемы Янова активно изучались в различ-
ных модификациях и обобщениях.
Схемы Янова можно рассматривать как подкласс стандартных
схем. Такое определение проще оригинального, так как оно не
использует интерпретированные логические операции в услов-
ных выражениях и понятие сдвига (дополнительного средства
управления воздействием преобразователей на распознаватели)
6* 163
J 781. Однако такое сужение класса не слишком существенно, тем
более, что главные проблемы имеют одинаковые решения в опре-
деляемом ниже и оригинальном классах схем Янова.
Схемами Янова называются схемы из подкласса стандартных
схем со следующим базисом:
(м, {/?>, /л... л.
{стоп (x)}(J {х : = /, (х) | i > 0} U {Pi I * > 0}).
Другими словами, базис класса схем Янова содержит
1) единственную переменную х;
2) только одноместные функциональные и предикатные сим-
волы;
3) только операторы присваивания вида xz— fa (х), условные
операторы вида pt (х) и заключительный оператор стоп (х).
Тот факт, что память схем Янова содержит всего лишь одну
переменную х, трактуется часто таким образом: в теории этих
схем память реальных программ считается монолитной, не разби-
той на отдельные ячейки, и внимание концентрируется на логиче-
ской структуре программ. Пример двух эквивалентных схем Яно-
ва приведен на рис. 7.11.
Рис. 7.11. Пример двух эквивалентных схем Янова
Отметим, что всякая схема Янова является сквозной, так что
описанный в § 2 алгоритм 9( распознавания эквивалентности
сквозных схем годится и для распознавания Эквивалентности
схем Янова.
В связи с тем, что статья Яиова «О логических схемах алго-
ритмов» [78] «не стала известна широкому кругу читателей, преж-
164
де всего из-за того, что написана довольно трудным языком, рас-
считанным в большей степени на специалистов по математиче-
ской логике, нежели на программистов» (Ершов [15]), а также
«вызвала значительный интерес и некоторое замешательство»
(Ратледж [136]), в начале 60-х гг. были предприняты попытки пе-
реизложить и упростить теорию схем Янова. Ратледж [136] уп-
ростил доказательство разрешимости проблемы эквивалентности,
моделируя простые схемы *) Янова конечными автоматами. Наи-
более известно переизложение теории схем Янова, выполненное
Ершовым [15]. В этой работе линейное представление схем, иду-
щее от операторного метода Ляпунова, заменено графовой формой
схем, что позволило упростить и сделать более наглядной систему
эквивалентных преобразований.
3 а д а в е 7.7. Покажите, что система преобразований, содержащая
правила, порождаемые схемами правил ЛТ1, ЛТ2, ЛТЗ, Ф1 и Ф2, представ-
ляет собой полную систему преобразований для функциональной эквива-
лентности схем Янова.
Указание. Проследите за процессом преобразования, с помощью которо-
го решается задание 7.6, и учтите те упрощения, которые можно внести
в этот процесс в связи с тем, что исходные схемы являются схемами Якова.
Работа Ершова дала импульс новым исследованиям схем Яно-
ва, особенно изучению различных обобщений этих схем. Система
преобразований схем Янова содержит схемы правил двух видов:
локальные (для применения которых к данному фрагменту до-
статочно иметь информацию о некоторой его заранее фиксирован-
ной окрестности) и нелокальные (для применения которых необ-
ходима информация о «почти всей» схеме в целом). Например,
схемы правил ЛТ7 (см. гл. 6) и Ф2 (см. задание 7.6) являются ло-
кальными, а, скажем, ЛТ1, ЛТ2 (см. гл. 6) и ПЗ у Ершова [15]
нелокальны. Янов [79] исследовал вопрос о том, можно ли заме-
нить нелокальные схемы правил конечным числом локальных
правил. Он установил, что в общем случае этого сделать нельзя,
и нашел положительное решение задачи для класса Як простых
схем Янова, удовлетворяющих следующим трем условиям:
(1) условия схем из Як — это произвольные выражения, за-
писанные с использованием логических операций ~|, Д* V наД
элементарными условиями из множества (х), . . ., рк (х)};
(2) все преобразователи схемы достижимы, т. е. выполняются
хотя бы при одной интерпретации;
(3) схема имеет универсальный сдвиг (в нашем варианте оп-
ределения схем Янова все схемы имеют универсальный сдвиг).
Сабельфельд [62] нашел общий критерий локальности систе-
мы эквивалентных преобразований схем Янова. Иткин [21] и
Каплан [НО] доказали разрешимость проблемы эквивалентно-
сти для схем Янова с повторными вхождениями одного и того же
преобразователя. Иткин построил также полную систему преоб-
*) Схема Якова называется простой, если в ней все операторы присваи-
вания различны, т. е. схема ие содержит двух вхождений одного к того же
функционального символа (именно простые схемы рассматривались Яновым).
165
разеваний для этого случая. Тузов [72, 73] исследовал схемы Яно-
ва с перестановочными преобразователями. В этом случае вместе
с простой схемой Янова задается конечное число соотношений
вида ftfj = fjfi, где ft, /у — функциональные символы. Тем самым
ограничиваются возможности интерпретации функциональных
символов. При определении отношения эквивалентности схем
(с использованием понятия свободной интерпретации) считается,
что термы-результаты равны с точностью до заданных соотноше-
ний перестановочности. Например, терм IJifjfiX равен терму
fififtf&t, если задана система соотношений {/j/2 = /j/3 s
— /з/i)- Тузов установил разрешимость такого обобщенного от-
ношения эквивалентности схем Янова. Аналогичный результат
был получен Летичевскнм как частный случай полугрупповой
эквивалентности [33]. Непомнящий [46] установил разрешимость
проблемы эквивалентности схем Янова с системами соотношений,
заданных полугруппами с определенными ограничениями. Эти
системы включают соотношения перестановочности.
Подловченко (54, 55] ввела и исследовала недетерминирован-
ные схемы Янова (A-схемы). В этих схемах вершины-распозна-
ватели заменены вершинами-фильтрами. Фильтр представляет
собой логическое выражение, однако между распознавателем и
вершиной-фильтром имеется различие, состоящее в следующем:
а) из вершины-фильтра выходит не ровно две дуги, как в схе-
мах Янова, а произвольное конечное число дуг;
б) при выполнении интерпретированной Я-схемы после вы-
числения значения предиката в фильтре возможен переход по лю-
бой из дуг, выходящих из фильтра, если это значение равно 1,
а в противном случае вычисления обрываются и текущее состояние
памяти объявляется результатом.
Подловченко показала, что для любой схемы Янова можно по-
строить эквивалентную недетерминированную схему, продемон-
стрировала разрешимость проблемы эквивалентности и построила
полную систему эквивалентных преобразований.
Как уже говорилось, включение в базис схем Янова единст-
венной переменной можно трактовать как исключение из схемы
информации о структуре памяти: каждый оператор присваивания
изменяет состояние всей памяти, значение каждого предиката вы-
числяется для состояния всей памяти. Таким образом, каждый
преобразователь автоматически влияет на все последующие рас-
познаватели. Чтобы сделать такое влияние более избирательным,
Янов ввел понятие сдвига, которое на уровне схем программ мо-
делирует структуру памяти реальных программ. Каждому преоб-
разователю сопоставлен набор предикатных символов, называе-
мый сдвигом этого оператора. Сдвиг накладывает ограничения на
класс возможных интерпретаций, а именно — если предикатный
символ р не входит в сдвиг некоторого оператора х : = / (х), то
при любой интерпретации I должно иметь место равенство
/ (р (/ (т))) = I (р (т)). Иткин расширил [23] класс схем Янова,
обобщив понятие сдвига таким образом, что сдвиг может содержать
166
ее только предикатные, но и функциональные символы. Тем са-
мым обобщенный сдвиг позволяет моделировать информационные
связи между операторами схемы. В классе обобщенных схем Яно-
ва Иткин ввел отношение так называемой комбинированной эк-
вивалентности, более сильное, чем функциональная эквивалент-
ность, но допускающее, тем не менее, выполнение как яновских
эквивалентных преобразований, так и преобразований, сохраняю-
щих логико-термальную эквивалентность. Показано, что комбини-
рованная эквивалентность разрешима для обобщенных простых
схем Янова.
Гарлэнд и Лакхэм [102], а также Летичевский [33] доказали,
что проблема функциональной эквивалентности остается разреши-
мой для класса схем Янова с засылками констант, т. е. когда раз-
решены операторы присваивания х : = а, а ЕЕ d (а) = 0.
Тот же самый эффект получается в результате добавления к бази-
су схем Янова специальной переменной, используемой только для
организации вспомогательных пересылок и в условных операто-
рах [140].
Для практики программирования главный интерес представ-
ляют не отрицательные результаты о неразрешимости таких про-
блем, как эквивалентность, тотальность, пустота или свобода,
а положительные результаты, связанные с выделением классов
схем, в которых такие проблемы разрешимы. Они используются
в оптимизации программ, при доказательстве правильности и по-
строении инструментальных систем преобразования программ.
Патерсон [126,127,119], доказав совместно с Лакхэмом и Пар-
ком неразрешимость проблемы функциональной эквивалентно-
сти стандартных схем, предпринял одновременно попытку вы-
делить разрешимые подклассы. Определив понятие свободной
схемы, он высказал гипотезу о разрешимости проблемы эквива-
лентности в классе свободных схем, однако эта гипотеза не под-
тверждена до сих пор, хотя и поддерживается многими исследова-
телями. Сама же проблема свободы неразрешима (см. гл. 5, § 3),
и не для всякой стандартной схемы существует эквивалентная
свободная схема.
Патерсон выделил класс либеральных схем. Стандартная схе-
ма S называется либеральной, если для любой свободной интер-
претации I любые термы-значения, вырабатываемые правыми
частями операторов присваивания (не пересылок) в протоколе про-
граммы (5, Z), не равны, т. е. никакой терм не может фигуриро-
вать дважды в протоколе как значение, присваиваемое (не пере-
сылкой) переменным из памяти схемы. Отметим здесь, что в силу
доказанного Непомнящим и Сабельфельдом [50] результата для
каждой стандартной схемы существует эквивалентная (в доволь-
но сильном смысле, более сильном даже, чем логико-термальная
эквивалентность) схема без пересылок.
В отличие от проблемы свободы проблема либеральности ока-
залась разрешимой. Установлена следующая связь между свобо-
дой и либеральностью: всякую либеральную схему можно пре-
167
образовать в эквивалентную свободную схему, но не наоборот.
Поскольку проблема либеральности оказалась «проще» проблемы
свободы, а либеральные схемы преобразуются в эквивалентные
свободные, проблема эквивалентности в классе либеральных схем
приобретает особый интерес: если она окажется неразрешимой,
то автоматически устанавливается неразрешимость проблемы эк-
вивалентности и в классе свободных схем. Пока обе эти пробле-
мы открыты.
В классе либеральных схем Патерсон выделил два интересных
подкласса — прогрессивные и консервативные схемы. В любой
цепочке прогрессивной схемы переменная, являющаяся результа-
том оператора присваивания, всегда используется в качестве ар-
гумента в следующем операторе цепочки, если только он есть.
Проблема эквивалентности оказывается разрешимой в классе
прогрессивных схем.
Сложнее обстоит дело с другим подклассом. Назовем опера-
тор присваивания невырожденным, если его переменная-резуль-
тат встречается среди аргументов, например х / (х, у, z). Схе-
ма называется консервативной, если все встречающиеся в ней
операторы присваивания являются невырожденными. Патерсон
только обратил внимание на класс консервативных схем, но не
исследовал его, и проблемы пустоты и эквивалентности остаются
открытыми для этого класса. Интересно, что большинство пред-
ложенных разными авторами подклассов стандартных схем с раз-
решимой функциональной эквивалентностью оказались или под-
классами класса консервативных схем, или близкими к нему.
В начале этой главы отмечалось, что разрешимым является
класс <У6 с базисом /й5 = ({xlt xa}, {f}, {р}, (xa : — / (хх), ха :=
:=/ (ха),стоп (xlt xa), p (Xj), p (Xj))). Характерным для этого клас-
са является то, что все функциональные и предикатные символы
одноместны (такие схемы называют унарными, или монадически-
ми) и переменные хх и ха разделены (независимы) в том смысле,
что при любой свободной интерпретации символ хх не входит ни
в один терм-значение переменной ха, а ха не входит ни в один терм-
значение переменной хх. Более общий класс схем &п, обладающих
этими двумя свойствами, называется классом монадических схем
с п независимыми ячейками и имеет следующий базис: ~
— ({хх, . . ., х„), {fi\ . . .), {pli\ . . .), {Xi := fj (x{) I 1 < i <
< n, j > 0} (j (pj (x.) | 1 < i < n, j > 0} (J {стоп (xt,..., x„)}).
Легко убедиться, что класс Уп является подклассом кон-
сервативных схем для любого п > 0. В работе [119) показано, что
унарные схемы с п независимыми ячейками можно моделировать
n-ленточными автоматами таким образом, что схема пуста (то-
тальна) тогда и только тогда, когда пуст (тотален) моделирующий
автомат, и две схемы эквивалентны тогда и только тогда, когда
эквивалентны моделирующие их автоматы. Отсюда сразу следует
решение проблем пустоты и тотальности в этом классе схем —
они разрешимы, так как разрешимы проблемы пустоты и тоталь-
168
ности для многоленточных автоматов (см. гл. 3, § 2). В гл. 3 бы-
ло доказано, что проблема эквивалентности двухленточных авто-
матов разрешима (этот результат получен Бердом [85] два года
спустя после публикации работы [119]), но она остается открытой
для автоматов с тремя и более лентами. Следовательно, проблема
эквивалентности разрешима в классе унарных схем с двумя
независимыми ячейками, но ждет решения для унарных схем
с тремя и большим количеством независимых ячеек. Отметим, что
в [119] доказан результат о равносильности класса п-ленточных
автоматов классу унарных схем с п независимыми ячейками: с по-
мощью специального моделирования автоматов схемами проблемы
пустоты, тотальности и эквивалентности для автоматов можно,
в свою очередь, свести к соответствующим проблемам для схем.
Заметим также, что класс схем Янова представляет собой класс,
унарных схем с одной независимой ячейкой, поэтому схемы Яно-
ва можно моделировать одноленточными автоматами методом,
описанным в работе [119].
Летичевский [33] показал разрешимость подкласса копсерва
тивных схем, в которых все операторы невырожденны, а услов-
ные операторы содержат один и тот же набор переменных, состав-
ленный из всех переменных памяти схемы. Петросян [52, 53] обоб-
щил этот результат на случай, когда каждый условный оператор
содержит один и тот же набор переменных, составленный из пере-
менных некоторой выделенной подпамяти схемы.
Годлевский [9, 10] доказал разрешимость эквивалентности
в следующем классе схем: все предикатные символы одноместны
и аргументом всех условных операторов является выделенная пе-
ременная х, а все присваивания переменной х имеют вид х :=
f (х, . . .), т. е. первым аргументом служит переменная х. Пе-
речисленные классы схем Летичевского, Петросяна и Годлевско-
го являются подклассами класса сквозных схем. Описанный
в этой главе алгоритм распознавания эквивалентности сквозных
схем был построен Сабельфельдом [69].
Непомнящий [48, 49, 125] довольно подробно исследовал раз-
личные базисы схем, близкие к «граничным» случаям с двумя пе-
ременными, когда добавление или удаление одного оператора кар-
динально меняет статус основных проблем. Он построил нераз-
решимый класс схем, который в начале этой главы был назван
классом и который уже неразрешимого класса из гл. 5.
Удаление любого оператора из базиса класса превращает его
в разрешимый класс. В этих же работах показана разрешимость
проблемы пустоты для классов <У7 и с/8.
. Годлевский [9] и Петросян [52] доказали неразрешимость про-
блемы пустоты в классе схем над базисом ({я, р), {/(1\ а(0,}<
{х : = / (я), у : = / (у), х : = а, у := а, р (я, у), стоп (я, у)}). Не-
помнящий доказал [49], что проблема пустоты остается неразре-
шимой для класса схем над базисом = ({я, у}, {fW, а<°>}, {р(2)},
(я := / (я), у := / (у), я := у, у := а, р (я, у), стоп (я, у)}), но
разрешима в классах схем над базисом, получающимся из базиса
169
Ar
заменой оператора у := а на оператор у := х или х := а.
В [49] был выделен замечательный граничный случай класса схем
над базисом ({х, у}, {а<°>, /(1>, gm}, {р^}, {x: = f(x), y:~g(y), <x:=
:= а, у := а>, p (x), p (у), стоп (x, p)}), в котором проблема тоталь-
ности разрешима, а проблемы пустоты и функциональной экви-
валентности неразрешимы. Здесь <х := а, у := а> -— так назы-
ваемый групповой оператор присваивания, который присваивает
значения переменным х и у «одновременно».
Если говорить о сложности алгоритмов, решающих основные
проблемы в разрешимых классах схем, то здесь мы отметим толь-
ко, что почти все они настолько сложны, что не может быть ника-
кой речи о их прямом практическом использовании. Исключение
составляют, пожалуй, только алгоритмы распознавания отноше-
ний, близких к отношению изоморфизма (где верхняя оценка
сложности имеет порядок О (nG (га)), см. гл. 3) и логико-термаль-
ной эквивалентности (где доказана полиномиальная верхняя оцен-
ка сложности). О сложности распознавания функциональной эк-
вивалентности даже в таком узком классе, каким являются прос-
тые ациклические схемы Янова, можно сказать, что к проблеме
распознавания эквивалентности для схем этого класса сводится
TVP-полная проблема выполнимости формул (бескванторной) ал-
гебры логики.
170
ГЛABA 8
РЕКУРСИВНЫЕ СХЕМЫ
В этой главе излагаются элементы теории рекурсивных схем,
которые моделируют рекурсивные методы программирования (ре-
курсивные языки и такие конструкции, как рекурсивные проце-
дуры в языках вроде Алгол-68 или Паскаль). Основное внима-
ние уделяется проблеме взаимной трансляции рекурсивных
и стандартных схем.
§ 1. Класс рекурсивных схем
1.1. Рекурсивное программирование. Среди упомянутых вы-
ше методов формализации понятия вычислимой функции метод
Тьюринга — Поста основан на уточнении понятия процесса вы-
числений, для чего используются абстрактные «машины», опи-
санные в точных математических терминах. Другой подход (ме-
тод Черча — Клини) основан на понятии рекурсивной функции.
Рекурсивная функция задается с помощью рекурсивных опреде-
лений. Рекурсивное определение позволяет связать искомое зна-
чение функции для заданных аргументов с известными значения-
ми той же функции при некоторых других аргументах. Эта связь
устанавливается с помощью универсального механизма рекурсии,
задающего механическую процедуру поиска значений функции.
Двум подходам к определению вычислимых функций соответст-
вуют два метода программирования этих функций — операторное
и рекурсивное программирование. При операторном методе про-
грамма представляет собой явно выписанную последовательность
описаний действий гипотетической вычислительной машины (по-
следовательность операторов, команд и т. п.).
Язык Фортран — типичный представитель операторных
языков. С другой стороны, рекурсивная программа — это сово-
купность рекурсивных определений, задающих рекурсивную
функцию, для которой аргументами служат начальные данные
программы, а значением — результат выполнения программы.
Известный язык рекурсивного программирования — язык Лисп —
предназначен для обработки символьной информации. В других
языках комбинируют оба метода программирования. Так, Пас-
каль — операторный язык с возможностью рекурсивного про-
граммирования, предоставляемой механизмом рекурсивных про-
цедур и функций.
171
Известным примером рекурсивно определяемой функции яв-
ляется факториальная функция FACT'. N—*-N, где N — мно-
жество целых неотрицательных чисел:
FACT (х) - { xxFACT {х_ 1)t
если х = О,
если х^>0.
Операторные программы, вычисляющие значения этой функции,
приведены в гл. 4. Эту же функцию можно запрограммировать
в некотором рекурсивном языке, базирующемся на механизме ре-
курсивных функций языка Паскаль:
FACT (о),
FACT (х) = если х = 0 то 1 иначе х X FACT (х — 1),
где а — некоторое целое неотрицательное число.
Выполнение этой программы для некоторого значения а (пусть
а = 4) может быть осуществлено следующим образом. В обе час-
ти рекурсивного определения вместо х подставляется 4, после чего
вычисляется правая часть определения. Вычисление правой час-
ти начинается с вычисления логического выражения. Если его
значение 1 (истина), то вычисляется левое функциональное выра-
жение (стоящее после то), а если его значение 0 (ложь) — вы-
числяется правое выражение (стоящее после иначе). Вычисление
функционального выражения сводится к его упрощению, т. е.
выполнению всех возможных вычислений. Если в упрощенном
выражении остается вхождение символа определяемой функции
FACT, то осуществляется переход к новому шагу выполнения
программы. На этом шаге вхождение FACT(m), где т — значение
внутри скобок после упрощения, заменяется левым (тп = 0) или
правым (тп 0) функциональным выражением, в котором все
вхождения х заменены на тп. Упрощения продолжаются до тех
пор, пока не будет получено выражение, не содержащее FACT
(в нашем случае это выражение — число).
FACT (4) = если 4 = 0 то 1 иначе 4 X FACT (4 — 1) =
= 4х FACT (3) = 4 X (если 3 = 0 то 1 иначе
3 X FACT (3 — 1)) = 4 X 3 X FACT (2) =
=12х (если 2 = 0 то 1 иначе 2 х FACT(2 — 1)) =
= 12 X 2 X FACT(1) = 24 X (если 1 = 0 то 1
иначе 1 х FACT (1 — 1)) =
= 24 х 1 X FACT(ty = 2Ах (если 0 =
= 0 то 1 иначе 0 X FACT(Q — 1)) = 24
Вычисление рекурсивной программы может завершиться за ко-
нечное число шагов с результатом, равным значению запрограм-
мированной функции для заданных аргументов (начальных зна-
чений переменных), но может и продолжаться бесконечно. В по-
следнем случае значение функции не определено.
Еще один популярный пример — рекурсивная программа, вы-
числяющая значения функции Аккермана А: № -* N:
172
А (о, b),
A (^i У) = если х = 0 то у 4- 1 иначе В (х, у),
В У) — если у = 0 то А (х — 1, 1) иначе С (х, у),
С (х, у) = А (х — 1, А (х, у — 1)).
Эта программа состоит из главного вызова А (а, Ь) и трех оп-
ределений функций. Первое, определение описывает функцию Ак-
кермана А через вспомогательную функцию В, которая задана,
в свою очередь, с помощью функций А и С. Последняя также оп-
ределена через функцию А. Здесь каждое определение, взятое
отдельно, само на себя не ссылается, но имеет место взаимная ре-
курсия, когда каждая из функций А, В, С косвенно определена
через саму себя.
Выполнение этой программы для а = b = 1 выглядит сле-
дующим образом (некоторые мелкие упрощения не выписаны):
А (1, 1) = если 1 = 0 то 2 иначе В (1, 1) = В (1, 1) — если
1 = 0 то А (0, 1) иначе С (1, 1) — С (1, 1) ==
— А (0, А (1, 0))= А (0, (если 1 = 0 то 1 иначе
В (1, 0))) = А (0, В (1, 0)) = А (0, (если 0 = 0 то
А (0, 1) иначе С (1, 0)) = А (0, И (0, 1)) =
—А (0, (если 0=0 то 2 иначе В (0, 1))) = А (0, 2) =
= если 0 = 0 то 2 4- 1 иначе В (0, 2) = 3.
Отметим, что в этом примере функциональное выражение со-
держит несколько вхождений символов определяемых функций
(например, А (0, А (1, 0))). Использованное нами правило под-
становки в этом случае требует, чтобы замещалось левое из самых
внутренних вхождений (в случае упомянутого терма — вхожде-
ние А (1, 0)).
Операторный и рекурсивный методы программирования имеют
свои достоинства и недостатки, обсуждать которые — не наша
задача (см. например, ставшую классической работу Дж. Бэку-
са [В4], обратившего внимание на преимущества функционального
стиля программирования). Но чтобы подготовить почву для та-
кого обсуждения, полезно формализовать оба метода. Стандарт-
ные схемы являются моделями операторных программ. Сейчас
вы введем рекурсивные схемы, которые служат абстракциями
рекурсивных программ, а в последующих параграфах проведем
сравнение этих моделей.
1.2. Определение рекурсивной схемы. Так же, как и стан-
дартные схемы, рекурсивные схемы определяются в некотором
базисе. Полный базис рекурсивных схем, как и базис стандартных
схем, включает четыре счетных множества символов: перемен-
ные, функциональные символы, предикатные символы, специаль-
ные символы.
Множества переменных и предикатных символов ничем не
отличаются от соответствующих множеств в базисе стандартных
схем. Множество специальных символов — другое, а именно:
(если, то, иначе, ( , ), , Что касается множества функциональ-
173
ных символов, то оно имеет единственное, но существенное отли-
чие от множества функциональных символов базиса стандартных
схем. Отличие состоит в том, что зто множество разбито на два
непересекающихся подмножества: множество базовых функцио-
нальных символов и множество определяемых функциональных
символов. Чтобы отличать их, будем определяемые функциональ-
ные символы обозначать прописными буквами, например, FW,
GW, НЮ, . . . (Такие буквы уже использовались для обозначения
функций. В рекурсивных схемах важно наглядно отделить базо-
вые и определяемые символы, поэтому мы пошли на двусмыслен-
ное использование прописных букв F, G, Н, . . ., надеясь, что
контекст поможет восстановить смысл обозначения.)
В базисе рекурсивных схем нет множества операторов, вместо
него — множество логических выражений и множество термов.
Простые термы определяются точно так же, как определялись
термы-выражения в стандартных схемах. Среди простых термов
выделим базовые термы, которые не содержат определяемых функ-
циональных символов, а также вызовы — термы вида F<n> (тЛ, . . .
. . ., тп), где тп . . ., тп — простые термы, а FW — определяемый
функциональный символ. Логическое выражение — слово вида
(т1г т8,___ тп), где p(n) — предикатный символ, тх, та,..., тп —
базовые термы. Терм — это 1) простой терм, или 2) условный терм,
т. е. слово вида
если л то тх иначе т„
где л — логическое выражение, тх и т, — простые термы, назы-
ваемые левой и соответственно правой альтернативой.
Примеры термов:
f(x,g(x,y))\
. ,, , .. } — базовые термы;
Л (Л (a)) J
f (F (х), g (х, F (у))) |
Я(Я(а)) )-простые термы;
Я (Я (а)) )~ вызовы’
если р (х, у) то h (h (а)) иначе F (х) — условный терм.
Наряду с обычным представлением термов будем использо-
вать бесскобочную форму:
если рху то hha иначе Fx.
Пусть Зв — некоторый базис. Расширим множество специаль-
ных символов дополнительным символом =.
Рекурсивным уравнением, или определением функции F назо-
вем слово вида
Лп> (хх, . . ., хп) = т (Xj, . . хп),
где — n-местный определяемый функциональный символ;
т (жх, . . хп) — терм, содержащий переменные из множества
174
переменных {xlt . . хп}, называемых формальными парамет-
рами (ФРП) функции F, и никаких других переменных.
Рекурсивной схемой называется лара (т, М), где т — терм,
называемый главным термом схемы (или ее входом), а М — такое
множество рекурсивных уравнений, что все определяемые функ-
циональные символы в левых частях уравнений различны и вся-
кий определяемый символ, встречающийся в правой части неко-
торого уравнения или в главном терме схемы, входит в левую
часть некоторого уравнения. Другими словами, в рекурсивной
схеме имеется определение всякой вызываемой в ней функции,
причем ровно одно.
Примеры рекурсивных схем:
1) Se-v F (®).
F (х) = если р (х) то а иначе g (х, F (Л (а:)));
2) 58.я: А (Ь, с),
А (х, у) = если р (х) то / (у) иначе В (х, у),
В (х, у) = если р (у) то A (g (х), а) иначе С (х, у),
С (х, у) = A (g (х), А (х, g (у)));
3) 5e.3: F (х),
F (х) — если р (х) то х иначе / (F (g (х)), F (h (х)))
1.3. Рекурсивная программа. Понятие интерпретации базиса,
введенное в гл. 4, полностью переносится на базисы рекурсивных
схем с одним лишь замечанием — определяемые функциональные
символы не интерпретируются. Определение свободной интерпре-
тации также остается в силе.
Пара (8, I), где 8 — рекурсивная схема в базисе Si, а I —
интерпретация этого базиса, называется рекурсивной программой.
Понятие выполнения рекурсивной программы определим с по- -
мощью протокола выполнения, который представляет собой ко-
нечную или бесконечную последовательность конфигураций. Кон-
фигурации определены с помощью понятия значения терма.
Так как мы сейчас рассматриваем термы, допускающие неинтер-
претируемые определяемые функциональные символы, необхо-
димо обобщить понятие значения (базового) терма, введенное
в п. 2.4 гл. 4.
Пусть т — терм, I — некоторая интерпретация, IV — неко-
торое состояние памяти, т. е. совокупность значений всех пере-
менных, входящих в терм (или в схему, содержащую этот терм).
Значение Т/ (И7) терма т при интерпретации I и состоянии памяти
W определяется следующим образом:
1) если х — базовый терм, то Т/ (И7) — значение этого терма,
определенное точно так, как это было сделано в п. 2.4 гл. 4;
2) если т — терм вида /'’<"> (тя, . . ., т„), то Т/ (И7) =
= F™ (т12 (И7).....хп1 (И7));
3) если х — терм вида /<п) (Тц . . ., хп) и хотя бы один из тер-
мов Tlt . . ., хп содержит определяемый функциональный символ,
то
Тг (И7) = ФС"> (ти (И7), . . ., тп1 (И7)),
175
где Ф<"> — символ функции I tjW), за которым в скобках сле-
дует список значений термов Tai (И7), . . ., тп/ (И7);
4) если т — условный терм вида
если р<"> (Tj, . . тп) то х{ иначе хт, то
т (W) — I XUеСЛИ 1 ‘ ’’Хп1 = *’
Xl' ' ~ ( хГ1 (И7) в противном случае.
Таким образом, в общем случае значения термов — это выра-
жения, содержащие элементы из области интерпретации, опре-
деляемые функциональные символы и символы конкретных функ-
ций.
Протокол выполнения рекурсивной программы (S, I) — это
последовательность конфигураций tlt ta, t3, . . . такая, что:
1) (И7,,), где тх — главный терм схемы 5, Wo —
начальное значение памяти, т. е. всех переменных схемы 8;
2) ti+1 получается из ti заменой в X, самого левого, самого
внутреннего вхождения вызова F<n> (dlt da, . . dn) (где F<”> —
некоторый определяемый символ, dlt da, . . ., dn g= Di) на зна-
чение терма в правой части уравнения F<n) (®lt . . ., —
= т(х1, . . ., хп) при интерпретации Z и значениях переменных:
W (Х1) = da, W (ха) = da....W (хп) = dn;
3) если tj не содержит определяемых функциональных сим-
волов, то ti — последняя конфигурация протокола.
Если протокол конечен, то программа (8, Z) останавливается
и последняя конфигурация в протоколе считается результатом
программы, если она представляет собой элемент из области ин-
терпретации. Если же последняя конфигурация — выражение,
составленное из символов функций и значений переменных, то
осуществляется вычисление этого выражения, и результат вы-
числения (элемент из области интерпретации) объявляется резуль-
татом программы. Программа (S, Z) зацикливается, если протокол
бесконечен.
Пример. Протокол выполнения программы («Sea, Zx), где
Zj — интерпретация из п. 2.5 гл. 4, выглядит следующим обра-
зом:
' Порядковый номер 1 2 3 4 5 6 Значение терма F(4) 4 х F (3) 4 X (3 X (F (2))) 4 X (3 X (2 X F (1))) 4 X (3 X (2 X (1 X F (0)))) 4 X (3 X (2 X (1 X 1))) = 24
Протокол выполнения программы (58Л, Za), где Za — интер-
претация из п. 2.5 гл. 4:
176
Порядковый Значение терма
номер
1 F (abc)
2 CONSCAR (abc, F (Ъс))
3 CONSCAR (abc, CONSCAR (be, F (c)))
4 CONSCAR (abc, CONSCAR (be,
CONSCAR (c, F (e))))
5 CONSCAR (abc, CONSCAR (be,
CONSCAR (c, e))) = abc.
Протокол выполнения программы (5e.lt Ih), где Ih — свободная
интерпретация из п. 3.2 гл. 4:
Порядковый номер 1 2 3 4 5 Значение терма Fx gxFhx gxghxFhhx gxghxghhxFhhhx gxghxghhxa
Отметим, что val (S6.j, /,) — val (<S4.a, Ij), val (5g.,, Z.) =#=
=#= val (S4.a, Zj) и val (Sg.!, Ih) ф val (54.а, где S4.a — стан-
дартная схема из гл. 4. После того как введено понятие выполнения рекурсивных
программ, можно дать определения пустоты, тотальности и функ-
циональной эквивалентности рекурсивных схем. Эти определе-
ния ничем не отличаются от соответствующих определений в п. 3.1
гл. 4, если в них заменить слово «стандартная схема» на «рекур-
сивная схема».
Задание 8.1.
А. Постройте протокол выполнения рекурсивной схемы 5s.*:
F(a),
F (х) — если р (х) то / (х) иначе F (F (g (х)))
при интерпретации Z: I (а) — 7,
если d>!°, / (/) (d) = d -1;
iWW-lQ, если d<10, Z (g) (d) = d + 2.
Б. Постройте протокол выполнения рекурсивной схемы Ss.s:
F(a),
F (х) = если р (х) то х иначе G (х),
G (х) = если q (х) то / (F (f(x))) иначе g (F (g (х)} )
при свободной интерпретации Z такой, что
{1, если число символов в бесскобочном терме-значении d
не больше 5,
О в противном случае;
{1, если число базовых функциональных символов в d
не больше 1,
О в противном случае.
177
Задание 8.2.
А. Определите подходящим образом понятие цепочки рекурсивной схе-
мы, понятие допустимой цепочки, свободной рекурсивной схемы.
Б. Покажите, что теоремы 4.1—4.3 о свободных интерпретациях пере-
носятся на случай рекурсивных схем.
§ 2. Проблемы трансляции
2.1. О сравнении классов схем. Программы для ЭВМ, будь
то программы, записанные на операторном языке, или программы
на рекурсивном языке, универсальны в том смысле, что любую
вычислимую функцию можно запрограммировать и найти ее
значения для заданных значений аргументов. При этом, как уже
указывалось, не требуется богатого набора программных прими-
тивов и базовых операций: достаточно тех средств, которые мо-
делируются стандартными схемами, плюс одна интерпретирован-
ная операция и один предикат. Это значит, что различные классы
программ не имеет смысла сравнивать по мощности, понимаемой
как способность реализовать различные алгоритмы,— все они
оказываются универсальными. В то же время программисты знают,
что одни программные примитивы являются «более выразитель-
ными», чем другие, что запись алгоритмов с привлечением рекур-
сии короче, чем итерационное представление, но вычисления по
такой программе, могут потребовать больше времени, и т. д. При
переходе к схемам программ возникает возможность поставить
и исследовать проблему выражения одних наборов примитивов
через другие в более чистом виде. Задачи такого типа образуют
сравнительную схематологию, основу которой составляют теоре-
мы о возможности или невозможности преобразования схем из
одного класса в схемы другого. При этом наряду с основной за-
дачей — выяснением соотношений между различными средствами
программирования — решается и другая, внутренняя задача схе-
матологии. Действительно, если мы умеем трансформировать один
класс схем в другой, то сможем переносить результаты, получен-
ные для некоторого класса схем, на другие классы.
В этой главе рассматриваются рекурсивные схемы, но так
как в следующей главе речь пойдет о других классах схем прог-
рамм, имеет смысл ввести необходимые понятия сравнительной
схематологии для произвольных классов схем программ.
Пусть «У — класс схем программ в некотором базисе Si, —
класс схем программ в базисе . Базис любого из рассматривае-
мых классов схем включает множества: переменных, базовых
функциональных символов, предикатных символов, другие мно-
жества, специфичные для данного класса (см. гл. 9).
Мы будем сравнивать классы схем, у которых базисы согла-
сованны в том смысле, что первые три из перечисленных множеств
одинаковы в данных базисах. Это дает возможность превращать
в программы схемы из разных классов с помощью одной и той же
интерпретации базисов. Например, полные базисы стандартных
и рекурсивных схем согласованны, т. е. определение функцио-
178
иальной эквивалентности может быть обобщено на схемы из раз-
ных классов.
Схема из класса <У и схема 8а из класса <У' функционально
эквивалентны, если для любой интерпретации I согласованных
базисов классов «У и <У' программы (5Х, 7), (5а, /) или обе
зацикливаются, или обе останавливаются с одним и тем же резуль-
татом.
Говорят, что класс схем & мощнее класса схем или класс
транслируем в класс Sf (обозначение: <У <У')» если для любой
схемы из <&’' существует эквивалентная ей схема в классе «У.
Класс & строго мощнее класса > &”), если Sf мощнее
еУ' и в 5^ существует схема, для которой нет эквивалентной схемы
в «У” (класс не транслируем в класс &). Классы и
равномощны, если <У мощнее У и <У' мощнее <У. Класс схем &
эффективно транслируем в класс схем У”, если существует алго-
ритм, преобразующий любую схему из & в эквивалентную схему
из <У'. Классы и <У' эффективно равномощны, если <У эффек-
тивно транслируем в <У' и if' эффективно транслируем в «У.
Ниже, когда устанавливается транслируемость одного класса
схем в другой или их равномощность, фактически демонстрируется
аффективная транслируемость или эффективная равномощность.
2.2. Трансляция стандартных схем в рекурсивные. В рекур-
сивных схемах результат поставляет ровно один терм, а в стан-
дартных схемах заключительный оператор может содержать
любой конечный набор термов и тогда результат программы —
не один элемент из области интерпретации, а набор таких эле-
ментов. Однако такое отличие не имеет принципиального значе-
ния для транслируемое™ схем. Можно было бы определить ре-
курсивные схемы, поставляющие в качестве результата наборы
термов, например, используя интерпретированную функцию пе-
чать (Tj, . . ., тп). Мы поступим проще — ограничим класс стан-
дартных схем схемами над базисом, содержащим заключительные
операторы только следующего вида: стоп (х), х €=
Т е о р е ма 8.1 (Маккарти). Класс стандартных схем транс-
лируем в класс рекурсивных схем.
Доказательство. Пусть исходная стандартная схема
задана в графовой форме. Доказательство будет состоять в непос-
редственном описании алгоритма трансляции, который состоит
из двух этапов.
На первом этапе с помощью эквивалентных преобразований
добьемся, чтобы к каждой вершине-преобразователю (помеченно-
му оператором присваивания) вела ровно одна дуга. Делается
это точно так же, как в п. 3.2 гл. 6 при приведении фрагментов.
Для этого достаточно применением ЛТ2 добиться, чтобы от каж-
дого преобразователя имелся хотя бы один путь к заключитель-
ному оператору, а затем применением правил копирования (см.
рис. 6.7, в) обеспечить выполнение требуемого условия.
Второй этап состоит в построении рекурсивной схемы Rs по
построенной на первом этапе стандартной схеме 5. Пусть Хз =
179
= {xlt . . xn} — память схемы S. Каждой вершине А схемы S,
не являющейся преобразователем, в соответствии с правилами,
перечисленными на рис. 8.1, сопоставим определение рекурсив-
ной функции Fa. На этом рисунке означает путь, начинаю-
щийся Д-дугой распознавателя А и кончающийся дугой, ведущей
к вершине ВА, отличной от преобразователя, a w — путь, начи-
нающийся выходной дугой начальной вершины и кончающийся
дугой, ведущей к вершине В, которая опять-такн отлична от пре-
образователя.
А I стоп (х)
5 С®!.-- .-Г„)
А I петля
(X,,..., хп ) = если П
то (t(W1,X1),...,t(W1,X/7))
иначе
о| СТАРТ(...) | ------»- ...4(Ю,ГЯ))
в
Рис. 8.1. Правила построения уравнений рекурсивной схемы Rs
Напомним, что t (w, т) — зто термальное значение (см. п. 3.5
в гл. 4) терма т для пути w. В качестве главного терма схемы R&
возьмем терм Fo (хъ . . ., хп).
Вот рекурсивная схема «S8.e, построенная описанным выше ал-
горитмом для стандартной схемы 54 2 из рис. 4.2:
Fo (х, у),
Fo (х> У) = F2 (х, °)’
Fa (х, у) = «сли Р (х) то F5 (х’ У) иначе Fa (h (х), g (х, у)),
Рь (х, У) = У-
Тот факт, что преобразование первого этапа алгоритма сохра-
няет эквивалентность, следует из теоремы 6.3 и корректности
лт-эквивалентности. Покажем, что рекурсивная схема Rg, по-
строенная на втором этапе, эквивалентна стандартной схеме 5.
Зафиксируем для этого произвольную интерпретацию I. Выписы-
вая протоколы выполнения программ (S, I) и (Rg, /), будем от-
мечать значения переменных в схемах при «прохождении» оче-
редной вершины А, отличной от преобразователя, и соответствен-
но при подстановке этих значений в определение рекурсивной
функции Fa- В начальный момент эти значения совпадают, так
как для любой переменной х начальное значение равно I (х). На-
180
чальной вершине схемы S соответствует главный терм схемы Rg.
Остается заметить, что если при переходе от распознавателя А
в протоколе программы (S, /) к следующему распознавателю или
заключительной вершине В, а также при переходе от вызова функ-
ции Fa в протоколе программы (Rs, I) к следующему вызову
Fc условия проверяются на одном и том же состоянии памяти,
то результаты проверки условий будут совпадать (так что В = С),
а изменение значений переменных xlt . . ., хп будет осуществлять-
ся по одним и тем же правилам: для перевычисления зтих значе-
ний в обоих случаях используются одни и те же термы, а именно
t (wi,, хг), . . .,t (шд, хп).
В протоколе выполнения программы (Rs, I) любое значение
терма содержит не более одного вхождения определяемого функ-
ционального символа. Если протокол программы (S, /) бесконе-
чен, то бесконечным будет и протокол программы (Rs, Г). В нем
с прохождением через очередной распознаватель А вызов функ-
ции Fa заменится на новый вызов Fb и т. д. Если же протокол
выполнения программы (S, I) конечен, то протокол выполнения
рекурсивной программы (Rt, /) тоже конечен, так как, согласно
установленной выше связи между протоколами, в рекурсивном
уравнении, соответствующем заключительной вершине, произойдет
замена вызова базовым термом. При этом val (S,I)-~ val (Rs, /). Q.
Задание 8.3.
А. Постройте протоколы выполнения программ (£в.«, ZJ, (5«.«, /»),
(Se.i, Zft), где и Za — интерпретации из п. 2.5 гл. 4, a Z/, — свободная ин-
терпретация из п. 3.2 этой же главы.
Б. Транслируйте в рекурсивные схемы стандартные схемы <S4.s, S4.4,.
St.b и St.»-
Отметим, что val (>S’8e, Ij) — val (*S8J, Д), где 6’81 — рекур-
сивная схема из п. 1.2 настоящей главы, а — интерпретация
из п. 2.5 гл. 4. Обе программы вычисляют 41, однако при других
интерпретациях результаты схем £вл и >V81 могут различаться,
так что рекурсивные схемы 8вл и Sg l неэквивалентны.
Рекурсивную схему назовем линейной, если в любом вызове
F (xlt . . ., тп) термы Тц . . ., тп (называемые также фактическими
параметрами этого вызова) являются базовыми. В доказательст-
ве теоремы 8.1 мы фактически доказали более сильное утвержде-
ние: класс стандартных схем эффективно транслируем в класс ли-
нейных рекурсивных схем. Описанный алгоритм трансляции стан-
дартных схем в рекурсивные не строит «оптимальные схемы». Из
него следует, что стандартная схема с т отличными от преобра-
зователей вершинами и п переменными транслируется в рекур-
сивную схему с т уравнениями» и с п переменными. Можно ли
сконструировать алгоритм, который транслировал бы любую стан-
дартную схему (или хотя бы любую унарную стандартную схему)
с п переменными в рекурсивную схему, в которой любая опреде-
ляемая функция имеет меньшее количество переменных, скажем,
п — 1? Ответ на этот вопрос, и ответ отрицательный, дал Чандра
(88]. Для следующей стандартной схемы 8В 3 с переменными ylt . . .
181
. . уп не существует эквивалентной рекурсивной схемы, в ко-
торой все определяемые функции содержали бы не более п — 1
переменных.
(старт,
1: У1 := а,
2: У, := / (У1),
3: Уз := / (Уа).
п: уп / (уп-1),
п 4- 1: если р (ух) то п 4- 2 иначе Зп 4- 1,
п 4- 2: если р (у2) то п 4- 3 иначе Зп 4- 1,
2п: если р (уп) то 2п 4-1 иначе Зп 4- 1,
2п 4- 1: У1 := g (ух),
2n 4- 2: Уз := g (у8),
Зп: Уп :=» g (Уп) на п 4-1
Зп 4- 1: стоп (yj)
Задание 8.4. Докажите утверждение о трансляции схемы S».,.
2.3 Трансляция рекурсивных схем в стандартные.
Теорема 8.2 (Патерсон — Хьюитт). Класс рекурсивных
схем не транслируем в класс стандартных схем.
Доказательство. Патерсон и Хьюитт привели при-
мер рекурсивной схемы, для которой не существует эквивалент-
ной стандартной схемы [129]. Это линейная схема Se 3 из примера
в п. 1.2 этой главы:
S8.S: F (*),
F (х) = если р (х) то х иначе / (F (g (х)), F (h (х))).
В общих словах, причина нетранслируемости этой схемы со-
•стоит в следующем. При варьировании интерпретаций возникает
необходимость запомнить сколь угодно большое число промежу-
точных значений, в то время как память любой стандартной схемы
-содержит фиксированное конечное число переменных.
Рассмотрим класс свободных интерпретаций {1п | п О},
в которых предикатный символ интерпретируется следующим об-
разом:
Ц₽)(т) =
1, если т содержит ровно п вхождений символов из
множества {g, h},
О в противном случае.
Результатом произвольной программы (58>3, /„) служит терм-
значение тп такой, что
т0 = ’х',
Ti = 7 (g (х), h (х))',
Тп = 7 (Тп-1 (g (*)), Tn_j (h (х))У.
182
Например, результатом программы (8В<3, Z2) является бесскобоч-
ный терм
Ь = ’ffggxhgxfghxhhx'.
Термы-результаты можно представить в виде следующих деревьев:
Zi (для тх), (для т2) и т. д., показанных на рис. 8.2. Вершины
Рис. 8.2. Представление термов-результатов в виде деревьев: а — Тх для
тх; б — для т2; в — Т3 для т3
деревьев перенумерованы по уровням — корень имеет номер 1,
номера вершин второго уровня 21 и 22 и т. д. В дереве jTn для тер-
ма тп число уровней равно п 4- 1.
Предположим, что существует стандартная схема S, эквива-
лентная схеме 88-3. Без потери общности можно предположить,
что схема S не содержит новых функциональных символов, и все
операторы присваивания, использующие символ /, имеют вид
у, := / (gji Ук). гДе У и Уь Ум ~ переменные из памяти схемы S.
Рассмотрим программу (S, /п). Если S ~ 8В-3, то val (8, In) =
= тп. Каждой вершине дерева Тп соответствует подтерм — про-
межуточное значение при вычислении терма тп. Подтерм одно-
значно восстанавливается из поддерева, корнем которого служит
эта вершина, и будет называться значением вершины. В прото-
коле выполнения программы каждому очередному выполнению
оператора у, := / (у/, у к) с двухместным функциональным симво-
лом /<2> соответствует продвижение вверх по дереву от двух сосед-
них вершин одного уровня к вершине следующего уровня. При
этом значение кащдой вершины дерева Тп должно запоминаться
183
и храниться до тех пор, пока пе станет возможным переместить-
ся на следующий уровень. Следующий фрагмент соответствует
выполнению оператора уА := / (у7, ук):
где у, хранит терм Т/, ук — терм тг, а у, — терм / тгтг. Перемен-
ная может быть или yJt или ук, но в целом такой фрагмент тре-
бует по крайней мере две переменные для запоминания промежу-
точных результатов.
Индукцией по п легко установить, что для вычисления терма
тп в программе (5, Z„) необходимо иметь n + 1 переменную для
запоминания промежуточных значений вершин дерева Тп. Дейст-
вительно, при п — 0 требуется одна переменная. Дерево Тп конст-
руируется из деревьев Тп_г и 7'n-i по следующей схеме:
Если Тп^ требует пг переменных и Тп-г — «2 переменных, то
дерево Тп потребует max (nx, n2) -f- 1 переменную, т. е., учиты-
вая начальный шаг индукции, Тп потребует п-j-l переменную.
Предположим, что стандартная схема S, эквивалентная ре-
курсивной схеме <S8<3, имеет к переменных. Результат рекурсив-
ной программы («Ь’8 Э, Zk) — терм тк. Для того, чтобы программа
(5, Zk) вычислила тот же терм, необходима к 4- 1 переменная,
что приводит к противоречию. Таким образом, не существует стан-
дартной схемы, эквивалентной рекурсивной схеме £8а3. [J
Итак, установлена транслируемость стандартных схем в ре-
курсивные и одновременно существование линейной рекурсивной
схемы, для которой нет эквивалентных стандартных схем. Эти два
факта объединены в следующей теореме.
Теорема 8.3. Класс рекурсивных схем строго мощнее клас-
са стандартных схем.
Доказательство. Прямое следствие из теорем 8.1
м 8.2. □
Задание 8.5. Установите, можно ли транслировать в стандартны»
схемы следующие рекурсивные схемы:
a) F (a), F (х) = если р (х) то / (х) иначе g (х, F (Л (х)));
б) схему S8.4.
§ 3. Линейные унарные рекурсивные схемы
3.1. Проблема трансляции. После того, как установлена не-
возможность трансляции произвольной (линейной) рекурсивной
схемы в стандартную, естественно начать поиск такого подкласса
рекурсивных схем, который транслируем в стандартные схемы.
Интерес представляет подкласс рекурсивных схем, построенный
по аналогии со схемами Янова.
Класс унарных рекурсивных схем имеет базис с единственной
переменной х и одноместными функциональными и предикатными
символами.
Класс линейных унарных рекурсивных схем (или класс схем де
Баккера — Скотта) — это подкласс унарных схем, в которых
всякий вызов содержит в качестве фактических параметров толь-
ко базовые термы. Например, рекурсивные схемы £8<4 и S8>5 из за-
дания 8.1 являются унарными, схема 58>5 — линейной унарной.
Теорема 8.4 (Патерсон — Хьюитт, Гарлэнд — Лакхзм).
Класс линейных унарных рекурсивных схем транслируем в класс
стандартных схем.
Доказательство. Предварительные за-
мечания. Не уменьшая общности, можно предполагать, что
все логические выражения имеют вид р (х), где х — переменная,
главный терм схемы — вид F (х), а сама рекурсивная схема R за-
дана в следующем виде: *)
Л (х),
Pi (х) = если Pi (х) то
иначе TiFr(i) 6>х (1 i n),
где Pi — некоторый предикатный символ; cq, р{, yit — цепоч-
ки из базовых функциональных символов; Рцц, FT(i) — опреде-
ляемые функциональные символы левой и, соответственно, пра
вой альтернатив, причем 0 I (г) п и 0 г (г) п. Усло-
вимся, что Fo — пустая цепочка, и если I (г) = 0, то cq пусто,
а если г (г) = 0, то у4 пусто. Выполнение схемы заканчивается,
когда оно достигает «вызова» Fo, поэтому такие альтернативы с ба-
зовыми термами назовем выходами схемы.
Отметим следующую особенность линейных унарных рекур-
сивных схем. При любой свободной интерпретации длина термов
в протоколе выполнения программы не уменьшается. При этом
каждый такой терм-значение содержит не более одного вхожде-
ния определяемого функционального символа. Если этот символ —
Fit то очередное значение в протоколе получается с помощью под-
•) Если правая часть некоторого уравнения — простой терм т, то его
можно заменить на условный терм: если р (х) то т иначе т, где р — произ-
вольный предикатный символ.
1.85
становии на его место одной из альтернатив i-го уравнения. Пусть
выход схемы достигается после т шагов выполнения схемы при
некоторой свободной интерпретации I. Результатом программы
(R, I) будет тогда бесскобочный терм-эначение
^PlPa ‘^ * Pm~l
левая часть правая часть
результата результата
где
( ₽q>(k), если (p4W)l (л^. . . ЛлХ)/ = 1,
I Л
( о<р(К) в противном случае,
( если (p<p(fcj)i (njt-j... n^xR — 1,
Pk— 1
I T<p(k) B противном случае,
для к = 1, . . т, а <р (А) — номер уравнения схемы, используе-
мого на А-м шаге построения протокола.
Алгоритм трансляции. Опишем способ построе-
ния стандартной схемы SR1 эквивалентной схеме R. В дополне-
ние к переменной х схема SR содержит еще три переменные и, v, w
и состоит из трех фрагментов-блоков А, В та С (см. рис. 8.4). Эти
блоки, в свою очередь, составлены из множества элементарных
фрагментов, которые строятся по уравнениям схемы R\ г-му урав-
нению соответствует фрагмент вида
a
(\у^)
y:=fty У= = М
L_-_|
b c
где у — одна из переменных и, v или w, а а, Ъ и с — метки; если
либо либо — пустая цепочка, соответствующий оператор
не включается во фрагмент. В приведенном ниже описании схемы
SR эти метки используются для понимания того, каким образом
соединяются фрагменты при построении SR. Когда соединяется
несколько фрагментов, всякий выход ведет к фрагменту, имеюще-
му ту же самую метку на входе.
Приведенный выше фрагмент, соответствующий t-му уравне-
нию, будем изображать следующим образом:
а
Г-Ц
Ь с
1НП
Первый блок схемы Sr (блок Л) составлен из п 4- 1 фрагмен-
та (рнс. 8.3, а), а их соединение определяется метками входных
и выходных дуг. Выход из блока А имеет метку 0. Блок изобра-
жен на рис. 8.4; цикл указывает, что соединения (с метками i ^>
0) производятся внутри блока. На рис. 8.3, б изображен блок
А для схемы £85.
1
а
Выход
из блока
б
Рис. 8.3. Построение блока А стандартной схемы SR, эквивалентной схеме
Я: а — фрагменты для сборки блока А; б — блок А для стандартной схемы
Sa.t
Понятно, что для свободной интерпретации I выход из
блока А программы (Sr, /) происходит со значением перемен-
ной и = 'Лпям . . . n^x', равным правой части результата
val (Sr, I). Таким образом, в блоках В и С к значению пере-
менной и должны быть применены функции, составляющие
левую часть результата схемы прн интерпретации I. Для сое-
динения фрагментов в блоках В а С использованы метки, пред-
ставляющие собой пары чисел (см. рис. 8.4). Внутри блока В вы-
ход фрагмента, перевычисляющего значения переменной v, сое-
диняется с фрагментом, перевычисляющим w, и наоборот, однако
выходы с метками 0/ фрагментов, перевычисляющих v, разрыва-
ют цикл в В и ведут к фрагментам, которые изменяют значение
переменной и. Блок В имеет п входов Вг, . . ., Вп. Если i-е урав-
нение содержит выход схемы R, то вход В, ведет к распознавателю-
187
< условием PiV, соответствующая выходная дуга которого (с мет-
кой 10) ведет к заключительному оператору стоп (и).
Эквивалентность схем В и Sr. Мы видели, что
к моменту выхода из блока А при выполнении программы (Sr, I)
переменная и имеет значение (лт лт_х . . . ЛзЛр;)/. Предполо-
жим, что переменной и к моменту очередного входа в блок В при-
оиоопо значение (pm-k-i • • • Pm-inmnmi • • • с некоторым
«па
к <Zm, так что следующим к и должно применяться pm_fc. Блок В
«ожидает» входа по метке Bt, где i — номер следующего уравне-
ния, которое используется при подстановке ожидаемого значения
(лк . . . яр:)/ переменной V. Это значит, что после т — к повторе-
ний «цикла» внутри блока В переменная v получит значение
(лт . . . njx)/, а переменная w — значение . Лдх)/, —
дело в том, что выход по метке С] из блока В произойдет раньше
(т — Л)-го присваивания переменной w. Таким образом, Рт-к бу-
дет применяться к значению переменной и точно так, как это де-
лается в схеме В с использованием /-го уравнения. После этого
блок С использует значение переменной w для того, чтобы вновь
установить v на следующее значение, ожидаемое в блоке В. Про-
исходит к 4- 1 повторений «цикла» в С, прежде чем w получит зна-
чение (лт . . . лхх)/, так что в момент выхода из блока С перемен-
ная v будет иметь значение (лк+1 . . . лх х)/, как и требовалось. На-
конец, если мы приходим к блоку В со значением переменной v =
= (лт . . . nxx)/, то выполнение программы заканчивается выпол-
нением оператора стоп (и).
Таким образом, описанная конструкция стандартной схемы
Sr позволяет восстанавливать левую часть результата програм-
мы (Я, I) при любой свободной интерпретации I. Если же про-
грамма (В, 7) зацикливается, то программа (Sr, /) зацикливается
уже в блоке А, что легко усматривается из структуры этого блока.
-Следовательно, построенная, стандартная схема Sr эквивалентна
исходной линейной унарной рекурсивной схеме В. Q
На рис. 8.5 изображена стандартная схема S8>#, эквивалентная
рекурсивной схеме 58>Б и построенная с помощью описанного в до-
казательстве алгоритма трансляции.
3.2. Праволинейиые унарные схемы. Как видно из доказатель-
ства теоремы 8.4, алгоритм трансляции линейных унарных рекур-
сивных схем в стандартные схемы достаточно сложен, и получаю-
щаяся схема громоздка. С трудностью реализации рекурсивных
процедур программисты столкнулись давно (в ряде ранних транс-
ляторов языка Алгол-60 рекурсивные процедуры не были реализо-
ваны). В следующей главе мы рассмотрим стандартные схемы, обо-
гащенные специальными программными примитивами или особой
организацией памяти, и эти новые средства позволяют значитель-
но упростить проблему трансляции рекурсии.
Класс линейных унарных рекурсивных схем не исчерпывает
все рекурсивные схемы, которые транслируются в стандартные
(например, схему £8<11 в задании 8.6, которая не является унар-
ной, можно транслировать). Но класс унарных схем не транслиру-
ем в класс стандартных схем. Примером унарной схемы, для ко-
торой не существует эквивалентной стандартной схемы, является
схема ^8.iq«
F(z),
F (х) = если р (х) то / (х) иначе g(F (F (h (х)))).
18»
В то же время класс стандартных схем не транслируем в класс
унарных схем (например* схема <58Л), поэтому эти классы схем ни
сравнимы по мощности.
В начале параграфа мы сравнили унарные рекурсивные схемы
со схемами Янова. Из последнего примера (схема 58Л0) ясно* чта
класс унарных рекурсивных схем мощнее класса схем Янова. Ка-
кой же подкласс унарных рекурсивных схем равномощен схемам
Янова?
1»()
Праволинейными унарными рекурсивными схемами называют
линейные унарные схемы, у которых термы-альтернативы в пра-
вых частях уравнений — это или базовые термы, или термы, начи-
нающиеся определяемым функциональным символом.
Теорема 8.5. Класс праволинейных унарных рекурсивных
схем и класс схем Янова равномощны.
Доказательство. Схемы Янова транслируемы в ре-
курсивные схемы как подкласс стандартных схем, и из способа
трансляции, предложенного в доказательстве теоремы 8.1, прямо
следует, что получаемые рекурсивные схемы являются праволиней-
яыми унарными.
Легко заметить, что для любой свободной интерпретации ре-
зультат val (S, I), где S — праволинейная унарная рекурсивная
схема, имеет вид (см. доказательство теоремы 8.4)
ЛтЛт_1 . . . л±х ,
где т — число значений в протоколе; лк (1 <1 к <1 т) — это Р<р(к>
или 6Ф(к); <р (к) — номер уравнения, используемого на к-м шаге
построения протокола.
Алгоритм трансляции праволинейных унарных схем в схемы
Янова теперь очевиден. Он совпадает с алгоритмом построения
блока А стандартной схемы Sr в доказательстве теоремы 8.4, за
исключением следующего: вместо переменной и используется
единственная в схеме переменная х, а выход из блока А присоеди-
няется к оператору стоп (х). Две переменные х и и в теореме 8.4
нужны были для того, чтобы сохранить для блоков В и С стандарт-
ной схемы Sr информацию о начальном значении х, а сейчас этого
не требуется делать. □
Задание 8.6. Транслируйте рекурсивные схемы:
a) Se.n: F (х),
F (х) = если р (х) то х иначе / (х, F (g (х)));
б) Sg,12: F (х),
F (х) = если р (х) то х иначе G (х),
G (х) = если д (х) то F (g (х)) иначе / (F (х)).
§ 4. Схемы е процедурами
4.1. Сравнение с классом рекурсивных схем. Схема с процеду-
рами — это модель алголоподобных программ с процедурами. Она
строится в объединенном базисе классов стандартных и рекурсив-
ных схем. Схема с процедурами состоит из двух частей — главной
схемы и множества схем процедур. Главная схема — это стандарт-
ная схема, в которой имеются операторы присваивания специаль-
ного вида х := F<n> (ylt . . ., уп), где х, уъ . . ., уп — переменные,
ft”) — определяемый функциональный символ. Такие операторы
называют операторами вызова процедур. Схема процедуры состоит
из заголовка и тела, разделенных символом равенства. Заголовок
схемы процедуры имеет тот же вид, что и левые части рекурсивных
уравнений: F<n> (жх, . . ., хп). Тело схемы процедуры — это стан-
дартная схема того же типа, что и главная схема. Заключитель-
191
ный оператор в теле процедуры всегда одноместен (стоп (z)). Па-
мять схемы процедуры (т. е. переменные, входящие в заголовок
тело схемы процедуры) не пересекается с памятью главной схе-
мы и памятями других схем процедур. Примеры схем с процеду-
рами:
а) 5влз: (старт (г),
1:
2:
3:
4:
5:
6:
F (у, v, w) = (старт,
1: если р (у) то 2 иначе 4,
2: y:=h(y),
3: v := G (у, w) иа 1,
4: если q (w) то 5 иначе 6,
5: у := v,
6: стоп (у))
G (t, г) — (старт,
1: если q (г) то 2 иначе 3,
2: t :=/(«),
3: стоп (£));
F (х) = (старт,
если р (х) то 2 иначе 3,
v х на 8,
z := g (х),
z := F (z),
и := h (х),
и F (и),
v := / (г, и),
z := х,
и а,
х : = F (х, z, и),
и:= Ь,
z : = F (z, х, и)
стоп (г))
б) 5ва<: (старт (х),
1: У : = F (х),
2: стоп {у})
1:
2:
3:
4:
5:
6:
7:
8: стоп (у)).
Выполнение интерпретированных схем с процедурами подоб-
но выполнению стандартных схем, но имеет следующие особенно-
сти.
1. Первой начинает выполняться интерпретированная главная
схема (главная программа), все операторы которой, отличные от
вызова процедуры, выполняются так же, как и операторы интер-
претированной стандартной схемы.
2. Выполнение оператора вызова к: х := F<n> (уъ . . ., уп)
(как в главной схеме, так и в телах процедур) при текущем состоя-
нии памяти IV включает следующие действия:
а) осуществляется переход к выполнению (интерпретирован-
ной) схемы процедуры (или процедуры) с заголовком (zj, . . .
. . ., хп), причем в качестве начального значения каждой перемен-
ной xit 1 i п, берется значение W (yt), а начальное значение
любой другой переменной z в теле процедуры равно I (г), где I —
интерпретация;
б) после завершения выполнения процедуры результат (зна-
чение переменной, упомянутой в заключительном операторе тела
процедуры) присваивается переменной х в операторе вызова к:
х := F (у1ч . . ., уп), а значение любой другой переменной у из па-
мяти главной схемы остается равным значению W (у);
в) осуществляется переход к выполнению оператора с меткой
к + 1 или оператора с меткой, указанной в переходе оператора
вызова.
192
3. Выполнение тела процедуры осуществляется точно так же,
как выполнение главной схемы.
Обозначим класс схем с процедурами & (Р).
Теорема 8.6. Класс рекурсивных схем, транслируем в класс
схем, с процедурами, т. е. & (К) <1 & (Р).
Д о к а з а т е л ь с т в о. Алгоритм трансляции рекурсивных
схем в схемы с процедурами:
1) строится главная схема вида
(старт (уи .... уп),
1: У := т (уь . . ., уп),
2: стоп (у)),
где У — новая переменная, не входящая в память рекурсивной схе-
мы, а т (ух, . . ., уп) — главный терм рекурсивной схемы;
2) памяти всех рекурсивных уравнений переименовываются
так, чтобы они взаимно не пересекались и не пересекались с па-
мятью главной схемы;
3) каждое рекурсивное уравнение
Ft {xlt . . x7l) = если р (xit, . . ., a:fl) то то иначе т/в
заменяется схемой процедуры
Ft (хх.....хп) = (старт,
1: если р (х,„ . . ., х^) то 2 иначе к,
2: S (v, Tjj на т,
к: S (у, ti0),
т: стоп (г)),
где S (v, тд) и S (v, Tj0) — фрагменты схем, называемые оператор-
ными раскрытиями простых термов Тц и Ti0. Операторное раскры-
тие S (и, т) простого терма т определяется следующим образом:
а) если т = х, то S (у, т) = v : = х;
б) если t = £(П) (тъ . . ., тп), где £<"> — базовый или опреде-
ляемый функциональный символ, то S (и, т) представляет собой
последовательность
alt и„ . . ., а„, v : = £<”> (zt.zn),
где zn . . ., zn — новые переменные, a
{z{: — х, если т{ — переменная х,
S (zit т{) в противном случае.
Например, S (у, f (F (g (x))t F (h (a:)))) — это последователь-
ность операторов и g (х), zx := F (и), w : = h (x), zt := F (u>),
v := f (zlt za).
На этом мы завершаем доказательство, считая, что содержатель-
ного анализа алгоритма трансляции и правил выполнения свобод-
но интерпретированных рекурсивных схем и схем с процедурами
достаточно для того, чтобы убедиться в эквивалентности исходной
построенной схем. Факт, что исходная и построенная схемы име-
ют разные памяти (в частности, в схеме с процедурами больше пе-
ременных за счет раскрытия термов), не вносит осложнений, там
как все добавляемые переменные используются в качестве времен-
7 В. Е. Котов. В. К. Сабельфельд
193
ных «рабочих ячеек», они не входят в заключительный оператор
главной схемы и их начальные значения, задаваемые интерпрета-
циями, не влияют на результаты. Q
Теорема 8.7. Класс схем с процедурами транслируем
в класс рекурсивных схем, т. е. Pf (Р) ^(Я).
Доказательство. Ниже описан несложный алгоритм
трансляции. Прежде всего, с помощью описанного в теореме 8.1
алгоритма главная схема S и тела схем процедур Pt, . . ., Рп не-
зависимо транслируются в рекурсивные схемы Rs и Rpt (г —
= 1, . . ., п). При этом не делается никаких различий между ба-
зовыми и определяемыми функциональными символами исходной
схемы. Пусть т0 — главный терм схемы Rs, а тг (i — 1, . . ., л) —
главный терм схемы Rp^ К системе рекурсивных уравнений, по-
лучающейся объединением уравнений схем Rs и Rpi (1 i <1 л),
добавим каждое из уравнений
Ft (xlt . . ., хп) = т„
где Ft (xt, . . ., хп) — заголовок схемы процедуры Pt, для г =
= 1, . . ., л. В качестве главного терма получающейся при этом
рекурсивной схемы возьмем терм т0. [3
Теорема 8.8. Класс рекурсивных схем и класс схем с проце-
дурами равномощны.
Доказательство. Следствие теорем 8.6 и 8.7. [3
Теорема 8.9. Класс схем с процедурами строго мощнее клас-
са стандартных схем, т. е. У < (Р), где — класс стандарт
ных схем.
Доказательство. Следствие теорем 8.3 и 8.8. [3
4.2. Частичная трансляция схем с процедурами. Хотя не су-
ществует алгоритма трансляции схем с процедурами в стандартные
схемы, рассмотрим преобразование схем с процедурами, которое
можно назвать частичной трансляцией. Преобразование представ-
ляет собой итеративный процесс, который всегда завершается по-
строением схемы, причем это или стандартная схема, или схема
с процедурами (часто с меньшим числом процедур, чем исходная).
Основу рассматриваемого преобразования составляет операция
подстановки тел схем процедур вместо операторов вызовов. Эта
операция — аналог известной в программировании открытой под-
становки процедур.
Подстановка вместо инструкции вызова
k: г : = (y1t . . ., у„) на I
тела схемы процедуры, определяющей функциональный символ
Ft, производится следующим образом. Схема процедуры копи-
руется, каждой переменной памяти этой схемы сопоставляется
взаимно однозначно новая переменная, а каждой метке в теле схе-
мы — новая метка, не встречающаяся в главной схеме и в телах
194
всех схем процедур. Все вхождения старых переменных и меток
в инструкции копии тела заменяются соответствующими новыми
переменными и метками. Заголовок копии и оператор старт в ко-
пии тела элиминируются, а метка I заменяется новой меткой т.
Заключительный оператор стоп (г) заменяется на z : = v на Z; инст-
рукция к: z Ft (уъ . . ., уп) — последовательностью инструк-
ций
fc: Xr := ylt . . .,хп := уп на т,
где хи . . ., хп — новые переменные копии схемы процедуры, со-
ответствующие старым переменным из заголовка этой схемы про-
цедуры. На этом подстановка завершается.
Например, подстановка вместо оператора вызова I: у F (у),
входящего в главную схему схемы 5в<м, тела схемы процедуры
следующим образом меняет главную схему:
(старт (х),
1: х1:= х на 9,
2: стоп (у),
9: если р (хг) то 10 иначе 11,
10; на 16,
11: zx := g(Xi),
12: Z1 := F (Z1),
13: ut:= h (x^,
14: := F (uj,
15: Vi := / (zlt wj,
16: у t— Vi на 2).
Начальный шаг частичной трансляции — сопоставление каж-
дой инструкции вызова в главной схеме и в схемах процедур вспо-
могательного списка определяемых функциональных символов.
Для инструкций вызова в главной схеме этот список пустой, а для
инструкций вызова в схемах процедур он состоит из одного сим-
вола, определяемого этой схемой процедуры.
Следующий шаг повторяется итеративно сначала для главной
схемы, затем для каждой схемы процедуры, затем снова для глав-
ной схемы и так далее, пока можно осуществлять хотя бы одну
подстановку. На этом шаге вместо каждой инструкции вызова
к: z : = Ft (уг...уп),
во вспомогательном списке которой (ГЛ, . . ., Fjz) нет символа
Flt подставляется тело схемы процедуры, определяющей функ-
циональный символ Ft. В списки всех новых инструкций вызова,
вошедших вместе с подставленным фрагментом, добавляются эле-
менты списка (Fj„ . . ., F}[) и символ Ft.
Если в главной схеме после некоторого очередного шага нет
инструкции вызова или нельзя осуществить ни одной из подста-
новок из-за невыполнения условия применения подстановки, час-
тичная трансляция заканчивается, а те схемы процедур, которые
определяют функциональные символы, не встречающиеся боль-
ше в главной схеме и ни в одной из схем процедур, элиминнруют-
7* 195
ся. В первом случае результат трансляции — стандартная схема,
а именно — главная схема без инструкций вызова. Во втором
случае получается схема с процедурами, в которой число проце-
дур и вызовов может уменьшиться по сравнению с исходной схе-
мой. Такую схему с процедурами будем называть приведенной.
Процесс частичной трансляции всегда завершается. Действи-
тельно, каждая подстановка или уменьшает число инструкций
вызова, или не уменьшает, но зато число элементов в списках
новых подставленных инструкций вызова увеличивается, по край-
ней мере, на единицу. Так как общее число определяемых функ-
циональных символов в схеме конечно, наступит момент, когда
очередную подстановку нельзя сделать. В этот момент в списке
любого вызова будут находиться символы всех тех определяемых
функций, при выполнении которых может возникнуть данный
вызов. Остается убедиться, что полученная схема, будь то стан-
дартная схема или приведенная схема с процедурами, эквивалент-
на исходной схеме. Чисто техническая работа по сравнению про-
токолов исходной и полученной схем при произвольной свобод-
ной интерпретации показывает, что это так.
Приведенная схема для S6 включает главную схему, по-
строенную выше, и ту же схему процедуры, что и в 58<м.
Если частичная трансляция завершилась построением приве-
денной схемы с процедурами, то это еще не значит, что исходную
(или построенную) схему нельзя транслировать в стандартную
схему. Алгоритм частичной трансляции обнаруживает отсутствие
или наличие «синтаксической» рекурсии. Но для некоторой схе-
мы 5 может случиться, что при любой интерпретации I во время
выполнения программы (5, I) ни одна из процедур не вызывается
повторно, пока не завершится выполнение предыдущего вызова
этой же процедуры. Это значит, что в схеме S нет, по существу,
рекурсии. Такие схемы транслируются в стандартные. Другой
пример рекурсивных схем и схем с процедурами, которые могут
быть пропущены алгоритмом частичной трансляции, — схемы беа
условных операторов (или логических выражений).
Краткий обзор и комментарии
Теоретическое изучение рекурсивного программирования бы-
ло начато Маккарти [121, 1221 в связи с его работами над языком
Лисп [43] и одновременно в связи с попытками создать основы
семантической теории программирования. В дальнейшем рекур-
сивные схемы и программы играли важную роль в развитии фор-
мальных методов описания и исследования семантики программ
и языков программирования, в теории правильности программ.
Схематологические аспекты рекурсивного программирования впер-
вые были исследованы Де Баккером и Скоттом [97], Стронгом
[138], Патерсоном и Хьюиттом [129].
Де Баккер и Скотт предложили унарные рекурсивные схемы
как обобщение схем Янова и инициировали изучение главных
196
проблем для рекурсивных схем. Так как класс рекурсивных схем
строго мощнее класса стандартных схем (см. теорему 8.3), не-
разрешимость всех главных проблем для рекурсивных схем мож-
но установить из их неразрешимости для стандартных схем.
С другой стороны, класс праволинейных унарных схем равномо-
щен классу схем Янова (см теорему 8.5), поэтому на этот класс
переносятся все «положительные» результаты из теории схем Яно-
ва. В настоящее время между этими двумя полюсами мало
существенных результатов. Гарлэнд и Лакхэм [1021 показали
разрешимость проблемы эквивалентности в классе линейных унар-
ных схем, и Сабельфельд [63J построил полную систему эквива-
лентных преобразований для этого класса в духе системы преоб-
разований Ершова для схем Янова. Наиболее полное исследова-
ние класса унарных схем выполнено Ашкрофтом, Манна и Пнуе-
ли [83], которые установили разрешимость проблем пустоты,
тотальности и свободы в этом классе, а также разрешимость про-
блемы эквивалентности в классе свободных унарных схем.
В классической работе [1021 Гарлэнд и Лакхэм высказали ги-
потезу о разрешимости функциональной эквивалентности в клас-
се унарных линейных рекурсивных схем с засылками констант,
т. е. схем, в которых разрешается использовать нульместные ба-
зовые функциональные символы. Однако все попытки применения
«техники следов» для построения распознающего алгоритма ока-
зались неудачными. Лисовик разработал новый метод (назвав его
методом жестких множеств), применением которого [36] доказал
гипотезу Гарлэнда — Лакхэма. Впрочем, другой алгоритм реше-
ния этой проблемы оказалось возможным извлечь из результатов
работ [107, 60].
Понятие унарной металинейной схемы отличается от унарной
линейной только тем, что снимаются все ограничения, которые
накладывались на главный терм схемы. Например,
Л № (Л («))).
(х) — если р (х) то х иначе g (Ft (/ (z))),
Fa (х) = если q (х) то / (F3 (g (х))) иначе (h (х)),
F3 (х) ~ если г (х) то х иначе F3 (g (h (z)))
— металинейная схема. Лисовик показал [37], что проблема эк-
вивалентности унарных металинейных рекурсивных схем с за-
сылками констант алгоритмически разрешима. Этот результат
был получен с помощью довольно длинной цепочки сведений,
в конечном счете проблема была сведена к решению системы ли-
нейных диофантовых уравнений.
В гл. 4 была определена логико-термальная эквивалентность,
оказавшаяся корректным и разрешимым отношением эквивалент-
ности. Характерная особенность лт-эквивалентпости состоит
в том, что ее определение не использует понятия интерпретации.
Несмотря на тот факт, что лт-эквивалентность существенно силь-
нее функциональной эквивалентности, набор преобразований,
сохраняющий лт-эквивалентность, оказался довольно широким
197
(см. гл. 6). Естественно попытаться ввести формальную эквива-
лентность, не использующую понятия интерпретации, и для ре-
курсивных схем. Такая эквивалентность, основанная на понятии
дерева развертки всех возможных выполнений схемы, была вве-
дена Розеном [134] под названием древесной эквивалентности
(tree equivalence).
Среди определяемых функциональных символов выделим осо-
бый символ й, d (й) =0, рекурсивное уравнение которого будет
иметь вид й = й, так что вычисление выражения й (как вызова
без фактических параметров) должно быть бесконечным при лю-
бой интерпретации. Будем предполагать, что область интерпре-
тации D всегда содержит по крайней мере два различных элемен-
та 1 и 0. Условное выражение
если л то а иначе р
будем записывать также в форме if (л, а, Р), используя трехмест-
ный базовый функциональный символ if, который может интер-
претироваться только такой трехместной функцией cond: D3 -> D,
для которой cond (1, а, р) — а и cond (0, а, Р) = р, но cond (л,
а, р) не определено, если л =# 1 и л =# 0.
Термы из множества Т всех термов могут рассматриваться
как деревья. Скажем, дерево
соответствует терму / (if (р (х, у), у, F (х)), G (а, г)). На мно-
жестве Т введем отношение частичного порядка, полагая
если терм t2 можно получить из терма заменой некоторых вхож-
дений й на элементы из Т. Например, й t для всех t Е Г.
В соответствии с доказанным в [3] множество Т можно пополнить
пределами всевозможных цепей элементов из Т, т. е. бесконечны-
ми деревьями (или макродеревъями). Результат пополнения —
множество S' с отношением частичного порядка ««^» — обладает
следующим свойством полноты: наименьшая верхняя грань lub (С)
всякой цепи С элементов из 3 принадлежит S'.
По рекурсивной схеме S построим последовательность термов
{Xn (iS), п >= О). Терм Хо (S) — это главный терм схемы S, а терм
ln+i (5) Для п > 0 получается из терма (5) открытой подста-
новкой всех самых внешних вызовов в Хп (5). Например, для схемы
5ваб: F (а, Ь),
F (х, у) — если р (х) то х иначе F (f (х), g (у))
198
получим
К (Seas) = F (а. V,
(Seas) = if (P («)> °> F (f («)» S (*)))>
К (Se.ls) = if (P (a), a, if (p(f (a)), f (a), F (f (f (a)), g (g(b))))).
Отображение p: T »-► T определим следующим образом:
P(*) =
х, если х = х, где хЕвЗР-,
/(p(Ti)....р(тп)), если т = /(т1,...,т„), где /—базо-
вый функциональный символ, j=£if и Vi(l<Ci^n)
i/(p(a),p(p),p(y)), если r=i/(a, 0, у), причем р(а)=/=£1
и либо р (0) =/= £1, либо р (у) =/= U;
О в остальных случаях.
det (5) = lub {р (kn (5)): n > 0} — детерминант схемы S. Схемы
jSj и 5а назовем древесно эквивалентными, если det (St) — det (S2).
Например, схема 5вл5 древесно эквивалентна следующей схеме
<^e.ie: F (а),
F (х) — если р (х) то х иначе F (f (х)}.
поскольку их общим детерминантом является макродерево
Проблема древесной эквивалентности оказалась равносильной
[93. 94, 101] проблеме эквивалентности детерминированных ма-
газинных автоматов, известной открытой проблеме в теории фор-
мальных языков. Что касается проблемы древесной пустоты
(det (5) = £2?), то в [67] описан алгоритм ее решения. Разрешимой
является также проблема древесной эквивалентности в подклассе
линейных (полиадических) рекурсивных схем [137].
Эквивалентные преобразования для рекурсивных схем про-
грамм рассматривались в работах [19, 66]. Условия применения
многих преобразований извлекаются при этом с помощью алго-
ритмов глобального анализа, обобщающих алгоритмы разметки
из гл. 2.
199
Стронг, Патерсон и Хьюитт исследовали задачу трансляции
рекурсивных схем в стандартные. Их работы открыли новый
раздел теории схем программ — сравнительную схематологию.
Задача сравнительной схематологии — изучение выразительных
возможностей различных средств (и методов) программирования,
изучение возможности транслировать один класс схем в другой
(более подробно эти вопросы рассмотрены в гл. 9). Стронг [138]
показал, что класс рекурсивных схем не транслируется в класс
стандартных схем (и даже в более общий класс счетчиковых схем,
см. теорему 9.2), и выделил некоторые подклассы транслируемых
схем. Одновременно Патерсон и Хьюитт предложили выразитель
ный пример рекурсивной схемы (схема 563), для которой не су-
ществует эквивалентной стандартной схемы. Они же анонсиро-
вали возможность трансляции линейных унарных схем, алгоритм:
трансляции был позднее предложен Гарлэндом и Лакхэмом [102].
ГЛАВА 9
ОБОГАЩЕННЫЕ СХЕМЫ
Стандартные схемы конструируются с привлечением мини-
мального набора программных примитивов из внушительного
арсенала средств, которыми располагает современный програм-
мист. В частности, в этих схемах очень просто устроена память —
конечное множество неинтерпретированных переменных. Мы же
видели в предыдущей главе, к каким трудностям приводит такая
простота: в теореме 8.2 именно конечность памяти указана как
причина нетранслируемости рекурсивной схемы 5g.3, а в теореме
8.4 отсутствие интерпретированных переменных типа счетчиков
делает построенную стандартную схему неоправданно громозд-
кой. Трудно представить себе достаточно содержательную реаль-
ную программу без использования таких конструкций, как про-
цедуры, счетчики, массивы, списки и т. д. Эта глава посвящена
расширениям класса стандартных схем, а именно схемам, в ко-
торые добавлены выделенные интерпретированные переменные
(с заданной областью интерпретации и допустимыми операциями)
или «динамические», потенциально бесконечные памяти специаль-
ной структуры.
Более конкретно будут рассмотрены схемы со счетчиками
(или счетчиковые схемы) и схемы с (одномерными) массивами.
Задача состоит в том, чтобы сравнить эти схемы между собой
по мощности, а также с рекурсивными и стандартными схемами.
Общая цель такого сравнения — выделить «универсальный» класс
схем, универсальный в том смысле, что любой из перечисленных
классов транслируем в этот выделенный.
§ 1. Классы обогащенных схем
1.1. Счетчики, магазины, массивы. Счетчик — интерпретиро-
ванная переменная, у которой областью значений является мно-
жество целых неотрицательных чисел; начальное значение счет-
чика равно 0. Счетчики входят как переменные только в специаль-
ные интерпретированные операторы, которые не содержат «обыч-
ных» переменных. Эти операторы добавляются вместе со счетчиком
в базис стандартных схем. Таких интерпретированных операторов
три:
с : = с + 1 — оператор прибавления единицы',
с := с — 1 — оператор вычитания единицы',
201
с = 0 — условный оператор проверки равенства счетчика нулю.
Если значение счетчика равно 0, то оператор вычитания единицы
не изменяет его, оно остается равным 0.
Магазин — неинтерпретированная переменная сложной струк-
туры. В процессе выполнения интерпретированной схемы состоя-
ние магазина — зто конечный набор элементов (d2, d2, . .., dn)
из области интерпретации. Начальное состояние — пустой набор
(магазин пуст). Значение dn называют верхушкой (непустого)
магазина. Магазин входит как переменная только в специальные
интерпретированные операторы трех типов:
М — х — запись в магазин;
х : — М — выборка из магазина;
М = 0 — условный оператор проверки пустоты магазина.
Здесь М — магазин; х — обычная переменная. Первый оператор
меняет состояние (d1T d2, . . dn) магазина М на состояние
(dn d2, . . dn, dn+1), где dn+1 — значение переменной х. После
выполнения этого оператора элемент dn+1 становится новой вер-
хушкой магазина. Второй оператор присваивает переменной х
значение, равное верхушке магазина, состояние которого меняется
с (d2, d2, . . ., dn) на (dA, d2, . . ., dn_j), при этом dn_^ ста-
новится новой верхушкой магазина. Если магазин М пуст, то
применение второго оператора оставляет его пустым, а перемен-
ная х не меняет своего значения. Третий оператор— предикат
проверки магазина на пустоту; если магазин пуст, то значение
предиката М — 0 равно 1, в противном случае — 0.
Массив — неинтерпретированная переменная сложной струк-
туры. При выполнении интерпретированной схемы состояние
массива — бесконечная последовательность (dt, d2, . . ., d,, . . .)
элементов из области интерпретации. Массивы входят только
в специальные интерпретированные операторы двух типов:
А [с] := х, х А (с), где А — массив; с — счетчик; [,] — спе-
циальные символы; [с] — целое число, равное текущему значе-
нию счетчика с. Первый оператор меняет состояние (d,, d2, . . .
. . ., d(c], . . .) массива А на новое состояние, которое отличается
от старого лишь тем, что элемент d[cj заменяется на значение пе-
ременной х. Второй оператор не меняет состояние массива, а при-
сваивает переменной х значение, равное [с]-му порядковому эле-
менту в состоянии массива. Начальное состояние массива интер-
претированной схемы определяется интерпретацией. Считается,
что это — бесконечная последовательность, состоящая из одного
и того же элемента d из области интерпретации, т. е. можно на-
чальное значение массива задать так: I (А) = d. Присутствие
массивов в схеме требует одновременного введения счетчиков.
1.2. Примеры обогащенных схем. Добавляя в полный базис
стандартных схем счетчики, массивы и магазины, можно образо-
вать различные классы обогащенных схем. Среди них нас в пер-
вую очередь интересуют «чистые» классы, которые получены за
счет расширения базиса одним видом дополнительных средств
(не считая того, что массивы требуют счетчиков).
202
Так, класс счетчиковых схем определяется следующим образом.
В полный базис стандартных схем добавляется счетное множество
счетчиков, а ко множеству операторов добавляются интерпрети-
рованные операторы над счетчиками описанного выше типа.
Класс магазинных схем образован добавлением в базис стандарт-
ных схем счетного множества магазинов, а во множество операто-
ров вводятся интерпретированные операторы над магазинами.
Класс схем с массивами — это расширение класса счетчиковых
схем за счет добавления счетного множества массивов и операто-
ров над ними.
Рис. 9.1. Стандартная и обогащенные схемы: а — стандартная схема
б — счетчяковая схема 5».t; в — магазинная схема 5».s; г — схема с масси-
вами
203
Мы будем наряду с «полными» чистыми классами упоминать
и их подклассы (например, класс схем с одним счетчиком), а также
«смешанные» классы обогащенных схем (например, класс схем
с одним счетчиком и одним магазином). Поэтому целесообразно
ввести следующую систему обозначений классов схем:
& — стандартные;
сУ (7?) — рекурсивные;
У (с) — счетчиковые;
(ЛГ) — магазинные;
<5? (4) — с массивами;
& (1с) — с одним счетчиком;
Sf (2с) — с двумя счетчиками;
<5? (2с, 1Л7) — с двумя счетчиками и одним магазином и т. д.
Понятие интерпретации и интерпретированных схем (программ)
переносится на обогащенные схемы естественным образом. Ново-
введенные переменные интерпретируются согласно правилам, упо-
мянутым при их определении. Семантика дополнительных опера-
торов также была разъяснена выше. Так как счетчики, магазины
и массивы не входят в заключительный оператор, определение
функциональной эквивалентности стандартных схем «автомати-
чески» переносится на обогащенные схемы, при этом как на схемы
внутри одного класса, так и на схемы из разных классов. По тем
же причинам остаются в силе определение свободных интерпрета-
ций и теоремы 4.1—4.3 о свободных интерпретациях.
На рис. 9.1 приведены примеры четырех схем — стандартной
5вл, счетчиковой $9Л, магазинной 5в<3 и схемы с массивами SeA.
Все они эквивалентны друг другу и рекурсивной схеме 5вл1 из
задания 8.6:
F(x),
F (х) = если р (х) то х иначе / (х, F (g (х))).
(В счетчиковой схеме 5вл использован не упомянутый выше
оператор пересылки значений счетчиков с3 : = сх. На самом деле
этот оператор — удобное сокращение фрагмента счетчиковых
схем, использующего три «базовых» оператора над счетчиками.
См. об этом подробнее в следующем параграфе.)
Задание 9.1. Покажите, что схемы $в.ц, 5вл, 5»л, 5».s и эк-
вивалентны.
§ 2. Проблемы трансляции
2.1. Счетчиковые и рекурсивные схемы. При определении
счетчика мы ввели три оператора над счетчиками: с := с + 1,
с : — с — 1 и с = 0. Формально в классе счетчиковых схем до-
пускается использование только этих операторов, однако удоб-
нее, по мере надобности, расширять этот «базовый» набор из трех
операторов другими операторами над счетчиками, как уже было
сделано в случае схемы 5вл. Но мы должны быть уверены, что
добавляемые операторы над счетчиками не выведут нас из класса
204
счетчиковых схем (такого, как мы его определили). Один из спо-
собов убедиться в этом — представить вводимый оператор как
фрагмент счетчиковой схемы, составленный из базовых операто-
ров. Например, введение в базис класса У (с) оператора над
счетчиками с2 := формально меняет определение класса, но
получающийся класс схем равномощен классу У (с), так как
этот оператор мощно заменить фрагментом, показанным на рис. 9.2.
Рис. 9.2. Расшифровка оператора := ct
Задание 9.2.
А. «Расшифруйте» операторы: засылки произвольного числа п в счет-
чик с := п, умножения на число с := с X п и деления на число с dn
с помощью трех базовых операторов. Используйте не более одного дополни-
тельного счетчика.
Б. Покажите, что предикат с mod п = 0, где п — некоторое число, а
с mod п — остаток от деления счетчика на п, можно представить через три
базовых оператора и один дополнительный счетчик.
Теорема 9.1 (Манна — Чандра). Класс счетчиковых схем
не транслируем в класс рекурсивных схем.
Доказательство. Счетчиковая схема S9.6 на рис. 9.3
не имеет эквивалентной рекурсивной схемы.
Отметим характерные особенности этой схемы. При любой
свободной интерпретации схемы 58-5 значения счетчика сх во
время выполнения программы пробегают некоторый начальный
отрезок последовательности чисел 0, 1, 2, 3, ... (в зависимости
от интерпретации предикатного символа р). Счетчик с2 принимает
при этом значения 0, 1, 0, 2, 1, 0, 3, 2, 1, 0, . . ., а переменная
у в условном операторе р (у) пробегает последовательность зна-
чений 'a', ’fa’, 'ga', 'fja, 'fga', 'fffa', . . ., 'jn'gn^n'a', где nx
и nt — текущие значения счетчиков q и, соответственно, ct.
Схема зацикливается при единственной свободной интерпретации
в которой (р) (т) — 1 для любого терма-значения т. При
любой другой свободной интерпретации I схема остановится после
первой же проверки предиката I (р), давшей значение 0.
205-
Рис 9.3. Счетчиковая схема Se-6, которую нельзя транслировать в рекурсив
иую схему
Предположим, что в классе 5^ (/?) существует схема 5, экви-
валентная схеме S9.5, и пусть п — максимальная местность опре-
деляемых функциональных символов, употребленных в схеме S.
Зафиксируем свободную интерпретацию /«,, о которой речь шла
выше. Множество всех значений, которые переменная у принимает
во время бесконечного выполнения программы (5, /«>), изобразим
в виде следующей таблицы.
Столбец 0 Столбец 1 Столбец 2 ... Столбец n Столбец остальных значений
а ga g’a - gn+lagn+*a
fa fga fg*a /g«a fgn+lafen+ta
f'a f*ga f*g*a ...
1яа isga f3g*a 13gna ...
/*« f*ga f*gna • . .
... • • • . • • • • • • - • • • •
В таблице выделены п+2 столбца: столбец 0, столбец 1,...
., столбец п, столбец остальных значений. Так как программа
(S, /<») должна зациклиться, а число столбцов в таблице конечно,
должен существовать определяемый функциональный символ F,
каждый аргумент которого при некотором повторном рекурсив-
ном обращении к уравнению, содержащему в левой части этот
символ (вызов F), заменяется значениями из того же столбца,
206
из которого уже бралось значение при некотором предыдущем
вызове. Предикат (р) тождественно истинен на всех термах-
значениях, поэтому повторные вызовы F происходят в том же по-
рядке, что и предыдущие обращения, и для значений аргументов,
выбираемых из тех же столбцов. Так как максимальное число
аргументов F не больше п, среди столбцов 0, 1, 2, . . п (их
п + 1) существует такой, термы из которого не используются
в качестве значений аргументов F при повторных вызовах F.
Следовательно, только конечное число термов из столбца I, 0
I п, будет появляться в процессе выполнения программы
(5, 7«>), и существует терм который никогда не станет зна-
чением аргумента условного оператора р (у).
Зафиксируем еще одну интерпретацию 7kJ, которая отлича-
ется от Л» лишь тем, что ZR1 (р)(' fkgla’) = 0, а для других термов
по-прежнему значение предиката —1. Терм '^ё1а' не будет предъ-
явлен предикату (р) при выполнении программы (S,
поэтому эта программа зациклится. В то же время программа
(59.5, 1к1) останавливается, так как рано или поздно переменная у
примет значение 'f^a'. Следовательно, схемы 59.5 и S неэкви-
валентны, что противоречит предположению. Q
Метод, которым доказана теорема, позволяет объяснить при-
чину невозможности транслировать произвольную счетчиковую
схему в рекурсивную. Счетчиковые схемы могут порождать (при
всевозможных свободных интерпретациях) богатые и разнообраз-
ные множества термов-результатов, которые не могут быть поро-
ждены механизмом рекурсии.
Теорема 9.2. Класс рекурсивных схем не транслируем
в класс счетчиковых схем.
Доказательство. Для рекурсивной схемы
F (х),
F (х) — если р (х) то х иначе / (F (g (х)), F (Л (г))),
которая не транслируется в стандартную схему, не существует
и эквивалентной счетчиковой схемы. Предоставляем читателю
убедиться самостоятельно, что доказательство теоремы 8.2 пол-
ностью проходит и для случая счетчиковых схем. В обоих случаях
причина невозможности транслировать эту схему одна и та же —
память конечна как в стандартных, так и в счетчиковых схемах. Q
Теорема 9.3. Класс счетчиковых схем и класс рекурсивных
схем не сравнимы по мощности.
Доказательство. Факт существования схем 59<5 и 58е3
(теоремы 9.1 и 9.2) непосредственно доказывает утверждение тео
ремы.
Задание 9.3.
А. Транслируйте в схему с одним счетчиком рекурсивную схему
из задания 8.1 А.
Б. Транслируйте рекурсивную схему 5в,6 из задания 8.1Б в счетчнко-
вую схему.
207
2.2. Счетчиковые и стандартные схемы.
Теорема 9.4. Класс счетчиковых схем строго мощнее
класса стандартных схем.
Доказательство. <5₽(с)^5₽по определению класса
У (с).
Счетчиковая схема 6'в 5 (см. рис. 9.3) не имеет эквивалентной
рекурсивной схемы. Для нее не может существовать и эквива-
лентной стандартной схемы, так как в противном случае суще-
ствовала бы (в силу теоремы 8.1) эквивалентная рекурсивная
схема. Следовательно, неверно, что У У (с), и класс У (с)
строго мощнее класса У. | I
Доказанная теорема констатирует тот факт, что имея в своем
распоряжении любое число счетчиков, мы получаем возможность
конструировать схемы более мощные, чем стандартные. Однако
известно, что добавление к базису стандартных схем лишь одного
счетчика не приводит к такому эффекту. Плейстед установил, что
класс схем У (1с) равномощен классу стандартных схем (130].
К сожалению, мы не можем изложить здесь доказательство этого
утверждения из-за его сложности. Более просто устанавливается
следующий результат, который сразу же вносит ясность в «проб-
лему числа счетчиков».
Теорема 9.5. Классы У {с) и У (2с) равномощны.
Доказательство. У(с)> У (2с) по определению.
Пусть схема S из класса У (с) содержит п счетчиков сп са, . . .
. . ., cf, . . ., сп. Упорядочим эти счетчики и каждый набор длины
п значений этих счетчиков кодируем взаимно однозначно сле-
дующим значением одного счетчика с (значение счетчика с£ будем
обозначать (cj):
2[с,] X 3[г,] X ... X Не,] X . . .Хг?»1,
где г,- — i-е простое число в последовательности всех простых
чисел. Если в схеме S заменить все вхождения оператора ct : =
:= Ci + 1, 1 <1 i n на оператор с : = с X rt, все вхождения
оператора ct с,- — 1 — на с : = c/rt и все вхождения предиката
ct = 0 — на с mod г, = 0, то получим счетчиковую схему, экви-
валентную схеме $. Построенную схему можно преобразовать
в счетчиковую схему из класса У (2с), что предлагалось сделать
самостоятельно в задании 9.2. Следовательно, У (2с) У (с),
откуда и из У (с) У (2с) получаем, что классы У (с) и У (2с)
равномощны. Q
Таким образом, необходимо два счетчика, чтобы достичь мощ-
ности полного класса счетчиковых схем.
2.3. Счетчиковые и магазинные схемы.
Теорема 9.6. Класс счетчиковых схем транслируем в класс
магазинных схем, т. е. У (М) У (с).
Доказательство. Принцип трансляции счетчиковых
схем в магазинные достаточно прост. Каждый счетчик с в исход-
208
ной счетчиковой схеме заменяется магазином Мс. Кроме того,
вводится одна дополнительная переменная х (на все счетчики) и
одна константа а. Переменной х сразу же после инструкции
старт присваивается константа: х := а. Каждое вхождение любого
из трех операторов над счетчиками заменяется оператором над
соответствующим магазином по следующим правилам:
оператор с z— с + 1 заменяется на Мо := х;
оператор с : = с — 1 — на х : — Мс‘,
оператор с = 0 — на 7ИС = 0.
Таким образом, магазин Мс имитирует работу счетчика: при-
бавлению единицы к счетчику соответствует увеличение «длины»
магазина на единицу; вычитанию единицы — уменьшение длины
магазина на единицу; когда значение счетчика равно 0, соответст-
вующий магазин пуст. Поэтому при выполнении интерпретиро-
ванных схем (исходной счетчиковой и построенной магазинной)
текущему значению счетчика, равному п, соответствует состояние
магазина (а, а,. . ,,а). Эквивалентность обеих схем очевидна. Д
п
Вопрос о трансляции магазинных схем в счетчиковые отложим
до п. 2.6 этой главы, где убедимся, что такая трансляция невоз-
можна, и сформулируем соответствующую теорему (теорему 9.14).
2.4. Магазинные схемы и схемы с массивами.
Теорема 9.7. Класс схем с массивами транслируем в класс
магазинных схем, т. е. & (М) & (А).
Доказательство. Прежде всего, все счетчики в схеме
с массивами S заменяются на магазины так, как это делалось
в доказательстве теоремы 9.6. Каждый массив А в схеме S заме-
няется парой магазинов Ма, Ма и переменной иА, а операторы
над массивами замещаются фрагментами магазинных схем. На
рис. 9.4, а показан фрагмент, замещающий оператор А [ с] := у,
на рис. 9.4, б — фрагмент, замещающий оператор у := А [с];
на рис. 9.4, в, г дана расшифровка совпадающих подфрагментов
обоих фрагментов. Переменные х, и а и z — новые переменные
в построенной магазинной схеме S', они не входили в память
схемы S. Переменная х играет ту же роль, что и в предыдущей
теореме, т. е. хранит константуч заполняющую «магазины-счет-
чики». Предполагается, что начальное значение переменной иА
при любой интерпретации I равно I (Л), эта переменная не меняет
своего значения при выполнении программы (S', 7). Переменная
z служит для организации обмена между магазинами МА и МА’-
Эквивалентность схем S и S' достаточно очевидна после со-
держательного анализа правил замены счетчиков, массивов и опе-
раторов над массивами, магазинами и показанными на рис. 9.4
фрагментами магазинных схем. При преобразовании схем с мас-
сивами в магазинные схемы использован довольно естественный
и понятный программистский прием. Магазин Ма отводится для
хранения состояний массива А, причем первый элемент состояния
всегда находится на верхушке магазина. Выборка элемента А [с]
в. Е. Котов, В. К. Сабельфельд 209
Перекачка
из Мд в Мд
элементов
А[0],... ,А[с-1]
Обратная
перекачка _
из Мд в Мд
а
Рис. 9.4. Замена операторов над массивами фрагментами магазинных схем:
л — фрагмент, заменяющий А [с] := у; б — фрагмент, заменяющий у :=
:= А [с]; в — перекачка из МА в МА, г — обратная перекачка из м'А в М4
из массива имитируется «перекачкой» элементов А [0], А [1], . . .
. . ., А [с — 1] из магазина МА в магазин МА, пока нужный эле-
мент не окажется верхушкой магазина МА. В зависимости от
того, требуется ли переслать этот элемент в переменную у или
на его место записать значение переменной у, используются соот-
ветствующие операторы над магазинами. Затем осуществляется
обратная перекачка из МА в МА для завершения формирования
нового «состояния массива». По определению, состояния масси-
ва — бесконечные последовательности элементов из области ин-
терпретации, а состояния магазинов — конечные последователь-
ности (перед выполнением программ (5, Z) и (S', I), где J —
210
произвольная интерпретация, состояние массива А — бесконеч-
ная последовательность, состоящая из одного и того же элемен-
та I (А), а все магазины в (S', I) пусты). Здесь на помощь прихо-
дит переменная и а, хранящая значение I (Л). Фрагменты мага-
зинной схемы на рис. 9.4 устроены таким образом, что магазин
МА на каждом шаге выполнения программы (S', А) хранит на-
чальную часть состояния массива А, длина которой равна макси-
мальному к данному моменту порядковому номеру элемента, вы-
биравшегося из массива или засланного в массив. Если же при
очередной имитации выборки из массива или засылки в массив
порядковый номер элемента больше глубины магазина (т. е. числа
элементов в его текущем состоянии), то используется перемен-
ная иА и механизм подгонки длин состояний при перекачке из
МА в МА (см. рис. 9.4, в, проверка Мд = 0 и последующая пере-
сылка Мд := uA). [j
Теорема 9.8. Класс магазинных схем транслируем в класс
схем с массивами, т. е. (Л) cf (М).
Доказательство. Алгоритм трансляции магазинных
схем в схемы с массивами проще, чем обратное преобразование.
Каждый магазин заменяется массивом Ам и счетчиком см, а опе-
раторы над магазинами замещаются следующими фрагментами
схем с массивами:
I: х : = М на 7с, заменяется на фрагмент
I: х : = Ам 1c.mL см • — см — 1 на Zc;
I: М : = х на к,— на фрагмент
I: см := см + 1, Ам 1см] := х на к;
I: если М = 0 то к иначе т — на оператор
I: если с — 0 то к иначе т.
Здесь также используется обычный программистский прием.
Элементы dx, d2, . . ., dn состояния магазина М становятся эле-
ментами состояния массива Ам с теми же порядковыми номерами.
Нулевой элемент состояния массива и элементы с номерами боль-
ше п равны I(Л) или содержат так называемый «мусор». Значение
счетчика в процессе выполнения построеннной интерпретиро-
ванной схемы с массивами указывает на «верхушку магазина»
в массиве Лм. Q1
Теорема 9.9. Классы & (А) и (М) равномощны.
Доказательство. Прямое следствие из теорем 9.7
и 9.8. □
Задание 9.4. Покажите, что классы S’ (Л) и S’ (1Л) равномощны.
2.5. Магазинные и рекурсивные схемы. В этом разделе мы по-
кажем, что рекурсивные схемы транслируются в магазинные,
и это не является неожиданностью, так как почти все практичес-
кие методы реализации рекурсии основаны на применении мага-
зинной (или стэковой) памяти.
8*
211
В предыдущей главе установлено, что рекурсивные схемы транс-
лируются в схемы с процедурами. Поэтому достаточно продемон-
стрировать транслируемость класса if (Р) в класс магазинных
схем. Описываемый алгоритм трансляции включает как первый
этап трансляцию схем с процедурами в класс схем с одним ма-
газином, но эти схемы обогащены дополнительным средством,
а именно — метками-символами и специально выделенной пере-
менной, значениями которой являются метки. Таким образом,
метки-символы могут запоминаться, в том числе в магазине,
и затем использоваться в переходах. Этот этап трансляции отсле-
живает практические методы реализации рекурсии. На втором
этапе осуществляется освобождение магазинной схемы от меток,
и результатом является схема из класса if (lA/j.
Промежуточная магазинная схема с метками принадлежит классу
if (IM, L). Схемы из этого класса — схемы с одним магазином и
со следующими особенностями:
а) инструкции не имеют числовых меток, но могут помечаться
метками-символами;
б) базис класса содержит выделенную интерпретированную
переменную, областью значений которой является множество
меток {Zlt L2, . . ., Lm};
в) все переходы в инструкциях присваивания и условных
операторах — метки-символы или выделенная переменная;
г) кроме того, выделенная переменная w может входить толь-
ко в специальные операторы засылки метки (w := L) и в опера-
торы над магазином (М := w, w := М).
Смысл использования меток-символов, выделенной перемен-
ной и модифицированных операторов при выполнении интерпре-
тированных схем из класса if (IM, L) не требует специальных
пояснений.
Лемма 9.1. Классы рекурсивных схем и схем с процедурами
транслируемы в класс if (IM, L).
Доказательство. Рекурсивная схема транслируется
в схему с процедурами посредством алгоритма из теоремы 8.6.
Пусть Z = {zj, z2, . . zj — множество переменных, получаю-
щееся в результате объединения памяти главной схемы и памяти
всех схем процедур исходной схемы с процедурами. Каждая
инструкция вызова
k : z := (уи . . ., уп) на т
заменяется следующим фрагментом:
к : М := Zj, . . ., М zt — запоминание состояния памяти
перед переходом к процедуре;
w := L |
} — запоминание метки возврата;
М : — w]
•= Уъ • • ; Уп иа — передача аргументов в за
головок процедуры и переход к процедуре;
212
L : z:= t на m — переменной z присваивается вычисленное
значение функции, где
М — магазин;
w — выделенная переменная для хранения меток-символов;
t — новая переменная, t Ejt Z;
L — метка-символ возврата.
Заголовок каждой схемы процедуры Ft fo, . . ., хп) и оператор
етарт элиминируются, а метка 1 в теле процедуры заменяется
меткой Lyt. Оператор стоп (0 в теле каждой схемы процедуры
заменяется фрагментом
t v,
w := М,
zt := М, . . zr := М на w.
Результат такого преобразования — магазинная схема с одним
магазином М и метками-символами, которые используются наря-
ду с метками-числами. Очевидным способом метки-числа можш>
элиминировать, заменив их в переходах метками-символами.
Полученная схема SL принадлежит классу У (IM, L). В том,
что схема и исходная схема эквивалентны, убеждает содер-
жательный анализ алгоритма трансляции. Магазин М может
хранить любое число меток-символов и последовательных набо-
ров значений переменных из Z. При рекурсивном вызове «старые»
значения этих переменных запоминаются в магазине вместе
с меткой возврата, указывающей контекст вызова, т. е. следующий
оператор, на который следует вернуться после того, как будет
получено значение вызываемой функции. Когда значение функ-
ции найдено, восстанавливается контекст и значения переменных
в этом контексте. Магазин оказывается пустым после возврата
в главную ‘ схему. Q
В качестве примера приведем магазинную схему с метками
5вв, эквивалентную рекурсивной схеме 58Л (см. пп. 1.2 и 2.3
предыдущей главы) и схеме с процедурами 58Д4 (см. п. 4.1 той же
главы). Напоминаем, что для этих схем не существует эквивалент-
ных стандартных и счетчиковых схем.
58еЯ: F (х),
F (х) — если р (х) то х иначе / (F (g (х)), F (Л (ж))),
(старт (х),
1: У := F (х),
2: етоп (у)),
F (х) — (старт,
1: если р (х) то 2 иначе 3,
2: v := х на 8,
3: z := g (х),
4: z : - F (z),
5: и h (х),
6: и : = F (и),
7: v ;= / (z, и),
8: стоп (0).
213
Условимся в примерах изображать последовательность опера-
торов М := у2, . . М := уг одним «оператором групповой за-
писи в магазин»: М (уг, . . уг), а последовательность опера-
торов yr := М, . . ут := М — одним «оператором групповой
выборки из магазина»: (г/п . . yr) := М. Аналогично, (хг, . . .
. . хг) := (У1< - - -, уг) — сокращенная запись «последователь-
ной групповой пересылки» хх := уъ . . хт := уг.
SB6: (старт (у, х, z, и, v),
М := (у, х, z, и, v),
w := Lo,
М := w,
х х на Lf,
У := t,
стоп (у),
LF: если р (х) то L1 иначе Л2,
Li. v := х на L&,
L2: z g (x),
M := (y, x, z, u, v),
w := L3
M := w,
x := z на Lp,
L3: z := t,
и := h (x),
M := (y, x, z, u, v),
w := L4,
M := w,
x и на Lp,
L^: и := t,
v "= f (z, u),
L6: t := v,
w :== M,
(v, u, z, x, у) := M на w).
Лемма 9.2. Пусть S — схема с процедурами, I — интер-
претация и во время выполнения программы (S, Г) некоторая про-
цедура вызывается рекурсивно, т. е. после некоторого шага началь-
ный оператор тела этой процедуры выполнился п раз (п 1),
а заключительный оператор — ни разу. Тогда для того, чтобы
заключительный оператор тела этой процедуры выполнился п
раз, необходимо, чтобы некоторый условный оператор р (хг, . . .
. . ., xt) выполнился дважды при разных состояниях памяти W и
W и Z(p)(Wi)...............W (xt)) ф I (р) (Ж Сч).......IF fo))-
Доказательство. Пусть кг, к2, . . ., кт — последова-
тельность меток инструкций тела процедуры, выписанная в том
порядке, в котором эти инструкции выполняются в программе
(5,1), причем fcj — 0 — метка начального оператора тела про-
цедуры, выполненного первый раз, кт = 0 — метка того же опе-
ратора, выполненного п-й раз, и в этой последовательности нет
ни одного вхождения метки заключительного оператора тела этой
процедуры. Далее, пусть к{, к2, . . к'г — последовательность
214
меток операторов тела процедуры, где fcj == 0 — метка n-го вы-
полнения начального оператора тела, а к'г — метка первого вы-
полнения заключительного оператора тела процедуры.
Если г т, то к'г =/= кт, так как к'г — метка заключительного
оператора, а кт не может метить заключительный оператор. Если
г т, то кт =# кт, так как кт — 0, а к'т не может метить началь-
ный оператор тела процедуры. В обоих случаях видно, что начала
последовательностей меток совпадают (по крайней мере, /q =
= к$, но затем последовательности различаются. Это значит, что
существует такое г, 1 < i < min (т, г), что kt — ki, но ki+l ф
Ф к'м. Но это может быть только в том случае, если к, и — два
вхождения метки одного и того же условного оператора, причем
результаты его выполнения в первом и во втором случае раз-
личны. Q
Лемма 9.3. Если S — приведенная схема с процедурами
(см. п. 4.2 гл. 8), то для любой интерпретации I, прежде чем
выполнится хотя бы один раз заключительный оператор в теле
любой процедуры, дважды вычисляется некоторый, один и тот же,
предикат I (р) при двух различных наборах аргументов (dn . . .
. . ., di) и (d[, . .., di), причем I(p)(du . . dt) =£ I (р) (di, . . .
• di).
Доказательство. Так как схема 5 получена частичной
трансляцией некоторой схемы с процедурами, в главной схеме
есть фрагменты-копии всех тел схем процедур и все оставшиеся
в главной схеме вызовы — рекурсивные вызовы. Поэтому перед
выполнением заключительного оператора в теле любой процедуры
обязательно дважды вычислится один и тот же предикат, причем
его значения будут различны (см. лемму 9.2). Q
Лемма 9.4. Магазинные схемы из класса cf (IM, L), по-
лученные трансляцией рекурсивных схем или схем с процедурами,
транслируемы в магазинные схемы из класса Sf (1Л1).
Доказательство. Пусть магазинная схема с мет-
ками получена из рекурсивной схемы или схемы с процедурами
с помощью алгоритма трансляции, описанного в доказательстве
леммы 9.1. Пусть М— магазин в схеме SL, w — единственная
выделенная переменная, значениями которой являются метки Ьг,
L2, • . ., Lm. Магазинная схема S из класса cf (iM), эквивалент-
ная схеме SL, строится из к + 1 вспомогательной схемы из класса
«У (iM), где к — число предикатных символов в схеме SL. Среди
этих вспомогательных схем есть схема 50, которую Грис и Кон-
стебль (92] назвали локатором, и схемы S2........Sk, назван-
ные ими рj-имитаторами схемы SL, 1 <1 i к. Схема ргимита-
тор эквивалентна схеме SL на множестве всех тех интерпретаций
Z, в которых I (р) обладает некоторым заданным свойством (о нем
речь пойдет ниже). Схема локатор So обнаруживает в схеме Sl
предикатный символ, который для данной интерпретации I об-
ладает заданным свойством, а если такого предикатного символа
£15.
не найдется, то локатор игнорирует рг-имитаторы, так как в этом
случае он сам способен повторить вычисления программы (5^, 7),
не используя переменную w.
Построение p-и митатора. Сначала покажем, как
строится р-имитатор схемы SL для произвольного предикатного
символа р. Для простоты полагаем, что р — одноместный символ.
Переменной w из схемы SL в р-имитаторе соответствует т
переменных wx, w2, . . wm, где т — число меток в схеме SL.
Преобразование схемы в р-имитатор осуществляется следующим
образом:
а) каждый оператор присваивания w := Lt, 1 i <1 т, за-
меняется последовательностью операторов w1 а, . . ., -—а,
wt :== Ь, wi+1 := а, . . ., wm := а, где а и Ь — некоторые констан
ты, добавляемые в базис схемы SL;
б) каждый оператор w : = М заменяется последовательностью
операторов wm := М, . . и\:~ М;
в) каждый оператор М := w заменяется последовательностью
операторов М := wx, . . ., М := wm;
г) каждый оператор присваивания х := т на w заменяется
фрагментом (рис. 9.5), где — метка оператора петля, нового
оператора, добавляемого в р-имитатор.
Таким образом, каждая метка оказы-
вается закодированной словом длины т
в алфавите {а, Ь), и смысл описанных
замен операторов становится понятным.
Построение р-имитатора схемы Sr. для
« местного предикатного символа р осу-
ществляется точно так же, но вместо кон-
стант а и b используются 2п констант:
и Соответственно
увеличивается число переменных и опера-
торов присваивания в правилах замены.
Отметим, что в схеме Si использование
переменной w ограничено: она не входит
в распознаватели и взаимодействует с ма-
газином так, что ей никогда не может быть
присвоено значение, отличное от меток из
(Zlf L2, . . ., Lm}. Поэтому несложно убе-
диться, что предлагаемое преобразование
схемы Sl в р-имитатор дает схему из
У (1Л7), эквивалентную схеме Si, но с одним ограничением: схе-
ма Sl и ее р-имитатор эквивалентны только на тех интерпрета-
циях 7, в которых 7 (р) (7 («)) = 0 и I (р) (/ (ft)) = 1.
р-имитатор схемы 5в в изображен на рис. 9.6. Так как в схеме
5в,6 переменная w запоминает только три метки Lo, Ls и Lit мы
упростили пример, не включив в область значений этой перемен-
ной другие метки.
Построение локатора. Чтобы исключить упо-
мянутое ограничение, используется локатор. Локатор So --
Рис. 9.5. Фрагмент
р-имитатора, заменяю-
щий инструкцию г т
на w.
216
СТАРТ (у, J, Z,U,V )
Рис. 9.6. р-имитатор схемы 5,.в
это схема из класса (IM), задача которой — для любой интерпре-
тации I обнаружить в схеме SL предикатный символ р<п), 1
«С i fc, и пару наборов значений аргументов (dlt . . dn) и
(<£v • dn) такие, чтобы I (р;) (du dn) =/= I (Pi) (d'u . . dn).
Найденный предикатный символ и пара наборов значений аргу-
ментов будут в дальнейшем использованы в имитаторе вместо
рассмотренного выше произвольного предикатного символа р и
констант.
Более точно, локатор 50 для схемы Sl, построенной по схеме
с процедурами, обладает следующими свойствами:
а) если для некоторой интерпретации I в протоколе выпол-
нения программы (5t, I) нет повторного вхождения какого-либо
предиката I (Pl) с разными вычисленными значениями, то про-
грамма (50, I) останавливается с результатом val (50, /), если и
только если останавливается программа (5/,, I), причем
val (Л’о,1) val (SL, I);
б) если для некоторой интерпретации I предикат I
вычисляется дважды при наборах dlt . . ., dn и d'u • . .« <4,
а I (Pi) (db . . dn) = 0 и / (Pi) (du . . <C) = i, то в локаторе
•S, выполняются следующие действия:
9 В. Е. Котов, В. К. Сабельфельд 217
(1) добавленным в локатор переменным vOi, . . vOn присваи-
ваются значения, соответственно: dlt . . dn;
(2) добавленным в локатор переменным vbl, . . vbn присваи-
ваются значения, соответственно: di, . . ., dn;
(3) осуществляется переход к выполнению добавленного в ло-
катор оператора Lm+i: петля, где Lm+i — новая метка.
Локатор для схемы Sl строится следующим образом (для про-
стоты все предикаты рг, р21 . . ., рк в схеме Sl считаем одномест-
ными, обобщение делается очевидным способом):
а) по рекурсивной схеме или схеме с процедурами, из которых
получена схема Sl, строится приведенная схема с процедурами
(см. гл. 8, п. 4.2);
б) приведенная схема транслируется в схему SL с помощью
алгоритма из леммы 9.1, и ясно, что схема Sl эквивалентна схе-
ме «Sl;
в) каждый условный оператор если р, (х) то иначе £а за-
меняется фрагментом, показанным на рис. 9.7;
Рис. 9.7. Фрагмент локатора,
заменяющий условный опера-
тор
г) из полученной схемы удаляются
все операторы, содержащие магазин
и выделенную переменную w, и затем
все операторы, из которых нельзя
попасть к заключительному операто-
ру, а «висячие» дуги присоединяются
к оператору петли.
Построенный таким образом лока-
тор принадлежит классу if и дейст-
вительно обладает теми свойствами,
которые были для него запланирова-
ны. Свойство а) обеспечивается тем,
что, в случае отсутствия в процессе
выполнения программы (Sl, I) по-
вторных вхождений предикатного
символа Pi с разными значениями
I (Pi) (Ф и I (р^) (d'), выполнение программы (50,1) протекает
так же, как и выполнение программы (SL, /). При этом исклю-
чение из схемы магазина и операторов с переменной w не влияет
на работу программы (50,'7), так как в этой программе нет повтор-
ных рекурсивных вызовов функций и, следовательно, нет необ-
ходимости запоминать контекст возврата (см. лемму 9.3). Свойство
б) обеспечивается тем, что как только для некоторого символа pt
будет обнаружено несовпадение I (р^) (d) Ф I (pt) (d'), произой-
дет переход на оператор Ьт+с. петля. Отсутствие магазина, пере-
менной w и использующих их операторов не влияет на поведение
локатора и в этом случае, так как прежде чем понадобится осу-
ществить возврат к месту вызова, обязательно обнаружится по-
вторное вхождение pt с отличным от предыдущего значением пре-
диката I (р^ (см. лемму 9.3) и осуществится переход к оператору
Lm+i' петля. При этом значения W (va) и W (vb) переменных va
218
стлгтсу.Кд,^)
Рис. 9.8. Локатор для схемы £,.«
я v* таковы, что
I(Pt)(W(va)) =0, I(Pi)(W(vb)) = i.
Локатор для схемы 5вл изображен на рис. 9.8. Он построен
по приведенной схеме с процедурами, полученной частичной транс-
ляцией схемы <Sg>u (см. также доказательство леммы 9.1), а при-
веденная схема имеет вид
(старт (х),
1: хх := х,
2: если р (xt) то 3 иначе 4,
3: :== хх на 9,
4: гх :== g (х,),
5: z, :== F (zj,
6: ux : = h (xx),
7: := F (ux),
8: Vi = / “i).
9: у := vx,
10: стоп (у))
F (x) = (старт,
1: если p (x) to 2 иначе 3,
219
2: v х на 8,
3: z : = g (ж),
4: z : = F (z),
5: и := h (x),
6: и := F (w),
7: v := / (z, iz),
8: стоп (v)).
Сборка схемы 5. Результирующая схема S из класса
2? (1Л7) собирается из локатора и р,-имитаторов схемы Sl.
Схема 5 начинается локатором 50, за которым следуют р;-имита-
торы Sx, Sa, . . ., Sk, где к — число предикатных символов в схе-
ме Sl- Однако как в локаторе, так и в р;-имитаторах делаются из-
менения, превращающие эту последовательность схем в одну
схему 5. Для каждой переменной у, из памяти схемы Sl, не счи-
тая выделенную переменную w, добавляется новая переменная щ,
и локатор начинается серией пересылок, назначение которых —
запомнить начальное состояние памяти, которое, возможно, по-
надобится для р2-имитатаров:
(старт (уь у2, . . .), и, := yt, Ug := уг, . . .).
В каждом р{-имитаторе оператор старт заменяется последователь-
ностью операторов:
Lm+t' Уг ми Уа иг, • • •»
а из локатора удаляются все операторы Lm+i: петля.
Таким образом, схемы 5lt S2, . . ., Sk оказываются присоеди-
ненными к схеме So. Далее, в каждом р,-имитаторе константы а и bf
где бы ни встречались, заменяются на переменные va и, соответ-
ственно, из локатора. (Эти переменные и переменные яв-
ляются единственными «глобальными» переменными схемы S.)
Построенная магазинная схема 5 из класса & (17И) эквива-
лентна схеме Sl. Действительно, для любой интерпретации /
первым начинает выполняться локатор. Если в процессе его вы-
полнения не встретился дважды один и тот же предикатный сим-
вол с разными значениями предиката, то выполнение программы
(S, I) происходит точно так же, как и программы (Sl, /), если
из нее удалить все операторы с переменной w. Выше мы видели,
что в этом случае программы (50,1) и (Sl, I) или обе зацикливают-
ся, или останавливаются с одинаковыми результатами. Если же
встретилось повторное вхождение предикатного символа pt со
значением предиката, отличным от предыдущего, то осуществляет-
ся переход на начало />,-имитатора. При этом значения перемен-
ных va и vb сохраняются и восстанавливается начальное состоя-
ние памяти. С этого момента можно забыть о том, что выполнялся
локатор, и рассматривать выполнение программы (S, /) как вы-
полнение программы («Sj, I), в которой значения IF (по) и W (vb)
переменных va и vb не меняются, а предикат I (pt) дает разные
значения: I (pt) (IF (ц>)) = 0 и / (/><) (W (vb)) = 1. Как уже от-
мечалось, программа (5it Z) эквивалентна программе (Sl, 7). Г~1
220
Теорема 9.10 (Грис—Констебль). Классы рекурсивных
схем и схем с процедурами транслируемы в класс магазинных схем,
в частности, в класс схем с одним магазином, т. е. & (К)
< У (1М) и У (Р)^& (Ш).
Доказательство. Алгоритм трансляции состоит в по-
следовательном применении преобразования рекурсивной схемы
в схему из класса & (IM, L) (см. лемму 9.1) и преобразования
полученной схемы в схему из класса (lAf) (см. лемму 9.4). Q
Отметим, что предложенный алгоритм трансляции рекурсивных
схем в магазинные дает схемы, в которых используются только
два оператора над магазином — оператор записи и оператор
выборки. Следовательно, для реализации рекурсии достаточно
более узкого класса магазинных схем, а именно — класса
<9* (1ЛГ) схем с одним магазином и без оператора проверки пусто-
ты магазина. Установлено [87], что классы 5? (Я), & (Р), & (1М)
и (12И) равномощны.
Задание 9.5.
А. Транслируйте в магазинные схемы рекурсивные схемы 58Л1 (см. за-
дание 8.6), У8.1 и Sg>2 (см. гл. 8, и. 1.2).
Б. Проверьте, упрощаются ли полученные схемы, если использовать
условный оператор проверки пустоты магазина.
Теорема 9.11. Класс магазинных схем не транслируем
в классы рекурсивных схем и схем с процедурами.
Доказат е л ь с т в о. Согласно теореме 9.1 существуют
счетчиковые схемы, которые нельзя транслировать в рекурсивные.
Но счетчиковые схемы транслируются в магазинные (теорема 9.6).
Если допустить, что любую магазинную схему можно трансли-
ровать в рекурсивную, то возникает противоречие. [3
Теорема 9.12. Класс магазинных схем строго мощнее клас-
са рекурсивных схем и схем с процедурами, т. е. У (М) > (Я)
и &(№) >&>№).
Доказательство. Следствие из теорем 9.3, 9.6 и 9.10. Г~1
2.6. Сравнительная схематология. Для того чтобы получить
полную картину соотношений между рассматриваемыми классами
схем, остается сравнить по мощности классы (Я) и (А),
& (с) и & (М), & (с) я У (А), & я& (М), яУ (А).
Теорема 9.13. Класс схем с массивами строго мощнее
классов рекурсивных схем и схем с процедурами, т. е. & (A)
><У(Я) и У (А) > (Я).
Док азательство. Так как класс & (М) строго мощнее
классов <5^ (Я) и У (Р) (см. теорему 9.12), а классы <У* (А) и 5” (М)
равномощны (см. теорему 9.9), класс & (А) строго мощнее класса
(Я) и класса & (Я). Q
Теорема 9.14. Класс магазинных схем строго мощнее
класса счетчиковых схем, т. е. У (М) > & (с).
221
Доказательство, £f (М) >> & (с) по теореме 9.6.
Если предположить, что классы & (М) в if (с) равномощвы,
то окажется (см. теорему 9.12), что класс У (с) строго мощнее
класса (/?), а это противоречит теореме 9.3. Q
Теорема 9.15. Класс схем с массивами строго мощнее клас-
ва счетчиковых схем, т. е. & (А) > if (с).
Доказательство, if (Л) if (с) по определению.
Если предположить равномощность классов ef (Л) в & (с), то
окажется (теорема 9.13), что класс (с) строго мощнее класса
8 (/?), а это противоречит теореме 9.3. □
Теорема 9.16. Класс магазинных схем, строго мощнее
класса стандартных схем, т. е. £f (М) > <У.
Доказательство. Следует из теорем 9.15 и 8.3. Q
Теорема 9.17. Класс схем с массивами строго мощнее
класса стандартных схем, т. е. У (Л)
Доказат е л ь с т в о. Следует из теорем 9.15 и 9.4. [~|
Диаграмма на рис. 9.9 дает полную информацию о сравнитель-
ной мощности классов схем &, & (с), & (/?), if (Р), Sf (М) в У (Л).
Стрелки указывают на возможность транслировать один класс
схем в другой, номера около стрелок — ссылки на теоремы.
Рве. 9.9. Сраввеиие полных чистых классов схем программ
Диаграмма на рис. 9.9 показывает, что классы магазинных
схем и схем с массивами являются универсальными в том смысле,
что схемы из любого класса можно транслировать в схемы, обо-
гащенные магазинами или массивами. В то же время, из этой диа-
граммы не видно, какое минимальное количество дополнительных
средств необходимо, чтобы достичь выразительной мощности того
или иного класса. В частности, в диаграмме нет информации о том,
какой класс является «минимальным универсальным», т. е. явля-
ясь универсальным, использует минимум дополнительных средств.
Диаграмма на рис. 9.10 дает частичный ответ на зти вопросы.
222
Рис. 9.10. Минимальные классы, равномощные полным классам
Чтобы не загромождать рисунок избыточной информацией, не-
которые стрелки, указывающие транзитивную транслируемость,
опущены.
Введены дополнительные обозначения: (п), где п — 1, 2, . . .,
обозначает класс стандартных схем, базис которого содержит
конечное число переменных, не большее п; (Л/) — класс ма-
газинных схем, в которых отсутствует условный оператор про-
верки пустоты магазина; (R, lu) — класс линейных унарных
рекурсивных схем; (R, rlu) — класс праволинейных унарных
рекурсивных схем; (R, п) — класс рекурсивных схем с п пере-
менными. Около стрелок, указывающих не обсуждавшиеся в этой
главе результаты, поставлены ссылки на литературу.
Диаграмма не требует специальных комментариев, за исклю-
чением одного: остается открытым вопрос о мощности класса схем
с двумя магазинами (2М). Существует гипотеза (87J, что этот
223
класс не является универсальным, хотя и «близок» к универсаль-
ным классам (iM, 2с), (ЭМ), if (1Л).
После того, как построена диаграмма сравнительной мощности
разных классов схем программ, естественно возникает вопрос,
какие свойства тех или иных программных средств (и методов
программирования) ответственны за положение соответствующего
класса схем в иерархии классов. Анализ доказательств позволяет
выделить следующие интуитивные факторы, определяющие мощ-
ность данного класса.
1. Объем памяти. Стандартные схемы имеют ограниченную
память. Возрастание числа переменных в стандартных схемах
увеличивает их мощность, но в ограниченных пределах. Счет-
чиковые схемы имеют также ограниченную память. Поэтому стан-
дартные и счетчиковые схемы, свободно интерпретированные, не
могут строить «слишком длинные» термы. Переход к рекурсивным
схемам, имеющим неограниченную «внутреннюю» память, введе-
ние магазинов и массивов, емкость которых не ограничена, сни-
мают этот недостаток стандартных и счетчиковых схем.
2. Гибкость управления. Добавление к стандартным схемам
счетчиков (более одного) дает дополнительную возможность кон-
тролировать ход выполнения интерпретированных схем и, тем
самым, удается более оперативно организовать «синхронизацию»
циклических фрагментов, прекращение выполнения и т. п.
Магазины и массивы сочетают возможности не ограниченной
памяти с возможностями счетчиков (магазины могут моделировать
счетчики, схемы с массивами содержат счетчики). Поэтому не уди-
вительно, что if (М) и if (А) — самые мощные из рассмотренных
классов. (Заметим, что если одного массива достаточно, чтобы
класс стал универсальным, одного магазина мало, так как он мо-
жет моделировать лиши один счетчик.)
Краткий обзор и комментарии
Работы Стронга (138, 139], Патерсона и Хьюитта [129] по ис-
следованию трансляции рекурсивных схем в стандартные и, в част-
ности, доказательство того факта, что класс рекурсивных схем
строго мощнее класса стандартных схем, а добавление счетчиков
увеличивает выразительные возможности схем, стимулировали
сравнительные исследования различных классов схем, полученных
обогащением стандартных и рекурсивных схем дополнительными
программными конструкциями. Достаточно полная сводка ре-
зультатов этих исследований со ссылками на работы, в которых
они были получены, содержится в диаграммах на рис. 9.9 и 9.10.
Из последней диаграммы видно, что наиболее активно изучались
магазинные схемы, и здесь еще работа ие завершена (открыта
проблема двух магазинов). В литературе рассматривались и дру-
гие обобщения стандартных и рекурсивных схем.
При доказательстве транслируемое™ классов if (R) п if (Р)
в класс if (М) использовались в качестве промежуточных схем
224
магазинные схемы, в которых есть возможность запоминать метки.
Лемма 9.4 говорит о том, что классы (IM, L) и if (iM) равно-
мощны. Более общин факт установлен Грисом и Констеблем [92]:
классы if (М), if (Л), if (М, L) и if (Л, L) равномощны, но пары
if (М), if (М, L) и if (Л), if (Л, L) не являются эффективно рав-
номощными, а именно: хотя для любой схемы из класса if (Л, L)
(или if (М, L)) существует эквивалентная схема в классе if (Л)
(или if (М)), эффективно транслировать первую во вторую нельзя.
Грис и Констебль [92], а также Браун и Шымански [87] обо-
гащали схемы маркерами. Каждая схема имеет конечное множе-
ство символов-маркеров {т1, та, . . ., тп}, интерпретированные
переменные для запоминания маркеров и два оператора над мар-
керами:
v := т — оператор запоминания маркера,
v — т — оператор проверки совпадения маркера, хранимого
в переменной v, с маркером т.
Показано, что класс if (Л, L) и класс if (Л, т) (т. е. класс схем
с массивами и маркерами) равномощны. Добавление же маркеров
в стандартные и рекурсивные схемы не увеличивает, против ожи-
дания, мощности зтих классов, т. е. классы if и if (т) равномощ-
ны и классы if (/?) и (R, т) равномощны С другой стороны,
усиление двумагазинных схем из класса if (2М) маркерами дает
класс if (2М, т), который равномощен классу if (М).
Введение многомерных массивов не увеличивает мощности
класса if (Л) [87].
Чандра [88] рассмотрел стандартные схемы, обогащенные оче-
редями. Очередь — это потенциально бесконечная память типа
FIFO (First-In-First-Out — данное, записанное первым, выби-
рается первым), в то время как магазин — память типа FILO
(First-In-Last-Out — данное, записанное последним, выбирается
первым). Состояние очереди — конечный набор элементов dlt
dt, . . ., dn из области интерпретации. Над очередями определены
три оператора:
q х — запись в очередь q;
х :-= q — выборка из очереди q;
q — 0 — проверка пустоты очереди q.
Оператор записи в очередь q := х меняет состояние очереди du
da, . . ., dn на новое состояние da, da, . . ., dn, d, где d — текущее
значение переменной х. Оператор х := q меняет состояние оче-
реди dj, da, . . ., dn на состояние da, . . ., dn, a d1 становится зна-
чением переменной х. Установлено, что класс схем с очередями
if (q) и класс схем с массивами if (Л) равномощны. В частности,
равномощны классы if (1g) и if (1Л), поэтому класс if (1g) строго
мощнее класса if (IM), и это говорит о том, что очередь является
более мощным средством, чем магазин.
Понятно, что обогащение стандартных схем такими известными
конструкциями, как операторы цикла, условные операторы типа
если (логическое выражение) то (оператор) иначе (оператор)
225
или введение блочной структуры не добавляют новых возможно-
стей: любая схема из такого обогащенного класса легко транс-
формируется в стандартную. Существенно новыми свойствами об-
ладают стандартные или рекурсивные схемы, если их расширить
за счет добавления проверки равенства термов, что было сделано
Чандрой и Манной [88, 901. Прежде всего следует отметить, что
для классов схем, с равенством теряют силу теоремы о свободных
(эрбрановых) интерпретациях (см. § 3 гл. 4). Так, следующая
схема iSg.7 из класса стандартных схем с равенством зацикливается
при некоторых интерпретациях, а при некоторых останавливается:
(старт,
1: х := а,
2: если х = b то 4 иначе 3,
3: петля,
4: стоп (г)).
Однако при любой свободной интерпретации эта схема зацик-
ливается, т. е. она является пустой на множестве свободных
интерпретаций, но не пустой на множестве всех интерпретаций.
Такие схемы называются иеэрбрановыми. Существуют и эрбра-
новы схемы с равенством. Легко убедиться, что проблема, явля-
ется ли данная схема эрбрановой, не будет частично разрешимой.
Введение проверок равенства термов отменяет и многие другие
теоремы о свойствах классов схем. Так, в классе схем Янова с
проверками все главные проблемы становятся неразрешимыми.
Введение проверок равенства увеличивает мощность стандарт-
ных схем, так что класс (=) строго мощнее класса У [88]. На-
пример, для схемы 1$8Л не существует эквивалентной стандартной
схемы. Более того, как показал Чандра [88], любой нз рассмот-
ренных нами чистых классов слабее соответствующего класса,
обогащенного проверками равенства. При этом проверки равен-
ства оказываются дополнением, ортогональным к другим рас-
смотренным обогащениям. Например, & (с) > S, & (—)>
& (с> —) > У (с). но классы У' (с) и & (—) несравнимы по мощно-
сти. В силу этой ортогональности классы & (А, =) и & (М, =)
оказываются «более универсальными», чем классы У (Л) и If (М).
Следует отметить, что «надбавка мощности», которую дают про-
верки равенства, зависит от сложности допускаемых к проверке
термов. Грис и Констебль [92] показали, что добавление к схеме
с массивами проверок равенства термов типа х — у, где х и у —
переменные, дает класс схем той же мощности, но этот класс не
транслируем эффективно в класс У (Л). Харник [104] установил,
что класс & (iAf, 1с, —) имеет ту же мощность, что и классы (М)
и <У (Л), чего нельзя сказать о классе У (1М, =). В обоих случаях
подразумевается, что допустимы только проверки типа х — у.
Когда в п. 2.6 этой главы говорилось об универсальных клас-
сах схем как о классах, в которые транслируются все другие клас-
сы, имелось в виду то, что круг сравниваемых типов схем ограни-
чен теми, что рассматривались в этой книге. Но такое определе-
ние универсальности относительно, так как появление новых,
226
более мощных, классов меняет ситуацию. Были предложены «аб-
солютные» определения универсальных классов [139, 70, 104].
В частности, Трахтенброт [70J сформулировал постулаты, которые
должны выполняться при интуитивно разумных определениях
схем программ и классов схем, и продемонстрировал, что при со-
блюдении этих постулатов можно доказать, что действительно
существуют абсолютно универсальные классы схем, например,
класс <5^ (Л, т, =). Все упоминаемые в этой книге классы схем
удовлетворяют предложенным постулатам, но один из этих по-
стулатов исключает недетерминированные и параллельные схемы,
поэтому класс (А, т, —) вновь может стать относительно уни-
версальным, если выйти за рамки последовательных детермини-
рованных схем. Действительно, Чандра [88] провел сравнитель-
ный анализ классов схем, допускающих недетерминизм выполне-
ния и особого рода параллелизм, и показал, что оба эти обога-
щения ортогональны другим обогащениям и друг другу.
Г Л А В A 10
СХЕМЫ СТРУКТУРИРОВАННЫХ ПРОГРАММ
Возрастающая сложность программ привлекает все большее
внимание к проблемам технологии программирования. Техноло-
гические соображения заставили, в первую очередь, пересмотреть
принципы организации программ, их структуру. Дейкстра [12)
первым высказался против неупорядоченного использования
переходов на метки, которое может привести и фактически при-
водит к переусложнению структуры программы, затрудняющему
ее понимание и декомпозицию на более простые фрагменты. Реа-
лизуя концепцию так называемого структурированного програм-
мирования, он предложил, в частности, отказаться от использо-
вания переходов в алголоподобных языках и ограничиться более
дисциплинирующими средствами управления вычислениями,
такими, как условные операторы алголовского типа и операторы
цикла. Следует заметить, что еще раньше в ряде теоретических
работ был исследован вопрос о сохранении функциональной мощ-
ности программ при наложении подобных структурных ограни-
чений. Так, Р. Петер * ••)), Бем и Якопини *•), Глушков (6) и ряд
других авторов установили, что структуру программ можно «ре-
гуляризовать» без уменьшения их функциональной мощности.
Проблемы структурированного программирования не были
обойдены вниманием схематологии, в результате чего появилась
серия работ, связанная с изучением мощности разных классов
структурированных схем и их основных свойств. В этой главе
рассмотрены основные факты, относящиеся к сопоставлению стан-
дартных и структурированных схем.
§ 1. Структурированные схемы
1.1. Класс структурированных схем. Класс структурирован-
ных схем будет определен в том же (полном) базнсе, который был
введен для класса стандартных схем (§ 2, гл. 4). Различия между
стандартными и структурированными схемами проявляются на
уровне структур схем. Вместо дополнительных специальных сим-
*) Р е t е г R. Graphschemata und rekursive Funktionen.— «Dialectics*,
1958, V. 12, P. 373—388.
••) BohmC., JacopiniG. Flow Diagrams, Turing Machines and
Languages with Only Two Formation Rules. — «Communication of ACM*.
1966, V. 9, № 5, P. 366—371.
228
волов, указанных в п. 2.2 гл. 4, вводятся символы {если, то,
иначе, пока, цикл, конец) Вместо инструкций с метками опреде-
ляются три типа схемных операторов в базисе 58: простой оператор,
условный оператор и операторы цикла.
Простой оператор — зто оператор присваивания, или началь-
ный оператор, или заключительный (все они — операторы базиса).
Условный оператор имеет вид
если л то ot иначе о0 конец,
где л — логическое выражение, и о0 — последовательности
(быть может, пустые) схемных операторов, среди которых нет ни
начального, ни заключительного.
Операторы цикла имеют вид
пока л цикл а конец или до л цикл а конец,
где л — логическое выражение, о — последовательность (быть
может, пустая) схемных операторов, среди которых нет ни на-
чального, ни заключительного.
Структурированной схемой в базисе 38 называется конечная
последовательность (оО) olt . . ., оп) схемных операторов в базисе
S3, где о0 — начальный оператор, оп — заключительный оператор,
остальные операторы — зто операторы присваивания, или услов-
ные операторы, или операторы цикла.
Примеры структурированных схем:
Схема 510Л
(старт (х),
У :=а,
до р (х) цикл
у := g(x, у)
х := h (х) конец,
стоп (х, у))
Схема
(старт (х),
У •= / (х),
если р (у) то иначе
У := / (У).
если р (х) то
пока р (х)
цикл х h (х) конец
иначе конец конец,
стоп (х, у)).
Пара (5, /), где S — структурированная схема в базисе 38,
а I — интерпретация этого базиса, называется структурирован-
ной программой.
Понятие выполнения структурированной программы опишем
менее формально, чем выполнение стандартной программы. По-
следовательность простых (интерпретированных) операторов вы-
полняется так же, как и последовательность аналогичных опе-
раторов стандартной схемы. Выполнение интерпретированного
условного оператора
если р (тх....тп) то ах иначе а0 конец
состоит из
(а) вычисления значения предиката 7(р) (т,/ (И7), . . ., (В7)),
где Tjj (И7) — значение интерпретированного терма при текущем
состоянии памяти W.
229
(б) выполнения последовательности alt если вычисленное зна-
чение предиката равно 1, или выполнения последовательности <7в,
если вычисленное значение —0.
Выполнение интерпретированного оператора цикла
пока р (тп . . тп) цикл о конец
состоит из
(а) вычисления значения предиката I (р) (BQ,. . .,xnj (W))
при текущем состоянии памяти W,
(б) выполнения последовательности о, если вычисленное зна-
чение предиката равно 1, и последующего перехода к шагу (а).
Выполнение интерпретированного оператора цикла
hi р|(т1> • - тп) Цикл о конец
Аналогично выполнению предыдущего оператора, но шаг (б) вы-
полняется в случав, когда значение предиката равно 0.
Если выполнение программы (S, /) завершается и W — за-
ключительное состояние памяти, то W (Z), где Z — набор выход-
ных переменных в заключительном операторе, является резуль-
татов val (S, Z) этой программы.
Йа структурированные схемы переносятся определения функ-
циональной эквивалентности и других главных свойств стандарт-
ных схем. Естественным образом отношение функциональной
эквивалентности распространяется на объединение классов струк-
турированных и стандартных схем. Можно убедиться, что струк-
турированная схема 51оа эквивалентна стандартной схеме из
«. 2.2 гл. 4. Все теоремы о свободных интерпретациях (п. 3.2 гл. 4)
сохраняют силу и для структурированных схем.
L2. Трансляций структурированных схем в стандартные.
Теорема 10.1. Класе структурированных схем трансли-
руем в класс стандартных схем.
Доказательство. Алгоритм трансляции структури-
рованных схем в стандартные достаточно прост. Все схемные опе-
раторы помечаются метками-числами в соответствии с порядком
як вхождения в структурированную схему. Условный оператор
к: если л то к 4- 1: ох иначе Г. о0 конец,
где к -f- 1 и I — метки первых операторов в последовательностях
<ц, заменяется на последовательность инструкций
к: если я то к 4- 1 иначе I, к 4- 1: ох на т, I: о0,
где т — метка оператора, следующего за условным оператором.
Если или <т0 — пустая последовательность, то к 4* 1 или, со-
ответственно, I должны равняться т, а соответствующие после-
довательности помеченных операторов отсутствуют в стандарт-
ной схеме.
Оператор цикла
к: пока я цикл к 4* 1: о конец
230
заменяется последовательностью операторов
к: если л то к + 1 иначе т, к + 1: о ва к,
где т — метка оператора, следующего за оператором цикла.
Оператор цикла
к: до л цикл к + 1: о конец
заменяется последовательностью операторов
kt если л то т иначе к + 1, к + 1: а на к,
где т — метка оператора, следующего за оператором цикла. Если
о — пустая последовательность, то первый оператор цикла за-
меняется на распознаватель
kt если я то Л иначе т,
а второй на
к: если л то т иначе к.
Последовательной заменой всех условных операторов и опе-
раторов цикла последовательностями инструкций строится стан-
дартная схема. Содержательный анализ правил замен убеждает,
что построенная схема эквивалентна исходной. £2
Стандартная схема <$10.3, эквивалентная структурированной
схеме Sio.21 имеет вид
(старт (ж),
1:у:=/(ж),
2: если р (у) то 7 иначе 3,
3: У := 1 (у),
4: если р (у) то 5 иначе 7,
5: если р (х) то 6 иначе 7,
6: х:= h (х) иа 5,
7: стоп (х, у)).
1.3. Трансляция стандартных схем в структурированные.
Структурированные программы универсальны в том смысле, что
набора предоставленных им программных средств достаточно для
описания любой вычислимой функции. Задача автоматического
преобразования стандартных схем в структурированные по-
разному формулировалась в разных работах с привлечением раз-
личных определений классов схем и отношений транслируемости
(82, 115, 116]. В рамках данного нами определения транслнруе-
мости (§ 2 гл. 8) и для введенного класса структурированных схем
ответ на вопрос о возможности трансляции стандартных схем в
структурированные носит отрицательный характер.
Теорема 10.2. Класс стандартных схем не транслируем
в класс структурированных схем.
Доказательство. На рис. 10.1 приведен пример стан-
дартной схемы для которой не существует эквивалентной
231
структурированной схемы. Предположим противное, и пусть S —
структурированная схема, эквивалентная схеме S10,4. На осно-
вании содержательного анализа схемы <$10.4 можно установить,
что эта схема является свободной и в схеме £ должен быть хотя
бы один оператор цикла, логическое выражение которого содер-
жит предикатный символ р или q (пусть, для определенности,
символ р). Кроме того, существуют свободные интерпретации,
при которых этот оператор выполняется. Зафиксируем такую ин-
терпретацию I следующим образом. Полагаем предикат Р — I (р)
тождественно равным 1, а предикат Q — I (о) выбираем так, чтобы
Рис. 10.1. Стандартная схема SM.4
Q (а) = 1 для всех термов-зна-
чений а, появляющихся при вы-
полнении программы (S, I) до
того момента, когда начнет вы-
полняться оператор цикла с пре-
дикатным символом р, и
Q (а) = 0 для всех остальных
термов-значений. Ясно, что про-
грамма (S, I) зацикливается (на
операторе цикла с предикатным
символом р). В то же время
программа (£10 4, I) останавли-
вается после некоторого выпол-
нения распознавателя с преди-
катным символом 9, так как
число термов а, при которых
Q (а) = 1, конечно, а переменная х получает все новые значения,
отличные от а. Из того факта, что (>S, /) зацикливается, а
(S’io.4, /) останавливается, следует, что предположение о суще-
ствовании схемы S, эквивалентной схеме 5ц>,4. было неверным. Q
Теорема 10.3. Класс стандартных схем строго мощнее
класса структурированных схем.
Доказательство. Следствие из теорем 10.1 н 10.2. Q
Таким образом, структурные ограничения, присущие струк-
турированным схемам, уменьшают их выразительные возможности,
-если сохраняется базис класса стандартных схем. В следующем
параграфе этот базис будет расширен, и это изменит ситуацию.
§ 2. Структурированные схемы
с логическими операциями
Второй класс структурированных схем, который рассматри-
вается здесь, обладает бблыпими возможностями за счет услож-
нения логических выражений в условных операторах и операторах
цикла. Если до сих пор логические выражения имели вид' р<п>
<q, . . ., тп), где р(П) — предикатный символ, т4, . . ., %п — тер-
мы, то в определяемом классе структурированных схем логиче-
232
ским выражением будем считать любую бескванторную логиче-
скую формулу, составленную из символов логических операций
(отрицание), Д (конъюнкция), V (дизъюнкция) и атомарных
формул, которыми являются логические выражения в старом
смысле. Примеры расширенных логических выражений:
~\Р (*) Л 9 (9. *).
Р (g (*, 0) V 9 (Л (*). х)-
Класс структурированных схем с логическими операциями
получается из класса структурированных схем, определенных
в предыдущем параграфе, добавлением в базис расширенных ло-
гических выражений.
' Проблема трансляции стандартных схем в структурированные
схемы с логическими операциями была исследована Ашкрофтом
и Манной [82], предложившими два алгоритма трансляции, каж-
дый из которых требовал расширения памяти. Мы рассмотрим
первый алгоритм, в нем расширение памяти осуществляется только
за счет добавления новых переменных — символов, в то время как
во втором алгоритме (хотя он проще и дает более «экономные*
схемы) требуется введение интерпретированных логических пе-
ременных.
Алгоритм Ашкрофта и Манны применим к стандартным схе-
мам, заданным в нормальной форме [100], которая показана на
Рис. 10.2. Нормальная форма стандартной схемы и нормальные фрагменты
рис. 10.2, а. Нормальный фрагмент определяется рекурсивно
через базовые нормальные фрагменты'.
(а) базовый нормальный фрагмент — это или преобразователь,
или распознаватель;
(б) фрагмент, получаемый композицией (рис. 10.2, б) или
зацикливанием (рис. 10.2, в) нормальных фрагментов, является
нормальным.
Оставляем читателю в качестве самостоятельного задания воз-
можность убедиться, что любую стандартную схему можно пред-
ставить в нормальной форме.
233
Теорема 10.4 (Ашкрофт — Манна). Класс стандартных
схем транслируем в класс структурированных схем с логическими
операциями.
Доказательство. Будет описан алгоритм преобразо-
вания, для которого исходная схема задана в нормальной форме.
Алгоритм сопоставляет каждому нормальному фрагменту & фраг-
мент структурированной схемы Ж, а каждому выходу из нормаль-
ного фрагмента — вспомогательную информацию, состоящую из
выходной последовательности (операторов присваивания) и вы-
ходного условия. Из фрагмента 3t, построенного по максималь-
ному нормальному фрагменту, и связанной с ним вспомогательной
информации конструируется результирующая схема.
Пусть & — базовый нормальный фрагмент. В этом случае
Ж — пустой фрагмент. Если & — оператор присваивания, то
выходная последовательность состоит из этого единственного
оператора, а выходное условие отсутствует. Если & — распозна-
ватель с логическим выражением л, то выходная последователь-
ность пуста, а два выходных условия — это л (для 1-дуги) и "Пл
(для 0-дуги).
Пусть & — композиция двух нормальных фрагментов Fj и
3% причем выход I фрагмента ведет на начало фрагмента F2.
Выходы фрагмента f — это выходы и кроме выхода i.
Рассмотрим разные случаи.
a) <Fa — базовый фрагмент, преобразователь х : — т. Выход-
ные условия всех выходов фрагмента & остаются теми же, какими
они были у выходов фрагментов и Выходные последова-
тельности для тех выходов, которые являются одновременно вы-
ходами 'Д, также не изменяются, а последовательности для тех
выходов, которые являются выходами фрагмента Fa, имеют вид
(ст£, х := т), где сц — выходная последовательность для выхода
г фрагмента Фрагмент Ж, соответствующий фрагменту Д,
совпадает с ЗД, соответствующим <Д.
б) — базовый фрагмент, распознаватель с логическим вы-
ражением л. Выходные последовательности для всех выходов &
остаются такими же, как и у соответствующих выходов фраг-
ментов Fi и Д2. Выходные условия тех выходов, которые явля-
ются выходами не меняются. Выходные условия тех выхо-
дов, которые были выходами фрагмента меняются на <р, Д л'
и ф; Д ~| л', где <р4 — выходное условие выхода i фрагмента
ал' — формула, получаемая из л и выходной последовательно-
сти щ того же выхода I следующим образом. Для последователь-
ности операторов <т{, которая рассматривается как свободно ин-
терпретированная цепочка преобразователей, находятся термаль-
ные значения тех переменных памяти, которые входят в логиче-
ское выражение л. Затем эти переменные замещаются в логиче-
ском выражении найденными термами, которые считаются тер-
мами-выражениями. Например, для последовательности (х := f (х),
V:=h(y), z := g (х, у)) и логического выражения р (х, / (z)}
получится выражение р (f (х), f (g (f (х), h (у)))).
234
Фрагмент ЭС, соответствующий фрагменту совпадает с фраг-
ментом соответствующим фрагменту
в) не является базовым фрагментом. В этом случае для
каждой той переменной памяти исходной схемы, которая входит
хотя бы в одно выходное условие фрагмента заводится пере-
менная-дублер. Выходные последовательности для выходов фраг-
мента 3- совпадают с выходными последовательностями соответ-
ствующих выходов фрагментов н &я. Для тех выходов, кото-
рые являются выходами фрагмента выходные условия полу-
чаются из соответствующих выходных условий фрагмента 3\
заменой всех встречающихся в них переменных исходной схемы
на переменные-дублеры. Для выходов $, являющихся выходами
фрагмента .?"а, выходные условия имеют вид <pj Д Лу, где <р4 — ус-
ловие* выхода i фрагмента но в нем все переменные заменены
на переменные-дублеры, а лу — условие выхода j фрагмента &я.
Фрагмент 3t, соответствующий фрагменту <F, имеет вид
: = х, . . ., zn : — у, если <р4 то сг£, Мя иначе конец), где 3tx, 9СЯ —
фрагменты, соответствующие и $ я, переменные zlt . . zn —
дублеры переменных х, . . у, а <р4 и — выходные условие к
последовательность выхода i фрагмента
Пусть $ — результат зацикливания фрагмента по неко-
торому выходу, предположим, для определенности, по первому.
Выходные последовательности для всех выходов, кроме первого,
сохраняются (первый выход теряет как выходную последователь-
ность, так н выходное условие). В качестве выходных условий
фрагмента $ берутся новые логические выражения Лу, состав-
ленные из тех же атомарных формул, что и старые выходные
условия <ру, но удовлетворяющие следующим требованиям:
(а) <ру ZD Лу для всех (старое условие имплицирует новое);
(б) пя V • • • V яп =1 (совокупность новых условий полна);
(в ) Лу Д лк = 0 для всех пар j и к таких, что j к =# 1 (новые
условия взаимно исключают друг друга).
Новые условия легко найти, если заметить, что выходные ус-
ловия представляют собой конъюнкции атомарных формул или
их отрицаний. Поэтому, если представить совокупность старых
условий в виде дерева, вершинами которого являются простые
логические выражения, а листьями — старые условия, то уда-
ление той вершины, которая ведет к фа, дает новое дерево, листья-
ми которого являются новые условия.
Фрагмент соответствующий имеет вид (3tx, пока фа
цикл ах, <КХ конец), где фа, — выходные условие и последова-
тельность для $х и 3fx — фрагмент, соответствующий
После того, как построены структурированные фрагменты,
выходные последовательности и условия для всех нормальных
фрагментов, начиная с базовых и кончая максимальным .Утат<
строится сама структурированная схема, которая имеет вид
(старт, ^шах,
если ла то ст1 иначе
если ла то о, иначе...
235
СТАРТ(X)
Рис. 10.3. Стандартная схема SM.g
если «п-! то on-i иначе стп конец . . . конец,
стоп (х, . . у)).
Здесь л1( .... лп-1 — выходные условия фрагмента /max,,
a ot, ...» оп— его выходные последовательности.
Содержательный анализ алгоритма показывает, что исходна»
стандартная схема и построенная структурированная эквивалент-
236
ны. Введение выходных последовательностей и условий для нор-
мальных фрагментов позволяет сначала расщепить заданную схе-
му на отдельные ветви-альтернативы, а затем скомпоновать из
них структурированные операторы. Дополнительные переменные
обеспечивают возможность «стягивания» разбросанных по схеме
условий выхода из цикла в одно условие проверки окончания
структурированного оператора цикла. С этой целью переменные-
дублеры запоминают состояния памяти в тех точках исходной
схемы, где возможны выходы из цикла в исходной схеме, а про-
верка осуществляется в одном месте. Q
В стандартной схеме S10.5 на рис. 10.3 выделены нормальные
фрагменты . . ., <F6, ^шах (более мелкие фрагменты не пока-
заны). Проиллюстрируем на примере этой схемы описанный выше
алгоритм. *В каждом из выделенных фрагментов выходы считаем
упорядоченными слева направо.
Для каждого фрагмента (i = 1, . . ., шах) выпишем выход-
ные последовательности и условия, а также фрагмент
Фрагмент
Вых. поел.: (х:~ g (х)), (х:= g (х)), (х: — g (х)).
Вых. усл.: р (х), ЙР (х) Л 9 (*)» ЙР (ж) Л (*)•
Фрагмент — пустой.
Фрагмент <Fa.
Вых. поел.: (х:= g (х)), (х:= g (х)).
Вых. усл.: q (х), П? («)•
Фрагмент ЗСаг
пока р (х) цикл х:— g (х) конец
Фрагмент &а.
Вых. поел.: (х:= / (х)), (х:= / (х)), (х: = / (х)).
Вых. усл.: q (х), П? (х) Д р (х), Й<? (ж) Л ПР (*)•
Фрагмент 3ta — пустой.
Фрагмент “Г*.
Вых. поел.: (х:=/(х)), (х:=/(х)).
Вых. усл.: р (х), Пр (*)•
Фрагмент 3£t:
пока q (х) цикл х : = / (х) конец
Фрагмент
Вых. поел.: (х:=/(х)), (х:==/(х)), (х:= g (х)).
Вых. усл.: q (у) Д р (х), q (у) Д ЙР (х), “]д (у),
где у — новая переменная, дублирующая х.
Фрагмент 3(t:
(5?а, у:— х, если q (х) то х: = g (х), иначе конец).
Фрагмент
Вых. поел.: (х: = / (х)), (х:= g (х)).
Вых. усл.: q (у), Й? (У)-
Фрагмент ^тат.
(Я?6, пока q (у) Д р (х) цикл х:= / (х), конец).
Искомая структурированная схема имеет вид:
(старт (х), пока р (х) цикл х:~ g (х) конец,
у:= х.
237-
«ели q (х)
то х: — g (х),
пока q (х) цикл х: — f (х) конец
иначе конец,
пока q (у) Д р (х) цикл
х’= f (х),
пока р (х) цикл х:— g (х) конец,
У- = х,
если q (х) то х:= g (*)»
пока q (х) цикл х:= / (х) конец
иначе конец
конец,
если q (у) то х:= / (х)
иначе х: = g (х) конец,
стоп (х)).
Переменная у используется для того, чтобы запомнить состоя-
ние памяти в точке а схемы £1в.9, где существует возможность
выхода из цикла, и проверить соответствующее условие выхода
а точке Ь, где также можно уйти из цикла, во состояние памяти
иное.
Приведенный пример показывает, что получающаяся струк-
турированная схема достаточно сложна и плохо обозрима. Ашкрофт
и Манна предложили другой алгоритм, который требует введе-
ния интерпретированных логических переменных со значениями
1 (истина) и 0 (ложь). Алгоритм позволяет строить структуриро
ванные схемы так, что при обратной трансляции с помощью ал
горитма, описанного в теореме 10.1, получаются стандартные схе-
мы той же структуры, что и исходные. Схема транслиру
ется таким методом в следующую структурированную схему, где
I — дополнительная логическан переменная:
(старт (х), t1,
пока t цикл
пока р (х) цикл х : = g (х) конец,
если q (х) то х : = £(*).
пока q (х) цикл х := / (х) конец,
если р (х) то x:^f (х).
иначе х := / (х), t := 0 конец
иначе х : — g (х), t: — 0 конец
конец,
стоп (х)).
Схему S10'6 нельзя транслировать в структурированную, ие
добавляя новых переменных.
3 а д а в и е 10.1.
А. Покажите, что класс структурированных схем с логическими опе-
рациями транслируем в класс стандартных схем.
Б. Постройте алгоритм трансляции стандартных схем в структурирован-
ные с логическими операциями, добавляя счетчики вместо логических пере-
менных.
В. Транслируйте в структурированные схемы St,a и 54.4 из гл. 4.
СПИСОК ЛИТЕРАТУРЫ
f
1. А х о А., X о и к р о ф т Дж., У л ь м а и Дж. Построение и анализ
вычислительных алгоритмов.— М.: Мир, 1979.— 536 с.
2. Баррон Д. Рекурсивные методы в программнроваинн.— М.: Мир,
1974.— 80 с.
3. Бнркгоф Г. Теория решеток,— М.: Наука, 1984.— 564 с.
4. Буд а А. О. Абстрактные машнны программ.— Препринт / ВЦ СО
АН СССР.— Новосибирск, 1978.— № 108.— 45 с.
5. БульоиковМ. А. Итеративные алгоритмы разметки в трансфор-
мационной машине//Программное обеспечение задач информатики:.
Сб. статен.— Новосибирск: ВЦ СО АН СССР, 1982.— С. 38—52.
6. Глушков В. М. Теория автоматов и формальные преобразования
мнкропрограмм И Кибернетика.— 1965.— № 5.— С. 1—9.
7. Глушков В. М., ЛетичевскийА. А. Теория дискретных
преобразователей И Избранные вопросы алгебры и логики.— Ново-
сибирск: ИМ СО АН СССР, 1973,— С. 5—39.
8. Годлевский А. Б. Некоторые специальные случаи проблемы
остановки и функциональной эквивалентности автоматов // Кибернети-
ка.— 1973,— № 4.— С. 90—97.
9. Годлевский А. Б. Об одном случае специальной проблемы функ-
циональной эквивалентности дискретных преобразователей // Кибер-
нетика.— 1974.— № 3.— С. 32—36.
10. Г о д л е в с к и й А. Б. Об одном разрешимом случае специальной
проблемы функциональной эквивалентности дискретных преобразова-
телей И Вопросы проектирования ЭВМ и других дискретных устройств. —
Киев: ИК АН СССР, 1974.— С. 16—40.
Н. Годлевский А. Б. О связи логико-термальной эквивалентности
схем программ с одним случаем специальной проблемы функциональ-
ной эквивалентности дискретных преобразователей П Кибернетика.—
1975, № 5.—С. 32-34.
12. Дал У., Дейкстра Э., Хоор К. Структурное программирова-
ние.—М.: Мир, 1975.— 248 с.
13. Ершов А. П. Операторные алгоритмы I И Проблемы кибернетики: Сб.
статей. Вып. 3.—М.: Фнзматгиз, I960.—С. 5—48.
14. Е р ш о в А. П. Сведение задачи экономии памяти при составлении
программ к задаче раскраски вершин графов И Док л. АН СССР.—
1962.— Т. 142, № 4, — С. 785—787.
15. Е р ш о в А. П. Об операторных схемах Янова И Проблемы киберне-
тики: Сб. статей. Вып. 20.— М.: Наука, 1967.— С. 181—200.
16. Е р ш о в А. П. Об операторных схемах над общей и распределенной
памятью // Кибернетика.— 1968, Mi 4.— С. 63—71.
17. Е р ш о в А. П. Современное состояние теория схем программ // Проб-
лемы кибернетики: Сб. статей. Вып. 27.— М.: Наука, 1973.— С. 87—НО.
18. Ершов А. П., Л я п у и о в А. А. О формализации понятия про-
граммы // Кибернетика.— 1967.— Л» 5.— С. 40—57.
239
IS. Ершов А. П., СабельфельдВ. К. Очерк схемной теории
рекурсивных программ И Трансляция н модели программ: Сб. статей.—
Новосибирск: ВЦ СО АН СССР, 1980.— С. 23—43.
20. Зыков А. А. Теория конечных графов.— Новосибирск: Наука,
1969.— 543 с.
21. И т к и и В. 3. Операторные схемы Янова с тождественными операто-
рами И Труды всесоюзной конференции по программированию (ВКП-
I), вып. А,— Киев: ИК АН УССР, 1968.— С. 27—46.
22. И т к и и В. Э. Логико-термальная эквивалентность схем программ И
Кибернетика,— 1972.— № 1.— С. 5—27.
23. И т к и и В. Э. Комбинированная эквивалентность схем программ //
Системное и теоретическое программирование: Тез. докл. III Всесоюзн.
симпозиума.— Кишинев. Изд-во Киш. Гос. Ун-та, 1974.— С. 174—177.
24. К а л у ж и и и Л. А. Об алгоритмизации математических задач И
Проблемы кибернетики: Сб. статей. Вып. 2.— М.: Фнзматгиз, 1959.—
С. 51—67.
25. Касьянов В. Н. Учет априорной информации при анализе свойств
состояний программ //Математическая теория программирования.— Но-
восибирск. ВЦ СО АН СССР, 1985.— С. 150—157.
26. К и и б е р Е. Б. Об одном классе многоленточных автоматов с разре-
шимой проблемой эквивалентности И Программирование.— 1983.—
№ 3,— С. 3—16.
27. К о т о в В. Е. Теория параллельного программирования: прикладные
аспекты // Кибернетика.— 1974.— № 1.— С. 1—16; № 2.— С. 1—18.
28. Кривицкий Н. А. Равносильные преобразования логических схем:
Автореф. дне... канд. физ-мат. наук.— М., 1959.— 24 с.
29. Крнницкнн Н. А. Равносильные преобразования алгоритмов и
программирование.— М.: Советское радио, 1970,— 304 с.
30. Л а в р о в С. С. Об экономии памяти в замкнутых операторных схе-
мах И ЖВМ и МФ, 1961.— Т. 1, № 4.— С. 687—701.
31. Летнчевскнй А. А. Функциональная- эквивалентность дискрет-
ных преобразователей I // Кибернетика.— 1969.— № 2.— С. 5—15.
32. Летнчевскнй А. А. Функциональная эквивалентность дискрет
ных преобразователей II // Кибернетика.— 1970.— № 2.— С. 14—28.
33. Летнчевскнй А. А. Функциональная эквивалентность дискрет
ных преобразователей III И Кибернетика.— 1972.— № 1.— С. 1—4.
34. Летнчевскнй А. А. Эквивалентность и оптимизация программ //
Теория программирования. Ч. 1.— Новосибирск: ВЦ СО АН СССР,
1972.— С. 166—180.
35. Летнчевскнй А. А. Практические методы распознавания экви
валентности дискретных преобразователей и схем программ И Кибер-
нетика.— 1973.— № 4.— С. 15—26.
36. Л и с о в и к Л. П. Проблема эквивалентности для преобразователей
над размеченными деревьями // Докл. АН УССР.— 1980.— № 6.—
С. 77—79.
37. Л и с о в и к Л. П. Металниейные схемы с засылками констант И Прог-
раммирование.— 1985.— № 2.— С. 29—38.
38. Л я п у и о в А. А. О логических схемах программ И Проблемы кибер
нетнкн: Сб. статей. Вып.1.— М.: Фнзматгиз, 1958.— С. 46—74.
39. Мальцев А. И. Алгоритмы и рекурсивные функции.— М.: Наука,
1965.— 391 с.
40. Марков А. А. Теория алгоритмов И Труды Матем. ни-та
им. В. А. Стеклова АН СССР, 1954.— Т. 42.— 376 с.
41. Мартынюк В. В. Выделение цепей в схемах алгоритмов И ЖВМ
и МФ, 1961.— Т. 1, № 1,— С. 151—162.
42. М а р т ы и ю к В. В. Об анализе графа переходов для операторной
схемы И ЖВМ и МФ, 1965.— Т. 5, № 2.— С. 298—310.
43. Маурер У. Введение в программирование на языке ЛИСП.— М-
Мир, 1976.— 104 с.
44. Минский М. Вычисления и автоматы.— М.: Мир, 1971.— 264 с.
240
45. НарнньяжнА. С. Теория параллельного программирования: фор-
мальные модели// Кибернетика.— 1974.— № 3.— С. 1—15; № 4.—
С. 1—14.
46. Непомнящий В. А. Об одном методе распознавания эквивалент-
ности схем программ и дискретных преобразователей // Труды всесоюз-
ной конференции по программированию (ВКП-2). Вып. К.— Новоси-
бирск: ВЦ СО АН СССР, 1970.- С. 49-63.
47. Непомнящий В. А. Критерии алгоритмической полноты систем
операций И Теория программирования: Сб. статей. Ч. 1.— Новосибирск,
1972.— С. 267—279.
48. Непомнящий В. А. О проблеме пустоты для схем программ I //
Программирование.— 1976.— № 4.— С. 43—51.
49. Непомнящий В. А. О проблеме пустоты для схем программ II //
Программирование. — 1977.— № 4. — С. 3—13.
50. Непомнящий В. А., СабельфельдВ. К. Элиминация пе-
ресылок в стандартных схемах программ И Программирование.— 1979.—
№ 4.— С. 34—43.
51. О ре О. Теория графов.—М.: Наука, 1968,—352 с.
52. П е т р о с я н Г. Н. Об одном базисе операторов и предикатов с не-
разрешимой проблемой пустоты//Кибернетика.— 1974.— № 5.—
С. 23-28.
53. Петросян Г. Н. Проблема включения на подпамяти для оператор-
ных схем и случай ее разрешения // Системное и теоретическое прог-
раммирование: Сб. статей.— Новосибирск: ВЦ СО АН СССР, 1974.—
С. 204—234.
54. Подловченко Р. И. Недетерминированные схемы алгоритмов //
Докл. АН СССР,- 1972.— Т. 207, № 4.— С. 789—792.
55. П о д л о в ч е н к о Р. И. Полная система подобных преобразований
недетерминированных схем алгоритмов // Докл. АН СССР.— 1973.—
Т. 212, № 1.— С. 64-66.
56. Подловченко Р. И. О понятиях и проблематике теории схем
алгоритмов над памятью // Системное и теоретическое программирова-
ние: Сб. статей.— Новосибирск: ВЦ СО АН СССР, 1974.— С. 130—151.
57. Подловченко Р. И. Интерпретационные и формальные отноше-
ния между схемами над памятью // Проблемы кибернетики: Сб. статей.
Вып. 30.— М.: Наука, 1975,— С. 277—292.
58. Подловченко Р. И. Функциональная н другие эквивалентности
схем программ//Проблемы кибернетики. Вып. 35.— М.: Наука,.
1979.— С. 185-198.
59. П о т т о с и н И. В. К задаче чистки циклов И Цифровая вычисли-
тельная техника н программирование: Сб. статей. Вып. 4.— М.: Со-
ветское радио, 1968.— С. 18—36.
60. Р е д ь к о В. Н., Л и с о в и к Л. П. Проблема эквивалентности для
конечноповоротных счетчиковых машин И Кибернетика.— 1980, № 4.—
С. 26—29.
61. Роджерс X. Теория рекурсивных функций н эффективная вычис-
лимость.— М.: Мнр, 1972.- 624 с.
62. Сабельфельд В. К. Критерий локальности преобразований опе-
раторных схем И Кибернетика,— 1971.— № 5.— С. 59—62.
63. СабельфельдВ. К. О преобразованиях унарных линейных ре-
курсивных схем И Кибернетика.— 1975.— № 5.— С. 56—63.
64. Сабельфельд В. К. Эквивалентные преобразования стандартных
схем//Проблемы программнровання. Со. статей.— Новосибирск:
ВЦ СО АН СССР, 1976.— С. 94—121.
65. СабельфельдВ. К. Полиномиальная оценка сложности распоз-
навания логико-термальной эквивалентности И Докл. АН СССР.—
1979.— Т. 249, № 4 — С. 793—796.
66. Сабельфельд В. К. Эквивалентные преобразования рекурсивных
схем программ// Оптимизация н преобразования программ: Сб. статей.
Ч. 1,— Новосибирск: ВЦ СО АН СССР, 1983.— С. 48—55.
241.
67. Сабельфельд В. К. О проблеме древесной пустоты для рекурсив-
ных схем программ // Проблемы системного и теоретического програм-
мирования: Сб. статей.— Новосибирск: НГУ, 1984.— С. 157—166.
68. Сабельфельд В. К. Метод разметки для глобального анализа
свойств,— Препринт / ВЦ СО АН СССР,—Новосибирск, 1986. № 699.—
20 с.
69. С а б е л ь ф е л ь д В. К. Функциональная эквивалентность сквоз-
ных схем И Тез. докл. II Всесоюзн. конф, по прикладной логике.—Ново-
сибирск: ИМ СО АН СССР, 1988.— С. 202—204.
70. Т р а х т е и б р о т Б. А. Об универсальных классах схем программ //
Теория программирования: Сб. статей. Ч. 1.— Новосибирск: ВЦ СО АН
СССР, 1972.— С. 239—249.
71. Т р а х т е н б р о т Б. А. Алгоритмы и вычислительные автоматы.—
М.: Советское радио, 1974.— 200 с.
72. Т у э о в В. А. Эквивалентность логических схем с перестановочными
операторами// Кибернетика.— 1970.— № 6.— С. 33—38.
73. Т у з о в В. А. Проблемы разрешения для граф-схем с перестановоч-
ными операторами II И Кибернетика.— 1971.— № 5.— С. 23—32.
74. Успенский В. А. Лекции о вычислимых функциях.— М.: Физ-
матгиз, 1960.— 492 с.
75. X а р а р и Ф. Теория графов.— М.: Мир, 1973.— 300 с.
76. Ш у к у р я н С. К. Разрешимость проблемы эквивалентности в одном
классе многоленточных многоголовочных автоматов и схем программ
над памятью И Кибернетика.— 1976.— № 4.— С. 12—16.
77. Я и о в Ю. И. О равносильности и преобразованиях схем программ И
Докл. АН СССР.— 1957,— Т. 113, № 1. — С. 39—42.
78. Я н о в Ю. И. О логических схемах алгоритмов И Проблемы киберне
тики: Сб. статен. Вып. 1.— М.: Физматгиэ, 1958.— С. 75—127.
79. Я и о в Ю. И. О локальных преобразованиях схем алгоритмов //
Проблемы кибернетики: Сб. статей. Вып. 20.— М.: Наука, 1968.—
С. 201—216.
80 Aho А. ¥., Ullman J. D. The Theory of Languages // Math. Syst
Theory.— 1968.—V. 2, № 2.—P. 97—125. (Русский перевод
A x о у А. В., Улман Дж. Д. Теория языков // Кибернетический
сборник. Новая серия: Сб. статей. Вып. 6.— М.:Мир, 1969.— С. 145
81. А 11 е n F. Е. A Basis for Program Optimization П Proc. IFIP Con
gress 71, Ljubljana, Yugoslavia, August 1971.— Amsterdam: North
Holl. Publ. Co.—1971.—P. 385—390.
82. Ashcroft E., Manna Z. The Translation of «Goto» Programs to
«While» Programs// Proc. IFIP Congress 71, Ljubljana, Yugoslavia, Au
gust 1971.— Amsterdam: North-Holl. Publ Co.— 1971.— P. 250—255
83. Ashcroft E., Manna Z., P n u e 1 i A. Decidable Properties of
Monadic Functional Schemes//!. ACM.— 1973.— V. 20, № 3.—
P. 489—499. (Русский перевод: Ашкрофт Э., Манна 3., Пнуели А.
Разрешимые свойства одноаргументных функциональных схем // Языки
и автоматы: Сб. статей.—М.: Мир, 1975.— С. 97—108.)
84. Backus !. Can Programming Be Liberated from the von Neuman
Style? A Functional Style and its Algebra of Programs // Comm. ACM.—
1978,— V. 21, № 24,— P. 613—641.
85. Bird M. The Equivalence Problem for Deterministic Two—Type
Automata//!. Computer and System Sci.— 1973.— V. 7, № 3.—
P. 218—236.
86. Bird R. Programs and Machines (An Introduction to the Theory of
Computation).— London: !ohn Wiley and Sons, 1976.— 214 p.
87. Brown S., Gries D., Szymanski T. Program Schemes
with Pushdown Stores//SIAM !. Computing.—1973.—V. 1, № 4.—
P. 242.
88. Chandra A. K. On the Properties and Applications of Program
Schemes//Ph. D. Thesis.—Stanford: Stanford Univ., 1973.
89. Chandra A. K. The Power of Parallelism and Nondeterminism in
Programming // Information Processing 74: Proc. IFIP Congress 74,
242
Stockholm, Sweden, Aug. 5—10, 1974.— Amsterdam.— North—Holl.
Publ. Co., 1974.— P. 461—465.
90. Chandra A. K., Manna Z. Program Shemes with Equality//
Proc. 4th Ann. ACM Symp. on Theory Comp.— Denver, 1972.— P. 52 —
64. (Русски* перевод: Чандра А. К., Манна 3. Схемы программ с ра-
венством И Теории программирования: Сб. статей. Ч. 1,— Новосибирск:
ВЦ СО АН СССР, 1972.—С. 200—238.)
91. С h u г с h A. An Unsolvable Problem of Elementary Number Theory //
Am. J. Math.—1936,—V. 58, № 2.—P. 345-363.
92. С о n s t a b 1 e R. L., G г i e a D. On Classes of Program Schemata //
SIAM J. Computing.—1973.—V. 1.—P. 66—118. (Русски* перевод:
Коистейбл P. Л., Грис Д. О классах схем программ // Кибернетиче-
ский сборник. Новая серия: Сб. статей. Вып. 14.—М.: Мир, 1977.—
С. 122-177.
93. Courcelle В. On jump deterministic pushdown automata // Math.
Systems Theory.—1977,— № 11,— P. 87—109.
94. Courcelle B. A representation of trees by languages // Theoretical
Computer Sci.—1978,— V. 6,— P. 255—279;— V. 7.— P. 25—55.
95. D a v i s M. Computability and Unsolvability.— N. Y.: McGraw-
Hill Book Co.—1958.—210 P.
96. De Bakker J. W. Semantics of Programming Languages // Advance»
in Information Systems Sciences.— N. Y.: Plenum Press, 1969.—
V. 2.— P. 173-227.
97. D e Bakker J. W., Scott D. A. Theory of Programs. Unpubli-
shed notes.— Vienna: IBM Seminar, 1969.
98. D о w n e у P. J., S e t h i R., Tarja n R. E. Variations on th»
common subexpression problem//I. ACM.—1980.— V. 27, №4.—
P. 758—771.
99. E 1 s p a s B., Levitt K., WaldingerR., Wakeman A.
An Assessment of Techniques for Proving Correctness // Computing Sur-
veys.-1972.—V. 4, №2.— P. 97—147.
100. Engeler E. E. Introduction to the Theory of Computation.—
N. Y.: Academic Press, 1973.
101. G a 11 i e r J. H. DPDA’s in <Atomic normal form» and application»
to equivalence problems//Theoretical Computer Sci.—1981.—V. 14,
№ 2.— P. 155-186.
102. Garland S. J., Luckham D. C. Program Schemes, Recursion-
Schemes and Formal Languages // J. Computer and System Sci.—1973.—
V. 7, №2.— P. 119—160. (Русский перевод: Гарлэнд С., Лакхэм Д.
Стандартные схемы, рекурсивные схемы н формальные языки // Ки-
бернетический сборник. Новая серия: Сб. статей. Вып. 13.— М.: Мир,
1976.—С. 73—119.)
103. Greibach S. A. Theory of Program Structures: Schemes, Semantics,
Verification//Lecture Notes in Computer Science. V. 36.— Berlin::
Springer Verlag, 1975.—364 p.
104. H a r n i k V. Effective Proper Procedures and Universal Classes of
Program Schemata // J. Computer and System Sci.—1975.— V. 10,
№ 1.— P. 44-61.
105. Ноаге C. A. R, Lauer P. E. Consistent and Complimentary For-
mal Theories of the Semantics of Programming Languages // Acta Infor-
matics.—1974.—V. 3, № 2.— P. 135—153.
106. Hopcroft J. E-, Ullman J. D. Formal Languages and Their
Relation to Automata.— Reading (Mass.): Addison-Wesley.—1969.—
242 p.
107. Ibarra О. H. Reversal-bounded multicounter machines and their
decision problems // J. ACM.—1978.— V. 25, № 1.— P. 116—133.
108. Itkin V. E., Zwinogrodzki Z. On Program Schemata Equi-
valence // J. Computer and System Sci.—1972.—V. 6, № 1.—
P. 88-101.
109. Kam J. B., Ullman J. D. Monotone data flow analysis frameworks//
Acta Informatica.—1977.—V. 7, 3.—P. 305-318.
243;
'<10. Kaplan D. M. Regular Expressions and the Equivalence of Pro-
grams//J. Computer and System Sci.—1969.—V. 4, № 3.—
P. 361-385.
ill. Karp R. M., Miller R. E. Parallel Program Schemata // J. Com-
puter and System Sci.—1969.— V. 3, № 2.— P. 147—195. (Русский пе-
ревод: Карп P. M., Миллер Р. Е. Параллельные схемы программ//
Кибернетический сборник. Новая серия: Сб. статей. Вып. 13.— М.:
Мир, 1976.— С. 5—61.)
'112. Kildall G. A. A unified approach to global program optimization //
Conf. Records of ACM Symp. on Principles of Programming Lang.—
Boston: MA, 1973.— P. 194-206.
113. К 1 e e n e S. C. General Recursive Functions of Natural Numbers //
Math. Ann.—1936,—V. 112, № 5,—P. 727—742.
114. К 6 n i g D. Theorie der endlichen und unendlichen Graphen.— Leip-
zig: Akademische Verlagsgesellschaft 1936.—258 p.
115. Kosaraju S. R. Analysis of Structured Programs // J. Computer and
System Sci.—1974,—V. 9, № 2,—P. 232—255.
116. Ledgard H. F, Marcotty M. A. Genealogy of Control Struc-
tures//Communs ACM.—1975,—V. 18, № 11,—P. 629—639.
117. Lewis H. R. A new decidable problem, with application//Proc.
18 Ann. Symp. on Foundations of Comp. Sci.—1979.— P. 62—73.
118. L о e c k h J. Computability and Decidability.— Berlin: Springer Ver-
lag, 1972.—76 p.
1119. Luck ham D. C., Park D. M., Paterson M. S. On Formali-
zed Computer Programs//J. Computer and System Sci.— 1970.—
V. 4, № 3.— P. 220—249. (Русский перевод: Лакхэм Д., Парк Д. М.,
Патерсон М. С. О формализованных машинных программах И Кибер-
нетический сборник. Новая серия: Сб. статей. Вып. 12.— М.: Мир,
1975.— С. 78-114.)
'120. Manna Z. Mathematical Theory of Computation.— N. Y.: McGraw-
Hill Book Co., 1974. — 448 P. (Русский перевод гл. 5: Манна 3. Теория
неподвижной точки программ.— Кибернетический сборник. Новая
серия: Сб. статей. Вып. 15.— М.: Мнр, 1978.— С. 38—100.)
121. McCarthy J. Towards a Mathematical Science of Computation //
Proc. IFIP Congress 1961.— Amsterdam: North-Holl. Publ. Co.—
1962.— P. 21—28.
122 McCarthy J. A Basis for a Mathematical Theory of Computation //
Computer Programming and Formal Systems.— Amsterdam: North-
Holl. Publ. Co.-1963 — P. 33-70.
123. Milner R. Equivalences on Program Schemes//J. Computer and
System Sci.—1970,—V. 4, № 3.—P. 205—219.
124. Morris J. H. Recursion Schemes with Lists 11 Proc, of the 4th Ann.
ACM Symp. on Theory of Comp.— Denver.—1972.— P. 35—43.
125. Nepomniaschy V. A. On Divergence Problem for Program
Schemes // Lecture Notes in Computer Sciences.— Berlin: Springer Ver-
lag, 1976,— V. 45.— P. 442-445.
126. Paterson M. S. Equivalence Problems in a Model of Computation:
Ph. D. Thesis.— Cambridge, 1967.—153 p.
127. Paterson M.S. Program Schemata//Machine Intelligence.—
Edinburg: Univ. Press, 1968.—V.3.— P. 19—31.
128. Paterson M. S. Decision Problems in Computational Models //
Proc. ACM Symp. Prov. Assert.— New Mexico: SIGPLAN Notices,
1972.— V. 7.— P. 74—82. (Русский перевод: Патерсон M. С. Пробле-
мы разрешимости в вычислительных моделях И Теория программиро-
вания: Сб. статей. Ч. 1.— Новосибирск: ВЦ СО АН СССР, 1972.—
С. 119—139.)
129. Paterson M.S., Hewitt С. Т. Comparative Schematology//
Proc, of the ACM Conf, on Concurrent Systems and Parallel Computati-
on.— N. ¥., 1970.— P. 119—127. (Русский перевод: Патерсон M. С.,
Хьюитт С. Е. Сравнительная схематология И Кибернетический сбор-
ник. Новая серия: Сб. статей. Вып. 13. — М.: Мир, 1976.— С. 62—72.)
244
130. Plaisted D. Program Schemes with Counters // Proc, of the 4th
Ann. ACM Symp. on Theory of Comp.— Denver, 1972.— P. 44—51.
131. Post E. L. Finite Combinatory Processes-Formulation I//Symb.
Logic.—1936.— V. 1, № 3.— P. 103—105.
132. Post E. L. A Variant of a Recursive Unsolvable Problem // Bull, of
Am. Math. Soc.—1946.-V. 52, № 4.—P. 264—268.
133. Rabin M. O., S с о 11 D. Finite Automata and Their Decision Prob-
lems // IBM J. Res. Dev.—1959.—V. 3, № 2.—P. 114—125. (Рус-
ский перевод: Рабии M. О., Скотт Д. Конечные автоматы и задачи их
разрешения//Кибернетический сборник. Новая серия: Сб. статей.
Вып. 4.—М.: Мир, 1962.—С. 58—91.)
134. Rosen В. К. Program equivalence and context—free grammars//
J. Computer and System Sci.— V. 11, № 3.— P. 358—374.
135. Rosenberg A. On Multi—Head Finite Automata // Proc, of the
5th Ann. Symp. on Switch. Theory and Log. Design.—1963.— P. 221—228.
136. Rutledge J. D. On lanov’s Program Schemata // J. ACM.—1964.—
V. 11, № 1.— P. 1—9.
137. Sabelfeld V. K. Tree equivalence of linear recursive schemata is
polynomial-time decidable//Information Processing Letters.—1981.—
V. 13, № 4.— P. 147—153.
138. Strong H. R. Translating Recursion Equations into Flow-Charts //
J. Computer and System Sci.—1971.— V. 5, № 3.— P. 254—285.
139. Strong H. R. High Level Languages of Maximum Power//Proc,
of the 12tn Annual IEEE Symp. on Switch, and Autom. Theory.—1971.—
P. 1—4.
140. Tokura N., Kasami T., Furuta Sh. lanov Schemas Aug-
mented by a Pushdown Memory // Proc, of the 15th Ann. IEEE Symp.
on Switch, and Autom. Theory.—1974.— P. 84—94.
141. Turing A. M. On Computable Numbers, with an Application to the
Entscheidungsproblem//Proc. London Math. Soc.—1936.— V. 42,
Ser. 2.— P. 230—235.
142. Walker S. A., Strong H. R. Characterizations of Flowchartable
Recursions// Proc, of the 4th Ann. ACM Symp. on Theory of Comp.—
Denver.—1972.— P. 18—34.
ОГЛАВЛЕНИЕ
Предисловие..................................................... 3
Глава 1. Вычислимость и разрешимость..........................
| 1. Вычислимые функции, алгоритмы............................
1.1. Функции.............................................
1.2. Словарные функции...................................
1.3. Вычислимые функции и машины Тьюринга................
1.4. Пример машины Тьюринга..............................
1.5. Словарное представление машины Тьюринга.............
f 2. Разрешимые и неразрешимые проблемы.......................
2.1. Массовые алгоритмические проблемы...................
2.2. Проблема остановки..................................
2.3. Проблема пустой ленты и метод сведения..............
2.4. Проблема зацикливания...............................
Краткий обзор и комментарии...................................
Глава 2. Графы и метод разметки...............................
| 1. Понятие графа............................................
1.1. Определение графа...................................
1.2. Связность и изоморфизм графов, деревья..............
| 2. Метод разметки и задача глобального анализа..............
2.1. Неформальное введение...............................
2.2. Формальная постановка задачи глобального анализа . . .
| 3. Решение задачи глобального анализа.......................
3.1. Процесс разметки....................................
3.2. Безопасность и единственность стационарной разметки ....
3.3. Точное решение задачи глобального анализа...........
Краткий обзор и комментарии...................................
Глава 3. Конечные автоматы....................................
| 1. Одноленточные автоматы.................................
1.1. Определение автомата.................................
1.2. Проблемы пустоты и эквивалентности...................
| 2. Многоленточные автоматы..................................
2.1. Определения..........................................
2.2. Свойства замкнутых диаграмм..........................
2.3. Процедура распознавания..............................
2.4. Предельная диаграмма.................................
2.5. Решение двухленточной проблемы.......................
| 3. Двухголовочпые автоматы..................................
3.1. Определение и пример.................................
3.2. Проблемы пустоты и эквивалентности...................
Краткий обзор и комментарии...................................
246
SBSSmSfcfcSgSS
Г л а в а 4. Стандартные схемы программ........................ 67
f 1. Схемы программ............................................ 67
1.1. Программы............................................. 67
1.2. От программ к схемам программ ........................ 69
J 2. Класс ставдартных схем.................................... 74
4 2.1. Базис..............«.................................. 74
2.2. Стандартная схема (графовая форма).................... 76
2.3. Стандартная схема (линейная форма)...............«... 77
2.4. Интерпретация, программа.............................. 79
2.5. Примеры программ...................................... 81
j 3. Эквивалентность и главные свойства стандартных схем .... 83
3.1. Эквивалентность, тотальность, пустота, свобода........ 83
3.2. Свободные интерпретации............................... 86
3.3. Согласованные свободные интерпретации................. 88
3.4. Основные теоремы о свободных интерпретациях........... 90
3.5. Определение логико-термальиой эквивалентности и ее кор-
ректность ................................................. 92
Краткий обзор и комментарии.................................... 94
Глава 5. Неразрешимые свойства стандартных схем................ 98
1 1. Двоичный двухголовочиый автомат........................... 98
$ 2. Моделирование двоичного автомата стандартной схемой .... 101
2.1 Класс <5\ стандартных схем............................ 101
2.2. Построение схемы, моделирующей автомат............... 102
J 3. Теоремы о неразрешимых свойствах стандартных схем .... 106
3.1. Проблемы пустоты и эквивалентности................... 106
3.2. Проблема тотальности................................. 106
3.3. Проблема свободы..................................... 108
Краткий обзор и комментарии.................................... НО
Глава 6. Логико-термальная эквивалентность стандартных схем 111
$ 1. Фрагменты и их преобразование............................. Ш
1.1. Фрагменты.............................................. Ш
1.2. Информационные маршруты, зацеплениость и влияние . . . 113
1.3. Формальные преобразования........................... 114
5 2. Инварианты н вх представление в виде сетей............. 116
2.1. Функциональные сети.................................. 116
2.2. Полурешетка приведенных сетей........................ 118
2.3 Нахождение инвариантов................................ 120
5 3. Алгоритм распознавания логико-термальной эквивалентности . . . 123
3.1. Система эквивалентных преобразований 2ЛТ............. 123
3.2. Приведение н согласование фрагментов................... 126
3.3. Полнота системы £лт.................................... 130
Краткий обзор и комментарии..................................... 133
Глава 7. Разрешимые подклассы стандартных схем................. 134
1 1. Свободные стандартные схемы............................... 136
1.1. Проблемы пустоты и тотальности........................ 136
1.2. Проблема изоморфизма.................................. 137
$ 2. Сквозные схемы............................................ 141
2.1. Определение сквозных схем............................. 141
2.2. Обобщение инвариантов................................. 143
2.3 Освобождение сквозных схем............................ 150
2.4. Алгоритм распознавания эквивалентности сквозных схем 153
2.5. Корректность алгоритма И.............................. 156
Краткий обзор и комментарии.................................. 163
Г л а в а 8. Рекурсивные схемы................................ 171
J 1. Класс рекурсивных схем................................... 171
1.1. Рекурсивное программирование......................... 171
1.2. Определение рекурсивной схемы........................ 173
1.3 Рекурсивная программа................................. 175
247
5 2. Проблемы трансляции...................................... 178
2.1. О сравнении классов схем............................. 178
2.2. Трансляция стандартных схем в рекурсивные.......... 179
2.3. Трансляция рекурсивных схем в стандартные.......... 182
5 3. Линейные унарные рекурсивные схемы....................... 185
3.1. Проблема трансляции.................................. 185
3.2. Праволинейные унарные схемы.......................... 189
{ 4. Схемы с процедурами...................................... 191
4.1. Сравнение с классом рекурсивных схем................. 191
4.2. Частичная трансляция схем с процедурами.............. 194
Краткий обзор и комментарии................................... 196
Глава 9. Обогащенные схемы.................................... 201
$ 1. Классы обогащенных схем................................. 201
1.1. Счетчики, магазины, массивы.......................... 201
1.2. Примеры обогащенных схем............................. 202
2. Проблемы трансляции..................................... 204
2.1. Счетчиковые и рекурсивные схемы...................... 204
2.2. Счетчиковые и стандартные схемы..................... 208
2.3. Счетчиковые и магазинные схемы....................... 208
2.4. Магазинные схемы и схемы с массивами................. 209
2.5. Магазинные и рекурсивные схемы....................... 211
2.6. Сравнительная схематология........................... 221
'Краткий обзор и комментарии.................................. 224
Глава 10. Схемы структурированных программ.................... 228
-j 1. Структурированные схемы................................. 228
1.1. Класс структурированных схем......................... 228
1.2. Трансляция структурированных схем в стандартные..... 230
1.3. Трансляция стандартных схем в структурированные . . . 231
t 2. Структурированные схемы с логическими операциями .... 232
Список литературы............................................. 239