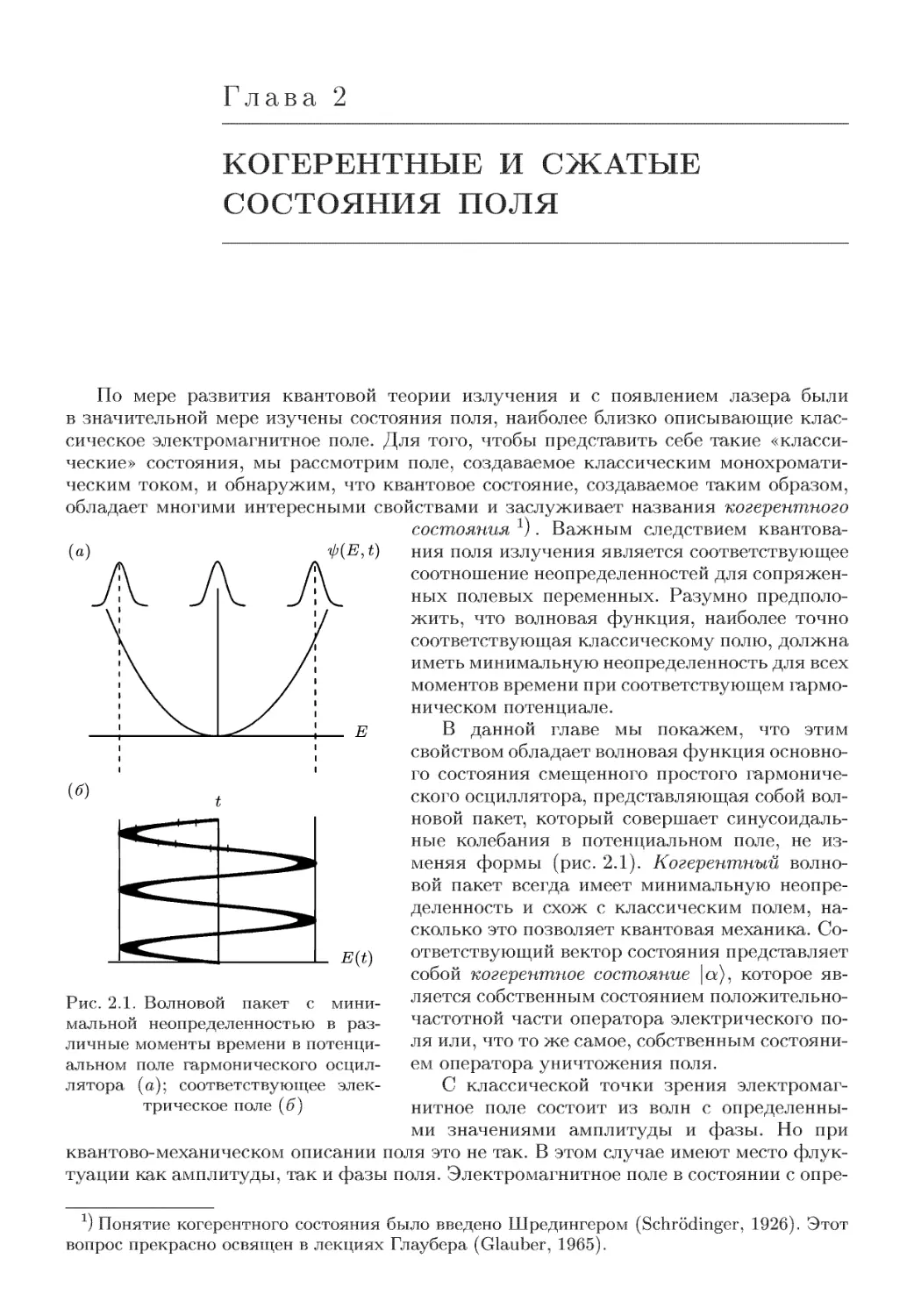
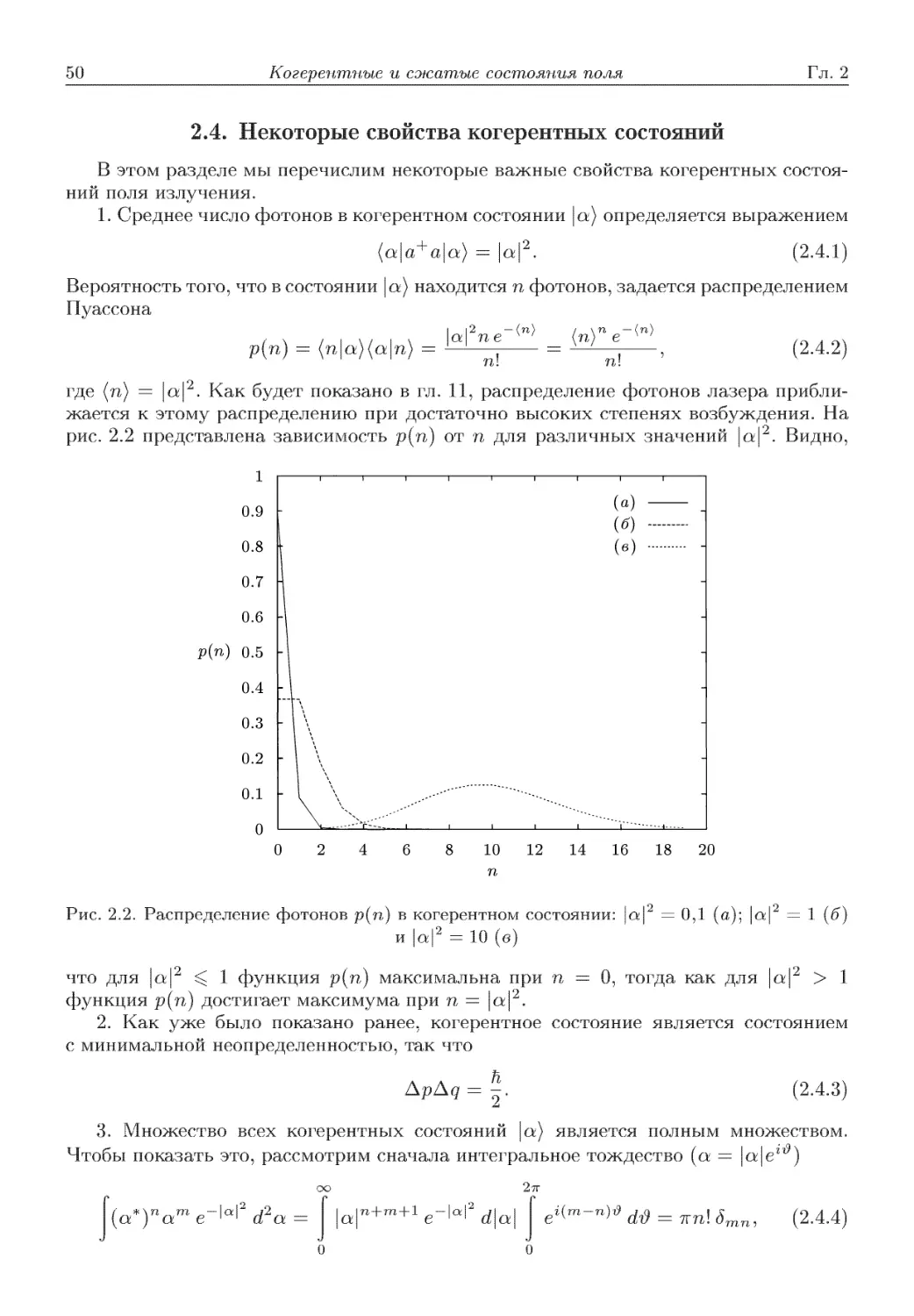
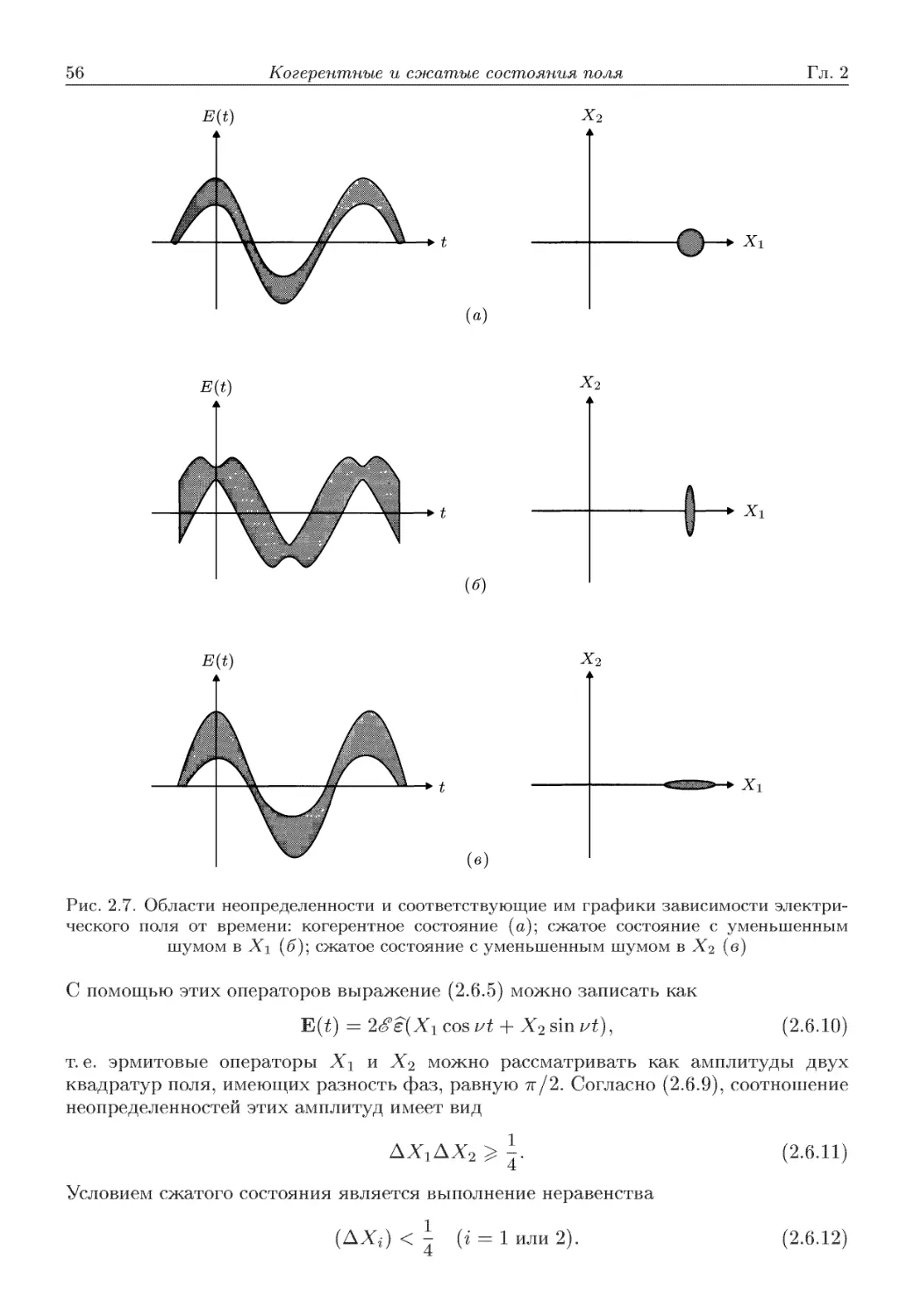
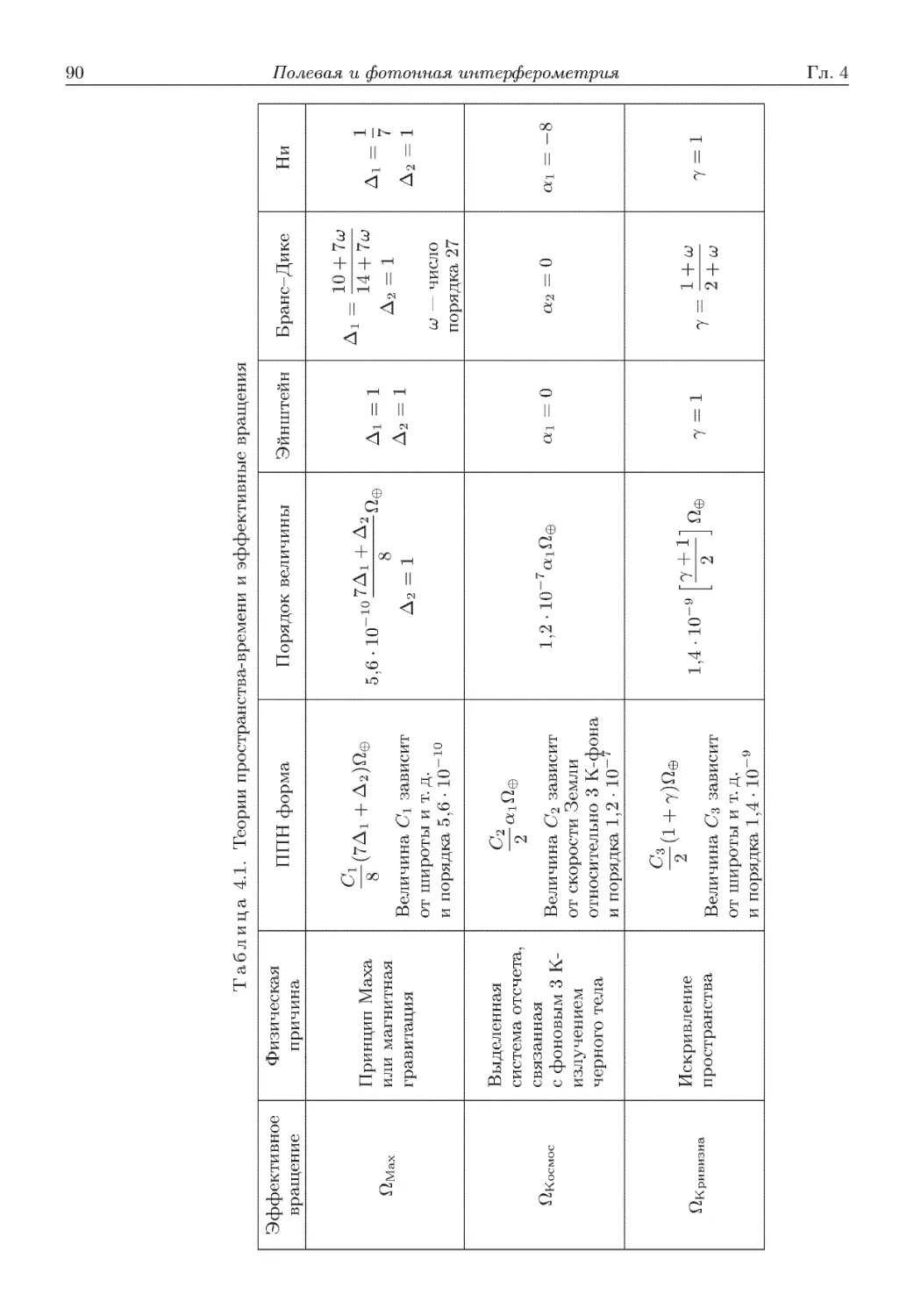
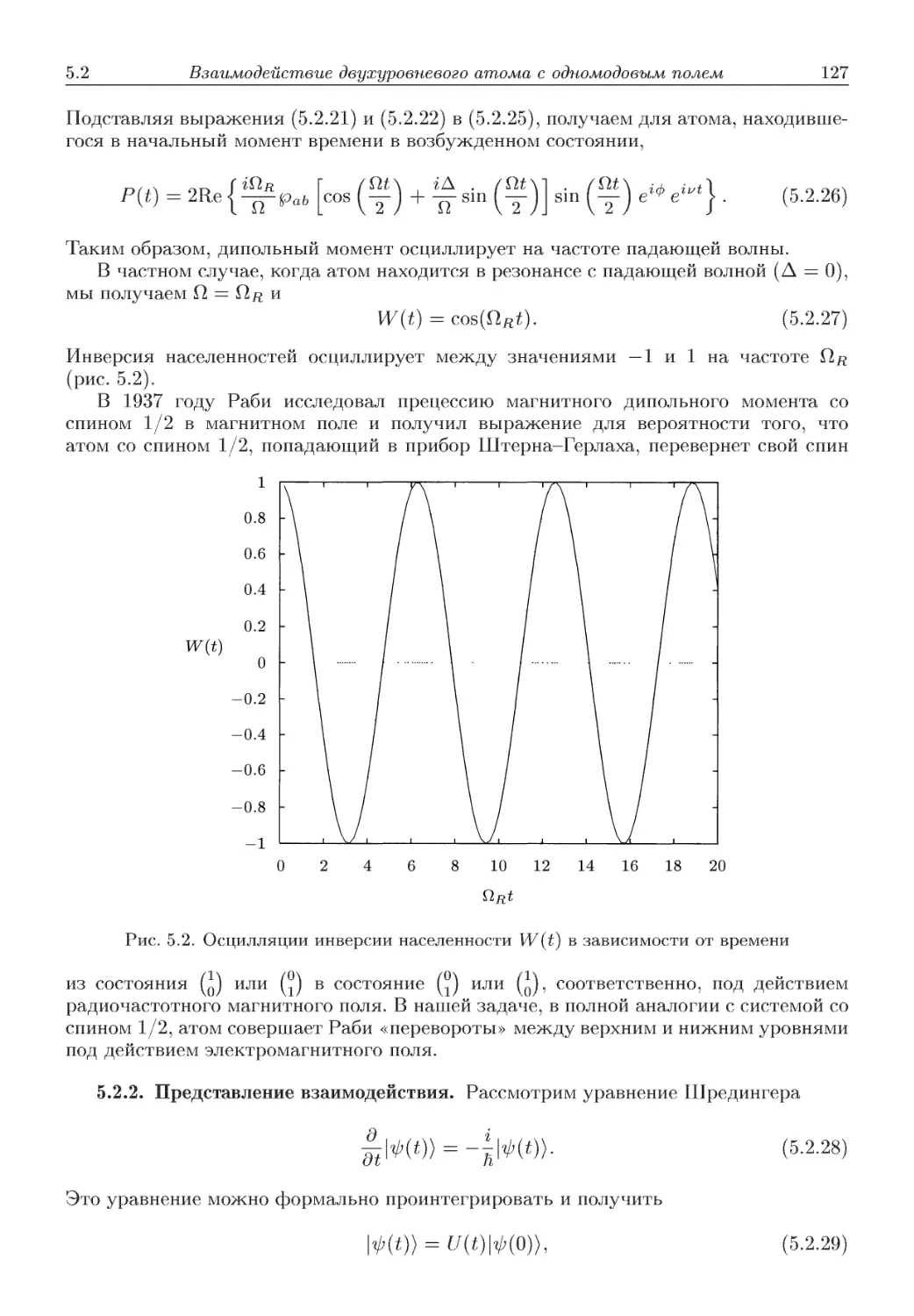
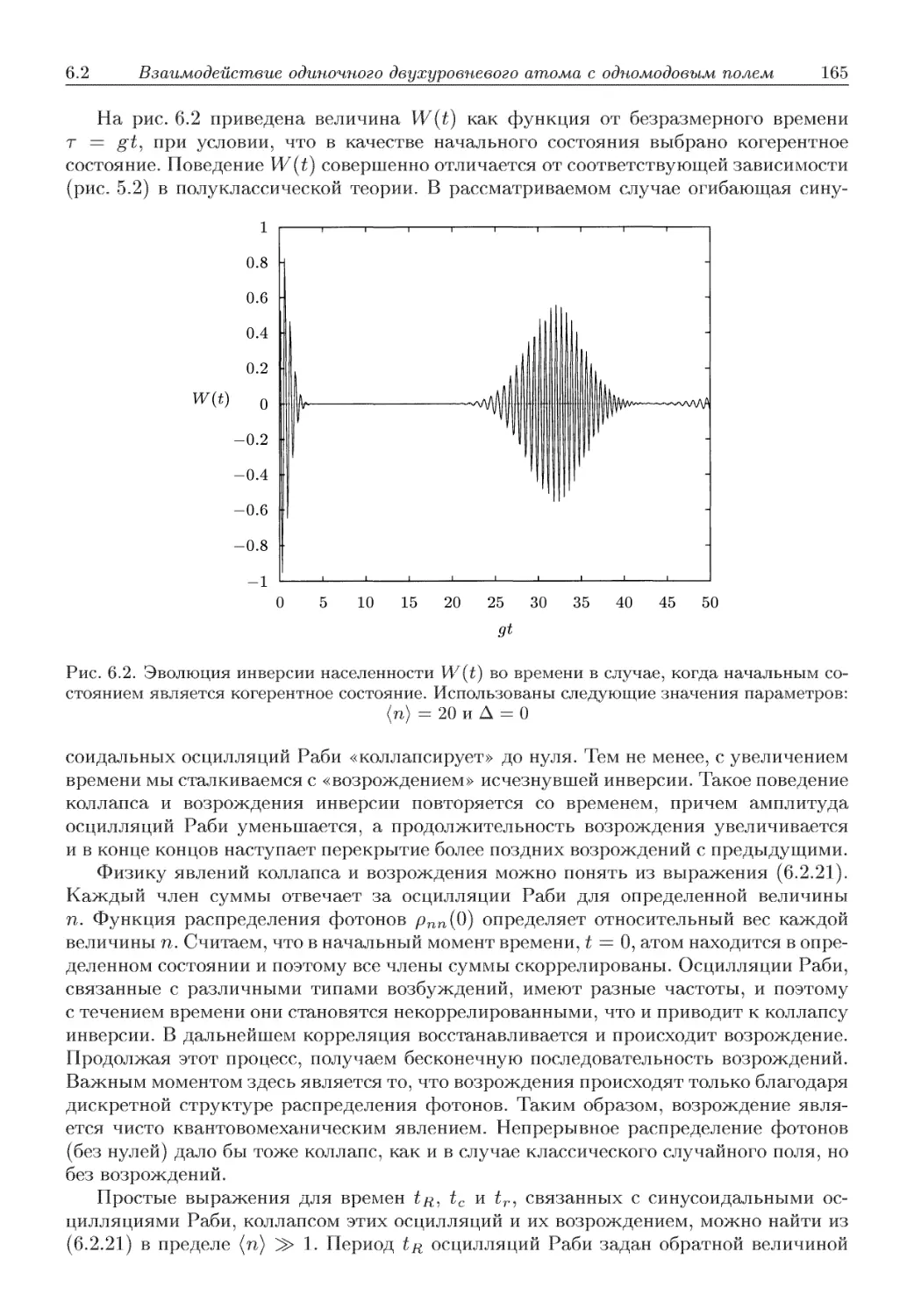
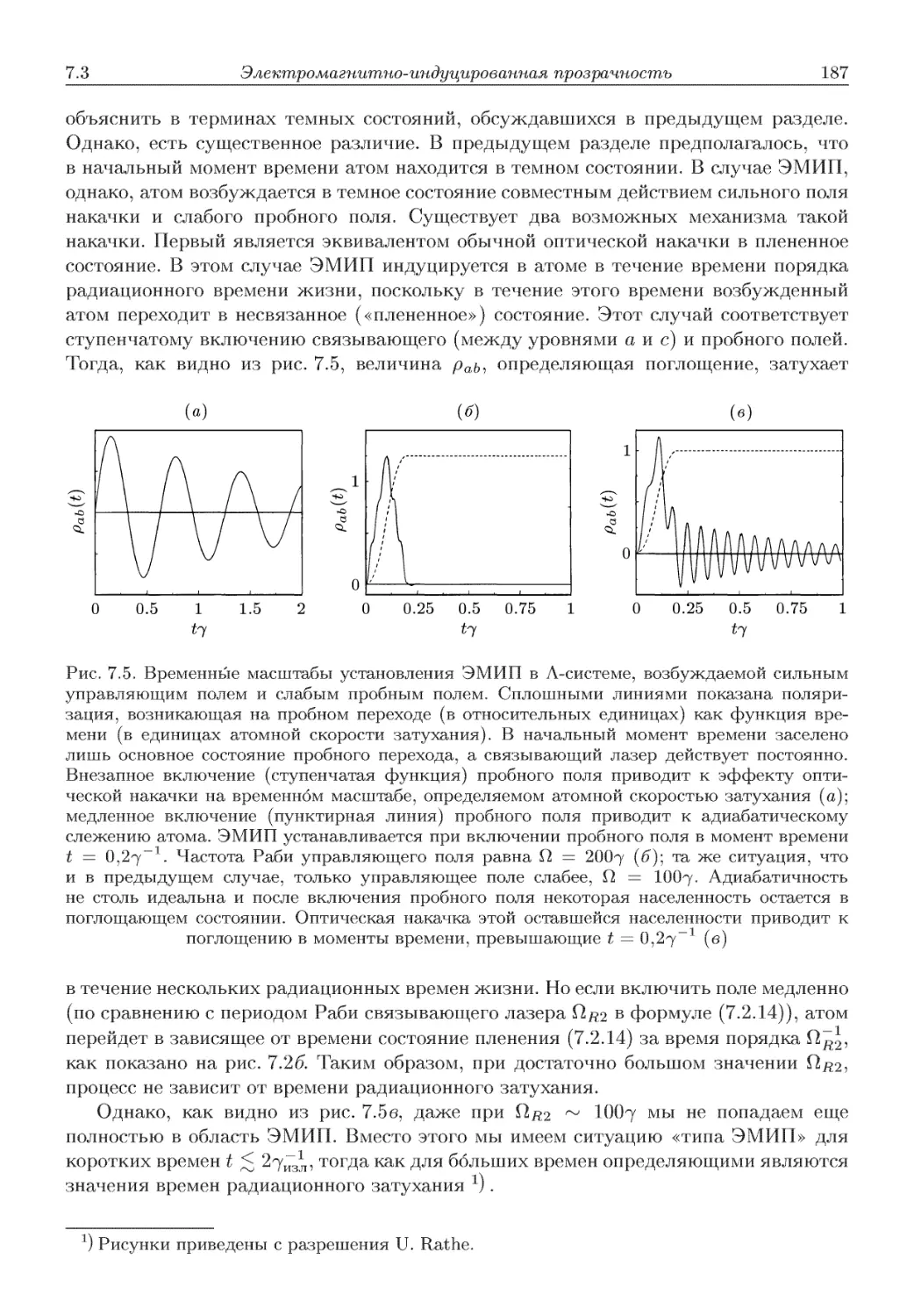
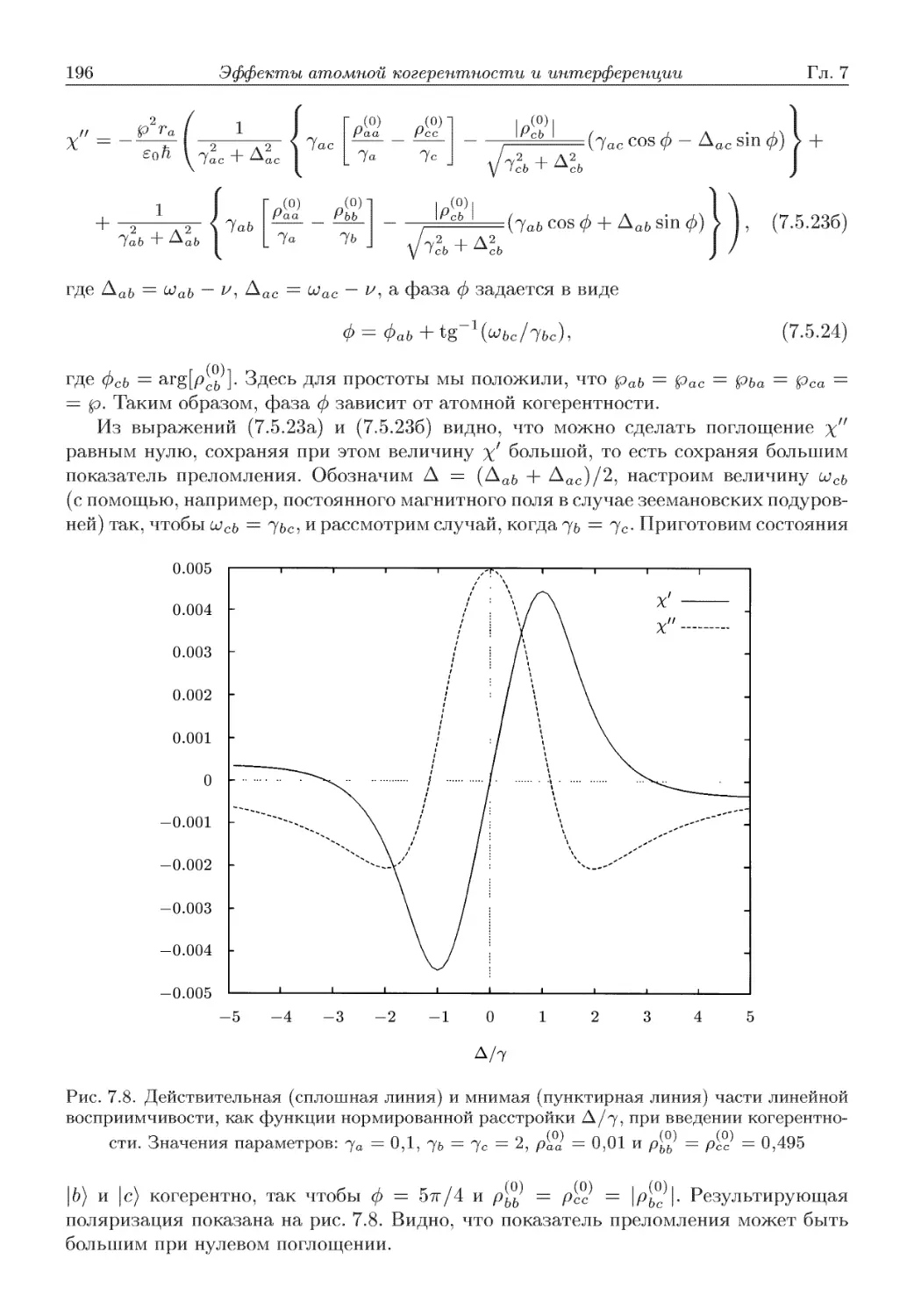
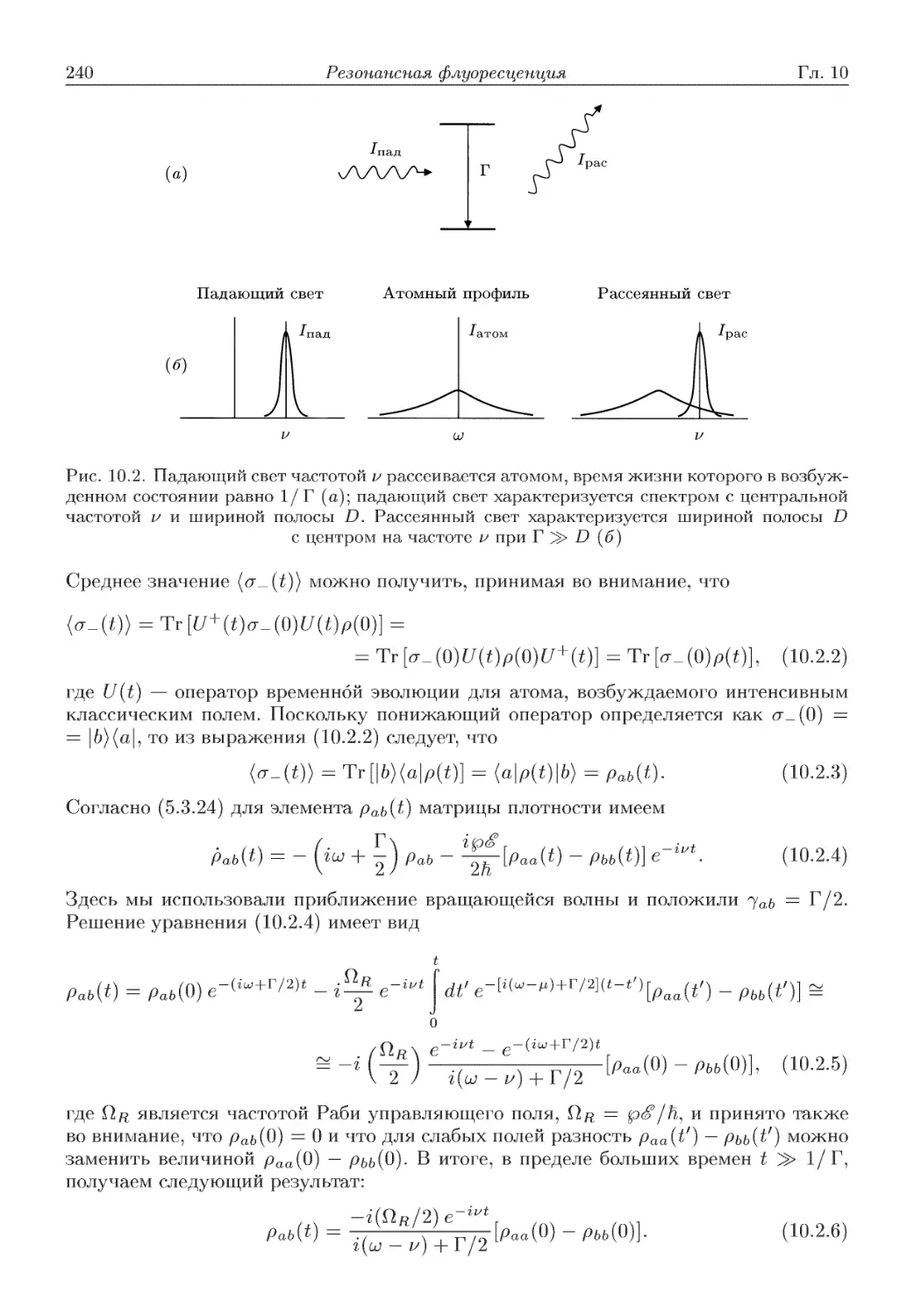
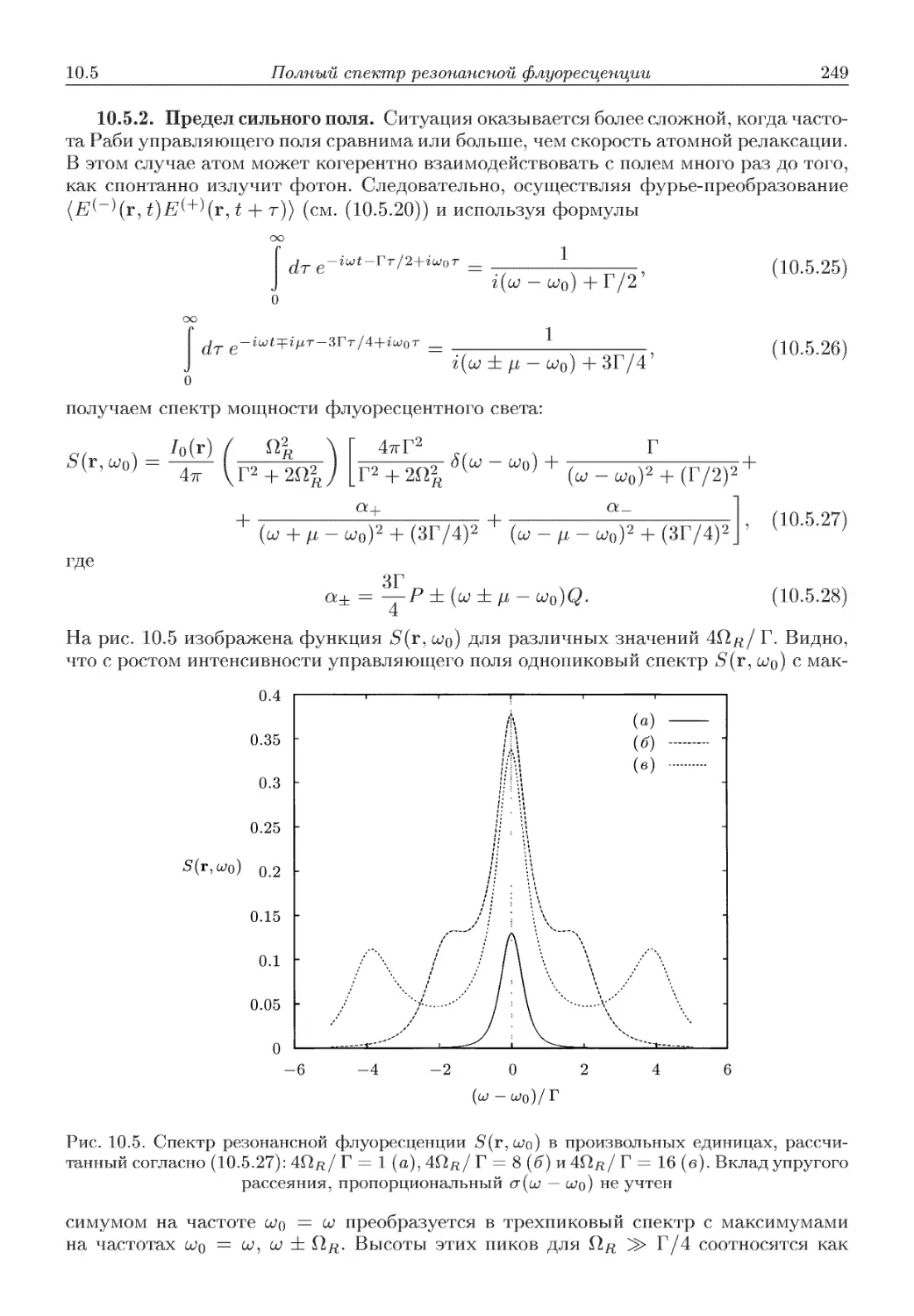
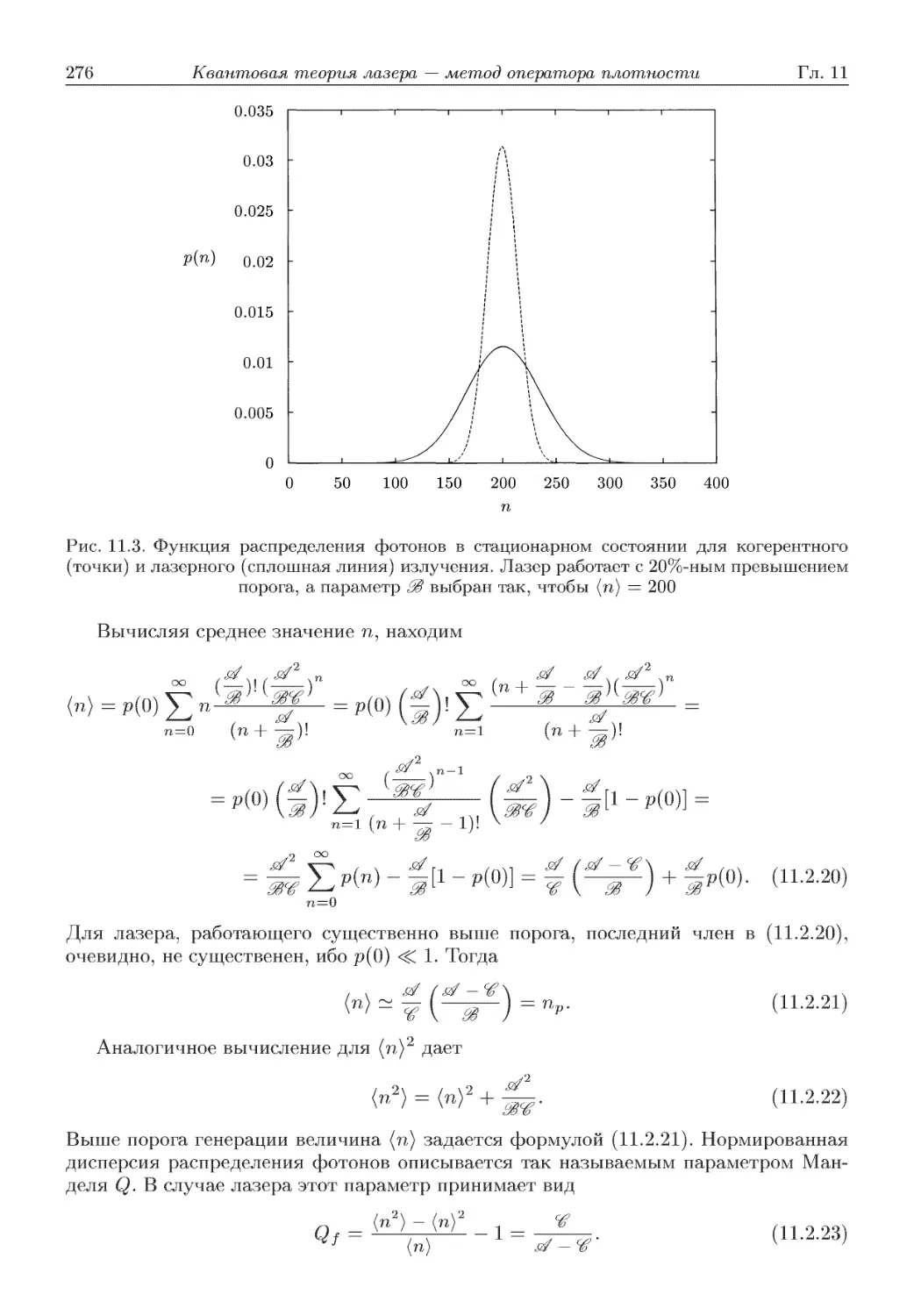
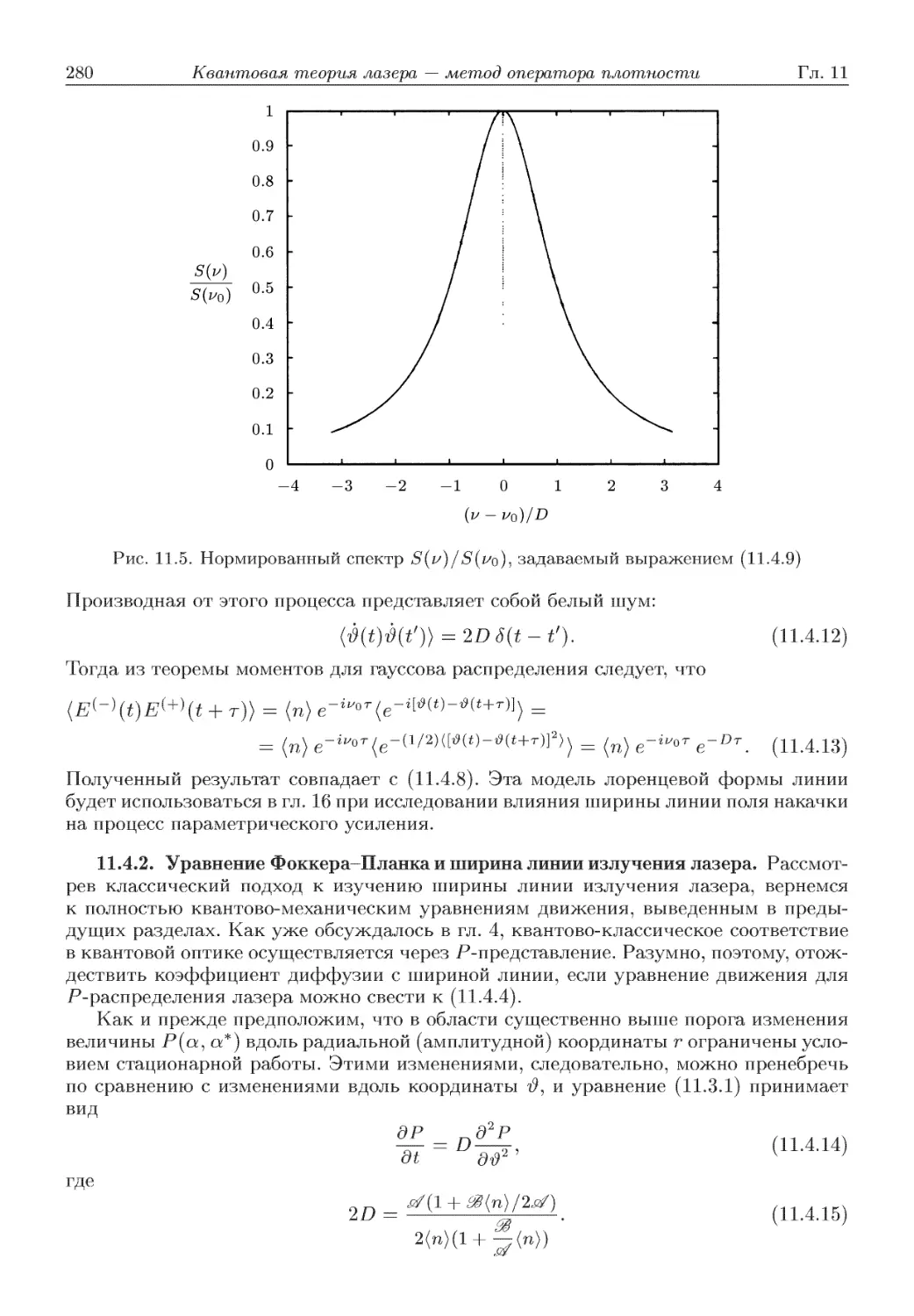
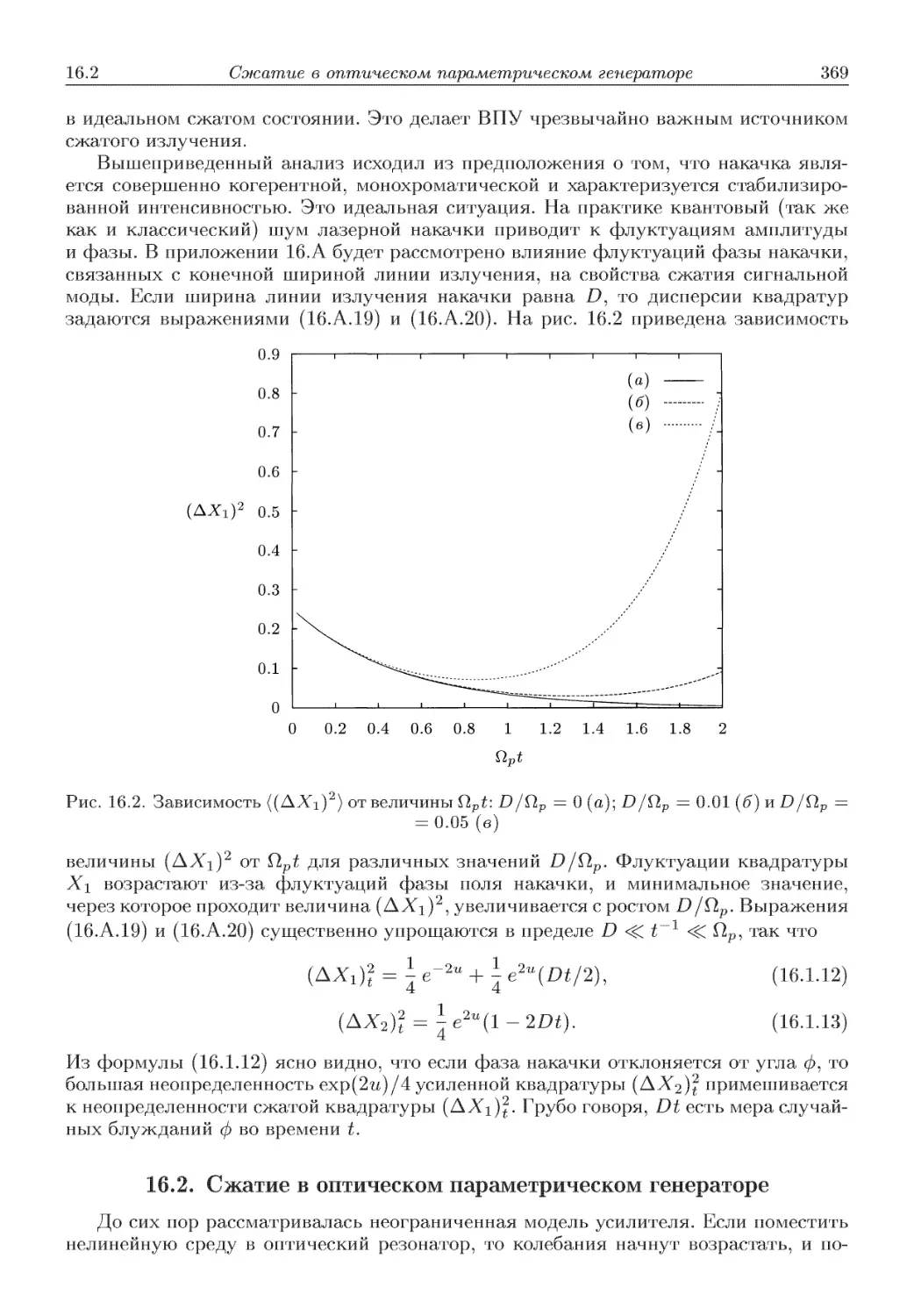
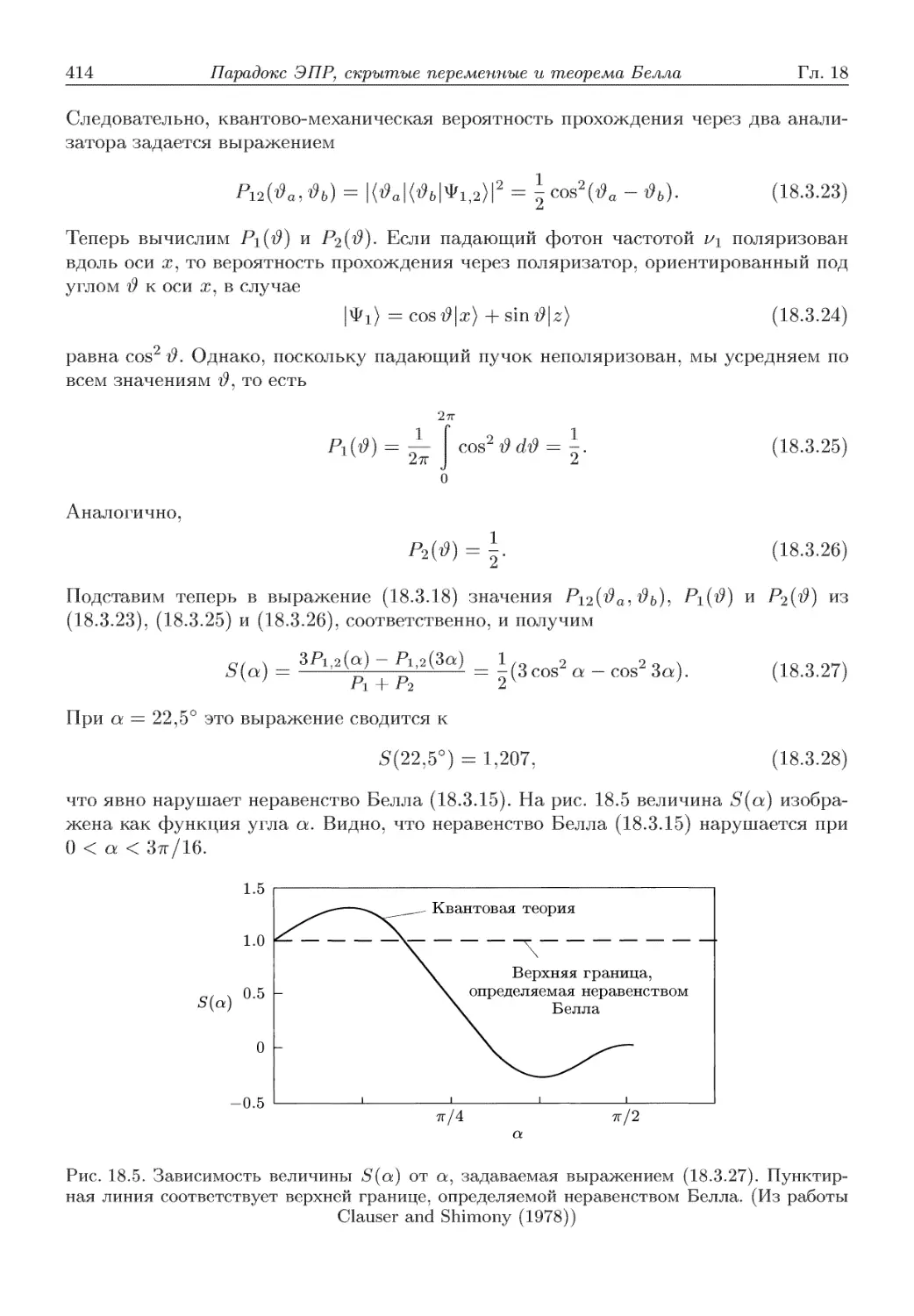
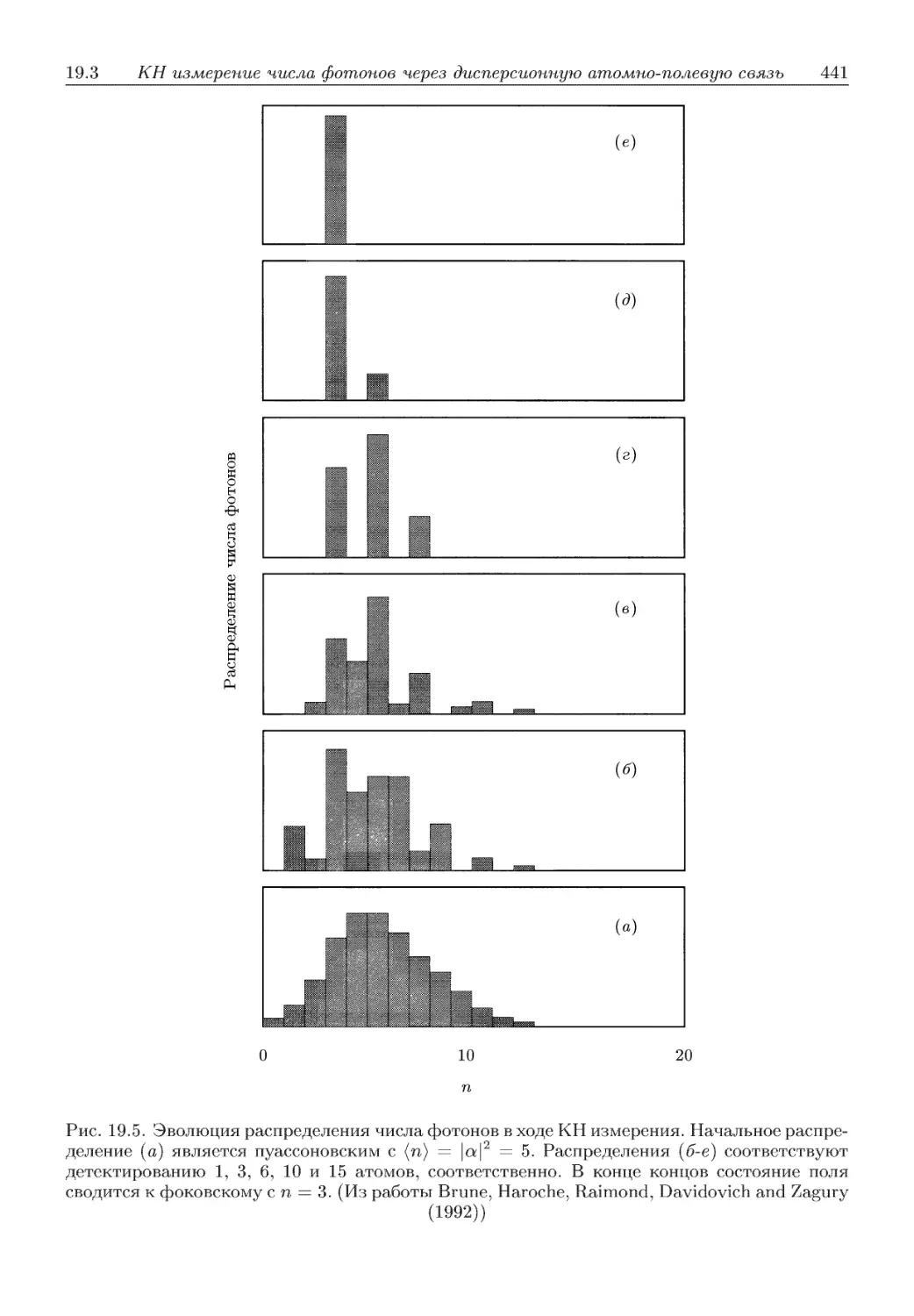
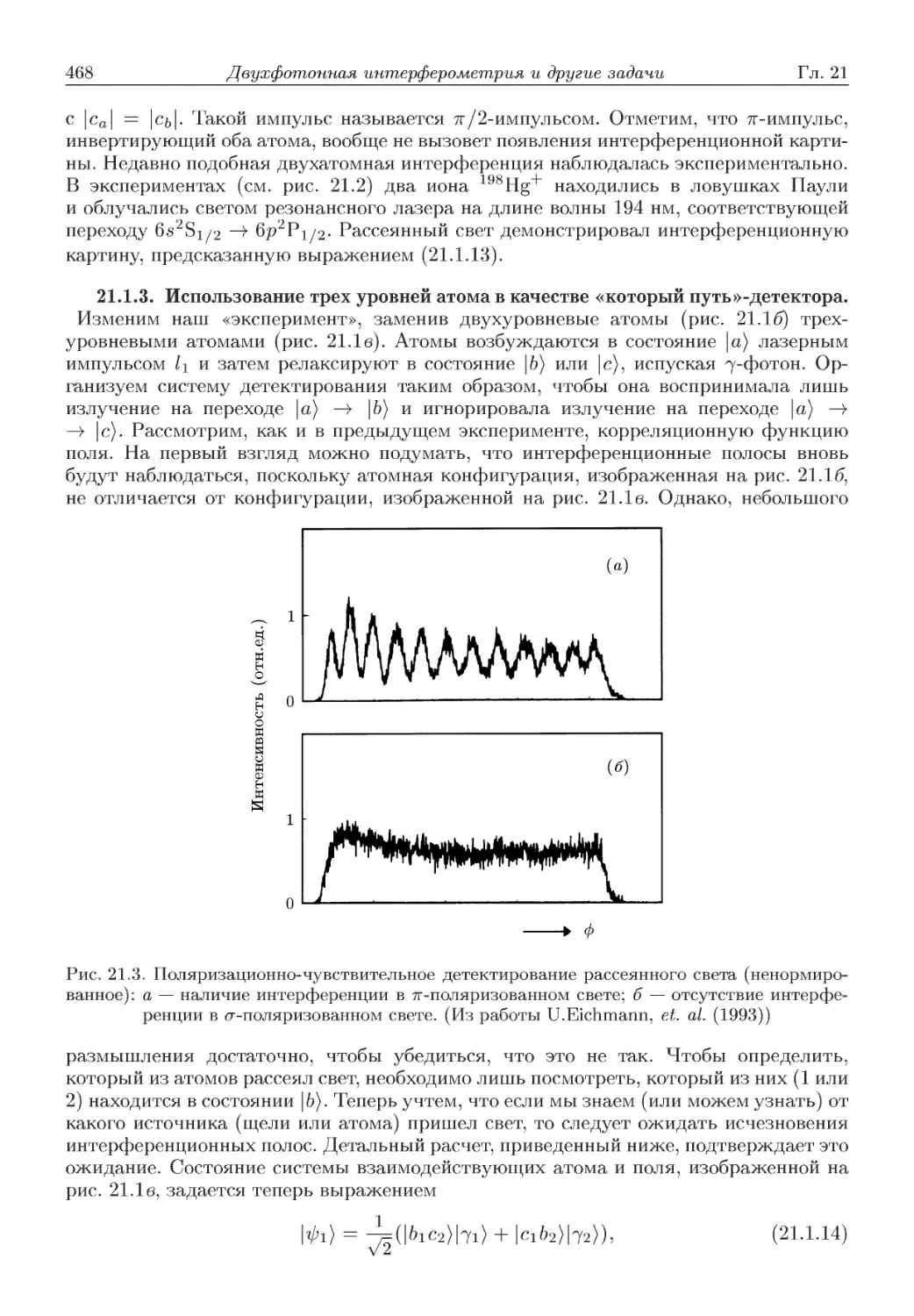
Автор: Скалли М.О. Зубайри М.С. Самарцева В.В.
Теги: оптика физика математическая физика спектроскопия издательство физматлит квантовая оптика
ISBN: 5-9221-0398-9
Год: 1997
Текст
QUANTUM OPTICS
Marian O. Scully
Texas AhM University and M'ax-Planck-Institut fur Quantenoptik
M. Suhail Zubairy
Quaid-i-Azam University
Cambridge University Press
1997
М.О. Скалли, М.С. Зубайри
КВАНТОВАЯ ОПТИКА
Перевод с английского
АЛ. КАЛАЧЁВА, ТТ МИТРОФАНОВОЙ, В.В. САМАРЦЕВА,
Р.Н. ШАХМУРАТОВА
Под редакцией
профессора В.В. САМАРЦЕВА
МОСКВА
ФИЗМАТЛИТ
УДК 535
ББК 22.34
С42
С калл и М. О., Зубайри М. С. Квантовая оптика: Пер. с англ. / Под ред.
В.В. Самарцева. - М.: ФИЗМАТЛИТ, 2003. - 512 с. - ISBN 5-9221-0398-9.
Книга знакомит читателя с современными проблемами квантовой оптики, такими как
лазерная генерация без инверсии, микромазеры, сжатые состояния света, атомная оптика
и лазерное охлаждение. Особое внимание уделяется различным проявлениям эффектов
квантовой интерференции, проблемам теории измерений и применению современной оптики
к исследованию основ квантовой механики.
Для широкого круга исследователей, работающих в области современной оптики, а так-
также для преподавателей, аспирантов и студентов соответствующих специальностей.
ISBN 5-9221-0398-9 (руССК.) @ Cambridge University Press, 1997
ISBN 0-521-43458 (англ.) © физматлит, 2003 (русск.)
Посвящается
Т. Т. Скалли и Н.Ф. Зубайри
и памяти
0.0. Скалли и ММ. Зубайри
ПРЕДИСЛОВИЕ
Квантовая оптика, представляющая собой синтез квантовой теории поля и фи™
зической оптики, испытывает в настоящее время революционные изменения. От
ранних исследований в области когерентных свойств излучения в 60-х гг., таких
как квантовая статистическая теория лазера, квантовая оптика эволюционировала
к современным вопросам, связанным, например, с исследованием роли сжатых со-
состояний поля излучения и атомной когерентности в подавлении квантового шума в
интерферометрии и оптических усилителях. С другой стороны, стали реальностью
такие, ранее казавшиеся немыслимыми, концепции, как лазер без инверсии насе-
ленностей и одноатомные (микро) мазер и лазер. Многие из этих идей являются
перспективными для создания новых устройств, обладающих чувствительностью,
существенно превышающей стандартные квантовые пределы. Кроме того, квантовая
оптика предоставляет новые мощные способы исследования таких фундаментальных
проблем квантовой механики, как дополнительность, скрытые параметры и другие,
являющиеся основными для квантовой физики и философии.
Целью данной книги является такое изложение этих и многих других захваты-
захватывающих результатов в области квантовой оптики, которое уделяло бы особое внима-
внимание фундаментальным принципам и их приложениям, что позволило бы студентам
проводить самостоятельные исследования в этой области. Эта книга (возникшая на
основе наших лекций, прочитанных в различных университетах, исследовательских
институтах и летних школах) может служить учебником для аспирантов, владеющих
некоторыми базовыми знаниями по квантовой механике и электродинамике. Каждая
глава сопровождается задачами и списком литературы. Некоторые задачи непосред-
непосредственно связаны с содержанием цитируемых статей. При составлении списков литера-
литературы мы стремились указать первоисточники и обзорные статьи для более глубокого
изучения, но не ставили перед собой задачу сделать эти списки исчерпывающими.
Формально книгу можно разделить на три части. В первых шести главах разраба™
тывается «инструментарий» квантовой оптики, а в последующих одиннадцати главах
этот «инструментарий» применяется к различным квантовым оптическим системам.
Последние четыре главы посвящены применению современной квантовой оптики к
исследованию основ квантовой механики.
6 Предисловие
Книга начинается с представления квантования поля излучения, в котором каж-
каждой моде поля ставится в соответствие квантованный гармонический осциллятор.
Стремление квантовать поле излучения во многих квантовых оптических системах
обусловлено такими явлениями, как квантовые биения, двухфотонная интерферомет-
интерферометрия и генерация неклассических состояний поля, например, фоковских состояний.
Некоторые из этих явлений по-новому освещают непростую концепцию фотона. В
первой части книги обсуждаются различные состояния радиационного поля, напри-
например когерентное и сжатое, и вводятся функции распределения, устанавливающие
связь между квантовой и классической теориями излучения. Затем развивается
квантовая теория когерентности в терминах корреляционных функций поля, состав-
составляющая основу для обсуждения результатов интерферометрических экспериментов.
Далее в книге развивается полуклассическая и квантовая теории взаимодействия
излучения с веществом. При этом основное внимание уделяется формированию тео-
теоретической базы, направленной на понимание многогранных проблем современной
квантовой оптики.
Во второй части книги эта теоретическая база применяется для развития теорий
атомного и полевого затухания, резонансной флуоресценции, функционирования ла-
лазера и микромазера, а также изучения свойств квантового шума в таких нелинейных
оптических процессах, как параметрическое усиление и четырехволновое смешение.
Подробно обсуждаются эффекты атомной когерентности в различных системах.
Например, роль атомной когерентности в подавлении поглощения приводит к таким
интересным эффектам, как лазерная генерация без инверсии населенностей и элек-
электромагнитно-индуцированная прозрачность. Атомная когерентность может играть
роль в подавлении шума спонтанной эмиссии Шавлова^Таунса в лазерах, также
как в корреляционных лазерах (КЛ). Такие КЛ-системы могут быть использованы,
например, в лазерных гироскопах и «бесшумовых» усилителях.
Третья часть книги посвящена приложению современной квантовой оптики к
рассмотрению фундаментальных вопросов, относящихся к основам квантовой меха-
механики, таких как теорема Белла, квантовые неразрушающие измерения, детекторы
типа «какой путь» и двухфотонная интерферометрия.
Мы очень благодарны многочисленным коллегам, друзьям и студентам, с которы-
которыми пришлось сотрудничать в процессе подготовки этой книги. Не имея возможности
отметить каждого индивидуально, позволим себе выразить благодарность лишь
некоторым из них.
Особенно благодарим С. Харриса, В. Лэмба, Дж. Швингера и Г. Вальтера, ко-
которые сильно повлияли на нас своим вкладом в физику вообще и плодотворным
сотрудничеством в частности. Их след в этой книге очевиден: без них не было бы
целых глав. Благодарим П. Найта за поддержку при написании книги. Неоценимую
помощь при рассмотрении различных тонких вопросов оказали его критические
замечания и дискуссии с ним, а также с Г. Агарвалом, Р. Арновиттом, К. Беднаром,
Дж. Берго, Л. Кохеном, Д. Доулингом, Д. Эберли, М. Флешхауером, Э. Фраем,
Д. Геа-Банаклочи, Р. Глаубером, Трунг-Данг Хо, X. Ли, Л. Нардуччи, Р. О'Коннелом,
Н. Рамзеем, У. Расе, В. Шлейчем, К. Водкиевичем, Б. Урке и Ши-Яо Цу. Один из
нас, М. Сушейл Зубайри, рад выразить благодарность комитету по атомной энергии
Пакистана за финансовую поддержку в течение нескольких лет и, в частности, его
председателю И. Ахмаду за его глубокий интерес и обязательность, сыгравшую
важную роль при завершении проекта. Марлан О. Скалли, со своей стороны, хо-
хотел бы поблагодарить за поддержку министерство военно-морских исследований и,
в частности, X. Пиллоффа, чья мудрость и увлеченность проявились во многих
успешных совместных проектах и конференциях, оказавших влияние на эту книгу.
Благодарим за финансовую поддержку исследовательский центр Хьюстона (HARC)
Предисловие
и фонд Велша. Спасибо Д. Вильяме за набор в редакторе Т^Х, а также Джиму и
Андре Байлей за гостеприимство на их ранчо, где была завершена рукопись.
Наконец, выражаем благодарность членам наших семей, за их поддержку и
понимание, особенно в периоды длительного отсутствия в последнее время, когда
эта книга обдумывалась, планировалась и писалась.
Марлан О. Скалли
М. Сушейл Зубайри
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Мы рады были узнать, что наша книга переводится в России. Всегда приятно,
когда чья-то работа выносится на широкое обсуждение. Надеемся, что наша книга
оправдает надежды российских студентов и исследователей. С ее помощью мы с
удовольствием разделим с читателями наш интерес к предмету квантовой оптики.
Квантовая оптика является быстро развивающейся областью науки. С момента
первого издания книги в 1997 году произошло много интересных и волнующих
событий. К ним относятся экспериментальная демонстрация новых эффектов атом-
атомной когерентности, таких как сверхмедленный свет, имеющий групповые скорости
порядка 10 м/с, бозе^эйнштейновская конденсация в разбавленных лазерно охлаж-
охлажденных атомных системах и различные аспекты квантовой информатики, включаю-
включающие квантовую когерентность и перепутанность. В данной книге изложены основы,
позволяющие изучить эти и другие недавно полученные результаты.
Мы выражаем благодарность профессору В.В. Самарцеву за его инициативу
и усилия, направленные на перевод «Квантовой оптики» на русский язык.
Марлан О. Скалли
М. Сушейл Зубайри
4 августа 2002 года
Глава 1
КВАНТОВАЯ ТЕОРИЯ
ИЗЛУЧЕНИЯ
Свет занимает особое место как в классическом, так и в квантово-механическом
описании явлений природы. Вспомним, что Ньютон, который внес фундаменталь-
фундаментальный вклад в оптику, был сторонником корпускулярной и противником волновой
теории света. Тем не менее, блестящее объединение электричества и магнетизма,
осуществленное Максвеллом, ясно показало, что свет следует понимать как волновой
процесс распространения в пространстве электрического и магнитного полей.
Ведущая роль света в определении границ познания в физике сохранилась и в
двадцатом веке с его ультрафиолетовой катастрофой, связанной с излучением чер-
черного тела, с одной стороны и фотоэлектрическим эффектом с другой. Именно тогда,
с введением Планком кванта действия, необходимого для объяснения спектра излу-
излучения черного тела, и началась эра квантовой механики. Дальнейшее развитие этих
идей привело Эйнштейна к объяснению фотоэлектрического эффекта и введению
понятия фотона.
Объединение волновых и корпускулярных свойств света удалось Дираку 1)' 2),
который в своей теории поля излучения, объяснил эффекты интерференции, а также
возбуждение отдельного атома в результате поглощения фотона. В этой главе, следуя
Дираку, каждой моде поля излучения мы ставим в соответствие квантованный гармо-
гармонический осциллятор, что составляет суть квантовой теории излучения. Интересным
следствием квантования излучения являются колебания, соответствующие нулевой
энергии, или так называемые вакуумные флуктуации. Эти флуктуации не имеют
классического аналога и лежат в основе многих интересных явлений квантовой
оптики. В гл. 5 и 7 обсуждается полу классическая теория взаимодействия поля
с атомом, в которой квантуется только атом, а поле рассматривается классически.
Такая теория может объяснить многие явления, наблюдаемые в современной оптике.
Тем не менее, квантование поля излучения необходимо для объяснения таких эффек-
эффектов, как спонтанное излучение, лэмбовский сдвиг, ширина линии излучения лазера,
эффект Казимира и полная статистика фотонов лазера. В действительности, каждый
из этих физических эффектов можно объяснить с точки зрения вакуумных флук-
флуктуации, возмущающих атомы. Например, часто говорят, что спонтанное излучение
возникает в результате «стимуляции» атома вакуумными флуктуациями. Однако,
имеются и другие, более существенные причины и логические аргументы в пользу
квантования поля излучения.
г) Пионерские работы Дирака (Dirac, 1927) и Ферми (Fermi, 1932) по квантовой теории
излучения следует прочитать каждому, кто изучает данный предмет. Превосходные совре-
современные исследования можно найти в книгах: (Loudon, 1973; Cohen-Tannoudji, Dupont-Roc,
and Crynberg, 1992; Welnberg, 1995; Pike and Sarkar, 1995).
) Вопросы квантовой оптики прекрасно изложены в книге (Mandel, Wolf, 1995) Ман-
дель Л., Вольф Э. Оптическая когерентность и квантовая оптика. Пер. с англ./ Под
ред. В.В. Самарцева — М.: Физматлит, 2000. — 896 с. — Примеч. ред. пер.
10 Квантовая теория излучения Гл. 1
В частности, задача о квантовых биениях дает нам простой пример того, что ре™
зультаты самосогласованных полностью квантовых вычислений качественно отлича-
отличаются от результатов, полученных с помощью полуклассической теории с учетом или
без учета вакуумных флуктуации. Другим экспериментом, для правильной интерпре-
интерпретации результатов которого необходима квантовая теория излучения, является двух-
фотонная интерферометрия и создание перепутанных состояний, соответствующих
такой конфигурации. Подробно это явление обсуждается в гл. 21. Дополнительными
аргументами в пользу квантования электромагнитного поля являются эксперимен-
экспериментальные наблюдения неклассических состояний поля излучения, таких как сжатые
состояния, субпуассоновская статистика фотонов и антигруппировка фотонов.
Представив это краткое обоснование квантовой теории излучения, приступим
к квантованию свободного электромагнитного поля.
1.1. Квантование свободного электромагнитного поля
Рассмотрение квантования электромагнитного поля в свободном пространстве
удобно начать с классического описания поля, основанного на уравнениях Максвел-
Максвелла. В единицах МКС эти уравнения выглядят следующим образом:
VxH=|, A.1.1a)
VxE = -^, A.1.16)
V-B = 0, A.1.1b)
V-D = 0; (l.l.lr)
материальные уравнения имеют вид
В = /i0H, A.1.2)
D = ?0Е. A.1.3)
Здесь eq и /хо — соответственно электрическая и магнитная постоянные,
где с — скорость света в вакууме.
Применяя оператор V к обеим частям уравнения A.1.16) и пользуясь уравнения™
ми A.1.1а), (l.l.lr), A.1.2) и A.1.3), получаем, что E(r, i) удовлетворяет волновому
уравнению
*=-?? = <>¦ A.1.4)
При выводе уравнения A.1.4) использовалось тождество V х (V х Е) — V(V • Е) —
-V2E.
1.1.1. Разложение по модам. Для начала рассмотрим электрическое поле в объ-
объемном резонаторе длиной L (рис. 1.1). Предположим, что поле поляризовано линейно
в направлении х и осуществим разложение по нормальным модам резонатора:
jqj(t)Sm(kjz), A.1.5)
где qj — амплитуда нормальной моды, имеющая размерность длины, kj = jn/'L
(j = 1,2,3,...) и
1.1
Квантование свободного электромагнитного поля
11
А
АЛЛА
V V V \J
Рис. 1.1. Электромагнитное поле частотой и внутри резонатора. В поперечном электромаг-
электромагнитном поле электрическое поле поляризовано в направлении х
где Vj = jttc/L — собственная частота резонатора, V = LA (А — площадь попе-
поперечного сечения оптического резонатора) — объем резонатора и rrij — константа,
имеющая размерность массы. Константа rrij введена исключительно для того, чтобы
провести аналогию между единичной модой электромагнитного поля и гармониче-
гармоническим осциллятором. Эквивалентный механический осциллятор будет иметь массу
rrij и декартову координату qj. Из A.1.5) находим выражение для ненулевой состав-
составляющей магнитного поля Ну в резонаторе г):
os(kjz). A-1-7)
Классический гамильтониан поля имеет вид
A.1.8)
где интегрирование проводится по объему резонатора. Подставляя в A.1.8) выраже-
выражения A.1.5) и A.1.7) для Ех и Ну, соответственно, получаем
1 \J1), A.1.9)
где pj = rrijqj — канонический импульс j-й моды. Выражение A.1.9) представляет
гамильтониан поля излучения в виде суммы энергий независимых осцилляторов.
Следовательно каждая мода поля динамически эквивалентна механическому гармо-
гармоническому осциллятору.
1.1.2. Квантование. Квантование в данной динамической задаче можно осу-
осуществить, полагая, что qj и pj представляют собой операторы, удовлетворяющие
коммутационным соотношениям
[qjiPjf] = ihSjj', A.1.10a)
[Qj,Qjf] = [PjjPj'] = 0. A.1.106)
) В настоящем рассмотрении квантования поля в вакууме мы оперируем векторами напря-
напряженности электрического и магнитного полей Е(г, t) и Н(г51). В материальной среде пред-
предпочтительнее работать с векторами D(r,t) и В(г,?) (см. Blalynlckl-BIrula and Blalynlckl-
Birula, 1976).
12 Квантовая теория излучения Гл. 1
Удобно осуществить каноническое преобразование и перейти к операторам uj и а+:
A.1.11а)
A.1.116)
Тогда гамильтониан A.1.9) приобретает вид
A.1.12)
Коммутационные соотношения между операторами аэ- и сЛ вытекают из соответ-
соответствующих соотношений для qj и pji
[аг,а+,] = 8ц., A.1.13)
[aj,aj,] = [a+,a+]=0. A.1.14)
По причинам, которые станут очевидными из последующего раздела, операторы
a,j и a~j получили названия операторов уничтожения и рождения соответственно.
Электрическое и магнитное поля, A.1.5) и A.1.7), выражаются через эти операторы
следующим образом:
Ex(z,t) = ^2%{^ е-*"** + а-f е{"**) sinkjz, A.1.15)
з
Hy(z,t) = -i?ocJ2^j(aJ ^iVjt ~ aj e*"**) cos kjz, A.1.16)
з
где величина
имеет размерность напряженности электрического поля.
До сих пор мы рассматривали квантование поля излучения в конечном одно-
одномерном резонаторе. Теперь можно осуществить квантование поля в неограниченном
свободном пространстве.
Рассмотрим поле, заключенное в достаточно большой, но ограниченной кубиче-
кубической полости со стороной L. Здесь под полостью подразумевается просто область
пространства, свойства границ которой не уточняются. Вместо решения в виде
стоячей волны, рассмотренного выше, рассмотрим решение в виде бегущей волны
и наложим периодические граничные условия.
Классические электрическое и магнитное поля могут быть разложены по плоским
волнам следующим образом:
Е(г, t)=Y, ^k«k е-'"*'-*-' + к.с, A.1.18)
к
Н(г, *) = —д J2 ^^^аи «.-'"»*+*•' + к.с, A.1.19)
к
где суммирование проводится по бесконечному дискретному множеству значений
волнового вектора к = (кх, ky, kz), е^ — единичный вектор поляризации, а^ —
1.1 Квантование свободного электромагнитного поля 13
безразмерная амплитуда и
В выражениях A.1.18) и A.1.19) «к.с.» означает комплексное сопряжение предыду-
предыдущего члена. Периодические граничные условия имеют вид
2тгпх j 2-кПу j 2жп2 , ч
Lj Lt Lt
где nXJ nyj nz — целые числа (О, =Ы, ±2, . . .). Совокупность чисел (пх, nyinz) опре-
определяет моду электромагнитного поля. Из уравнения (l.l.lr) следует, что должно
выполняться равенство
k-ek = 0, A.1.22)
т. е. поля являются чисто поперечными. Таким образом, существуют два независимых
направления поляризации еь для каждого к.
Переход от дискретного распределения по модам к непрерывному осуществляет-
осуществляется путем замены суммирования интегрированием в выражениях A.1.18) и A.1.19)
согласно правилу
A.1.23)
где множитель 2 возникает вследствие учета двух возможных состояний поляриза-
поляризации.
Во многих задачах нас будет интересовать плотность мод в интервале частот i/,
v + dv. Эту величину можно найти, осуществив переход от прямоугольных коор-
координат (kxi kyj kz) к полярным координатам (к sin § cos ф, к sin § sin ф, к cos #). Тогда
элемент объема в k-пространстве имеет вид
2
d к = к dk sin i9 d§ dф = ^- dv sin i? d$ d(b. A.1.24)
с
Полное число мод в объеме Ь'л с частотами, лежащими в интервале i/, v + dv,
определяется выражением
2тг
L \2 2
2W ~?
inti \ d</>=^Tdi'. A.1.25)
J тг с
О О
Таким образом, число мод с частотами, лежащими в интервале v,v-\- dv, равно
D(u)du= ^rdu, A.1.26)
7Г С
где величина D(u) называется плотностью мод.
Как и ранее, квантование поля излучения осуществляем путем замены величин а^
и а? операторами гармонического осциллятора а^ и а?, соответственно, удовлетво-
удовлетворяющими коммутационному соотношению [«к,а?] = 1- Квантованные и магнитное
поля имеют вид
Е(г, t) = J2 ek^kOk e-*-*'-1-*" + э.с, A.1.27)
к
Н/ #\ 1 \ "Л *?¦ ^ ^к /э —ii/i.t-\-i\c-r I /1 1 оо\
(Г, tj = > <^как е 1 Э.С, A.1.АО)
к
14 Квантовая теория излучения Гл. 1
где «э.с.» означает эрмитово сопряжение предыдущего члена. Как правило, раз™
деляют положительно- и отрицательно-частотные части этих полевых операторов.
Например, оператор электрического поля Е(г, t) записывается в виде
E(r,i) = E(+>(M) + E<-)(r,t), A.1.29)
где
(+> ^-^(+*r, A.1.30)
53il/fct-ik-p. A.1.31)
к
Здесь оператор E^(i% t) содержит только операторы уничтожения, а сопряженный
ему оператор E^(r, t) — только операторы рождения.
1.1.3. Коммутационные соотношения между электрическими и магнитными со-
составляющими поля. Важным следствием применения квантовых условий A.1.13)
и A.1.14) является то, что напряженности электрического и магнитного полей не
могут быть измерены одновременно, поскольку соответствующие операторы не ком-
коммутируют друг с другом. Для того, чтобы это показать, перепишем разложения по
модам A.1.27) и A.1.28) для E(r, t) и H(r, t), соответственно, выразив в явном виде
наличие двух состояний поляризации, обозначаемых символом А,
Е(Г, t) =
k,A
Н(г, t) = — У kXgk #kQk л е-^**+л-г + э.с. A.1.33)
k,A
Соответствующие коммутационные соотношения между операторами flk,A и ak A
имеют вид
[ак,А,ак',А'] = [ак,А'ак',А'1 =0' laK^^ahf,X'} = ^kk'*AA'- A.1.34)
Отсюда следует, что равновременнбй коммутатор между составляющими поля опре-
определяется выражением
[??ш(г, t), Hy(r>, *)] = ^ Е eta[^*- - 4A,)*-][e'k-('-r') - е-л'<'-''>], A.1.35)
k,A
где e^i (i = ж, у, z) является г-й составляющей е^ . Далее, с помощью операторного
тождества из задачи 1.9, запишем
€4) f = 1, A-1.36)
где е^ е\ , еjj. е\ и кк — диадные произведения, ькалярно умножив выражение
A.1.36) на декартов единичный вектор ё^ слева и на ej справа, молено показать, что
Теперь с помощью A.1.37) можно осуществить суммирование по состояниям поля™
ризации в выражении A.1.35). Результирующее выражение для коммутатора имеет
1.2 Фоковские состояния или представление чисел заполнения 15
вид
[^(г, *), Яу(г', t)} = ^ J^ Ы^Мг~Г>) ~~ е-*'Ь-*\ A.1.38)
к
Перейдем от суммирования к интегрированию согласно правилу
3fc. A.1.39)
Множитель 2, в отличие от A.1.23), здесь отсутствует, так как в данном случае
суммирование по двум состояниям поляризации проведено в явном виде. Получаем
[Ех(т, t), Hy(v', t)} = ~ihc2j-z 6™(т - г'). A.1.40)
В общем случае
\Ej(r,t),Hj(r',t)} = 0 (j = x,y,z), A.1.41)
[?,-(r, *), Я*(г', *)] = ~if^§i <5C)(r - г'), A.1-42)
где j, k и I соответствуют циклической перестановке ж, у и z. Следовательно
можно заключить, что параллельные составляющие Е и Н могут быть измерены
одновременно, тогда как перпендикулярные друг другу составляющие — нет.
1.2. Фоковские состояния или представление чисел заполнения
В этом разделе мы для начала ограничимся рассмотрением единичной моды поля
с частотой и и операторами рождения и уничтожения а+ и а, соответственно. Пусть
\п) — собственное энергетическое состояние, относящееся к собственному значению
энергии Еп, т.е.
Ж\п) = Пи (а+а + -} \п) = Еп\п). A.2.1)
Если подействовать оператором а слева, то с помощью коммутационного соотно-
соотношения [а, а+] = 1 и после некоторой перестановки получаем
Жа\п) = (Еп - hv)a\n). A.2.2)
Это означает, что состояние
\п-1) = —\п) A.2.3)
также является собственным энергетическим состоянием, но относящимся к меньше-
меньшему собственному значению:
Еп^г = Еп^ Пи. A.2.4)
В выражении A.2.3) ап — константа, которая определяется из условия нормировки
(п-1|п-1) = 1. A.2.5)
Повторяя эту процедуру п раз, мы движемся в сторону уменьшения энергии каждый
раз на величину hi/, пока не придем к выражению
= {Е0 - hi/)a\0). A.2.6)
Здесь Eq — энергия основного состояния, так что величина (Е® — Ни) должна соот-
соответствовать собственному значению энергии, меньшему, чем Eq. Поскольку значения
16 Квантовая теория излучения Гл. 1
энергии меньшие, чем Eq, для осциллятора не допустимы, следует сделать вывод, что
а|0)=0. A.2.7)
Состояние |0) известно как вакуумное состояние. Используя это соотношение, можно
найти значение Eq из уравнения для собственных значений:
= ?0|0). A-2.8)
Получаем
^о = \hv. A.2.9)
Тогда из выражения A.2.4) следует, что
Еп = (п+ i) hi/. A.2.10)
Из выражения A.2.1) получаем
а+а\п) = п\п), A.2.11)
т. е. собственное состояние оператора энергии является также собственным состоя-
состоянием оператора «числа частиц»:
п = а+а. A.1.12)
Теперь можно вычислить нормировочную константу ап в выражении A.2.3):
/п _ \\п _ ]\ = (в]а+а п) = П (п\п) = П =1 A2 13)
Если приравнять нулю фазу нормировочной константы anj то ап = у/п. Уравнение
A.2.3) в этом случае принимает вид
а\п) = у/п\п- 1). A.2.14)
Аналогичные рассуждения молено повторить для оператора а+. В результате полу-
получаем
а+\п) = л/п + 1 \п + 1). A.2.15)
Многократное применение этого уравнения дает
\п) = ^т^-10)- A.2.16)
vn!
Полезно интерпретировать собственные значения оператора энергии A.2.10) как
наличие п квантов или фотонов с энергией hi/. Собственные состояния |п) называют-
называются состояниями Фока или состояниями с определенным числом частиц. Они образуют
полную систему, т. е.
со
?|п)(п| = 1. A.2.17)
п=0
Собственные значения оператора энергии являются дискретными в отличие от клас-
классической электромагнитной теории, согласно которой энергия может иметь любое
значение. Тем не менее, среднее значение энергии может принимать различные значе-
значения, поскольку вектор состояния, в общем случае, представляет собой произвольную
суперпозицию энергетических собственных состояний, т. е.
№> = У>п|п>, A.2.18)
1.2 Фоковские состояния или представление чисел заполнения 17
Еп+1 = (п + 3/2)/ш
#2 = 5/2 Ни
Ех = 3/2 /ш
Ео = 1/2 Пи
Рис. 1.2. Схема энергетических уровней системы квантовомеханических гармонических ос-
осцилляторов, соответствующей электромагнитному полю. Оператор рождения а+ добавляет
квант энергии hi/, а оператор уничтожения а отнимает аналогичное количество энергии
где сп — комплексные коэффициенты. Остаточная энергия Ни/2^ соответствующая
Ео, называется энергией нулевых колебаний. На рис. 1.2 показана схема энерге-
энергетических уровней системы квантово-механических осцилляторов, соответствующей
электромагнитному полю.
Важным свойством состояния с определенным числом частиц \п) является то, что
соответствующее среднее значение оператора одномодового линейно поляризованно™
го поля
E(r, t) = ia е-^*+*к'г + эх. A.2.19)
обращается в нуль, т. е.
(п\Е\п) = 0. A.2.20)
Однако среднее значение оператора интенсивности Е2 определяется выражением
{п\Е2\п)^2\?\2(п+\), A.2.21)
т. е. существуют флуктуации поля относительно его нулевого среднего по ансамблю.
Интересно отметить, что ненулевые флуктуации существуют также и для вакуумного
состояния |0). Как уже упоминалось ранее, эти вакуумные флуктуации лежат в осно-
основе многих интересных явлений в квантовой оптике. Например, можно считать, что
они стимулируют спонтанное излучение возбужденного атома. Они же отвечают
за лэмбовский сдвиг 2Р1^2 —> 25i/2 уровней энергии атома водорода. В частности,
в разд. 1.3 мы рассмотрим, каким образом вакуумные флуктуации электромагнит-
электромагнитного поля приводят к лэмбовскому сдвигу.
Операторы а и а+ называют операторами уничтожения и рождения фотонов,
поскольку, как видно из выражений A.2.14) и A.2.15), они переводят состояние с п
фотонами в состояние сп~1 или п + 1 фотонами, соответственно. Эти операторы
сами по себе не являются эрмитовыми а ф а+ и не соответствуют наблюдаемым
физическим величинам таким, как амплитуды электрического и магнитного полей.
18 Квантовая теория излучения Гл. 1
Однако, некоторые их комбинации, например, а\ = (а + «+)/2 и а^ = (« — a+)/2i,
являются эрмитовыми.
До сих пор мы рассматривали одномодовое поле и нашли, что в общем случае,
волновая функция может быть представлена в виде линейной суперпозиции состоя-
состояний числа фотонов \п). Теперь применим этот формализм к случаю многомодовых
полей.
Гамильтониан Ж в выражении A.1.12) можно переписать в виде
Ж = ^Ж^ A.2.22)
к
где
= Пик (а+ак + ±) . A.2.23)
Энергетическое собственное состояние |вк) оператора Ж\^ определяется по аналогии
с одномодовым полем через уравнение для собственных значений энергии:
k + 1) |nk). A.2.24)
Общее собственное состояние оператора Ж может, следовательно, иметь nkl
фотонов в первой моде, п^2 — во второй, пк| — в 1-й и так далее, и может быть
записано как |тгк1)|пк2) . . . |/iki) • • . или более компактно:
nkl,nk2J. . . ,rck,,. . .) = |{nk}>. A.2.25)
Операторы уничтожения и рождения aki и а^ понижают или повышают значение
только 1-го элемента, т. е.
CL\c, Tit-, , П\сп •>•••-, Tile, ,...) = \/тЬ\г, П\гл , ТЬ\г* •> • • • 1 71W, — 1, . . .) , A.2.26)
~т~ \ / i I i \ / Л п?*т\
/| ! a^i | ^тэ | ^тэ | \ ^ / f»~i | _|— I ТЭ | "Т11 1Э1 —\— I ) II /,/,(%
Общий вектор состояния поля представляет собой линейную суперпозицию этих
собственных состояний:
х |nkl,nk2J... ,пкм...) = ^ с{пк}|{^к})- A.2.28)
Это суперпозиция более общего вида, чем
.., A-2.29)
где |^к|) — векторы состояния отдельных мод. Выражение A.2.28) содержит как
векторы состояния типа A.2.29), так и более общие состояния, имеющие корреляции
между модами поля, которые могут возникать в результате взаимодействия различ™
ных мод поля с системой в целом.
1.3. Лэмбовскжй сдвиг
Точное определение лэмбовского сдвига между 25i/2 и 2Рг/2 уровнями атома
водорода фактически дало толчок к развитию современной квантовой электроди-
электродинамики (КЭД). Согласно теории Дирака уровни 2S±/2 и 2Pj/2 должны были бы
1.3 Лэмбовский сдвиг 19
иметь одинаковые энергии. Однако излучательные поправки, возникающие благода-
благодаря взаимодействию между атомным электроном и вакуумом, приводят к увеличению
энергии уровня 2#1/2 относительно уровня 2Pi/2 приблизительно на 1057 МГц.
Первоначальные попытки рассчитать эти излучательные поправки, вызванные
вакуумом, не имели успеха, поскольку они приводили к бесконечным сдвигам уров-
уровней. Однако замечательные измерения Лэмба и Резерфорда послужили стимулом
к созданию теории перенормировки, оказавшейся весьма успешной в устранении этих
расход имостей.
По случаю шестидесятипятилетия Лэмба, Фриман Дайсон писал (Dyson, 1978):
«Ваша работа, посвященная тонкой структуре атома водорода, немед-
немедленно вызвала волну прогресса в квантовой электродинамике, которая и ме-
меня привела к славе и успеху. Вы проделали тяжелую, скучную, поисковую
работу. Как только Вы положили начало этой волне, дорога для нас, тео-
теоретиков, стала легкой. И после того, как мы стремительно достигли берега
с нашими изящными, прихотливыми теориями, Вы упорно продолжали за-
заниматься своей экспериментальной работой. В течение многих последующих
лет Вы напряженно трудились, добывая из атома водорода точные данные,
чтобы дать прочную основу всем нашим гипотезам. . .
Годы, когда лэмбовский сдвиг являлся центральной темой в физике, стали
золотым временем для всех физиков моего поколения. Вы первым увидели,
что этот незначительный сдвиг, неуловимый и трудно измеримый, принци-
принципиальным образом прояснит наши представления о частицах и полях.»
Вскоре после того, как были доложены экспериментальные результаты, Бете,
воспользовавшись идеей Крамерса, Швингера и Вайскопфа о «вычитании» бесконеч-
бесконечностей, осуществил несложный нерелятивисткий расчет, который качественно согла-
согласовался с теорией. В дальнейшем на основе этого расчета возникла полностью реля-
тивстская теория, количественно согласующаяся с экспериментами Кроля и Лэмба,
Френча и Вайскопфа. Этот расчет также явился предшественником современной
квантовой электродинамики КЭД в том виде, как она была развита Швингером,
Фейнманом и Дайсоном.
Блестящее согласие между полностью квантовой теорией излучения и вещества
и экспериментом, достигнутое на примере лэмбовского сдвига, обеспечило сильный
довод в пользу квантования поля излучения. Однако подробный расчет лэмбовского
сдвига увел бы нас далеко от главного направления квантовой оптики. Поэтому
мы ограничимся тем, что приведем эвристический вывод сдвига электромагнитного
уровня, следуя Вел тону.
Влияние вакуумных флуктуации электрического и магнитного полей приводит
к отклонению электрона в атоме водорода от стандартных орбит, определяемых
кулоновским потенциалом взаимодействия с протоном ^е2/4тгеог, т. е. г —> г + Sr,
где Sr — смещение положения электрона, вызванное флуктуирующими полями. Из-
Изменение потенциальной энергии, а, следовательно, и соответствующий сдвиг уровня,
определяется выражением
AV = V(r + Sr) - V(r) = St-4V + |(<Jr • VJV(t) + ... . A.3.1)
Поскольку флуктуации изотропны, то (Eг)вак = 0, и первым членом можно прене-
пренебречь. Кроме того,
<(<5r-VJ>BaK=^((<5rJ>BaKV2, A.3.2)
20 Квантовая теория излучения Гл. 1
опять же в силу изотропности флуктуации. Таким образом, получаем
где (. . .)ат — квантовое среднее по атомным состояниям.
Для 2Я-состояния атома водорода
A.3.4)
где ао = 47rsoli2/me2 (m — масса электрона) представляет собой радиус Бора. При
выводе предыдущего соотношения мы воспользовались выражениями
V2 C) = -4тг$(г), A.3.5)
Для Р-состояний нерелятивистская волновая функция в начале координат обраща-
обращается в нуль. Следовательно, и энергетический сдвиг в этом случае также равен нулю.
Теперь рассмотрим множитель {ErJ)Bavi в выражении A.3.3), обусловленный
вакуумными флуктуациями. Классическое уравнение движения для смещения элек-
электрона (Jr)k, вызванного единичной модой поля с волновым вектором к и частотой
i/, имеет вид
т?>{6г)ъ = -еЕк. A.3.7)
Это уравнение справедливо в том случае, если частота поля и больше, чем частота
орбиты Бора i/q, т.е. если v > же/а®. Для поля, осциллирующего на частоте i/,
6r(t) = 5r@) e^iut + к.с. A.3.8)
Тогда
(<Ик - -^272Е^ A-3-9)
тс к
где согласно выражению A.1.27)
Ек = #к(ак е-<"*+*-' + э.с). A-З.Ю)
Суммируя по всем модам, получаем
(У (i)(L3-n)
тс к I /-^ \тс к
7 к х
где была осуществлена подстановка @ь = (hck/2eoVI^2. В случае непрерывного
распределения по модам суммирование в A.3.11) заменяется интегрированием (см.
A.1.23)). Тогда, интегрируя по углам, получаем
1.4 Квантовые биения 21
Полученный результат расходится. Однако, как было отмечено ранее, данный метод
справедлив только для v > тгс/ао? т-е- Для к > ж/щ. Он также справедлив только
для длин волн, превышающих комптоновскую длину волны, т. е. для к < тс/Н, по-
поскольку при vIс = р/ тс = Нк/тс < 1 начинают сказываться магнитные эффекты.
Этот метод не применим, если рассматривать электрон как релятивистскую частицу.
Таким образом, мы можем выбрать нижний и верхний пределы интегрирования
в выражении A.3.12) равными тг/ао и mc/h, соответственно. Тогда
Подставляя A.3.4) и A.3.13) в A.3.3), получаем следующее выражение для вели-
величины лэмбовского сдвига
который соответствует частотному сдвигу, равному приблизительно 1 ГГц. Учиты-
Учитывая, что в расчете нами были сделаны достаточно грубые приближения, можно
считать, что этот результат хорошо согласуется с экспериментальным значением.
В заключение отметим замечательные достижения в физике лэмбовского сдвига,
которые стали возможными благодаря методам современной квантовой оптики, а
именно, определение радиационного сдвига 1Я-состояния с помощью точных изме-
измерений частоты двухфотонного перехода IS — 25, впервые осуществленных Ханшем
с сотрудниками.
1.4. Квантовые биения
За прошедшие десятилетия был предложен ряд теорий, альтернативных КЭД.
Одна из таких теорий основана на стохастической электродинамике. В этом случае
вещество рассматривается квантово-механически, тогда как излучение описывается
уравнениями Максвелла, к которым добавлены вакуумные флуктуации. Казалось,
что в этом представлении, почти все квантовые явления, такие как спонтанное
излучение, лэмбовский сдвиг и ширина линии излучения лазера, молено описать
с помощью полуклассической теории.
Однако, явление квантовых биений (Svanberg, 1991) представляет собой простой
пример того, что результаты полностью самосогласованного квантового вычисления
существенно отличаются от результатов, полученных с помощью полуклассической
теории (ПКТ), даже дополненной понятием вакуумных флуктуации. Это хороший
пример задачи, которая в рамках полу классической теории не может быть объяснена
даже качественно, не говоря уже о проведении вычислений.
В последующих главах мы представим усовершенствованные теории взаимо-
взаимодействия атома с полем, основанные на полуклассическом и полностью квантово-
механическом подходах. Однако, в этом разделе с помощью квантовой электроди-
электродинамики и полуклассической теории мы обсудим квантовые биения в трехуровневых
атомных системах, исходя из простейших соображений. Рассмотрим два различных
типа трехуровневых атомов с так называемыми V- и Л-конфигурациями, являющи-
являющимися когерентной суперпозицией всех трех состояний. Обе системы будут сначала
рассмотрены полу классически, а затем с помощью методов КЭД с целью сравнения
результатов этих двух подходов.
22
Квантовая теория излучения
Гл. 1
i=a,b,c
+ c1\c,lVl)+c2\c,lv
i=a,b,c
(а)
(б)
Рис. 1.3. Трехуровневые атомные структуры для квантовых биений: (а) — V-типа; (б) —
Л-типа
Как показано на рис. 1.3, ансамбль атомов, приготовленных в когерентной супер-
суперпозиции состояний, описывается вектором состояния
— iujnt \ I —iujht \ ь\ i
С*И,
A.4.1)
где са, сь и сс — амплитуды вероятности того, что атом находится в состоянии
|а), \Ь) и |с), соответственно. Кроме того, если не обращающиеся в нуль дипольные
матричные элементы обозначить следующим образом:
ъас = е{а
= еF|г|с) (атомы V-типа),
, = e(a\r\b) (атомы Л-типа),
A.4.2)
где обозначения V и Л пояснены на рис. 1.3, то состояние A.4.1) подразумевает, что
каждый атом содержит два микроскопических осциллирующих диполя, а именно,
P(t) = 3?ac{c*acc) eivit + &ьс(с*ьсс) eiV2t + к.с. (атомы V-типа),
P(t) = ^ас{с*аСс) eWlt + ^ab(clcb) e^2* + к.с. (атомы Л-типа),
A.4.3)
где v\ = ша — ujcj i/2 = ^ь — ^с для атомов V-типа, ш i/\ = ша — шь? 1/2 = wa — шс
для атомов Л-типа. В этом случае, с полуклассической точки зрения излучаемое поле
представляет собой сумму двух членов:
Ег(+) = Sx e^ivit + cf2 e^il/2t. A-4.4)
Тогда очевидно, что функция отклика квадратичного детектора содержит интерфе-
интерференционный член или так называемый тон биений:
I С7( + )|2 \/р |2 || I /э [2 I, Г/г>* л> гЛ{^\ ^v"l)^ j_ т/ л 1 /1 /1 К^
[ tL I — |©i [ -г |<$21 '1^1 ^2 б тК.С]. ^1.4.0j
Такой тон биений часто наблюдается в экспериментах по электронно-пучковой (beam-
foil) спектроскопии.
В заключение в качестве основного вывода отметим, что согласно ПКТ такой
интерференционный член имеет место для атомов как V-, так и Л-типа.
Рассмотрим теперь эту же задачу с точки зрения КЭД. Для атома V-типа
вычислим тон биений:
(*)), A.4.6)
1.5 Что есть свет? Понятие фотона 23
где El' и Е^ пропорциональны операторным выражениям а^ exp (iv\t)
и а,2 ехр (—гг/2^)? соответственно. С учетом выражения для |t/vW) (см. рис. 1.3а),
выражение A.4.6) приводится к виду
^(UCUa+a^l^) е^-^)'(с|с), A.4.7)
где ж — константа. Следовательно, тон биений, вычисленный с помощью квантовой
электродинамики, определяется выражением
A.4.8)
С другой стороны, для атомов Л-типа имеем
<^л(*) | ^1~) (*)^+) (*) |^л(*)> • A-4.9)
С учетом выражения для |^л(^)) (см. рис. 1.36) получаем
x'il^latazlO^) е^-^г(с\Ь) = х' ег^-^ {с\Ь}. A.4.10)
=0
Суммируя КЭД рассуждения, получаем, что
атомы \Лтипа: (^v(t)\E^] (^E^ (t)\i)V(t)) = х
атомы Л-типа: (фА(г)\Е^](t)E^](t)\i;A(t)) = 0,
тогда как ПКТ вычисления дают ненулевое значение амплитуды тона биений для
атомов как 1/-, так и Л-типа.
Следующие рассуждения, основанные на квантовой теории измерений, дают нам
некоторое понимание физики недостающих биений. Когерентно возбужденный атом
V-типа релаксирует, испуская фотон частоты v\ или vi- Поскольку оба перехода
приводят к одному и тому же конечному атомному состоянию, нельзя определить,
каким путем^ v\ или v^, ре-лаксировал атом. Аналогично задаче Юнга с двойной
щелью, эта неопределенность в траектории атома приводит к интерференции между
фотонами с частотами и\ и 1/2, вызывая квантовые биения. Дополняющий характер
информации типа какой путь и возникновение квантовых биений будут подробно
обсуждаться в гл. 19. Когерентно возбужденный атом Л-типа также релаксирует,
испуская фотон частоты v\ или ь>ч- Однако теперь, спустя значительное время после
испускания фотона, наблюдение за атомом могло бы дать нам информацию о том,
какой путь релаксации A или 2) имел место (атом находится в состоянии \с) или \Ь)).
Следовательно, в этом случае биений быть не должно.
Очевидным является вывод о том, что (в отличие от результатов ПКТ) результаты
вычислений, полученные с помощью КЭД, согласуются с основными положениями
квантовой теории.
1.5. Что есть свет? Понятие фотона
Квантовая теория излучения (с учетом определенных предположений о пере™
нормировке) достаточно полно описывает взаимодействие излучения с веществом.
Несмотря на это, заманчиво доказать, что концептуальные основы квантовой теории
излучения и понятие фотона лучше всего рассматривать через классическое поле
и флуктуации, связанные с вакуумом. Однако успехи квантовой оптики выдвинули
новые аргументы в пользу квантования электромагнитного поля, и вместе с ними
возникло более глубокое понимание сущности фотонов. При рассмотрении таких при-
примеров, как квантовые биения, квантовое стирающее устройство, некоторые явления
24 Квантовая теория излучения Гл. 1
двухфотонной интерференции, становится необходимым, как будет показано далее,
рассматривать фотон как квантово-механический объект, физика которого гораздо
глубже, чем та, что следует из полуклассической теории, дополненной логикой ваку-
вакуумных флуктуации. Заметим также, что существуют серьезные вопросы, касающиеся
метрики в теории квантованного поля. В одной из своих последних статей Фейнман г)
делает интересные замечания о возможности более глубокого понимания теории
перенормировки путем сочетания концепции отрицательной вероятности с физикой
индефинитной метрики. Некоторые из этих идей и обобщений нашего понимания
концепции фотона являются предметом обсуждения в заключительном разделе этой
главы.
1.5.1. Вакуумные флуктуации и понятие фотона. Несмотря на то, что формаль-
пая квантовая теория излучения и квантовая электродинамика достигли поразитель-
поразительного успеха в объяснении взаимодействия электромагнитного излучения с веществом,
существуют и определенные принципиальные проблемы. Например, различные рас-
расходимости, возникающие при вычислении таких величин, как лэмбовский сдвиг
и аномальный магнитный момент. С другой стороны, как будет показано в последую-
последующих главах этой книги, существует много процессов, связанных с взаимодействием
излучения и вещества, которые можно объяснить в рамках полу классической теории,
когда поле рассматривается классически, а вещество — квантово-механически. К
числу физических явлений, которые могут быть полностью или в значительной
степени описаны полу классически, относится фотоэлектрический эффект, который
впервые был объяснен подобным образом Вентцелем в 1927 году. Вынужденное
излучение, резонансная флуоресценция и многие другие эффекты не требуют для
своего объяснения полного аппарата квантовой теории излучения. В этих случаях
предпочтительнее использовать полуклассический анализ.
Отметим далее, что два облачка, возникшие на горизонте физики в начале два-
двадцатого столетия, были также связаны с электромагнитным излучением. Читатель,
без сомнения, помнит, что единственными двумя вопросами, которые не были вполне
поняты в физике в то время, являлись нулевой результат эксперимента Майкельсона™
Морли и катастрофа Релея-Джинса (так называемая УФ-катастрофа), связанная
с излучением черного тела. Эксперимент Майкельсона^Морли привел к возникно-
возникновению специальной теории относительности, которая поставила неизбежный крест
на классической механике и электродинамике, а разрешение Планком проблемы
катастрофы Релея—Джинса положило начало квантовой механике.
Однако, интересно и важно то, что ни одно из этих явлений не повлекло за
собой возникновения концепции фотона. В первом случае, Эйнштейн, в основном,
размышлял о преобразованиях уравнений Максвелла. В свою очередь, Планк кван-
квантовал энергию осцилляторов в пределах полости, не прибегая к квантованию поля
излучения. То есть в этот момент ни квантовая теория излучения, ни идеальная
концепция фотона не были задуманы.
Впервые понятие фотона было введено Эйнштейном при объяснении фотоэлек-
фотоэлектрического эффекта. Отметим вновь, что это явление в значительной мере может
быть описано полу классически. Напомним читателю, что существуют три законо-
закономерности фотоэлектрического эффекта, которые должна объяснить любая теория.
Во-первых, когда свет частоты и падает на фотоэмиссионную поверхность, энергия
испускаемых электронов Те удовлетворяет уравнению
Й1/ = Ф + Те, A.5.1)
1) В книге Negative Probabilities in Quantum Mechanics, ed. B. Hiley and F. Peat, Routledge,
London A978).
1.5
Что есть свет? Понятие фотона
25
где Ф — работа выхода, представляющая собой характеристику конкретного мате™
риала. Во-вторых, скорость эмиссии электронов пропорциональна интенсивности
электрического поля падающего света. В третьих, отсутствует задержка во времени
между моментом, когда свет достигает светочувствительной поверхности, и момен-
моментом фотоэлектронной эмиссии. Первые два свойства можно, в отличие от того,
что написано в большинстве учебников, полностью объяснить с помощью простого
квантования атомов фотодетектора. Однако, третий результат, а именно, полное
отсутствие временной задержки, является более тонким. Можно резонно заметить,
что квантовая механика учит нас, что скорость испускания конечна даже для малых
времен, т. е. времен порядка нескольких оптических периодов поля излучения. Тем
не менее, можно показать, что понятие фотона здесь действительно явно обозначено
в том смысле, что под угрозой находится закон сохранения энергии. А именно,
если бы только момент начала взаимодействия поля излучения с атомами и мо-
момент эмиссии фотоэлектрона разделял малый интервал времени т, то количество
энергии, падающей на поверхность, определялось бы выражением е$Е2Ат, где А —
сечение падающего пучка. Для достаточно коротких времен, энергия, падающая на
фотодетектор, вероятно, не превышает Ф. Отсюда ясно видно, закон сохранения
энергии не выполняется, если придерживаться полуклассической точки зрения. Од™
нако, концепция фотона, согласно которой испускание фотоэлектрона предполагает
уничтожение фотона, полностью устраняет эту проблему, что является одним из
достижений квантовой теории поля.
В любом случае, надо отдать должное глубокому пониманию физики Эйнштей-
Эйнштейном, которое позволило ему ввести понятие фотона исходя из столь ограниченных
и, в некоторых отношениях, противоречивых данных. Отметив ряд достоинств по-
полуклассической теории, рассмотрим теперь, в каких случаях она несостоятельна.
Квантовая механика
Статистическое суммирование
i
V
X
[V
x E(i
Электродинамика
1 д2
о^-Р
го,
¦» Самосогласованное
*)
поле: Е;
Рис. 1.4. Уравнения самосогласованной полуклассической теории. Некоторое поле Е;(го, t)
возмущает г-й атом согласно законам квантовой механики, индуцируя электрический ди-
польный момент. Значения дипольных моментов атомов, локализованных в точке го, скла-
складываются, образуя макроскопическую поляризацию Р(го,?). Эта поляризация действует
как источник в уравнениях Максвелла для поля Е(го, t). В завершение цикла вычислений
записывается условие самосогласованности, состоящее в том, что предполагаемое поле
Е'(го,1) приравнивается создаваемому полю Е(го, t)
26 Квантовая теория излучения Гл. 1
В дискуссиях на эту тему часто слышится утверждение, что недостатком полу-
полуклассической теории является отсутствие обратного действия поля на атом. Это,
разумеется, не так, поскольку обратное действие можно учесть, решая самосогласо-
самосогласованную задачу (см. рис. 1.4). Мы видим, что поле входит в уравнение Шредингера,
индуцируя дипольный момент у невозмущенного атома. Затем этот диполь излу-
излучает и является источником поглощения, вынужденного излучения, резонансной
флуоресценции и т. д. Теперь учтем, что излучение, испускаемое диполем, само по
себе является источником возмущения атомной волновой функции (т. е. обратного
действия) в самосогласованной задаче, как показано на рис. 1.4. Однако успехи
полу классической теории на этом и заканчиваются. Обратимся теперь к задачам,
которые ей не под силу. Покажем, как в этих случаях работает полу классическая
теория с учетом вакуумных флуктуации.
1.5.2. Вакуумные флуктуации. Возможно наиболее важным примером ситуации,
которую нельзя описать с помощью полуклассической теории (рис. 1.4), является
спонтанное излучение света. Заметим, что атом, изначально находящийся в возбуж-
возбужденном состоянии, так и останется возбужденным, поскольку, находясь в чистом
квантовом состоянии, он не имеет дипольного момента, и, следовательно, никогда
не начнет излучать. Эта ситуация соответствует неустойчивому равновесию, и атом
остается в возбужденном состоянии в течение долгого, потенциально бесконечного,
времени, если не будет флуктуации, запускающих процесс. Кроме того, хорошим
примером физической задачи, объяснить которую возможно только учитывая влия-
влияние вакуума, является лэмбовский сдвиг. Как уже упоминалось, решение Дирака
для атома водорода дает полное вырождение между 22Я]_/2 и ^Pi/i уровнями
атома водорода. Однако при учете вакуумных флуктуации, как показано в разд. 1.3,
лэмбовский сдвиг можно объяснить качественно. Другие явления, такие как рас-
распределение Планка для излучения черного тела и ширина линии излучения лазера,
также можно описать в рамках такой полуклассической теории с учетом вакуум-
вакуумных флуктуации. Таким образом в ранние 70-е годы сложилось общее мнение, что
вакуумные флуктуации играют очень важную роль в нашем понимании концепции
фотона и что, возможно, наилучшим подходом к решению такого рода задач является
теория классического поля с учетом вакуумного шума или неопределенности. Рас-
Рассмотрение сжатия как перераспределения этой неопределенности (см. гл. 2) и другие
родственные физические темы подтверждают эту точку зрения. Однако мы вскоре
поймем, что такая концепция фотона, будучи полезной, недостаточно полна. Далее
мы обратимся к более глубокому и более значительному обоснованию квантования
поля излучения.
1.5.3. Квантовые биения, квантовое стирающее устройство, теорема Белла и дру-
другие задачи. Как обсуждалось нами в разд. 1.4, существование квантовых биений
в ансамбле атомов V-типа, в противоположность отсутствию таковых в ансамбле
с атомной конфигурацией Л-типа, создает основу для альтернативного довода в поль™
зу квантования поля излучения, не связанного с обсуждавшимися ранее вакуумными
флуктуациями. Квантовые биения являют собой пример несостоятельности полу-
полуклассической теории, дополненной учетом вакуумных флуктуации, в объяснении
физики этого явления. Отсюда позднее возникли понятия квантового стирающего
устройства и явления двухфотонной корреляции при интерференции. В итоге было
показано, что предыдущие доводы и утверждения о том, что «фотоны интерфе-
интерферируют только сами с собой» следует понимать только в рамках экспериментов
типа экспериментов Юнга с двойной щелью и не следует распространять за эти
пределы. Особую важность приобретают здесь перепутанные состояния фотонов.
Подобные перепутанные состояния используются в оптических тестах неравенств
1.5 Что есть свет? Понятие фотона 27
Белла, и можно было бы показать, что они дают более глубокое понимание концепции
фотона и, фактически, всей квантовой механики. Как обсуждается в последней главе
этой книги, результатом недавних исследований в области квантовой оптики явилось
более глубокое понимание природы квантовой теории света.
1.5.4. «Волновая функция фотонов». Заголовок этого раздела помещен в кавыч-
ки по двум причинам. Во-первых, он совпадает с названием раздела в классической
книге Пауэра (Power, 1964) по квантовой электродинамике. Во-вторых, кавычки
служат читателю предупреждением о том, что, строго говоря, «волновой функции
фотона» не существует. В частности, Пауэр, а также Крамере обращают особое вни-
внимание на то, что фотон не следует рассматривать *) как нерелятивистскую частицу.
С другой стороны, ряд физиков утверждают, что одиночный фотон в свободном
пространстве аналогичен мезону, если предположить массу мезона стремящейся
к нулю. Таким образом, интересно рассмотреть обоснованность аргументов в пользу
и против понятия «волновой функции фотона».
Философский принцип корпускулярно-волнового дуализма света привел де Брой-
ля к идее о том, что электроны ведут себя как волны. Однако, с точки зрения
современной квантовой оптики, волновая механика Максвелла^Шредингера ясно
различает световые волны и волны частиц вещества. Интерференция и дифракция
волн материи составляют суть квантовой механики. В свою очередь, соответствую-
соответствующее поведение света описывается классическими уравнениями Максвелла.
Возникает естественный вопрос: можем ли мы рассматривать электрическое поле
света как своего рода «волновую функцию фотона»? В своей книге по квантовой ме-
механике Крамере в разделе «Волновая функция фотона: обоснование и определение»
спрашивает:
«В какой мере и с какой степенью точности можно уверенно говорить
о соответствии между полем излучения и ансамблем независимых частиц?
Когда в 1924 году де Бройль предположил, что частицы вещества долж-
должны обладать волновыми свойствами . . ., тогда эта идея имела большое
эвристическое значение. Теперь, когда волновая механика стала последо-
последовательной теорией, возникает вопрос, можно ли рассматривать уравнения
Максвелла как вариант уравнения Шредингера для частиц света вместо то-
того, чтобы рассматривать их, как мы это делали до сих пор, как классические
уравнения движения, которые могут быть записаны в виде волнового урав-
уравнения и, в дальнейшем, квантованы. Или же оба подхода эквивалентны?»
В конце раздела Крамере отвечает на свой вопрос следующим образом:
«Ответ на вопрос заданный в начале этого раздела таков, что говоря
о поле излучения, нельзя использовать понятие частиц в том же смысле,
как это делается в (нерелятивистской) квантовой механике в отношении
систем материальных точек.»
Доводы Крамерса в пользу этого заключения аналогичны доводам, ясно сформу-
сформулированным Пауэром (в разд. 5.1 «Волновая функция фотонов»):
«Таким образом, естественно задаться вопросом, что представляют собой
функции ф для фотонов? Строго говоря, таких волновых функций нет!
Говоря о поле излучения, нельзя говорить о частицах в том же смысле,
как о системах частиц в элементарной квантовой механике. Дело в том, что
) См. также работу (Blalymlckl-BIrula, 1994).
28 Квантовая теория излучения Гл. 1
решения волнового уравнения в виде зависящей от времени волновой функ-
функции Шредингара, соответствующей энергии Е\, имеют круговую частоту
ш\ = +Е\/Н, тогда как монохроматические решения волнового уравнения
содержат положительно- и отрицательно-частотные части =bcj^. Поля Е
и В, удовлетворяющие уравнениям Максвелла в свободном пространстве,
а, следовательно, удовлетворяющие и волновому уравнению, являются дей-
действительными и не являются собственными функциями оператора ihd/dt.
Шредингеровская волна, соответствующая заданной энергии, должна быть
комплексной.»
То есть, реальная электрическая волна (выражение A.1.27)) содержит члены,
пропорциональные как ехр (—г */&?), так и ехр (г */&?), тогда как волна содержит только
члены, пропорциональные ехр (—ivpt). Мы вернемся к этому вопросу позднее, но сна-
сначала вспомним аргументы Бома, касающиеся данного вопроса, из его классической
книги «Квантовая теория». Он пишет:
«Вероятность того, что электрон находится в пределах интервала от х
до х + dx равна
Р(х) = ф*(х)ф(х) dx.»
Затем он проводит аналогию со светом и продолжает:
«Строго говоря, функция, отражающая вероятность найти световой
квант в заданной точке, не существует. Если заданная область велика по
сравнению с длиной волны, то приближенно получаем
Но в случае, когда область вполне определена, и(х) не имеет смысла».
Далее Бом утверждает, что для вещества
«имеет место ток вероятности
S = ^
удовлетворяющий уравнению
но отмечает, что
«соответствующей величины для света не существует».
Мы согласны с выводом Крамерса и Бома, а именно с тем, что понятие волновой
функции фотона может вводить в заблуждение и его следует использовать с боль-
большой осторожностью. Однако, как мы увидим, все приведенные возражения можно
преодолеть.
Начнем с того, что в полуклассической теории мы имеем дело с волновым
описанием (классического) излучения и (квантовым) веществом. Только когда мы
приступаем к квантованию поля излучения, уравнения для системы «излучение^
вещество» рассматриваются с единых позиций. В этой полностью квантовой тео-
теории полезно рассматривать вещество с выгодных позиций вторичного квантования.
Вспомним процедуру квантования, изложенную в разд. 1.1, когда фурье-амплитуды
поля заменяются операторами. Рассмотрим классическое комплексное поле E(r,t)
1.5 Что есть свет? Понятие фотона 29
поляризованного света. Поскольку свет поляризован, векторным характером поля
можно пренебречь. При переходе от классического описания поля к квантовому,
коэффициенты собственных функций поля Ut(r) заменяются операторами, т.е.
^]r), A.5.2)
к
где «к — амплитуды классического поля, заменяется выражением
kake-^[/k(r), A.5.3)
где at — квантовые полевые операторы.
Теперь соответствующую процедуру квантования можно и нужно применить к ве-
веществу. Например, волновая функция системы, обладающей массой (атом, электрон,
мезон и т.д.), описывается суперпозицией состояний
r), A.5.4)
Р
где ир = Е/h, cp — амплитуда вероятности частицы в состоянии фр(г). Например,
для частицы с импульсом р имеем
фр(т) = -±=е*-'. A.5.5)
Процедура вторичного квантования заключается в том, чтобы заменить каждую
амплитуду вероятности ср оператором уничтожения с*р, который подчиняется ком-
коммутационным соотношениям Ферми-Дирака или Бозе-Эйнштейна, и т. д. В этом
случае волновая функция становится оператором
ф(г,1) = ^2сРе-^фр(г), A.5.6)
Р
A.5.6) который уничтожает частицу в точке г, а состояние системы описывается
вектором состояния \ф). На этом этапе как вещество, так и фотоны описываются
квантованными полями, а состояние фотонного и/или мезонного поля описывается
вектором состояния \ф). Логика полуклассического подхода и логика полного вторич-
вторичного квантования при рассмотрении системы «излучение^вещество» представлены
на рис. 1.5.
Заметим, что термин «вторичное квантование» уместен только в отношении поля
вещества, поскольку мы вводим операторы вторично. То есть мы сначала полагаем
рх —>> (h/i)d/dx и т.д., а затем заменяем амплитуды вероятности операторами
cp(t) —>> Cp(t). Однако, в случае фотона дело обстоит иначе, так как h возникает
только один раз. В этом смысле квантование поля излучения можно считать проце-
процедурой «первичного» квантования.
Теперь рассмотрим ситуацию с противоположной точки зрения. Представим себе,
что мы сначала изучили фотоны, мезоны и т. п. с позиций полностью квантованного
поля. Волновая функция частицы получается из вектора состояния путем взятия
скалярного произведения собственного вектора оператора положения |г) и вектора
состояния \t/)(t)):
Ф(г,*) = <>#(*)>¦ A.5.7)
Напомним, что состояние |г) можно записать как
|г> = ^+(г)|0), A.5.8)
30
Квантовая теория излучения
Гл. 1
Полуклассическая
теория
Квантово-полевая
теория
Свет
E(r,t)
? Е = -fJL0P
Максвелл
E(r,t) = ^Qk(t)f/k(r)
к
Дирак
Вещество
Шредингер
р
Швингер
Рис. 1.5. В полуклассической теории излучения и вещества «поля» рассматриваются с по-
помощью уравнений Максвелла и Шредингера. Оба поля обнаруживают волновой характер,
но h появляется только в уравнении для вещества. Полностью квантовая теория, например,
Дирака и Швингера, позволяет рассматривать излучение и вещество с единых позиций
то есть оператор рождения
A.5.9)
действуя на вакуум, создает частицу в точке г. Таким образом, из A.5.7) и A.5.8) мы
получаем привычное выражение для волновой функции вещества,
Ф(г, ?) = (О\ф(г)\ф(г)}. A.5.10)
Возникает естественный вопрос, нельзя ли записать для фотона выражение типа
A.5.7)? Строго говоря, ответ должен быть отрицательным, поскольку состояния |г)
для фотона не существует.
Имея это в виду, забежим вперед и зададим практический вопрос: какова веро-
вероятность того, что однофотонное состояние поля излучения, а именно
}>. A-5.11)
где {п} обозначает множество состояний с одним (и только одним) фотоном в каждой
моде к, приведет к испусканию фотоэлектрона детектором (атомом), помещенным
в точку г?
В частности, состояние A.5.11) может возникнуть в результате перехода возбуж-
возбужденного атома в основное состояние. К этому примеру мы вернемся позднее. В любом
случае, имеется в виду волновой пакет, представляющий одиночный фотон, распро-
распространяющийся в пространстве, а амплитуды вероятности c^nj содержат информа-
информацию, обычно соответствующую фурье^коэффициентам однофотонного импульса.
Как будет показано в разд. 4.2, вероятность возбуждения атома (детектирующего
атома) в точке г определяется выражением
A.5.12)
где оператор уничтожения
, t) задается формулой
A.5.13)
1.5 Что есть свет? Понятие фотона 31
а оператор рождения E(~\r,t) ~~ выражением, комплексно сопряженным выраже-
выражению A.5.13). Вставим в выражение A.5.12) сумму по полному множеству состояний,
2 ll^'IKf^'ll = 1? и запишем
t) ex J](^|E^(r,t)|K})(K}|^+)(r,t)|^). A.5.14)
in'}
Поскольку в состоянии ф находится только один фотон, и оператор E(~*~'(r,t) уни-
уничтожает его, только вакуумный член |0)@| будет давать вклад в A.5.14). Отсюда,
Рф(г, t) ее (ф\Е(-\г, *)|0><0|?7<+>(г, 1)\ф), A.5.15)
что приводит нас к следующему определению «электрического поля», связанного
с однофотонным состоянием \ф7):
Ф^(г, t) = @\E^(r, t)\i/>7). A.5.16)
Для состояния |^7), возникшего в результате релаксации атома (выражение
F.3.24)), находим
A.5.17)
где #о — константа, г — расстояние от атома до детектора, в (ж) — обычная ступенча-
ступенчатая функция, Г — скорость релаксации атома. Заметим, что волновой пакет A.5.17)
имеет ярко выраженный максимум на частоте атомного перехода из. Это верно для
всех волновых пакетов, рассматриваемых в этом разделе.
Запишем A.5.16) более подробно, используя положительно-частотную часть вы-
выражения A.1.32) для оператора уничтожения электрического поля,
A.5.18)
V ZuCn ?
k,A
Как упоминалось в предыдущем разделе, поле имеет ярко выраженный максимум
на частоте ш, что позволяет заменить медленно меняющуюся частоту v^ под знаком
квадратного корня наши записать
Сравнение A.5.19) с волновой функцией A.5.4) приводит к следующему выражению
для амплитуды вероятности фотодетектирования:
^ %\ф7). A.5.20)
Иначе говоря,
ф*(г.*) = У§-^(г»*)- A-5-21)
Можно записать уравнение движения для ^7(r,t) с помощью уравнений Макс-
Максвелла, связывающих электрическое A.5.16) и магнитное поля:
, t) = <0|H«(r, t)\Vl). A.5.22)
32
Квантовая теория излучения
Гл. 1
Здесь HM(r,t) — положительно-частотная часть оператора магнитного поля
A.1.33), которую мы запишем в виде
к,Л
A.5.23)
Используя выражения A.5.22) и A.5.23) и проводя те же операции, что и в случае
(г, t), находим
к,Л
-ю =
Xy(r,t). A.5.24)
Теперь можно записать уравнения Максвелла A.1.1) для кр1 (выражение A.5.21))
и Xj (выражение A.5.24)) в виде
A.5.25а)
v
V
= 0.
A.5.256)
A.5.25в)
A.5.25г)
Перепишем систему уравнений A.5.25а-1.5.25г) в более предпочтительной с эстети-
эстетической точки зрения матричной форме, представив (р и х в виде матриц-столбцов
размером 1x3:
'Хх
Ху
IXzl
A.5.26)
Тогда (см. задачу 1.7) уравнения Максвелла A.5.25а-1.5.25г) приобретают вид
О ^cs •
A.5.27а)
A.5.276)
где sx, sy и sz — матрицы размером 3x3, определенные в задаче 1.7, р — обычный
оператор импульса (h/i)V.
Интересно сравнить уравнения Максвелла A.5.27а,б) с уравнениями Дирака -1)
для нейтрино:
-са-р]
•р О
ikdt \хЛ ~[с<т-\
A.5.28)
где двухкомпонентные спиноры (р^ и х-ц формируют волновую функцию Дирака для
нейтрино
A.5.29)
1) Аналогия между уравнениями Максвелла и Дирака хорошо известна (см., например,
BtalyntckKBIrula, 1994).
1.5
Что есть свет? Понятие фотона
33
Ф -
7 "
Вооружившись уравнениями движения A.5.27а,б), легко получить уравнение
непрерывности
— Ф+Ф7 = -V • j, A.5.30)
где
A.5.31)
A.5.32)
A.5.33)
а плотность тока j определяется формулой (см. задачу
где оператор «скорости» имеет вид
0 -
Сравнение Ф7 с Ф-. представлено на рис. 1.6.
Квантовая теория
поля
«Волновая» механика
Классический
предел: эйконал
Фотон
ми
Лучевая оптика
S \п ds = 0
Принцип Ферма
Нейтрино
ф" = 111
Классическая механика
<5 [ L dt = 0
Принцип Гамильтона
Рис. 1.6. Аналогия в описании фотона и нейтрино. В классическом пределе (последняя
строка) свет описывается с помощью геометрической оптики, а вещество — с помощью
сходного принципа Гамильтона. Квантовое теоретическое описание фотона и нейтрино
в первой строке также вполне симметрично. В строке, соответствующей «волновой» ме-
механике, представлены уравнения движения для Ф7(г? 0 и
Несмотря на замечательное сходство в уравнениях движения фотона и нейтрино,
необходимо отметить важные принципиальные различия. Например, если рассмот-
рассмотреть уравнения A.5.28) для электрона в нерелятивистском пределе, то получим,
в частности, соотношение для плоской волны вида
(р,
электр
он V** j t) —
1
A.5.34)
где kz = pz/h и ujk = p2z/2mh. Теперь, чтобы придать электрону импульс в направ-
направлении х достаточно применить операцию exp (ikxx)^ где х = д/дкх. Таким образом,
новый импульс определяется выражением
k = exkx^ezkz. A.5.35)
Теперь рассмотрим подобного рода операцию в отношении A.5.20). Если изна-
изначально записать ip(r,t) для плоской волны, распространяющейся в направлении z
2 М.О. Скалли, М.С. Зубайри
34
Квантовая теория излучения
Гл. 1
и поляризованной в направлении ж,
= ex
A.5.36)
а затем применить операцию exp(ikxx)j то, вероятно, можно было бы записать новую
функцию
<p(r,t) =ex
Но в этом случае уравнение Максвелла A.5.276) более не справедливо:
V- (р =
дх
/0.
A.5.37)
A.5.38)
Это лишь один пример того, насколько «волновая функция» фотона отличается
от волновой функции нерелятивистской частицы, обладающей массой, и насколько
неверным может быть представление «фотон как частица».
В качестве другого, еще более яркого примера, рассмотрим двухфотонные явле-
явления, а именно двухфотонное испускание и детектирование (рис. 1.7). Как подробно
обсуждается в гл. 4, вероятность того, что два фотоэлектрона будут зафиксированы
детекторами D\ и D2, определяется двухфотонной корреляционной функцией. Вы-
Вычислим двухфотонную корреляционную функцию
G^O-b^ra,^) = (ф\Е^\т1,Ь1)Е^(т2,г2)Е^\т2,Ь2)Е(-+\т1,и)\ф) A.5.39)
для двух детекторов, расположенных в точках ri и г 2 в случае, когда взаимодействие
с фотонным полем, описываемым \ф), включается в моменты времени t\ и ^2,
соответственно (рис. 1.7).
Рис. 1.7. Трехуровневый атом, расположенный в точке г, релаксирует с уровня \а) на
уровень \Ь) со скоростью ja и с уровня \Ь) на уровень \с) — со скоростью 7&- Детекторы
D\ и ?>2, расположенные в точках ri игг, включаются в моменты времени t\ и ti
Заметим, что в процесс излучения одиночного атома вовлечены только два
тона, так что
1.5 Что есть свет? Понятие фотона 35
= (ф\Е[-)Е<-)\О)(О\Е<+)Е[+)\ф), A.5.40)
и, следовательно, имеется амплитуда двухфотонного детектирования
A.5.41)
которую нам следует рассмотреть.
Для начала рассмотрим случай, когда скорости релаксации с уровня \а) на
уровень |6), 7а? и с уровня \Ь) на уровень |с), 7ь? таковы, что 7а ^ 76? т-е- атом
очень быстро релаксирует на уровень |6), а затем, спустя некоторое время, — на
уровень \v). В этом случае (см. разд. 21.4.1)
ФB)(Г1, h; Г2, t2) = *a(ri, *1)Ф^(Г2, *2) + Ф^(Г1, <1)Фа(г2, *2), A-5-42)
где
фа(г., Ц) = -?- в (ti - —) е-7Л«.-Аг-,/С)е-гШа6(*,-Дг,/С); A.5.43а)
-^(П-Аг,/с)е-гшЬс(П-Аг,/с)^ A.5.436)
Здесь г = 1,2, шаь и шьс — атомные частоты переходов \а) —> \Ь) и \Ь) —> |с), Аг{ —
расстояние от атома до i~ro детектора, ^аш^ь^ константы. Прямая аналогия между
выражениями A.5.43а) и A.5.436) и амплитудой единичного фотодетектирования
A.5.17) очевидна. Мы, без сомнения, имеем здесь выражение Бозе-Эйнштейна в том
виде, как его можно было бы записать для двух атомов гелия.
Однако ситуация совершенно меняется, если обратиться к случаю 7ь ^ jaj T-e-
когда атомы в течение некоторого времени релаксируют на уровень |6), а затем бы-
быстро переходят на уровень |с). Тогда, согласно разд. 21.4.1, амплитуда двухфотонного
детектирования имеет вид
ФB)(гь h;r2,t2) = ^^- ехр [-(шас + la) [tl - ^)] в (tl - ^
+ Aо2). A.5.44)
Смысл очевиден. Когда 7а ^ 7ь? имеет место испускание фактически независи-
независимых фотонов. Когда же ja ^C jc, два события сильно коррелированы, а представле-
представление «фотон как частица» неверно.
В заключение можно сказать, что несмотря на то, что мы, пожалуй, преодолели
основное возражение Крамерса (амплитуда вероятности @\Е\ф) пропорциональна
только е^гшг) и частично справились с возражениями Бома (акты фотодектирова™
ния фактически локализованы *) на расстояниях, не превышающих длину волны),
буквальное представление о <p(r, t), как о волновой функции частицы может ввести
1) Однако заметим, что локализация фотона (в отличие от локализуемое™ амплитуды
вероятности детектирования фотона) качественно отличается от локализации частицы,
обладающей массой, например, электрона. Электрон можно поместить в малый объем,
линейные размеры которого меньше или равны комптоновской длине волны. Фотон же
невозможно поместить или втиснуть в объем, линейные размеры которого меньше длины
волны фотона. См. работу Deutsch and Garrison A991).
36
Квантовая теория излучения
Гл. 1
в заблуждение. Физика фотона существенно отличается от физики шредингеровских
частиц.
Приемлемая рабочая философия «фотона» удачно сформулирована Лэмбом:
«Что же делать далее? Мы можем и должны использовать квантовую
теорию излучения. Ферми показал как делать это на примере полос Липп™
мана. Идея проста, но детали несколько неприятны. Правильные обозначе-
обозначения и большая практика облегчают задачу. Начнем с того, что определим
в какой мере необходимо учесть влияние «вселенной». Определим, какие
нормальные моды необходимы для адекватного описания. Решим, каким
образом моделировать источники света и определим, как они управляют
системой.»
Именно этим мы будем заниматься в последующих двадцати главах.
Приложение 1.А
Эквивалентность многочастичного бозе-газа и ансамбля
квантованных гармонических осцилляторов
В разд. 1.1. мы квантовали поле излучения, сопоставляя каждой моде поля кван-
квантованный простой гармонический осциллятор. Эта процедура привела нас к введе-
введению состояний Фока (или состояний с определенным числом частиц) поля, содер-
содержащих, для каждого осциллятора, п фотонов, и связанных с ними операторов а
и а+, которые уничтожают и рождают фотоны. В данном разделе мы покажем, что
ансамбль гармонических осцилляторов динамически эквивалентен многочастичному
бозе-газу.
Рассмотрим бозе-газ из N частиц, заключенный в объеме V. JV-частичную волно-
волновую функцию можно записать путем симметризации произведения одночастичных
волновых функций ipa(r):
1/2
ЛП
, A.A.1)
где Р обозначает перестановку среди N частиц. Целые числа ns (s = р, q, . . . , к, . . .)
представляют собой числа заполнения одночастичных волновых функций t/?s(fj),
такие что
и ns может принимать значения 0,l,2,...,iV. Одночастичная волновая функция
свободной частицы задается выражением
A.А.З)
Здесь h& — импульс частицы.
П.1.А Эквивалентность бозе-газа и ансамбля гармонических осцилляторов 37
Пусть для N частиц, взаимодействующих друг с другом, потенциал равен
N
В результате взаимодействия частица из состояния ^p(rj) может перейти в состояние
^k(rj). Амплитуда перехода для этого процесса пропорциональна
Например, если свободная частица с импульсом Н\а, рассеиваясь на фононной волне
с волновым вектором к
переходит в состояние с импульсом Яр, то
= Щ 5{р + к - к). A.А.7)
Теперь рассмотрим многочастичный вариант этой задачи.
Прежде чем обратиться к общему случаю бозе-газа из N частиц внутри объема 1/,
рассмотрим простой случай трехбозонной системы. Волновая функция трехчастич-
ной системы, для которой изначально пр = 2, п^ = 1, задается выражением
В результате взаимодействия между частицами через потенциал A.А.4) с N = 3 одна
частица переходит из состояния р в состояние к, т. е.
Тогда трехчастичный матричный элемент этого процесса имеет вид
з
n dr2 dr3^;=ljnk=2(rb г2, г3) J^ v(ri)^lP=2,nk=i^u г2, г3). A.А.10)
г = 1
3
Теперь учтем, что каждая частица в сумме J2 v(rj) Дает одинаковый вклад, так что
г=1
3
можно просто выбрать частицу, скажем частицу 1, и заменить ^ множителем 3.
г=1
Тогда
ЛГЗ = 3
38
Квантовая теория излучения
Гл. 1
Если умножить и разделить каждое из выражений в квадратных скобках на у/2
и воспользоваться выражением A.А.1) для Ф^ =1 =1(г2, гз), то получим
Поскольку двухчастичная волновая функция нормирована, то
.^з = л/2 л/2 VkP, (LA.13)
где Vkp определяется выражением A.А.5).
Далее проведем аналогичный анализ для случая перехода одиночной частицы
из начального состояния A.А.1) в результате взаимодействия A.А.4) в конечное
состояние:
Фпр-1,пЧ)...,пк + 1,...(ГЬ Г2, • • • , Глг) = [
(np-l)!nql...(nh
1/2
, A.A.14)
Вычисляем матричный элемент
ri... drNV%*_ln^ Пк+1(гг,г2,..., rN) x
,r2,
По аналогии с трехчастичным случаем, устанавливаем, что все перестановки иден-
N
тичны, и заменяем ^ ^(г^) на Nv(ri). Тогда A.А.15) можно выразить через (N —
— 1)-частичные волновые функции в виде
, ...,rN)x
?^p(ri)<Anq,...,nk,...(r2,...,l
/nk ¦
Таким образом, мы видим, что многочастичный характер задачи заключается
в множителях у/пр и у/п^ + 1, соответствующих удалению (уничтожению) частицы
в состоянии фр и добавлению (рождению) частицы в состоянии ф^.
Естественно (и значительно удобнее!) ввести многочастичный вектор состояния
г) г) т \ (Л А 17)
и операторы, которые переводят векторы состояния из одного в другой, меняя
число частиц в различных состояниях. С этой целью введем операторы уничтожения
Задачи к гл. 1 39
(поглощения) для нашей бозонной системы,
ар\пр,пЧ1. . . , Пк, • • •> = л/п^\пр - l,nq,. . . ,
и соответствующие операторы рождения:
a+|np,nq,. . . ,nkj.
Из определений следует, что имеют место коммутационные соотношения
K,a+] = SP,P, A.A.20)
[ap,ap.] = [a+,a+] = 0, A.A.21)
что очевидно, если рассматривать действие этих упорядоченных операций на век-
векторы состояния. Для того чтобы восстановить результаты вычисления матричного
элемента, необходимо ввести гамильтониан взаимодействия
и гамильтониан свободной частицы
stj/y \. г -f- /1 А QO\
<тс = 2* ttpftp- A.A.2S)
р
Резюме: физический смысл имеет заполнение состояний числа частиц, где
информация содержится в состояниях \пр) и матричных элементах vtp =
= J e/i?(r)i;(r)^p(r). То есть, нет смысла беспокоиться о сложных комбинациях,
обо всем этом самым замечательным образом позаботится операторный формализм.
Однако главным в этом разделе является не удобство операторного подхода, а
скорее глубокая взаимосвязь между многобозонной квантовой механикой и механи-
механикой квантованных гармонических осцилляторов. Говоря словами Дирака:
«Динамическая система, состоящая из ансамбля одинаковых бозонов,
эквивалентна динамической системе, состоящей из ансамбля осцилляторов.
Они представляют собой совершенно одинаковые системы, рассматривав™
мые с различных точек зрения. Каждому независимому бозонному состоя-
состоянию соответствует осциллятор. Это один из наиболее фундаментальных ре-
результатов квантовой механики, дающий возможность объединить волновую
и корпускулярную теории света.»
Однако же фундаментальные различия столь же сильны, как и аналогия
«бозон»—«ансамбль осцилляторов». Например, в задаче об осцилляторе мы, в итоге,
получаем вклад вакуумных флуктуации, отсутствующий в случае совокупности
бозонов. В разд. 1.3 вакуумное состояние электромагнитного поля использовалось
для вычисления лэмбовского сдвига.
Задачи
1.1. Поле излучения в пустом кубическом резонаторе со стороной L удовлетворяет
волновому уравнению
с2 dt2 ~
40 Квантовая теория излучения Гл. 1
и условию кулоновской калибровки V • А = 0. Покажите, что решение, удовле-
удовлетворяющее граничным условиям, имеет следующие составляющие:
Лж(г, t) = Ax(t) cos (kxx) sin (kyy) sin (kzz),
Ay(r, t) = Ay(t) sin (kxx) cos (kyy) sin (kzz),
Az(r, t) = Az(t) sin (kxx) sin (kyy) cos (kzz),
где A(t) не зависит от положения, а компоненты волнового вектора к определя-
определяются выражением A.1.21). Покажите, что целые числа nxiny^nz в выражении
A.1.21) таковы, что только одно из них может быть равным нулю в данный
момент времени.
1.2. Пусть А и В — два некоммутирующих оператора, удовлетворяющих условию
[[А, В], А] = [[А, В], В] =0.
Покажите, что
еА+в = е~^л'Б1 еЛ ев = е+^А'Б1 ев ел.
Данное выражение представляет собой частный случай так называемой теоре-
теоремы Бейкера-Хаусдорфа теории групп.
1.3. Пусть А и В — два некоммутирующих оператора, а — параметр. Покажите,
что
2
е~аАВ еаА = В - а[А, В] + ^И, И, В]] + . . .
1.4. Пусть /(а, а+) — функция, разложимая в степенной ряд по а и а+. Покажите,
что
а) [a,f(a,a+)] = ^:,
б) \а , f (а. а )] = ——
с/а
в) е-аа+а/(а, а+) еаа+а = /(а еа, а+ е""),
где а — параметр.
1.5. Покажите, что
+ + i + +I
Г — OLCL CL~\ / — OL -| \ — СХп п Г"Т" — OCCL CL~\ ( OL i\ — OLU CL "Т"
I Сд/ * C^ I — I C-' JL I \Z/ \Ju * I IL*/ « t^ 1 — I C^ JL I C-' CJ/ *
где а — параметр.
1.6. Покажите, что гамильтониан свободного поля
можно выразить через состояния с определенным числом частиц в виде
и,следовательно,
Список литературы к гл. 1
41
1.7. Покажите, что уравнения Максвелла в свободном пространстве можно записать
в виде выражений A.5.27а) и A.5.276). Для этого сначала покажите, что
c?" V Л
где Ё = У^Е и Й =
Н. Затем докажите, что
s • VV = V х V,
'О О Г
0 0 0
-10 0
V-H = 0,
"О -1 О'
1 О О
0 0 0
где s и V в левой части выражения рассматриваются как вектор-столбцы 1 х
х 3. Воспользуйтесь этим тождеством для того, чтобы получить выражения
A.5.27а) и A.5.276).
1.8. Получите выражение A.5.32) для плотности тока вероятности, записав уравне-
уравнения движения для у?7 и %7 в виде
и учитывая, что s+ = —s.
1.9. Докажите, что
= 1, вычислив скалярное произведение с произвольным
вектором v. Следовательно, если ёх = е^. , е2 = Щ^ и ез = к/А;, то получаем
выражение A.1.36). Можно также получить выражение A.1.37), полагая, что
к, #, ф — полярные координаты волнового вектора к, так что
k = k(sm 'д cos 0, sin $ sin ф, cos #).
Тогда два поперечных вектора поляризации могут быть записаны в виде
Щ^ = (sin 0, — cos <^5 0), е^. = (cos # cos ф, cos # sin <^5 — sin $),
и можно показать, что
fcki fckj "г fcki fckj "" °*J ^2 5
где г,,7 обозначают декартовы компоненты. Покажите это путем прямой под-
подстановки.
Список литературы
Квантование поля излучения
DIrac, P. A. M. Proc. Roy. Soc. A 114, 243 A927).
Fermi, E. Rev. Mod. Phys. 4, 87 A932).
Некоторые полезные книги по квантовой теории излучения
и квантовой оптике
Heitler, W. The Quantum Theory of Radiation, (Oxford University Press, New York 1954).
[Гайтлер В. Квантовая теория излучения (ИЛ, Москва, 1956).]
Kramers, H. A. Quantum Mechanics, (North-Holland, Amsterdam 1958).
42 Список литературы к гл. 1
Power, E. A. Introductory Quantum Electrodynamics, (Longman, London 1964).
Klauder, J. R. and Sudarshan, E. C. G. Fundamentals of Quantum Optics, (W.A. Benjamin,
New York 1970). [Клаудер Дж., Сударшан Э. Основы квантовой оптики (Мир, Москва,
1970).]
*Ахманов С.А., Чиркин А.С. Статистические явления в нелинейной оптике (МГУ, Моск-
Москва, 1971).
Perina, J. Coherence of Light, (Van Nostrand, London 1972). [Перина Я. Когерентность света
(Мир, Москва, 1974).]
Haake, F. Statistical Treatment of Open Systems by Generalised Master Equations, (Springer
Tracts in Modern Physics, Vol. 66), (Springer-Verlag, Berlin 1973)
Loudon, R. The Quantum Theory of Light, (Oxford University Press, New York 1973). [Лоудон Р.
Квантовая теория света (Мир, Москва, 1983).]
Louisell, W. H. Quantum Statistical Properties of Radiation, (John Wiley, New York 1973)
Agarwal, G. S. Quantum Statistical Theories of Spontaneous Emission, (Springer Tracts in
Modern Physics, Vol. 70), (Springer-Verlag, Berlin 1974).
Nussenzveig, H. M. Introduction to Quantum Optics, (Gordon and Breach, New York 1974).
Allen, L. and Eberly, J. H. Optical Resonance and Two-Level Atoms, (John Wiley, New York
1975). [Аллен Л., Эберли Дж. Оптический резонанс и двухуровневые атомы (Мир,
Москва, 1978).]
Bialynickl-BIrula, I. and Blalynlcka-BIrula, Z. Quantum Electrodynamics, (Pergamon Press,
Oxford 1976).
Sargent III, M., Scully, M. O. and Lamb, W. E., Jr. Laser Physics, (Addlson-Wesley, Mass. 1974).
*Рытов СМ., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику
(Наука, Москва, 1978).
*Клышко Д.Н. Фотоны и нелинейная оптика (Наука, Москва, 1980).
Itzykson, С. and Zuber, J. В. Quantum Field Theory, (McGraw Hill, New York 1980).
Haken, H. Light, Vols. I and II, (North-Holland, Amsterdam 1981).
*Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую радиофизику и
оптику (Наука, Москва, 1981).
Knight, P. L. and Allen, L. Concepts of Quantum Optics, (Pergamon Press, Oxford 1983).
Perlna, J. Quantum Statistics of Linear and Nonlinear Optical Phenomena, (D. Reidel, Dordrecht
1984). [Перина Я. Квантовая статистика линейных и нелинейных оптических явлений
(Мир, Москва, 1987).]
Cohen-Tannoudji, С., Dupont-Roc J. and Grynberg G. Photons and Atoms. Introduction to
Quantum Electrodynamics, (Wiley, New York 1989).
Meystre, P. and Sargent III, M. Elements of Quantum Optics, (Springer-Verlag, Berlin 1990).
Shore, B. W. The Theory of Coherent Atomic Excitation, Vols. 1 and 2, (John Wiley, New York
1990).
*Килин С.Я. Квантовая оптика: поля и их детектирование (Наука и техника, Минск,
1990).
Gardiner, С. W. Quantum Noise, (Springer-Verlag, Berlin 1991).
Cohen-Tannoudji, C., Dupont-Roc, J. and Grynberg, G. Atom-Photon Interactions, (Wiley, New
York 1992).
Carmichael, H. An Open Systems Approach to Quantum Optics, (Springer-Verlag, Berlin 1993).
Milonni, P. W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics, (Aca-
(Academic, New York 1994).
Vogel, W. and Welsch, D.-G. Lectures on Quantum Optics, (Akademie Verlag, Berlin 1994).
Список литературы к гл. 1 43
Perina, J., Hradil, Z. and Jurco, В. Quantum Optics and Fundamentals of Physics, (Kluwer,
Dordrecht 1994).
Walls, D. F. and Mllburn, G. J. Quantum Optics, (Springer-Verlag, Berlin 1994).
Mandel, L. and Wolf, E. Optical Coherence and Quantum Optics, (Cambridge, London 1995).
[Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика (Физматлит,
Москва, 2000).]
Welnberg, S. Theory of Quantum Fields, (Cambridge, London 1995).
Pike, E. R. and Sarkar, S. Quantum Theory of Radiation, (Cambridge, London 1995).
Leonhardt, U. Measuring the Quantum State of Light, (Cambridge, London 1997).
Лэмбовский сдвиг
Lamb, W. E., Jr. and Retherford, R. C. Phys. Rev. 72, 241 A947).
Bethe, H. Phys. Rev. 72, 339 A947).
Welton, T. A. Phys. Rev. 74, 1157 A948). Вычисляя лэмбовский сдвиг, мы следовали просто-
простому, хотя и не строгому, подходу, изложенному в этой статье.
Kroll, N. Н. and Lamb, W. E., Jr., Phys. Rev. 75, 388 A949).
French, J. B. and Weisskopf, V. F. Phys. Rev. 75, 1240 A949).
Dyson's, F. letter, In Lamb, W. E., Jr., A Festschrift on the Occasion of his 65th Birthday, ed.
D. ter Haar and M. O. Scully (North-Holland, Amsterdam 1978), p. XXXVI.
Hildum, E. A., Boest, IL, Mclntyre, D. H., Beausoleil, R. G., and Hansch, T. W. Phys. Rev. Lett
56, 576 A986). В этой статье сообщается о первом точном измерении энергетического
интервала IS — 2S в атоме водорода.
Квантовые биения
Corney, A. and Series, G. W. Proc. Phys. Soc. 83, 207 A964).
Chow, W. W., Scully, M. O. and Stoner, J. O., Jr., Phys. Rev. A 11, 1380 A975).
Herman, R. M., Groth, H., Kornbllth, R. and Eberly, J. H. Phys. Rev. A 11, 1389 A975).
Khoo, I. C. and Eberly, J. H. Phys. Rev. A 14, 2174 A976).
Jaynes, E. T. In Foundations of Radiation Theory and Quantum, Electrodynamics, ed. A. O.
Barut (Plenum, New York 1980).
Scully, M. O. In Foundations of Radiation Theory and Quantum Electrodynamics, ed. A. O.
Barut (Plenum, New York 1980).
Svanberg, S. Atomic and Molecular Spedroscopy, (Springer-Verlag, Berlin, 1991).
* Александров Е.Б., Хвостенко Г. И., Чайка М.П. Интерференция атомных состояний (На-
(Наука, Москва, 1991).
Локализуемость фотонов и электронов. «Волновая функция фотона»
Newton, Т. D. and WIgner, E. P. Rev. Mod. Phys. 21, 400 A949).
Mandel, L. Phys. Rev. 144, 1071 A961).
Jauch, J. M. and Piron, C. Helv. Phys. Ada 40, 559 A967).
Amreln, W. O. Helv. Phys. Ada 42, 149 A969).
Cook, R. J. Phys. Rev. A 25, 2164 A982); ibid 26, 2754 A982).
Pike, E. R. and Sarkar, S. Phys. Rev. A 35, 926 A987).
Deutsch, I. H. and Garrison, J. С Phys. Rev. 43, 2498 A991).
Bialynicki-Birula, I. Ada Phys. Polonica A 86, 97 A994).
Lamb, W. E., Jr., Appl. Phys. В 60, 77 A995).
Глава 2
КОГЕРЕНТНЫЕ И СЖАТЫЕ
СОСТОЯНИЯ ПОЛЯ
По мере развития квантовой теории излучения и с появлением лазера были
в значительной мере изучены состояния поля, наиболее близко описывающие клас-
классическое электромагнитное поле. Для того, чтобы представить себе такие «класси-
«классические» состояния, мы рассмотрим поле, создаваемое классическим монохромати-
монохроматическим током, и обнаружим, что квантовое состояние, создаваемое таким образом,
обладает многими интересными свойствами и заслуживает названия когерентного
состояния г). Важным следствием квантова-
квантования поля излучения является соответствующее
соотношение неопределенностей для сопряжен-
сопряженных полевых переменных. Разумно предполо-
предположить, что волновая функция, наиболее точно
соответствующая классическому полю, должна
иметь минимальную неопределенность для всех
моментов времени при соответствующем гармо-
гармоническом потенциале.
В данной главе мы покажем, что этим
свойством обладает волновая функция основно-
основного состояния смещенного простого гармониче-
гармонического осциллятора, представляющая собой вол-
волновой пакет, который совершает синусоидаль-
синусоидальные колебания в потенциальном поле, не из-
изменяя формы (рис. 2.1). Когерентный волно-
волновой пакет всегда имеет минимальную неопре-
неопределенность и схож с классическим полем, на-
насколько это позволяет квантовая механика. Со-
Соответствующий вектор состояния представляет
которое яв-
собой когерентное состояние
а)
ляется собственным состоянием положительно-
частотной части оператора электрического по-
поля или, что то же самое, собственным состояни-
состоянием оператора уничтожения поля.
С классической точки зрения электромаг-
электромагнитное поле состоит из волн с определенны-
определенными значениями амплитуды и фазы. Но при
квантово-механическом описании поля это не так. В этом случае имеют место флук-
флуктуации как амплитуды, так и фазы поля. Электромагнитное поле в состоянии с опре-
Рис. 2.1. Волновой пакет с мини-
минимальной неопределенностью в раз-
различные моменты времени в потенци-
потенциальном поле гармонического осцил-
осциллятора (а); соответствующее элек-
электрическое поле (б)
1) Понятие когерентного состояния было введено Шредингером (Schrodlnger, 1926). Этот
вопрос прекрасно освящен в лекциях Глаубера (Glauber, 1965).
2.1 Излучение классического тока 45
деленным числом частиц \п) имеет вполне определенную амплитуду, но полностью
неопределенную фазу, тогда как поле в когерентном состоянии имеет одинаковые
величины неопределенностей для этих двух переменных. Можно также описывать
поле с помощью двух сопряженных квадратурных составляющих. Неопределенности
двух сопряженных переменных удовлетворяют принципу неопределенности Гейзен-
берга, так что произведение неопределенностей двух переменных больше или равно
одной второй модуля среднего значения коммутатора этих переменных (см. выра-
выражение B.6.2) ниже). Поле в когерентном состоянии представляет собой состояние
с минимальной неопределенностью, причем неопределенности двух квадратурных
составляющих равны между собой.
Рассмотрев когерентные состояния поля излучения, мы обратимся к так называ-
емым сжатым состояниям. В принципе, возможно создать состояния, для которых
флуктуации одной квадратурной составляющей будут ниже квантового предела. Это
происходит за счет усиления флуктуации канонически сопряженной квадратуры,
так что принцип неопределенности Гейзенберга не нарушается. Такие состояния по™
ля излучения называются сжатыми состояниями. Квадратуру электромагнитного
поля, флуктуации которой меньше стандартного квантового предела, перспективно
использовать в оптической связи, фотодетектировании, детектировании гравитаци-
гравитационных волн и усилении, свободном от шумов. В данной главе мы физически обоснуем
и сформулируем определение и свойства сжатых состояний, обращая особое внима-
внимание на так называемые сжатые когерентные состояния, являющиеся результатом
действия «оператора сжатия» на когерентное состояние.
2.1. Излучение классического тока
В данном разделе мы дадим определение когерентного состояния и покажем, что
поле, создаваемое классическим распределением тока, находится в таком состоянии.
Под классическим током мы подразумеваем ток, который можно описать заданным
вектором J(r, t), который не является оператором. Рассмотрим взаимодействие этого
тока и векторного потенциала, задаваемого оператором (ср. выражение A.1.27)
и разд. 5.1)
А(г, t) = -i^2~ ek^kak e~il/kt+ilc'T + э.с. B.1.1)
k
Гамильтониан, описывающий взаимодействие поля с током, имеет вид
(r,t)- A(r,t)d3r, B.1.2)
а вектор состояния \rf(t)) полной системы удовлетворяет уравнению Шредингера
в картине взаимодействия:
Векторная функция J(r, ?) коммутирует сама с собой в различные моменты
времени, но для оператора А(г, t), а, следовательно, и для энергии взаимодействия
У(?), это не так. Таким образом, обычно нельзя просто проинтегрировать уравнение
Шредингера и записать
\ф{Ь)) = ехр
B.1.4)
46 Когерентные и сжатые состояния поля Гл. 2
Однако различные коммутаторы, вводимые при проведении корректного интегриро-
интегрирования B.1.4), приводят к появлению в нем общего фазового множителя, который мы
опускаем. С учетом B.1.1) и B.1.2) экспонента в B.1.4) принимает вид
ехр
t
i
о
B.1.5)
к
где зависящая от времени комплексная амплитуда ак определяется выражением
t'
iff • / .,
ак = т—4с dt1 dre^ • Л„(г, t) eWkt ~гк'г. B.1.6)
Ai/fe J J
о
В B.1.6) индекс v в обозначении тока диполя Л„(г, ?) означает наличие монохро-
монохроматического диполя, осциллирующего на частоте v = ск. Если начальное состояние
является вакуумным |0), то вектор состояния B.1.4) принимает вид
- a?ak)|0)k. B.1.7)
Это состояние поля излучения называется когерентным состоянием и обозначается
как |{ок}). Очевидно, что многомодовое когерентное состояние B.1.7) молено пред-
представить в виде произведения одномодовых когерентных состояний |ak):
где
|ak> = exp(aka+ - okak)|0)k. B.1.9)
В оставшейся части этой главы мы, в основном, будем иметь дело с одномодовым
когерентным состоянием. Поэтому опустим индекс к в определении B.1.9) и запишем
а) = ехр(сш+ - a*a)|0). B.1.10)
Далее мы представим альтернативные подходы к понятию когерентного состояния.
2.2. Когерентное состояние как собственное состояние
оператора уничтожения ж как смещенное состояние
гармонического осциллятора
Выражение B,1 10'1 было получено нами для случая, когда под когерентным со-
состоянием поля излучения \а) понималось состояние поля, создаваемого классически
осциллирующим распределением тока. Аналогичное выражение для \а) можно по-
получить, определив когерентное состояние поля, как собственное состояние оператора
уничтожения а с собственным значением а, т. е.
а\а) = а\а). B.2.1)
Состояние \а) можно выразить через состояния с определенным числом частиц |п)
следующим образом:
\а) = е~'а' ^2 \ Л л) B 2 2)
2.2 Когерентное состояние как собственное состояние оператора уничтожения 47
Учитывая, что \п) = [(a+)n/\/n[]|0), последнее выражение можно записать в виде
Отметим далее, что поскольку ехр (^а*а)|0) = |0), выражение B.2.3) можно пере-
писать как
|a) = D(a)|0), B.2.4)
где
D(a) = e~|a|2/2 еаа+ е~а*а. B.2.5)
Теперь учтем, что согласно формуле Бейкера-Хаусдорфа для двух произвольных
операторов А и Я, таких что
[[А,В],А] = [[А,В]В]=0, B.2.6)
верно тождество
еА+в = е~[А'в]/2 еА ев.
B.2.7)
Если положить А = сш+, В = ^а*в, то
D(a) = eaa+^a*a, B.2.8)
что согласуется с выражением B.1.10). В эквивалентном антинормально упорядо-
упорядоченном виде оператор D(a) записывается как
Оператор D(a) является унитарным оператором, т.е.
D+(a) = D(-a) = [D(a)]^1. B.2.10)
Он действует как оператор смещения на амплитуды а и а+, т. е.
D~1(a)aD(a) = а + а, B.2.11)
и [а)а U\OL) = а ¦+¦ а . {Л.АЛЛ)
Свойство смещения можно доказать, записав
D-1{a)aD{a) = ea*a е~аа+аеаа+ е^а*а, B.2.13)
где для О~г(а) использовано выражение B.2.9), а для D(a) — выражение B.2.5).
Для любых операторов А и В
2
е^аАВеаА = В - а[А, В] + ^-[А, [А, В]] + . . . . B.2.14)
Для А = а+, В = а, это выражение принимает вид
e"aa+aeQa+ = а + а. B.2.15)
Применяя полученный результат в B.2.13), получаем свойство смещения B.2.11) для
D(ol). Свойство смещения B.2.12) можно доказать аналогичным образом.
Согласно выражению B.2.4), когерентное состояние получается в результате при-
применения оператора смещения к вакуумному состоянию. Следовательно, когерентное
состояние представляет собой смещенное основное состояние гармонического осцил-
осциллятора.
48 Когерентные и сжатые состояния поля Гл. 2
2.3. Что когерентно в когерентных состояниях?
Для ответа на этот вопрос полезно рассмотреть координатное представление
состояния с определенным числом частиц \п) для осциллятора. Координатное пред-
представление
п) определяется выражением
фп(д) = (д\п). B.3.1)
Из A.1.11) следует, что
где нами было использовано соотношение р = —ihd/dq. Тогда A.2.7) приводит
к уравнению
(^Я + Пщ)фо(я) = О- B-3.3)
Нормированное решение этого уравнения имеет вид
V B.3.4)
Собственные функции высшего порядка в координатном представлении можно по-
получить из выражений A.2.16), B.3.1) и B.3.2):
B-n!I/2 "
fo{q), B.3.5)
где Нп — полиномы Эрмита. Они представляют собой хорошо известные собственные
функции гармонического осциллятора. Можно показать, что эти волновые функции
удовлетворяют условию ортонормированности
что
т. B.3.6)
Из определения волновых функций гармонического осциллятора фп{ч) следует,
оо
(Я)= J Ф*п(я)яФп(я)с1я = 0. B.3.7)
— оо
Аналогично
(р) = 0, B.3.8)
(р2) = hu(n + \), B.3.9)
B.3.10)
2.3 Что когерентно в когерентных состояниях? 49
Следовательно, неопределенности обобщенного импульса и координаты определяют-
определяются выражениями
(АрJ = (р2) - (рJ = hu(n+\), B.3.11)
(AqJ = l(n+\). B.3.12)
Произведение неопределенностей равно
ApAq= (n+i)ft. B.3.13)
Это произведение принимает минимальное возможное значение, равное Я/2, для
волновой функции основного состояния (f)®(q).
Особый интерес представляет волновой пакет, сохраняющий одно и то же значе-
значение среднеквадратичного отклонения Ад, претерпевая простое гармоническое дви-
движение. Такая волновая функция наиболее близко соответствовала бы классическому
полю. Предположим, что в момент времени t = 0 волновая функция i/j(q,i) имеет
вид волнового пакета с минимальной неопределенностью B.3.4), смещенного в в
положительном направлении q на величину д0. Тогда
1/4
[^A B-ЗЛ4)
Временная эволюция этого волнового пакета рассмотрена в задаче 2.3, где пока™
зано, что исходный волновой пакет вида B.3.14) имеет следствием то, что в после-
последующие моменты времени плотность вероятности задается выражением
1/2
[?2] B.3.15)
Отметим, что волновой пакет B.3.14) осциллирует в потенциальном поле гармони-
гармонического осциллятора, не меняя формы, т. е. он не расплывается или когерирует.
Сравним его с волновым пакетом, который при t = 0 имеет вид дельта-функции,
при vt = тг/2 становится плоской волной и вновь приобретает вид дельта-функции
при vt = тг (см. подробнее в разд. 2.5). Хотя дельтаобразный пакет возвращается
к своей изначальной форме в конце периода, его среднеквадратичное отклонение
сильно зависит от времени, т. е. он не когерирует.
Произведение неопределенностей волнового пакета ф имеет минимальное разре-
разрешенное квантовой механикой значение, а именно АрAg = h/2. Следовательно, такие
состояния являются наиболее близким квантово-механическим аналогом свободного
классического одномодового поля.
Волновой пакет с минимальной неопределенностью B.3.14), козерирующий в по-
потенциальном поле гармонического осциллятора, задается выражением (задача 2.4)
п=0
B-3.16)
где а = (|//2ЯI/2до? и нами использовано соотношение ф{с[) = (q\n). Состояние
|а), соответствующее i/>(q, 0), следовательно, имеет разложение по состояниям числа
частиц, идентичное разложению когерентного состояния (выражение B.2.2)). Вол-
Волновой пакет с минимальной неопределенностью tpiq^O)? таким образом, является
координатным представлением когерентного состояния.
50
Когерентные и сжатые состояния поля
Гл. 2
2.4. Некоторые свойства когерентных состояний
В этом разделе мы перечислим некоторые важные свойства когерентных состоя-
состояний поля излучения.
1. Среднее число фотонов в когерентном состоянии \а) определяется выражением
_ |Л |2
(а\а а
B.4.1)
Вероятность того, что в состоянии |а) находится п фотонов, задается распределением
Пуассона
р(п) = (п\а)(а\п) =
(п)пе~{п)
B.4.2)
где (п) = \а\2. Как будет показано в гл. 11, распределение фотонов лазера прибли-
приближается к этому распределению при достаточно высоких степенях возбуждения. На
рис. 2.2 представлена зависимость р{п) от п для различных значений |о|2. Видно,
(а)
(б)
(в)
10 12 14 16 18 20
п
Рис. 2.2. Распределение фотонов р(п) в когерентном состоянии: \а\2 = 0,1 (а); |а|2 = 1 (б)
и \а\2 = 10 (в)
что для |а|2 ^ 1 функция р(п) максимальна при п = 0, тогда как для |а|2 > 1
функция р(п) достигает максимума при п = |«|2-
2. Как уже было показано ранее, когерентное состояние является состоянием
с минимальной неопределенностью, так что
' 2"
3. Множ:ество всех когерентных состояний \а) является полным множеством.
Чтобы показать это, рассмотрим сначала интегральное тождество (а = |а|е )
B.4.3)
2тг
' d\a\ [ t
B.4.4)
2.5 Физика сжатого состояния 51
где интегрирование осуществляется по всей комплексной плоскости. Из этого тож-
тождества с учетом разложения B.2.2) для когерентных состояний следует, что
а)(а\ d2a = тг ^|в)(в|. B.4.5)
п
Поскольку фоковские состояния \п) образуют полное ортонормированное множество,
сумма по п представляет собой единичный оператор. Тогда
1 I \ / « ,2
7Г
a)(a\d2a = 1. B.4.6)
Полученное выражение представляет собой соотношение полноты для когерентных
состояний.
4. Два когерентных состояния, соответствующих различным собственным значе-
значениям а и а' не являются ортогональными, т. е.
(a\af) = ехр ( —-
и
\(а\а)\2 = ехр(-|а - а'\2). B.4.8)
Видно, что если а — а' значительно больше единицы, то состояния \а) и \af) почти
ортогональны друг другу. Степень перекрытия этих волновых функций определяет
величину скалярного произведения (а\аг). Следствием отсутствия ортогональности
(выражение B.4.7)) является то, что любое когерентное состояние можно выразить
через другие когерентные состояния:
\а) = - \d2a'\a')(a'\a) = - fdVla') ехр (--Id2 + а'* а - -\а'\2) . BА9)
7TJ 7Г J V 2 2 /
Это означает, что когерентные состояния переполнены.
2.5. Физика сжатого состояния
Естествознание, представляющее собой синтез эксперимента и теории, изобилует
замечательными примерами успешного взаимодействия экспериментальной и теоре-
теоретической мысли. «Ультрафиолетовая катастрофа», связанная с излучением черного
тела, послужила причиной введения Планком понятия кванта. Эти соображения при-
привели Эйнштейна к понятию «спонтанного излучения», что позволило объяснить раз-
различия между распределениями излучения Планка и Вина. Понятие вынужденного
излучения привело к развитию физики лазера, который стал символом современной
эры квантовой оптики.
Сжатые состояния поля излучения станут в ближайшем будущем еще одним
примером плодотворной связи эксперимента и теории. Сами по себе, сжатые состоя-
состояния поля не представляют особого интереса. Например, состояния с определенным
числом фотонов п безусловно существуют, но как их создать, и кому это нужно?
Ответ на вопрос «кому это нужно?», в частности, лежит в области поиска грави-
гравитационных волн. Как будет показано в дальнейшем, в гл. 4, ускорение удаленной
материи, например, взрыв сверхновой, ведет к незначительному воздействию на
лабораторные приборы. Например, осциллирующая гравитационная волна может
возбудить механический осциллятор, который, в этом случае, будет детектором
гравитационных волн.
Однако, амплитуды осцилляции, создаваемых многими источниками гравитаци-
гравитационного излучения, предположительно, будут значительно меньше ширины волновой
52
Когерентные и сжатые состояния поля
Гл. 2
функции основного состояния. Это побуждает нас задуматься о сжатии волновой
функции основного состояния (нулевого шума) квантово-механических осциллято-
осцилляторов.
То, что такое «сжатие» в принципе возможно, становится ясным из рассмотрения
элементарной квантовой механики простого гармонического осциллятора (ПГО). Как
показано на рис. 2.3, волновой пакет, обладающий ярко выраженным максимумом
Рис. 2.3. Эволюция сжатого состояния простого гармонического осциллятора
(т. е. сжатый) в начальный момент времени, будет периодически растягиваться
и вновь возвращаться в исходное состояние. Для того, чтобы пояснить ситуацию,
вкратце рассмотрим временную эволюцию ПГО г). Напомним, что волновая функ-
функция в момент времени t связана с волновой функцией в начальный момент времени
соотношением
',0), B.5.1)
где хорошо известная из учебников по квантовой механике функция распространения
ПГО имеет вид
Здесь т и v — масса и частота осциллятора.
Теперь, если в начальный момент времени t = 0 мы имеем дельтаобразный
волновой пакет г/?(ж',0) = 5(xf — жо), то в момент времени t = тг/2и волновая
функция становится плоской волной. То есть, наше сжатое состояние эволюционирует
во времени следующим образом:
, t = 0) = 5(х —
ф(х, t = тг/2и) = 4/ ™— ехр
ф(х, t = тг/*/) = 8{х +
B.5.3а)
B.5.36)
B.5.3в)
) См., например, книгу Sargent, Scully and Lamb A974), приложение Н.
2.5
Физика сжатого состояния
53
Таким образом, из выражений B.5.3) и рис. 2.3 видно, что если в начале имеется
дельтаобразное или сжатое состояние, то мы будем возвращаться к нему каждые
пол-периода. В этом смысле, возможно своего рода «стробоскопическое» измере-
измерение, когда наблюдение за осциллятором осуществляется в моменты времени t =
= 0, тг/j/, 2тг/|/, . . ., не будучи ограничено шириной волновой функции основного
состояния.
Обосновав и проиллюстрировав сжатые состояния, перейдем к более глубокой их
трактовке. С этой целью рассмотрим мысленный эксперимент, демонстрирующий
то, каким образом можно было бы при-
приготовить такие состояния. Для начала
вкратце обсудим, как можно приготовить
когерентное состояние.
В классической механике ПГО мож-
можно привести в движение, растянув пру-
пружину таким образом, что осцилляции бу- У^ ^ ^ ,
дут происходить относительно нового по-
положения равновесия (рис. 2.4). В кван-
квантовой механике можно проделать то же
самое, но следует уточнить, каким обра-
образом мы приготовим начальное состояние
ПГО. Пусть ПГО представляет собой ча-
частицу массой га, с зарядом е в поле Eq I—О О О О О О ш m> e
(рис. 2.4). Тогда гамильтониан имеет вид
ж¦ =
zm z
который можно записать как
2
B.5.4а)
Рис. 2.4. Потенциал, отмеченный пунктир-
пунктирной линей, вызывает осцилляции частицы
с массой m и зарядом е относительно по-
положения х = 0. Приложение постоянного
электрического поля эквивалентно растя-
растяжению пружины до нового положения рав-
равновесия ж о 5 относительно которого будет
совершать осцилляции точечный заряд
к ) 2k{ к
B.5.46)
В B.5.46) отражен хорошо известный
факт, что приложение линейного потен-
потенциала к ПГО приводит к смещению его
положения равновесия. Очевидно, такими
же будут и решения. Таким образом, приготовлено смещенное основное состояние
(рис. 2.4). При отключении постоянного электрического поля, т.е. при Eq = 0, будет
иметь место когерентное состояние |а), осциллирующее без изменения формы.
Необходимо отметить, что приложение постоянного электрического поля к ПГО
математически эквивалентно действию оператора смещения B.2.8) на состояние |0)
(рис. 2.4).
Рассмотрим далее, как приготовить сжатое состояние. Предположим, что мы
вновь прилагаем постоянное электрическое поле, но на сей раз введем некий барьер,
ограничивающий ПГО пределами конечной области, как показано на рис. 2.5а.
В этом случае, волновой пакет, вероятно, деформируется или «сожмется» при
столкновении с барьером. Также следует ожидать, что квадратичный потенциал
смещения, изображенный на рис. 2.56, создаст сжатый волновой пакет. Чтобы по-
показать, что это действительно так, рассмотрим гамильтониан ПГО в присутствии
квадратичного потенциала:
\
Ж = ?- + \кх2 - еЕ0(ах - 6х2),
B.5.5а)
54
Когерентные и сжатые состояния поля
Гл. 2
:Я га, е g
Одр Q 0> ># К Барьер
/ Смещенный
«искаженный »
потенциал ПГО
х
Смещенный
«суженный»
потенциал ПГО
V = -еЕ0(ах -Ъх2)
Исходное основное
состояние
Сжатое
основное
состояние
Рис. 2.6. Сжатие волнового пакета сме-
смещенным «суженным» квадратичным по-
тенциалом ПГО
Рис. 2.5. Потенциал ПГО сначала смеща-
ется постоянным электрическим полем, а
затем «искажается» барьерами, которые
ограничивают осцилляции заряда в преде-
пределах конечной области (а); потенциал ПГО
смещается и «сужается» квадратичным по-
потенциалом смещения (б)
где член ах приводит к смещению осциллятора, а член Ъх2 вводится в качестве
барьера, «сжимающего волновой пакет». Перепишем B.5.5а) в виде
¦ 2еЬЕд)х —
B.5.56)
Из B.5.56) видно, что вновь имеет место смещенное основное состояние, но на этот
раз с большей эффективной жесткостью пружины, к1 = к + 2еЬЕ®. Это, безусловно,
означает, что имеется сжатый смещенный волновой пакет, показанный на рис. 2.6.
Это и есть желаемый результат.
В заключение заметим, что для создания когерентного состояния важна именно
та часть линейного потенциала смещения, которая содержит оператор рождения.
В то же время при создании сжатого когерентного состояния оказываются важны
двухфотонные а+2 и а2 вклады, содержащиеся в члене Ъх2 в выражении B.5.5).
2.6 Сжатые состояния и соотношение неопределенности 55
2.6. Сжатые состояния ж соотношение неопределенности
Обосновав изучение и природу сжатых состояний, рассмотрим, какими еще свой™
ствами они могут обладать. Рассмотрим два эрмитовых оператора А и Я, удовле-
удовлетворяющих коммутационному соотношению
[A,B] = iC. B.6.1)
Согласно принципу неопределенности Гейзенберга произведение неопределенностей
в определении средних значений двух переменных А и В задается выражением
АААВ > 1\{С)\. B.6.2)
Состояние системы называется сжатым состоянием, если неопределенность одной из
наблюдаемых (скажем А) удовлетворяет неравенству
(ДАJ < ||<С>|. B.6.3)
Если, помимо условия B.6.3), среднеквадратичные отклонения удовлетворяют также
соотношению минимальной неопределенности
АААВ=\\(С)\, B.6.4)
то такое состояние называется идеальным сжатым состоянием.
Таким образом, в сжатом состоянии величина квантовых флуктуации одной из
переменных становится меньше, чем в симметричном состоянии с минимальной не-
неопределенностью [(АЛJ = (АВJ = 1@I/2], за счет соответствующего увеличения
флуктуации сопряженной переменной. При этом соотношение неопределенностей
не нарушается.
В качестве примера рассмотрим квантованное одномодовое электрическое поле
частотой и:
E(t) = Se{a eTilJt + а+ eivt), B.6.5)
где а и а+ удовлетворяют коммутационному соотношению
[а,а+] = 1. B.6.6)
Введем эрмитовые операторы амплитуды
Х1 = \(а + а+), B.6.7)
X2 = j-.(a-a+). B.6.8)
Очевидно, что Х\ и Х2, по существу, представляют собой операторы безразмерных
координаты и импульса:
у Ы1 UlU ( ix
х = ——™ (а + бг ),
Из B.6.6) следует, что Х\ и Х2 удовлетворяют коммутационному соотношению
[ХиХ2]=г-. B.6.9)
56
Когерентные и сжатые состояния поля
Гл. 2
(а)
(б)
E(t)
Х2
(в)
Рис. 2.7. Области неопределенности и соответствующие им графики зависимости электри-
электрического поля от времени: когерентное состояние (а); сжатое состояние с уменьшенным
шумом в Х\ (б); сжатое состояние с уменьшенным шумом в Х2 (в)
С помощью этих операторов выражение B.6.5) можно записать как
E(t) = 2&ё(Х1 cos vt + X2 sin vt), B.6.10)
т. е. эрмитовые операторы Х\ и Х^ можно рассматривать как амплитуды двух
квадратур поля, имеющих разность фаз, равную тг/2. Согласно B.6.9), соотношение
неопределенностей этих амплитуд имеет вид
I\XiI\X2 ^ —. B.0.11)
Условием сж:атого состояния является выполнение неравенства
B.6.12)
2.7 Оператор сэюатия и сжатые когерентные состояния 57
Если, наряду с B.6.12), выполняется равенство
AXlAX2 = i, B.6.13)
то имеет место идеальное сжатое состояние.
В следующем разделе мы рассмотрим двухфотонное когерентное состояние, ко-
которое является примером идеального сжатого состояния. А пока отметим, что коге-
когерентное состояние \а) и фоковское состояние \п) не являются сжатыми состояниями.
Из B.6.7) следует, что в случае когерентного состояния
= \(а\[а2 + аа+ + а+а + (а+J]\а) - \{(а\(а + а+)\а)]2 = \ B.6.14)
И
(АХ2J = \. B.6.15)
По аналогии, для фоковского состояния,
(АХгJ = {n\Xl\n) - {{п\Хг\п)J = \{2п + 1), B.6.16)
(АХ2J = iBn + l). B.6.17)
На рис. 2.7 изображены области неопределенности для Х\ и Х^ и соответствую-
соответствующие им зависимости электрического поля от времени для когерентного состояния,
сжатого состояния с уменьшенным шумом в Х\ и сжатого состояния с уменьшенным
шумом в X*i. Каждая точка в области неопределенности для различных состояний
соответствует волне с определенной амплитудой и определенной фазой. Следователь-
Следовательно, суммирование всех таких волн в пределах этой области дает неопределенности
электрического поля, которые представлены на графике в виде заштрихованной
области. Электрическое поле в когерентном состоянии (рис. 2.7а), для которого
неопределенности величин Х\ и Х2 равны, имеет постоянное значение среднеквадра-
среднеквадратичного отклонения. Электрическое поле в сжатом состоянии с уменьшенным шумом
в Х\ (рис. 2.76") обладает уменьшенной амплитудной неопределенностью за счет
увеличения фазовой неопределенности, тогда как для электрического поля в сжатом
состоянии с уменьшенным шумом в Х2 (рис. 2.7в) ситуация прямо противоположна.
2.7. Оператор сжатия ж сжатые когерентные состояния
В разд. 2.5 упоминалось, что квадратичные по х члены, т. е. члены вида (а + а+J,
играют важную роль в создании сжатых состояний. Учитывая это, имеет смысл
рассмотреть вырожденные параметрические процессы в связи с созданием таких
состояний поля излучения. Действительно, как показано в гл. 16, физику сжатых
состояний, в основном, можно подробно рассмотреть на примере вырожденного
параметрического процесса. Соответствующий двухфотонный гамильтониан молено
записать в виде
Jf = ih(ga+2-g*a2), B.7.1)
где g — константа взаимодействия. В результате создается состояние поля вида
B.7.2)
58 Когерентные и сжатые состояния поля Гл. 2
что приводит нас к определению унитарного оператора сжатия
S@ = exp (^V - \ia+2) , B.7.3)
где ? = г exp (i#) — произвольное комплексное число. Легко видеть, что
S+(C) = S-\0 = S(-C). B.7.4)
Непосредственное применение формулы
еАВ е~А = В + [А,В} + ±{А, [А, В}} + ... B.7.5)
приводит к следующим полезным свойствам преобразования с помощью унитарного
оператора сжатия:
= achr - а+ е^ shr, B.7.6)
= а+ ch г - а е'^ sh г. B.7.7)
Определив повернутую на угол $ /2 комплексную амплитуду как
Y1+iY2 = (X1+iX2)e-ii>/2, B.7.8)
из B.7.6) получим
= Y1 e~r + iY2 er. B.7.9)
Сжатое когерентное состояние |ск,?) получается в результате воздействия на
вакуумное состояние оператора смещения D(a) и последующего воздействия на
полученное состояние оператора сжатия Я(^), т.е.
\a,0 = S(OD(a)\0), B.7.10)
где а = \a\exp (i(p). Как уже упоминалось ранее, когерентное состояние создается
членами, линейными по а и а+, под знаком экспоненты, тогда как для создания
сжатого состояния необходимы квадратичные члены.
В дальнейшем мы обсудим некоторые свойства сжатого когерентного состояния
поскольку оно является каноническим примером сжатого состояния.
2.7.1. Дисперсия квадратур. Средние значения операторов в состоянии |а,?)
можно найти, воспользовавшись определением B.7.10) и свойствами операторов
смещения и сжатия B.7.3). Тогда
(а) = (а,?\а\а,?) = @\D+(a)S+(OaS(OD(a)\0) =
= (а\(а ch г - а+ еы sh r)\a) = achr - а* е^ shr, B.7.11)
(а2) = ((а+J)* = (Q\D^(a)S^(Oa2S(OD(a)\0) = (а|5+@а5@5+@а5@|а> =
= a2 ch2 г + (a*J e2i^ sh2 г - 2\а\2 е^ sh r ch г - е^ ch r sh r, B.7.12)
(а+а) = |o|2(ch2r + sh2r) - (а*J ei# shr chr - a2e^shrchr + sh2 r. B.7.13)
С помощью этих средних значений можно вычислить дисперсии повернутых ампли™
туд Y\ и Y*i- Подставляя выражения для Х\ и Х2 из B.6.7) и B.6.8), получаем
Y±+iY2 = ae~ii?/2, B.7.14)
2.8
Многомодовое сжатие
59
так что
= (Y2) - (УгJ = \(
¦ аа -\- а а) (
% B.7.15)
\е2г, B.7.16)
= \- B-7.17)
Следовательно сжатое когерентное состояние является идеальным сжатым состояни-
состоянием. Как показано на рис. 2.8, в плоскости комплексной амплитуды область неопреде-
AY2
Yi
У" AYi
Рис. 2.8. Область ошибок сжатого когерентного состояния
ленности, имеющая форму круга для когерентного состояния, сжимается в эллипс
той же площади. Главные оси эллипса направлены вдоль Yi и Y^ повернутых на угол
#/2 относительно Х\ и Х2, соответственно. Степень сжатия определяется величиной
г = |?|, которая получила название параметра сжатия.
2.8. Многомодовое сжатие
Одномодовое двухфотонное когерентное состояние можно обобщить на случай
многомодового сжатого состояния, используя генератор, который содержит про-
произведения операторов уничтожения (и рождения) для пар коррелированных мод,
расположенных симметрично относительно моды, с частотой, скажем, v. Для начала
рассмотрим простейший случай двухмодового сжатия, а затем обобщим его на слу-
случай многомодового сжатия. Двухмодовое сжатое состояние получается в результате
действия унитарного оператора
= е^
B.8.1)
на двухмодовый вакуум.
60 Когерентные и сжатые состояния поля Гл. 2
Чтобы показать, что операторы, связывающие две моды, обладают способностью
к сжатию, введем коллективные операторы рождения и уничтожения:
b = —^= [п ¦ / ¦+• ег а _ /] , B.8.2)
v 2
6 = —7= \аи+у' Н" е а _ '1 • B.8.3)
V 2
Квадратурные компоненты задаются выражениями
&2 = ~:(^ "" Ь ). B.8.5)
Соответствующее соотношение неопределенностей имеет вид
A6iA62 ^ i. B.8.6)
Дисперсии двух составляющих в двухмодовом сжатом вакуумном состоянии равны
(АЬгJ = \ [exp(^2r) cos2 (^ - |) + expBr) sin2 (^ - |)] , B.8.7)
(А62J = i [expBr) cos2 (f ^ f) + exp(^2r) sin2 (^ - |)] . B.8.8)
В двух частных случаях при 8 — § = 0 и тг, имеет место идеальное сжатое состояние
с уменьшенными флуктуациями величин Ь\ и 62, соответственно.
Аналогичным образом можно сжать многомодовое вакуумное состояние. Опера-
Оператор многомодового сжатия определяется выражением
S\Hy)\ = I ^ exP [Civ'W+v'av-v' ~ ?("')^+„>а1;-„>] • B-8-9)
Здесь интегрирование осуществляется по положительной частотной области и ?(v) =
= г (и) ехр [i#]. Многомодовое сжатое когерентное состояние можно получить, по
аналогии с B.7.10), первоначально смещая вакуумное состояние, а затем сжимая
полученное состояние с помощью многомодовых операторов смещения и сжатия:
M"UM> = S[?(v)]D[a(v)]\0), B.8.10)
где |0) — многомодовое вакуумное состояние.
Задачи
2.1. Покал^ите, что
а+ а)(а\ = ( а* + ^^ ) а)(а| и а)(а|а = (а + т^^г ) \а)(а .
\ oolJ \ оа у
2.2. Покажите, что среднее значение оператора смещения D{a) для поля теплового
источника определяется выражением
а2
)> = ехр
где (п) — среднее число фотонов поля.
Задачи к гл. 2 61
2.3. Временная эволюция волнового пакета B.3.14) определяется уравнением Шре™
дингера для гармонического осциллятора:
п2 д2 ^
Общее решение этого уравнения можно выразить через стационарные волновые
функции следующим образом:
ею
п=0
где Еп = (п + l/2)hu, an — произвольные коэффициенты. Используя условия
ортонормированности волновых функций </)n(q), найдите ап, доказав тем са~
мым B.3.15).
2.4. Получите выражение B.3.16).
2.5. Альтернативное определение для сжатого когерентного состояния имеет вид
где ? = rexp(i#). Покажите, что дисперсии квадратурных составляющих
и У2, таких что
определяются выражениями
2.6. Рассмотрите двухмодовое сжатое состояние, определяемое выражением
где
Di(ai) = exp (ataf - a*a,i) (i = 1, 2)
— оператор смещения для двух мод, описываемых операторами уничтожения
и рождения а% и а^~,
5i2@ = ехР (Г«1«2 + ^atai)
— оператор двухмодового сжатия, |0) — двухмодовое вакуумное состояние.
Покажите, что каждая мода в отдельности не является сжатой. (Указание: см.
Barnett and Knight, 1985.)
2.7. Говорят, что состояние сжато в N-м порядке, если ((AXi)N) (i = 1 или 2)
меньше, чем соответствующее значение для когерентного состояния. Здесь
Покажите, что условием сжатия JV~ro порядка является выполнение неравен™
ства
62 Когерентные и сжатые состояния поля Гл. 2
где
(Указание: см. Hong and Mandel, 1985.)
2.8. Рассмотрите эрмитовы операторы, соответствующие действительной и мнимой
составляющим квадрата комплексной амплитуды поля:
Х1 = 1(а2 + а+2), Х2 = 1(а2-а+2).
Покажите, что условие сжатия имеет вид
(AXf) < (а+а) + i (г = 1 или 2).
л
Этот вид сжатия называется амплитудно-квадратичным сжатием. Покажите,
что амплитудно-квадратичное сжатие является неклассическим эффектом.
(Указание: см. Hillery, 1987).
Список литературы
Когерентные состояния поля излучения
Schrodlnger, E. Naturwissenschaften 14, 664 A926).
Kennard, E. H. Z. Physik 44, 326 A927).
Glauber, R. J. Phys. Rev. 130, 2529 A963).
Glauber, R. J. In Quantum Optics and Electronics, Les Houches, ed. C. DeWItt, A. Blandln, and
C. Cohen-TannoudjI (Gordon and Breach, New York 1965). [Глаубер Р. В кн. Квантовая
оптика и радиофизика (Мир, Москва, 1966), с. 91-279.]
Mandel, L. and Wolf, E. Rev. Mod. Phys. 37, 231 A965).
*Клышко Д.Н. Фотоны и нелинейная оптика (Наука, Москва, 1980).
Klauder, J. R. and Skagerstam, В. S. Coherent States, (World Scientific, Singapore 1985). Эта
книга представляет собой превосходное собрание статей по когерентным состояниям.
*Килин С.Я. Квантовая оптика: поля и их детектирование (Наука и техника, Минск,
1990).
Обзоры по сжатым состояниям
Walls, D. F. Nature 306, 141 A983).
Leuchs, G. In Non-equilibrium Quantum Statistical Physics, ed. G. T. Moore and M. O. Scully
(Plenum, New York 1985), p. 329.
Loudon, R. and Knight, P. L. J. Mod. Opt 84, 709 A987).
Zaheer, K. and Zubairy, M. S. In Advances in Atomic, Molecular and Optical Physics Vol. 28,
ed. D. R. Bates and B. Bederson (Academic Press, New York 1990), p. 143.
*Ахманов С.А., Белинский А.В., Чиркин А.С. В кн. Новые физические методы оптической
обработки информации, ред. Ахманов С.А., Воронцов М.А. (Наука, Москва, 1990), с. 83.
Сжатое когерентное состояние
Stoler, D. Phys. Rev. D 1, 3217 A970).
Lu, С. Y. E. Lett. Nuovo Cim. 2, 1241 A971).
Список литературы к гл. 2 63
Sargent III, M., Scully, М. О. and Lamb, W. E., Jr., Laser Physics, (Addlson-Wesley, Mass.
1974).
Yuen, H. P. Phys. Rev. A 13, 2226 A976).
Hollenhorst, J. N. Phys. Rev. D 19, 1669 A979).
Schletch, W. and Wheeler, J. A. Nature 326, 574 A987); J. Opt Soc. Am. В 4, 1715 A987).
Применение сжатых состояний в интерферометрии
Caves, С. М. Phys. Rev. D 23, 1693 A981).
Xiao, M., Wu, L. A., and Kimble, H. J. Phys. Rev. Lett 59, 278 A987).
Gea-Banacloche, J. and Leuchs, G. J. Opt Soc. Am. В 4, 1667 A987).
Многомодовое сжатие
Caves, С. М. Phys. Rev. D 26, 1817 A982).
Harriett, S. M. and Knight, P. L. J. Opt Soc. Am. В 2, 467 A985).
Caves, C. M. and Schumaker, B. L. Phys. Rev. A 31, 3068 A985).
Schumaker, B. L. and Caves, С. М. Phys. Rev. A 31, 3093 A985).
Сжатие высшего порядка
Fisher, R. A., Nieto, M. M. and Sandberg, V. D. Phys. Rev. D 29, 1107 A984).
Hillery, M., Zubalry, M. S. and Wodkiewlez, K. Phys. Lett ЮЗА, 259 A984).
D'Arlano, G., RasettI, M. and Vadacchino, N. Phys. Rev. D 32, 1034 A985).
Hong, С. К. and Mandel, L. Phys. Rev. Lett 54, 323 A985).
Braunstein, S. L. and McLachlam, R. I. Phys. Rev. A 35, 1659 A987).
Hillery, M. Phys. Rev. A 36, 3796 A987); Opt. Commun. 62, 135 A987).
Глава 3
ТЕОРИЯ КВАНТОВЫХ
РАСПРЕДЕЛЕНИЙ
И ЧАСТИЧНО КОГЕРЕНТНОЕ
ИЗЛУЧЕНИЕ
В предыдущих главах было показано, что существуют квантовые флуктуации
в состояниях, соответствующих классически вполне определенным электромагнит-
электромагнитным полям. В общем случае, для описания флуктуации необходим оператор плот-
плотности. Однако, существует альтернативное, но эквивалентное описание с помощью
функций распределения. В данной главе мы продолжаем исследование квантовых
статистических явлений, развивая сначала теорию квазиклассических распределе-
распределений. Это интересно по нескольким причинам.
Во первых, необходимо расширить квантовую теорию излучения с тем, чтобы
рассмотреть неквантовые стохастические эффекты, такие как тепловые флуктуа-
флуктуации. Это является важной составляющей теории частичной когерентности. Кроме
того, такие распределения делают понятной связь между классической и квантовой
теориями. Ярчайшим примером является распределение Вигнера г).
В данной главе вводятся различные функции распределения. Сюда входит пред-
представление когерентных состояний или Р-распределение Глаубера^Сударшана. С его
помощью вычисляются нормально упорядоченные корреляционные функции поле-
полевых операторов. Как будет показано в следующей главе, Р-распределение устанав-
устанавливает соответствие между квантовой и классической теориями когерентности. Для
некоторых состояний поля эта функция распределения не обладает всеми свойства-
свойствами классических функций распределения, например, она может быть отрицатель-
отрицательной. Помимо представления когерентных состояний, мы обсудим так называемое
Q-распределение, связанное с антинормально упорядоченными корреляционными
функциями, а также приведем другие функции распределения и их свойства.
3.1. Представление когерентных состояний
Изучение связи квантовой и классической теорий представляет значительный ин-
интерес. Эта связь нигде не проявляется так ярко, как в квантовой оптике, где мы часто
сталкиваемся с задачей описания полей, которые весьма близки к классическим,
1) Первое квазиклассическое распределение (WIgner, 1932) было введено для волновой
функции. В более поздней работе (Moyal, 1949) распределение Вигнера было получено
с помощью характеристических функций. Обзоры данного вопроса даны в работах Hillery,
O'Connel, Scully and WIgner A984) и Relchl A980). Рекомендуем также прочесть весьма
хорошо написанные учебники (Louisell, 1974; Walls and Mllburn, 1994 и Cohen, 1995),
расширяющие концепцию квазиклассического распределения.
3.1
Представление когерентных состояний
65
но обладают важными квантовыми свойствами. Когерентные состояния являются
весьма подходящими для такого рода исследований. Чтобы показать, почему это
так, напомним, что в случае флуктуирующего классического поля мы, как правило,
имеем дело с распределением вероятности Р{<е) для комплексной амплитуды поля
<?= Ще^ (рис. 3.1).
Рис. 3.1. Флуктуирующее классическое поле как функция времени в случае сильно флукту-
флуктуирующего поля (сплошная линия) и в случае стабилизированного поля (пунктирная линия)
(а); соответствующие распределения вероятности (б")
В квантово-механических задачах в основе распределения вероятности системы
лежит статистический оператор или оператор плотности, который определяется
следующим образом. Предположим известно, что система находится в состоянии \ф).
Тогда, среднее значение оператора О равно
(О) км = (Ф\О\ф}< C.1.1)
Однако, как правило, можно говорить лишь о вероятности Рф того, что система
находится в состоянии |^), и, следовательно, необходимо также провести усреднение
по ансамблю:
<{О)
км)ансамбль =
C.1.2)
Далее, используя свойство полноты ^2п |п)(п|=1, можно записать, что
п). C.1.3)
П ф
П ф
Таким образом, поле излучения, в общем случае, описывается оператором плот-
плотности
р = ^Рф\ф)(ф\, C.1.4)
Ф
где Рф — вероятность того, что система находится в состоянии \ф). Тогда среднее
значение любого оператора поля О определяется выражением
(О)=Тг(Ор),
C.1.5)
3 М.О. Скалли, М.С. Зубайри
66 Теория квантовых распределений и частично когерентное излучение Гл. 3
где Тг означает след. Оператор плотности можно разложить по состояниям чисел
заполнения фотонов:
Р = ^2^2\П)(П\р\т)(т\ = ^2^2рпт\п)(т\. C.1.6)
п т п т
Также возможно осуществить разложение по когерентным состояниям:
C-1.7)
Следуя Глауберу, определим Д-распределение как
R(a*,/3) = {а\р\/3} ef (H'+I^l2), C.1.8)
так что оператор плотности может быть записан в виде
l2!3|2)_ C.L9)
Таким образом, для того чтобы точно определить оператор плотности, мы использо-
использовали два индекса п и га, или а и C.
Далее мы установим связь с Р(<*), разработав диагональное представление по
когерентным состояниям. То есть, ниже мы выразим оператор плотности р через
диагональные пары |а)(а|.
3.1.1. Определение представления когерентных состояний. Рассмотрим опера-
оператор О]\г(<2,О'+), представляющий собой нормально упорядоченную функцию опера-
операторов а и а+ (все операторы рождения а+ стоят слева от операторов уничтожения
а), т. е.
ON(a, а+) = J2 J2 Спт(а+)пат. C.1.10)
п т
Заметим, что любой оператор, зависящий от а и а+, можно привести к нормально
упорядоченному виду, используя коммутационное соотношение [а, а+] = 1. Напри™
мер, а2а+ = а+а2 + 2а. Тогда для среднего значения оператора Одг(а,а+) можно
записать
(ON(a, о+)> = Tr [PON(a, a+)] =
Определим оператор (см. приложение З.А)
5(а* -а+)8(а-а) = \ [ехр[-/3(а* - а+)} ехр[/3*(а - a)} d2f3, C.1.12а)
тг J
или
6 (а* - а+) 5(а-а) = \\ exp[-i/3(a* - а+I exp[-i/3*(a - a)] d2f3. C.1.126)
тг J
Далее в тексте мы будем попеременно использовать эквивалентные друг другу
выражения C.1.12а) и C.1.126). Тогда C.1.11) можно переписать в виде
(ON(a, а+)) = И2" X) Z) СптТт \Р 6(а* ~ а+) *(" " «)](«*)"«"* =
^ п m
= ld2aP(a,a*)ON(a,a*), C.1.13)
j
3.1 Представление когерентных состояний 67
где
Р(а, а*) = Тг [р 6{а* - а+) 6{а - а)]. C.1.14)
Из C.1.13) видно, что с помощью функции Р(о, о*) можно вычислить средние значе-
значения любой нормально упорядоченной функции операторов а и в+, используя методы
классической статистической механики. В силу эрмитовости оператора плотности р,
функция распределения Р(а,а*) является действительной. Кроме того, поскольку
Тг (р) = 1, Р(а, а*) нормирована на единицу, т. е.
(a,a*)d2a = 1. C.1.15)
Функция Р(а, а*) известна как Р-представление или Р-распределение по когерент™
ным состояниям. Термин Р-представление состояния р возник благодаря тому,
что существует диагональное разложение оператора плотности р по когерентным
состояниям вида г)
р = I Р(а, a*)\a){a\ d2a, C.1.16)
Равнозначность определений C.1.14) и C.1.16) для Р(о, а*) можно легко доказать,
подставляя выражение C.1.16) для р в C.1.14). В следующей главе будет показано,
что Р(а,а*) устанавливает соответствие между классической и квантовой теория-
теориями когерентности. Прежде чем рассмотреть некоторые примеры Р-распределений,
приведем простой алгоритм, позволяющий найти Р(а, а:*), зная р. Пусть |/3) и —1/3)
являются когерентными состояниями с собственными значениями оператора а, рав-
равными /3 и —/3, соответственно. Тогда, учитывая B.4.7),
= Р(а, а*)(-Р\а){а\Р) d2a =
j
= е^ f[P(a, а*) еЧа|2] е^а^^а d2a. C.1.17)
Заметим здесь, что если а = ха + гг/а и /3 = х@ + гг/^, то d2a = с!жа с^г/а и /За* —
— /3*а = 2i{y^xa — Х/зУа), а выражение C.1.17) приобретает вид
{^Х а j У а) ^ а а j 6 ЛХ а dya. yo.L.LOj
Таким образом, (—/3|р|/3) е'^' представляет собой двумерное фурье-преобразование
от Р(а, а*) е^'а1 . Отсюда видна полезность матричного элемента (—/3|р|/3), посколь-
поскольку обратное фурье-преобразование позволяет легко выразить Р(а, а*) через опера-
оператор плотности р. Осуществляя обратное преобразование Фурье C.1.17), получаем
) При переводе книги для обозначения функции Р(а,а*), соответствующей оператору
плотности в базисе когерентных состояний, использовался термин «Р-распределение» (в ли-
литературе часто еще используется термин «весовая функция»). Термин «Р-представление»
использовался для обозначения разложения вида C.1.16). То же самое касается Q- и W-
распределений и представлений, рассматриваемых далее. — Примеч. ред. пер.
68 Теория квантовых распределений и частично когерентное излучение Гл. 3
искомое выражение:
Р(а,а*) = ^^\ \{-{3\р\Р)е{Х'
^- \(-Р\р\Р) е^2 е-Ра*+Р*а d2f3. C.1.19)
3.1.2. Примеры распределений по когерентным состояниям. В качестве первого
примера, вычислим Р(о, а*) для теплового излучения. Поле, излучаемое источником
в состоянии теплового равновесия при температуре Т, описывается каноническим
ансамблем:
где ^в — постоянная Больцмана, Ж9 = hu{a+а + 1/2) — гамильтониан свободного
поля. Для простоты ограничимся рассмотрением одной моды поля. Подставляя
выражение для Ж в C.1.20), получаем
C.1.21)
*—— L \ п-В 1- / Л \ гьп J- /
П
Соответственно,
(п) = Тг (а+ар) = [ехр (^т) - l] • C.1.22)
Таким образом, выражение C.1.21) можно переписать в виде
р = V ——тт п)(п\. C.1.23)
Отсюда следует хорошо известный результат, что распределение фотонов в тепловом
поле описывается распределением Бозе-Эйнштейна, т. е.
Рпт = (п\р\п) = +{Г?^))П+г ¦ C-1.24)
Теперь подставим выражение C.1.23) для р в C.1.19). Заметим, что
'V "Л \/ / о\ \/ I /3\
п
е ГИРИ М"М _е „.„I 1Д12Л , JM I C.1.25)
1 + <п> „
и,следовательно,
р(а, „•) = ^1 Г е-|/3|2/A + 1/(п» е-/3а'+а/3* d2^ = 1 е-|а!2/(«> (ЗЛ.26)
V ^ 7r2(l + (n»J H n(n) V ^
т. е. Р-распределение теплового излучения является гауссовым. В качестве другого
примера, рассмотрим Р-распределение когерентного состояния \olq). В этом случае
р = |«о)(«о|, так что
^РЫЫ/3) = ехр(-|ао|2 ^ \Р\2 ^ ао0* + pal). C.1.27)
3.2 Q -представление 69
Тогда из C.1.19) следует, что
р(а а*\ = J_ е1«|2-|«о|2 Г е-/3(а*-а;)+/Г (а-ао) ^ = ДB)/ _ ч C.1.28)
7Г J
7Г
т. е. Р-представление когерентного состояния представляет собой двумерную дельта-
функцию.
Хотя Р-распределение позволяет нам вычислять нормально упорядоченные кор-
корреляционные функции полевых операторов а и а+, оно не является неотрицательно
определенным и, как таковое, не является функцией распределения для некоторых
состояний поля. Это легко показать, вычисляя Р-представление состояния с опреде-
определенным числом частиц |п), для которого р = \п)(п\, и
<-/3|р|/3) = (-/ЗНН/З) = exp(-|/?|2)('1)^|/3i . C.1.29)
Соответствующее Р-представление, таким образом, имеет вид
пда*п
d/j^ n! дапда
Для п > 0 это выражение, очевидно, не является неотрицательно определенной
функцией, и, следовательно, состояние с определенным числом частиц не имеет
хорошо определенного Р-представления.
В следующей главе будет показано, что как только распределение фотонов ста-
становится уже, чем распределение Пуассона, как это происходит в случае состояния
с определенным числом частиц |га), функция Р(а,а*) становится нерегулярной.
Это та цена, которую мы платим за вынужденное приведение квантовой теории
в соответствие с классической, т. е. за то, что мы используем Р(а, а*) вместо, скажем,
3.2. Q-представленже
Подобно Р-распределению, связанному с вычислением нормально упорядочен-
упорядоченных корреляционных функций полевых операторов а и а", можно ввести другие
функции распределения, соответствующие другим типам упорядочений. Функция
распределения, позволяющая находить антинормально упорядоченные корреляци-
корреляционные функции, представляет собой так называемое Q-распределение. Оно опреде-
определяется следующим образом:
Q(a, а*) = Тг [р 5(а - а) 8(а* - а+)]. C.2.1)
Отсюда, вставляя разложение единицы B.4.6) между 5(а —а) и 8(а* — а+) и используя
B.2.1), получаем, что
- а')\а')(а'\ 8[(а* - (а')*]} = ±Тт{р\а)(а\) = \{а\
Q(a,a*) = ^Тт\ё?а'[р6(а- а)\а')(а'\6(а* - а+)] =
= ±Тт{р\а)(а\) = \{
C.2.2)
70 Теория квантовых распределений и частично когерентное излучение Гл. 3
то есть, функция Q(a,a*) пропорциональна диагональному элементу оператора
плотности в представлении по когерентным состояниям. Из свойства полноты коге-
когерентных состояний \а) (выражение B.4.6)) и условия Тг (р) = 1 следует, что Q(ck, ск*)
нормирована на единицу, то есть
Для того чтобы увидеть, как антинормально упорядоченные корреляционные
функции операторов а и а+ вычисляются с помощью <3™РаспРеДеления5 определим
сначала антинормально упорядоченную функцию Од (а, а+),
О ( + )^\^\^d n( +)m C 2 4)
п т
Отсюда следует, что
(ОА(а,а+)) = Тг[ОА(а,а+)р] =
птТт\- lan\a)(a\(a+)mpd2a) =
1ж J J
)\ql,ol )С/д(а,о; Jd а, (о.2.5)
J
где, в первой строке, вставили
- a)(a\d2a = 1. C.2.6)
71 J
В отличие от Р-распределения, функция Q(ot, а*) является неотрицательно опре-
определенной и ограниченной. В этом можно убедиться, подставляя р из C.1.4) в C.2.2).
Получаем
^)\2. C.2.7)
Ф
Поскольку |(^|а)|2 ^ 1, имеем
Q(a,a*)^^. C.2.8)
Q-распределение можно связать с Р-распределением, вычислив диагональный
элемент р по когерентным состояниям в C.1.16). Результат имеет вид
Q(a, a*) = if Р(а', а'*) е"!"-"'!2 d2a'. C.2.9)
Например, функция Q(ct, а*) для состояния с определенным числом частиц \п)
имеет вид
Q(a, а*) = Ц(п\а}\2 = ^"^f", C.2.10)
то есть является регулярной функцией. Q-распределение для сжатого состояния
определяется в разд. 3.5.
3.3. Распределение Вмгнера-Вейля
До сих пор мы рассматривали различные функции распределения, а именно Р-
и Q-распределения, отвечающие, соответственно, нормальному и антинормальному
3.3 Распределение Вигнера-Вейля 71
упорядочениям операторов а и а+. Подобным образом можно вывести функции
распределения, отвечающие другим упорядочениям.
Короче говоря, мы ввели функции
Р(а, о*) = Тг [<5(о* - а+) 5(а - а)р], C.3.1а)
Q(a, а*) = Тг [5(а - а) 6(а* - а+)р], C.3.16)
которые можно записать через так называемые характеристические функции. На-
Например, подставляя C.1.126) в C.3.1а), получаем
if
^ J
где характеристическая функция С^(/3,/3*) определяется как
Cw(/3,/3*) = Tr(eif3a+ eif3*ap) . C.3.3)
Аналогично молено записать C.3.16) в виде
Q{a,a*) = \ 1ё2Ре^^а^^*аС{а)(Р,Р*), C.3.4)
где характеристическая функция
G(а)(/5,/Г) = Tr(eiC*aeif3a+ р) . C.3.5)
Другое полезное распределение, введенное Вигнером и Вейлем, определяется как
W(a,a*) = Д^ \A2(Зе^а*^*аС{з)((],/3*), C.3.6)
^ J
где характеристическая функция С^(/3,/3*) задается выра^сением
f~^(s) { Я Й*\ Ту (ю^@а +*Д*а гА (Q Q I7^
Эта функция распределения VK(a, а*) отвечает симметричному упорядочению. Ее
можно использовать для вычисления средних значений произвольных симметрично
упорядоченных функций а и а+ в классической манере. Например,
а+а) = Г W{a, a*)aa* d2a. C.3i
В приложении З.Б описывается процедура нахождения очисловых функций
05(a,a*), соответствующих симметрично упорядоченной форме оператора
О(а,а+).
Исторически, распределение VF(a, а*) было введено через операторы координаты
q и импульса р в виде, эквивалентном следующему
W(p,q) = —^2 f do- f drei(Tp+<T9)Tr[e-i(TP+^p]. C.3.9)
Bтг) J J
Чтобы привести это выражение к виду, введенному Вигнером, воспользуемся
операторным тождеством
еА еВ е-[А,В}/2
72 Теория квантовых распределений и частично когерентное излучение Гл. 3
справедливом, когда коммутатор [А, В] коммутирует с операторами Л и В, и запи-
запишем C.3.9) в виде
, q) = —^2 \da\dr ei{rp+aq) Tr [e^irp e^iaq e^ihar/2p) . C.3.10)
B7Г) J J
Используя циклическую перестановку под знаком следа, получаем
W(p, q) = —l— [ da [ dr ei{Tp+aq) Tr (e^ir^2 e~iaqp e~irp/2) e~ih(JTl2. CJ.11)
Отсюда, записывая след в координатном представлении, получаем
x dq'{q'\ e~iTp/2 e~iaqp e~iTp/2\qf) e~ih<TTl2. C.3.12)
Отмечая, что exp(—irp/2)\qf) = \qf — hr/2) и т.д., находим
o,q) = —Ц^ Ida \dr \ dqf eia{q~q>) {q' + Пт/2\р\Ч' - hr/2) eirp. C.3.13)
Bтг) J J J
Наконец, интегрирование по а дает функцию <5(g — g;), что позволяет осуществить
интегрирование по q'. В результате, обозначая у = —Нт/2, записываем VK(p, q)
в обычном виде
(р' q) = ~k\dy e~i2vp/h(<i - у\р\я + у)- (з-3-14)
Функция Вигнера вида C.3.14) широко использовалась при решении множе-
множества задач. В следующем разделе мы установим связь этой функции с Р- и Q-
распределениями.
3.4. Обобщенное представление оператора плотности ж связь между
P-j Q- ж ^-распределениями
Ниже будет представлено обобщенное представление оператора плотности, перво-
первоначально введенное Кохеном, и примененное к квантовой оптике Агарвалом и Воль™
фом. Р-, Q- и FK-распределения получаются из обобщенного распределения как
частные случаи.
Обобщенное представление i^(^)(a>a ) оператора плотности имеет вид
р = тг I F(o)(a, a*)A(o)(a - a, a* - a+) d2a, CA1)
где
(o)(« - a, a* - a+) = \ [exp[ft(/3, /3*)] ехр[^/3(а* - a+) + ^*(a - a)
7Г
Здесь функция О(/3, /3*) (такая, что О@, 0) = 0) характеризует различные упорядо™
чения. Например, если О(/3,/3*) = ^|/3|2/2, то имеем F^°^(a,a*) = P(a,a*), а если
I, то F^\a, a*) = Q(a, a*).
Чтобы показать это явным образом, рассмотрим сначала функцию
I/Qi2
C.4.3)
3.4 Обобщенное представление оператора плотности 73
Из B.2.6) и B.2.7) следует, что
ехр (-Щ- + Д«+ - ^а) = ехр(-/Г а) ехр(/3а+), C.4.4)
и получаем
-а, а*- а+) =
тг3
. C.4.5)
Подставляя это выражение для A(o)(a^a, a* — a+) в формулу C.4.1), вновь получаем
определение Р-предетавления C.1.16), где F^(a, a*) = P(a, a*).
С другой стороны, если выбрать О(/3,/3*) = |/3|2/2, то
-/3(а*-а+) е/?-(а-а) ^ (д.4.6)
Из C.4.1) следует, что
i^pla/) = [ F^(a, «^(a'lA^^a - а, а* - а+)|с/) d2a. CA7)
Однако из C.4.6) получаем
(а'|Д(">(а - а, а* - а+)|а;) = \ f<a;|e-^a*-a+) е^^аЦа'} d2f3 =
тг J
= Л fe-^(a""a/")+^(a"a/)d2i8 = ^(a-a/). C.4.8)
7Г J
Выполняя интегрирование по а в C.4.7), вновь получаем C.2.2), где Q(a,a*) =
Другое распределение, введенное Вигнером и Вейлем, получается при правиль-
правильном выборе О, а именно, при О(а, а*) = 0. Для этого обратим выражение C.4.1),
используя функцию
А(О)(а ^а,а*^ а+) = \ f ехр[-П(^, /3*)] ехр[/3(а* - а+) - Г (а - «)] ^2^- C.4.9)
тг J
Мож:но показать (см. задачу 3.3), что
Тг [Д(п)(а - а, а* - а+)Д(П)(с/ - а, а'* - а+I = - ё{2)(а - а'). C.4.10)
7Г
Тогда из C.4.1) следует, что
F^(a, a*) = Тг [рА{п)(а - a, a* - о+)]. C.4.11)
Из C.4.9) и C.4.11) получаем
W(a,a*) = \ [тфехр(^/За++/Га)]ехр(/За* - /3*а) d2p. C.4.12)
7Г J
Это выралсение, как и ожидалось, совпадает с C.3.6), в котором величина /3 заменя-
заменяется величиной —г/3, а /3* — величиной г/3*. Выражения C.1.14) для Р-распределения
74 Теория квантовых распределений и частично когерентное излучение Гл. 3
и C.2.2) для <3~РаспРеДеления получаются из C.4.11), при
и О(/3,/3*) = |/3|2/2, соответственно.
Далее выведем явное выражение для распределения Вигнера-Вейля W(a,a*).
Прежде всего отметим, что W(a, а*) является фурье-образом функции
Кроме того, ехр(^2|о|2) является фурье-образом функции ехр(—|/3|2/2)/2тг, то есть
ехр(-2|а|2) = ^ |ехр (-\\Р\2) ехрЦЗа* - /Га) d2f3. C.4.13)
Тогда, согласно теореме о свертке,
W{a, а*) ехр(-2|а|2) = Г С(/3, /3*) ехр(/3а* - р*а) d2p, (ЗАМ)
j
где С(Р,Р*) является сверткой:
(^) 2^. C.4.15)
Явное выражение для С(/3^ /3*) можно получить, используя тождество B.2.7) и встав-
вставляя разложение единицы по когерентным состояниям B.4.6), следующим образом:
exp (-\\0- Pi\2 ~ \\Hi\2) d2p! d2f32 d2f33
2
x d2/3id2/32d2/33. C.4.16)
После интегрирования по /3i выражение C.4.16) принимает вид
(/32| - /3/2) d2h d2fo = ^(/3/2|Н - /3/2).
C.4.17)
Наконец, подставляя С(/3,/3*) из C.4.17) в C.4.14) и меняя переменные интегриро-
интегрирования /3, /3* на —2/3, ^2/3*, получаем
2 9 Г 9
И^(а, а*) = — ехрB|а|2) (-Р\р\Р) ехр[-2(/За* - /3*а)] d2/3. C.4.18)
^ J
Это выражение, очень похожее на соответствующее выражение для Р-распределения
C.1.19), молено использовать для вычисления распределения Вигнера^Вейля для
заданного оператора плотности поля.
3.5. Q-представление сжатого когерентного состояния
В этом разделе мы выведем (^-распределение для сжатого когерентного состояния
|/3,0. Согласно C.2.2)
3.5 Q-представление сжатого когерентного состояния 75
Теперь учтем, что
(а\Р, О = {a\S(?)D(p)\0) = (a\S(?)\P). C.5.2)
Следовательно, нам необходимо вычислить функцию (а|
Используя свойства когерентного состояния и свойство преобразования B.7.7)
оператора 5(?), получаем
{a\S(Z)\0) = ±r(a\a+
= ±r{a\S(Z)S+(Oa+S(O\{3) = ±r(a\S(t)(a+ ch r - а~" shr)|/?) =
= 4 [chr (^ + \C*) - e-**/3shr] (a\S@\C). C.5.3)
Таким образом, функция {(%\S(^)\f3) удовлетворяет следующему дифференциально-
дифференциальному уравнению:
[ch гщ-р е-1» sh г + (^/3* ch r - а*)] <а|5(?)|/3} = 0. C.5.4)
Решение этого уравнения имеет вид
(а|5(е)|/3) = A-exp(-i|/3|2 + a*/3sechr+ ^ e^/32thr) . C.5.5)
Вид множителя К, зависящего в общем случае от а, а*, /3*, г и #, можно найти,
используя свойство унитарности оператора 5(?). Из
01«> C.5.6)
следует, что
= К(Р, /3*, а*, г, 1? + тг) ехр[-^|а|2-^е-^a2 th r] . C.5.7)
Таким образом, /С имеет вид
/Г(а,а*,/Г,г,<9) = (sechrj^exp [-||«|2 - | е'*(а*Jthr] . C.5.8)
Коэффициент (sechrI/2 выбран таким, чтобы удовлетворялось условие нормировки
d2a = l. C.5.9)
Подставляя это выражение для К в C.5.5), получаем
= (sechrI/2x
х exp {-^(|«|2 + |Д|2) + o*/3sechr - ^[eii9(a*J - е"**/32] thr} . C.5.10)
76
Теория квантовых распределений и частично когерентное излучение
Гл. 3
Следовательно, Q-распределение для состояния |/3, ?) имеет вид
<Э(а,а*) = ^^^ехр| - (\а\2 + |/3|2) + (а*/? + 0*а) sechr-
- J[e*V2 " Г2) + е""(а2 - /З2)] thr j>. C.5.11)
На рис. 3.2 величина Q(a, а*) = Q(XUX2) (Хг = (а + а*)/2, Х2 = (а - a*)/2i)
изображена как функция амплитуд Х\ и Х^ двух квадратур. Ясно видно, что
дисперсии квадратур Х\ и Х^ в состоянии \/3,?) не равны между собой. Исполь™
зуя выражение C.5.10) для (a\S(?)\/3}
Q(Xi,x2) можно вычислить функцию распределе™
ния фотонов в сжатом когерентном со-
состоянии.
Функция распределения фотонов р(п)
для поля в состоянии |/3, ?) задается вы-
выражением
р(п) = Кп|/3,О|2- C-5.12)
Величину G11/3, ?) можно найти, записы-
записывая
п=0
C.5.13)
Рис. 3.2. Величина Q(а, а*) = Q(Xi,X2) и разлагая правую часть выражения
как функция амплитуд Хг и Х2 в сжатом C.5.10) в ряд по степеням а* с помощью
когерентном состоя™™. (Из Pf о™ Yuen, производящей функции полиномов
„Р. Phys. Rev. A 13, 2226 A976).)
та Hn(z):
Hn{z)tn^
n=0
C.5.14)
Сравнивая полученное разложение с разложением в формуле C.5.13), получаем
, О -
2 '
»(Р thг)] Нп
C.5.15)
Следовательно, функция распределения фотонов р(п) для идеального сжатого со-
состояния имеет вид
2
( \ (th^)W / i
/Зе-*
"n'chr ' I " ' ' 2L ' - ' J j | '"VV2chrshr,
C.5.16)
Как правило, источники сжатого света создают поле излучения в сжатом вакуум-
вакуумном состоянии |0, ?). Однако схемы детектирования добавляют к нему когерентную
составляющую. Следовательно, детектируемое состояние описывается распределе-
распределением C.5.16). Флуктуации среднего числа фотонов можно найти либо из C.5.16),
3.5
Q -представление сжатого когерентного состояния
77
р(п)
О 10 20 30 40 50 60 70 80 90 100
Рис. 3.3. Сравнение функции распределения фотонов для когерентного состояния \а) с
= 60 (сплошная линия) и для сжатого состояния |/3,?) (/3 = |/3|ехр(г0), ? = rexp(i#))
с |/312 = 60, г = 0.6 и 0 = #/2 (пунктирная линия)
0.25
0.15
0.05
0 10 20 30 40 50 60 70 80 90 100
п
Рис. 3.4. Функция распределения фотонов р(п) для двухфотонного когерентного состояния
C.5.16) при |/3|2 = 60 и г = 1.6. Сжатая составляющая больше, чем когерентная составляю-
составляющая, и сжатие происходит вдоль когерентной амплитуды
используя
C.5.17)
п=0
78 Теория квантовых распределений и частично когерентное излучение Гл. 3
0.2
0.15
р(п)
0.05
Рис. 3.5. Функция распределения фотонов р(п) для сжатого вакуумного состояния при
г = 1.6
либо используя свойства B.7.6) и B.7.7) унитарного преобразования, осуществляе-
осуществляемого оператором сжатия. В результате получаем
(AnJ = |^|2[ch 4r - cos(# - 2ф) sh 4r] + 2 sh2 r ch2 r. C.5.18)
Далее рассмотрим три случая, представляющих для нас интерес. В первом случае,
когда \Р\2 ^> sh r, когерентная составляющая больше, чем сжатая составляющая.
На рис. 3.3 приведены для сравнения распределения вероятности для сжатого и ко-
когерентного состояний. Если сжатие происходит вдоль когерентной амплитуды, то
состояние имеет субпуассоновскую статистику фотонов. Во втором случае (рис. 3.4),
когда сжатая составляющая больше, чем когерентная составляющая, сжатое состоя-
состояние демонстрирует осцилляции. Главный максимум, также как и последующие, уже,
чем соответствующее значение у/п. Однако полное распределение имеет суперпуас-
соновскую статистику. Наконец, в случае нулевого смещения, то есть в случае сжатого
вакуумного состояния, функция распределения C.5.16) сводится к
рBп) = ^ j^J (| th г) " , рBп + 1) = 0. C.5.19)
В этих выражениях ненулевое значение четных членов обусловлено сжатием вакуума
и ясно показывает «двухфотонную» природу поля. На рис. 3.5 показано распределе-
распределение вероятности C.5.19). Распределение имеет острый пик при п = 0 и очень длинный
хвост, аналогично тепловому распределению.
Приложение З.А
Проверка соотношений C.1.12а, 3.1.126)
Можно проверить, что двумерная дельта-функция имеет вид C.1.12а)
5(а* - а+) 6(а - а) = Д- [ехр[-/3(а* - а+)\ ехр[/Г (а - а)] d2f3, C.A.1)
"¦ J
П.З.А Проверка соотношений C.1.12а, 3.1.126) 79
вычисляя средние значения в когерентном состоянии I7) обеих частей выражения
(З.А.1). В самом деле, поступая таким образом и используя то, что I7) является
собственным состоянием оператора уничтожения а с собственным значением 7?
получаем
6(а* - 7*) 6(а - 7) = \ [ехр[-/3(а* - 7*)] ехР[/Г (о - 7)] d2f3. C.A.2)
Если записать а = ха + iya, /3 = жд + iy@ и j = z7 + %7, то получим <i2/3 = dxp dy@,
и правая часть выражения (З.А.2) принимает вид
[
ехр[-/3(а* - 7*)] ехр[-/Г (а -
= —
7Г J
= 5[lm (а - 7)] S[^ {<* - 7)] = S{a - 7) S(a* - 7*), C.A.3)
где во второй строке величины 2х@ и 2ур заменены величинами х@ и у^, соответ™
ственно, и использовано следующее выражение для дельта-функции:
сю
eikx
6(х) = ^ [ eikx dk. C.A.4)
— ОО
Выражение C.1.126)
S(a* - а+) <*(а - а) = -^ [exp[^i/3(a* - а+I exp[^i/3*(a - аI d2j3 C.A.5)
тг J
можно получить из (З.А.1) простой заменой переменных: /3 —>> г/3 и /3* —>- —if]*.
Другая формула для антинормально упорядоченной двумерной дельта-функции,
а именно,
<*(а - а) 5(а* - а+) = \ \ ехр[^*(а - а)} ехр[^(а* - а+)] d2/3, C.A.6)
7Г J
которая использовалась в определении (^-распределения C.2.1), мож:ет быть прове-
проверена путем вставки
^J27 = l C.A.7)
следующим образом:
-р- \exp{C*(a-a)}expl-C(a*-a+)]d2p = -^ I [ е"*(а-°>|7><7| е~^а'-а+^ d2f3 d21 =
(а-7)|7><7| е-«а*-^*) d2f3 d27 =^js(a- -у)|-у><-у| 5(а* - 7*) А =
= 6{а - a) (^|7><7l d2-yj 5{а* - а+) = д(а - а) 5{а* - а+). (З.А.8)
80
Теория квантовых распределений и частично когерентное излучение Гл. 3
Приложение З.Б
О-числовая функция, соответствующая распределению
Вигнера-Вейля
Для заданного оператора О(а,а+) и распределения Вигнера-Вейля W(a^a*)
вычислим функцию Оя(а, ск*), такую что
{О{а, а+)) = Tr (Op) = I d2a0s(a, a*)W{a, о*). (З.Б.1)
Напомним, что распределение Вигнера^Вейля определяется как (см. C.3.6) и C.3.7))
W(a,a*) = \ [ё2рТг(е^*а+^а+ р) e^iC*a^iCa\ (З.Б.2)
где характеристическая функция
Cis\/3,f3*)= \eil5'a+ilia'W{a,a*)d2a^
= Тг(е^'а+^а+р) = Tr(ei/3a+ ei/3'a е~№2/2р). (З.Б.З)
В последней строке выралсения (З.Б.З) использована формула Бэйкера^Хаусдорфа.
Теперь для произвольного нормально упорядоченного оператора О(а^а^) можно
записать
О(а, а+) = J2 cn,ma+nam. (З.Б.4)
п,пъ
Нетрудно показать, что
д
а1 =
Тогда
(а) =
I3*=I3=O
2i\ [d(iB*)^2i
•=/3=0
= dzaOs(a, a*)W(a, а*), (З.Б.5)
откуда
d(iC) 2%
Г) + 2г
. (З.Б.6)
Выражение (З.Б.6) и есть требуемый результат. Рассмотрим некоторые примеры:
а) О(а, e+) = a+a,
г\ / *\ ^_
2i
2i
C*=C=0
= а*а--; (З.Б.7)
Задачи к гл.
81
б) О(а,а+) = (а+Jа,
2i
/3*=/3=O
/3*=/3=O
= -^- + а* (а*а - \) = «*2« - «*• (З.Б.8)
Оператор, соответствующий функции распределения Вигнера в координатно-им-
пульсном представлении, приводится в книге Cohen A986).
Задачи
3.1. Покажите, что
l(aa+ + a+a) = [ W(a, a*)\a\2 d2a,
где W(a, a*) — распределение Вигнера-Вейля.
3.2. Покажите, что
Tr[D(a)] =ж8{2\а), Тг [D{a)D+{af)] = ж 8{2){а - а'),
где D{ol) — оператор смещения. Используя эти результаты, покажите, что
Тг [Д(")(а - а, а* - a+)A(O)(a; - а, а*; - а+)] = - ё{2)(а - af).
Операторы А^°) и Д определяются выражениями C.4.2) и C.4.9), соответ-
соответственно.
3.3. Покажите, что распределение Вигнера^Вейля VK(a:, a*) можно выразить через
Р~распределение F(a, a*), используя соотношение
W{a, «*) = f
3.4. Определите Q(a, а*) и VF(a, а*) для когерентного состояния и теплового со-
состояния поля.
82 Теория квантовых распределений и частично когерентное излучение Гл. 3
Список литературы
Р-представление
Glauber, R. J. Phys. Rev. 131, 2766 A963).
Sudarshan, E. С. G. Phys. Rev. Lett 10, 277 A963).
Walls, D. F. and Mllburn, G. J. Quantum Optics, (Springer-Verlag, Berlin 1994).
Q-j Вмгнера-Вейля и другие распределения
WIgner, E. Phys. Rev. 40, 749 A932).
Moyal, J. Proc. Cambridge Phil. Soc. 45, 99 A949).
Kano, Y. J. Math. Phys. 6, 1913 A965).
Klauder, J. R., McKenna, J. and Currie, D. G. J. Math. Phys. 6, 734 A965).
Mehta, C. L. and Sudarshan, E. C. G. Phys. Rev. 138, B274 A965).
Cohen, L. J. Math. Phys. 7, 781 A966).
Lax, M. 1968 Brandis Lectures on Fluctuation and Coherence Phenomena (Gordon and Breach,
New York 1968).
Cahill, K. E. and Glauber, R. J. Phys. Rev. 177, 1857 A969).
Agarwal, G. S. and Wolf, E. Phys. Rev. D 2, 2161, 2187, 2206 A970).
Louisell, W. Quantum Statistical Properties of Radiation, (Wiley, New York 1974).
Carruthers, P. and Zacharlaser, F. Phys. Rev. D 13, 950 A976).
Reichl, L. А. A Modern Course in Statistical Physics, (University of Texas Press 1980).
Hillery, M., O'Connell, R. F., Scully, M. O. and WIgner, E. P. Phys. Rep. 106, 123 A984).
Cohen, L. In Frontiers of Nonequilibrium Statistical Physics, ed. G. T. Moore and M. O. Scully
(Plenum, New York 1986), p. 97.
Cohen, L. Time Frequency Analysis, (Prentice Hall, New York 1995). W. Vogel and D.-G. Welsch,
Lectures on Quantum Optics, (Akademe Verlag, Berlin 1994).
Глава 4
ПОЛЕВАЯ И ФОТОННАЯ
ИНТЕРФЕРОМЕТРИЯ
Оптическая интерферометрия лежала в основе революции, приведшей к новой
эре физики двадцатого столетия. Например, ключевой эксперимент в поддержку
специальной теории относительности, показывающий, что не существует детекти-
детектируемого движения относительно «эфира», был сделан с помощью интерферометра
Майкельсона.
Замечательная заслуга Майкельсона состоит в том, что та же концепция интер-
интерферометра стала центральной для детекторов гравитационных волн, которые пред-
предвещают новое понимание общей теории относительности и астрофизики в двадцать
первом веке. То же произошло и с интерферометрами Саньяка и Маха^Цендера,
обсуждаемыми в этой главе. Отметим, кроме того, что звездный интерферометр
Хэнбери-Брауна-Твисса г) стал движущей силой в наступлении новой эры квантовой
оптики.
Все это побуждает нас развивать теорию интерферометрии, основанной на кор-
корреляции поля (амплитуды) и фотонов (интенсивности). При этом мы обнаружим,
что предмет рассмотрения предоставляет нам тонкий прибор для изучения микро-
и макромира, то есть объектов квантовой механики и общей теории относительности.
Таким образом, в данной главе разрабатываются основы для изучения квантовых
статистических корреляций света. Квантовые корреляционные функции поля обос-
обосновываются с точки зрения теории фотодетектирования. Многие экспериментально
наблюдаемые величины, такие как статистика фотоэлектронов и спектральное рас-
распределение поля, могут быть связаны с соответствующими функциями корреляции
поля. Эти функции корреляции необходимы для описания эксперимента Юнга с дву-
двумя щелями и понятия спектра мощности света. Функции корреляции интенсивности
соответствуют, обычно, измерениям корреляций интенсивность—интенсивность, что
требуется для описания знаменитого эффекта Хэнбери-Брауна-Твисса и других
экспериментов по двухфотонной интерференции, обсуждаемых в этой главе.
Квантовая теория когерентности позволяет также исследовать состояния по-
поля, демонстрирующие неклассические свойства, то есть состояния, которые нельзя
описать классической статистической теорией. Такие состояния возникают тогда,
когда явно проявляется квантовая природа света. Примерами являются состояния
с определенным числом фотонов и сжатые состояния поля излучения.
В следующих двух разделах мы обсудим применение!пс1ехОтносительности тео-
теория (общая) интерферометрии в астрофизике и общей теории относительности, а
затем обратимся к общему рассмотрению оптики фотонов.
) См. пионерскую работу Hanbury-Brown and Twlss A954; 1956). С педагогической точки
зрения превосходное рассмотрение сделано в работах Fano A961); Glauber A965); Baym
A969), см. также обзор Hanbury-Brown A974).
84
Полевая и фотонная интерферометрия
Гл.4
4.1. Интерферометр как космический датчик
Основы физики неразрывно связаны с искривленным пространством-временем.
Понятие «пространство-время» введено Минковским, показавшим, что физические
события (например испускание фотона) лучше всего представлять происходящими
в (плоском) четырехмерном пространстве, имеющем одну временную и три про-
пространственных координаты. Прилагательное «искривленный» отображает ситуацию,
когда в задаче учитывается гравитация. То есть, согласно общей теории относитель™
ности Эйнштейна, гравитация представляется нам как возникающая в результате
(или описываемая посредством) искривления четырехмерного пространства. Это
искривление, в свою очередь, возникает из-за присутствия в космосе массивных тел,
таких как Земля, Солнце, крабовидная туманность и т. д.
Многие теоретики считают общую теорию относительности самой красивой из
всех физических теорий. Однако из-за малости константы гравитационного взаи-
взаимодействия, G = 6,67 • 1СП8 см3 г™1 с™2, экспериментальные проверки этой теории
были крайне редкими. Это было подчеркнуто Мизнером, Торном и Уилером, которые
заметили:
«В первую половину века своей жизни, общая теория относительности
была раем для теоретиков и адом для экспериментаторов».
Однако, благодаря достижениям современной лазерной оптики, были разработа-
разработаны (и продолжают разрабатываться) новые тесты метрической теории гравитации
(общей теории относительности). Оптический интерферометр стал главным инстру-
инструментом этих астрофизических и общерелятивистских исследований.
4.1.1. Интерферометр Майкельсона и общая теория относительности. Как отме-
отмечалось выше, интерферометр Майкельсона использовался в эксперименте по обна-
обнаружению движения относительно эфира и стал одним из ключевых экспериментов
для разработки специальной теории относительности и современной физики.
В настоящее время строится интерферометр типа Майкельсона, предназначенный
для детектирования гравитационных волн. Действие гравитационного излучения,
(а)
\w\\\\\ м2
Светоделитель
Детектор
Рис. 4.1. Внешний лазер освещает интерферометр Майкельсона, который находится под
действием гравитационной волны, обозначаемой через hy,u («); увеличение эффективной
оптической длины пути в плечах интерферометра Майкельсона за счет внесения в них
резонаторов, многократно отражающих проходящий через них свет (б)
4.1 Интерферометр как космический датчик 85
фактически, состоит в изменении длины пути, проходимого светом в одном из плеч
интерферометра (см. рис. 4.1), и, следовательно, в формировании фазового сдвига.
То, каким образом возникает этот фазовый сдвиг, можно представить двумя различ-
различными способами: A) гравитационная волна изменяет расстояние между зеркалами,
и B) гравитационная волна изменяет или возмущает пространство-время, действуя
подобно диэлектрику. Здесь мы примем первую точку зрения.
В стационарной (ньютоновской) теории гравитации скалярный потенциал Ф
(в свободном пространстве) удовлетворяет уравнению Лапласа
?2Ф = 0, D.1.1)
тогда как в нестационарной (эйнштейновской) теории гравитации, тензорное поле J
Ф//1/(г, t), где индексы /л и и пробегают значения от 1 до 4, удовлетворяет волновому
уравнению движения
(^J^ D.1.2)
Следовательно, гравитационные эффекты распространяются со скоростью света с
из своего источника (двойные звезды, взорвавшиеся галактики и т. д.) в нашу ла-
лабораторию на земле. Эта «гравитационная волна» заставляет точки лаборатории
испытывать крошечные по амплитуде колебания.
Схема измерения гравитационных волн (^-волн) основана на интерферометре
Майкельсона. Влияние гравитационного излучения состоит в растяжении или сжатии
цилиндра длиной L, расположенного перпендикулярно направлению распростране-
распространения. Например, гравитационная волна частотой i/g будет изменять расстояние Lx
между зеркалом Mi и светоделителем (рис. 4.1а) по закону
Lx = L[l + h0 cos(^t)], D.1.3)
где L — длина плеча интерферометра в отсутствии гравитационной волны и ho
— амплитуда гравитационной волны, имеющая порядок величины ^ 10™21 для
реальных источников.
Следовательно, между световыми пучками, прошедшим через два плеча интер-
интерферометра, возникает разность фаз
5 = k(Lx - Ly) = kLh0 cos(i/gt). D-1.4)
4.1а, будет опреде
D.1.5)
Поэтому интенсивность, регистрируемая детектором на рис. 4.1а, будет определяться
по формуле
/ /0(l + cos5),
где /о — интенсивность падающего света.
В реальных экспериментах в двух плечах интерферометра Майкельсона исполь-
используются резонаторы (рис. 4.1 б). Теперь сигнал, обусловленный гравитационной вол-
волной, преобразуется в зависящий от времени фазовый сдвиг, описываемый формулой
D.1.4), в которой Lx заменяется эффективной длиной пути L, равной, в сущности,
числу отражений, умноженному на длину плеча L. Следовательно, на временах
t ^C i^Z1 фазовый сдвиг, индуцированный ^-волной, равен А'ё^ = uLh^/c^ где
и — частота лазерного излучения. Фундаментальным квантовым пределом в таком
эксперименте является «дробовой шум фотонов». Обозначая среднее число лазерных
1) Обсуждение общей теории относительности, ориентированное на студентов, изучающих
современную квантовую оптику, имеется в работе Schleich and Scully A984).
Полевая и фотонная интерферометрия
Гл.4
фотонов через п, мощность на детекторе через Р, и полагая, в данном разделе, кван-
квантовую эффективность детектора равной единице, получаем что неопределенность
фазы, обусловленная дробовым шумом при измерении в течение времени ?ш, имеет
вид
A^^ = i/^ D.1.6)
Приравнивая Д#'р) и А#те, находим минимальное значение амплитуды ^-волны,
регистрируемое в данной пассивной системе,
D.1.7)
где введена скорость затухания резонатора ^f = с/L.
4.1.2. Кольцевой интерферометр Саньмка. В 1913 году Саньяк рассмотрел ис™
пользование кольцевого резонатора для поиска «течения эфира» относительно вра-
вращающейся системы координат. Однако, как часто бывает, его результаты оказа-
оказались полезными в областях, о которых сам Саньяк и не мечтал. Как показано на
рис. 4.2, физика эффекта Саньяка состоит просто в том, что короткому импульсу
A(t = 0)
A(t =
Рис. 4.2. Схема кольцевого интерферометра Саньяка
света требуется больше времени для того, чтобы «вернуться» к источнику, если он
распространяется по направлению вращения интерферометра, и меньше времени,
если он распространяется против направления вращения.
Для количественного описания рассмотрим рис. 4.2. На нем показано, что ла~
зерный свет входит в интерферометр в точке А и расщепляется светоделителем на
пучки, распространяющиеся по часовой стрелке (Ч) и против часовой (ПЧ) стрелки.
Если интерферометр не вращается, то Ч- и ПЧ-пучки вновь встретятся в точке А
спустя время
*=*?, D.1.8)
4.1 Интерферометр как космический датчик 87
где b ~~ радиус кольца. Однако, если интерферометр вращается с угловой скоростью
Ог вокруг оси, проходящей через его центр и перпендикулярной его плоскости, то
пучки вновь встретятся со светоделителем в различные моменты времени, поскольку
Ч~пучок (сонаправленный с Ог) должен пройти путь немного больший, чем 2тгЬ,
чтобы совершить один полный оборот, так как интерферометр за время обхода
поворачивается на малый угол. Аналогично, ПЧ-пучок за один оборот должен пройти
путь немного меньший, чем 2тгЪ. Если обозначить время обхода Ч-пучка через t+, a
ПЧ^пучка через t~, то величина t+ дается выражением
где в первой строчке 6Ort+ — длина дуги, на которую повернется интерферометр до
момента возвращения Ч-пучка к светоделителю. Аналогично
ЬпгГ 2пЬ / Ш *
Разность между t+ и t равна
с
+
\ С /
4^ , D.1.10)
с —
J <С с2
Для разумных значений Ъ и Ог величина FОГJ <С с2, так что
D.1.11)
разность оптических путей обхода интерферометра AL определяется выражением
^ ±. D.1.12)
Из D.1.12) видно, что разность оптических путей обхода, согласно данному анализу,
прямо пропорциональна скорости вращения интерферометра. Более общий подход,
справедливый для интерферометра произвольной формы, приводит к результату
AL = 4°г 'zA, D.1.13)
где А — площадь области, ограниченной траекторией света, и z — единичный вектор,
нормальный к поверхности интерферометра.
Эффективность интерферометра Саньяка ограничивается тем, что разность оп-
оптических путей обхода D.1.12) существенно меньше длины волны света. (Например,
если b = 1 и Ог = 10 град/час, то AL = 4.1 • 10™12 м.) На первый взгляд может
показаться, что использование кольцевых лазерных гироскопов, в качестве чувстви-
чувствительных к вращению устройств, является практически нецелесообразным, поскольку
желательна чувствительность 10~3 град/час и выше. Однако существуют две схемы,
значительно повышающие чувствительность кольцевых лазерных гироскопов.
В первой схеме общая длина пути обхода увеличивается путем использования
оптических волокон километровой длины в качестве резонатора интерферометра.
Для того чтобы увидеть, как это увеличивает чувствительность гироскопа, пре-
преобразуем D.1.12) к более общему виду. Из D.1.12) следует, что разность фаз Д#
между противоположно распространяющимися пучками после одного обхода дается
выражением
^. D.1.14)
Полевая и фотонная интерферометрия
Гл.4
где Л = А/2тг — приведенная длина волны лазерного излучения и А = тгб2 — площадь
области, ограниченной пучками света. Выражение D.1.14) справедливо для одного
витка кругового обхода. При использовании оптического волокна, свет, обычно,
проходит по катушке с волокном радиуса b со множеством витков. В частности, если
такая катушка содержит N витков, то формула D.1.14) принимает вид
м = ъ**ъ2мпг Dлл5)
или
4пЬЬПг
с\
D.1.16)
где L = 2тгbN — общая длина оптического волокна. Выражение D.1.16) представ-
представляет собой важный результат, состоящий в том, что фазовый сдвиг, создаваемый
вращением кольцевого волоконного интерферометра Саньяка, возрастает линейно
с увеличением общей длины оптического волокна.
Во второй схеме расчет делается на увеличение сигнала кольцевого лазерного
гироскопа за счет введения активной лазерной среды в кольцевой резонатор. Эта
схема показана на рис. 4.3. Для удобства, до конца этого раздела такую схему
Рис. 4.3. Схема активного кольцевого лазерного гироскопа
будем называть активным кольцевым лазерным гироскопом. Тогда Ч- и ПЧ-моды
кольцевого лазера имеют различные частоты вследствие разности эффективных
длин оптических путей обхода, обусловленной вращением резонатора. Таким обра-
образом, имеются лишь колебания на частотах, удовлетворяющих условию резонанса,
отвечающего эффективным значениям длины резонатора L± для Ч- и ПЧ-пучков,
соответственно, а именно
т7ГС //11 in\
i/± = -р—, D.1.17)
Ь± '
где т — целое число и
L+ = L
D.1.18)
4.1 Интерферометр как космический датчик 89
С учетом D.1.17) разность частот Ч- и ПЧ-пучков можно приближенно записать
в виде
А ттгс ттгс mircAL AL ,. л ^_ч
д„ = „_ _ „+= __ _ __ й ___ = „_ D.1.19)
Приближение возникает потому, что полагаем L+L^ = L2.
Здесь необходимо сделать пару существенных замечаний. Первое состоит в том,
что при использовании активного кольцевого лазерного гироскопа измеряется именно
разность частот (а не разность длин оптических путей) противоположно распростра-
распространяющихся пучков. Эта разность частот, как правило, измеряется гетеродинированием
двух выходных пучков. Кроме того отметим, что разность частот D.1.19) в и/' L раз
больше разности длин оптических путей D.1.12). Такой большой масштабный мно-
множитель, а также относительная простота измерений малых разностей частот, делают
активный кольцевой лазерный гироскоп наиболее распространенным и, в настоящее
время, наиболее чувствительным интерферометрическим датчиком вращения.
Подстановка D.1.12) в D.1.19) дает (для обхода по круговой траектории)
Отметим, что Аи не зависит от общей длины резонатора, так что в активных лазер-
лазерных кольцевых гироскопах использование длинных катушек с оптическим волокном
не позволяет достичь большего масштабного множителя. В случае произвольной
геометрии резонатора выражение D.1.20) принимает вид
^ D.1.21)
где А — площадь области, ограниченной траекторией света, ир — ее периметр. Коэф-
Коэффициент пропорциональности 4А/Хр между Аи и Ог часто называется масштабным
множителем и в дальнейшем будет обозначаться через S.
4.1.3. Предполагаемая проверка метрических теорий гравитации с помощью
кольцевого лазера. Недавний прогресс в исследованиях с помощью лазерных ги-
гироскопов показал, что в принципе молено измерить скорости вращения вплоть до
1СР10Оф, где Оф — скорость вращения Земли. Учитывая это, можно теперь пред-
представить эксперименты, чувствительные к маховскому увлечению системы отсчета
(эффект Лензе^Тирринга), к существованию выделенной системы отсчета во все-
вселенной (космология выделенной системы отсчета) и к локальному искривлению
пространства^времени.
С тех пор, как Эйнштейн сформулировал общую теорию относительности, появи-
появилось много других альтернативных теорий гравитации, например Бранеа—Дике и Ни.
Эти теории, мотивированные различными соображениями, приводят к различным
предсказаниям для упомянутых выше эффектов. Для систематического сравнения
различных теорий с экспериментом были разработаны теоретические основы пара-
параметризованного постньютоновского (ППН) формализма, предоставляющего способы
изучения очень широкого класса метрических теорий гравитации в условиях слабого
поля и медленного движения солнечной системы.
Для помещенного на поверхность Земли сверхчувствительного кольцевого ла~
зерного резонатора, в зависимости от выбора метрической теории гравитации
и пространства^времени, можно ожидать нескольких «эффективных вращений».
Это вкратце отражено на рис. 4.4 и в табл. 4.1. Видно, что помимо вращения кольца
со скоростью Qo и вращения Земли со скоростью Оф, имеется три других вклада,
соответствующих ОМах, Окосмос и 0КрИВИЗна, соответственно.
90
Полевая и фотонная интерферометрия
Гл.4
э g
а
а
I
О
о
т—I
ю
I
О
я
Cq СО О <М
я
5 *
61
m о о
ь
Н
о
ави
го
со
оЗ
S
S
с
Be.
s
3
о
35
1
О
t—1
щ
а
о
s
СО
ш е
к
PQ
S
фек
0)
CD
S
К
ш
hred
а
G
4.1
Интерферометр как космический датчик
91
Первое из этих эффективных вращений, Омах, рассматривается как «слабое» под-
подтверждение принципа Маха. То есть, гироскоп испытывает эффективное вращение
даже если он зафиксирован относительно неподвижных звезд (т.е., если движение
Земли учтено, так что Oq и Оф непосредственно не влияют на кольцевой резонатор).
Кольцевой
лазер
Саньяка
Рис. 4.4. Использование кольцевого лазерного интерферометра Саньяка для проверки мет-
метрических теорий гравитации
Это эффективное вращение обусловлено исключительно тем, что мы находимся
около другого массивного тела — Земли. Другая интерпретация состоит в том,
что это вращение рассматривается как вариант магнитной гравитации, аналогичной
магнитному моменту вращающегося электрона.
Второй вклад, Окосмос, возникает из-за наличия выделенной (покоящейся) систе-
системы координат. Можно считать, что эта «выделенная система отсчета» связана с суще-
существованием фонового излучения черного тела, имеющего температуру 3 К. В общей
теории относительности Эйнштейна отсутствуют выделенные системы отсчета, тогда
как согласно теории Ни вселенная покоится в выделенной системе отсчета. Этот
эффект особенно интересен, поскольку он один из наименее обоснованных в физике
гравитации.
Последний член, 0КрИВИЗна, обусловлен тем, что используется искривленная про-
пространственная метрика. Подобная физика «искривленного пространства» приводит
к искривлению лучей света звезд, гравитационному красному смещению и т. д.
Приложение инструментов современной квантовой оптики к проблемам гравита-
гравитационной физики требует героической и творческой работы. Однако ясно, что такая
работа принесет богатые дивиденды как в фундаментальной, так и в прикладной
науке.
4.1.4. Звездный интерферометр Майкельсона. Рассмотрим простую двойную (то
есть с двойным источником) интерферометрическую установку, изображенную на
рис. 4.5. На рис. 4.5а изображена двойная звезда, «посылающая» на Землю излуче-
излучение с волновыми векторами кик'. Требуется измерить угловое расстояние ф между
ними.
Один из способов сделать это состоит в том, чтобы собрать свет с помощью
зеркал Mi и Л#2 (рис. 4.56") и направить его на фотодетектор, расположенный в точке
92
Полевая и фотонная интерферометрия
Гл.4
.'к'
Земля
(а)
lfk'
}
Мл
1*1
м2
Р
(б)
S S'
|к-к'
/
/
ф1
?'k'
7
к
/
/
1
1
]:
Го
(г)
М2
Рис. 4.5. Волновые векторы ki и кг, характеризующие излучение, приходящее на Землю от
двойной звезды (а); схема звездного интерферометра Майкельсона, предназначенного для
измерения углового расстояния между двойными звездами (б); отфильтрованное излуче-
излучение звезды S, падающее на зеркала Mi и Мг, характеризуется фазовыми множителями
ехр(—i*/fc? + ikri) и ехр(—ii/д.^ + ikr2), соответственно, в то время как излучение звезды Sr
характеризуется множителями exp(—ii^'kt + ik'ri) и exp(—ii/k't + ik'r2) (в); иллюстрация
того, что при малых углах (к — k')(ri — Г2) = |к — k^rocos^A « фкго, ибо |к — к;| с± А;0
и cos<f) ~ 1 (г)
Р такой, что пути М\Р и М2Р равны между собой. Тогда фототок определяется
выражением
= я(Е*Е) =
ik'r2)
ik''r2)|2) =
|??k,|2)
K.c]
к.с.]>, D.1.22)
где сделано упрощающее предположение, что свет, приходящий от звезд, отфиль™
трован, так что молено положить и^ = и^> и, следовательно, временные множители
типа expii/^t и expii/^/t сокращаются в выражении D.1.22). Кроме того, поскольку
излучение звезды является тепловым, (Еъ) = (Е^?) = 0 и (E^E^t) = (Е^)(Е^) =
= 0. Наконец отметим, что к — не представляющая интерес константа, зависящая от
характеристик фотодетектора, расстояния до звезды и т. д.
/ = 2к1®{2 + cos[k • (п - г2)] + cos[k; • (п - г2)]} =
= 4ж/0{1 + cos[(k + к;) • (п - г2)/2] + cos[(k - к;) • (п - г2)/2]}. D.1.23)
Из рис. 4.5г видно, что (к — к') • (ri — г2) = фкг®^ так что D.1.23) можно записать
в виде
/ =
+ cos[(k + к') ¦ (п - г2)/2] cosGrr0^/A)},
D.1.24)
где учтено, что |к| = |к'| = 2тг/А. Таким образом, видно, что фототок будет содер-
содержать интерференционный член, который модулируется при изменении го и может
4.1
Интерферометр как космический датчик
93
использоваться для определения ф, путем изменения г о вплоть до того момента, когда
ТГГоф/А = 7Г И Т. Д.
Эта удобная схема применялась для исследования нескольких близкорасположен-
близкорасположенных двойных звезд. К сожалению, атмосферные и инструментальные флуктуации
непосредственно входят в член cos[(k + k;) • (i*i — Г2)/2] в выражении D.1.24) и огра-
ограничивают полезность такого подхода. Именно здесь на сцену выходят Хэнбери™Браун
и Твисс.
4.1.5. Интерферометр Хэнбери-Брауна^Твисса.
Сущность звездного интерферометра Хэнбери-Брауна-Твисса (ХБ-Т) состоит
в следующем. Рассмотрим два фотодетектора в точках А\ и А^ с радиус-векторами
ri и Г2, соответственно, как показано на рис. 4.6. Тогда имеем следующие фототоки:
к.с.]} (г = 1, 2),
D.1.25)
и фазовая информация содержится в членах exp[i(k — к')г].
Что если перемножить токи детекторов (расположенных в точках А\ и
рис. 4.6)? Из D.1.25) тогда получим
на
\Ek,\2J)
к.с.]}, D.1.26)
где использован тот факт, что (| Е^ |2 Е? E^r) = 0 и т. д. Видно, что имеется требуемый
низкочастотный интерференционный член. Однако чувствительные к атмосфере
члены типа cos[(k + k;) • (ri — Г2)/2] отсутствуют. В этом и состоит суть оригинальной
идеи Хэнбери-Брауна и Твисса.
73
Pi
..А
Bi
С
Рис. 4.6. Схема звездного интерферометра интенсивности Хэнбери-Брауна-Твисса: Pi
и ?2 — фотодетекторы, А\ ж А^ — зеркала, В\ и Вч — усилители, т — время задержки, С
— умножитель, М — интегратор
94 Полевая и фотонная интерферометрия Гл. 4
Справедливости ради отметим, что презентация эффекта Хэнбери-Брауна и Твис-
са вызвала бурный интерес. Возникло много вопросов, например, каким образом,
создавая биения фототоков, мы получаем информацию о фазе? Не нарушает ли это
каким-нибудь образом квантовую механику? И как насчет утверждения Дирака, что
фотоны интерферируют сами с собой? Проблемы снимаются, если рассмотреть кван-
квантовую теорию детектирования и корреляций фотонов, к чему мы сейчас и переходим.
4.2. Детектирование фотонов и квантовые функции когерентности
Более полное изложение теории фотодетектирования приводится в разд. 6.5.
Здесь мы представим эвристический вывод вероятности фотодетектирования
и функции корреляции, достаточный для целей данной главы.
Как показано в гл. 1, оператор поля E(r, i) можно разделить на положительно-
и отрицательно-частотные части:
H(r,f), D.2.1)
где
— -»1/**+»кт? D.2.2)
il/fet"ik-r. D.2.3)
k
Далее будем полагать, для простоты, что поле является линейно поляризованным,
так что будем иметь дело со скалярными величинами ?^+^(r,t) = ?• E^(r,t)
и #(-)(r,*) = e-E^)(r,t).
В оптическом диапазоне, для локальных измерений поля обычно используются
детекторы, основанные на фотоэлектрическом эффекте. Схематично можно пред-
представить себе, что атом в основном состоянии помещается в поле излучения в точку
г. Затем наблюдаются фотоэлектроны, возникающие в результате фотоионизации.
В таких поглощающих детекторах измерения являются разрушающими, поскольку
фотоны, ответственные за возникновение фотоэлектронов, исчезают. Следовательно,
в этом случае вклад дает лишь оператор уничтожения Е^+\ Вероятность перехода
детектирующего атома в возбужденное состояние вследствие поглощения фотона из
поля в точке г между моментами времени t и t + dt, пропорциональна iui(r, t) dt, где
t)\i>\2, D.2.4)
|г) — начальное состояние поля до процесса детектироавния и |/) — конечное состоя-
состояние, в котором поле можно обнаружить по окончании процесса. Конечное состояние
поля никогда не измеряется. Следовательно можно просуммировать по конечным
состояниям:
_ t)|i), D.2.5)
где в последней строке использовано соотношение полноты
D.2.6)
4.2 Детектирование фотонов и квантовые функции когерентности 95
Таким образом, скорость счета фотонов wi пропорциональна среднему значению по™
ложительно определенного эрмитового оператора ?л '(г, t)E^(r, t), вычисленного
в начальном состоянии поля |г). На практике, однако, состояние |г) почти никогда
точно не известно. Поскольку точное знание поля обычно отсутствует, прибегают
к статистическому описанию, усредняя по всем возможным реализациям начального
поля:
Wl(r, t) = 5>|Z?(-V, t)E(+\r, t)\i). D.2.7)
i
Если ввести оператор плотности для поля
Р = ?ВД<*|, D-2.8)
г
то можно переписать D.2.7) в виде
«;i(г, t) = Тг [р?(-)(г, *)Я<+>(г, *)]. D.2.9)
Определим функцию корреляции первого порядка поля
G^n, r2; tut2) = Tr [p^-)(n, *i)tf (+)(г2, t2)] = (?/(-)(n, ti)E(+)(r2, *2)>.
D.2.10)
В оптике, обычно, имеют дело со статистически стационарными полями, то есть кор™
реляционные функции поля не изменяются при смещениях временной переменной.
В этом случае корреляционная функция 6r^(i*i, 1*2; ^ъ ^2) зависит от t% и ti лишь
через разность т = t^ ~~ t\, то есть
GA)(rbr2; tt,t2) = GW(rb r2; r). D.2.11)
Скорость счета гох, записанная через G^\ имеет вид
гух = СA)(г,г;0). D.2.12)
Рассмотрим теперь скорость совместного счета на двух фотодетекторах, рас-
расположенных в точках ri и 1*2- Совместная вероятность наблюдения одной фото-
ионазации в точке Г2 в интервале между ti и ti + dti и другой фотоионизации
в точке ri в интервале между 1\ и t\ + dt\, где t\ ^ t^, пропорциональна величине
W2(rb*i;r2,?2)d?i dt2, где
w2(ruti;r2it2) = |(/|Е(+)(г2,*2)^+)(п,*1)|г)|2. D.2.13)
Отсюда, суммируя по всем конечным состояниям и усредняя, как и прежде, по всем
возможным реализациям начального состояния поля, получаем
t«2(ri, in г2, t2) = Тг [рЕ^-Цп, Ь)Е(-Хг2, t2)E^(r2, Ь)Е<-+\Г1,Ь)]. D.2.14)
Совместная вероятность фотодетектирования определяется, таким образом, кван-
тово^механической функцией корреляции второго порядка
= Тг [р^-)(Г1, *i)tf<->(r2,
\Ы<\,и)). D.2.15)
96 Полевая и фотонная интерферометрия Гл. 4
В общем случае можно определить функцию корреляции п-го порядка
= Tr [p(n, x)(„, n)(n+1, n+1)Bn, 2n)]
= <?<->(!•!,*!) . . . Я(->(г„, *„)^(+)(г„+1, tn+l) ¦ ¦ ¦ ?(+)(r2n, *2n)>- D-2.16)
В этом определении функции корреляции н-го порядка содержится равное число
операторов рождения и уничтожения, поскольку такие функции корреляции изме-
измеряются в типичных экспериментах по многофотонному счету.
Из предыдущего ясно, что функции корреляции полевых операторов, которые
встречаются в любом эксперименте по детектированию фотонов, основанном на
фотоэлектрическом эффекте, являются нормально упорядоченными (то есть, все
операторы уничтожения находятся справа, а все операторы рождения — слева).
Например, средняя интенсивность света в точке г в момент времени t равна
t)), D.2.17)
а измеряемая функция корреляции интенсивности имеет вид
<?(->(г, t)E^(r, i)B(+)(r, t)?(+>(r, t)),
отличающийся от (/(г, t)/(r, t)).
Можно определить квантово-механические степени когерентности первого и вто-
второго порядков в точке г как
^(г,г) D_2Д8)
у <?(-)(г, t)E(+)(r, t))(E(-)(r, t + т)Е(+)(г, t + т)}
„B)(г т) = (E^-\r,t)E^-\r,t + r)E^(T,t + r)E^(T,t)) ( ,
g {'} {E^(rt)E^(rt)){E^(rt + )E^(rt + ))' ( '
где поле предполагается статистически стационарным. В определении g-^(r, т) было
выбрано не только нормальное упорядочение полевых операторов в числителе, но
и определенное упорядочение по времени. Это временное упорядочение является
следствием использованного выше способа вычисления скорости фотоэлектронного
счета (отметим, что ti ^ t\ в D.2.14)). Значительно более простой вид этих величин
получается в частном случае, когда поле излучения содержит лишь одну моду. Тогда,
после подстановки разложений по модам величин Е^ и Е^ (D.2.2) и D.2.3))
в выражения D.2.18) и D.2.19), большая часть множителей сокращается, и остается
<а+(*)а(*+ г)), D.2.20)
^(г)+.
(а а)
g{2) / ч = (a+(t)+(t + )(
{а+а}2
Поскольку процессы фотодетектирования подразумевают лишь нормально упо-
упорядоченные корреляционные функции, соответствие между классической и кванто-
квантовой теориями когерентности задается Р-распределением P(ct, а*). Это получается
потому, что квантово-механические средние значения нормально упорядоченных
функций вычисляются с помощью Р-распределения точно также, как вычисля-
вычислялись бы соответствующие классические функции когерентности с помощью клас-
классической функции распределения. Однако Р-распределение не имеет всех свойств
классической функции распределения. В частности, как обсуждалось в разд. 3.1,
4.3
Когерентность первого порядка
97
Р-распределение не является неотрицательно определенным. Световые поля, для
которых Р-распределение не является регулярной функцией, демонстрируют не-
неклассические свойства. Некоторые из них будут рассматриваться в разд. 4.4.
Теперь, в рамках квантовой теории когерентности, найдем нормированную функ-
функцию корреляции #'2'(т) для тепловых и когерентных полей. Р-распределение одно-
модового поля теплового источника задается распределением Гаусса (см. C.1.26)):
' Ы2 /(п\\ (А 9 99)
Тогда
о/ *
Р(а7 а
1 4 i2
\а а а
= 2.
D.2.23)
В случае же лазера, работающего выше порога, поле находится в когерентном со-
состоянии
)? для которого (см. C.1.28))
Р(а,а*) =
Тогда нормированная функция корреляции имеет вид
D.2.24)
D.2.25)
4.3. Когерентность первого порядка и эксперименты типа Юнга
с двумя источниками
4.3.1. Эксперимент Юнга с двойной щелью. Одним из классических экспери-
экспериментов, демонстрирующих свойства когерентности света первого порядка является
эксперимент Юнга с двойной щелью (см. рис. 4.7). Сложное поле, создаваемое ква™
зимонохроматическим источником света, расщепляется с помощью непрозрачного
экрана Si, расположенного поперек пучка, с двумя точечными отверстиями Р\ш Р2.
Положительно-частотную часть оператора поля в точке Р на экране S2 в момент
Si S2
Рис. 4.7. Схема идеализированного эксперимента Юнга с двойной щелью
4 М.О. Скалли, М.С. Зубайри
98 Полевая и фотонная интерферометрия Гл. 4
времени t можно аппроксимировать линейной комбинацией операторов, представ-
представляющих поле в точках Р% и Р2 в более ранние моменты времени:
, t) = КгЕ^(гъг - U) + К2Е^{т2, t ^ t2), D.3.1)
где t^ = s^/c (i = 1,2) — время распространения света из точечного отверстия Pi
в точку Р, i*i и г2 — радиус-векторы точечных отверстий Pi и Р2, соответственно.
Коэффициенты К\ и Кч зависят от размера и геометрии точечных отверстий. Из
теории дифракции следует, что К\ и К2 являются чисто мнимыми величинами.
Фотодетектор, помещенный в точку Р, измеряет интенсивность
\К2
2Тг [pEl-Цп, t -
2Тг [РЕ{-\г2, t - t2)E^(r2, t - t2)]+
+ 2Re {K{K2Tr [pfi(-)(n, t - <i)??(+)(r2, t - t2)]}. D.3.2)
Это выражение можно переписать через функцию корреляции первого порядка
^^, Г2; t\, <г) следующим образом:
+ 2Re [/CJ/CaG^Cri, r2; t-tut- t2)]. D.3.3)
В случае статистически стационарных полей выражение D.3.3) для средней интен-
интенсивности в точке Р принимает вид
(/(г, i)> = iK^G^in, n; 0) + |X2|2GA)(r2, r2; 0) + 2Re [ATJ ATaG^Cn, r2; r)],
D.3.4)
где г = ^i — t2. Следовательно средняя интенсивность (/(г, t)} не зависит от време-
времени t.
Первые два члена в D.3.4) представляют собой средние интенсивности света
в точке Р, приходящего из точечных отверстий Pi и Р2, соответственно. Однако
последний член дает вклад, обусловленный светом, приходящим из обоих отверстий,
и отвечает за интерференцию. Для того чтобы увидеть это явным образом, запишем
(/«(г)) = \К#вЫ{тип; 0) (г = 1, 2) D.3.5)
и определим нормированную функцию корреляции первого порядка
ь г2; г) = G(r"r2iT) D.3.6)
y'GA)(ri)ri;0)GA)(r2)r2;0)
Выражение D.3.4) переписывается через g^{v\, r2; т) следующим образом:
(/(г, t)) = </A)(r)) + (/B)(r)) + 2[(/A)(r))(/B'(r))]1/2Re ^(ri.rj; т)]. D.3.7)
Функцию корреляции представим в виде
gA)(ri, г2; т) = |gW(ri, r2; r)| eia^'r^~^\ D.3.8)
где a(ri, г2; т) = argfg'^^ri, r2; г)] + щт и щ — частота поля. Тогда
1, r2; r)| cosHn, r2; r) - щт]. D.3.9)
4.3 Когерентность первого порядка 99
В случае квазимонохроматических источников света величины (/^(г)}, (/B)(г)),
^(^(п, Г2; т)| и a(ri, Г2; т) изменяются медленно при перемещении точки на экране.
Однако функция косинуса изменяется быстро, поскольку содержит величину щт =
= vo(si — S2)/c, что приводит к синусоидальному изменению интенсивности на
экране.
Физический смысл величины g^{ri, Г2; т) можно понять, если рассмотреть вид-
ность интерференционных полос на экране. Видность, являющаяся мерой контраст-
контрастности интерференционных полос, определяется как
тт \Дг)/тах — \i(r)/mln
и =
(/(r))max+(/(r))min
D.J.I0)
где (/(г)}max и (^(r))min — максимальное и минимальное значения средней интен-
интенсивности, соответственно, в окрестности точки Р. В хорошем приближении они
соответствуют значениям +1 и —1 функции cos[a(ri, 1*2; т)^1/от] в выражении D.3.9).
Тогда
то есть, видность полос пропорциональна абсолютному значению величины
g*^(i*i, 1*2;т)? которая называется комплексной степенью когерентности. В част-
частности, если средние значения интенсивностей двух пучков одинаковы, (/^(г)) =
= (/B)(г)), то видность 17 равна |g"^(ri, 1*2; т)|- Таким образом, если g^iri, Г2; т) =
= 0, то никаких полос в окрестности точки Р не образуется, так что можно
предположить, что два пучка света, достигающие точки Р являются взаимно
некогерентными. Максимальная видность полос в окрестности точки Р получается
тогда, когда |#A)(г1,Г2;т)| = 1, и два пучка света, достигающие точки Р, являются
полностью взаимно когерентными. Это имеет место, если
(?7(->(гь *)?7<+>(г2, t + г)) = S *(гь *К(г2, * + г). D.3.12)
Промежуточные случаи, когда 0 < |g"^(ri, Г25 т)| < 1? описывают частичную
когерентность.
Например, излучение источника света со спектром, имеющим доплеровское уши-
рение типа теплового источника, описывается выражением
?^(гьг2;т) = #о2ехр(-г^от - т2/2тс2), D.3.13)
где тс — постоянная величина. Ясно, что если разность хода ст становится суще-
существенно больше, чем етс, то |#A'(г1,Г2;т)| = ехр(^т2/2т<?) устремляется к нулю,
и интерференционные полосы исчезают. Константа тс, которая связана со спектраль-
спектральной шириной света (как показано ниже), является, таким образом, мерой времени
когерентности света.
Важным свойством функции корреляции первого порядка
, г; т) = (Е^(т, t)tf (+)(r, t + т)>
является то, что она связывается фурье-преобразованием со спектром мощности
S(r,t) статистически стационарного поля в точке г, то есть
г;т)е^г. D.3.14)
100
Полевая и фотонная интерферометрия
Гл.4
Следовательно, для вычисления спектра мощности необходима функция корреляции
первого порядка при положительных значениях т.
Рассмотрим пример источника света с доплеровски уширенным спектром, для ко-
которого функция корреляции первого порядка задается выражением D.3.13). Спектр
мощности источника, вычисленный по формуле D.3.14), равен
хр[—(*/ — щJт^ /2]. D.3.15)
Это гауссов спектр, центрированный на частоте и = щ и имеющий полную ширину
на половине высоты, равную 2л/2\п2/тс. Таким образом, величина 1/тс, обратная
времени когерентности светового поля, является мерой спектральной ширины света.
4.3.2. Эксперимент Юнга с двумя атомами г). Рассмотрим эксперимент Юнга,
схема которого показана на рис. 4.8. Два атома расположены в точках S и S'. В мо-
момент времени t = 0 оба атома взаимодействуют с одиночным фотоном, обозначаемым
Рис. 4.8. Схема эксперимента типа Юнга, использующего излучение двух атомов
через |0), в результате чего какой-либо из атомов может перейти в возбужденное
состояние. Таким образом мы имеем состояние
а(\а, bf) + \Ь, af))\0) + /3\Ь, Ь')\ф), D.3.16)
где |а), \Ь) и |а;), \bf) — возбужденное и основное состояния атомов в точках S
и Sf, соответственно, а а и /3 — амплитуды вероятности состояний с возбужденными
и невозбужденными атомами, соответственно. Следовательно с вероятностью |а|2
путем поглощения одного фотона получаем состояние
D.3.17)
" ^2
С течением времени это состояние распадается в следующее:
|-0(оо)) = —^\Ь, 6;)(|7) + |т'))? D.3.18)
где I7) и jf) — состояния фотонов, соответствующие испусканию из точек S ш Sf. Для
целей настоящего раздела достаточно считать, что I7) и 7;) являются состояниями
1) Этот раздел основан на работе Scully and Drtihl, Phys. Rev. Л 25, 2208 A982).
4.4 Когерентность второго порядка 101
плоской волны |lie) и |1к;)? гДе к/^ и к;/^; — единичные векторы, направленные из
точек S и S1 в точку г детектора (рис. 4.8). Тем не менее, вопрос как выбрать состоя™
ния I7) и |7;) наиболее простыми, но в тоже время верно отражающими физическую
ситуацию, является важным и тонким, и рассматривается в приложении 4.А.
Корреляционная функция 6r^(r, r; t, t) принимает теперь вид
GA)(r,r;M) = (V'(oo)|?'(-)(r)?'(+)(r)|^(oo)) = GA)(r, r;0), D.3.19)
где отмечено, что зависящие от времени множители сокращаются, поскольку и^ =
= j/fc/. Используя условие полноты (как при выводе формулы A.5.15)), можно запи-
записать
GA>(r,r;0) = *J(r)**(r), D.3.20)
где
Ф,(г) = <0|?<+>(г)№(оо)> = ^ (eik-r + еЛ'"). D.3.21)
Таким образом, видно, что возникает интерференционная картина, задаваемая
выражением
GA)(r, г; 0) = <42{1 + cos[(k - к') • г]}, D.3.22)
которое, как показано в приложении 4.А, можно записать в обычном виде:
GA)(r,r;0) = ?g [l + cos^d-r)| = gg [1 + cosBkxd/D)]. D.3.23)
4.4. Когерентность второго порядка
В предыдущем разделе рассматривались корреляционные функции первого по-
рядка и их свойства. Если поля обладают одинаковыми спектральными свойствами,
то невозможно распознать их природу, исходя лишь из функции корреляции первого
порядка. Например, излучение лазера и излучение обычного теплового источника
имеют одинаковые свойства когерентности первого порядка. Однако это не так, если
речь идет о свойствах когерентности второго и более высокого порядка. Поэтому
далее мы рассмотрим применения корреляционных функций второго порядка.
4.4.1. Физика эффекта Хэнбери-Брауна^Твисса. Вооруженные теорией фото™
электронных корреляций, вернемся к эффекту Хэнбери-Брауна—Твисса. Для начала
рассмотрим состояние \ф) = |lk, Ik')? T0 есть случай двух независимых фотонов, один
из которых имеет импульс к, а второй — импульс к;. Ясно, что функцию корреляции
второго порядка можно теперь записать в виде
i, r2; t, t) = (lk, lk, |Е(-)(гь
D.4.1)
Используя соотношение J^in} l{n})({n}l = 1> получаем, что
DA2)
Ы
Поскольку |lk, It/) является двухфотонным состоянием, которое уничтожается дей-
действием оператора E^(r2j t)E^(ri, t), остается лишь член |0)@|.
102 Полевая и фотонная интерферометрия Гл. 4
С учетом вышесказанного видно, что в случае двух одиночных фотонов можно
записать
G^(ru r2; t, t) = ФB>*(гь t; г2, *)фB)(гь t; r2, *), D.4.3)
где
фB)(гь*;г2,г) = (O|/?W(r2,i)^(+)(ri,O|lk,lk'). D.4.4)
Поскольку
E^(ri,t) = ?'k(ake-i''t+ik-r*+ak,e-il't+ik'-r>) (г = 1,2), D.4.5)
получаем
g* е^@|ак, eik''riak
так что
GB)(rb r2; t, t) = 244{1 + cos[(k - k;) . (n - г2)]}. DА7)
Интерференция интенсивности для двух атомов. Рассмотрим случай двух ато-
атомов, расположенных в точках S и Sf (рис. 4.9), когда каждый из них первоначально
находится в возбужденном состоянии, то есть
D.4.8)
Спустя время, существенно большее времени затухания, это состояние примет вид
\ф(оо)) = |6, bf)\j, 7')? D.4.9)
где, как и в предыдущем разделе, можно считать, что I7) = |lie), \У) = |lk')-
Тогда двухфотонная корреляционная функция совпадает с функцией, определяемой
выражениями D.4.1) и D.4.7).
S S
1
2
Рис. 4.9. Графическое представление членов в выражении D.4.6)
Обратимся теперь к случаю некогерентного возбуждения атомов, с тем чтобы
показать действительную мощь эффекта ХБ—Т. Предположим, что атомы, распо-
расположенные в точках S и S\ возбуждаются электронным ударом. Тогда в некоторый
момент времени, допустим t = 0, имеем состояние вида
= N е^\а, а'} + |/3| (е^\а, b>) + ew'|6, a')) + \l\\b, Ь')} ® |0), D.4.10)
которое (см. приложение 4.А) эволюционирует в состояние
Нос)} = [|а| e^|lk, 1к,> + |/3| (ew|lk> + ew'|lk,)) + |7||0>] ® |6, Ь'), D.4.11)
где ф^ 1? и # — случайные фазы, обусловленные, например, случайным характером
моментов времени, соответствующих возбуждению атомов.
В этом случае интерференционные члены, содержащиеся в функции корреляции
первого порядка, умножаются на фазовый множитель, по которому необходимо
4.4 Когерентность второго порядка 103
провести усреднение, то есть
Г/^A)/г г./\1 , v /р-Ц#-д')\ p-i(h-hf)-r (ЛЛЛОЛ
[Ur yL , i , ?/jjперекрестные интерференционные члены * \с / с • ^.^t.JLZjj
Эта величина обращается в нуль вследствие случайного характера § и §'. Следо-
Следовательно, можно было бы заключить, что атомы, описываемые состоянием D.4.11),
никогда не создадут интерференционной картины. Однако это не так. Если восполь-
воспользоваться выражением D.4.11) для вычисления 6Л2^(гх, гг; ?,?), то найдем, что
) r2; t, t) = H2(lk, l^lE^^E^
= 2|a|Vk4{l + cos[(k - k') • (r! - r2)]}. D.4.13)
Здесь мы вновь видим, что случайные фазы, разрушающие когерентность первого
порядка, не влияют на когерентности типа ХБ-Т второго порядка.
Эффект Хэнбери-Брауна-Твисса для теплового и лазерного излучений. Обратим-
Обратимся теперь к случаю многофотонных состояний, отвечающих тепловому и лазерному
излучениям, и вычислим корреляции ХБ—Т для двух источников такого излучения,
расположенных в точках S ш Sf.
Как и прежде, нам необходимо вычислить скорость совпадений фотоотсчетов
в детекторах, расположенных в точках ri и Г2, причем скорость задается функцией
корреляции второго порядка
GB)(rbr2;M) = (?j(-)(rbf)?;(-)(r2,i)i?(+)(r2,i)^(+)(ri,i)). D.4.14)
Рассмотрим случай, когда основные члены в операторах электрического поля ?7(r^, i)
(г = 1, 2) имеют вид
Я(+)(г4, *) = <?k(ak e-^+ik-r- + ak< е-""+Л'"Р0, D.4.15)
где кик'- волновые векторы излучения, приходящего из точек S и S1. Кроме того,
как и прежде, и = с|к| = с|к'|. Отмечая, что в случае излучения, создаваемого теп-
тепловым источником, лазером со случайной фазой, а также двумя атомами, остаются
лишь «парные» упорядочения операторов (см. приложение 4.Б), получаем
x (ak егк"Г2 + ak/
o+a+ak/ak[l + е<("')-(п-Р2)Л DА16)
Если предположить, что (nk) = (nk/) = (n) и, аналогично, (nk) = (nk,) = (н2), то
D.4.16) можно записать в виде
b r2; *, t) = 2<fk4 ((п2) - (п) + (пJ {1 + cos[(k - к') • (п - г2)]}). D.4.17)
Далее вычислим (п2) для двух различных случаев: излучение звезд и излучение
лазера со случайной фазой.
1. Звезды. Излучение звезд является тепловым, поэтому
(n2) = 2(nJ + (n), (n) = [exp(hv/kBT) -
1-1
104 Полевая и фотонная интерферометрия Гл. 4
так что из D.4.17) следует, что
GB)(ri, г2; t, t) = 244 B(нJ + (пJ {1 + cos[(k - k;) . (n - г2)]}). D.4.18)
Последний член в D.4.18) соответствует эффекту Хэнбери-Брауна^Твисса и позво-
позволяет измерить угол между кик' (см. обсуждение, следующее за формулой D.1.24)).
2. Лазеры. В области, существенно превышающей порог, статистика фотонов
лазера является пуассоновской, поэтому (п2) = (вJ + (п), и
GB)(ri,r2; t, t) = ISt ((nf + (nJ {1 + cos[(k - k') • (n - r2)]}). D.4.19)
Таким образом, в обоих случаях можно измерить угловое расстояние, устранив
влияние возмущающих членов типа cos[(k + k;) • (ri — Г2)/2], которые мешают работе
звездного интерферометра Майкельсона.
Эффект Хэнбери-Брауна-Твисса в случае пространственной интерференции
нейтронов. Теперь уже ясно (вопреки тому, что часто можно услышать и прочи-
прочитать), что интерференционная картина ХБ—Т, или интерференционные перекрестные
члены в выражении для G'2'(ri,r2), не имеет никакого отношения к бозонному
характеру фотонов. То есть, как показано в двух предыдущих разделах, перекрест-
перекрестные интерференционные члены ХБ—Т появляются для излучения, испущенного как
двумя независимыми атомами, так и лазерами. В обоих этих случаях «группировка
бозонов» отсутствует.
Кроме того, из выражения D.4.4) и рис. 4.9 ясно, что эффект переносится также
и на нейтроны. В этом случае операторы уничтожения фотонов, такие как D.4.5),
заменяются фермионными операторами вида
ф{тиЬ) = ck е-*"*+*-г« + Ck, е-«"*+*'->ч, D.4.20)
где операторы уничтожения фермионов е^ и с^/ подчиняются антикоммутационным
соотношениям
4Ck'ck = ^k,k'' D.4.21)
44 = 0, D.4.22)
Ck,Ck = 0. D.4.23)
Теперь выражение D.4.4) заменяется двухфермионной волновой функцией
= e-2-4<0|ckeik-r2ck, eik'-ri|lk, Ik') + e-M"'@|ck, е*'-'Ч eikri|lk, lk'>, D-4-24)
и поскольку
@|ckck,|lk,lk'} = @|ckck,C+c+|0} = -<0|ckc+|0)@|ck,c+|0} = -1, D.4.25)
в то время как для второго члена из D.4.24) та же операторная алгебра дает +1, то
фермион-фермионная функция корреляции принимает вид
G<2>(ri, г2; t,t)=2{l- cos[(k - k') • (n - г2)]} . D.4.26)
Таким образом, эффект Хэнбери-Брауна^Твисса в случае двух точечных ис-
источников (S и S' на рис. 4.9), испускающих нейтроны или /3-частицы, работает
также хорошо, как и в случае источников 7-излучения или о-частиц. Единственное
различие заключается в знаке интерференционного члена.
4.4
Когерентность второго порядка
105
4.4.2. Гомодинное детектирование сжатых состояний. Как показано выше, пря-
прямые эксперименты по счету фотонов, в которых свет, имеющий распределение
фотонов р(п), падает непосредственно на фотодетектор, дают лишь информацию
о среднем числе фотонов и моментах более высокого порядка. Такие измерения
интенсивности, следовательно, не чувствительны к сжатию, а чувствительны к ан-
антигруппировке или к суб- и суперпуассоновской статистике, то есть к эффектам,
которые наблюдаются и в случае несжатых полей. Детектирование сжатых состоя-
состояний, с другой стороны, требует фазово-чувствительной схемы, при помощи которой
измеряется дисперсия квадратуры поля. В этом разделе рассматривается задача
детектирования сжатых состояний поля излучения с помощью гомодинирования.
Схема гомодинного детектирования показана на рис. 4.10. Входное поле скла™
дывается с полем гетеродина на свободном от потерь светоделителе, имеющем ко-
коэффициент пропускания Т и коэффициент отражения R, так что R + Т = 1.
Детектор 2
а
А
Светоделитель
Гете{
d
/?
/
Ъ
ЮДИН
с
Фазовращатель
Детектор 1
¦
Балансное
гомодинирование
ф
Обычное
гомодинирование
Рис. 4.10. Схема гомодинного детектирования
Моды входного поля и поля гетеродина описываются операторами уничтожения а
и 6, соответственно. Тогда, обозначая аналогичные операторы двух выходных мод,
достигающих детекторов 1 и 2, через end, соответственно, получаем
c = Vfa^ гу/1-Т 6, D.4.27)
d = iVl-Ta + Vfb. D.4.28)
Возникающая разность фаз между отраженной и прошедшей волнами, равная тг/2
для симметричного светоделителя, учтена при помощи множителя г в выражениях
D.4.27) и D.4.28). Сигналы, измеряемые двумя детекторами, определяются операто™
рами
г+ р — Тп^'п -4- A ¦
<U Ls A %Jj Hi \^ \ X
d+d = A - Т)а+а + ТЪ+Ъ - г
- Т) {а+Ъ -
- Т) (а+Ъ -
D.4.29)
D.4.30)
Поскольку частота гетеродина совпадает с частотой входного поля, эти операторы
не зависят от времени. Далее мы рассмотрим обычное и балансное гомодиннное
детектирование.
Обычное гомодинное детектирование. В случае обычного гомодинного детекти™
рования коэффициент пропускания светоделителя близок к единице, то есть
Т > Я, D.4.31)
106 Полевая и фотонная интерферометрия Гл. 4
и измеряется лишь фототок детектора 1. Мода гетеродина возбуждается в когерент-
когерентное состояние |/3/) с большой амплитудой и фазой ф\. Из D.4.29) следует, что сигнал,
достигающий детектора 1, дается выражением
(с+с) = Т(а+а) + A - Т)Щ2 - 2у/ТA - Т)\/31\(Х(ф1 + тг/2)>, D.4.32)
где
Х{ф) = Хф = ±(ае-'ф + а+е'ф). D.4.33)
Видно, что сигнал содержит часть входных фотонов, прошедшую через светодели-
светоделитель, отраженное поле гетеродина и, самое главное, член, описывающий интерфе-
интерференцию входящего поля и поля гетеродина. Именно этот интерференционный член
содержит квадратуру входного поля, зависящую от фазы гетеродина. В этой схеме
детектирования используется мощный гетеродин, так что
A-Т)|/3,|2»Т(а+а). D.4.34)
Неравенства D.4.31) и D.4.34) вместе означают, что почти все поле на входе достигает
фотодетектора, но часть поля гетеродина, достигающая детектора, все еще домини-
доминирует. Следовательно, первым членом в D.4.32) можно пренебречь и среднее число
фотонов в моде с равно
(пс) = A - Т)Щ2 - 2^ТA-Т)Щ(Х(ф1 + тг/2)). D.4.35)
Первый член составляет известное постоянное значение, которое можно вычесть
из сигнала, так что оставшийся сигнал будет содержать лишь квадратуру входного
поля.
Моды входного поля и поля гетеродина являются независимыми, то есть (ab) =
= (а)(Ъ). Флуктуации числа фотонов можно тогда легко вычислить, используя
D.4.29) и D.4.30),
(АпсJ = A - Т)|йГ{A - Т) + ЩАХ(ф1 + тг/2)]2}. DА36)
При выводе D.4.36) использовано неравенство D.4.34) и оставлены члены второго
порядка по |/3/|. Видно, что шум сигнала содержит отраженный шум гетеродина
(первый член) и прошедший шум входной квадратуры (второй член). Если поле
на входе является некогерентным (или вакуумным), то [АХ(ф1 + тг/2)]2 = 1/4, и
оставшийся член представляет собой дробовой шум гетеродина. Условие сжатия на
входе имеет вид
[( )]2<1 D.4.37)
для тех значений фазы ф\ гетеродина, при которых сжата квадратура Х\ или Х^-
На практике сначала блокируют вход и определяют уровень дробового шума.
Затем входное поле допускается на светоделитель и определяется уровень дисперсии
по отношению к уровню дробового шума. Таким образом, сжатие проявляется при
гомодинном детектировании как субпуассоновская статистика.
Отметим, однако, что измерения интенсивности при гомодинном детектировании
существенно отличаются от измерений при прямом детектировании, то есть: а)
флуктуации интенсивности в этом случае непосредственно определяют флуктуации
квадратуры на входе, и б) сигнал и его дисперсия зависят от фазы гетеродина,
являющейся внешним параметром.
4.4 Когерентность второго порядка 107
Балансное гомодинное детектирование. Обсуждая выражение D.4.35), мы пред-
предположили, что поле гетеродина является идеально когерентным и пренебрегли избы-
избыточным шумом гетеродина. В схеме гомодинного детектирования нельзя подавить
дробовой и избыточный шум гетеродина, проникающий за счет отражения от свето-
светоделителя, поскольку коэффициент пропускания Т, в принципе, не может быть рав-
равным 1. Следовательно, обычное гомодинное детектирование ограничивается шумом
гетеродина. В частности, детектирование не является квантово ограниченным, если
прошедший входной шум меньше, чем отраженный шум гетеродина, что может быть
в том случае, когда входной шум слишком мал.
Альтернативная схема основана на двухканальном гомодинном детектировании,
в которой сопоставляется выход двух каналов светоделителя. Тот факт, что неинтер-
ференционные члены для двух каналов имеют одинаковый знак, а интерференцион-
интерференционные члены — разный знак (см. выражения D.4.29) и D.4.30)), молено использовать
для полного исключения неинтерференционных членов. В этой схеме используется
светоделитель 50/50 и определяется разность показаний двух детекторов. Выходной
сигнал задается оператором
ncd = с+с - d+d = -г(а+Ь - Ъ+а). D.4.38)
Тогда измеряемый сигнал равен
(ncd) = -2\р1\(Х(ф1 + тг/2)>. D.4.39)
Видно, что вклад гетеродина исключен, и остался лишь результат интерференции
между средним полем гетеродина и входной квадратурой. Дисперсия выходного
сигнала получается равной
(AncdJ = А\/31\2[АХ(ф, + тг/2)]2. D.4.40)
Здесь вновь предполагается, что гетеродин является мощным. Доминирующий член
связан лишь с интерференцией между шумом входного сигнала и мощностью ге-
гетеродина, а шум последнего полностью исключен. Это делает требование сильного
гетеродина в данном случае менее жестким.
Измерение фазовой неопределенности г) . Использование балансного гомодинно-
гомодинного детектирования в прецизионной интерферометрии приводит к нескольким ин-
интересным результатам. Здесь мы рассмотрим применение балансного гомодинного
детектирования к измерению фазовой неопределенности оптических сигналов. Схема
измерения показана на рис. 4.11, где изображен интерферометр Маха^Цендера, со-
содержащий в верхнем плече фазово-чувствительный элемент и работающий в баланс-
балансном режиме. Фазово-чувствительный элемент вносит фазовый сдвиг фр, например,
за счет эффекта Керра, рассмотренного в разд. 19.2.
Предположим, что Mi и Мч на рис. 4.11 являются светоделителями 50/50 и до-
допустим, что длины двух путей между ними одинаковы. Операторы уничтожения
различных мод, изображенных на рис. 4.11, связываются друг с другом при помощи
1) Изложение в данном разделе следует, в частности, неопубликованной лекции В. Yurke,
которому авторы выражают свою признательность.
108
Полевая и фотонная интерферометрия
Гл.4
Керровская среда
М2
>-¦
Рис. 4.11. Интерферометр Маха-Цендера, содержащий в верхнем плече фазово-чувстви-
тельный элемент и работающий в балансном режиме. Операторы а и b представляют собой
операторы уничтожения фотонов в модах сигнального поля и поля гетеродина
соотношении
а! =
У =
-L(
с =
d = ±={
ibf
+ b'
)Ь],
DА41)
DA42)
DА43)
D.4.44)
Здесь, как и прежде, предполагается фазовый сдвиг у отраженного поля, равный
тг/2.
Сигнал на выходе балансного гомодинного детектора задается оператором
= с+ с —
= (b+b — а+а) cos фр — (а
sin
D.4.45)
Если мода гетеродина находится в когерентном состоянии |/3/) с большой амплитудой,
а сигнальная мода — в вакуумном состоянии |0), то сигнал определяется выражением
(ncd) = nl cos <
D.4.46)
где щ = |й|2-
4.4 Когерентность второго порядка 109
Интересно отметить, что для фр = тг/2
ncd = ^(a+b^b+aI D.4.47)
то есть ncd не зависит от операторов числа фотонов, и система, изображенная на
рис. 4.11, в сущности эквивалентна балансному гомодинному детектору, изображен-
изображенному на рис. 4.10.
Теперь учтем, что в случае сигнальной моды, находящейся в вакуумном состоя-
состоянии, разностный оператор D.4.47) имеет дисперсию
(ДпыJ = |/3,|2 = п,. D-4.48)
Эту величину можно связать с погрешностью фазы, заметив, что из D.4.46) следует
д(пса) . ,
= гцятф
дфр
и в балансном режиме, когда фр = тг/2, имеем
d{ncd)
дфр
Следовательно погрешность фазы задается выражением
D.4.49)
D.4.50)
АЛ — ^ncd _ s/щ _ 1 (Л Л
Ф ~ \д(пса)/дфр\ - ~W - ^/Щ- ( •
Если теперь взять сигнал в сжатом вакуумном состоянии |0, ?), где ^ =
то
(ncd) = (ni + sh2 r) cos фр = rii cos Фр- D.4.52)
В балансном режиме (фр = тг/2) \d(ncd)/дфр\ = п/, и
{AncdJ = ni[ch2r-cos(#- 2^|)sh2r] + sh2 r, D.4.53)
где использованы выражения B.7.11)—B.7.13). Если положить & = 2<^/, то выражение
D.4.53) принимает вид
(AncdJ = nz e^2r + sh2 r, D.4.54)
и в случае п/ ^> 1 можно пренебречь членом sh2 r в D.4.54) и получить следующее
выражение для уменьшенного фазового шума:
4.4.3. Интерференция двух фотонов. Рассмотрим эксперимент, в котором изме-
измеряется зависимость совместной вероятности детектирования двух фотонов в двух
точках от расстояния между точками. Этот эксперимент по двухфотонной интер-
интерференции является примером эксперимента по корреляции интенсивности, в кото-
котором предсказания квантовой теории существенно отличаются от соответствующих
предсказаний классической теории когерентности. Экспериментальные результаты
согласуются с предсказаниями квантовой теории когерентности при таком выборе
параметров, когда классическая и квантовая теории приводят к различным результа-
результатам. Существование неклассических эффектов в двухфотонной интерференции есть
всего лишь один пример из огромного числа тех явлений, в которых явно проявляется
квантовая природа света. Некоторые из этих явлений рассматриваются в этой книге,
в частности, в гл. 21.
В двухфотонном интерферометре две волны света, имеющие случайные фазы
и узкую спектральную ширину, падают одновременно на поверхность светоделителя.
110
Полевая и фотонная интерферометрия
Гл.4
Отраженные и прошедшие волны приходят вместе на детекторы Da и D&, распо-
расположенные в точках га и г^5 соответственно (рис. 4.12). Выходные сигналы, после
усиления, посылаются на коррелятор. Измеренная скорость совпадений является
Рис. 4.12. Схема эксперимента по двухфотонной интерференции. (Из работы Gil and Man-
del, 1989)
мерой совместной вероятности детектирования Р(жа, хъ) ёха ёх^ при детектирова-
детектировании в точках ха и хъ, задаваемых с точностью 5ха и 8хъ- Здесь ха и хь являются
проекциями векторов та и Г5 на векторы к2 — ki и кг — ki, соответственно (см.
рис. 4.12), где ki и к2 — волновые векторы, соответствующие ki и к2 после отражения
на светоделителе.
Как обсуждалось в разд. 4.2, совместная вероятность детектирования определя-
определяется величиной W2- Таким образом
Р{ха, хь) =
D.4.56)
где каш щ — множители, зависящие от характеристик детекторов. Вычислим теперь
совместную вероятность детектирования для падающих коррелированных фотонов
в рамках квантовой и классической теорий когерентности.
Если рассматривать светоделитель О (см. рис. 4.12) как источник, то положи-
положительно-частотные части Е^(ха) и Е^>(хъ) можно записать в виде
л/Т'
а2
D.4.57)
D.4.58)
где R и Т — коэффициенты отражения и пропускания светоделителя, ai и й2 —
операторы уничтожения полей на входе в светоделитель, и S = (hi//2eqVI^2. Если
светоделитель является 50%-ным , то R = Т = 1/2. Выражения D.4.57) и D.4.58)
4.4
Когерентность второго порядка
111
тогда упрощаются и принимают вид
a2
DА59)
DA60)
Начальным состоянием поля (при подаче двух одиночных фотонов) является
двухфотонное фоковское состояние |li, I2). Такое состояние молено получить в про-
процессе вырожденного параметрического усиления в нелинейной среде (гл. 16). Следо-
Следовательно, совместная плотность вероятности детектирования D.4.56) определяется
выражением
Р(ха, хь) = >саяьA1,12\Е^Цха)Е(--\хь)Е(-+\хь)Е^\ха)\11,12> =
\1 - cos[(k2 - kx) ¦ ra - (k2 - ki) ¦ r6]}, D.4.61)
где использованы выражения D.4.59) и D.4.60) для Е^(жа), Е^{хь) и эрмитово
сопряженных им величин. Если угол § между ki и к2 и между к2 и ki очень мал, то
соответствующая интерференционная картина имеет расстояние между полосами,
равное
2тг 2тг
где k = |ki| =
L~ 27Г
~ |ki - k2
, и мы получаем
Р(ха,хъ) = ->
|k2-ki
{l -
cos
)] } .
D.4.62)
D.4.63)
Таким образом, совместная вероятность детектирования является модулированной
в отношении переменной ха — хь по закону косинуса, причем видность
U =
" m
= 1.
D.4.64)
Следовательно, имеется интерференция двух двухфотонных амплитуд, связанная
с тем, что оба фотона отражаются и оба пропускаются светоделителем.
Видность, равная единице, означает, что если фотон регистрируется в точке жо, то
существуют определенные положения ж^? гДе второй фотон невозможно обнаружить,
и наоборот. Эта ситуация противоречит классической оптике (как будет показано
ниже), которая предсказывает отличное от нуля поле в обоих положениях ха и хъ-
Теперь вычислим видность, рассматривая падающие поля классически. Опера-
Операторы а\ и а,2 в выражениях D.4.59) и D.4.60) можно заменить классическими с-
числовыми амплитудами ос\ и «2 j соответственно. Предположим также, что поля
имеют случайные фазы. Это разумное предположение, поскольку однофотонные
состояния имеют произвольную фазу. Следовательно, классические средние по ан-
ансамблю зависящих от фазы величин, таких как ot\ и |oi|2a2? обращаются в нуль.
Совместная вероятность детектирования P(xaj хъ) задается выражением D.4.56),
в котором теперь Е^ и Е^ являются классическими с-числовыми полями, и угло™
вые скобки обозначают классическое среднее по ансамблю. Нетрудно показать, что
а, хь) = \
h?) ~ 2(hh)
(Жа - хь)/2],
D.4.65)
112 Полевая и фотонная интерферометрия Гл. 4
где I\ = <f2|oi|2 и /2 = <f2|a2|2- Видность U интерференционной картины задается
выражением
U = Щ1й . D.4.66)
Поскольку G2) + (if) > 2A112),
U^\, D.4.67)
что задает классический предел. Отсюда видно, что видность не может превышать
50%, в противоположность предсказанию квантовой механики.
Таким образом, наблюдение видности, превышающей 50%, свидетельствует о не-
неклассическом поведении света. В двухфотонных интерференционных экспериментах
наблюдалась видность свыше 75%.
4.4.4. Антигруппировка фотонов, пуассоновский и субпуассоновский свет.
В разд. 4.2 было показано, что соответствие между квантовой и классической
теориями когерентности устанавливается через Р-распределение. Однако Р-
распределение не имеет всех свойств классической функции распределения.
Таким образом, возможно, что некоторые неравенства для корреляционных
функций, которые явно предполагают регулярное распределение вероятности,
могут не удовлетворяться. Нарушение этих неравенств для определенных полей
излучения явилось бы явным доказательством квантовой природы света. В этом
разделе мы рассмотрим некоторые примеры таких полей.
В классической теории когерентности операторы поля заменяются с-числовыми
полями. Для таких полей из неравенства Шварца | (а*Ь)\2 ^ (|а|2)(|6|2) (где а = /(г, i)
и Ъ = /(г, t + г)) следует, что
|(/(r, i)/(r, t + т))|2 ^ </2(r, i))(/2(r, t + r)). D.4.68)
Соответствующее неравенство в квантовой теории когерентности получается заме-
заменой произведения интенсивностей в угловых скобках соответствующими нормально
упорядоченными операторами, то есть
|(: /(г, <)/(г, t + т) :}|2 < (: /2(t, *) :)(: /2(t, t + т) :), D.4.69)
где символ : : обозначает нормальное упорядочение, при котором операторы рожде-
рождения расположены слева от операторов уничтожения. Это неравенство удовлетворяет-
удовлетворяется для полей с регулярным Р^распределением. Из определения g^2\r) (см. D.2.21))
следует, что в случае статистически стационарных полей этому неравенству можно
придать следующий простой вид:
gW{T)^gB\$). D.4.70)
Это неравенство, как мы видели, удовлетворяется для теплового и когерентного
полей. Напомним, что g^2\r), по определению, является мерой корреляций фотонов
в моменты времени tit + r. Если поле удовлетворяет неравенству g^2\r) < g^@)
при т < тс, то фотоны демонстрируют избыточную корреляцию на временах,
меньших времени корреляции тс. Это называется группировкой фотонов^ поскольку
фотоны стремятся распределиться преимущественно по группам, а не случайным
образом. Когда такой свет падает на фотодетектор, фотонные пары с меньшим интер-
интервалом регистрируются чаще, чем фотонные пары с большим интервалом (рис. 4.13а).
Примером поля, демонстрирующего явление группировки фотонов, является поле
теплового источника.
4.4
Когерентность второго порядка
113
В некоторых квантовых оптических системах неравенство D.4.70) может нару-
нарушаться, и мы получаем
ГB)@). D.4.71)
g{2){r) >
Этот результат соответствует явлению антигруппировки фотонов, что является
противоположным эффектом, при котором фотонные пары с меньшим интервалом
(а)
{б)
(в)
Рис. 4.13. Распределение фотоотсчетов во времени в случае: группировки фотонов (а),
пуассоновского распределения фотонов (б") и антигруппировки фотонов (в) в световых
пучках
регистрируются реже, чем фотонные пары с большим интервалом (рис. 4.13в). Анти-
Антигруппировка фотонов в процессе резонансной флуоресценции атома будет рассмот-
рассмотрена в разд. 10.6.
Еще одним неклассическим неравенством является неравенство
g-B)@) < 1, D.4.72)
которое справедливо для полей, Р-распределение которых не является неотрица-
неотрицательно определенным. Для того чтобы явно это показать, перепишем сначала это
неравенство в виде (см. D.2.21))
0,
или в Р-представлении,
0.
D.4.73)
D.4.74)
Поскольку величина (|«|2 — (а+а)J является положительно определенной для всех
значений а, единственный способ удовлетворить неравенству заключается в том,
чтобы сделать величину Р(о, а*) отрицательной, хотя бы при некоторых значениях
а. Неравенство D.4.72) удовлетворяется для полей, функция распределения кото-
которых уже, чем распределение Пуассона. Такие поля называются субпуассоновскими.
Подобным образом, поля, для которых #'2'@) = 1 и g^@) > 1, называются
114 Полевая и фотонная интерферометрия Гл. 4
пуассоновскими и суперпуассоновскими соответственно. Например, тепловое поле,
для которого g^ @) = 2, является суперпуассоновским, поле в когерентном состоя-
состоянии |ао)? Для которого ^2^@) = 1, является пуассоновским, а поле в состоянии
с определенным числом частиц |по), для которого g^@) = 1 — I/no, является
субпуассоновским.
Из предыдущего рассуждения очевидно, что можно создать много других состоя-
состояний, для которых Р-распределение не будет регулярным. Одним из них является
сжатое состояние поля излучения. Для того чтобы это показать, выразим (АХ^J
(г = 1, 2) в виде среднего по Р-распределению:
2 = \ + 0 A*i О2 =
= \ {l + \ d2aP{a, а*)[(а + а*) - ((а) + (а*))]2} . D.4.75)
Условие сжатия (АХ{J < 1/4 (г = 1 или 2) требует, чтобы величина Р(а, а*) была
отрицательной, хотя бы при некоторых значениях а, то есть не была «неотрица-
«неотрицательно определенной». Таким образом, сжатое состояние поля излучения является
неклассическим состоянием.
4.5. Счет и статистика фотонов
В этом разделе мы определим статистику фотоэлектронного счета, которая со-
создается полностью квантово-механическим полем. Задачу, состоящую в нахождении
распределения фотоотсчетов исходя из статистики фотонов, можно решить полно-
полностью квантово-механически. Здесь приводится простой вывод соотношения между
этими распределениями, основанный на простом вероятностном рассуждении.
Пусть вероятность испускания фотоэлектрона детектором, взаимодействующим
в течение некоторого времени с полем, имеющим только один фотон |1), равна rj.
Квантовая эффективность 77 зависит от характеристик атомов детектора и времени
взаимодействия. Тогда, если поле излучения находится в состоянии |п), то вероят-
вероятность Ргп обнаружения т фотоэлектронов пропорциональна величине г]т, которую
нужно умножить на вероятность того, что (п — т) квантов не поглотились, то есть
на величину A — rj)n^m. Таким образом,
рш] ^ ^Ч1 - V)n^m< D.5.1)
Однако нам не известно, какие т фотонов поглотились из исходного числа фотонов
п, поэтому необходимо добавить комбинаторный множитель
\{ ]) D.5.2)
mj
Это есть распределение Бернулли для т удачных исходов (отсчетов) и n - m
неудачных, когда каждый из исходов имеет вероятность rj. Поскольку распределение
значений п задается функцией распределения фотонов рпп, необходимо умножить
D.5.2) на рпп и просуммировать по тг,
Pm = Y,P(rn]Pnn, D.5.3)
П.4.А
Интерференция с двумя источниками
115
что приводит к следующему выражению для распределения фотоэлектронного счета:
= Е
D.5.4)
Это выражение справедливо при всех значениях т\ (О ^J rj ^ 1). Для того чтобы
определить статистику фотонов по счету фотоэлектронов, необходимо, очевидно,
чтобы 7] = 1. В этом случае из D.5.4) следует, что
Pm=Pmm- D.5.5)
Во всех остальных случаях, когда г) < 1, наблюдаемая статистика фотоэлектронов
может существенно отличаться от статистики фотонов.
С другой стороны, величину Рш можно выразить через Р-распределение Р(а, о*)
поля, записывая
-е~|а|2, D.5.6)
так что выражение D.5.4) принимает вид
Pm = \d2a V
Р(а,а')
Поменяв п на I + т и просуммировав по I, получаем
D.5.7)
Отметим, что это выражение можно обратить, то есть можно Р-распределение поля
выразить через Рт, при условии, что р диагональна в в-представлении.
Приложение 4.А
Классическое и квантовое описания интерференции с двумя
источниками
При корректном классическом описании эксперимента Юнга, излучение от двух
щелей представляется в виде сферических волн. Выражение для интенсивности на
•и
z -d
D
Рис. 4.14. Схема, иллюстрирующая плоско-волновое рассмотрение эксперимента Юнга
экране в обозначениях рис. 4.14 имеет вид
¦ +
ёе%
D.А.1)
116 Полевая и фотонная интерферометрия Гл. 4
а интерференционный перекрестный член задается выражением
/12 = ?!?е«(п-га)+кх> D.А.2)
Г1Г2
Поскольку Fi52 = л/D2 + (х =р dJ = D + d2/BD)=pxd/'D, где знак « —» соответствует
источнику 1, а знак «+» соответствует источнику 2, имеем
I12c±flfe-2ikxd/D + K.c. D.A.3)
Однако некоторые авторы приводят плоско-волновое описание эксперимента Юн-
Юнга, считая при этом, что излучение в точке детектора г состоит из двух плоских волн.
В этом случае
/(г) = |A eikl'r + <% eik2"r|2 , D.A.4)
и интерференционный перекрестный член имеет вид
/12(r) = cfo*cfo ei(kl"k2)'r + к.с. D.А.5)
Следовательно, если записать, в обозначениях рис. 4.14, что kj = k('zcosf&i+xsm'&i),
то получим к^ • г = k(Dcos#« + xsin&i) = k(D =p xd/D), где знак « —» и «+»
соответствуют источникам 1 и 2. В результате
/12(г) = 4*^о e-2ikxdlD + к.с, D.А.6)
в соответствии со сферически-волновым описанием.
Квантово-полевое описание эксперимента Юнга хорошо поясняется наглядным
примером, в котором две щели заменяются двумя атомами (см. разд. 4.3.2 и 21.1).
В этом случае вектор состояния фотона, испущенного г-м атомом, задается выраже-
выражением
D.А.7)
к Х1/Ьг ш' ~*~ll ' *
где g"k — константа, зависящая от величины атомно-полевого взаимодействия, из
— частота перехода атома между состояниями |а) и |6), Г — скорость релаксации
на переходе \а) -^ \Ъ) и d^ — радиус-вектор г-го атома. Корреляционная функция
рассеянного поля записывается тогда в виде
2
, D.А.8)
где $ — эффективное электрическое поле. Таким образом, получается тот же резуль-
результат, что и при классическом сферически-волновом описании.
В заключение отметим, что однофотонные плоско-волновые состояния также
можно использовать для иллюстрации интерференционных полос, создаваемых дву-
двумя источниками. Очевидно, что если поле излучения источника 1 описывается од-
нофотонным состоянием |lki)? а поле излучения источника 2 — состоянием |lk2)? т0
GA)(r,r;0) =
\
\ |@|i?(r, t)|lkl> + @|??(г, t)|lk2)|2 = « |eikl'r + eik2r|2 . D.А.9)
Здесь опять наблюдается интерференция как в классическом случае, что оправды-
оправдывает использование обоих состояний |7i) и |lki) для описания эксперимента Юнга.
Задачи к гл. 4 117
Приложение 4.Б
Вычисление корреляционной функции второго порядка
Из выражений D.4.14) и D.4.15) имеем (обращаем внимание на то, что некоторые
члены подчеркнуты)
GB)(ri,r2;M) =
B) + 4'B)][акB) + ак,B)][акA) + а
[а+A)а+B)акB)ак,A) + а+A)а+B)ак,B)акA) + а+A)а
+ а+A)а+B)окB)ак.A) + a+(l)a+B)ак>B)акA)+
+ [а+A)а+B)акB)акA) + о+A)о+ B)ак,B)ак,A)] +
+ а+A)а+B)окB)ак.A) + о+A)а+B)ак.B)акA)+
+ [а+A)а+B)окB)акA) + а+A)а
+ а+A)а+B)ак>B)ак>A)+
+ [вк'A)«к'B)«кB)ак'A) + а+ A)о+ B)ак/B)акA)+
+ о+A)а+B)окB)окA)]>, D.Б.1)
где
a+(i) = a+e-ikr% а+ (г) = а+ е"*'"'. D.Б.2)
Все члены в последнем выражении, заключенные в квадратные скобки, обращаются
в нуль, если рассматривается излучение звезд, лазеров со случайной фазой, тепло-
тепловых источников и атомов. Таким образом, удерживая лишь подчеркнутые члены,
получаем
ь r2; t, t) = g?(a
+ o+o+akak/[l + e-*(k-k')-(n-P2)] + a+a+ak/ak[i + ei(k-k')-(pi-ra)]^ DBJ)
Задачи
4.1. Покажите, что состояние поля излучения, являющееся суперпозицией вакуум-
вакуумного состояния и однофотонного состояния, то есть 1^) = fto|0) + ai|l), где ciq
и ai — комплексные коэффициенты, является неклассическим состоянием.
4.2. Пусть тп = (а+пап) есть п-й момент интенсивности. Рассмотрим матрицу
л¦ =
1 7711
mi ??i2
Покажите, что для классического Р-распределения det Ж должен быть поло™
жительно определенным. (Указание: см. работу G.S. Agarwal and К. Тага, Phys.
Rev. A 46, 485 A992).)
118 Полевая и фотонная интерферометрия Гл. 4
4.3. Рассмотрим состояние, описываемое оператором плотности
где <Ж — нормировочный множитель и к = hu / k^T.
1. Покажите, что это состояние переходит, в фоковское состояние, если к —>•
—>• оо, и в состояние теплового поля, если к -Л 0.
2. Найдите g"'2'@) и покажите, что статистика фотонов является субпуассо-
новской, если п < yjm/(m + 1), где п = [ехр(х) — I].
4.4. Найдите функцию распределения фотоэлектронов Рш для поля, находящегося
в когерентном состоянии |а), в состоянии с определенным числом фотонов
и для одномодового поля теплового источника при температуре Т.
Список литературы
Обзорные статьи по теории оптической когерентности
Glauber, R. J. In Quantum Optics and Electronics, Les Houches, ed. C. DeWItt, A. Blandln, and
C. Cohen-TannoudjI (Gordon and Breach, New York 1965). [Глаубер Р. В кн. Квантовая
оптика и радиофизика (Мир, Москва, 1966), с. 91-279.]
Mandel, L. and Wolf, E. Rev. Mod. Phys. 37, 231 A965).
Mandel, L. and Wolf, E. editors, Selected Papers on Coherence and Fluctuations of Light, Vols.
1 and 2 (Dover, New York 1970). Этот двухтомник является превосходным собранием
статей по теории оптической когерентности, вышедших до 1966 года.
Glauber, R. J. In Quantum Optics, ed. S. Kay and A. Maltland (Academic, New York 1970).
Mandel, L. In Progress in Optics, Vol. 13, ed. E. Wolf (North^Holland, Amsterdam 1976).
Loudon, R. Rep. Prog. Phys. 43, 913 A980).
Paul, H. Rev. Mod. Phys. 54, 1061 A982).
Интерферометр Саньяка и кольцевой лазерный гироскоп
Sagnac, G. С. R. Acad. Sci. 157, 708 A913).
Aronowltz, F. In Laser Applications, ed. M. Ross (Academic, New York 1971), p. 113.
Chow, W. W., GearBanacloche, J., Pedrotti, L. M., Sanders, V. E., Schlelch, W. and Scully, M.
O. Rev. Mod. Phys. 57, 61 A985).
Применение кольцевых лазерных гироскопов в исследованиях
по общей теории относительности
Scully, M. О., Zubalry, M. S. and Haugan, M. P. Phys. Rev. A 24, 2009 A981).
Schlelch, W. and Scully, M. O. «General Relativity and Modern Optics» In Modern Trends
in Atomic and Molecular Physics, Proceedings of Les Houches Summer School, Session
XXXVIII, ed. R. Stora and G. Grynberg (North-Holland, Amsterdam 1984).
Эксперимент Хэнбери-Врауна—Твисса
Hanbury-Brown, H. and Twlss, R. Q. Phil. Mag. 45, 663 A954); Nature 178, 1046 A956); Proc.
Roy. Soc. A242, 300 A957).
Forrester, A., Gudmundsen, R. and Johnson, P. Phys. Rev. 99, 1691 A955).
Purcell, E. M. Nature 178, 1449 A956).
Fano, U. Am. J. Phys. 29, 539 A961).
Список литературы к гл. 4 119
Baym, G. Lectures on Quantum Mechanics, (Benjamin Pub., New York 1969), p. 431.
Hanbury-Brown, R. The Intensity Interferometer (Taylor and Frances, London 1974).
Эксперимент по двухфотонной корреляции
Mandel, L. Phys. Rev. A 28, 929 A983).
Ghosh, R. and Mandel, L. Phys. Rev. Lett 59, 1903 A987).
Ou, Z. Y. and Mandel, L. Phys. Rev. Lett 62, 2941 A989).
*Бурлаков А.В., Клышко Д.Н., Кулик СП., Пенин А.Н., Чехова М.В. Письма ЖЭТФ 65,
20 A997).
*Бурлаков А.В., Клышко Д.Н., Кулик СП., Чехова М.В. Письма ЖЭТФ 69, 788 A999).
*Burlakov A.V., Chekhova M.V., Karabutova O.A., Kulik S.P. Phys. Rev. A 63, 053801 B001).
Счет и статистика фотонов
Mandel, L. Proc. Phys. Soc. 72, 1037 A958).
Mandel, L. In Progress in Optics, Vol. 2, ed. E. Wolf (North-Holland, Amsterdam 1963), p. 181.
Kelley, P. L. and Kleiner, W. H. Phys. Rev. 136, A316 A964).
Scully, M. O. and Lamb, W. E., Jr., Phys. Rev. 179, 368 A969).
*Горбачев В.П., Жилиба А.И., Трубилко А.И. Изв. РАН, сер.физ. 66, 345 B002).
Спектр мощности
Eberly, J. H. and Wodkiewicz, К. J. Opt. Soc. Am. 67, 1252 A977). В этой статье обсуждается
спектр мощности нестационарных полей.
Eberly, J. H., Kunasz, С. V. and Wodkiewicz, К. J. Phys. В 13, 217 A980).
Cresser, J. D. Phys. Rep. 94, 47 A983). В этой работе сделан исчерпывающий обзор по данной
теме.
Балансное гомодинное детектирование
Yuen, H. P. and Chan, V. W. S. Opt Lett 8, 177 A983).
Walker, N. G. and Carrol, J. E. Opt Quantum Electron. 18, 355 A986).
Глава 5
ВЗАИМОДЕЙСТВИЕ АТОМА
С ПОЛЕМ —
ПОЛУКЛАССИЧЕСКАЯ
ТЕОРИЯ
Поведение двухуровневого атома в одномодовом электромагнитном поле является
одной из простейших, но нетривиальных, задач в проблеме взаимодействия атома
с полем. Двухуровневое описание атома справедливо, когда из всех уровней энергии
только два находятся в резонансе с возбуждающим полем или незначительно от-
отстроены от резонанса. Используя некоторые реалистические предположения, можно
свести проблему к точно решаемой, что позволяет прояснить основные особенности
взаимодействия атома с полем.
В этой главе представлена полуклассическая теория взаимодействия одиночного
двухуровневого атома с одномодовым полем, в которой атом рассматривается как
квантовая двухуровневая система, а поле описывается классически. Полная кванто™
вомеханическая теория будет дана в гл. 6.
Существует формальная аналогия между двухуровневым атомом и спином 1/2,
имеющим два возможных состояния. В дипольном приближении, когда длина волны
излучения больше размера атома, взаимодействие атома с полем эквивалентно вза-
взаимодействию частицы, имеющей спин 1/2, с переменным магнитным полем. Точно
также, как под действием переменного магнитного поля спин 1/2 совершает, так
называемые, осцилляции Раби между состояниями спин-вверх и спин-вниз, двух-
двухуровневый атом испытывает оптические осцилляции Раби под действием электро-
электромагнитного поля. Эти осцилляции затухают, если атомные уровни имеют конечное
время жизни. Понимание этой простой модели взаимодействия атома с полем позво-
позволяет рассмотреть более сложные проблемы, включающие взаимодействие ансамбля
атомов с полем. Среди таких проблем в качестве наиболее значимого примера может
быть назван лазер. Его мы обсудим позже в этой главе 1).
5.1. Гамильтониан взаимодействия атома с полем
Электрон, имеющий заряд е и массу га, взаимодействующий с внешним электро-
электромагнитным полем, описывается гамильтонианом минимального взаимодействия:
ж = i[p "eA(r'i)]2 + ef/(r'l) + v(r)' EЛЛ)
1) Полуклассическая теория лазера, развитая школами Лэмба и Хакена (см. Lamb, 1963;
1964 и Haken, 1964), является пионерским вкладом в эту проблему. Теория Лэмба берет
начало от связанной системы уравнений Максвелла и Шредингера, в то время как Хакен
с соавторами использует полу классический (факторизованный) предел квантовых полей.
5.1 Гамильтониан взаимодействия атома с полем 121
где р — канонический оператор импульса, А(г, ?) и f/(r, ?) — векторный и скалярный
потенциалы внешнего поля, соответственно, и V(r) — электростатический потенциал,
который обычно является потенциалом атомной связи. В этом разделе мы сначала
выведем этот гамильтониан, используя калибровочную инвариантность, а затем при-
приведем его к виду, пригодному для описания взаимодействия двухуровневого атома
с полем излучения.
5.1.1. Лсжальнам калибровочнам (фазовам) инвариантность и гамильтониан ми-
минимального взаимодействия. Движение свободного электрона Движение свободного
электрона описывается уравнением Шредингера описывается уравнением Шредин-
гера:
-?*¦-«?, E.1.2,
при этом
P(r,t) = Hr,i)|2 E-1.3)
есть плотность вероятности нахождения электрона в положении г в момент времени
t. Из уравнения E.1.2) следует, что если ^(r, t) является решением, то ф(т^ t) =
= ф(т, t) exp(ix) — тоже решение, где % — произвольная постоянная фаза. Произ-
Произвольный выбор х не влияет на плотность вероятности P(r, t). Таким образом, выбор
фазы волновой функции ^(r, t) абсолютно произволен и две функции, отличающиеся
только фазовым множителем, представляют одно и то же физическое состояние.
Между тем, ситуация выглядит иначе, если фаза может локально изменяться,
т.е., она является функцией от пространственных координат и времени, т.е.,
i/>(r,t) ^^(r,t)eix(r't}. E.1.4)
Вероятность P(r, t) не изменяется под действием такого преобразования, но урав-
уравнение Шредингера E.1.2) уже не удовлетворяется. Чтобы сохранить локальную
калибровочную (фазовую) инвариантность, мы должны модифицировать уравнение
Шредингера, добавив новые члены к E.1.2):
где A(r, t) и U(r,t) — функции, которые необходимо подставить в E.1.2), для того
чтобы осуществить преобразование E.1.4). Они задаются следующим образом:
A(r,f)^A(r,i) + ^VX(r,f), E.1.6)
U(v,t)^U(T,t)-^(v,t). E.1.7)
Функции А (г, t) и U(r,t) отождествляются с векторным и скалярным потенциалами
электромагнитного поля, соответственно. Они являются калибровочно зависимыми
потенциалами. Калибровочно независимыми величинами являются электрическое
и магнитное поля:
В = V х А. E.1.9)
Уравнение E.1.5), являющееся логическим расширением E.1.2), вследствие требова-
требования локальной (фазовой) инвариантности, имеет вид
= гПдф/дг, E.1.10)
122 Взаимодействие атома с полем — полуклассическая теория Гл. 5
где Ж — гамильтониан минимального взаимодействия (напомним, что р = —i
определенный выражением E.1.1). Уравнение Шредингера E.1.5) описывает вза-
взаимодействие электрона с заданным электромагнитным полем. Электрон задается
волновой функцией ф(г,г), тогда как поле описывается векторным и скалярным
потенциалами А и 17, соответственно.
Интересно отметить, что гамильтониан E.1.1) был «выведен» из соображений
калибровочной инвариантности, и он выражен с помощью калибровочно завися-
зависящих величин A(r, t) и U(r,t). Поэтому векторный и скалярный потенциалы име-
имеют большее физическое значение, чем им обычно приписывается. Они введены не
просто для математического упрощения в задачах, связанных с «наблюдаемыми»
электрическим и магнитным полями, а появляются естественным образом в любом
калибровочно (фазово-) инвариантном рассмотрении.
Следует также отметить, что уравнение Шредингера плюс концепция локальной
калибровочной инвариантности привели нас к необходимости введения электромаг-
электромагнитного поля. Таким образом, можно доказать, и мы доказываем, что «фотон»
(в нашем случае — его классический аналог) «появился» из уравнения Шредингера
и соображений калибровочной инвариантности.
Здесь мы опробировали одну из наиболее фундаментальных концепций совре-
современной физики, а именно концепцию калибровочной теории поля. Калибровочная
теория привела Стивена Вайнберга и Абдуса Салама к созданию единой теории
слабых и электромагнитных взаимодействий.
5.1.2. Дипольное приближение и (г • Е)-гамильтониан. Теперь рассмотрим элек-
электрон, связанный потенциалом V(r) с центром сил (ядром), расположенным в точке г.
Гамильтониан минимального взаимодействия E.1.1), описывающий взаимодействие
атома и поля излучения, можно упростить, используя дипольное приближение.
Атом целиком помещается в плоскую электромагнитную волну, которая описывается
векторным потенциалом А(го + г, ?). Этот векторный потенциал можно записать
в дипольном приближении, когда к • г <С 1, следующим образом:
А(г0 + г, t) = A(t) exp[ik • (г0 + г)] =
= A(t) exp(ik • го)A + гк ¦ г + ...) ~ A(t) exp(ik • г0). E.1.11)
Уравнение Шредингера для этой задачи (в дипольном приближении) задано выра-
выражением E.1.5), в котором А(г, t) = A(i*o,t), т.е.,
"<? [V - <f А<*ъ*)f + П')} *(*>*) = ^
где добавлен потенциал связи V(r). Отметим, что в уравнении E.1.12), и далее во
всей книге, используется радиационная калибровка, в которой
U(r,t) = 0, E.1.13)
V-A = 0. E.1.14)
В гамильтониан добавлен член V(r), обусловленный электростатическим потенциа-
потенциалом, связывающим электрон с ядром.
Продолжая упрощать уравнение E.1.12), определим новую волновую функцию
</>(r, t) так, что
V(r, t) = exp [jA(ro,t) ¦ г] «Яг, t), E.1.15)
5.1 Гамильтониан взаимодействия атома с полем 123
Подставляя E.1.15) в E.1.12), находим
ih — А • r^»(r, t) + ф(г, t) exp f —A • r J =
= exp [Ц-А -r) \^—-\- V(r) ф(т, t). E.1.16)
Это уравнение, после сокращения экспоненциальных множителей и выполнения
некоторых преобразований, принимает простой вид
, t) = [Жо - ег • Е(г0, *)]0(г, t), E.1.17)
где использовано соотношение Е = -Аи
^o = |^ + V(r), E.1.18)
— невозмущенный гамильтониан электрона. Отметим, что полный гамильтониан
Ж = ЖО + ЖЪ E.1.19)
где
Жг = -er.E(ro,t), E.1.20)
выражен через калибровочно независимое поле Е. В дальнейшем этот гамильтониан
будет использоваться для изучения взаимодействия атома с полем. Отметим, что этот
гамильтониан был получен из радиационно калибровочного гамильтониана E.1.12)
с помощью применения калибровочного преобразования %(r, t) = —еА(го,?) • г/К.
5.1.3. (р • А)-гамильтониан. Во многих учебниках можно найти атомно-полевой
гамильтониан, выраженный через канонический импульс р и векторный потенциал
А, вместо простого калибровочно инвариантного выражения E.1.17). Это приводит
к большой путанице и ошибкам. Поэтому мы рассмотрим эту проблему более по-
подробно. Опять выберем радиационную калибровку, в которой U(r,t) = 0 и V • А = 0.
В квантовой механике условие V • А = 0 подразумевает, что [р, А] = 0. Поэтому
полный гамильтониан E.1.1) можно записать как
Jq; = Дд ~\- ^25 (O.l.Zl)
где Ж® задается выражением E.1.18), и в дипольном приближении E.1.11)
Ж2 = -—р • А(г0, t) + — A2(r0j t). E.1.22)
тгь Лтгь
Тогда уравнение Шредингера приобретает вид
2 1 д
fo р • А(г0, t) + -^Л2(г0, t) ф(т, t) = ih—ф(т, t). E.1.23)
В уравнении E.1.23) член с А2 обычно мал, и им можно пренебречь. Тогда волновая
функция ^(r, i) удовлетворяет уравнению движения
%Пщф{т, t) = [Жо - ^р • А(г0) t)] ^(r, t), E.1.24)
которое соответствует гамильтониану
Ж1 = Жо - ^р • А(г0, t), E.1.25)
= -—p-A(ro,t). E.1.26)
Tfl
124
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
Два разных гамильтониана Ж\ и Ж^^ заданные выражениями E.1.20) и E.1.26),
соответственно, оказывается приводят к разным физическим результатам, так как
их матричные элементы, вычисленные по собственным состояниям невозмущенного
гамильтониана Жо^ определенного выражением E.1.18), не одинаковы. Для того,
чтобы это явно продемонстрировать, рассмотрим взаимодействие поля линейно-
поляризованной монохроматической плоской волны с атомом, помещенным в точку
г о = 0. Тогда электрическое поле приобретает вид
E@,t) = ?cosvt, E.1.27)
и соответствующий векторный потенциал в радиационной калибровке имеет вид
A@,t) = ? sin vt.
E.1.28)
Теперь рассмотрим не зависящие от времени амплитуды соответствующих величин,
связанных с Ж\ и Ж^^
E.1.29а)
E.1.296)
Можно связать W\ и
E.1.30)
Тогда для матричных элементов операторов W\ и VK2, вычисленных между началь-
начальным собственным состоянием \г) гамильтониана Жо (Жо\г) = huj{\i) и конечным
собственным состоянием |/) (^о|/) = hu)f\f)\ находим отношение
заметив
W2 =
, что
= -ег-^,
mi/
-m(z/R)[r,
(f\W2
(e/m»)(f\p\i)-?
E.1.31)
где ш = ujf — Шг — частота перехода. Следовательно матричные элементы двух
гамильтонианов взаимодействия Ж\ и Ж2 отличаются, и относятся друг к другу как
частота перехода к частоте поля. Как еще было отмечено Лэмбом, это приводит к от-
отличию таких измеряемых величин, как скорости переходов. Решение этой проблемы
представлено в приложении 5.А.
5.2. Взаимодействие двухуровневого атома с одномодовым полем
5.2.1. Метод амплитуд веромтности. Рассмотрим взаимодействие одномодового
поля излучения частотой v с двухуровневым атомом (рис. 5.1). Пусть \а) и \Ь) пред-
представляют собой верхнее и нижнее состояния атома,
о) т. е. они являются собственными состояниями невоз-
невозмущенной части гамильтониана Жо с собственными
значениями Кша и Ишь-) соответственно. Волновую
функцию двухуровневого атома можно записать
в виде
где Са и Сь — амплитуды вероятности нахождения
\Ъ) атома в состояниях \а) и |6), соответственно. Эво-
Эволюция атома описывается уравнением Шредингера
Рис. 5.1. Взаимодействие двух-
двухуровневого атома с одномодо- |^(^)) = ——J4?\ib(t)), E.2.2)
вым полем "-
5.2 Взаимодействие двухуровневого атома с одномодовым полем 125
с гамильтонианом
где Ж® и Ж\ — невозмущенная часть и взаимодействие, соответственно. Используя
условие полноты \а)(а\ + \b)(b\ = 1, можно записать Ж® как
Жо = (\а)(а\ + \Ь)(Ь\)Ж0(\а)(а\ + |6)F|) = Нша\а)(а\ + Пшь\Ь)(Ь\, E.2.4)
где учтено, что Жо\а) = hwa\a) и Жо\Ь) = Ншъ\Ь). Аналогичным образом, часть
гамильтониана Ж\^ которая описывает взаимодействие атома с полем излучения,
можно записать в виде
Жг = -exE{t) = -е(\а)(а\ + \b)(b\)x(\a)(a\ + \b)(b\)E(z, t) =
= ^{pab\a)(b\ + pba\b)(a\)E(t), E.2.5)
где раь = p^a = e(a\x\b) — матричный элемент электрического дипольного момента
и E(t) — поле в точке нахождения атома. Здесь предполагается, что электрическое
поле линейно поляризовано вдоль оси х. В дипольном приближении это поле можно
записать в виде
E(t) = #cosz/t, E.2.6)
где S — амплитуда поля и v = ск — его частота. Уравнения движения для амплитуд
Са и Сь можно записать следующим образом:
Са = -г^аСа + Шд е~*ф cos(ut)Cbj E-2.7)
дь = -г^ьСь + i^R е~1ф cos(ut)Ca, E.2.8)
где частота Раби Од определена как
и ф — фаза дипольного матричного элемента: ра^ = |раь|ехр(^)- Для того, чтобы
найти Са и Сь, сначала запишем уравнения движения для медленно меняющихся
амплитуд:
са = Сае{ш"\ E.2.10)
c6 = Cbeiw**. E.2.11)
Тогда из уравнений E.2.7) и E.2.8) следует, что
са = ^е-^сье^ш-^, E.2.12)
сь = ^е1фсае-1^-^\ E.2.13)
где ш = ша — шь — частота атомного перехода. При выводе уравнений E.2.12)
и E.2.13) в приближении вращающейся волны мы пренебрегли в правой части члена-
членами с противоположным вращением поляризацией, пропорциональными exp[zbi(o; +
+ v)t]. В общем случае это хорошее приближение. Более того, в некоторых случаях
(как будет показано ниже в разд. 5.2.3) члены с «противоположным вращением»
никогда не проявляются, и уравнения E.2.12)—E.2.13) являются точными.
126 Взаимодействие атома с полем — полуклассическая теория Гл. 5
Решения для са и съ можно записать следующим образом:
ca(t) = (п1 eim'2 + a2 e~im'2) eiAt'2, E.2.14)
cb(t) = (Ьг eiut'2 + b2 e-iut'2) e~iA^2, E.2.15)
где A = uj — i/,
О = yJil2R + (a; - vJ , E.2.16)
и ai, «2? b\ и ^2 — константы интегрирования, которые находятся из начальных
условий:
аг = -^[(П - Д)с„@) + Од е-*фсь(О)], E.2.17)
а2 = ^[(О + Д)со@) - ОЯ е-^сь(О)], E.2.18)
6i = ^[@ + Д)сь(О) + Од е'*со@)], E.2.19)
Ь2 = ^[@ - Д)сь(О) - Од е'*с„(О)]. E.2.20)
Затем находим
с^) = {с-(°)[СО8(т)-^81п(т)] +
'2, E.2.21)
E.2.22)
Нетрудно убедиться, что
kaW|2 + \чШ2 = 1. E.2.23)
Это есть простой закон сохранения вероятности, поскольку атом находится в состоя™
нии \а) или \Ъ).
Если предположить, что атом первоначально находился в состоянии |а), то
со@) = 1, сь(О) = 0. В этом случае вероятности нахождения атома в состояниях
\а) и \Ь) в момент времени t задаются величинами |ca(t)|2 и |c5(t)|2. Инверсия
населенностей определяется выражением
= |ca(t)|2 - \cb(t)\2 = (^-^) sin2 3) + cos2 f^) . E.2.24)
Под действием поля индуцируется дипольный момент между двумя атомными
уровнями. Этот индуцированный момент выражается через наблюдаемую величину
оператора дипольного момента
P(t) = е(фA)\гЩ1)) = С*аСьРаЬ + к.с. = c*acbPab eiut + к.с. E.2.25)
5.2
Взаимодействие двухуровневого атома с одномодовым полем
127
Подставляя выражения E.2.21) и E.2.22) в E.2.25), получаем для атома, находивше™
гося в начальный момент времени в возбужденном состоянии,
P(t) =
^pa6 [cos (Ц.)
sin
» е™} . E.2.26)
Таким образом, дипольный момент осциллирует на частоте падающей волны.
В частном случае, когда атом находится в резонансе с падающей волной (А = 0),
мы получаем О = Од и
W(t) = cos(?lRt). E.2.27)
Инверсия населенностей осциллирует между значениями — 1 и 1 на частоте Од
(рис. 5.2).
В 1937 году Раби исследовал прецессию магнитного дипольного момента со
спином 1/2 в магнитном поле и получил выражение для вероятности того, что
атом со спином 1/2, попадающий в прибор Штерна-Герлаха, перевернет свой спин
W(t)
Рис. 5.2. Осцилляции инверсии населенности W{i) в зависимости от времени
из состояния @) или (-J в состояние (-J или @), соответственно, под действием
радиочастотного магнитного поля. В нашей задаче, в полной аналогии с системой со
спином 1/2, атом совершает Раби «перевороты» между верхним и нижним уровнями
под действием электромагнитного поля.
5.2.2. Представление взаимодействия. Рассмотрим уравнение Шредингера
Это уравнение можно формально проинтегрировать и получить
= иA)\ф@)),
E.2.28)
E.2.29)
128
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
где унитарный оператор эволюции во времени определяется выражением
U(t) = ~Ж\]{€), E.2.30)
и 17@) = 1.
В представлении взаимодействия существует удобный подход к решению задачи
взаимодействия атома с полем, в котором предполагается, что зависимость от време-
времени вектора состояния возникает только благодаря энергии взаимодействия. При этом
вектор состояния \%jji) в представлении взаимодействия определяется выражением
где
Тогда
и следовательно, из уравнений E.2.28), E.2.31) и E.2.32), получаем
E.2.31)
E.2.32)
E.2.33)
E.2.34)
1/1/ I Ь
Здесь
y(t) = U?(t)Jff{Uo{t) E.2.35)
— гамильтониан в представлении взаимодействия. Любой оператор О в представле-
представлении Шредингера преобразуется, соответственно, как
Oi{t) = Uo~(t)OUo(t). E.2.36)
В этом можно убедиться из выражения для наблюдаемой величины:
(О) = (i)(t)\O\tj)(t)) = {il>i(t)\U?OU0(t)\il>i(t)) = (^/(t)|O/|^/(t)). E.2.37)
Формальное решение уравнения E.2.34) имеет вид
E.2.38)
где
f//(t) =
E.2.39)
~i \y{r)dT
о
— оператор временной эволюции в представлении взаимодействия, и 3~ — оператор
временного упорядочения, который является формой сокращенной записи для вы-
выражения
j)
.... E.2.40)
о о
5.2 Взаимодействие двухуровневого атома с одномодовым полем 129
Для того, чтобы продемонстрировать преимущество этого формализма, рассмот-
рассмотрим взаимодействие двухуровневого атома с монохроматическим полем частоты
и. Гамильтониан в этом случае дается выражениями E.2.3), E.2.4) и E.2.5). Из
равенства
Жоп = {hoja)n\a)(a\ + {hojb)n\b)(b\ E.2.41)
следует, что
U0(t) = exp (^^) = ехр(-га;а*)|а)(а| + ехр(-го;ь*)|Ь>(Ь|. E.2.42)
Поэтому для атома, находящегося в точке z = 0, гамильтониан в представлении
взаимодействия задается выражением
= -Юци?№(е-*ф\а)(Ь\ + ei4>\b){a\)U0{t)
ei(w+i/)t + е*ф\Ь)(а\ e-i(w+I/)t], E.2.43)
где А = lj — I/. Члены, пропорциональные exp[±i(cj + v)t], изменяются очень быстро
и их средние на временном масштабе, превышающем 1/V, равны нулю. Поэтому в
приближении вращающейся волны этими членами можно пренебречь. Упрощенный
гамильтониан в представлении взаимодействия имеет вид
^(Ь\ + е'*\Ь){а\), E.2.44)
в котором мы предположили, что выполняется резонансное условие А = 0. Оператор
временной эволюции в представлении взаимодействия Uj{t) можно получить прямо
из E.2.39), используя
) () Щ
2п+1 {Ъ.2ЛЪ)
(^) П (е-*\а)(Ь\ + е'*\Ь){а\).
Окончательное выражение для 17/(t) имеет вид
Uj(t) = cos (^) (|о)(а| + |6)F|) + isin (^) (е-'*|о)F| + е^|6)(а|). E.2.46)
Если атом первоначально находился в возбужденном состоянии(|V*@)) = |^)), то
\№) = Ui(t)\a) = cos (^f) \a) + isin (^*) e^\b), E.2.47)
и мы получаем амплитуды вероятности
ca(t) = (а\ф) = cos (^) , E.2.48а)
cb(t) = (Ь\ф) = г sin (^) е'*, E.2.486)
что согласуется с выражениями E.2.21) и E.2.22).
5 М.О. Скалли, М.С. Зубайри
130 Взаимодействие атома с полем — полуклассическая теория Гл. 5
5.2.3. За пределами приближения вращающейся волны. В квантовой оптике
часто встречается, так называемое, приближение вращающейся волны, которое уже
обсуждалось в связи с уравнением E.2.13). Конечно, это хорошее приближение,
в котором удерживаются только те члены в гамильтониане, которые сохраняют
энергию.
Более того, как будет показано ниже, существуют ситуации, когда это приближе-
приближение является «точным», поскольку во всех практических задачах «члены с противо-
противоположным вращением» никогда не появляются. Рассмотрим атом водорода, который
находится в сильном магнитном поле и взаимодействует с монохроматическим полем
т = +1
Свет с левой круговой
поляризацией т = 0
Рис. 5.3. Взаимодействие падающей электромагнитной волны с водородом (ридберговским
атомом) в случае, когда разность энергий em=i — Еъ намного больше, чем em=_i — еь
(рис. 5.3). Если уровни хорошо разрешены по энергии, то можно сконцентрироваться
на рассмотрении только двух уровней (см. задачу 5.7), для которых
фа(г) = —(х - гу) ехр(-г/2а0), E.2.49а)
фь(г) = —== ехр(^г/а0), E.2.496)
где а® — РаДиУс Бора.
Используя дипольное приближение (см. разд. 5.1.2) и помещая атом в начало
координат так, что R = 0, получаем гамильтониан в представлении взаимодействия
У = -er(*) -E(t), E.2.50а)
где
r(t) = е{Ж°гг е^Жо\ E.2.506)
поэтому
yab(t) = -erab(t) ¦ Е(*) = -erab ¦ Е(*) eiwt, E.2.51a)
%a(t) = -evba(t) ¦ E(t) = -evba ¦ E(t) e~iut, E.2.516)
где ш — частота атома.
Теперь, в случае линейной поляризации, когда
E(t) = xgcosvt, E.2.52)
5.2 Взаимодействие двухуровневого атома с одномодовым полем 131
выражения E.2.51а, 5.2.516) и E.2.52) означают, что
yab(t) = - ex abi cos uteiujt =
= -exa6|[e^+^ + e-<("-">*] - -exab^ е~^-^\ E.2.53)
а также
%a(t) = -exbaS* cos иte^iujt =
^*» «) ^ e^^K E.2.54)
Таким образом, приближение вращающейся волны заключается в пренебрежении
членами с противоположным вращением, которые пропорциональны ехр[±г(о; + и)}.
Теперь рассмотрим случай волны с левой круговой поляризацией (ЛКП), которая
связывает состояния фа(г) и фь(г)^ заданные выражением E.2.49). Электрическое
поле имеет вид
E(t) = xS cos vt - yS sin ut. E.2.55)
При этом выражения E.2.53) и E.2.54) приобретают вид
rab(t) = -e?{xab cos vt + уаЬ sin vt) ei0J\ E.2.56a)
%a(t) = -eS{xba cos vt + yba sin vt) е~1ш\ E.2.566)
где, согласно E.2.49а) и E.2.546), можно записать
exab = Ф1(г)хфь(г) dr = р, E.2.57а)
г
ехЬа = Ф1(г)уфь(г) dr = -ip, E.2.576)
а также ехЬа = р и еуЬа = гр. Тогда выражения E.2.56а) и E.2.566) принимают
простой вид:
s vt - i sin vt) eiujt = -pi e-%{v-w)t^ E.2.58a)
%a(t) = -pcf(cos vt + i sin vt) e^iojt = -pi е^~ш)\ E.2.586)
и члены с противоположным вращением не появляются.
В заключение отметим, что хотя и отсутствуют члены с противоположным
вращением типа ен^+^К? которые связаны с волной ЛКП, вызывающей переходы
Am = — 1, но существуют члены с противоположным вращением, связанные с ЛКП
и переходами в состояние п = 2, I = 1, га/ = +1, т.е. с Атл = +1. Обычно говорят,
что такие переходы исчезают благодаря правилам отбора по угловому моменту.
Здесь они принимаются «исчезающе малыми», так как они ведут себя как члены
с противоположным вращением. То есть, они разрешены в том смысле, что атом
совершает переход в возбужденное состояние с излучением фотона. Такие члены
могут быть существенно меньше обычных членов с противоположным вращением
(см. задачу 5.7).
132 Взаимодействие атома с полем — полуклассическая теория Гл. 5
5.3. Оператор плотности для двухуровневого атома г)
Для заданной физической системы существует вектор состояния \ф), который
содержит всю возможную информацию о системе. Если мы хотим извлечь часть
информации о системе, то нам нужно вычислить среднее значение соответствующего
оператора О,
E.3.1)
Во многих случаях мы можем не знать \ф), но нам достаточно знать вероятность Рф
того, что система находится в состоянии |^). В такой ситуации нам не только нужно
взять квантово-механическое среднее, но также усреднить по ансамблю большого
числа идентичных, одинаково приготовленных систем. Вместо E.3.1) имеем теперь
(см. разд. 3.3)
<(О)кМ>анСамбль = Тг (Ор) , E.3.2)
где оператор плотности р определяется выражением
^ E.3.3)
Можно заметить, что
Тг(Ор) = Тг (рО). E.3.4)
В частном случае, когда все Рф равны нулю, за исключением величины, соответ-
соответствующей состоянию |^о), имеем
Р=Ш(Фо\, E.3.5)
и это состояние называется чистым состоянием. Из условия сохранения вероятности
следует, что Тг (р) = 1. Кроме того, для чистого состояния
Тг(р2) = 1. E.3.6)
5.3.1. Уравнение движения для оператора плотности. Уравнение движения для
оператора плотности можно получить из уравнения Шредингера:
\ E.3.7)
Взяв производную по времени от р (выражение E.3.3)), получим
где Рф не зависит от времени. Используя уравнение E.3.7), чтобы заменить \ф) и (ф\
в E.3.8), получаем
р=~[Ж,р]. E.3.9)
1) Наиболее полное описание вынужденного излучения, развитое Лэмбом и Скалли (Lamb
and Scully, 1971), можно найти в главе III книги Sargent, Scully and Lamb A974).
5.3 Оператор плотности для двухуровневого атома 133
Уравнение E.3.9) часто называют уравнением Лиувилля или Фон Неймана. Оно
является более общим, чем уравнение Шредингера, поскольку оно использует опе-
оператор плотности вместо определенного вектора состояния и поэтому может дать как
квантово-механическую, так и статистическую информацию.
В уравнении E.3.9) не учтен распад уровней за счет спонтанного излучения.
Возбужденные уровни атома могут также распадаться благодаря столкновениям или
другим явлениям. Конечное время жизни атомных уровней можно просто ввести,
добавив феноменологические времена распада в уравнения для оператора плотности
E.3.9) (см. также задачу 5.2).
Скорости распада можно включить в уравнение E.3.9) с помощью релаксацией™
ной матрицы Г, которая определяется выражением
(гс|Г|т) = jnSnm. E.3.10)
С этим дополнением уравнение движения для оператора плотности приобретает вид
р = -^[Ж, р] - \{Т, р}, E.3.11)
где {Г, р\ = Г^ + дТ. В общем случае, релаксационные процессы оказываются более
сложными.
Матричный элемент ij уравнения E.3.11) имеет вид
1
к к
Эта формула оказывается полезной для описания многоуровневых систем.
5.3.2. Двухуровневый атом. Теперь вновь рассмотрим двухуровневую атомную
систему, состояние которой является линейной комбинацией состояний \а) и |6), т.е.
\ф) = Са\а) + Съ\Ъ). Тогда оператор плотности можно записать как
Р = \Ф)(Ф\ = [Ca{t)\a) + Cb(t)\b)][C:(t)(a\ + C6*(*)<&|] =
= \Са\2\а){а\ + СаС1\а){Ъ\ + CbC*\b)(a\ + |СЬ|2|Ь)(Ь|. E.3.13)
Матричные элементы будут иметь вид
Раа = {а\р\а) = \Ca(t)\2, E.3.14)
Раь = (а\р\Ь) = Ca(t)Cb(t)*, E.3.15)
РЬа = РаЫ E-3.16)
Рьь = (b\p\b) = \Cb(t)\2. E.3.17)
Оператор плотности в матричном виде можно записать как
р = (Раа раЬ) . E.3.18)
\Pba Pbb/ X ;
Очевидно, что раа и р^ь являются вероятностями нахождения в верхнем и нижнем
состояниях, соответственно. Для того чтобы понять смысл недиагональных элемен-
элементов, необходимо вспомнить, что атомная поляризация (см. E.2.25)) двухуровневого
атома (в точке z) есть
P(z, t) = CaClpba + к.с. = pab{z, t)pba + к.с. E.3.19)
134 Взаимодействие атома с полем — полуклассическая теория Гл. 5
Таким образом мы видим, что недиагональные элементы определяют атомную по™
ляризацию.
Можно было бы найти эту форму для р прямо из E.3.5), вспомнив, что в спинор-
ных обозначениях
Ш = (С*а С*ь). E.3.20)
Тогда, перемножая матрицы, получаем
/с \ /|са|2 cac*h\
р=(СЛ(С*а С?)= ( ' ' "). E.3.21)
сьс* \С
Ь\
Уравнения движения для элементов матрицы плотности можно вывести из урав-
уравнения E.3.12) с гамильтонианом, заданным выражениями E.2.4) и E.2.5). Результат
имеет вид
Раа = -JaPaa + ^[pab^pba ~ K.C.], E.3.22)
РЪЪ = ^ibPbb - J^PabEpba ~ К.С.], E.3.23)
РаЪ = ~{Ш + гЧаЪ)раЪ ~ ^pabE(paa ~~ рЬЬ), E.3.24)
где 7аЬ = (т« Н~ 7ь)/2 Gа и 7ь определяются выражением E.3.10)), и E(t) задается
выражением E.2.6). В приближении вращающейся волны функция cos(isi) заменя™
ется в уравнениях E.3.22)-E.3.24) функцией exp(—ii/t)/2.
5.3.3. Учет упругих столкновений между атомами. Физическая интерпретация
элементов матрицы плотности позволяет нам включить в эти уравнения члены,
связанные с определенными процессами. Одним из таких процессов является упругое
столкновение между атомами в газе.
В частности, во время столкновения атомов уровни энергии испытывают случай-
случайные штарковские сдвиги без изменения состояния и скорость распада раъ увеличива-
увеличивается без существенного изменения ja и 7ь- Изменение скорости распада раъ можно
просто вычислить следующим способом.
Предположим, что случайные сдвиги Штарка включены в уравнение E.3.24)
путем добавления случайных сдвигов 5w(t) к частоте а;. Пренебрегая, для простоты,
взаимодействием атома с полем, можно записать уравнение движения для элементов
матрицы плотности раъ следующим образом:
Pab = ^[i^ + iS(jj(t) + JabjPab- E.3.25)
Формально интегрируя E.3.25), получаем
Pab(t) =exp
-{ш + jab)t - г dt'8uj(tf)
о
раЬ@). E.3.26)
Выполним теперь статистическое усреднение уравнения E.3.26) по случайным изме-
изменениям 8uj(t). Это усреднение затрагивает только множитель <5o;(t), так что требуется
t
найти (ехр[-г \dt'Su(t')]).
5.4 Уравнения Максвелла-Шредингера 135
Функция 8ш имеет столько же положительных значений, сколько и отрицатель™
ных. Следовательно, среднее по ансамблю (Suj(t)) равно нулю. Более того, поскольку
изменения Suj(t) обычно происходят очень быстро по сравнению с другими измене-
изменениями, развивающимися на таких масштабах как 1/7а&? полагаем, что
{Sw{t) 6w(t')) = 27ph S(t - t'), E.3.27)
где 7ph — константа. Также положим, что euj(t) описывается случайным гауссовым
процессом, так что справедлива хорошо известная теорема моментов для гауссова
процесса. В этих условиях получаем
ехр
г
-г \dt'8uj{tl)
E.3.28)
что дает для среднего от E.3.26) следующее выражение:
РаЪ = ехр[-(го; + jab + jph)t]pab(O). E.3.29)
Следовательно, дифференцируя это выражение и добавляя член взаимодействия,
получаем модифицированное уравнение движения для раь:
РаЪ = ~(iw + j)pab - ^pabE(z, t)(paa - pbb), E.3.30)
где 7 = 7ab + 7Ph — новая скорость распада. Уравнение E.3.30) является уравнением,
усредненным по столкновениям.
5.4. Уравнения Максвелла-Шредингера
Взаимодействие одиночного атома с одномодовым полем, которое обсуждалось
в предыдущих параграфах, представляет собой простую идеализированную систе-
систему. Во многих задачах квантовой оптики вызывает интерес взаимодействие поля
излучения с большим числом атомов. Первым примером такой системы является
одномодовый лазер, в котором возбужденные накачкой атомы взаимодействуют
с электромагнитным полем внутри резонатора. Другие примеры относятся к про™
хождению когерентного импульса и оптической бистабильности.
В этом разделе для рассмотрения таких задач развивается математический
аппарат, который основан на самосогласованной системе уравнений для вещества
и поля. Этот набор уравнений и его модификации позволяют работать со многими
полу классическими задачами, в которых атомы описываются квантовомеханически,
а поле — полу классически.
При данном полуклассическом атомно-полевом взаимодействии классическое по-
поле индуцирует в среде электрический дипольный момент согласно законам квантовой
механики. Чтобы упростить статистическое суммирование отдельных дипольных
моментов, необходимое для получения макроскопической поляризации среды, ис-
используется матрица плотности. Хотя полу классический подход является очень хоро-
хорошим для описания многих задач, представляющих интерес при изучении заданной
системы, он, тем не менее, не достаточен для получения информации о квантово
статистических свойствах света. Эти аспекты будут представлены в следующих
главах, где поле излучения описывается квантово-механически.
136 Взаимодействие атома с полем — полуклассическая теория Гл. 5
5.4.1. Матрица населенности и уравнение движения длм нее. Рассмотрим взаи-
взаимодействие электромагнитного поля со средой, состоящей из двухуровневых атомов
с однородно уширенной линией. Отдельные атомы описываются оператором плотно-
плотности (см. выражения E.3.14)-E.3.17))
p(z, t, t0) = J^ P^{z, t, to)\a)@l E.4.1)
где a^f3 = a, b и pap(z,t,to) — элементы матрицы плотности отдельного атома
в момент времени t в точке z, который начинает взаимодействовать с полем в на-
начальный момент времени to- Начальный момент времени to может быть случайным.
Элементы матрицы плотности отдельного атома pa^(z, t, to) удовлетворяют уравне-
уравнениям движения E.3.22), E.3.23) и E.3.30). Если состояние атома в момент накачки
записывается как
р(Мо,М = ?р$1<*><01, E.4.2)
ТО
pap{z,U,U) = p(*l. E.4.3)
Влияние тех атомов, которые возбуждаются в процессе накачки со скоростью
ra(zjto) атомов в секунду в единице объема, учитывается путем суммирования по
начальным временам. Результирующая матрица населенности определяется как
t t
dtora(z,to)pap(z,t,to)\a)(l3\. (БАЛ)
Обычно скорость возбуждения ra(z,to) изменяется медленно и ее можно считать
постоянной. Макроскопическая поляризация среды, P(z,t), создается ансамблем
атомов, которые прибывают в точку z в момент времени t, независимо от времени
их возбуждения, т. е.,
t
Г г
P(z,t)= dtora(z,to)TT[pp(z,t,to)] = ^2
«0
-ОО «.0-ОО
E.4.5)
где р — оператор дипольного момента, и во второй строке мы подставили p(z, t, to)
из E.4.1). Для двухуровневого атома, у которого раь = рьа = р5 получаем
Р(М) = р[Раб(М) + к.с.]. E.4.6)
Таким образом, недиагональные элементы матрицы населенности определяют ма-
макроскопическую поляризацию.
Уравнения движения для элементов матрицы населенности p(z,t) можно полу™
чить, взяв производную по времени от выражения E.4.4) и используя уравнения
E.3.22), E.3.23) и E.3.30). Например, если атомы некогерентно возбуждаются на
уровни \а) и \Ь) с постоянной скоростью ra (pafj = pbj = 0), тогда
Раа = Аа - JaPaa + ^(РЕPba ~ K.C.), E.4.7)
Ръъ = Аб - ^ьРьь ^ -^{рЕръа ^ к.с), E.4.8)
Pab = ~(iw + l)pab - ^рЕ(раа - pbb), E.4.9)
5.4
Уравнения Максвелла-Шредингера
137
где Ла = гаpad и Л5 = rapbb . Эти уравнения для среды двухуровневых атомов связа-
связаны с полем Е. Условие самосогласованности требует, чтобы уравнение движения для
поля Е определялось матричными элементами атомной населенности. В следующем
параграфе мы выведем это уравнение для одномомодовой бегущей волны.
5.4.2. Уравнения Максвелла длм медленно меняющихся функций поля. Элек-
Электромагнитное поле излучения описывается уравнениями Максвелла:
V-D = O,
V-B = 0,
m
' at'
&D
r at'
где
= /i0H,
EA10)
E.4.11)
EA12)
Здесь Р — макроскопическая поляризация среды. Для того чтобы избежать решения
сложной задачи с граничными условиями, рассмотрим среду с проводимостью а. Эта
проводимость введена для того, чтобы феноменологически учесть линейные потери,
обусловленные наличием какой-либо поглощающей фоновой среды, а также потери,
связанные с дифракцией и пропусканием зеркал. Объединив роторные уравнения,
взяв соответствующие временные производные и воспользовавшись выражением
E.4.12), получим волновое уравнение
E.4.13)
Таким образом, поляризация P(r,t) действует как член-источник в уравнении для
поля излучения. Рассмотрим ситуацию, в которой поле излучения взаимодействует
с двухуровневыми атомами внутри однонаправленного кольцевого резонатора, пока-
показанного на рис. 5.4. Обычно в резонаторе существуют обе бегущие волны. Однона-
Рис. 5.4. Схема лазера в однонаправленной кольцевой конфигурации
правленное распространение достигается с помощью устройства внутри резонатора,
обеспечивающего большие потери для одной из бегущих волн. Обычно интенсивность
поля изменяется медленно поперек оси лазера на масштабах порядка оптической
длины волны. Поэтому мы пренебрегаем зависимостью Е от х и у, т. е.
E.4.14)
138 Взаимодействие атома с полем — полуклассическая теория Гл. 5
Тогда уравнение E.4.13) упрощается и принимает вид
д2Р ( .
E.4.15)
д2Е , дЕ 1 д2Е д2Р
+
]t ¦ г df ^u df
Поле частотой v записывается в виде бегущей волны:
E(z, t) = \g{z, t) e-i\"t-kz^z,t)\ + KX_} EA16)
где e(z,i) и ф(г^) ~~ медленно меняющиеся функции координаты и времени; к =
= и /с. Для задачи лазерной генерации к = ^с/с, где vc — частота резонатора.
В общем случае ё(z, t) — комплексная функция; тем не менее, в этом и последующих
разделах мы считаем ее действительной величиной.
Если поле задается выражением E.4.16), то отклик среды, в пренебрежении
высшими гармониками, определяется поляризацией
F(z, t) = \&{z, t) е-№-ь*+Ф(*>*)] + K.c#j E.4.17)
где &(z,i) — медленно меняющаяся функция координаты и времени.
Медленно меняющаяся комплексная поляризация &(z,t) выражается через мат-
матрицу населенности путем отождествления положительно^частотных частей в выра™
жениях E.4.6) и E.4.17):
tJ^\zч t) '^ АрраЬ в . (о.4.1о)
Подставим выражения E.4.16) и E.4.17) для E{z^t) и P(z,t) в уравнение E.4.15)
и сделаем следующие приближения:
ifT Ж E.4.20)
Эти приближения медленно меняющихся амплитуд и фаз оправданы, когда J3, ф
и & изменяются незначительно на масштабах периода оптической частоты. Так как
уравнение E.4.15) можно переписать в виде
д 1 д\ ( 8 1 д\ „ дЕ д2Р (хл<>л\
получаем
^ + iM = _X(f_J_fcIm^5 E.4.23)
dz с dt 2ео х '
9± + 191 = к_Ц_ 1 ^-iRe^, E.4.24)
dz с dt с 2е0 х J
где к = a/2eqc — коэффициент линейных потерь.
Уравнения E.4.7)-E.4.9), E.4.23) и E.4.24) формируют самосогласованный на-
набор уравнений. Этот набор уравнений является отправным пунктом для изучения
многих систем, включающих взаимодействие поля излучения с ансамблем атомов.
Обобщение этого набора уравнений на случай многоуровневой атомной системы
и многомодового поля очевидно.
В следующем разделе в качестве важного примера применения этого набора
уравнений мы представим полуклассическую теорию лазера.
5.5 Полу классическая теория лазера 139
5.5. Полуклассическая теория лазера
В этом разделе, мы сначала изложим в общих чертах основные принципы лазер-
лазерной генерации, а затем представим теорию лазера в том виде, как она впервые была
развита Лэмбом с соавторами. Будут также выведены пороговые условия генерации
и уравнения эволюции для электромагнитного поля.
5.5.1. Принцип работы 1). В 1954 году Гордон, Зейгер и Таунс показали, что
можно осуществить генерацию когерентного электромагнитного излучения в радио-
радиочастотном диапазоне с помощью, так называемого, мазера (maser — аббревиатура
выражения microwave amplification by stimulated emission of radiation). Первая ма-
зерная генерация наблюдалась в аммиаке.
Принцип работы мазера был распространен на оптическую область частот ТТТа-
вловым и Таунсом а также Прохоровым 2), так что получился лазер (laser — аббревиа-
аббревиатура выражения light amplification by stimulated emission of radiation). Лазер состоит
из набора атомов, взаимодействующих с электромагнитным полем внутри резона-
резонатора. Резонатор поддерживает только определенный набор мод, соответствующих
дискретной последовательности собственных частот. Активные атомы, т. е. атомы,
возбужденные в процессе накачки на верхний уровень лазерного перехода, находятся
в резонансе с одной из собственных частот резонатора. Резонансное электромаг-
электромагнитное поле вызывает вынужденное излучение и атомы передают свою энергию
возбуждения полю излучения. Испущенное излучение остается в резонансе. Если
верхний уровень достаточно населен, то это излучение вызывает последующие пере-
переходы в других атомах. Таким образом, вся энергия возбуждения атомов передается
в одну моду поля излучения.
Первая импульсная лазерная генерация была продемонстрирована в рубине Мей-
маном. Гелий-неоновый газовый лазер, первый лазер непрерывного действия (лазер
непрерывной волны), был построен Джаваном 3). С тех пор во многих системах
была продемонстрирована лазерная генерация когерентного света, простирающегося
от инфракрасной до ультрафиолетовой области частот. Они включают лазеры на
красителях, химические лазеры и полупроводниковые лазеры. Также был разработан
новый класс лазеров, в которых используются электроны в периодическом магнит-
магнитном поле (названных лазерами на свободных электронах).
Из нашего обсуждения принципа работы лазера следует, что лазерная теория
должна включать три основных элемента — активную среду (двухуровневые атомы
с инверсией населенности), механизм накачки на верхний лазерный уровень и ради™
ационные потери, обусловленные резонатором. Последовательная полу классическая
теория лазера была развита Лэмбом.
5.5.2. Полуклассическая теория Лэмба. Рассмотрим полуклассическую теорию
лазера для простого случая линейно поляризованного электрического поля в од-
однонаправленном кольцевом резонаторе с двухуровневыми однородно уширенными
активными атомами.
) В 1939 г. В.А. Фабрикант впервые сформулировал в диссертации принцип усиления
волны при ее прохождении через вещество. В 1951 г. на эту идею было выдано авторское
свидетельство. — Примеч. ред. пер.
) В список упомянутых ученых следует, безусловно, внести и Н.Г. Басова. — Примеч. ред.
пер.
3) Наряду с А. Джаваном, следует назвать также У. Беннета и Д. Гарриота. — Примеч.
ред. пер.
140 Взаимодействие атома с полем — полуклассическая теория Гл. 5
Временную зависимость электрического поля <f(z,t) можно отделить от про-
пространственной части, разлагая поле по нормальным модам резонатора. В кольцевом
резонаторе только определенные дискретные моды достигают ощутимой величины,
а именно те, частоты которых удовлетворяют соотношению
^ш = ~^~ = ктс, E.5.1)
где S — окружность кольца, т — большое целое число (обычно порядка 106) и кт —
соответствующее волновое число. Здесь мы рассматриваем одиночную моду с функ-
функциями однонаправленной моды (бегущей волны) U(z) = exp(ifcz) (рис. 5.4).
В данной задаче уравнения движения для амплитуды поля E.4.23) и фазы E.4.24)
сводятся к следующим:
ж = \«*-\{т№> E-5-2а)
где ис — частота резонатора и j = Gа + 7ь)/2. В уравнении E.5.2а) величина к
заменена величиной ^/2с, где ^ = uc/Q {Q — добротность резонатора), для учета
потерь на зеркалах резонатора. Поляризация ^, возбуждающая поле в выражении
E.4.18), определяется уравнением E.4.9) и имеет вид
'. E.5.3)
При условии, что амплитуда ^(tf) и разность населенности раа — р^ь существенно
не изменяются на временах порядка 1/7? интеграл E.5.3) можно легко вычислить,
ибо данные члены можно тогда вынести из под знака интеграла. Это решение
приводит к скоростным уравнениям для атомной населенности. Такое приближение
является точным в стационарном состоянии (^ = 0). Мы получаем следующие
выражения:
-^(*). E.5.46)
Подставляя E.5.4) в уравнения движения для раа и р^ь (E-4.7) и E.4.8)), получаем
скоростные уравнения
Раа = Аа - JaPaa ~ Щраа ~ Pbb) , E.5.5a)
Pbb = Aft - JbPbb + ЩРаа ~ Pbb), E.5.56)
где постоянная скорости
) , J ()
J 7 + (u) — u)
Очевидно, что постоянная скорости R, определяющая скорость, с которой изменяется
5.5 Полу классическая теория лазера 141
разность населенностей со временем, зависит в основном от скорости, с которой
изменяется общая интенсивность поля. Следовательно, приближение скоростных
уравнений заключается в предположении, что огибающая электрического поля слабо
изменяется на временах жизни возбужденного состояния атома. Из E.5.5) мож-
можно найти разность населенностей в стационарном состоянии. Эту разность можно
подставить обратно в уравнения для Im & и Re & и, таким образом, определить
составляющие поляризации.
В стационарном состоянии (раа = ръъ = 0) уравнения E.5.5) дают
где Nq = Аа7а^1 — А^Ть и ^s = ТаТь/^Т- Поэтому разность населенностей задается
значением iVo? ПРИ отсутствии поля, деленным на величину, которая увеличивается
с ростом интенсивности электрического поля.
Комбинируя E.5.7) с выражениями E.5.4) и E.5.2), получаем уравнения для
амплитуды и частоты:
)g \ E-5-8)
E.5.9)
где V — объем резонатора, и
-5 — 2, E.5.10а)
2е0У/ '
Здесь sz/ — параметр линейного усиления и S3 — параметр насыщения.
Теперь определим безразмерную интенсивность
E.5.106)
E.5.11)
которая соответствует «числу фотонов» в лазере. (Здесь ?®?>2Vf2 — полная энергия
в лазерном луче и Ни — энергия, соответствующая одному фотону.) Эта формулиров-
формулировка будет еще усилена в гл. 11 при изучении квантовой теории лазера. Из уравнений
E.5.8) и E.5.9) следует, что
E.5.12)
E.5.13)
При слабом возбуждении (Шп/^f <С 1) можно построить теорию возмущений,
разлагая в ряд знаменатели в уравнениях E.5.12) и E.5.13), что приводит к
п = (^ - <g)n - mn1, E.5.14)
и + ф = ис + (^у-^) (^ - @п). E.5.15)
142
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
Уравнения E.5.14) и E.5.15) являются основными уравнениями лазера. Как будет
показано ниже, они описывают пороговое условие генерации, стационарную и пе-
переходную интенсивности лазера, а также затягивание частоты благодаря наличию
усиливающей среды.
Из уравнения E.5.14) сразу видно, что в стационарном случае (п = 0) имеем п =
= 0 до тех пор, пока не выполнится условие ?&>*€. Когда srf > *€, стационарная
интенсивность задается выражением
n° = n = ^ir"- E-5Л6)
Таким образом, условие порога лазерной генерации имеет вид s^ = ^, т. е. усиление
равно потерям в резонаторе.
На рис. 5.5 изображена зависимость стационарной интенсивности от расстройки
А = ш — и. Согласно уравнению E.5.15), частота осцилляции и сама зависит от
интенсивности. Между тем, при вычислении различных коэффициентов, хорошим
приближением можно считать и = ь?с.
J.UU
140
120
100
80
60
40
20
п
-0.4 -0.3 -0.2 -0.1 0 0.1
А/7
0.2 0.3
0.4
Рис. 5.5. Зависимость стационарной интенсивности по от расстройки A/j. Здесь исполь-
использованы следующие значения параметров:
= 1 мкс^1, ^2и/S
V = КГ3 мкс
= 1.15 мкс
Уравнение E.5.15), определяющее частоту, предсказывает затягивание частоты
генерации от частоты пассивного резонатора к центру линии. В частности, в стаци-
стационарном режиме (ф = 0)
E.5.17)
где
27
— фактор стабилизации. Уравнение E.5.17) можно интерпретировать как уравнение
для центра масс, в котором частота генерации и равна взвешенному среднему от ис
5.6 Физическая картина вынуэюденного испускания и поглощения 143
ишс весами 1 и .У7, соответственно. Обычно ^ <С 27 и поэтому и = ис^шо и затянута
ближе к атомной частоте ш. Это явление называется затягиванием мод.
5.6. Физическая картина вынужденного испускания н поглощения
Для того чтобы лучше понять физику, стоящую за вынужденным излуче-
излучением и поглощением, рассмотрим атом, взаимодействующий с полем E(z,t) =
= ${z, i) cos(ut ~~ kz) в точке z = 0. Как и прежде, амплитуды Са и Съ определяются
уравнениями E.2.7) и E.2.8), а медленно меняющиеся амплитуды са = Са e%UJat
и С5 = Сь etuJbt определяются уравнениями E.2.12) и E.2.13) соответственно. Для
простоты рассмотрим точный резонанс А = из — и = 0. Тогда решение E.2.21)—
E.2.22) принимает вид
ca(t) = [co@) cos (^) + гсь(О) sin (^*)] , E.6.1а)
cb(t) = [сь@) cos (^) + ice@) sin (^)] , E.6.16)
где мы предположили, что матричный элемент является действительной величиной
?Paij = S^ba = &• Теперь в первом порядке теории возмущений можно просто
вычислить раь = cacjj e~tujt для случаев, когда атом находится в возбужденном
состоянии и в основном состоянии.
В первом случае (вынужденное излучение), когда со@) = 1 и с&@) = 0, для
атома, прошедшего через резонатор за время т, в первом порядке находим
са{т) ^ 1, E.6.2а)
Сь(г)^г^. E.6.26)
Тогда поляризация имеет вид (см. E.4.18))
9 = 2рРаЬ eil/T ^ -ipuRT. E.6.3)
В случае поглощения, в начальный момент времени са@) = 0 и сь@) = 1, и в
первом порядке получаем
са(т) - i^f, E.6.4а)
сь(т) 9* 1, E.6.46)
И
& = ipuRT. E.6.5)
Теперь, используя уравнение E.4.23), для атома, первоначально находившегося в воз-
возбужденном состоянии, имеем
±«? *?,,, E.6.6)
с at 2e0 h
где мы пренебрегли потерями резонатора. Из уравнения E.6.6) следует, что измене™
ние электрического поля за время т имеет вид
^^-^т2, E.6.7)
т. е. падающая волна испытывает усиление.
144
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
Подобным образом, для атома, первоначально находившегося в основном состоя-
состоянии, получаем
и поэтому
с dt 2e0 h '
ск
E.6.8)
E.6.9)
т. е. падающая волна испытывает поглощение. Таким образом, атом действует, по
существу, как крошечный осциллирующий электронный ток, индуцированный па-
падающей световой волной. Тогда ослабление падающей волны происходит в резуль-
результате излучения этого тока, деструктивно интерферирующего с падающим светом
(рис. 5.6). Эту простую физическую картину вынужденного излучения и поглощения
(а)
(б)
Рис. 5.6. Излучение: конструктивная интерференция индуцированного излучения диполя и
падающей волны (а); поглощение: деструктивная интерференция индуцированного излуче-
излучения диполя и падающей волны (б)
можно расширить, чтобы объяснить более сложные явления, такие как лазерная
генерация без инверсии (см. разд. 7.3.1).
5.7. Спектроскопия с временным разрешением
В предыдущем разделе мы увидели, насколько проста и интуитивно красива
концепция вынужденного излучения и поглощения в рамках полуклассической тео-
теории излучения. В качестве примера необычной, противоречащей интуиции, физики
в рамках той же полуклассической теории мы закончим эту главу обсуждением
спектроскопии с временным разрешением.
В обычной спектроскопии предел разрешения по энергии между двумя состояни-
состояниями \а) и \Ь) определяется суммой скоростей релаксации ja и 7ь из этих состояний.
В этом разделе описывается метод спектроскопии, который обеспечивает разре-
шение, превосходящее пределы естественного уширения линии. Наши соображения
основаны на том факте, что в переходном режиме вероятность индуцированных
переходов в двухуровневой системе, взаимодействующей с монохроматическим элек-
электромагнитным полем, не определяется лоренцианом с шириной GО + 7ь)/2 = Jab?
а скорее задана лоренцианом с шириной (уа — 7ь)/2 = ^аь- Лоренцева ширина 7аб5
которая обычно встречается в атомной физике, восстанавливается только в соответ-
соответствующем пределе.
5.7
Спектроскопия с временным разрешением
145
Приступим к рассмотрению экспериментальной ситуации, в которой ансамбль
двухуровневых атомов в момент времени t = to возбуждается в состояние \Ь)
некоторым «мгновенным» механизмом возбуждения, например, пикосекундным оп-
оптическим импульсом. Затем возбужденные атомы подвергаются действию монохро-
монохроматического, но перестраиваемого, поля излучения.
Рассмотрим схему уровней, изображенную на рис. 5.7. Там показан атом с двумя
нестабильными состояниями \а) и \Ь) и слабое поле, возбуждающее атом из нижнего
Рис. 5.7. Энергетическая диаграмма уровней, на которой показано, что атом из основного
состояния возбуждается в состояние |6), затем взаимодействует с резонансным полем,
переводящим атом из состояния \Ь) в состояние |а), с последующим переходом в состояния
\d) и \с) со скоростями 7а и 7ь, соответственно
состояния \Ь) в верхнее \а). Если добавить нижние состояния (|с) и |<i)), в которые
переходят \а) и |6), то эту систему можно рассматривать как четырехуровневый
атом. То есть, мы имеем атом в состоянии \Ь) в момент времени to, возбуждаем атом
в состояние |а), и считаем число атомов, накопившихся в состоянии |с), начиная
с момента to до конечного времени t. Скорость счета измеряется как функция
расстройки между лазерной и атомной частотами.
Далее, решая уравнения движения для матрицы плотности E.3.22)-E.3.24) с точ™
ностью до первого неисчезающего члена, находим элемент paa(t)- Результат имеет
вид
Х2
- 2
cos
где 8аь = {la ~~ 7fe)/2, Од — частота Раби возбуждаемого перехода иА- расстройка
между частотой лазера и шаь- Ключевым пунктом является то, что лоренцев мно-
множитель в E.7.1) имеет ширину 7а — 7ь? a не 1а + 1ь-
Теперь предположим, что мы считаем число фотонов, испущенных возбужденным
атомом, когда он совершает переход \а) —>• |с). Оно будет равно полному числу ато-
мов, накопившихся на уровне |с), и определяется простым скоростным уравнением
Pcc{t,t0) =lPaa(t,t0), E.7.2)
где обозначения напоминают нам, что атомы первоначально были возбуждены в мо~
мент времени to- Тогда полное число спонтанно испущенных фотонов, начиная с мо-
момента времени to до достаточно большого времени, прошедшего после возбуждения
146
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
в состояние |6), задается выражением
где 77 — константа, определяемая эффективностью детектирования фотона.
Подставляя E.7.1) в E.7.3), находим
То есть, когда мы выполняем вышеописанную процедуру, накапливая фотоны,
испущенные на переходе \а) —> |с), начиная от to до бесконечно большого времени, то
возвращаемся к обычному лоренциану с шириной 7аЬ- Этот результат обнадеживает,
так как во многих экспериментах именно Tab определяет разрешение.
Рис. 5.8. Сигнал ^{т\ наблюдаемый во время-задержанной спектроскопии при различных
значениях т. Для простоты все кривые нормированы. В действительности, как следует
из формулы E.7.6), максимумы кривых, которые соответствуют большим значениям т,
существенно меньше. Тем не менее, сужение линии может оказаться полезным (см. FIgger
and Walther, 1974)
Давайте теперь подождем до момента времени to + т, прежде чем начать прини-
принимать какие-либо отсчеты счетчика. То есть, будем измерять
N(A,t0
paa(A,t,t0)dt.
E.7.5)
to+т
Подставляя E.7.1) в E.7.5), находим (См. Meystre, Scully, and Walter, 1980)
1
+
П.5.А Эквивалентность (г • Е)- г/ (р • А)-гамильтонианов 147
Идея прозрачна. Когда мы задерживаем наблюдение, оказывается, что линия
сужается, что видно из сравнения E.7.4) и E.7.6). Зависимость E.7.6) представлена
на рис. 5.8 для различных значений задержки во времени.
В заключение отметим, что, как еще было указано Фиггером и Вальтером, су-
сужение линии в спектроскопии с временным разрешением обеспечивает высокое спек-
спектральное разрешение в том смысле, что мы можем разрешить близко расположенные
линии. Тем не менее, для частот атомного перехода ша1, это более высокое разрешение
не всегда приводит к более высокой экспериментальной точности получаемого
результата. Причина этого — экспоненциальное затухание сигнала с увеличением
времени задержки, проявляющееся через множители ехр(^7ат) и ехр(^7ьт) в вьь
ражении E.7.6). Мы вернемся к вопросу увеличения спектрального разрешения в
последующих главах, например, в разд. 21.7.
Приложение 5.А
Эквивалентность (г • Е)- и (р • А)-гамильтонианов
В разд. 5.1 было отмечено, что в радиационной калибровке (R—калибровке) и в
дипольном приближении (А(г, ?), ?/(r, i)) = (A(?), 0) калибровочное преобразование
приводит к калибровке @, —Е(?) -г). Заметим, что калибровка @, —Е(?) -г) приводит
к электрическому дипольному взаимодействию Ж (выражение E.1.19)) и поэтому
мы называем его калибровкой электрического поля (IiJ-калибровка). Поэтому два
гамильтониана Ж (см. E.1.19)) и Ж1 (см. E.1.21)) связаны через калибровочное
преобразование E.А.1). Калибровочное преобразование требует преобразования по-
потенциалов, согласно E.1.6) и E.1.7), и волновых функций согласно E.1.4). Для фи™
зически измеряемых величин получаются неидентичные, неправильные результаты
в различных калибровках, если выполнить только одно из этих двух преобразований.
Обсудим, как обращаться с волновой функцией в двух различных калибровках для
того, чтобы получить калибровочно-инвариантные физические предсказания. Одна-
Однако, прежде чем это сделать, давайте кратко обсудим некоторые примеры физических
величин.
5.АЛ. Форм-инвариантные физические величины. Форм-инвариантная физи™
ческая величина определяется как величина, соответствующий оператор Gx =
= G(AXJ Ux) которой является инвариантным по форме при унитарном преобра-
преобразовании T(r, t) = exp[ix(r, t)], т. е.
Gx> = TGXT+, E.A.2)
где волновая функция в калибровке х преобразуется в калибровку х' с помощью
унитарного преобразования
iPx,(r,t) = T(r,t)i>x(r,t). E.A.3)
Разница между физическими и нефизическими величинами лежит в калибровочной
инвариантности собственных значений. Собственные значения физической величины
одинаковы во всех калибровках, в то время как собственные значения нефизических
величин зависят от выбранной калибровки. Для того чтобы это показать, обозначим
148 Взаимодействие атома с полем — полуклассическая теория Гл. 5
собственные значения и собственные состояния оператора Gx через gn и |Сх,п}?
соответственно:
Gx\Zx,n)=gn\tx,n). E.A.4)
Только для физических величин собственные значения gn калибровочно инвариант-
инвариантны, т. е.
Gx,|?x',n> = TGxT+T\iXtn) = Tgn\iXtn) = gn\ix.,n). E.A.5)
Следовательно, нефизические величины могут быть использованы только как вы-
вычислительные инструменты.
Теперь рассмотрим некоторые примеры физических и нефизических величин.
Отправным пунктом в этих рассуждениях является тот факт, что операторы г
и Р (р = —*^V), связанные с координатой и каноническим импульсом частицы,
одинаковы во всех калибровках. То есть р представляется оператором —ihV во всех
калибровках. Это гарантирует, что коммутационное соотношение [r^p^] = ihejk
выполняется в любой калибровке. При таком критерии оператор механического
момента
тгх = р — eAx(r, t) E.А.6)
является физической измеряемой величиной, поскольку
ТпхТ+ = Т[р - еАх(г, t)]T+ = р - еАх - ftV% = р - еДх/ = тгх/. E.А.7)
Аналогично, оператор мгновенной энергии системы, состоящий из кинетической
энергии и статического потенциала (обычно, атомного связывающего потенциала),
Sx = ^[v-eAx{v,t)f + V{r), E.A.8)
представляет физическую величину, также как и любой другой оператор, который
является только функцией других физических величин, типа тг%.
С другой стороны, канонический импульс р не является физической величиной,
поскольку
ТрТ+ =р-ГОх/р. E.А.9)
Аналогичным образом, оператор Ж® = р2/2т (не зависящий от потенциалов) не яв-
является физической величиной, поскольку
ТЖ0Т+ =Жо-^{р-УХ + (Vx) • Р] + ?(VxJ ф Жо. E.А.10)
В общем случае, любой оператор, который является функцией только нефизических
величин, таких как канонический импульс р или векторный и скалярный потенциалы
Ах и Ux, представляет собой нефизическую величину. Полный гамильтониан
Ж* = ^[р - eAx(r, t)f + ellx(r, t) + V(r). E.A.11)
также является нефизической величиной, поскольку он зависит от скалярного по-
потенциала Ux.
Поэтому мы приходим к выводу, что временная эволюция физической системы
определяется такими гамильтонианами, как Жх или Ж®, которые, в общем случае, не
являются наблюдаемыми величинами. Физическими величинами являются, напри-
например, механический импульс и мгновенная энергия системы.
П.5.А Эквивалентность (г • Е)~ и (р • А.)-гамильтонианов 149
5.А.2. Вероятности переходов в двухуровневом атоме. В этом разделе мы огра-
ограничимся обсуждением длинноволнового дипольного приближения (ДДП), в котором
потенциал А можно рассматривать как не зависящий от г, т.е. А(г, i) = A(t).
Поскольку оператор энергии <§х (см. E.А.8)) зависит от времени, его собственные
состояния |ах(?)), где а = а, 6, и его собственные значения Еа = !гша в общем
случае также зависят от времени, а именно
?x\ax(t)) = Ea\ax(t)). E.A.12)
Тем не менее в ДДП собственные значения «§х не зависят от времени. Это можно
показать с помощью калибровочного преобразования E.А.1). В ДДП
[^] [Р - eA(t)]2 exp [*^] = v\ E.A.13)
так что
ехр Y— cfxexp Y— = Ж®. E.А.14)
Тогда, собственное состояние \otx) связано с собственным состоянием
л. / ч гамиль-
гамильтониана Жо соотношением
ах) = ехр ^— |o:(t)), E.A.15)
и собственные значения i?a оператора ёх совпадают с не зависящими от времени
собственными значениями Еа гамильтониана Жд^ так как собственные значения
физических величин не зависят от калибровки.
В Е'-калибровке оператор невозмущенной энергии $е равен невозмущенному
гамильтониану Ж®. Следовательно, собственные состояния Жд являются также соб-
собственными состояниями $е- Поэтому только в Е-калибровке волновая функция
разлагается по собственным состояниям энергии, и коэффициенты ca(t), где а =
= а, 6, в формулах E.2.10) и E.2.11) интерпретируются как амплитуды вероятности
нахождения системы в собственном состоянии наблюдаемой энергии. В любой другой
калибровке Жд — нефизическая величина, и ее состояния не являются собственными
состояниями энергии системы. Тогда коэффициенты разложения ca(t) в выражениях
E.2.10) и E.2.11) являются амплитудами вероятности найти систему в собственном
состоянии гамильтониана Жд. Между тем, если Жд — нефизическая величина, то
эта вероятность зависит от калибровки, и ее нужно отличать от измеряемой,
калибровочно-инвариантной вероятности найти систему в собственном состоянии
энергии.
Поэтому полезно разложить волновую функцию системы по собственным состоя-
состояниям оператора энергии #х:
\Фх(г)) = da(t) e~iuJat\ax) + db(t) e~iuJbt\bx). E.A.16)
Тогда коэффициенты разложения da и d^ совпадают с амплитудами вероятности
переходов системы в собственные состояния \ах) и \ЬХ) оператора энергии $х с соб-
собственными значениями Нша и
da{t) = (ax\il>x(t)) eiu-\ E.A.17)
db{t) ^ {bx\i,x{t)) e^. E.Д.18)
150
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
Теперь явно покажем, что эти амплитуды калибровочно инвариантны.
В I^-калибровке амплитуда вероятности da(t) задается в виде
df (<) = {a\U0{t)U?\t)\b) e--*,
а в Я-калибровке — в виде
d^(t) = (а\ ехр
где Uo{t) = ехр(-
\Ь)
E.А.19)
E.А.20)
E.А.21)
Здесь мы полагаем, что атом первоначально находился в основном состоянии \Ь).
Аналогичные выражения существуют для амплитуд d^{i) и d^(t). В первом порядке
ггA)
теории возмущении оператор эволюции во времени и г принимает вид
E.А.22)
а амплитуда вероятности возбужденного состояния в iiJ-калибровке описывается
выражением
¦i<
= ^ • <а
r|fc) dn
j
о
-. E.А.23)
Сравним этот результат с соответствующим результатом в R-калибровке. В первом
порядке теории возмущений
1+»бА@)т1 ^eiUatm E>A824)
в низшем порядке по «й^ получаем
Используя E.1.26), E.2.32) и
Из E.1.30) имеем ра5 = +гтштаъ и, определяя ё = ius^', получаем
егД(-
E.A.25)
П.5.Б Векторная модель матрицы плотности 151
Таким образом, амплитуды df' (t) и d^(t) оказываются идентичными. Это разреша-
разрешает г) очевидное противоречие, отмеченное в конце разд. 5.1.
Приложение 5.Б
Векторная модель матрицы плотности
Физическое описание матрицы плотности можно получить, приведя уравнения
E.3.22), E.3.23) и E.3.30) к виду, эквивалентному уравнениям Блоха, применяемым
в теории ядерного магнитного резонанса. Рассматриваемая проблема двухуровне-
двухуровневой системы, взаимодействующей с электромагнитным полем, похожа на задачу о
магнитном диполе со спином 1/2, испытывающим прецессию в магнитном поле. Эта
формальная аналогия привела к предсказанию, наблюдению и пониманию физики
большого числа явлений, связанных с распространением когерентного импульса
в системе двухуровневых атомов.
Введем действительные величины
Ri= Раье^ + к.с, E.Б.1)
R2 = ipabeil/t+K.c, E.Б.2)
R-i^Paa-рЬЬ- E-Б.З)
Эти величины являются составляющими вектора R, заданного выражением
R = fliei + Я2е2 + Д3е3, E.Б.4)
где ei, ё2 и ез образуют набор взаимно перпендикулярных единичных векторов.
Здесь R\ и R,2 представляют атомный дипольный момент, а R$ — разность населен-
ностей между уровнями \а) и \Ъ).
Из уравнений E.3.22), E.3.23) и E.3.30) следует, что в приближении вращающейся
волны (при 0 = 0)
^ E.Б.5)
E.Б.6)
^ E.Б.7)
где мы положили ja = 7ь = l/^i и 7 = 1/^2- Величины Т\ и Т^ соответственно
называются продольным и поперечным временами релаксации по аналогии с соот-
соответствующими величинами в уравнениях Блоха. Уравнения E.Б.5)—E.Б.7) называют
оптическими уравнениями Блоха.
Когда Т\ = Т2, эти уравнения можно записать в следующей компактной форме:
R= -™R-[-Rx О, E.Б.8)
где эффективное поле задано выражением
- Де2. E.Б.9)
) Представленное описание слишком упрощено в том плане, что не учитываются эффекты
атомной релаксации. Рассмотрение более общего случая можно найти в работе Lamb,
SchJtcher and Scully A987).
152
Взаимодействие атома с полем — полуклассическая теория
Гл. 5
Зависимость R от времени, задаваемая выражением E.Б.8), хорошо известна из клас-
классической механики. Вектор R прецессирует по часовой стрелке вокруг эффективного
поля О, затухая по амплитуде. Прецессия в случае точного резонанса и в случае
Ш < V
(а) (б)
Рис. 5.9. Прецессия вектора Блоха R вокруг эффективного поля О: А = 0 (а) иД/0 (б)
небольшой отстройки от резонанса изображены на рис. 5.9. Физически вектор R,
направленный вдоль ез (Кз = 1, R\ = R2 = 0), изображает систему, находящуюся
в возбужденном состоянии, когда раа = 1, ръъ = 0. Аналогичным образом вектор R,
направленный вдоль — е"з? изображает систему в ее основном состоянии.
Приложение 5.В
Физика квазимод лазера, основанная на модах вселенной г)
Многие теории лазеров, например, та, что представлена в разд. 5.5, описывают
электромагнитное поле с помощью дискретного набора квазимод резонатора лазера,
каждая из которых имеет конечную добротность Q. В данном разделе эта теория
обобщается на случай лазера с резонатором, который моделируется полупрозрачной
стенкой в качестве одного из зеркал, так что теперь присутствует множество мод
«вселенной», соответствующих каждой квазимоде. Здесь мы покажем, что нормаль-
нормальные моды вселенной, связанные с одной «модой», при определенных условиях могут
синхронизоваться, и может восстановиться «5-образная линия излучения лазера.
Рассмотрим нормальные моды для комбинированной системы, состоящей из ла-
лазерного резонатора, связанного с внешним миром. Изобразим «вселенную» с помо-
помощью существенно большего резонатора, имеющего идеально отражающие стенки.
Простая одномерная модель, которая имеет основные черты такой комбинированной
системы, показана на рис. 5.10. Зеркала в точках z = L и -Lq являются абсолютно
отражающими, в то время как зеркало в точке z = 0 — полупрозрачное. Область 1
соответствует резонатору лазера, а область 2 — остальной части вселенной.
Представим полупрозрачное зеркало в виде очень тонкой пластинки с очень боль-
большой диэлектрической константой. В качестве идеализации такого зеркала выберем
1) Для дальнейшего чтения рекомендуем Lang, Scully and Lamb A973).
П.5.В
Физика квазимод лазера, основанная на модах вселенной
153
Область 2
Область 1
7
/
/
/
/
/
•. : •: •
• • *•• •• •
.• •
-L0
О
Рис. 5.10. Резонатор с утечкой, который состоит из идеального зеркала, расположенного
в точке z = L, и полупрозрачного зеркала, расположенного в точке z = 0. Смежный
резонатор, который вместе с резонатором с утечкой объемлет всю вселенную, состоит из
идеального зеркала, расположенного в точке z = —Lq (Lq —^ ооM и зеркала, расположенного
в точке z = 0
диэлектрическую константу в окрестности точки z = 0, равную
ф) = eo[l + 77<*(z)], E.B.1)
где 1) — параметр с размерностью длины, который определяет прозрачность этой
пластинки.
Функции нормальных мод этой системы можно получить, решая уравнения
Максвелла с соответствующими граничными условиями (см. задачу 5.6). Для тех
нормальных мод, которые имеют частоту f&(= ck), близкую к «резонансной» частоте
щ(= ско), собственные функции всего резонатора имеют вид
Mksmk(z - L) (z > 0),
Ck sin k(z + L) (z<0),
E.B.2)
где ^k — фазовый множитель, который меняется между значениями 1 и — 1 при
возрастании к от одного значения до следующего. Коэффициенты М^ в E.В.2) имеют
вид
= ^ [(I/*-i/oJ + ^
E.B.3)
где <& — спектральная полоса, связанная с прозрачностью зеркала и определяемая
выражением
«if =-^^- = -^-, E.B.4)
где
Л =
Г) I/Q
ко '
а частота щ для п-й квазимоды дается выражением
. (п7Г
щ = ск0 = ±
E.В.6)
Произвольное неуправляемое поле во всем резонаторе можно выразить через
положительно-частотную часть поля:
E.В.7)
154 Взаимодействие атома с полем — полуклассическая теория Гл. 5
что можно рассматривать как сумму мод большого резонатора, т. е. «вселенной».
Теперь продемонстрируем, что полу прозрачность зеркал приводит к затуханию
свободных колебаний в лазерном резонаторе. Предположим, что в момент времени
t = 0 лазерный резонатор (область 1) содержит поле вида
#(+)(*, 0) = l^ole-^sinfcoOz- Ь), E.В.8)
в то время как вне резонатора, т. е. в области 2, поля нет. В этом случае коэффициенты
<?&(()) находим, умножая E.В.8) на функцию Uk{z), задаваемую выражением E.В.2),
и интегрируя по z. Результат имеет вид
E.B.9)
Поэтому на более поздних временах, t > 0,
E(z, t) = №o\L/Lo) X) MkUk(z) e-^+rt. E.B.10)
к
Суммирование можно приближенно заменить интегрированием, если частотный
интервал между нормальными модами мал по сравнению с сё). После выполнения
интегрирования по к в E.В.10), явное выражение для E(z, i) в резонаторе лазера
приобретает вид
E{+\z, 0) = Ко| sin ko{z - L) e-*("*t+?>)-*V2e E.B.11)
Выралсение E.В.11) означает, что поле, локализованное в резонаторе лазера, экспо-
экспоненциально затухает со скоростью ^/2, благодаря утечке через зеркало.
Задачи
5.1. Покажите, что уравнение Шредингера E.1.5) инвариантно при локальных
калибровочных преобразованиях E.1.4), E.1.6) и E.1.7).
5.2. Конечность времени жизни атомных уровней можно описать, добавляя фено-
феноменологические релаксационные члены в уравнения для амплитуд вероятности
E.2.12) и E.2.13):
^ у гфсь, сь = -^сь + -у- е%фса,
где 7 — константа затухания ш ш = и. Покажите, что для атома, первоначально
находившегося в состоянии |а), инверсия в момент времени t имеет вид
W(t) = e^7*cos(OKt).
5.3. Найдите решение уравнения E.Б.8) (при 7\ —> оо)
для R@) = 0. Дайте физическую интерпретацию этого решения.
Задачи к гл. 5 155
5.4. Покажите, что в общем случае
где равенство справедливо только для чистого состояния.
5.5. Рассмотрите трехуровневый атом, взаимодействующий с классическим полем
частотой и. Переходы \а) —» \Ъ) и \Ь) —>> \с) разрешены, тогда как переход \а) -^
—>• \с) —запрещен. Также предполагается, что ша — шь = шъ^шс = и. Предпола-
Предполагая, что атом первоначально находился на уровне |с), и применяя приближение
вращающейся волны, найдите вероятности того, что атом находится на уровнях
а) и |с).
5.6. Электромагнитное поле во всем резонаторе (области 1 и 2 на рис. 5.10) удовле-
удовлетворяет волновому уравнению Максвелла
где Е можно записать как Е = Uk{z) exp(—гг/^t).
1. Найдите Uk{z) в виде E.В.2) и докажите что
Ml tg2kL + l
it tgJ ifeZ, + (Л tg AjZ, - IJ '
где величина Л задается выражением E.В.5). Выведите уравнение E.В.З).
2. Покажите, что
dzUk(z)Ukf(z)s(z) = 01
где e(z) = 6qA + rjS(z)). (Указание: см. работу Lang, R., Scully, M.O. and
Lamb, W.E., Jr. Phys. Rev. A 7, 1788 A973).)
5.7. Уровень m = +1 на рис. 5.3 слабо связан с уровнем фь{г) светом с левой кру-
круговой поляризацией через противоположно вращающиеся члены в выражении
E.2.55). Отметим, что в этом случае (переход т = 0 —> т = +1) обычно
исключают такую связь на основании того, что для перехода m = 0^m = +l
необходим свет с правой круговой поляризацией.
1. Покажите, что если определить
где tj — несущественная константа [у64тшд ао]^1, то
yafb(t) = ^е# dr Фа(г) r-(x cos vt—y sin ut) фь(г) etuJa'bt = —p^ e2^'6^^.
156 Взаимодействие атома с полем — полуклассическая теория Гл. 5
2. Покажите, на определенном примере, что члены с противоположным вра-
вращением, связанные с переходами \Ь) —>• |а;M которые пропорциональны
[<ша'Ь + И™1? могут оказаться намного меньше обычных членов с противо-
противоположным вращением [u^H-i/]. (Указание: рассмотрите атом Ридберга,
в котором шаъ = (л)а'Ь — 10° Гц. Если теперь приложить поле порядка 104Гс,
то можно сделать шаъ порядка 103 Гс за счет зеемановского сдвига, в то
время как шац, ~ Ю10 Гс.)
Список литературы
Монографии
*Файн В.М., Ханин Я.И. Квантовая радиофизика (Сов. радио, Москва, 1965).
* Карлов Н.В. Лекции по квантовой электронике (Наука, Москва, 1983).
*Альперин М.М., Клубис Я.Д., Хижняк А.И. Введение в физику двухуровневых систем
(Hayкова думка, Киев, 1987).
Saleh, В. Е. A. and Telch, М. С. Fundamentals of Photonics, (Wiley-Intersclence, New York
1991).
*Ахманов С.А., Никитин СЮ. Физическая оптика (МГУ, Москва, 1998).
*Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика (Физматлит,
Москва, 2000).
Гамильтониан взаимодействия атома с полем
Goppert-Mayer, M. Ann. Phys. (Leipzig) Э, 273 A931).
Power, E. A. and Zlenau, S. Philos. Tran. Roy. Soc. London 251, 427 A959).
Cohen-Tannoudji, C, Dupont-Roc, J. and Grynberg, G. Atom-Photon Interactions, (Wiley, New
York 1992).
Взаимодействие двухуровневого атома с одномодовым полем
Bethe, H. A. In Quantentheorie, Vol. 24/1 of Handbuch der Physik, 2nd ed. (Springer, Berlin
1933), p. 273.
Lamb, W. E. and Retherford, R. C. Phys. Rev. 72, 339 A947).
Feynman, R. P., Vernon, F. L. and Hellworth, R. W. J. Appl. Phys. 28, 49 A957).
Jaynes, E. T. and Cummlngs, F. W. Proc. IEEE 51, 89 A963).
Allen, L. and Eberly, J. Optical Resonance and Two Level Atoms, (Wiley, New York 1975).
[Аллен Л., Эберли Дж. Оптический резонанс и двухуровневые атомы (Мир, Москва,
1978).]
Stenholm, S. Foundations of Laser Spectroscopy, (Wiley, New York 1984).
*Осадько И.С. Селективная спектроскопия одиночных молекул (Физматлит, Москва, 2000).
Экспериментальная реализация двухуровневого атома
Abate, J. A. Opt Commun. 10, 269 A974).
Grove, R. E., Wu, F. Y. and Ezekiel, S. Phys. Rev. A 15, 227 A977).
Meschede, D., Walther, H. and Muller, G. Phys. Rev. Lett 54, 551 A985).
Сравнение (р • А)- и (г • Е)-гамильтонианов
Lamb, W. E., Jr., Proc. Scuola Internazionale di Fisica Course XXXI, Academic Press 1963.
Haken, H. Z. Phys. 181, 96 A964).
Список литературы к гл. 5 157
Lamb, W. E., Jr., Phys. Rev. 85, 259 A952).
Yang, К. Н. Ann. Phys. (NY) 101, 62 A976).
Kobe, D. H. and Smirl, A. L. Am. J. Phys. 46, 624 A978).
Schllcher, R. R., Becker, W., Bergou, J. and Scully, M. O. In Quantum Electrodynamics and
Quantum Optics, ed. A. O. Barat (Plenum, New York 1984), p. 405.
Becker, W. Opt Commun. 56, 107 A985).
Lamb, W. E., Jr., Schllcher, R. R. and Scully, M. O. Phys. Rev. A 36, 2763 A987).
Мазер
Gordon, J. P., Zelger, H. J. and Townes, С. Н. Phys. Rev. 95, 282 A954); ibid. 99, 1264 A955).
Лазер
Malman, Т. Н. Nature 187, 493 A960).
Javan, A., Bennet, W. R., Jr., and Herrlot, D. R. Phys. Rev. Lett 6, 106 A961).
Полуклассическая теория лазера
Prokhorov, A. M. Sov. Phys. JETP 34, 1658 A958).
Schawlow, A. L. and Townes, С. Н. Phys. Rev. 112, 1940 A958).
Haken, H. and Sauermann, H. Z. Phys. 173, 261 A963); ibid. 176, 47 A963).
Proc. Enrico Fermi School of Physics, Course XXXI, p. 78 A963)
Lamb, W. E., Jr., Phys. Rev. 134, A1429 A964).
Sargent III, M., Lamb, W. E., Jr. and Fork, R. L. Phys. Rev. 164, 450 A967).
Stenholm, S. and Lamb, W. E., Jr., Phys. Rev. 181, 618 A969).
Haken, H. Laser Theory, (Springer, Berlin 1970).
Lamb, W. and Scully, M. OSA Spring 1971, p. 66.
Sargent III, M., Scully, M. and Lamb, W. E., Jr., Laser Physics (Addlson-Wesley, Reading, MA
1974).
Siegman, A. E. Lasers (Univ. ScL Books, Mill Valley, CA 1986).
Milonni, P. and Eberly, J. Lasers (Wiley, New York 1988).
* Боровский А.В., Галкин А. Л. Лазерная физика (Изд. атом, техн., Москва, 1996).
Лазерный усилитель
АгессЫ, F. Т. and Bonifacio, R. IEEE Journal of Quantum Electronics QE-1, 169 A965).
Hopf, F. A. and Scully, M. O. Phys. Rev. 179, 399 A969).
* Карлов Н.В., Маненков А. А. Квантовые усилители (ВИНИТИ, Москва, 1966).
Моды лазерного резонатора
Fox, A. G. and Li, Т. Bell System Tech. J. 40, 453 A961).
Boyd, G. D. and Gordon, J. P. Bell System Tech. J. 40, 489 A961).
*Файн В.М., Ханин Я.И. Квантовая радиофизика (Сов. радио, Москва, 1965).
Spencer, М. В. and Lamb, W. E., Jr., Phys. Rev. A 5, 884 A972).
Lang, R., Scully, M. O. and Lamb, W. E., Jr., Phys. Rev. A 7, 1788 A973).
Lang, R. and Scully, M. O. Opt. Commun. 9, 331 A973).
Ujihara, K. Phys. Rev. A 12, 148 A975); ibid. 16, 652 A977).
*Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн (Наука, Москва, 1979).
*Ораевский А.Н., УФЫ 164, 415 A994); Квантовая электроника 29, 137 A994).
158 Список литературы к гл. 5
Спектроскопия с временным разрешением
FIgger, H. and Walther, H. Z. Phys. 267, 1 A974).
Meystre, P., Scully, M. and Walther, H. Opt. Commun. 33, 153 A980).
*Набойкин Ю.В., Самарцев В.В., Зиновьев П.В., Силаева Н.Б. Когерентная спектроскопия
молекулярных кристаллов (Наукова думка, Киев, 1986).
*Кессель А.Р., Моисеев С.А. Письма ЖЭТФ 58, 77 A994).
Demtroder, W. Laser Speciroscopy, (Springer, Berlin 1995). [Демтредер В. Лазерная спектро-
спектроскопия (Наука, Москва, 1995).]
*Mohan, R.K., Luo, В., Kroll, S., Malr, A. Phys. Rev. A 58, 4348 A998).
Глава 6
ВЗАИМОДЕЙСТВИЕ АТОМА
С ПОЛЕМ — КВАНТОВАЯ
ТЕОРИЯ
В предыдущих главах, касающихся взаимодействия поля излучения с веществом,
поле предполагалось классическим. Во многих случаях это предположение справед-
справедливо. Тем не менее есть много примеров, когда классическое поле не может описать
экспериментально наблюдаемые результаты, и необходимо квантовое описание поля.
Это, например, справедливо для спонтанного излучения атома, которое феноменоло-
феноменологически описывалось в гл. 5. Для строгого описания распада возбужденного атомного
состояния в свободном пространстве необходимо рассмотреть взаимодействие атома
с вакуумными модами «вселенной». Даже в простейшей системе, которая включает
в себя взаимодействие одномодового излучения с одиночным двухуровневым атомом,
предсказания динамики атома в полуклассической теории и полностью квантовой
теории существенно отличаются. В отсутствие процессов распада полу классическая
теория предсказывает осцилляции Раби для атомной инверсии населенности, тогда
как квантовая теория предсказывает некие явления коллапса и возрождения. Эти
интересные предсказания квантовой теории поля были уже экспериментально про-
проверены.
В этой главе мы обсудим взаимодействие квантованного поля излучения с двух-
двухуровневой атомной системой, которое описывается гамильтонианом в дипольном
приближении и приближении вращающейся волны. Для одномодового поля гамиль-
гамильтониан сводится к очень простой форме. По ряду причин — это особенно приме-
примечательный гамильтониан в квантовой оптике. Во-первых, для него задачу молено
решить точно при произвольной константе связи, и он демонстрирует некоторые
истинные квантово-механические эффекты, такие как коллапс атомной инверсии с
последующими периодическими возрождениями. Во-вторых, он дает простейшую ил-
иллюстрацию спонтанного излучения и поэтому объясняет эффекты различных видов
статистики поля в более сложных системах, таких как микромазер и лазер, которые
мы рассмотрим в последующих главах. В-третьих, и пожалуй это самое главное,
благодаря замечательным успехам в развитии микроволновых резонаторов с высокой
добротностью Q г) такой гамильтониан стало возможным воплотить в эксперименте.
Спонтанный распад атомного уровня описывается с помощью рассмотрения вза-
взаимодействия двухуровневого атома с модами вселенной в вакуумном состоянии.
Мы исследуем состояние поля, которое рождается в процессе испускания кванта
энергии, равного разности энергий атомных уровней. Такое состояние можно считать
однофотонным состоянием.
) Здесь можно выделить микромазер Вальтера с соавторами, который обсуждается
в гл. 13. См. также статью Ароша и Клеппнера в Physics Today (Haroche and Kleppner, 1989),
которая дает очень хорошее представление о квантовой электродинамике для резонатора.
160 Взаимодействие атома с полем — квантовая теория Гл. 6
6.1. Гамильтониан взаимодействия атома с полем
Взаимодействие поля излучения Е с одноэлектронным атомом можно описать
в дипольном приближении следующим гамильтонианом:
Ж = ЖА + ЖР - ег • Е. F.1.1)
Здесь Жа и Жр — энергии атома и поля излучения, соответственно, в отсутствие
взаимодействия, иг — радиус-вектор электрона. В дипольном приближении поле
предполагается однородным по всему атому.
Энергия свободного поля Жр выражается через операторы рождения и уничто-
уничтожения следующим образом:
к
Можно выразить Жа и ег через операторы атомных переходов:
°а = \Ш- F.1.3)
Как и ранее, {|г)} представляет собой полный набор собственных энергетических
состояний атома, т.е. J^i l*)(*l = 1- Тогда из уравнения для собственного значения
Ж^\ъ) = Ei\i) следует, что
Yi Y^icrii. F.1.4)
г i
А также
где pij = e(i|r|j) — матричный элемент электрического дипольного перехода. В ди-
дипольном приближении оператор электрического поля вычисляется в координатах
точечного атома. Из уравнения A.1.27) следует, что для атома, находящегося в начале
системы координат, имеем выражение
E = 53?k<?k(ok + a+), F.1.6)
к
где <lk = (^|/ife/2so^I • Здесь, для простоты, мы используем базис линейной поля-
поляризации и действительные единичные векторы поляризации.
Следовательно, подставляя Жа, Жр^ ег и Е из F.1.2), F.1.4), F.1.5) и F.1.6)
в выражение F.1.1), получаем
Ж =
k i i,j k
где
g« = _?«ipA. F.L8)
В выражении F.1.7) мы опустили в первом члене энергию нулевых колебаний. Далее
в этой главе, для простоты, будем считать ^^j действительной величиной.
Теперь приступим к рассмотрению двухуровневого атома. В случае, когда 0^аь =
= ?^baj запишем
6.1 Гамильтониан взаимодействия атома с полем 161
Тогда гамильтониан приобретает следующий вид:
к + (Еаааа + Ebabb) + h^g^{aab + aba){a^ + a+). F.1.10)
к к
Второй член в уравнении F.1.10) можно записать как
Еаааа + ЕьаЬЪ = \Пш{ааа - аьь) + \{Еа + Еь), F.1.11)
где использованы соотношения (Еа — Еь) = Яш, и ааа + (Тьъ = 1- Членом с постоянной
энергией (Еа + Еь)/2 можно пренебречь. Если использовать обозначения
(Jz = (Jaa - (ТЬЪ = \п) (п\ - \Ь){Ъ\, F.1.12)
а+ = ааЬ = \а){Ь\, F.1.13)
<т- = <тьа = \Ь)(а\, F.1.14)
то гамильтониан F.1.10) приобретает вид
Ж = ^2^ика^а^ + 2^cjctz + Я^^к(сг+ + cr^)(ak + a?). F.1.15)
к к
Из тождества
kij, ^fcl] = CTi/^-fe - (TkjSu F.1.16)
следует, что <j+, а_ и <rz удовлетворяют алгебре спина 1/2 для матриц Паули, т.е.
[<7_,<7+] = -<7г, F.1.17)
[G_,Gг] =2<7_. F.1.18)
В матричном виде сг+, сг^ и сг^ записываются следующим образом:
/0 0\ /0 1\ /1 0
Оператор <т^ переводит атом из верхнего состояния в нижнее состояние, тогда как
сг+ переводит атом из нижнего состояния в верхнее состояние.
В выражении F.1.15) энергия взаимодействия состоит из четырех членов. Член
a^(j_ описывает процесс, в котором атом переводится из верхнего состояния в ниж-
нижнее состояние и испускается фотон моды к. Член а^а^. описывает противоположный
процесс. Энергия сохраняется в обоих случаях. Член а^а^ описывает процесс, в кото-
котором атом переходит из верхнего состояния в нижнее состояние и фотон уничтожается,
что приводит к потере энергии, примерно равной 2huj. Аналогично ajtr+ описывает
процесс с увеличением энергии на 2huj.
Пренебрежение членами, которые не сохраняют энергию, соответствует прибли-
приближению вращающейся волны. В результате такого приближения получается упрощен™
ный гамильтониан, который имеет вид
\ ак °"-)- F.1.20)
Гамильтониан такого вида, который описывает взаимодействие одиночного атома
с многомодовым полем, является отправной точкой во многих расчетах в области
квантовой оптики.
6 М.О. Скалли, М.С. Зубайри
162 Взаимодействие атома с полем — квантовая теория Гл. 6
6.2. Взаимодействие одиночного двухуровневого атома с одномодовым
полем
Из F.1.20) следует, что взаимодействие одномодового квантованного поля часто-
частоты и с одиночным двухуровневым атомом описывается гамильтонианом
Ж = Жп + Жх, F.2.1)
где
Жг = hg{a+a + а+а^). F.2.3)
Здесь индекс константы взаимодействия g опущен. Гамильтониан, заданный вы-
выражениями F.2.1)-F.2.3), описывает взаимодействие атома с полем в дипольном
приближении и в приближении вращающейся волны. Как будет показано ниже,
этот важный для квантовой оптики гамильтониан дает нам точно решаемый пример
атомно-полевого взаимодействия.
Удобно работать в представлении взаимодействия. Гамильтониан в этом пред-
представлении имеет вид
Используя формулу
еаЛв ^аЛ = в + а[д щ + |! [ д [д ?]] + ..., F.2.5)
нетрудно убедиться, что
ei^a+ata e-iva+at = fl g-ii/t ? F-2.6)
Комбинируя выражения F.2.1)-F.2.3), F.2.4), F.2.6) и F.2.7), получаем
Г = hg{a+a eiAt + a+a^ e^iAt), F.2.8)
где А = ш — u.
В этом разделе мы представим три различных, но эквивалентных метода решения
задачи эволюции системы «атом + поле», описываемой гамильтонианом F.2.1)—
F.2.3). Первый метод основан на решении уравнений для амплитуд вероятности,
второй — на использовании операторов Гейзенберга для поля и атома, третий — на
унитарном операторе эволюции во времени.
6.2.1. Метод амплитуд вероятности. Сначала решим уравнение движения для
|^), т.е.
ift^f = r№>. F.2.9)
В любой момент времени t вектор состояния \ip(t)) является линейной комбинацией
состояний \а, п) и |6, п). Здесь |а, п) — состояние системы, при котором атом находит-
находится в возбужденном состоянии |а), а поле имеет п фотонов. Аналогично описывается
состояние |6, п). Используя представление взаимодействия, вводим медленно меняю-
меняющиеся амплитуды вероятности сп)П и сьуП- Поэтому вектор состояния имеет вид
>]. F.2.10)
6.2
Взаимодействие одиночного двухуровневого атома с одномодовым полем
163
Взаимодействие F.2.8) может вызывать только переходы между состояниями |а, п)
и |6, п + 1). Поэтому рассмотрим эволюцию амплитуд вероятности са?п и сь,п+1- Урав-
Уравнения движения для амплитуд са}П и C5,n+i можно получить, подставляя сначала
выражения F.2.10) и F.2.8) для \ip(t)} и У в уравнение F.2.9), а затем проецируя
результат соответственно на(а,п|иF,п +
В результате получаем
г А*
F.2.11)
F.2.12)
Эта связанная система уравнений очень похожа на ту, которая была получена в полу-
полуклассическом описании (ср. с E.2.12) и E.2.13)). Эти уравнения можно решить точно
при определенных начальных условиях. Общее решение для амплитуд вероятности
имеет вид
(+\ - / (п\ \ (?hd\ _ i*. - f^l\] _
Ca^n{^LJ — л Ca,n\}j) COS II „ Sin I J
^ L \ ^ / *'n V <" / -I
2igy/n + 1 fm /Ont\ 1 iAt/2 ffi2144
tont\ . гА . /Ont\l
—^—J + ^- Sin |^—^—J J -
F.2.14)
где
O^ = A2 + 4g-2(n + 1). F.2.15)
Если атом первоначально находился в возбужденном состоянии |а), то cOjn@) =
= сп@), и C5,n+i@) = 0. Здесь сп@) — амплитуда вероятности только для поля.
Тогда получаем
= cn@)[cos(^)
гД
At/2
F.2.16)
F.2.17)
Эти уравнения дают полное решение задачи. Из них можно получить все основные
физические величины, относящиеся к квантованному полю и атому. Выражения
для |ca>ri|2 и |с5)П|2 представляют собой вероятности того, что в момент времени t
имеется п фотонов и атом находится соответственно в состоянии \а) или \Ь). Поэтому
вероятность р(п) того, что в момент времени t в поле имеется п фотонов, можно
получить, взяв след по атомным состояниям, т. е.
р(п) = \ca,n{t)\2 + \cbjn{t)\2 = Pnn@)x
X COS
(?)
F.2.18)
где рпп = \cn
— вероятность того, что в момент времени t = 0 в поле имеется
п фотонов. На рис. 6.1 представлен график зависимости р(п) для начального коге-
когерентного состояния:
Рпп@) =
F.2.19)
164
Взаимодействие атома с полем — квантовая теория
Гл.6
р(п)
О 10 20 30 40 50 60 70 80 90 100
Рис. 6.1. Зависимость р(п), задаваемая формулой F.2.18), которая справедлива если в
качестве начального состояния взято когерентное состояние поля. Использованы следующие
значения параметров: А = 0, (п) = 25 и gt = 10
Другой важной величиной является инверсия VF(t), которая связана с вероятно-
вероятностями
Ca,n(t)\2 и |сб,п(
выражением
F.2.20)
Подставляя ca?n(t) и с&}П(?) из выражений F.2.16) и F.2.17), после некоторых пре-
преобразований получаем
ui
¦ cos{Q.nt) .
F.2.21)
Интересно отметить, что если даже взять в качестве начального состояния ваку-
вакуумное поле (рпп@) = <5„оM то
W(t) =
cos[(A
4]
F.2.22)
т. е. имеют место осцилляции Раби. Этот результат совершенно отличается от пред-
предсказаний полу классической теории, рассмотренной в гл. 5. В полу классической тео-
теории атом, находящийся в возбужденном состоянии, не может совершить переход
в нижнее состояние в отсутствие возбуждающего поля. В полностью квантово-
механическом описании переход из верхнего состояния в нижнее состояние становит-
становится возможным в вакууме благодаря спонтанному излучению. Процесс, описываемый
формулой F.2.22), является самым простым примером спонтанного излучения, в ко-
котором спонтанно испущенный фотон вносит вклад в рассматриваемую одиночную
моду. Подробный анализ спонтанного излучения атома в свободном пространстве,
обусловленного наличием бесконечного числа вакуумных мод, будет рассмотрен
в следующем параграфе.
6.2 Взаимодействие одиночного двухуровневого атома с одномодовым полем 165
На рис. 6.2 приведена величина W(t) как функция от безразмерного времени
т = gt, при условии, что в качестве начального состояния выбрано когерентное
состояние. Поведение W(t) совершенно отличается от соответствующей зависимости
(рис. 5.2) в полуклассической теории. В рассматриваемом случае огибающая сину-
Рис. 6.2. Эволюция инверсии населенности W(t) во времени в случае, когда начальным со-
состоянием является когерентное состояние. Использованы следующие значения параметров:
(п) = 20 и А = 0
соидальных осцилляции Раби «коллапсирует» до нуля. Тем не менее, с увеличением
времени мы сталкиваемся с «возрождением» исчезнувшей инверсии. Такое поведение
коллапса и возрождения инверсии повторяется со временем, причем амплитуда
осцилляции Раби уменьшается, а продолжительность возрождения увеличивается
и в конце концов наступает перекрытие более поздних возрождений с предыдущими.
Физику явлений коллапса и возрождения можно понять из выражения F.2.21).
Каждый член суммы отвечает за осцилляции Раби для определенной величины
п. Функция распределения фотонов рпп@) определяет относительный вес каждой
величины п. Считаем, что в начальный момент времени, t = 0, атом находится в опре-
определенном состоянии и поэтому все члены суммы скоррелированы. Осцилляции Раби,
связанные с различными типами возбуждений, имеют разные частоты, и поэтому
с течением времени они становятся некоррелированными, что и приводит к коллапсу
инверсии. В дальнейшем корреляция восстанавливается и происходит возрождение.
Продолжая этот процесс, получаем бесконечную последовательность возрождений.
Важным моментом здесь является то, что возрождения происходят только благодаря
дискретной структуре распределения фотонов. Таким образом, возрождение явля-
является чисто квантовомеханическим явлением. Непрерывное распределение фотонов
(без нулей) дало бы тоже коллапс, как и в случае классического случайного поля, но
без возрождений.
Простые выражения для времен ?#, tc и tr, связанных с синусоидальными ос™
цилляциями Раби, коллапсом этих осцилляции и их возрождением, можно найти из
F.2.21) в пределе (п) ^> 1. Период tn осцилляции Раби задан обратной величиной
166 Взаимодействие атома с полем — квантовая теория Гл. 6
частоты Раби Оп при п = (п), т.е.
Как упоминалось ранее, эти осцилляции Раби продолжаются до момента времени
коллапса tc, когда колебания, связанные с различными значениями п, становятся
некоррелированными. Теперь учтем, что для распределения Пуассона F.2.19) пер-
первоначально когерентного поля среднеквадратичный разброс числа фотонов An равен
у(п) • Поэтому оценку tc можно получить из условия
(п, /— - О г—) tc - 1. F.2.24)
V (n) + \/(n) (n)-y/(n)J с х J
Поскольку (п) ^> \/(п) в пределе (п) ^> 1, выражение F.2.24) дает
[А2 + 4g2
В случае точного резонанса, А = 0, время коллапса tc равно l/2g и не зависит
от среднего числа фотонов (п). При отличной от нуля расстройке, tc увеличивается
с ростом (п). Промежуток времени tr между возрождениями можно найти из условия
(О(п) - ft<n>_i)tr = 2тгт (т = 1, 2, . . .), F.2.26)
т. е. возрождения имеют место, когда фазы колебаний соседних членов в F.2.21)
отличаются на число, кратное 2тг. В пределе (п) ^> 1 вновь получаем
F-227)
где тя — целое число. Отсюда видно, что возрождения происходят через регулярные
интервалы времени.
6.2.2. Метод оператора Гейзенберга. До сих пор мы рассматривали задачу взаи™
модействия одномодового квантованного поля с одиночным двухуровневым атомом
в картине взаимодействия. Ниже дано решение этой же задачи в представлении
Гейзенберга. В частности, мы решаем операторные уравнения для атомного и по-
полевого операторов a(i) и a±(t). Эти решения могут быть особенно полезными для
вычисления многовременных корреляционных функций, необходимых при изучении
спектральных свойств поля. Уравнения Гейзенберга для операторов а, а^ и az
получаются из гамильтониана F.2.1):
а= ^[а,Ж] = -iua-iga^, F.2.28)
а^ = —iuja^ + igaza, F.2.29)
az = 2ig(a+a^ - сг+а). F.2.30)
6.2 Взаимодействие одиночного двухуровневого атома с одномодовым полем 167
Для того чтобы облегчить решение этих связанных операторных уравнений, опреде-
определим следующие интегралы движения:
N = а+а + а+а^, F.2.31)
С = ^Aaz + g(a+a + а+<т_). F.2.32)
Т.е. N и С коммутируют с гамильтонианом: [JV, Ж] = [С, Ж\ = 0. Здесь N —
оператор, который описывает полное возбуждение в системе «атом + поле», а С
— интеграл обмена энергией.
Сначала выведем уравнение движения для атомного понижающего оператора а^
—. Из уравнения F.2.29) следует, что
а^ = ^i6d<T^+ig"(«Tza+«7za) = —iuja^—2g (a^a^a—a^a )~^ugaza—g <7_, F.2.33)
где во второй строчке подставлены значения az и а из уравнений F.2.30) и F.2.28),
соответственно. Легко убедиться, что
g2(a+a-a - а+а2) = -i (у + с) <т_ + (иС - ^Д2 + ^д) а., F.2.34)
gaza = —ia^ + w<7_. F.2.35)
Подставляя эти выражения в F.2.33), получаем необходимое уравнение для а^:
а^ + 2i(u - С)а^ + Bi/G - и2 + #2)сг- = °- F.2.36)
Аналогичным образом получаем
а + 2i(v - С)а + Bi/C - и2 + g-2)a = 0. F.2.37)
Эти уравнения можно непосредственно решить и получить выражения для а^
и a(t):
a-{t) = [<T+(t)}+ = e-ivt eict I f cosxt + iC^^j <r_@) - ig^^a@) I , F.2.38)
W-.f лп+ Г/ . ^-y sin жЬ \ /лЧ . sin >^i /л\1 /л ^ ллч
гз tut jO«'IL/t' I лЛС -^,j- «/ » 1 n I ex \ n fr /x 1П1 ffi 9 4Qi
— fc. fc. I ШЬ ль — l\y I Ulxjj — fcg, и 1Uj , I O.Zi.oy J
где я — интеграл движения,
Га2 2 11/2
ж = — + g2{N + 1) , F.2.40)
который коммутирует с С, т. е. [G, х] = 0. При выводе F.2.38) и F.2.39) мы исполь-
использовали соотношения
С2 = — +^2iV, F.2.41)
^сг2а = 2Са^ + A<j^ — ga. F.2.42)
Выражения F.2.38) и F.2.39) дают полное решение задачи взаимодействия двух-
двухуровневого атома с одномодовым полем в представлении Гейзенберга. Все интере-
интересующие нас величины можно найти из этих решений. Например, выражение для
инверсии W(t) F.2.21) можно получить из F.2.38), используя соотношение
W(t) = (a, a\az(t)\a, a) = 2(а, a\a+(t)<T-(t)\a, a) - 1. F.2.43)
Здесь мы предположили, что первоначально атом находился в возбужденном состоя-
состоянии |а), а поле — в когерентном состоянии |а).
168
Взаимодействие атома с полем — квантовая теория
Гл.6
Как уже упоминалось, особым преимуществом работы в картине Гейзенберга яв-
является простота вычисления многовременных корреляционных функций. В качестве
примера воспользуемся выражением F.2.38), чтобы построить диполь-дипольную
корреляционную функцию (задача 6.5):
(а, а|а+(?)сг_(?)|а, а) = е г1/т 'а' х
X > L 5" COS о ~
х {(П„ + AJ e"ifW2 + (^ _ ДJ еа
где Оп задается выражением F.2.15).
гД
sin ( -
)cos[On(r ¦
F.2.44)
6.2.3. Метод унитарного оператора эволюции. Другим эквивалентным подходом
для решения задачи взаимодействия атома с полем является поиск решения с по-
помощью унитарного оператора эволюции во времени. Во многих задачах, в которых
эволюция системы унитарна, т. е. когда нет диссипации, этот подход может оказаться
самым простым. Для нашей задачи взаимодействия двухуровневого атома с одномо™
довым квантованным полем унитарный оператор эволюции во времени имеет вид
U(t) =
F.2.45)
где гамильтониан в картине взаимодействия *f при точном резонансе имеет вид (см.
F.2.8) при А = 0)
Г = hg{a+a + а+<7_). F.2.46)
Здесь сг+ = \а)(Ь\ и а^ = \Ь)(а\. Используя
(G+а + а+ст^J1 = (аа+)||а)(а| + (а+аI\Ь)(Ь1 F.2.47)
(а+а + а+а^J|+1 = (аа+)|а|а)F| + а+(аа+)||6)(а|, F.2.48)
получаем
U(t) = cos (g'tVa+a + 1 )|«)(а| + cos (gtva+a)\b)(b\ —
. sin (gWa+a + 1) . + s!n(g-tVa+a + l)
^^ . a|a)(o| — га |o)(a . (o.z.49j
Вектор состояния в момент времени t выражается через вектор состояния в момент
времени t = 0 следующим образом:
\Ф(г)) = U(t)\tp(Q)}. F.2.50)
В качестве демонстрации эквивалентности этого метода всем предыдущим подхо-
подходам вычислим амплитуды вероятности ca?n(t) и C5)W+i(t) для атома, первоначально
находившегося в возбужденном состоянии |а), и поля, представляющего собой ли-
линейную комбинацию состояний с определенным числом частиц, т. е.
п=0
)\а,п). F.2.51)
Подставляя U(t) и |^@)) из F.2.49) и F.2.51), соответственно, в F.2.50), получаем
а,п) -zsin(#*>/n + l)|b,7i + l)]. F.2.52)
6.3 Теория Вайскопфа-Вигнера спонтанного излучения двухуровневого атома 169
Таким образом,
со,„(«) = (а, пЩ1)) = с„@) cos {gWn + 1), F.2.53)
cb,n+i(t) = -гс„@) sin (g*Vn + 1), F.2.54)
в полном согласии с выражениями F.2.16) и F.2.17) при А = 0.
6.3. Теория Вайскопфа-Вигнера спонтанного излучения
двухуровневого атома
В предыдущем разделе было показано, что атом, находящийся в возбужденном
состоянии, может со временем совершать переходы в основное состояние и обратно
даже в отсутствие приложенного поля. Тем не менее, эксперимент показывает, что
в возбужденном состоянии атом распадается с характерным временем жизни в ниж-
нижнее состояние, и он не совершает переходов вверх и вниз. В уравнениях для матрицы
плотности атома такой распад атома был учтен феноменологически (см. задачу
5.2). В нашей модели спонтанного излучения, которая обсуждалась в предыдущем
разделе, распад не учитывался, поскольку мы рассматривали только одну моду поля.
Чтобы должным образом учесть распад атома, нужно включить в рассмотрение кон-
континуум мод, соответствующий квантованию бесконечно протяженного резонатора.
Для этой системы в представлении взаимодействия гамильтониан в приближении
вращающейся волны имеет вид
^ = Й$>?(гоУ+ак е'*"-"*)* + э.с], F.3.1)
к
где gv(ro) = g"i-exp(—гк • r0), т.е. пространственная зависимость учтена в явном
виде. Здесь tq — радиус-вектор положения атома. Гамильтониан в представлении
взаимодействия получаем тем же методом, который был описан в начале разд. 6.2.
Предположим, что в момент времени t = 0 атом находился в возбужденном состоянии
|а), а моды поля — в вакуумном состоянии |0). Поэтому вектор состояния имеет вид
53ь>к|6,1к>, F.3.2)
к
где
са@) = 1, сь>к@) = 0. F.3.3)
Мы хотим найти состояние атома и состояние поля излучения через некоторый проме-
промежуток времени, когда атом начнет излучать фотоны. Мы найдем его в приближении
Вайскопфа-Вигнера.
Из уравнения Шредингера,
Ш)) = -{пт), F-3-4)
получим уравнение движения для амплитуд вероятности са и с^^:
ca(t) = -i Y, SkM e^-^Cb.kW, F.3.5)
к
сь,к(*) = -igk(ro) e'^-^cait). F.3.6)
170 Взаимодействие атома с полем — квантовая теория Гл. 6
Для того чтобы получить уравнения, содержащие только са, сначала проинтегри-
проинтегрируем уравнение F.3.6),
t
cb>k(*) = -igM^dt'e-^-^'cait'). F.3.7)
о
Подставляя это выражение для C5?k B уравнение F.3.5), получаем
t
Л' е'("-'*»*-'')со(<'). F.3.8)
к о
Это выражение все еще остается точным уравнением. Мы заменили два линейных
дифференциальных уравнения одним линейным интегродифференциальным урав-
уравнением. В качестве следующего шага сделаем некоторые приближения.
Предполагая, что моды поля близко расположены по частоте, можно заменить
сумму по к интегралом
2тт 7Г оо
0 0 0
[cWsini? [ dkk2, F.3.9)
где V — объем квантования. Из F.1.8) следует, что
^ cos2t>, F.3.10)
где v — угол между дипольным моментом атома trab и вектором поляризации
электрического поля е^. Тогда уравнение F.3.8) принимает вид
оо t
2 Г Г
ca(t) = - Bж)ЧПе с3 dukUk dt' ег{ш^ик){1^г }ca(t;), F.3.11)
о о
где выполнено интегрирование по $ и ф и использовано соотношение к = ^к/с-
В спектре излучения интенсивность света, которая связана с полем, испущенным
атомом, должна быть центрирована на частоте атомного перехода ш. Величина v\
изменяется незначительно около частоты и^ = cj, для которой интеграл по времени
в уравнении F.3.11) дает основной вклад. Поэтому молено заменить и^ величиной
о;3, а нижний предел в интегрировании по ик устремить к — оо. Интеграл
duk e^-^X*-*') = 2тг 8{t - tf) F.3.12)
— оо
дает следующее уравнение для ca(i) в приближении Вайскопфа-Вигнера:
с (t) — — — с (t) С6 Я "Ш
2
где константа распада имеет вид
Г = —!— 4ш p3ab. F.3.14)
/|— 31гс3 V ;
Решение уравнения F.3.13) дает
П), F.3.15)
6.3 Теория Вайскопфа-Вигнера спонтанного излучения двухуровневого атома 171
т.е. возбужденное состояние \а) атома в вакууме распадается экспоненциально со
временем жизни т = 1/ Г.
В процессе спонтанного распада атом излучает квант энергии, равный Еа — Е^ =
= hi/. Теперь найдем состояние волны, испущенной в течение процесса спонтанного
излучения.
Сперва вычислим коэффициенты Cb^(t). Подставляя решение для ca(t) в урав-
уравнение F.3.7), находим
t
сьм(*) = -^k(ro) j dt' е-<(«-".)*'-г*'/2 = gk(ro) [ ке_^) + гТ/2 j , F.3.16)
О
о
^1-ы) + гГ/2
так что
к
Далее, вводя состояние поля
Е-гкт0
8*1 ^.г/9|1к) F.3.18)
к
на временах, больших по сравнению с радиационным распадом t ^> 1/ Г, получаем
\ф) —>• |6)|7о)- Здесь индекс «О» в |7о) напоминает нам, что это состояние соответ-
соответствует атому, расположенному в точке г0. Оно является линейной суперпозицией
однофотонных состояний с различными волновыми векторами.
На больших временах корреляционная функция первого порядка 6r^(i% r; t, t)
определяется следующим выражением:
GA)(r,r;M) =
= Ы\Е^(г, t)E^(r, t)|7o) = Ы\Е^(т, t)\0)@\E^(r, *)|-уо>- F-3.19)
Здесь вставлено разложение по полному набору состояний и, поскольку выживает
только вакуумное состояние, а другие состояния приводят к нулю, мы сохраняем
только вакуумное состояние. Мы также предположили, что поле линейно поляризова-
поляризовано, скажем вдоль оси х. Как обсуждалось в разд. 4.2, функция G^(r, г; t, i) пропор-
пропорциональна вероятности зарегистрировать фотон в момент времени t фотодетектором,
находящимся в точке г. Согласно F.3.19), С7A)(г, г; t, t) = \@\E^(r,t)\jQ}\2. Таким
образом, функцию
Ф7(г,<) = <О|Я<+>(г,*)|7о> F.3.20)
мож:но интерпретировать как некий вид волновой функции фотона. Это сделано по
аналогии с соответствующей волновой функцией частицы (см. разд. 1.5).
Из определений E^(r,t) и |7о) (выражения A.1.30) и F.3.18)), находим
Теперь вычислим эту функцию, сначала преобразуя сумму в интеграл с помощью
выражения F.3.9). Однако, мы выбрасываем множитель 2 из этого выражения, так
172
Взаимодействие атома с полем — квантовая теория
Гл.6
как предполагается, что поле поляризовано вдоль оси х. Интегрирование по ф и $
можно выполнить, выбирая систему координат, в которой вектор г — го направлен
вдоль оси z, дипольный момент атома составляет угол rj с осью z в плоскости xz,
и волновой вектор к имеет составляющие
к = k (sin $ cos фх + sin $ sin фу + cos #
Окончательное выражение для @\E^(r^ t)\jo) имеет вид г)
— е
1:
F.3.22)
F.3.23)
где Аг = |г — Гд|. В вышеприведенном интеграле член exp[^i(^Ar + i/fct)] отвечает за
приходящую волну и поэтому мы им пренебрегаем. Так же, как в теории спонтанного
излучения Вайскопфа^Вигнера, мы предположим, что величина и^ слабо меняется
Im/c
+> Re к
С2
Рис. 6.3. Контур интегрирования, используемый при вычислении F.3.23). Путь интегриро-
интегрирования замыкается в верхней полуплоскости с помощью полуокружности Ci, если t < Аг/с,
или в нижней полуплоскости с помощью С2, если t > Аг/с
около Pk = ш и поэтому ее можно заменить величиной ш2, а нижний предел интегри-
интегрирования распространить до ^оо. Используя эти приближения, приходим к интегралу
ехр(—ii/fet + wu At I с)
- ш) + гГ/2
Этот интеграл вычисляется с помощью метода контурного интегрирования (рис. 6.3).
Если t < Аг/с, контур лежит в верхней полуплоскости, а если t > Аг/с — в нижней
1) Выражение F.3.23) можно вывести более полным и строгим способом, используя метод,
описанный в приложении 10.А.
6.4
Двухфотонное каскадное излучение
173
полуплоскости. Выполняя интегрирование, находим
-<(t-Ar/c)(w-<r/2)
где в — единичная ступенчатая функция и
Аг
F.3.25)
Тогда получаем
Здесь ступенчатая функция появляется из-за того, что сигнал не может распростра-
распространяться быстрее скорости света.
6.4. Двухфотонное каскадное излучение
В этом разделе мы рассмотрим спонтанное излучение в трехуровневом атоме,
имеющем каскадную конфигурацию переходов (рис. 6.4). Атом в верхнем состоянии
\а) испускает k-фотон частоты и^ и переходит в состояние |6), которое в свою очередь
распадается в состояние \с) с испусканием q-фотона
частоты i/q. Гамильтониан системы в картине взаи-
модействия имеет вид
Ч к
э.с], F.4.1)
где 4Ч = W)(bl af = 1^)(С1 и ^, ,ч
константы взаимодействия для переходов \а) —> \Ь)
и \Ь) —> |с), соответственно.
Теперь состояние системы «атом + поле» описы- \с
вается выражением
\фA)) = ca(t)\a, 0) + У^ сЬ;к|6, 1к)+
Рис. 6.4. Схема распада воз-
бужденного состояния трех™
уровневого атома благодаря
спонтанному излучению в кас-
cC5k,q|c, Ik, lq). F.4.2) кадной конфигурации
Как и в разд. 6.3, амплитуды вероятности са,
ниям движения
cc,k>q = -*?b,q(ro)cb,k
и cC)k,q удовлетворяют уравне-
уравне--^, F.4.3)
)Сс>к,ч e*^"".)*, F.4.4)
-"»)'. F.4.5)
174 Взаимодействие атома с полем — квантовая теория Гл. 6
Поступая также, как в разд. 6.3, приходим к тому, что в приближении Вайскопфа-
Вигнера
к
где Га — скорость перехода атома из состояния \а) в состояние \Ь). Более того, видно,
что второй член в уравнении F.4.4) отвечает за переход из 16) в |с), и можно записать
где Г5 — скорость перехода из \Ь) в |с). Подставляя выражения F.4.6) и F.4.7)
в F.4.3)—F.4.5) получаем в окончательном виде удобные уравнения движения для
системы «атом + поле»:
са^~са, F.4.8)
cc,k,q = -igb,4(ro)cbM е-*^-"')*, F.4.10)
где в первом члене уравнения F.4.9) величина ca(t) заменена функцией exp(^Fat/2).
В этой задаче основной интерес представляет состояние поля на больших време-
временах t ^> Г,!^1. Поэтому мы хотим узнать cC5k,q(oo) при условии, когда са(оо)
и С5;к(°°) стремятся к нулю.
После выполнения простого интегрирования уравнения F.4.9) получаем
t
ch h(t) = -%к k(rn) \ dt' е~^шаъ~^кI'~та1'/2 e~rb(t~tf)f2 _
— ^Sa,k\4)j -J7- ; ; x 7 p p ч J9 • F.4.11)
Это выражение для сь^A) можно подставить в уравнение F.4.10), а получившееся
уравнение проинтегрировать. В результате на больших временах имеем следующий
предел для cC)k,q(?):
uk + Uq- Шас) ~ Га/2 i(vq ~~ UJbc) - ГЬ
_ ™*(k+q)-r0
[«(i/fc + Fg - шас) - ra/2}[i(uq - ujbc) - Гь/2]' l ' }
Поскольку в пределе больших времен обе величины ca{t) и с^к(?) равны нулю, мы
подставляем cC)k,q(oo) из F.4.12) в F.4.2) и находим, что состояние поля излучения
имеет вид
— i(k+q)-r0
k,q
где |7, ф) представляет собой двухфотонное состояние.
6.5 Вероятности возбуждения для одиночных и парных фотоэлектронных событий 175
Более детально мы воспользуемся этим результатом в гл. 21, когда мы будем
использовать двухфотонную корреляционную функцию для того, чтобы прийти
к более глубокому пониманию основ квантовой механики.
6.5. Вероятности возбуждения для одиночных и парных
фотоэлектронных событий
В разд. 4.2 были приведены эвристические аргументы, показывающие, что веро-
вероятность фотодетектирования определяется нормально упорядоченной корреляцион-
корреляционной функцией поля. Здесь мы выведем вероятность воз-
возбуждения для одиночного и парного фотоэлектронных *
событий, используя формализм взаимодействия системы
«атом + поле», развитый в этой главе 1).
Рассмотрим взаимодействие линейно поляризованно-
поляризованного поля, которое описывается полевыми операторами
E^(r,t) и i?(~)(r, ?), с атомной системой, характеризу-
характеризуемой основным состоянием \Ь) и набором возбужденных
состояний \a,j) (рис. 6.5). Предположим, что атом первона-
чально находится в состоянии |6), а поле — в состоянии |г).
В приближении вращающейся волны гамильтониан в пред-
представлении взаимодействия имеет вид
з)
г = -
з
Состояние системы «атом
задается выражением
, t) ex.p(iujajjbt) + э.с. F.5.1)
поле» в момент времени t
1-х
F.5.2)
Вычисляя среднее значение оператора проектирования
ность возбуждения атома в состояние |ftj), т. е.
Рис. 6.5. Схема уровней,
используемая для описа-
описания процесса фотодетек-
фотодетектирования. Атом совер-
совершает переход из состоя-
состояния \Ь) во множество со-
состояний \a,j)
bj}{aj\, находим вероят-
paj,b
t t
о о
где состояние \ф) подставлено из F.5.2). Если мы хотим найти только вероятность
возбуждения, мы должны просуммировать по всем возбужденным состояниям \dj).
В случае, когда ^^.ь слабо зависит от j, можно положить S^\.b — ?^2. Следователь-
Следовательно, для широкополосного детектора суммирование по j для функции exp[io;ai (ti —1^2)]
приводит к эффективной S(ti — ^2)-функции, и мы получаем
F.5.4)
1) Замечательное описание этой проблемы можно найти в лекциях Глаубера (Les Houches
lectures of Glauber, 1965).
176
Взаимодействие атома с полем — квантовая теория
Гл.6
где к ~~ константа. В случае смешанных состояний выражение F.5.4) принимает вид
F.5.5)
Теперь рассмотрим атомы, расположенные в точках i*i и Г2, и найдем вероятность
совместного отсчета Pi2, т.е. ищем среднее значение оператора фотовозбуждения
для обоих атомов, т. е. а = 1 и 2. По аналогии с уравнением F.5.5) запишем
,t1)]. F.5.6)
О О
Таким образом Pi 2 задается корреляционной функцией второго порядка операторов
поля.
Задачи
6.1. Модель, которую иногда рассматривают для изучения взаимодействия атома
с полем в резонаторе без потерь, описывается гамильтонианом
в обычных обозначениях. Отметим, что взаимодействие зависит от интенсивно-
интенсивности. Вычислите атомную инверсию и рассмотрите ее эволюцию на различных
временных масштабах, т. е. на периоде осцилляции Раби, временах коллапса
и временах возрождения для случаев, когда в начальный момент времени поле
находится (а) в когерентном состоянии и (б) в тепловом состоянии.
6.2. Вычислите в дипольном приближении и приближении вращающейся волны
инверсию населенности двухуровневого атома, взаимодействующего с одно-
модовым квантованным полем излучения, для произвольного времени ?, при
условии, что при t = 0 поле находится в когерентном состоянии |а), а атом
НаХОДИТСЯ В СОСТОЯНИИ |^)атом = (\а) +
+ е~*ф\Ь))/у/2) (\а)и |Ъ) ^возбужденное 1а'
и основное состояния соответственно).
Обсудите условия, при которых населен-
населенности обоих состояний остаются «пле-
«плененными».
6.3. Рассмотрите атомную систему, показан-
показанную на рис. 6.6, с двумя близко располо-
расположенными верхними уровнями, соответ-
соответствующими состояниям |а) и |а;), и ниж-
нижним уровнем, соответствующим состоя- Рис. 6.6. Радиационный распад двух
нию \Ь). Правила отбора и энергетиче- состояний \а) и \а'), разделенных не-
ский интервал между состояниями |о> большим энергетическим интервалом,
I /\ „ в общее состояние о)
и \а ) таковы, что они взаимодействуют ' '
а')
Список литературы к гл. 6 177
с одинаковыми вакуумными модами. Взаимодействие этой системы с мно
гомодовым вакуумным полем описывается гамильтонианом в представлении
взаимодействия
Здесь aj — оператор рождения моды с волновым вектором к и ш^ = ша — ш^,
ша>ъ = ooai —ujf,. Выведите для этой трехуровневой системы уравнения движения
для амплитуд вероятности и покажите, что эффекты квантовой интерференции
возникают благодаря совместному использованию общих вакуумных мод двумя
верхними уровнями. [Указание: см. работу Zhu, NarduccI and Scully, Phys. Rev.
A 52, 6 A995).]
6.4. Покажите, что если выполняются соотношения С = До^/2 + g(a+a + а+сг„)
и N = а^а + <т+<т^, то
6.5. Докажите соотношение F.2.44).
Список литературы
Обзорные статьи и монографии по двухуровневым системам,
взаимодействующим с одномодовым квантовым полем
Stenholm, S. Phys. Rep. 6, 1 A973).
Sargent III, M., Scully, M. and Lamb, W. E., Jr., Laser Physics, (Addlson-Wesley, Reading, MA,
1974).
Allen, L. and Eberly, J. H. Optical Resonance and Two-Level Atoms, (John Wiley, New York,
1975). [Аллен Л., Эберли Дж. Оптический резонанс и двухуровневые атомы (Мир,
Москва, 1978).]
Knight, P. L. and Milonni, P. W. Phys. Rep. 66, 21 A980).
Stenholm, S. Foundations of Laser Spectroscopy, (Wiley, New York, 1984).
Cohen-TannoudjI, G., Dupont-Roc, J. and Grynberg, G. Photons and Atoms. Introduction to
Quantum Electrodynamics, (Wiley, New York 1989).
Haroche, S. and Kleppner, D. Physics Today 42, Jan. 24 A989).
Cohen-TannoudjI, C, Dupont-Roc, J. and Grynberg, G. Atom-Photon Interactions, (Wiley, New
York 1992).
Shore, B. W. and Knight, P. L. J. Mod. Opt 40, 1195 A993).
Berman, P. ed., Cavity Quantum Electro•dynamics^(Acad. Press, New York 1994).
Walls, D. F. and Milburn, G. J. Quantum Optics, (Springer-Verlag, Berlin 1994).
Статьи общего характера
Jaynes, E. Т. and Cummlngs, F. W. Proc. IEEE 51, 89 A963).
Glauber, R. J. In Quantum Optics and Electronics, Les Houches, ed. C. DeWItt, A. Blandln, and
C. Cohen-TannoudjI (Gordon and Breach, New York 1965).
Scully, M. O. and Lamb, W. E., Jr., Phys. Rev. 159, 208 A967).
Tavis, M. and Cummlngs, F. W. Phys. Rev. 188, 692 A969).
Meystre, P., Quattropani, A. and Baltes, H. P. Phys. Lett 49A, 85 A974).
178 Список литературы к гл. 6
von Foerster, Т. J. Phys. A 8, 95 A975).
Ackerhalt, J. R. and Rzazewski, K. Phys. Rev. A 12, 2549 A975).
Narozhny, N. В., Sanchez-Mondragon, J. J. and Eberly, J. H. Phys. Rev. A 23, 236 A981).
Knight, P. L. and Radmore, P. M. Phys. Rev. A 26, 676 A982).
Zaheer, K. and Zubairy, M. S. Phys. Rev. A 37, 1628 A988).
Eiselt, J. and RIsken, H. Opt. Commun. 72, 351 A989); Phys. Rev. A 43, 346 A991).
Quang, Т., Knight, P. L. and Buzek, V. Phys. Rev. A 44, 6092 A991).
*Bykov, V.P. Radiation of atoms in a resonant environment (World Scientific: Singapore, 1993).
Обобщенные модели квантованных атомно-полевых взаимодействий
Cook, R. J. and Shore, B. W. Phys. Rev. A 20, 539 A979).
Kumar, S. and Mehta, C. L. Phys. Rev. A 21, 1573 A980).
Buck, B. and Sukumar, C. V. Phys. Lett A 81, 132 A981).
Singh, S. Phys. Rev. A 25, 3206 A982).
Bogolubov, N. N., Jr., Le Klen, F. and Shumovsky, A. S. Phys. Lett. A 101, 201 A984); ibid.
107, 456 A985).
Deng, Z. Opt Commun. 54, 222 A985).
Seke, J. J. Opt Soc. Am. В 2, 968 A985).
Abdel-Hafez, A. M., Obada, A. S. F. and Ahmad, M. M. A. Phys. Rev. A 35, 1634 A987).
Alsing, P. and Zubairy, M. S. J. Opt Soc. Am. В 4, 177 A987).
Iqbal, M. S., Mahmood, S., Razml, M. S. K. and Zubairy, M. S. J. Opt. Soc. Am. В 5, 1312
A988).
Purl, R. R. and Bullough, R. K. J. Opt Soc. Am. В 5, 2021 A988).
Buzek, V. and Jex, I. J. Mod. Opt 36, 1427 A989).
Sharma, M. P., Cardimona, D. A. and Gavrielldes, A. J. Opt. Soc. Am. В 6, 1942 A989).
Buzek, V. Phys. Rev. A 39, 3196 A989); J. Mod. Opt 37, 1033 A990).
Adam, G., Seke, J. and Hittmair, O. Phys. Rev. A 42, 5522 A990).
Joshi, A. and Purl, R. R. Phys. Rev. A 42, 4336 A990).
Toor, A. H. and Zubairy, M. S. Phys. Rev. A 45, 4951 A992).
*Юкалов В.И. Изв. РАН, сер.физ. 64, 2039 B000).
Мвления коллапса и возрождения
Eberly, J. H., Narozhny, N. В. and Sanchez-Mondragon, J. J. Phys. Rev. Lett 44, 1323 A980).
Rempe, G. and Walther, H. Phys. Rev. Lett. 58, 353 A987).
Flelschhauer, M. and Schlekh, W. Phys. Rev. A 47, 4258 A993).
Сжатие и антигруппировка фотонов при взаимодействии атома с
полем
Meystre, P. and Zubairy, M. S. Phys. Lett A 89, 390 A982).
*Голубев Ю.М., Соколов И.В. ЖЭТФ 87, 408 A984).
Knight, P. L. Phys. Scripta 33 (Т12), 51 A986).
Bogolubov, N. N., Jr., Le Klen, F. and Shumovsky, A. S. Europhys. Lett 4, 281 A987).
Aravind, P. K. and Hu, G. Physica С 150, 427 A988).
Gerry, С. С. Phys. Rev. A 37, 2683 A988).
Kuklinski, J. R. and Madajczyk, J. L. Phys. Rev. A 37, 3175 A988).
Список литературы к гл. 6 179
Kim, M. S., De Oliveira, F. A. M. and Knight, P. L. J. Mod. Optics 37, 659 A990).
Mahran, M. H. Phys. Rev. A 42, 4199 A990).
Mir, M. A. and Razmi, M. S. K. Phys. Rev. A 44, 6071 A991).
*Gorbachev, V.N., Gziliba, A.I. Quant Opt 5, 193 A993).
*Горохов А.В. Изв. РАН, сер.физ. 64, 2030 B000).
Когерентная суперпозиция при взаимодействии атома с полем
Phoenix, S. J. D. and Knight, P. L. Ann. Phys. (NY) 186, 381 A988).
Zaheer, K. and Zubairy, M. S. Phys. Rev. A 89, 2000 A989).
Gea-Banacloche, J. Phys. Rev. Lett 65, 3385 A990).
Sherman, B. and Kurizki, G. Phys. Rev. A 45, 7674 A992).
Приближение Вайскопфа^Вигнера
Welsskopf, V. and WIgner, E. Z. Phys. 63, 54 A930).
Sargent III, M., Scully, M. and Lamb, W. E., Jr., Laser Physics, (Addison-Wesley, Reading, MA
1974) p. 236.
Louisell, W. Quantum Statistical Properties of Radiation, (Wiley, New York 1974).
Kimble, H. J., Mezzacappa, A. and Milonni, P. W. Phys. Rev. A 31, 3686 A985).
Двухфотонные эффекты и каскадное излучение
Holt, H. Phys. Rev. Lett 19, 1275 A967).
Narducd, L. M., Scully, M. O., Oppo, G.-L., Ru, P. and Tredlcce, J. R. Phys. Rev. A 42, 1630
A990).
Zhu, Y.-F., Gauthier, D. J, and Mossberg, T. W. Phys. Rev. Lett 66, 2460 A991).
Huang, H. and Eberly, J. H. J. Mod. Opt 40, 915 A993).
Глава 7
ЛАЗЕРНАЯ ГЕНЕРАЦИЯ
БЕЗ ИНВЕРСИИ И ДРУГИЕ
ЭФФЕКТЫ АТОМНОЙ
КОГЕРЕНТНОСТИ
И ИНТЕРФЕРЕНЦИИ
Эффекты квантовой когерентности, а также корреляций в атомной физике и тео-
теории излучения имеют много интересных и неожиданных проявлений. Например, в ан-
ансамбле атомов, находящихся в когерентной суперпозиции состояний, наблюдаются
эффект Ханле, квантовые биения, фотонное эхо, самоиндуцированная прозрачность
и когерентные рамановские биения г). В разд. 1.4 уже говорилось, что квантовые
биения являются одним из наиболее веских оснований для квантования поля излу-
излучения.
Другим интересным следствием приготовления атомной системы в когерентной
суперпозиции состояний является то, что при определенных условиях можно изба-
избавиться от поглощения за счет атомной когерентности. Такие атомные состояния на-
называются состояниями пленения 2). Наблюдение резонансов без поглощения повлия-
повлияло на концепции лазерной генерации без инверсии (ЛГБИ) 3), увеличения показателя
преломления, сопровождающегося исчезновением поглощения, и электромагнитно-
индуцированной прозрачности.
Основная идея лазерной генерации без инверсии состоит в исчезновении поглоще-
поглощения благодаря атомной когерентности и интерференции. Это явление лежит также
в основе электромагнитно-индуцированной прозрачности. Обычно оно наблюдается
в трехуровневой атомной системе, имеющей два когерентных пути поглощения,
которые могут деструктивно интерферировать, что и ведет к исчезновению по-
поглощения. В результате, небольшая населенность возбужденного состояния может
приводить к результирующему усилению. Родственным эффектом является резо-
резонансное увеличение показателя преломления в отсутствие поглощения в ансамбле
фазово-когерентных атомов (фазеониум). В газообразном фазеониуме, у которого
1) Рекомендуем ознакомиться с оригинальными исследованиями по самоиндуцированной
прозрачности (McCall and Hahn, 1969) и когерентным переходным явлениям, таким как
когерентные рамановские биения (Brewer and Hahn, 1973), близкими по духу к данной главе.
2) Превосходным обзором по когерентному пленению населенности является работа Ari-
mondo A996).
) Хотя возможность ЛГБИ была отмечена много лет назад (Hansch and Toschek, 1970;
Popov, Popov and Ravtian, 1970; Arkhpkln and Heller, 1983), серьезные исследования по
этой теме начались лишь недавно (Kocharovskaya and Khanin, 1988; Harris, 1989; Scully,
Zhu and Gavrlelldes, 1989). Сейчас выполнены решающие эксперименты, которые ясно
демонстрируют справедливость этой идеи.
7.1
Эффект Ханле
181
возбужденный уровень не заселен, исчезновение поглощения всегда соответствует
исчезновению преломления. Однако, если небольшая часть атомов находится в воз-
возбужденном состоянии, то поглощение обращается в нуль с небольшой отстройкой
от резонанса, там где действительная часть восприимчивости имеет существенное
значение. Это и приводит к возможности высокого значения показателя преломления
в непоглощающей среде.
В этой главе мы рассмотрим эти новые явления, в которых явно видно влияние
атомной когерентности.
7.1. Эффект Ханле
Эксперимент Ханле является одной из наиболее ясных и старейших демонстра-
демонстраций той ситуации, в которой атомная когерентность играет важную роль. Пусть
ансамбль атомов, помещенных в слабое магнитное поле, освещается импульсом света,
поляризованным вдоль оси х. Регистрируется поляризация света, переизлучаемого
1-
т = +1
О
-1
т = О
Рис. 7.1. Иллюстрация эксперимента Ханле и схема атомных уровней
в направлении оси z. Оказывается, что в слабом магнитном поле переизлученный
свет может быть поляризован вдоль оси у, как показано на рис. 7.1.
Чтобы понять, каким образом атомы, возбуждаемые светом, поляризованным
вдоль оси ж, переизлучают свет, поляризованный вдоль оси г/, необходимо вычислить
дипольный момент, индуцированный падающим излучением. Пусть атом в началь-
начальный момент времени находился в основном состоянии,
И0)> = |0>. G.1.1)
Далее электрическое поле
E(r, t) = ж Jo cos(% - ut) G.1.2)
вызывает переходы на уровни т = =Ы, и волновая функция атома принимает вид
\Ф(г)) = с+ ехр(га;+*)|+) + с^ ехр(га;_*)|-) + со|О). G.1.3)
Частоты ш± равны
ш± = v ± А,
G.1.4)
182
Эффекты атомной когерентности и интерференции
Гл.7
где А — величина расщепления уровней в магнитном поле. Тогда дипольный момент
атома равен
+ A)t + f/sin(V + A)t] +p^[xcos(V - A)t - ysln(u - A)t], G.1.5)
где p± — поляризация, соответствующая величине р±,о = c±cq5 то есть
р± = е(±|а;|О>(р±,о + э.с.). G.1.6)
Далее будем рассматривать случай, когда р_|_ = р^ = р. Тогда выражение G.1.5)
принимает вид
(P(t)) = р cos ut(x cos At + у sin At).
G-1-7)
Интенсивность и поляризация излучения такого атомного диполя и являются интере-
интересующими нас функциями времени. Согласно G.1.7), если поместить детектор в точке
х = хд на оси ж, то никакого переизлучения не будет регистрироваться в случае,
когда приложенное магнитное поле if, а значит и А, равны нулю. Для конечных
значений А, однако, будет наблюдаться модулированное поле излучения вдоль оси
ж, зависимость которого от времени будет иметь вид
= Sq cos vt sin At.
G.1.S
Причиной такой модуляции является индуцированная когерентность между уровня-
уровнями |+) и |—). Этим уровням соответствуют неравные нулю элементы р±. В общем
случае, говорят, что атомная когерентность существует, если матрица плотности
имеет отличные от нуля недиагональные элементы.
7.2. Когерентное пленение — темные состояния
Интересным явлением, в котором по-новому проявляется когерентная суперпози-
суперпозиция атомных состояний, является когерентное пленение. Если атом находится в ко-
когерентной суперпозиции состояний, то можно при определенных условиях аннулиро-
аннулировать поглощение или излучение. Такие атомы являются практически прозрачными
для падающего света даже при наличии резонансных переходов. В этом разделе
обсуждается эффект когерентного пленения в трехуровневой атомной системе.
Когерентные суперпозиции атомных состояний трехуровневых атомов имеют
множество интересных приложений. Таковыми являются лазерная генерация без
инверсии и увеличение показателя прелом-
преломления в непоглощающей среде, обсуждаемые
в этой главе. Другими интересными приложе-
приложениями являются квантовые биения (разд. 1.4)
и корреляционный лазер (гл. 14).
Рассмотрим когерентное пленение в трех-
трехуровневом атоме, взаимодействующем с дву™
мя полями, имеющими частоты v\ и г/2> как
показано на рис. 7.2. Предположим, что атом
имеет так называемую Л-конфигурацию уров-
Рис. 7.2. Взаимодействие трехуровне-
трехуровневого атома, имеющего Л-конфигура-
Л-конфигурацию переходов, с двумя полями с ча-
частотами U\ И 1/2
ней, когда два нижних уровня \Ъ) и \с) связы-
связываются с одним верхним уровнем \а). Другими
возможными конфигурациями уровней явля-
являются V- и каскадная конфигурации.
7.2
Когерентное пленение — темные состояния
183
Гамильтониан такой системы, в приближении вращающейся волны, получает-
получается соответствующим обобщением гамильтониана двухуровневого атома, взаимодей-
взаимодействующего с одномодовым полем (выражения E.2.3)-E.2.5)), на случай трехуровне-
трехуровневого атома, взаимодействующего с двухмодовым полем:
где
Жо = Пша\а)(а\ + Пшь\Ь)(Ь\ + Пис\с)(с
G.2.1)
G.2.2)
э.с).
Здесь Од1 ехр(—г0х) и 0^2 exp(^i<^2) — комплексные частоты Раби, соответствую-
соответствующие взаимодействию мод поля, имеющих частоты ^ и ^, с атомными переходами
\а) —> \Ь) и |а) —} \с) соответственно. Здесь предполагается, что дипольно разрешены
лишь переходы \а) —> \Ь) и \а) —> |с).
Волновая функция атома может быть записана в виде
= ca(t)
cb(t)
cc{t)
G.2.4)
Уравнения движения для амплитуд вероятности ca(t), Cb(t) и cc(t) выводятся из
уравнения Шредингера Иг\ф) = Ж\ф) и имеют вид
са = fan е-^сь + UR2 е-**асс), G.2.5)
C6=^fimei*1ce, G.2.6)
, G.2.7)
где мы предположили, что поля резонансны переходам \а) —> \Ь) и \а) —> |с), то есть
^аЪ = ^1 И Шас = 1/2.
Предположим теперь, что начальное атомное состояние является суперпозицией
состояний \Ъ) и \с):
\ф@)) =
G.2.8)
Решение уравнений G.2.5)—G.2.7), удовлетворяющее начальному условию G.2.8),
имеет вид
(t) =
= ^2 {["д2 + "hi cos (Sit/2)] cos (#/2) -
G.2.9)
Cc(t) = 1{[Л2Д1 + Sl2R2 cos (Ш/2)]
- 2SIR1SIR2 e*^1-*2-^ sin2 (Ш/4) sin (#/2)}, G.2.10)
^ sin (#/2) -
- 2ОШОЯ2 е~{(ф1~ф2) sin2 (Ш/4) cos (#/2)}, G.2.11)
где О = (Од-| + ^яг) • ОчевиДно) чт0 когерентное пленение имеет место в случае,
когда
^Я1 = ^Я2, <? = тг/2, ф1-ф2-'ф = ±1Г. G.2.12)
184
Эффекты атомной когерентности и интерференции
Гл.7
При этих условиях
,-1ф
G.2.13a)
G.2.136)
G.2.13в)
то есть, населенность захваченав нижних состояниях и поглощение отсутствует даже
в присутствии поля. В данном трехуровневом атоме когерентное пленение имеет ме-
место вследствие деструктивной квантовой интерференции между двумя переходами.
В заключение отметим, что существует интересное следствие когерентного плене-
пленения населенности (КПН) в случае адиабатического включения и выключения поля
в выражении G.2.3). То есть, пусть в начальный момент времени атом находится
в состоянии |6), ?Iri = 0, и величина 0^2 конечна. Затем будем выключать 0^2
при медленном включении Пш. Тогда атом закончит эволюцию в состоянии |с). Это
становится ясным, если представить, что атом находится в зависящем от времени
состоянии пленения:
№)) =
l\b)-toRi(t)e-ifpi\c)
G.2.14)
UR2
см. задачу 7.3.
В этом разделе мы рассмотрели случай, когда атом в начальный момент времени
находится в непоглощающем состоянии. Интересный аспект КПН состоит в том, что
оно может иметь место даже тогда, когда атом не находится в темном состоянии
в момент t = 0. Фактически, атом можно привести в это состояние путем, на-
например, непрерывного действия электромагнитных полей и спонтанного излучения
(аналогично механизму оптической накачки) с помощью адиабатического переноса
населенности. Пример этого приводится в следующем разделе.
Связывающее
поле
с)
7.3. Электромагнмтно-жндуцжрованная прозрачность
В предыдущем разделе рассматривалось явление когерентного пленения населен-
населенности с помощью трехуровневой системы, в которой нижние состояния существуют
в виде когерентной суперпозиции. В этом
разделе рассматривается другое родствен™
ное явление — электромагнитно-индуциро-
электромагнитно-индуцированная прозрачность (ЭМИП), впервые ис-
исследованное Харрисом с сотрудниками, при
котором квантовая интерференция появля-
появляется вследствие воздействия на два верх-
верхних уровня трехуровневой атомной системы
сильным когерентным полем (см. рис. 7.3).
При определенных условиях среда становит-
ся фактически прозрачной (поглощение рав-
равно нулю) по отношению к пробному полю.
Рассмотрим замкнутую трехуровневую
систему, показанную на рис. 7.3. Уровни \а)
и \Ь) связываются пробным полем, имеющем
амплитуду $ и частоту и. Нас будет интере-
интересовать дисперсия и поглощение этого поля.
/\/\/v>
Пробное
поле
\Ь)
Рис. 7.3. Схема возбуждения трехуров-
трехуровневой системы в режиме электромагнит-
электромагнитно-индуцированной прозрачности
7.3 Электромагнитно-индуцированная прозрачность 185
Верхний уровень \а) связывается с уровнем \с) сильным когерентным полем частоты
Vp, комплексная частота Раби которого равна Г^ехр(—г<^). Скорости затухания
недиагональных элементов ра5, рас и РсЪ обозначим, соответственно, через 7ъ 72
и 7з-
Гамильтониан взаимодействия атома с двумя полями вновь задается выражени-
выражениями G.2.1)—G.2.3), но с подстановками:
Ош е~*ф1 e~ivit = ^j^ e~il/\ пт e~i<t>2 e~il/2t = п^ е~1ф^ е"^*. G.3.1)
Уравнения движения для элементов матрицы плотности р^ и рс^ имеют вид
Раь = -(iu>ab + 7iW - \^f~ e-ivt{Paa - рьь) + ^ e"'*" е-^рсь, G.3.2)
Pcb = -(шсь + ls)Pcb -\^jf- e~ivtPca + '-^ j*» е^раь, G.3.3)
Рас = -(iUac + li)Pac + \^f е~ШPbc - *"м е^" ^^\раа - Pec)- G.3.3)
Как было показано ранее, дисперсия и поглощение определяются величиной ра^, то
есть нам нужно вычислить поляризацию в низшем порядке по S. Однако, поскольку
когерентное поле, связывающее уровни \а) и |с), является сильным, относительно
него задача должна решаться точно, и необходимо удерживать Ом во всех порядках.
Поскольку в начальный момент времени атомы находятся в состоянии |6),
J0) _ 1 @) _ @) _ @) _ 0 /7 о к\
Pbb — -1' Раа — Рсс ~ Рса ~ У* {(.д.Э)
Подставляя эти значения матричных элементов в G.3.2) и G.3.3) и делая замену
Pab^pabe-iu\ G.3.6)
Рсъ = Рсье-*1'+ш™)\ G.3.7)
получаем следующую систему уравнений:
Раь = "G1 + i^)Pab +1^ + 1"/* е-{ф-рсЬ, G.3.8)
Рсь = -Gз + iA)Pcb + \^ е-*»раЬ, G.3.8)
где А = (л)аъ — и — отстройка пробного поля, так же предположим, что v^ = шас.
Полученную систему уравнений можно решить, например, переписав ее сначала
в матричном виде:
Д=-МД + Л, G.3.10)
где
R= /J' м= а/\ю р*ф^ 'Уо+^д м А=\ аЬо ' G-ЗЛ1)
и затем интегрируя
Я(*) = [ e~M{t~tf)Adtf = М~гА. G.3.12)
— сю
Это дает
2ft[Gl + гД)Gз
186
Эффекты атомной когерентности и интерференции
Гл.7
Используя соотношение 0^ = б®х^ вместе с определением E.4.18) комплексной
поляризации, получаем следующее выражение для действительной и мнимой частей
комплексной восприимчивости \ = х' Н~ ^х":
X1 =
X =
eohz
где Na — плотность атомов и
Z = (А2 - 717з -
— [ТзG1 + 7з) + (А2 - 717з - f
[A2Gi + 7з) ~ 7з(А2 - 7i73 -
+ А2G1 + 7зJ-
G.3.14)
G.3.15)
G.3.16)
Из выражений E.4.23) и E.4.24) ясно видно, что х' и х" связаны с дисперсией и по-
поглощением, соответственно. Более детальное обсуждение будет сделано в разд. 7.5.
На рис. 7.4 приведена зависимость х! и х" от величины расстройки А, выра-
выраженной в единицах 71? Для случая, когда О^ = 271 и 71 ^ 7з Gз = 10^47i)-
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-2.5 -2 -1.5 -1 -0.5
Рис. 7.4. Действительная (сплошная линия) и мнимая (пунктирная линия) части линейной
восприимчивости (в относительных единицах), как функции нормированной расстройки
А/71
Видно, что при нулевой расстройке А = 0, обе величины х' и х" равны нулю, то
есть поглощение почти отсутствует там, где показатель преломления равен единице.
Таким образом, среда становится прозрачной при воздействии сильного когерентного
поля. Это пример светоиндуцированной прозрачности.
Отметим, что при резонансе х' = 0? и величина х" пропорциональна 7з- По™
скольку последняя величина представляет собой скорость релаксации дипольно за-
запрещенного перехода, она может быть очень малой. Физику явления ЭМИП можно
7.3
Электромагнитно-индуцированная прозрачность
187
объяснить в терминах темных состояний, обсуждавшихся в предыдущем разделе.
Однако, есть существенное различие. В предыдущем разделе предполагалось, что
в начальный момент времени атом находится в темном состоянии. В случае ЭМИП,
однако, атом возбуждается в темное состояние совместным действием сильного поля
накачки и слабого пробного поля. Существует два возможных механизма такой
накачки. Первый является эквивалентом обычной оптической накачки в плененное
состояние. В этом случае ЭМИП индуцируется в атоме в течение времени порядка
радиационного времени жизни, поскольку в течение этого времени возбужденный
атом переходит в несвязанное («плененное») состояние. Этот случай соответствует
ступенчатому включению связывающего (между уровнями а и с) и пробного полей.
Тогда, как видно из рис. 7.5, величина pat, определяющая поглощение, затухает
Рис. 7.5. Временные масштабы установления ЭМИП в Л-системе, возбуждаемой сильным
управляющим полем и слабым пробным полем. Сплошными линиями показана поляри-
поляризация, возникающая на пробном переходе (в относительных единицах) как функция вре-
времени (в единицах атомной скорости затухания). В начальный момент времени заселено
лишь основное состояние пробного перехода, а связывающий лазер действует постоянно.
Внезапное включение (ступенчатая функция) пробного поля приводит к эффекту опти-
оптической накачки на временном масштабе, определяемом атомной скоростью затухания (а);
медленное включение (пунктирная линия) пробного поля приводит к адиабатическому
слежению атома. ЭМИП устанавливается при включении пробного поля в момент времени
t = 0527~1- Частота Раби управляющего поля равна О = 2007 (б); та же ситуация, что
и в предыдущем случае, только управляющее поле слабее, О = 1007- Адиабатичность
не столь идеальна и после включения пробного поля некоторая населенность остается в
поглощающем состоянии. Оптическая накачка этой оставшейся населенности приводит к
поглощению в моменты времени, превышающие t = 0,27™Х (в)
в течение нескольких радиационных времен жизни. Но если включить поле медленно
(по сравнению с периодом Раби связывающего лазера 0^2 в формуле G.2.14)), атом
перейдет в зависящее от времени состояние пленения G.2.14) за время порядка О^?
как показано на рис. 7.25. Таким образом, при достаточно большом значении Од25
процесс не зависит от времени радиационного затухания.
Однако, как видно из рис. 7.5в, даже при 0^2 ~ ЮО7 мы не попадаем еще
полностью в область ЭМИП. Вместо этого мы имеем ситуацию «типа ЭМИП» для
коротких времен t < 27^, тогда как для больших времен определяющими являются
значения времен радиационного затухания г).
1) Рисунки приведены с разрешения U. Rathe.
188
Эффекты атомной когерентности и интерференции
Гл.7
7.4. Лазерная генерация без инверсии
Увидев, что когерентная суперпозиция дублета основного состояния может при-
привести к исчезновению поглощения, зададимся естественным вопросом: возможна
ли лазерная генерация, если в основном дублете находится
больше атомов, чем в возбужденном состоянии |а). В об-
общем случае (см. разд. 5.5) лазеру требуется инверсия на-
населенности для того, чтобы преодолеть поглощение ато-
атомами, находящимися в основном состоянии. Но что если
организовать дело так («сфазировать» атомы), чтобы по-
поглощение исчезло? Будет ли тогда лазерная генерация без
\Ь) \ * А инверсии? Ответ: «Да». В этом разделе будут рассмотрены
ситуации, когда лазерная генерация без инверсии возни-
возникает в когерентно приготовленной трехуровневой атомной
системе (рис. 7.6). С этой целью мы сначала очень просто
обсудим физику лазерной генерации без инверсии (ЛГБИ),
а затем приступим к более серьезному рассмотрению про-
проблемы.
Рис. 7.6. Трехуровневая
атомная система в поле
с частотой и
7.4.1. Концепция ЛГБИ. Рассмотрим вновь Д-систему, показанную на рис. 7.2,
где верхний уровень \а) связывается с нижними уровнями \Ъ) и \с) с помощью двух
полей, имеющих частоты v\ и vi- Будем считать, что дипольно разрешены только
два перехода \а) —>• \Ъ) и \а) —>> |е), и что выполняются условия резонанса ша5 =
= и\ и шас = 1/2- Гамильтониан системы задается выражениями G.2.1)-G.2.3), а
уравнения движения для амплитуд вероятности — выражениями G.2.5)—G.2.7).
Рассмотрим случай, когда в начальный момент времени заселены только два ниж-
нижних состояния \Ь) и |с), причем населенность их одинакова, а фазы их фиксированы,
так что
са@)=0, сь@) = ^=, сс(О) =
Это частный случай начального условия G.2.8), когда
Таким образом из решения G.2.9)—G.2.11) следует, что в низшем порядке
г (f) с* j fOD1 Р^гф1 .
Если
f
выражение G.4.3) принимает вид
= ^я,
Это означает, что поглощение исчезает (|ca(t)|2 = 0), если
то есть вновь получаем условия G.2.12) для когерентного пленения.
В случае, когда в начальный момент времени атом возбужден, то есть
са@) = 1, сь@) = сс@) = 0,
G.4.1)
G.4.2)
G.4.3)
G.4.4)
G.4.5)
G.4.6)
G.4.7)
7.4 Лазерная генерация без инверсии 189
решение уравнений G.2.5)-G.2.7) имеет вид
ca{t) = cos (^) , G.4.8)
ШХ G.4.9)
а - V 2 ! ¦ GА1°)
При fit ^C 1 приближенно получаем
G.4.11а)
Cc(t)-^. G.4.116)
Тогда вероятность излучения равна
Q2t2
' + |cc(t)|2 = ——, G.4.12)
то есть является величиной положительной и не зависящей от фаз. Таким образом,
если в системе выполняются условия G.4.2), G.4.4) и G.4.6) для исчезновения погло-
поглощения, то будет иметь место результирующее усиление даже в отсутствии инверсии
населенности.
7.4.2. ЛГБМ с точки зрения лазерной физики: простое рассмотрение. Рассмот-
Рассмотрим систему трехуровневых атомов, взаимодействующих с лазерным полем в резона-
резонаторе. Модель, которую мы будем рассматривать, иллюстрируется на рис. 7.6. Атомы
имеют один верхний уровень \а) и два нижних уровня \Ь) и \с) с энергиями Нша,
hujb, hujc и скоростями релаксации уа, 7ь? 1с соответственно. Переходы \а) —> \Ь)
и \а) —> \с) индуцируются теперь одним классическим полем частоты и. Переход
\Ь) —>• \с) дипольно запрещен. Атомы накачиваются со скоростью га в когерентную
суперпозицию состояний
P{U) = Р™\а)("\ + Р(ьь\Ь)(Ь\ + Р<?\с)(с\ + №\Ъ){с\ + Р{с°ь]\с)(Ь\. G.4.13)
Здесь раа (ск = а, 6, с) — населенности уровней и paai (ol ф af) — атомные
когерентности.
Прежде чем представить детальную теорию, дадим простое доказательство того,
как исчезновение поглощения в данной системе может привести к лазерной генерации
без инверсии.
Поскольку состояния \Ь) и \с) независимы, вероятность излучения задается вы-
выражением
Р»зл ^Рь + Рс^ (|*o^b|V2 + |xa^c|V2)pi°a\ G.4.14)
где ка^ь и ка^с — постоянные, зависящие от матричного элемента перехода между
соответствующими состояниями и от связи атома с полем. С другой стороны, веро-
вероятность поглощения записывается в виде
Рпогл = х\сь + Сс| V2 = ж[р<°> + pW + р%> + р%>]. G.4.15)
Поэтому скорость роста амплитуды лазерного поля, при подходящих условиях, при-
принимает вид
190 Эффекты атомной когерентности и интерференции Гл. 7
Здесь я/ — постоянная величина. Таким образом, если величины р^с , р^сЬ , р^ и Дс
взаимно сокращаются, то
$ = у Р<2*, G-4.17)
и мы можем получить лазерную генерацию даже тогда, когда только малая часть
атомов находится в возбужденном состоянии |а), то есть когда раа < (рьь + Рсс)-
С физической точки зрения, исчезновение поглощения в рассмотренной трехуров-
трехуровневой системе является проявлением квантовой когерентности. Если атом совершает
переход из верхнего состояния в два нижних, то полная вероятность перехода есть
сумма вероятностей переходов \а) —> \Ь) и \а) —> \с). Однако вероятность перехода
из двух нижних уровней в один верхний получается возведением в квадрат суммы
двух амплитуд вероятности. Если имеет место когерентность между двумя нижними
состояниями, то появляются интерференционные члены, дающие нуль в вероятности
перехода, соответствующего поглощению фотона.
7.4.3. Анализ ЛГБИ. Для более строгого рассмотрения роли атомной когерент-
когерентности в лазерной генерации без инверсии, обратимся к полуклассической теории,
в которой поле рассматривается классически, и ограничимся линейным анализом
проблемы, удерживая члены до второго порядка по константе взаимодействия атома
с полем. Уравнение движения для амплитуды поля в данной задаче имеет вид (см.
разд. 5.4)
g{t) = -—lm{eivt[pcaPac(t) + pbaPab(t)]}. G.4.18)
Уравнения для различных элементов матрицы населенности можно получить обоб-
обобщением метода, развитого в разд. 5.5.
В данном случае имеем 3 х 3-матрицу населенности
t
I to, G.4.19)
где суммирование по а и /3 включает состояния |а), \Ъ) и |с), и атомы возбуждаются
в процессе накачки с постоянной скоростью га в когерентную суперпозицию состоя-
состояний G.4.13). Для данной задачи, когда одномодовое поле частотой и и амплитудой
#(t) взаимодействует с трехуровневой атомной системой, гамильтониан взаимодей-
взаимодействия задается выражениями G.2.1)—G.2.3) с заменой
пш e~i4>1 e~il/lt = ^^ e~iv\ пш e~i(f>2 e~il/2t = ^^ e~ivK G.4.20)
В результате уравнения движения для элементов матрицы населенности имеют вид
раЬ = ^{iujab + lab)pab ^\^ е~ш{раа - рьь) + \^jf e~-Vc6, GA21)
Рас = ~{шас + 1ас)Рас -\^Y~ е~Ш(Раа - Рсс) + \ ^ e~ivt РЬс, G.4.22)
Раа = rapW ^ Japaa, G.4.23)
Рьь = rbpfb - jbPbb, G.4.24)
Рсс = rcpfj - JcPccj G.4.25)
Pbc = rapf] - (iujbc + jbc)pbc- G.4.26)
7.4
Лазерная генерация без инверсии
191
Здесь отсутствуют члены взаимодействия в уравнениях для paaj
поскольку мы ограничились линейным приближением.
Решение этих уравнений нулевого порядка, а именно
Рсс и
J
г ЛО)^ П @)
' aPaa ai® ~ Л Fao ч
7a
G.4.28)
G.4.29)
G.4.29)
можно подставить в уравнения G.4.21) и G.4.22) для раЬ и рас. Интегрируя резуль™
тирующие уравнения, находим, что
—
ъъ
Рсс =
1ъ J
^J
^а
_@)
Pab\J) —
//0* л@)
76
76c
Pac
'a 'c
G432)
При выводе этих уравнений мы предположили, что ?(t) является медленно ме-
меняющейся функцией времени t в течение атомного времени жизни, и потому $(to)
заменили величиной &(t). Подставляя обратно эти выражения для раъ и рас в G.4.18),
получаем
G.4.33)
где
7a с
2 , д 2 I
lac T ^
7a
lah
r
a 2
lab
j|pa?
(A + i^gC){iuJbc - 7bc)
. Gac +
(A - г7аб)(г
@)
@)
baPacPcb
G.4.34)
G.4.35)
G.4.36)
G.4.37)
G.4.37)
и А = v - шаЬ = шас - и = шЬс/2.
192 Эффекты атомной когерентности и интерференции Гл. 7
В уравнении G.4.33) член ?/aaj пропорциональный раа;, отвечает за усиление.
Он содержит две части, соответствующие процессам излучения при переходе из
состояния |а) в состояния \Ь) и |с). Члены ^6 и <^са пропорциональные pbb и рсс. ,
соответственно, отвечают за потери при поглощении в ходе перехода из состояний
\Ъ) и \с) в состояние \а). Это обычные слагаемые для полуклассической теории,
в которой требуется инверсия населенности для результирующего усиления. Однако
теперь, благодаря атомной когерентности, имеются зависящие от фазы члены ^ьс
и s^cbj пропорциональные, соответственно, рЬс и рсЬ . Поэтому возможно, что при
определенном выборе параметров члены ^г4ь и «й^.с, отвечающие за поглощение,
и члены 8&ъс и ^cbj отвечающие за когерентность, сокращаются, что и приводит
к лазерной генерации без инверсии. Это имеет место в двух случаях:
7а =76= 7с =7, Рас = РаЬ = Р, 7 > "Ьс, P^J = \йы! I ^. G-4'39)
7a<76, 7c = 76 = 7, Pac = Pab = Pi 7 = ^ab, PbJ = {pbJ \ e*"/2 , G.4.40)
где 2|рЬс| = pbb + pcc. Тогда
i(t) = —<f, G.4.41)
где
staa = ^ra Jp| 2pW, G.4.42)
соответственно. Таким образом, при условиях G.4.39) или G.4.40), любая малая
населенность верхнего уровня приводит к усилению.
7.5. Увеличение показателя преломления е помощью квантовой
когерентности
Значение показателя преломления оптической среды может достигать 10 или 100
на частотах близких к резонансу. Цена, которую необходимо заплатить за такую
высокую дисперсию, состоит, обычно, в высоком поглощении. Однако, благодаря
атомной когерентности или интерференционным эффектам, приводящим к таким
явлениям как корреляционный лазер или лазерная генерация без инверсии, можно
получить прозрачную среду со сверхвысоким показателем преломления. В этом
разделе будет рассмотрена ситуация, когда когерентность и интерференционные
эффекты приводят к большому значению показателя преломления, в то время как
поглощение остается очень малым или исчезает вовсе.
Линейный отклик атомной системы на электрическое поле Е описывается ком-
комплексной поляризацией
сю
P(z, t) = s0 [ x(r)E(z, t - т) dr, G.5.1)
о
7.5 Увеличение показателя преломления с помощью квантовой когерентности 193
которая появляется в виде вынуждающего члена в волновом уравнении для электри-
электрического поля (уравнение E.4.15) при <т = 0):
02Е 1 02Е 02Р (Г7Г оЧ
^о^г- G.5.2)
at
oz с at at
В уравнении G.5.1)
X = х' + X" G.5.3)
представляет собой восприимчивость, а %' ш х" — ее действительная и мнимая части
соответственно.
Для плоской волны с частотой i/,
E(z, t) = \i e-i(^-kz) + KX>j (j^^
A
из G.5.1) получаем
P(z, t) = ^*[хП е-'("*-*г) + X{-v) е<("*-*г)], G.5.5)
где x{v) — фурье™образ x(t). Сравнение с E.4.17) (при ф = 0) дает
&(z,t) = eo?x. G-5.6)
Таким образом, записывая х = X1 + ^х"ч получаем
G-5.7)
G-5.8)
Следовательно, подставив выражения для Re & и Im & в E.4.23) и E.4.24), получа-
получаем, что величины \' и х" описывают, соответственно, дисперсию и потери на единицу
длины волны.
Теперь свяжем действительную и мнимую части восприимчивости с показателем
преломления и коэффициентом поглощения среды.
Подставляя Е и Р из выражений G.5.4) и G.5.5), соответственно, в уравнение
G.5.2), получаем дисперсионное соотношение
к2 - ^п2 = 0, G.5.9)
с
где
n2(i/) = l+ *(!/). G.5.10)
Как обычно, к = ип/с. Если nf и п" есть действительная и мнимая части п, то есть
n = nf + in", G.5.11)
то п' представляет собой показатель преломления среды, а п" — коэффициент
поглощения. Согласно определению п" среда будет поглощающей, если п" > 0,
и усиливающей, если п" < 0. Объединяя G.5.10) и G.5.11), получаем
n' + in" = A + х' + гх") ' = [A + xO + x' ] '4exp[islgn(x/;)^/2], G.5.12)
где ft = tg^1[|x//|/(l + x')]- Тогда
G.5.13)
n =
7 М.О. Скалли, М.С. Зубайри
194 Эффекты атомной когерентности и интерференции Гл. 7
Отметим, что в случае, когда %; > 0 и %; ^> |х/;|,
п'~A + Х'I/2, G.5.15)
п" ~ 0, G.5.16)
то есть имеем большой показатель преломления и маленький коэффициент поглоще-
поглощения. Прежде чем обсуждать увеличение показателя преломления с одновременным
уменьшением поглощения за счет квантовой когерентности, покажем сначала, что
подобный эффект отсутствует в обычной двухуровневой системе.
Для двухуровневой системы действительную и мнимую части восприимчивости
можно получить подстановкой Re 3^ и Im 3^ из формул E.5.4) в выражения G.5.7)
и G.5.8). В результате находим, что
/ _ Pr- A \JQ) _ J0)i G к 17а\
X - eoh<ya у* + А2[Раа PbbU G.5.17а)
„ = _ V_la_ " Г @) _ W| Gl
?о^7ь 7 + A
где А = ш ~~ и; также было использовано линейное приближение
раа = —pW, G.5.18а)
J (X
Раа = —pfb- G.5.186)
Здесь 7 = (la Н" 7ь)/2, и будем считать, что уа = 7ь- Для замкнутой системы,
содержащей Na атомов в единице объема, величины га/уа и га/уь в выражениях
G.5.18а) и G.5.186) заменяются величиной ЛГО, так что формулы G.5.17а) и G.5.176)
принимают вид
Эти зависимости изображены на рис. 7.7. Условия %' ^> 1 и х; > |хя| не удовле-
удовлетворяются ни при каких значениях отстройки. Например, для перехода \Ь) —> \а)
(р1°2 = 0, р^ = 1) имеем х' = х", когда А = 7 и
^a G.5.20)
для 7 = 7d гДе
f4 G.5.21)
— скорость радиационного затухания между уровнями \а) и \Ь). Таким образом, для
длины волны 1 мкм и Na ^j 1016 атом-см™3 (газ при давлении одна атмосфера) имеем
%' ~ Ю4, то есть большой показатель преломления. Однако также и х" ^ Ю4? гДе
х" фактически характеризует потери на единицу длины волны. Следовательно свет
поглотился бы полностью на расстоянии существенно меньшем длины волны. Таким
образом, высокому показателю преломления соответствует сильное поглощение.
Однако ситуация существенно меняется в случае трехуровневых схем (типа той,
что рассматривалась в предыдущем разделе), где устанавливается атомная когерент-
когерентность и имеют место эффекты квантовой интерференции.
7.5 Увеличение показателя преломления с помощью квантовой когерентности 195
0.6
0.4
0.2 -
0 -
-0.2 -
-0.4 -
-0.6
у
у'
х'
х" -
i i i i
-2.5 -2 -1.5 -1 -0.5 0 0.5
А/7
1.5
2.5
Рис. 7.7. Действительная (сплошная линия) и мнимая (пунктирная линия) части линейной
восприимчивости двухуровневого газа (в относительных единицах), как функции нормиро-
л / г-> @) п @) -,
ванной расстройки /1/7- одесь раа = и и pbb = 1
Рассмотрим трехуровневую систему с парой близко лежащих нижних уровней,
в которой устанавливается когерентность между состояниями дублета с помощью
какого-то внешнего воздействия, как это обсуждалось в разд. 7.3. Предполагая, что
дипольно разрешенными являются переходы между верхним синглетом \а) и двумя
близко расположенными нижними уровнями \Ъ) и |с), получаем, что линейная вос-
восприимчивость системы равна
Х =
& _ 2 (РЬаРаЬ Рсарас\ ^iut
EoS1 v sqS1 eo(o J
G.5.22)
где элементы матрицы населенности ра^ и рас задаются выражениями G.4.31)
и G.4.32). Подставляя эти значения ра5 и рас в G.5.22), после некоторой перестановки
получаем
lib'
Paa
la
lb
, G.5.23a)
196
Эффекты атомной когерентности и интерференции
Гл. 7
- Aacsin<
lab + ^ab I I Та Jb
где Аа5 = и)аъ ~~ v, Аас = шас — ы,ъ> фаза ф задается в виде
, G.5.236)
G.5.24)
где фсЬ = arg[p;fe}]. Здесь для простоты мы положили, что раЬ = рас = рЬа = Рса =
= р. Таким образом, фаза ф зависит от атомной когерентности.
Из выражений G.5.23а) и G.5.236) видно, что можно сделать поглощение х"
равным нулю, сохраняя при этом величину х' большой, то есть сохраняя большим
показатель преломления. Обозначим А = (Аа5 + Дас)/2, настроим величину шсъ
(с помощью, например, постоянного магнитного поля в случае зеемановских подуров-
подуровней) так, чтобы шсь = 7Ьс? и рассмотрим случай, когда 7ь = 7с- Приготовим состояния
-0.005
-5 -4 -3 -2 -1
0
А/7
Рис. 7.8. Действительная (сплошная линия) и мнимая (пунктирная линия) части линейной
восприимчивости, как функции нормированной расстройки А/7, при введении когерентно-
когерентности. Значения параметров: ja = 0,1, jb = Jc = 2, раа = 0,01 и р^ = piJ = 0,495
\b) и |с) когерентно, так чтобы ф = 5тг/4 и р^ = рсс = \Рьс\- Результирующая
поляризация показана на рис. 7.8. Видно, что показатель преломления может быть
большим при нулевом поглощении.
7.6
Точное решение простой модели
197
7.6. Когерентное пленение, лазерная генерация без инверсии
ж электромагнжтно-мндуцмрованная прозрачность: точное решение
простой модели
В предыдущих разделах было показано, что пленение населенности, лазерная
генерация без инверсии и электромагнитно-индуцированная прозрачность являются
следствиями квантовой когерентности и интерференции. Чтобы дать единое описа-
Пробное
поле
Связывающее
поле
Рис. 7.9. Схема уровней энергии и порядок возбуждения в случае единого рассмотрения
когерентного пленения населенности, лазерной генерации без инверсии и электромагнитно-
индуцированной прозрачности
ние этих явлений в одной системе, рассмотрим систему трехуровневых атомов в Л-
конфигурации, когда скорости релаксации всех уровней равны j (рис. 7.9).
Если для атома в начальном состоянии
\ф@)) = са@)\а) + сь{О)\Ь) + сс(О)|с>, G.6.1)
то состояние атома в момент времени t будет иметь вид (задача 7.2)
№(*)> = A(t)\a) + B(t)\b) + C(t)\c), G.6.2a)
где
A(t) = L@)cos(m/2)-ic6@)^-sin(m/2)-icc@)^sm(m/2)je-7t/2, G.6.2a)
B{t) = { -
sin(m/2) + c6@)
cos(m/2)
¦ cos
e~7t/25 G.6.26)
198 Эффекты атомной когерентности и интерференции Гл. 7
= I - гса(О)— sin(m/2) + сь@)
сс@) [^ + ^ cos(m/2)j \ e^l\ G.6.2b)
Од1 и Од2 — частоты Раби, отвечающие резонансным полям, действующим на
переходах \а) —> \Ь) и \а) —>> |с), соответственно, и
Это общее решение можно использовать при соответствующих начальных условиях
для получения результатов, относящихся к захвату населенности, лазерной генера-
генерации без инверсии и электромагнитно-индуцированной прозрачности.
а) Если атомы приготовлены в когерентной суперпозиции нижних состояний, то
есть
И0)> = ^|6>-^|с>, G.6.4)
то получаем плененное состояние, если 7 = 0. Это можно проверить подставляя
са@) = 0, сь@) = пт/п и сс@) = -Пях/П в выражение G.6.2).
б) Рассмотрим теперь лазерную генерацию без инверсии. Как обсуждалось ранее,
усиление на единицу длины в лазере пропорционально мнимой части поляри-
поляризации Im &. Если вводить атомы в состояние \а) со скоростью га, то
= jra ca(t,to)c*b(t,to)dto =
t
if sinw - *°)] e(t"t0) = 4r°w
e
Здесь ca(t, to) = cos[O(t — to)/2] и с^(^, to) = -iO^i sin[O(t — to)/2]/0 — ампли-
амплитуды вероятности того, что атом находится в состоянии \а) и |6), соответственно,
удовлетворяющие тому начальному условию, что атомы переведены в состоя-
состояние \а) в момент времени to- Таким образом, получаем лазерную генерацию
без инверсии. Если еще одновременно переводить атомы в состояние пленения
(Q,R2\b) — Hj^i|c))/O, то получим лазерную генерацию без инверсии поскольку
плененные атомы не влияют на усиление.
в) Наконец рассмотрим свободную от затухания Л электромагнитно-индуциро-
электромагнитно-индуцированную прозрачность. Полагая j = 0 и рассматривая атомы переведенные
в состояние |6), получаем
Го2
\ JL Д2
1 ^Д1
COS
[
^Ч ИЛ
Tj|6>
и0й2
о2
о2
- cos
2
Список литературы к гл. 7
199
Теперь вероятность поглощения фотона пробного поля (то есть вероятность
возбуждения атома в состояние \а)) задается выражением
и обращается в нуль в пределе 0^2
но-индуцированной прозрачности.
чт0 и соответствует электромагнит-
электромагнитЗадачи
7.1. Рассмотрим трехуровневый атом в Л-конфигурации, как показано на рис. 7.9.
Гамильтониан взаимодействия атома с полем в представлении взаимодействия
и в условиях точного резонанса имеет вид
У =
|а)(с|+э.с.,
где Од1 и Од2 — частоты Раби, связанные с полями, действующими на перехо-
переходах \а) —)- \Ъ) и \а) —>• |с) соответственно.
1. Покажите, что собственные векторы гамильтониана имеют вид
где О = \/Щц + Од2 . Найдите соответствующие собственные значения.
2. Добавив одинаковые постоянные релаксации j для трех уровней, пока-
покажите, что решение уравнения Шредингера, удовлетворяющее начальному
условию G.6.1), задается выражениями G.6.2а)-G.6.2г) (см. работу Scully,
1994).
7.2. Используя адиабатическую теорию возмущений, покажите, что атом, находя-
находящийся в состоянии G.2.14), будет оставаться в этом состоянии. (Указание: см.
работу Kukllnsky, Gaubatz, Hioe and Bergmann, 1989.)
Список литературы
Эффект Ханле, фотонное эхо, самоиндуцированная прозрачность
и когерентные рамановские биения
Hanle, W. Z. Phys. 80, 93 A924).
Brelt, G. Rev. Mod. Phys. 5, 91 A933).
Abella, I., Kurnit, N. and Hartmann, S. Phys. Rev. 141, 391 A966).
Scully, M., Stephen, M. J. and Burnham, D. C. Phys. Rev. 171, 213 A968).
McCall, S. and Hahn, E. Phys. Rev. 183, 457 A969).
200 Список литературы к гл. 7
Shoemaker, R. and Brewer, R. Phys. Rev. Lett. 28, 1430 A972).
Brewer, R. and Hahn, E. Phys. Rev. A8, 464 A973).
*Маныкин Э.А., Самарцев В.В. Оптическая эхо-спектроскопия (Наука, Москва, 1984).
*Голенищев-Кутузов В.А., Самарцев В.В., Хабибуллин Б.М. Импульсная оптическая и
акустическая когерентная спектроскопия (Наука, Москва, 1988).
Scully, M. О., Fearn, H. and Atherton, В. W. In New Frontiers in Quantum Electrodynamics
and Quantum Optics, ed. A. O. Barut (Plenum, New York 1989)
*Ахмедиев Н.Н., Самарцев В.В. В кн. Новые физические принципы обработки информации,
ред. Ахманов С.А., Воронцов М.А. (Наука, Москва, 1990), с.326-359.
* Евсеев И.В., Ермаченко В.М., Самарцев В.В. Деполяризующие столкновения в нелинейной
электродинамике (Наука, Москва, 1992).
*Калачев А.А., Самарцев В.В. Фотонное эхо и его применение (КГУ, Казань, 1998).
*MaImIstov A.I., Basharov A.M. Nonlinear optics waves (Klawer Academic Publishers, London
1999).
*Рубцова Н.Н. Изв. РАН, сер.физ. 66, 302 B002).
Когерентное пленение
Alzetta, G., Gozzlni, A., Mol, L. and Orriols, G. Nuovo Cimento 36B, 5 A976).
Arimondo, E. and Orriols, G. Nuovo Cimento Lett 17, 333 A976).
Whltley, R. M. and Stroud, C. R., Jr., Phys. Rev. A 14, 1498 A976).
Gray, H. R., Whltley, R. M. and Stroud, C. R., Jr., Opt Lett 3, 218 A978).
Alzetta, G., Mol, L. and Orriols, G. Nuovo Cimento 52B, 209 A979).
Stettler, J. D., Bowden, C. M., Witriol, N. M. and Eberly, J. H. Phys. Lett 73Л, 171 A979).
Radmore, P. M. and Knight, P. L. J. Phys. В 15, 561 A982); Phys. Lett 102A, 180 A984).
Dalton, D. J. and Knight, P. L. Opt Commun. 42, 411 A982).
Swain, S. J. Phys. В 15, 3405 A982).
Agarwal, G. S. and Nayak, N. J. Phys. В 19, 3375 A986).
Zaheer, K. and Zubairy, M. S. Phys. Rev. A 39, 2000 A989).
Arimondo, E. In Progress in Optics ed. E. Wolf, 35, 257 A996).
Лазерная генерация без инверсии
Javan, A. Phys. Rev. 107, 1579 A956).
Hansch, Т. W. and Toschek, P. E. Z. Phys, 236, 213 A970).
Popov, Т., Popov, A. and Ravtian, S. JETP Lett 30, 466 A970).
Arkhlpkln, V. and Heller, Yu., Phys. Lett 48A, 12 A983).
Kocharovskaya, O. and Khanln, Ya. I. Pis'ma Zh. Eksp. Teor. Fiz. 48, 581 A988) (JETP Lett
48, 630 A988)).
Harris, S. E. Phys. Rev. Lett 62, 1033 A989).
Scully, M. O., Zhu, S.-Y. and Gavrielldes, A. Phys. Rev. Lett 62, 2813 A989).
Harris, S. E. and Macklin, J. H. Phys. Rev. A 40, 4135 A989).
Imamoglu, A. Phys. Rev. A 40, 2835 A989).
Lyras, A., Tang, X., Lambropoulos, P. and Zhang, J. Phys. Rev. A 40, 4131 A989).
Kocharovskaya, O. and Mandel, P. Phys. Rev. A 42, 523 A990).
Fill, E. E., Scully, M. O. and Zhu, S.-Y. Opt Commun. 77, 36 A990).
Kocharovskaya, O., Li, R.-D. and Mandel, P. Opt Commun. 77, 215 A990).
Список литературы к гл. 7 201
Blok, V. R. and Krochik, G. M. Phys. Rev. A 41, 1517 A990).
Agarwal, G. S., Ravi, S. and Cooper, J. Phys. Rev. A 41, 4721 A990); ibid. 41, 4727 A990).
Baslle, S. and Lambropoulos, P. Opt. Commun. 78, 163 A990).
Imamoglu, A., Field, J. E. and Harris, S. E. Phys. Rev. Lett 66, 1154 A991).
Agarwal, G. S. Phys. Rev. A 44, R28 A991).
Narducci, L. M., Doss, H. M., Ru, P., Scully, M. O. and Keitel, C. Opt Commun. 81, 379 A991).
Bergou, J. A. and Bogar, P. Phys. Rev. A 43, 4889 A991).
Kocharovskaya, O. Phys. Rep. 219, 175 A992).
Scully, M. Phys. Rep. 219, 191 A992).
Scully, M. O., Zhu, S.-Y. and Fearn, H. Z. Phys. D 22, 471 A992).
Fleischhauer, M., Keitel, C. H., Narducci, L. M., Scully, M. O., Zhu, S.-Y. and Zubairy, M. S.
Opt Commun. 94, 599 A992).
Scully, M. O. Quantum Optics 6, 203 A994).
Kocharovskaya, O. and Mandel, P. Quantum Optics 6, 217 A994).
*Malyshev, V.A., Ryzhov, I.V., Trifonov, E.D., Zaitsev, A.I. Laser Physics 8, 494 A998).
*Shakhmuratov, R.N., Kozyreff, G., Coussement, R., Odeurs, J., Mandel, P. Opt. Commun. 179,
525 B000).
Экспериментальная демонстрация усиления света и лазерной
генерации без инверсии
Nottelmann, A., Peters, С. and Lange, W. Phys. Rev. Lett 70, 1783 A993).
Fry, E. S., Li, X., NIkonov, D., Padmabandu, G. G., Scully, M. O., Smith, A. V., Tittel, F. K.,
Wang, C., Wilkinson, S. R. and Zhu, S.-Y. Phys. Rev. Lett 70, 3235 A993).
van der Veer, W. E., van Diest, R. J. J., Donszelmann, A. and van Linden van den Heuvell, H.
B. Phys. Rev. Lett 70, 3243 A993).
ZIbrov, A. S., Lukln, M. D., NIkonov, D. E., Hollberg, L. W., Scully, M. O., Velichansky, V. L.
and Robinson, H. G. Phys. Rev. Lett 75, 1499 A995).
Padmabandu, G. G., Welch, G. R., Shvbin, I. N., Fry, E. S., NIkonov, D. E., Lukln, M. D. and
Scully, M. O. Phys. Rev. Lett 76, 2053 A996).
Увеличение показателя преломления с помощью квантовой
когерентности
Scully, M. О. Phys. Rev. Lett 67, 1855 A991).
Fleischhauer, M., Keitel, С. Н., Scully, M. О. and Su, С. Opt Commun. 87, 109 A992).
Fleischhauer, M., Keitel, C. H., Scully, M. O., Su, C., Ulrich, В. Т. and Zhu, S.-Y. Phys. Rev. A
46, 1468 A992).
Scully, M. O. and Zhu, S.-Y. Opt Commun. 87, 134 A992).
WIlson-Gordon, A. D. and Friedmann, H. Opt Commun. 94, 238 A992).
Rathe, U., Fleischhauer, M., Zhu, S.-Y., Hansch, T. W. and Scully, M. O. Phys. Rev. A 47, 4994
A993).
Sultana, S. and Zubairy, M. S. Phys. Rev. A 49, 438 A994).
Kocharovskaya, O., Mandel, P. and Scully, M. Phys. Rev. Lett 74, 2451 A995).
Электромагнитно-индуцированная прозрачность
Harris, S. E., Field, J. E. and Imamoglu, A. Phys. Rev. Lett 64, 1107 A990).
Hahn, K. H., King, D. A. and Harris, S. E. Phys. Rev. Lett 65, 2777 A990).
202 Список литературы к гл. 7
Boiler, K.-J., Imamoglu, A. and Harris, S. E. Phys. Rev. Lett 66, 2593 A991). В статье
сообщается о первом наблюдении ЭМИП.
Field, J. E., Hahn, К. Н. and Harris, S. E. Phys. Rev. Lett 67, 3062 A991).
Hakuta, K., Marmet, L. and Stolcheff, B. Phys. Rev. Lett 66, 596, A991).
*Шахмуратов Р.Н., Сабо А., Козырев Г., Куссемент Р., Одюрс Дж., Мандель П. Изв. РАН,
сер.физ. 64, 1963 B000).
* Сазонов СВ. Изв. РАН, сер.физ. 66, 353 B002).
Адиабатическим перенос населенности в трехуровневых системах
KukJtnskt, Л. R., Gaubatz, U., Hioe, F. Т. and Bergmann, K. Phys. Rev. A. 40, 6741 A989).
Oreg, J., Hioe, F. T. and Eberly, J. H. Phys. Rev. A 29, 690 A984).
Wilkinson, S. R., Smith, A. V., Scully, M. O. and Fry, E. S. Phys. Rev. A 53, 126 A996).
Явление интерференции Фано
Fano, U. Phys. Rev. 124, 1866 A961).
Fano, U. and Rail, A. Atomic Collisions and Spectra, (Academic Press, New York 1986).
Глава 8
КВАНТОВАЯ ТЕОРИЯ
РЕЛАКСАЦИИ — МЕТОДЫ
ОПЕРАТОРА ПЛОТНОСТИ
И ВОЛНОВОЙ ФУНКЦИИ
Во многих задачах квантовой оптики релаксация играет важную роль. Среди
них можно, например, отметить распад атома из возбужденного состояния в нижнее
состояние и затухание поля излучения внутри резонатора с частично прозрачны-
прозрачными зеркалами. В общем случае релаксация системы обусловлена взаимодействием
с резервуаром с большим числом степеней свободы. Между тем, нас интересует
только эволюция переменных системы. Чтобы решить эту проблему, необходимо
вывести уравнения движения интересующей нас системы, взяв след по переменным
резервуара. Существует несколько различных подходов к решению этой задачи.
В этом разделе мы представим теорию релаксации, основанную на использовании
оператора плотности, в которой переменные резервуара исключаются с помощью вве-
введения приведенного оператора плотности системы в представлении Шредингера (или
представлении взаимодействия). Мы также представим подход «квантовых скачков»
к теории релаксации. В следующих главах релаксация системы будет рассмотрена
с привлечением метода оператора шума в представлении Гейзенберга.
Понять механизм релаксации можно, рассматривая распад атома из возбуж-
возбужденного состояния внутри резонатора. Атом можно рассматривать как одиночную
систему, связанную с полем излучения внутри резонатора. Даже в отсутствие фо-
фотонов в резонаторе существуют квантовые флуктуации, связанные с вакуумным
состоянием. Как уже обсуждалось в гл. 1, поле можно представить как большой набор
гармонических осцилляторов, каждый из которых соответствует отдельной моде
резонатора. С увеличением размеров резонатора плотность мод увеличивается, и в
свободном пространстве мы получаем континуум мод. Поэтому среди них существует
«мода резонатора», которая находится в резонансе с атомным переходом.
Атом тоже можно представить как осциллятор, причем возбужденный атом
соответствует осциллятору в возбужденном состоянии. Взаимодействие атома с боль-
большим числом осцилляторов (соответствующих большому числу мод поля) приводит
к релаксации. Это означает, что энергия, первоначально принадлежавшая атому,
распределится между затухающими осцилляторами, вызывая таким образом переход
атома в нижнее состояние.
Диссипация энергии сопровождается флуктуациями. На примере систем, изуча-
изучаемых в этой и последующих главах, мы познакомимся с этим аспектом релаксации,
который в более формальном виде выражен в так называемой флуктуационно-
диссипационной теореме. Прежде чем рассматривать релаксацию атома и поля, обу-
обусловленную резервуаром гармонических осцилляторов (бозонных) мод, рассмотрим
общую теорию резервуара.
204 Квантовая теория релаксации — оператор плотности Гл. 8
8.1. Общая теория резервуара
Рассмотрим в общем виде некую систему Я, которая взаимодействует с резерву-
резервуаром R. Комбинированный оператор плотности обозначим через Psr- Приведенный
оператор плотности системы ps получается путем взятия следа по координатам
резервуара, т. е.
Ps = Ttr(Psr). (8.1.1)
Пусть У(€) — энергия взаимодействия системы с резервуаром. Тогда уравнение
движения для Psr имеет вид
ihpSR = [r(t),psn(t)]. (8.1.2)
Это уравнение можно формально проинтегрировать и мы получаем
t
Psn(t) = psr(U) - \ JV(*'), pSR{t')] dt'. (8.1.3)
ti
Здесь t{ — время, когда начинается взаимодействие. Подставляя psR.{t) обратно
в уравнение (8.1.2), получаем уравнение движения
t
PSR = ~[П*),РЗЛ(и)] ~ jf jVW, №), PSR(t')}] dt'. (8.1.4)
ti
Если бы энергия взаимодействия У{1) равнялась нулю, то система и резервуар
были бы независимы друг от друга и оператор плотности psu можно было бы пред-
представить в виде прямого произведения psu{t) = Ps(t) ® Pr{U), где мы предполагаем,
что резервуар находится в тепловом равновесии. В случае, когда ^ мало, ищем
решение уравнения (8.1.4) в виде
PsR(t) = Ps(t) <S> pR{U) + Pc(t), (8.1.5)
где pc(t) — члены более высоких порядков по У'. Для того чтобы удовлетворить
условию (8.1.1), потребуем, чтобы
Тг[рс(<)]=0. (8.1.6)
Если psR{t) из (8.1.5) подставить в интеграл из (8.1.4), и оставить только члены
порядка не выше Т^2, то получим
ps = -^Тг \ПЬ), Ps(t) ® PR(U)} - ± j[Y(t), [T(t'), ps(t') ® pr(U)}} dt'. (8.1.7)
U
Приведенный оператор плотности ps(t), определяющий статистические свойства
системы, зависит от предыдущей истории, начиная с момента времени t = ti до t'.
Это видно из уравнения (8.1.7), так как ps(tf) оказывается под интегралом. Между
тем, обычно, резервуар является протяженной открытой системой, имеющей много
степеней свободы. Более того, как будет показано на частном примере в следующем
разделе, наличие большого числа степеней свободы резервуара (мод, фононов, и т. д.)
приводит к дельта-функции S(t — tf). Следовательно, оператор плотности системы
Ps(tf) можно заменить оператором ps(t), и процесс тогда называется марковским.
Это предположение разумно, поскольку релаксация разрушает память о прошлом.
8.2 Релаксация атома, вызванная тепловым и сжатым вакуумным резервуарами 205
Теперь уравнение (8.1.7) принимает вид
t
ps = -^Tr [T(t),ps{t) 0 pR(U)] ^ ^ Г[Г(t), [y(tf), Ps(t) 0 pR(U)]] dtf. (8.1.8)
и
Это уравнение справедливо для системы, описываемой оператором р^? которая вза-
взаимодействует с резервуаром, описываемым оператором рц. В следующих разделах
будут рассмотрены несколько примеров взаимодействия системы с резервуаром.
8.2. Релаксация атома, вызванная тепловым и сжатым вакуумным
резервуарами
Спонтанный переход атома из возбужденного состояния можно объяснить на при-
примере простой модели, в которой атом связан с резервуаром простых гармонических
осцилляторов. Аналогичным образом, релаксацию поля излучения внутри резона-
резонатора можно описать с помощью модели, в которой интересующая нас мода связана
с полным набором мод резервуара. Эти задачи интересны не только для физики
лазеров и мазеров, но также и для квантовой теории пассивных интерферометров,
например таких, которые используются для детектирования гравитационных волн.
Сначала рассмотрим радиационный распад возбужденного состояния двухуров-
двухуровневого атома, вызываемый резервуаром простых гармонических осцилляторов, ко-
которые описываются операторами уничтожения (рождения) Ь^ (б?) и плотностью
распределения частот v^ = ck. В представлении взаимодействия и приближении
вращающейся волны гамильтониан взаимодействия имеет простой вид
к
где а^ = \Ь)(а\ и а+ = \а)(Ь\ выражены через векторы возбужденного (\а)) и основно-
основного (\Ь)) состояний. Теперь система соответствует двухуровневому атому (ps = Ратом)-
Подставляя энергию взаимодействия У (выражение (8.2.1)) в уравнение движения
(8.1.7) для ps = Ратом, получаем
k,k'
+ [a+a^paTOM(tf) — a^paTOM(tf)a+] е %^ш Vk^1 г^ш Vk>t '(b^b^t) +э.с.}, (8.2.2)
где средние значения относятся к начальному состоянию резервуара. С этого момента
мы выбираем частную модель состояний резервуара.
8.2.1. Тепловой резервуар. В качестве первого примера предположим, что пере-
переменные резервуара распределены по некоррелированной тепловой равновесной смеси
состояний. Приведенный оператор плотности такого резервуара является многомо-
довым обобщением теплового оператора, а именно
PR = П I1 " exp ("TZ^ J | ехр ( -
к
206 Квантовая теория релаксации — оператор плотности Гл. 8
где &в — постоянная Больцмана и Т — температура. Легко показать, что
(Ьк> = Н) = 0, (8.2.4а)
> = "к?кк<, (8.2.46)
(ггк + 1Нкк<, (8.2.4в)
F+6+) = 0, (8.2.4г)
где среднее число бозонов
Подставляя средние значения из (8.2.4) в уравнение (8.2.2), получаем
о it 1 — do it 1 (j-j-l (Tib- ~\~ l) e* l/k)\f' * )\ _i_ ^ q /'g 2 ^^
Теперь выполним ту ж:е процедуру, что была сделана в теории спонтанного излучения
Вайскопфа-Вигнера.
Сумму по к можно заменить интегралом с помощью стандартного рецепта (см.
F.3.9)):
2тг тг оо
к
I d§ sin I? \ dkk2, (8.2.7)
J J
()
0 0 0
где V — объем квантования. Интегрирование в уравнении (8.2.6) можно выполнить
в приближении Вайскопфа-Вигнера, как уже обсуждалось в разд. 6.3. Тогда мы
получаем интегралы вида F.3.12). Таким образом, находим приведенный оператор
ПЛОТНОСТИ Ратом,
р
Ратом {t) = -птепл-[<т^о-+ратом(^) — a+paTOM(t)a^] —
_ р
- (птепл + l)-[a+(j^paTOM(i) - a^paTOM(t)(j+} + э.с, (8.2.8)
где тгтепл = nko (k0 = ш/с) и
1 4а^ь (829)
— скорость релаксации атома, идентичная константе релаксации F.3.14), выведенной
в теории спонтанного излучения Вайскопфа-Вигнера. При выводе уравнения (8.2.8)
мы воспользовались величиной g^ из F.1.8).
Теперь уравнение движения для элементов матрицы плотности атома можно
получить из уравнения (8.2.8):
Раа = («|ратОм|а) = ^(^тепл + 1)Граа + ^теплГ Pbb, (8.2.10a)
РаЪ = Р*Ьа = - (^тепл + |) ГраЬ, (8.2.106)
Pbb = ^^теплГрбЬ + (^тепл + 1)Граа. (8.2.10в)
Отметим, что раа + рьъ = 0. Это соотношение справедливо благодаря тому, что
мы рассматриваем переход из верхнего состояния \а) только в нижнее состояние
8.2 Релаксация атома, вызванная тепловым и сжатым вакуумным резервуарами 207
\Ь). Поэтому, согласно условию сохранения вероятности, подразумевается, что раа +
+ рьь = 1- Эта ситуация отличается от той, которая обсуждалась в разд. 5.3, где
атомные состояния \а) и \Ъ) распадались в другие состояния через безызлучательные
переходы. При нулевой температуре (ггТепл = 0) уравнения сводятся к следующим:
Раа = -Г>аа, (8.2.11а)
РаЪ = ^\раЪ, (8.2.116)
Уравнение (8.2.11а) представляет собой как раз результат Вайскопфа-Вигнера
F.3.15).
8.2.2. Резервуар сжатого вакуума. Во втором примере рассматривается ситу™
ация, когда атом связан с резервуаром сжатого вакуумного поля. Приведенный
оператор плотности резервуара имеет вид
(Ок|5+@, (8-2.12)
где оператор сжатия (см. выражение B.8.9) с 6к = b(ck) и т. д.) определяется
выражением
ЖО = ехр(Г&к0+кЬк0-к - ^0+к&+ _к), (8.2.13)
где ? = г ехр(г$), г — параметр сжатия и § — опорная фаза сжатого поля. Многомодо™
вое сжатое поле не является просто произведением независимо сжатых мод, а скорее
существует корреляция между модами, симметрично расположенными относительно
центральной, резонансной частоты v = cko сжимающего устройства. Следуя методу,
который использовался при выводе соотношений B.7.6) и B.7.7), получаем
_k0 = 6kch(r) - Ь^^е'* sh(r), (8.2.14a)
-ko = b+ ch(r) - 62ko_k e-ie sh(r). (8.2.146)
Аналогичные выражения существуют для S^ „^ftkS'ko—k и ^k -k^k ^ko-k- Поэтому
вычисление средних значений, таких как (b^br/), мож:но упростить, записав
(b+bv) = П(°Ч1^ч b?S4$4 bk,S4\O4). (8.2.15)
q
Следовательно
(&k> = (b?) = 0, (8.2.16a)
(b+bv) = sh2 (rNw, (8.2.166)
) =ch2 (rMw, (8.2.16b)
w sh(r) ch(r) <5k',2k0-k, (8.2.16r)
^ Mr) ch(r) ^,2ko_k. (8.2.16д)
208 Квантовая теория релаксации — оператор плотности Гл. 8
Подставляя выражения (8.2.16а-8.2.16д) в уравнение (8.2.2) и поступая также, как
и при выводе уравнения (8.2.8), получаем
тр
Ратом = ~ "^ ch2(r)( 2 + )
тр
- - sh2(r)(cr_cr+paTOM - 2<т+/эатом<т_ + /эатомо
-re-iiJsh(r)ch(r)cr_paTOMcr_ -re^sh(r)ch(r)o-+/0aTOM<7+. (8.2.17)
При выводе уравнения (8.2.17) было использовано соотношение а^а^ = 0"+<т+ = 0.
Из (8.2.17) следует, что уравнения движения для средних значений операторов
ах = (<т^ + а+)/2, (Ту = {а ^ — a+)/2i и az = Bсг+«7^ — 1) имеют вид
<*х) = -?е2г<О, (8.2.18а)
<*»> = -|егЫ, (8-2-186)
(&z) = -r[2sh2(r) + 1](ctz) - Г = -Г2(а2) - Г, (8.2.18b)
где Yz = F[2sh2(r) + 1], и выбрана фаза $ = 0. Поэтому ясно, что резервуар
сжатого вакуума приводит к фазово-чувствительной релаксации атома. Синфазная
и квадратурная составляющие, (сгж) и («т^), дипольного момента атома релаксируют
с различными скоростями, в зависимости от его начальной фазы относительно фазы
'д сжатого вакуума.
8.3. Релаксация поля
Метод, развитый в предыдущем параграфе, можно применить к затуханию моды
электромагнитного поля частотой и внутри резонатора. Вместо (8.2.1) теперь вос-
воспользуемся гамильтонианом взаимодействия в виде
1/ = h^g^lae^^k)t + a+b^ei{iJ^k)% (8.3.1)
k
где а (а+) — оператор уничтожения (рождения) интересующей нас моды. Операторы
6к и Ь^ описывают моды резервуара, вызывающие затухание поля. Для потерь,
обусловленных пропусканием, они в действительности представляют собой поле вне
резонатора.
Уравнение движения для приведенного оператора плотности поля можно легко
получить, так как его вывод точно такой же, как и для атомной системы, которая уже
обсуждалась в предыдущем разделе. Это можно сделать, заменив а^ и сг+ полевыми
операторами а и а+, соответственно.
Когда моды 6к изначально находятся в тепловой равновесной смеси состояний
(8.2.3), тогда результат имеет вид
С/У Cj??
р = -^птепл{аа+р-2а+ ра + раа+) - -^(птепл + 1)(а+ар - 2ара+ +ра+а), (8.3.2)
где, как и ранее, *€ — постоянная затухания, и птетш = ^к0 — среднее число квантов
(на частоте и) в тепловом резервуаре. Здесь р — приведенный оператор плотности
для поля. В частности, при нулевой температуре (птепл = 0),
р = j{a^ap - 2ара+ + ра+а). (8.3.3)
8.4
Уравнение Фоккера-Планка
209
Если все потери являются потерями, обусловленными пропусканием, тогда *€ можно
связать с добротностью Q резонатора с помощью соотношения ^ = v/Q.
Когда моды 6к изначально находятся в состоянии сжатого вакуума (выражение
(8.2.12)), то получается следующее уравнение движения для приведенного оператора
плотности р
р =
CJ?
1)(а+ар - 2ара
ра+а) N(aa+р - 2а+ра
М(аар - 2ара + раа) -\ М*(а+а+р - 2а+ра+
(8.3.4)
где N = sh2(r) и М = ch(r) sh(r) exp(-i'd). Это уравнение описывает, например,
эволюцию поля в резонаторе, связанном через частично прозрачное зеркало с внеш-
внешним полем, которое находится в состоянии сжатого вакуума. Уравнение движения в
случае теплового резервуара (8.3.2) можно получить из уравнения (8.3.4) с помощью
подстановки N —> WTenjl, M —>• 0. Однако в случае резервуара сжатого вакуума
параметры N и М связаны друг с другом соотношением \М\ = [N(N +
8.4. Уравнение Фоккера-Планка
Особенно интересным представлением, в которое молено преобразовать уравнение
движения для оператора плотности, является представление когерентных состояний
или Р—представление, уже обсуждавшееся в гл. 3. В этом параграфе мы выведем
уравнение движения для Р-распределения, которое соответствует уравнению (8.3.2)
для оператора плотности моды гармонического осциллятора, затухающей при взаи-
взаимодействии с тепловым резервуаром, заполненным гармоническими осцилляторами.
Итоговое уравнение будет иметь вид уравнения Фоккера-Планка. Решение этого
уравнения раскроет некоторые интересные черты временной эволюции распределе-
распределения поля.
Подставим Р-представление оператора плотности C.1.16)
р= P{(%j ol*, t)\a){(x\ d a (8.4.1)
в уравнение (8.3.2). Тогда получаем
P(a,a*Jt)\a)(a\d2a =
d a—
a\t){a+a\a){a\ - 2а\а)(а\а+ + \а)(а\а+а)
Из соотношений
= а\а)(а
\а)(а
а){а\а =
а1 = а
а)(а\,
(8.4.2)
;8.4.3а)
;8.4.3б)
;8.4.3в)
(8.4.3г)
210
Квантовая теория релаксации — оператор плотности
Гл.8
следует, что
аа '
а)(а\ — 2а+ \а) (а\а + \а)(а
аа ' =
¦см а*\ \а)(а
д Л д2
да да* дада*
* ИИ, (8.4.4)
а а\а)(а\ — 2а\а)(а\а + \а)(а\а а =
Теперь подставим (8.4.4) и (8.4.5) в уравнение (8.4.2) и проинтегрируем результат по
частям. Выполняя это, получаем
= аР(а,а*,?)|а)(а|
Поскольку на бесконечности распределение стремится к нулю, уравнение (8.4.6)
приобретает вид
Р(а, a*,t) (a^-\a)(a\) d2a = - \ \^-аР(а, a*,t)] \a)(a\ d2a. (8.4.7)
х J х да' ' х / J Ida x 7J ' ' х ' х 7
Аналогичным образом
4 d2a= I \^L—P(a,a*,t)\ \a)(a\d2a. (8.4.
Тогда из уравнения (8.4.2) имеем
- Ц [{1а + ^+Ш—о?^
a>(a|d»a. (8.4.9)
Приравнивая коэффициенты при |a)(a| под знаками интегралов, получаем уравне-
ние движения для Р(ск, ск*, t) в виде
(8.4.10)
Это и есть уравнение Фоккера^Планка для Р-распределения.
Найдем теперь решение уравнения Фоккера^Планка. Предположим, что поле
изначально находится в когерентном состоянии |ооЬ т-е-
-а0). (8.4.11)
8.4
Уравнение Фоккера-Планка
211
В гауссовом представлении ^-функции имеем
Р(а,а*,0) = lim — ехр
Поэтому мы ищем решение уравнения (8.4.10) в виде
Р(а, а*, 0) = ехр[-а(*) + b(t)a + c(t)a* - d(t)aa*]
при начальных условиях
а@) = ^ + 1п(тгб;),
6@) = а*0/е,
с@) =
d@) =
(8.4.12)
(8.4.13)
(8.4.14а)
(8.4.146)
(8.4.14в)
(8.4.14г)
Подставляя выражение (8.4.13) для Р(а,а*,?) и выполняя необходимые операции
дифференцирования по t и а, получаем
— а
со* —
еплFс- d)
a + f | - nTenjlcd)a* - (d - nTemirf2)H | •
(8A15)
Сравнение членов, пропорциональных |о|25 с**, а и единице, приводит к следующей
системе дифференциальных уравнений:
d = ^{d - nTenjId2), (8.4.16a)
(8.4.166)
(8.4.16в)
a = -^[1 + нтеплFс - d)]. (8.4.16г)
Решение этих уравнений при начальных условиях (8.4.14а)—(8.4.14г) имеет вид
«о е
14.176)
8.4.17в)
1 |_ 1п{тг[птеплA — е~^ь) + ? е~^*]}. (8.4.17г)
татеПлA - е €t) + e е~^*
Подстановка этих решений в уравнение (8.4.13) приводит к гауссову виду Р(а, а*, ?):
212
Квантовая теория релаксации — оператор плотности
Гл.8
где
8А19)
— дисперсия функции Гаусса около ее среднего значения,
a0U(t) = а0 e-vt/2-м. (8А20)
В выражении (8.4.20) мы включили множитель ехр(—г*/?), возвращаясь обратно из
представления взаимодействия в представление Шредингера.
Дисперсия D(t) растет, начиная с нулевого значения, в то время как центр гауссо-
гауссова распределения циркулирует по экспоненциальной спирали, заданной выражением
(8.4.20). Это показано на рис. 8.1, где Р-распределение изображено как функция
P{a,a*,t)
P(a,a*,t = 0)
Ima
Re a
Без затухания
С затуханием
(экспоненциальная спираль)
Рис. 8.1. Р-представление для комплексной амплитуды моды гармонического осциллятора,
затухающей при взаимодействии с тепловым резервуаром. Мода гармонического осцилля-
осциллятора начинает эволюцию из когерентного состояния \а) в момент времени t = 0, а среднее
значение амплитуды движется по экспоненциальной спирали, непрерывно уменьшаясь по
модулю, в то время как дисперсия амплитуды растет
комплексной амплитуды а. Когда время t намного больше, чем время затухания (^7~1,
распределение поля приходит к равновесию с осцилляторным тепловым резервуаром.
В этом стационарном состоянии дисперсия принимает свое предельное значение
^тепл? и распределение Гаусса центрировано в начале системы координат. Таким
образом, поле передает свое первоначальное возбуждение в тепловой резервуар
осцилляторов, но приобретает шум в процессе затухания. Это является проявлением
флуктуационно-диссипационной теоремы, т. е. диссипация через тепловой резервуар
осцилляторов сопровождается флуктуациями. Мы обсудим это в следующей главе.
Интересно отметить, что если взять тепловой резервуар, находящийся при нуле-
нулевой температуре, (птепл = 0), то дисперсия D(t) остается нулевой для всех значений
времен и Р(а, a*, i) всегда остается ^-функцией, т. е.
Р(а, a*,t) = 8{2)[а - a0U{t)]. (8A21)
Состояние поля остается для всех времен чистым когерентным состоянием. Эта
форма диссипация полностью свободна от шума.
8.5 Описание релаксации с помощью «квантовых скачков» 213
8.5. Описание релаксации с помощью «квантовых скачков»
Исторически понятия квантовых скачков и мгновенного коллапса волновой функ™
ции восходят к ранним дням становления квантовой механики, когда Эйнштейн вы-
высказывал свою озабоченность по поводу исходящей сферической волны, «коллапси-
рующей» при детектировании фотоэлектрона; и к представлениям Бора, касающимся
излучения света, когда атом «прыгает» между боровскими орбитами.
Между тем, с приходом квантовой механики вопрос о квантовых скачках в целом
стал приобретать новые перспективы. Были введены представления об атомных
переходах и часто можно было встретить утверждение, что «нет таких вещей как
квантовые скачки».
Недавно в работе Демельта и других было ясно показано, что резкие скачки
появляются во многих явлениях квантовой оптики. К таким примерам можно отнести
блестящую работу, посвященную одиночному иону в ловушке Паули.
Совсем недавно был развит новый подход «квантовых скачков» к проблеме дис™
сипации, и здесь можно встретить такие названия и концепции как: метод Монте
Карло, квантовые траектории, коллапс или редукция вектора состояния, отсутствие
отсчета или «нулевое» измерение, и матрица условной вероятности. Здесь мы кратко
познакомим вас с этими интересными идеями применительно к релаксации или
диссипации в квантовой оптике.
8.5.1. Условные операторы плотности и нулевое измерение. В предыдущих раз-
разделах этой главы была развита теория релаксации или диссипации в квантовой меха-
механике с точки зрения оператора плотности. Теория обычно приводит к уравнению вида
(8.3.3), которое описывает затухание отдельной моды резонатора при температуре
Т = 0. При выводе уравнения использовалась модель резервуара с большим числом
осцилляторов, например, взаимодействие мод резонатора с внешними фононами. Тем
Рис. 8.2. Пучок двухуровневых атомов, находящихся в основном состоянии |6), проходит
через резонатор
не менее результат (8.3.3) не зависит от модели и здесь мы вновь исследуем эту
проблему, используя другую модель, которая приведет нас естественным образом к
другой точке зрения, касающейся процессов диссипации.
Рассмотрим модель, изображенную на рис. 8.2, в которой атомы, находящиеся
в основном состоянии, пропускаются через резонатор, настроенный на частоту атом™
ного перехода, т. е. гамильтониан в представлении взаимодействия имеет вид
У = hg(a+\b){a\ + \a){b\a). (8.5.1)
214 Квантовая теория релаксации — оператор плотности Гл. 8
Рассмотрим оператор плотности поля p(t + т) в момент времени t + т, который
получается в результате иыжекции атомов, находящихся в основном состоянии, в ре-
резонатор в момент времени t, т. е.
p(t + т) = Тгатом [e-ir^hp{t) 0 \Ь)(Ь\ eir^n] =
= (а|Ратом-поле(* + т)\п) + <6|ратом-поле(^ + т)\Ъ). (8.5.2)
Естественно отождествить два члена в (8.5.2) с «условными» операторами плот™
ности, т. е.
Pa{t + т) = условный оператор плотности поля, атом возбужден =
= (а\ e-irT/hp(t) <g> \Ь)(Ь\ eirr/h\a}, (8.5.3а)
Pb(t + т) = условный оператор плотности поля, атом не возбужден =
= (b\ e-iyr/hp(t) ® \b)(b\ eirT'h\b). (8.5.36)
Можно рассматривать ра и р^ как условные операторы плотности, соответствую-
соответствующие тому, что в пучке атомов мы зарегистрировали отсчет (атом возбужден) или
не зарегистрировали его (атом находится в основном состоянии). Таким образом,
атомный пучок выполняет две функции: он является механизмом диссипации и он
также является своего рода пробником или фотодетектором для поля.
Далее отметим, что на малых временах т можно разложить множители
ехр(±1Ут/Н) и получить, что
pa(i + т) ^ g2T2ap(t)a+, (8.5.4а)
pb(t + т) ^ p{t) ^ \g2r2[a+ap{t) + p{t)a+a] ^ e^Rra+ap(t) e^Rra+a, (8.5.46)
где Д = g2r/2.
Теперь сделаем следующий важный шаг. Устремим т->0и допустим, что выра-
выражение (8.5.4а) связано с «квантовым скачком» фотопоглощения в момент времени
t. Тогда, если рассматривать процесс, в котором наблюдается п отсчетов в моменты
времени t\, ti, • • • , tn, при отсутствии отсчетов в промежутках между этими момен-
моментами, то условный оператор плотности имеет вид
pW = [e-s(t-tn)ae-s(tn-tn.1) _^aе-*(*2-*1)ае-*
х e^a+ е"^*2"*1) . . . a+ e^^^a+e"^^]/ Tr, (8.5.5)
где S = i?a+a, и след в знаменателе — нормировочный множитель. Выражение
можно упростить, учитывая то, что, например,
e-S(t2-t1)ae-St1 _ e^Ra+a{t2^t
at г a g- Ra+ at! _ e~ Ra+at2 e~
5
Это соотношение можно использовать многократно и привести выражение (8.5.5)
к простому виду
— Ra~*~ at n /f\\ +n —- Ra' at
(n) = e a p@)a e
Tv[p@)a+ne-2Ra atan]
где разнообразные множители типа ехр(—Д^х) сокращаются благодаря нормировке.
Выражение (8.5.7) (и его обобщения) является основным результатом этого раздела.
8.5 Описание релаксации с помощью «квантовых скачков» 215
В частности, если взять в качестве р@) оператор плотности чистого состояния р@) =
= \ф(О))(ф(О)\, то (8.5.7) можно записать следующим образом:
— Ra' at n
e a
Уравнение (8.5.8) является исходным для наиболее простого и естественного введе-
введения метода волновой функции в описании диссипативных процессов.
8.5.2. Метод Монте Жарло для волновой функции при описании релаксации.
Пользуясь результатом предыдущего раздела, т.е. выражением (8.5.8), представим
здесь краткий расчет затухания в рамках метода волновой функции. Для того, чтобы
раскрыть основные идеи, мы продолжим рассмотрение простой задачи релаксации
одномодового поля, но возьмем более общий резервуар, такой, как разд. 8.3. Таким
образом, скорость релаксации R больше не определяется временем т, а задается
более короткими временами корреляции резервуара. Выражение (8.5.8) приводит
нас к записи «условного вектора состояния»
— Ra ' a8t n\ / /.\\
№<">(* + 6t)) = , в а Wt)) (8.5.9)
<\J(il>(t)\a+n e^2Ra+aStan\i)(t))
представляющего собой состояние поля, возникающее из \фA)) при условии, что п
фотонов поглотилось в течение времени St. В частности, особый интерес представ™
ляют собой состояния, включающие в себя только одно событие поглощения или ни
одного. Состояние в момент времени t + St для п = 0 (ноль измерений), имеет вид
St)) = «l*'» S '~**У*Ж*)), (8.5.10а)
где (а+а) = (ip(t)\a^a\ip(t)); а состояние, соответствующее п = 1, (квантовый
скачок) есть
+ st)) = **№)) ~ -7=н;№)). (8.6.106)
Например, если начальное квантовое состояние полевой моды имеет вид
(8.5.11)
то (8.5.10а) и (8.5.106) означают условные векторы состояния
( }
St)) = -™|0). (8.5.126)
ll2
Между тем, мы хотим описать эволюцию из состояния |^>(?)), заданного выражением
(8.5.11), в более общее состояние в последующие моменты времени, которое должно
стать в конце концов состоянием |0). Как видно из (8.5.10а) в течение времени St не-
ненормированное состояние «нет отсчета» или «нулевое измерение» \ф) удовлетворяет
уравнению движения
1*@)(« + *))-|*@)@) = -Дв+а|^»)(*)>, (8.5.13а)
О ь
216 Квантовая теория релаксации — оператор плотности Гл. 8
то есть
^№@)(*)> = -jr(-ihRa+a)\&°\t)). (8.5.136)
Таким образом, в отсутствие поглощения мы вынуждены описывать временную
эволюцию ненормированного вектора состояния с помощью неунитарного уравнения
Шредингера
которое определяется неэрмитовым гамильтонианом
Уг = —ihRa+ а. (8.5.15)
Конечно, развитие во времени, которое подразумевается в уравнении (8.5.14),
прерывается в случайные моменты времени квантовыми скачками или коллапсами
волновой функции. Когда такой коллапс происходит, состояние задается вектором
|0). Это происходит только один раз. Начиная с этого момента времени и далее поле
находится в вакуумном состоянии. Продолжая рассмотрение нашего простого приме™
ра, заметим, что, согласно уравнению (8.5.14), ненормированный вектор состояния
\ф{Ь)) = co(t)\O) + ci(t)|l) (8.5.16)
удовлетворяет простым уравнениям движения
co(t) = O,
которые означают, что
cQ{t) = со@),
Соответствующие нормированные амплитуды вероятности имеют вид
. со(р)
, /п\ 12 g — 2Rt '
-Rt
(8.5.
(8.5.
(8.5.
(8.5.
(8.5.
(8.5.
17а)
176)
18а)
186)
19а)
196)
Таким образом, мы имеем полностью когерентную эволюцию условного вектора
состояния до точки коллапса,
c@)|0) + c@)e-^[l)
+ ici@)|2 е-2я*
Отметим, что при t —>• оо состояние IV7 @)) ~* |0)« Получилось так, как должно
было быть, поскольку условное состояние \ф^A)} является следствием допущения,
что ни один фотон не поглотился. Поэтому, если по прошествии большого времени мы
ни разу не зафиксировали «отсчет», то из этого следует вывод, что мы должны были
все время находиться в вакуумном состоянии |0). Подводя итог, можно заключить,
что согласно уравнению (8.5.14) поле развивается, начиная с момента t = 0 до
8.5 Описание релаксации с помощью «квантовых скачков» 217
некоторого момента времени t, и между t и t + St происходит скачок, т. е.
(8.5.21а)
«нет отсчетов» при 0 —} t
(8.5.216)
| коллапс при t —)¦ t + St
= |0), (8.5.21в)
где co(t) и ci(t) в (8.5.216) задаются выражениями (8.5.19а) и (8.5.196), а (8.5.21в)
следует из (8.5.106). Теперь вспомним, что вероятность коллапса или скачка в момент
времени t задается оператором плотности, обусловленным событием поглощения
одного фотона, т.е., «отсчетом». Имея это в виду, запишем уравнение (8.3.3) при
R = tf/2 в виде
Р =
(8.5.22)
= р(нет отсчета) + р(отсчет).
Следовательно, вероятность коллапса между t и t + St определяется выражением
= 2RStTr[p(t)a^a] =
= 2R6t(il>(t)\a+a\il>(t)) = 2ш№^. (8.5.23)
Поэтому, для данной задачи, из уравнений (8.5.16)-(8.5.19б) и (8.5.23) вытекает
следующее выражение для вероятности скачка:
I (f)\\2 —%R~t
Jtlm?e-^ (8-5-24)
Наконец, переведем вышесказанное в диаграмму вероятности найти фотон в ре-
резонаторе по истечении времени t, при условии, что cq@) = 0 и ci@) = 1, т.е.
когда Рскачок(^) = 2RSt. Сделаем это с помощью метода Монте Карло следующим
образом. Во-первых, начнем рассмотрение поля в состоянии |1) с ci@) = 1 и выберем
число между 0 и 1, используя компьютерный генератор случайных чисел. Если число
меньше, чем РСКач<ж@), то считается, что скачок или коллапс произошел, и число
фотонов полагается равным нулю. Между тем, более вероятно, что это число будет
больше, чем РСкачок5 и тогда мы заново проводим расчет |^(t)) с помощью выражения
(8.5.20) и затем начинаем все снова. Эту процедуру повторяем п раз до тех пор пока
случайное число не окажется меньше, чем РСкачсж(^) в (8.5.24). После этого сделаем
218 Квантовая теория релаксации — оператор плотности Гл. 8
запись в нашу таблицу следующим образом:
«эволюция»
= St \Ф№)) = coFt)\0) +
«эволюция»
t = 2St 1^B^)) = co{2St)\O)
«эволюция»
(8.5.25)
«эволюция»
t = nSt \i>(n6t)) = co(nSt)\O) + ct(n5t)\l)
«коллапс»
Нет необходимости говорить, что простой предыдущий пример был выбран в пе-
педагогических целях. Методом квантовых скачков Монте Карло можно решить, и бы-
было решено, множество более сложных задач. Среди них можно отметить спонтанное
излучение, резонансную флуоресценцию, доплеровское охлаждение, пленение насе-
населенности и линию темного резонанса х), и это составляет лишь малую часть списка.
В заключение отметим, что метод, представленный в этом разделе, часто называ-
называют «методом квантовых траекторий». Также можно отметить интересную работу
Виллиса Лэмба, в которой рассчитаны траектории гауссовых волновых пакетов
с целью разработки квантовой теории некоторых проблем, связанных с процессом
измерения. Эта работа также предполагает компьютерный анализ, чтобы наглядно
изобразить (случайные) результаты эксперимента.
Задачи
8.1. Выведите соотношения (8.2.14а) и (8.2.146) и используйте эти результаты для
того, чтобы рассчитать корреляционные функции (8.2.16а)-(8.2.16д).
8.2. Уравнение движения для приведенного оператора плотности, описывающего
поле одномодового резонатора, взаимодействующего с вакуумным резервуаром
через частично пропускающее зеркало, имеет вид
• _ Л-( +
А
1) Имеется ввиду определенное сочетание частот поля накачки и пробного поля, при
которых возникает пленение населенности в темном состоянии. — Примеч. ред. пер.
Список литературы к гл. 8 219
Здесь ^ — скорость затухания, связанная с добротностью Q резонатора соот-
соотношением *$ = и I' Q. Выведите уравнения движения для соответствующих ве-
величин и затем решите их чтобы показать, что среднеквадратичные отклонения
(AXi)| и (ДХг)?, где Х\ = (а + а+)/2 и Х^ = (а — a+)/2i, увеличиваются бла-
благодаря диссипации (флуктуационно-диссипационная теорема!). Эту ситуацию
можно рассматривать как случай бозонной моды, некоррелированной с полем
резонатора, которая входит в резонатор через частично пропускающее зеркало,
и следовательно добавляет некоррелированный шум.
8.3. Если резервуар из предыдущей задачи находится в состоянии многомодового
сжатого вакуума, то уравнение движения для приведенного оператора плот-
плотности имеет вид (8.3.4). Как и в предыдущем случае, вычислите среднеквад-
среднеквадратичные отклонения (AXi)| и (ДХг)^. Можно ли подавить в этой ситуации
добавочный шум?
8.4. Для теплового резервуара
С/? С/У
р = — т^(^тепл + l)(tt+ttP — 2ара+ + ра+а) — ^rnTeilJl(aa+р — 2а+ра + раа+),
где птеПл — среднее число фотонов в резервуаре. Выведите соответствующее
уравнение для (^-распределения и решите его.
8.5. Выведите уравнения (8.2.18а)-(8.2.18с).
Список литературы
Квантовая теория релаксации и диссипации
Lax, M. Phys. Rev. 145, 110 A966).
Weidlich, W. RIsken, H. and Haken, H. Z. Phys. 201, 369 A967).
Haken, H. Laser Theory, (Springer, Berlin 1970).
Loulsell, W. Quantum Statistical Properties of Radiation, (Wiley, New York 1974).
Sargent III, M., Scully, M. and Lamb, W. В., Jr., Laser Physics (Addlson-Wesley, Reading, MA
1974).
*Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую радиофизику и
оптику (Наука, Москва, 1981).
*Coleman, A. J., Yukalov, V. I. Reduced density matrixes (Springer, Berlin 2000).
Релаксация в условиях сжатого вакуума
Collett, M. J. and Gardiner, С. W. Phys. Rev. A 30, 1386 A984).
Gardiner, С W. Phys. Rev. Lett. 56, 1917 A986).
Gea-Banacloche, J., Scully, M. O. and Zubairy, M. S. Phys. Scripta T21, 81 A988).
Р-представление моды гармонического осциллятора, затухающей
при взаимодействии с тепловым резервуаром
Glauber, R. J. In Quantum Optics and Electronics, Les Houches, ed. C. DeWItt, A. Blanch,
and C. Cohen-Tannoudji (Gordon and Breach, New York 1965), p. 331. [Глаубер Р. В кн.
Квантовая оптика и квантовая радиофизика (Мир, Москва, 1966), с. 91-279.]
Glauber, R. J. In New Techniques and Ideas in Quantum Measurement Theory. Annals of the
New York Academy of Sciences, Vol. 480, ed. D. M. Greenberger A986), p. 336.
220 Список литературы к гл.
Квантовые скачки
Dehmelt, Н. J. Bull. Am. Phys. Soc. 20, 60 A975).
Cook, R. J. and Kimble, H. J. Phys. Rev. Lett. 54, 1023 A985).
Cohen-Tanoudji, C. and Dallbard, J. Europhys. Lett. 1, 441 A986).
Nagoumey, W., Sandberg, J. and Dehmelt, H. Phys. Rev. Lett. 56, 2797 A986).
Sauter, Th., Blatt, R., Neuhauser, W. and Toschek, P. E. Opt. Gommun. 60, 287 A986).
Schenzle, A., DeVoe, R. G. and Brewer, R. G. Phys. Rev. A 33, 2127 A986).
Nlenhuis, G. Phys. Rev. A 35, 4639 A987).
Zoller, P., Marte, M. and Walls, D. F. Phys. Rev. A 35, 198 A987).
PorratI, M. and Puttermann, S. Phys. Rev. A 36, 925 A987).
Reynaud, S., Dalibard, J. and Cohen-Tannoudji, C. IEEE Journal of Quantum Electronics 24,
1395 A988).
Bergqulst, J. C., Itano, W. M., Hulet, R. G. and Wineland, D. J. Phys. Scripta T22, 79 A988).
Общая теория непрерывных измерений
Srlnlvas, M. D. and Davles, E. B. Opt. Ada 28, 981 A981).
Ueda, M. and Kitagawa, M. K. Phys. Rev. Lett 68, 3424 A992).
Метод Монте Карло для волновой функции
Dallbard, J., Castln, Y. and M0lmer, K. Phys. Rev. Lett 68, 580 A992).
Carmichael, H. J. An Open Systems Approach to Quantum Optics (Springer-Verlag, Berlin 1993).
Квантовая теория измерения и траекторий
Lamb, W. E., Jr., Physics Today, 22, 23 A969); Proc. 2nd Int. Symp. Found, of Quant. Mech.
(Tokyo 1986), p. 185.
Lamb, W. E., Jr., in New Techniques and Ideas in Quantum Measurement Theory. Annals of
the New York Academy of Sciences, Vol. 480, ed. D. M. Greenberger A986), p. 407.
Lamb, W. E., Jr., in Quantum Measurement and Chaos, ed. E. Pike and S. Sarkar (Plenum, New
York 1987), p. 183.
Глава 9
КВАНТОВАЯ ТЕОРИЯ
РЕЛАКСАЦИИ — МЕТОД
ГЕЙЗЕНБЕРГА-ЛАНЖЕВЕНА
В предыдущей главе было получено уравнение движения для системы, эволю-
эволюционирующей под влиянием ненаблюдаемой системы (резервуара). При этом ис-
использовался метод оператора плотности и расчет производился в представлении
взаимодействия. В этой главе та же задача взаимодействия системы и резервуара ре-
решается методом Гейзенберга^Ланжевена. При этом мы снова исключаем переменные
резервуара. Результирующие уравнения для операторов системы содержат, помимо
релаксационных членов, операторы шума, вызывающие флуктуации. Эти уравнения
имеют вид классических уравнений Ланжевена, описывающих, например, броунов-
броуновское движение частицы, подвешенной в жидкости. Метод Гейзенберга-Ланжевена,
рассматриваемый в этой главе, особенно подходит для вычисления двухвременных
корреляционных функций операторов системы, которые требуются, например, для
определения спектральной ширины лазера.
Сначала рассматривается релаксация гармонического осциллятора, обусловлен-
обусловленная взаимодействием с резервуаром, состоящим из множества других простых гармо-
гармонических осцилляторов. Эта система описывает, например, затухание одномодового
поля в резонаторе, имеющем зеркала с потерями. В этом случае резервуар состоит
из большого числа мод фононного типа, возбуждаемых в зеркалах. Кроме того,
рассматривается затухание поля, обусловленное взаимодействием его с атомным ре-
резервуаром. Интересным приложением теории взаимодействия системы с резервуаром
является эволюция атома в резонаторе с потерями. Показано, что скорость спонтан-
спонтанного перехода атома может существенно возрасти, если его поместить в резонатор.
9.1. Простое рассмотрение релаксации через резервуар осцилляторов:
марковский белый шум
Рассмотрим систему, состоящую из одномодового поля частоты i/, взаимодей-
взаимодействующего с резервуаром. Поле описывается оператором уничтожения a(t). В ка-
качестве резервуара можно взять произвольный большой ансамбль систем, имеющий
много степеней свободы. Предположим, что резервуар состоит из множества осцилля-
осцилляторов (например фононов, других фотонных мод и т.д.), имеющих близкие частоты
Vk и операторы уничтожения (рождения) b^ (b?). Такая система, следовательно, опи™
сывает затухание гармонического осциллятора, обусловленное взаимодействием с ре™
зервуаром, состоящим из множества других простых гармонических осцилляторов.
222 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
Эволюция системы «поле + резервуар» во времени определяется гамильтонианом
Ж = ЖО + ЖЪ (ЭЛЛ)
(9.1.2)
. (9.1.3)
Как и прежде, Ж® — энергия свободного поля и мод резервуара, а Ж\ — энергия вза-
взаимодействия. Операторы поля коммутируют с операторами резервуара в заданный
момент времени. Отметим, что в (9.1.3) сделано обычное приближение вращающейся
волны.
Уравнения движения Гейзенберга для операторов системы имеют вид
а = у:[Ж,а] = -iva{t) - i^gMt), (9.1.4)
k
6k = -zi/fcftk(*) - ig^a{t). (9.1.5)
Нас интересует замкнутое уравнение для оператора гармонического осциллятора
a(t). Уравнение для оператора резервуара b^(t) можно формально проинтегрировать
и получить
t
= МО) е-'"*« - igA dt'a(t') e-^C-*'). (9.1.6)
О
Здесь первый член описывает свободную эволюцию мод резервуара, тогда как второй
член является результатом взаимодействия этих мод с гармоническим осциллятором.
Операторы резервуара b^(t) можно исключить, подставляя формальное решение для
в уравнение (9.1.4). В результате получим
а = -iva -Y^A. \dt'a(t') e-'"*(*-«'> + fa(t), (9.1.7)
-"»'. (9.1.8)
Оператор fa(t) в уравнении (9.1.7) является оператором шума, поскольку он зависит
от операторов резервуара &к@). Таким образом, эволюция средних значений, содер-
содержащих оператор гармонического осциллятора, зависит от флуктуации резервуара.
Оператор шума изменяется быстро, ибо содержит все частоты резервуара. Высо™
кочастотную зависимость оператора a(t) от времени можно исключить, переходя
к медленно меняющемуся оператору уничтожения
a(t) = a{t)eilJK (9.1.9)
Видно, что
[a(t),a+(t)] = l, (9.1.10)
9.1 Марковский белый шум 223
и уравнение (9.1.7) сводится к
t
di'a{tf) e-^h-^it-t1) + Fa(t), (9.1.11)
k
Интегрирование по времени в (9.1.11) аналогично тому, которое встречалось в теории
Вайскопфа-Вигнера (разд. 6.3). Как и в приближении Вайскопфа-Вигнера, сумми-
суммирование в (9.1.11) приводит к функции S(t — tf), после чего интегрирование становится
осуществимым. В результате получаем
dt'a(t') e"^*-1^*-*') ~ ^S(t), (9.1.13)
к о
где константа затухания
<? = 2n[g(u)}2D(u). (9.1.14)
Здесь g{y) = gi//c — константа взаимодействия, вычисляемая при к = г^/с, и D{y) =
= Vu2 /ж2сл (где V — объем квантования) — плотность состояний (см. A.1.26)).
Таким образом, уравнение (9.1.11) можно заменить уравнением Ланжевена:
2 = -i^a + Fa[t), (9.1.15)
z
где Fa(t) — оператор шума, зависящий от переменных резервуара.
Интересно отметить, что присутствие оператора шума в уравнении (9.1.15) не-
необходимо для сохранения коммутационного соотношения (9.1.10) в любой момент
времени. В отсутствии шумового члена (Fa(t) = 0) уравнение (9.1.15) можно решить
и получить
'Г/-#\ 7iff\\ ю""^^/^ /Q 1 ЛРЛ
Если оператор а удовлетворяет коммутационному соотношению (9.1.10) в момент
времени t = 0, то
[a(t),S (t7)] = e~ , (9.1.17)
что соответствует нарушению коммутационного соотношения. Оператор шума,
имеющий подходящие корреляционные свойства, помогает сохранить коммута-
коммутационное соотношение (9.1.10) в любой момент времени. Наличие в уравнении
(9.1.15) шумового члена вместе с релаксационным членом является проявлением
флуктуационно-диссипационной теоремы статистической механики, то есть
диссипация всегда сопровождается флуктуациями.
Предположим, что резервуар находится в состоянии теплового равновесия, так
что
= 0, (9.1.18)
W, (9.1.19)
Fk(ON+ @)) = (nk + 1) cW, (9.1.20)
<Ы0)М0)> = Н @)Ь?@)> = 0. (9.1.21)
224 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
Используя эти соотношения вместе с выражением для оператора шума (9.1.12),
можно вычислить следующие корреляционные функции первого и второго порядков,
содержащие Fa(i).
1. Из (9.1.18) сразу следует, что средние по резервуарам значения операторов
Fa(t) и F-'it) обращаются в нуль, то есть
(F~a(t))R^(F±(t))R = 0. (9.1.22)
2. Используя (9.1.19), получаем
(F±(t)F5(t'))R =
к к'
OG
* кПк6 к =\^Ш»ь)\пЫе * duk. (9.1.23)
В последней строке мы перешли обычным образом от дискретного представления
к непрерывному. Теперь можно вытащить за знак интеграла медленно меняющиеся
члены D(yk), g{yk) ш ^(ук) ПРИ значении и^ = v и заменить интеграл E-функцией.
В результате получим
(F^(t)F~a(t'))R = Кптепл S(t - *'), (9-1.24)
где $ задается выражением (9.1.14) и птеш1 = n(uk)- По аналогии с классической
теорией Ланжевеыа, определим коэффициент диффузии D^+^ для а+й с помощью
соотношения
(F^(t)Fa(tf))R = 2(D^+^)R 6(t - tf), (9.1.25)
Тогда из (9.1.24) получаем следующее выражение для коэффициента диффузии:
2(^й+й)я = ^тепл- (9.1.26)
Подобным образом можно показать, что
(Fa{t)F±{t'))R = ^{птепл + 1) S(t ^ t;), (9.1.27)
(Fa(t)Fa(t'))R = (F^(t)F^(tf))R = 0, (9.1.28)
так что
2(ОШ+)Я = ^{птепл + 1), (9.1.29)
(Daa)R={Da+a+)R = O- (9-1.30)
3. Вычислим теперь (F-'(tOi{t)}r. Эта величина понадобится при выводе урав-
уравнения движения для (а+й)д. Решая уравнение (9.1.15), получаем
t'
a(t) = S@) exp (~т"М + dt' exp ^y (t — t;) Fa{t!). (9.1.31)
о
Тогда
t(t)a(t))R = <Fa+(t))*o@)exp (-|<
+ jd«'exp[-|(<-*')] (F±(t)Fz(t'))R. (9.1.32)
9.2 Немарковский окрашенный шум 225
Здесь предполагается, что Fa(t) и 2@) являются статистически независимыми. Из
(9.1.22) и (9.1.24) следует, что
(F^(t)a(t))R = ^птепл = <Я5+5>я. (9.1.33)
Аналогично можно показать, что
(a+(t)Fs(t))R = |птепл. (9.1.34)
Эти корреляционные функции будут использоваться при выводе уравнений дви-
движения для корреляционных функций поля в разд. 9.3. Далее мы рассмотрим за-
затухание одномодового поля, взаимодействующего с атомным резервуаром, а также
расширим и усилим данное рассмотрение резервуара осцилляторов. Главным резуль-
результатом этого будет корреляционная функция оператора шума, которая не является
дельта-функцией и, следовательно, соответствует «окрашенному» шуму, а не белому
шуму, рассмотренному в этом разделе.
9.2. Расширенное рассмотрение релаксации через резервуары атомов
и осцилляторов: немарковский окрашенный шум
В этом разделе мы расширяем наш подход к задаче релаксации, предполагая
на этот раз конечные значения времен корреляции (то есть, не дельта-функции).
Вначале рассматривается механизм релаксации поля через взаимодействие с двух-
двухуровневыми атомами, проходящими через резонатор и распределенными по закону
Больцмана. Атомы предполагаются долгоживущими и моноэнергетическими, так что
они взаимодействуют с полем в резонаторе в течение фиксированного времени т.
Затем мы возвращаемся к модели резервуара осцилляторов, обобщая рассмотрение
и выходя за пределы марковского приближения.
9.2.1. Метод атомного резервуара г). Рассмотрим затухание одномодового поля,
обусловленное взаимодействием с атомами. Гамильтониан для данной задачи имеет
вид
Ж = ЖО + ЖЪ (9.2.1)
-hi/^al, (9.2.2)
г
Yy,T)a+aiL+*.c.], (9.2.3)
г
где а\ и ог_ ~~ операторы, соответствующие г-му атому, и /(^,?,т) — функция,
описывающая появление атома в момент времени ti и его исчезновение в более позд-
поздний момент времени t{ + т. В этом смысле функция /(tj, ?, т) является ступенчатой
функцией, имеющей значения
J <*<**+'. (9.2.4)
0, в противном случае.
Для простоты предположим, что влетающие атомы находятся в резонансе с полем.
Используя данный гамильтониан, записываем уравнения движения для полевых
1) Для дальнейшего знакомства с материалом см. гл. 12 и работу Scully, Siissmann and
Benkert A988).
8 M.O. Скалли, М.С. Зубайри
226 Квантовая теория релаксации — метод Гейзенберга—Ланжевена Гл. 9
и атомных операторов в представлении взаимодействия:
a(t) = -igY^f(ti,t,T)<ri(t), (9.2.5)
а{_A) = 1ё/(и,1,т)а1аA). (9.2.6)
Как и прежде, нас интересует замкнутое уравнение для оператора a(t). Интегриро-
Интегрирование уравнения для атомного оператора (9.2.6) дает
t
at(t) = al(U) + ig I dtff(U, t\ T)a\{t')a[t'). (9.2.7)
Подставляя это выражение для <т!_(?) в уравнение для оператора поля, получаем
t
dt'f(U, t, T)f(U, t1, т)а1(гг)а(^) - ig^f(U,t, r)cr!_(^). (9.2.8)
Если поле не меняется существенно в течение времени прохождения атомов, то
оператор a(tf) в уравнении (9.2.8) можно заменить оператором a(t). В линейном
приближении оператор и\ (tf) также заменяется своим значением в момент инжекции
alz(ti). Результирующее уравнение имеет вид
<i = -^fa + Fa(*), (9.2.9)
где
t
г',т)<тЦи), (9.2.10)
Fa(t) = ig^ff{ti,t,T)<Ti_(U). (9.2.11)
Здесь константа затухания ^ является положительной величиной, поскольку на-
начальное значение инверсии az(t{) является отрицательным в условиях теплового
равновесия.
Можно показать, что оператор шума Fa(t) имеет моменты
<Fa(t))=0, (9.2.12)
<F+(t)Fe(t')> = g2 Y, f(U, t, T)f(tj,t', т)(<т*+(и)<тЦЬ)) =
= g2[l + exp(hv/kBT)]-1YJf(ti,t,T)f(ti,t',T), (9.2.13)
i
где учтено, что для атомов, находящихся в состоянии теплового равновесия при
температуре Т, имеет место соотношение
{(т{+(и)а1(^)} = 5ij[l + ехр(Й1/ /'квТ)}^1, (9.2.14)
9.2
Немарковский окрашенный шум
227
которое получается из стационарного решения уравнений (8.2.10а) и (8.2.10в) с ис-
использованием формулы (8.2.5). Заменяя сумми™
рование по г в (9.2.13) интегрированием по вре™ (F%(t)Fa(tf)}
мени инжекции
aF
(9.2.15)
где га — скорость инжекции атомов в резонатор,
находим
->*
x f dtif(U,t,T)f(ti,tf,T). (9.2.16)
„qq Рис. 9.1. Корреляционная функция
шума {F^(t)Fa(t;)), задаваемая вы-
Интегрирование можно выполнить, например, ражением (9.2.20)
записывая
f(U,t,т) = Q(t - U) - в(* - г - U), (9.2.17)
где в — единичная ступенчатая функция, и используя соотношение
[ dU. (9.2.18)
j J
— oo —oo
Тогда получаем
^tf)^e(t^tf -r)]
- tf) - Q(t - t1 + r)] | dt» + [B{tf -t)- e(t' -t-
dt{+
—oo
t —r
f d^. (9.2.19)
Внимательный анализ показывает, что правая часть выражения (9.2.19) равна нулю,
до тех пор пока не выполнится условие т ^ |? — ?'|, при удовлетворении которого
правая часть становится равной т — |? —?'|. Таким образом, корреляционная функция
(9.2.16) задается выражением
(F+(t)Fa(t')) =
а
0,
если I* ~ 1'\ ^ т'
в противном случае,
(9.2.20)
где ар = ra<g*2r2[l + exp(lw/квТ)] *, и имеет вид, как показано на рис. 9.1. Это один
из простейших примеров «окрашенного» шума.
8*
228 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
9.2.2. Обобщенное рассмотрение задачи осцилляторного резервуара г). Рас™
смотрим теперь задачу теплового резервуара, состоящего из множества осцилля-
осцилляторов. В случае, когда осциллятор, характеризуемый импульсом р и координатой ж,
взаимодействует с резервуаром осцилляторов, имеющих импульс pj и координату q$,
гамильтониан «системы + резервуара» можно записать в виде
з
Отметим, что в таком виде гамильтониан (9.2.21) записан без приближения вра-
вращающейся волны. Используя стандартные коммутационные соотношения [ж,р] = ih
и [qj,Pk] = i^Sjkj находим
m
(9.2.22а)
р= А[р5 Ж] = -mz/2z + ^miu;|(gi -ж), (9.2.226)
з
(9'2-22в)
Pi = UPi^] = ~т^2М - ж)' (9.2.22г)
Дифференцируя уравнения (9.2.22а) и (9.2.22в) и используя (9.2.226) и (9.2.22г),
находим
x(t) = -v2x(t) + J2 ^wj[9i(*) - ж(*)]. (9.2.23а)
i
qj(t) =-u,][qj(t) - x(t)]. (9.2.236)
Прямой подстановкой можно проверить, что решение для qj(t) записывается в виде
qj{t)-x(t) = q?(t)- [ dt'cos[ojj(t-t')]x(t'), (9.2.24)
где q^(t) — решение задачи в отсутствие взаимодействия (ж = 0):
д°(*) = д.С08а;,-* + р,-^^. (9.2.25)
Здесь gj и pj — обычные зависящие от времени операторы координаты и импульса.
Подставляя (9.2.24) в (9.2.23а), находим
t
г
mx(t)+ dtffi(t-tf)x(tf)^mu2x(t) = F(t), (9.2.26)
j
где релаксационная функция задается выражением
fj,(t - tf) = ^wiju'jcoslujjit - t')], (9.2.27a)
1) Изложение этого раздела следует работе Ford, Lewis and O'Connell A988).
9.3 Уравнения двиэшения для корреляционных функций поля 229
а оператор шума принимает вид
= Vm^^-W. (9.2.276)
Уравнение (9.2.26), написанное в таком виде, очень похоже на уравнение (9.1.11).
Однако задачу можно обобщить и учесть эффекты памяти, записывая следующее
общее выражение для затухающего осциллятора:
t
г
mx(t)+ dt'ii{t-tl)x{tt) + mu2x{t) = F(t), (9.2.28)
— со
где
[dR^ + O+^fithf^^^^-O]^ (9.2.29)
и Ji — фурье-образ функции /J,(i).
В случае постоянного затухания, который представляет для нас наибольший
интерес, Re [//(о; + iO+)] = Г, и корреляционная функция принимает вид
оо
\{F{t)F{t') + F(t')F(t)) = I [ dtohtocth (J^.) cos{u;(t - t')] =
(9.2.30)
Отметим, что выражение (9.2.30), приближаясь в пределе к 8(t — ^)-функции, в об-
общем случае выходит за пределы марковского приближения, то есть подразумевает
окрашенный шум.
9.3. Уравнения движения для корреляционных функций поля
Теперь можно вывести уравнения движения для среднего значения оператора
a(t) и оператора числа частиц й+2. Поскольку (Fa(t))n = 0, из (9.1.15) следует, что
?tDt))R = -\v(a(t))R. (9.3.1)
Видно, что среднее значение оператора системы стремится со временем к нулю.
Отметим, что усреднение в уравнении (9.3.1) осуществляется лишь по переменным
резервуара, так что остается оператор по полевым координатам.
Эволюция среднего значения полевого оператора числа частиц задается уравне-
уравнением
= -4f(a+(t)a(t))R + (F^(t)a(t))R + (а+ (t) F~a{t)) R = -^ (a+(t)a(t)) R
(9.3.2)
230 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
Таким образом, стационарное значение оператора числа частиц (а~*~ (t)a(t)} r равно
^тепл (умноженное на единичный оператор поля). Оно не равно нулю, в противопо-
противоположность значениям (a^~(t))fi и (а(?))д, стремящимся со временем к нулю в соответ-
соответствии с (9.3.1).
Аналогично можно показать, что
ft(a(t)Z+(t))R = -V(a(t)a+(t))R + V{nTenjl + l). (9.3.3)
Объединяя (9.3.2) и (9.3.3), видим, что коммутатор [й(?), a+(t)] сохраняет свое сред-
среднее по резервуару значение, равное единице, а не стремится к нулю.
Рассуждая таким же образом, как при выводе уравнений движения для (d(t))ц
и (S+(t)a(t)}^ (уравнения (9.3.1) и (9.3.2)), можно показать, что для произвольного
произведения операторов рождения и уничтожения имеет место уравнение
^(E+Г5")д = -|(m + n)((a+)mUn)R + Ътпптеил{{Ъ+)т-Чп-1)н. (9.3.4)
В переменных а и а+ (см. (9.1.9)) оно имеет вид
ft((a+)man)R = [iv{m - п) - |(ш + п)] х
пл((а+)т-1а"-1)д. (9.3.5)
Это уравнение обычным образом описывает влияние резервуара.
Как отмечалось ранее, настоящий подход Гейзнберга^Ланжевена к квантовой
теории релаксации особенно удобен для вычисления многовременных корреляцион-
корреляционных функций. Это можно оценить на простом примере затухания поля частотой v
в резонаторе со скоростью ^ = и/Q. Здесь Q — добротность резонатора.
Оператор поля а = a(t) exp(ii/t) подчиняется уравнению
Z = -^a + F7i(t), (9.3.6)
решение которого имеет вид (при т > 0)
dtf exp [—^(U + г - tf)j F5(t;). (9.3.7)
Следовательно, поскольку (а~*~(t{)Fa(tf)}r = (a+ (ti)}n(Fa(tf)}r = 0, получаем
(9.3.8)
то есть, функция корреляции поля затухает со временем экспоненциально. Спектр
поля можно получить, выполняя фурье-преобразование функции корреляции:
(a+{U)a{U + г)>я = (а+(и)а(и + т))я e^il/T = (n) exp (^iur - ^т) , (9.3.9)
где (п) — среднее число фотонов в начальный момент времени t{. В результате
получаем (см. D.3.14))
S(U) = I Re\(a+(t)a(t + r))R e^ dr = М ^ _ ^Ц^ (9.3.10)
9.4 Флуктуационно-диссипационная теорема и формула Эйнштейна 231
— распределение Лоренца, центрированное на частоте ш = и и имеющее полуширину
I//2Q.
Приближенное выражение для плотности мод пустого резонатора Dc(uj) получа-
получается делением S(uj) на (п), то есть
Следовательно, плотность состояний внутри резонатора существенно отличается от
плотности состояний в свободном пространстве (см. A.1.26)).
9.4. Флуктуацмонно-диссмпацжонная теорема и формула Эйнштейна
Теперь установим связь между настоящим квантовым ланжевеновским и клас-
классическим подходами. В разд. 9.1 была получена корреляционная функция второго
порядка ланжевеновского шума Fa(t):
епл S(t - t'). (9.4.1)
Интегрируя обе части, получаем
сю
*==*- \ {F±{t)F~a{t>))Rdt>. (9.4.2)
— ОО
Это выражение означает, что скорость затухания системы ^ определяется флукту™
ациями резервуара. Таким образом, флуктуации, индуцируемые резервуаром, вы-
вызывают рассеяние энергии в системе. Это одна из формулировок флуктуационно-
диссипационной теоремы.
Теперь воспользуемся уравнением (9.1.15) и соотношением (9.1.26), чтобы пере-
переписать (9.3.2) в виде
я f Fa {t)
(9.4.3)
Это есть формула Эйнштейна, определяющая коэффициент диффузии. Мы выводим
ее для задачи затухающего гармонического осциллятора. Однако можно показать,
что это соотношение справедливо для многих более общих задач, связанных с систе-
системой и резервуаром. Подобным образом можно вывести соотношение
(9.4.4)
Формула Эйнштейна связывает члены дрейфа [da/dt — Fa{t)] и [da~*~ /dt — F~^(t)}
с коэффициентами диффузии. При решении многих интересных задач эта формула
предоставляет чрезвычайно простой способ вычисления коэффициента диффузии.
Формулу Эйнштейна можно использовать для определения коэффициентов диф-
диффузии непосредственно из уравнений для матрицы плотности. Чтобы пояснить,
как это делается, рассмотрим простой пример затухания поля при взаимодействии
232 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
с тепловым резервуаром, (8.3.2). Из этого уравнения следует, что
'da
= -у<*>, (9-4-5)
^(а+«) = -^((а+а) - птепл), (9.4.7)
При выводе этих уравнений использовались возможность циклической перестановки
операторов под знаком следа (то есть, Тг (ABC) = Тг (CAB) и т.д.) и коммутаци-
коммутационное соотношение [а, а+] = 1. Теперь величины [da/'dt — Fa(t)] и [da+ /dt — F^~(t)]
можно получить из (9.4.5) и (9.4.6), соответственно, убирая знак среднего значения
в правой части. В результате
? - *.(*)
= -f о, (9.4.S
2
= -|о+. (9-4.9)
Подставляя (9.4.7)-(9.4.9) в соотношение (9.4.3), получаем
2(D5+5) = ^птепл, (9.4.10)
в соответствии с (9.1.26).
9.5. Атом в резонаторе с потерями
Очень простым применением математического формализма, развитого в этой
главе, является исследование эволюции одиночного двухуровневого атома, приготов-
приготовленного изначально в верхнем состоянии |«), в условиях резонанса атомного перехода
и моды резонатора. В частности, оказывается, что скорость спонтанного излучения
атома в резонаторе существенно выше, чем в свободном пространстве. Фактор увели-
увеличения можно получить строгим образом в рамках квантово-механического анализа,
при котором затухание резонатора рассматривается через взаимодействие одномо-
дового поля с резервуаром, состоящим из большого числа простых гармонических
осцилляторов. Это интересное явление мы поясним сначала с помощью эвристиче-
эвристического рассуждения.
Напомним (см. разд. 6.3), что спонтанное излучение атома в свободном про-
пространстве рассматривалось нами так, что атом взаимодействовал с континуумом
мод электромагнитного поля. Скорость затухания Г (выражение F.3.14)) можно
переписать в виде
Г = 27r(|g-(o;)|2)D(a;), (9.5.1)
где угловые скобки обозначают среднее по направлению, g(uj) — вакуумная частота
Раби и D(uj) = Vuj2/тг2с3 — плотность состояний на частоте атомного перехода ш.
Следовательно, скорость спонтанного затухания пропорциональна плотности состоя-
состояний. Структура мод вакуумного поля резко изменяется в резонаторе, размер которого
сравним с длиной волны. В резонаторе добротности Q, плотность мод Dc(uj) можно
аппроксимировать лоренцевой функцией (9.3.12)
9.5 Атом в резонаторе с потерями 233
Следовательно, скорость спонтанного затухания атома в резонаторе получается пу-
путем замены D(uj) в выражении (9.5.1) плотностью Dc(uj):
rc^27v{\g(co)\2)Dc(co). (9.5.3)
Если резонатор настроен на частоту, близкую к атомной частоте перехода, то
Dc(w) ~ 2<2/тгш, и
2 (ш^Л /2Q4 BT\
Таким образом, с точностью до геометрического множителя порядка единицы (для
нижайшей моды резонатора ш = тгс/L, где L — длина резонатора, этот множитель
равен 2/тг2), скорость спонтанного затухания в резонаторе в Q раз больше, чем
скорость затухания в свободном пространстве.
Возрастание скорости спонтанного излучения можно еще объяснить по-другому,
используя понятие мнимого заряда. Влияние зеркал резонатора на эволюцию атома
можно имитировать, поменяв зеркала на создаваемые ими образы атома, число
которых равно Q. Поскольку резонатор настроен на частоту атомного перехода,
диполи всех этих образов находятся в фазе с диполем атома. Следовательно, они
действуют как Q сонаправленных антенн, находящихся в фазе. Каждая антенна
в этом массиве излучает в Q раз быстрее, чем отдельная антенна. Поэтому энергия
атома рассеивается в Q раз быстрее, чем в свободном пространстве.
Обратимся теперь к строгому выводу скорости атомного затухания в резонаторе.
Рассмотрим систему из двухуровневого атома, взаимодействующего с одномодовым
электромагнитным полем внутри резонатора. Резонатор взаимодействует с тепловым
резервуаром через свои стенки. Таким образом, гамильтониан системы и резервуара
записывается в виде
(9.5.5)
JfF = Ниа+а, (9.5.6)
ЖА = \hvaz, (9.5.7)
(9.5.8)
(9.5.9)
(9.5.10)
Здесь J^?f и Ж*а — гамильтонианы свободных поля и атома, соответственно, J^af
— оператор взаимодействия атома с одномодовым полем резонатора, Ж'и — га-
гамильтониан резервуара и Жрк — оператор взаимодействия поля с резервуаром.
Вследствие потерь на зеркалах, моды резервуара соответствуют вакуумным модам,
проникающим в резонатор через частично пропускающие зеркала. Полагаем, что
моды резервуара находятся в состоянии теплового равновесия при температуре Т.
Интересующими нас величинами являются энергия поля (а+а) и инверсия атома
(crz). Уравнение движения для произвольного оператора вида (а+)ш'ап'О а (где О а —
атомный оператор, например а+, а^ az) имеет вид
ft{(a+)manOA] = -1-[{а+)тапОА,ЖР + Жа + Жар] + (^[(a+)ma"])д ОА,
R (9.5.11)
234 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
где (d[{aJr)man}/ dt) r задается выражением (9.3.5). Используя это уравнение, можно
вывести следующие уравнения для средних значений (а+а) и (az):
= zg-(a_|_a - a^cr_) — w(a^a) + WnTenjl, (9.5.12)
.. = ^z^g4<r+a — a^u^). (9.5.13)
at
Угловые скобки обозначают одновременно среднее значение по резервуару
и квантово-механическое среднее значение. Эти уравнения содержат среднее
значение эрмитового оператора (а^а — сг^а+), для которого уравнение движения
в свою очередь содержит величину (a^aza) и т. д. В общем случае получается
бесконечная система уравнений, которую нельзя решить аналитически. Однако
ситуация существенно упрощается, если в начальный момент времени атом находится
в возбужденном состоянии |а), поле внутри резонатора — в вакуумном состоянии
|0), а резонатор находится при нулевой температуре (птепл = 0). Поле может
содержать самое большее один фотон, так что состояние поля внутри резонатора
в произвольный момент времени t является линейной суперпозицией вакуумного
состояния |0) и однофотонного состояния |1). Следовательно, средние значения
операторов, содержащих вторые и более высокие степени полевых операторов а
и а+, например ((a+J<rza2), равны нулю в каждый момент времени. При этих
условиях получаем следующую замкнутую систему уравнений:
--gAx -^(а+а), (9.5.14)
*&± = -2gA1. (9.5.15)
^ = g(<Tz) + 2^Л2 + g - |аь (9.5.16)
—— = —gA\ — <^?A2j (9.5.17)
где
-a+(j^}, (9.5.18)
A2 = (a+aza). (9.5.19)
Отметим, что в уравнении (9.5.17), в свете вышесказанного, мы пренебрегли членом,
пропорциональным (а+а+а2 — (а+Jаа^). Четыре уравнения (9.5.14)-(9.5.17) можно
решить, например, используя метод преобразований Лапласа. Решения для (a^~a)t
и ((Tz)t, удовлетворяющие начальным условиям (а+а)о = ^4i@) = ^2@) = 0 и (az) =
= 1, имеют вид
(^2 le2I/2] -(^2-i6g2I/2*/2\ (9-5_21)
9.5
Атом в резонаторе с потерями
235
На рис. 9.2 изображена вероятность нахождения атома в возбужденном состоянии
Ра = A + (crz))/2 как функция времени при различных значениях ff/Ag. Здесь мы
видим переход от затухающих осцилляции Раби к апериодическому движению.
Ра
Рис. 9.2. Вероятность Ра как функция безразмерного времени gt: *&/4g = 0.1 (а); Ч
= 10 [б)
Это различие в поведении можно легко показать, рассматривая два предельных
случая решения (9.5.21). Если ^ <С 4#, то атомная инверсия (az(t)} и вероятность
Ра принимают простой вид,
(9.5.22)
(9.5.23)
соответствующий затухающим осцилляциям Раби частоты 2g. В противоположном
пределе ^ ^> 4g получаем
(п (f\\ — I _i_ о р-4я2*/^ (Q К 9А\
р ( + \ 0 — ^g t/^ (Q К ^КЛ
то есть атом затухает экспоненциально со скоростью
гг =
(9.5.26)
Если не считать тривиального множителя 3, это выражение идентично выражению
(9.5.4), полученному с помощью эвристических рассуждений, учитывающих плотно-
плотности состояний. Множитель 3 исчезает, если в выражении (9.5.26) заменить величину
g2 ее средним значением по различным ориентациям.
236 Квантовая теория релаксации — метод Гейзенберга-Ланэюевена Гл. 9
Задачи
9.1. Одиночная мода частотой v взаимодействует с тепловым резервуаром. Эволю-
Эволюция системы «поле + резервуар» описывается уравнением Ланжевена
где a(i) = a(i)exp(ii/t), a — оператор уничтожения фотона в моде поля.
Вычислите дисперсию (АХ\J (где Х\ = (а + а+)/2) в момент времени t,
выразив ее через дисперсию в начальный момент времени t = 0.
9.2. Вычислите корреляционную функцию (F+(t)Fa(t;)), задаваемую выражением
(9.2.13), при следующих условиях:
,,. . ч Ге-г(*-**\ если U ^ t < U + т,
f(ti,t,T) = <
[0, в противном случае.
9.3. Вычислите корреляционные функции второго порядка (F~^(t)Fa(tf))ji,
(Fa(t)F±(t'))R, (Fa(t)Fa(t'))R и {F±(t)F?(t'))R ланжевеновского оператора
в случае, когда резервуаром является многомодовый сжатый вакуум.
9.4. Выведите уравнение движения для среднего значения произвольного произве-
произведения операторов рождения и уничтожения ((а+)тап) в случае: (а) теплового
резервуара и (б) сжатого резервуара.
9.5. Пусть резервуар находится в состоянии сжатого вакуума. Вычислите коэффи-
коэффициент диффузии D^+, используя уравнение движения для оператора плот-
плотности моды поля и формулу Эйнштейна. Проверьте результаты, сравнивая их
с результатами теории Ланжевена.
Список литературы
Метод Гейзенберга—Ланжевена в квантовой теории релаксации
и связанные с этим задачи
Lax, M. Phys. Rev. 145, 110 A966).
Ford, G. W., Lewis, J. T. and F. O'Connell, R. Phys. Rev. A 37, 4419 A988).
Scully, M. O., Siissmann, G. and Benkert, С Phys. Rev. Lett 60, 1014 A988).
Атом в резонаторе с потерями
Purcell, E. M. Phys. Rev. 69, 681 A946).
Milonni, P. W. and Knight, P. L. Opt Commun. 9, 119 A973).
Haroche, S. In High Resolution Laser Spectroscopy, ed. K. Shimoda (Springer-Verlag, Berlin
1976).
Kleppner, D. Phys. Rev. Lett. 47, 233 A981).
*Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую радиофизику и
оптику (Наука, Москва, 1981).
Sachdev, S. Phys. Rev. A 29, 2627 A984).
Haroche, S. and Ralmond, J. M. In Advances in Atomic and Molecular Physics^ Vol. 20, ed.
D. Bates and B. Bederson (Academic Press, New York 1985), p. 347.
Список литературы к гл. 9 237
Gallas, J. A., Leuchs, G., Walther, H. and FIgger, H. In Advances in Atomic and Molecular
Physics, Vol. 20, ed. D. Bates and B. Bederson (Academic Press, New York 1985), p. 413.
* Быков В.П., Шепелев Г.В. Квантовая электроника 9, 1844 A986).
Эксперименты по усилению или подавлению спонтанного излучения
в резонаторе
Goy, P., Raimond, J. M., Gross, M. and Haroche, S. Phys. Rev. Lett. 50, 1903 A983).
Gabrlelse, G., Van Dyck, R., Jr., Schwlnberg, P. and Dehmelt, H. Bull Am. Phys. Soc. 29, 926
A984).
Глава 10
РЕЗОНАНСНАЯ
ФЛУОРЕСЦЕНЦИЯ
Явление резонансной флуоресценции интересно проявлениями квантовой теории
света, и в нем высвечивается «фактическая область» применений материала гл. 8 и 9.
В процессе этого явления двухуровневый атом, обычно, возбуждается непрерывным
резонансным лазерным полем, а измеряются спектральные и квантовые статистиче-
статистические свойства флуоресцентного света, испущенного атомом. Экспериментально это
может быть достигнуто путем рассеяния лазерного излучения на коллимированном
атомном пучке, когда направления
Атомный лазерного пучка, атомного пучка
ПУЧОК и оси детектора являются взаимно
перпендикулярными (рис. 10.1).
Если возбуждающее (управляю-
(управляющее) поле монохроматично, то при
слабой интенсивности возбуждения
атом поглощает фотон на частоте
возбуждения и переизлучает его на
той же частоте вследствие сохране-
сохранения энергии. Спектральная ширина
флуоресцентного света является, по-
поэтому, очень узкой. Ситуация, од-
однако, становится существенно более
сложной с ростом интенсивности воз-
возбуждения, когда частота Раби, соот-
соответствующая управляющему полю,
становится сравнимой или большей,
чем атомная ширина линии. При та-
таких интенсивностях осцилляции Ра-
Раби проявляются в модуляции кванто-
V J Детектор
Рис. 10.1. Схема эксперимента по резонансной
флуоресценции. Направления атомного пучка,
лазерного пучка, а а также оси детектора вза-
взаимно перпендикулярны
вого дипольного момента, и в спектре 1) излучения возникают боковые компоненты.
Это так называемое динамическое штарковское расщепление является интересным
свойством атомно-полевого взаимодействия. Кроме того, флуоресцентный свет обна-
обнаруживает определенные неклассические свойства, такие как антигруппировка фото-
фотонов и сжатие.
В этой главе развита теория резонансной флуоресценции, объясняющая эти явле-
явления. Для начала будет установлена связь между полевыми операторами, необходи-
необходимыми для определения характеристик рассеянного света, и атомными дипольными
) Полный расчет спектра был впервые выполнен Моллоу (Mollow, 1969). Прекрасное
физическое объяснение с использованием «одетых состояний» было позднее дано С. Cohen-
TannoudjI с соавторами (см., например, Cohen-TannoudjI and Reynaud, 1976).
10.2 Введение в теорию спектра резонансной флуоресценции 239
операторами в соответствующий более ранний момент времени. Дипольные корре-
корреляционные функции будут при этом рассчитываться полу классически, а сильное
управляющее поле рассматривается классически. Рассмотрена также задача о резо-
резонансной флуоресценции системы V-типа. В этом случае наблюдается представляю-
представляющее интерес «сужение линии». Нами представлена упрощенная трактовка задачи,
отражающая физическую суть.
10.1. Оператор электрического поля для спонтанного излучения
одиночного атома
Начнем с рассмотрения двухуровневого атома, расположенного в точке с радиус-
вектором Го и подвергающегося воздействию сильного непрерывного лазерного поля.
Это взаимодействие можно рассматривать полу классически, как это сделано в гл. 5.
Возмущенный атом возбуждается в верхнее энергетическое состояние и затем из-
излучает спонтанно по всем направлениям (см. гл. 6). Оператор поля в точке г, ассо-
ассоциируемый с этим флуоресцентным полем излучения, зависит от соответствующего
атомного оператора в момент времени запаздывания, равный времени распростра-
распространения из Го в точку г. В приложении 10.А получено соотношение, позволяющее нам
изучать спектральные свойства флуоресцентного света путем упрощенного расчета
соответствующих корреляционных функций, содержащих атомные операторы воз-
возбужденного атома.
Как показано в приложении 10.А, делая, по-существу, приближение Вайскопфа—
Вигнера, мы находим, что оператор поля Ел+^ в точке г определяется выражением
,?„. (t - ?^i) , A0.1.1)
0| Vе/
и аналогичным для Е' '(г, ?). Выражение A0.1.1) указывает, что положительно-
частотная часть оператора поля пропорциональна атомному понижающему опера-
оператору в момент времени запаздывания.
В выражении A0.1.1), справедливом только в дальней зоне, диполь предпола-
предполагается расположенным в плоскости xz под углом tj к оси z, частота ш — атомная
частота перехода, а р ~~ матричный элемент диполя на переходе между двумя
состояниями. Видно, что в приближении дальней зоны рассеянное поле поляризовано
в ж-направлении.
10.2. Введение в теорию спектра резонансной флуоресценции
10.2.1. Предел слабого управляющего поля. До погружения в детальные вычис-
вычисления, воспользуемся простыми аргументами для понимания спектральных свойств
флуоресцентного света.
На рис. 10.2 поле со спектральной шириной D и средней частотой v воздействует
на атом со спектральной шириной Г и средней частотой из. Поле наводит в атоме
дипольный момент, который определяет излучаемый или рассеянный свет согласно
выражению A0.1.1). А именно, если вычислить среднее значение выражения A0.1.1),
то найдем
240
Резонансная флуоресценция
Гл. 10
(а)
¦Гла
Падающий свет
Атомный профиль
(б)
Рассеянный свет
-Трас
Рис. 10.2. Падающий свет частотой и рассеивается атомом, время жизни которого в возбуж-
возбужденном состоянии равно 1/Г (а); падающий свет характеризуется спектром с центральной
частотой и и шириной полосы D. Рассеянный свет характеризуется шириной полосы D
с центром на частоте и при Г ^> D (б)
Среднее значение (сг_(?)) молено получить, принимая во внимание, что
, A0.2.2)
где U(i) — оператор временной эволюции для атома, возбуждаемого интенсивным
классическим полем. Поскольку понижающий оператор определяется как 0"_(О) =
= \Ь)(а\, то из выражения A0.2.2) следует, что
A0.2.3)
A0.2.4)
(a-(t)) = Tr[|6><a|p(t)] = (a\p{t)\b) = pab(t).
Согласно E.3.24) для элемента pab(t) матрицы плотности имеем
[Paa(t)-Pbb(t)]e-
pab{t) = - [iuj+^j Pah- ^
Здесь мы использовали приближение вращающейся волны и положили 7аб = Г/2.
Решение уравнения A0.2.4) имеет вид
Pab(t) = Раб
— г~
= -г
п
f)
(uj - и) + Г/2
-[р««@)-Рбь@)], (Ю.2.5)
где Од является частотой Раби управляющего поля, Од = р$j%, и принято также
во внимание, что раь(Щ = 0 и что для слабых полей разность paa(tf) — Pbb(tf) можно
заменить величиной раа(Щ — Рьь(Щ- В итоге, в пределе больших времен t ^ 1/ Г,
получаем следующий результат:
A0.2.6)
10.2
Введение в теорию спектра резонансной флуоресценции
241
Выражение A0.2.6) свидетельствует о том, что диполь осциллирует на частоте
управляющего поля, а не на атомной частоте. Из A0.2.1) и A0.2.6) видно, что поле,
излучаемое в некотором новом направлении, имеет тот же спектр, что и управляющее
поле, если его спектральная ширина D мала по сравнению с Г (см. рис. 10.2). Другими
словами, для поля, обратная спектральная ширина которого равна 1/D, вследствие
его конечной продолжительности, мы представляем атомный отклик как отклик
возбуждаемого осциллятора с частотой управляющего поля. Атомный осциллятор
рассеивает до тех пор, пока он возбуждается, т.е. в пределах времени 1/D. Таким
образом, флуоресцентный свет, вызванный спектрально узким управляющим полем,
также имеет узкую спектральную ширину.
10.2.2. Предел сильного поля: появление боковых полос. Ситуация, описанная
выше, соответствует слабой интенсивности возбуждения. Когда же частота Раби,
соответствующая управляющему полю Од, становится сравнимой или большей,
чем спектральная ширина атома Г, в спектре флуоресцентного света появляются
сателлиты, что приводит к трехпиковому спектру. Возникновение боковых полос на
частотах v + Од и i/ — Од обязано модуляции дипольного момента осцилляциями
Раби. Физическое толкование такого интересного поведения можно дать, рассмотрев
атомно-полевое взаимодействие в представлении «одетого» атома. Гамильтониан
взаимодействия квантованной полевой моды, резонансно взаимодействующей с двух™
уровневым атомом, в приближении вра-
вращающейся волны имеет вид (см. F.2.8))
tft = сЖО Т" еЯ>1 =
= —az + Twor a + ng{<j+a + a^a^).
A0.2.7)
Рассмотрим случай, когда ш = i/, так
что в представлении взаимодействия
имеем гамильтониан
Г = hg((i+a + a+cj^). A0.2.8)
Путем прямой подстановки молено по-
показать, что собственные состояния га-
гамильтониана A0.2.8) имеют вид
, A0.2.9)
т
п
1
ш-П
Т
п
1
п + 1 квантов
ш + П
п квантов
Рис. 10.3. Расщепление атомных состояний
при динамическом эффекте Штарка
с собственными значениями +Шп/2
и — М2п/2, соответственно, где Оп =
= 2g-\fn + 1 — «обобщенная» частота Раби. Таким образом, ранее вырожденные
состояния |а, п) и |6,п + 1) расщепляются на дублеты «одетых» состояний, раз-
разделенных частотой Оп, как показано на рис. 10.3. Такое расщепление называется
динамическим штарковским расщеплением. Динамические штарковски расщеплен-
расщепленные дублеты имеют почти равный интервал при п ^> 1. Как показано на рис. 10.3,
спектр однофотонного спонтанного распада состоит из триплета линий, разделенных
частотой Раби Оп с центральной линией, обусловленной двумя равными вкладами.
10.2.3. Ширины трех пиков в пределе очень сильного поля. Из разд. 10.2.1.
и 10.2.2 видно, что явные спектральные особенности, такие как дельтаобразный
спектр в пределе слабого поля и появление трех пиков в пределе сильного поля,
242 Резонансная флуоресценция Гл. 10
легко объяснимы, чего нельзя сказать о ширинах этих пиков. Как будет видно далее,
ширина центрального пика равна Г/2, а ширины боковых полос — ЗГ/4. В чем причи-
причина этого различия? Традиционный расчет трехпикового спектра достаточно сложен
(см. разд. 10.5 и приложение 10.Б). Дадим простой вывод для случая, когда частота
Раби много больше, чем скорость атомного распада. Для начала предположим, что
распределение фотонов поля имеет острый максимум в окрестности среднего числа
фотонов гг, так что можно записать
Un^uw=uR. A0.2.10)
В этом случае индекс фотона в выражении A0.2.9) для собственных состояний можно
опустить
|±> = -^(|о)±|6». A0.2.11)
Полученное выражение представляет собой собственные состояния полуклассическо-
полуклассического гамильтониана взаимодействия [выражение E.2.54) при ф = тг]
У=^(\а)(Ь\ + \Ь)(а\), A0.2.12)
такие что
У|±) = ±^Я|±). A0.2.13)
Вооружившись этими обозначениями и предположениями, приступим к вычисле-
вычислению оператора плотности возбуждаемого и затухающего атома. Атомный оператор
плотности подчиняется уравнению движения (в представлении взаимодействия)
[У,р]+^Р, A0.2.14)
где релаксационный член находится из (8.2.8) (в пределе птепл = 0) и имеет вид
Г
{а+а^р 2а^ра+ + ра+а^). A0.2.15)
Для начала найдем среднее (а_(?)), которое в базисе «одетого» состояния имеет
вид (см. задачу 10.2)
(а_(*)> е*"* = \{P++(t) - p—{t) - p+_(i) + />_+(*)]. A0.2.16)
Учитывая, что р = 1 — р++ и р |_ = р* , для вычисления (<7_(?)) достаточно
найти р_|__|_(?) и р^ (t). Запишем уравнения движения для р++ и^ , используя
выражения A0.2.14) и A0.2.15) (см. приложение 10.Б),
l1-, A0.2.17а)
Г Г
-р.+ - -. A0.2.176)
Кроме того, в секулярном приближении, которое справедливо для сильных полей,
таких что Од >» Г, последними двумя членами в уравнении A0.2.176) можно
пренебречь (поскольку они приводят к быстро осциллирующим членам):
A0.2.18)
10.3 Теория анализатора спектра 243
Решая A0.2.17а) и A0.2.18), находим
p++(t) = Р++@) е~г*/2 + 1A - е~г*/2), A0.2.19а)
р+^ (t) = р+^ @) е-^я^зг*/4в A0.2.196)
В заключение, подставим выражения A0.2.19а) и A0.2.196) в A0.2.16) и получим
<<т_(*)> е-4 = \{[2Р++@) - 1] е"г*/2 - [р+.@) е"^™/4 _ кх]}> A0220)
Из выражения A0.2.20) с учетом A0.2.1) следует несколько интересных момен-
моментов. Прежде всего, имеется центральная составляющая, спадающая как функция
ехр(—Г?/2), что подразумевает наличие центрального пика с шириной Г/2, и два
сателлита на частотах ±Од с ширинами ЗГ/4. Таким образом, имеется простой способ
вычисления ширины линий.
Однако, как видно из A0.2.19а), стационарное значение р++@) равно 1/2, и,
следовательно, первый член в A0.2.20) обращается в нуль. Более того, в пределе
Од ^> Г, стационарное значение р^ @) стремится к нулю, и наш диполь, следо™
вательно, исчезает. Дело в том, что следует подробнее рассмотреть, в чем состоит
суть вычисления (и измерения!) спектра рассеянного света. Этим мы и займемся
в следующем разделе.
10.3. Теория анализатора спектра
Для ответа на вопрос, возникший в предыдущем разделе, мы пересмотрим и углу-
углубим наш подход к процессу измерения спектра рассеянного излучения. С этой целью
рассмотрим модель анализатора спектра (см. рис. 10.4). Имеется атомный детектор
Анализатор спектра
\P)—J
Атомный детектор
• Затвор
Управляющее \
поле \
Рассеивающий атом
Рис. 10.4. Схема установки модели анализатора спектра
с двумя «узкими» уровнями, соответствующими состояниям \а) и |/3), разделенными
энергией Нша. После того, как в момент времени to затвор открывается, рассеянный
свет облучает атом вплоть до момента времени to + Т, когда затвор закрывается.
Потребуем, чтобы время Т было много больше, чем обратная спектральная
ширина 1/ Г рассеянного света. В этих условиях атомный детектор возбуждается
на верхний уровень с вероятностью Р(ша). Затем «смотрим», возбужден ли атом,
записываем результат наблюдения, переводим атом в основное состояние |/3) и по-
повторяем измерение много раз.
Далее мы «перестраиваем атомный детектор», изменяя ша (например, варьируя
внешнее магнитное поле) и повторяем последовательность действий, изложенную
244 Резонансная флуоресценция Гл. 10
в предыдущем абзаце. В заключение, строим зависимость вероятности Р(ша) от
частоты о;а, чтобы получить спектр рассеянного света.
Вышеприведенная умозрительная схема анализатора спектра дает нам операци-
операционное определение спектрального профиля. Теперь не составляет труда рассчитать
Р(ша), используя выражение F.5.3), что в принятых обозначениях приводит к сле-
следующему результату:
, t2)) e-*"«(*i-*2). (ю.3.1)
to t0
Здесь ра@ является обычным дипольным матричным элементом, а (...) — среднее по
операторам рождения и уничтожения поля, означающее Тг [pjr . . .], где рр — опера-
оператор плотности поля. Еще точнее, спектр, определенный выражением A0.3.1), можно
записать через корреляционную функцию 6Л^(г, г; ti, i^) (выражение D.2.10)). Вы-
Выражение A0.3.1) тогда будет иметь вид
Р{ша,Т) = ^0- j dh j dt2G^(T, r; h, t2) e-^a^-*») 5 A0.3.2)
*o to
где G^^(r, r; ti, ^2) =Tr[E(~\r,ti)E^(r,t2)pF]- Из приложения 10.Д следует, что
эта вероятность пропорциональна спектру мощности рассеянного света и равна (для
стационарных полей)
Р(ша) = к \ drG{1) (г, г; 0, т) eiw«T + к.с, A0.3.3)
где к является константой, зависящей от эффективности детектора и т. д.
В данной задаче о резонансной флуоресценции можно с помощью A0.1.1) записать
A0.3.3) в виде
где г = |г — го | ир — атомный оператор плотности.
Но как вычислить двухвременное среднее в выражении A0.3.4)? В разд. 10.2 мы
имели дело исключительно с одновременными средними значениями
<<7_(*)>=Тг[<7_@)р(<)]. A0.3.5)
Возникает вопрос, можно ли использовать A0.3.5) для вычисления двухвременных
средних значений, аналогичных тем, что имеют место в A0.3.4)? В следующем
разделе показано, как это можно сделать.
10.4. От одновременных к двухвременным средним: теорема
регрессии Онсагера-Лакса
При изучении спектральной плотности и антигруппировки фотонов флуоресцент-
флуоресцентного света нами будут использоваться следующие двухвременные корреляционные
функции: (<т+(?)<т_(? + г)) и ((T+(t)cr+(t + r)a^(t + т)<т_(?)). В общем случае, для
вычисления двухвременных корреляционных функций не достаточно решения для
оператора плотности. Необходимо определить распределение вероятности перехода.
Однако, при определенных условиях, теорема квантовой регрессии позволяет нам
10.4 Теорема регрессии Онсазера-Лакса 245
получить двухвременную корреляционную функцию из одновременной корреляци-
корреляционной функции.
Полный оператор плотности в момент времени т при т ^ 0 выражается через
оператор плотности в более ранний момент времени t = 0 следующим образом:
р(т) = U(t)p@)U+(t), A0.4.1)
где U(t) является унитарным оператором временной эволюции для полной системы.
Здесь p(t) является оператором плотности для полной системы «атом + резервуар».
Предполагается, что оператор плотности резервуара рд@) не связан с атомным
оператором плотности ратом@) в начальный (более ранний) момент времени t = 0,
т. е.
р@) = рд@)®ратОм@). A0.4.2)
Приведенный оператор матрицы плотности для атома в момент времени т, таким
образом, можно получить, взяв «след» по переменным резервуара, т. е.
Ратом(т) = Тгд [ВДрД@) ® Ра,ом@)и+(т)}. A0.4.3)
Тогда среднее значение <т_ (т) определяется как
(ст_(т)} = Тгатом Тгд [<т-@)ра(т) ® ра«ш(т)] =
= Тгатом {а_@)Тгя [{/(т)рн@) ® />ато„@){/+(т)]}, A0.4.4)
в то время как двухвременная корреляционная функция записывается в виде
<<7+@)<7_(т)> = ТгатомТгд [<Т+@)(Т-(т)рЯ@) О Ратом(О)] =
= Тгатом {а+@)Тгд [U+(t)<7.(Q)U(t)Pr@) ® ратом@)]} =
= Тгатом (ст_@)Тгд {{/(т)рд@) ® baTOM@)a+@)]f/+(T)}). A0.4.5)
Сравнивая выражения A0.4.5) и A0.4.4), молено легко вычислить (<т+@)сг^(т)},
используя Ратом@)сг+@) вместо ратом@) В выражении A0.4.4). Очевидно, что двух-
двухвременную корреляционную функцию можно получить, зная одновременные средние
значения. Ключевым предположением является выражение A0.4.2), которое обычно
именуется марковским приближением.
Более общая формулировка квантовой теоремы регрессии состоит в том, что,
если для некоторого оператора О,
<д(* + т)) = Х>л-(т)<б,-(*)>, A0.4.6)
3
то
(di(t)d(t + r)dk(t)) = Y, а^т){д^)д^)дк{1)). (ю.4.7)
3
Осуществив эти предварительные шаги, возвратимся к задаче разд. 10.2.2. Ис-
Используя выражения A0.Б.28) и A0.Б.29), можно записать A0.2.20) в представлении
«неодетых» состояний как
(а_(т)) е*- = \{Tv i\b){a\p@)} + Tr [\a){b\p@)}} е^'2-
J {\a)(a\p@)] - 1 - Tr [|b)(o|p@)] + Tr [|а)F|р@)]} е"ЗГт/4 e~in^+
[\a)(a\p@)} - 1 + Tr [|6)<a|p@)] - Tr [\a)(b\p(O)}} е"ЗГт/4 еш«т, A0.4.8)
246 Резонансная флуоресценция Гл. 10
где использовано также соотношение Pij(O) = Тг (|j)(i|p(O)). Если теперь заменить
р@) величиной р@)<т_|_@), как предложено выше, то получим
= ±Tr [\а)(а\р{0)]
- Tr [\a)(a\p@)]} e^/4 e~in^+
Тг [\а){а\р@)}} е^Гт'А еш«т. A0.4.9)
Для стационарного состояния раа = р^ = 1/2, ра5 = ръа = 0, и окончательный вид
двухвременнбй корреляционной функции задается формулой
) ~1шт. A0.4.10)
В этом результате содержатся физические основы трехпикового резонансного спек-
спектра флуоресценции, включая ширины пиков. Данный результат A0.4.10), получен-
полученный в приближении сильного поля, распространен в разд. 10.5 на случай обычных
полей.
10.5. Полный спектр резонансной флуоресценции
В этом разделе вычисляется полный спектр мощности излучения, рассеянного
двухуровневым атомом, возбуждаемым полем произвольной величины. Предполо-
Предположим, что атом изолирован и зафиксирован в определенной точке пространства.
Нас интересует поле, излучения вдоль оси х. Поэтому оператор поля в A0.1.1)
можно рассматривать как скаляр. Спектр мощности S(t,ujq) флуоресцентного
света в некоторой выбранной точке г в дальнем поле получается путем фурье-
преобразования относительно т нормально упорядоченной корреляционной функции
поля {E^(r,t)E^(r,t^r)} (см. приложение 10.Д):
сю
5(г, ш0) = - Re [ dr(?/(-)(r, t)^(+)(r, t + r)> eiw°T. A0.5.1)
я" J
Здесь мы предположили, что поле в стационарном состоянии является статистически
стационарным, т. е. полевая корреляционная функция не зависит от начального
момента времени, так что корреляционная функция (E(~\r, i)E^(r, t + т)} зависит
только от разницы значений времени т.
Из A0.1.1) следует, что
t + r)) = /0(г)<<7+(*)G_(* + т)>, A0.5.2)
где
'-го
Двухвременную корреляционную функцию (<т+(?)а_(? + т)) можно вычислить с по-
помощью квантовой теоремы регрессии, зная соответствующие одновременные корре-
корреляционные функции. Таким образом, нам необходимы средние значения дипольных
10.5 Полный спектр резонансной флуоресценции 247
операторов в представлении взаимодействия, (а+(?)) = Pba(t) exP {iojt), (сг_(?)) =
= pab(i) exp (—iwt), и оператора инверсии (<rz(t)) = [paa(t) — рьб(?)]. ^се корреляци-
корреляционные функции высших порядков могут быть получены из них. Например,
0, A0.5.4а)
= ((az(t)} + l)/2. A0.5.46)
Как показано в приложении 10.Б (см., также, приложение 10.В), точное решение
уравнения Лиувилля A0.2.14) приводит к выражениям
= ai(r) + a2(T){a-(t)) eiut + о3(т)(<7+(*)> e~iut + а4{т){(аz{t)) + l)/2, A0.5.5)
z(t + T)) + l)/2 = paa(t + T) =
= 61 (r) + &2(t)(<x_(*)> е<ш* + Ь3(т)(а+(*)> е"*"' + b4(r)((az(t)) + l)/2, A0.5.6)
где
f^ { ""* h (^) H} (io-5-7)
[rsin/xr + 4/xcos/xr], A0.5.8)
zw 2 8/x
аз(т) = - е~Гт/2 [rsinjtir + 4/х cos fir], A0.5.9)
Л o/x
a4(r) = ^^ е^ЗГт/4 sin /xr, A0.5.10)
/i
— (cos цт H sin/irj е^ЗГг^4 , A0.5.11)
62(r) = ^ е-ЗГт/48т/гг, A0.5.12)
2/i
63(T) = -— е"ЗГт/4 sin /iT, A0.5.13)
64(r) = е^ЗГт/4 [cos /it - — sin /it] , A0.5.14)
M=l0^^—J . A0.5.15)
Нас будут интересовать стационарные свойства рассеянного поля. В стационарном
состоянии (t —> сю) средние значения различных атомных операторов являются
независимыми от начальных условий. Отсюда следует, что
lim (<T-(t)) eiujt = ai(oo) = ^ R^ , A0.5.16)
t—too I + zilp
:Ы°°)=га"пп2- (Ю-5.17)
Теперь вычисление двухвременной корреляционной функции (a_|_(t)<j_(t + г)), как
было показано в разд. 10.4, формально идентично вычислению одновременного сред-
среднего значения {<J—(t + г)), за исключением того, что вместо приведенного оператора
248 Резонансная флуоресценция Гл. 10
плотности ратом(^) следует использовать неэрмитов оператор paTOM(t)cr+(t). Следо-
Следовательно, из A0.5.5) следует, что
i / \/ /л\ /j-W —lUJt i / \l /j.\ Г /j.\
+ a3\TJ\{J+(*jcr+\^j/ e + a4\Tj\cr+VVLcr^\^J "
= {ai(r)(a+(t)} + a2(r)[(az(t)) + 1/2]}- A0.5.18)
В стационарном состоянии из A0.5.16) и A0.5.17) следует, что
(a^(t)(j^(t + т))сс = [ai(r)aj(oo) + a2(rNi(oo)] e^iwr. A0.5.19)
Подставляя различные коэффициенты из выражений A0.5.7), A0.5.8), A0.5.16)
и A0.5.17) в A0.5.19), получим следующее точное выражение для полевой двухвре™
менной корреляционной функции:
r+(t)a-(t + T))cc =
ul \ ( Г2 е~Гг/2
э^ЗГт/4 \
[e™^r(F + iQ) + e^r(F - iQ)] У A0.5.20)
4
где /q (г) определяется выражением A0.5.3), а безразмерные константы Р и Q имеют
вид
— Г2 Г 10О2 — Г2
Выражение для спектра мощности можно получить, выполняя фурье-преобразо-
вание (E(~)(r,t)E(+)(r,t + г)) (см. A0.5.1)). Как уже было показано в разд. 10.2
и 10.4, спектр демонстрирует удивительно разное поведение в слабо- и сильнополевом
пределах. Поэтому мы рассмотрим их отдельно.
10.5.1. Предел слабого поля. Выражение A0.5.20) значительно упрощается в пре-
пределе слабого поля, когда
Г2д<^. A0.5.22)
Частота Раби управляющего поля в этом пределе много меньше скорости спонтанного
испускания фотонов. Поэтому атом ведет себя как сверхзатухающий квантовый
гармонический осциллятор. Из определения fi (см. A0.5.15)) следует, что в этом
пределе /i = гГ/4. Первый член в фигурных скобках в выражении A0.5.20) в этом
случае будет порядка единицы, второй и третий члены взаимно уничтожаются, а
четвертый член равен нулю. Получаем
(Д(->(г, *)?7<+)(г, t + г)) - /0(г)(Пд/ ГJ е-*шт. A0.5.23)
Следовательно, спектр мощности излученного поля имеет вид
5(г, w0) = /о(г)(Пя/ ГJ <*(w - ^о), A0.5.24)
т. е. спектр определяется ^-функцией. Результат не является неожиданным, посколь-
поскольку при монохроматическом резонансном управляющем поле атом поглощает фотон
на частоте возбуждения, а закон сохранения энергии требует, чтобы испущенный
фотон имел ту же частоту, в соответствии с предсказаниями для упругого релеевского
рассеяния. Таким образом мы вновь получаем результаты разд. 10.2.1.
10.5
Полный спектр резонансной флуоресценции
249
10.5.2. Предел сильного полм. Ситуация оказывается более сложной, когда часто-
частота Раби управляющего поля сравнима или больше, чем скорость атомной релаксации.
В этом случае атом может когерентно взаимодействовать с полем много раз до того,
как спонтанно излучит фотон. Следовательно, осуществляя фурье-преобразование
r,t + т)) (см. A0.5.20)) и используя формулы
э-гш1-Тт/2+1ш®т _
A0.5.25)
A0.5.26)
получаем спектр мощности флуоресцентного света:
S(Y Шо) = ML>
4тг
: + (Г/2J
(и-
(ЗГ/4J
(ш
- м - о;0J
о;0J + (ЗГ/4J
где
зг
зг
= —rP ±(ш ± /1 -
A0.5.27)
A0.5.28)
На рис. 10.5 изображена функция Sf(r, ujq) для различных значений 4Од/ Г. Видно,
что с ростом интенсивности управляющего поля однопиковый спектр S(t,cjq) с мак-
Рис. 10.5. Спектр резонансной флуоресценции S(r, шо) в произвольных единицах, рассчи-
рассчитанный согласно A0.5.27): 4ОД/ Г = 1 (а), 4ОЯ/ Г = 8 (б) и 4ОЯ/ Г = 16 (в). Вклад упругого
рассеяния, пропорциональный а(ш — Шо) не учтен
симумом на частоте ujq = ш преобразуется в трехпиковый спектр с максимумами
на частотах ujq = a;, cj ± Од. Высоты этих пиков для Од ^> Г/4 соотносятся как
250 Резонансная флуоресценция Гл. 10
1:3:1. Упругий релеевский пик при ш® = ш теряется в этом пределе. Такое поведение
аналитически следует из выражения A0.5.26) в пределе Од >> Г/4. Тогда
*(Г,.О)=/О(Г)Г ЗГ/4
8тг ^
Г , ЗГ/4
+ (и - w0J + (Г/2J + (ш + пк- и0J + (ЗГ/4J ' A0-5-29)
что согласуется с выражением A0.4.10). Ширина пиков с центрами на частотах ш® =
= ш — Од, ш и ш + Од равна ЗГ/4, Г/2 и ЗГ/4, соответственно. Однако интегральные
интенсивности пиков соотносятся как 1:2:1.
10.6. Антжгруппжровка фотонов
Покажем, что рассеянное поле при резонансной флуоресценции обнаруживает
неклассическое поведение, связанное с антигруппировкой фотонов. Для того, что-
чтобы вычислить нормированную корреляционную функцию второго порядка #'2'(т)
(выражение D.2.21)), сначала определим двухвременную корреляционную функцию
(сг+(?)<т+(? + т)сг_(? + т)<т_(?)) из выражения A0.5.6). Используя квантовую теорему
регрессии, получаем
{<r+{t)a+{t + r)a.(t + T)<r-(t)) = <<т+(*)(М* + т)
= b1(T)(a+(t)a.(t)) + b2(T)(a+(t)a.(t)a.(t)) eiut + b3(r)(a+(t)a+(t)a.(t)) е~*шЬ +
+ b4(T){a+{t)(az{t) + l)<7_(*)>/2 = Ь1(т)((<7г(*)> + 1)/2. A0.6.1)
Для стационарного состояния из выражения A0.5.6) имеем
(a+(t)a+{t + т)<т_(* + r)cr-(t))cc = 61(т)Ь1(оо). A0.6.2)
Подставляя различные коэффициенты из A0.5.11) и A0.5.17) в A0.6.2), получаем
(cr+(t)a+(t + т)<7_(* + т)<т_(г))сс =
(cos "т+Ъsin
Из A0.6.3) с учетом A0.1.1) и D.2.21) следует, что
ЗГ
т) = 1 - (cos цт + ^ sin /и-) е"ЗГт/4. A0.6.4)
На рис. 10.6 величина g^(r) представлена как функция временной задержки т
для различных значений нормированной частоты Раби управляющего поля. Видно,
что gB\r) = 0 для т = 0, и gB\r) > 0 с ростом т. Следовательно
g{2)(T)>gW@), A0.6.5)
что соответствует явлению антигруппировки фотонов (см. D.4.71)).
В случае слабого управляющего поля, когда Од 4С Г/4, величина g^2\r) увели™
чивается монотонно от 0 до 1 с ростом т. В случае же сильного управляющего поля,
когда Од ^> Г/4, величина #'2'(т) демонстрирует осцилляционную зависимость от
т. Амплитуда этих осцилляции спадает с ростом т, а функция g^(r) стремится
к единице при т —> ос.
10.7
Резонансная флуоресценция возбуждаемой V-системы
251
Рис. 10.6. Нормированная корреляционная функция второго порядка g^ (t) как функция
безразмерной задержки Гт: 4Од/ Г = 0.1 (а), 4Од/ Г = 10 (б)
Легко понять физическую причину антигруппировки фотонов в резонансной
флуоресценции. После испускания фотона атом возвращается в основное состояние,
и для того, чтобы вновь возбудить атом в верхнее состояние, из которого может
быть испущен следующий фотон, управляющему полю необходимо некоторое время.
В среднем, эта задержка порядка периода Раби О^ , что можно видеть из выраже-
выражения A0.6.4) в пределе Од ^> Г/4. Следовательно, спонтанно испущенные фотоны
демонстрируют тенденцию к антигруппировке для малых времен задержек т.
10.7. Резонансная флуоресценция возбуждаемой ^-системы
В заключение обсудим флуоресценцию трехуровневого атома г), возбуждаемого
двумя когерентными полями (см. рис. 10.7). Основное отличие от традиционной
схемы резонансной флуоресценции состоит в наличии второго управляющего по-
поля. В результате не только возникают каче-
качественные изменения в форме спектров ис-
испускания и поглощения, но меняется также
и ширина линии в том смысле, что она ста-
становится зависимой от атомных параметров
и от относительной интенсивности полей.
В частности, ширины и пиковые ампли-
амплитуды спектральных компонент могут зна-
значительно отличаться от таковых для слу-
случая традиционной резонансной флуорес-
флуоресценции, в которой двухуровневая система
возбуждается единственным близким к ре-
резонансу полем (см. рис. 10.8).
Рис. 10.7. Схематичное представление V-
модели. i/i и 1/2 — несущие частоты управ-
управляющих полей
1) Для ознакомления с простой физической трактовкой см. (Keltel, NarduccI and Scully,
1995). Классической является экспериментальная работа Zhu, Gauthler and Mossberg A991).
252
Резонансная флуоресценция
Гл. 10
Пусть атом переходит из возбужденных состояний (см. рис. 10.7), \а) и \Ь) в со™
стояние \с) со скоростями Га и Г&, и мы предположим, что Га ^> IV Более того,
предположим, что частоты Раби
управляющих полей, связывающие
\а) и \с) (Ош) и |Ь) и \с) (пт) та-
ковы, что Од2 ^ ^Я1- В этом слу-
случае наблюдается спектральное суже-
сужение (см. рис. 10.8). В следующих не-
нескольких параграфах мы представим
эвристическую трактовку задачи.
Начнем с разложения атомного
дипольного оператора по наиболее
естественному набору состояний —
«одетым» состояниям системы «атом
+ управляющее поле» — и найдем
скорости релаксации «одетых» ко-
когерентных составляющих, которые
определяют ширины линий спектра
резонансной флуоресценции в при-
приближении сильного управляющего
поля. Мы получим точное выражение
для скорости затухания, определяю™
щей ширину одной из крайних боко-
вых полос, и идентифицируем вкла-
вклады, вносимые двумя возбужденными
состояниями в этот распад «одетой»
когерентности. Оказывается, что ва-
вакуумные флуктуации на частотах, близких к частоте одного из двух разрешенных
атомных переходов, могут подавляться флуктуациями на частотах, близких к часто-
частоте другого перехода, благодаря взаимной связи, которую «одетые» состояния полной
системы вызывают между «неодетыми» возбужденными атомными состояниями.
«Одетые» состояния являются собственными состояниями гамильтониана систе-
системы «атом + управляющее поле»:
-10
Рис. 10.8. Спектр спонтанного излучения на пе-
переходе а) —Ь с) в случае резонансных управ-
управляющих полей: стандартный спектр для случая
резонансного управляющего поля, связывающе-
связывающего состояния \а) и \с) (а); то же, но для случая
сильного управляющего поля на переходе \Ь) —^
—^ \с) (б). (Из статьи Narducci, Scully, Oppo, Ru,
and Tredlcce, 1990.)
= hgl(\c)(a
a)(c\ai) + hg2(\c)(b\at + \b)(c\a2),
A0.7.1)
где Hi и а2 являются операторами уничтожения фотонов полевых мод, чьи фоковские
состояния обозначены как \п) и |т), соответственно. Эти собственные состояния при-
приведены на рис. 10.9, а матричные элементы перехода между «одетыми» состояниями,
связанные со спонтанным излучением фотона, показаны на рис. 10.10. Как следует из
рис. 10.10, теперь возможны по пять линий на обоих \а) —>• \с) и \Ь) —> \с) переходах,
хотя на этом рисунке отражены лишь по три линии на каждом переходе.
Ширины спектральных составляющих определяются временной эволюцией со-
соответствующих «одетых» когерентностей. В качестве яркого примера, рассмотрим
составляющую дипольного оператора (см. A0.2.16))
1 • *
/ {4-\\ Т N \/ I (-f\~\ ( | \ —%шасъ (Л С\ 7 ^)\
которая осциллирует с частотой шас + 20, где
¦ "Я2 '
A0.7.3)
10.7
Резонансная флуоресценция возбуждаемой V-системы
253
, п,т) = —;=[|с, п,т)
a,n — 1,га)
, п,га — 1)]
|0, п,т) = cos ^|a, n — 1,?тг) + sin #16, n,m — 1}]
—, п,т) = —=\\с,п,т) — sin#|a,n — l.m) — cos#|b, n,m — 1I
2
Переходы
на частоте a;a
-\-,n - l,m) — —=[\c,n - l,
2
sin6'|a,n - 2,m) + cos0\b,n - l,m - 1)]
|0, n — l,m) = cos^|a,n — 2,ra) — sin^|b, n — l,m — 1)]
— ,n — l,m) = —=[|c, n — l,77i) — sin 01 a, n — 2,m) — cos 9\b, n — l.m — 1I
' ' t / C\ LI' ' / I ' 'I \ ' ' /J
2
sin Q — —
COS б zz
Рис. 10.9. Собственные состояния, соответствующие п фотонам в первом управляющем поле
и m фотонам — во втором, распадающиеся в состояния с п —1 и т фотонами, соответственно.
Часть состояний, связанных с переходами на частоте шас, выделена волнистой линией
ujac'- |(±,n,m|r|±,n — 1,га)| = — sin в\(а, п — 1, m|r|c, n — 1, т)\
4
4
— ,п— 1,?тг)|2 = - sin2 9\(а,п — 1,т\т\с,п — 1,ш)
: |@,n,m|r| —, п — 1,?тг)|2 = - cos2 0|(a,n — l,m|r|c, n — 1,?тг)
Рис. 10.10. Распад состояний с числом фотонов п и тп в управляющих полях в состояния
с числами п — 1, m и п, тп — 1 фотонов, соответственно. В окрестности обеих частот шас
и шъс будут наблюдаться по пять пиков, из которых только три отражены на рисунке.
Приведены матричные элементы тп, mn и пг2П на n, m —> и — 1, ж-фотонных переходах.
См. обозначения на рис. 10.6
254 Резонансная флуоресценция Гл. 10
Если внешние управляющие поля являются достаточно сильными или, точнее, если
эффективная частота Раби О много больше, чем обе скорости спонтанного распада
верхних атомных состояний, можно воспользоваться секулярным приближением
и получить (см. приложение 10.Д)
р+- = -2Ш/9+_ - 7+-Р+-, A0-7.4)
где
Ясно, что когда Га ^> Г^, но Од2 ^> ОдЬ ширина линии на частоте шас + 20
становится равной Г^.
Таким образом, можно сказать, что вакуумное взаимодействие, связанное с \Ь) —>
—>¦ \с) переходом, определяет ширину пика |а) —>> |с) на частоте о;ас + 2О. Этот эффект
наблюдался экспериментально.
Приложение 10. А
Оператор электрического поля в приближении дальней зоны
Начнем с рассмотрения взаимодействия двухуровневого атома с полем излуче-
излучения, которое в приближении вращающейся волны описывается гамильтонианом (см.
F.2.20))
к,Л к,Л
Здесь учтено взаимодействие между атомом и всеми полевыми модами, характе-
характеризующимися волновым вектором к и поляризацией Л. Далее введем медленно
меняющиеся операторы й^д и <т_, такие что
flk,A(t) = aKX(t) e~^\ A0.A.2a)
a-(t) = a-(t) e^iujK A0.A.26)
Уравнения движения Гейзенберга для этих операторов имеют вид
5k?A(t) = -ig^xa-{t) e-<(w-^)t-ik.rOj (Ю.А.За)
(T—\t) = > ^^kjA^z v*jttk,A e • (lU.A.tjOj
k,A
Можно формально проинтегрировать эти уравнения и получить
t
aKX(t) = 2k>A@) - ig^x e-tiv-^-^o difa^(tf) e^""^)^-*'), A0.A.4a)
о
5^ (t) = a^ @) + J^ ^k,A ei(w^I/k)t+ik-r° f citVz (t;)Sk,A e^^-^^*"*^. A0.A.46)
k,A I
Первые члены в этих выражениях соответствуют свободной эволюции полевых
и атомных операторов в отсутствие взаимодействия. В следующих разделах нас будет
интересовать вклад в поле, обусловленный его взаимодействием с атомом.
П. 10.А Оператор электрического поля в приближении дальней зоны 255
Из A.1.30) следует, что положительно-частотная часть оператора электрического
поля имеет вид
Е(+>(г,*) = ^^4A)ak,A(t)eik-r, A0.A.5)
к,Л
где <#к = (hvk/2eoVI/2. Подставляя выражение для a^\(t) из A0.А.2а) и A0.А.4а),
получаем
х [ dt'a- (tf) е*^-^)(*-*'), A0.А.6)
о
где было использовано определение g^ из F.1.8) и осуществлена замена суммы
интегралом согласно правилу
Учитывая, что (см. A.1.36))
получаем оператор векторного поля в удобном виде:
sin0
x f Л75_(tf) е*^-^)(*-*'), A0.А.7)
Затем предположим, что линия, соединяющая атом с наблюдателем, направлена
вдоль оси z, которая параллельна вектору г^г0, а электрический диполь расположен
в плоскости xz под углом rj к оси z (см. рис. 10.11). Тогда векторы к и р в полярных
координатах записываются следующим образом:
k = k(x sin § cos (p + у sin # sin у? + zcos#), A0.A.8)
p = p(xsinrj + zcosfj). A0.A.9)
Рассмотрим сначала интегрирования по углам в выражении A0.А.7). Интегриро-
Интегрирование по (р дает для я>составляющей
2тг
о
2тг
— sin $ cos 9?(sin 77 sin 1? cos 99 + cos 77 cos #)] = 2тгр sin 77 A sin2 # J ,
A0.A.10)
Резонансная флуоресценция
Гл. 10
Рис. 10.11. Вектор дипольного момента атома и вектор к электрического поля в полярных
координатах
для у-составляющеи
2тг
0
d<P \У- Р^
(ij • kl f k •
2тг
—sine sin (
(p + cos 77 cos $)] = 0,
A0.A.11)
и для z-составляющеи
2тг
к)(к • р)'
z - @ — тт^ I = I <i^p[cos 77 — cos #(sin 77 sin § cos <p + cos 77 cos #)] =
0
= 2тгр cos 77A — cos2 #) = 2тгр cos 77 sin2 §. A0.A.12)
Таким образом, ^-составляющая электрического поля обращается в нуль. Далее
рассмотрим интегрирование по i9 в A0.А.7). Записывая
гк-(г — г0) ik\(r—ro)\ cost?
и осуществляя замену переменных /i = cos#, получаем для ж-составляющей
о
= 27Tpsin?]
а для z-составляющей
io4j[i-i(i-
г/г|г - r0
h О
-r0
, A0.A.13)
- /i2) eik^r°
О
r-rolV
A0.А.14)
П.10.Б
Уравнения двиэшения для матрицы плотности
257
где использованы результаты A0.А.10) и A0.А.12). В области дальнего поля членами,
пропорциональными ОA/|г — го|2), можно пренебречь, и ^-составляющая электри-
электрического поля также обращается в нуль. Комбинируя A0.А.7) и A0.А. 13), получаем
— ro
r-r0| _ е-г
|г-г0|) [dt>z
(ю.А.15)
Далее по аналогии с теорией Вайскопфа-Вигнера осуществим замену к2
2
—> (cl?/cJ, распространим передел интегрирования по к до ^
рования по /г, получим
—>•
и, после интегри™
t
ro|/c) dt'a-{t'N(t-t'+ Г^Г° j . A0.A.16)
Пренебрегая вкладом входящей волны и возвращаясь к <т_(?) (см. A0.А.26)), легко
получаем выражение A0.1.1).
Приложение 10. Б
Уравнения движения для матрицы плотности и их точное
решение в базисе «одетых» состояний
10.Б.1. Вывод уравненим движения в базисе «одетых» состояний. В разд. 10.2
было показано, что в пределе сильного поля и в рамках секулярного приближения
решение системы в базисе «одетых» состояний объясняет положения и ширины
спектральных линий без сложных расчетов. Более того, как будет показано далее,
точное решение задачи в базисе «одетых» состояний также требует меньших усилий,
чем в базисе «неодетых» состояний.
Для начала заметим, что из выражения A0.2.11) следует
)), (Ю.БЛа)
)). A0.Б.16)
yz
С помощью этих формул запишем гамильтониан взаимодействия l^7, выразив пони-
понижающий и повышающий операторы а+ и а^ через состояния |±):
*- = \ь)(а\ = g
(I+X+I-I-X-I), (ю.в.2)
¦I+X-I-I-X+I-I-X-I), (ю.Б.3)
9 М.О. Скалли, М.С. Зубайри
258 Резонансная флуоресценция Гл. 10
а+а. = \а)(а\ = \(\+)(+\ + \+)(-\ + \-)(+\ + |+>(-|). (Ю.Б.4)
Подставляя выражения A0.Б.2)—A0.Б.4) в A0.2.14) и используя соответствующие
матричные элементы оператора плотности, получаем
Р++ = ~^Р++ + 4 ' (Ю.Б.5а)
/ЗГ \ Г Г
Р+- = - (Т + Ми) Р+- - JP-+ - 2 . A0.Б.56)
ЗГ \ Г Г
ш] ^+ - ^Р+^ - 2". (Ю.Б.бв)
10.Б.2. Решение уравнений движения. Достоинство базиса «одетых» состояний
состоит в том, что уравнение A0.Б.5а) не связано с уравнениями A0.Б.56) и (Ю.Б.бв).
Решение для р++ Уже найдено в A0.2.19а). Для того чтобы получить решения для
р^ и р |_, удобно переписать A0.Б.56) и (Ю.Б.бв) в матричной форме:
R(t) = -MR(t) + В, A0.Б.6)
где
M i ' Г/4 ЗГ/4-zftJ'
A0.Б.9)
Для того чтобы решить уравнение A0.Б.6), найдем собственные состояния и соб-
собственные значения матрицы М, такие что
(i = 1, 2). A0.Б.10)
Следовательно, матрица, состоящая из собственных векторов (матриц-столбцов) v^
имеет вид
V = (vi v2), A0.Б.11)
и
MV = (Aivi A2v2). A0.Б.12)
Нам также понадобится матрица, обратная У, которую можно найти традиционными
матричными методами и записать в виде матрицы, состоящей из векторов-строк:
V-1 = (I]) ¦ (Ю.Б.13)
Студентам, изучающим современную квантовую механику (и лучше знакомым
с обозначениями Дирака, чем с матричными обозначениями) может помочь следую-
следующее замечание:
Vi ^ \i), vj ^ (j\. A0.Б.14)
Теперь учтем, что (т.е., согласно нашему определению V^1)
1 = 1, A0.Б.15)
П.10.Б Уравнения двиэшения для матрицы плотности 259
A0.Б. 15) можно записать через собственные векторы и обратные к ним в виде
= (vi v2) (Y*) = vivi + v2v2 = 1, A0.Б.16)
(вновь отметим, что это аналогично выражению |1)A| + |2)B| = 1).
С помощью A0.Б.15) можно записать A0.Б.6) как
R(t) = -1
ИЛИ
— [V^Rit)] = -(V^1 MV^V^1 R(t)] + Vх В. A0.Б.18)
Поскольку
V~XMV = ()} ?)=D, A0.Б.19)
TO
— [V^R^t)] = -DlV^Rit)] + V^B. A0.Б.20)
Решение этого уравнения имеет вид
Из A0.Б.21) сразу же следует, что
R(t) = (V e-DtV~1)R@) + VD^A - e'^V^B. A0.Б.22)
Принимая во внимание тот факт, что D является диагональной, e~Dt записывается
в виде
~ /^—^i* о \
A0.Б.23)
Теперь очевидно, что зная собственные значения и собственные векторы, р^ (t)
и р y(f) можно получить из A0.Б.22) непосредственным перемножением матриц.
В нашей задаче собственные значения М равны
ЗГ / 9
Ai,2 = —±г/х, fi = y/?l2R- (Г/4J, A0.Б.24)
и отвечают собственным состояниям
vi = (C0St) , v2 = (~Smf) , A0.Б.25)
1 \sini;/ ' z \ cos 17 / ' v ;
где tgi? = — Dг/ Г)(Од — /x). Теперь можно построить У, V, D, и после некоторых
алгебраических преобразований мы приходим к следующему выражению для р^ (t):
1 . Г
р^ = — B/i cos fit — 2Шд sin /it) e^ *' /?_| @) sin /it e
2/i 4/i,
Г(Г/2 - »
2^д
260 Резонансная флуоресценция Гл. 10
Подставляя выражение A0.2.19а) для p++(t) и выражение A0.Б.26) для р_| (t)
в формулу
0"- = Раъ = Р++ - Ит (р+_) - -, A0.Б.27)
и отмечая, что
= -A + РаЬ + РЬа), A0.Б.28)
Р+~ = \@Раа ~ 1 " РаЬ + Рба), A0.Б.29)
получаем выражения для (<т_(?+т)) и (<rz(t+r)) вида A0.5.5)—A0.5.14), необходимые
для вычисления спектра мощности. Для сравнения мы вкратце изложили решение
той же задачи в привычном базисе «неодетых» состояний в приложении 10.В, ис-
используя несколько иную технику расчета.
Приложение 10. В
Уравнения движения для матрицы плотности и их точное
решение в базисе «неодетых» состояний
Поучительно решить задачу резонансной флуоресценции в базисе «неодетых»
состояний исключительно для того, чтобы показать, насколько проще она решается
в базисе «одетых» состояний. Уравнения движения для различных элементов матри-
матрицы плотности можно получить из A0.2.14) и A0.2.15) путем подстановки выражения
для ^ из A0.2.12) и последующего подбора соответствующих матричных элементов
оператора плотности. Результирующие уравнения можно записать в компактной
матричной форме следующим образом:
R(t) = -MR(t) + B, A0.B.1)
где (при рьъ = 1 - раа)
/Pah\
A0.В.2)
М = ( -Шд/2 Г Шя/2 | , A0.В.З)
A0.В.4)
Разительное отличие уравнений AО.Б.5а)-AО.Б.5в) (или A0.Б.6)) от A0.В.1)
заключается в том, что в системе уравнений AО.Б.5а)-AО.Б.5в) уравнение A0.Б.5а)
не связано с остальными, тогда как в A0.В.1) все три уравнения для ра5, раа и Pba
взаимосвязаны. Это означает, что в базисе «неодетых» состояний нам придется
оперировать матрицами размера 3 х 3 в отличие от матриц размера 2 х 2 в базисе
«одетых» состояний.
Для решения уравнения A0.В. 1) сначала находим собственные значения матрицы
М, которые имеют вид
Г ЗГ ЗГ
Ai = -, А2 = —+ гм, А3 = — — i/A, A0.B.5)
А 4 4
П. 10.Г Спектр мощности в стационарном режиме 261
где, как и прежде, /i = \/П|» ~~ Г2/16 . Вновь обозначая собственные векторы и обрат-
обратные им векторы через V/ и V/ (/ = 1,2,3), соответственно, по аналогии с A0.Б.16)
имеем
з
]TV = L A0.B.6)
С помощью A0.В.6) можно показать, что
з
e^MtO = 5^(v/O)vz e~Xl\ A0.B.7)
i=i
где О — матрица-столбец размера 3x1. Теперь можно найти решение:
M^Bjwi e^XlT} + M~XB. A0.B.8)
Определяя обратную матрицу М^1 и подставляя различные величины в A0.В.8),
можно получить выражения A0.5.5)—A0.5.14) для {®~{t + г)) и (az(t + г)) (зада™
ча 10.3).
Приложение 10. Г
Спектр мощности в стационарном режиме
Согласно теореме Винера-Хинчина, спектр мощности выражается через двухвре™
менную корреляционную функцию поля излучения следующим образом:
т т
%) = 7" Urn I \dt
о о
В стационарном режиме корреляционная функция (E^'fyE^'ft')} зависит только
от разности значений времени т = t — t\ и выражение A0.Г.1) принимает вид
о \о t
Т t T — t
\
0 0 0
A0.Г.2)
При условии, что операторы поля коррелируют только при малых значениях вре-
времени, можно распространить верхний предел интегрирования по т до бесконечности,
не внося значительных изменений. Поскольку
)*) A0.Г.З)
262 Резонансная флуоресценция Гл. 10
из A0.Г.2) следует, что
оо
S(ujq) = - Re [ dr{E^@)E^\r)} eiwor. A0.Г.4)
Приложение 10. Д
Вывод формулы A0.7.5)
Отметим, что в обычных обозначениях оператор релаксации в представлении
«одетых» состояний имеет вид
затухание
и после вставки полного набора состояний
(dP+-{t)
I dt
затухание
(Ю.Д-2)
В пределе сильного поля остаются только члены типа р^ , что приводит к выраже-
выражению
затухание
у<«1+> + Па){а\-) - 2{+\с)(а\+){-\а)(с\-))р+--
-\Ь)(Ь\-)-:
¦+_ = -7+-. (Ю.Д.З)
Таким образом, р^ (t) ~ е~7+-*р_| @), т.е. диполь Pac(t) = рас(сгас(^)) С(>
держит компоненту, которая спадает как е^7+™*, и, следовательно, (cr+c(O)crac(t))
(согласно теореме регрессии) ведет себя также.
Задачи к гл. 10 263
Задачи
10.1. Покажите, что атомно-полевые «одетые» состояния | + ,тг) и | —,п), определен-
определенные в A0.2.9), являются собственными состояниями гамильтониана A0.2.8)
с соответствующими собственными значениями i?(dz,n) = ±М!п/2, где Оте =
= 2gy/n + 1.
10.2. 1. Покажите, что полнота типа |+)(+| + |~)(~| = 1 эквивалентна |а)(«| +
+ |Ь)(Ь| = 1.
2. Используя предыдущий результат покажите, что
= (+\а.\+)(+\р\+) + (+\а.\-)(-\р\+) +
Заметим, что в отличие от A0.2.2) здесь появляется множитель elujt,
поскольку мы работаем в представлении взаимодействия.
3. Покажите, что
(+\<т\+) = (+\Ь)(а\+) = ±,
4. Учитывая все полученные выше результаты, докажите справедливость
выражения A0.2.16).
10.3. Получите выражения A0.5.5)—A0.5.14), следуя методу, изложенному в прило-
приложении 10.В.
10.4. Рассмотрите резонансную флуоресценцию двухуровневого атома, затухающую
благодаря многомодовому сжатому вакууму. В этом случае уравнение движе-
движения для атомного оператора плотности имеет вид (см. (8.2.17))
i Г
Р = ~т[У, Р] ~ 77 ch2 (r)({J+{J- 2 + )
h a
р
sh (r)((j
- Г е^ы sh (r) eh (r)a^pa^ - Г еы sh (r) ch
где г — параметр сжатия, $ — опорная фаза сжатого поля, 'У — гамильтониан
A0.2.12) в представлении взаимодействия. Получите выражение для спектра
резонансной флуоресценции в случае сильного когерентного управляющего
поля. Покажите, что ширину центрального пика в трехпиковом спектре можно
сузить по сравнению с соответствующей шириной в случае атомного распада
в вакууме за счет соответствующего подбора •&. (Указание: см. Carmichael, H.J.,
Lane, A.S. and Walls, D.F. Phys. Rev. Lett 58, 2539 A987).)
264 Резонансная флуоресценция Гл. 10
Список литературы
Обзорные статьи
Knight, P. L. and Milonni, P. W. Phys. Rep. 66, 23 A980).
Loudon, R. Rep. Prog. Phys. 43, 227 A980).
Mollow, B. R. In Progress in Optics, Vol. 19, ed. E. Wolf (North-Holland, Amsterdam 1981).
Трехпиковый спектр
Burshteln, A. I. Sov. Phys. JETP 21, 567 A965); ibid. 22, 939 A966).
Newstein, M. Phys. Rev. 167, 89 A968).
Mollow, B. R. Phys. Rev. 188, 1969 A969).
Kimble, H. J. and Mandel, L. Phys. Rev. A 13, 2123 A976).
Cohen-Tannoudji, C. and Reynaud, S. J. Phys. B: Atom. Molec. Phys. 10, 345 A976).
Renaud, В., Whitley, R. M. and Stroud, C. R., Jr., J. Phys. B: Atom. Molec. Phys. 19, L9 A976).
Wodklewlcz, K. and Eberly, J. H. Ann. Phys. 101, 574 A976).
Eberly, J. H., Kunasz, C. V. and Wodklewlcz, K. J. Phys. В 13, 217 A980).
Cardimona, D. Raymer, M. and Stroud, C. J. Phys. B. 15, 55 A982).
Sargent III, M., Zubairy, M. S. and de Martini, F. Opt Lett 8, 76 A983).
Экспериментальное наблюдение трехпикового спектра
Schuda, F., Stroud, С. R., Jr., and Hercher, M. J. Phys. B: Atom. Molec. Phys. 198, L7 A974).
Walther, H. In Laser Spectroscopy, ed. S. Haroche, J. C. Pebay-Peyroula, T. W. Hansch, and S.
E. Harris (Springer™Verlag, Berlin 1975).
Wu, F. Y., Grove, R. E. and Ezekiel, S. Phys. Rev. Lett 35, 1426 A975).
Hartig, W., Rasmussen, W., Schleder, R. and Walther, H. Z. Physik A 278, 205 A976).
Grove, R. E., Wu, F. Y. and Ezekiel, S. Phys. Rev. A 15, 227 A977).
Сужение естественно уширенных линий и резонансная
флуоресценция ^/-системы
Narducci, L. M., Scully, М. О., Oppo, G.-L., Ru, P. and Tredicce, J. R. Phys. Rev. A 42, 1630
A990).
Zhu, Y.-F., Gauthier, D. J. and Mossberg, T. W. Phys. Rev. Lett 66, 2460 A991).
Keitel, C. H., Narducci, L. M. and Scully, M. O. Appl. Phys. В 60, S153 A995).
Антигруппировка и сжатие
Carmichael, Н. J. and Walls, D. F. J. Phys. В 9, L43 A976); ibid. 9, 1199 A976).
Kimble, H. J. and Mandel, L. Phys. Rev. A 13, 2133 A976).
Cohen-Tannoudji, D. In Frontiers in Laser Spectroscopy Vol. 1, ed. R. Balian, S. Haroche, and
S. Liberman (North-Holland, Amsterdam 1977).
Walls, D. F. and Zoller, P. Phys. Rev. Lett 47, 709 A981).
Mandel, L. Phys. Rev. Lett 49, 136 A982).
Short, R. and Mandel, L. Phys.. Rev. Lett. 51, 384 A983).
*Голубев Ю.М., Соколов И.В. ЖЭТФ 87, 408 A984).
*Gorbachev V.N., Zhiliba A.I. Quant. Opt 5, 193 A993).
*Горохов А.В. Изв. РАН, сер.физ. 64, 2030 B002).
Список литературы к гл. 10 265
Экспериментальное наблюдение антигруппировки фотонов
Kimble, H. J., Dagenals, M. and Mandel, L. Phys. Rev. Lett 39, 691 A977).
Dagenals, M. and Mandel, L. Phys. Rev. A 18, 2217 A978).
Cresser, J. D., Hager, J., Leuchs, G., Ratelke, M. and Walther, H. In Dissipative Systems in
Quantum Optics, ed. R. Bonifacio, (Springer-Verlag, Berlin 1982).
Эффект флуктуации накачки
Kimble, H. J. and Mandel, L. Phys. Rev. A 15, 689 A977).
Knight, P. L., Molander, W. A. and Stroud, C. R., Jr., Phys. Rev. A 17, 1547 A979).
Raymer, M. G. and Cooper, J. Phys. Rev. A 20, 2238 A979).
Теорема квантовой регрессии
Onsager, L. Phys. Rev. 37, 405 A931).
Lax, M. Phys. Rev. 129, 2342 A963).
Глава 11
КВАНТОВАЯ ТЕОРИЯ
ЛАЗЕРА — МЕТОД ОПЕРАТОРА
ПЛОТНОСТИ
В гл. 5 и 7 теория лазера излагалась таким образом, что свет описывался как
классическое поле, подчиняющееся уравнениям Максвелла, тогда как лазерная сре-
среда представлялась множеством атомов, динамика которых описывалась уравнени-
уравнением Шредингера. Такая полуклассическая теория поведения лазера достаточна для
описания широкого круга явлений. Однако, существует много вопросов, ответы на
которые требуют полностью квантовой теории излучения. Например, статистика
фотонов и ширина линии излучения лазера могут быть правильно поняты лишь
с помощью полностью квантовой теории лазера.
Ширина линии излучения лазера является важной величиной. Например, она
определяет фундаментальный предел работы активного кольцевого лазерного гиро-
гироскопа. Первый полностью квантовый вывод выражения для спектральной ширины
лазера был сделан методом оператора квантового шума 1) и был настолько общим,
что включал в себя даже проблему ширины линии излучения полупроводникового
лазера. Этот вывод излагается в гл. 12.
Статистическое распределение фотонов лазера интересно по нескольким причи-
причинам. Исторически сложилось так, что статистика фотонов изначально предполага-
предполагалась бозе—эйнштейновской. Небольшое размышление показывает, что этого не мо-
может быть, поскольку лазер работает в условиях, далеких от термодинамического
равновесия. С другой стороны, существовала теория, согласно которой множество
атомов, осциллирующих в фазе, создает, в сущности, классический ток, который
генерирует когерентное состояние. Статистика последнего является пуассоновской.
Однако, например, статистика фотонов типичного гелий-неонового лазера суще-
существенно отличается от пуассоновской. Конечно, существенно выше порога, стационар-
стационарное статистическое распределение фотонов лазера является пуассоновским. Первый
вывод статистики фотонов лазера использовал формализм матрицы плотности 2)
и представлен в данной главе.
Существует глубокий смысл в том, что поведение лазера вблизи порога ана-
аналогично фазовому переходу второго рода 3). Это можно правильно понять лишь
) Рассмотрение с помощью оператора квантового шума было представлено М. Лаксом на
конференции «Физика квантовой электроники» в 1965 г.; см. Proceedings of the Int. Conf. on
the Phys. of Quantum Electronics, ed. P. Kelley, B. Lax, and P. Tannenwald (New York, 1966).
) Рассмотрение с помощью матрицы плотности, развитое Скалли, Лэмбом и Стефаном,
также было представлено на конференции «Физика квантовой электроники» в 1965 г; (см.
Scully, Lamb and Stephen, 1966). Очень ясное изложение вопроса можно найти в книгах
Loudon A970); Pike and Sarkar A996).
3) См. (Graham and Haken, 1970; DIGiorglo and Scully, 1970). Блестящее изложение расчета
приводится в работе Haken A975).
11.1
Уравнение двиэшения для матрицы плотности
267
в контексте полностью квантовой теории лазера, как это делается в данной главе.
В заключение заметим, что микромазер, в смысле реального устройства, есть модель,
для правильного понимания работы которой требуется квантовая теория лазера.
Такое описание дано в гл. 13.
11.1. Уравнение движения для матрицы плотности
Рассмотрев полу классическую теорию в гл. 5, а также затухание квантовых си™
стем в гл. 8 и 9, перейдем теперь к «фотонному» описанию работы лазера. Квантовая
теория лазерного излучения, в сущности, есть проблема неравновесной квантовой
статистической механики. Нашей задачей будет вывод «крупномасштабного» урав-
уравнения движения для матрицы плотности лазерного излучения, отражающего процесс
добавления (и последующего устранения) множества возбужденных атомов. Мы
выведем это уравнение двумя способами.
Метод 1. Рассмотрим систему атомов в резонаторе, структура уровней которых
изображена на рис. 11.1. Для описания лазерной генерации теория должна задать
Рис. 11.1. Схема уровней энергии, поясняющая работу лазера. Лазерная генерация проис-
происходит на переходе между двумя возбужденными состояниями \а) и |6), имеющем частоту ш.
Состояние \а) возбуждается со скоростью га, при этом состояния \а) и \Ь) релаксируют
в состояния с) и \d), соответственно, со скоростями уа и "уь* Состояния \а), \с) и \d)
релаксируют в состояние \g) со скоростями уё, yc и у а, соответственно
механизмы накачки и релаксации. Для описания действия накачки предположим,
что атомы усиливающей среды переводятся в верхнее возбужденное состояние \а)
из основного состояния \g) в случайные моменты времени to со скоростью Ао.
Релаксация из состояний \а) и \Ь) может происходить в состояния \с) и |d), со™
ответственно, со скоростями ja и 7ь? а Уже из этих состояний в основное \g) со
скоростями, соответственно, jc и 7d (рис. 11.1). Скорость релаксации из состояния
268 Квантовая теория лазера — метод оператора плотности Гл. 11
\а) в состояние \g) обозначим через jg. Для простоты предположим, что 7а = 7ь =
= 7? и рассмотрим лазер, настроенный в резонанс с атомами. Детали механизма
затухания поля в резонаторе не очень важны для теории лазера. В полуклассической
теории затухание описывалось омическими токами (разд. 5.5). Здесь можно пред-
предположить, что существуют только потери при пропускании, которые объясняются
взаимодействием поля излучения внутри резонатора с резервуаром вакуумных мод,
представляющим окружающий мир (моды «вселенной» 1)) так, как он видится через
частично пропускающие зеркала.
В данном подходе будем искать сначала квантово-механический аналог уравнений
Максвелла для поля и выражение, соответствующее атомной поляризации. Метод 1
будем излагать, подчеркивая связь с полуклассической теорией.
Гамильтониан взаимодействия для активных атомов, резонансных одномодовому
лазерному полю, в представлении взаимодействия и в приближении вращающейся
волны (выражение F.2.8)) имеет вид
где а^_ = (|а)F|)г и аг_ = (|6)(а|)г — повышающий и понижающий операторы для
i-го атома, соответственно. Здесь учтено лишь взаимодействие с полем на переходе
между состояниями \а) и \Ъ). Возбуждение посредством накачки из состояния \g)
в состояние \а) и релаксация состояний будут учтены феноменологически, как это
делалось в полуклассической теории лазера.
Уравнение движения для матрицы плотности лазерного поля, учитывающее вза-
взаимодействие с активной лазерной средой и механизм релаксации, имеет вид
/W = -^Тгатомы [Г,/»]„,„/ + (^р)п,п', (П.1.1)
где, как следует из (8.3.3),
nin> = -| (п + п')рпп, + <gy/{n + l){n' + l)pn+lin,+1. A1.1.2)
Слагаемое в A1.1.1), описывающее лазерную генерацию, расписывается следующим
образом:
) =-|тгатомы [У, р]п,п, = -А^[У,р]{а} {а} ,, A1.1.3a)
усиление "- Л х—^
{«}
где {а} = «1, «2, • • • , «jv («i = Q> или b) обозначает состояние всех N атомов лазера.
Его можно упростить, записывая в виде
4 ? Е^Л.«;«*.«'' A1л-36)
ai = a,b г
где
Рпп' = ^Р{а'},п;{а'},п'(*) A1.1.3в)
{«}
— проекция матрицы плотности для системы атомов и поля на пространство со™
стояний г-го атома и поля, {«'} = «i, . . . «i-i? «i+i? • • • aN- Используя A1.1.36)
г) См. работы Lang, R., Scully, M.O. and Lamb, W.E., Jr., Phys. Rev. A 7, 1788 A973); Lang,
R. and Scully, M.O. Opt Commun. 9, 331 A973).
11.1 Уравнение двиэшения для матрицы плотности 269
и A1.1.3в), запишем вклад лазерной генерации в изменение величины р в формуле
A1.1.3а) следующим образом:
. I t А1 атомы [г 1 Р\п,п'
С /усиление *^
где
Здесь отметим, что члены типа J^ p^n 6n+1(t, t^), где t^ — время инжекции j-ro
атома, являются полностью квантовым аналогом матрицы населенности E.4.4).
Таким образом, имеет смысл ввести обобщенную матрицу населенности, элементы
которой
Рап}Ъп+^ = У ;РЪап,Ъп+1\1-> ^)-
i
Уравнение A1.1.3г) можно переписать через элементы матрицы населенности в виде
I —77— J — ~TV^on,bn+lP6n+l,on ~ Pan,bnf + 1 ^Ьта/^1,ап/ +
\ 01 /усиление '*'
+ %п,ап-1Рап-1,Ьп' ~ РЪп,an1-\Уan'-!№')• (И-1-4)
Теперь предположим, что рассматривая атомно-полевую матрицу населенности
для г-го атома можно учитывать влияние остальных атомов только через их вклад
в pnnf(t) (так же как в полуклассическом случае влияние на г-й атом остальных
атомов определялось коллективным полем E(t)). Тогда уравнения движения для
матрицы населенности рапфп> = (а, ^|ратом—поле|Д, п') можно записать в виде
— т{Уап,Ьп+1РЬп+1,ап' "" Pan^n' + l^bn' + l^n'), A1.1.5a)
Pan,an' — ^aPgn,gn' 7 Pan, an' 7g Pan, an'
i
h
Г) l t i i — — 17 л 1 /1-1 — — I ir *> 1 1 /71. lit. /11 — /) /У /ж /ill I I I I Г1О I
r O7i j 07i ~r l I !r an ,on -\- L *- \ r an ,оп-\- i t' 07i-|- i ,on -\-1 t' an }an r an }on -\- i / 5 ^j-jL.jL.<j'\j|y
Pbn+l,anf :=: ~7 Pbn+l^an' ~ Tx^bn+l^anPan^an' ~~~~ Pbn+l,bn' + l'bn' -\-l,an' ) 1 A1.1.OBJ
Pbn+l,6n' + l = ~7Pbn + l,bn' + l "" т(%п+1,апРап,Ьп' + 1 ~ РЬп+1,ап'Уап',bn' + l) i A1.1.5r)
Penmen' — TPan,anf 'УсРсп^сп'
Pdn,dnf = lPbn,bnl — ldPdn,dn
Pgn,gnf — ^aPgn^gn1 i Tg"Pan,an' T 7cPcn,cn' ^
где член Aapg.n)g-n/ в уравнении A1.1.5а) соответствует возбу^«дению в процессе
накачки из состояния \g) только в состояние \а). Отметим, что уравнение A1.1.5ж)
является довольно общим и справедливо для более сложных схем, например когда
атомы, находящиеся в состояниях \а) и \Ь) могут релаксировать во многие другие
состояния, а возбуждение в процессе накачки в состояния \а) и \Ъ) может осуще-
осуществляться из любого произвольного состояния. Как будет показано ниже, для вывода
270 Квантовая теория лазера — метод оператора плотности Гл. 11
уравнения движения полевой матрицы плотности необходимы только уравнения
A1.1.5а)—A1.1.5г) и A1.1.4). Таким образом, справедлива эффективная двухуров-
двухуровневая картина.
Далее найдем компоненты элементов матрицы плотности рьп+i,апЧ Pan,bnf+ii
Pan-i,bnf и рьп,ап'-1- Сначала предположим, что скорость релаксации с уровня \а)
на уровень \g) мала, так что в уравнениях A1.1.5а) и A1.1.5ж) можно пренебречь
членами, пропорциональными jg. Тогда из A1.1.5д)—A1.1.5ж) следует, что в стаци-
стационарном состоянии
Pgn,gnf = Т-(Рап,ап' + РЬп,Ьп')т A1.1.6)
Предположим, что 7o7rf ^ 7 5 так чт0 в стационарном состоянии pCn,cnf =
= Pdn,dnf — 0. Это условие гарантирует, что как только атомы в процессе релаксации
перешли из состояний \а) и \Ь) в состояния \с) и |d), соответственно, они быстро
окажутся в состоянии |g*M из которого возбудятся в состояние \а) в процессе накачки.
Таким образом, поскольку
Рпп' — Pan,an' i Pbn,bnf > Pcn,cnf i Pdn,dnf i Pgn,gn' i ^Il.I.iaJ
имеем
Pan,anf + Pbn,bnf — Pnnf ~ Pgnignf, A1.1.76)
и вырал^ение A1.1.6) дает
/у
Pgn,gn> — , Рпп'- A1.1.8)
Теперь уравнение A1.1.5а) можно переписать в виде
Pan,an' — raPnnf ~ JPan,an' ~ T (^an,bn+lPbn+l,an; — Pan^bn'+ l^bn'+ l,an') i A1.1.9)
гДе ra = 7^a/G H" Aa) — эффективная скорость накачки. В результате уравне-
уравнение A1.1.9) вместе с уравнениями A1.1.56)—A1.1.5д) образуют замкнутую систему
уравнений для матричных элементов, соответствующих лазерным уровням |а) и \Ъ).
Решения этих уравнений движения для элементов panybn+i{t) и т.п. приводятся
в приложении 11.А.
Подставляя различные компоненты атомно-полевой матрицы населенности из
приложения 11.А в A1.1.4), находим уравнение движения для рпп/, описывающее
воздействие активной среды,
\ St /усиление V 1 + J^nn>^Ш) РпП
где введены линейный коэффициент усиления
о 2
7
коэффициент самонасыщения
т = %^^ (и.1.12)
11.1
Уравнение двимсения для матрицы плотности
271
и безразмерные множители
Л»' = ±(п + 1 + п' + 1)+[П П)^, A1.1.13а)
jYnn, = i(n + 1 + ri + 1) + —16^; ¦ A1.1.136)
Коэффициенты усиления и насыщения &/ и ^ соответствуют коэффициентам
E.5.10) полуклассической теории лазера в случае накачки на верхний уровень и ну-
нулевой отстройки. Связь между данным квантовым рассмотрением и полуклассиче-
полуклассическими результатами будет показана в конце этого раздела.
Добавляя (n|j?fp|n') из A1.1.2) находим
Рпп> =
(п + l)(nf
A1.1.14)
Полученное уравнение составляет наш основной результат. В частности, для диа-
диагональных элементов рпп = р(п), соответствующих вероятности обнаружить п
фотонов в поле лазера, имеем уравнение движения
р(п) = -
+ ^{п + 1)р(п + 1). A1.1.15)
Важно отметить, что диагональные элементы связаны только с диагональными, а
недиагональные элементы, в общем случае, связаны только с теми недиагональными,
которые имеют ту же разность п — п1.
Уравнению A1.1.15) для функции распределения фотонов можно придать про-
простой физический смысл, разлагая в ряд члены знаменателя в A1.1.15) и используя
диаграмму потоков вероятности (рис. 11.2). Мы видим, что есть всевозможные
га + 1
п- 1
^ (п + 1)р(п + 1)
*(п + 1Мп) "
VnP(n)
*«„(«-1)
38 (п + 1Jр(п) • • •
Рис. 11.2. Диаграмма потоков вероятности для лазера
«потоки» вероятности между состоянием |п) и соседними состояниями |п+1) и |п —1).
Например, член «2^(п + 1)р(п) представляет собой поток вероятности от состояния \п)
к состоянию \n-\-1), обусловленный испусканием фотонов атомами, находившимися
первоначально в верхних состояниях. Здесь sin есть скорость вынужденного излу-
излучения, ^ — скорость спонтанного излучения и эти скорости умножаются на р(п),
для того чтобы дать полную скорость потока вероятности. Поскольку вероятность
вытекает из р(п), этот член отрицателен. Первый член в разложении множителя
в квадратных скобках из A1.1.5), а именно 38(п + 1Jр(п) = я/(п + 1)C8/^/)(п +
+ 1)р(п), соответствует процессу, в котором фотоны излучаются, а затем перепогло-
перепоглощаются. Скорость перепоглощения равна C8/^/)(п + 1). Аналогичные разложения
существуют для остальных членов, включая члены потерь.
272 Квантовая теория лазера — метод оператора плотности Гл. 11
Метод 2. Как подчеркивалось ранее, каждый атом в газовом лазере передает
свою энергию полю независимо от других, если не считать того, что поле, с ко-
которым он взаимодействует, создано другими атомами. Принимая это во внимание,
рассмотрим изменение матрицы плотности поля излучения, возникающее вследствие
инжекции в момент времени to одного атома, возбужденного в процессе накачки
в верхнее состояние \а). В представлении чисел заполнения это изменение запишется
в виде
Spnn* = Рпп'{4 + Г) - /W(*o)> A1.1.16)
где время т больше атомного времени жизни, но меньше времени, характеризующего
рост или спад поля излучения. Тогда макроскопическое изменение матрицы плотно-
плотности Арпп/ вследствие действия N атомов на поле в течение интервала времени At
равно
A/W = N5pnn, = raAt8pnn4 A1.1.17)
где га — скорость инжекции атомов.
Обратимся теперь к определению величины Spnnr, фигурирующей в A1.1.16).
Чтобы найти pnni (tg+т) необходимо проследить за эволюцией объединенной системы
«атом + поле» до момента времени to + т и затем взять след от матрицы плотности
по атомным состояниям N:
Pnn'(to + T) = ^Pa,n;«5n'(*0 + т) (а = п,Ь). A1.1.18)
а
«Крупномасштабная» производная от матрицы плотности лазерного поля Ар/At =
= га8р получается комбинированием выражений A1.1.16)—A1.1.18):
/8рп^\ = Га[рап^п/^0 + Т) + PbnMf(t0 + Т) ^ ра„,ап/(*о)]. (И.1.19)
\ ОС /усиление
В адиабатическом приближении время to в этом выражении заменяется временем t.
Поскольку в данном рассмотрении атомы возбуждаются в процессе накачки в со-
состояние |а), PbnM'i^o) = О-
Величины pan,anf(t + т), Pbn,bn'(^ + т) и Pan,an'(t) нетрудно определить, решая
уравнения для амплитуд вероятности сап и сьп+1 (уравнения F.2.11) и F.2.12)).
В случае резонанса А = ш — и = 0 решения выглядят следующим образом:
A1.1.20)
A1.1.21)
откуда
Pan}an'(t + Т) = pnn>(t) COs(g-TVnTT) COs(g-T\/n/ + 1 ), A1.1.22)
A1.1.23)
A1.1.24)
поскольку при т = 0,
Pnn'(t) = \can(t)\2. A1.1.25)
Результирующее уравнение для приведенной матрицы плотности поля имеет вид
Spn,n> \
О* /усиление
'n')Pn-l,n'-l. A1.1.26)
11.2 Статистика лазерных фотонов 273
Отметим, что это уравнение было получено для системы, в которой двухуровневые
атомы переводятся в верхнее состояние \а) в случайные моменты времени со скоро-
скоростью га и взаимодействуют с полем излучения в течение времени т. Такая модель,
и следовательно уравнение A1.1.26), непосредственно имеет отношение к проблеме
квантовой статистики микромазера, которая будет рассматриваться в гл. 13.
Используя A1.1.26) можно получить уравнение A1.1.10). С этой целью рассмот-
рассмотрим атом, переведенный в состояние \а) в момент времени равный нулю, который
релаксирует из состояний \а) и \Ь) в состояния \с) и |rf), как показано на рис. 11.1, со
скоростью 7 = 1а = 1ь- Вероятность того, что атом останется в состояниях \а) и \Ь)
спустя время т равна
P(r)dr = 7 е^7Г dr. A1.1.27)
Следовательно, усредняя A1.1.26) по этому распределению получаем «крупномас-
«крупномасштабное» уравнение для матрицы плотности лазерного излучения:
сю
Оь /усиление
A1.1.28)
Вычисляя интегралы приходим к уравнению A1.1.10). Детали расчета приводятся
в задаче 11.7.
Чтобы связать данную квантовую теорию лазера с полуклассической теорией,
рассмотренной в разд. 5.5, выведем из A1.1.15) уравнение для среднего числа фото-
фотонов (п). В области порога генерации, когда 38{п) /'si <C 1, получаем (разложив в ряд
знаменатели первых двух членов в правой части)
оо
d{n) - ^ пр(п) = {st- <tf)(n) ~~ 38((п + IJ) + si. A1.1.29)
п=0
Это уравнение сводится к E.5.16) в пределе (п) > 1 и (п2) = (^J. Таким образом,
полуклассическая теория справедлива при больших числах фотонов и в ситуациях,
когда справедливо приближение
(п2) = (пJ. A1.1.30)
Член si в уравнении A1.1.29), отсутствующий в полуклассическом уравнении,
отвечает за спонтанное излучение в моду лазерного поля. Видно, что если в началь-
начальный момент времени п = 0, то согласно полуклассическому уравнению поле остается
равным нулю и в последующие моменты времени. Наоборот, согласно квантовому
уравнению A1.1.29) поле может вырасти с нулевого значения благодаря члену si,
отвечающему за спонтанное излучение.
11.2. Статистика лазерных фотонов
Как показано в предыдущем разделе, вероятность pnn(t) = p(n) обнаружить
п фотонов в лазерном поле изменяется со временем вследствие усиления за счет
вынужденного излучения и потерь резонатора. В данном разделе будут рассмот-
рассмотрены стационарные решения уравнения движения A1.1.15) для рпп и определена
статистика числа фотонов в стационарном режиме.
274 Квантовая теория лазера — метод оператора плотности Гл. 11
Перед тем как обсуждать общее решение уравнения A1.1.15), рассмотрим два
предельных случая работы лазера.
11.2.1. Линейное приближение (8ё = 0). Уравнение движения A1.1.15) для
функции распределения фотонов р(п) в стационарном состоянии (р(п) = 0) сводится
к следующему:
-st{n + 1)р(п) + ^пр(п - 1) - ^пр(п) + &(п + 1)р(п + 1) = 0. A1.2.1)
Из условия детального равновесия следует, что дифференциальное уравнение вто-
второго порядка A1.2.1) сводится к эквивалентной системе двух дифференциальных
уравнений первого порядка:
?/пр(п - 1) - ^пр(п) = 0, A1.2.2)
st(n + l)p(n) ~~ tf{n + 1)р(п + 1) = 0. A1.2.3)
Решение этих уравнений имеет вид
A1.2.4)
Константа р@) определяется из условия нормировки:
оо
^р(п) = 1. A1.2.5)
Когда «g/ < ^, получаем
р@) = (l - f) , (И-2.6)
так что
Поскольку в линейном приближении решение для р(п) не существует при ^ ^ ^,
условие «й^ = ^ мож:но рассматривать как пороговое. Следовательно, ниже порога
генерации, стационарное решение есть, в сущности, решение для излучения черного
тела:
где эффективная температура Т задается соотношением
ехр(--
11.2.2. Лазер, работающий существенно выше порога («g/ >» ^). В этом случае
насыщение настолько сильное, что ^Ш{п) /'&& ^ 1. Тогда в знаменателях из правой
части уравнения A1.1.15) молено пренебречь единицей по сравнению с величиной
Зёп/я/. Результирующее стационарное уравнение для р(п) имеет вид
~р(п) + ^р(п - 1) - tfnp(n) + tf{n + l)p(n + 1) = 0. A1.2.10)
Это уравнение опять решается с привлечением условия детального равновесия, ко-
которое означает, что
^р(п - 1) - <ifnp(n) = 0. A1.2.11)
11.2
Статистика лазерных фотонов
275
Нормированное решение этих уравнений имеет вид
где
(п) = |?.
A1.2.12)
A1.2.13)
Таким образом, статистика фотонов лазера, работающего существенно выше порога,
задается распределением Пуассона, характеризующим когерентное состояние поля.
11.2.3. Точное решение. Рассмотрев два предельных случая, дадим общее ста™
ционарное решение уравнения A1.1.15). Из условия детального равновесия следует,
что
^ = 0. A1.2.14)
Решение этого уравнения, очевидно, имеет вид
k=i
где р@) определяется из условия нормировки
ется произведением п сомножителей вида (
+
= 1. Величина р(п) явля-
являг. В случае, когда
каждый из этих сомножителей больше единицы, тогда как при к > пр эти сомно-
сомножители меньше единицы. Следовательно с увеличением п величина р(п) растет
пока п ^ Пр, а затем монотонно убывает до нуля при п > пр. Таким образом,
распределение достигает максимума при
Выражение A1.2.15) можно записать в более удобной форме:
A1.2.18)
Нормировочный множитель р@) выражается через вырожденные гипергеометриче-
гипергеометрические функции:
р@) =
)!
-1
На рис. 11.3 приведено распределение фотонов р(п) A1.2.18) для лазера, работаю-
щего с 20%-ным превышением порога.
276
Квантовая теория лазера — метод оператора плотности
Гл. 11
0.035
0.03
0.025
0.02
0.015
0.01
0.005
0
\ \
\ \
\
О 50 100 150 200 250 300 350 400
п
Рис. 11.3. Функция распределения фотонов в стационарном состоянии для когерентного
(точки) и лазерного (сплошная линия) излучения. Лазер работает с 20%-ным превышением
порога, а параметр & выбран так, чтобы (п) = 200
Вычисляя среднее значение п, находим
)
Для лазера, работающего существенно выше порога, последний член в A1.2.20),
очевидно, не существенен, ибо р@) <С 1. Тогда
= пр. A1.2.21)
Аналогичное вычисление для (пJ дает
A1.2.22)
Выше порога генерации величина (п) задается формулой A1.2.21). Нормированная
дисперсия распределения фотонов описывается так называемым параметром Ман-
деля Q. В случае лазера этот параметр принимает вид
(п2) - (nf
(п)
- 1 =
A1.2.23)
11.4 Естественная ширина 277
Поскольку Qf > 0 выше порога {srf > ff), поле является суперпуассоновским. Однако
существенно выше порога («й^ ^> сё?) величина Q f стремится к нулю, что соответству-
соответствует пуассоновскому распределению и согласуется с предшествующим анализом.
11.3. Лазер в Р-представлении
В гл. 3 было показано, что Р-распределение устанавливает соответствие меж-
между классической и квантовой теориями когерентности. Поэтому интересно найти
Р-распределение для лазера, исходя из которого довольно просто вычисляются
все нормально упорядоченные корреляционные функции операторов поля. Однако
существуют и другие преимущества использования Р-представления. Как будет
показано в следующем разделе, вычисление естественной ширины лазерной линии
сильно облегчается при использовании уравнения движения для Р-распределения.
Эта задача является довольно сложной в рамках метода оператора плотности. Кроме
того, Р-представление помогает установить соответствие между методом оператора
плотности, рассмотренным в разд. 11.1 и методом уравнения Ланжевена, который
будет рассматриваться в следующей главе.
Как показано в приложении 11.Б, уравнение движения для Р(о, a*, t) записыва-
записывается в виде
dt 2 \гдгГ 2гдгГдг 2r2
16 tf*d
Здесь совершен переход от независимых комплексных переменных а, а* к полярным
координатам г, #, с использованием соотношения
а = ге^. A1.3.2)
Это уравнение содержит производные всех порядков по г и $.
Вблизи порога стационарное решение уравнения A1.3.1), как показано в прило-
приложении 11.Б, имеет вид
а
\а\ \ , A1.3.3)
где JV1 — нормировочная константа.
11.4. Естественная ширина
До сих пор рассматривались статистические характеристики лазерного поля,
связанные с диагональными матричными элементами рпп приведенного оператора
плотности поля. Квантовые флуктуации, ответственные за флуктуации числа фото-
фотонов поля, отвечают и за фазовые флуктуации, приводя к конечной ширине линии
излучения лазера.
Детальный вывод выражения для естественной ширины линии должен включать
вычисление двухвременнбй корреляционной функции (E('(t)E^'(t + г)) поля.
Согласно выражению D.3.14) преобразование Фурье этой двухвременнбй корреля-
корреляционной функции дает спектр поля и, следовательно, ширину линии. Это довольно
тяжелый процесс, поскольку для него требуется нестационарное решение уравнения
A1.1.14) для недиагональных матричных элементов рпп/ или уравнения A1.3.1)
для соответствующего Р-распределения. Здесь мы воспользуемся простым методом,
278
Квантовая теория лазера — метод оператора плотности
Гл. 11
дающим желаемый результат при вычислении коэффициента фазовой диффузии
в уравнении Фоккера^Планка для Р-распределения. Однако сначала, для обоснова-
обоснования этого подхода, рассмотрим модель уширения линии излучения лазера за счет
фазовой диффузии.
11.4.1. Модель фазовой диффузии. Для того чтобы рассматривать фазовые
флуктуации лазерного поля, представим напряженность электрического поля в виде
комплексного вектора (рис. 11.4), испытывающего малые изменения фазы вследствие
Ima
••'•Г
•••••• •
* • • •
* • *
* • * * m
• •
•'•••:$
/ * y.
• * •
• * • * • •*'
у.
•
•
•
* •«
1
'.;. •
vV«
Re a
Рис. 11.4. Представление напряженности электромагнитного поля на комплексной плоско-
плоскости. Фаза диффундирует вследствие спонтанного излучения
актов спонтанного излучения. Поскольку эти малые изменения носят абсолютно
случайный характер, фаза постепенно диффундирует и становится распределенной
равномерно по углу 2тг. Предположим, что малое изменение фазы из-за одного акта
спонтанного испускания происходит за время, намного меньшее времени, в течение
которого происходит общая эволюция поля.
Рассмотрим ситуацию, когда лазер работает существенно выше порога, так что
амплитудными флуктуациями можно пренебречь. В этом случае поле E^(t) можно
записать в виде
Е^ (t) = \/{п) explicit) — ii^o^L A1.4.1)
где (п) — среднее число фотонов частоты щ в стационарном состоянии поля. Ско-
Скорость спонтанного излучения равна &/. Вследствие случайных актов спонтанного
испускания, вектор электрического поля (фазор) совершает случайные блуждания.
Пренебрегая амплитудными флуктуациями, получаем одномерное случайное блуж-
блуждание по угловой координате. Согласно теории случайного блуждания, вероятность
перемещения на расстояние I за g/t шагов равна
¦- ехр
A1.4.2)
11.4 Естественная ширина 279
Выражая ее через угловое смещение #, получаем
где использовано I = у/\ть) $ (см. рис. 11.4). Легко показать, что Р(#) удовлетворяет
уравнению фазовой диффузии
ЯР Я2 р
Ч- = O^-V, A1.4.4)
где
D^-f-,. A1.4.5)
Цп) v f
Таким образом, простая модель, в которой акты спонтанного излучения вызывают
случайное блуждание конца вектора электрического поля (фазора), приводит к урав-
уравнению фазовой диффузии для Р(#).
Теперь рассмотрим корреляционную функцию второго порядка (E('(t)E^)(t +
+ г)). Предположим, что поле является статистически стационарным и требуется
лишь определить величину (Е^@)Е^'(т)). Из рис. 11.4 видно, что
г)} = (?(->@)?(+)(т)) = (п) е-™от(е1*). A1.4.6)
Из выражения A1.4.3) следует, что
<cos0)= \p{d)e^dd = e-DT, A1.4.7)
так что
(#(-)(*)#(+)(* + т)) = (п) eTilJQT^DT. A1A8)
Тогда спектр мощности получается путем фурье-преобразования корреляционной
функции второго порядка (см. D.3.14)), т.е.
+ г)) е- dr = ^(|/_^а + да- (П.4.9)
Это есть распределение Лоренца, центрированное на частоте и = щ и имеющее
полуширину (ширину на половине высоты)
2D = Wr AL4-10)
как показано на рис. 11.5.
Этот простой вывод выражения для ширины лазерной линии, основанный на
модели фазовой диффузии, показывает, что коэффициент диффузии в уравнении
для распределения вероятности определяет ширину линии. В следующем разделе мы
воспользуемся этим результатом при выводе выражения для ширины линии лазера,
исходя из уравнения Фоккера—Планка, полученного в предыдущем разделе.
Рассмотренная выше модель фазовой диффузии дает обоснование чрезвычай™
но простому подходу ко многим интересующим проблемам. Поле E(t) с конечной
шириной линии 2D можно описать выражением A1.4.1), в котором предполагается,
что $(?) является случайной гауссовой фазой, совершающей броуновское движение,
описываемое так называемым стохастическим процессом Винера^Леви:
= о, <0(*Ж*')> = ?>(< + *'-!*-«'!)• (пап)
280
Квантовая теория лазера — метод оператора плотности
Гл. 11
-4-3-2-10 1 2 3 4
Рис. 11.5. Нормированный спектр S(y)/Я(щ), задаваемый выражением A1.4.9)
Производная от этого процесса представляет собой белый шум:
ee = 2D S(i - i').
A1.4.12)
Тогда из теоремы моментов для гауссова распределения следует, что
— (и у р
— IVQT I —\
-Dr
= (п) e-i»or(e
Полученный результат совпадает с A1.4.8). Эта модель лоренцевой формы линии
будет использоваться в гл. 16 при исследовании влияния ширины линии поля накачки
на процесс параметрического усиления.
11.4.2. Уравнение Фоккера^Планка и ширина линии излучения лазера. Рассмот-
Рассмотрев классический подход к изучению ширины линии излучения лазера, вернемся
к полностью квантово-механическим уравнениям движения, выведенным в преды-
предыдущих разделах. Как уже обсуждалось в гл. 4, квантово-классическое соответствие
в квантовой оптике осуществляется через Р-представление. Разумно, поэтому, отож-
отождествить коэффициент диффузии с шириной линии, если уравнение движения для
Р-распределения лазера можно свести к A1.4.4).
Как и прежде предположим, что в области существенно выше порога изменения
величины Р(ск, а*) вдоль радиальной (амплитудной) координаты г ограничены усло-
условием стационарной работы. Этими изменениями, следовательно, можно пренебречь
по сравнению с изменениями вдоль координаты #, и уравнение A1.3.1) принимает
вид
dt ~
д2Р
где
2D =
A1.4.14)
A1.4.15)
11.5 Недиагональные элементы и ширина линии излучения лазера 281
При выводе этого уравнения величину г2 заменили величиной (п) и предположили
(п) ^> 1 >> 381?0. Из выражения для (п) A1.2.21) следует, что
A1.4.16)
""- Цп) '
Вблизи порога, когда ?/ ~ J3,
Это выражение для коэффициента диффузии, а следовательно и для ширины линии,
идентично выражению, полученному в ходе эвристических рассуждений, основанных
на модели фазовой диффузии.
Интересно отметить, что выражение A1.4.17) для лазерной ширины линии вблизи
порога можно вывести из лазерного уравнения движения в линейном приближении
[ЗВ = 0, см. A1.4.15)). Кроме того, член потерь, пропорциональный ^, не входит
прямо в коэффициент диффузии. Следовательно, для работы вблизи порога (но
с достаточным превышением его, так чтобы изменения величины Р вдоль радиальной
координаты ограничивались ее стационарным значением) ширину линии лазера
просто можно получить в линейном приближении без члена потерь (до тех пор пока
потери резонатора описываются взаимодействием с тепловым резервуаром при ну-
нулевой температуре). Среднее число фотонов (п), однако, зависит от коэффициентов
насыщения и потерь. Это упрощение будет использовано при вычислении ширины
линии излучения лазера в более сложных лазерных системах, таких как в гл. 14.
11.5. Неджагональные элементы ж ширина линии излучения лазера
Как обсуждалось ранее, строгий вывод выражения для ширины линии излу-
излучения лазера требует вычисления двухвременной корреляционной функции поля
(E('(t)E^'(t + г)). Из-за очевидной сложности вычисления этой функции мы
последовали в предыдущем разделе простому подходу, основанному на модели фа-
фазовой диффузии. Здесь будет описан альтернативный подход к вычислению ширины
линии излучения лазера, основанный на вычислении недиагональных элементов
приведенной матрицы плотности поля.
Напомним (разд. 10.4), что в марковском приближении (которое справедливо
для решения рассматриваемой задачи) справедлива квантовая теорема регрессии,
то есть зависимость двухвременной корреляционной функции от времени идентична
зависимости среднего значения поля (E~(t)} от времени. Таким образом, определе-
определение (E~(t)} дало бы значение лазерной ширины линии. Теперь учтем, что величина
(E~(t)} связана с недиагональным матричным элементом приведенного оператора
плотности поля выражением
п=0
Следовательно, затухание недиагонального матричного элемента pn,n+i(?) означает
одновременное затухание поля, приводящее к уширению линии излучения. В этом
разделе будет описан простой метод вычисления /0n,n+i(?) И вновь получены резуль-
результаты, касающиеся ширины линии излучения лазера.
282 Квантовая теория лазера — метод оператора плотности Гл. 11
Будем исходить из уравнения движения A1.1.14) для матрицы плотности
— (к)
Рп,п+к = Рп •
•(к) = _ ( Ж,п+к^ \ (к) , Г у/п(п + к)я/ 1 (к)
) РП l 1^1
2 п
Перепишем его, добавляя и вычитая соответствующие члены:
•(к) = _ ( Ж,п+к^ \ (к) , Г у/п(п + к)я/ 1 (к)
<^гп — 1,п-\-к
- у у- ¦ ~,у- ¦ ~ ¦ ~,~ | (Л) _ Vl^ + 1ДП-ЦС + lj^ | n{k)_
[ 1 + ^,n+fc^/=c/ j [ 1 + сЛ^п-
1
9f [^77 -I- 1 V« -4- J^ 4-
— 2^n P™ Cn-lPn-l icn
где
A1.5.5)
Здесь безразмерные множители jYnn> и J^^ni задаются выражениями A1.1.13а)
и A1.1.136). Уравнение движения для рп A1.5.2) связывает рп лишь с ближай-
(к) (к) ,
шими соседними элементами, а именно рп+-± и р^_1? но не вносит связи по ^-индексу.
Таким образом, перед нами трехчленное дифференциальное рекуррентное соотноше-
соотношение между сложными, но не зависящими от времени коэффициентами. Далее будет
описан приближенный, но аналитический метод вывода нижайшего собственного
значения, исходя из условия детального равновесия.
Условие детального равновесия имеет вид сп рп = ^n-i-iPn-i-i (и' следовательно,
условие c^j.j/o^j.j = dn р„, ) и предполагает, что
п (к)
Ц
Ро Ц^у ро 11 х + л +к_1
j=l 3 j=l
Таким образом, из A1.5.2) следует, что
D^) j (fc) | [D<Vitf>]} (Ц.5.7)
11.6 Поведение лазера вблизи порога и фазовый переход второго рода 283
До сих пор вычисление носило точный характер. Теперь разложим экспоненты и в
низшем порядке найдем
Здесь мы предположили, что
l^n - ^n-ll = 9l^^ ~ ^п-1 ^ = о ^^^ ^ ^ -1' A1.5.9)
^ 1
2
at
аналогичное выражение имеем для |-/}„_)_j — Dn |. Это условие выполняется, когда
/Лп является медленно меняющейся функцией от п. Тогда из выражений A1.5.6)
и A1.5.8) следует, что
A1.5.10)
у / р числа
(п). Соотношение A1.5.10) сводит выражение A1.5.1) к следующему:
где на последнем шаге величину пв/ii^ заменили средним значением числа фотонов
A1.5.11)
Учитывая A1.5.3), получаем для ширины линии 2D лазера в пределе (п) ^> 1
выражение
2D - »(п) - I [-Щ- - {п)A + {п)^/^)\ ¦ (П.5.12)
Вторым членом в A1.5.12) можно пренебречь по сравнению с первым при всех
значениях 3§(п) /??. Таким образом, получаем
в полном согласии с A1.4.16).
11.6. Аналогия между поведением лазера вблизи порога и фазовым
переходом второго рода
В этом разделе мы рассмотрим возможность полезных аналогий между теорией
лазера и другими разделами неравновесной статистической механики. Фактически
интересное сравнение можно сделать между фазовыми переходами второго рода
в ферромагнетиках и полупроводниках и лазером, работающим вблизи порога ге-
генерации. Целью данного раздела является демонстрация того, что поведение лазера
вблизи порога аналогично фазовому переходу второго рода.
Аналогия становится очевидной, если вспомнить, что обычное рассмотрение
лазера проводится в рамках самосогласованной теории поля. При анализе пред-
предполагается, что каждый атом образует излучающий диполь в электромагнитном
поле, создаваемом всеми другими атомами. Поле излучения, создаваемое множе-
множеством излучающих атомов, вычисляется тогда самосогласованным образом. В этом
отношении физика лазера схожа с физикой ферромагнетика, в котором каждый
спин «чувствует» среднее магнитное поле, создаваемое всеми остальными спинами,
и выстраивается вдоль него, давая таким образом вклад в среднее магнитное по-
поле. Формальное сходство между макроскопическими уравнениями, описывающими
284 Квантовая теория лазера — метод оператора плотности Гл. 11
свойства лазера, и уравнениями, описывающими ферромагнетик, является пора-
поразительным и предполагает отождествление лазерного поля с параметром порядка
в ферромагнетике, а атомной инверсии населенностей — с температурой. Следуя
этой точки зрения, покажем, что теория лазера может быть рассмотрена на языке
фазовых переходов второго рода.
Стационарное решение для Р-распределения Р(а, а*) задается выражением
A1.3.3). Среднее значение (Е) безразмерного оператора электрического поля Е =
= (а + а*)/2, соответственно, удовлетворяет уравнению
{я/ ~~ Ъ){Е) ~~ М(Е3) = 0. A1.6.1)
Если лазер работает не слишком близко к порогу, то (Е3) можно заменить в полу-
полуклассическом пределе величиной (i^K, так что
= 0. A1.6.2)
Пороговое условие определяется в разд. 11.2 как я/ = *€. Полагая «я^ = аа^ ^8 =
= бег и *$ = acrti запишем стационарное решение уравнения A1.6.2) в виде
{0, если а — at ^. 0 (ниже порога),
— ( 1 , если а — at > 0 (выше порога).
Теперь рассмотрим теорию молекулярного поля в ферромагнетике. Пусть система
содержит N магнитных атомов в единице объема, и каждый атом имеет магнитный
момент /л. Средняя намагниченность (М) является функцией температуры Т систе-
системы и внешнего магнитного поля Н.
В случае невзаимодействующих спинов (М) задается выражением
(|), A1.6.4)
где А;в — постоянная Больцмана. Случай взаимодействующих спинов, естественно,
намного сложнее, и точного решения для трехмерной системы не существует. Про-
Простейшее приближенное решение было получено Вейссом, в рамках теории, обычно
называемой теорией молекулярного поля. В этой модели эффект взаимодействия
спинов учитывается просто добавлением к внешнему полю внутреннего поля If, ко-
которое вычисляется самосогласованно и пропорционально величине (М) с константой
пропорциональности Л. Уравнение состояния ферромагнетика можно вывести из
A1.6.4), подставляя вместо Н сумму Н + ХМ и разлагая в ряд по степеням (М).
В результате имеем
, A1.6.5)
I fb?5 ± U \ 1ЬЦ J- / I
откуда
Я = af(T - TC){M) + SN^T2(H + MM)f = a\T - TC)(M) + ЪГТ(М)\ A1.6.6)
где
а = «, 1С = —: , о = о—т. A1.6.7)
Здесь сделана подстановка Н = а1 (Т — ТС)(М) в кубическом члене из первой строки
выражения A1.6.6).
11.6 Поведение лазера вблизи порога и фазовый переход второго рода 285
Из A1.6.6) получаем следующее соотношение между М и Т при Н = 0:
{0,если Т - Тс ^ 0,
га'?/Т ^Т\11/2 A1.6.
Выражения A1.6.3) для лазера и A1.6.8) для ферромагнетика формально одинаковы.
Огибающая электрического поля Е соответствует статической намагниченности М,
являющейся параметром порядка для ферромагнитного перехода. Инверсия насе-
ленностей а, если не учитывать изменение знака, соответствует температуре Т.
Чтобы установить полную аналогию, необходимо расширить теорию лазера,
включив в нее внешнее поле. Напомним, что равновесное среднее по ансамблю
значение намагниченности может быть равно нулю только в присутствии внешнего
магнитного поля с определенной ориентацией. Аналогичная ситуация с лазером про-
происходит при введении внешнего классического поля в лазерный резонатор. Это при-
приводит к добавочной поляризации J? exp(—ivt) активной среды. Амплитуда У есть
не зависящая от времени действительная величина, определяющая интенсивность
внешнего поля. Предполагается также, что внешнее поле имеет то же направление
поляризации, что и лазерная мода.
Квантовую теорию лазера можно расширить, включив в нее внешнее поле. Ста-
Стационарное решение для Р-распределения в присутствии внешнего поля находится
в виде
Р(а, а ) ~ ^р ехр [{ ^ ) Н ~ ^Н + ~^~(а + а )\ > A1.6.9)
где c/Vf — нормирующий множитель. При 5? = 0 это решение сводится к A1.3.3).
Данное выражение для Р(а, а*) можно переписать через эффективную свободную
энергию G в виде
Р(х, у) = ±г ехр [-^^] , (П.6.10)
где х = (а + а*)/2 и у = (а — а*)/2г — декартовы координаты,
G(x, у) = \а{а - at)(x2 + у2) + \Ъа(х2 + у2J -Ух + в0 A1.6.11)
и К = а/4 — четверть коэффициента усиления для одного атома. Здесь отметим,
что я/ -& = а(а - at), и в$ = Ьа.
Рассмотрим теперь соответствующее выражение для плотности вероятности
Р(М) намагниченности М ферромагнитной системы вблизи фазового перехода.
В состоянии теплового равновесия эта плотность определяется выражением
[^], A1.6.12)
где
F(M) = ^af(T - ТС)М2 + Ъ)'ТМ'Л - НМ + Fo, A1.6.13)
причем Fo зависит от Т и Н. Сходство выражений A1.6.2) для Р(М) и A1.6.10) для
Р(х^у) очевидно, и означает, что функцию G{x^y) можно интерпретировать как
функцию типа термодинамической энергии. То, что распределение вероятности для
лазерного поля A1.6.10) и соответствующий термодинамический результат A1.6.12)
находятся в таком близком соответствии, является сильным доводом в пользу ана-
аналогии между областью лазерного порога генерации и фазовым переходом второго
рода.
286
Квантовая теория лазера — метод оператора плотности
Гл. 11
Близкая аналогия между поведением лазера вблизи порога генерации и фазовым
переходом второго рода ясно показывает, что кооперативное явление может раз™
виваться даже в условиях, далеких от теплового равновесия. Другими примерами
являются мягкие моды в сегнетоэлектрике, химические реакции и турбулентность.
Использование этих идей привело к новым открытиям в фундаментальной и при-
прикладной науке, от лазеров до компьютеров, и далее в социологии. Понятие переходов
типа порядок—беспорядок, происходящих в условиях далеких от состояния теплового
равновесия, привело ко многим интересным нововведениям. Мы завершим главу
несколькими примерами.
В лазерной физике нарушение симметрии посредством внешнего поля наводит на
мысль о том, что массив из N маломощных лазеров с синхронизированными фазами
может служить средством достижения высокой фокальной мощности (растущей
как iV2), за счет преодоления рандомизации Шавлова^Таунса. Отметим также, что
переход типа порядок—беспорядок, встречающийся в явлении оптической бистабиль-
ности, тесно связан с поведением лазера вблизи порога в присутствии внешнего
поля. Более того, переход к хаосу через многократные бифуркации является есте-
естественным расширением аналогии с лазерным фазовым переходом. Наконец, отметим
недавнее красивое исследование по гидродинамике, проведенное путем изучения
схожего поведения поперечной модовой структуры лазера. Аналогия между вынуж-
вынуждаемыми параметрическими системами и динамикой мягких мод в сегнетоэлектрике
привела Ландауэра к новым идеям в информатике. Подобным образом переходы
типа порядок—беспорядок, происходящие в химических реакциях и даже изучаемые
в социологии, плодотворно исследованы с позиций физики фазовых переходов, про-
происходящих в условиях, далеких от термодинамического равновесия.
Приложение 11. А
Решение уравнений для элементов матрицы плотности
Решение системы уравнений A1.1.9) и A1.1.56)—A1.1.5г) облегчается, если пере-
переписать ее в матричном виде:
Д=-МД + Л, A1.А.1)
где
R =
РЬп+1,ап'
М =
7 -ig^n1 + 1
—ig^n1 + 1 7
ig^s/n + 1 О
О ig\Jn + 1
>n
+ 1
0
7
-igy/rPTT
in'
T
0
0
0
0
ig\/n + 1
—ig^Jn1 + 1
7
A1.А.2)
A1.А.З)
A1.А.4)
П. 11.Б Точное решение для Р-распределения лазера 287
Формальное интегрирование уравнения A1.АЛ) дает
R(t)=
Здесь мы сделали адиабатическое приближение, предположив, что поле заметно
не меняется в течение времен жизни атомных состояний. Это позволяет рассматри-
рассматривать А в A1.А.5) как не зависящую от времени величину. Поскольку нас интересуют
матричные элементы pan,bn'+i ш Pbn+i,anfi требуется определить лишь (M^1Ji
и (М™1)з1- Результирующие выражения для требуемых матричных элементов имеют
вид
%Гё- п) + 12]рппЧ (И.А.6)
Pbn+l,an> = ГаР^М-1)^ = "^^^"^(П - П*) + *у2]Рпп>, (П.А.7)
где
\М\ = det М = 74 + %g2l2(n + 1 + п; + 1) + g-4(n - n'J- A1.A.8)
Матричные элементы рап—1,Ъп' и Pbn,anf — i получаются из A1.А.6) и A1.А.7), соот-
соответственно, путем замены величин п, п1 величинами п — 1, п' — 1.
Приложение 11. Б
Точное решение для Р-раепределения лазера
Рассмотрим основное уравнение A1.1.14) для матричных элементов. Если опре-
определить вспомогательную величину
/inn' = (l + ^nn) РппЧ A1.Б.1)
то уравнение A1.1.14) будет равносильно следующей системе уравнений:
+ 2^(п + 1 + п' + 1) + j^(n - nff /w = pnn>.
В Р-представлении матричный элемент рпп' задается в виде
Pnn.{t)= [^аР(а,а',<)е-'а1ааДаД- (П-Б.4)
J vnlvn'!
Определим другую вспомогательную функцию М(а, «*), соответствующую /хпп',
Используя эти соотношения, уравнения A1.Б.2) и A1.Б.3) можно преобразовать
в эквивалентную систему уравнений для Р ш М.
288
Квантовая теория лазера — метод оператора плотности
Гл. 11
Различные члены в A1.Б.2) и A1.Б.3) можно записать через Р ш М следующим
образом:
+ 1 + П + l)fJbnn' =
= Id2 a 1
J
да
an(a*)n' е^а^] М(а,а*) =
v ' J v }
- ПJ[1пп? =
= Id2a -1 ^ Г(«^-«*7^т
J \Jn\ Vfi7! L\ c^a <9a
J
n\ yn'l
д д
дада* ~а~да~
a
,a*)l, A1.
= d2ae^2af^a ^— \(-j-a-
Р(а,а*I . A1.Б.10)
Раскрывая члены в уравнениях A1.Б.2) и A1.Б.3) с помощью выражений A1.Б.6)™
A1.Б.8), после некоторых преобразований получаем
dt
д д
дада*
х М(а, а*) +
| (J-a + ^
(J
a
(а, а*),
Б1
Уравнения A1.Б.11) и A1.Б.12) принимают более удобный вид, если перейти от не™
зависимых комплексных переменных а, а* к полярным координатам г, #, используя
П. 11.Б Точное решение для Р-распределения лазера 289
соотношение
Тогда
д 1 д 2 1.0
4г2 V' ^г' ^г
В результате, уравнения A1.Б.11) и A1.Б.12) принимают вид
_ '102 I д д
dt 2 \^гс)г 2г дг дг
1 - —л \~^~г2 - 2A + г2)] - ^^т ДД М(г, #) = Р(г, 1?). A1.Б.17)
2i2f [Г ОГ J 16 .g/ 0>i9 J
Уравнение для Р можно получить, подставляя М из A1.Б.17) в уравнение A1.Б.16):
дР ^ fldo 1 д д 1 д2 0ё д
- 2A + г2)! - ^ЛГ ^ + - f 'IгЛ Р. (П.Б.18)
у Jl 1п^2д^2) 2 \гдг ) х }
\ г дг
Это уравнение содержит производные всех порядков по г и гд.
В стационарном состоянии (dP/dt = 0) Р-распределение является функцией
лишь от модуля а (то есть \а\ = г), поскольку все недиагональные элементы рпп>
равны нулю. Уравнения A1.Б.16) и A1.Б.17) сводятся к
-т (^ ^ - f 1-4)м+? (
2 \г дг 2г дг дг/ 2 \г
Если теперь ввести переменную интенсивности
1 = г2 = \а\2,
то уравнения A1.Б.19) и A1.Б.20) существенно упрощаются:
Эти уравнения решаются относительно М путем исключения Р. Результат имеет
вид
M(I) = I const' (Х " ^Jj exP(J)' если ^J ^ х' A1.Б.24)
I 0, в противном случае.
10 М.О. Скалли, М.С. Зубайри
290 Квантовая теория лазера — метод оператора плотности Гл. 11
Тогда Р-распределение находим из A1.Б.23):
если/^1 (Ц.Б.25)
=)^[1-^1) ехРG)' если-^-
Здесь сЖ — нормирующий множитель. Наличие в A1.Б.18) производных всех по-
порядков приводит к стационарному состоянию, которое описывается неаналитической
функцией от / = |а|2.
Р-распределение позволяет вычислить все нормально-упорядоченные моменты
оператора числа частиц а+а, исходя из первого:
((а+)тат) = | dIImP(I) = [|J - | - (m - 1)
+Г-2ат-2), m > 1. A1.Б.26)
Вблизи порога среднее значение интенсивности / = |о|2 мало, и справедливо неравен-
неравенство (Ш^/s^2)\a\2 «С 1. Множитель перед экспоненциальной функцией в A1.Б.25)
записывается приближенно в виде
где сделано приближение srf е2± *$ в |а|4-члене разложения экспоненты. Следователь-
Следовательно Р-распределение (выражение A1.Б.25)) имеет вид
где сЖ; — нормирующий множитель. Ограничение на / в A1.Б.25) теперь, очевидно,
можно убрать, ибо распределение A1.Б.28) никогда не перейдет в область отрица-
отрицательных значений, так что величину \а\ можно считать изменяющейся от 0 до оо.
Задачи
11.1. Рассмотрим одномодовый двухфотонный лазер, в котором атомы, находящиеся
в возбужденном состоянии |а), совершают переход через виртуальное состояние
в нижнее состояние |6), испуская два фотона частотой и. Предположим, что по-
потери на зеркале резонатора являются линейными. Исходя из эффективного га-
гамильтониана, записанного в представлении взаимодействия в условиях точного
резонанса (шаь = 2и) У = hg[a^a2 + (a~*~J<r_], выведите уравнение движения
для элементов pnni приведенной матрицы плотности поля. Покажите, что Qf =
= 1/2, если лазер работает высоко над порогом.
11.2. Рассмотрим лазер с насыщаемым поглотителем, то есть лазер, резонатор кото-
которого в дополнение к активной среде содержит поглощающую среду. Усиливаю-
Усиливающая среда состоит из двухуровневых атомов, характеризуемых состояниями
а) и |6), которые накачиваются в возбужденное состояние \а) со скоростью
rai. Поглотитель также состоит из двухуровневых атомов, характеризуемых
Список литературы к гл. 11 291
состояниями \с) и \d), но атомы накачиваются в нижнее состояние \d) со скоро-
скоростью га2. Предполагая точный резонанс для обоих типов атомов (ша5 = bJcd =
= и\ выведите уравнение движения для приведенной матрицы плотности поля.
Получите стационарное решение для функции распределения фотонов р(п), а
затем выражение для среднего числа фотонов (п). (Указание: см. работу Roy,
R. Phys. Rev. A 20, 2093 A979).)
11.3. Покажите, что в линейном режиме (Зё = 0) уравнение A1.1.14) для рпп>
эквивалентно следующему уравнению движения для приведенного оператора
плотности поля:
р = (аа^ р ~~ 2в+ра + раа^) (а^ар ~~ 2ара~*~ + ра^а).
А А
11.4. Выведите A1.2.22).
11.5. Выведите уравнение движения для рпп'^ описывающее одномодовый лазер
в условиях отсутствия резонанса между полем и атомами, то есть, когда А =
= ш - и ф 0.
11.6. Вычислите ширину линии излучения лазера, используя метод коэффициента
диффузии из разд. 11.4, в случае, когда потери резонатора описываются взаи-
взаимодействием с тепловым резервуаром, находящимся при температуре Т.
11.7. Выведите уравнение движения для диагональных элементов матрицы плотно-
плотности, используя метод усреднения по временам жизни. С этой целью выведите со-
соотношение A1.1.28), учитывая A1.1.27). Выполните интегрирование в A1.1.28),
предполагая п = п1'. Указание: начните с уравнения
о
и покажите, что
7
о
где Qn = gy/n. Это приведет к уравнению
dt
Список литературы
Теория лазера, метод оператора плотности
Scully, М. О., Lamb, W. E., Jr. and Stephen, M. J. Proceedings of the International Conference
on the Physics of Quantum Electronics, Puerto Rico, 1965, ed. P. Kelley, B. Lax, and P.
Tannanwald (New York, 1966), p. 75.
Fleck, J., Jr., Phys. Rev. 149, 309 A966).
Scully, M. O. and Lamb, W. E., Jr., Phys. Rev. 159, 208 A967); ibid. 179, 368 A969).
Pine, E. R. Riv. Nuovo Cimento, Numero Speclale 1, 277 A969).
10*
292 Список литературы к гл. 11
Scully, M. Proceedings of the International School of Physics «Enrico Fermi», Course XLII ed.
R. Glauber (Academic Press, New York 1969).
Sargent III, M., Scully, M. O. and Lamb, W. E., Jr., Appl. Opt 9, 2423 A970).
Scully, M. O., Kim, D. M. and Lamb, W. E., Jr., Phys. Rev. A 2, 2529 A970); ibid. 2, 2534
A970).
Wang, Y. R. and Lamb, W. E., Jr., Phys. Rev. A 8, 866 A973).
Stenholm, S. Phys. Rep. 6C, 1 A973).
Loudon, R. The Quantum Theory of Light, (Oxford University Press, New York 1973). [Лоудон
P. Квантовая теория света (Мир, Москва, 1976).]
Lugiato, L. A. Physics 81 А, 565 A976).
Pike, E. R. and Sarkar, S. Quantum Theory of Radiation, (Cambridge, London 1996).
*Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика (Физматлит,
Москва, 2000).
Теория лазера, метод Фоккера^Планка
RIsken, Н. Z. Phys. 191, 186 A965); In Progress in Optics, Vol. 8, ed. E. Wolf (North-Holland,
Amsterdam 1970).
Hemstead, R. D. and Lax, M. Phys. Rev. 161, 350 A967).
RIsken, H. and Vollmer, H. D. Z. Phys. 201, 323 A967).
Haken, H. Z. Phys. 219, 246 A969).
Grossmann, S. and RIchter, P. H. Z. Phys. 249, 43 A971).
Graham, R. and Smith, W. A. Opt Commun. 7, 289 A973).
Mandel, P. Physica (Utr.) 77, 174 A974).
Casagrande, F. and Lugiato, L. A. Phys. Rev. A 14, 778 A976).
Arecchi, F. T. and RIcca, A. M. Phys. Rev. A 15, 308 A977).
Tehrani, M. M. and Mandel, L. Phys. Rev. A 17, 677 A978); ibid. 17, 694 A978).
Аналогия между поведением лазера вблизи порога и фазовым
переходом и связанные с этим работы
DIGiorgio, V. and Scully, M. О. Phys. Rev. A 2, 1170 A970).
Graham, R. and Haken, H. Z. Phys. 237, 31 A970).
Landauer, R. IBM Journal of Res. and Dev. 14, 152 A970).
Landauer, R. F err о electrics 2, 47 A971).
Glandsdorff, P. and Prlgoglne, I. Thermodynamic Theory of Structure, Stability, and Fluctua-
Fluctuations, (Wiley, New York 1971).
Haken, H. Rev. Mod. Phys. 47, 67 A975).
Scott, J. F., Sargent III, M. and Cantrell, C. Opt Commun. 15, 13 A975).
Chow, W. W., Scully, M. O. and van Stryland, E. W. Opt Commun. 15, 6 A975).
Weidlich, W. Concepts and Models of a Quantitative Sociology: the Dynamics of Interacting
Population, (Springer, Berlin 1983).
*Yukalov V.I., Shumovsky A.S. Lectures on phase transitions (Wourd Scientific: Singapore,
1990).
Gatti, A. and Lugiato, L. A. Phys. Rev. A 52, 1675 A995).
Глава 12
КВАНТОВАЯ ТЕОРИЯ
ЛАЗЕРА — МЕТОД
ГЕЙЗЕНБЕРГА-ЛАНЖЕВЕНА
В этой главе будет представлена теория лазера, основанная на методе Гейзен-
берга-Ланжевена г). Это совершенно другой метод, но он полностью эквивалентен
методу оператора плотности, рассмотренному в предыдущей главе. В общем случае,
метод оператора плотности лучше подходит для изучения статистики фотонов поля
излучения, тогда как метод Гейзенберга—Ланжевена имеет определенные преимуще-
преимущества вычислительного характера при определении коэффициентов фазовой диффу-
диффузии и, следовательно, ширины линии излучения лазера.
В разд. 12.1 описан простой метод определения ширины линии излучения лазера,
основанный на линейной теории. Этот анализ интересен и полезен потому, в частно-
частности, что учитывает эффекты атомной памяти, что трудно сделать в рамках теории,
основанной на методе оператора плотности. В разд. 12.2—12.4 изложена полная не-
нелинейная теория лазера и заново получены все важные величины, характеризующие
квантовые статистические свойства поля излучения.
12.1. Простой расчет ширины линии излучения лазера методом
Ланжевена, учитывающий эффекты атомной памяти 2)
Полная нелинейная квантовая теория лазера, обсуждавшаяся в предыдущей
главе, рассматривает наиболее интересные квантовые статистические свойства поля
излучения. Однако, во многих практически значимых задачах нет необходимости
в таком детальном рассмотрении. Например, как было видно в предыдущей главе,
естественную ширину линии излучения лазера можно определить из линеаризован-
линеаризованной теории. То есть, полная нелинейная теория служит для определения амплитуды
поля, а фазовые флуктуации в области рабочей точки описываются линейной тео-
теорией. В этом разделе будет представлена простая линейная ланжевеновская теория
лазера, в которой атомное время жизни учитывается в эффективном гамильтониане.
Преимущество этого простого подхода состоит в том, что его можно легко расширить,
как будет показано ниже, с целью учета эффектов атомной памяти и вычисления
естественной ширины линии излучения других квантовых оптических систем.
) Оригинальное рассмотрение Лакса (Lax, 1966; 1968) изложено в методичной форме Лью-
селлом (Louisell, 1974). Особенно полезным является расчет ширины линии, выполненный
Хакеном (Haken, 1970). Отметим также книгу Sargent, Scully, and Lamb A974).
2) Раздел основан на работе Scully, Siissmann and Benkert A988).
294
Квантовая теория лазера — метод Гейзенберга-Ланэюевена
Гл. 12
Эффективный гамильтониан системы двухуровневых атомов, взаимодействую-
взаимодействующих с одномодовым полем в условиях точного резонанса, в представлении взаимо-
взаимодействия имеет вид
Ж = hg^2 ffatjKa+ai + а{а). A2.1.1)
з
Здесь введена функция f(t,tj), определяющая взаимодействие j-ro атома, переве-
переведенного в момент времени tj в верхнее состояние, с полем излучения. Для опреде-
определенности запишем f(t,tj) в виде
/(*, tj) = @(t - tj) exp[-7(* - tj)/V2], A2.1.2)
где Q(t) — обычная ступенчатая функция. Функция /(?, tj) изображена на рис. 12.1.
Здесь экспоненциальный множитель ехр[^7(^ ~ ^j)/v2] моделирует релаксацию
/(Mi)
Рис. 12.1. Функция взаимодействия f{t,tj), определяющая взаимодействие j-ro атома
и электромагнитного поля
атомов лазера. Таким образом атомная релаксация включена в эффективный га-
гамильтониан.
Уравнения движения Гейзенберга для операторов поля и атомных дипольных
моментов имеют вид
f(t,
сг- =igf{t,tj)<Tia.
A2.1.3)
A2.1.4)
Эффекты потерь резонатора учтены в уравнении A2.1.3) через скорость затухания
резонатора ^ и соответствующий ей оператор ланжевеновского шума F^. При
нулевой температуре (птепл = 0) все нормально упорядоченные корреляционные
функции величины F<g> равны нулю.
12.1 Простой расчет, учитывающий эффекты атомной памяти 295
Формальное интегрирование уравнения A2.1.4) дает
t
<xi =<rL(tj) + ig \dt'f(t',tj)<Ti(t')a(t'). A2.1.5)
Отметим, что определение функции f(tf,tj) позволяет устремить нижний предел
интегрирования в A2.1.5) к —оо. Подстановка этого выражения в A2.1.3) приводит
к результату
"Е-
з
dt'J^f(t,tj)f(t\tj)ai(t')a(t') + Fv(t) + Fa(t), A2.1.6)
где
Fa(t) = -ig^fi^t^alitj) A2.1.7)
з
— шум, возникающий в поле из-за взаимодействия с лазерными атомами.
Уравнение A2.1.6) для оператора поля а молено упростить, если предположить,
что линейный коэффициент усиления определяется, главным образом, мгновенным
значением поля излучения. Такое приближение имеет силу, если оператор элек-
электрического поля a(t) медленно меняется в течение атомного времени жизни 7-
Это условие удовлетворяется, если j >> сё). Тогда можно заменить оператор a(tf)
в интеграле A2.1.6) оператором a(i) и вынести его из-под знака интеграла. Кроме
того, ограничимся линейным приближением по оператору поля. В этом случае можно
аппроксимировать оператор разности населенностей (rz{tf) его средним значением
в начальный момент времени, (a3z(tj)) = 1. В результате получаем следующее
уравнение для оператора a(t):
2
в котором линейный коэффициент усиления ^ определен в виде
t
^ tj). A2.1.9)
Если предположить, что скорость инжекции атомов га является постоянной вели-
величиной, то можно заменить суммирование по атомам интегрированием по временам
инжекции, то есть
оо
г
dtj. A2.1.10)
Используя определение A2.1.2) функции взаимодействия f(t,tj) и вычисляя остав-
оставшиеся интегралы, получаем следующий линейный коэффициент усиления
^=J^pL^ A2.1.11)
7
который совпадает с линейным коэффициентом усиления, полученным ранее (см.
выражение A1.1.11)).
Теперь обратимся к вычислению корреляционной функции операторов шума
в уравнении A2.1.8). При нулевой температуре (птепл = 0) нормально упорядоченные
296 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
корреляционные функции операторов Fc^ равны нулю (формулы (9.1.24), (9.1.27)
и (9.1.28)). Таким образом, оператор шума F^ не дает вклада в ширину линии
излучения лазера. Это будет показано явно при строгом рассмотрении в следующих
разделах. Из A2.1.7) находим
O> = g2
Все атомы находятся в начальный момент времени в возбужденном состоянии \а)
и полностью независимы друг от друга. Таким образом,
(a{{tj)ak_{tk)) = 8jk. A2.1.13)
Если опять заменить суммирование по атомам интегрированием по моментам време-
времени инжекции, то получим
(F+(t)Fa(t>)) = ^^= exp (--^|i - t'|) . A2.1.14)
Интересно отметить, что шум не является ^-коррелированным. События спонтанного
испускания нельзя больше рассматривать как мгновенные импульсы. Вместо этого
событие спонтанного испускания размазано по характерному временному интервалу
7, в течение которого испускается фотон. Такие эффекты памяти, обусловленные
атомами, приводят к окрашенному шуму вместо белого шума.
В пределе j^1 —>> 0 вновь получаем белый шум:
(F+(t)Fa(t')) =?/6{t- f). A2.1.15)
Эта E-корреляция операторов шума является результатом предположения, что вре-
временная эволюция атома происходит намного быстрее эволюции поля излучения.
Аналогичным образом находим
(Fa(t)Fa(t')) = (F+(t)F+(t')) = 0. A2.1.16)
То, что обе корреляционные функции в A2.1.16) равны нулю, есть прямое следствие
начального состояния атомов и ограничения линейным приближением по полю.
Чтобы получить выражение для коэффициента фазовой диффузии электромаг-
электромагнитного поля отождествим операторное уравнение Ланжевена A2.1.8) с соответ-
соответствующим с-числовым уравнением. Это можно сделать заменив операторы а и Fa(t)
комплексными переменными а. и J^"a(t), соответственно. Результирующее уравнение
имеет вид
а = ^(я/ - &)а + &а. A2.1.17)
Если выбрать классическую функцию шума ^a(t) так, чтобы она имела корре-
корреляционные функции вида A2.1.15) и A2.1.16), то все произведения комплексных
переменных а будут соответствовать нормально упорядоченным произведениям опе-
операторов а.
Поскольку нас интересуют фазовые флуктуации лазерного поля, удобно работать
в полярных координатах г и #, определяемых соотношением а = г ехр(г$). Тогда из
A2.1.17) следует, что
•& = &<>{t), A2.1.18)
где
(^y A2.1.19)
12.2
Квантовые уравнения Ланэюевена
297
Если пренебречь амплитудными флуктуациями, то есть предположить, что \а\2 =
= (п), где (п) — стационарное среднее число фотонов в лазерном поле, то из
выражений A2.1.15) и A2.1.16) следует, что
> = ^*(*-*')- A2.1.20)
A2.1.21)
Сравнение с формулой A1.4.12) приводит к выражению
в согласии с результатами предыдущей главы 1).
12.2. Квантовые уравнения Ланжевена
В этом разделе будут выведены квантовые уравнения Гейзенберга—Ланжевена
для полевых и атомных переменных, с учетом всех нелинейных эффектов насы-
насыщения. Из полученной системы уравнений можно определить статистику фотонов
и ширину линии излучения лазера.
Рис. 12.2. Физическая модель лазера: атомы (изображенные в виде точек) проходят через
лазерный резонатор
На рис. 12.2 изображена физическая модель лазера. Множество трехуровневых
атомов взаимодействует с одной модой поля излучения внутри лазерного резонатора.
Атомы находятся в начальный момент времени в состоянии |а), и два верхних состоя-
состояния \а) и \Ь) являются рабочими. Нижнее атомное состояние |с), далекое от резонанса,
1) Дальнейшее обобщение результатов этого раздела, учитывающее эффекты памяти,
можно найти в работе Scully, Siissmann, and Benkert A988).
298 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
так что ооас,шьс ^> ^аб? является неактивным основным состоянием, в которое
атомы релаксируют со скоростью 7- Гамильтониан такой системы в представлении
взаимодействия и в приближении вращающейся волны имеет вид
<Ж = сЖАР + <У^игР + ^2F5 (lZ.Z.lj
где Жар — гамильтониан взаимодействия атомов с полем, а Жиг р и Жц2 а описывают
взаимодействие поля и атомной системы с резервуарами гармонических осциллято-
осцилляторов, имеющих наборы близких частот vq и vk и операторы уничтожения сч и 6к5
соответственно:
Жар = hg^2e(t - tj)(a^aJL +<т^_а), A2.2.2)
з
RlF = hJ2gi4LaexP[-i("-vq)t} + *-c; A2-2-3)
q
2)<сЬкехр[г(шас - vk)t] + g^'^сЬкехр[г(а;бс - икЩ} + ъ.с,
A2.2.4)
где Q(t) — единичная ступенчатая функция, а3^ = \b)jj(a\ и сг^ = \d)jj(b\ — повы-
повышающий и понижающий операторы, соответственно, для j-ro атома. Предположим,
A) B)
что константы взаимодействия g*, ^q и g^. являются действительными величинами,
и что
aim = \n)jj(m\ (п? rn = a,,b, с). A2.2.5)
Мы предположили, для простоты, что частота лазерного перехода \а) —> \Ь) равна
частоте поля, то есть шаь = v. Влияние всех атомов учитывается в гамильтониане
Жарч где ступенчатая функция отвечает тому факту, что j-й атом начинает взаи-
взаимодействовать с полем в момент инжекции tj. Такой подход немного отличается от
метода оператора плотности, где влияние большого числа атомов описывалось при
помощи матрицы населенности.
Уравнения движения Гейзенберга для различных атомных, полевых и резервуар-
ных переменных записываются в следующем виде:
а = -ig^Qit - tj)**. - iX^Cqe**"-"')*, A2.2.6)
3 Ч
*3L=ige(t-tj)(*ia-*ib)a +
"*)*, A2.2.7)
k
&ia = igQ(t - t^a+ai - a{a) -
- i Y, gPaieb e^«-"*)* + i E g^KoL e-^—)*, A2.2.8)
k k
k
+ iY^g^bt^b e-^-»^, A2.2.9)
A2.2.10)
-'(«-c-^)t]. A2.2.11)
12.2 Квантовые уравнения Ланэюевена 299
Формально интегрируя уравнения A2.2.10) и A2.2.11) и подставляя величины cq
и 6к в уравнения A2.2.6)-A2.2.9) (см. разд. 9.1), находим следующие квантовые
уравнения Ланжевена для полевых и атомных операторов:
а = -fa - ig^B(t - tj)ai + F<v(t), A2.2.12)
з
at = --rat + ig&(t - tj)(aia - a{b)a + F^t), A2.2.13)
(a+crJL - <r3+a) + F>aa{t), A2.2.14)
Hb = -1< - ig®(t - tj)(a+ai - aj+a) + F^t), A2.2.15)
где ^ — обычная скорость затухания резонатора И7- атомная скорость релаксации,
которая, для простоты, считается одинаковой для обоих возбужденных атомных
уровней. При выводе этих скоростей затухания было сделано обычное приближение
Вайскопфа-Вигнера (см. разд. 6.3).
Операторы F в правой части уравнений A2.2.12)—A2.2.15) есть ланжевеновские
операторы шума, появляющиеся вследствие взаимодействия с тепловым резервуаром
и имеющие вид
F*(t) = -г^41)сЧ(°)е'A/~^' A2.2.16)
A2.2.17)
FL(t) = шШ J2 *к }М0) e*^--^)* + э.с, A2.2.18)
к
^ь(*) = Чс(*)Е^к)Ьк@)е4^-"*)* + э.с. A2.2.19)
к
Операторы F<g имеют нормально упорядоченные корреляционные функции:
<*V(*)> = о,
- t'), A2.2.20)
Для простоты предположим, что тепловой резервуар находится при нулевой темпера™
туре, так что 7гтепл = 0. Интересующие нас ненулевые моменты атомных операторов
шума при нулевой температуре имеют вид
= a,b),
')
Следующим шагом будет переход от операторов, соответствующих отдельным
атомам, к операторам, описывающим макроскопические атомные характеристики.
Это окажется необходимым для приближенных методов, используемых далее в этом
300
Квантовая теория лазера — метод Гейзенберга-Ланэюевена
Гл. 12
разделе. Несмотря на то, что индивидуальные атомные операторы очень чувстви-
чувствительны к адиабатическому приближению, усредненные макроскопические величины
можно рассматривать таким способом. Пусть, следовательно,
M(t) = -i
A2.2.22)
A2.2.23)
A2.2.24)
Оператор М есть макроскопическая атомная поляризация. Множитель (—*)
в A2.2.22) введен для удобства вычислений. Операторы Na и N^ определяют число
атомов в двух возбужденных атомных состояниях \а) и \Ь) соответственно. С учетом
этих определений уравнение A2.2.12) для электромагнитного поля запишется в виде
а = -|о + gM
Fv(t).
A2.2.25)
Уравнения Ланжевена для атомных операторов можно найти, дифференцируя вы™
ражения A2.2.22)-A2.2.24) и подставляя соответствующие величины из A2.2.13)-
A2.2.15). Например, для оператора Na получаем
G(t -
J«(<i) - 7^a - g(a+M + M+a)
- tj)Faa1(t). A2.2.26)
Первый член в правой части A2.2.26) соответствует возбуждению атомов в процессе
накачки в верхнее состояние. Чтобы прояснить это, вычислим среднее значение
первого члена:
¦ A2-2-27)
Здесь учтено, что атомы находятся в начальный момент времени в верхнем возбуж-
возбужденном состоянии, так что {o~3aa{tj)) = 1. Индекс S при угловых скобках в A2.2.27)
означает, что необходимо еще усреднить по моментам времени инжекции, то есть
усреднить по флуктуациям накачки. Пусть средняя, не зависящая от времени, ско-
скорость инжекции равна га. Тогда результат усреднения запишем в виде
dtj8{t -tj) = ra.
A2.2.28)
Выражение A2.2.27) можно рассматривать как альтернативное для определения
усредненной скорости атомной инжекции га.
Чтобы отделить в A2.2.26) члены дрейфа от шумовых членов, добавим и вычтем
среднее значение первого члена и получим
a = ra- 1Na - g{a+M + M+a) + Fa(t),
A2.2.29)
12.2 Квантовые уравнения Ланэюевена 301
где
Fa(t) = ?e(t - WHait) + ?*(* - *>?«(*;) -r«- A2*2-30)
i i
Оператор ,Fa есть оператор полного шума для атомной величины Na. Он содержит
вклады атомной релаксации, индуцированной резервуаром, и флуктуации накачки.
Нетрудно проверить, что среднее значение оператора Fa(t) равно нулю для любых
моментов времени.
Подобным образом можно вывести уравнения для оставшихся атомных операто-
операторов:
Nh = ^jNb + g(a+M + М+а) + Fb(t), A2.2.31)
М = ^jM + g(Na - Nb)a + FM(t), A2.2.32)
где
!> i ]T (* - trfvibitj), A2.2.33)
S(-f - *i)ff-(*i)- A2.2.34)
i i
Отметим, что в выражениях A2.2.31) и A2.2.32) отсутствует член накачки, поскольку
предполагается, что атомы в начальный момент времени находятся в возбужденном
состоянии \а).
Корреляционные функции шума можно вычислить следующим образом:
(Fa{t)Fa{t')) =
s
A2.2.35)
Здесь статистическое среднее по временам инжекции, обозначаемое индексом 5,
отделено от квантово-механического среднего. Чтобы вычислить члены в A2.2.35)
отметим, что индивидуальные атомы абсолютно не зависят друг от друга. Поэтому
первое слагаемое в выражении A2.2.35) содержит вклады только членов с j = к.
Кроме того, среднее значение (o"oa(^j)°"aa(^fe)) в0 ВТОРОМ слагаемом факторизуется
для j ф к в виде (c»"ia(^j))(craa(^)} = 1 {{ааа[^з)) = 1 для всех атомов, первоначально
находящихся в возбужденном состоянии). Поэтому
-t'). A2.2.36)
302 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
На последнем шаге вывода были использованы определения A2.2.23) и A2.2.28)
операторов Na и га, соответственно, а также соотношения
*') = га *(*-*'), A2-2.37)
rl A2.2.38)
Аналогичным образом молено вычислить остальные ненулевые корреляционные
функции:
(Fb(t)Fb(tf)} = j(Nb) S(t - i'), A2.2.39a)
(Fb(t)FM(tf)) = j(M) 6{t - tf), A2.2.396)
(F+ (t)FM{t')) = D(Na) + ra) S(t - t'), A2.2.39b)
(Fa(t)FM(tf)} = 7(M+) S(t - tf). A2.2.39r)
Прежде чем решать уравнения A2.2.25), A2.2.29), A2.2.31) и A2.2.32) для четырех
макроскопических величин, преобразуем операторные уравнения Ланжевена в соот-
соответствующие с-числовые уравнения. Это упростит расчет.
12.3. Вывод с-чмеловых уравнений Ланжевена
Чтобы преобразовать операторные уравнения, необходимо определить некоторое
упорядочение операторов, которому будут соответствовать с-числовые уравнения.
Это необходимо, поскольку с-числа коммутируют друг с другом, а операторы нет.
Поэтому однозначное соответствие между операторными и с-числовыми уравне-
уравнениями Ланжевена можно получить, только если определить соответствие между
произведениями с-чисел и произведениями операторов. Здесь мы выберем нормаль-
нормальное упорядочение а+, М+, Naj Nb, M, аи выведем четыре с-числовых уравнения
Ланжевена для переменных а, Ж^ J/a и ^Жь, так чтобы уравнения для их пер-
первых и вторых моментов совпадали с операторными. Уравнения A2.2.25), A2.2.29),
A2.2.31) и B1.2.32) уже записаны в нужном порядке, так что сразу получаем
a = ~a + gj? + &v, A2.3.1)
JK = —1je + g(jVa-jVb)a + &jK, A2.3.2)
Ла = га - -у^а - g(a*^ + Jt*a) + &a, A2.3.3)
J-b = -1j^b + g(a*^ + ^*a) + ^b. A2.3.4)
Функции J2" в уравнениях A2.3.1)—A2.3.4) опять являются типичными ланжевенов-
скими флуктуационными силами, имеющими средние значения
(^k(t)) = 0, A2.3.5)
(^k(t)^i(t')) = BDkl) S(t - t'), A2.3.6)
где J^k и &i могут быть любыми из указанных выше. Коэффициенты диффузии
D^i определяются теперь исходя из требования, чтобы уравнения движения для
вторых моментов также совпадали с соответствующими операторными уравнениями.
Нетрудно показать, что коэффициенты диффузии для флуктуационной силы
12.3 Вывод с~числовых уравнений Ланэюевена 303
такие же, как и для нормально упорядоченного оператора шума i<V, так что
?><*?• ^ = 0, ZW = 0. A2.3.7)
Однако некоторые коэффициенты диффузии изменяются при переходе от опера-
операторного к с-числовому уравнению. Например, вычислим коэффициент Dj?j?. Из
операторного уравнения A2.2.32) получаем
^(M(t)M{t)) = ~27(ММ)+
+ g[((Na - Nb)Ma) + (M(Na - Nb)a)] + (MFM) + (FMM). A2.3.8)
Второй член в квадратных скобках не соответствует выбранному типу упорядочения,
поскольку оператор М находится слева от Na и А^,. Поэтому необходимо восполь-
воспользоваться коммутационным соотношением [М, Na — Nb] = 2М, чтобы привести этот
член к нужному порядку. Кроме того, последние два слагаемых обращаются в нуль,
так что получаем
ft(M(t)M(t)) = -27(ММ) + 2g({Na - Nb)Ma) + 2g(Ma). A2.3.9)
Воспользуемся теперь уравнением A2.3.2), чтобы получить соответствующее с-
числовое уравнение
j-t{JZ{t)Jt(t)) = -27(Ж40 + 2g{(rJ<a - jrb)jga) + BД^). A2.3.10)
Если потребовать, чтобы левые части уравнений A2.3.9) и A2.3.10) совпадали, то
коэффициент диффузии Djiji следует записать в виде
Оставшиеся ненулевые с-числовые коэффициенты диффузии вычисляются анало™
гично:
^Вж,ж = 7^ + га, A2.3.12а)
A2.3.126)
A2.3.12b)
2Daa = jj^a + Га _ g(a*jK + Л*6), A2.3.12г)
2Dbb = 1j?b - g{a*JH + Л*а), A2.3.12д)
2Dab = g{a*jK + Л*а). A2.3.12е)
Теперь можно решать уравнения Ланжевена A2.3.1)—A2.3.4). Обычно скорость атом-
атомной релаксации j существенно больше скорости затухания поля *€, так что эволюция
атомных переменных происходит намного быстрее, чем эволюция поля. В этом случае
можно адиабатически исключить атомные переменные Л, jVa и jVb и вывести
уравнение только для поля а. Для этого сначала в уравнении A2.3.2) положим
производную по времени равной нулю и получим адиабатическое значение атомной
поляризации
^?=-(Лг-Л)а+-^. A2.3.13)
304 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
Подстановка этого результата в уравнения для */#, jVa и J/^ дает
Z М? ^)« + «^ + ^>>, A2.3.14)
7
= Га - j^a - ^(Лг - Л)а*а - -(&*жа + а*&ж) + &а, A2.3.15)
J/b = ->yjrb + 1i-(^a- Л)а*а - -{&*жа + а&ж) + &ь. A2.3.16)
Теперь адиабатически исключим населенности jVa и ^, полагая их производные
по времени равными нулю. При этом уравнения A2.3.15) и A2.3.16) сводятся к си-
системе двух линейных уравнений и легко решаются. Результат имеет вид
A2.3.17)
A2.3.18)
7
где / — интенсивность \а\2 поля излучения, а шумовые функции ^а и % определя-
определяются выражениями
% = ^a (^\yga + a ^Ji)i A2.Л.19)
<^, 4Г, i <§" / ^-* ^, _|_ ^ * (Ж Л (л 9 о 9fi\
7
Подставим теперь выражения A2.3.17) и A2.3.18) в уравнение A2.3.14) и получим
уравнение движения для электромагнитного поля:
А^~|а+ / ^ х +^а, A2.3.21)
в котором флуктуационная сила ^а задается в виде
2
М + / (ХСЯ ч (а %) A2.3.22)
7 E
Параметры «й^ и ^ являются коэффициентами усиления и насыщения лазера, опре-
определенными ранее (см. выражения A1.1.11) и A1.1.12)). Флуктуационная сила ^а
характеризуется корреляционными функциями
(^a(t)) = 0, A2.3.23а)
f)) = BDa*a) 5(t - t;), A2.3.236)
tf)) = BDaa) S(t - tf). A2.3.23b)
12.4 Статистика фотонов и ширина линии излучения лазера 305
Коэффициенты диффузии Da*a и Daa определяют интенсивность шума и могут
быть вычислены исходя из определения ^а. Длинный, но простой расчет приводит
к результату (см. задачу 12.3)
2Daa = BDa.a.y = - ®а% C + §l) . A2.3.25)
Полученные результаты можно теперь использовать для анализа стационарного
режима работы и квантовых флуктуации лазера.
12.4. Статистика фотонов и ширина линии излучения лазера
Нас интересуют свойства интенсивности и фазы лазерного излучения. Перейдем
в полярную систему координат, используя определение
а = л/7ехр(г#). A2.4.1)
Дифференцируя по времени и сравнивая действительные и мнимые части с уравне-
уравнением A2.3.21), получаем следующие уравнения Ланжевена для переменных /иЛ
# = F*, A2.4.2)
/ = -Sf/ + —^ + ^, A2АЗ)
где
F# = Im (^) , A2.4.4)
F, = 21 Re (^) . A2.4.5)
В выражении A2.4.5) опущены индуцированные шумом дрейфовые члены, которые
намного меньше оставшихся величин. Коэффициенты диффузии для операторов
шума F$ и Fj имеют вид
«( ?) A2.4.6)
1 + —J
Прежде чем рассматривать статистику фотонов и естественную ширину линии излу-
излучения, отметим, что коэффициент диффузии D$$ совпадает с коэффициентом диф-
диффузии A1.4.15), если величину / заменить средним числом фотонов (п) в стационар-
стационарном состоянии. Далее в этом разделе будет установлено прямое соответствие между
методом оператора плотности (и соответствующим Р-распределением), обсуждав-
обсуждавшимся в предыдущих разделах, и рассматриваемым здесь методом Ланжевена.
Чтобы установить соответствие между величиной / и статистикой фотонов ла-
лазера, напомним, что при переходе от операторных уравнений A2.2.25), A2.2.29),
306 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
A2.2.31) и A2.2.32) к очисловым уравнениям A2.3.1)—A2.3.4) было выбрано нор-
нормальное упорядочение. Следовательно, интенсивность / соответствует нормально
упорядоченным произведениям полевых операторов. Среднее число фотонов (п)
и дисперсия числа фотонов определяются выражениями
(п) = (а+а) = (I), A2.4.8)
(ДпJ = (а+аа+а) - (а+аJ =
= (а+а+аа) + (а+а) - (а+аJ = (I2) + (I) - (IJ = (AIJ + (I). A2.4.9)
Из A2.4.3) следует, что в стационарном состоянии, когда (/) = 0, имеем
/-^LA=0, A2.4.10)
\1 + ^7/
где учтено, что (Fj(t)) = 0. Если предположить, что (/г) = (/)г, то
A2.4.11)
Для определения флуктуации величины / сначала линеаризуем уравнение
A2.4.3) около стационарного значения. Определяя А/ = / — /q и используя
выражение A2.4.11) для среднего числа фотонов в стационарном состоянии, находим
dt l + —(
= -ЪA0+А1) + ^ ; , 2 +^/ =
-7^0
^ F,. A2.4.12)
Следовательно,
|2 ^ 2 A2.4.13)
Корреляционную функцию (AI(t)Fj(t)) можно найти, используя методы, разрабо-
разработанные в разд. 9.1. Из формального решения уравнения A2.4.12) следует, что
= AI@)(Fr(t)) exp [~(* ~
dt'exp [-JK " Ш - *')] (^/(*')^(*)> = (Dn), A2.4.14)
где использованы соотношения (Fj(t)) = 0 и (F/(t/)F/(t)) = 2(?>//) S(t — t'). Таким
образом, стационарное решение уравнения A2.4.13) имеет вид
f^(Du). A2.4.15)
12.4 Статистика фотонов и ширина линии излучения лазера 307
Подставляя ((А/J} и (/) из A2.4.15) и A2.4.11) в формулу A2.4.9), получаем
(AnJ = ^ (п). A2.4.16)
Нормированная дисперсия распределения фотонов определяется параметром Ман-
деля Q для поля и равна
Выражения A2.4.11) и A2.4.17) совпадают с результатами A1.2.21) и A1.2.23), полу-
полученными в разд. 11.2 методом оператора плотности.
Теперь рассмотрим фазовую скорость диффузии, которая вычисляется с помо-
помощью уравнения A2.4.2). Интегрируя последнее, получаем
t
= \
dt'F#(t'), A2.4.18)
так что
Подставляя BD$$) из A2.4.6) в A2.4.19) и используя выражение A2.4.11) для
среднего числа фотонов в стационарном состоянии, находим, после интегрирования
по времени, что
(#2> = -!-г + ^r^-t. A2.4.20)
х ' Цп) Цп) у J
Постоянная интегрирования 1/4(п) в A2.4.20) обусловлена вкладом вакуумных
флуктуации и будет детально обсуждаться в разд. 14.5. Второй член в A2.4.20)
показывает, что фаза диффундирует линейно во времени, а скорость диффузии
(«й^ + ef )/4(п) определяет естественную ширину линии излучения лазера.
Связь между методом оператора плотности и методом Ланжевена можно устано-
установить через уравнение для функции распределения поля. В приложении 11.Б было вы-
выведено уравнение движения для Р-распределения (уравнения A1.Б.1) и A1.Б.2)), ко-
которое эквивалентно соответствующему уравнению для матрицы плотности A1.1.14)
лазерного поля. Теперь учтем, что если случайная комплексная переменная а удо-
удовлетворяет уравнению Ланжевена A2.3.21) с корреляционными функциями вида
A2.3.23а)-A2.3.23в), то, согласно теореме о стохастических процессах, распределение
вероятности Р(о, а*) удовлетворяет уравнению Фоккера^Планка:
dt 2 да _
A2.4.21)
Поскольку для перехода от операторных уравнений к с-числовым уравнениям было
выбрано нормальное упорядочение, следует ожидать, что Р(ск, о*) отвечает вычис-
вычислению нормально упорядоченных корреляционных функций. Это соответствует Р-
представлению поля. Нетрудно показать, что если пренебречь производными третье-
третьего и более высокого порядка (что можно обосновать из масштабных соображений),
308 Квантовая теория лазера — метод Гейзенберга-Ланэюевена Гл. 12
то уравнения A1.Б.11) и A1.Б.12) оказываются идентичными уравнению A2.4.21).
Это и доказывает эквивалентность двух подходов.
Задачи
12.1. 1. Выведите уравнения движения для с-числовых полевых и атомных пере-
переменных а, е^, j?a и jV^^ соответствующие антинормальному упорядоче-
упорядочению операторов а, М, Na, Nb, M+, а+.
2. Найдите ненулевые коэффициенты диффузии, связанные с лаыжевенов-
скими флуктуационными силами в уравнениях движения для а, */#, сЖа
и jVb.
3. Выведите уравнение движения для электромагнитного поля а, адиабати-
адиабатически исключая атомные переменные.
12.2. Выведите формулы A2.3.12а)-A2.3.12е).
12.3. Выведите формулы A2.3.24) и A2.3.25).
Список литературы
Ланжевеновская теорим лазера
*Файн В.М., Ханин Я.И. Квантовая радиофизика (Сов. радио, Москва, 1965).
Lax, M. In Physics of Quantum Electronics, ed. P. L. Kelley, B. Lax, and P. E. Tannenwald
(McGraw Hill, New York 1966), p. 735.
*Микаэлян А.Л., Тер-Микаелян М.Л., Турков Ю.Г. Оптические квантовые генераторы на
твердом теле (Сов. радио, Москва, 1967).
Lax, M. In Statistical Physics, Phase Transition, and Superconductivity, Vol. II, ed. M. Chretien,
E. P. Gross, and S. Dreser (Gordon and Breach, New York 1968).
Louisell, W. Quantum Statistical Properties of Radiation, (Wiley, New York 1974).
Haken, H. Laser Theory, (Springer, Berlin 1970).
Haken, H. Light, Vols. I and II, (North-Holland, Amsterdam 1981).
Flelschhauer, M. Phys. Rev. A 50, 2773 A994).
Sargent III, M., Scully, M. and Lamb, W. E., Jr., Laser Physics, (Addlson-Welsley, Reading,
MA, 1974).
Эффекты атомной памятм в лазере
Haake, F. Z. Phys. 227, 179 A969).
Scully, M. O., Siissmann, G. and Benkert, C. Phys. Rev. Lett. 60, 1014 A988).
Scully, M. O., Zubairy, M. S. and Wodklewicz, K. Opt Commun. 65, 440 A988).
Benkert, C, Scully, M. O. and Sussmann, G. Phys. Rev. A 41, 6119 A990).
Эффекты синхронизации мод и окрашенный шум
Chow, W. W., Scully, M. О. and Van Stryland, E. Opt Commun. 15, 6 A975).
Cresser, J. D., Louisell, W. H., Meystre, P., Schlekh, W. and Scully, M. O. Phys. Rev. A 25,
2214 A982).
Graham, R., Hohnenback, M. and Schenzle, A. Phys. Rev. Lett 48, 1396 A982).
Fox, R. F., James, G. E. and Roy, R. Phys. Rev. Lett 52, 1778 A984).
Список литературы к гл. 12 309
Влияние статистики накачки
Golubev, M. and Sokolov, I. V. Zh. Eksp. Tear. Fiz. 87, 408 A984) (Sov. Phys. JETP 60, 234
A984)).
Yamamoto, Y., Machlda, S. and Nilsson, O. Phys. Rev. A 34, 4025 A986).
Machlda, S., Yamamoto, Y. and Itaya, K. Phys. Rev. Lett 58, 1000 A987).
Marte, M. A., Ritsch, H. and Walls, D. F. Phys. Rev. Lett. 61, 1093 A988).
Bergou, J., Davldovlch, L., Orszag, M., Benkert, C, Hillery, M. and Scully, M. O. Phys. Rev. A
40, 5073 A989) (метод оператора плотности).
Haake, F., Tan, S. M. and Walls, D. F. Phys. Rev. A 40, 7121 A989).
Benkert, C, Scully, M. O., Bergou, J., Davldovlch, L., Hillery, M. and Orszag, M. Phys. Rev. A
41, 2756 A990) (метод Ланжевена).
Briegel, H.-J., Englert, B.-G., GInzel, C. and Schenzle, A. Phys. Rev. A 49, 5019 A994).
Fontenelle, M. T. and Davldovlch, L. Phys. Rev. A 51, 2560 A995).
Глава 13
ТЕОРИЯ МИКРОМАЗЕРА
Разработка одноатомного мазера или микромазера -1) позволяет детально иссле-
исследовать взаимодействие атома с полем. Ситуация здесь очень близка к идеальному
случаю взаимодействия одного двухуровневого атома с одномодовым квантовым
полем, рассмотренному в разд. 6.2. В микромазере поток двухуровневых атомов
направляется в сверхпроводящий резонатор, имеющий высокую добротность. Ско-
Скорость поступления атомов может быть такой, что в каждый момент времени только
один атом находится внутри резонатора. Благодаря высокой добротности резонатора
время затухания излучения намного больше характерного времени взаимодействия
атома с полем, которое задается обратной однофотонной частотой Раби. Поэтому
поле внутри резонатора растет, если среднее время между моментами поступления
атомов в резонатор меньше времени затухания резонатора. Таким образом, микро-
микромазер позволяет поддерживать генерацию при условии, что в резонаторе в среднем
находится менее одного атома.
Реализация одноатомного мазера или микромазера стала возможной благодаря
грандиозному прогрессу в конструировании сверхпроводящих резонаторов, а также
благодаря сильному лазерному возбуждению атомов, называемых атомами Ридбер-
га. Добротность сверхпроводящих резонаторов достаточно высока для того, чтобы
наблюдать периодический обмен энергией между атомом и полем резонатора. Инте-
Интересные свойства атомов Ридберга делают их идеальными для микромазеров. У такого
атома вероятность вынужденных переходов между соседними уровнями становится
очень большой и изменяется пропорционально тг4, где п — главное квантовое число.
Следовательно, нескольких фотонов достаточно для насыщения перехода между
соседними уровнями. В добавок, время жизни возбужденного состояния для случая
спонтанного перехода оказывается очень большим.
На рис. 13.1 приведена общая схема прекрасного эксперимента, выполненного
в институте квантовой оптики имени Макса Планка (Гархинг, Германия), в котором
реализована идея микромазера. Сильно коллимированный пучок атомов рубидия
пропускается через селектор скоростей Физо. Перед входом в резонатор атомы
возбуждаются на верхний мазерный уровень 63р3/2- Сверхпроводящий ниобиевый
резонатор охлаждается до температуры 0,5 К с помощью гелиевого CНе) криостата.
При такой низкой температуре число тепловых фотонов снижается до 0,15 на частоте
21,5 ГГц. Добротность резонатора равна 3 • 1010, что соответствует времени жизни
фотона 0,2 с. Исследуются мазерные переходы с уровня бЗрз/2 на уровень 6Ы3/2
(частота 21,5 ГГц). Среднее время пролета ридберговских атомов сквозь резонатор
равно 50 мкс, а поток атомов уменьшается до значения 1750 атом/с. Прошедшие
через резонатор ридберговские атомы, находящиеся на вернем и нижнем уровнях,
) Первый микромазер был построен Мешедом, Вальтером и Мюллером (Meschede, Walter,
and Miiller, 1985). Обзор основополагающих более ранних работ см. в работе Haroche and
Ralmond A985).
13.1 Уравнение двиэшения для матрицы плотности 311
Каналотропные
детекторы
Е \Е
Возбужденные Резонатор Поле ионизации Поле ионизации
ридберговские атомы микромазера из верхнего из нижнего
состояния состояния
Рис. 13.1. Схема эксперимента, демонстрирующего работу микромазера (из работы
Rempe, G., Schmldt-Kaler, F. and Walther, H. Phys. Rev. Lett 64, 2783 A990))
регистрируются двумя разными полевыми ионизационными детекторами. Напря-
Напряженность поля ионизации подбирается такой, чтобы в первом детекторе атомы, нахо-
находящиеся в верхнем состоянии ионизировались, а находящиеся в нижнем состоянии —
нет.
Статистика фотонов в микромазере обнаруживает много интересных свойств,
включая субпуассоновский характер. Используя резонатор с достаточно высокой
добротностью можно даже генерировать состояния с определенным числом фотонов.
Если в резонаторе отсутствуют тепловые фотоны, что достигается охлаждением
резонатора до очень низкой температуры, возникают интересные особенности типа
плененных состояний.
В этой главе изучаются эти интересные свойства фотонной статистики, а также
ширина линии излучения микромазера. Приложение микромазеров к проблеме кван-
квантовых измерений будет рассматриваться в гл. 19 и 20.
13.1. Уравнение движения для матрицы плотности
Рассмотрим одномодовый резонатор, в который вводятся возбужденные двух-
двухуровневые атомы со скоростью достаточно низкой, чтобы в каждый момент времени
в резонаторе находился самое большее один атом. Затухание резонатора полагается
настолько малым, что им можно пренебречь в течение времени взаимодействия.
Времена жизни всех уровней также полагаются намного большими, чем время вза-
взаимодействия атома с полем в резонаторе мазера. Таким образом, можно пренебречь
процессами спонтанного распада (на другие уровни или в другие моды) и считать,
что совместная эволюция одномодового поля и атома является унитарной.
Чтобы получить «крупномасштабное» уравнение движения для приведенной
матрицы плотности поля необходимо сложить вклады всех атомов, поступающих
в резонатор в случайные моменты времени со скоростью га и взаимодействующих
с полем излучения в резонаторе в течение фиксированного времени т до момента
выхода из резонатора (см. разд. 11.1, метод 2). Результирующее уравнение имеет вид
(уравнение A1.1.26))
усиление
7)pn^i,n^i. A3.1.1)
312
Теория микромазера
Гл. 13
-у [2птепл(п + п' + 1) + (п + п')],
Добавим вклад потерь резонатора (уравнение (8.3.2)):
Это приводит к следующему уравнению движения для матрицы плотности в пред-
представлении чисел заполнения (где рпп> = (n\p\nf), n, п' = 0,1, . . .):
где
) cos{gry/n' + 1)] —
A3.1.4)
L)(n' + l)]1/2, A3.1.5)
сП}П? = ^(птеш1 + 1) VW7. A3.1.6)
Это уравнение является основой большинства исследований квантовых статиста™
ческих свойств излучения в микромазере. Диагональные элементы р(п) = рПги
представляющие собой вероятность обнаружить в поле п фотонов, удовлетворяют
уравнению движения
р(п) = ап^пр(п) + bn^i}n^ip(n — 1) + cn+ijn+ip(?i + 1), A3.1.7)
где
) - ЩптеплBп + 1) + п], A3.1.8)
Т) + ^птепл(п + 1), A3.1.9)
,епл + 1)п. A3.1.10)
bn,n' = га sin(g-T
аП)П = -г а
ЬП}п = Га Sin2 (g
Cn?n =
Отметим также, что
ап,п + ЬП}П + сп>п = 0.
13.2. Статистика фотонов в стационарном состоянии
A3.1.11)
Стационарное распределение числа фотонов можно получить из уравнения
A3.1.7), полагая р(п) = 0, как это делалось в гл. 11. Результирующее уравнение
{ra sI
плB
птеплBп
эквивалентно следующим рекуррентным соотношениям:
[г а Sin2 {gT^/n) + ^Птеплп]р(п - 1) = ^(пТепл ^
[rasin2(^rV^ + 1) ¦"
откуда
1)р(п + 1),
= 0 A3.2.1)
A3.2.2)
A3.2.4)
где р{0) определяется из условия нормировки:
A3.2.5)
13.2
Статистика фотонов в стационарном состоянии
313
Выражение A3.2.4) является основным результатом этого раздела, поскольку из него
можно получить все свойства статистики фотонов в микромазере.
Прежде чем обсуждать поведение стационарной функции распределения фотонов
р(п), найдем пороговое условие для микромазера. Для этого достаточно использовать
линейное приближение, в котором
г, A3.2.6)
и уравнение A3.1.7) сводится к следующему:
р(п) = -[ra(gr)
¦ 1) +
+ ra{gTJnp(n - 1) + Щп + 1)р(п + 1). A3.2.7)
Здесь мы предположили, что птепл = 0. Теперь можно проследить за ростом поля,
исходя из уравнения для среднего числа фотонов,
(п) = J^ пР(п) = [ra{grf - Щ[п) + ra{grf
п=0
A3.2.S
Последний член является следствием спонтанного излучения. Ясно видно, что поле
растет, когда
га(ётJ > V. A3.2.9)
Таким образом, условие ra{grJ = & определяет порог генерации микромазера.
Ниже порога (ra(grJ < $) поле должно исчезнуть. Отсюда естественным образом
определяется нормированное время взаимодействия:
A3.2.10)
которое равно единице на пороге генерации
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
(N)
/
1 1 1 1 1
(а) -
(б) -
10
12
14
Рис. 13.2. Нормированное среднее число фотонов (N) в стационарном состоянии как функ-
функция нормированного времени взаимодействия твз при птеПл = 0.1: iVBO36 = 20 (а) и iVBO36 =
= 2000 (б)
314
Теория микромазера
Гл. 13
На рис. 13.2 изображена зависимость нормированного числа фотонов,
iVBO36
]np(n),
A3.2.11)
n=0
от величины твз для iVBO36 = ra/^ = 20 и 2000, и при условии, что птепл = ОД.
Параметр iVBO36 = ra/& представляет собой среднее число атомов, проходящих через
резонатор в течение времени жизни поля. Среднее число фотонов остается практиче-
практически равным нулю для малых твз, однако на пороге (твз) = 1 величина (п) становится
конечной и быстро растет почти до единицы ((n) = iVBO36) с увеличением твз. Затем
среднее число фотонов падает, достигая минимума при твз ~ 2тг, после чего скачком
возрастает до большего значения. Такое колебательное поведение продолжается, хотя
и становится менее отчетливым, при дальнейшем увеличении значения твз.
На рис. 13.3 изображен параметр Манделя Q,
Q
(n>
A3.2.12)
как функция величины твз. Сразу над порогом распределение фотонов сначала
становится сильно суперпуассоновским (Qf ^> 0), а затем параметр Q падает ниже
пуассоновского уровня Qf = 0. С увеличением твз суперпуассоновские пики появля-
появляются приблизительно с интервалом 2тг, чередуясь с субпуассоновской статистикой.
Q
Рис. 13.3. Параметр Манделя как функция нормированного времени взаимодействия твз
При iVBO36 = 200 И Птепл = 0.1
Генерирование субпуассоновской статистики в стационарном состоянии является ин™
тересной чертой микромазера. В следующем разделе будет показано, как микромазер
может генерировать состояния с определенным числом фотонов.
До сих пор рассматривалось поведение первых двух моментов функции распреде-
распределения фотонов в стационарном состоянии. На рис. 13.4 приведена зависимость р(п)
от п при различных значениях времени взаимодействия. Когда твз = Зтг, очевидно,
имеем субпуассоновское поведение. Однако, когда твз = 15тг, распределение не имеет
13.3
Состояние с определенным числом частиц
315
О 10 20 30 40 50 60 70 80 90 100
Рис. 13.4. Функция распределения фотонов в стационарном состоянии при iYBO36 = 200
и Жгепл = 0.1: твз = Зтг (а) и твз = 15тг (б). Распределение имеет три пика при значении
Твз = 15?Г
более одного пика. Такое многопиковое распределение является еще одной особенно-
особенностью микромазера.
13.3. Создание состояния с определенным числом фотонов
в высокодобротном микромазере
В этом разделе обсуждаются два возможных способа создания состояния с опре-
определенным числом фотонов в высокодобротном микромазере, а именно: 1) схема
редукции состояния, когда вывод о статистике делается на основе осмотра рид™
берговских атомов при выходе их из резонатора и 2) схема состояния пленения,
в которой время взаимодействия выбрано таким, чтобы вероятность испускания при
определенном числе фотонов была мала, и поле обрезалось на этом числе фотонов.
Чтобы экспериментально получить состояние поля с точно известным числом
фотонов, необходимо выполнение двух условий. Первое касается температуры. Теп™
ловые фотоны должны быть подавлены, поскольку они индуцируют распад и влияют
на статистику, так что получается суперпозиция состояний с определенным числом
фотонов. Тепловые фотоны можно устранить, охлаждая резонатор до достаточно
низкой температуры. Среднее число тепловых фотонов на частоте 20 ГГц равно 3 х
х 10^5 при Т = 0,1 К. Второе условие состоит в том, чтобы фотоны, запасенные
в резонаторе, не терялись во время эксперимента, то есть необходим резонатор,
потерями которого за это время можно пренебречь. Время жизни фотонов опреде-
определяется скоростью затухания S1 = и/'Q. Поскольку добротность Q резонатора может
достигать значения 1011, времена жизни фотонов с микроволновой частотой около
20 ГГц получаются равными нескольким секундам.
13.3.1. Редукция состояния. Рассмотрим экспериментальную установку типа
той, которая изображена на рис. 13.1. Атомы в возбужденном состоянии влетают
в пустой резонатор, то есть поле в начальный момент времени находится в вакуумном
316
Теория микромазера
Гл. 13
состоянии |0). Вылетев из резонатора, атомы анализируются статическим электри-
электрическим полем, ионизирующим все атомы, находящиеся на верхнем энергетическом
уровне. Все те атомы, которые не ионизируются, испустили фотон в резонаторе.
Подсчитав эти атомы (с помощью электронного детектироания, как показано на
рис. 13.1), можно сделать вывод о числе фотонов в поле мазера. Отметим, что
редукция состояния и связанные с ней идеи теории измерений имеют принципиальное
значение для этой схемы. При определении состояния выходящих атомов, число
фотонов в резонаторе становится точно известным, то есть поле переводится в чистое
состояние с определенным числом фотонов. Поскольку первоначально излучение
в резонаторе отсутствует, поле всегда находится в состоянии с определенным числом
фотонов, когда атом попадает в резонатор. Вследствие взаимодействия атома с по-
полем, находящимся в состоянии |п), последнее переходит в суперпозицию состояний
\п) и \n-\-1). В результате последующего измерения атомного состояния эта суперпо-
суперпозиция переводится в одно из состояний \п) или \п + 1), в зависимости от результата
измерения.
Теперь, имея нулевые потери в резонаторе, будем сохранять состояние с опреде-
определенным числом фотонов, поскольку в данном эксперименте излучение не покидает
резонатор. Однако мы получим лишь априорные вероятности, согласно которым,
в данной схеме редукции состояния, в действительности генерируется состояние
с определенным числом фотонов. Эти априорные вероятности не должны противоре-
противоречить статистическим распределениям фотонов. Например, если бы поле излучения
находилось в когерентном состоянии, то любой лазер или любая рассматриваемая
система была бы в бесконечной суперпозиции состояний с определенным числом
фотонов. В данном же случае каждая система находится в конкретном состоянии
с определенным числом фотонов. Однако до эксперимента не известно, какое это
будет состояние. Поэтому необходимо повторить эксперимент многократно с одним
и тем же общим числом атомов, получая, таким образом, большое число различных
состояний с определенным числом фотонов. Распределение чисел фотонов будет
задаваться априорным распределением вероятности, которое сейчас будет вычис-
вычислено. Необходимо подчеркнуть, что число атомов, покидающих резонатор в нижнем
состоянии, равно числу фотонов в резонаторе только в том случае, если последний
является резонатором без потерь.
Перейдем теперь к вычислению вероятности Рп(т) того, что в поле будет п
фотонов, после того как т атомов пройдут через резонатор. Для этого выведем
рекуррентное соотношение. Оператор эволюции U(t) системы, состоящей из двух-
двухуровневого атома, взаимодействующего с полем, задается выражением F.2.49), т.е.
U (г) =
a+a )\b)(b\ —
i \/u • + sIn(^rVa+a +1) |LX/ /iooi\
a\a)(b\ — га^ L\b){a . A3.3.1)
Предположим, что первоначально атом находится в верхнем состоянии |в), а поле —
в состоянии с определенным числом фотонов \п). Следовательно, оператор плотности
системы «атом + поле» имеет вид |a,n)(a,n|. Спустя время взаимодействия т
получаем
= и(т)\а,п}(а,п\и+(т) =
= cos
а, п)(а, п\ + sin2 (gr у/п + 1 )|6, п +
, n\ —
, п + 1| —
^ п + 1|]. A3.3.2)
13.3
Состояние с определенным числом частиц
317
Состояние поля излучения определяется теперь через редукцию состояния. То есть,
если окажется, что атом находится в верхнем состоянии |а), то оператор плотности
A3.3.2) сведется к следующему:
р(т) = cos2 (gr у/п + 1 )|а, п){а, п\, A3.3.3)
а если атом будет обнаружен в состоянии |6), то оператор плотности запишется в виде
A3.3.4)
р(т) = sm2(g-rVn + l)|6, п + 1>(Ь, п +
Отсюда находим, что вероятность того, что поле останется в состоянии |п), равна
с(п) = cos (gT-y/n + 1),
а вероятность перехода его в состояние \п + 1} имеет вид
s(n) = sin2 (gry/n + 1).
После прохождения га —1 атома поле будет в состоянии \п) с вероятностью Рп(т —
— 1) и в состоянии |п — 1) с вероятностью Pn_i(ra — 1). Тогда вероятность того, что
поле будет в состоянии |п), после того, как в резонаторе побывало га атомов, равна
Рп{т) = с(п)Рп(т - 1) + 8(п ^ l)Pn_i(m - 1). A3.3.5)
Предположим, что поле в начальный момент времени находится в вакуумном состоя™
нии |0), то есть Ро(О) = 1. Тогда для одного атома имеем РоA) = с@) и Pi(l) = s@),
для двух атомов имеем
A3.3.6)
и т.д.
Распределение вероятности Рп(т) может быть найдено численно как функция
числа прошедших атомов для различных значений gr. На рис. 13.5 приведены
результаты расчетов для различного числа атомов, вплоть до 1000.
Pi B) = c(l)Pi(l) + s@)Po(l) = e@)[c@) + c(l)],
Рп(т)
10
20
30 40
n
50
60
70
Рис. 13.5. Вероятность обнаружить п фотонов в резонаторе после прохождения через него
т атомов при gr = 0.4 (из работы Krause, Scully and Walther A987))
318 Теория микромазера Гл. 13
Очевидно, что вероятность Рп(т) очень сильно зависит от значения gr. Этот па™
раметр меняется экспериментально путем изменения скорости атомного пучка. Если
gr < 1, то в распределении фотонов развивается пик, перемещающийся в сторону
больших чисел фотонов по мере возрастания числа прошедших атомов. Теоретически
величина s(uq) может стать равной 0, так что распределение вероятности будет S-
функцией в стационарном состоянии. Этот случай будет обсуждаться ниже. Однако
в любом эксперименте распределение скоростей атомного пучка никогда не бывает
таким острым. Поэтому высота пика распределения вероятности уменьшается при
увеличении числа вводимых атомов, и новый пик развивается перед следующим
барьером Bтг/'grJ. Таким образом, реализация состояния с определенным числом
фотонов связана с детектированием через выходящие атомы.
Скорость атомов сама по себе не является усложняющим фактором в данной схеме
создания n-состояния. Она приводит к изменению вероятности испускания фотона,
но для эксперимента важно лишь, испущен фотон или нет. Главная идея получения
информации о поле через наблюдение за атомами остается в силе независимо от
усложняющих факторов типа движения атомов. Однако, если эксперимент повторять
многократно, то статистика получаемых чисел фотонов в состояниях с определенным
числом фотонов будет меняться.
13.3.2. Состояния пленения. В общем случае, как показано в разд. 13.2, в микро-
мазере достигается стационарное состояние вследствие потерь в резонаторе. В такой
ситуации статистика поля существенно зависит от длительности взаимодействия т.
Вообще говоря, стационарное состояние не существует для резонатора без потерь,
поскольку атомы в возбужденных состояниях непрерывно вводятся в резонатор.
Однако стационарное состояние можно получить в резонаторе без потерь, выбирая
время взаимодействия таким, чтобы вероятность испускания при определенном числе
фотонов становилась малой, так что поле обрезалось бы на этом числе фотонов.
Такое состояние называется состоянием пленения. В этом разделе обсуждается схема,
основанная на манипуляции временами взаимодействия с целью получения чистых
состояний с определенным числом фотонов.
Рассмотрим установку, в которой атомы, находящиеся в возбужденном состоянии
влетают в пустой резонатор. Если время взаимодействия атомов с полем выбрать так,
чтобы для nq фотонов внутри резонатора выполнялось условие
gTyfnq + 1 = qn (9 = 1,2,3,...), A3.3.7)
то возбужденный атом испытает q осцилляции Раби и останется в резонаторе в воз-
возбужденном состоянии. Говорят, что мазер находится в восходящем состоянии пле-
пленения, поскольку по мере поступления инвертированных атомов поток вероятности
от состояния nq к состоянию nq + 1 не возникает, и поле мазера эволюционирует
в состояние \nq).
С другой стороны, если
gT^=q7T (g = 1,2,3,...), A3.3.8)
то атом, входящий в резонатор в основном состоянии, испытает q осцилляции Раби
и покинет резонатор в том же состоянии. Говорят, что мазер находится в нисходящем
состоянии пленения. Ясно, что состояние с определенным числом фотонов, непосред-
непосредственно следующее за нисходящим состоянием пленения, есть восходящее состояние
пленения. В обоих случаях атомы, влетающие в резонатор, воспринимают поле как
2дтг-импульс, и стационарное состояние достигается даже в отсутствии потерь, так
что
p(ti+1) = р{и), ti+1 = U + r-1. A3.3.9)
13.3
Состояние с определенным числом частиц
319
Выражение A3.3.9) есть общепринятый критерий стационарного состояния микрома-
микромазера, несмотря на тот факт, что поле изменяется в течение времени взаимодействия т.
Покажем теперь, как состояние с определенным числом фотонов возникает из
точного решения основного уравнения A3.1.1) для микромазера.
Уравнение A3.1.1) для функции распределения фотонов (без членов потерь)
можно переписать в матричном виде следующим образом:
R = -MR,
A3.3.10)
где
R(t) =
A3.3.11)
м =
«о
-а0
сц
-сц
A3.3.12)
p(l, t) = (l\pF(t)\l) ИСЦ = -Та Sin2 (
Определим собственное значение А/ матрицы М, соответствующее правому соб-
собственному состоянию,
и левому собственному состоянию,
следующими соотношениями:
МАг =
BiM = XtBh
A3.3.13)
A3.3.14)
A3.3.15)
A3.3.16)
Если уравнение A3.3.15) умножить на B\i слева, уравнение A3.3.16) для V умножить
на А\ справа, а затем вычесть одно из другого, то получим соотношение ортогональ-
ортогональности
BlfAi = Sti4 A3.3.17)
при условии, что Л| ф Л// или Л/, Л|/ не вырождены.
С учетом A3.3.15) решение уравнения A3.3.10) имеет вид
A3.3.18)
1=0
320 Теория микромазера Гл. 13
В тех случаях, когда собственные значения не вырождены, коэффициент С/ можно
определить, используя условие ортогональности A3.3.17), так что
d = Я,Я@). A3.3.19)
Из A3.3.18) и A3.3.19) следует, что
#"» е-А'*р(<7, 0). A3.3.20)
1=0 q=0
То есть функция распределения фотонов полностью определяется собственными
значениями Л/ и элементами правого и левого собственных состояний А\ и В[.
Собственные значения А/ матрицы М, удовлетворяющие уравнению
det(M-Af7) = 0, A3.3.21)
где / — единичная матрица, имеют вид
Л| = щ = -ra stn2(gWl + l). A3.3.22)
Когда 0 ^ I ^ по и gry/rtQ + 1 = ^? имеем Л/ / Л// при I / 1;. Подстановка выражения
A3.3.22) в A3.3.15) и A3.3.16) приводит к следующим рекуррентным соотношениям
между матричными элементами а1п и /3':
-an-io^.-L + ana^ = a|a^5 A3.3.23)
ag-i/3g-i - ag-ii8g = a/i8g-i. A3.3.24)
Многократно применяя рекуррентные соотношения A3.3.23) и A3.3.24), получаем
Ш /(«r - «l), П > Z,
n = /, A3.3.25)
n</,
-aO» ^ < ^
g = I, A3.3.26)
q>L
Формула A3.3.20) вместе с выражениями для Л/, а^ и /3' полностью определяют
эволюцию оператора плотности во времени.
Пусть начальное состояние поля является вакуумным. При этом p(g,0) = Sqg.
Время взаимодействия выберем так, чтобы gr^/riQ + 1 = тг. Тогда апо = 0. При этих
условиях выражение для функции распределения фотонов существенно упрощается
и принимает вид
{еа°* п = 0
Y^n' IVm-1 -a,t/nn ( \\ \/ A3.3.27)
Е/=о [Пг=о аг е а'у Пгро(«1 - ar)J , п ^ 1. v ;
В стационарном состоянии (t —> оо) величина р{п, оо) равна нулю при п ф п®. Един-
Единственный член, дающий ненулевой вклад в сумму, есть член I = п®. Следовательно,
стационарное распределение фотонов рсс(п) имеет вид
Рсс(п) = 5ппо, A3.3.28)
т. е. является функцией распределения фотонов фоковского состояния.
13.4
Ширина линии излучения микромазера
321
13.4. Ширина линии излучения микромазера
Обратимся теперь к вычислению спектра микромазера. Расчет будет основан
на вычислении недиагональных элементов полевой матрицы плотности, таким же
образом, как это делалось в разд. 11.5 для лазера.
Уравнение движения для матрицы плотности pn,n+k = Рп A3.1.3) молено
переписать в виде A1.5.2), но с другими коэффициентами:
= 2Га sin2 [^
, A3.4.1)
A3.4.2)
A3АЗ)
Следуя той же процедуре, что была использована в разд. 11.5, получаем следующее
выражение для ширины линии излучения микромазера:
(eJ + 1}, A3А4)
где использовано разложение квадратных корней из A3.4.1) при (п) >> 1.
На рис. 13.6 изображена зависимость этой приближенной константы фазовой
диффузии D от нормированного времени взаимодействия твз = ET\fral^ = 50
для vajS = 50 атомов и птеПл = Ю^4 тепловых фотонов. Острые пики на фоне
монотонного увеличения D напоминают состояния пленения.
0.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Рис. 13.6. Относительная ширина линии D/^, определяемая формулой A3.4.4), как функ-
функция времени взаимодействия твз при га/^ = 50 и ffTerM = 10~4. На вставке показана точная
зависимость, полученная на основе численного решения уравнения для матрицы плотности
A3.1.3) для больших значений времени твз при га/^ = 20 и тгтеПл = 1
11 М.О. Скалли, М.С. Зубайри
322 Теория микромазера Гл. 13
Отметим, что фазовая диффузия особенно велика, когда мазер заперт в состоянии
пленения, то есть, когда величина (п) зафиксирована в одном из острых минимумов.
Выражение A3.4.4) обнаруживает такое поведение в пределе коротких времен вза-
взаимодействия или больших чисел фотонов, то есть, когда gr/^{пI'2 «С 1. Разлагая
тогда функцию синуса в ряд, приходим к выражению Шавлова-Таунса A1.5.13) для
ширины линии:
^ + УB+ 1)
2Д= ^
где
^ = гаё2т2. A3.4.6)
Сложный характер поведения ширины линии микромазера проистекает из слож-
сложной зависимости величины (п), входящей в знаменатель, от параметра накачки.
Наличие функции синуса в A3.4.4) означает колебательное поведение ширины линии
в пределе больших твз. Это подтверждается точными численными расчетами (см.
вставку на рис. 13.6).
Задачи
13.1. Покажите, что в полуклассическом приближении, когда (пг) = {п)г и (п) ^>
^> 1, нормированное среднее число фотонов (N) = (п)/NBO3^ в микромазере
определяется по формуле sin (твз\/(-/V)) = (N). Отсюда покажите, что при
больших значениях твз может быть более одного стационарного значения (N).
13.2. Покажите, что вероятность Рп(тп) обнаружить п фотонов в резонаторе ми-
микромазера после прохождения m двухуровневых атомов через первоначально
пустой резонатор задается выражением
71 — 1 П 771 — 1
Рим = п Ф) Е П с(ь-)'
г=0 *i=0 j=n
(*т-1<-..<»«)
где
Е П
ij=O j=n
im-2 m — 1
... E Пс(ь)' т
in=Oin+1=O iTO_1=0 j=n
15 rn = n, n ^ 0,
0, m < n или n < 0
и [] =1. (Указание: см. работу Krause, Scully, Walther, and Walther, 1989.)
i=0
Список литературы
* Обзоры
* Вальтер Г. УФЯ 166, 777 A996).
Список литературы к гл. 13 323
Эксперимент
Meschede, D., Walther, H. and Muller, G. Phys. Rev. Lett 54, 551 A985).
Haroche, S. and Raimond, J. M. In Advances in Atomic and Molecular Physics, Vol. 20, ed. D.
R. Bates and B. Bederson (Academic, New York 1985), p. 350.
Gallas, G. A. C., Leuchs, G., Walther, H. and Figger, H. In Advances in Atomic and Molecular
Physics, Vol. 20, ed. D. R. Bates and B. Bederson (Academic, New York 1985), p. 414.
Rempe, G., Walther, H. and Klein, N. Phys. Rev. Lett 58, 353 A987).
Теория
Fillpowlcz, P., Javanalnen, J. and Meystre, P. Phys. Rev. A 34, 3077 A986).
Lugiato, L. A., Scully, M. O. and Walther, H. Phys. Rev. A 36, 740 A987).
Статистика фотонов, определяемая через статистику атомов
Vogel, W., Welsch, D.-G. and Lelne, L. J. Opt Soc. Am. B. 4, 1633 A987).
Rempe, G. and Walther, H. Phys. Rev. A 42, 1650 A990).
Paul, H. and RIchter, Th. Opt Commun. 85, 508 A991).
Briegel, H.-J., Englert, B.-G., SterpI, N. and Walther, H. Phys. Rev. A 49, 2962 A994).
Wagner, C, Schenzle, A. and Walther, H. Opt Commun. 107, 318 A994).
Bardroff, P. J., Mayr, E. and Schleich, W. Phys. Rev. A 51, 4369 A995).
Bardroff, P. J., Mayr, E., Schleich, W. P., Domokos, P., Brune, M., Raimond, J.M. and Haroche,
S. Phys. Rev. A 53 2736 A996).
Двухфотонный микромазер
Brune, M., Raimond, J. M. and Haroche, S. Phys. Rev. A 35, 154 A987).
Davldovlch, L., Raimond, J. M., Brune, M. and Haroche, S. Phys. Rev. A 36, 3771 A987).
Ashraf, L, GearBanacloche, J. and Zubairy, M. S. Phys. Rev. A 42, 6704 A990).
Ashraf, I. and Zubairy, M. S. Opt Commun. 77, 85 A990).
Создание состояний с определенным числом фотонов и состояний
пленения
Fillpowlcz, P., Javanalnen, J. and Meystre, P. J. Opt Soc. Am. В 3, 906 A986).
Krause, J., Scully, M. O. and Walther, H. Phys. Rev. A 36, 4547 A987).
Krause, J., Scully, M. O., Walther, T. and Walther, H. Phys. Rev. A 39, 1915 A989).
Slosser, J. J., Meystre, P. and Braunsteln, S. L. Phys. Rev. Lett 63, 934 A989).
Qamar, S., Zaheer, K. and Zubairy, M. S. Opt. Commun. 78, 341 A990).
Спектр микромазера
Qamar, S. and Zubairy, M. S. Phys. Rev. A 44, 7804 A991).
Scully, M. O., Walther, H., Agarwal, G. S., Quang, T. and Schleich, W. Phys. Rev. A 44, 5992
A991).
Lu, N. Phys. Rev. Lett 70, 912 A993); Phys. Rev. A 47, 1347 A993).
Quang, Т., Agarwal, G. S., Bergou, J., Scully, M. O., Walther, H., Vogel, K. and Schleich, W.
Phys. Rev. A 48, 803 A993).
Микролазер
An, K., Childs, J. J., Desarl, R. R. and Feld, M. S. Phys. Rev. Lett 73, 3375 A994).
An, K. and Feld, M. S. Phys. Rev. A 52, 1691 A995).
11*
Глава 14
КОРРЕЛЯЦИОННЫЙ ЛАЗЕР:
КОНЦЕПЦИЯ, ТЕОРИЯ
И АНАЛИЗ
Как обсуждалось в последних трех главах, фундаментальным источником шума
в лазере является спонтанное излучение. Простая наглядная модель происхождения
ширины линии излучения лазера представляет ее как следствие случайного процесса
фазовой диффузии, возникающего благодаря добавлению спонтанного излучения
фотонов со случайными фазами к лазерному полю. В этой главе мы показываем,
что квантовый шум, приводящий к уширению лазерной линии, может быть подав-
подавлен ниже стандартного уровня, то есть предела Шавлова-Таунса, путем создания
атомных систем в когерентной суперпозиции состояний, как в эффекте Ханле или
экспериментах по квантовым биениям, обсуждавшимся в гл. 7. Спонтанное излучение
в таких системах называется коррелированным. Лазеры, работающие посредством
такого фазово-когерентного атомного ансамбля, будем называть корреляционными
лазерами (КЛ) 1). Интересным аспектом КЛ является то, что квантовый шум спон-
спонтанного излучения на связанных переходах можно устранить, создавая корреляции
двух актов спонтанного излучения.
Существует много схем подавления квантового шума ниже стандартного уров-
уровня. В двухмодовых схемах корреляция двух актов спонтанного испускания в две
различные моды устанавливается с помощью атомной когерентности, так что от-
относительная фаза между ними не диффундирует или не флуктуирует. В лазере
Ханле и лазере квантовых биений это достигается когерентной накачкой атомов,
так что каждый спонтанно излучающий атом вносит равный вклад в две моды
излучения, что приводит к сокращению или далее исчезновению шума разности
фаз. В двухфотонном КЛ каскадный переход трехуровневых атомов связан лишь
с одной модой поля излучения. Точно определенная когерентность между верхним
и нижним состояниями приводит к корреляции света, излучаемого на переходе \а) -^
—> \Ь) и последующем переходе \Ь) —> \с) (см. рис. 14.8).
В этой главе описываются микроскопические теории этих схем для корреляцион-
корреляционных лазеров и определяются условия, при которых имеет место подавление квантово-
квантового шума. При работе лазера Ханле и лазера квантовых биений происходит обращение
в нуль константы диффузии относительной фазы, а в случае двухфотонного К Л еще
и сжатие фазы.
1) Простейшее рассмотрение КЛ основано на методе квантовых уравнений Ланжевена
(Scully, 1985). Здесь представлен анализ в рамках формализма матрицы плотности и урав-
уравнения Фоккера-Планка (Scully and Zubalry, 1987), поскольку его легче обобщить, учитывая,
например, нелинейные эффекты (Krause and Scully, 1987).
14.1 Концепция корреляционного лазера 325
Для простоты ограничимся линейной теорией. В ходе обсуждения естественной
ширины линии излучения одномодового лазера (разд. 11.4) мы увидели, что для вы-
вычисления ширины спектра в областях выше порога генерации достаточно линейного
анализа. Он быстрее выявляет физику явлений, а полностью нелинейный анализ
(Krause, and Scully, 1987) оправдывает такой подход.
14.1. Концепция корреляционного лазера
Во многих областях современной науки существует большая потребность в высо-
высокоточных лазерных интерферометрических измерениях. Например, интерферометр
Майкельсона служит основой современных попыток зарегистрировать гравитаци-
гравитационное излучение, а лазерный гироскоп, использующий кольцевой интерферометр
Саньяка, часто работает на стандартном квантовом «пределе». Как обсуждалось
в разд. 4.1, кольцевой интерферометр Саньяка используется для измерения скоростей
вращения. Для того чтобы определить назначение корреляционного лазера, мы
рассмотрим здесь квантовые пределы пассивного и активного лазерных гироскопов.
Напомним (разд. 4.1.2), что в оптическом кольце радиуса 6, вращающемся со
скоростью Ог, разность фаз А# между противоположно распространяющимися
лазерными пучками после одного обхода задается выражением (см. D.1.14))
Дг9 ^} (млл)
сХ
где Л = А/2тг — приведенная длина волны.
Однако, поскольку мы имеем дело с высококачественным оптическим резона™
тором, характеризуемым скоростью затухания ^, свет обойдет кольцо N раз, где
N = с<^7™1/2тг6, и фактический сдвиг фаз (фазовый сигнал) между противоположно
распространяющимися волнами будет равен
Д^сигн = NA<3 = S^ пг (пассивный), A4.1.2)
где S = 26/Л.
С другой стороны напомним, что квантовый шум (в случае, когда квантовая
эффективность равна единице) таков, что А#погр ~ 1/у^, где п ~~ измеренное
число фотонов (фотоэлектронов), равное Ptm/hi/ (P — мощность лазера, tm — время
измерения). Таким образом,
-— (пассивный). A4.1.3)
Приравнивая A4.1.2) и A4.1.3), находим обычное значение квантового предела ла-
лазерного гироскопа:
(пассивный). A4.1.4)
Сейчас подходим к интересному моменту. Активный лазерный гироскоп работает
на разности частот противоположно распространяющихся волн. Если время одного
оборота для пучков, распространяющихся по часовой (Ч) и против часовой (ПЧ)
стрелки, обозначить как t+ иГ, соответственно, то частоты i/+ и г/_, соответствую™
щие Ч- и ПЧ-пучкам, задаются условиями резонанса ct = тжс/V±, где т — четное
целое число. Следовательно, подставляя t+ и t~ из D.1.9), в низшем порядке по 6Ог/с
имеем
A4.1.5)
326 Корреляционный лазер: концепция, теория и анализ Гл. 14
где v = тттс/2тгЬ. Тогда разность частот Аи = 2иЬПг/с создает фазу активного
сигнала
Д^сигн = Д^то = Stm?lr (активный). A4.1.6)
Сравнивая A4.1.2) и A4.1.6), видим, что фазовый сигнал в активном гироскопе
на много порядков больше, чем в пассивном, ибо, например, tm ~ 1 с, но <Ё?~1 ~
~ 10~-™-10~ с. Именно по этой причине коммерческие лазерные гироскопы, обычно,
являются активными.
Но каково отношение сигнал/шум в активном гироскопе? Кажется естественным
(и многие попали в эту ловушку), что нужно объединить ошибку A4.1.3), связанную
с дробовым шумом, вместе с сигналом A4.1.6) и найти
(предел активного гироскопа). A4.1.7)
Хорошая новость — то, что выражение A4.1.7) устанавливает предел, существенно
лучший предела пассивного гироскопа A4.1.4), а плохая новость — то, что это
выражение ошибочное. Как было показано в ходе рассмотрения фазовой диффузии,
индуцированной спонтанным шумом, погрешность фазы $, выросшая за время tmi
равна А#погр = \/'Dtm , где D — скорость фазовой диффузии (выражение A1.4.11)).
Кроме того, поскольку D ~ ^/ (п) и (п) = Р^^1 /hu, имеем
^ Jw^ /шум спонтанного излучениях
— © tm у pt \в активном гироскопе ) '
/шум спонтанного излучениях
\в активном гироскопе )
Таким образом, видно, что благодаря множителю ^гт фазовый шум A4.1.8) намного
больше, чем A4.1.3). Наконец, если использовать выражения A4.1.8) и A4.1.6) вместе
(как и следует делать), то вновь получим стандартный предел A4.1.4). То есть,
для активного и пассивного устройств предел получается одинаковым. Естественно
приходим к вопросу: существует ли способ сделать активное устройство, избежав
при этом шума спонтанного излучения? Этот вопрос является отправной точкой
в изучении корреляционного лазера, к чему мы сейчас и приступаем.
14.2. Корреляционный лазер Ханле: метод оператора плотности
В предыдущем разделе мы напомнили, что в активных лазерных интерферомет-
рических экспериментах предельным источником квантового шума часто являются
флуктуации относительного фазового угла, связанные со спонтанным излучением.
Сейчас будет показано, что диффузия относительного фазового угла между двумя
такими лазерными модами может быть устранена путем создания лазерной среды, со-
состоящей из «трехуровневых» атомов, и таким ее расположением, чтобы два перехода
\а) О \с) и \Ь) О \с) возбуждали двойной резонатор (см. рис. 14.1). Таким способом
можно по-разному влиять на оптические пути внешним воздействием (например,
гравитационной волной или частотным сдвигом Саньяка).
Атомные переходы, возбуждающие два оптических пути, являются сильно корре-
коррелированными, когда верхние состояния \а) и \Ь) создаются в когерентной суперпози™
ции, как в случае эффекта Ханле или экспериментах по квантовым биениям. В случае
эффекта Ханле, в качестве состояний \а) и \Ъ) можно взять состояния «линейной
поляризации», образованные из одного состояния «эллиптической поляризации»,
как показано на рис. 14.1а. В случае квантовых биений когерентное смешивание
создается сильным внешним микроволновым сигналом, как показано на рис. 14.2а.
Поля, излучаемые атомами в первом случае (рис. 14.1), различаются поляризацией,
14.2
Корреляционный лазер Ханле: метод оператора плотности
327
Когерентность,
индуцированная поляризацией
Усиливающая
среда
Двойной резонатор
(а)
(б)
Рис. 14.1. Лазер Ханле. Когерентное возбуждение атомов на лазерные уровни а) и \Ь)
с помощью соответствующим образом поляризованного пучка накачки. Переходы с воз-
возбужденных состояний в основное \с) различаются поляризацией (а). Схема лазера Ханле,
использующая когерентно возбужденные атомы в качестве активной среды. Чувствитель-
Чувствительные к поляризации зеркала разделяют моды поляризации в двойном резонаторе (б)
«ЛААА,
Усиливающая
среда
Когерентность, индуцированная
микроволновым полем
(а)
Двойной резонатор
{б)
Рис. 14.2. Лазер квантовых биений. Приготовление атомов в когерентной суперпозиции
верхних состояний \а) и \Ь) с помощью внешнего поля, имеющего эффективную частоту
Раби Од. Два лазерных перехода частоты v\ и vi делят общий нижний уровень \с) (а).
Схема лазера квантовых биений с двойным резонатором (б)
тогда как поля, излучаемые атомами во втором случае (рис. 14.2), различаются
частотой.
В обоих упомянутых случаях тон биений гетеродина между двумя спонтанно
излучаемыми полями 1 и 2 показывает, что они сильно коррелированы. Чтобы
увидеть это, рассмотрим атомы, взаимодействующие с квантованным полем, как
показано на рис. 14.2. Вектор состояния задается выражением
= а
1} 02)
ь 02) + 7i|c, Ц, 02
7а
A4.2.1)
где |1^) — состояние a^|0f), г = 1, 2 и щ (ai) — оператор рождения (уничтожения)
фотонов частоты и^. Теперь видно, что среднее значение оператора электрического
328 Корреляционный лазер: концепция, теория и анализ Гл. 14
поля Е{ ,
A42.2)
вычисленное с помощью A4.2.1), равно нулю, поскольку состояния \а), \b) и \с)
ортогональны. Аналогичные рассуждения показывают, что Е^ также обращается
в нуль. Однако перекрестный член не равен нулю:
(ф|?;(-)?7^+)|ф) =^1V27J72(c|c>exp[-i(k1 -k2)-r + i(t,1 - u2)t]. A4.2.3)
То есть, спонтанно испущенные фотоны частотой v\ и и2 являются коррелированны-
коррелированными.
Под влиянием предыдущих рассуждений, перейдем к исследованию диффузии
относительного фазового угла в двойных резонаторах, изображенных на рис. 14.16
и рис. 14.25.
В случае лазера Ханле имеем активную среду, состоящую из трехуровневых
атомов, находящихся в когерентной суперпозиции верхних состояний \а) и \Ь) и ре™
лаксирующих в состояние |е), с испусканием излучения различной поляризации
(рис. 14.1). В двойном резонаторе эти две волны взаимодействуют с активной средой
при помощи поляризационно-чувствительного зеркала.
Гамильтониан атомно-полевой системы в приближении волны вращающейся по-
поляризации задается выражением
Ж = ЖО + ЖЪ A4.2.4)
где
^ ^ 2j A4.2.5)
Жг = hgiai\a)(c\ + hg2a2\b)(c\ + э.с. A4.2.6)
Здесь gi и gi — константы взаимодействия для переходов \а) —>• \с) и \Ъ) —>•
—>¦ |с), соответственно. Если верхние состояния \а) и \Ь) соответствуют зеемановским
подуровням вырожденного верхнего состояния, то в отсутствии внешнего магнитного
поля имеем ша с± шь, так что волны, испущенные атомами на переходах |а) —>- \с)
и \Ъ) —ь |с), различаются поляризацией, но имеют практически одинаковую частоту
(i/-i_ = и2 = v). Если теперь преобразовать гамильтониан A4.2.4) в представление
взаимодействия относительно J#q, to получим
iAt
a)(c| + hg2a2 eiAt|6)(c| + эх., A4.2.7)
где А = ша — шс — и = шь — шс — и — расстройка, которую будем считать одинаковой
для обоих переходов.
Предположим, что атомы находятся в когерентной суперпозиции двух верхних
состояний. Следовательно атомный оператор плотности имеет вид
(Ь\) =
™ 1°> ^ A4.2.8)
Здесь ф — некоторая фиксированная относительная фаза между верхними состоя™
ниями и pajj = \pal\ ехр(г<^) — начальная когерентность.
14.2 Корреляционный лазер Ханле: метод оператора плотности 329
Уравнение для приведенного оператора плотности поля р получается взятием
следа по атомным переменным х), что приводит к результату
Р 7-^ Гатом [ У , Ратом—поле]
= -^([Уас, Рса] + [%с, Pah] + [%а, Рас] + [%Ь, РЬс}), A4.2.9)
где Ратом—поле обозначает полный атомно-полевой оператор плотности и Уас =
= hgiaiexp(iAi), Уьс = %^2 exp(iAt). Атомные матричные элементы рас и ръс
можно вычислить в первом порядке по константам взаимодействия gi, решая соот-
соответствующие уравнения.
Уравнения движения для рас и р^с имеют вид
Рас = ^JPac ^ -^{УасРсс ~ Раа^ас ~ Pab'f), A4.2.10)
Pbc = -1РЪс - ^(%сРсс ^ Pbb%c ^ Pba^)- A4.2.11)
Здесь 7 — атомная скорость затухания, которую, для простоты, будем считать
одинаковой для всех уровней. Уравнения движения нулевого порядка для рсс, раа,
Рьь и Pab имеют вид
Рсс = -7Рсс A4.2.12)
Раа = Гпр^р-7Раа, A4.2.13)
Рьь = Гар^р - 7Рьь, A4.2.14)
Pab = Гар^ьР ~ 7РаЬ, A4.2.15)
где га — скорость перевода атомов в когерентную суперпозицию A4.2.8). Стационар™
ное решение этих уравнений записывается следующим образом:
Рсс = 0, A4.2.16)
Раа = JP^P, A4.2.17)
Рьь = "fp^P, A4-2.18)
Следовательно, подставляя эти выражения для матричных элементов нулевого по-
порядка в уравнения A4.2.10) и A4.2.11) и затем интегрируя, получаем
Pac(t) = ij± j dt0 e-^-^[p^palgl eiAt° + p™pa2g2
) С этого момента р без индексов соответствует приведенному оператору плотности,
Рполе = Тгатом ратом^поле- Наличие индексов, рас = (а|Ратом-—-ооле |с), означает матричный
элемент полного оператора плотности, взятый между атомными состояниями.
330 Корреляционный лазер: концепция, теория и анализ Гл. 14
^) {1 sAt°]. A4.2.21)
Остальные матричные элементы в A4.2.9) определяются при помощи соотношений
Pea = Ptc И рсЬ = ptc.
Подставляя рас и рьс из A4.2.20) и A4.2.21) в уравнение A4.2.9), получаем
следующее основное уравнение для атомно-полевого оператора плотности р:
Р = -^ii{pa\ai - afpat) - -а22{ра2^ - а^ра2)-
^ ^«i2(p«2af ~ a>tPaz) е%Ф ~ ^a2i{pai®>t ^ a^pai) е^гф + э.с, A4.2.22)
где
@)
В этом уравнении члены, пропорциональные оц и «22? описывают усиление двух
мод, которые приводят к обычным выражениям для ширины линии, рассмотренным
в разд. 11.4. Однако члены, пропорциональные ql\2 и «21, чувствительны к фазе
и возникают вследствие создания верхних уровней \а) и \Ь) в когерентной суперпози-
суперпозиции. В уравнение A4.2.22) не включены члены, описывающие затухание резонатора,
поскольку они не вносят вклада в коэффициенты фазовой диффузии в последующих
вычислениях.
Для того чтобы исследовать фазовый шум, преобразуем уравнение A4.2.22) в эк-
эквивалентное уравнение Фоккера^Планка для Р-распределения P{ot\, aj, «2, a^) ПРИ
помощи следующих подстановок:
щр<—У щР,
A4.2.27)
ро.% <—> yoii - t^tJ P,
где i = 1,2. Результирующее уравнение Фоккера^Планка имеет вид
аР _
dt ~
Теперь определим полярные координаты rj, fij (j = 1,2) с помощью соотношения
olj = Vj exp(i#j), а также разностную и среднюю угловые переменные $ = #i — #2 и
14.2
Корреляционный лазер Ханле: метод оператора плотности
331
2. Тогда
д _ e~iel / а 1 0 \
^m ~ 2 van + ^i Ш1) '
а _ е~'*2 / д 1 а \
A42.29)
A4.2.30)
A4.2.31)
A4.2.32)
Выше порога флуктуации амплитуды малы, и ими можно пренебречь. Это означает,
что Р можно считать не зависящей от г\ и Г2, а зависящей лишь от д и /л. Переменные
ri и Г2 можно заменить их средними значениями yj(п\) и у/{п2) в стационарном
состоянии. Точные выражения для (п\) и {п2) можно определить путем нелинейного
анализа. При этих условиях уравнение A4.2.28) сводится к следующему виду:
д2
где
j-,(D^P), A4.2.33)
A4.2.34)
A4.2.35)
A4.2.36)
A4.2.37)
A4.2.38)
+ К.С,
к.с.
и ф = i9 — ф.
Физический смысл членов в A4.2.33) следующий. Коэффициенты d# и d^ есть
коэффициенты дрейфа относительно переменных д = i?i — #2 и /х = (#i + ^2)/2,
a D^i? и ^Vju — соответствующие коэффициенты диффузии. Главной особенностью
коэффициентов диффузии и дрейфа является то, что они явно зависят от фазы, и эти
фазовые зависимости возникают вследствие внесенной когерентности. Более простой
вид коэффициентов получается в случае, когда
J0) _ J0) _ | (о). _ | (о), _ 1
Раа — Pbb — \Pab I ~ \Pba I ~ о'
A4.2.39)
g\ = ^2 = g и (rii) = (n2) = (п). При этих условиях
«11 = «12 = «21 = «22 =
7G
A4.2.40)
332
Корреляционный лазер: концепция, теория и анализ
Гл. 14
i
= О,
A4.2.41)
A4.2.42)
A4.2.43)
A4.2.44)
A4.2.45)
где sz/ = 2rag2/(j2 + A2) — линейный коэффициент усиления.
Из уравнения Фоккера-Планка A4.2.33) получаем следующее уравнение движе-
движения для относительной фазы:
-^-@) = (d#). A4.2.46)
Синхронизация фаз (или запирание относительной фазы) ((#) = const) имеет место
для тех значений #, при которых коэффициент дрейфа обращается в нуль. Это
происходит тогда, когда ф = 0, то есть $ = ф. Кроме того коэффициент диффузии
относительного фазового угла (см. A4.2.43)), пропорциональный величине (l^cos ф),
обращается в нуль при ф равном нулю. Таким образом, в лазере Ханле возникает
режим работы корреляционного лазера (КЛ).
Интересно отметить, что условия, при которых исчезает диффузия относительной
фазы # = t?i — ^25 не приводят к обращению в нуль D^^, где fi = (#i + $2)/2.
Физику подавления флуктуации относительной фазы $, вызванных спонтанным
излучением, можно понять, обратившись к рис. 14.3, где на комплексной а-плоскости
Ima
1тск
Re a
-> Re
(а)
(б)
Рис. 14.3. Наглядное представление эффекта КЛ. События спонтанного испускания в две
моды являются сильно коррелированными, так что относительные фазы до (а) и после (б)
спонтанного испускания одинаковы
изображено «случайное блуждание» фаз электрического поля двух мод. Если прене-
пренебречь флуктуациями амплитуд, то флуктуации фазы поля, связанные со спонтанным
излучением, позволяют концам вектора напряженности поля диффундировать по
кругу в комплексной плоскости. Если D§§ = 0, то спонтанное излучение в обе
моды становится сильно коррелированным, так что относительный фазовый угол
14.3 Лазер квантовых биений: качественное описание 333
$ «запирается» в определенном значении. Однако средняя фаза характеризуется
ненулевой диффузией.
14.3. Лазер квантовых биений: качественное описание
Лазер квантовых биений, также как и лазер Ханле, состоит из трехуровневых
атомов с ^-конфигурацией переходов, которые возбуждаются в процессе накачки
в верхнее состояние \а) внутри двойного резонатора (рис. 14.2). Когерентность между
верхними состояниями \а) и \Ь) создается внешним полем, характеризуемым частотой
Раби Од ехр(—г0), где Од и ф — действительная амплитуда и фаза. Предполагается,
что переходы \а) —>> \с) и \Ъ) —>• \с) разрешены в дипольном приближении, а переход
\а) —> |6), следовательно, запрещен. Внешнее поле, приводящее к когерентности
между состояниями, может быть сильным магнитным полем в случае магнитного
дипольно-разрешенного перехода. Переход \а) —> \Ь) рассматривается полуклас-
полуклассически, в произвольном порядке по частоте Раби. Переходы \а) —> \с) и \Ь) —>
—>• \с) рассматриваются полностью квантово-механически, но с точностью до второго
порядка по константам взаимодействия. Расчет, приведенный в приложении 14.А,
вновь показывает, что квантовый шум спонтанного излучения в относительном фа-
фазовом угле можно сделать равным нулю. Здесь представлено простое наглядное 1)
рассмотрение проблемы, приводящее к тому же результату интуитивным путем.
В схеме КЛ квантовых биений два электрических поля S\ = r\ exp(i#i) и $ч =
= Г2 exp(i#2) с медленно меняющимися амплитудами rj и фазами fij (j = 1, 2) син-
синхронизированы постоянным относительным фазовым углом #q- Эта синхронизация
фаз описывается в простейшем случае следующим уравнением Адлера для разности
фаз (см. задачу 14.3):
# = a-6sin#, A4.3.1)
где а = vi — 1/2 — разность собственных частот Uj двух резонаторов, а величина Ь
пропорциональна коэффициенту усиления.
Перейдем во вращающуюся систему координат, в которой поля S\ и ^ являются
медленно меняющимися и имеют относительный фазовый угол #о = sin^1(a/6),
определяемый формулой A4.3.1). Таким образом, S\ = \/{п) exp(^i#0/2) и <f2 =
= \/{п) exp(i#o/2). Здесь мы предположили симметричную конфигурацию, когда
г\ = Г2 = \/(n)j и (п) обозначает среднее число фотонов в стационарном состоянии.
Вследствие спонтанного излучения электрические поля Sj (j = 1, 2) флуктуиру-
флуктуируют, так что
Sij = Fj(t), A4.3.2)
где Fj — гауссовы источники шума:
(Fi) = (FJ(t)Ffe(t')>=0 (j, k = 1,2), A4.3.3)
{F*{t)Fk{t'))^2Djk5{t-t') {j,k = l,2). A4.3.4)
Отметим, что акты спонтанного излучения из двух когерентно возбужденных состоя-
состояний являются сильно коррелированными, как показано для лазера Ханле. В резуль-
результате этого, перекрестный коэффициент диффузии Di2 можно сделать отличным от
нуля.
) Для дальнейшего чтения см. работу Schlelch and Scully A988).
334
Корреляционный лазер: концепция, теория и анализ
Гл. 14
+0/2)
Рис. 14.4. Фазовая диаграмма спонтанного излучения в лазере с синхронизированными
фазами. Напряженности электрического поля S\ и $ъ имеют фиксированную относительную
фазу 'д. Флуктуация SS'j (j = 1, 2) вызывает изменение фазы S'&j, задаваемое выражениями
A4.3.5) и A4.3.6)
Рассмотрим теперь влияние флуктуационных сил F\ и F2 на относительную
разность фаз # (см. рис. 14.4). Фазовый сдвиг S&i обусловлен актом спонтанного
испускания SS'i и при |<5<fi| <C л/(п) задается выражением
§/2) =
Re
. A4.3.5)
Аналогично
Следовательно полная флуктуация <5# =
и с учетом A4.3.2),
1 г
- F2St)
- Re F?2) sin(i?/2)]. A4.3.6)
• <5#2 разности фаз # равна
h<J<?2)], A4.3.7)
F25t)]. A4 Ji
14.3 Лазер квантовых биений: качественное описание 335
Определяя Sfi/St = (9#/с^)|флук, находим
l (Ft ~~ F2) + sin(^/2)Re (Fx + F2)]. A4.3.9)
флук
Прибавляя этот результат к детерминистическому уравнению A4.3.1), приходим
к геометрически обоснованному уравнению движения:
•д = a- 6sln# + cos(#/2)F^ + sin(#/2)F+. A4.3.10)
На последнем шаге мы ввели гауссовы силы Ланжевена F^ = Im(Fi — F2)/ у/{ть)
и F+ = Re(Fi + F2)I\/{n), имеющие, согласно выражениям A4.3.3) и A4.3.4),
следующие свойства:
<^_) = (^+} = 0, A4.3.11а)
t')) = т\[Ои + D22 - 2Re(D12)] 5(t - t'), A4.3.116)
t')) = ^y[?>u + D22 + 2Re(D12)} S(t - t'), A4.
Здесь учтено, что D12 = Z^i (что следует из A4.3.4)). В соответствии с A4.3.116)
и A4.3.11в) корреляция источников шума F\ и F^, то есть то, что Dyi ф 0, приводит
к снижению шума у F^ и соответствующему увеличению шума у F_|_. Следовательно,
силы Ланж:евена F^ и F+ являются коррелированными, что отражается формулой
A4.3.11г). Вклад косинуса или синуса в уравнении движения для $ A4.3.10) зависит
от степени корреляции между F\ и F2.
В отсутствие корреляции, то есть когда D\2 = 0, обе случайные силы F^ и F+
имеют равный вес, и выражение A4.3.7) упрощается путем введения гауссова шума
F = cos(#/2)F^ + sin(#/2)F+, имеющего, согласно формулам A4.3.11), следующие
свойства:
(F) = 0, A4.3.12)
(F(t)F(tf)) = 29S(t - t;), A4.3.13)
где 9 = D/(n). Здесь, и до конца раздела, полагается, что ?)ц = D22 = D.
Уравнение движения для § A4.3.10) сводится, следовательно, к уравнению для так
называемого лазера с синхронизацией фаз (ЛСФ):
$ = а- bsine + F(t). A4.3.14)
Обратимся теперь к случаю максимальной корреляции, когда Оц = D22 = 2Re D12
и, следовательно, (F_(t)F_(t')) = 0. Для простоты предположим, что lmDi2 =
= 0, так что (F^F+) = 0. Поскольку (F_) = 0 и F^ является гауссовым шумом, все
корреляционные функции более высокого порядка также равны нулю. Следовательно
F^ = 0. В результате уравнение A4.3.10) упрощается до уравнения движения для
разности фаз в корреляционном лазере:
A4.3.15)
где, согласно A4.2.11в),
(F+(t)F+(t')) = 2B^) S(t - t1). A4.3.16)
336
Корреляционный лазер: концепция, теория и анализ
Гл. 14
Сравнивая A4.2.16) и A4.3.13), мы видим, что интенсивность коррелированного
шума в два раза больше интенсивности некоррелированного шума F. Подчеркнем,
кроме того, что два уравнения движения для #, A4.3.14) и A4.3.15), существенно от-
отличаются друг от друга. В A4.3.15) шум F+ умножается на нелинейную функцию сто-
стохастической переменной $. Особенно отметим, что ((S'dJ) = 4(D/(n)) sin2(rd/2)ei =
= 2(D/(n))(l — cosset. Это и есть желаемый результат.
14.4. Голографмческжй лазер
В предыдущих разделах рассматривались лазеры, основанные на эффекте Ханле
и квантовых биениях, в которых трехуровневые атомы поддерживают две лазерные
моды, соответствующие переходам из двух когерентно созданных верхних состояний
в общее основное состояние. В этом разделе рассматривается голографический лазер,
активная среда которого состоит из двухуровневых атомов, находящихся в кольцевом
резонаторе. Режим КЛ может быть достигнут для двух противоположно распростра-
распространяющихся бегущих волн с помощью пространственной модуляции активной среды.
В этом случае спонтанный шум подавляется точно также, как в трехуровневых
лазерах, рассмотренных выше.
Обоснование данному варианту КЛ проистекает из области когерентной фурье-
оптики и голографии. Напомним, что в процессе создания голограммы фотопла-
фотопластинка облучается двумя пучками света, как показано на рис. 14.5а. Эти два пучка
(а)
Опорный
пучок
Объект
Считывающий пучок
Фотопластинка
* (
Мнимое
изображение
{б)
Рассеянный
свет
Фотопластинка
Рис. 14.5. Процесс создания голограммы: интерференционная картина, создаваемая объ-
объектным и опорным (записывающим) пучком, записывается на фотопластинке (а); после
проявления опорный (теперь уже считывающий) пучок рассеивается на голограмме, созда-
создавая мнимое изображение объекта (б)
света (опорный и объектный) интерферируют, создавая на фотопластинке гологра-
фическое распределение плотности или модуляцию. Затем информация, записанная
на фотопластинке, считывается при подаче исходного (теперь уже считывающего)
опорного светового пучка, который рассеивается слоями полученной голограммы,
создавая, таким образом, новый объектный пучок (рис. 14.56).
По аналогии можно ожидать, что слоистая активная среда будет создавать силь-
сильную связь между двумя противоположно распространяющимися модами кольцевого
лазера. Эта взаимосвязь будет такой, что две моды станут сильно коррелированными
и можно ожидать, что эта корреляция перенесется также и на квантовые характе-
характеристики поля. Такой тип кольцевого лазера называется поэтому гол ©графическим
лазером (ГЛ).
14.4
Голографический лазер
337
В ГЛ активная среда, находящаяся в кольцевом резонаторе, состоит из тонких
слоев (см. работы Scully, 1987; Raja, Brueck, Scully and Lee, 1991), разделенных
одинаковым пространственным интервалом (рис. 14.6). Когерентное взаимодействие
двух противоположно распространяю-
распространяющихся мод кольцевого резонатора воз-
возникает в результате обратного рассея-
рассеяния. При рассеянии назад света од-
одной моды слоем усиливающей среды
получается конструктивная интерфе-
интерференция, если фазы отраженной части
пучка и противоположно распростра-
распространяющегося пучка согласованы. Два по-
поля в кольцевом резонаторе можно опи-
описать волновыми векторами &i, к2, с ча-
частотами */]_, v2 и амплитудой So, кото-
которую будем полагать одинаковой у обо-
обоих пучков, так что
Ег = Soexpftfaz- Pit)},
A4.4.1)
При отражении в момент времени to,
фазы двух пучков должны быть рав-
равными, с точностью до целого кратного
' Зеркала
Усиливающая среда
Слои активных
атомов
A4.4.2)
где zq — координата отражающего
слоя. Отсюда получаем
(Jfci+A^o-^i-^^o = 2ttj. A4.4.3)
Поскольку v\ = i/2, условие на zq име-
имеет вид
го = _М_ = ^, A4.4.4)
ибо к\ ^ к2.
Из этого эвристического рассуж-
рассуждения мы заключаем, что слои уси-
усиливающей среды должны быть рас-
пол ожены в точках z = (tt/Ic)j, для
того чтобы была максимальная связь
между модами. Фактически, такой же
результат получается и из детального
анализа.
Как и в предыдущих линейных тео-
ч
-«-
Рис. 14.6. Голографический лазер. Слоистая
среда помещается в кольцевой резонатор. Две
моды бегущей волны частично отражаются
различными атомными слоями. Отраженный
свет конструктивно интерферирует с противо-
противоположно распространяющейся модой, подав-
подавляя фазовый шум. (Из работы Krause and
Scully A987))
риях лазеров, основанных на эффекте
Ханле и квантовых биениях, будем описывать обе моды операторами рождения
и уничтожения ai, af и a2l aj. Обе моды взаимодействуют с одними и теми же двух-
двухуровневыми атомами усиливающей среды. Здесь допустим, что собственные частоты
«пустого резонатора» ис\ и ис2 отличаются от рабочих частот v\ и и2 лазерных полей,
338 Корреляционный лазер: концепция, теория и анализ Гл. 14
поскольку, как видно из D.1.19), это необходимо для работы лазерного гироскопа.
Взаимодействие между пучками и лазерной средой описывается гамильтонианом
^ = hucia^ai + huC2O^a2 + huja\a)(a\ + Ни
+ % E Ш*)\"Ш*э + U;{z)a+\b)(a\], A4.4.5)
J = l,2
где |а) и \b) — верхнее и нижнее атомные состояния, разделенные энергетическим
интервалом ш = ша — о^, и Uj(z) (j = 1, 2) — функции нормальных мод. В картине
взаимодействия гамильтониан сводится к следующему:
Г = Н(ис1 - vjatm + h(vc2 - У2)а+а2 + hg[\a)(b\A(z, t) + A+(z, t)\b){a\], A4.4.6)
где комбинированный оператор A(z,t) задается выражением
A(z, t) = ai exp(iAit)(/i(z) + a2 e^p(iA2t)U2(z) A4.4.7)
и Ai = lj — vi, A2 = u) — U2- Координата z отсчитывается вдоль пучков, так
что усиливающая среда простирается от z = —1/2 до z = 1/2, и предполагается,
что протяженность среды в направлении, перпендикулярном направлению пучка,
не зависит от z.
Следуя методу, изложенному в разд. 14.2 для лазера Ханле, можно вывести
следующее уравнение движения для приведенного оператора плотности поля:
р = -%{ус\ - i/i)[afai,p] - i{uC2 - ^2)[«^«2, р\-
1/2
dzn{z)[A{z)A+{z)p^2A+{z)pA{z) + pA{z)A+{z% A4A8)
-1/2
где &/ = 2rag2 /у2 — обычный коэффициент усиления, а суммирование по атомам
в резонаторе выполнено путем пространственного интегрирования с плотностью
атомов n(z). Для простоты предположим далее, что v\ = 1/2 = ^ci = ^с2 = ш-
Функции нормальных мод U±(z) и U2{z) для бегущих волн имеют вид
Ut(z) = eik\ A4.4.9а)
U2(z) = e~ik\ A4.4.96)
В этом случае уравнение A4.4.8) сводится к A4.2.22) с ф = 0. Коэффициенты a^j
для голографического лазера задаются выражениями
1/2 1/2
Г Г
aj:j=^ n(z)\Uj(z)\2 dz = si n(z)dz (j = 1,2), A4.4.10)
j j
-1/2 -1/2
1/2 1/2
a12 = a*21 = si I n{z)U1{z)U2{z)dz = si I n(z)e2ikzdz. A4.4.11)
-1/2 -1/2
Как показано для лазера Ханле, коэффициент диффузии D$$ относительной фазы
#1 — #2 равен (выражение A4.2.36))
2Dm = -Цац + а22 - а12 е^ - а21 ew), A4A12)
где мы предположили, что (п\) = (п2) = (п).
14.5 Квантовые флуктуации фазы и амплитуды 339
Если усиливающая среда не является пространственно модулированной, то есть
n(z) = по, то величины «12 и «2i получаются порядка скц/fe, то есть являются очень
малыми на оптических частотах по сравнению с ац и в выражении A4.4.12) ими
можно пренебречь. В этом случае мы не получаем подавления шума относительного
фазового угла и из A4.4.12) имеем
2Dm = ?ii A4.4.13)
Из A4.4.10) и A4.4.11) следует, что модуляция, при которой коэффициенты усиления
равны между собой, должна быть такой, чтобы плотность атомов была велика,
главным образом, в тех точках, где expBifez) с± 1, т.е. в точках z = nj/k^ где
j — целое число. В принципе, хотелось бы иметь ^-функции в этих точках, но на
практике получатся пики плотности, имеющие ширину А. Если предположить, что
эти пики имеют гауссову форму (см. Krause and Scully, 1987), то функция плотности
n(z) между точками z = -1/2 и z = 1/2 будет выглядеть следующим образом:
In2
= Е ^п(—) аехр -дз-{*-р
i L
где jo = 1к/2ж и по — константа.
В этом случае получаем для интегралов из A4.4.10) и A4.4.11) следующие выра-
выражения:
1/2
f n(z)dz = n0, A4.4.15а)
-1/2
1/2 / л2 2\
| n(z)e2ikzdz = noe^p(^^^) . A4.4.156)
-1/2
Видно, что интегралы приблизительно равны, если ширина А намного меньше 1/к.
Этот результат (выражение A4.4.15)) остается справедливым и тогда, когда лишь
каждый п-й пик (п — положительное целое) в формуле A4.1.14) отличен от нуля. Из
A4.4.10) и A4.4.11) сразу видно, что все коэффициенты усиления равны между собой
(оц = «22 = ol\2 = tt2iM чт0 и требуется для получения нулевого коэффициента
диффузии
14.5. Квантовые флуктуации фазы и амплитуды
Как показано в гл. 2, сжатые вакуумные флуктуации поля излучения связаны
с разложением амплитуды электрического поля на косинусоидальную и синусоидаль-
синусоидальную составляющие. Это означает, что оператор уничтожения для электрического
поля записывается в виде а = а\ + Ш2? гДе oi и «2 — эрмитовы амплитуды
двух квадратурных составляющих. Квантово-механические свойства этих амплитуд
предполагают соотношение неопределенностей
АагАа2 ^ 1/4. A4.5.1)
Сжатыми состояниями света являются состояния, для которых
(AaiJ или (Аа2J < 1/4. A4.5.2)
Это есть стандартное определение сжатия.
340
Корреляционный лазер: концепция, теория и анализ
Гл. 14
Флуктуации амплитуды и фазы являются величинами, представляющими фу и™
даментальный интерес для лазерной физики. Как показано в гл. 11, в области суще-
существенно выше порога флуктуации амплитуды достаточно малы, и происходят вокруг
постоянного значения, которое в полу классическом приближении равно \/(п), где
(п) — среднее число фотонов в стационарном состоянии. Далее мы будем связывать
флуктуации фазы и амплитуды в лазере с эрмитовыми операторами а\ и а^. Сначала
приведем рассуждения, использующие простую полу классическую картину лазерно-
лазерного излучения.
Ima
-> Re a
Рис. 14.7. Амплитудная 8а\\ и фазовая ё$ флуктуации комплексной амплитуды а
Пусть флуктуация <5ац, как показано на рис. 14.7, соответствует чисто амплитуд-
амплитудной флуктуации величины а. Из простых тригонометрических соображений получа-
получаем следующие соотношения:
Sa\\ = \8а\ co
8а± = \8а\ si
ёа е
2г
A4.5.3)
A4.5.4)
где 8а = \8а\ ехр(г$). В этих формулах #0 — мгновенная фаза полуклассического
электрического поля и § — фаза флуктуационного смещения 8а. Члены 8а\\ и 8а±
относятся к следующим зависящим от #о амплитудам:
A4.5.5)
A4.5.6)
В этих амплитудах узнаются стандартные квадратуры а\ и <22, повернутые на угол
#о п0 отношению к направлению, задаваемому амплитудой а электрического поля.
Для флуктуации, приводящих к малому изменению фазы 8$ и амплитуды <5г, имеем
а е
а е~*1
2
уо _
*
а
*
а
е
i'&n
е и
8а\\ =
A4.5.7)
A4.5.8)
14.5 Квантовые флуктуации фазы и амплитуды 341
Здесь на последнем этапе мы заменили величину а полуклассическим выражением
\/{п), поскольку в повернутой системе координат ее фаза равна нулю, и аппрок-
симировали значение тангенса значением аргумента. Эти соотношения позволяют
приблизительно отождествить флуктуации амплитуды и фазы с флуктуациями за-
зависящих от фазы величин <2i(#q) и o^^q).
До этого момента наши рассуждения были полуклассическими. Теперь распро-
распространим наши выводы на квантовый случай. С этой целью заменим классические
амплитуды а и а* в выражениях A4.5.5) и A4.5.6) бозе-операторами уничтожения
и рождения а и а+, и свяжем фазу #о с поворотом эрмитовых наблюдаемых. Такое
унитарное преобразование оставляет коммутационное соотношение без изменения,
т.е. [ai(#o)? ^2(^0)] = */2, и можно видеть, что соотношение неопределенности
A4.5.1) инвариантно относительно произвольных поворотов на угол #q. Это озна-
означает, что обобщая полуклассические флуктуации амплитуды и фазы, мы получаем
следующие квантово-механические выражения:
{EамJ) = <Да?@о)>, A4.5.9)
= ^у(Да^о)}, A4.5.10)
где правые части выражений A4.5.9) и A4.5.10) являются здесь квантово-механичес-
кими дисперсиями операторов ai(#o) и а2(^о)- Из этих определений и соотношения
A4.5.1) получаем следующее соотношение неопределенностей между фазой и ампли-
амплитудой:
J> ? ^. A4.5.11)
Отметим, что это определение свободно от проблем, связанных с попытками скон-
сконструировать оператор квантовой фазы. Оно имеет ясный физический смысл и свя-
связывает простым образом флуктуации фазы и амплитуды с точно определенными
квантово-механическими наблюдаемыми а^ и й2-
Квантово-механические дисперсии Да?(#о) {i = 1, 2) можно переписать в виде,
содержащем лишь нормально упорядоченные операторы (нормально упорядоченные
дисперсии) и вклад коммутатора:
Да2@о) =: Aa?(tfo) : +\. A4.5.12)
Такое представление квантово-механических флуктуации окажется крайне полез-
полезным при рассмотрении работы К Л с учетом эффектов сжатия. Напомним, что сжа-
сжатыми состояниями света являются состояния, в которых : Аа^(#о) : или : Аа|(#о) :
меньше нуля.
Используя A4.5.12), можно переписать A4.5.9) и A4.5.10) в следующем виде:
((ИJ) = Щ + (:М2:)- A4-5.13)
(Fallf) = \ + (:Eallf:), A4.5.14)
где символические выражения (: F$J :) и (: (<5«цJ :) обозначают нормально упо™
рядоченные дисперсии величин ai($o) и «2(^0O как в формулах A4.5.9) и A4.5.10).
В сжатых состояниях эти «нормально упорядоченные» флуктуации фазы и ампли-
амплитуды становятся отрицательными.
342 Корреляционный лазер: концепция, теория и анализ Гл. 14
Появление нормально упорядоченных операторов в наших выражениях полезно
в том отношении, что всякий раз, когда подразумевается нормально упорядоченное
квантовое среднее значение, естественным образом используется Р-представление.
14.6. Двухфотонный корреляционный лазер
До сих пор мы рассматривали схемы коррелированного спонтанного излучения,
в которых создается корреляция актов спонтанного испускания в две различные
моды поля излучения, так что относительная фаза между ними не диффундирует.
В данном разделе мы рассмотрим другой тип корреляционного лазера, в котором
каскадный переход трехуровневых атомов (рис. 14.8) связывается лишь с одной модой
Приготовление
состояния Двухфотонный КЛ
Рис. 14.8. Схема двухфотонного корреляционного лазера. Приготовление состояния (пер-
(первый резонатор) отделено от работы лазера (второй резонатор). В первом резонаторе атомы
приготовляются в когерентной суперпозиции путем, например, прохождения через фольгу
или около острия ножа, или путем оптической накачки. Затем они вводятся во второй резо-
резонатор, где происходит лазерная генерация. Два перехода \а) —>> \Ъ) и \Ь) —ь \с) связываются
одной модой поля излучения
поля излучения. В этой схеме можно не только снизить шум спонтанной фазовой
диффузии ниже предела Шавлова—Таунса, но и получить сжатие фазового шума.
14.6.1. Теорим. Данная схема подразумевает, что в лазерный резонатор со скоро™
стью г а вводятся трехуровневые атомы, имеющие каскадную конфигурацию у ров-
го) /. ч @) | @) /. ,ч
ней, населенности ри [г = а, с) и начальную когерентность рас! = \рас ехр(г<р).
Предполагается, что частота перехода на промежуточный уровень \Ь) отстроена от
лазерной частоты v на величину А, то есть А = cj^c ~~ ^ и шас = 2*л Гамильтониан
в представлении взаимодействия имеет вид
Г = П{ис - и)а+а + hg(a e~iAt\a)(b\ + a eiAt\b)(c\ + эх.), A4.6.1)
где i/c — собственная частота пустого резонатора.
Следуя методу, использованному при выводе основного уравнения для приве-
приведенного оператора плотности поля р в случае лазера Ханле, получаем следующее
уравнение в рассматриваемом случае:
р = {
+ р{^(ра+а+ - а+ра+) + pi°J(paa - ара)] + эх.} - %{ус - и)[а+а, р], A4.6.2)
где jSf = 7/G - гД) и ^ = 2rag2/j2.
Для того чтобы изучить фазовый шум, преобразуем уравнение A4.6.2) в эквива-
эквивалентное уравнение Фоккера^Планка для Р-распределения Р(а, а*). Как и в случае
лазера Ханле предположим, что можно пренебречь амплитудными флуктуациями.
Соответствующее уравнение Фоккера^Планка относительно фазовой переменной $
получается подстановкой а ~ у/(п) ехр(г#), где (п) — среднее число фотонов в поле.
14.6 Двухфотонный корреляционный лазер 343
Результат имеет вид (задача 14.4)
Ж'-М^П + ^чП A4.6-3)
где
d* = Im{ - f>[p&> - pW] - i{uc -„) + f?(J? - _S?>(°> e™}, A4.6.4)
D™ = (?)f {^ + ^>i°2 +2Re[p(°a)^e2^]}. A4.6.5)
Условие синхронизации фаз можно получить из следующего уравнения для фазы:
^<0> = <d*> = -^|jgf|2[pW - р(°) - 2|p(°a)|(cos(^ - 20))] + «/ - *с. A4.6.6)
Из A4.6.6) получаем уравнение затягивания частоты,
«/ = ^ + ^Иа[рЙ>-р?)], A4.6.7)
и уравнение синхронизации фаз,
^f p<°>Kcos(^ - 20)). A4.6.8)
Синхронизация фаз имеет место для
f J A4.6.9)
Это значение # гарантирует, что d(d#)/dt < 0 при # = #0.
При условии синхронизации фаз A4.6.9) коэффициент диффузии принимает вид
A4-6.10)
Ясно, что вклад атомной когерентности, в отличие от вклада населенности, зависит
от расстройки. Режим К Л получается тогда, когда раа = \рсаЩ/l- При pad <
< I Pea AI/7 имеем ?)(i?o) < 0 и можно получить, как показано ниже, фазовое сжатие.
Ранее было показано, что неопределенность фазы в стационарном состоянии
равна
<ИJ> = щ + 0 0МJ:>, A4-6.11)
где первый член соответствует дробовому шуму, вызванному вакуумными флукту-
ациями, а второй член — шуму спонтанного излучения. Для того чтобы связать
коэффициент фазовой диффузии с шумом фазовой переменной лазера, получим из
уравнения Фоккера-Планка уравнение движения для (: (S'dJ :) в виде
ff(: EtiJ :) = 2(: d#60 :> + 2(Dm), A4.6.12)
где 5$ = i? — (#). В стационарном состоянии фаза запирается в среднем значении
& = #о? Для которого d$0 = 0. Это значение стабильно, если dd$Q/дё < 0. Разлагая
в A4.6.12) величину d# в точке #о в РЯД с точностью до членов первого порядка, то
есть
d6~d6o +^50 = ^60, A4.6.13)
344 Корреляционный лазер: концепция, теория и анализ Гл. 14
получаем
|^р. A4.6.14)
Подставляя это значение в A4.6.11) получаем, что стационарное значение дисперсии
фазы равно
dd$
-i
Таким образом, при стабильной синхронизации фаз знак величины (D$$) определяет,
будет ли добавочный шум, обусловленный спонтанным излучением, добавляться или
вычитаться из вакуумного шума. При (D##) < 0 фазовые флуктуации сжимаются
ниже вакуумного уровня. Подставляя в A4.6.15) выражения A4.6.10) и A4.6.4)
для D($o) и (d"&)i соответственно, получаем общий фазовый шум в стационарном
состоянии:
ЫШ (шиб)
Следовательно, фазовое сжатие в лазере получается при paaj < \рас: |А.
Для того чтобы показать, что сжатие и усиление в лазере совместимы, отметим,
что линейный коэффициент усиления G двухфотонного КЛ, определяемый уравне-
уравнением
*® A4.6.17)
можно найти из A4.6.2). Результат имеет вид
G = ^\Щ2 Ш - Рс7] - —ШI sin@ - 2#) \. A4.6.18)
I I ^аа ГСС J ^ |Гас W /J \ /
Выралсение содержит два вида членов: s^\J^\2 [раа — Рсс] — обычный коэффициент
усиления, а оставшаяся часть — зависящий от фазы добавочный коэффициент,
обусловленный коррелированным излучением. При условии синхронизации фаз ко-
коэффициент G принимает вид
G = ^И2 {[pW - pg)] + ^|^} . A4.6.19)
Оптимизация этого выражения в отношении |А|/7 дает, что максимум усиления
получается при
М = ^^ A4.6.20)
При выводе этого условия мы учли, что |J?|2 зависит от |Д|/7 и положили \рас \2 =
@) @) @) @) 1 т-1
= Раа Рсс при ркаа + рсс = 1- Ьсли это условие выполняется, то
), A4.6.21)
Эти выражения для коэффициента усиления и фазового шума необыкновенно
просты. Усиление определяется лишь населенностью верхнего уровня и не зависит от
начальной населенности нижнего состояния |с). Поэтому возможно результирующее
усиление вынужденного излучения и, следовательно, лазерная генерация, даже в
14.6
Двухфотонный корреляционный лазер
345
отсутствии инверсии. Причиной этого является квантовая интерференция, возни-
возникающая из-за исходного состояния атомной системы в когерентной суперпозиции
состояний. Эта интерференция исключает поглощение излучения атомами, разрешая
тем не менее испускание. Из выражения A4.6.22) для фазового шума видно, что
фазовое сжатие имеет место при 0 < раа < 0,5, причем максимальное 50%-ное
сжатие получается при pal — 0. Таким образом, сжатие совместимо с усилением, что
означает возможность создания мощного источника сжатого света.
14.6.2. Эвристический расчет двухфотонного КЛ. Как описано выше, двухфо-
двухфотонный КЛ состоит из когерентно приготовленных трехуровневых атомов, взаи-
взаимодействующих с одной модой поля резонатора. Например, атомы можно ввести
в резонатор, предварительно приготовив их в когерентной суперпозиции атомных
состояний (рис. 14.8). Эта атомная когерентность приводит к «коррелированному
излучению» на последовательных переходах \а) —>• \Ь) и \Ь) —> \с). Складывая вклады
переходов \а) —» \Ь) и \Ъ) —> |с), находим, что фаза результирующего электрического
поля не зависит от фазы состояния \Ь) и (спонтанно) излучаемое поле определяется
лишь когерентностью между верхним и нижним состояниями. В момент спонтан-
спонтанного испускания атом совершает спонтанный переход, например из состояния \а)
в состояние \Ь). Вследствие случайного характера этого перехода, приобретаемая
фаза состояния \Ь) не определяется атомной когерентностью и является совершенно
случайной. Однако при последующем переходе из состояния \Ъ) в состояние \с) атом
«вспоминает» произвольную фазу состояния |6), так что, в коррелированном лазе-
лазере, фазовая когерентность двухфотонного перехода сохраняется. Другими словами,
шум, созданный спонтанным переходом из состояния \а) в состояние |6), компенси-
компенсируется последующим переходом из \Ь) в |с), так что суммарное электрическое поле
всегда имеет одну и ту же фазу (рис. 14.9). Эта фаза полностью определяется атом-
А
Фас/2
Рис. 14.9. Два события спонтанного излучения в двухфотонном КЛ, вклады которых в элек-
электрическое поле обозначены через векторы Ь$\ и 6^2 на комплексной (^-плоскости, оставляют
фазу результирующего электрического поля неизменной. Таким образом, фазовый шум
не добавляется
ной когерентностью между верхним и нижним состояниями. Следовательно, в КЛ
подавляется «шум», создаваемый актами спонтанного излучения, чем и объясняется
снижение фазового шума в двухфотонном КЛ.
Чтобы сделать рассуждения более конкретными, объясним теперь с помощью
несложных рассуждений, каким образом атомная когерентность может привести
346 Корреляционный лазер: концепция, теория и анализ Гл. 14
к значительному снижению фазового шума в двухфотонном коррелированном ла-
лазере, и выведем уравнения, подтверждающие наши наглядные, физически интуи-
интуитивные рассуждения.
Рассмотрим сначала трехуровневый атом (рис. 14.8), взаимодействующий резо-
резонансно с одной модой поля излучения на переходах \а) —>• \Ь) и \Ь) —> \с). Предполо-
Предположим, что до взаимодействия с полем излучения создана когерентность между тремя
уровнями, так что вектор атомного состояния можно записать в виде
\t/>(t)) = са е{фа e~iuJat\a) + съ ei<t>b e~iuJbt\b) + сс е*ф° е^Шсг\с), A4.6.23)
где са, С5 и сс — действительные числа. Поляризация на переходе \а) —> \Ь) задается
выражением (см. E.4.6))
Pab{t) = p\Pab\ е-«ш*-ф*ь) + к.с. = 2р\раЬ\ cos(ujt - фаЬ), A4.6.24)
где
P = erba. A4.6.25)
Последняя часть A4.6.24) записана в предположении, что матричный элемент гьа
является действительным. Кроме того, использованы обозначения фаЬ = фа ^ Фъ
и ш = ша — шь. Аналогично для перехода \Ь) —> \с) находим
Pbc(t) = 2p\pbc\ cos(ut - фЬс). A4.6.26)
Для простоты рассмотрим резонансный случай, когда частота переходов \а) —$> \Ь)
и \Ь) —> \с) совпадает с частотой поля излучения. Кроме того, положим Г5а = ^сЪ-
Полная поляризация атома определяется тогда суммой Раъ{$) и Pbcif)'-
P(i) = 2p[\pab\ cos(ujt - фаЬ) + |рЬс| cos(ujt - фЬс)} = 2pl cos(out - ф0), A4.6.27)
где
I = \/\раъ\2 + \рьс? + 2|раЬ||р6с| cos(^ab - фЪс). A4.6.28)
Фаза фд поляризации задается выражениями
COS <^о = (\Pab\ COS фаь + \pbc\ COS фьс)/1, A4.6.29)
sin ф0 = {\раь\ sin фаь + \pbc\ sin фьс)/1- A4.6.30)
В частном случае, когда величина \раь\ равна \pbc\t выражения A4.6.28) и A4.6.30)
можно упростить:
I = 2\pab\ cos[D>ab - фЬс)/2]. A4.6.31)
Используя тригонометрические тождества cos a + cos/3 = 2cos[(a + /3)/2]cos[(a —
- 15)/2} и sin a + sin j5 = 2 sin[(a + /3)/2] cos[(a - /3)/2], находим
<Ao = \{ФаЬ + ФЬс) = \фас- A4.6.32)
Видно, что фаза поляризации атома совершенно не зависит от фазы фь. Этот ре-
результат окажется важным при обсуждении влияния на систему актов спонтанного
излучения. Поскольку испущенное электромагнитное поле пропорционально атомной
поляризации, можно заключить, что в двухфотонном КЛ вектор электрического
поля определяется фазой ф®^ задаваемой выражением A4.6.30). Это показано на
рис. 14.9.
Обратимся теперь к анализу шума спонтанного излучения. Хотя чисто полу-
полуклассическая теория не объясняет спонтанное излучение, представим последнее сле-
следующим образом. При спонтанном переходе атома из возбужденного состояния \а)
П. 14.А Спонтанный шум в лазере квантовых биений 347
в промежуточное \Ь) создается поляризация
Pab(t) = 5Pcos(ujt - fab). A46.33)
Здесь SP — поляризация атома, приходящаяся на один фотон и ^аъ = фа ^ Сь-
Отметим, что в отличие от вынужденного перехода, фаза ?& не определяется фазой
фъч а является совершенно произвольной. Этим моделируется случайный характер
актов спонтанного излучения. Последующий спонтанный переход атома из состояния
\Ъ) в состояние \с) характеризуется аналогичной поляризацией атома:
Pbc(t) = 5Pcos{ujt - f6c), A46.34)
где ^5с = Сь — Фс- Полная поляризация и, следовательно, полный вклад спонтанного
излучения в электромагнитное поле получается в результате сложения A4.6.33)
и A4.6.34) и оказывается пропорциональным
P(t) ос SPcos(ujt - fac). A46.35)
Видно, что случайная фаза ?& сокращается, и что суммарная поляризация всегда
имеет фазу фаа которая задается атомной когерентностью. Это показано на рис. 14.9.
Каждый шумовой вклад спонтанного перехода \а) —>> \Ь) компенсируется вкладом
последующего перехода \Ъ) ~~> \c) таким образом, что результирующая фаза (корре-
(коррелированного) двухфотонного излучения равна фас для всех атомов. Следовательно,
если фаза двухфотонного шума совпадает с фазой поля излучения, то все вклады
двухфотонного шума имеют одинаковую фазу, то есть «свободны» от шума. Это
и есть полное подавление шума в двухфотонном корреляционном лазере.
Приложение 14.А
Спонтанный шум в лазере квантовых биений
Система атомов и поля в лазере квантовых биений описываются тем же гамиль-
гамильтонианом, что и в лазере Ханле, то есть выражениями A4.2.4), A4.2.5) и A4.2.6).
Однако имеется дополнительный член в Ж\, возникающий вследствие взаимодей-
взаимодействия когерентного поля с атомной системой, который имеет вид
где Од — частота Раби и Ф — фаза матричного элемента дипольного момента. Главное
отличие данной схемы от лазера Ханле состоит в том, что атомы, возбужденные
некогерентно в состояние |а), переводятся внешним полем в когерентную суперпо™
зицию верхних состояний, тогда как в случае лазера Ханле атомы уже находятся
в когерентной суперпозиции состояний до начала взаимодействия с лазерным полем.
Гамильтониан в картине взаимодействия записывается в виде
V = %(aj eiAt\a){c\ + а2 eiAt\b)(c\) - ^ е-**|а)<Ь| + э.с, A4.А.2)
где А = ша — шс — и\ = ujfj — u)c ~~ U2 — расстройка между полем и атомами, и мы
для простоты предположили, что v\ — u<i = 1/3 = ^ab- Уравнение движения для
приведенного оператора плотности поля можно получить, как и прежде, взяв след
по атомным переменным:
Р = -у:(№с, Pea] + [%c, Pcb] + [%а, Рас] + [%b, Pbc])- A4.A.3)
348 Корреляционный лазер: концепция, теория и анализ Гл. 14
Матричные элементы оператора плотности рас и р^с получаются из решения следую™
щего матричного уравнения:
R = -MR - igA eiA\ A4.A.4)
где
A4.А.5)
м=\ т. ... 2 Ь A4А-6)
\а2Рсс ~ Pbba2 ~~ РЪаа1/
Ясно, что здесь, в отличие от случая лазера Ханле, элементы рас и рьс связаны
внешним полем Пцехр(гф) даже в нулевом порядке по константе взаимодействия g.
Решение уравнения A6.А.4), линейное по g, имеет вид
t
R(t) = ^ig I dt0 e-M(^t®)AeiAto = -ig{M + iAI^A eiA\ A4.A.8)
J
— oo
где / — единичная матрица. Здесь
где D = G + *АJ + ^я/4. Тогда из A4.А.5)-A4.А.7) следует, что
Pac{t) = ~Щ G +
eiA\
^ e^(aipcc - Раа
+ G + iA)(a2pcc -
Следующий шаг состоит в нахождении paai p^, рсс и раъ в нулевом порядке по
g. Поскольку атомы первоначально возбуждаются в процессе накачки в состояние
\а) со скоростью го, имеем рсс = 0, и величины paa, р^ь и Раб определяются при
полуклассическом рассмотрении перехода \а) —> \Ъ) в произвольном порядке по Од.
Уравнения движения для матричных элементов оператора плотности имеют вид
R = -MR + B, A4.A.12)
П.14.А
Спонтанный шум в лазере квантовых биений
349
где
fPaa
д = I Pab
М =
.«.„..
\
О
A4.А.13)
2 2
Решением уравнения A4.A. 12) является
t
[ dtoe-X7('-'o)B =
7 /
A4.А.14)
A4.А.15)
Для нахождения Д необходимо найти лишь Мп , М21 , М31 и М41 . Вычисляя эти
элементы и подставляя их в A4.А. 15), получаем
A4.А.16)
Pab = raM2{p = -—f^^UR e^^p, A4.A.17)
Рьь = тамА{р = -^№р, A4.А.18)
\м\
Подставим теперь выражения A4.А.16)-A4.А.18) для элементов раа, ръъ и раь,
учитывая, что рсс = 0, в формулы A4.А.10) и A4.А.11). Результирующие выражения
для рас и р5с5 а также комплексно сопряженные им, можно, в свою очередь, подста-
подставить в A4.А.3). Тогда получаем следующее уравнение движения для приведенного
оператора плотности поля:
р = ^
где
— а~1 ра2)
э-с-? A4.А.19)
«и =
B72
«12 =
7 -
: = д^(П-<7)-7-»(А+ Он/2)
350 Корреляционный лазер: концепция, теория и анализ Гл. 14
«21= g2ra fBj2
Y + (A-UR/2Y
i о_/ом ^ A4_д_22)
a22 = 27G'+tf,H -3,:: г::;а("-'7)+.уа. ;г:г::уа("+'7) ^ A4.А.23)
Отметим, что уравнение A4. А. 19) для лазера квантовых биений совпадает по виду
с уравнением A4.2.22) для лазера Ханле. Однако коэффициенты aij (г = 1, 2) в слу™
чае лазера квантовых биений являются более сложными. Как и при рассмотрении
лазера Ханле, уравнение A4.А. 19) можно преобразовать в эквивалентное уравнение
Фоккера-Планка для /^распределения. В пренебрежении флуктуациями амплитуды
получаем уравнение вида A4.2.33) в переменных относительной # = i^i — #2 и средней
^ = (#1 + #2)/2 фазы.
Режим КЛ достигается в лазере квантовых биений при выполнении следующих
условий:
Д = ^, Пд»7, A4.А.24)
то есть, величина расстройки должна быть равна половине частоты Раби возбуж-
возбуждающего поля, которое когерентно смешивает состояния \а) и |6), и обе эти величины
должны существенно превышать скорость затухания атомов. При этих условиях
2
Re an = Re а22 ~ ^г, A4.А.25)
27
^ A4.A.26)
7
Тогда из A4.2.36) в случае (fii) = G12) = (п) получаем
?)^~^(l-cos^), A4.A.27)
где &/ = 2g2ra/j2 — обычный коэффициент усиления и ф = $ — <^>. Коэффициент
диффузии обращается в нуль, если ^ = 0.
Задачи
14.1. Рассмотрим двухфотонный КЛ, в котором атомы вводятся в резонатор, имея
@) @) @)
начальные населенности paaj Ръъ •> Рсс и начальные когерентности
@) @)* | @), /. , ч @) @)* | (О). /• , х
Pab = Pba = \Раь\ехР(гФаь), РЬс = РСЬ = \Pbc I ехР(г<1>Ьс),
о@) _ @)* _ \п@)\е (АЛ )
Рас ~~ Рса — \Рас I G^P\l(Pac) ?
где |a), \b) и |с) соответствуют верхнему, среднему и нижнему уровням трех-
трехуровневой системы с каскадной конфигурацией переходов. Предположим, что
расстройки Шаь — и и ш^с — ^ равны нулю. Найдите условие синхронизации фаз
и фазовый шум ((S'dJ) в стационарном состоянии при наличии этой синхро™
низации. Определите условия, при которых достигаются режим К Л и фазовое
сжатие. (Указание: см. работу Scully, Wodkiewlcz, Zubairy, Bergou, Lu and Meyer
terVehn A988).)
Задачи к гл. 14 351
14.2. Рассмотрим двойной двухфотонный КЛ, в котором четырехуровневые ато-
атомы (см. рис. 14.10) вводятся в резонатор, имея начальные населенности pad,
@) @) @) @) @) г @) @)* @)
Рсс, Рм и начальные когерентности pyj, pKJ, pxj [р]/ = р\/ и р\/ =
= \р\л \ exp(i«^jj)]. Состояния \с) и \d) рассматриваются как почти вырожденное
состояние. Предполагается, что имеет место двухфотонный резонанс, а в отно-
отношении однофотонного резонанса уровень \Ь) смещен по частоте на величину А.
Выведите уравнение движения для приведенного оператора плотности поля.
Найдите условие синхронизации фаз и стационарное значение фазового шума
((ё$J). Покажите, что при оптимальных условиях фазовое сжатие совместимо
с инверсией населенностей. (Указание: см. работу Bergou, Benkert at.al. A990).)
14.3. Рассмотрим следующее общее уравнение Фоккера^Планка для Р-распределе-
ния:
где da = Ra + С*а*, Daa = (Da*a*)* = \D\ exp(i^>a), a R и G — совершенно
произвольные комплексные параметры. В полярных координатах это уравнение
переписывается в виде
дР 1 д ( т д , m 1 д ( дР.
Найдите drj d#, Drr, D$$ и Dr#, выразив их через Я, С, \D\ и фа. Найдите
условие синхронизации фаз и затем условие полного подавления фазового шу-
шума. Пренебрегите флуктуациями амплитуды, т.е. замените г величиной \/(п).
14.4. Выведите коэффициенты диффузии Daaj Da*a и Da*a*^ соответствующие
уравнению для оператора плотности поля A4.6.2), используя соотношения
Эйнштейна, а также уравнение Фоккера^Планка для Р(аа*). Используя эти
результаты, найдите
14.5. 1. Покажите, что для лазера квантовых биений, описываемого уравнением
A4.А. 19) для оператора плотности поля, в котором 0 = 0, имеют место
уравнения
-
2. Используя полученные уравнения, выведите уравнение вида A4.3.1) для
относительной фазы § = §г — §2^ записывая {а\) = у/{п) exp(i#i — ivit),
(«2) = \/{п) exp(i#2 — ivi€). Покажите также, что все a^j (h j = 1, 2)
равны нулю.
352 Корреляционный лазер: концепция, теория и анализ Гл. 14
Список литературы
Лазер квантовых биений
Scully, M. О. Phys. Rev. Lett 55, 2802 A985).
Scully, M. О. and Zubatry, M. S. Phys. Rev. A 35, 752 A987).
Bergou, J., Orszag, M. and Scully, M. O. Phys. Rev. A 38, 754 A988).
Zaheer, K. and Zubalry, M. S. Phys. Rev. A 38, 5227 A988).
Swain, S. J. Mod. Opt 35, 1 A988).
Ansari, N. A. and Zubalry, M. S. Phys. Rev. A 40, 5690 A989).
Rathe, U. W. and Scully, M. O. Phys. Rev. A 52, 3193 A995).
Лазер Ханле
Bergou, J., Orszag, M. and Scully, M. O. Phys. Rev. A 38, 768 A988).
Dalton, B. J. In New Frontiers in Quantum Electrodynamics and Quantum Optics, ed. A. O.
Barut (Plenum Press, New York 1990), p. 167.
Голографический лазер
Krause, J. and Scully, M. O. Phys. Rev. A 36, 1771 A987).
Scully, M. O. Phys. Rev. A 35, 452 A987).
Brueck, S. R. J., Raja, M. Y. A., Orsinki, M., Schaus, C. F., Mahbodzadeh, M. and Dahlhaus,
K. J. SPIE 1043, 111 A988).
Raja, M. Y. A., Brueck, S. R. J., Scully, M. O. and Lee, С Phys. Rev. A 44, 4599 A991).
Двухфотонный корреляционный лазер
Scully, M. О., Wodkiewlcz, К., Zubairy, M. S., Bergou, J., Lu, N. and Meyer ter Vehn, J. Phys.
Rev. Lett. 60, 1832 A988).
Lu, N. and Zhu, S. Y. Phys. Rev. A 40, 5735 A989); ibid. 41, 2865 A990).
Ansari, N. A., GearBanacloche, J. and Zubalry, M. S. Phys. Rev. A 41, 5179 A990).
Bergou, J., Benkert, C, Davldovlch, L., Scully, M. O., Zhu, S.-Y. and Zubalry, M. S. Phys. Rev.
A 42, 5544 A990).
Наглядное представление корреляционного лазера
Schlelch, W. and Scully, M. O. Phys. Rev. A 37, 1261 A988).
Schlekh, W., Scully, M. O. and von Garssen, H.-G. Phys. Rev. A 37, 3010 A988).
Фазовое сжатие
Bergou, J., Orszag, M., Scully, M. O. and Wodkiewlcz, K. Phys. Rev. A 39, 5136 A989).
Эксперименты с корреляционным лазером
Ohtsu, M. and Liou, K.-Y. Appl. Phys. Lett. 52, 10 A988).
Winters, M. P., Hall, J. L. and Toschek, P. E. Phys. Rev. Lett 65, 3116 A990).
Sterner, I., Schanz, L. and Toschek, P. E. In Proceedings of the Twelfth International Conference
on Laser Spectroscopy, Island of Capri, Italy (June 11-16, 1995).
Глава 15
ФАЗОВАЯ
ЧУВСТВИТЕЛЬНОСТЬ
В КВАНТОВЫХ ОПТИЧЕСКИХ
СИСТЕМАХ: ПРИЛОЖЕНИЯ
В предыдущей главе было показано, что фазовая чувствительность, обуслов™
ленная атомной когерентностью, может привести к подавлению шума спонтанного
излучения. Ранее, в гл. 8, обсуждалась роль сжатого вакуума в установлении фазово™
чувствительного затухания. В этой главе рассматриваются возможные приложения
этих идей.
В качестве первого примера показано, что чувствительность кольцевого лазерного
интерферометра с модулированной активной средой (голографический лазер) может
быть увеличена сверх обычного квантового предела. Затем рассматривается кван™
товая теория линейных усилителей и показано, что если усилитель состоит из трех-
трехуровневых атомов, находящихся в когерентной суперпозиции атомных состояний, как
в двухфотонном КЛ, то можно получить усиление свободное от шума. В конце главы
демонстрируется, что естественная ширина линии излучения лазера уменьшается,
если поле внутри резонатора связано с резервуаром гармонических осцилляторов,
находящимся в сжатом вакуумном состоянии. Эти примеры иллюстрируют ту боль-
большую роль, которую может играть фазовая чувствительность в подавлении шума.
15.1. КЛ-гжроскоп
Развив в разд. 14.4 теорию кольцевого корреляционного лазера, вернемся к во-
просу, поставленному в начале гл. 14, а именно, в какой степени можно сделать
активный гироскоп свободным от шума спонтанного излучения? Как показано в при™
ложении 15.А, относительный фазовый угол между двумя модами кольцевого КЛ-
гироскопа (см. рис. 15.1а)
^ = (I/1_I/2)t-tf1+tf2 A5.1.1)
удовлетворяет уравнению синхронизации [уравнение A5.А. 16) при Sc = 0]
ф = Sur - <я/тпф + &ф, A5.1.2)
где S — масштабный множитель из разд. 14.1, а именно S = 4 А /Ар, где А — площадь,
охватываемая гироскопом, и р — его периметр, А = А/2тг — приведенная длина
волны, Ог — скорость вращения. Величина srf в уравнении A5.1.2) есть линейный
коэффициент усиления, одинаковый для обеих мод, а источник шума &${€) опреде™
ляется соотношением (см. приложение 15.А)
(J^(i)^(i')} = 2п(ф) S(t - *'), A5.1.3)
12 М.О. Скалли, М.С. Зубайри
354 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
где
щA-созф), (ШЛА)
и (п) — среднее число фотонов, которое будет считаться одинаковым для обеих мод.
Запишем ф в виде
A5.1.5)
где ф® — среднее значение, а 8ф — вызванное шумом отклонение от фд. Теперь
учтем, что поскольку SQ,r <С «й/, то ф® <С 1, так что в хорошем приближении имеем
sin^o — ^о? и из A5.1.2) следует, что
ф0 = 5Or/j#, когда tm ~ лГ. A5.1.6)
Кроме того, уравнение A5.1.2) означает, что флуктуации 8ф вокруг значения фд
определяются выражением
t
= I dt1 exp[^j#(t - tf)]^(tf), A5.1.7)
о
и из A5.1.7), A5.1.3) и A5.1.4) имеем
поскольку фо <С 1. Следовательно предельным источником шума теперь является
дробовой шум. Погрешность фазы тогда равна 5ф ~ 1/(пI/2, где (п) — среднее
число фотонов, детектированных за время tm, то есть (п) = Pdtm/hv, где Р^
— лазерная мощность на детекторе. В случае з/ ~ <#, величина Р^ равна общей
излучаемой мощности Р. Приравнивая погрешность дробового шума 8ф сигналу
фо, заданному выражением A5.1.6), находим наименьшее значение детектируемой
скорости вращения:
A5.1.9)
Очевидно, что предел A5.1.9) КЛ-гироскопа является обычным квантовым пре-
пределом, задаваемым выражениями A4.1.4) или A4.1.8), ибо «й^ « $. Однако отметим,
что время измерения tm в выражении A5.1.9) имеет порядок «й^, тогда как в случае
обычного квантового предела величина tm не ограничена. Таким образом, похоже на
то, что КЛ-гироскоп имеет худшую чувствительность. Но это неверно, поскольку
можно сделать так, чтобы гироскоп достиг значения ф® за время ей/™1, записать
значение фо, разблокировать гироскоп, например путем вибрации или другими спо-
способами, затем «выключить» вибрацию и позволить гироскопу опять возвратиться
к своему заблокированному значению ф®. Это можно повторить N раз за время т ^>
^> ей/^1, где N ~ т/ей/^1 = ^т. Так что, если переписать выражение A5.1.9) для
im = s?/^1 в виде
/ *..
A5.1.10)
то можно улучшить результат, умножив его на множитель 1/yiV = 1/у/&/т , и по-
получить
/ *.. -, П^
A5.1.11)
15.1
КЛ-гироскоп
355
Таким образом, предел измерений A5.1.11) КЛ-гироскопа в случае «многих из-
измерений» не ограничен короткими временами, и результат совпадает с обычным
квантовым пределом.
N
\
Е2
\
\
Модулированная среда
(а)
м6
м2
м4
Модулированная среда
Детектор
(б)
Рис. 15.1. Кольцевой корреляционный лазер, в котором корреляция создается слоистой или
модулированной усиливающей средой (а); КЛ-гироскоп, излучение которого извлекается
с помощью зеркал Mi и Л#2 и возвращается с помощью зеркал М% и Me, что приводит
к увеличению чувствительности гироскопа (б). (Из работы Scully A987).)
Однако отметим, что чувствительность КЛ-гироскопа A5.1.9) можно улучшить,
используя контролируемое обратное рассеяние (рис. 15.16). Как показано в приложе-
приложении 15.А, уравнение для ф в этом случае принимает вид
ф = Sur -{srf - %)81пф + #^(t), A5.1.12)
где
A5.1.13)
12*
356 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
Здесь р — периметр кольца, Т ~~ коэффициент пропускания зеркал Mi и М2 (см.
рис. 15.16) и Rc ~~ коэффициент отражения зеркал М^ и Mg. Теперь получаем
больший сигнал
ф0 = Jur^ , A5.1.14)
и поэтому
A5.1.15)
Наконец отметим, что мощность Р^ равна не общей излучаемой мощности Р, а лишь
{^d/^)P (гДе ^*d — ?& — ^c)j поскольку вход детектора М$ выделяет лишь часть
$dllS общей излучаемой мощности. Кроме того, множитель («й^' — <?с)/'$ в выражении
A5.1.15) равен S^jS^ так что с учетом соотношения Р^ = («f^/J^P получаем
A5.1.16)
где е = 1/y/cetm и где учтено, что t^1 ~ («я/ — (fc) = ^. Таким образом, в рамках
нашей идеальной модели чувствительность гироскопа увеличилась в е раз. Подчерк™
нем, что в данном вычислении игнорируются потери зеркал из-за поглощения $а.
Если учесть такие потери в простейших моделях, то множитель е определяется вели-
величиной Saj\$a + <?). В заключение можно сказать, что: A) КЛ-гироскоп, в принципе,
имеет чувствительность, превышающую обычный квантовый предел 1); B) этому
устройству не мешает обычная проблема захвата в «мертвой зоне», возникающая
при низких скоростях вращения.
15.2. Процесс линейного усиления: общее описание
Линейный усилитель представляет собой усилитель, выход которого линейно
зависит от входа. Такое широкое определение, требующее лишь линейности работы,
позволяет единым образом рассчитать квантовые пределы для таких устройств,
не вдаваясь в детали их внутренней работы.
Усилители играют важную роль в процессе измерения, поскольку они наводят
мост между квантовым и классическим мирами. Не считая этого, существует мно-
множество других применений. В системах связи, например, может оказаться выгоднее
заменить повторитель в оптоволоконном соединении усилителем или же использо-
использовать последний для повышения детектирующей способности приемника.
Интересный вопрос состоит в том, можно ли клонировать фотон с помощью
усилителя. Такое точное удвоение фотонов позволило бы преодолеть ограничения,
налагаемые принципом неопределенности в интерференционных и корреляционных
экспериментах. Поскольку усиление в оптических усилителях достигается за счет из-
лучательного процесса, на него неизменно оказывает влияние спонтанное излучение.
Это налагает фундаментальные квантовые пределы на отношение сигнал/шум на
выходе.
Процесс линейного усиления описывается следующим преобразованием, связы-
связывающим операторы уничтожения авх и ашъш на входе и выходе, соответственно:
A5.2.1)
1) Подобная возвратная схема, примененная к КЛ-детектированию гравитационных волн,
также увеличивает чувствительность (см. Scully and Gea-Banacloche, 1986).
15.2 Процесс линейного усиления: общее описание 357
где G — коэффициент усиления, а второй член необходим по соображениям непро-
непротиворечивости, так чтобы удовлетворить коммутационному соотношению на выхо-
выходе. Здесь F^ — оператор, удовлетворяющий коммутационному соотношению для
бозонов [F, F^~] = 1 и коммутирующий с авх. Определим теперь две эрмитовы
квадратуры Х$ и Х#+7г/2*
Дисперсии этих квадратур равны
2 f 2, A5.2.3)
/ / я/2J, A5.2.4)
где
f^^Fe^ + f+e^). A5.2.5)
Первый член в выражениях для дисперсии представляет собой усиленный шум на
входе, а второй член — добавочный шум^ обусловленный усилением. Такой, завися-
зависящий от усиления шум, есть проявление флуктуационно-диссипационной теоремы,
обсуждавшейся в разд. 9.4.
В этой связи возникает два вопроса. Первый состоит в том, могут ли на выходе
линейного усилителя проявляться неклассические свойства, если таковые имеются на
входе? Второй — может ли усилитель генерировать на выходе сжатое поле? Ответы
на эти вопросы приводят к разделению усилителей на два класса, а именно, фазово-
чувствительные и фазово-нечувствительные усилители. В фазово-нечувствительном
усилителе две квадратуры обрабатываются одинаково, то есть усиливаются в одина-
одинаковой степени и приобретают одинаковый (фазово-нечувствительный) шум. В таком
усилителе нет преимущественной фазы, и фазовый сдвиг на входе приводит к такому
же фазовому сдвигу на выходе. Наоборот, фазово-чувствительный усилитель обраба-
обрабатывает две квадратуры по-разному, добавляя разный шум. Например, добавочный
шум у одной квадратуры может быть уменьшен за счет увеличения добавочного
шума в сопряженной квадратуре.
Для усиления сигнала необходим резервуар энергии, которую можно передать
сигналу. Однако резервуар, находящийся при высокой температуре, просто давал
бы сигналу тепловой шум. Поэтому, модель усилителя включает взаимодействие
бозонной моды с резервуаром инвертированных гармонических осцилляторов. Такой
резервуар не имеет основного состояния, зато состояния инвертированных гармони-
гармонических осцилляторов имеют верхнюю границу. Этот усилитель все еще добавляет
тепловой шум в систему, поскольку состояние резервуара напоминает каноническое
распределение с отрицательной температурой. Практическая реализация этой мо-
модели состоит из множества инвертированных двухуровневых атомов. В этом случае
линейность работы означает, что происходят лишь однофотонные процессы. Ситу-
Ситуация соответствует беззеркальному лазеру, возмущенному слабым внешним полем.
В следующем разделе будут рассмотрены свойства такой системы и явно показано,
что она добавляет к сигналу фазово-нечувствительный шум.
Фазово-чувствительный усилитель можно создать путем оснащения (Stenholm,
1986) или изменения резервуара, создавая в последнем состояние сжатого ваку-
вакуума, центрированного на частоте усиливаемой моды. Бозонные моды резервуара
удовлетворяют коммутационным соотношениям (8.2.16). Основное уравнение для
358 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
усилителя, резервуар которого состоит из «сжатого белого шума», имеет вид
р = -^N{a+ap - 2ара+ + ра+а) ~~ ~-{N + 1){аа+р - 2а+ра + раа+) +
+ ^М*(аар - 2ара + раа) + ^-M{a+a+p - 2а+ра^ + ра+а+), A5.2.6)
где sz/ — коэффициент усиления. Члены, пропорциональные М или М*, отвечают
за фазовую чувствительность усилителя. Примером физической реализации фазово-
чувствительного усилителя является двухфотонный К Л. Эта система обсуждается
в разд. 15.4.
15.3. Фазово-нечувствжтельное усиление в двухуровневых системах 1)
Гамильтониан взаимодействия для любого заданного атома в представлении вза-
взаимодействия, в условиях точного резонанса и в приближении вращающейся волны,
имеет вид
A5.3.1)
Атомы вводятся в резонатор со скоростью га в состоянии некогерентной суперпози-
суперпозиции верхнего \а) и нижнего \Ь) состояний, то есть в начальный момент времени t{
/W,(i*) = P™\a)(a\ + Р(ьь]\Ь)(Ь1 A5-3-2)
@) @) r I \ IL\
где раа и pbb — вероятности возбуждения в состояния \а) и \о) соответственно.
Следуя методам, развитым в гл. 11, получаем обычное в квантовой теории лазера
уравнение движения для приведенного оператора плотности поля:
р = -^{р^}(аа+р - 2а+ра + раа+) + р^(а+ар - 2ара+ + ра+а% A5.3.3)
где ей/ = 2rag2 /j2 — коэффициент усиления, га — скорость поступления (инжекции)
атомов в состоянии A5.3.2) и 7 — атомная скорость релаксации. В данном уравнении
(о) (о) / ч
члены, пропорциональные раа и pbb , соответствуют усилению (за счет излучения)
и потерям (за счет поглощения) соответственно. Как будет показано далее, резуль-
(о) (о)
тирующее усиление достигается тогда, когда раа > р\^ •
Уравнение A5.3.3) молено решить для произвольных моментов времени. Здесь мы
воспользуемся им, чтобы получить уравнения движения для различных моментов
полевых операторов а и а+:
^ Й) A5-3-4)
A5.3.5)
| A5.3.6)
Систему уравнений A5.3.4)—A5.3.6) можно решить точно, получив следующий ре-
результат:
A5.3.7)
г) См., например, работу Caves A982).
15.4 Усиление свободное от шума 359
„(о)
(a+a)t = С(а+аH + (G - 1) {0)раа , A5.3.8)
Раа — РъЬ
(a2)t = G(a2}0, A5.3.9)
где
С = ехр(Дф<?а>-р?)]*) A5.3.10)
— коэффициент усиления. Выражения A5.3.7)—A5.3.10) можно рассматривать как
соотношения, связывающие вход и выход усилителя: среднее значение в момент
времени t есть выход усилителя, выраженный через вход (среднее значение в момент
t = 0). Ясно, что усиление имеет место (G > 1), если pal > pbb , и система действует
как аттенюатор (G < 1), если pia < р^ь •
Определим теперь две квадратуры Х$ и X#+n/2i аналогично A5.2.3) и A5.2.4),
с помощью соотношения
Х<> = \{а+е** + ае{*). A5.3.11)
Здесь умножение на экспоненциальные множители означает просто произвольное
вращение в комплексной Х-плоскости, оставляющее неизменными коммутационные
соотношения. Из A5.3.7)-A5.3.9) следует, что
(X#)t = VG {ХвH, A5.3.12)
(AXl)t = G(AX$H + (G- \)JT, A5.3.13)
где
Видно, что две квадратурные составляющие Х$ и Х^+7Г/2 подвергаются одинаковому
усилению (G\ = G2 = С), и что добавочный шум одинаков для обеих квадратур
и не зависит от угла #, то есть AJ^f = А#"| = (G — 1)^Ж. Таким образом, рас-
сматриваемый усилитель является фазово-сохраняющим, фазово-нечувствительным
усилителем. Из выражения A5.3.13) видно также, что максимальный коэффициент
усиления, сохраняющий какое-нибудь сжатие на выходе, есть
^t + f A5.3.15)
(jo + JY
так что в случае сильно сж:атого входа ((ДХ|)о = 0) и р\1 = 1 получаем Gmax =
= 2. Это значение обычно называют пределом клонирования. Таким образом, любое
сжатие на входе исчезает в процессе усиления вследствие фазово^нечувствительного
добавочного шума.
15.4. Фазово-чувствжтельное усиление с помощью двухфотонного
корреляционного лазера: усиление свободное от шума г)
В этом разделе будет рассмотрен двухфотонный линейный усилитель, фазовая
чувствительность в котором создается путем приготовления активной среды, то есть
атомов, в когерентной суперпозиции состояний.
) Следуя работе Scully and Zubalry A988).
360 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
Система состоит из трехуровневых атомов с каскадной конфигурацией переходов
между состояниями |а), \Ь) и |с). Предположим, что бозонная мода частоты v резо-
резонансна обоим атомным переходам. Гамильтониан взаимодействия в представлении
взаимодействия и в приближении вращающейся волны имеет вид
У = Пё[а+{\Ь)(а\ + |с}F|) + (И<6| + \Ь){с\)а]. A5.4.1)
Рассмотрим ситуацию, когда атомы вводятся в резонатор в когерентной суперпози-
суперпозиции состояний \а) и \с) со скоростью га. Оператор плотности атомов в начальный
момент времени равен
(с\- A5.4.2)
rj @) @)* \ I \ @)
адесь р^с = Рса — начальная когерентность между состояниями а) и |с), а раа
@)
и рсс — населенности соответствующих уровней.
Следуя той же процедуре, что использовалась в разд. 11.1, получаем следующее
уравнение движения для приведенного оператора плотности:
р = -ур1°2(аа+р - 2а+ра + раа+) - уР^(ааР ~ 2аРа
+ pa+a+) - ур^(а+ар - 2ара+ + ра+а). A5.4.3)
Члены, пропорциональные ра1 и р\.с , соответствуют обычным процессам усиле™
ния и поглощения, так же как в уравнении A5.3.3). Однако теперь имеются еще
(о) (о) 1
и аномальные члены, пропорциональные рас и рхса;, которые и отвечают за фазово™
чувствительную работу усилителя.
Из A5.4.3) следует, что
" (а)и A5А4)
A5А5)
A5А6)
Эти уравнения решаются точно, и мы получаем
(a)t = VG(a)o, A5.4.7)
„@)
(a+a)t = G(a+aH+ (/°" (O)(G-1), A5.4.8)
Раа Рас
(a2)t = G(a2H- /°° (G-1), A5.4.9)
Раа - Рас'
@") @*)
где G = ехр{^/[раа — Pccjt} — коэффициент усиления.
Теперь можно рассчитать эволюцию квадратурных составляющих, определенных
соотношением A5.3.11). Из выражения A5.4.7) и комплексно сопряженного ему
следует, что
Шум квадратуры Х$ равен
A5А11)
15.5 Лазер с инжекцией сжатого вакуума 361
где
"* A5412)
!>). A5.4.13)
Выражение A5.4.11) по форме напоминает A5.3.13), но теперь добавочный шум, то
есть второй член, зависит от фазового угла $. Определяя параметр е так, чтобы
@) = 1±? @) = 1^? @) = A^е2I/2 . ,
гаа 2 ' "сс 2 ' 2 ' ^jl«j>.-±.jl-*_/
получаем
Следовательно сигнал {Х#} можно усилить (G ^> 1), не внося добавочный шум
& <С 1), если выполняются следующие условия:
B# — ф) = 0, е —ь 0, srft —ь оо, j#te = конечная величина. A5.4.16)
При этом J/®+pii2 —>" оо, то есть добавочный шум одной квадратуры уменьшается
за счет увеличения добавочного шума второй квадратуры, так что (<Л# + ^Д^+тг/г) =
= 1/2е > 1/2.
15.5. Лазер с жнжекцмей сжатого вакуума
В гл. 11 было показано, что в отсутствие каких-либо источников шума (например,
тепловых или механических) ширина линии излучения лазера определяется спон-
спонтанным излучением. В рамках простой наглядной модели (см. разд. 11.4) уширение
спектра представляется как следствие случайного процесса фазовой диффузии, воз-
возникающего из-за добавления к лазерному полю спонтанно испущенных фотонов со
случайными фазами. В обычном лазере вакуум проникает в резонатор через выход-
выходное зеркало, так что некоторые спонтанно испущенные фотоны являются следствием
усиления вакуумных флуктуации. Если вакуум заменить сжатым вакуумом^ то
фазы спонтанно испущенных фотонов будут упорядочены, что приведет к уменьше-
уменьшению фазовой диффузии и, следовательно, к уменьшению ширины линии излучения
лазера.
Рассмотрим кольцевой лазер с одной модой бегущей волны (рис. 15.2), работаю-
работающий выше порога генерации. Внешнее поле связывается с полем внутри резонатора
через выходное зеркало. Предполагается, что внешнее поле находится в состоянии
сжатого вакуума, центрированного на рабочей частоте лазера v = cJcq, которое
задается вектором состояния (см. выражения (8.2.12) и (8.2.13)):
o_k)\Ok), A5.5.1)
где ? = гехр(гф). Потеря излучения через пропускающее зеркало, следовательно,
определяется взаимодействием излучения внутри резонатора с резервуаром сжатых
вакуумных мод гармонических осцилляторов. Это учтено в уравнении (8.3.4).
Таким образом, влияние сжатого вакуума учитывается в основном уравнении
лазера заменой члена, описывающего потери резонатора (8.3.3), выражением (8.3.4).
362 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
Сжатый вакуум \
Рис. 15.2. Схема кольцевого лазера, предназначенная для связывания сжатого вакуума
(пунктирная линия) с полем внутри резонатора
В линейном приближении имеем г)
р = (сш+р — 2а^ ра + ^)
(N
CJ?
С/
- 2ара + раа) + -
a^~ р —
- 2а
ра
A5.5.2)
^i<^). В уравнении A5.5.2) величина я/ есть
где N = sh2(r) и М = ch(r) sh(r)
обычный коэффициент линейного усиления.
Соответствующий коэффициент диффузии D$$ можно определить либо из соот-
соотношения Эйнштейна (разд. 9.4), либо преобразуя уравнение для оператора плотности
в эквивалентное уравнение Фоккера-Планка для Р-распределения с помощью соот-
соотношений A4.2.27). Окончательное выражение для коэффициента фазовой диффузии
имеет вид
2{n)
r-shrch
Если выбрать фазу сжатого поля в виде ф = 2$, то получим
A+
A5.5.3)
A5-5-4)
) Этот интересный результат был впервые получен в работе Gea-Banacloche A987). Важно
отметить, однако, что это приводит лишь к 50%-му уменьшению обычной ширины линии
излучения лазера. Однако, если сжатый вакуум вносится в корреляционный лазер, то
система может стать, например, мощным источником сжатого света (см. работу Bergou,
Lu and Scully A989)).
П. 15. А Анализ К Л-гироскопа с реинэюекцией 363
где в последней строке величина $ заменена величиной «й^, что является хорошим
приближением для лазера, работающего вблизи порога генерации. Сравнивая вы-
выражения A5.5.4) и A1.4.17), приходим к выводу, что при взаимодействии лазера со
сжатым вакуумом, в противоположность обычному вакууму, возможно уменьшение
до пятидесяти процентов скорости фазовой диффузии лазера и, соответственно, его
ширины линии излучения.
Приложение 15. А
Анализ КЛ-гироскопа с реинжекщией 1)
Напомним, что уравнение движения для оператора плотности, описывающего
излучение голографического КЛ, записывается через операторы уничтожения (рож-
(рождения) aj (a~j), j = 1, 2 в виде (см. уравнение A4.4.8))
р(аъ af, а2, а%) = -г{усХ - i'i)[а^аь р] - i{uc2 - ^)[а^«2, р]~
1/2
-у |
-1/2
A5.А.1)
где ис\ и ис2 — собственные частоты «пустого резонатора», и\жи2 — рабочие частоты,
sz/ — коэффициент усиления и n(z) — плотность лазерных атомов. Оператор поля
A(z), записанный через функцию Uj(z) нормальной моды резонатора, имеет вид
A(z) = аг exp(iAit)!7i(z) + а2 exp(iA2t)U2(z), A5.A.2)
где Дх = шаъ — v\ и А2 = ujab — ^2- Наконец, потери резонатора за счет пропускания
учтены при помощи оператора Лиувилля:
^fjP = -^(a'fajp - 2а j pal- + ра^а5). A5.А.З)
Удобно резюмировать информацию, содержащуюся в уравнении A5.А.1), исполь-
используя квантовое уравнение Ланжевена, то есть
(ц = -г(*/С1 - i/i)ai + -ацаг + -а12а2 егФ - ^\аг + Fb A5.A.4)
а2 = -i{vc2 - и2)а2 + -а22а2 + -а21аг е~гФ - -^2а2 + F2. A5.A.5)
Ланжевеновские операторы шума, фигурирующие в уравнениях A5.А.4) и A5.А.5),
определяются соотношениями
(F+WFjit1)} = 2Dij S(t - t'), A5.A.6)
где матрица коэффициентов диффузии Dij имеет вид
[D«] = \ [, f" + а\ гФ (a" + t21^"! - A5.А.7)
4 \(а21 + «12) егФ «22 + «22 /
Фазовый угол Ф равен {ь?\ — v^t. В рамках данного обсуждения будем считать, что
коэффициенты усиления равны, то есть ац = «22 = <*--
г) См. работу Scully A987).
364 Фазовая чувствительность в квантовых оптических системах: приложения Гл. 15
Коэффициенты взаимодействия а12 и a2i зависят от пространственного распре-
распределения активной среды. Например, если активная среда распределена равномерно
в области —1/2 ^ х ^ 1/2, то а\ч = «21 = 0. Однако если усиливающая среда
модулирована и распределена по закону A4.4.14), как в голографическом лазере (см.
рис. 15.1а), то «12 = «21 = ol. То есть получаем сильную корреляцию между модами
1 и 2. Отметим, в частности, что перекрестные коэффициенты диффузии D\2 и ^21
отличны от нуля в случае модулированной усиливающей среды, но равны нулю, когда
лазерная среда накачана однородно. Как показано в разд. 14.4, конечное значение D\2
может привести к гашению спонтанных флуктуации относительного фазового угла.
Рассмотрим теперь применение такого голографического КЛ к проблеме лазерного
гироскопа.
Отметим, что неотъемлемыми составляющими работы обычного гироскопа явля-
являются усиление, потери и взаимодействие мод через обратное рассеяние. Обобщая
динамику КЛ, описываемую уравнениями A5.А.4) и A5.А.5), на предмет учета
эффектов возврата (см. рис. 15.16), и переписывая уравнения движения через пере-
переменные амплитуды и фазы, определяемые соотношением а,{ = г^ ехр (г#$), получаем
рабочие уравнения КЛ-гироскопа:
2fi = оцГ1 + ai2r2cos^ — ^ri + ^i2r2 cos(ф + ф), A5.А.8)
2f2 = «22^2 + «217*1 COS^ — ^2Г2 + ^21^1 COs(^ + ф) , A5.А.9)
/' 1 (
2 \
«12 V «21 — I Sin ф-
п Г2/
~ \
где относительный фазовый угол ф определяется в виде
а коэффициент потерь и коэффициент взаимодействия через обратное рассеяние (см.
рис. 15.16) равны
<jfx = #2 = <«? = -A - Я), A5.А.12)
g12 g21 %
Здесь р — периметр кольца, R и Т — коэффициенты отражения и пропускания
зеркал Mi и М2 (рис. 15.16), соответственно, и Rc — коэффициент отражения зеркал
Л#5 и Mq. Дополнительный набег фазы 0, возникающий при обратном рассеянии,
зависит от положения внешних зеркал М§ и Mq. Наконец источник шума в уравнении
A5.А.10) определяется из A5.1.3) и A5.1.4) и записывается в виде
- t'), A5.A.14)
где скорость фазовой диффузии в физически интересном случае, когда г\ =
= г2 = \/(п), равна
Aф) A5А15)
В этом случае (в предположении, что ф = тг) рабочее уравнение A5.А. 10) прини-
принимает вид
ф = Sur - {si - <gc) sln^
Список литературы к гл. 15 365
где, напоминаем, ис\ ~~ ^с2 = SQ,r, Or — скорость вращения гироскопа, S — масштаб-
масштабный множитель, введенный в конце разд. 4.1.
Задачи
15.1. Рассмотрим двухфотонный линейный усилитель, в котором когерентность
между верхним \а) и нижним \с) состояниями создается с помощью вынуж-
вынуждающего классического поля частоты Раби О. Гамильтониан системы «атом +
поле» в представлении взаимодействия имеет вид
У = hg[a+(\b){a\ + \с)(Ь\) + (\а)(Ь\ + \Ь)(с\)а] - i™(\a)(c\ - \с)(а\),
где мы предположили, что фаза вынуждающего поля ф = ^тг/2. Будем считать,
что скорости релаксации j одинаковы для всех трех уровней.
1. Получите уравнение движения для приведенного оператора плотности
поля р;
2. Определив квадратуры Х\ = (а + а+)/2 и Х2 = (a^a+)/2i, показать, что
(AX2Jt = G2(AX2f0 + ,yK2(G2 - 1).
Найдите Gi, G2, ^Ж\ и J/^-
3. Покажите, что в случае, когда j ^> О, усилитель становится нечувстви-
нечувствительным к фазе. (Указание: см. работу Ansari, Gea-Banacloche and Zubalry
A990).)
15.2. Рассмотрим фазово-нечувствительный усилитель, соответствующий модели,
обсуждаемой в разд. 15.3. Покажите, что если поле на входе является тепловым,
то поле на выходе также является тепловым.
15.3. Вычислите нормально упорядоченную дисперсию числа фотонов,
(: An :)\ = {a+a+aa)t - ((a+a)tJ,
в фазово-чувствительном усилителе, рассмотренном в разд. 15.4. Покажите,
что добавочный шум зависит не только от начальных атомных параметров, но
и от состояния поля на входе. Может ли добавочный шум быть отрицательным?
Если да, то получите соответствующие условия, которым должны удовлетво™
рять поле на входе и параметры усилителя.
Список литературы
КЛ-гироскоп и детектор гравитационных волн
Scully, M. О. and Gea-Banacloche, J. Phys. Rev. A 34, 4043 A986).
Scully, M. O. Phys. Rev. A 35, 452 A987).
*Andrianov S.N., Samartsev V.V. Laser Physics 11, 542 B001); Proc. SPIE 4605, 228 B001).
Квантовая теория линейного усиления
Caves, С. М. Phys. Rev. D 26, 1817 A982).
366 Список литературы к гл. 15
Zaheer, К. and Zubairy, M. S. In New Frontiers in Quantum Electrodynamics and Quantum
Optics, ed. A. O. Barat (Plenum, New York, 1990), p. 203.
*Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика (Физматлит,
Москва, 2000).
Модели нечувствительных к фазе усилителей
Shlmoda, К., Takahasi, H. and Townes, С. Н. J. Phys. Soc. Japan 12, 687 A957).
Наш, Н. A. and Mullen, J. A. Phys. Rev. 128, 2407 A962).
Scully, M. O. and Lamb, W. E., Jr., Phys. Rev. 159, 208 A967).
Carusotto, S. Phys. Rev. A 11, 1629 A975).
Abraham, N. B. and Smith, S. R. Phys. Rev. A 15, 421 A977).
Rockower, E. В., Abraham, N. B. and Smith, S. R. Phys. Rev. A 17, 1100 A978).
Frlberg, S. and Mandel, L. Opt Commun. 46, 141 A983).
Loudon, R. and Shepherd, T. J. Opt Ada 31, 1243 A984).
Hong, C. K., Frlberg, S. and Mandel, L. J. Opt Soc. Am. В 2, 494 A985).
Glauber, R. J. In Frontiers in Quantum Optics, ed. E. R. Pike and S. Sarkar (Hilger, London
1986).
Stenholm, S. Opt Commun. 58, 177 A986).
Модели чувствительных к фазе усилителей
Dupertuls, M. A., Barnett, S. M. and Stenholm, S. J. Opt Soc. Am. В 4, 1102 A987); ibid. 4,
1124 A987).
Dupertuls, M. A. and Stenholm, S. J. Opt Soc. Am. В 4, 1094 A987); Phys. Rev. A 87, 1226
A988).
Mllburn, G. J., Steyn-Ross, M. L. and Walls, D. F. Phys. Rev. A 35, 4443 A987).
Scully, M. O. and Zubairy, M. S. Opt. Commun. 66, 303 A988).
Zaheer, K. and Zubairy, M. S. Opt Commun. 69, 37 A988).
Ansari, N. A., GearBanacloche, J. and Zubairy, M. S. Phys. Rev. A 41 5179 A990).
Kim, M. S. and Buzek, V. Phys. Rev. A 47, 610 A993).
*Калачев А.А., Самарцев В.В. Квантовая электроника 32, No.8 B002).
Лазер с инжекцией сжатого вакуума
Imoto, N., Наш, Н. A. and Yamamoto, Y. Phys. Rev. A 32, 2287 A985).
Stenholm, S. Phys. Scripta T12, 56 A986)
Gea-Banacloche, J. Phys. Rev. Lett. 59, 543 A987).
Marte, M. A. M. and Walls, D. F. Phys. Rev. A 37, 1235 A988).
Marte, M. A. M., RItsch, H. and Walls, D. F. Phys. Rev. A 38, 3577 A988).
Bergou, J., Lu, N. and Scully, M. Opt. Commun. 73, 57 A989).
Ginzel, C., Schack, R. and Schenzle, A. J. Opt Soc. Am. В 8, 1704 A991).
Глава 16
СЖАТИЕ С ПОМОЩЬЮ
НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ
ПРОЦЕССОВ
Если пучки света взаимодействуют внутри нелинейной среды, то могут генериро-
генерироваться новые гармоники. Именно так происходит в оптических параметрических про-
процессах и процессах четырехволнового смешения. В параметрическом усилителе пучок
накачки генерирует сигнальный и холостой пучки, взаимодействуя с х -нелинейной
средой, тогда как в процессе четырехволнового смешения два пучка взаимодействуют
с сигнальным пучком в х -нелинейной среде, возбуждая сопряженный пучок. Эти
процессы давно рассматривались как важные источники сжатого света, что нашло
свое экспериментальное подтверждение.
В данной главе описываются квантовые статистические свойства излучения для
этих нелинейных оптических процессов, особенно те свойства, которые связаны со
сжатыми состояниями *).
16.1. Вырожденное параметрическое усиление
Параметрический усилитель или параметрический преобразователь частоты вниз
состоит по сути из двух мод, обычно называемых сигнальной и холостой, с часто-
частотами vs и i>i, соответственно, связанных через нелинейную среду, например х
нелинейный кристалл, с модой накачки, имеющей частоту i/p, так что
ир = и8 + щ. A6.1.1)
Обычно предполагается, что поле накачки находится в когерентном состоянии с боль-
большой амплитудой, создавая, следовательно, классически модулированное взаимодей-
взаимодействие сигнальной и холостой мод. Если частоты сигнальной и холостой мод одина-
одинаковы, то говорят, что усилитель работает в вырожденном режиме. Полностью кван-
квантовый гамильтониан невырожденного параметрического усилителя в представлении
взаимодействия и в приближении вращающейся волны имеет вид
Г = hx(a+afb + а8аф+). A6.1.2)
Здесь Ъ и as (ац) — операторы уничтожения фотонов в моде накачки и сигнальной
(холостой) модах, соответственно, ах — константа взаимодействия, зависящая от
тензора восприимчивости второго порядка, являющегося посредником взаимодей-
взаимодействия.
Вследствие двухфотонной природы взаимодействия, лежащей в основе парамет-
параметрического процесса, последний давно рассматривался как источник сжатого света,
• Прекрасное изложение данной темы можно найти в книге Walls and Mllburn A994).
368
Сжатие с помощью нелинейных оптических процессов
Гл. 16
что и было подтверждено экспериментально. В невырожденном режиме усилитель
создает поле в двухмодовом сжатом состоянии, тогда как вырожденный параметра
ческий усилитель (ВПУ), для которого ир = 2и и i/8 = щ = и (см. рис. 16.1), создает
одномодовое сжатое состояние.
Нелинейная среда
Рис. 16.1. Геометрия параметрического усиления
В этом разделе будет рассмотрено вырожденное параметрическое усиление, а
также обсуждены характеристики и возможности генерации сжатых состояний.
Гамильтониан, описывающий вырожденное параметрическое усиление в пред-
представлении взаимодействия имеет вид
Г = Пж{а+2Ь + а26+). A6.1.3)
В параметрическом приближении поле накачки рассматривают классически и исто-
истощением накачки пренебрегают. Тогда гамильтониан A6.1.3) принимает вид
Г = йк(Зр(а+2 е~{ф + а2 е1ф), A6.1.4)
где /Зр и ф ~~ действительная амплитуда и фаза когерентного поля накачки. Такое
приближение справедливо в условиях, когда
ж1 —» 0, /Зр —> оо, KJ3pt = const. A6.1.5)
Уравнения Гейзенберга для сигнальной моды имеют вид
A6.1.6)
ирьь ^ . A6.1.7)
Здесь Ор = 2х/3р — эффективная частота Раби. Решение уравнений A6.1.6) и A6.1.7)
приводит к следующим выражениям для средних значений операторов:
a(t) = а0 ch(Opt) - ie+ sh(upt) е^1ф, A6.1.8)
а = —ъ\1ра ' е
а+ = гО„а ег
a+(t) = а+
гщ s
е{ф
A6.1.9)
где а® = а@). Отметим, что при ф = тг/2 эти выражения совпадают с преобразовани-
преобразованиями B.7.6) и B.7.7). Следовательно, если сигнальное поле находится первоначально
в вакуумном состоянии, то дисперсии квадратур Х\ = (а + а+)/2 и Х\ = (a^a+)/2i
задаются выражениями (см. формулы B.7.15) и B.7.16))
! = ^е~2г\ A6.1.10)
2 = ^е2г\ A6.1.11)
где и = Q,pt — эффективный параметр сжатия. Выражения A6.1.10) и A6.1.11)
показывают, что поле на выходе ВПУ можно сжать на 100%, и оно находится
16.2
Сжатие в оптическом параметрическом генераторе
369
в идеальном сжатом состоянии. Это делает ВПУ чрезвычайно важным источником
сжатого излучения.
Вышеприведенный анализ исходил из предположения о том, что накачка явля™
ется совершенно когерентной, монохроматической и характеризуется стабилизиро-
стабилизированной интенсивностью. Это идеальная ситуация. На практике квантовый (так же
как и классический) шум лазерной накачки приводит к флуктуациям амплитуды
и фазы. В приложении 16.А будет рассмотрено влияние флуктуации фазы накачки,
связанных с конечной шириной линии излучения, на свойства сжатия сигнальной
моды. Если ширина линии излучения накачки равна D, то дисперсии квадратур
задаются выражениями A6.А.19) и A6.А.20). На рис. 16.2 приведена зависимость
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
(а)
(б)
(в)
0 0.2 0.4 0.6 0.8
1.2 1.4 1.6 1.8
Рис. 16.2. Зависимость <(AXiJ) от величины upt: D/Up = 0 (a); D/Up = 0.01 (б) и D/Up =
= 0.05 (в)
величины (AXiJ от ilpt для различных значений D/?1р. Флуктуации квадратуры
Х1 возрастают из-за флуктуации фазы поля накачки, и минимальное значение,
через которое проходит величина (AXiJ, увеличивается с ростом D/Ор. Выражения
A6.А. 19) и A6.А.20) существенно упрощаются в пределе D <C t^1 <C Ор, так что
1 -•>,, , 1 9«/^. /«ч A6.1.12)
A6.1.13)
Из формулы A6.1.12) ясно видно, что если фаза накачки отклоняется от угла ф^ то
большая неопределенность ехрBгх)/4 усиленной квадратуры (АХ2)^ примешивается
к неопределенности сжатой квадратуры (AXi)^. Грубо говоря, Dt есть мера случай-
случайных блужданий ф во времени t.
16.2. Сжатие в оптическом параметрическом генераторе
До сих пор рассматривалась неограниченная модель усилителя. Если поместить
нелинейную среду в оптический резонатор, то колебания начнут возрастать, и по-
370 Сжатие с помощью нелинейных оптических процессов Гл. 16
лучится оптический параметрический генератор (ОПГ). Такой метод сжатия пред-
предпочтительнее, поскольку, обычно, взаимодействие очень слабо и удержание света
в резонаторе помогает получить заметный эффект, существенно увеличивая время
взаимодействия. Рассмотрение сигнального поля должно теперь учитывать потери
на одном или двух выходных зеркалах. Далее для простоты будем рассматривать
случай, когда частично пропускающим является одно зеркало.
Используя методы, развитые в гл. 9, можно вывести следующее уравнение Гей-
зенберга-Ланжевена для полевых операторов а и а+:
а = -Ора+ - у а + F(t), A6.2.1)
а+ = ^пра - ^а+ + F+(t). A6.2.2)
Здесь ё описывает затухание резонатора, F(t) — оператор шума (ср. (9.1.15)), и фаза
поля накачки выбрана равной ф = тг/2. Среднее значение оператора шума равно
нулю, то есть
(F(t)) = 0. A6.2.3)
Кроме того
{F(t)F(t')} = {F+(t)F(t')} = {F+(t)F+(t')} = 0, A6.2.4)
t'). A6.2.5)
Для того, чтобы рассмотреть свойства сжатия сигнальной моды в стационарном
состоянии, вычислим (а), (а2) и (а+а). Из уравнений A6.2.1) и A6.2.2) следует, что
средние значения (а) и (а+) удовлетворяют следующей системе уравнений:
ft{a) = -Up{a+) - |<а>, A6.2.6)
^<а+) = -пр(а) - |(а+), A6.2.7)
где использовано (F(t)) = (F~*~(t)} = 0. Решение этих уравнений имеет вид
(a)t = [<о0> ch(fipt) - (а+)о sh(upt)\ e^*/2, A6.2.8)
(a+)t = [(а+> ch(upt) - (аH sh(Upt)} e^^2. A6.2.9)
Из полученных соотношений видно, что для ОПГ, работающего ниже порога (^/2 >
> Ор), в стационарном состоянии имеем
(а>сс = (а+)сс = 0. A6.2.10)
Рассмотрим теперь билинейные величины (а2), («+2) и (а+а). Из соотношений
A6.2.3) и A6.2.4) следует, что величины
Аг = (а2), A6.2.11)
Л2 = ((аа+ + а+а)), A6.2.12)
А3 = (а+2) A6.2.13)
удовлетворяют следующей системе уравнений:
Аг = -прА2 - ЪАг + ((aF + Fa)), A6.2.14)
А2 = -2прА3 - 2прАг - ^А2 + ((aF+ + F+a + а+F + Fa+)), A6.2.15)
А3 = -прА2 - ^А3 + <(a+F+ + F+o+)). A6.2.16)
16.2 Сжатие в оптическом параметрическом генераторе 371
Для нахождения величин, содержащих операторы шума F и F+, сначала перепишем
A6.2.1) и A6.2.2) в матричной форме:
&^ A6.2.17)
A6.2.18)
& = [/+] . A6.2.20)
Формальное решение уравнения A6.2.17) имеет вид
)dt\ A6.2.21)
Умножая A6.2.21) на J^+(t) слева и используя свойства A6.2.3)-A6.2.5) вместе
с предположением, что полевые операторы в начальный момент времени t = 0
статистически не зависят от флуктуации, то есть (aF)F(t)} = 0 и т.д., получаем
Аналогично
Это означает, что все корреляционные функции, содержащие операторы шума,
в уравнениях A6.2.14)—A6.2.16) равны нулю, за исключением (Fa+) = (aF~*~) =
= ^/2. Уравнения A6.2.14)—A6.2.16) поэтому упрощаются и принимают вид
Аг = -прЛ2 - ^Лъ A6.2.24)
А2 = -2прА'Л - 2прАг - ^А2 + ^, A6.2.25)
Л3 = -прА2 - ^Л3. A6.2.26)
Это три линейных дифференциальных уравнения с тремя неизвестными, которые
можно решить точно. В данном случае нас интересует лишь стационарное решение.
Используя несложные алгебраические преобразования, находим
= (а2)сс =
2 ,
- п2р]'
A6.2.27)
р]
А2 = ((аа+ + а+а))сс = % ^, A6.2.28)
u И 4[(^/2J - п2р]' l ;
-&nv
Чтобы проанализировать сжатие, выразим поле через эрмитовы операторы:
A6.2.30)
A6.2.31)
372 Сжатие с помощью нелинейных оптических процессов Гл. 16
Соответствующие дисперсии в стационарном состоянии равны
\ 2 е^ + а+2 е^)}^
а2
A6-2.32)
Здесь $ = 0. Видно, что максимальное сжатие в ОПГ достигается на пороге
генерации A^р = ^/2), при этом
(ДХ^сс = i. A6.2.34)
Однако это соответствует лишь 50%-му сжатию по сравнению с вакуумным
уровнем. Причина такого умеренного сжатия объясняется вакуумными флуктуаци-
ями, проникающими в резонатор сквозь частично пропускающее зеркало. С другой
стороны, ОПГ можно рассматривать как источник коррелированных пар фотонов
(сигнальный + холостой), а зеркало резонатора — как устройство, позволяющее
каким-то отдельным фотонам вырваться из каждой пары, в результате чего теряется
квантовая корреляция, а вместе с ней и сжатие.
Теоретический предел 50%-го сжатия не только непривлекателен, но и не отра-
отражает реальной экспериментальной ситуации, касающейся поля вокруг резонатора,
степень сжатия которого может в действительности заметно отличаться от степени
сжатия поля внутри резонатора. Мы остановимся на этой проблеме в следующем
разделе.
16.3. Сжатие на выходе резонатора
Теоретический предел сжатия внутри резонатора ОПГ, равный 50%, немного
разочаровал нас. В этом разделе будет показано, тем не менее, что поле, выходящее из
ОПГ, является идеально сжатым г). Прежде всего покажем, что связь между полем
внутри резонатора и полем вокруг резонатора не является тривиальной, особенно
если рассматривать антинормально упорядоченные средние значения, характери-
зующие сжатие. Частично отражающее выходное зеркало не только выпускает поле
из резонатора, но и позволяет внешнему полю (вакууму) просачиваться внутрь
резонатора. Очевидно, что поле резонатора и входящее поле становятся со време-
временем коррелированными. Эта корреляция делает возможным взаимное уничтожение
остаточных флуктуации в спектре пропущенного наружу поля резонатора и соответ-
соответствующих флуктуации отраженного внешнего поля, что приводит к почти полному
многомодовому или спектральному сжатию на соответствующей частоте.
Соотношение между полями внутри и вне резонатора можно представить сле-
следующим образом. Рассмотрим сначала поле амплитуды EBX(t), проникающее внутрь
пустого резонатора длины L сквозь одиночное полупрозрачное зеркало, имеющее
коэффициент отражения R и коэффициент пропускания Т. Рост поля резонатора
^рез описывается, при точном резонансе, следующим уравнением:
e3(t - 2L/c) + VfEBX(t), A6.3.1)
) Этот важный результат был впервые получен в работе Yurke A984).
16.3 Сжатие на выходе резонатора 373
где 2L/с — время пролета через резонатор туда и обратно, и мы предположили,
что нет никаких потерь, кроме тех, что обусловлены полупрозрачным зеркалом.
Здесь учтено, что при отражении от среды с более низким показателем преломления
фаза изменяется на тг, а при отражении в обратном порядке фаза не меняется.
Если амплитуды в уравнении A6.3.1) являются медленно меняющимися (Epe3(t —
— 2L/c) ~ Epe3(t) — BLI'c)dEpe3/'dt), и коэффициент отражения зеркала высокий
(R ~ 1), то это уравнение можно заменить следующим:
dEpe3 <? cVT /1ftQM
где $ ~ сТ/2L. Уравнение A6.3.2) является основным рабочим уравнением для
так называемой проблемы «внутреннее поле — внешнее поле». Его строгий вывод,
основанный на методе «мод вселенной» (приложение 5.В), дается в приложении 16.Б.
Сходство последнего уравнения с A6.2.1) означает, что в случае квантованного
поля оператор силы Ланжевена F(t) можно отождествить с вакуумным полем во™
круг резонатора, просачивающимся внутрь резонатора. Действительно, записывая
положительно-частотную часть входящего поля EB-X(t),
Пе-^-^Ы^ A6.3.3)
где 6BX(i/) — операторы многомодового поля, находящегося в вакуумном состоянии,
легко проверить, что E^x(t) действительно обладает свойствами A6.2.3)—A6.2.5) лан-
жевеновского оператора F. Нормировка, принятая в A6.3.3), соответствует одномер-
одномерному бегущему полю с поперечной площадью квантования А. Операторы рождения
и уничтожения подчиняются перестановочным соотношениям [6(i/), Ь^{и)\ = 8 (у —
— и'). Кроме того, сделано предположение, что интегрирование по частоте распро-
распространяется на интервал больший, чем полоса пропускания резонатора, но меньший,
чем центральная частота i/q, поэтому величину л/щ вынесли за знак интеграла.
Подставляя A6.3.3) в уравнение A6.3.2) и записывая положительно-частотную
часть поля резонатора в виде Ерез = (JIi/q/Ае^АЬI' 2а, получаем
где использовано приближение *€ ~ cT/2L, означающее высокий коэффициент
отражения зеркала. Это уравнение согласуется с A6.2.1) (где Ир = 0 в случае пустого
резонатора), если
-<(—о)*
Aб.з.5)
что, как отмечено выше, дает правильные корреляционные свойства для F(i), если
предположить, что состояние входного поля, на которое действуют операторы 6BX(i/),
является вакуумным.
Чтобы прочувствовать далеко идущие последствия этого отождествления ланже-
веновского оператора F(i) с входящим вакуумным полем, заметим, что выходное
поле является комбинацией отраженного входного поля и пропущенного поля резо-
резонатора, т. е.
#вых(*) = -VREm(t) + Vf Epe3(t). A6.3.6)
Возможность наблюдения большего сжатия за пределами резонатора, чем внутри
него, возникает из-за того, что два поля, складываемые в правой части выраже-
выражения A6.3.6), в действительности коррелируют, в силу A6.3.1). Формулы A6.2.22)
374 Сжатие с помощью нелинейных оптических процессов Гл. 16
и A6.2.23) описывают корреляции между ланжевеновским оператором F, пропорци-
пропорциональным i?BX, и оператором моды поля внутри резонатора a(t), пропорциональным
Epe3(t)j если резонатор содержит среду параметрического усилителя. Сжатие вы-
выходного поля является результатом частичного взаимного сокращения флуктуации
спектральных составляющих Евх и (уже частично сжатыми) флуктуациями a(t).
Записывая эквивалент выражения A6.3.6) для положительно-частотных частей
поля и осуществляя преобразование Фурье, получаем
Ьвых(|/) = ^У/Я6ВХ(|/) + V2ir<&a(v), A6.3.7)
где оператор a(t) записан в виде
(х/) e-i{v-VQ)t dv. A6.3.8)
Точный вид фурье-составляющих ~a(v) поля внутри резонатора легко находится
из точного решения A6.2.21). Предположим сначала, что имеет место стационарный
режим, так что первый член, пропорциональный начальному значению поля внутри
резонатора, исчезает. Тогда, из A6.2.21), с учетом отождествления A6.3.5), явно
видно, что поле внутри резонатора растет со временем из входного вакуумного поля.
Имеем
t
a(t) = \
О
_ I L
0
Подставляя A6.3.5) и выполняя интегрирование по времени, получаем
В пределе стационарного состояния, то есть в пределе больших значений време-
времени, затухающими экспоненциальными множителями в A6.3.10) можно пренебречь.
Кроме того, во втором интеграле можно заменить переменную интегрирования и
симметричной частотой 2i/q — и. В результате
a(t) = /*?[([^-г(,-,о)]6вхИ-^B,о-,)| l{v_Va)t
Используя A6.3.11) и A6.3.8), можно найти фурье-составляющую ~о>{у) и подста-
подставить ее в A6.3.7). Результат имеет вид
2г• (lb.3.12)
Далее, в соответствии с приближениями, сделанными ранее, предположим, что ко-
коэффициент отражения настолько высок, что R в первом члене можно положить
равным 1. Выражение A6.3.12) демонстрирует возможность взаимных сокраще-
сокращений флуктуации спектральных составляющих внутрирезонаторного поля (последний
16.4 Четырехволновое смешение 375
член) и отраженного входного поля (первый член). Результирующее сжатие может
оказаться намного больше, чем сжатие внутри резонатора.
Добавляя к A6.3.12) эрмитово сопряженное ему выражение, взятое на симмет-
симметричной частоте 2i/q — i/, получаем
f ] -^)]- A6.3.13)
Отсюда, зная степень сжатия входного поля на какой-то частоте, можно сразу
вычислить степень сжатия выходного поля. Отметим, что это выражение является
достаточно общим, в том отношении, что оно справедливо даже тогда, когда внешнее
поле не находится в вакуумном состоянии.
Теперь определим квадратурные переменные:
*i»«M = \[ьвыхЫ + ь^Ы], х1вхы = \[ьвхы + 6+ (!/„)] A6.3.14)
на центральной частоте v = щ. Из A6.3.13) следует, что отношение дисперсий
выходной и входной квадратур XiBbIX и Х]_вх определяется формулой
[АХ1вЫхЫ]2 _
Для ОПГ вблизи порога Ор ~ ^/2, и согласно A6.3.15) для этой квадратуры
получается по существу идеальное сжатие. (Отметим, что это справедливо незави-
независимо от состояния на входе.) Снижение шума на остальных частотах, то есть спектр
сжатия, определяется из A6.3.13):
= 1 ^^ « ¦ A6.3.16)
(#/2 + прJ + (у - щJ К ;
Это есть перевернутое лоренцево распределение, ширина которого порядка ширины
линии резонатора (ибо в области ниже порога Ор ^ ?*/2).
16.4. Четырехволновое сметпенже
Четырехволновое смешение представляет собой нелинейный процесс, при котором
две плоские волны накачки, распространяющиеся навстречу друг другу, взаимодей-
взаимодействуют в нелинейной среде с пробным полем, имеющим произвольное направление
распространения по отношению к волнам накачки, и создают четвертую (выходную)
волну. Характер нелинейной среды при четырехволновом смешении проявляется в
нелинейной восприимчивости х^ • Две волны накачки и пробная волна связываются
через х ? создавая четвертую волну, которая пропорциональна комплексно сопря-
сопряженной пробной волне.
Значительный интерес к процессу четырехволнового смешения обусловлен воз-
возможностью создавать в ходе этого процесса фазово-сопряженные волны, что находит
применение в адаптивной оптике. Явление фазового сопряжения подразумевает
возбуждение волны, комплексно сопряженной падающей волне лишь в пространстве,
но не во времени, то есть пробная волна E(r, t) = Re{c^(r) exp[i(k • г — ^t)}} преоб-
преобразуется в фазово-сопряженную волну Е'фс(г, t) = Re {<#*(r) exp[^i(k • г + vt)}}. Это
равносильно тому, что пространственная часть E(r,t) остается неизменной, а знак
t меняется. Таким образом фазовое сопряжение эквивалентно обращению времени.
Эти свойства фазово-сопряженных зеркал можно использовать для восстановления
сильно искаженных волн, дважды пропуская их через искажающую среду.
376
Сжатие с помощью нелинейных оптических процессов
Гл. 16
Кроме того, четырехволновое смешение является важным источником сжатого
света. Самая первая генерация сжатого состояния была сделана в режиме четырех™
волнового смешения.
В данном разделе излагается теория четырехволнового смешения в хC)-нелиней-
ной среде и рассматривается генерация сжатого состояния.
16.4.1. Усиление и генерация при четырехволновом смешении. Рассмотрим гео-
геометрию эксперимента, приведенную на рис. 16.3. Две интенсивные волны накачки
1^2 и Кч1, распространяющиеся в противоположных направлениях, взаимодействуют
с двумя слабыми полями Е\ и Е% (все одной частоты и) внутри нелинейной среды,
Е3{0)
z = L
Рис. 16.3. Геометрия четырехволнового смешения
характеризуемой нелинейной восприимчивостью третьего порядка х^ • Поля Е\ и Е$
также распространяются в противоположных направлениях, но отличающихся от
направлений распространения волн Е2 и Еч'. Предположим, что поля Ej (j = 1, 2,
2;, 3) линейно поляризованы и запишем их в виде
Ej(r,t) = ^;(г)е*<г-"*)+к.с, A6.4.1)
где <oj(t) — медленно меняющиеся величины, в общем случае комплексные. Направ-
Направления распространения волн подразумевают, что
ki+ks = 0, k2 + k2/=0. A6.4.2)
Покажем теперь, что если в присутствии волн накачки Еч и Еч1 на нелинейный кри™
сталл падает сигнальное поле Ei, то создается новое поле Е$, фазово-сопряженное
полю Ei. Будем исходить из волнового уравнения (см. E.4.15))
д2Р
A6.43)
где
Е = Ег + Е2 + Е2> + Е3 A6.4.4)
— полное поле иР- нелинейная поляризация, связывающая волны, которая внутри
Х^-среды записывается в виде
Р = хC)^3. A6.4.5)
Ввиду A6.4.4) очевидно, что поляризация содержит большое число членов, по-
разному зависящих от пространственных координат. Однако мы сохраним лишь
члены, содержащие exp(ikj • г) (j = 1,2,2',3), поскольку они могут действовать
16.4
Четырехволновое смешение
377
как согласованные по фазе члены источника в уравнении A6.4.3) для четырех
взаимодействующих полей A6.4.1).
Подставим теперь выражения A6.4.1), A6.4.4) и A6.4.5) для E(r,t) и Р(г, t)
в уравнение A6.4.3). При этом будем считать z координатой, измеряемой в направле-
направлении распространения поля Е\. Кроме того, воспользуемся приближением медленно
меняющихся амплитуд:
A6.4.6)
dz1
При этих условиях сигнальное и сопряженное поля подчиняются следующей системе
уравнений:
dz
^ = - (—) h,
dz \eocj
где
Pi =
Л^
8
|
ъ2 /а*
?!*).
A6
A6.
A6.
.4.7)
.4.8)
.4.9)
A6.4.10)
Поскольку предполагается, что сигнальное S\ и сопряженное S^ поля намного слабее
полей накачки Si и #2;, можно пренебречь первыми двумя членами в выражениях
A6.4.9) и A6.4.10). Кроме того, предположим, что поля накачки не истощаются.
Тогда уравнения A6.4.7) и A6.4.8) записываются в виде
dz
где
(з)
A6.4.11)
A6.4.12)
A6.4.13)
A6.4.14)
Это система связанных линейных уравнений, которую можно решить точно, задавая
граничные условия.
Тем не менее, приведем эту систему уравнений к более простому виду заменой
переменных:
= S\ e
При этом уравнения A6.4.11) и A6.4.12) сводятся к уравнениям
dz
d7
A6.4.15)
A6.4.16)
A6.4.17)
A6.4.18)
378 Сжатие с помощью нелинейных оптических процессов Гл. 16
Амплитуда генерируемого поля &$ определяется лишь комплексно сопряженной
амплитудой сигнального поля, что и приводит к фазовому сопряжению.
Если задать поля на границах нелинейного кристалла z = 0 и z = L, то решение
системы уравнений A6.4.17) и A6.4.18) запишется в виде
4- COSI(:,7^)]^@), A6-4.19)
kcos(\m\L) лу J ' cos(\k\L)
~;@). A6.4.20)
cos(|x|L) 1V r
Особенно интересен случай, когда на входе имеется одно поле ^i(Q) при z = 0, а
^з(Ь) = 0. Тогда амплитуды полей на выходе имеют вид
gl(L) = -flM— A6.4.21)
cos(|>f|L)
<?з@) = щ tg(|x|L)/l@). A6.4.22)
Интересно отметить, что при тг/4 < |x|L < Зтг/4,
|<?з@)| > |<?i@)|, A6.4.23)
то есть амплитуда отраженной волны больше, чем амплитуда падающей. Таким
образом, устройство работает как отражающий усилитель. Из A6.4.21) также следует,
что
\ii{L)\ > |А@)|, A6.4.24)
то есть интенсивность прошедшей сигнальной волны всегда больше интенсивности
падающей волны. Усиление отраженной фазово-сопряженной волны и прошедшей
сигнальной волны происходит потому, что среда накачивается приложенными извне
волнами, которые могут подводить энергию. В представлении чисел заполнения про™
цесс четырехволнового смешения молено описать как процесс, при котором в каждой
из двух волн накачки уничтожается, а к сигнальной и фазово-сопряженной волнам
добавляется, по одному фотону.
Когда \x\L = тг/2, имеем
М'з(О) ©i(L) (ла . ^-х
—=з —У СЮ, —^ —У ОО, ( lb.4.Z0)
I /? (С\\ I I /? (С\\ I
<55 1 I U ) \(о 11 U I
что соответствует генерации. Здесь, однако, требуется осторожность, поскольку
предположение об отсутствии истощения накачки неприменимо к случаю \к\Ь =
= тг/2.
16.4.2. Сжатие при четырехволновом смешении. Данный классический анализ
можно расширить до феноменологического квантового рассмотрения, если заменить
переменные поля S\ и <^з в уравнениях A6.4.17) и A6.4.18) операторами а\ и аз-
Тогда
^ = ixa+ A6.4.26)
dz 3 ' v ;
das
1b
= -Ыа\. A6.4.27)
16.4 Четырехволновое смешение 379
Для простоты предположим, что к = \к\. Решение этих операторных уравнений
можно получить из классических решений A6.4.19) и A6.4.20):
ai(L) = itg(xL)a+(L) + sec(^L)ai(O), A6.4.28)
аз@) = sec(xL)a3(L) + itg(xL)a+@). A6.4.29)
Эти решения аналогичны соответствующим решениям для полевых операторов в слу-
случае параметрического усиления, обсуждавшегося в разд. 16.1. Поэтому естественно
далее рассмотреть свойства сжатия поля излучения в процессе четырехволнового
смешения. Определим квадратурные составляющие сигнального и сопряженного
полей:
aji = \(aj+af), A6.4.30)
oi2 = ^(Oi-ot), A6.4.31)
где j = 1, 3. Предположим, что входные поля «i@) и a$(L) находятся в когерентном
состоянии. Для флуктуации квадратурных составляющих полей на выходе получаем
Аа2и(Ь) = Да§,@) = \[l + 2tg2(^L)], A6.4.32)
где I = 1,2. Согласно A6.4.32) флуктуации поля на выходе увеличиваются в про-
процессе четырехволнового смешения. Это не удивительно, поскольку выходные поля
усилены, а как мы уже знаем, усиление, в общем случае, добавляет шум.
Если вместо этого рассмотреть моду с/, образуемую линейной комбинацией вход-
входных мод,
d= -^(ai + a3)eii9, A6.4.33)
то канонически сопряженные эрмитовы амплитудные операторы запишутся в сле-
следующем виде:
^ A6.4.34)
^ A6.4.35)
АЪ
Дисперсия величины d\ выражается через корреляционные функции операторов
поля ai(L) и аз@) следующим образом:
(a+@)a3@)> + (a+(L)a3@)) + (a^(O)ai(L))}-
¦кх. A6.4.36)
Аналогичное выражение можно получить и для (Де^J- Подставляя а±(Ь) и а^@) из
формул A6.4.28) и A6.4.29), соответственно, в выражение A6.4.36), получаем, когда
'д = тг/4 и входные поля находятся в когерентном состоянии,
2 = ^[sec(^L) - tg(^L)]2. A6.4.37)
Аналогично
(Дс12J = ^[sec(>fL) + tg(>fL)]2. A6.4.38)
380 Сжатие с помощью нелинейных оптических процессов Гл. 16
При увеличении кЬ флуктуации величины d\ становятся меньше 1/4 и в конце
концов обращаются в нуль при кЬ —$> тг/2. Следовательно, амплитуда d\ является
сжатой. Из A6.4.37) и A6.4.38) следует, что
ЫгЫ2 = i, A6.4.39)
то есть данное сжатое состояние является идеально сжатым.
Приложение 16. А
Влияние фазовых флуктуации накачки на сжатие
при вырожденном параметрическом усилении г)
В разд. 16.1 отмечалось, что предположение о совершенно когерентной монохро-
монохроматической накачке со стабилизированной интенсивностью соответствует идеальной
ситуации в вырожденном параметрическом усилении. На практике лазерная накач-
накачка имеет конечную спектральную ширину, возникающую в результате флуктуации
поля. В этом приложении будет рассмотрено влияние фазовых флуктуации лазерной
накачки в параметрическом усилителе на дисперсии квадратур, и особенно на сжатие
сигнального поля.
Диффузию фазы можно описать следующим образом:
ф(г) = фо + 8ф(г), (шла)
где <^о — фиксированная фаза, которую в данном случае будем считать равной тг/2,
и 8ф(г) — случайная фаза с нулевым средним, то есть (ёф(г)) = 0. Предположим,
что 6ф@) = 0. Как обсуждалось в разд. 11.4, поле накачки имеет лоренцеву форму
линии с фазово-индуцированной шириной D, если производная от случайной фазы
§ф(г) является белым шумом, то есть
E<j>(tM<j>(t')) = ID S(t - tf). A6.A.2)
Определим, прежде всего, среднее значение оператора аа^ + а+а. Из уравнений
движения Гейзенберга A6.1.6) и A6.1.7) получаем следующее стохастическое муль-
мультипликативное уравнение:
Ф = [Мо + i#(t)Mi]#, A6.A.3)
где
A6.А.4)
A6.А.5)
A6.А.6)
) См. работу Wodklewicz and Zubalry A983).
П. 16.А Влияние фазовых флуктуации накачки 381
Отметим, что оператор аа+ + а+а не связан непосредственно с а2 и а+2. Чтобы
определить стохастическое среднее значение оператора аа+ + а+а, необходимо вы-
вычислить две вспомогательные величины (а2 егёф) и (а+2 е^%5<^). Можно показать,
что в случае флуктуирующей случайной фазы S<j)(i), описываемой стохастическим
процессом Винера-Леви, справеливо следующее точное уравнение:
(Ф) = (м0 - 1)М2)(Ф), A6.А.7)
где Мо и Mi ~~ произвольные независящие от времени матрицы. Это матричное
уравнение с конкретными матрицами Ф, Мо и Mi, заданными выражениями A6.А.4)-
A6.А.6), можно решить точно, используя, например, преобразование Лапласа. Для
вакуумного начального состояния сигнальной моды получаем
^- eZ (Z + I>J. A6.A.8)
с
Вычисляя корни алгебраического уравнения в знаменателе выражения A6. А.8) и вы-
выбирая должным образом контур интегрирования G, находим явную зависимость от
времени:
{а+а + aa+)t = 1"-^ sh(fjbt) + ch(/it)l e^Dt/2, A6.A.9)
где
Наконец, последняя величина, необходимая для определения сжатия, есть стоха-
стохастическое среднее (а2). Вновь из уравнений движения Гейзенберга с флуктуирующей
фазой получаем мультипликативное стохастическое уравнение вида A6.А.З), где
/ а2 \
ф = ( е-{8ф{а+а + аа+) j A6.A.11)
A6.А.12)
A6.А.13)
Как и в предыдущем случае стохастическое среднее значение (Ф) удовлетворяет
точному дифференциальному уравнению A6.А.7) с матрицами Mq и Mi, определяе-
определяемыми теперь выражениями A6.А. 12) и A6.А. 13). При нашем конкретном начальном
условии лапласово изображение решения имеет следующий вид:
(а2), = [ ^fl ]
l ]¦
+ DD2 ^ 4U2p)z ^ 8п2рD
С
Соответственно, точная зависимость от времени задается выражением
{п }t - ~ 2s (ААЖА
382 Сжатие с помощью нелинейных оптических процессов Гл. 16
где Х{ — корни следующего кубического уравнения:
Л3 + 5DA2 + 4(D2 - п2р)Х - HU2pD = 0. A6.А.16)
Эти корни можно найти точно, используя формулу Кардано. Однако приемлемое
понимание физики процесса можно получить, решая это кубическое уравнение в ре™
алистическом пределе малых фазовых флуктуации (по сравнению с вынуждающей
частотой Раби, то есть, когда D <С Ор). В этом пределе
Ai ~-2D, А2 ~ 2пр - 3D/2, А3 ~ -2пр - 3D/2 A6.А.17)
и, соответственно,
/п2\ ^ r-2Dt D^P Bnp-3D/2)t 2Qp + 5Р/2
1 ;* fiJD2/ 4BOp + D/2) +
"С°- A6'АЛ8)
Из A6.А.9) и A6.А. 18) получаем следующие формулы для дисперсии эрмитовых
амплитуд при наличии флуктуации лазерной фазы (с приближенными корнями А^):
-2Ш
2BОР + D/2)
(о2
^-± е
4 [ 20; -
2BОр + D/2) 2BOp - D/2)
chB0 t
Это и есть требуемые выражения для дисперсии эрмитовых амплитуд в присутствии
флуктуации поля накачки.
Приложение 16. Б
Квантово-полевое рассмотрение задачи «вход^выход»,
приводящее к выражению A6.3.4) г)
Рассмотрим односторонний резонатор, ограниченный идеально отражающим зер-
зеркалом в точке z = L и частично пропускающим зеркалом в точке z = 0. Пусть
последнее характеризуется коэффициентами отражения и пропускания —yR и уГ
для полей, падающих на него нормально слева, и yR и уТ для полей, падающих
на него нормально справа. Поскольку Т ф 0, строго говоря, нельзя определить
нормальные моды, ограниченные исключительно пространством внутри резонатора.
Чтобы сохранить полезность концепции нормальных мод для данной задачи, введем
вспомогательное идеально отражающее зеркало в точке z = —Lg < 0 и положим
1) Из работы Gea-Banacloche et.al. A990).
П.16.Б Квантово-полевое рассмотрение задачи «вход-выход» 383
L® —>> оо в конце расчета, как это делалось в приложении 5.В (см. рис. 5.10).
Положительно частотную часть квантованного поля можно теперь определить в виде
(см. A.1.15))
где
а модовые функции Uk{z) имеют вид (см. E.В.12))
Отметим, что выражение A6.Б. 1) определяет квантованное поле таким образом,
что нетрудно установить операторы входящего, выходящего и внутрирезонаторного
полей. В области z < 0, скажем в точке z = 0~, части выражения A6.Б.1), бегу-
бегущие вправо и влево, есть соответственно входное и выходное поля, тогда как поле
в области z > 0 (скажем часть, распространяющаяся вправо в точке z = 0+) есть
внутрирезонаторное поле. Положительно-частотные части этих полей записываются
в виде
^е"' A6-Б-6)
A6.Б.7)
Принято определять (как было сделано в приложении 5.В) оператор уничтожения
а внутри резонатора на частоте щ квазимоды так, чтобы по всей квазимоде оператор
а вел себя как одномодовый оператор уничтожения, в том смысле, что [а, а+] = 1.
Если ограничить квазинепрерывное суммирование по к в A6.Б.6) одной квазимодой,
Щ ~ 2L < Vh < Щ + 2L' A6.Б.8)
то молено записать ограниченную сумму, обозначаемую штрихом сверху, в виде
E$'(t) = 0a(t)e-ikoL (ko = vo/c), A6.Б.9)
где
В пределе Lq —>• оо это выражение принимает вид (при
¦ |2 ^ '""к ^и U/X,,\ ^*,/K~^j _ ,ь^к A6 Б 11)
384 Сжатие с помощью нелинейных оптических процессов Гл. 16
где для Мк использовано выражение E.В.З). Другими словами, величину ?рез (t)
с точностью до фазового множителя можно записать в виде
- <16B12»
Тогда, используя A6.Б.6), можно записать выражение для a(t) непосредственно
через операторы уничтожения ак в модах всего пространства:
1/2 ,
к
Теперь можно вывести операторное уравнение, описывающее затухание поля
внутри пустого резонатора. В этом случае можно записать, что
ak(t) = ofc@) e^kt A6.Б.14)
и,следовательно,
Г X1/2
\
a(t - 2L/6) = г \jr-j ]Г Мкпк е^' A6.Б.15)
к
где использовано соотношение 2щЬ/с = 2птг. Тогда, используя уравнение
Мк e^ikL = \fReikLMk + Vf'ik eikL°, A6.Б.16)
получаем
E?>(t). A6.Б.17)
Наконец приближение
позволяет записать (для R ~ 1), что
Это уравнение можно свести к уравнению A6.3.4) с помощью A6.Б.12).
Задачи
16.1. Рассмотрим процесс вырожденного параметрического усиления в парамет-
параметрическом приближении (гамильтониан A6.1.4)). Определите дисперсии двух
квадратур при произвольном значении фазы ф поля накачки. Следует пред по™
ложить, что сигнальное поле находится первоначально в вакуумном состоянии.
Покажите, что квадратуры сжимаются только при значениях фазы в области
ф = тг/2. Каков физический смысл этого результата?
16.2. Рассмотрим процесс невырожденного параметрического усиления (гамильто-
(гамильтониан A6.1.2)) в параметрическом приближении, b —$> j3p exp(—г0). Покажите,
Список литературы к гл. 16 385
что в этом случае нарушается неравенство Коши-Шварца:
{a+a+a8as)t(afafaiai)t ^ ((а+а+оца^J.
Предположите, что сигнальные и холостые поля находятся первоначально в ва-
вакуумном состоянии.
16.3. Рассмотрим вырожденный параметрический генератор, у которого одно зерка-
зеркало оптического резонатора частично пропускающее. Пусть через это зеркало
вместо обычного вакуума с полем внутри резонатора связывается многомо-
довый сжатый вакуум, центрированный на частоте и8. Запишите уравнения
движения для (а), (а2) и (а^а). Покажите, что стационарное сжатие поля
внутри резонатора на пороге накачки может превышать 50%.
16.4. Уравнение движения для оператора плотности р сигнального поля вырожден-
вырожденного параметрического генератора имеет вид
р = ~^[У, р] - ~^{а+аР
где *? — гамильтониан взаимодействия A6.1.4).
1. Выведите уравнения движения для (а), (а2) и (а+а) в случае, когда
фаза поля накачки равна тг/2. Сравните эти уравнения с теми, что были
выведены в разд. 16.2 методом Гейзенберга^Ланжевена
2. Решая эти уравнения, покажите, что
(Д*!)? = GiiAX^l + ^A - Gi), (AX2Jt = G2(AX2J0 + ад - G2)
Найдите G±, C25 ^1 и ^2-
16.5. Рассмотрим процесс вырожденного параметрического усиления в параметри-
параметрическом приближении (гамильтониан A6.1.4)). Предположим, что поле накачки
не имеет фазовых флуктуации ф = фо^ то имеет амплитудные флуктуации
(Зр = /Зо + Pi(t)- Случайная амплитуда /3i(t) с нулевым средним, (/5i(t)) = 0,
описывается так называемым процессом Орнштейна-Уленбека:
Найдите (a)t, (fl2)t и {o^o)t ш покажите, что сжатие уменьшается при увели-
увеличении Г.
Список литературы
Монографии
Bloemberger, N. Nonlinear Optics, (Benjamin, New York 1965).
*Клышко Д.Н. Фотоны и нелинейная оптика (Наука, Москва, 1980).
Shen, Y. R. The Principles of Nonlinear Optics^ (Wlley-Intersclence, New York 1984).
*Килин С.Я. Квантовая оптика: поля и их детектирование (Наука и техника, Минск,
1990).
Walls, D. F. and Mllburn, G. J. Quantum Optics, (Springer, New York 1994).
*Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика (Физматлит,
Москва, 2000).
13 М.О. Скалли, М.С. Зубайри
386 Список литературы к гл. 16
Параметрическое усиление
Louisell, W. Н., Yariv, A. and Siegmann, A. E. Phys. Rev. 124, 1646 A961).
Gordon, J. P., Louisell, W. H. and Walker, L. P. Phys. Rev. 129, 481 A963).
Gordon, J. P., Walker, L. R. and Louisell, W. H. Phys. Rev. 130, 806 A963).
Mollow, B. R. and Glauber, R. J. Phys. Rev. 160, 1076 A967); ibid. 160, 1097 A967).
Субпуассоновская статистика и сжатие света при параметрических
процессах
Ralford, M. Т. Phys. Rev. А 2,1541 A970); ibid. 9, 2060 A974).
Stoler, D. Phys. Rev. Lett 33, 1397 A974).
Yuen, H. P. Phys. Rev. A 13, 2226 A976).
Mista, L., Perlnova, V., Perlna, J. and Brounerova, Z. Act. Phys. Pol. A 51, 739 A977).
Mllburn, G. J. and Walls, D. F. Opt Commun. 39, 401 A981).
Jakeman, E. J. and Walker, J. G. Opt. Commun. 55, 219 A985); Opt. Acta 32, 1303 A985).
Rauf, Z. and Zubairy, M. S. Phys. Rev. A 36, 1481 A987).
Bjork, G. and Yamamoto, Y. Phys. Rev. A 37,125 A988); ibid. 37,1991 A988).
Zhu, S.-Y. Phys. Lett A 151, 529 A990).
Anwar, J. and Zubairy, M. S. Phys. Rev. A 45, 1804 A992).
Сжатие на выходе из резонатора
Yurke, В. Phys. Rev. A 29, 408 A984).
Collett, M. J. and Gardiner, С. W. Phys. Rev. A 30, 1386 A984).
Gardiner, C. W. and Collett, M. J. Phys. Rev. A 31, 3761 A985).
Carmichael, H. J. J. Opt Soc. Am. В 4, 1588 A987).
Collett, M. J., Loudon, R. and Gardiner, C. W. J. Mod. Opt 34, 881 A987).
Gea-Banacloche, J., Lu5 N., PedrottI, L. M., Prasad, S., Scully, M. O. and Wodklewicz, K. Phys.
Rev. A 41, 369 A990); ibid. 41, 381 A990).
Роль флуктуации накачки
Hillery, M. and Zubairy, M. S. Phys. Rev. A 26, 451 A982).
Wodklewicz, K. and Zubairy, M. S. Phys. Rev. A 27, 2003 A983).
Scharf, G. and Walls, D. F. Opt. Commun. 50, 245 A984).
Caves, С M. and Crouch, D. D. J. Opt Soc. Am. В 4, 1535 A987).
Crouch, D. D. and Braunsteln, S. L. Phys. Rev. A 36, 4696 A988).
Gea-Banacloche, J. and Zubairy, M. S. Phys. Rev. A 42, 1742 A990).
Полуклассическая теория четырехволнового смешения
Yariv, A. and Pepper, D. M. Opt. Lett 1, 16 A977).
Abrams, R. L. and LInd, R. С Opt Lett 2, 94 A978).
Yariv, A. Opt Commun. 25, 23 A978).
Fu, T. and Sargent III, M. Opt Lett 5, 433 A980).
Boyd, R. W., Raymer, M. G., Narum, P. and Harter, D. J. Phys. Rev. A 24, 411 A981).
Saxena, R. and Agarwal, G. S. Phys. Rev. A 31, 877 A985).
*3ельдович Б.Я., Пилипецкий Н.Ф., Шкунов В.В. Обращение волнового фронта (Наука,
Москва, 1985).
Список литературы к гл. 16 387
"Четырехволновое смешение в атомной среде
Reid, M. D. and Walls, D. F. Phys. Rev. A SO, 343 A984).
Sargent III, M., Holm, D. A. and Zubalry, M. S. Phys. Rev. A 31, 3112 A985).
Stenholm, S., Holm, D. A. and Sargent III, M. Phys. Rev. A 31, 3124 A985).
Holm, D. A., Sargent III, M. and Hoffer, L. M. Phys. Rev. A 32, 963 A985).
Agarwal, G. S. Phys. Rev. A 84, 4055 A986).
Сжатие и неклассические эффекты при четырехволновом смешении
Yuen, H. P. and Shapiro, J. H. Opt Lett 4, 334 A979).
Kumar, P. and Shapiro, J. H. Phys. Rev. A 80, 1508 A984).
Reid, M. D. and Walls, F. D. Opt. Commun. 50, 406 A984); Phys. Rev. A 31, 1622 A985); ibid.
32, 392 A985).
*Slusher, R.E., Hollberg, L.W., Yurke, В., Mertz, J.C. and Valley, J.F. Phys. Rev. Lett 55, 2409
A985).
Holm, D. A., Sargent III, M. and Capron, B. A. Opt. Lett 7, 443 A986).
Ansarl, N. A. and Zubalry, M. S. Phys. Rev. A 38, 2380 A988).
Экпериментальное наблюдение сжатия
Slusher, R. E., Hollberg, L. W., Yurke, В., Mertz, J. C. and Valley, J. F. Phys. Rev. Lett 55,
2409 A985).
Shelby, R. M., Levenson, M. D., Parlmutter, S., Devoe, R. and Walls, D. F. Phys. Rev. Lett 57,
691 A986).
Slusher, R. E., Yurke, В., Grangier, P., LaPorta, A., Walls, D. F. and Reid, M. D. J. Opt Soc.
Am. В 4, 1453 A987).
Wu, L. A., Xiao, M. and Kimble, H. J. J. Opt Soc. Am. В 4, 1465 A987).
Orozco, L. A., Raizen, M. G., Xiao, M., Brecha, R. J. and Kimble, H. J. J. Opt Soc. Am. В 4,
1490 A987).
13*
Глава 17
АТОМНАЯ ОПТИКА
Интерферометрия волн вещества ведет начало с момента возникновения кванто-
квантовой механики, т. е. с ранних экспериментов по дифракции электрона. Более совре-
современные эксперименты нейтронной интерферометрии дали новое понимание многих
фундаментальных аспектов квантовой механики. Сейчас уже существует атомная
интерферометрия, которая является в перспективе новой областью оптики — оптики
волн вещества. Эта область чрезвычайно интересна, поскольку потенциальная чув-
чувствительность интерферометров волн вещества существенно превосходит чувстви-
чувствительность их световолновых или «фотонных» аналогов.
В этой главе мы рассмотрим физику воздействия светоиндуцированных сил на дви-
движение центра масс атомов г) и их применение в оптике (рис. 17.1). Наиболее заметной
из них является отдача, связанная с испусканием и поглощением света. Это «радиа-
ционное давление» лежит в основе лазерно-индуцированного охлаждения J' J.
Другим очень важным механическим эффектом является градиентная сила,
обязанная, например, поперечным изменениям в лазерном пучке. Эти существенно
полуклассические силы полезны в управлении и захвате нейтральных атомов.
Рассмотрев основные силы, позволяющие нам охлаждать, управлять и захваты-
захватывать атомы, мы перейдем к оптике волн де Бройля атомных центров масс, т. е. к атом-
атомной оптике. Согласно общей направленности представленного текста, мы сфокусиру-
сфокусируем наше внимание на квантовых пределах интерферометрии волн вещества. Будет
проведен анализ гироскопа волн вещества как очевидного продолжения лазерного
гироскопа, а также их сходства и относительных достоинств каждого из них.
В заключение мы установим «предел отдачи» в лазерном охлаждении и покажем,
что этот предел можно устранить посредством атомных когерентных эффектов.
17.1. Механическое действие света
Вследствие законов сохранения энергии и импульса, атомы могут испытывать
воздействие светоиндуцированных сил при взаимодействии с полем излучения.
В этом разделе обсуждается применение этих сил для отклонения, охлаждения
и дифракции атомных пучков. Обсуждается также градиентная сила, возникающая
в результате поперечной нестабильности лазерного поля.
1) В основе понимания физики этих сил лежат фундаментальные работы Дж. Максвелла
и П.Н. Лебедева (см. библиографию, где новые ссылки отмечены звездочкой). — Примеч.
ред. пер.
2) При дальнейшем чтении см. Proceedings of the CXII Enrico Fermi School, ed. by Arimondo,
Philips, and Stramla A992).
) Начиная с 1995 г., ведутся активные исследования проблемы лазерного охлаждения
твердых тел. В 1975 г. получен патент США на создание лазерного рефрижератора, и в
настоящее время предпринимаются активные усилия по его практической реализации. Биб-
Библиография основных публикаций по этой проблеме содержится в конце главы. — Примеч.
ред. пер.
17.1 Механическое действие света 389
17.1.1. Отклонение атомов. При поглощении или испускании атомом фотона
частотой и из светового пучка происходит перенос импульса отдачи Ар = hk = hi//с
между атомом и полем. Если вслед за поглощением следует вынужденное излуче-
излучение, то перенос результирующего импульса к атому отсутствует, так как импульс,
переносимый в процессе поглощения, компенсируется равным, но противоположным
по знаку, импульсом в процессе вынужденного излучения. Если же за поглощением
следует спонтанное излучение, то происходит перенос результирующего импульса
к атому, поскольку спонтанное излучение в произвольных направлениях, в среднем,
не дает вклада в импульс. Если этот процесс (поглощение с последующим спонтанным
излучением) происходит большое число раз, то имеет место существенный перенос
импульса от светового пучка к атому, вызывающий отклонение атома. Далее мы
получим выражение для отклонения или силы отдачи атомов.
Как уже упоминалось, атом испытывает импульс отдачи Ар = hk при каждом акте
излучения. Следовательно, абсорбционная сила атома Fa определяется формулой
Fa = rhk, A7.1.1)
где г — скорость излучательного перехода или суммарная скорость флуоресценции.
Для неподвижного двухуровневого атома с частотой перехода ш скорость г пропор-
пропорциональна населенности верхнего уровня атома раа:
г = ГРаа, A7.1.2)
где Г — скорость спонтанного излучения на переходе из возбужденного состояния \а)
в основное состояние \Ь).
Взаимодействие двухуровневого атома с полем излучения частотой v описывается
следующей системой уравнений для элементов матрицы плотности:
РаЬ = - (гД + 0 раЬ + i^RPaa ~ |^Я, A7.1.3)
Раа = ~Граа + ^^(Pab ~~ РЬа), A7.1.4)
РЬа = ^Д ~ ^] РЬа ~ iuRpaa + ^ОЯ. A7.1.5)
Эти уравнения получаются путем обобщения уравнений A0.В.1)-A0.В.4) с учетом
расстройки А = lj — I/. Здесь Пц — частота Раби, связанная со световым пучком.
Стационарное решение уравнений A7.1.3)—A7.1.5) имеет вид
Раа = —о—^# т- A7.1.6)
Следовательно, абсорбционная сила равна
К = ЬкТ—2—^| т A7.1.7)
и направлена так же, как и падающий пучок.
17.1.2. Лазерное охлаждение г). До сих пор мы исследовали силу воздействия
светового пучка на атом, находящийся в покое. Если же атом движется со скоростью
v коллинеарно световому пучку, то обнаруживается доплеровский сдвиг частоты
v =h kv^ где и — частота светового пучка. Знак + (или —) соответствует ситуации,
1) Концепция лазерного охлаждения впервые предложена в работе Hansch and Schawlow
A975) для свободных атомов и в работе Wineland and Dehmelt A975) для атомов в ловушке.
390 Атомная оптика Гл. 17
когда атом движется в противоположном (или том же) направлении, что и световой
пучок. Тогда выражение для абсорбционной силы Fa приобретает вид
О2
5-^ т- A7.1.8)
При отсутствии насыщения (Од = 0 в знаменателе) и при малой скорости атома,
знаменатель можно разложить в ряд. Конечное выражение для Fa имеет вид
Fa = Fo±@mv, A7.1.9)
где
Fo = ПкТ AfR 2J A7.1.10)
4A2 + Г2 х J
/3 = 8М2Г "f* ¦ A7.1.11)
Первый член в выражении A7.1.9) является постоянной отклоняющей силой, в то
время как второй член, пропорциональный атомной скорости, ведет себя подобно
силе трения.
Если атом помещен в стоячую волну 1), он чувствует воздействие двух проти-
противоположно распространяющихся волн, одна из которых имеет то же направление,
что и скорость атома, а другая — противоположное направление. Предположим,
что силы, обусловленные этими двумя пучками, накладываются друг на друга.
Следовательно суммарная сила, действующая на атом в поле стоячей волны, равна
Стоячая волна = {Fo - j3mv) - (Fo + /3mv) = -2pmv, A7.1.12)
т. е. отклоняющие силы компенсируются, и остаются лишь силы трения обоих пуч-
пучков. Сила трения отвечает за снижение скорости атома, приводящее к лазерному
охлаждению.
Процесс лазерного охлаждения можно трактовать следующим образом. Если А >
> 0, т. е. ш > и, то поле, движущееся в противоположном направлении по отношению
к атому, оказывается доплеровски сдвинутым, что в итоге компенсирует расстройку.
Следовательно, атом будет тормозиться. Благодаря этому механизму атомы могут
быть замедлены до скорости сверхмедленной атомной мелассы.
17.1.3. Атомнам дифракция. При взаимодействии пучка атомов с периодической
структурой стоячей волны происходит дифракционное рассеяние. Оно разбрасывает
атомный пучок по многим направлениям, как это показано на рис. 17.1а. Это явление
аналогично рассеянию световой волны на оптической решетке. При соответствующих
условиях атомный пучок можно заставить дифрагировать только в двух направлени-
направлениях, т. е. создать атомный делитель пучка. Такой делитель пучка можно использовать
в атомных интерферометрах.
Мы изложим простой вывод этого эффекта, пренебрегая внутренней двухуровне-
двухуровневой структурой атома.
Дипольное резонансное взаимодействие атома со стоячей волной в z-направлении
описывается гамильтонианом
Жг = p^osinkz, A7.1.13)
1) Впервые проблема локализации нейтрального атома в поле стоячей световой волны была
поставлена Летоховым B.C. (*Летохов, 1968). — Примеч. ред. пер.
17.1
Механическое действие света
391
(а)
(а)
{б)
Рис. 17.1. Взаимодействие атомного пучка со стоячей волной может сопровождаться атом-
атомной дифракцией (а); градиентная сила поля может заставить атомы отражаться подобно
тому, как световой пучок отражается от зеркала (б); атомный пучок может быть сфокуси-
сфокусирован градиентной силой электромагнитного поля (в)
где р — атомный дипольный момент. Если атом изначально находится в собственном
состоянии с импульсом hk®, т. е. ф(г,0) = ехр (ikoz), то можно найти зависящую от
времени волновую функцию
nhk
kz)
-*вых
A7.1.14)
где Од = pS'o/h — частота Раби, Jn
— функция Бесселя п-го порядка. Им-
Импульсное представление для 4p(z,t), т.е.
i/>(p,t), получается с помощью фурье-
преобразования выражения A7.1.14):
Лазерный пучок
п=—оо Рис. 17.2. Атомный пучок с волновым
A7.1.15) вектором ко может приобрести момент
Это выражение описывает дифракцион- пНк при прохождении через стоячую вол»
ное рассеяние на множество составляющих ШУ, что приводит к атомной дифракции
с различными импульсами, кратными им-
импульсу фотона Нк. Дифракционное рассеяние обусловлено тем фактом, что атом,
проходя через стоячую волну, может обмениваться целым числом фотонов, имеющих
импульс Нк в направлении +z или —z (см. рис. 17.2).
17.1.4. Полуклассическая градиентная сила. Рассмотрим силу, действующую на
атом, находящийся в резонаторе в той области поля, которая имеет сильные попереч-
поперечные колебания. В частности, такая ситуация имеет место в сильно сфокусированном
гауссовом лазерном пучке. Вычислим величину этой градиентной силы.
Гамильтониан взаимодействия атома с полем в дипольном приближении можно
записать в виде
Jffi = -pE(r,t), A7.1.16)
392 Атомная оптика Гл. 17
где E(r,i) для светового пучка, распространяющегося в направлении z, имеет вид
Е(т, t) = \go(x, у) е-*(-*-*«) + к.с. A7.1.17)
В полуклассическом приближении оператор дипольного момента р в выражении
A7.1.16) можно заменить его средним значением:
(р) = РаЬРаЬ е'^*-**) + к.с. A7.1.18)
Таким образом, в приближении вращающейся волны энергия взаимодействия равна
^ba+pab), A7.1.19)
где Од = раь^)/Я — частота Раби, которую мы предполагаем действительной
величиной.
Стационарное решение уравнений A7.1.3)—A7.1.5) имеет вид
2Qfl(A + iF/2) Г17 1 9A^
Pab = о 9 ^5 A7.1.ДЛ
что приводит к выражению
4А2 + Г2 + 2^ V ;
На атом, помещенный в область поля, будет действовать сила (для Од <С Г)
F = -V±WX = --^-,V±nl(x, у), A7.1.22)
где V^ — поперечный градиент. Для плоской волны Од не зависит от поперечных
координат, и эта сила обращается в нуль. Но в случае сфокусированного пучка
с шириной а, когда
IV^I ~ ^, A7.1.23)
сила A7.1.22) становится равной
F= 2hT2\- A7Л.24)
аDА2 + Г2) V ;
Таким образом, полуклассическая градиентная сила пропорциональна расстройке, а
ее направление зависит от знака А. При положительной расстройке сила направлена
вдоль градиента поля. Следовательно, эта сила заставляет атомы отскакивать подоб-
подобно тому, как световой пучок отражается от зеркала (рис. 17.16). В противоположном
случае атомный пучок может испытывать фокусировку. Тогда ситуация подобна той,
что имеет место при использовании цилиндрических линз (рис. 17.1 в) г).
17.2. Атомная интерферометрия
В этом разделе развивается теория атомных интерферометров на языке опе-
операторного формализма. Это формализм будет использован в следующем разделе
при изучении квантового предела полной чувствительности прибора. Мы также
) Вопрос о том, что градиентная сила в случае пучка атомов, движущихся коллинеарно
лазерному пучку, может приводить к фокусировке и дефокусировке, впервые рассмотрен
Аскарьяном Г.А. (*Аскарьян, 1962). — Примеч. ред. пер.
17.2
Атомная интерферометрия
393
рассматриваем возможность использования атомного интерферометра в качестве
детектора вращения или гироскопа.
17.2.1. Атомный интерферометр Маха-Цендера. На рис. 17.3 изображена схема,
в соответствии с которой поток из N атомов распространяется через интерферометр
Маха^Цендера в течение времени измерения tm. Атомы разделяются делителем
пучка 1, распространяются по маршрутам а или /3, отражаются зеркалами и затем
Детектор а
Зеркало
Атомный
пучок
Делитель
пучка 1
Зеркало
Детектор i
(а)
(б)
Рис. 17.3. Схема атомного интерферометра Маха-Цендера (а); суммарное изменение фазы,
вызванное делителями пучка и зеркалами, в верхней и нижней ветвях E). (Из работы Scully
and Dowllng A993))
рекомбинируют в делителе пучка 2. Рекомбинированные атомы детектируются верх-
верхним детектором а или нижним детектором 6, где записываются интерференционные
полосы.
Предположим, что при отражении от поверхности делителя пучка частицы при-
приобретают незначительный фазовый сдвиг, который мы примем равным тг/2, но
который, в действительности, зависит от структуры делителя пучка. В свою очередь,
при прохождении через делитель пучка атом приобретает фазовый сдвиг (pi (i =
= 1,2 для первого и второго делителей пучка, соответственно). На рис. 17.36показан
совокупный результат воздействия этих различных процессов на волновую функцию
ф, приводящий к волновой функции фа^ соответствующей верхнему детектору, а
394
Атомная оптика
Гл. 17
именно
Фа = \ ^all ~ e-ik{la-le\ A7.2.1)
фь = % e^b[l + e-ih^-^\ A7.2.2)
где да = тг/2 + kla + (р2, $ь = kla + ipi + y?2 и гДе? без потери общности, мы
положили (fi = (f2 = тг- Здесь А; — атомное волновое число, 1а и 1р — проходимые
пути по верхней и нижней ветвям, соответственно. Теперь представим, что пучок
рекомбинируется вторым делителем пучка, а детекторы а и 6, изображенные на
рис. 17.3а, подсчитывают число атомов по мере их прибытия в рекомбинированный
верхний или нижний пучок, соответственно. Если каждому из N атомов присвоить
индекс г = 1, . . . , N по мере их прохождения через интерферометр в течение
времени измерения ?ш, то соответствующий вектор состояния \(f)i для г-го атома
в интерферометре после рекомбинации определяется выражением
I'd a i®b
где (pap = кAа — l/з)- Очевидно, что это состояние является суперпозицией состояний
с определенным числом частиц
|1О, 0&) и |0а, 1&), отвечающих атому, падающему на
верхний или нижний детектор, соответственно. Тогда вектор состояния |Ф)лг Для
iV-атомного состояния представляет собой прямое произведение индивидуальных
атомных состояний, а именно
N
A7.2.4)
г=1
Пусть с^i и caji (а = а, Ъ) — операторы рождения и уничтожения, соответ-
соответственно, действующие на состояния с определенным числом частиц \na,nb)i, где
соответствующие операторам числа частиц па^ = с^ }Са^ собственные значения па
и пъ равны 0 или 1. Тогда оператор числа частиц Na для числа атомов в верхнем
и нижнем состояниях определяется выражением
N
(а = а, 6),
A7-2.5)
а оператор с удовлетворяет коммутационным соотношениям
[c<M<i±<i<v,;] = <%, A7-2.6)
где знаки плюс или минус указывают на статистику Бозе или Ферми соответственно.
Статистическая природа атомов оказывается важной в условиях, когда плотность
частиц в интерферометре столь велика, что в данный момент времени в пределах
длины когерентности находится более чем один атом, или когда атомы поступают
на вход интерферометра коррелировано. Средние значения {Ма)м этих операторов
числа частиц A7.2.5) определяются формулами
A7.2.7)
17.2 Атомная интерферометрия 395
Это дает следующие выражения для среднего числа атомов в ветвях а и /3:
(Na)N = N sin2
(Nb)N = Ncos2 фа0/2,
которые определяют сигнал.
17.2.2. Атомный гироскоп. Теперь рассмотрим идеальный атомный интерферо-
интерферометр, используемый в качестве датчика вращения или гироскопа. Как показано на
рис. 17.4, атомный интерферометр состоит из полукруглых плеч.
61 = Ъпг-Kd/v
Рис. 17.4. Схема атомного интерферометра с полукруглыми плечами, используемого в ка-
качестве датчика вращения или гироскопа
Если образовавшаяся петля вращается с угловой скоростью Ог вокруг оси, про-
проходящей через центр перпендикулярно плоскости петли, то разность хода противо-
противоположно распространяющихся пучков равна (см. D.1.12))
AL = ^^, A7.2.10)
V
где Ъ — радиус петли, v — атомная скорость. Разность хода превращается в разность
фаз Саньяка,
™%± ™^ A7.2.11)
A7.2.12)
жением
А# = . A7.2.13)
Оно справедливо как для атомных, так и для световых интерферометров, если,
в случае фотона, определить его эффективную массу т1 из уравнения
ш7с2 = Ни. A7.2.14)
Поскольку «масса» фотона определяется оптическими энергиями порядка нес-
нескольких эВ, тогда как атомные массы — порядка 103 МэВ, очевидно, что гироскопы
А4% ^,
vX vX
где А — площадь петли, а величина
Л = —
mv
— атомная длина волны де Бройля. Тогда разность фаз определяется выражением
396 Атомная оптика Гл. 17
волн вещества потенциально имеют сигнал, на много порядков превышающий сигнал
лазерных гироскопов. Однако, для того чтобы определить минимальную скорость
вращения, необходимо рассмотреть шум в атомном интерферометре, к которому мы
обратимся в следующем разделе.
17.3. Квантовый шум в атомном интерферометре
Вычислим флуктуации квантового шума, используя формализм вторичного кван-
квантования, изложенный ранее. С учетом определений для оператора числа частиц Na
A7.2.5) и вектора состояния |Ф)дг A7.2.4), а также коммутационных соотношений
A7.2.6) можно записать
N N
i = l j=l
N
г = 1
iV
г = 1
^V 2 Л + +
= — Sin <?>ад ± > г(ИСст гСст гС<^ *С<^ г^/г (СГ = а?^)? A7.3.1)
где, как и ранее, верхняя и нижняя составляющие соответствуют а = а или 6, а
знаки ± указывают на статистику частиц: знак «плюс» для бозонов, знак «минус»
для фермионов. Заметим, что зависящий от статистики член в выражении A7.3.1)
является суммой неотрицательных матричных элементов, так что его вклад является
неотрицательным или неположительным в зависимости от того, какой знак стоит
перед суммой. Количественный анализ вклада члена, зависящего от статистики,
нуждается в специфической модели когерентности между атомами в плотном пучке.
Однако, можно качественно утверждать, что для достаточно высоких плотностей ис-
использование фермионных атомов приводит к низкому квантово-шумовому пределу.
Это происходит потому, что последний член будет отрицательным. Бозоны будут при-
приводить к противоположному эффекту. Во многих экспериментах, представляющих
интерес, интенсивность пучка столь мала, что в заданный момент времени в пределах
длины когерентности находится только один атом. В этом случае зависящий от
статистики член в выражении A7.3.1) равен нулю, и мы приходим к результату
,. A7.3.2)
Отметим, что этот результат зависит от полного числа атомов N. Теперь сигнал
в каждой из ветвей Na определяется выражением A7.2.9).
Квантовые флуктуации Aipa@ измеряемой разности фаз (ра@ можно определить
как (см. D.4.51))
17.4 Пределы лазерного охлаждения 397
Этот результат не зависит от (рар. На первый взгляд такая независимость может
показаться неожиданной, но она является прямым следствием того факта, что кван™
товый шум (ANa) пропорционален крутизне сигнала (Na) для верхнего и нижнего
состояний числа частиц, рассматриваемых в этом разделе.
В заключение применим полученный результат к задаче гироскопа. Отметим,
что число атомов N равно jimi где j — атомный поток (в единицах атом -с™1), попа-
попадающий на детектор. Из A7.3.3) получаем минимальный регистрируемый фазовый
сдвиг (рт-т = 1/Vjtm • Приравнивая его к фазе сигнала, полученной ранее, ^сигнал =
= 4ДтПг/1г, находим минимальную регистрируемую скорость вращения
^± (вещество). A7.3.4)
r 2Am x/7-L
у J L lib
Это выралсение необходимо сравнить с выражением, полученным для оптического
интерферометра, когда поток j равен мощности Р, деленной на энергию фотона 7ш,
где т1 ~~ эффективная масса фотона, определяемая как т1 = hu / с2. Как уже
упоминалось ранее, типичное значение эффективной массы фотона дает увеличение
чувствительности в 1010 раз. Однако, это увеличение компенсируется низким значе-
значением потока частиц, характерным для атомов. В итоге, чувствительность лазерного
гироскопа увеличивается относительно чувствительности гироскопов волн материи
примерно в 102 раз. Кроме того, атомы совершают не более одного обхода интерферо-
интерферометра, тогда как в кольцевом лазерном гироскопе фотоны совершают большое число
(г& 104) обходов, что приводит к дополнительному увеличению чувствительности
в 104 раз в пользу лазерной системы. Несмотря на это, гироскопы волн вещества
остаются в 104 раз чувствительнее.
17.4. Пределы лазерного охлаждения
17.4.1. Предел отдачи. Обратимся к вопросу о разбросе скоростей, т. е. к флук-
туациям в распределении момента, связанным с лазерным охлаждением. После по-
поглощения п фотонов z-составляющая атомного импульса определяется выражением
р = Ро + nhk + ^Rfccostfj, A7.4.1)
i=i
где hk cos 'dj — проекция на ось z для j-ro спонтанно испущенного фотона.
Отметим, что как число актов поглощения п, так и направления излучения
фотонов, являются случайными переменными. Далее мы приведем эвристический
вывод флуктуациий радиационного давления, возникающих благодаря этим двум
случайным процессам.
Рассматривая флуктуации, возникающие за счет спонтанного излучения (СИ),
отметим, что число актов СИ в секунду равно
^ = ГРвозб, A7.4.2)
где Г — скорость спонтанного излучения, Рвозб — вероятность того, что лазерно-
вынуждаемый атом находится в возбужденном состоянии. Диффузия импульса за
398 Атомная оптика Гл. 17
время At характеризуется выражением
Ар2 = (р2) - (рJ. A7.4.3)
Поскольку (р) обращается в нуль в силу большого числа актов СИ, имеем
Ар2 = (hkf^At = h2k2^-At. A7.4.4)
(ль Л
Здесь в последней строчке мы учли, что dN/dt = Г/2, так как РВозб =^ 1/2 для
релаксирующего двухуровневого атома.
Учитывая, что коэффициент диффузии равен 2Dch = Ар2/At, имеем
^си = \h2k2Y, A7.4.5)
что представляет собой коэффициент диффузии импульса, обусловленной спонтан-
спонтанным излучением.
Также существуют флуктуации радиационного давления, обусловленные флук-
туациями числа актов поглощения, приводящими к атомному возбуждению. Ока-
Оказывается, что этот источник шума фактически равен источнику флуктуации СИ.
Следовательно флуктуации, обусловленные излучением и поглощением, характери-
характеризуются диффузией в скоростях, определяемой как
D = ^-^. A7.4.6)
m
Таким образом, можно записать уравнение Фоккера~Планка для плотности вероят-
вероятности P(v,i) в пространстве скоростей:
где коэффициент дрейфа (затухания) d определяет процесс охлаждения, а коэффи-
коэффициент диффузии (флуктуации) D определяет эффективную температуру охлажден-
охлажденного газа.
Из A7.4.7) видно, что в стационарном состоянии
P(v) = Р@)ехр
V
¦ [d(v')lD(v')dvf
Тогда учитывая, что максимальное затухание имеет место, когда А и Од в A7.1.11)
порядка Г, имеем d « hk2v/mg^ и взяв D(v) из A7.4.6), записываем распределение
скоростей A7.4.8) в виде
^^fy A7.4.9)
Сравнивая A7.4.9) с обычным больцмановским распределением
, A7.4.10)
получаем эффективную температуру лазерно-охлажденного газа
17.4 Пределы лазерного охлаждения 399
Выражение A7.4.11) называется «пределом отдачи» в лазерном охлаждении, кото-
который составляет порядка нескольких микрокельвинов 1). Такие низкие температуры
представляют интерес во многих отношениях, но ситуация становится еще лучше,
когда мы воспользуемся эффектом атомной когерентности, т. е. пленением населен-
населенности, как будет показано в следующем разделе.
17.4.2. Селективное по скорости когерентное пленение населенности 2). В пре-
дыдущем разделе мы установили, что для двухуровневых атомов предел отдачи
в лазерном охлаждении определяется выражением A7.4.11). Но если распространить
наш анализ на многоуровневые атомы и, в частности, на атомы с двумя нижними
уровнями, то оказывается возможным охлаждение вне предела отдачи.
Для того чтобы показать это, рассмотрим ситуацию, отраженную на рис. 17.5.
Атом с импульсом pz = р управляется двумя полями с поляризациями сг+ и а".
Селективное по скорости когерентное пленение населенности (ССКПН) происходит
тогда, когда атом после возбуждения попадает в состояние
-^[\Ь+,р + Щ + \Ь.,р- Нк)]. A7.4.12)
Положим, что взаимодействие с лазерным полем имеет вид
у = 5р[_|а)F_| е-К"Ь-кг+ф) + |а^6+| e-i(«,t+**+«fr)] + эх>? A7.4.13)
где матричные элементы выбраны таким образом, что рпуь_ и ра,ь+ отличаются
знаком. Из A7.4.12) и A7.4.13) видно, что
{a,p\V\VNC{P)) = 0. A7.4.14)
После того, как атом возбуждается в состояние |а,р), он может спонтанно ис-
испустить фотон в любом направлении, и атомный момент может измениться на
любую величину q в пределах от hk до —hk. Но когда происходит переход в нижнее
несвязанное состояние, он прекратит поглощать лазерные фотоны.
Для того чтобы прояснить, что происходит при ССКПН, рассмотрим ситуации,
в которых спонтанно испущенный фотон оставляет атом в суперпозиции двух состоя-
состояний:
fy A7.4.15а)
= -^(\Ь+,р + hk) -\Ь.,р- hk)). A7.4.156)
) В этой главе обсуждается лишь проблема лазерного охлаждения газов. Между тем,
в последние годы проводятся экспериментальные и теоретические исследования лазерного
охлаждения твердых тел. Первый эксперимент в этом направлении был поставлен Р. Эпстей-
ном с коллегами из Национальной лаборатории Лос-Аламоса в 1975 году. В настоящее время
достигнуто лазерное охлаждение тяжелометаллического стекла, легированного трехвалент-
трехвалентным иттербием, на 65°С, начиная от комнатной температуры (*Gosnell, 1999). С теорией
лазерного охлаждения твердых тел можно ознакомиться в книге * Андрианов, Самарцев
A998). Библиография основных публикаций содержится в конце главы. — Примеч. ред.
пер.
) Хорошее объяснение оригинальной идеи см. в статье Aspect A., Arimondo E., Kaiser R.,
Vantseenkiste N. and Cohen-TannoudjI С. J. Opt. Soc. Am. В 6, 2112 A989). Другая удачная
схема охлаждения дана в статье Kasevlch M. and Chu S. Phys. Rev. Lett. 69, 1741 A992).
400 Атомная оптика Гл. 17
\b-,p-hk)
Рис. 17.5. Атом, перемещающийся в направлении z и имеющий импульс р, во время перехода
из состояния |6_) нижнего уровня (J = 1, т = —1) в состояние \а) верхнего уровня (J = 1,
т = 0) с помощью <т+-излучения и из состояния |6) нижнего уровня (J = 1, m = +1)
а) с помощью о""""""-излучения. Импульс атома в состояниях 6±, связываемых
в состояние
через возбужденное состояние с импульсом р, равен р ± hk
Однако эти состояния, в общем случае, связаны оператором кинетической энер-
энергии, т. е.
<*с(?)|^|Ф*с(?)> = ^. A7-4.16)
Следовательно атом, который переходит в состояние \Wnc(q)}, %Дет эволюцио™
нировать в суперпозицию \^nc{q)) и |^c(tf))> благодаря не обращающемуся в нуль
матричному элементу A7.4.16) оператора кинетической энергии, связывающего эти
состояния. Однако при q = 0 эти состояния не связаны, и |Флгс@)) является «идеаль™
ным» состоянием пленения.
Резюме: многоуровневый атом, типа изображенного на рис. 17.5, можно охладить
ниже Тотдачи = КГ/кв благодаря ССКЗН. Атомы захватываются в несвязанное
состояние |Фдго@)}, соответствующее нулевой скорости. В настоящее время ССКПН
используется для получения температур в области нанокельвинов.
Задачи
17.1. Из выражения A7.1.15) видно, что атом испытывает дифракционное рассеяние
в стоячей волне с компонентами импульса, пространственно разделенными
импульсом фотона hk. Покажите, что ширина импульса определяется выра-
выражением
Список литературы
Обзорные статьи и книги по механическому действию света
Toschek, P. E. In New Trends in Atomic Physics, Vol. 1, Les Houches 1982, Session XXXVIII,
ed. G. Grynberg and R. Stora (North-Holland, Amsterdam 1984).
Stenholm, S. Rev. Mod. Phys. 58, 699 A986).
Список литературы к гл. 17 401
MInogIn, V. G. and Letokhov, V. S. Laser Light Pressure on Atoms, (Gordon and Breach,
New York 1987). [Миногин В.Г., Летохов B.C. Давление лазерного излучения на атомы
(Наука, Москва, 1986).]
Kazantsev, A. P., Surdutovlch, G. J. and Yakovlev, V. P. Mechanical Action of Light on
Atoms, (World Scientific, Singapore 1990). [Казанцев А.П., Сурдатович Г.И., Яковлев В.П.
Механическое действие света на атомы (Наука, Москва, 1991).]
Articles in Laser Manipulation of Atoms and Ions, Proceedings of the International School of
Physics «Enrico Fermi», Course CXIII, ed. E. Arimondo, W. D. Phillips, and F. Strumia
(North-Holland, Amsterdam 1992).
* Андрианов С.Н., Самарцев В.В. Оптическое сверхизлучение и лазерное охлаждение в
твердых телах (КГУ, Казань, 1998).
*Mungan, С. Е. and Gosnell, T. R. Advances in atomic, molecular and optical physics 40, 161
A999)
Лазерное охлаждение и радиационное давление
* Лебедев П.Н., Избранные сочинения, (ГИТТЛ, Москва-Ленинград 1949)
* Maxwell, J.C. A Treatise on Electricity and Magnetism, (Dover, New York 1954)
Letokhov, V. S. JETP Lett 1, 272 A968) [Летохов B.C., Письма в ЖЭТФ 7, 348 A968)].
*Казанцев, А.П. ЖЭТФ 63, 1628 A972)
Hansch, Т. W. and Schawlow, A. L. Opt Commun. 13, 68 A975).
Wineland, D. and Dehmelt, H. Bull Am. Phys. Soc. 20, 637 A975).
Ashkln, A. Phys. Rev. Lett 40, 729 A978).
*WIneland, D.I., Drulllnger, R.E. and Walls, F.L. Phys. Rev. Lett 40, 1639 A978)
*Балыкин В.И., Летохов B.C., Мишин В.И. Письма в ЖЭТФ 29, 614 A979); ЖЭТФ 78,
1376 A980)
Javanalnen, J. and Stenholm, S. Appl. Phys. 21, 283 A980); ibid. 24, 71 A981); ibid. 24, 151
A981).
Chu, S., Hallberg, L., Bjorkholm, J. E., Cable, A. and Ashkin, A. Phys. Rev. Lett. 55, 48 A985).
Chu, S., Bjorkholm, J. E., Ashkln, A. and Cable, A. Phys. Rev. Lett 57, 314 A986).
Lett, P. D., Watts, R. N., Westbrook, C. I., Phillips, W. D., Gould, P. L. and Met calf, H. J. Phys.
Rev. Lett. 62, 1118 A988).
Diedrlch, F., Bergquist, J. C, Itano, W. M. and Wineland, D. J. Phys. Rev. Lett. 62, 403 A989).
Dallbard, J. and Cohen-Tannoudji, C. J. Opt Soc. Am. В 6, 2023 A989).
Castln, Y., Wallis, H. and Dallbard, J. J. Opt Soc. Am. В 6, 2046 A989).
Ungar, P. J., Weiss, D. S., Riis, E. and Chu, S. J. Opt Am. Soc. В 6, 2058 A989).
Shevy, Y. Phys. Rev. Lett 64, 2905 A990).
Salomon, C, Dalibard, J., Aspect, A., Metcalf, A. and Cohen-Tannoudji, C. Phys. Rev. Lett. 65,
559 A990).
* Cohen-Tannoudji, C.H. and Fillips, W.D. Physics Today 43, 33 A990)
*Chu, S. Science 253, 861 A991)
Storey, E. P., Collett, M. J. and Walls, D. F. Phys. Rev. Lett 68, 472 A992).
Атомная дифракция и атомный делитель пучка
*AshkIn, A. Science 210, 1081 A980)
Moskowltz, P. E., Gould, P. L., Atlas, S. R. and Pritchard, D. E. Phys. Rev. Lett. 51, 370 A983).
Tangvy, C, Reynaud, S. and Cohen-Tannoudji, С J. Phys. В 17, 4623 A984).
Gould, P. L., Ruff, G. A. and Pritchard, D. E. Phys. Rev. Lett 56, 827 A986).
402 Список литературы к гл. 17
Martin, P. J., Gould, P. L., Oldaker, В. G., Miklich, A. H. and PItchard, D. E. Phys. Rev. A 36,
2495 A987).
Martin, P. J., Oldaker, B. G., Miklich, A. H. and PItchard, D. E. Phys. Rev. A 60, 515 A988).
Meystre, P., Schumacher, E. and Stenholm, S. Opt Gommun. 73, 443 A989).
Wright, E. M. and Meystre, P. Opt Gommun. 75, 388 A990).
Gould, P. L., Martin, P. G., Ruff, G. A., Stoner, R. E., Picque, J.-L. and Pritchard, D. E. Phys.
Rev. A 43, 585 A991).
Akulin, V. M., Kien, F. L. and Schleich, W. P. Phys. Rev. A 44, 1462 A991).
Shore, B. W., Meystre, P. and Stenholm, S. J. Opt Soc. Am. В 8, 903 A991).
Tan, S. M. and Walls, D. F. Phys. Rev. A 44, R2779 A991).
Wilkens, M., Schumacher, E. and Meystre, P. Opt. Gommun. 86, 34 A991).
Атомное зеркало и линзы, градиентная сила
*Аскарьян, Г.А. ЖЭТФ 42, 1567 A962)
Pearson, D. В. Phys. Rev. Lett. 41, 1361 A978); Opt. Lett 5, 111 A980).
Cook, R. and Hill, R. Opt Commun. 48, 258 A982).
Balykin, V. I., Letokhov, V. S., Minogin, V. G. and Zueva, T. Z. Appl. Phys. В 35, 149 A984).
Balykin, V. L, Letokhov, V. S., Ovchinnikov, Yu. B. and SIdorov, A. I. Phys. Rev. Lett 60, 2137
A988).
Нейтронная интерферометрия
Collela, R., Overhauser, A. W. and Werner, S. A. Phys. Rev. Lett 34, 1472 A975).
Zeilinger, A. Z. Phys. В 25, 97 A976).
Rauch, H., Treimer, W. and Bonse, U. Phys. Lett A 47, 369 A977).
Werner, S. A., Staudemann, J.-L. and Collela, R. Phys. Rev. Lett 42, 1103 A979).
Badurek, G., Rauch, H., Summhammer, J., Kischko, U. and Zeilinger, A. Physics В 151, 82
A988).
Шум в атомном интерферометрии
Yurke, В. Phys. Rev. Lett 56, 1515 A986).
Carnal, О. and Mlynek, J. Phys. Rev. Lett 66, 2689 A991).
Keith, D. W., Ekstrom, C. R., Turchette, Q. A. and Pritchard, D. E. Phys. Rev. Lett 66, 2693
A991).
Riehle, F., Kisters, Т., Witte, A., Helmeche, J. and Borde, D. E. Phys. Rev. Lett 67, 177 A991).
Kasevich, M. and Chu, S. Phys. Rev. Lett. 67, 181 A991).
Scully, M. O. and Dowling, J. P. Phys. Rev. A 48, 3186 A993).
Пределы лазерного охлаждения
*Миногин В.Г., Летохов B.C. Давление лазерного излучения на атомы (Наука, Москва,
1986).
Kazantsev, A. P., Surdovich, G. I. and Yakovlev, V. P. Mechanical Action of Light on Atoms,
(World Scientific, Singapore 1990). [Казанцев А.П., Сурдатович Г.И., Яковлев В.П. Меха-
Механическое действие света на атомы (Наука, Москва, 1991).]
Stenholm, S. in Laser Manipulation of Atoms and Ions (Proc. International School of Physics)
ed. E. Arimondo, W. D. Phillips, and F. Strumina (North-Holland, Amsterdam 1992), p. 53.
Aspect, A., Emile, O., Gerz, C, Kaiser, R., Vansteenkiste, N., Wallis, H. and Cohen-Tannoudji,
C. ibid., p. 401.
Список литературы к гл. 17 403
* Лазерное охлаждение твердых тел
*Epsteln, R.I., Buchwald, M.I., Edwards, B.C., Gosnell, T.R. and Mungan, C.E. Nature 377,
500 A995).
*Epstein, R.I., Edwards, B.C., Buchwald, M.I. and Gosnell T.R. Fluorescent refrigeration, Patent
USA, 5.447.032 (Sep 5, 1995).
*Andrianov, S.N. and Samartsev, V.V. Laser Physics 6, 759 A996); 6, 949 A996); 7, 314 A997).
*Kalachev, A.A. and Samartsev V.V. Laser Physics 6, 27 A996); 7, 476 A997).
*Ораевский А.Н. Квантовая электроника 23, 1045 A996).
*3адерновский А.А., Ривлин Л.А. Квантовая Электроника 23, 1100 A996).
* Андрианов С.Н., Самарцев В.В. Оптическое сверхизлучение и лазерное охлаждение в
твердых телах (КГУ, Казань, 1998).
* Mungan, C.E. and Gosnell, T.R. Advances in atomic, molecular and optical physics 40, 161
A999).
* Gosnell, T.R. Optics Lett 24, 1041 A999).
*Hoyt, C.W., Shelk-Bahae, M., Epstein, R.I., Edwards, B.C. and Anderson, J.E. Phys. Rev. Lett
85, 3600 B000).
*Petrashkin, S.V. and Samartsev, V.V. Laser Physics 11, 948 B001).
Глава 18
ПАРАДОКС ЭЙНШТЕЙНА,
ПОДОЛЬСКОГО, РОЗЕНА,
СКРЫТЫЕ ПЕРЕМЕННЫЕ
И ТЕОРЕМА БЕЛЛА
Квантовая механика является чрезвычайно успешной теорией, занимающей уни-
уникальное место в истории науки. Она раскрыла тайны, простирающиеся от макро-
макроскопической сверхпроводимости до микроскопической теории элементарных частиц,
глубоко проникнув в природу вакуума с одной стороны и описание нуклона с другой.
Целые новые области физики, такие как квантовая оптика и квантовая электроника,
обязаны своим существованием квантовой механике.
Однако, несмотря на ошеломляющие успехи квантовой механики отсутствует
общее согласие по принципиальным основам и интерпретации предмета. Теория
дает однозначную информацию об исходе измерения физического объекта. Однако
многие чувствуют, что она не дает удовлетворительного ответа на вопрос, какого
характера «реальность» мы должны приписать физическим объектам между актами
измерения.
Принципиальная трудность возникает потому, что волновая функция \ф) за-
задается, обычно, как когерентная суперпозиция всевозможных различных исходов
эксперимента. Если обозначить множество состояний, соответствующих возможным
исходам эксперимента, через |^)j, то \ф) = ]Г^. Cj|i/?j), где Cj = (г/>^ф). Вероятность
исхода \xjj)j равна pj = \cj\2. В процессе измерения происходит так называемый кол-
коллапс волновой функцииш выбирается одно, определенное состояние \ф)j физического
объекта. Трудность возникает при интерпретации механизма, с помощью которого
это определенное состояние выбирается из всех возможных.
Важным следствием формализма квантовой механики является то, что он, по-
видимому, не допускает локального описания событий, в том смысле, который будет
обсуждаться ниже. С другой стороны, локальную теорию можно построить, но при
этом возникают трудности, связанные с отрицательными вероятностями.
Этот контринтуитивный аспект квантовой механики был предметом спора с пер-
первых дней ее существования. В частности, Эйнштейн, Подольский и Розен пред™
положили, на основе мысленного эксперимента, что квантовая механика является
неполной теорией. В отсутствие конкретных экспериментов, проверяющих аспекты
реальности и локальности квантовой механики, споры по основам последней про-
продолжались долгие годы, оставаясь, по сути, философскими.
Однако ситуация существенно изменилась, когда в 1964 году Дж.С. Белл сфор-
сформулировал определенные неравенства, называемые теперь неравенствами Белла 1),
) Замечательное обсуждение вопроса имеется в работах Mermln A990a,b).
18.1 Парадокс Эйнштейна, Подольского, Розена 405
которые всегда должны выполняться для любой теории, удовлетворяющей интуи-
интуитивно понятным представлениям о реальности и локальности. Одним из наиболее
интересных результатов современной физики является то, что согласно квантовой
механике, в определенных ситуациях неравенства Белла нарушаются, и что резуль-
результаты экспериментов согласуются с предсказаниями квантовой теории.
В этой главе анализируются аргументы Эйнштейна, Подольского и Розена, ка-
касающиеся неполноты квантовой механики. Затем обсуждаются неравенство Белла
и квантово-механические результаты, нарушающие его. Противоречие между нера-
неравенством Белла и предсказаниями квантовой механики обостряется при изучении
различных альтернативных теорий, среди которых наиболее известными являются
теории скрытых переменных (параметров) (СП). Для того чтобы лучше понять
проблему, мы покажем, что можно развить «нелокальную» теорию скрытых пере-
переменных, согласующуюся с квантовой теорией. В заключение, будет показано, что
в квантовой механике нарушается также более современный критерий локальности
— так называемое равенство Гринбергера-Хорна-Цейлингера (ГХЦ).
Данная глава и две последующие касаются проблем интерпретации квантовой
механики. При обсуждении этих вопросов мы следуем примеру Лэмба (Lamb, 1969),
а именно, развиваем исследование, анализируя прибор, разработанный для соот-
соответствующих измерений. Это усиливает аргументы и всегда напоминает о цели
исследования.
18.1. Парадокс Эйнштейна, Подольского, Розена
В 1935 году Эйнштейн, Подольский и Розен представили рассуждение, показы-
показывающее, что существуют ситуации, в которых общая вероятностная схема квантовой
теории кажется неполной. Здесь мы изложим вариант этого рассуждения, следуя
Бому.
Рассмотрим двухкомпонентную систему, состоящую из двух частиц со спином
1/2 (например, молекулу Hg2). До некоторого момента времени t = 0 эти частицы
считаются находящимися в связанном состоянии с нулевым моментом количества
движения. Обозначим соответствующий вектор состояния через |Фх,2)- Б момент
времени t = 0 мы «выключаем» связывающий потенциал (например, путем фо-
фоторасщепления молекулы), не сообщая системе момент количества движения и не
возмущая спины каким-либо образом. Отдельные части системы теперь свободны
и их можно разнести в противоположные стороны лаборатории (или, фактически,
вселенной). Теперь рассмотрим две схемы экспериментальных установок, показанные
на рис. 18.1.
Сначала рассмотрим случай, когда измеряется z-составляющая спина 1, как
показано на рис. 18.1а. До измерения вектор состояния системы имеет вид
I*l,2> = ^(|tl,4.2>-|-k,t2», A8-1.1)
где | ¦fi, 4-2) обозначает состояние, когда частица 1 имеет проекцию спина, равную
+1/2, а частица 2 — проекцию спина, равную — 1/2 (относительно оси z) и т. д.
Теперь одна из версий рассуждения Эйнштейна, Подольского, Розена будет зву™
чать следующим образом.
1. Выберем произвольное направление, которое будем считать осью z, и пропу-
пропустим один атом Hg (скажем атом 1) через прибор Штерна-Герлаха (ПШГ), ориен™
тированный вдоль оси z. В результате частица отклонится либо в направлении +z,
либо в направлении — z. Пусть это будет -\-z. Следовательно, известно, что частица
находится в состоянии со значением az, равным +1.
406
Парадокс ЭПР, скрытые переменные и теорема Белла
Гл. 18
О
1 Д 2
Спин 2
(а)
Спин 1
Рис. 18.1. Схема мысленного эксперимента ЭПР. Система со спином, равным нулю (напри-
(например, ортоводород), расщепляется внешним полем. Две частицы со спином 1/2 (протоны)
распространяются в противоположных направлениях. Частица 1 проходит через прибор
Штерна—Герлаха: а — ориентированный вдоль оси z и б — ориентированный вдоль оси ж
2. Зная, что спин частицы 1 направлен вверх, мы заключаем, что спин частицы
2 направлен вниз. Но если теперь пропустить атом 2 через ПШГ, ориентированный
вдоль оси ж, то обнаружится, что частица 2 имеет определенный спин вдоль оси х
(либо в направлении +ж, либо в направлении —ж), то есть будет известно значение ах.
3. Следовательно, продолжая рассуждение, мы знаем теперь обе проекции (z и х)
спина частицы 2, что нарушает принцип дополнительности.
Приведенную версию парадокса Эйнштейна, Подольского, Розена, сконцентри-
сконцентрированную на аппаратном нарушении дополнительности («определены» как сгж, так
и crz), имеет смысл сформулировать иначе, рассматривая векторы состояния.
Сначала рассмотрим случай, когда измеряется z-составляющая спина 1, как
показано на рис. 18.1а. До измерения, выполняемого (в некоторый момент времени
to) над частицей 1, вектор состояния системы имеет вид
A8.1.2)
18.1 Парадокс Эйнштейна, Подольского, Розена 407
где гф< обозначает состояние до (t < to) «осмотра» частицы 1. Если теперь после
измерения, сделанного над частицей 1, оказывается, что она находится в состоянии,
скажем, | 4i)? то состояние частицы 2 записывается в виде
\ф>) = \Ь). A8.1.3)
Здесь Ф2 обозначает состояние системы 2 после (t > to) измерения, выполненного
над частицей 1.
Здесь Эйнштейн, Подольский, Розен рассуждают следующим образом: поскольку
в момент измерения две системы больше не взаимодействуют, то во второй системе
не происходит никакого реального изменения, являющегося следствием того, что
может произойти с первой системой. То есть, между системами нет взаимодействия.
Более того, утверждают ЭПР, поскольку, осматривая частицу 1, мы не влияем на
частицу 2, состояние частицы 2 должно быть одинаковым до и после измерения. То
есть
\ф<) = \ф>) = ||2), A8.1.4)
где ip2 ш Ф2 обозначают состояния «до» и «после».
Но мы с тем же успехом могли бы измерить ж-составляющую спина частицы 1
(рис. 18.16). Поэтому естественно описывать спины через состояния | ± х)
\±х) = \±) = -^(|t) ± 14)), A8.1.5)
так что синглетное состояние до измерения равно
1^1<,2> = ^A + Ь-2>-|-1+2». A8.1-6)
Теперь, после обнаружения спина 1, скажем, в состоянии | — i), получаем
1^) = 1+2), A8.1.7)
что означает
а это очень неудовлетворительное положение вещей! Поскольку, говоря словами
Эйнштейна, Подольского, Розена:
«Таким образом, можно приписать два различных вектора состояния
(в наших обозначениях | fo) и | +2)) одной и той же реальности.»
Один из способов решения этой проблемы состоит в том, чтобы рассматривать
подсистему (например, только частицу 2), используя формализм оператора плотно-
плотности. В общем случае, когда рассматривается комбинированная система, состоящая
из двух подсистем А и В, и нас интересуют лишь средние значения операторов Qai
относящихся к одной только системе Л, то есть
Q = Q®1B, A8.1.9)
то вводится, обычно, приведенный оператор плотности рд. То есть, выражая среднее
значение через полный оператор плотности ра,в, имеем
(Q) = Тгд1В {PABQ) = 53(o, b\PABQ\a, Ъ) =
а,Ь
~ ~ ~ \а) = Tra (paQа), A8.1.10)
408 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
где приведенный оператор плотности для системы А имеет вид
РА*)' A8.1.11)
Следовательно, будет правильным рассматривать оператор плотности системы 2 (до
осмотра системы 1). Для первого эксперимента этот оператор имеет вид
P2~(i) = Tri [pi^(i)] = (ti IV^KV^I ti) + D-1 {Фг^кФгА 4-1) =
1 1 /1 0\
2 2 \0 l/2
Подобным образом оператор плотности, соответствующий второму эксперименту,
имеет вид
<Г /тт\ гтп Г
Р2 (И; = 11"! [р__
= ^(|-2>(-2| + |+2>(+2|), A8.1.13)
или, выражая через спиноры | ^2) и | 4-2)?
Р2<(") = \[(\Ь) - \i2))((U - (|2|) + «t2| + D.2|)(|t2> + 14-2»] =
= f ШСЫ +14-2><4-2|) = \ (J J) ¦ A8.1.14)
Следовательно,
р<A) = р<(Ц). A8.1.15)
Это равенство отражает внутреннюю непротиворечивость квантовой теории. То
есть, используя надлежащий формализм оператора плотности, мы не получаем два
различных описания одной и той же частицы.
Однако, несмотря на то, что методы квантовой механики могут быть сдела-
сделаны самосогласованными 1), квантовая механика кажется необычной. Более того,
именно искусное использование «перепутанных» (например, спиновых синглетных)
состояний, введенных Эйнштейном, Подольским, Розеном и расширенных Беллом,
показывает, насколько необычным в действительности является квантовый мир.
Неспособность квантовой механики дать точные предсказания для исходов не-
некоторых измерений заставила Эйнштейна, Подольского, Розена постулировать су-
существование «скрытых» переменных, которые неизвестны и, возможно, неизмеряе-
мы. Ожидалось, что введение этих скрытых переменных восстановило бы полноту
и детерминизм квантовой теории. Основой для количественной проверки теорий
скрытых переменных являются неравенства Белла, которые будут рассматриваться
ниже. Показано, что выполняя корреляционные эксперименты типа тех, что рассмот-
рассмотрены в рассуждении Эйнштейна, Подольского, Розена, можно найти различие между
предсказаниями некоторых теорий скрытых переменных и квантовой механики.
18.2. Неравенство Белла
Рассмотрим мысленный эксперимент Эйнштейна, Подольского, Розена, проил-
проиллюстрированный на рис. 18.2. Система с нулевым спином «расщепляется» на две
г) См. также работу Griffiths, R.B. Phys. Rev. Lett. 70, 2201 A993) по последовательной
интерпретации квантовой механики через квантовые траектории и ссылки в ней.
18.2
Неравенство Белла
409
частицы со спином 1/2, имеющие теперь антикоррелированные значения проекции
спина на любую заданную ось. С целью доказательства теоремы Белла, рассмотрим
вероятность того, что частица 1 пройдет через прибор Штерна-Герлаха (ПШГх),
ориентированный под углом #а к вертикальному направлению (+z), а частица 2
пройдет через прибор Штерна-Герлаха (ПШГг), ориентированный под углом #5
к вертикальному направлению (см. рис. 18.2). Обозначим эту совместную вероят™
Рис. 18.2. Схема мысленного эксперимента ЭПР. Система со спином, равным нулю (напри-
(например, ортоводород), расщепляется внешним полем. Две частицы со спином 1/2 (протоны)
распространяются в противоположных направлениях и проходят через приборы Штерна-
Герлаха, ориентированные под углом #а к вертикали {-\-z) для частицы 1 и под углом #ь для
частицы 2. Для примера показано, что частица со спином вверх «пройдет» через нижнее
отверстие
ность прохождения через Р(#а> $ь) =
обозначение
Ъ- Для продолжения доказательства введем
Частица 1 Частица 2
(+ - О I - + О
A8.2.1)
Здесь левая часть в скобках относится к частице 1, а правая — к частице 2. В каж-
каждой части имеется три «позиции», в которые мы поместили либо знак плюс, либо
знак минус, либо кружок. Первая, вторая и третья позиции зарезервированы для
информации, касающейся прохождения через ПШГ, ориентированный под углом
$о, #ь и ^С5 соответственно. Знак плюс соответствует прохождению, знак минус —
блокированию. Кружок означает, что эта совместная вероятность не содержит ин™
формации о прохождении при данном значении угла. Например, в выражении A8.2.1)
первый знак + означает, что частица 1 проходит через ПШГ, ориентированный под
углом i?a, но частица 2 при этом не проходит через ПШГ, ориентированный под
углом #а, что отмечено знаком —. Аналогично, если частица 2 проходит через ПШГ,
ориентированный под углом #ь, мы помещаем знак + во вторую позицию в правой
части и, следовательно, знак — во вторую позицию в левой части, относящейся
к частице 1.
Теперь, объяснив обозначения в общем случае, вернемся к выражению A8.2.1).
Напомним, что Ра^ обозначает вероятность того, что частица 1 пройдет через ПШГх,
ориентированный под углом #а к оси z, а частица 2 пройдет через ПШГ2, ориентиро-
ориентированный под углом i?5 к вертикальному направлению. Таким же образом записываем
Рьс = р(О + - I О - +),
Рас = Р(+ О " I " О +)•
A8.2.2)
A8.2.3)
410 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
Польза такого обозначения станет очевидной на следующем этапе рассуждения.
Хотя совместная вероятность Раь ничего не говорит о прохождении при значении
угла #с, мы знаем, что для любой заданной частицы сумма вероятности прохождения
ее через ПШГ, ориентированный под углом #с к вертикали, и вероятности непро-
непрохождения ее через этот прибор, равна единице. Используя этот факт и учитывая
антикорреляцию проекций спина, записываем
Раь = Р{+ ~ О I " + О) = Р(+ ~ + I " + ") + Р(+ ~ ~ I " + +)• A8.2.4)
Аналогично
Рьс = Р(О + - IО - +) = Р(+ + -
Рас = Р{+ О - I - О +) = Р(+ + -
- - +) + Р{- + - | + - +), A8.2.5)
+) + Р(+ | - + +). A8.2.6)
Имея A8.2.4)—A8.2.6), нетрудно продолжить доказательство теоремы Белла. Сло-
Сложим РаЬ и РЬс:
Раь + Рьс
+ Р(+ + - | +) + Р(- + - | + - +). A8.2.7)
Отметим, что с учетом A8.2.6) выражение A8.2.7) можно записать в виде
РаЬ + Pbc^ Рас + Р(+ ~ +\~ + -) + Р(- + - | + " +)¦ A8.2.8)
Поскольку вероятности должны быть положительными, получаем
РаЬ + Рьс^ Рас* A8.2.9)
На этом доказательство теоремы Белла закончено.
18.3. Квантовое вычисление корреляций в теореме Белла
Квантовое вычисление вероятности прохождения частицы со спином 1/2, описы-
описываемой вектором состояния |Ф), через ПШГ, ориентированный под углом $, осуще-
осуществляется по формуле
\ A8-3-1)
где состояние |#) получается вращением состояния «спин вверх» вокруг оси у:
|#) = е-^^/2||>. A8.3.2)
Здесь напомним, что
'-(! J). «-.-С "о')- '.-6 Л) <«¦•¦»
И
it) = (о) , Ш=(?). A8-3-4)
Выражение A8.3.1) можно переписать в виде
Рф@) = (Ф|#)(#|Ф). A8.3.5)
Теперь рассмотрим оператор проектирования |#)(#|, полезную величину, опреде-
определяемую как
тг<, = |0)@|. A8.3.6)
С учетом A8.3.2) это выражение можно записать следующим образом:
^"/2, A8.3.7)
18.3 Квантовое вычисление корреляций в теореме Белла 411
и с помощью соотношения
находим, что A8.3.7) принимает вид
тт.? = - A + (jz cos # + стж sin #). A8.3.9)
Из предыдущего обсуждения мы знаем, что вероятность одновременного про-
прохождения частиц, описываемых синглетным спиновым состоянием A8.1.1), через
приборы Штерна-Герлаха, ориентированные под углами #а и #55 равна
РаЬ = (*1,2\**У?\*1,2)> A8.3.10)
где операторы проектирования тг^ и тг^ соответствуют частицам 1 и 2. После
небольших преобразований (см. задачу 18.3) находим
РаЬ = \[1~ COs(tfa - вь)] = \ Sin2 (^-=^) • A8.3.11)
Теперь учтем, что при выводе неравенства Белла A8.2.9) мы рассматривали толь-
только три угла. Следовательно, можно использовать квантово-механический результат
= 2 sm { 2 ] A8.3.12)
для проверки того, «удовлетворяет» ли квантовая механика теореме Белла. То есть,
справедлива ли «квантовая версия» неравенства Белла,
Для ответа на этот вопрос достаточно рассмотреть лишь углы #а = 0, #5 = тг/4
и #с = тг/2, при которых A8.3.13) означает, что
2 sin2 — ^ sin2 —,
или
0,15 ^ 0,25, A8.3.14)
что неверно. Следовательно, квантовая механика нарушает неравенство Белла!
Таким образом, получается, что предсказания квантовой механики и теории
скрытых переменных не согласуются между собой. Было поставлено, и продолжают
ставиться, много экспериментов, и все они до сих пор подтверждают квантовую меха-
механику, как мы увидим ниже. И хотя имеется несколько «лазеек», оставляющих вопрос
открытым, большинство ученых сейчас уверены, что окончательный эксперимент 1)
подтвердит квантовую механику.
Где сделана ошибка при выводе теоремы Белла? Каким образом эти простые
рассуждения оказались неправильными? Возможно лучшим способом ответить на
эти вопросы является изучение простых примеров, рассматриваемых в следующем
разделе.
г) См. работы Kwlat, Eberhard, Steinberg and Chiao A994); Fry, Walther and LI A995).
412 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
Отметим, что существует множество других неравенств Белла. Одна из полезных
форм неравенства Белла (которая, обычно, проверяется экспериментально) принад-
принадлежит Клаузеру и Хорну и записывается в виде (см. задачу 18.1)
5^1, A8.3.15)
где
и Pi{d'a) (р2($ь)) ~~ вероятность прохождения частицы 1 B) через прибор Штерна-
Герлаха, ориентированный под углом $^ (#ь).
Во многих экспериментах по проверке неравенств Белла определенные симметрии
помогают упростить неравенство A8.3.15). В этих экспериментах Pi(i^) и Р2($ь)
не зависят от углов $^ и #5? соответственно, то есть Pi($^) = Pi и Р2(^ь) = ^2- Кроме
того, совместные вероятности Pi2(^a)^6) зависят лишь от абсолютного значения
разности углов #а и t^ то есть Pi2(^a? $&) = ^i2(|^a "" $ь|)- Предположим, что #а,
#5, ^ь и #д в формуле A8.3.16) выбраны так, что
|0« - 0*1 = К " ^б1 = \К - $'ь\ = f h?« - ^1 = "• A8.3.17)
Тогда
= ЗР12(а)-Р12(За)^
П + F2
Большинство экспериментов являются вариациями эксперимента, в котором
измеряются корреляции поляризации фотонов, испущенных последовательно при
каскадном переходе атома. В таких экспериментах трехуровневый атом переходит,
Рис. 18.3. Схема рабочих уровней кальция. Пунктирной линией показан двухфотонный путь
возбуждения в состояние Ар So
например, с уровня J = 0 на уровень J = 1, а затем на уровень J = 0, который
соответствует основному состоянию атома. В типичном случае используются атомы
кальция. Уровень 4р2 1S'o заселяется с помощью двухфотонного возбуждения ла-
лазерным излучением. Затем атомы релаксируют в состояние 4s2 1AS'o через уровень
Pi, испуская два фотона на длинах волн 5513 А и 4227 А (см. рис. 18.3).
18.3
Квантовое вычисление корреляций в теореме Белла
413
Благодаря сохранению четности и момента импульса, имеется сильная корреляция
поляризации испущенных фотонов.
Схема эксперимента показана на рис. 18.4. Пара коррелированных фотонов
видимого диапазона испускается в ходе атомного каскадного перехода в хорошо
стабилизированном, высокоэффективном источнике S. Эти фотоны проходят через
Контроль четырехкратных
совпадений
Рис. 18.4. Схема эксперимента по корреляции фотонов при двухфотонном каскадном излу-
излучении, предназначенного для проверки неравенства Белла. (Из работы Aspect, Dallbard and
Roger A982))
переключающие устройства С\ и Сг, за которыми следуют два поляризатора с двумя
различными ориентациями: §а и §'а в области 1, и #5 и $'ъ в области 2. Совместные ве-
вероятности измеряются с помощью фотоумножителей ФЭУ1, ФЭУ2, ФЭУ1; и ФЭУ2;
и схемы совпадений.
Два фотона различаются длиной волны или частотой. Предположим, что излу™
чающий атом находится в начале системы координат и рассмотрим испущенные
фотоны, распространяющиеся в противоположные стороны по направлениям ±т/.
Оптический фильтр в направлении -\-у пропускает лишь фотоны на частоте */]_, а
фильтр в направлении —у — лишь фотоны на частоте vi- Поскольку реализуется
переход J = 0^J = l^J = 0, начальное и конечное состояния атома имеют
нулевой момент количества движения и одинаковую четность. Таким же образом,
двухфотонное состояние должно иметь нулевой момент количества движения и по™
ложительную четность. Состояние поляризации двух фотонов, после прохождения
через фильтры имеет вид
1
A8.3.19)
где R и L соответствуют правой и левой круговой поляризации, а индексы 1 и 2 —
фотонам частотой v\ и v^, соответственно. Переход в базис состояний линейной
поляризации |ж), \z) позволяет переписать вектор состояния A8.3.19) в виде
1
|ф1,2) = —7={\Z\)\Z2) + |Я1>|Ж2». A8.3.20)
Совместное измерение линейных поляризаций с помощью анализаторов, ориентиро-
ориентированных под углом §а и #5 к оси zi проецирует состояние A8.3.20) на два состояния
поляризации:
sio
A8.3.21)
A8.3.22)
414
Парадокс ЭПР, скрытые переменные и теорема Белла
Гл. 18
Следовательно, квантово-механическая вероятность прохождения через два анали-
анализатора задается выражением
Теперь вычислим Pi($) и Р2{'&). Если падающий фотон частотой v\ поляризован
вдоль оси ж, то вероятность прохождения через поляризатор, ориентированный под
углом § к оси ж, в случае
|ФХ> = cos Щх) + sin ф) A8.3.24)
равна cos2 #. Однако, поскольку падающий пучок неполяризован, мы усредняем по
всем значениям #, то есть
2тг
Аналогично,
Подставим теперь в выражение A8.3.18) значения Р\2{
A8.3.23), A8.3.25) и A8.3.26), соответственно, и получим
S(a) = 1>2 pi + p^'2 = -(Scos2 a -
При а = 22,5° это выражение сводится к
5B2,5°) = 1,207,
A8.3.25)
A8.3.26)
и P2(ti) из
A8.3.27)
A8.3.28)
что явно нарушает неравенство Белла A8.3.15). На рис. 18.5 величина S(a) изобра-
изображена как функция угла а. Видно, что неравенство Белла A8.3.15) нарушается при
0 < а < Зтг/16.
1.5
S(a)
-0.5
Квантовая теория
Верхняя граница,
определяемая неравенством
Белла
тг/4
тг/2
Рис. 18.5. Зависимость величины S(a) от а, задаваемая выражением A8.3.27). Пунктир-
Пунктирная линия соответствует верхней границе, определяемой неравенством Белла. (Из работы
Clauser and Shlmony A978))
18.4 Скрытые переменные с точки зрения квантовой оптики 415
18.4. Скрытые переменные с точки зрения квантовой оптики г)
В своей академической книге по теории скрытых переменных (СП) Белифант
показывает, что теории СП не столь далеки от квантовой механики (КМ), как это
может показаться. Рассуждения и наблюдения Белифанта побуждают нас применить
теорию квантового распределения к системе спинов 1/2, поскольку она в большой
степени соответствует квантовой оптике. При этом мы предлагаем теорию скрытых
переменных, которая согласуется с квантовой теорией во всем, что касается двухча-
двухчастичных корреляционных экспериментов, но, очевидно, является нелокальной.
Для начала напомним, что совместная вероятность прохождения частицы 1 через
ПШГ, ориентированный под углом Фа к вертикальному (-\-z) направлению, и частицы
2 через ПШГ, ориентированный под углом #5 K вертикали, определяется корреляци-
корреляционной функцией
Pl2(t?e,t?6) = <*l41>S)|*). A8'4Л)
и для спинового синглета имеем (см. A8.3.11))
\ (KM). A8.4.2)
Теперь рассмотрим ту же проблему, следуя Белинфанту. Для придания теориям
скрытых переменных характера перспективных, потребуем, чтобы они давали ре-
результаты, совпадающие с квантово-механическими, по крайней мере в простейших
случаях. Например, в случае неполяризованного пучка лишь 1/2 частиц должна
проходить через данный ПШГ. Далее вероятность прохождения через второй ПШГ,
помещенный вслед за первым (вертикальным) ПШГ под углом $ к нему, должна
определяться величиной (f |тг#| f), равной A + cos#)/2. Или в более общем случае,
если спин, вышедший из ПШГ, ориентированного под углом а, поступает затем
в ПШГ, наклоненный под углом § к вертикали, то вероятность выхода частицы из
второго ПШГ равна
i[l + cos@-a)]. A8.4.3)
Таким образом, можно сказать, что «скрытая переменная» а определяет, пройдет ли
частица через прибор, угол наклона $ которого определяется экспериментатором.
Имея это в виду, определим функцию вероятности скрытой переменной,
5rtf(a) = i[l + cos(i9-a)], A8.4.4)
как функцию, дающую вероятность «одновременного прохождения» через приборы
Штерна-Герлаха, ориентированные под углом § и а.
Теперь рассмотрим случай, когда два спина синглетной системы (рис. 18.2), один
из которых (спин 1) поляризован под углом а, а второй (спин 2) — под углом /3,
являются коррелированными, так что
I{a,P)dadp A8A5)
есть вероятность того, что спины имеют поляризации а и /3, тогда как остальные
скрытые переменные распределены случайно. Для случая максимальной корреляции
1) В этом разделе мы следуем работе Scully A983). Для дальнейшего чтения рекомендуем
Mermtn A993).
416 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
поляризации Белифант делает разумное предположение:
1(а,0) = 6(а-0-п)±. A8.4.6)
Зададимся теперь вопросом: какова вероятность одновременного прохождения
спинов 1 и 2 через систему двух ПШГ, изображенную на рис. 18.2? То есть, чему равна
величина P^i^a^b) в теории скрытых переменных? Следуя вышеприведенным
рассуждениям и учитывая A8.4.4) и A8.4.5), разумно ответить, что
f?(a). A8.4.7)
Учитывая A8.4.6) и A8.4.4), получаем
Г Г
Pi2(^a^b)= \ \dadp8{a- /3 -тг)х
J J
I Г "I i /А /1 \ 1 Г il i /А \1 / И О /I О \
х — < - 1 + cos(i75 — о) - 1 + cos(i/a — а)\> . A8.4.8)
2тг 12 2 J
Выполняя простое интегрирование в A8.4.8), находим
(СП). A8.4.9)
Для нас представляет интерес то, что имеется совершенно четкое различие между
квантовой корреляцией A8.4.2) и результатом теории скрытых переменных A8.4.9).
Что мы должны думать о предсказании теории скрытых переменных A8.4.9)?
Оно не так уж отличается от квантового предсказания. Нет ли в выражении A8.4.9)
«зародыша» истины или аргументов, ведущих к ней? В этой связи мы процитируем
Белифанта (Belinfante, 1973):
«Поляризационная (спиновая) скрытая переменная, введенная здесь,
является, конечно, величиной, не существующей в квантовой теории . . .
в квантовой теории даже не существует такого понятия как а».
Далее мы докажем, что строгое квантово-механическое рассмотрение этой про-
проблемы можно сделать, фактически, с помощью угловой переменной а. При этом
придется пересмотреть корреляционную функцию A8.4.7), и путем простого рас-
расширения A8.4.6) мы восстановим квантовый результат A8.4.2) с помощью теории
«скрытой переменной», сделанной «по образу и подобию» квантовой теории.
Приступая к квантово-механическому описанию корреляции спина 1/2, вычислим
сначала двумерную функцию распределения спина,
Ft(mz,mx) = Тг [рё(тх - ax)S(mz - az)], A8.4.10)
для случая, когда р = | f)(t I? T0 есть для частицы со спином вверх. Как показано
в приложении 18.А,
Pt(mz,mx) = \[8{тх + 1) S(mz - 1) + 6(тх - 1) S(mz - 1)]. A8.4.11)
Обращаясь к рис. 18.6, мы видим, что квантовая функция распределения для со-
состояния | f) соответствует равным примесям «вероятности», отвечающей значениям
±тг/4.
Выражение A8.4.11) можно переписать через угол а (см. рис. 18.6), такой что
тх = т sin а и mz = m cos а. В результате получим
Pt(o, т) = | \б (а - j\ + б(а + j)"U(m - V2 ).
A8.4.12а)
18.4
Скрытые переменные с точки зрения квантовой оптики
417
Спин вверх
Рис. 18.6. Описание частицы со «спином вверх» в теории квантового распределения
Аналогично, для «спина вниз»
~ т) +5(а + т)}S(m^ ^)- A8.4.126)
Теперь перепишем оператор тг$ A8.3.7) в соответствующем ему с-числовом представ-
представлении, то есть
1
= - A + mz cos $ + тх sin §).
Записанное через величины шиа, это выражение принимает вид
- a)].
= -[1
A8А13)
A8.4.14)
Длину т вектора в A8.4.14) можно определить из требования, чтобы величина
(f |тго| f) была равна единице, то есть
1=
l + mcos|L A8.4.15)
L
Это дает значение т, равное у2 .
В заключение отметим, что плотность вероятности, вычисленная для состояния,
соответствующего произвольному углу </>, определяется выражением
A8А16)
Чтобы установить связь с теорией скрытых переменных Белифанта, отметим, что
функции вероятности/проекции в теории скрытой переменной и в квантовой теории,
то есть тг#(а) A8.4.4) и тг$(о) A8.4.14), довольно похожи. Действительно, квантовые
плотности вероятности, задаваемые формулой A8.4.16), подразумевают, что в наших
рассуждениях со скрытой переменной вводятся похожие плотности вероятности, а
именно
Р+ф(а) = ё(а-ф).
Связь двух теорий отражена в табл. 18.1.
14 М.О. Скалли, М.С. Зубайри
A8.4.17)
418
Парадокс ЭПР, скрытые переменные и теорема Белла
Гл. 18
Таблица 18.1. Результаты, подчеркивающие близкое сходство между одночастичным
описанием в квантовой механике и настоящей теорией СП
Проекционная
функция
Распределение
вероятности для
спина вверх
Вероятность
прохождения
Квантовая механика
7г$(а) = -[1 + mcos($ — a)]
т = V2
Pt(a) = ±[*(a-?)+«(a+?)]
^t = [ Pt(a)iro(a) da = 1
Теория СП
7г^(а) = -[1 + cos(# - а)}
Pt(a) = S(a)
&T = 1 Pt(a)n0(a) da = 1
Распространим теперь результаты, собранные в табл. 18.1, на случай синглета
двух частиц со спином 1/2, ориентируясь на соответствующую теорию СП, которая
предлагает такие исследования. Для антикоррелированного (синглетного) состояния
пары частиц со спином 1/2,
-1+2»,
имеем соответствующее распределение вероятности:
A8.4.18)
A8А19)
В выражении A8.4.19) р = |Ф)(Ф|, где |Ф) задается выражением A8.4.18), ах
и (iz — обычные операторы Паули для г-й частицы (г = 1,2), а nix и тп^ —
соответствующие квазиклассические переменные.
Теперь нам необходимо сделать вычисление P(m^, m^2^), подобное тому, которое
делалось для Р(т). После некоторых преобразований находим, что
5{а-
где а и C — угловые переменные, соответствующие частицам 1 и 2. Физический смысл
различных членов в выражении A8.4.20) поясняется на рис. 18.7 для случая ф = 0.
Сразу замечаем, что фактор «антикорреляции спинов», имеющийся в A8.4.20), то
есть S(а — /3 — тг), совпадает с тем, что содержится в функции Белифанта /(а,/3),
задаваемой выражением A8.4.5). Различие, конечно, в том, что данный результат
непосредственно следует из квантовой теории. Более того, член в фигурных скобках
соответствует сумме одночастичных функций плотности вероятности для спинов,
направленных вдоль -\-ф и — ф.
Принимая во внимание выражения A8.4.6), A8.4.16), A8.4.17) и A8.4.20), логично
рассмотреть функцию вероятности «скрытой переменной»
Рф(а,,
= 5(а-/3- тг) - [6 {а -ф)
5(а-ф- тг)
A8.4.21)
18.4
Скрытые переменные с точки зрения квантовой оптики
419
Антикорреляция спинов Вверх
Вниз
Рис. 18.7. Физическая интерпретация совместной плотности вероятности для функции
спин—спиновой корреляции
Вероятности совместного счета, такие как A8.4.9), легко вычисляются с помощью
общего выражения
г г
, рOг§ь{рOг$а{а) аа ар. Aо.4.II)
Данная «теория» скрытых переменных подразумевает подстановку выражений
A8.4.4) и A8.4.21) в A8.4.22), что дает
(а^ф^ тг)]
х i [1 + cos(#6 - /3)] i [1 + cos(#a - a)} da dp A8.4.23)
или, после вычисления пары простых интегралов,
A8.4.24)
при ф = §а. Полученный результат A8.4.24) согласуется с предсказанием квантовой
механики A8.4.2). Результаты двух теорий подытожены в табл. 18.2.
Таблица 18.2. Соответствие между двухчастичными функциями корреляции спинов
в теории СП Белифанте, квантовой механике и настоящей теории СП
Теория СП
Белифанте
КМ
Настоящая
теория СП
Двухчастичное распределение
±6(а-/3п)
\б(а-/3-п)х
*{\[*(«-Ф-!)+'{«-Ф+Ф
8(а-р- тг)^[6(а -ф) + 8(а-ф- тг)]
Совместная вероятность
| [l - | cos(tfa - 0ь)]
i[l-cos(i?0-tfb)]
i[l-C0s(i?o-1?b)]
14*
420 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
В заключение обратимся к вопросу: в чем различие между данной теорией
СП, согласующейся с квантовой механикой, и рассмотрением Белла (воплощенным
в неравенстве Белла), отличающимся от КМ? Ответ следующий: данная теория СП,
прежде всего, включает отрицательную вероятность и, кроме того, теория является
нелокальной.
Говоря о первом аспекте — отрицательной вероятности, напомним общую форму
классического описания Pi2($aj $ь)> задаваемую выражением A8.4.22).
В выражении A8.4.22) величины тг$а (о) и тг$ь(/3) представляют собой вероятности
того, что частица 2 со «скрытой» переменной а пройдет через ПШГх, ориентирован-
ориентированный под углом #а к вертикали, а частица 1 со «скрытой» переменной C пройдет через
ПШГ1, ориентиованный под углом ёь к вертикали. Классически эти вероятности,
конечно, положительны. Функция Рф(а, C) описывает корреляцию между перемен-
переменными а и р. Таким образом, интегрирование по этим величинам дает совместную
вероятность прохождения Fi2(^a? $&)• Общий вид Pi2(#a> $ь)> полученный из теории
квантовых распределений очень походит на классический (ср. A8.4.22)) и задается
выражением
J J
Как и в классическом случае величина Рф(а^ /3) играет роль функции корреляции
между переменными а и /3. Однако операторы проектирования ж$ь([3) и тг$а(а),
имеющие вид
тг^а(а) = -[1 + V2cos(#a - а)], A8.4.26а)
а 2
ж®ъ{C) = -[1 + \/2cos(#b - /?)], A8.4.266)
могут быть теперь отрицательными. В этом состоит существенное различие между
классическим и квантовым описаниями проблемы Эйнштейна, Подольского, Розе-
на спинового синглета. Функции тг#ь(/3) и тг#а(а), являющиеся наиболее близкими
квантовыми аналогами классических вероятностей тт$ь(C) и тг^а(а), могут быть
отрицательными. Напомним, что доказательство теоремы Белла не имеет силы, если
допустить отрицательные вероятности.
Мы показали, что попытка сделать квантовую механику похожей на классическую
требует, чтобы было установлено соответствие между классическими вероятностями
и функциями теории квантовых распределений, которые не являются положительно
полуопределенными. Таким образом, мы видим (на этом примере), каким образом
в квантовой механике нарушается теорема Белла.
Обратимся теперь к более тонкому, но важному вопросу. Вычисляя /^(^а? $ь)
с помощью функции Ро(а^ /3), задаваемой выражением A8.4.20) при ф = 0, находим
х i[l + mcos(tfb -/3)]i[l + mcos(#a- a)] da dC = i[l - cos@e - t?6)]. A8.4.27)
18.5 Теорема Белла без неравенств: равенство Гринбергера-Хорна-Цейлингера 421
Этот результат совпадает с тем, что получается при использовании Рф(а,/3) из
A8.4.20). Этого и следовало ожидать, ибо использование как сферически симмет-
симметричного состояния
|Ф> = ^Iltib) ~~ \Ub)] -> Ро(<*,Р), A8.4.28а)
так и
|Ф> = ^[|+i - 2) - |-1 + 2)] -»• РФ(а, /3), A8.4.286)
должно давать одинаковый результат.
Однако, если в рамках данной теории СП вычислить Рш^а^ь) с помощью
функции Рд(а, /3), заданной на рис. 18.7, то получим
Pi2(#a,0b)= [ 1б{а-Р-<к)±[6(а) + 6(а-<1г)]х
х \[l + cos(#b - /?)]i[l + cos(#a - a)] da d/3, A8.4.29)
A A
что дает
~ ( \ ^ \ ^ ( \ ^ ( \1
4 L 2 2 J
Этот результат согласуется с квантовым предсказанием, только если #5 = 0.
Физическое содержание и интерпретация функций прохождения (проектирова-
(проектирования), например тг^(а), и распределения условной вероятности Рф(а, /3) различаются
в квантовой теории и в представленной теории СП. Также приготовление состояний
и экспериментальная параметризация играют разные роли в этих теориях.
В квантовой теории приготовление состояния означает выбор \ф), то есть
(а, /3), а рассматриваемый эксперимент говорит нам, какой оператор, например тго,
мы должны вычислить. Однако, если заменить Рф{а^C) функцией Ро(а,/3), вычис-
вычисление не должно измениться, поскольку рассматривается сферически симметричное
состояние. _
С другой стороны, в представленной теории СП выбор Ро(а,/?), для данной
сферически симметричной проблемы, должен «соответствовать» выбору тг#(а), как
показывают вычисления выражений A8.4.29), A8.4.30) и A8.4.26а,б). Как Po(a1f3)J
так и п$(а) подразумевают приготовление состояния и конкретизацию эксперимента.
Таким образом, хотя данная теория СП воспроизводит квантовую спин-спиновую
корреляционную функцию, она отличается от квантовой теории в этом важном
вопросе. Мы видим, следовательно, что данная теория СП является нелокальной.
18.5. Теорема Белла без неравенств: равенство
Гринбергера-Хорна-Цейлмнгера
Результаты разд. 18.3 говорят о том, что квантовая теория, а не теории скрытых
переменных, подтверждаются экспериментами, хотя результаты теории СП неприем-
неприемлемы лишь в некоторых областях значений угла а. Кроме того, мы видели, что можно
даже развить (нелокальную) теорию СП, согласующуюся с квантовой механикой.
Было бы очень интересным найти ситуацию, в которой корреляции теории СП и
квантовой механики полностью противоречат друг другу. Именно этому и посвящен
данный раздел.
Гринбергер, Хорн и Цейлингер показали, рассматривая определенные трехча-
стичные корреляционные эксперименты, что результаты теорий СП и квантовой
422 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
механики полностью противоречат друг другу. В работе Гринбергера, Хорна и Цей™
лингера отсутствуют неравенства, и предсказания теорий СП и квантовой механики
просто разные. Это дает более сильное опровержение теорий СП.
Рассмотрим трехчастичное состояние
|ФK = ^(Ititzts) - I-U42.U» A8.5.1)
вместо предыдущего двухчастичного состояния
|Ф>2 = ^(Itll2> - |llt2». A8.5.2)
Состояние |Ф)з является собственным состоянием операторов ах <ту <ту ,
A) B) C) A) B) C) гл
(Ту (Тх & у и (Ту (Ту <7х • ^то молено проверить, вспоминая, что
°x\t) = \l), <т*|4-> = |Т>, <ry\t) = i\l), <ry\i) = -ift), A8.5.3)
так что, например,
^ ] = |Ф>з- A8.5.4)
Таким образом, |ФK является собственным состоянием оператора ах ау ау с соб™
ственным значением +1. Аналогично можно показать, что |Ф)з является также
g. A) B) C) A) B) C) g.
собственным состоянием операторов ау ох ®у и а у ау ох с собственным зна-
значением +1.
Следовательно, мы имеем новый тип корреляции Эйнштейна, Подольского, Розе-
на состоящей в том, что если измеренные значения ау и ау оба окажутся равными
+1, то значение ах также должно быть равно +1. Однако, если ау и ау окажутся
равными +1 и — 1, соответственно, то ах будет равно — 1. Так что получаем новый
тип «действия Эйнштейна, Подольского, Розена на расстоянии».
Теперь отметим, что
^1)^2)^3)|Ф)з = -|Ф)з, A8.5.5)
поскольку
^A)^B)^C) = _Г(ТA)(ТB) C)пг A) B) C)и A) B) CI /jg 5 g4
X X X IX у у J L у X у J L у у X J \iUil/tU/
(напомним, что ахау = —ауах (г = 1,2,3)), и действие операторов каждого
из трех наборов в квадратных скобках на |Ф)з дает +|Ф)з- Следовательно, измере-
A) B) (з) з
ние ах , ах и ах всегда приводит к ситуации, когда произведение трех исходов
равно — 1.
Теперь рассмотрим предсказания исходов по теории СП. Каждому оператору ах
U) (г) (г)
и ст^ мы приписываем соответствующую классическую величину тх и ту , где
rrix и ту могут принимать значения +1 или — 1. Из A8.5.4) следует, что
m^m^mf = +1, A8.5.7)
m^m^m^ = +1, A8.5.8)
m^m^m^ = +1. A8.5.9)
18.6 Квантовая криптография 423
Следовательно,
[m^mfmf)[m^m^mf}[m^m^m^] = +1 A8.5.10)
ИЛИ
m^m^m^[m^]2\mff[mf]2 = +1. A8.5.11)
Поскольку [ту ]2 = +1 и т. д.,
т^т^т^ = +1, A8.5.12)
в противоположность квантовому предсказанию A8.5.5), согласно которому эта ве-
величина должна быть равна — 1.
18.6. Квантовая криптография
Интересное приложение квантовой корреляции между одиночными фотонами си-
системы ЭПР-типа, рассмотренной в разд. 18.1, лежит в области квантовой криптогра-
криптографии. Как обсуждалось ранее, измерение квантовой системы в общем случае вызывает
возмущение последней и дает лишь неполную информацию о состоянии системы до
измерения. В квантовой криптографии этот аспект квантовой механики используется
для такой связи между двумя участниками, отправителем и получателем, которая
остается абсолютной тайной даже при наличии подслушивания.
При любом секретном обмене информации данные (обычно, последовательность
битов 1 и 0) комбинируются со случайной последовательностью битов, называемой
ключом, и посылаются по коммуникационному каналу. Ключ известен лишь отпра-
отправителю и получателю. Случайный характер ключа гарантирует, что передаваемые
данные также являются случайными и недоступны для подслушивающего, не имею-
имеющего ключа. Безопасность канала, следовательно, зависит от секретности ключа.
Проблема классического канала, в принципе, состоит в том, что подслушивание
может происходить в тайне от отправителя или получателя. Это не так в случае
квантовой криптографии, в которой, как мы увидим ниже, подслушивание возмуща-
возмущает измеряемую последовательность, так что это можно зафиксировать. Далее будут
рассмотрены различные квантовые криптографические системы.
18.6.1. Протокол Беннота^Брассарда. В этой схеме квантовый криптографиче-
криптографический прибор состоит из передатчика и приемника. На конце передатчика отправитель
посылает фотоны в одном из четырех состояний поляризации, характеризуемых угла-
углами 0°, 45°, 90° и 135° по отношению к вертикальному направлению. Два состояния
поляризации, например 0° и 45°, обозначают бит 0, тогда как другие два, 90° и 135°,
обозначают 1. Поток фотонов, поляризованный соответствующим образом, представ-
представляет таким образом последовательность единиц и нулей. На принимающем конце
получатель измеряет поляризацию приходящих фотонов, выбирая случайно базис
ф (поляризатор ориентирован вертикально) или (?§) (поляризатор ориентирован под
углом 45°). Согласно законам квантовой механики получатель может различить
прямолинейную поляризацию (углы 0° и 90°) или диагональную поляризацию (углы
45° и 135°), но не обе сразу.
Если базис, выбранный получателем, совпадает с базисом отправителя, то поля-
поляризация полученного фотона полностью коррелирует с поляризацией отправленно-
отправленного. Таким образом, фотон, поляризованный под углом 90°, который прошел через
поляризатор, ориентированный вертикально, будет зарегистрирован как фотон, по-
поляризованный под углом 90° и т. д. Однако такая корреляция отсутствует, если базис,
выбранный получателем, является сопряженным базису отправителя, то есть фотон,
424 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
поляризованный под углом 90° будет с равной вероятностью зарегистрирован как
фотон, поляризованный под углом 45° или 135°, если поляризатор получателя ори-
ориентирован под углом 45°. Таким образом, последовательность поляризаций, характе-
характеризуемая углами 0°, 90°, 135°, 0°, 45°, 135°, 45°, 45°, 90°, полученная с помощью по-
последовательности базисов (?§), ф, ф, C)? (8)? ®? Ф? ®? Ф? может дать на выходе по-
последовательность 135°, 90°, 0°, 45°, 45°, 135°, 90°, 45°, 90°. Получатель записывает ре-
результаты измерений тайным образом, а через открытый канал он и отправитель срав-
сравнивают последовательности своих базисов. Они сохраняют значения, полученные при
одинаковом базисе, и отбрасывают оставшиеся. Таким образом, в вышеприведенном
примере результаты 2, 5, 6, 8 и 9 сохраняются, а результаты 1, 3, 4, и 7 отбрасываются.
При переводе в биты 0и1A0101в указанном примере) получается ключ.
В протоколе Беннета-Брассарда выбор базиса полностью скрыт от подслуши-
подслушивающего. Пассивное подслушивание в этом протоколе невозможно, поскольку лю-
любая попытка этого приведет к несоответствию последовательностей. Отправитель
и получатель могут догадаться о подслушивании, сравнивая часть данных. В случае
несоответствия они могут забраковать свои данные и начать сначала.
18.6.2. Жвантовая криптография, основанная на теореме Белла. Эта возможная
схема квантовой криптографии основана на мысленном эксперименте Эйнштейна,
Подольского, Розена (разд. 18.2), а теорема Белла используется для проверки на под-
подслушивание. Установка похожа на ту, что использовалась для проверки неравенства
Белла (рис. 18.4). Канал состоит из источника, испускающего пары частиц со спином
1/2, находящиеся в синглетном состоянии. Частицы разлетаются в противоположные
стороны, к отправителю и получателю, которые затем измеряют различные состав-
составляющие поляризации, как в эксперименте по неравенству Белла. После того, как
будут сделаны измерения составляющих поляризации, отправитель и получатель
сравнивают через открытый канал последовательность ориентации их анализаторов.
Они делят свои измерения на две группы. В первую группу включаются те измере-
измерения, при которых их анализаторы были ориентированы одинаково, а во вторую те,
при которых анализаторы были ориентированы по-разному. Все те измерения, при
которых любому из них не удалось зарегистрировать частицу, отбрасываются.
Результат первой группы измерений не доступен на открытом канале и исполь-
используется для формирования ключа, ибо измерения полностью коррелированы. Резуль-
Результат второй группы измерений пересылается между отправителем и получателем
по открытому каналу и результирующие данные используются для вычисления
величины 5, задаваемой выражением A8.3.16). Если не было прослушивания, то
результат должен совпадать с предсказаниями квантовой механики. Таким образом
осуществляется тест на подслушивание.
Приложение 18. А
Квантовая функция распределения для одиночной частицы
со «спином вверх»
Приступая к о-описанию задачи спинового синглета, рассмотрим сначала среднее
значение оператора Q(aXJ cr^, crz), вычисляемое с помощью оператора плотности р:
Вводя операторную <5-функцию
^b)], A8.A.2)
П. 18.Б Квантовая функция распределения для двух частиц 425
где b ~~ оператор (например, az) и Р ~~ связанная с ним классическая переменная
(например, mz), можно записать оператор Q(crXJ ay,az) в виде
г
Q(ax, ay, az) = d3mQ(mx,my,mz) 5(mx - ax) S(my - ay) S(mz - az). A8.A.3)
Подставляя A8.A.3) в выражение A8.А.1), находим, что среднее значение оператора
Q задается выражением
mP{mx^my^mzlt)Q{mx^myimzI A8.А.4)
где
Р(тх, myimZJt) = Тг [p(t) 8{тх - ах) 5(ту - ау) S(mz - az)}. A8.А.5)
Напомним, однако (см. разд. 18.4), что нас будут интересовать лишь операторы
Q, содержащие ах и aZJ например тг^, так что можно ограничиться рассмотрением
операторных разложений вида
Г Г
Q(dXJ az) = Q{mx,mz) S(mx — ax) S(mz - az) dmx dmz
и соответствующей квантовой функцией распределения
P(mx,mz,t) = Tr [p(t) 6(mx - ax) 8{mz - - M A8.A.6)
Функция распределения A8.A.6) является средством, с помощью которого молено
осуществить квантовое рассмотрение данной задачи для спина 1/2 с использованием
угла а. Далее мы рассмотрим простую задачу одиночной частицы со «спином вверх».
Для случая «спин вверх» оператор плотности, очевидно, имеет вид
A8-А.7)
а соответствующая функция распределения
Pt(mx,mz) = Tr [|t)(t| 5(тх - ах) S(mz - az)} =
= (t| S(mx - ax) 5(mz - <rz)|f>. A8.A.8)
Последнее выражение, с учетом A8.А.2), принимает вид
A8.А.9)
Приложение 18. Б
Квантовая функция распределения для двух частиц
Здесь мы заполним пробел между выражениями A8.4.19) и A8.4.20). Сначала
заметим, что A8.4.19) можно записать в виде
)|>
A8.Б.1)
426
Парадокс ЭПР, скрытые переменные и теорема Белла
Гл. 18
|Ф) = -y=(|ti4-2> - |4it2» = A8.Б.2)
= —Wl+i - 2) - hi + 2)), A8.Б.З)
V 2
где, в рамках данного приложения, | f) — положительное собственное состояние
оператора aZJ |+) — положительное состояние оператора ах. Следовательно, (±| f) =
= 1/л/2, (±|4-) = =Ы/\/2, так что, например,
С функцией от оператора можно обращаться следующим образом: разложить объект
действия по собственным состояниям, после чего заменить функцию от операторов
функцией от собственных значений. В данном случае, в частности,
-±=
. A8.Б.4)
-L[
Объединяя с A8.Б.1), получаем
^Ч-П-и,
]. A8.Б.5)
1) 5(m{x
{2) -
1)+
+ 1)+
- 1)+
1)]. A8.Б.6)
Теперь, считая, как и прежде, что угол а определяет ориентацию вектора т^, угол
/3 ориентацию вектора т^2\ а ф задает произвольную ориентацию оси z, последнее
выражение можно записать в виде
61 а-
Зтг
4
ill, A8.B.7)
что совпадает с A8.4.20).
Задачи к гл. 18 427
Задачи
18.1. 1. Рассмотрим четыре числа Ж]_, Ж2, х$ и Ж4, такие что 0 ^ Х{ < 1, (г =
= 1,2,3,4). Покажите, что значения функции X = х\Х2 — х\Х4 + Ж2Ж3 +
+ Ж3Ж4 — Х2 — Жз ограничиваются неравенством — 1 ^ X ^ 0.
2. Полагая в предыдущем неравенстве х\ = Pi(/x,#a), Х2 = ^(/^^б)? жз =
= Pi(/x, $^) и Ж4 = РгСм? ${,)? докажите неравенство Белла
где
Здесь Fi(/i,#a) и F2(/i,#5) — вероятности детектирования частиц 1 и 2
при ориентации приборов Штерна-Герлаха (рис. 18.2) под углом ^ и if^
соответственно, где fi — скрытые переменные, «полностью» описывающие
процесс испускания в источнике и dA — мера переменных /х. Далее, Pi(#^)
и Р2($ь) — вероятности прохождения частиц 1 и 2 через соответствующие
приборы Штерна-Герлаха, ориентированные под углом t^ и #55 соответ™
ственно, и Pi2($ai $ь) — совместная вероятность того, что частицы 1 и 2
пройдут через соответствующие им приборы Штерна^Герлаха, ориентиро-
ориентированные под углом #а и #55 соответственно. (Указание: см. работу Clauser
and Home, A974).]
18.2. 1. Покажите, что exp(—ifday/2) = cos(#/2) — iay sin(i9/2)
2. Используя полученный результат, покажите, что
2) = -A +
А
18.3. Для спинового синглетного состояния |#i52) = [| ti, 4-2} — 1 11? Тг)]/\/2 покажите,
что
где
4? = ^ [1 + 41' COS ^a + ^i^ Sin
Здесь ах и (iz — матрицы Паули для г-то спина.
18.4. Покажите, что |Ф)з = (| tit2ts) ~ I ^1^24-2))/\^2 есть собственное состояние
A) B) C) A) B) C)
операторов а у а^ ®у ж иу иу ах .
428 Парадокс ЭПР, скрытые переменные и теорема Белла Гл. 18
Список литературы
Теория измерений
Lamb, W. E., Jr. Physics Today, 22, 23 A969).
* Брагинский В.Б., Халил Ф.Я. Квантовые измерения (Наука, Москва, 1990).
ЭПР-парадсжс
Einstein, A., Podolsky, В. and Rosen, N. Phys. Rev. 47, 777 A935).
Bohr, N. Phys. Rev. 48, 696 A935). Ответ Бора Эйнштейну, Подольскому и Розену дошел до
нас в виде так называемой копенгагенской интерпретации квантовой механики.
Bohm, D. Quantum Theory, (Prentice Hall, Englewood Cliffs, NJ 1951).
Belinfante, F. A Survey of Hidden Variable Theories, (Pergamon, New York 1973).
Cantrell, C. D. and Scully, M. O. Phys. Rep. С 43, 499 A978).
*Клышко Д.Н. Фотоны и нелинейная оптика (Наука, Москва, 1980).
*Килин С.Я. УФН 169, 508 A999)
*Гадомский О.Н., Антипин К.К. Proc. SPIE 4061, 37 A999).
Горбачев В.Н., Трубилко А.И. ЖЭТФ 118, 1036 B000).
*Менский М.Б. УФН 170, 631 B000).
*Баргатин И.В., Гришанин Б.А., Задков В.Н. УФН 171, 625 B001).
Неравенство Белла
Bell, J. S. Physics I, 195 A965); Rev. Mod. Phys. 38, 447 A966).
WIgner, E. P. Am. J. Phys. 38, 1005 A970).
Clauser, J. F. and Home, M. A. Phys. Rev. D 10, 526 A974).
Clauser, J. F. and Shlmony, A. Rep. Prog. Phys. 41, 1881 A978). Прекрасный обзор по данной
теме.
Pipkin, F. M. In Advances in Atomic and Molecular Physics, Vol. 14, ed. D. R. Bates and B.
Bederson (Academic, New York 1978), p. 281.
de' Espagnat, B. Set. Am. 241, 158 (Nov. 1979). В этой работе приводится общепринятый
вывод неравенства Белла.
Scully, M. О. Phys. Rev, D 28, 2477 A983).
PedrottI, L. M. and Scully, M. O. In Quantum Electrodynamics and Quantum Optics, ed. A. O.
Barut (Plenum, New York 1984).
Mermln, N. D. Rev. Mod. Phys. 65, 803 A993).
Оптические проверки неравенства Белла
Freedman, S. J. and Clauser, J. F. Phys. Rev. Lett. 28, 938 A972).
Fry, E. S. and Thompson, R. C. Phys. Rev. Lett. 37, 465 A976).
Aspect, A., Grangler, P. and Roger, G. Phys. Rev. Lett 49, 91 A982).
Aspect, A., Dallbard, J. and Roger, G. Phys. Rev. Lett 49, 1804 A982).
Ou, Z. Y. and Mandel, L. Phys. Rev. Lett 61, 50 A988).
Shlh, Y. H. and Alley, С. О. Phys. Rev. Lett 61, 2921 A988).
Kwlat, P. G., Eberhard, P. H., Steinberg, A. M. and Chiao, R. Y. Phys. Rev. A 49, 3209 A994).
Fry, E. S., Walther, T. and Li, S. Phys. Rev. A 52, 4381 A995).
Список литературы к гл. 18 429
Равенство Гринбергера^Хорна^Цейлмнгера (ГХЦ)
Greenberger, D. M., Home, M. and Zelllnger, A. In Bell's Theorem, Quantum Theory, and
Conceptions of the Universe, ed. M. Kafatos (Kluwer, Dordrecht 1989), p. 73.
Mermin, N. D. Am. J. Phys. 58, 731 A990a); Physics Today 43 F), 9 A990b).
Greenberger, D. M., Home, M. A., Shlmony, A. and Zelllnger, A. Am. J. Phys. 58, 1131 A990).
Функции распределения для спина 1/2
Stratnovich, R. L. Sov. Phys. JETP 4, 891 A957).
Arecchi, F., Courtens, E., Gllmore, R. and Thomas, H. Phys. Rev. A 6,2211 A972).
Cohen, L. and Scully, M. O. Found. Phys. 16, 295 A986).
Chandler, C, Cohen, L., Lee, C, Scully, M. O. and Wodklewlcz, K. Found. Phys. 22, 867 A992).
Dowling, J. P., Agarwal, G. S. and Schlelch, W. P. Phys. Rev. A 49,4101 A994).
Scully, M. O. and Wodklewlcz, K. Found. Phys. 24, 85 A994).
Квантовая криптография
Bennett, С. Н. and Brassard, G. In Proceedings of IEEE International Conference on Computers,
Systems, and Signal Processing, Banglore, India (IEEE, New York, 1984), p. 175. В работе
излагается протокол Беннета—Брассарда.
Ekert, А. К. Phys. Rev. Lett. 67, 661 A991). В этой статье описана квантовая криптография,
основанная на теореме Белла.
Bennett, С. Н. Phys. Rev. Lett 68, 3121 A992).
Bennett, С. Н., Brassard, G. and Mermin, N. D. Phys. Rev. Lett. 68, 557 A992).
Townsend, P. D., Rarity, J. G. and Tapster, P. R. Electron. Lett. 29, 634 A993).
Huttner, В., Imoto, N., Gisin, N. and Мог, Т. Phys. Rev. A 51, 1863 A995).
*Burlakov, A.V., Chekhova, M.V., Karabutova, O.A., Klyshko, D.N. and Kulik, S.P. Phys. Rev.
A 60, R4209 A999).
Глава 19
КВАНТОВЫЕ
НЕРАЗРУШАЮЩИЕ
ИЗМЕРЕНИЯ х)
Во многих квантовых системах процесс измерения наблюдаемой величины вносит
шум, так что последовательные измерения одной и той же наблюдаемой дают разные
результаты. Простейшим примером квантовой системы является свободная частица,
описываемая гамильтонианом
*=?, A9.1)
где р — оператор импульса и т — масса частицы. Оператор координаты х можно
измерить с произвольной точностью путем мгновенного измерения. Однако, согласно
соотношению неопределенностей Гейзенберга между х и р, первоначальное точное
измерение х резко возмущает р, так что
^ A9-2)
В течение последующей свободной эволюции импульс р вносит изменения в ж в со™
ответствии с уравнением
х = ^[х,Ж] = — A9.3)
гН1 J т
^ A9.4)
В результате
[Ax{t)f = [Дх@)]° + [*№]\* > [Д,@)Г+Щ2^, A9.5)
то есть точность второго измерения уменьшается.
В квантовых оптических системах детектирование полевых переменных осуще-
осуществляется, обычно, методами счета фотонов, которые возмущают поле. Как след-
следствие, последовательные измерения полевых переменных дают разные результаты.
Желательно рассмотреть схемы, позволяющие избежать обратного действия изме™
рения на детектируемую наблюдаемую. Такое измерение, при котором осуществля-
осуществляется контроль за наблюдаемой и ее можно измерять многократно, так что результат
каждого измерения полностью определяется результатом начального, точного изме-
измерения, называется квантовым неразрушающим (КН) измерением.
) Стандартным обзором по этой теме является Caves, Thorne, Drever, Sandberg and
Zimmermann A980). Глубокий анализ проблемы содержится в более поздней книге Braglnsky
and Khalili A992).
19.1 Условия для КН измерений 431
В этой главе мы определим сначала условия для КН измерений в квантовой систе-
системе общего вида, а затем обсудим схемы КН измерения числа фотонов в определенных
квантовых оптических системах.
19.1. Условия для КН измерений
В общем случае КН измерений сигнальная наблюдаемая Ag квантовой системы
S измеряется путем детектирования изменения наблюдаемой Ар пробной системы
Р, взаимодействующей с Я в течение времени измерения Т, без возмущения после-
последующей эволюции Ag- Таким образом можно получить последовательность точных
измерений величины As, таких, что результат каждого измерения полностью пред-
предсказывается по результату предыдущего измерения. Такая наблюдаемая называется
КН-наблюдаемой.
Полный гамильтониан системы S-P записывается в виде
Ж = ЖБ + ЖР + Ж}, A9.1.1)
где J^s, Жр и Ж\ — гамильтонианы, описывающие исследуемую систему, пробную
систему и их взаимодействие, соответственно. Уравнения движения для операторов
As и Ар имеют вид
A9.1.2а)
= [Ар,ЖР + «#}]. A9.1.26)
Определим теперь условия, определяющие процесс КН измерения. Измерение яв-
является типа КН, если измеряемая наблюдаемая As, пробная или считывающая
наблюдаемая Ар ш гамильтониан взаимодействия Ж\ удовлетворяют следующим
условиям.
1. Поскольку As подлежит измерению, гамильтониан Ж{ должен быть функцией
от As, то есть
§?#0. A..1.3)
2. Поскольку пробная система Р используется для измерения As, наблюдаемая
Ар не может быть интегралом движения, то есть Ар ф 0. Следовательно, коммута-
коммутатор Ар ш Ж\ должен быть отличным от нуля:
[АР,Ж1]ф0. A9.1.4)
3. Наблюдаемая As не должна изменяться при взаимодействии пробной системой
в течение измерения, так что
\А3,Ж1\ = 0. A9.1.5)
4. Гамильтониан Жб не является функцией наблюдаемой Acs, сопряженной к As,
то есть
|f = 0. A9.1.6)
Это требование гарантирует, что движение As не станет непредсказуемым вследствие
неопределенности, накладываемой на сопряженную переменную Acs при измерении
As, и что измерение As не влияет на саму As-
Условия A9.1.3)—A9.1.6) определяют процесс КН измерения. Рассмотрим теперь
схемы КН измерений, в которых измеряется число фотонов.
432
Квантовые неразрушающие измерения
Гл. 19
19.2. КН измерение числа фотонов с помощью оптического эффекта
Керра
Показатель преломления многих материалов можно описать соотношением
2 A9.2.1)
где по — обычный показатель преломления в случае слабого поля ш П2 — постоя-
постоянная, определяющая скорость изменения показателя преломления при изменении
интенсивности света. Если мощная сигнальная волна падает на такой нелинейный
материал, то она вызывает изменение показателя преломления, так что слабая
пробная волна, проходя через материал, испытывает сдвиг фазы, пропорциональный
интенсивности сигнальной волны. Изменение показателя преломления, описываемое
формулой A9.2.1), называется оптическим эффектом Керра. В этом разделе мы
опишем схему КН измерения, основанную на эффекте Керра, в которой измеряется
число фотонов сигнальной волны путем измерения фазы опорной волны.
Схема КН измерения числа фотонов сигнальной волны показана на рис. 19.1.
Пробная волна испытывает сдвиг фазы вследствие изменения показателя прелом-
преломления, который пропорционален интенсивности сигнальной волны в керровской
as
Сигнал
Mi
z = L
Пробный
лазер
Керровская среда
М2
V
аР
Светоделитель 1
Светоделитель 2
\|
Детектор
Рис. 19.1. Схема КН измерения числа фотонов сигнального поля. Пробная, опорная и сиг-
сигнальная волны обозначены операторами уничтожения ар, аг и as, соответственно. Ваку-
Вакуумные флуктуации (оператор Ъ) примешиваются на светоделителе 1. Зеркала Mi и Mi
являются прозрачными для сигнальной волны. (Из работы Imoto, Наш, and Yamamoto
A985))
среде. Сигнальная волна проходит через керровскую среду без изменения числа
фотонов, так что фаза пробной волны модулируется числом фотонов сигнальной
волны. Фазовый сдвиг пробной волны измеряется с помощью фототока балансного
детектора. На рис. 19.1 коэффициент пропускания зеркал Mi и M<i равен нулю для
частоты сигнального поля ug и равен единице для частоты пробного поля up, так
что интерферометр создается лишь для пробного поля.
Гамильтониан взаимодействия сигнальной и пробной волны в керровской среде
имеет вид
где
Ж. = hus
A9.2.3)
19.2 КН измерение числа фотонов с помощью оптического эффекта Керра 433
ЖР = hup (а+аР + i) , A9.2.4)
A9.2.5)
Здесь к — постоянная взаимодействия, зависящая от нелинейной восприимчивости
третьего порядка, вследствие эффекта Керра. КН-наблюдаемая, которую нужно
измерить, есть оператор числа фотонов:
As = a+as, A9.2.6)
а пробная, или считывающая наблюдаемая — подходящий фазовый оператор. Фазо-
Фазовый оператор фр можно определить с помощью соотношений
1ехр(г0р), A9.2.7)
/-1. A9.2.8)
Можно проверить, что exp(i^>p) и ехр(—г<^р) не являются эрмитовыми операторами
и, следовательно, не описывают наблюдаемые свойства поля. Однако их комбинации,
cos«^p = -[ехр(г^р) + ехр(—г^р)], A9.2.9а)
А
ыпфр = -r[exp(i^F) — ехр(—г0р)], A9.2.96)
лъ
являются эрмитовыми операторами. Последние можно рассматривать как квантово-
механические операторы, представляющие наблюдаемые фазовые свойства электро™
магнитного поля. Таким образом, можно выбрать
АР = s!n^F. A9.2.10)
Из A9.2.7), A9.2.8) и A9.2.10) следует, что в переменных ар и Ор
h
Ар = h { г4-—ар ~ °р г^—) • A9-2Л1)
Al yapap + l Vарар + 1
Можно проверить, что условия A9.1.3)—A9.1.6) соблюдаются для операторов Ар
и Ag (см. задачу 19.2), так что данная схема обеспечивает КН измерение числа фо-
фотонов сигнальной волны Ag = a^as- В частности видно, что As является интегралом
движения.
Уравнение движения Гейзенберга для оператора пробного поля ар в керровской
среде имеет вид
аР = -ъкА8аР. A9.2.12)
Это уравнение эволюции во времени можно переписать в виде уравнения эволюции
в пространстве для рассматриваемой задачи бегущей волны, заменяя t величиной
— z/v, в случае распространения в направлении +z со скоростью v, то есть
jz ^. A9.2.13)
Интегрируя A9.2.13) от z = 0 до z = L, получаем
ap(L) = exp ^ASLJ aP@), A9.2.14)
где учтено, что As является интегралом движения. Оператор kAsL/v в выражении
A9.2.14) соответствует фазовому сдвигу оператора ар. Оператор Ар для пробного
434 Квантовые неразрушающие измерения Гл. 19
поля в точке z = L задается тогда формулой
1 аР@) exp (^Asb) -
^Asb)a+@) / =1 ¦ A9.2.15)
v J Va+@)aP@) + lJ
Этот фазовый сдвиг пробного поля, а следовательно и число фотонов сигнального
поля, можно измерить балансным детектором.
Рассмотрим выход балансного детектора, изображенного на рис. 19.1, где указа-
указаны операторы уничтожения для каждой части интерферометра. Как обсуждалось
в разд. 4.4, выходной сигнал двухканального гомодинного детектора описывается
оператором
ncd = d+d-c+c. A9.2.16)
Операторы с и d относятся к полю на входе, операторы аий-к пробному полю на
выходе и вакуумным флуктуациям, соответственно. Пробное поле ар и опорное поле
аг связаны саиб соотношениями
A9.2.17)
A9.2.18)
где 7\ — коэффициент пропускания светоделителя 1, и мы предположили, что
фазовый сдвиг в отраженной моде равен тг/2. Керровская среда вызывает сдвиг фазы
пробной волны в соответствии с выражением A9.2.14),
а'Р = exp \i (^ASL + \ jl oP@), A9.2.19)
где сдвиг фазы на тг/2 добавляется путем настройки интерферометра. Вводя коэф-
коэффициент пропускания Т^ светоделителя 2, запишем поля с и d в виде
+ гу/\-Т2аг, A9.2.20)
A9.2.21)
Из A9.2.16)-A9.2.21) следует, что при Т2 = 0,5,
ncd = 2^A-^) (a+a - 6+6) sin (^As) - 2iT1{a+b - b+a) sin (^A
^i^As^j + 6+aexp (г^Л5)] . A9.2.22)
Поскольку поле b находится в вакуумном состоянии,
/ , yrh
(ncd) = I\f 1 ill — 11) (a a) (Aq). (ly.i.io)
v
где использовано приближение sinfaLAs/v) ~ xLAg/v^ которое справедливо, если
kLAs/v <C 1. Таким образом, измеряемый фототок балансного детектора пропор-
пропорционален среднему числу фотонов сигнального поля.
19.3 КН измерение числа фотонов через дисперсионную атомно-полевую связь 435
19.3. КН измерение числа фотонов через дисперсионную
атомно-полевую связь г)
В гл. 13 обсуждались возможные схемы создания состояний с определенным чис-
числом частиц в микромазере. Рассмотрим теперь КН-метод измерения числа фотонов
в состоянии с определенным числом частиц |п), приготовленном в высокодобротном
резонаторе. Этот метод основан на детектировании дисперсионного фазового сдвига,
создаваемого полем резонатора у волновой функции нерезонансных атомов, проходя-
проходящих через резонатор. Этот сдвиг можно измерить путем атомной интерферометрии,
используя описываемый ниже метод Рамзи.
В данном КН-методе пробной системой являет- ^
ся не поле, а пучок атомов, взаимодействующих
нелинейно и нерезонансно с сигнальным полем.
Рассмотрим трехуровневую атомную си-
систему с каскадной конфигурацией переходов
(рис. 19.2). Переходы \а) —> \Ь) и \Ь) —> \с) разре-
разрешены, а переход \а) —>> \с) запрещен. Частота v
моды резонатора отстроена от частоты перехода
\а) —>> \Ь) на величину Д = i/ — шаь^ которая
предполагается малой по сравнению с шаь и ча-
частотами всех остальных переходов, в частности
перехода \Ь) —>> \с). В результате, нерезонанс-
нерезонансное взаимодействие атомов с полем затрагивает
лишь состояния \а) и |6), а состояние \с) остается
невозмущенным.
Физика КН измерения числа фотонов в ре-
резонаторе состоит в том, что взаимодействие не-
нерезонансного поля с атомом вносит дисперси-
дисперсионный энергетический сдвиг (поглощения нет)
в состояние \Ь^п) (атом в состоянии \Ь) и по-
поле в состоянии с определенным числом частиц
|п)), пропорциональный числу фотонов п в поле.
Этот энергетический сдвиг детектируется путем
измерения дефазировки, накапливаемой между
состояниями \Ь) и |с), методом (Рамзи) раздельных осциллирующих полей. Тот факт,
что энергетический сдвиг зависит от п, является результатом дисперсионного эффек-
эффекта, не влияющего на число фотонов, и отвечает за неразрушающий характер метода.
Прежде чем рассматривать установку Рамзи для КН измерения, найдем диспер-
дисперсионный энергетический сдвиг дь состояния |6, п).
Взаимодействие атома с полем описывается гамильтонианом (см. F.2.1)-F.2.3))
i
i
J
т
V
j
ЫЪс
г
Рис. 19.2. Трехуровневая атомная
система, предназначенная для КН
измерения числа фотонов с помо-
помощью дисперсионного атомно-поле-
вого взаимодействия
Ж=^(\а)(а\-\Ь)(Ь\)
hg(\a)(b\a + a+\b)(a\),
A9.3.1)
где учитывается лишь взаимодействие поля частоты и с уровнями \а) и |6) и пренебре-
гается далеко отстроенным уровнем |с). Гамильтониан Ж можно диагонализовать
и получить атомно-полевые «одетые» состояния,
,?i- I) -sin#n|fc,n), A9.3.2a)
n- l)+cos#n|6,n), A9.3.26)
1) Этот раздел основан на работе Вшпе, Haroche, Lefevre, Ralmond and Zagury A990).
436 Квантовые неразрушающие измерения Гл. 19
с соответствующими собственными значениями:
Е+п = ft [(га - 1)и + |wa6] - ^(Оп - А), A9.3.3а)
Е-п = ft (rai/ - \шаЬ^ + ^(Оп - А), A9.3.36)
где
, A9.3.4)
ig2n
==, A9.3.5)
Оп = ^/А2 + 4g-2ra. A9.3.6)
Предположим, что А существенно больше, чем 2g^/n, так что
—«- <С 1. A9.3.7)
Простой анализ показывает, что если условие A9.3.7) выполняется, то cos#n ~ 1
и sin §n ~ 0, поэтому
|+) ~ |а,п- 1), A9.3.8а)
-> ~ |Ь,п>, A9.3.86)
с соответствующими собственными значениями:
\^, A9.3.9а)
^. A9.3.96)
Результирующий эффект состоит в том, что число фотонов не меняется, но состояние
|6, п), имеющее невозмущенное значение энергии Я(ш/ — шаь/2), испытывает энерге-
энергетический сдвиг
hSb(n) = ^^. A9.3.10)
Энергетический сдвиг, приходящийся на один фотон, hg2/А, может быть большим
в системах ридберговских атомов. При подходящих значениях расстройки величина
сдвига ридберговских уровней щелочных атомов, приходящаяся на один фотон,
может достигать значения 1015 с. Важным моментом данного анализа является то,
что энергетический сдвиг пропорционален числу фотонов сигнального поля и имеет
дисперсионный характер, то есть этот сдвиг не сопровождается поглощением фото-
фотонов.
Теперь ограничим наше рассмотрение атомным гильбертовым пространством,
натянутым лишь на состояния \Ь) и |е). Эффективный гамильтониан атомно-полевого
взаимодействия запишем в виде
Ж = Жа + Щ + Жи A9.3.11)
19.3 КН измерение числа фотонов через дисперсионную атомно-полевую связь 437
где
Жа = ^^аг, A9.3.12)
A9.3.13)
A9.3.14)
где az = (|6)F| — |с)(с|), <7+ = |Ь)(с| и а— = |с)F|. Видно, что этот эффективный
гамильтониан вносит фазовый сдвиг в состояние |6), пропорциональный величине
5ь(п), а состояние \с) оставляет неизменным. Отметим, что п представляет собой
собственное значение сигнальной наблюдаемой As = a^as- В качестве пробной
наблюдаемой Ар выберем оператор атомного дипольного момента
Ар = п
A9.3.15)
Операторы Ag и Ар удовлетворяют критериям КН измерения. Рассматриваемый
случай аналогичен случаю с оптическим эффектом Керра, обсуждавшимся в преды-
предыдущем разделе, только теперь операторы ар~ и ар заменены атомными операторами
сг+ и сг^, соответственно.
Рассмотрим метод раздельных осциллирующих полей Рамзи для детектирования
дефазировки, накапливаемой между состояниями \Ь) и |е). Схема установки, pea™
лизующей этот метод, приведена на рис. 19.3. Резонатор, содержащий п фотонов,
Лазерное поле
+
микроволновое поле
Резонатор
Ri
1С
Рис. 19.3. Схема КН измерения числа фотонов с помощью дисперсионного атомно-полевого
взаимодействия. Атомы, приготовленные в состоянии |6) лазерным возбуждением, проходят
последовательно зону микроволнового поля Ri, резонатор и зону микроволнового поля R2,
после чего их состояние (|6) или с)) определяется полевым ионизационным счетчиком 1С.
(Из работы Brane, Haroche, Lefevre, Ralmond and Zagury A990))
помещается между двумя зонами R\ и R2 поля, возбуждающего переход \Ь) —>
—>• |с). Вначале каж:дый атом приготавливается в состоянии \Ь) путем лазерного
возбуждения. Затем он взаимодействует в первой зоне R\ с микроволновым полем,
настроенным на частоту г/г, резонансную с переходом \Ь) —>• |с), и таким образом
переводится в когерентную суперпозицию состояний \Ь) и |с). До взаимодействия
со вторым микроволновым полем в зоне i^25 настроенным на частоту i/r, атом про-
проходит через резонатор. При прохождении через резонатор амплитуда состояния \Ь)
приобретает фазовый сдвиг, пропорциональный ёь(п). В конце, после прохождения
зоны i?2, атом детектируется в состоянии \Ь) или \с) полевым ионизационным счетчи-
счетчиком. Вероятность обнару^сить атом в состоянии \Ъ) или \с) является периодической
438 Квантовые неразрушающие измерения Гл. 19
функцией от 5ь(п) и, следовательно, приводит к характерным интерференционным
полосам, интервал между которыми зависит от числа фотонов в резонаторе. Эти
полосы Рамзи можно использовать для непрерывного контроля (мониторинга) числа
фотонов в ходе КН измерения.
Если атом, имеющий скорость v, пройдет через резонатор, содержащий п фото™
нов, то атомно-полевая система окажется в суперпозиционном состоянии:
1Сон™е> = сь,п\Ь, п) + сС)П|с, п). A9.3.16)
Найдем теперь амплитуды вероятности сь^п и сс,п обнаружить атом в состояниях \Ъ)
и |с), соответственно, после прохождения им микроволновых полей и поля резонато™
ра, при условии, что резонатор содержит п фотонов. Предположим, для простоты,
что микроволновые поля в зонах R\ и R2 являются резонансными переходу \Ъ) —>-
—> |с), однородными в этих зонах и характеризуются частотой Раби Од, которую
будем считать действительной. Начальные условия для амплитуд вероятности, до
вхождения атома в зону i?i, имеют вид
сь,п = 1, сс<п = 0. A9.3.17)
Эволюция этих амплитуд в ходе взаимодействия атома с микроволновым полем
в области Ri в течение времени т = L/v (где L ~~ длина зон Ri и #2, a v — скорость
атома) задается уравнениями (см. E.2.12) и E.2.13))
сь}п = i^cc,n, A9.3.18а)
cc,n = i^c6,n. A9.3.186)
Решение этих уравнений, удовлетворяющее граничным условиям A9.3.17), в момент
времени т равно (см. E.2.12) и E.2.13))
cb,n = cos (^) , A9.3.19а)
сс,п = г sin (^f-). A9.3.196)
После прохождения через резонатор, содержащий п фотонов, амплитуда С5,п при-
приобретает фазовый сдвиг 5ь(п)тс = g2nrc/A (где тс = Lc/v — время, проведенное
атомом в резонаторе), в то время как сС)П остается неизменной. Поэтому на входе
в зону i?2 атомные амплитуды имеют вид
= cos (^f-) exp (-i^) , A9.3.20)
(^) A9.3.21)
В зоне 1^2 амплитуды вновь эволюционируют согласно уравнениям A9.3.18а,б),
которые можно решить, задавая начальные условия в виде A9.3.20) и A9.3.21). Тогда,
после прохождения зоны R2 атомные амплитуды определяются выражениями (см.
E.2.21) и E.2.22))
cbjfl = cos^ [^^) exp I -г^^ J - sin' [^^J , A9.3.22)
cc?n
2
exp I -ig Т^П 1+1
L V / J
= i sln(uRr) [exp f-i^^] + ll . A9.3.23)
19.3 КН измерение числа фотонов через дисперсионную атомно-полевую связь
439
Эти выражения значительно упрощаются, если частота Раби Пц микроволновых
полей и время взаимодействия т выбираются такими, чтобы Пцт = тг/2, и мы
получаем следующие вероятности обнаружить атом в состояниях \Ь) и \с):
Рь = \cb, |2
Рс. = кг..
1 — cos
¦ cos
g2rcn
2
g rcn
A
A9.3.24a)
A9.3.246)
Это периодические функции от п, демонстрирующие характерную структуру ин-
интерференционных полос, интервал между которыми зависит от п. Таким образом,
регистрируя атомы в состояниях \Ь) или |е), можно измерить число фотонов в резо-
резонаторе.
Колебательную природу вероятностей Рь и Рс можно понять с точки зрения
процесса атомной интерференции. Амплитуда вероятности сС)П обнаружить атом
в состоянии |с), если первоначально он находится в состоянии |6), содержит два
члена (см. A9.3.23)). Член в скобках, равный единице, соответствует процессу, при
котором атом переводится из состояния \Ь) в состояние \с) в зоне i?i, так что он
не испытывает фазовый сдвиг, проходя через поле резонатора, и в зоне R2 остается
в состоянии |с). Член e^p(—ig2Tcn/А) соответствует процессу, при котором атом
не совершает переход в состояние \с) и испытывает фазовый сдвиг внутри резонатора.
Вероятность Рс равна квадрату суммы амплитуд, соответствующих этим процессам,
что и приводит к интерференционной картине, описываемой выражением A9.3.246).
Другими словами, атом приготавливается в зоне R\ в когерентной суперпозиции двух
состояний, одно из которых изменяется полем резонатора, а другое нет. Когда атом
детектируется в состоянии \Ь) или |с), невозможно сказать, каким путем система
совершила эволюцию, и результирующая вероятность детектирования проявляет
соответствующую квантовую когерентность в виде интерференционной картины
Рамзи. Роль информации типа «какой путь» в квантовых интерференционных экс-
экспериментах будет детально обсуждаться в следующей главе.
Рассмотрим более сложную, но более реалистичную ситуацию, когда начальное
состояние поля в резонаторе не является состоянием числа частиц, а является супер-
суперпозицией таковых, то есть задается выражением
\ф) = ^Ъп\п). A9.3.25)
п
Примером такого состояния поля является когерентное состояние |а), для которого
(см. B.2.2))
Ьп =
A9.3.26)
После взаимодействия с атомом, имеющим скорость v, состояние атомно-полевой
системы задается суперпозицией вида
1^конечнП°ле) = 7. Ьп[сьуп\Ь^ п) + сС)П|с, п)}. A9.3.27)
Система атом—поле, очевидно, находится в перепутанном состоянии, которое нельзя
выразить в виде произведения атомных и полевых состояний, что означает сильную
корреляцию между атомными и полевыми подсистемами.
440
Квантовые неразрушающие измерения
Гл. 19
Обнаружение атома в состоянии, скажем, |6), проецирует состояние A9.3.27)
в состояние
/Г 11/2
J2 Ьпсь1П\Ь, п) / \J2 Ы2\съА2 > A9.3.28)
что приводит к распутыванию системы. Состояние поля является теперь суперпози-
суперпозицией состояний с определенным числом фотонов, имеющих амплитудв! вероятности,
задаваемые, с точностью до нормировочного множителя, величиной Ъпсъ^п- По су™
Атом, обнаруженный
в состоянии \с
Атом, обнаруженный
в состоянии \Ь)
(а)
Рис. 19.4. Преобразование начального пуассоновского распределения с (п) = |а|2 = 10 при
детектировании одиночного атома. Начальное распределение |6П| (график а) умножается
на осциллирующую интерференционную функцию |ci(?i)|2 (г = Ь или с) (график б). В ре-
результирующих распределениях (график в) числа фотонов, ближайшие к темным полосам,
опустошаются. Картины, получаемые при детектировании атома в состояниях \Ь) и |с),
дополняют друг друга. (Из работы Brane, Haroche, Ralmond, Davldovlch and Zagury A992))
ществу, распределение числа фотонов умножается на осциллирующую функцию от
ni |c6,n|2- На рис. 19.4 видно, как распределение числа фотонов
р(п) =
\Ьп
(г = b или с),
A9.3.29)
соответствующее сначала когерентному состоянию (величина Ьп задается выраже-
выражением A9.3.26)), преобразуется после обнаружения атома в состоянии \Ь) или |с).
Состояния с числами фотонов, при которых интерференционная функция |с^п|2
равна нулю, практически опустошены.
Если большое число атомов, имеющих случайные значения скорости v (случайные
значения тс в выражениях A9.2.22) и A9.2.23)), проходят через установку Рамзи
и обнаруживаются в состояниях \Ь) или |с), то остальные числа фотонов подавляются.
Опустошение продолжается до тех пор, пока не получится состояние с одним опреде-
определенным числом фотонов. Состояние с определенным числом фотонов достигается
в резонаторе, как показано на рис. 19.5, даже в отсутствие энергообмена между
атомами и полем. Такой процесс без рассеяния энергии представляет собой КН
измерение числа фотонов в резонаторе.
19.3 КН измерение числа фотонов через дисперсионную атомно-полевую связь 441
(в)
(г)
(в)
а)
10
п
20
Рис. 19.5. Эволюция распределения числа фотонов в ходе КН измерения. Начальное распре-
распределение (а) является пуассоновским с (п) = а\ =5. Распределения (б-е) соответствуют
детектированию 1, 3, 6, 10 и 15 атомов, соответственно. В конце концов состояние поля
сводится к фоковскому сп = 3. (Из работы Brune, Haroche, Ralmond, Davidovlch and Zagury
A992))
442 Квантовые неразрушающие измерения Гл. 19
19.4. КН измерения в оптических параметрических процессах
В этом разделе мы рассмотрим КН измерения в оптических параметрических
процессах, характеризуемых обобщенным соотношением между входящими и выхо-
выходящими модами вида
п _ pitiif, _i_ <$ pWi+^fp-Wh -4~pi(^h+) f1Q4 1a"l
ивых — c "вх Т^ с ус t/BX ~г с fBX/5 ^ly.i.idj
/l — p^2h A- <$ ?>*(&2 + Ф)( — p^^ a -A- p^ n+' ^ ИПД1^
иВЫХ С "ВХ "Т «У С \С "'ВХ « С авХ/5 ^JL^.^t. JLUj
где авх, аВых5 ^вх и &вых — операторы уничтожения для мод, входящих и покидаю-
покидающих черный ящищ представляющий КН измеритель или усилитель без обратного
действия, и *$ — коэффициент усиления. Преобразования типа A9.4.1), связываю-
связывающие вход и выход, не обязательно являются результатом действия одного устрой-
устройства, а могут быть результатом действия подходящей комбинации параметрических
устройств, как будет показано на примере из данного раздела.
Для того чтобы показать, что черный ящик, характеризуемый преобразованиями
входа—выхода A9.4.1), осуществляет КН измерения, определим операторы квадра-
квадратурных составляющих для мод входящего поля,
Х^х(ф) = ^^(е^г1^авх + e^aij, A9.4.2)
V2
уф\ = —— f e ttBX — е о-вхЬ AУ.4.о)
V 2
XB*(il)\ — -—(p-Wh 4~р{^Ь+) A®АА\
rb \*Р) — гг\е °вх с C/BXj ^ly.^.OJ
V2
и для мод выходящего поля,
. + Ф) = ^=(е-^+Мавш + е^^+^а+ых), A9А6)
. i Y7/ — /~^ "вых е авых/5 у1У.Ч:.1)
Xf IX(#! + -0) = ^(е^г№+фNвых + ег№+фN+ых), A9.4.8)
Тогда из A9.4.1) следует, что
(ф), A9.4.10)
A9.4.11)
A9.4.12)
». A9.4.13)
Из этих соотношений сразу видно, что нам удалось избежать обратного действия.
Согласно A9.4.13) составляющая Уьвых(#2 + Ф) несет информацию о y<fx('0), так что
измеряется составляющая Уа(ф) входящего сигнала. Однако, из A9.4.11) видно, что
составляющая V?fx('0) остается чистой, а весь шум обратного действия
согласно A9.4.10), приходится на в сопряженную переменную Ха.
19.4
КН измерения в оптических параметрических процессах
443
Рассмотрим теперь пример КН-соотношений входа-выхода A9.4.1) в системе,
состоящей из параметрических устройств, как показано на рис. 19.6. Сигнальное
поле, распространяющееся на участках Hi, &i, c\ и d\, имеет частоту x/s, а пробное или
считывающее поле, распространяющееся на участках а2^ Ъч, с2 и d2j имеет частоту i/r.
>
>
по
ЧП1
bi
>
ь2
ПУ
ci
С2
ЧП2
>
>
d2
Рис. 19.6. Схема КН-усилителя, составленного из преобразователей частоты ИП1, ИП2
и параметрического усилителя ПУ. Сигнальное поле, распространяющееся на участках ai,
&i, ci и rfi, имеет частоту i/s, а пробное поле, распространяющееся на участках е&2, 62, С2
и с?2, имеет частоту иг. Преобразователи ИП1 и ИП2 возбуждаются в процессе накачки на
разностной частоте v8 — иг |, тогда как усилитель ПУ — на суммарной частоте и3-\-иг. Здесь
показаны пучки накачки. (Из работы Yurke A985))
Преобразователи частоты ИП1 и ИП2 возбуждают в процессе накачки на разност-
разностной частоте i/s — i/rn описываются, в параметрическом приближении (см. разд. 16.1),
гамильтонианом в представлении взаимодействия:
Ж =
A9.4.14)
Здесь к ~~ постоянная связи, зависящая от нелинейной восприимчивости среды, C\
и ф\ — амплитуда и фаза классического поля накачки, a as и аг — операторы уни-
уничтожения фотонов сигнального и считывающего полей. Гейзенберговские уравнения
движения для операторов as и аг имеют вид
as = -Ых{5\ат е~{ф1, A9.4.15)
ar = -imfads е{ф1. A9.4.16)
Решение этих уравнений записывается следующим образом:
п ( Т\ nr\o( is й I IгЛп (С\\ i а\\л( ч* й Т I п\п (С\\ ю^^Ф1 (Лп Л Л 7*л\
Ugllj} — LObl y?\\J\ JLj/Clclgiyi — l Ы11\ Mi fJi Ju / CJUr\\J J С , I ly.^.l/ a> j
ar{L) = cos(xi/3iL/c)ar@) - i sm(xi^iL/c)as(O) ei4>1, A9.4.176)
где L — длина нелинейной среды, а время t заменено величиной L/c, где с — скорость
света. Соотношения входа^выхода для преобразователей частоты ИП1 и ИП2, изоб-
изображенных на рис. 19.6, получаются, следовательно, путем соответствующей замены
as@), ar@), cl8(L) и ar(L) в выражениях A9.4.17а) и A9.4.176) величинами а1? а2?
Ъ\ и Ъ2 для ИП1 и величинами ci, c2, d\ и d2 для ИП2. Результирующие уравнения
имеют вид
С?2 — —Ъ ( 1 — Л-| )
di = К\С\ —- i(l —-
d2 = -гA ^
е*ф1сг + Кгс2,
A9.4.18)
A9.4.19)
A9.4.20)
A9.4.21)
где Кг = cos(xi/3iL/c).
Параметрический усилитель ПУ, изображенный на рис. 19.6, возбуждается в про-
процессе накачки на суммарной частоте vs + vr и описывается, в параметрическом
приближении, гамильтонианом в представлении взаимодействия (см. A6.1.2)):
Ж = Пкф2{а^а^ e~i4>2 + asar ei<f>2). A9.4.22)
444 Квантовые неразрушающие измерения Гл. 19
Соответствующие уравнения движения для операторов as и а+,
а8 = -гя2р2а^ е^2, A9.4.23а)
а+ = гк2C2а8е1ф\ A9.4.236)
имеют решение
as(L) = ав@) сЦк2/32Ь/с) - ш+@) sh(^2/32L/c) е~^2, A9.4.24)
ar(L) = ar@)ch(x2/32L/c) - ш+@) sh(x2/32L/c) e"^2. A9.4.25)
Соотношение между операторами поля &i, 62, ci и С2 (рис. 19.6) получаются тогда
заменой as@), ar@), cl8(L) и ar(L) в выражениях A9.4.24) и A9.4.25) величинами
&ъ ^2 ? Ci и с2, соответственно, что дает
С1 = К2Ъг - г{К\ - 1I/2 е~{ф2Ь%, A9.4.26)
С2 = ^i{Kl - II/2 е-*ф*Ъ$ + К262, A9.4.27)
где К2 = сЬ(ж2/32Ь/с).
Мы хотим выразить выходные операторы d\ и d2 через входные операторы а\
и а2. Из соотношений A9.4.18)-A9.4.21), A9.4.26) и A9.4.27) получаем
di = К2B^2 - l)ai - 2iKtK2{l - KlI^2 e^i<f>1a2 - i{K2 - lI/2 е~*ф2а?,
A9.4.28)
d2 = K2{2Kl - l)o2 - 2iK1K2(l - i^iI/2 e^oi - i(i^22 - 1I/2 e"^2of. A9.4.29)
Если величины /fi и К2 подобрать (подбирая амплитуды накачки) так, чтобы
то выражения A9.4.28) и A9.4.29) сводятся к
1ф1а2 + е~{ф2а%), A9.4.31)
d2 = а2 - г{К\ - 1I/2(е{ф1аг + е~^2а+). A9.4.32)
Эти соотношения имеют тот же вид, что и A9.4.1), если
ф1 = ф-ф-^, A9.4.33)
Ф2 = ~{Ф + Ф)-^- A9.4.34)
Таким образом, цепь параметрических устройств, изображенная на рис. 19.6,
способна осуществлять КН измерения полевых переменных, если должным образом
настроены амплитуды и фазы полей накачки преобразователей частоты и парамет-
параметрического усилителя.
Список литературы к гл. 19 445
Задачи
19.1. Докажите следующие свойства операторов фазы cos ф и sin ф, введенных с по-
помощью соотношений A9.2.9):
(п — 1| cos ф\п) = (п\ cos ф\п — 1) = -,
(п — 1| sin ф\п) = —(п\ cos ф\п — 1) = —,
[cos ф1 sin ф] = —¦ а+ — а — 1 ,
[а^а, cos </>] = —г sin 0,
[а+а, sin ф] = i cos 0.
19.2. Покажите, что As и Лр, задаваемые выражениями A9.2.6) и A9.2.11), удо-
влетворяют условиям КН измерений, если гамильтониан имеет вид A9.2.2)—
A9.2.5).
19.3. Покажите, что выралсение A9.4.16) определяется однозначно из A9.4.1а), если
потребовать, чтобы оператор 6ВЫХ зависел линейно от операторов 6ВХ, авх и а^,
и чтобы операторы рождения и уничтожения удовлетворяли коммутационным
соотношениям
Кх,«+Х] = 1, [&вх,Ь+х] = 1,
при равных нулю всех остальных независимых коммутационных соотношениях
между операторами рождения и уничтожения входящего поля, и
Кых, а+ыХ] = 1, [Ьвых, Ь+ых] = 1,
при равных нулю всех остальных независимых коммутационных соотношениях
между операторами рождения и уничтожения выходящего поля.
Список литературы
Концепция квантового неразрушающего (КН-) измерения
Braglnsky, V. В., Vorontsov, Y. I. and Khalili, F. I. Zh. Eksp. Tear, Fiz. 73, 1340 A977) (Sov.
Phys. JETP 46, 705 A977)).
Braglnsky, V. В., Vorontsov, Y. I. and Khalili, F. Y. Zh. Exsp. Tear. Fiz. 73, 1340 A977) (Sov.
Phys. JETP 46, 705 A977)).
Unrah, W. G. Phys. Rev. D 18, 1764 A978).
Caves, C. M., Thome, K. S., Drever, R. W. D., Sandberg, V. D. and Zimmerman, M. Rev. Mod.
Phys. 52, 341 A980).
*Багаев С.Н., Чеботаев В.П. УФН 148, 143 A980).
Braglnsky, V. В. and Khalili, F. Y. Quantum Measurement, (Cambridge Univ. Press, 1992).
[Брагинский В.Б., Халил Ф.Я. Квантовые измерения (Наука, Москва, 1990).]
КН-схемы
Mllburn, G. J. and Walls, D. F. Phys. Rev. A 28, 2065 A983).
Hillery, M. and Scully, M. O. In Quantum Optics, Experimental Gravity and Measurement
Theory, ed. P. Meystre and M. O. Scully (Plenum, New York 1983), p. 661.
446 Список литературы к гл. 19
Yurke, В. and Corruccini, L. R. Phys. Rev. A 30, 895 A984).
Imoto, N., Наш, Н. A. and Yamamoto, Y. Phys. Rev. A 32, 2287 A985).
Yurke, B. J. Opt Soc. Am. В 2, 732 A985).
Brane, M., Haroche, S., Lefevre, V., Ralmond, J. M. and Zagury, N. Phys. Rev. Lett. 65, 976
A990).
Levenson, M. D. Phys. Rev. A 42, 2935 A990).
Holland, M. J., Walls, D. F. and Zoller, P. Phys. Rev. Lett 67, 1716 A991).
Shlmlzu, A. Phys. Rev. A 43, 3819 A991).
Brane, M., Haroche, S., Ralmond, J. M., Davidovlch, L. and Zagury, N. Phys. Rev. A 45, 5193
A992).
Haroche, S., Brune, M. and Ralmond, J. M. Appl. Phys. В 54, 355 A992); J. Phys. II France 2,
659 A992).
Экспериментальные демонстрации КН-схем
Levenson, M. D., Shelby, R. M., Reid, M. and Walls, D. F. Phys. Rev. Lett 57, 2473 A986).
Imoto, N., Watkins, S. and Sasaki, Y. Opt Commun. 61, 159 A987).
LaPorta, A., Slusher, R. E. and Yurke, B. Phys. Rev. Lett 62, 28 A989).
Grangler, P., Roch, J. F. and Roger, G. Phys. Rev. Lett 66, 1418 A991).
Метод Рамзи раздельных осциллирующих полем
Ramsey, N. F. Molecular Beams, (Oxford University Press, New York 1985).
Глава 20
КВАНТОВЫЕ ОПТИЧЕСКИЕ
ТЕСТЫ
НА ДОПОЛНИТЕЛЬНОСТЬ х
Дополнительность, например корпускулярно-волновой дуализм природы, лежит
в основе квантовой механики. Он отличает мир квантовых явлений от реальности
классической физики. В 1920-х годах квантовая теория была еще новой, и примеры,
использовавшиеся для иллюстрации дополнительности, подчеркивали у квантово-
механических объектов, будь это фотон или массивная частица, свойства положения
(корпускулярность) и импульса (волнообразность). В этом состоит историческая
причина того, почему дополнительность часто поверхностно отождествляется с так
называемым корпускулярно-волновым дуализмом материи.
Однако дополнительность является более общим понятием. Говорят, что две
наблюдаемые являются дополнительными^ если точное знание одной из них озна-
означает, что все возможные исходы измерения другой являются равновероятными.
Проиллюстрируем это двумя противоположными примерами. Первый пример — это
положение и импульс (вдоль одного направления) частицы. Если, скажем, положение
предопределено, то результат измерения импульса нельзя предсказать; все значения
импульса имеют одинаковую вероятность (в широком диапазоне). Второй пример —
две ортогональные составляющие спина 1/2. Если, скажем, вертикальная состав-
составляющая спина имеет определенное значение («вверх» или «вниз»), то при измерении
горизонтальной составляющей оба значения (например «влево» или «вправо») будут
появляться с вероятностью 50%. Таким образом, в микромире полное знание, в смыс-
смысле классической физики, недоступно. Классическим примером слияния волнового
и корпускулярного поведения является эксперимент Юнга с двумя щелями. До
тех пор пока в этом эксперименте невозможно сказать, через какую щель прошел
свет, наблюдается интерференционная картина. Другими словами, любая попытка
увеличить информацию о пути прохождения света возмущает свет так, что интер-
интерференционные полосы размываются. Этот момент особенно проясняется в спорах
Эйнштейна и Бора, чьи доводы мы воспроизводим в следующих абзацах.
Эйнштейн предлагает нам рассмотреть эксперимент Юнга с двумя щелями, в ко-
котором щели могут испытывать отдачу, как показано на рис. 20.1. Интерференци-
Интерференционная картина создается, например, путем измерения выходного сигнала массива
фотодетекторов, обусловленного прохождением света через щели. Если масса экрана
(узла с двумя щелями) достаточно мала, то он отталкивается, когда свет излучается
заданной щелью. Тогда, в силу закона сохранения импульса, можно сказать, какой
волновой вектор, ki или кг, имеет фотон (см. рис. 20.1). То есть, можно иметь тогда
информацию о том, по которому пути прошел свет.
1) Материал этой главы взят из работ Scully, Englert and Schwlnger A989); Scully, Englert
and Walther A991).
448
Квантовые оптические тесты на дополнительность
Гл.20
Плоская волна
Экран с интерференционными полосами
Экран без интерференционных полос
Рис. 20.1. Схема эксперимента с двойной щелью. В этом мысленном эксперименте экран со
щелями может испытывать отдачу, демонстрируя, через какую щель прошел фотон
Однако Бор замечает, что плоскость, испытывающая отдачу, также должна рас-
рассматриваться по законам квантовой механики. В частности, Бор доказывает, что
положение плоскости известно лишь с точностью Аж, вследствие принципа неопре-
неопределенности. Эта погрешность будет приводить к случайному фазовому сдвигу Аф
световых пучков, который будет разрушать интерференционную картину.
Эти доводы случайной фазы, показывающие, как информация типа «который
путь» разрушает в заданной экспериментальной установке моменты, связанные
с когерентной волнообразной интерференцией, являются привлекательными. Они
соответствуют духу гейзенберговского j-микроскопа. Во всех этих доводах отме-
отмечается, что акт измерения неизменно возмущает измеряемую систему, и потеря
когерентности является неизбежным результатом этого возмущения 1).
В другом примере, более соответствующим духу данной главы, Фейнман (Feyn-
man, 1965) заменяет фотоны электронами. Вследствие хорошо известной волновой
природы материи, интерференция между электронами, проходящими через щели
(рис. 20.2), должна приводить к обычной интерференционной картине на экране.
В этой схеме имеется дополнительное средство контроля за интерферирующими
частицами, ибо за электронами молено наблюдать, например, путем рассеяния света.
Это отражено на рис. 20.2, где показан источник света, рассеиваемого в окрестности
той или иной щели, в зависимости от того, через какую щель проникает электрон.
Далее Фейнман объясняет, что эта процедура наблюдения разрушает интерферен-
интерференционные полосы, видимые на экране. Он завершает свой анализ этого интересного
примера следующим утверждением:
«Если прибор способен определить, через какую щель прошел электрон,
то он не может быть столь деликатным, чтобы существенным образом не раз-
разрушить интерференционную картину. Никто никогда не находил (и даже
не помышлял) способа обойти принцип неопределенности».
В экспериментальных ситуациях, обсуждавшихся до сих пор, как и во всех стан-
стандартных примерах, включая знаменитый гейзенберговский микроскоп, дополнитель-
дополнительность подкреплялась соотношением неопределенности Гейзенберга для переменных
«координата—импульс». Всегда ли работает такой механизм? Нет! Как мы увидим,
) См., однако, работу Wooters and Zurek A979).
20.1
«Который путь»-детектор на основе микромазера
449
Плоская
электронная волна
Экран с интерференционными полосами
Экран без интерференционных полос
Рис. 20.2. Фейнмановская версия эксперимента с двойной щелью. В данном случае интерфе-
интерферируют электроны, а рассеяние фотонов используется для определения их положения сразу
после прохождения щелей, что демонстрирует, через какую щель электрон достиг экрана
возможно, как в принципе, так и на практике, поставить эксперименты, которые дают
информацию «который путь» с помощью детекторов, не возмущающих систему
каким-либо заметным образом.
В этой главе рассматриваются некоторые оптические системы, в которых потеря
когерентности, вызываемая информацией «который путь», т.е. наличием «который
путь»-детектора, происходит просто благодаря установлению квантовых корреля-
корреляций 1) и никак не связана с большими факторами случайной фазы, как в случае
эйнштейновских щелей, испытывающих отдачу, или гейзенберговского микроскопа.
Таким образом, принцип дополнительности проявляется, хотя соотношение неопре-
деленностеи координаты и импульса не играет роли ].
20.1. «Который путь»-детектор на основе микромазера
Рассмотрим двухщелевой эксперимент с атомами, изображенный на рис. 20.3. На-
Набор широких щелей коллимирует два атомных пучка, падающих на две узкие щели,
являющиеся источником интерференционной картины. Установка дополнена двумя
высокодобротными резонаторами микромазеров и лазерным пучком, переводящим
атомы из нижнего состояния \Ь) в возбужденное \а). Длина резонатора подобрана
так, чтобы ридберговский атом, проходя через резонатор, совершил переход \а) —»
—>• \Ъ) с вероятностью, равной единице, даже при отсутствии фотонов в резонаторе,
спонтанно испуская микроволновый фотон.
В отсутствии системы резонаторов атомный пучок, прошедший через двойную
щель, описывается вектором состояния
1
B0.1.1)
1) Другое более раннее обсуждение этого вопроса см. в работе Scully, Shea and McCullen
A978).
) Отметим, что анализ можно переделать, так что он «будет выглядеть» как будто
случайное фазирование, вызываемое обратным действием измерения, разрушило интер-
интерференционную картину (см. Stern, Aharonov and Imry, 1990). Мы обсудим это в разд. 20.3.
15 М.О. Скалли, М.С. Зубайри
450
Квантовые оптические тесты на дополнительность
Гл.20
где г — радиус-вектор центра масс, а г обозначает внутреннее состояние атома.
Следовательно, плотность вероятности обнаружить частицы в точке экрана г = R,
задается квадратом модуля функции Ф(Н):
Отметим, что перекрестный член Ф1Ф2 + Ф2Ф1 соответствует обычной интерферен-
интерференции.
Теперь рассмотрим ситуацию, когда лазер включен и ультрахолодные (ваку-
(вакуумные) микромазерные резонаторы размещены на обоих путях, как показано на
рис. 20.3. До того, как атомы войдут в резонаторы, лазерный пучок возбуждает их
Микромазеры
Коллима- Резонатор 1
торы
р(П)
Резонатор 2
волна Лазерный пучок
Экран с интерференционными полосами
Экран без интерференционных полос
Рис. 20.3. Схема эксперимента с двойной щелью на атомах. [Из работы (Scully, Englert and
Walther, 1991).]
в долгоживущее ридберговское состояние \а). После того, как атомы пройдут через
резонаторы и совершат переход \а) —> |6), испуская спонтанно фотон, состояние кор-
коррелированной системы атомного пучка и мазерного резонатора задается выражением
1
= —[ф1{т)\1102)
B0.1.3)
где, например, |I1O2) обозначает состояние, в котором есть один фотон в резонаторе 1
и ни одного в резонаторе 2. Отметим, что, в отличие от B0.1.1), эта функция ф(т) не
является произведением двух множителей, один из которых относится к атомным, а
другой — к фотонным степеням свободы. Система и детектор стали перепутанными
за счет взаимодействия. В противоположность выражению B0.1.2), плотность веро-
вероятности в плоскости экрана задается теперь в виде
P(R) = \[
B0.1.4)
Но поскольку (I1O2|0iI2) обращается в нуль, интерференционные члены исчезают,
так что
/L/, |2 i L/, |2\
B0.1.5)
и интерференционных полос теперь нет.
Микромазеры служат в качестве «который путь»-детекторов, только если один
добавочный фотон, оставленный атомом, изменяет поле фотонов детектируемым
20.2 Резонансное взаимодействие атомов с микроволновым полем 451
образом. Следовательно, будет ли доступна информация «который путь» или нет
зависит от того, в каких состояниях находятся в начальный момент времени фотоны
в резонаторах. Одна из крайних ситуаций — ни одного фотона в начале и один
фотон в одном из детекторов в конце — только что рассмотрена. Ясно, что в этом
случае можно сказать, через какой резонатор и, следовательно, через какую щель
атом попадает на экран. Ситуация совершенно меняется, когда резонаторы содержат
классическое микроволновое излучение с большим (средним) числом фотонов, п\
и П2, имеющим разброс, равный корню квадратному из этого числа. Например,
изменение числа фотонов в резонаторе 1 происходит теперь от значения п\ ± уп\
до п\ + 1 =Ь уп\ . Это изменение невозможно зарегистрировать, поскольку уп\ ^> 1,
так что информация «который путь» недоступна.
В последнем случае (классическое излучение в микроволновых резонаторах)
невозможно сказать, через какую щель атом достигнет экрана и интерференционная
картина получается точно такой же, как и в отсутствии микроволновых резонато-
резонаторов. Наоборот, резонаторы, не содержащие фотонов в начальный момент времени,
запоминают информацию «который путь», и поэтому интерференционная картина
исчезает. Она заменяется некогерентной суперпозицией B0.1.5) картин от одиночных
щелей.
Таким образом, мы показали, что интерференционный перекрестный член
^i(r)^2(r)(li02|0il2) B0.1.6)
обращается в нуль, поскольку (I1O2IQ1I2) = 0. Но откуда мы знаем, что «принцип
неопределенности» не приводит к тому, что Ф2Ф1 та>кжв обращается в нуль? В этом
случае мы могли бы доказать, что именно появление факторов случайной фазы,
вследствие взаимодействия с полем, ответственно за потерю интерференции. Далее
будет показано, что это не так.
20.2. Резонансное взаимодействие атомов с микроволновым полем
ж его влияние на движение центра масс атома 1)
Резонансный атомно-полевой гамильтониан для данной задачи имеет вид
Ti fid) 1
Ж = — + — az + Пша+а + hgU(z)JS, B0.2.1)
где
j? = ст+а + а+G^. B0.2.2)
Здесь к обычному гамильтониану взаимодействия двухуровневого атома с одномодо-
вым полем F.2.8) добавлен член р2/2т, связанный с движением центра масс атома.
В выражении B0.2.1) р является one™
ратором импульса центра масс атома,
имеющего массу т, а функция U(z)
описывает пространственную зависи-
зависимость связи между атомным переходом
и фотонами мазера. В идеальном случае и L
это плоская функция, изображенная на Ри^ 2QA функция (jfz\
рис. 20.4.
1) Дальнейшее обсуждение вопроса имеется в работе Englert, Schwlnger and Scully A990).
15*
452
Квантовые оптические тесты на дополнительность
Гл.20
Теперь учтем, что собственные состояния оператора J/ задаются выражением
1
1-5—, III/ — .— I \Uj, ILj < ") '" i^ //5 \Zj\J.Zj.OI
а соответствующие собственные значения равны ±\/п + 1 (см. разд. 10.2.2). Соб-
Собственные значения гамильтониана системы (постоянные) принимают вид
2
z < 0 : # = #-,
0 < z
>I: J
± hgs/n +1,
" 2m'
следовательно,
B0.2.4a)
B0.2.46)
B0.2.4b)
B0.2.5)
2m 2m - •"*> * - ¦
или
P± = (P2 T 2m%Vn + 1I/2. B0.2.6)
Поскольку энергия центра масс существенно превосходит энергию взаимодействия,
B0.2.7)
mhg /—
p± = pt—aV^-
Рассмотрим теперь случай, когда атомы входят в резонатор, содержащий п
фотонов, будучи в возбужденном состоянии |а), то есть
ф(г = 0) = |а, п) = —=
и на выходе из резонатора z = I имеем
„/./у _ /Л _ _J_n_i_ n\ r,^ip+1/^ _|_ ^Х р-«2
Ц/У/С — l I — __ I "у", II// С ~т~ 5 /
B0.2.8
, B0.2.9)
где и0 = р/т.
Видно, что фазовые факторы p±l/h, возникающие благодаря взаимодействию
с полем, не являются случайными, в отличие от фактора Раби gr\/n + 1, где т =
= 1/vq — время пролета.
В приложении 20. А сделан точный расчет для полной задачи, включающей (почти
незаметную) отдачу фотонов и показано, что случайные фазы не появляются и в этом
случае.
Дело в том, что микромазерные «который путь»-детекторы не приводят к случай™
ной фазе при взаимодействии атома с полем. Атомно-полевое взаимодействие не вы-
вызывает существенного изменения в пространственной волновой функции атомов.
Именно корреляция волновой функции центра масс и фотонных степеней свободы
в резонаторах ответственна за потерю интерференции.
20.3. Квантовое стирающее устройство
В предыдущих разделах мы видели, что именно корреляции между системой
и детектором отвечают за глубокие воздействия измерительного прибора на рас-
рассматриваемую систему. Не удивительно, что когерентность разрушается, как только
20.3
Квантовое стирающее устройство
453
получается информация «который путь». Однако разрушение интерференционного
(волнообразного) поведения, рассмотренное в разд. 20.2, не содержало неконтроли-
неконтролируемых актов рассеяния.
Возникает вопрос, можно ли восстановить перекрестные члены когерентной ин-
интерференции путем удаления («стирания») информации типа «который путь», содер-
содержащейся в детекторах. В этом смысле мы рассматриваем здесь задачу квантового
стирающего устройства. Отметим, что если рассматривать когерентность, теряемую
вследствие случайного рассеяния или иных стохастических возмущений, как пола-
полагалось в начале главы, этот вопрос никогда бы не возник. Фактически, мы увидим,
что интерференционные эффекты можно восстановить путем манипулирования «ко-
«который путь»-детекторами спустя много времени после прохождения атомов через
резонаторы.
Рассмотрим схему системы «атомный пучок + микромазер», изображенную на
рис. 20.5. Атомы проходят через два мазерных детектора, но сейчас мы представим
себе, что «который путь»™детекторы разделены комбинацией заслонка-детектор.
Теперь мы имеем конфигурацию, в которой возможно квантовое стирание. В част-
частности, рассмотрим систему резонаторов, изображенную на рис. 20.5а. Две заслонки
Микромазеры
Коллима- Резонатор 1
торы
Резонатор 2
и
"темная волна Лазерный пучок
Экран с интерференционными полосами
Экран без интерференционных полос
Да
Нет
Рис. 20.5. Квантовое стирающее устройство, в котором электрооптические заслонки изо-
изолируют микроволновые фотоны в двух резонаторах от стенки детектора, поглощающей
микроволновые фотоны и действующей как фотодетектор (а). Плотность атомов на экране,
зависящая от того, наблюдался ли фотоотсчет на стенке детектора («да») или не наблюдался
(«нет»), демонстрирующая то обстоятельство, что корреляции между событием на экране
и фотоотсчетом стирающего устройства являются необходимыми для восстановления ин-
интерференционной картины (б). (Из работы Scully, Englert and Walther A991))
расположены так, что будучи закрытыми, они ограничивают излучение, оставляя его
либо в верхнем, либо в нижнем резонаторе. Далее представим себе, что при открытых
заслонках свет имеет возможность взаимодействовать со стенкой детектора. Таким
образом, излучение, остающееся либо в верхнем, либо в нижнем резонаторе, в зави-
зависимости от того, по какому пути прошел атом, будет теперь поглощаться и можно
сказать, что память о прохождении (информация «который путь») будет стираться.
Можно ли сейчас (после стирания) восстановить интерференционные полосы?
Ответ является положительным, но как это возможно? Атом удалился далеко от ми™
кромазерных резонаторов, так что не может быть и мысли о каком-либо физическом
воздействии на волновую функцию атомного центра масс. Тот факт, что эта ситуация
454 Квантовые оптические тесты на дополнительность Гл. 20
кажется парадоксальной, был отмечен Джейнсом г):
«Мы имеем полный ЭПР (Эйнштейн—Подольский—Розен) парадокс —
и более того. Применяя или не применяя механизм стирания до измерения
состояния микроволновых резонаторов, мы можем, по желанию, привести
атомный пучок в одно из двух состояний: A) состояние с известным путем
и невозможностью интерференционных эффектов при дальнейших измере-
измерениях; B) состояние, в котором представлены обе функции ф\ и фч c из-
известной относительной фазой. В этом случае интерференционные эффекты
не только наблюдаемы, но и предсказуемы. И мы можем решать, что делать,
после того, как взаимодействие закончилось и атом находится далеко от
резонаторов, так что не может быть и мысли о каком-либо физическом
воздействии на волновую функцию атомного центра масс!
Отсюда вполне ясно, что настоящая квантовая теория не только не ис-
использует, она даже не отваживается упоминать, понятие «реальной физи-
физической ситуации». Защитники теории говорят, что это понятие является
философски наивным, возврат к устаревшим способам мышления, и что
осознание этого составляет глубокое новое знание о природе науки. Я го-
говорю, что эта теория составляет крайнюю иррациональность, что где-то
в этой теории утратилось различие между реальностью и нашим знанием о
реальности, и результат имеет характер скорее средневековой черной магии,
чем науки. Я надеялся, что квантовая оптика, с ее огромными новыми тех-
технологическими возможностями, способна предоставить экспериментальный
ключ к разрешению этих противоречий».
Приступим к разрешению «парадокса Джейнса», расширяя математическое опи-
описание и учитывая детектор, находящийся первоначально в основном состоянии \d).
Имеем
ф(г) = ¦^={ф1(г)\1102) + V>2(r)|0il2>]|fc)|d) B0.3.1)
вместо B0.1.3). После поглощения фотона детектор оказывается в возбужденном
состоянии |е).
Удобно ввести симметричное ф+ и антисимметричное ф_ атомные состояния,
определяемые как
ф±(г) = ^=[фг(г)±ф2(г)}. B0.3.2)
Таким же образом вводятся симметричное |+) и антисимметричное |—) состояния
полей излучения в резонаторах, содержащих «какой путь»-информацию,
|±) = -^(|1102>±|0i12». B0.3.3)
С учетом B0.3.2) и B0.3.3) состояние B0.3.1) системы «атомный пучок + поле
в резонаторе + детектор» записывается как
ф(г) = -Lfo&+(r)|+) + V-(r)|-)]|6)|d>. B0.3.4)
Рассмотрим теперь взаимодействие между полем излучения, находящимся в резо-
резонаторе, и детектором. Как уже отмечалось ранее, мы представляем себе детектор,
) См. работу Jaynes A980). Квантовое стирающее устройство было независимо впервые
предложено в работе Scully and Driihl A982), а связь между этой работой и парадоксом
Джейнса была впервые установлена в работе Scully, Englert and Walther A992).
20.3 Квантовое стирающее устройство 455
состоящий из атома, который имеет нижнее состояние \d) и возбужденное состояние
|е). Гамильтониан взаимодействия между полем и детектором зависит от симмет-
симметричных комбинаций полевых переменных, так что только симметричное состояние
|+) полей будет задействовано. Тогда находим, что действие детектора (стирающего
устройства) создает состояние
V(r) = ^=[ф+(т)\0102)\е) + ^_(r)|->|d>]|6), B0.3.5)
то есть, симметричное взаимодействие изменяет только симметричное состояние
поля |+). Антисимметричное состояние |—) остается неизменным.
Атомная плотность вероятности на экране для состояния B0.3.4) выглядит сле-
следующим образом:
P(R) = \[ф+*(К)ф+(К)+ф.*(П)ф.(Щ = i[^(R)^(R)+^2*(R)V2(R)], B0.3.6)
и не дает никаких интерференционных полос, до тех пор пока конечное состояние
детектора неизвестно. Но, если задать вопрос, какова плотность вероятности Pe(R)
обнаружить и детектор в возбужденном состоянии, и атом в точке R, экрана, то
ответом будет
Pe(R) = |V4(R)|2 = \ [№i (R) I2 + 1^2 (R) Г] + Re h/4 (КШЫ)]. B0.3.7)
Это выражение демонстрирует те же полосы, что и B0.1.2), показанные сплошной
линией на рис. 20.55. Наоборот, плотность вероятности P^(R) обнаружить и детектор
в невозбужденном состоянии, и атом в точке R экрана равна
Pd(R) = |^-(R)|2 = ^^i(R)|2 + ^2(R)|2]-Re[^*(R)^2(R)], B0.3.8)
что дает «антиполосы», обозначенные пунктирной линией на рис. 20.55. Если не учи-
учитывать сигнал стирающего устройства, получаем суперпозицию B0.3.6), равную
половине суммы Ре и Р^, которая не имеет полос и, конечно, эквивалентна B0.1.5)
(см. рис. 20.3).
Дадим физическую интерпретацию этого расчета. После того, как атом переме-
переместился из источника (печи) на экран, проходя через микромазеры и оставляя свой
контрольный фотон, мы фиксируем событие где-то на экране. Затем возвращаемся
к «который путь»-микромазерам, открываем заслонки и делаем возможным погло-
поглощение микроволнового фотона. Наблюдая фотоотсчет в детекторе, мы знаем, что
стирание закончено. В этом случае атом учитывается как «да»-атом.
Далее мы ждем, пока второй атом пройдет через систему от источника до экрана.
Вновь фиксируем событие на экране и затем возвращаемся к микромазерам. На
этот раз предположим, что при открытии заслонки мы не наблюдаем фотоотсчета
в детекторе квантового стирающего устройства. Это будет в половине случаев, как
объяснялось выше. Теперь атом учитывается как «нет»-атом.
Повторяем указанную последовательность много раз. Очевидно, что «да»-атомы
построят полосы, изображенные сплошной линией на рис. 20.5, а «нет»-атомы со-
создадут «антиполосы», отмеченные пунктиром. В заключение отметим, что полосы
и «антиполосы» исчезнут, если не соотносить их с состоянием детектора стирающего
устройства.
Представив физику квантового стирающего устройства, обратимся к схеме, экс-
экспериментально более реализуемой, которая имеет много общего с идеей квантового
стирающего устройства. Рассмотрим изображенную на рис. 20.6 антисимметричную
456
Квантовые оптические тесты на дополнительность
Гл.20
ситуацию, когда резонатор 1 настроен на переход \а) —> |6), а резонатор 2 — на
переход \а) -^ \с).
Даже если резонаторы содержат классическое микроволновое излучение, как
будем полагать впоследствии, и, следовательно, не сохраняют информацию «который
путь», на экране не будет интерференционных полос, поскольку внутренние атомные
состояния \Ь) и \с) являются ортогональными. Это аналогично исчезновению интер-
интерференционных членов в B0.1.4), если не считать того, что теперь атомы сами несут
информацию «который путь».
Последнее обстоятельство вновь провоцирует вопрос: можно ли индуцировать
переходы \Ь) —» \с) в атомах, прошедших резонатор 1, так чтобы информация «кото™
рый путь» стерлась и, в связи с этим, интерференционная картина появилась вновь?
Ответ будет положительным. Экспериментальная реализация, однако, дело тонкое,
поскольку необходимо тщательно контролировать фазы различных классических
полей. Чтобы пояснить это, предположим, что между резонатором 1 и плоскостью
Источник
радиочастотного
Микромазеры напряжения
Коллима-
Коллиматоры
Резонатор 1
I,
Mill
\а)
\Ъ)
NIMI III IIIIIIIIII
IIIMIIIIMIIIIIIIIIIIIIIIIIII
и
Плоская
атомная волна
Резонатор 2
Лазерный пучок
Экран с интерференционными полосами
Экран без интерференционных полос
Рис. 20.6. Асимметричная установка, в которой резонатор 1 индуцирует переход \а) —^
—>- |6) и резонатор 2 индуцирует переход \а) —^ \с). «Который путь»-информация стирается
радиочастотным полем катушки, в которой совершается переход \b) —t \c). (Из работы
Scully, Englert and Walther A991))
щелей помещена катушка, к которой подводится напряжение радиочастотой 50 МГц,
имеющее подходящую величину, для того чтобы гарантировать переход \Ь) —> \с) (см.
рис. 20.6). В области интерференции состояние атома, по существу, записывается как
-±=
B0.3.9)
где относительный фазовый угол E определяется фазами микроволновых полей
в двух мазерных резонаторах и радиочастотным полем катушки. Поскольку эти
поля имеют разные частоты, величина /3 относится к определенному мгновению или
моменту времени, скажем, когда атом возбужден в состояние \а) лазерным пучком.
Плотность вероятности в плоскости экрана,
P(R) = |V(R)|2 = \
Re
B0.3.10)
20.4 Квантовые оптические полосы Рамзи 457
содержит теперь интерференционный член, сильно зависящий от /3. Поэтому, если
значение C меняется от атома к атому, интерференционная картина не возникает. Это
довольно хорошо иллюстрирует вездесущее явление потери когерентности, вызыва-
вызываемой случайными фазами. Следовательно, для восстановления интерференционных
полос мы должны гарантировать одинаковое значение фазового угла /3 у всех атомов.
В случае установки, изображенной на рис. 20.6, это достигается подгонкой фазы
радиочастотного излучения катушки к фазам, которые имеют микроволновые поля
резонаторов в момент возбуждения атомов лазером. Дополнительным преимуще-
преимуществом такой схемы является возможность менять выбранное значение /3, что позво-
позволяет смещать интерференционную картину на экране. Таким образом, контроль 1)
над фазовым углом /3 представляет собой переключатель, с помощью которого
экспериментатор может включать и выключать интерференционные полосы, или
перемещать их.
20.4. Квантовые оптические полосы Рамзи
Другим интересным примером, позволяющим исследовать, каким образом про-
процесс измерения (присутствие детектора) влияет на исследуемую систему, является
возможный эксперимент с квантовыми оптическими полосами Рамзи. Такая возмож-
возможность существует благодаря тому, что в микромазере можно создавать состояния
с определенным числом частиц поля излучения, как обсуждалось в разд. 13.3. Данная
схема близка к тому, чтобы быть реализованной как противоположность экспе-
эксперименту с двумя щелями, дополненному микромазерными резонаторами, который
обсуждался в предыдущем разделе.
Рассмотрим интерферометр, в котором двухуровневый атом проходит последова-
последовательно два одинаковых высокодобротных резонатора микромазеров, как показано на
рис. 20.7. Перед входом в первый резонатор атомы находятся либо в верхнем |а), либо
в нижнем \Ь) состоянии. После выхода из второго резонатора внутреннее состояние
атома тестируется путем (селективной по состояниям) ионизации полем, так что
измеряется вероятность того, что атом заканчивает свое движение в возбужденном
состоянии. Для каждого начального состояния существует два различных пути, по
которым может быть достигнуто конечное возбужденное состояние (см. рис. 20.7). До
тех пор пока отсутствует информация о том, какая альтернатива реализована, можно
наблюдать интерференцию. С другой стороны, если «который путь»-информация
сохраняется в резонаторах, то интерференция невозможна вследствие дополнитель-
дополнительности.
Можно показать, используя решения F.2.13) и F.2.14) для амплитуд вероятности,
описывающих взаимодействие двухуровневого атома с одномодовым квантованным
полем излучения, что вероятности обнаружить атом в верхнем состоянии \а) после
прохождения им двух микромазерных резонаторов равны (см. задачу 20.1)
= (С+С1)(С+С2)
- 2Re ({C+a+S1)(C+a2S2} eiAT), B0.4.1)
2Re (Eia+Ci)(C2+a252) eiAT). B0.4.2)
1) Точка зрения «корреляция между системой и детектором разрушает интерференцию»
(как противоположность точке зрения случайных фаз) получает здесь сильную поддержку.
Если сосредоточиться на точке зрения «случайной фазы обратного действия», то мы, скорее
всего, не достигнем данного результата.
458
Квантовые оптические тесты на дополнительность
Гл.20
(а)
(б)
Рис. 20.7. Альтернативные пути достижения конечного возбужденного состояния. Если
атом сначала находится в возбужденном состоянии (а), то число фотонов изменяется либо
ни в одном, либо в обоих резонаторах. Если атом сначала находится в основном состоянии
(б"), то число фотонов изменяется либо в первом, либо во втором резонаторе. (Из работы
Englert, Walther and Scully A991))
Здесь Ра (P^ ) — вероятность обнаружить атом в верхнем состоянии в случае,
когда атом находился вначале в верхнем (нижнем) состоянии, А = ша1, — и —
расстройка между атомом и полем, Т — время, необходимое атому для прохождения
расстояния между резонаторами, и
2gsm
= cos
B0.4.3)
B0.4.4)
где clj и а^ (j = 1,2) — операторы уничтожения и рождения фотона в поле j-
го резонатора, g — константа взаимодействия атома с полем, т — длительность
взаимодействия между атомом и одним из полей резонаторов, и величины Sj и Cj
получаются при замене uju^ произведением a^aj. Средние значения в выражениях
B0.4.1) и B0.4.2) относятся к моменту времени, предшествующему входу атома
в первый резонатор, так что это средние значения полей в их начальном состоянии.
При выводе B0.4.1) и B0.4.2) пренебрегалось затуханием резонаторов и спонтанным
распадом возбужденного состояния атома.
Рассмотрим теперь две различные ситуации. В первом случае прдположим, что
начальные состояния полей в микромазерных резонаторах являются классическими
состояниями (когерентные состояния с большой амплитудой). Далее предположим,
20.4 Квантовые оптические полосы Рамзи 459
для простоты, что средние числа фотонов в этих состояниях равны между собой
((а{ а\) = (ajа2) = п) ш велики (п ^> 1, (A/2gJI и такие что
cos(gy/nr) = sin(gy/nr) = —т=. B0.4.5)
При этих условиях выражения B0.4.1) и B0.4.2) существенно упрощаются. Если
через ф обозначить относительную фазу полей в резонаторах, то вероятность обна-
обнаружить атом в возбужденном конечном состоянии запишется в виде
Р(а±] = \ [1 Т cos(AT + ф)}. B0.4.6)
Очевидно, что при изменении Т (например, вследствие изменения расстояния между
резонаторами) наблюдаются полосы Рамзи. Эти полосы Рамзи означают наличие
когерентной суперпозиции двух атомных состояний в области между резонаторами.
Информация «который путь» не сохраняется и, следовательно, интерференция воз™
можна.
В другой крайней ситуации полагаем, что в обоих резонаторах поля приготовле-
приготовлены в состояниях с определенным числом частиц. Альтернативы, изображенные на
рис. 20.7, соответствуют тогда следующим изменениям состояний:
а)
б)
71, п)
П, п)
га, п) или |га + 1, га - 1), B0.4.7)
га - 1, га) или |га, n - 1). B0.4.8)
Следовательно, конечные значения чисел фотонов в резонаторах показывают, какой
из путей реализовался в действительности, так что интерференция невозможна. Это
сразу видно из выражений B0.4.1) и B0.4.2), в которых интерференционные члены
обращаются в нуль, если начальными состояниями являются состояния с определен-
определенным числом частиц. При этих условиях
PW = \ B0.4.8)
то есть, вероятности обнаружить атом в конце пути в верхнем состоянии не демон-
демонстрируют полосы Рамзи.
Таким образом, создавая поля в микромазерных резонаторах в состоянии с опре-
определенным числом частиц или в классических состояниях (соответствующих коге-
когерентным состояниям с большой амплитудой), экспериментатор может получить либо
информацию «который путь», либо полосы Рамзи. И то, и другое, одновременно
невозможно. Интересно отметить, что потеря способности к интерференции, вызы-
вызываемая состояниями с определенным числом частиц, не имеет ничего общего ни со
случайными фазами, ни с соотношениями неопределенностей Гейзенберга. Именно
ортогональность, или, говоря на физическом языке, различимость двух конечных
состояний в выражениях B0.4.7), вызывает эту потерю.
Таким образом, атомный интерферометр можно использовать для демонстрации
того, как дополнительность подкрепляется механизмом, отличающимся от случай-
случайных фаз или ограничений, налагаемых произведением неопределенностей. Полосы
Рамзи исчезают каждый раз, как только резонаторы микромазеров содержат ин-
информацию о том, какая альтернатива реализована. Хотя довольно трудно извлечь
эту информацию, она имеет место независимо от того, следят за ней или нет. Одного
лишь факта, что мы в принципе имеем информацию «который путь», достаточно для
уничтожения полос.
460
Квантовые оптические тесты на дополнительность
Гл. 20
Приложение 20.А
Эффект отдачи в «который путь»-детекторе на основе
микромазера г)
Запишем волновую функцию атомов, находящихся в щелях, z = 0, в виде
перепутанного состояния
\ф(х, у, 0)) = А(х - d/2, y)\l1,02)i/;i(x)g1(x, y)+
+ А(х + d/2, y)|0i, U)il>i(x)g2(x, у), B0.A.1)
где А(х ± d/2, у) — функции диафрагм, отличные от нуля лишь в окрестности точек
х — =F<i/2, у — 0, функция ?pi(x) — амплитуда вероятности до взаимодействия,
У +¦
Рис. 20.8. Ориентация резонаторов и направление вектора напряженности электрического
поля в них. Резонаторы показаны с точки зрения наблюдателя, находящегося на экране.
Кружки обозначают отверстия, через которые атомы достигают наблюдателя
а функции gi(x,y) и g2(x,y) суммируют эффект взаимодействия и определяют
вероятности того, что атом испустит фотон в резонаторе 1 и 2, соответственно.
1) Раздел основан на работах Englert et. al. A994); Yelin et. al. A996).
П.20.А Отдача в «который путь»-детекторе на основе микромазера 461
В случае модовых функций U(x,y) = cos(ky), соответствующих геометрии,
изображенной на рис. 20.8, функции g\ и gi задаются выражениями
g-1(a?,y) = sin[g cos(ky)r] при х > 0, B0.А.2а)
g2(xJy) = sin[g*cos(A;i/)r] при х < 0. B0.А.26)
Для того чтобы рассчитать интерференционную картину, необходимо сначала
найти волновую функцию на экране z = D, выразив ее через волновую функцию на
диафрагме z = 0. Это соотношение выглядит следующим образом:
ф(х, у, D) = фг(х, у, D) + ф2(х, у, D), B0.А.З)
где
фг(х,у,О) = dx' dy'G(x,y, D;x' ,у' ,0)х
х A(xf - d/2, j/7)|1ь 02)i/>i(x')gl(x', yf), B0.А.4)
ф2(х, y,D)=ll dx' dy'G{x, y, D; xf, t/', 0) x
x A(xf + d/2, j/OIOi, U)^i{x')g2{x', yf), B0.A.5)
и С(ж, |/, D; x;, |/;, 0) — функция Грина для волны, имеющей длину волны де Бройля
G{x, у, D; х\ у\ 0) = jYexp f ^§Ч(^ - ^J + (ж/ " 2/'J]} ¦ B0.А.6)
Множитель сЖ содержит все, не относящиеся к делу, постоянные величины. Эта
функция Грина применима в случае дифракции Фраунгофера, когда экран располо-
расположен далеко от щелей, и рассеяние происходит на малые углы.
Чтобы вероятность отсутствия излучения в любом из микроволновых резонаторов
была мала, положим gr = тг/2. Остается лишь задать gi^{x, у) в точках х = dzd/2,
у = 0 диафрагмы. При данных условиях
gi,2(x,y) -1-^fcV, B0.A.7)
где у изменяется поперек диафрагм, так что зависимость gi^i^^y) определяется
масштабами, устанавливаемыми шириной щели а (~ 5 нм). Таким образом, откло™
нение от единицы в выражении B0.А.7) приблизительно равно (каL" ^ [102 м^1E •
• 10~9 м)]4 ~ 10™25, что является пренебрежимо малой величиной.
Имея теперь составляющие выражения B0.А.3), приступим к вычислению вет-
ветвей волновой функции центра масс в плоскости экрана и, таким образом, к явной
демонстрации того, что способность к интерференции не потерялась в результате
взаимодействия. Для простоты, возьмем гауссову функцию диафрагмы
А(х т d/2, у) = exp {-^[(x ± d/2J + z/2]} . B0.A.8)
Верхняя щель дает
ф^х, у, D) = ,Л11 dx' dy' еХр {-^[(ж - x'f + (у - у1J}} х
х exp {-^[(x ± d/2J + у2}} [l - ^fcVJ . B0.A.9)
Аналогичное выражение получается и для ф2(х^У^^).
462 Квантовые оптические тесты на дополнительность Гл. 20
Интерференционная картина от двух щелей определяется выражением
Re [ф;(х, у, О)ф1(х, у, D)] = Re [фЦ-х, у, О)фг(х, у, D)]. B0.A.10)
В отсутствие взаимодействия атома с фотоном она задается выражением
exp p ^tW)] cos
где b = XdBD/2na. Согласно этому выражению, интервал между полосами равен
2nab/d = \$bD / d. Таким образом, интерференционная картина не уничтожается
эффектами поперечной отдачи.
Задачи
20.1. Выведите выражения B0.4.1) и B0.4.2).
20.2. Определите, сохраняется или нет информация «который путь» в атомном
интерферометре, рассмотренном в разд. 20.4, если поле излучения в резона-
резонаторах микромазеров находится: а) в одномодовом поле теплового источника
с температурой Т; б) в сжатом вакуумном состоянии |?,0) и в) в состоянии,
описываемом оператором плотности
п=0
Список литературы
Работы общего характера
Feynman, R., Lelghton, R. and Sands, M. The Feynman Lectures on Physics, Vol. Ill, (Addlson
Wesley, Reading, MA 1965).
Scully, M. O., Shea, R. and McCullen, J. D. Phys. Rep. 43, 485 A978).
Wheeler, J. A. In Problems in the Foundations of Physics, ed. G. T. di Francia (North-Holland,
Amsterdam 1979).
Wootters, H. W. K. and Zurek, W. H. Phys. Rev. D 19, 473 A979).
Barut, A., Meystre, P. and Scully, M. O. Laser Focus (Oct. 1982), pp. 49^56.
Wheeler, A. and Zurek, W. H. Quantum Theory and Measurement (Princeton Univ. Press, 1983)
Englert, В., Schwinger, J. and Scully, M. O. Found. Phys. 18, 1045 A988).
Schwinger, J., Scully, M. O. and Englert, B.-G. Z. Phys. D 10, 135 A988).
Scully, M. O., Englert, B.-G. and Schwinger, J. Phys. Rev. A 40, 1775 A989).
Englert, B.-G., Scully, M. O. and Walther, H. Scl Am. 271, 56 A994).
Микромазерный «какой путь»-детектор
Scully, M. О. and Walther, H. Phys. Rev. A 39, 5229 A989).
Stern, A., Aharonov, Y. and Imry, Y. Phys. Rev. A 41, 3436 A990).
Scully, M. O., Englert, B.-G. and Walther, H. Nature 351, 111 A991).
Tan, S. M. and Walls, D. F. Phys. Rev. A 47, 4663 A993).
Список литературы к гл. 20 463
Движение центра масс мазерных атомов
Englert, B.-G., Schwinger, J., Barat, А. О. and Scully, M. O. Europhys. Lett 14, 25 A991).
Haroche, S., Brune, M. and Ralmond, J. M. Europhys. Lett. 14, 19 A991).
Englert, B.-G., Schwinger, J. and Scully, M. O. In New Frontiers in Quantum Electrodynamics
and Quantum Optics, ed. A. O. Barut (Plenum, New York, 1990).
Englert, B.-G., Fearn, H., Scully, M. O. and Walther, H. In Quantum Interferometry, (World
Scientific, Singapore, 1994), p. 103.
Yelin, S. F., Bednar, C. J. and Hu, C.-R. Opt Commun. 136, 171 A997).
Квантовые оптические полосы Рамзи
Englert, B.-G., Walther, H. and Scully, M. O. Appl. Phys. В 54, 366 A991).
Квантовое стирающее устройство
Jaynes, E. In Foundation of Radiation Theory and Quantum Electronics, ed. A. O. Barut
(Plenum, New York 1980), p. 37.
Scully, M. O. and Driihl, K. Phys. Rev. A 25, 2208 A982).
Hlllery, M. and Scully, M. O. In Quantum Optics, Experimental Gravity and Measurement
Theory, ed. P. Meystre and M. O. Scully (Plenum, New York 1983), p. 65.
Ou, Z. Y., Wang, L. J., Zou, X. Y. and Mandel, L. Phys. Rev. A 41, 566 A990).
Zajonc, A. G., Wang, L. J., Zou, X. Y. and Mandel, L. Nature 858, 507 A991).
Zou, X. Y., Wang, L. J. and Mandel, L. Phys. Rev. Lett 67, 318 A991).
Kwiat, P. G., Steinberg, A. M. and Chlao, R. Y. Phys. Rev. A 45, 7729 A992); ibid. 49, 61 A994).
Herzog, T. J., Kwiat, P. G., Weinfurter, H. and Zeillnger, A. Phys. Rev. Lett 75, 3034 A995).
Глава 21
ДВУХФОТОННАЯ
ИНТЕРФЕРОМЕТРИЯ,
ПРОБЛЕМА КВАНТОВОГО
ИЗМЕРЕНИЯ И ДРУГИЕ ЗАДАЧИ
Как было показано в предыдущей главе, результат эксперимента существенно
зависит от процесса наблюдения и сбора информации или, по крайней мере, от
вероятности «знания» (независимо от того, потрудились мы «посмотреть» на систему
или нет). Например, в случае микромазерного «который путь»-детектора нет необхо-
необходимости «смотреть» или «опрашивать» мазеры, для того чтобы лишиться интерфе-
интерференции. Достаточно того, что существует возможность получить соответствующую
информацию. Эксперименты такого типа являются ярким примером того, насколько
важна информация «который путь» (или «1\?е1спег-1У\^у»-информация).
В данной главе проблема квантового стирающего «который путь»-устройства
рассматривается с иной точки зрения. Сначала обсуждается интерференция света,
рассеянного простыми атомными системами г), состоящими из одиночных атомов,
расположенных в двух соседних точках. Эта простая модель позволяет нам дале-
далеко продвинуться в понимании таких проблем как дополнительность, задержанный
выбор и квантовое стирающее устройство, работа которого описывается с помощью
полевых и фотонных корреляционных функций, то есть G^{r^t) и 6Л2^(г, г;; t, tf).
В конце главы будет показано, что такие исследования могут, в принципе, привести
даже к новым видам спектроскопии высокого разрешения.
21.1. Полевая корреляционная функция света, рассеянного двумя
атомами
С тем чтобы подготовить почву для наших исследований рассмотрим «двухще-
левой» эксперимент, в котором щели заменены двумя двухуровневыми атомами,
резонансными лазерному импульсу /i, как показано на рис. 21.1а. Корреляционная
функция поля
, t) = (ф\Е(-\г, t)E(+Hr, 1)\ф) B1.1.1)
описывает интерференционную картину, создаваемую рассеянным светом.
1) Для дальнейшего чтения об атомных «который путь»-детекторах см. Scully and Driihl
A982); Elchmann, Bergqutst, at. al. A993).
21.1
Полевая корреляционная функция света, рассеянного двумя атомами
465
(а)
(б)
(в)
(г)
Рис. 21.1. Свет I освещает атомы, расположенные в создают на экране интерференционную
картину (а); двухуровневые атомы возбуждаются лазерным импульсом h (б); трехуровне-
трехуровневые атомы возбуждаются импульсом 1\ на переходе с) —> а), после чего следует испускание
7-фотонов на переходе \а) —>> \Ь) (в); то же самое, что и в случае в, но на переходе \Ь) —>> \b)f
действует второй импульс 1%. Переход \b)f —^ с) приводит к испусканию с^-фотона (г). (Из
работы Scully and Driihl A982))
Здесь положительно-частотная часть поля E^+^(r,t) задается обычным рядом
Фурье, содержащим операторы уничтожения а^ (как в A.1.30)):
^кт-^ B1.1.2)
Соответствующее выражение получается и для отрицательно-частотной части
Е^' (г, t). Относящаяся к делу часть системы «атом + рассеянное поле» описывается
теперь вектором состояния
1
B1.1.3)
Вектор состояния фотона, рассеянного г-м атомом, задается выражением F.3.18)
в виде
B1.1.4)
466 Двухфотонная интерферометрия и другие задачи Гл. 21
где g"^ — константа, зависящая от эффективности взаимодействия атома с полем,
ш — частота перехода между состояниями \а) и \Ь) атома, Г — скорость релаксации
на переходе \а) —> \Ь) и г^ — радиус-вектор г-го атома. Из выражений B1.1.1)—B1.1.4)
находим, что корреляционная функция рассеянного света равна
+ |72» =
\ г, t)\l2)\2 = ||*i(r, t) + Ф2(г, t)\2, B1.1.5)
и из F.3.24) имеем
Ф4(г, t) = @|?7(+)(г, *)Ы = ^г ® (* " ^) е-(-+г/2)(*"д^/с), B1.1.6)
где Аг^ = |г — г^| представляет собой расстояние от г-го атома до детектора. Таким
образом, имеем следующий перекрестный интерференционный член:
ф1ф2 + к.с. = -?&?- Q(t- Агг/с) @(t- Дг2/с) х
где ^о = ш/с.
Выраж:ение B1.1.7) описывает ни что иное, как интерференционную картину
в эксперименте Юнга с двумя щелями, обобщенную на случай рассматриваемой
задачи рассеяния. Отметим, что когда фотоны 71 и 72 приходят на детектор «од-
«одновременно», возникают интерференционные полосы. Если же нет «перекрывания»,
то есть время когерентности рассеянного света слишком мало, то не будет и ин-
интерференции. Это есть временной вариант утверждения, сформулированного для
частотной области и состоящего в том, что некогерентный свет не создает интерфе-
интерференционной картины. Очевидно, что мы использовали не самый простой, хотя все же
и занятный, способ получить этот элементарный результат. В заключение отметим,
что в приложении 21.А изложен операторный подход к решению данной задачи. Он
оказывается полезным в более сложных ситуациях.
21.1.1. Коррелмционнам функция G^1' (r, t) при рассеянии двумя возбужденны-
возбужденными атомами. Воспользуемся нашим операторным формализмом для того, чтобы
определить, будут ли два возбужденных атома, расположенных в точках ri и Г2,
создавать интерференционную картину (см. рис. 21.1а). Как и прежде предположим,
что атомы расположены достаточно далеко друг от друга и кооперативными эффек-
эффектами можно пренебречь. Пусть в начальный момент времени t = 0 атомы находятся
в состоянии
). Для значений времени t ^> 1/ Г состоянием системы будет
B1.1.8)
и корреляционная функция теперь будет иметь вид
г,
= |Ф1(г, t)\2 + |Ф2(г, t)\2 + [Ф1(г, *)Ф2(г, «)Ы71> + к.с]. B1.1.9)
Видно, что интерференционная картина, определяемая последним членом выраже-
выражения B1.1.9), пропорциональна величине G2|7i)- Из определения |7i) B1.1.4) следует
21.1
Полевая корреляционная функция света, рассеянного двумя атомами
467
(задача 21.2), что
G2|7l) =
Следовательно, если |ri — Г21
будет слабо выраженной.
А, то |G2|7i)l
B1.1.10)
и интерференционная картина
21.1.2. Возбуждение лазерным излучением. Теперь посмотрим, что произойдет,
если осуществлять двухатомный эксперимент при помощи лазерного импульса. Бу-
Будем полагать, что импульс является достаточно мощным, так что его можно считать
классическим, и что его длительность существенно короче времени затухания ато-
атомов. Это означает, что импульс практически мгновенно переводит атомы в некоторую
суперпозицию основного и возбужденного состояний. Для определенности предполо-
предположим, что до того, как импульс достиг одного из атомов, последний находился в со-
состоянии \Ъ). Сразу после прохождения импульса, атом окажется в состоянии са\а) +
+ сь|6), где \са\2 + \съ\2 = 1. Следовательно, в момент t = 0 (сразу после прохождения
импульса) двухатомная система (предполагаем, что импульс возбуждает оба атома)
будет в состоянии
\Ф) = (co|oi> + cb\h))(ca\a2) + сь|62})|0) =
= (cl\aia2) + cacb\aib2) + cbca\bia2} + cg|6162>)[0>. B1.1.11)
Спустя время t ^> 1/ Г состояние B1.1.11) принимает вид
\Ф) = ^|7172> + CaCbhl) + CbCa\l2) + сЦО). B1.1.12)
Вычислим теперь корреляционную функцию. Если предположить, что атомы распо-
расположены достаточно далеко друг от друга, так что G2I71) — 0? тогда
+ \cacb\2) + 2|cac6|2Re [#i(r, *)Ф2(г, t)]. B1.1.13)
Последний член в выражении B1.1.13) является интерференционным и образу-
образуется из членов выражения B1.1.11), в которых лишь один из двух атомов является
возбужденным. Каким должен быть возбуждающий импульс, чтобы интерферен-
интерференционная картина была наиболее яркой? Интерференционный член пропорционален
|сась|2 = lca|2(l — lca|2)- Эта величина имеет максимальное значение, когда |са|2 =
= 1/2, так что нужно взять импульс, который будет создавать атомное состояние
Световой пучок
194 нм
Рис. 21.2. Свет, рассеянный двумя ионами (изображенными в виде двух кружков около
цента ловушки) отображается на детектор D% с поляризатора Р. Детектор D\ служит
в качестве устройства, контролирующего число ионов. (Из работы U.EIchmann, et. at A993))
468
Двухфотонная интерферометрия и другие задачи
Гл. 21
с \са\ = |q,|. Такой импульс называется тг/2-импульсом. Отметим, что тг-импульс,
инвертирующий оба атома, вообще не вызовет появления интерференционной карта™
ны. Недавно подобная двухатомная интерференция наблюдалась экспериментально.
В экспериментах (см. рис. 21.2) два иона 198Hg находились в ловушках Паули
и облучались светом резонансного лазера на длине волны 194 нм, соответствующей
переходу 6s2Si/2 —* 6jo2Pi/2- Рассеянный свет демонстрировал интерференционную
картину, предсказанную выражением B1.1.13).
21.1.3. Использование трех уровней атома в качестве «которым путь»-детектора.
Изменим наш «эксперимент», заменив двухуровневые атомы (рис. 21.16) трех™
уровневыми атомами (рис. 21.1 в). Атомы возбуждаются в состояние \а) лазерным
импульсом 1\ и затем релаксируют в состояние \Ь) или |с), испуская 7~фотон- Ор-
Организуем систему детектирования таким образом, чтобы она воспринимала лишь
излучение на переходе \а) —> \Ь) и игнорировала излучение на переходе \а) —>
—> \с). Рассмотрим, как и в предыдущем эксперименте, корреляционную функцию
поля. На первый взгляд можно подумать, что интерференционные полосы вновь
будут наблюдаться, поскольку атомная конфигурация, изображенная на рис. 21.16",
не отличается от конфигурации, изображенной на рис. 21.1в. Однако, небольшого
Рис. 21.3. Поляризационно-чувствительное детектирование рассеянного света (ненормиро-
(ненормированное): а — наличие интерференции в тг-поляризованном свете; б — отсутствие интерфе-
интерференции в сг-поляризованном свете. (Из работы U.EIchmann, et. al. A993))
размышления достаточно, чтобы убедиться, что это не так. Чтобы определить,
который из атомов рассеял свет, необходимо лишь посмотреть, который из них A или
2) находится в состоянии \Ъ). Теперь учтем, что если мы знаем (или можем узнать) от
какого источника (щели или атома) пришел свет, то следует ожидать исчезновения
интерференционных полос. Детальный расчет, приведенный ниже, подтверждает это
ожидание. Состояние системы взаимодействующих атома и поля, изображенной на
рис. 21.1 в, задается теперь выражением
&
|С1&2>|72»,
B1.1.14)
21.2 Свет, рассеянный двумя многоуровневыми атомами 469
и корреляционная функция поля в таком состоянии имеет вид
, t) = |(|Ф!(г, t)\2 + |Ф2(г, t)\2 + [Ф1(г, *)Ф2(г, i)FlC2|Cl62) + к.с.]) =
= ^(|Ф1(г,*)|2 + |Ф2(г^)|2). B1.1.15)
Из B1.1.15) видно, что интерференционные члены исчезли, в согласии с нашим
интуитивным представлением, обсуждавшимся ранее, поскольку состояния \Ъ) и \с)
являются ортогональными. Полезность такого простого «который путь»-устройства
была подтверждена Эйхманном с сотрудниками 1). Когда они поставили экспери-
эксперимент таким образом, что затухание на переходе \а) —> \Ь) (рис. 21.1в) имело место
с излучением света ст-поляризации, интерференция не наблюдалась. Однако, когда
они наблюдали свет, соответствующий переходу \а) —>• |с), предполагающий тг-
поляризацию, интерференция имела место. Эти результаты приведены на рис. 21.3.
21.2. Полевая ж фотонная корреляции света, рассеянного двумя
многоуровневыми атомами: квантовое стирающее устройство
Как было показано в разд. 21.1.3, трехуровневые атомы, изображенные на
рис. 21.1в, предоставляют возможную информацию «который путь», приводящую
к потере интерференции. А именно, интерференционные члены в функции корре-
корреляции поля B1.1.15) умножаются на атомное внутреннее произведение (&1C2IC162)
и, поэтому, обращаются в нуль. Возникает вопрос 2): что если «заставить» атомы
переходить из состояния | Ь) в состояние | с), так чтобы эти состояния больше не были
ортогональными? Если бы удалось добиться этого, то возникла бы интересная ситу-
ситуация. А именно, 7™ФОТОНЫ были бы уже на пути к детекторам (то есть, далеко от
атомов 1 и 2), а полосы пытались бы появиться или нет в зависимости от того, что
мы делаем с атомами спустя много времени после того, как произошло испускание
7™фотона.
Предположим, что состояния \Ь) и \с) связываются с помощью подходящего
лазерного или микроволнового поля. Тогда, унитарная эволюция атомов 1 и 2 на
переходе \Ь) —> \с) означает, что
<bic2|cib2> -»• (bic2\U+U\Clb2). B1.2.1)
Если оператор эволюции во времени является унитарным, то U+U = 1, и мы видим,
следовательно, что нам не удалось создать полосы, воздействуя вторым импульсом.
Еще удивительнее, если бы смогла работать какая-нибудь другая схема, разработан-
разработанная для восстановления интерференционных полос. Тем не менее, наличие информа-
информации, содержащейся в трехуровневых атомах, аналогично обладанию информацией,
хранящейся в виде результатов наблюдения, а известно, что процесс наблюдения
изменяет вектор состояния неунитарным образом. Более наглядно вопрос можно
поставить так: можно ли стереть информацию (память), запертую в атомах, и таким
образом восстановить полосы? Под влиянием этих рассуждений, рассмотрим сле-
следующее стирающее (информацию) устройство. Пусть атомы 1 и 2 имеют чуть более
сложную структуру уровней, содержащую четыре уровня, как показано на рис. 21.1г.
Второй лазерный импульс 1ч настроен в резонанс с переходом \b) —> \bf) и устроен так,
) Eichmann et. al. A993). Рекомендуем прочитать эту классическую работу.
) Отметим, что данное описание концепции квантового стирающего устройства является
продолжением гл. 20 (см. Scully and Driihl, 1982) и представлено здесь в «независимой»
манере.
470
Двухфотонная интерферометрия и другие задачи
Гл. 21
что переносит 100% населенности из \Ь) в \bf). To есть, пусть второй импульс является
тг-импульсом. Последнее означает, что огибающая лазерного импульса удовлетворяет
условию
B1.2.2)
где ръь1 — матричный элемент дипольного момента, связывающего состояния \Ь)
и \bf). Такой тг-импульс переводит каждый атом, который встретится ему в состоя-
состоянии |6), в состояние \bf). Следовательно, состояние системы после взаимодействия
с импульсом 1ч имеет вид
\Ф^) = ^^(l^ic2)|7i) H~ Ici^з) 1тз))- B1.2.3)
Однако, как отмечено на рис. 21.1 г, состояние \Ъ') сильно связано с |с), так
что спустя короткий промежуток времени можно считать, что г-й атом распался
в состояние |с), испустив фотон, который обозначим через ф{. Состояние фотона \ф)
совпадает с состоянием I7), с очевидными изменениями волнового вектора, скорости
затухания и т. д. Вектор состояния после ^-испускания записывается в виде
\
1^з) =:: —т= СI ci сз) [1 ^1 Ti} "I" 1^272)])* B1.2.4)
Рассмотрим далее экспериментальную ситуацию, в которой состояния фотонов
ф\ и фч<, фактически, «сводятся» к вакуумным состояниям с возбуждением общего
фотодетектора. Эта ситуация отражена на рис. 21.4. Фотодетектирование ^-фотона
7-детектор
Падающий
импульс
72
Атом 2
\Ь)
ф- детектор
Структура уровней
атомов 1 и 2
Рис. 21.4. Схема двухатомного корреляционного эксперимента
21.2 Свет, рассеянный двумя многоуровневыми атомами 471
(в точке г; и в момент tf) с последующим детектированием 7™излучения (в точке г
и в момент t) описывается функцией корреляции интенсивности
, r'; t, t') = (V|?H(r, <)Я<->(г', t')EM(v', t')?(+)(r, 1)Щ, B1.2.5)
где \ф) задается выражением B1.2.4). Упростим ситуацию, рассматривая атомы,
изображенные на рис. 21.1г, и предполагая, что при переходе \а) —> \Ь) испускается
7™фотон, а переход \Ь) —> \с) сопровождается испусканием 0-фотона. То есть будем
считать, что взаимодействие с уровнем \bf) всегда «включено», и что состояние,
называемое |6), в действительности есть \bf). Или можно считать, что начальное
возбуждение \с) —> \а) является двухфотонным, причем оба перехода |а) —)> \Ъ) и
\Ь) —>> \с) разрешены. Приступим к вычислению C^(r, r;, t, t;), определяя состояния
^-фотонов,
как и в случае 7-ф°тонов- Теперь получаем следующую амплитуду вероятности ф-
фотона:
() = Ф0,г(М), B1.2.7)
где здесь и далее индексы ф и j относятся к фотонам, а индекс г — к атомам. Для
7~фотона аналог выра^сения B1.2.7) имеет вид
= Ф7>гМ). B1.2.8)
Следовательно, двухфотонная корреляционная функция B1.2.5) принимает вид
фг) + \12ф2)) =
Ф7>1(г, *)Ф0,1(г', *') + Ф7>2(г, *)Ф0J(г', t')\2. B1.2.9)
Здесь перекрестные члены вновь создают интерференционную картину. Интерферен-
Интерференция не получилась бы, если бы измерялся лишь один 7-фотон- Измерение (^-фотона
необходимо для стирания информации о пути 7-фотона (то есть о том, каким атомом,
1 или 2, он рассеялся).
21.2.1. Альтернативный фотонный базис. Существенного упрощения можно до-
достичь, переходя к другому базису. С этой целью перепишем состояние B1.2.3) через
симметричные и антисимметричные комбинации. То есть, если определить фотонные
состояния как
1Ы = ^(Ы±Ы), B1-2.10)
где х есть ф либо 7? т0 выражение B1.2.4) можно записать следующим образом:
\ф) = ±[\С1с2)(\ф+1+) + \ф--г-))]. B1.2.11)
Однако, если |г — i*i| = |г — г2|, то
<0|?7<+>(г, €)\ф.) = ^(**,i(r, *) - Ф«,2(г, *)) = 0, B1.2.12)
поскольку, как видно из B1.1.6), Ф^Дг, t) зависит лишь от Аг{ = |г — г^|, и в
случае симметричного расположения Ф^д = ^ф,2- Поскольку все члены типа
472 Двухфотонная интерферометрия и другие задачи Гл. 21
, t)\(j)-) обращаются в нуль, можно записать корреляционную функцию в ±-
базисе следующим образом:
i> + ЫФ2)) =
= \{{1+ф+\ + i-у.ф. |)Я<">(г, t)E^(r', t')E^(r', t')E^(r, г)(\-у+ф+) + \-у.ф.)) =
= 1<7+0+|Я(->(г, t)??(-)(r', i')#(+)(r', i')^(+)(r, t)|-y+0+>. B1.2.13)
Видно, что вклад дают лишь состояния ф+. Это означает, что для заданного
ансамбля актов рассеяния, \ф+)-половина актов приводит к отсчету, тогда как \ф^}-
половина не приводит к отсчету. Если удерживать только те акты, которые приводят
к отсчету <^-фотона, то в статистическом распределении отсчетов 7~ФОТОНОВ на
экране обнаружатся интерференционные полосы. С другой стороны, если не снимать
показаний счетчика <^-фотонов и удерживать все акты рассеяния, то никакой ин-
интерференционной картины в полном ансамбле отсчетов 7-фотонов не обнаружится.
Следовательно, в этом эксперименте полный ансамбль актов рассеяния разлагается
на два подансамбля, демонстрирующих интерференционные полосы и «антиполосы».
21.3. Экспериментальная проверка неравенства Белла через
двухфотонные корреляции
Двухатомный эксперимент, приведенный на рис. 21.4, имеет все основные состав-
составляющие, необходимые для проверки неравенства Белла. Напомним, что коррели-
коррелированное состояние, являющееся результатом двухфотонного испускания атомами
в точках 1 и 2, имеет вид
\Ф) = ±(ЫФ1) + ЫФ2)), B1.3.1)
и результирующая совместная вероятность Р^ф детектирования фотона в обоих j-
и <^>™счетчиках вычисляется с помощью корреляционной функции второго порядка.
То, что в данной конфигурации возможна экспериментальная проверка теоремы
Белла х), легче всего установить, обращаясь к экспериментам по корреляции поля-
поляризации, рассмотренным в разд. 18.3. В этих экспериментах (см. рис. 18.4) в ходе
каскадных переходов генерировалось «поляризационно коррелированное фотонное
состояние», такое как
\ф) = ±(\1хфх) + \ъфу)). B1.3.2)
Затем измерялось распределение совместных фотоотсчетов Р7ф, как функция угла
между анализаторами 1 и 2. Ясно, что имеется прямое соответствие между двумя
задачами, и что анализ атомного каскадного эксперимента можно применить, с оче-
очевидными изменениями, к данной задаче с двумя атомами. Таким образом, корре-
корреляции, подразумевающие двухфотонное состояние B1.3.1), могли бы предоставить
новый тест теорий скрытых переменных, основанный на теореме Белла.
1) Простое обсуждение теоремы Белла и двухфотонных корреляций с этой точки зрения
имеется в работе Scully A981).
21.3 Экспериментальная проверка неравенства Белла. Двухфотонные корреляции 473
Двухфотонные состояния генерируются в процессе параметрического преобразо-
преобразования частоты вниз. Напомним (гл. 16), что в процессе невырожденного парамет™
рического усиления взаимодействие волны накачки частотой ин с х -нелинейным
кристаллом приводит к появлению сигнальной и холостой волн, имеющих частоты ис
и j/x, соответственно, так что иш = ис + г/х. В экспериментах по проверке неравенства
Белла выполняются корреляционные измерения смешанных сигнальных и холостых
фотонов при различных вариантах ориентации двух линейных поляризаторов.
В работе Shlh and Alley A988) (см. также Franson, 1989) выполнен эксперимент,
основанный на создании коррелированного двухфотонного состояния, генерируемого
в процессе параметрического преобразования частоты вниз в нелинейном кристалле.
Для создания коррелированных пар фотонов в данном эксперименте (рис. 21.5) через
нелинейный кристалл дейтерированного дигидрофосфата калия (KD*P) посылалось
излучение с длиной волны 266 нм. Каждый фотон переводился в состояние с опреде-
опредеНейтр.
Призма 2 Фильтр
/3-ВаВ2О4
М
Рис. 21.5. Схема эксперимента по проверке неравенства Белла. (Из работы Shlh and Alley
A988))
474
Двухфотонная интерферометрия и другие задачи
Гл. 21
ленной поляризацией с помощью четверть-волновых пластинок (А/4), помещенных
на путях А и В, преобразующих состояния линейной поляризации в состояния
круговой поляризации. Фотоны совмещались на светоделителе (BS). Таким путем,
используя схему совпадений, наблюдались поляризации ЭПР-типа и было показано,
что неравенство Белла нарушается.
В похожем эксперименте (Ou and Mandel, 1988) было показано, что нарушает-
нарушается не только неравенство Белла, но и предсказания для совместной вероятности,
полученные в рамках классической волновой теории. Как показано на рис. 21.6,
в данном эксперименте УФ свет накачки падает на нелинейный кристалл дигидро-
УФ
Рис. 21.6. Схема эксперимента по проверке неравенства Белла. (Из работы Ou and Mandel
A988))
фосфата калия (KDP), и в процессе параметрического преобразования частоты вниз
образуются сигнальные и холостые фотоны. Если для вырожденного параметриче-
параметрического процесса (ус = */х) выполняется условие фазового синхронизма, сигнальные
и холостые фотоны выходят под малыми углами к пучку накачки. Эти фотоны
являются линейно поляризованными, и их векторы напряженности электрического
поля направлены перпендикулярно рисунку. Холостые фотоны проходят через 90° -
вращатель поляризации, тогда как сигнальные фотоны проходят через компенси-
компенсирующую стеклянную пластинку С\ для создания одинаковой задержки во времени.
Затем два пучка с противоположных сторон падают на светоделитель (BS), что
приводит к образованию двух пучков, состоящих из смешанных сигнальных и холо™
стых фотонов. Эти пучки проходят через линейные поляризаторы, устанавливаемые
под регулируемыми углами #i и #2 и попадают на два фотодетектора, связанные
со схемой совпадений. Как и прежде, совместный счет фотонов является мерой
совместной вероятности /^(^ъ^) детектирования двух фотонов двух линейных
поляризаторов при различных значениях #i и #2-
21.4. Двухфотонная каскадная интерферометрия
В разд. 21.2 рассматривалось двухфотонное излучение двух отдельных атомов
в контексте мысленного эксперимента с квантовым стирающим устройством. Посту-
Поступая так, мы пришли к состоянию поля, соответствующему прерванной эмиссии, так
что первый и второй фотоны были задержаны друг относительно друга. Как будет
21.4
Двухфотонная каскадная интерферометрия
475
показано в этом разделе, это имеет много общего с задачей двухфотонного каскадного
излучения из разд. 6.4. В частности, задача прерванного двухфотонного каскадного
излучения и общее соотношение для двухфотонного каскадного излучения, опреде-
определяемое формулой F.4.13), дают такую же функцию Ф^2\ когда время жизни на
промежуточном уровне существенно превосходит время жизни на возбужденном
уровне.
В настоящем разделе рассматривается двухфотонная корреляционная функция,
соответствующая двухфотонному каскадному излучению, и полученные результаты
используются для анализа интерферометра Франсона^Чиао.
21.4.1. Двухфотонные корреляции при каскадном излучении атома. Поле излу-
излучения, создаваемое в процессе прерванного каскадного излучения одиночного атома
(как в разд. 21.2), имеет вид
B1-4.1)
где I7) и \ф) задаются выражениями вида B1.1.4). Тогда из B1.2.9) видно, что
корреляционную функцию фотонов можно записать как
rf; t, tf) =
, t; г', *'
B1.4.2)
причем
Ф<2>(г, t; r', *') = Ф7(г, г)*ф(т', t') + Ф7(г', *')Ф*(г, t), B1.4.3)
где Ф7 и Ч?ф — амплитуды вероятности того, что 7- и с^-фотоны возбудят детекторы
в точке г в момент времени t ив точке г; в момент времени t'.
Теперь рассмотрим задачу корреляции фотонов, когда трехуровневые атомы
имеют узкий верхний уровень и короткоживущее
промежуточное состояние (см. рис. 21.7). Мы ви-
видим, что данная атомная конфигурация является I
противоположной той, что рассматривалась в за-
задаче квантового стирающего устройства, в которой
верхний уровень был широким, а промежуточный —
узким. В случае, изображенном на рис. 21.7 (долго- ,
живущее верхнее состояние \а) и короткоживущее
состояние |6)), состояние поля излучения нельзя
записать в простом факторизованном виде, как в
задаче квантового стирающего устройства, и оно
принимает вид |
Ть
Рис. 21.7. Радиационное ушире-
ние верхнего и промежуточного
уровней трехуровневого атома,
имеющего каскадную конфигу-
конфигурацию переходов, в случае, ког-
когда Гь > Га
N>> = 5>k,q|lklq>, B1ЛЛ)
k,q
гДв Ck?q задаются формулой F.4.12). Ключевым мо-
моментом является то, что энергия еа — ес = huj^ +
+ ^cjq, так что к- и q-фотоны являются коррелиро-
коррелированными. Поэтому и не получается факторизован-
ного вектора состояния вида B1.4.1). Как и прежде, будем искать двухфотонную
корреляционную функцию
GB)(rb r2; ti,t2) = (ф\Е^(гъ11)Е^(т2, t2)E^(rut1)E^(r2j t2)\il>),
соответствующую двум детекторам в точках гх и Г2. Взаимодействие с фотонным
полем, описываемым вектором \ф), включается в моменты времени t\ и t2, соот-
соответственно. В приложении 21.Б показано, что бЛ2^ определяется теперь амплитудой
476 Двухфотонная интерферометрия и другие задачи Гл. 21
вероятности двойного фотовозбуждения:
ехр [- («,ас + ?) (tl - ^)] 9 (tl -
), B1.4.5)
где к — несущественная константа и Ari = |г^ — г|. Вновь подчеркнем, что
не имеет простого факторизованного вида B1.4.3). Отметим также, что выражение
B1.4.5), в общем случае, справедливо при любых значениях Га и Г&. Поскольку
Ф^(г1, ti; Г2, ^) не равна нулю лишь в моменты времени t\ = Аг\/с +
выражение B1.4.5) можно записать в виде (при Га ^> Г^)
x exp [ ( !±) (t
J J в
[- (ш5с + !±) (t2 - ^)] 0 (h - ^ + ОСГ)) + (lo 2) -
x ехр [- [гшЬс + |) (t2 - ^)] в (t2 -^)+(lH 2), B1.4.6)
то есть, в пределе Га ^> Г^ выражение B1.4.5) принимает факторизованный вид.
Это интуитивно понятно, поскольку задача прерванного каскадного излучения есть,
по существу, задача, в которой состояние \Ь) является «долгоживущим», и мы с удо-
удовлетворением видим, что фB\ задаваемая выражением B1.4.6), имеет вид B1.4.3).
21.4.2. Интерферометрия Франсона^Чиао. Обратимся теперь к интересному
примеру двухфотонной корреляционной интерферометрии, впервые предложенной
Франсоном (Franson, 1989) и реализованной Чиао с сотрудниками (Kwait, Steinberg
and Chiao, 1992). Схема установки приведена на рис. 21.8. Здесь мы видим двухфотон™
ный интерферометр с одиночным возбужденным трехуровневым атомом в качестве
источника света. При распаде из верхнего состояния \а) в промежуточное \Ь) со скоро-
скоростью Га и из \Ь) в основное состояние \с) со скоростью Г^ атом испускает два фотона j
и ф, соответственно. Излучение распространяется от атома к детекторам D\ и Di по
короткому и длинному оптическим путям, длиной S и L, определяемым светоделите-
светоделителями BS и зеркалами М. Теперь учтем, что длина когерентности излученного света
существенно меньше разности хода в двух плечах интерферометра Маха-Цендера
(BS-M-M-BS и BS-BS на рис. 21.8). Следовательно, можно ожидать, что никаких
интерференционных полос не наблюдается, что, в действительности, соответствует
случаю, когда смотрят на любой из двух детекторов по отдельности. То есть, коге-
когерентность G^ отсутствует. Однако, если посмотреть на корреляцию фотоотсчетов
в детекторах D\ и Di, то есть рассмотреть функцию G^2\ то должна обнаружиться
интерференция. Приступим к анализу этой задачи, моделируя действие делителей
пучка и зеркал путем гейзенберговского рассмотрения операторов
\ U)}, B1.4.7)
21.4
Двухфотонная каскадная интерферометрия
477
Рис. 21.8. Двухфотонный интерферометр с трехуровневым возбужденным атомом в каче-
качестве источника света. Переходя в процессе релаксации из верхнего состояния \а) в проме-
промежуточное \Ь) со скоростью Га и из состояния \Ь) в основное состояние \с) со скоростью Гь,
атом испускает два фотона j и ф, соответственно. Излучение распространяется от атома
к двум детекторам D\ и Di по короткому и длинному оптическим путям (длины S и L),
задаваемым светоделителями BS и зеркалами М
где величины Si и Li описывают короткий и длинный пути, соответственно. Исполь-
Используя двухфотонное состояние |Ф), задаваемое выражением F.4.13), функцию
можно записать через амплитуду парной вероятности
= Ф*A,2)ФA,2),
B1.4.S
где
^ B1.4.9)
Для простоты рассмотрим ситуацию, когда детекторы расположены в точках i*i =
= ^1*2. Тогда
, 2) = ФEЬ h; 52, t2)
i; L2,
B1.4.10)
где
тAо2), B1.4.11)
величина г» = 5» или L^ (г = 1,2), ха = 7rgako^koD(ujab)/ko, щ =
= 7TgbqoS>qoD(ujbc)/qQ, k0 = шаЬ/с, g0 = ^Ъс/с и D(u) = 1/|/2/тт2с3 — плотность мод
в свободном пространстве.
Полезно классифицировать различные члены в B1.4.10) так, как показано на
рис. 21.9. Каждая из четырех комбинаций путей симметрична и изображена при
помощи диаграммы. Например, в случае ФEь t\] Ь2, ?2) первая диаграмма (соот™
ветствующая В12) обозначает фотон ф^ избравший короткий путь к детектору Di,
и фотон 7? избравший длинный путь к детектору D2.
478 Двухфотонная интерферометрия и другие задачи Гл. 21
Теперь можно понять физику задачи и существенно сократить вычисления, пред-
предполагая, что Га С Г5 и L ~ 5 > сГ^ . То есть, предположим, что атом переходит
из \Ь) в \с) очень быстро, так что испускание 7™Фотона (переход \а) —> \Ь)) сопро™
вождается испусканием 0-фотона (переход \Ь) —> |с)). Тогда вклад в функцию
1 Ф
1;S2,t2) = А12 + А21 = * • >
2 1
7
Ф
i;L2,t2) = B12 + B2i = «J~~L . >
2 1
Ф
7
i;52,t2) = С12 + С21 = ^
2
Рис. 21.9. Диаграммы, соответствующие различным членам выражения B1.4.10). Напри-
Например В\2 можно рассматривать как вклад, вносимый фотоном 7, избравшим длинный путь
к детектору ZJ, и фотоном ф, избравшим короткий путь к детектору Т)\
будут давать только первая и последняя линии на рис. 21.9, то есть ФEх, t\\ S2, ti)
и \H(Li, t\] h<i, t'l)- Остальные члены Ф(Я1, t\\ L2, ?2) и ^(^1)^15*^25^2) будут обра-
обращаться в нуль, поскольку 7™ и <^>™фотоны никогда не будут «перекрываться» в детек-
детекторах.
Это делает расчеты существенно короче, и мы находим, что совместная вероят™
ность отсчетов задается выражением
оо оо
, 2) = \ dh I <Й2|ВД, *i; S2, t2) + Ф(?ь ti; Ь2, t2)|2. B1A12)
Вычисление интегралов в B1.4.12) приводит к простому выражению:
РA, 2) = jf^r [2 + ехр (-^) со8(швст)] , B1.4.13)
где N = (KaKfj/2S ЬJ, шас = ша5 + ш^с ит = (L- S) /с, и мы положили Si = S2 = S
ш Li = L2 = L.
21.5. Двухчастичная интерферометрия с помощью нелинейного
преобразования частоты вниз ж отобранных по моменту фотонных пар
В пионерской работе Home, Shimony and Zeilinger A989) Хорн, Симони и Цай-
лингер (ХСЦ) исследовали проблему двухфотонной интерферометрии и предложили
схему, в которой на выходе нелинейного кристалла выделяются четыре пучка (см.
рис. 21.10). Здесь используется тот факт, что согласно требованию фазового синхро™
низма кд + ко = к^ + к^> = к, где к — волновой вектор возбуждающего лазерного
поля. Если обнаружится фотон с волновым вектором, скажем кд, то его коррели-
коррелированный по преобразованию частоты вниз партнер будет обнаружен с волновым
21.5
Двухчастичная интерферометрия
479
Рис. 21.10. Взаиморасположение четырех пучков, отобранных на выходе преобразователя
частоты вниз S. Диафрагма, расположенная по ходу излучения за источником Я, нормальна
к направлению падающего пучка /. Отверстия, из которых выходят пучки А и D, лежат на
окружности, центрированной вокруг /. При этом отверстия, из которых выходят пучки В
и С, лежат на другой окружности, центрированной вокруг /. Линия пересечения плоскости
АС с плоскостью BD совпадает с /. В эксперименте сводятся пучки А и D и пучки В и С.
(Из работы Home, Shlmony and Zelllnger A989))
Рис. 21.11. Установка по двухчастичной интерферометрии с регулируемыми фазовращате-
фазовращателями. Источник S испускает две частицы 1 и 2 в четыре пучка Л, В, С и D. Индекс г (г =
= 1,2) обозначает частицу, регистрируемую детекторами Ui и Li. Состояние пары задается
выражением B1.5.1), представляющим собой суперпозицию двух амплитуд: A) частица 1
в пучке А и частица 2 в пучке С и B) частица 1 в пучке D и частица 2 в пучке В. Два пучка
А и D частицы 1 приобретают регулируемую разность фаз ф\ до рекомбинации в точке
01 на полусеребреном зеркале Н\ (интерферометрия Маха-Цендера). Подобным образом,
два пучка В и С частицы 2 приобретают регулируемую разность фаз ф2 до рекомбинации
в точке 02 на полусеребреном зеркале Нч. Наблюдаемыми величинами являются скорости
счета двухчастичного совпадения, как функции ф\ и ф<±. (Из работы Home, Shlmony and
Zelllnger A989))
вектором kc. В работе ХСЦ показано, что если два пучка смешиваются на одном
детекторе, а два — на другом, то скорости совпадений G^ будут демонстрировать
интерференцию, а скорости счета одиночных детекторов G^ — нет. Предложенная
ими схема эксперимента показана на рис. 21.11. В процессе нелинейного преобразо-
480
Двухфотонная интерферометрия и другие задачи
Гл. 21
вания создается коррелированное состояние
1^ = |lkAllcc) ~l~ |lk?)lks)« B1.5.1)
21.5.1. Интерферометрия на основе преобразования частоты вниз с двумя ис-
источниками. Работа ХСЦ побудила Али и Шиха, а также Манделя с коллегами,
приступить к выполнению нескольких красивых экспериментов по двухфотонной
интерференции, используя схему двойного преобразования частоты вниз. В одном из
экспериментов, принципиальная схема которого изображена на рис. 21.12, Оу, Ванг,
Рис. 21.12. Схема двухфотонного интерференционного эксперимента с двумя преобразова-
преобразователями частоты вниз. (Из работы Ou, Wang, Zou and Mandel A990))
Зоу и Мандель (ОВЗМ) использовали два нелинейных кристалла ЫЮз, обозначен™
ные здесь как NL1 и NL2, каждый из которых создавал пары фотонов в процессе
параметрического преобразования частоты вниз. Излучение каждого из кристаллов
падало на светоделители BSa и BSb и комбинированные сигналы попадали в де-
детекторы Da и Dr. Чтобы проанализировать задачу в простом, но полном виде,
обратимся к схеме из разд. 21.2 и рассмотрим случай, когда NL1 и NL2 являют-
являются простейшими в природе преобразователями частоты вниз, а именно, простыми
трехуровневыми атомами, изображенными на рис. 21.1. Естественно, использование
простого атомного преобразователя частоты вниз является идеализацией. С помо-
помощью установки, изображенной на рис. 21.13, можно организовать эксперимент, следуя
ХСЦ, так чтобы 7™фотон в некотором направлении всегда сопровождался 0-фотоном,
благодаря фазовому синхронизму. Однако это не соответствует случаю атомных пре-
преобразователей частоты вниз. Тем не менее, корреляции будут наблюдаться, и общие
принципы остаются прежними.
Физика реального эксперимента ОВЗМ и эксперимента, поставленного по схеме,
изображенной на рис. 21.13, одинакова, так что продолжим рассуждения, анализируя
рис. 21.13. В этом случае к рассматриваемой задаче можно сразу применить резуль™
таты разд. 21.2 (см. выражение B1.2.9)):
, r'; t, t') = |Ф7(|г - п|, *)|2|\М|г' -
|Ф7(|г-г2|,*)|2|Ф0(|г'-г2|,О|2+
[Ф7(|г -
- г2|,
- Г2
к.с], B1.5.2)
где обозначения такие же, как на рис. 21.4, за исключением того, что длины путей
|г — Ti\ и |г; — i^| (г = {1, 2}) являются теперь длинами изогнутых оптических путей
21.5
Двухчастичная интерферометрия
481
DB
Рис. 21.13. Одноатомный преобразователь частоты вниз, предназначенный для анализа
интерференционного эксперимента ОВЗМ из рис. 21.12
с учетом светоделителей. Подставляя Ф7 и Ф^> из B1.1.6) в B1.5.2), получаем
-An/c)e (t
-%0(*- Ar2/c)e~(f-
•2 A #0T 0(t-Ari/c)e"
?- Ar[/c)e~
-(*-Дг1/с)Г
^Q(t'-Arf2/c)e
\(t-Ar2/c)e~
- Ar2
B1.5.3)
где Ar^ = |r — r^ | и Ar\ = |г' —г^|. Таким образом, при изменении относительных фаз,
например путем изменения положения атомов г^, должна появляться интерферен-
интерференционная зависимость от разности хода, что подтверждается экспериментом ОВЗМ.
В другом оригинальном эксперименте по двойному преобразованию частоты вниз
(см. рис. 21.14), Зоу, Ванг и Мандель (ЗВМ) показали, что конфигурацию рис. 21.12
можно изменить таким образом, что смешение холостых фотонов восстанавливает
интерференцию без необходимости детектировать совпадения. На рис. 21.14 изоб-
изображены два нелинейных кристалла NL1 и NL2, которые возбуждаются когерентно
в процессе накачки и создают две пары сигнальных и холостых пучков в процессе
спонтанного параметрического преобразования частоты вниз. Затем два холостых
фотона совмещаются по направлению и детектируются одним общим фотодетек-
фотодетектором Di, что делает их неразличимыми. Два сигнальных фотона соединяются на
детекторе Ds. Спрашивается, будут ли эти два пучка интерферировать? Необходимо
16 М.О. Скалли, М.С. Зубайри
482
Двухфотонная интерферометрия и другие задачи
Гл. 21
от аргонового лазера
Рис. 21.14. Схема интерференционного эксперимента. (Из работы Zou, Wang and Mandel
A991))
отметить, что интенсивность холостого пучка, приходящего из NL1, слишком мала,
чтобы индуцировать какое-либо вынужденное преобразование частоты вниз в кри-
кристалле NL2, так что детектируемая когерентность, безусловно, не является резуль-
результатом процесса вынужденного излучения, приводящего, очевидно, к когерентным
сигнальным пучкам.
Результат состоит в следующем: сигнальные пучки являются когерентыми и,
следовательно, интерферируют, если холостые пучки сливаются, и — не когерент-
когерентными, если холостые пучки различимы. (Холостые пучки можно сделать различи-
различимыми, помещая перегородку между кристаллами NL1 и NL2.) Это можно понять
с точки зрения «который путь»-информации. Рассмотрим сначала случай, когда
между кристаллами NL1 и NL2 поставлена перегородка. Если фотон измеряется
детектором D8, тогда, посмотрев на Di, можно сказать, откуда пришла пара фотонов,
из NL1 или NL2: если детектор Di также регистрирует фотон, то фотонная пара
должна исходить из NL2, в противном случае она должна исходить из NL1. Дру-
Другими словами, поставив перегородку, мы получаем «который путь»-информацию,
поэтому сигнальные пучки не интерферируют. Однако в отсутствии перегородки
не существует способа определить, какой кристалл испустил сигнальный фотон,
зарегистрированный детектором Ds, поскольку Di отметит фотон в любом случае.
Таким образом, без перегородки мы не имеем информации «который путь» и, сле-
следовательно, должны складывать амплитуды вероятности вместо вероятностей, что
и приводит к интерференции.
Тем не менее отметим, что интерференция, которую наблюдали Мандель с сотруд-
сотрудниками, обусловлена когерентностью первого порядка сигнальных пучков. Другими
словами, детектор Di с таким же успехом можно убрать из эксперимента. Именно
возможность получить информацию «который путь» оказывает воздействие на
интерференцию.
Приступим к анализу задачи, вновь используя одноатомные преобразователи
частоты вниз, см. рис. 21.15. Функция когерентности первого порядка, соответствую-
соответствующая установке из рис. 21.15, имеет вид
к.с]. B1.5.4)
21.5
Двухчастичная интерферометрия
483
71
Рис. 21.15. Одноатомный преобразователь частоты вниз, предназначенный для анализа
интерференционного эксперимента ЗВМ из рис. 21.14
Смещение В So, мкм
0.4 0.6 0.8
а$
Фаза, хтг
Рис. 21.16. Скорость счета фотонов Rs как функция смещения светоделителя В So в случае
когда между NL1 и NL2 вставлен: нейтральный светофильтр с коэффициентом пропускания
Т = 0,91 (а); перегородка с Т = 0 (б). Точки — экспериментальные данные, кривая —
аппроксимация синусоидальной функцией с периодом 394 нм. (Из работы Zou, Wang and
Mandel, 1991))
Можно показать, что для межатомных расстояний, превышающих оптические длины
волн, состояния |7г) являются ортогональными. Следовательно, интерференционный
член в B1.5.4) обращается в нуль, и фотоны \ф{) не интерферируют. Этот результат
16*
484 Двухфотонная интерферометрия и другие задачи Гл. 21
не удивителен, поскольку 7~фотон несет информацию «который путь» относительно
процесса излучения.
Чтобы вновь получить интерференцию, поступим также, как в разд. 21.2: располо-
расположим 7~фотодетектор в точке г. Подходящим выражением теперь является функция
корреляции второго порядка:
G<2>(r, г'; *, *') = (фг^-Цг',
2|?7<-)(r', t')E^(v', t')\4>2)(l2\E(-\r, *)?7<
(> ^ ^ <>, t)\l2) + k.c], B1.5.5)
и интерференция восстанавливается.
Но, и это является интригующим моментом в работе ЗВМ, если должным образом
расположить преобразователи частоты 1 и 2 по одной линии, то можно гарантиро-
гарантировать, что |7i) = G2M и функция корреляции первого порядка B1.5.4) демонстрирует
когерентность! Это «разумно» с точки зрения ортодоксальной квантовой механики,
утверждающей, что теперь у нас нет больше информации «который путь», и интер-
интерференция восстанавливается.
Более того, если поместить перегородку, например зеркало, между преобразова-
преобразователями 1 и 2, то интерференция исчезнет. Это происходит потому, что внутреннее
произведение G1I72) обращается теперь в нуль, поскольку |7i) и I72) являются
ортогональными. Физически это означает, что теперь имеется информация «который
путь». Эти результаты подтвердились в эксперименте ЗВМ (см. рис. 21.16).
21.6. Эксперимент Зоу^Ванга^Манделя с точки зрения вакуумных
флуктуации
Общей чертой квантового стирающего устройства, микромазерного «который
путь»-детектора и экспериментов Манделя является то, что для их полного пони-
понимания, очевидно, необходимо привлечь квантовую электродинамику (КЭД). Есте-
Естественно возникает вопрос, существует ли простая механистическая картина, спо-
способная помочь лучше понять физику (Scully and Rathe, 1994). В этом отношении
мы рассматриваем данную ситуацию почти также, как рассматривается лэмбовский
сдвиг в КЭД. Не может быть сомнений, что КЭД дает превосходное объяснение
эффекта. Но мы рады, что имеются также эвристическое описание Велтона на языке
вакуумных флуктуации, приводящие к простому пониманию физики. Конечно, рас-
рассуждения Велтона не заменяют КЭД, но они доставляют удовольствие. Мотивируя
свои действия таким образом, дадим в общих чертах простое наглядное объяснение
эксперимента ЗВМ. Для этого обратимся к понятию стохастически флуктуирующих
электромагнитных полей.
Для нашего «объяснения» эксперимента ЗВМ, основанного на классических
флуктуирующих полях, заменим два нелинейных кристалла двумя атомами 1 и 2,
каждый из которых имеет три уровня |а), \Ъ) и |с). Как отмечалось выше, чтобы
компенсировать отсутствие направленности спонтанного излучения, мы навязываем
направленность холостому и сигнальному полям. Это можно сделать, например, по-
помещая два атома в оптические волноводы, отвечающие соответствующим частотам.
Эти два атома возбуждаются слабым полем накачки и, возбудившись, испускают два
классических поля ji и ф{, где г = 1, 2 (рис. 21.15). Состояние каждого атома после
возбуждения \ф) = са\а) + сс|с). Такой атом подвергается возмущениям со стороны
вакуумных флуктуации, что вызывает некоторый перенос населенности с уровня \а)
на уровень |6), так что
сс\с). B1.6.1)
21.6 Эксперимент Зоу-Ванга-Манделя с точки зрения вакуумных флуктуации 485
Амплитуда 5сь имеет случайную фазу ф7^, определяемую индуцирующим полем,
поэтому дипольный момент, формируемый на переходе между уровнями \а) и |6),
излучает с фазой фа^ — ф1^- Как только некоторая населенность будет перенесена
на уровень |6), также начнет излучать диполь на переходе \Ъ) —>• \с). Фаза этого
излучения ф1^ — фс,%-> гДе Фа,1 — Фс,{? есть относительная фаза между состояниями
\а) и \с) (г-го атома), определяемая слабым падающим полем, вызывающим переход
\с) —> \а). Отметим, что мы не учитывали вакуумные флуктуации, действующие на
переходе \Ь) —> |с), поскольку они являются величиной второго порядка по полю.
Таким образом, полные дипольные моменты имеют вид
Pi = Pab\ca\\Scb\ e^p{-iujabt + 1(фп1{ - 07,*)] +
+ рьс|сь||с5сс| e^p[-iujbct + г(ф7,1 — Фс,{)] +
+ члены более высокого порядка. B1.6.2)
Эти диполи излучают поля
Ei(r, t) = ЕУ(т, t) + E?(r, t), B1.6.3)
где два вклада с различными частотами задаются выражениями
E7(r, t) = |^7(r)| exp[-iwO6< + t(^Oii - ф1А) + ik^i ¦ (г - г4)], B1.6.4)
E?(r, t) = |<^*(г)| exp[-iw6ct + г(ф1Л - фсА) + ik0)i ¦ (г - п)]. B1.6.5)
Для того чтобы найти степень когерентности этих полей, рассчитаем классиче-
классический аналог функции когерентности Глаубера:
, t) = {E*(r, t)E(r, <)). B1.6.6)
Ключевой член в разложении данного выражения в соответствии с формулой
B1.6.3), определяющий степень когерентности, есть перекрестный двухатомный член
х exp[i(<^c?i - фс^2) - ik^i • (г - n) + ik^?2 • (г - г2)] + . . . . B1.6.7)
В данном случае, усреднение по статистически независимым вакуумным фазам ф1^
дает нуль. Следовательно, подход вакуумных флуктуации, как и КЭД, приводит
к отсутствию интерференции.
Рассмотрим эксперимент ЗВМ с позиций КЭД. Взаимодействие атомов с полем
накачки и последующее затухание приводит к интерференции, как обсуждалось
в разд. 21.5. Главный член в выражении для функции когерентности первого порядка,
определяющий, будут ли наблюдаться интерференционные полосы, имеет вид
GW(t, t) = {фг\Е^(г, t)Ei+\v, ?)|<ЫЫ72> + ¦ ¦ ¦ ¦ B1-6.8)
Если перегородка удерживает холостой фотон 71 от перекрывания с фотоном 72 ? т0
|Ti) и I72) являются состояниями двух различных мод и ортогональны, т.е.
в КЭД перегородка есть: G1I72) = 0 =^ интерференции нет. B1.6.9)
Однако, если перегородка отсутствует, то эти два фотона соответствуют состояниям
одной моды, т. е.
в КЭД перегородки нет: GI7) = 1 =^ интерференция есть. B1.6.10)
Обращаясь теперь к описанию на языке вакуумных флуктуации (ВФ), отметим,
что подходящая функция когерентности первого порядка, задаваемая выражением
486 Двухфотонная интерферометрия и другие задачи Гл. 21
B1.6.7), имеет вид
GA)(r, t) = {E*(r, t)E(r, t)) = х(ехр[-г@7>1 - фъ2)]) + • • ¦, B1.6.11)
где выписан лишь ключевой член. При наличии перегородки две вакуумные фазы
являются статистически независимыми и процесс усреднения приводит к нулю, т. е.
ВФ, перегородка есть:
(ехр[—г@7д — ф7^)]) = 0 =^> интерференции нет. B1.6.12)
Если перегородку убрать, то вакуумное поле, стимулирующее эмиссию в атоме 1,
достигает атома 2 и, следовательно, сообщает обоим атомам одинаковую фазу. Таким
образом, усреднение в этом случае дает единицу (поскольку <^>7д = ф7^), т.е.
ВФ, перегородки нет:
(ехр[—г@7д — 0-у,2)]) = 1 =^ интерференция есть. B1.6.13)
Резюме: описание на языке вакуумных флуктуации дает тот же результат, что
и КЭД, согласующийся с «псевдо-ЗВМ»-экспериментом.
В общем случае, стохастическая электродинамика часто оказывается полезной
для физического понимания. Подчеркнем, однако, что настоящий эвристический
подход не является заменой полному анализу КЭД. В действительности, на неко-
некоторые задачи стохастическая электродинамика дает ответы, противоречащие КЭД.
Примером является анализ квантовых биений в Л-системах, представленный в гл. 1.
В данной задаче мы также окажемся в затруднении, если будем развивать логику
вакуумных флуктуации слишком далеко.
21.7. Спектроскопия высокого разрешения на основе двухфотонной
каскадной интерферометрии г)
Завершая эту главу, покажем, что можно достичь нового типа сужения ли™
нии спонтанного излучения, используя двухфотонные корреляционные измерения
атомного каскадного излучения. Спектральная ширина оптического перехода между
двумя атомными состояниями \а) и |6), измеряемая обычными спектроскопическими
способами, определяется суммой скоростей излучательной релаксации Га + Г 5 из
этих двух состояний. Исключением является случай спектроскопии с временным
разрешением (разд. 5.7), где разрешение определяется величиной Га — Г&.
Следует отметить, что, используя подобные схемы измерений, мы имеем дело
с обычными однофотонными событиями, то есть с испусканием и поглощением
одного фотона. Однако, как будет показано далее, ситуация радикально меняется,
если вместо этого рассмотреть схему двухфотонного коррелированного спонтанного
излучения и двухфотонного детектирования (рис. 21.17). В этом случае оказывается,
что функция корреляции второго порядка демонстрирует спектральную ширину,
равную Га, независимо от значения Г&, где Га — скорость релаксации с уровня \а)
на уровень \Ь) и Г 5 — скорость релаксации с уровня \Ь) на уровень |с).
Отметим, что (однофотонная) спектроскопия с временным разрешением, рассмотрен-
рассмотренная в гл. 5, наиболее полезна в случае, когда Га = Г&, поскольку сужение линии
определяется величиной Гд^Г^. Однако (двухфотонная) каскадная корреляционная
интерферометрия дает, в принципе, улучшенное разрешение в случае, когда Г 5 ^> Го.
Рассмотрим схему эксперимента, изображенную на рис. 21.17, с двумя атомами,
расположенными в точках г и s, и двумя детекторами, расположенными в точках ri
) Для дальнейшего чтения рекомендуем работу Rather and Scully A994).
21.7
Спектроскопия высокого разрешения
487
Рис. 21.17. Два трехуровневых атома подвергаются воздействию слабого поля, так что
возбуждается либо атом в точке г, либо атом в точке s
и Г2- Приготовим систему таким образом, чтобы один атом находился в возбужденном
состоянии |а), второй — в основном состоянии |с), а поле — в вакуумном состоянии
|0). Такое начальное атомно-полевое состояние можно записать следующим образом:
1
~ л/2
Для времени t ^> Г^ *, Г^1 это состояние примет вид
B1.7.1)
Фг) + |^s50s)M B1.7.2)
v ^
где \фТ1фт) и \ф8,ф3) — состояния поля, создаваемые атомами, имеющими радиус-
векторы г и s, соответственно, причем \ф) (\ф)) отвечает переходу \а) —> \Ъ) (\Ъ) —>•
—>• |с)). Такие состояния задаются выралсением F.4.13), которое в настоящих обозна-
обозначениях записывается в виде
где вектор d равен г или s.
Соответствующая амплитуда двухфотонной вероятности,
B1.7.4)
позволяет вычислить совместную вероятность отсчета двух детекторов в точках
и Г2- Имеем
ею со
о о
где функцию корреляции интенсивности
(см. разд. 21.4.2)
b r2; *ь t2) =
T2; tut2), B1.7.5)
, 1*2; ^ъ ^г) можно записать в виде
ti; г2) «2)ФB)(гь «i; г2, *2). B1.7.6)
488
Двухфотонная интерферометрия и другие задачи
Гл. 21
Подстановка \ф) из B1.7.2) в B1.7.4) дает
ФB)(гь *1; г2, <2) = -^
, Фг) +
^ ,«1;г2,*2)]) B1.7.7)
где Ф^2)(г1,г2;*1,*2) = <0|?7(+>(n,*i)?7<+>(r2,t2)№d,&i) (d равен г или s). Исполь-
зуя B1.7.3), находим (см. приложение 21.Б)
[-{
iwab + ^
- ^)] в
Ф<2)(
гь h; г2,
В выражениях B1.7.8) и B1.7.9) г; =
^) ( ^)] Aо 2), B1.7.8)
= Ф<2)(гь ix; г2, *2)|Г1_ц4. B1.7.9)
|г; — г| м s^ — |sj — s| (г — 1, 2), х— несуществен-
несущественная постоянная величина, и 0(а?) — обычная ступенчатая функция. Обозначение
A -О- 2) в формуле B1.7.8) означает, что ша;,-фотон направляется к детектору D2,
а Шьс-фотон — к детектору D\. В заключение отметим, что такие же рассуждения
можно провести и для атома, расположенного в точке s. Соответствующая амплитуда
двухфотонной вероятности Фд (ri, ti; Г2, ^) определяется формулой B1.7.9).
Для того чтобы упростить вычисление рассмотрим схему на рис. 21.17 в случае,
когда S2 > Г2 и si = r\. С учетом этого подставим B1.7.8) и B1.7.9) в выражение
B1.7.6) и выполним интегрирование в B1.7.5). После довольно длинного вычисления
находим
где
/(г, А) = cos шЬст +
g(r, A) = cosшьсТ - — si
cos шаЪт,
(Я.7.10)
B1.7.11)
Т (cosujabT - — sinшаьт) . B1.7.12)
V i а /
В выражении B1.7.10) А = шаь — и)ьс, т = («2 — t^)Jc и с — скорость света.
Именно наличие здесь острой лоренцевой функции с шириной Га представляет для
нас интерес, поскольку обычно (то есть в случае некоррелированного спонтанного
излучения) ожидается ширина Га + IV На рис. 21.18 с целью демонстрации су-
сужения линии изображена функция g(r, А)/(А2 + Г2) при различных значениях т.
В частности, пунктирная линия, соответствующая т = 6Г, имеет ширину, равную
приблизительно Га независимо от значения FV
Член, пропорциональный (А2 + Г2)™1 в выражении B1.7.10), позволяет нам
следующим образом представить себе измерение с высоким разрешением частот
атомных переходов шаь и ш^. Как показано на рис. 21.19, в качестве промежуточного
уровня \Ъ) атомного каскадного перехода можно взять магнитный подуровень с m =
= — 1, так что можно варьировать величину А = шаЬ — ш^с вокруг значения А =
= 0, прилагая магнитное поле. Таким образом можно пройти по контуру острого
21.7
Спектроскопия высокого разрешения
489
Рис. 21.18. Составляющая g(r, A)/(A2 + (Га/2J) совместной вероятности счета в спектро-
спектроскопии коррелированного излучения при различных значениях т. Для простоты все кривые
нормированы
лоренциана (А2 + Гд)м1 и с хорошей точностью измерить напряженность магнитного
поля ?»q, для которого А = 0. Зная это значение BQj можно определить разность
— промежуточное
несмещенных частот переходов \а) О |&о) и |&о) ^ |СЬ гДе
состояние с т = 0. Эта процедура позволяет, в принципе, измерить ша^ ~~ шьос^
с точностью до ширины уровня \а). Дополнительное измерение величины шаъ$ +
+ шьос = шас также можно выполнить с точностью до Га. В результате, мы имеем
возможность определить значения шаь0 и ш^с с точностью, определяемой лишь
значением Га.
Здесь, однако, отметим, что величина gij^ А) зависит от А точно также, как
знаменатель лоренциана. Эта функциональная зависимость такова, что при малых
т <С Гд х сигнал g(Tj А)/(А2+Гд) стремится к постоянному значению, не зависящему
от А. Следовательно, задержка во времени т должна быть порядка Г. Это, однако,
ведет к экспоненциальному уменьшению амплитуды сигнала из-за наличия множи-
Рис. 21.19. Каскадное излучение, «настроенное» внешним магнитным полем так, чтобы
шаь_ = шь^с ~ cjq- В этом случае величина А = шаь_ — ооь^с варьируется вокруг нулевого
значения. (Состояние |6_) соответствует состоянию \Ь) при вычислении.)
490 Двухфотонная интерферометрия и другие задачи Гл. 21
теля ехр(—Г^т) в выражении B1.7.10) и, очевидно, к колебательному поведению
сигнала из-за наличия функций синус и косинус в выражении B1.7.10). Оба эффекта
хорошо известны из спектроскопии с временным разрешением (см. разд. 5.7).
Внимательный читатель вполне может спросить: какова физика этого «двухфо-
тонного сужения линии»? Ответ на этот оправданный вопрос можно найти в лите-
литературе (см., например, Rathe and Scully A994)).
Приложение 21.А
Рассеяние двумя атомами: операторный подход
Для рассмотрения задачи из разд. 21.1, а также более сложных задач из гл. 21,
удобно использовать операторный формализм. С этой целью введем оператор jf,
определяемый следующим образом:
к
откуда, с учетом B1.1.4), следует, что
l7i> = 7!+|0>. B1.A.2)
Используя последнее выражение, можно переписать корреляционную функцию в ви-
виде
^W() ^)()tOl+|0). B1.A.3)
Далее, операторное произведение ?л+^(г, ?Oi можно записать следующим образом:
, *) + [Я(+)(г, t), 7l+], B1.A.4)
где [E^(r, t), 7i~] ~~ обычный коммутатор.
Это удобно, поскольку 7i"^'^+Hr? ^)|0) = 0 И5 следовательно, из B1.А.3) и B1.А.4)
имеем
(> M (>г, t), 7l+]|0)|2 , B1.А.5)
что легко вычисляется, ибо (задача 21.1)
К0|[?7<+>(г, t), 7+]|0)| = ^- в(<-Дп/с) e-(t-An/c)(ic+r/2) _ ф7(дГ1) t). B1.A.6)
Применим этот подход к последней двухатомной задаче. Как и прежде, пред™
положим, что имеются два атома в точках ri и Г2, и что в момент времени t = 0
они находятся в состоянии (l/\/2)(|ai&2) + |^i^2))|0), то есть один атом возбужден,
а второй нет. Для времен t ^> 1/7 состояние системы примет вид (если атомы
расположены достаточно далеко друг от друга, так что вероятность поглощения
одним атомом фотона, испущенного другим атомом, мала, т.е., если |ri — Г21 1^> А)
-L(|71) + |72})|61Ь2) = -J=Gl+ + Ъ+)|0}|6162). B1.А.7)
П.21.Б
Двухфотонная корреляционная функция
491
Тогда корреляционная функция имеет вид
7+
72+)|0) =
, t) + Ф7(Дг2, *)|2. B1.A.
Перекрестный член в выражении B1.А.8) отвечает за интерференционные эффек-
эффекты и описывает полосы, которые создавались бы на экране, задерживающем свет,
испущенный атомами. В этом можно убедиться, вычислив перекрестный член и об-
обнаружив, что в случае, когда |г| >> |ri|, |r2|, имеем
2Re [Ф;
г2, t)} = ^§-Q(t- г/с)
cos[k0(r2 -
]. B1.А.9)
Функция косинус описывает интерференционную картину. Например, если ri =
= (а/2)? и 1*2 = ™(а/2)?, и экран расположен перпендикулярно оси х на расстоянии
R от начала системы координат, то интервал между полосами интерференции будет
равен Л Я/а, где Л — длина волны света.
Приложение 21.Б
Вычисление двухфотонной корреляционной функции
в случае каскадного излучения атома
В случае каскадного излучения одиночного атома испускаются лишь два фотона,
так что
поэтому именно двухфотонная «волновая функция»
представляет интерес. Воспользовавшись тем фактом, что
?(ri,*i) = X)Oke~<l'*t<"Hk"P< (* = 1,
к
и взяв |^) из F.4.13), получим
ФB)(гь h; г2, t2) =
B1.Б.2)
k,q p,s
- wac) - Га/2][г(|/д - шЬс) - Гь/2]
1 \
j J-q/ —
k,q
— ik-r — iq-r
e
[i{uk + vq- uac) - ra/2][i(vq - шьс) - Гь/2]
. B1.Б.З)
492
Двухфотонная интерферометрия и другие задачи
Гл. 21
Для того чтобы вычислить Ф^2\ заменим суммы по к и q интегралами, вычислим
все константы связи и плотность атомных состояний в области резонансов ско = шаь
и ego = ^Ьс5 выберем ось z для интегрирования по к и q так, чтобы Дгх = Гх — г
и Аг2 = Г2 — г для первого члена в скобках и Г2 — г и гх — г для второго члена.
Выполнив все эти действия, записываем выражение B1.Б.3) в виде
СО 7Г
Г Г
L?^i5r2?^2) = ~ \ к dk
J J
sin
2тг со 7Г
г г
d(/)k \ q dq \ sin #9 <
ооо
1
2тг
[i(ck + cq - ujac) - Га/2][г(сА; - u)bc) - Tb/2]
2)]х
. B1.Б.4)
Интегрирование по углам дает
dkdq
-icfctw
V
-icgt2/ -iqrAr2 _ iqAr2\
[г(сА; + eg - шас) - Fa/2][i(ck - шЬс) - Гь/2]
о о
+ A**2). B1. Б. 5)
Теперь выполним интегрирование по модулю волновых векторов. Пределы инте-
интегрирования по к и q можно расширить до — оо, вследствие пикообразного характера
лоренцевых функций. Контур по к замыкается в нижней полуплоскости (рис. 21.20а),
Irak
Iraq
, Re к
X
ко
X
Qo
(а)
(б)
Рис. 21.20. Полюс ^о = {^ас — гГа/2)/с — g и контур интегрирования для eti > An.
Интеграл B1.Б.5) обращается в нуль, когда ct\ < An (а); полюс до = (^бс — гГь/2)/с — д
и контур интегрирования для (?2 — Дгг/е) > (?i — An/с) E)
если с?х > ^Г1 и в верхней полуплоскости, если ct\ < Дгх- Следовательно, пре-
пренебрегая нефизическими приходящими волнами, пропорциональными множителю
), находим
/B
/с),
в*!-^ dq
2 - Ar2/c) - (t! - Ап/с)]}
i(cq — ojbc) — Г5/2
2). B1.Б.6)
П.21.В Совместная вероятность отсчета в интерферометрии Франсона-Чиао 493
Аналогично выполняется интегрирование по q с использованием контура, изобра-
изображенного на рис. 21.205, и мы находим, что
+ A<->2), B1.Б.7)
где к= B7rLk(k)()
Приложение 21.В
Вычисление совместной вероятности отсчета
в интерферометрии Франсона-Чиао
Согласно F.4.13) двухфотонное состояние, создаваемое в процессе каскадного из-
излучения одиночного возбужденного трехуровневого атома, расположенного в начале
системы координат, имеет вид перепутанного состояния:
_ g-ik-d-iq-d
a l |lk l) BLR1)
•/ I \ Tl /О1Г'/ \ T-l /Г>1 К? -*-а/* ^ JL . JLJ» . JL ^
;(i/fc + i/g — Шас) — ra/2j[*(j/g — LJbc) — Гь/2] ч/
k,q
Состояние |Ф) позволяет вычислить совместную вероятность отсчета, то есть сов-
совместную вероятность того, что оба детектора, изображенные на рис. 21.8, возбужда-
возбуждаются (в пределах бесконечного окна совпадения). Эта вероятность пропорциональна
интегралу
оо оо
РA,2) = [ <Й1 [ <Й2?B>A,2) B1.В.2)
о о
от глауберовской функции когерентности второго порядка
GB)(l, 2) = Ф*A, 2)ФA, 2), B1.В.З)
где «амплитуда вероятности фотон-электронной пары» ФA, 2) задается выражением
B1.4.10).
Используя B1.4.10) и обозначения из рис. 21.9, находим в результате довольно
длинного вычисления в случае, когда Si = S2 = S « L\ = Li = L, T = (L — S)/с
2) = \dtA ^2{[(Hi2|2 + IB12I2 + \Cl2\2 + \D12\2) + A «¦ 2)]x +
° ° +[(Л12?>12 + к.с.) + A++2)]2+
+ [(A*12B12 + C*12D12 + k.c.) + (lo 2)]3+
+ [(A*12C12 + B*12D12 + k.c.) + A «• 2)]4+
+ [(B*12C12 + k.c.) + (lo 2)]5+
[{A*12B21 + C*12A21 + C*2B21 + C*12D21 + D*12B21 + k.c.) + (!<->¦ 2)]e} = B1.B.4)
494
Двухфотонная интерферометрия и другие задачи
Гл. 21
2ке
С08(шасТ) + |
1 al Ь J2 [lalb
cos(a;abT)
СО8(ШЬСТ)
^ а1 Ь
- cos(AT)
4А2
cos(ujabT) -
2А
cos(AT) - ^ sln(AT)] |j , B1.B.5)
где к = {KaKb/2SLJ, a;ac = шаъ + Ш5С, А = шаЬ — шьс- Выралсения в квадратных
скобках в формуле B1.В.4), пронумерованные индексами, являются источниками
соответствующих членов в B1.В.5) 1).
(а)
(б)
Рис. 21.21. Области интегрирования при вычислении различных членов в выражении
B1.Б.4) для совместной вероятности счета РA, 2) в интерферометрии Франсона-Чиао: член
B1.В.6) (а); член Ci2B2i (б)
В качестве примера, рассмотрим интегрирование по t\ и t^ для члена
A\2D12 + к.с. = f e(rb~ra)tl~rbt2+ra(L+s)/2C cosKcT)e(tl - L/c) e(t2 - О,
B1.BJ)
ведущего к осцилляциям на суммарной частоте шаь- Область интегрирования изоб-
изображена на рис. 21.21а. Получаем
оо оо
к.с.) =
о о
-cos(cjacT). B1.В.7)
L/c
1) Эти члены анализировались в работе Meyer, Agarwal, Huang and Scully A994).
Список литературы к гл. 21 495
Для некоторых других членов области интегрирования оказываются немного более
сложными, особенно в случае конечного окна совпадения. Например, на рис. 21.216
показана область интегрирования для члена С^Дп с окном совпадения То.
Задачи
21.1. Используя результаты разд. 6.3, покажите, что
где
#kexp(-ikri)
к
21.2. Покажите, что
' г2 - :
где |7г) {i = 1, 2) — однофотонные состояния, задаваемые формулой B1.1.4).
Список литературы
Другие «какой путь»-детекторы
Scully, М. О., Shea, R., and McCullen, J. Phys. Rep. 43, 486 A978).
Scully, M. O., Englert, B.-G. and Schwlnger, J. Phys. Rev. A 40, 1775 A989).
Рассеяние света атомами: квантовая интерференция, корреляция
фотонов и теорема Белла
Scully, М. О. Laser Spectroscopy V, ed. M. Kellar and B. Stoichoff A981), p. 41.
Scully, M. O. and Driihl, K. Phys. Rev. A 25, 2208 A982).
Hlllery, M. and Scully, M. O. In Quantum Optics, Experimental Gravity, and Measurement
Theory, ed. P. Meystre and M. O. Scully (Plenum, New York 1983), p. 65.
Mandel, L. Phys. Rev. A 28, 929 A983).
Fearn, H. and Loudon, R. Opt Gommun. 64, 485 A987); J. Opt Soc. Am. В 6, 917 A989).
Meyer, G. M., Agarwal, G. S., Huang, H. and Scully, M. O. in Proceedings of the NATO Advanced
Study Institute on Electron Theory and Quantum Electrodynamics, (Edlrne, Turkey, 1994).
Интерференционные эксперименты
Horne, M. A., Shlmony, A. and Zeillnger, A. Phys. Rev. Lett 62, 2209 A989).
Ekhmann, U., Bergquist, J. C., Bellinger, J. J., Gilligan, J. M., Itano, W. M., Wineland, D. J.
and Raizen, M. G. Phys. Rev. Lett. 70, 2359 A993).
*Mohan, P.K., Luo, В., Kroll, S. and Mair, A. Phys. Rev. A 58, 4348 A998).
Квантовая интерференция в параметрических преобразователях
частоты вниз
Hong, С. К., Ou, Z. Y. and Mandel, L. Phys. Rev. Lett 59, 2044 A987).
Ou, Z. Y. and Mandel, L. Phys. Rev. Lett 61, 50 A988).
Shih, Y. H. and Alley, С. О. Phys. Rev. Lett. 61, 2921 A988).
496 Список литературы к гл. 21
Franson, J. D. Phys. Rev. Lett 62, 2205 A989).
Ou, Z. Y., Wang, L. J., Zou, X. Y. and Mandel, L. Phys. Rev. A 41, 566 A990).
Ou, Z. Y., Zou, X. Y., Wang, L. J. and Mandel, L. Phys. Rev. Lett. 65, 821 A990); Phys. Rev.
A 42, 2957 A990).
Rarity, G. and Tapster, P. R. Phys. Rev. Lett 64, 2495 A990).
Zou, X. Y., Wang, L. J. and Mandel, L. Phys. Rev. Lett. 67, 318 A991).
Kwiat, P. G., Steinberg, A. M. and Chlao, R. Y. Phys. Rev. A 45, 7729 A992).
Kelss, T. E., Shlh, Y. H., Serglenko, A. V. and Alley, С. О. Phys. Rev. Lett 71, 3833 A993).
Scully, M. O. and Rathe, U. W. Opt Commun. 110, 373 A994).
Shlh, Y. H. and Serglenko, A. V. Phys. Rev. A 50, 2564 A994).
Shlh, Y. H., Serglenko, A. V., Rubin, M. H., Kelss, Т. Е. and Alley, С. О. Phys. Rev. A 50, 23
A994).
Herzog, T. J., Kwiat, P. G., Weinfurter, H. and Zeilinger, A. Phys. Rev. Lett 75, 3034 A995).
Kwait, P. G., Mattle, K., Weinfurter, H., Zeilenger, A., Serglenko, A. V. and Shih, Y. Phys. Rev.
Lett 75, 4337 A995).
Strekalov, D. V., Serglenko, A. V., Klyshko, D. N. and Shih, Y. H. Phys. Rev. Lett 74, 3600
A995).
Pittman, Т. В., Strekalov, D. V., Migdall, A., Rubin, M. H., Sergienko, A. V. and Shlh, Y. H.
Phys. Rev. Lett. 77, 1917 A996).
*Burlakov, A.V., Chekhova, M.V., Klyshko, D.N., Kulik, S.P., Penln, A.N., Shlh Y.H. and
Strekalov D.V. Phys. Rev. A 56, 3214 A997).
*Бурлаков А.В., Клышко Д.Н., Кулик СП., Пенин А.Н., Чехова М.В. Письма ЖЭТФ 65,
20 A997).
*Бурлаков А.В., Кулик СП., Пенин А.Н., Чехова М.В. ЖЭТФ 113, 1991 A998).
*Бурлаков А.В., Клышко Д.П., Клышко СП., Чехова М.В. Письма ЖЭТФ 69, 788 A999).
*Burlakov, A.V., Chekhova, M.V., Karabutova, O.A., Klyshko, D.N. and Kulik, S.P. Phys. Rev.
A 60, R4209 A999).
*Корыстов Д.Ю., Кулик СП., Пенин А.П. Квантовая электроника 30, 922 B000).
*Burlakov, A.V., Chekhova, M.V., Karabutova, O.A. and Kulik, S.P. Phys. Rev. A 63, 053801
B001).
*Nagasako, E.M., Bentley, S.I., Boyd, R.W. and Agarwal, G.S. Phys. Rev. A 64, 043802 B001).
Сужение линии путем коррелированного спонтанного излучения
Huang, H. and Eberly, J. H. J. Mod. Opt 40, 915 A993).
Scully, M. O., Rathe, U. W., Chang, S., Agarwal, G. S. Opt Commun. 136, 39 A997).
Rathe, U. W. and Scully, M. O. Lett Math. Phys. 34, 297 A995).
Rathe, U. W. and Scully, M. O. Annals of the New York Academy of Sciences 755, 28 A995).
* Квантовая информатика
*Bouwmeester, D., Ekert, A., Zeilinger, A. (Eds.) The physics of quantum Information, Springer-
Verlag, Berlin, 2000 (Бауместер Д., Экерт А., Цайлингер А. Физика квантовой информа-
информации. М. Постмаркет, 2002.)
*Валиев К.А., Кокин А.А. Квантовые компьютеры: надежды и реальность. Ижевск, 2001.
*Кессель А.Р., Ермаков В.Л. ЖЭТФ 117, 517 B000).
*Ermakov V.L., Kessel A.R., Samartsev V.V. SPIE Proceedings 4061, 79 (quant-ph/0001090).
*MoIseev S.A., Kroll S. Phys.Rev.Lett 87, 173601 B001).
*Ребане А.К. Изв. РАН, сер.физ. 66, 297 B002).
предметный указатель
Абсорбционная сила, 390
Адиабатический перенос населенности,
184
Адиабатическое исключение (перемен-
(переменных), 303
Адиабатическое приближение, 272
Амплитуда перехода, 37
Амплитудные флуктуации, 340
Аномальный магнитный момент, 24
Антигруппировка фотонов, 10, 112, 113,
249, 250
Антикорреляция спинов, 418
Антинормальное упорядочение, 70
Атом
движение центра масс, 388, 451
дифракция, 390
отклонение, 389
релаксация, 205
Атом в резонаторе с потерями, 232
Атома с полем взаимодействие, 120, 159
квантовая теория, 159
полуклассическая теория, 120
Атомная интерферометрия, 392
Атомная когерентность, 343, 347, 388
Атомная меласса, 390
Атомная оптика, 388
Атомного перехода оператор, 160
Атомного резервуара метод, 225
Атомные эффекты памяти, 293
Атомный гироскоп, 395
Атомный интерферометр, 395, 396
Балансное гомодинное детектирование,
107
Безразмерная интенсивность, 141
Бейкера-Хаусдорфа
теорема, 40
формула, 47, 80
Белла
неравенство, 404, 408, 412, 414, 427,
472
теорема, 26, 409, 410, 420, 421, 424
Белый шум, 221, 380
сжатый, 358
Беннета-Брассарда протокол, 423
Бернулли распределение, 114
Блоха уравнения, 152
Бозе—Эйнштейна распределение, 68, 266
Бозе-газ многочастичный, 36, 37
Больцмана распределение, 398
Бора орбита, 213
Бора радиус, 20, 130
Броуновское движение, 279
Вайскопфа— Вигнера приближение, 169,
170, 206, 223, 239, 299
Вайскопфа—Вигнера теория спонтанного
излучения, 169, 172, 206
Вакуумные флуктуации, 9, 17, 19—21, 24,
26, 39, 307, 343, 434, 484, 485
сжатые, 76, 109, 207
Вектор состояния
многочастичный, 38
редукция, 213
условный, 215
фотона, 116, 171, 465
Векторная модель оператора плотности,
151
Векторного потенциала оператор, 45
Вероятность перехода, 94
Взаимодействия картина, 127
Вигнера функция распределения, 72, 81
Вигнера-Вейля распределение, 70, 73, 74,
81
Видность, 111, 112
498
Предметный указатель
Винера-Леви стохастический процесс,
279
Винера-Хинчина теорема, 261
Водорода атом, 130
Возбуждаемая У-система, 251
Волн вещества гироскоп, 396
Волн вещества интерферометр, 388
Волновая функция
двухфермионная, 104
коллапс, 404
метод Монте Карло, 215, 218
фотонов, 27
Волновое уравнение, 39, 85, 137, 155, 376
Волновой пакет, 49, 52-54
с минимальной неопределенностью,
44,49
сжатый смещенный, 54
Восприимчивость, 193-195
Временное упорядочение, 96, 129
Вторичное квантование, 29
Выделенная система отсчета, 91
Вынужденное излучение, 24, 142
Вырожденное параметрическое усиление,
57, 367, 368, 380, 384, 385
Высокого разрешения спектроскопия, 486
Гамильтона принцип, 33
Гамильтониан, 11, 18, 45, 53, 120, 147, 161,
233
двухфотонный, 57
картина взаимодействия, 129, 169
минимального взаимодействия, 121
неэрмитовый, 216
Гармонический осциллятор, 48, 52
квантованный, 36, 39
операторы, 13
простой, 11, 44, 49, 52
смещенный, 46
функция распространения, 52
Гауссов случайный процесс, 135
Гауссова статистика, 68, 135, 211
Гейзенберга микроскоп, 448, 449
Гейзенберга оператора метод, 166
Гейзенберга принцип неопределенности,
45, 448, 451
соотношение, 55, 448
Гейзенберга-Ланжевена метод, 221, 230,
293
Гейзенберга-Ланжевена уравнение, 370
Генерация
при четырехволновом смешении, 376
Гетеродин, 105
Гильбертово пространство, 436
Голографический лазер, 336
Гомодинное детектирование, 105, 434
балансное, 107, 108
Гравитационная волна, 84
Гравитационное красное смещение, 91
Гравитационных волн детектор, 45, 51
Градиентная сила, 388, 391
Грина функция, 461
Гринбертера-Хорна-Цейлинтера равен-
равенство, 405, 421
Группировка фотонов, 112
Двухатомная корреляция, 470
Двухвременная корреляционная функ-
функция, 244, 248, 261
Двухмодовое сжатое состояние, 61
Двухуровневый атом, 120, 124, 133, 162
Двухфотонная интерференция, 23, 83
Двухфотонная интерферометрия, 474,
486
Двухфотонная корреляционная функ-
функция, 34, 471, 472, 475, 491
Двухфотонного детектирования ампли-
амплитуда, 35
Двухфотонное каскадное излучение, 173
Двухфотонное фоковское состояние, 111
Двухфотонный интерферометр, 109
Де Бройля длина волны, 395
Делитель пучка, 393
Дельта-функция, 79, 211
двумерная, 69, 78
Детектирование фотонов, 94
Динамическое штарковское расщепление,
238, 241
Дипольного момента оператор, 136
матричный элемент, 125, 160, 485
Дипольное приближение, 122, 123, 147,
160, 391
Дирака уравнение, 32
Дисперсионный энергетический сдвиг,
435
Дисперсия, 186, 193
Диффузии коэффициент, 224, 280, 297,
305, 331-333, 338, 363, 398
Дополнительность, 406, 447, 448
Дрейфа коэффициент, 331, 332, 398
Дробовой шум, 343
Дробовой шум фотонов, 86
Естественная ширина, 277
Звездный интерферометр
Майкельсона, 91
интенсивности, 83, 93
Зоу-Ванга-Манделя-эксперимент, 481,
484
Излучение классического тока, 45
Импульса оператор, 32
Предметный указатель
499
Инверсия населенностей, 127, 164
Интенсивности корреляция, 83, 96, 471
Интерференция двух фотонов, 109
Интерференция интенсивности, 102
Интерферометр
Маха-Цендера атомный, 393
Интерферометрия, 83
атомная, 392
двухфотонная, 109, 464
двухчастичная, 478
на основе преобразования частоты
вниз, 480
нейтронная, 388
КН-наблюдаемая, 431
Казимира эффект, 9
iiJ-калибровка, 147
Калибровочная инвариантность, 121
Калибровочная теория поля, 122
Канонический импульс, 11, 148, 149
Кардано формула, 382
Каскадная интерферометрия, 486
Квадратурная дисперсия, 58
Квазиклассическое распределение, 64
Квазимода, 153
Квантование поля излучения, 10, 12
Квантовая интерференция, 177, 184
Квантовая когерентность, 94, 192
Квантовая криптография, 423
Квантовая теорема регрессии, 245, 281
Квантовая теория измерений, 23
Квантовая теория когерентности, 67
Квантовая электродинамика, 21
Квантовая эффективность, 114
Квантовое неразрушающее измерение,
430-432, 435, 442, 445
Квантовое распределение, 64, 424
Квантовое стирающее устройство, 23, 26,
452, 469, 475
Квантовое уравнение Ланжевена, 297,
299, 363
Квантовой фазы оператор, 341
Квантовые биения, 10, 21, 23, 26, 324
лазер, 324, 333, 337, 347, 350
Квантовые флуктуации, 277, 339, 379, 396
фазы и амплитуды, 339
Квантовый гармонический осциллятор,
17, 36, 248
Квантовый скачок, 203, 213
Квантовых траекторий метод, 218, 408
Керра эффект, 107, 432, 433
Классическая теория когерентности, 67
Клонирования предел, 359
Когерентная суперпозиция, 21, 198, 328,
437
Когерентное пленение, 182, 183, 188, 197
Когерентное пленение населенности, 399
селективное по скорости, 399
Когерентное состояние, 44-47, 49, 50, 57,
61, 66, 75, 81, 439
представление, 64, 67
сжатое, 58, 61, 74
Когерентность
внесенная, 331
второго порядка, 101
первого порядка, 97
потеря, 457
степень, 96, 485
частичная, 99
Когерентные рамановские биения, 180
Коллапс и возрождение, 159, 165
Кольцевой
лазерный гироскоп, 87, 88, 325
резонатор, 337
Коммутационные соотношения, 12, 14, 15,
148
Бозе-Эйнштейна, 29
Ферми-Дирака, 29
между электрическими и магнитны-
магнитными составляющими поля, 15
Комптоновская длина волны, 20, 35
Корпускулярно-волновой дуализм, 27,
447
Коррелированное спонтанное излучение,
324, 486
Корреляционный лазер, 324-326, 336
Ханле эффект, 326
гироскоп, 353, 356, 363
двухфотонный, 342, 344, 345, 350,
353, 359
«Который путь»-детектор, 449, 464
микромазер, 449, 460
«Который путь»-информация, 439
Информация, 449
информация «который путь», 450, 459,
484
Коши-Шварца неравенство, 385
Крабовидная туманность, 84
Крупнозернистое уравнение движения,
272
Крупномасштабное уравнение движения,
311
Кулоновская калибровка, 40
Лазер
Ланжевена теория, 293
гироскоп, 364
гол ©графический, 336
квантовая теория, 266, 293
квантовых биений, 333
корреляционный, 324
на свободных электронах, 140
500
Предметный указатель
пол у классическая теория, 139
порог, 142, 274, 283, 285
принцип работы, 139
с инжекцией сжатого вакуума, 361
с насыщаемым поглотителем, 290
с синхронизацией фаз, 335
со случайной фазой, 117
ширина линии излучения, 9, 26, 266,
279-281, 305, 324
Лазерная генерация без инверсии, 180,
188, 197, 198
Лазерно-индуцированное охлаждение,
388
Лазерное охлаждение, 389, 390
предел отдачи, 399
пределы, 397
Лазерный гироскоп, 87, 325
Ланжевена уравнение, 221, 299, 302
Ланжевеновская сила, 335
Ланжевеновская теория лазера, 293
Ланжевеновский оператор, 294, 373
Ланжевеновский шум, 231
Лапласа уравнение, 85
Лензе-Тирринга эффект, 89
Линейный
коэффициент потерь, 139
коэффициент усиления, 141, 270, 295
процесс усиления, 356
усилитель, 356
Липпмана полосы, 36
Лиувилля уравнение, 133, 247
Локализация фотона, 35
Локальная калибровочная (фазовая)
инвариантность, 121
Локальности аспекты квантовой механи-
механики, 404
Лоренца распределение, 231, 232, 279
Лэмбовская полуклассическая теория
лазера, 140
Лэмбовский сдвиг, 9, 17, 18, 24, 26, 39, 484
Магнитная постоянная, 10
Магнитное поле, 12, 121
квантованное, 13
классическое, 10, 12
оператор, 32
Майкельсона интерферометр, 83-85, 325
звездный, 91
Майкельсона-Морли эксперимент, 24
Максвелла уравнения, 10, 21, 24, 32, 137,
153, 268
Максвелла-Шредингера уравнения, 135
Манделя параметр Q, 276, 307, 314
Марковский процесс, 204
Марковское приближение, 225, 229, 245,
281
Масштабный множитель, 89, 353
Матрица населенности, 136, 269
Маха принцип, 91
Маха-Цендера интерферометр, 83, 107,
476
атомный, 393
Маховское увлечение системы отсчета, 89
Медленно меняющиеся амплитуды, 125
приближение, 138, 377
Мезонное поле, 29
Механическое действие света, 389
Микромазер, 159, 273, 310, 312, 319, 321,
449, 455, 484
ширина линии излучения, 321
Минимального взаимодействия гамиль-
гамильтониан, 121
Многовременные корреляционные функ-
функции, 168
Многомодовое сжатие, 59
Модулированная усиливающая среда, 364
Молекулярного поля теория, 284
Моментов теорема, 135
Наблюдаемые, 122, 431
КН-, 431
сопряженные, 431
Накачка, 139, 184, 187, 267, 324, 367, 369
скорость, 190, 270
флуктуации фазы, 369, 380
Намагниченность, 284
Насыщения параметр, 141
Невырожденный параметрический уси-
усилитель, 367, 384
Нейтрино, 32
Нелокальность, 421
Немарковский шум, 225
Неодетое состояние, 261
Непрерывности уравнение, 33
Нормальное упорядочение, 66, 70, 96, 112,
302, 305, 341
Нормальные моды, 10, 140, 363
Нормировки условие, 15
Нулевое измерение, 213
Обратное действие, 442
Обратное рассеяние, 337, 364
Обращение времени, 375
Одетого атома картина, 241
Одетое состояние, 252, 257, 263, 435
Однородно уширенный, 136
Однофотонное состояние, 171
Окрашенный шум, 225, 229, 296
Онсагера-Лакса теорема регрессии, 244
Оператор
квантовый полевой, 29
плотности, 65, 72, 95, 132, 203, 245
Предметный указатель
501
проектирования, 175, 410
рождения, 12, 39, 66, 445
сжатия, 57, 207
смещения, 47, 60, 81
унитарный, 47
уничтожения, 12, 39, 66, 94, 356, 445
фазы, 433, 445
фермионный, 104
числа фотонов, 433
шума, 294
эволюции во времени, 128, 150, 168,
316
Оператор плотности, 132, 151
векторная модель, 151
приведенный, 204, 407
уравнение движения, 133
условный, 213
Оператора эволюции метод, 168
Оптический параметрический генератор,
369, 372
Оптический параметрический процесс,
442
Орнштейна-Уленбека процесс, 385
Относительности теория (общая), 83
Отрицательные вероятности, 404
Парадокс ЭПР, 405, 406
Параметризованный постньютоновский
формализм, 89
Параметрический преобразователь ча-
частоты вниз, 367, 478
Параметрическое приближение, 368, 384,
385
Параметрическое усиление, 367, 443
Паули ловушка, 467
Паули матрицы, 161
Планка распределение, 26
Плотность мод, 13
Плотность состояний внутри резонатора,
231
Поглощения коэффициент, 193
Показателя преломления увеличение, 192
Полевая
интерферометрия, 83
корреляционная функция, 464
Полнота, 51, 65
Полу классическая теория, 21, 29
Полу классическая теория лазера, 139
Поляризация, 134, 346
Поперечное время релаксации, 152
Потоков вероятности диаграмма, 271
Приближение вращающейся волны, 126,
129, 131, 155, 159, 161, 360, 367
за пределами, 130
Приготовление состояния, 421
Проводимость, 137
Продольное время релаксации, 152
Просветление среды, 184, 186, 188
Пуассона распределение, 50, 166, 266, 275
Раби осцилляции, 120, 159, 164, 165, 318
затухающие, 235
Раби перевороты, 127, 176
Раби частота, 183, 232, 249, 250, 310, 333,
347, 365, 382, 391, 392, 438
Радиационная калибровка, 147
Радиационное давление, 388
Разложение поля по модам, 10
Рамзи метод раздельных осциллирующих
полей, 435, 437
Рамзи полосы, 438, 457, 459
Р-раепределение, 64, 67, 68, 70, 72, 81, 97,
112-115, 117, 210, 277, 280, 284,
287, 305, 307, 330, 342, 350, 351
когерентного состояния, 68
лазера, 277
одномодового поля теплового источ-
источника, 97
состояния с определенным числом
частиц, 69
теплового поля, 68
Q-распределение, 64, 69, 70, 72, 79
сжатого когерентного состояния, 74
состояния с определенным числом
частиц, 70
Реальности аспекты квантовой механики,
404
Редукция состояния, 315
Резонансная флуоресценция, 24, 113, 238,
239, 251, 260, 264
возбуждаемой У-системы, 251
спектр, 239, 246
Резонатор, 10
двойной, 326
кольцевой, 137, 337
с потерями, 232
Релаксации константа, 223, 294
Релаксация, 203, 221, 242
Релея пик, 249
Релея рассеяние, 249
Релея-Джинса катастрофа, 24
Ридберговский атом, 310
Ридберговское состояние, 450
Рождения оператор, 12, 39, 445
Самоиндуцированная прозрачность, 180
Самонасыщения коэффициент, 270
Самосогласованные уравнения, 26, 139
Саньяка кольцевой интерферометр, 86,
88, 325
Саньяка разность фаз, 395
Сверхпроводимость, 404
502
Предметный указатель
Свет
круговая поляризация, 131, 399, 413
линейная поляризация, 125, 131, 413
механическое действие, 389
Светоделитель, 105
Секулярное приближение, 242
Сжатие
N-ro порядка, 61
амплитудно-квадратичное, 62
в оптическом параметрическом гене-
генераторе, 369
многомодовое, 59, 372
на выходе резонатора, 372
спектр, 375
фазового шума, 342
Сжатия оператор, 45, 57, 58
Сжатия параметр, 59, 368
Сжатое когерентное состояние, 45, 57, 58,
60, 61, 74
Q-распределение, 74
многомодовое, 60
Сжатое состояние, 10, 44, 45, 51, 56, 76,
105, 114, 341, 367
генерация, 368, 369
двухмодовое, 59, 61, 368
детектирование, 105
идеальное, 55, 368, 380
Сжатые вакуумные флуктуации, 339
Сжатый вакуум, 109, 207, 236, 357, 361,
363
инжекция в лазер, 361
многомодовый, 207, 264, 385
Сжатый вакуумный резервуар, 205, 207,
236
Сигнальная мода, 367
Сильного поля предел, 249
Симметричное упорядочение, 71
Система спина 1/2, 120, 127
Системы с резервуаром взаимодействие,
204
Скорости оператор, 33
Скоростное уравнение, 141
Скрытые переменные, 405, 415, 416
Слабого поля предел, 248
Случайная фаза, 102, 347, 380, 485
Смещения оператор, 47, 60, 81
Совместная вероятность детектирования,
110, 176, 472, 478, 487, 493
Соотношение неопределенностей, 55, 430
между фазой и амплитудой, 341
Состояние пленения, 180, 184, 318
Состояние с определенным числом ча-
частиц, 45, 48, 49, 66, 69, 70
Состояние с определенным числом ча-
частиц, 15, 16, 315, 440
Спектр мощности, 248, 261, 279
Спектральный анализатор, 243
Спектроскопия с временным разрешени-
разрешением, 145
Спиновая функция корреляции, 419
Спиновое синглетное состояние, 405, 408,
418, 427
Спонтанное излучение, 51, 164, 324, 343,
345-347, 356, 397
возрастание скорости, 233
коррелированное, 324, 486
шум, 324, 326, 343, 347
Стабилизации фактор, 142
Статистика фотонов, 266, 305, 312
лазера, 273
микромазера, 311
Статистическое распределение фотонов
лазера, 266
Стационарное поле, 95, 261
Степень когерентности
второго порядка, 96, 101
первого порядка, 96
Столкновения, 134
Субпуассоновская статистика, 77, 311, 314
Сужение линии, 146, 252, 486
Суперпуассоновская статистика, 78, 314
Сферическая волна, 115
Счет фотонов, 114
Темное состояние, 182
Теплового источника поле, 60, 68, 81
Тепловой резервуар, 205
Ток
классический, 45
плотность, 33, 41
Трехпиковый спектр, 241, 249
Трехуровневый атом, 182, 251, 297, 328,
333, 412, 435, 468, 487
Трехчастичное состояние, 422
Ультрафиолетовая катастрофа, 24, 51
Уничтожения оператор, 12, 39, 94, 356,
445
Упругие столкновения, 134
Усиление
при четырехволновом смешении, 376
свободное от шума, 45, 353
фазово-нечувствительное, 358
фазово-чувствительное, 359
Усиления коэффициент, 270
Условие детального равновесия, 274, 282
Фазеониум, 180
Фазовая неопределенность, 107
Фазово-нечувствительный добавочный
шум, 359
Фазово-нечувствительный усилитель,
357, 359, 365
Предметный указатель
503
Фазово-чувствительный усилитель, 357-
359
Фазовое сопряжение, 375
Фазовой диффузии модель, 278, 279
Фазовые флуктуации, 341
Фазовый оператор, 433, 445
Фазовый переход второго рода, 266, 283,
286
Фано интерференция, 202
Ферма принцип, 33
Ферми статистика, 394
Ферромагнетик, 283
Флуктуационно-диссипационная теоре-
теорема, 203, 223, 231, 357
Фока состояние, 15, 16, 57, 118
Фоккера-Планка уравнение, 209, 210, 278,
280, 330, 332, 342, 343, 350, 362,
398
Фон Неймана уравнение, 133
Фотовозбуждения оператор, 176
Фотодетектирования теория, 83
Фотодетектор, 105
Фотон, 23
Фотонная интерферометрия, 109
Фотонная корреляция, 469
Фотонное поле, 29
Фотонное эхо, 180
Фототок, 92
Фотоэлектрический эффект, 9, 24, 94
Франсона-Чиао интерферометрия, 475,
476, 493
Фраунгофера дифракция, 461
Функция корреляции, 95
п-го порядка, 96
второго порядка, 95, 117, 176
двухфотонная, 34, 471, 475, 491
интенсивности, 471
первого порядка, 95, 98, 99
поля, 464
Функция распределения фотонов, 291,
320
для идеального сжатого состояния,
76
Ханле лазер, 328, 338, 342, 347, 350
Хайле эффект, 181, 324, 326, 337
Характеристическая функция, 71
Холостая мода, 367
Хэнбери-Брауна-Твисса интерферометр,
93
Хэнбери-Брауна-Твисса эффект, 83, 93,
101, 104
для лазерного излучения, 103
для нейтронов, 104
для теплового излучения, 103
"Частотный преобразователь, 443
Черного тела излучение, 9, 24
Планка распределение, 26
Четверть-волновая пластина, 474
Четность, 413
Четырехволновое смешение, 367, 375
сжатие, 378
Шавлова-Таунса предел, 324, 342
Шавлова—Таунса рандомизация фаз, 286
Шавлова-Таунса ширина линии, 283, 322
Шварца неравенство, 112
Широкополосный детектор, 175
Шредингера уравнение, 26, 45, 121, 125,
127, 132
Штарковский сдвиг, 134
Штерна-Герлаха прибор, 405, 409, 412,
427
Шум в атомном интерферометре, 396
ЭПР-парадокс, 454
Электрическая постоянная, 10
Электрическое поле, 12, 121
калибровка, 147
квантованное, 13
классическое, 10, 12
оператор, 14, 30, 94, 239
приближение дальней зоны, 254
Электромагнитно-индуцированная про-
прозрачность, 180,184,186,197-199
Электромагнитное поле, 121, 137
Элементарные частицы, 404
Энергия нулевых колебаний, 17
Эрмита полином, 48, 76
Эффективная масса фотона, 395
Эффективное вращение, 89
Эффективное поле, 152
Юнга эксперимент с двойной щелью, 26,
83, 97, 447
ОГЛАВЛЕНИЕ
Предисловие .................................................. 5
Предисловие к русскому изданию .................................... 8
Глава 1. Квантовая теория излучения
1.1. Квантование свободного электромагнитного поля ..................... 10
1.1.1. Разложение по модам A0). 1.1.2. Квантование A1). 1.1.3. Коммута-
Коммутационные соотношения между электрическими и магнитными составляющими
поля A4).
1.2. Фоковские состояния или представление чисел заполнения .............. 15
1.3. Лэмбовский сдвиг ........................................... 18
1.4. Квантовые биения ........................................... 21
1.5. Что есть свет? Понятие фотона ................................. 23
1.5.1. Вакуумные флуктуации и понятие фотона B4). 1.5.2. Вакуумные флук-
флуктуации B6). 1.5.3. Квантовые биения, квантовое стирающее устройство, теоре-
теорема Белла и другие задачи B6). 1.5.4. «Волновая функция фотонов» B7).
Задачи ...................................................... 39
Список литературы.............................................. 41
Глава 2. Когерентные и сжатые состояния поля
2.1. Излучение классического тока .................................. 45
2.2. Когерентное состояние как собственное состояние оператора уничтожения и как
смещенное состояние гармонического осциллятора .................... 46
2.3. Что когерентно в когерентных состояниях? ......................... 48
2.4. Некоторые свойства когерентных состояний ......................... 50
2.5. Физика сжатого состояния ..................................... 51
2.6. Сжатые состояния и соотношение неопределенности ................... 55
2.7. Оператор сжатия и сжатые когерентные состояния .................... 57
2.7.1. Дисперсия квадратур E8).
2.8. Многомодовое сжатие ........................................ 59
Задачи ...................................................... 60
Список литературы.............................................. 62
Глава 3. Теория квантовых распределений и частично когерентное
излучение
3.1. Представление когерентных состояний ............................ 64
3.1.1. Определение представления когерентных состояний F6). 3.1.2. Примеры
распределений по когерентным состояниям F8).
3.2. Q-представление ............................................ 69
Оглавление 505
3.3. Распределение Вигнера-Вейля .................................. 70
3.4. Обобщенное представление оператора плотности и связь между Р-, Q- и W-
распределениями ........................................... 72
3.5. Q-представление сжатого когерентного состояния ..................... 74
Приложение З.А. Проверка соотношений C.1.12а, 3.1.126) .................. 78
Приложение З.Б. О-числовая функция, соответствующая распределению Вигаера--
Вейля ................................................... 80
Задачи ...................................................... 81
Список литературы.............................................. 82
Глава 4. Полевая и фотонная интерферометрия
4.1. Интерферометр как космический датчик ........................... 84
4.1.1. Интерферометр Майкельсона и общая теория относительности (84).
4.1.2. Кольцевой интерферометр Саньяка (86). 4.1.3. Предполагаемая
проверка метрических теорий гравитации с помощью кольцевого лазера (89).
4.1.4. Звездный интерферометр Майкельсона (91). 4.1.5. Интерферометр
Хэнбери-Брауна-Твисса (93).
4.2. Детектирование фотонов и квантовые функции когерентности ............ 94
4.3. Когерентность первого порядка и эксперименты типа Юнга с двумя источниками 97
4.3.1. Эксперимент Юнга с двойной щелью (97). 4.3.2. Эксперимент Юнга
с двумя атомами A00).
4.4. Когерентность второго порядка ................................. 101
4.4.1. Физика эффекта Хэнбери-Брауна^Твисса A01). 4.4.2. Гомодинное детек-
детектирование сжатых состояний A05). 4.4.3. Интерференция двух фотонов A09).
4.4.4. Антигруппировка фотонов, пуассоновский и субпуассоновский свет A12).
4.5. Счет и статистика фотонов .................................... 114
Приложение 4.А. Классическое и квантовое описания интерференции с двумя ис-
источниками ................................................ 115
Приложение 4.Б. Вычисление корреляционной функции второго порядка ....... 117
Задачи ...................................................... 117
Список литературы.............................................. 118
Глава 5. Взаимодействие атома с полем — полуклассическая теория
5.1. Гамильтониан взаимодействия атома с полем ........................ 120
5.1.1. Локальная калибровочная (фазовая) инвариантность и гамильтониан ми-
минимального взаимодействия A21). 5.1.2. Дипольное приближение и (г • Е)-
гамильтониан A22). 5.1.3. (р • А)-гамильтониан A23).
5.2. Взаимодействие двухуровневого атома с одномодовым полем ............. 124
5.2.1. Метод амплитуд вероятности A24). 5.2.2. Представление взаимодей-
взаимодействия A27). 5.2.3. За пределами приближения вращающейся волны A30).
5.3. Оператор плотности для двухуровневого атома ...................... 132
5.3.1. Уравнение движения для оператора плотности A32). 5.3.2. Двухуровне-
Двухуровневый атом A33). 5.3.3. Учет упругих столкновений между атомами A34).
5.4. Уравнения Максвелла-Шредингера .............................. 135
5.4.1. Матрица населенности и уравнение движения для нее A36). 5.4.2. Урав-
Уравнения Максвелла для медленно меняющихся функций поля A37).
5.5. Полуклассическая теория лазера ................................ 139
5.5.1. Принцип работы A39). 5.5.2. Полуклассическая теория Лэмба A39).
5.6. Физическая картина вынужденного испускания и поглощения ............ 143
5.7. Спектроскопия с временным разрешением .......................... 144
Приложение 5.А. Эквивалентность (г • Е)- и (р • А)-гамильтонианов .......... 147
5.А.1. Форм-инвариантные физические величины A47). 5.А.2. Вероятности
переходов в двухуровневом атоме A49).
Приложение 5.Б. Векторная модель матрицы плотности ................... 151
Приложение 5.В. Физика квазимод лазера, основанная на модах вселенной ...... 152
506 Оглавление
Задачи ...................................................... 154
Список литературы.............................................. 156
Глава 6. Взаимодействие атома с полем — квантовая теорим
6.1. Гамильтониан взаимодействия атома с полем ........................ 160
6.2. Взаимодействие одиночного двухуровневого атома с одномодовым полем .... 162
6.2.1. Метод амплитуд вероятности A62). 6.2.2. Метод оператора Гейзенбер-
га A66). 6.2.3. Метод унитарного оператора эволюции A68).
6.3. Теория Вайскопфа-Вигнера спонтанного излучения двухуровневого атома . . . 169
6.4. Двухфотонное каскадное излучение .............................. 173
6.5. Вероятности возбуждения для одиночных и парных фотоэлектронных событий 175
Задачи ...................................................... 176
Список литературы.............................................. 177
Глава 7. Лазерная генерация без инверсии и другие эффекты атом-
атомной когерентности и интерференции
7.1. Эффект Ханле ............................................. 181
7.2. Когерентное пленение — темные состояния ......................... 182
7.3. Электромагнитно-индуцированная прозрачность ..................... 184
7.4. Лазерная генерация без инверсии ................................ 188
7.4.1. Концепция ЛГБИ A88). 7.4.2. ЛГБИ с точки зрения лазерной физики:
простое рассмотрение A89). 7.4.3. Анализ ЛГБИ A90).
7.5. Увеличение показателя преломления с помощью квантовой когерентности . . . 192
7.6. Когерентное пленение, лазерная генерация без инверсии и электромагнитно-
индуцированная прозрачность: точное решение простой модели ........... 197
Задачи ...................................................... 199
Список литературы.............................................. 199
Глава 8. Квантовая теория релаксации — методы оператора плот-
плотности и волновой функции
8.1. Общая теория резервуара ..................................... 204
8.2. Релаксация атома, вызванная тепловым и сжатым вакуумным резервуарами . . 205
8.2.1. Тепловой резервуар B05). 8.2.2. Резервуар сжатого вакуума B07).
8.3. Релаксация поля ............................................ 208
8.4. Уравнение Фоккера-Планка .................................... 209
8.5. Описание релаксации с помощью «квантовых скачков» ................. 213
8.5.1. Условные операторы плотности и нулевое измерение B13). 8.5.2. Метод
Монте Карло для волновой функции при описании релаксации B15).
Задачи ...................................................... 218
Список литературы.............................................. 219
Глава 9. Квантовая теория релаксации — метод Гейзенберга—
Ланжевена
9.1. Простое рассмотрение релаксации через резервуар осцилляторов: марковский
белый шум................................................ 221
9.2. Расширенное рассмотрение релаксации через резервуары атомов и осциллято-
осцилляторов: немарковский окрашенный шум .............................. 225
9.2.1. Метод атомного резервуара B25). 9.2.2. Обобщенное рассмотрение задачи
осцилляторного резервуара B28).
9.3. Уравнения движения для корреляционных функций поля ............... 229
9.4. Флуктуационно-диссипационная теорема и формула Эйнштейна .......... 231
9.5. Атом в резонаторе с потерями .................................. 232
Задачи ...................................................... 236
Список литературы.............................................. 236
Оглавление 507
Глава 10. Резонансная флуоресценция
10.1. Оператор электрического поля для спонтанного излучения одиночного атома . 239
10.2. Введение в теорию спектра резонансной флуоресценции ................ 239
10.2.1. Предел слабого управляющего поля B39). 10.2.2. Предел сильного поля:
появление боковых полос B41). 10.2.3. Ширины трех пиков в пределе очень
сильного поля B41).
10.3. Теория анализатора спектра. ................................... 243
10.4. От одновременных к двухвременным средним: теорема регрессии Онсагера-
Лакса ................................................... 244
10.5. Полный спектр резонансной флуоресценции ......................... 246
10.5.1. Предел слабого поля B48). 10.5.2. Предел сильного поля B49).
10.6. Антигруппировка фотонов ..................................... 250
10.7. Резонансная флуоресценция возбуждаемой F-системы ................. 251
Приложение 10.А. Оператор электрического поля в приближении дальней зоны . . 254
Приложение 10.Б. Уравнения движения для матрицы плотности и их точное реше-
решение в базисе «одетых» состояний ................................ 257
10.Б.1. Вывод уравнения движения в базисе «одетых» состояний B57).
10.Б.2. Решение уравнений движения B58).
Приложение 10.В. Уравнения движения для матрицы плотности и их точное реше-
решение в базисе «неодетых» состояний ............................... 260
Приложение 10.Г. Спектр мощности в стационарном режиме ................ 261
Приложение 10.Д. Вывод формулы A0.7.5) ............................ 262
Задачи ...................................................... 263
Список литературы.............................................. 264
Глава 11. Квантовая теория лазера — метод оператора плотности
11.1. Уравнение движения для матрицы плотности ....................... 267
11.2. Статистика лазерных фотонов .................................. 273
11.2.1. Линейное приближение iJM = 0) B74). 11.2.2. Лазер, работающий суще-
существенно выше порога (srf ^> ^) B74). 11.2.3. Точное решение B75).
11.3. Лазер в Р-представлении ...................................... 277
11.4. Естественная ширина ........................................ 277
11.4.1. Модель фазовой диффузии B78). 11.4.2. Уравнение Фоккера-Планка
и ширина линии излучения лазера B80).
11.5. Недиагональные элементы и ширина линии излучения лазера ............ 281
11.6. Аналогия между поведением лазера вблизи порога и фазовым переходом второго
рода .................................................... 283
Приложение 11.А. Решение уравнений для элементов матрицы плотности ....... 286
Приложение 11.Б. Точное решение для лазера в Р-представлении ............ 287
Задачи ...................................................... 290
Список литературы.............................................. 291
Глава 12. Квантовая теория лазера — метод Гейзенберга^Ланжеве-
на
12.1. Простой расчет ширины линии излучения лазера методом Ланжевена, учиты-
учитывающий эффекты атомной памяти ............................... 293
12.2. Квантовые уравнения Ланжевена ................................ 297
12.3. Вывод с-числовых уравнений Ланжевена ........................... 302
12.4. Статистика фотонов и ширина линии излучения лазера. ................ 305
Задачи ...................................................... 308
Список литературы.............................................. 308
Глава 13. Теория микромазера
13.1. Уравнение движения для матрицы плотности ....................... 311
13.2. Статистика фотонов в стационарном состоянии ...................... 312
508 Оглавление
13.3. Создание состояния с определенным числом фотонов в высокодобротном микро-
микромазере ................................................... 315
13.3.1. Редукция состояния C15). 13.3.2. Состояния пленения C18).
13.4. Ширина линии излучения микромазера ............................ 321
Задачи ...................................................... 322
Список литературы.............................................. 322
Глава 14. Корреляционный лазер: концепция, теория и анализ
14.1. Концепция корреляционного лазера .............................. 325
14.2. Корреляционный лазер Ханле: метод оператора плотности .............. 326
14.3. Лазер квантовых биений: качественное описание ..................... 333
14.4. Голографический лазер ....................................... 336
14.5. Квантовые флуктуации фазы и амплитуды ......................... 339
14.6. Двухфотонный корреляционный лазер ............................ 342
14.6.1. Теория C42). 14.6.2. Эвристический расчет двухфотонного КЛ C45).
Приложение 14.А. Спонтанный шум в лазере квантовых биений ............. 347
Задачи ...................................................... 350
Список литературы.............................................. 352
Глава 15. Фазовая чувствительность в квантовых оптических си-
системах: приложения
15.1. КЛ-гироскоп .............................................. 353
15.2. Процесс линейного усиления: общее описание ........................ 356
15.3. Фазово-нечувствительное усиление в двухуровневых системах ............ 358
15.4. Фазово-чувствительное усиление с помощью двухфотонного корреляционного
лазера: усиление свободное от шума .............................. 359
15.5. Лазер с инжекцией сжатого вакуума .............................. 361
Приложение 15.А. Анализ КЛ-гироскопа с реинжекцией ................... 363
Задачи ...................................................... 365
Список литературы.............................................. 365
Глава 16. Сжатие с помощью нелинейных оптических процессов
16.1. Вырожденное параметрическое усиление ........................... 367
16.2. Сжатие в оптическом параметрическом генераторе .................... 369
16.3. Сжатие на выходе резонатора. .................................. 372
16.4. Четырехволновое смешение .................................... 375
16.4.1. Усиление и генерация при четырехволновом смешении C76).
16.4.2. Сжатие при четырехволновом смешении C78).
Приложение 16.А. Влияние фазовых флуктуации накачки на сжатие при вырожден-
вырожденном параметрическом усилении ................................. 380
Приложение 16.Б. Квантово-полевое рассмотрение задачи «вход—выход», приводя-
приводящее к выражению A6.3.4) ..................................... 382
Задачи ...................................................... 384
Список литературы.............................................. 385
Глава 17. Атомная оптика
17.1. Механическое действие света ................................... 388
17.1.1. Отклонение атомов C89). 17.1.2. Лазерное охлаждение C89).
17.1.3. Атомная дифракция C90). 17.1.4. Полуклассическая градиентная
сила C91).
17.2. Атомная интерферометрия .................................... 392
17.2.1. Атомный интерферометр Маха-Цендера C93). 17.2.2. Атомный гиро-
гироскоп C95).
17.3. Квантовый шум в атомном интерферометре ......................... 396
17.4. Пределы лазерного охлаждения ................................. 397
Оглавление 509
17.4.1. Предел отдачи C97). 17.4.2. Селективное по скорости когерентное пле-
пленение населенности C99).
Задачи ...................................................... 400
Список литературы.............................................. 400
Глава 18. Парадокс Эйнштейна, Подольского, Розена, скрытые пе-
переменные и теорема Белла
18.1. Парадокс Эйнштейна, Подольского, Розена ......................... 405
18.2. Неравенство Белла .......................................... 408
18.3. Квантовое вычисление корреляций в теореме Белла ................... 410
18.4. Скрытые переменные с точки зрения квантовой оптики ................ 415
18.5. Теорема Белла без неравенств: равенство Гринбергера-Хорна-Цейлингера . . . 421
18.6. Квантовая криптография ..................................... 423
18.6.1. Протокол Беннета-Брассарда D23). 18.6.2. Квантовая криптография,
основанная на теореме Белла D24).
Приложение 18.А. Квантовая функция распределения для одиночной частицы со
спином вверх .............................................. 424
Приложение 18.Б. Квантовая функция распределения для двух частиц ........ 425
Задачи ...................................................... 427
Список литературы.............................................. 428
Глава 19. Квантовые неразрушающие измерения
19.1. Условия для КН измерений .................................... 431
19.2. КН измерение числа фотонов с помощью оптического эффекта Керра ...... 432
19.3. КН измерение числа фотонов через дисперсионную атомно-полевую связь .... 435
19.4. КН измерения в оптических параметрических процессах ................ 442
Задачи ...................................................... 445
Список литературы.............................................. 445
Глава 20. Квантовые оптические тесты на дополнительность
20.1. «Который путь»-детектор на основе микромазера. .................... 449
20.2. Резонансное взаимодействие атомов с микроволновым полем и его влияние на
движение центра масс атома ................................... 451
20.3. Квантовое стирающее устройство ................................ 452
20.4. Квантовые оптические полосы Рамзи ............................. 457
Приложение 20.А. Эффект отдачи в детекторе типа «который путь» на основе
микромазера .............................................. 460
Задачи ...................................................... 462
Список литературы.............................................. 462
Глава 21. Двухфотонная интерферометрия, проблема квантового
измерения и другие задачи
21.1. Полевая корреляционная функция света, рассеянного двумя атомами ....... 464
21.1.1. Корреляционная функция G^(r,?) при рассеянии двумя возбужденны-
возбужденными атомами D66). 21.1.2. Возбуждение лазерным излучением D67). 21.1.3. Ис-
Использование трех уровней атома в качестве «который путь»-детектора D68).
21.2. Полевая и фотонная корреляции света, рассеянного двумя многоуровневыми
атомами: квантовое стирающее устройство ......................... 469
21.2.1. Альтернативный фотонный базис D71).
21.3. Экспериментальная проверка неравенства Белла через двухфотонные корреля-
корреляции ..................................................... 472
21.4. Двухфотонная каскадная интерферометрия ......................... 474
21.4.1. Двухфотонные корреляции при каскадном излучении атома D75).
21.4.2. Интерферометрия Франсона—Чиао D76).
510 Оглавление
21.5. Двухчастичная интерферометрия с помощью нелинейного преобразования ча-
частоты вниз и отобранных по моменту фотонных пар ................... 478
21.5.1. Интерферометрия на основе преобразования частоты вниз с двумя ис-
источниками D80).
21.6. Эксперимент Зоу-Ванга-Манделя с точки зрения вакуумных флуктуации .... 484
21.7. Спектроскопия высокого разрешения на основе двухфотонной каскадной интер-
интерферометрии ............................................... 486
Приложение 21.А. Рассеяние двумя атомами: операторный подход ............ 490
Приложение 21.Б. Вычисление двухфотонной корреляционной функции в случае
каскадного излучения атома. ................................... 491
Приложение 21.В. Вычисление совместной вероятности отсчета в интерферометрии
Франсона-Чиао ............................................ 493
Задачи ...................................................... 495
Список литературы.............................................. 495
Предметный указатель ........................................... 497
Оглавление ................................................... 504
ОБ АВТОРАХ
Шарлем, О. Скалли удостоен многочисленных наград за свои пи-
пионерские работы в области науки и за преподавательскую деятель-
деятельность по обе стороны Атлантики. Среди них: медаль Адольфа Ломба
Оптического Общества Америки, медаль Элиота Крессона Общества
Франклина, стипендия Гуггенхейма, премия Александра фон Гумболь-
Гумбольдта. М.О. Скалли — действительный член Общества Макса Планка
и член Американского Физического Общества, Оптического Общества
Америки и Американской ассоциации содействия науке. Преподавал
в Йельском университете, Массачусетском технологическом институ-
институте, университете штата Аризона, университете штата Нью-Мексико.
В настоящее время М.О. Скалли является заслуженным профессором
физики, директором центра теоретической физики университета штата
Техас, одним из директоров лазерной лаборатории штата Техас и пригла-
приглашенным научным сотрудником института квантовой оптики им. Макса
Планка.
Ш. Сухейл Зубайри защитил диссертацию в университете г. Ро-
честера в 1978 году. Занимался научной работой и преподавал в уни-
университете г. Рочестера, университете штата Аризона и университете
штата Нью-Мексико. С 1984 года работает в университете им. Каид-э-
Азама в Исламабаде, где он в настоящее время является профессором и
деканом факультета электроники. Занимал приглашенные должности в
институте квантовой оптики им. Макса Планка, университете г. Уль-
ма, университете штата Нью-Мексико и университете г. Кампинаса.
М.С. Зубайри был ассоциированным членом Международного Центра
Теоретической Физики (г. Триест). В 1993 году президент Пакистана
наградил его Звездой Имтиаза. Пакистанская Академия Наук наградила
М.С. Зубайри премией Салама по физике и золотой медалью Академии.
М.С. Зубайри — действительный член Пакистанской Академии Наук и
Оптического Общества Америки.
Научное издание
С К АЛ Л И Марлен Орвил
ЗУ Б АИР И Мухаммад Сухейл
КВАНТОВАЯ ОПТИКА
Редактор М.Б. Козинцова
Оригинал-макет: Е.Ю. Морозов
ЛР №071930 от 06.07.99. Подписано в печать 03.03.03. Формат 70x100/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 41,48. Уч.-изд. л. 56.
Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3.
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72.
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
ISBN 5-9221-0398-9
9 78592203985