Автор: Полубаринова-Кочина П.Я.
Теги: движение жидкостей гидродинамика гидрогеология гидрология
Год: 1977
Текст
П. Я. ПОЛУБАРИНОВА-КОЧИНА
ТЕОРИЯ ДВИЖЕНИЯ
ГРУНТОВЫХ ВОД
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия для студентов университетов,
обучающихся по специальности «Механика*
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1 977
532
П53
УДК 532.5
Теория движения грунтовых вод. П о л у б а р и но в а-Ко ч и н а П. Я.
Изд. 2-е, Главная редакция физико-математической литературы издательства
«Наука», М., 1977, 664 стр.
Книга посвящена в основном математическим методам исследования дви-
движений грунтовых (или подземных) вод.
В разделе об установившихся движениях рассмотрены методы, появив-
появившиеся или получившие дальнейшее развитие после основоположных работ
II. Е. Жуковского^ Н. Н. Павловского: применение теории конформных отоб-
отображений, краевых задач теории функций, аналитической теории линейных
дифференциальных уравнений к задачам о движении воды под плотинами,
в теле земляных плотин, при фильтрации из каналов, в линзах пресной воды
и т. д. Уделено внимание также гидравлическим теориям.
Раздел неустановившихся движений, значительно расширенный по срав-
сравнению с первым изданием, посвящен главным образом гидравлическим теори-
теориям, получившим широкое развитие в последние годы. Рассмотрены задачи, свя-
связанные с орошением.
Книга предназначена для студентов, научных работников и инженеров,
владеющих математикой в объеме вуза, интересующихся теоретическими воп-
вопросами гидротехники и мелиорации.
Табл. 14, илл. 354, библ. 475.
Пелагея Яковлевна Полу бар иное а-Конина
ТЕОРИЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
М., 1977 г., 664 стр. с илл.
Редактор Г. К. Михайлов.
Техн. редактор С. Я. Шкляр. Корректор М. Л.Медведская.
Сдано в набор 2.07.77. Подписано к печати 5.12.77. Бумага 60X90Vie тип. N& I. Физ. печ.
л. 41,5. Условн. печ. л. 41,5. Уч.-изд. л. 40,41. Тираж 5500 экз. Заказ 672
Цена книги 1 р. 80 к.
Издательство «Наука». Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении
Соколовой Союзполиграфпрома при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект, 29.
о 20303—181 |О_ _- © Главная редакция
П ' \oi-t I физико-математической литературы
Obo(Uz)// издательства «Наука», 1977, с изменениями
ОГЛАВЛЕНИЕ
Из предисловия к первому изданию 9
Предисловие ко второму изданию 11
Введение 13
Часть первая
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
Глава /. Физические и математические основы теории движения грунто-
грунтовых вод 17
§ 1. Состав грунта A7). § 2. Пористость грунта B1). § 3. Электро-
Электромолекулярные силы в грунте B4). § 4. Различные состояния воды
в грунте B4). § 5. Скорость фильтрации B8). § 6. Опытные законы
фильтрации C0). § 7. Коэффициент фильтрации C2). § 8. Пределы при-
применимости линейного закона фильтрации и нелинейные законы C5).
§ 9. Капиллярность C6). § 10. Водопроницаемость грунта при неполном
его насыщении C7). § 11. О фильтрационных аномалиях в пористых
средах C9). § 12. Уравнения движения грунтовых вод D3).
Глава II. Плоские движения в вертикальной плоскости 48
А. Общие вопросы 48
§ 1. Уравнения плоского движения D8). § 2. Граничные условия
в плоском установившемся движении D9) § 3. Условия на границе раз-
раздела грунтов E2). § 4. Годограф скорости E3). § 5. Поведение скорости
в угловых точках области движения E6). § 6. Примеры построения годо-
годографа скорости E8). § 7. Треугольник фильтрации F3). § 8. Силы, дей-
действующие на частицы грунта F4). § 9. Уравнения движения при нели-
нелинейных законах фильтрации F7).
Б.. Простейшие примеры плоских движений 73
§ 10. Предварительные замечания G3). § 11. Дренажная щель на во-
доупоре G4). § 12. Горизонтальная дрена при отсутствии водоупора;
изолинии грунтового потока G6). § 13. Плоский флютбет в слое беско-
бесконечной глубины G8). § 14. Шпунт в проницаемом грунте бесконечной
глубины (84). § 15. Флютбет с дренажным отверстием (87).
Глава III. Напорная фильтрация под гидротехническими сооружениями 89
А. Многоугольные области в задачах о напорной
фильтрации. Общие теоремы 89
§ 1. Постановка задачи (Н. Н. Павловский) (89). § 2. Конформное
отображение многоугольника на полуплоскость (89). § 3. Отображение
прямоугольника на полуплоскость (93). § 4. Основной прямоугольник
задач напорной фильтрации (95). § 5. Теорема единственности (97).
§ 6. О движении граничных точек отображаемых областей (99).
4 ОГЛАВЛЕНИЕ
Б. Фильтрация под флютбетами 103
§ 7. Плоский флютбет в слое конечной глубины A03). § 8. Флютбет
при наличии дренирующего основания A07).
В. Обтекание сооружений со шпунтами 109
§ 9. Отображение на полуплоскость многоугольника, все стороны
которого проходят через одну точку A09). § 10. Обтекание наклонного
шпунта A11). § П. Шпунт при наличии водоупора или дренирующего
основания A12). § 12. Плоский флютбет со шпунтом в грунте конечной
глубины A14).
Г. Многошпунтовые схемы 118
§ 13. Метод фрагментов A18). § 14. Многошпунтовые схемы в грунте
бесконечной глубины A20). § 15. Метод фильтрационных сопротивле-
сопротивлений A22).
Д. Гидродинамические реакции на основание пло-
плотины 125
§ 16. Главный вектор сил давления A25). § 17. Главный момент сил
давления A30).
Глава IV. Функция Жуковского и ее приложения. Применение функ-
функциональных уравнений 132
А. Применение функции Жуковского 132
§ 1. Функция Жуковского A32). § 2. Шпунт Жуковского A33).
§ 3. Одиночная дрена A36). § 4. Приток к системе дрен при наличии
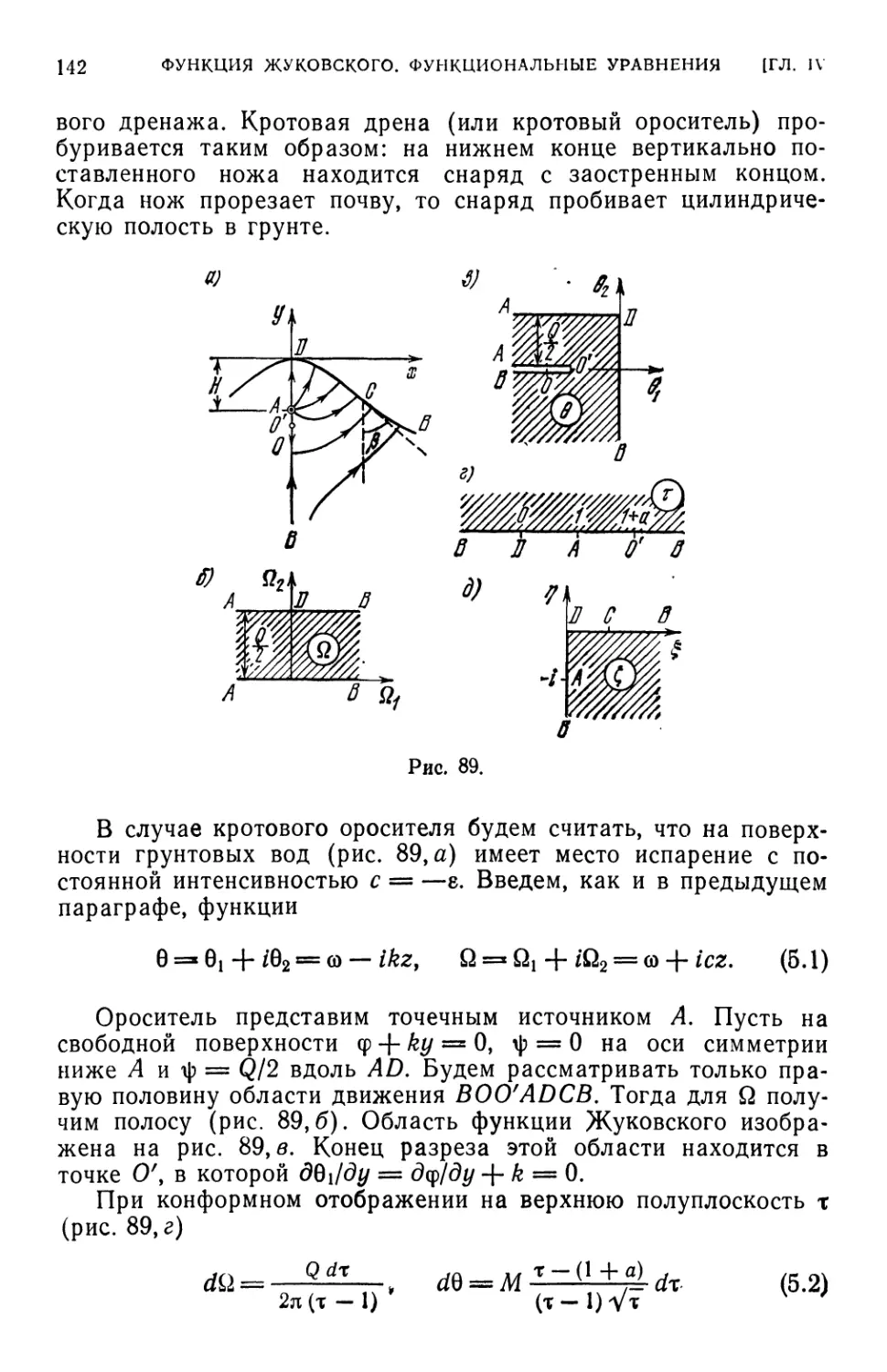
инфильтрации A38). § 5. Кротовый ороситель и кротовая дрена A41).
§ 6. Фильтрация из канала в симметрично расположенные водоприем-
водоприемники A45). § 7. Полуобратные методы решения задач A48).
Б. Применение функциональных уравнений 150
§ 8. Движение грунтовых вод по наклонному водоупору A50).
§ 9. Каналы криволинейного очертания A53). § 10. Земляные плотины
на водопроницаемых основаниях A57). § И. Перемычка Н. М. Герсева-
нова A62).
Глава V. Применение метода инверсии 164
А. Фильтрация из каналов и приток к дренам 164
§ 1. Некоторые свойства инверсии A64). § 2. Фильтрация из канала
трапецеидального сечения A65). § 3. Канал трапецеидального сечения
при учете капиллярности A74). § 4. Канал с малым уровнем воды при
наличии капиллярности A77). § 5. Приток грунтовых вод к дренажной
канаве трапецеидального сечения A81). § 6. Несовершенная галерея
в безнапорном пласте A82).
Б. Флютбет сучастками постоянной скорости 186
§ 7. Заглубленный флютбет со сглаженными углами A86). § 8. Флют-
Флютбет без вертикальных стенок A92). § 9. Контур постоянной скоро-
скорости A93). § 10. «Обтекаемые» флютбет и шпунт в грунте бесконечной
глубины A96).
Глава VI. Смешанная задача теории функций и ее приложения к тео-
теории фильтрации 202
§ 1. Определение аналитической функции по ее действительной части
на действительной оси B02). § 2. Смешанная задача теории функ-
функций B06). § 3. Частный случай задачи B08). § 4. Земляная плотина тра-
ОГЛАВЛЕНИЕ 5
пецеидального профиля на непроницаемом основании при наличии дре-
дренажа B11). § 5. О приведении к смешанной задаче теории аналитиче-
аналитических функций в общем случае плоской задачи фильтрации B31).
§ 6. О фильтрации при наличии дрены или канала в случае наклонного
водоупора B31).
Глава VII. Применение аналитической теории линейных дифференциаль-
дифференциальных уравнений 240
A. Общая теория 240
§ 1. Вводные замечания B40). §,2. Условия на действительной оси
для двух основных функций B40). § 3. Задача определения двух функ-
функций по условиям на действительной оси B42). § 4. Уравнение с тремя
регулярными особыми точками B46). § 5. Гипергеометрические функции
и их свойства B48). § 6. Общий случай кругового многоугольника B50).
§ 7. Случай действительных показателей; второй вывод характеристи-
характеристического уравнения B56). § 8. Показатели для основных случаев теории
фильтрации B59).
Б. Задача о прямоугольной перемычке 264
§ 9. Расход прямоугольной перемычки и совершенного колодца B64).
§ 10. Построение решения для перемычки B68).
B. Задача о перемычке в форме прямоугольной тра-
трапеции 280
§ 11. Фильтрация в трапецеидальной перемычке при испарении B80).
§ 12. Фильтрация в трапецеидальной перемычке в отсутствие испаре-
испарения B84). § 13. О теоремах существования и единственности для задач
о плотинах B89).
Глава VIII. Фильтрация в неоднородных и анизотропных грунтах.
Фильтрация двух жидкостей . . . 291
A. Неоднородные грунты 291
§ 1. Флютбет на двуслойном основании со слоями одинаковой тол-
толщины B91). § 2. Шпунт на двуслойном основании со слоями одинако-
одинаковой толщины C03). § 3. Точечные шпунты в двуслойном грунте C09).
§ 4. Точечный вихрь в многослойной области C12). § 5. Простейшие
движения в слоистых грунтах C17). § 6. Напорная фильтрация в неод-
неоднородных пластах C20).
Б. Анизотропные грунты 323
§ 7. Уравнения движения и примеры C23). § 8. Задача об обтекании
шпунта C26). § 9. Предельно-анизотропные грунты C27).
B. Две жидкости разной плотности 330
§ 10. О движении двух жидкостей разной плотности C30). § 11. Об-
Обтекание точечного шпунта при наличии неподвижного подстилающего .
слоя тяжелой жидкости C33). § 12. О линзе пресной воды над соленой
водой C34). § 13. Фильтрация из канала при наличии засоленных под-
подпорных вод C38).
Глава IX. Колодцы и скважины. Горизонтальные дрены 341
А. Совершенные скважины 341
§ 1. Совершенная скважина в центре пласта C41). § 2. Скважина,
эксцентрично расположенная в круговом пласте C44). § 3. Случай про-
произвольного контура C46). § 4. Об интерференции скважин C48). § 5. При-
Приток к совершенным скважинам в неоднородной среде C50).
б ОГЛАВЛЕНИЕ
Б. Горизонтальные дрены 353
§ 6. Применение метода источников к задачам о горизонтальном
дренаже C53). § 7. Подземный водозабор, питающийся водами соседнего
водоносного пласта C55).
В. Движение в пластах, граничащих со слабо прони-
проницаемы ми пластами 357
§ 8. Вывод уравнений C57). § 9. Движение в одном проницаемом
пласте C60). § 10. Совершенные скважины в напорном пласте C60).
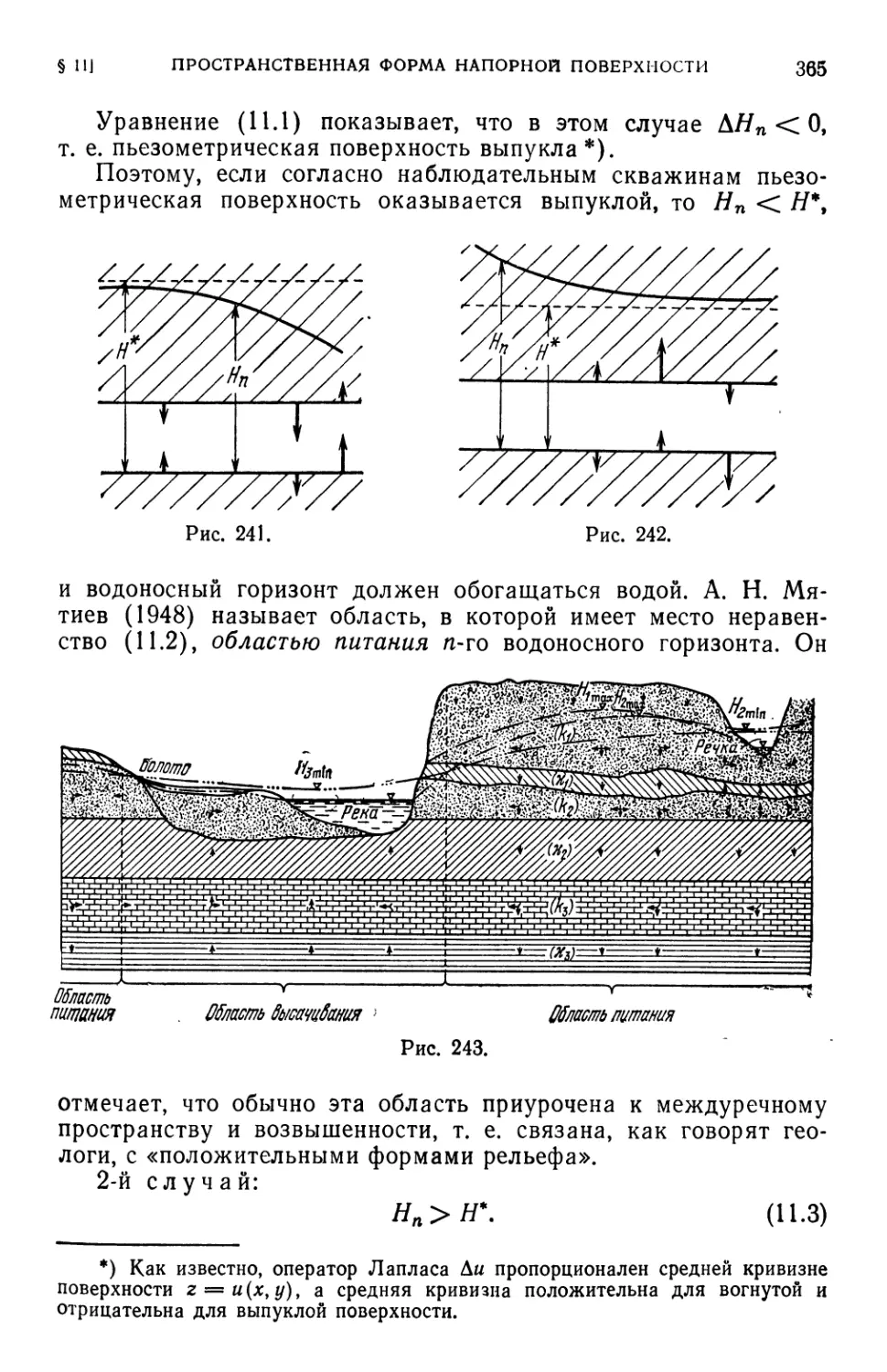
§ 11. О пространственной форме напорной поверхности C64).
Г. Некоторые пространственные задачи 366
§ 12. Несовершенные скважины в полупространстве C66). § 13. Источ-
Источник между двумя горизонтальными плоскостями C67). § 14. Скважина
в пласте с конечным радиусом контура питания C71). § 15. О наклонной
и горизонтальной скважинах в безграничном пространстве C74).
§ 16. Скважина в полупространстве с горизонтальной плоскостью рав-
равного потенциала C76).
Глава X. Гидравлическая теор/.л установившихся движений 381
A. Безнапорные движения при наличии водоупора381
§ 1. Гидравлическая теория и ее основные положения C81).
§ 2. Плоское течение с горизонтальным водоупором C85). § 3. Свобод-
Свободная поверхность при инфильтрации или испарении C86). § 4. Фильтрация
в грунтах, слабо неоднородных по вертикали C87). § б. Фильтрация
в двуслойном грунте с наклонной линией раздела C89).
Б. Безнапорные пространственные и полунапорные
движения 391
§ 6. Связь между пространственными безнапорными и плоскими
напорными движениями C91). § 7. Напорно-безнапорные движения C92).
§ 8. Фильтрация в обход сооружений C94).
B. Движения в пластах с перетоками 398
§ 9. Скважина в безнапорном пласте со слабо проницаемым основа-
основанием C98). § 10. О некоторых движениях с начальными градиен-
градиентами D02).
Часть вторая
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
Глава XI. Об инерционных членах при неустановившихся движениях.
Напорные движения 406
§ 1. О напорных движениях при действующих напорах, зависящих
от времени D06). § 2. О влиянии волнения на фильтрацию под гидро-
гидротехническими сооружениями D09). § 3. Одномерные движения по верти-
вертикали при постоянном действующем напоре D13). § 4. Вертикальная
фильтрация при заданной подаче воды D16). § 5. Вертикальная фильт-
фильтрация в двуслойном грунте D18). § 6. Уравнения неустановившихся дви-
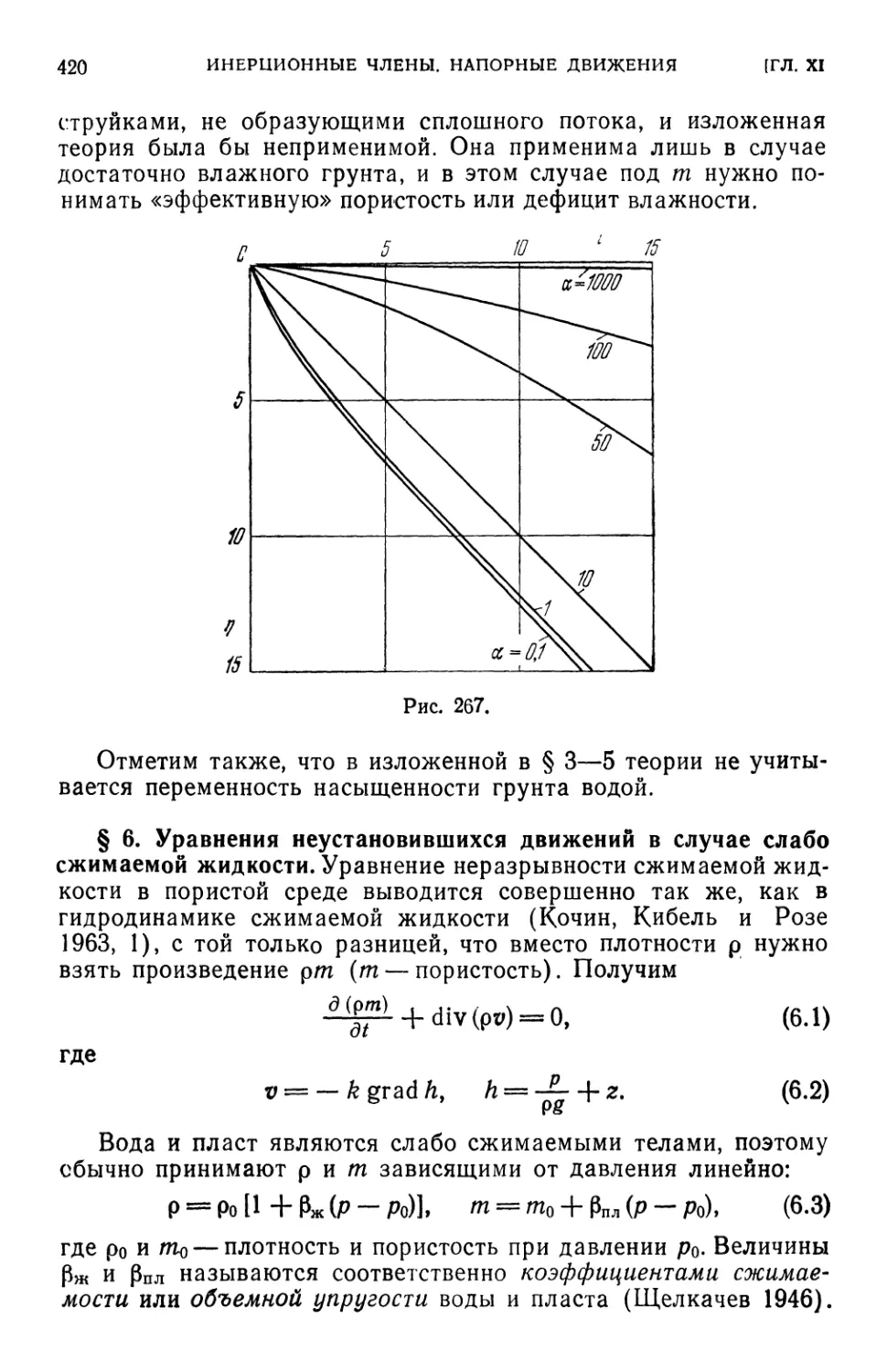
движений в случае слабо сжимаемой жидкости D20). § 7. Скважина в пла-
пласте с непроницаемым водоупором D23). § 8. Скважина в пласте с пере-
перетоками D26).
Глава XII. Нелинейные задачи неустановившихся движений со свобод-
свободной поверхностью 431
§ 1. Вывод основных соотношений D31). § 2. Вывод нелинейного
уравнения D32). § 3. Метод малого параметра D33). § 4. Фильтрация
при изменении уровня воды в водохранилище D34). § 5. Численное ив>
ОГЛАВЛЕНИЕ 7
тегрирование D38). § б. Фильтрация из грунта в пустой бассейн D40).
§ 7. Фильтрация в грунте с нулевым уровнем грунтовых вод D42).
§ 8. Другая форма нелинейного уравнения D45). § 9. Равномерный подъем
уровня воды в канале; решения нелинейного уравнения типа источ-
источника D46). § 10. Задача Буссинеска D48). § 11. Теоремы существования
и некоторые свойства нелинейных уравнений теории фильтрации D50).
Глава XIII. Линеаризованные уравнения неустановившихся безнапорных
движений 452
§ 1. Неустановившиеся движения в безнапорном пласте D52).
§ 2. Просачивание из канала при горизонтальном водоупоре и отсутст-
отсутствии инфильтрации D54). § 3. Приток к скважине в безнапорном пла-
пласте D56). § 4. Скважина в круговой области D57). § 5. Фильтрация
к скважинам при наклонном водоупоре со слабым уклоном D63).
§ 6. Неустановившиеся движения при коэффициенте фильтрации, слабо
меняющемся с высотой D66). § 7. Перемещение поверхности раздела
между двумя жидкостями разной плотности D69). § 8. Пример прост-
пространственной задачи D70).
Глава XIV. Динамика грунтовых вод при поливах 477
А. Образование и растекание бугров грунтовых вод 477
§1.0 поливах и растекании бугров грунтовых вод D77). § 2. Расте-
Растекание бугров D78). § 3. Некоторые случаи поливов D82). § 4. Учет
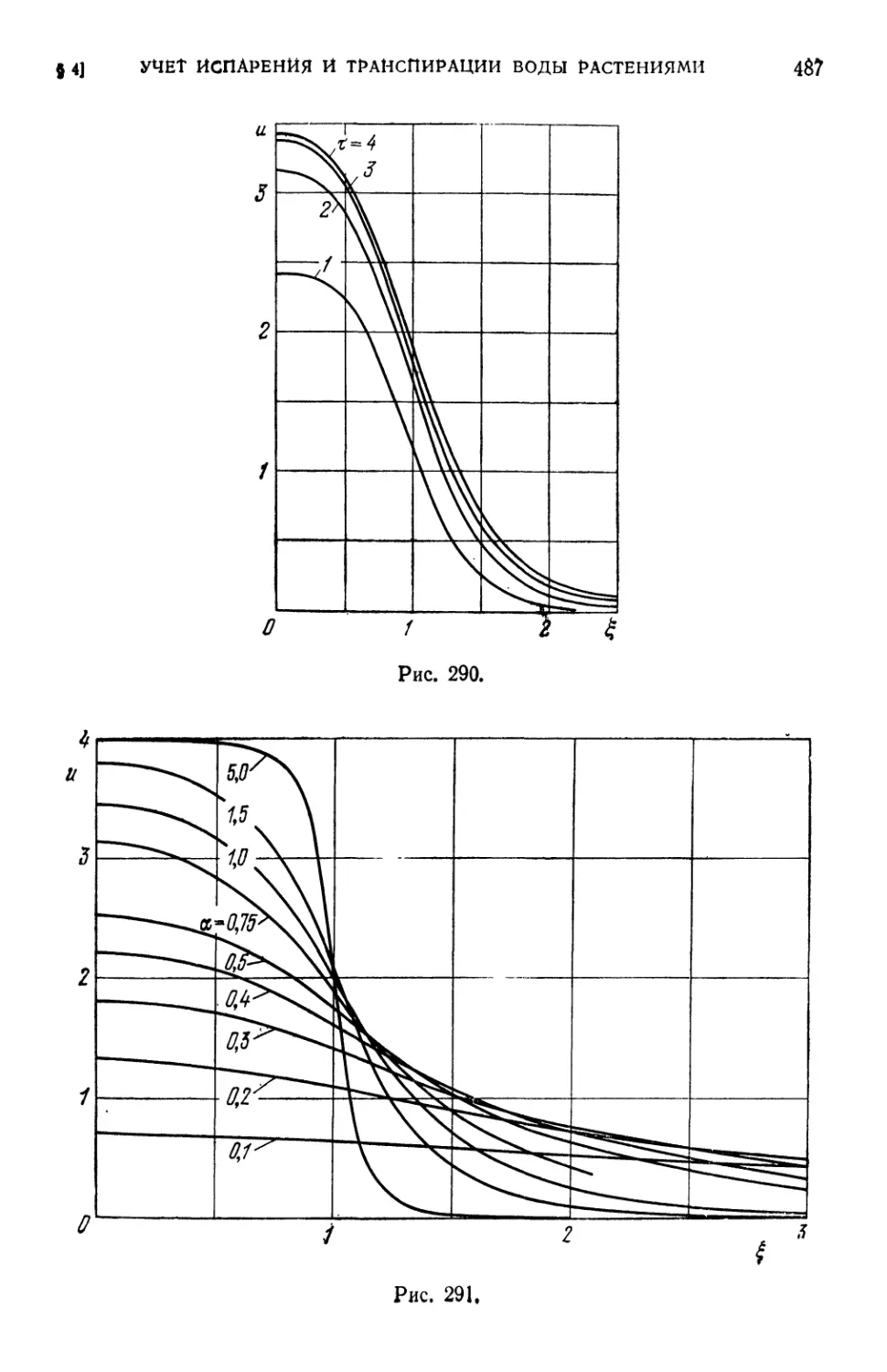
испарения и транспирации воды растениями D85).
Б. О регулировании уровня грунтовых вод при оро-
орошении 488
§ 5. Постановка задачи D88). § 6. Одномерная задача с непрони-
непроницаемым водоупором D89). § 7. Движения с перетоками D96). § S. На-
Начально-краевая задача для движения с перетоками D99). § 9. Случай
переменных уровней воды в каналах E02).
Глава XV. Некоторые вопросы, связанные с орошением 504
А. О фильтрации при неполном насыщении 504
§ 1. Фильтрация в почве при неполном насыщении E04). § 2. Приб-
Приближенное решение простейших задач E06). § 3. Статистический споеоб
определения коэффициентов фильтрации и диффузии E08).
Б. Некоторые вопросы засоления и рассоления
грунтов 511
§ 4. Основные уравнения диффузии и рассоления E11). § 5. Расп-
Распространение индикатора в пористой среде E13). § 6. Модель процесса
конвективного солепакопления в почве E15). § 7. Задача о растворении
и вымыве солей E20). § 8. Два случая точного решения задачи о рас-
рассолении E23).
Глава XVI. Об определении параметров пласта 529
§ 1. Об определении коэффициента фильтрации E29). § 2. О неко-
некоторых обратных задачах уравнений параболического типа E32). § 3. Опре-
Определение переменной проницаемости пласта по натурным наблюдениям
в случае осевой симметрии E35). § 4. О корректности определения коэф-
коэффициента фильтрации E39). § 5. О методе модулирующих функций E40).
§ 6. Метод наименьших квадратов E43).
8 ОГЛАВЛЕНИЕ
Глава XVII. Гидродинамическая теория неустановившихся движений
грунтовых вод 547
§ 1. Условие на свободной поверхности E47). § 2. Задачи о расте-
растекании бугров грунтовых вод в полуплоскости E50). § 3. Те же задачи
при линеаризованном условии E55). § 4. Задача о растекании бугра
грунтовых вод в слое конечной глубины на горизонтальном водо-
упоре E61). § 5. Неустановившийся приток грунтовых вод к точечному
стоку E62). § 6. Задача о стягивании контура нефтеносности E66).
Часть третья
ПРИБЛИЖЕННЫЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИЗУЧЕНИЯ
ДВИЖЕНИЙ ГРУНТОВЫХ ВОД
Глава XVIII. Установившиеся движения грунтовых вод 568
А. Графические и численные методы расчета 568
§ 1. Графический способ построения гидродинамической сетки E68).
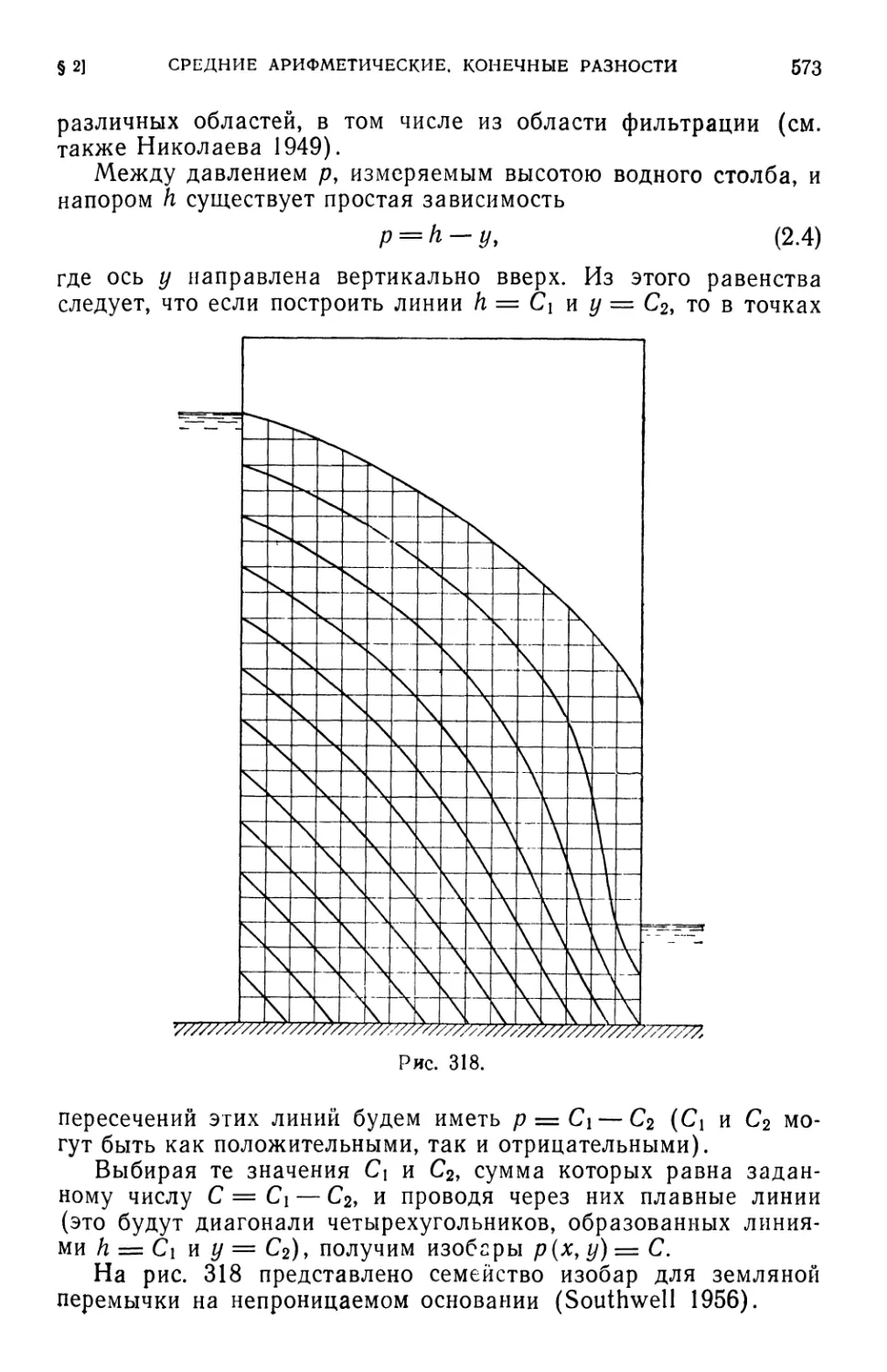
§ 2. Способ средних арифметических, конечные разности E71). § 3. Сетка
в осесимметричном движении E77). § 4. Метод суммарных представле-
представлений E81). § 5. Графо-аналитические построения безнапорных движений
с помощью рассмотрения фиктивного течения в области годографа
скорости E84). § 6. Графоаналитический способ расчета пространствен-
пространственных движений E92). & 7. Метод конечных элементов для интегриро-
интегрирования эллиптических уравнений E95).
Б. Метод электрогидродинамических аналогий (ЭГДА) 601
§ 8. Основные соотношения метода ЭГДА F01). § 9. Применения
метода ЭГДА и другие методы аналогового моделирования F04).
Глава XIX. Неустановившиеся движения грунтовых вод 607
А. Аналитические и численные методы расчета . . •. 607
§ 1. Метод последовательной смены стационарных состояний F07).
§ 2. Радиус влияния скважины; зона влияния F12). § 3. Метод конеч-
конечных разностей F14). § 4. О методе статистических испытаний (метод
Монте-Карло) F17). § 5. Вариационно-разностный метод F20). § 6. Дви-
Движение под действием источников и стоков с нелинейным условием
на свободной поверхности F23).
Б. Опыты в щелевых и грунтовых лотках, натурные
наблюдения 628
§ 7. Теория щелевого лотка F28). § 8. Опыты в грунтовых лотках
и натурные наблюдения F35). § 9. Пример комбинации разных спосо-
способов (задача о промывках) F37).
Литература • 641
Именной указатель 661
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
В основу настоящей книги положены лекции, которые были
прочитаны мной несколько раз в Московском государственном
университете имени М. В. Ломоносова для студентов-гидроме-
студентов-гидромехаников механико-математического факультета. Содержание
лекций в книге значительно расширено.
Материал книги расположен в основном по методам мате-
математического исследования и частично по объектам изучения.
Мне хотелось дать такое изложение математических методов
исследования в гидромеханике грунтового потока, чтобы лица,
изучающие настоящую книгу, могли усвоить эти методы и быть
в состоянии прилагать их к решению новых задач фильтрации.
Однако вследствие обширности имеющегося материала по этому
разделу гидромеханики пришлось ограничить себя в выборе за-
задач. Так как автор не является специалистом-практиком, то
этот выбор диктовался, быть может, несколько субъективными
представлениями, а также желанием дать иллюстративный ма-
материал для математических методов.
Основное содержание книги составляет изложение теории
движения грунтовой воды, рассматриваемой как несжимаемая
жидкость в случае, когда можно считать закон фильтрации ли-
линейным и можно пренебрегать наличием воздуха в грунте. По-
Поэтому разделы, касающиеся других случаев, выделены в мел-
мелкий шрифт. Этим же шрифтом выделены громоздкие решения
некоторых задач, представляющие принципиальный интерес, но
еще мало использованные для приложений.
Там, где это возможно, задачи приводятся доведенными до
численных или графических результатов, причем указывается,
где можно найти данные расчетов, если из-за экономии места
они не приведены.
Г. Н. Положим предоставил в мое распоряжение свои
исследования по вариационным задачам и другим вопросам,
Ю ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
С. Н. Нумеров —дополнительные исследования и вычисления
к своим задачам, изложенным здесь в § 4 и 7 главы VI, за чго
я выражаю им обоим глубокую благодарность.
Г. К. Михайлов проделал большую работу при подготовке
книги к печати; он произвел некоторые дополнительные вычис-
вычисления; рядом его советов я воспользовалась, в особенности по
главе первой; кроме того, им написан § 12 главы VII. Разно-
Разнообразную помощь мне оказывали М. М. Семчинова и другие
сотрудники Института механики Академии наук Союза ССР,
а также Н. Н. Кочина. Выражаю им всем искреннюю благо-
благодарность.
П. Полубаринова-Кочина
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
За четверть века, прошедшую со времени появле-
появления первого издания этой книги A952 г.), теория
фильтрации и ее часть — теория движения грунтовых
вод получили широкое развитие благодаря трудам
исследователей во многих странах. Поэтому теперь
мою книгу правильнее было бы назвать «Введением
в теорию движения грунтовых вод».
Основной характер книги остался прежним, но
она подверглась некоторым деформациям.
В первом издании обширной была часть первая,
посвященная установившимся движениям. Здесь ста-
старый материал несколько сокращен, выброшены неко-
некоторые громоздкие или менее интересные примеры,
а также несущественные рисунки; кое-где сокращены
математические выкладки. Те или иные добавления
сделаны почти во всех главах. Приближенные методы
расширены и выделены в часть третью.
Часть вторая, посвященная неустановившимся
движениям, расширена; она содержит семь глав вме-
вместо прежних пяти. Новыми являются главы XV, XVI
и вторая часть главы XIV.
Литература по теории движения грунтовых вод
достигла за последние десятилетия практически не-
необозримого объема. В связи с этим в одной книге
невозможно отразить сколько-нибудь представительно
все существующие направления исследований. Не
ставя себе вовсе этой цели, я отдавала предпочтение
при выборе материала преимущественно работам,
близким мне по стилю, и работам моих учеников. По-
Последнее особенно характерно для второй части книги.
предисловие: ко второму изданию
Это обстоятельство читатель должен постоянно иметь
в виду при работе с книгой.
Глава XVI написана для настоящего издания
И. Б. Басовичем, а вторая часть главы XIV — Н. Н. Ко-
чиной, которая оказала также большую помощь по
всей книге, за что я им обоим очень признательна.
Особую благодарность я должна принести редактору
книги Г. К. Михайлову, который не только заботился
об улучшении изложения материала, но и вникал и
его содержание, дав мне ряд очень ценных советов.
Я благодарю также моих бывших сотрудниц
Н. В. Волженскую и В. М. Егорову за помощь прд.
оформлении рукописи книги.
П. Полубаринова-Конина
ВВЕДЕНИЕ
Главное содержание настоящей книги составляет изложение
математических теорий, применяемых к исследованию движений
грунтовых вод. Гидрогеологи называют грунтовыми подземные
воды верхнего горизонта. В этой книге затрагиваются и движе-
движения в нижележащих пластах.
Начало развития теории движения подземных вод относится
к 50-м годам прошлого века, когда инженер А. Дарси A803—
1858) стал работать над проектом системы водоснабжения
г. Дижона (Франция). В 1856 г. Дарси выпустил книгу, содер-
содержащую подробный отчет, исторические сведения и описание
опытов по фильтрации воды через песок в цилиндре. Дарси
установил простейший закон просачивания воды в песке, на-
названный его именем. Многочисленные опыты других исследова-
исследователей подтвердили справедливость закона Дарси в определен-
определенных условиях для ряда грунтов и установили границы его при-
применимости.
Ж. Дюпюи A804—1866) дал основы гидравлической теории
движения грунтовых вод, рассмотрел неравномерные движения
при наклонном водоупоре, вывел формулы для дебитов притока
к дрене и к колодцу, которые названы его именем.
Ж. Буссинеск A842—1929) внес дальнейший вклад в разви-
развитие гидравлической теории, вывел условия на свободной по-
поверхности грунтового потока, решил ряд задач о неустановив-
неустановившихся его движениях.
В Германии А.Тим A836—1908),главный инженер-строитель
Дрездена, пришел к ряду тех же результатов, что и Дюпюи;
формулы последнего для дебита иногда называют формулами
Дюпюи — Тима.
Ф.Форхгеймер A852—1933), профессор гидравлики в Ахене,
затем в Граце, ввел в рассмотрение гидродинамические сетки
14 ВВЕДЕНИЕ
движения, указал переход от напорного движения к безнапор-
безнапорному, применяя уравнение Лапласа к квадрату напора, развил
теорию колодцев.
Ч. Сликтер A864—1946) в США провел ряд исследований
независимо от европейских ученых, не зная их работ, и повто-
повторил ряд их результатов. В работе 1899 г. ему принадлежит
изучение движения жидкости в идеальном грунте, состоящем из
шариков одинакового размера при различных способах их
укладки.
К 1889 г. относится первая работа Н. Е. Жуковского
A847—1921) по теории фильтрации: «Теоретическое исследо-
исследование о движении подпочвенных вод», в которой он выводит
дифференциальные уравнения фильтрации. В следующей ра-
работе, 1890 г.: «О влиянии давления на насыщенные водою
пески», Жуковский пользуется результатами наблюдений
К. Э. Лембке над колодцами Костромской губернии. Лембке
опубликовал ряд теоретических работ, начиная с 1886 г., где
он, в частности, применяет к неустановившимся движениям
грунтовых вод приближенный метод, который позже был вновь
открыт и развит И. А. Чарным и др. и назван методом после-
последовательной смены стационарных состояний. v
В России большую роль для своего времени сыграла книга
А. А. Краснопольского A912) о грунтовых и артезианских ко-
колодцах. В ней изложены имевшиеся к тому времени теоретиче-
теоретические результаты, а также исследования самого автора по филь-
фильтрации в трещиноватых породах — нелинейный закон филь-
фильтрации.
Значительного развития теория фильтрации достигла в
СССР.
Н. Н. Павловским A884—1937) была создана строгая мате-
математическая теория движения грунтовых вод под гидротехниче-
гидротехническими сооружениями; она была изложена в его книге 1922 г.
Эти исследования были продолжены в многочисленных работах
его учеников и последователей. Н. Н. Павловскому принадле-
принадлежат и первые работы по некоторым безнапорным движениям.
Одновременно такие движения стал изучать В. В. Ведерни-
Ведерников, в частности, задачи о каналах, с применением метода ин-
инверсии.
ВВЕДЕНИЕ 15
Н. Н. Павловский положил начало применению эксперимен-
экспериментального метода электрогидродинамических аналогий (ЭГДА),
который получил дальнейшее развитие в трудах П. Ф. Фильча-
кова и Н. И. Дружинина и в настоящее время широко исполь-
используется в научно-исследовательских и проектных организациях.
Работы Н. Н. Павловского привлекли внимание Н. Е. Жу-
Жуковского, который снова начал думать о задачах подземной
гидромеханики и дал в 1920 г. постановку задач, приведших
к понятиям о «дрене Жуковского» и «шпунте Жуковского» (ра-
(работа Жуковского была опубликована посмертно в 1923 г.). Так
называемая функция Жуковского применяется теперь при ре-
решении ряда задач о движениях со свободной поверхностью.
С. Н. Нумеров A939) развил собственный метод решения
фильтрационных задач — приведение к смешанной задаче тео-
теории аналитических функций, аналогичный предложенному не-
несколько позже и затем широко развитому Ф. Д. Гаховым
и Н. И. Мусхелишвили методу краевых задач.
Возможность применения к ряду задач фильтрации анали-
аналитической теории линейных дифференциальных уравнений была
указана Н. Е. Кочиным и получила развитие в работах
П. Я. Полубариновой-Кочиной, Б. К. Ризенкампфа и других
в конце 30-х и в 40-х годах.
Г. Н. Положему A914—1968) принадлежат значительные ис-
исследования по применению вариационных принципов в теории
движения грунтовых вод, некоторым приближенным методам,
применению обобщенных аналитических функций.
Н. К. Гиринский и А. Н. Мятиев в 1946—1947 гг. дали тео-
теорию движения подземных вод в проницаемых пластах, чередую-
чередующихся со слабо проницаемыми, — то, что теперь получило за
границей название теории перетекания. Начала этой теории,
остававшиеся неизвестными советским авторам, были еще
раньше опубликованы в Голландии. В настоящее время теория
перетекания получила значительное развитие в ряде стран. Та-
Такая же судьба постигла многие другие исследования, которые
были переоткрыты в разных странах из-за незнания языка или
малой осведомленности авторов.
Ряд новых направлений в теории фильтрации, в частности,
в задачах диффузии и растворения солей, начат Н. Н. Вериги-
Ным и развивается его учениками.
16 ВВЕДЕНИЕ
И. А. Чарный A909—1967) дал свои знаменитые формулы
для дебита перемычки и колодца, совпавшие внешне с форму-
формулами Дюпюи.
В последние десятилетия исследования движений жидкостей
в подземных пластах ведутся очень интенсивно как в Советском
Союзе, так и за рубежом, о чем можно получить представление,
если рассмотреть список литературы в конце настоящей книги *)
и выделить в нем работы, вышедшие в свет после 1950 г. В связи
с появившимися возможностями расчетов на ЭВМ появилась
большая литература по приближенным методам. В ряде горо-
городов СССР и других стран сложились свои школы по теории
движений как воды, так и нефти и газа в подземных пластах.
В настоящей книге представлена лишь незначительная часть
накопившихся обширных исследований.
*) Список литературы составлен в алфавитном порядке авторов и
ссылки на него даются по фамилии автора и году публикации соответствую-
соответствующей работы.
Часть первая
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
Глава I
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
§ 1. Состав грунта. Прежде чем перейти к изложению мате-
математических теорий движения грунтовых вод, приведем в крат-
кратких чертах, не вдаваясь в детали, основные сведения о свой-
свойствах грунта.
Грунт следует рассматривать как единую систему, состоя-
состоящую из минеральных частиц, коллоидных частиц, окружающей
их воды с растворенными в ней солями и газообразной фазы
(воздух, пары воды). С этой точки зрения то, что обычно назы-
называют грунтом, составляет собственно твердую фазу грунта.
Ниже будет дано формальное определение термина грунто-
грунтовые воды (см. § 4). Здесь же мы отметим, что Н. Е. Жуковский
называл эти воды подпочвенными и говорил о просачивании их
через плотины. Эти выражения сразу дают наглядное пред-
представление о том, какое явление рассматривается. Укоренив-
Укоренившийся у нас термин фильтрация равносилен понятию просачи-
просачивания, т. е. медленного движения в пористой среде.
Движение грунтовых вод происходит в верхнем слое земной
коры. Обычно представляют основной интерес верхние водопро-
водопроницаемые горизонты, на глубине нескольких метров или не-
нескольких десятков метров. Однако полное изучение движения
грунтовых вод и взаимодействия между водами отдельных го-
горизонтов требует знания и того, что делается на больших глу-
глубинах. Современные методы бурения позволяют получать сква-
скважины глубиной в несколько километров.
Грунты можно разделить на скальные и нескальные, или
рыхлые. Нескальные грунты образуются путем разрушения
скальных пород. Они образуют грунты двух основных видов;
грунты типа песков (несвязные) и типа глин (связные) (Прик-
лонский 1955).
18 ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. I
Типичный песок в сухом состоянии представляет сыпучее
тело, которое по мере увлажнения переходит временно в связ-
связное состояние. Влажность песка колеблется в небольших преде-
пределах, и при любой степени увлажнения песок лишен пластич-
пластичности, т. е. свойства сохранять данную ему форму. Песок
сильно водопроницаем, не набухает, обладает незначитель-
незначительным капиллярным поднятием воды и при высыхании не дает
усадки.
Глина может быть в трех состояниях: текучем, пластичном
и твердом. Связность глины может быть настолько высокой, что
при ее разработке применяются иногда взрывные работы. Влаж-
Влажность глин может колебаться в очень широких пределах. Глина
слабо водопроницаема, а в пластичном состоянии практически
непроницаема, набухает сильно, имеет большое капиллярное
поднятие, при высыхании дает большую усадку, причем умень-
уменьшение ее объема сопровождается растрескиванием.
Песчинки имеют вид зерен, приближающихся к кубической
или округлой форме, глинистые же частицы имеют форму че-
чешуек или пластинок. Удельная поверхность частиц глин значи-
значительно больше, чем частиц песков, что является одной из причин
больших молекулярных сил взаимодействия между частицами
глины и воды.
Свойства обычных грунтов являются промежуточными
между свойствами песков и глин (супесиу суглинки).
Грунты, у которых содержание глинистых частиц превышает
60% (по объему) от общего количества частиц, называют тя-
тяжелыми глинами; те же, в которых количество глинистых частиц
колеблется между 30 и 60%, называют глинами. Суглинки
(разделяемые на тяжелые, средние и легкие) содержат от 10 до
30% глинистых частиц, супеси (тяжелые и легкие) — от 3 до
10% и, наконец, пески могут содержать до 3% глинистых
частиц.
В строительной практике применяется классификация частиц
грунта по их размерам, приведенная в таблице 1 (Аравин и Ну-
Нумеров 1948). Существуют и другие разделения частиц по их
крупности. Так, например, если частицы грунта имеют диаметр
больше 3 мм, то почвоведы говорят, что они составляют каме-
каменистую часть почвы; частицы от 3 до 0,01 мм называют «физиче-
«физическим» песком, мельче 0,01 мм—«физической» глиной; частицы
мельче 0,001 мм называют иногда илом, мельче 0,0001 мм —
коллоидными частицами. Ниже (см. § 4) будет указана важная
роль коллоидных частиц во взаимодействии между водой и
частицами грунта и влияние их на физические свойства грунта
(Качинский 1975; Сергеев 1952).
Разрез верхнего слоя земной коры на глубину порядка не-
нескольких десятков метров показывает, что грунт обычно имеет
СОСТАВ ГРУНТА
19
слоистую структуру. В пределах каждого слоя грунт состоит
из частиц различной формы и крупности (таблица 1).
Таблица 1
Диаметры фракций, составляющих грунт
Наименование фракций
Глинистые
Пылеватые
Песчаные
Гравелистые
Галька
Валуны
мелкие
[ крупные
очень мелкие
мелкие
средние
крупные
мелкие
средние
, крупные
Диаметры
в мм
< 0,005
0,005—0,01
0,01—0,05
0,05-0,25
0,25-0,5
0,5-1,0
1,0-2,0
2,0-4,0
4,0-10
10—20
20—60
>60
Под почвой понимают поверхностные слои грунта, обладаю-
обладающие плодородием, переработанные и измененные совместным
действием климата, растительных и животных организмов и
деятельностью человека. Фильтрация воды в почве имеет свои
особенности по сравнению с фильтрацией в грунте, которые мы
будем иногда отмечать. Исследуя явления, имеющие место как
в почвах, так и в грунтах, употребляют также название почво-
грунты.
Чтобы получить понятие о составе данного грунта, произво-
производят анализ крупности его составных чаотей или фракций, на-
например, при помощи просеивания грунта через ряд сит с отвер-
отверстиями разных размеров.
Стремление охарактеризовать крупность грунта одним чис-
числом приводит к понятию гранулометрического показателя, ко-
который разными авторами определяется по-разному — некото-
некоторыми, например, как средний или эффективный диаметр частиц
^Эф. За него иногда принимают диаметр ^ю, равный диаметру
отверстия сита, сквозь которое просеивается 10% от пробы
грунта по весу (и на котором остается 90% по весу).
В качестве примера в таблице 2 дается гранулометрический
состав образца овражного песка (Черкасов 1958). В приведен-
приведенном составе песка пять мелких фракций дают в сумме 0,66 +
+ 0,66+1,32 + 2,27 + 3,08 = 7,99%, т. е. на 2% меньше 10%.
Это означает, что d\0 лежит в промежутке между 0,10 и 0,25 мм.
Интерполяция дает dio = 0,11 мм.
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. 1
Таблица 2
Гранулометрический состав овражного песка
Диаметры ча-
частиц в мм
Фракции в %
от веса сухой
почвы
1,0-0,25
40,70
0,25-0,10
51,32
0,10-0,05
3,08
0,05-0,01
2,27
0,01-0,005
1,32
0,005-0,0025
0,66
< 0,0025
0,66
75
50
25
/
/
/
1
- —
Рпс. 1.
Сыпучие материалы входят в состав осадочных горных по-
пород, образующихся в результате механического разрушения ра-
ранее существовавших пород.
100%\ 1 1 i i i i При этом частицы претерпе-
претерпевают дальнейшие изменения
степени дробления, формы,
окатанности и т. п. на их
пути к месту формирования
осадочной породы. А.Н. Кол-
Колмогоров A941) показал, что
при определенных условиях
последовательного дробле-
дробления частиц их размеры под-
подчиняются логарифмически
нормальному закону распре-
распределения. И действительно,
распределение логарифма
диаметра частиц во многих
случаях бывает близким к
нормальному, а отклонения
от этого закона рассматри-
рассматриваются как свидетельство
того, что данный грунт яв-
является смесью разных есте-
естественных грунтов.
На рис. I дана кривая
механического, или грануло-
гранулометрического, анализа грун-
грунта средней крупности (При-
клонский 1955): по оси абс-
абсцисс откладываются диаметры частиц грунта в мм, по оси орди-
ординат—процентные отношения суммарного веса частиц, меньших
данного диаметра, к весу всех частиц исследуемого образца. На
рис. 2 та же кривая дана в полулогарифмическом масштабе: по
оси абсцисс отложены логарифмы диаметров частиц грунта. На
этом же рисунке пунктирной линией показана кривая распреде-
распределения для того же грунта, которая, как видно, близка к логарифм
мически-нормальной.
100%
75
25
—-
J
/
/
/
/
f ^r
f
1
J
\
\
1
/
\
\
/
\
\
\
\
4,
0,01
0,1
Рис. 2.
с!,мм
10
ПОРИСТОСТЬ ГРУНТА 21
§ 2. Пористость грунта. Возьмем некоторый образец грунта
объема V. Пусть объем всех пор в этом образце будет V\. Отно-
Отношение V\ к V называется пористостью грунта, порозностью или
скважностью. Обозначим эту величину буквой а:
а— v .
Другими словами, пористость есть суммарный объем всех
пор, имеющихся в единице объема грунта.
Пористость зависит от характера грунта, от его геологиче-
геологического происхождения, от испытываемого им давления, обра-
обработки почвы и т. д.; она зависит от утрамбовки грунта (что
часто наблюдается в лабораторных условиях) и может изме-
изменяться со временем.
Поперечный размер отдельной поры колеблется от 2—3 см
до малых долей микрона.
Если бы грунт состоял из шариков одинакового размера, то можно
было бы найти теоретически пористость при различных правильных распо-
расположениях частиц. Так, при кубическом расположении шаров (когда шары
можно считать вписанными в кубическую решетку) примем V = d3, где
d — диаметр шара; тогда У] = сР—(я/6)сC (разность между объемами куба
и шара). Для пористости получаем
0—lL-l-i-0,476...
В книгах по теории фильтрации кубическое расположение рассматри-
рассматривается как наименее плотное из всех правильных расположений, в качестве
же наиболее плотного указывается «ромбоэд-
«ромбоэдрическое» расположение, которое получится,
если уложить наиболее плотно ряд шаров
на плоскости (рис. 3) и затем такие ряды
накладывать один на другой так, чтобы ша-
шары второго ряда попадали в углубления пер-
первого. При этом пористость будет равна
(Slichler 1899)
ael_ WL-0.2G0...
о —
Последнее значение а есть действитель-
действительное наименьшее, что же касается кубической
укладки, то она является наименее плотной лишь среди вполне
однородных укладок. Чтобы пояснить это, заметим, что в ромбоэдрической
укладке каждый шар соприкасается с двенадцатью шарами: так, на рис. 3
заштрихованный шар граничит с шестью шарами, центры которых лежат
в одной плоскости, и, кроме того, с не изображенными на чертеже тремя
шарами верхнего и тремя шарами нижнего ряда. В кубической же укладке
каждый шар соприкасается с шестью шарами Были рассмотрены укладки,
при которых каждый шар касается четырех шаров (Гильберт и Кон-Фосссн
1951). Одна из них, «тетраэдральная», при которой указанные четыре шара
размещаются в вершинах тетраэдра (внутри которого находится первый
ШаР)> дает пористость 0,660 (рис. 4,а). Другая укладка, еще более разре-
22
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[ГЛ. I
женная, дает пористость, равную 0,876 (рис. 4,6). Это, по-видимому, наи-
наибольшая из известных пористость правильной твердой решетки одинаковых
шаров, при которой шары удерживаются друг другом (последнее обстоятель-
обстоятельство обеспечивается тем,
что каждый шар касается
четырех шаров, центры ко-
которых не лежат в одной
плоскости). Рис. 4 сделан
Г. К. Михайловым A952,1).
В естественных грун-
грунтах пористость должна
меняться в широких
пределах, так как
структура грунтов мо-
может быть сложной и
разнообразной. Так,
почвы имеют сложную
комковатую структуру.
На рис. 5 дан пример
неоднородной глини-
глинистой породы, состоя-
состоящей из крупных песча-
песчаных зерен (У), мелких
пылеватых зерен (J?),
неуплотненных глини-
глинистых частиц в порах между крупными частицами C) и уплот-
уплотненных глинистых частиц на контакте между крупными части-
частицами D) (Роде 1965).
В таблице 3 даются значения пористости для ряда грунтов
(Аравин и Нумеров 1948).
Таблица 3
Паристость грунтов
Рис. 4.
Наименование грунта
Пористость
Гравий (с диаметром частиц от 2 до 20 мм)
Пески (с диаметром частиц от 0,05 до 2 мм)
Супесь
Суглинок
Глинистый грунт
Торфяной грунт
0,30—0,40
0,30—0,45
0,35-0,45
0,35-0,50
0,40-0,55
0,60—0,80
В книге А. А. Роде A965) пределы пористости почвы ука-
указаны от 25 до 90% и выше.
Для трещиноватых горных пород по аналогии вводится по-
понятие трещиноватости, т. е. отношения объема трещин образца
данного грунта к общему объему образца (Ломизе 1951),
§2]
ПОРИСТОСТЬ ГРУНТА
23
Бывает, что после дождя уровень грунтовых вод, залегаю-
залегающих на некоторой глубине под поверхностью земли, сильно под-
поднимается. Так, если дождя выпало 2—3 см, то грунтовые воды
могут подняться на 20—30 см. Если бы непосредственно над
свободной поверхностью грунтовых вод грунт был сухим, то,
принимая во внимание значения пористости, приведенные в таб-
таблице 3, можно было бы ожидать подъема грунтовых вод, пре-
превышающего высоту выпавших осадков максимум в 3—4 раза.
Рис. 5,
Получающиеся же 10—12-кратные подъемы объясняются тем,
что у поверхности грунтовых вод грунт является увлажненным,
что уменьшает объем просветов между частицами грунта, мо-
могущих быть заполненными водой. Нужно еще заметить, что при
подъеме грунтовых вод не весь объем этих просветов будет за-
заполняться водой, так как в порах остается некоторое количе-
количество защемленного воздуха. При опускании уровня грунтовых
вод от воды освобождается также не весь объем порового про-
пространства, так как грунт остается влажным.
В связи с этим вводят понятие об активной пористости грун-
грунта, взятого из зоны осушения или зоны, прилегающей к поверх-
поверхности грунтовых вод: это есть отношение объема пор, не заня-
занятых связанной с грунтом водой, к общему объему образца.
Активная пористость может быть порядка 0,1 и меньше.
24
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[ГЛ. I
§ 3. Электромолекулярные силы в грунте. Между твердыми
частицами грунта и водой существуют электромолекулярные
силы взаимодействия. Вода состоит из полярных молекул с
ионами водорода, заряженными положительно, и ионами кисло-
кислорода, заряженными отрицательно. При действии внешнего
электрического поля происходит поляризация молекул и ориен-
ориентация диполей воды в элек-
электрическом поле (Цытович
1963).
Так как диэлектрическая
постоянная твердых частиц
сильно отличается от ди-
диэлектрической постоянной
воды, то при соприкоснове-
соприкосновении частиц грунта с водой
возникает электрическое по-
поле с избыточной энергией на
поверхности частиц грунта
и диполи воды притягивают-
притягиваются к поверхности минераль-
минеральных частиц.
Силы притяжения дей-
действуют на весьма близких
расстояниях от поверхности
частицы: до 0,01 мкм для
очень чистых неполярных
неполимерных жидкостей до
10 мкм для полимерных рас-
растворов A мкм = 0,001 мм).
Величина молекулярных сил
огромна у поверхности час-
частицы (порядка десятков ты-
тысяч килограммов на квад-
квадратный сантиметр) и быстро убывает с расстоянием. Область си-
силового действия измеряется толщиной нескольких слоев молекул.
На рис. 6 показана схема взаимодействия молекулярных сил
на границе раздела воды и твердой частицы. Рис. 6, а представ-
представляет в увеличенном виде часть рис. 6,6. На ней показана ориен-
ориентация диполей воды возле глинистой частицы (Цытович 1963).
Электрический заряд глинистых фракций имеет большое
значение при осушении грунтов методом электродренажа (Ло-
мизе и Нетушил 1958).
§ 4. Различные состояния воды в грунте. Молекулы воды, не-
непосредственно окружающие частицу грунта, подвержены столь
большим силам притяжения (см. § 3), что они оказываются
Прочно обязанная
(адсорбированная)
Рыхло оВязанная
'(лиосордиробанная)
язанная\ ^ Сдоёодная дода
<0%5мкм
Рис. 6.
§ 4] РАЗЛИЧНЫЕ СОСТОЯНИЯ ВОДЫ В ГРУНТЕ 25
прочно связанными с поверхностью частиц. Это те частицы
воды, которые не удается отделить даже центрифугированием,
развивающим силы, в несколько десятков тысяч раз превосхо-
превосходящие силу тяжести. Эти молекулы образуют так называемую
прочно связанную воду. Слои прочно связанной воды, толщина
которых имеет порядок нескольких десятков рядов молекул, в
свою очередь связывают и ориентируют прилегающие к ним
молекулы воды. Последние образуют рыхло связанную воду.
Провести строгую границу между прочно связанной и рыхло
связанной водой трудно.
Основы классификации видов влаги в почвах и грунтах были
даны А. Ф. Лебедевым A936). Он различает следующие формы
воды в грунтах: 1) водяной пар, 2) гигроскопическую воду,
3) пленочную воду, 4) гравитационную воду, 5) воду в твердом
состоянии, 6) кристаллическую воду и 7) химически связанную
воду. Последние три категории А. Ф. Лебедев не изучал. Рас-
Рассмотрим четыре первые.
1. Водяной пар заполняет все свободные пустоты грунта и
передвигается из областей с повышенным давлением в области
с более низким давлением. А. Ф. Лебедев считал конденсацию
перемещающихся в грунте паров воды одной из причин образо-
образования грунтовых вод, особенно в глубоких горизонтах.
2. Гигроскопическая вода — это вода, конденсирующаяся на
поверхности частиц. Если сухой грунт поместить во влажный
воздух, то частицы грунта будут адсорбировать пары, вес
грунта будет увеличиваться, пока не достигнет некоторой вели-
величины, соответствующей максимальной гигроскопичности. Для
различных грунтов максимальная гигроскопичность может иметь
такие значения: для песков — около 1%, для пыли — до 7%, для
глины — до 17% от веса сухого вещества.
Согласно А. Ф. Лебедеву гигроскопическая вода может пе-
передвигаться в грунте, только переходя в парообразное со-
состояние.
3. Пленочная вода образуется на частицах под влиянием
молекулярных сил сцепления. Она удерживается с большой си-
силой и не может быть удалена из грунта центрифугированием с
ускорением, в десятки тысяч раз превышающим ускорение силы
тяжести. Пленочная вода способна передвигаться как жидкость
от более толстых пленок к более тонким. Сила тяжести не ока-
оказывает влияния на движение пленочной влаги. Влажность грун-
грунта, отвечающая максимальной толщине пленочной воды, на-
названа Лебедевым максимальной молекулярной влагоемкостью.
Пленочная вода удаляется при высушивании грунта.
4. Гравитационная вода — это вода свободная, не подвер-
подверженная действию сил притяжения к поверхности твердых ча-
частиц. Она передвигается под влиянием силы тяжести, в ней
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[гл. i
Смотродая mpyfia 0ля
наблюдения грунтовых Зад
Лодерхность пдчды
действует только гидродинамическое давление. Мы будем назы-
называть гравитационную воду грунтовой водой и будем в дальней-
дальнейшем изучать законы движения именно грунтовой воды.
К грунтовым водам причисляют обычно и капиллярную
воду — это вода, заполняющая частично или полностью поры
грунта и имеющая поверх-
поверхность, ограниченную вогну-
вогнутыми менисками (см. § 9).
Отметим, что некоторые ще-
щелочные воды могут давать
выпуклые мениски и отри-
отрицательную высоту капил-
капиллярного поднятия, т. е. ка-
капиллярное опускание.
Представления А. Ф. Ле-
Лебедева были уточнены и до-
дополнены последующими ис-
исследованиями ряда ученых.
В настоящее время прида-
придается большое значение роли
коллоидных частиц в грун-
грунте. Коллоидные вещества
откладываются на поверх-
поверхности минеральных зерен в
виде тонких оболочек. Сор-
Сорбируемые водяные пары
впитываются этими оболоч-
оболочками, входя с ними в хими-
химическое взаимодействие.
Электрически заряженные
коллоидные частицы, назы-
называемые мицеллами, сорби-
сорбируют пары воды до извест-
известного предела максимальной
Рис. 7. гигроскопичности, о которой
мы говорили выше. Этот
предел характеризуется прекращением выделения теплоты сма-
смачивания. В дальнейшем коллоидная оболочка может набухать,
впитывая капельно-жидкую влагу без выделения тепла.
Таким образом, частицы влажного грунта имеют гигроскопи-
гигроскопическую оболочку, а при дальнейшем увлажнении грунта, после
освобождения всей теплоты смачивания, они приобретают пле-
пленочную воду. В натуре частицы грунта сближены между собой
так, что пленочный слой не развивается до наибольшего воз-
возможного предела. В углах пор между частицами грунта соби-
собирается вода, поверхность которой образует мениск поверхно-
§4]
РАЗЛИЧНЫЕ СОСТОЯНИЯ ВОДЫ В ГРУНТЕ
27
стного натяжения. При дальнейшем увлажнении грунта скопле-
скопления воды в уголках пор увеличиваются, и их мениски соприка-
соприкасаются. В поре остается просвет, по которому может переме-
перемещаться вода.
Когда вода заполняет все поры (в них может оставаться
некоторое количество воздуха), то она получает способность
передвигаться (за исключением пленочной воды) под влиянием
силы тяжести. Такая вода, как мы уже говорили, называется
гравитационной, или грунтовой. Движение этой воды в пористой
среде называется фильтрацией.
Таким образом, физическая картина движения воды в грунте
является сложной. В любом грунте, полностью или не полно-
полностью насыщенном водой, имеется вода, не участвующая в дви-
движении, связанная адсорбционными силами со скелетом грунта.
Вследствие обволакивания частиц грунта прочно связанной
водой увеличивается объем твердой фазы и сокращается объем
пор грунтовой массы. Величина связанной воды меняется от не-
нескольких процентов от пористости для песков до полной пори-
пористости для некоторых глин. В последних движение возможно
лишь при приложении сил, превышающих силы адсорбции.
Рис. 8.
Рис. 9.
В глинисто-коллоидных фракциях имеют место явления
коагуляции и пептизации, которые ведут к образованию агрега-
агрегатов или распаду их, что в итоге меняет гранулометрический со-
состав, а вместе с тем и удельную поверхность твердой фазы
грунта.
На рис. 7 приведена схема различных форм воды в грунте,
данная Н. А. Качинским A975). На ней цифрой 1 обозначена
частица почвы, 2 — вода выпавшего дождя, 3 — пленка гигро-
гигроскопической воды, 4 — почвенный воздух с парами воды, 5 — во-
вода пленочная, под которой Н. А. Качинский понимает воду,
рыхло связанную с почвой, 6 — зона открытой капиллярной
воды, где вода и воздух заполняют поры вперемежку, 7 —
28
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[ГЛ. I
капиллярная вода, 8 — зона замкнутой капиллярной воды, 9 —
уровень грунтовой воды, 10 — грунтовая вода.
Для отдельного просвета между зернами грунта, в случае,
когда вода еще не стала гравитационной, будем иметь картину,
изображенную на рис. 8: в уголках между песчинками имеются
капиллярные мениски, внутренняя область заполнена воздухом.
Что касается грунтовой воды, то, как мы уже отмечали
выше, она обычно не заполняет полностью всю область между
частицами грунта, так как в последней остаются пузырьки воз-
воздуха. Можно схематизировать движение грунтовой воды так,
как это изображено на рис. 9, где внутренний кружок соответ-
соответствует пузырьку воздуха.
§ 5. Скорость фильтрации. Под скоростью фильтрации пони-
понимают расход жидкости, т. е. объем жидкости, протекающей в
единицу времени через единицу площади, выделенную в пори-
пористой среде.
Вспомним, как определяется расход жидкости в гидродина-
гидродинамике (Кочин, Кибель и Розе 1963, 1). Пусть имеется элементар-
элементарная площадка S (рис. 10), через которую проходит жидкость со
скоростью, представляемой вектором и. Количество жидкости,
Рис. Ю.
Рис. 11.
протекающее в единицу времени через S, равно объему ци-
цилиндра, построенного на S и и, а так как высота этого цилиндра
равна ип — нормальной к площадке S составляющей скорости,
то расход Q через площадку S равен Q = Sun. Если в данной
точке вращать элементарную площадку и восстанавливать нор-
нормали к ней, то направление я, соответствующее наибольшему
расходу, будет являться направлением вектора скорости.
Обратимся к движению жидкости в пористой среде. Пред-
Представим себе площадку в грунте, содержащую сечения зерен
грунта и просветы между этими сечениями (рис. 11). Движение
жидкости между зернами грунта носит сложный характер, по-
§5]
СКОРОСТЬ ФИЛЬТРАЦИИ
29
этому принято рассматривать не скорости в отдельных точках
жидкости, а средние значения этих скоростей.
Пусть вектор средней скорости частиц жидкости в области
площадки S будет и. Площадь просветов, находящихся на пло-
площадке S, обозначим через Si. Положим
Si
и назовем т поверхностной пористостью или просветностью.
Расход через площадку S будет
Q = Sxun = mSun.
Расход через площадку, величина которой равна единице, ра-
равен пгип и называется скоростью фильтрации.
Вектор скорости фильтрации имеет величину тиу равную
максимальному значению тип при различных положениях пло-
площадки S, и направлен по нормали к той площадке, через кото-
которую проходит наибольший расход.
Если вектор и скорости частицы имеет составляющими
их, иуу uZy то для вектора скорости фильтрации v составляющие
будут
vx = тих,
vy = тиуу
v2 = muz.
E.1)
Для того чтобы определить поверхностную пористость неко-
некоторого образца, можно было бы поступить так, как это делают
в некоторых специальных лабораториях: образец, вынутый из
грунта с помощью цилиндрической трубки
с острыми краями (такой образец назы-
называют керном), пропитывают склеивающим
веществом и затем делают ряд тонких сре-
срезов этого образца. Положив срезы под
микроскоп, можно измерить площади про-
просветов и взять их отношения к площади се-
сечения образца. Среднее из этих величин по
всем взятым сечениям дает среднюю по-
поверхностную пористость взятого образца.
Однако такой способ ее определения сло-
сложен. Вместе с тем очевидно, что описанный прием определения
поверхностной пористости даст для нашего цилиндрического
образца величину средней пористости грунта.
В самом деле, предполагая, что среда статистически одно-
однородна, обозначим через S\(z) площадь пор в сечении цилиндра
на расстоянии z от его основания (рис. 12). Пусть m(z) будет
просветностью этого сечения, т. е.
Л
Рис. 12.
30 ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. 1
где S —площадь основания цилиндра. Тогда среднее значение
просветности т будет равно
я
m = -jj\m{z) dz.
о
Это выражение можно представить так:
я я
Здесь HS = V — объем рассматриваемого цилиндра, а инте-
интеграл равен объему V\ всех пор в данном образце. Поэтому
средняя просветность или поверхностная пористость т равна
средней объемной пористости а:
В дальнейшем мы не будем делать различия между поверх-
поверхностной пористостью и объемной и будем обозначать ту и дру-
другую величины буквой а или буквой т.
§ 6. Опытные законы фильтрации. Прежде чем перейти к из-
изложению результатов экспериментальных исследований движе-
движения воды в трубках с грунтом, напомним некоторые сведения из
области гидродинамики (см., например, Кочин, Кибель и Розе
1963, 1).
Если несжимаемая невязкая жидкость движется в трубке —
горизонтальной или наклонной — с гладкими стенками, причем
движение установившееся, то имеет место уравнение Бернулли
^ + z + -|- = const. F.1)
Здесь р — плотность жидкости, g— ускорение силы тяжести,
р— давление, и — скорость, z — геометрическая высота; вели-
величина p/pg называется пьезометрической (т. е. обусловленной
давлением) высотой, a u2/2g носит название скоростной высоты,
или скоростного напора.
Уравнение Бернулли говорит, что для всех точек трубки сум-
сумма трех высот остается постоянной величиной. Сумма двух
первых членов уравнения F.1) называется напором, или пьезо-
пьезометрическим напором. Обозначим его через А:
h =¦?-+*• F-2)
$61
ОПЫТНЫЕ ЗАКОНЫ ФИЛЬТРАЦИИ
31
Теперь можно переписать уравнение F.1) в виде
и2
/г + ^ = const.
F.3)
Отсюда видно, что если бы жидкость двигалась в трубке без
сопротивления и с постоянной скоростью, то напор во всех
точках трубки был бы один и тот же. Внутреннее трение учиты-
учитывается в гидравлике введением
в уравнение F.3) поправочных
членов.
В случае движения жидко-
жидкости в пористой среде многочис-
многочисленные опыты, проведенные во
многих лабораториях, над ус-
установившимся движением (во-
(воды и других жидкостей, напри-
например нефти) приводят к сле-
следующим результатам.
Возьмем две точки на оси
трубки (рис. 13) на расстоя-
расстоянии As друг от друга и поме-
поместим в них концы пьезометров — открытых трубок. В пьезомет-
пьезометрах вода поднимается соответственно на высоты h\ и /i2, отсчи-
отсчитываемые от произвольной горизонтальной плоскости, причем h
определяется формулой F.2).
В гидравлике рассматривают величину /, которую называют
гидравлическим уклоном или градиентом напора, определяя ее
как отношение потерь напора Д/i =/ii — h2 к пути As или, в
общем случае, как производную от h по пути s, взятую со
знаком минус:
Рис. 13.
i.
ds
F.4)
Эксперименты показывают, что скорость фильтрации яв-
является функцией от гидравлического уклона, или уклон есть
функция скорости:
/-Ф(о). F.5)
Такой характер рассматриваемых движений вызывается тем,
что при фильтрации в пористой среде жидкость испытывает,
вследствие влияния вязкости, большое сопротивление.
Для многих грунтов (пески, глины, торфяные грунты, мелко-
мелкотрещиноватые скальные грунты и т. д.) имеет место линейная
зависимость скорости фильтрации от пьезометрического уклона:
v = k' — k%. F-6)
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
ГГЛ. I
где коэффициент пропорциональности k называется коэффи-
коэффициентом фильтрации. Коэффициент фильтрации имеет размер-
размерность скорости; он равен скорости фильтрации при гидравличе-
гидравлическом уклоне, равном единице. Часто мы будем обозначать его
также через и.
Равенство F.6) было установлено Дарси (Darcy 1856) и
называется законом Дарси.
5)
Рис. 14.
На рис. 14 в виде примера приведены две схемы опыта, мо-
могущего служить проверкой закона фильтрации. Песок в трубках
удерживается от размыва с помощью сетки или натянутой
марли.
При рассмотрении этих простейших схем гидравлический
уклон / берется равным отношению разности напоров Н к дли-
длине пути фильтрации s, так что скорость фильтрации будет
F.7)
-*4-
В плотных глинах и тяжелых суглинках, в которых вода со-
содержится в молекулярно связанном виде, явление фильтрации
возникает лишь тогда% когда величина градиента напора пре-
превышает некоторое значение fe, называемое начальным градиен-
градиентом. В этом случае уравнение F.6) заменяется таким (Пузы-
ревская 1931):
= k (J — /о)« F.8)
Для очень плотных глин /0 может достигать значений, равных
20—30.
§ 7. Коэффициент фильтрации. Коэффициент фильтрации дан-
данного образца грунта может быть о* ределен на одном из прибо-
приборов, изображенных на рис. 14, а, б. На рис. 15 приведена более
КОЭФФИЦИЕНТ ФИЛЬТРАЦИЙ
подробная схема такого прибора, снабженного пьезометриче-
пьезометрическими трубками.
Если нужно ориентировочно определить коэффициент филь-
фильтрации в природных условиях, то можно взять образцы грунта
(по возможности, ненарушенной структуры) и испытать их в
указанном приборе. Однако этот спо-
способ недостаточно надежен, так как он
может не дать характеристики всей
области в целом. Прибегают к поле-
полевым способам определения коэффи-
коэффициента фильтрации по откачкам из
скважин (см. главы IX и XVI), кото-
которые дают наиболее надежное значение
этой величины. При этом получается
некоторое среднее значение коэффи-
коэффициента фильтрации для рассматривае-
рассматриваемой области движения. В таблице 4
дан порядок значений коэффициента
фильтрации для различных грунтов
(Черкасов 1958).
Коэффициент фильтрации зависит
от свойств грунта, величины и формы
его зерен, а также от жидкости, про-
протекающей в грунте, в частности от ее
вязкости, а следовательно и темпера-
температуры.
Обычно коэффициент фильтрации,
определенный тем или иным путем, *
относят' к температуре 0° или 10 °С.
Тогда коэффициент фильтрации при температуре /°С вычис-
вычисляется по формулам вида
k = k0 (I + 0,0337/ + 0,000221/2) (формула Пуазейля),
k = kl0 @,7 + 0,030 (формула Хазена).
Н. Е. Жуковский A889) обратил внимание на зависимость
коэффициента фильтрации от атмосферного давления. Наблю-
Наблюдения показывают, что высота грунтовых вод в буровых сква-
скважинах уменьшается с увеличением атмосферного давления и
увеличивается с его уменьшением. Жуковский это объясняет
тем, что при падении давления упругие пузырьки воздуха, на-
находящиеся в водоносном слое (они могут приноситься дожде-
дождевыми водами), расширяются и выталкивают грунтовые воды.
Уровень их в колодцах поднимается, а ключи текут быстрее.
При увеличении давления будет обратная картина.
Но и при постоянном давлении наличие в грунтовой воде пу-
пузырьков воздуха изменяет степень водопроницаемости грунта,
2 П Я. Полубаринова-Кочина
34
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. I
Таблица 4
Коэффициенты фильтрации грунтов
Наименование грунта
Песок чистый
Песок глинистый
Супесок
Суглинок карбонатный
Глина
Глина солонцеватая
Лёсс карбонатный
Лёсс бескарбонатный
Солончак
Солонец столбчатый
Тор(
Торс
Торс
Торс
> осоковый мало разложившийся
) средне разложившийся
) сфагновый молодой
) сфагновый старый
Коэффициент фильтрации
k, см1сек
1,0-0,01
0,01-0,005
0,005-0,003
0,001-0,00005
0,0005-0,000005
0,000001-0,0000003
0,0005-0,0001
0,00005-0,00001
0,001-0,0001
0,000001-0,0000003
0,006-0,002
0,0008-0,0002
0,002—00002
0,002-00001
которая не остается постоянной при производстве более или
менее длительного опыта. Изменение коэффициента фильтрации
во времени может обусловливаться и другими физическими и
химическими процессами (например, выщелачиванием раствори-
растворимых солей), а также биологическими процессами в почве.
В теории фильтрации нефти вместо коэффициента фильтра-
фильтрации рассматривают другую величину, называемую проницаемо-
проницаемостью грунта. Учитывая большой диапазон изменения вязкости
нефтей, при изучении их движения в горизонтальной трубке
удобнее записывать скорость фильтрации в виде
v = — ¦
dp
ds
G.1)
где коэффициент ko зависит только от свойств грунта и назы-
называется проницаемостью грунта, \х — вязкость нефти, р — давле-
давление. Если рассматривается движение в вертикальной плоскости
или пространстве, то в этой формуле следует заменить р на
Р + Ре*-
Как нетрудно видеть, коэффициент фильтрации k связан
с проницаемостью &о соотношением
~ |1 ~ V
Здесь v = fx/p — кинематическая вязкость жидкости.
Существуют формулы, выражающие зависимость коэффи-
коэффициента фильтрации от пористости и от данных механического
§ 8] ПРИМЕНИМОСТЬ ЗАКОНА ДАРСИ И НЕЛИНЕЙНЫЕ ЗАКОНЫ 35
состава грунта. Приведем в качестве примера формулу Козени
(Kozeny 1931):
где |л — вязкость жидкости, d — эффективный диаметр частиц
(см. § 1), а—-пористость, р— коэффициент, который Козени
считает постоянным (для воды).
§ 8. Пределы применимости линейного закона фильтрации и
нелинейные законы. Многочисленные опыты показали, что линей-
линейный закон Дарси F.6) имеет определенные пределы применимо-
применимости. Так, для однородных грунтов (песка, гравия) закон Дарси
имеет место лишь при выполнении для числа Рейнольдса нера-
неравенства (Павловский 1922)
Re = H±<^A (8.1)
(обозначения те же, что и в конце § 7). Здесь А— число, для
которого разные авторы дают различные значения, заключаю-
заключающиеся в пределах от 3 до 10.
Если принять v = 0,018 см2/сек (для воды), то
vd < 0,070 - 0,075, (8.2)
где v выражается в см/сек, d — в сантиметрах (Аравин и Нуме-
Нумеров 1948).
Должен существовать и нижний предел применимости за-
закона Дарси, когда начинает сильно сказываться действие моле-
молекулярных сил, на что указал Н. Н. Павловский A922).
За пределами линейного закона фильтрации, например для
крупнозернистых грунтов или при больших скоростях движения,
принимают на основании опытов иные зависимости между v и /.
Так, рассматривают полином второй степени
/ = Av + Bv2,
реже — полином третьей степени или одночленную зависимость
вида
v = CJn.
Постоянные Л, В, С, п определяются из опыта.
Н. К. Гиринский A947), изучая приток грунтовых вод к сква-
скважинам, пришел к заключению, что для большинства грунтов
(рыхлых) отклонения от закона Дарси могут иметь место лишь
в непосредственной близости от скважины. При этом он указы-
указывает, что обычно зона нарушения закона Дарси является и
зоной нарушения естественного состояния грунта под влиянием
36
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
(ГЛ. I
бурения и суффозионных (т. е. связанных с выносом частиц)
процессов, происходящих при прокачке скважины.
В трещиноватых породах возможны более значительные от-
отклонения от линейного закона фильтрации (Ломизе 1951).
Отметим, что вдоль бетонного основания плотины может
иметь место так называемая контактная фильтрация, при кото-
которой образуется слой воды между грунтом и плотиной. Движе-
Движение жидкости в таком слое не подчиняется обычным законам
фильтрации (Аравин и Нумеров 1948).
§ 9. Капиллярность. Если мы опустим конец трубки с песком
в воду, то увидим, что вода в трубке будет подниматься сначала
быстро, затем все медленнее, наконец, ее передвижение станет
незаметным для глаза. Обозначим высо-
ту наибольшего поднятия воды (вернее,
ее среднее значение но контуру трубки)
через Лк и назовем ее статической высо-
высотой капиллярного поднятия.
Предположим, что основание трубки
АВ (рис. 16) соприкасается с поверх-
поверхностью воды в сосуде. Тогда вдоль АВ
будем иметь атмосферное давление. Мо-
Молекулярные силы, заставляющие жид-
жидкость подниматься между песчинками,
действуют так, что в смоченной части
— — трубки будет иметь место давление ниже
. . атмосферного (вакуум). Если принять
Рис. 16. атмосферное давление равным нулю, то
давление в области ABCD придется
считать отрицательным и на поверхности CD равным — pghK.
Или, если атмосферное давление обозначить через ра> то на по-
поверхности CD
А
щ
С
В
—
h
i
к
- —^
Это условие, которое должно выполняться на свободной по-
поверхности грунтовых вод, было указано Н. Е. Жуковским A923)
и применено В. В. Ведерниковым, а потом и другими авторами
при решении ряда задач (см. главу V).
Отметим, что верхний слой грунта (почва) является струк-
структурным, т. е. таким, в котором элементарные частицы объеди-
объединены в агрегаты минеральных частиц, сцементированных пере-
перегноем. Между комками диаметром 1—5 мм образуются круп-
крупные поры. В структурном грунте капиллярность почти не наблю-
наблюдается. Мала она и в крупнозернистых грунтах. Однако есть
грунты, в которых капиллярное поднятие достигает высоты
3—5 м (Качинский 1975).
Ю]
ВОДОПРОНИЦАЕМОСТЬ ГРУНТА ПРИ НЕПОЛНОМ НАСЫЩЕНИИ
37
В таблице 5 приведены границы значений высот капилляр-
капиллярного поднятия в некоторых грунтах (Черкасов 1958).
Таблица 5
Высоты капиллярного поднятия в грунтах
Грунт
Глина
Суглинок
Супесок
Песчаная почва
ftK (см)
400-200
300-150
150-100
100-50
Грунт
Лёсс туркестанский
Подзол
Торф
Солонец и солончак
hK (см)
450-250
35-40
120-150
12
Как известно, высота поднятия воды в капиллярной трубке,
смачиваемой водой, зависит от кривизны мениска и для круглой
трубки равны 2о/(уг), где а —поверхностное натяжение воды,
г—радиус трубки, у — объемный вес воды.
Поры почвы представляют собой сложный «лабиринт пу-
пустот», а потому для высоты капиллярного поднятия будет иметь
место более сложная зависимость. Для песка предложена при-
приближенная формула (Черкасов 1958)
* г\ лг 1 — #1 1
h = 0,45 ¦;— СМ9
к ' т dl0 *
где т — пористость, dro — эффективный диаметр частиц грунта
в см (см. стр. 19).
§ 10. Водопроницаемость грунта при неполном его насыщении. Здесь крат-
кратко излагаются результаты исследований С. Ф. Аверьянова A949, 1), пред-
представляющие первую попытку теоретиче-
теоретического освещения вопроса о зависимости
коэффициента фильтрации от степени
увлажнения грунта.
Обозначим пористость грунта через а,
количество связанной воды в долях от
общего объема грунта через wq, полную
влагоемкость в природных условиях, т. е.
с учетом наличия некоторого количества
зажатого воздуха, через W\. Действитель-
Действительную степень насыщения (влажность) обо-
обозначим через w. Тогла будем иметь нера-
неравенства о ^ W\ > w > wo. Если нет зажа-
зажатого воздуха, то w\ = о.
Предположим, что грунт не полностью
насыщен, обладая влажностью w. Обозна-
Обозначим через kw коэффициент фильтрации при
неполном насыщении. Будем иметь kw =
= 0 при w = w0, при w = о должно быть
kw — к, где k — коэффициент фильтрации при полном насыщении. В общем
случае положим kw — ak.
С Ф. Аверьянов рассматривает следующую схему движения вязкой
жидкоеiи в капиллярной трубке (рис. 17). В центральной части трубки цилин-
Рис. 17,
38
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[ГЛ. I
дрическая область радиуса Ri заполнена воздухом; кольцевая область, ограни-
ограниченная окружностями радиусов /?о и R[} заполнена движущейся вязкой жид-
жидкостью. При этом окружность радиуса Ro есть граница между гравитационной
и связанной водой. С. Ф. Аверьянов принимает, что скорость вдоль трубки
равна нулю при г — ROy а при г = R\ достигает наибольшего значения.
20
0,8 . W
ги
Тогда, как известно и курса гидродинамики, скорость течения вязкой
жидкости в горизонтальной цилиндрической трубке будет
4vA/
г2 + a In г + b
(ЮЛ)
где и — скорость течения на расстоянии г от продольной оси трубки при
разности Ар давлений, приложенных на расстоянии Д/, v— кинематический
коэффициент вязкости. В нашем случае получим
Расход Q определим по формуле
ur dry
что дает
§vA/
4*!1п $
) ФИЛЬТРАЦИОННЫЕ АНОМАЛИИ В ПОРИСТЫХ СРЕДАХ 39
Введем относительную влажность w° с учетом связанной воды:
мО до — w0 .. о — w
О — Wo О — W0
Но, как видно из рис. 17, имеем
-w0 nR0 RQ V o-w0
В результате отношение -jr- можно выразить через о/°. Таким путем
АО
С. Ф. Аверьянов приходит к зависимости а от w°, которую он для упроще-
упрощения представляет затем в виде степенной функции:
а = w° Cw° - 2) - 2 A - w°J In A - w°) « w°n,
причем принимает п = 3, 5. Сопоставление имеющихся опытных результатов,
полученных разными авторами, с теоретической кривой дало, как это ни уди-
удивительно при сделанных искусственных предположениях, хороший результат
(рис. 18).
Дальше, в главе XV, будет идти речь о статистических методах опре-
определения зависимости kw от w.
§ И. О фильтрационных аномалиях в пористых средах. Мы уже говорили
в § 3 о молекулярно-поверхностных силах на границе соприкосновения
жидкости с твердым телом. В жидкости могут также наблюдаться аномаль-
аномальные явления под влиянием коллоидных частиц и частиц или молекул других
поверхностно-активных веществ, которые могут образовывать определенные
решетчатые структуры в микрообъеме.
В вязкой жидкости поверхностные силы имеют кроме нормальной и ка-
касательные составляющие. Если движение происходит в плоскости xz парал-
параллельно оси ху то касательное напряжение или сила трения определяется фор-
формулой Ньютона (Кочин, Кибель и Розе 1963, 2)
du /HIV
т = и17, A1.1)
где и — скорость, параллельная оси х, \х — вязкость.
При движении вязкой несжимаемой жидкости в щели между плоско-
плоскостями г = db R для скорости и получено уравнение
u=-iri?(«2-z2)=w}{R2-z2)' AL2)
а для течения в трубке радиуса R
В этих формулах / — градиент напора, равный
j—™--L2L (a—E-Y A1.4)
дх pi' дх \ рй ) '
40 ФИЗИЧЕСКИЕ Й MATEMAtH4ECKtfE ОСНОВЫ ТЕОРИИ [ГЛ. 1
Будем обозначать через ? как г, так и г. Тогда для силы трения т, дей-
действующей на расстоянии ? от оси х или от плоскости ху, имеет место равен-
равенство
т „ du
причем 6 = 0 для щели и б = 1 для трубки. Вблизи твердой стенки, при
% = R, имеем
При движении жидкости в пористой среде следует учесть добавочное
сдвиговое напряжение т0, аналогично тому, как это делается для неньюто-
неньютоновских жидкостей в модели Бингама — Шведова (Рейнер 1947), и написать
вместо A1.5) такое уравнение:
В книге М. Рейнера A947) ю рассматривается как постоянная, и после
интегрирования A1.6) для средней скорости движения получается так назы-
называемое уравнение Букингема — Рейнера (см ниже уравнение A1.22) для
вязкопластических тел).
М. А. Саттаров A972) предлагает обобщить равенство A1.6), считая т0
функцией от g:
(H.7)
Это дает более широкие возможности рассмотрения различных аномалий
движения жидкостей в пористых средах Автор, в частности, полагает, что
основные аномалии проявляются в молекулярно-поверхностных взаимодей-
взаимодействиях: жидкость — пористый скелет и жидкость — взвешенная частица по-
поверхностно-активного вещества.
Из (П-6) можно найти положение экстремума скорости, полагая
du/dl = 0:
Рассмотрим два случая: 1) | = 0, 2) ? = ?ь где ?i удовлетворяет урав-
уравнению
h - Mpja) AT (Si) (I Ei К Л). (И 8)
Поведение u(Q в точках 5 = 0 и ? = ?ь в соответствии с физическими
особенностями взаимодействия системы жидкость — пористый скелет, позво-
позволяет выделить следующие две основные группы жидкостей.
Группа А. Возле стенок трубки (или щели) в некотором кольце (или
в полосах) ?i<l?l<# действуют силы сцепления, и здесь связанная
жидкость остается неподвижной. Во внутренней области трубки (или щели)
жидкость движется так, что при ? = 0 ее скорость максимальна, а при
g ===== g, она обращается в нуль. Отсюда получается условие N@)= 0. Такому
условию удовлетворяет, например, функция вида
(я>0) A1.9)
(М. А. Саттаровым A972, 1973) рассмотрен также случай N(%) = a%eml).
§ II] ФИЛЬТРАЦИОННЫЕ АНОМАЛИИ В ПОРИСТЫХ СРЕДАХ 41
Условие максимума скорости в точке ? = 0, г. е. условие d2u/d%2 < 0 при
g = 0, требует выполнения неравенства п ^ 1. При этом N(%) будет воз-
возрастающей функцией.
При выполнении условия прилипания w(?i)=0 для скорости получаем
Расход через площадь поперечного сечения трубки радиуса R или щели
единичной длины с раскрытием 2R определяется по формуле
Ь
<Э = BлN ( utdl (б-0, 1), A1.11)
а для скорости фильтрации, которую можно записать в виде
v = oQ: [яб^+1B-6)] F = 0, I)
(а — эффективная пористость), получается выражение
v » Л, (/-/,), A1.12)
причем из A1.11) можно получить
С возрастанием напора / активная ширина просвета ^i» а следовательно,
и величина 1\ должны увеличиваться.
Если |i -> R, то имеем
Г L
lim k\-=*=k =¦ const.
При дальнейшем увеличении / картина движения сохраняется до дости-
достижения некоторого значения /Кр — критического градиента, при котором ла-
ламинарный характер течения нарушается.
Для NA) вида A1.9) получены такие формулы для скорости фильт-
фильтрации:
п+\
l при °<'<'* (ИЛ5)
при JR<J<JKp, A1-16)
где
V
42 ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. I
Группа Б. Течение жидкостей этой группы начинается сразу во всей
трубке, причем средняя часть, в которой (б— 1M) < g < gi, движется с по-
постоянной скоростью (как твердый стержень), а жидкость в полосах или в
кольце gi<[g|</? имеет максимум скорости при |g| = gi и обращается
в нуль у стенки грубки или щели, т.е. при |g|=/?. Скорость в точке g
будет иметь вид
(П.17)
"~ 2A+б)ц VJV *'
(при gi < | g | < /?),
R
V = 2A + 6) p, {R2 "" ll) "" J ^
C0"St
(при Ш<Ы
При этом gi удовлетворяет уравнению A1.8). Из этого уравнения видно,
что каждому заданному значению ?i соответствует определенное значение /,
Если gi -»- R, то
Л"^^^ ^^"—^"* (Н-19)
Если gj -> 0, то
hm /j = /0 = — lira — . A1.20)
Этот предел может не существовать, так как величина J\ должна увеличи-
увеличиваться при ?i->0. В частности, это будет для W(g), имеющих вид A1.9) при
п < 1.
М. А. Саттаров A972, 1973) показал, что для /V(g) вида A1.9) скорость
фильтрации через поперечное сечение трубки радиуса R или щели ширины
2R можно представить в виде
Л+6+2
(Н.21)
Отсюда при п = A — б) /4, т. е. при я = *U для щели и гг = 0 для труб-
трубки, получается формула Букингема — Рейнера (Рейнер 1947)
Интересно, что один и тот же результат получился для разных моделей:
для трубки при постоянном предельном напряжении сдвига то = ^N и для
щелевой модели при то = \xaR(l/R)x^.
§
УРАВНЕНИЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
43
0,5
О
/
//,
///
/ /
/ /
/ /
/ /
/
У /
/
/
//
/
/
/
/
О?
W
Рис. 19.
/
2,0
Если /я// достаточно мало, так что можно пренебречь его третьей сте-
степенью, то получим линейную форму зависимости v от / с начальным гради-
градиентом
3 + 6 1,0
к
На рис. 19 построены графики
зависимости vjk от / при движе-
движении в трубке F= 1): для слу-
случая А сплошные линии по урав-
уравнениям A1.15) и A1.16) при/л =
= 2 и для случая Б пунктирные
линии по уравнению A1.21) при
/0 = 0,2. Заметим, что кривые
группы Б можно разделить на
два типа: имеющие асимптоту —
это случай — 2 < п < 1 (вязко-
пластические жидкости), и без
асимптоты — это случай п < — 2
(так называемые пластичные тела).
Предполагается, что в дей-
действительности модель А имеет
место для чистых жидкостей, а
модель Б — для вязкопластических
тел и для жидкостей с неустойчи-
неустойчивым структурным строением.
Рассмотренная выше модель С. Ф. Аверьянова (см. § 10) была бы част-
частным случаем модели Б при N(Q = 0, если предположить отсутствие движе-
движения во внутреннем ядре.
§ 12. Уравнения движения грунтовых вод. Выше было сказа-
сказано о том, что вода в пористых породах может находиться в
различных состояниях. Мы будем заниматься вопросами движе-
движения гравитационной воды.
В каждой из пор грунта происходит сложное движение с
изменением скорости и ускорения по величине и направлению
от точки к точке. Поры имеют различное направление и различ-
различную форму стенок, а потому в каждом выделенном объеме
грунта должны иметься самые разнообразные по величине и на-
направлению скорости. Поэтому невозможно рассматривать ско-
скорости отдельных частиц.
Правильнее было бы рассматривать средние значения ско-
скоростей в некотором объеме. В теории фильтрации принято
рассматривать не скорости, а расходы через определенную пло-
площадку. Будем вектор расхода через единичную площадку обо-
обозначать через v. Если средняя скорость частиц некоторого
объема ес?ь и, то мы можем отнести ее к центру тяжести этого
объема, координаты которого обозначим через (x,y,z). При-
Примем вектор и имеющим составляющие dx/dt, dy/dt, dz/dt. Тог-
Тогда, обозначая пористость грунта через а, можем написать
v = ou, A2.1)
44
ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
[ГЛ. I
т. е. если составляющие вектора v обозначить через vXy vy, vz, то
dx dy dz /t o Пч
Уу = СГ-т7-» V,. = О —rr i Vy = О —jt • A2.2)
x dt У dt ' * dt v '
В гидродинамике при выводе уравнений движения рассмат-
рассматривают ускорения частиц жидкости, которые выражаются через
скорости так:
dux dux Л" Л" ^"
^«*
и т. д.
dt dt ¦ dx "х ^ dy "v r .
Уравнения движения отдельных частиц жидкости в порах
можно написать таким образом:
dux 1 dp , с
р dx ' 'Х9
dt
duy
L2L
p ду
A2.3)
dt p dz
Здесь p — давление жидкости, р — плотность, g — ускорение
силы тяжести, ось z направлена вверх. Через /х, fyj fz обозна-
обозначены составляющие условных сил сопротивления, которые как
бы испытывает частица жидкости в поре. Эти силы сопротивле-
сопротивления зависят от внутреннего трения жидкости.
Считая скорости их, иу, иг и их производные по координатам
малыми, произведениями их пренебрегают, оставляя в выраже-
выражениях составляющих ускорения лишь члены dujdt, duv/dt, dujdt.
Некоторое обоснование того, что можно отбрасывать конвективную часть
ускорения (сил инерции), приводит С. Н. Нумеров A968). Он заменяет в
уравнениях A2.3) скорости частиц на скорости фильтрации согласно A2.1)
и переписывает эти уравнения в векторной форме, присоединяя уравнение
неразрывности A2.16):
div*-Of 4zr^r
A2.4)
Функцию f(v) i
равной
go dt 'go'*
¦¦¦ J/v, выражающую закон сопротивления, он полагает
[ (у) ess a + bv, A2.5)
т. е. выбирает квадратичный закон сопротивления (при b = 0 получим закон
Дарси). Далее С. Н. Нумеров рассматривает два случая установившегося
одномерного движения: 1) осесимметричное течение при наличии бесконеч-
бесконечного прямолинейного источника (или стока) и 2) радиальное течение с то-
точечным источником (стоком).
Случай 1. Уравнения A2.4) принимают вид
dH
dr
-f bv2 = О,
A2.6)
H
2go2
§ 12] Уравнения движения грунтовых вод 45
Здесь г — расстояние точек области движения от источника, Н — полный
напор, равный гидравлическому только в пренебрежении квадратом скорости.
Из A2.6) получаем rv — А = const, т.е. v = Л/гу и
dH аЛ . , Л
dv v
что дает после интегрирования
Н = h + у^2" = яЛ 1п у + * Av + в A2-7)
(В = const).
Для параметра Ь Линдквист (Lindqvist 1933) дал такую формулу.
*~^. 02.8)
где cf — средний диаметр частиц пористой среды.
Рассмотрим величину
равную отношению члена в уравнении A2.7), обусловленного конвективной
частью ускорения, к члену, обусловленному квадратичной частью силы сопро-
сопротивления. С учетом того, что vr = Л, заменяя Ь согласно A2.8), получим
<12Л0>
Случай 2 рассматривается аналогично. Для него r2v = Л2,
dH a A ЬАл/v
dv 2^/v 2
откуда
= 0,
f|2 _
A2.11)
3
3d
40a2r '
A2.12)
Выражения A2.10) и A2.12) отличаются лишь числовым множителем.
Чтобы рассматривать фильтрующуюся жидкость как сплошную среду, мы
должны считать, что элементарный объем этой среды должен содержать до-
достаточно большое количество ее частиц, а тогда допустимые значения вели-
величины г должны быть значительно больше величины d. При этом е будет
малой величиной, и конвективной частью ускорения в уравнениях движения
можно пренебречь. Если мы принимаем закон Дарси, пренебрегая квадра-
квадратичным членом сопротивления, то вместе с тем можем в рассмотренных зада-
задачах отбросить и конвективные члены.
При этом уравнения A2.3) становятся линейными. Теперь
нетрудно произвести их осреднение по некоторому объему, доста-
достаточно малому, чтобы учесть изменения скорости от одного места
движения к другому, но достаточно большому по сравнению с
размерами пор. Тогда можно будет под их% иу, uZi p> fXi fy, fz
46 ФИЗИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ [ГЛ. I
понимать их средние значения по объему. При этом под /х, fv, fz
будем понимать составляющие сил сопротивления, полученные
из опыта.
Таким образом, закон Дарси можно истолковать как линей-
линейный закон сопротивления, т. е. такой закон, при котором сопро-
сопротивление пропорционально первой степени скорости фильтра-
фильтрации. Запишем эту зависимость в виде
f — 1*L f - gVy ' f - gv* no 13\
Считая, что коэффициент k сохраняет для неустановивше-
неустановившегося движения то же значение, что и для установившегося, пе-
перепишем линеаризованные и осредненные уравнения A2.3) с
помощью A2.13) и A2.1) в виде (Жуковский 1889)
L. д°* 1_ dp gvx
a dt ~~~~"р' дх k ¦
1 dvy I dp gvy
0 dt p ду k '
1 dv2 ]_AL g^z _
a dt p dz k
A2.14)
Можно показать, что при реальных значениях коэффициента
фильтрации (k = 1 — 100 м/сутки) членами, содержащими диф-
дифференцирование по времени, можно пренебречь.
В самом деле, каждое из уравнений A2.14) имеет вид (Ри-
зенкампф 1938, 1)
Введем переменную U=V — X/, выражающую отклонение V
от Xf. Получим
a dt a dt X '
Если df/dt остается ограниченным при всех /, то член Л =
= (K/a)df/dt будет очень малым. Так, полагая fe=100м/сутки—
= 1,864 м/сек и g= 10 м/сек2, получим X = 1/8640 сек, и чле-
членом Л действительно можно пренебречь, если df/dt не очень
велико (см. главу XI). Остающееся уравнение
dil _ _а г7
dt ~ Ки
по интегрировании дает
§ 12] УРАВНЕНИЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД 47
Правая часть здесь стремится к нулю настолько быстро, что
уже через доли секунды можно считать U = О, V = X/, т. е.
пренебречь членами
1 dvx I dVy I dv2
о* dt • ~о~дГ' ~о~~дГ'
Тогда уравнения A2.14) можно переписать, введя гидравличе-
гидравлический напор ft, в виде
v = - k grad ft (ft = -^- + z). A2.15)
Линейные инерционные члены сохраняют только в отдельных
случаях, например для вывода соотношений подобия.
Движения, в которых можно пренебречь силами инерции по
сравнению с силами трения, называют по Стоксу (см., напри-
например, Прандтль 1951) ползущими. В них обычно сопротивление
пропорционально первой степени скорости.
Уравнения A2.14) содержат четыре неизвестные функции:
Vx, vyt vz и р. Присоединим к этим уравнениям уравнение нераз-
неразрывности. Вывод его проводится так же, как в общей гидроди-
гидродинамике (Кочин, Кибель и Розе 1963, 1). Выделяя элементарный
объем пористой среды в форме параллелепипеда с ребрами dx,
dy, dz и подсчитывая проходящие через него объемы жидкости
(расходы), получим для случая несжимаемой жидкости уравне-
уравнение неразрывности в виде
4^+4^+^=о. A2.16)
дх ' ду ' dz ^ '
Это уравнение имеет тот же вид, что и в общей гидродинамике
несжимаемой жидкости.
Из соотношения A2.15) следует, что скорость фильтрации
имеет (при постоянном k) потенциал
ф(х, */, z) = - k {-^ + z) + С = - kh + С A2.17)
(С —произвольная постоянная), так что
v = grad ф = - k grad ft (ft = ^~ + z) . A2.18)
Из уравнения неразрывности следует, что потенциал скоро-
скорости удовлетворяет уравнению Лапласа
Глава II
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
А. ОБЩИЕ ВОПРОСЫ
§ 1. Уравнения плоского движения. Уравнения плоского дви-
движения грунтовых вод можно написать (при постоянном k)
в виде (см. уравнение A2.18) главы I)
д(р * dh дер , dh
1Л 1Ч
если мы обозначим для простоты через и и v компоненты
скорости фильтрации vx и vy. Принимая ось у вертикальной и
направленной вверх, а ось х горизонтальной, будем иметь
h = Jg + у + Сь ф = "" k Hi + у) + С>' {L2)
Если же ось у направлена вниз, то
Согласно уравнению A2.19) главы I для постоянного k
имеем
д»-Ц- + ^-°- 0-3)
Из уравнения неразрывности
вытекает, что существует функция тока *ф (jc, у), такая, что
u — ^L v— _^L n
Сопоставляя A.1) и A.5), получаем
дф д\\> ду дг|)
дх ду ' ду дх
§ 2] ГРАНИЧНЫЕ УСЛОВИЯ В УСТАНОВИВШЕМСЯ ДВИЖЕНИИ 49
Это условия Коши — Римана (Даламбера — Эйлера). Если они
выполняются, то, как известно, линейная комбинация функций
ф И ф
© = <р + п|> A.6)
является функцией комплексного переменного z = x + iy. Функ-
Функцию со называют комплексным потенциалом.
§ 2. Граничные условия в плоском установившемся движении.
На рис. 20 представлен вертикальный разрез водосливной пло-
плотины, нормальный к оси плотины. Подземное основание ее, на-
называемое флютбетом, состоит из понура /, служащего для
v////////////////////////////////
Рис. 20.
удлинения путей фильтрации под плотиной, водобоя 2, воспри-
воспринимающего удары падающей воды и также удлиняющего пути
фильтрации, сливной части или рисбермы 5, защищающей русло
от размыва и обеспечивающей безопасный выход фильтрацион-
фильтрационных вод в нижний бьеф, и, наконец, шпунтов или зубьев 4, т. е.
заглубленных в основание вертикальных стенок, служащих
также для удлинения пути фильтрации.
Понур в плотине может и отсутствовать. Рисберма устраи-
устраивается водопроницаемой, и при фильтрационных расчетах ее
основание не включается в подземный контур гидротехнического
сооружения.
В глухой плотине, не пропускающей через себя воду, рис-
рисберма и водобой отсутствуют (Гришин 1962; Чугаев 1974).
На рис. 21 представлена схематично земляная плотина, че-
через тело которой просачивается вода.
При рассмотрении задач о фильтрации воды под гидротехни-
гидротехническими сооружениями, в теле земляных плотин, а также при
просачивании воды в почву из каналов и т. п. мы встречаемся
с четырьмя видами границ области движения (Павловский 1922;
Ведерников 1939).
1. Непроницаемые границы. Эго подземные кон-
контуры гидротехнических сооружений (рис. 20), а также границы
50
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
области движения и непроницаемого или слабо проницаемого
грунта (последний называют водоупором).
Непроницаемые границы являются линиями тока, а потому
вдоль них функция тока должна иметь постоянное значение
э = const.
B.1)
Обычно непроницаемые границы схематизируются отрез-
отрезками прямых. Пусть уравнение такого отрезка (например, ВС
на рис. 21) будет
с{=0. B.2)
Уравнения B.1) и B.2) можно рассматривать как два условия,
которые должны выполняться вдоль непроницаемой границы.
2. Границы водных бассейнов. При больших раз-
размерах водного бассейна можно считать, что в нем давление
распределяется по гидростатическому закону. Поэтому в про-
произвольной точке М, находящейся на границе АВ между грунтом
и водоемом (рис. 21), на высоте у,
отсчитываемой от дна верхнего бье-
бьефа (вообще говоря, от произвольной
горизонтальной оси х)у для давле-
давления будем иметь выражение
p = pu + pg(H{- у), B.3)
где ра — давление на поверхности
Рис- 21. бассейна, равное атмосферному дав-
давлению. Второе слагаемое формулы
B.3) выражает вес столба жидкости, действующего на единич-
единичную площадку в точке М.
Подставляя B.3) в формулу A.2) для ф, получим
Таким образом,
Ф = const
B.4)
B.5)
вдоль водной границы; другими словами, водная граница яв-
является линией равного потенциала.
Предполагая, что водная граница представляет отрезок
прямой
а2х + Ь2у + с2 = 0, B.6)
мы будем в дальнейшем рассматривать B.5) и B.6) как два
условия на границе водного бассейна.
3. Линии свободной поверхности представляют
линии раздела между влажным и сухим грунтом. Принято рас-
§ 21 ГРАНИЧНЫЕ УСЛОВИЯ В УСТАНОВИВШЕМСЯ ДВИЖЕНИИ 51
сматривать два вида условий для давления на свободной по-
поверхности.
а) Это давление обычно считают равным атмосферному, так
как на свободной поверхности поры грунта сообщаются между
собой и с атмосферным воздухом. Можно принять атмосферное
давление равным нулю (ра = 0). На линии свободной поверхно-
поверхности, которую также называют кривой депрессии, на основании
A.2) получаем условие
Ф -f- ky = const. B.7)
Если ось у направлена вниз, то B.7) заменяется уравнением
ф — ky = const. B.70
б) При наличии капиллярности грунта принимают, что на
свободной поверхности давление имеет постоянное значение,
меньшее атмосферного на величину, соответствующую высоте
капиллярного поднятия воды в грунте (Жуковский 1890; Ведер-
Ведерников 1939):
h B.8)
Наблюдения показывают, что обычно при движении грунто-
грунтовых вод для hK в формуле B.8) следует брать значение, мень-
меньшее получающегося при подъеме воды в трубке с грунтом, о ко-
котором мы говорили в § 9 главы I (см. дальше § 4 главы V).
Подставляя вместо р его значение B.8) в формулу A.2), мы
получим опять условие B.7), но лишь с другим значением по-
постоянной.
Одной из важнейших задач теории движения грунтовых вод
является отыскание вида депрессионной кривой, уравнение ко-
которой заранее не известно. На ней должно выполняться еще
одно условие: она должна быть линией тока, т. е. на ней должно
соблюдаться условие
а|) = const. B.9)
Таким образом, на линии свободной поверхности выпол-
выполняются два условия — B.7) и B.9).
Представляет интерес случай, когда на свободную поверх-
поверхность выпадают осадки или просачивается вода (вследствие
полива, при таянии снега и т. п.). В этом случае говорят, что
имеется инфильтрация с поверхности земли на свободную по-
поверхность грунтовых вод. Обычно принимают следующий закон
притока влаги на свободную поверхность: расход воды через
какую-нибудь часть свободной поверхности пропорционален
горизонтальной проекции дуги этой поверхности, или, иначе,
пропорционален разности абсцисс концов этой дуги:
4>-4>о = е(*-хо). BЛ0)
52
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
Сдободиая
¦ подерхность
Рис. 22.
Здесь г|; и \|э0 — значения функции тока соответственно в точках
свободной поверхности с абсциссами х и х0 (рис. 22), е — коли-
количество воды, поступающей в единицу времени на единицу длины
горизонтальной проекции дуги депрессионной кривой. Для слу-
случая инфильтрации е больше нуля.
Этот же закон, выражаемый равенством B.10), прини-
принимается и в случае испарения со свободной поверхности с той
ч ^ лишь разницей, что е будет отри-
отрицательно. Однако для испарения
равенство B.10) менее обосно-
обосновано, чем для инфильтрации.
Дальше мы встретимся и с дру-
другими законами испарения.
Таким образом, можно счи-
считать, что на свободной поверхно-
поверхности выполняются условия B.7)
и B.10), причем е может быть
положительным, отрицательным
или равным нулю.
4. Промежутки высачивания. В земляной плотине
могут существовать участки, где вода из тела плотины выса-
высачивается не в водный бассейн, а прямо в атмосферу (рис. 21,
отрезок ED). Такие участки называются промежутками выса-
высачивания. Они имеются также на стенках колодцев, дренажных
канав и т. п. Вдоль них давление должно равняться атмосфер-
атмосферному, т. е. должно выполняться условие B.7). Если промежуток
высачивания прямолинеен, то к этому условию присоединяется
еще уравнение прямой
a& + b,y + cs = 0. B.11)
§ 3. Условия на границе раздела грунтов. Допустим, что грун-
грунтовая вода проходит через два грунта с различными коэффи-
коэффициентами фильтрации k\ и k2y граничащих друг с другом по
линии KL (рис. 23).
Обозначая комплексные потенциалы первой и второй сред
соответственно через (Oi и сог"
= ф!
ф2
будем иметь для потенциалов скорости выражения
C2, C.1)
где р\ и 02—соответственно давления в первой и второй средах.
Так как на границе двух сред давление должно меняться не-
непрерывно, то р\ = р2 в каждой точке линии KL, и из C.1) полу-
§4]
ГОДОГРАФ СКОРОСТИ
чаем, выбирая произвольные постоянные равными нулю, что на
линии раздела двух грунтов
ф! Ф2
C.2)
Другое условие получим, исходя из того, что нормальная к
линии раздела составляющая скорости должна быть непрерыв-
непрерывной. Если v\n и v2n — нормальные составляющие вектора скоро-
скорости при подходе к линии раздела из
первой и из второй сред, то на KL
Vin = V2n- Если ввести функции тока
г|I и гр2 для той и другой сред, то
последнее равенство можно запи-
записать в виде
ds
ds
\К
Рис. 23.
где s — длина дуги линии раздела.
Интегрируя полученное соотноше-
соотношение по s и выбирая постоянную ин-
интегрирования равной нулю, получим на линии раздела KL
*i=*2- C.3)
Уравнения C.2) и C.3) представляют условия, которые
должны выполняться на границе двух сред.
Продифференцируем теперь C.2) вдоль дуги линии раздела.
Получим
1 dgpi 1 дф2
k\ ds k2 ds '
или, вводя касательные составляющие скорости v\s и v2s,
Как видно из рис. 23,
где ai и аг — углы между нормалью к линии раздела и векто-
векторами скорости. На основании зависимостей между нормаль-
нормальными и касательными составляющими скоростей отсюда можно
получить «закон преломления» для двуслойной среды:
tgcti _ tga2 ,o а\
§ 4. Годограф скорости. Комплексный потенциал со представ-
представляет функцию неременной z— комплексной координаты точек
области движения: со = со (г).
S4 Плоские движения в вертикальной плоскости [гл. п
Комплексной скоростью называется производная
-— = u — iv. D.1)
Она является, так же как и со, функцией комплексного пере-
переменного г:
w гз и —• iv = w (г). D.2)
Область комплексно сопряженной с w величины w = u + iv
называют годографом скорости. Очевидно, что области измене-
изменения www отличаются лишь зеркальным отображением в оси и.
Поэтому для большей наглядности в дальнейшем мы будем рас-
рассматривать вместо плоскости w плоскость годографа скорости.
Если граница области движения состоит из прямолинейных
отрезков и депрессионной кривой, то, как мы сейчас покажем,
соответствующая область плоскости (и, v) будет ограничена
прямыми и дугами окружностей (Девисон 1938).
Для доказательства рассмотрим различные виды границ.
При этом вместо плоскости u — iv будем, как сказано, рассмат-
рассматривать плоскость и + iv. Нас будут интересовать величины
углов, а они те же, чго и на плоскости u — iv (направление
отсчета у них будет противоположное).
1. На непроницаемой границе вектор скорости направлен
вдоль этой границы. Поэтому, если непроницаемая стенка со-
составляет угол а с осью абсцисс, то проекции скорости связаны
уравнением
V = tga, D.3)
т. е. на плоскости (и, v) имеем прямую, проходящую через на-
начало координат и параллельную границе.
2. Граница водного бассейна является эквипотенциальной
линией, а потому вектор скорости перпендикулярен к этой гра-
границе. Если уравнение границы есть y = xtga-\-b, то конец
вектора скорости должен лежать на прямой
-?•= — ctga, D.4)
проходящей через начало координат плоскости (и, v) и перпен-
перпендикулярной к рассматриваемой границе.
3. Вдоль свободной поверхности имеем уравнение B.7):
<$-\-ky = const. Дифференцируя его по s, где s — длина дуги
депрессионной кривой, получим
§ 4] ГОДОГРАФ СКОРОСТИ 55
Отсюда, умножая почленно на dcp/ds, получаем
V ds ) ' ds ds
Но dq>/ds есть величина вектора скорости, поэтому
ds ) U ^ V ' ds ds
и условие на свободной поверхности можно переписать так:
и2 + v2 + kv = 0. D.6.)
Это уравнение окружности радиуса k/2 с центром в точке
@, —Л/2), касающейся оси абсцисс в начале координат и от-
отсекающей на оси ординат отрезок, величина которого равна
коэффициенту фильтрации k.
При наличии инфильтрации или испарения на свободной
поверхности имеем уравнения
Ф + ky = const, -ф — гх = const. D.7)
Уравнение D.5) здесь также имеет место, однако ду/ds уже
не является величиной полной скорости, а равно проекции ско-
скорости на направление касательной к депрессионной кривой.
Обозначая через а угол касательной с осью и, получим
+ и sin а, -^|- = sina, D.8)
на основании чего уравнение D.5) примет вид
и cos a + v sin a + k sin a = 0. D.9)
Дифференцирование второго из уравнений D.7) по s при-
приводит к уравнению
и sin a — v cos a — ecosa = 0, D.10)
так как имеют место соотношения
-0j- = — vn = и sin a — v cos a.
Исключив переменную а из уравнений D.9) и D.10), получим
и2 + v2 + (k + в) v + fee = 0. D.11)
Это уравнение окружности, проходящей через точки @, —е) и
@, —k), имеющей центр в точке @, —(г + к)/2) и радиус,
равный (к — г) 12 (рис. 24,а). Очевидно, что при е = 0 из D.11)
получим уравнение D.6). При е < 0 получаем случай испарения
до свободной поверхности (рис. 24,6).
56
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
4. На промежутке высачивания, где давление постоянно,
имеет место уравнение D.5), а также уравнение D.9), причем
в последнем а теперь обозначает постоянный угол, который
образуется промежутком высачивания с осью абсцисс. Поэтому
для промежутка высачивания на плоскости (и, v) имеет место
уравнение прямой
и cos a + и sin a + fesina = 0, D.12)
проходящей через точку @, —k) и перпендикулярной к самому
промежутку высачивания.
Ук
sffk
Рис. 24.
Рассмотрение условий на границах, встречающихся в широ-
широком круге задач фильтрации, приводит к заключению, что на
плоскости u-{-iv, а следовательно, и на плоскости u — iv грани-
границами области являются отрезки прямых или дуги окружности.
Если прямую интерпретировать как окружность бесконечно
большого радиуса, то можно сказать, что область w ограничена
дугами окружностей.
Прежде чем перейти к примерам построения годографа ско-
скорости, рассмотрим вопрос о поведении отображающих функций
вблизи вершины угла. Это позволит нам составить представ-
представление о значениях скорости в угловых точках области движения
и облегчит задачу построения годографа скорости.
§ 5. Поведение скорости в угловых точках области движения.
Допустим, что в состав границы области г, которую мы хотим
отобразить на полуплоскость, входят отрезки двух пересекаю-
пересекающихся прямых АВ и АС. Рассмотрим поведение отображающей
функции вблизи вершины угла области фильтрации (рис. 25)
(см., например, Ризенкампф 1938, 2).
При отображении угла ВАС на верхнюю полуплоскость пло-
плоскости ?—? + ir\ угол па переходит в угол я. Будем рассмат-
рассматривать вместо г функцию U = гЧа. Примем ее аргумент равным
§ 5] Поведение скорости в угловых Точках §7
нулю при ? = ? > 0. Тогда при обходе точки ? = 0 на угол л
в положительном направлении аргумент z получит значение
ал, z приобретет множитель еап\ а г1/а — множитель eni. По-
Поэтому U вдоль АВ будет иметь значение
Таким образом, ?/ принимает действительные значения вдоль
отрезка ВАС. В окрестности точки ? = 0 функция U анали-
тична, однозначна и непрерывна вплоть до действительной оси.
По принципу симметрии (Смирнов 1974) такую функцию можно
продолжить в нижнюю полуплоскость. Следовательно, U будет
П
а)
Рис. 25.
аналитической в точке ? = 0 и будет разлагаться в ряд по сте-
степеням ?. Так как она обращается в нуль при ? = 0, то это раз-
разложение имеет вид
Отсюда
a.^+ ...Г
Так как (а, + а2?> + ...)а можно разложить в ряд по сте-
степеням ?, то получаем
z = ?а (б0 + &i? + Ы2 +...)• E.1)
Если аналитическая функция вблизи некоторой точки ? = ?э
представима в виде обобщенного степенного ряда
сходящегося в некоторой окрестности точки ?о, то говорят, что
go ^сть регулярная особая точка функции. Таким образом, вер-
вершина, в которой сходятся два прямолинейных отрезка границы
области, есть регулярная особая точка функции, совершающей
конформное отображение данной области на полуплоскость.
58 Плоские Движения 6 вертикальной плоскости [Гл. И
Рассмотрим различные случаи угловых точек.
1. Угловая точка на непроницаемой границе.
Вдоль этой границы ty = const; следовательно, для комплекс-
комплексного потенциала точка ? = 0, в которую мы переведем рассма-
рассматриваемую угловую точку, при отображении на полуплоскость ?
будет обыкновенной точкой, в которой будем иметь
со = с0 + с,С + erf2 + ... E.2)
С помощью E.1) и E.2) находим выражение комплексной ско-
скорости в виде
% = V-a(eo + e& +...)• E.3)
Из E.3) видно, что если угол па < я, то скорость при ? = О
будет равна нулю; если угол больше я, то эта скорость обра-
обращается в бесконечность.
2. Угловая точка на границе водоема. Здесь
вдоль ломаной линии qp = const, поэтому для со точка ? = О
опять будет обыкновенной и скорость будет иметь вид E.3).
3. Угловая точка на пересечении прямолиней-
прямолинейной границы водоема и прямолинейной непро-
непроницаемой границы. Тогда в точке А комплексный потен-
потенциал меняет условие Re со = const на условие Im со = const и
его разложение около ? = О имеет вид
с1?+ ...)• E.4)
Из E.1) и E.4) получаем
-37 = ?''¦-" (eo + *iE+ ...)• E.5)
Из этого равенства видно, что если а < 72, т. е. если угол
в точке А острый, то скорость будет равна нулю; если этот
угол тупой, то скорость обращается в бесконечность. В случае
прямого угла будем иметь конечное значение скорости.
§ 6. Примеры построения годографа скорости. Для безнапор-
безнапорного движения, т. е. движения со свободной поверхностью, бы-
бывает полезно построить годограф скорости.
В этом параграфе рассматриваются примеры построения
годографа скорости для земляных плотин. Поэтому приведем
здесь несколько рисунков, дающих представление о форме су-
существующих земляных плотин, построенных в разное время в
разных странах.
На рис. 26 приведены профили некоторых земляных плотин
средней высоты, причем отмечены размеры в метрах и уклоны
§б]
ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА СКОРОСТИ
59
откосов. Среди них отметим первую — Змеиногорскую плотину,
построенную на Алтае в 1780 г. русским гидротехником
К. Д. Фроловым. Для нее характерны крутые откосы, причем
верховой откос представляет выпуклую (по отношению к пло-
плотине) ломаную линию. Согласно исследованиям предыдущего
параграфа скорость в вершине этой ломаной линии равна нулю.
Ниже мы приводим годограф ско-
скорости такой плотины (рис. 31).
В качестве примера высокой зем-
земляной плотины на рис. 26 приве-
приведена Мингечаурская плотина
(в Азербайджане), ее наиболь-
наибольшая высота 80 м9 длина по греб-
гребню 1550 м.
Возьмем в качестве примера
простейшую плотину с наклон-
наклонным верховым откосом CD
(рис. 27), лежащую на непрони-
непроницаемом дренированном основа-
основании DE (EF — линия дренажа).
В земляной плотине обычно
глубина воды Н в верхнем бьефе
мала по сравнению с длиной ос-
основания плотины L. Предполо-
Предположим, что отношение Н к L на-
настолько мало, что перпендикуляр
CN к линии CD в точке С пере-
пересекает основание плотины DE
(рис. 27). В этом случае депрес-
сионная кривая должна иметь
точку перегиба. Действительно, в
противном случае депрессионная
кривая вся лежала бы под пря-
прямой CN, что, очевидно, невоз-
невозможно, так как вода, накапливаясь в теле плотины, должна
иметь выход в дренажную щель EF.
Обратимся к годографу скорости (рис. 28). Он ограничен
согласно D.6) окружностью и2 + v2 + kv = 0, соответствующей
свободной поверхности, прямой, проходящей через начало ко-
координат и перпендикулярной к верховому откосу плотины, осью
и, соответствующей непроницаемому основанию плотины, и, на-
наконец, осью v, отвечающей линии дренажа. Учитывая наличие
точки перегиба у депрессионной кривой, нужно провести надрез
по дуге окружности. С увеличением HjL надрез СВ уменьшается
и при некотором определенном значении H/L исчезает; при даль-
дальнейшем увеличении H/L появится надрез СВХ вдоль прямой
Рис. 26.
60
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
DC. Это означает, что точка перегиба С, в которой величина
скорости имеет наименьшее значение, дойдя до откоса, исчезнет,
а вместо нее на откосе появляется точка с максимумом скоро-
скорости. С увеличением H/L эта точка будет перемещаться вниз по
откосу, причем величина максимума увеличивается.
a w
Г
Рис. 27.
¦Рис. 28.
Вычисления для двух значений угла 0 показывают, что точка
перегиба исчезает при значениях (Полубаринова-Кочина
1939, 3)
-~ = 1,16 sin 9 = 0,820 для 0 = ^-,
^ = 1,19 sin Э = 0,232 для 6 = -^.
Обычно в плотинах отношение H/L имеет меньшие значе-
значения, чем только что приведенные, и поэтому, как правило, де-
прессионная кривая имеет точку перегиба.
Рассмотрим еще пример изменения годографа скорости. На
рис. 29 представлена симметричная плотина с наклонными от-
откосами, угол между которыми Э острый. Пусть Нх и Я2 —глу-
—глубины воды в верхнем и нижнем бьефах, L — длина непроницае-
непроницаемого основания. Обозначим Н = Н\ — Н2.
Если значение отношения H\jL мало, то точке перегиба сво-
свободной поверхности соответствует точка В на годографе скоро-
скорости (рис. 30). При возрастании величины H\\L точка В стре-
стремится к точке С; затем вместо надреза СВ появится надрез
СВи который при максимальном подъеме воды перед плотиной
перейдет в отрезок СВ2, причем часть СВ2А первоначальной об-
области годографа исчезнет. При Э = я/2 точки С и А на годо-
годографе скорости совпадут, надрез СВХ станет невозможным.
Таким образом, при 0 = я/2 точка перегиба всегда существует,
кроме предельного случая подъема воды перед плотиной.
§6]
ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА СКОРОСТИ
61
Если Э > я/2, то всегда, даже и при полном подъеме воды
в верхнем бьефе, будет существовать свободная поверхность, на
которой имеется точка перегиба. Годограф скорости всегда бу-
будет иметь разрез АВ по дуге окружности (так как точка С на
годографе скорости в этом случае будет ниже точки А).
При #2 = 0, т. е. при отсутствии воды в нижнем бьефе, точка
Е годографа скорости займе! положение Е\ и верхняя часть
годографа отпадет.
У//Л П У///////////////////////////////\с///, Т
Рис. 29.
Рис 30.
Если будем отодвигать основание плотины DF вниз в беско-
бесконечность, то получим
Н\ «
Н2
Я,
' ОО.
При этом на годографе скорости разрез FED исчезнет. Он
исчезнет также, если, полагая L к Н\ (или Н2) неизменными,
устремлять #2 к Нх (или #i к Я2). Но в этом случае движение
стремится к покою, для которого годограф скорости сводится
к точке. Таким образом, здесь, как и в предыдущем случае, при
стремлении к покою нарушается непрерывность изменения ско-
скорости.
На рис. 31 дан годограф скорости плотины Фролова для
случая отсутствия воды в нижнем бьефе. Если бы откос ABC
состоял из одной прямой, то разрез AN В исчез бы. Если бы
угол ABC был больше л, в точке В скорость была бы равна оо.
На рис. 32 представлена плотина на непроницаемом основа-
основании конечной глубины с горизонтальным отрезком дренажа
GF; годограф скорости для нее дан на рис. 33. В бесконечно
удаленных точках А и К скорость равна нулю, поэтому точки
А и К будут на годографе скорости в начале координат. Далее,
вдоль АВ имеем и = 0, v направлена вниз, причем увеличи-
увеличивается при движении от Л к В. Так как в точке В Ихмеем разрыв
62
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
в направлении скорости, то по свойству функции комплексного
переменного u-\-iv может равняться в этой точке или нулю, или
бесконечности. В данном случае угол в точке В больше я,
следовательно, и + iv = °о. Дальше вектор скорости меняет
F
У ^о
Рис. 31.
направление, делаясь перпендикулярным к границе BD\ на го-
годографе имеем отрезок BCD, причем С —точка, в которой ско-
скорость имеет наименьшее значение, a D — точка пересечения с
К
Рис. 32.
окружностью, которая соответствует свободной поверхности.
Точке перегиба линии свободной поверхности Е соответствует
на годографе скорости вершина кругового разреза Е. По дуге
окружности мы должны дойти до точки F и затем перемещаться
вдоль оси vt так как вдоль отрезка дренажа FG скорость на-
направлена перендикулярно к отрезку. В точке G скорость обра-
§7]
ТРЕУГОЛЬНИК ФИЛЬТРАЦИИ
щается в бесконечность, меняя направление при переходе на
отрезок GK. В бесконечно удаленной точке /С, как уже сказано,
скорость равна нулю. Вдоль непроницаемого основания скорость
направлена вправо, принимая в некоторой точке L максималь-
максимальное значение, изображаемое на годогра-
годографе скорости отрезком KL. Всей линии АК
соответствует на годографе скорости от-
отрезок ALK, проходимый в прямом и об-
обратном направлении (Полубаринова-Ко-
чина 1940, 3).
На рис. 33 имеем двулистную область, ^
так как часть плоскости {и, v) покрыта
два раза областью изменения перемен-
переменной и + iv. Когда идем в плоскости z
вдоль контура ABD, то область движения
остается справа, на годографе же скоро-
скорости при этом область находится налево
от контура (так как u+iv является функ-
функцией от г, а не от г), что изображено
штриховкой вблизи контура.
р ур
Рассмотренные примеры показывают,
ф
ВП
Рис 33.
р
что построение годографа скорости, во-
вообще говоря, сложно; поэтому желатель-
но при решении задач обходиться без
годографа скорости. Такие методы в применении к некоторым
задачам будут указаны в главе VI.
§ 7. Треугольник фильтрации. Под треугольником фильтра-
фильтрации будем понимать треугольник (Ризенкампф 1938, 1), по-
построенный на векторах, которые получаются, если взять гра-
градиент от обеих частей уравнения
Это уравнение вытекает из A.2), если положить
где y ~~ объемный вес жидкости, ра—атмосферное давление.
Получим
~ grad p = grad h ~ /, G.1)
где / — единичный вектор, направленный вверх по вертикали.
Такой треугольник изображен на рис. 34.
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. It
Равенство G.1) можно представить в другом виде, умножив
его почленно на коэффициент фильтрации к и приняв во внима-
внимание, что
- k grad h = v, G.2)
где v — вектор скорости фильтрации. Тогда
Рассмотрим плоскость годографа скорости. На ней пункти-
пунктиром построена окружность
и2 + v2 + kv = О,
соответствующая свободной поверхности грунтового потока. Из
v
\""
Рис. 35.
рассмотрения рис. 35 видно, что на свободной поверхности век-
векторы v и (&/Y)grad p ортогональны.
§ 8. Силы, действующие на частицы грунта. В вопросах проч-
прочности и устойчивости гидротехнических сооружений важное зна-
значение имеет изучение силового воздействия воды, протекающей
в грунте под сооружением.
Задача эта рассматривалась многими учеными: Н. П. Пузы-
ревским, Н. Н. Павловским, К. Терцаги, Н. М. Герсевановым
и др. При этом вопрос о физической природе фильтрационных
сил вызывал дискуссию (Рельтов, Чугаев и Вяземский 1949).
Здесь приводится изложение в форме, данной в работе Б. К. Ри-
зенкампфа A938, 1).
Выделим единицу объема пористого тела и найдем равно-
равнодействующую F сил, действующих на твердые частицы этого
объема. Эта сила может рассматриваться как геометрическая
сумма следующих сил:
1. Вес F\ сухих частиц выделенного объема. Эта сила на-
направлена по вертикали вниз и равна по величине произведению
§ 8] СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЧАСТИЦЫ ГРУНТА 65
пу\, где Yi—объемный вес материала частиц, п = 1—т —
объем твердых частиц в единице объема пористого тела. Таким
образом, можем написать, обозначая через / единичный вектор,
направленный вверх по вертикали, равенство
2. Сила F2 давления воды на твердые частицы в единице
объема пористого тела. Так как действие давления на единицу
объема пористого тела равно —grad/?, то для F2 имеем
F2— — ngrad p.
3. В качестве третьей силы Б. К. Ризенкампф рассматривает
силу Fz — увлекающее действие фильтрующейся воды на твер-
твердые частицы, заключенные в единице объема пористого тела.
Это действие равно и противоположно сопротивлению единицы
объема пористого тела. Сопротивление же, отнесенное к единице
массы воды, определяется равенством
«—*•¦
Так как масса воды в объеме грунта, равном единице, равна
/пр, где р — плотность воды, то получаем
Величина F$ носит название фильтрационной силы.
Геометрическая сумма fb F2 и jF3 дает равнодействующую
F = — aiyi/ — п grad p + ^-v.
Преобразуем полученное выражение двумя способами, ис-
используя уравнения G.1) и G.2) и исключая с их помощью один
раз р, другой раз v:
F = — grad p —
Здесь введено обозначение
Величина уо представляет вес единицы объема пористого тела
с заключенной в нем водой.
Силу F можно построить с помощью диаграммы рис. 36, на
которой даны оба указанных представления F.
3 П. Я, Полубарииова Кочина
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. I!
Вектор F можно представить через силовую функцию
V = — yh — п (yi — у) у — — р — Yo# H~ const
в виде F = grad V. Нетрудно убедиться в том, что V удовлетво-
удовлетворяет уравнению Лапласа.
Все приведенные в этом пункте рассуждения годятся как для
плоскости, так и для пространства.
В случае плоского движения, кроме функции V7, можно вве-
ввести функцию [/, гармонически сопряженную с 1/, так что
Линии V = const суть линии равного потенциала силы F, урав-
уравнение U = const определяет силовые линии поля силы F.
Если жидкость находится в покое, то v = 0 и
что выражает закон Архимеда: сила, действующая на грунто-
грунтовый скелет, равна весу скелета, умень-
уменьшенному на вес вытесненной им воды.
Если давление в жидкости постоян-
постоянно, то она движется лишь под дей-
действием силы тяжести. В этом случае
т.е. к весу грунтового остова присо-
присоединяется вес воды в порах.
Б. К. Ризенкампфом указана воз-
возможность вычисления напряжений в
грунте, через который просачивается
вода.
Если обозначить через ох и оу нор-
нормальные напряжения на площадках
пористого тела, перпендикулярных к
осям х и уу а через хху — касательное напряжение на этих
площадках, то на основании уравнений равновесия сплошной
среды будем иметь
Рис. 36.
дх
ху
дт
ху
дои
дх
дх
где
дх '
F — ^L
У~ ду '
§ 9] УРАВНЕНИЯ ДВИЖЕНИЯ ПРИ НЕЛИНЕЙНЫХ ЗАКОНАХ 67
Если пористое тело подчиняется закону Гука, то, вводя
функцию напряжений Ф(х, у) с помощью уравнений
~ ду2 V> ТхУ—
ду2 V> ТхУ— дхду* °У~~дхт~~У>
найдем, что Ф удовлетворяет бигармоническому уравнению
§ 9. Уравнения движения при нелинейных законах фильтрации. Теория
этих уравнений развита в работе С. А. Христиановича A940).
Как было указано в § б первой главы, движение грунтовых вод в общем
случае подчиняется зависимости вида
/ = ф(Г), (9.1)
связывающей гидравлический уклон / = —dh/ds со скоростью фильтрации W.
Рассмотрим уравнения плоского установившегося движения
<9-2>
или
Считая жидкость несжимаемой, присоединим к ним уравнение неразрывности
Введем обозначение
W
Можно рассматривать условно К как коэффициент фильтрации, зависящий
от скорости. Исключая h из (9.2), получим
Вместо и и v можно принять в качестве новых функций величину век-
вектора скорости W и угол его с осью абсцисс О:
Тогда вместо (9.3) и (9.5) получим такую систему уравнений:
Ф' (W
б*
68
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
Из уравнения неразрывности вытекает существование функции тока г|э — та-
такой, что
дх
ду
• и = W cos Ф.
(9.7)
Пусть имеем некоторую функцию F(xf у) координат ху у. Если введем
новые независимые переменные h и г|э, то получим на основании (9.2) такие
выражения:
(9.8)
4^ = - Ф (W) sin 1
ду v
dF t XV7 л dF
-rj- + U^cosO-—--.
С помощью этих формул система (9.6) приводится к виду
= 0, ** itf^'nm я
dh
dh ^ [Ф (W)]2
(9.9)
Прежде чем идти дальше, рассмотрим вопрос о приведении системы
квазилинейных уравнений к каноническому виду. Пусть дана система
ди
ди
dv
dv
ди
W
ди
dv
W
dv
••еь
• е2у
(9.10)
коэффициенты которой а**, 6гл и вА суть функции от х, у, и и v.
Для нахождения уравнений характеристик присоединим к уравнениям
(9.10) уравнения
ди
_
ди
_
/л11.
(9Л1)
Будем решать систему уравнений (9.10) — (9.11) относительно производных
ди/дх, ди/ду, dv/dxy dvjdy. Для этого перепишем (9.11) так:
ди
дх
du
~ dx
ди
ду
dy
dx*
dv
dx
dv
— dx
dv
dy
dy
dx '
Обозначим с(г//с(л; через Я и подставим значения (9.12) в (9.10). Получим
систему двух уравнении, линейных относительно ди/ду и dvjdy: •
(9.13)
Отсюда найдем
ди , ., ,. Eу da rfy
— -f- (&12 — ai2A) -щ = ei — an -^ ai2"rf7"»
ди д, dti rftt rfy
+ ( Л) е « a
Аи
Л '
dv
§ 9]
где
УРАВНЕНИЯ ДВИЖЕНИЯ ПРИ НЕЛИНЕЙНЫХ ЗАКОНАХ
bn-
Ь 2\ — 0-2\Ь b22 — #22^
— ^и _ dv
du dv
(?2 — 021 ~~j 022 ~»— #22 — 022^
69
du
— an ——
dv
, . du dv
Уравнения характеристик получаются из условия, что вдоль них не
существует единственного решения для ди/ду, dv/dy, т.е. из уравнений Д=0,
Ди = О, Д« = 0. Одно из этих уравнений есть следствие двух других.
Раскрывая определители Д и Ди и вводя обозначения
012
= 0.
612
622
flu
021
0.1
a2
012
022
E
— A
~~ '
012
022
^11
bn
Ь\\ Ь\2
bi\ bi2
= F
= С
e\ b\2
e2 b22
Ь\2
Ь22
= M,
012
022
2B
получим такие уравнения:
ЛЯ2 + 2ВХ + С = О,
Решая первое из них относительно X, будем иметь
В VВ2 - АС
Если
А = Л
V- АС< О,
(9.14)
то говорят, что данная система эллиптического типа. Предполагая это усло-
условие выполненным, положим
A.I — Р + iQ,
где
В л/АС-В*
Можем написать уравнения характеристик в виде
dy = Xxdxy (9.15)
(Е + Х{А) du + D dv + (М + Mi) dx = 0. (9.16)
Допустим, что найдено некоторое решение системы (9.10) и = и(ху у),
v = v(x,y). ]з,ля определения характеристик, отвечающих этому решению,
подставим в Р и Q вместо и и v их значения и(х,у), v(xfy). Пусть общий
70 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
интеграл (9.15) будет ц(*, У) + i v(*, у) = const, Дифференцируя это соотно-
соотношение и используя (9.15), найдем
-?• (ц + /v) + (P + IQ) -щ (ц + «V) = 0.
Разделение действительной и мнимой частей дает
4ML + ^|iL_Q^l = Ol *L+QV)L+p*L = o. (9.17)
дх ду ду дх ду ду
Рассмотрим систему уравнений (9.10) и (9.17), принимая за независимые
переменные \х и v, а за искомые функции х> у, и и у. Формулы перехода бу-
будут иметь вид
дх -~ Л dv ' d*/ "~~ A dv' дх~~ А дц* ду ~" Л dfx' ( j
где
a "" dji dv d\i dv "" v L V (?Ц / "h V dv
Сделаем замену переменных в (9.17) и (9.10), причем в последних урав-
уравнениях производные ди/дх, ди/ду, ... заменим через производные по \х и v
с использованием соотношений (9.17) и (9.18). Получим систему
(9.19)
которую можно назвать канонической системой. В ней ху у, и и v являются
функциями параметров (Л и v. Решение этой системы при отличном от нуля
определителе Д будет также решением исходной системы.
Полученная система не меняется, если заменить \i и v переменными ц*
и v*, где (Л* + tv* = f(\i + iv)— аналитическая функция. Если уравнения ха-
характеристик допускают интегрируемую комбинацию, т. е. если существует
соотношение
р (ху у, и, v) + iq (x, yt u> v) = const,
справедливое в силу уравнений (9.15) и (9.16), то, если принять р и q за но-
новые неизвестные вместо х, у или м, у, два уравнения системы будут уравне-
уравнениями Коши — Римана, т. е. р + Щ будет аналитической функцией |1 + iv.
Вернемся теперь к системе (9.9). Вместо х> уу и и v в нее входят г|), Л,
W и б1. Каноническая система с параметрами \i и v будет для системы (9.9)
иметь такой вид:
dv дц d\i ' d\i \
/-. IS Ц/ W I W **' \ W / Oil
:U' ^JT
"у и^Ф(и^) dv дц
(9.20)
dv
§ 9) уравнения Движения при нелинейных законах 71
Вместо функции W введем фиктивную скорость фильтрации W* и пере-
переменную S с помощью равенства
$LdW. (9.21)
Для закона Дарси W* = cW (с — постоянная интегрирования), для степен-
степенного закона / = U?Y/k
V
(при y = 1 величина k обращается в коэффициент фильтрации, а степенной
закон в закон Дарси).
Теперь можно переписать систему (9.20) так:
д In ИГ dft = Q din Г* aft
dv ди, да dv ,-
[ (9.22)
d\i dv * dv d\i * j
где
ф (W) I Ф(Ц^)
L ^—г"- Д/ »7 ^/^ = L (ИИ- (9-23)
Для степенного закона
С помощью формул (9.8) можно найти производные от х и у по h и \|к
dx __ cos ft djc sin ft d# sin ft dy cos ft
~dh~~~~ Ф(Н^) ' ^vjT"~ Г~' Ж"""" ФAГ) ' ThjT8*5 Г *
Отсюда для л: и г/ найдем выражения в виде криволинейных интегралов
cos ft ,, , sin ft ,л f sin ft ,, cos ft
S co
JA
Рассмотрим условия на границах области движения (подробнее об этих
условиях см. в § 2 главы II).
Вдоль прямолинейных непроницаемых стенок \|) = const и ft = const.
Вдоль дрямолинейной границы водоема h = const, ft = const.
Вдоль свободной поверхности г|) = const и давление постоянно, т. е.
р = р^г(/| —^)= const. Дифференцируя последнее равенство вдоль свобод-
свободной поверхности, получим
(Ю у2 Ф (W) у
4 =
дх * ду dx dx ~~ U W и W и
или ФA^)+ sin ft = 0. Получаем некоторую замкнутую кривую на плоско-
плоскости и, v.
Вдоль промежутка высачивания — отрезка прямой под углом ft0 к оси
х — имеем постоянство давления. Дифференцируя вдоль этого отрезка урав-
уравнение р = const, получим
или
+v
72 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
что можно привести к виду
Ф (W) cos (в - О0) + sin в0 = О,
При решении конкретных задач рекомендуется на плоскости р, v рас-
рассматривать область, соответствующую движению, удовлетворяющему за-
закону Дарси, и затем искать поправки на отклонение от этого закона.
Примеры. Система уравнений (9.2) —(9.3) легко интегрируется в слу-
случае одномерных движений. Так, для осесимметричного движения h = h(r),
W= W(r), где г — расстояние от оси симметрии, причем скорость направ-
направлена по радиусу-вектору, имеем из (9.3)
jL(Wr)=0, *--?-. (9.24)
где Q — постоянный расход. Из (9.2) тогда получаем (Нумеров 1969)
h (г) = - \ Ф (-^г) dr + const. (9.25)
Случай Ф (W) а=я (а + bW) W соответствует квадратичному закону филь-
фильтрации
grad h = -(a + bW)W (a > О, Ъ > 0). (9.26)
Для точечного стока согласно (9.24) получим
Этот пример был использован С Н. Нумеровым A969) для иллюстрации
сходимости предложенного им метода последовательных приближении при
решении системы
grad h = — (а + bW) W, div W= 0. (9.23)
Метод Нумерова состоит в следующем. Решаем уравнение (9.26) относи-
относительно W:
lF-2|gradA|:[a(l + д/l + ^-1 grad
(9.29)
Так как скорость направлена противоположно градиенту напора, то можно
положить
л/\ + ~^
(9.30)
В исходном приближении |grad/i| в выражении величины Я прини-
принимается таким, как в случае фильтрации по закону Дарси. Далее, решая
уравнение
div (Я grad h) = 0, (9.31)
найдем первое приближение h\(x, у, z). Подставляя в выражение для к
(9.30) вместо |grad/i| величину |grad/i]|, найдем во втором приближении
lh(*, У> z) и grad h2 и т. д.
В. В. Соколовским A949) рассмотрен частный случай, когда
W
Ф (W) =
§ 10] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 73
Это соотношение, выбранное из соображения интегрируемости уравне^
ний характеристик, может на некотором интервале значений W дать оценку
решения в случае отклонения от линейного закона фильтрации.
Если в системе (9.20) положить
ц + /v = S — Л,
где S определяется формулой (9.21), то вместо системы уравнений (9.20)
получим такую систему:
Ф2(^) ^ , dh _0 ф ** дк -о
в которой независимыми переменными являются W и Ф. Это соответствует
преобразованию годографа, примененному С. А. Чаплыгиным в теории газо-
газовых струй.
Уравнение (9.32) оказалось удобным в задачах о фильтрации с началь-
начальным (предельным) градиентом. Для фильтрации вязкопластических жидко-
жидкостей или воды в глинизированных породах принимают (Ентов 1967)
ф(Г) = \Г + Л при IPX),
0<O(U7)<A, при IF —0. ( ' '
Особенность фильтрации с предельным градиентом — возможность обра-
образования застойных зон, т. е. областей, в которых градиент напора меньше
предельного и движение отсутствует. Если имеются две скважины в обыч-
обычном потоке, то между ними найдется нейтральная точка, в которой скорость
равна нулю. При наличии начального градиента вместо точки будет целая
область, напоминающая бубновый туз, с точками возврата в вершинах. Тео-
Теория таких движений развита В. М. Битовым и др. (см. Бернадинер и Ен-
Ентов 1975).
Б. ПРОСТЕЙШИЕ ПРИМЕРЫ ПЛОСКИХ ДВИЖЕНИЙ
§ 10. Предварительные замечания. Рассмотрим несколько
примеров движения грунтовых вод. При этом остановимся лишь
на таких случаях, для которых точное решение получается срав-
сравнительно просто. Более сложные задачи будут рассматриваться
дальше при помощи специальных методов математического ана-
анализа, разработанных различными авторами применительно к от-
отдельным группам задач теории фильтрации.
Движения грунтовых вод делятся на напорные, безнапорные
и полунапорные, или напорно-безнапорные.
Напорным движением в теории фильтрации называют такое
движение, в котором нет свободной поверхности. Таково движе-
движение грунтовой воды под гидротехническим сооружением, проис-
происходящее под влиянием разности напоров в верхнем и нижнем
бьефах, или поток воды к скважинам в водоносном пласте,
ограниченном непроницаемыми поверхностями. В напорном дви-
движении всегда сверху имеется твердая стенка, границы области
Движения бывают лишь двух типов: линии тока и линии равного
потенциала.
74 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
Безнапорным движением называется такое, в котором об-
область движения ограничена сверху свободной поверхностью
(или, по крайней мере, имеются промежутки высачивания).
Наконец, полунапорная фильтрация характеризуется тем,
что фильтрационный поток сначала соприкасается с подземным
контуром сооружения, а затем отрывается от него, образуя сво-
свободную поверхность. Полунапорное движение имеет место под
сооружениями, ниже которых имеется значительное падение
уровня грунтовых вод, например под водосбросами и напор-
напорными бассейнами гидростанций. Полунапорные движения будут
рассмотрены в главе X.
Нижеследующие § 11 и 12 этой главы посвящены безнапор-
безнапорным движениям, остальные — напорным.
§ 11. Дренажная щель на водоупоре. Будем искать z как
функцию от (о «= ф + fy> причем зададимся простейшим (после
линейного) видом функциональной зависимости, положив
2 = Л©2, A1.1)
где Л — пока неопределенная постоянная.
Посмотрим, может ли рассматриваемое течение иметь сво-
свободную поверхность. На последней должно выполняться усло-
условие равенства нулю давления qp + ky = 0, равносильное усло-
условию B.7) при const = 0, а также условие, что линия свободной
поверхности есть линия тока: г|) = г|?о.
Подставляя в правую часть A1.1) значения ф=—ky, \|)=%ь
получим
Отделение действительной и мнимой частей дает для действи-
действительного А
Для выполнения последнего из двух равенств необходимо,
что8ы
Тогда свободной поверхностью будет парабола
Теперь подставим найденное значение Л в уравнение A1.1)
и, разделив в нем действительную и мнимую части, найдем за-
зависимость координат х и у от функций ф и г|>:
11]
ДРЕНАЖНАЯ ЩЕЛЬ НА ВОДОУПОРЕ
75
При \|) = 0 линией тока является отрицательная часть оси #,
так как при этом имеем, считая г|?о > О,
Другие линии тока получим, давая в A1.4) постоянные зна-
значения \|). Это — софокусные параболы с фокусом в начале коор-
координат (рис. 37,а).
Наконец, положив в A1.4) ф=0, получим эквипотенциаль
у—°» х—
Это часть положительной оси абсцисс. Мы возьмем ее отрезок
Тогда линии тока \|э = О и гр = \ро = Q (Q — расход дренаж-
дренажной щели) вместе с линией равного потенциала ф = 0 образуют
область движения, отвечающего притоку грунтовой воды из бес-
бесконечности к дренажной щели О А (рис. 37, а). Эквипотенциали
будут параболами, ортогональными к параболам — линиям
тока.
Длина отрезка дренажа ОА — d связана с расходом Q ра-
равенством
<«-#•
Следовательно, расход пропорционален ширине щели:
A1.5)
76
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
Приведенная задача была рассмотрена Ф. Форхгеймером
и И. Козени. Затем Н. Н. Павловский A937) получил ее ре-
решение прямым путем, задаваясь граничными условиями на трех
частях контура, ограничивающего область движения, и строя
годограф скорости, который, как нетрудно видеть, имеет вид
рис. 37,6.
Возвращаясь к уравнению свободной поверхности A1.3),
возьмем на ней две точки с координатами (хиу{) и (х2,у2)
и подставим их соответственно в уравнение A1.3). Вычитая за-
затем почленно полученные тождества, найдем для расхода вы-
выражение
У2 - У\
y\-yj
2 (л:2 — ЛГ1
(П.6)
Совершенно такая же формула для расхода получается в гид-
гидравлической теории установившегося движения (см. главу X),
где ее принято называть формулой Дюпюи (Dupuit 1863).
§ 12. Горизонтальная дрена при отсутствии водоупора; изо-
изолинии грунтового потока. Этот случай получается из только что
рассмотренного, если к области движения, выбранной нами
Рис. 38.
в § И, присоединить нижнюю полуплоскость (рис. 38). Все ли-
линии тока являются софокусными параболами. Для их построе-
построения нужно давать г|) значения от ф0 До —оо.
Помимо линий тока и линий равного потенциала, представ-
представляют интерес линии равного давления или изобары грунтового
12]
ГОРИЗОНТАЛЬНАЯ ДРЕНА ПРИ ОТСУТСТВИИ ВОДОУПОРА
77
потока. Чтобы построить семейство изобар, вспомним зависи-
зависимость между потенциалом скорости и давлением A.2). Прини-
Принимая С\ = 0, ее можно переписать так:
откуда видно, что графическое сложение эквипотенциалей и ли-
линий у = const дает изобары.
На рис. 39 построено семейство изобар (сплошные линии)
с помощью графического сложения эквипотенциалей (пунктир-
(пунктирные линии) и горизонтальных прямых у = const.
Рис. 39.
Помимо ортогональной сетки, образованной семейством ли-
линий тока и линий равного потенциала, принято еще рассматри-
рассматривать семейство изовел или изотах, т. е. линий равной скорости,
и изоклин, т. е. линий, вдоль которых вектор скорости имеет
одно и то же направление. Сетки изотах, как указал Н. Н. Пав-
Павловский, полезны для расчета суффозии, т. е. явления выноса
мелких частиц грунта, которое в ряде случаев может приводить
к авариям плотин.
Возьмем логарифм комплексной скорости и разделим в нем
действительную и мнимую части:
In w = lg | w I + / arg w = In W — /0
78
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
[ГЛ. II
(W — величина скорости, О — угол между вектором скорости
и осью абсцисс). Так как действительная и мнимая части In до
являются гармоническими функциями, то линии
In W = const, О = const
образуют ортогональные семейства.
Для рассматриваемого нами простейшего примера нетрудно
найти уравнения изоклин и изотах. Действительно, имеем на
основании A1.1) и A1.2):
@
/
= V ~
W
Отсюда логарифм комплексной скорости
In w = In д/- *f- -1 (in \z | + I arctg |) .
При этом видно, что изотахи суть концентрические окруж-
окружности г = const с центром в фокусе парабол, изоклины —лучи,
исходящие из фокуса (рис. 40).
//////////////////////////////////////////77//////7/////////////////W
Рис. 40.
Величина скорости равна коэффициенту фильтрации вдоль
той окружности, которая касается свободной поверхности (в ме-
месте подхода этой поверхности к отрезку дренажа).
§ 13. Плоский флютбет в слое бесконечной глубины. Рассмот-
Рассмотрим теперь простейший пример напорного движения грунтовых
вод под гидротехническим сооружением — обтекание плоского
флютбета в грунте бесконечной глубины (рис. 41).
§18]
ПЛОСКИЙ ФЛЮТБЕТ В СЛОЕ БЕСКОНЕЧНОЙ ГЛУБИНЫ
79
В этом случае можно построить решение по особенностям
комплексной скорости w = u — iv, рассматриваемой как функ-
функция от z.
В самом деле, на отрезках АВ и СА (рис. 41) имеем и = О,
вдоль флютбета ВС имеем v = 0; другими словами, w прини-
Рис. 41.
мает действительные значения на отрезке ВС, т. е. при — / <
< х < / (ВС = 21), и чисто мнимые значения при |*|>/.
Рассмотрим функцию -д// — z . Она действительна при z =
= х < I и имеет чисто мнимые значения при z = х > /. Функ-
Функция V + z -действительна при z = х> — I и чисто мнима при
г = х <1 —I. Поэтому функция л/12 — г2, принимая действи-
действительные значения на отрезке (—/, /), является чисто мнимой
вне этого отрезка на действительной оси. Нужно поставить ес-
естественное в данной задаче условие —обращение скорости
в нуль на бесконечности. Тогда за w может быть принята
функция
м м
<13Л)
где М — некоторая постоянная.
Выражение w, как нетрудно видеть, удовлетворяет усло-
условиям: v = 0 при |*| </ и и = 0 при |*| >/. Но это не един-
единственная функция, удовлетворяющая данным условиям. Так,
можно было бы выражение A3.1) умножить на рациональную
функцию с действительными коэффициентами, в которой сте-
степень числителя не превышает степени знаменателя.
Например, можно взять за w функцию
, ЩГ'Г , , A3.2)
где т и п — целые числа, причем
80 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
Однако функция A3.2) будет иметь дополнительные особен-
особенности в точках z = а и с\ если же, например, а = /, то при
z = I (в точке С) получается более сложная особенность, чем
это отвечает нашей задаче: в то время как вектор скорости в
этой точке (рис. 41) должен поворачиваться на прямой угол, по
формуле A3.2) он поворачивается на угол я(т + ]/2)-
Таким образом, чтобы задача была определенной с матема-
математической точки зрения, нужно задаться порядком бесконечности
функции в особой точке.
Если считать —I < а < /, то формула A3.2) дает функцию,
имеющую особую точку при z = а, т. е. на флютбете. При
п = 0, т=\ эта особая точка — источник или сток. Это заме-
замечание мы используем ниже, при решении задачи о дренажной
трубе под флютбетом (см. § 15).
В формуле A3.1) нужно определить значение постоянной М.
Для этого обратимся к комплексному потенциалу. Интегрируя
уравнение
_ dco _ М
~~ dz~ */l2 — z2 '
найдем
(о = ф -f гф = М arcsin у + N. A3.3)
Примем вдоль флютбета гр = 0.
Перепишем формулу A.2), выражающую зависимость между
потенциалом скорости и давлением, в таком виде:
Произвольная постоянная С\ выбрана так, чтобы значение ф
вдоль нижнего бьефа было равно нулю (атмосферное давление
считается равным нулю). Вдоль границы верхнего бьефа имеем
p = pgH\. Поэтому вдоль /4В, учитывая, что у = 0 вдоль верх-
верхнего бьефа, получим
где Н = Я1 — #2 — действующий напор.
Теперь, полагая в A3.3) z = ±1 и принимая во внимание,
что в этих точках ф = 0, а ф соответственно равно 0 и —kH,
найдем
kH . z kH kH z /1ОГЧ
со = — arcsin у 2" = ~ arccos у. A3.5)
Отсюда для z будем иметь
?• A3.6)
§ 13]
ПЛОСКИЙ ФЛЮТБЕТ В СЛОЕ БЕСКОНЕЧНОЙ ГЛУБИНЫ
81
Разделяя здесь действительную и мнимую части, получим
х = / cos ф* ch \|)*, y= — /sinq^shit»*, A3.7)
где принято
Р —~Ш> Ф —Тн-
A3.8)
kH* ^ ~ кН
Давая -ф* постоянное значение /ф* = /ф*, получим линии тока-
эллипсы с фокусами в точках ± /:
У2 _
* I
A3.9)
При Ф* = Ф* получим эквипотенциали — софокусные гиперболы
/COS ф! /sin (fj
На рис. 41 построены линии тока и линии равного потен-
потенциала. По их густоте можно судить о величинах средних ско-
скоростей.
1
\
1
V
V
/
J
2
1
0
^
-г
-д
1
Щ
У
1
U
V
ч
Рис. 42.
Для вычисления скорости в любой точке z = x-fiy служит
Д
формула
ьи
пл/12-г2
В частности, для скорости вдоль флютбета (рис. 42) имеем
A3.11)
кН
я V/2 -
82 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
и вдоль границ верхнего и нижнего бьефов (знак — для верх-
верхнего, знак + для нижнего бьефа)
Ш
Это редкий по простоте случай, когда возможно дать явные
величины составляющих скорости и и v в любой точке (х,у)
области движения:
=
kH д
я У 2"
kH
/У(/2-*2 +
У(/2-
У2J
-X2
+ У
+
+
2J
4х2у2 + I2
У2J + 4х2у
+ 4х2у2 -
—
2
I2
х2+ у2
»
+ х*-у*
V я л/2
причем верхний знак имеет место для х < 0, нижний для х > 0.
Важным элементом движения является давление или напор
вдоль основания гидротехнического сооружения. Так как вдоль
последнего г|э=О, то из A3.5) получаем, полагая h = —(p/kt
что вдоль флютбета
, // х
h = — arccos-y.
Так как вдоль флютбета у = 0, то давление пропорционально h:
р = pgh = -Ц^- arccos у.
Распределение напора вдоль нашего флютбета можно полу-
получить как предельный случай напоров при Т/1 = оо (см. рис. 61
в главе III).
Представляет интерес вычисление расхода г^ через отрезок
нижнего бьефа, от точки х = I до точки х = х,0. Для его под-
подсчета можно воспользоваться первым из уравнений A3.7), по-
положив в нем ф = 0, х = хо. Тогда получим
kH xn kH
= — arch-^ = — In
A3.12)
При удалении х0 на бесконечность расход ф0 становится беско-
бесконечно большим. Мы увидим дальше, что для проницаемого слоя
конечной глубины полный расход получается конечным.
В § 8 настоящей главы мы ввели силовую функцию V для
вектора F — равнодействующей сил, действующих на частицы
грунта:
О'
§13]
ПЛОСКИЙ ФЛЮТБЕТ В СЛОЕ БЕСКОНЕЧНОЙ ГЛУБИНЫ
83
На рис. 43 построены линии V = const для плоского флют-
бета. На этом же рисунке построены для одного частного слу-
случая линии U = const, вдоль которых направлен вектор F. При
наложении этих семейств друг на друга получилась ортого-
ортогональная сетка. Из рассмотрения рис. 43 видно, что вектор F
всюду направлен вниз, за исключением области а возле ниж-
нижнего бьефа, где вертикальная составляющая этого вектора на-
направлена вверх. Здесь возможно выпирание грунта и вынос час-
частиц вверх.
H-WL
Рис. 43.
Замечание 1. Постоянную С2 во второй из формул A.2)
можно выбрать иначе. Можно, например, поставить условие,
чтобы значения потенциала скорости вдоль верхнего и нижнего
бьефов были равны по величине, но противоположны по знаку.
Тогда получим
2 =
Н\ + Яг
Н\ + Яг
Значения ф вдоль верхнего и нижнего бьефов соответственно
будут
_ , Hl~H2 __ kH _u Нх-Н2 _kH
Ф1— * 2 — 2 , ф2 —« 2 ~ 2 '
84 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
Комплексный потенциал будет связан с z зависимостью
со = Ф + *Ф = ~arcsin7 • A3.13)
Замечание 2. Линии тока непосредственно под гидротех-
гидротехническим сооружением зависят от формы подземного контура
этого сооружения. Но по мере удаления в глубину слоя и в обе
стороны от основания сооружения это влияние будет все мень-
меньше. Линии тока становятся близкими к полуокружностям.
Иначе говоря, при удалении в глубь водопроницаемого слоя
на достаточно большое расстояние от сооружения можно счи-
считать размеры последнего исчезающе малыми. Поэтому условия
на бесконечности будут для действительного контура такими
же, как для «точечного флютбета», т. е. такого флютбета, для
которого / = 0. Для этого случая формула A3.11) дает
^ A3.14)
TLIZ
Комплексный потенциал «точечного флютбета» будет
© = q> + n|) = -^-lnz + C. A3.15)
Другими словами, точечный вихрь интенсивности Г = 2kH
дает схему течения на далеких расстояниях от сооружения,
а именно, начиная с того места, где линии тока практически на-
начинают совпадать с полуокружностями (что будет для г > 2L,
где L — ширина сооружения).
§ 14. Шпунт в проницаемом грунте бесконечной глубины. Для
уменьшения давления на плотину и уменьшения выходных ско-
скоростей движения под основанием гидротехнических сооружений
Рис. 44.
устраивают шпунтовые ряды, обычно из металлических фигур-
фигурных пластин. Для того чтобы между шпунтинами не было ще-
щелей, им придают особую форму (на рис. 44 дан пример сечения
двух шпунтин).
Если повернуть чертеж рис. 41 на 90°, то получим другое
движение, представленное на рис. 45. На нем изображен вер-
вертикальный отрезок длины S, который обтекается грунтовой во-
водой под влиянием разности напоров Н.
141
ШПУНТ В ПРОНИЦАЕМОМ ГРУНТЕ БЕСКОНЕЧНОЙ ГЛУБИНЫ
Комплексная скорость и комплексный потенциал здесь
имеют вид
km 1
Знак плюс берется для правой части чертежа.
Линии тока суть половины эллипсов, эквипогенциали —ор-
—ортогональные к ним гиперболы. На рис. 45 построена сетка дви-
движения.
Рис. 45.
На рис. 46 построены линии V = const и U = const, по-
подобно тому как это сделано в § 13 для случая плоского
флютбета. Из этой фигуры видно, что за шпунтом имеется об-
область, обозначенная буквой а, внутри которой сила F имеет
вертикальную составляющую, направленную кверху. В этой
области частицы грунта могут всплывать. На рис. 47 представ-
представлены три случая, соответствующие трем значениям отношения
Н к S. В последнем из них, для Н = S, область а очень мала —
положение ее указано стрелкой. Однако такая область за бес-
бесконечно тонким шпунтом всегда должна существовать (Ризен-
кампф 1938, 1).
86
ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
Можно поставить задачу: найти такую глубину 5 забивки
шпунта, чтобы вдоль границы нижнего бьефа вертикальная
Рис. 46.
Рис. 47.
составляющая Fy не была отрицательной. Для решения этой за-
задачи заметим, что вдоль границы нижнего бьефа
w==0' °-,VW
Наибольшее значение вертикальной составляющей скорости
фильтрации равно kH/(nS)y поэтому для точки выхода
§ 15]
ФЛЮТБЕТ С ДРЕНАЖНЫМ ОТВЕРСТИЕМ
87
Если мы хотим, чтобы в этой точке выполнялось неравенство
Fy ^ 0, то должны взять длину шпунта не меньше, чем
1 теп (yi — Y) '
§ 15. Флютбет с дренажным отверстием. Иногда под флютбе-
тами устраивают отверстия для уменьшения давления. Пред-
Предположим, что имеется труба в форме полуцилиндра, поме-
помещенного непосредственно под флютбетом (рис. 48). Пусть
центр трубы находится в точке
х = а.
Согласно замечанию, сде-
сделанному в § 13, мы можем ис-
искать решение в виде
кИ ,
w = а — iv =
л V/2 -
М
(z-a)Y/2-z2 '
A6.1)
Рис. 48.
ибо каждое из слагаемых правой части удовлетворяет гранич-
граничным условиям для w, а второе слагаемое дает особенность типа
стока в точке z = a.
Рис. 49.
Если в точке z = а имеется сток интенсивности Q', то w
должно иметь вид
где F(z)—голоморфная функция в точке z = а. При этом
88 ПЛОСКИЕ ДВИЖЕНИЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ [ГЛ. II
Q' == 2Q, где Q — дебит полуцилиндрической трубы, рассчитан-
рассчитанный на единицу длины трубы. Выражение
_ _01= 0.
является вычетом w(z), который можно вычислить как предел
lim [{г - a) w (z)}= ,Л—.
z->a У Г — а*
Отсюда находим
kH(z-a)
На рис. 49 дана гидродинамическая сетка для случая про-
проницаемого грунта конечной глубины. Более сложные схемы рас-
рассмотрены в работе Н. Т. Мелещенко A936).
Глава HI
НАПОРНАЯ ФИЛЬТРАЦИЯ
ПОД ГИДРОТЕХНИЧЕСКИМИ СООРУЖЕНИЯМИ
А. МНОГОУГОЛЬНЫЕ ОБЛАСТИ В ЗАДАЧАХ О НАПОРНОЙ
ФИЛЬТРАЦИИ. ОБЩИЕ ТЕОРЕМЫ
§ 1. Постановка задачи (Н. Н. Павловский). В 1922 г. вышла
в свет книга Н. Н. Павловского, в которой он дал математиче-
математическую теорию напорного движения грунтовых вод под гидротех-
гидротехническими сооружениями, т. е. иод плотинами, шлюзами, пере-
перепадами, водоспусками и т. п. Н. Н. Павловский подверг иссле-
исследованию большое количество задач, для многих из которых дал
расчетные формулы и вспомогательные графики. Ряд советских
ученых продолжил и дополнил эти исследования.
Н. Н. Павловским рассмотрена следующая общая задача:
контур основания гидротехнического сооружения и граница во-
доунора состоят из отрезков прямых линий, границы верхнего
и нижнего бьефов также прямолинейны (см. рис. 20). Другими
словами, область движения z представляет многоугольник. На
плоскости комплексного потенциала со также получается много-
многоугольник, а именно, прямоугольник со сторонами \|) = \|эь г|? = г^2,
ф = Фь Ф = Ф2-
Введем вспомогательную комплексную переменную ? (ее на-
называют параметрической переменной), на верхнюю или нижнюю
полуплоскость которой будем отображать две области: область
функции z и область функции со = ф + 'Ф- Имея z = Fx (?)
и со = /72(?)> можно найти все элементы движения; например,
скорость получим с помощью формулы
-4. ал)
Конформное отображение многоугольника на полуплоскость
производится с помощью, формулы Кристоффеля — Шварца.
§ 2. Конформное отображение многоугольника на полу-
полуплоскость. Пусть имеем многоугольник с вершинами А\,А2, ...
..., An-ltAn на плоскости z (рис.50). Отобразим его, например,
90
НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ
[ГЛ. III
на верхнюю полуплоскость плоскости ?. Предположим, что
вершины многоугольника перешли в точки действительной оси
с абсциссами соответственно ? = аь а2, ..., ап-ь ап. Формула
Кристоффеля — Шварца имеет
^>. ^ вид (Лаврентьев и Шабат 1973)
0 ^
/ \ ^
... (? —ал)а«~^? +W. B.1)
Здесь аь ot2, ..., ап — деленные
на я величины углов многоуголь-
многоугольника.
Проверим справедливость фор-
формулы B.1) и укажем способ оп-
определения постоянных Му N,
Начнем с рассмотрения отрез-
отрезка А\А2 и перепишем подынте-
подынтегральную функцию B.1) так,
чтобы она была действительна и
положительна на отрезке А{А2
плоскости ?. Для этого доста-
достаточно заменить разности ? — а2,
..., ? — ап разностями а2 — g, ..., ап — ^, заменив постоянную
М на новую неизвестную постоянную М\. Перейдем от неопре-
неопределенного интеграла B.1) к определенному, в пределах от ах
до ?:
Рис. 50.
= Afi J (С -
1 (а2 -
... (а, -
B.2)
Здесь zx — комплексная координата вершины многоугольника А{.
Обозначим подынтегральную функцию B.2) черев Ф{{$,
Ф1($ = &-а1)а1-1(а2-ф-1 ... (an-Qan-\ и рассмотрим диф-
дифференциал z вдоль отрезка Л^а: d2 = М{Ф{ @ d?. Пусть отре-
отрезок А{А2 составляет угол ф! с осью абсцисс. Положив
М{ = ре*'**,
где р — положительная постоянная, получим
z= |
B.3)
Так как ®i(^) > 0 вдоль АХА2, то dz действительно соответствует
прямолинейному отрезку, составляющему угол сд{ с осью
абсцисс.
§ 2] ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКА НА ПОЛУПЛОСКОСТЬ 91
Придя в точку Л2, мы должны положить ? = а2, z = z2y где
г2— координата вершины А2. Принимая во внимание B.3), по-
получим
J1(OdS + zI. B.4)
Обозначим длину стороны многоугольника АХА2 через /12.
Тогда можно написать
и B.4) по сокращении на е1^ даст
B-5)
Отсюда можно было бы найти р, если бы были известны пара-
параметры аи 02, • • •, fln.
Перейдем к отрезку Л2Лз. Для этого на плоскости ? мы
должны обойти точку ? = а2 по полукругу в направлении часо-
часовой стрелки (рис. 50). Величина а2— ? станет теперь отрица-
отрицательной, причем, если мы выбрали arg(a2— ?) = 0 для ? =
= I < 02, то после обхода точки ? — а2 аргумент а2—? будет
равен —я, и можно написать, что на отрезке А2АЪ
02 - ? = e~ni 102 - ? | = (? - 02) е-"*.
Множитель же (а2 — ?)а2~! перейдет в
(? - a2)ai~l e~ni (а'-° = (? - а2)а^! е*'™* 1.
Но угол я — яа2 есть угол поворота вектора А\А2 при переходе
его в положение вектора А2А3.
Введя обозначения
qpi + л — яа2 = ф2,
а — а,)"» (S — «2Г2 («з — С) ... (а„-0а^=Ф2@,
получим вместо B.4)
а. ?
z= ре' ^ J Ф, (?) 4 + ?е'^ \ Ф, @ d? + z, =
ai a;
= 2г2 - z, + ре/(Р.е<"-"аг) г \ Ф2 (С) 4 + ги
а*
ИЛИ
с
J B.6)
92 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Функция d>2(?) принимает положительные значения вдоль Л2Л3.
Обозначим через /2з длину стороны многоугольника Л2Л3. Тогда
из последней формулы, полагая ? = а3 в верхнем пределе инте-
интеграла, получим
z3 - z2 = ре'
Ф2 @ dl, l2i = р \ Ф2 (?) d?. B.7)
Продолжая таким же образом дальше, получим уравнения, ана-
аналогичные B.5) и B.7), для других сгорон многоугольника. Од-
Однако уравнения для двух последних сторон, Ап.лАп и АпАи не
будут независимыми ог предыдущих. В самом деле, при задан-
заданных вершинах Ах и Ап_{ и заданных углах па\ и nan-i в этих
вершинах положение вершины Ап является вполне определен-
определенным, и, значит, равенства, относящиеся к сторонам Ап^Ап
и АпА\, не дадут нам новых соотношений. Примем в качестве
последнего из уравнений типа B.5), B.7) уравнение
B.8)
аП-2
где
Формулы B.5), B.7), ..., B.8) дают п — 2 уравнений, содер-
содержащих п-\- 1 параметров: р, ab a2, ..., ап\ три из этих парамет-
параметров остаются произвольными. Можно задать произвольно, на-
например, три из величин аь аг, ..., Яп-
Это находится в соответствии с тем обстоятельством, что
дробно-линейное преобразование с действительными коэффи-
коэффициентами
t==-gi + i B.9)
переводит полуплоскость ^ в полуплоскость & с сохранением
действительной оси; параметрами а, C, у» б> точнее, отношением
трех из них к четвертому, можно распорядиться так, чтобы три
произвольные точки действительной оси ? перешли в три задан-
заданные точки действительной оси плоскости ?ь
Нетрудно проверить, что подынтегральное выражение фор-
формулы B.1) сохраняет свой вид, если мы от переменной ? перей-
перейдем к переменной ^ с помощью формулы B.9). В самом деле,
при этом получим соотношение вида
Мх (I - a,)"' (I - а2Г>-1 ... (С - aj"» dl =
= м <С'-»'>а'~'--- (?i-ft>.)tt>t~'<*Ci
(C + *)a'+-+a-ll+a '
§3]
ОТОБРАЖЕНИЕ ПРЯМОУГОЛЬНИКА НА ПОЛУПЛОСКОСТЬ
93
Но по свойству углов многоугольника сц + «2 + ... + 0Ln =
= п — 2, и, следовательно, знаменатель правой части обра-
обращается в единицу.
Часто принимают в качестве трех специальных значений as
значения 0, 1, оо.
Отметим, что в формуле B.1) переход к ап = оо можно сде-
сделать, переписав эту формулу в виде
где М3 = М(-ап)ап{.
Полагая ?/an->0 при an—юо, получим, что формула Кри-
стоффеля —Шварца сохраняет свой вид, если одна из вершин
многоугольника переводится в бес-
бесконечно удаленную точку плоскости
?, причем соответствующий этой
точке множитель в формуле B.1)
заменяется единицей.
Если какая-нибудь вершина, на-
например Л2, удаляется на бесконеч-
бесконечность так, что прилежащие к ней
стороны становятся параллельными
(рис. 51, а), то нужно взять а2 = 0.
При дальнейшем разворачивании
сторон А\А2 и АЪА2, когда они пе-
перестанут быть параллельными, но
вершина А2 будет бесконечно уда-
удаленной точкой (рис. 51,6), угол яа2
следует считать отрицательным, а
именно, яа2 = —яа, где яа—угол,
образованный продолжениями сто-
сторон АХА2 и АЪА2.
Формула B.1) справедлива и
для многолистного многоугольника, т. е. расположенного на не-
нескольких листах римановой поверхности.
Определение п — 3 из постоянных аь а2, ..., ап интеграла
Кристоффеля — Шварца представляет трудности при сколько-
нибудь значительном числе вершин многоугольника. В книгах
П. Ф. Фильчакова A964, 1970) приводится ряд способов для их
определения при помощи графо-аналитических приемов, обоб-
обобщенных степенных рядов, аналитического продолжения, элек-
электромоделирования.
§ 3. Отображение прямоугольника на полуплоскости. По-
Построим отображение прямоугольника ABCD плоскости z
(рис. 52) на нижнюю полуплоскость плоскости параметрической
94
НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ
[ГЛ. III
комплексной переменной ?. Вследствие симметрии отображаемой
фигуры удобно перевести две смежные вершины прямоуголь-
прямоугольника— выберем вершины В и С — в точки 5 = ±1 соответ-
соответственно, с тем чтобы вершины А и D перешли в симметрично
расположенные точки плоскости ?, которые можно обозначить
через ±\/k (k — некоторое число, меньшее единицы, подлежащее
в дальнейшем определению). Так как углы при всех вершинах
прямые, то и все показатели as рав-
равны 72 и ae—1=—7г (s= 1,2,3,4).
Формула Кристоффеля — Шварца
примет при этом вид
t
z = -
_J
-E2)(l-'
C.1)
где К — полный эллиптический инте-
интеграл *) при модуле k:
К
-\
V(i — с2) (i —
nil
Рис. 52.
Vl -k2
sin2 ф
C.2)
Вводя обозначение эллиптического интеграла первого рода
ф
Л
или, полагая sin ф =
можем написать
, ft)==
in?) fe)].
C.3)
C.4)
Обозначив, как это принято, полный эллиптический интеграл
первого рода при модуле k'^-yfl — k2 через К', получим со-
соотношение
*) Необходимые здесь и далее сведения из теории эллиптических инте-
интегралов и эллиптических функций читатель найдет в справочниках И. С. Град-
штейна и И. М. Рыжика A962) и А. М. Журавского A941).
§41
ПРЯМОУГОЛЬНИК ЗАДАЧ НАПОРНОЙ ФИЛЬТРАЦИИ
95
Если заданы длины Lx и L2, то отсюда найдем по специаль-
специальным таблицам модуль k (Журавский 1941; Аравин и Нумеров
1948 —изд. 2).
Очевидно, что смещение прямоугольника ABCD в плоско-
плоскости z, без его поворота, добавит лишь в формулы C.1) и C.4)
слагаемое zB. Формула же C.5) при этом не изменится.
§ 4. Основной прямоугольник задач напорной фильтрации.
Обращаясь к типовому случаю обтекания основания гидротех-
гидротехнического сооружения, изображенному на рис. 53, выпишем ус-
условия на границах области движения для функций ф и \|> или
в
\
р
\
<—
'///у
т.
ш
г,
—x/f—ъ.
^^%^
v9?svyyW
Р
у///////////////////////////////////////////.
? А
В "\ С ЦЕ
Рис. 53.
о л
соответственно пропорциональных им напора h = —ф/х и функ-
функции приведенного расхода q = —i|)/x*). Значения ф мы выби-
выбираем так, как это сделано нами в § 13 главы II для обтекания
плоского флютбета, т. е. ф = —хЯ вдоль дна верхнего бьефа
и ф—0 вдоль дна нижнего бьефа (рис. 53). Вдоль основания
сооружения примем ^ = 0, а вдоль границы водоупора пусть
i|)= — Q, или q = q° = — (Q > 0). D.1)
Величина q° = Q/x является приведенным расходом, т. е. рас-
расходом при х=1, рассчитанным на единицу длины плотины
(в направлении, перпендикулярном к течению грунтовых вод).
На рис. 54 приведен прямоугольник, отвечающий области
движения ABCD на плоскостях комплексного потенциала со
и комплексной переменной —со/х = h + iq.
*) Здесь и во всей главе III коэффициент фильтрации обозначается че-
через х, так как через k обозначен модуль эллиптических интегралов.
96 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
При отображении прямоугольника ABCD (рис. 54) на ниж-
нижнюю полуплоскость плоскости ? (рис. 53) получим
со = ф + д|) = — ^ [К — F (arcsin ?, k)]9
h + iq = -ътт[К — F(arcsin ?, k)].
Обращение эллиптического интеграла
есть эллиптический синус ?
По формуле D.2) получаем для ?:
спи <ло\
D.3)
где
2/Ссо
и
сп и = V1 — sn2 и, dn w = V1 — fe2 sn2 и.
Заменяя в C.5) отрезок L2 на Q/x и L\ на Я (рис. 54), по-
получим
Q = -^-. D.5)
Если бы мы знали Н и Q, то нашли бы & из соотношения
/С _ Q
Но обычно расход Q является неизвестным, модуль же k опре-
определяется из условия, что известны некоторые размеры обла-
области Z.
Если водоупор отсутствует, т. е. если он находится настолько
глубоко, что можно считать грунт простирающимся вниз до бес-
бесконечности, то прямоугольник плоскости (о переходит в полупо-
полуполосу. Можно получить отображение полуполосы на полуплос-
полуплоскость непосредственно, а можно положить k = 0 в предыдущих
формулах и учесть, что К = я/2 при k = 0.
Эллиптический интеграл первого рода C.3) при k = 0 дает
arcsin ?. Из уравнений D.2) получаем
(о = ф + гф = arcsin ? — — ) = arccos ?, D.6)
JX \ ^ / JX
Л+ /</ =-f arccos ?, D.7)
§ 5] ТЕОРЕМА ЕДИНСТВЕННОСТИ 97
откуда
? = cos^. D.8)
Иногда принимают условия на границах бьефов в виде ф =
= ±х#/2. Тогда формулы D.2) несколько видоизменяются.
§ 5. Теорема единственности. Задача о напорной фильтрации
под гидротехническими сооружениями относится к числу так
называемых смешанных задач теории потенциала, т. е. таких
задач, в которых на различных участках контура задаются по-
поочередно ф (ф = const на границах бассейнов) и дф/ддг
(ду/дп = 0 на непроницаемых границах), где ф — потенциал
скорости. Как известно, если на всем контуре области задана
функция ф и требуется найти значение ф внутри области, то
задача называется задачей Дирихле; если задано значение нор-
нормальной производной на контуре области дф/ддг, то задача об
отыскании функции ф внутри области называется задачей Ней-
Неймана. В курсах анализа доказывается единственность решения
задач Дирихле и Неймана при
определенных условиях.
Н. Н. Павловский A922)
исследовал вопрос о единст-
единственности решения задачи о на-
напорной фильтрации под гидро-
гидротехническими сооружениями.
Предположим, что движе-
движение происходит в области D,
изображенной на рис. 55. Эта
область ограничена линиями, Рис. 55.
вдоль которых ф = const или
\|) = const; вдоль последних ду/дп = 0. При этом для доказа-
доказательства единственности решения такой задачи нет надобности
предполагать границы прямолинейными — они могут быть кри-
криволинейными, удовлетворяющими условиям, которые обычно
ставятся при рассмотрении задач Дирихле и Неймана (Смир-
(Смирнов 1974).
Рассмотрим сначала случай, когда фильтрация происходит
в конечной области D, ограниченной линиями тока и линиями
равного потенциала.
Допустим, что существуют две гармонические функции,
ф(*> у) и ф1(#, у) у удовлетворяющие условиям на границах:
Ф = const на контурах (У) и B), дц/дп = 0 на контурах C)
и D). Докажем, что ф (х, у) = ф1 (*, у).
Для этого составим разность w = у(х,у)—<р\(х,у). На-
Напишем формулу Грина для двух функций и(х,у), v(x,y)f
4 П. Я. Полубаринова-Кочина
98 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
непрерывных в области D вместе с первыми и вторыми произ-
производными:
Здесь dv/dn — производная по внешней нормали к контуру С
области. Приняв и— v = w, получим
Так как Д<р = Aqpi = Ддо = 0, то в правой части последнего ра-
равенства остается один контурный интеграл. Но и этот интеграл
равен нулю, так как на границах (/) и B) функция w = 0, а на
границах C), D) ее нормальная производная равна нулю. По-
Поэтому остается равенство
$$[(?)'+(?)>*-»•
Интеграл от суммы квадратов может равняться нулю только
в случае, если каждое слагаемое равно нулю:
дГ — °' ду — °"
Отсюда следует, что w = const, а так как на некоторых грани-
границах w = 0, то w н= 0.
Этим и доказывается единственность решения смешанной
задачи о фильтрации указанного вида в конечной области.
Если фильтрация происходит в водопроницаемом слое бес-
бесконечной глубины, то можно сначала ограничить область полу-
полуокружностью большого радиуса /?, на которой ду/дп имеет по-
порядок скорости (см. § 13 главы II), т.е. порядок I//?2. Поэтому
так как ds = RdQy а функция ф порядка In/?, получаем оценку
^\^RdB = n^-+0 при R->oo.
(Я) 0
Следовательно, предыдущие заключения и здесь остаются в
силе.
Для области, ограниченной водоупором, но простирающейся
в стороны до бесконечности, теорема единственности также мо-
может быть получена предельным переходом от случая конечной
области.
§ б] ДВИЖЕНИЕ ГРАНИЧНЫХ ТОЧЕК ОТОБРАЖАЕМЫХ ОБЛАСТЕЙ 99
§ 6. О движении граничных точек отображаемых областей.
Вопрос о характере движения граничных точек отображаемых
областей представляет интерес для теории фильтрации, так как
позволяет получать некоторые качественные выводы относи-
относительно изменения расхода при деформации контура области
движения. Так как доказательство следующих теорем опи-
опирается на так называемую лемму Шварца, то мы приведем
здесь формулировку этой леммы (Привалов 1977).
Лемма Шварца. Если функция ш = /(г), голоморфная
(или аналитическая) в круге |z|< 1, удовлетворяет условию
f@) = 0 F.1)
и если \f(z)\<\ при |z|<l, то имеем |f(z)|<|z| всюду в
круге |<z|< 1. Если равенство |/(z)| = |z| имеет место хотя бы
в одной внутренней точке (кроме точки z = 0, в которой это
равенство выполняется по условию), то оно имеет место во всех
точках области, и тогда f{z) = eaiz.
Другими словами, лемма Шварца утверждает, что если при
условии F.1) модуль отображающей функции меньше единицы,
то он будет в соответствующих точках и
меньше модуля z. Геометрически это озна-
означает, что если w =/(z) переводит область
единичного круга в область, внутреннюю по
отношению к этому кругу, то с помощью
функции f(z) всякая точка либо прибли-
приближается к началу координат, либо отобра-
отображение представляет вращение около начала.
Обозначим через g (рис. 56) данную
область, содержащуюся в круге радиуса Рис- 56-
единица, через g* — область круга. Точка О
является неподвижной точкой преобразования области g в об-
область g*. Когда область g переходит в область g*, точка О яв-
является отталкивающей, так как она раздвигает точки области g,
приближая их к контуру круга.
Если вместо круга взять произвольную область, содержа-
содержащую данную область g, то лемма Шварца остается в силе.
В качестве неподвижной точки может быть взята любая внут-
внутренняя точка, в том числе и бесконечно удаленная точка, кото-
которая рассматривается при этом как внутренняя точка области.
Теперь приведем теоремы Г. Н. Положего о движении гра-
граничных точек отображаемых областей в изложении автора
(Положий 1953—1955).
Пусть будет G — односвязная область в плоскости z=x+iy,
G* — односвязная область, содержащая G и имеющая с G час-
частично общую границу в виде некоторой жордановой кривой Г.
100 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Теорема. При конформном отображении односвязной об-
области G на произвольную область G*, содержащую G и имею-
имеющую с G частично общую границу в виде некоторой жордано-
вой кривой Г, на открытой (т. е. не содержащей своих концов)
кривой Г не может быть больше трех неподвижных точек. Если
таких точек имеется три, то две крайние из них — притягиваю-
притягивающие, а средняя — отталкивающая; если таких точек только две,
то одна из них — притягивающая, другая —непритягивающая.
В самом деле, при наличии на открытой кривой Г трех не-
неподвижных точек без ограничения общности можем считать,
что G* совпадает с верхней полу-
полуплоскостью (рис. 57), G — с об-
областью, лежащей в верхней полу-
полуплоскости, Г —с интервалом веще-
вещественной оси, лежащим вне отрезка
[а, Ь] (—1 < а ^ Ь < 1), и непод-
неподвижные точки — с точками г=1,
z = оо и z = —1. Пусть Я есть об-
область, полученная склеиванием об-
области G с областью, ей симметрич-
симметричной относительно вещественной оси,
Рис. 57, н* — ее образ в плоскости функции
w = f(z), отображающей G на G*.
Область Я, разрезанная вдоль отрезков [—1,а] и [6,1], оче-
очевидно, преобразуется функцией w = f(z) в плоскость, раз-
разрезанную вдоль отрезка [—1, 1], и, следовательно, по лемме
Шварца точка z = оо должна быть отталкивающей неподвиж-
неподвижной точкой и никаких других неподвижных точек на интервале
Ы>1 не будет. Область Я, разрезанная вдоль отрезков
[— 1,а] и [&, 1— е], где 0< е < 1 — Ъ, преобразуется функцией
w = f(z) в плоскость, разрезанную вдоль некоторого отрезка
[—1,1—е'] (е/>0). Предположение о том, что е' ^ е, приво-
приводит к противоречию с тем, что при отображении какой-либо об-
области на область, ей внутреннюю, может быть не больше одной
внутренней неподвижной точки. Следовательно, точка z = 1
будет притягивающей неподвижной точкой и на интервале F,1)
никаких неподвижных точек не будет. Область Я, разрезанная
вдоль отрезков [—1 + е, а] и [6, 1] @ <е < 1 + я), преобра-
преобразуется функцией w = f(z) в плоскость, разрезанную вдоль от-
отрезка [—1 + в', 1], где е7 — некоторое положительное число.
Предположив, что е" ^ е, также приходим к противоречию.
Следовательно, точка z = —1 также будет притягивающей
неподвижной точкой и на интервале (—1,а) неподвижных то-
точек нет. В том случае, когда на открытой кривой Г имеются
только две неподвижные точки, отобразим область G на G* так,
чтобы эти две неподвижные точки были притягивающими. Это
§ б] ДВИЖЕНИЕ ГРАНИЧНЫХ ТОЧЕК ОТОБРАЖАЕМЫХ ОБЛАСТЕЙ Ю1
возможно в силу вышесказанного. Отображая теперь область G*
саму на себя с помощью дробно-линейного преобразования при
тех же заданных неподвижных точках, видим, что одна из них
будет притягивающей, а другая — непритягивающей. Этим тео-
теорема доказана.
Следствие 1. Если Р и Q — концы кривой Г, то при нали-
наличии на открытой кривой Г трех неподвижных точек Л, В, С все
точки полузакрытой кривой [Р, В) (т. е. содержащей точку Р
и не содержащей точки В), кроме точки Л, и все точки полуза-
полузакрытой кривой [S,Q), кроме точки С, получают ненулевые сме-
смещения в направлении к точке Л и соответственно в направлении
к точке С.
Следствие 2. В случае, когда на открытой кривой Г
имеется только две неподвижные точки Л и В (если для опре-
определенности считать притягивающей точку Л), все точки полу-
полузакрытой кривой [Р,В), кроме точки Л, получают ненулевые
смещения в направлении к точке Л, а все точки открытой кри-
кривой (В, Q) получают ненулевые смещения в одном и том же
направлении по отношению к точке 5.
Следствие 3 (о закрепленном конце). Если конец Q кри-
кривой Г закреплен и на открытой кривой Г имеются две непо-
неподвижные точки Л и В, то все точки полузакрытой кривой [Р,В),
кроме точки Л, получают ненулевые смещения в направлении
к точке Л, а все точки открытой кривой (Л,<2), кроме точки В,
получают ненулевые смещения в направлении от точки В.
Следствие 4 (о закрепленных концах). Если концы Р и Q
кривой Г закреплены и на открытой кривой Г имеется непо-
неподвижная точка Л, то все точки открытой кривой Г, кроме
точки Л, получают ненулевые смещения в направлении от
точки Л.
Следствие 5. Пусть G* — область, содержащая односвяз-
ную область G и имеющая с G частично общую границу в виде
нескольких жордановых кривых. Если при отображении G на
О* на одной из этих кривых имеются три или только две непо-
неподвижные точки, то на каждой другой из этих кривых может
быть не больше одной неподвижной точки, и если такая точка
имеется, то она притягивающая.
Теорема. Пусть О и G* — односвязные области, частично
содержащие друг друга и имеющие в качестве общей части гра-
границ только две жордановы кривые. Тогда, если на одной из
этих кривых имеется неподвижная точка, то на другой из них
может быть не больше двух неподвижных точек, и если такие
две точки имеются, то одна из них притягивающая, а другая
отталкивающая.
В самом деле, отображение G на G* с тремя неподвижными
точками можно получить путем выдавливания той части гра-
Ю2 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
ницы G, которая находится внутри G*, и путем вдавливания той
части границы G, которая находится вне G*. При этом по пре-
предыдущей теореме из двух неподвижных точек, лежащих на од-
одной и той же жордановой кривой, одна будет притягивающей,
другая отталкивающей и никаких других неподвижных точек
на данной жордановой кривой быть не может.
Следствие (о свободной средней точке). Пусть границы
односвязных областей G и G* составлены из общей им жорда-
жордановой кривой Г и соответственно из жордановых кривых у и у*>
пересекающихся в некоторой точке Р. Тогда при отображении
G на G* при условии, что концы кривой Г закреплены и одна
из точек открытой кривой остается неподвижной, точка Р полу-
получает ненулевое смещение вдоль кривой у* в направлении к ее
концу, подходящему к границе области G изнутри.
Рассмотрим несколько простейших следствий из приведен-
приведенных выше теорем (Положий 1953—1955).
Пусть имеем движение грунтовых вод под гидротехническим
сооружением произвольного очертания (рис. 55) с водоупором
произвольной формы AD, с границами водоемов АВ и CD.
Точки А и D могут быть и не в бесконечности. Граничные кри-
кривые пусть будут кусочно-гладкие.
Обозначим через G область движения ABCDA. Пусть G\ —
область с теми же вершинами Л, В, С и D, но полученная из G
путем деформации некоторых границ, которые заменяются ку-
кусочно-гладкими кривыми, лежащими частично или полностью
внутри G. Тогда имеет место
Теорема 1. При неизменном напоре расход уменьшится,
если деформированы (вдавлены) непроницаемые границы ВС
или ЛЬ, и увеличится, если деформированы границы водоемов
АВ или CD.
В самом деле, пусть g\— образ G\ на плоскости комплекс-
комплексного потенциала со. Отобразим прямоугольник g\ на нижнюю
полуплоскость ? при неподвижных точках ? = —1, 1, l/k. В силу
теоремы о движении граничных точек точка ? = — l/k прибли-
приблизится к точке ? = —1 при изменении ВС или DA и удалится
от точки ? = —1, если изменяются АВ или CD. В первом слу-
случае Q уменьшается, во втором — увеличивается.
Теорема 2. При неизменном напоре Н величина вектора
скорости фильтрации на общей части границ областей G и G\
уменьшается вблизи точек В и С, если G\ получается из G из-
изменением непроницаемой границы ВС, и уменьшается вблизи D
и Л, если изменяется водоупор AD.
Действительно, пусть g\ — образ G на плоскости со. Пусть
область G\ получена из G заменой ВС. Отобразим g* на G* при
неподвижных точках В*, С*, D*. При эгом В* и С* будут при-
притягивающими точками.
§7]
ПЛОСКИЙ ФЛЮТБЕТ В СЛОЕ КОНЕЧНОЙ ГЛУБИНЫ
103
Следствие. Если при изменении ВС некоторые части ВВГ
и С'С остаются общими для G и Gb то давление во всех точ-
точках ВВГ увеличивается, а во всех точках С'С уменьшается.
В частности, из изложенных предложений вытекает, что
если в границе водоема нижнего бьефа сделать выемку, то вы-
выходные скорости, т. е. скорости вдоль границы нижнего водоема
вблизи точки С, уменьшатся (при этом Q увеличится). Выход-
Выходные скорости уменьшатся также, если на границе верхнего
бьефа устроить бугор (расход при этом уменьшится).
В другой форме вариационные принципы и их применение
к задачам о напорной фильтрации даны М. А. Лаврентьевым
A946) (см. также Лаврентьев и Шабат 1973).
Б. ФИЛЬТРАЦИЯ ПОД ФЛЮТБЕТАМИ
§ 7. Плоский флютбет в слое конечной глубины. Теперь мы
перейдем к рассмотрению отдельных групп задач о движении
грунтовых вод под гидротехническими сооружениями и начнем
с задач об обтекании флютбетов. Простейшая задача такого
рода — обтекание плоского
флютбета в грунте бесконеч-
бесконечной глубины — рассмотрена
в § 13 главы II. Теперь рас-
рассмотрим более сложный слу-
случай — обтекание плоского
флютбета в слое конечной
глубины (рис. 58). Область
движения — полоса, которую
нам нужно отобразить на 'л.
полуплоскость ? так, как это
изображено на рис. 58. С по-
помощью формулы Кристоф-
феля — Шварца B.1) полу-
получим
'/////Z77/////77////V77777/
= М . 1+
2k ш 1 -
G.1)
Пусть ширина флютбета ВС равна 21. Тогда при ?= ±1 имеем
z= ±/ и
G.2)
1 -Л *
Далее, обход точки ?=1/& в положительном направлении в
нижней полуплоскости соответствует переходу с отрезка CD
104 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
плоскости z на отрезок DE, что даст для In A—kZ) прираще-
приращение ш; следовательно, приращение г, которое мы обозначим
через Дг, будет
А М , л Mni
А* = -2л(-ш) = 2Г'
Коэффициент М9 как это видно из формулы G.2), — действи-
действительное число; следовательно, мы получили для Дг чисто мни-
мнимое значение. Это соответствует изменению мнимой части г,
т. е. ординаты у, со значения у = 0 на значение у = —Т. Дру-
Другими словами, Дг = —77 и
По формуле G.2)
Отсюда
G.3)
В уравнении D.3), связывающем со и ?, положим на этот раз
тогда
, 1 + kt ill
Расход вычисляется по формуле D.5):
Формула G.4) дает зависимость z от комплексного потен-
потенциала. Обращая G.4), получим
tt-thg-. G.6)
Обратим внимание на выражение производной правой части
равенства G.4):
Л l+*simV _ о. сп«
Выпишем разложение en u/dn и в тригонометрический ряд
СП U Я
пи Зпи
cosw cosir , cos"
. Wl/i\ , UWW\ . ОЯ/\
sh -7ГТГ- sh -1777— sh
ЭП11
Q IV" I
2,i\ J
§7]
ПЛОСКИЙ ФЛЮТБЕТ В СЛОЕ КОНЕЧНОЙ ГЛУБИНЫ
105
Тогда, интегрируя по и, получим г в виде ряда
f. пи , Зли , 5яы т
sinw «in— ^ sta-g^
сЬя/Г Q „u Зя/Г + е u 5я/С "• •
shF 3sh-2T" ^"ЙГ J
2/C
Здесь и= %н =—jf{h-\-iq). Отделяя в полученном ряде
действительную часть от мнимой, найдем
4Т_ Г sin (я/г*) ch (лд*) _ sin (ЗяУ) ch (Зпд*) , ]
я L sh а 3 sh (За) > ' " J'
___ 4Г Г cos (я/г*) sh (лд*)
У— л L sha
cos (ЗлН*) sh (Злдщ)
3 sh Ca)
G.7)
где
2К *
По этим формулам можно строить сетку линий q~ const и
h = const.
Напор вдоль флютбета полу- ^====fr
чим, подставляя g из G.6) в D.2)
и полагая г = д;:
th
= -о7г/7 arcsin
2д
ял:
2Г
th
я/
2Г
.*.
G.8) Рис. 59.
Для скорости найдем, дифференцируя D.2) и G.4),
rfoo t dz
17
AkKT
что дает с помощью G.6) для правой половины рис. 58:
Ch-7T7=-
АКТ
y\Jsha"nZ" sh
(/ + *) . я(/-г)
2Г Sn 271
G.10)
В частности, вдоль границы нижнего бьефа, где z ==*>/,
я/
кНл
V-
ch-
2f
2Г
1JB
JL
H
0,8
0,6
0,4
0,2
\
\
\
Т\
У/////
-
У//////////
¦*-—.—
У/////
— -
1.11
о г
6 8 10 12
Рис. 60.
ft
7"
§ 8]
ФЛЮТБЕТ ПРИ НАЛИЧИИ ДРЕНИРУЮЩЕГО ОСНОВАНИЯ
107
и вдоль непроницаемого основания, где
nl
= x — Ti,
и —
ch
2Т
АКТ
V
c
2Г
На рис. 59 указана сетка линий тока и линий равного по-
потенциала при Т = 2/. На рис. 60 построена кривая зависимости
приведенного расхода от размеров области движения. На
рис. 61 даны графики распределения напора вдоль флютбета.
§ 8. Флютбет при наличии дренирующего основания. В при-
природе встречаются случаи, когда под основным слоем грунта, в
котором находится флютбет, залегает хорошо водопроницаемый
пласт такой, что его коэффициент
фильтрации значительно больше
коэффициента фильтрации вышеле-
вышележащего слоя. Тогда можно считать,
что на границе двух слоев напор
имеет постоянное значение. Эту
Рис. 63.
задачу можно рассматривать как частный случай задачи о те-
течении под флютбетом в двуслойном грунте (см. § 1 главы VIII).
Рассмотрим обтекание плоского флютбета (рис. 62). Об-
Область движения здесь та же, что и в предыдущем случае. Ее
отображение на полуплоскость ? (рис. 63) дает
где
~ к 2T '
k = th -^jT.
(8.1)
(8.2)
Будем считать, что вдоль границы AD напор постоянен и по-
потенциал ф =*—xHq (#i > #о > #2). Тогда на плоскости ком-
комплексного потенциала получаем полуполосу с разрезом (рис.63).
108 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
Пусть точка F плоскости ю переходит в точку ? = а. Соот-
Соответствие остальных точек указано на рисунке. Получаем
со =
—с2
- М [- ^ ardg (A Vr=^) + f arctg (-^f^)] - xtf,. (8.3)
Обход особых точек С и D в положительном направлении, б
и А — в отрицательном по полуокружностям в нижней полу-
полуплоскости дает для со полувычеты, равные скачкам при пере-
переходе с отрезка CD на FD и с АВ на AF. Получаем равенства
Из этой системы уравнений находим
Для ш при этом равенство (8.3) дает
-^, (8.4)
Подставляя (8.1) и (8.2), окончательно получим
2Г
arccos I —^- | - *Я2. (8.6)
Отсюда найдем напор вдоль флютбета, полагая z = x и
считая, что h — — ф/х — Я2:
Для сравнения рассматриваемого случая с флютбетом при
наличии водоупора вычислим значение h в середине флютбета,
§ 9] ОТОБРАЖЕНИЕ ЗВЕЗДООБРАЗНОГО МНОГОУГОЛЬНИКА 109
при х = 0. Получим
h = h0-4 + 2Яо~*' ~"> arccosf—^
в то время как для флютбета при наличии водоупора
Мы считали, что Н{> Но> Н2. Если это неравенство не
выполнено, то область со рис. 63 изменится, но можно показать,
что все формулы сохранятся.
При Но = (#i + Н2)/2 все вычисления упрощаются. Линии
тока станут симметричными относительно оси ординат, которая
будет линией равного напора h = Я/2.
Этот именно случай является предельным для неоднород-
неоднородного грунта (см. § 1 главы VIII). Расход через всю линию CD
(рис. 62) при #2 < #о < Яь каковой случай мы и рассматри-
рассматриваем, бесконечно велик, причем часть воды переходит из верх-
верхнего бьефа в нижний, часть — из верхнего бьефа в нижний слой
грунта и часть — из нижнего слоя грунта в нижний бьеф.
Приведем еще формулу для комплексной скорости
и — iv = yt
yshibi?±
BT 2T
В. ОБТЕКАНИЕ СООРУЖЕНИЙ СО ШПУНТАМИ
§ 9. Отображение на полуплоскость многоугольника, все сто-
стороны которого проходят через одну точку. Дан «звездообразный»
многоугольник, т. е. такой, все стороны которого (или их про-
продолжения) проходят через одну точку (рис. 64). Пусть эта точка
будет началом координат плоскости w, а область, которую мы
хотим отобразить на полуплоскость, имеет границу ABCDEFA.
Обозначим углы, образованные линиями АВ, BCD, DE, ...
с осью абсцисс, соответственно через паи яа2> яаз, ...
Составим функцию
w = Сет** (а{ - Qan-ai (а2 - ф~а> ... (ап - 0а»-'"а» (9.1)
и покажем, что она производит конформное отображение звез-
звездообразной области ABCD ... на верхнюю полуплоскость плос-
плоскости ? (рис. 64). Здесь С —действительная постоянная, яап —
угол с осью абсцисс отрезка ANFE, точка N которого переходит
в точку I = оо.
по
НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ
[ГЛ III
Действительно, возьмем логарифм от (9.1)
In w = In | до | + I arg до = In С + nani + (an — aj) In (a{ — ?) +
- a2) In @2 - ?) + ... + (<хя-, - ая) In (ая - ?). (9.2)
Рассматривая действительные значения ?, лежащие между —оо
и аи и считая arg(ai — ?)= ... = arg(an —Е) = 0, видим, что
все слагаемые правой части (9.2) имеют действительное значе-
значение, кроме nani. Поэтому arg w = пап на отрезке ЛМ, что как
раз соответствует условию задачи.
Рис. 64.
Далее, переходя на отрезок АВ, обойдем точку А в отрица-
отрицательном направлении по полуокружности, причем ln(fli — ?)
получит приращение —я/, а (ап — ai)ln(ai — ?) получит прира-
приращение —ni(an — ai). Это будет изменением In w при обходе
точки А. При этом
arg w = шп — зх (ая — щ) = яа1э
что соответствует значению arg до на отрезке АВ. Обход точки В
даст изменение In w на —jii (o&i — аг). Следовательно, получим,
что arg до = лаг вдоль отрезка BCD.
Продолжая идти дальше, убедимся в справедливости фор-
формулы (9.1).
Заметим, что отображение звездообразной области на полу-
полуплоскость можно произвести и с помощью формулы Кристоф-
феля —Шварца. Так как конформное отображение звездооб-
звездообразной области на полуплоскость единственно (при трех фик-
фиксированных вершинах), то интеграл Кристоффеля — Шварца
должен совпасть с выражением (9.1); следовательно, в данном
случае этот интеграл вычисляется в конечном виде.
§ 10]
ОБТЕКАНИЕ НАКЛОННОГО ШПУНТА
111
Следует обратить внимание на то, что в формуле (9.1) со-
содержатся аффиксы аи ..., ап не всех вершин многоугольника,
а только тех, в которых происходит изменение направления
ограничивающего отрезка.
§ 10. Обтекание наклонного шпунта. В главе II мы рассмотре-
рассмотрели обтекание вертикального шпунта в слое бесконечной глу-
глубины. Здесь мы рассмотрим наклонный шпунт. Из таких шпун-
шпунтов устраивают иногда противофильтрационные завесы. К за-
задаче о косом шпунте, как мы
увидим ниже, сводится задача
об обтекании прямого шпунта
в анизотропном грунте. На-
Наклонный шпунт изображен на
рис. 65 (Веригин 1940).
Отобразим область ABCDA
(рис. 65) на нижнюю полу-
Рис. 66.
плоскость ? так, чтобы вершины 5, С, D перешли соответствен-
соответственно в точки ? = —1, а, 1.
По формуле (9.1) имеем
z = C(l+?I~Y(l-?)Y. (ЮЛ)
Сопоставим этот результат с тем, что дает нам формула
Кристоффеля — Шварца в применении к многоугольнику
рис. 66: У
С
A + ?ГУ E - а) A - Qy d?. A0.2)
Интеграл в формуле A0.2) в общем случае не выражается
в элементарных функциях, но в данном случае, когда вершины
многоугольника В и D совпадают, это имеет место. Мы можем
приравнять выражения A0.1) и A0.2), а затем, дифференцируя
это тождество, получим
Отсюда А = —С, а= \ —2у.
112 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
Таким образом, сравнение с формулой Кристоффеля —
Шварца позволило нам определить значение параметра а — аф-
аффикса конца шпунта на плоскости ?. Можно было бы найти
это значение и из условия, что при ? — а скорость равна бес-
бесконечности.
Найдем постоянную С. Концу шпунта отвечает значение
г = 5ехр(—nyi), где 5 — длина шпунта. Полагая в формуле
A0.1) ? = я, найдем
и равенство A0.1) примет вид
г _ se-** (j?r)'~V (-и)" (« = 1 - 2Y). (Ю.З)
Область на плоскости комплексного потенциала представ-
представляет полуполосу, конформное отображение которой на полу-
полуплоскость ? дает
со = — arcsin ?.
Отсюда
? = sin-2?-. A0.4)
В главе XVIII (рис. 321) приведена гидродинамическая
сетка для косого шпунта.
§ 11. Шпунт при наличии водоупора или дренирующего ос-
основания. Для случая, изображенного на рис. 67, решение
строится совершенно так же, как для плоского флютбета в § 7.
Поэтому приведем без вывода отно-
J/f сящиеся сюда результаты,
-л* Расход под шпунтом равен
Рис. 67.
причем
2Г
Комплексный потенциал имеет вид
где
V
у/7 (arcsin S,
ch w-
nS . nz
§ П] ШПУНТ ПРИ НАЛИЧИИ ВОДОУПОРА
Скорость фильтрации равна
w = и — iv =
из
2
-С05
W
На рис. 68 дана сетка для частного случая шпунта 5 = Т/2
(Hoffmann 1934). На рис. 69 построен график зависимости
Рис. 68.
U
1,0
0,8
0,6
?
0,2
\
\
Л
HZ
0,8 1,0
S
Рис. 69.
приведенного расхода q* = Q/(yM) и относительной выходной
скорости v* = v0S/(kH) в точке z = 0 от величины S/T. Выходная
П4 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
скорость определяется формулой
Для случая шпунта при наличии дренирующего основания
ввиду аналогии задачи с той, которая приведена в § 8, ограни-
ограничимся лишь окончательными формулами (Гиринский 1936).
Комплексный потенциал здесь имеет вид
Г, , и (*w\]
со = —и —• B#0 ~ #i — Н2)т + 17 arcsinI ^- — нЯ2.
1 Zl In 1 ЗХо II
L V^if/J
Распределение напора вдоль низовой грани шпунта:
A = (Ho_^)f + !arcs,n|
вдоль верховой грани имеем
h = Нх + (я0 - -2l+?l) f —И- arcsin |
Скорость фильтрации определяется формулой
Н_ т
Нх + Н2 , 2 Ch 2Г
§ 12. Плоский флютбет со шпунтом в грунте конечной глуби-
глубины. Имеем плоский флютбет со шпунтом длины S, разделяющим
флютбет на отрезки с длинами 1\ и /2 (рис. 70). Глубина прони-
проницаемого слоя пусть будет Г.
Излагая решение задачи по Н. Н. Павловскому A922), вы-
выберем оси координат, в отличие от обыкновения, так, как ука-
указано на рис. 70. Отобразим область движения на полуплос-
полуплоскость ?, причем занумеруем вершины областей. Пусть точки /,
2, ..., 7 области z переходят в точки ?i, ?2, ..., ?7 области ?.
Область z имеет прямые углы в точках ? = ±а, угол, рав-
равный 2я, в точке 2, для которой ? = 0, и нулевые углы в точках
? = ±1. Поэтому отображение области движения на нижнюю
полуплоскость плоскости ? дает
A2.1)
§ 12] ФЛЮТБЕТ СО ШПУНТОМ В ГРУНТЕ КОНЕЧНОЙ ГЛУБИНЫ
Окончательно для z получим
Ц5
Решая это уравнение относительно ?, найдем
-0'24д2-^. A2.3)
Знак плюс соответствует правой полуплоскости, минус —- левой,
6 \7
? ^ л?
b * 5
1 О) Ti
У////////////////////////////////////
Т~Р
ij ir tt C b is
При этом
__ . л§_ ,_ nS_
Следовательно, для ? можем написать
A2.4)
^ + tg2-§-. A2.5)
В частности, для концов флютбета z = — lx и г = 12 получим
соответственно
cos
A2.6)
Пб НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
Перейдем теперь к конформному отображению прямоугольника
плоскости cD = qp + n|) на полуплоскость ?. Так как вершины
прямоугольника переходят при этом в точки ?4, ?б> ?б> &7> т0
будем иметь
» = а\
A2.7)
Введем функцию и с помощью подстановки
(?5 ~ fee) Vfe — ?4) (fe5 — S7) Vfe4 — fee)
Находя отсюда ? — J4> ^ — ?5, ... и подставляя в A2.7), получим
) - Се) (Сб ~ Ет)'
Тогда формула обращения интеграла A2.7) будет иметь вид
где
Рассмотрим вершины прямоугольника. При ? = ?5 имеем,
как и должно быть, о = 0. При ? = ?4 получаем
Так как при ? = ?4 должно быть со = — /Q, то предыдущее
равенство дает Q = —AK'lv- Далее, при ? = ?7 имеем
sn(|i©/i4)= 1/&. Следовательно,
Но вершине ?7 соответствует со = —кН — QI. Сравнивая эти
выражения, найдем
Модуль k согласно A2.8) и A2.1) выражается так:
причем Pi и Рг определяются формулами A2.6). Таким обра-
образом, мы имеем полное решение задачи.
12]
ФЛЮТБЕТ СО ШПУНТОМ В ГРУНТЕ КОНЕЧНОЙ ГЛУБИНЫ
117
Отметим, что для симметричного случая расположения
шпунта, когда Pi = р2 = Р, получаем
A2.10)
причем
Формула A2.10) соответствует преобразованию Ландена.
Ч -0,75 -0,5 -0,15 0 0,25 0,5 0,75 fft
Рис. 71
Рис. 72.
Между полными эллиптическими интегралами модулей & и
существует соотношение
K'(k) _ К'(ft
К (k) 2K (Р) *
]18 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Поэтому для симметричного расположения шпунта формула
расхода может быть переписана в том виде, в каком мы имели
ее уже не раз:
п
W 2/C(p) '
У Н. Т. Мелещенко A937) приведены различные номо-
номограммы для подобных случаев. На рис. 71 показано влияние
симметричного шпунта на распределение напора вдоль флют-
бета: перед шпунтом давление поднимается, за ним — сильно
падает. На рис. 72 дана сетка движения для одного случая не-
несимметричного расположения шпунта.
Г. МНОГОШПУНТОВЫЕ СХЕМЫ
§ 13. Метод фрагментов. Если рассматривается флютбет с
несколькими шпунтами, то формула для отображения области
движения на полуплоскость сильно усложняется. При этом уве-
увеличивается число параметров, подлежащих определению, так
как каждый шпунт дает две или три новые вершины в области
движения. Ряд случаев с двумя, тремя и даже четырьмя шпун-
шпунтами исследовали с помощью точной теории Н. Н. Павловский
A922), В. С. Козлов A941), П. Ф. Фильчаков A959—1960)
и другие авторы, но вычисления в этих случаях сложны.
Н. Н. Павловский предложил приближенный метод фраг-
фрагментов, который применим для многошпунтовой схемы в случае
(Г)
>
\B)\ C) Г
'///////////у
У//
У/////
х \
\ \ (п)
У/////////////////,
Рис. 73.
проницаемого слоя конечной глубины. Этот метод состоит в том,
что область движения разбивается вертикальными прямыми,
проходящими через концы шпунтов, на участки — фрагменты
и линии раздела (пунктирные прямые рис. 73) принимаются за
линии равного напора. В действительности они отличаются от
эквипотенциалей, но тем ближе к ним, чем меньше глубина про-
проницаемого слоя.
Предположим, что можно рассчитать движение для каждого
из п фрагментов нашей области. В частности, допустим, что
13]
МЕТОД ФРАГМЕНТОВ
119
вычислен расход каждого фрагмента
A3.1)
1где Нт — потеря напора при фильтрации через m-й фрагмент,
а Фт— модуль формы этого фрагмента, т. е. безразмерная
величина, зависящая от формы фрагмента. Так, для n-го фраг-
фрагмента (рис. 73) на основании формул § 11 имеем Фп = 2К/К'
при k = sin(nS/2T).
Так как расход через все фрагменты один и тот же, то
Ф,
Ф2
Складывая числители и знаменатели написанных отношений,
получим
2
Но сумма всех потерь напора равна действующему напору Н
(разности уровней воды в верхнем и нижнем бьефах). Поэтому
окончательно расход выразит-
выразится так:
A3.2)
т-1
A)
Каждый из потерянных яа-
поров можно теперь вычислить
по формуле
Фт " A3.3)
C)
Н.
» i -
V//////////////////////////////////////
Рис. 74.
т-1
Зная все напоры Ят, можно произвести расчет элементов
движения каждого типового фрагмента, а следовательно, и про-
произвольной области. Рассмотренный способ называется последо-
последовательным фрагментированием.
В. С. Козловым построен ряд номограмм, которые приве-
приведены в его книге A941). Формулы для модулей формы фраг-
фрагментов различного типа можно найти в книге В. И. Аравина
и С. Н. Нумерова A948 —изд. 2).
Другой способ разбивки потока — по линиям, близким к ли-
линиям тока, — называется параллельным фрагментированием
(Девисон 1937, 2). На рис. 74 представлен пример такого фраг-
ментирования: пунктирные линии принимаются за линии тока.
120 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Здесь для каждого фрагмента имеем
Qm = igf (m=l, 2,..., п),
причем потери напора в каждом фрагменте будут одинаковым^:
#! = #2 = ... = Нп. Полный фильтрационный расход Q ра-
равен сумме частных расходов: Q = Qi + Q2+ ... + Qn-
Доказано, что метод фрагментов, основанный на введении
искусственных эквипотенциалей в напорном потоке, не может
занижать величину расхода против точного решения. При вве-
введении в напорном потоке искусственных линий тока величина
фильтрационного расхода, напротив, не может быть больше, чем
при точном решении (Девисон 1937, 2; Дольский 1963).
§ 14. Многошпунтовые схемы в грунте бесконечной глубины.
В случае проницаемого слоя большой глубины метод фрагмен-
фрагментов становится неприменимым. Н. Т. Мелещенко A940) пред-
предложил для этого случая метод разворачивания шпунтов, раз-
развитый П. Ф. Фильчаковым
U
"]j JH 7/ A951, 1964). Сущность ме-
^ I J тода можно пояснить на
I двухшпунтовой схеме плос-
q /Г кого флютбета (рис. 75).
ф (р )
Произведем конформное
рис. 75. отображение на нижнюю по-
полуплоскость ? области дви-
движения со шпунтом BCD, выбросив второй шпунт. Выберем ото-
отображение в такой форме:
S-V^T^5. A4.1)
Оно разворачивает шпунт длины 5 в отрезок BCD оси ?, при-
причем ширина отрезка будет равной 2S. Разделяя в A4.1) дей-
действительную и мнимую части, получим
I2 = ¦§¦ W(S2 + x2-yr + 4xY + S2 + х2 - у2],
: \ A4.2)
ri2= y W(S2 + x2- ff + 4x2y2 - S2 - x2 + y2].
На рис. 76 представлена сетка линий х = const, у = const
на плоскости х, у и на плоскости ?, х\ при 5=1.
Второй шпунт расположен на расстоянии / от первого. Под-
Подставив х = 1 в A4.2) и полагая #->оо, найдем, раскрыв неоп-
оеделенность,
lim ?2 = /2
§ И]
ШПУНТЫ В ГРУНТЕ БЕСКОНЕЧНОЙ ГЛУБИНЫ
121
Следовательно, та кривая, в которую перейдет линия х = /
после преобразования A4.1), имеет асимптоту 1 — 1. На оси g
эта кривая отсекает отрезок
A4.3)
Чем больше /, тем меньше gi отличается от / и тем меньше,
следовательно, искажается второй шпунт.
Итак, теперь на плоскости ? вместо двух прямолинейных
шпунтов имеется один, несколько искривленный. Заменяя его
близким к нему вертикальным отрезком, длину которого обо-
обозначим через S2, вместо двухшпунтовой схемы получим более
простую одношпунтовую.
-5-4-3-2-1 113 4 5
в\ U
:-/; е им)
Если произведем еще одно преобразование на новую полу-
полуплоскость ?', то контур ABCDEFGH развернется в флютбет
некоторой общей длины L. Новое преобразование будет
A4.4)
Напор вдоль такого флютбета распределяется по закону
(см. § 13 главы II)
где g' —расстояние от левого конца флютбета.
122 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Перенеся это распределение с помощью обратных преобра-
преобразований на первоначальный контор со шпунтами, получим при-
приближенное значение напора в точках этого контура.
Вычисление выходной скорости можно произвести так. После
первого преобразования, когда получился флютбет с одним
шпунтом, вычислим скорость для этого случая, равную d/dt
Тогда скорость на плоскости z будет
dm d(o dz
w :
что даст более простое выражение для скорости, чем при пря-
прямом решении задачи для первоначальной схемы.
Если число шпунтов больше двух, то процесс выпрямления
шпунтов можно продолжить до получения простой схемы.
П. Ф. Фильчаков обратил внимание на то, что линии
у = const рис. 76 с глубиной выпрямляются, становясь почти
горизонтальными прямыми на глубине 4—5 длин шпунта. По-
Поэтому метод выпрямления шпунтов применим и для слоя конеч-
конечной глубины. П. Ф. Фильчаковым A951) даны таблицы для рас-
расчета плоских флютбетов со шпунтами в слое бесконечной глу-
глубины. С помощью схемы одноступенчатого перепада дается
приближенный способ расчета также для флютбетов конечной
толщины. Различные задачи рассмотрены методом последова-
последовательных конформных отображений А. Я. Олейником A965)
и другими.
П. Ф. Фильчакову принадлежат и более общие способы рас-
расчета движения грунтовых вод, основанные на развитых им при-
приближенных методах конформных отображений A964).
§ 15. Метод фильтрационных сопротивлений. В большинстве
фильтрационных потоков зоны резко изменяющегося течения
локализованы и отделены друг от друга зонами равномерного
потока большой протяженности, в которых напор по кровле
пласта стремится асимптотически к линейной функции. В со-
соседней зоне эпюра напоров будет иная, со своей асимптотой, но
если удается добиться того, чтобы эти эпюры в промежуточной
зоне достаточно точно стыковывались, то будет получено при-
приближенное решение задачи.
Метод фильтрационных сопротивлений был предложен
С. Н. Нумеровым A953, 1) (см. также Аравин и Нумеров 1953,
1948 — изд. 2). Он развит применительно ко многим задачам не
только напорных, но и безнапорных (где асимптотическая пря-
прямая заменяется асимптотической параболой), а также напорно-
безнапорных движений (см. «Развитие исследований ...» 1969;
Нумеров и Барсегян 1966)
16]
МЕТОД ФИЛЬТРАЦИОННЫХ СОПРОТИВЛЕНИЙ
123
Поясним метод С. Н. Нумерова на примере плотины с пону-
понуром, водобоем и флютбетом с двумя шпунтами (рис. 77). Для
этого нам понадобятся две первые из пяти основных форм на-
напорной резко изменяющейся фильтрации, рассмотренных
С. Н. Нумеровым (другие его схемы относятся к фильтрации
У////7//////^//^
Рис. 77.
вблизи дренажа тела бетонной плотины и вблизи створа сква-
скважин, служащих для уменьшения противодавления по подошве
плотины).
Схема 1 (рис. 78). Она имеет место при обтекании внут-
внутренних шпунтов, а также вблизи сопряжения тела бетонной пло-
плотины с понуром, который является слабо проницаемым, но мо-
может считаться непроницаемым.
На рисунке изображено течение между твердыми стенками
со шпунтом ВС. Линии напора в левой и правой частях течения
имеют асимптотами соответственно прямые
(в явном виде эти уравнения нами не будут использованы).
124
НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ
[ГЛ. III
щ
\
I
\
ЧЬА
\Ah
""" •— — .
График напоров по верхней водонепроницаемой поверхности
(сплошные кривые, рис. 78) может быть приближенно пред-
представлен двумя прямыми (пунктирные линии на рис. 78), являю-
являющимися асимптотами графика напора. Высота ступеньки при-
приближенного графика напоров
\ может быть выражена так:
ДД = фдг, где дополнительное
фильтрационное сопротивление
Ф зависит от параметров S/T\
и Т2/Ти причем q = Q/x —
приведенный удельный филь-
фильтрационный расход.
Графики зависимости вели-
величины Ф от ее аргументов при-
приведены на рис. 79.
Максимальное расхождение
Рис. 78. точного графика напоров с
приближенным будет в точках
А и В рис. 78. Разности точных и приближенных значений
напоров в точках А и В составляют AhA = qfA и Ыгв = qfB,
IA и /Б — функции от S/T\ и Гг/Гь Графики этих функ-
функций также построены С. Н. Ну-
меровым A953, 1) (см. так-
также Аравин и Нумеров 1948 —
изд. 2).
Схема 2 (рис. 80). Она
имеет место вблизи верховой
грани непроницаемого (или
/'////////////////////////У////////////////////////
где
ф
0,8
0,5
/
'А
¦ 1/
11
7 77.
Ti '7
Щ
о)
J
/
у
//
/
/,
./
Л
/
/
/
/
' У
/
7
/
/
Горцзонт 8о0ы
А
0.8
'////'////////77////////////////'/////////V
Рис. 79.
Рис. 80.
принимаемого за непроницаемый) понура или вблизи низовой
грани водобоя (принимаемого за вполне проницаемый). Для
этой схемы также рассчитывается высота ступеньки приближен-
приближенного графика напоров ДА = ф#. Графики Ф E/Гь Т2/Т\) пред-
представлены на рис. 81. В точке В (рис. 80) разность точного и
§ 16]
главный вектор сил давления
125
2,0
Ф
зоне
приближенного значений напоров может быть также представ-
представлена в виде ДА* = qfB, где fB — функция аргументов S/Tx и
Т2/Т\; ее графики также даны С. Н. Нумеровым.
Вернемся теперь к рис. 77. По графикам рис. 78 при S/T\ =
= 13,5: 27,0 = 0,5 и Т21ТХ = 24,3: 27,0 = 0,9 найдем для сред-
средней зоны резко изменяющейся
фильтрации Ф = 0,65. Для
верховой зоны по графикам
рис. 81 при S/T\ = 0 и Т2/Т\ =
= 27,0 : 30,0 = 0,9 находим
ф = 0,58. В низовой
S/Г, =2,7:27,0=0,1
= 24,3 : 27,0 = 0,9, поэтому
ф = 0,67. Под понуром, в зоне
равномерной фильтрации, Ф =
= 54,0:27,0 = 2,0. Наконец, в
зоне равномерной фильтрации
в основании флютбета плоти-
плотины Ф = 30,0: 24,3= 1,23. Об-
Общее фильтрационное сопротив-
сопротивление при фильтрации в ос-
основании гидросооружения Ф =
58 200 065 123 +
у
у
У
у
1?
/
у
/
4 Л.
0,8 ^
//
/С
У
У
1
1
1
f /
у
/
/
J
/
f I
/
/
/ /
/
/
1 к
/ 1
1
/
/
0,2
0,6 s 0,8
Рис. 81.
= 0,58 + 2,00 + 0,65 + 1,23 +
+ 0,67 = 5,13.
Так как напор на гидросо-
гидросооружении Я «= 1о,0 м, то q =
= Я/Ф = 16,0: 5,13 = 2,93 м. Потери напора, соответствующие
найденным фильтрационным сопротивлениям, вычисляются по
формуле ДА=2,93Ф и получаются соответственно равными
1,7 м, 5,9 м, 1,9 ж, 3,6 ж и 1,9 ж. По этим потерям построен гра-
график напоров по подошве гидросооружения в первом приближе-
приближении, он изображен на рис. 77 пунктирной линией. После введе-
введения поправок к напорам в точках В\, А2, В2 и В3 на рис. 77
построена уточненная (сплошная) кривая распределения напо-
напоров. Исправленные величины напоров даны в скобках.
Д. ГИДРОДИНАМИЧЕСКИЕ РЕАКЦИИ
НА ОСНОВАНИЕ ПЛОТИНЫ
§ 16. Главный вектор сил давления. Рассматривая плоское
движение грунтовых вод под гидротехническим сооружением,
выделим часть этого сооружения, ограниченную двумя вер-
вертикальными плоскостями, одна из которых есть плоскость
рис. 82, другая, ей параллельная, отстоит от нее на единицу
длины.
126
НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ
[ГЛ. III
Обозначим через а угол нормали к контуру с осью х
(рис. 83) и через 8 —угол между касательной к контуру
и осью х. При этом положительным направлением дуги будем
Hi
Рис. 82.
считать направление от точки В к точке С контура основания,
а положительным направлением нормали —направление внутрь
области движения. Тогда направление п будет соответствовать
направлению оси х, направление
касательной — направлению оси у.
Обозначим через dF элемент си-
силы давления, действующий на пло-
площадку в виде криволинейного пря-
прямоугольника, одна сторона которого
есть элемент дуги ds контура ВС,
; другая имеет длину, равную едини-
' це, и направлена перпендикулярно
к плоскости чертежа.
Так как давление р направлено
по нормали к контуру и противопо-
противоположно выбранному нами направлению нормали, то будем иметь,
полагая
dF = dX + idY, A6.1)
следующие выражения проекций dX и dY силы dF на оси коор-
координат:
dX = — р cos (n, jc) ds — — р cos a ds,
dY = — р cos (n, y)ds= — p sin a ds.
По чертежу рис. 83 видно, что
cos а = sin 8, since = — cos 8, A6.2)
Рис. 83.
§ 16] ГЛАВНЫVI ВЕКТОР СИЛ ДАВЛЕНИЯ 127
Поэтому можно написать
dX + i dY = — р (sin в — / cos 6) ds = pi (cos 6 + / sin 0) ds,
или dF = dX + i dY = pi {dx + / dy) = pi dz.
Производя интегрирование по контуру ВС, найдем главный
вектор сил давления на основание плотины
F = X + iY = i [ pdz. A6.3)
ВС
Мы видели в главе II, что давление р в любой точке грун-
грунтового потока выражается через напорную функцию таким
образом:
(ty), A6.4)
где у = 98 — объемный вес воды.
Подставляя A6.4) в A6.3), найдем
X+iY = iy \{h-y)dz, A6.5)
ВС
или, разделяя действительные и мнимые части,
Х=-у \{h-y)dyy Y = y J(A-y)djc. A6.6)
ВС ВС
ВС ВС
Рассмотрим крайние точки б и С, в которых основание пло-
плотины соединяется с границей воды в верхнем и нижнем водое-
водоемах. Обозначим через Hi и Н2 уровни воды в верхнем и ниж-
нижнем бьефах, отсчитываемые от произвольно выбранной оси х>
ординаты точек В и С через у\ и у2, давления в точках В и С
через р\ и /?2- Тогда
-у = //<-^ h(xhyi) = Hi (i=i,2).
Предположим, что известно распределение напора вдоль
основания плотины, и пусть эпюра давлений изображена на
рис. 82 вертикальной штриховкой. При этом считаем, что пря-
прямые, параллельные оси ординат, пересекают контур ВС лишь
в одной точке.
Тогда величина У, определяемая уравнением A6.6), будет
равна весу вертикально заштрихованной области рис. 82, если
бы она была заполнена водой. Так как Н2 < h < Яь то для ве-
величины Y получаем неравенства
Y \ {H2-y)dx<Y<y J (Hx-y)dx.
ВС ВС
128 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. III
Г. Н. Положки ввел обозначения для верхнего и нижнего
гидростатических давлений Гв и Гн, полагая
Гв = V J (#1 - У) dx9 Г„ « у $ (#2 - У) dx. A6.7)
ВС ВС
Очевидно, что Гн есть вес воды в объеме, образованном движе-
движением площади ВСС2В2 на единицу длины перпендикулярно к
площади чертежа. Тогда так же Гв есть вес воды в объеме, об-
образованном площадью ВСС\ВХ.
Следуя Г. Н. Положему, введем понятие о среднем гидро-
гидростатическом давлении
\(Ц) A6.8)
ВС
В случае симметричной области вертикальная составляющая
сил давления равна среднему гидростатическому давлению:
У = гср. В общем случае можно написать
v Г Л #1 + #г\л, С/Я,+#2 \,
7 = Y J \h ^H~J dx + Y ) ( I ~~ y) dx>
ВС
x. A6.9)
ВС ВС
или
ВС
Интегрированием по частям можно преобразовать интеграл
в A6.9):
ВС ВС
Если ось у провести на равном расстоянии от точек В и С,
ТО X!+*2 = 0> И МЫ ПОЛУЧИМ
\dh. A6.10)
По этой формуле нетрудно подсчитать У, например, в том слу-
случае, когда построено семейство линий равного напора.
Предположим, что прямая, параллельная оси х, пересекает
контур ВС лишь в одной точке. (Это может иметь место в пере-
перепадах и быстротоках, но не имеет места в плотинах.) В этом
случае можно дать неравенство для X:
§ 16] ГЛАВНЫЙ ВЕКТОР СИЛ ДАВЛЕНИЯ 129
Здесь у\ и у2— ординаты точек В и С. Обозначим высоту
\у\ — f/21 через d. Если расположить ось абсцисс посредине
между у = ух и у = у2, то будем иметь ух + у2 = 0, и можно
написать
yH2d<\X\<yH{d.
При этом Нх и Н2 отсчитываются от указанной средней линии.
Интегрируя выражение A6.6) для X по частям, получим
Х=-у{Н2у2-НхУх) + у J ydh. A6.11)
ВС
Обращаясь к общему случаю контура ВС, обозначим через
т)! и т]2 ординаты самой верхней и самой нижней точек контура
ВС. Тогда для интеграла
будем иметь оценку
уч\2Н <у ^
ВС
где Н = Н2-НХ.
Отметим, что в формулах A6.10) и A6.11) под знаком ин-
интеграла можно заменить h на Q = h + Щ\ так как q постоянно
вдоль контура ВС, то можно принять q = 0. Получим
Я! Я,
или
Иг
я,
где
Вср = у{Н1 + Н2)у2 при
Знание вертикальной составляющей сил давления У имеет
важное значение в вопросе о невсплывании плотины. Обозначим
через У вес плотины, через У" — вертикальную составляющую
равнодействующей сил давления жидкости на наземную часть
плотины. Тогда, считая, что отсутствуют силы сцепления между
основанием плотины и частицами грунта, получаем необходи-
необходимое условие для невсплывания: Y" -\- У > Y.
В гидротехнике рассматривается величина
, Y" 4- Г
5 П. Я. Полубаринова Кочина
130 НАПОРНАЯ ФИЛЬТРАЦИЯ ПОД СООРУЖЕНИЯМИ [ГЛ. Ill
называемая коэффициентом устойчивости на всплывание (Гри-
(Гришин 1962). Неравенства, установленные для У, дают возмож-
возможность также получить оценку для k*.
Вопросы силового воздействия грунтового потока на скелет
грунта и на подошву сооружений представляют значительный
практический интерес, так как решение их определяет многие
детали гидротехнического проектирования. Можно указать на
специальную дискуссию, посвященную этим вопросам (Рельтов,
Чугаев и Вяземский 1949).
§ 17. Главный момент сил давления. Для выяснения вопроса
об устойчивости гидротехнического сооружения представляет
интерес вычисление главного момента сил давления относитель-
относительно прямой, перпендикулярной к плоскости поперечного сечения
плотины, или, что то же, момента относительно некоторой точки
г0 плоскости поперечного сечения плотины. В особенности ин-
интересен случай, когда z0 совпадает с одним из концов плотины.
Пусть 2о = Хо + Ч/о. Выражение главного момента М сил
давления относительно г0 имеет вид
М = ~"~ \ Р^х"хо)cos (я> У) —(У — Уо)cos (я> *)] ds, A7.1)
ВС
или (см. рис. 83)
м =
ВС
= у \ pd\z-ZQ\2.
ВС
Подставляя сюда p = y(h — у) и производя интегрирование
по частям, будем иметь
ВС
я,
J \ \z-Zo\4h. A7.2)
Для последнего слагаемого можно дать следующие неравен-
неравенства, если принять z0 за одну из крайних точек, B(zi) или С )
Положим Zq = z\. Тогда
я,
\d\z-z{\2 + l. ^ \Z-Zx?dh.
ВС Нг
A7.3)
§ 17] ГЛАВНЫЙ МОМЕНТ СИЛ ДАВЛЕНИЯ 131
Теперь примем во внимание, что 0 <; |аг — 2Ti| < \z2 — zx\. От-
Отсюда следует неравенство
г1
Яг
Остальные члены формулы для М{гх) вычисляются согласно
геометрической форме плотины.
В качестве примера найдем результирующий вектор и мо-
момент сил давления на плоский флютбет в слое бесконечной глу-
глубины, приняв за г0 левый конец флютбета, примыкающий к
верхнему бьефу. Для этого случая мы нашли выражение напора
в виде
С помощью формул A6.7) получаем Х = 09
-I
Здесь В = 21 — ширина основания плотины. По формуле A7.3)
найдем, так как у нас Z\ = — I, у = О,
i[
- #2 dX
Вычислив интеграл в правой части, для опрокидывающего мо-
момента относительно точки z0 = —/ получаем
в2.
Очевидно, что для момента относительно точки zo = I будем
иметь
М(/) = -уЗЯ* + 5//' В\
Глава IV
ФУНКЦИЯ ЖУКОВСКОГО И ЕЕ ПРИЛОЖЕНИЯ.
ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
А. ПРИМЕНЕНИЕ ФУНКЦИИ ЖУКОВСКОГО
§ 1. Функция Жуковского. В плоском установившемся движе-
движении грунтовых вод между потенциалом скорости и давлением
имеет место зависимость (см. § 11 главы I)
которую можно переписать в виде
-¦^Г/^Ф По-
Последовательно, выражение
eI==q> + ty--JLp A.1)
лишь постоянным множителем отличается от давления. Функ-
Функция 0i является гармонической по х, у, так как tp и у— гармони-
гармонические функции. Сопряженной с 0i является функция
62 = *-**. A.2)
Обозначим 0] + *02 через 0:
в = в! + Ю2 = ш — ikz (со = ф + п|), z = x+iy). A.3)
Функцию A.3) будем называть функцией Жуковского (Жу-
(Жуковский 1923).
Если по аналогии с A.1) ввести обозначение
62=-^-Р'. A.4)
то
0 = -jg(P + ifO. A.5)
§ 2] ШПУНТ ЖУКОВСКОГО 133
Можно назвать комплексным давлением выражение
Р = /? + *>', A.6)
и тогда функция Жуковского будет пропорциональна комплекс-
комплексному давлению.
На свободной поверхности грунтового потока давление равно
атмосферному. При наличии капиллярности, как мы видели (см.
§ 2 главы II), давление также является постоянным. Если при-
принять атмосферное давление равным нулю, то на границе капил-
капиллярной каймы следует положить
p=-pg7zK, A.7)
где hK — высота капиллярного поднятия воды в грунте.
Таким образом, на свободной поверхности действительная
часть функции Жуковского является постоянной. Это и обуслов-
обусловливает значение функции Жуковского.
Вместо A1) и A.2) можно написать соотношения, содер-
содержащие напор и приведенный расход: h = —y/k и q = -—г|э/&.
Приняв pg" = 1 и измеряя р и р' высотой водяного столба, бу-
будем иметь
P = h — y, p' = q + x.
В § 2—7 мы покажем применение функции Жуковского к
различным задачам.
§ 2. Шпунт Жуковского. В качестве первого примера рассмот-
рассмотрим задачу Н. Е. Жуковского о шпунте.
Пусть шпунт ВС обтекается под действием напора Н
(рис. 84). Тогда за шпунтом вода поднимается на некоторую
высоту CD и образует свободную поверхность DAy на которой
имеем условие
e,=q> + ty = *AK. B.1)
Вдоль границы АВ
ф=-&#. B.2)
Вдоль линии BCDA положим
г1> = 0. B.3)
Так как уравнение линии АВ есть у = 0, то вместе с тем
вдоль АВ
;/ = -&//. B.4)
Далее, так как вдоль шпунта BCD имеем х = 0, то вдоль него
62 = i|5-/b = 0. B.5)
134
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
На плоскости функции Жуковского (рис. 85) получаем для
области движения ABCDA полуполосу; отображение ее на ниж-
нижнюю полуплоскость плоскости i дает
K arcsing-fe
B.6)
С другой стороны, на плоскости комплексного потенциала со
имеем простую область— прямой угол (рис. 85), так как вдоль
линии АВ у нас ф = —fe#,
а вдоль всей остальной грани-
границы ф = 0. Следовательно, мо-
можем положить
со
+ kH = М У ? + 1 •
Для определения М положим
?= 1. Тогда, так как в точке
В
Рис. 84.
Рис. 85.
D имеем ф = — ky + khK, a y — —d (d — длина отрезка BD)%
то
Находя отсюда М, получим
B.7)
Исключая (о из B.6) и B.7), получим для z уравнение
С. B.8)
Для того чтобы найти скорость в любой точке области движе-
движения, продифференцируем по ? уравнения B.6) и B.7):
da -udz_kH + hK I da k(H + hK + d)
ШПУНТ ЖУКОВСКОГО
135
Разделив почленно левые и правые части полученных уравне-
уравнений, найдем
1 — 'k — — 2У^ __н + hK
с/со
На конце шпунта в точке z = —SI скорость обращается в бес-
бесконечность, а обратная ей величина dz/d(o — в нуль. При этом
для значения ?, соответствующего концу шпунта, получаем
8 ( Н + Нк ^ B.9)
Подстановка этого выражения в B.8) дает длину шпунта
4 (// + Лк)
¦arcsin-
B.10)
Зависимость между о и Э получается с помощью уравнений
B.6) и B.7) в виде
со
= - k [H - (Я + hK + d) cos ^-+*ff ].
Вдоль свободной поверхности ф + ky = fe/zK, -ф = 0, 6 =
= — ikx-\-khK и (о = ф= — ky + fe/zK. Поэтому для свободной
поверхности получается уравнение цепной линии
7JJ- B-И)
Приведенное решение принадлежит В. В. Ведерникову A939).
Н. Е. Жуковский строил выражения для ю и 6 как функ-
функции от вспомогательной комплексной переменной в виде ин-
интегралов, подынтегральные функции которых он находил по ха-
характеру особенностей — в данной задаче эти функции содержат
квадратные корни в знаменателях, так как углы рассматривае-
рассматриваемых областей прямые (см. рис. 85).
Таблица 6
Зависимость величины dj(H + Лк) от Sj{H + hK)
s
Я + Лк
d
Я + Лк
S-d
Я + Лк
0
-0,363
0,363
0,074
-0,2
0,274
0,213
0
0,213
0,64
0,5
0,14
1,10
1
0,10
2,066
2
0,066
136
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
В заключение приведем таблицу 6 зависимости величины
d/{H + hl{) от SI(H + hK), вычисленную В. В. Ведерниковым.
Отрицательные значения d/(H-\-hK) означают, что вода за
шпунтом поднимается выше точки В (рис. 84).
Отметим, что действие капиллярности сказывается в этой за-
задаче таким образом, как если бы вместо действующего напора
Н имелся напор, увеличенный на высоту капиллярного подня-
поднятия, т. е. равный Н + hK.
§ 3. Одиночная дрена. Эта задача также рассмотрена
Н. Е. Жуковским A923). Осушительную канаву или дрену с
очень малой глубиной воды в ней можно схематически предста-
представить в виде щели, изобра-
изображенной на рис. 86.
На линиях АВ и FA,
являющихся свободными
поверхностями, давление
постоянно. Примем его
равным нулю. Тогда мож-
можно записать условие для
потенциала скорости на
свободной поверхности
в виде
ф + ky = 0. C.1)
Контур дрены BCDEF
является эквипотенци-
алью (линией равного напора) ср = 0. Так как для этого конту-
контура у = 0, то условие C.1) выполняется также и на нем.
Таким образом, для функции Жуковского A.3) действитель-
действительная часть равна нулю для всего контура области движения.
Введем вспомогательную переменную ? так, чтобы полуплоско-
полуплоскости ? отвечала полуплоскость 0. Тогда можем принять
е = а?, C.2)
где а — постоянная, которую определим в дальнейшем.
Линии АВ и FA суть линии тока. Обозначим через Q вели-
величину полного расхода дрены (на единицу ее длины). Можем
принять ф = — Q/2 вдоль FA и г|з = Q/2 вдоль АВ.
Отображение области комплексного потенциала со на ниж-
нижнюю полуплоскость плоскости ? (рис. 87) дает
Рис. 86.
С
со =
Vl-?2
C.3)
ОДИНОЧНАЯ ДРЕНА
137
Решив это уравнение относительно ?, найдем
Я0/
= sin-
Q '
со — ikz=* a sin
71Ш
C.4)
Подставляя это выражение ? в C.2) и заменяя Э на со — ikz,
получим
C.5)
Решим это уравнение относительно z:
со а ясо/
C.6)
Для определения постоянной а положим z = bJ2y где Ь\— ши-
ширина промежутка В/7 (рис. 86). При этом в точке F имеем
(рис. 87) ф = 0, ф = — Q/2. Поэтому
C.6) дает
«--«й+ 7-)- C.7)
Из уравнения C.6), дифференци-
дифференцируя его по со, найдем величину dz/dco,
обратную скорости фильтрации:
dz 1 _J ая Я0/ /q n\
В точке ?" — конце дренажной щели
скорость бесконечно велика и, следо-
следовательно, l/w = 0. Это дает
л о/ Qi 2Q
Q аи я (Q + /j^i)
C.9)
Рис. 87.
В точке ?, кроме того, ф = 0. Пусть Q' обозначает расход через
отрезок CDE. Тогда в точке Е будет \() = —Q'/2 и со = —Q'i/2.
Подставляя это значение со в C.9) и решая последнее уравне-
уравнение относительно Q', найдем
О' = 2 — arccos 2Q
я я (С
C.10)
Теперь определим ширину щели по дну CDE = Ь. В точке ?
имеем z = b/2 и со = —Q4/2. Подставляя эти значения в C.6),
получим, учитывая C.7), C.9) и C.10),
4Q2
2Q
2Q
(З.П)
Наконец, найдем уравнение ветви свободной поверхности FA.
Для этого в уравнение C.6) подставим <р = —ky и \|) = —Q/2,
138 ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
Получим
_ % + Т XQ_ * v /_^_ „Ч
г ~ 6/ l2fe f 2JSin\ Q 2 )•
Полагая г = х-\-1у, после сокращений находим
Как и в шпунте Жуковского, в качестве кривой депрессии мы
получили цепную линию. Б. К. Ризенкампф заметил A940, 1),
что задача о дрене Жуковского может быть получена из задачи
о шпунте Жуковского (при отсутствии капиллярного поднятия
в грунте), если сделать замену функции z на —iz, со на /0 и 0
на /со.
Уравнение C.12) можно переписать в форме
Если известна какая-нибудь точка (хи у\) депрессионной линии
грунтового потока, а также отрезок Ь> то уравнения C.11) и
C.13) позволяют вычислить приведенный расход QJk дрены и
величину Ьх.
Любую из эквипотенциалей вблизи контура BCDEF можно
принять за очертание дрены. Если данная дрена имеет форму,
отличающуюся от этих эквипотенциалей (обычно сечение дре-
дренажной канавы вертикальной плоскостью имеет форму пря-
прямоугольника, трапеции или некоторой плавной линии), то
вблизи нее форма депрессионной кривой будет иная, но на до-
достаточно больших расстояниях от дрены уравнение депрессион-
депрессионной кривой будет очень близким к C.13).
В. И. Аравин A936) рассмотрел примеры дрен Жуковского
с построением сеток движения для различных значений 6, вклю-
включая случай Ъ\ = 0. Здесь ветви депрессионной кривой полу-
получаются смыкающимися в одной точке, в середине дрены — такую
дрену называют затопленной. Полагая Ъ\ = 0, из C.11) по-
получим
§ 4. Приток к системе дрен при наличии инфильтрации.
Обычно дрены предназначаются для того, чтобы отводить из
почвы излишки грунтовых вод. Для этого дренажные канавы
делаются с уклоном, чтобы вода из них могла стекать в коллек-
§4}
ПРИТОК К СИСТЕМЕ ДРЕН ПРИ НАЛИЧИИ ИНФИЛЬТРАЦИИ
139
торы — большие дрены, из которых вода отводится самотеком
или перекачивается в реки или большие каналы.
Дрены питаются за счет инфильтрации, т. е. поступления
воды с поверхности почвы вследствие дождей, поливов, проса-
просачивания тающего снега и т. п.
Рассмотрим задачу о притоке грунтовых вод в систему боль-
большого числа прямолинейных горизонтальных дрен, представляю-
представляющих бесконечно тонкие щели, расположенные на одинаковой
глубине, на равном расстоянии друг от друга, в водопроницае-
водопроницаемом слое бесконечной глубины (Аравин и Нумеров 1953).
б)
С В А
А
Рис. 88.
Обозначим через е постоянную интенсивность инфильтрации.
Если выделим часть потока (рис. 88, а), ограниченную верти-
вертикальными линиями тока, находящимися посредине между со-
соседними дренами, то получим область движения с вертикаль-
вертикальными твердыми стенками и горизонтальными водопроницаемы-
водопроницаемыми границами (стенки щелей). В этом случае, кроме функции
Жуковского
е = со-/&2 = е1 + /е2, D.1)
рассмотрим еще введенную Б. В. Девисоном и Б. К. Ризенкамп-
фом функцию
Q = со — iez = Й! + ^2, D.2)
140 ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
у которой мнимая часть имеет постоянное значение на свобод-
свободной поверхности:
Q2 = <ф — гх = const. D.3)
Если найдем Э и Q, то z и со будут определяться из уравнений
г = -^т F - Q), со = -Л-^ (Ш - еЭ). D.4)
Обозначим через Q полный расход каждой из дрен, через
Qi — расход, поступающий в дрену из толщи грунта. Тогда ин-
фильтрационный расход дрены Q2:
Q2 = Q-Qi = e (/-&,), D.5)
где / — расстояние между соседними дренами, Ь\ — внутренний
размер дренажной щели С'С.
Пусть ф = 0 на контуре дрены С'В'ОВС и г|) = 0 на оси сим-
симметрии АО области движения. Конформное отображение полу-
полуполос областей Q и Э (рис. 88, в—г) на нижнюю полуплоскость
плоскости ? (рис. 88,6) дает
6 = - JL (Qj + kl)arcsinС, Q = - /(Q^e6l) arcsin -J-, D.6)
где
a~Sin 2(Ql+kl) '
Подставляя D.6) в DА)9 найдем
* = п(^,е) [(Qi + *0 arcsin ? - (Q + eft,) arcsin i] • D.8)
Вдоль правой ветви кривой депрессии CD (которая симмет-
симметрична левой ветви) ? = ach[(? — e)ny/(Q + e&i)], и уравнение
свободной поверхности можно написать в виде
Полагая в D.9) х = 1/2 и j/ = W, где Я — максимальная
отметка кривой депрессии, получим
Для того чтобы определить ширину щели Ь, заметим, что в
точке В абсцисса х, рассматриваемая как функция от ? = ?,
§ Б] КРОТОВЫЙ ОРОСИТЕЛЬ И КРОТОВАЯ ДРЕНА 141
достигает экстремума. Полагая dz/d?=0, С. Н. Нумеров получил
где
Сетка движения в рассматриваемой задаче такова, что на
некотором расстоянии внизу линии тока становятся почти верти-
вертикальными, а линии равного потенциала — почти горизонталь-
горизонтальными. При глубине |*/|>/ практически последние можно счи-
считать горизонтальными отрезками. Для напора h на такой линии,
отсчитанного от отметки дрены, имеет место равенство
Из D.13), зная напор в толще грунта на некоторой глубине,
можно найти Qi, зная Q.
Если дрены питаются только за счет инфильтрации на
свободную поверхность, то Qi=0, Q==Q2==e(/ — b{) и р =
= sin(e/&). Если они питаются только за счет притока воды из
толщи грунта, то е = 0 и Q = Q\. Заметим, что из полученного
решения без учета инфильтрации можно найти решение задачи
при учете инфильтрации, изменив все линейные размеры в
A—г/k) раз и заменив расход Q на Q-\-eb[.
В рассмотренной задаче причиной подъема уровня грунто-
грунтовых вод и, возможно, заболачивания являются не только атмо-
атмосферные осадки или поливы, но и фильтрация из пласта с на-
напорными артезианскими водами вверх через покрывающую
этот пласт толщу земли. Другими словами, питание дрены, пред-
предназначенной отводить излишки воды, происходит также снизу.
Поэтому установившееся движение оказывается возможным и
при отсутствии инфильтрации.
Решение задачи о притоке к системам дрен в области, огра-
ограниченной снизу линией равного напора (причем контур дрены
рассматривается как малая окружность около точечного стока),
было дано В. В. Ведерниковым A939).
Заметим, что применение функции Жуковского удобно в тех
случаях, когда имеем, помимо свободной поверхности, горизон-
горизонтальные линии равного потенциала и вертикальные линии тока
в области движения. Ряд примеров такого рода рассмотрен
Ф. Б. Нельсоном-Скорняковым A947).
§ 5. Кротовый ороситель и кротовая дрена. Эти задачи рас-
рассмотрены Б. К. Ризенкампфом A940, 1). Они могут представить
интерес при исследовании работы кротового полива или крото-
142
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. IV
вого дренажа. Кротовая дрена (или кротовый ороситель) про-
пробуривается таким образом: на нижнем конце вертикально по-
поставленного ножа находится снаряд с заостренным концом.
Когда нож прорезает почву, то снаряд пробивает цилиндриче-
цилиндрическую полость в грунте.
В
д)
ш
1
А
В 0
'о'
и
в
g
Рис. 89.
В случае кротового оросителя будем считать, что на поверх-
поверхности грунтовых вод (рис. 89, а) имеет место испарение с по-
постоянной интенсивностью с = —е. Введем, как и в предыдущем
параграфе, функции
е
F.1)
Ороситель представим точечным источником Л. Пусть на
свободной поверхности <р + ky = 0, ф = 0 на оси симметрии
ниже А и ф = Q/2 вдоль AD. Будем рассматривать только пра-
правую половину области движения BOO'ADCB. Тогда для Q полу-
получим полосу (рис. 89,6). Область функции Жуковского изобра-
изображена на рис. 89, в. Конец разреза этой области находится в
точке О', в которой dQildy = ду/ду + k — 0.
При конформном отображении на верхнюю полуплоскость т
(рис. 89, г)
2я(т-1)
§ 5) КРОТОВЫЙ ОРОСИТЕЛЬ И КРОТОВАЯ ДРЕНА 143
Подстановка л/% = it, переводит полуплоскость т в угол обла-
области ? (рис. 89,<3), в результате чего получаем
Отсюда найдем
+aM Q-
Так как точка ? = —i соответствует точке Л области дви-
движения, где z имеет конечное значение, то нужно положить
Q/Bn) + aM = 0, откуда
Интегрируя и считая 2 = 0 при ? = 0, получаем
Так как при ? = —/ имеем z= — /Я, то
(ft + c)-Jtf = 4" + 1п2- E.6)
Уравнение свободной поверхности получим, полагая ? = ?:
У = — (ьл-л« lnVl +I2. E.7)
В точке перегиба линии свободной поверхности, как нетрудно
Л
видеть, ? = лЛ -\-а. Обозначая через р угол касательной в точке
перегиба с вертикалью, найдем, что
Ветви кривой депрессии E 7) уходят вниз на бесконечность.
Пусть Ао будет напор по контуру трубы оросителя. С помо-
помощью формулы E.1) можем написать для со выражение
= - icz + JLln(l + I2) E.9)
144
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
Полагая ? = —/ -f ?', z = —iH
малой окрестности точки А
г', будем иметь в бесконечно
(б. 10)
причем на основании E.5) имеем с точностью до малых выс-
высшего порядка
* 2я(? + *)со5р • ^#11'
Положим теперь z' = ReiQy где R — радиус трубы. Подставляя
это выражение в E.11) и E.10) и отделяя действительную часть
от мнимой, найдем
2nk
4я/? (k + с) cos ft
Q
E.12)
Если угол р = 0, то точка перегиба ухо-
уходит на бесконечность, параметр а будет
равен бесконечности, и из E.6) получим
,. In 2 Q
я k + с '
н Свободная поверхность будет иметь
асимптоту х = Ql[2(k + с)] (рис. 90).
Скорость на бесконечности будет ?/«> =
= —&, в то время как в общем случае
Точно так же решается задача для осушительной трубы
(дрены) при наличии инфильтрации, т. е. при с = —е < 0.
Рис. 90.
Н *2?
1
д
Рис. 91.
Можно получить это решение из предыдущего, заменяя Q на
—Q и полагая —а = Ъ > 0.
Уравнение свободной поверхности будет иметь вид
?li*Jl?Lx=_L_arctgS, Jii
(б.13)
§ 6]
ФИЛЬТРАЦИЯ ИЗ КАНАЛА В ВОДОПРИЕМНИКИ
145
где
Ь =
1 + sec
tgp
причем р — угол между вертикалью и касательной в точке пере-
перегиба С (рис. 91). Для глубины Н залегания трубы будем иметь
уравнение
(k + )
и
Н =
sec ft
Л
I-
¦L-
-If
А а:
Q
Формула E.12) для напора сохраняет свой вид.
Если угол Р = 0, то точки перегиба сливаются и образуют
точку заострения (рис. 92). В формулах E.13) нужно при этом
положить b = 1.
§ 6. Фильтрация из канала в симметрично расположенные
водоприемники. Схема задачи представлена на рис. 93. Канал
DE имеет простейшую форму горизонтального отрезка. Дрены,
в которые поступает вода,
имеют вид горизонтальных
отрезков АВ к GA с щеля-
щелями С В и GF.
Как и в предыдущей за-
задаче, здесь вдоль всего кон-
контура мы имеем qp + ку=0 *)
и при отображении на по-
полуплоскость ? (рис. 93) для
функции Жуковского полу-
получаем, учитывая соответст-
соответствие бесконечно удаленных
точек,
= до — ikz = а?. F.1)
Положим вдоль отрезков
ABC и FGA потенциал ско-
скорости равным нулю. Тогда
вдоль DE будем иметь
ф = —хГ, где Т — высота
основания канала относи-
относительно дрен.
Обозначая полный расход на единицу длины канала через
Q, положим, что г|з = Q/2 вдоль EF и чр= —Q/2 вдоль CD,
Тогда на плоскости © (рис. 93) получим* прямоугольник, для
которого отображение на нижнюю полуплоскость плоскости ?
*) В § б и 7 коэффициент фильтрации обозначен через к.
146
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
дает (см. аналогичные задачи в главе III)
t
Qi
@ =
Vd - V) A - &?)
F.2)
F.3)
F.4)
F.5)
F.6)
Из этого уравнения, зная 1/Т и L/T, можно определить значение
k, которое позволит затем вычислить расход по формуле F.3).
Расход связан с напором соотношением
п_ 2хТК
Как нетрудно проверить, a = -j(Q — к1), откуда
i
Полагая g=l/fe и z = L/2, получим
Сравнивая это с F.3), получим
К
Рис. 94.
Можно вместо L ввести другую величину, а именно, расстояние
U от уреза воды в канале до уреза воды в водоприемнике, или,
иначе, проекцию EF па ось х (рис. 93). Величины Z, L и 1Х свя-
связаны соотношениями
ФИЛЬТРАЦИЯ ИЗ КАНАЛА В ВОДОПРИЕМНИКИ
147
При этом F.6) перепишется так:
т
2k
— k т
К'
F.7)
В. В. Ведерников A939)
QI(kT) от 1/Т и /i/7\ На
рис. 94 представлена гидро-
гидромеханическая сетка движе-
движения, рассчитанная В. В. Ве-
Ведерниковым для одного ча-
частного случая; на ней нане-
нанесены значения q* = —if>/Q
и h* = —<р/(иГ).
Фильтрация из ка-
канала при водоприем-
водоприемнике с одной сторо-
н ы. Эта задача (рис. 95) ре-
решается аналогично предыду-
предыдущей. Здесь опять получим
6 = а?. Для со получаем
вычислил таблицу зависимости
П
г
- С) A - С)
Е
Л
1
г< XT >
t
р.
А
Рис. 95.
Подстановка ? = et2y е = k2
приводит интеграл для со
к нормальной форме; выразим теперь величины со и 0 через /:
0 =
dt
-t2)(\ -k2t2)
Здесь а! и с' — постоянные, подлежащие определению.
Дальнейшие вычисления, которые мы опускаем, дают зави-
зависимость, аналогичную F.7):
JL= k* ll i K
т IF т к''
причем для расхода получается формула
_Q_^ J & и
кТ ~ Т h'2 T
к
К' '
F.8)
F.9)
148
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
На рис. 96 дана сетка движения, построенная для частного
случая В. В. Ведерниковым A939). На ней нанесены значения
q*=zyp/Q и
канала.
= ф/(хГ), а линия А* = 0,2 принята за контур
§ 7. Полуобратные методы решения задач. Под полуобрат-
полуобратными методами понимают такие методы, когда строится реше-
решение задачи, удовлетворяющее только части заранее заданных
краевых условий, в то время как некоторые краевые условия
получаются в процессе самого реше-
решения и несколько отличаются от за-
заданных.
Так, например, строгий расчет
фильтрации в теле земляных пло-
плотин очень сложен. Ему будут посвя-
посвящены в значительной степени главы
VI и VII. Здесь же мы рассмотрим
упрощенную схему, позволяющую
рассчитывать фильтрацию в теле
земляной плотины на проницаемом
основании конечной глубины при
отказе от условия о горизонтальности водоупора. На рис. 97
изображена земляная плотина (Вощинин 1939), в верхнем и
нижнем бьефах которой слой воды очень мал. Разность уровней
воды равна Н. Проницаемое основание снизу ограничено ли-
линией, форма которой заранее не известна; это линия тока, опре-
определяемая из искусственного условия: на ней должно быть по-
постоянным выражение ф + ху. Это условие возникает из того
обстоятельства, что на свободной поверхности ф + и?/ = const,
Рис. 97.
§71
ПОЛУОБРАТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
149
вдоль границ водоемов у = const и ф = const, а следовательно
и ф + ху = const. Поэтому, если принять на свободной поверх-
поверхности ф + ку = 0 и на линии водоупора АВ положить ф + ку =
= —кТ, то на плоскости функции Жуковского
е = со — iy
+ ;е2
G.1)
получим полосу ширины Т (рис. 98).
Сравнив рассматриваемую задачу с задачей об обтекании
флютбета в проницаемом слое глубины Т (рис. 58), видим, что
область движения здесь
аналогична области функ-
функции Жуковского. Об-
Область комплексного по-
потенциала той и другой за-
задач одна и та же.
Подобно формуле
G.4) главы III для г,
здесь будем иметь для 0:
?=т(
2T%
G.2)
Рис. 98,
Для ? как функции от
со можем воспользоваться формулой D.3) главы III:
и =¦
G.3)
Из формул G.2) и G.3) найдем z как функцию от со:
/со Г . dn и + fe en и
к я dn и — kcnu *
Как и в случае § 4 главы III, будем иметь
k = th "оуГ .
G.4)
Уравнение свободной поверхности получается симметричным
относительно средней точки М (рис. 97). Линия водоупора на
бесконечности слева и справа отстоит от соответствующей гра-
границы верхнего или нижнего бьефа на расстояние Г, следова-
следовательно, водоупор понижается на величину Н при переходе от
х sss—оо к х = +оо. На рис. 97 пунктиром указаны «среднее»
положение горизонтального водоупора и одна из эквипотенциа-
лей области движения, каждая из которых может быть принята
150
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. IV
за новую линию верхового откоса плотины, переходящую в ли-
линию дна водохранилища.
Частный случай задачи Т = оо был исследован ранее и
приведен в книге Ф. Б. Нельсона-Скорнякова A947), где рас-
рассмотрены с помощью функции Жуковского также другие схемы.
Приведем еще один простой пример полуобратного решения
задачи о притоке воды к осушительной канаве криволинейного
профиля. М. И. Базанов A938)
рассмотрел задачу о притоке
из бесконечности к канаве, в
которой слой воды бесконечно
тонок (точнее говоря, к пустой
канаве). Здесь весь периметр
канавы является линией выса-
чивания, и по всему контуру
области движения имеем усло-
условие 0i = const, т. е. область
движения представляется на
плоскости функции Жуковско-
Жуковского полуплоскостью. Форма ка-
канавы определяется условием,
что на плоскости инверсии го-
годографа скорости l/w (см.
§ 1 главы V) ей отвечает дуга
некоторой окружности. При
этом решение получается с по-
помощью конформных отображений. М. И. Базанов нашел для
расхода Q, притекающего к канаве, зависимость Q = хяЯ, где
Н — высота участка высачивания на откосы канавы. На рис. 99
приведена сетка, построенная Базановым для случая b/Н = 2,43
(АВ— зона высачивания, ВС— кривая депрессии).
Рис. 99.
Б. ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
§ 8. Движение грунтовых вод по наклонному водоупору. Ре-
Решение ряда задач теории движения грунтовых вод было полу-
получено Б. К. Ризенкампфом A940, 1) и Н. М. Герсевановым
A943, 1950) с помощью функциональных уравнений. Сущность
их метода состоит в следующем. Пусть комплексная перемен-
переменная z = х + iy будет выражена как функция от со = ф + *ф:
z = х + iy = F (со). Тогда z=*x— iy = F (со) (со = <р — гф), откуда
У =
(8.1)
(8.2)
§8]
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД ПО НАКЛОННОМУ ВОДОУПОРУ
151
Задание граничных условий позволяет в некоторых случаях
найти функцию ^((о). Б. К. Ризенкампф A940, 1) задавался ус-
условиями на двух линиях тока и получил решение задачи о филь-
фильтрации со свободной поверхностью по наклонному водоупору и
о фильтрации из каналов (см. § 9).
Н. М. Герсеванов A943) рассмотрел ряд задач для случая,
когда областью комплексного потенциала является прямоуголь-
прямоугольник (см. § 10 и 11).
Рассмотрим движение грунто-
грунтовых вод по наклонному водо-
водоупору. Пусть поток грунтовых вод
течет со свободной поверхностью, /- \
имея линией тока наклонную пря- / чЛ4
мую, составляющую угол а с го- хх4
ризонтальной осью х (рис. 100)
Уравнение этой прямой напишем
в виде
х sin а + у cos а = 0. (8.3)
Пусть г|) = 0 на этой прямой. На
свободной поверхности положим
•ф = Q. В уравнении (8.3) под- рис юо.
ставим вместо х и у их выра-
выражения (8.1) и (8.2) и учтем, что г|) = 0 вдоль прямой (8.3).
Получим
sin a [F (Ф) + F (Ф)] +
[F (Ф) - F (<р)] = 0,
откуда
Заменяя в последнем уравнении ф на со, получим
(8.4)
o) = F((o). (8.5)
Теперь рассмотрим условие на свободной поверхности. По-
Полагая \|) = Q, получим со = ф + iQ. Кроме того, на свободной
поверхности
k •
(8.6)
Подставляя в уравнение (8.6) выражения (8.2) и г|? = Q,
получим
(8.7)
152 ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
Положим ф — /Q = co. Тогда q> + iQ = © + 2/Q, и последнее ра-
равенство можно написать в виде
F(© + 2/Q) _ /?(©) = - -f- (© + /Q).
На основании (8.5)
F (со + 2/Q) - e2"*F (со) = - -^- + -^-. (8.8)
Это линейное уравнение в конечных разностях, решение ко-
которого мы составим из двух частей. Прежде всего найдем ча-
частное решение неоднородного уравнения (8.8) в виде линейной
функции от со:
F,(co) = Ao + B.
Подстановка этого выражения в (8.8) дает
Теперь найдем общее решение однородного уравнения
F (со + 2/Q) - e^F (со) = 0. (8.9)
Для этого заменим искомую функцию F((o) новой функцией
/(со), полагая
/?(©) = ем»/(©). (8.10)
Подставив (8.10) в (8.9), получим
еМ {»+2iQ)f (со + 2/Q) - eMw+2'af ((О) == 0.
Подберем постоянную М так, чтобы для /(со) получилось урав-
уравнение
Очевидно, за /(со) можно принять любую периодическую функ-
функцию периода 2iQ. Что касается числа М9 то оно имеет значение
М = (a + mt)/Q, где дг — любое целое число. Таким образом,
общее решение уравнения (8.8) может быть представлено в виде
а+пя __ja
z==F{(i)) = e Q u)f(@) + _?__((B + Qctga)> (8.11)
причем f (со) — произвольная периодическая функция с перио-
периодом 2/Q.
Отметим частный случай, полагая
д = 0, /(со) = const = iL
§ 91 КАНАЛЫ КРИВОЛИНЕЙНОГО ОЧЕРТАНИЯ
Тогда вместо (8.11) можно написать
153
zeia =
ze
sin а
Далее, вводя обозначение
и отделяя в (8.12) действительную часть от мнимой, найдем
=х cos a—у sin a
1 /
in a \
—
*He
+ (p+Qctg
(8.13)
На рис. 100 представлено семейство линий г|э = Q, которые
являются, при различных Q, возможными линиями свободной
поверхности. Они имеют асимптоты г\ = у cos a + x sin a = Я.
Для расхода получается выражение Q = &#sina.
Если считать угол а малым, так что sin a ^ a, tga « а, то
соответствующее семейство кривых депрессии совпадает с полу-
получающимся в гидравлической теории неравномерного движения
грунтовых вод (Dupuit 1863; Павловский 1930).
§ 9. Каналы криволинейного очертания. В уравнении (8.11)
примем a = я/2 и перепишем, по предложению Н. М. Герсева-
нова A943, 1950), это уравнение в виде
°° B/1+1) JtQ)
Аяв 2« ~х + С' (9Л>
Рис
С помощью уравнения (9.1) Н. М. Герсе-
ванов предложил рассматривать задачи о
фильтрации воды из каналов, подбирая
коэффициенты Ап так, чтобы получить за-
заданную форму поперечного сечения ка-
нала.
Однако выяснилось (Цицкишвили 1957, 1), что здесь возни-
возникает опасность получения многолистных решений, когда контур
поперечного сечения канала оказывается самопересекающимся
и, следовательно, нереальным (рис. 101). Все же некоторые кри-
криволинейные формы каналов, в том числе уже исследованные
раньше другими авторами, на этом пуги получить можно.
1. Горизонтальный канал (канал бесконечно малой
глубины). Если в (9.1) принять А = — Л_1 = Л/2, С = 0, все
остальные Ап положить равными нулю, то получим
ясо
/со
154
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ IIVL IV
Полагая здесь <р= — ky и
х = ЛсЬ
==Q, получим уравнение
nky | Q
Q" "• /г '
(9.3)
которое можно считать уравнением свободной поверхности. По-
Положив в (9.2) г|) = 0, найдем
*/ = 0, (9.4)
что может быть принято за уравнение контура канала. Постоян-
Постоянная А остается неопределенной, т. е. получаем целое семейство
свободных поверхностей (рис. 102).
Для определения А нужно задаваться
каким-нибудь условием, например за-
задать точку, через которую проходит
свободная поверхность. При А = 0
уравнение свободной поверхности бу-
будет х = Q/k = В/2, где В — ширина
канала. Расход всего канала будет
Оканала = 2Q = kB.
При А Ф 0 скорость на бесконечно-
бесконечности равна нулю, и в этом случае гово-
говорят, что имеет место фильтрация с
подпором; при А = 0 комплексная ско-
скорость всюду в потоке, в том числе и на бесконечности, равна
d<u/dz = iky т. е. v = — &, и говорят о фильтрации без подпора
(Аверьянов 1956).
2. Каналы Козени криволинейного очерта-
очертания. Их можно получить, взяв в (8.12) а= ±я/2. Для а = я/2
Рис. 102.
Я(О
Разделение действительной и мнимой частей дает
Яф Яф
(9.5)
2Q к *
Уравнение свободной поверхности получим, полагая i|)==Qh
Ф = — ky:
nky
x = He~~ + -f. (9.6)
При ф = 0 найдем линию, которая может быть принята за
контур поперечного сечения канала:
ГГ TCI]) TJ . TCI]) . i|) /Q ^V
У " COS n« i X tl SHI nn I г~ ^У. /)
§9]
КАНАЛЫ КРИВОЛИНЕЙНОГО ОЧЕРТАНИЯ
155
или, по исключении if> (для правой части),
х =
- arccos JL.
(9.8)
Эта линия — удлиненная циклоида или трохоида (рис. 103).
Для нахождения зависимости расхода Q от глубины и ши-
ширины канала рассмотрим точку х = В/2, у = 0, в которой
Ф == 0 и г|; = Q. Подстановка в (9.7) дает В/2 = Я + Q/&, от-
откуда для полного расхода канала получим
Скорость на бесконечности в этом течении равна нулю, в чем
нетрудно убедиться, дифференцируя (9.5):
dz
Hni ъ? i
dm 2Q ^ k
оо.
Таким образом, имеет место движение с подпором, как будто
на бесконечности имеется твердая стенка.
Если в (8.12) положим а = —я/2, то получим
=-^--Hie
(9.10)
или
Яф
к 2Q и к
За контур поперечного сечения канала примем ф = 0, что
дает укороченную циклоиду (рис. 104):
или
(9.11)
Полагая х = В/2, у = 0, найдем для Q
156
ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
и для полного расхода канала
О =* 20==: k (В -4- 2//). (9.12)
Уравнение свободной поверхности получается при i|) = Q и
x = f-HiW. (9.13)
Линия свободной поверхности имеет при у->— оо асимптоту
л: = Q/fe = S/2 + Я. Скорость на бесконечности здесь равна
коэффициенту фильтрации k (движение без подпора).
Рис. 106.
Если обратимся к рис. 100, то можно заметить, что пунктир-
пунктирные линии представляют возможные формы поперечных сече-
сечений каналов, если взять соответственно а = я/2 или а = —я/2.
На рис. 105 изображено по В. В. Ведерникову несколько
поперечных сечений каналов с эпюрами скоростей вдоль пери-
§ 10] ЗЕМЛЯНЫЕ ПЛОТИНЫ НА ВОДОПРОНИЦАЕМЫХ ОСНОВАНИЯХ 157
метра канала (без подпора). На рис. 106 приводятся гидроди-
гидродинамическая сетка движения и семейство изобар для канала при
В/Н = 2.
Заметим, что ветви депрессионной кривой очень быстро при-
приближаются к асимптоте: на глубине \у\ = г/2{В + 2Н) абсцисса
отличается от х^ на величину, меньшую 0,01 Н. Можно считать,
что уже на этой глубине имеется дренирующий пласт, погло-
поглощающий воду.
Криволинейные формы каналов были получены для течений
без подпора И. Козени (Kozeny 1931), затем другим путем
Н. Н. Павловским A936, 1 и 2) и В. В. Ведерниковым A939).
§ 10. Земляные плотины на водопроницаемых основаниях.
В случае горизонтального водоупора а = 0 и уравнение (8.8)
принимает вид*)
/4©) = --^ + -^-§ (ЮЛ)
а его общее решение
г = F (о) = --^- + f, (о, 2/Q), A0.2)
1де fi (со, 2iQ)— периодическая функция с периодом 2iQ.
Б. К. Ризенкампф A940, 1) рассмотрел при помощи уравне-
уравнения A0.2) случай плотины на непроницаемом основании с дре-
дренажем.
Можно высказать общие соображения о виде функции
/(со, 2iQ) для случая плотины на проницаемом основании ко-
конечной глубины (рис. 107, а) с произвольной формой откосов **).
Для таких областей движения характерно наличие скачка орди-
ординаты при х = ±оо. Поэтому, если положить
U (о, 21Q) = М In о + N In (о + кН) + /2 (о, 2/Q),
то при переходе около точки со = 0 с отрезка АВ на отрезок AD
(рис. 107,6) слагаемое Mlnco получит приращение (nf2)Mi,
что должно равняться приращению z на iyAy где уА — ордината
дна нижнего бьефа при х = —оо. Отсюда
М = — и л.
*) В § 10 коэффициент фильтрации обозначен через ус.
**) То обстоятельство, что на рис. 107 направление течения принято про-
противоположным указанному на рис. 100, не имеет принципиального значения.
При значении г|) = 0 на водоупоре теперь -ф = —Q на свободной поверхности.
158 ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [I7L IV
Точно так же найдем
где у в — ордината контура верхнего бьефа при х = -f-°°.
Функцию f2(co, 2iQ) будем считать однозначной аналитиче-
аналитической функцией. Введем другую аналитическую функцию
ю
А
)
\
н
~т
Уа
У>
л
Л ///////////////у
/
J
4
V
Jr
\
Л
\и
У////////////////////У
ч?_______ # -^
V •
\
ф~0
lii
in
—Г"
Ув
\ ?
7/////////////////////^
В
В
ип
л
Рис. 107.
Р
f(co, 2/Q), характеризующуюся тем, что f(co, 2/Q): со отлична от
нуля при со = 0. Тогда для f2 примем выражение
Ысо, 2/Q) =
,M + Blnt_W_ +
+Bne
J,
а для z
2 = -^- + Л1п/((о, 2jQ) + S!nf(«) + xW> 2/Q) +
Q J- (Ю.З)
Заметим, что для функции f, стоящей под знаком In, достаточно
иметь период AQi и удовлетворять соотношению /(со, 2Qi) =
«5= С/(со), где С — постоянная,
§ 101 ЗЕМЛЯНЫЕ ПЛОТИНЫ НА ВОДОПРОНИЦАЕМЫХ ОСНОВАНИЯХ 169
Среди функций A0.3) должны найтись такие, которые дадут
форму откосов, близкую к форме откосов действительных пло-
плотин. Но так как здесь промежуток высачивания в явной форме
не учтен, то вблизи нижнего бьефа могут получиться особенные
формы плотин, с выемкой, как изображено на рис. 107.
В. И. Меньшикова A960) рассмотрела ряд примеров, часть
которых мы разберем.
Пример 1. В нижнем бьефе есть вода (рис. 107). Выберем
функции /иг следующим образом:
f (о, 2iQ) = ish -g-, An — 09 Bn = 0, A0.4)
"' ° l ясо 2 , * я(со + хЯ) , ~ . .„ /1/Чг-\
h-щ -yBlnsh v zq—L + Ci+tC2. A0.5)
Разделение действительной и мнимой частей дает
lD + C,. A0.6,
Для выбранного расположения осей координат получаем
~ Q I 2 11 як# п .
Cl = "ST + Т Ув 1П Ch Q" ' С2 = ^ + Ул ~ Ув'
Нетрудно написать уравнения линий границ верхнего и ниж-
нижнего бьефов и свободной поверхности, полагая соответственно
Ф = —кН и ф=0 при —Q < ф < 0, г|з = —Q при —хЯ < ф < 0.
При этом, обозначая через L проекцию линии DC на ось х, на-
находим
т %Н2 . 2 . . \11 як#
1 = Q" + -^(Уа + У в) In ch -2Q-,
откуда мол<но вычислить приведенный расход Q/x, если заданы
Н, L и уА + ув.
На рис. 107 построена сетка движения для одного частного
случая (у\1Н = 1,6, ув/Н = 2,0, Q/(xH) = я/5).
Пример 2. Нулевой уровень воды в нижнем бьефе при
совпадении уровней дна верхнего и нижнего бьефов (рис. 108).
Этот случай движения будем иметь, заменив в A0.5) гипербо-
гиперболические синусы эллиптическими:
160 функция Жуковского, функциональные уравнения (гл. iv
где К — полный эллиптический интеграл первого рода при мо-
модуле k. При этом
Тогда, имея в виду формулу
1
14 '~ ksn(t, k) 9
можем объединить два члена в A0.7):
причем
Здесь для криволинейного откоса, вдоль которого <р = —х#
и —Q < ф < 0, имеем
х2Я2~ф2 2 . г, / /Сф Л1 , Q Яф .
вдоль свободной поверхности, где г|з = — Q и — х/У < ср < 0
Для проекции линии DC на ось х получается уравнение
, xtf2 . 2 . 1
На рис. 108 приведена сетка движения лля уо/Н = 3, &2 = 0,4.
При этом для расхода получается величина Q/(kH) = 0,9. Уклон
верхового откоса в точке С
dy _%Н _К'
а dx — Q ~ К '
В таблице 7 приведены результаты расчетов С}/(кН)у а и
L/# для ряда значений k2 и t/o/#» а на рис. 109 — графики зави-
зависимости Q/(kH) от L/H при различных значениях уо/Н.
Пример 3. Фильтрация из водоема (рис. ПО). Он получен
В. И. Меньшиковой с помощью уравнения
со2 2 . ,i ясо
Zy]nthly
Здесь получается почти прямолинейный откос. Прямая DA —
эквипотенциаль, ВА — твердая стенка, т. е. дно водоема непро-
непроницаемо, что ограничивает интерес задачи. На рис. НО взято
уо/Н = 2, Q/(//) 04
У//////////////////////////д
Рис. 108.
Л-
н~и
Ю 15
и
Н
Рис. 109.
Рис. ПО.
6 П. Я. Полубаринова-Кочина
162 ФУНКЦИЯ ЖУКОВСКОГО. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IV
Таблица 7
Зависимость Q/(xH) от L/H и уо/Н
кг'0
10-
10 8
1(Г
10
1(Гз
10"
10
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
Q
иЯ
0,122
0,133
0,148
0,166
0,189
0,220
0,262
0,325
0,426
0,625
0,735
0,826
0,911
1,00
1,10
1,21
1,36
1,60
а
7°
8°
9°
10°
11°
13°
15°
18°
23°
32°
36е
40°
42°
45°
47°
50°
53°
58°
{/о/Я = 0
4,63
4,18
3,74
3,30
2,86
2,42
1,98
1,54
1,17
0,80
0,68
0,61
0,65
0,50
0,45
0,41
0,37
0,31
{/о/Я = 1
11,43
10,33
9,23
8,13
7,04
5,94
4,84
3,74
2,64
1,53
1,19
0,99
0,84
0,72
0,62
0,52
0,44
0,34
t/o/Я - 2
13,26
11,43
9,60
7,77
5,94
4,11
2,27
1,70
1,37
1,13
0,94
0,78
0,64
0,51
0,38
Уо1Н « 3
13,17
10,70
8,14
5,57
3,00
2,21
1,75
1,42
1,16
0,94
0,75
0,58
0,41
{/о/Я - 4
15,93
13,19
10,34
7,04
3,73
2,72
2,14
1,72
1,38
1,10
0,86
0,65
0,45
§ И. Перемычка Н. М. Герсеванова. Решение Н. М. Герсе-
ванова задачи о перемычке — земляной плотине прямоугольного
сечения — интересно отметить потому, что ошибочное предполо-
предположение автора (крупного специали-
специалиста по механике грунтов) привело
к объяснению приближенной мате-
математической теории.
Н. М. Герсеванов думал, что дви-
движение происходит так, как указа-
указано на рис. 111 сплошной линией
АМСУ т. е. что свободная поверх-
поверхность имеет точку перегиба и входит
в нижний бьеф как раз на уровне
горизонта воды в нем. При этом
промежуток высачивания отсутст-
отсутствует и на плоскости со = ф + tip
имеем прямоугольник. Разыскивается решение в виде A0.3) при
А = В = 0. Коэффициенты Ап и Вп определяются из условий на
границах х = 0 и х = I, что дает
Рис. 111.
Z —— ~"~
_2Q
оо
I
(-1
тп
A1.1)
11)
ПЕРЕМЫЧКА Н. М. ГЕРСЕВАНОВА
163
Для расхода через перемычку при этом получается формула
Дюпюи
A1.2)
2L
Оказалось, что свободная по-
А
А. Р. Цицкишвили A957, 2) произвел расчет гидродинамиче-
гидродинамической сетки по формуле A1.1)
верхность имеет своеобраз-
своеобразный вид (см. рис. 112 и 113):
основная ее часть АВ близ-
близка к точному решению (см.
§ 10 главы VII), но есть ду-
дуга ВС, выходящая за пре-
пределы плотины. Однако если
Рис. 112.
Рис. ИЗ.
эту дугу отбросить, то остальная картина будет близка к полу-
получаемой в точном решении. Формула A1.2) является точной.
Таким образом, решение Н. М. Герсеванова можно рассматри-
рассматривать как хорошее приближенное решение (см. Герсеванов 1943,
1950),
Глава V
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
А. ФИЛЬТРАЦИЯ ИЗ КАНАЛОВ И ПРИТОК К ДРЕНАМ
§ 1. Некоторые свойства инверсии. Преобразованием обрат-
обратными радиусами-векторами или инверсией в окружности К ра-
радиуса R с центром в точке С называется преобразование, при
котором точка М, лежащая на луче СМУ переходит в точку М'
на том же луче (рис. 114), причем СМ • СМ' = R2. Координаты
точки М'(х'у у') связаны с координатами
точки М (ху у) уравнениями
, R2x
Отсюда
/ I . / л\ \Х ~т~ llf)
* +ч/ - Х2 + у; x_iy-
что можно записать, вводя комплексные
числа z = х + iy, z' = / + iy\ z = x— iy,
таким образом:
*-=•?. ал)
R2
Преобразование
Рис. 114.
2/ = ^L
z
A.2)
представляет соединение инверсии с отражением в действитель-
действительной оси плоскости z. В этом случае имеем
„/ R2x ,/ R2y
При инверсии точки, лежащие на окружности К (рис. 114),
преобразуются сами в себя. Центр окружности переходит в бес-
бесконечно удаленную точку, бесконечно удаленная точка перехо-
переходит в центр окружности. При инверсии всякая окружность или
прямая переходит в окружность или прямую.
Заметим, что мы обычно будем строить область функции
u^-iv и искать выражение для 1/ш= 1/(и — iv), т. е. пользо-
% 2] ФИЛЬТРАЦИЯ ИЗ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ 165
ваться отображением вида A.1), которое представляет чистую
инверсию области {и, v)y без отражения в оси абсцисс.
Возвратимся к рис. 114. Рассмотрим окружность К', про-
проходящую через центр С окружности. Точка С преобразуется
в бесконечно удаленную точку, точки А и В остаются неподвиж-
неподвижными. Следовательно, окружность К' переходит в прямую, про-
проходящую через точки А и В. Отсюда получается такое след-
следствие.
Пусть имеем область, ограниченную дугами окружностей
(прямые линии, которые мы можем считать окружностями
бесконечно большого радиуса, могут также входить в число гра-
границ области), причем все эти окружности или их продолжения
пересекаются в одной точке. Тогда, приняв точку пересечения
окружностей за центр инверсии С и выбрав произвольно ра-
радиус /?, применим преобразование инверсии к заданной области.
Все границы рассматриваемой области перейдут в отрезки пря-
прямых линий, и, следовательно, в результате инверсии мы получим
прямолинейный многоугольник.
Это свойство инверсии было использовано Н. Н. Павловским,
В. В. Ведерниковым, а также другими авторами для решения
различных задач по фильтрации, когда на годографе скорости
получаются линии, проходящие через одну точку.
В начале этой главы рассматриваются задачи о фильтрации
из каналов трапецеидального сечения. Целью исследования яв-
является выяснение вопроса о зависимости расхода и вида сво-
свободной поверхности от формы канала. Влияние капиллярности
грунта на фильтрацию из каналов рассмотрено на случаях ка-
канала трапецеидального сечения и широкого канала (или канала
с малым слоем воды).
В этой же главе рассмотрена задача о притоке грунтовых
вод к дренажной канаве трапецеидального сечения с малым ко-
количеством воды в ней.
Задача о несовершенной галерее в безнапорном пласте пред-
представляет плоский аналог задачи о несовершенной скважине.
При ее решении также применим метод инверсии.
Наконец, с помощью метода инверсии рассмотрена задача о
плавных контурах оснований гидротехнических сооружений.
§ 2. Фильтрация из канала трапецеидального сечения. Реше-
Решение этой задачи было дано В. В. Ведерниковым A939) с помо-
помощью применения преобразования инверсии к области комплекс-
комплексной скорости. Впоследствии Б. К. Ризенкампф A940, 1) пред-
представил это решение в виде рядов. Ю. Д. Соколов A951,2) дал
другую форму решения.
Все указанные авторы рассматривали так называемое дви-
движение без подпора, при котором скорость внизу на бесконечно-
166 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ [ГЛ. V
сти равна по величине коэффициенту фильтрации. С. Ф. Аверья-
Аверьянов A956) обратил внимание на значение фильтрации с под-
подпором, когда скорость на бесконечности принимается равной
нулю, и рассмотрел простейший случай — канал бесконечно
малой глубины. А. Р. Цицкишвили A957, 1) комбинируя ме-
методы В. В. Ведерникова и Б. К. Ризенкампфа, дал решение
задачи о фильтрации из канала трапецеидального сечения, как
с подпором, так и без подпора, которое охватывает и все ука-
указанные выше случаи. Здесь мы приводим решение А. Р. Циц-
Цицкишвили.
Введем видоизмененный комплексный потенциал Q, полагая
V), B.1)
т. е.
Ф = — -5-ф, Чг=— -^-г|), B.2)
причем Q — полный расход канала (расход через сечение
E'D'CDE—рис. 115,а). Примем вдоль свободной поверхности
EFA (которая может иметь точку перегиба F) ? = 0, вдоль АС
будет Ч? = я/2.
Обозначим через Q\ расход через отрезок DE, и пусть W = 0
в точке D. Тогда
9=-^-. B.3)
Вдоль смоченного периметра канала полагаем Ф = 0. Область
функции Q — полуполоса (рис. 115,6), конформное отображение
которой на верхнюю полуплоскость плоскости вспомогательного
комплексного переменного ? (рис. 115, в) имеет вид
? = sin2(/Q). B.4)
Далее проводится инверсия области годографа скорости
(рис. 115, г) в единичном круге с центром в начале координат
и вводится функция
w _ 1 __ dz _ n dz {0 -v
w aco Q dQ x '
Для функции W (рис. 115,5) по формуле Кристоффеля —
Шварца можно написать
w
k ) cv.+«(C_e)i-
§ 2) ФИЛЬТРАЦИЯ ИЗ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ
167
(здесь яа — угол откоса канала к горизонту). Для определения
йостоянной М заметим, что W = (—i-\-tgna)/k при ? = 0.
Рис. 115.
Интеграл B.6) в пределах @, а) выражается через эйлеровы ин-
интегралы, что дает
V
B.8)
B.9)
B.10)
Уя Г (а) [с + a (I-2a)] '
При 1 = а имеем Q = 8/ (рис. 115,6), поэтому
а = sin2 8.
Вместо с введем параметр Я, полагая
Возьмем дифференциал
dW = -
Ml (Я sine+
168 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ 1ГЛ. V
и, принимая во внимание, что согласно B.4) ? = sin2(j'Q) =
¦и — (eQ — e"nJ/4, введем еще одну переменную T = e~2Q. Тогда
получим
= -М=г Га sin0 - A~ТJ1 Ф (т) Л, B.11)
где
Функция ф(т) разлагается в ряд по степеням т:
... + а„т* + ..., B.13)
сходящийся при |т|<1. Предлагается такой способ опреде-
определения коэффициентов ап. Возьмем логарифмическую производ-
производную от ф(т):
•Ф' (т) __ 1 , 2а , 2A — g) (cos 29-т) _
<р (т) ~~ 1 + т "*" 1 — т "*" 1 — 2тcos29 + т2 "~
1 - 2 cos 29 (т - т3) - т4 '
причем
( А2= 1 +2A— cos20)a,
B.1
BЛ5)
Для определения коэффициентов аи ..., ап, ... перепишем урав-
уравнение B.14) так:
а{ + 2а2т + За3т2 + ...) [1 - 2cos2e(t - т3) - т4] =
= A + ахх + а2т2 + а3т3 + ...) (Д, + Дт + Л2т2 + т3).
Раскрывая скобки и приравнивая коэффициенты при одинако-
одинаковых степенях т, получим
а\ = А),
2а2 = Лоа! + А + 2а! cos 20,
За3 = А0а2 + Ахах + А2 + 4а2 cos 28,
4а4 = Л0а3 + ^i^2 + А2а{ + \ — 2а{ cos 20 + 6а3 cos 20,
ап+{ = Лоад + Ая/i-i + Л^-2 + (п — 2) art-3 +
+ 2 cos 20 [пап — (п — 2) ая-2].
B.16)
§ 2] ФИЛЬТРАЦИЯ ИЗ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ 169
Принимая во внимание B.15), можно последовательно опреде-
определить аь а2, ... Уравнение B.11) теперь перепишем в виде
dW=Tw
a*(xn~l -2т"+тЛ+1
Интегрирование этого уравнения дает
11dx-
А)
(,.7,
Вспоминая, что W — — (л/Q) dz/dQ и т — е~2а, произведем
интегрирование по Q и найдем г в виде ряда
9-B/i-l)Q
2. B.18)
Вдоль свободной поверхности со = — /?г/, поэтому Q = kny/Q
и из уравнений B.18) найдем
+ ° с ' ' **я\B/1-1)*
Произвольные постоянные С! и С2 определяются путем та-
таких рассуждений. В точке С (рис. 115,C) функция IF имеет
чисто мнимое значение; так как Q = ш"/2, то все члены ряда
BЛ7) имеют также мнимое значение (коэффициенты а\, а2, ...
Действительны), поэтому и С\ должно быть мнимым. Значение
170 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ [ГЛ. V
С\ = —l/k находится из условия, что правая часть уравнения
B.19) действительна на свободной поверхности, вдоль которой
и С2 должно быть действительным. Из уравнения B.18) для
точки С, где х = 0 и у = —Я, имеем Я = я*/2, все слагаемые
чисто мнимые, кроме двух последних, откуда и получаем
C Q/2
()
Полагая в уравнении B.19) х = В/2 и у = 0, найдем
З2 -*" Zj я V Bл - О2 Bл
IJ
B.20)
В средней точке канала С имеем Q —ш'/2 и у*** — Я, по-
поэтому из B.18) находим
Умножая B.21) на 2 и сложив с B.20), получим
B.22)
где \xQ определяется с помощью уравнения
J h
n 4 2B/1- IJ B/1+ IJ h 2Bai + 3J
rt-l
Перепишем выражение B.7) для М с учетом B.8) и B.9):
М = -= ^±±^ . B.24)
4п [Я + A- 2а) sin 9] Г (а) V '
При \-\-^(\ —2а)sin8 = 0 имеем М = оо, следовательно,
fio = O при *, = — (! — 2a)sin9? B.26)
ФИЛЬТРАЦИЯ ИЗ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ
171
расход Q при этом равен нулю, движения нет (вся нижняя полу-
полуплоскость заполнена жидкостью). Параметр X может изменяться
в пределах
— A — 2a)sin6<A,<oo.
Если А, = оо, то М = 0, но
lim (MX) = i— = МЬ
я-»оо уя Г (а)
и все формулы упрощаются:
Но
R Q 8MtQ
B.26)
B.27)
tt-0
Dя
„=1
an 1
2/i + D» h
J
«« 1
J
B.28)
Уравнение свободной поверхности теперь также не будет со-
содержать параметра к. Согласно B.9) при % = оо имеем с = оо,
точка перегиба F уходит на бесконечность. На годографе ско-
скорости точка F переходит в F2, верхняя часть годографа отпа-
отпадает, на бесконечности (А = F2) скорость фильтрации равна k
и подпор отсутствует.
Рассмотрим частный случай горизонтального канала (с бес-
бесконечно малым уровнем воды). При 6 = 0 для функции <р(т)
получаем
/ \ * +т
Интегрируя теперь два раза уравнение B.11) и полагая
т = е~2а, получим уравнение
$] B-29)
Принимая в нем ф = 0, ф = —ky, Q = kny/Q, найдем уравнение
свободной поверхности; оно будет иметь вид
<230»
причем
\7'2
Применение метода инверсии
[ГЛ. V
А^ Р. Цицкишвили A957, 1) провел расчеты для ряда зна-
значений К. Мы здесь приводим лишь графики, относящиеся к
случаю Я = оо.
Рис. 116.
По формулам B.28) вычислены значения |х0 в зависимости
от Q\/Q при различных а и значения Н/В в зависимости от а
при различных Q\/Q (рис.
116 и 117). По ним при за-
заданных Н/В и а можно най-
найти Qi/Q и jLi0, а следователь-
следовательно и Q/k.
Для простейшего случая
Н/В = О по уравнению
B.30) построены графики
свободной поверхности при
различных X: это поверну-
повернутые на 90° цепные линии
(рис. 102). При X = оо пра-
правая линия свободной поверх-
поверхности переходит в прямую
х = l/2Q/k, скорость на бес-
бесконечности равна k. При от-
отличном от бесконечности X
для его определения нужно
задать дополнительное условие, например, задать какую-нибудь
точку на свободной поверхности.
В. В. Ведерников A939) также решал задачу о трапецеи-
трапецеидальном канале, применяя метод инверсии к годографу скорости
Рис. И 7.
§2]
ФИЛЬТРАЦИЯ ИЗ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ
173
(случая с подпором он не рассматривал). Вычислив ряд опре-
определенных интегралов, он нашел зависимости расходов от раз-
размеров канала и построил для некоторых случаев линии свобод-
свободной поверхности.
В. В. Ведерников записывает формулу полного фильтрацион-
фильтрационного расхода канала в виде Q = k(B + ЛЯ), где А зависит от
угла р = яа и отношения В/Н. В таблице 8 представлена за-
зависимость между величинами Л, В/Н, feS/Q, kb/Q, kHJQ, Q2/Q
и р, выраженным в градусах. Буквой Q2 обозначен расход через
дно канала.
Таблица 8
Зависимость kb/Q, kB/Q, kH/Q, Q2/Qt А и В/Н от ?
для канала трапецеидального сечения
3
45°
30°
22° 30'
kb
Q
0
0,167
0,304
0,479
0,609
0,706
1
0
0,204
0,353
0,530
0,653
1
0
0,229
0,384
0,559
0,678
1
kB
Q
0,500
0,545
0,595
0,676
0,746
0,802
1
0,656
0,684
0,720
0,777
0,824
1
0,736
0,757
0,786
0,829
0,855
1
kH
Q
0,250
0,189
0,146
0,0986
0,0682
0,0480
0
0,189
0,139
0,106
0,0713
0,0494
0
0,152
0,109
0,0832
0,0569
0,0387
0
Q
0
0,333
0,500
0,667
0,770
0,839
1
0
0,333
0,500
0,667
0,770
1
0
0,333
0,500
0,667
0,770
1
A
2,00
240
2,78
3,29
3,73
4,12
1,82
2,28
2,63
3,13
3,65
1,74
2,22
2,68
8,05
3,48
в
H
№
4,08
6,86
10,9
16,7
00
3,46
4,93
3,78
10,9
16,7
00
4,82
6,92
9,45
14,8
22,3
00
Интересно вспомнить, что для криволинейных каналов, рас-
рассмотренных в главе IV, по формуле (9.12) мы имели для А
значение А = 2. Таблица 8 показывает, что для практически
интересных каналов трапецеидального сечения А меняется в
пределах от 2 до 4.
На рис. 118 дана рассчитанная В. В. Ведерниковым картина
течения из канала трапецеидального сечения для р = 45°,
В/Н = 5,16, 6/Я = 3,16: распределение скоростей вдоль пери-
периметра канала и форма свободной поверхности. Если, как в этом
174
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
примере, скорость фильтрации на бесконечности равна коэффи-
коэффициенту фильтрации, то это соответствует тому, что на боль-
большой глубине имеется дренирующий слой. Для случая конечной
Рис. 118.
глубины дренирующего слоя задача о фильтрации из трапецеи-
трапецеидального канала была решена Ю. Д. Соколовым A951,2).
§ 3. Канал трапецеидального сечения при учете капилляр-
капиллярности. Явление капиллярности играет большую роль при движе-
движении грунтовых вод со свободной поверхностью. Под действием
капиллярных сил расширяется пло-
площадь, смоченная водой, и увеличи-
увеличивается расход.
Пусть имеем канал с произволь-
произвольной формой поперечного сечения
(рис. 119). Пунктирная линия озна-
означает свободную поверхность при
отсутствии капиллярности, сплош-
сплошная— при наличии ее. В последнем
случае принимается, что на де-
прессионной кривой давление по-
постоянно и равно атмосферному, уменьшенному на величину yhK
(где hK — высота капиллярного поднятия, у— объемный вес
жидкости), т. е. р = р& — уЬк на свободной поверхности (Жуков-
(Жуковский 1923; Ведерников 1940):
Откосы канала АВ и А'ВГ (рис. 119) В. В. Ведерников, а
вместе с ним и другие авторы принимают за твердые стенки, на
которых функция тока имеет поеюянное значение. При этом
Рис. 119.
§3]
КАНАЛ ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ
175
условии применимы изложенные методы решения задач по тео-
теории фильтрации.
В. В. Ведерников A940) дал общие формулы для фильтра-
фильтрации из канала трапецеидального сечения (рис. 120) при учете
капиллярности.
У ? Г \ff F Е и с а
Формула для зависимости от ? величины, обратной комплекс-
комплексной скорости w = и — iv, имеет вид
dz _ 1
da* w
+ ¦
C.1)
где б2 = /3//4, а величины J\, /2, /3 и /4 имеют значения
со
г _ Г г] (б2 + Л2) dr\
1 "J (P2 + Л2I1 Vl — ti2(y2 + T]2)I+a '
о
2 *"" J (ft2 __ Г
Vl - S2 (y2 - ?2I+a '
1
J (?2-
176 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ [ГЛ. V
Для комплексного потенциала получаем
© = ф + и|) = -iL arcsin ?, C.2)
где Q —расход канала. Зависимость г от ^ дается формулой
—fi=. C.3)
Введем еще интегралы
. * С (б2 - V) dj
arcsin c гв'с»I-^'?»>¦+» Vn=Tr •
о
1
arcsin
и
о
/ = \ (arcb Р — arch ?) (g2 — б2) ? ^g
7~J «2-p2I-a(Y2-C2)I+aVcr::T'
Параметры Р и y определятся следующими уравнениями:
В /б + /в cos яа
6 /б
В о /б + /в cos яа
C.4)
Здесь В — ширина зеркала воды в канале, Ь — ширина канала
по дну, Н — глубина воды в канале.
Расход на единицу длины канала определяется по формуле
Q = k(B + AH)f C.6)
где
А п (Л + /2) — 2 G5 + /8 cos яа)
Л== /б81пяа •
Можно также определить расход по формуле Q = kNB, где
Для высоты Яо (см. рис. 120, а) имеем
Здесь hH — высота капиллярного поднятия для данного грунта,
КАНАЛ С МАЛЫМ УРОВНЕМ ВОДЫ
177
В. В. Ведерниковым произведены вычисления для одиночного
откоса (а = lU, таблица 9) и для вертикальной щели (а= 7з
и В = 0, таблица 10).
Таблица 9
Результаты расчета для одиночного откоса (а = !/4)
в
я
2,0
4,1
8,3
22,8
2,0
3,8
К
н
7,3
12,6
22,0
51,2
3,0
4,8
А
16,0
27,1
46,8
106,8
8,8
13,9
Яо
"к
0,246
0,240
0,233
0,225
0,285
0,273
В
Я
7,2
19,7
2,0
3,4
5,8
13,2
К
н
8,0
18,6
0,97
1,46
2,2
4,1
А
22,9
48,2
4,7
6,6
9,5
16,5
_Яо_
"к
0,254
0,248
0,320
0,315
0,306
0,287
Таблица 10
Результаты расчета для вертикальной щели (а = V2)
"к
я
0
0,75
1,9
А
2,8
3,7
6,8
Яо
К
1,0
0,58
0,55
К
н
3,2
27,4
А
9,6
43,7
лк
0,48
0,33
Отметим, что высота поднятия воды по откосам получается
меньшей, чем высота статического капиллярного поднятия.
В дополнение к изложенному рассмотрим в следующем па-
параграфе еще один, более простой случай фильтрации из канала,
который можно исследовать, следуя Б. К. Ризенкампфу A940, 1).
§ 4. Канал с малым уровнем воды при наличии капилляр-
капиллярности. Если уровень воды в канале близок к нулю, то расход
Qo на фильтрацию из канала в случае отсутствия капиллярного
поднятия близок к величине
Qo = kb (b — ширина канала).
D.1)
Предположим, что имеем фильтрацию из канала D'D в
грунт, капиллярная высота которого есть hK (рис. 121,а). Тогда
будет иметь место растекание в стороны. При этом горизон-
горизонтальные отрезки CD, CD' принимаются за линии тока, и годо-
годограф скорости будет иметь вид рис. 121,6, где изображена
половина области годографа, соответствующая правой половине
178
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
!гл. v
области движения жидкости. В точке D скорость равна беско-
бесконечности, в точке С — нулю, на бесконечности в А она равна
коэффициенту фильтрации k.
Область комплексного потенциала представлена на рис. 121,#.
Приняв значение ф = 0 вдоль OD, гр = 0 вдоль DCA, получим
в точке С для ф значение ф = khK. Вдоль оси симметрии ОА
примем г|) = —Q/2, где Q — расход
всего канала.
Отобразим область комплексного
потенциала на полуплоскость ?
(рис. 121, г):
© = --5?-arccos(l-2?)f
«sirr
2я
яю/
"О""
:-stf-S. D.2)
С
А
0\
U
А.
Полагая ? = — а2 и со = khK9 получим
D.3)
Q
б)
О А
Обращаясь к годографу скорости,
произведем инверсию области ско-
скорости в круге радиуса 1 с центром
в начале координат. Получим полу-
полуполосу. Ее отображение на полу-
полуплоскость ? • представляется с по-
помощью интеграла
1 dz _ .
и — iv d®
Рис. 121.
Условия
0, u — iv =
dz 2i ,
ж = --?гагс^-„
Обозначим для краткости
пш г.
2М .
¦ — arctg
а
где М и N — постоянные,
оо и ?==оо, и = — k дают
" 2/ , / 1 . яа
- = ~^rarct&Tsln-7
—
Q -"¦ -- Q
и рассмотрим тригонометрический ряд
dz
A@
2/ .„.!„ sinQ li_V -igfl-iin s\nBn — 1)Q
CL Z\,k / ' 2fl — 1
(a = sh a),
D.4)
D.5)
D.6)
D.7)
§ 4] КАНАЛ С МАЛЫМ УРОВНЕМ ВОДЫ 179
который получается из известного ряда
ЯГСЫ 2Р sin * — 9 V л2«-1 sinBtt-l)*.
1 — р ^^ Z/Z — 1
я=1
Нетрудно видеть, что ряд D.7) сходится в полосе — khK < qp <
< + khK. Интегрируя его почленно и учитывая, что г = 0 при
© = — Q//2, найдем z:
*— kn2 Lu* B/г-1J . \t.°)
я-1
Полагая в D.8) ? = 0 и ? = — а2, получим соответственно
со = О, Q = 0 и со = khK, Q = m. Поэтому найдем для ширины
канала
()
я-1
и для ширины смоченной поверху части грунта
4Q
я-1
I е
^ V4 1 я2
откуда следует равенство I если учесть, что > <2п—\J sss"8"
V я-1
+ |И2а). D.11)
По заданной ширине канала ft и величине Ак из D.9) и
D.10), или D.11), найдем ширину В и расход Q. Так как на
бесконечности скорость равна коэффициенту фильтрации, то
ширина потока просачивающейся воды на бесконечности
Д = Т D12)
Ряды D.9) и D.10) хорошо сходятся для больших значений
а, но медленно сходятся для малых а. Поэтому преобразуем
D.9), воспользовавшись представлением
L Bд
я-1
|30 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
и разложениями в ряды
1ГЛ, V
где
-gn i зл '
Окончательно для В найдем
4«[Jl2JLflni-l>la-^4.—-^-+ 1 D13)
^[Т+Г! Т 36^7200 635040 ^"-J* K '
36
7200 635040
г>
На рис. 122 построены графики зависимостей Q/Qo, Boo/B,
BJb от hjb. Здесь Qo = &&—- расход из канала при hK = 0.
Рассмотрение графиков показывает, что влияние капилляр-
капиллярности на фильтрацию является значительным. При этом роль
капиллярности возрастает с
возрастанием отношения hjb.
В действительных условиях
статическое капиллярное под-
поднятие часто бывает порядка
нескольких десятков сантимет-
сантиметров, а иногда достигает двух-
трех метров. Учитывая непол-
неполное- насыщение капиллярной
зоны грунта водой, при рас-
рассмотрении движения грунтовых
вод нужно брать в расчет не
статическое поднятие, а лишь
его некоторую долю. Если
возьмем hK = 7зЛКс> где hK0 —
0 0,5 1,0 высота статического поднятия,
it то получим величину, могу-
могущую достигать значения в I м
Рис. 122. и более. При ширине канала
в 10 м будем иметь hjb =
= 0,1; как видно из рис. 122, расход увеличивается на 40%, а
разность В — b будет равна 0,9 м. При меньшей ширине канала
изменения расхода и величины растекания поверху будут еще
значительнее.
Отметим, что зависимость В/b от hjb получается близкой
к линейной. Для 0 <. hH< \,\Ь можно принять В = b + 0,8Лк.
Н. Н. Веригин A949,3) рассмотрел вопрос об учете капил-
капиллярности при фильтрации из канала почти полукруглого сече-
сечения; в нем растекание в стороны будет еще сильнее, чем в слу-
/
/
/
/
/
b
Дренажная канава трапецеидального сечения
181
чае широкого канала. Эта задача применима к фильтрации из
оросителя ирригационной системы (ширина такого оросителя
бывает порядка 20—30 см).
Отметим, что почва со струк-
структурным грунтом обладает сла-
слабой капиллярностью.
§ 5. Приток грунтовых вод
к дренажной канаве трапеце-
трапецеидального сечения. Решение
этой задачи было дано В. В.
Ведерниковым A948). Его ис-
исследование дополнено Ю. Д.
Соколовым A951,1).
Канава изображена на рис.
123, а. Высотой воды в канаве
пренебрегают, так как при на-
наличии воды решение задачи
сильно усложняется.
Вдоль всего контура области
движения мы имеем здесь
условие ф + ky = 0; поэтому
удобно использовать функцию
Жуковского
Э в= со — ikz ss
\О U
Годограф скорости (рис.
123,6) имеет границами дугу
окружности и прямые, причем
все они пересекаются в одной
точке F, где и = 0, v = —k.
Инверсия в окружности с цент-
центром в точке F дает много-
многоугольник (рис. 123, в), который
уже нетрудно отобразить на
полуплоскость ? (рис. 123,г). Приведем окончательные резуль-
результаты:
8)
Рис. 123.
E.1)
г= —
ЯГ(У
\1-U
kB + Q
2{vQ + k)
С E.2)
182
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
где Vo — значение скорости фильтрации в точке О. Это уравне-
уравнение было дано В. В. Ведерниковым, который более детально ис-
исследовал случай а = !/г» т- е- случай вертикальных откосов
(В = Ь). Здесь все формулы значительно упрощаются, так как
все интегралы выражаются в явном виде через элементарные
функции. Для полного расхода Q и ординаты Н получены фор-
формулы
kbX \
'» I
E.3)
где
E.4)
Задавая различные значения к между нулем и единицей, можно
вычислить соответствующие значения Ql{kb)y Hjb и vo/k.
Отметим, что при а= 1, когда откосы становятся горизон-
горизонтальными, получаем дрену Жуковского. Другой частный случай,
когда вся канава сводится к
вертикальной щели, пред-
представлен на рис. 124 (Ведер-
(Ведерников 1948), где дана гидро-
гидродинамическая сетка движе-
движения и пунктиром указаны
изобары (Q — полный рас-
расход щелевой канавы).
§ 6. Несовершенная гале-
галерея в безнапорном пласте.
Вертикальная скважина для
откачки воды обычно со-
состоит из металлической тру-
трубы, в нижней части которой
имеется фильтр, т. е. перфо-
перфорированный участок — на
нем пробиты круглые или
щелевидные отверстия, че-
через которые вода из пласта
входит в трубу. Если бы
труба была перфорирована по всей длине (или если бы скважи-
скважина вовсе не была обсажена трубой), то можно было бы назвать
эту скважину совершенной и для вычисления ее дебита в безна-
безнапорном движении служила бы формула Дюпюи —Чарного
(см. § 9 главы VII).
Но обычно фильтр занимает лишь часть трубы, поэтому
промежуток высачивания отсутствует и верхняя часть трубы
Рис. 124.
НЕСОВЕРШЕННАЯ ГАЛЕРЕЯ В БЕЗНАПОРНОМ ПЛАСТЕ
183
непроницаема. Решение такой задачи в точной постановке
представляет большие трудности. П. Я. Полубаринова-Кочина,
В. А. Постнов и В. Н. Эмих A967) рассмотрели плоский аналог
этой задачи, что может дать некоторое представление о возмож-
возможной зависимости фильтрационных характеристик от степени не-
несовершенства скважины.
шшжж
8)
Область фильтрации представлена на рис. 125, а. Ограни-
Ограничимся рассмотрением случая, когда водоприемная часть галереи
ВС примыкает к непроницаемой горизонтальной подошве пла-
пласта. Ордината у свободной поверхности, возрастая по мере уда-
удаления от галереи, делается неограниченной. Действительно, в
противном случае мы имели бы у dy/dx-+0 при я—>—оо и ра-
расход потока был бы неограниченно убывающим при х-+—оо,
что невозможно при стационарном режиме. Мы будем прини-
принимать за левую границу потока одну из эквипотенциалей А{А2,
получаемых из решения.
Произведем конформное отображение области комплексного
потенциала со (рис. 125,6) и области dz/da>— инверсии годо*
184 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ [ТЛ. V
графа скорости (рис. 125, в, г) на верхнюю полуплоскость вспо-
вспомогательной комплексной переменной ? (рис. 125, д). По фор-
формуле Кристоффеля — Шварца найдем
со = _ i? in (VC + УГ11^ ) - kH2 + *Q, F.1)
-,l. F.2)
с/со fell I Va-1 /a-lVs-aJ *
Здесь & — коэффициент фильтрации пласта, Н2 — уровень воды
в галерее, Q — расход потока, подлежащий определению, а и
Р — параметры конформного отображения.
Полагая в F.1) ? = а, со = —kH0 + iQ (Яо — неизвестное
значение ординаты свободной поверхности в точке D), получим
соотношение
Но = Я2 + || In (Va + л/^=П). F.3)
Дифференцируя далее F.1) по ? и перемножая получаемое
выражение с равенством F.2), имеем
dz = Q Г1п УС^^Ч-Уе — 1 1 .P-q 1 I ,
d? Ь;2 L Va-1 VCE-D о-1 Vt(C-a) J
+ -^- . ' F.4)
Допустим, что на некотором расстоянии L от галереи най-
найдена путем замера ордината Н свободной поверхности. Если
обозначить через у соответствующее значение параметра ? при
2 = —L + Ш, то, беря интеграл от F.4), получим
- a + Vg - 1 \ dl ,
Va-1 ) VCEO
+Min^v^vy - jj + f^g-intve+ye-i )+h2j
(M = 2|^y-) F.5)
и затем найдем
НЕСОВЕРШЕННАЯ ГАЛЕРЕЯ В БЕЗНАПОРНОМ ПЛАСТЕ 185
Далее, рассмотрев участки ВС и CD, найдем из F.5)
Н2 _ я, = -^ \М arccos -^ - \
kn2 I Va J
arcsin
o-l Vt
(t-l) J
F.7)
rr 2Q ., .
1 ^2 L
где
51П ~t=- + \ In I , 2_ 1 te r I ,
Va J V. Va-1 / VC(l-t) J
F.8)
Наибольший интерес представляют зависимости величин Q
и Яо от параметров Я2 и Н{ (отношение последних характери-
характеризует степень заглубления экрана). На рис. 126 и 127 представ-
представлены зависимости Qo = 2Q/(nkH) и Но/Н от HJH при
№
0,05
^,/75-
^
0,2
—
\
75
Hz/H-0,9
о,г
о,$
Рис. 126.
Рис. 127.
различных значениях Н2/Н и L/Я = 5. Проведенная на рис. 126
пунктиром дуга параболы представляет собой зависимость, со-
соответствующую формуле Дюпюи
H2-H]
2Z
F.9)
186
Применение метода инверсии
1ГЛ. V
Как видно из графиков, дебит несовершенной галереи зависит
от величины понижения в большей мере, чем от степени несо-
несовершенства.
-1,582-
Рис. 128.
На рис. 128 приведены кривые свободной поверхности при
L/# = 2,5 (для верхней кривой HJH = 0,01, для нижней
#/Я 04)
Б. ФЛЮТБЕТ С УЧАСТКАМИ ПОСТОЯННОЙ СКОРОСТИ
§ 7. Заглубленный флютбет со сглаженными углами. На
рис. 20 (стр. 49) приведено типовое очертание подземного кон-
контура плотины.
Пользуясь формулой для скорости фильтрации V = kJy где
/ — градиент напора, можно сделать грубую оценку средней
скорости фильтрации, если принять среднее значение / равным
просто отношению действующего напора Н ко всей длине пути
фильтрации, т. е. к длине L подземного контура:
V ср = kj Ср ==: к —J- ¦
Из наблюдений установлено, что размываемость грунта и
его деформации зависят не от скоростей, но от градиентов на-
напора, причем критический градиент, т. е. такой, при котором на-
начинается опасная для размыва деформация грунта, близок к
единице. Исходя из этого, можно было бы принять длину кон-
контура, скажем, в полтора раза большей Я, тогда УСр не будет
превышать критического значения скорости. Однако в потоке
возможны местные скорости, значительно превышающие сред-
средние. Так, на концах плоского флютбета, на концах шпунта, в
вершинах заглубленного флютбета и т. п. теоретически эти ско-
скорости получаются бесконечно большими, какова бы ни была
длина флютбета или шпунта. На самом деле мы, конечно, не
будем иметь бесконечных скоростей, но каковы эти скорости —
на этот вопрос обычно применяемая теория не дает ответа.
А. П. Вощинин A950) поставил задачу об идеальном под-
подземном контуре сооружения, т. е. таком, во всех точках которого
§7]
ЗАГЛУБЛЕННЫЙ ФЛЮТБЕТ СО СГЛАЖЕННЫМИ УГЛАМИ
187
скорость имеет одно и то же значение. Для грунта бесконечной
глубины, граничащего с верхним и нижним бьефами по горизон-
Рис. 129,
Е
А
В-
Bf
Рис. 130.
тальной прямой, идеальным контуром будет полуокружность.
Однако полукруглый контур не-
неприемлем из практических сооб-
соображений.
Рассмотрим более общую за-
задачу. Пусть контур основания
F А 0 Bj ty \ С Сг Вх1 Л Е F
гидротехнического сооружения (рис. 129) состоит из среднего
горизонтального отрезка СХСС2, примыкающих к нему дуг кри-
кривых В\С\ и C2Di с постоянной величиной скорости обтекания
|^|== w0 и вертикальных отрезков ВВ{ и DD
*) Частные случаи этой задачи были рассмотрены ранее (И. Н. Кочина
и Полубаринова-Кочина 1952; Полубаринова-Кочина 1952, 1), причем в их
решение вкралась ошибка, которая будет нами отмечена ниже (см. § 9).
188 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ 1ГЛ. V
Годограф скорости представлен на рис. 130, на рис. 131, а
дан контур соответствующей области функции w2y на рис. 131,6
изображена область инверсии функции w2 -\-wl в единичной
окружности L с центром в точке (DbSi), или, иначе, область
функции U — 1 j(w2 + wQ.
При конформном отображении последней области на ниж-
нижнюю полуплоскость вспомогательного переменного ? (рис. 132, а)
имеем *)
причем постоянные Mt n N определяются из условий да = w0
при ? = а и oj = 0 при ? = 1/fe. Получаем
/ iVi-fe^ A/g2-«2 ^
Пооле ряда преобразований найдем
Начинаем с рассмотрения участка контура С<?)\. В точке С<±
имеем ? = а, ю = Юо, в точке Di ^=р и ш = —ш0. Для пере-
перехода на отрезок СС2 делаем обход около точки С2 по часовой
стрелке на угол я, т. е. заменяем -y/tf — a2 на —-/Уа2~--?2- По-
Получим
В частности, при ? = 0, т. е. в точке С, имеем
v ^. G.4)
V р — сг
Для того чтобы перейти на линию FE, делаем два обхода,
около точек g = ft и g= 1/fe. Тогда Ур2 — ^2 перейдем в / У^2 — р2,
У1 — &2?2 в i^k%2— 1 и для до получим
w - Н ^ГГ?5Г ^^^^ - Vrr^ V^^ G.6)
Vp'a2 v^2e2 i
*) Через k здесь и в последующих параграфах главы V обозначен пара-
параметр, являющийся модулем эллиптических интегралов (см. ниже).
i 7] ЗАГЛУБЛЕННЫЙ ФЛЮТББТ СО СГЛАЖЕННЫМИ УГЛАМИ
В точке F при ? = оо
189
G.6)
# V р — о
(при этом ^F < wc).
Для потенциала скорости со имеем (см., например, § 3 гла
вы III) согласно рис. 132,6
xff f
2л J
G.7)
Так как w = da/dz = ((((&№?): (dz/dt), то для d^/d^, после
ряда преобразований, из G.2) и G.7) получаем
-k2?)
откуда
%H
2Kw0 Vp2 — a2
Введем обозначение
- a2
G.10)
Полагая в G.9) верхний предел интегралов ? = р и принимая
во внимание, что при этом г = / — rfi/ (рис. 129), найдем
- /, - a vr^
После перехода на отрезок
? а=з 1, найдем
, имея в виду, что z = / при
190 ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
а с учетом второй из формул G.11)
МЗ)
Теперь в выражении для z G.9), для перехода на линию DE,
обойдем точку ? = 1 по полуокружности в положительном на-
направлении. Тогда Vl—?2 перейдет в /д/?2—1 и, учитывая
равенство для d\ G.12), можно написать
l
7.U)
Под знаком интегралов в G.14) выделим особенность в точке
?=l/fe. Для этого заменим соответственно множители при
1: A— k%2) на
-а2 , /1-
2-l "" v l-
Тогда G.14) можно будет переписать так:
_ - У" 2 Vl — fe2a2 Vl-fe2p2 f d
Z — A\ F J 1 -
L 1
Здесь второе и третье слагаемые уже не содержат особенности,
а от первого члена получаем
Л i о-о я-о-1 A 4- Ш A — k)
<* — л (\ /?2r*2W1 h^Pr) Ш— ¦—SJL-1 L
* ЬЬ' V V1 Л u J \1 * г / П ЪТ\ 1\ Л- Ь\
+
§ 1) ЗАГУБЛЕННЫЙ ФЛЮТБЕТ СО СГЛАЖЕННЫМИ УГЛАМИ 191
Обход точки ? = l/k в положительном направлении дает для
In A—fe?) приращение ш, а для z приращение —П; поэтому,
сокращая на —i, найдем
Tl G.16)
Для А у нас есть выражение G.10), поэтому G.16) дает
т %кН /A -k2a2){\ -k2§2)
1 ^ 2Kw0k'k Л/ Р2 - a2
откуда получаем для напорного градиента
, _ ^о __ пН I (\-kW)(\^W)
а также
Т Ь'Ь
А , G.18)
я V(l ^a2) (I ^2p2)
Теперь нам остается найти формулы для 1\ и / в отдельности.
Для этого обойдем точку ? = а в отрицательном направлении
и заменим во втором члене G.9) д/?2—-а2 на — / л/а2 — ?2. По-
Получим
а
Так как z = -—di при ? = 0, то отсюда найдем
а
+ Vi-*2P2W^t#-7t?WI. G-19)
а из G.11)
lv)- G-20)
192 Применение метода инверсии Сгл, v
Отметим, что расход Q, на основании G.7), получается, как
мы уже не раз имели, равным
G.21)
Перейдем теперь к частным случаям.
§ 8. Флютбет без вертикальных стенок. Рассмотрим флютбет,
в котором вертикальные отрезки ВВ\ и D\D отсутствуют. Для
этого достаточно положить во всех полученных в § 7 формулах
р = 1. Из G.2) будем иметь
(8.1)
Скорость в точке С согласно G.4)
™'(8.2)
(8.з,
Скорость в точке F согласно G.6)
Зависимость г от ? получим на основании G.9), причем пер-
первый интеграл здесь представляется в конечном виде, а со-
согласно G.16) и G.18)
А = кН — — k (8 4)
2Ka'wQ я Vl- k2a2 '
Для напорного градиента /0 на основании G.17) напишем
Jn» ИЛИ
0 х 2KTka' Г/о
Окончательно для z найдем
Я __ 2Ш ,« ,
ИЛИ —- / =г . \О.О
г—Al 2k ln
$91
КОНТУР ПОСТОЯННОЙ СКОРОСТИ
193
или, подставляя значение А из (8.4),
(8.6)
Отделяя здесь действительную часть от мнимой и полагая
? = ?, напишем уравнения криволинейной части контура C2DX
(рис. 129 при DX = D);
_J[_I (I + kl) A — ka)
X 2jt A — kl) i
Tk'k Г
' ~ n Vl —k2a2 J
42-a2 dt
— d.
(8.7)
Полагая |=1, найдем
/ — /. =-^7— In
Tk'k
(8.8)
- - я vr^^ J v i — e2 i — п* •
Наконец, для /! и / согласно G.19) и G.20) получим
a
/ Т 1- l+ka i Г ^^ f / a2 -- ?2 ^i
/i =— In / \ Л/ E
2я l~^a я Vl — ^2a2 J V 1 — V- i_^
я VT=
(8.9)
(8.10)
Расход Q по-прежнему определяется формулой G.21).
§ 9. Контур постоянной скорости. Теперь, для того чтобы по-
получить случай контура постоянной скорости, остается в получен-
полученных формулах положить a = 0.
Для комплексной скорости из (8.1) получим
(9.1)
Скорость в точке С, теперь совпадающей с С| и С2, равна
в точке F водоупора
7 П. Я. Полубаринова-Кочнна
194
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
Положим в уравнениях (8.7) а = 0. Во втором из этих урав-
уравнений произведем интегрирование, принимая во внимание, что
j Vi — c2ci —
Получим уравнения контура постоянной скорости
т
y=-L [arctg
¦arctgy]-d.
Так как при ?=1 имеем * = / и ^/ = 0, то
Т k Т
= — arctg -jT- = — arcsin
Отсюда для k имеем два выражения:
k = th -jr- == SHI -y- .
Уравнения контура BCD окончательно напишем так:
2я
(9.3)
(9.4)
(9.5)
(9.6)
Напишем еще на основании формулы (8.5) выражение для
HI (Г/о):
-iL=|/Cft. (9.7)
Давая k ряд значений от k = О до k = 1, из (9.4) найдем,
что (ЦТ изменяется от 0 до Г/2. При k = 1 получим предельный
случай — горизонтальную прямую*)
71 1 1 + 5 Т /п
2я 1 — g 2
В таблице 11 приведена зависимость величин //Г, H/(TJ0) и
Q/(kH) от d/Г или fe.
Та бли ца 11
Зависимость ЦТ и H/(TJ0) от J/T
d/T
k
ЦТ
Я/(Г/0)
QI(*H)
0,1
0,309
0,102
0,317
0,808
0,2
0,588
0,214
0,623
0,578
0,3
0,809
0,359
1,04
0,433
0,4
0,951
0,586
1,57
0,309
0,45
0,988
0,812
2,05
0,244
0,48
0,998
1,12
2,67
0,186
*) В указанных на стр. 187 статье и книге во всех формулах вместо Г
ошибочно фигурирует величина 2Т. В качестве предельной линии там оши-
ошибочно указана прямая у = — Т.
§9]
КОНТУР ПОСТОЯННОЙ СКОРОСТИ
195
На рис. 133 построено семейство контуров флютбета постоян-
постоянной скорости, на рис. 134 даны кривые зависимости d/T G),
QI(hH) B) и Я/(По) C) от ЦТ.
х;
i_
1
т
1
\
и
У Т
TJo
^ ь
\
157
05 "
—п.
t
Н
J
у
J
.. , d
'—Т"
1
У
ом
J"
- т
Рис. 133.
Плоский (незаглубленный) флютбет. Для конт-
контроля рассмотрим другой частный случай: а=1, 0=1. Здесь
при а->1 имеем ш0->оо, поэтому
удобнее исходить из выражения
G.3) для wy в котором мы сначала
положим р = 1, а для w0 исполь-
используем уравнение (8.5):
w = •
2KTka'
¦X
X
Для перехода к пределу при а -
перепишем это выражение так:
2KTk
. \/
ч/ У 1 — к L,
Vl - k2a2 Vl -V 4- k' л/aF^l
Теперь видно, что при а->1
клН
w =
4KTk
(9.8)
Рис. 134.
Как раз такое выражение мы имели в § 7 главы III (формула
G.9)) для плоского флютбета в слое конечной глубины; там же
7*
196
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
для полуширины флютбета / была получена формула (см.
G.2))
1 = ^^Т^7- (9.9)
Сравнение этого выражения с выражением (9.4) для флютбета
постоянной скорости показывает, что при одном и том же k
такой же расход Q будет иметь место для плоского флютбета
вдвое большей ширины.
§ 10. «Обтекаемые» флютбет и шпунт в грунте бесконечной
глубины. Случай грунта бесконечной глубины получим, если во
всех формулах § 7 положим k = 0. Так, из G.2) будем иметь
У р2 - а2
из G.9), принимая во внимание, что /С@) = я/2,
(ЮЛ)
JlWo
A0.2)
Уравнение криволинейной части контура C2D{ (рис. 129) полу-
получим, полагая ? = ? и разделяя в A0.2) действительные и мни-
мнимые части:
^f dl+lu
A0.3)
Выражение G.10) для А дает
А = -
Н
— а2
—а2
для вертикальных размеров dy d\ из G.12) и G.13) получаем
§ 101 «ОБТЕКАЕМЫЕ» ФЛЮТБЕТ И ШПУНТ 197
Длины 1{ и / получим из G.19) и G.20):
,а а .
/l = А(\ Vr=f di+\ Vt^f d4'
^o о '
Расход Q = оо.
Рассмотрим частные случаи.
Случай 1. Вертикальные отрезки ВВ\ и D{D отсутствуют.
Здесь Р=1, поэтому уравнения криволинейной части контура
A0.3) теперь имеют вид
/То Г"Т~
¦dt, — d @<g<l), A0.8)
Н
Из этих уравнений получаем, полагая ?=1, * = / и у = 0:
Уравнения A0.8) можно переписать, использовав A0.9), так:
1
A0.10)
Из A0.6) и A0.7) при р=1 найдем
'
A0.11)
Интеграл, входящий в выражения для / и 1и приведем к кано-
каноническому виду, полагая ? = a/ = asinq):
a 1
WT^^ = a2WT^W dt = E(a)-a'2K{a)
о о
(a'2=l-a2), A0.12)
198
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
где ?(а) и /С (а) — полные эллиптические интегралы. Теперь
A0.11) можно переписать так:
/ = А [1 + Е(а) - а'2К (а)], /, = А [а + Е(а) - Л (а)]. A0.13)
Интеграл, входящий в A0.10), преобразуем подстановкой
~?2 =777-cos ф или ? =
Будем иметь
=? (ф> a°
I 0
A0.15)
где ?(qp, fe) и F(yyk)—эллиптические интегралы второго и пер-
первого рода. Поэтому уравнения A0.10) для криволинейной части
контура перепишутся так:
U = л(лЛ - a/2sin29 - a), I
у = Л[?(Ф, aO-a2f(9, a0]. J
х - U =
Можно определить А и a no двум заданным величинам, напри-
например / и dy в то время как 1\ определится из A0.9). Но мы в двух
о noi ощ 0,03
0,01
од
0,03
0,04
0f05
0,08
0,07
Рис. 135.
0,05
~* И
\ н
¦77=5,4
Н ч /
/
/
А
'/
II
1
л
/\
л
V
/
н
Рис. 136.
примерах зададимся значениями /о и а, а по ним вычислим
IIН, li/H и djH. Положим /0 = 1, a = cos 10° и cos 15°. Тогда
соответственно а' = sin 10° = 0,174 и sin 15° = 0,259, А/Н =
= 1,84 и 1,24. Затем по формулам A0.9) и A0.11) найдем
(/ — l\)/H, djH и IJH и по уравнениям A0.16) вычислим коор-
Ю]
«ОБТЕКАЕМЫЕ» ФЛЮТБЕТ И ШПУНТ
199
динаты точек закругленного конца флютбета. Результаты ра-
расчета представлены на рис. 135; полученные кривые близки к
четвертям эллипсов с полуосями / —1\ и d, изображенным на
рисунке пунктиром. На рис. 136 построены кривые зависимостей
/о (/-/,)/Я и/od/Я от Я/(Л/0).
Случай 2. Горизонтальный отрезок С1С2 отсутствует. При
этом в уравнениях A0.1) и A0.2) а = 0. Этот случай соответ-
соответствует «обтекаемому» шпунту или зубу, имеющему некоторую
толщину 21 и длину d\y с насадкой внизу в виде
контура постоянной скорости (рис. 137). ^
Уравнение A0.1) при а = 0 примет вид
уравнение A0.2) дает
A0.17)
-di, A0.18)
Л
- - 1 jj>
= -ттг. (Ю.19) -J
Рис. 137.
Здесь d — общая длина шпунта, вместе с насадкой.
Уравнения A0.3) криволинейной части перейдут в такие:
I
A0.20)
или, после подстановки ? = p/ =
. A0.21)
При ^ = Р, т. е. ф = я/2, имеем х = /, y = — du поэтому
1 = В[Еф) - р/2/С(Р)], d - dx =5A - Р0. A0.22)
Для нахождения d перейдем на правую вертикальную гра-
ницу шпунта, обойдя на угол я точку ? = Р- При этом VP2 ~" S2
перейдет в / д/^2 — Р2 и A0.18) даст
2 =
A0.23)
200
ПРИМЕНЕНИЕ МЕТОДА ИНВЕРСИИ
[ГЛ. V
Наконец, полагая ?=1 и <г = /, найдем
d = В
- В
A0.24)
Найдем еще выражение выходной скорости или выходного
градиента /i = V\/k, i. е. скорости около шпунта на выходе в
щ
A)
0,75
0,50
0,25
/
/
X
<
\
\
ол
03
0J
2
Рис. 138.
у//////////////////////////////////////////////.
Ю
Рис. 139.
нижний бьеф (в точке D рис. 129). Для этого в A0.17) заменим
V — S2 на ^ VS2 — Р2 и положим ?=1:
^1 = -Шо(Р/-1) = шоA~р/), /i=/o(l-P'). (Ю.25)
По полученным формулам проведены расчеты, результаты
которых представлены на рис. 138 в виде кривых зависимостей
djd {1) и //о/Я B) от H/(Jod).
§ Ю] «ОБТЕКАЕМЫЕ» ФЛЮТБЕТ И ШПУНТ 201
Задачу можно обобщить, рассматривая годограф скорости,
изображенный на рис. 139, а Это двулистная область, состоя-
состоящая из дуг окружностей заданных радиусов и прямолинейных
разрезов. Область движения изображена на рис. 139,6. Для
функции W = In w на дугах окружностей имеем постоянное зна-
значение Re W = In V, вдоль лучей Im W = argw постоянна. Зави-
Зависимость ш от ^ можно найти с помощью применения интеграла
типа Коши (см. главу VI).
Казанской школой математиков, в которой развиваются ме-
методы решения обратных краевых задач теории аналитических
функций (см. книги: Нужин и Тумашев 1965; Нужин и Ильин-
Ильинский 1963; Ильинский 1966), широко представлены и решения
обратных задач теории фильтрации. Это задачи об определении
подземного контура плотины, удовлетворяющего наперед за-
заданным условиям: с заданной эпюрой скоростей, с заданными
распределением напора вдоль водонепроницаемых участков и
значениями функции тока на водопроницаемых, с заданной эпю-
эпюрой скоростей по дну нижнего бьефа и т. п. Исследованы во-
вопросы однолистности решений указанных задач (Аксентьев
1959), обычно возникающие в теории обратных краевых задач
(например, относящихся к теории крыла). Обзорная статья по
обратным краевым задачам в теории фильтрации имеется в
книге «Развитие исследований по теории фильтрации в СССР»
A969).
Глава VI
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
И ЕЕ ПРИЛОЖЕНИЯ К ТЕОРИИ ФИЛЬТРАЦИИ
§ 1. Определение аналитической функции по ее действитель-
действительной части на действительной оси. Пусть дана аналитическая
функция /(?) в верхней полуплоскости, непрерывная вплоть до
действительной оси и имеющая предельное значение /о на бес-
бесконечности
Положим для определенности, что при больших по модулю
значениях ?
Последнее равенство означает, что существует отличный от
нуля предел
H
Применим теорему Коши *) к функции /(?), взяв замкнутый
контур, состоящий из отрезка действительной оси (—/?, R) и по-
полуокружности С радиуса /?, проходимой в положительном на-
направлении (рис. 140). Получим для точки ?, лежащей внутри
контура:
R
i{t)dt 1 ] [ l(x)dr
Т )
-R С
Устремляя R к бесконечности, получим
„,
2ш J т - ? — 2 '
С
*) См., например, курс В. И. Смирнова A969) или монографию
. И. Мусхелишвили A968).
§ 1] ОПРЕДЕЛЕНИЕ ФУНКЦИИ ПО ЕЕ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ
так как
203
1 Г f о d% __ jiff о _ 1 с
2я/ J т - I ~ 2ш ~ 2 ' °>
С
а второе слагаемое дает нуль. Таким образом,
^ + f
0-2)
Возьмем точку ? = ?— щ в нижней полуплоскости. Она яв-
является внешней по отношению ко взятому нами контуру; как из-
известно из теории функций комп-
комплексного переменного, интеграл
в правой части равенства A.1)
будет равен нулю, следовательно,
будет равен нулю и предел его,
выражаемый правой частью ра-
равенства A.2):
о
2ш J t - i
— oo
R
Рис. 140.
В равенстве A.3) заменим все комплексные числа на сопря-
сопряженные. Получим
L
2ш
Ut)dt , h
/-^2'
Теперь вычтем почленно из A.2) равенство A.4). Получим
Полагая
f = ф -J- /i]^ ^0 = ф0 -|- /-ф0)
перепишем последнее равенство в следующем виде:
A.5)
A.6)
Точно так же, складывая почленно A.2) и A.4), получим вы-
выражение аналитической функции /(?) в верхней полуплоскости
204 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
через значения мнимой ее части на оси абсцисс:
W+*- (L7)
Перед интегралами A.6) и A.7) нужно взять знак минус, если
? — точка нижней полуплоскости.
Рассмотрим интеграл
и будем искать предельное значение функции ?/(?), когда точка
? стремится к некоторой точке g действительной оси. Для этого
возьмем на действительной оси две точки М{(—?ь 0) и Л12(Ег, 0)
и будем искать предел выражения
dt
)
Этот предел будет существовать при \\ = |2 в смысле главного
значения, если со удовлетворяет, например, условиям Гельде-
ра — Липшица и выполнены условия сходимости для U. Поэто-
Поэтому, когда ? стремится к точке g из верхней полуплоскости,
С помощью уравнения A.8) из формулы A.6) получим, пола-
полагая со = 2ф,
/Юф© + ^ J U=AffiLЛ + АКь. A-9)
В правой части A.9) действительная часть равна ср(|), что и
доказывает, что функция /(?), построенная по формуле A.6),
действительно удовлетворяет поставленному условию.
Такая же проверка применима к уравнению A.7).
Если на некоторой части оси g, например вне отрезка (а, 6),
функция (p(g) = O, то в формуле A.6) можно взять пределы
а и 6 и написать выражение для /(?) так:
Тогда при переходе на ось g будем различать два случая:
§ 1] ОПРЕДЕЛЕНИЕ ФУНКЦИИ ПО ЕЕ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ 205
1) если а < I < b, то
2) если
находится вне промежутка (a, 6), то
ь
-I-
В качестве примера рассмотрим схему движения, изображен-
изображенную на рис. 141. Дождь падает полосой на увлажненный грунт
глубины Т. Грунтовые воды растекаются так, что линии АВ и
А'В' можно считать твердыми стенками. Тогда на отрезке В'СВ
будем иметь условие v =
= —е, где е есть интенсив-
интенсивность дождя, т. е. количество
его, выпадающее на единицу
площади в единицу времени.
На остальных границах об-
области движения v = 0. Ото-
Отображая область движения
на нижнюю полуплоскость
(рис. 141), получим (напри-
(например, с помощью формулы
Кристоффеля — Шварца)
зависимость между ? и z:
• I-
ф-ех
б
zt—s
б' С В
; = acth|f. A.10)
Рис. 141.
Для того чтобы найти зависимость комплексной скорости
w = u — iv от ?, воспользуемся формулой A.7) этой главы,
дающей значение функции в нижней полуплоскости, когда из-
известны значения ее мнимой части на действительной оси, причем
w = 0 на бесконечности:
w
ОО 1
_1 1 vdl __ е \ dl __ e «
(lid
ъ ъ *• ъ I •
-оо -1
Исключая ? из уравнений A.10) и A.11), найдем w как функ-
функцию г:
206 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
Так как при ?=1 имеем г = / + 77, то из A.10) найдем
§ 2. Смешанная задача теории функций. Рассмотрим задачу:
найти функцию ну = /(?), голоморфную в верхней полуплоско-
полуплоскости и непрерывно продолжимую на действительную ось ?, за
исключением, быть может, отдельных точек, при подходе к ко-
которым /(?) имеет порядок роста, меньший единицы, если ш
удовлетворяет условию
сA) на оси g. B.1)
Здесь с (|) — кусочно-непрерывная функция, удовлетворяю-
удовлетворяющая условию Гельдера на каждом открытом отрезке между точ-
точками разрыва аи а2, ..., ап\ co(g) ку-
$k G\ сочно-постоянна.
^^ Сначала обратимся к однородной
i *- задаче, когда сA) = 0, считая (о(|) =
Of аг ак аА+1 ? = яал на отрезке (аи, ah+\) (рис. 142).
Рис 142. В § 9 главы III мы имели пример
такой задачи, отображая конформно
на полуплоскость многоугольник, ограниченный прямы-
прямыми, проходящими через начало координат. В самом деле,
уравнение B.1) при сA) = 0 дает (w = и + iv) прямую
ucosjtafc — us\nnah = 0. Решение указанной задачи было дано
формулой (9.1) главы III (С — действительная постоянная):
ю, = С."»' (а, - С)""" (а, - СH1" ... (ап - Qa^'\ B.2)
Однако однородные условия B.1) будут также удовлетво-
удовлетворены, если в выражении B.2) каждый из показателей увеличим
или уменьшим на целое число.
По поводу выбора показателей заметим следующее. Обозна-
Обозначим через yh скачок со(|)/я при обходе точки ah (рис. 142):
Y* = a*-i—aik (t = l,2 й), ап+1 = ах. B.3)
Можно выбрать целые числа Хь. так, чтобы выполнялись нера-
неравенства — 1 <Yfc + ta< 1- Если yh — целое, то, положив Хь. =
= —уь> получим единственное число у* + А* = 0, удовлетво-
удовлетворяющее этому условию; если у^ — не целое, то существует два
значения kh> при которых удовлетворяются соответственно не-
неравенства
- К Vk + К < 0, 0 < у, + Xk < 1. B.4)
Если в B.2) заменить yk на ун + Хн из первого неравенства
B.4), то ww обращается в бесконечность порядка <1 в точке а&;
§ 2] СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ 207
такого типа решения часто встречаются в теории фильтрации.
Но иногда ищется решение, ограниченное при ? = ah. Тогда
нужно взять Xk удовлетворяющим второму из условий B.4).
Остановившись на определенном выборе Хд, введем обозна-
обозначения
6* = 4k + К = а*-! — <*Л + ЛЛ. B.5)
Выделим те точки аи #2, ..., aqy в которых 0 ^ Ьк < 1 (в точ-
точках а9+ь .. •, ап имеем, следовательно, —1 < бд < 0).
Выражение
Т @ = О™*' fj (а, - ?)9* = i-*Ce™nl Д fe - I)'* B.6)
называют*) канонической функцией класса h(a\,...,aq) (С —
действительная постоянная, которую можно принять равной
единице). Индексом к решения класса h(a\9...9aq) называется
число
х=-(в,+в2+ ... +ЙЛ) = —(Я,+Л2+ ... +К). B.7)
Обращаясь к неоднородному условию B.1), перепишем его
так:
- 4 И*) - «(I) ^ Щ = с (I) е*» ®. B.8)
Функция B.6) удовлетворяет уравнению ТA)—Г(?)е2г@ = 0.
Подставляя найденное отсюда выражение e2i(d = Т/Т в B.8)
и разделив его почленно на Г, получим
Приходим к задаче об определении функции, голоморфной
в верхней полуплоскости, по ее мнимой части на действитель-
действительной оси (см. § 1). Для ее решения нужно еще задаться усло-
условием для сA) на бесконечности. При этом будем различать два
случая.
1. Пусть индекс х ^ 0. Это значит, что Г(?) при ? = оо об-
обращается в нуль порядка х. Потребуем для c(Q при подходе
к g = ±oo выполнения неравенства
I /о\ Л I ^ лУ1 /о < /\\
(А, М, а — постоянные, а > 0; А = 0 при х > 0).
Для получения общего решения класса h(au. ..,ая), огра-
ограниченного на бесконечности, следует ввести в формулу A.7)
*) См., например, монографию Н. И. Мусхелишвили A968).
208 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
вместо постоянной полином степени х. Тогда
где Со, Си ..., С„— действительные постоянные.
2. Если х < 0, то решение класса h(au...9aq), вообще го-
говоря, не существует. В самом деле, в этом случае Г(?) при
?-*оо обращается в бесконечность порядка —х. Разлагая
подынтегральную функцию B.11) по степеням 1/?, получим
Отсюда видно, что для существования решения, имеющего ко-
конечный предел при ?->оо, необходимо обращение в нуль всех
членов ряда, включая член с |~х~!; получим условия
c{l)f(^dl =0 (m = 0, 1, 2, .... -х-1), B.12)
при выполнении которых и при условии Со = ... = Сх = 0
существует решение, ограниченное на бесконечности.
Если ищется решение, могущее обращаться в бесконечность
порядка р при ?-~*оо (р —целое положительное число), то до-
достаточно в B.11) взять полином степени х + р, а не х. Если
решение должно обращаться в нуль на бесконечности, то нужно
в B.11) положить Со = 0.
§ 3. Частный случай задачи. Пусть U — совокупность отрез-
отрезков действительной оси (ai, bi), (a2, Ь2)> ..., {an,bn)9 L" —ос-
—остальная часть действительной оси (рис. 143). Требуется найти
функцию /(?), голоморфную в верхней полуплоскости, ограни-
ограниченную на бесконечности и в точ-
^-^ ках аи, а при подходе к точкам
@ Ьи имеющую порядок роста, мень-
^^ ^яя | ший единицы, по контурному ус-
z bz an I ловию
c{i) на L\
Рис- 143' lmw = c($ на L\ C.1)
где с(|) в интервалах между точками аи и Ьи удовлетворяет
условию Гельдера, а при подходе к бесконечности — условию
B.10). Примем ап =0 и со = 0 на L" и со = — я/2 на U в B.1),
а скачки в точках а& и bh соответственно равными 1/2 и —72-
Индекс х класса А(аь...,ап) равен нулю, и функция B.6)
§3]
имеет вид
ЧАСТНЫЙ СЛУЧАЙ ЗАДАЧИ
209
¦-П
Решением класса h(au ..., ап) будет
-оой-1
с-**1
C.2)
где Со — действительная постоянная.
Если потребовать в точках а* лишь выполнения условия,
что порядок роста в них меньше единицы, то решением, огра-
ограниченным на бесконечности, будет
C.3)
где Со, С), ..., С„ — действительные постоянные, со = 0 на Z/
и со = —я/2 на L'.
Рис. 144.
В качестве примера рассмотрим задачу о плоском напорном
движении под п плотинами в произвольной области (рис. 144),
Для которой построим комплексный потенциал как функ-
функцию от ?.
Пусть на действительной оси плоскости ? точкам Л, Ви
С\у ..., J5n, Cn, D соответствуют точки а, Ьи с\9 ..., bn, cn, d.
Действительная часть функции со = ф + /ф принимает на от-
отрезках abu C\b2y ...» cnd постоянные значения —хЯт, мнимая
Часть — на отрезках Ь\С\, ..., Ьпсп постоянные значения Qm}
210 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
а на da — Qn+i. Производная dco/d?, взятая вдоль действитель-
действительной оси плоскости ?, будет иметь действительную часть равной
нулю на отрезках cmbm+u мнимую часть равной нулю на Ьтст.
Поэтому dco/d? можно представить в виде
C.4)
X (? — d), если точки А и D не совпадают, и /?(?) = (?;— Ь\)Х
X (? — ?*i) ... (?—&п) (? — ^п), если эти точки совпадают (водо-
упор отсутствует).
Полином Р(?) должен быть степени не выше /г+1 при на-
наличии водоупора и не выше п— 1 при его отсутствии. В самом
деле, в первом случае имеем при ? = со, предполагая кон-
контур AD гладким, конечную скорость в точке плоскости 2, пере-
переходящей в бесконечно далекую точку плоскости ?; во втором
случае dco/d? = ОA/?).
Интегрируя dco/d? в пределах fem, cw и cm, bm+u найдем
> т 5 vra c"Qlfl+l""Qm'( }
Пусть заданы значения части величин Ни /72, ..., Нп+\, Qu
Q2, ..., Qn+ь з именно, /г+1 из них при А Ф D и п из них
при Л = D. Тогда уравне-
уравнения C.5) позволяют опре-
определить коэффициенты поли-
полинома Я(?); после этого
из остальных уравнений
C.5) определятся оставшие-
оставшиеся неизвестными величины
Нт и Qm.
Рис. 145. Отметим, что определи-
определитель системы, служащей для
определения коэффициентов полинома Я(?), отличен от нуля
(Положий 1954,2).
На рис. 145 представлен плоский разрезной флютбет на про-
проницаемом слое конечной глубины. Для частного случая равных
длин флютбета / приведем без вывода основные результаты.
Расход отверстия между двумя элементами флютбета *)
*) Э § 3 и 4 главы VI коэффициент фильтрации обозначен через К
§4)
ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ
211
где #ь #2, Я3— напоры в каждом из водоемов и модуль эллип-
эллиптических интегралов
sti
2Т
sh-
2Г
Зависимость между комплексным потенциалом и координа-
координатой z можно представить в виде
© = - ? (Я, - 2Я2 + Я3) F (arcsin Л, *'),
где
sh
А,=
sh
2T
Заканчивая на этом изложение случаев обтекания флютбе-
тов, заметим, что Н. Н. Павловский рассмотрел обтекание за-
заглубленного прямоугольного флютбета. Имеются исследования
по обтеканию плоского флютбета в слое конечной глубины,
цельного и разрезного, с учетом наличия дрен. Результаты этих
исследований приведены в книге В. И. Аравина и С. Н. Нуме-
рова A948) и в работе Н. Т. Мелещенко A937). В последней
рассмотрена также задача о плоском флютбете при наклонном
водоупоре.
§ 4. Земляная плотина трапецеидального профиля на непро-
непроницаемом основании при наличии дренажа. Приведем решение
С. Н. Нумерова A942) задачи о трапецеидальной плотине
(см. также Аравин и Нумеров 1953). Рассмотрим фильтрацию
в земляной плотине, построенной на непроницаемом основании,
V///////////V/////////////////////////R X////////////////////// ЗГ
4
Рис. 146.
с Дренажем или обратным фильтром в виде призмы. Наклонная
прямая CGB (рис. 146), вообще говоря, состоит из отрезка
BG — границы нижнего бьефа и отрезка GC — промежутка
212
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
[ГЛ. VI
высачивания. Это вносит усложнение в годограф скорости
(рис. 147).
В частных случаях промежуток высачивания может отсут-
отсутствовать. Так, если разрез GFB удлиняется и точка F займет
положение F\, нижний кусок области годографа отпадает и
остается заштрихованная область (рис. 147). При этом депрес-
сионная кривая будет ортогональна к низовому откосу, точка С
совпадет с F\.
При построении годографа мы исходили из предположения,
что депрессионная кривая имеет одчу точку перегиба Е. Но
можно предположить, что на свободной поверхности имеются
/Н* ?+)*
Рис. 148.
две точки перегиба — К и Е. В этом случае, пройдя по окруж-
окружности дугу DE (рис. 148), мы возвращаемся по разрезу к точке
/(, затем опять поднимаемся по дуге окружности, перейдя на
другой лист римановой поверхности, до точки С (лежащей над
точкой А на втором листе). От точки С мы идем по прямой СВ.
Тогда в случае вырождения годографа, для которого отпадает
промежуток высачивания, в точке С выхода депрессионной кри-
кривой на низовой откос скорость равна нулю, и касательная к сво-
свободной поверхности горизонтальна.
Из рассмотренного примера видно, насколько сложной мо-
может оказаться область годографа и какое большое число пара-
параметров может содержать формула Кристоффеля — Шварца.
С. Н. Нумеров дает решение задачи, предполагая промежу-
промежуток высачивания отсутствующим и точки Си G (рис. 146) сов-
совпадающими. Тогда границами области движения. ABCD яв-
являются линии тока и эквипотенциали. Положим ф ===== 0 вдоль АВ
и г|) = Q вдоль CD, и пусть потенциал скорости связан с
§ 4} ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ
давлением равенством
213
D.1)
так что потенциал скорости имеет значения ф = -ьх///2 соот-
соответственно на границах верхнего и нижнего бьефов, причем
it TJ ГТ
Область комплексного потенциала представлена на рис. 149.
Отображая ее на верхнюю полуплоскость плоскости ?, получим
аналогично тому, как мы это
делали в ряде случаев,
@=-
где
Я/2
О
V(i — s2) (y2 —
D.2)
А ? в
Рис. 149.
Приведем интеграл D.2) к каноническому виду, полагая ? — yt.
Получим
> = — \ , . . . = — /Marcsin—, YI- D.3)
2/с J V(l — t2) A — y2t2) 2/C V Y /
@ =
Приняв ? = g, будем идти вдоль действительной оси плоско-
плоскости ?. Для промежутка y < ^ < 1 имеем
_ кн %т Г d/
~ 2 + 2/С J V(/2- 1)A -Y2^2
2)
= — + ^Г Г F ^arcsin у
Последнее выражение получается путем подстановки
, yJJ . D.4)
Отсюда, в частности, полагая | = 1, найдем формулу для рас-
расхода:
¦Х.НК'
D.5)
214 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
Используя это равенство, перепишем D.4) для у < | < 1 так:
co(l) = ^f+/Q[l-^1]. D-6)
Здесь принято
^^. D.7)
Аналогичным образом для промежутка —1 <С ? <—у по-
получим такое выражение:
j?[J^U] D.8)
где Я имеет значение D.7).
Теперь будем согласно С. Н. Нумерову A942) рассматри-
рассматривать z как функцию со. Вместо г (со) удобнее рассматривать
другую функцию, получаемую из следующих соображений. Если
бы мы вместо действительной депрессионной кривой рассмат-
рассматривали параболу для течения с горизонтальной дренажной
щелью, исходящей из точки В, то соответствующее течение оп-
определялось бы уравнением (см. § 11 главы II)
Введем функцию Z(co) с помощью равенства Z = z — z* — I:
z((o) = ;t + <y=*(cD) + ^[*(//|2+//2) -о]2. D.9)
Для этой функции получаем следующие условия на отдель-
отдельных частях области движения.
На ЛВ, где г|> = 0 и у = О,
У = 0. D.10)
На линии ВС, уравнение которой можно написать в виде
л: sin Pjc — г/ cos pjt = / sin рте и вдоль которой ф = х#/2, получаем
%Н\ \ Н2 cos ря sin ря о
D.11)
Вдоль свободной поверхности CD, где у = к(Н{-\- Н2)/2 —ку
и \|) = Q, получаем опять
Г = 0. D.12)
Наконец, вдоль верхового откоса DA, где ср = —хЯ/2 и урав-
уравнение которого имеет вид х sin an — у cos ая = 0, получаем
уравнение
? sin ая Я, cos ая sin ая _
L_ + _!_ ф___ф2. D.13)
§4)
ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ
215
Таким образом, задача свелась к следующей: на сторонах
прямоугольника плоскости со заданы линейные комбинации
функций X и У; найти функцию X + iY внутри прямоуголь-
прямоугольника со. Это так называемая задача Римана — Гильберта. Далее
С. Н. Нумеров заменяет область со полуплоскостью плоскости ?,
на которую отображает область движения, и затем приемом,
указанным у нас в § 2 этой главы, сводит задачу к задаче
Дирихле.
Мы получим зависимость со от ?, выражающуюся форму-
формулами D.6) и D.8), для двух отрезков оси ?, на которых имеются
ненулевые условия D.11) и D.13). Принимая во внимание, что
на этих отрезках соответственно ср = ±х#/2, найдем по фор-
формулам D.6) и D.8), что в обоих случаях, для y^5^ 1 и Для
D.14)
Подставим это выражение -ф в равенства D.11) и D.13). После
простых преобразований получим
для y < I < 1
X (I) sin ря - Y (I) cos ря = Re [/' ("*)z] =
D.15)
для —¦ 1 < I < — Y
X (I) sin ая — Y (I) cos ая = Re
о ^,
У = 0.
для
и
При этом
b0 = I sin ря + H2 cos ря -f
u и а~ ОэтРя и
O\ = и^2СО5рЯ —, c?2
i sin ая Q sin ая
a0 = #! cos
п\ = Я| cqs ад -j-
2% '
Q sin ая
D.16)
216
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
[ГЛ. VI
Отсюда видно, что на отрезках действительной оси получи-
получились такие условия, какие были у нас отмечены в § 2.
Составим функцию
Т(?>) = i (у — ?N(y + ?I~аA — ?)!~0A + ?)а- D.17)
Эта функция принимает чисто мнимые значения для действи-
действительных значений ? = ?, причем —y < 5 < Y- Примем ее аргу-
аргумент равным я/2 для 0 < g < y« Тогда на различных участках
действительной оси | для Г(?) будем иметь следующие выра-
выражения:
для |?|<Y
для y < Е < 1
для — 1 < ? < — y
r(E) = (Y-^(-Y
ДЛЯ — ОО < I < —
ДЛЯ 1 < I < ОО
DЛ8)
Произведение r(?)Z(?) будет чисто мнимым для |||<y и
|5|> 1, т. е. для него действительная часть равна нулю на этих
промежутках.
На промежутках y<?<1 и —1 < | <—y известна дей-
действительная часть функции T(\)Z(\). Для того чтобы можно
было применить формулу Коши в целях отыскания T(t,)Z(l),
нужно исследовать это произведение при ? = оо.
Так как Z(?)— аналитическая функция, ограниченная на
всей полуплоскости ?, то на бесконечности она разлагается в ряд
Лорана вида
D.19)
При этом, заметив, что на отрезках |?|>1 мнимая часть Z
равна нулю (У = 0), по принципу симметрии Шварца для функ-
функции Z(?) получим следующее свойство: она принимает в сопря-
сопряженных точках ? и ? сопряженные значения. Отсюда вытекает,
что коэффициенты сп должны быть действительными числами.
§4) ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ 21?
Что касается Г(^), то около ? = оо можно положить
j ил j>2 ^ j УЛ ( j I jA ^ j М Z' j i }\а _
причем все коэффициенты dn действительны.
Произведение 7*(E)Z(E) на бесконечности имеет вид
Т (Е) Z (Е) = — /соЕ2 — i (с\ + corfi) E -~ i (c2 + ^i^i + c0d2) + ...
Функция
У (?) = Г (?) Z (Е) + /соЕ2 + / (Ci + cod!) ? D.20)
будет ограниченной на бесконечности, и ее удобно принять
в качестве вспомогательной функции. На тех участках, где
У = 0, новая функция обладает тем свойством, что ее действи-
действительная часть равна нулю. Что касается остальных отрезков, то
на них нетрудно найти значение действительной части этой
функции. Получаем
id (ЮМЕ) Д^ v<E<l.
fc(E)ME) Для -KE<-Y, D.21)
0 • для \Ц< у и Ш >1,
Xi(E) и %2(Ю имеют значения D.15), причем
Задача оказалась сведенной к задаче Дирихле, для решения
которой применима формула A.6) этой главы:
где С — произвольная действительная постоянная.
Подставим в D.22) выражение D.20) для ИР(Е) и, использо-
использовав равенство D.17), получим, сокращая на /,
(codi + cl)t> + CqI2 + (у — tf (у + ?)[~а {I — S)I~3A +E)aZ(g) =
-l
218 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
Полученное уравнение содержит неизвестные постоянные с0, с{
и С. Их можно исключить, полагая в D.23) последовательно
? = ±У и ± 1. При ? = у
1
+ ) + CY2
-1
Вычитая это выражение из D.23) и сокращая получающийся
результат на Y—"?> получим
- (Y - S)^
— _± С f @ dt
~ п ) (/-Y)(>-?) '
Вычитая из этого равенства аналогичное соотношение, соответ*
ствующее ? = —Y» получим
- (y - S)e"' (Y + ?Га A - О1"8 A + 0а Z @ =
п J (<-Y)(
Полагая ?, = 1 и вычитая соответствующие уравнения, исклю-
исключим со и найдем
Y- 0e"!(Y+0"e(l -D~e(l +0aZ(Q =
1 С n*)dt
Наконец, положим в последнем уравнении ? = —1. Так как ле-
левая часть при этом обратится в нуль, то правая даст следующее
уравнение:
Вычитая из правой части D.24) левую часть D.25), приведем
D.24) к более симметричному виду. После этого, решая D.24)
§ 4] ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ 219
относительно Z(?), получим
X
I
(-, f{t)dt D26)
3 (Y2 -12) A - п (< - с) * к '
-1
Наконец, вспоминая зависимость D.9) между Z и z, напишем
уравнение для г(?):
1
л
И 2 ^z я J (Y2 — <2)(! — '2)(< — S) '
D.27)
2xQ _J
где Г, (?) = (Y - ?)'"
Уравнение D.25) содержит неизвестный параметр у и может
служить для определения значения этого параметра. Когда най-
найдено у, расход Q определится по формуле D.5).
Перепишем более подробно уравнение D.25), используя вы-
выражения D.21) и D.15):
F
К' К' (Y(
1
(±^>\^^= 0. D.28)
K> к" ) (/2 - y2) A - t2)
Здесь
Уравнение D.28) можно переписать иначе, вводя обозначения
-Y
-1
-1
где *(t)_
220 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ% VI
а также
1
][ = \ ф{ (/) F (arcsin ^X T i2 , VI *,
J \ V /
где Ф, @ = (/ - Y)e-' (/ + YH A - 0~b A + /)°-'.
Теперь перепишем D.28) в виде
^^ |/i + -^-/- = O. D.29)
Для случаев, имеющих место на практике, обычно 1/Н > 10.
При этом параметр у очень близок к единице, у' очень близко
к нулю. Интегралы ]п и Уп можно тогда упростить, принимая
/48. Y') «В, у« 1.
Рассмотрим интеграл /0. Положим
(Y + ОМ-а+/)¦-(J)
e482 Bl. D-30)
Подынтегральную функцию в /0 заменим на
A+/)-'(/-Y)~e0 - 0е"'«^-V)'e(l-0е. D.31)
Тогда интеграл
1
Y
приводится к бета-функции подстановкой 1 — / = A — v) s:
Точно так же найдем приближенное равенство J'o«я/Bsin Ря).
На основании рядов D.30) и D.31) можно сделать оценку
принятых приближений.
§ 4] ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ 221
В интеграле J\ примем
Fyarcsin—^—, у'j » arcsin 7—.
Тогда, применяя те же упрощения, что для /0, напишем
1
У, » т j (/ - v)~e (I - О"" arcsin VT^1T A.
Y
Сделаем подстановку
Тогда
Точно так же
Здесь через /! (а) и f3(«) обозначены функции, представляемые
соответствующими определенными интегралами.
Переходя к интегралу /[, напишем
Аналогично
Равенство D.29) содержит величину К'. Для у' близких к
нулю можно принять К' ~ я/2.
Интересно отметить, что параметр y совсем исчез из всех
приближенных формул.
Подставим теперь найденные приближенные выражения ин-
интегралов /0, /ь ... в D.29). Сократив на общий множитель я/2,
получим
~& ~ Ж^ ~ «i/i (о) + *¦/> A ~ Р) - 2a2f3 («) + 262f3 A ~Р) = 0.
222 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
Наконец, принимая во внимание равенства D.16), напишем
— Г#! cos cut — ---sin cut) fi{a) + (H2cos$n — -—sinfto) fi(l—p)—
~^sinan/3(a) + |-sinpn/3(l-p) = 0.
Отсюда можно найти приближенное равенство для /:
+ sin ря fx A - р) + sin ая /3 (a) - sin Ря f3 A - p)].
Введем еще обозначение
f 2 (<*) = fi(a) — / з (<*) =
о
Тогда можно переписать уравнение для / так:
х (я2 — Н2Л
1 ™ 2Q + Я* tct? aJt "" C0S aJt f 1 (a^ "" Я2 [ctg Ря —
— cos ря f! A — p)] — -~ [— sin ая /2 (a) + sin ря f2 A — p)].
Выполним еще одно преобразование, использовав свойство
функций /i(l—P) и /2A— Р)> которое мы получим, если в ра-
равенстве
1
о
положим /= 1 —т. Будем иметь
1 1
Ml - Р) = $ ctg-з ( «) rfT - 5 т ctg-з («) Л - ^ - Л ф).
о о
Аналогично найдем
fsd -Р) = т 5 A -r^ctg-
о
1
§4]
ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ
223
Подставляя полученные выражения в формулу для /, после про-
простых преобразований окончательно получим
х (Н1 — И?)
1 ~ 2Q + Н\ [ctg an — cos an f{ (a)] — H2 cos $n f{ ф) —
- -J [ 1 - sin сея /2 (а) - sin ffct /8 ф)]. D.32)
Эта приближенная формула обладает большой степенью точ-
точности для широких плотин. Для функций fi, f2 и /3 вычислены
таблицы (Нумеров 1946; Аравин и Нумеров 1948, 1953).
0,05
0,15 0,25 0,35 а
4JJ0
0,320
0,310
0,300
0,290
г
n
и,
п
\
п
и,
3 -
40
\
\
\
100-
095-
090-
\
'1 Is
I
085Л
\
\
/
\
\
ч
г
у ft «Я
\
/
)
\
/
\
_
/
s
f3fr
/
/
)
У
/
/
У
/
у
/
/
ff»
У
i
/
/
х.)
/
1
1
А
/
/
7
Ц470
o,w
0,430
0,410
0,05 0,10
0,15
Рис. 150.
0,20 л 0,25
(для fzuf$)
0,390
В частном случае прямоугольной перемычки с горизонталь-
горизонтальным дренажем, т. е. при a = V2 и р = 0, полагая Н\ = Я,
#2 = 0, получим из D.32)
1 ~ 2Q 6х '
откуда для Q находим приближенное равенство
По вычислениям С. Н. Нумерова П. А. Шанкиным A947, 2)
построены графики зависимости fu f2 и /3 от а, изображенные на
рис. 150.
224 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
Уравнение депрессионной кривой. Для получе-
получения уравнения кривой депрессии в уравнении D.27) нужно по-
положить со = ф + iQ = к{Н\ + Н2)/2 — ку + iQ. Тогда
(Y - >)l~P (- Y - 0а A - /K A + t)l~a (t - I)
_ \ \ К А /
J (^ - YI (Y + 0а A - 0е A + /)!"а (/ - 6) J '
Рассмотрим левую часть кривой депрессии, для которой
—оо < g < —1. Для у ~ 1 уравнение D.33) можно упростить,
подобно тому как мы это делали выше при вычислении интегра-
интегралов ]\ и /г- Принимая К' « я/2, получим
х « ^- 4- — 4- — (I — I) (— v — 1)а (— 1 — ?){~а X
Y
Здесь для F можно написать приближенное равенство
. л/Т^Т д vr^F
Отметим, что во втором интеграле разность / — ? заменена на
1 — ?. Это допустимо в силу того, что в данном случае в ряде
1 1
при Y^U 1<^<Y> I — g > 2 можно принять
/-6 1-6 '
После таких же упрощений уравнение D.28) принимает вид
4а2 г2 1 и 261 D _ Ab2 v2
•dt.
Y
- Y _ ^"i r- __ ^ n2 • I, ^t/1 n _ ^t/2
§ 4J ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ 225
Умножив обе части этого равенства на
вычтем его почленно из D.34). Под знаком первого интеграла,
где / « —1, можно принять 1 — / » 2. Поэтому из D.34) полу-
получаем следующее уравнение:
щ2 i Q ,
**Й+ +
-V
(-Y--OaO + Ol~a(>-?)
Теперь введем новую переменную интегрирования с по-
помощью зависимости
t = JL. D.35)
Получим
i
о
При этом можно принять
arcsin
in л/уЕг~т & arcsin д/ t __ ,
так как A — /)/A+y) ^ 1- Заменяя в последнем выражении
arcsin на arctg соответствующего аргумента, получим
F « arctg д/j^ •
Далее по формуле D.35) найдем
F» arctg (д/ZIELtg-f-). D.37)
В силу уравнения D.3) имеем
И для — оо < | < — 1
8 П. Я. Полубаринова-Кочина
226 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ, VI
На основании D.5) получаем
Для левой ветви депрессионной кривой, для которой у
близко к Ни можно написать
у _ к (Я! + Н2) ну к (Н{ -у) %Н __ к (Hi -у) К
Q ~ 2Q Q Q 2Q ~ Q К' '
Пользуясь формулами (см. Градштейн и Рыжик 1962)
у \ "Т > У) sn (a:, y) ' dn (a:, y) '
получим
. / vt % (Hi — у) \
1 an I д , y I
D.38)
sn
Возвращаясь к D.37), положим
Последнее выражение можно принять в силу того, что при
Y « 1 с высокой степенью точности A — ?)/(y — ?) « 1. На осно-
основании D.38) получаем
D.39)
Поэтому D.37) принимает вид
где и имеет значение D.39).
Теперь, принимая во внимание значение величины а0 со-
согласно D.16) и учитывая равенство @ < а < {/2)
sin ая
§ 4] ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ 227
напишем уравнение левой части депрессионной кривой в виде
2Q
tf,ctgcut —
о
]
2 / я2 J
На основании D.16)
п —U гп" гттт Q Sin аП п —
ai — л 1 cos ал; —, а2^
Поэтому удобно ввести обозначения
F( („, а) = -^L J ctg-2. (?E) arctg („ tg f) dr,
о
F2(«, a) =
Тогда окончательно уравнение левой ветви депрессионной кри-
кривой запишется в форме
,.iWzlL + „, [ctgan_,,(„, =4^1, .)] +
+ -|tg<»P!(thS^L, a). D.40)
Аналогичным путем получается уравнение правой части
депрессионной кривой:
где
F3 (и, Р) = l^lJL \ tgi-20 ^ arcctg («tg ~^) rfr,
О
1
^) arcctg2 (и tg-?) dr.
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
1ГЛ, VJ
1,0 0,8 0,6
2)
0,2 и О
0,30
0,10
0,10
6
А
f
<?,
р\
-«^
*?
А
п
ч
У,
2
ч
^>
„^
//
У,
(и
Ч,
^"
А
у
/
)
ч
ч
Z
У
у
<
><
ч
<
ч
I
ч
/
4s
ч,
/И
у
ч
Sk
у
У
Ль
м
S
4^ <?« о,е о,8 и 1,0
Рис. 151.
0,2 Ofi 0,6 0,8 1,0
Рис. I52.
§4]
ЗЕМЛЯНАЯ ПЛОТИНА ТРАПЕЦЕИДАЛЬНОГО ПРОФИЛЯ
229
С. Н. Нумеров A946) составил таблицы значений функций
F\{uy а), F2(u,a), Fs(u9a) и FA(u, а). На рис. 151 и 152 приве-
приведены графики этих функций (Шанкин 1947,2).
Для плотины с горизонтальным дренажем (Нумеров 1939)
р = 0, и положение всей кривой депрессии может быть опреде-
определено одним уравнением, совпадающим с D.40) при замене Н
на Н\\
/ л/ „
2Q
2 r* f f-f ft \ ~]
— -f-tflctgcm; — Fx f thxrc—^p-, ajj +
На рис. 153 приведена для примера депрессионная кривая, по-
построенная для случая Q = 0,2хЯ, / « 3.16Я, a = 0,25 (Нуме-
(Нумеров 1939)
1,0
0,6
0,2
О
t
А
/
%
/
/
/
—
^—.
\
\
НО ?
н
Рис. 153.
Для прямоугольных перемычек с горизонтальным дренажем
(а = 7г, Р = 0) уравнение кривой депрессии принимает вид
_ н2-у2 Q F /, 1 Н — у \
где
F {и) = — \ arctg (wtg ^) Fl —— arctg (wtg %f) 1 dr.
0
На рис. 154 приведен график зависимости F от w.
С помощью D.41) можно найти для окрестности точки
С —выхода депрессионной кривой в нижний бьеф — выражение
производной
щ-л
230
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
(ГЛ. VI
При и -> О оба интеграла стремятся к бесконечности и, вообще
говоря, dx/dy~-+ =fcoo. Для уточнения вопроса о знаке сделаем
подстановку utg{m/2) = tg(jis/2), что даст
X
ctg23 Г~-J ^5 Г s ctg2e у~2~) ds
1 +«2Ctg2 (-y-J J 1 +«2ctg2^-y-J J
D.42)
Отсюда найдем предел выражения
Знак производной
зависит от знака величины
При Л = 0 для dx/dy получается конечное, отличное от нуля
значение Если А > 0 то rfx/dy > 00 т е кривая депрессии
р д /y
значение. Если А > 0, то
0,30
0,26
0,22
0,18
0,1b
0,10
0 0,2
I
1
1
/
f
/
I
/
/
V
/
/
—00, т. е. кривая депрессии
подходит к низовому откосу го-
горизонтально. Если А < 0, т. е.
dx/dy -> + 00, то кривая депрес-
депрессии подходит к низовому откосу,
имея касательную, направленную
вдоль откоса к его подошве. Оче-
Очевидно, последняя форма движе-
движения физически нереальна, и этот
случай соответствует движению
с участком высачивания.
0,8 0,8 1,0
Рис. 154.
Рис. 155.
Таким образом, для отсутствия участка высачивания необхо-
необходимо и достаточно, чтобы выполнялось условие А ^ 0, т. е.
Способы приближенного вычисления величины промежутка
высачивания указаны в цитированной книге В. И. Аравина и
С. Н. Нумерова A948).
§ 6) ДРЕНЫ И КАНАЛЫ В СЛУЧАЕ НАКЛОННОГО ВОДОУПОРА 231
На рис. 155 представлена кривая депрессии, рассчитанная
по формулам С. Н. Нумерова. В ней имеется та же особенность,
которая была отмечена в § И главы IV по поводу перемычки
Н. М. Герсеванова: выход фильтрационного потока и свободной
поверхности во внешнюю область; если отбросить эту часть по-
потока, то получится приближенная форма свободной поверхно-
поверхности и отрезка высачивания.
§ 5. О приведении к смешанной задаче теории аналитических
функций в общем случае плоской задачи фильтрации. В примере
земляной плотины с дренажем (см. § 4), когда промежуток вы-
высачивания считался отсутствующим, была известна область со —
в задаче § 4 это прямоугольник, искомой же являлась функция
2A). На отдельных примерах С. Н. Нумеров обобщил трактовку
указанного метода, приведя решение к двум смешанным зада-
задачам в полуплоскости для двух из функций z(t), (о(?) и 8(?)
(Аравин и Нумеров 1953; Нумеров 1954, 3). Эти примеры: сим-
симметричный приток жидкости к вертикальной дренажной щели,
расположенной в проницаемом слое конечной глубины, и филь-
фильтрация в полубесконечном массиве к откосу сухого бьефа, опи-
опирающемуся на полосообразное основание, подстилаемое водо-
упором. Каждая из указанных смешанных задач в граничных
условиях для искомых функций на некоторых участках действи-
действительной оси полуплоскости ? содержит неизвестные функции.
Автор приводит задачу к системе интегральных уравнений типа
Фредгольма второго рода с регулярными или сингулярными яд-
ядрами. В названных работах изложен один из возможных спосо-
способов решения интегральных уравнений, основанный на приведе-
приведении их к вполне регулярной бесконечной системе алгебраиче-
алгебраических линейных уравнений и решении этой системы методом по-
последовательных приближений.
Следует отметить, что С. Н. Нумеров использовал в 1939 г.
свой метод решения смешанной задачи в полуплоскости, осно-
основанный на применении интеграла Коши, независимо от Ф. Д. Га-
хова и Н. И. Мусхелишвили, которые в дальнейшем широко
развили соответствующий общий метод. Эта работа С. Н. Ну-
Нумерова, посвященная частной задаче теории фильтрации, оста-
осталась неизвестной математикам.
§ 6. О фильтрации при наличии дрены или канала в случае
наклонного водоупора. Схема рассматриваемого движения дана
на рис. 156. Дрена имеет вид горизонтальной щели, граница во-
доупора составляет угол an с горизонтальной прямой (Нумеров
1951, 1; Аравин и Нумеров 1953).
Обозначим через Q и Q\ расходы соответственно на беско-
бесконечности слева и на бесконечности справа; при этом величина
232
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
(ГЛ. VI
Рис. 156.
©
§6)
ДРЕНЫ И КАНАЛЫ В СЛУЧАЕ НАКЛОННОГО ВОДОУПОРА
233
Qi может быть отрицательна, если приток к дрене происходит
и из бесконечности справа.
Будем различать четыре случая:
1) всесторонний приток воды к дрене, когда расход Q боль-
больше расхода Q\\ при этом правая ветвь депрессионной кривой
имеет максимум в точке ветвления потока Мо (рис. 157);
2) расход из дрены в грунт, т. е. фильтрация из канала; при
этом левая часть кривой депрессии имеет минимум в точке Мо
(рис. 158);
Рис. 160.
3) в верховой части дрены имеет место приток грунтовых
вод, в низовой — просачивание из дрены в грунт, и точка вет-
ветвления Мо расположена на дрене
(рис. 159);
4) поток поступает в дрену с
двух сторон из бесконечности, и точ-
точка ветвления Мо находится на водо-
упоре, а расход Qi отрицателен
(рис. 160).
Соответствующие области комплексного потенциала со =
= Ф + /ф изображены на тех же рис. 157—160.
Конформное отображение области со на полуплоскость ?
(рис. 161) во всех случаях дает *)
2 1 2 /1 [
@= — /Q Qarch , Н—Q{ arsh л/ ¦
я VK я41 V B(l-
С)
F.1)
В самом деле, пусть конец разреза на плоскости со, т. е. точ-
точка Af0, переходит в точку а плоскости ?. Тогда формула Кри-
стоффеля — Шварца, примененная к любой из трех фигур
*) Четвертый случай здесь не рассматривается. С. Н. Нумеров A947, 1)
*1ал его решение для а — 0, т. е. для горизонтального водоупора.
234 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
плоскости со, даст
@ =
= Ма[—/е + M(l-g)t dS, F.2)
Учитывая, что полувычет первого интеграла правой части около
точки ? = О равен —iQ, а полувычет второго около ? = 1 есть
—t'Qi, и вычислив указанные интегралы, придем к формуле
F.1).
Теперь введем в рассмотрение функцию Жуковского
в = 8, + /62 = © — ikz. F.3)
Для промежутков (—оо, 0) и A,оо), т. е. вдоль депрессион-
ной кривой и вдоль контура дрены, давление равно атмосфер-
атмосферному, а потому
Im (iQ) = 8! = Ф + ky = 0. F.4)
На промежутке 0 < ? < 1 имеем
х sin an + У cos an = — Т cos an, \f> = — Q. F.5)
В силу F.3) 9j = ф -]- fer/, 62 = i|) — kxt г потому F.5) пере-
перепишется так:
Im [ieaniQ] = — 92 sin an + 8! cos an =
= — kT cos an + Q sin ая + Ф (?) cos an, F.6)
причем
1/й <6-7>
Бесконечно удаленная точка плоскости ? для 9 является
нулем. Применяя формулу A.7) к функции
получим
, Q to cosajt a/f. ni-af '~a A -Qa@^ /a q\
+ T~"? —?(?--1) J p— . F.8)
0
Определение постоянных. Уравнения F.1) и F.8)
содержат две неизвестные постоянные: Q\ и р. Величина Q яв-
является заданной, она выражается через глубину h потока на
бесконечности слева:
¦— = h sin an cos an. F.9)
§ 6] ДРЕНЫ И КАНАЛЫ В СЛУЧАЕ НАКЛОННОГО ВОДОУПОРА 235
Точно так же имеем, обозначая через hx глубину потока справа
на бесконечности:
"?- = /*! sin ал; cos ая. F.10)
Условия z (оо) = 0, ср = Ф = 0 и 2 A/р) = /, ф = 0, -ф = Q — Q{ дают
1
t, F.11)
^r. F-12)
о
С. Н. Нумеров, считая заданным р, а искомыми h и h\> пере-
переписывал последние равенства в виде системы двух уравнений,
линейных относительно h и h\. Для облегчения вычислений ко-
коэффициентов этих уравнений он дал ряд упрощенных формул.
В. Н. Эмих и Е. М. Эмих A968) предложили другой способ
вычислений. По формулам F.9) и F.1Q) можно ввести h и h\
вместо Q и Qi и разрешить F.11) относительно h\\
- <613>
Внося выражение F.13) в F.12), получим / как функцию от па-
параметра р (при заданном К)\
Z = F(P). F.14)
На ЭВМ из этого уравнения при заданных h и / можно найти р,
причем доказана однозначная разрешимость этого уравнения.
С помощью уравнения F.1) можно написать уравнения вет-
ветвей свободной поверхности. Для правой ветви
Ф 2Q ,1 2Q,
= —~ = -^-arch —7= ^
k nk Vpi я*
/ 1 — 6
л К
Vf(g-
Приравнивая нулю производную по I
dy = 1 (ц__ Qi УГ^ТЛ
-Р5 V I 6-1 /
d\ jxAjVi -Р5 V I 6
236 СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ [ГЛ. VI
и имея в виду, что Qx :Q = Aj :А, найдем
Превышение отметки максимума над горизонтом воды в дрене
F.17)
В силу условия для ?тах заключаться в промежутке A,
имеем
откуда получаем неравенство
fn Vl - р #
Точно так же для левой ветви депрессионнои кривой в слу-
случае фильтрации из канала получаем значение минимальной
ординаты
_, 2Qi « л I Vl — Р (Aj Vl — Р — h) ,a ло\
+ ltFarch v h$— FЛ8)
при условии
Случай малого уклона. Если угол ая мал, то ряд
формул можно упростить. А именно, положим
tgcwi = / F.19)
и обозначим через Qo = Q — Q\ фильтрационный расход еди-
единицы погонной длины дрены. Положим также
Тогда получаются приближенные равенства:
Ус 1 f^, fp п /^. t л—2v U —. ^' >»^ 71 /Л 01 \
л » г ' j fe sin ая cos ая v y
§6] ДРЕНЫ И КАНАЛЫ В СЛУЧАР НАКЛОННОГО ВОДОУПОРА 237
Далее, найдены приближенные значения экстремальных
ординат депрессионной кривой при малых ал:
-»«5 [
причем h* = h/T > eY,
*-~ 1 [тarchV г--* -archV^d-e-v) J•
причем й* < e-v. Отсюда следует, что при /г* > ^ имеем случай
всестороннего притока грунтовых вод к дрене, при h* < e-Y —
случай фильтрации из канала в грунт. Для е-ч ^.h*^e^ имеет
место случай рис. 160.
Для внешней и внутренней ширин щели Ь и Ь\ (рис. 156) по-
получены приближенные выражения
*»«x(is— 0' <6-22)
где
F.23)
Формулы F.22) являются точными в случае одиночной дрены
в безграничном массиве грунта, что видно из формулы C.11)
главы IV (в которой Q соответствует нашему Qq)%
При Ь\ = 0 имеем б = 2/я, поэтому здесь
«0,262 ^. F.24)
По формулам F.22) найдем разность
26
Щ\ , , г - - arccos б]. F.25)
k I jt(Vl-62+ 1) я J v
Производная этого выражения положительна:
д(Ь-Ьх) _ Qo 1 - л/Т=У п (д_я №\
Следовательно, при заданном приведенном расходе дрены
разность между ее внешней и внутренней шириной уменьшается
с ростом внутренней ширины. Наибольшее значение этой разно-
разности будет при Ь\ = 0, оно равно 0,262Q0/fe. В случае фильтрации
воды из дрены в грунт имеем Ь = Ь\.
Рассмотрим частный случай: фильтрацию из канала при от-
отсутствии естественного потока (рис. 162). В этом случае Q = 0.
СМЕШАННАЯ ЗАДАЧА ТЕОРИИ ФУНКЦИЙ
[ГЛ. VI
Рис. 162.
Рис. 163.
Рис. 164.
§ 6] ДРЕНЫ И КАНАЛЫ В СЛУЧАЕ НАКЛОННОГО ВОДОУПОРА 239
Найдем границу распространения подтопления каналом L и от-
отметку Н кривой депрессии на этой границе. Рассматривая про-
промежуток —оо < ? ^ 0, напишем с помощью F.8), учитывая,
что на свободной поверхности ф = —kyy
х = — Т ctg cut —
-!&«»«*<-0" 0 -i)'ir°(l -/Г1 arsh
^_,
Положив t = — ?т под знаком интеграла в выражении для х
и переходя к пределу при ?->0, найдем
L, = Т ctg ая + -^- ctg ая arch
nk
H =
l — В 2Qi
Другой частный случай: приток к горизонтальному фильтру
(рис. 163). Здесь имеем 6 = оо, Ql = 0i p=l, поэтому фор-
формулы F.1) и F.8) дают
2Q , 1 .^
(о= —arch—j=r — rQ,
г = — T ctg ая + —¦ + -т-arch —j= +
Уравнение ветви свободной поверхности получим, полагая
? = i и рассматривая ? в промежутке (—со, 0):
х = — Т ctg ая —
Для ширины верхней части щели &ф найдена приближенная
формула
На рис. 164 дана фотография эксперимента в щелевом лотке
^Р фильтрации из канала над наклонным водоупором
(В. Н. Эмих и Е. М. Эмих 1968).
Глава VII
ПРИМЕНЕНИЕ АНАЛИТИЧЕСКОЙ ТЕОРИИ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
А. ОБЩАЯ ТЕОРИЯ
§ 1. Вводные замечания. Как известно (Полубаринова-Ко-
чина 1938), идею применения к задачам о движении грунтовых
вод аналитической теории линейных дифференциальных урав-
уравнений дал Н. Е. Кочин. Эта мысль была принята за основу ме-
метода, развитого в работах автора A938—1939), а также
Б. К. Ризенкампфа A940, 1). Метод был применен к решению
задач о фильтрации в земляных плотинах: в прямоугольной пе-
перемычке и плотине, поперечное сечение которой представляет
прямоугольную трапецию. В случае более сложных плотин при-
приходим к дифференциальным уравнениям с большим числом па-
параметров, подлежащих определению, что затрудняет эффектив-
эффективное применение метода. Эта трудность аналогична той, с кото-
которой встречаемся, применяя формулу Кристоффеля — Шварца
к многоугольнику с большим числом сторон.
С помощью аналитической теории дифференциальных урав-
уравнений удалось решить несколько задач о линзах пресной воды
над засоленной грунтовой водой, а также несколько задач о
фильтрации в двух грунтах различной водопроницаемости (см.
главу VIII).
§ 2. Условия на действительной оси для двух основных функ-
функций. В главе II были рассмотрены условия на границах, которые
являются отрезками прямых и депрессионными кривыми. Мож-
Можно заметить (см. § 2 главы II), что все эти условия представ-
представляются или в виде равенства нулю линейных функций от коор-
координат (уравнения прямых) или линейных функций от коорди-
координаты и потенциала скорости или функции тока. Другими сло-
словами, на каждой из границ контурные условия могут быть пред-
представлены в виде двух уравнений вида
k\x + lxy + юкр + nrf = Р>\ /2 1)
k2x + l2ij + m2^ + n2^ = q9 )
где коэффициенты суть постоянные.
§ 2] УСЛОВИЯ НА ДЕЙСТВИТЕЛЬНОЙ ОСИ ДЛЯ ДВУХ ФУНКЦИЙ 241
Уравнения B.1) можно записать, пользуясь знаком мнимой
части функции Im в таком виде:
Im (kz + /со) = р, Im (mz + ам>) = q. B.2)
Здесь k, ly ту п— комплексные, р и q — действительные числа.
Можно проверить, что для всех границ, которые мы рассмо-
рассмотрели, определитель
k l
т п
отличен от нуля, за исключением одного совершенно частного
случая инфильтрации на свободной поверхности, когда интен-
интенсивность инфильтрации е равна коэффициенту фильтрации
грунта (см. формулу B.10) главы II).
В дальнейшем будем отображать область движения и об-
область комплексной скорости на полуплоскость вспомогательной
комплексной переменной ?. При этом границы области перей-
перейдут в отрезки действительной оси плоскости ?; поэтому значе-
значения ?, соответствующие контуру области движения, будут дей-
действительны.
Продифференцируем B.1) или B.2) по действительной пе-
переменной ? и введем обозначения
F — *Ш 7 — — f 9 Ч\
t - df Z - df ^
Тогда вместо условий B.2) получим однородные условия сле-
следующего вида:
Im (kZ + IF) = 0, Im {mZ + nF) = 0. B.4)
Именно исходя из них и удается построить всю теорию, разви-
развиваемую в настоящей главе.
Уравнения B.4) показывают, что величины kZ-\-lF и mZ +*
-f nF принимают действительные значения на соответствующем
отрезке действительной оси. Но тогда и отношение этих величин
будет принимать только действительные значения, так что мож-
можно написать, например, такое равенство:
•1ли, разделив числитель и знаменатель на Z,
242 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
Замечая, что
F dca # dz d®
Y~ir:~di'^"d7
получаем уравнение
Это уравнение определяет на плоскости w окружность. В са-
самом деле, дробно-линейное преобразование w\ = (k + to)/(m+
+ nw) переводит окружность плоскости w в окружность пло-
плоскости W\ и обратно. Но это преобразование переводит уравне-
уравнение B.5) в уравнение Im w\ = 0, т. е. в уравнение действитель-
действительной оси плоскости о>ь которая является окружностью в обоб-
обобщенном смысле и переходит, следовательно, в некоторую окруж-
окружность плоскости w-
Непосредственно видно, что окружность B.5) проходит че-
через точки w = —k/l и w = —т/п.
§ 3. Задача определения двух функций по условиям на дейст-
действительной оси. Пусть функции F и Z комплексной перемен-
переменной ? удовлетворяют на отрезках действительной оси условиям
вида
Im (ksZ + 1SF) = 0, Im {msZ + nsF) = 0 {s = 1, 2, ..., n). C.1)
Возьмем два соседних участка М\М2 и М2М3 оси ? и выпи-
выпишем относящиеся к ним условия (рис. 165): \m(k\Z-\-l\F) =0
и Im(tri\Z + n\F) = 0 на М\М2, lm(k2Z + 12F) = 0 и \m(m2Z +
+ n2F) = 0 на М2МЪ.
Рис. 166.
Покажем, что F и Z при обходе особой точки, например М2,
претерпевают линейную подстановку.
Продолжим функции на нижнюю полуплоскость и применим
принцип симметрии Шварца в его простейшей форме: если
функция f(z) аналитична в области G, примыкающей к действи-
действительной оси, и непрерывна вплоть до отрезка АВ, причем на от-
отрезке АВ имеется условие Im/(z) = 0, то f(z) может быть про-
продолжена в нижнюю полуплоскость так, что в сопряженных точ-
точках функция принимает сопряженные значения (рис. 166). Дру-
§ 3] ОПРЕДЕЛЕНИЕ ДВУХ ФУНКЦИЙ ПО УСЛОВИЯМ НА ОСИ 243
гими словами, если мы в нижней полуплоскости возьмем точку
z*, причем г* = z = х — iy, то получим, обозначая через /*
значение аналитического продолжения, что
П**) = Ш- C.2)
Применим это правило к линейным комбинациям Z и F, вхо-
входящим в условия на отрезке М\М2. Сделаем надрез вдоль от-
отрезка М2М$ и обозначим соответствующие точки на верхней и
нижней сторонах разреза через Мг и М" (рис. 165). Значения
функций F и Z после обхода особой точки M2i когда мы попа-
попадаем в точку М", обозначим через F* и Z*. Тогда на основании
равенства C.2) будем иметь
kxZ* + 1XF* = k{Z + i\F, mxZ* + nxF* = mxZ + n,F. C.3)
Перепишем условия на отрезке М2М3 в виде
k2Z + 12F — k2Z — 12F = 0, m2Z -\-rhF — m2! — n2F = 0. C.4)
Из уравнений C.4) и C.3) можно исключить F и Z. Тогда полу-
получим зависимость Т7* и Z* от Т7 и Z вида
= aZ+pr, г =YZ+or. C.5)
Итак, функции F и Z действительно претерпевают линейную
подстановку при обходе вокруг особой точки.
С помощью характеристического уравнения (Смирнов 1969)
= 0 C.6)
a-Я
можно привести C.5) к каноническому виду. Это значит, что
существуют функции U и У, претерпевающие при обходе особых
точек подстановку
U* = h'U, V*=*V'V, C.7)
где А/ и А," — корни характеристического уравнения, причем F
и Z являются линейными комбинациями этих функций.
Равенство C.7) имеет место, если А/ не равно А,". В случае
кратного корня уравнения C.6) каноническая подстановка
имеет вид
U* = XV, V* = aU In ? + k'V. C.8)
Введем числа а7 и а", полагая
a — 2я/ • a ~ 2ш '
Пусть точке М2 соответствует значение 5> равное go- Функции
244 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
при обходе особой точки ?0 в положительном направлении на
угол 2я переходят соответственно в
(С - ?о)а" = Я" (С
отношения же
E - ?о)а' ' (С - ?о)а"
при этом не претерпевают изменений, т. е. остаются однознач-
однозначными функциями. Следовательно, они могут быть представлены
рядами Лорана около ? = ?0. Для U и V получаем поэтому
-?о)а' Z
(ЗЛО)
Z "
Если %' = АЛ, то первое выражение сохраняется, второе же бу-
будет, вообще говоря, содержать 1п(? — ?о):
K-ot/intt-bo + t/ z ^(c-w*. (зло
ft = —оо
Если ряды Лорана в формулах C.10) и C.11) содержат
лишь конечное число членов с отрицательной степенью ? — ?о>
точка ?0 называется регулярной особой точкой. Так как показа-
показатели а! и а" определяются формулами C.9) лишь с точностью
до целых слагаемых, то можно изменить их значения так, чтобы
в этом случае степенные ряды не содержали членов с отрица-
отрицательной степенью ? — ?о-
Можно представить каноническую систему функций U и V
в окрестности регулярной особой точки ? = ?0 в следующем
виде:
; C.12)
V = (?-?</'? MS - ?o)ft + а?Лп (? - i
fe-0
причем по и &о отличны от нуля. Если а' — а" не есть целое
число или нуль, то следует считать a = 0.
Для упрощения характеристического уравнения C.6) заме-
заменим функции Z и F их линейными комбинациями, положив
Z, == k2Z + У7, F{ = m2Z + n2F. C.13)
Тогда на отрезке М2МЪ будем иметь
ImZ! = 0, ImF1 = 0. C.14)
ОПРЕДЕЛЕНИЕ ДВУХ ФУНКЦИЙ ПО УСЛОВИЯМ НА ОСИ
245
На отрезке МХМ2 получим условие того же вида, что и раньше,
но с другими коэффициентами. Положим, что на М\М2
lFl) = 0, lm(mZl+nFl) = 0. C.15)
Тогда уравнения C.3) и C.4) упростятся:
откуда
kn — ml ,
kn — ml
km — km
In —In
kn — ml J
kn — mi
C.16)
1 kn — mlllkn — ml
Характеристическое уравнение будет иметь вид
kn — ml л in — in
kn — ml
km — km
kn — ml
kn — ml
kn — mi
kn — ml
= 0.
C.17)
Корни этого уравнения А/ и Я" должны совпадать с корнями
уравнения C.6), так как Z\ и Fu как линейные комбинации Z
и F, должны принадлежать тем же показателям. По найденным
V и Я" с помощью C.9) определяются показатели а7 и а".
Рассматривая поведение функций со(?) и z(?) около особых
точек области движения (см. ниже § 8), можно убедиться в том,
что все встречающиеся в наших задачах о движении грунтовых
вод особые точки являются регулярными особыми точками
функций F = dajdl и Z = dz/dt,.
Из аналитической теории линейных дифференциальных ура-
уравнений известно (Смирнов 1969; Голубев 1950), что две линейно
независимые функции U и У, имеющие точку ?0 регулярной осо-
особой точкой, т. е. представимые вблизи этой точки в форме
C.12), являются системой решений линейного дифференциаль-
дифференциального уравнения
= 0, C.18)
C.19)
где p(Q и q(?) имеют вид
(C —Co
Здесь р\ (?) и q\ (Z) — функции, регулярные в точке ?0, т. е. раз-
разлагающиеся в ряды по целым положительным степеням ? — ?0-
Функции Z и F имеют каждую из особых точек регулярной
особой точкой и могут быть представлены в виде линейных ком-
комбинаций двух линейно независимых решений уравнения C.18)
246 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
с коэффициентами вида C.19). Уравнение C.18), все особые
точки которого являются регулярными, называется уравнением
класса Фукса (Смирнов 1969; Голубев 1950).
§ 4. Уравнение с тремя регулярными особыми точками.
В этом случае можно полностью построить линейное дифферен-
дифференциальное уравнение задачи.
Можем считать согласно сказанному выше, что на плоскости
? особыми точками являются 0, 1 и оо.
Предположим, что один из показателей у каждой из особых
точек на конечном расстоянии равен нулю. Другими словами,
пусть показатели около особых точек будут: 0 и а около ? = 0,
0 и р около ? = 1, у и у' около ? = оо, причем а, р, y и у' — дей-
действительные числа. Ветвь аналитической функции У, принадле-
принадлежащей этим показателям, обозначим с помощью символа Ри-
мана Р:
@ 1 оо )
Y = P\O oY 5 . D.1)
U P Y' )
Дифференциальное уравнение для У имеет вид (Уиттекер и
Ватсон 1962; Голубев 1950)
^)^ 0. D.2)
При этом сумма всех показателей должна равняться единице
(соотношение Фукса)
D.3)
Обозначим через ?/, V фундаментальную каноническую си-
систему решений уравнения D.2) около точки ? = 0:
D.4)
Около точки ?=1 систему линейно независимых интегралов
примем в виде
~ D.5)
Около ? = оо можно принять фундаментальную систему ре-
решений в виде
+*+*+¦••).
§4]
УРАВНЕНИЕ С ТРЕМЯ РЕГУЛЯРНЫМИ ОСОБЫМИ ТОЧКАМИ
247
Будем считать для простоты аир отличными от целых чи-
чисел и нуля. Коэффиценты пи #2, • • •, Ьи &2, • • •, Си 42, ... рядов
D.4) — D.6) —действительные числа. При этом ряды D.4) схо-
сходятся в круге Со (рис. 167) с центром в точке ? = 0, проходя-
проходящем через ближайшую особую точку, т. е. ?=1; ряды D.5)
сходятся в круге Сь для которого |?— 1| < 1; ряды D.6) схо-
сходятся для |?| > 1, т. е. вне круга Со.
Уравнение D.2) связано с задачей о конформном отображе-
отображении кругового треугольника на полуплоскость. Для того чтобы
это показать, составим функцию
V ?а A + ait, + ...) (Л7\
где |и — заданная вещественная постоянная. Для определенно-
определенности будем считать аир положительными.
Рис. 167.
Рис. 168.
Для ? = 5 @ < | < 1) функция w принимает действитель-
действительные значения; значит, w при этом пробегает некоторый отрезок
оси абсцисс. При ? = % < 0 имеем (считая arg ? = О при ? =
= g>0): ?a = enia(—g)a. Следовательно, w пробегает точки
отрезка прямой АС (рис. 168).
Дробно-линейное преобразование
AU + BV
Bw
cu + dv
переводит прямые в окружности, и, следовательно, в окрестно-
окрестности точки ? = 0 некоторому отрезку действительной оси ? = |
отвечают дуги пересекающихся окружностей.
Для рассмотрения окрестности особой точки ? = 1 перейдем
от системы функций U, V к системе f/i, V\ с помощью вспомога-
вспомогательной подстановки
qVu V — rUx + sV{.
D.9)
248 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
С помощью D.9) можно переписать D.7) так:
Рассуждения, аналогичные предыдущим, показывают, что в
точках i = 1 и ? = оо также получаем пересечения дуг окруж-
окружностей. Имеет место теорема: функции вида D.7) или D.8) пре-
преобразуют конформно верхнюю полуплоскость в круговой тре-
треугольник, не имеющий внутри точек разветвления.
§ 5. Гипергеометрические функции и их свойства. Гипергео-
Гипергеометрической функцией называется функция
r-i/ ¦• \ * \ 0,0 \ CL \(Х -т- 1 ) О \ О "т* 1 ) 9 i /г* а \
F(а, Ь, с, х) = 1 + — х + \.2.с(с+\) х + • • • (б-1)
Она является частным решением следующего уравнения:
хA - x)Y" + [с - (а + Ъ + 1)х] Г - abY = 0, E.2)
называемого уравнением гипергеометрического ряда. Уравнение
E.2) получается из D.2), если положить у = а, у' = Ь, а =
= 1 — с, р = с — а — 6, с учетом соотношения D.3). Всякое
решение этого уравнения выражается с помощью символа Ри-
мана (Смирнов 1969; Голубев 1950):
•0 оо 1
0 а 0 х \. E.3)
1-е Ь с — a — b
Отметим свойство символа Римана для любого числа особых
точек. Пусхь
( а, а2 ... ап оо ч
= P< оц «2 ... ап а х >.
I в в, ... в„ в )
E.4)
Р
Если в выражении У выделим множитель (х — ai)?, то во вто-
втором множителе показатели около точки х = а\ уменьшатся на
р и будут, следовательно, а\ — р, Pi — р, а около бесконечно да-
далекой точки показатели увеличатся на ру так что вместо аир
будем иметь а + Р, Р + Р- Другими словами,
а,
Р.
по ...
а2 ...
Р2 ...
ап о
Рм м
х \ =
г п\ а2 ... ап оо ч
а,-р а2...а,г а + р Л
I В. — о Во ... В« В + о J
00
E.5)
§ 5] ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ СВОЙСТВА 249
В частности, можно с помощью этого преобразования получить
функцию Римана, имеющую по одному равному нулю показа-
показателю около каждой особой точки на конечном расстоянии.
Пользуясь символом Римана, можно отыскивать другие ре-
решения гипергеометрического уравнения. Так, для получения ре-
решения уравнения E.2) около х = 0, отличного от F(a,b9 с9х)9
выделим множитель хх~с в E.3). Получим
/ О ОО 1 ч
Y = x]-cP< с— \ а+\— с О х\ =
О оо 1ч
О а+\-с О х I. E.6)
с — \ 6 + 1 — с с — а — b )
Выражение, являющееся множителем при xl~c9 есть гипергео-
гипергеометрическая функция, в которой первыми аргументами являют-
являются показатели на бесконечности а + 1 — с и b + 1 — с9 третий
же аргумент представляет дополнение до единицы отличного от
нуля показателя при х = 0. Таким образом, получаем
Y = x]'cF(a+l -с9 Ь+ 1 -с9 2-с9 х).
Эта функция линейно независима с F(a9 b9 c9 x), поэтому в каче-
качестве фундаментальной системы решений около х = 0 для урав-
уравнения E.2) мы имеем
U = F{a9 Ь9 с9 х)9 V=x'-cF{a+l-c9 b + I - с9 2 - с9 х). E.7)
Аналогично можно найти системы решений около особых точек
х = 1 и х = оо:
1— (а9 , а+ —с+ , — х)9 1
F/1 \С — п — и r> i I fill 41^'
1 = A — л:) F(с — а9 с — Ь9 с — а — b + \9 1 — х)\ )
b-c+\9 6-a + l, 7).
Ряды E.7) сходятся при |х|<1, ряды E.8) при \х—1|<
< 1, ряды E.9) при |*| > 1.
Замена х соответственно на 1-х, \/х9 1/A—х), (х—1)/*
и х/(х— 1) меняет коэффициенты уравнения, но сохраняет в ка-
качестве особых точек 0, 1 и оо.
Отсюда можно найти новые формы интегралов уравнения
E.2). Вместе с уже указанными получаются 24 формы-Куммера.
250
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ. VII
Между различными ветвями гипергеометрической функции
существует линейная зависимость, выражаемая вспомогатель-
вспомогательной подстановкой вида D.9). Так,
F(atb9 c,z) = pF(a, b,a + b+\-c, 1
E.10)
zl'cF(a+l -с, b+ 1 -с, 2-е, z)=
где
Г (с) Г (с - а - Ь)
Т(с-а)Т{с-Ь) '
Т(с)Т(а + Ь-<
Г~~ Т(а)Т(Ь)
_TB-c)T(c-a-b) _ Г B - с) Г (a + b - с)
Г~" Г A-a) Г A-6) ' 5~~ Г(а + 1 _
E.11)
Если с — а — ft > 0, то гипергеометрический ряд сходится при
г=1. Поэтому из E.11) для этого случая получаем
F(a Ь С 1)аГ(с)Г(с-а-6)
а) Г
E.12)
§ 6. Общий случай кругового многоугольника.Предположим, что имеем
круговой многоугольник, т. е. многоугольник, ограниченный дугами окружно-
окружностей
F.1)
Углы в вершинах многоугольника обозначены через паи яа2, • • •v+
Отобразим его конформно на верхнюю полуплоскость вспомогательного ком-
комплексного переменного ?. Пусть вершины многоугольника переходят в точки
вещественной оси а3 (s = 1, 2, ..., v -f 1), причем пусть av+1 = оо. Если вы-
выберем произвольно аффиксы еще двух точек а8у то положение остальных то-
точек будет вполне определенным (но заранее неизвестным) для данного мно-
многоугольника.
Функцию w можно представить в виде отношения двух линейно неза-
независимых частных решений дифференциального уравнения
Y".
1 — а2
1 — av
(С — «О (С — «2> ... (С — «v)
F.2)
Здесь oti, аг, . •., av суть деленные на я углы в вершинах многоугольника,
переходящих при конформном отображении в точки вещественной оси ?> ле-
лежащие на конечном расстоянии, av+1 и а^+1 таковы, что
F.3)
§ 6] ОБЩИЙ СЛУЧАЙ КРУГОВОГО МНОГОУГОЛЬНИКА 251
есть угол при вершине, переходящей в точку ? = °°). При этом между
числами as (s = 1, 2, ..., v), a^,+1 и av+1 должно выполняться соотноше-
соотношение Фукса
"
а, + а2 + ... + av + с^+1 + а"+1 = v - 1. F.4)
Здесь v — число особых точек, находящихся на конечном расстоянии от на-
начала. Наконец, величины Х\, Я2,..., A,v-2 в уравнении F.2) представляют
так называемые акцессорные параметры, которые заранее не известны. В слу-
случае кругового треугольника эти параметры, как мы видели, отсутствуют, что
и облегчает решение задачи.
Обозначим линейно независимые интегралы уравнения F.2) около точ-
точки а8 через Ua и Va. Тогда величина w будет дробно-линейной функцией
от них:
AUS + BVS
W~ CUS + DVS' F'5)
где Л, В, С и D — постоянные.
Рассмотрим частные случаи круговых многоугольников.
1. Треугольник. Вернемся к треугольнику рис. 168 и выясним связь
постоянной [I в формуле D.7) с размерами треугольника ABC (рис. 168),
которые можно выразить через отрезки а и т.
Прежде всего отметим, что произвольный круговой треугольник с отлич-
отличным от нуля углом яа можно с помощью дробно-линейного преобразования
перевести в треугольник с двумя прямолинейными сторонами вида рис. 168.
При этом уравнения сторон АВ и АС можно записать соответственно в виде
Imoy = O. 1т(ея'аш) = 0, F.6)
а уравнение окружности ВС в виде
Для рассматриваемого треугольника имеют место уравнения D.7)" и D.9),
причем р, ду г, s и [х — действительные числа.
Если перейти с отрезка @, 1) плоскости ? на отрезок ?> 1, то там
функция Vi уже не будет иметь действительных значений. Можно положить
V\ = e~nt^Vf. где функция V имеет действительные значения при ?>1.
Тогда получим
grc'P (ю - or) = gttfg (цг - pa) U{ + ([is - да) Vf
су - т """ (цг - рх) U, + (\is - дх) e~mVr '
Если выполняется уравнение F.7), то необходимо должны одновременно
выполняться равенства
Im [еш ([хг - рх) (цг - рог)] = О,
Im И3 ([is - qx) ([is - да)] = О,
Im \e7ni* ([ir - pa) (ps - gx)] — 0
Так как ps — gr = 0, то одновременно \ir—pa = 0 и [is — gx = 0, от-
кУДа для \х получаем два выражения: [х = gx/s и [х = ра/r. Для совместности
этих равенств необходимо, чтобы
^—^. F.8)
a gr N
252
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
В теории гипергеометрических функций выводится соотношение
_ps_ sin я (а + у) sin я (ft + у)
qr sin яу sin яу'
С другой стороны, рассматривая треугольник ЛВС, найдем для косинуса
угла при вершине С
a cos я (а — ft) — т cos я (а + ft)
т — а
cos я (у — у') =
F.9)
F.10)
Решив последнее уравнение относительно т/а, получим выражение, стоящее
в правой части F.9), что и доказывает справедливость тождества F.8).
Уравнение D.7) дает вполне
определенное (и единственное со-
согласно теореме Римана о кон-
конформном отображении) выраже-
выражение функции, отображающей
треугольник ABC на полупло-
j,, уду• VwJ^ скость так, чтобы вершины его
X -т*-Гп перешли соответственно в точки
О, 1, оо.
2. Четырехугольник.
Аналогичным образом можно рас-
рассмотреть четырехугольник с не-
неравными нулю углами. С по-
помощью дробно-линейного преоб-
преобразования переведем его в четы-
четырехугольник, две смежные сторо-
стороны которого суть прямые. Пусть
это будет четырехугольник, представленный на рис. 169. Напишем уравнения
его сторон в форме
F.11)
Рис. 169.
Im w = 0, Im {e~niaw) = 0,
Im
-0. F.12)
Для отыскания функции, дающей конформное отображение внутренности
нашего четырехугольника на верхнюю полуплоскость ? с переходом точек А,
В, С и D плоскости z соответственно в точки 0, 1, о и оо плоскости ?, соста-
составим линейное дифференциальное уравнение второго порядка
1 -а
1-1
1 —-
бб- (с - Я)
Г=0. F.13)
Это уравнение определяет функцию, две ветви которой имеют около осо-
особых точек показатели, соответственно равные 0 и .а около ? = 0, 0 и Р около
? = 1, 0 и у около ? = а, у и у' около ? = оо. Эти показатели должны
удовлетворять соотношению Фукса ос + |3 + у + 6 + 6'=2.
Уравнение F.13), в отличие от уравнения, соответствующего треуголь-
треугольнику, кроме заданных параметров а, C, у, 6 и 6' содержит еще два неизвест-
неизвестных параметра а и Я, которые зависят как от углов данного четырехуголь-
четырехугольника, так и от других параметров, определяющих этот четырехугольник. По-
Поэтому нужно получить два соотношения, могущих послужить для определения
а и X.
Фундаментальные канонические системы решений уравнения F.13) обо-
обозначим соответственно через (U, V), (Ui} Vi), (Ua, Va), (?/», V\»). Коэффи-
§ 6] ОБЩИЙ СЛУЧАЙ КРУГОВОГО МНОГОУГОЛЬНИКА 253
циенты рядов для этих функций будут теперь зависеть не только от показа-
показателей, но и от а и Я.
Функция, отображающая конформно рассматриваемый четырехугольник
на полуплоскость, имеет около точки ? = О вид D.7). Подстановка этого вы-
выражения в первое из уравнений F.12) приводит к двум выражениям для \i:
|л = pxjs и \i = pojs. Для того чтобы эти выражения совпадали, необхо-
необходимо выполнение соотношения
которое теперь представляет уравнение, также содержащее неизвестные а и X.
Для того чтобы получить еще одно уравнение между а и X, обратимся
к неиспользованному еще нами последнему из уравнений F.12) четвертой
стороны четырехугольника. Для этого перейдем от системы (U, V) решений
около точки ? == 0 к системе решений (Ua, Va) около точки 1 = а. В рас-
рассматриваемом случае а < О, т. е. отрезок (а, 0) лежит влево от точки ? = 0.
Поэтому на отрезке (а, 0) решение U имеет действительные значения, а ре-
решение V имеет вид V = eniaV , где функция V принимает только действи-
действительные значения. Вспомогательная подстановка, переводящая (U, V) в
(Ua> Va), имеет вид
V = PcVa + ЯсУа « Pj>a + Яа
V - enla (raUa + saVa) = e*ia (raVa
где коэффициенты ра, qa, ra и sa—действительные числа. Вторые равенства
относятся к значениям ? < а, для которых функция Va имеет действительные
значения.
Так как согласно D.7)
Яе^(гаиа
U+
то последнее из уравнений F.12) дает
Im Г e"'V ((ir" ~ VlPa) Ua + ((iSfl " а2"а) Va 1 0
L (цла - т2ра) Ua + (ц8а - xaqa) e^V'a J
Отсюда вытекает необходимость выполнения условий \хга — а2ра = 0 и
\xsa — т2^а = 0, т. е. равенств для ц: ц == paor2/rfl = <7aT2/sa. Это дает нам
уравнение
которое вместе с F.14) образует систему двух уравнений для определения
значений X и а.
Заметим, что в случае четырехугольника уравнение, соответствующее
Уравнению F.10) для треугольника, имеет вид
соэя F — 6') = ai%2 cos л (а + Р — У) + cr2Ti cos я (а — Р + у) _
(CTi — Т,)(ОГ2-Т2)
_giT1cosjt(a+ B +у) + cr2T2cosn(a — р — у) + 2 (а^ + tit2) sin яр sin яу
— Т2)
254
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ. VII
Некоторые свойства конформного отображения четырехугольника рассмо-
рассмотрены в специальных работах (Смирнов 1918; Heun 1899).
3. Многоугольники с разрезами. Во многих задачах теории
фильтрации на годографе скорости имеются разрезы. Для примера рассмо-
рассмотрим пятиугольник рис. 170. Обозначим через D конец разреза. Около точки D
угол многоугольника равен 2я, следовательно, показатели около этой точки
можно принять равными @,2). В этом слу-
случае можно найти алгебраическое уравнение,
связывающее параметры задачи.
Поясним это на простейшем случае кру-
Я(8-г)^~№>( \ гового четырехугольника с разрезом. Соответ-
Соответствующее ему дифференциальное уравнение
F.2) перепишем в виде
В
Рис. 170.
1 (?-а) (?-&)(?-с) ~' VW-1V"
Пусть точка ? = с соответствует вершине D четырехугольника, так что
С = —1; одной из его вершин пусть отвечает ? = оо. При этом
/?(?)—?(?- %) = Е1 + Е0, Е = ъ'г", F.17)
так что я(е' — е") есть угол при вершине, удаляемой на бесконечность.
Обозначив коэффициенты уравнения F.16) через /?(?) и q(t>), напишем
~г* Р \ъ) * "Т" Q \ъ) •* ==5 ^* ^o.loj
Составим дифференциальное уравнение для производной У = W. Его
можно представить в виде
W" + P(t)W + Q (g) W — 0, F.19)
причем
~-q + p' -P-. F.20)
Канонические интегралы для Y около точки ? == с имеют вид
Yx = а0 + «1 (Е — с) + а2 (I — сJ + ..., F.21)
Y2 = b2(t)- сJ + ЬгA- с)ь + ..., F.22)
причем а0 Ф 0, Ь^Ф 0, ai # 0. Последнее неравенство видно из непосред-
непосредственной подстановки ряда F.21) в уравнение F.16).
Логарифм 1п(? — с) в выражении У2 отсутствует. Действительно, най-
найдется дробно-линейное преобразование
Wx~~ kYx+lY2 '
переводящее разрез, составленный дугой окружности, в прямолинейный раз-
разрез (рис. 170). Но около точки D разложение функции ач должно иметь вид
Wi = (? — сJР(?>—с), где Р(? — с)—аналитическая функция, что было бы
невозможно, если бы У2 содержала 1п(? — с).
Из выражений F.21) и F.22) следует, что около ? = с интегралы урав-
уравнения F.19) принадлежат показателям @, 1), другими словами, ? = с теперь
будет обыкновенной точкой.
6] ОБЩИЙ СЛУЧАЙ КРУГОВОГО МНОГОУГОЛЬНИКА 255
Имея в виду, что
p(g l-a ^l-b^ 1-е' q (t_e)
?? + ?„ = ?(? -Я,),
составим выражения для Р (?). Q (?) (считаем пока Е Ф 0):
lw E - в) (Е - *) E - с) i~
Д [/?'(?) 1 ! 1 С Г R'(Z) 1 1_Т
E-*L«(C) 5-в S — 6J 5-cL /?E) С-о 5-6J-
В рассматриваемом нами случае С = —1 и точка ? = с не должна быть
полюсом коэффициента Q(?) уравнения F.19). Поэтому
-a F.23)
Иначе говоря, получаем квадратное уравнение для акцессорного параметра
_4^Il^y+7J-x + ^-+|^ = 0. F.24)
Если Е = О, то имеем уравнение первой степени для акцессорного пара-
параметра Ео'.
(с — а) (с — Ь) с —а с — Ь
Оно может быть получено переходом к пределу при Х->-оо, причем
—ЕХ = Ео.
В задачах о фильтрации в земляных плотинах годограф скорости имеет
5, 7 и т. д. особых точек, с одним, двумя и большим числом разрезов. Усло-
Условие для конца разреза получается аналогично F.25). Если принять с = 0 и
заметить, что А = 1 — а, В = 1 — р, то уравнения F.24) и F.25) примут
особенно простой вид
Отметим еще случай пятиугольника, для которого вместо F.16) будем
*ть упявнение
иметь уравнение
F'27)
Будем считать D = —1. Полином /?(?) можно представить в одном из
Двух видов:
R (О = ? (С - *1) F - Я2), Я (С) = ^S2 + ?,С + ^о
Условие в точке ?> = rf может быть записано в следующей форме:
R (d) ^W , Л-1 , В— 1 . С-1
(d - a) (d - b) (d - с) "*" R(d) ~*~ d - а ~*~ d - b ~*~ d - с и<
256 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ (ГЛ. VII
Полагая А = 1 — а, В = 1 — р, С = 1 — у, Я = ее' и раскрывая R (d) и
R' (d), можем записать его в виде
es'(d — \i)(d — X2) 1 1 а
"Г '
(d — a) (d — b) (d — с) ~ d - X{ ~ d - Я2 d - а
--^Т~-^7 = 0. F.28)
При ее' = 0 будем иметь другую форму:
Eid + Ep Ег а g у_
(d - a) (d - b) (d - с) ^ E{d + Ео d-a d — b d - с
Наконец, приняв d = 0, получим соответственно
Недавно А. Р. Цицкишвили A973, 1974) предложил для общего случая
кругового многоугольника применить теорию сопряжения для нескольких не-
неизвестных функций (Н. П. Векуа 1970) и теорию И. А. Лаппо-Данилевского
систем линейных дифференциальных уравнений. Это дает возможность полу-
получить систему уравнений для параметров задачи о конформном отображении
круговых многоугольников.
Некоторые частные типы круговых многоугольников с числом вершин,
большим трех, рассмотрены в работах Э. Н. Береславского A972). В частно-
частности, для случая, когда числа Л, В, С, все равны V2, решение уравнения F.16)
сводится к уравнению Ламе, которое решается в 8-функциях (Уиттекер и
Ватсон 1962).
§ 7. Случай действительных показателей; второй вывод ха-
характеристического уравнения. Вернемся к вопросу об определе-
определении показателей около особых точек (см. § 3). Нас специально
будет интересовать случай, когда о! и а!' действительны. Не-
Нетрудно убедиться, что необходимым и достаточным условием
действительности а' и а" является условие пересечения окруж-
окружностей
полученных из уравнений C.14) и C.15), где W\ = F\/Z\. Дей-
Действительно, если окружности G.1) пересекаются, то а' — о!' —
действительное число, так как я(а' — а")—угол между этими
окружностями. Тогда отношение А/Д" должно по модулю рав*
няться единице. Координаты точек пересечения являются кор-
корнями уравнения
о , Ш — kn + kh — im , km — km л /7 o\
w2 -\ ¦—*-= w + ——j— = 0> G-2)
In —In in— In
§ 7] СЛУЧАЙ ДЕЙСТВИТЕЛЬНЫХ ПОКАЗАТЕЛЕЙ 257
Принимая во внимание неравенство (Ш — ~1пJ < 0, найдем,
что эти корни действительны при условии
(kn — kn + lm - Imf -4 (km — km) (In - In) < 0. G.3)
Так как произведение W есть действительное число, то из дей-
действительности числа а/ — а" вытекает действительность чисел
а' и а". В самом деле, если в уравнении C.17) положить
K(kn— ml) =|, то для I будем иметь уравнение
где А — kn — ml, В = 1п — /Я, С = km — km. Условие, что
корни g' и g" — комплексные сопряженные, состоит в том, что
(А-\-АJ— 4(АА—ВС) < 0, что совпадает с условием G.3).
При этом |Г/Г| = |W| = 1.
Предполагая теперь выполненными условия действительно-
действительности показателей а/ и а" около ? = 0, вернемся к условиям на
отрезках вида C.1). Предположим, что
G.4)
где
U = f Za^, V = ta'f,bnta, G.5)
/l=»0 /2 = 0
причем для простоты считаем, что в этих разложениях члены
с In ? отсутствуют.
Тогда первое из условий на отрезке М2М3 (рис. 165) можно
согласно G.4) представить в виде
Im {k2Z + 12F) = Im [(k2A + 12C) U + (k2B + 12D) V] = 0. G.6)
Если показатели около всех особых точек действительны, что
считаем выполненным, то коэффициенты в разложениях G.5)
будут действительными. Поэтому G.6) можно представить в
виде
U Im (k2A + 12C) + V Im (k2B + 12D) = 0.
Так как функции U и V линейно независимы, то коэффициенты
при них должны равняться нулю:
Im (k2A + 12C) = 0, Im (k2B + /2D) = 0. G.7)
Таким же образом получим еще два уравнения
Im (т2А + п2С) = 0, Im (т2В + щ€) = 0. G.8)
Перейдем теперь с отрезка М2М$ на отрезок М\М2, совершив
обход около точки ? = 0 по полуокружности в верхней полу-
полуплоскости. Если на отрезке М2МЪ считать arg ? = 0, то arg ? =
9 П. Я, Полубаринова-Кочина
258 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
= п на отрезке MxM2i а следовательно, на отрезке МХМ2 при
Полагая для ? = ?<0 U = ел(а'и\ V = ePia"V9 где U' и V'
действительны при ? < 0, на отрезке МХМ2 получим
Im (kxZ + hF) = Im [(kxA + 1{C) enia'U' + {kxB + 1XD) е*1*У] = 0.
Отсюда
Im [(kxA + Щ enia'] = 0, Im [(kxB + 1XD) enia"] = 0. G.9)
Аналогичным путем найдем
Im \(mxA + nxC) e*ia'] = 0, Im [{mxB + nxD) enia"] = 0. G.10)
Полученные восемь уравнений G.7) —G.10) распадаются на
две группы, в одну из которых входят А и С, в другую В
и D. Перепишем уравнения первой группы, вводя комплексно
сопряженные числа:
k2A + /2С — k2A — /2С = 0,
щА + щС — т2А — п2С = 0,
(У А Л- 1 С\ otniof Ъ Л IP П
уК>Х/~1 ^^ ^Х\^) & fvjyl I XKj U,
(тхА + пхС) e27lia' — тхА — пхС = 0.
Для того чтобы система G.11) имела отличные от нуля ре-
решения, необходимо равенство нулю определителя
Лпт' 1 ?т
G.11)
mi
и
я,
= 0.
Если в этом определителе заменить а! на а", то получим
условие того, что система уравнений для В и D имеет отличные
от нуля решения.
Это показывает, что e2nia' и e2nia" являются корнями сле-
следующего уравнения второй степени относительно Я:
Ы hX ki U
Ш\Х ti\X th\ h\
k2 l2 k2 /2
= 0.
G.12)
/722 ^2 ^2 ^
Получили, таким образом, характеристическое уравнение для
% = e2nia. Хотя при выводе мы пользовались условием вещест-
вещественности а' и а!', однако уравнение G.12) годится и для ком-
ПОКАЗАТЕЛИ ДЛЯ ОСНОВНЫХ СЛУЧАЕВ ТЕОРИИ
259
плексных а', а"', в чем можно убедиться, преобразовав уравне-
уравнение C.6) к виду G.12).
Предложен также способ получения показателей около регу-
регулярных особых точек в тригонометрической форме (Kravtchenko
и др. 1955, 1 и 2).
§ 8. Показатели для основных случаев теории фильтрации.
Приведем результаты, относящиеся к способу определения по-
показателей около особых точек для различных комбинаций гра-
граничных условий, которые встречаются при изучении движения
грунтовых вод.
Рассмотрим некоторые комбинации границ, которые могут
встретиться в задачах о земляных плотинах (Ризенкампф 1940,
1). Границами области фильтрации могут быть (а) прямолиней-
прямолинейные непроницаемые стенки, (б) прямолинейные границы водое-
водоемов, (в) прямолинейные промежутки высачивания, (г) свобод-
свободные поверхности, вдоль которых может происходить испарение
воды (или к которым может притекать вода извне). Всего имеем
шесть возможных случаев соединений {аб), (ав), (аг), (бе),
(бг), (вг) вышеуказанных границ.
1. Случай (аб). Пусть откос плотины составляет угол яа
с линией непроницаемого основания (рис. 171). Тогда конформ-
конформное отображение области г на полуплоскость ? вблизи точки 5,
если считать, что точка В переходит в начало координат плоско-
плоскости ?, имеет вид
Для функции Z получаем
Следовательно, функция Z принадлежит показателю а—1.
260
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ. VII
На плоскости со = q> + ftp в точке В сходятся линии ф
= const и г|) = const; поэтому
т. е. функция F принадлежит показателю —7г-
Таким образом, для функций Z и F имеем показатели а— 1,
-Vs.
Если угол jta прямой, то показатели будут —7г, —lfo- В этом
случае на годографе скорости точка В будет обыкновенной точ-
точкой. Подстановка
приводит к функциям Z\ и F\y для которых точка В является
также обыкновенной точкой, т. е. разложения этих функций
имеют вид
Такие точки, особенность в которых можно устранить под-
подстановкой вида U = ?т?Л, можно назвать устранимыми осо-
особыми точками (Ризенкампф 1940, 1). В нашем случае можно
Рис. 172.
составить линейную комбинацию функций Z\ и F\, принадлежа-
принадлежащую показателю +1, и считать, что функции Z\ и F\ принадле-
принадлежат показателям 0 и 1, а функции Z и F—показателям —7г
и1/*
2. Случай (ав). Непроницаемая стенка соединяется с про-
промежутком высачивания (рис. 172). Как и в предыдущем случае,
для Z имеем
§8]
ПОКАЗАТЕЛИ ДЛЯ ОСНОВНЫХ СЛУЧАЕВ ТЕОРИИ
26!
Рассмотрим плоскость комплексной скорости. На ней имеем
прямые, пересекающиеся в точке В под углом я(!/2 — а)- Сле-
Следовательно, для и — iv получим
Отсюда
Таким образом, функции Z и F будут принадлежать показать
лям а— 1, —Уг- Здесь, в отличие от предыдущего случая, при
а = У2 разложения для Z и F содержат логарифмический член.
Действительно, в этом случае на пло-
плоскости и — iv прямые становятся па-
параллельными, а потому
МБ
Следовательно, F = Zm In g + ...
3. Случай (аг). Непроницаемая
стенка соединяется со свободной по-
поверхностью (рис. 173). На поверх-
поверхности СВ происходит испарение интен- Рис 173.
сивности с (или имеется инфильтра-
инфильтрация интенсивности е = —с), так что \|э + сх = const. Кроме того,
вдоль СВ давление постоянно, т. е. ф + ky = const. Уравнение
стенки АВ пусть имеет вид у cos яа — х sin яа = 0; вдоль стенки
г|) = const.
Условия на отрезках АВ и ВС плоскости ? имеют вид Im F =
= 0 и Im(Ze-rt'e) =0 на АВ, lm{iF + kZ) =0 и " "" "
'+ ciZ) = 0 на ВС.
Составим характеристическое уравнение:
0
k
cl
0 еп1а 0
Я 0 1
1 k -t
I -ci 1
= 0.
Это уравнение приводится к виду
cos
Каждый раз, когда [(k — с)/(k + с)]2 cos2па <. 1 (в частно-
частности, это неравенство имеет место при с > 0, т. е. в случае испа-
испарения), в выражении для
- enia [4+7 cos ™ ± '¦ V1 ~ (
262
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
(ГЛ. VII
можно положить [(k — c)/(k + с)] cos яа = cos яб, и будем
ИМеТЬ X — ?Лг'(а+6),
Искомые показатели около особой точки В, определяемые
по формулам Г\ = In %'lBni), r2 = In \"'/}{2ni), будут соответст-
соответственно 7г(а + б)+т и 7г(а—
— б) + т\ где т и т!— целые
числа и 0 < б < 1.
Рассмотрение годографа ско-
скорости (рис. 174) показывает, что
т = —1, т' == 0, причем яб есть
дополнение до я угла ABC на го-
годографе скорости; при этом угол
яр, образуемый стенкой и ли-
линией свободной поверхности, оп-
определяется через величины а и
б: яр = я(а + б)/2.
В данном случае показатели
системы функций Z и F имеют
вид 7г (а — б) и 72 (а + б) — 1.
4. Случай (бв). Прямоли-
Прямолинейная граница водоема являет-
является и прямолинейной границей промежутка высачивания
(рис. 175).
Здесь на плоскости г, а следовательно и для функции Z,
имеем обыкновенную точку 5 = 0: Z = а0 + ai? + ...
Рис. 174.
Рис. 175.
На плоскости и — iv точка В находится на бесконечности и
представляет пересечение двух параллельных прямых, перпен-
перпендикулярных к прямой ABC плоскости z. Поэтому около точки В
и — ш = Со In ? + ...
Показатель системы функций Z и F есть двукратный нуль
@,0).
5. Случай (бг). Свободная поверхность при наличии ин-
инфильтрации или испарения соединяется с границей водного бас-
бассейна (рис. 176). Условия на линии АВ будут такие же, как в
§8]
ПОКАЗАТЕЛИ ДЛЯ ОСНОВНЫХ СЛУЧАЕВ ТЕОРИИ
263
третьем случае, а условия на отрезке ВС, наклоненном под уг-
углом па к горизонту, имеют вид
Im (Z<r«'a) = 0, Im(i'F) = 0.
Соответствующее характеристическое уравнение
kx ix k —i
ciX X — ci 1
e-nia о enia 0
0 i 0 -/
= 0
приводится к виду
Отсюда
k + c
k — c
k + с
eni (у,-а) cos я ^ _ a
яA-а)±
-a) = 0.
cos:
Полагая при fe>c — [(ft —¦ c)/(k + c)]cosji(V2 — «) = cos яб,
получим Я = ешA/2~а + б), откуда для показателей получаем
значения У2 (V2 — a + б) —• 1 и V2 (V2 — a — 6) или — г/А—
-V2(a-6) и 74 — V» (а+ 6).
Если нет испарения, т. е. с = 0, то б = a + V2, и показатели
будут —72 и —а.
Область годографа скорости для рассматриваемого случая
изображена на рис. 177.
Рис. 177.
©
6. Случай (вг). Свободная поверхность при наличии ис-
испарения (инфильтрации) граничит с прямолинейным промежут-
промежутком высачивания (рис. 178). Условия на отрезках АВ и ВС пло-
плоскости I имеют вид lm(Ze-*ia) = 0 и lm(iF + kZ) = 0 на АВ,
lm{F+ciZ) =0и lm(iF + kZ) = 0 на ВС.
264
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
(ГЛ. VII
Характеристическое уравнение здесь имеет корни К\ = 1,
А,2= — ёШа = е2п1{1/2+а). Отсюда нетрудно прийти к заключению,
что около вершины В показатели будут 0 и а—xk- Если откос
составляет тупой угол с линией горизонта, то яр = я, а если
острый, то яр = я (а + 72).
В заключение сделаем замечание относительно показателей
около бесконечно удаленной точки (Ризенкампф 1940, 1).
Если считать, что данной вершине В соответствует беско-
бесконечно удаленная точка плоскости ?, то полученные выше зна-
значения показателей нужно увеличить на две единицы. В самом
деле, положим ? = 1/т. Тогда точка ? = оо перейдет в точку
т = 0; после преобразования к новой переменной функций Z =
= dz/dt, и F = da/dZ, получим выражения
гт dz _*> „ d(d 2
dx
dx
откуда и следует высказанное утверждение.
Б. ЗАДАЧА О ПРЯМОУГОЛЬНОЙ ПЕРЕМЫЧКЕ
§ 9. Расход прямоугольной перемычки и совершенного ко-
колодца. На рис. 179 представлена перемычка с откосами ВС и
AD на непроницаемом горизонтальном основании CD длины /.
Высота воды в нижнем бьефе Н%,
в верхнем Н\. Требуется определить
элементы движения, в том числе
высоту #о промежутка высачивания
АЕ (см. § 2 главы II).
Прежде всего обратимся к зада-
задаче об определении полного расхода
перемычки (И. А. Чарный 1951, 1).
Пусть имеем установившееся
движение с потенциалом скорости
ф(*,У), причем на свободной по-
поверхности АВ удовлетворяется усло-
условие постоянства давления
Рис- 179> Ф (х, y) + ky = 0. (9.1)
Обозначим ординату свободной поверхности через У = Y(x),
тогда на свободной поверхности будем иметь тождество
Вдоль откоса ВС для <р имеем значение
ф@, y)= — kHu
вдоль ED
(9.3)
(9.4)
§ 9] РАСХОД ПРЯМОУГОЛЬНОЙ ПЕРЕМЫЧКИ И КОЛОДЦА 265
Вдоль промежутка высачивания АЕ должно выполняться
условие (9.1): q>(/, y) + ky = O.
Вычислим расход через произвольное вертикальное сечение
перемычки. Очевидно,
\
Рассмотрим интеграл
Y(x)
i = \ <p(x, y)<fy (9.6)
О
и составим производную от него по я:
у
С помощью (9.2) можно написать
s\ dJ , т/\ dY dJ i ,,; а?К
Интегрируя это уравнение, получим
у
Учитывая, что при х = 0 имеем У = ЯЬ найдем
Hi
kHl
Учитывая (9.3) и вычитая почленно последние равенства, по-
получим
Q* = \ Ф (*> У) dy H—-—g— • (9-9)
о
Теперь положим х = /. При этом интеграл правой части ра-
разобьем на два и используем соотношение (9.4):
2
-k \
= - kHi - 41(н, + НоJ - н$].
266 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
После этого уравнение (9.9) дает
При этом #о выпадает из правой части и остается
(9.10)
Полученная формула для расхода прямоугольной перемычки
совпадает с формулой Дюпюи, которую мы отметили в § 11
главы II (см. также § 2
главы X).
Точно так же выводит-
выводится формула расхода для
осесимметричной задачи
в случае совершенного ко-
колодца.
Рассмотрим колодец
радиуса б, в котором во-
вода стоит на уровне Н2.
Пусть цилиндрическая
Рис. 180. поверхность г = R есть
поверхность равного по-
потенциала (рис. 180), а ординаты свободной поверхности z =
= Н2 + Но при г — б и z = Hi при г = R.
В цилиндрических координатах (rf z) имеем потенциал ско-
скорости ф(г, z), так что проекции скорости равны vr = dcp/dr, vz =
= dyjdz. На свободной поверхности имеем соотношение, выра-
выражающее постоянство давления:
ф(г, z) + kz = 0. (9.11)
Расход через произвольный цилиндр радиуса г, ось которого
совпадает с осью z, выражается так:
(9.12)
где z есть ордината свободной поверхности. Если положим
In г
2я
•=х,
то задача сводится к предыдущему случаю перемычки.
Для получения окончательного результата достаточно в
выражении расхода (9.10) заменить 1 = х2 — хх величиной
§ 9] РАСХОД ПРЯМОУГОЛЬНОЙ ПЕРЕМЫЧКИ И КОЛОДЦА 267
(In R — In 6)/Bя), что и даст формулу Дюпюи для колодца (см.
§ 6 главы X):
Q- lnR/6 • (9ЛЗ)
Таким образом, не имея в настоящее время точного решения
задачи о безнапорном притоке жидкости к колодцу, мы имеем,
однако, точную формулу для расхода колодца.
Другой вывод несколько обобщенной формулы Чарного для
перемычки может быть дан с помощью применения теоремы
Коши, говорящей, что интеграл от аналитической функции по
замкнутому контуру равен нулю. Функция со (г) = ф + ар яв-
является аналитической, не имеющей особенностей в области дви-
движения, ограниченной контуром Г = ABCDEA (рис. 179). Инте-
Интеграл по этому контуру от со dzy а также его мнимая часть равны
нулю:
Im \ со dz = \ ф dy + а|) dx = 0.
Г ABCDEA
Примем, что на свободной поверхности АВ имеет место инфиль-
инфильтрация (или испарение) постоянной интенсивности е (см. § 2
главы II). Обозначая через Q\ расход через верхнюю грань ВС
плотины, получим, что \|? = e#+Qi вдоль АВ и \р = 0 вдоль
CD. Подставляя под знаком второго из интегралов вместо ф и
ф соответствующие выражения на отдельных участках контура,
начиная с АВУ напишем
я, о о
Н2+Н9 I Я,
И 2 Яа4*Яо
kH2dy- J kydy = 0. (9.14)
я2
При постоянных k и г интегрирование выполняется, и после про-
простых преобразований получаем
ft__-+42^. (9,5)
На низовой части плотины к этому расходу прибавится расход
инфильтрации е/ и общий выходной расход Q2 будет равен
(9,6)
В случае инфильтрации свободная поверхность, конечно, не-
несколько возвышается над уровнем верхнего бьефа у точки В
268 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
(рис. 179), и над точкой В образуется второй промежуток вы-
сачивания. Однако на окончательных формулах (9.15) и (9.16)
это не сказывается.
Обобщение формул (9.15) и (9.16) на случай, когда е зави-
зависит от х, a ft зависит от у, было дано И. А. Чарным A953), а
также С. Н. Нумеровым A953, 2) применившим потенциал Ги-
ринского:
{Hi-y)k{y)dy-\{H2-y)k{y)dy\.
о о о J
(9.17)
Ю. С. Лапшин показал, что уравнение (9.14) сохраняется и
для кусочно-постоянной зависимости k (у) в случае горизонталь-
горизонтальных прослоек с участками напорно-безнапорного движения.
§ 10. Построение решения для перемычки. Решение этой за*
дачи было получено первоначально Б. Б. Девисоном A932) и
Г. Гамелем (Hamel 1934) как решение задачи Дирихле. Здесь
дается более простое решение *).
Пользуясь результатами § 8, найдем показатели системы
функций Z и F для рассматриваемой задачи (рис. 179, 181).
Около точки А (? = 0) имеет место шестой случай, поэтому
показатели (здесь а = 7г) будут 0, 0. Около точки В (? = 1)
имеет место пятый случай, причем показатели равны —7г> —7г.
Около точки С (? as а) соответственно первому случаю имеем
показатели —7г> 7г> причем здесь особенность является устра-
устранимой. Точка D (I as b) аналогична точке С, и около нее пока-
показатели будут —7г» 7г- Около точки Е (? = оо) имеем четвертый
случай, которому соответствует кратный корень характеристи-
характеристического уравнения, равный нулю. Так как эта особая точка —
бесконечно удаленная, то показатели около нее будут 2, 2 (см.
конец § 8).
Функции F и Z являются различными ветвями функции, ко-
которая может быть представлена с помощью символа Римана:
-1 1 1 2
2 2 2 Z
(ЮЛ)
*) Связь обоих решений показана в книге П. Я. Полубариновой-Кочиной
A942, 1).
§ 10J ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ 269
Отметим, что сумма всех показателей равна трем, следова-
следовательно, условие Фукса F.4) здесь выполняется (число особых
точек v + 1 равно пяти).
Применяя E.6) к функции У*, можем написать
( 1 а Ъ оо
о о о о |
О 0 1 1 1
— С) (С — «) (С —
(Ю.2)
Введенная новая функция У в точках ? = а и ? = Ъ имеет
показатели 0 и 1 и, как было указано выше, в своих разложе-
разложениях не содержит логарифмических членов. Поэтому ? = а и
? = Ъ являются обыкновенными точками и могут быть исклю-
исключены из рассмотрения, т. е. функция У имеет лишь три особые
точки и может быть обозначена так:
A0.3)
Функция У есть решение уравнения D.2), в котором а = р = О,
у = у' = у2 и которое можно записать так:
СA-ОУ* + A-20Г-|г = 0. A0.4)
При этом, если U и V — его линейно независимые интегралы, то
F AU + BV 7 CU + DV ,1П-,
V(l С) (С а) (С 6)
F 7
V(l - С) (С - а) (С - Ь) V(l — С) (С — а) (С —
Около ? = 0 имеем интеграл этого уравнения, представляю-
представляющийся в виде гипергеометрической функции E.1) при а = 7г»
A0.6)
Рассмотрим определенный интеграл
Я/2
J V '
270 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
Гипергеометрическая функция A0.6) лишь постоянным множи-
множителем отличается от этого полного эллиптического интеграла
первого рода, рассматриваемого как функция от квадрата мо-
модуля k2 = ?. Следовательно, в качестве одного из частных ре-
решений уравнения A0.4) можем взять
Я/2
[ dq> [ dt (Ю.8)
1
=[
J
При замене ? на 1 — ? уравнение A0.4) не меняется, поэтому
V = K(l-Q = K' (k/2 =1-?) A0.9)
также является решением нашего уравнения, регулярным около
точки ? = 1.
Ряд для /((?) сходится при |?| < 1, т. е. в круге Со
(рис. 167), ряд К{\ —?) в круге Си для которого |?— 1| = 1.
Выясним, как ведет себя /СA — ?) при ? = 0.
Между /С и /(' существует соотношение, получаемое с по-
помощью теоремы об определителе Вронского (Смирнов 1969):
Его можно переписать в виде
— с) ~~
где ^i(?) -—ряд по целым положительным степеням ?. Отсюда,
интегрируя, найдем
где Р(?) имеет вид
Таким образом, /СA—?) представляет решение, имеющее
логарифмическую особенность около точки ? = 0; следова-
следовательно, K{t) и /СA—?) линейно независимы и образуют фун-
фундаментальную систему решений около ? = 0:
[/ = #(?), V = iC(l — О- (Ю.12)
На основании формул E.10) и аналогичных им находим, что
A0ЛЗ)
§ Ю]
ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ
271
есть фундаментальная система интегралов уравнения A0.4).
Ряды для функций A0.13) сходятся при |?| > 1.
Заменяя ? на 1 — ?, из A0.13) найдем новую систему инте-
интегралов
A0Н)
А
\
д
ж
С
л
Щ
?
ряды для которых сходятся вне круга
d (рис. 167).
Конформное отображение модуляр-
модулярного треугольника плоскости до =
= и — iv (рис. 181) на верхнюю полу-
полуплоскость ? производится по формуле
W '¦
А д С В ?
Рис. 181.
Рассматривая промежуток @,1) для
?, имеем такое соответствие точек ?
и w: w = xi при ? = 0, w = 0 при
? = 1 и w = хA + 0/2 при ? = 72- Отсюда найдем ¦)
(О- IK A-
A0.15)
Если точка ? находится в верхней полуплоскости, то имеют
место соотношения
С их помощью найдем для отрезка 1 < ? < оо
ЧУ)
" * Чт) '
для отрезка — оо < g < О
A0.16)
A0.17)
A0.18)
*) В этом параграфе коэффициент фильтрации обозначен через к.
272 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
Справедливость A0.17) и A0.18) проверяется непосредственно
из рассмотрения рис. 181.
Теперь нетрудно составить выражения для функций F и Z,
исходя из A0.5), с учетом того, что числители этих выражений
должны быть пропорциональны соответственно числителям и
знаменателям формул A0.15), A0.17) и A0.18).
Введем обозначения
f (Л = KJQ f (п=_. К A -1)
11 \«/ /71 ZT-, ZT77 ZT * ' 2 \т>/
h@ =
V(l - C)(fl — EM*
\ 1 — С /
VC(C-l)(C-e)
-0 '
-5)
(*-C)
(*-C)
A-
Vt(
Vt(
V g — l
5) V(e - S)
v S
:c-i)«-«
J
)
)
i)(b-?>) '
)
A0.19)
Получим, вводя некоторую постоянную Л, вдоль отрезков
действительной оси ? = ?:
для 0 < g < 1
2=-3f+^=-^If,@-ff2@], F = -$~-*Aft®i A0.20)
для — оо < g < 0
для 1 < ? < а
для а<?,<Ь
-li = -x^f6@; A0.22)
2 = 4НЛ№> /? = Ц-=^^@; (Ю.23)
для Ь < $ < оо
^ ^оЮ. (Ю.24)
§ 10] ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ 273
Производя интегрирование по ? в соответствующих пределах,
найдем формулы для длин отрезков Яь I, Я2, Яо и для рас-
расходов Q, Q2, Qo через отрезки соответственно Нь Я2, Яо:
ь
а
оо
= а\ Ы?)С
а
= хЛ J f6(?)d
1
0
= >сЛ ^ f4(?)'
Я, = Л J /5 (?) d?,
i
0
Н0 = А J /3(?)d?
— оо
оо
Ь
CIl.»
A0.25)
;, (Ю.26)
X, (Ю.27)
A0.28)
Если ввести интегралы
Js= \ f,E)rfC, (Ю.29)
где a8 и bs — соответствующие значения пределов интегрирова-
интегрирования, то из выведенной формулы Дюпюи для полного расхода Q
следует такое соотношение между тремя из этих интегралов:
2/6/7 = ]\ - /°9. A0.30)
Для удобства вычислений введем обозначения
а = у, Р = ~ @<а<р<1) A0.31)
и сделаем в интегралах для /, Нх и Я2 подстановку
A0.32)
Далее, заменим т новыми выражениями, различными для раз-
разных интервалов, делающими подынтегральную функцию конеч-
конечной на пределах интегрирования. А именно, положим
p)sin2x при 1<?<а, Л
(P-ct)sin2x при а < t < ft, \ A0.33)
2 ПРИ b <1<оо. )
274 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
Вводя еще обозначение 2Ал/аЬ=С, получим следующие
формулы:
я/2
t *(« + (Р-«>"х) d% AО.з4)
Vl - а - (Р - a) sin2 х
Я/2
iicaH.(i-l»rin»x)rfXt A0.35)
1 J Vp-a+(l-p)sin2X V
Л/2
В интегралах для Но и Qo введем подстановку 1/A— ?) =
2t), что даст
н с\ к (*>*%) an * ж %dX A0>37)
J V(l-a, sin2 x) A - P. sin2 x)
V(l-a,sin2x)(l-Pisin2x)
Здесь положено
a, = 1 - a, p! = 1 - p. A0.39)
Остается преобразовать интеграл Q2. Полагая (?—1)/? =
= т=1— asin2x, будем иметь
Я/2
\ ^0cxsi2x)sinJcijL
V(l — a sin2 %) (P — a sin2 %)
Наконец, найдем уравнение депрессионной кривой в пара-
параметрической форме. Для этого отделим действительную часть от
мнимой в первом из уравнений A0.19) и введем подстановку
? = sin2 %. Получим
x = l_r \ % (sin2 %) sin % i
о V(l-asin2Yj(l--Psin2Yj
J V(l-asin2x)(l-psin2x)
A0.41)
Постоянная С остается произвольной; можно, например, счи-
считать ее равной единице.
§ 10] ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ 275
Полагая в полученных уравнениях % = я/2, найдем другое
выражение для /, а также равенство для Н\ — Я2 — #о:
Я/2
=С\
J
л » \- — w*" л// V* Р ***П Л/
Я/2
/С (cos2 x) sin х d%
= -4=r [ К {a, dn2 u) du. A0.43)
Va, J
-4=
Va, J
На рис. 182—188 представлены результаты расчетов по при-
приведенным формулам для прямоугольных перемычек.
Отметим частные случаи.
1. Случай а = 0, р = 1. Это значит, что в нижнем бьефе
нет воды и длина основания перемычки бесконечно велика
(рис. 189, а). Для отрезка высачивания из A0.37) получаем
Я/2
A0.44)
(здесь G= 1 — -от + -нг" + ... =0,915 966 —постоянная Ката-
лана). Расход Q = Q0 определится из A0.38):
Я/2
о
Отсюда найдем зависимость между Q и Яо:
Q = -2g? #0= 1,3469хЯ0. A0.45)
Уравнение депрессионной кривой упрощается, и его можно
написать в виде
где Х\ = / — х, т. е. абсцисса Х\ отсчитывается от точки на низо-
низовом откосе в сторону верхового откоса перемычки.
оВ таблице 12 приведена зависимость координат депрессион-
нои кривой xi и у\ от параметра /п, вычисленная по формулам
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1Г
05 1,0 1,5 2М 2,5 , 3,0
Рис. 182.
к
0,8
0,5
0,1
\
у
IS
\
\|
\
Г
1
\
-ш, ля
777/
\
0,2 0,4 0,6 0,8 f
Рис. 183.
Ю]
ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ
0,5
0,4
0,3
0,2
0,1
0
-«5=;
1 —¦—,
Ч
\
2 N,
¦н, 1 ¦
\
N
0,2 0,4 0,6 0,8
Рис. 184.
Н, '
0,2 0,4 0,6 0.3 „ 1,0
0.1
Рис. 185.
0,5 1,0 1,5 2,0 2,5 1,0 3,5 ff
Рис. 186.
1,0
0,8
0,6
0,2
\\
H,i
Hf
^Hi
Hf
_ j
=====
=====
•'
¦¦
В - —
J 4 5 6
Рис. 187.
Pi
/
/
/
¦
7 "^
г "^
N
'//////У/////'
/
/
/
/
/
1
7
h xH0
- A-
xH0\
''///////////7/7777777/
г ь ^ 8 н в)
Рис. 188.
Ф
Рис. 189.
ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ ПЕРЕМЫЧКИ
279
Таблица 12
Зависимость координат депрессионной кривой от параметра т
в случае отсутствия воды в нижнем бьефе для бесконечно широхой
перемычки
т
Xi
У\
т
У\
т
х{
У\
0
0
0
0,80
1,533
1,568
1 —10~7
43,784
13,005
0,05
0,036
0,084
0,90
2,370
2,133
1-ю-8
55,321
14,813
0,10
0,073
0,160
0,99
5,977
3,961
1 —Ю-9
68,184
16,622
0,25
0,250
0,445
0,999
10,890
5,771
1—ю-12
114,72
22,047
0,50
0,593
0,773
0,9999
17,126
7,579
1-ю-15
173,19
22,472
0,60
0,805
0,976
1-10~б
24,686
9,388
1-10-18
243,59
32,898
0,70
1,094
1,226
1-ю-8
33,572
11,196
1—Ю-24
420,18
43,748
A0.46) при С = 1. Для того чтобы получить ординаты депрес-
депрессионной кривой у = f/i + Но, нужно к значениям у\ таблицы 12
прибавить величину Яо = 1,8319. На графике депрессионной
кривой (рис. 190) величина Но принята равной единице, поэтому
—-*.
)
16
*****
1
д
6
4
1
0
b
If
z
\
\
и
0,675
Рис. 190.
при его построении все значения Х\ и ух из таблицы 12 разде-
лены^на 1,8319. При этом согласно A0.45) расход Q = 1,3469k.
Такой же расход через горизонтальный отрезок d дренажа дает
парабола с параметром р = 2d = 1,3469 (см. формулу A1.5)
главы II). На рис. 190 она показана пунктиром — это асимпто-
асимптотическая парабола для построенной депрессионной кривой.
Заметим, что рассмотренный случай отсутствия воды в ниж-
нижнем бьефе бесконечно широкой перемычки эквивалентен задаче
о притоке воды из бесконечности к канаве с вертикальными
стенками при отсутствии в ней воды.
280 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ [ГЛ. VII
В случае перемычки с конечной, но достаточно большой ши-
шириной основания равенство A0.45) выполняется приближенно.
Так, при ЦН\ > 1 имеем Q « 1,35хЯ0; при 1\Н\ < 1 равенство
A0.45) становится все менее точным по мере приближения
//#! к нулю (рис. 188). При / = оо, но отличном от нуля #2,
т. е. при наличии воды в нижнем бьефе, отношение Qo/(kHo) из-
изменяется в пределах от 1,347 до 1, когда Н2/Н0 растет от 0 до оо.
2. Случай а = р = 0. Это случай бесконечно глубокой
перемычки без воды в нижнем бьефе. Обозначим через Н' отре-
отрезок, изображенный на рис. 189,6. Формула A0.42) дает / =
= Ся2/4. По формуле A0.41) получаем
я/2
#' = С$ /С (cos2 -ф) sin -ф d-ф = 2CG.
о
Отсюда найдем И' = 8Gl/n2 = 0,7425/.
3. Случай а = Р=1. Этому случаю соответствует
рис. 189, в. Формулы A0.37) и A0.38) дают
Но» С J К (t2) tdt = C9 Qo = хС J К A - f) t dt = xC.
о о
Следовательно, Qo = x#0.
В. ЗАДАЧА О ПЕРЕМЫЧКЕ В ФОРМЕ ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ
§11. Фильтрация в трапецеидальной перемычке при испаре-
испарении. Будем называть перемычкой не только плотину с вертикаль-
вертикальными откосами, но и плотину, у которой верховой откос верти-
вертикален, а низовой имеет форму прямой, составляющей с горизон-
горизонтальной осью угол Э = яа, не превышающий я.
Пусть имеем перемычку на непроницаемом основании
(рис. 191, а).
В верхнем бьефе глубина воды равна Я, в нижнем бьефе
воды нет, так что жидкость просачивается через откос, являю-
являющийся промежутком высачивания. Со свободной поверхности
происходит испарение таким образом, что на СВ
я|) + сх = const, (П.1)
где с > 0. Годограф скорости представлен на рис. 191,6.
Отметим, что линия С В не есть линия тока и угол 9i = паи
составляемый линией свободной поверхности с горизонталью, не
равен нулю. Как видно из годографа скорости, отрезок ОС ра-
равен -y/kc; с другой стороны, рассматривая бесконечно малую
11]
ТРАПЕЦЕИДАЛЬНАЯ ПЕРКМЫЧКА ПРИ ИСПАРЕНИИ
281
окрестность точки С и заменяя прилежащую к ней часть сво-
свободной поверхности отрезком прямой, получим, что градиент
М
Рис. 191.
напора в точке С равен tg9i, а скорость фильтрации ОС—
= k tg 0i. Отсюда _
tg0j — tgnoi = А/-г-. (П.2)
Пусть на действительной оси вспомогательной плоскости ?
точки Л, В, С и D переходят соответственно в точки ? = О, 1, оо,
—а (рис. 192). При ? = — а
имеем устранимую особенность
с показателем —7г Для функ-
функций F и Z. Положив
и
Ш
ж
А
в
A1.3)
Рис. 192.
для функций F\ и Z\ около особых точек получим показатели
—72 и a — 1 при ? = 0, 1 + еи 1-е при ? = оо, 0 и 1/2 — а при
Функции Z\ и Fi представляют линейные комбинации двух
ветвей функции Римана:
о
оо
1
от — 1 1-е -пГ —
00
о у + е °
282
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
Около точки ? = 0 линейно независимые ветви функции
выражаются через гипергеометрические функции U и V:
¦ = ?'~cF(a-c+l, b-c+l, 2-е, ?) =
== ? 2f ((T -f" 8, О — 8, /
A1.4)
Функции F и Z, удовлетворяющие всем условиям на отрез-
отрезках действительной оси, имеют вид
F=
= BA — / tg 9)
V
A1.5)
Здесь В — постоянная, подлежащая определению, г и р — ко-
коэффициенты вспомогательной подстановки (см. формулы
E.12)). Отношение r/р выражается через гамма-функции (при-
(принято б = 1 — о):
Г B - с) Г (с - а) Г (с - Ь)
Г A- а) Г A-6) Г (с)
cos jte
|—б)г(й-в)Г(б+в).
Формулы A1.5) нетрудно проверить, переходя от одного отрезка
к другому.
Длина / основания плотины находится по формуле
(И.6)
Для расхода получается выражение
(Ц.7)
Отметим частный случай, когда 9 = л. Это значит, что
мы имеем горизонтальный отрезок дренажа. Формулы A1.4)
§ И] ТРАПЕЦЕИДАЛЬНАЯ ПЕРЕМЫЧКА ПРИ ИСПАРЕНИИ
перейдут в такие:
^ + 8> Т""-8' "»
283
A1.8)
Гауссом были найдены выражения
т»
2е sin t cos t '
При /-> oo параметр а -* oo и формулы A1.5) упрощают-
упрощаются. Подстановка ? = sin2 / приводит к интегралам, которые
выражаются в конечном виде (здесь А=— ИтВ1л/а при
а = оо):
= -^ 5 sin Bе/) Л = -
- cos BeO],
cos Bе/) Л = -^- Л sin
(Н.9)
При этом начало координат перенесено в точку В выхода сво-
свободной поверхности в дренаж (на низовой откос). Длина от-
отрезка /0 найдется из A1.9) при t = я/2, когда х = 0 и у = 0:
Полагая во втором из уравнений A1.9) t = я/2, ср = 0 и
\|) = Q, найдем зависимость между расходом Q и отрезком
Дренажа /0:
Для того чтобы найти уравнение свободной поверхности, по-
положим ф + ky = 0 и г|) + сх = 0; при этом t = я/2 + Л, где Л > 0.
Получим гиперболу
A1.10)
284 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
§ 12. Фильтрация в трапецеидальной перемычке в отсутствие
испарения. Для частного случая задачи предыдущего параграфа,
когда величина с = О, т. е. испарение отсутствует, получаем
следующие формулы:
/()
J A-*)'-аУ* Vl-(l+a)x
J
l
I
Г2A — о) (У2 — a) sin2 6 f F A — а, 1 — о, э/2 - а, 1 - *) ,
Г2C/2 — а) cos6 J (I — л:)а~1/2 V^MFoT X'
or, a
A2.1)
В случае бесконечно широкой плотины (/ = оо) С. В. Фаль-
ковичем (Полубаринова-Кочина и Фалькович 1947) найдено вы-
выражение для klo/Q непосредственно в функции от угла наклона
низового откоса:
я/2
kL 4 f 1-9J X
~тг = —т\ (ctgx) lnctg-Trdx. A2.2)
о
Формулы A2.1) преобразованы Г. К. Михайловым A953, 1)
к виду, удобному для вычислений. Для этого гипергеометриче-
гипергеометрические функции были разложены в ряды и затем подынтеграль-
подынтегральные функции почленно интегрировались.
По полученным формулам были проведены вычисления.
Путем предельного перехода при сг->0 Г. К. Михайлов по-
получил из приведенных формул простую формулу
И1
при а-> 72 путем такого же предельного перехода им была по-
получена формула
^ = A#_(l_AjlnTJ_. A2.4)
Здесь ht = H/H\ и Qx—Q/Qq, где Qo = kH\jL — расход при
наибольшем напоре Н = Н\.
§ 12]
ТРАПЕЦЕИДАЛЬНАЯ ПЕРЕМЫЧКА В ОТСУТСТВИЕ ИСПАРЕНИЯ
285
Следует отметить, что при а = 0 и а — 1/2 расчетная схема
плотины теряет смысл, но формулы A2.3) и A2.4) сохраняют
свое значение. Их можно рассматривать как приближенные при
Графики формул A2.3) (/) и A2.4) B), а также результаты
вычислений при а =0,1 C) и а = 0,25 D) приведены на
рис. 193. Как видно из рис. 193, формулы A2.3) и A2.4) дают
близкие кривые, между которыми лежат кривые для всех пря-
прямых наклонов низового откоса
(а<72). %0
К этим же граничным кри- f#
вым можно прийти и другим
путем. Рассмотрим для этого W
сначала плотину, сложенную
из анизотропного горизонталь- 05
но-слоистого грунта, для кото-
которого ky = 0 (см. § 9 главы
VIII). Движение в таком грун- %4
те происходит по горизонталь-
горизонтальным прямым, причем
0,2
и
Ux
dx
-^
1
7
' h
п
/
0,2 0,4
0,8
Рис. 193.
Выделим элементарную го-
горизонтальную полоску на вы-
высоте у от водоупора (рис.
191, а). Длина такой полоски
равна 1У = / — ydgQ = /A — yjHx). Разность напоров на ее
концах составляет Н — у. Поэтому
-у _^ Шг н-у
A2.5)
Расход найдем из формулы
В обозначениях #¦ и Л* формула A2.6) совпадает с приве-
приведенной выше формулой A2.4). Формула A2.6) была дана и ре-
рекомендована в качестве приближенной для изотропных плотин
Н. Т. Мелещенко A932).
Рассмотрим теперь фильтрацию в вертикально-слоистом
гРунте при ky = оо. В этом случае вертикали х = const являют-
Ся линиями равного потенциала. Эта схема есть точная ин-
интерпретация уравнения Дюпюи, описывающего неравномерное
Движение грунтовых вод в гидравлической теории (см. § 1—2
286 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
главы X). При этом линия свободной поверхности представляется
параболой Дюпюи вида у2 = ах + Ъ. Найдем постоянные а и Ь
из условия, что парабола проходит через точку С (О, Я) и пере-
пересекает прямую низового откоса в некоторой точке В(хо,уо)
(рис. 191, а). Очевидно,
Расход Q через сечение CD составляет
гг2 _ „2
Во всем треугольнике ABB' горизонтальная скорость фильтра-
фильтрации постоянна. Разность напоров в точках В' к А равна уо> дли-
длина пути фильтрации между ними / — х0. Поэтому фильтрацион-
фильтрационный расход в сечении ВВ\ равный расходу в сечении CD, со-
составляет
e. A2.8)
Присоединяя к соотношениям A2.7) и A2.8) условие, что точка
(х0, у0) лежит на прямой низового откоса, получим окончательно
для фильтрационного расхода формулу
Я2 A2.9)
* / + V/2 - Я2 ctg2 9
В обозначениях ?* и /i* формула A2.9) принимает вид формулы
A2.3). Формула A2.9) была рекомендована Н. Н. Павловским
в качестве приближенной для изотропных плотин A931).
Так как кривые зависимостей q^ = q^(h^) для случая изо-
изотропного грунта следует предполагать лежащими между кри-
кривыми формул A2.6) и A2.9), то приведенные соображения о
фильтрации в предельно-анизотропных грунтах позволяют до-
довольно точно оценить величину фильтрационного расхода в пло-
плотине. Применение модели предельно-анизотропных грунтов ока-
оказывается полезным и в некоторых других задачах теории филь-
фильтрации (см. § 9 главы VIII).
Кривые расходов q* = q*{K) в реальных плотинах, как по-
показывает рис. 193, получаются очень близкими к кривой, по-
построенной по формуле A2.3) или, что то же, по формуле A2.9).
Поэтому для практических расчетов можно рекомендовать фор-
формулу Н. Н. Павловского A2.9).
Что касается зависимости отношения величины участка вы-
сачивания к фильтрационному расходу klo/Q от угла наклона
низового откоса, то эта зависимость получается, как показы-
§ 12]
ТРАПЕЦЕИДАЛЬНАЯ ПЕРЕМЫЧКА В ОТСУТСТВИЕ ИСПАРЕНИЯ
287
вают расчеты, практически одной и той же для всех реальных
плотин. При значениях #//, не превышающих практически встре-
встречающихся, отношение klo/Q зависит только от угла наклона ни-
низового откоса к горизонту. Поэтому для этого отношения можно
использовать формулу С. В. Фальковича A2.2), которую
Г. К. Михайлов привел к двойному ряду
л2 La
Т (т - \ +2о)
(n + оJ Г (- 1 + 2а) т\
A2.10)
Ha рис. 194 приведен график этой зависимости, причем для
удобства при 0 < л/2 вместо klo/Q отложены значения
kl0 sin 6/Q, чаще встречающиеся в практических подсчетах. При
5,0
2,0
1,0
\
\
\
>
\
\
Г Р -
к10йп8 -
t
\
/
ч
/
щ
klg
—.
*--
0 Ж 60° 90° 110° 150° 180°
в
Рис. 194.
9 < я/2 формула A2.10) может быть с точностью свыше 3%
представлена приближенной зависимостью (Михайлов 1953, 1)
/г/0 a ctg 9 + 6 — а
Q " 4 sinG
A2.11)
где а = 4 при ctg 9 > 1 и а = 3 при ctg б < 1.
Для того чтобы перейти от рассмотренной схемы к реаль-
реальным профилям плотин, необходимо рассмотреть различные на-
наклоны верхового откоса, отличные от вертикального. Известно,
что уклон верхового откоса плотины оказывает малое влияние
на величину фильтрационного расхода. В связи с этим часто
288
ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ VII
используют для расчета плотин прием приведения наклонного
верхового откоса к вертикальному путем замены действительной
плотины в расчетной схеме эквивалентной ей в смысле вели-
величины фильтрационного расхода плотиной с вертикальным вер-
верховым откосом.
Для ширины основания Д/э эквивалентного прямоугольника,
заменяющего в указанном смысле треугольник верховного от-
откоса, были предложены различные полуэмпирические формулы.
Рис. 195.
Г. К. Михайлов из анализа существующих гидромеханических
исследований нашел, что при tg г|з <С 4/з эта величина довольно
точно выражается формулой
A2.12)
где i|) — угол наклона верхового откоса к горизонту. При
tg\|)>4/3 формула A2.12) может быть заменена более точной
для этого интервала зависимостью
4 = -у COS 1
A2.13)
Влияние воды в нижнем бьефе. Для получения
ориентировочной оценки влияния глубины воды в нижнем
бьефе на расход плотины Г. К. Михайлов рассмотрел треуголь-
§ 131 tEOPEMbt CVlUECfBOBAHra И ЕДИНСТВЕННОСТИ Ш
ную плотину при наибольшем уровне воды в верхнем бьефе, до-
достигающем гребня треугольника. Для такой плотины с поло-
пологими откосами, когда угол при вершине больше прямого, при
максимальном заполнении верхнего бьефа сохраняется участок
свободной поверхности; точное решение задачи в этом случае
является сложным. Если же угол при вершине меньше пря-
прямого, то грунтовый поток сплошь заполняет треугольник пло-
плотины. Точное решение задачи в этой постановке может быть по-
получено с помощью конформного отображения треугольника пло-
плотины на пятиугольник области годографа скорости.
На рис. 195 даны графики, характеризующие влияние воды
в нижнем бьефе на фильтрационный расход плотины. Под Qmax
здесь понимается фильтрационный расход при отсутствии воды
в нижнем бьефе. Задача о фильтрации в подобных треугольных
плотинах без воды в нижнем бьефе была рассмотрена
М. М. Моргулисом (см. Нельсон-Скорняков 1949).
Как видно из рис. 195, встречающиеся на практике неболь-
небольшие подтопления плотины водой со стороны нижнего бьефа
уменьшают расход воды в плотине, но немного. Чем положе ни-
низовой откос, тем меньше влияние подтопления на расход.
Ряд схем для земляных плотин при наклонном водоупоре рас-
рассмотрен А. М. Мхитаряном A954, 1957) (см. также Мхитарян и
Фомин 1959).
§ 13. О теоремах существования и единственности для задач
о плотинах. Вопросы существования и единственности решения
задач фильтрации со свободной поверхностью являются слож-
сложными. Так, в § 11 главы IV было показано, что в постановке
Н. М. Герсеванова задача о прямоугольной перемычке полу-
получила физически невозможное решение: исключение промежутка
высачивания привело к появлению разреза DE (рис. ИЗ), и ли-
линия свободной поверхности вышла за естественные пределы.
Если задача о плотинах с наклонными откосами решается с по-
помощью построения годографа скорости, то появляются разрезы
на его плоскости, возможно появление многолистных областей
(см., например, главу VI), возникает вопрос о единственности
определения параметров.
Вопросами единственности и существования решений для
фильтрации в земляных плотинах занимается группа итальян-
итальянских ученых. Ими исследованы некоторые случаи перемычек
(Байокки и Мадженес 1974).
Для прямоугольной перемычки (рис. 179) предлагается ме-
метод, основная идея которого состоит в том, что делается за-
замена неизвестных функций ф(х, у) и ^(х, у)у позволяющая све-
свести исходную «линейную» задачу в неизвестной области Q к
«нелинейной» краевой задаче в прямоугольнике D с основанием
Ю П. Я. Полубаринова-Кочина
290 ТЕОРИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VII
(О, /) и высотой Н\. Функции ф и \|) продолжаются во всю об-
область D:
f
Ф (х, у) в Qy ( ф (jc, у) в Q,
% bD-Q, * (О bD — Q;
через Q и J5 обозначены соответствующие области с включением
их границ.
Задача сводится к вариационным неравенствам или к мини-
минимизации некоторого функционала, а для такой задачи единст-
единственность решения в определенном классе функций доказана.
Несколько сложнее доказательство теоремы существования.
В упомянутой выше статье, со ссылкой на другие работы
К- Байокки, утверждается, что в уравнении свободной поверх-
поверхности у = %(#) функция %(х) аналитична при 0 < х < / и что
Х(/)>#2 (Рис- 179), что свидетельствует о наличии промежутка
высачивания.
Там же трактуются также случаи прямоугольной перемычки,
у которой верховой откос в верхней части содержит вертикаль-
вертикальную твердую стенку или заменен наклонным. Для них решение
также существует и единственно.
К. Байокки (Baiocchi 1974 и др.) рассмотрел и случай пло-
плотин криволинейного очертания, однако вопрос о промежутке
высачивания здесь не вполне ясен.
Г. Стампаккья A974) доказал существование и единствен-
единственность решения и построил вычислительный алгоритм для спе-
специальной пространственной схемы, допускающей применение
метода Байокки: плотина ограничена двумя цилиндрическими
поверхностями так, что в каждом поперечном сечении верти-
вертикальной плоскостью, параллельной общему направлению потока
воды в реке, получается картина, отвечающая прямоугольной
перемычке.
Указана возможность обобщения рассмотренных задач на
случай, когда ср(#, у) удовлетворяет уравнению div k grad cp = О,
если коэффициент фильтрации k(xy у) не зависит от одной из пе-
переменных и кусочно-постоянен относительно другой (слоистые
плотины).
Согласно утверждению авторов, предлагаемый ими метод
позволил провести расчеты для широкого класса фильтрацион-
фильтрационных задач.
Глава VIII
ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ
И АНИЗОТРОПНЫХ ГРУНТАХ.
ФИЛЬТРАЦИЯ ДВУХ ЖИДКОСТЕЙ
А. НЕОДНОРОДНЫЕ ГРУНТЫ
§ 1. Флютбет на двуслойном основании со слоями одинаковой
толщины. Рассмотрим следующую задачу. В полосе глубины Т
с коэффициентом фильтрации к\ имеется плоский флютбет (ос-
(основание гидротехнического сооружения, имеющее вид горизон-
горизонтального отрезка) шириной 2/. Нижний слой, также глубины Г,
имеет коэффициент фильт-
фильтрации Х2 и лежит на непро-
непроницаемом основании (рис.
196). Требуется определить
все элементы движения (По-
лубаринова-Кочина, 1939, 4,
1942, 1).
Величины, относящиеся
к первой области, снабдим
индексом 1, а ко второй об-
области — индексом 2. Будем
рассматривать только пра< Рис- 196-
вую половину чертежа. Вы-
Выпишем условия, которые должны выполняться на контуре обла-
областей AXDCBA и АВЕА2.
Границы водоемов представляют эквипотенциальные линии.
Следовательно, на них можно принять условия:
вдоль границы левого водоема
Н?
77777777777777777777777777777777777777777777?
на
И
Ф1 = — Щ ~2>
Н
A.1)
A.2)
где Н = Н1 — Я2 — действующий напор.
Ш*
292 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Вследствие симметричности потока на линии Сб, которая
также является линией равного потенциала,
ф1=0. A.3)
Линия BE также должна быть эквипотенциалью, так что на
ней фг = const. Положим на BE
ф2 = 0. A.4)
Далее, CD и ЕА2 являются линиями тока. Положим
на ЕА2
ф2 = 0, A.5)
на CD
t|)i = Q. A.6)
На границе АВ двух сред должны выполняться условия (см.
§ 3 главы II)
Отобразим область A\DCBEA2 плоскости z = х + W на над-
надрезанную плоскость комплексного переменного ? (рис. 197) так,
iF^-D Im(Fi)~O Im(iF<j)=O Im(ff~f2)**0
^r r r }
ПОд А
(ФШ///////МУ/. ^?ч (оо)
At
. iff if?
/m(fz)-ff lm(iFz)
Рис. 197.
чтобы область A\DCBA перешла в верхнюю полуплоскость, а
область АВЕА2 — в нижнюю.
Зависимость между г и ? будет иметь вид
«. \ + а , I — Д ^у. тег п Яч
С,— о I о СП—7j7-t \i'°)
где а —аффикс точек С и ? на плоскости ?. Полагая в уравне-
уравнении A.8) I = 0 и z = I + 77, найдем
a = th2if. A.9)
Таким образом, по заданным / и Т легко вычислить а,
§ 1] ФЛЮТБЕТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ 293
Будем рассматривать комплексные потенциалы coi = <pi +
+ ii|)i и оJ = Ф2 + ^2 первой и второй областей движения. На
плоскости ? функция coi (?) рассматривается в верхней полупло-
полуплоскости, о)г(О —в нижней. Через функции o)i и оJ можно выра-
выразить условия на границах:
на DA{
на CD
на СВ
на BE
на ЕА2
Im (/ol>i) = щ -q"
Im(co1) = Q,
Im(/(o1) = 0,
Im (/o2) = 0,
Im (co2) = 0,
на ЛЯ lm(-^--^) = 0, Im (со, - <»2) = 0.
Для получения однородных условий на контуре введем функ-
функции F\ = d^xldl, и 7*2 = doJ/d?. Соответствующие условия вы-
выписаны возле каждого отрезка на рис. 197.
В точке С (рис. 197) сходятся линии qpi = const (CB) и
ф, = const (CD), следовательно, на плоскости комплексного по-
потенциала здесь имеем прямой угол. Поэтому разложение o)i (?)
около точки ? = а должно иметь вид (см. § 5 главы II)
а{ (? - а) + ...].
Точно так же в точке Е функция @2(?) имеет вид
Отсюда для функций F\ (?) и F2 (?) получаем
A.10)
где <Di(?) и Ф2(^) —функции, имеющие точку ? = а обыкновен-
обыкновенной точкой. Будем рассматривать вместо Fi и F2 функции Ф] и
Ф* Вдоль действительной оси полуплоскости ? при ? = g > a
радикал V? ~~ я имеет действительные значения, следовательно,
условия для функций Ф] и Ф2 направо от точки а будут такими
же, как и для Л и F2. При ? = g < а радикал д/? — а имеет
мнимые значения, вследствие чего условия на отрезках A\D, DC
и А2Е изменятся так, как указано на рис. 198.
294 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Функции F\ и F2 должны быть аналитическими функциями
соответственно в верхней и нижней полуплоскостях, имеющими
регулярные особенности в точках ?= 0, 1, а, оо. Предположим,
что каждая из этих функций может быть продолжена в другую
полуплоскость, и попытаемся искать F\ и F2 как решения линей-
линейного дифференциального уравнения второго порядка.
1т(Ф1-Ф1)-0
ПФ1 ^
1тAФ2) ш0 /^ \ "#Г ~ ~#р
Рис. 198.
Исследуем поведение рассматриваемых функций около осо-
особых точек.
1. Около ? = 0. Функция coi (g) должна иметь вид
так как здесь сходятся линия тока и эквипотенциальная линия.
Тогда
т. е. F\(Z), а значит, и Oi(^) принадлежат показателю —!/г. Для
f2(?) точка ^=0 является обыкновенной, т. е. показатель в ней
равен нулю как для /7г(^), так и для
(Е)
2. Около 5=1. Предположим, что
функции Ф] и Ф2 могут быть продолже-
ны через отрезок В А. Сделаем надрез
вдоль отрезка DB (рис. 199). Изменим
Рис. 199. несколько обозначения. А именно, сохра-
сохраним обозначения Ф1 и Ф2 для значений
рассматриваемых функций на нижней стороне разреза и обо-
обозначим через ф[, Фг значения тех же функций на верхней
стороне разреза. Тогда разность Ф] — Ф2 перейдет в Ф| — Ф2»
Но так как вдоль ВА разность Ф] — Ф2 принимает действитель-
действительные значения, то в точке М\ которую можно рассматривать
как сопряженную с Af, эта разность заменится на сопряженное
§ 1] ФЛЮТБЕТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ 295
выражение
Ф1 —Ф; = Ф,—ф2. A.11)
Точно так же второе условие на отрезке АВ дает
/ф! /ф* /ф, /ф9
х, х2 ~ х, "^ х2 • KlAZ)
Решая эти уравнения относительно ф\ и Ф*2, получим
Щ -Х2 l Xi Х2 I
j (U3)
Что касается условий на отрезке DCB, то в наших новых
обозначениях они должны быть представлены в виде
1т(/Ф1) = 0, 1т(/Ф2) = 0,
или иначе __ __
ф; + Ф1 = 0, Ф2 + Ф2 = 0, A.14)
откуда ф! = — ф! и Ф^= —Ф2. В равенстве A.13) для Ф*и
заменяя все величины им сопряженными, получим
Сложив последнее равенство с равенством A.13) для Ф* и при*
нимая во внимание A.14), найдем, что Ф] + Ф\ =0. Поэтому
функции Ф* и Ф2 можно выразить через функции Ф1 и Ф2:
ф;= *'+*' ф ?^1_ ф )
2 Х2 —X! ] Н2 — Xi 2 ^
Как нетрудно убедиться, характеристическое уравнение
имеет корни X = 1, А/= —1. Показатели, при которых функ-
функции o)i и оJ остаются ограниченными в точке В, соответственно
будут
In Я Л , In Г 1
2m ' Y 2я/ 2 *
3. Около ? = оо. Положительный обход вокруг бесконечно
удаленной точки может быть заменен отрицательным обходом
вокруг точек D и В. При этом рассматриваемые функции будут
§96 НЕОДНОРОДНЫЕ Й AHH3OfPOnHbIE *ТУН1Ы [ГЛ. Vtll
продолжены через отрезок В А, следовательно, формулы A.13)
сохраняются и в этом случае. Если через Фх и Ф2 обозначить
значения функций до обхода, т. е. на верхнем краю разреза
(ьис 200) а через Ф\ и ф'-их значения после обхода, т. е. на
нижнем краю разреза, то условия на AD будут иметь_вид
Im(Oi) = 0, 1т(/Ф2) = 0, или Ф1=
—* /Ti*
Во втором из уравнений A.13)
заменим все величины на сопряжен-
сопряженные. Получим
Рис. 200. ^*^^ф^ = 1^^ф1^1^:^Ф2'
Складывая полученное равенство со вторым из равенств A.13),
найдем
откУДа *,
Подставив Ф, и Ф2 в уравнение A.13), получим
Характеристическое уравнение имеет корни
Положим
Тогда lejw Г = е-2пе', откуда
Условие ограниченности функций ©! и со2 при $==оо дает
для яия' значения п = п' = \, так что р= 1 +е и р = 1 — е.
Предполагая, что Ф, и Ф2 не имеют никаких других особых
точек получаем, что функции Ф, и Ф2 представляют ветви
§ n
ФЛЮТБЕТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ
297
функции Римана
( О оо 1
у = р < О а О
11— с Ь с — а — J
О оо
О 1 +е
= я< 1 Iere у г^. A.17)
"^^ !"^8 ""Т
Имеем а=1+е, 6 = 1 —е, с=3/2.
Функции (t>! и Ф2 будут линейными комбинациями интегра-
интегралов уравнения
или
A.18)
А именно, около ? = 0 можно взять фундаментальную систему
решений
A.19)
функции можно пред-
предПолученные гипергеометрические
ставить в виде (Gauss 1888)
\ , 1 1 Л
— ?
A.20)
(УГ=
Функции Ф] и Ф2 выражаются линейно через U и V: Ф\ =
= Л^ + ВТ, Ф2 = С7!/ + D'V, где Л7, В7, С и D'- комплекс-
комплексные постоянные.
Так как на отрезке DB, где 0 < ?< 1, функции f/ и У при-
принимают действительные значения, то для выполнения условия
lm(i<b[) = 1гп(/Ф2) =0 необходимо, чтобы постоянные А\ В\
С и D' были чисто мнимыми. Поэтому, меняя обозначения,
имеем Ф! = AiU + BiV и Ф2 = СШ + DiV, где Л, В, С и D —
действительные постоянные. Для того чтобы на промежутке AD,
где ? < 0, функция Ф] принимала действительные, а функция
298 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Ф2 чисто мнимые значения, необходимо, чтобы выполнялись ра-
равенства А = D = 0. Поэтому
•.-«"-^(т+'-т-'-т-О-
или
ф] = —/ Bi . [(Vi — с + л/--!J8 + (лЛ — ? — V^
2 Vcd —о
A.21)
Предположим теперь, что ? > 1. Тогда, совершив обход во-
вокруг точки ? = 1 по полуокружности, получим
смотря по тому, в какой полуплоскости рассматривается функ-
функция, в верхней или нижней. Для функции G>i нужно взять знак
минус, для функции Ф2 — знак плюс.
Точно так же при переходе от значений ? <С 0 к значениям
? > 0 получаем
причем минус относится к функции Фь а плюс — к Ф2.
При ? > 1 функции Ф] и Ф2 можно представить в виде
ф = Bi
1 2 iVc«D v
2 4е/ УЕ(Е — 1)
Условие Im (Ф! — Ф2) = 0 при ?> 1 приводит к равенству
Im ( — Ве~ш + -—- еяв') = В sin en + ~- cos ел = О,
откуда С = — 2е tg гпВ.
Второе условие на отрезке АВ выполняется тождественно.
Для функций F{ и F2 получаем на основании A.10) и A.21)
р __ Bi
В tg ея [(У 1 — S + V — g)g — (У1 — ? — У —
2 Ус A — е> (ё^117^)
§ I] ФЛЮТБЕТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ 299
Вдоль отрезка а < ? < 1 будем считать все корни VI»
д/l — ?, л/^ — а положительными и V~"? = *'V?-
Переходя на отрезок 0 < ? < а, после обхода точки ? = а
будем иметь
ь V? — а = ~ i V'а —
Поэтому для 0 < ? < a
р _d^ _В (л/Т=1 + / УП2в + (УГ=ё - /
Проинтегрируем A.24) вдоль отрезка CD в пределах от
? = 0 до ? = а. Положив ? = sin2t, получим
arcsin Va
а = 2В f cosBex).x
J у a — sin2 т
Заметим, что конформное отображение полуполосы А2ЕВСАХ
на разрезанную плоскость ? определяется уравнением
S = -Lt^+i^chiIi=l+*'2sh2JH-, (L27)
причем
Л/2 = 1 — Л2Э k2 = a = th2(Xl\ h = -?r. A.28)
Так как co1 = xi#/2 + Q/ при ? = 0 и (o1=Q/ при ? = а, то
A.26) дает
arcsin ft
Р Х1Я /_ [ cos Bет) ^т ( 9Q.
В~ 4Г' У"~ J У^-81п»т' (К29)
Подстановка sinT = fesint/ дает
Я/2
, Г cos Bе arcsin (A; sin т')) d%' /t олх
/==J Vl-^sin^T- • (L30)
Если проинтегрируем A.25) в пределах @, а), то получим
значение ф2 потенциала скорости в точке D\ (рис. 196), симме-
симметричной с точкой D относительно оси х:
arcsin k
(ф2)о_*?/2, /2==
300 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Теперь вернемся к отрезку а < ? < 1, т. е. к выражениям
A.23). Подстановка ?=sin2t и интегрирование в пределах
(а, 1) для Сдадут
Я/2
cos Bет) dx ^ . Пк.
arcsin k
я/2
f sin Bет) dx
arcsin k
Здесь Qo — значение ^ и ф2 в точке В (рис. 196), Q —полный
расход фильтрационного потока. Вычитание полученных выра-
выражений дает, после подстановки я/2 —t = t',
arcsin к
п 2В [ cos Bex/) dx'
c
f
J
^ cos яе J Vcos2 x' — k2 *
Используя A.29), получим
r\ 2J3 v y,\H J\
1 2cosjie /
причем
arcsin k я/2
cos Be arcsfn (kf sfn т)) rfr
f cos Bет') rfx' f
J Y^^2 _ Sin2 X' J
о v « — ы" «- о
В то же время, как нетрудно видеть,
Я/2
/
A, y3= С f^** A.34)
ZJ J Vsin2T —^2
i fe
J
arcsin
Перейдем теперь к формулам для скоростей на различных
отрезках границ области движения.
Для комплексной скорости имеем
«.-'».—IT—^-g- («-1. 2), A.35)
причем
Д?? 26'2Jt , яг • яг , #* и яг
shc fe ASn
1. Вдоль отрезка а<?< 1 получим
1] ФЛЮТБЕТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ 301
Имея в виду, что ?= 1 — k'2sm2(ly) = sin2r, т. е.
r ())
у ? (
х = arccos {kr sin (Яг/)), найдем окончательно
cos Be arccos (fe' sin Xy))
27
ВДОЛЬ CBy
V 1 — я г sin-
tg яе sin Be arccos (kr sin
-fc/2 sin2
ВДОЛЬ Bt.
Видим, что при у = 0 щ/и2 = ctg2 пг = ^
2. Возьмем 0 < ? < а. Вдоль отрезков CZ) и ?D] имеем
22
arccos
VI -
sin Be arcsin (/г' ch Яле))
==-^ ВА°ЛЬ
о / / 5
ZJ V1 - k' ch2 (Ял:)
Отметим, что в точке ?>ь где л; = /, сЬ2(Я/) = 1//г'2, для ^
получается неопределенность 0/0, раскрыв которую, найдем
{u2)Dx = —-—т • (* • 36)
3. Пусть — оо < ? < 0. При переходе через точку ? = 0
в формулах A.23) V? перейдет соответственно в /д/ — ? и
— /V""?- Поэтому получим
и для скоростей
fe" ch (Я*) + М]28 + U'2 ch (Я*) - М]2е ~ л
——*—др ^ — вдоль ?>ЛЬ
/^'сЬ(Яа:) + М]2е— [k'ch(Xx) — Л1]28 ^ „
¦ rz ВДОЛЬ UiA2i
2/
где M = ()
Прил: = / для и2 получается неопределенность, по раскрытии
которой находим прежнее выражение A.36).
4. Наконец, пусть будет 1 < ? < оо. Здесь 2 = л;, ?=1 -f-
2 и
%iHX cos яе [Л' sh (Kx) + N]2B +[N-k' sh (Я*)]°е
= 47 й '
[k' sh (Kx) + УУ]26 - [/V - fe' sh (Ял:)]28
_
t,1= _. _
где ^ V
302
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
1ГЛ. VIII
Что касается и2 и v2, то нетрудно проверить, что для них
2 (/)
имеют место равенства щ = щ tg2 пг = (щ
Н
щ и v2 =
Q 0,0/ 0,1 0,5 1 2
0,8
Цб-т
ОМ
OJ 0,2 0,3
Рис. 201.
l_L
--
К
О
/
/
/ /
¦ \
\\
\\\
\\\
\\\
II III
/ill
/ /я
//If
///III
'III
Wl
Ш
s
]
0,5
На рис. 201 даны графики
зависимости СЦ{щН) от
Графики зависимости Q/(%{H)
от IJT даны на рис. 202.
U
0,8
0,5
0,2
\
\
А
\
Л
V
\
\
\
\
\
\
\
ч
\
N
\
N
35
—
2 3 4 5 5 7 8
Рис. 202.
Заметим, что при е = 0, т. е. х2 = 0, имеем движение в одно-
однородном верхнем слое грунта глубины Т с коэффициентом филь-
фильтрации Иь
В заключение отметим частные случаи.
1. х2 = 0, т. е. нижний слой непроницаем. Тогда
** 2 / 2К ' "- — "" 2Г f
где К и К' — полные эллиптические интегралы модулей k и ft'
соответственно,
§ 2J
ШПУНТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ
303
2. xi = %2, тогда tg ле = 1, e = lU. Имеем однородный грунт
толщиной 27\
3. к2 = оо, tg ле = оо, е = 7г. Здесь ось х будет проницае-
проницаемой границей, на ней ф = const.
Заметим, что Ле Ван Тьемом предложен несколько иной путь
для решения рассмотренной задачи (Le Van Thiem 1962).
§ 2. Шпунт на двуслойном основании со слоями одинаковой
толщины. В двуслойном грунте, состоящем из двух горизон-
горизонтальных слоев (рис. 203) одинаковой толщины Г, расположен
шпунт, глубина забивки ко-
которого равна S. Коэффи-
Коэффициенты фильтрации этих
слоев равны соответственно
К\ И %2.
В этой задаче приходит-
приходится различать три случая.
1. Пусть S < Т. Как и в
задаче § 1, отобразим об-
область ABCDAi на верхнюю, Рис. 203.
а область АВЕА2 на ниж-
нижнюю полуплоскость плоскости комплексного переменного ?, как
это показано на рис. 204.
> 1т(ЪН
Y/////////////////////////////////////////A 2
Y
в
С
Y
В
\
А
(со;
iff iF2
4
Рис. 204.
Зависимость между z и ? будет опять выражаться форму-
формулой A.8)
г — 1 +а л- l ~a pb -5JL
ь 2 2 Т '
но в ней а имеет другое значение. В самом деле, принимая здесь
?== 0, z= (T — S)i, найдем
4. 2
B.1)
304 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VII!
Введем обозначения
sin J!^L — k cos-^- = &/; B.2)
тогда а *= — k2/k'2. Положим и здесь
Fl= Ф| , F2= ф2
Тогда для функций Ф1 и Ф2 будут выполняться на отрезках
(—оо, 0), @, 1) и A, оо) те же условия, что и в предыдущей за-
задаче. Следовательно, решение будет выражаться через те же
функции A.20), и для F{ и F2 получим те же уравнения A.23).
Но постоянная В здесь имеет другое значение. А именно, инте-
интегрируя в формуле A.24) от а до 0, найдем
В Г
2 3
V —СA — С)(С —а)
Подстановка ? = asin2q) дает B = Xi#//, где
Я/2 _ _
, 9 Г (У 1 + Ь sin2 ф + У b sin фJе + (У 1 + b sin2 ф — У 6 sin фJе
"~ 3 Vl + 6sin2m
о
причем 6 = — a = k2/k'2. Полагая ф = зт/2 —а, найдем
где
Я/2 К
6
у
Я/2 А
f (У1 — /г2 sin2 ф + k cos ф)8 * f / j , / Ч9р ,
= \ — ; ^ф = \ (dn w + k cn и)?е dw,
J VI — /г2 sin2 Ф J
nil
(Vl
(Vi
— k2 sin
Vi-
— /г2 sin
2 ff
)fe2
) + k COS ф)°8
sin2 ф
) — k COS ф)^8
VF
B.3)
a dnw и cn« — эллиптические функции.
Далее, беря в выражении A.24) для ©[ пределы —оо и а,
найдем расход
± (
2 J, Vco-««-«)
— 00
§ 21 ШПУИТ НА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ
Полагая
305
= a cosec2 ф = Т2 , М = V1 — kr sin2 ср,
k' sin2 ф
получим
Можно вычислить расход Q иначе — как сумму расходов че-
через отрезки ЕВ и ВС. Ниже приводится полученная таким обра-
образом формула для Q, которая была использована при числовых
расчетах. Не останавливаясь ни вычислениях, ограничимся при-
приведением окончательных результатов.
Для S < Т будем иметь
где
B.5)
}
a /i и /2 определяются формулами B.3). Далее, выражения
комплексных скоростей для первого и второго слоев имеют вид
у
X
[- sin (Я/2) + N]2B + [- sin (%iz) -
n [sin (Я12) + iV]28 - [sin (Я/2) -
47 (/,+/,) У^
i2e
B.7)
где
В частности, для выходной скорости у0» т- е. скорости
в точке D шпунта, имеем
47
Л (/,
При е = 0, т. е. при Х2 = 0, получаем однослойный грунт
глубины Т. При этом
306 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ 1ГЛ. VIII
где К — полный эллиптический интеграл первого рода с моду-
модулем k = sin(nS/2T)y а К' — такой же интеграл с дополнитель-
дополнительным модулем. При е = XU имеем однослойный грунт глубины
27. При е = 72> т. е. Х2 = оо, получаем задачу § 11 главы III
о шпунте при наличии дренирующего основания. Здесь
2. Для S>T имеют место формулы
х,//я/ f- sin (Я/г) + N]2e - [- sin (Я/2) - N]2e
щ — tV{ = —
Здесь
4770 N
%\Hn tg ел [sin (Я/г) + Щ2е + [sin (Я/г) - N]q
/28
/
sinen
Для расхода и выходной скорости имеем
_
2
27T(e) [-sin (Я/z)]18'
я ViT г (у2 + в)
2ГГ(е) [-sin
На рис. 205—208 приведены графики зависимости величин
V
Q/(k\H) и 2Tv0I{k\H) от параметра e = (l/n)arctg V^Mi и отно-
отношения S/Br).
Н. К. Калининым указаны некоторые приближенные приемы
решения задач о фильтрации в двуслойной среде A941). Им же
дано точное решение задачи о фильтрации через двуслойный
A952).
При е = 0, т. е. И2 = О, движения нет: Q = О, vQ = О.
3. Наконец, положим S = Г. Этот случай был рассмотрен ]
Н. К. Гиринским A947). Он может быть получен как из случая \
S < Г, так и из случая S > Т при k = 1 и &' = 0, что дает ]
5
1
П Г G2 + в) .?
Mi — Ш] =
ШПУНТ ПА ДВУХ СЛОЯХ ОДИНАКОВОЙ ТОЛЩИНЫ
0,1 0,2 0,3 Ot s
Рис. 205.
10
1,2
0,8
\
\
\
\
ч
Ч
0J0-
е
S~L
—¦ 1
035
0,30
0,25
QJ5
\05
——.
"^—
•—
——
-
—-—.
=====
\
\
\
J
0,2 0,4 0,6
Рис. 206.
S
IT
308
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
. vm
Рис. 207.
0,01 0J
0,1 0,2 0,5
Рис. 208.
§3]
точечные шпунты в Двуслойном грунте
309
§ 3. Точечные шпунты в двуслойном грунте. Рассмотрим здесь
две схемы (Полубаринова-Кочина 1942, 1).
1. Два несимметрично расположенных точеч-
точечных шпунта. Этот случай изображен на рис. 209, а.
Если отобразить конформно область движения на надрезан-
надрезанную плоскость ? (рис. 209,6), то получим, что на верхнем краю
разреза есть особенность в точке ? = —а, а на нижнем краю
разреза —особенность в точке ? = —Ь.
Проанализировав решение задачи для двух точечных шпун-
шпунтов, изображенных на рис. 209, но в однородной среде, т. е. при
X! = иг, можно попытаться искать
функции F\ и F2 для задачи с двумя
различными коэффициентами фильт-
фильтрации в виде
• 5 + hVR
Условия, которые должны выпол-
выполняться на отрезках надрезанной плос-
плоскости ?, приводят к таким соотношениям между постоянными:
К = Л, М = С, L= {щЫ\)В, N= (x2/xi)Z); таким образом,
выражения для F\ и F2 примут вид
(с + a)
¦
*)Vt(i-o
2 =
Беря полувычеты функций Fi и F2 около точек 5 = —а и
» ~ ~Ь, найдем (Ни Н2 — разности уровней воды в водоемах)
я-ZL^Ve + Вл/\+а
л/а A + а)
= *,#,,
+ b)
s-^Vi+<
Va(l
Xi
= 0,
= 0.
310 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Отображение области z на полуплоскость ? дается, как и
раньше, формулой
Поэтому a = sh2(Mx)9 b = sh2(Xl2), где Я, = я/2Г, а /, и /2 —
отрезков ВС и CF Aи /2 > 0).
Для постоянных получим значения
длины
Окончательные формулы для скоростей имеют такой вид:
[Н{ Г— ch (Я/i) sh (Яг) + -~- sh (Я/i) ch (Яг)] ff 1
. sh (Я (/, + г)) sh (Я (/, - г)) sh (Я A2 - г)) J '
( „ Я2 Teh (Я/2) sh (Яг) + ^L sh (Я/2) ch (ЯгI
А ( sh (Я (/, + г)) sh (Я (/2 + г)) sh (Я (/2 - г)) J ' J
Если точка М на границе среднего водоема, в которой ско-
скорость обращается в нуль, лежит во второй области (где х > 0),
то абсцисса х0 этой точки определяется уравнением
#i sh (I (/2 + х0)) sh (X (/2 - хо)) =
= #2 [ch (Я,у sh (Ях0) + — sh (Я/2) ch м] sh (Я (/! + х0)). C.2)
Если эта точка лежит в первой области, то в уравнении C.2)
нужно заменить Я2, /2, и2 на Яь /1э Xj и хо на — х0.
Положив для краткости Х1{ = а1э Kl2 = ct2, Я^Я! = ц, х^ = v,
получим из уравнения C.2)
,1 я^о М- (ch a2 shaj + vsha2ch ai) .
. V[|a (ch а2 shai — v sh a2 ch aQ + sh 2a2]2 + 2\i (v + 1) sh 2a2 sh (a2 — ai)
' 2 ch a2 (cha2 + fi ch ai)
При /i = /2 = /, т. е. при а1 = а2, последнее уравнение приобре-
приобретает вид
и ПХ0_ Х;Я| — Х2Я2 , Jt/_
ХП 2Г ~ х, (//i + Я2) Ш 2Г #
ТОЧЕЧНЫЕ ШПУНТЫ В ДВУСЛОЙНОМ ГРУНТЕ
311
2. Точечный шпунт в бесконечной полупло*
скости. Положим в формулах предыдущего случая //2 = 0.
Тогда будем иметь шпунт лишь в точке г = — 1Х. Обозначим
/1==/, Н{ = Н. Тогда формулы C.1) примут вид
- ch (XI) sh (кг) + -~ sJi (XI) ch (кг)
sh (X (I + z)) sh (X (I — z))
1
C.3)
sh
Рассмотрим теперь случай грунта бесконечной глубины, т. е.
положим Г = оо (Я = 0). Уравнения C.3) после преобразований
примут вид
и2 — w2—
и2 —'
Ш 1 + Z '
C.4)
На рис. 210 построены линии тока и эквипотенциали для то-
точечного шпунта, когда т/щ = 7з-
Рис. 210.
Интегрируя уравнения C.4), получим для комплексного по-
потенциала обеих областей соответственно
! (z) = ^f [In (/ + г) + [х In (/ - z)] + Си
312 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Нетрудно видеть, что в первой (левой) области линии тока пред-
представляют «обобщенные лемнискаты», т. е. линии, уравнение ко-
которых есть |/ + г|.|/ —г|»* = const. Во второй (правой) обла-
области линии тока являются дугами окружностей.
§ 4. Точечный вихрь в многослойной области. Для решения
задачи о движении грунтовых вод под гидротехническими соору-
сооружениями^ среде, состоящей из горизонтальных слоев грунта
различной проницаемости, можно поступить подобно тому, как
это делается в гидродинамике в задаче об обтекании тел, а
именно, заменить контур основания гидротехнического сооруже-
сооружения системой точечных вихрей и подбирать плотность интенсив-
интенсивности этих вихрей так, чтобы удовлетворялось условие на кон-
2 туре — нормальная составляющая ско-
°^J рости равна нулю (Полубаринова-Ко-
** чина 1942, 1).
^ч!> (g) Для составления интегрального
уравнения, которому должна удовлет-
(Sj^ ворять интенсивность источников, нуж-
— но найти выражение комплексного по-
потенциала точечного вихря в многослой-
'
Тп
7777777777777777777777777777777777 НОЙ ОблаСТИ.
Рис. 211. На рис. 211 изображен горизон-
горизонтальный слой грунта толщины d\ с
коэффициентом фильтрации ки далее слой толщины d2 с коэф-
коэффициентом фильтрации к2 и т.д., наконец, нижний слой грунта
толщины dn с коэффициентом фильтрации хп.
Наряду с величинами dr будем рассматривать их суммы Тг
так что Г, = du T2 == dx + d2i ..., Тп = dx + d2 + ... + dn. Ли-
Линия у = —Тп представляет непроницаемую границу.
В точке zo = хо + iyQ верхнего слоя поместим точечный
вихрь, интенсивность которого равна единице.
Обозначим через wr = ur — ivr комплексную скорость в точ-
точке г, принадлежащей r-му слою, обусловленную наличием то-
точечного вихря в точке z0. Будем искать функцию wr в виде инте-
интеграла Фурье
\ Аг{а)е1™ +Br(a)e~i**]da (r = 2, 3, ..., п), D.1)
о
где Аг(а) и Вг(а) — комплексные функции действительной пе-
переменной а.
Что касается скорости в точке верхнего слоя, содержащего
точечный вихрь, то в ее выражении выделим член
1 1
$ 41 ТОЧЕЧНЫЙ ВЙХРЪ В МНОГОСЛОЙНОЙ ОБЛАСТИ 313
Вдоль оси х, соответствующей границе водного бассейна, гори-
горизонтальная составляющая скорости равна нулю, что можно за-
записать так: Im(Wi) =0. Отсюда следует, что функция комп-
комплексного переменного iw\ может быть продолжена в верхнюю
полуплоскость (в область, представляющую полосу между пря-
прямыми у = 0 и у = +o?i), причем в точке z функция iw\ перехо-
переходит в —Ш\. Это позволяет искать W\ в виде
О
где
А (<*)*=-Л, (а). D.3)
На непроницаемой границе нижнего п-го слоя вертикальная
скорость должна равняться нулю. Это определяет зависимость
между Ап (а) и Вп (а) вида
На границе раздела r-го и (г + 1)-го слоев нормальная к
границе составляющая скорости должна быть непрерывна, каса-
касательные же составляющие пропорциональны соответствующим
коэффициентам фильтрации. Поэтому при у = —Тг имеем
или иначе
Im(ayr+1) = Im wn xrRe(^r+1) = xr+1 Re(ayr).
Наконец, последнее условие можно переписать так:
wr+l — wr+{ = wr — wn
При z = x — Tri имеем
оо
шг+1B) = 5 и+,(о)Лв+|" +Br+I(o)e-V-'e*]da,
О
оо
«V(*)= \ [Ar{a)eTra+lax + fir(a)e-V-'«]rfa.
О
Условия D.5) должны выполняться не только для самих
Функций, но и для их подынтегральных выражений. Поэтому
3l4 НЕОДНОРОДНЫЕ И ШИЗОТРОПНЫЕ ГРУНТЫ [1 Л. VIII
получаем
(Лг+1 - Ar)eTra+iax + (Sr+1 - Br) <rV-<- =
= (Ar+i - A,)eTr«-iax + (Br+l - Br)e-Tra+i"\
Эти уравнения должны выполняться тождественно относи-
относительно х, поэтому можно приравнять между собой коэффициен-
коэффициенты при eiax и e~iax. Это даст четыре уравнения, из которых вы-
выпишем два:
- Аг)ет'а - Eг+1 - Вг)е~тг* = 0, |
Два других уравнения получим, если заменим в D.6) все ком-
комплексные величины их сопряженными.
Уравнения D.6) имеют место для г = 2, 3, ..., п—1. Что
касается линии у = —d\ = —Гь то для того, чтобы использо-
использовать условие на ней, представим главную часть выражения W\
в виде определенного интеграла:
оо
—1— = / \ e-ia (*-*.> da при Im (z — zQ) < 0.
Z Zq J
0
Вдоль линии у = —7*1 условие \m(z — z0) < 0, равно как и
условие Im(z — г0) < 0, выполнено. Поэтому функцию w\(z)
можно представить в виде
wx (z) = ^ [л, (a) eia* + 5, (a) e~ia* + ^e'ia <*-*•> ch(ay0)] da
о
(У-Уо< 0),
а при z~x — T{i в виде
о;, (г) = ^ [л, (а) вг'а+/ах + 5, (а) ?Г
о
§4]
ТОЧЕЧНЫЙ ВИХРЬ В МНОГОСЛОЙНОЙ ОБЛАСТИ
315
Условия на линии раздела дают
(Ах - А2) ет^ - (В, - В2) е~т« = ~ е-т
+ М2)^« + (хД - хД) *-'«« = D.7)
ch (ау0) = *,
Введя обозначения
е2V = <хг,
систему уравнений D.3), D.4), D.6) и D.7) можно переписать
в виде
а2Л2 - В2 -
а2Л2 + В2 —
3 = 0,
В частности, при п = 2 получаем
(а, + 1) Л, + (а2 — а,) Л2 = 6, (а, — 1) Л! — Я (а2 + а{) А2 = — 6,
откуда найдем
л __ 1 ch (ayо) [xi ch (tf2a) - ^2 sh (rf2aI ^-/n^-w,»
1 2л x2 sh (d,a) sh (d2a) + x, ch (d,a) ch (d2a) e
и =
2
J
ch
= J ( ^/oxero
2 2л x2 sh (d,a) sh (d2a) + xi ch (d,a) ch (d2a)
где Г = d, + d2.
Для комплексных скоростей первой и второй областей дви-
движения будем иметь
оо
= ^ j N (a) cos (a B — z0)) da,
316
где
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
[ГЛ. VIII
w, ч ch (аур) [xi ch (d2a) — x2 sh (d2a)]
W ~ (xj + x2) ch (Га) + (xi - x2) ch ((d, - d2) a) '
w/ ч ch (af/p)
* ' (x, + x2) ch (Га) + (xi — x2) ch ((d{ — d2) a) '
Отметим частные случаи.
1. щ = 0, т. е. нижний слой непроницаемый. Тогда
= — F
csch
cscn
2d,
ccch
cscn
2d,
2. X2 = °o, т. е. линия у = —d\ представляет линию равного
напора. Тогда
1
3. Нижний слой бесконечно глубокий, т. е. d2 = оо. Этот слу-
случай был рассмотрен Б. К. Ризенкампфом A940, 2). Для него
можно написать (считая вихрь находящимся на оси х, т. е.
)
ch (d,a) + x2 sh (dxa)
или в виде ряда по степеням Х = (щ — к2I(к\ +н2):
1 1 к(г-хо) , Я2B~а:о)
(г) =
2я/ 2 - х
0
л/
B - ^0)
- + ¦
Перейдем теперь к составлению интегрального уравнения.
Пусть основание гидротехнического сооружения ограничено ли-
линией АВ (рис. 212). Отразив эту ли-
линию в оси абсцисс, получим замк-
замкнутый контур С. Будем считать, что
контур С в каждой точке имеет ка-
касательную. Распределим вдоль кон-
контура С вихри с интенсивностью
T(s)ds на элементе дуги ds. Обозна-
Обозначим через w(z9 z0) комплексную ско-
скорость, происходящую от действия
вихря с интенсивностью, равной еди-
единице, в точке 20. Тогда элемент дуги
ds будет вызывать в точке z скорость T(s)w(z, zo)ds. При этом
2о = Xq{s) + iyo(s) будет функцией дуги s. Скорость W(z),
происходящая от действия на точку z системы всех вихрей.
V///////////////7////////////////////
Рис. 212.
§5] ПРОСТЕЙШИЕ ДВИЖЕНИЯ В СЛОИСТЫХ ГРУНТАХ 317
распределенных по контуру С, будет
W{z)= \r(s)w(z, zQ)ds. D.9)
с
Положим
w(ZyZf)) = ±r-J— + O(z9 *0),
где Ф(г, Zq) —голоморфная функция. Будем приближать точку
г к точке контура zK = Ъ(о), где а —длина дуги в точке zK.
В пределе для интеграла типа Коши (Смирнов 1967) получим
F (а) — угол касательной с осью х)
Умножив D.9) почленно на eiQW и перейдя к пределу при
z-+ zK, получим
W (zK) ei в <°> = IГ (а) + JL J Г (s) w (гк, г0) ^ в.(а
с
Но W(zK)eiQW= Vt — iVni где ^ — проекция скорости на ка-
касательную к контуру, Vn — проекция на нормаль. Поэтому, от-
отделив в D.11) действительную часть от мнимой и учитывая, что
на контуре Vt = Г(а), Vn = 0, получим два интегральных ура-
уравнения: уравнение второго рода с обыкновенным ядром
, s)ds9
где ?(а, s) = t/(a, s) sin 9 (а) — v (a, s) cos 9 (а), и уравнение пер-
первого рода с несобственным ядром
T(s)G(o, s)ds = 0,
с
где G (a, s) = u (a, s) cos 9 (а) + v (a, s) sin 9 (а).
Н. К. Калининым A941) и Б. К. Ризенкампфом A940, 2)
указаны некоторые возможности для отыскания решения по-
последнего уравнения для плоского флютбета.
§ 5. Простейшие движения в слоистых грунтах. Остановимся
на простейших одномерных движениях в неоднородных грунтах
(Dupuit 1863).
318
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
[ГЛ. VIII
1. Фильтрация вдоль напластования. Схема та-
такого движения изображена на рис. 213: грунт состоит из парал-
параллельных (горизонтальных) слоев, толщины которых d[td2t ...
..., dn. Коэффициенты фильтрации слоев обозначены соответ-
соответственно через k\9 k2t ..., kn. Первый и по-
последний слои граничат с водоупорами.
Расход, проходящий вдоль напласто-
напластования через каждый слой, вычисляется
по элементарной формуле, вытекающей
непосредственно из закона Дарси:
Qi = -ki]bi2lL-dim E.1)
d.
Здесь Н2 — Н{ — разность напоров на
Рис. 213. концах рассматриваемого слоя, L — дли-
длина пути фильтрации.
Для суммарного расхода через всю толщину грунта полу-
получаем выражение
E.2)
Разделив расход на площадь поперечного сечения потока,
получим среднюю скорость фильтрации и. Принимая толщину
слоя в направлении, перпендикулярном к плоскости чертежа, за
единицу, получим, что площадь Q численно равна общей глу-
глубине потока:
Поэтому для средней скорости потока получим
Н\ - Н2
или
и= k-
E.3)
E.4)
Можно назвать k эквивалентным коэффициентом фильтра-
фильтрации, это среднее значение, взвешенное по толщинам слоев, ко-
коэффициентов фильтрации отдельных слоев. Движение происхо-
происходит так, как если бы мы имели однородный грунт с коэффи-
коэффициентом фильтрации, равным среднему коэффициенту фильтра-
фильтрации всех слоев.
2. Фильтрация поперек напластования. До-
Допустим, что движение происходит в таком же грунте, как и в
§5]
ПРОСТЕЙШИЕ ДВИЖЕНИЯ В СЛОИСТЫХ ГРУНТАХ
31$
предыдущем случае, но скорость движения направлена поперек
напластования — по вертикали (рис. 214); над верхним слоем
имеется напор воды Ни а под нижним слоем — напор Н2.
Вдоль линий раздела грунтов значения напоров неизвестны;
обозначим их соответственно через Аь А2, ..., An_i, так что в
основании 1-го слоя напор составляет Аг-.
Применяя к каждому из слоев формулу Дарси, обозначим
через Vi скорость в i-м слое:
hi-hi-,
In
E.5)
Все эти скорости равны между собой, так как жидкость счи-
считается несжимаемой, а движение одномерным (уравнение нераз-
неразрывности дает при этом постоянное зна-
значение скорости).
Приравнивая между собой выражения
E.5), получим п—1 уравнений для п—1
неизвестных Аь А2, ..., hn-\ (первое из
уравнений — тождество, введенное для
удобства вычислений):
а1(А, —//,) = а,(А,—#!>,
а3(А, — //i) = а, (Л3 — Л2),
©
Рис. 214.
ап (Л, - //,) = а, (Н2 - Ал_,),
где а* = U/ki. Складывая левые и правые части этих уравне-
уравнений, получим
(а,+а2+ ... +*n)(hx-Hl) = al(H2-Hl),
откуда будем иметь для у,, а следовательно, и для всех vt:
— Н\ Н2 — Н\
* «1 а, + а2 + • • • + <*/г
Обозначая через v общее выражение скорости, получим
U
¦+?+•••+&'
E.6)
E.7)
Можно сделать приведение этой скорости к какому-нибудь
слою грунта, например верхнему, написав ее так:
Н\ — Н2
Т-1*. E-8)
320 -НЕОДНОРОДНЫЕ Й АНИЗОТРОПНЫЕ ГРУНТЬт ГГЛ. VIII
Величину L можно назвать эквивалентной или приведенной
длиной.
Но можно иначе интерпретировать формулу E.7), полагая
?+¦?+•••+-(НЬ (б-9)
Тогда
v=kJL^, k== E.io)
k{ ^ k2 "Г * * * "Г kn
Здесь k — эквивалентный коэффициент фильтрации, дающий ту
же скорость, что и неоднородный грунт, при толщине однород*
ного слоя, равной общей толщине неоднородного грунта.
§ 6. Напорная фильтрация в неоднородных пластах. Фильтра-
Фильтрации несжимаемой жидкости в неоднородной пористой среде по-
посвящено много работ. Результаты ряда исследований изложены
в книге Г. В. Голубева и Г. Г. Тумашева A972).
Ограничимся рассмотрением одного довольно общего метода
решения задач напорной фильтрации в неоднородном плоском
пласте.
Считая коэффициент фильтрации k(x,y) непрерывной и диф-
дифференцируемой функцией координат, для напора h(x,y) будем
иметь уравнение
Авторы применяют метод Бергмана A964) к решению задач
о притоке жидкости к скважинам.
Предполагая, что k(x,y) нигде не обращается в нуль, поло-
положим, как это делали хмногие авторы,
у). F.2)
Тогда для U {х, у) будем иметь уравнение
bU + g{x,y)U = 0, F.3)
причем g(x, у) определяется из соотношения
AV* + *(*. 0)V*-=O. F.4)
Далее вводятся функции комплексного переменного Wn(z) и
функции An(z, г), где г = х + iy и S — х — iy. Функция U(x, у)
ищется в виде
U (х, у) = Re ? Ап (г, z) Wn (z), F.5)
/i=Q
§ 6] НАПОРНАЯ ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ ПЛАСТАХ 321
где An(z, z) —искомые перменные коэффициенты, a Wn(z) удо-
удовлетворяют соотношениям
4^=гп-,. F.6)
dz n l v '
Подстановка F.5) в F.3) дает
где
1 S _ I Х -. i= Ч
F.8)
Из F.6) получаем представление Wn(z) через H^o(^)s кото-
которая остается пока произвольной:
?"'"
-1)!
Теперь ряд F.5) можно представить в виде
U {х9 у) = Re ^о B) + \ N (z, г9 t) Wo (/) A J, F.10)
где
N(zt z, t) = Yj An(z, г) ^G-^ni - FЛ1)
Интегральный оператор в уравнении F.10) переводит произ-
произвольную аналитическую функцию W0(z) в решение уравнения
F.3), так что фильтрационному потоку в однородной среде с на-
напором А = Re Wo (г) ставится в соответствие некоторое филь-
фильтрационное течение в неоднородной среде с проницаемостью
Ь(х,у).
Для применимости интегрального оператора F.10) к крае-
краевым задачам необходимо, чтобы ядро оператора N(z,z,t) в об-
области фильтрации было равномерно и абсолютно сходящимся.
Рассмотрим несколько примеров.
1. Для линейного распределения проницаемости пласта за-
задача решалась (Г. В. Голубев 1966) по методу И. Н. Векуа
A948). Пусть k(x9y) = Ml +a*). Тогда
G (г, z) = 7 ^ (X = const),
г
(я= 1, 2, . ..)•
U П. Я. Полубаринова-Кочина
322 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. Vtlt
Здесь
n+ I), ^о== 1,
W
2п (п - 1)! A + ах)" *
Выбирая Я = а2/16, получим а1 = а2 = 1/2- Тогда
2 ' 2 ' !' 2 A + fl
где F(a, 6, с, л:) — гипергеометрическая функция. Ряд F.12) схо-
сходится абсолютно и равномерно при
a (z -t)
2A +ах)
я в качестве области сходимости для ядра N(zizit) можно
взять круг с радиусом R = B/a)min(l + #*)•
Это решение можно рассматривать как мажоранту в круго-
круговой области для решений, соответствующих некоторому классу
проницаемостей.
2. Если принять g{x,y) == X2 = const, то получается
и N (г, 2, t) принимает вид
оо
x7°Jz~Z
Для случая, когда функция k{x,y) удовлетворяет одному из
уравнений
различными авторами решен ряд краевых задач, так же как для
осесимметричной задачи с k(xy у) = f(r)y г==л/х2 + у2 (Г. В. Го-
Голубев 1966; Голубев и Тумашев 1972).
3. Пусть имеем при г = 0 точечную скважину с дебитом Q
в горизонтальном пласте мощности Г, причем контуром пита-
питания является окружность радиуса р0:
h = H0 при р = У х2 + #2 = ро,
lim (&kT-z--ds\ = Q
§ 7] УРАВНЕНИЯ ДВИЖЕНИЯ И ПРИМЕРЫ 323
(здесь y — произвольный контур, охватывающий скважину, п —
внутренняя нормаль к контуру). Решение ищется в виде
ж Г с 1
h = Ho + -7==Re\Wo(z)+\N{z, z,t)Wo(t)dt\.
Аналитическая функция Wq(z) с логарифмической особен-
особенностью представляется в таком виде:
"inz
Q
w=0 / 2яЯУ*@, 0)
Постоянные ат выбираются так, чтобы выполнялось краевое
условие
Re [in z + ? amzm + j ^V (z, z, t) (In / + J amA dt\ = 0
L m=0 0 ^ m=0 ^ -I
при \z\ — р0.
Для определения коэффициентов ат получается бесконечная
система алгебраических уравнений; обрезая ее, находят реше-
решение и проводят расчеты.
Б. АНИЗОТРОПНЫЕ ГРУНТЫ
§ 7. Уравнения движения и примеры. Известно, что в лессо-
лессовых грунтах водопроницаемость в вертикальном направлении
больше, чем в горизонтальном, в ряде других грунтов имеем
обратную картину — проницаемость в горизонтальном направ-
направлении больше, чем в вертикальном.
Анизотропным грунтом называется такой грунт, у которого
величина коэффициента фильтрации в данной точке области
движения зависит от направления.
В. И. Аравин исследовал общие законы анизотропии в пло-
плоской задаче (Аравин 1937), а также рассмотрел частные распо-
расположения слоев в виде концентрических окружностей и в виде
пучков прямых. Мы ограничиваемся рассмотрением однородной
анизотропии, для которой коэффициент фильтрации вдоль ка-
каждой прямой является постоянным.
Для изотропного грунта мы имели основную зависимость
Для линейного закона фильтрации V = —k grad /г, где k — ко-
коэффициент фильтрации, напор h связан с давлением формулой
h==ji + y- GЛ)
324
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
[ГЛ. VIII
В случае однородно-анизотропного грунта можно выбрать
за оси координат g, ц (рис. 215) главные оси анизотропии грун-
грунта — они взаимно перпендикулярны, вдоль них коэффициенты
фильтрации k\ и кч имеют постоянные значения (максимальное
и минимальное). Составляющие скорости
вдоль главных направлений будут
u= — k— = — к — G2)
1 dl ' 2 drj # \ '
Уравнение неразрывности
* ди , dv
Рис. 215.
приводит к уравнению для h:
G.3)
Если в это уравнение ввести новые координаты
;-. G.4)
где k0— произвольная постоянная, имеющая размерность ско-
скорости, то получим уравнение Лапласа
d2h , d2h
При этом для ft будут иметь место такие равенства:
h = -^- +1 sin a + т] cos а =
го
G.5)
Условия постоянства давления на некоторых границах (на
свободной поверхности, вдоль промежутка высачивания) в ко-
координатах (хиу\) приводят к несколько более сложным выра-
выражениям, чем соответствующие выражения для изотропного грун-
грунта (см., например, Полубаринова-Кочина 1940, 2). Г. К. Михай-
Михайлов A954) предлагает более простой путь, вводя другое преоб-
преобразование координат, а именно,
X = bx + ]iy, Y = y, G.6)
причем X и \х выбираются так, чтобы в переменных (X, Y) ура-
уравнение G.3) стало уравнением Лапласа:
1
'дХ2 "*" dY2
§7]
УРАВНЕНИЯ ДВИЖЕНИЯ И ПРИМЕРЫ
325
Так как координаты (л:, у) связаны с координатами (|, ц) фор-
формулами
х = \ cos а — т] sin а, у = ? sin а + Ц cos а, G.7)
для X и jlx получаются такие выражения:
. k\ sin2 a + k2 cos2 а (&2 —
л/Щ
G-8)
Предлагается далее рассматривать фиктивное течение в пло-
плоскости (X, У), приняв ось X за горизонтальную, а ось У за вер-
вертикальную прямые и вводя коэффициент фильтрации k*=* л/ k{k2*
Так как теперь для напора h имеем
h(X, У) = -^- + У, G.9)
то условие постоянства давления в координатах (X, У) имеет
тот же вид, что и в координатах (л:, у):
—^- = /г — К == /г — у = const.
G.10)
Вводя составляющие фиктивной скорости
и * дХ '
dh
dY
G.11)
можно из G.10) получить уравнения для годографа скорости в
плоскости ([/, V), в частности, уравнение окружности для сво-
свободной поверхности и прямой для промежутка высачивания.
Поэтому для решения ряда задач ^
о фильтрации в однородно-анизо-
однородно-анизотропных грунтах достаточно ре-
решить соответствующую задачу
для изотропного грунта в коор-
координатах (X, У) и затем перейти к
переменным (л:, у) по формулам
G.6) и G.8).
В качестве примера найдено
уравнение свободной поверхно-
поверхности для притока по горизонтальному водоупору из бесконечно-
бесконечности (рис. 216) для однородно-анизотропного грунта. Для изо-
изотропного грунта мы имели «дрену на водоупоре» (см. § 11 гла-
главы II), уравнение свободной поверхности которой в координа-
координатах (Ху У) можно записать в виде
Рис. 216.
¦4-и
G.12)
326 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
где Q — удельный (т. е. на единицу ширины потока) фильтра-
фильтрационный расход дренажа, / — длина участка высачивания в
дренаж.
Подставляя в G.12) X и У из уравнений G.5) и G.8), най-
найдем искомое уравнение свободной поверхности
Ф = Q^ 2Q *» sin2 а + Ъ cos2 а Г __ (fe, - Ь) sin а cos а 1 ^ 3)
* ^0 ^0 ^k^2 |_ ^ sin2 а + k2 C0S2 а ^J V
Полагая у = 0 и л: = /, найдем для участка дренажа
/ — J9G 14)
1 2 u1^
J 9 G 14)
2 ki sin2 а + k2 cos2 а ' u#1^
§ 8. Задача об обтекании шпунта. В напорных движениях
обычно в качестве границ области рассматривают отрезки пря-
прямых линий. Если в случае однородной анизотропии пользоваться
преобразованиями координат G.7) и G.4), то зависимость ме-
между первоначальными координатами (л:, у) и координатами
(*ь У\), приводящими к уравнению Лапласа, будет
cos а —- ух V&2 sin а> У=== xi V^i s^n а "Ь У\ V^2cos а- (8.1)
По способу, предложенному Г. К. Михайловым A954), ура-
уравнение Лапласа получается в независимых переменных (X, У),
связь которых с (х, у) согласно G.6) можно переписать так:
х = |*--?-У, y = Y9 (8.2)
где X и A определяются по формулам G.8).
Видим, что в обоих способах прямые линии плоскости (л:, у)
переходят в прямые линии вспомогательных плоскостей, однако
преимущество формул (8.2) состоит в том, что согласно им го-
горизонтальные прямые у = const переходят в горизонтальные же
прямые У = const.
Что касается вертикальных отрезков, в частности шпунтов,
то их уравнения, как в системе координат (х\9ух), так и в си-
системе (X, У), переходят, вообще говоря, в наклонные прямые.
Ось х = 0 переходит в прямую
Y X
причем для тангенса угла 6 наклона шпунта получаем
tg6 = -^ ^Ш- . (8.3)
6 (k2 — h) sin a cos a v '
Следовательно, вертикальный шпунт перейдет в наклонный на
плоскости (X, У). В случае бесконечно глубокого грунта была
рассмотрена задача об обтекании косого шпунта (см. § 10 гла-
главы III), но уже ее решение достаточно сложно. В главе XVIII
§ 9) ПРЕДЕЛЬНО-АНИЗОТРОПНЫЕ ГРУНТЫ 32?
приведен пример построения гидродинамических сеток на пло-
плоскости (Ху Y) около наклонного шпунта с пересчетом их на ли-
линии основной области движения в плоскости (я, у). Построение
этих изолиний возможно на основе следующих свойств фиктив-
фиктивного течения.
Для U и V, определенных формулой G.11), имеет место ура-
уравнение неразрывности
дХ "^ dY ~U'
это показывает, что существует «функция тока» Ч; = — k q (X, Y)
такая, что
п — J^L— — ьЁ± у — д^ — ъ dq
и ~ dY ~~ к dY ' v ~ дХ ~ к дХ '
Сравнивая эти выражения с выражениями G.11) для U и
V, видим, что функция h + iq может рассматриваться как функ-
функция комплексного переменного X + iY, а эквипотенциали h =
= const и линии тока q = const фиктивного течения взаимно
ортогональны. Пересчет координат этих линий по формулам
(8.2) даст изолинии на плоскости (х, у) действительного те-
течения.
§ 9. Предельно-анизотропные грунты. Пусть область филь-
фильтрации ограничена снизу горизонтальным водоупором, причем
грунт однородно-анизотропен и главные оси анизотропии напра-
направлены горизонтально и вертикально. Обозначая коэффициенты
фильтрации соответственно через k\ и k2i напишем для состав-
составляющих скорости фильтрации
dh I dh A р . \ /г\ л\
Г. К. Михайловым A953, 2) введены в рассмотрение пре-
предельные значения k2 = 0 и k2 = оо, которые он называет соот-
соответственно верхним (k2 = 0) и нижним (k2 = оо) пределами
анизотропии. При k2 = 0 вертикальная составляющая скорости
v = 0 при k2 = оо из условия конечности v следует dh/dy = 0,
т. е. напор h не зависит от у, эквипотенциали течения всюду вер-
вертикальны. В ряде случаев можно установить предельные значе-
значения расходов, а для неустановившихся движений и скоростей
перемещения языков грунтовых вод между предельными значе-
значениями должны лежать значения этих величин для 0 <С k2 < оо.
В качестве первого примера возьмем прямоугольную пере-
перемычку (рис. 217). При k2 = 0 дело обстоит так, как будто все
Движение происходит по тонким горизонтальным прослойкам,
вдоль которых сохраняется постоянная скорость, пропорцио-
пропорциональная разности капоров.
328
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
[ГЛ. VIII
Для вычисления полного расхода через левую вертикаль ра-
разобьем область фильтрации на две: 1) 0 < J/ < Я2 и 2) Н2 ^
^ у ^ Н\. В первой по всем прослойкам имеем горизонтальную
скорость
HH (9.2)
и расход, вытекающий в нижний бьеф, равен
я,
о
Во второй области, в полосе, находящейся на высоте у от
основания плотины, перепад напоров будет Н\ — у и скорость
У\
V///////////
Рис. 217.
HZ
Y////////' ¦
Рис. 218.
на выходе через промежуток высачивания будет и = k\ (H\ —
— y)\U а вдоль всего «участка выхода», который мы должны
считать отрезком высоты Н\ — Я2, расход будет
(9.4)
Складывая Q\ и Q2, получим для общего расхода
(9.6)
Верхний расход совпал с действительным, значение которого
дается формулой Дюпюи — Чарного. Форма свободной поверх-
поверхности здесь не учитывалась, как будто все течение происходит
по горизонталям.
В случае k2 = оо рассмотрим произвольное вертикальное се-
сечение области движения с ординатой свободной поверхности у
(рис. 218). Расход через любое из таких сечений равен QH. Ori
§9]
ПРЕДЕЛЬНО-АНИЗОТРОПНЫЕ ГРУНТЫ
329
определяется, как в гидравлической постановке, произведением
у на скорость и = —kidy/dx:
л и <.Ау
(9.6)
Интегрируя это уравнение, получим
qhX=-Z1- + C. (9.7)
При х = / пусть выходная ордината свободной поверхности бу-
будет уо. Так как при х = 0 имеем у = Ни то из (9.7) найдем
(9.8)
где уо—величина, неизвестная заранее. Из условия конечности
скоростей следует, что г/о = H2i и для расхода QH в нижнем пре-
пределе анизотропии также получается фор-
формула Дюпюи — Чарного.
Г. К. Михайлов A953,2) рассмотрел
также перемычку на наклонном водоупо-
ре, когда главные оси анизотропии на-
направлены соответственно параллельно и
перпендикулярно плоскости водоупора,
которая составляет угол а с горизонталь-
горизонтальной плоскостью (рис. 219), причем
в нижнем бьефе вода отсутствует.
Здесь QB вычисляется аналогично Q2
формулы (9.4), причем координаты (х, у)
нужно преобразовать к координатам
(*b#i)> что приводит к замене Н\—у
под знаком интеграла в (9.4) на (Н — у) cos a + l sin а. Поэто-
Поэтому будем иметь для k2 = О
Рис. 219.
В случае нижнего предела анизотропии градиент напора
нужно выразить в уравнении (9.6) через координаты Х\ и у{.
Тогда
п . sinadxi — cos a dy\
что после интегрирования и подстановки Х\ = 0, у\ = Н даст
__0^1п «и (9Л0)
330 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Равенства (9.9), (9.10) принимают простой вид при введении
безразмерных величин
а именно,
9в=1+^. 1 + Р = ^н In ^^гг •
При р->оо имеем #в->1, qH-*l и отношение
* Ян Qn ^ 1
о = — =-л—> 1.
<7в Qb
При р->0 получается qB-*oo и Qh-^00, но
При других значениях р б< 1; б принимает наименьшее
значение 6 = 0,836 при f$ = 1,10. Отсюда можно сделать прав-
правдоподобный вывод, что действительные значения фильтрацион-
фильтрационного расхода в перемычках рассматриваемого типа могут отли-
отличаться от даваемого формулой (9.9) не более чем на 16,4%.
Для случаев предельной анизотропии рассмотрены также
(Михайлов 1953, 2) задачи фильтрации по нелинейным зако-
законам фильтрации —степенному и квадратичному — и найдены
верхний и нижний расходы для перемычки и для колодца. Тес-
Тесные границы получены в случае неустановившихся движений
при перемещении языка грунтовых вод по водоупору. Об этом
будет сказано в § 7 главы XII.
В. ДВЕ ЖИДКОСТИ РАЗНОЙ ПЛОТНОСТИ
§ 10. О движении двух жидкостей разной плотности. Задача
о фильтрации двух жидкостей разной плотности возникает, на-
например, в случае, когда при движении воды под плотиной на
некоторой глубине имеется слой соленой воды, образовавшейся
вследствие того, что проницаемый слой лежит на толще камен-
каменной соли; морские воды, проникая в грунт, могут находиться под
пресными грунтовыми водами; на разных глубинах грунтовые
воды могут иметь различную минерализацию, в то время как
воды, фильтрующиеся с поверхности, являются пресными.
В качестве примера остановимся на случае (Полубаринова-
Кочина 1942, 1), когда на некоторой глубине под гидротехни-
гидротехническим сооружением имеется слой соленой воды A'D'D"A'\ на-
находящийся над непроницаемой толщей соли (рис. 220, а). Весь
слой грунта ADD"А" считается однородным, т. е. состоящим из
одной и той же породы.
ДВИЖЕНИЕ ДВУХ ЖИДКОСТЕЙ РАЗНОЙ ПЛОТНОСТИ
331
Предполагается, что после возведения гидротехнического со-
сооружения будет происходить отжим рассола так, что левая
часть линии A'D' будет понижаться, правая подниматься.
Будем считать обе жидкости несжимаемыми, обладающими
соответственно плотностями pi и рг, причем рг > рь Примем,
учитывая, что коэффициент фильтрации зависит не только от
грунта, но и от жидкости, в частности от ее вязкости, коэффи-
Рис. 220.
циенты фильтрации грунта в двух рассматриваемых областях
движения равными соответственно k\ и k^.
Напишем уравнения для скоростей щ, vt (t = 1,2) каждой
из двух жидкостей:
Ut = -
(/=1,2).
(ЮЛ)
Условие равенства давлений на линии раздела приводит к
уравнению
= (р2 —Pl)r/
A0.2)
на линии раздела.
Кроме того, линия раздела должна быть линией тока, т. е.
на ней ^i = const, г|J = const.
Если рассмотрим плоскость комплексного потенциала coi =
= Ф1 + ity\ для первой области, то на ней получим прямоуголь-
прямоугольник A'D'CB (рис. 220, б). Следовательно, ф конечно во всей этой
области.
Перейдем ко второй области. Если бы в ней было возможно
движение, то на плоскости ее комплексного потенциала о>2 =
= ф2 + а|>2 мы получили бы полосу A'D'D/fA" (рис. 220,в),
Откуда следует, что ф2=±оо, когда х=±оо. Но тогда из
332 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
уравнения A0.2) следовало бы, что и cpi = ±00 при х= ±оо,
что невозможно. Следовательно, в случае установившегося дви-
движения жидкость в нижней области должна оставаться в покое.
Таким образом, задача сводится к определению движения в
одной области, причем для линии раздела получаются условия,
совершенно аналогичные тем, какие имеют место на линии сво-
свободной поверхности. А именно, полагая в уравнении A0.2) ве-
величину ф2 постоянной, его можно представить в виДе
ф1 - су = const = С, c={^—\)kx. A0.3)
Величина коэффициента фильтрации второй среды не во-
вошла в условие задачи.
Очевидно, что на годографе скорости уравнению A0.3) со-
соответствует окружность (см. § 4 главы II)
u2 + v2-cv = 0. A0.4)
Пусть имеем гидротехническое сооружение произвольной
формы. На границах водоемов АВ и CD (рис. 220) потенциал
скорости имеет постоянные значения. Положим ц>\ = —k\Hj2 на
АВ и ф! = ki/H/2 на CD. Обозначим глубины потока движущей-
движущейся жидкости для х = —оо и х = +оо соответственно через h' и
А". Из уравнения A0.3), заменяя постоянную, будем иметь: при
х = q=oo соответственно
иг k\H \П h" ^\Н 1 Г
Отсюда С = —{W + h")/2.
Для установившегося движения в конечной области должно
было бы выполняться условие равенства первоначальной и окон-
окончательной площадей соленых вод. В рассматриваемом случае
эти площади бесконечны, поэтому заменим указанное условие
следующим: будем считать полусумму глубин V и h" равной
глубине верхнего слоя в состоянии равновесия
^4^ = Л,. (Ю.5)
Тогда С —-~h{ и
h=h, + — -А1+2ЫР1_,)
" — "! 2с ~ "» 2(p2/Pl — 1) '
Разность глубин равна
~~ ~~ p2/pi — 1
§11)
ОБТЕКАНИЕ ТОЧЕЧНОГО ШПУНТА
333
Таким образом, глубина вытеснения будет тем больше, чем
меньше разность плотностей pi и р2.
Если окажется, что
h
2
—2—
2(Р2/Р1-1) '
то правый конец линии раздела будет упираться в границу
А'г
t, ¦
^ \н
в
тж.
h"\ С
Ф/У/////////////Ш^^^
Рис. 221.
нижнего водоема. Если глубина Л2 нижнего слоя удовлетворяет
неравенству
то линия раздела упирается в линию водоупора. Таким обра-
образом, возможны четыре вида линии раздела, изображенные на
рис. 221.
§ 11. Обтекание точечного шпунта при наличии неподвижного
подстилающего слоя тяжелой жидкости. Рассмотрим случай 1
рис. 221. Принимая <р = — kH/2 вдоль АВУ <р = kH/2 вдоль ВС,
М5 = 0 вдоль AfDC\ получим
kH . .
со = arcsin?.
old
На плоскости годографа скорости w имеем полуплоскость
с разрезом по окружности A0.4). Инверсия в окружности
334 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
единичного радиуса с центром в начале координат даст область
функции d/d
При 111 < 1 имеем Im dz/dco = 1/c, при | g | > 1 Re dzjd® = О, при
? = oo dz/dco = 0. Это дает
C = —, Z) = -. A1.3)
ca с v '
Найдем из A1.2) и A1.1) величину dz/dt, и проинтегрируем
ее по ?. Учитывая, что обход точек ?=±1 дает приращения
для г, соответственно равные —h"i и h'i, для которых имеют
место равенства A0.6), найдем
~ 0 + М2^ 1П О + 0 +
^ + -^-ln2-fA,. A1.4)
Уравнение линии раздела получим при —1 < ? < 1:
Если между h\ w H имеет место зависимость
и и и
U к\Н п
1 = ^Г= 2(p2/Pl — 1) '
то уравнение линии раздела принимает вид
x=ij4n [2A+0], y = -^-arcsinC —Л,. A1.6)
А. Т. Павлов A942) и В. А. Брагинская A942) рассмотрели
случаи заглубленного шпунта и плоского флютбета; дано реше-
решение тех же задач и для анизотропного грунта.
§ 12. О линзе пресной воды над соленой водой. По-видимому,
первое (гидравлическое) решение задачи о движении пресных
вод над солеными принадлежит Ф. Форхгеймеру A935), кото-
который ссылается на наблюдения Герцберга (Herzberg 1901), ка-
касающиеся равновесия пресных и соленых вод. Японские ученые
(см. Kitagava 1940) дали некоторые обобщения решений Форх-
геймера и провели ряд сравнений теории с экспериментами и
наблюдениями в натуре (на полуострове в Японии). Э. Чайлдс
§ 12]
ЛИНЗА ПРЕСНОЙ ВОДЫ НАД СОЛЕНОЙ ВОДОЙ
335
провел ряд опытов по применению метода электрогидродинами-
электрогидродинамических аналогий к таким задачам. В Советском Союзе разра-
разработкой вопросов движения двух жидкостей различной плотно-
плотности, и притом в неоднородных грунтах, занимался Н. К. Гирин-
ский A955).
Ф. Форхгеймер рассматривал гидравлически задачу о линзе
пресной воды, которая может образоваться в теле острова, по-
получающего питание пресными дождевыми водами. Эти послед-
последние продавливают первоначально горизонтальную поверхность
соленой морской воды и обра-
образуют выпуклую свободную по-
поверхность (рис. 222). Для отно-
отношения отрезков Н\ и #2 имеем
условие равновесия
Н2 = Pi
Н\ Р2 — Pi
Пресная
A2.1)
Соленая 6ода
Рис. 222.
где pi — плотность пресной, р2 — плотность соленой воды. Сво-
Свободная поверхность по Форхгеймеру — эллипс с отношением по-
полуосей
Нл = /MPpPi) A22)
L у «р2
где 2L — ширина линзы, k — коэффицент фильтрации, е — по-
постоянная интенсивность инфильтрации на единицу длины по-
потока.
Ниже рассматривается задача о плоском движении пресной
воды в линзе при условии оттока этой воды в горизонтальные
дренажные щели.
Рассматриваемая схема представлена на рис. 223. Как мы
видели выше (§ 10), нижняя, более плотная жидкость должна
оставаться неподвижной. Тогда годограф скорости для правой
половины области, занятой пресной водой, будет иметь вид
рис. 224. На нем полуокружность ВА, соответствующая свобод-
свободной поверхности, проходит через точки v = —k и v = —е, по-
полуокружность DE проходит через начало координат и имеет
диаметр с (см. формулу A0.4)).
Будем рассматривать указанные полуокружности как линии
равного потенциала течения, вызванного источником и стоком
одинаковой интенсивности Q, помещенными соответственно в не-
некоторых точках w = ai и w = — Ы. Можно установить соответ-
соответствие между w = da)/dz и вспомогательной комплексной пере-
переменной т (рис. 224), рассматривая последнюю как комплексный
потенциал течения на плоскости w и принимая Q = я:
(w + bi) 2abi ch т
т_ 1 |
2
Ь (w — ai)
(а + b) sh т — (а — b) ch т
336 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
Используя очевидное соотношение
dco # dz
можно написать
[ГЛ. VIII
A2.4)
^- = 2аЫ А (х) chT, -g. = А (х) [(а + 6) shx — (а — 6)chx]. A2.5)
Исследование поведения dco/dt и rfz/dx в особых точках показы-
показывает, что А (т) — постоянная.
Рис. 223.
Интегрирование A2.5) с учетом геометрических размеров
области движения (рис. 223) дает
со = i
где
(k — г)
к
J
-V
е, что
(е +с) /Ли
— shr
(k + с) (8 4
скорость
- с) а
в точке
1 X) -
х,
+ ь
с,
/ /
для
ь ^
(Р2-Р,)Л
Pi
которой т = т
A2.6)
A2.7)
1, обра-
щается в бесконечность, дает
A2.8)
§ 12] ЛИНЗА ПРЕСНОЙ ВОДЫ НАД СОЛЕНОЙ ВОДОЙ 337
откуда можно найти длину L отрезка ОС или, наоборот, выра-
выразить через L остальные отрезки:
_ / А /
н /
е) (Л + с + е) ' п^~ь У (k- e)(k + с + е) '
т / (k-{-с) (г-\-с) tj j I
> == L Л I т,—; ;—^— , П о == L Л -
' V 0 (k + С + 8) ' Z У I
г 2 г 2 гг2 г2 гг2
/у = L\ — П | = Ь2 — По.
A2.9)
Полный расход Q и расходы Q\ и Q2 соответственно через
отрезки СВ и CD определяются по формулам
A2.10)
Вводя обозначение т = т' + it" и отделяя в A2.6) действи-
действительную и мнимую части, получим
Ф = — сН2 ch %' sin т", гр = сЯ2 sh т' cos т/г, A2.11)
л: = L2 (ch т' — v sh т') cos xn\ у = L2 (sh %' — v ch т7) sin т/г. A2.12)
Чтобы построить линии тока, положим
sht/cosT// = C A2.13)
и будем давать С равноотстоящие постоянные значения 0 ^
^ С ^ sh ji., причем 0 ^ х' ^ (г, 0 ^ %" ^ я/2. Исключая при
помощи A2.13) одну из переменных, например т", из уравнений
A2.12), получим уравнения линий тока в параметрической
форме
UC , u / и /\ L2 У sh2 т' - С2 / u , u ,ч
л:==-^1~7-(сЬт7 —vshxO, У = sh т/ (sh т7 - v ch т7).
A2.14)
Для построения эквипотенциалей полагаем
chT/sint// = D A2.15)
и даем D ряд значений, 0 <С D ^ ch \i. Уравнения эквипотен-
эквипотенциалей можно представить в виде
A2.16)
При этом (х можно определить из одного из уравнений
338
НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ
[ГЛ. VIII
Свободная поверхность представляет половину эллипса с по-
полуосями Li, #1, линия раздела между пресной и соленой во-
водой— полуэллипс с полуосями L2, #2. При с = оо получается
задача В. А. Васильева A955) о форме бугра грунтовых вод
между двумя дренами на водоупоре при наличии инфильтрации.
При е = 0 задача теряет смысл, однако отношение Нъ1Н\ имеет
предел, соответствующий равновесному соотношению Н2/Н\ =
= Pl/(p2 — pi).
I I I I I I 1 1 I 1 ! I 1 1 I 1 1 I
Рис. 225.
На рис. 225 построена сетка для случая е = с = &/4.
Ю. И. Капранов A973) обобщил эту задачу на случай беско-
бесконечной системы горизонтальных щелевидных дрен.
§ 13. Фильтрация из канала при наличии засоленных подпор-
подпорных вод. Обычно в местах, нуждающихся в орошении, грунтовые
воды вблизи свободной поверхности бывают в той или иной
степени засоленными. Поэтому фильтрующаяся из канала вода,
продавливая соленые грунтовые воды, образует на них прес-
пресную линзу. При близком к поверхности земли залегании грунто-
грунтовых вод имеет место испарение со свободной поверхности. Тог-
Тогда возможно установившееся движение, при котором линза
пресной воды сохраняет свои размеры, причем нижняя, более
тяжелая жидкость остается неподвижной. Задача состоит в
определении границ линзы.
Для простоты будем считать, что слой воды в канале тонкий
(рис. 226), так что форма поперечного сечения канала не играет
§ 13]
ФИЛЬТРАЦИЯ ИЗ КАНАЛА НАД ЗАСОЛЕННЫМИ ВОДАМИ
339
роли. Такая задача рассматривалась В. Н. Эмихом A962, 1966)
следующим образом.
н
х
А
й)
В
Рис. 226.
На свободной поверхности давление постоянно, поэтому
вдоль CD и C'Df можно положить
ф-)-/г# = О. A3.1)
Примем, что испарение со свободной поверхности происхо-
происходит с постоянной интенсивностью е (<0) на единицу площади
горизонтальной проекции свобод-
свободной поверхности. Тогда для функ-
функции тока г|) на свободной поверх-
поверхности будем иметь
-Ф —ex = const. A3.2)
При переходе через поверх-
поверхность раздела (С'ВС) мы имели
условие A0.3), которое теперь за-
запишем в виде
<p—cy = {k + c)T на С ВС, A3.3)
где Т — глубина залегания го-
горизонта покоящихся грунтовых
вод.
Ограничимся в силу симмет-
симметрии задачи рассмотрением обла-
области движения ABCD (рис. 22G) и
предположим, что эта область
плоскости z отображена на верх- Рис. 227.
нюю полуплоскость вспомогатель-
вспомогательного комплексного переменного ? (рис. 227, я), причем угловым
точкам области движения Л, В, С и D приводятся в соответствие
на действительной оси полуплоскости ? точки с абсциссами я,
1» оо и 0 (аффикс а подлежит определению). На плоскости го-
Дографа скорости область движения ABCD имеет вид, приве-
приведенный на рис. 227,6,
340 НЕОДНОРОДНЫЕ И АНИЗОТРОПНЫЕ ГРУНТЫ [ГЛ. VIII
Для функций Z = dz/dt, и F = df/dt, граничные условия при-
принимают вид
Im {Fi — cZ) = 0, ImF = 0 на ВС,
i = 0 на CD.
Кроме того, на DAB выполняются очевидные условия
1 = 0, ImZ = 0 на DA,
лп к A3.5)
= 0 на АВ. х v 7
Для рассматриваемой задачи В. Н. Эмихом A962) получено
эффективное решение. Уравнение свободной поверхности CD
можно представить в виде (см. Полубаринова-Кочина и др.
1969)
где
2bk
@<t<oo).
Уравнение линии раздела ВС двух жидкостей имеет вид
х
с cos яб J Vch21 — a ~~ ' \ • )
2 =
т = arsh д/^ — 1 @ < т < оо).
В. Н. Эмих рассмотрел также случай, когда интенсивность
испарения е есть линейная функция ординаты свободной по-
поверхности (Полубаринова-Кочина и др. 1969; Эмих 1966), а
Ю. И. Капранов A973) — случай линейной зависимости интен-
интенсивности испарения от х и у.
Глава IX
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
А. СОВЕРШЕННЫЕ СКВАЖИНЫ
§ 1. Совершенная скважина в центре пласта. Будем рас-
рассматривать движение жидкости — воды или нефти —в прони-
проницаемом пласте (обычно состоящем из песка или песчаника),
ограниченном двумя горизонтальными непроницаемыми слоями.
Скважину цилиндрической формы считаем пробуренной через
весь пласт — такая скважина называется совершенной или пол-
полной в отличие от несовершенной, за-
глубленной лишь частично в прони-
проницаемый пласт.
Движение в таком пласте можно
считать плоскопараллельным.
Рассмотрим осесимметричный
-приток к скважине радиуса гс
(рис. 228). Вычислим расход Q че-
через цилиндрическую поверхность
произвольного радиуса г и высоты Т.
Он равен
Q = 2jtrTv, A.1)
где v — величина скорости фильтра-
фильтрации, зависящая только от г. Жид-
Жидкость считается несжимаемой, дви-
движение установившимся, напорным,
т. е. не образующим свободной по-
поверхности. При этих условиях рас-
расход Q через цилиндр любого радиу-
радиуса г должен быть постоянным. Следовательно, скорость v будет
обратно пропорциональной расстоянию. Принимая во внимание
направление этой скорости к центру скважины, который мы по-
помещаем в начале координат, и введя обозначение радиальной
скорости иг, получим
Ф S 0.2)
Рис. 228.
342 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
Интегрируя это уравнение, найдем потенциал скорости или про-
пропорциональный ему напор
к
A.3)
Будем предполагать, что известен напор Н2 на расстоянии R
от центра скважины. Это дает
Предположим еще, что известен напор Н{ на самой скважине,
т. е. при г = гс. Тогда будем иметь
Из последних двух уравнений можно исключить С, после чего
получим уравнение для определения расхода скважины (Du-
puit 1863)
2nkT(H2-Hl) . ,
У- ПГ(ГО * A-4)
Это основная формула, по которой рассчитывают дебит сква-
скважины. Для напора h получаем уравнение
Заметим, что говорят о радиусе влияния скважины, как о
таком расстоянии, на которое распространяется влияние дан-
данной скважины. Однако это понятие в случае уравнения A.5)
остается неопределенным, так как зависимость напора h от
радиуса-вектора является логарифмической и h возрастает до
бесконечности при г—>оо. Дальше мы вернемся к этому вопросу
(см. § 2 главы XIX).
В. Н. Щелкачев и Г. В. Пыхачев A939) предложили вместо
понятия радиуса влияния другое понятие — радиуса контура пи-
питания скважины. Это понятие имеет значение при рассмотрении
нефтеносного пласта, который бывает — при так называемом
водонапорном режиме — окружен областью питания, в которой
накапливаются запасы воды. Граница между областью грунта,
насыщенного нефтью или водой, и областью его питания назы-
называется контуром питания. Собственно говоря, любую постоян-
постоянную изобару, или (что то же, при горизонтальном движении)
линию равного напора, можно условно принять за контур пи-
питания.
Напомним, что при изучении движения нефти вместо на-
напора рассматривают давление р, связанное с напором при
§ 1] СОВЕРШЕННАЯ СКВАЖИНА В ЦЕНТРЕ ПЛАСТА 343
горизонтальном движении равенством
а вместо коэффициента фильтрации k — проницаемость пласта
&о, причем (v — динамическая вязкость нефти)
k = *f A.7)
(см. § 7 главы I).
Полагая р = рс и г = гс на периметре скважины, г = R и
р = Рн на контуре питания (область питания считается кругом,
концентричным с контуром скважины), получим формулу деби-
дебита скважины в виде
Q2nkoT (fa — рс) п оЧ
= ^ , A.8)
где \х — вязкость нефти.
Возвращаясь к формуле A.4), заметим, что ею пользуются
в гидрогеологии для вычисления коэффициента фильтрации по
данным откачки из скважины. При этом нужно знать мощность
проницаемого слоя Т и значения напоров Н\ и Н2 в скважине
и на расстоянии R от нее. Величина Н2 есть напор в одной из
наблюдательных скважин, которые обычно пробуриваются во-
вокруг действующей.
В дальнейшем будем рассматривать течения грунтовых вод
в пластах единичной мощности, полагая Т = I. При этом ис-
используются обычные представления плоской задачи гидроди-
гидродинамики.
Часто в* напорных пластах имеется установившееся тече-
течение грунтовых вод. Для упрощения расчета скважин в таких
пластах скважины обычно заменяют точечными стоками и вы-
выбирают затем за периметр скважины подходящую замкнутую
эквипотенциаль в окрестности стока. Рассмотрим здесь про-
простейшую задачу о точечной скважине с дебитом Q в однород-
однородном потоке грунтовых вод (рис. 229). Пусть поток грунтовых
вод имеет в бесконечности скорость ?/, направленную парал-
параллельно и противоположно оси х. Тогда комплексный потенциал
течения со будет складываться из комплексного потенциала рав-
равномерного потока o)i = —Uz и комплексного потенциала точеч-
точечного стока оJ = — (С?/2яIп г\
ы= — Uz —In 2 + С. A.9)
Отсюда для потенциала скорости и функции тока имеем
344
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
Функцию arctg(ylx) будем считать здесь определенной на пло-
плоскости {х,у) с разрезом вдоль оси абсцисс при х > 0. Тогда,
если принять Сг = зх/2, получим для распадающейся на две
ветви линии тока г|? = 0 (рис. 229) уравнение
A.10)
Это уравнение описывает полупрямую у = 0 (х < 0) и кривую
с асимптотами у = ±Q/B/7), пересекающую ось ординат в
'///////////////////////////////////
Рис. 229.
точках у = +Q/Df/) и ось абсцисс в точке х == — Q/BnU),
в которой поток разветвляется и скорость равна нулю. Область,
ограниченную линией A.10), можно назвать областью питания
колодца (рис. 229).
§ 2. Скважина, эксцентрично расположенная в круговом
пласте. Пусть контуром питания будет окружность радиуса R
с центром в начале координат (рис. 230). Мощность пласта
принимаем равной единице. Скважина радиуса б помещается
6 точке М{(х\,у\). Возьмем произвольную точку М области Ц
§2]
ЭКСЦЕНТРИЧНО РАСПОЛОЖЕННАЯ СКВАЖИНА
345
обозначим через г комплексную координату этой точки, через
Z\ — координату точки М\. Через Q\ обозначим дебит скважины
с центром в точке М\.
Тогда комплексный потенциал течения со (г) можно полу-
получить, поместив сток интенсивности Q\ в точке М\ и источник
той же интенсивности в точке М\ (с комплексной координатой
z2 = R2/z\), представляющей инверсию точки Mi в круге радиу-
радиуса R (см. § 1 главы V):
B.1)
Здесь Q\ — расход стока, помещенного в точке Ми которая рас-
рассматривается как центр скважины, С{ — постоянная, пока про-
произвольная. Функция ф(х, у) является действительной частью
выражения B.1), поэтому она может быть представлена в виде
^L
ф (X, у) = - ^L (in | Z - 2, | - If!
R
B.2)
Вблизи скважины линии равного напора близки к окружно-
окружностям, поэтому за периметр скважины приближенно можно при-
принять одну из таких линий, близкую к окружности радиуса б.
0,2
0,6 0,8 1,0
Рис. 230.
Рис. 231.
Вдоль периметра скважины напор по условию равен Яс; пусть
А = Яс в точке z = z\ +6. На контуре питания напор равен Нк.
В частности, h = HK в точке, для которой z = R (рис. 230).
Это дает окончательно
п _ 2я/г (Нк - Яс) (9 оч
где R\ — расстояние точки Mi от начала координат. Если сква-
скважина центральная, т. е. находится в центре окружности, то ее
346 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
дебит равен
Составим отношение
__ 2nk(HK-Hc)
vo — in /{ - in б
Q\ = in p
Qo in (p — рг/р) '
где р = Я/6, pi = Ri/8.
На рис. 231 представлена зависимость величины Qi/Qo от
R\/R при заданном р = 100. Видим, что дебит скважины резко
возрастает при ее приближении к контуру питания.
§ 3. Случай произвольного контура. Рассмотрим пласт S,
ограниченный произвольным контуром питания L со скважиной
в точке М\ (рис. 232). Совершим конформное отображение
внутренности круга |Z|=/? на внутренность области S пло-
плоскости z с помощью преобразования
Z = F(z). C.1)
Пусть при этом контур круга радиуса
R плоскости Z перейдет в контур L.
Тогда напор h(x,y) = —ф/& в области S
будет выражаться формулой, которую
получим из B.3) заменой z на F(z) со-
согласно C.1):
* h(x и)- Ql In Я!^*)-^*')! i г C2)
Рис. 232. П(Х> У) - 2nk 1П I** - F (z) Fjzl)\ + C' {6'2)
где z\—комплексная координата точки М{.
Условие, что в точке z = Z\ -\- б напор h = HCi если прене-
пренебречь малыми высшего порядка для б, дает*)
Уравнение контура L согласно равенству C.1) будет
\F(z)\ = R. C.4)
Возьмем произвольную точку г0 контура L. В этой точке,
как и вдоль всего контура L, пусть напор равен Нк. Из C.2)
*) В самом деле,
§ 3] СЛУЧАЙ ПРОИЗВОЛЬНОГО КОНТУРА 347
имеем тогда
flK = _Qi-in *\Fto)-i[M\ +с. C<5)
2nk \R*-F(zo)F{zl)\ ^ V '
Принимая во внимание, что \ F(zo)\ = R, найдем
R\F(zo)-FM\ я1 С_я
и из уравнения C.3) получим окончательно
п 2я/г (Як - Яс)
In (R2 - | /?(*,) |2) - In
В качестве примера вытянутой области естественно взять
эллипс. Функция, дающая конформное отображение внутренно-
внутренности эллипса на внутренность единичного круга, имеет вид
Z = F (г) = ^Y sn (-^ arcsin f), C.8)
где k* — модуль эллиптического интеграла /С, определяемый с
помощью равенства
X = ^Г arth 7 " ^Гln T=T'
Здесь c2 = a? — б2, а и 6 — полуоси эллипса. Составим произ-
производную
V
pf B) = ^VFcn^dniL) H==^arcsin±. (ЗЛ0)
n ус2 — z2 n с
С помощью формулы C.9) найдем для дебита скважины,
находящейся в точке ги выражение
Q 2jtfe (ЯК — НС) /g j .4
1п(A - k* sn2 и,) д/с2 - г] ) - In (а | сп и, dn и{ \) '
Здесь
щ = —arcsin-1-, а=
где 6, как и выше, есть радиус скважины.
Если скважина находится в центре эллипса, то
г\ 2jtfe (Нк — Нс)
348
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
Отсюда для отношения дебита скважины в эллиптической
области к дебиту Qo скважины в круговой области радиуса R,
центр которой совпадает с центром эллипса, получаем
Q\ t R t nc
-^- = 1п —: jn ¦=-.
Qo б 2 6/С yk*
Рассмотрим скважину в бесконечной полосе (между двумя
каналами). В этом случае (рис. 233) комп-
лексный потенциал имеет вид
. C.13)
Для напора имеем выражение
— In | sin (¦§- (г + а)) | ] + С. C.14)
Рис. 233.
В точке z = a + 6 на скважине h = Hc и
Яс = ^ fin (яб) - In Ы sin ^)] + С. C.15)
В точке z = I считаем h = Як. Отсюда дебит скважины
k (Нк - Яс)
Qi =
па
C.16)
§ 4. Об интерференции скважин. С увеличением числа совер-
совершенных скважин, пробуриваемых в пласте, суммарный дебит
скважин при одинаковых разностях напоров Нк — Нс увеличи-
увеличивается. Однако это увеличение не пропорционально числу сква-
скважин, а суммарный дебит п одинаковых скважин меньше, чем
n-кратный дебит одной скважины. Это явление называют интер-
интерференцией скважин: скважины оказывают влияние друг на
друга, уменьшая дебит каждой из них. При этом, чем большее
число скважин будет находиться на данной площади, тем мень-
меньше будет каждой скважины. При некотором значении п = N
дальнейшее увеличение числа скважин уже станет невыгодным,
так как затраты на скважину не окупят того малого прираще-
ни*я суммарного дебита, которое получится за счет (Л/ -f- 1) -й
скважины. Вопросы о наивыгоднейшем числе скважин имеют
важное значение в теории фильтрации нефти.
Ограничимся рассмотрением простейшего случая двух сква-
скважин. Поместив в точках z = ±a по стоку одинаковой интенсив-
интенсивности Q, получим схему двух скважин в безграничном пласте.
§ 4) ИНТЕРФЕРЕНЦИЯ СКВАЖИН 349
Комплексный потенциал такого течения будет
со = ф + /* = —^-1п[B-а)B + а)] + С, D.1)
где Q — дебит каждой из скважин. Поэтому, отделяя в D.1)
действительную часть, можем написать
А--2-йГ»иB-а)B + аI + С,. D.2)
Для определения постоянной С\ и дебита Q нам нужны два
условия.
Считая, что радиус скважины б мал по сравнению с расстоя-
расстоянием 2а между скважинами, примем за контур поперечного се-
сечения скважины изобару, проходящую через точку z = а + б.
При указанных условиях эта изобара близка к окружности ра-
радиуса б с центром в точке а.
На скважине пусть напор равен Нс. Тогда формула D.2)
даст, после пренебрежения величиной б2,
^ 1. D.3)
В течении с двумя скважинами эквипотенциали, охватывающие
обе скважины, представляют семейство лемнискат. Однако на
достаточно большом расстоянии от начала эти лемнискаты ста-
становятся близкими к окружностям. Считая R достаточно боль-
большим по сравнению с а, предположим, что при г = R напор ра-
равен Нк (контурному напору). Подставляя в D.2) г = R и Н =
= Як, получим
Вычитая D.3) из D.4), получим
я н in
Отсюда найдем расход каждой из скважин:
^f^r. D.5)
ln
2аЬ
Сравним этот расход с расходом одиночной скважины ра-
радиуса б, центр которой находится в начале координат, для ко-
которой напоры при г = б и г = R соответственно равны Яс и
Нк. Как мы видели (см. § 1), этот дебит, который мы обозначим
через Qb равен
^^. D.6)
350 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
Отношение Q/Q{ равно
[ГЛ. IX
_Q_
1п
. R
1пТ
R2
R
Так как мы считаем, что R > и, "-о второе слагаемое знаме-
знаменателя положительно и Q/Qi < 1.
§ 5. Приток к совершенным скважинам в неоднородной среде.
Вторую задачу из § 3 главы VIII можно интерпретировать ина-
иначе, заменив точечный вихрь точечным источником. Для этого
Рис. 234
достаточно поменять роли ф и \|). А именно, допустим, что на-
напорный пласт, в котором порисходит движение жидкости к со-
совершенной скважине, состоит из двух полуплоскостей с коэф-
коэффициентами фильтрации k\ и k2 (рис. 234), причем линия раз-
раздела грунтов является осью абсцисс.
Тогда, обозначая через Q дебит скважины, можно напи-
написать для первой и второй областей, если скважина находится в
§ 5] Приток к скважинам в неоднородной среде 351
первой области в точке г0,
E.1)
Для дебита скважины получается формула
П 2л&1 (Як — Яс)
Q =—?— ?-
E.2)
где б —радиус скважины, 6 —расстояние скважины от оси абс-
абсцисс, #к —напор при \z — zo\ = R, Нс — напор при г — г0 = б,
причем принято, что R/b » 1 и 6/6 <С 1.
Формулы E.1) могут быть получены также при помощи тео-
теоремы об окружности для случая фильтрации в неоднородном
пласте. Эта теорема представляет обобщение известной в тео-
теоретической гидродинамике теоремы об окружности (Милн-Том-
сон 1964).
Теорема об окружности применительно к фильтрационным
движениям была дана Шт. Георгицэ в 1957 г. и К. Якобом в
1959 г. (см. Gheorghita 1966) и была ими применена к равно-
равномерному потоку с постоянной скоростью на бесконечности. Ряд
обобщений теоремы дал Шт. Георгицэ, который занимался мно-
многими вопросами о течениях в неоднородных пластах. Некоторые
общие математические исследования в этой области провела
Э. Унгуряну-Давид (см., например, Ungureanu 1969).
Для линии раздела грунтов — кривой второго порядка реше-
решение построено О. В. Голубевой и А. Я. Шпилевым A967). За-
Задачи с эллиптическим контуром рассматривались также
Шт. Георгицэ и Э. Унгуряну.
Приведем изложение теоремы об окружности по О. В. Голу-
Голубевой A966), которая получила эту теорему независимо от пре-
предыдущих исследователей и применила ее к течениям с источни-
источниками и стоками.
Пусть фильтрация в безграничном пласте с постоянным ко-
коэффициентом фильтрации k\ определяется комплексным потен-
потенциалом <o = /(z), причем особые точки f(z) располагаются
только вне (только внутри) окружности |z| = /?. Далее, пусть
будет внутренность (внешность) этой окружности заполнена
грунтом с коэффициентом фильтрации k2. Тогда комплексный
потенциал ом течения вне (внутри) окружности и комплексный
потенциал со2 течения внутри (вне) окружности будут иметь вид
. E.3)
КОЛОДЦЫ И СК&АЖМНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
Теорема об окружности получается отсюда как частный слу-
случай при Х=1. Нетрудно проверить, что на линии раздела двух
грунтов zz = R2 выполняют-
выполняются необходимые условия
ф,/*1 = ф2/&2 и ^1 = ^2-
Если граница раздела
между двумя грунтами —
ось у = О, то уравнения
E.3) заменяются следую-
следующими:
со2 = A-Я)/(г). E.4)
Пример. Скважина
(точечный сток) находится
в точке z = Zq безгранично-
безграничного пласта с коэффициентом
фильтрации k\, причем име-
Рис. 235. ется круговое включение с
коэффициентом фильтрации
k2 при |г|</? (рис. 235). Тогда, обозначая через Q дебит
стока, получим в случае, когда точка z0 находится вне круга
f (z) = —о— In (z — Zq), E.5)
co2 = —
-*) In
E.6)
Видно, что особыми точками coi являются, кроме z = z0, так-
также z = R2/z0 внутри круга и г = оо вне круга.
Если точка г0 находится внутри круга |г| = /?, то исходная
функция E.5) содержит особенность при z = оо и условие тео-
теоремы об окружности (особенности должны быть только в одной
области) не выполняется. Правильный результат получим, если
во второе из выражений E.6) введем слагаемое —(ф/2I
E.7)
Здесь в области |,г|</? имеет место коэффициент фильтрации
*ь a fe2 —в области |г| > R.
Если скважина находится в точке 20 в области, ограничен-
ограниченной окружностью радиуса г= 1, где грунт имеет коэффициент
§ 6] ЗАДАЧИ О ГОРИЗОНТАЛЬНОМ ДРЕНАЖЕ 353
фильтрации &i, а в кольцевой области, между окружностями ра-
радиусов 1 и /?, находится грунт с коэффициентом фильтрации &2,
причем внешняя окружность является эквипотенциалью, то
имеем такие формулы для скоростей (Полубаринова-Кочина
1952, 1):
5.8)
Л. И. Костицына обобщила теорему об окружности на слу-
случай двух концентрических окружностей. Используя ее резуль-
результаты, формулы E.8) можно представить в таком виде:
q (i — я) Г i . v ял v я*-1
2jt Lz ~ z° n\z ~Z{)IR \z~~ ** I*1
E.9)
Б. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
§ 6. Применение метода источников к задачам о горизонталь-
горизонтальном дренаже. Поверхность земли может оказаться заболоченной
по разным причинам: вследствие выхода грунтовых вод на дан-
данный участок, под влиянием атмосферных осадков, при поливах,
предназначенных для промывки засоленных почв, и т. д.
Рассмотрим случай, когда над горизонтальной поверхностью
грунта находится слой воды высоты Я. На некоторой глубине d
от поверхности заложена горизонтальная труба радиуса 6, соби-
собирающая воду и отводящая ее в какой-нибудь коллектор.
Будем считать, что примерно в центре трубы находится то-
точечный сток, расход которого на единицу длины трубы равен Q,
и пусть ось абсцисс совпадает с поверхностью грунта, а коорди-
координаты центра стока будут @,—d). В точке @, d) поместим источ-
источник такой же интенсивности, как сток. Тогда для комплексного
потенциала скорости будем иметь
12 П. Я. Полубарииооп Кочина
354
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
Произвольная постоянная выбрана равной —kH для того, чтобы
удовлетворить условию ф=—kH на поверхности грунта (у=0).
Предположим, что на контуре дренажной трубы напор ра-
равен //Др, тогда
Q
У— \nBd/6) *
На рис. 236 представлена сетка движения и эпюра скоростей на
поверхности грунта, построенные В. В. Ведерниковым A939)
Рис. 236.
для одного частного случая. Он решал эту задачу, так же как
и следующие в этом параграфе, методом конформного отобра-
отображения области движения и области комплексного потенциала
на полуплоскость.
Рис. 237.
В случае бесчисленного множества параллельных дренаж-
дренажных труб, находящихся на расстоянии / друг от друга (рис.237),
будем иметь
sin (-5- (z - d/)
Q i
sin
— kH.
§7]
ПОДЗЕМНЫЙ ВОДОЗАБОР
355
Полагая ф = —kHw при х = 0 и у = —
ражение расхода
2пк{И-М„)
* — , . 2nd, . яб *
In sh —j In sh —-j—
б, получим вы-
выЗаметим, что мы считаем 8/1 настолько малым, что вместо
sh (яб//) можно взять яб//. Этим объясняется различие во внеш-
внешнем виде формул, даваемых в подобных задачах различными
авторами.
Рис. 238.
Аналогичным образом рассматривается случай дрены на
водоупоре (рис. 238). Обозначая через Т глубину проницаемого
слоя и располагая поочередно источники и стоки вдоль верти-
вертикали на расстояниях ±2пТ от основного стока, имеем здесь
Q
th
K(z-iT)
4Т
— kH.
При этом Q — расход единицы длины дрены, равный половине
расхода стока, помещенного в ее центре:
kn (Я - ядр) kn (Я - ядр)
Q:
In th
2Т
In
яб
2Т
§ 7. Подземный водозабор, питающийся водами соседнего
водоносного пласта. Предположим, что напорный водоносный
пласт, простирающийся вниз до бесконечности, имеет естествен-
естественный напор #о (отсчитываемый от его кровли) и коэффициент
фильтрации k. Сверху он ограничен слабо проницаемым слоем
пород мощности Т с коэффициентом фильтрации k\. Над этим
слоем залегает хорошо проницаемый артезианский пласт с есте-
естественным постоянным напором Hi или слой воды глубины Нх—
~Т\. В некоторой точке M(z = z0) нижнего пласта помещен
точечный сток (рис. 239). Изобару его, близкую к окружности,
можно принять за контур дрены (Веригин 1949, 1).
12*
366
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
Считая фильтрацию в слабо проницаемом слое происходя-
происходящей по вертикали, примем, что вертикальная составляющая
скорости фильтрации на кровле нижнего водоносного пласта
Рис. 239.
определяется непосредственно по формуле закона Дарси (см.
также ниже § 8):
, —ft.J^—^.+i), G.1)
где h{ = fti (*) — напор на кровле водоносного пласта.
Составим функцию
Если найдем W7 = F (z), то после интегрирования получим
<о = е-а* [ еа* [F (z) — b]dz + Се~аг, G.3)
где
а
ik,
Нетрудно видеть, что в случае одного стока, помещенного в
точке 2 = Zq, имеем (D — постоянная)
В случае бесконечного ряда стоков, отстоящих от точки z
на расстояниях 2nl (п = ± 1, ±2, .. .)>
§ 8] ВЫВОД УРАВНЕНИЙ 357
В самом деле, так как при z = x имеем в обоих случаях
lmF(z) = 0, то
поэтому условие G.1) оказывается выполненным. Обычно при-
принятые условия на бесконечности также выполняются.
Постоянные С и D определяются из условий ф = —� при
х = оо, \ju — г|)в = Q. Для определения расхода дрены Q слу-
служит условие h = #дР в верхней точке дрены (при z = Zq-\-6i,
где б — радиус дрены).
В. ДВИЖЕНИЕ В ПЛАСТАХ, ГРАНИЧАЩИХ СО СЛАБО
ПРОНИЦАЕМЫМИ ПЛАСТАМИ
§ 8. Вывод уравнений. Напорное движение грунтовых вод к
совершенным, т. е. проходящим через весь пласт, колодцам вы-
выше рассматривалось как плоское движение, а скважины интер-
интерпретировались с помощью источников и стоков.
Однако в действительности абсолютно непроницаемых «во-
«водоупорных» пластов нет. Обычно хорошо проницаемые пласты
перемежаются со слабо проницаемыми. Отношение коэффициен-
коэффициентов фильтрации двух соседних слоев может быть порядка 10~5—
10~10, и все же слабо проницаемый грунт может оказывать
влияние на общую картину фильтрации, если она происходит
на большой площади. Теория движения в таких пластах с пере-
перетоками развита А. Н. Мятиевым A946—1948) и Н. К. Гирин-
ским A947).
Предположим, что горизонтальные слои хорошо проницае-
проницаемых грунтов перемежаются со слабо проницаемыми грунтами.
Пусть /г-й водопроницаемый слой имеет мощность (толщину) dn
и коэффициент фильтрации kUi нижележащий слой плохо про-
проницаемого грунта — толщину бп и коэффициент фильтрации хп,
вышележащий плохо проницаемый слой — толщину 6n-i и коэф-
коэффициент фильтрации xn_i (считаем величины %nlkn и кп-\/Ьп
малыми). Каждая линия тока, переходящая из слоя dn в ни-
нижележащий, будет преломляться, причем, как было указано в
§ 3 главы II, если линия тока образует с нормалью к границе
двух грунтов углы а и р, то
Для любого значения а, отличного от я/2, получаем вследствие
предположенной малости отношения кп : kn, что угол р будет
малым, и, следовательно, после преломления линии тока в сла-
слабо проницаемом грунте будут близки к вертикальным прямым.
Этим замечанием мы воспользуемся ниже.
358 КОЛОДЦЫ И СКВАЖИНЫ, ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
Обозначим через и, v, w проекции на оси х, у, z скорости
фильтрации в какой-нибудь точке М(х, у, z) хорошо проницае-
проницаемого пласта толщины Т и примем для простоты начало коорди-
координат лежащим на основании этого пласта. Считая жидкость не-
несжимаемой, т. е. плотность ее постоянной, будем иметь уравне-
уравнение неразрывности
_fL + i! + -jL==O. (8.2)
дх ' ду ' dz v '
Предположим, что горизонтальные скорости мало меняются
с высотой, и введем в рассмотрение средние по высоте значения
этих скоростей U и У, полагая
т т
U {*, У) = — \ и (*» #> z) dz> V (*> y) = —\v (*> У> z)dz-
о о
Проинтегрируем уравнение (8.2) по z (как это делают ино-
иногда в динамической метеорологии, принимая за Т толщину слоя
атмосферы). Примем во внимание равенства
дх ™ дх Г дх ' J ду ™ л ду '
0 0 0
а также то, что интегрирование третьего члена уравнения (8.2)
дает
Sdw
где W\—значение вертикальной скорости на нижней, w2 — на
верхней границе пласта.
Теперь уравнение неразрывности примет вид
Пусть напорная функция неосредненного движения будет
h(x, у, z), так что
и dh I dh * dh
Применив осреднение к горизонтальным составляющим скоро-
скорости и и v, мы тем самым осредним и напорную функцию
§ 8} ВЫВОД УРАВНЕНИЙ 359
h{x,yyz). Будем обозначать осредненное значение этой функ-
функции через Н(х,у):
т
Н(х9 y) = — \h (xy у, z) dz.
<Г
Тогда можно написать U = —k дН/дх и V = —кдН/ду.
Применяя эти равенства к n-му проницаемому пласту, по-
получим
Un = -knl§-, Vn = -kn^. (8.4)
Теперь найдем выражения вертикальных скоростей w\ и w2
на кровле и подошве n-го пласта. Согласно сделанному выше
замечанию можно считать, что фильтрация в слабо проницае-
проницаемом пласте происходит по вертикали. Обозначая напорные
функции для (rz-f-l)-ro и (п—1)-го проницаемых пластов со-
соответственно через Яп+1 и #п-ь по закону Дарси будем иметь
(так как скорость фильтрации при наших предположениях бу-
будет пропорциональна разностям напоров на границах плохо
проницаемого пласта и обратно пропорциональна его толщине)
Hn . (8.5)
При Нп+1 > Нп получаем wx > 0 и наоборот.
Подставляя выражения (8.4) и (8.5) в уравнение (8,3), по-
получим (dn — мощность п-го пласта)
Нп —-Яц-1
(8.6)
Введем следующие обозначения:
(8.7)
(8.8)
Тогда уравнение (8.6) перепишется в виде
ф- + Хф- - ап (Я„ - Hi) - 0. (8.9)
Если пьезометрические напоры #n_i и #n+i в соседних пла-
пластах изменяются настолько слабо, что их можно считать по-
постоянными, то и Н*п будет постоянным. Если же #n-i и Нп+\
360
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
(ГЛ, IX
переменны, то нужно составлять и для них уравнения, анало-
аналогичные (8.9). Если нижележащий или вышележащий пласт со-
совершенно непроницаем, то соответствующее значение хп или
Ип-1 равно нулю.
§ 9. Движение в одном проницаемом пласте. Предположим,
что движение происходит параллельно оси х. Отбросим значок
п в уравнении (8.9) и перепишем это уравнение применительно
к рассматриваемому случаю в виде
= 0.
(9.1)
Общее решение этого уравнения можно представить в виде
Н-Н* = Схе~х V3" + С2ех V*.
Нужно поставить два граничных условия для определения
постоянных С\ и Сг. Так, С\ и Сг будут определены, если будут
известны значения напора Я в двух точках пласта. Если рас-
рассматривается приток жидкости из бесконечности, например,
приток из бесконечности справа к
ханаве, то, поставив условие конеч-
конечности напора при л:=+°°» полу-
получим, что С2 = 0 и
Зная величину напора в какой-ни-
какой-нибудь точке, определим С\. Напри-
Например, если Я = Н\ при х = 0, то
H = H* + {Hl- И*) е~х V?. (9.2)
Величина Я* будет в этом случае
напором при х = оо.
Если Hi > //*, то кривая (9.2) лежит над асимптотой Н =
= Я* и вогнута кверху; если Н\ < Я*, то кривая лежит под
своей асимптотой и выпукла (рис. 240). Направление выпукло-
выпуклости пьезометрической кривой можно определить непосредствен-
непосредственно из уравнения (9.1), переписав его так:
Рис. 240.
Так как а > 0, то при Н > Н* вторая производная положи-
положительна, т. е. кривая вогнута, при Я <С Я* она, наоборот, выпукла.
§ 10. Совершенные скважины в напорном пласте. Предполо-
Предположим сначала, что имеется одна цилиндрическая скважина, ось
которой совпадает с осью z и приток к которой со всех сторон
одинаков, так что течение не зависит от полярного угла, а за-
§ 10] СОВЕРШЕННЫЕ СКВАЖИНЫ В НАПОРНОМ ПЛАСТЕ 361
висит только от радиуса-вектора г. Оператор Лапласа приве-
приведется при этом к виду
i д'н — d2fI I ! dH
дх2 "•" ду2 ~ dr2 "•" г dr '
и вместо (8.9) будем иметь (отбрасывая значок п)
Это уравнение Бесселя, общее решение которого представляется
в виде
Н-Н* = С Jo (ar) + С2К0 (аг), A0.2)
где /о — цилиндрическая функция мнимого аргумента нулевого
порядка первого рода, Ко — соответствующая функция второго
рода.
Если известно значение напора на двух окружностях радиу-
радиусов г\ и г2, то постоянные С\ и Сг определяются.
Рассматривая движение в бесконечном пласте, поставим
условие: Я должно оставаться ограниченным при г, стремящем-
стремящемся к бесконечности. Так как функция 10(х) неограниченно воз-
возрастает при увеличении аргумента, то следует положить С\=0.
Получаем
Н-Н* = С2К0(аг). A0.3)
Функция Ко(х) стремится к нулю при возрастании х; поэтому
Я стремится к Я* при г—>оо. Следовательно, Я* есть невозму-
невозмущенное значение напора. Можно ввести величину S = Н* — Н,
называемую понижением напора. Тогда для 5 получаем выра-
выражение
S = -C2K0(ar). A0.4)
Обозначим радиус скважины через гс и вычислим расход Qc
через боковую поверхность цилиндра радиуса гс, пересекающе-
пересекающего весь пласт, мощность которого обозначим через Т:
A0.5)
где Vc — скорость течения на стенке цилиндра. Имеем
4l arc), A0.6)
где К\ — цилиндрическая функция мнимого аргумента второго
рода первого порядка.
362 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
Подставляя A0.6) в A0.5), найдем
U2~~ 2nkrcaKi(arc)T •
и уравнение A0.3) дает
S-H -Н- ШгаТ КЛаГс) . A0.7)
Так как через горизонтальные плоскости, ограничивающие
хорошо проницаемый пласт, происходит просачивание жидко-
жидкости, то расход Qr через цилиндр радиуса г будет зависеть от г.
Мы получим Qr, заменяя в A0.7) гс на г:
Qr = 2nkrTaC2Ki (ar).
Деля это выражение на A0.7), получим
Если х < 0,02, то можно пользоваться приближенными фор-
формулами (С — эйлерова постоянная)
#о (х) « ~ In х + In 2 - С = 0,1159 - In х, A0.9)
/Ci(*)«-i-. A0.10)
Обычно arc < 0,02; поэтому К\ (arc) « l/(arc), и формулу A0.7)
можно заменить такой:
Я-W»- ЩтКо(аг\ A0.11)
или
S~W*°(ar). A0Л2)
Полагая в уравнении A0.8) г = гс, найдем понижение напора
на скважине:
гг* г/ /„ \ о /„ \ Qc /Co (arc)
Я - Я (гс) - S (гс) - 1ШГ аге/с, (агс) '
где Я(гс)—напор на стенках скважины. Воспользовавшись при-
приближенными выражениями для Ко и К\9 напишем
Отсюда для дебита скважины находим
п 2nkT [Я' - Н (гс)] р* Ы23 /iniQ\
Ус~ In (R*/rc) ' *=~Г~- A0ЛЗ>
Сравним эту формулу с формулой A.4), полученной для дебита
совершенного колодца в плдсте без перетоков, которую можно
§ 10) СОВЕРШЕННЫЕ СКВАЖИНЫ В НАПОРНОМ ПЛАСТЕ 363
переписать так:
Здесь H(R) —напор в точке, лежащей на расстоянии R (произ-
(произвольном) от центра колодца, в то время как Н* формулы
A0.13) есть напор при г = оо. В знаменателе A0.13) вместо R
стоит R* — выражение, зависящее (через а) от интенсивности
фильтрации через слабо проницаемые грунты, которые в фор-
формуле A0.14) рассматриваются как совершенно непроницаемые.
Вычисления А. Н. Мятиева A947) показывают, что Q тем
ближе к Qc, чем ближе R к гс.
Если производится откачка воды из скважины, то на неко-
некоторых расстояниях от нее гь г%, ..., гп могут быть расположены
наблюдательные колодцы, в которых отмечаются понижения
напора соответственно Si,S2> •••, Sn. Имея по крайней мере
две пары значений (r>S), можно вычислить величины а и kT.
Если считать вышележащий пласт совершенно непроницаемым,
то можно по формуле (8.7), зная мощность подстилающего сла-
слабо проницаемого пласта, вычислить коэффициент фильтрации
последнего.
По данным наблюдений можно вычислить два параметра,
входящих в уравнение A0.12): А = Q/BnkT) и а. Эти пара-
параметры характеризуют суммарно свойства пласта. Если известны
некоторые из величин, от которых зависят Л и а, то можно вы-
вычислить еще какие-нибудь из мощностей слоев и коэффициен-
коэффициентов фильтрации.
В действительности обычно не бывает известной достаточно
точно ни одна из величин 6*, щ, &ь поэтому можно, когда изве-
известно Q, смотреть на величины а и kT как на некоторые постоян-
постоянные, суммарно характеризующие область движения грунтовых
вод. Опытные откачки дают возможность определить эти важ-
важные постоянные.
Перейдем теперь к случаю п совершенных скважин, центры
которых находятся в точках (х\,у\), ..., {хПууп). Обозначим
через Г{ расстояние от произвольной точки (х, у) до точки
(хи Уг):
г, = У(х-х,J+(*/-</<J.
Функция Ko(ari) при любых значениях (хи у{) является реше-
решением уравнения
Поэтому понижение от действия всех скважин будет равно сум-
сумме понижений, вызываемых отдельными скважинами. С помощью
364 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
формулы A0.7) можем написать
2nkrciaT Ki (arci)
Движение подземных вод в системе нескольких водоносных
пластов исследовал Н. К. Гиринский A951). Взаимодействие
группы скважин и ряд других вопросов о движении подземных
вод при наличии перетоков через слабо проницаемые пласты
рассмотрены в книге П. Я. Полубариновой-Кочиной с соавто-
соавторами A969).
§ 11. О пространственной форме напорной поверхности. Пере-
Перепишем уравнение (8.9) для пьезометрического напора п-то пла-
пласта Нп{х,у) в виде
tb- = a?{Hn-H\ A1.1)
где Н* согласно (8.8) есть некоторое среднее из значений напо-
напоров в двух соседних с n-м водопроницаемых пластах. Это вели-
величина напора, который обеспечивается в n-м пласте двумя со-
соседними пластами, так как уравнение A1.1) имеет частное
решение Нп = Я*, соответствующее покою (считаем Н* по-
постоянным).
Предположим, что под влиянием каких-нибудь причин (на-
(например, откачки или нагнетания) происходит движение грун-
грунтовых вод. Рассмотрим два случая.
1-й ел у ч а й:
Нп<Н\ A1.2)
При этом суммарная вертикальная скорость
будет направлена внутрь пласта. Следовательно, п-й горизонт
обогащается водой других горизонтов. Так как величина
w=-ё=г{Нп ~ Нп-х)+~й~{Нп ~ Нп+х)
состоит из двух слагаемых (скоростей просачивания через каж-
каждую из двух границ n-го пласта), то одна из этих скоростей мо-
может быть направлена и из пласта, но другая скорость, направ-
направленная внутрь, должна быть при этом больше. Поэтому мы по-
получаем три возможности, схематически изображенные на
рис. 241 посредством стрелок различной длины.
§ 11]
ПРОСТРАНСТВЕННАЯ ФОРМА НАПОРНОЙ ПОВЕРХНОСТИ
365
Уравнение A1.1) показывает, что в этом случае Д#п < О,
т. е. пьезометрическая поверхность выпукла*).
Поэтому, если согласно наблюдательным скважинам пьезо-
пьезометрическая поверхность оказывается выпуклой, то Нп < #*,
Рис. 241.
и водоносный горизонт должен обогащаться водой. А. Н. Мя-
тиев A948) называет область, в которой имеет место неравен-
неравенство A1.2), областью питания п-го водоносного горизонта. Он
Область
пищания
Область литания
Рис. 243.
отмечает, что обычно эта область приурочена к междуречному
пространству и возвышенности, т. е. связана, как говорят гео-
геологи, с «положительными формами рельефа».
2-й случай:
Нп>Н\ A1.3)
*) Как известно, оператор Лапласа Аи пропорционален средней кривизне
поверхности z = u(xyy)y а средняя кривизна положительна для вогнутой и
отрицательна для выпуклой поверхности.
366 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
При этом имеем общее вытекание из я-го пласта (см. три воз-
возможных случая на рис. 242), и поверхность пьезометрического
напора вогнута. А. Н. Мятиев называет такую область областью
высачивания п-го горизонта. Он отмечает, что обычно такие
области приурочены к речным долинам, котловинам и впади-
впадинам, т. е. связаны с «отрицательными формами» рельефа мест-
местности. На рис. 243 дана схема А. Н. Мятиева движения под-
подземных вод в междуречном массиве. А. И. Силин-Бекчурин
A951), приводя схему Мятиева, отмечает, что она относится
лишь к верхним горизонтам.
Г. НЕКОТОРЫЕ ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
§ 12. Несовершенные скважины в полупространстве. Несовер-
Несовершенной по степени вскрытия пласта скважиной называется сква-
скважина, не доходящая до основания проницаемого пласта. В пла-
пласте бесконечной глубины скважина всегда будет несовершенной.
Пусть дана скважина в пласте, занимающем все нижнее
полупространство. Разместим вдоль оси скважины стоки. Для
пространственного стока в точке ? на оси скважины потенциал
скорости выражается так:
1 A2.1)
2J + г2 V
где г2 = х2 + у2. Горизонтальная плоскость z = О является при
этом твердой стенкой. Поэтому продолжим ось скважины вверх
и возьмем интеграл от выражения A2.1) в пределах от —I до/.
Получим
Интенсивность стоков q(t) надо подобрать так, чтобы на по-
поверхности цилиндра радиуса гс иметь постоянное значение по-
потенциала. Кроме того, на дне цилиндра должно выполняться
некоторое заданное условие. В такой постановке задача очень
сложна.
Обычно принимают интенсивность q постоянной вдоль всей
скважины. Тогда интеграл A2.2) легко вычисляется:
ф(г, z) = J^ln^L^+r2 + {l~z\ A2.3)
где Q = lq — расход скважины.
Поверхности равного потенциала здесь будут эллипсоидами
вращения с фокусами в точках @, 0, /) и @, 0, — /). Следова-
§ 13] ИСТОЧНИК МЕЖДУ ГОРИЗОНТАЛЬНЫМИ ПЛОСКОСТЯМИ 367
тельно, поверхность скважины заменяется поверхностью узкого
эллипсоида. Можно подобрать полуоси этого эллипсоида так,
чтобы объем эллипсоида был равен объему цилиндрической
скважины. Получим
где Sc — понижение напора на скважине.
Положив в формуле A2.3) z = О, получим распределение
потенциала вдоль кровли пласта:
„(г, 0)-|rln VFTP + '. A2.5)
Потенциалы линейных источников, которые мы помещаем
внутрь скважин, можно складывать. Можно, в частности, та-
таким образом вычислить распределение напора от нескольких
скважин.
Если перейти к безнапорному движению, считая; что пло-
плоскость z = О была поверхностью грунтовых вод до устройства
скважины, то можно принять, что после устройства скважины
свободная поверхность определяется уравнением z=—ф(г, 0)/k,
т. е. считать, что депрессионная поверхность совпадает с по-
поверхностью пьезометрического напора напорного движения.
Заметим, что при построении потенциала скорости с по-
помощью стоков, распределенных вдоль оси скважины, для полу-
получения более точного решения можно было бы задаться иным
распределением интенсивности. Очевидно, что q{l) должно уве-
увеличиваться при приближении к концам отрезка (—/, /). В соот-
соответствующей плоской задаче распределение q{t) имеет вид
Если принять этот же закон для пространственного случая,
то получится приближенное решение в виде эллиптического ин-
интеграла, тем более точное, чем меньше радиус скважины гс.
Если к выражению A2.6) прибавить целый многочлен относи-
относительно ?, то можно подобрать еще более точное решение (Mus-
kat 1932).
§ 13. Источник между двумя горизонтальными плоскостями.
Прежде чем переходить к несовершенной скважине в слое ко-
конечной глубины, приведем несколько формул для источников в
пласте, ограниченном горизонтальными плоскостями. Представ-
Представляют интерес два основных случая: когда источник находится в
области, ограниченной двумя параллельными непроницаемыми
368 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
плоскостями, и когда одна из граничных плоскостей непрони-
непроницаема, а другая есть плоскость равного потенциала.
Пусть сток помещен в точке М, которая имеет координаты
(О, 0, ?). Для первой задачи мы можем поместить стоки в точ-
точках, симметричных с данной точкой относительно обеих ограни-
ограничивающих плоскостей, 2 = 0 и г = с, затем продолжить про-
процесс отражения, перейдя к плоскостям z = nc, z = —пс. Взяв
у всех источников одинаковую интенсивность и написав ряд
для потенциала скорости
д f 1 , 1 ,
Ф ~ 4я I Yr2 + (г - ?J Vr2 + (г + ?J
»
SJ
. у г
/if^ooL
видим, что ряд является расходящимся. М. Маскет A949) дает
выражения, пригодные для малых значений г, и другие, удоб-
удобные для больших значений г.
Здесь мы приведем выражения в виде определенных инте-
интегралов двух функций: 1) функции ?/(г, г, ?), обращающейся в
нуль на двух плоскостях z = ±с и имеющей в точке z = ? осо-
особенность типа источника, так что
и-
Vr2 + (z - tJ
есть регулярная гармоническая функция вблизи точки @, 0, ?)';
2) функции V(r9 2, ?), для которой нормальная производная
равна нулю на стенках, т. е. dV/dz = 0 при г = ±с. В точке
г = ? характер особенности тот же, что и у функции U.
Имеем (Bateman 1932)
U = \ g (z, 0 /о (/г) Л, V = J y (г, О Л> (/г) Л,
о о
где /0 (*) — цилиндрическая функция нулевого порядка,
shB/c)
!2 ch (/ (c - z)) ch (/ (c +
sh (lie)
2ch(f(c
shB/c)
§ 13] ИСТОЧНИК МЕЖДУ ГОРИЗОНТАЛЬНЫМИ ПЛОСКОСТЯМИ 369
Можно представить U и V также в другом виде, выделив
в них слагаемое
оо
\ *-Ч*-
Другими словами, положим
g (г, O = e-'l«-ti + A(z, 0, у (г, Q = e-4*-U+ r\(z, Q,
где функции
h(z t\ = e'cchУ(г~Ы~chV(г + О)
остаются непрерывными. Теперь имеем
оо
J ,B, QJ0(rl)dl.
о о
Тогда потенциалы
оо оо
U{ = J Л (г, О /о (г, О Л, 1Л = J л (г, ?) /о (
остаются непрерывными при z = ?, так же как производные
Можно проверить, что все поставленные для U и V условия
удовлетворяются, и, следовательно, U и V являются искомыми
функциями Грина, дающими источник между твердыми стенка-
стенками или плоскостями равного напора (Bateman 1932).
Однако интеграл для V\ является расходящимся. Можно
исправить его, вычтя «бесконечную постоянную»— другой рас-
расходящийся интеграл. Тогда получим
Если имеем источник между двумя плоскостями, из которых
одна — плоскость тока, другая — плоскость равного потенциа-
потенциала, то для этой задачи можно построить решение в виде ряда,
который, являясь знакопеременным с убывающими членами,
будет сходиться. Этот ряд имеет вид {z = 0 — непроницаемая
370 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
плоскость, z = с — эквипотенциальная поверхность)
со
I/= У ( 1)ЯГ ! ! 1
^ L V'2 + (z + 2пс - ?J Vr2 + (z + 2пс + ?J J '
П= — оо
Для г < с можно пользоваться этим рядом, приняв в расчет
несколько первых его членов. Для больших г можно взять раз-
разложение в тригонометрический ряд по s\x\{mnzj2c) (т = 2п + 1):
ynz I . Skz , . Stcz i
= a{ sin-^г + a3sin-2^~ + as sin-g^- + •••
Коэффициенты этого ряда вычисляются так:
1 С _. rnnz V4* / i\n Г 1
0 /i=»-oo
1
Vr2 + (z + 2«c + S)
Если положить z + 2rac -? = ти соответственно z + 2ис + С = Ti
то, изменяя в каждом слагаемом пределы интегрирования,
найдем
2 .
Но имеет место равенство
oo
„ , ч f cos и du
АО B) = \ —— --it- ,
J (U2 + Z2)'2
где /(o(^)—цилиндрическая функция мнимого аргумента нуле-
нулевого порядка второго рода. Поэтому окончательно можно на-
написать
T/__J_V4 . Bд+ 1)яг . Bп+ 1)яС у / B/1+ 1)яг N
— г / v Sln 2г Sln 9г °l 2r J*
/1 = 0
Отметим, что для больших г имеет место асимптотическое
представление
14]
ПЛАСТ С КОНЕЧНЫМ РАДИУСОМ КОНТУРА ПИТАНИЯ
371
У///////////////////////Л
•R
§ 14. Скважина в пласте с конечным радиусом контура пита-
питания. Рассмотрим осесимметричный приток к точечному стоку с
координатами г = О, г = ?, расположенному в круговом одно-
однородно-анизотропном пласте конечного радиуса R (рис. 244) в
простейшем предположении об анизотропии, когда в горизон-
горизонтальных плоскостях грунт изотропен
(Стклянин 1962).
В области, содержащей источники
или стоки, для потенциала скорости
вместо уравнения Лапласа можно на-
написать уравнение Пуассона (Иваненко
и Соколов 1951)
Дф = Чг(л:, у, г), A4.1)
ч
где А — оператор Лапласа, ф — потен-
потенциал скорости, 4я — плотность источ- ^ис. 244.
ников как функция координат. В слу-
случае одного точечного стока интенсивности q можно A4.1) перь
писать в виде
где г — радиальная координата, z — направленная вниз верти-
вертикальная координата, ft— горизонтальная и kz — вертикальная
составляющие коэффициента фильтрации, б (л:) —дельта-функ-
—дельта-функция
=0 при хфО, 6(х) = оо при * =
6{x)dx
у
\ оо
Будем считать кровлю (г = 0) и подошву (г = Т) пласта
непроницаемыми, т. е.
-g- = 0 при ^==0 и
A4.3)
На внешнем контуре (г = R) примем ф = 0 (если при г = R
Ф = ф0, то, заменяя ф на ф1 + Фо, получим задачу A4.2) —A4.3)
для ф1 с ф1 = 0 при г = R).
Задачу будем решать методом интегральных преобразова-
преобразований. К A4.2) применим преобразование Ханкеля с конечными
пределами (Снеддон 1955)
R
(?f A4.4)
R
Ф* (г, ц,) = \ ф (г, z) r h (?jf) dr,
где щ —положительный корень уравнения /0((хг)=0, J0(x) —
функция Бесселя первого рода нулевого порядка (Янке, Эмде
372
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
и Леш 1968). Левая часть уравнения A4.2) даст
К*
К* д\ 1 <?ф 1 д\
Так как
то после преобразования уравнение {14.9Л и условия A4.3) при-
примут вид
' 1 d2 ц2Л # q 1
= 0 при z = 0 и 2 = Г.
Теперь к A4.6) применим косинус-преобразование
1<
: = 9 (л, щ).
Так как
6B — ?) COS -p-rf2 =
COS
то из A4.6) получаем
По найденной двойной трансформанте ф**, дважды применяя
формулу обращения (Трантер 1956), найдем
i
J_ A cos [ия (г - PIT) + cos
s [яя (г + О/Г] 1 /0(Фг//?)
fill? J /?(й|)
§ 14] ПЛАСТ С КОНЕЧНЫМ РАДИУСОМ КОНТУРА ПИТАНИЯ 373
где J\ (x) — функция Бесселя первого рода первого порядка. Ряд
в квадратных скобках можно просуммировать (Снеддон 1955),
тогда получим
Ф(г, г; ?) =
^х (Т - 1 z - ? 1)//?) + ch (^х (Т - z - ?)//?) /Q
д% у
~ 2^ ft
Введя безразмерные величины р = /*//?, t/ = z/T> Po =
т] = ?/Г, последнее равенство можно переписать так:
ф(р. у; чIу>т»=гФ(»э р;
Ю. И. Стклянин нашел также потенциал скорости ф для
линии стоков с постоянной интенсивностью q = qo для 0^2^/
(^ = 0 для l^z^T). В безразмерных параметрах будем иметь
Ф(р, у) = т\
о
Интегрирование дает
(^
Так как имеет место соотношение
то окончательно можем написать
Q Q Д ch (ц,у/Ро) sh (|if A - р)/Ро) /0
^U-^ + S-JL-^
причем здесь введен полный расход линии стоков Q = qol.
Полученное уравнение является приближенным уравнением
для потенциала скорости несовершенной бесконечно тонкой
скважины.
374
КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ
[ГЛ. IX
М. Маскет A949) нашел формулу дебита несовершенной
скважины в изотропном пласте конечной мощности, распределяя
вдоль оси скважины точечные стоки, интенсивность которых он
подбирал так, чтобы на поверхности скважины радиуса гс по-
потенциал скорости был постоянным:
2nkl Д#
A4.7)
in 4r
где
Г @,875ft) Г @,125ft)
- 0,875ft) Г A -0,125ft)
V
\
\
N
и &Н — разность напоров на контуре питания радиуса /? и на
скважине. График функции f (ft) приведен на рис. 245.
Для группы несовершенных скважин И. А. Чарный A948)
предложил приближенный метод вычисления дебита. Приняв,
что на некотором удалении от несовершенной скважины поток
можно считать плоскопараллель-
f(fi) \ ным (это расстояние равно при-
примерно мощности пласта), И. А.
Чарный выделяет цилиндриче-
цилиндрическую поверхность, которую мож-
можно считать поверхностью равного
потенциала. Тогда к каждой из
скважин можно применить фор-
формулу Маскета. Потенциалы на
выделенных около каждой сква-
скважины цилиндрических поверхно-
поверхностях определяются из системы ли-
линейных уравнений, в которые вой-
войдут дебиты скважин.
Б. И. Сегал A946) рассматривал пространственную решетку
несовершенных скважин. Он помещает вдоль оси скважин ли-
линию стоков, интенсивность которой подбирает в виде полинома
второй степени относительно ординаты точек стока, и, кроме
того, на нижнем конце скважины помещает точечный сток. Ин-
Интенсивность последнего, а также коэффициенты указанного по-
полинома, подбираются путем вычислений.
§ 15. О наклонной и горизонтальной скважинах в безгранич-
безграничном пространстве. Системы горизонтальных скважин находят
широкое применение при устройстве водозаборных сооружений.
Наклонные скважины встречаются при бурении нефти, так как
вместо горизонтальной иногда бывает удобнее прокладывать
наклонную скважину под небольшим углом к горизонту.
П. Я. Полубаринова-Кочина A955, 1956) дала приближенное
0,2 0,4 0,6 0,8 1,0
Рис. 245.
§ 15]
НАКЛОННАЯ И ГОРИЗОНТАЛЬНАЯ СКВАЖИНЫ
375
решение задачи о наклонных скважинах известным методом
распределенных источников постоянной интенсивности.
Обозначим через q интенсивность стока, рассчитанную на
единицу дуги кривой L. На элементе дуги будем иметь расход
q ds. Потенциал скорости, вызываемый действием стоков, рас-
распределенных вдоль линии L, находящейся в безграничном про-
пространстве, имеет вид
Здесь s — длина дуги, отсчитываемая от какой-нибудь точки
линии L, g, т) и ? — координаты точек
этой линии.
Если принять q постоянным вдоль
всей линии L, то обозначив через /
длину кривой L, получим для полного
расхода жидкости, притекающей к L,
выражение
Q = lq. A5.2)
Предположим, что ось скважины
представляет отрезок прямой между
точками M\(Xi,yuZ\) и М2(х2, у2, z2) Рис.246,
(рис. 246). Распределим вдоль этого
отрезка стоки постоянной интенсивности (на единицу длины),
равной q. Потенциал скорости получающегося при этом движе-
движения будет
м2
\WT==J^ww=w, A5.3)
где М(х, у, z) —произвольная точка пространства, W(g, т), ?) —
точка отрезка М\М2. Обозначая через s длину дуги, отсчитывае-
отсчитываемую от точки М\ вдоль отрезка М{М2, через / — длину отрезка
M\M2i а через cos a, cos p, cosy — направляющие косинусы
этого отрезка, можем написать
I = х{ + s cos а, л = ух + 5 cos р, ? = zx + s cos у,
Z
Тогда подкоренное выражение интеграла A5.3) примет вид
(* -1J + (У - ЛJ + (г - If = г] - 2rlss + s2,
где
— х{) cos a + {у — у,) cos p + (z — z,) cos у.
376 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ (ГЛ. IX
Величина г\8 представляет проекцию отрезка МХМ на направ-
направление отрезка М\М2 (рис. 246). Теперь для A5.3) будем иметь
У. г)—
A6.4)
Здесь р — расстояние от точки М(х, у, г) до отрезка M,AJ2:
Вводя в рассмотрение расстояние г2 от точки М до М2 и
проекцию отрезка ММ2 на направление М\М2у которую обозна-
обозначим через r2s, получим
r2s = (*2 — х)cos а + (У2 — У)cos Р + te — z)cos Y = / — 'is-
Выражение A5.4) теперь можно переписать так:
Ф(х, у, г) = ^\п^±^ = ^п
§ 16. Скважина в полупространстве с горизонтальной пло-
плоскостью равного потенциала. Предствим себе, что под горизон-
горизонтальной поверхностью, покрытой слоем воды глубины Я, за-
заложена в грунте наклонная скважина, из
которой откачивается вода (обычно от-
откачка ведется через вертикальную тру-
трубу). Пусть скважина представлена от-
отрезком М'{М'2 (рис. 247), концы кото-
которого имеют координаты Щ{х{, у[9 — z{)y
М'2 (х2, у2, — г2). Отразив этот отрезок
относительно плоскости z = 0, представ-
представляющей поверхность грунта, получим
отрезок М\М2 с концами М{(х\, yuz\)t
М2(х2, у2, г2).
Рис 247- Отрезок М\М'г нагрузим стоками, а
отрезок М\М2 — источниками интенсив-
интенсивности q. Потенциал скорости фильтрации будет иметь вид
Ф(х, у, ^-JLl^ + ^^ + ^
4я p'2(r,+rls)(r2
что можно переписать в виде
у. г)=^Ы^^Щ + С, A6.1)
4я (г2 + r2s) (г, - г, J
§ 16] СКВАЖИНА В ПОЛУПРОСТРАНСТВЕ 377
r[9 r2, r[8, r2s имеем
причем г и rls, r2, r2s определяются формулами § 15, а для
,-УаУ+(,— - • <16-2>
r\s = (л: — л^) cos a + (г/ — */,) cos р + (г + гЛ cos y, )
Г2«= (xo — x)cos а + {У2 "~ ^) cos P -~ (z + ^2) cos y. J
Так как при 2 = 0 имеем rx=r\, r2 = r'2, rls = r'ls, r2s=*r'2st
то ф(х, у, 0) =0. Если скважина находится в грунте с коэффи-
коэффициентом фильтрации k под слоем воды, глубина которой равна
Я, то удобно принять, что потенциал скорости на плоскости
2 = 0 равен — kH. Тогда вместо A6.1) напишем
{r{+r2s)(rl-rls)
- kH. A6.4)
Эквипотенциальные поверхности в случае одной скважины,
рассмотренной в § 15, являются эллипсоидами вращения. В слу-
случае двух наклонных скважин близкими к эллипсоидам враще-
вращения будут лишь те поверхности равного потенциала, которые
достаточно тесно охватывают отрезок М\Мъ или М\М2. Рассмот-
Рассмотрим эквипотенциальную поверхность, охватывающую отрезок
М\М\ настолько тесно, что поперечное сечение ее, образованное
плоскостью, проходящей через середину отрезка М{Мо и пер-
перпендикулярное к нему, можно было бы принять за окружность.
Обозначим через хОу у0, —z0 координаты середины отрезка
М'\М\ через б — радиус указанного почти кругового сечения.
Возьмем произвольную точку Мь этого сечения, координаты ко-
которой можно записать в виде
хЛ = *о + б cos а<ъ Уь = Уо + б cos p0, z6 =— zo +6cosyQ. A6.5)
Теперь в формуле A6.4) положим М = 7Иб, т. е. х = х6, у =
= Уь и z = г6. Тогда будем иметь приближенные соотношения
Кроме того,
^ = ^ = Т- A6-7)
Что же касается величин гь г2, Г\8 и r2s, то для их вычисления
можно приближенно заменить Мб серединой отрезка М[Мъ т.е.
378 колодцы и скважины, горизонтальные дрены [гл. IX
*б> Уь> Z6 заменить соответственно на xOi уОу —zq. Получим
r2 _ J_ /2 I Ay у r — —1 — Ay Z°~~ Zl
' 1 4l ~ ™ori> Ms 2 0 /
Значение напора на выбранной эквипотенциальной поверх-
поверхности обозначим через Яс, т. е.
<pc=--fe#c. A6.9)
Подстановка выражений A6.6) —A6.9) в формулу A6.4) дает
klH-Hj^JL In '2 [V/WTg^-f 4,0 (г0 - g|)// - 1/2] A6Л0)
4я б2 [V/74 + 4гог! + 4г0 (г0 - 2,)/ + //2]
Отсюда для полного дебита отрезка MWi, равного Q = ql, на-
находим следующее выражение:
w— in(//6)_e •
где
V/2/4 + 420*! + 42о Bо - zi)// - //2
В частном случае горизонтальной скважины выражение для
Э, входящее в формулу для Q, упрощается и получаем, полагая
Z\ = Z2 = ZOi
I |
2
Если длина скважины настолько велика, что можно пренебречь
величиной 16zo по сравнению с /2, то можно написать
Q_2nkl(H-Hc) A614)
W~ lnB2o/6) * U°-i^
Это известная формула дебита отрезка длины I бесконечно
длинной горизонтальной скважины.
Отметим другой частный случай — вертикальной скважины,
заложенной в грунте под поверхностью воды. Так как в этом
случае
Z{ = Z0 — у/, 22 = 20 + у/, A6.15)
то получаем
e=4lni^h-- A6Л6)
§ 16]
СКВАЖИНА В ПОЛУПРОСТРАНСТВЕ
379
Для того чтобы иметь возможность сравнивать работу дрен
при различных их наклонах, преобразуем формулу A6.12),
вводя вместо Z\ и z2 величины Z\ и у по формулам
z2 = z{ + I cos y, zu = zx + у cos у.
Кроме того, введем безразмерную величину
A6.17)
A6.18)
Тогда 9 будет зависеть от 1Х и у:
'f Ч- в B Н- /д cos у) A +/1cos'v)
/1cosY)cosy
+ 8 B + /j cos y) + 2 B + /j cos Y) cos у -
A6.19)
Отметим предельный случай /! = oo. Для него имеем
+8cos2y +2cos2y+1
A6.20)
в
0,8
Для всех скважин, кроме горизонтальной, предельное зна-
значение 0 имеет конечное значение. На рис.248 представлены гра-
графики зависимости 8 от U при раз-
различных значениях y- Как видно, >
8 мало меняется для скважин, в
близких к вертикальным, и силь-
но возрастает при приближении
к горизонтальному положению.
Так как 8 является вычитаемым
в знаменателе формулы A6.11),
то с увеличением 9 дебит сква-
скважины увеличивается. Поэтому де-
дебит горизонтальной скважины
(при одной и той же длине сква-
скважин) больше дебита наклонной
скважины, если напор на этих
скважинах одинаков и если верх-
верхний конец скважины остается неизменным (так что скважина
вращается вокруг него, как вокруг неподвижной точки). На
рис. 248 даны значения y лишь в пределах от 0 до 90°. При уве-
увеличении угла (от 90 до 180°) можно использовать те же гра-
графики, беря вместо у величину 180° — у и вместо l\ = l/z{ ве-
величину /2 = //г2.
Если вращать отрезок М\М'2 вокруг его середины (сохраняя
длину),то можно написать формулу, выражающую зависимость
^—
^-——
s= =
0°
_ео°х
—
10 10
50
Рис. 248.
380 КОЛОДЦЫ И СКВАЖИНЫ. ГОРИЗОНТАЛЬНЫЕ ДРЕНЫ [ГЛ. IX
Э от у:
e=llnV^8B + /0cos1 + 4cosY+/0 / ±Ч
2 <s/tt + *B + lo«*y) +4cosy-/0 Z°
Вместо действительной скважины, ограниченной цилиндриче-
цилиндрической поверхностью, мы имели скважину, ограниченную почти
эллипсоидальной поверхностью. Можно условиться установить
некоторый принцип соответствия между ними. Например, после-
последовав примеру Н. К. Гиринского A950), рассматривавшего
одну вертикальную скважину, можно цилиндрической скважи-
скважине длины / и радиуса гс привести в соответствие эллипсоидаль-
эллипсоидальную поверхность, у которой большая ось равна длине скважи-
скважины, причем объем «эллипсоида» равен объему цилиндра. Тогда
из соотношения nr2cl = 2/3nlb2 получим, что 6=гсд/3/2. Прини-
Принимаем 6 = & « 1,22гс.
Отметим также, что при таком рассмотрении задачи полу-
получается приток и через концы скважины. Если донного притока
нет, то можно учесть частично это обстоятельство, поместив
источники подходящей интенсивности на концах скважины. Ряд
задач о скважине конечной длины в различных условиях рас-
рассмотрен Г. А. Разумовым A962).
Глава X
ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ
УСТАНОВИВШИХСЯ ДВИЖЕНИЙ
А. БЕЗНАПОРНЫЕ ДВИЖЕНИЯ ПРИ НАЛИЧИИ ВОДОУПОРА
§ 1. Гидравлическая теория и ее основные положения. Под
гидравлической теорией мы будем понимать такую теорию, в
которой применяется осреднение потока по высоте. Тем самым
уменьшается число измерений в изучаемом движении: плоская
задача превращается в одномерную, т. е. такую, в которой эле-
элементы движения зависят лишь от одной координаты (л:), если
движение происходит в вертикальной плоскости (#,?), и в
двумерную, с координатами (х, у), если рассматривается дви-
движение в трехмерном пространстве (х, у, z).
В гидродинамической теории рассматриваются все — два или
три—измерения, отвечающих данной, задаче. При этом могут
вводиться те или иные упрощения, например, в граничных усло-
условиях и т. д.
При современном развитии гидравлической теории в неко-
некоторых задачах приходится пользоваться сложным математиче-
математическим аппаратом, поэтому нельзя уже противопоставлять гидрав-
гидравлическую теорию гидродинамической как простую теорию.
Сравнение для ряда задач гидравлических и гидродинамиче-
гидродинамических решений показывает, что во многих случаях гидравличе-
гидравлические теории дают хорошие результаты.
При расчете фильтрации через земляные плотины приме-
применяются методы, которые можно назвать полугидравлическими:
плотина разбивается на участки, из которых средний рассчи-
рассчитывается по формуле Дюпюи, а участки, примыкающие к верх-
верхнему и нижнему бьефам, рассчитываются различными искус-
искусственными приемами.
Свободная поверхность грунтового потока бывает слабо изо-
изогнутой, если поток охватывает большую площадь, например,
когда рассматривается фильтрация из канала в реку, фильтра-
фильтрация при орошении и т. п. Такой поток может занимать пло-
площадь, измеряемую квадратными километрами, в то время как
глубина потока измеряется в метрах или десятках метров и
382 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
на больших протяжениях — за исключением областей, приле-
прилежащих непосредственно к каналу или реке, — изменяется лишь
на доли метра.
На границах области движения, т. е. возле самых рек и ка-
каналов, поверхность потока может оказаться сильно изогнутой,
непосредственно под каналом течение носит пространственный
характер. В этих частях потока требуются более точные методы
исследования.
Что касается тех участков течения, на которых оно является
слабо изменяющимся от точки к точке, и где скорости близки
к горизонтальным, то для них применима гидравлическая тео-
теория. Эта теория у нас уже встречалась при изучении напорных
движений (см. § 8 главы IX). Здесь мы останавливаемся на
безнапорных движениях (Dupuit 1863).
Вспомним условие, которое должно выполняться на свобод-
свободной поверхности: это условие постоянства давления, т. е. равен-
равенства его атмосферному давлению (или капиллярному).
Зависимость между потенциалом скорости и давлением
имеет вид (см. § 11 главы I)
<p = -k{-^ + z) = -kh, A.1)
где
A = z + -?-, A.2)
причем h есть функция от координат х, у и z. Считая атмосфер-
атмосферное давление равным нулю, получим из A.2) условие на сво-
свободной поверхности в виде
h(x, у, z) = z, A.3)
или согласно A.1)
Если поверхность грунтового потока слабо изогнута, то это
значит, что z слабо изменяется, колеблясь около некоторого
среднего значения г0. Разложим h в ряд по степеням z — z0:
h (х, у, z) = h (х, у, z0) + (-I7) (z - z0) + ... A.4)
Будем считать малой величину dh/dz, пропорциональную верти-
вертикальной скорости, и произведением этой величины на малую
величину z — z0 будем пренебрегать. Другими словами, заме-
заменяем действительный напор h(xtyyz) величиной h(x, у, г0), за-
зависящей от средней глубины потока ?о, но не зависящей от ко-
координаты z. Будем его обозначать через h(x,y).
§ 1] ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ И ЕЕ ОСНОВНЫЕ ПОЛОЖЕНИЯ 383
Это означает, что напор считается постоянным вдоль каж-
каждой вертикали, или, иначе, поверхности равного напора прини-
принимаются за вертикальные цилиндрические поверхности. В пло-
плоском течении линии равного напора будут вертикальными пря-
прямыми. (Ниже мы увидим, что в это основное предположение
гидравлической теории можно будет внести некоторые по-
поправки.)
Теперь можно считать уравнение A.3), приняв вместо
h(x,yyz) осредненное по высоте значение h(xyy), уравнением
свободной поверхности:
z = h(x, у). A.5)
Таким образом, в гидравлической теории напор в каком-нибудь
сечении принимается за уровень воды в этом сечении.
Выведем уравнение неразрывности для потока со
слабо изменяющейся свободной поверхностью.
Горизонтальные составляющие скорости и и v вы-
выражаются через напор h(x,y) при помощи равенств
* dh I dh /i ~\
дх ду v '
Выделим в жидкости элементарный столб, ограни-
ограниченный сверху свободной поверхностью, снизу — го-
горизонтальной плоскостью (л:, у), представляющей для &
простоты основание проницаемого пласта, с боков —
вертикальными плоскостями, образующими в основа- ™u z^-
нии прямоугольник со сторонами dx и dy (рис. 249).
Расход через левую грань полученного тела равен площади
грани h dy, умноженной на скорость и. Обозначим через qx
расход в направлении оси х (на единицу длины в направлении
оси у). Тогда расход через левую грань тела будет равен
A.7)
Здесь h и dh/dx берутся в точке (х,у). Расход через правую
грань равен такому же выражению A.7), в котором надо лишь
заменить х на х + dx:
ГУ. A.8)
Разность между количеством жидкости, вытекающим в еди-
единицу времени через грань x-\-dx, и количеством ее, втекающим
через грань х, равна {qx+<ix — Qx)dy; по формуле Лагранжа
384 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
(где 1~ некоторое число, лежащее между х и x-\-dx), и изме-
изменение расхода в направлении оси х преобразуется так:
(Ях+лх -qx)dy = 2g-dxdy=-k-gr(h -§-) dx dy. A.9)
Точно так же найдем изменение расхода в направлении оси у:
xdy. A.10)
В выражениях A.9) и A.10) нужно считать независимые пере-
переменные равными величинам g, т), лежащим соответственно меж-
ду х и х + dx, у и у + dy. При переходе к пределу, когда dx-+0
и dy-+Oy получим вместо (§, т)) значение (л:,у).
Общее изменение расхода через боковые грани, равное сум-
сумме выражений A.9) и A.10), в установившемся движении не-
несжимаемой жидкости может компенсироваться поступлением
или оттоком жидкости сверху или через основание пласта.
Сверху на свободную поверхность может падать дождь или
вода при поливе — эти явления называют инфильтрацией; испа-
испарение дает отток жидкости с поверхности. Через основание пла-
пласта может происходить слабое просачивание, если нижележа-
нижележащий пласт является не абсолютно водоупорным (что обычно и
имеет место в действительности), но слабо проницаемым. Такой
случай будет рассмотрен ниже в этой же главе. Пусть на еди-
единицу площади (горизонтальной проекции свободной поверхно-
поверхности) поступает сверху расход е и снизу расход wq. На площад-
площадку dx dy соответствующие расходы будут:
edxdy, wodxdy. A-11)
Складывая выражения A.9) и A.10) и приравнивая их
сумме A.11), после деления на dx dy получим
dqx , дЯу
дх ' ду 1
ИЛИ
Величина е положительна, если вода поступает в область
движения, т. е. в случае инфильтрации или в случае превыше-
превышения интенсивности инфильтрации над интенсивностью испаре-
испарения, и отрицательна в случае испарения или преобладания ис-
испарения над инфильтрацией. Вертикальная скорость w0 поло-
положительна, если вода просачивается из нижнего грунта в верх-
верхний, и отрицательна в обратном случае.
ПЛОСКОЕ ТЕЧЕНИЕ С ГОРИЗОНТАЛЬНЫМ ВОДОУПОРОМ
385
Если основание грунта непроницаемо и отсутствуют инфиль-
инфильтрация и испарение, то е = w0 = 0 и уравнение A.12) можно
переписать в виде
О \П ) ¦ О \П ) q /л л л\
В этом случае функция h2 удовлетворяет уравнению Лапласа.
§ 2. Плоское течение с горизонтальным водоупором. Рассмот-
Рассмотрим движение грунтового потока в плоскости (х>г) (рис. 250).
Уравнение A.13) переходит
в данном случае в следующее:
d2 (h2)
dx2
= 0.
Интегрирование дает параболу
(А и В — произвольные посто-
постоянные)
B.2)
Рис. 250.
Можно также получить эту параболу, исходя из выражения
расхода q через сечение х (рассчитанного на единицу длины
потока в направлении, перпендикулярном к оси х)
q=-kh^j. B.3)
Интегрируя это уравнение и подставляя координаты точек
(*i,/*i)> (x2, h2), после преобразований получим
<2-4>
Формула B.4) называется формулой Дюпюи.
Мы видели, что такая же формула получается при точном
решении двумерной задачи о притоке к горизонтальной дрене
(см. § 11 главы II). В § 9 главы VII эта же формула выведена
для земляной перемычки, где, однако, ft2 не есть ордината сво-
свободной поверхности.
Мы уже указывали, что в гидравлической теории вертикаль-
вертикальными скоростями обычно пренебрегают. Однако можно дать
способ приближенного учета вертикальных скоростей в потоке.
Напишем уравнение неразрывности
ди , dw
дх "+" dt
= 0
и проинтегрируем его по -г, помня, что у нас и есть функ-
функция только от х, определяемая уравнением и = —kdh/dx.
13 П. Я. Полубаринова-Кочина
3^6 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
Учитывая, что на водоупоре при -г «в 0 вертикальная скорость
равна нулю, получим
Так как d2h\dx2 не зависит от г, то интегрирование дает w =
=¦= kz d2h/dx2. С помощью выражения B.3) найдем вторую про-
производную:
dx* 1№
Отсюда
На свободной поверхности, где z = hy имеем
w kh2 * \kh ) '
Отсюда видно, что над непроницаемым водоупором верти-
вертикальная скорость отрицательна, величина ее пропорциональна
высоте.
§ 3. Свободная поверхность при инфильтрации или испарении.
В уравнении A.12) примем w0 &= 0, но оставим слагаемое е,
определяющее инфильтрацию или испарение. Ограничиваясь
рассмотрением плоского движения, перепишем уравнение A.12)
так (см., например, Аравин и Нумеров 1948):
Интегрирование его дает
2. C.2)
В случае инфильтрации, при е > 0, имеем уравнение эллип-
эллипса, в случае испарения, когда можно положить е = —е (е > 0),
получим уравнение гиперболы
АЛ2-**2 —С^ + Св. C.3)
Для определения постоянных С\ и С2 нужно задать два усло-
условия, например две точки свободной поверхности. Перемещая
начало координат вдоль оси х, можно добиться, в частности,
обращения С\ в нуль.
ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ ПО ВЕРТИКАЛИ ГРУНТАХ
387
Пусть, например, фильтрация происходит через прямоуголь-
прямоугольный массив грунта из бассейна глубины Н\ в бассейн глубины
Я2 и на поверхности имеет место инфильтрация (рис. 251). Обо-
Обозначим максимальную ординату свободной поверхности через
Я, расстояние ее от водных бассейнов соответственно через L\
и L2 и совместим с ней начало координат. Учитывая, что
при этом С\ = О, перепишем
уравнение C.2) следующим
образом:
При этом, полагая х = —L\, Hi
h = Н\ и х = L2, h «=« Я2, по- ±
лучим зависимости
U2 I 8 Г2 ?72
Рис. 261.
Н'а + ±Ц«*Н'. C.4)
Обозначая расстояние между водоприемниками через L, будем
иметь уравнение
LX+L2 = L. C.5)
Два уравнетя C.4) и уравнение C.5), в которых L, Яь Я2
являются заданными, служат для определения неизвестных Lu
Ь2иН.
Что касается случая испарения, то здесь представляются две
возможности в зависимости от знака С2 (если выбрать С\ = 0),
так как может получиться одна из двух сопряженных гипербол.
В случае вырождения свободная поверхность обращается в от-
отрезки двух, прямых.
§ 4. Фильтрация в грунтах, слабо неоднородных по вертикали.
Мы уже встречались в § 5 главы VIII с простейшими напорны-
напорными движениями в неоднородных (слоистых) грунтах. Рассмот-
Рассмотрим здесь движение со свободной поверхностью в грунте, коэф-
коэффициент фильтрации которого является функцией от высоты г.
Вычислим расход qx в направлении оси х, протекающий че-
через прямоугольник высоты Л, основание которого равно единице
длины и плоскость которого перпендикулярна к оси х. Разби-
Разбивая h на элементы dz, весь прямоугольник разобьем на эле-
элементарные прямоугольники с расходами —k(z)(dh/dx)dz. Про-
Проинтегрировав это выражение по 2 в пределах от нуля до /г,
найдем расход qx через упомянутый прямоугольник высоты h:
h
^dz = —d±\k{z)dz. D.1)
13»
388 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
Здесь dh/dx можно вынести за знак интеграла, так как h со-
согласно рассматриваемой гидравлической теории не зависит от
г (см. § 1).
Точно так же определяется расход qy через площадку высо-
высоты h с основанием, равным единице, перпендикулярную к оси у:
h
k {z) dz. D.2)
о
H. К. Гиринский A946) ввел функцию, которую теперь на-
называют потенциалом Гиринского:
h
ф (х, y)=\(z — h)k (z) dz. D.3)
о
Через- нее, как нетрудно проверить, просто выражаются qx и qy:
_ дФ _ дФ
Если грунт однороден, то
h
= -^f. D.5)
Функция D.3), как нетрудно проверить, удовлетворяет уравне-
уравнению Лапласа по переменным я, у. Таким образом, функция
Ф(х, у) представляет обобщение функции — kh2/2 на случай
грунта, неоднородного по вертикали.
Пример. В качестве примера непрерывного изменения
k(z) с высотой возьмем случай линейной зависимости k(z) =
= &оA + Ьг). Подстановка этого выражения в D.3) и интегри-
интегрирование дают для движения в плоскости х> z
OW = ^if«^. D.6)
Считая расход q постоянным для всех х и полагая d<D/dx = q9
после интегрирования получим
Ф = <7* + С, D.7)
где С —произвольная постоянная. В силу D.6) будем иметь
уравнение параболы третьей степени
или
l^^-^ + c,. D.8)
§5]
двуслойный грунт с наклонной линией раздела
389
Задание двух точек (хи hx) и (x2,h2) свободной поверхности
дает нам
k0 (Л2 - hx) [л2 + Л, + | (Л22 + Л,А, + Л*)]
о — —
Если & > 0, то коэффициент фильтрации возрастает с высо-
высотой, а абсолютное значение q больше, чем при Ь = 0; если
Ь < 0, то k убывает с высотой, и q по абсолютной величине
меньше, чем при Ь = 0.
Ь<0
Рис. 252.
Рис. 263.
Исследование формы свободной поверхности (можно при-
принять С\ = 0) показывает, что при Ь > 0 получается кривая
(рис. 252), лежащая ниже параболы
При Ь < 0 в качестве возможной формы свободной поверхности
получается лишь участок кривой, на котором h меняется от
нуля до h\ = —l/b, а х — от нуля до х\ =—&о/C<7&2), т. е.
участок от точки перегиба до нижней вершины параболы. Это-
Этому участку отвечает изменение коэффициента фильтрации от ko
до нуля (рис. 253).
§ 5. Фильтрация в двуслойном грунте с наклонной линией
раздела. Рассмотрим двуслойный массив грунта, расположенный
на горизонтальном водоупоре. Пусть прямолинейная граница
раздела грунтов наклонена под не слишком большим углом а к
горизонту и уравнение ее имеет вид y=ix,rnei=tga (рис.254).
Верхний грунт имеет коэффициент фильтрации fe, а нижний
—k0. Полуось у = 0 (х^О) является при этом границей водо-
упора, и движение рассматривается только в области х ^ 0.
Будем считать, что градиент напора постоянен вдоль каж-
каждой вертикали, и вычислим фильтрационный расход q, проте-
протекающий через вертикальное сечение ABC с глубиной h (рис.254).
390
ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИИ [ГЛ. X
Вычисляя расход по отдельности через отрезки AB = ix и ?С=
= h — ix, получим
При этом q > О для течений, направленных вправо, и ?<0 для
течений, направленных влево. Поскольку фильтрационный рас-
расход потока грунтовых вод q постоянен, перепишем полученное
уравнение так:
Это линейное уравнение пер-
первого порядка. Общий его инте-
интеграл имеет вид
h — Ix+H = Ceh/Hi E.2)
где
1=(\ —-^Л/ И — -2-
\ k I> п— иг
Рис. 264. Интегральные кривые имеют
асимптоту h = Ix — H.
Произвольная постоянная С может быть определена, на-
например, из условия прохождения интегральной кривой (депрес-
сионной линии) через некоторую заданную точку (xuh\). Для
Рис. 255.
определения отношения qjk (или величины Я) следует задать
еще одну точку (х2, h2) на депрессионной линии.
§ 6] СВЯЗЬ МЕЖДУ НАПОРНЫМИ И БЕЗНАПОРНЫМИ ДВИЖЕНИЯМИ 391
Решения E.2) имеют смысл лишь при х ^ 0 и h ^ ix, т. е.
в области верхнего грунта. На рис. 255 представлены четыре
возможных случая расположения депрессионных линий в зави-
зависимости от знака величин k — k0 и q. Пунктиром на рисунке
указаны не отвечающие реальным движениям ветви решений
E.2). По поводу последнего случая (k < k0, q>0) заметим,
что если отношение ko/k велико, то асимптота будет близка к
вертикали и депрессионная линия может оказаться сильно изо-
изогнутой, тогда излагаемая гидравлическая теория неприменима.
При k0 = О рассматриваемые течения обращаются в тече-
течения в однородном грунте по наклонному водоупору. Асимптоты
при этом параллельны водоупору и из четырех указанных на
рис. 255 случаев остаются только два различных. Эти течения
были рассмотрены Ж. Дюпюи (Dupuit 1863) и подробно иссле-
исследованы позже Н. Н. Павловским A930). В частности, при / = 0
из уравнения E.1) получим параболу Дюпюи.
Б. БЕЗНАПОРНЫЕ ПРОСТРАНСТВЕННЫЕ И ПОЛУНАПОРНЫВ
ДВИЖЕНИЯ
§ 6. Связь между пространственными безнапорными и пло-
плоскими напорными движениями. В § 1 было выяснено, что задача
о пространственном движении грунтовых вод при условии сла-
слабой изменяемости свободной поверхности при наличии горизон-
горизонтального водоупора приводится к уравнению Лапласа для функ-
функции h2(x,y). При этом h(xyy) есть осредненный по высоте на-
напор и вместе с тем ордината точки свободной поверхности.
С другой стороны, в плоском напорном движении, в пласте,
ограниченном двумя горизонтальными плоскостями, напорная
функция, которую мы обозначим через hE(xty), удовлетворяет
уравнению Лапласа Д/гн »= 0.
Если граничные условия для двух задач одинаковы, то меж-
между h2 и hE должна существовать линейная зависимость.
В дальнейшем удобно использовать введенное Н. Н. Пав-
Павловским понятие о приведенном напоре hr = h/H, т. е. напоре,
деленном на действующий напор Н. При этом Павловский при-
принимал, что hr = 1 вдоль границы верхнего бьефа и hr = 0
вдоль границы нижнего бьефа.
Допустим, что действительный напор h вдоль верхнего бьефа
равен Аь вдоль нижнего — h2. Тогда зависимость между h и hr
можно выразить с помощью уравнения
l • {0Л)
л,-л2
В более общем случае, когда задано соответствие между напо-
напорами h и hr в двух произвольных точках, причем значению h=
392 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
= hi соответствует Аг = Аг1, а значению A = А2 отвечает hr =
= Аг2, будем иметь
hr - hr2
Теперь приведем в соответствие два движения — безнапорное и
напорное. Тогда в левой части уравнения F.2) нужно заменить
A, Aj и А2 соответственно на А2, Н\ и h\, и мы получим соотноше-
соотношение Форхгеймера (Форхгеймер 1935; см. также, например, Ара-
вин 1947)'
^2—%=hJ~~hru • F-3)
л, - п2 лг1 - hr2
В качестве примера рассмотрим приток к котловану, круг-
круглому в плане. Такой котлован есть не что иное, как скважина
большого радиуса. Обозначим этот радиус через гь а соответ-
соответствующее значение А через h\. Пусть при г = г2 напор А = А2.
Соответствующее напорное движение определяется функцией
Аг вида
Аг==Л1пг + В. F.4)
Пусть при /*==/*! имеем Аг = Агь при г = г2 Аг = Аг2, где Ari и
Аг2 — произвольные числа. Из F.2) с помощью F.4) получим
hr~hr2 д
Тогда F.3) дает
Отсюда с помощью равенства
где Г2 — радиус скважины, получаем формулу Дюпюи для де-
дебита скважины Q (см. также § 9 главы VII):
F.5)
§ 7. Напорно-безнапорные движения. В § 10 главы II упоми-
упоминалось о существовании таких движений, для которых область
движения распадается на ряд областей с безнапорным и напор-
напорным движениями (Аравин и Нумеров 1948).
Так, может случиться, что напорный поток под флютбетом
отрывается и дальнейшее движение происходит с образованием
свободной поверхности CD (рис. 256). В области / имеем на-
§7]
НАПОРНО-БЕЗНАПОРНЫЕ ДВИЖЕНИЯ
393
порное движение, в области 2— безнапорное. На границе меж-
между ними, которую можно принять за линию равного напора,
h = hu (напор пограничного сечения). В данном случае hn= Т.
~/////s/////////////////////////////////////уvv/7
Рис. 256.
Для области 1 применима формула F.2), которую можно пе-
переписать, принимая во внимание, что h2 = Г, h\ = Н\-\- Г, йгз=
= hm и hr\ = 1, следующим образом:
1-лг
Через hrn обозначен неизвестный пока приведенный напор на
границе раздела. Для области 2 нужно воспользоваться форму-
формулой F.3), которая дает, если учесть, что теперь h\ =» Г, п2 *¦=
= #2, К\ = hm и hr2 = 0:
T2-Hl
G.2)
Для определения неизвестного напора пограничного сечения hrn
можно воспользоваться условием равенства расходов через это
сечение в областях 1 и 2.
В качестве примера рассмотрим подробнее случай, изобра-
изображенный на рис. 256. Грунтовый поток, обтекая флютбет, отры-
отрывается от него в точке С, образуя свободную поверхность CD
и впадая дальше в реку или дрену. Разбивая течение на две
части, применяем к левой части формулу для расхода при об-
обтекании плоского флютбета ширины 21 (см. § 7 главы III):
Для правого участка вычисляем расход по формуле Дюпюи:
Г2 — Я2
2 (L - /р
Сравнение этих формул позволяет найти положение точки от-
отрыва потока, т. е. отрезок /.
394
ГИДРАВЛИЧЕСКАЯ ТРОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИИ [ГЛ. X
§ 8. Фильтрация в обход сооружений. Рассмотрим движение
грунтовых вод в берегах реки, вызванное разностью уровней во-
воды в верхнем и нижнем бьефах плотины, снабженной противо-
фильтрационной завесой. Завеса представляет собой вертикаль-
вертикальную стенку, расположенную вдоль берега или врезанную в бе-
берег, предназначенную для уменьшения фильтрации из водохра-
водохранилища (верхнего бьефа) в нижний бьеф.
Предположим, что поток грунтовых вод до возведения соору-
сооружений был направлен из бесконечности нормально к прямоли-
прямолинейному участку реки и имел постоянную скорость v = kl, где
Рис. 267.
СЕ
Рис. 258.
/ — первоначальный градиент потока. Пусть берега реки верти-
вертикальны и доходят до горизонтального водоупора, служащего
также основанием сооружений (Веригин 1947).
На рис. 257 и 258 представлены два простейших типа за-
завес—продольная и поперечная. Берег реки совмещен с осью х,
и движение происходит в верхней полуплоскости чертежа. Воз-
Возведенные сооружения нарушают первоначальный поток и со-
создают дополнительный поток из верхнего в нижний бьеф. При
этом возможны два случая разветвления потока: когда точка
нулевой скорости N находится вне завесы (на рисунках слева)
и когда она попадает на завесу (на рисунках справа).
§8]
ФИЛЬТРАЦИЯ В ОБХОД СООРУЖЕНИЙ
895
Сначала найдем решение для напорного потока, соответ-
соответствующего принятым на рис. 257 и 258 схемам. Область комп-
комплексного потенциала ш = ф + u|> имеет вид, изображенный на
А И С Е
Рис. 259.
рис. 259 и 260. Отображение любой из них на полуплоскость Z
дает
СО'
Для отрезка — 1 < ? < 1
где Н = Нх — #2, а Н{ и Я2 — напоры соответственно в верхнем
и нижнем бьефах. Для отрезка — оо <с ? < — 1 имеем
G) = "
ikH
ikH
Отображая на полуплоскость область движения, получим со-
соответственно: для продольной завесы (Ь — половина ширины за-
завесы)
z «ftg, (8.1)
для поперечной
г = I Уё^Т. (8.2)
396 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
Координаты точки разветвления потока находятся из условия
v = —kl и и = О на бесконечности. Отсюда получаем для про-
продольной завесы а = Н/(nib), для поперечной завесы (которая
называется шпорой) а = Н/(п11).
В результате комплексный потенциал со выразится в зави-
зависимости от z следующим образом. Для продольной завесы: на
отрезке CDE
(о = — ' — — klb l\ *2 ?(#i+#2)
я Ь \j b2 2 '
на линии АС
ю = -— arch ( — -J-) — ^^ Л/"Р" — 1 — kH\;
для поперечной завесы: на отрезке CDE
(плюс для —1 < ? < 0, минус для 0 < ? < 1), на линии АС
со = —l-^- arsh у + iklz — kHx.
При а ^—1 отсутствует фильтрация из верхнего бьефа в
нижний. В общем случае ширина зоны обходной фильтрации в
области верхнего бьефа будет для продольной завесы В =
= L — by для поперечной В = L. Величина L определяется из
уравнений (8.1) и (8.2) при ? = —а и z = —L.
Для продольной завесы получаем выражение напора за за-
завесой
1 X2 Н
и выражение расхода
Q = kHA, A = l(archl-VTTIF), B = ltf-t>9 (8.3)
где
Р = ^. (8.4)
Для потока с точкой разветвления на завесе имеем Q = 0 и
В = 0. Минимальная длина завесы lm = 26m, при которой об-
обходная фильтрация из верхнего бьефа в нижний отсутствует,
выражается таким образом:
где S = H/I — расстояние от линии берега до линии пересече-
пересечения горизонта верхнего бьефа с первоначальной плоскостью
пьезометрических напоров.
§ 8] ФИЛЬТРАЦИЯ В ОБХОД СООРУЖЕНИЙ 397
В случае поперечной завесы получаем для напора на завесе
h = з ± — arccos f + Iy
(плюс для левой и минус для правой стороны завесы). Для по-
потоков первого типа расход определяется по формулам (8.3) и
(8.4), где вместо Ь берется полная длина поперечной завесы /.
Ширина зоны обходной фильтрации
Для потоков второго типа Q = О и В = 0. Предельная длина
завесы находится из условия отсутствия обходной фильтрации:
1т~ я/ я °'
Отсюда видно, что для достижения отсутствия обходной
фильтрации продольная завеса должна быть вдвое длиннее по-
поперечной.
Переходя к безнапорному потоку, мы должны заменить h
на h2. Получим для продольной завесы
h2 + hl h2 — hi ( z >
h2 = —Цл Re I arcsin -г
z я v о >
a = (h\ — h2)/{nlb). В случае движения первого типа
Г dh (ki f1 dh2
Q = — k \ h -^— dx = Re I -7Г \ —r-
-L ч -а
где h{ и h2 — напоры в верхнем и нижнем бьефах,
о 1 nib Tib
= hi—h2, S = ho/I. Для величины В получаем
Для движений второго типа Q = 0, ? = 0 и а=1, поэтому
m m я/ я
Для поперечной завесы имеют место равенства
z\ . h\-h\
398 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИИ [ГЛ. X
В случае течения второго типа, когда Q = 0, В = 0 и <х=1,
h0 = S
я/ я
; По О
Настоящий раздел изложен по статье Н. Н. Веригина A947).
В других работах (Аравин 1940, 2; Недрига 1947) эти вопросы
рассматриваются несколько иначе; там также дается решение
задачи для случая комбинации шпоры и плоского устоя.
В. ДВИЖЕНИЯ В ПЛАСТАХ С ПЕРЕТОКАМИ
§ 9. Скважина в безнапорном пласте со слабо проницаемым
основанием*). Пусть водоносный пласт с коэффициентом филь-
фильтрации k подстилается слабо проницаемым горизонтальным)
прослоем (толщины d с коэффициентом фильтрации х), ниже
которого расположен хорошо проницаемый мощный пласт с по-
постоянным напором Н. Тогда из нижнего пласта будет происхо-
происходить подпитывание верхнего пласта с интенсивностью
где h — напор в верхнем водоносном пласте, который будем от-
отсчитывать от его основания.
Рассмотрим совершенную вертикальную скважину радиуса
гс, пересекающую весь водоносный пласт; пусть в ней поддер-
поддерживается напор hc. Пренебрегая вертикальными составляющими
скорости фильтрации, будем считать поток плоскорадиальным
и осесимметричным. Тогда уравнение движения грунтовых вод
A.12) в отсутствие инфильтрации на свободной поверхности
(е = 0) примет вид
Зададим следующие граничные условия:
h = hc при r = rCi h = H при г->оо. (9.2)
Решение уравнения (9.1) при условиях (9.2) существует и
единственно, причем ему соответствует одно и только одно зна-
значение (dh/dr)rarc (см. Клоков 1969), т. е. при условиях (9.2) де-
дебит скважины совершенно определенный. Однако проинтегри-
проинтегрировать нелинейное уравнение (9.1) в замкнутой форме не уда-
удается, поэтому его приходится либо линеаризовать, либо решать
численно.
*) Этот параграф излагается по книге П. Я. Полубариновой-Кочиной,
В. Г. Пряжинской и В. Н. Эмиха A969).
§ 9] ПЛАСТ СО СЛАБО ПРОНИЦАЕМЫМ ОСНОВАНИЕМ 399
Первый способ линеаризации уравнения (9.1) (линеариза-
(линеаризация по ft), примененный А. Н. Мятиевым A948), состоит в за-
замене в (9.1) переменного множителя ft при dh/dr некоторым
постоянным значением Л*, что равносильно осреднению мощно-
мощности потока. Если исходить из того, что на некотором расстоянии
от скважины со все большей точностью начинает выполняться
приближенное равенство ft « Я, то можно положить ft* = #
(А. Н. Мятиев предлагал принять /i»/ic). Тогда вместо урав-
уравнения (9.1) получим следующее:
Однако такая линеаризация не всегда удачна. Полубарино-
вой-Кочиной A960, 1) предложен способ линеаризации уравне-
уравнения (9.1) по ft2. Умножим второй член левой части уравнения
(9.1) на (ft + H)/2h*9 где величина ft* выбирается с-таким рас-
расчетом, чтобы эта дробь была по возможности ближе к единице.
Если принять ft* да Я, то указанное условие выполняется с лю-
любой точностью, начиная с некоторого расстояния от скважины.
Вместо уравнения (9.1) получим теперь следующее линейное от-
относительно ft2 уравнение:
Уравнения (9.3) и (9.4) являются уравнениями Бесселя от-
относительно ft — Н и ft2—Н2 соответственно. Их решения пред-
представляют линейную комбинацию функций /о (cor) и Ко (cor)
((о2 = x/(kdH)), причем, если потребовать от решений выпол-
выполнения второго из условий (9.2), то остаются лишь функции
Ко (cor) (ибо lim/0(cor)= oo при г->оо). Итак, выражения
(9.5)
суть решения соответствующих уравнений (9.3) и (9.4), удов-
удовлетворяющие второму условию (9.2).
Формула для дебита скважины, на основании (9.6), будет
/ dh\ nk(H2-h\)
Q = 2nk [rh ^)г__гс- >o((or/ Кг (согс). (9.7)
Вследствие малости величины югс можно принять (см. фор-
формулы A0.9) и A0.10) главы IX)
Ы2) Ki(*rJm-±-, (9.8)
400 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
и (9.7) перепишется так:
Для расхода получается такое же выражение, какое он
имеет в случае непроницаемого водоупора при наличии цилинд-
цилиндрического контура питания с радиусом R* = 1,123/со и напором
Я. Отметим, что при линеаризации по h для дебита получается
формула вида A.4) главы IX, как для напорного пласта.
Обе схемы безнапорного движения — с непроницаемым во-
доупором при контуре питания радиуса /?* и со слабо проницае-
проницаемым основанием при том же R* — имеют одинаковые дебиты,
но кривые свободной поверхности будут различаться. В частно-
частности, при г = R* для слабо проницаемого водоупора уровень h
определится из равенства
1Й |^. (9.10)
Чем меньше проницаемость водоупора, а, следовательно, и со,
тем больше R* и тем меньше различие между h и Я, определяе-
определяемое формулой (9.10). Поэтому при малых со (порядка 10~4—
10~б лН), когда эта разница становится пренебрежимо малой,
величину /?* = 1,123/со можно условно принять за радиус влия-
влияния скважины.
Предположим далее, что в условиях установившегося прито-
притока к скважине в некоторых двух точках измерены (при помощи
наблюдательных скважин) уровни свободной поверхности, т. е.
имеем h = Н\ при г = Г\ и h = Я2 при г = гг. Подставив эти
условия в уравнение свободной поверхности (9.6), получим
Ко (юг,) (Я2 - hi) = Ко (сог2) (Я2 - /г2). (9.11)
Из этого соотношения можно определить со, а, следовательно,
проводимость прослойки, подстилающей водоносный горизонт.
При достаточно малых co/*i и сог2 можно воспользоваться
приближенным равенством A0.9) главы IX и преобразовать
(9.11) следующим образом:
со я2-!, я2-/*; t
In = —z г In /*i г> г In Го,
1,123 h\-h\ h2~h\
откуда
1 ===—2 а2~~' 2 ==:—*> 2~~' J0 == » ^20 === •
§ 9] ПЛАСТ СО СЛАБО ПРОНИЦАЕМЫМ ОСНОВАНИЕМ 401
Заметим, что судить о степени малости величин (ог\ и (ог2 до
вычисления со можно, лишь имея предварительное представле-
представление о порядке со; после же подсчета со по формуле (9.12) станет
ясным, насколько обосновано допущение о его малости. Если же
заранее нет уверенности в том, что соп и сог2 достаточно малы,
то для вычисления со следует пользоваться более точной зави-
зависимостью (9.11).
Описанный способ определения коэффициента фильтрации
слабо проницаемой прослойки был предложен А. Н. Мятиевым
A948).
Хотя уравнение (9.1), как это отмечалось выше, не интегрируется в за-
замкнутой форме, его решение, удовлетворяющее условиям (9.2), можно оце-
оценить, например, при помощи соответствующего (удовлетворяющего тем же
граничным условиям) решения (9.6) уравнения (9.4). Сделаем в (9.1) и (9.4)
замену: г = ер, h = zH. Тогда эти уравнения примут соответственно вид (Ме-
ламед 1963)
где со2 = %\{k dH). Штрихами обозначены производные по р. Граничные
условия (9.2) преобразуются в следующие:
z = zo = -i^- ПРИ р = Ро = 1пгс, 2=1 при р->со. (9.15)
Вычитая (9.13) из (9.14), получаем
и" = юУр [и - A - гJ], u^z2 - 4)- (9.16)
Потребуем пока, чтобы решения z и гB) уравнений (9.13) и (9.14) удо-
удовлетворяли первому из условий (9.15), а вместо второго поставим следую-
следующее: г (р0) = г\ (р0) = Zq, т. е. для обоих уравнений ставится задача Коши
при одинаковых начальных условиях. Тогда начальные данные задачи Коши
для уравнения (9.16) таковы:
и (ро) = и' (ро) = 0. (9.17)
В силу (9.16) м"(ро) < 0 и согласно (9.17) в окрестности ром'(р) < 0 и
убывает, а значит, м(р)<0 и также убывает. Так будет продолжаться и
дальше, ибо превращению и из отрицательной величины в положительную
должно предшествовать изменение знака с минуса на плюс у первой, а стало
быть, и у второй производной; между тем последняя согласно (9.18) не мо-
может стать положительной раньше и. Итак, и = г1 — z^ < 0 для р0 < р < оо,
т.е. интегральная кривая уравнения (9.14), выходящая из той же точки на
стенке скважины и под тем же углом, что и кривая уравнения (9.13), оказы-
оказывается выше последней, все больше отклоняясь от нее с ростом р (и' < 0).
Если же решения уравнений (9.13) и (9.14) подчинить теперь условиям
(9.15), то интегральная кривая уравнения (9.14), линеаризованного по /г2,
расположится ниже соответствующей кривой нелинейного уравнения (9.13).
Выше было выяснено, что соответствующая кривая уравнения (9.3), линеари-
линеаризованного по /г, окажется еще ниже.
Такое расположение кривых было обнаружено и в результате непосред-
непосредственного сравнения решений уравнений (9.1), (9.3) и (9.4) при условиях
402
ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
(9.2), сделанного С. Т. Рыбаковой A962). Интегрирование уравнения (9.1)
осуществлялось на ЭВМ как решение задачи Коши, причем значение h0 за-
задавалось, а значение h'c определялось в некотором интервале так, чтобы
решение соответствующей задачи Коши удовлетворяло второму условию (9.2).
Как указывалось в начале параграфа, это значение tiz единственно. Если
начальное значение производной выбрано большим h!z (h! (p0) > /^),
то lim/i(p)=oo при р->-оо, и при численном интегрировании с некоторых
пор оказывается ft(p)>l; если же h' (р0) < h'c> то lim/i(p)=— <х> при
р-^оо, и при интегрировании h(p) начинает с некоторых пор убывать. Эти
признаки и были использованы: при проявлении одного из них интегрирова-
интегрирование с выбранным Л'(ро) прекращалось и одновременно, в зависимости от того,
какой признак проявлялся, делалось заключение о том, является ли вы-
выбранное А'(Ро) ббльшим или меньшим истинного значения tic (соответствую-
(соответствующего условиям (9.2)). В результате исходный интервал, в котором должно
находиться А^, сужался до заданных
размеров, которые и определяют точ-
точность вычисления h'c. Интегрирова-
Интегрирование велось по схеме Рунге — Кутта,
причем величина шага определенным
образом увеличивалась с ростом г.
Оказалось, что для указан-
указанной задачи линеаризация по
h2 дает хорошее приближение
к численному решению нели-
нелинейного уравнения (9.4), в то
время как при линеаризации
по h свободная поверхность и
дебит сильно занижены, а для
малых понижений формула
для дебита оказывается совер-
совершенно неверной.
На рис. 261 представлены
кривые депрессии при различ-
различных уровнях воды в скважине для нелинейного уравнения (9.1)
(или, что то же, при линеаризации по h2) — сплошные линии и
при линеаризации по h — пунктирная линия.
§ 10. О некоторых движениях с начальными градиентами.
В последнее время поднялся интерес к движениям с начальными
градиентами (о них говорилось в главе I), причем даны реше-
решения ряда задач и в гидравлической постановке. В качестве при-
примера рассмотрим задачу В. И. Пеньковского и С. Т. Рыбаковой
A968) о фильтрации с учетом начальных градиентов пласта и
слабо проницаемого основания.
Пусть, как и в предыдущем параграфе, движение грунтовых
вод происходит в водоносном пласте, подстилаемом слабо про-
проницаемым горизонтальным прослоем, ниже которого находится
Рис. 261.
§ 10] НЕКОТОРЫЕ ДВИЖЕНИЯ С НАЧАЛЬНЫМИ ГРАДИЕНТАМИ 403
мощный хорошо проницаемый горизонт с постоянным напором.
Начальные градиенты рассматриваемого пласта и слабо прони-
проницаемого прослоя обозначим соответственно через /о и J\. Фильт-
Фильтрация в верхнем пласте пусть происходит в горизонтальном на-
направлении вдоль пласта со скоростью фильтрации
а в слабо проницаемом прослое — по вертикали со скоростью
Здесь k и к — коэффициенты фильтрации рассматриваемого пла-
пласта и слабо проницаемого прослоя соответственно, d—мощность
последнего, Я—напор в нижележащем горизонте, отсчитывае-
отсчитываемый от основания рассматриваемого пласта.
В случае одномерного безнапорного движения дифференци-
дифференциальное уравнение A.12) примет вид
* (^- А)+ «-0. (Ю.З)
Здесь е — скорость равномерной инфильтрации вдоль свободной
поверхности.
Остановимся на задаче о расчете горизонтального дренажа.
Предположим, что горизонтальные дренажные канавы, проре-
прорезающие водоносный пласт до его основания, расположены на
расстоянии 2/ одна от другой, симметрично относительно оси
у. Таким образом, решение уравнения A0.3) ищется при усло-
условиях
h = hQ и -^ = -/0 при х = 0 (й(-*) = А(*)). A0.4)
Второе из этих условий есть результат того, что скорость в точке
х = 0 должна быть равной нулю.
Предполагается, что переток через слабо проницаемый про-
прослой происходит по всей длине междренного пространства, т.е.
для всех 0 < х <с: / выполняется неравенство (Я — h)/d>J{ и,
кроме того, при 0 < х ^ / справедливо другое неравенство:
—dh/dx > /о, т. е. предполагается, что в исследуемой области нет
застойных зон. В противном случае область фильтрации нужно
разбить на отдельные части и определение ординат свободной
поверхности h{x) сведется к решению системы уравнений, каж-
каждое из которых справедливо в определенных пределах измене-
изменения х.
404 ГИДРАВЛИЧЕСКАЯ ТЕОРИЯ УСТАНОВИВШИХСЯ ДВИЖЕНИЙ [ГЛ. X
Введем безразмерные величины
где принято
Теперь можно переписать задачу A0.3) — A0.4) так:
^-O-O, A0.7)
т]=т]о, ||-=-'о при | = 0. A0.8)
Решение этой задачи найдено численными методами с ис-
использованием ЭВМ и приближенными с помощью линеариза-
линеаризации уравнения A0.7).
По первому способу линеаризации в уравнении A0.7) мно-
множитель ц при производной dr\/dl заменяется некоторой средней
величиной т)* (можно принять ее равной г\о). Тогда будем иметь
Решение этого уравнения при условиях A0.8) имеет вид
j , A-т)о)Р2-/о Рх1 __ A — ло)Р1 — ^о Pl6 (
1 ' Pl—P2 P\—P2 V
где
При втором способе линеаризации уравнение A0.7) заме-
заменяется следующим:
f^W-l)==O, A0.12)
где rii =A + Ло)/2. Его решение при условиях A0.8) имеет вид
1 * Si — S2
Здесь
Сравнение решений A0.10) и A0.13) с точным решением по-
показывает, что линеаризация по ц2 дает несколько лучший ре-
результат.
§ Ю] НЕКОТОРЫЕ ДВИЖЕНИЯ С НАЧАЛЬНЫМИ ГРАДИЕНТАМИ 405
Как видно из уравнений A0.7), A0.8) и дальнейших, вели-
величина J\ начального градиента слабо проницаемой прослойки не
входит в них явным образом. Полученные решения годятся и
при /0 = 0. Наличие начального градиента J\ улучшает работу
дренажа, так как в этом случае уменьшается подпитывание
дренируемого пласта через слабо проницаемый водоупор на-
напорными водами нижележащего горизонта. Пренебрежение ве-
величиной /о ведет к сильному завышению уровней в дренах при
заданных ординате свободной поверхности в середине междренья
и расстоянии между дренами, и это завышение тем больше, чем
больше величина начального градиента /0.
Рассмотрим числовой пример: г|о = 0,8 и /0 = 0,22. Если без-
безразмерное расстояние & = /со равно 0,7, то уровень в дрене
ць = hi/Hi получается равным 0,732, в то время как при /0 = 0
этот уровень равен 0,544. Задаваясь относительными глубинами
ц0 и r\i, можно определить расстояние между дренами с учетом
действия /о и без него. Пусть по-прежнему г\о = 0,8 и 10 = 0,22,
но т]/ = 0,5. Для этого случая & получается равным 0,765 и
1,285 соответственно для to = 0,22 и /о = 0. Таким образом,
если не принять во внимание наличия /0, то расстояние между
дренами получается завышенным почти в 1,7 раза. Поэтому при
расчете работы дренажа важно, кроме таких параметров, как
коэффициенты фильтрации, знать также значения начальных
градиентов.
В. И. Пеньковским и С. Т. Рыбаковой рассмотрены также
задачи о неустановившихся движениях при наличии начальных
градиентов (Пеньковский и Рыбакова 1969; Рыбакова 1969).
Часть вторая
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
Глава XI
ОБ ИНЕРЦИОННЫХ ЧЛЕНАХ
ПРИ НЕУСТАНОВИВШИХСЯ ДВИЖЕНИЯХ.
НАПОРНЫЕ ДВИЖЕНИЯ
§1.0 напорных движениях при действующих напорах, зави-
зависящих от времени. В § 12 главы I была дана оценка линейной
части инерционных членов и было выяснено, что при тех значе-
значениях коэффициентов фильтрации, которые имеют место в ре-
реальных условиях, членами
1 ди 1 dv n n
следует, как правило, пренебрегать.
В связи с этим простое решение получает задача о неуста-
неустановившемся движении в напорном пласте, возникающем за счет
того, что в водоемах уровень воды изменяется со временем.
А именно, допустим, что имеется п водоемов, в которых уровень
воды соответственно равен #i(/)> #2@» •••> Hn(t)f где #i@>
H2(t)y ..., Hn(t) — заданные функции времени. Между водое-
водоемами находятся основания гидротехнических сооружений
(рис. 262). Тогда, если имеем решение такой же задачи с по-
постоянными значениями Яь Я2, ..., Нп, то это же решение го-
годится и для переменных //™(/), B которых время / следует рас-
рассматривать как параметр (Девисон 1938).
Возьмем простейший случай обтекания плоского флютбета
ширины 2/ в проницаемом слое бесконечной глубины, причем
будем считать, что в верхнем бьефе имеем постоянный уровень
Hi = h\, а в нижнем бьефе отметка уровня меняется по закону
#2 (/) = h2 + a sin (It), причем h2 > a, h\> h2 + a.
Тогда достаточно в полученные в главе II формулы A3.5)
и A3.11) для комплексного потенциала и скорости подставить
in
НАПОРЫ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ .
407
заданные значения Hx{t) и H2(t). Получим, в частности,
w >
-и — iv >
k [hx - h2 - a sin (%t)\
n V/2 - z2
A.2)
Обратимся теперь к другому решению этой же задачи, когда
учитываются члены вида A.1) в уравнениях движения, и пока-
покажем иллюзорность этого учета.
Рис. 262.
Если напишем уравнения плоского движения с учетом членов
A.1), но. с отброшенными квадратичными членами в выражении
ускорения, то будем иметь уравнения движения
J^du^ 1 dp gu
т dt р дх k '
1 dv
1 dp
m dt p dy k *
и уравнение неразрывности
Их
ду
Если ввести величины
k ди j,
^-dt' V
k dv
то уравнения A.3) и A.4) напишутся так:
Введем обозначение
A.3)
A.4)
A.5)
A.6)
A.7)
A.8)
408 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ [ГЛ. XI
Тогда будем иметь
Ш' ду ' ^ # '
причем функция ф удовлетворяет уравнению Лапласа.
Если известны U (х, у, t) и V {х, у, t), то составляющие ско-
скорости фильтрации и, v определятся как решения линейных
уравнений A.5) в следующем виде (a = mg/k):
t
и = иое~а V-^ + ae-at \ eatU {t) dt,
A.10)
-о* J eatV (t) dt.
и
Выражение комплексной скорости можно написать так:
t
w = u — iv = woe~a <*-'•> + <>>e-at [ eatW (x, y, t) dt, A.11)
где W = U — iV9 wo(x, y) — значение w при t = t0.
При этом для величины W будет иметь место выражение,
которое получается из теории установившихся движений, т. е.
для нашего примера
ЫЪЫ A.12)
W = U-iV= я
п V/2 - z2
Для скорости и —iv находим после интегрирования
w == woe~a ('-'•> -1 , k ¦. i Uhx - h2) A — ^"a «-'•>) -
Я V/2 — Z2 L
„ sin (Xt) - (к/а) cos (Xt) , ^,fl^..^sl
Оценим члены, входящие в это выражение. Чтобы получить
большее влияние членов, содержащих параметр а, нужно взять
такие значения k и т, при которых этот параметр по возмож-
возможности мал. Поэтому примем ?=100 м/сутки = 1/864 м/сек>
m = 0,1, g = 9,8 м/свк2. Тогда будем иметь a = mg/k ^
^ 850 1/се/с и множитель е~850^~^о) будет порядка 0,001 уже при
t — to = 0,01 ге/с.
Следовательно, из решения A.13) можно выбросить все
члены, содержащие укаванный малый множитель. При этом по-
получим выражение
w
Ь \h и п sin (Xt) -(Я/a) cos (Яр 1 n
§ 2] ВЛИЯНИЕ ВОЛНЕНИЯ НА ФИЛЬТРАЦИЮ 409
которое Девисон считал соответствующим значению /о = — °°>
т. е. соответствующим процессу, устанавливающемуся через до-
достаточно большой промежуток времени.
Но и в остающемся теперь выражении члены, содержащие
а, чрезвычайно малы. В самом деле, % есть частота колебания
воды в нижнем бьефе; она обратна периоду колебаний Г. Если
принять период колебаний порядка долей минуты, например,
считать Т = 2яД = 10 сек, то будем иметь К/а « 0,001.
Следовательно, член (Va)cos(M) может быть ощутимым
лишь при очень малых периодах колебаний, имеющих порядок
долей секунды для сильно проницаемого грунта и еще меньших
для слабо проницаемых грунтов. При обычных же условиях чле-
членами с К/а также можно пренебречь, и остается формула, полу-
получаемая без учета инерционных членов.
§ 2. О влиянии волнения на фильтрацию под гидротехничес-
гидротехническими сооружениями. В задачах об установившихся движениях
грунтовых вод под гидротехническими сооружениями предпо-
предполагалось, что вода в бассейнах, граничащих с областью фильт-
фильтрации, неподвижна, т. е. что поверхность воды в водоеме пред-
представляет горизонтальную плоскость. Однако в действительности
часто наблюдается волнение свободной поверхности бассейнов,
что изменяет картину фильтрации под плотиной, причем влия-
влияние волнения особенно сказывается в нижнем бьефе (Аравин
1940,3).
Рассмотрим плоский флютбет ширины 2/ в грунте бесконеч-
бесконечной глубины. Предположим, что напоры по дну верхнего и ниж-
нижнего бьефов Нх и #2 заданы в виде функций х и t: H\ (х, t) и
Н2{х,г). Примем \р = 0 вдоль основания плотины. Тогда полу-
получим задачу об определении в нижней полуплоскости комплекс-
комплексного потенциала со (г, t)t для которого известна мнимая часть на
отрезке (—/, /) и действительная часть на отрезках (— сю, —/)
и (/, оо). Применим формулу A.6) главы VI к функции
#Ь^ B.0
При этом примем л/z2 — I2 = + У*2 — I2 для / < х < оо; тогда
для — оо < х < — / будет / /
Полагая ю = ф + гф, получим
<а(г, t) = 1 С Ф(С
Уг2-/2 ni J (?-z)V?2-/2
—-оо
Знак минус появился перед интегралом в силу того, что разы-
разыскивается значение функции в нижней полуплоскости. Постоян-
410
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
[ГЛ. XI
ное слагаемое в формуле B.2) равно нулю, так как вблизи
z = оо
со (z) = О (In z), lim
Окончательно напишем
Vz2 - /2
1!
— *
0.
@B,/) =
J (E-*)Vt2-/2
яг (с,
B.3)
В качестве примера возьмем случай
Н{ (х, t) = Нг = const,
Я2 (л:, /) = Я2 + (Л sin — + В cos ¦
sin (a/),
B.4)
что соответствует стоячим волнам в нижнем бьефе. Суммируя
влияние стоячих волн, можно получить произвольные колебания.
После подстановки B.4) в B.3) и частичного интегрирова-
интегрирования будем иметь со (z, t) = ио (z) -f- o)i (z, t), где
B.5)
Здесь а>о(г) — комплексный потенциал установившегося течения
(при Л = Б = 0), coiB,/) определяет дополнительное течение,
возникающее из-за наличия волнения в бьефе.
Нас будет интересовать распределение напора h\ (x, /) вдоль
основания плотины, т. е. для —/ ^ х <g /. Будем иметь
(*,/)¦
n
(С-.
Введем безразмерные величины
B.6)
§2] ВЛИЯНИЕ ВОЛНЕНИЯ НА ФИЛЬТРАЦИЮ 411
и напишем (Басович 1974, 1)
Й! (X, т) = - Vl~*2 [AI(a9X) + BJ (a, Z)] sinт, B.7)
где
sin
Па у\ _
Преобразуем интегралы B.8), выделив в них особенность
при 1 = Х:
(а, X) -
f(x) =
sin (aX),
UxcsmX
V
B.9)
Далее, так как
sin (a|) = sin И(|-
= cos (aX) sin (a A - X)) + sin (aA) cos (a (? — X)),
то /(a, X) можно представить в виде
/ (a, X) = cos {aX) К (а, X) + sin (aX) L(a, X) + f(X) sin (aX),
причем
- x) V?2 -
Продифференцируем /С (a, Jf) по параметру a, что допустимо,
так как К (а, X) — равномерно сходящийся интеграл. Тогда
'« (а, X)
= i [/, (a) sin (aX) - ^Vo (a) cos {aX)},
412 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ [ГЛ. XI
где /0(а) и No(a) -— цилиндрические функции (Градштейн и
Рыжик 1962):
оо оо
, , 2 f sin (g?) dl кг (П\— 2 [
/o \P>) = — \ /fc2 , » NQ(a) = \
я j V!2- 1 я J ?
Если теперь проинтегрировать K!a (я> Ю по а> то найдем
а
К (а, X) = | J [/о (а,) sin (а^) - Wo (а,) cos (а,*)] rffll.
о
Аналогично получим
а
L (а, X) = - j \ [No (а,) sin (а,*) + /0 (а,) cos (а, А)] йа„
о
и для /(а, X) можно написать
/(a, X) = /,(a,
а
/, (а, X) = f \ [- Wo (a,) cos ((а, - а) X) + /0 (a,) sin ((а, - а) X)] da,.
о
Таким же образом найдем
/(a, *) = /,(a, X) + f(X)cos(aX), B.10)
где
/, (а, X) = - у J [Wo (a,) sin ((а, -а)Х) + /0 (a,) cos ((а, - а) X)] da,.
о
Теперь, если напор в нижнем бьефе задан в виде стоячей
волны B.4), то
А, (*, /) = (A sin 22- + В cos ?f) sin (at),
и в силу B.7) —B.10) можем написать
А, (X, т) = - [А Г (а, Х) + ВГ (а, X)] sinт, B.11)
где
Г (а, Х) = -1[УГ=^Р/,(а
Г {а, Х) = ^[л/Т^П('Ч1(а, X) + (arcsinZ + f) cos(aX)].
§3]
ОДНОМЕРНЫЕ ДВИЖЕНИЯ ПО ВЕРТИКАЛИ
413
Здесь а = nil с, I — полуширина флютбета, с — полудлина
волны.
0,5
-0,5
V
V
ft
V
i
a~5n
V
-1,0 -0,5 О
Рис. 263.
На рис. 263 и 264 построены графики /* и /* в зависимости
от X для нескольких значений а (Басович 1974, I).
§ 3. Одномерные движения по вертикали при постоянном
Действующем напоре. Будем рассматривать просачивание воды
в грунт по вертикали, считая коэффициент фильтрации k и по-
пористость т постоянными величинами.
414
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
[ГЛ. XI
Возьмем уравнения движения A2.3) главы I, выписанные
для средних истинных скоростей движения жидкости в порах с
сохранением инерционных членов. Направляя ось у вертикально
вниз, получим
дпу дпу 1 dp mg
Остальные уравнения отсутствуют, так как движение считается
одномерным, происходящим параллельно оси у. При этом урав-
уравнение неразрывности принимает вид
дии
ду v
Это показывает, что иу зависит только от времени. Поэтому
C.1) можно переписать, вводя вместо иу скорость фильтрации
v согласно соотношению иу = v/m, следующим
-^г-^^-утг образом.»
О
1 и
in 1
т .' ~ р ar/T^ k v*
Но мы показали в § 1 (а также в главе II), что
членом (l/m)dv/dt можно пренебречь во всех
практически интересных случаях. Поэтому, вво-
вводя напор
Фронт
промачибания
У
мы возвращаемся к закону Дарси
C.3)
C.4)
Рис. 265. применимому, следовательно, и в случае неуста-
неустановившихся движений.
Предположим теперь, что вода просачивается в грунт под
постоянным напором Н (рис. 265), причем в момент времени t
она просочилась на глубину уо от дна водоема. В начальный мо-
момент времени t = 0 пусть у0 = 0.
Так как v = v(t) зависит только от времени и не зависит
от у, то согласно C.4) h есть линейная функция от у:
h(y, t) = a(t)y + b(t). (З.б)
При у = 0 напор равен Н: h @, t) = b (t) = H. При у = у0, счи-
считая атмосферное давление равным нулю, имеем согласно C.3)
h {у0, t) = - К - Уо = ау0 + Я, C.6)
где через Лк обозначена высота капиллярного поднятия в грунте.
§3]
ОДНОМЕРНЫЕ ДВИЖЕНИЯ ПО ВЕРТИКАЛИ
415
Поэтому для а можем написать согласно C.5) и C.6) такое
выражение:
a = |L=_iL±A±lL. C.7)
Скорость фильтрации v связана с производной dyjdt соотно-
соотношением (т — пористость
или недостаток насыще- . г 4Я
ния грунта)
v=m^f. C.8)
Сопоставление C.7) и C.8)
с C.4) приводит к уравне-
уравнению для у0:
15
5
dy0
dt
Я + /гк + у о
10
/Л
C.9)
Отметим, что согласно
полученному уравнению
капиллярная высота при-
прибавляется к действующе-
действующему напору так, как буд-
будто вместо напора Н
мы имеем напор Н + hv.
Из уравнения C.9), полагая уо = 0 при t
интегрирования
Уо ,
— ¦ -
\
v/k
Рис. 266.
О, найдем после
Вводя безразмерны* величины
kt
т
Лк)
C.10)
C.11)
C.12)
График зависимости ц от т изображен на рис. 266. Здесь же
представлена зависимость безразмерной скорости v/k от т.
Для малых значений г\ можно произвести обращение уравне-
уравнения C.12), если разложить 1пA +т|) в степенной ряд. Получим
перепишем C.10) следующим образом:
откуда найдем, извлекая квадратный корень,
= г,-|т12 + ^г1з+... C.14)
4t6 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ [ГЛ. XI
Положим
И C.15)
и будем искать tj в виде ряда по степеням \х:
ti = jx + V + Bjx3+ ..., C.16)
где Л, В, ... — неизвестные пока коэффициенты. Подставив вы-
выражение C.16) в C.14) и сравнивая коэффициенты при одина-
одинаковых степенях ц, найдем
^+|-1Г + ^т^+ ... C.17)
§ 4. Вертикальная фильтрация при заданной подаче воды.
Рассмотрим сначала такую задачу. Допустим, что некоторое ко-
количество воды мгновенно выливается на горизонтальную поверх-
поверхность грунта и в дальнейшем вода больше не подливается. Обо-
Обозначим через Q количество воды, поданной на единицу площади
поверхности грунта. Тогда к некоторому моменту времени / ве-
величина Q будет складываться из воды, находящейся в слое глу-
глубины H(t) над поверхностью грунта, и воды в смоченном слое
грунта глубины у0: Q = H{t)-\- туо.
Если теперь в уравнение C.9) подставим вместо Н его зна-
значение Н = Q — myOi то получим уравнение
¦
\-m
m^ k k{xm) DI)
Решение этого уравнения имеет вид C.12), если положить
_ 1 — т _ k(\-mJ ,
и считать, как и в предыдущем параграфе, что у0 = 0 при t = 0.
В действительности невозможно осуществить внезапный на-
налив воды на поверхность грунта на заданную конечную высоту
Н. А если бы это и было возможно, то имел бы место разрыв
давления в начальный момент времени, когда уо = 0. В самом
деле, при этом столб воды высоты Н оказывает на горизонталь-
горизонтальную площадку в плоскости у = 0 давление, равное весу этого
столба. С другой стороны, на границе грунта, т. е. при у = 0,
давление равно нулю (или соответствует капиллярному вакууму
при учете капиллярности). Этим разрывом давления и объяс-
объясняется то, что в рассмотренных выше задачах в начальный мо-
момент времени получается бесконечная скорость.
В связи с тем, что в действительности вода всегда подли-
подливается постепенно (это же имеет место и при наполнении ка-
канала), рассмотрим следующую более общую задачу. Предполо-
§ 4] ФИЛЬТРАЦИЯ ПРИ ЗАДАННОЙ ПОДАЧЕ ВОДЫ 417
жим, что на поверхность грунта подается постоянный расход q
(на единицу площади), так что к моменту времени t общее ко-
количество поданной воды Q = qt. Это количество воды идет на
образование столба воды высоты H(t) над поверхностью грунта
и на смачивание грунта на глубину у0, т. е. qt = Н (t) -j- my$.
Подставляя выражение H(t) отсюда в уравнение C.9), получим
mgsak 9 {42)
Рассмотрим прежде всего частный случай Ак = 0, т. е. пре-
пренебрежем влиянием капиллярности. Уравнение
^ D.3)
имеет частное решение вида
yo = ct. D.4)
Для определения значения постоянной с подставим D.4) в
D.3), тогда получим квадратное уравнение для с: тс2 — k[q +
+ A—т)с\. Из двух корней этого уравнения возьмем положи-
положительный, так как интересующее нас течение направлено вниз:
г A — ту , kq
2m г 'V 4m5 ¦ ~m" '
Так как полученное решение удовлетворяет начальному условию
г/0@) = 0, то оно является как раз тем решением, которое нам
нужно.
Отсюда видно, что если подавать на поверхность постоянный
расход q, то вода будет просачиваться в грунт с постоянной
скоростью. При этом уровень воды над поверхностью грунта
H(t) будет линейной функцией времени
H(t)=(q-mc)t. D.5)
Очевидно, что для возможности движения должно выпол-
выполняться неравенство q ^ тс. В случае знака равенства будем
иметь просачивание при отсутствии слоя воды над поверхностью
грунта, это просачивание будет происходить со скоростью с =
Если обратиться к общему случаю уравнения D.2), когда
учитывается капиллярность грунта, то решение его имеет более
сложный вид. А именно, подстановка t + hK/q = т приводит
Уравнение D.2) к однородному:
т dyp _ /с 9Т + П — т) Уо
т /с
14 П. Я, Полубаринова-Кочина
418 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ {ГЛ. XI
Общий интеграл его можно написать в виде
С% = (А - иГ'''-а (В + и)~>1г+а, и = ^, D.6)
где
k(\-m) lk*
ы h V—
k A - т)
D.7)
Уравнения D.6) представляют т и г/о в параметрической фор-
форме, в функциях параметра и. Исключая и, можно написать об-
общий интеграл D.6) в виде
(Ах - уо)%+а (Вт + «/о)* = С,. D.8)
Условие f/o = 0 при t = 0 дает начальное значение т = То =
= hK/q. Поэтому находим для произвольной постоянной С\ сле-
следующее выражение:
Ci-4IA+efiVi-e-k. D.9)
§ 5. Вертикальная фильтрация в двуслойном грунте. Рассмот-
Рассмотрим задачу о вертикальной фильтрации воды в двуслойном
грунте, когда в поверхностном слое толщины d коэффициент
фильтрации и пористость имеют соответственно значения k\ и
ть в нижнем бесконечном слое — значения k2 и т2. Над грун-
грунтом находится слой воды глубины Я. Глубину воды, просочив-
просочившейся в грунт к моменту времени t, обозначим по-прежнему че-
через уо. Из условия неразрывности потока следует, что скорости
фильтрации V\ и с/2 обоих слоев равны и зависят только от
времени:
0j ш=г V2 = V (t). F.1)
Положим, что v\ = dcpi/dy и v2 = ду2/ду, причем потенциалы
в каждом из слоев определяются формулами
) E-2)
Так как cpi и фг должны удовлетворять уравнению Лапласа по
у> то имеем для qpi и фг, как и для h в случае однородного
грунта, линейные функции от у: cpi = v{t)y + bi(t),y2 = v(t)y-\i
b{t)
§ б] ВЕРТИКАЛЬНАЯ ФИЛЬТРАЦИЯ В ДВУСЛОЙНОМ ГРУНТЕ 419
На границе двух грунтов при у = d имеем из условия ра-
равенства давлений соотношение qpi/&i = Ф2/&2, которое приводится
к виду (vd + b{)jk\ = {vd + b2)/k2. Далее, при у = 0 имеем
Ф1 = *1= —k\Hi\ при у = уо — ф2 = vyo + b2 = k2(hK + yQ).
Исключая из последних уравнений Ь\ и Ъ^ получим для проса-
просачивания в нижнем слое грунта
Интегрирование последнего уравнения дает
Здесь введены обозначения
и за начальный момент времени t = 0 принят момент начала
просачивания в нижний слой. Очевидно, что просачивание в
верхнем слое грунта при сделанных предположениях рассчи-
рассчитывается по формулам предыдущих параграфов.
Выделим случай, когда верхний слой грунта тонок. Это имеет
место, в частности, в случае кольматажа. Так, часто создают
искусственные условия для уплотнения грунта на дне канала,
вводя в канал мутную воду, содержащую мелкие глинистые ча-
частицы. Закольматированный слой может иметь толщину поряд-
порядка 10—20 еж.
Предположим, что d мало по сравнению с величиной Н + /iK,
и введем обозначения
Тогда, отбрасывая d под знаком логарифма (но сохраняя его
в выражении для Л), получим уравнение
т = л-A-ЛIпA+т)). E.5)
Давая здесь А различные значения, можно построить графики
зависимости г\ от т. На рис. 267 приведены такие кривые для
d/(H-\- hK) = 0,1 и различных значений а = ?2/61. Видно, что
кольматаж может в значительной степени уменьшить скорость
просачивания воды в грунт.
Следует отметить, что если бы вода, пройдя через слой ма-
малопроницаемого грунта, попадала в достаточно сухой грунт, то
просачивание в этом последнем происходило бы отдельными
14*
420
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
[ГЛ. XI
струйками, не образующими сплошного потока, и изложенная
теория была бы неприменимой. Она применима лишь в случае
достаточно влажного грунта, и в этом случае под т нужно по-
понимать «эффективную» пористость или дефицит влажности.
Ю
15
10
15
\
а-1000
Рис. 267.
Отметим также, что в изложенной в § 3—5 теории не учиты-
учитывается переменность насыщенности грунта водой.
§ 6. Уравнения неустановившихся движений в случае слабо
сжимаемой жидкости. Уравнение неразрывности сжимаемой жид-
жидкости в пористой среде выводится совершенно так же, как в
гидродинамике сжимаемой жидкости (Кочин, Кибель и Розе
1963, I), с той только разницей, что вместо плотности р нужно
взять произведение рт (т — пористость). Получим
где
t> = —fegradft, h = -?-
F.2)
Вода и пласт являются слабо сжимаемыми телами, поэтому
обычно принимают ри/n зависящими от давления линейно:
Р = Ро [1 + Рж (Р — Ро)]> т = то + Рпл (Р - Ро), F.3)
где ро и пц — плотность и пористость при давлении /?0. Величины
рж и рПл называются соответственно коэффициентами сжимае-
сжимаемости или объемной упругости воды и пласта (Щелкачев 1946).
§ б] УРАВНЕНИЯ ДВИЖЕНИЯ СЛАБО СЖИМАЕМОЙ ЖИДКОСТИ 421
Они заключаются в таких пределах для воды и грунта:
рж = B,7 + 5) 10 ат~\ (Зпл = @,3 -*- 2) 1(Г5 апГ1.
Перемножая р и т и отбрасывая члены второго порядка ма-
малости, получаем
9т == рсш0 + РоР (р ~ Ро)< Р = АПоРж + рпл, F.4)
и тогда изменение массы по времени будет
-Р2Р^. F.5)
Здесь можно р0 заменить на р ввиду малости рж.
Развернем выражение div(pt>):
dvx dvu dvz\ до до до
Из F.3) получаем
1 = Мо1-Ржр1 = р2м1-. F.7)
Таким же образом найдем
Подстановка в F.1) дает, по сокращении на р,
?(*?)+¦&(*¦?)+?(*?)+
Обычно членом, содержащим прямые скобки, пренебрегают
и полагают k = const. Тогда остается линейное уравнение
dh ь( дЧ , d*h , d2h
или
-§ = а,ДЙ, F.10)
где
Величина а# носит название коэффициента пьезопроводности.
Это уравнение выведено В. Н. Щелкачевым A946). Рассмот-
Рассмотренный вид движения называется упругим режимом. Его рас-
рассматривают, в частности, для слабо проницаемой прослойки
422
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
[ГЛ. XI
между водоносными пластами, где происходят перетоки по вер-
вертикали (Jacob 1950) и где оно принимает вид
dh
d2h
F.11)
Рассмотрим движение жидкости в напорном пласте. Обычно
мощность пласта Т мала по сравнению с горизонтальными раз-
размерами. Поэтому проинтегрируем F.10) по z в пределах @, Г).
Полагая
получаем для h° уравнение
- FЛ2)
Если рассматриваемый водопроницаемый пласт мощности Т
ограничен слабо проницаемыми пластами мощностей Т\ и Т2
с коэффициентами фильтрации соответственно k\ и k2 и напо-
напорами Н\ и #2 (рис 268), то в си-
силу условия неразрывности будем
иметь
дг JT ' V дг
Отбрасывая нолик у Л°, пере-
перечу* пишем F.12) в виде
Рис. 268.
При этом H{(z,t) и H2(z,t) должны удовлетворять уравне-
уравнениям вида F.11). Если не учитывать сжимаемости при пере-
перетоках, то можно написать (Н\ — h)/T\ вместо (dH\/dz)T и
{h — Н2)/Т2 вместо (дН^дг)^
При сделанных допущениях уравнение F.13) примет вид
F.14)
FЛ5)
или
§ 7] СКВАЖИНА В ПЛАСТЕ С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ 423
Здесь
5 FЛ6)
Можно записать уравнение F.15) иначе, введя обозначения
.( к,
Получим, отбрасывая индекс у а„,:
Уравнение F.18) имеет частное решение h = H — это предель-
предельное состояние напорного пласта при ?->оо.
Если жидкость и пласт считаются несжимаемыми, т. е. р = О,
то в уравнении F.14) член с dh/dt отсутствует и получается та-
такое же уравнение, как при установившемся движении. Зависи-
Зависимость от времени может войти при этом в решение лишь через
граничные условия.
§ 7. Скважина в пласте с непроницаемым водоупором. Рас-
Рассмотрим осесимметричное движение в пласте мощности Т. Для
него уравнение F.18) запишется так (при & = 0):
dh а д ( dh
Величина а — коэффициент пьезопроводности — имеет вид
k
у (
¦Р* G.2)
(Рж — коэффициент сжимаемости жидкости, рпл — то же для
пласта).
Будем искать автомодельное решение, зависящее от комби-
комбинации независимых переменных | = г2/Dа/). При этом уравне-
уравнение G.1) приведется к обыкновенному дифференциальному
уравнению
искомое решение которого имеет вид
424 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ [ГЛ. XI
Произвольные постоянные С! и С2 выбираются из условий, что
при t = 0 (т. е. | = 0) напор h (/% 0) имеет постоянное значение
#о, а дебит скважины бесконечно малого радиуса, ось которой
расположена вдоль оси ординат, есть постоянная величина Q.
Тогда h(r,t) запишется в виде
л-Я + Е
где Ei — интегральная экспоненциальная функция
-i^-. G.4)
Формулу G.3) принято называть формулой Тейса (Theis
1935). Почти одновременно эту формулу получил М. Маскет
A949). Сам Ч. В. Тейс отметил, что эту формулу ему указал
Любин (Lubin).
Составим выражение для расхода Qo через цилиндрическую
поверхность радиуса /*с> пересекающую весь пласт, т. е. расхода
совершенной скважины радиуса гс:
Qo- - 2nrcTk(^-)_r =Qexp(—^). G.5)
Отсюда видно, что для скважины конечного радиуса дебит Qo
меняется со временем, возрастая от нуля при t = 0 до Q при
f = oo. Однако при обычных значениях гс (порядка 0,1 м) и
обычных значениях а приближение Qo к Q происходит настолько
быстро, что можно считать дебит скважины радиуса гс постоян-
постоянным и равным Q.
Напор на поверхности скважины является переменным:
Для достаточно малых значений аргумента экспоненциаль-
экспоненциального интеграла имеем приближенную формулу (Бейтмен и Эр-
дейи 1973—1974) Ei (—х) = In х + С, где С = In у = 0,577 — эй-
эйлерова постоянная (у = 1,78). Существует такая оценка этой
формулы: для 0 <.х <. \/у ее ошибка 8 < х/\\п(ух)\. Поэтому
для достаточно больших значений t можно написать прибли-
приближенное выражение
h(r, 0 = Я0—^(ln-^--lnY). G.7)
Оно тем более годится для г = гс, где гс — радиус скважины.
§ 71 СКВАЖИНА В ПЛАСТЕ С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ 425
Введем обозначение понижения на скважине S = Но — Лскв
и перепишем последнее уравнение, полагая в нем г = гс.
Получим
4nK r\
Введя обозначения
напишем зависимость между S и In/ в виде (см. Бузинов и
Умрихин 1964; Чернов и др. 1960)
S = A + B\nt. G.10)
Следовательно, если построить график зависимости S от
In t, то угловой коэффициент получающейся при этом прямой
будет равен В, а начальная ордината (при t = 1) будет равна
А. Отсюда, если известны Г, Q и гс, можно найти k и а, а если
известно а, то можно найти гс. Однако при этом получается,
вообще говоря, не действительный радиус скважины, а так на-
называемый приведенный радиус г'с: это радиус такой скважины,
которая давала бы тот же дебит Q при тех же параметрах
пласта, но не имела бы сопротивлений (фильтра, труб и т. п.)
действительной скважины. По величине отношения г'с/гс можно
судить о сопротивлениях фильтра и труб.
Наблюдения за остановленной скважиной дают другой спо-
способ определения одного из параметров пласта. Предположим,
что происходила откачка из скважины в течение промежутка
времени /ь а затем откачка была прекращена. Тогда восстанов-
восстановление напора в точке г пласта будет происходить согласно
формуле
-Ei(-ik)}- с7-11)
Действительно, G.11) является решением уравнения G.1), удов-
удовлетворяющим условию, что при / = 0 (момент остановки)
и обращающимся в Яо при г= оо.
Выражению G.11) дают такую интерпретацию. Предполо-
Предположим, что откачка с дебитом Q продолжается и после t = t\9 a
затем начинает действовать нагнетательная скважина с тем же
дебитом Q. В результате получится нулевой дебит, а возле
скважины будет происходить восстановление уровне
426
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
[ГЛ. XI
Для достаточно больших значений /, пользуясь формулой
G.7), найдем
•Но — fl= *
G.12)
Откладывая по оси абсцисс значения 1пA+^д), а по оси ор-
ординат значения 5, получим
уравнение прямой с угловым
коэффициентом В = Q,
Изложенная теория
75
S,cm
t
•
У
X
:
50
Рис 269
%№Н
150
поль-
пользуется в настоящее время боль-
большой известностью (см., напри-
50 \— —I Ъг~А 1 мер , Де Уист 1969) и широко
применяется для определения
параметров пластов как в слу-
случаях водяных, так и нефтяных
25\ о!ч 1 "I скважин. В. Н. Щелкачев
A946) одним из первых стал
применять ее к различным за-
задачам. В частности, он сопо-
сопоставил результаты наблюдений
над уровнем в одной останов-
остановленной нефтяной скважине с
результатами расчета и по-
получил хорошее совпадение
(рис. 269)
В случае группы скважин можно складывать решения, соот-
соответствующие отдельным скважинам.
§ 8. Скважина в пласте с перетоками. Будем рассматривать
линейное уравнение вида F.18) для осесимметричного случая:
(8.1)
где а — коэффициент пьезопроводности G.2), Ъ — коэффициент,
характеризующий перетоки F.17) через слабо проницаемые
пласты.
Для уравнения (8.1) существует решение, полученное
Ч. Э. Джейкобом и М. С. Хантушем (см. Хантуш 1964, 1, 2).
Чтобы его получить, применим преобразование Лапласа, пола-
полагая (Снеддон 1955)
U (г, р) = \ А (г,
о
§ 8] СКВАЖИНА В ПЛАСТЕ С ПЕРЕТОКАМИ 427
Для U(r>p) получим обыкновенное дифференциальное урав-
уравнение
решение которого, соответствующее начальному и граничному
условиям для h(r,t):
А (г, 0) = Я0, 2якТг^-\ =Q,
имеет такой вид:
Функции /C0(Vap) соответствует оригинал
±-
По теореме смещения преобразованию /^(p + n) соответствует
оригинал e~ntf(t). В рассматриваемом случае
Наконец, множитель 1/р в выражении для изображения
функции даст интеграл
Замена переменной r2/Dat) = u приводит к интегралу
J
о /?
и, наконец, для Л (г, /) получаем
428
ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ
|ГЛ. XI
Введем величину 5 = д/а/&, называемую коэффициентом
связи, и функцию
W (и, ±) -
(8.4)
Функция W протабулирована (Хантуш 1964, 2) и для нее
11
W
10
8
В
4
2
О
10
I =
г/0-0
4f
/77
—80-
100"
^r
\
s
-6
n-f
10~° 10
Рис. 270.
~г
построены графики (Бочевер и Веригин 1961). На рис. 270
дана зависимость W от и для различных г/В.
Формулу (8.3) можно переписать теперь так:
Заметим, что интеграл
подстановкой а/и = у приводится к виду
§ 8] СКВАЖИНА В ПЛАСТЕ С ПЕРЕТОКАМИ 429
Последний интеграл представляет цилиндрическую функцию
второго рода мнимого аргумента 2/СоB л/а), так как
«.«-¦И «К-»-¦?)¦?¦
(8.6)
Таким образом, можем написать
/ (а, Р) = 2 Ко B д/а) - / (а, |) . (8.7)
Положим
г2 о г2 _а_ оЛ_
a~AB2i ?~'Ш1 J~'W*
Тогда
t) + w
Чтобы найти выражение расхода Q(r, t) через цилиндри-
цилиндрическую поверхность радиуса г, воспользуемся вторым из ра-
равенств (8.8); получим
Q(r, i) = 2nkrT^r =
Здесь использовано соотношение Ко{х) = — К\{х).
При г->0 имеем
При / > 0 интеграл в правой части (8.9) остается ограни-
ограниченным и его произведение на г2 стремится к нулю при г->0.
Поэтому limr>0Q(r, 0 = Q'» следовательно, скважина бесконечно
тонкого радиуса имеет постоянный расход Q. Для скважины
конечного радиуса может служить формула (8.9), если поло-
положить в ней г*=г0.
430 ИНЕРЦИОННЫЕ ЧЛЕНЫ. НАПОРНЫЕ ДВИЖЕНИЯ [ГЛ. XI
Введем обозначения
Тогда формулы (8.8) и (8.9) можно переписать в виде
(8.10)
В главе XIII для безнапорных движений рассмотрены и за-
задачи о скважине конечного радиуса. Все полученные там резуль-
результаты нетрудно перенести также на случай напорного пласта.
Глава XII
НЕЛИНЕЙНЫЕ ЗАДАЧИ НЕУСТАНОВИВШИХСЯ
ДВИЖЕНИИ СО СВОБОДНОЙ ПОВЕРХНОСТЬЮ
§ 1. Вывод основных соотношений. В общем случае, если не
учитывать инерционные члены в уравнениях движения, движе-
движение грунтовых вод при постоянном коэффициенте фильтрации
k определяется уравнениями (см. § 12 главы I)
причем
Здесь и, v К w — проекции скорости фильтрации, так что
где dx/df, dy/Л, d^/df — проекции скорости частицы жидкости,
т — пористость грунта, k — коэффициент фильтрации, р — дав-
давление, р — плотность, g — ускорение силы тяжести. Ось z на-
направлена вверх. Пусть уравнение свободной поверхности имеет
вид F(xt у у z, t) = 0. Дифференцируя его по времени и пользуясь
равенствами A.4), получим
dF.dF.dF . dF л п -ч
Если уравнение свободной поверхности написать в виде z =
= 6(х, у, t), или 8(х, у, t) — z = O, то вместо A.5) будем иметь
На свободной поверхности, где давление р постоянно, из A.3)
следует уравнение
ф (х, у у z, t) + kzm* const. A.7)
432 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ [ГЛ. XII
Ограничимся здесь для простоты случаем, когда массив од-
однородного грунта подстилается горизонтальным основанием.
Первое допущение. Будем считать, что свободная по-
поверхность слабо изогнута и колеблется около средней высоты
йо. Тогда, разлагая функцию ф в ряд по степеням z — h0 и пре-
пренебрегая членами высшего порядка, будем иметь на свободной
поверхности
ф (х, yf z, t) = ф (*, у, ft0, f) -f -JL (z — й0) + ... « ф (х, у, й0, t),
и уравнение A.7) можно переписать так:
Постоянную, входящую в уравнение A.7), можно считать вклю-
включенной в функцию ф. Таким образом, если бы мы нашли потен-
потенциал скорости, то уравнение A.8) было бы уравнением свобод-
свободной поверхности.
Второе допущение. Будем считать, что горизонтальные
скорости не зависят от высоты г. Тогда уравнение неразрывно-
неразрывности A.2) можно проинтегрировать по г. Получим
ди . d
или
w(x, у, z, t) = — г(7 + |^) +®о(х, У, t). A.9)
Здесь Wo—вертикальная скорость на нижнем основании пласта
при 2 = 0. Но так как мы, в сущности, осреднили наше движе-
движение по высоте, то можем включить в выражение w0 и другие
факторы, создающие вертикальную скорость, например, выра-
выражения, учитывающие инфильтрацию или испарение со свобод-
свободной поверхности.
Уравнение A.9) дает линейную зависимость вертикальной
скорости w от z.
§ 2. Вывод нелинейного уравнения. Покажем, что из уравне-
уравнения A.6) при сделанных двух допущениях можно получить не-
нелинейное уравнение Буссинеска (Boussinesq 1904). Введем в
рассмотрение функцию h{x,yyt)y связанную с потенциалом ско-
скорости ф(я, у у йо, t) соотношением
A —f. B.1)
§ 31 МЕТОД МАЛОГО ПАРАМЕТРА 433
Тогда уравнение свободной поверхности примет вид
z = A(*. y,t), B.2)
а для горизонтальных скоростей будем иметь выражения
Уравнение A.6) с учетом B.3) даст
) +
Для w возьмем A.9), положив z = h. Тогда B.4) примет вид
dh
m
что можно также переписать в виде
dh k Г d (и dh\ , d (,_ dh \ \ , _wo_ /^ ^\
§ 3. Метод малого параметра. Рассмотрим уравнение одно-
одномерного движения
в котором Я будем считать некоторым малым параметром;
f{xyt)—функция, учитывающая внешние воздействия на поток:
инфильтрацию, испарение и т. д.
Если положить
h (xt t) = H0 + X ЯA, (х9 t) + X2H{2) {X,t)+ ..., C.2)
где Яо — некоторая постоянная, то, подставляя ряд C.2) в урав-
уравнение C.1) и приравнивая коэффициенты при одинаковых сте-
степенях X, получим для определения ЯA), ЯB) и т. д. систему урав-
уравнений
дНф) д2Н^2\ о, d
-дГ=а-д^-+1п-д7\л^-дг;' \ (з.з)
При рассмотрении движения на отрезке @, /) сюда надо
присоединить начальные и граничные условия
h(x, O) = q>(x), C.4)
) = F2(t). C.5)
434 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИИ [ГЛ. XII
Практически вычисление большого числа членов ряда C.2)
невозможно, но второе приближение иногда удается получить без
труда. Примером является случай фильтрации из водохрани-
водохранилища, рассматриваемый ниже, когда вычислены члены до треть-
третьего порядка включительно. Сходимость ряда при этом не ис-
исследована.
§ 4. Фильтрация при изменении уровня воды в водохрани-
водохранилище. Рассмотрим подробно простейшую задачу, а именно, за-
задачу об интегрировании нелинейного уравнения
L = ±J-(h2L
dt т дх V дх
на полупрямой х^О при начальном л граничном условиях
Л(х, 0)-Яя, А (О, /) = #ь D.2)
где Н\ и #2 — постоянные, что соответствует случаям внезапного
подъема (#i > Я2) или опускания (Нх < Н2) уровня воды в во-
водоеме (рис. 271).
Подробный разбор этой задачи интересен потому, что он
дает возможность сравнения решений, получаемых после линеа-
линеаризации уравнения D.1), с точ-
точным его решением. При этом
существуют два простейших
способа линеаризации этого
уравнения, которые мы будем
называть соответственно пер-
первым и вторым.
Первый способ состоит в
том, что множитель h в круг-
Рис 271, лой скобке уравнения D.1)
заменяется некоторым постоян-
постоянным значением /icp. Тогда получается линейное уравнение
dh d2h
V7777777J/77777777777777777SS77777S77777,
где постоянная величина а = khcvlm называется коэффициен-
коэффициентом уровнепроводности (Шестаков 1973).
При втором способе (см., например, Веригин 1949, 2) в ка-
качестве неизвестной функции принимается не /г, а /г2. Полагая
А2 = и, D.4)
получим такое уравнение:
ди k /— д2и
§ 4J ИЗМЕНЕНИЕ УРОВНЯ ВОДЫ ВОДОХРАНИЛИЩЕ 435
Теперь заменим в нем л]и постоянным значением ЛСр- Тогда бу-
будем иметь линейное уравнение
ди д2и
a
где a = khc?/m.
Доводом в пользу введения второго способа линеаризации
является то обстоятельство, что при переходе от неустановив-
неустановившегося движения к установившемуся при первом способе линеа-
линеаризации получаем для h уравнение d2h/dx2 = 0, дающее в каче-
качестве решения линейную функцию h = С\Х + С2. При втором же
способе линеаризации имеем уравнение d2h2/dx2 = О, общее ре-
решение которого дает h2 = Схх + С2.
Другими словами, при первом способе линеаризации для
установившегося движения уравнение свободной поверхности
дает прямую, что не соответствует действительности, в то время
как при втором способе для свободной поверхности получаем
параболу Дюпюи.
Далее мы увидим, что в некоторых случаях более близкие к
точному решению результаты будут получаться при первом спо-
способе линеаризации, в других случаях — при втором.
В рассматриваемой задаче х изменяется в пределах от нуля
до бесконечности, и граничное и начальное условия таковы, что
им удовлетворяет автомодельное решение, получаемое подста-
подстановкой
где a — постоянная, которую мы выберем в дальнейшем.
При этом уравнение D.1) перейдет в обыкновенное нелиней-
нелинейное дифференциальное уравнение
ma2 dh п
ПГЧ-^0- D.7)
Введя еще подстановки
/7 Ikhc
получим уравнение (Полубаринова-Кочина 1949, 2)
4л0
4? ЖГ. D.8)
Наряду с этим уравнением будем рассматривать уравнение, по-
получаемое из D.8) подстановкой и2 = v (Полубаринова-Кочина
1948), т. е. уравнение
-??-+ *LiL = 0. D.9)
dx\2 yv dr\
436
НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ
[ГЛ. XII
Будем искать решение каждого из уравнений D.8) и D.9)
в виде рядов по степеням параметров / и X соответственно
u=l+lul + Pu2 + Pu3 + ..., D.10)
v=l+Xv{+X2v2 + X3v3 + ... D.11)
При этом можно за /icp принять по произволу как Яь так и
#2. Если хотим получить пучок кривых, проходящих через на-
начальную точку, то положим Лср = #ь если же хотим получить
кривые, сходящиеся на бесконечности, то примем /icp = Я2.
В том и другом случаях для определения коэффициентов
ряда D.10) получаем такую систему уравнений:
D.12)
Для коэффициентов ряда D.11) получаются уравнения с более
простыми правыми частями:
D.13)
Обратимся к первому случаю, когда Лср = #1. Подчиним
функции щ и vt условиям щ @) = и2 @) = ... = 0, Vx @) =
= V2 @) = . . . = 0, U2 (оо) = % (оо) == . . . = 0, V2 (оо) = 03 (°°) = . ..
...=0. Чтобы удовлетворить условиям на бесконечности
и (оо) = Hz/Hi, v (оо) == (HJHiJ, нужно принять соответственно
откуда для параметров / и Я получаем значения
гг2 гг2
/У2 — М{
Я,
D.14)
(ниже мы увидим, что щ (оо) = У! (оо) = 1).
Первое приближение дает как для иь так и для v{ функцию
е~кг dX = erf ч.
. 15)
§ 4] ИЗМЕНЕНИЕ УРОВНЯ ВОДЫ В ВОДОХРАНИЛИЩЕ 437
Для вторых приближений получаем соответственно
«. (л) - ? а - «-""> - т^е-Ч - ти« + (т - ?)">• <4Л6)
^.--^.. D.17)
Наконец, для третьих приближений находим такие выражения:
0 -7Ь-^^-^^-^Ф^ V3). DЛ8)
-1 с2 - r2U е-* - -^ «-»* _ 1^1 ф (г, д/3 )•
4 16
Если обратимся ко второму случаю, т. е. примем /icp = #2,
то удобнее будет ввести другие обозначения, отыскивая решение
уравнения D.9) в виде ряда
+ ..., D.20)
где функции Wi по-прежнему удовлетворяют уравнениям D.13),
но при других граничных условиях. Последние выберем таким
образом: ^i(oo) = до2(оо)= ... =0, w2{0) = wd@) = ... = 0.
Тогда получим
- ^ ^+^w ^^^ D-22)
Значение параметра \х определяется из условия 1 + \x,wx @) =
= НЦНЪ так что vl^W-HDIhI
С помощью полученных формул были произведены вычис-
вычисления. При этом оказалось, что для крайних случаев — фильтра-
фильтрации в грунт при нулевом уровне грунтовых вод (Н2 = 0) и
фильтрации в пустой водоем (Н\ = 0)—принятая степень при-
приближения, при которой мы ограничились членами до третьего
порядка включительно, недостаточна. Эти случаи были иссле-
исследованы отдельно с помощью численного интегрирования.
438 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ [ГЛ. XII
§ 5. Численное интегрирование. Введя подстановку
W2 = ?, E.1)
приведем уравнение D.8) к следующему:
\d2u2 , 2 du_ 0
или в развернутом виде к такому:
ии" + и'2 + 1и' = 0. E.2)
Будем искать решение уравнения E.2) для малых значений §
(при Аср = Н{) в виде ряда
//
u=l+ufe + -?Tl2 + ... E.3)
Положим ^ = а, где а будет выбираться произвольно. Тогда
найдем и% = - а\ и\и = За3 - а, и™ = - 15а4 + 6а2, и* = 105а5 -
— 49а3 + За, и%1 = — 945а6 + 504а4 — 52а?, и™ = 10395а7 —
- 6237а5 + 882а3 - 15а.
Давая а ряд значений, можно построить семейство интег-
интегральных кривых уравнения E.2). Начиная с некоторых значе-
значений g, ряд E.3) становится непригодным для вычислений, и при-
приходится обращаться к численному интегрированию уравнения
E.2). Таким способом было построено семейство интегральных
кривых уравнения E.2) для а = ±0,1, ±0,2, ..., ±0,6. Все эти
кривые имеют асимптотами прямые, параллельные оси ?. С по-
помощью интерполирования кривые были пересчитаны так, чтобы
асимптотами оказались равноотстоящие по и прямые. Резуль-
Результаты расчетов представлены на рис. 272, где принято ЛСр = Hi-
Кривой, доходящей до оси абсцисс, соответствует значение а =
= —0,628.
Таблицы зависимости и(г\) приведены в книге Г. И. Барен-
блатта, В. М. Ентова и В. М. Рыжика A972). Там же рассмот-
рассмотрены более общие случаи автомодельных решений для уравне-
уравнений движения жидкостей и газов в пористой среде (см. также
Баренблатт 1952, 2).
Можно перестроить графики рис. 272 несколько иначе. Обо-
Обозначим через Д# превышение уровня воды в канале над перво-
первоначальным уровнем грунтовых вод (Д# = Н\ — Н2) и введем
отношение р = Д#/#2. Теперь построим для различных значе-
значений р графики зависимости от rj величины щ = (А — Я2)/ДЯ,
где А —глубина потока (рис. 273). Если бы мы линеаризовали
уравнение D.1), то получили бы одну кривую для всех р (см.
§2 главы XIII).
$5]
2,0
и
1,6
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
43&
0,8
>
6
-^—
.—
—-—
ч
\
^—
.
-
—¦—
~.—¦
—
¦—¦—
¦
—-—
——
-——¦
—
—-
-
^--
^
« — —
- ¦
—
с
ОЛ 0,8 t;2 1,6 2,0
Рис. 272.
Щ
0,8
0,6
0,1
0 0,1 0.4 0,6 0,8 W
Рис. 273.
\
\
V
\
л
1,1 i4
440 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ [ГЛ. XII
§ 6. Фильтрация из грунта в пустой бассейн. Этот частный
случай уравнения D.8) можно свести к такой системе двух урав-
уравнений, которые позволяют использовать частично результаты
вычислений, проведенных в теории пограничного слоя пластин-
пластинки, и получить затем в явной форме решение рассматриваемой
задачи для малых значений независимой переменной т). Перепи-
Перепишем уравнение D.8) в виде
^ + 2п-0, F.1)
где штрих обозначает производную по т). Теперь введем новую
вспомогательную переменную ? и будем считать и и г\ функ-
функциями от ?, причем переменную ? определим равенством
dy\jdX, = и. Следовательно, если бы мы нашли и как функцию от
?, то получили бы ц в виде
rf?. F.2)
0
Теперь имеем
dt\ , du 1 du 1 d2y\
aj d\\ и dt, и a?2
откуда
¦ I —— I — -Д- 2т|=== О
du \ dll" ) du
и, наконец,
^L + 2T1i!lL = 0 F3)
Будем искать решение F.3) в виде степенного ряда
Г) = 00 ~
при условиях ri@) = 0, ^(О) = 0, ri/(oo)= 1.
Такое решение мы можем взять непосредственно из теории
пограничного слоя. Для г\ как функции от ? получим ряд (см.
Кочин, Кибель и Розе 1963, 2)
(а = 0,33206).
Взяв его производную по ?, найдем и в функции от ?:
U = 2aS-4r«2C4+^Fa^-1^rat10+ ... F.6)
Пусть
"''1 E!)~Vl = 0,4873 л/ц, X = dh E\)-'h ?.
§ 61 ФИЛЬТРАЦИЯ ИЗ ГРУНТА В ПУСТОЙ БАССЕЙН
Тогда вместо F.4) получим
441
Обращение этого ряда дает
Подставляя это выражение для X в ряд F.5) для и, оконча-
окончательно найдем
||* —~тг,/li -J- ...I, \Р#Ч/
где 5 = 2a/!15v< = 2,3652.
С помощью ряда F.4) были произведены вычисления до
г] =0,6; дальнейшие расчеты проводились с помощью числен-
численного интегрирования по формуле F.2). Результаты расчетов
представлены на рис. 274 (где принято /гср = #2)
и
0,8
0,6
0,2
V
/
$>
0,2 0^
0,6 0,8 iff
Рис. 274.
D
Интересно сравнить найденное точное решение с приближен-
приближенными, получаемыми посредством первого и второго (см. § 4)
способов линеаризации (см. уравнения D.3) и D.5)). В обоих
случаях мы принимаем /гср = #2. Для первого способа линеа-
линеаризации решение имеет вид
и =
F.7)
442 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ [ГЛ. XII
Для второго способа линеаризации получаем
м = мB)=л/ф(т,). F.8)
Из рис. 274 видно, что первый способ линеаризации дает в этом
случае очень плохой результат, в то время как второй дает ре-
решение, довольно близкое к точному.
§ 7. Фильтрация в грунте с нулевым уровнем грунтовых вод.
Другой крайний случай, для которого принятая в § 4 степень
точности — до третьих степеней параметра включительно — не-
недостаточна, есть случай фильтрации из водоема в грунт, в ко-
котором до наполнения водоема не было грунтовых вод (но кото-
который мог, конечно, быть влажным; в этом случае пористость
будет заменена недостатком насыщенности или активной пори-
пористостью— см. § 2 главы I).
Для этого случая интегральная кривая была построена с по-
помощью следующего разложения в ряд (Полубаринова-Кочина
1952, 3). Если в уравнении E.2) положить и = О, то, считая
и" Ф оо, будем иметь и/(и/ + ?) = 0. Отсюда, если и! Ф0, по-
получим
' + 0. G.1)
Предполагая, что в рассматриваемом случае интегральная
кривая пересекает ось абсцисс, обозначим абсциссу точки пе-
пересечения через с. В этой точке
и = 0, и' = — с. G.2)
Дифференцируя последовательно E.2) и используя G.2), най-
найдем разложение и в ряд по степеням разности I — с:
ll(S-cM A-е)* . п .
86 400c3 230 400c4 "*"••• \'•*'
Положим в полученном равенстве | = 0. Будем иметь (при
АСр = Н\)
1=с^' Х
Сложив быстро убывающие члены ряда, стоящего в скобках,
найдем с2, а затем с = 1,14277 ...
С помощью ряда G.3) получена таблица 13 зависимости и
от ?.
§71
ГРУНТ С НУЛЕВЫМ УРОВНЕМ ГРУНТОВЫХ ВОД 443
Таблица 13
1
и
1
и
0
1
0,7
0,458
Зависимость
0,1
0,936
0,8
0,363
0,2
0,867
0,9
0,263
и от
0,3
0,794
1
0,4
0,716
1,0
0,158
0,5
0,635
1,1
0,0487
0,6
0,549
1,143
0
Нетрудно пересчитать эту таблицу, перейдя от независимой
переменной | к переменной т]=|/У2. Не приводя этого пере-
пересчета, мы даем график (рис. 275), где построена зависимость
и от г), а также приведены кривые 1—Ф(л) и лЛ ~ФСп)» яв"
ляющиеся соответственно решениями уравнения движения, ли-
линеаризованного по первому и по второму способам. В отличие
аг $4 qt -0,8 w
Рис. 275.
от случая, рассмотренного в § 6, здесь второй способ линеари-
линеаризации, когда за неизвестную функцию принимается /i2, дает зна-
значительно худший результат.
Возвращаясь к точному уравнению G.3) для линии свобод-
свободной поверхности, заметим, что выше мы взяли лишь часть этой
линии для 0 <: I ^: с, так как отрицательные значения и не
имеют смысла. Для g > с следует принять и = 0. При этом и'
будет претерпевать разрыв непрерывности при \ = с, но вели-
величина ии\ пропорциональная расходу в сечениях потока, остается
непрерывной.
444
НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ
[ГЛ. XII
Интересно, что в рассматриваемом крайнем случае язык
грунтовых вод перемещается с конечной скоростью (при / > 0).
Из условия I = с находим, принимая во внимание соотношения
D.6) и E.1), абсциссу переднего края языка
х =
2kH,t
т
и затем скорость распространения переднего края
dx _ с
dt
G.4)
G.5)
Нужно иметь в виду, что интегрирование нелинейного урав-
уравнения дает форму депрессионной кривой более точно, чем ин-
интегрирование линеаризованных уравнений, однако все же при
1,0
и
0,8
Цв
0,2
:\
NT.
ч
» Ч.
ч
ч
\
ч
ч
ч
fv
* л фильтрационный лоток >
о««* щелевой лоток
\
\
4f\
\
\
\
0%2
0,6 0,8
iff
1,1
Рис. 276.
этом получается лишь гидравлическое решение, т. е. осреднен-
ное по высоте. Точное решение двумерной задачи нам не изве-
известно. Г. К. Михайлов A953, 2) обратил внимание на то, что
уравнение Буссинеска для перемещающегося языка грунтовых
вод (случай этого параграфа) точно соответствует анизотроп-
анизотропному грунту с ky = оо (см. § 9 главы VIII).
Для случая ky = 0 все линии тока горизонтальны и поэтому
уравнение депрессионной кривой принимает вид
dx = k Нх-у gv
dt т х \ • /
§8]
ДРУГАЯ ФОРМА НЕЛИНЕЙНОГО УРАВНЕНИЯ
445
Интегрирование его, считая у = const и полагая х = О при
/ = О, дает для депрессионной кривой уравнение
2kt
G.7)
или, в предыдущих обозначениях, и = 1 — §2.
Опыты (Семчинова 1953) показали, что форма депрессион-
депрессионной кривой в плоской задаче является промежуточной между
формами кривых G.3) и G.7). На рис. 276 приведены обе тео-
теоретические кривые, нижние концы которых совмещены в одной
точке. Точки, полученные в результате ряда экспериментов,
укладываются в области, ограниченной кривыми G.3) и G.7),
§ 8. Другая форма нелинейного уравнения. Для построения
интегральных кривых уравнения E.2) в § 5 было применено
численное интегрирование при заданных значениях а. При этом
были найдены значения #«>. Интерполированием был сделан
расчет для равноотстоящих значений {/«>. Можно избежать ин-
интерполирования, если преобразовать уравнение E.2) соответ-
соответствующим образом.
На рис. 277 построено в несколько видоизмененной форме
семейство кривых (Aronofsky и Jenkins 1952), представляющих
зависимость величины
h (л, t) -- Hi _ и - 6 (а — ЛЛ
/72 ~~* iil' 1 — О \ /22 /
от х\ = х V^/B -y/kH2t). Для и(ц) = h/H2 выше было получено
Дифференциальное уравнение D.8) ии"+ и'2+ 2ци'— 0. Для
и2{ц) будем иметь такое уравнение:
-О- (8.1)
446 НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ [ГЛ. XII
При 6= 1 (#i =Я2), когда движение отсутствует, и = 1,
.однако уравнение (8.1) имеет решение и2 = erf гь т. е.
Это решение линеаризованного уравнения. Представленное на
рис. 277 пунктирной линией, оно разделяет линии, для которых
#i < #2, от линий, для которых Hi > H2. Интегральная линия
при #2 = 0 остается невыявленной, но другие линии резко от-
отличаются друг от друга.
§ 9. Равномерный подъем уровня воды в канале; решения не-
нелинейного уравнения типа источника. Можно обобщить задачу,
рассмотренную в предыдущих параграфах этой главы (Барен-
блатт 1952, 1). Нелинейное дифференциальное уравнение
dt п дх2 ™л'
в случае, если ищется его решение, удовлетворяющее условиям
h (х9 0) = 0, h @, 0 = atp (p > 0), (9.2)
с помощью подстановок
h= at"f&), б-тЬ**'1*'*""]"* (9.3)
приводится к обыкновенному дифференциальному уравнению
При этом для f должны выполняться условия
f@)=l, /(oo) = 0. (9.6)
Если решение уравнения (9.1) должно удовлетворять условиям
А(*,0) = 0, i*BA--t/' (q>0), (9.6)
то подстановка
2 ^2<7+1 Я-fe 2fe <7Q-fe)-fe
*+1 (9.7)
приводит к уравнению
причем ставится условие d\\ @)/^|== — 1.
$ 9] РАВНОМЕРНЫЙ ПОДЪЕМ УРОВНЯ ВОДЫ В КАНАЛЕ 447
Специальный интерес представляет частный случай /7=1,
k = 2, соответствующий равномерному подъему воды в канале.
При этом уравнение (9.4) приводится к такому:
U f 4 (9.9)
^4=
а у at
Нетрудно обнаружить, что это уравнение имеет решение вида
f = 1 + &|. Подстановка этого выражения в уравнение (9.9)
дает для постоянной b значения ± l/V2> из которых мы выби-
выбираем отрицательное.
Функция, заданная соотношениями
V2 _ \ (9.10)
/ = 0 для л/2 < ? < оо, J
дает непрерывное решение уравнения (9.9) с непрерывным зна-
значением величины //', пропорциональной расходу. Оно соответ-
соответствует поставленной задаче.
Возвращаясь к функции А, получим решение, отвечающее ус-
условиям h(x> 0) = 0 и А@, t) = at для уравнения
~df = ~2m~!h?~' (9Л1)
в следующем виде:
(9.12)
:0
Следовательно, депрессионная линия представляет отрезок пря-
прямой, перемещающейся параллельно самой себе (рис. 278) с по-
постоянной скоростью распространения переднего края
dx
dt
Опыты в щелевом лотке хорошо подтверждают эту картину.
Можно получить также решение типа источника для урав-
уравнения (9.11) в случае симметрии относительно оси ординат (Ба-
ренблатт 1952,2):
Его можно рассматривать как частный случай растекания бугра
грунтовых вод по поверхности водоупора, которое подробно об-
обсуждается в § 1 и 2 главы XIV.
448
НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ
[ГЛ. XII
В случае цилиндрической симметрии вместо (9.11) имеем
уравнение
dt — г дг V дг
Решение типа мгновенного источника здесь имеет вид
Оно представляет схему растекания осесимметричного бугра
грунтовых вод при сосредоточенном поливе по поверхности во-
доупора. В обоих случаях свободная поверхность имеет в се-
сечении вид параболы, расширяющейся со временем (рис. 279).
Н
Рис. 278.
Рис. 279.
Однако наибольшая абсцисса увеличивается по различным за-
законам: в плоской задаче пропорционально tx/\ в осесимметрич-
ной пропорционально /1/а.
Отметим неавтомодельное точное решение уравнения D.1),
найденное Ю. Д. Соколовым A956):
в котором а, Ь и с — произвольные постоянные.
§ 10. Задача Буссинеска. Буссинеск (Boussinesq 1904) искал
решение уравнения
dt ~ т дх \П дх )
в виде произведения двух функций
h = T(t)X(x),
A0.1)
A0.2)
из которых одна зависит от времени, другая от координаты.
§ Ю] ЗАДАЧА БУССИНЕСКА 449
Подставляя A0.2) в A0.1) и разделяя переменные, получим
Г _ k (XX'Y _ _ я
где А — произвольная постоянная. Уравнение A0.3) распадает-
распадается на два —для Т и для X. Интегрирование каждого из них
дает
1
В выражении для х заменим произвольные постоянные но-
новыми, полагая
х
UM /!E по.5)
Считая X изменяющимся от нуля до Я, выберем постоянную D
так, чтобы иметь х = L при X = Н. Тогда
3L
где В обозначает бета-функцию. Равенство A0.6) можно полу-
получить, преобразуя интеграл с помощью подстановки X3 = Я3т:
3Z;= 1,16-4=-.
В выражении для Т выберем постоянную С равной единице,
чтобы иметь Т = 1 при t = 0.
Обозначая через f(x/L) = X/H обращение уравнения A0.6)
и учитывая зависимость А от Z), можем переписать A0.2) в виде
График функции Y = f(x/L) представлен на рис. 280. Его
можно рассматривать как начальную форму кривой депрессии,
15 И. Я. 11ол>барипова Ко чин а
450
НЕЛИНЕЙНЫЕ ЗАДАЧИ БЕЗНАПОРНЫХ ДВИЖЕНИЙ
[ГЛ. XII
которая затем будет понижаться согласно A0.7). Эта схема со-
соответствует задаче о бесконечном ряде дрен, лежащих на водо-
упоре, причем начальная
поверхность имеет уравне-
уравнение Ао = Hf(x/L). Для рас-
расхода каждой из дрен най-
найдем выражение, составляя
произведение 2kh dhjdx и
переходя к пределу при
\J26kH2
Рис. 280.
A0.8)
Буссинеск пытался дока-
доказать устойчивость рассмот-
рассмотренного движения, назван-
названного им «упорядоченным ре-
режимом». Однако он лишь
обнаружил существование
класса возмущений, которые
стремятся к нулю при t -> оо быстрее, чем А, что недостаточно-
для полного доказательства устойчивости.
§ 11. Теоремы существования и некоторые свойства нелиней-
нелинейных уравнений теории фильтрации. В задаче § 7 — о фильтрации
в грунт с нулевым уровнем воды в нем — обнаруживается осо-
особенность: конечная скорость распространения передней границы
возмущенной области движения. Это свойство нелинейных урав-
уравнений параболического типа было обнаружено в работах
Я. Б. Зельдовича и А. С. Компанейца (I960) и Г. И. Барен*
блатта A952, 1). В дальнейшем Г. И. Баренблатт и М. И. Ви-
шик A956) доказали, что конечной является также скорость
распространения передней границы возмущенной области для
пологих безнапорных движений (а также для широкого класса
более общих задач) при начальных распределениях напора,
равных нулю вне некоторой конечной области.
При нестационарной фильтрации газа в одномерной пори-
пористой среде движение газа описывается уравнениями (см., на-
например, Баренблатт, Ентов и Рыжик 1972)
ди
dt
(ИЛ)
где функция ср(и) {и — давление газа) определена для и
q/(tt) > 0 при м>0и ф'@) = 0- Для политропного газа q(u
— аип\ при п = 2 приходим к уравнению Буссинеска D.1).
0,
§ U] ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СВОЙСТВА УРАВНЕНИЙ 451
В работах О. А. Олейник, А. С. Калашникова и Чжоу Юй-
линя A958) и А. С. Калашникова A967) исследованы вопросы
существования и единственности решений краевых задач и за-
задачи Коши для уравнения A1.1) При этом особое место зани-
занимает исследование решения при нулевом начальном условии
и(Ху 0) = 0, простейшие случаи которого указаны в § 6 и 7.
Так, линия ABC (рис. 272) не является интегральной кривой
(в обычном смысле) дифференциального уравнения F.2), так
как в точке В производная у нее терпит разрыв непрерывности.
В таких случаях в указанных работах доказывается, что урав-
уравнение A1.1) имеет обобщенное решение в смысле С. Л. Собо-
Соболева A966). Так, в случае задачи Коши обобщенным решением
называется неотрицательная, непрерывная и ограниченная в по-
полосе G{— оо <jc < оо, 0 ^ t <^ Т) функция и(х, t)y если суще-
существует обобщенная в смысле Соболева производная ду(и)/дх
(в рассматриваемой задаче она существует в обычном смысле),
ограниченная в G, и для любой непрерывно дифференцируемой
в G функции f{x,t), равной нулю вне конечной области и при
/ = Г, выполняется равенство
оо
\f@.x)u{x,0)dx~0. A1.2)
Показано, что во всех точках, где уравнение A1.1) не вы-
вырождается (вырождение имеет место при и = 0), обобщенное
решение имеет непрерывные производные, входящие в A1.1),
и удовлетворяет этому уравнению.
Заметим, что для получения уравнения A1.2) нужно умно-
умножить обе части уравнения A1.1) на f{x,t) и проинтегрировать
по области G. Интегрирование по частям приведет к (П.2)
(Смирнов 1969; Соболев 1966).
Глава XIII
ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ
НЕУСТАНОВИВШИХСЯ БЕЗНАПОРНЫХ ДВИЖЕНИИ
§ 1. Неустановившиеся движения в безнапорном пласте. Для
неустановившегося движения при горизонтальном водоупоре мы
имели уравнение B.5) в главе XII. Выведем более общее урав-
уравнение Буссинеска, считая, что граница водоупора — некоторая
слабо изменяющаяся поверхность
z=-T0(x,y). A.1)
Пусть имеем уравнение свободной поверхности
z = h(x,y,i). A.2)
Тогда область, занятая водой, будет определяться в каждом
вертикальном сечении высотой
Q{x,y). A.3)
Выделим столб воды в грунте высотой T{x,yJ) с площадью
основания ДхДг/. Через поверхность этого объема, перпендику-
перпендикулярную к оси х, будет проходить в единицу времени количество
жидкости
Tvx А/у = — kT-^ Ну.
Изменение этого количества при выходе из рассматриваемого
объема через поверхность, соответствующую сечению х-\-Ах>
равно
^^(^) A.4)
Для сечений, перпендикулярных к оси у, получим изменение ко-
количества воды
]L(^) A.6)
Складывая A.4) и A.5), будем иметь общее количество
жидкости, вытекающее (или втекающее) из рассматриваемого
§ 1] НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ В БЕЗНАПОРНОМ ПЛАСТЕ 453
столба в единицу времени. Оно компенсируется изменением во
времени высоты столба жидкости, умноженной на пористость:
^Д*Д</. A.6)
Складывая A.4) — A.6) и сократив на ДяД*/, можем написать
уравнение
В это уравнение можно также ввести величину w0 — разность
между инфильтрацией и испарением на единицу площади гори-
горизонтальной проекции поверхности грунтовых вод.
Введем еще одно обозначение
kT = K. A.8)
Величина К называется, как и в случае напорного движения,
проводимостью пласта. Здесь эта величина является функцией
времени, но обычно ее заменяют осредненным значением, и
притом не только по времени, но и по координатам, считая
K&{kT)cv или K~{kh)Cp- Заметим, что если \h(x,yft)\ мало
по сравнению с Т0(х,у), то T(x,y,t)& T0(x,y).
Окончательно напишем уравнение безнапорного неустановив-
неустановившегося движения в виде
д (mh) д („ dh \ . д
В случае постоянных m и К оно перепишется так:
2h . d2h
=-^)' AЛ0)
Величина а — коэффициент уровнепроводности — имеет вид
а = - (или а = -^). A.11)
Если имеем горизонтальный водоупор, так что Т0(х, у) = О,
то получаем нелинейное уравнение, так как в A.3) T(x,yJ) =
b{t)
_(khL)+(kh). A.12)
дх \ дх ) ' ду \ ду ) v '
Часто рассматривают m и k как постоянные. Если добавить
в правой части A.12) еще перетоки из нижнего слабо проницае-
проницаемого прослоя
«"=-¦?• (А-Я),
454 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ 1ГЛ. XIII
где k* — коэффициент фильтрации и d— толщина слабо прони-
проницаемого прослоя, а Н — постоянный напор под слабо прони-
проницаемым прослоем, отсчитываемый от основания пласта, то полу-
получим уравнение
где а = k/tn и Ъ = kj(tnd).
§ 2. Просачивание из канала при горизонтальном водоупоре
и отсутствии инфильтрации. Будем рассматривать линеаризован-
линеаризованное уравнение неустановившегося движения.
Прежде всего рассмотрим случай фильтрации из канала при
изменении в нем уровня —эту задачу мы уже исследовали в
§ 4 — 8 главы XII, как решение нелинейного уравнения.
Пусть уровень грунтовых вод в начальный момент времени
t = 0 постоянен и равен Яо. В дальнейшем в канале поддержи-
поддерживается постоянный уровень Н\ = #0 ~Ь ^- Тогда, принимая, что
ордината свободной поверхности h(x,t) удовлетворяет уравне-
уравнению (см. A.10))
дН п дЧ (О П
где а = &Лср/т, получаем известное из теории теплопроводности
решение
h (x,t) = H0 + Heric (j±=r). B.2)
Здесь erfc есть дополнение интеграла вероятности:
В практических задачах обычно представляет особый инте-
интерес промежуток времени, за который ордината свободной по-
поверхности достигнет той или иной величины. Обозначим через у
заданное значение ординаты кривой депрессии, отсчитываемое
от Яо: y = h(x,t)—Яо. Тогда из B.2) получим
И — U / Y \
_ ?L nrf / I (О *Х\
н ~enL/- I- \z-6>
По таблицам функции erf (g) можно найти отсюда значение ее
аргумента, а затем и время t.
С. Ф. Аверьянов A956) рассмотрел определение момента
времени, когда уровень грунтовых вод достигает высоты, состав-
составляющей заданную долю от высоты Н (т. е. добавочной высоты
ПРОСАЧИВАНИЕ ИЗ КАПАЛА БЕЗ ИНФИЛЬТРАЦИИ
455
Таблица 14
Значения коэффициента Ц достижения величины z/H
Z
-#
ign
z
н
0,01
3190
3,504
0,60
0,704
-0,141
0,03 0,05 0,10
353 127 31,5
2,548 2,104 1,50
0,70 0,80
0,463 0,305
-0,334 —0,516
0,20
7,69
0,886
0,90
0,184
-0,735
0,30 0,40
3,26 1,81
0,526 0,258
0,95
0,130
-0,886
0,50
1,10
0,041
0,99
0,0752
-1,124
к первоначальной высоте Яо). Введем еще одно обозначение:
2=яЯ — у. По формуле B.3) имеем
B.4)
н
При заданном z отсюда получим для t выражение вида
kht
ср
B.5)
?
Коэффициент (л, зависящий от г/Я, можно назвать коэффициен-
коэффициентом достижения величины
г/Я. В таблице 14 приве- ^
дены значения ц в функ- J
ции от z/H. График этой »
зависимости представлен на ;<
рис. 281.
Рассмотренные задачи ф
имеют применение в вопро-
вопросах засоления почв, которое
может иметь место при вы-
высоком подъеме грунтовых
вод. Именно, если грунтовые
воды будут находиться на
глубине 2—3 м от поверх-
поверхности земли, то вода при на-
наличии интенсивного испаре-
испарения будет подниматься
вверх и выносить с собой
растворенные в ней соли
(Ковда 1946). Высокое стояние грунтовых вод может вызвать
также заболачивание почвы.
Как видно из формулы B.5), важное значение для опреде-
определения времени достижения того или иного подъема воды имеет
значение величины т.
\
\
\
\
1 ' ' h
101 10й
Рис. 281.
456 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XIII
§ 3. Приток к скважине в безнапорном пласте. Рассмотрим
осесимметричный приток к скважине в пласге с первоначально
постоянным уровнем грунтовых вод при внезапном понижении
уровня воды в скважине. Для осесимметричного движения при
w = О уравнение A.10) имеет тот же вид, что и уравнение G,1)
главы XI (но при а, определяемом вторым из равенств A.11)).
Поэтому и формула G.3) главы XI годится (с учетом изменения
значения величины а) для определения притока к скважине, при-
причем теперь z = h(x, у, t) является уравнением свободной по-
поверхности.
Предположим, что основание пласта мало отличается от го-
горизонтальной плоскости. Тогда можно положить Т(х> y>t)»
^ h(x,y,t) и получить уравнение вида A.12). Применяя к нему
второй способ линеаризации, получим для функции и = Л2 'урав-
'уравнение того же вида, что и G.1) главы XI:
ди а д ( ди
где /icp — мощность водоносного слоя грунта (может быть, иначе,
чем раньше, осредненная). Теперь для вычисления дебита Q
скважины радиуса гс нужно положить
причем
поэтому
Q = nrckC{
и для К1 получаем выражение (ср. формулу G.3) главы XI)
где Яс = Л(гс, t) — глубина воды в скважине.
Для скважины при слабо проницаемом прослое в основании
можно взять уравнение (ср. уравнение A.13))
dh2 а д
где Я —постоянный напор в нижнем водоносном горизонте. Точ-
Точно так же, как в § 8 главы XI, можно получить его решение для
§ 4] СКВАЖИНЫ В КРУГОВОЙ ОБЛАСТИ 457
скважин бесконечно малого радиуса:
где функция W(uy r/b) определена равенством (8.4) главы XI.
§ 4. Скважины в круговой области. Предположим, что на
площади, подлежащей орошению, распределено более или менее
равномерно большое количество скважин. Тогда каждая сква-
скважина будет иметь свою область влияния и будет в основном
отсасывать воду из некоторого цилиндра, окружающего сква-
скважину. Если область действия скважины достаточно велика, то
неправильный (в плане) контур, ограничивающий соответствую-
соответствующую площадь 2, можно заменить окружностью и, таким обра-
образом, рассматривать движение в круговом цилиндре — вода как
бы откачивается из бочки некоторого радиуса R.
Случай постоянного уровня воды в скважине
конечного радиуса. В случае неустановившегося осесим-
метричного движения грунтовых вод в безнапорном пласте с
учетом слабой проницаемости нижележащего прослоя и ин-
инфильтрации сверху напорная функция Л (г, t) удовлетворяет сле-
следующему линеаризованному уравнению:
dt
где
dh _ I и-п , 1 и и \ t /#_ гг \ I _.. (А \\
k* e
—т, w = —
md /n
k — коэффициент фильтрации водоносного пласта, т — пори-
пористость грунта, k* — коэффициент фильтрации подстилающего
прослоя, d — его толщина, Но — напор в водоносном пласте
ниже слабо проницаемого прослоя, /icp—некоторое среднее зна-
значение глубины потока, е — интенсивность инфильтрации на по-
поверхности грунтовых вод.
Уравнение D.1) отличается от A.10) членом, определяющим
перетоки из нижележащего водоносного пласта через слабо
проницаемый промежуточный прослой.
Предположим, что интенсивность инфильтрации постоянна и
что скважина радиуса гс работает при постоянном уровне Нс
воды в ней. Напор Но считаем постоянным. На границе г = R
области действия скважины, как на твердой стенке цилиндра,
dh/dr = O. В начальный момент времени /г (г, 0) = Я0. Тогда
относительно функции S (г, t)=h (г, /) — Яо, определяющей
458 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ 1ГЛ. XIII
понижение напора в пласте, получаем краевую задачу
dS sd2S I dS
dt V дг2 г дг
S(r, 0) = 0,
D.2)
где Я = Нс — Яо.
Дальнейшее изложение ведется по статье Т. И. Матвеенко
A974).
Применив интегральное преобразование Лапласа (см., на-
например, Свешников и Тихонов 1974) относительно переменной /,
получаем для изображения
оо
7>,P)=J e-"'S(r,/)*
о
следующую задачу:
+ lEL-L±JLT + JiL = o
1 г dr а ' ар '
Общим решением задачи D.3) будет функция
Т( \ w \ Hp + Hb -w /0 (cor) ^i (со/?) + Ко (о)г) /t (о)/?)
м^. р; = р (р + Ь) -г р(р + ь) /о (с0Лс) /Ci ((Di?) + Ко {@Гс)
где со2 = (р + ^)/а» ^B) И К\(z)— цилиндрические функции
мнимого аргумента соответственно первого и второго рода по-
порядка L
По формуле обращения Римана — Меллина
S(r, 0 ~Jr (!-«-") +
V+joo
1 f
i
+ Hb-y /о (cor) /С, (о>/?) + /Со (^>г) /, ((oJ?) , , ....
Р' К '
где интегрирование проводится по произвольной прямой (v > 0),
параллельной мнимой оси.
Подынтегральная функция относительно р однозначна ц
обладает простыми полюсами в точках р = 0, р = —ft,
pkx=z—b— as\ (k = 1, 2, 3, ...), где sh — корни уравнения
/о (rcs) Yx (Rs) - /, (/?5) r0 M = 0. D.6)
Здесь J%{z)y Yh(z)—цилиндрические функции соответственно
первого и второго рода порядка К. Как известно (см., например,
§ 4] СКВАЖИНЫ В КРУГОВОЙ ОБЛАСТИ 459
Янке, Эмде и Леш 1968), корни уравнения D.5) действительные
и простые. Так как у нас выполнены все условия леммы Жор-
дана (см. Свешников и Тихонов 1974), то для вычисления ин-
интеграла D.3) достаточно найти сумму вычетов подынтегральной
функции во всех полюсах.
После вычислений находим искомую функцию
S{r, t) = h(r, t)-H0 =
b b 4VMV?LV!)W?)
A (r)
J0(rcSk)-J\ {Xsk)
Из асимптотических разложений цилиндрических функций
следует, что
а поэтому, если в D.5) положить 6 = 0, т. е. считать основание
совершенно непроницаемым, то
Для D.7) можно получить более простое приближенное вы-
выражение, ограничившись первым членом бесконечного ряда
(Аверьянов и Усенко 1961).
Случай постоянного дебита. В отличие от пре-
предыдущего случая будем теперь считать заданным и постоянным
460 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ, XIII
не уровень воды в скважине радиуса гс, а ее дебит Q. Тогда для
функции S(r, t) получим краевую задачу
S(r,0) = 0, ^(rc,O = g
где р = — Q/{2nkrchcv).
Аналогично предыдущему для изображения по Лапласу
Г (г, р) функции S(r, t) находим
JL л-
рсо /(, (со/?) /, (согс) - /, (со/?) /Ci (согс) "Г р (р + ft) •
где, как и ранее, со2 =(р-\-Ь)/а. Первое слагаемое в равенстве
D.9) четное, и, следовательно, функция однозначна. Так как
выполнены все условия леммы Жордана, то для нахождения
оригинала достаточно найти сумму вычетов функции
1 Кх (со/?) /о (cor) + /i (со/?) Ко (cor) ePt
рсо К\ (со/?) Л (согс) - Л (со/?) К\ (согс) с
в ее особых точках (полюсах) /? = 0, р= — 6, pk = — Ъ — as\
(k = \, 2, 3, ...), где sk — корни уравнения
Известно, что все sfe действительные и простые.
После вычислений и преобразований находим
'?'('-V/i:) ,
т^г' - Dло)
где
I 4] СКВАЖИНЫ В КРУГОВОЙ ОБЛАСТИ 461
В случае непроницаемого основания после перехода в D.10)
к пределу при &->0 находим
ft (г, О = Яо +
Для бесконечно тонкой скважины, вместо задания
ПрИ r = rCi имеем граничное условие l\mr-*o(rdS/dr) = v9 где
v = — Q/BnkhcP).
Решением операторного уравнения D.3), удовлетворяющим
граничным условиям
будет функция
Как и ранее, для нахождения оригинала достаточно найти
сумму вычетов функции
Кх (со/?) /0 (cor) + Л (со/?) /Со (юг) t
plx (со/?)
во всех ее особых точках. Особыми точками этой функции
являются полюсы р = 0, р= — b9 pk = — b — as\ (k = 1, 2, 3,...),
где sk (они вещественны) — корни уравнения Jl(Rs) = 0.
После вычислений и преобразований находим
\ \ и / \ у u / \ v1*/ >¦ \ и / i
462 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XIII
Из асимптотического разложения цилиндрических функций
следует, что
77—т ° ^Г VtJ + Mr VtJ ~
lim I > v »/ I0[r л/4) + Ко[гл/-)--jgre-" 1 =
вв — I Г I ^ I 2Д /
Следовательно, для совершенно непроницаемого основания
/г (г, /) = #о + ДО/ +
fe-i
Нетрудно проверить выполнение начального условия, вос-
воспользовавшись соотношением
если pfe — корни уравнения /i(PJe=0 (у нас $k = Rsk и р = г//?).
При достаточно больших значениях / бесконечным рядом
в D.12) можно пренебречь, и тогда h(r, t) будет линейной функ-
функцией времени. В частности, на скважине (хотя мы приняли для
упрощения формул скважину бесконечно тонкой, теперь в полу-
полученные формулы имеем право подставить радиус скважины гс)
будем иметь
D.13)
При w = 0 множитель при /, т. е. угловой коэффициент прямой
h = A+Bty равен (Albert 1960)
_ Q 2khcp Qhcp Qhcp
и 5B=E —
mR2
где V — объем жидкости в пласте. Зная две из трех величин т,
R и ЛСр (в случае напорного пласта вместо /icp будет фигуриро-
фигурировать мощность пласта), по объему V откачиваемой жидкости
можно определить третью величину.
В безнапорном движении образуется свободная поверх-
поверхность — воронка депрессии. Через достаточно большой проме-
промежуток времени она начнет снижаться, как показывает уравне*
§5]
СКВАЖИНЫ ПРИ ВОДОУПОРЕ СО СЛАБЫМ УКЛОНОМ
463
ние D.12), с постоянной скоростью Q/(nmR2)—w. Задавшись
допустимым понижением S за промежуток времени t, можно
найти величину дебита, при которой такое понижение не будет
превзойдено:
л < ^m/?2<s 4- R2
t
При достаточно больших значениях t степень заглубления
воронки депрессии S (или воронки напора) можно определить
по формуле
§ 5. Фильтрация к скважинам при наклонном водоупоре со
слабым уклоном. Направим ось х по горизонтали в сторону
подъема плоскости водоупора и обозначим через а угол между
водоупором и осью х (на рис. 282 дано сечение потока плоско-
плоскостью у = 0). Тогда для водоупора будем иметь уравнение г =
= ix, где i = tg a « а. Пе-
Переписывая это уравнение в
виде A.1), получим
Введем далее согласно A.2)
глубину потока над водо-
водоупором
Т (х, y,t) = h (х, у, 0 — ix.
(б'2) Рис. 282.
При этом уравнение движения A.7) при постоянных m и k при-
примет вид
Произведя линеаризацию уравнения (б.З), будем иметь
дТ
дТ
kT
cp
= 4)- F-4)
Здесь Гср — некоторое среднее значение глубины грунтовых вод.
Положим далее
у,
E.6)
где
= Т(х, у, 0), а =
464 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XIII
причем функцию То(#, у) будем считать удовлетворяющей урав-
уравнению Лапласа. Будем искать для v решение с осевой симме-
симметрией относительно вертикальной оси г, совмещенной с осью
скважины. Для v (r, /) получим уравнение
—(? + f?) ('-VF+7) E.6)
Применим к v (г, t) преобразование Лапласа
оо
V(r,p)=\ ь{г,г)е-РЧи F.7)
О
Для V (г, р) будем иметь уравнение
#+!•?-*>'-* <м»
общее решение которого имеет вид
V (г, р) = С,*о (г д/l) + С*7° (г Д/Ю • E-9)
где /Со и /0 — модифицированные функции Бесселя, С\ и С2 —
постоянные.
Пусть скважина нулевого радиуса действует с постоянным
дебитом Q, тогда начальное и граничные условия будут иметь
вид
Г(г, 0) = Г0, o(r,0) = 0,
)^ ()re0 E.10)
T(ooyT) = TQy О(ооэ0 = 0 J
Здесь принято во внимание, что
( x). E.11)
r=-0
В E.9) нужно принять С2 = 0, так как у->0 при г->оо.
С помощью второго из условий E.10) находим
E.12)
Из таблиц перехода от изображений к оригиналу и из тео-
теоремы умножения (Erdelyi и др. 1954) найдем
f 5] СКВАЖИНЫ ПРИ ВОДОУПОРЕ СО СЛАБЫМ УКЛОНОМ 465
Полагая Л2 =* г'7DаА,), получим
ехр(-Я--^)-^, E.14)
г2/Dа<)
где к\ заменено под знаком интеграла на А,.
При <х = р = 0 это решение переходит в решение задачи
о бесконечно тонкой скважине при горизонтальном водоупоре.
Воспользуемся интегральным представлением функции Ко{х):
О
Тогда можно написать
и Т (х, г, t) перепишется в таком виде:
Т(х, r,t) =
„ у
E.15)
Вместо ординаты свободной поверхности можно рассматри-
рассматривать понижение S (х, yyj) = То — Т (х, уу t). Тогда будем иметь,
вводя обозначения гл/$/а = р и р/ = т,
PV4T
ИЛИ
Q
" 4nkTc[)
Для малых т предпочтительна формула E.16), для больших —
E.17).
466
ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
[ГЛ. XIII
Интеграл, входящий в полученные формулы, табулирован
М. С. Хантушем A964, 1).
Для случая п скважин, проекции которых на плоскость (х, у)
определяются координатами (xut/i), решение для малых т за-
записывается в виде, аналогичном E.16);
Z
exp(-A,-4)?. F.
18)
где
А. Бегматовым A964) проведены вычисления понижений при
откачке из одной, двух и трех скважин, а также для цепочек
Z,M
t=0
Рис. 283.
скважин. На рис. 283 представлен случай трех скважин с оди-
одинаковыми дебитами Q = 20 л/сек, для k = 20 м/сут, Гср = 25 м9
m = 0, 2, i = 0,005, при г0 = 0,2 ж. Время t задается в сутках.
§ 6. Неустановившиеся движения при коэффициенте фильтра-
фильтрации, слабо меняющемся с высотой. Некоторые задачи об устано-
установившихся движениях в неоднородных грунтах были рассмотрены
в § 4 главы X. Там же введен потенциал Н. К. Гиринского A947)
для безнапорного движения
it.
<D{x,y)'=\(x-fi)k(z)dz.
F.1)
§ б] ДВИЖЕНИЯ В НЕОДНОРОДНЫХ ПО ВЕРТИКАЛИ ГРУНТАХ 467
Здесь h — напор, который можно рассматривать как функцию
от х, у и t, k — коэффициент фильтрации, зависящий от высоты.
При этом считается, что k мало меняется с высотой. Для безна-
безнапорного движения h принимается за ординату свободной поверх-
поверхности.
В случае неустановившегося движения можно составить
уравнение движения следующим образом.
Обозначим через т пористость грунта, которую будем счи-
считать постоянной во времени. Тогда, выражая условие, что из-
изменение расхода по координатам компенсируется изменением по
времени величины mft, можем написать
д2Ф , д2Ф d(mh) ,fi ~
дх2 + ду2 — — dt # 'b#^
Далее имеем
-^=Ф/(/гLг- F.3)
ОТ ОТ
Исключая dh/dt из F.2) и F.3), получим
дФ __ Ф'(h) / д2Ф д2Ф
dt т \ дх2 * ду2
Если считать, что величина Ф'(К) мало меняется, т. е.
h
— -jjj- Ф' (h) = -i- \ k {z) dz « a = const, F.5)
о
то получим уравнение теплопроводности
д®_ = а I д2Ф , _^Ф\ f66x
Возьмем в качестве примера двухслойный массив грунта, рас-
расположенный на горизонтальном водоупоре. В нижнем слое глу-
глубины Т пусть коэффициент фильтрации равен k0 и активная по-
пористость т0, в верхнем соответствующие величины обозначены
через k и т. Свободную поверхность будем считать находящейся
в верхнем слое грунта.
Тогда, вводя обозначение (J в ko/k, получим следующее вы-
выражение для Ф в верхнем слое:
ф = k0 \ (z - h) dz + k J (z - h) dz =
о т
468 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. ХШ
При этом в качестве а можно принять величину
к0Т + к (Аср - Т) /*ср + (р - 1) Т
а = = к , F.8)
где АСр есть средняя глубина потока.
Рассмотрим фильтрацию из канала с вертикальным откосом,
доходящим до водоупора. Принимая А (я, 0) = Яо, А@, /)==
= Н\ > Но и считая h ограниченным при х = оо, напишем на-
начальное и граничное условия для Ф:
:Ф2, F.9)
Ф@, 0 = -^{[Я]+(Р-1)Г]2 + р(р-1)Г2}=Ф1. F.10)
Для Ф(*, 0 получим известное решение
Щх9 t) = {O2-Ol)ert(j:^ + Ol. F.11)
При этом
^[ ]~Я0). F.12)
Выражение расхода в сечении х имеет вид
При х = 0 получаем
Для однородного грунта, полагая Ао = k> имеем для расхода
выражение
Составив отношение расходов, получим
Г" = * + (р — U'ff I и • • F.15)
Заметим, что в уравнение теплопроводности, а следовательно,
и в решение этого уравнения время входит с множителем а.
Обозначим этот множитель для однородного грунта через по.
Составив отношение
§ 7] ПОВЕРХНОСТЬ РАЗДЕЛА МЕЖДУ ДВУМЯ ЖИДКОСТЯМИ 469
легко видеть, что при р < 1 имеет место неравенство а < а0,
а при р > 1 — обратное неравенство а > а0. Это показывает,
что в первом случае процесс (при прочих равных условиях) бу-
будет для неоднородного грунта более медленным, чем для одно-
однородного (такого, как верхний грунт), во втором случае будем
иметь обратное явление.
Чтобы найти форму свободной поверхности в различные мо-
моменты времени, достаточно написать выражение для Ф, под-
подставив в него правую часть F.7).
§ 7. Перемещение поверхности раздела между двумя жидко-
жидкостями разной плотности. Мы уже говорили о существующих в
природе движениях двух жидкостей различной плотности,
в частности пресной и соленой воды (см. главу VIII). Рассмо-
Рассмотрим здесь уравнения, определяющие положение поверхности
раздела таких жидкостей в различные моменты времени, при
обычно принимаемом условии слабой изменяемости этой поверх-
поверхности.
Пусть имеем две жидкости: верхнюю, для которой все вели-
величины обозначим индексом 1, и нижнюю, с большей плотностью,
которой соответствует индекс 2. Для потенциалов скорости бу-
будем иметь соответственно
4fi) <7Л>
G-2)
Условие непрерывности давления на линии раздела (Pi =
дает
откуда получаем приближенное уравнение линии раздела
z = а2ф! (х, уу А, 0 — а2ф2 {х, у, h, t) = 6 (х, у, t)9 G.3)
где
п Pi п Р2
Ql~~ MP2-Pi) ' 2~~ MP2~Pi) '
Дифференцируя это уравнение вдоль поверхности раздела и
подставляя в него один раз скорости ии v\ и W\> другой раз иъ
v% и w2, получим два уравнения на поверхности раздела:
дб . дб . дб л
470 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XIII
Предположим, как и раньше, что горизонтальные скорости не
зависят от z. Тогда из уравнения неразрывности получаем для
нижнего грунта
где w2q — скорость при 2 = 0, и для верхнего грунта
wl0. G.6)
Здесь z — высота свободной поверхности, на которой мы при-
принимаем г = —cpi/fci. Поэтому для w\ можно еще написать
Величина Дою—вертикальная скорость на свободной поверх-
поверхности, происходящая от действия осадков, испарения и т. п.
Подставляя полученные выражения для W\ и w2 в уравне-
уравнения G.4), получим систему двух нелинейных уравнений с част-
частными производными относительно функций ф1 и ф2 (величина б
может быть исключена из этих уравнений с помощью уравне-
уравнения 6 = aicpi — 0С2Ф2). Возможна линеаризация этих уравнений,
на чем мы не останавливаемся. Для случая перемещения языка
нижней жидкости в напорном пласте нелинейная однородная
система может быть сведена к системе обыкновенных дифферен-
дифференциальных уравнений (Полубаринова-Кочина 1949, 2). Была
рассмотрена (Полубаринова-Кочина 1950) задача о перемеще-
перемещении поверхности раздела между пресной и соленой водой под
флютбетом с учетом линейных инерционных членов, причем за-
задача была сведена к телеграфному уравнению. На основании
изложенного в главе XI не имеет смысла учитывать эти члены,
а тогда вместо телеграфного уравнения получается более про-
простое уравнение теплопроводности. Задачу о двухжидкостной си-
системе рассматривал также Н. К- Гиринский A947).
§ 8. Пример пространственной задачи. Рассмотрим плановую
задачу о течении в верхней полуплоскости плоскости (х, у).
Пусть ось х представляет собой вертикальный берег доходящего
до горизонтального водоупора канала. В начальный момент вре-
времени имеется постоянная глубина грунтовых вод Но и уровень
воды в канале внезапно изменяется так, что в одной части его,
при х < 0, устанавливается глубина воды Ни а в другой, при
х > 0, — глубина #2> которые затем поддерживаются постоян-
постоянными. Требуется найти уравнение свободной поверхности грун-
грунтовых вод г = h(x, yy t) в полуплоскости у > 0, т.е. по одну
сторону канала.
8] ПРИМЕР ПРОСТРАНСТВЕННОЙ ЗАДАЧИ 471
Искомая функция h удовлетворяет следующему уравнению:
2h , d2h
Решение уравнения теплопроводности (8.1) при начальном
условии
h(x9 у, 0) = /(x, у) (8.2)
и граничном условии
h{x9 0, t) = F(x, () (8.3)
имеет вид (Карслоу и Егер 1964; Соболев 1966)
оо оо
О —ею
В рассматриваемом случае
Г Н\ при х < О,
Нз при х>0. (8.5)
Так как граничная функция F(x, t) не зависит от времени, то
предварительно преобразуем второй интеграл, выполнив в нем
интегрирование по т. Получим
оо оо
— оо О
Подставим теперь в эту формулу выражения (8.5) и при-
примем во внимание равенство
472 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ 1ГЛ. XIII
Подстановка g — jc = т| дает
Ч2 + У2\ rfti
Ш I r\2 + у2 '
о
что можно переписать еще так:
h(х, у, t) = Н0erf (-U) + Hl±M?С ехр(-*+?)_*!_
+ (Я,-Я2)УГ (_jii±ji\_^t (8>
1 я J г \ Ш ) п2 + у2 к
о
Интеграл с постоянными пределами, входящий в последнюю
формулу, приводится к функции ошибок, а именно,
(8.9)
Для вывода равенства (8.9) заметим, что
00 оо
(«g)rf6, J e--co
Поэтому можно произвести такие преобразования интеграла
оо оо оо
~п ««'+»•) -у^о- = - \ dA e-»w-^-««' cos(«|) du =
oo
оо оо
— [
л J + J J
oo
Подстановка ?/B<\Лг ) + Л-\/^ =^ Дает J = erfc(h'>/n ).
§ 81 ПРИМЕР ПРОСТРАНСТВЕННОЙ ЗАДАЧИ 473
Использовав (8.9), приведем выражение (8.8) к виду
Из (8.10) следует, что напорная функция h состоит из трех
слагаемых: первое получается от первоначального уровня грун-
грунтовых вод, второе соответствует одномерной задаче с постоян-
постоянным напором (Н{ + Я2)/2, а третье, зависящее от х> определяет
асимметрию течения вследствие разности напоров в верхнем и
нижнем бьефах.
При / = оо получаем установившееся движение, для кото-
которого уравнение свободной поверхности имеет вид
w+^^^^^^^> (8Л1)
Это—уравнение винтовой поверхности: она образована пря-
прямыми лучами, исходящими из различных точек оси z и лежа-
лежащих в горизонтальных плоскостях, и имеет форму веера, развер-
развернутого на 180°.
Теперь рассмотрим ту же задачу в предположении, что об-
область движения подстилается слабо проницаемым грунтом тол-
толщины d с коэффициентом фильтрации &* (ср. § 1 и 4). Тогда
можно принять уравнение
Положим, что начальная высота грунтовых вод совпадает
с напором #о, и пусть
h = H0 + e-btu. (8.13)
Требуется определить движение в полуплоскости у > 0, если
дано, что Н = Но при / = 0, а при t > 0 и у = 0
Нх при х < 0,
_/ н ' (8.14)
#2 ПрИ X > 0. V '
Для функции и эти условия принимают вид
и = 0 при / = 0,
u = {H{-Ho)ebt при х<0, у = оЛ (8.15)
u = (H2-H0)ebt при х>0, у = 0
Поскольку функция и(х, уу t) удовлетворяет уравнению (8.1),
решение для и можно найти с помощью формулы (8.4),
474 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XII!
подставив в нее /(|, х\) — 0 и
Ъ-Ндё* при ?<0,
Hi-H^e^ при 1>0.
Тогда получим
О —оо
{^i^?)l^. (8Лв)
О О
Введем подстановки
'У-УУ-О, ^-y + f2^^ (8.17)
соответственно для первого и второго из интегралов формулы
(8.16). Переставляя пределы, получим окончательно
О и,
Г
?
I b(H2-Ho)y f f -«-?
^ 4jta J J
0 a; i
Здесь введены обозначения
У2
Найдем форму свободной поверхности в предельном случае при
/ = оо. Это будет форма свободной поверхности в установив-
установившемся движении. Нам нужно вычислить интеграл
_*,_?.
к dX. (8.20)
о
Подстановка X = л/с е~* приводит этот интеграл к такому:
оо
/ = Vc" J в-2^<*'-'Л. (8.21)
§ 8] ПРИМЕР ПРОСТРАНСТВЕННОЙ ЗАДАЧИ 475
Существует следующее представление модифицированной функ-
функции Бесселя второго рода:
APW 2 slnpji ~ 2 ) е "'•
Таким образом, J = 2л/с К\Bл/с ).
Подставив полученное выражение в формулу (8.18) и заме-
заменив в первом из интегралов | -\- х на ?, а во втором | — х на ?,
получим
д:
F(?)rf5, (8.23)
О
где
В частном случае Hi = Я2 получаем одномерную задачу
о вытекании воды из канала. Решение будет зависеть лишь от
координаты у, и вместо (8.12) будем иметь
Подстановка (8.13) приводит это уравнение к обычному урав-
уравнению теплопроводности, решение которого, удовлетворяющее
условиям и(у, O) = f(y), u@f t)= F(t), имеет вид (см. Соболев
1966)
оо
2 [F(t - JL.) e-n> dr] U = -4=1 • (8.24)
Vn J V 4a4V V 2л/at J
476 ЛИНЕАРИЗОВАННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. XIII
В рассматриваемом случае f(y) — H0, F(t) = ebi(Ht — Яо) и
(8.24) дает
h {у, t) = Яо + (Я2 - Яо) е-и erf ц +
+ (Я, - Яо) [ch д/4 у -1 ехр (д/| г/) erf (|) +
+ т ехР (- VI"у)ег{ (л)]' (8<25)
где
2 у
При выводе формулы (8.25) использовано выражение интеграла
Для установившегося движения при / = оо получаем из (8.25)
простую форму свободной поверхности: h(y, оо) = #0 +
+ (#i — #о)ехр(— л/b/a у). Она же может быть получена из
уравнения (8.23) при Я1 = Я2.
Глава XIV
ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ
А. ОБРАЗОВАНИЕ И РАСТЕКАНИЕ БУГРОВ ГРУНТОВЫХ ВОД
§ 1. О поливах и растекании бугров грунтовых вод. При оро-
орошении или при прохождении дождя происходят сложные явле-
явления в верхних слоях грунта. Вода впитывается почвой, имею-
имеющей определенную сложную структуру, и поглощается корневой
системой растений. Затем, поступая в листья растений, вода ис-
испаряется — говорят, что происходит транспирация влаги расте-
растениями. Часть поливной воды испаряется с поверхности орошае-
орошаемого участка.
Под зоной поверхностного увлажнения грунта образуется
зона капиллярно-подвешенной влаги. Ниже залегает воздухона-
сыщенная зона, называемая зоной аэрации грунта, еще ниже
имеется поток грунтовых вод, с каймой капиллярного подъема
над ним.
Идеальным представляется случай, когда влага сохраняется
в двух верхних зонах, не просачиваясь ниже. Однако, как пра-
правило, при обычных способах орошения влага не удерживается
полностью во взвешенном состоянии. Отдельными струйками
или каплями она проходит через зону аэрации и попадает на
поверхность грунтового потока или его капиллярной каймы —
эта часть поливной или дождевой воды составляет инфильтра-
инфильтрацию на поверхность грунтовых вод. С самой поверхности может
происходить также испарение.
После полива (или выпадения дождя) на поверхности грун-
грунтового потока образуется бугор, который в дальнейшем мед-
медленно рассасывается, создавая местное повышение уровня. Ча-
Часто бывает, что это повышение, достигающее иногда одного
метра в год и больше, через несколько лет приводит к засоле-
засолению (см. главу XV) или заболачиванию орошаемого участка.
Кроме поливов и выпадения атмосферных осадков потери на
фильтрацию из поверхностных вод могут создаваться за счет не-
несовершенства поливных устройств, фильтрации из оросительных
каналов и т. п.
Для описания того, что происходит на поверхности грунто-
грунтовых вод, при наличии подстилающего грунт горизонтального
478 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
водоупора служит выведенное ранее (см. § 1 главы XIII) урав-
уравнение типа уравнения теплопроводности
dh ( d2h . d2h
а+
где
khcp w(x9y,t)
Здесь w(x, yi t)= e — с — разность между инфильтрацией и ис-
испарением, а глубина h отсчитывается от водоупора.
Будем рассматривать безграничную область плоскости (я, у)у
над некоторой частью которой производится полив, при усло-
условии, что в то же время происходит растекание ранее образовав-
образовавшихся бугров.
Если начальная форма поверхности грунтового потока есть
h(x9 у, 0)= ho(x, у), то решение уравнения A.1) имеет вид (Со-
(Соболев 1966)
оо оо
h (х, у, t) = j^j J J exp (- ^-) h0 (xu yx) dx1 dyx +
yutl)dxldyl, A.2)
— oo —oo
oo oo
— OO —<X5
где r2 = (x-x[J + {y-ylJ.
Для плоскопараллельного движения на плоскости (jc, h)
вместо A.1) будем иметь уравнение
а его решение для h(я, 0) = h0(x) принимает вид
оо
h (х, t) = —=• t exp (- ^^-^Л К (хх) dxx +
§ 2. Растекание бугров. При поливе или дожде происходит
просачивание воды в грунт, а после их прекращения происходит
растекание образовавшегося бугра или столба грунтовых вод.
Если не учитывается инфильтрация или испарение, то форма
бугров, изменяющаяся со временем, определяется первыми сла-
слагаемыми формул A.2) и A.4).
§ в] РАСТЕКАНИЕ БУГРОВ 479
Одним из простейших случаев будет растекание бугра, в на-
начальный момент представлявшего столб в виде прямоуголь-
прямоугольного параллелепипеда высотою ДЯ над прямоугольником
(—R ^ х ^ R, —R\ ^ у ^ R\). При этом начальное положение
свободной поверхности грунтовых вод записывается в виде
|>tf, \y\>R{
ho(x,
и
ho(x>
y) = h
у) — ft
Jo = const
^ = Яо + А/:
при
l при
По формуле A.2) имеем (при w = 0)
-R
Подстановка хх — х = 2л/а( и, у{— у = 2 л/at v приводит к ра-
равенству
h (*, у, 0 = Яо + ~ \ е~« da \ е~« dv
Каждый из сомножителей правой части представляет раз-
разность значений функции ошибок erf z. С учетом нечетности этой
функции имеем
B.1)
f Azi + erf-^iY
2 л/at 2 V at )
В центре прямоугольника (при х = у = 0) формула B.1) дает
h @, 0, t) = H0 + АЯ erf X erf Я! B.2)
|Л= 7=" » Ai = 7==г)«
V 2^at l 2 Vat )
Введем безразмерные величины
т==_, „(T) = -i_J , й = т, B.3)
480 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Тогда получим
u(x) = erl-4=rerl-?=r. B.4)
Для больших значений т имеем и(х)« 4п/(ят).
При п = оо имеем случай плоского течения в плоскости
(х, А), другими словами, случай растекания полосы:
B.6)
На рис. 284 представлены формы поперечных сечений бугров
в координатах (и, g), где ? = x/R> при т = 0, т=1ит = 4
(Муминов 1967): сплошные кривые отвечают значению п = оо,
а пунктирные — п = 1.
На рис. 285 представлены графики понижения бугра в центре
прямоугольника для различных значений п. Кривые зависимо-
зависимости максимальной ординаты от времени сначала круто спадают,
затем растекание становится все более медленным.
Заметим, что в формулах B.1) и B.5) любой момент вре-
времени / = t\ может быть принят за начальный, тогда начальная
форма бугра будет некоторой плавной поверхностью.
Если начальная функция А0(л;, у) представляется в виде
суммы нескольких слагаемых, то и h(x> у> t) будет суммой соот-
соответствующих слагаемых.
На рис. 286 представлена зависимость от т уровней грунто-
грунтовых вод для середины бугра в случае растекания полосы, а так-
также для точек I = x/R = 1 и | = 2.
Отметим еще один случай, когда решение уравнения A.1)
получается в конечном виде; при
Ло (*, у) = А ехр (- а2х2 - РУ) B.6)
имеем
а2*2
1 + 4а2а/ 1 -
B.7)
Простой результат, получается для периодической функции
ho(x) = A cos(ax) (Кочина 1951):
h (л:, t) = A cos (a*) exp (— a2at). B,8)
При растекании бугра наибольшие ординаты его снижаются,
другие несколько приподнимаются, так, что общий объем в силу
несжимаемости жидкости все время остается постоянным. По-
Поэтому один бугор действует на другой всегда таким образом, что
в каждый момент в той или иной мере повышает его ординаты
и замедляет растекание.
РАСТЕКАНИЕ БУГРОВ
481
и
0,8
0,6
€,2
\
-
1,0
и
0.8
0,6
0,2
О
0,5
1 2
Рис. 284.
\
\
-~—
oo
1 ^.
— -
1 и
Рис. 285.
'
\
/
10 W
Рис. 285.
50
16 П. Я. Полубаринова-Кочина
482 динамика грунтовых вод при поливах [гл. xiv
§ 3. Некоторые случаи поливов. Будем считать, что полив
производится с постоянной во времени интенсивностью, т. е. что
в формуле A.2) /(*, */, t) не зависит от /. Тогда под знаком ин-
интеграла можно сделать замену переменной / —1\ на /. Получим
(считая ho(x, у) = Но)
" J
—oo —oo
Предположим, что полив производится по поверхности пря-
прямоугольника (—R ^ х ^ /?, —/?i ^ у ^ Ri), над которым w =
s= e = const, причем вне прямоугольника w = 0. Тогда по фор-
формуле C.1) будем иметь
f() f
-R -Я,
Применяя те же подстановки, что и в задаче о растекании,
найдем
at
X (
V
erf-^ +erf ^-^
2 л/at 2 л/at
Случай полива бесконечной полосы —R ^ x ^ R может
быть рассмотрен при помощи формулы A.4) или получен из
C.2) при /?i = оо:
t
А (*, 0 = Яо + •? J (erf f^f + erff^f) di. C.3)
Здесь интегрирование по частям приводит для
и &т)»5?-[А (*,/)-#<,] (S = f« Т = 1") C'4)
к такому выражению:
и (I, x) = F (I, т) + F (-1, т) + 6 (| - IJ, C.5)
} 3) НЕКОТОРЫЕ СЛУЧАИ ПОЛИВОВ 483
где 6 = 0 при Ш< 1, 6=1 при |?|> 1,
Интеграл в правой части формулы C.3) можно представить
в компактной форме (Аверьянов 1956, 1959):
C.6)
где
оо оо
i2 erf с г = \ dz2\ erf с z{ dzu erf с z = 1 — erf z. C.7)
z z2
Функции inerfc2 протабулированы в книге А. В. Лыкова и
Ю. А. Михайлова A963).
Возвращаясь к формуле C.2), рассмотрим подъем в центре
прямоугольной площади при х = у = 0:
t
h @, 0, 0 = Но + ^ J erf Я erf Kx dt9 C.8)
о
где
2 Vat 2 Vat
Для малых значений t аргументы сомножителей под знаком
интеграла велики. Применим асимптотическую формулу
ошибка которой не превосходит первого из отбрасываемых чле-
членов ряда. Мы отбросим 1/Bл:2). Тогда будем иметь
А @, 0, /) « #о + ¦?¦/ — Ajj; [f (*) + f (^i)l - 2/ fx (P), C.9)
где ___
/ (a) =« -3S2- H 3 h 3— erfca,
e-3 o? j_ d2
Это показывает, что для достаточно малых значений t подъем
центра бугра происходит равномерно со скоростью г/т. Продол-
Продолжительность стадии равномерного подъема зависит от размеров
поливного участка. При заданном R она наибольшая для Ri =
16*
484
ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ
[ГЛ. XIV
= оо, т. е. для полосы. В этом случае точное равенство имеет
простой вид
«(O,T)-x-[(,+i)erfcTir-Vf-p(-J-)]. (ЗЛО)
При т > 0, 1 линия и @, т) отклоняется от прямой. На
рис. 287 даны графики зависимости иA, т) от т для ряда зна-
значений g; на рис. 288—-зависимость от I для ряда значений т.
и
////
г
tmff/,
fa,
(У
ш
и
5
—-^
—^
-^
—
*—¦—.
——
50
Рис. 287.
/ 2
Рис. 288.
О
0,5
1,0
1,5
2,0
V
Май
1
\
Т ППП/ffi
f\
J
Июнь
лолид Цроли
\
VJ
\
Июль
Жполиб
\
V
Адгуст
Яполив
\
Сентябрь
Рис. 289.
Формулы A.2) и A.4) позволяют решать задачи о сериях
поливов, когда в разные промежутки времени происходят по-
поливы разной интенсивности. Для таких задач решения приве-
приведены Чжан Вэй-цинем A959).
На рис. 289 представлены кривые подъема грунтовых вод и
их дальнейшего опускания для натурных наблюдений на одном
§ 4] УЧЕТ ИСПАРЕНИЯ И ТРАНСПИРАЦИИ ВОДЫ РАСТЕНИЯМИ 485
из участков орошения (Крылов 1947) (по оси ординат отло-
отложены глубины в метрах, отсчитываемые от поверхности земли).
Сравнение с ними приведенных выше теоретических кривых по-
показывает, что общий характер тех и других одинаков.
Отметим, что наблюдения над уровнем грунтовых вод во
время полива и в следующий за ним период могут дать возмож-
возможность вычислить важную численную характеристику грунта —
величину а = khcp/m. Эта величина учитывает суммарно водо-
водопроницаемость грунта и глубину слоя грунтовых вод.
§ 4. Учет испарения и транспирации воды растениями. В лет-
летнее время большую роль в режиме грунтовых вод играет испа-
испарение воды, причем оно может происходить или непосредственно
с поверхности грунтовых вод, или через посредство растений,
которые впитывают из почвы влагу, испаряющуюся затем с по-
поверхности листьев (транспирация).
На основании ряда наблюдений на орошаемых участках
М. М. Крыловым A947) исследована зависимость интенсивно-
интенсивности испарения и транспирации от глубины залегания свободной
поверхности грунтовых вод. Эта зависимость оказалась близкой
к линейной. Обозначив интенсивность испарения через с, можно
написать эту зависимость в виде с = р — ау, где у — ордината,
отсчитываемая от поверхности земли, которая считается гори-
горизонтальной плоскостью. Полагая у + h = /, где / — расстояние
от поверхности земли до водоупора, получим c = a{h — /) + р.
Обращаясь теперь к уравнению A.1), введем величину w/m
в виде
Здесь учтена также инфильтрация, интенсивность которой обо-
обозначена через е, и введены обозначения Ь = а/т, Н = 1—р/а.
Вместо A.3) получим уравнение
dh d2h i // rr\ i в / л cw
_==a___fe(A_//) + _. D.2)
Это же самое уравнение, лишь с другими значениями по-
постоянных 6 и Я, получается при учете вертикальной скорости,
которая имеет место на границе со слабо проницаемым про-
прослоем.
Приведем решение уравнения D.2) для случая полосообраз-
ного дождя (или полива). Выпишем здесь без вывода соответ-
соответствующие формулы, введя безразмерные величины
и—Пг(А-Я). 6—j-. *2 = W, a—g-. D.3)
486 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Для иA, т) будем иметь при полосообразном поливе с учетом
испарения (или слабого просачивания в нижележащий грунт)
при UK 1
и = А -2,-[erf (^ЦЬ») +erf
- е-* »+« erf с (аA+6) - т) - е~** "-» erfc (a{l~l) - т) -
_ ^ad+y erfc (аAт+6) + т) - ***<i-$> erfc (аA~ё) + т); D.4)
при |?| > 1
и = - 2*-[erf ««±il - erf -^ii] -
erfc (a(gT+1) -T)-**»<*+»erfc (qFT+1) + т) +
) . D.5)
(^} + т)
В рассматриваемом случае линии свободной поверхности не
будут неограниченно подниматься вверх, как это имело место
в случае отсутствия испарения; они будут стремиться к предель-
предельному положению. Именно, при /-»-оо (соответственно) внутри
и вне участка ||| < 1
н->4A --e~2a ch 2a?), и -> Ае~^ sh 2a. D.6)
На рис. 290 даны графики зависимости а от \ при а = 1 для
нескольких моментов времени. На рис. 291 показаны предельные
положения свободной поверхности для ряда значений пара-
параметра а.
Растекание бугра грунтовых вод при наличии
испарения. Будем считать, как и в § 4, испарение линейной
функцией /г, инфильтрацию будем считать отсутствующей (е=0)
или включенной в слагаемое ЪН. Тогда после подстановки
h-H = e-btU D.7)
для U получим уравнение теплопроводности. Его решение для
растекания полосообразного столба воды, в начальный момент
расположенного над отрезком |я|</?, имеет вид B.5), а для
нашего случая из D.7) получим
А <*. 0 - * + е- [ЯО - Я + М. ^rf f^f + erf $+?)]. D.8)
Здесь Но — первоначальная глубина грунтовых вод, АЯ — вы-
высота столба воды над первоначальным уровнем. Как видно, при
t-+oo глубину грунтовых вод h стремится к постоянному значе-
значению //==/ — р//
4] учет испарения и транспирации воды растениями
48?
488 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Б. О РЕГУЛИРОВАНИИ УРОВНЯ ГРУНТОВЫХ ВОД
ПРИ ОРОШЕНИИ
§ 5. Постановка задачи. При орошении больших площадей
возникает опасность подъема грунтовых вод. Если уровень
h (x, у, t) поднимается выше некоторого уровня /7#, начиная
с которого испарение становится интенсивным, то появляется за-
засоление или заболачивание почвы. Если полив происходит с от-
откачкой подземных вод, то понижение уровня ниже некоторой
величины #** может оказаться нежелательным, так как повле-
повлечет истощение водоносного пласта. В связи с этим желательно
такое регулирование процесса орошения, чтобы полив выклю-
выключался при достижении в некоторой выбранной точке уровня //*
и включался вновь, когда уровень в этой точке понизится до #**.
При этом уровень грунтовых вод будет описываться уравнением
где а = khcvjm, b = kj(tnd), H — постоянный напор в подсти-
подстилающем слабо проницаемое основание пласте, k^ и d — коэффи-
коэффициент фильтрации и толщина слабо проницаемого основания,
(х°, у°) — контрольная точка, по
поведению уровня грунтовых
вод в которой принимается реше-
решение о включении или прекраще-
прекращении полива.
Для F(h{x°,y°,t)) примемсле-
дующие условия:
( а{ при h < #„,
I —¦
Рис. 292. I — 0*2 при h > #„,.
Здесь о\ = (е — с)/т, ог = с/т, где е — интенсивность инфиль-
инфильтрации, с — интенсивность испарения.
Нужно решить уравнение E.1) с некоторыми начальными ч
граничными условиями.
График функции F(h(x°> y°>t)) дан на рис. 292. Он характе-
характеризуется наличием при #** < h < #* участка неоднозначности.
Выбор значения F на этом участке зависит от того, каким было
значение F для предыдущих моментов времени, соответствую-
соответствующих участкам однозначности. Уравнение E.1) представляет
уравнение релейного типа, соответствующее включениям и вы-
выключениям некоторого механизма. Такого рода задачи рассмо-
рассмотрены Н. Н. Кочиной A971 — 1973).
§ 6] ОДНОМЕРНАЯ ЗАДАЧА С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ 489
§ 6. Одномерная задача с непроницаемым водоупором. Будем
предполагать, что грунтовые воды занимают область 0 < х < /
между каналами (или дренами) с уровнями воды Н\ и Н2 со-
соответственно. В точке х = х° @ < х° < /) измеряется уровень
грунтовых вод ft. Когда этот уровень достигает величины #*, по-
полив прекращается и начинается вновь, когда h уменьшится
до #**.
Это задача сводится к нахождению решения уравнения теп-
теплопроводности с правой частью, релейно зависящей от уровня
грунтовых вод в точке х° с граничными условиями
Полагая в E.1)
h (*, 0 = #1 + (#2 — Hx)± + u (*, /), 6 = 0, F.2)
сведем задачу к нахождению решения и(х, t) уравнения
^ = aJ? + F(u(x°,t)), F.3)
где
0! ПрИ U (Х°, 0 < Ы„
при и (х°у t) > и^,
с условиями
и @,0 = 0, и (/,0 = 0 F.5)
("** < и*> °\ > 0, 0*2 > 0). Здесь введены обозначения
¦4- F-6)
И*0, 0) = [ __\
Уравнению F.3) — F.4) и граничным условиям F.5) удовле-
удовлетворяют стационарные решения
*(*)== ¦?*('-*). F.7)
*>(х) = -%.хA-х). F.8)
Исследование методом малых возмущений показывает, что
эти стационарные решения устойчивы (Кочина 1972).
Рассмотрим теперь решение задачи F.3) — F.5) с начальным
условием
и(*,0) = Ф(*), F.9)
где Ф (jc) = ф (х) -Н{- (Н2 - Нх)± , ф W = Л (jc, 0).
Будем считать для определенности, что /7(w)=ai при
(p(xo)<a* и F(u) = — a2 при ф(хо)>а*. Тогда решение за-
задачи F.3) —F.5), F.9) до некоторого момента времени будет
490 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
описываться выражениями
оо
и, (х, /) = ? {С„ехр(-аД0 - <т1а„[1-ехр(-Л2„/)]Ьт^, F.10)
зт2^. F.11)
/1-1
Формула F.10) имеет место при ф(#°)<«*, F.11)—при
ф(*°)> ".-
Здесь введены обозначения
_ яУ^Г/г _ 2/Ч(-1)п- 1] , « 2 у /61„ч
Сп и Dn — коэффициенты Фурье функции ф(х), которую считаем
удовлетворяющей условиям Дирихле:
F.13)
Нетрудно убедиться, что при стремлении времени / к беско-
бесконечности решение U\{x, t), определенное формулой F.10), стре-
стремится к v(x), решение и2(х, t) F.11)—к w(x). Таким образом,
если q>(*°)|< v(x°) < и*, то при неограниченном возрастании
времени / решение F.10) стремится к стационарному решению
v (х). Аналогично, если ф(#°)> и* и w(x°)> и**, то F.11) стре-
мится к стационарному решению ay(x). Можно видеть, что в за-
зависимости от соотношений между величинами и*, и**, v(x°) и
w(x°) осуществляется один из четырех случаев поведения реше-
решения задачи.
Примерный вид зависимости и(х°, t) для этих случаев пред-
представлен соответственно на рис. 293—296.
Случай 1: и** < w (х°) < v (х°) < и*. Если ф (х°) < и* ре-
решение описывается формулой F.10). При /-*оо U\(x, t)->v(x),
т. е. решение стремится к стационарному решению F.7)
(рис. 293, кривые 1). Здесь предположено, что ф(#°) < v(x°).
Если v(x°) < ф(а:°) < и^ то возможен также случай, аналогич-
аналогичный представленному на рис. 295, кривая 5.
При ф(#°)> и* решение описывается формулой F.11). При
t-+oo u2(x, t)->w(x), т.е. решение стремится к стационарному
решению F.8) (рис. 293, кривая 2).
Случай 2: w(x°) < и„ < v (х°) < и*. Для q>(*°) < «„ ре-
решение описывается формулой F.10). При /->оо их{х, t)~>v(x)
(рис. 294, кривые 3).
Если ф(х°)> и*, решение дается формулой F.11) и2{х, t) до
момента времени / = Ти когда и2(х°, Г1)== и**. Начина^ с MQ'
§6] ОДНОМЕРНАЯ ЗАДАЧА С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ 491
менТа / = Тх решение описывается формулой F.10) для U\(x, t),
в которой t следует заменить на /— Гь а Сп — коэффициенты
Фурье функции и2(х, Т\), где и2(х, t) дано выражением F.11).
При t-+oo u\{x,t)->v{x) (рис. 294, кривая 4).
Рис. 293.
Рис. 294.
Рис. 295.
Рис. 296.
Случай 3: и„ < w (х°) < и* < v (х°). В случае ф (*°) < иф
решение дается формулой F.10) для и\(х9 t) до момента / = Ти
когда u\(xo,T\) = u*. Начиная с момента Ти решение описы-
описывается выражениями F.11), где нужно t заменить на t—Т{,
a Dn — коэффициенты Фурье функции и,\(х,Т\). При /->оо
{, t)-> w(x) (рис. 295, кривые 5).
Если ф(л:о)>^*, решение дается формулой F.11). При
>oo u2{x, t)->w(x) (рис. 295, кривая 6).
492 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Возможны еще картины, аналогичные описанным выше.
Случай 4: w (х°) < и^ < и* < v (х°). При ф (х°) < и# ре-
решение описывается формулой F.10) до момента t = Гь когда
Щ{х°> Т\)=и+, затем формулой F.11), пока не будет t = Т2,
где и2(х°, Т2) = и** и т. д. Следовательно, решение имеет коле-
колебательный характер. Н. Н. Кочина A972) выписала это реше-
решение и показала, что при w \х°) < и** < и* < v (x°) оно стре-
стремится к периодическому (рис. 296, кривая 7), которое мы сей-
сейчас рассмотрим.
Из сказанного в начале § 5 следует, что оптимальным яв-
является четвертый режим.
Для ф(х°)>и* решение снова имеет колебательный харак-
характер, описываясь то формулой F.11), то формулой F.10), и при
безграничном росте времени / стремится к периодическому
(рис. 296, кривая 8).
Таким образом, решение начально-краевой задачи асимпто-
асимптотически стремится либо к одному из двух устойчивых стацио-
стационарных решений, либо к периодическому решению.
Будем искать периодическое решение задачи F.3) — F.4)
с граничными условиями F.5). Начальное условие заранее не
задаем, оно получится из условия периодичности.
Предположим, что имеются два значения Тх и Г, удовлетво-
удовлетворяющие условиям
и(х°,Т1) = и„ и(х°9Т) = и„. F.14)
Здесь Т\ — продолжительность стадии полива, Т — период коле-
колебания. Введем обозначения
при Г</<Г J F 5)
Тогда F = о\ для щ(х, t), F = — о2 для и2(х, t).
Запишем выражения для функций U\(x, t) и и2(ху t) в виде
рядов
F.16)
«2 (*, 0 = 2 (D«exP (- я« С -
где
)»
_ 2Р [(-I)»-1) 2 _
"— ая3л3 ' "—
§6] ОДНОМЕРНАЯ ЗАДАЧА С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ
493
Чтобы решение было периодическим, должны выполняться ра-
равенства
Щ (х, 0) = щ (х, Г), щ (*, Тг) = щ (х, Тх). F.18)
В силу соотношений F.16) и F.17) из равенств F.18) выте-
вытекают выражения для постоянных Сп и Dn'
_ «л [- gi (Уп - 6/t) + сг2 A — у„)]
F.19)
где
Из F.17) и F.19) ясно, что ряды F.16) равномерно схо-
сходятся.
Величины Т\ и Т найдутся как наименьшие корни уравнений
и{х°, Т{)= и* и и(х°, Т)= и„.
В силу F.16) и F.19)
(Р/г -
sin ~Г —
«я I- gi (Y/i - 6/t) + сг2 A —
Рассмотрим простой случай о\ =
F.19) и F.20) примут вид
sin / —
F.20)
= а, Г = 271!. Формулы
1 -- р„ . ппх°
/г-1
F.21)
Пусть х° = 1/2. Тогда в силу F.17) из F.21) найдем
Г _ = 4/2 а ]~&k-i с =0
w. = -
ая3 Z-. B/г— IK l+p2ft_,
fti
F.22)
ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Рассмотрим функцию
Bk-о3 \ + hk-i(Ti) •
Ясно, что у@) = 0, y/G1i)>0. При стремлении Г! к беско-
бесконечности у стремится к величине
Zj Bfc — IK ='32"#
Отсюда получаем следующий результат: единственный ко-
корень Т\ > О уравнения F.22) существует, если выполнено не-
неравенство
* " Та ^ Т'
Таким образом, при этом условии существует единственное
решение рассматриваемой задачи. Оно описывается формулами
F.16), где Сп и Dn даны равенствами F.21) —F.22).
При о\ = 02 = а и Т = 2Т\ формула F.21) дает
Sin
• /2(Т я3 Z-f B^— IK l+p2fc-,
Из F.23) легко видеть, что [/*@)= 0. С ростом ii = аТ{/Р,
как показывают расчеты, U^ растет, причем при стремлении ц
к бесконечности О* стремится к
и°°— 2 / \1 I ) '
Следовательно, и в этом случае при U* < f/oo существует
единственное решение ц.
В общем случае из формул F.20), вводя обозначения
у _ аи* у _ аи„ x = ^lL т = аТУ s = — F 24)
* /2(Ti ' ** /2(Ti ' /2 /2 ' (Ti '
получаем такие выражения для функций U^(xux) и Um(xux):
п = JL V [1 — p2fe-i — ^p2fe-i A — V2fe-i)]
U* я3 ? {2k 1K A р?)
L
я3
[y2fe-i A — p2fe-i) — s A — v2fe-i)] . _
/Of. 1 \Q / 1 Л \1 will
F.25)
где
hk-i = exp (- д2 BЛ - IJ tO, Y2*-i = exp(- д2 Bft - IJ (t - x{)).
§ 6] ОДНОМЕРНАЯ ЗАДАЧА С НЕПРОНИЦАЕМЫМ ВОДОУПОРОМ
495
Из F.25) ясно, что при стремлении ti и т — х\ к бесконеч-
бесконечности U* и и** стремятся соответственно к (Л» и —sUoo.
0,15
0,15
0,10
0,05-
-0,05
-0,10
0,05
/
5 6
Y^—Т
::»- - .-
/
\^-
^>^.
I -
^-
[±
2
1
2
•3
^6
0,15 0,5 0,75
Рис. 297.
0,15
0,10
0,05 \
1,0
0,25 0,50 0,75
Рис. 298
-0,05
-0,10
fx
.
ч
us
Рис. 299.
На рис. 297 построены графики функции [/#, определенной
формулой F.23), в зависимости от х\ для различных значений
496 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ 1ГЛ. XIV
параметра х°/1. На рис. 298 для случая s = 0,5, т = Зп по-
построены зависимости 1/# и ?/** от Ть При этом на рис. 297 и 298
кривым 1 — 6 соответствуют пары значений х°/1 0,08333 и
0,91667, 0,16667 и 0,83333, 0,25 и 0,75, 0,33333 и 0,66667, 0,41667
и 0,58333, 0,5.
На рис. 299 построены графики функций U* и [/** в зависи-
зависимости от х\ для случая s = 0,5, х°/1 = 0,5, т = vti (/ — v = 4,
2 — v = 2, 3 — v = 4/3).
Из вида кривых t/.(n, t) и 1/»#(ть t), аналогичных построен-
построенным на рис. 297—299, ясно, что каждой паре значений I/, и 1/м,
удовлетворяющих неравенствам —slloo < ?/** < U* < ?Л», со-
соответствует единственная пара значений х\ и т.
Используя асимптотическое поведение решений краевых за-
задач для параболических уравнений, можно показать, что рас-
рассмотренные выше случаи верны и для более широкого класса
задач.
§ 7. Движения с перетоками. На практике часто встречаются
случаи, когда основание слабо проницаемо. Будем считать его
также горизонтальным, имеющим постоянную мощность d и ко-
коэффициент фильтрации ?*, причем k4 <C k.
Интенсивность испарения будем предполагать равной
(vft + M-)m- Нужно считать, что здесь либо v = 0, \х > 0, либо
v > 0, \х < 0, причем в последнем случае полученные резуль-
результаты будут верны для уровней грунтовых вод, не меньших ве-
величины — (Ll/V.
Мы можем также приближенно учесть вертикальную откачку
грунтовых вод, «размазывая» скважины вертикального дренажа
по всей области 0 < х < / между дренами или каналами и пе-
перенося граничные условия на скважинах в дифференциальное
уравнение добавлением как бы «испарения» с соответствующей
интенсивностью (см., например, Чиркин и Шульгин 1964).
Рассматриваемая начально-краевая задача сводится к на-
нахождению решения неоднородного уравнения теплопроводности
(Кочина 1973,2)
w=a If -b (h - H) + F№> '))> G-i)
где теперь, в отличие от E.1), Ь = kj(tnd) + v, a
Г а, при h (*°, 0 < Я,
(а, = г/т — vH — ц, сг2 = vtf + ц), с граничными условиями
h(O,t) = Hu h(l,t) = H2 G.3)
и начальным условием
h{x, 0) = q>(*). G.4)
§71
ДВИЖЕНИЕ С ПЕРЕТОКАМИ
497
Здесь е — интенсивность инфильтрации, b = kJ(md)-{- v,
k*(H — h)fd — скорость просачивания через слабо проницаемое
основание. В выражение для Ь включено влияние не только
слабо проницаемого основания, но и испарения, если оно проис-
происходит по линейному закону.
Можно убедиться, что уравнение G.1) — G.2) с условиями
G.3) при этом имеет устойчивые стационарные решения 1>о(*)
и wo(x):
Здесь
С,= (Я2-Я---^-
sh
1
shvT''
sh A/ —
sh
А / — /
V а
» ехР (- tit) sin-=Ji @ < / < Г,),
G.5)
G.6)
Периодическое решение задачи дается зависимостью
(х, t) = Hi+ i V Щ (^, 0 (* = 1. 2), G.7)
где
щ (Ху t) = v {х) -
«а (х, 0 = а» (*) + 2] Оге ехр (- Я2ге (/ - Г,)) sin ^р (Г, < / < Т),
. . ^ _ - е„ A - у„) г, _. е„ A - рп)
/2 -to, ьп— fTI^- , ^„ — , _Ьп ,
2 (or, + a2)
498 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ [ГЛ. XIV
Здесь vni wn и 6„ — коэффициенты Фурье функций
iK*) = M*)-tfi-(tf2-tfiO'
w(x) = w0 (x) - #1 - (Я2 - Я,) j,
6 (л:) = у (л:) — ш (л:).
Величины 7^ и Т2 = Т— 7^ находятся как наименьшие корни
из системы двух уравнений
G.8)
оо
Т\ "V* А У/г 0 — Р/г) _• ftfl*° ,. _Л1 /vo\
Здесь по-прежнему
Из G.7) и G.5) видно, что
w{x°)
G.9)
При Т\ = Т2 = 0 функции ф^, Г2) и ^(Гь Г2) не являются
непрерывными. Из вида G.8) функций V\ = ф(Гь Т2) и V2 =
= ^(^ь Г2) легко показать, что паре значений V\ и К2, удовле-
удовлетворяющих неравенствам w(x°)— v(x°)< V\ < 0, 0 < К2 <
< v(x°)— w(x°), V2— V\ < y(JC°)— «;(jc°), соответствует одно-
однозначным образом пара значений 7^ и Г2, не обращающихся
в нуль одновременно.
Таким образом, каждой паре значений и* и и**, удовлетво-
удовлетворяющих неравенствам ^(л:°)< и^ < и* < v(x°), соответствует
одна пара значений Т{ Ф 0 и Т2 Ф 0.
Рассматривая вместо периодического решения G.7) перио-
периодическое решение, состоящее не из двух кусков щ{х, t) и и2(х, /),
а из 2т кусков u2j+l (x, t) и u2j+2(x, t) (j = 0, 1, 2, ..., m— 1),
можно видеть, что все куски с нечетными и четными индексами
совпадают между собой (u2j+\(xt t) = щ{х, t), w2j+2(a:, /) =
= U2{x> t)y j = 1, 2, ..., m — 1). Отсюда следует единственность
периодического решения G.7).
§ 8] ПЛЧАЛЬНО-КРАЕВАЯ ЗАДАЧА С ПЕРЕТОКАМИ 499
§ 8. Начально-краевая задача для движения с перетоками.
Обратимся к начально-краевой задаче G.1) — G.4)'. Если реше-
решение этой задачи существует, оно имеет вид
(*, /) = v {Х) ¦
?<? , / = 0,1.2,3,..., Г(о) = о),
/-о /-о /
/-0
/=0 /=0
(8Л)
= щ (xyt) — Hx j (/==1,2).
Здесь С{п — коэффициенты Фурье функции ф(л:) — v{x), Т{\+1)
и Ги+1) — наименьшие корни уравнений
Mi I*, 2u" +?t 1 = м». w-? I*. 2j " 1 = м„. (8.2)
\ /=0 / \ /-0 /
Функции v{x) и ^(л:) даются формулами G.7) и G.5).
Из формул (8.1) и (8.2) следуют соотношения
(8.3)
/г-1
При этом Р</) =
В силу равенств
'-° Ч "° ' - (8.4)
SoO
Динамика грунтовых вод при поливах
[гл. xiv
получаем зависимости
n n
= 6
n
Здесь 6„ — функции, определяемые из G.7).
Из формул (8.5) вытекают равенства
П UL П
) ) = Q J}il+\tk+\)
л л л
где введены обозначения
ГС *> = l — v(n + vUN(^ — v(/>B(/)v(f-n 4-
B^. *) = 1 — rw 4- B^V') — e^v^-^BC-1) 4-
/I x r/l «^ r/i Vrt Нл Гл Нл П^
(8.6)
(8.7)
При этом в формулах (8.6) за k может быть принято любое
число k^ 1.
После некоторых преобразований уравнения (8.2) с учетом
(8.1) и (8.6) для достаточно больших значений / приведутся
к виду
W "О +
«1, (8.8)
sin
(8.9)
fl-1
8] НАЧАЛЬНО-КРАЕВАЯ ЗАДАЧА С ЙЁРЕТОКАМИ
Здесь использованы обозначения (8.6) и положено также
у» = q [и, - v (x°)], Y(,0) = Р к» - w (х0)],
и„ — w (x°) — 8, sin—J .
(8.10)
В рассматриваемом случае 4 (§ 6) выполняются неравенства
а. - о (*°) < 0, а„ - а; (*°) > 0. (8.11)
Из формул (8.8) — (8.11) можно видеть, что уравнения
(8.8) — (8.9) при любых значениях р{0) и y!0) имеют хотя бы по
одному решению. Если имеется несколько решений уравне-
уравнений (8.8) — (8.9) pj?+1) и y(/+1)> то берем наибольшие из этих зна-
значений.
Можно показать, что имеют место следующие зависимости:
limp'/+»=p HmYi'+1> = Y,, (8.12)
где Pj =exp(-~ЦТ^ и y{ =exp( —A,2(T — T{}) — рассмотренные
выше величины для периодического решения G.7). Можно ви-
видеть, что величины р(/> и y\i\ определяющиеся из уравнений
(8.8) —(8.9), ограничены, если и* — и** > О > 0 (что всегда со-
соответствует физическим условиям):
Р«Ш < Г < Ртах < 1. YmIn < Y(/> < Vmax < I- (8.13)
Пусть i достаточно велико. Константы pmln, Ymin, Pmax, Ymax
определяются методом последовательных приближений из урав-
уравнений, аналогичных (8.8) — (8.9).
Пользуясь формулами (8.8) и (8.9) для величин р|?+1) и у(/+1)
и оценками (8.13), можно показать, что существует такое число
0 < X < 1, что для достаточно больших значений i выполняются
неравенства
| | f | | / y!7) I < еГ-1 (8.14)
где
, _ (п-\)п . (п-\)п . , . п(п + \) . 9 я (/г+ 1) . ,
502 ДИНАМИКА ГРУНТОВЫХ ВОД ПРИ ПОЛИВАХ (ГЛ. XIV
если при / = 1,2,...,/ имеют место неравенства
е, | Y(/+1) - У\п | < е. (8.15)
С помощью (8.14) можно оценить разность |Р(/+Р) — P(/+I) |
при любом р = 2, 3, ... Используя неравенство треугольника
р(/+Р-0 —
I р(/+Р) — р(/ + 1) I <^ I р(/ + р) — р(/ + Р-1) I -|_ I р
и устремляя в формуле (8.14) п к бесконечности, можно пока-
показать, что выполнен необходимый и достаточный признак суще-
существования предела Pi последовательности р(,л. Аналогично до-
доказывается и существование предела Yi последовательности
Y</>. Подстановка Р(/) = Р1, Y(/) = Y1 в (8.8) — (8.9) дает G.8).
Результаты, аналогичные изложенным выше для одномер-
одномерного случая, получены также для задачи, описываемой уравне-
уравнением E.1) в случае прямоугольной области.
Заметим, что периодическое решение G.7), частным случаем
которого при Ь = 0 является решение F.16), F.17), F.19), оп-
определяет автоколебательный процесс, т. е. процесс, характер ко-
которого определяется свойствами самой системы, создающей эти
незатухающие колебания. Действительно, продолжительность
стадии полива Т\ и период автоколебания Т находятся из урав-
уравнений G.8) или F.20), т.е. определяются параметрами нашей
задачи.
§ 9. Случай переменных уровней воды в каналах. Пусть
теперь уровни воды в каналах или дренах зависят от времени:
hi = hi(t) (i = 1, 2). Тогда начально-краевая задача сводится
к решению уравнения G.1) — G.2) с начальным условием G.4)
и граничными условиями (Кочина 1973, 1)
А@,/) = tfi@, h(ltt) = H2@, (9.1)
В этом случае вместо G.9) имеем следующие соотношения:
и. @ = Н. - Я, (/) - [Н2 (/) - Я, (/)] 4-,
(9.2)
«.. (/) = я„ - я, @ - [я2 @ - я, @]^-. '
Предположим теперь, что выполнены условия
= 0 (/=1,2). (9.3)
§ 9] СЛУЧАЙ ПЕРЕМЕННЫХ УРОВНЕЙ ВОДЫ В КАНАЛАХ
Тогда из формул (9.2) получим
lim и„ (/) = Н„-Н1оо — (Я2оо - Н{ J -у- = ммо
503
(9.4)
Можно показать, что тогда указанные выше четыре случая
поведения решения соответствующих начально-краевых задач
верны и для этой задачи, если в формулах G.5) —G.9) заменить
величины Нг на Hioo (i = 1, 2). При этом в четвертом случае,
когда выполнены неравенства и^ — ^(л:0) <0, и^*оо — Woo{x°) >
> 0, аналогичные (8.11), имеют место зависимости (8.12) и ре-
решение асимптотически стремится к периодическому решению
G.7) (соответствующему указанной выше замене).
Глава XV
НЕКОТОРЫЕ ВОПРОСЫ,
СВЯЗАННЫЕ С ОРОШЕНИЕМ
А. О ФИЛЬТРАЦИИ ПРИ НЕПОЛНОМ НАСЫЩЕНИИ
§ 1. Фильтрация в почве при неполном насыщении. Почва
представляет собой трехфазную систему — твердые частицы,
вода и воздух с парами воды. Насыщенность почвы влагой яв-
является переменной. В теории движения почвенной влаги при
неполном насыщении считают, что давление и коэффициент во-
водопроницаемости — заданные функции насыщенности, причем
движением воздуха пренебрегают.
Было сделано наблюдение, что почвенные агрегаты содер-
содержат два вида пор — «капиллярные» и «некапиллярные». Дру-
Другими словами, имеются поры двух порядков крупности, причем
«капиллярные» поры обусловливают водоудерживающую спо-
способность почв, «некапиллярные» определяют быстрое просачи-
просачивание воды в почву. Считается, что для идеальной почвы сум-
суммарные объемы каждой из систем пор должны быть примерно
одинаковыми (Baver 1956). Такая почва имеет достаточную
аэрацию, хорошие проницаемость и водоудерживающую способ-
способность.
В нефтяной гидродинамике исследуется фильтрация в пла-
пластах, содержащих систему трещин и капиллярных пор (Барен-
блатт, Желтов и Кочина 1960). В неустановившихся течениях
могут оказаться существенными перетоки жидкости из одной
системы пор в другую. Такую модель можно перенести на дви-
движения воды в почве. Теорию движений газо- и водонефтяных
смесей можно было бы также использовать при изучении филь-
фильтрации воды в почве. Мы ограничимся простейшим рассмотре-
рассмотрением вопроса.
При выводе уравнения для насыщенности w грунта влагой
(влажности) исходят из уравнения неразрывности, которое вы-
выражает тот факт, что изменение массы жидкости, вытекающей
3 единицу времени из элементарного объема, компенсируется
§ 1) ФИЛЬТРАЦИЯ В ПОЧВЕ ПРИ НЕПОЛНОМ НАСЫЩЕНИИ 505
изменением насыщенности внутри этого объема:
dvx , dvy dvz dw
где vx, vy> vz — компоненты скорости фильтрации.
При неполной насыщенности грунта считают, что имеет ме-
место закон Дарси в форме
vx = -k(w)-%±r, Vy = -k(w)^, vz=-k{w)-^, A.2)
где напор h = ply + z. Здесь k(w)—коэффициент водопрони-
водопроницаемости при влажности w.
Уравнение A.1) с учетом A.2) можно переписать в виде
dw д_ (k(w) dp \ , J_ / k (w) dp \ . д ( k(w) dp \
dt ~ дх \ y dx ) + dy \ у dy ) + dz [ у dz )
A.3)
Для k(w) имеется, например, формула С. Ф. Аверьянова (см.
§ 10 главы I)
где т — пористость, w0 — количество связанной воды в единице
объема грунта, k\ — коэффициент фильтрации при полном на-
насыщении (когда w = т).
На границе фаз вода — воздух действуют капиллярные силы,
обусловливающие разность между давлениями в жидкости (р)
и в воздухе (рв):
P — Pb = Pk(w), A.5)
причем обычно pK{w) определяется с помощью полуэмпириче-
полуэмпирических формул. Давление воздуха будем считать постоянным, по-
полагая рв = 0. Чем меньше w, тем больше pK(w): при очень ма-
малой насыщенности пор водой она адсорбируется на поверхности
твердых частиц — образуется прочно связанная вода, которую
трудно отделить даже при очень больших скоростях центрифу-
центрифугирования. При увеличении w появляются слои рыхло связанной
влаги, при еще большей насыщенности она делается, наконец,
способной двигаться под влиянием силы тяжести (см. § 4
главы I). Зависимость pK(w) от w при малых значениях w носит
гиперболообразный характер. Мы будем применять формулу
С. Ф. Аверьянова
W
506 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ {ГЛ. XV
Здесь ро — давление при влажности w0 связанной воды, wn —
полная влагоемкость, т. е. влагоемкость, соответствующая ат-
атмосферному давлению р = 0.
§ 2. Приближенное решение простейших задач. В случае дви-
движения влаги по вертикали И. И. Крамаровская (Кулабухова
1967) предложила следующий приближенный прием решения.
Пусть w(z, t) удовлетворяет начальному и граничному усло-
условиям w (z, 0) = w2 и w @, /) = W\.
Допустим, что в момент времени t область, смоченная проса-
просачивающейся влагой, распространилась до уровня z = /(/). Тре-
Требуется найти зависимость / от t и распределение w с глубиной
(или высотой) в зависимости от /.
Зададимся простейшей зависимостью между координатой z
какой-нибудь точки жидкости и насыщенностью в ней w:
2 °
ДОТ — W'
4
B.1)
Выделим столб грунта между плоскостями z = 0 и z = /(/)
с площадью основания, равной единице, и составим уравнение
баланса
t i(t)
[= J [w{zyf)-w2]dz,
о
дифференцируя которое по времени и учитывая B.1), получим
М0,/) = Л-зр B.2)
где
1 J w2)
3 W\ + W2
С другой стороны, по обобщенному закону Дарси
Принимая формулы С. Ф. Аверьянова A.4) и A.6), получим
Vz@,t) = -k(wx)Uffe2-. B.3)
где
wl — Wq
2] ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПРОСТЕЙШИХ ЗАДАЧ 507
Интегрируя B.2), найдем
Будем считать W\ > w2, тогда В > 0. Рассмотрим два
случая.
Случай 1: /(/)>0, т.е. происходит капиллярное подня-
поднятие жидкости вверх. На рис. 300 приведены кривые, рассчитан-
рассчитанные по формулам B.1) и B.5) при следующих значениях пара-
параметров: wn = т = w\ = 0,4, w2 = 0,2, w0 — 0,04. Безразмерные
координаты \ и т определяются формулами
у. __ V [l —{wolwnf] _ powo (m — шрK'5 ,
^ poWo * у [1 — (wo/wnK] ki
При малых значениях / можно написать в формуле B.5)
вместо логарифма два первых члена его разложения в ряд по
степеням /. Получим
В уравнении B.5) при t-+oo имеем /->S, т.е. В является
высотой капиллярного поднятия.
Случай 2: /@<0> т- е. имеет место просачивание влаги
вниз (рис. 301). Вычисления проведены для тех же значений
параметров, что и в первом случае. Для удобства введем обо-
обозначение /(/)=—L(t), тогда вместо B.5) будем иметь урав-
уравнение
btl (±) B.6)
Теперь L(t) неограниченно возрастает. В обоих случаях, со-
согласно принятому допущению B.1), влажность w изменяется
с глубиной по параболе.
Для одномерного уравнения A.3), т.е. такого, в котором от-
отсутствуют производные по х и по у, преобразованного так, что
искомой функцией является z(w9 t), Дж. Филипом A972) был
предложен метод разложения z(w, t) в ряд по степеням tl/*.
B. И. Пеньковским A964) (см. также Полубаринова-Кочина
и др. 1969) этот способ был применен к отысканию первых чле-
членов ряда для pK{w) и k(w), взятых по формулам, предложенным
C. Ф. Аверьяновым. В линеаризованной постановке две задачи
рассмотрены И. И. Кулабуховой A959)—о линейном и точеч-
точечном оросителях.
508
НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ
[ГЛ. XV
С другими подходами к расчетам фильтрации при неполном
насыщении грунта можно познакомиться по многочисленным
0,20 0,24 0,28 ОД DJ6 №
w
Рис. 300.
\
\
*
.
Г-оо
\
s\
112,5 S
4J?4
^20,7
s
JO
\
L
/
/
/
3,0/
/
/
/
1
/
/
/,
7
/
У
J
Ц20 0,24 0,28 ОД ОМ ОАО
w
Рис. 301.
работам Дж. Филипа (см., например, его обзор в сборнике «Изо-
«Изотермическое передвижение влаги в зоне аэрации», 1972 г.).
§ 3. Статистический способ определения коэффициентов
фильтрации и диффузии. Уравнение A.3) для одномерной филь-
фильтрации вдоль оси z может быть записано так:
Здесь D(w) можно назвать коэффициентом диффузии.
В. И. Пеньковским A964) предложена модель почвогрунта,
представляющая систему параллельных капилляров с радиу-
радиусами, распределенными по логарифмически нормальному закону
с плотностью
§ 3] СТАТИСТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ 509
где /г, г0 и а — некоторые постоянные параметры. Тогда мате-
математическое ожидание N пор в единичном поперечном сечении
образца будет
оо
N = \ ф (г) dr = У 2я /ггоа ехр ~-.
о
Площадь всех пор выразится интегралом
оо
я\ /*2ф (г) dr = nNr\ ехр Dа2) = т, C.1)
о
где т — пористость грунта.
По формуле Гагена — Пуазейля для расхода q через капил-
капилляр радиуса г имеем (Кочин, Кибель и Розе 1963, 2)
яг4 др
а для расхода Q через единичное поперечное сечение образца
о
где pi — вязкость жидкости. Принимая закон Дарси в форме
п ko dp
получаем для проницаемости
C.2)
Полученные выражения для пористости и проницаемости
грунта могут быть использованы для выбора параметров r0, n
и а при переходе от реального грунта к модели. Недостающее
соотношение может быть получено из формулы для всасываю-
всасывающей силы почвы при некотором значении влажности w.
Рассмотрим теперь равновесное состояние влаги в вертикаль-
вертикально расположенном образце. По формуле Лапласа для высоты
капиллярного поднятия Лк(г) над зеркалом грунтовых вод
имеем
где С — постоянная, зависящая от гидрофильности капилляра.
Так как на уровне h > hK(r) могут быть заполнены только поры
510 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
с радиусом, меньшим чем г (поры с большими радиусами пу-
пусты), то насыщенность s = w/tn на высоте hK(r) и относитель-
относительная проницаемость f{r)=k(r)/ko определяются по формулам
C.4)
т
k(r
k0
)
Введем
г
m о
г
0 0
обозначение
H1+er
1 Ti
-2LI +
D 1
r
1
V2"
. 1
,aV2"
3a Yl
го V2 JJ '
nr 5aYl
"го V2-JJ
ят
ал/2 г0
и перепишем первое из уравнений C.4) так:
Обозначим через inv оператор взятия обратной функции. Тогда
для R можно написать
# = J|- + inv erf Bs - 1) C.6)
и затем выразить f (г) как функцию от 5. Полагая f{ (r) = f(r (s)),
получим
fi (s) =4"d + erf (inv erf Bs - 1) - a aJ2)]. C.7)
Из C.5) и C.6) найдем зависимость г от s:
г = г0 ехр (За2) ехр (а л/2 inv erf Bs — 1)). C.8)
По формуле C.3) можно найти капиллярное давление p{s) —
= — hK(r(s)) как функцию насыщенности s = w/tn, если под-
подставить г из C.8) в C.3), что дает
р (s) = - ~- ехр (- За2) ехр (— а л/2 inv erf Bs - 1)). C.9)
Из уравнений C.1) и C.2) можно исключить N и выразить
параметр а через k0, m и г0:
„ l I7~sh
C.10)
Тогда множитель ехр (—За2) можно заменить выражением
a3/e, где а = mrlj(SkQ).
ОСНОВНЫЕ УРАВНЕНИЯ ДИФФУЗИИ И РАССЛОЕЙЙЯ
611
На рис. 302 приведены графики функций /i(s) и p(s) (Пень-
ковский и Рыбакова 1966).
Аналогично можно получить формулу для всасывающей силы
^(s) единичного сечения образца, равной суммарному капил-
капиллярному давлению, разви-
развиваемому менисками в неза- ^д
полненных капиллярах:
оо
p*{r)= \ P{r)y{r)dr.
о
При этом
$(s) = Cna д/л/2[1 +
+ erf (inverfBs-l) +
В частности, максималь-
максимальную всасывающую силу бу-
будет развивать сухая почва,
для которой s = 0: ^max =
= л/2п С па.
0,1 0,4 0,6 О98 W
8
Рис. 302.
л/2п С па.
Пользуясь формулами C.7) и C.9), можно определить ко-
коэффициент диффузии влаги
где Х = invert Bs— 1).
В работе М. И. Вайнера A963) с помощью статистического
метода построены характеристики двухфазного потока и полу-
получены зависимости капиллярного давления и фазовых проницае-
мостей от насыщенности. При этом автор исходит из понятия
эффективного гидравлического радиуса пор и принимает лога-
логарифмически нормальный закон распределения пор по этим ра-
радиусам.
Б. НЕКОТОРЫЕ ВОПРОСЫ ЗАСОЛЕНИЯ И РАССОЛЕНИЯ ГРУНТОВ
§ 4. Основные уравнения диффузии и рассоления. Грунтовые
воды всегда содержат то или иное количество растворимых со-
солей. Некоторое количество солей находится в грунте в твердой
фазе, они могут быть сорбированными на частицах грунта и де-
512 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
сорбироваться с их поверхности, или быть рассеянными внутри
пор. Имеет место то или иное первичное засоление почв и грун-
грунтов, в результате ирригации наблюдается вторичное засоление.
Оно объясняется тем, что при подъеме грунтовых вод, когда они
приблизятся к поверхности земли на достаточно близкое рас-
расстояние (обычно меньшее трех метров), испарение с их поверх-
поверхности становится особенно интенсивным, и соли выносятся
в верхние части грунта и на его поверхность. При этом сни-
снижается плодородие почвы, а через некоторый промежуток вре-
времени она может стать совсем бесплодной. Поэтому вопросы вод-
водно-солевого режима почв и грунтов имеют первостепенное значе-
значение для мелиорации.
В жидкости с концентрацией соли с, движущейся со скоро-
скоростью v параллельно оси х> имеет место диффузия, уравнение ко-
которой записывается в виде
дс ~ д2с дс ,д « ч
dt дх2 дх ' v • /
Здесь D — коэффициент диффузии, т. е. параметр, характеризую-
характеризующий диффузионные свойства среды и растворимого вещества.
При движении жидкости в пористой среде нужно учитывать
изменение по времени не только массовой концентрации тс
(т — пористость) вещества в жидкой фазе, но и концентрации N
твердой фазы, причем обе концентрации рассчитываются на
единицу объема пористой среды (вместе с жидкостью). В общем
виде для несжимаемой жидкости, движущейся в пористой среде
со скоростью фильтрации v(v\y v2i ^з), можно ввести понятие
массовой скорости и(щ, и2, и^) вещества, ассоциированного
с жидкостью (см., например, Веригин и Шержуков 1969):
Ui^ViC-D^ (/=1,2,3). D.2)
Тогда уравнения диффузии и массообмена при полном на-
насыщении почвы влагой можно написать в виде
з
Еди{ dN д (тс)
dxt dt * dt ' V • /
-тт- = / (с, N). D.4)
ot
К этим уравнениям присоединяют уравнения фильтрации
»' = -*-!г- (/=1, 2, 3),
§ 5] РАСПРОСТРАНЕНИЕ ИНДИКАТОРА В ПОРИСТОЙ СРЕДЕ 613
где h e= ply, и уравнение неразрывности для жидкости
Функция f(c, N)y входящая в D.4), обычно берется в такой
форме:
f(ct N) = -6(c,-c)N\ D.6)
так что
^=-6(c,-c)N\ D.7)
где с* —концентрация насыщения.
Показатель а ^ 0 выбирается опытным путем. При а = О
в выражении D.6) N выпадает, и если подставить D.7) в D.3),
то получим уравнение для с:
D.8)
Обзор работ по диффузии и массообмену в пористых средах
можно найти, например, в сборнике «Развитие исследований по
теории фильтрации в СССР» A969). Здесь рассматривается не-
несколько частных задач, имеющих значение для мелиорации и
гидрогеологии.
§ 5. Распространение индикатора в пористой среде. Для оп-
определения скорости течения грунтовых вод пользуются различ-
различными индикаторами — красящими или радиоактивными веще-
веществами, перемещающимися со скоростью движения частиц воды.
Однако замечено, что в наблюдательной скважине индикатор
появляется раньше, чем частицы жидкости. Это объясняется тем,
что в потоке происходит диффузионное перемешивание.
Рассмотрим частный случай уравнения D.3) при N = О,
D.; = D — const для одномерного движения вдоль оси х со ско-
скоростью 0i = v rs const (Бан и др. 1962):
Пусть начальная концентрация задана так: с(х, 0)=0 при
\х\ > а, с(х,0)хв 1 при |л:| < а, с = 0 на бесконечности. Тогда,
как нетрудно проверить, решение будет иметь вид
с(g, t) = ±rerf( S+f-Л - erf ( l,ZJL)\, E.2)
Vfe> ; 2L \2^Dt/m ) \2^Dt/m Л V
где g = x — vt/tn.
17 Па Ян Полубаринова-Кочииа
514
НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ
[ГЛ. XV
В системе координат, движущейся вместе с жидкостью, по-
получаем семейство кривых, аналогичных представленным на
рис. 303, вершина которых перемещается вместе с жидкостью,
а размытый край уходит вперед. Точки и кружки на рисунке
отвечают опытам Коха и Слобода (Koch и Slobod 1957).
Если коэффициент D очень мал, так что диффузией можно
пренебречь, то вместо параболического уравнения E.1) полу-
получим уравнение гиперболического типа
дс
дс
(б.З)
F.4)
(б.б)
уравнение характеристик которого
dt c dx
т v
дает прямые
х - / *= const.
т
Общее решение уравнения (б.З) имеет вид
c(*f 0-вб-
где Ф(х)—произвольная функция, определенная, если известно
начальное распределение концентрации. Вдоль характеристик
E.5) концентрация сохраняет постоянное значение.
Если в начальный момент концентрация постоянна и равна
с0, а на границе х = 0 при / > 0 подается постоянная концен-
концентрация С\9 то растворенная жидкость будет перемещаться в виде
§6] МОДЕЛЬ ПРОЦЕССА КОНВЕКТИВНОГО СОЛЕНАКОПЛЕНИЯ 515
ступеньки: в сечении х в момент времени / будет с = с0, если
х > vt/m, и с = си если х < vt/m. При наличии диффузии,
когда D ф О, будет происходить размыв.
Вычисленные в опытных условиях значения коэффициента
диффузии.в пористой среде оказались на несколько порядков
больше, чем при молекулярной диффузии в воде. Ряд экспери-
экспериментов показал прямую пропорциональность между коэффициен-
коэффициентом диффузии и скоростью фильтрации, в других случаях ко-
коэффициент диффузии оказался линейной или более сложной
функцией скорости.
При движении в пористой среде различают молекулярную
диффузию и «конвективную» или «механическую» диффузию
(см. Сафмэн 1960). Последняя представляет процесс, возникаю-
возникающий из-за неупорядоченности картины линий тока, проходящих
между частицами грунта, и из-за того, что элементы жидкости,
которые первоначально находились рядом, стремятся отделиться
друг от друга. При этом имеется аналогия с турбулентной диф-
диффузией, однако в то время как в последней играет роль беспо-
беспорядочность в самом потоке, в конвективной диффузии не-
неупорядоченность линий тока происходит из-за сложности гео-
геометрической структуры среды. Отмечу, что Ф. Сафмэн в своих
исследованиях опирался на теорию Дж. И. Тейлора (Taylor
1953; Saffman и Taylor 1958).
Рядом авторов, начиная, по-видимому, с А. Шейдеггера
(в середине 50-х годов), предложены статистические методы ис-
исследования диффузионных явлений. При этом различают про-
продольную дисперсию (рассеяние) частиц, т.е. дисперсию в направ-
направлении средней скорости движения жидкости, и боковую или по-
поперечную — в перпендикулярных направлениях. Продольная
дисперсия изучалась Ф. Сафмэном A960), для поперечной же он
не получил удовлетворительных результатов. Об исследованиях
по продольной и поперечной диффузии см. в сборнике «Развитие
исследований по теории фильтрации в СССР» A969) и в книге
А. Бана и др. A962). Частная модель, построенная на предпо-
предположении, что пульсирующие скорости не могут быть направлены
против средней скорости течения, рассмотрена А. Б. Казанским
A973).
§ 6. Модель процесса конвективного соленакопления в почве.
Такая модель предложена В. И. Пеньковским A971) для слу-
случая внутрипочвенного испарения в зоне капиллярной каймы.
Для определения величины суммарного испарения из всего
почвенного слоя (зоны аэрации) С. Ф. Аверьяновым A956) пред-
предложена формула
17*
516 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
где бо — интенсивность испарения с поверхности почвы при очень
высоком стоянии грунтовых вод, у поверхности земли, d — глу-
глубина залегания грунтовых вод, d* — критическая глубина, т. е.
такая, что при d > d* можно считать е = 0. Для критической
глубины имеется зависимость от средней годовой температуры
данного района /°Ц (Ковда 1946—1947):
/°Ц) см. F.2)
Для установившегося распределения содержания влаги в ка-
капиллярной кайме С. Ф. Аверьянов дал эмпирическую формулу
(Аверьянов и Дзя Да-лин 1960)
w (x) = r
где m — пористость, w0 — наименьшая влагоемкость или содер-
содержание связанной воды, hK— максимальная высота капиллярного
поднятия, а ось х направлена по вертикали вверх.
Рассмотрим, как это сделано С. Ф. Аверьяновым A956), от-
отдельную пору капиллярной каймы, содержащей как жидкую, так
и газовую фазу. Последнюю будем считать заполняющей сфе-
сферический пузырек радиуса R\ (см. § 10. главы I) или часть его.
Делается предположение, что интенсивность q(x) испарения
влаги внутри пузырька в слое, отстоящем на расстояние х от
поверхности грунтовых вод, пропорциональна /??, в то время как
часть объема поры, занятая газовой фазой, пропорциональна
объему У =4/зяЯ? = /и —до; поэтому можно принять q = AV2/*.
На рассматриваемом уровне х капиллярной каймы имеется оп-
определенное значение влажности w — w(x), а капиллярное дав-
давление (всасывание) определяется величиной кривизны поверх-
поверхности раздела на границе фаз, т.е. значением R\. Суммируя
вклады всех пор на элементарной площадке сечения ху можно
принять
) = A(m-w)v\ F.4)
причем w(x) определяется по F.3).
Суммарное испарение влаги 8 из зоны капиллярной каймы
выражается через q(x) таким образом:
8=5 q{x)dx. F.5)
о
Подставляя сюда F.4), после интегрирования найдем
Л 20е (« + „.)
3hK Cm + 5доо) (т — Доо)
(б>6)
§ 6] МОДЕЛЬ ПРОЦЕССА КОНВЕКТИВНОГО СОЛЕНАКОПЛЕНИЯ 517
В неполностью насыщенных средах диффузионный перенос
солей уменьшается с уменьшением насыщенности среды раство-
раствором, а также за счет осмотического переноса влаги. Считая,
кроме того, испарение настолько интенсивным, что процесс кон-
конвективного переноса солей преобладает над диффузионным,
можно записать уравнения сохранения масс растворенного ве-
вещества и почвенной воды соответственно в виде
^^Г». ? —«С* F.7)
Здесь v(x)—объемная скорость фильтрации в сечении х капил-
капиллярной зоны, q(x) определяется формулами F.4) — F.6). Из
второго уравнения системы F.7) и из условия v@)= г найдем
v (х) _ v (х) _ 1 / 1 - s У/з 1+ 3S ,
Где s = w/tn — насыщенность водой порового пространства ка-
капиллярной зоны, So = Wo/m — насыщенность связанной воды.
Так как v не зависит от /, то первое из уравнений F.7) можно
переписать в виде
d(cv) , w d(cv) _ п .„ 0,
~дГ + Т ~дГ — и* ^'yj
Это линейное однородное уравнение для функции W = cv. Ин-
Интегрируя уравнение
получим уравнение характеристики, проходящей через точку
(*о, 0):
X
$§"^. FЛ0)
где х0 лежит между 0 и Ак.
Запишем уравнение характеристики, проходящей через точку
х = 0, / = 0, в виде х = x*(t). Тогда можно рассматривать две
области: под линией х = x*(t) и над нею. Обозначим соответ-
соответствующие им решения уравнения F.9) через С\(ху t) и с2(х, t):
( c{(x,t) при x>x.(t)9
с(х, t) = < . л . /л F.11)
I c2{x, t) при х< х.(/).
Для функции с\(х, t) примем условие
с,(х,0)-/(х), F.12)
518 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
где f(x)~ начальное распределение концентрации раствора в ка-
капиллярной кайме. Во второй области примем граничное условие
FЛЗ)
где ср(/)—изменение во времени концентрации солей в грунто-
грунтовых водах, питающих капиллярную кайму.
Общий интеграл уравнения F.9) имеет вид
сх (*, /) v (х) = Ф (/ - /, (х) + /, (*<>)),
где Ф — произвольная функция. Вдоль характеристики
/ = U*)-U*o) F.14)
имеем С\(х, t)v(x) = Ф@). При / = 0 и х = х0 это уравнение
дает f(х0)v(xq) = Ф@). Исключая Ф@) из последних уравне-
уравнений, получим
c,feO-f(y. F.15)
Вместе с уравнением F.14) получаем решение задачи F.7) —
F.12) в параметрической форме с параметром Xq.
Аналогично найдем, что функция с2(х> /), т.е. решение за-
задачи F.7) — F.13), будет иметь вид
с2(х, 0 = ф(/~Ш)-^у. F.16)
Если ф(/)= со = const, т. е. концентрация солей в питающих
капиллярную кайму грунтовых водах постоянна, то из F.16)
с учетом F.8) получим
« . 5
С2 (X, t) = Cq 1 —
+
if s° J
На рис. 304 приведены графики кривых т = т*(?) — т*(?о),
где т = et/(ahK) и | = */Ак, построенные для разных значений
go с помощью формулы F.10) при w0 = 0,2, а = 0,5.
На рис. 305 дан график зависимости c2/cq от ?, вычисленный
по формулам F.17) и F.3). Концентрация соли возрастает
с возрастанием Е-; если она станет равной концентрации предель-
предельного насыщения с^ для данного вида соли, то с этого момента,
определяемого по кривой ?0 = 0, начинается процесс кристал-
кристаллизации соли (см. рис. 304).
В грунтовых водах обычно растворены разные соли с раз-
различными значениями предельной концентрации. В процессе ис-
испарения происходит их стратификация, при которой в нижних
слоях почвы откладываются труднорастворимые соли (такие,
§6]
МОДЕЛЬ ПРОЦЕССА КОНВЕКТИВНОГО СОЛЕНАКОПЛЕНИЯ
519
как гипс), а в верхних слоях— легкорастворимые (MgCl, NaCl
и др.)»
1,0
х
0,5
ь-у,
А
/ /0,8
1,0
0,8
0,6
0,2
0
/
{
I
У
—
US
Рис. 304.
W
3
Рис. 305.
В частном случае, когда испарение начинается после полива
почвы водой с некоторой концентрацией cUi для испарения
с верхнего края каймы х = /iK
будем иметь v = 0 согласно 0^ 41 4!t М^ М Л"
F.8) и w = w0 согласно F.3),
а уравнения F.7) примут вид
dc V
Интегрирование дает
с = сп ехр
( А (т - шо)'/з Л
V Wo )'
F.18)
0,6
Момент начала кристалли- ff,8
зации t\ или Ti = etj(mhl{) по-
получим из F.18), полагая с =
\
\
у
—*-\
/
7
/
f,S
20m (m + wo) cn
Рис. 306.
На рис. 306 построены графики распределения по глубине
капиллярной каймы безразмерной скорости v/e (по формуле
F.8)) и С\/с0 = v(xo)/v(x) при /(xo)=l для момента т = 0,2.
При этом значения | и |о берутся с рис. 304 при т = 0,2.
520 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
§ 7. Задача о растворении и вымыве солей. Для случая дви-
движения параллельно оси *, когда скорость фильтрации раствора
значительно больше скорости диффузии растворенного веще-
вещества, т. е. число Пекле Pe = vl/D велико (/— характерный раз-
размер), вместо системы D.3) — D.4) можно рассматривать систему
дс , дс , dN г, \
dN*_ ^ т а [ GЛ)
Будем считать ось х направленной по вертикали вниз, а ско-
скорость промывки v постоянной.
Система G.1) является квазилинейной системой гиперболи-
гиперболического типа с двумя семействами характеристик: х = const и
х — vt/m = const.
В. И. Пеньковский A969) дал решение задач о рассолении
для а = 1 и а = 0,5. Мы ограничимся случаем а = 1.
Вводя безразмерные величины
где / — некоторый характерный линейный размер, и новые не-
независимые переменные
v — Х v — mx~vt П Я\
Х\ J 9 Х2 J 9 \1 *О)
перепишем G.1) в виде
дС_ дп л дп
к\ дх2
си ип л on п ~ч ,_ ,ч
Система G.4) решается в области Х\ > 0, аг2 < 0 при усло-
условиях
С = 0 при хг=09 *2<0, |
п = F (*,) при х2 = 0, *, > 0. j ( }
Заданная функция F(xi) считается дифференцируемой. Из G.4)
находим
Г 1 1 д Inn 1 д2 In п . дп л
L~X~~~Z~dxT' T дх2дх{ +~дх7 = {)'
Интегрируя второе уравнение по х2 и используя второе из уело*
вий G.5), получим
1 д In п . 1 д In F , „ .- _v
§7)
ЗАДАЧА О РАСТВОРЕНИИ И ВЫМЫВЕ СОЛЕЙ
521
Перепишем G.7) в виде
п
п
или
n'F-F'n
Интегрируя полученное уравнение по хи получим
a\F{x)dx\, G.8)
о '
где Ф(л:2)— произвольная функция.
В первом из уравнений G.6) положим Х\ = О и с = 0;
тогда, используя G.5), найдем п@, х2) = F@)exp(ax2). От-
Отсюда ^ „ „ , п _
ф , ч
1 _ ехр (о*2)
И ИЗ G.8)
п(хи т) =
— 1 + ехр (— am (jci — т))
, G.9)
где
F(x)dx
),
0,2
0,6
0,8
1,0
\\l у
1 /
/v
11
III
II/ *
11/ 1
i
%
i \
1
К
I)
1
4
/
[\
\
? \
\
/
/
/
6
1
A
X/
Л
\
\
\
\ <r
\ T
т=0"
\
s
\
\
N
N
\
N
V
N
\
\
\
N
\
i
\
\
1
О
0,8 0,3 1,0
ml l* Рис. 307.
Функция С(хьт) находится теперь из уравнений G.6):
С (Xi, т) = х - 1 + ехр (- am (хх - т))'
G.10)
На рис. 307 графики функций п и С, построенные по урав-
уравнениям G.9) и G.10), представлены соответственно сплошными
и пунктирными линиями. В вычислениях было принято т = 0,5,
a = l, F(*,) = 5exp(—4*,).
Для определения скорости v при промывке в неполностью
насыщенной пористой среде можно воспользоваться формулой
С. Ф. Аверьянова (см. § 10 главы I)
т — wo
G.11)
522 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
Если известна скорость промывки v ^ /г, то из G.11) можно
определить величину w\ = w — Wo, характеризующую часть
влаги, принимающую участие в движении:
G.12)
В уравнениях рассмотренной в этом параграфе задачи нужно
при этом заменить т на W\. Если еще сделать предположение,
что концентрация поливной воды сп Ф О, то в формулах вместо
с* нужно взять с*— сп.
При указанных соглашениях можно, исходя из G.9), напи-
написать уравнение для N(x9 t):
N (х, t) = F {х) у—гг тт^ тт—гт-, G.13)
4 ' ' v 7 У — 14- руп Aло)х (г — nt пи 11 ' \ * /
• ехр (Xw\ (x — vt/wi)) '
где
%=а_= аАс>-сп) Y = exp(^\F(x)dx\, G.14)
F(x)—функция, через которую выражается начальная функ-
функция N(x, 0).
В условиях промывок сп/с* является малой величиной.
В. И. Пеньковский, разлагая правую часть G.13) по степеням
cjc* и удерживая два члена ряда, получил приближенную фор-
формулу для N(x, t):
N {х, t)« F (x) ехр (tow, (x - -^-)) X
))]±\\ G.15)
причем Vc» « ajv.
С помощью G.15) можно вывести уравнение для величины
промывной нормы Q путем таких рассуждений. Для нижнего
фронта погружающегося столба воды при заданной величине Q
имеем
Q. G.16)
Введем величину Ncp — среднее, окончательное, допустимое
солесодержание в слое мощности /:
Nc9-\\N(x,t)dx. G.17)
§ 8] ДВА СЛУЧАЯ ТОЧНОГО РЕШЕНИЯ О РАССОЛЕНИИ 5°й
Проинтегрируем G.15) по х от 0 до I и разделим на /. Вводя
Q согласно G.16), получим уравнение для Q:
где
j\ G.19)
О О О
Для Q получается такое выражение:
Q = 1 In -А- +1 In ( 2~ [Л + /2 + V(/i + /2J - 4/2ЛГср]) . G.20)
Из двух корней уравнения GЛ8) выбирается меньший, т.е.
отвечающий большему значению Q.
В. И. Пеньковским A969) дана приближенная формула
При больших с# выражение для /2 мало, /i можно рассма-
рассматривать как некоторое исходное солесодержание #ср и вместо
G.21) написать приближенную формулу
Q«iln|k G.22)
Формула G.22) известна в мелиоративной практике как эм-
эмпирическая формула Волобуева — Панина (Панин 1968). Для
константы А, дается таблица значений применительно к различ-
различным видам засоления и различным почвам (Мариночкина и
Пеньковский 197Б).
§ 8. Два случая точного решения задачи о рассолении. Рас-
Рассмотрим одномерное движение вдоль оси х, которую будем счи-
считать направленной вниз по вертикали.
Если на входе, при х = 0, подавать в сухой грунт (точнее —
не содержащий гравитационную воду) пресную воду или воду
слабой концентрации Со, то можно различать 1) область с по-
подвижной границей 0^a;^a;i(/), в которой происходит лишь
перераспределение концентрации с(х, /) за счет диффузии, и
2) область Xi(t)^ х ^. Xo(t), в которой происходит полный пе-
переход солей из твердой фазы в раствор. Граница xo(t) пере-
перемещается вместе с частицами жидкости и определяется урав-
уравнением
^t. (8.1)
524 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
Случай 1. Рассматривая эту задачу, Ю. И. Капранов
A972) принял, что в предположении о достаточно быстром рас-
растворении солей ширину второй зоны можно считать равной
нулю, т.е. положить X\(t) = Xo(t), а все влияние второй зоны
внести в граничное условие в такой форме:
mD-^ = Nov, x = ±U (8.2)
где Nq — коэффициент объемного засоления. Засоленность по-
подаваемой воды можно принять равной нулю и считать
с (О, /) = 0. (8.3)
Ю. И. Капранов рассмотрел также другой вид граничного ус-
условия (D дс/дх = vQ при х = 0), но мы здесь ограничиваемся
условием (8.3).
Введем безразмерные переменные
$=%х, т=^-/, аF, т) = ^с(х, t) (8.4)
и функцию
Тогда задача может быть сформулирована так: найти функ-
функцию и(?, т), удовлетворяющую следующему из E.1) уравнению;
ит = ^-^ @<?<т), (8.6)
граничному условию
и@, т) = 0 при т>0 (8.7)
и условию
1^=1 при ? = т>0. (8.8)
Функция a(g, т) ищется в подвижной области, ограниченной
линией I = т, для т > 0. Если продолжить иA, х) на весь квад-
квадрант g > 0, т > 0 как решение уравнения (8.6) при начальном
условии u(i, 0)= uo(l), для которого
Ио(О) = Оэ (8.9)
то решение при определенных ограничениях на рост uo(Q будет
единственным и может быть представлено в виде
(8.10)
В случае подвижной границы начальное условие не имеет
смысла. Однако при специальном выборе в (8.10) функции ио(|)
§ 8] ДВА СЛУЧАЯ ТОЧНОГО РЕШЕНИЯ О РАССОЛЕНИИ 525
возможно удовлетворить условию (8.8). Для нахождения иоA)
вычислим и\ по уравнению (8.10) и подставим в (8.8). Получим
интегральное уравнение
s g (s, t) f (s) ds = 2т, f (s) = «o (s) A + e-*). (8.11)
0
Так как
\ sg(s, %)ds = — Л/— ехрГ — -j-J,
о
то нетрудно в (8.11) произвести интегрирование по частям и по-
получить интегральное уравнение
оо
[g(s,x)f'{s)ds=l, (8.12)
решение которого имеет вид /'(?)== 2. Следовательно, /(?)
= 2g + С. Полагая С = 0, так как ио(О) = 0, найдем
Теперь по уравнению (8.10) найдем и(|, т):
s9%)-g& + st%)]ds. (8.14)
о chy
Полученное решение непрерывно вместе с и^ в треугольной
области 0 2-е: g ^ т. Уравнение (8.14) показывает, что при фикси-
фиксированном х концентрация с ростом / очень быстро стремится
к нулю, но на фронте g = т при больших т имеет место рост
и(ху т) = 2 д/т/я +0A), что налагает ограничения на примени-
применимость предложенной схемы при больших t.
Случай 2. Теперь предположим, что начальное объемное
засоление почвы не постоянно, но определяется заданной функ-
функцией ф(#). Концентрацию сп промывной воды будем считать по-
постоянной. В. И. Пеньковский и С. Т. Рыбакова A975) рассмо-
рассмотрели такую задачу: дано уравнение E.1)
% v @<<(fl) (8.15)
526 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
и граничные условия
— D -г—\- v (с — сп) = О при х = О,
г> дс . у. dx0 /j\
D -gj = cp {x0) -jj~ при x = xQ(t).
Как и выше, *0(/)= vt/m есть фронт продвижения воды.
Вместо х и t введем переменные ? и т согласно равенствам
(8.4), вместо с (я, f)— новую функцию
Это приводит к простейшему уравнению теплопроводности
4 | @<Б<т) (8.18)
и граничным условиям
dv \ *
при ? = 0,
--?) при | = т,
(8.19)
Уравнение (8.18) имеет однопараметрическое решение вида
W F, т, а) = *-** [Л (а) sin (og) + В (а) cos
Первое из условий (8.19) удовлетворяется при В (а) = 2а А (а).
Искомое решение а(?, т) представляется в виде
v (|, т) = J A (a) [sin (а|) + 2а cos (а|)] е-°'* rfa. (8.20)
Удовлетворяя граничному условию при ? = т, для Л (а) по-
получаем интегральное уравнение
Л (а) [(| - a2) sin (at) + a cos (ат)] exp [(j - а2) т ] da = 1 / (т).
(8.21)
Для некоторого упрощения уравнения проинтегрируем (8.21) по
§ 8] ДВА СЛУЧАЯ ТОЧНОГО РЕШЕНИЯ О РАССОЛЕНИИ 527
т в пределах от 0 до т. Получим, изменяя порядок интегриро-
интегрирования (что законно в силу равномерной сходимости по /),
A (a) sin (at) exp [(-j- — а2) т] da — - F (т), (8.22)
о
где
Считая А (а) непрерывной функцией в промежутке @, оо),
причем Л@)=0, В. И. Пеньковский находит А (а) путем при-
применения двукратного прямого и одного обратного преобразова-
преобразования Лапласа, обозначаемых так:
lp (h) = ] e~Psh (s) ds = H (/?), L71 (Н)=-^т J epsH (p) dp=A (s).
0 a-*oo
Теперь к обеим частям уравнения (8.22) применим преобразо-
преобразование LP2, что приводит к уравнению
оо
\ А (а) г^ i^r - у Lp, (F). (8.23)
о а2 + [р + а2 - jJ
Разложение на простейшие дроби дает
ар 1 Г a a
Умножая обе части уравнения (8.23) на р и применяя опе-
операцию L7\ после ряда преобразований найдем
оо
I L7l (pLp, (F)) -= (sh|) J Л (a) sin (as) da.
О
Введем функцию
L7l(pLp>(F)) = ±(sh^yl L7l(Lp>(f)), (8.24)
являющуюся синус-преобразованием функции Л (а). По формуле
528 НЕКОТОРЫЕ ВОПРОСЫ, СВЯЗАННЫЕ С ОРОШЕНИЕМ [ГЛ. XV
обращения найдем
оо
А(а) = -\ Ц (s) sin (as) ds. (8.25)
О
Подстановка этого выражения в (8.20) даст и(?, т). Для вычис-
вычислений удобно предварительно преобразовать (8.20) с помощью
формулы (Градштейн и Рыжик 1962, стр. 494)
e~aH sin (sa) sin (|a) da = -~ G (|, s; т), (8.26)
о
где
Подставляя (8.25) в (8.20), изменяя порядок интегрирова-
интегрирования и учитывая формулу (8.26), получим
l, s;
|^(|, s; x)]ds =
s. (8.27)
В качестве примера положим, что /(|)=ехр(—\х21)
(jjt = const). Такое распределение объемного засоления почвы
близко к случаю, когда кристаллы легкорастворимых солей ска-
скапливаются вблизи дневной поверхности почвы. Тогда последо-
последовательно имеем
2|»2sh-|
Глава XVI
ОБ ОПРЕДЕЛЕНИИ ПАРАМЕТРОВ ПЛАСТА
§ 1. Об определении коэффициента фильтрации. Обратные
задачи для дифференциальных уравнений в частных производ-
производных привлекают в последнее время внимание специалистов в са-
самых разных областях механики и физики.
Это связано с тем, что во многих случаях решение обратной
задачи является залогом успешного решения исследуемой пря-
прямой задачи и получения более полного и правильного представ-
представления о реально происходящих физических процессах.
Современные вычислительные средства — аналоговые и циф-
цифровые машины — позволяют с большой степенью точности ре-
решать дифференциальные уравнения, моделирующие тот или иной
физический процесс. Однако удовлетворительный результат мо-
может быть достигнут только в том случае, когда есть хорошее со-
соответствие между выбранной моделью (в данном случае речь
идет о дифференциальных уравнениях) и реальным объектом.
Одним из необходимых условий такого соответствия является
правильное задание коэффициентов дифференциального урав-
уравнения, которые являются некоторыми физическими и механиче-
механическими параметрами исследуемого объекта.
Примерами таких параметров могут служить коэффициент
теплопроводности, коэффициент диффузии, фильтрационные па-
параметры грунтов и т. д.
Весьма актуальна эта проблема в теории фильтрации, кото-
которая тесно связана с разработкой нефтяных и газовых место-
месторождений, с мелиорацией земель и с рядом других народнохо-
народнохозяйственных задач.
Все это делает задачу определения коллекторских свойств
пластов важной с практической и теоретической точек зре-
зрения.
В литературе имеется большое количество работ, посвящен-
посвященных этой важной проблеме. Методы решения обсуждаемых во-
вопросов весьма разнообразны и зависят от тех конкретных задач,
которые ставят перед собой различные авторы. Однако можно
выделить два принципиально различных подхода к задачам оп-
определения фильтрационных параметров грунтов.
530 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Первый подход основан на физико-механическом анализе
грунта, например, по исследованию керновых проб. Некоторые
из методов такого анализа опираются на статистическую теорию
проницаемости. Сущность последней заключается в том, что по-
пористая среда, в которой происходит фильтрация вязкой жидко-
жидкости, рассматривается как система упорядоченных или случайным
образом ориентированных в пространстве капилляров с различ-
различными диаметрами. Коэффициент фильтрации среды в таких мо-
моделях зависит от пористости среды и функции распределения
капилляров по размерам (одна из таких моделей описана в § 3
главы XV).
Существенным недостатком физико-механического анализа
грунта является небольшое, в сравнении с размерами исследуе-
исследуемых объектов, количество возможных замеров, когда большая
часть пласта остается практически неизученной.
Второй подход заключается в решении обратных задач для
дифференциальных уравнений, моделирующих процесс фильтра-
фильтрации. Коэффициенты этих уравнений являются искомыми осред-
ненными фильтрационными параметрами и определяются по не-
некоторым известным характеристикам решений исходных диффе-
дифференциальных уравнений.
Необходимая информация для сопоставления с решениями
дифференциальных уравнений получается на основе изучения
каких-либо гидродинамических характеристик течения в пла-
пластах, например, с помощью проведения экспериментальных от-
откачек, наблюдения за изменением уровня грунтовых вод или
изучения карт изобар, составляемых для эксплуатируемых неф-
нефтяных месторождений.
Наибольшее количество работ в литературе посвящено за-
задаче определения постоянного осредненного фильтрационного
параметра (чаще всего это коэффициент фильтрации) гидроди-
гидродинамическими методами, т. е. по наблюдениям за давлением и
расходом в скважинах при различных режимах эксплуатации.
Наиболее простая формула для определения коэффициента
фильтрации при установившемся режиме откачки — формула
Дюпюи (см. § 9 главы VII, а также § 1 главы IX). Большое рас-
распространение получили методы определения параметров пласта,
основанные на теории неустановившейся фильтрации жидкости.
О некоторых из них говорилось, в частности, выше в § 7 и 8
главы XI.
Рассмотрим здесь лишь один способ, использующий преоб-
преобразование Лапласа. Он был предложен Г. И. Баренблаттом
и др. A957) применительно к уравнению
§ I) ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ФИЛЬТРАЦИИ 631
но нетрудно обобщить его и на уравнение с перетоками
а[ + )bS (S-Я-Л). A.2)
Это сделано А. Б. Бегматовым (см. Полубаринова-Кочина и др.
1969).
Применим преобразование Лапласа
оо
S*(r, p)=J e-i*S(r, t)dt A.3)
О
к уравнению A.2), когда ищется его решение при условиях
(Г — мощность пласта)
S (г, 0) = 0, S (оо, I) = 0, 2nkTr 4г = Q. A.4)
Получим (ср. формулу (8.2) главы XI)
Я+^-фг-О- 0-5)
Решение этого уравнения, ограниченное на бесконечности,
представляется функцией Бесселя второго рода:
В частном случае 6 = 0 эта функция переходит в
Ее оригиналом является интегральный экспоненциал (ср. фор-
формулу G.3) главы XI).
Оригинал изображения A.6) дает функцию (8.3) главы XI
для течения с перетоками.
Но можно оперировать с функцией A.7), не возвращаясь
к оригиналу. Величину /?, размерность которой есть Н, заме-
заменяют, полагая р = 1/т, и проводят вычисления неизвестной кон-
константы а по формуле
предварительно подвергнув известные значения S(r,t) преобра-
преобразованию
S*(r, т)=^ е х S(r, t)dt.
о
При этом верхний предел заменяется некоторым достаточно
большим числом Af.
532 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Этот способ и границы его применения обсуждаются в ряде
книг (Баренблатт, Ентов и Рыжик 1972; Полубаринова-Кочина,
Пряжинская и Эмих 1969). В первой из указанных книг рас-
рассмотрены также случаи неоднородного пласта.
§ 2. О некоторых обратных задачах уравнений параболическо-
параболического типа. В теории фильтрации представляют интерес обратные
задачи для уравнений параболического типа, в которых решение
считается известным в некоторой фиксированной точке про-
пространства во все моменты времени, а искомым является какой-
нибудь параметр уравнения — функция координат. Возникает
вопрос, возможно ли решение такой задачи: по наблюдениям
в одной точке определить распределение в пространстве, напри-
например, коэффициента фильтрации.
В статье М. М. Лаврентьева и К. Г. Резницкой A973) сфор-
сформулированы теоремы единственности поставленной задачи для
четырех случаев уравнений параболического типа, в которых
искомый параметр является функцией только одной коорди-
координаты.
Первая задача формулируется следующим образом. Пусть
и(х, у, t) есть решение (обобщенное) уравнения
+p{y)u> BЛ)
удовлетворяющее начальным и краевым условиям
и\Ы0 = 6(хN(у), -fj-l^-O, uoo = 0f B.2)
где через «<» обозначено значение функции и на бесконечности
(при г2 + у2-*-оо), б (л:)—дельта-функция, определяемая соот-
соотношениями
б(х) = 0 при хфО,
Здесь р(у)—искомая функция, непрерывная и ограниченная,
причем \р{у)\^ Ро (ро — постоянная). Задача состоит в опре-
определении функции р(у), если известна функция и(х, у, t) при
всех />0 в некоторой фиксированной точке (#о, 0).
Пусть и(х0, 0, t)= ф(^)—заданная ограниченная бесконечно
дифференцируемая функция. Обозначим через А отображение,
переводящее р(у) в <р(/):
Л/? = Ф. B.3)
Теорема утверждает, что решение уравнения B.3) единствен-
единственно в классе непрерывных ограниченных функций.
§ 2] ОБРАТНЫЕ ЗАДАЧИ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА 533
Применительно к теории фильтрации эту задачу можно ин-
интерпретировать, принимая и равным напору h(xy у, t), следую-
следующим образом. Скважина имитируется точечным стоком в начале
координат, возмущающим пласт в начальный момент времени,
причем ось х является осью симметрии движения. В точке
(Хо, 0) проводятся замеры h(x, у, t) в разные моменты времени.
Требуется определить параметр р{у), зависящий от координаты
у — этот параметр может характеризовать имеющие место пе-
перетоки через слабо проницаемые пласты.
Во второй задаче рассматривается уравнение
при условиях
= 0. B.5)
Задача состоит в отыскании p(z) по уравнению типа B.3). Тео-
Теорема утверждает, что ее решение также единственно в классе
непрерывных функций.
В третьей задаче речь идет об уравнении
/ ч ди д2и . д2и /л «ч
¦*&>-«—a?"+eF B'6)
(— оо < х < оо, #^0, t^O), решение которого и(х, у, z, t) удо-
удовлетворяет условиям
^| моо = 0. B.7)
Считается заданной функция и(хо, #о> 0= ф@; задача состоит
в определении \i(y) по ф@- Доказано, что решение задачи един-
единственно в классе непрерывных и ограниченных функций, удо-
удовлетворяющих условиям
|i,. B.8)
Четвертый случай совершенно аналогичен третьему, только
вместо декартовых координат в нем фигурируют, как и во вто-
втором случае, цилиндрические координаты.
Для доказательства упомянутых теорем используются пре-
преобразования Лапласа и Фурье, спектральная теория обыкновен-
обыкновенных дифференциальных уравнений второго порядка и решение
обратной задачи Штурма — Лиувилля.
Полное решение задачи, аналогичной указанным, но имею-
имеющей непосредственное отношение к теории фильтрации, дано
И. Б. Басовичем A974, 2, 3). Это решение будет приведено
ниже.
534 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
В статье Г. Шавана (Chavent 1969) рассматривается уравне-
уравнение более общего вида
ди д ( , ч ди \ . д ( , ч ди \ /п гл
Неизвестная функция а(х, у) ищется по известному в некоторой
области решению и(х, у, t) методами теории оптимального уп-
управления системами с распределенными параметрами.
Задача сводится к минимизации функционала
т
I (а (х, у)) = J J [и Ос, у, t) - щ (х9 уу О]2 dx dy dt,
О Q
в котором и(ху у, t)—решение уравнения B.9), ио(х, у, t)—экс-
t)—экспериментально полученное решение этого уравнения. Для
и(х, у у t) задаются начальное и краевое условия.
В. Я. Булыгин A974) рассмотрел уравнение вида B.9) со
свободным членом, переписанное в форме
да ди . да ди . А о ди . р, .ч /п л лХ
^Г-б7 + 17-^ + аАы = Р^Г + /(;с>у'0' B10)
где а (л:, у) может обозначать коэффициент фильтрации ила
гидропроводность пласта, и(х, уу t)—напор или давление,
/(*> У» t) характеризует плотность отбора с единицы площади
пласта. Спрашивается, можно ли определить а(х, у), зная
u(x,y,t) в отдельных точках пласта в разные моменты t. Автор
делает по этому поводу следующие замечания. Если а(х, у) из-
известно на некотором контуре, то задача Коши для уравнения
в частных производных первого порядка относительно а условно
корректна в смысле Тихонова (Тихонов и Арсенин 1974), однако
задача построения производных от u(x,y,t) по равномерным
приближениям функции некорректна.
Рассматривая уравнение B.10) для ряда моментов времени,
можно получить для величин а, да/дх, да/ду систему уравнений
+
( — значение и в /-й момент времени). Если система пере-
переопределена, то ее можно нормализовать. Для решения системы
требуется хорошая ее обусловленность, т. е. значения коэффи-
коэффициентов системы должны хорошо различаться, что на практике
обычно не выполняется. В. Я- Булыгин A974) дает советы по
использованию метода регуляризации для получения устойчи-
устойчивого решения плохо обусловленной системы.
§ 3] ОПРЕДЕЛЕНИЕ ПЕРЕМЕННОЙ ПРОНИЦАЕМОСТИ ПЛАСТА 535
§ 3. Определение переменной проницаемости пласта по на-
натурным наблюдениям в случае осевой симметрии. Пусть имеется
круговой пласт радиуса R и центральная скважина радиуса гс.
Будем считать коэффициент фильтрации пласта k(r) пере-
переменным, зависящим только от радиуса г.
Изменение давления в пласте описывается уравнением
и граничными условиями
p(R,t) = O, p(r,0) = 0, 2кгск{гс)Щ =4@. C.2)
1
Пусть задано дополнительное граничное условие
Р(гс, 0 = ф@, C.?)
означающее, что производятся замеры давления на скважине.
Займемся отысканием положительной, непрерывно диффе-
дифференцируемой на отрезке [гс, R] функции &(г), при которой вы-
выполняются условия C.2) и C.3) (Басович 1974, 2, 3).
Применим преобразование Лапласа к уравнению C.1) и гра-
граничным условиям C.2) и C.3). Положим
Р (г, s) = \ e~stp (r, t)dt, Q (s) = -^ \ e~stq (t) dt,
Ф (s) B J e-siq> (О Л.
о
Тогда будем иметь
C.5)
C.6)
p\r_r ==фE). C.7)
Решим уравнение (З.б) при граничных условиях C.6). Введем
функцию p*(r, s):
P(r,s) = p*(r,s) + Q(s)9(r), C.8)
где
г R
536 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Функция p*(r, s) удовлетворяет уравнению
frp* + frQ(s)p(r) = ±±(rk(r)l?) C.10)
и граничным условиям
Ц- р<и==0- (ЗЛ1)
Решение уравнения (ЗЛО) будем искать в виде ряда по соб-
собственным функциям оператора
^{^ C.12)
причем
4
Пусть
оо
Р* (г, s) = ? сп (s) рп (г), C.13)
/1=1
где рп (г) — нормированные собственные функции оператора
C.12). Подставим C.13) в уравнение C.10):
PsJC cnpn(r) + $sQ(s)ZVnPn(r) = -ZKcnPn(rY C.14)
Здесь
оо R
Лг) = р(г), \in=\p(r)rPn(r)dn
поэтому из C.14) получим
_ Ps Q (s) \in
— АЛ + sB *
Рассмотрим коэффициент цЛ:
f I f
M-ii = \ г Р« (г) Р (^) ^ = Т" \ LP«P (г) ^г =
(ЗЛ5)
Интегрируя C.15) два раза по частям и учитывая, что ip = 0
и р(/?) = 0, получим
р ЛаЫ. Cлб)
Ад
§ 31 ОПРЕДЕЛЕНИЕ ПЕРЕМЕННОЙ ПРОНИЦАЕМОСТИ ПЛАСТА 537
Тогда
оо
p/f $)— n*(r §\ J_ П<с\ъ (Л Q^n/o\V Pn(fc)
В силу теоремы Мерсера (см., например, Владимиров 1971)
ряд C.17) сходится равномерно на [rc, R]. Полагая в C.17)
г = гс и воспользовавшись равенством C.7), получим
Q(s)
/1=1 Л=-1
Здесь ап — нормировочный множитель оператора C.12):
где рп(г) — собственная функция оператора C.12) и рп(гс)=1.
Из C.18) видно, что Я„ — полюсы функции Ф (—tyPVQ (—VP).
Покажем, что по известному набору {ап, Хп} можно опре-
определить функцию k (г). Для ?того сведем задачу определения k (r)
к обратной задаче Штурма — Лиувилля.
В уравнении C.12) сделаем замену переменных:
где
г
dr
Тогда получим
-2"-Н(л:)г = цг, C.19)
причем
|^@) = 0, г(я)=0 C.20)
538 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Собственные числа оператора C.12) пропорциональны Хп: \in =
= В2Хп/п2, а нормировочные множители
Рл ~~ BQ @) а*'
Для \хп и рл справедливы асимптотические формулы
VUT=" + ! + 0(!), Ai = T + 0(-i-). C.22)
Отсюда находим константы
fi = jtlim-=., 6@) = —Нта„.
Таким образом, для оператора C.19) известен набор {\xni Prt},
по которому функция 1(х) определяется однозначно (Гельфанд
и Левитан 1951; Левитан и Гасымов 1964).
Пусть i|)(x, jli) — решение уравнения C.19), удовлетворяющее
условиям
¦ @, l*)-l. tf@, 10--Щ-. C.23)
Как известно, существует ядро К(х> t) такое, что
х
¦ (х, v) = cos (х лДх) + ^К(х, t) cos (/ Vl*") dt. C.24)
о
Ядро К(х9 t) определяется из интегрального уравнения
х
Их, у) + \К(Х, s)f(s, y)ds + K(x, </) = 0.
о
Здесь
где
а (\х) при \i < О,
a (\i) — спектральная функция оператора C.19):
§ 4] КОРРЕКТНОСТЬ ОПРЕДЕЛЕНИЯ ПРОНИЦАЕМОСТИ 539
Но функция л/б(л;)/Э@) удовлетворяет тому же уравнению
и тем же граничным условиям, что и i|j0 (х) = а|) (х, 0), следо-
следовательно,
В(х) = В@)^0(х). C.25)
Зная 8(х), нетрудно определить ft (г). Действительно, урав-
уравнение
равносильно уравнению
dr В
r-d7=Tr
интегрируя которое, найдем
C.26)
Из C.24) следует, что функция а|эо(л:) выражается через
ортогонализирующее ядро К{ху /) при \х = 0:
Ъ>(х)=1 + [к(х, t)dt.
Таким образом, получено выражение ft (г) в параметрической
форме. Вместе с тем доказано следующее: если существует по-
положительная, непрерывно дифференцируемая на [rCj R] функ-
функция ft (г), при которой выполняются условия C.1) — C.3), то она
единственная и определяется равенствами C.26).
§ 4. О корректности определения коэффициента фильтрации. Выше было
дано определение зависимости k(г) по заданным функциям ф(/) и q(t). На
практике исходные функции ф(/) и q(t) всегда бывают заданы с некоторой
погрешностью, что, естественно, влияет на точность определения коэффици-
коэффициента k (г).
Как и все задачи подобного типа, задача определения неизвестного коэф-
коэффициента дифференциального уравнения по переопределенной системе гра-
граничных условий некорректна в классическом смысле. Однако при некоторых
априорных предположениях о функции k (r) можно доказать условную кор-
корректность или корректность по Тихонову рассматриваемой обратной задачи.
Обозначим через Н множество функций {k(r)}, таких, что k(r) непрерыв-
непрерывны вместе с производными первого и второго порядка в [г0, R], причем
0<*i<jfe(r)<*,<oof \k'(r)\<Mu \k"(r)\<M*.
540 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Фиксируем некоторую функцию q(t)y для которой существует преобразо-
преобразование Лапласа C.4).
Пусть Ад — оператор, ставящий в соответствие всякой функции &(г)еН
функцию ф@= р(гс, 0» гДе Р(г> 0—решение уравнения C.1) при граничных
условиях C.2).
Обозначим через Uq множество функций ср(/) = Aqk (r) при &(r)eHfc
Тогда на Uq определен обратный оператор А~'<р (t) = k (г). И. Б. Басович
A974,2) показал корректность обратной задачи в классе функций й(г)еН,
т. е. доказал, что если для <р и фп е Uq
IIФ-Фи II- max |ф(*)-фя(/)| —> 0, D.1)
/е@. оо) п+°°
ТО
и^-А-\\^к(г)-кя(гЦ~гтвх^\к(г)-кп(г)\;^>аО. D.2)
Доказательство основывается на непрерывной зависимости спектральных
параметров оператора Штурма — Лиувилля от исходных данных задачи и
существенно опирается на теорему В. А. Марченко A972) об устойчивости
восстановления обыкновенного дифференциального уравнения по его спек-
спектральной функции.
§ 5. О методе модулирующих функций. В некоторых практи-
практических задачах нет необходимости в детальном исследовании
коллекторских свойств пласта, а можно ограничиться лишь ос-
редненными по всей области значениями фильтрационных пара-
параметров. В этом случае течение жидкости в пористой среде опи-
описывается уравнениями с постоянными коэффициентами.
В настоящем параграфе будет рассмотрен метод модулирую-
модулирующих функций для определения постоянных коэффициентов диф-
дифференциального уравнения по известному в некоторой области
решению этого уравнения (см. Басович 1973). Этот метод был
предложен ранее (Loeb и Cahen 1963, 1965) и затем применен
к определению гидрогеологических параметров пласта, пара-
параметров задачи о рассолении почвогрунтов и некоторым другим
обратным задачам фильтрации (Георгиевский 1971; Георгиев-
Георгиевский, Мироничева и Шульгин 1968).
Рассмотрим уравнение (см. § 6 главы XI)
|* **) E.1)
в котором величины я, Ь и с будем считать постоянными, под-
подлежащими определению.
Предположим, что на площади прямоугольника П = [О, А] X
X [О, В] проводятся систематические наблюдения за уровнем
грунтовых вод. Функцию h(x, у, t) будем считать известной
в параллелепипеде П X [О, Т]. Прежде всего выясним, одно-
однозначно ли определяются коэффициенты a, b и с по заданному
решению уравнения F.1).
§ 5] МЕТОД МОДУЛИРУЮЩИХ ФУНКЦИЙ 541
Изменяя обозначения, перепишем E.1) так:
-||L = х Aft + М + ц (>i = ai X = — b, \х = ЬН+ с). E.2)
Предположим, что, кроме чисел к, X и jx, уравнение E.2)
удовлетворяется также при значениях параметров х', АЛ \х':
-g^x'AA + b'A + ji'. E.3)
Тогда, вычитая почленно E.3) из E.2), получим
oft + M<o = O (xo = x — и', Я0 = Я — А/, м-о = М- — М-^)- E.4
(Заметим, что если найдется функция h(x, */, /), удовлетворяю-
удовлетворяющая уравнению E.2) при некотором наборе параметров х, А,, \х
и одновременно уравнению E.4) при наборе хо, Аю, М-о, то она
удовлетворяет уравнению E.2) и при любом наборе х + 5ио,
А, + sA,0, \i + «Мю, где s — произвольное число.)
Рассмотрим два случая.
1. ко = 0; тогда Ко ф 0, иначе было бы и juio = 0. Из E.4)
находим h = — [iofko = const.
2. хо Ф 0. Находим Aft из E.4) и подставляем в E.2):
^r=--^(hh + \io) + Xh + ii = yh + ?>t E.5)
где
Интегрирование по / дает
h = C{x9 у)еУ' + Но, E.6)
где
h ЦХр — ЦрХ
Подстановка E.6) в E.4) приводит к уравнению
х0ДС^< + Х0Сё" + \х0 + hho = 0,
откуда следует
АС + ^ С = 0, цо + Мо = 0. E.7)
Хо
Таким образом, для решений вида E.6) при условии E.7)
обратная задача определения постоянных х, А, и jm решается не-
неоднозначно. Рассмотрев случай y = 0» -можно получить выра-
выражение для всего класса функций, удовлетворяющих исходному
уравнению E.1) при различных наборах параметров. Обозна-
Обозначим множество таких функций через W.
Перейдем теперь к рассмотрению метода модулирующих
функций.
542 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Пусть задано решение h (х, у, t) уравнения E.1), не при-
принадлежащее множеству W.
Умножим обе части E.1) на функции вида
Ф*(*. У, /) = Х*(')ф| (*)**&).
причем
Х*@) = Х,(Г) = 0 (»=1,2,3),
Ф< @) = Ф, (А)=Ф; @) = Ф; (А) = о,
Ь @) = ^ (в) = ф; @)=ч>; (В) = о.
Примерами таких функций могут служить
&(/) = sin^-f <р,(*) = *|||(Л-*)'1 (m, /i>2) и т.д.
После интегрирования по частям в параллелепипеде П X
X [0, Т] получим систему линейных уравнений для определе-
определения постоянных а, Ь и с:
- J hOU dV=a J h ДФ, dV-b J ЛФ, dF + FЯ + с) J OtdV. E.9)
v к v v
Здесь I/ = П X [0, Л» dV = dxdydt, пределы интегрирова-
интегрирования по х9 у, t соответственно будут @, Л), @,5), @, Г). Заме-
Заметим, что для определения коэффициентов в уравнении E.9) не
требуется проведения численного дифференцирования решения
h(x,y,t) и не нужно задавать краевые условия на сторонах
прямоугольника — в этом сущность метода модулирующих функ-
функций. Выбрав три функции Фг (i = 1,2,3) так, чтобы детерми-
детерминант соответствующей системы линейных уравнений отличал-
отличался от нуля (для решений h(x, у, /), не принадлежащих мно-
множеству W, это всегда можно сделать), однозначно определим
постоянные а, Ь и с, решив систему E.9).
Однако на практике функция h(x,y,t) бывает известна с
некоторой погрешностью. В этом случае решение системы E.9)
будет зависеть от выбора модулирующих функций, которые
следует задавать так, чтобы получить как можно лучше обус-
обусловленную систему линейных уравнений. Имеются рекоменда-
рекомендации по выбору модулирующих функций (Георгиевский 1971;
Басович 1973). Для решения плохо обусловленных линейных
систем нужно применять регуляризацию (Тихонов и Арсенин
1974).
Заметим, что для успешного применения этого метода при
выборе модулирующих функций нужно руководствоваться не-
некоторыми априорными предположениями о решении исходного
уравнения и точности экспериментального задания этого ре-
решения.
§ 6] МЕТОД' НАИМЕНЬШИХ КВАДРАТОВ 643
Приведем небольшой пример. Рассмотрим уравнение
dh _ d2h
dt ~К~дхт'
Оно имеет частное решение
Заменим приближенно s\n(nx/a) полиномом 4л:(а — х)/а29
а множитель ехр(—я2х//а2) линейной функцией 1-Я/, где К —
некоторая постоянная. Тогда, взяв в качестве модулирующей
функции (р(х) = хп(а —х)п (п — целое > 1), получим из рас-
расчета приближенное значение коэффициента уровнепроводности
—i- Л,Г^ 2а2 Bп + 3) B/х + 2)
/С
Степень точности приближенного значения к* будет зависеть
от удачи в подборе К и Т (приближение к синусоиде оказалось
очень хорошим).
Если в случае уравнения E.1) сомножители в выражении
E.8) взять в виде фг(х) =xk(a — xI, %i(y)=ym(b — у)п и да-
давать ky U m> n различные целые значения ^2, то система урав-
уравнений для параметров получается плохо обусловленной, так
как коэффициенты одного уравнения мало отличаются от коэф-
коэффициентов других уравнений (см. Полубаринова-Кочина, Пря-
•кинская и Эмих 1969).
§ 6. Метод наименьших квадратов. Естественным обобщением
изложенного в предыдущем параграфе способа решения обрат-
обратных задач является метод наименьших квадратов (Басович
1973).
Введем обозначения
-§T~fo. M = fb h = f29 1-я/а-
Тогда уравнение E.2) можно записать в виде
fo-Z^ifc F.1)
Здесь через U обозначены искомые значения параметров. Пред-
Предположим, что нам известны приближенные значения /q, f\> f'2, /3
функций /о, /ь /г, /з и известно, что
« = 0, 1,2,3). F.2)
544 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
Составим выражение
ф (*,, х2, х3) = (/; - t f'txi9 r0 - t /;*,). (б.з)
Скалярное произведение (f, ф) определяется формулой
а в т
tf' ф)==$ И /(*' у' Оф(*' у' O^rfy*. F.4)
0 0 0
В развернутом виде можно написать
з з
Ф =
# Е
Z
bOt
F.5)
где
В качестве искомых приближений Я,* предлагается принять
значения л:^, дающие минимум квадратичной формы F.3), т.е.
удовлетворяющие системе
2 X ад+ 6, = 0 (t=l,2,3).
/1
F.7)
Определитель этой системы есть определитель Грамма функ-
функций /;, /;, г3:
()
0S./O
()
(f*Q
Будем считать функции /', f2, f3 линейно независимыми;
тогда определитель G (fj) должен быть отличным от нуля (Гант-
махер 1967). Так как доказано, что всегда G(/^)^0, то в дан-
данном случае он больше нуля. Отсюда следует, что квадратичная
форма F.5) положительно определенная.
Обозначим через Я* (/=1, 2, 3) решение системы F.7) — это
приближенные значения искомых hi.
Пусть
Тогда
Ы<8
0 = 0,1,2,3).
Е
Е
§ б] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 545
Положим Xt—Xh где Xt удовлетворяют уравнению
fo=thfi-
Тогда
?=-1
где
/ 3 \2
М = \
Чтобы получить оценку для разностей X. — Я* между точными
и приближенными значениями параметров, положим Z>i=xi — X*
|* = Я. —Я*. Тогда
Так как матрица пц положительно определенная, то Ф(^)
можно привести ортогональным преобразованием к виду
где |л? — собственные числа матрицы aifi обладающие свойством
О < \1Х < \i2 < |i3- Тогда
Окончательно получим
I*, Z
Здесь jjti >0—наименьшее собственное число матрицы ац.
Для того чтобы избежать дифференцирования эксперимен-
экспериментальной функции h(xy у, /), можно выразить квадратичную
форму Ф(Х{) через коэффициенты Фурье функций ft (/ = 0,1,
2, 3) относительно какой-нибудь полной ортонормированной
П. Я* Полубаринова-Кочина
546 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАСТА [ГЛ. XVI
системы функций Fh{x} у, /), обладающей следующими свой-
свойствами:
Fk(x, У, 0) = Fk{xt y,T)*=0 {х9 уеП),
Fk{x, yy O = -f-f (*, у, /) = 0 (х, г/еГ).
Здесь через Г обозначена граница прямоугольника П, dFk/dn —¦
нормальная производная на Г,
3 \2
— Z XiCkl
\2
где ^, = (F,, /,) (/ = 0,1,2,3).
В силу свойств функций Fh при вычислении коэффициентов
chi можно воспользоваться интегрированием по частям и избе-
избежать тем самым дифференцирования экспериментальной функ-
функции h(x, у, t).
Глава XVII
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ
НЕУСТАНОВИВШИХСЯ ДВИЖЕНИЙ
ГРУНТОВЫХ ВОД
§ 1. Условие на свободной поверхности. До сих пор мы зани-
занимались изучением неустановившихся движений грунтовых вод
со слабо изменяющейся свободной поверхностью, происходя-
происходящих в слое конечной глубины. Такие движения мы рассматри-
рассматривали «гидравлически», т.е. считая горизонтальные скорости не
меняющимися по высоте (вертикальные скорости при этом счи-
считаются малыми) и тем самым уменьшая число независимых
переменных на единицу.
В случае, когда нужно учесть форму границ области движе-
движения, когда в пласте есть особенности — например, имеются дре-
дренажные трубы, когда поток простирается вниз на большую глу-
глубину и т. п., такой метод рассмотрения задач недостаточен.
В главе XI мы пришли к заключению, что в неустановив-
неустановившихся движениях грунтовых вод можно полностью пренебрегать
инерционными членами и принять, что вектор скорости фильтра-
фильтрации имеет потенциал ф(л:, у, t):
A.1)
удовлетворяющий уравнению Лапласа
0 + |^ = О. A.2)
Функция ф связана с давлением равенством
с A.3)
(ось у направлена вверх).
Потенциал ф(л:, у, t) содержит время t лишь в качестве пара-
параметра. В неустановившемся движении со свободной поверх-
поверхностью зависимость ср от времени входит в условие на этой по-
поверхности. Выведем это условие.
18*
548 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ [ГЛ. XVII
Принимая давление на свободной поверхности постоянным)
из A.3) получаем условие на депрессионной кривой (постоян-
(постоянная С принята равной нулю)
(p+ky = O. A.4)
Предположим, что на линии L свободной поверхности грун-
грунтового потока некоторая функция остается все время равной
нулю:
F(x, у, 0 = 0. A.5)
Если в момент времени t + А/ линия L перешла в Z/, то некото-
некоторая точка М(х, у) линии L перейдет в точку М'(х-\-Ах, у-\-Ау)
линии Lf. (Можно рассматривать L как линию разрыва, причем
мы рассматриваем этот разрыв как стационарный (Кочин, Ки-
бель и Розе 1963, 2)). Тогда
F(x + bxy у + Ьу, / + Д0 = 0. A.6)
Вычитая A.5) из A.6), деля на At и переходя к пределу при
Д?-*0, получим уравнение
dF_,dF dx , dF dy ___ п (] -,
dt "+" dx dt ^^dj dt ""U- Ki'l}
С помощью A.1) имеем
(m — пористость или недостаток насыщения грунта). Подставив
эти выражения в A.7), найдем условие на свободной поверх-
поверхности
«?+#?+??-•¦ A-9)
В частности, приняв F = y+ky и учитывая, что
dF dqp dF _d(p dF дф , ,
~W — 1Г ' dx ~ ~dx * dy dy"^ '
найдем уравнение для ф:
которое должно выполняться на свободной поверхности (Bous-
sinesq 1904).
Перейдем к преобразованию этого условия к комплексным
переменным. Будем рассматривать одновременно комплексный
потенциал со = ф + гф и функцию Жуковского (см. главу IV)
0 = о — ikz = (ф + ky) + i($ — kx). A.11)
§ 1] УСЛОВИЕ НА СВОБОДНОЙ ПОВЕРХНОСТИ 549
Переписав уравнение A.10) в виде
нетрудно обнаружить, что его можно заменить следующим урав-
уравнением:
(см. Калинин и Полубаринова-Кочина 1947), что можно также
представить в форме
^r^7+I1 + mL + J° AЛ2)
Здесь чертой наверху отмечается сопряженная величина.
Предположим, что область, занятая движущейся жидкостью,
отображена конформно на полуплоскость вспомогательного ком-
комплексного переменного ? = g + lr\ так, что свободная поверх-
поверхность все время соответствует действительной оси. Обозначая
отображающие функции через z = z(t),t) и ? = ?(z, f) и пере-
переходя к переменным ? и t, будем иметь
д 6 (г, 0 _ д 0 (?, /) . дб i /^ = а ? (г, /) \ ^ 1д,
Замечая затем, что на депрессионной кривой при ? = ?
у dt dt
перепишем условие A.12) в виде
day df[ _d?_ д^_ , ^со ^8 д^ _??_ ,
Так как при дифференцировании по действительной пере-
переменной ? = ! имеет место равенство
ае(?,
и так как dtjdz= \/(dz/dQ и dtjdz*** l/(dz/d?), то получаем
Далее, если подставить в уравнение г = /(?, 0 величину
? = ?(z, /), то получим тождество z = f (?B, 0> 0 дифференци-
дифференцируя которое частным образом по /, найдем
550 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ [ГЛ. XVII
Отсюда имеем
что дает возможность переписать A.15) в виде
да) да f dz дг дг дг \ п ,- «~ч
или в других обозначениях
«>»(##)—'¦»(?)• с-18»
Если вернуться к функции Жуковского, то условиями на
линии свободной поверхности будут уравнения
(дгЪг\ 1 т /d9\ k т /. dz\ ,. 1ПЧ
Для отдельных групп задач бывает известно выражение
функций 9(?) или (о(?), что дает возможность привести уравне-
уравнения A.18) и A.19) к условию для функции z(?, f) на свободной
поверхности.
§ 2. Задачи о растекании бугров грунтовых вод в полуплос-
полуплоскости. После дождя, после прекращения полива и т. п. поверх-
поверхность грунтовых вод принимает бугристую форму, которая затем
постепенно выравнивается. Такого рода задача — о деформации
депрессионной кривой, уравнение которой в начальный момент
времени задано, для области потока, простирающейся вниз на
бесконечность, — является простейшей задачей с граничным
условием A.19).
Здесь функция Жуковского может быть принята просто про-
пропорциональной ?, а именно, 0 = — ikH^t где Я —некоторая по-
постоянная, имеющая размерность длины. В самом деле, вспом-
вспомним, что 0 пропорциональна комплексному давлению (см. § 1
главы IV):
е = —?(р + *У)- B.1)
При т] = 0 имеем /7 = 0 и Re0 = 0. На бесконечности давление
ведет себя, как в случае невозмущенной поверхности, т.е. как
pgt\. Поэтому
0 === (о — ikz = — ikHl. B.?)
При этом мы считаем, что функция, отображающая область
движения на полуплоскость ?, имеет вид
2 = ?Я + Ф(?, /), B.3)
где ФE»0 голоморфна в нижней полуплоскости.
§ 2] РАСТЕКАНИЕ БУГРОВ ГРУНТОВЫХ ВОД В ПОЛУПЛОСКОСТИ 551
Подставляя B.2) во второе из уравнений A.19), получим
условие на свободной поверхности для 2E, t):
дг дг , ki дг\ kH . . /л .,
+ ) ПРИ S = 8- B-4)
Условие B.4) можно переписать несколько иначе:
k дг . . дг дг \ kH * * /л г\
иж + 'жж)^— при ?-8- B-5)
Если ввести безразмерную комплексную координату z*=z/H
и безразмерное время т = kt/ (тН), то условие B.5) несколько
упростится:
( ^lb С-8. B-50
Теперь нетрудно также получить условие для комплексного
потенциала со на свободной поверхности. На основании B.2)
имеем
«•E, T)-C-^cD(Cf т). B.6)
Введем безразмерный комплексный потенциал со* == со/(&#).
Тогда
дг,, . . доа» ^г,, . dflf
55 ~ 55 ' dt ~l дх *
Подставляя эти выражения в B.5/), после простых преобра-
преобразований получим
*) (*?) «-5- С17)
В левой части имеем линейное выражение относительно про-
производных, в правой стоит произведение производных. Если от-
отбросить правую часть, то условие B.7) значительно упрощается.
Л. А. Галин A951) предложил применять метод последователь-
последовательных приближений.
Опустим далее для простоты звездочки в индексах у г и со,
помня, что они теперь безразмерны.
Примем первое приближение (о<!)E, t) удовлетворяющим ли-
линейному условию (при этом учтено, что Reco^ = Re со)
и начальному условию (соо(?) —заданная функция)
со") (С, 0)-«о@. B-9)
552
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ
[ГЛ. XVII
Найдя ©W(?,t) и подставив его в правую часть B.7), будем
считать, что (оB)(?, т) удовлетворяет граничному условию
при S =
и начальному условию ш<2>(?, 0)= (Оо(?)- Этот процесс можно
продолжить.
Рис. 308.
Был рассмотрен пример. Пусть при т = 0 грунтовые воды
занимают область, отображаемую на полуплоскость посредством
функции
так что при ? = I имеем уравнения депрессионной кривой (на
рис. 308 это кривая т = 0)
Л. А. Галиным A951) даны первое и второе приближения
для этого примера:
B.12)
§ 2] РАСТЕКАНИЕ БУГРОВ ГРУНТОВЫХ ВОД В ПОЛУПЛОСКОСТИ
553
Отсюда, полагая ? = ? и разделяя в выражении для 2A)(?> т)
действительную и мнимую части, получим уравнение свободной
поверхности первого приближения в виде
*."-Е+Б, + G+Т).. W-vT{i+'xy.. B-13)
На рис. 308 представлены кривые первого приближения, по-
построенные по B.13) для разных значений т при а = 0,5.
Зависимость от т максимальной ординаты свободной поверх-
поверхности имеет в первом приближении вид
Для второго приближения
+ T •
4A +т) + 2A +тJ 4A +т)
г]-
"' " i ~г i L*\i-r'bJ *\i-rir M'T'WJ
На рис. 309 представлены графики зависимостей у[{) @, т) и
>@, т) от т при а = 0,5с
V
— —
—«•¦¦иг
и 1 2 5 4 5
Рис. 309.
Э. Г. Кучеренко A955) нашла точное решение как этой за-
задачи, так и несколько более общей. А именно, она обнаружила
существование функции г(?, ti), удовлетворяющей условию
B.57) и имеющей вид
z = <
BЛ4)
где с, Ьу ah и Ah являются некоторыми функциями п=т + С,
а С — постоянная, которую определим дальше. Аналогичные ре-
решения рассматриваются в задаче о перемещении контура нефте-
нефтеносности (Куфарев и др. 1947, 1950, 1, 2, 1963; Виноградов и
Куфарев 1948).
554 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ [ГЛ. XVII
Частным случаем B.14) является выражение
При этом y является постоянной,
A = 2X(X-xl)-iD2, а = -•¦§¦-/(А,-т,)
где Я — положительный корень уравнения
SV - 4х^ + (т? - Dx) X2 + ^ = 0.
Если постоянные Di и D2 удовлетворяют неравенствам D\ > 0,
D\ > 3DL то такой корень существует.
Уравнение B.14) дает решение задачи о растекании некото-
некоторой волнообразной поверхности грунтовых вод, уравнение
B.15) — одного бугра над наклонной плоскостью с углом на-
наклона Y- При y = 0» Z>2 = 0, D{ = D выражение B.15) упро-
упрощается:
г=?+1^> B.16)
причем А = 2К(к — ti), a = iky К есть положительный корень
уравнения
ЗЯ2 - 4т^ + х\ - D = 0.
Пример Л. А. Галина получается отсюда, если положить
Решение представляется уравнением B.16), в котором
;A[2(+l) + B]
Нетрудно видеть, что при т = 0 получается В = а + 1, А = а
и a = i, что соответствует уравнению B.11). Наибольшая орди
ната растекающегося бугра получается из B.16) при ? = 0:
или
]
B.17)
§ 3] ТЕ ЖЕ ЗАДАЧИ ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ 555
При а = 0,5 кривая зависимости */*@, т), выражаемой точ-
точным решением B.17), практически совпадает со вторым прибли-
приближением Л. А. Галина — верхней линией рис. 309.
Заметим, что методика, изложенная в § 1, была применена
и к другим задачам. Группа задач была рассмотрена Н. К. Ка-
Калининым, в том числе задачи о неустановившейся фильтрации
в случае дрены в водопроницаемом слое бесконечной (Калинин
и Полубаринова-Кочина 1947) и конечной глубины (Калинин
1948). Решение строилось в виде рядов по степеням времени t.
Задачам, которые рассматриваются с помощью формул § 1,
предшествовали задачи о стягивании контура нефтеносности
(у нас простейшая из таких задач указана в § 6). В них течение
рассматривается в горизонтальной плоскости, следовательно, без
учета силы тяжести, когда формулы немного проще, чем в § 1.
Для такого рода задач доказано, что их решение в виде рядов
по степеням t сходится, но радиус сходимости не определен. На
практике удается определить коэффициенты разложения по сте-
степеням t лишь для небольшого числа членов ряда, так как с каж-
каждым следующим членом их вид усложняется.
Отметим, что Г. Даган рассматривал также пространствен-
пространственные задачи растекания грунтовых вод (Dagan 1964, 1967). При
этом он применял метод разложения решения по степеням ма-
малого параметра.
§ 3. Те же задачи при линеаризованном условии. Отбросив
в уравнении A.10) члены (ду/дхJу {ду/дуJу получим линейное
условие на депрессионной кривой
*L + c|l = 0 (с--!). C.1)
Считая свободную поверхность слабо изогнутой, перенесем
граничное условие на ось абсцисс. При этом уравнение свобод-
свободной поверхности будем определять из условия A.4); переписав
его в виде у = —ф(х, у, t)/k и полагая в правой части у = 0,
окончательно примем уравнение свободной поверхности в форме
C.2)
Сделанные допущения соответствуют тем, которые принимаются
в гидродинамической теории длинных волн.
Рассмотрим задачу: грунтовые воды занимают нижнюю полу-
полуплоскость у < 0. В начальный момент времени линия свободной
поверхности имеет форму кривой, заданной уравнением
y = f(x). C.3)
556 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ ttVI. XVII
Сопоставляя C.2) и C.3), найдем граничное значение для
Ф(х, у, 0 при / = 0:
<f(x,0,0) = -kf{x). C.4)
Зная значение гармонической функции на действительной
оси и задавшись условием, что ф обращается в нуль на беско-
бесконечности, можно построить начальное значение функции
ю = Ф + *ф с помощью интеграла (см. Кочина 1951):
Теперь сделаем замечание по поводу равенства C.1). Так
как функция ф является гармонической, то такова же будет в
нижней полуплоскости и функция
Из условия, что Q)(x,y9t) = Q на оси х и Ф(х> у, t) ограничена
на бесконечности, вытекает, что <b(x,y,t) равна нулю на всей
полуплоскости, т.е. уравнение C.1) имеет место для всей полу-
полуплоскости. Отсюда следует, что ф(х, у, t) зависит от линейной
комбинации у и t: ф (х, у, t) = ф (х, у — ct).
Это же относится и к комплексному потенциалу. Поэтому
для нахождения со (г, t) достаточно в полученном выражении
для со (г) заменить г — х + iy на х + i(y — ct):
у, /)=
Отделив действительную часть, найдем ф(л:, у, t). Положив в
полученном выражении у = 0, по формуле C.2) найдем урав-
уравнение свободной поверхности:
п
Эти же результаты можно получить другим путем, дающим
сразу наглядную геометрическую картину движения (Кочина,
1951).
Сначала рассмотрим случай, когда начальное возмущение
сосредоточено в бесконечно малой окрестности точки х = О,
у = 0. Пусть 5 будет величиной площади, заключенной между
профилем начального возмущения свободной поверхности и
осью х.
§ 3] ТЕ ЖЕ ЗАДАЧИ ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ 657
По примеру Н. Е. Кочина A935), применившего принцип
размерности к одной задаче теории волн, составим безразмер-
безразмерное выражение
Ф (О» У» О У _г//,\
которое является функцией от единственной безразмерной пере-
переменной и = ct/y. Условие C.1) должно, как сказано выше, удо-
удовлетворяться не только на границе, но и во всей области дви-
движения. Функция ф@, */, t) также удовлетворяет уравнению C.1).
Подставляя выражение
ф@, У, t) = ^-U(u)
в уравнение C.1), получим уравнение U'(l — и) = U, общее ре-
решение которого имеет вид (А — произвольная постоянная)
г 1 — А — Ау
и 1-й y-ct '
Следовательно, для ф@, у, /) получаем выражение
Заменив в нем у на у — ix, получим комплексный потенциал
оB, t) рассматриваемого неустановившегося движения:
iAcS
со (г, t) = ф (*, у, t) + ity {х, у, () = z __ ш .
Отделив в нем действительную часть от мнимой, найдем
/ А — AcS (У *""ct^ — AcSx
ф (х, у, t)— (y_ ctJ + х2 , У— {у_ ctJ + Х2 •
Чтобы получить уравнение свободной поверхности, нужно в
выражении для ф(я, у, t) положить у = 0. Получим
_ Ac2St
У ~ k (c2t2 + х2) '
Определим произвольную постоянную А так, чтобы площадь,
ограниченная осью абсцисс и линией свободной поверхности,
равнялась S: А =1г1(ск). Следовательно,
Уравнение свободной поверхности окончательно запишется так:
_ cSt
У — я (х2 + сН2) '
558
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ
(ГЛ. XVII
Как видно из выражения для комплексного потенциала, при
этом имеет место течение с диполем в точке z = id. В началь-
начальный момент времени диполь находится в начале координат, за-
затем он перемещается вверх по оси ординат со скоростью
с = k/т. Таким образом, для моментов времени, близких к на-
начальному, диполь попадает в область движения. Найдем момент
времени, когда диполь окажется в вершине свободной поверх-
поверхности. Для этого нужно максимальную ординату свободной по-
поверхности S/(nct) приравнять величине ct. Получим
Для t>t\ область движения уже не будет содержать особен-
особенностей. Если принять за начальный момент времени значение
t0 > t\, то получим движение без особенностей с начальной фор-
формой свободной поверхности
__ cSt0
У
ct
Мгновенные линии тока в рассматриваемом течении суть
окружности (рис. 310), проходящие через точку х = 0, у = ct
и касающиеся оси ординат, мгно-
мгновенные линии равного потенциа-
потенциала — ортогональные к ним ок-
окружности.
В общем случае, когда на-
х чальная форма свободной поверх-
поверхности задана уравнением у =
= f(x), решение задачи, т. е.
значение потенциала скорости,
получим, заменив в выражениях
C.8) S на /(g)rfg, х на х — I и
проинтегрировав по | в пределах от — оо до оо. В результате по-
получим те же выражения C.6) и C.7).
Если сделать в C.7) подстановку g — х = cttga, то получим
другое выражение для у (х> t):
Я/2
Рис. 310.
У(х, /) = -i-
ctiga)da.
C.70
-Я/2
Из него видно, что у(х, O) = f(x) при / = 0.
Рассмотрим в качестве примера случай прямоугольного в
начальный момент времени бугра, когда начальная форма сво-
свободной поверхности задается уравнениями
\х\> К.
§3]
ТЕ ЖЕ ЗАДАЧИ ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ
559
Форма свободной поверхности в последующие моменты времени
определится уравнением
ct )•
Комплексный потенциал течения
z — R —
C.10)
(З.юо
представляет плоскопараллельное течение с парой вихрей в точ-
точках (±/?, ct). Эти точечные вихри перемещаются вверх парал-
параллельно оси ординат со скоростью с = k/m (рис. 311). В началь-
начальный момент времени особые
точки (±#, 0) находятся на
свободной поверхности. Они
сходят с нее в момент вре-
времени tu определяемый урав-
уравнением
Если рассматривать уравне-
уравнение свободной поверхности рис зи.
в момент времени / > t\9 то
особые точки течения будут уже находиться вне области, заня-
занятой движущейся жидкостью.
Мгновенные линии тока здесь — аполлониевы окружности,
мгновенные линии равного потенциала—ортогональные к ним
окружности.
Пространственные задачи можно рассматривать
аналогичным образом (Кочина 1953). Вместо условий A.4) и
A.10) теперь на свободной поверхности будут иметь место усло-
условия (ось z направлена вверх по вертикали)
дер
Будем считать эти условия выполненными на плоскости
2 = 0. Пренебрегая квадратичными членами, получим при z — 0
C.11)
Отсюда следует, что <p = <p(x, у, z — ct) и уравнение свободной
поверхности будет
Ф (х, у, — ct)
k
z —— — ¦
C.12)
560
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ
[ГЛ XVII
Пусть на свободной поверхности задано условие ф(я, у, 0) =
= — kf(x, у). Решив задачу Дирихле для нижнего полупрост-
полупространства, найдем
= 4r \ \
(г - ct) f (g, т)) d\ dr\
l(x - IJ + (У - r\J + (z -
C.13)
В качестве примера рассмотрим случай бугра, имеющего на-
начальную форму в виде параллелепипеда, причем 1(х,у)=Н
внутри прямоугольника |*|</?, \y\<R\ и f(x,y)=O вне его.
Решение уравнения Аф = 0 для данной задачи имеет вид
ф (х9 у, z, /) =
kHr"'" "ч ' "(-Я, -Rx) -F(-Rf RX)-F{R, -R{)]>
где функция ^(р, pj). определена равенством
= arctg-
(x + p) (y + Pi)
(z - ct) У (г - ctJ + (x + pJ + (y + PlJ
Устремляя сторону R{ прямоугольника к нулю, получим в
пределе поверхность вида (Q — объем растекающейся воды)
Q ct г х + /? * — /? "I
L V(* + /^J + у2 + c2t2 У(* — /?J + г/2 + с2/2 J "
2я
c2t2)
Если, кроме того, R стремится к нулю, то получаем урав-
уравнение
. ч Q, с? . 2
' 2я (r2 + c2^2)Vi(
Если постоянное начальное возвышение уровня грунтовых вод Н
имеется только внутри круга радиуса /?, то форма свободной
поверхности выражается через
гипергеометрические функции,
а для максимальной ординаты
(при г = 0), получаем (Кочи-
па 1953)
Di
В случае полива по бо-
бороздам поверхность грунто-
грунтовых вод приобретает волнистый
характер, причем непосредст-
рис 312. венно под бороздой получает-
получается бугор грунтовой воды. По-
Поэтому зададимся начальной формой бугра в виде синусоиды у =
= a sin (соя). Тогда нетрудно получить уравнение депрессионной
§ 41 БУГРЫ ГРУНТОВЫХ ВОД В СЛОЕ КОНЕЧНОЙ ГЛУБИНЫ 561
кривой для последующих моментов времени (Кочина 1951):
у = ае-ш $\п{ш).
Линии тока имеют вид, показанный на рис. 312.
§ 4. Задача о растекании бугра грунтовых вод в слое конеч-
конечной глубины на горизонтальном водоупоре. В этом случае имеем
такие условия (в линеаризованной форме):
дф • к дф ~ т г ^
~dt +7Г7Г = 0 при У = н> I
4 п п DЛ)
-~ = 0 при и = О, I
оу r J
где Я — некоторая средняя начальная глубина грунтовых вод
в пласте. Кроме того, должно быть удовлетворено начальное
условие
ф = — ?/г0 (х) при / = 0 и у = Н. D.2)
Здесь ho{x)— начальная глубина грунтовых вод (Галин 1951).
Будем искать гармоническую функцию ф(я, #, t) в случае
симметричной задачи в форме интеграла Фурье
оо
Ф (*, У, 0 = J A (a, t) ch {ay) cos {ax) da. D.3)
о
Построенная функция удовлетворяет второму из условий D.1).
Чтобы выполнялось первое из этих условий, необходимо выпол-
выполнение равенства
(дф . к дф \
~дГ~*"~т~ду')у-Н~
оо
= \ [ch (аЯ) -—¦ + ^ A sh (аЯ)] cos {ax) da = 0. D.4)
о
Отсюда следует, что функция Л (а, /) должна удовлетворять
уравнению
ch (аЯ) -^- + ~- Ла sh (аЯ) = 0. D.5)
Так как ф(я, Я, 0) = — kho{x) при / = 0, то из D.3) получаем
оо
— kh0 (х) = J Л (а, 0) ch (аЯ) cos (ax) da. D. G)
о
562 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ [ГЛ. XVII
Решение уравнения D.5) можно написать в виде
и, следовательно, для qp(jt, у, t) будем иметь
оо
Ф(х, у,Ъ = \а (а, 0) ch (ay) cos (ax) exp (- ^Ш1 ,) da. D.7)
0
Функция Л (а, 0) находится обращением уравнения D.6):
оо
-,.)cos (
о
В частном случае, когда ho{x) = /го== const на участке
— а < х <а и ho = O вне этого участка, получим
а
о
Отсюда найдем значение потенциала скорости
sin (aa) Ch (a^/) cos
) ach(a//)
о
и глубины грунтовых вод
8in(cuQcos(cu) exp ^_ feathjaff)
§ 5. Неустановившийся приток грунтовых вод к точечному
стоку. К решению задачи о неустановившемся притоке к сква-
скважине В. К. Беляковой (Кузьминой) A956) применен метод ис-
источников и стоков. Задача решается в приближенной постановке,
так как граничное условие, которое должно выполняться на сво-
свободной поверхности, заранее неизвестной, сносится на горизон-
горизонтальную плоскость, и само это условие берется в линеаризован-
линеаризованной форме.
В том случае, когда рабочая часть скважины мала по сравне-
сравнению с глубиной вскрытия пласта, ее можно заменить простран-
пространственным стоком.
Считаем, что движение происходит в однородном, неограни-
неограниченно простирающемся вниз пласте, причем первоначальное
положение свободной поверхности совпадает с горизонтальной
§ 5] НЕУСТАНОВИВШИЙСЯ ПРИТОК К ТОЧЕЧНОМУ СТОКУ 563
плоскостью. Сток интенсивности Q(t) помещен на глубине Я
под этой плоскостью в точке с координатами @, 0, —Я). По-
Потенциал скорости ф(я, у, z, t), создаваемый стоком, будем счи-
считать удовлетворяющим условию
дф | д(р ~ г\ ( k \ /г- i\
-5Г + с17 = 0 ПРИ 2==0 Г = 1г)' EЛ)
а также начальному условию
Ф (*,</, 0, 0) = 0. F.2)
Наряду со стоком в точке @, 0, —Я) поместим источник
той же интенсивности Q(t) в точке (О, О, Я), симметричной со
стоком относительно плоскости 2 = 0. Представим ф(х, у, z, t)
в следующем виде:
Ф (*, у, z, 0 =
^ Q @ 1 _ Q @ 1 j
+ Ф1(^, У, 2, /)• E.3)
Рассматривая условие E.1) для ф! (л:, у, z, t) получим
2 = 0. E.4)
+ С
dt dz 2я аг Va:2 + У2 + (^ - НJ
Таким образом, для построения решения нужно определить
гармоническую в нижнем полупространстве функцию фЬ удо-
удовлетворяющую при 2 = 0 условию E.4).
Имея в виду известную формулу (Градштейн и Рыжик 1962)
E.5)
где Jo (кг) — функция Бесселя, ищем у{ в виде следующего
определенного интеграла:
оо
Ф, (х, у, z, t) = ^- \ А (Я, 0 /0(X, /V<*-"> dX.
о
Вычисления дают
t
А(Х, t) = -j\kQ(т)есК<т"«dr,
о
564
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ
[ГЛ. XVII
и потенциал скорости принимает вид
ф (*, */, z, /) =
_ cn*L I Q (О
4я У*2 + у2 + (г + ЯJ
оо
о
2я л/х2 + у2 + (г-НJ
t
Q(x)ecM*-*4%. E.6)
Для определения расхода необходимы дополнительные усло-
условия. Так, при Q = Qo = const интегрирование в формуле E.6)
выполняется; воспользовавшись равенством E.5), найдем
ф [X, У> *> )—
4я
- НJ
Qo
1
2я У*2 + у2 + (z - Н - с/J #
Потенциалу скорости здесь можно дать кинематическую ин-
интерпретацию: движение можно рассматривать как создаваемое
JSZ.
— —
1 —
——¦—-
—
6
Рис. 313.
10 12
двумя стоками интенсивности Qo, помещенными в точках
(О,О,—Я) и (О, О, Я), и источником удвоенной интенсивности
2Qo, перемещающимся по оси z вверх со скоростью, равной с>
причем этот источник в начальный момент находится в точке
(О, О, Я).
Свободная поверхность определяется уравнением
ф (*> У у 0, /) + kz ¦= 0, F.7)
что дает для данного случая
^ Qo Г
. ~ ~~ 2nk L У
1
+ у< + Н< Мх< + Г + К" + cty A
На рис. 313 показан вид свободной поверхности, при Q ==
с^= 500 см3/сек, ? = 0,1 см/сек, т = 0,33, Я = 5 л, для f =
= 10 А«(/Н, 60 Л1«« И ОО.
§ 5] НЕУСТАНОВИВШИЙСЯ ПРИТОК К ТОЧЕЧНОМУ СТОКУ 565
Если расход Q(t) не постоянен, то можно найти для его
определения интегральное уравнение. Положим, что ф = ф0 на
некоторой эквипотенциали, близкой к сфере малого радиуса
г = а, проходящей через точку (а, О, —Я). Подставляя коорди-
координаты этой точки в E.6), получим уравнение Вольтерра второго
рода:
t
»-<W + *S0H^v,." ,_,,,.*. E-8)
где
7
У а2
Можно искать его решение в виде ряда
Q(t) = qQ + Xqi(t) + l2
Тогда для q{(t) получаем
1
1 I ^
При достаточно малом Я, ограничиваясь первым приближением,
получим
^ W ^ чо ^ д/а2 + 4#2 Va2 + BЯ + ctJ J
При /->оо расход Q(t) будет стремиться к пределу
Таким образом, расход Q(f) с течением времени меняется
в пределах q0 (A — а/Н) ^ Q @ < <7о.
Приток грунтовых вод к стоку, расположен-
расположенному над водоупором. В этом случае, кроме граничного
условия E.1), должно выполняться условие
|7 = 0 при г=-7\ E.9)
где Г —начальная глубина грунтовых вод.
Потенциал скорости ищется в виде
An л/х2+у2+(г+Н)г
566 ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ 1ГЛ. XVII
Удовлетворяя условиям E.1) и F.9), получим
ф (х, У, г, 0 =
= Q(t) I , Q (*) 1 _
4я V*2 + У2 + (г + ЯJ 4я V** + У2 + (г + 271 - ЯJ
О
где \x = ckth{XT).
Для Q = Qo = const потенциал скорости принимает вид
+
. », *, о=
^== ^2 + (х+нJ + ^___(г+2г_я),
¦?¦ \ е~кн х t-T™T) [e%x+e~K {z+2T)] J°{Xr) dx -
о
An у I — e
[eK* + е~^'+Щ JQ (Kr) dk.
В. К. Беляковой A956) найдены также решения задачи о
вертикальной скважине, рассматриваемой как линия стоков по-
постоянной интенсивности, о стоке в неоднородном грунте и о
скважине в неоднородном грунте. Несколько случаев движения
при наличии стоков были исследованы Е. М. Мальгиновой
A967, 1972).
§ в. Задача о стягивании контура нефтеносности. Несколько более про-
простой и более изученной является следующая задача. В горизонтальной пло-
плоскости в начальный момент времени задана площадь, занятая жидкостью
(нефтью). Внутри контура L, ограничивающего эту область, заданы скважины
в виде точечных источников. Спрашивается, как будет деформироваться со
временем контур L, если считать, что на нем давление остается все время
постоянным (Лейбензон 1934, 1947; Полубаринова-Кочина 1945, 2; Галин
1945).
Это упрощенная схема задачи о передвижении нефти, окруженной водой
в напорном пласте. Дело в том, что для уравнений плоского движения воды
и нефти можно принять такие уравнения:
v = --^gradp, v. = --^-gradp.. F.1)
Здесь ko — проницаемость грунта; величины без «звездочек» относятся к об-
области, занятой нефтью, а со «звездочкой» — к области, занятой окружающей
нефть водой. Если считать, что вязкость воды очень мала по сравнению
с вязкостью нефти, так что коэффициент \i* можно принять равным нулю,
то следует принять р+ = const (иначе v* будет обращаться в бесконечность).
§ 6] ЗАДАЧА О СТЯГИВАНИИ КОНТУРА НЕФТЕНОСНОСТИ 567
Отсюда следует, что давление на контуре L не должно зависеть от коорди-
координат и может быть функцией только времени, в частности, быть постоянным.
Тогда и потенциал скорости, пропорциональный в данном случае давлению,
должен сохранять постоянное значение на контуре. Дифференцируя уравнение
<р (*,#,/) = const на L по времени так, как мы это делали в § 1, получим
уравнение
которое должно выполняться на L во все время движения.
В работах П. П. Куфарева A950, 1, 2) получены в замкнутой форме
решения задач об одной скважине и рядах равноотстоящих скважин для
полуплоскости, полосы и окружности в качестве контура L. Простейшей за-
задачей является задача о кардиоиде, уравнение которой в начальный момент
времени задано в виде
z~at + bl\ ? = е<0 @<8<2я),
причем считается, что 0 < b/а < 1/2, т.е. что кардиоида не имеет угловой
точки. Тогда, если центр скважины находится в точке z = 0, в последующие
моменты времени уравнение контура L имеет вид (Полубаринова-Кочина
1945, 2)
где А\ и А2 являются функциями времени.
Когда Ai станет равным 2Лг, у кардиоиды образуется точка возврата,
область течения сделается многолистной и решение уже не будет иметь фи-
физического смысла. Это же обстоятельство — появление угловых точек на кон-
контуре и одновременно многолистности решения раньше, чем точки контура дой-
дойдут до контура скважин (последние считаются близкими к окружностям, ра-
радиус которых мал по сравнению с размерами области), — имеет место во всех
указанных выше задачах — это результат нелинейности условия на свободной
поверхности.
Существование решения для малых t доказано при довольно общих пред-
предположениях о начальной форме контура (Куфарев 1950, 1,2).
Указанное свойство — потеря однолистности — ограничивает интерес к
теории в этой простейшей постановке.
Часть третья
ПРИБЛИЖЕННЫЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ
ИЗУЧЕНИЯ ДВИЖЕНИЙ ГРУНТОВЫХ ВОД
Глава XVIII
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
А. ГРАФИЧЕСКИЕ И ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
§ 1. Графический способ построения гидродинамической сетки.
Построение сетки линий тока и линий равного потенциала, кото-
которую называют иногда гидродинамической сеткой или сеткой
движения, имеет большое значение для изучения плоских уста-
установившихся течений. По этой сетке виден характер течения и
можно найти средние скорости в различных местах области дви-
движения (см., например, Гиринский 1939).
При изучении движения грунтовых вод иногда бывает удоб-
удобно функцию тока и потенциал скорости заменить пропорцио-
пропорциональными им функциями приведенного расхода q = — ty/k и
напора h = —q>/k. Комплексный потенциал со = ф + п|э заме-
заменится при этом выражением со* = h + Щ- Функция со* = h + iq,
так же, как и со, является функцией комплексного переменного
г, ее действительная и мнимая части суть гармонические функ-
функции (k считается постоянным).
Сетка ф = const, \|) = const может быть выбрана изотерми-
изотермической, т.е. образующей криволинейные квадраты. В самом
деле, пусть в точке А (рис. 314) An означает расстояние между
соседними линиями тока ^ = ^i и ф = г|?2 = tyi + Аг|), As —
расстояние между соседними эквипотенциалями ф = ф1 и ф =
= ф2 = ф! -f- Аф- Скорость в точке А приближенно равна
Аш Аф
Vа « ir-tt -Xх-.
л As А/г
Если выбрать Аф = Ая|?, то получим, что As = An, т. е. две со-
соседние стороны криволинейного прямоугольника ABCD оказы-
оказываются равными. Это свойство и называют изотермичностью
сетки.
§1]
ГРАФИЧЕСКОЕ ПОСТРОЕНИЕ ГИДРОДИНАМИЧЕСКОЙ СЕТКИ
569
При желании можно строить и сетку прямоугольников с за-
заданным отношением сторон. Полагая Дф = ЛД\|>, где к — задан-
заданное число, получим, что As = Я An.
Примеры гидродинамических сеток были приведены в главах
ц — V для простейших случаев движения, когда линии тока и
линии равного потенциала представляют-
представляются простыми кривыми, уравнения кото-
которых легко написать. В более сложных
случаях пользуются приближенными ме-
методами. Укажем главнейшие из них.
Рассмотрим для примера напорное
движение под гидротехническим соору-
сооружением произвольной формы (рис. 315).
Известны две линии тока или приве-
приведенного расхода: контур основания
гидротехнического сооружения и грани-
граница водоупора, а также две линии рав-
равного напора — границы верхнего и
нижнего бьефов. Последние мы мо-
можем принять за линии h = И и h = 0.
Проведем на глаз несколько примерно равноотстоящих ли-
линий тока. На рис. 315 это четыре криволинейные линии тока,
лежащие между граничными линиями q = 0 и q = qo, причем
величина q0 заранее не известна.
Рис. 315.
Теперь будем строить линии равного напора. Начнем, напри-
например, с линии, ближайшей к линии АВ. Около отрезков ВВ\,
BiB2, ... построим криволинейные квадраты. Отметим, что кри-
криволинейный прямоугольник можно считать квадратом, если дли-
длины его средних линий оказываются равными.
Квадраты, примыкающие к линии АВ рис. 315, оказались
такими, что их стороны (отмеченные пунктиром) не составляют
продолжения одна другой, т.е. не образуют линии равного на-
напора, как это должно было бы иметь место. Следовательно, нам
нужно поправить линии тока, уменьшив прежде всего отрезок
570 установившиеся движения грунтовых вод [гл. xviii
ВВ\. Выправив первый ряд клеток, переходят ко второму и т.д.
Последний ряд, примыкающий к линии CD, как правило, будет
состоять не из квадратов, а из прямоугольников. После первого
цикла построений получим сетку, приведенную на рис. 316. Да-
Далее эту сетку можно дополнительно уточнять, более тщательно
выполняя условия ортогональности линий и «квадратности»
ячеек сетки.
Для проверки правильности сетки можно провести диаго-
диагонали квадратов, которые должны также образовать ортогональ-
ортогональную сетку.
Рис. 316.
Около особых точек вместо квадратов получаются другие
фигуры. Так, линии равных напоров, оканчивающиеся в углах
водонепроницаемого контура, делят эти углы пополам. В конце
шпунта касательная к линии равного напора является продол-
продолжением шпунта.
Теперь допустим, что мы построили всю сетку, причем кон-
контур ВС оказался разбитым на s участков (s может быть и дроб-
дробным числом, если последний ряд клеток состоит из прямоуголь-
прямоугольников). Тогда линии равного напора будут иметь отметки h = 0,
H/sy 2H/s, ..., Н. Сетка строилась как изотермическая; следо-
следовательно, отрезок qo/n (где п — число участков, на которые ока-
оказались разбитыми линии АВ и CD) должен равняться H/s:
qQ/n = H/s. Отсюда найдем приближенное значение приведен-
приведенного расхода ^о и действительного расхода Q:
Вместо сетки квадратов можно было бы строить сетку пря-
прямоугольников, сохраняя пропорциональность сторон всех прямо-
прямоугольников (Панов 1951).
Если грунт простирается вниз на бесконечность, то в каче-
качестве линии тока q = q0 можно взять полуокружность достаточно
большого радиуса, равного примерно утроенной длине флютбета
(см. § 13 главы II).
§ 2] СРЕДНИЕ АРИФМЕТИЧЕСКИЕ. КОНЕЧНЫЕ РАЗНОСТИ 571
В безнапорном движении на депрессионной кривой должно
выполняться условие h = у или Aft = Ay, где Aft —падение на-
напора между двумя эквипотенциалями, а Ау — расстояние по вер-
вертикали между точками кривой депрессии.
§ 2. Способ средних арифметических, конечные разности.
Этот способ основан на свойстве гармонической функции, со-
согласно которому значение функции в некоторой точке равно
среднему из ее значений на окружности, в центре которой нахо-
находится взятая точка:
2Я
Фо= ~^
о
Здесь фо —значение гармонической функции в центре окружно-
окружности, фм — значение ее в точках окружности.
Отсюда получается приближенная формула
где фь ф2, ... —значения ф в равноотстоящих точках по кон-
контуру окружности. В частности, если ограничиться четырьмя точ-
точками, то
^^Jt±Sl+Si±SLt B.1)
причем взятые точки будут находиться в вершинах квадрата, а
Фо будет значением функции в центре квадрата.
Допустим теперь, что грубо система изолиний у нас построе-
построена на бумаге, разграфленной квадратами. Интерполированием
между соседними изолиниями найдем приближенные значения
функции в вершинах квадратов Mit Их средние арифметические
принимаем за значения функции в центре квадратов. Средние
арифметические значений в центрах квадратов дадут уточнен-
уточненные значения функции в вершинах М{. Продолжая этот процесс,
получим систему чисел, стремящихся к определенным преде-
пределам— значениям искомой гармонической функции в вершинах
квадратов (Панов 1951). Практически после 3—4 шагов значе-
значения функции в вершинах перестают изменяться. Имея значения
функции в вершинах квадратов, можно провести систему изоли-
изолиний, т. е. линий, соединяющих одинаковые значения функции
(при этом, конечно, придется большую часть точек получать ин-
интерполированием).
Таким способом можно построить одно семейство линий, на-
например, эквипотенциалей. Другое семейство — линий тока — мо-
можно строить как ортогональное к первому или же независимо
от первого тем же способом средних арифметических.
572
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
Существуют различные упрощения и усовершенствования
указанных методов.
На рис. 317 построены линии тока для флютбета с тремя
шпунтами в слое конечной глубины (Козлов 1941).
Формулу B.1) можно получить иначе, рассмотрев метод ко-
конечных разностей в применении к уравнению Лапласа (см., на-
например, Годунов и Рябенький 1973). Этот способ состоит в том,
\
\
\
\
\\
^—
^-—
—
.—--
... —
\)
)
/
1
Рис. 317,
что вместо уравнения Аи = О рассматривают соответствующее
ему разностное уравнение
»хх + Uyy = 0, B.2)
где
"хх = "гг И* + А, у) — 2и (х, у) + и {х — А, у)],
1
h) — 2и{х, у) + и(х, у — А)],
или в других обозначениях
(
Следовательно, уравнение B.2) заменяется уравнением
и*+1. * + % /+i - 4^, / + ик-и i + uky {-x = 0. B.3)
Из формулы B.3) можно получить формулу B.1) для икл.
Задаваясь значениями функции на контуре области или зна-
значениями ее нормальной производной, которую при этом надо
выразить через разности, или, наконец, задавая на одних частях
контура значения функции, на других — значения нормальной
производной, можно получить систему уравнений для uhti.
Обычно число уравнений и число неизвестных получаются очень
большими.
Способы упрощенного решения этих систем рассмотрены раз-
различными авторами. Р. В. Сауселлом (Southwell 1966) и его со-
соавторами эти методы применены к решению ряда примеров из
СРЕДНИЕ АРИФМЕТИЧЕСКИЕ, КОНЕЧНЫЕ РАЗНОСТИ
673
различных областей, в том числе из области фильтрации (см.
также Николаева 1949).
Между давлением /?, измеряемым высотою водного столба, и
напором h существует простая зависимость
р = Гг — у, B.4)
где ось у направлена вертикально вверх. Из этого равенства
следует, что если построить линии h = С\ и у = С2, то в точках
'/////////л
¦/7777,
Рис. 318.
пересечений этих линий будем иметь р = С\ — С2 (С{ и С2 мо-
могут быть как положительными, так и отрицательными).
Выбирая те значения С\ и С2, сумма которых равна задан-
заданному числу С = С\ — С2, и проводя через них плавные линии
(это будут диагонали четырехугольников, образованных линия-
линиями А = Ci и у = С2), получим изобсры р(х,у)= С.
На рис. 318 представлено семейство изобар для земляной
перемычки на непроницаемом основании (Southwell 1956).
574
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
Отметим, что при построении изолиний для случая фильтра-
фильтрации в земляной плотине мы сталкиваемся с тем затруднением,
что линия свободной поверхности заранее не известна, и ее надо
определять подбором как линию тока, вдоль которой h = у.
Используя то обстоятельство, что депрессионная кривая яв-
является изобарой, можно найти, что вдоль депрессионной кривой
должно выполняться соотношение
дп
(Aif у),
B.5)
где п — внешняя к области движения нормаль к линии свобод-
свободной поверхности.
Уравнение B.5) можно вывести из условия, что на свобод-
свободной поверхности
I. B.6)
дп
Так как ф = — k (р + у) (при pg = 1), то
2.
дп
4?-
дп
B.7)
Р-Ро
Но dyjdn, как видно из рис. 319, равно косинусу угла между
нормалью п и осью у: dy/dn = sin a = cos (я, у). Подставляя
это значение dy/dn в уравнение
B.7), получим соотношение B.5).
Оно может служить для проверки
правильности построения депрес-
депрессионной кривой или для построения-
изобары р = ри когда известна де-
депрессионная кривая — изобара р =
= р0. В последнем случае имеем
приближенное равенство
(n, у),
B.8)
Рис. 319.
позволяющее, построив нормали в
ряде точек свободной поверхности и
вычислив в них cos(n,y), найти длины отрезков нормали An
между линиями р0 и рх.
В первом издании настоящей книги (Полубаринова-Кочина
1952, 1) формула B.8) была использована для построения фор-
формы свободной поверхности при неустановившейся фильтрации —
вытекания воды из каналов в грунт (см. § 5 главы XVI первого
издания). Однако лица, пробовавшие применять этот способ к
отдельным задачам, заметили, что счет получается неустойчи-
неустойчивым: при небольшой деформации изобары угол нормали к ней
может сильно изменяться. Поэтому ^тот способ нельзя рекомен-
рекомендовать. Приведенные в первом издании книги примеры, получен-
§2]
СРЕДНИЕ АРИФМЕТИЧЕСКИЕ, КОНЕЧНЫЕ РАЗНОСТИ
675
ные с его помощью, могут иметь лишь иллюстративный ха-
характер.
Применение метода сеток в случае анизо-
анизотропных грунтов. Рассмотрим следующий пример (Козлов
1941). Задан флютбет (рис. 320) с размерами /i = 6 м, /2=10 ж,
S = 3,5 м. Коэффициенты фильтрации в направлении глав-
главных осей анизотропии имеют следующие значения: k\ =
=а 0,000049 м/сек, k2 = 0,000004 м/сек, так что «коэффициент
анизотропии» v = k2/ki =0,0816. Угол между осью х и главной
осью фильтрации |, который характеризует наклон слоистости,
19°Г
Рис. 320.
Требуется построить сетку движения. Вспоминая результаты
§ 8 главы VIII, перейдем от координат х, у к координатам X, Y.
Воспользовавшись формулой (8.3) главы VIII для тангенса
угла 6 косого шпунта с осью X
& (k2 — k\) sin a cos a '
для рассматриваемого примера найдем tgб = —|- 1 и 6 = я/4.
По первому из уравнений G.6) главы VIII при у = 0 имеем
v л k\ sin2 a + k2 cos2 а
А = АХ = 7г=Г= Х>
по второму уравнению при л: = 0 получим
Y = — X =
(k2 — k{) sin a cos a
X.
576
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
Отсюда можно найти длины преобразованных отрезков флют-
бета и шпунта (рис. 321) /1 = 8,92 м, &= 14,87 м, S* = 11,64 м.
В осях координат X, У на рис. 321 дана сетка движения.
h/H-1,0
Рис. 321.
Уравнения (8.2) главы VIII позволяют сделать пересчет по-
полученной сетки, перенеся ее на плоскость х, у. Новая, уже не
ортогональная сетка представлена на рис. 320.
Отметим, что сетка рис. 321 может строиться указанными
выше графическими методами, но может быть получена и иначе,
Рис. 322,
например, В. С. Козловым A941) она была построена по методу
электрогидродинамических аналогий, о котором говорится ниже
(§9).
Для неоднородных грунтов при переходе из одного
слоя в другой нужно учитывать закон преломления линий тока
на границе раздела двух грунтов. Приемы построения сеток в
СЕТКА В ОСЕСПММЕТРИЧНОМ ДВИЖЕНИИ
577
неоднородных грунтах развиты в работах Н. К. Гиринского
A939) и С. Ф. Аверьянова A949, 3).
На рис. 322 дан пример сетки для фильтрации иод флютбетом
в основании из двух различных грунтов (Фильчаков 1960).
§ 3. Сетка в осесимметричном движении. В случае движения
несжимаемой жидкости с осевой симметрией существует функция
тока ф, через которую составляющие скорости выражаются сле-
следующим образом: 7.
г дг
1 <
C.1)
дг
Ось г — ось вращения, г — поляр-
полярный радиус-вектор.
Функция г|? удовлетворяет
уравнению
дг2
:^ + 44--l-tl = o. C.2)
дг2
дг
Если движение имеет потен*
циал скорости ф, то для послед-
последнего получаем в цилиндрических
д2ф , д2ф , 1 д
дг2 ' дг- ' г д
Рис. 323с
координатах
уравнение
C.3)
Допустим, что построена сетка линий г|) = const и ф = const.
Эти линии взаимно ортогональны, но из них нельзя образовать
изотермическую сетку, т. е. сетку квадратов. В самом деле, из
равенств C.1) и из свойства функции ф имеем
1 д\|з дф дф 1 dib
°г1С=7""д5~ = ~дГ' Vz ==~дг~ = ~~'Т'~дГ-
Если давать ф и ф равноотстоящие значения, полагая Дг|) = Дф,
то получим, что должны выполняться условия
г kz^ = Дгф, Дгф = г Дгг C.4)
Индекс ф или \|) указывает, между какими линиями берется при-
приращение.
Выведем формулу для вычисления значения ф0 функции тока
i|) в центре квадрата со сторонами 2п, если известны значения
этой функции г|)а, -фь, tyc, tyd в вершинах квадрата (рис. 323).
Проведем линии ^ = i|?a, ..., гр = -ф^ через вершины квадрата
и вычислим расход между поверхностями вращения яр = tj>a и
19 П. Я. Полубаринова-Кочина
678 установившиеся движпшя грунтовых вод [гл. xviii
^ = гро- Элементарный расход dQ между поверхностями г|) и
г|) + Л|5 равен
dQ = 2nrvz dr = -2n-^r dr.
Отсюда, выбирая соответствующим образом значение постоян-
постоянной интегрирования, получим
Q = -2*t(^-i|)a). C.5)
Для расхода qao между поверхностями tya и ^о находим, при-
принимая во внимание, что расходы через стороны а$ и Оа оди-
одинаковы:
= 2я (г - -у ) ПУг
ЯаО = Яаа + Q4 = Qaa +
Отсюда, выражая расходы через значения функции тока по
формуле C.5) и сокращая на 2л, получим
Фо = Ф« + (г — у) nv2 + rnvr
Таким же образом, подсчитав расход между поверхностями
и урь, будем иметь
Точно так же получим
Фо = Ъс — у + -f) ПХ)г — (Г + /Z) tlVn
Фо = ^ + (г — -g-j /гуг — (Г — П) ПЮГ.
Складывая все четыре выражения для яро и деля сумму на че-
четыре, найдем
% + Я'ь + %+% п2
Фо = 5 2" У;г#
При этом для vz можно взять одно из следующих приближен-
приближенных выражений:
z г дг ~ г 2п г 2п г An
Рассмотрим пример применения графического метода.
Сетка для установившегося движения при
наливе воды в скважину (осевая симметрия).
В полевых условиях проницаемость грунта определяется в основ-
основном двумя методами: методом откачки и методом нагнетания.
Частным случаем нагнетания является налив воды в скважину.
СЕТКА В ОСЕСИММЕТРИЧНОМ ДВИЖЕНИИ
579
Предположим, что нам удалось осуществить установившееся
движение при наливе в скважину — для этого нужно вести опыт
до тех пор, пока расход, подаваемый в скважину, практически
d
АН
АН
Рис. 324,
станет постоянным. В. М. Насберг A950) рассмотрел частный
случай, когда отношение высоты столба воды в скважине над ее
дном к диаметру скважины h/d = 50. Действующий напор, от-
отсчитываемый от некоторой плоскости а\С\ (рис. 324), обозначим
через Я. Поверхности равного напора построены через равные
интервалы напоров Д#, причем
C.6)
19*
680 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
где р — число поясов напора. Поверхности тока построены че-
через равные интервалы расходов, т.е. расходы AQ каждой коль-
кольцевой трубки тока, протекающей между любыми двумя смеж-
смежными поверхностями токов, должны быть одинаковы:
AQ = -f. C.7)
где Q — полный расход скважины, t — число трубок тока, рав-
равное числу поверхностей тока, принятых для построения.
Согласно условию h = z на свободной поверхности расстоя-
расстояние между горизонтальными плоскостями, проведенными через
линии, образованные пересечением двух соседних эквипотенци-
эквипотенциальных поверхностей с поверхностью депрессии, должны быть
одинаковы и равны АН.
При построении сетки можно использовать методы, приме-
применяемые при построении электростатических полей с осевой сим-
симметрией (Корсунцев 1937).
Назовем величину
Atf = ?^- = const C.8)
приведенным сопротивлением участка трубки тока, заключенно-
заключенного между смежными эквипотенциальными поверхностями. Из
C.1) следуют приближенные равенства
Аф 1 Аг|) Аф 1 As
As г Ал ' Аф г An *
где As и Д/г откладываются по взаимно перпендикулярным на-
направлениям. Полагая Аф = k Д#, 2я Аф = AQ, As = /, An = ft,
получим А/? = l/{2nrb). Для г, малых по сравнению с Ь
(рис. 324 — вблизи скважины), поверхности тока близки к гори-
горизонтальным плоскостям, поверхности равного напора — к вер-
вертикальным цилиндрам, и для расхода AQ можно принять фор-
формулу A.4) главы IX. Поэтому AR = In (г\1г2)/BпЬ).
В последних формулах введены следующие обозначения
(рис. 325): /—средняя длина участка трубки тока, заключенно-
заключенного между смежными эквипотенциальными поверхностями (/ =
= АВ на рис. 325), ft —средняя ширина меридионального се-
сечения участка трубки тока (b = CD), 2nrb — площадь среднего
поперечного сечения участка трубки тока, г —расстояние от се-
середины сечения трубки тока до оси скважины (г = ОЕ), Г\ —
расстояние от точки С до оси скважины, Гг — расстояние от точ-
точки D до оси скважины.
Из равенств C.6) — C.8) получается формула для определе-
определения коэффициента фильтрации k:
h_^R_ Р п__ _М- Ln — СП
§4]
МЕТОД СУММАРНЫХ ПРЕДСТАВЛЕНИЙ
581
Из этой формулы видно, что, зная постоянную С и определив
из опыта значение расхода Q, можно вычислить искомый коэф-
коэффициент фильтрации.
Постоянная С имеет размерность [L~2]. Поэтому, чтобы по-
получить величину С, отвечающую натуре, нужно постоянную Ст,
Рис. 325.
найденную по чертежу сетки, построенному в масштабе 1 : т,
разделить на т2. Получим
с = -~р-. (зло)
На сетке рис. 324 принято /i/d=50, Ai= 175 мм, Д# = 20 мм,
/=6, Д/? = 3,82-10~3 мм~1. По уравнению C.9) получаем
С ^ А/? ! =31 S 1(Г6 !
LSfJ t MM
§ 4. Метод суммарных представлений. Как было показано
выше, в теории фильтрации ряд задач сводится к уравнению
Гельмгольца
= const), D.1)
для которого ищется решение краевой задачи.
Рассмотрим в качестве области движения прямоугольник D%
по контуру Г которого задаются краевые условия
Ыи\г = Ф(х,у) D.2)
(iV —оператор граничных условий).
Напишем соответствующее уравнению D.1) конечноразно-
стное уравнение
ДАм - 2с и {хь yk) = / (xh yk), D.3)
которое рассматривается в сеточном прямоугольнике с коорди-
координатами узлов Xi = х0 + ih, yk = Уо + khx = yQ + kh/y (t=0,1,...
682 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
..., т + 1; k = 0, 1, ..., п + 1) и отношением сторон в элемен-
элементарном прямоугольнике h/h\ = у. На границе Г области D бу-
будем иметь конечно-разностный оператор
у*)- D.4)
В качестве Д^и возьмем построенный по пяти узлам оператор
= тт (Щ-и k - 2и/§ л + и ) + (" 2и + и )
Л"
= -1- (щ-и k - 2 A + Y2)"/. fe + Mj+i, Л + Y2^, fe-i + Y2«f, fe+i), D.5)
где ulk = u{xi9yk), y = h/h{.
Г. Н. Положему A962) принадлежит введение метода реше-
решения краевых задач конечно-разностных уравнений для некото-
некоторых канонических областей, названного методом суммарных
представлений. В нем решение конечно-разностной задачи вве-
введением специальной Р-трансформации сводится к решению
обыкновенного конечно-разностного уравнения. Это решение за-
записывается в замкнутой форме, представляющей дискретный
аналог представления решений линейных дифференциальных
уравнений при помощи интегральных представлений с исполь-
использованием функции Грина. Мы ограничимся тем, что выпишем
окончательный результат (Ляшко и др. 1974) для задачи Ди-
Дирихле в случае прямоугольной области.
Считаем, что в граничных точках на параллельных оси х
сторонах прямоугольника (л;*, уо) и (л:г-, уп+\) известны значе-
значения функции u(xh yh). Возьмем t-e сечение и введем вдоль него
/г-мерные векторы
ui = u{xi) = {uiu щъ ..., uln), fi = {fn, •••> ftn)*
©* = @ М = Ко, 0, ..., 0, щщ я+1}, Hi = h2fi — y4
(t=l, 2, ..., m). Далее вводится квадратная матрица чисел
{}
(/, k=l9 2, ..,, щ\ 9^ —корни уравнения sin (л + 1)8 = 0).
Кроме того, вводятся три диагональные матрицы
с элементами по диагоналям ц?, vlk, ^у~р'(цй — v*)~'' пРичем
§ 4] МЕТОД СУММАРНЫХ ПРЕДСТАВЛЕНИЙ 583
(/е = 1, 2, ..., п). Теперь можно выписать решение нашей за-
задачи в очень компактной векторной форме
и (*,) = Р L'A + v'B - ? G (i - p) P*H (xp)} D.6)
(i = 0, 1, ..., m+1). Здесь P*— транспонированная матрица
по отношению к матрице Р, А = {Ah} и В = {Bh} — векторы по-
постоянных Ah, Bh (k= 1, 2, ..., п), которые определяются из
граничных условий на параллельных оси у участках границы
области D. А именно, предположим, что {ион} = #A), {um+\th} =
= н<2) (к=1, 2, ..., п) — заданные постоянные векторы'. По-
Положив 1 = 0 и t = m+l в уравнении D.6), получим систему
двух векторных уравнений для А и В:
D.7)
pUm+lA + vm+*B- ? G(m+\-p)P*Hp\ = uW.
Умножим левую и правую части уравнений D.7) на Р\
Так как произведение Р*Р=1, то получим
т
А + В - Z G (- р) Р*НР = PV1),
1
_ v^+l JB — Z G (т + 1 - р) Р*НР = Р*ФК
р-1
Решением последней системы являются векторы
а = д-1 (vV° - Л в=л-1 (v-V° - фB))>
где
fWeWHl G(-p)P*Hp,
1
фB) = р*„B) + ? G (т _|_ J _ р) р«Я
1
Аналогичным образом дается представление решения урав-
уравнения D.3) для граничных условий второго рода и смешанных
краевых условий. Особенностью метода суммарных представле-
представлений является то, что подавляющая часть неизвестных, входящих
в конечноразностную задачу, не участвует в процессе счета. При
этом решение может быть найдено в любом отдельном узле сет-
сетки без одновременного нахождения решения в остальных узлах.
584
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
(ГЛ. XVIII
Метод Г. Н. Положего развивался им и рядом других авто-
авторов и применялся к конкретным задачам. Так, был рассмотрен
случай, когда область D — полуполоса или полоса, когда она
может быть разбита на прямоугольники, для которых устанав-
устанавливаются условия на участках «сшивания», для» кусочно-неодно-
кусочно-неоднородных слоев.
§ 5. Графо-аналитические построения безнапорных движений
с помощью рассмотрения фиктивного течения в области годо-
годографа скорости. Предположим, что мы отобразили плоскость
комплексного потенциала о на плоскость комплексной скорости
w = u — iv. Тогда со (до) будет представлять течение в области
годографа скорости, т. е. фиктивное течение, на границах кото-
которого выполняются те же условия для ф и ^, что и для действи-
действительного течения на плоскости z (Weinig и Schields 1936).
Рис. 326.
В качестве примера рассмотрим приток из бесконечности к
вертикальному откосу на непроницаемом водоупоре, когда вода
в нижнем бьефе отсутствует (Breitenoder 1942) (рис. 326). Это —
частный случай прямоугольной перемычки, рассмотренной у нас
в главе VII.
На рис. 327 построен годограф скорости перемычки. Свобод-
Свободной поверхности отвечает дуга окружности и2 + v2 + kv = 0, не-
непроницаемому основанию — ось и, промежутку высачивания —
прямая, параллельная оси абсцисс и проходящая через точку
и=0, v=—k. На плоскости годографа линии АВ и АС являют-
являются линиями тока фиктивного течения. Примем вдоль них соот-
соответственно ф = О и г|?=1. (Когда мы найдем величину расхо-
расхода Q, то умножим значения функции тока на него.)
§5]
ФИКТИВНОЕ ТЕЧЕНИЕ В ОБЛАСТИ ГОДОГРАФА СКОРОСТИ
585
Линия ВС есть промежуток высачивания. Чтобы исследовать
поведение линий тока вдоль этой прямой, можно построить се-
семейство изоклин на плоскости (и, v). Это — пучок прямых, исхо-
исходящих из начала координат (они не изображены на рис. 327).
Угол 9 каждой из них с осью абсцисс меняется от нуля в точке
С до —90° в точке В.
Так как область z отображается на область u-\-iv конформ-
конформно, с сохранением углов (но с измененным направлением отсче-
отсчета углов), то на плоскости годографа линии тока должны пере-
пересекать прямую ВС под тем же углом а, под каким линии тока
плоскости z пересекают промежуток высачивания. При этом а
представляет дополнение угла 0 до —90°.
В
Разметив вдоль отрезка ВС рис. 327 значения а, можем по-
построить семейство линий тока, исходящих из вершины Л, и ли-
линий равного потенциала. Эквипотенциаль, исходящую из вер-
вершины В, принимаем за нулевую. В точке А эквипотенциали сгу-
сгущаются до ф = оо и скорость фиктивного течения здесь будет
бесконечно велика.
Построение сетки в области течения. Линиям
тока фиктивного течения отвечают линии тока действительного
течения на плоскости z. To же относится к эквипотенциалям.
Выясним вопрос о том, как перенести эти изолинии с плоскости
и -f- iv (или w = и — iv) на плоскость х + iy-
Из уравнения
dz
получаем
f den f dсо
J w J // — iv
E.1)
686
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
Вводя величину скорости V и угол вектора скорости с осью
абсцисс 8, имеем
u-iv
Выражение
можно разбить на действительную и мнимую части, и тогда
получим
= \у (cos Э dy — sin 0 da|>) + i\ у- (sin 9 ^ф + cos 0 rf\|)). E.2)
Вдоль линии тока d^ = 0, а потому линия тока плоскости z
определится уравнениями
ф|
cos 9
sinB
E.3)
Ф1
Вдоль эквипотенциален dq> = 0, и поэтому уравнения линии
равного потенциала на плоскости течения будут представляться
10 . в виде
0,8
0,5
\
1
\
V
\
V
-
% -—
cose
E.4)
Здесь ф! и \fi — некоторые произ-
произвольно выбранные значения ф и г|?.
(/Л——I 1 т NL 1 Если на плоскости годографа
построена сетка линий ф = const
и ф = const, то, производя графиче-
0 0,5 1,0 ское или численное интегрирование
Р по формулам E.3) и E.4), можно
Рис. 328. построить сетку движения на
плоскости z.
В качестве примера возьмем эквипотенциаль ф = 0 фиктив-
фиктивного течения (рис. 327). Взяв на ней точки со значениями \|э =
= 0, 74, 2Д, 3U, 1, снимем в этих точках значения V и 0 и по-
построим графики величин cos9/V и sinB/V как функции от \|э
(рис. 328). Произведя численное интегрирование, получим зна-
значения хну для эквипотенциали ф = 0. Интеграл для у в пре-
§ 5] ФИКТИВНОЕ ТЕЧЕНИЕ В ОБЛАСТИ ГОДОГРАФА СКОРОСТИ 687
делах от 0 до 1 даст приведенную длину промежутка высачи-
вания
1
kH0
Q
S
Проведенные вычисления дают для ординаты Но = ВС
(рис. 326) значение 0,744 Q/k. Более точно, как было показано
в § 10 главы VII, должно быть Но = 0,7425 Q/k— различие все-
всего в 0,2%. Если произвести интегрирование по другим изоли-
изолиниям ф и г|) плоскости годографа, то получим сетку плоскости z
(рис. 326). В частности, интегрируя вдоль полуокружности го-
годографа скорости, получим координаты точек депрессионной
кривой. Условие ф + &(?/ — Я0) = 0 на свободной поверхности
может служить для проверки правильности построения этой
кривой.
Изоклины и изотахи фиктивного течения. Рас-
Рассматривая комплексный потенциал со как функцию от до, мы
можем взять производную от нее по до:
•Й—tf-VV*. FJ3>
которая будет представлять комплексную скорость фиктивного
течения. При этом V* будет величиной скорости, 9*—углом,
образованным вектором скорости с осью и. Взяв In до* и отделив
в нем действительную часть от мнимой, получим
Линии V* = const и 0* = const образуют ортогональную сет-
сетку изотах и изоклин фиктивного течения. С помощью этой сет-
сетки можно уточнять построение линий тока и линий равного по-
потенциала фиктивного течения.
Допустим, что у нас грубо построена сетка фиктивного тече-
течения (желательно построить густую сетку). Будем проводить ка-
касательные к линиям тока под одним и тем же углом 0° к оси
абсцисс и соединим плавной линией точки, отвечающие этому
углу. Это будет изоклина р°. Построив систему изоклин, отве-
отвечающих, например, значениям C° = 0°, 5°, 10°, ..., проведем
ортогональные к ним линии V* = const. Если получим изотерми-
изотермическую сетку, то значения V* вдоль соседних изотах будут удов-
удовлетворять соотношению ln(K*+1/F*) =агс5°== л/36, или
При этом значение V*, вначале произвольное, может быть опре-
определено в конце всех построений.
§ 5] ФИКТИВНОЕ ТЕЧЕНИЕ В ОБЛАСТИ ГОДОГРАФА СКОРОСТИ 589
Полученную таким образом сетку надо выравнивать до тех
пор, пока не получится правильная система квадратов.
Внутри области годографа встречаются точки, в которых
пересекаются изоклины с одинаковым значением, обычно под
прямым углом. В этой же точке пересекутся и изотахи, также
под прямым углом, составив с изоклинами углы в 45°. Такая
особая точка является точкой разветвления. Для рассматривае-
рассматриваемого примера изоклины и изотахи фиктивного течения изобра-
изображены на рис. 329. Они имеют только одну точку разветвления.
Проведя касательную в какой-нибудь точке полукруга годо-
годографа скорости, найдем угол, соответствующий той изоклине,
которая проходит через эту точку. Изоклины выходят из полу-
полукруга и частью уходят на бесконечность, частью втекают в ниж-
нижнюю часть полукруга.
От системы изоклин и изотах фиктивного течения можно
перейти к системе линий ф = const и г|) = const на плоскости
годографа, если проинтегрировать уравнение E.5) по произволь-
произвольному пути в плоскости w. Положим
ю = J I/Vе* Аи, E.6)
и пусть dw = e°s ds, где ds —элемент дуги выбранной кривой,
в8 — угол касательной к этой дуге с осью абсцисс. Тогда будем
иметь
со =
So
ИЛИ
" V cos (9S - 9*) ds, ф = jj У sin (в, - 9) ds. E.7)
Здесь So — начальное, s — конечное значения длины дуги инте-
интегрирования. Значения ф и ф в какой-нибудь точке, полученные
по различным путям интегрирования, должны совпадать.
С помощью интегралов E.7) можно найти значения потен-
потенциала скорости и функции тока в различных точках области го-
годографа и, таким образом, уточнить построение сетки.
С помощью такого приема Ф. Вайниг и А. Шильдс, а затем
М. Брайтенодер рассмотрели несколько примеров. Рис.330 и 331
изображают построение течения в случае притока грунтовых
вод к канаве прямоугольного сечения.
Г. К. Михайлов A956) применил метод Вайнига и Шильдса,
в комбинации с методом ЭГДА, к решению задачи о форме дре-
дренажного устройства. В простейшем случае дренажа, представ-
представляемого бесконечно тонкой щелью (см. § 12 главы II), на одном
590
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
конце щели решение дает бесконечную скорость. Считая, что
дрена есть щель конечной ширины, снабженная оголовком,
Г. К, Михайлов определял такой оголовок, вдоль которого
Рис. 330.
величина скорости (или градиент фильтрационного потока) имеет
постоянное значение. В результате он получил форму оголовка
и дал приближенную зависимость градиента от расхода дрены
и толщины ее оголовка.
§ б]
ФИКТИВНОЕ ТЕЧЕНИЕ В ОБЛАСТИ ГОДОГРАФА СКОРОСТИ
691
Можно указать способ определения радиусов кривизны ли-
линий \|э = const и ф = const, что дает возможность более точного
построения этих линий, как состоящих из дуг окружностей кри-
кривизны. Способ этот основан на следующей теореме (Barillon
Рис. 331.
1936). Пусть даны линии <р = С,г, ф = Сф и диагональные к ним
линии С45° и Ci35°. Тогда центры кривизны диагональных линий
находятся на одной прямой
с центрами кривизны линии
тока и эквипотенциали
(рис. 332). При этом на-
направление этой прямой со-
совпадает с направлением ка-
касательной к контуру видоиз-
видоизмененного годографа ско-
скорости, под которым понима-
понимается линия, описанная кон-
концом вектора, исходящего из
произвольного полюса Q, ве-
величина которого равна вели-
величине вектора скорости, но который составляет прямой угол с на-
направлением скорости.
Так, на рис. 332 линия MN есть линия тока, Q — полюс видо-
видоизмененного годографа. Если известен центр кривизны С^ и
если мы знаем направление касательной к видоизмененному го-
годографу МГ, то, проведя через точку С^ прямую, параллельную
МТ, найдем ось, на которой лежат Сф, С45° и Ci35°.
592
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVITI
§ 6. Графо-аналитический способ расчета пространственных
движений. В естественных условиях плоские течения грунтовых
вод встречаются очень редко, действительные движения бывают
трехмерными. На рис. 333 приведены примеры пространствен-
пространственных движений. На схеме а показан грунтовый поток, образован-
образованный просачиванием воды, являющимся следствием фильтрацион-
фильтрационных потерь оросительной системы. Схема б представляет типич-
типичный случай выклинивания грунтового потока в пойму реки. На
схеме в изображен грунтовый поток, образующийся от инфильт-
инфильтрации атмосферных осадков и выходящий на склоны оврагов.
И-орошаемый
массид
Ю
Рис. 333.
Схема г изображает фильтрацию из водохранилища и обтека-
обтекание плотины.
С. Ф. Аверьянов A949,3), приводя эти схемы, указывает,
какие задачи встают при их рассмотрении. Для схемы а возни-
возникает вопрос о подъеме грунтовых вод и возможном засолении
сельскохозяйственных земель. Дело в том, что если поверхность
грунтовых вод близка к поверхности земли, то могут наступить
интенсивное испарение грунтовых вод и поднятие их по капил-
капиллярам грунта; при этом из почвы выносятся соли на поверхность
земли (см. раздел Б главы XV). Для случая б возникает вопрос
о возможности улучшения сельскохозяйственного использования
поймы реки и ее осушения. Для схемы в бывает важно устано-
установить место наиболее интенсивного выхода грунтового потока и
определить необходимые мероприятия по борьбе с оползнями.
Для случая г важно суметь определить потери на фильтрацию
из водохранилища и найти меры борьбы с подъемом грунтовых
вод на прилегающих к нему сельскохозяйственных землях.
Для численного расчета пространственных установившихся
движений С. Ф. Аверьянов предложил следующий метод.
В пространстве вместо линий тока нужно рассматривать по-
поверхности тока, образующие трубки тока или шнуры течения,
§ 6] РАСЧЕТ ПРОСТРАНСТВЕННЫХ ДВИЖЕНИЙ 593
вместо линий равного напора (или потенциала)—поверхности
равного напора (или потенциала). Последние ортогональны ли-
линиям тока.
Вдоль каждой трубки тока расход является постоянным.
Можно провести поверхности равного напора так, чтобы паде-
падения напора между соседними поверхностями были равны. Если
п — число проведенных таким образом поверхностей, то nAh=
= #, где Н — разность напоров начальной и конечной эквипо-
эквипотенциальных поверхностей, а Ah есть падение напора между со-
соседними поверхностями.
Рассмотрим элементарный шнур течения с элементарным
расходом AQ. Для элемента этого шнура, отсеченного соседни-
соседними эквипотенциальными поверхностями, элементарный расход
выражается так:
Д<2 = М1д/Д&. FЛ)
Здесь k — коэффициент фильтрации, А/— длина элемента шну-
шнура, А6 — ширина, At — глубина этого элемента.
Заменяя Ah равным ему выражением Н/п, получим
= const-
Разобьем область движения на такие шнуры, расходы вдоль
которых равны между собой, т. е. для которых AQ = const. Так
как kH/n постоянно, то мы должны иметь
= const. F.3)
Это условие вместе с условием ортогональности линий тока к
поверхностям равного напора дает критерий правильности по-
построения пространственной решетки.
Для потоков, занимающих большую площадь и имеющих
слабо изменяющуюся свободную поверхность, как уже указы-
указывалось в главе X, можно принять, что поверхности равного на-
напора являются цилиндрическими поверхностями с вертикальны-
вертикальными образующими. Суммируя в этом случае шнуры по вертика-
вертикали, получим для расхода AQ через пачку шнуров следующее
выражение:
AQ = kAh^-. F.4)
Здесь / — средняя глубина потока для пачки шнуров, располо-
расположенных на одной вертикали.
При этом для одной пачки шнуров должно быть соблюдено
условие
if F-5)
694 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
Можно назвать т коэффициентом формы пространственной
сетки. *
Полный расход потока при т =- const для всей сетки равен
Q^kkhmx^-^mx, F.6)
где m — число пачек шнуров по ширине потока, п — число экви-
эквипотенциальных поверхностей.
Отсюда следует, что если построить в плане сетку с соблю-
соблюдением постоянства коэффициента формы т, то по ней можно
получить все характеристики потока. Эквипотенциальные по-
поверхности в плане будут линиями равного напора для напорно-
напорного потока и гидроизогипсами, т. е. линиями равной высоты сво-
свободной поверхности, для свободного (безнапорного) потока. По
ним можно определить расходы и скорости отдельных элемен-
элементов потока. При этом элементы сетки будут криволинейными
прямоугольниками с переменным отношением сторон, так как
для пространственного потока соблюдается условие F.3), но не
условие Д&/Д/ = const, имеющее место для плоского потока.
Лишь при постоянной глубине потока / пространственная сетка
обращается в плоскую.
При больших значениях по сравнению с / величин В и L —
общей ширины и длины потока — в качестве первого приближе-
приближения можно взять сетку плоского потока для постоянной глу-
глубины потока /Ср, равной среднему значению глубин / потока.
Затем эту сетку можно исправить сдвиганием эквипотенциалей
и линий тока при сохранении их ортогональности и при соблюде-
соблюдении для каждого параллелепипеда сетки условия F.5).
В общем случае, когда поверхности равного напора не яв-
являются цилиндрическими поверхностями с вертикальными обра-
образующими, полный расход потока получается суммированием
выражений F.2):
m r
где m и г —число шнуров по ширине и глубине потока.
В случае, когда образование потока происходит только за
счет инфильтрации постоянной интенсивности е, для любого па-
параллелепипеда сетки получаем
где S — площадь питания, равная площади всех квадратов сет-
сетки от рассматриваемого места до водораздела (истока потока);
AQ уже не будет постоянным по длине шнура. Критерием пра-
§ 71 МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ 595
вильности построения пространственной сетки будет теперь со-
соблюдение равенств
е 1 _±ьь_
T~M~~s~KF~consl-
Если грунт неоднороден (т. е. коэффициент фильтрации не
является постоянным), то напор
k pg ^
не будет удовлетворять уравнению Лапласа. Но если уравнения
Дарси
1 dh , dh i dh
имеют место, то они показывают, что расход AQ по-прежнему
будет выражаться формулой F.4). Однако условие F.5) не бу-
будет выполняться; вместо него будем иметь соотношение
AQ , ttab
где k — осредненный по вертикали коэффициент фильтрации.
§ 7. Метод конечных элементов для интегрирования эллипти-
эллиптических уравнений*). В последнее время большое применение на-
находят вариационные методы решения уравнений эллиптического
и параболического типа (см., например, Зенкевич и Цанг 1974).
Остановимся здесь на так называемом методе конечных элемен-
элементов (для уравнения нестационарной фильтрации в главе XIX
будет рассмотрен вариационно-разностный метод).
Пусть дано уравнение
d ( dh \ ,п 1Ч
GЛ)
где р\{х,у) и р2{х,у) —заданные функции я, у. Требуется най-
найти его решение в области Z), ограниченной контуром L, при
условии, что на контуре значения h(x,y) известны:
h(x,y)\L = f(x9y). G.2)
Будем искать минимум функционала
J]} G.3)
D
при условии, что h(x,y) удовлетворяет условию G.2).
¦) При составлении этого параграфа был использован отчет В. А. Ва-
Васильева.
596 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
Как известно (см., например, Михлин 1970), если интеграл
минимизируется, то необходимым условием является то, что
функция F должна удовлетворять дифференциальному уравне-
уравнению Эйлера
д Г dF }\ д \
'дх 1д(ди/дх)\~ ду [
д (ди/ду)}
в той же области, а и(хуу) удовлетворяет тем же граничным
условиям. При достаточно широких условиях задача G.1) — G.2)
эквивалентна задаче G.3) — G.2).
Можно интерпретировать выражение G.3) для / как энер-
энергию, запасенную жидкостью в данной области на фиксирован-
фиксированный момент времени.
й)
Рис. 334.
Разобьем всю область D на треугольники произвольного
вида (см. рис. 334) и пронумеруем их от 1 до jV, а все верши-
вершины—от 1 до М. Выделим какой-нибудь треугольник А (*,/,&)
с вершинами Mi(xuyi)i Mj(Xj9yj), Mk(Xh,yh)- Обозначим зна-
значения h(xyy) в узлах через ft*, hjy А*. В пределах каждого тре-
треугольника h(x,y) считается представимой линейной функцией
координат:
А (х9 у) = а{ + а2х + аъу. G.4)
Следовательно,
A (xi9 tji) = hi = al + а2х( +
h (xi% yj) = hJ = al+ a2xj
b yk) = hk = щ + a2xk + a3yk.
§7]
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
597
Из этой системы уравнений находим as и подставляем в G.4).
Получим
h (х, у) = Ntht + Njhj + Nkhb G.5)
где
= -gj- (as + bsx + csy) (s = i9 /, k).
G.6)
При этом
= xkyt — xtyki ak = xtyf — xfyh G.7)
bj = yk — yh bk = yl — yj, G.8)
cJ-=xi — xki ck = xf — xh G.9)
- yj)l G.10)
Теперь интеграл / по треугольной области будет функцией hiy
hh hk:
J(h(x, y)) = r{hi9hhhk).
Чтобы найти минимум /* по переменным hh hh hk, полагаем
i^l = — = J*?- == О
dhi dhj dhk
Получаются основные уравнения метода конечных элемен-
элементов для треугольной области, которые можно записать в матрич-
матричной форме:
{} G.11)
Здесь [g] — квадратная матрица
u + gik) gt
Г
= \
L
gik
==-4b(p\bibf + p2cicJ)i
= -45- (p\bibk + p2CiCk)y
= 45- {p\bibk + p2c}ck)
G.12)
G.13)
(функции p, (x, у) и р2 (х, у) в пределах каждой треугольной
ячейки считаются постоянными). Далее, имеем {/г}, {бш/3} —
698
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
матрицы-столбцы:
{4-}-
G.14)
G.15)
В развернутом виде уравнения G.11) имеют вид
gu {h, - ht) + gik (А» - Ы) = qu
Ski (A* - h,) + gl{ (hi - hj) = q,,
gjk (A, — hk) + gik (hi — hk) = qk,
G.16)
где qt = 6Wi/3 и т. д.
Структура этих уравнений позволяет трактовать коэффи-
коэффициенты gij как «проводимости» некоторых фиктивных трубок,
по которым жидкость якобы перемещается от одного узла тре-
треугольника к другому. Матрицу G.12) называют матрицей фильт-
фильтрационных проводимостей треугольного элемента. Эта матрица
симметрична: gij = gjii... Для программирования ее записы-
записывают в виде
[g] = [A]"lT X [В] X [А]~\ G.17)
где
лг uf
ИГ—я-
26
К , И]Г = ^- ai bi с!
ГО 0 0 1
[В] = О Р1 0 .
Loo p2 J
G.18)
G.19)
Для составления системы уравнений для всех неизвестных ht
в области D нужно объединить матрицы проводимости для
всех элементов области. Получается система уравнений вида
[G] X {Я} = {Q}, G.20)
где
hi
h2
(Q} =
§7]
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
599
Составление матрицы [G] является трудоемким, оно произ-
производится по тем же правилам, которые разработаны в электро-
электротехнике при составлении баланса токов в замкнутых и разветв-
разветвленных цепях (Бессонов 1967).
Поясним на простом примере, как строится система уравне-
уравнений G.20). Предварительно перепишем систему уравнений
G.16), снабдив в ней все gik значком / в знак принадлежности
их ячейке с номером /:
Рассмотрим схему из шести треугольных элементов с семью
вершинами (рис. 334,6) и составим для них шесть систем урав-
уравнений вида G.21). Выпишем лишь какие-нибудь две из них:
например, для первого элемента с узлами /, 3 и 4:
для четвертого элемента с узлами 3, 5 и 6:
- (ей + 40 К + 8\ьК + g\zK = <&
ё!А - (8U + ej.) К + §1А = €
~ (^бз + в&) К = <¦
G-22)
G-23)
Всего получим 18 уравнений с 7 значениями А: Аь ..., Л7. Их
группировка в систему из 7 уравнений производится так. Три
уравнения, правые части которых содержат ?ь 42 и q7, встре-
встречающиеся лишь по одному разу (что видно и по ячейкам с но-
номерами 1, 6 и 5), выписываются без изменений, так что для
первого уравнения объединенной системы
/i-l
будет, согласно первому из уравнений G.22),
Gll = - (*1з + 8\i)> G12 = G15 = G16 = GI7 = О'
Так же составим вторую и седьмую строки матрицы G.
Далее, заметим, что величина q^ (с разными верхними знач-
значками) встречается четыре раза: во втором из уравнении G.22),
600
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
1ГЛ. XVIII
в первом из уравнений G.23) и еще в двух невыписанных урав-
уравнениях. Сложим почленно четыре соответствующих уравнения.
В правой части объединенного уравнения получим
Суммируя коэффициенты при hu h2, ..., hlf найдем
31 &31» ^32 &32'
ek
Нетрудно заметить правило составления элементов G^. Для
диагональных элементов имеем
Недиагональные элементы можно составить, рассматривая на
рис. 334 отрезок (f, ft): если он примыкает только к одной ячей-
ячейке /, то Gik = glik, если к двум ячейкам 1\ и l2i то Gik = g\lk + g\\9
если узлы i и k не лежат на одном отрезке, то Gih = 0.
Для нашего примера можно записать систему уравнений
20)
G.20) i
з виде
0
Gsi
Gv
о 1
0
0
0
G22
G32
0
G52
0
0
G,3
G23
G33
G43
|о!з
0
0,4
0
G34
G44
Gt4
0
G25
G35
G45
G75
0
0
G36
G46
G56
0
0 -
0
1 0
G47
G57
O77_
X
Ail
hi
h3
ht
h5
h.
= ¦
Q.
Q2
Qs
Qt
Q5
Qe
Q
Матрица G симметрична: Gih=Ghu она имеет ленточную
структуру, т. е. Gij = 0, как только |i —/| > Я/, где Я/ — ши-
ширина ленты матрицы проводимостей.
Если граничное условие отличается от G.22)—обычно оно
задается в виде
-j^- cos (/1,
cos (л,
= 0,
то в выражении G.3) для J(h) добавляется интеграл по кон-
контуру L, ограничивающему область D:
\ qh ds + ^ \
L L
ds
L L
и ищется минимум такого расширенного функционала.
§8]
ОСНОВНЫЕ СООТНОШЕНИЯ МЕТОДА ЭГДА
601
На рис. 335 представлены результаты расчета линий равно-
равного напора, выполненного О. Зенкевичем с соавторами (см. Зен-
Зенкевич и Цанг 1974) для обтекания плотины в сильно неоднород-
неоднородной анизотропной среде с криволинейными границами. Главные
Рис. 335.
оси анизотропии каждого слоя вместе с коэффициентами филь-
фильтрации вдоль них указаны на рисунке в виде построенных в оди-
одинаковом масштабе взаимно ортогональных векторов.
Б. МЕТОД ЭЛЕКТРОГИДРОДИНАМИЧЕСКИХ АНАЛОГИЙ (ЭГДА)
§ 8. Основные соотношения метода ЭГДА. Между установив-
установившимся движением грунтовых вод и движением электрического
тока существует аналогия, выражающаяся в том, что оба явле-
явления описываются с помощью дифференциальных уравнений
одного и того же вида с одинаковыми граничными условиями.
Эта аналогия была использована Н. Н. Павловским, который
еще в 1918 г. применил ее для экспериментального решения ря-
ряда задач, встречающихся при изучении движения грунтовых вод
(Павловский 1922).
Предположим, что у нас имеется тонкий слой жидкого или
твердого проводника (теперь получила широкое применение
электропроводная бумага), толщина которого z может быть
переменной. Дифференциальные уравнения установившегося
602
УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XVIII
движения электрического тока имеют вид
tx — ~~ С дх '
d{zix) ,
— с
дУ
ду '
дх
(8.1)
(8.2)
где lXj iy — компоненты плотности тока, V — электрический по-
потенциал или функция напряжения, с — коэффициент электро-
электропроводности, х, у — координаты точек электрической модели.
Введем функцию тока W с помощью равенств
дх — *"у> ду "*'
Сравнивая эти выражения с (8.1), получим
дУ 1 dW дУ \ дУ
дх cz ду * ду cz дх '
Обратимся теперь к уравнениям теории фильтрации
дх
ду
(8.3)
(8.4)
(8.5)
(8.6)
где h — напор. Введя функцию тока -ф, найдем зависимость
между Лиф:
dh 1 дф dh 1 дф ,~ -v
ТИпГ' ~ЛГ~Т~' '°''J
дх
дх '
Сравнение (8.7) и (8.4) показывает, что линиям тока грунтово-
грунтового потока отвечают линии электрического тока, а линиям равно-
равного напора — линии равного элек-
электрического потенциала. Если смоде-
смоделировать дно по условию k = cz и
построить область, заполненную
проводником, подобную области
грунтового потока (рис. 336), то, из-
измеряя электрический потенциал в
различных точках, будем знать про-
пропорциональную ему величину напо-
напора, измерение плотности тока в от-
отдельных точках даст величину ско-
скорости, а величина силы тока будет пропорциональна расходу
потока.
С. А. Христианович A940) указал применение способа ЭГДА
для случаев, когда движение грунтовых вод не удовлетворяет
линейному закону Дарси и коэффициент фильтрации k является
функцией скорости.
Рис. 336.
§ 8] ОСНОВНЫЕ СООТНОШЕНИЯ МЕТОДА ЭГДА 603
В случае движения в однородной среде, когда k = const,
с = const и z = const, уравнения для V и h будут уравнениями
Лапласа:
При рассмотрении основных задач теории фильтрации мы
имели граничные условия такого рода: на границах водоемов
h = const, на твердых стенках и депрессионной кривой dh/dn=
=0. На электрической модели нетрудно осуществить на задан-
заданной линии условия вида V = const или dV/dn = 0.
Модели фильтрационных областей изготовляются из провод-
проводников, имеющих большое сопротивление: это пластинки из ста-
станиоля толщиной 0,01—0,02 мм, электролиты — жидкости или
растворы солей, графит или смесь его с мрамором, студнеобраз-
студнеобразная масса из желатина или агар-агара в растворе поваренной
соли, электропроводная бумага и т. д. Для осуществления кон-
контура равного напряжения устанавливают латунные шины с нич-
ничтожно малым сопротивлением (по отношению к сопротивлению
проводника, из которого сделана область движения).На рис.336
такие шины обозначены цифрой 1.
Для получения на модели линии, соответствующей линии
тока фильтрационного движения, нужно вдоль соответствующе-
соответствующего участка контура поставить изоляцию — парафин, воск, стекло
и т. п. Для проводящей бумаги изолятором является воздух,
поэтому линия тока — просто край обрезанной соответствующим
образом бумаги.
Вдоль промежутка высачивания, как известно, потенциал
скорости и напор являются линейными функциями ординаты:
h = у + const. Для задания напряжения по закону прямой ли-
линии применяют коллекторную шину B на рис. 336). В простей-
простейшем виде эта шина может состоять из ряда чередующихся ла-
латунных и эбонитовых пластинок.
На свободной поверхности также должно выполняться усло-
условие h = у + const. Кроме того, свободная поверхность является
(без учета инфильтрации или испарения) линией тока. Однако
форма этой линии заранее не известна и ее приходится подби-
подбирать так, чтобы выполнялись два условия: V = ay + b, dV/dn=
= 0. Поэтому обычно поступают так: верхнюю часть модели
обрезают по предполагаемой форме кривой депрессии, но с за-
запасом. Получив для этой области линии равного напряжения,
отыскивают точки пересечения этих линий с прямым у = const
и соединяют их плавной линией. Делают обрез по новой линии
(с запасом) и т. д.
604 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
Когда модель области движения готова, то параллельно ей
в электрическую сеть включается потенциометр, т. е. проводник,
в каждой точке которого заранее известно напряжение, если ве-
величина силы тока вдоль него не изменяется. Модель и потен-
потенциометр соединяются между собой мостиком Уитстона. В слу-
случае отсутствия в соединительной ветви электрического тока на-
напряжение в потенциометре равно напряжению в модели.
Прибор ЭГДА может работать как на постоянном, так и на
переменном токе.
В состав установки ЭГДА входит телефон (или другой ин-
индикатор— обычно световой); отсутствие или минимум звука
указывает на то, что в данной точке модели напряжение такое
же, какое установлено на потенциометре. Можно просто следить
за стрелкой гальванометра.
Определив на модели ряд точек одного и того же напряже-
напряжения, их соединяют плавной линией и получают линию равного
напряжения.
Линии тока можно строить как ортогональные к линиям рав-
равного потенциала. Однако можно строить их и независимо, по-
поставив задачу так, чтобы линии тока и эквипотенциала поменя-
поменялись местами.
Для определения фильтрационного расхода Q вдоль дуги
линии равного напора нужно сопоставить формулу
L
где / — длина дуги линии равного напора, с формулой для силы
тока /, проходящего через дугу равного напряжения:
дУ
ds
L
Некоторыми авторами рекомендуются методы, основанные
на измерении плотности тока, а не потенциала в различных
точках модели (Христианович 1940).
§ 9. Применения метода ЭГДА и другие методы аналогового
моделирования. В случае, если нужно смоделировать область,
состоящую из нескольких участков с различными проницаемо-
стями, пользуются различными электролитами или, как уже
указано, одним и тем же электролитом различной глубины.
Удобно использование бумаги различной электропроводности
(Фильчаков и Панчишин 1961).
В настоящее время находит также широкое применение мо-
моделирование методом ЭГДА пространственных движений (Дру-
(Дружинин 1966).
со
606 УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XVIII
Н. И. Дружинин обследовал с помощью пространственного
прибора ЭГДА обширные области подземных вод: Кулундин-
скую степь, Туркмению и т. д.
Метод ЭГДА получил широкое распространение в различных
научно-исследовательских институтах и проектных организа-
организациях. С его помощью строят сетки движения для моделей ре-
реальных гидротехнических сооружений. На рис. 337 и 338 приве-
приведены примеры такого рода (Фильчаков 1960). На рис. 337 вид-
видно, как велико влияние щели, которая может образоваться в
шпунте.
Применялся метод ЭГДА и в исследованиях общего харак-
характера. Так, С. М. Проскурников (см. Девисон 1938) провел ис-
исследования фильтрации через перемычки и трапецеидальные
плотины, причем получил зависимости расхода и высоты проме-
промежутка высачивания от уклона откоса (другой откос вертикаль-
вертикальный), а также через плотины с двумя наклонными откосами.
П. Ф. Фильчаков A949) рассматривал модели течения через
прямоугольную перемычку и другие плотины при разнородных
грунтах.
Широкое применение, главным образом в области гидрав-
гидравлики нефтяного пласта, находит прибор, называемый электроин-
электроинтегратором. Он относится к числу сеточных моделей (Толстов
1942; Гутенмахер и др. 1953).
Разработка конструкции универсальных сеточных электроин-
электроинтеграторов была проведена под руководством Л. И. Гутенма-
хера. В отличие от сплошных моделей ЭГДА в сеточных инте-
интеграторах имеется сетка электрических сопротивлений, в узловых
точках которой располагаются емкости.
В. С. Лукьяновым A960) был разработан сеточный гидрав-
гидравлический интегратор для решения тепловых задач. Он состоит
из сетки гидравлических сопротивлений, к которым в узловых
точках присоединены гидравлические емкости — трубки. Гидрав-
Гидравлические сопротивления образуют трубки, в которых сопротив-
сопротивление меняется за счет изменения длины кольцевого канала.
Гидравлические интеграторы применяются для прогноза ре-
режима грунтовых вод, электрические — для расчета фильтрации
в нефтеносных пластах.
Описание сеточных интеграторов и других аналоговых при-
приборов имеются в ряде книг (Вевиоровская, Кравченко и Румян-
Румянцев 1962; Жернов и Шестаков 1971; Де Уист 1969). В двух пер-
первых из них даны примеры моделирования фильтрации подзем-
подземных вод для конкретных водоносных бассейнов,
Глава XIX
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
А. АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
§ 1. Метод последовательной смены стационарных состояний.
В некоторых случаях возможно применение приближенного ме-
метода, при котором движение в каждый момент времени рассмат-
рассматривается как установившееся, но граница области движения,
относительно которой делаются те или иные упрощающие пред-
предположения, перемещается. При этом расход за элементарный
промежуток времени равен изменению площади, занятой жид-
жидкостью, за этот промежуток.
По-видимому, первое исследование такого рода принадлежит
К. Э. Лембке A886). Он рассмотрел задачи об осушении водо-
водоносного слоя при наличии горизон-
горизонтальной дрены и при наличии верти- J J j J | J
кальной скважины. Остановимся на
первой из этих задач.
Предположим, что над рассмат-
рассматриваемой площадью имеет место ин-
инфильтрация с постоянной интенсив-
интенсивностью е. В точке В (рис. 339)
имеется дренажное устройство.
В моменты времени t и t + dt осу- Рис 339.
шенная площадь пусть будет соот-
соответственно ABD и A\BD. Предположим, что, согласно гидравли-
гидравлической теории установившегося движения грунтовых вод с по-
постоянным расходом, линия АВ является параболой у2 = —H2x/L,
где L — длина (AD), меняющаяся со временем, а Я— мощность
водоносного слоя (BD). Тогда расход рассматриваемого потока
в единицу времени будет
<7 = — ky -r~ — k -от~.
Количество воды, полученной за промежуток времени dt из
части водоносного слоя, осушенной эксплуатацией, равно qdt\
с другой стороны, оно равно умноженному на пористость
608 неустановившийся движения грунтовых вод [Гл. xix
изменению площади ABD (которая равна tfL/З), сложенному
с количеством жидкости, принятым поверхностью АВ за счет ин-
инфильтрации. В результате будем иметь уравнение
q dt = k ^dt = % И dl + U dt. A.1)
Интегрируя это уравнение с учетом начального условия L@) =
= 0, получим
При /-*оо найдем предельное значение длины водосборного
сооружения, соответствующей установившемуся движению:
(L3)
К. Э. Лембке назвал Loo пределом радиуса водосборного соору-
сооружения.
Изменение расхода со временем выражается формулой
При / = оо получим значение расхода в установившемся дви-
движении, когда весь он образуется за счет инфильтрации
A.5)
К. Э. Лембке рассмотрел также случай, когда размеры водо-
водоносного слоя не позволяют линии депрессии достичь длины, со-
соответствующей нормальному действию дренажа, и различает
две стадии движения, во второй из которых депрессионная кри-
кривая понижается, сохраняя длину.
В частном случае, когда инфильтрация отсутствует, уравне-
уравнение A.1) после интегрирования дает
. I SkHt 1 ТОЛ I kHt /Л «ч
L= а/ = 1,732 д/ . A.6)
С помощью такого же приема можно получить приближен-
приближенное решение задачи о продвижении языка грунтовых вод по го-
горизонтальному водоупору при истечении из водоема с верти-
вертикальной стенкой, доходящей до водоупора, с учетом испарения
со свободной поверхности с постоянной интенсивностью с. Так
как теперь нужно рассматривать смоченную площадь ABC, ве-
величина которой равна 2UHL, то в решениях задачи A.2) и A.6)
нужно будет Уз заменить на 2/3. Получим
A.7)
§ 1]
ПОСЛЕДОВАТЕЛЬНАЯ СМЕНА СТАЦИОНАРНЫХ СОСТОЯНИЙ
609»
а при отсутствии испарения
kHt
Здесь L —расстояние, на которое продвинулся язык грунтовых
вод от вертикальной стенки водоема.
Последняя задача — о языке грунтовых вод при наличии*
испарения— рассматривалась также В.М. Маккавеевым A937).
Развитие метода последовательной смены стационарных со-
состояний и само название метода принадлежат И. А. Чарному
A948, 1949). Идея этого способа
встречается у Л. С. Лейбензона
A934).
Укажем здесь на примере воз-
возможность применения этого мето-
метода для решения некоторых за-
задач, рассматриваемых как дву-
двумерные (Полубаринова-Кочина
1951, 1).
Пусть имеем систему равно-
равноотстоящих горизонтальных дрен.
Линия ВС представляет границу
водоупора, центры дрен распо-
расположены на расстоянии Ь от водо-
водоупора (рис. 340). Поместим в
центры дрен точечные стоки ин-
интенсивности Q и рассмотрим бес-
бесконечную цепочку стоков в точках z=bi, ±2l+bi, ±4/ -\-bi, ...
Такую же цепочку стоков поместим в симметричных относи-
относительно оси абсцисс точках z = —Ы, ±21 — Ы, ±4/ — Ы, ...
Комплексный потенциал такого течения, как известно и*
курса гидродинамики (Кочин и др. 1963, 1), имеет вид
д
Рис. 340.
ш= —~- In (sin
п (г - Ы)
2/
sin
п (z + Ы)
2/
с-
Отделив действительную часть от мнимой, получим выражение
потенциала скорости
ф_?1п[(сЬ^ _COSILL)
A.10)
Сделаем предположение, что выражение A.10) имеет место
и при неустановившемся движении, причем расход будет функ-
функцией времени, подлежащей определению. В начальный момент
7г20 П. Я. Полубаринова-Кочина
^610 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
времени уравнение свободной поверхности пусть будет у = Яо.
В дальнейшем свободная поверхность будет изменять свою
форму. Но мы сначала сделаем предположение, что она пред-
представляет все время горизонтальный отрезок y = h(t), понижаю-
понижающийся с течением времени. Другими словами, мы принимаем
прямую y = h(t) за некоторую среднюю линию, около которой
колеблется действительная свободная поверхность.
Расход скважины за промежуток времени dt равен измене-
изменению за этот же промежуток времени площади, занятой водой,
в пределах области влияния одной скважины. Это дает урав-
уравнение
= — 2ldh. A.11)
Для того чтобы найти выражение расхода Q, поступим так.
Сначала возьмем на свободной поверхности точку Е над дре-
дреной (х = 0). Для нее у = A— r\\. Считая, что на свободной по-
поверхности имеет место капиллярное поднятие высоты Ак, будем
иметь на ней условие ф = —k(y — Ак), что дает в точке Е
<р = — k(h — г]1 — Ак).
Подставим эти выражения в A.10), причем в правой части
уравнения пренебрежем величиной г\\ по сравнению с А:
— /г (/г — ri! — /гк) ==
A.12)
Точно так же, рассматривая точку D и полагая х=1, у=Н-\-у\2,
кр = —k(h + тJ — hK), получим уравнение
Возьмем полусумму левых и правых частей последних уравне-
уравнений и пренебрежем в левой части величиной г\\ — г\2 по сравне-
сравнению с А. После некоторых преобразований получим
A.14)
Теперь предположим, что на контуре дрены, которую будем
считать окружностью радиуса б (этот радиус считаем малым
но сравнению с основными размерами области движения / и А),
«апор равен Ад и, следовательно, потенциал скорости равен
—&АД. В частности, можно считать, что в точке я=0, у=Ь + 8
потенциал скорости равен —&АД. Подстановка этого значения в
уравнение A.10) дает
4)(^^])C. A.15)
§ 1]
ПОСЛЕДОВАТЕЛЬНАЯ СМЕНА СТАЦИОНАРНЫХ СОСТОЯНИЙ
61 Г
Вычитая A.15) из A.14), исключим постоянную С и полу-
получим выражение расхода дренажной трубы (единицы ее длины)
Akn (h-hK- hjy)
Q =
где
-sh—J.
A.16),
A.17),
Подставим полученное выражение для расхода в формулу
A.11) и разделим в полученном таким образом уравнении пе-
переменные. После некоторых преобразований, интегрируя, по-
получим
h , Г 1 ( , 2nh _, 2nb
_
2nk
—
—
dh.
После того как найдена зависимость h от /, с помощью ра-
равенства A.16) можно вычислить значения Q в функции от /.
Рис. 341.
Для того чтобы получить приближенное уравнение свобод-
свободной поверхности, воспользуемся уравнением для потенциала-
скорости A.10), из которого исключим произвольную постоян-
постоянную с помощью A.14). Принимая во внимание, что на свобод-
свободной поверхности ф = —k{y — /iK), получим
п (h — b) пх \ ( , п (h -f b) nx\
. cos_)(ch_L_ cos_)
ch-
In
A.19),
V»20*
•612 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Полагая b = О, получим частный случай дрены на водоупо-
ре. На рис. 341 даны два положения свободной поверхности в
/глицериновом щелевом лотке, соответствующем дрене на водо-
упоре (о щелевом лотке см. ниже § 7).
Для случая дрены на водоупоре было произведено сравнение
результатов вычислений с результатами экспериментов в щеле-
щелевом лотке (Полубаринова-Кочина 1949,2). Для среднего сниже-
снижения уровня лучшие результаты получились бы при рассмотре-
рассмотрении потока конечной глубины, когда со выражается через эллип-
эллиптические функции.
§ 2. Радиус влияния скважины; зона влияния. При откачке
воды свободная поверхность грунтового потока начинает дефор-
деформироваться вблизи скважины и можно, с той или иной степенью
точности, выделить область возмущенного потока из первона-
первоначальной области. Если грунт однороден и транзитный поток
отсутствует, при горизонтальном водоупоре воронка депрессии
будет осесимметричной, и можно говорить о радиусе влияния
или радиусе действия скважины, т. е. о таком расстоянии от оси
скважины, на котором воронка депрессии «кончается»: это крат-
кратчайшее расстояние от оси скважины, на котором уровень воды
•становится практически равным первоначальному. При таком
¦определении величина радиуса влияния зависит от точности
замеров уровня. Но для практики большая точность обычно и
не требуется, тем более, что радиус влияния в формуле Дюпюи
входит под знаком логарифма
(Полубаринова-Кочина 1960, 2).
Для неустановившихся дви-
движений существует такой способ
определения радиуса влияния:
если формулу для дебита сква-
скважины можно представить в виде
х формулы Дюпюи
Рис. 342. У In [ro/R (/)] '
где R(t)—некоторая функция времени, то R{t) можно принять
за радиус влияния. При этом для непроницаемого водоупора
рядом исследователей была получена формула вида R = a^kt9
где а — некоторая постоянная, зависящая от параметров пласта.
Естественным способом для определения радиуса влияния
(или зоны влияния) является метод последовательной смены
¦стационарных состояний или его обобщения (Чарный 1956):
«ведь в нем как раз предполагается, что область движения раз-
разделяется на две области — возмущенную и невозмущенную.
§ 2] РАДИУС ВЛИЯНИЯ СКВАЖИНЫ; ЗОНА ВЛИЯНИЯ 613
Сначала рассмотрим галерею в неустановившемся потоке
при слабо проницаемом водоупоре. Возьмем нелинейное урав-
уравнение A.13) главы XIII, положив в нем dh/dy = 0:
—- — a—-.[li—-\ — b(h — H) [а= — tb=—^r). B.1)
dt дх \ дх ) v ' V т* md ) v ;
Будем искать решение этого уравнения при условиях h(x, 0) =
= Я, А@,0=^0, h(oott)=H.
Разделим действительную область движения на возмущен-
возмущенную область AD (рис. 342) и невозмущенную область за нею.
Пусть AD = L(t), и положим, что h(x,t) представляется в воз-
возмущенной области дугой эллипса ВС:
Я2 — Н2
h? = H2 jj-^{L — xf при
x ^ L (/), I
x^L(t). )
h = H при
Проинтегрируем почленно B.1) по х в пределах от 0 до L(t).
Обозначив через S интеграл
о
и сделав подставки в B.1), получим соотношение
причем
-arcsin
= (H-A)L, А = -^
7о
Отсюда найдем уравнение для L(i):
^ ^(H-A)L*. B.4)
Интегрирование его дает при L@) = 0
(-^-). B.5)
kd(H2-Hl)
Предел L (/) при t = oo равен
причем B2 = (H2-Hq)I(H-A).
20 П. Я. Полубаринова Кочина
614 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
При изменении y = HQ/H от единицы до нуля В2 изменяется
в узких^ пределах, от #/A—я/4) до 4#, а fi — от 2,16 У#
до 2 УЖ Можно принять В = 2,08 д/Т/*, тогда 1^2,08 Уfe dtf/fe,,.
При другом выборе функции h(x,L) мы получили бы другой
множитель перед знаком корня в последнем выражении для Loo.
Коэффициент v при t представляет очень малую величину.
Разлагая экспоненту в B.5) в ряд по степеням t, получим
-2.08
Отсюда видно, что для малых значений t влияние слабо
нроницаемого основания практически не сказывается, и лишь в
дальнейшем в формуле B.6) начинает сказываться влияние вто-
второго члена ряда. Стремление L(t) к пределу происходит мед-
медленно.
Величина L(t) представляет ширину полосы, занятой движу-
движущейся жидкостью, — ее можно назвать зоной влияния галереи.
В случае осесимметричного движения можно провести ана-
аналогичные рассуждения, но выкладки будут значительно слож-
сложнее. Для предельного значения радиуса влияния получается
формула вида (Полубаринова-Кочина 1960, 2).
где а зависит от //, Но и гс (гс — радиус скважины). В случае
простейшего выбора аппроксимирующей зависимости h(x, t) лля
возмущенной области в виде
и2
h =
приближенное значение а получается равным 2,82.
§ 3. Метод конечных разностей. В настоящее время этот ме-
метод в разных вариантах широко применяется для численного
решения уравнений параболического типа (см., например, Бере-
зин и Жидков 1962). В теории фильтрации одним из первых,
применявших этот метод, был Г. Н. Каменский A943). Он де-
делал расчеты для участка канала Москва — Волга, рассматривая
задачу как одномерную, в которой ордината свободной поверх-
поверхности h(x, у, t) удовлетворяет уравнению
dh _ k d2h2 . w mv
dt ~ 2m dx2 "t" m ' ^ '
§ 3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 615
Здесь w — инфильтрация сверху, т — пористость или недоста-
недостаток насыщения. Ордината свободной поверхности h отсчиты-
вается от водоупора.
Уравнение B.1) можно заменить уравнением в конечных
разностях
h —>
где индексы t — 1, i, t+1 обозначают последовательные сече-
сечения грунтового потока, Ах— расстояния между сечениями, чис-
числа /, /+1—порядковые индексы для моментов времени, At —
расчетные промежутки времени.
Для вычислений формула C.2) переписывается в виде, ре-
решенном относительно Лг, j+i-
hi,l+l=hiJ+-^T(hUul-2hlf + hU.i) + ^L, C.3)
причем нужно исходить из заданных начальных и граничных
условий.
С помощью конечных разностей можно вести расчет и для
случая, когда граница водоупора является криволинейной по-
поверхностью. Пусть уравнение этой поверхности имеет вид z =
= —То(х). Отсчитывая ординату свободной поверхности от не-
некоторой горизонтальной линии, обозначим разность h — Го, т.е.
глубину потока, отсчитываемую от водоупора, через Т. Тогда
уравнение C.1) нужно будет заменить таким:
dt — m дх V дх ) ^ m ' {6'V
а уравнение C.3) — следующим уравнением:
Ы.,+, = htt, + -^г Tt,, (hl+u, - 2hlt / + *,_,,,) + -?- At. C.5)
Для простейшего линейного уравнения
формула, соответствующая C.3), имеет вид
(« 2akt \ . а М .
Решение данного дифференциального уравнения C.6) в каждой
точке будет равно решению соответствующего аппроксимирую-
аппроксимирующего разностного уравнения C.7) плюс ошибка аппроксимации.
Если ошибка затухает при уменьшении Ал: и А/, то разностный
метод называется устойчивым, решение разностного уравнения
20*
616 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
при достаточно малых Ал: и А/ близко к решению дифферен-
дифференциального и стремится к этому решению при неограниченном
измельчении сетки.
Для неустойчивой разностной схемы ошибка аппроксимации
увеличивается при измельчении сетки и решение разностного
уравнения не стремится к решению дифференциального урав-
уравнения.
Уравнение C.7) представляет так называемую явную схему,
т. е. такую, в которой индекс / + 1 стоит только при ординате
в левой части уравнения. Для того чтобы схема C.7) была
устойчивой, необходимо выполнение условия
^<1. C.8)
Если это условие не выполняется, то пользуются неявными
схемами, в которых индекс /+ 1 входит в обе части уравнения.
Эти схемы всегда устойчивы, но вычисления по ним сложнее —
применяется метод прогонки (Березин и Жидков 1962).
В качестве наглядной иллюстрации метода конечных разно-
разностей может служить графический способ.
Графический способ интегрирования урав-
уравнения теплопроводности. В статье Ю. Ф. Харкеевича
A950) указан такой способ.
При специальном выборе А/ и Ajc, а именно, при
Д/=4н"' C.9)
уравнение C.7) упрощается и принимает следующий вид:
(tt + tt)- (ЗЛО)
Введем систему координат (х, t, и) (рис. 343). Допустим,
что нам нужно найти решение уравнения C.6) при начальном
условии
C.11)
и граничных условиях
и@, /) = ф,(/), иA, /) = Ф2(/). C.12)
На оси х отложим длину / и разделим ее на п частей, каж-
каждая из которых будет равна Ал: = 1/п. На плоскости t = 0 по-
построим линию и = /(#), а на плоскостях х = 0 и х = I соответ-
соответственно линии u = (f\(t) и « = ф2@. Вдоль оси t будем откла-
откладывать отрезки А/, вычисленные по формуле C.9).
Теперь, рассматривая ординаты начальной кривой Що и «го,
возьмем согласно формуле C.10) их полусумму. Получим орди-
§4]
МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
617
нату п\\. Можно полусумму ординат определять с помощью
приложения линейки к точкам uQq и ^о и проведения средней
ординаты.
Приложив линейку к концам ординат и{0 и а30, отмечаем
точку пересечения этой прямой на ординате ^о, отрезок которой
от оси х до отмеченной точ-
точки дает ординату и2\ и т. д.
Полученные ординаты пере-
переносим параллельно оси и в
точки A,1), B,1), ...,
(л— 1,1) первого слоя. Сое-
Соединив концы ординат аОь
«и, ..., «ni плавной линией,
получим кривую для момен-
момента времени tx = kt.
Построив средние ариф- J
метические ординат этой ^
кривой и перенеся их в точ- г
киA,2), B,2),..., (л-1,2),
будем иметь величины ор-
ординат U02, «12, • • -, «п2, ПО
которым построим кривую
для следующего момента
времени t2 = 2 At, и т. д.
При построении рекомен-
рекомендуется изображать область
(х, t) в виде прямоугольни-
прямоугольника (рис. 343), а ординаты и
в виде вертикальных отрез-
отрезков. В упомянутой статье
(Харкеевич 1950) рассматривается уравнение теплопроводности
для трех независимых переменных (#, #, 0, а также для четы-
четырех— (xyyyz, t).
§ 4. О методе статистических испытаний (метод Монте-Кар-
Монте-Карло). В последнее время к решению фильтрационных задач часто
применяется метод статистических испытаний (см., например,
Швидлер 1963, 1, 2; Абуталиев и др. 1968). Не входя в детали,
поясним основную идею метода в применении к приближенному
интегрированию уравнения теплопроводности, причем исполь-
используем статью В. Н. Эмиха A968), который на одной задаче вы-
выяснил особенности этого метода, и условия, при которых его при-
применение выгодно.
Уравнение
Рис. 343.
618 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
будем рассматривать в области G (О < х < х0, О < у < у0>
О < / < оо) при условиях
h (х, у9 0) = #0 (х, У), h @, у, t) = Нх {у, /), h (xQy У, t) = Н2 (уу /),
h (х9 0, t) = #3 (х, 0, Л (*, уо, 0 = #4 (*, 0. D.2)
Уравнения D.2) можно рассматривать как краевые условия,
заданные на границе Г области G, представляющей полубеско-
полубесконечный прямой параллелепипед. Немногим сложнее было бы
рассматривать полубесконечный цилиндр с направляющей на
плоскости (х, у), удовлетворяющей достаточно широким усло-
условиям.
Покроем область G пространственно-временной сеткой с
шагами А1 по пространственным координатам и Д? по времени.
Составим систему конечноразностных уравнений, соответствую-
соответствующих уравнению D.1):
+ -др- (At-i, /.s-i + A/+i. /. s-i + А/, /-1,s-i + hi, /+i, s-i) D.3)
(i, U s=\, 2, ...).
Перенумеруем узлы, образовавшиеся на начальной плоско-
плоскости s = 0 и боковых гранях. Тогда вместо D.2) будем иметь
условия
hi,f,s\r = fir (г=1, 2, ..., Я),
причем берутся все узлы вплоть до (s—1)-го слоя по t.
По методу статистических испытаний определение величины
hi, j, s осуществляется путем реализации процесса блуждания
фиктивной частицы из узла (t, /, s). Каждый шаг блуждания
представляет переход частицы из данного узла в один из свя-
связанных с ним по схеме D.3). Переход в соседний узел должен
выполняться с вероятностью, равной коэффициенту при соответ-
соответствующем значении h в этом узле, который теперь принимается
за узел отправления. Блуждание прекращается, когда частица
попадает на границу Г области G, причем фиксируется
«штраф» — значение hr в узле попадания. Затем частица вновь
начинает блуждать из узла (/, /, s). При многократном повто-
повторении блужданий вычисляется статистическая оценка математи-
математического ожидания штрафа в узле (t, /, s), которое (см., напри-
например, Швидлер 1963, 1) равно величине hit jf s, что можно запи-
записать так:
ht,,,s=Zb!,),,shr, D.4)
§ 4] МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ 619
где 6^/, 5 — вероятность попадания частицы из узла (i, /, s) в
r-й граничный узел. Она определяется как отношение числа
попаданий к общему числу испытаний.
Шаги Д/ и At выбираются из условия
Л/2 ^ 4 • D.0)
При нарушении этого неравенства вероятность перехода
блуждающей частицы из данного узла в непосредственно под
ним расположенный была бы отрицательной, вместе с тем усло-
условие D.5) есть условие устойчивости явной схемы D.3).
Если принять аД//Д/2 = 74, то уравнения D.3) становятся
особенно простыми:
^/./.s = -j(^t-i,/,s-i + A* + i,/.s-i + A/./-ilS-i + A/,/+i,s-i)- D.6)
Согласно D.6) блуждающая частица на каждом шаге долж-
должна переходить с вероятностью lU в один из четырех узлов
(s— 1)-го слоя по / и через я шагов выйдет на начальный слой,
или же при меньшем, чем s, числе шагов выйдет на боковую
поверхность.
При этом процесс блужданий должен быть случайным, что
осуществляется следующим образом. Отрезок @,1) делится на
четыре равные части (так как у нас каждая из четырех вероят-
вероятностей равна lU). Берется случайное число, лежащее между
нулем и единицей, — такие числа вырабатываются датчиками
по специальной программе ЭВМ (см., например, Ляшенко 1971).
Частица перейдет в тот или иной из четырех узлов в зависимо-
зависимости от того, в какой из четырех отрезков попадет случайное
число т). Для того чтобы при многократном розыгрыше блужда-
блуждания частота попаданий из данного узла в соседний соответство-
соответствовала вероятности этого события, случайные числа должны рав-
равномерно распределяться в интервале @, 1).
Очень важен вопрос о числе N блужданий, который должна
произвести частица, выходящая из узла (t, /, s), для того, чтобы
величина hit$tS в формуле D.4) была определена с достаточной
точностью и вместе с тем без излишних затрат машинного вре-
времени.
В. Н. Эмих A968) рассмотрел «задачу Г. Н. Каменского»:
область фильтрации — квадрант, ограниченный с двух сторон
каналами, вдоль которых сохраняется уровень воды h = Ни в
начальный момент времени во всей области фильтрации h = Яо
(#i и Яо— постоянные). Точное решение этой задачи имеет
вид
h (х, у, /) = Я, - (Я1 - Но) erf -^— erf jJj= . D.7)
620 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Г. Н. Каменский A958) применил к решению этой задачи для
частных условий метод конечных разностей по схеме D.3). Рас-
Рассматривая задачу с помощью метода статистических испытаний,
В. Н. Эмих определил на основе некоторых теоретических оце-
оценок в качестве достаточного значение N = 900 и провел расчеты
для yV = 1000 и N = 10000 для искомой функции h(x,yj) в
диагональных узлах A,1), B,2), ..., G,7) при /=1500 сут.
Число испытаний N = 1000 оказалось достаточным.
Погрешность разностной аппроксимации переплетается с
ошибкой метода статистических испытаний (вероятностной
ошибкой). В. Н. Эмих провел сопоставление расчетов по методу
Монте-Карло, по явной и неявной конечноразностным схемам, с
расчетом по формуле D.7) и пришел к следующему выводу.
Метод Монте-Карло дает значительный выигрыш во времени по
сравнению с конечноразностными методами в случаях, когда
требуется долгосрочный прогноз режима фильтрации в отдель-
отдельных точках области. При этом неявная схема оказывается не-
невыгодной: для получения решения в одной точке по явной схеме
Монте-Карло затрачивалось около 10 сек машинного времени,
по неявной — около 30 сек. При вычислении непосредственно по
разностным схемам время исчислялось минутами, так как тре-
требовалось проведение расчетов для всех предыдущих временных
слоев.
В цитируемой статье В. Н. Эмиха рассмотрены вопросы уче-
учета гидравлической связи с соседними горизонтами, неоднород-
неоднородности грунтов, наличия скважин. Коснемся здесь только послед-
последнего вопроса. Пусть имеется скважина с заданным дебитом Q.
Распределим равномерно дебит по квадратной ячейке площади
Д/2, в центре которой находится узел (t, /), ближе других к сква-
скважине. Предыдущая явная схема D.6), сохраняющаяся для дру-
других узлов, для узла (i,j), который принято называть особым,
заменяется таким уравнением:
hi,f, s==if (^t-i,/, s-i + hi+\t /, s-i + hlt /—i, s-\ + hlt j+i s-i) m д/2
(s=l, 2, ...)•
При попадании частицы в особый узел из общей суммы на-
накопленного штрафа вычитается величина (At/mAl2)Q и блуж-
блуждание продолжается до выхода на границу или начальный слой.
§ 5. Вариационно-разностный метод. Рассмотрим еще один
метод решения широкого класса задач о неустановившихся дви-
движениях подземных вод (Джаныбеков и Мурзакматов 1974; Мур-
закматов 1975), который проиллюстрируем на двух основных
случаях — одномерного и двумерного движения.
§ 5] ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД 621
1. Одномерный случай. Пусть дано уравнение
Г(Х, 0-^ = ^ (/?(*, 1)?)-д(х, t)h + w(x, t), E.1)
которое рассматривается в промежутке а ^ х ^ Ь при 0 < / ^
^ Т. Ищется решение, удовлетворяющее краевым условиям
а также начальному условию h (лс, 0) = F(х). Коэффициенты
уравнений E.1) и E.2), свободные члены и начальная функция
F(x) удовлетворяют определенным условиям гладкости, обеспе-
обеспечивающим принадлежность решения данному классу.
К уравнению E.1) применяется метод прямых по t с заме-
заменой dh/dt в момент t = tK выражением
dh hk — /г/г— i - v у /с о\
-Qf = ^ > * = '*--<л-1- E.3)
В уравнении E.1) положим один раз t = tk, другой раз
t = tk-\> Первое из получающихся таким образом уравнений
умножим почленно на а, второе — на 1—аи сложим (а — про-
произвольное число, 0 < а ^ 1). Получим уравнение
где
hk = h(xy tk), Pk = p(x, tk)9 ... (k = l, 2, ..., л),
— Qk = 7 [агЛ + A - «) r*-i] + a^,
- ^ = a^, + A - a) t^-, + -^ [ark + A - a) r*-,] -
E#5)
Доказано, что решение задачи E.4) —E.2) — E.3) можно
свести к нахождению функции ftA, дающей минимум функциона-
функционала (см. Михлин 1970)
ъ
в \{ т
( ) ahnk (у 6АЛ„6 — ««) • E-6)
Здесь /ioft и Л„ь — значения Л в крайних точках й-го слоя.
622 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Функция hk(x) на каждом промежутке Xi-i ^ х ^ х{ ищется
в виде линейной комбинации
hk(x) = ^p^-h{i-l)k-XXi-x hik E.7)
(x]l^l=xi — xi-i\ i=h 2, ..., n),
где hik есть искомое приближенное значение hh в точке хг.
Поступая аналогично тому, как это было сделано в § 7 гла-
главы XVIII при отыскании минимума интеграла J(h), можно по-
получить трехдиагональную систему алгебраических уравнений
относительно й^, которая решается методом прогонки. Интегра-
Интегралы, через которые выражаются прогоночные коэффициенты, вы-
вычисляются по тем или иным квадратурным формулам.
Можно для получения большей точности аппроксимировать
hk(x) кусочно-кубическими полиномами (сплайнами) (см. Мар-
чук 1972; Алберг и др. 1972):
hk(x) =
Числа A/f определяются из системы уравнений, выражаю-
выражающих условие гладкости первой производной многочлена E.8) в
узлах сетки. При этом приближенное решение получается не-
непрерывным.
2. Двумерный случай. Уравнение
t л dh "I
-q(x, y, t)h + w(xt y,t) E.9)
при 0 < t ^ T рассматривается в прямоугольнике или в обла-
области D с криволинейной границей L, заключенной в прямоуголь-
прямоугольнике. Ограничимся разбором первой краевой задачи, когда
функция й(лг, у, /) задана вдоль контура области D. После при-
применения к E.9) метода прямых по t будем иметь аналогично
E.6) минимизирующий функционал
D
В главе XVIII мы имели подобный функционал G.3), для
минимизации которого был указан метод конечных элементов.
§ 6] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ИСТОЧНИКОВ И СТОКОВ 623
Было отмечено, что этот метод является трудоемким для реали-
реализации на ЭВМ. В работах Ч. Джаныбекова и М. У. Мурзакма-
това рекомендуется «расщепление» функционала E.10) и сведе-
сведение его к одномерным функционалам. Применяя локально-
одномерный метод (Самарский 1962), на слое (tk,tk-\) вместо
уравнения E.9) рассматривают последовательность двух одно-
одномерных уравнений типа E.4), решение которых сводится к ми-
минимизации следующих функционалов:
J - ЪЛ, * } Л». E.12)
rB)
В выражении для гр^ принимается h{i)h-i = hh-u где hh-\ счи-
считается уже вычисленным. Во втором функционале при вычисле-
вычислении \|J/i найденные величины h{i)h принимаются за h^h-i- Вычис-
Вычисленные затем значения h^)k принимаются за решение задачи
при t = th:hh = h(x, у, th) = h{2)k. При этом Qh = Q{h + Q2k и
\ph = yplh -f- \p2ft (разбивка функций Qk = Q (x, y, th) и tyh =
= ty(x, У> h) произвольна); QSh и tySk (s = 1, 2) выражаются ана-
аналогично E.5). Пределы интегралов (х*0, xf]) и (у[1), у{р) — ко-
координаты точек пересечения кривой L с прямыми y=yj и x=xt
соответственно.
Результаты, получаемые при решении одномерной задачи
вдоль одной из координатных осей, служат начальными усло-
условиями для другой одномерной задачи, решаемой вдоль другой
координатной оси. Такой локально-одномерный метод приме-
применяется и для решения третьей краевой задачи, когда задается
на контуре L условие вида
Р\ ^ cos (л, х) + p2-0jj- cos (л, у) + р (х, y,t)h = a {x} yy t)
для всех / в промежутке 0 < t ^ Т.
Авторы рассмотрели также ряд эадач фильтрации в много-
многослойных пластах, в том числе и для случая нелинейных урав-
уравнений.
§ 6. Движение под действием источников и стоков с нелиней-
нелинейным условием на свободной поверхности. Такую задачу рассмат-
рассматривал А. Бегматов A973,1974).Мы ограничимся рассмотрением
двумерного движения в вертикальной плоскости (х,у).
624 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Пусть в начальный момент грунтовые воды занимают поло-
полосу 0 ^ у ^ #о, —°° < х < °°» причем плоскость у = 0 совпа-
совпадает с водоупором, где ду/ду = 0. Потенциал скорости ф(л:, у, t)
удовлетворяет уравнению Лапласа
& + ?-<>• <61>
Пусть уравнение линии свободной поверхности L в резуль-
результате действия источников или стоков имеет вид
F(x,y9t) = y-r\(xtt) = O. F.2)
Тогда на свободной поверхности выполняются два условия:
условие постоянства давления
Ф (*> У> t) + ky = const F.3)
и условие стационарности L, рассматриваемой как поверхность
разрыва,
tn-^j- + gradF • gradqp = O на L. F.4)
Уравнение F.4) легко получается, если рассмотреть уравнение
F.2) в момент времени t + At, когда точка х, у перейдет в точ-
точку (х + Ах, у + Ау):
F (х + Ах, у + Ay, t + At) = 0. F.5)
Вычитая F.2) из F.5), разделив на At и перейдя к пределу
при А/—>(), получим
dF . dF dx . dF dy _n
dt """ dx dt ~*~ dy dt ~U*
Наконец, учитывая, что m(dx/dy) = ду/дх и m(dy/dt) = ду/ду,
получим F.4).
По аналогии с тем, как действовал В. Л. Данилов A957,
1962) в задаче о перемещении контура нефтеносности, потен-
потенциал скорости фильтрации ф ищется в виде
ф(*, У, 0 = \ 9 (s, t) G (x, I; t) ds + фо (х, у, t) + С. F.6)
Здесь фо—известная функция, учитывающая действие источни-
источников и удовлетворяющая условию дщ!ду — 0 при у = 0, р — не-
неизвестная плотность потенциала простого слоя по искомой ли-
линии L, G(x, |;0— функция Грина для полуплоскости, причем
? — координата точки контура L.
Для решения поставленной задачи — отыскания функций
ф(х, #, t) и y](jc, t)~ применяется следующий прием. Предпола-
Предполагается, что область над поверхностью грунтовых вод занята
§ 6] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ИСТОЧНИКОВ И СТОКОВ 625
фиктивной жидкостью, давление которой удовлетворяет уравне-
уравнению Лапласа, и что граница раздела L между водой и этой
жидкостью является стационарной поверхностью раздела. Тогда
на этой поверхности должны выполняться условия непрерыв-
непрерывности давления и нормальных составляющих скорости филь-
фильтрации:
Р+ = Р~, K = v~. F.7)
Здесь pf и v+—значения давления и нормальной скорости
фильтрации при подходе к L изнутри, р~ и v~ — извне, п —
внутренняя нормаль.
Решение уравнения Лапласа для р ищется во всей области,
занимаемой водой и фиктивной жидкостью в виде р =
= —у(ф/^+*/)> гДе Ф определяется формулой F.6).
Первое из условий F.7) удовлетворяется в силу непрерыв-
непрерывности ф. Второе условие и свойство нормальной производной
потенциала простого слоя (см., например, Курант и Гильберт
1951) дают
1Л_ др+ др~ _ /JM^__JV\ дф+ ду+ ( .
к Р ~ дп дп ~\k- к ) дп дп КУ Y h
где |ы~, &~, y~ — вязкость, коэффициент фильтрации и удельный
вес фиктивной жидкости. Теперь, считая \i~ и у~ исчезающе ма-
малыми (что соответствует постоянству давления на L), получим
Используя свойство нормальной производной простого слоя при
подходе к L, имеем
Из уравнения F.4) находим
_ пи.эР_ w (бло)
дп dt дп VI + (дц/дхJ v
Подставляя F.8) и F.10) в F.9), получим интегро-диффе-
ренциальное уравнение для r\(x, t):
17-= S ^^KMi 0<Ъ + Цх.Ь F.11)
626 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Здесь ц (х, 0) = "По = const,
/( = 2(gradG • grad F)L, F.12)
во
f (x, t) = ± + 4- \K(x, I; t)dl + ± (grad Фо • grad F) \L. F.13)
А. Бегматов A974) предлагает приближенный способ инте-
интегрирования уравнения F.11). Разбивая рассматриваемый про-
промежуток времени на малые отрезки [/п-ь tn\ линеаризуем урав-
уравнение F.11) на каждом отрезке; вычисляем ядро К и свобод-
свободный член при у = г\(ху /n-i), т.е. заменив L для t^(tn-\ytn] на
Ln-X = ?*-*„__,. При этом на каждом отрезке интегро-дифферен-
циальное уравнение сводится к интегральному уравнению Фред-
гольма второго рода:
dt - ) [ dt «<n_, («)
— оо
А. Бегматов доказал однозначную разрешимость этого урав-
уравнения.
Пример. Требуется определить понижение уровня грунто-
грунтовых вод в горизонтальном, простирающемся до бесконечности
пласте конечной мощности, с непроницаемой подошвой, под дей-
действием горизонтальной дренажной трубы. Если действие трубы
заменить действием стока, расположенного в ее центре @, с),
имеющего расход q{t) на единицу длины трубы, то в F.12)
нужно положить
6. 01
т (х - IJ + h (х, о + ч (I. О]2 '
где
г2 = (х -1J + (У ~ ЧJ, г*2 = (х - IJ + (у + пJ,
На первом отрезке 0</^/! имеем
§ 6] ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ИСТОЧНИКОВ И СТОКОВ 627
Поэтому уравнение F.14) при п=1 примет вид
дх)A, t) d% . 2
+
I a, u-p' + ^ + L
F.15)
Для удобства будем отсчитывать уровень грунтовых вод от
стока, полагая г\о = уо + с. Тогда уравнение F.15) перепишется
так:
din , JL
- IY + 4
q(t) Г
-I
Уо , J/0 +2с
+ 2 + 0 +
К этому уравнению применяется преобразование Фурье. Исполь-
Используя теорему о сверткак, получаем
Ф ("S?") +вф J^j
или
П^ Я ch (ac)
5"
Здесь
Возвращаясь к оригиналу, из F.16) получим (Градштейн и
Рыжик 1962, стр. 518)
_ ch (a (i/o + c))
о
cos
Уо + с l Уо +
Отсюда, интегрируя по t, находим
1 cos "o . v ch
2(уо+с)
+СО5_яс ]
+ с * уо + с о
628
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
1ГЛ. XIX
Для пласта неограниченной мощности, устремляя с к оо и
раскрывая неопределенность, получим
t
1 Уо
?\яШх.
На последующих отрезках времени приходится применять
численные методы решения уравнения Фредгольма F.11). Для
уравнений подобного вида В. Л. Даниловым A957) предложен
аналог метода Эйлера. В других задачах А. Бегматов применял
обобщенный метод Ньютона (см. Канторович 1949).
Б. ОПЫТЫ В ЩЕЛЕВЫХ И ГРУНТОВЫХ ЛОТКАХ,
НАТУРНЫЕ НАБЛЮДЕНИЯ
§ 7. Теория щелевого лотка. Известно, что плоское безвихре-
безвихревое движение хорошо воспроизводится посредством пропуска-
пропускания вязкой жидкости между двумя параллельными пластинка-
пластинками, достаточно близкими друг к другу.
-5и
////////У,
Рис 344.
Аналогия между ламинарным движением жидкости в щели
между параллельными пластинками и движением воды в грунте
с постоянным коэффициентом фильтрации была использована
Е. А. Замариным. Прибор, названный щелевым лотком (рис. 344),
был изобретен X. С. Хиле-Шоу и применялся Н. Е. Жуковским
для демонстрации обтекания крыла ламинарным потоком. В на-
настоящее время он широко распространен в научно-исследова-
научно-исследовательских и учебных лабораториях. Щелевой лоток удобен тем,
что дает наглядную картину движения, легко позволяет воспро-
§7]
ТЕОРИЯ ЩЕЛЕВОГО ЛОТКА
629
изводить неустановившееся движение. В противоположность
прибору ЭГДА здесь свободная поверхность образуется автома-
автоматически.
Теория щелевого лотка изложена В. И. Аравиным A965).
В курсах гидродинамики рассматривается задача о движе-
движении вязкой несжимаемой жидкости между двумя параллельны-
параллельными плоскими стенками
(рис. 345). Пусть движение У\
будет одномерным, происхо-
происходящим параллельно оси х,
так что v = w = 0.
Как известно (Кочин
и др. 1963, 2), в этом случае
имеет место уравнение
др _ д2и
дх ~~ ^ дг2 '
у///////////////////////////////////.
G.1)
Рис. 345.
где \х — вязкость жидкости,
причем др/дх здесь будет
величиной постоянной.
Интегрирование уравне-
уравнения G.1) по г в пределах от
а до г, принимая во внимание условия прилипания жидкости к
стенкам, т. е условия и = 0 при z = ±а, дает
Интегрируя полученное выражение скорости по г в пределах от
—а до а, найдем расход жидкости через поперечное сечение
щели (считая толщину слоя в направлении, параллельном оси у
(рис. 345), равной единице)
2<23 др
У 3(л дх
Отсюда для средней скорости и* движения параллельно оси х
получаем
G.2)
а2 др
~3\i дх
Если учитывать действие силы тяжести, то в формуле G.2)
вместо давления нужно взять величину Р = р + pgy или про-
пропорциональную ей величину— напор h = у + p/(pg). В послед-
последнем случае уравнение G.2) примет вид
a2g dh n оч
".в-"з7"а7' G>3)
где v = ц/р —кинематический коэффициент вязкости.
630 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
Обратимся теперь к двумерному течению между параллель-
параллельными стенками, т. е. такому, в котором составляющая скорости
по оси z (рис. 345) равна нулю, но и и v отличны от нуля. Тог-
Тогда будем иметь систему уравнений движения вязкой жидкости
du I dp
4Z- = _li?-
dt p ду
G.4)
Движение вязкой жидкости в узкой щели, как и движение
жидкости в пористой среде, относится к числу «ползущих» дви-
движений (см. § 12 главы I). Эти движения характеризуются ма-
малыми скоростями, т. е. такими, что можно пренебречь в левой
части уравнений G.4) инерционными членами, а в правых ча-
частях этих уравнений — значениями вторых производных по ко-
координатам х и у по сравнению с производными по г.
Так же как в случае одномерного движения, будем иметь
для средних значений составляющих скорости и% и v* в узкой
щели выражения
и— -??•— v--?^-— G>)
и*~ 3v дх • v*~ 3v ду ' [ 0)
Обозначим входящий в эти выражения коэффициент ga'2/{3v)
через а. Величину а называют коэффициентом проницаемости
щели. Перепишем теперь уравнения G.5) в виде
dh dh
Уравнение неразрывности для несжимаемой жидкости
ди„ . ду„ __q
дх "•" ду
приводит к уравнению Лапласа для h.
Сопоставляя уравнения G.6) с уравнениями теории фильт-
фильтрации
— *&• v = ~kW' G'7>
видим полную аналогию между ними. Граничные условия в ще-
щелевом лотке такие же, как для грунтового потока.
По законам движения вязкой жидкости она прилипает к
стенкам, на которых скорости равны нулю, образуя погранич-
пограничный слой. Однако этот слой чрезвычайно тонок, и, как показы-
показывают опыты по обтеканию профилей, картина линий тока в ще-
щелевом лотке совпадает с той, которая получается при теоретиче-
теоретическом решении задачи об обтекании плоского профиля.
«TJ
ТЕОРИЯ ЩЕЛЕВОГО ЛОТКА
631
Заметим еще, что выведенные формулы для движения в
щели предполагают ламинарный характер течения, поэтому
число Рейнольдса для щели Re = 1/a/v, где V—характерная
скорость течения, не должно превосходить критического значе-
значения, в качестве которого В. И. Аравин A965) предлагает брать
ReKP = 500.
Для очень узких щелей закон распределения скоростей G.6)
становится несправедливым. Однако для обычных опытов с
глицерином при размерах щели порядка 1 мм или долей мил-
миллиметра этой опасности не возникает.
Наконец, отметим, что установившаяся картина ламинарного
течения наблюдается на некотором расстоянии / от входа в
модель. Имеется указание (Аравин 1965), что I ж 0,1 a Re.
Определение картины фильтрации. Фильтрация
через тело плотины моделируется так: в широкую коробку
с глицерином вставляется из
парафина модель плотины
(abcdefgh на рис. 346), причем
слой парафина должен быть
таким, чтобы щель между стек-
стеклом и парафином была доста-
достаточно узкой. На рис. 346 дан
вид модели плотины в щелевом
лотке; верхний и нижний бье-
бьефы моделируются с помощью Рис. 346.
коробок, более широких, чем
щель лотка. Стеклянные цилиндры по бокам лотка служат
для поддержания желаемых уровней жидкости на границах
лотка.
Формулы G.5) показывают, что если нужно получить опреде-
определенное значение проницаемости, то ширину щели 2а нужно
брать тем меньшей, чем меньше вязкость жидкости, с которой
проводится эксперимент. Если пропускать воду, то нужно брать
щель порядка 0,1—0,3 мм, для глицерина можно брать 1—2 мм.
Предположим теперь, что имеем одинаковых размеров грун-
грунтовый лоток (например, с песком) и щелевой лоток (с глицери-
глицерином или водой). Расход грунтового потока в лотке на единицу
его ширины (перпендикулярно к плоскости чертежа, т.е. по
оси z) обозначим через qM. Расход щелевой модели (через всю
ширину 2а щели) обозначим через qm. Имеем
ь dh
где s — направление линии тока. В грунтовом и щелевом лотках
мы устанавливаем одинаковые действующие напоры и все гео-
геометрические размеры берем одинаковыми. Тогда для расхода
632 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
<7щ через щель ширины 2а можно написать
dh o
<7Щ = —а-^2а.
Сопоставляя формулы для qu и ^щ, получаем
Ям _ k
qm 2aa '
Предположим теперь, что на щелевом лотке грунтовый поток
выполняется в масштабе К. Это значит, что все длины грунто-
грунтового потока в натуре в X раз больше длин щелевого лотка. Тог-
Тогда, так как скорости потока в грунтовом лотке и в натуре оди-
одинаковы, то расход натуры qH будет в X раз больше расхода грун-
грунтовой модели qM- Следовательно, получаем
=
qm 2aa
Принимая во внимание G.6) и G.5), получим формулу перехо-
перехода от расхода в щелевом лотке #щ к расходу в натуре qu:
<7н = -2^зг<7щ. G.8)
Моделирование неоднородных грунтов. Рас-
Рассмотрим лоток, состоящий из двух частей с различными прони-
цаемостями, т.е. с различными ширинами щелей в них. Пусть в
первой области полуширина щели будет аи во второй — а2. Вме-
Вместо вектора средней скорости введем вектор расхода W с со-
составляющими
И^ = ?* = 2аи,= -р-!?, ry = <7y = 2ai>,= -p-g-f G.9)
где р = 2аа (величина р называется второй проницаемостью
щели). Обозначив индексами / и 2 величины, относящиеся соот-
соответственно к первой и второй области щелевого лотка с различ-
различными проницаемостями. Легко показать (ср. § 3 главы II), что
для отношения касательных составляющих W8\ и Ws2 вдоль ли-
линии раздела имеют место соотношения
ws2 tge2 p2 '
где 8i и 02 — углы, образованные векторами W\ и W2 с нор-
нормалью к линии раздела.
Для неоднородных грунтов мы имели тот же закон прелом-
преломления линий тока, где вместо Рь р2 входят ku k2. Поэтому
$ Я теория щелеёого лотка
Применив формулу G.8) к обоим грунтам, получим
633
откуда найдем
Bа
G.10)
Итак, отношение коэффициентов фильтрации пропорцио-
пропорционально отношению кубов ширин щелей. Это дает возможность
моделировать грунты, довольно сильно различающиеся по про-
проницаемости.
На щелевом лотке можно учитывать капиллярность грунта*
радиальное течение можно моделировать, делая щель перемен-
переменной ширины.
Рис. 347.
На рис. 347 дана фотография картины установившегося дви-
движения при фильтрации из канала, когда проницаемость верх-
верхнего слоя грунта меньше проницаемости нижнего.
Неустановившиеся движения. Пренебрегая квадратичной ча-
частью инерционных членов в уравнениях движения, можно написать дифферен-
дифференциальные уравнения плоского движения грунтовых вод (в натурных уело-
ВИЯХ) В ВИДв
1 ди __ 1 dp g
т dt - J~d7~~ku>
GЛ1)
dt
p dy
Величины, относящиеся к движению в грунтовой модели, будем снабжать
индексом «м»: им, им, ...
Предположим, что мы переходим от натуры к грунтовой модели вводя
масштабные коэффициенты таким образом:
ttl шШт "/7l^M' "
G.12)
21 П. Я, Полубариаоаа Конина
634 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД (ГЛ. XIX
Масштаб пьезометрических высот, т.е. величин p/(pg)t и линейный масштаб
обозначим через X:
i-Jlii, х = кхы. G.13)
Подставляя во второе из уравнений G.11) выражения G.12) и G.13), получим
ХУ «V 1 дры g_ __
bmUmu dtu рм дхы Xkku v M *' К ' '
Для того чтобы уравнение G.14) имело тот же вид, что и уравнение G.11),
необходимо выполнение равенств
Отсюда следует, что
Теперь вместо G.14) будем иметь
^-^^J-^.JL G16)
тм dtu рм дхи ?м
Эти соотношения показывают, что чем больше Xh, т. е. чем мелкозернистее
грунт модели, тем меньшие скорости и тем меньшие промежутки времени бу-
будут получаться на модели (если тм = т, т. е. пористость грунта в натуре и
на модели одна и та же).
Напишем теперь уравнения неустановившегося движения для щелевой
модели, снабжая все соответствующие величины значком «щ»:
дищ 1 дрщg
рщ дх
dtm рщ ду т ищ g*
Допустим, что грунтовая и щелевая модели у нас выполнены в одинако-
одинаковом масштабе.
Сравним грунтовый поток в натуре с потоком в щелевом лотке; для
этого в формулах G.12) заменим индекс «м» на индекс «щ», принимая во
внимание, что тщ = 1 и km = а. Получим и = КУищ, v = ХуУщ, / = Мщ,
т = Кт, k = XhOL. Таким образом, масштаб Кт не может быть выбран произ-
произвольно; этот масштаб равен величине пористости грунта.
Ширину щели можно рассчитать, задавшись каким-нибудь из масштабов,
например h. Имеем а = k/Kk. Но согласно G.15) Kk = iv = him = A,<m;
следовательно, а = k/(mkt) и Xt = k/(am). Принимая во внимание значе-
значение а согласно G.5), получим для масштаба времени выражение
откуда полуширина щели
V
§8]
ОПЫТЫ В ГРУНТОВЫХ ЛОТКАХ И НАТУРНЫЕ НАБЛЮДЕНИЯ
635
Последняя формула позволяет найти ширину щели, если мы знаем k и т для
данного грунта и v для щелевой модели и задаемся определенным масшта-
масштабом времени Kt, желая получить на модели более быстрое движение, чем в
натуре. Если на щелевом лотке длительность некоторого процесса будет /щ,
то для натуры соответствующая продолжительность времени будет ta =» Мщ-
Для зависимости между расходом потока в натуре (на единицу ширины
потока) и расходом через щель лотка ^щ имеем по-прежнему формулу G.8).
Пример применения щелевого лотка для иллюстрации неустановившегося
движения был приведен в главе XII (здесь см. рис. 341, 347 и 350).
§ 8. Опыты в грунтовых лотках и натурные наблюдения.
Для изучения особенностей движения грунтовых вод в различ-
различных условиях устраивают грунтовые лотки — коробки, напол-
наполненные грунтом. В стенках лотков проделывают отверстия, ко-
которые соединяют с помощью резиновых трубок со стеклянными
трубками — пьезометрами. Последние показывают, какой напор
имеется в той точке грунта, в которую введен конец трубки.
:-2-:'-.:з
_4V... -?¦
^^
:¦••.••*;:•.¦;
з^г—^
ill
щ
=-^ 1
2 J <
f 6
' 6
¦ /
т
Рис. 348
На рис. 348 представлена схема грунтового лотка, в котором
вода просачивается под влиянием разности напоров. Пьезоме-
Пьезометры показывают значения напора в точках 1, 2, ..., помещен-
помещенных на дне лотка. При слабо изменяющейся свободной поверх-
поверхности эти значения были бы близкими к ординатам свободной
поверхности потока, если бы в грунте не было капиллярного
поднятия. Но в верхней части грунта всегда наблюдается ка-
капиллярная кайма большей или меньшей высоты. Если поме-
поместить в грунте частицы марганцовокислого калия, то они дадут
во время движения воды в грунте следы в виде окрашенных по-
полос, соответствующих линиям тока. Такие линии тока будут на-
наблюдаться и в капиллярной кайме (рис. 348). Однако, если
вставить в грунт прозрачные перфорированные трубки, то уров-
уровни воды в них не будут доходить до конца смоченного грунта,
а будут примерно соответствовать границе смоченной области
при отсутствии капиллярности. Отметим, что само введение этих
трубок несколько нарушает первоначальное движение.
21*
636 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
М. М. Семчиновой были проведены в грунтовом и щелевом
лотках опыты по вытеканию воды из канала. На рис. 349 пока-
показаны линии свободной поверхности и линии раздела между вы-
вытекающей (окрашенной) водой и первоначальной —вытесняемой
(неокрашенной). В щелевом лотке (рис. 350) условия опыта не-
несколько иные: окрашенная вода сначала проходит через более
Время § минутах
Рис. 349.
узкую щель («слабо проницаемый грунт»), потом попадает на
свободную поверхность «грунтового потока» — глицерин нахо-
находящийся в более широкой щели. При этом образуется как бы
инфильтрация на свободную поверхность. Общим для явлений
Рис. 350.
представленных на рис. 349 и 350, является то, что верхняя
жидкость глубоко продавливает нижнюю, заставляя ее припод-
приподниматься вблизи границы соприкосновения жидкостей.
Большое значение имеет постановка натурных наблюдений
над уровнем грунтовых вод в области проектируемых сооруже-
сооружении и в области уже построенных. В ряде книг можно найти
изложение основных методов наблюдений грунтового потока в
натуре (Гиринский 1950; Альтовский 1962).
Для того чтобы определить отметки зеркала грунтовых вод
закладывают в ряде точек буровые скважины. В них опускают
рейку, штангу или стальную рулетку, на конце которых имеется
ПРИМЕР КОМБИНАЦИИ РАЗНЫХ СПОСОБОВ
637
то или иное устройство, позволяющее наблюдать момент сопри-
коскновеиия его с водой: хлопушка, свисток, контактный ци-
цилиндр, дающий замыкание контакта, которое вызывает световой
или звуковой сигнал, и т.д. При этом скважины или шурфы
(ямы, вырываемые при близком к поверхности земли залегании
грунтовых вод) должны быть занивелированы.
На основании замеров залегания поверхности грунтового по-
потока проводят гидроизогипсы, т. е. линии равных уровней грунто-
грунтовых вод. Линии, ортогональные к гидроизогипсам, проведенные в
сторону их падения, определяют направление движения грунто-
грунтовых вод.
Для нахождения средней скорости движения грунтовых вод
можно в выработку пустить индикатор — красящее вещество,
соль и т. п., который затем улавливается в наблюдательном пун-
пункте с помощью проб воды через определенные промежутки вре-
времени. Расстояние между выработками, деленное на время про-
прохождения, дает среднюю скорость движения.
§ 9. Пример комбинации разных способов (задача о промыв-
промывках). Если имеет место вторичное засоление почвы и грунта,
то обычно осенью или зимой организуют промывки, заливая
большие площади водой, которая потом отводится с помощью
дрен в реку.
Рис. 351.
Предположим, что имеется система горизонтальных парал-
параллельных друг другу дрен, расстояния между которыми одинако-
одинаковы и которые заложены на некоторой глубине под поверхностью
земли. Если залить всю орошаемую площадь водой (рис. 351),
то интенсивная промывка будет над дреной (которая рассмат-
рассматривается как линейный сток), в отдалении же от нее течение
воды, а следовательно и рассоление, будет медленным. Движе-
Движение, представленное на рис. 351, легко изучается методом кон-
конформных отображений.
638
НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД
[ГЛ. XIX
Если заливать водой не всю поверхность, а только полосу
посредине между дренами (рис. 352), то рассоление начнется
под полосой и поток будет в значительной части области дви-
движения почти горизонтальным. Такая промывка носит название
боковой (по А. С. Калашникову). При боковой промывке
образуется свободная поверхность и задача усложняется.
В. Н. Эмихом (отчет 1975 г.) дано решение такой задачи. Она
характерна тем, что годограф скорости получается двулистным
А д С
Рис. 352.
и на депрессионной кривой возможны две точки перегиба. Не
останавливаясь подробнее на этом случае, отметим лишь упро-
упрощенную постановку, указав отдельные ее этапы.
1. На рис. 352 представлена принятая схема движения: ли-
линия свободной поверхности сносится на прямую АВ, на которой
•ф = const. Отрезок ВС — эквипотенциаль, вдоль нее произво-
производится затопление, точка F — центр дренажной трубы, контур
которой — одна из эквипотенциалей, близких к окружности ра-
радиуса, малого по сравнению с другими размерами области дви-
движения, ED и DC — твердые стенки.
Применяя конформное отображение областей г и со на полу-
полуплоскость вспомогательной комплексной переменной ?, для слу-
случаев рис. 351 и рис. 352 В. Н. Эмих получает решения вида
z = F\(Q и со = F2(?) и затем находит z = F(e(co)) =
((p + |))
Давая \|) ряд значений, он получает z = х + iy как функцию
от ф и вычисляет с помощью ЭВМ координаты (х, у) отдельных
точек линий тока. Таким образом найдены эквипотенциали и
построены гидродинамические сетки на рис. 352. Но можно эти
же результаты получить графическим путем или на приборе
ЭГДА.
2. Промывные воды рассоляют грунт и выводят соли в дре-
дрену. Чтобы получить наглядное представление об этом процессе,
интересно рассмотреть фронт вытеснения засоленных грунтовых
§9)
КОМБИНАЦИЙ 1>АЗ*ШХ Ci
639
вод поступающей промывной водой (которая засоляется по пу-
пути). С этой целью В. Н. Эмих исследует перемещение линии ме-
меченых частиц, а именно, частиц, занимавших в начальных мо-
момент отрезок ВС.
59$
Рис. 353.
__-—
-| ~Г~
—
г —
\
\
\
—X "
N
.
— \
'tm3/fifffs\
Рис. 354.
Если идти вдоль линии тока, то, обозначив через s длину
дуги, можно написать уравнение
ds дф
т
dt
откуда
-
ds •
ds
ду/ds '
(9.1)
(9.2)
где t\ — момент достижения точки s\.
Вместо (9.1) и (9.2) можно написать приближенные ра-
равенства
(AsJ
= > т
Aqp #
640 НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ ГРУНТОВЫХ ВОД [ГЛ. XIX
В особенности простыми будут вычисления, если взять Аф по-
постоянным.
Соединив точки на линиях тока, отвечающие одному и тому
же значению t\> получим для этого момента линию фронта вы-
вытесняющей жидкости. На рис. 353 построены такие линии (для
полного затопления сплошные, для полосообразного —пунктир-
—пунктирные) с помеченными на них значениями условного времени;
штрих-пунктиром отмечено приближенное положение кривой де-
депрессии. Рисунок показывает различный характер течения при
двух рассмотренных способах полива и — на этом примере — бо-
более быстрое вытеснение засоленных вод путем боковой про-
промывки.
3. На рис. 354 представлены результаты опыта в щелевом
лотке. Четыре сплошные линии -—депрессионная кривая и ли-
линии тока, отмеченные красящим индикатором (раствором мар-
марганцовки). Пунктирные линии — линии отмеченных частиц (при
t = 3 и 10 мин), в момент t = 0 расположенных на отрезке за-
затопления. Они построены по данным о распространении индика-
индикатора вдоль линий тока. При t = 30 мин индикатор заполнил
всю область движения.
ЛИТЕРАТУРА
Абрамов С. К., Бабушкин В. Д. A955) Методы расчета притока
воды к буровым скважинам. М., Госстройиздат, 384 с.
Абуталиев Ф. Б., Абуталиев Э. Б. A968) Методы решения задач
подземной гидромеханики на ЭВМ. Ташкент, «ФАН», 196 с.
Абуталиев Ф. Б., Ходжибаев Н. Н., Умаров У., Измаи-
Измаилов И. И. A972) Методы математического моделирования гидрогеологиче-
гидрогеологических процессов. М., «Недра», 64 с.
Аверьянов С. Ф. A949, 1) Зависимость водопроницаемости почво-
грунтов от содержания в них воздуха. Докл. АН СССР 69, № 2, 141—144.
Аверьянов С. Ф. A949, 2) Приближенная оценка роли фильтрации
в зоне «капиллярной каймы». Докл. АН СССР 69, № 3, 309—312.
Аверьянов С. Ф. A949, 3) Об изучении режима грунтовых вод мето-
методом построения сеток движения. Докл. ВАСХНИЛ, № 4, 36—40.
Аверьянов С. Ф. A956) Фильтрация из каналов и ее влияние на
режим грунтовых вод. В сб.: Влияние оросительных систем на режим грунто-
грунтовых вод. М., АН СССР, с. 85—441.
Аверьянов С. Ф. A959) Рассоляющее действие фильтрации из канала.
В сб.: Влияние орошения на режим грунтовых вод. М., АН СССР, с. 44—120.
Аверьянов С. Ф. A965) Некоторые вопросы предупреждения засоле-
засоления орошаемых земель и меры борьбы с ними в Европейской части СССР.
В сб.: Орошаемое земледелие в Европейской части СССР. М., «Колос»,
с. 90—151.
Аверьянов С. Ф., Дзя Да-лин A960) К теории промывки засо-
засоленных почв. Докл. ТСХА, № 56, 15—20.
Аверьянов С. Ф., Усенко В. С. A961) Способ расчета системати-
систематического вертикального дренажа. В сб.: Управление поверхностными и под-
подземными водными ресурсами и их использование. М., АН СССР, с. 145—
160.
Аксентьев Л. А. A959) Достаточные условия однолистности решения
обратной задачи теории фильтрации. Усп. мат. н. 14, № 4, 133—140.
Алберг Дж., Нильсон Э., Уолш Дж. A972) Теория сплайнов и
ее приложения (пер. с англ.). М., «Мир», 316 с.
Альтовский М. Е., ред. A962) Справочник гидрогеолога. М., Госгеол-
техиздат, 626 с.
Ар а вин В. И. A936) Приток грунтовых вод к водосборам. Изв. Н.-иссл.
ин-та гидротехн. 18, 4—43.
Ар а вин В. И. A937) К вопросу о фильтрации в анизотропно-водопро-
анизотропно-водопроницаемых грунтах. Тр. Ленингр. индустр. ин-та, № 9, вып. 2, 3—12.
Аравин В. И. A940, 1) Фильтрация в анизотропно-водопроницаемом
грунте. Тр. Ленингр. индустр. ин-та, № 1, вып. 1, 1—14.
Аравин В. И. A940, 2) Расчет фильтрации в обход гидротехнических
сооружений. Изв. Н.-иссл. ин-та гидротехн. 27, 53—59.
Аравин В. И. A940, 3) О влиянии волнения на фильтрацию под
гидротехническими сооружениями. Изв. Н.-иссл. ин-та гидротехн. 28, 109—
115.
Аравин В. И. A947) Приближенные способы фильтрационного расчета
флютбетов з случаях пространственной фильтрации. Тр. Ленингр. политехи,
ин-та, № 4, 133-140.
642 ЛИТЕРАТУРА
Аравин В. И. A965) Вопросы исследования неустановившейся и осе-
симметричной фильтрации при поМощи вязкостной аналогии. Изв. Всес.
н.-иссл. ин-та гидротехн. 78, 204—213.
Аравин В. И., Нумеров С. Н. A948) Фильтрационные расчеты гид-
гидротехнических сооружений. М., Стройиздат, 227 с; изд. 2. Л. -^ М., 1955,
292 с.
Аравин В. И., Нумеров С. Н. A953) Теория движения жидкостей и
газов в недеформируемой пористой среде. М., Гостехиздат, 616 с.
Бабушка И., Витасек Э., Прагер М. A969) Численные процессы
решения дифференциальных уравнений (пер. с англ.). М., «Мир», 368 с.
Базанов М. И. A938) Исследование фильтрации для случая притока
воды к осушительным каналам. Прикл. мат. и мех. 2, № 2, 223—244.
Байокки К., Мадженес Э. A974) О задачах со свободной грани-
границей, связанных с течением жидкости через пористые материалы. Усп. мат. н.
29, № 2 A76), 50—69.
Бан А., Богомолова А. Ф., Максимов В. А., Николаев-
Николаевский В. Н., О г а н д ж а н я н ц В. Г., Рыжик В. М. A962) Влияние свойств
горных пород на движение в них жидкости. М., Гостоптехиздат, 276 с.
Баренблатт Г. И. A952, 1) О некоторых неустановившихся движе-
движениях жидкости и газа в пористой среде. Прикл. мат. и мех. 16, № 1, 67—78.
Баренблатт Г. И. A952, 2) Об автомодельных движениях сжимаемой
жидкости в пористой среде. Прикл. мат. и мех. 16, № 6, 679—698.
Баренблатт Г. И. A953) Об одном классе точных решений плоской
одномерной задачи нестационарной фильтрации газа в пористой среде. Прикл.
мат. и мех. 17, № 6, 739—742.
Баренблатт Г. И., Борисов Ю. П., Каменецкий С. Г., Кры-
Крылов А. П. A957) Об определении параметров нефтеносного пласта по дан-
данным о восстановлении давления в остановленных скважинах. Изв. АН СССР,
Отд. техн. н., № И, 84—91.
Баренблатт Г. И., Вишик М. И. A956) О конечной скорости рас-
распространения в задачах нестационарной фильтрации жидкости и газа. Прикл.
мат. и мех. 20, № 3, 411— 417.
Баренблатт Г. И., Ентов В. М., Рыжик В. М. A972) Теория не-
нестационарной фильтрации жидкости и газа. М., «Недра», 288 с.
Баренблатт Г. И., Желтов Ю. П., Кочина И. Н. A960) Об
основных представлениях теории фильтрации однородных жидкостей в тре-
трещиноватых породах. Прикл. мат. и мех. 24, № 5, 852—864.
Басович И. Б. A973) Об определении параметров пласта с примене-
применением модулирующих функций. Изв. АН СССР, мех. жидк. и газа, № 5,
154-158.
Басович И. Б. A974, 1) О влиянии волнения на фильтрацию под гид-
гидротехническими сооружениями. Изв. АН СССР, мех. жидк. и газа, № 4,
161—164.
Басович И. Б. A974, 2) Определение переменной проницаемости пла-
пласта в случае радиальной симметрии по опытным откачкам из центральной
скважины. Прикл. мат. и мех. 38, № 3, 514—522.
Басович И. Б. A974, 3) Определение неизвестных параметров нефте-
нефтеносного пласта при наличии перетоков через слабопроницаемый пласт и ин-
инфильтрации. Ж. прикл. мех. и техн. физ., № 5, 80—85.
Бегматов А. A964) О неустановившейся фильтрации грунтовых вод
при наклонном водоупоре. Изв. АН СССР. мех. и машиностр., № 6, 167—171.
Бегматов А. A973) Об асимптотических решениях некоторых плоских
задач фильтрации и диффузии со свободной границей. В сб.: Краевые задачи
для дифференциальных уравнений, № 3. Ташкент, «ФАН», с. 136—144.
Бегматов А. A974) К вопросу определения свободной поверхности
грунтовых вод. В сб.: Краевые задачи для дифференциальных уравнений,
№ 4. Ташкент, «ФАН», с. 99—108.
ЛИТЕРАТУРА 643
Бейтмен Г., Эрдейи А. A973—1974) Высшие трансцендентные функ-
функции (пер. с англ.), т. 1—2. М., «Наука», 294+295 с.
Белаш П. М. A964) Основы вычислительной техники. М., «Недра», 329 с.
Белякова (Кузьмина) В. К. A956) Неустановившийся приток грунто-
грунтовых вод к скважинам. Прикл. мат. и мех. 20, № 1, 109—115.
Бергман С. A964) Интегральные операторы в теории линейных урав-
уравнений с частными производными (пер. с англ.). М., «Мир», 305 с.
Березин И. С., Жидков Н. П. A962) Методы вычислений, т. 1—2.
М., Физматгиз, 464 + 639 с.
Береславский Э. Н. A972) О конформном отображении пятиуголь-
пятиугольника с круговым разрезом. В сб.: Вопросы прикладной математики и геомет-
геометрического моделирования. Ленингр. инж.-стр. ин-т, с. 12—15.
Бернадинер М. Г., Ентов В. М. A975) Гидродинамическая теория
фильтрации аномальных жидкостей. М., «Наука», 199 с.
Бессонов Л. А. A967) Теоретические основы электротехники. Изд. 5.
М., «Высшая школа», 775 с.
Бочевер Ф. М., Веригин Н. Н. A961) Методическое пособие по
расчетам эксплуатационных запасов подземных вод для водоснабжения. М.,
Госстройиздат, 199 с.
Бочевер Ф. М., Гармонов И. В., Лебедев А. В., Шеста-
к о в В. М. A965) Основы гидрогеологических расчетов. М., «Недра», 306 с.
Брагинская В. А. A942) Некоторые задачи фильтрации в анизотроп-
анизотропном грунте. Прикл. мат. и мех. 6, № 2—3, 229—240.
Бузинов С. Н., Умрихин И. Д. A964) Исследование пластов и сква-
скважин при упругом режиме фильтрации. М., «Недра», 272 с.
Булыгин В. Я. A974) Гидромеханика нефтяного пласта. М., «Недра»,
230 с.
Бэр Я., Заславски Д., Ирмей С. A971) Физико-математические
основы фильтрации воды (пер. с англ.). М., «Мир», 452 с.
Вайнер М. И. A963) Статистические критерии подобия при фильтра-
фильтрации жидкости в однородной пористой среде. Изв. АН СССР, мех. и маши-
ностр., № 5, 144—148.
Васильев В. А. A955) О форме бугра грунтовых вод между двумя
дренами на водоупоре при наличии инфильтрации. Поикл. мат. и мех. 19, № 1,
106—108.
Васильев С. В., Веригин Н. Н., Г л е й з е р Б. А., Разумов Г. А.,
Рудаков В. К., Саркисян В. С, Шержуков Б. С. A970) Ме-
Методы фильтрационных расчетов гидромелиоративных систем. М., «Колос»,
440 с.
Вевиоровская М. А., Кравченко И. П., Румянцев С. А. A962)
Методы гидравлических аналогий В. С. Лукьянова и метод электрогидроди-
электрогидродинамических аналогий Н. Н. Павловского применительно к фильтрационным
расчетам. Моск. ун-т, 257 с.
Ведерников В. В. A939) Теория фильтрации и ее применение в об-
области ирригации и дренажа. М. — Л., Госстройиздат, 248 с.
Ведерников В. В. A940) Учет влияния капиллярности грунта на
фильтрацию из каналов. Докл. АН СССР 28, № 5, 408—410.
Ведерников В. В. A947) Итоги исследований по физической картине
фильтрации. Докл. АН СССР 55, № 3, 203—206.
Ведерников В. В. A948) К теории дренажа. Докл. АН СССР 59, № 6,
Ю69—1072.
Ведерников В. В. A949) Фильтрация при наличии дренирующего
или водоносного слоя. Докл. АН СССР 69, № 5, 618—622.
Веку а И. Н. A948) Новые методы решения эллиптических уравнений.
М. — Л., Гостехиздат, 296 с.
Веку а Н. П. A970) Системы сингулярных интегральных уравнений и
некоторые граничные задачи. Изд. 2. М., «Наука», 379 с.
644 ЛИТЕРАТУРА
Веригин Н. Н. A940) Фильтрация в основании плотин с наклонными
завесами и шпунтами. Гидротехн. стр-во, № 2, 30—33.
Веригин Н. Н. A947) Фильтрация в обход плотин и эффективность
противофильтрационных завес. Гидротехн. стр-во, № 5, 10—14.
Веригин Н. Н. A949, 1) К вопросу о расчете подземных водозаборов
в условиях плоского движения грунтовых вод. Докл. АН СССР 64, № 2,
183—186.
Веригин Н. Н. A949, 2) О неустановившемся движении грунтовых
вод вблизи водохранилищ. Докл. АН СССР 66, № 6, 1067—1070.
Веригин Н. Н. A949, 3) Фильтрация воды из оросителя ирригацион-
ирригационной системы. Докл. АН СССР 66, № 4, 589—592.
Веригин Н. Н. A951) О фильтрации из каналов в сухой грунт. Докл.
АН СССР 79, № 4, 581—584 (исправл.: 1952, 82, № 4, с. 836).
Веригин Н. Н. A953) Некоторые вопросы химической гидродинамики,
представляющие интерес для мелиорации и гидротехники. Изв. АН СССР,
Отд. техн. н., № 10, 1369—1382.
Веригин Н. Н., Шержуков Б. С. A969) Диффузия и массообмен
при фильтрации жидкости в пористых средах. В кн.: Развитие исследо-
исследований по теории фильтрации в СССР A917—1967) М., «Наука», с. 237—
313.
Веригин Н. Н., Шержуков Б. С, Шапинская Г. П. A967)
К расчету промывания засоленных почв при действии дренажа. Тр. коорд.
совещ. по гидротехн. 35, 27—36.
Виноградов Ю. П. A954) Один частный случай теории фильтрации.
Научн. тр. Кемеровск. горн, ин-та 1, 132—138.
Виноградов Ю. П., Куфарев П. П. A948) Об одной задаче филь-
фильтрации. Прикл. мат. и мех. 12, № 2, 181—198.
Владимиров В. С. A971) Уравнения математической физики. М.,
«Наука», 512 с.
Вощинин А. П. A939) Движение грунтовых вод в теле и основании
однородной земляной плотины с горизонтальным фильтром при конечной глу-
глубине проницаемого основания. Докл. АН СССР 25, № 9, 733—735.
Вощинин А. П. A950) О применении обтекаемых и ребристых под-
подземных контуров при постройке гидротехнических сооружений на проницае-
проницаемом основании. Инж. сб. 7, 15—20.
Галин Л. А. A945) Неустановившаяся фильтрация со свободной по-
поверхностью. Докл. АН СССР 47, № 4, 250—253.
Галин Л. А. A951) Некоторые задачи неустановившегося движения
грунтовых вод. Прикл. мат. и мех. 15, № 6, 654—678.
Гантмахер Ф. Р. A967) Теория матриц. Изд. 3. М., «Наука»,
575 с.
Гельфанд И. М., Левитан Б. М. A951) Об определении дифферен-
дифференциального уравнения по его спектральной функции. Изв. АН СССР, сер. мат.
15, № 5, 309—360.
Георгиевский В. Б. A971) Унифицированные алгоритмы для опре-
определения фильтрационных параметров (справочник). Киев, «Наукова думка»,
328 с.
Георгиевский В. Б., Мироничева Г. В., Шульгин Д. Ф. A968)
Метод определения параметров в задачах по рассолению почвогрунтов. Изв.
АН УзбССР, сер. техн., № 5, 33-38.
Герсеванов Н. М. A943) Приложение функционального анализа при
решении задач по фильтрации грунтовых вод. Изв. АН СССР, Отд. техн. н.,
№ 7, 73—89.
Герсеванов Н. М. A950) Итерационное исчисление и его приложе-
приложения. М., Машстройиздат, 69 с.
Гильберт Д., Кон-Фоссен С. A951) Наглядная геометрия. Изд. 2.
М., Гостехиздат, 352 с.
ЛИТЕРАТУРА 645
Гиринский Н. К. A936) Основы теории движения грунтовых вод под
гидротехническими сооружениями при наличии по нижней поверхности грунта
напора постоянной величины. Гидротехн. стр-во, № 6, 22—28.
Гиринский Н. К. A939) Графическое построение гидродинамических
сеток. Научн. зап. Моск. гидромелиор. ин-та, 7, № 11, 3—22.
Гиринский Н. К. A946) Комплексный потенциал потока со свободной
поверхностью в пласте относительно малой мощности при /г = /(г). Докл.
АН СССР 51, № 5, 337-338.
Гиринский Н. К. A947) Некоторые вопросы динамики подземных
вод. Гидрогеол. и инж. геол., № 9, 3—102.
Гиринский Н. К. A950) Определение коэффициента фильтрации по
данным откачек при неустановившихся дебите и понижениях. М., Госгеолиз-
дат, 136 с.
Гиринский Н. К. A951) Расчет притока воды в подземные выработки
в условиях взаимодействия подземных вод пяти, семи водоносных пластов.
В кн.: Методы исследований и расчетов при инженерно-геологических и гидро-
гидрогеологических работах. М., Госгеолиздат, с. 99—149.
Гиринский Н. К. A955) Фильтрация подземных сильно минерализо-
минерализованных вод и рассолов в море. Тр. Лаб. гидрогеол. пробл. АН СССР
12, 3—47.
Годунов С. К., Рябенький В. С. A973) Разностные схемы, введе-
введение в теорию. М., «Наука», 400 с.
Голубев В. В. A950) Лекции по аналитической теории дифферен-
дифференциальных уравнений. Изд. 2. М. — Л., Гостехиздат, 436 с.
Голубев В. В. A961) Однозначные аналитические функции, автоморф-
ные функции. М., Физматгиз, 455 с.
Голубев Г. В. A966) К задаче об определении поля давлений в не-
неоднородной пористой среде. Изв. АН СССР, мех. жидк. и газа, № 4,
152-154.
Голубев Г. В., Тумашев Г. Г. A972) Фильтрация несжимаемой
жидкости в неоднородной пористой среде. Казан, ун-т, 195 с.
Голубева О. В. A950) Уравнения двумерных движений идеальной
жидкости по криволинейной поверхности и их применения в теории фильтра-
фильтрации. Прикл. мат. и мех. 14, № 3, 287—294.
Голубева О. В. A966) Обобщение теоремы об окружности на филь-
фильтрационные течения (к вопросу о течениях в кусочно-неоднородных грунтах).
Изв. АН СССР, мех. жидк. и газа, № 1, 113—116.
Голубева О. В., Шпилевой А. Я. A967) О плоской фильтрации в
средах с непрерывно изменяющейся проницаемостью вдоль кривых второго
порядка. Изв. АН СССР, мех. жидк. и газа, № 2, 174—179.
Градштейн И. С, Рыжик И. М. A962) Таблицы интегралов, сумм,
рядов и произведений. Изд. 4. М., Физматгиз, 1100 с.
Гришин М. М. A962) Гидротехнические сооружения. М., Строй-
издат, 764 с.
Гусейн-Заде М. А. A965) Особенности движения жидкости в не-
неоднородном пласте. М., «Недра», 276 с.
Гутенмахер Л. И., Корольков Н. В., Клабукова Л. С, Ни-
Николаев Н. С, Маруашвили Т. И. A953) Руководство к электроинтегра-
электроинтеграторам типа ЭИ-12. М., АН СССР, 204 стр.
Данилов В. Л. A957) Интегро-дифференциальные уравнения движения
границы раздела двух жидкостей в пористых средах. Изв. Казан, фил. АН
СССР, сер. физ.-мат. и техн. н., № 11, 99—133.
Данилов В. Л. A962) Об одном аналитическом методе решения за-
задачи стягивания контура нефтеносности. Изв. АН СССР, мех. и машиностр.,
№ 1, 185—188.
Девисон Б. Б. A932) Об установившемся движении грунтовых вод
через земляные плотины. Уч. зап. Гос. гидрол. ин-та 6, 11—19.
646
Дев и сон, Б, Б. A937, 1) Некоторые случаи плоского установившегося
движения грунтов'ых вод при наличии испарения. Тр. Гос. гидрол. ин-та, № 5,
183—193.
Девисон Б. Б. A937, 2) К вопросу об одном приеме упрощенного
расчета напорного движения грунтовых вод. Тр. Гос. гидрол. ин-та, № 5,
194—199.
Девисон Б. Б. A937, 3) О неустановившемся движении грунтовых
вод без свободной поверхности. Тр. Гос. гидрол. ин-та, № 5, 212—217.
Девисон Б. Б. A938) Движение грунтовых вод. В кн.: Христиано-
вич С. А., Михлин С. Г., Девисон Б. Б. Некоторые новые вопросы механики
сплошной среды. Л., АН СССР, с. 219—356.
Де У ист Р. A969—1970) Гидрогеология с основами гидрологии суши,
т. 1—2 (пер. с англ.). М., «Мир», 312 + 252 с.
Джаны беков Ч., Мурзакматов М. У. A974) Вариационно-раз-
Вариационно-разностный метод решения задач подземной фильтрации. Изв. АН КиргССР.
Рукопись деп. в ВИНИТИ 29 янв. 1974, № 182-74, 77 с.
Дольский В. Е. A963) Оценка погрешности метода фрагментов при
фильтрационном расчете. Докл. АН УССР, № 7, 861—866.
Дружинин Н. И. A956) Метод электрогидродинамических аналогий
и его применение при исследовании фильтрации. М. — Л., Госэнергоиздат,
347 с.
Дружинин Н. И. A966) Изучение региональных потоков подземных
вод методом электрогидродинамических аналогий. М., «Недра», 336 с.
Ентов В. М. A967) О некоторых двумерных задачах теории фильтра-
фильтрации с предельным градиентом. Прикл. мат. и мех. 31, № 5. 820—833.
Жернов И. Е., Шестаков В. М. A971) Моделирование фильтрации
подземных вод. М., «Недра», 224 с.
Жуковский Н. Е. A889) Теоретическое исследование о движении
подпочвенных вод. Ж. Русск. физ.-хим. об-ва 21, № 1, 1—20. Собр. соч., т. 3.
М., Гостехиздат, 1949, с. 184—206.
Жуковский Н. Е. A890) О влиянии давления на насыщенные водою
пески. Собр. соч., т. 7. М., Гостехиздат, 1950, с. 73—89.
Жуковский Н. Е. A923) Просачивание воды через плотины. Собр.
соч., т. 7. М., Гостехиздат, 1950, с. 297—332.
Журавский А. М. A941) Справочник по эллиптическим функциям.
М. - Л., АН СССР, 236 с.
Зельдович Я. Б., КомпанеецА. С. A950) К теории распростране-
распространения тепла при теплопроводности, зависящей от температуры. В сб.: К 70-ле-
70-летию академика А. Ф. Иоффе. Л. — М., АН СССР, с. 67—71.
Зенкевич О. К., Цанг И. A974) Метод конечных элементов в теории
сооружений и в механике сплошных сред. М., «Недра», 239 с.
Ивакин В. В. A947) О фильтрации при нагнетании в ненасыщенный
водой грунт. Изв. АН СССР, Отд. техн. н., № 6, 669—679.
Иваненко Д. Д., Соколов А. А. A951) Классическая теория поля.
Изд. 2. М. —Л., Гостехиздат, 480 с.
Ильин А. М., Калашников А. С, Олейник О. А. A962) Линей-
Линейные уравнения второго порядка параболического типа. Усп. мат. н. 17, № 3,
3-146.
Ильинский Н. Б. A966) Обратная задача напорной фильтрации для
основания с дренажами. Тр. семинара по обратным краевым задачам, № 3,
Казан, ун-т, с. 47—52.
Ильинский Н. Б., Фомин В. М., Шешуков Е. Г. A972) Приме-
Применение метода Бергмана — Назарова к решению уравнений нелинейной теории
фильтрации. В сб.: Вычисл. и прикл. мат. 17, 3—18.
Казанский А. Б. A973) Теория фильтрационной диффузии и приложе-
приложение ее к задачам гидрологии и гидрогеологии. М., «Наука», 136 с.
ЛИТЕРАТУРА 647
Калашников А. С. A967) О возникновении особенностей у решений
уравнения нестационарной фильтрации. Ж. вычисл. мат. и мат. физ 7, № 2
440—444.
Калинин Н. К. A941) Некоторые приближенные приемы решения за-
задачи о фильтрации в двуслойной среде. Докл. АН СССР 30, № 7, 593—597.
Калинин Н. К. A948) О неустановившейся фильтрации в случае дре-
дрены в водопроницаемом слое конечной глубины. Прикл. мат. и мех. 12, № 2
199—206.
Калинин Н. К. A952) Фильтрация через двухслойный клин. Прикл.
мат и мех. 16, № 2, 213—222.
Калинин Н. К., Полубаринова-Кочина П. Я. A947) О не-
неустановившихся движениях грунтовых вод со свободной поверхностью. Прикл.
мат. и мех. 11, № 2, 231—236.
Каменский Г. Н. A943) Основы динамики подземных вод. Изд. 2. М.,
Госгеолиздат, 248 с.
Каменский Г. Н. A958) Методика прогноза изменений режима грун-
грунтовых вод и развитие подтопления в зоне подпора. Тр. Лаб. гидрогеол. пробл.
АН СССР 20, 29—54.
Каменский Г. Н., Гавич И. К., Мясникова Н. А., Семено-
Семенова С. М. A960) Гидродинамические основы изучения режима грунтовых вод
и его изменение под влиянием искусственных факторов (метод конечных раз-
разностей). Тр. Лаб. гидрогеол. пробл. АН СССР 26, 190 с.
Каменский Г. Н., Корчебоков Н. А., Разин К. И. A935) Дви-
Движение подземных вод в неоднородных пластах. М. — Л., ОНТИ, 168 с.
Канторович Л. В. A949) О методе Ньютона. Тр. Мат. ин-та АН
СССР 28, 104—144.
Канторович Л. В., Крылов В. И. A962) Приближенные методы
высшего анализа. Изд. 5. М. — Л., Физматгиз, 708 с.
Капранов Ю. И. A972) О некоторых точных решениях в задачах
рассоления грунтов. Изв. АН СССР, мех. жидк. и газа, № 1, 177—180.
Капранов Ю. И. A973) О форме линзы пресных вод при линейном
законе испарения. Прикл. мат. и мех. 37, № 3, 497—504.
Карслоу Г., Егер Д. A964) Теплопроводность твердых тел (пер. с
англ.). М., «Наука», 487 с.
Качинский Н. А. A975) Почва, ее свойства и жизнь. Изд. 3. М.,
«Наука», 294 с.
Клоков Ю. А. A959) Одна предельная краевая задача для уравнения
х- + rf(xyx')+cp(x)= 0. Изв. вузов, математика, № 6, 72—80.
Ков да В. А. A946—1947) Происхождение и режим засоленных почв,
ч. 1—2. М. —Л., АН СССР, 573 с.
Козлов В. С. A940) К вопросу о расчете движения воды под- гидро-
гидротехническими сооружениями в анизотропно-проницаемых грунтах. Изв. АН
СССР, Отд. техн. н., № 3, 59—79.
Козлов В. С. A941) Гидромеханический расчет флютбетов. М. — Л.,
Госэнергоиздат, 279 с.
Коллинз Р. A964) Течения жидкостей через пористые материалы. М.,
«Мир», 351 с.
Колмогоров А. Н. A941) О логарифмически нормальном законе рас-
распределения размеров частиц при дроблении. Докл. АН СССР 31, № 2, 99—101.
Коппенфельс В., Штальман Ф. A963) Практика конформных
отображений (пер. с нем.). М., ИЛ, 406 с.
Корсунцев А. В. A937) Подсобная номограмма для построения элек-
электрических полей с осевой симметрией. Электричество, № 14, 50—51.
Костяков А. Н. A960) Основы мелиорации. Изд. 6. М., Сельхозгиз,
622 с.
Костяков А. Н., Фаворин Н. Н., Аверьянов С. Ф. A956) Влия-
Влияние оросительных систем на режим грунтовых вод. М., АН СССР, 452 С,
648 ЛИТЕРАТУРА
Ко чин Н. Е. A935) К теории волн Коши — Пуассона. Тр. Мат. ин-та
АН СССР, 9, 167-187.
Кочин Н. Е., Кибель И. А., Розе Н. В A963, 1) Теоретическая
гидромеханика, ч. 1. Изд. 6. М., Физматгиз, 583 с.
Кочин Н. Е., Кибель И. А., Розе Н. В. A963, 2) Теоретическая
гидромеханика, ч. 2. Изд. 4. М., Физматгиз, 727 с.
Кочина И. Н., Полубаринова-Кочина П. Я. A952) О примене-
применении плавных контуров основания гидротехнических сооружений. Прикл. мат.
и мех. 16, № 1, 55—66.
Кочина Н. Н A951) Плоская задача о растекании бугра грунтовых
вод в слое бесконечной глубины. Прикл. мат. и мех. 15, № 6, 679—682.
Кочина Н. Н. A953) Некоторые вопросы пространственного растека-
растекания грунтовых вод. Прикл. мат. и мех. 17, № 3, 377—381.
Кочина Н. Н. A971) Об изменении уровня грунтовых вод при поливах.
Ж. прикл. мех. и техн. физ., № 4, 87—94.
Кочина Н. Н. A972) О некоторых нелинейных задачах уравнения теп-
теплопроводности. Ж. прик. мех. и техн. физ., № 3, 123—128.
Кочина Н. Н. A973, 1) Вопросы регулирования уровня грунтовых вод
при поливах. Докл. АН СССР 213, № 1, 51—54.
Кочина Н. Н. A973, 2) О регулировании уровня грунтовых вод при
орошении. Ж. прикл. мех. и техн. физ., № 5, 125—133.
Краснопольский А. А. A912) Грунтовые и артезианские колодцы.
Спб., 177 с.
Крылов М. М. A947) К изучению динамики баланса грунтовых вод
в целях гидрогеологического прогноза. Изв. АН УзбССР, № 2, 106—117.
Кулабухова (Крамаровская) И. И. A959) Две задачи неустановив-
неустановившейся фильтрации при неполном насыщении грунта. Изв. АН СССР, мех. и
машиностр., № 3, 196—201.
Кулабухова (Крамаровская) И. И. A967) О фильтрации при неполном
насыщении грунта. Докл. АН УзбССР, № 8, 10—12.
Курант Р., Гильберт Д. A951) Методы математической физики,
г. 1—2 (пер. с нем.). М. — Л., Гостехиздат, 476+544 с.
Куфарев П. П. A950, 1) Решение задачи о контуре нефтеносности
для полосы с цепочкой скважин. Докл. АН СССР 75, № 2, 353—355.
Куфарев П. П. A950, 2) Задача о контуре нефтеносности для круга
при любом числе скважин. Докл. АН СССР 75, № 4, 507—510. •
Куфарев П. П., Виноградов Ю. П. A947) О некоторых частных
решениях задачи фильтрации. Докл. АН СССР 57, № 4, 335—338.
Куфарев П. П., Пряжинская В. Г. A963) Об одной системе инте-
интегральных уравнений в теории движения грунтовых вод. Тр. Томск, ун-та 163,
63—72:
Кучеренко Э. Г. A955) Об одном частном решении задачи о движе-
движении грунтовых вод. Уч. зап. Томск, ун-та 25, 113—114.
Лаврентьев М. А. A946) Конформные отображения с приложениями
к некоторым вопросам механики. М. — Л., Гостехиздат, 159 с.
Лаврентьев М. А., Шабат Б. В. A973) Методы теории функций
комплексного переменного. Изд. 4. М., «Наука», 736 с.
Лаврентьев М. М., Резницкая К. Г. A973) Теорема единствен-
единственности некоторых нелинейных обратных задач уравнения параболического
типа. Докл. АН СССР 208, № 3, 531—532.
Ладыженская О. А. A957) Метод конечных разностей в теории
уравнений с частными производными. Усп. мат. н. 12, № 5, 123—149.
Лебедев А. Ф. A936) Почвенные и грунтовые воды. Изд. 4. М. — Л.,
АН СССР, 316 с.
Левитан Б. М., Гасымов М. Г A964) Определение дифференци-
дифференциального оператора по двум спектрам. Усп. мат. н. 19, № 2 A16),
3-63.
ЛИТЕРАТУРА 649
Лейбензон Л. С. A934) Руководство по нефтепромысловой механике,
ч. 2: Подземная гидравлика воды, нефти и газа. М. — Грозн. — Л. — Новосиб.,
Горгеолнефтеиздат, 352 с.
Лейбензон Л. С. A947) Движение природных жидкостей и газов в
пористой среде. М. — Л., Гостехиздат, 244 с.
Лембке К. Э. A886—1888) Движение грунтовых вод и теория водо-
водосборных сооружений. Инженер, № 2 A886), № 17—19 A888).
Ломизе Г. М. A951) Фильтрация в трещиноватых породах. М. — Л.,
Госэнергоиздат, 127 с.
Ломизе Г. М., Нетушил А. В. A958) Электроосмотическое водо-
понижение. М. — Л., Госэнергоиздат, 176 с.
Лукьянов В. С, Вевиоровская М. А. (I960) Применение метода
гидравлических аналогий к исследованию фильтрации грунтовых вод. В сб.:
Проблемы гидрогеологии. М., Госгеолиздат, с. 194—206.
Лыков А. В., Михайлов Ю. А. A963) Теория тепло- и массопере-
носа. М. — Л., Госэнергоиздат, 535 с.
Ляшенко В. Ф. A971) Программирование для цифровых вычислитель-
вычислительных машин М-20, БЭСМ-ЗМ, БЭСМ-4, М-220. Тбил. ун-т, 432 с.
Ляшко И. И., Великоиваненко И. М., Лаврик В. И., Мистец-
кий Г. Е. A974) Метод мажорантных областей в теории фильтрации. Киев,
«Наукова думка», 200 с.
Маккавеев В. М. A937) Частный случай неустановившегося движе-
движения грунтовых вод со свободной поверхностью (к вопросу о заболачивании
поймы). Тр. Гос. гидрол. ин-та, № 5, 218—222.
Малый нова Е. М. A967) Пространственные задачи нестационарной
фильтрации жидкости. Педаг. ин-т, Ростов-на-Дону.
Малы и но в а Е. М. A972) Некоторые задачи нестационарной филь-
фильтрации жидкости. В сб.: Математика и механика. Ростов-на-Дону, с. 26—30.
Мариночкина А. С, Пеньковский В. И. A975) К определению
промывных норм при капитальных промывках. Почвоведение, № 12, 90—93.
Марченко В. А. A972) Спектральная теория операторов Штурма —
Лиувилля. Киев, «Наукова думка», 219 с.
М арчу к Г. И. A972). Методы вычислительной математики. Новосиб.,
«Наука», 474 с.
М аскет М. A949) Течение однородных жидкостей в пористой среде
(пер. с англ.). М. — Л., Гостоптехиздат, 628 с.
Матвеенко Т. И. A974) Некоторые задачи о неустановившемся при-
притоке жидкости к скважине в круговой области с учетом слабой проницаемо-
проницаемости водоупора. Вычисл. и прикл. мат. (Киев), № 24, 27—32.
Меламед В. Г. A963) К расчету дебита скважины в безнапорном дви-
движении со слабопроницаемым водоупором. Изв. АН СССР, мех. и машиностр.,
№ 5, 160—161.
Мелещенко Н. Т. A932) О расчете фильтрации через земляные пло-
плотины по методу проф. Н. Н. Павловского. Гидротехн. стр-во, № 2—3, 21—24.
Мелещенко Н. Т. A936) Расчет движения грунтовых вод под соору-
сооружениями, имеющими дренажные отверстия. Изв. Н.-иссл. ин-та гидротехн. 19,
25—48.
Мелещенко Н. Т. A937) Движение грунтовых вод под гидротехниче-
гидротехническими сооружениями (методы расчета). Л. — М., ОНТИ, 91 с.
Мелещенко Н. Т. A940) Приближенный метод расчета фильтрации
под сооружениями, расположенными на безграничном проницаемом основа-
основании. Изв. Н.- иссл. ин-та гидротехн. 28, 267—272.
Меньшикова В. И. (I960) Несколько обратных задач теории безнапор-
безнапорных движений грунтовых вод. Изв. АН СССР, мех. и машипостр., № 2, 159—166.
Мизес Р., Шиффер М. A955) О методе Бергмана интегрирования
плоского движения сжимаемой жидкости (пер. с англ.). В сб.: Проблемы
механики, ИЛ, с. 489—518.
650 ЛИТЕРАТУРА
Милн-Томсон Л. М. A964) Теоретическая гидродинамика (пер. с
англ.). М., «Мир», 655 с.
Минский Е. М. A958) Статистическое обоснование уравнений фильтра-
фильтрационного движения. Докл. АН СССР 118, № 2, 255—258.
Мироненко В. А., Шестаков В. М. A974) Основы гидрогеомеха-
ники. М., «Недра», 295 с.
Михайлов Г. К. A951) К задаче о фильтрации в анизотропных зем-
земляных плотинах трапецоидального профиля на горизонтальном водоупоре.
Докл. АН СССР 80, № 4, 553-556.
Михайлов Г. К. A952, 1) К геометрии фиктивного грунта. Прикл. мат.
и мех. 16, № 4, 511—512.
Михайлов Г. К. A952, 2) О фильтрации в трапецеидальных плотинах
на горизонтальном водоупоре. Гидротехн. и мелиорация, № 1, 33—42.
Михайлов Г. К. A953, 1) О фильтрации в трапецеидальных плотинах
с вертикальным верховым откосом. Прикл. мат. и мех. 17, № 2, 189—199.
Михайлов Г. К. A953, 2) Применение модели предельно анизотроп-
анизотропных грунтов для оценки решений некоторых краевых задач о движении по-
потока грунтовых вод по водоупору. Инж. сб. 15, 159—168.
Михайлов Г. К. A954) Упрощение способа расчета фильтрации в од-
однородно-анизотропном грунте. Инж. сб. 19, 159—160.
Михайлов Г. К. A956) О максимальных градиентах близ дренажа
земляных плотин. Изв. АН СССР, Отд. техн. н., № 2, 109—112.
Михайлов Г. К., Николаевский В. Н. A970) Движение жидко-
жидкостей и газов в пористых средах. В сб.: Механика в СССР за 50 лет, т. 2. М.,
«Наука», с. 585—648.
Михлин С. Г. A970) Вариационные методы в математической физике.
Изд. 2. М., «Наука», 512 с.
Муминов С. Н. A967) О поливах и растеканиях бугров грунтовых
вод. Ж. прикл. мех. и техн. физ., № 3, 134—137.
Мурзакматов М. У. A975) Применение вариационно-разностного ме-
метода к решению задач фильтрации подземных вод. Фрунзе, АН Кирг. ССР,
18 с.
Мусхелишвили Н. И. A968) Сингулярные интегральные уравнения.
Изд. 2. М., Физматгиз, 599 с.
Мхитарян А. М. A953) К расчету фильтрации через земляные пло-
плотины. Инж. сб. 14, 142—156.
Мхитарян А. М. A954) О фильтрации воды через земляную плотину
с экраном и понуром на проницаемом основании с наклонным водоупором.
Укр. мат. ж. 6, № 4, 448—456.
Мхитарян А. М. A957) Фильтрация из канала на наклонном водо-
водоупоре. Научн. тр. Куйбышевск. индустр. ин-та 7, 139—142.
Мхитарян А. М., Фомин М. М. A959) Гидромеханический расчет
фильтрации через земляную плотину на водопроницаемом основании при на-
наличии воды в нижнем бьефе. В кн.: Фильтрационные расчеты гидротехниче-
гидротехнических сооружений. Киев, АН УССР, с. 70—77.
Мятиев А. Н. A946) Действие колодца в напорном бассейне подзем-
подземных вод. Изв. Туркм. фил. АН СССР, № 3—4, 43—50.
Мятиев А. Н. A947) Напорный комплекс подземных вод и колодцы.
Изв. АН СССР, Отд. техн. н., № 9, 1069—1088.
Мятиев А. Н. A948) Задача о колодцах в горизонте грунтовых вод.
Изв. АН СССР, Отд. техн. н., № 3, 293—300.
Назаров Г. И. A966) Точное решение уравнений газовой динамики.
Изв. АН СССР, мех. жидк. и газа, № 3, 113—120.
Насберг В. М. A950) Гидродинамическая сетка при фильтрации без
подпора из скважины и применение сетки для определения водопроницаемо-
водопроницаемости грунта. Изв. Тбил. н.-иссл. ин-та сооруж. и гидроэнергетики 3,
15-25,
ЛИТЕРАТУРА 651
Насберг В. М. A951) Вопрос о фильтрации при нагнетании в нена-
ненасыщенный водой грунт. Изв. АН СССР, Отд. техн. н., № 9, 1415—1429.
Недр иг а В. П. A947) Расчет фильтрации в обход гидротехнических
сооружений. Гидротехн. стр-во, № 5, 15—18.
Нельсон-Скорняков Ф. Б. A947) Фильтрация в однородной среде.
М., «Советская наука», 280 с. Изд. 2, 1949, 568 с.
Нерпин С. В., Чудновский А. Ф. A967) Физика почвы. М., «Нау-
«Наука», 584 с.
Николаева М. В. A949) О релаксационном методе Саусвелла. Тр.
Мат. ин-та АН СССР 28, 160—182.
Николаевский В. Н., Басниев К. С, Горбунов А. Т., Зо-
Зотов Г. А. A970) Механика насыщенных пористых сред. М., «Недра», 336 с.
Нужин М. Т., Ильинский Н. Б. A963) Методы построения подзем-
подземного контура гидротехнических сооружений. Обратные краевые задачи теории
фильтрации. Казан, ун-т, 139 с.
Нужин М. Т., Тумашев Г. Г. A965) Обратные краевые задачи и их
приложения. Изд. 2. Казан, ун-т, 333 с.
Нумеров С. Н. A939) О фильтрации в земляных плотинах с дренажем
на водопроницаемых основаниях. Изв. Н.-иссл. ин-та гидротехн. 25, 115—135.
Нумеров С. Н. A940, 1) О фильтрации через земляные плотины с
дренажем на водопроницаемых основаниях. Изв. Н.-иссл. ин-та гидротехн. 27,
60—73.
Нумеров С. Н. A940, 2) Гидромеханический метод расчета береговой
дрены. Изв. Н.-иссл. ин-та гидротехн. 28, 91—108.
Нумеров С. Н. A940, 3) Об учете инфильтрации или испарения воды
со свободной поверхности при расчете движения грунтовых вод. Прикл. мат.
и мех. 4, № 5-6, 11 — 17.
Нумеров С. Н. A942) Решение задач о фильтрации без промежутков
высачивания и инфильтрации или испарения воды со свободных поверхностей.
Прикл мат. и мех. 4, № 1, 75—86.
Нумеров С. Н. A946) Практический способ фильтрационного расчета
земляных плотин с дренажем на водонепроницаемых основаниях при нали-
наличии воды в нижнем бьефе. Изв. Н.-иссл. ин-та гидротехн. 31, 273—276.
Нумеров С. Н. A947, 1) Фильтрационные расчеты горизонтального
дренажа гидростанций и промышленных сооружений (при конечной глубине
водопроницаемого слоя). Изв. Всес. н.-иссл. ин-та гидротехн. 34, 43—54.
Нумеров С. Н. A947, 2) О фильтрации из каналов деривационных
ГЭС и ирригационных систем. Изв. Всес. н.-иссл. ин-та гидротехн. 34, 85—98.
Нумеров С. Н. A948, 1) Медленно-изменяющаяся неустановившаяся
фильтрация. Изв. Всес. н.-иссл. ин-та гидротехн. 37, 3—29.
Нумеров С. Н. A948, 2) Применение метода фрагментов при расчетах
плоской, напорной, неустановившейся фильтрации. Тр. Ленингр. политехи,
ин-та, № 5, 208—213.
Нумеров С. Н. A951, 1) О фильтрации к горизонтальной дрене в слу-
случае наклонного водоупора. Изв. Всес. н.-иссл. ин-та гидротехн. 46, 72—85.
Нумеров С. Н. A951, 2) О притоке грунтовых вод к прямоугольной
траншее. Изв. Всес. н.-иссл. ин-та гидротехн. 46, 202—206.
Нумеров С. Н. A953, 1) Приближенный способ расчета напорной
фильтрации в основании гидротехнических сооружений. Изв. Всес. н.-иссл.
ин-та гидротехн. 50, 71—90.
Нумеров С. Н. A953, 2) Обобщение формулы Дюпюи. Изв. Всес.
н.-иссл. ин-та гидротехн. 50, 197—202.
Нумеров С. Н. A954, 1) О фильтрации к несовершенной дренажной
траншее в горизонтальном артезианском пласте. Изв. Всес. н.-иссл. ин-та
гидротехн. 52, 119—130.
Нумеров С. Н. A954, 2) Об одном способе решения фильтрационных
задач. Изв. АН СССР, Отд. техн. п., № 4, 133—139.
652 ЛИТЕРАТУРА
Нумеров С. Н. A954, 3) Методы исследования плоской установив-
установившейся фильтрации (тяжелой несжимаемой жидкости) в однородной среде. М.,
Ин-т механики АН СССР, 18 с.
Нумеров С. Н. A956) О фильтрации в полубесконечном грунтовом
массиве. Изв. АН СССР, Отд. техн. н., № 4, 58—74.
Нумеров С. Н. A968) О необходимости учета сил инерции в основных
уравнениях теории фильтрации. В сб.: Вопросы прикладной математики и гео-
геометрического моделирования. Ленингр. инж.-стр. ин-т, с. 18—21.
Нумеров С. Н. A969) Об одном методе расчета нелинейной фильтра-
фильтрации жидкости. В сб.: Вопросы прикладной математики и геометрического мо-
моделирования. Ленингр. инж.-стр. ин-т, с. 27—32.
Нумеров С. Н., Барсегян Р. М. A966) О дополнительных фильтра-
фильтрационных сопротивлениях несовершенных скважин и дренажных траншей при
фильтрации жидкости в многослойных горизонтальных пластах. Тр. коорд.
совещаний по гидротехн. 25, 124—138.
Нумеров С. Н., Петров Н. Г. A972) О плоской установившейся
фильтрации в двухслойном основании недренированной бетонной плотины.
В сб.: Вопросы прикладной математики и геометрического моделирования.
Ленингр. инж.-стр. ин-т, с. 23—30.
Олейник А. Я. A965) Расчет прерывистых дренажей в земляных пло-
плотинах методом последовательных конформных отображений. В кн.: Исследо-
Исследования по прикладной гидродинамике. Киев, «Наукова думка», с. 248—261.
Олейник А. Я., Насиковский В. П. A970) Методы расчета мелио-
мелиоративного дренажа в неоднордоно-слоистых грунтах (пособие для расчета).
Киев, «Урожай», 230 с.
Олейник О. А., Калашников А. С, Чжоу Юй-линь. A958) За-
Задача Коши и краевые задачи для уравнении типа нестационарной фильтра-
фильтрации. Изв. АН СССР, сер. мат. 22, № 5, 667—704.
Павлов А. Т. A942) Установившееся движение грунтовых вод при двух
слоях жидкости различной плотности. Прикл. мат. и мех. 6, № 2—3, 221—228.
Павловский Н. Н. A922) Теория движения грунтовых вод под гидро-
гидротехническими сооружениями и ее основные положения. Пгр., XIX + 753 с.;
Собр. соч., т. 2. М.— Л., АН СССР, 1956.
Павловский Н. Н. A930) Неравномерное движение грунтовых вод.
М., Гостехиздат, 58 с.
Павловский Н. Н. A931) О фильтрации воды через земляные плоти-
плотины. Л., Кубуч, 259 с.
Павловский Н. Н. A932) Неравномерное движение грунтовых вод
(дальнейшее развитие вопроса). Л., Кубуч, 80 с.
Павловский Н. Н. (Ш36, 1) Основы метода гидромеханического ре-
решения задачи о свободной фильтрации из открытых русел. Изв. Н.-иссл. ин-та
гидротехн. 19, 5—24.
Павловский Н. Н. A936, 2) Свободная фильтрация на бесконечность
из открытых русел с круговой основой формы. Изв. Н.-иссл. ин-та гидротехн.
19, 49—79.
Павловский Н. Н. A937) О притоке воды к горизонтальным фильтрам.
Изв. Н.-иссл. ин-та гидротехн. 21, 5—21.
Панин П. С. A968) Процессы солеотдачи в промываемых толщах почв.
Новосиб., «Наука», 303 с.
Панов Д. Ю. A951) Справочник по численному решению уравнений в
частных производных. Изд. 5. М. — Л., Гостехиздат, 183 с.
Пеньковский В. И. A964) О коэффициенте диффузии уравнения дви-
движения влаги в почвогрунтах. Изв. АН СССР, мех. и машиностр., № 6, 149—-
152.
Пеньковский В. И. A968) Две модельные задачи о движении агрес-
агрессивной жидкости в пористой среде. Ж. прикл. мех. и техн. физ., № 6,
155-158.
ЛИТЕРАТУРА 653
Пеньковский В. И. A969) Одномерная задача растворения и вы-
мыва солей при фильтрации с большими значениями критерия Пекле. Ж.
прикл. мех. и техн. физ., № 2, 148—152.
Пеньковский В. И. A971) Конвективное соленакопление в капил-
капиллярной кайме, вызванное испарением почвенных вод. Почвоведение, № 11,
137—140.
Пеньковский В. И., Постнов В. А. A968) О фильтрации раство-
растворов при больших значениях критерия Пекле. Изв. АН СССР, мех. жидк. и
газа, № 2, 145—147.
Пеньковский В. И., Рыбакова С. Т. A966) К задаче о неустано-
неустановившейся фильтрации при неполной насыщенности грунта. Изв. АН СССР,
мех. жидк. и газа, № 3, 148—152.
Пеньковский В. И., Рыбакова С. Т. A968) Фильтрация в напор-
напорном пласте с учетом начальных градиентов кровли и подошвы. Изв. АН
СССР, мех. жидк. и газа, № 6, 173—177.
Пеньковский В. И., Рыбакова С. Т. A969) О влиянии начальных
градиентов напора на фильтрацию в слоистых грунтах. Динамика сплошной
среды (Новосибирск) 2, 100—ИЗ.
Пеньковский В. И., Рыбакова С. Т. A975) Прогноз водносоле-
вого режима на орошаемых территориях. В сб.: Природные условия Западной
Сибири и переброска стока рек в Среднюю Азию. Новосиб., «Наука», с. 101—
ИЗ.
Плешакова Л. М., Пряжинская В. Г. A965) О некоторых мето-
методах численного решения одной задачи пространственной неустановившейся
фильтрации. Ж- прикл. мех. и техн. физ., № 2, 141—142.
Положий Г. Н. A953) Метод движения граничных точек и мажорант-
мажорантных облстей в теории фильтрации. Укр. мат. ж. 5, № 4, 380—400.
Положий Г. Н. A954, 1) О краевых задачах теории функций ком-
комплексного переменного в теории фильтрации. Уч. зап. Киевск. ун-та 13, № 8,
121—123.
Положий Г. Н A954, 2) Вариационные теоремы плоской и осесиммет-
ричной фильтрации в однородной и неоднородных средах, метод сохранения
области. Укр. мат. ж. 6, № 3, 333—348.
Положий Г. Н. A955) Об одном дополнении к теореме о движении
граничных точек. Укр. мат. ж» 7, № 3, 339—342.
Положий Г. Н. A962) Численное решение двумерных и трехмерных
краевых задач математической физики и функции дискретного аргумента.
Киевск. ун-т, 161 с.
Полубаринова-Кочина П. Я. A938) Применение теории линей-
линейных дифференциальных уравнений к некоторым случаям движения грунтовой
воды. Изв. АН СССР, сер. мат., № 3, 371—398.
Полубаринова-Кочина П. Я. A939, 1) Применение теории линей-
линейных дифференциальных уравнений к некоторым задачам о движении грун-
грунтовых вод (случай трех особых точек). Изв. АН СССР, сер. мат., № 3,
329—350.
Полубаринова-Кочина П. Я. A939, 2) То же название (число
особых точек больше трех). Изв. АН СССР, сер. мат., № 5-6, 579—602.
Полубаринова-Кочина П. Я. A939, 3) О непрерывном изменении
годографа скорости в плоском установившемся движении грунтовых вод.
Докл. АН СССР 24, № 4, 327—330.
Полубаринова-Кочина П. Я. A939, 4) Простейшие случаи дви-
движения грунтовой воды в двух слоях с различными коэффициентами фильтра-
фильтрации. Изв. АН СССР, Отд. техн. н., № 6, 75—88.
Полубаринова-Кочина П. Я- A940, 1) Расчет фильтрации через
земляную перемычку. Прикл. мат. и мех. 4, № 1, 53—64.
Полубаринова-Кочина П. Я. A940, 2) О фильтрации в анизот-
анизотропном грунте. Прикл. мат. и мех. 4, № 2, 101—104.
654 ЛИТЕРАТУРА
Полубаринова-Кочина П. Я. A940, 3) Движение грунтовых вод
в дренированной плотине. Уч. зап. Моск. ун-та 39, 91—102.
Полубаринова-Кочина П. Я. A942, 1) Некоторые задачи пло-
плоского движения грунтовых вод. М.—Л., АН СССР, 144 с.
Полубаринова-Кочина П. Я. A942, 2) О притоке жидкости к
скважинам в неоднородной среде. Докл. АН СССР 34, № 2, 46—51.
Полубаринова-Кочина П. Я. A945, 1) О неустановившихся дви-
движениях в теории фильтрации. Прикл. мат. и мех. 9, № 1, 79—90.
Полубаринова-Кочина П. Я. A945, 2) К вопросу о перемещении
контура нефтеносности. Докл. АН СССР 47, № 4, 254—257.
Полубаринова-Кочина П. Я. A948) Об одном нелинейном урав-
уравнении в частных производных, встречающемся в теории фильтрации. Докл.
АН СССР 63, № 6, 623—626.
Полубаринова-Кочина П. Я. A949, 1) О неустановившихся дви-
движениях грунтовых вод при фильтрации из водохранилищ. Прикл. мат. и мех.
13, № 2, 187—206.
Полубаринова-Кочина П. Я. A949, 2) О некоторых неустано-
неустановившихся движениях грунтовых вод. Изв. АН СССР, Отд. техн. н., № 6,
838—846
Полубаринова-Кочина П. Я. A950) Об источниках и стоках на
поверхности. Прикл. мат. и мех. 14, № 1, 57—64.
Полубаринова-Кочина П. Я- A952, 1) Теория движения грунто-
грунтовых вод. М., Гостехиздат, 676 с.
Полубаринова-Кочина П. Я- A952, 2) О фильтрации в двух
грунтах с наклонной линией раздела. Изв. АН СССР, Отд. техн. н., № 1,
11—20.
Полубаринова-Кочина П. Я. A952, 3) О перемещении языка
грунтовых вод при фильтрации из канала. Докл. АН СССР 82, № 6, 853—855.
Полубаринова-Кочина П. Я- A955) Задача о системе горизон-
горизонтальных скважин. Arch. mech. stosow. 7, № 3, 287—300
Полубаринова-Кочина П. Я. A956) О наклонных и горизонталь-
горизонтальных скважинах конечной длины. Прикл. мат. и мех. 20, № 1, 95—108.
Полубаринова-Кочина П. Я. A960, 1) О дебите скважины в
безнапорном движении со слабопроницаемым водоупором. Изв. АН СССР
мех. и машиностр., № 3, 155—156.
Полубаринова-Кочина П. Я. A960, 2) О радиусе влияния сква-
скважины. Изв. СО АН СССР, № 5, 20—29.
Полубаринова-Кочина П. Я. A973) К вопросу о модулирующих
функциях. Изв. АН СССР, мех. жидк. и газа, № 5, 152—153.
Полубаринова-Кочина П. Я. A975) По поводу вопроса о моду-
модулирующих функциях. Изв. АН СССР, мех. жидк. и газа, № 5, 174—175.
Полубаринова-Кочина П. Я., Постнов В. А., Эмих В. Н.
A967) Установившаяся фильтрация к несовершенной галерее в безнапорном
пласте. Изв. АН СССР, мех. жидк. и газа, № 4, 97—100.
Полубаринова-Кочина П. Я-, Пряжинская В. Г., Эмих В. Н.
A969) Математические методы в вопросах орошения. М., «Наука», 414 с.
Полубаринова-Кочина П. Я., Фалькович С. В. A947) Теория
фильтрации жидкостей в пористых средах. Прикл. мат. и мех. 11, № 6, 629—
674.
Прандтль Л. A951) Гидроаэромеханика (пер. с нем.). Изд. 2. М.,
ИЛ, 576 с.
Привалов И. И. A977) Введение в теорию функций комплексного
переменного. Изд. 12. М., «Наука», 444 с.
Приклонский В. А. A955) Грунтоведение, ч. 1. Изд. 3. М., Госгеол-
техиздат, 431 с.
Проскурников С. М. A937) Новые расчетные данные по фильтрации
через земляные перемычки. Тр. Гос. гидрол. ин-та, № 5, 162—182.
ЛИТЕРАТУРА 655
Пузыревская Т. Н. A931) ^Просачивание воды через песчаные грун-
грунты. Изв. Н.-иссл. ин-та гидротехн. 1, 251—258.
Развитие исследований по теории фильтрации в СССР A917—1967). М.,
«Наука», 545 с. A969).
Разумов Г. А. A962) Расчет радиальных систем горизонтальных сква-
скважин. Тр. Лаб. инж. гидрогеол. ВОДГЕО, № 4, 28—50.
Рейнер М. A947) Десять лекций по теоретической реологии (пер. с
англ.). М. — Л., Гостехиздат, 134 с.
Рейнер М. A965) Реология (пер. с англ.). М., «Наука», 223 с.
Рельтов Б. Ф., Чугаев Р. Р., Вяземский О. В. A949) Статьи
о давлении воды на основание гидротехнического сооружения. Изв. Всес.
н.-иссл. ин-та гидротехн. 41, 18—39.
Ризенкампф Б. К. A938, 1) Гидравлика грунтовых вод, ч. 1. Уч. зап.
Саратовск. ун-та, сер. физ.-мат. ин-та 14, № 1, 89—ИЗ.
Ризенкампф Б. К. A938, 2) Гидравлика грунтовых вод, ч. 2. Уч. зап.
Саратовск. ун-та, сер. физ.-мат. ин-та 14, № 2, 181—205.
Ризенкампф Б. К. A940, 1) Гидравлика грунтовых вод, ч.З. Уч. зап.
Саратовск. ун-та 15, № 5, 3—93.
Ризенкампф Б. К. A940, 2) Об одном случае фильтрации воды в мно-
многослойном грунте. Уч. зап. Саратовск. ун-та 15, № 5, 94—100.
Ризенкампф Б. К., Калинин Н. К- A941) Движение грунтовых вод
в трех измерениях с эллипсоидальной свободной поверхностью. Прикл мат
и мех. 5, № 2, 283—286.
Роде А. А. A965—1969) Основы учения о почвенной влаге, т. 1—2. Л.,
Гидрометеоиздат, 664 + 287 с.
Рыбакова С. Т. A962) К задаче о дебите скважины в безнапорном
движении со слабопроницаемым водоупором. Ж. прикл. мех. и техн. физ
№ 3, 113—116. * ''
Рыбакова С. Т. A969) К расчету горизонтального дренажа с учетом
начальных градиентов дренируемого пласта и слабопроницаемого водоупора
Изв. АН СССР, мех. жидк. и газа, № 2, 159—161.
Самарский А. А. A962) Об одном экономичном разностном методе
решения многомерного параболического уравнения в произвольной области.
Ж. вычисл. мат. и мат. физ. 2, № 5, 787—811.
Самарский А. А. A971) Введение в теорию разностных схем. М.,
«Наука», 552 с.
Самарский А. А., Гулин А. В. A973) Устойчивость разностных
схем. М., «Наука», 415 с.
Саттаров М. А. A972) Некоторые модели фильтрации в пористых
средах. Докл. АН СССР 203, № 1, 54—57.
Саттаров М. А. A973) К изучению особенностей течения жидкостей
через пористые среды. Изв. АН СССР, мех. жидк. и газа, № 5,
163—167.
Сафмэн П. A960) Теория дисперсии в пористой среде (пер. с англ.).
Сб. пер. «Механика», № 2, 3—33.
Свешников А. Г., Тихонов А. Н. A974) Теория функций комплекс-
комплексной переменной. Изд. 3. М., «Наука», 319 с.
С era л Б. И. A946) Некоторые пространственные задачи теории потен-
потенциала и их приложения. Изв. АН СССР, сер. мат. 10, № 4, 323—358.
Седов Л. И. A966) Плоские задачи гидродинамики и аэродинамики.
Изд. 2. М ., «Наука», 448 с.
Седов Л. И. A977) Методы подобия и размерности в механике. Изд. 8.
М., «Наука», 440 с.
Семчинова М. М. A953) Сравнение опытных данных с теорией для-
случая неустановившейся фильтрации из канала, расположенного на гори-
горизонтальном водоупоре. Инж. сб. 15, 195—2Q(X
556 ЛИТЕРАТУРА
Семчинова М. М. A957) Оценка формулы М. Борели по эксперимен-
экспериментальным данным В. И. Аравина в случае притока к одному совершенному
колодцу. Изв. АН СССР, Отд. техн. н., № 3, 173—176.
Сергеев Е. М. A952) Общее грунтоведение. Моск. ун-т, 384 с.
Силин-Бекчурин А. И. A951) Специальная гидрогеология. М., Гос-
геолиздат, 395 с.
Смирнов В. И. A918) Задача обращения линейного дифференциаль-
дифференциального уравнения второго порядка с четырьмя особыми точками. Пгр., XVI+
+ 317 с.
Смирнов В. И. A969) Курс высшей математики, т. 3, ч. 2. Изд. 8. М.,
«Наука», 672 с.
Смирнов В. И. A974) Курс высшей математики, т. 2, Изд. 21. М.,
«Наука», 655 с.
Снеддон И. A955) Преобразования Фурье. М., ИЛ, 668 с.
Соболев С. Л. A966) Уравнения математической физики. Изд. 4. М.,
«Наука», 443 с.
Соколов Ю. Д. A951, 1) О притоке грунтовых вод к дренажной ка-
канаве трапецеидального сечения. Прикл. мат. и мех. 15, № 6, 683—
688.
Соколов Ю. Д. A951, 2) О расчете фильтрации из канала трапецеи-
трапецеидального сечения. Докл. АН СССР 79, № 5, 759—762.
Соколов Ю. Д. A956) О некоторых частных решениях уравнения
Буссинеска. Укр. мат. ж. 8, № 1, 48—54.
Соколовский В. В. A949) О нелинейной фильтрации грунтовых вод.
Прикл. мат. и мех. 13, № 5, 525—536.
Стампаккья Г. A974) О фильтрации жидкости через пористую среду
с переменным поперечным сечением. Усп. мат. н. 29, № 4A78), 89—101.
Стклянин Ю. И. A962) Точное решение задачи о потенциале точеч-
точечного стока в однородно-анизотропном пласте с осевой симметрией и конечным
радиусом контура питания. Ж прикл. мех. и техн. физ., № 2.
Тихонов А. Н. A963) О решении некорректно поставленных задач и
методе регуляризации. Докл. АН СССР 151, № 3, 501—504.
Тихонов А. Н., Арсен ин В. Я. A974) Методы решения некорректных
задач. М., «Наука», 223 с.
Тихонов А. Н., Иванов В. К., Лаврентьев М. М. A970) Некор-
Некорректно поставленные задачи. В кн.: Дифференциальные уравнения с частными
производными. М., «Наука», с. 224—238.
Тихонов А. Н., Самарский А. А. A972) Уравнения математической
физики. Изд. 4. М., «Наука», 735 с.
Толстов Ю. Г. A942) Применение метода электрического моделирова-
моделирования физических явлений к решению некоторых задач подземной гидравлики.
Ж. техн. физ. 12, № 10, 587—606.
Тр а н тер К. Дж. A956) Интегральные преобразования в математиче-
математической физике (пер. с англ.). М., Гостехиздат, 204 с.
Уиттекер Э. Т., Ватсон Дж. Н. A962) Курс современного анализа,
ч. 1 (пер. с англ.). Изд. 2. М., Физматгиз, 343 с.
Усенко В. С. A972) Искусственное восполнение запасов и инфильтра-
ционные водозаборы подземных вод. Минск, Наука и техника, 253 с.
Филип Дж. Р. A972) Теория инфильтрации (пер. с англ.). В кн.: Изо-
Изотермическое передвижение влаги в зоне аэрации. Л. — М., Гидромегеоиздат,
с. 6—71.
Фильчаков П. Ф. A949) Электромоделирование задач фильтрации в
разнородном грунте. Докл. АН СССР 66, № 4, 593—596.
Фильчаков П. Ф. A951) Приближенный метод гидромеханического
расчета плотин. Киев, АН УССР, 68 с.
Фильчаков П. Ф. A959—1960) Теория фильтрации под гидротехниче*
скими сооружениями, т. 1—2. Киев, АН УССР, 308 + 256 с.
ЛИТЕРАТУРА 657
Фильчаков П. Ф. A964) Приближенные методы конформных отобра-
отображений. Киев, «Наукова думка», 532 с.
Фильчаков П. Ф. A970) Численные и графические методы приклад-
прикладной математики (справочник). Киев, «Наукова думка», 791 с.
Фильчаков П. Ф., Нанчишин В. И. A961) Интегратор ЭГДА, мо-
моделирование потенциальных полей на электропроводной бумаге. Киев,
АН УССР, 171 с.
Форхгеймер Ф. A935) Гидравлика (пер. с нем.), М. — Л., ОНТИ,
615 с.
Хан туш М. С. A964, 1) Новое в теории перетекания (пер. с англ.).
В сб.: Вопросы гидрогеологических расчетов. М., «Мир», с. 43—60.
Хантуш М. С. A964, 2) Анализ данных опытных откачек из скважин
в водоносных горизонтах с перетеканием (пер. с англ.). В сб.: Вопросы гидро-
гидрогеологических расчетов. М., «Мир», с. 27—42.
Харкеевич Ю. Ф. A950) Графическое решение уравнения в частных
производных параболического вида. Прикл. мат. и мех. 14, № 3, 303—310.
Харченко С. И. A975) Гидрология орошаемых земель. Л., Гидро-
метеоиздат, 374 с.
Христианович С. А. A940) Движение грунтовых вод, не следующее
закону Дарси. Прикл. мат. и мех. 4, № 1, 33—52.
Цицкишвили А. Р. A957, 1) Фильтрация из канала трапецеидаль-
трапецеидального сечения. Изв. СССР, Отд. техн. н., № 3, 125—133.
Цицкишвили А. Р. A957, 2) Об итерационном методе Н. М. Герсе-
ванова. Прикл. мат. и мех. 21, № 2, 291—296.
Цицкишвили А. Р. A973) О конформном отображении полуплоско-
полуплоскости на круговые многоугольники. Докл. АН СССР 211, № 2, 300—303.
Цицкишвили А. Р. A974) Применение метода И. А. Лаппо-Данилев-
ского к отысканию функций, конформно отображающих полуплоскость на
круговые многоугольники. Дифференциальные уравнения 10, № 3, 458—
469.
Цытович Н. А. A963) Механика грунтов. Изд. 4. М., Госстройиздат,
636 с.
Чайлдс Э. A973) Физические основы гидрологии почв (пер. с англ.).
Л., Гидрометеоиздат, 427 с.
Ч арный И. А. A948) Подземная гидромеханика. М. — Л., Гостехиздат,
196 с.
Ч арный И. А. A949) Метод последовательной смены стационарных
состояний и его приложение к задачам нестационарной фильтрации жидкости
и газов. Изв. АН СССР, Отд. техн. н., № 3, 323—342.
Ч арный И. А. A951, 1) Строгое доказательство формул Дюпюи для
безнапорной фильтрации с промежутком высачивания. Докл. АН СССР 79,
№ 6, 937—940.
Ч арный И. А. A951, 2) О величине промежутка высачивания при без-
безнапорной фильтрации. Докл. АН СССР 80, № 1, 29—33.
Ч арный И. А. A953) Безнапорная фильтрация в среде с переменной
вдоль вертикали проницаемостью. Докл. АН СССР 88, № 5, 765—768.
Ч арный И. А. A956) Основы подземной гидравлики. М., Гостоптехиз-
дат, 260 с.
Чарный И. А. A963) Подземная гидрогазодинамика. М., Гостоптех*
издат, 396 с.
Черкасов А. А. A958) Мелиорация и сельскохозяйственное водоснаб*
жение. Изд. 4. М., Сельхозгиз, 376 с.
Чернов Б. С, Б а зло в М. Н., Жуков А. И. A960) Гидродинамйче*
ские методы исследования скважин и пластов. М., Гостоптехиздат, 319 с.
Чернов ал В. Т. A961) О решении некоторых задач нестационарной
фильтрации при помощи интегратора ЭГДА. Укр. мат. ж. 13, № 2*
235-239.
658 Литература
Ч ж а н В э й - ц и н ь A959) Неустановившийся режим грунтовых вод
под влиянием орошения. В сб.: Влияние орошения на режим грунтовых вод
(сб. 2). М., АН СССР, с. 121—162.
Чирки н М. П., Шульгин Д. Ф. A964) О движении солей в капил-
капиллярной зоне грунта при наличии испарения. Тр. Ташк. ун-та 242, 100—103.
Чу га ев Р. Р. A974) Подземный контур гидротехнических сооружений.
Изд. 2. Л., «Энергия», 237 с.
Шаманский В. Е. A969) Численное решение задач фильтрации грун-
грунтовых вод на ЭЦВМ. Киев, «Наукова думка», 375 с.
Шанкин П. А. A947, 1) Исследование фильтрации в построенных гид-
гидротехнических сооружениях. М., Речиздат, 176 с.
Шанкин П. А. A947, 2) Расчет фильтрации в земляных плотинах.
М. —Л., Речиздат, 180 с.
Швидлер М. И. A963, 1) Решение плоских фильтрационных задач ме-
методом Монте-Карло. Изв. АН СССР, мех. и машиностр., № 1, 141—145.
Швидлер М. И. A963, 2) Фильтрационные течения в неоднородных
средах. М., Гостоптехиздат, 136 с.
Шейдеггер А. Э. (I960) Физика течения жидкостей через пористые
среды (пер. с англ.). М., Гостоптехиздат, 250 с.
Шестаков В. М. A965) Теоретические основы оценки подпора, водо-
понижения и дренажа. Моск. ун-т, 233 с.
Шестаков В. М. A973) Динамика подземных вод. Моск. ун-т,
327 с..
Шульгин Д. Ф. A969) К расчету опреснения засоленных пород при
промывке. Вопросы механики 7 (Ташкент), с. 137—143.
Щелкачев В. Н. A946) Основные уравнения движения жидкости в
упругой пористой среде. Докл. АН СССР 52, № 2, 103—106.
Щелкачев В. Н. A959) Разработка нефтеводоносных пластов при
упругом режиме. М., Гостоптехиздат, 467 с.
Щелкачев В. Н., Лапук Б. Б. A949) Подземная гидравлика. М.—Л.,
Гостоптехиздат, 524 с.
Щелкачев В. Н., Пыхачев Г. Б. A939) Интерференция скважин и
теория пластовых водонапорных систем. Баку, АзГОНТИ, 286 с.
Эмих В. Н. A962) Фильтрация с полосы при наличии соленых подпор-
подпорных вод. Ж. прикл. мех. и техн. физ., № 2, 145—149.
Эмих В. Н. A966) О форме линзы пресных вод при фильтрации из
канала. Изв. АН СССР, мех. жидк. и газа, № 2, 115—119.
Эмих В. Н. A968) Решение одной плановой задачи неустановившейся
фильтрации грунтовых вод методом статистических испытаний. Ж. прикл. мех.
и техн. физ., № 4, 163—168.
Эм их В. Н., Эм их Е. М. A968) К задаче о канале (дрене) над пото-
потоком грунтовых вод по наклонному водоупору. Ж. прикл. мех. и техн. физ.,
№ 3, 153-158.
Яненко Н. Н. A967) Метод дробных шагов решения многомерных за-
задач математической физики. Новосиб., «Наука», 196 с.
Янке Е., Эм де Ф., Л еш Ф. A968) Специальные функции (пер. с нем.).
Изд. 2. М., «Наука», 344 с.
Albert Р. A960) Methode d'estimation des reserves. С. г. 6-emes jour-
nees de l'hydraulique (Nancy) 2, question 6, n° 4,560—566.
Aronofsky J. S., Jenkins R. A952) Unsteady flow of gas through
porous media, one-dimensional case. Proc. 1st US Nat. Congr. Appl. Mech.,
763—771.
Baiocchi С A974) Probleme a frontiere libre en hydraulique. С. г. Acad.
sci. A278, n° 18, 1201—1203.
В aril Ion E. G. A936) Note sur les rayons de courbure intervenant dans
la construction des resaux hydrodynamiques. Rev. gen. hydraulique, n° 8, 411—
415.
ЛИТЕРАТУРА 659
Bateman H. A932) Partial differential equations of mathematical phy-
physics. Cambridge, Univ. Press, 522 p.
BaverLD. A956) Soil physics. 3rd ed. N. Y., Wiley, London, Chapman, 489 p.
Boussinesq J. A904) Recherches theoriques sur l'ecoulement des nappes
d'eau infiltrees dans le sol et sur le debit des sources. J. math, pures et appl.
10, n° 1, 5—78 (Complement, n° 4, 363—394).
Breitenoder M. A942) Ebene Grundwasserstromungen mit freier Ober-
flache. Berlin, Springer-Verlag, vi + 128 S.
Chavent G. A969) Sur une methode de resolution du probleme inverse
dans les equations aux derivees partielles paraboliques. С. г. Acad. sci. A269,
n°24, 1135—1138.
Chi Ids E. С A969) An introduction to the physical basis of soil water
phenomena. London e. a., J. Wiley, xiii + 493 p.
Dachler R. A932) Ueber Sickerwasserstromungen in geschichtetem Ma-
Material. Wasserwirtschaft, H. 2, 15—20.
Dachler R. A936) Grundwasserstromung. Wien, Springer-Verlag, vi +
+ 142 S.
Dagan G. A964) Second-order linearized theory of free-surface flow in
porous media. Houille blanche 19, n° 8, 901—910.
Dagan G. A967) Linearized solutions of free-surface groundwater flow.
J. Geophys. Res. 72, n° 4, 1183—1193.
Darcy H. A856) Les fontaines publiques de la ville de Dijon. Paris,
647 p.
De Glee G. J. A930) Over grondwaterstromingen by wateronttrekking by
middel van putten. Delft.
De Wiest R. J. M. A965) Geohydrology. N. Y. a o., Wiley, 366 p.
Dupuit J. A863) Etudes theoriques et pratiques sur le mouvement des
eaux. 2-е ed. Paris, 304 p.
Erdelyi A., Magnus W., Oberhettinger R, Tricomi P. G.
A954) Tables of integral transforms, v. 1. N. Y. a. o., McGraw-Hill, xx + 391 p.
Ferrari F. A964) Theorie du puits. Application a la methode de Porchet.
Houille blanche 19, n° 8, 911—919.
Gauss K. A888) Allgemeine Untersuchungen uber die unendliche Reihe
1 + ap/(l y)x -f ... Berlin, Springer-Verlag, 86 S.
Gheorghita $t. I. A966) Metode matematice fn hidrogazodinamica
subterana. Bucuresti, ed. Acad. RSR, 583 p.
Hamel G. A934) Ueber Grundwasserstromung. Z. angew. Math, und
Mech. 14, H. 3, 129—157.
Hamel G., Gunther E. A935) Numerische Durchrechnung zu der Ab-
handlung uber Grundwaserstromung. Z. angew. Math, und Mech. 15, H. 5,
255—265.
Hantush M. S. A964) Hydraulics of wells. Adv. Hydroscience 1, 201 —
291.
Herzberg A. A901) Die Wasserversorgung einiger Nordseebader. J. Gas-
beleuchtung und Wasserwirtschaft 44.
Heun K. A899) Zur Theorie der Riemannschen Funktionen zweiter Ord-
nung mit vier Verzweigungspunkten. Math. Ann. 33, 161—179.
Hoffmann R. A934) Grundwasserstromung unter Wehren. Wasserwirt-
Wasserwirtschaft, H. 18—19, 20-21.
Hunt B. W. A970) Unsteady seepage toward narrow ditch. J. Hydraulic
Div. Proc. Amer. Soc. Civil Engrs 96, n° 10, 1953—1956.
Jacob C. E. A946) Radial flow in a leaky artesian aquifer. Trans. Amer.
Geophys. Union 27, n° 11, 198—205.
Jacob С E. A950) Flow of ground water. In: H. Rouse (ed.) Engineering
hydraulics. N. Y., p. 321- 386.
Kitagava Kiugoro A940) Un aspect de developpement des etudes
des eaux souterraines au Japan. Japan. J. Astron. and Geophys. 17.
660 ЛИТЕРАТУРА
Koch H. A., Slobod R. L. A957) Miscible slug process. J. Petrol. Tech-
nol, n° 2, 40—47 (Trans. AIME 210).
Kozeny J. A931) Grundwasserbewegung bei freiem Spiegel, Fluss- und
Kanal-versickerung. Wasserkraft und Wasserwirtschaft, H. 3, 28—31.
Kravtchenko J., Sauvage de Saint-Marc G., Boreli M.
A955, 1) Sur les singularites des ecoulements plans et premanentes des nappes
souterraines pesantes. Houille blanche 10, n° 1, 47—62.
Kravtchenko J., Sauvage de Saint-Marc G., Boreli M.
A955, 2) Etude d'une singularite dans les ecoulements plans des liquides pe-
sants en milieux poreux. Houille blanche 10, n° 4, 533—542.
Le Van Thiem A962) Об одной задаче фильтрации в двухслойном
грунте (на вьетн. яз.). Thong bao khoa hoc 1, n° 1, 19—25.
Lindqvist E. A933) On the flow of water through porous soil, ler Con-
gres des grands barrages (Stockholm), v. 5, 81—101.
Loeb J., Cahen G. A963) Extraction,, a partir des enregistrements me-
sures, des parametres dynamiques d'un systeme. Automatisme 8, n° 12, 479—486.
Loeb J. M., Cahen G. M. A965) More about process identification.
J. IEEE, Trans. Automatic Control AC-10, n° 3, 359—361.
Musk at M. A933) Potential distributions in large cylindrical disks with
partially penetrating electrodes. Physics. 4, n° 4, 129—147.
Musk at M. A937) The flow of homogeneous fluids through porous media.
N. Y. —London, McGraw-Hill, xix + 763 p.
Philip J. R. A957) Numerical solution of equations of the diffusion type
with diffusivitiy concentration dependend, 2. Austral. J. Phys. 10, n° 1, 29—42.
Picard E. A928) Traite d'analyse, t. 3. 3-е ed. Paris, Gauthier-Villars,
xii + 660 p.
Saffman P. J. A959) A theory of dispersion in porous media. J. Fluid
Mech. 6, n° 3, 321—349.
Saffman P. J., Taylor G. I. A958) The penetration of a fluid into
a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc.
Roy. Soc. London A245, n° 1242, 312—329.
Schaffernak F. A933) Erforschung der physikalischen Gesetze, nach
welchem die Durchsickerung des Wassers durch eine Talsperre oder den Unter-
grund stattfindet. Wasserwirtschaft, H. 30, 10—20.
Scheidegger A. E. A974) The physics of flow through porous media.
3d ed. Univ. Toronto Press, xv + 353 p.
Schneebeli G. A966) Hydraulique souterraine. Paris, 191 p.
Slichter Ch. A899) Theoretical investigation on the motion of ground
waters. XIX Annual Rept, U. S. Geol. Survey A897—1898), pt 2, p. 295—384.
Southwell R. V. A952—1956) Relaxation methods in theoretical phy-
physics, v. 1—2. Oxford, Univ. Press, 522 p.
Taylor G. I. A953) Dispersion of soluble matter in solvent flowing
slowly through a tube. Proc. Roy. Soc. London A219, n° 1137, 186—203.
Taylor G. I. A971) A model for the boundary condition of a porous
material, pt 1. J. Fluid Mech. 49, n° 2, 319—326.
Theis С V. A935) The relation between the lowering of the piesometric
surface and the rate and duration of discharge of a well using ground-water
storage. Trans. Amer. Geophys. Union 16, 519—524.
Ungureanu E. A969) Sur le mouvement des fluides dans les milieux
poreux non homogenes. С. г. Acad. sci. A268, n° 3, 181—183.
Wei nig F., Schields A. A936) Graphisches Verfahren zur Ermittlung
der Sickerstromung durch Staudammen. Wasserkraft und Wasserwirtschaft,
H. 18, 233-240.
ИМЕННОЙ УКАЗАТЕЛЬ
Абрамов С. К. 64Я
Абуталиев Ф. Б. 617, 641
Абуталиев Э. Б. 641
Аверьянов С. Ф. 37—39, 43, 154, 166, 454, 459,
483, 505-507, 615, 516, 521, 576, 592,
641, 647
Аксентьев Л. А. 201, 641
Алберг Дж. (Ahlberg J. Н.) 622, 641
Альбер П. (Albert P.) 462, 658
Альтовский М. Е. 636, 641
Аравин В. И. 18, 22, 36, 95, 119, 122, 124,
138, 139, 211, 223, 230, 231, 323, 386, 392,
398, 409, 629, 631, 641, 642
Аронофски Дж. (Aronofsky J. S.) 445, 658
Арсенин В. Я. 634, 542, 656
Ватсон Дж. И. (Watson G. N.) 246, 256, 656
Вевиоровская М. А. 606, 643, 649
Ведерников В. В. 14, 36, 49, 51, 135, 136, 141
147, 156, 157, 165, 166, 172—175, 177, 181
182, 354, 643
Векуа И. Н. 321, 643
Векуа Н. П. 256, 643
Веригин Н. Н. 15, 111, 180, 355, 394, 398,
428, 434, 512, 643, 644
Виноградов Ю. П. 553, 644, 648
Витасек Э. (Vita"sek E.) 642
Вишик М. И. 450
Владимиров В. С. 644
Волженская Н. В. 12
Вощинин А. П. 148, 186, 644
Вяземский О. В. 64, 130, 655
Бабушка И. (Babuska I.) 642
Бабушкин В. Д. 641
Базанов М. И. 150, 642
Базлов М. Н. 657
Байокки К. (Baiocchi С.) 289, 290, 642, 658
Бан А. (Вйп А.) 513, 515, 642
Баренблатт Г. И. 438, 446, 447, 450, 504, 530,
532, 642
Барийон Э. Ж. (Barillon E. G.) 591, 658
Барсегян Р. М. 122, 652
Басниев К. С. 651
Басович И. Б. 12, 413, 533, 535, 540, 542,
543, 642
Бегматов А. 466, 531, 623, 626, 628, 642
Бейвер Л. Д. (Baver L. D.) 504, 659
Бейтмен X. (Bateman H.) 369, 424, 643, 659
Белаш П. М. 643
Белякова (Кузьмина) В. К. 562, 566, 643
Бергман С. (Bergman S.) 643
Березин И. С. 614, 616, 643
Береславский Э. Н. 256, 643
Бернадинер М. Г. 73, 643
Бессонов Л. Л. 599, 643
Богомолова А. Ф. 642
Борели М. (BoreH M.) 660
Бочевер Ф. М. 428, 643
Брагинская В. А. 334, 643
Брайтенодер М. (Breiten6der M.) 584, 589,
659
Бузинов С. Н. 425, 643
Булыгин В. Я. 534, 643
Буссинеск Ж. (Boussinesq J.) 13, 432, 443,
450, 659
Бэр Я. (Bear J.) 643
Вайнер М. И. 511, 643
Вайниг Ф. (Weinig F.) 584, 589, 660
•Васильев В. А. 338, 595, 643
Васильев С, В. 643
Гавич И. К. 647
Галин Л. А. 651, 652, 554, 555, 561, 566, 644
Гамель Г. (Hamel G.) 268, 659
Гантмахер Ф. Р. 544, 644
Гармонов И. В. 643
Гасымов М. Г. 538, 648
Гаусс К. Ф. (Gauss К. F.) 659
Гахов Ф. Д. 15, 231
Гельфанд И. М. 638, 644
Георгиевский В. Б. 540, 542, 644
Георгицэ Шт. (Gheorghita St. I.) 351, 659
Герсеванов Н. М. 64, 150, 151, 153, 162, 163,
231, 289, 644
Герцберг A. (Herzberg A.) 334, 659
Гильберт Д. (Hilbert D.) 21, 625, 644, 648
Гирйнский Н. К. 15, 35, 114, 306, 335, 357,
364, 380, 388, 466, 470, 568, 576, 636, 645
Глейзер Б. А. 643
Годунов С. К. 572, 645
Голубев В. В. 245, 246, 248, 645
Голубев Г. В. 320, 321, 322, 645
Голубева О. В. 351, 645
Горбунов А. Т. 651
Градштейн И. С. 94, 226, 412, 528, 563, 627.
645
Гришин М. М. 49, 130, 645
Гулин А. В. 655
Гусейн-Заде М. А. 645
Гутенмахер Л. И. 606. 645
Гюнтер Э. (Gunther E.) 659
Даган Г, (Dagarj G.) 555, 659
Данилов В. Л. 624, 628, 645
Дарси A. (Parcy H.) 13, 32, 659
Дахлер P. (Dachler R.) 659
Девисон Б. Б. (Davison В.) 54, 119, 139,
268. 406, 606, 645, 646
Де Глэ Г. И. (De Glee G. J.) 659
662
ИМЕННОЙ УКАЗАТЕЛЬ
Де Уист P. (De Wiest R. J. M.) 426, 606,
646. 659
Джанмбеков Ч. 620, 623, 646
Джейкоб Ч. Э. (Jacob С. Е.) 426, 659
Дженкинс P. (Jenkins R.) 445, 658
Дзя Да-Лин 516, 641
Дольский В. Е. 646
Дружинин Н. И. 15, 604, 606, 646
Дюпюи Ж. (Dupuit J.) 13, 76, 153, 317, 342,
382, 391, 659
Егер Дж. К. (Jaeger J. С.) 647
Егорова В. М. 12
Ентов В. М. 73, 438, 450, 532, 643, 646
Желтов Ю. П. 504, 642
Жернов И. Е. 606, 646
Жидков Н.'П. 614, 616, 643
Жуков А. И. 657
Жуковский Н. Е. 14, 15, 17, 33, 36, 46, 51,
132. 133, 135, 174, 628, 646
Журавский А. М. 94, 95, 646
Замарин Е. А. 628
Заславски Д. (Zaslavsky D.) 643
Зельдович Я. Б. 450, 646
Зенкевич О. К. (Zienkiewicz О. С.) 595,
601. 646
Зотов Г. А. 651
Ивакин В. В. 646
Иваненко Д. Д. 371, 646
Иванов В. К. 656
Измаилов И. И. 641
Ильин А. М. 646
Ильинский Н. Б. 201, 646, 651
Ирмей С. (Irmay S.) 643
Казанский А. Б. 515, 646
Калашников А. С. 451, 638, 646, 647, 652
Калинин Н. К. 306, 317, 549, 555, 647, 655
Каменский Г. Н. 614, 619, 620, 647
Канторович Л. В. 628, 647
Капранов Ю. И. 338, 340, 524, 647
Карслоу Г. (Carslaw H. S.) 647
Качинский Н. А. 18, 27, 36, 647
Казн Ж. (Cahen G.) 540, 660
Кибель И. А. 28, 30, 39, 47, 420, 440, 548, 648
Китагава К. (Kitagava К.) 334, 659
Клабукова Л. С. 645
Клоков Ю. А. 647
Ков да В. А. 455, 516, 647
Козени И. (Kozeny J.) 35, 76, 154, 660
Козлов В. С. 118, 119, 572, 575, 576, 647
Коллинз P. (Collins R. Е.) 647
Колмогоров А. Н. 20, 647
Компанеец А. С. 450, 646
Кон-Фоссен С. (Cohn-Vossen S.) 21, 614
Коппенфельс В. (Koppenfels W.) 647
Корольков Н. В. 645
Корсунцев А. В. 580, 647
Корчебоков Н. А. 647
Костицын Л. И. 353
Костяков А. Н. 647
Кох X. A. (Koch H. А.) 514, 659
Кочин Н.'Е. 15, 28, 30, 39, 47, 240, 420, 440,
548, 557, 609, 629, 648
Кочина И. Н. 187, 504, 642, 648
Кочина Н. Н. 10, 12, 480, 488, 489, 492, 496,
556, 559-561, 648
Кравченко Ж. (Kravtchenko J.) 259, 660
Кравченко И. П. 606, 643
Крамаровская И. И. см. Кулабухова И. И.
Краснопольский А. А. 14, 648
Крылов В. И. 647
Крылов М. М. 485, 648
Кузьмина В. К. *см. Белякова В. К.,
Кулабухова (Крамаровская) И. И. 506, 507,
648
Куммер 3. (Kummer E.) 249
Курант P. (Courant R.) 625, 648
Куфарев П. П. 553, 567, 644, 648
Кучеренко Э. Г. 553, 648
Лаврентьев М. А. 90, 103, 648
Лаврентьев М. М. 532, 648, 656
Ладыженская О. А. 648
Лаппо-Данилевский И. А. 256
Лапук Б. Б. 658
Лапшин Ю. С. 268
Ле Ван Тьем (Le Van Thiem) 303, 660
Лебедев А. В. 643
Лебедев А. Ф. 25, 26, 648
Левитан Б. М. 538, 644, 648
Лейбензон Л. С. 566, 609, 649
Лембке К. Э. 14, 607, 608, 649
Леш Ф. (L6sch F.) 372, 459, 658
Линдквист Э. (Lindqvist E.) 46, 660
Ломизе Г. М. 22, 24, 36, 649
Лоэб Ж. (Loeb J.) 540, 660
Лукьянов В. С. 606, 649
Лыков А. В. 483, 649
Любии (Lubin) 424
Ляшенко В. Ф. 619, 649
Ляшко И. И. 582, 649
Магнус В. (Magnus W.) 659
Мадженес Э. (Magenes E.) 289, 642
Маккавеев В. М. 609, 649
Максимов В. А. 642
Мальгинова Е. М. 566, 649
Мариночкина А. С. 523, 649
Маруашвили Т. И. 645
Марченко В. А. 540. 649
Марчук Г. И. 622, 649
Маскет М. см. Мускат М.
Матвеенко Т. И. 458, 649
Меламед В. Г. 401, 649
Мелещенко Н. Т. 8S, 11& 120, 211, 285, 649
Меньшикова В. И. 159, 649
Мизес P. (Mises R.) 649
Милн-Томсон Л. М. (Milne-Thomson L М )
351, 650
Минский Е. М. 650
Мироненко В. А. 650
Мироничева Г. В. 540, 644
Михайлов Г. К. Ю, 12, 22, 284, 287, 238, 324,
326, 327, 329, 330, 444, 589, 590, 650
Михайлов Ю. А. 483, 649
Михлин С. Г. 596. 621, 650
Моргулис М. М. 289
Муминов С. Н. 480, 660
ИМЕННОЙ УКАЗАТЕЛЬ
663
Мурзакматов М. У. 620, 623, 646, 650
Мускаг М. (Muskat M.) 367, 368, 374, 424,
649, 660
Мусхелишвили Н. И. 15, 202, 207, 231, 650
Мхитарян А. М. 289, 650
Мясникова Н. А. 647
Мятиев А. Н. 15, 357, 363, 365, 366. 399. 401.
650
Рейнер М. (Reiner M.) 40, 42, 655
Рельтов Б. Ф. 64, 130, 655
Ризенкампф Б. К. 15, 56, 63, 65, 66, 85, 138,
139, 141, 150, 151, 157, 165, 166, 177, 240,
260, 264, 316, 317, 655
Роде А. А. 22. 655
Розе Н. В. 28, 30, 39. 47, 420, 440, 548, 648
Назаров Г. И. 650
Насберг В. М. 579, 650, 651
Насиковский В. П. 652
Нёдрига В. П. 398, 651
Нельсон-Скорняков Ф. Б. 150, 289, 651
Нерпин С. В. 651
Нетушил А. В. 24, 649
Николаев Н. С. 645
Николаева М. В. 573, 651
Николаевский В. Н. 642, 650, 651
Нильсои Э. (Nilson E. N.) 641
Нужин М. Т. 201, 651
Нумеров С. Н. 9, 15, 18, 22, 36, 44, 72. 95,
119, 122—125, 135, 139, 141, 211, 212, 214,
215, 223, 229-231, 233, 235, 268, 386, 392,
642, 651, 652
Оберхеттингер Ф. (Oberhettinger F.) 659
Оганджанянц В. Г. 642
Олейник А. Я. 122, 451, 652
Олейнпк О. А. 646, 652
Павлов А. Т. 334, 652
Павловский Н. Н. 14, 15, 35, 49, 64, 76, 77,
89, 97, 114, 118, 153, 157, 165, 211, 286,
391, 601, 652
Панин П. С. 523, 652
Панов Д. Ю. 570, 571, 652
Панчишин В. И. 604, 657
Пеньковский В. И. 402, 405, 507, 508, 511.
515, 520, 522, 523, 525, 527, 649, 652, 653
Петров Н. Г. 652
Пикар Э. (Picard E.) 660
Плешакова Л. М. 653
Положий Г. Н. 9, 15, 99, 102, 128, 582, 584,
653
Полубаринова-Кочина П. Я. 15, 60, 63, 183,
187, 240, 268, 284, 291, 309, 312, 324, 330,
340, 353, 364, 374, 398, 435, 442, 470, 507,
531, 532, 543, 549, 555, 566, 567, 574, 609,
612, 614, 647, 648, 653, 654
Постнов В. А. 183, 653, 654
Прагер М. (Pra"ger M.) 642
Прандтль Л. (Prandtl L.) 47, 654
Привалов И. И. 99, 654
Приклонский В. А. 17, 20, 654
Проскурников С. М. 606, 654
Пряжинская В. Г. 398, 532, 543, 648, 653, 654
Пуазейль Ж. Л. (Poiseuille J. L.) 33
Пузыревская Т. Н. 32, 655
Пузыревский Н. П. 64
Пыхачев Г. Б. 342, 658
Разин К. И. 647
Разумов Г. А. 380, 643, 655
Резницкая К. Г. 532, 648
Рудаков В. К. 643
Румянцев С. А. 606, 643
Рыбакова С. Т. 402, 405, 511, 525, 653, 655
Рыжик В. М. 438, 450, 532, 642
Рыжик И. М. 94, 226, 412, 528, 563, 627, 645
Рябенький В. С. 572, 645
Самарский А. А. 623, 655, 656
Саркисян В. С. 643
Саттаров М. А. 40, 42, 655
Сауселл Р. В. (Southwell R. V.) 572, 573,
660
Сафмэн Ф. (Saffman Ph. J.) 515, 655. 660
Свешников А. Г. 458, 459, 655
Сегал Б. И. 374, 655
Седов Л. И. 655
Семенова С. М. 647
Семчинова М. М. 10, 445, 636, 655, 656
Сергеев Е. М. 18, 656
Силин-Бекчурин А. И. 366, 656
Сликтер Ч. (Slichter Ch.) 14, 21, 660
Слобод Р. Л. (Slobod R. L.) 514, 659
Смирнов В. И. 57, 97, 202, 245, 246, 248, 254,
270, 317, 451, 656
Снеддон И. (Sneddon I. N.) 373, 426, 656
Соболев С. Л. 451, 478, 656
Соваж-де-Сен-Марк Ж. (Sauvage de Saint-
Marc G.) 660
Соколов А. А. 371, 646
Соколов Ю. Д. 165, 174, 181, 448, 656
Соколовский В. В. 72, 656
Стампаккья Г. (Stampacchia G.) 290, 656
Стклянин Ю. И. 371, 373, 656
Стоке Дж. (Stokes G. G.) 47
Тейлор Дж. И. (Taylor G. I.) 515, 660
Тейс Ч. В. (Theis С. V.) 424, 660
Терцаги К. (Terzaghi К.) 64
Тим A. (Thiem A.) 13
Тихонов А. Н. 458, 459, 534, 542, 655, 656
Толстов Ю. Г. 606, 656
Трантер К. Дж. (Tranter С. J.) 372, 656
Трикоми Ф. Г. (Tricomi F. G.) 659
Тумашев Г. Г. 201, 320, 322, 645, 651
Уиттекер Э. Т. (Whittaker E. Т.) 246, 256,
656
Умаров У. 641
Умрихин И. Д. 425, 643
Унгупяну-Давид Э. (Ungureanu-David E.)
351, 660
Уолш Дж. (Walsh J. L.) 641
Усенко В. С. 459, 641, 656
664
ИМЁНИОЙ
Фаворин Н. Н. 647
Фалькович С. В. 284, 287, 654
Феррари Ф. (Ferrari F.) 659
Филип Дж. P. (Philip J. R.) 507, 656, 660
Фильчаков П. Ф. 15, 93, 118, 120, 122, 677,
604, 606, 656, 657
Фомин В. М. 646
Фомин М. М. 289, 650
Форхгеймер Ф. (Forchheimer Ph.) 13, 76,
334, 335, 392, 657
Фролов К. Д. 59
Хазен A. (Hazen A.) 33
Хант Б. У. (Hunt В. W.) 659
Хантуш М. С. (Hantush M. S.) 426, 428, 466,
657, 659
Харкеевич Ю. Ф. 616, 617, 657
Харченко С. И. 657
Хиле-Шоу X. С. (Hele-Shaw H. S.) 628
Ходжибаев Н. Н. 641
Хойн К. (Heun К.) 254, 659
Хоффманн P. (Hoffmann R.) ИЗ, 659
Христианович С. А. 67, 602, 604, 657
Чиркин М. П. 496, 658
Чугаев Р. Р. 49, 64, 130, 655, 658
Чудновский А. Ф. 651
Шабат Б. В. 90, 103, 648
Шаван Г. (Chavent G.) 534, 659
Шаманский В. Е. 658
Шанкин П. А. 223, 229, 658
Шапинская Г. П. 644
Шаффернак Ф. (Schaffernak F.) 660
Швидлер М. И. 617, 618, 658
Шейдеггер А. Э. (Scheidegger A. E.) 515,
658, 660
Шержуков Б. С. 512, 643, 644
Шестаков В. М. 434, 606, 643, 646, 650, 658
Шешуков Е. Г. 646
Шильдс A. (Schields A.) 584, 589, 660
Шиффер М. (Schiffer M. М.) 649
Шнеебели Ж. (Schneebeli G.) 660
Шпилевой А. Я. 351. 645
Штальман Ф. (Stallmann F.) 647
Шульгин Д. Ф. 496, 540, 644, 658
Цанг И. (Cheung Y. К.) 595, 601. 646
Цицкишвили А. Р. 153, 163, 166, 172, 256, 657
Цытович Н. А. 24, 657
Чайлдс Э. (Childs E. С.) 334, 657, 659
Чаплыгин С. А. 73
Чарный И. А. 14, 16. 264, 268, 374, 609, 612,
657
Черкасов А. А. 19, 33, 37, 657
Чернов Б. С. 425, 657
Черновал В. Т. 657
Чжан Вэй-цинь 484, 658
Чжоу Юй-линь 451, 652
Щелкачев В. Н. 342, 420, 421, 426. 658
Эмде Ф. (Emde F.) 371, 459, 658
Эмих В. Н. 183, 235, 239, 339, 340, 398, 532,
543, 617, 619, 620, 638, 639, 654, 658
Эмих Е. Н. 235, 239, 658
Эрдейи A. (Erdelyi A.) 424, 464. 643, 659
Якоб К. (Iacob С.) 351
Яненко Н. Н. 658
Янке Е. (Jahnke E.) 371, 459. 658