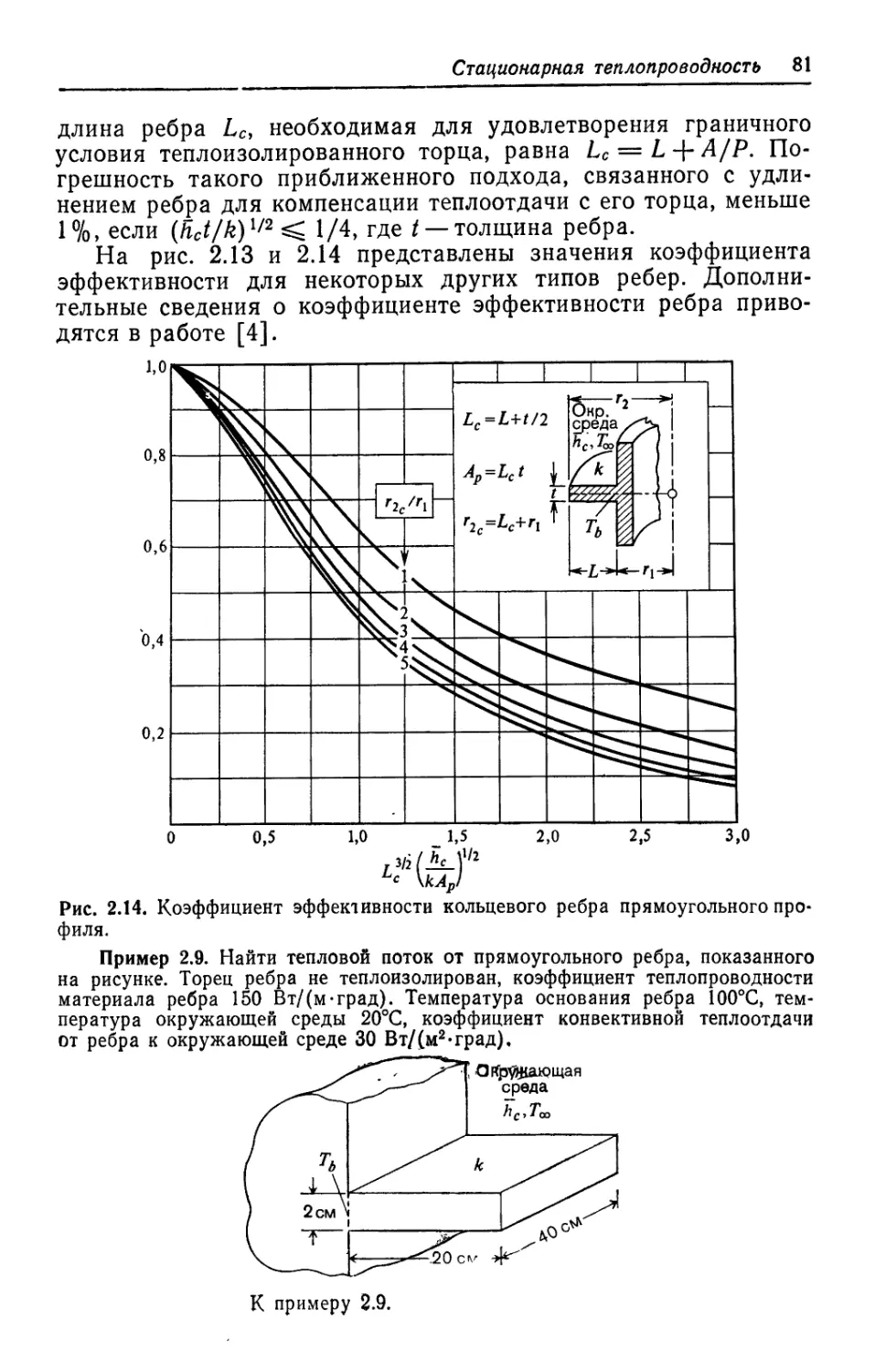
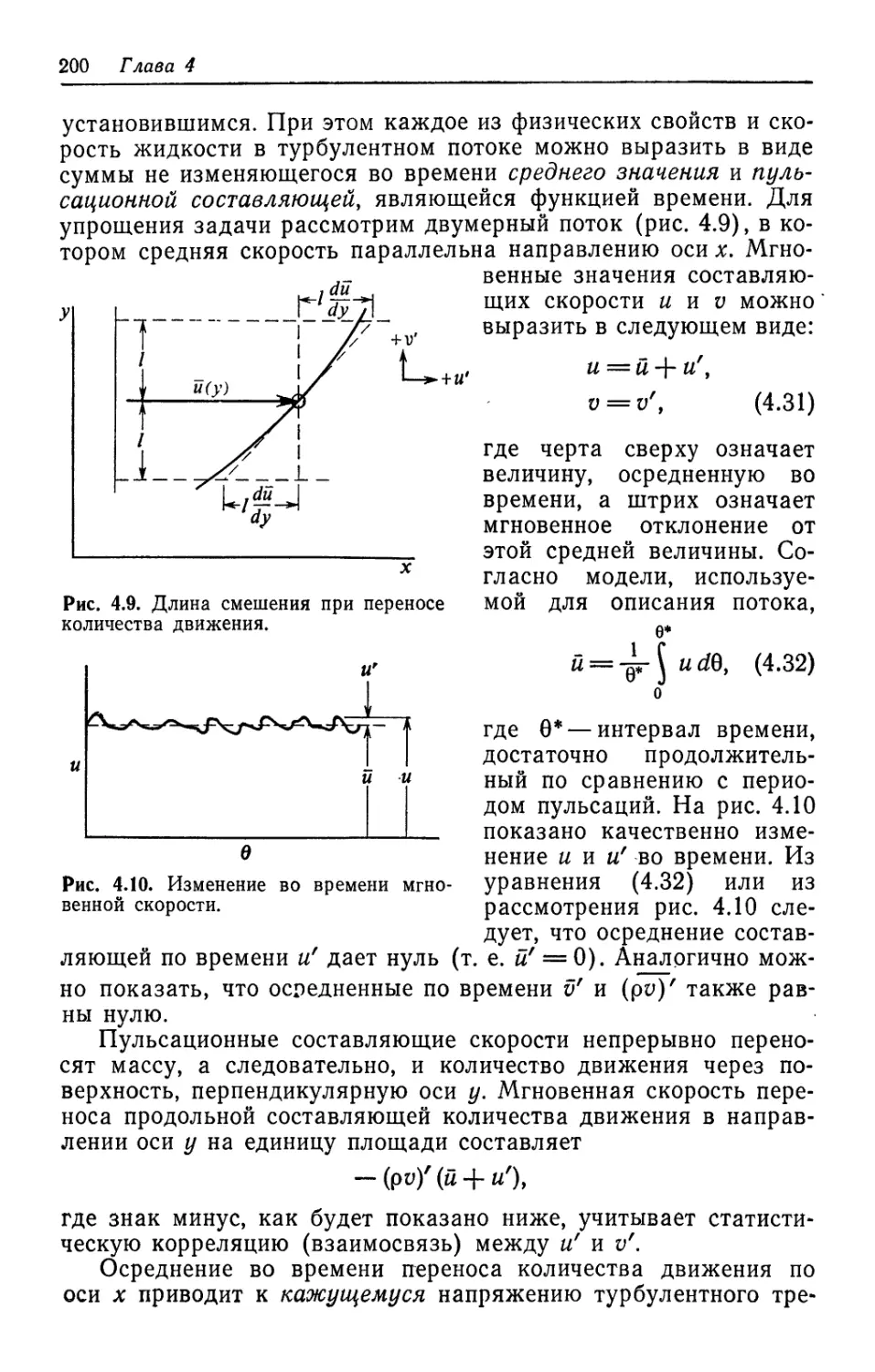
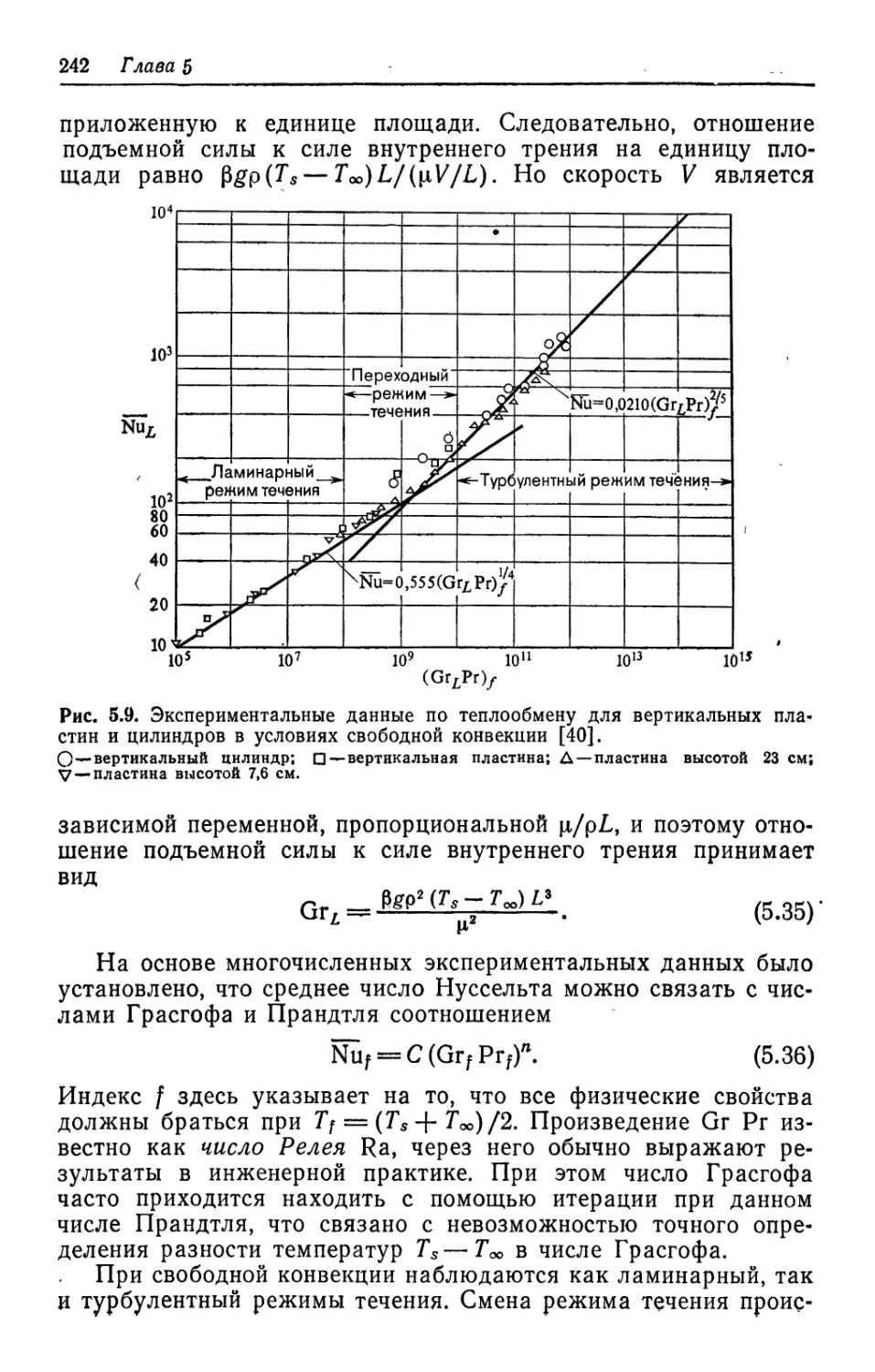
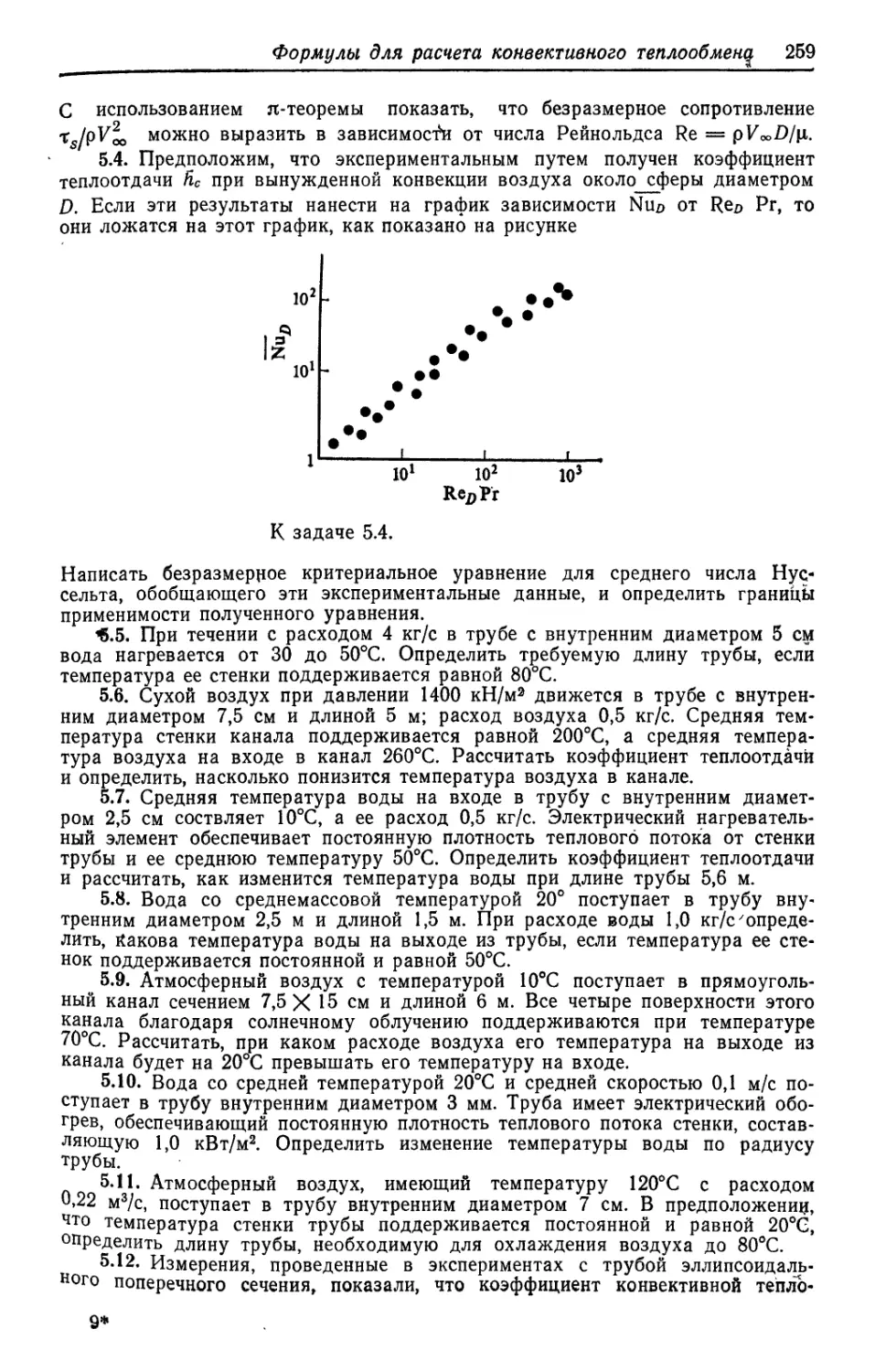
Теги: теплопроводность теплопередача теплоэнергетика теплотехника теплообмен
Год: 1983
Текст
BASIC HEAT
TRANSFER
Frank Kreith
Solar Energy Research Insiittv
University of Colorado
William Z. Black
Georgia Institute of Technology
Harper and Row, Publishers, Mew York
Cambridge, Hagerstown, Philadelphia,
San Francisco, London, Mexico City,
Sao Paulo, Sydney
1980
основы
ТЕПЛОПЕРЕДАЧИ
Ф.Крейт, УБлэк
Перевод с английского
под редакцией
д-ра техн. наук, профессора
И. А. Анфимова
Москва «Мир» 1983
ББК 31.31
К 79
УДК 536.2
Крейт Ф., Блэк У.
Основы теплопередачи: Пер. с англ.—М.: Мир, 1983.—
2 с. ил.
512 с, ил.
Вводный курс инженерной теплопередачи, написанный американскими авто-
авторами. Излагаются основы стационарной и нестационарной теплопроводности,
конвективного теплообмена и теплообмена излучением. Рассмотрены теплообмен
при конденсации и кипении, теплопередача в теплообменниках и тепловых тру-
трубах, а также массообмен. Авторы ориентируют читателя на использование вы-
вычислительной техники.
Для инженеров, а также студентов старших курсов инженерных специаль-
специальностей вузов.
2303010000-305
К 041@1)-83
Редакция литературы по новой 1ехнике
Copyright © 1980 by Frank Kreith and William Z. Black
© Перевод на русский язык, «Мир», 1983
ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ИЗДАНИЯ
Процессы теплообмена и связанного с ним массообмена
играют исключительно важную роль в природе и технике. От
них зависит температурный режим окружающей среды и жилых
помещений, они определяют протекание рабочего процесса в
различных технологических установках и т. п. Неудивительно
поэтому, что теория теплообмена интенсивно развивалась, осо-
особенно в последние десятилетия в связи с потребностями тепло-
теплоэнергетики, атомной энергетики, космонавтики и некоторых дру-
других областей техники.
По теплообмену имеется обширная литература, включающая
многочисленные учебники, монографии и справочники. Несмотря
на это, данная книга должна вызвать интерес советских чита-
читателей. Во-первых, по характеру изложения эта книга простая и
ясная. Ее чтение не требует глубоких специальных знаний. Она
ориентирует читателя на самостоятельное проведение инженер-
инженерных расчетов. Интересны примеры расчетов, носящие сугубо
прикладной, иногда даже бытовой характер, на примере кото-
которых автор показывает, как можно, делая типовые допущения,
свести довольно сложные по своей начальной постановке задачи
к простому решению.
Во-вторых, книгу отличает наличие программ на языке Фор-
Фортран. Это, безусловно, вполне современно. Сейчас инженеры не
удовлетворяются только логарифмической линейкой или элек-
электронным калькулятором, но и широко применяют ЭВМ, как пра-
правило пользуясь сравнительно простыми алгоритмами и про-
программами. Именно такие программы приводят авторы книги.
В-третьих, рассмотрен довольно широкий круг вопросов, от
традиционных для курсов теплопередачи (теплопроводность,
конвекция, излучение) до новых (тепловые трубы, солнечные
коллекторы), интерес к которым возрос в связи с топливно-энер-
топливно-энергетическим кризисом.
В Советском Союзе издано довольно много книг по теплопе-
теплопередаче— как отечественных авторов, так и переводных. Список
некоторых из них приведен в приложении. Но если читатель не-
недостаточно знаком с теорией теплопередачи, а ему надо самому
провести некоторые простейшие тепловые расчеты той или иной
системы, то можно порекомендовать именно эту книгу. Полагаю,
6 Предисловие редактора русского издания
что книга будет встречена с интересом также специалиста-
специалистами-теплотехниками и всеми инженерами и научными работни-
работниками, которым приходится иметь дело с процессами тепло- и
массообмена.
Перевод книги выполнен канд. техн. наук С. С. Ченцовым
(гл. 1—3, приложение), канд. техн. наук В. И. Кабаковым
(гл. 4, 5), д-ром техн. наук Б. А. Хрусталевым (гл. 6) и канд.
техн. наук В. М. Жуковым (гл. 7, 8).
Н. Л. Анфимов
Литература !
1. Авдуевский В. С. и др. Основы теплопередачи в авиационной и ракет-
ракетно-космической технике.— М.: Машиностроение, 1975.
2. Ивановский М. Н. и др. Физические основы тепловых труб. — М.2
Атомиздат, 1978.
3. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. —
4-е изд., перераб. и доп. — М.: Энергоиздат, 1981.
4. Кошкин В. К., Калинин Э. К. Теплообменные аппараты и теплоноси-
теплоносители.— М.: Машиностроение, 1971.
5. Кутателадзе С. С. Основы теории теплообмена. — 5-е изд., перераб. и
доп.—М.: Атомиздат, 1979.
6. Лыков А. В. Теория теплопроводности. — М.: Высшая школа, 1967.
7. Лыков А. В. Тепломассообмен: Справочник.—М.: Энергия, 1971.
8. Михеев М. А., Михеева И. М. Основы теплопередачи. — 2-е изд. — М.:
Энергия, 1977.
9. Теория тепломассообмена/Под ред. А. И. Леонтьева. — М.: Высшая
школа, 1979.
10. Теплотехнический справочник: В 2-х томах/Под ред. В. Н. Юрьева
и П. Д. Лебедева.— 2-е изд., перераб. — М.: Энергия, 1976.—Т. 2.
11. Юдаев Б. Н. Теплопередача. — М.: Высшая школа, 1973.
ПРЕДИСЛОВИЕ
Эта книга является начальным курсом инженерной теплопе-
теплопередачи. Такой курс читается в течение одного семестра студен-
студентам младших курсов или четверти семестра студентам стар-
старших курсов любых инженерных специальностей. Предполага-
Предполагается, что читатели знакомы с основами физики, термодинамики
и теории обыкновенных дифференциальных уравнений, а также
располагают некоторыми знаниями в области гидромеханики.
Материал представлен в соответствии с классической линией
изложения первоначального текста Крейта с акцентом на реше-
решение инженерных задач и на использование вычислительных ма-
машин. В ходе изложения особое внимание уделяется физическому
пониманию процессов переноса тепла и способам применения
необходимых предположений и упрощений в реальных задачах,
позволяющим найти инженерное решение. В книге используется
международная система единиц СИ.
Задачи теплопроводности решаются как аналитическими, так
и численными методами с привлечением численных методов ре-
решения на ЭВМ. При анализе задач конвективного теплообмена
для ламинарного и турбулентного режимов течения сначала
представлены аналитические решения, а затем приведены эмпи-
эмпирические формулы для тел различной формы, наиболее важных
в инженерной практике. Число корреляционных соотношений
сведено к минимуму, чтобы читателю было проще находить чис-
численный ответ. Указаны способы правильного выбора определяю-
определяющей температуры, которую нужно использовать в эмпирических
формулах для каждой из наиболее важных геометрических кон-
конфигураций. Для решения задач теплообмена излучением приме-
применен метод тепловых цепей, который также был использован при
совместном анализе всех процессов теплопередачи с единых
методологических позиций.
В главе, посвященной теплообменникам, представлены метод
среднелогарифмйческого температурного напора и метод, осно-
основанный на использовании понятия эффективности теплообмен*
Ника, причем указаны преимущества и недостатки каждого из
них. Кроме того, в отдельных разделах этой главы описаны
современные теплообменные устройства: тепловые трубы, реге-
регенеративные теплообменники с насадкой и солнечные коллекторы.
8 Предисловие
Задачи в конце каждой\главы расположены в порядке возра-
возрастания сложности. В первых нескольких задачах нужно про-
провести расчет обычными методами; в остальных требуется сде-
сделать инженерные предположения и проявить творческий подход
к решению.
В приложениях содержатся таблицы теплофизических ха-
характеристик, которые помогают изложению материала и реше-
решению помещенных в книге задач. Все приведенные в книге ответы
на задачи были получены с помощью теплофизических свойств,
указанных в этих таблицах. Однако, если нужна более полная
информация о теплофизических свойствах, следует обратиться к
соответствующим справочникам.
Мы старались избежать перегрузки квдги специальными све-
сведениями и представить материалы, полезные для многих сторон
инженерной деятельности. Мы не претендуем на оригиналь-
оригинальность, но надеемся, что наш стиль изложения поможет студен-
студентам учиться, а преподавателям учить их.
Фрэнк Крейт
Уильям Блэк
ОБОЗНАЧЕНИЯ
а — ускорение;
а — скорость звука;
А — площадь (поперечного сечения);
As — площадь поверхности;
с — удельная теплоемкость;
с — скорость света;
ср — удельная теплоемкость при постоянном давлении;
cv — удельная теплоемкость при постоянном объеме;
С — теплоемкость;
С. — коэффициент трения;
С — мольная концентрация;
Dh — эквивалентный (гидравлический) диаметр;
D — диаметр;
D — коэффициент диффузии;
Е — энергия;
Е — плотность потока собственного излучения излучающего тела или
газа;
Е — электрический потенциал;
f — коэффициент трения;
F — сила;
-угловой коэффициент излучения от поверхности / к поверхно-
поверхности 2;
g — ускорение свободного падения;
G = pF — плотность потока массы;
G — плотность потока падающего излучения;
h — постоянная Планка;
hc — коэффициент конвективной теплоотдачи поверхности;
i — удельная энтальпия;
/ — интенсивность излучения;
/ — сила электрического тока;
/ — параметр теплообмена;
/ — плотность потока эффективного излучения;
k — постоянная Больцмана;
k — коэффициент теплопроводности;
I — длина;
/ — длина пути перемешивания Прандтля;
L — линейный размер;
гп — масса;
т — массовый расход;
Ш — молекулярный вес;
М — число Маха;
N — число молекул;
N — поток массы;
Р — периметр;
р — давление;
Я — тепловой поток;
10 Обозначения
q" — плотность теплового потока;
qG — интенсивность тепловыделения в единице объема;
Q — количество тепла;
Q = VA — объемный расход;
г — радиус;
г — коэффициент восстановления;
R — коэффициент загрязнения;
R — газовая постоянная;
Ru — универсальная газовая постоянная;
R — термическое сопротивление;
5 — формфактор теплопроводности;
t — время;
t — толщина;
Т — температура;
и — местная скорость вдоль поверхности;
U — внутренняя энергия;
U — суммарный коэффициент теплопередачи;
v — местная скорость по нормали к поверхности;
v — удельный объем;
V — скорость;
V — объем;
х — координата, направленная обычно вдоль поверхности;
X — мольная долевая концентрация;
у — координата, направленная обычно по нормали к поверхности;
z — координата;
а — поглощательная способность;
а — коэффициент температуропроводности;
Р — термический коэффициент объемного расширения;
V — отношение удельных теплоемкостей;
6 — толщина пленки;
6 — толщина динамического пограничного слоя;
6^ — толщина теплового пограничного слоя;
Д — изменение, конечная разность;
е — излучательная способность (степень черноты);
е — коэффициент турбулентной диффузии;
вн — коэффициент турбулентной температуропроводности;
ем — коэффициент турбулентной вязкости;
Т] — коэффициент динамической вязкости;
т| — эффективность, к. п. д.;
8 — нормальный угол;
G — разность температур, температурный напор;
Я — длина волны;
|i — коэффициент динамической вязкости;
v — коэффициент кинематической вязкости;
v — частота;
| ~ безразмерная координата;
л — безразмерный комплекс параметров;
р — плотность;
р — отражательная способность;
а — постоянная Стефана — Больцмана;
а — поверхностное натяжение;
х — безразмерное время;
т — пропускательная способность;
т — напряжение трения;
Ф — угловая координата;
со — телесный угол;
со — долевая массовая концентрация,
Глава 1
ПРИНЦИПЫ ТЕПЛОПЕРЕДАЧИ
1.1. ВВЕДЕНИЕ
Если где-либо в пространстве возникла разность темпера-
температур, энергия переносится из области высокой температуры в
область низкой температуры. В соответствии с концепциями
термодинамики энергия, перенесенная вследствие разности тем-
температур, называется теплом. Хотя законы термодинамики отно-
относятся к переносу энергии, они применимы лишь для систем, на-
находящихся в равновесии. Поэтому с их помощью можно рассчи-
рассчитать количество энергии, необходимое для перехода системы из
одного равновесного состояния в другое, но нельзя определить,
какое время займет этот переход. Теория теплопередачи допол-
дополняет первый и второй законы классической термодинамики,
предлагая методы, позволяющие найти скорости переноса
энергии.
Чтобы нагляднее показать различие в видах информации,
полученных с помощью термодинамики и теплопередачи, рас-
рассмотрим нагрев стального стержня в горячей воде. Законы тер-
термодинамики, с одной стороны, позволяют рассчитать конечную
температуру, после того как две системы достигнут равновесия,
и количество энергии, перенесенное при переходе от начального
равновесного состояния к конечному, но они не дают возмож-
возможности определить скорость переноса тепла и температуру
стержня по истечении заданного промежутка времени или най-
найти, через какое время температура стержня достигнет задан-
заданного значения. С другой стороны, теория теплопередачи позво-
позволяет вычислить скорость переноса тепла от воды к стальному
стержню, а затем на основании этой информации рассчитать,
как изменяются по времени температуры стержня и воды.
При полном анализе переноса тепла необходимо рассмотреть
три различных механизма теплопередачи: теплопроводность,
конвекцию и излучение. Для правильного выбора конструкции и
анализа работы теплообменников и преобразователей энергии
нужно знать особенности всех трех механизмов переноса тепла
и их взаимодействия между собой. В этой главе мы рассмотрим
основные принципы теории теплопередачи и некоторые простей-
простейшие приложения. В следующих главах будет подробно описан
каждый из видов теплопередачи. .
12 Глава 1
1.2. ТЕПЛОПРОВОДНОСТЬ (КОНДУКТИВНЫЙ ПЕРЕНОС ТЕПЛА)
Теплопроводность является единственным видом теплопере-
теплопередачи в непрозрачной твердой среде. Если в такой среде сущест-
существует градиент температуры, тепло переносится из высокотемпе-
высокотемпературной области в низкотемпературную. Скорость переноса
Направление теплового потока
,dr yr
*Jx-yS
s>^-
v + лг
Направление теплового потока
Т(х)
>> + х > +х
Рис. 1.1а. Схема, иллюстрирующая правило знаков для теплопроводности.
тепла вследствие теплопроводности (кондуктивный тепловой
поток qk) пропорциональна градиенту температуры dT/dx и
площади поверхности Л, че-
через которую идет поток теп-
тепла (рис. 1.1а), или
qk~A(dT/dx)9 A.1)
где Т — температура, х— на-
направление теплового потока.
Действительная скорость пе-
переноса тепла зависит от коэф-
коэффициента теплопроводности
k — теплофизической характе-
характеристики среды. Следовательно,
скорость переноса тепла мож-
можно выразить количественно со-
соотношением
qk = -kA (dT/dx). A.2)
Знак минус обусловлен вторым законом термодинамики, соглас-
согласно которому тепло должно переноситься в направлении сниже-
снижения температуры. Градиент dT/dx будет отрицательным, если
температура снижается в направлении возрастания х (рис. 1.16).
Если считать тепло, переносимое в направлении положительной
оси х, положительной величиной, необходимо в правой части
соотношения A.2) поставить знак минус.
Рис. 1.16. Направление кондуктивно-
го теплового потока.
/ — профиль температуры; 2—градиент
температуры dT/dx,
Принципы теплопередачи 13
Соотношение A.2) называется законом теплопроводности
Фурье1) и служит для определения коэффициента теплопровод-
теплопроводности k. Если площадь выражена в квадратных метрах, темпе-
температура— в Кельвинах, а тепловой поток — в ваттах, то k имеет
размерность Вт/(м-К).
Плоская стенка
Простым примером использования закона Фурье является
задача о теплопередаче через плоскую стенку (рис. 1.2). Если
обе поверхности стенки имеют постоянные, но различные темпе-
температуры, тепло будет переноситься только в одном направлении,
по нормали к поверхностям стенки.
Если коэффициент теплопроводно-
теплопроводности яьляется постоянной величи-
величиной, после интегрирования соотно-
соотношения A.2) получаем
/v/1 /*Т1 ?Т1 \
. . RA /Т» *р \ /1 О\
где L — толщина стенки, Тх — тем-
температура левой поверхности (х=0),
Т2 — температура правой поверхно-
поверхности (х = L).
-71
Рис. 1.2. Теплопроводность че-
через плоскую стенку с постоян-
постоянным коэффициентом теплопро-
теплопроводности.
Пример 1.1. Стеклянная витрина мага-
магазина имеет площадь 12 м2 и толщину 1 см.
Коэффициент теплопроводности стекла
0,8 Вт/(м-град). В холодный день темпе-
температура внешней поверхности стекла со-
составляет 272 К (— 1°СJ), а температура внутренней поверхности 276 К
(+3°С). Найти: а) тепловой поток через стекло и б) температуру в сред-
среднем сечении между внешней и внутренней поверхностями стекла
Решение, а) Тепловой поток через стекло равен
б) Температура в среднем сечении (Т при L/2) равна 274 К, среднему зна-
значению между температурами внешней и внутренней поверхностей стекла»
так как в стекле создается линейный профиль температуры.
. Для многих материалов коэффициент теплопроводности не
является постоянной величиной, а зависит от температуры. За*
J) Фурье A768—1830 гг.) — французский математик, внесший существен*
ный вклад в теорию теплопроводности [1].
2) В закон Фурье можно подставлять температуры, выраженные в граду*
сах Цельсия или Кельвина, поскольку, хотя шкалы .Цельсия и Кельвина от*
личаются на 273°, величина разности температур одна и та же. Другими ело»
вами, градиент температуры ГС/м равен градиенту температуры 1 К/м.
14 Глава 1
частую эту зависимость в определенных интервалах темпера-
температуры можно аппроксимировать линейной функцией
где ко — коэффициент теплопроводности при некоторой харак-
характерной температуре, р — эмпирическая постоянная. В таких слу-
случаях, как показано подробнее в гл. 2, интегрируя соотношение
A.2), получаем
йлй
A.5)
A-6)
где km — значение k при средней температуре (Т\-\-Т2)/%
Многослойная плоская стенка
Если происходит кондуктивный перенос тепла через не-
несколько стенок, находящихся в тепловом контакте друг с дру-
Профйль
/температуры
Рис. 1.3. Одномерная теплопроводность через многослойную стенку и ее элек-
электрический аналог.
гом, что характерно, например, для многослойных стен боль-
большинства зданий, анализ становится лишь немного сложнее. Од-
Однако, как показано на рис. 1.3 для случая трехслойной стенки,
градиенты температуры в различных слоях неодинаковы. Можно
Принципы теплопередачи 15
выразить тепловые потоки для каждого слоя и приравнять их
друг другу:
(Г3-Г4). A.7)
Исключая в соотношениях A.7) промежуточные температуры
Т2 и 73, получаем следующее выражение для теплового потока:
„ Т1 — Т4 п оч
Для многослойной стенки из Af слоев, находящихся в иде-
идеальном тепловом контакте, тепловой поток выражается фор-
формулой
т т т т
A.9)
т,-т,
Т\ ~~
где Ti — температура поверхности первого слоя, a T^+i — тем-
температура поверхности N-ro слоя.
Пример 1.2. Стенка печи (рис. 1.4) состоит из внутреннего слоя нержа-
нержавеющей стали толщиной 1,2 см, покрытого внешним слоем асбестовой изо-
изоляции толщиной 5 см. Температура внутренней поверхности нержавеющей
Wf/
ш
2
¦:".'.' ..:'?':'."'¦''•."•"* •:¦.''•!'.•
к{Л
Рис. 1.4. Схема стенки печи для примера 1.2.
/ — нержавеющая сталь; 2— асбест.
стали равна 800 К, а температура наружной поверхности асбеста 350 К.
Найти плотность теплового потока через стенку печи и температуру контакт-
контактной поверхности стали и асбеста. Коэффициенты теплопроводности для ста-
стали и асбеста равны соответственно 6i= 19 Вт/(м-град), ?2= 0,7 Вт/(м-град).
18 Глава 1
Решение. Тепловой поток равен
а
ЧЬ LxlkxA + L2/k2A •
Плотность теплового потока составляет
qk Тх - Т2 800 - 350
= 6245 Вт/м2.
A Lxlkx + L2/k2 0,012/19 + 0,05/0,7
Температура на контактной поверхности Тх определяется из уравнения
Отсюда находим Тх
Яь (Lx \ ( 0,012 \
-^ XJ-) = 800 ~ 6245 (—Jq—) = 796 К.
Следовательно, перепад температур на нержавеющей стали составляет всего
лишь около 4 К, перепад температур на асбесте 446 К.
Электрическая аналогия для теплопроводности
В этом месте изложения целесообразно указать иной под-
подход к анализу проблем теплопередачи, который можно приме-
применить и в более сложных задачах и который будет использован
в следующих главах. Этот новый подход, в котором применяются
концепции теории электрических цепей, часто называют анало-
аналогией между переносом тепла и электричества. Если считать, что
тепловой поток аналогичен электрическому току, комплекс
L/kA рассматривать как сопротивление, а разность температур
как аналог разности потенциалов, то соотношение A.2) можно
записать в форме, аналогичной закону Ома в электротехнике:
qk = ATfRk> A.10)
где АТ = (Т\ — Т2) — перепад температур (термический потен-
потенциал), Rk = L/kA — термическое сопротивление. Обратная
величина термического сопротивления называется тепловой
проводимостью, а отношение &/L, тепловая проводимость на еди-
единицу площади, — удельной тепловой проводимостью для кондук-
тивного теплового потока. Аналогичным образом можно обоб-
обобщить соотношение A.8) для теплового потока через трехслой-
трехслойную стенку (рис. 1.3) в виде
где АТ = Тх-Ть RA=(L/kA)Ai RB = (L/kA)B, Rc = (L/kA)c.
Электротепловую аналогию можно использовать и для ре-
решения более сложных задач.. Например, во многих случаях про-
процесс теплопроводности протекает в материалах, расположенных
Принципы теплопередачи 17
параллельно. На рис. 1.5 показана плита, состоящая из двух
материалов, расположенных параллельно и имеющих попереч-
поперечные сечения А\ и А2\ справа на рисунке представлена соответ-
соответствующая тепловая цепь. Чтобы решить эту задачу, отметим,
что при заданном перепаде температур поперек плиты каждый
слой составной конструкции можно рассматривать отдельно при
условии, что для каждой из двух секций кондуктивный перенос
тепла можно считать одномерным. Если разность температур
между контактирующими материалами мала, тепловой поток
г
го к
Рис. 1.5. Теплопроводность через составную стенку из двух параллельных
секций.
вдоль слоев будет намного больше теплового потока в попереч-
поперечном направлении и задачу можно считать одномерной без сколь-
сколько-нибудь серьезной потери точности.
Поскольку тепловые потоки для различных материалов мож-
можно рассматривать по отдельности, общий тепловой поток пред-
представляет собой их арифметическую сумму:
Отметим, что общая площадь, которую пересекает, тепловой по-
поток, равна сумме двух отдельных площадей и что обратная ве-
величина суммарного термического сопротивления равна сумме
обратных величин отдельных термических сопротивлений. Как
видно из рис. 1.5, тепловая цепь для этой задачи представляет
собой параллельное соединение двух термических сопротивле-
сопротивлений R\ И /?2-
Более сложным примером использования понятия тепловых
цепей является задача о передаче тепла через составную стен-
стенку, которая должна представляться с помощью последователь-
последовательно и параллельно соединенных термических сопротивлений
18 Глава 1
(рис. 1.6). Для этой системы термическое сопротивление сред-
среднего слоя R2 (рис. 1.6) выражается формулой
р В^С /1 iq\
A.14)
а тепловой поток определяется следующим образом:
^J ft
где N — число слоев, Rn — термическое сопротивление каждого
слоя, АГполн — разность температур двух внешних поверхностей.
Рис. 1.6. Тепловая цепь с параллельно и последовательно соединенными эле-
элементами.
При анализе данного примера с помощью метода тепловых
цепей предполагалось, что поток тепла является одномерным.
Если термические сопротивления RB и Re сильно отличаются
друг от друга, могут проявиться существенные двумерные эф-
эффекты. Такие двумерные задачи теплопроводности будут рас-
рассмотрены в гл. 2.
Контактное термическое сопротивление
Если различные теплопроводящие слои находятся в контакте
(рис. 1.4), на поверхности раздела твердых тел часто возникает
термическое сопротивление. Это термическое сопротивление, ко-
которое обычно называют контактным термическим сопротивле-
сопротивлением, возникает, когда поверхности двух материалов недоста-
Принципы теплопередачи 19
точно плотно прижаты друг к другу и между ними остается
тонкий слой жидкости или газа. Исследование сильно увели-
увеличенной картины контакта между двумя твердыми поверхностями
показывает, что материалы касаются друг друга только верши-
вершинами профилей шероховатости поверхностей, а впадины кон-
контактирующих поверхностей заполнены инородной средой, воз-
возможно воздухом, жидкостью или вакуумом.
Контактное термическое сопротивление зависит прежде
всего от шероховатости поверхностей; давления, прижимаю-
прижимающего две поверхности друг к другу; среды в районе контактной
поверхности и температуры в зоне контакта. Механизм тепло-
теплопередачи в районе контактирующих поверхностей довольно сло-
сложен. В местах непосредственного контакта твердых поверхно-
поверхностей осуществляется процесс теплопроводности, а перенос тепла
через зазоры, заполненные жидкостью или газам, производится
путем конвекции и излучения.
Если плотность теплового потока через две контактирующие
поверхности составляет q/A, а разность температур поперек
заполненного жидкостью или газом зазора, который разделяет
две твердые поверхности, равна ДГ*, то контактное термическое
сопротивление Ri определяется выражением
Считается, что две поверхности находятся в идеальном тепло-
вом контакте, когда контактное термическое сопротивление
стремится к нулю и на поверхности раздела нет перепада темпе-
температур. При неидеальном тепловом контакте на поверхности раз-
раздела существует перепад температур.
В большинстве задач, приведенных в конце главы, не учи-
учитывается термическое сопротивление на поверхности раздела,
хотя оно всегда возникает при механическом соединении твер-
твердых тел. Несмотря на это, всегда следует иметь в виду сущест-
существование этого сопротивления и соответствующего перепада тем-
температур поперек зоны контакта. Для сильно шероховатых по-
поверхностей и при небольших стягивающих давлениях перепад
температур поперек зоны контакта может быть значительным и
его нужно учитывать.
Проблема контактного термического сопротивления доста-
достаточно сложна, и пока нет единой теории или серии эксперимен-
экспериментальных данных, которые позволяли бы достаточно точно рас-
рассчитывать это сопротивление в инженерных задачах. Более де-
детальный анализ данной проблемы можно найти в работах
[2,3].
Пример 1.3. Стена здания состоит из слоя обычного кирпича [Li=0,l м,
& = 0,7 Вт/(м-град)] и слоя гипсовой штукатурки [L2 = 0,038 м, k =
— 0,48 Вт/(м-град)]. Сравнить тепловые потоки через эту стену и через
20 Глава 1
такую же стену с термическим сопротивлением на поверхности раздела
между кирпичом и штукатуркой, равным 0,1 град/Вт.
Решение. Плотность теплового потока через идеализированную стену при
разности температур 1 К равна
1 1
4
qk
A (Ti - То)
L2/k2 = 0,100/0,70 + 0,038/0,48
Поверхность раздела представляется третьим, последовательно соединенным
термическим сопротивлением, после чего плотность теплового потока записы-
записывается в виде
аи 1 1
A (Tt - Го)
0,222 + 0,1
Коэффициент теплопроводности
Коэффициент теплопроводности— это характеристика ма-
материала, определенная соотношением A.2). Его нельзя рассчи-
рассчитать теоретически (исключение составляют лишь газы при низ-
низких температурах). Поэтому имеющиеся сведения о коэффи-
коэффициентах теплопроводности различных материалов основаны на
экспериментальных данных. В общем случае коэффициент теп-
теплопроводности материала зависит от температуры, но во мно-
многих практических задачах можно получить достаточно точные
результаты, применяя постоянное значение k при средней темпе-
температуре системы. В табл. 1.1 указаны типичные значения коэф-
коэффициента теплопроводности для некоторых металлов, неметал-
неметаллических твердых веществ, жидкостей и газов, чтобы проиллю-
проиллюстрировать порядок величин kf ожидаемых на практике. Допол-
Дополнительные данные представлены в приложениях IV—VII.
Таблица 1.1
Коэффициенты теплопроводности некоторых металлов, неметаллических
твердых веществ, жидкостей и газов
Материал
Медь
Алюминий
Углеродистая
сталь
Стекло
Пластики
Вода
Коэффициент тепло-
теплопроводности
при 300 К, Вт/(м»град)
386
204
54
0,75
0,2-0,3
0,6
Материал
Этиленгликоль
Моторное масло
Фреон (жидкий)
Водород
Воздух
Коэффициент тепло-
теплопроводности
при 300 К, Вт/(м«град)
0,25
0Д5
0,07
0,18
0,026
Механизм теплопроводности в газах можно качественно объ-
объяснить с помощью кинетической теории. Все молекулы газа на-
находятся в хаотическом движении и обмениваются энергией и
импульсом при столкновениях друг с другом. Чем выше темпе-
Принципы теплопередачи 21
ратура газа, тем больше кинетическая энергия молекул, поэтому
молекула, движущаяся из высокотемпературной области в низ-
низкотемпературную, переносит кинетическую энергию на молеку-
молекулярном уровне в область низкой температуры. При столкновении
с "молекулой, обладающей меньшей кинетической энергией, про-
происходит передача энер-
энергии, которая с макроско-
макроскопической точки зрения и
является переносом теп-
тепла. Физический механизм
0,8
[0,7
Г 0,6
; 0,5
}0,4
0,3
i 0,2
0,1
0
3
\
—-2
— 5
¦ээг
\i
Не
.
=====
о2
—
V2
6
250 350
450 550 650
Температура, К
750 850
теплопроводности в ка-
капельных жидкостях каче-
качественно аналогичен опи-
описанному, но поскольку
молекулы в жидкостях
расположены ближе друг
к другу и их силовые по-
поля играют существенную
роль при переносе энер-
энергии путем соударений,
картина явления еще
сложнее, чем в газах.
На рис. 1.7 показано
изменение коэффициентов
теплопроводности некото-
некоторых газов с изменением
температуры. Значения ко-
коэффициента теплопровод-
теплопроводности газов практически
не зависят от давления,
исключая условия, близ-
близкие к критической точке.
Согласно результатам упрощенного расчета, основанного на
кинетической модели обмена, коэффициент теплопроводности
газов пропорционален квадратному корню из абсолютной темпе-
температуры.
На рис. 1.7 также показаны в зависимости от температуры
значения коэффициента теплопроводности для некоторых жид-
жидкостей. Можно видеть, что коэффициенты теплопроводности
жидкостей, за исключением воды, уменьшаются с ростом темпе-
температуры, но это изменение столь мало, что в большинстве прак-
практических задач коэффициент теплопроводности можно считать
постоянным и равным значению, соответствующему некоторой
средней температуре; давление практически не влияет на вели-
величину k для жидкостей.
На рис. 1.8 представлены зависимости коэффициента тепло-
теплопроводности некоторых металлических и неметаллических
Рис. 1.7. Изменение коэффициентов тепло-
теплопроводности различных газов и жидкостей
в зависимости от температуры.
1 — вода (на линии насыщения); 2—глицерин;
3—бензол; 4—легкое масло; 5— фреон-12; 6—воз-
6—воздух.
22 Глава 1
&
твердых веществ. В твердых телах энергия переносится свобод-
свободными электронами, а также при колебаниях кристаллической ре-
решетки. В общем случае наиболее важную роль играет движение
свободных электронов, а поскольку в хороших проводниках элек-
электричества движется много свободных электронов, хорошие про-
проводники электричества
являются и хорошими
проводниками тепла (на-
(например, медь, серебро,
алюминий). С другой сто-
стороны, хорошие электро-
электроизоляторы являются и хо-
хорошими теплоизолятора-
ми (например, стекло и
пластмассы). Однако в
лучших теплоизоляторах
высокая эффективность
теплоизоляции достига-
достигается за счет пористой
структуры, заполненной
газом. В таких материа-
материалах перенос тепла может
осуществляться несколь-
несколькими способами: путем
теплопроводности через
волокнистый или пори-
пористый материал; путем
теплопроводности и(или)
конвекции через воздух
в порах и путем радиа-
радиационного теплообмена
между элементами струк-
450
400
350
300
250
200
150
100
50
0
—-
.
-
-——
— —
— 1
-3
250 350
450 550 650
Температура, К
750 850
Рис. 1,8. Изменение коэффициентов тепло-
теплопроводности некоторых металлов в зависи-
зависимости от температуры.
1—-медь; 2 — алюминий; 3—углеродистая сталь;
4 — нержавеющая сталь 18-8.
туры твердого материала,
что особенно важно при
высоких температурах или в условиях вакуума. Для использо-
использования в криогенных установках при очень низких температурах,
до 25 К, разработаны специальные типы материалов с повышен-
повышенными теплоизоляционными свойствами. Такая суперизоляция
состоит из ряда слоев хорошо отражающего материала, разде-
разделенных вакуумированными промежутками, чтобы свести к ми-
минимуму теплопроводность и конвекцию. Эффективный коэффи-
коэффициент теплопроводности такой изоляции может достигать очень
низких величин, порядка 0,02 Вт/(м-град). Более полные све-
сведения о суперизоляции1) можно найти в работах [4, 5].
1) В отечественной литературе применяется термин «сэкранно-вакуумная
тепловая изоляция (ЭВТИ)», — Прим. пер*
Принципы теплопередачи 23
1.3. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
Если жидкость (или газ) вступает в контакт с поверхностью
твердого тела, имеющей другую температуру, протекающий
процесс обмена тепловой энергией называется конвективным
теплообменом. Такой процесс часто встречается в жизни, но
подробно описать его механизм довольно сложно. В этой ввод-
вводной главе мы не будем пытаться охватить аналитические ме-
методы, а постараемся привести основные соотношения, позволяю-
позволяющие рассчитать конвективные тепловые потоки в тех подсисте-
подсистемах, которые играют существенную роль в общих системах
нагрева или охлаждения.
Различают два вида конвекции: естественную, или свобод-
свободную, конвекцию и вынужденную конвекцию. В конвекции пер-
первого вида движущая сила обусловлена разностью плотностей
жидкости, вызванной ее контактом с поверхностью, имеющей
другую температуру, вследствие чего возникают подъемные
(архимедовы) силы. Типичными примерами такой конвекции яв-
являются теплоотдача от стен или крыши здания в безветренный
день, конвекция в сосуде с жидкостью, в которую погружена
нагревательная спираль, или теплоотдача от солнечного коллек-
коллектора в безветренную погоду.
Вынужденная конвекция происходит в условиях, когда под
действием внешней движущей силы жидкость обтекает поверх-
поверхность, имеющую более высокую или более низкую температуру,
чем сама жидкость. Поскольку скорость жидкости при вынуж-
вынужденной конвекции больше, чем* при свободной, в этом случае
может быть передано больше тепла при заданном перепаде тем*
ператур. Это возрастание теплового потока компенсируется ра^
ботой, затрачиваемой для приведения жидкости в движение. Но
независимо от того, является ли конвекция свободной или вы-
вынужденной, тепловой поток qc можно выразить с помощью за-
закона Ньютона при охлаждении:
qc=hcA{Ts-TUx), A.16)
Таблица 1.2
Приближенные значения коэффициента
конвективной теплоотдачи
Вид конвекции и среда
Свободная конвекция, воздух
Свободная конвекция, вода
Вынужденная конвекция, воздух
Вынужденная конвекция, вода
Кипящая вода
Конденсирующийся водяной пар
Вт/(м?трад)
5-25
20-100
10—200
50—10 000
3 000—100 000
5 000-100 000
24 Глава 1
где Re — удельная тепловая проводимость для конвекции или
средний коэффициент конвективной теплоотдачи на поверхности
раздела жидкости и твердого тела, Вт/(м2-град); Л —площадь
поверхности, омываемой жидкостью, м2; Ts — температура по-
поверхности, К; 77foo — температура невозмущенной жидкости вда-
вдали от поверхности теплообмена, К. Соотношение AЛ6) служит
только для определения Яс- Численное значение hc можно найти
теоретически или экспериментально. Размерность hc в системе
СИ — Вт/(м2-град). В табл. 1.2 указаны некоторые приближен-
приближенные значения коэффициента конвективной теплоотдачи, вклю-
включая случаи кипения и конденсации, которые обычно относятся
к области конвекции1).
Пример 1.4. Вода с температурой 300 К омывает одну сторону пластины
с размерами 1X2 м, температура которой поддерживается равной 400 К.
Рассчитать конвективный тепловой поток от пластины к воде, если коэффи-
коэффициент конвективной теплоотдачи составляет 200 Вт/(м2-град).
Решение. Вычисляя тепловой поток по формуле A.16), получаем ,
qc = НСА (Ts - Tft „) = 200 • 2 • D00 - 300) = 40 000 Вт.
Методы расчета коэффициента теплоотдачи рассмотрены в
гл. 4 и 5. Здесь мы просто опишем физический процесс и ука-
укажем основные особенности конвективного переноса тепла к по-
потоку жидкости. На рис. 1.9 показана нагретая плоская пластина,
Поток жидкости
У
:\
и(у) 1 '
\т(у)
дт \
жжшжжжжжж
Конвективный I I
тепловой 2/|Ов Ts
поток qc
Рис. 1.9. Профили скорости и температуры при вынужденной конвекции около
нагретой пластины.
охлаждаемая обтекающим ее воздушным потоком. Кроме того,
показаны профили скорости и температуры. Прежде всего от-
отметим, что из-за действия сил вязкости скорость и (у) умень-
уменьшается по направлению к стенке. Поскольку скорость слоя
жидкости, примыкающего к стенке, равна нулю, плотность
1) Процессы кипения и конденсации сопровождаются фазовыми превра-
превращениями и имеют много специфических особенностей, вследствие чего как
в отечественной, так и в зарубежной литературе они обычно рассматрива-
рассматриваются как самостоятельные разделы теории теплообмена.—Прим. ред.
Принципы теплопередачи 25
теплового потока (тепловой поток на единицу площади1)) от
стенки к этому слою жидкости определяется только теплопро-
теплопроводностью
дТ ,- tm „ ч A17)
Щ- = а' к.
ду
Хотя при рассмотрении процесса с такой точки зрения предпо-
предполагается, что передача тепла осуществляется теплопроводно-
теплопроводностью, градиент температуры на стенке (дТ/ду)\у=о определя-
определяется скоростью переноса
тепла жидкостью от стен-
стенки в основной поток. По-
Поэтому градиент темпера-
температуры на стенке зависит
от поля течения, и чем
выше скорость течения,
тем больше и градиент
температуры, и тепловой
поток. В то же время су-
существенную роль играет
и коэффициент теплопро-
теплопроводности жидкости. На-
Например, величина kf для
воды примерно на поря-
порядок больше, чем для воз-
воздуха; поэтому, как указа-
Рис. 1.10. Профили скорости и температуры
но в табл 1 2 коэсЬби- при свободной конвекции около нагретой
' ' ^^ пластины, отклоненной от горизонтали на
циент конвективной теп- угол р г
лоотдачи для воды боль-
больше, чем воздуха.
Аналогичные особенности имеет и свободная конвекция
(рис. 1.10). Основное отличие заключается в том, что в усло-
условиях вынужденной конвекции скорость при удалении от стенки
приближается к скорости набегающего потока, обусловленной
внешней силой, а в условиях свободной конвекции скорость при
удалении от пластины сначала возрастает, а затем под дейст-
действием вязкости довольно быстро снижается до нуля, в то время
как разность плотностей изменяется медленнее. Однако в конце
концов подъемная сила также уменьшается, по мере того как
плотность жидкости приближается к плотности окружающей
среды; это вызывает повышение скорости до некоторого макси-
максимального значения, а затем ее падение до нуля на достаточно
большом расстоянии от нагретой поверхности. Температурные
поля при свободной и вынужденной конвекции аналогичны по
*) В тексте одним штрихом обозначена величина, приходящаяся на еди-
единицу длины, двумя штрихами —на единицу площади, тремя —на единицу
объема.
26 Глава 1
форме, и в обоих случаях механизмом переноса тепла на по-
поверхности раздела между жидкостью и твердым телом является
теплопроводность.
Проведенное обсуждение позволяет сделать вывод, что коэф-
коэффициент конвективной теплоотдачи зависит от плотности, вяз-
вязкости и скорости жидкости, а также от ее теплофизических
свойств (коэффициента теплопроводности и удельной теплоем-
теплоемкости). В то время как при вынужденной конвекции движение
среды обычно создается насо-
насосом или вентилятором и его
скорость можно непосредст-
непосредственно измерить, при свободной
конвекции скорость зависит от
перепада температур между
стенкой и жидкостью, коэффи-
коэффициента теплового расширения
жидкости (который определя-
определяет изменение плотности на
единицу перепада температур)
и силового поля, которое в си*
стемах, расположенных на
земле, обусловлено просто си*
лой тяжести.
Рис. 1.11. Тепловая цепь для тепло-
теплопередачи через плоскую стенку при
наличии конвекции на обеих поверх-
поверхностях.
Конвективный теплообмен
также можно рассматривать в
рамках концепции тепловых цепей. Исходя из соотношения
A.16), определим термическое сопротивление для конвектив-
конвективного переноса тепла формулой
R0*=*l/heA, A.18)
и это термическое сопротивление на поверхности раздела между
жидкостью и твердым телом можно легко включить в тепловую
цепь. Например, на рис. 1.11 показана схема теплопередачи от
внутренней среды помещения с температурой Ti через стенку
во внешнюю атмосферу с температурой То. Тепловой поток опре-
определяется соотношением
А2 "Г A3
где Rx = 1/Яс, Л #2 = L/kA, Я3 = 1/Яс, о А.
Пример 1.5. Кирпичная стена толщиной 0,1 м [k = 0,7 Вт/(м-град)]
обдувается холодным ветром с температурой 270 К при коэффициенте кон-
конвективной теплоотдачи 40 Вт/(м2-град). С другой стороны стены находится
неподвижный воздух с температурой 330 К при коэффициенте конвективной
теплоотдачи 10 Вт/(м2-град). Рассчитать тепловой поток на единицу пло-
площади (плотность теплового потока).
Принципы теплопередачи 27
Решение. По формулам A.19) вычисляем три термических сопротив-
сопротивления:
/?! = ^ = —— = 0,025 град/Вт,
пСу0А 40-1
Яг =* -=-^— «= —~ « 0Д0 град/Вт.
й A 101
вна
Следовательно, плотность теплового потока равна
± _ 330-270
Л 0,025 + 0,143 + 0,10
1.4. РАДИАЦИОННЫЙ ТЕПЛООБМЕН
В то время как теплопроводность и конвективный тепло-
теплообмен могут осуществляться лишь в материальной среде, пере-
перенос тепла излучением может происходить даже в абсолютном
вакууме. При радиационном теплообмене энергия переносится
в виде электромагнитных волн, которые распространяются со
скоростью света. Существует много различных видов электро-
электромагнитного излучения (например, рентгеновские лучи), но мы
будем рассматривать лишь тепловое излучение, которое пере*
носит энергию в виде тепла.
Количество энергии, переносимое от поверхности в виде теп-
теплового излучения, зависит от абсолютной температуры и свойств
поверхности. Идеальный излучатель, или абсолютно черное
тело1), испускает со своей поверхности радиационный тепловой
поток qr, определяемый формулой
qr = о АТ\ A.20)
qr выражается в ваттах, если площадь поверхности А выражена
в квадратных метрах, температура поверхности Г — в кель-
винах, а размерный коэффициент су, называемый постоян-
постоянной Стефана — Больцмана, в системе единиц СИ равен
5,67-Ю-8 Вт/(м2-град4).
Соотношение A.20) показывает, что радиационный тепловой
поток, испускаемый абсолютно черной поверхностью, пропор-
пропорционален четвертой степени абсолютной температуры. Хотя ве-
величина теплового потока излучения, испускаемого телом, не
зависит от окружающих условий, для расчета результирующего
переноса тепла излучением необходимо знать температуры по-
поверхности двух или более тел, между которыми происходит ра-
радиационный теплообмен. Если черное тело излучает в окружаю-
окружающую его замкнутую полость с абсолютно черной поверхностью
*) Более подробно физический смысл этих терминов будет рассмотрен
в гл. 6.
28 Глава 1
(которая полностью поглощает все падающее на нее излучение),
результирующий радиационный тепловой поток определяется
соотношением
q^aA^T'-Tt), A.21)
где Т\ — температура черного тела в Кельвинах, а Т2 — темпе-
температура поверхности полости в Кельвинах.
Реальные тела не являются идеальными излучателями, они
излучают тепло менее интенсивно, чем абсолютно черное тело.
Если они при некоторой температуре испускают на каждой
длине волны одинаковую долю излучения черного тела с той
же температурой, они называются серыми телами. Радиацион-
Радиационный тепловой поток от серого тела равен гвАТА. Результирую-
Результирующий тепловой поток от серого тела с температурой Т\ к окру-
окружающему его абсолютно черному телу с температурой Т2 вы-
выражается формулой
*, = <МЛ(Г}-73), A-22)
где е — излучательная способность (степень черноты) серой по-
поверхности, равная отношению потока излучения серой поверх-
поверхности к потоку излучения идеального излучателя при той же са-
самой температуре.
Пример 1.6. Рассчитать радиационный тепловой поток, испускаемый в
пространство верхней поверхностью горизонтальной квадратной плоской пла-
пластины размерами 2 X 2 м с температурой 500 К и степенью черноты 0,6.
Решение. По формуле A.20) вычислим радиационный тепловой поток от
абсолютно черного тела с температурой 500 К
qr = 5,67 • 10~8 • 4 • E00L = 14 180 Вт.
Однако, поскольку степень черноты излучающей поверхности равна 0,6,
действительный тепловой поток будет равен 0,6-14 180 = 8508 Вт.
Если ни одно из двух тел не является идеальным излучате-
излучателем и если тела занимают определенное геометрическое поло-
положение друг относительно друга, результирующий радиационный
тепловой поток между ними определяется выражением
ЧГ = ^^2(Т\-Ц)9 A.23)
где Si—2 — коэффициент в соотношении для радиационного теп-
теплового потока от идеального излучателя, учитывающий степени
черноты и относительное расположение реальных тел.
Во многих инженерных задачах излучение действует наряду
с другими видами теплопередачи. Зачастую можно упростить
решение таких задач, используя термическое сопротивление для
излучения Rr. Величина Rr определяется аналогично термиче-
термическому сопротивлению для конвекции или теплопроводности.
Принципы теплопередачи 29
Если радиационный тепловой поток записать в виде
*-^. A-24)
то, используя соотношение A.23), можно получить следующую
формулу для термического сопротивления:
Кроме того, можно определить удельную тепловую проводи-
проводимость для излучения hr
г 1 *Si-2Gi-7i)
К = YT^—т~^?—' A>26)
где ТГ2 — подходящая характерная температура, выбор которой
часто диктуется уравнением конвекции.
Пример 1.7. Рассчитать удельную радиационную тепловую проводимость
для небольшого сферического спая термопары, расположенного в большой
абсолютно черной трубе, по которой продувается воздух. Температура тру-
трубы 300 К, температура термопары 500 К, степень черноты термопары 0,3.
Решение. Используя соотношения A.2) и A.26) в предположении, что
характерной температурой является температура трубы 7V получаем
= 5,67 • 1(Г8 • 0,3 E002 + 3003) (800) = 4,63 Вт/(м2 • град).
1.5. СЛОЖНЫЙ ТЕПЛООБМЕН
На практике тепло обычно переносится ступенчатым образом
через ряд различных последовательно соединенных элементов
и зачастую два механизма теплопередачи действуют парал-
параллельно. Примером такой ситуации является теплопередача от
продуктов сгорания в камере ракетного двигателя через тонкую
стенку к потоку охладителя в кольцевом канале с внешней сто-
стороны стенки (рис. 1.12).
Продукты сгорания содержат газы СО, СО2 и Н2О, которые
испускают и поглощают излучение. Следовательно, в первом
элементе системы тепло переносится от горячей газовой среды
к внутренней поверхности стенки ракетного двигателя конвек-
конвекцией и излучением, действующими параллельно. Суммарный
тепловой поток q к поверхности стенки на некотором расстоянии
от сопла определяется выражением
Я = Чс + Чг = hcA (Tg - Tsg) + hrA (Tg - T8g),
или </ = (M + M (Tg - Tsg) = --* J^?, A.27)
30 Глава 1 -
где Tg — температура горячего газа, Tsg — температура внутрен-
внутренней поверхности стенки, R\ = 1/{Нг + Яс)А — суммарное терми-
термическое сопротивление первого элемента системы. В стационар-
стационарных условиях кондуктивный тепловой поток через стенку (вто-
(второй элемент системы) равен тепловому потоку, поступающему
в стенку,
и А Т Т
а = аь = — (Т — Г)=-2? — A28)
Li * Д2
где Tsc — температура поверхности стенки со стороны охлади-
охладителя, R2— термическое сопротивление второго элемента систе-
системы. После прохождения через стенку, в третьем элементе си-
Т -^ Т -ш. Т
R2 *3
Рис. 1.12. Теплопередача в ракетном двигателе,
а—физическая схема; б—тепловая цепь.
стемы, тепло передается охладителю конвекцией. Тепловой по-
поток в этом последнем элементе выражается формулой
п п h А (Т Т\ IT T\IT? (\ 9Q\
Ч — Чс — псЛ К1 sc — 1 с) — К1 sc — L сП^Ъу Vl .Zyj
где Тс — температура охладителя, /?3 — термическое сопротив-
сопротивление третьего элемента системы. Следует отметить, что через
he обозначена в общем случае удельная конвективная тепловая
проводимость, но численные значения этого коэффициента для
первого и третьего элементов системы зависят от многих факто-
факторов и, как правило, отличны друг от друга. Кроме того, площади
поверхностей во всех трех элементах системы, по которой рас-
распространяется тепловой поток, не одинаковы. Но поскольку
стенка очень тонкая, изменение площади поверхности теплооб-
теплообмена настолько мало, что в рассматриваемой системе им можно
пренебречь.
Принципы теплопередачи 31
На практике часто известны лишь температуры горячего
газа и охладителя. Если, приравнивая друг другу соотношения
A.27), A.28) и A.29), исключить промежуточные температуры,
получим следующее выражение для теплового потока:
т — т
Где Термические сопротивления всех трех последовательно сое-
соединенных элементов, или ступеней, теплового потока опреде-
определены соотношениями A.27), A.28) и A.29).
В соотношении A.30) тепловой поток выражен через полный
перепад температур и характеристики теплообмена каждого
элемента на пути теплового потока. Исходя из этого соотноше-
ния, можно количественно оценить важность каждого термиче-
ского сопротивления на этом пути. Анализ порядка величины
членов, входящих в знаменатель, часто помогает упростить за-
задачу. При преобладающей величине одного из членов в ряде
случаев остальными можно пренебречь. Упростив методы рас-
расчета отдельных термических сопротивлений и коэффициентов
тепловой проводимости, мы сможем применять такой прибли-
приближенный подход во многих численных примерах. Однако в не-
некоторых задачах, особенно в расчетах конструкции теплообмен-
теплообменников, удобно упростить соотношение A.30), объединив все
отдельные термические сопротивления, или коэффициенты тепло-
тепловой проводимости, в один параметр, называемый суммарной
удельной тепловой проводимостью, или суммарным коэффициен-
коэффициентом пропускания тепла, или суммарным коэффицентом тепло-
теплопередачи U. Применение суммарного коэффициента теплопере-
теплопередачи позволяет упростить выкладки, при этом важно не
забывать о сравнительной роли каждой составляющей коэффи-
коэффициента U,
Применяя в соотношении A.30) суммарный коэффициент
Теплопередачи, получаем
A.31)
где
Суммарный коэффициент теплопередачи U может относиться к
любой выбранной площади поверхности. Следовательно, чтобы
избежать недоразумений, нужно всегда определять площадь, со-
соответствующую этому коэффициенту. Дополнительные сведения
о суммарном коэффициенте теплопередачи U будут представ-
представлены в последующих главах.
В дальнейшем мы увидим, что суммарный коэффициент теп-
теплопередачи удобно применить в задачах о тепловых системах,
32 Глава 1
состоящих из нескольких последовательно соединенных элемен-
элементов. Анализ теплообмена на границах тела сложной формы и
в задачах нестационарной теплопроводности можно упростить,
применяя суммарный коэффициент удельной тепловой проводи-
проводимости поверхности Я. Этот коэффициент, называемый также
удельной тепловой проводимостью поверхности, учитывает кон-
конвективный и радиационный теплообмен между поверхностью и
средой и определяется выражением
h = hc + hr. A.33)
Удельная тепловая проводимость поверхности определяет сред-
средний суммарный тепловой поток к единице площади твердой по-
поверхности, омываемой жидкостью, при единичном температур-
температурном перепаде. Ее размерность Вт/(м2*град).
Пример 1.8. Температура стенки паропровода диаметром 0,5 м (в = 0,9)
равна 500 К. Паропровод расположен в помещении с температурой воздуха
300 К, коэффициент конвективной теплоотдачи от его поверхности к окру-
окружающему воздуху равен 20 Вт/(м2-град). Рассчитать суммарную удельную
тепловую проводимость поверхности и тепловые потери на единицу длины
паропровода.
Решение. Эту задачу можно идеализировать, считая, что малый объект
(паропровод) находится внутри большой абсолютно черной полости (поме-
(помещение). В таком случае коэффициент теплоотдачи излучением равен
Йг == ore (^ + 7|) (Т{ + Т2) — 13,9 Вт/(м2. град),
суммарная удельная тепловая проводимость поверхности равна
h -в hc + hr = 20 + 13,9 = 33,9 Вт/(м2 • град),
а тепловые потери на единицу длины Aм) паропровода равны
q = nDLh (ГПаропр — ^воздух) = я • 0,5 • 1.33,9 -200 = 10 650 Вт.
Пример 1.9. Максимальная температура стенки авиационного теплооб-
теплообменника (рис. 1.13) не должна превышать 800 К. Для условий, указанных
ниже, определить максимально допустимое удельное термическое сопротивле-
сопротивление на 1 м2 площади металлической стенки между горячим газом, с одной
стороны, и холодным газом — с другой. Температура горячего газа
Tg = 1300 К, удельная тепловая проводимость стенки со стороны горячего
газа hi = 200 Вт/(м2-град). Удельная тепловая проводимость стенки со сто-
стороны холодного газа Яс = 400 Вт/(м2-град), температура охлаждающего
газа Тс = 300 К.
Решение. В стационарных условиях плотность теплового потока q/A от
газа к горячей поверхности стенки равна плотности теплового потока q/A от
горячей поверхности стенки через стенку к холодному газу, или
q Т -Т то-тс 1300-800 1300-300
А ~ J?i ~" Л, + Я, + «8 1/200 A/200) + R2 + A/400)'
где Tsg — температура горячей поверхности стенки. Подставляя численные
значения удельных термических сопротивлений и температуру, получаем
1300 — 800 1300 — 300
0,005 — R2 + 0,0075 '
Принципы теплопередачи 33
Отсюда находим /^2 = 0,0025 (м2-град/Вт). Если удельное термическое со-
сопротивление будет больше 0,0025 (м2-град/Вт), температура внутренней по-
поверхности стенки будет выше 800 К.
а
Металлическая стенка
Горячий газ
(Горячая поверхность)
Охладитель
(Холодная поверхность)
Рис. 1.13. Физическая схема и тепловая цепь для примера 1.9.
а —физическая схема; б—детализированная тепловая цепь; в — упрощенная тепловая цепь»
1.6. РАЗМЕРНЫЕ ВЕЛИЧИНЫ И ЕДИНИЦЫ ИЗМЕРЕНИЯ
Размерной величиной называется любая измеряемая вели*
чина. Например, пространство, занятое предметом, определяется
размерной величиной, называемой объемом. Расстояние между
двумя точками определяется размерной величиной, называемой
длиной. В теории теплопередачи нам встречаются обычно сле-
следующие размерные величины: длина, время, масса, сила, коли-
количество тепла и температура.
Прежде чем проводить численные расчеты, нужно выразить
каждую размерную величину в определенных воспроизводимых
единицах измерения. Единицы измерения — это произвольно вы-
выбранные меры, которые позволяют определить количественно
каждую размерную величину. Например, метр — единица из-
измерения размерной величины длины. Применяются и другие
2 Зак 187
34 Глава 1
единицы, позволяющие измерить длину. Назовем некоторые из
них: фут, ярд, миля, миллиметр, сантиметр, километр.
В настоящее время в мире используется несколько различ-
различных систем единиц измерения. В промышленности, науке и тех-
технике быстро распространяется и становится общепринятой си-
система СИ (международная система единиц). Система СИ была
принята Международной организацией по стандартизации и ре-
рекомендована многочисленным национальным организациям по
стандартизации. Поэтому в нашей книге используется система
единиц СИ.
Таблица 1.3
Основные и производные единицы измерения
в различных системах
Размерная
величина
Длина
Время
Сила
Масса
Температура
Количество тепла
Система
СИ
М
С
Н
кг
К
Дж
мкс
м
с
Н
кг
°С
кал
сгс
см
с
дина
г
°С
кал
Техническая
СССР
М
С
КГ
м-1 -кГ-с2
°С
кал
США
фут
с
фунт силы
фунт массы
°F
БТЕ
В табл. 1.3 указаны основные единицы измерения системы
СИ и других общеупотребляемых систем.
1.7. ТЕОРИЯ РАЗМЕРНОСТЕЙ
Неудобства, возникающие при переходе от одной системы
единиц к другой, часто можно избежать, используя безразмер-
безразмерные параметры, величины которых одинаковы в любой системе
единиц. Процесс определения соответствующих безразмерных
параметров описывается с помощью теории размерностей. Эта
теория не только позволяет найти безразмерные комбинации не-
нескольких переменных, не зависящие от системы единиц, но и
облегчает интерпретацию экспериментальных данных.
Самый серьезный недостаток теории размерностей состоит в
том, что она не дает сведений о природе явления. Чтобы при-
применять теорию размерностей, нужно заранее знать, какие пере-
переменные оказывают влияние на рассматриваемое явление, и успех
или неудача зависят от правильности выбора этих переменных.
Поэтому необходимо иметь хотя бы предварительную теорию
или глубокое физическое понимание явления, чтобы применить
теорию размерностей. Однако, если определяющие переменные
Принципы теплопередачи 35
известны, теорию размерностей можно применить в большинстве
задач, используя методику, которую мы опишем ниже1).
Основные размерные величины и формулы размерности
Первый шаг состоит в выборе системы основных размерных
величин. Выбрать основные размерные величины можно произ-
произвольно, но через них должны выражаться формулы размерности
всех определяющих переменных. В системе СИ основными раз-
размерными величинами являются длина L, время 0, температура Т
и масса М.
Формула размерности физической величины вытекает из оп-
определения или из физических законов. Например, формула раз-
размерности длины стержня записывается по определению как
[L]2). Средняя скорость частицы жидкости равна расстоянию,
Таблица 1.4
Обозначения и размерности некоторых физических
Физическая величина
Длина
Время
Масса
Сила
Температура
Тепловая энергия
Скорость
Ускорение
Работа
Давление
Плотность
Внутренняя энергия
Энтальпия
Удельная теплоемкость
Динамическая вязкость
Кинематическая вязкость
Коэффициент теплопроводности
Коэффициент температуропроводности
Термическое сопротивление
Термический коэффициент объемного расширения
Поверхностное натяжение
Трение на единицу площади
Удельная тепловая проводимость
Массовый расход
величин
Обозначение
L, х
t
М
F
Т
Q
V
а> S
W
р
р
и
h
с
ц
v =^м,/р
k
а
R
а
X
he
m
Размерность
в системе MLQT
L
0
М
т
MU/Q2
L/B
i/e2
ML2/W
M/WL
M/L*
LW
L2/92
LWT
M/LQ
ьщ
ML/WT
L2/B
№jML2
\/T
M/W
M/L92 .
М/83Г
M/e
1) Здесь мы не описываем алгебраическую теорию размерностей. Стро--
гое и содержательное изложение математических основ этой теории можно
найти в гл. 3 и 4 работы [7].
2) Квадратные скобки означают, что величина. и.ме.е/г формулу размерно-»
сти, стоящую в скобках
2*
36 Глава 1
деленному на время, которое было затрачено на преодоление
этого расстояния. Следовательно, формула размерности ско-
скорости [L/0] или [L0-1] (т. е. длина, деленная на время). Ско-
Скорость может быть выражена в метрах в секунду, футах в се-
секунду или милях в час, поскольку все эти единицы измерения
представляют собой длину, деленную на время. В табл. 1.4 пред-
представлены обозначения и формулы размерности физических ве-
величин, часто встречающихся в задачах теплопередачи.
я-теорема Бэкингема
Чтобы найти число независимых безразмерных комбинаций,
необходимое для того, чтобы получить соотношение, описываю-
описывающее физическое явление, можно использовать я-теорему Бэкин-
Бэкингема1). Согласно этой теореме, число независимых безразмер-
безразмерных комбинаций из физических переменных, существенных в
рассматриваемой задаче, равно общему числу этих физических
переменных п (например, плотность, вязкость, коэффициент
теплоотдачи) за вычетом числа основных размерных величин т,
необходимых для того, чтобы выразить формулы размерности п
физических величин. Если обозначить эти комбинации (комп-
(комплексы) через пи Яг, ..., то уравнение, выражающее связь ме-
между переменными, имеет решение вида
F(nlt л2, я3, ...) = 0. A.34)
В задаче с пятью физическими величинами и тремя основными
размерными величинами п — т = 2 и решение имеет вид
F(nu я2) = 0, A.35)
или
f() A.36)
Экспериментальные данные для такой задачи удобно предста-
представить в виде зависимости щ от л2. Полученная эмпирическая
кривая определяет функциональную связь щ и я2, которую
нельзя найти на основании теории размерностей.
Для явления, которое можно описать тремя безразмерными
комплексами (т. е. если /г-— т = 3), уравнение A.34) прини-
принимает вид
/7(я1, я2, я3) = 0, A.37)
или оно может быть переписано в виде
Щ = / (яг. *з). A.38)
1) Согласно более строгому правилу, предложенному Ван-Дристом [6],
я-теорема справедлива до тех пор, пока система уравнений, полученная пу-
путем приравнивания нулю показателей степени при каждой основной размер-
размерной величине, остается линейно независимой. Если одно из уравнений системы
является линейной комбинацией одного или более других уравнений (т. е.
если уравнения линейно зависимы), число безразмерных комплексов равно
общему числу переменных п минус число независимых уравнений.
Принципы теплопередачи 37
В этом случае экспериментальные данные можно связать, по-
построив зависимости К! от Я2 при различных значениях яз. Иногда
можно скомбинировать один параметр из двух комплексов л и
построить единую зависимость этого комбинированного пара-
параметра от оставшегося комплекса, как это будет показано в гл.5.
Определение безразмерных комплексов
Опишем простой метод определения безразмерных комплек-
комплексов, применяя его к задаче теплопроводности и к задаче тече-
течения жидкости.
Пример 1.10. Определить безразмерные параметры, связывающие макси-
максимальную температуру Тт в пластине толщиной L с коэффициентом теплопро-
теплопроводности 6, если в пластине происходит равномерное тепловыделение с объ-
объемной скоростью qG , температура одной поверхности поддерживается по-
постоянной и равной ft, а вторая поверхность теплоизолирована.
Решение. Сначала запишем я в виде произведения переменных, каждая
из которых возведена в неизвестную степень,
а затем подставим формулы размерносш из табл. 1.4:
Чтобы величина я была безразмерной, показатели степени при каждой основ-
основной размерной величине по отдельности должны давать в сумме нуль. При-
Приравнивая сумму показателей при каждой основной размерной величине нулю,
получим следующую систему уравнений:
а Ч- b — с = 0 для Г,
с -f- е = 0 для М,
— Ъс — Зе = 0 для 9,
с + d — е = 0 для L
Очевидно, что для каждого набора значений a, b, cy d и е, при котором удо-
удовлетворяется эта система уравнений, величина я безразмерна. Имеется пять
неизвестных и только четыре уравнения. Заметим, что условия для М и 9
приводят к одному и тому же уравнению, так что имеется не четыре, а
только три независимых уравнения. Поэтому для каждого безразмерного
комплекса можно произвольно выбирать значения двух показателей степени.
Единственное ограничение при этом — каждое выбранное значение должно
не зависеть от остальных. Указанное условие выполняется, если определитель,
составленный из коэффициентов при оставшихся показателях, не равен нулю.
Поскольку мы хотим в итоге найти Тт, примем показатель степени при
этой переменной а равным 1. Поскольку мы хотим, чтобы величина q? была
независимой переменной, мы не будем комбинировать ее с Тт и примем ее
показатель степени е равным 0. В результате получим систему уравнений
1 + Ь — с « 0,
с + 0 = 0,
с + d - 0 = 0.
38 Глава 1
Решая эту систему, находим Ь = —1, с = О, d = 0, и, таким образом, пер-
первым безразмерным критерием является отношение максимальной температуры
к температуре поверхности щ — 7m/7Y
Чтобы найти я2, примем а = 0, чтобы величина Тт выпала, а затем
примем е = 1, чтобы независимая переменная qG входила в соотношение
для я2 в первой степени. Решая систему уравнений при выбранных значениях
а и е, получим с = —1, Ь = —1, d = 2, следовательно,
Итак, решение рассматриваемой задачи можно выразить в общей функцио-
функциональной форме A.36)
ТГ"
Анализ размерности не позволяет найти конкретную функциональную связь
между Я! и Яг, но в гл. 2 будет показано, что эта связь имеет вид
Пример 1.11. Найти безразмерные параметры, связывающие результаты
измерения падения давления Ар в трубе диаметром D и длиной L, если в ней
со средней скоростью V течет жидкость, вязкость которой ц, а плотность р.
Решение. В задаче шесть переменных, но только три основные размерные
величины, что приводит к трем независимым уравнениям. Следовательно, при
определении каждого из безразмерных параметров я нужно выбрать три пе-
переменные. В приведенной ниже таблице указаны переменные рассматриваемой
задачи, их размерности и показатели степени.
Переменная
L
Ар
9
D
Размерность
\М1Ш]
ID
[Ai/iei
Показатель
степени
а
Ь
с
d
е
1
Запишем общее соотношение
Для нахождения первого безразмерного комплекса примем а = 1, Ъ = О,
с = 0, что дает следующую систему уравнений:
e + / = 0 для L,
е =5 0 для М,
— е-~ f=sO для 9.
Отсюда d = —1 и
пдекса примем а —
LID, Для определения второго безразмерного ком-
0^ Ь «я \% Решая полученную систему уравнений, на*
Принципы теплопередачи 39
ходим Л2 = Ap/pV2. Аналогичным образом, полагая е = 1, а = Ь = 0, на-
находим третий безразмерный комплекс яз = |i./pVD. Чтобы связать экспери-
экспериментальные данные, можно построить зависимости я2 от яз при различных
значениях Я1. Однако в инженерной практике удобно использовать отношение
Я2/Я1, называемое коэффициентом трения f. Более того, можно показать тео-
теоретически, что
f =
На рис. 1.14 представлены экспериментальные данные, построенные в виде
Зависимости Я2/Л1 от обратной величины яз. Как будет отмечено в гл. 4>
\
V
\
А
V
\
\
\
-
г
V
\
\
\
к
ч
2'
,v
V
1
0 6
* s ¦
#^
_n.-i>
2 UUL
SZ) 507
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
Рис. 1Л4. Соотношение между коэффициентом трения f и числом РейнольДса
Rez) для гладких труб и труб с искусственной шероховатостью. (Зависимость
ig^Am) от1еA/яз) [8].)
/ — ламинарное течение; 2—турбулентное течение в гладких трубах.
6 2,8 3,0 3,2 3,4 3,6 3,8 4,0" 4,2 4,4 4,6 4,8 5,0 5,2 5? 5,6 5,8
если 1/яз меньше примерно 2300, течение является ламинарным и f = Яг/Яг5525
*= 64яз. Однако при 1/яз > 2300 вид функциональной зависимости между /
и яз изменяется, поскольку «ламинарный» режим течения переходит в «тур-
«турбулентный». Разумеется, анализ размерности не позволяет предсказать это
физическое явление. Кроме того, при турбулентном режиме течения на ве-
величину f влияет не только яз, но и шероховатость поверхности. Об этом убе-
убедительно свидетельствуют представленные На рис. 1.14 экспериментальные
результаты для я2/я1 в зависимости от я^ при ламинарном и турбулентном
режимах течения. Экспериментальные данные для турбулентного течения по-
показывают отчетливо выраженную зависимость от отношения средней высоты
элементов шероховатости поверхности к к диаметру трубы Ъ. Однако для
гладких труб эмпирическое соотношение
Яз/Я1 = f tt 0,046rtf - 0,046/Re^2
позволяет связать экспериментальные данные в широком диапазоне значений
"з [8].
40 Глава 1
Литература
1. Fourier J. В., Theorie analytique de la chaleur, Paris, 1822.
2. Rohesenow W. M., Hartnett J. P., eds., Handbook o! Heat Transfer,
Sec. 3 (by P. J. Schneider), McGraw, N. Y., 1973.
3. Veizirogen T. N., Correlation of Thermal Contact Conductance Experi-
Experimental Results, Prog. Astron. Aero., 20, Academic Press, N. Y., 1967.
4. Vance R. W., Duke W. M., eds., Applied Cryogenic Engineering, Wiley,
N. Y., 1962.
5. Barron R., Cryogenic Systems, McGraw, N. Y., 1967.
6. Van Driest E. R., On Dimensional Analysis and the Presentation of
Data in Fluid Flow Problems, /. Appl. Mech., 13 A940).
7. Langhaar H. L., Dimensional Analysis and Theory of Models, Wiley,
N. Y., 1951.
8. Nikuradse J., Gesetzmassigkeiten der turbulenten Stromung in glatten
Rohren, VDI Forschungsheft, vol. 356, 1932; Stromungsgesetze in rauhen Roh-
ren, VDI Forschungsheft, vol. 361, 1933.
ЗАДАЧИ
Задачи в этой главе сгруппированы по тематике разделов, как указано в
следующей таблице.
Номера задач
1.1—1.18
1.19—1.25
1.31—1.34
1.35—1.37
1.38—1.41
Раздел
1.2
1.3
1.4
1.5
1.7
Тема
Теплопроводность
Конвективный теплооб-
теплообмен
Радиационный теплооб-
теплообмен
Сложный теплообмен
Теория размерностей
1.1. Определить плотность теплового потока через кирпичную стену [k =
я= 0,3 Вт/(м-град)], если одна ее поверхность имеет температуру 25°С, а
другая — 10°С. Толщина стенки 10 см.
1.2. Стенка печи изготовлена из силикатного кирпича [Л = 1,1 Вт/м X
Хград)], температура ее внутренней поверхности 450°С Толщина стенки
30 см, температура ее наружной поверхности 55°С. -Найти плотность тепло-
теплового потока через стенку.
1.3. Плотность теплового потока через плоскую стенку составляет
1000 Вт/м2. Одна поверхность стенки имеет температуру 100°С. Коэффициент,
теплопроводности стенки 28 Вт/(м-град), ее толщина 25 см. Найти темпе-
температуру второй поверхности стенки.
1.4. Распределение температуры по толщине плоской стенки с коэффи-
коэффициентом теплопроводности 2 Вт/(м-град) имеет вид Т(х) = 100+150*, где
температура Т выражена в градусах Цельсия, а координата х — в метрах и
измеряется от одной поверхности стенки. Найти плотность кондуктивного
теплового потока через стенку. В каком направлении течет тепловой поток?
В направлении возрастания х или в противоположном направлении?
1.5. Кондуктивный тепловой поток через пластину из плексигласа [k =
= 0,195 Вт/(м-град)] толщиной 1 см равен 300 Вт. Площадь поверхности
пластины 2 м2. Температура одной поверхности поддерживается равной 30°С.
Найти температуру второй поверхности пластины и температуру ее среднего
сечения.
и 1.6. Термическое сопротивление стены жилого дома равно 9 град/Вт.
Найти тепловой поток через стену площадью 30 м2, если перепад темпера-
температур на стене составляет 30°С.
1.7. Для описания термического сопротивления изоляции часто приме-
применяют коэффициент R = L/k, где L — толщина изоляции. Рассчитать коэффи-
коэффициент R для 10-сантиметрового слоя следующих материалов: стекловолокна,
штукатурки, фанеры и обычного кирпича. Использовать значения коэффи-
коэффициента теплопроводности, приведенные в табл. П. IV. 3,
42 Глава 1
1.8. С точки зрения теплопередачи является ли нержавеющая сталь хо-
хорошим материалом для кухонной посуды? Какие факторы, кроме теплопере-
теплопередачи, должны учитываться при конструировании товаров широкого потреб-
потребления типа кухонной посуды?
1.9. Несколько стержней диаметром 1 см и длиной 10 см теплоизолиро-
теплоизолированы по боковой поверхности. С одной стороны концы стержней имеют тем-
температуру 100°С, с другой 0°С, так что кондуктивный тепловой поток направ-
направлен по оси. Найти значения теплового потока для стержней из меди (а), алю-
алюминия (б), нержавеющей стали (в), асбеста (г), картона (д) и стекловолокна
(е). Использовать коэффициенты теплопроводности, приведенные в прило-
приложении n.iv.
1.10. Тонкий плоский нагреватель площадью 0,2 м2 с температурой 200°С
помещен между двумя слоями теплоизоляции с коэффициентом теплопровод-
теплопроводности к = 0,35 Вт/(м-град). Мощность нагревателя 1000 Вт. Рассчитать тол-
толщину теплоизоляции, при которой температура ее внешней поверхности не
превышает 50°С.
1.11. Изменение коэффициента теплопроводности материала в зависимо-
зависимости от температуры описывается выражением к = 2,2 + 4-10~4 Г, где к вы-
выражается в Вт/(м-град), а Т — в Кельвинах. Найти тепловой поток, если две
тонкие пластины, разделенные слоем этого материала толщиной 40 см, имеют
температуры 100 и 200°С. Площадь поперечного сечения материала 1,8 м2.
1.12. Проинтегрировать соотношение A.2) для случая плоской стенки,
коэффициент теплопроводности которой линейно зависит от температуры, и
проверить формулу A.6).
1.13. Найти плотность теплового потока через плоскую стенку, коэффи-
коэффициент теплопроводности которой изменяется по квадратичному закону к =»
= ko(l + ВТ + СТ2). Выразить полученный результат через kOy Bt С, темпе-
температуры обеих поверхностей стенки Т\ и Т2 и толщину стенки L. Рассчитать
плотность теплового потока через стенку при Т{ = 200°С, Т2 = 500°С, L =
= 15 см, k0 = 15 Вт/(м-град), В = Ю-4 Кг1, С = 10"8 К~2.
1.14. Металлическую стенку рефрижератора нужно покрыть слоем пено*
пластовой теплоизоляции с коэффициентом теплопроводности 0,03 Вт/(м X
Хград). Температура внутри рефрижератора поддерживается равной —20°С.
Его хладопроизводительность 2 кВт, а площадь поверхности стенок 100 м2.
Найти минимальную толщину изоляции, при которой на внешней ее поверх-
поверхности не происходит конденсации, если точка росы окружающего воздуха вне
рефрижератора равна 15°С.
1.15. Предположим, что происходит одномерный кондуктивный перенос
тепла через составную стенку, показанную на рисунке.
/7
Г = 5004s
К задаче 1.15.
-Г=100°1
lj> И
а) Составить тепловую цепь для этой стенки, используя общепринятые
обозначения для всех сопротивлений и потенциалов.
б) Найти тепловой поток через сгенку.
в) Найти температуру левой поверхности материала D. если кА =
= 75 Вт/(м-град), LA = 20 см, кв = 60 Вт/(м-град), LB = Lc =
= 25. см, кс == 58 Вт/(м-град), LD = 40 см? кр = 20 Вт/(м-град),
44 = Ad = 2 м2, А$ = Aq,
Принципы теплопередачи 43
1.16. Стационарный профиль температуры в двухслойной стенке показан
на рисунке. Какой материал имеет больший коэффициент теплопроводности?
Обоснуйте свой ответ.
Материал 2 '
т
Материал 1
——-
К задаче 1.16.
1.17. Левая поверхность многослойной стенки, показанной на рисунке
омывается водой с температурой 70°С. Коэффициент конвективной теплоот
дачи на этой поверхности равен 60 Вт/(м2-град). Найти величину kx.
Г=50°С-
к = 200 Вт/ (м- град)
4-
= 60Вт/(м2-град)
Г„г70°С
<—30 см-
-25см->|<-15см
?=30Вт/(мтрад)
К задаче 1.17.
1.18. На рисунке показан стационарный профиль температуры в трех-
трехслойной стенке. Выбрать правильное неравенство из следующих: а) kA >
> kB > kc\ б) kA > kc > kB\ в) kB > kA > kc\ г) kc> kA> kB\ Д) kc >
> ka > kA.
Т(хУ
К задаче 1.18.
1.19. В безветренный день коэффициент конвективной теплоотдачи крыши
Здания равен 6 Вт/(м2*град). Найти конвективный тепловой поток от крыши,
если температура внутренней поверхности крыши 15°С, а температура окру-
окружающего воздуха —5°С. Площадь поверхности крыши 400 м2. Рассчитать
тепловой поток, если подул ветер и величина Re возросла до 85 Вт/(м2-град).
1.20. Найти конвективный тепловой поток от шарикоподшипника диа-
диаметром 1 см, имеющего температуру 200°С, который погружен в масло с тем-
температурой 100°С. Принять h = 1000 Вт/(м2-град).
1.21. Рассчитать конвективный тепловой поток от пластины с темпера-
температурой 200°С к окружающему воздуху с температурой 30°С. Коэффициент
конвективной теплоотдачи от пластины к воздуху 30 Вт/(м2-град), а пло-
Щадь поверхности пластины 10 м2.
44 Глава 1
1.22. Электрический нагреватель мощностью 1000 Вт с площадью по-
поверхности 0,1 м2 работает в среде с температурой 20°С. Рассчитать темпера-
температуру поверхности нагревателя для следующих условий:
з) нагреватель находится в воздухе, Яс = 30 Вт/(м2-град);
б) нагреватель находится в спокойной воде, he = 500 Вт/(м2-град);
в) нагреватель находится в перемешиваемой воде, Яс = 5000 Вт/(м2Х
Хград).
1.23. Электрический нагреватель мощностью 100 Вт находится в воздухе
с температурой 20°С, hc = 50 Вт/(м2-град). Какова должна быть минималь-
минимальная площадь поверхности нагревателя, чтобы температура его поверхности
не превышала 60°С?
1.24. Воздух с температурой 20°С омывает верхнюю поверхность гори-
горизонтальной плиты из чистого железа толщиной 10 см. Коэффициент конвек-
конвективной теплоотдачи 20 Вт/(м2-град), и к этой поверхности подводится внеш-
внешний радиационный тепловой поток плотностью 350 Вт/м2. От нижней поверх-
поверхности во внешнюю среду отводится тепловой поток плотностью 200 Вт/м2.
Составить тепловую цепь для этой задачи и рассчитать установившиеся тем-
температуры обеих поверхностей железной плиты.
1.25. Одна поверхность плоской пластины омывается жидкостью с тем-
температурой 20°С. С этой стороны поверхность стенки покрыта слоем теплоизо-
теплоизоляции толщиной 4 см с коэффициентом теплопроводности 0,5 Вт/(м-град).
Температура поверхности под изоляцией поддерживается равной 500°С. Рас-
Рассчитать коэффициент конвективной теплоотдачи на внешней поверхности изо-
изоляции, при которой температура этой поверхности не будет превышать 50°С.
Рассчитать плотность теплового потока через изоляцию.
1.26. Составная стенка, показанная на рисунке, состоит из двух различ-
различных материалов. Одна поверхность стенки имеет постоянную температуру
20°С, а вторая омывается воздухом с температурой 150°С,
60 см
60 см
20° С <
60 см
56 Вт/См-град)
*=52Вт/(мград)
/Гс=5Вт/(м2.Град)
К задаче 1.26.
а) Составить тепловую цепь для этой задачи.
б) Рассчитать все термические сопротивления.
в) Определить тепловой поток через стенку на единицу ширины стенки.
г) Рассчитать температуру поверхности стенки, омываемой воздухом.
1.27. Две металлические пластины плотно прижаты друг к другу шеро-
шероховатыми поверхностями. Одна пластина толщиной 15 см имеет коэффициент
теплопроводности ? = 45 Вт/(м-град), а вторая, толщиной 25 см, имеет ко-
коэффициент теплопроводности k = 70 Вт/(м-град). Удельное контактное тер-
термическое сопротивление между двумя пластинами 10~2 м2-град/Вт. Полный
перепад температур между внешними поверхностями обеих пластин 400°С.
а) Составить тепловую цепь системы.
б) Определить плотность теплового потока через поверхность.
Принципы теплопередачи 45
в) Рассчитать перепад температур на поверхности раздела.
г) Определить плотность теплового потока в предположении об отсут-
отсутствии контактного термического сопротивления.
1.28. Небольшой транзистор выделяет мощность 250 мВт. Его нужно ох-
охлаждать с помощью алюминиевого радиатора, имеющего общую площадь по-
поверхности 10 см2. Температура воздуха, окружающего радиатор, 25°С, коэф-
коэффициент конвективной теплоотдачи на поверхности ребер радиатора
12 Вт/(м2-град). Поскольку ребра радиатора из алюминия, их термическое
сопротивление мало и можно считать, что они изотермичны по всей их по-
поверхности. Найти установившуюся рабочую температуру транзистора.
1.29. В задаче 1.28 контактное термическое сопротивление между корпу-
корпусом транзистора и радиатором равно 60 град/Вт. Составить тепловую цепь
системы. Определить все термические сопротивления. Рассчитать рабочую
температуру транзистора. Найти перепад температуры на контактном сопро-
сопротивлении. Предложить пути устранения контактного сопротивления.
1.30. На рисунке показано поперечное сечение типичного потолка жилого
дома. Составить тепловую цепь типичной секции потолка. Рассчитать плот-
плотность теплового потока через потолок. Где уходит больше тепла — через пере-
перемычки или через изоляцию? Задачу теплопроводности считать одномерной.
Тсо= -10° С
Л =20 Вт/(м2-град)
6 см
-30 см
Изоляция из рыхлого
стекловолокна
Перемычки
изсосны
2 см
Штукатурка
К задаче 1.30.
Гда=25С
/Гс = 10Вт/(м2-град)
1.31. Абсолютно черное тело с площадью поверхности 0,1 м2 излучает в
холодную окружающую среду, Найти радиационный тепловой поток от тела
при температуре 27, 527 и 1027°С.
1.32. Нить электрической лампочки мощностью 100 Вт излучает как аб-
абсолютно черное тело в вакууме. Диаметр нити 0,13 мм, ее длина 7 см. Пре-
Пренебрегая кондуктивными потерями тепла из нити, рассчитать ее температуру.
1.33. Степень черноты серого тела с площадью поверхности 10 см2 равна
0,3. Найти радиационный тепловой поток при температуре 1000 К.
1.34. Серое тело с площадью поверхности 1 м2 и степенью черноты 0,5,
имеющее температуру 700°С, находится в большой черной камере с темпера-
температурой 100°С. Найти результирующий радиационный тепловой поток между
серым телом и камерой.
1.35. Рассчитать суммарный коэффициент теплопередачи V для условий
задачи 1.15. В качестве характерной площади принять AD.
1.36. Рассчитать суммарный коэффициент теплопередачи U для условий
задачи 1.26. В качестве характерной площади принять суммарную площадь
поперечного сечения стенки.
1.37. Рассчитать суммарный коэффициент теплопередачи U для условий
задачи 1.30. В качестве характерной площади принять площадь поперечного
сечения 1 м2.
1.38. Известно, что местная температура в ребре определяется следую-
следующими физическими параметрами: коэффициентом конвективной теплоотдачи
46 Глава 1
между ребром и окружающей средой — Fic, коэффициентом теплопроводности
материала ребра — k, характерным линейным размером ребра — L, темпера-
температурой окружающей среды — Гоо, температурой основания ребра — Г&, коорди-
координатой, измеряемой от основания ребра, —х.
Используя я-теорему Бэкингема, показать, что распределение темпера-
температуры в ребре можно описать с помощью следующих безразмерных парамет-
параметров: безразмерной температуры [Т(х)—Тоо]1(Ть — Гоо), безразмерного тер-
термического сопротивления HcL/k и безразмерной координаты x/L
1.39. Подставляя размерности для каждого физического параметра, при-
приведенного в табл. П.Х. 1, показать, что каждый комплекс является безраз-
безразмерной величиной.
1.40. Известно, что в задачах нестационарной теплопроводности распре-
распределение местной температуры в твердом теле определяется следующими фи-
физическими параметрами: плотностью твердого тела р, его удельной тепло-
теплоемкостью ср, характерным размером L, коэффициентом теплопроводности ма-
материала k, временем /, линейной координатой х.
Применяя я-теорему Бэкингема, показать, что распределение безразмер-
безразмерной температуры можно выразить с помощью безразмерных параметров x/L
и числа Фурье kt/pcpL2.
1.41. Если нагретое тело поместить в поток более холодной жидкости, то
с его поверхности будет отводиться тепло вследствие вынужденной конвек-
конвекции. Процесс теплообмена в этих условиях определяется следующими физи-
физическими параметрами: коэффициентом конвективной теплоотдачи hC) ха-
характерным размером поверхности L, плотностью жидкости р, скоростью по-
потока V, коэффициентом теплопроводности жидкости k, ее удельной теплоем-
теплоемкостью Ср И ВЯЗКОСТЬЮ \1.
Применяя я-теорему Бэкингема, показать, что процесс теплообмена опре-
определяется следующими тремя безразмерными параметрами: числом Нуссельта
HcL/k, числом Рейнольдса pVX/jx и числом Прандтля \x,cPlk.
Глава 2
СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
2.1. ВВЕДЕНИЕ
Теплопроводностью (кондуктивным переносом тепла) назы-
называется вид теплопередачи, при котором тепло распространяется
из области высокой температуры в область низкой температуры
вследствие прямого контакта между молекулами среды. Связь
кондуктивного теплового потока с распределением температуры
в среде определяется законом Фурье.
Процесс теплопроводности может происходить в твердых ве-
веществах, капельных жидкостях и газах. Однако в циркулирую-
циркулирующих жидкостях и газах он обычно действует совместно с кон-
конвекцией. Следовательно, «чистая» теплопроводность имеет место
в основном в сплошных твердых телах, где движение материала
ограничено. В этой главе будем считать, что теплопроводящей
средой является твердое тело, хотя полученные закономерности
применимы также к жидкостям и газам, конвективное движе-
движение которых ограничено.
При рассмотрении проблемы теплопроводности ее можно
разделить на три основные части. Первая — задачи стационар-
стационарной теплопроводности, в которых температура зависит только
от одной пространственной координаты (разд. 2.3 — 2.6). Вто-
Вторая— задачи стационарной теплопроводности, в которых тем-
температура зависит от двух или трех пространственных координат
(разд. 2.7). Третья — задачи нестационарной теплопроводности.
Этой теме посвящена гл. 3.
При изложении теории теплопередачи следует отметить важ-
важность применения цифровых вычислительных машин и програм-
программирования численных расчетов, поскольку часто встречаются за-
задачи, которые оказываются слишком сложными или трудоем-
трудоемкими для ручного счета. Чтобы найти решение в таких случаях,
мы часто обращаемся к ЭВМ и ручным калькуляторам, инже-
инженерным или программируемым. Чтобы показать типы программ,
которые применяются для решения задач теплопроводности, в
эту главу включены четыре программы численного расчета. Про-
Программы написаны в общей форме, чтобы их можно было при-
применять для решения широкого класса задач.
В следующем разделе выводится общее уравнение теплопро-
теплопроводности. Большая часть материала, представленного в этой
главе, начинается с решения уравнения теплопроводности. Оно
позволяет найти распределение температуры в твердом
48 Глава 2
после чего можно с помощью закона Фурье рассчитать кондук-
тивный тепловой поток,
2.2. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Уравнение теплопроводности является математическим выра-
выражением закона сохранения энергии в твердом веществе. Оно
выводится из рассмотрения баланса энергии для элементарного
объема материала, в котором происходит кондуктивный перенос
тепла. Предполагается, что в твердом теле переносом тепла кон-
конвекцией и излучением можно пренебречь. Кондуктивный тепло-
тепловой поток связан с распределением температуры в твердом теле
законом Фурье (уравнение 1.2).
При составлении баланса энергии учитывается возможное
генерирование энергии внутри материала. Типичными приме-
примерами генерирования энергии в твердом теле служат тепловыде-
тепловыделение при химических реакциях, омический нагрев при пропу-
пропускании электрического тока и тепловыделение вследствие ядер-
ядерных реакций.
Общее уравнение теплопроводности учитывает аккумулиро-
аккумулирование энергии внутри материала. Согласно законам термоди-
термодинамики, внутренняя энергия материала возрастает при повыше-
повышении температуры. Следовательно, количество энергии, аккуму-
аккумулированное в твердом теле, увеличивается, если температура
повышается со временем, и уменьшается, если температура соот-
соответственно снижается. Если температура материала остается
постоянной, энергия не аккумулируется, и тогда мы говорим,
что имеют место стационарные условия.
Проблемы теплопередачи подразделяются на несколько ос-
основных категорий в соответствии с тем, от каких переменных
зависит температура. Если температура не зависит от времени,
задачу называют стационарной, или установившейся. Если тем-
температура зависит от времени, задачу называют нестационарной,
или переходной. Кроме того, задачи классифицируются по числу
пространственных координат, от которых зависит температура.
Если температура зависит только от одной координаты, задачу
называют одномерной. Если температура зависит от двух или
трех пространственных координат, ее называют соответственно
двумерной или трехмерной. Если температура зависит от вре-
времени и координаты х в прямоугольной системе координат, т. е.
T = T(x,t), то мы имеем дело с одномерной нестационарной
задачей. Если Т= T(r,Q) в цилиндрической системе координат,
то мы рассматриваем двумерную стационарную задачу.
Прямоугольные координаты
Чтобы упростить вывод уравнения теплопроводности, рас-
рассмотрим одномерную прямоугольную систему координат (рис. 2.1)
и предположим, что температура твердого тела зависит толькд
Стационарная теплопроводность 49
от координаты х и времени, т. е. Г= T(x,t). Кроме того, пред-
предположим, что и коэффициент теплопроводности &, и плотность
р, и удельная теплоемкость с твердого материала постоянны.
Влияние переменности коэффициента теплопроводности k рас-
рассмотрено в разд. 2.4.
я(х) •
q(x + hx)
-л: *f«—Дх—*\
Рис. 2.1. Контрольный объем в прямоугольных координатах.
Применим закон сохранения энергии к контрольному объему,
показанному на рис. 2.1:
Г Энергия, подводимая в конт-"|
I рольный объем вследствие
L теплопроводности
г Энергия, отводимая из
I контрольного объема
I вследствие теплопровод-
L ности
["Энергия, генерируемая"]
I + I внутри контрольного =
J L-объема J
, ["Энергия, аккумулированная"]
[.внутри контрольного объема]*
B.1)
Выражая два члена, обусловленные теплопроводностью, с по-
помощью закона Фурье и обозначая через q'^' интенсивность
внутреннего тепловыделения в единице объема, записываем ра-
равенство B.1) в форме
-kA^(xy
дТ
9АЬхс^. B.2)
Разделив на объем контрольного объема ААх и выполнив не-
несложные преобразования, получаем
дТ
_
дТ
Ь
-рсж.
B.3)
50 Глава 2
Если перейти к пределу при Дх-^0, первый член в левой части
уравнения B.3) станет по определению второй производной
температуры по х и уравнение примет вид
k-^r + QG =РСЖ- <2'4)
Уравнение B.4) не является общим уравнением теплопровод-
теплопроводности, так как оно выведено в предположении об одномерном
распределении температуры. Если теперь снять это ограниче-
ограничение и считать, что температура зависит от всех трех линейных
координат и времени, т. е. Т= T(x,y,z,t), в уравнение войдут
члены, аналогичные первому члену в уравнении B.4), которые
выражают кондуктивные тепловые потоки в направлениях у и
г. В таком случае получаем трехмерную форму уравнения теп-
теплопроводности
Важно понимать физический смысл каждого члена, входя-
входящего в уравнение B.5). Первые три члена в левой части урав-
уравнения выражают результирующую скорость переноса тепла в
контрольный объем вследствие теплопроводности (на единицу
объема). Последний член в левой части — это скорость внутрен-
внутреннего тепловыделения в единице объема. Правая часть уравне-
уравнения B.5) выражает скорость изменения внутренней энергии ма-
материала на единицу объема. Каждый из членов имеет размер-
размерность энергии, отнесенной к единице времени и единице объема.
В системе СИ каждый член имеет размерность [Вт/м3].
Уравнение B.5) часто применяется в форме
д2т д2т д2т цш х дТ
+ + + B)
где коэффициент температуропроводности а представляет собой
следующую комбинацию теплофизических свойств материала:
а = k/pc. B.7)
Коэффициент температуропроводности имеет размерность м2/с.
Численные значения коэффициента теплопроводности, плот-
плотности, удельной теплоемкости и коэффициента температуропро-
температуропроводности для различных материалов, применяющихся в инже-
инженерной практике, приведены в приложениях.
Нам редко приходится определять распределение темпера-
температуры в твердом теле, решая общее уравнение теплопроводности
B.6), что требует решения дифференциального уравнения в
частных производных. В большинстве практических задач мож-
можно сделать упрощающие предположения, которые позволяют ис-
исключить тот или иной член из уравнения теплопроводности, что
Стационарная теплопроводность 51
часто дает возможность упростить задачу и отыскание решения.
Рассмотрим несколько частных случаев уравнения теплопровод-
теплопроводности, а соответствующие примеры будут представлены в по-
последних разделах этой главы.
Если температура материала не зависит от времени, задача
становится стационарной и аккумулирования энергии в мате-
материале не происходит. В таком случае уравнение стационарной
трехмерной теплопроводности записывается в прямоугольных
координатах следующим образом:
д2т
B-8)
Если задача не только стационарная, но и не происходит
тепловыделения внутри материала, то уравнение теплопровод-
теплопроводности упрощается еще более и принимает вид
Это уравнение, называемое уравнением Лапласа, встречается в
различных областях науки.
Если в установившихся условиях при отсутствии тепловыде-
тепловыделения рассматривается одномерная задача, т. е. температура
зависит только от координаты х, уравнение теплопроводности
становится обыкновенным дифференциальным уравнением
•S?—°- BЛ0>
Безразмерная форма уравнения теплопроводности
Уравнение теплопроводности, записанное в форме B.6), яв-
является размерным. Часто удобнее переписать это уравнение
таким образом, чтобы каждый член стал безразмерным. Выпол-
Выполнив это, мы найдем безразмерные параметры, определяющие
процесс теплопроводности. Приведем одномерное уравнение
теплопроводности B.4) к безразмерному виду, вводя безразмер-
безразмерную температуру
8 /Г B.11)
безразмерную пространственную координату
l = x/Lr B.12)
и безразмерное время
т = ///г. B.13)
Величины 7V, Lr и tr — это характерные значения температуры,
длины и времени соответственно. Выбор характерных значений
произволен, хотя, когда задача полностью определена, нужно
выбирать значения, имеющие физический смысл. Вместо отно-
отношения температур обычно удобнее применять относительную
52 Глава 2
избыточную температуру; выбор безразмерных параметров из-
изменяется от задачи к задаче. Безразмерные параметры часто вы-
выбирают таким образом, чтобы их значения изменялись в удоб-
удобных пределах, например от 0 до 1. За Lr обычно принимается
максимальная координата х в системе, для которой находится
распределение температуры.
Подставив определенные таким образом безразмерные вели-
величины температуры, линейной координаты и времени в уравнение
B.4), получаем безразмерное уравнение теплопроводности
Безразмерный параметр atr/L2r называется числом Фурье и обо-
обозначается символом Fo:
Fo = at r/L2r. B.15)
Выбор характерных значений времени и длины, входящих в
число Фурье, изменяется от задачи к задаче, но функциональ-
функциональный вид соотношения между ними остается неизменным. Число
Фурье всегда равно коэффициенту температуропроводности, ум-
умноженному на время и деленному на квадрат характерной
длины.
Число Фурье представляет собой отношение скорости кон-
дуктивного переноса тепла к скорости аккумулирования энергии
в материале. Число Фурье является важным безразмерным кри-
критерием в задачах нестационарной теплопроводности, и оно часто
будет фигурировать в ходе дальнейшего изложения.
Вторым безразмерным параметром в уравнении B.14) яв-
является член, включающий тепловыделение. Будем применять
безразмерный параметр тепловыделения <7с определяемый фор-
формулой
Чо = Чтг- BЛ6)
Этот параметр представляет собой отношение количества
тепла, генерируемого внутри тела за единицу времени, к коли-
количеству тепла, перенесенного теплопроводностью через рассмат-
рассматриваемый объем в единицу времени.
Итак, одномерное уравнение теплопроводности записывается
в безразмерной форме следующим образом:
|т + **-КГ&- BЛ7)
Пример 2.1. Найти упрощенную форму общего уравнения теплопровод-
теплопроводности для установившегося одномерного кондуктивного переноса тепла в
прямоугольном твердом теле с постоянными теплофизическими свойствами
при отсутствии внутреннего тепловыделения. Решить полученное уравнение
Стационарная теплопроводность 53
теплопроводности и выразить распределение температуры в твердом теле и
тепловой поток через постоянные интегрирования.
Решение. Общее уравнение теплопроводности имеет вид
д2Т дЧ ,д2Т\ ,// дТ
Поскольку рассматривается одномерная стационарная задача, температура не
зависит от времени и является функцией только одной из трех линейных ко-
координат. Если предположить, что Т зависит только от х, то dT/dt=d2T/dy2=
= д2Т/дг2 = 0. Кроме того, поскольку отсутствует внутреннее тепловыделе-
тепловыделение, <7g/===0-
Уравнение теплопроводности в упрощенной форме записывается следую-
следующим образом:
d2T/dx2 = 0.
Интегрируя дважды это дифференциальное уравнение второго порядка, нахо-
находим распределение температуры, выраженное через две постоянные интегри-
интегрирования Ci и С2:
Т = Схх + С2.
Значения этих двух постоянных определяются для конкретной задачи из двух
граничных условий.
Кондуктивный тепловой поток через твердое тело в направлении х опре-
определяется законом Фурье:
4 dx
Отметим, что тепловой поток является однородным в соответствии с приме-
примерами 1.1 и 1.2, т. е. в установившихся условиях он остается одинаковым во
всех точках твердого тела.
Цилиндрические координаты
Уравнение теплопроводности в форме B.6) применимо толь-
только для прямоугольной системы координат. Члены, выражающие
тепловыделение и аккумулирование энергии, инвариантны отно-
относительно системы координат, но члены, выражающие результи-
результирующий кондуктивный тепловой поток, зависят от геометрии и,
следовательно, от системы координат. Зависимость от принятой
в задаче системы координат можно исключить, если выразить
кондуктивные члены с помощью оператора Лапласа. Форма
лапласиана различна для различных систем координат. В при-
приложении I представлена форма лапласиана для прямоугольной,
цилиндрической и сферической систем координат. С использова-
использованием лапласиана уравнение теплопроводности записывается сле-
следующим образом:
Для общей нестационарной трехмерной задачи в цилиндри-
цилиндрических координатах Т = Г (г, <J>, г, t). Цилиндрическая система
54 Глава 2
координат показана на рис. 2.2а. Если выражение для лап-
лапласиана подставить в уравнение B.18), общее уравнение тепло-
теплопроводности в цилиндрических координатах примет вид
дт
аг
Если нестационарная температура в цилиндре изменяется
в одном направлении, т. е. Т = T(r,t)9 то для этого частного
случая уравнение теплопровод-
dz
ности упростится:
1 д ( дТ\
Яд 1 ЗТ
Рис. 2.2а. Цилиндрическая система
координат.
B.20)
Далее, если температура по-
постоянна по времени и изме-
изменяется только в радиальном на-
направлении, уравнение тепло-
теплопроводности сводится к сле-
следующему:
d( dT'' -"- = 0.B.21)
Отметим, что температура, определяемая уравнением B.21), за-
зависит теперь только от переменной г и это уравнение является
обыкновенным дифференциальным уравнением.
Когда внутреннее тепловыделение отсутствует, а температура
зависит только от радиуса, стационарное уравнение теплопро-
теплопроводности в цилиндрических координатах принимает вид
dT
B.22)
Пример 2.2. Выразить стационарное распределение температуры и тепло-
тепловой поток для цилиндра длиной / через две постоянные интегрирования. Тем-
Температура зависит только от радиуса, внутреннего тепловыделения в цилиндре
не происходит.
Решение. В условиях задачи применимо уравнение B.22)
Чг
После первого интегрирования по радиусу получаем
г (dT/dr) = С{
cfT/dr и Ci/r.
или
В результате второго интегрирования находим
Т = Ci In r + С2.
Стационарная теплопроводность 55
Постоянные интегрирования можно определить, как только будут заданы два
граничных условия. Тепловой поток через поверхность цилиндра произволь-
произвольного радиуса г выражается формулой
qz==^kA^j-^-k Bnd) -^- = — 2лЫС1.
Заметим, что в установившихся условиях тепловой поток через любую ци-
цилиндрическую поверхность является постоянной величиной.
Сферические координаты
Для тела сферической формы, когда температура зависит от
трех координат и времени, т. е. Т = Т(г, 8, ф, t), общее уравне-
уравнение теплопроводности с учетом генерирования энергии записы-
записывается в виде
дТ
1
дТг
r2 sin2 9 дФ2
Рис. 2.26. Сферическая система коорди-
координат.
+ !LL?L B 23)
Сферическая система коор-
координат показана на рис. 2.26.
Из уравнения B.23) мож-
можно получить упрощенные
уравнения для одномерной стационарной теплопроводности и
одномерной нестационарной теплопроводности в сферических
координатах. Эти упрощенные уравнения предлагается вывести
в качестве упражнения.
2.3. ОДНОМЕРНАЯ СТАЦИОНАРНАЯ ЗАДАЧА
ТЕПЛОПРОВОДНОСТИ ПРИ ОТСУТСТВИИ ВНУТРЕННЕГО
ТЕПЛОВЫДЕЛЕНИЯ
Применим уравнение теплопроводности для решения задач,
в которых температура зависит только от одной линейной коор-
координаты. Примем, что в прямоугольной системе координат тем-
температура будет зависеть только от х, а в цилиндрической и сфе-
сферической системах координат — только от радиуса. Предпола-
Предполагается, что коэффициент теплопроводности является постоянной
величиной, а тепловыделение отсутствует.
Применим общую методику решения, состоящую из двух
этапов. На первом этапе из решения соответствующего упро-
упрощенного уравнения теплопроводности находится распределение
температуры. С этой целью отыскивается аналитическое реше-
решение дифференциального уравнения второго порядка. После того
56 Глава 2
как решение дифференциального уравнения записано в общем
виде, с помощью двух граничных условий определяются две
постоянные интегрирования. На втором этапе с помощью закона
Фурье вычисляется кондуктивный тепловой поток через твердое
тело.
Прямоугольные координаты
Стационарное одномерное распределение температуры в пря-
прямоугольной плоской стенке при отсутствии внутреннего тепло-
тепловыделения описывается упрощен-
упрощенным уравнением теплопроводности
B.10)
Решение этого дифференциального
уравнения с использованием двух
постоянных интегрирования Сх и Сг
имеет вид (см. пример 2.1)
Т (х) = Схх + С2.
Значения этих постоянных мож-
можно найти, если заданы два гранич-
граничных условия. Предположим, что в
качестве этих условий заданы тем-
температуры на двух поверхностях
стенки (рис. 2.3): Т@) = Тх и T(L)=T2. Применяя эти гранич-
граничные условия, получаем следующее распределение безразмерной
температуры стенки:
Рис. 2.3. Одномерная задача
теплопроводности в прямоуголь-
прямоугольных координатах и граничные
условия.
Т(х)-Тх
X
B.24)
Следовательно, температура изменяется линейно по х. Тепло-
Тепловой поток через стенку определяется законом Фурье:
п —- —. Ъ А = Ь А (О ОК\
Тепловой поток на единицу площади называется плотностью теп-
теплового потока и обозначается q". Двойной штрих означает, что
величина^ рассчитана на единицу площади. Для плоской стенки
а" = — ==
k (Т, - т2)
Л~ L
Если записать соотношение B.25) в форме закона Ома:
АГ AT
B.26)
Стационарная теплопроводность 57
Материал 2
то термическое сопротивление плоской стенки, как отмечалось
в гл. 1, выражается формулой
r* = Ta- B.27)
Кондуктивный тепловой поток через плоскую стенку обусловлен,
перепадом температур поперек стенки, и его распространению
противодействует термическое сопротивление, пропорциональное
толщине стенки и обратно про-
пропорциональное коэффициенту теп-
теплопроводности стенки и площади
ее поперечного сечения.
Если кондуктивный перенос
тепла осуществляется через со-
составную (многослойную) плоскую
стенку, распределение темпера-
температуры и тепловой поток можно
найти, предполагая, что тепло те-
течет по эквивалентной тепловой
цепи, представляющей сумму тер-
термических сопротивлений, соответ-
соответствующих отдельным слоям из
различных материалов.
В качестве примера тепловой
цепи рассмотрим плоскую стенку
(индекс 1), покрытую двумя
слоями различных изоляционных
материалов (индексы 2 и 3). Гео- Л пл „
метпия чалачи покяяяна ня Рис'2А Последовательная тепловая
метрия задачи показана на цепь> прямоугольные координаты.
рис. 2.4. Один и тот же тепловой
поток проходит последовательно
через каждое термическое сопротивление, и, следовательно,
тепловая цепь состоит из последовательно соединенных тер-
термических сопротивлений. Если известны свойства всех трех
материалов, заданы геометрические характеристики и темпера-
температуры на двух внешних поверхностях, тепловой поток можно
найти с помощью соотношения, аналогичного закону Ома [см.
выражение A.14)]:
Rt
АГп
B.28)
Поскольку тепловой поток через многослойную стенку известен,
можно найти температуры на поверхностях раздела материалов,
применяя закон Ома для каждого слоя. Например, температуру
Тх на поверхности раздела материалов I и 2 можно рассчитать
58 Глава 2
по формуле
B.29)
Часто в многослойных стенках слои материалов располо-
расположены так, что тепловой поток через них течет скорее парал-
параллельно, чем последовательно. В таком случае в тепловую цепь
включаются участки из параллельно соединенных термических
сопротивлений. Типичный пример такой стенки показан на
рис. 1.6.
Тепловой поток определяется по формуле
Отдельные термические сопротивления выражаются соотноше*
нием .
Промежуточные температуры типа Тх можно найти из уравне*
ния B.29).
Предполагается, что при параллельном соединении термиче*
ских сопротивлений /?2 и /?3 тепловой поток остается одномер-
одномерным; если же сопротивления R2 и /?3 заметно отличаются друг
от друга, могут стать существенными двумерные эффекты
(разд. 2.7).
Цилиндрические координаты
Из задач теплопроводности для тел цилиндрической формы
чаще всего встречается задача о кондуктивном тепловом потоке
через длинный полый цилиндр (рис. 2.5). Известно, что темпе-
ратура внутренней поверхности цилиндра равна Г/, а темпера-
температура наружной поверхности То. Стационарное распределение
температуры в твердом теле с постоянными теплофизическими
свойствами при отсутствии внутреннего тепловыделения опреде-
определяется решением уравнения B.22) при двух граничных усло-
условиях: Г(г,)== Ti\ T(ro)= То. Решение для местной температуры
Т(г) имеет вид (см. пример 2.2)
TM-^ + Vo-Td^fc. B.31)
Выражение B.31) записывается в безразмерной форме следую-
следующим образом:
Т (г) - Т{ _ in (rln)
То - Т i "In (ro/n) •
Следовательно, температура изменяется в радиальном направ-
направлении по логарифмическому закону.
Поскольку распределение температуры известно, тепловой
поток вдоль радиуса цилиндра можно найти с помощью закона
Стационарная теплопроводность 59
Фурье для цилиндрической системы координат,
q = -kA(r)^- = -kBnrl)^, B.33)
clt аг
где / — длина цилиндра.
Дифференцируя распределение температуры B.31) и под-
подставляя полученный результат в соотношение B.33), получаем
/71 гг
B.34)
ч~ 1п(
Выражение B.34) записано в форме закона Ома, и знаме-
знаменатель представляет собой термическое сопротивление полого
цилиндра:
2nkl
Принципы последователь-
последовательного и параллельного соедине-
Рис. 2.5. Одномерная задача теп-
теплопроводности в цилиндрических
координатах и граничные условия.
Рис. 2,6/ Последовательная тепловая
цепь, цилиндрические координаты.
ния термических сопротивлений в цепь, справедливые для плоской
стенки в прямоугольной системе координат, можно применить и
для задачи о теплопроводности в полом цилиндре. Предполо-
Предположим, например, что жидкость течет в трубе, покрытой тепло-
теплоизоляционным материалом (рис. 2.6). Известно, что средняя
температура жидкости равна Т\, а температура внешней поверх-
поверхности изоляции Гг- Характеристики материала трубы обозна-
обозначены индексом 1, а изоляции — индексом 2. Конвективное тер-
термическое сопротивление жидкости определяется формулой
60 Глава 2
A.18). Конвективное термическое сопротивление жидкости
нужно соединить последовательно с двумя кондуктивными тер-
термическими сопротивлениями для двух твердых материалов, по-
поскольку тепловой поток распространяется последовательно че-
через каждый из этих материалов.
Тепловой поток в этой задаче выражается соотношением
*L) = huh
Rt Лолн 1 , In (r2/r,) , In (г3/г2)
B.36)
Термическое сопротивление, входящее в соотношение B.36),
является суммой всех термических сопротивлений между двумя
известными температурами.
Если известны температуры Тх
и Т2, то полное сопротивление
должно равняться сумме толь-
только кондуктивных сопротивле-
сопротивлений трубы и изоляции. Темпе-
Температура Тх при известном теп-
тепловом потоке находится из со-
соотношения
Воздух
4 =
In (nlr{)l2nkxl
In (г3/г2)/2яй2/"
B.37)
Воздух
Пример 2.3. В алюминиевой тру-
трубе \kp = 185 Вт/(м-град)] течет во-
водяной пар при температуре Ts =
= 110°С. Внутренний диаметр трубы
10 см, наружный диаметр 12 см. Тру-
Труба расположена в помещении с тем-
температурой 30°С, коэффициент конвек-
конвективной теплоотдачи от трубы к воз-
воздуху Нсо равен 15 Вт/(м2-град). Най-
Найти тепловой поток на единицу дли-
длины, если труба не теплоизолирована.
Чтобы снизить тепловые потери от трубы, она была покрыта слоем изо-l
ляции [kj = 0,2 Вт/(м-град)] толщиной 5 см. Найти тепловой поток на еди-
единицу длины от теплоизолированной трубы. Предположить, что конвективное
термическое сопротивление пара пренебрежимо мало.
Решение. Для трубы без теплоизоляции наиболее существенными являют-
являются кондуктивное термическое сопротивление самой трубы и конвективное тер-
термическое сопротивление комнатного воздуха. Поскольку конвективным терми-
термическим сопротивлением пара можно пренебречь, температура внутренней по-
поверхности трубы равна температуре пара. Тепловой поток на единицу длины
трубы в обозначениях, показанных на рисунке, выражается соотношением
К примеру 2.3.
т-т
s о
110-30
In
+ \l2nr2hco
In F/5)/2я • 185 + 1/2я • 0,06 . 15
80
1,57-
0,177
452 Вт/м.
Стационарная теплопроводность 61
Для трубы с теплоизоляцией нужно добавить термическое сопротивление изо-
изоляции, и соотношение для теплового потока примет вид
я т-т
In (r2fr{) In (г8/га) .
2nkp 2nkJ
1
2nr3hco
110-30
In F/5)
2Я-185
In A1/6)
2л-0,2
2я-0,11 • 15
80
1,57-1<Г
0,482+ 0,096
= 138 Вт/.м.
Использование теплоизоляции позволяет втрое снизить потери тепла паром.
Отметим, что в обоих случаях можно пренебречь кондуктивным термиче-
термическим сопротивлением алюминиевой трубы без сколько-нибудь заметного сни-
снижения точности результатов расчета теплового потока.
Сферические координаты
Распределение температуры и тепловой поток для полого
шара определяются таким же образом, как для полого ци-
цилиндра и плоской стенки.
Стационарное одномерное
распределение температуры
при отсутствии внутреннего
тепловыделения определяет-
определяется из решения упрощенного
уравнения теплопроводно-
теплопроводности, записанного в сфериче-
сферических координатах. Это урав-
уравнение имеет вид
г2 dr
dr
d2(rT)
dr2
= 0.
Рис. 2,7. Одномерная задача теплопро-
теплопроводности в сферических координатах и
граничные условия.
Предполагаем, что гранич-
граничными условиями являются
заданные температуры внут-
внутренней и наружной поверх-
поверхностей шара (рис. 2.7):
T(n)=Ti\ Т(го)=То. В таком случае распределение темпера-
температуры в полом шаре определяется соотношением
т (г) - Tt _
To-Tt -
то
-v-
B.38)
Следовательно, температура полого шара изменяется в ради-
радиальном направлении по гиперболическому закону.
62 Глава 2
Тепловой поток через стенку шара можно найти, применяя
закон Фурье к соотношению B.38). В итоге получаем
q = Ti -Jo—. B.39)
Таким образом, термическое сопротивление стенки шара выра-
выражается формулой
% B-40)
Суммарный коэффициент теплопередачи
Как показано в гл. 1, если в задаче теплообмена участвует
несколько термических сопротивлений, соединенных последова-
последовательно, параллельно или комбинированно, удобно ввести сум-
суммарный коэффициент теплопередачи, или суммарную удельную
тепловую проводимость. Суммарный коэффициент теплопере-
теплопередачи обозначается через U и определяется формулой
q = UA(AT)nonH. B.41)
Величина U играет ту же роль, что и коэффициент конвектив-
конвективной теплоотдачи Л. И U, и h имеют размерность Вт/(м2-град).
Если соотношение B.41) сравнить с равенством
• <2-42>
лн
то видно, что U можно выразить через полное термическое со-
сопротивление цепи:
В качестве примера использования суммарного коэффициента
теплопередачи рассмотрим трехслойную плоскую стенку, пока-
показанную на рис. 2.4. Величина U в этой задаче находится по
формуле
В этом примере площади поперечного сечения всех трех мате-
материалов одинаковы, поэтому нет сомнений, какую площадь нуж-
нужно использовать в соотношении B.43). Однако если площади
для каждого термического сопротивления различны, нужно быть
последовательными при выборе площади, входящей в соотно-
соотношение B.43).
Случаю переменной площади соответствует задача о много-
многослойной цилиндрической стенке с последовательным соедине-
соединением термических сопротивлений. Величину UA для тепловой
цепи (рис. 2.6) можно определить из формулы
= UA (А7-)полн =
info/r,)
h6Bnrxl) 2л/М
Стационарная теплопроводность бЗ
или
UA=-
In (Г2/Г1) In (Г3/Г2)
2fe/
Отметим, что произведение UA постоянно, но величина U зави-
зависит от выбора соответствующей площади. Предположим, напри-
например, что за характерную площадь мы приняли площадь вну-
внутренней поверхности трубы At = 2nr\l. В таком случае величина
U, рассчитанная по Л/, равна
г г !
1 Hln
1 |
Й
In (гз/г>)
k2
Если величина U рассчитана по
площади наружной поверхности
трубы А о = 2яг3/, то
1
1п
1п
o-VA WVo
Несмотря на то что значения Ui
и [/о различны, произведение LJA
всегда постоянно: UtAi = UOAO.
Пример 2.4, По пластмассовой тру-
трубе [? = 0,5 Вт/(м-град)] течет жид-
жидкость, причем коэффициент конвективной
теплоотдачи равен 300 Вт/(м2«град).
Средняя температура жидкости 100°С. Внутренний диаметр трубы 3 см, на-
наружный 4 см. Рассчитать температуру наружной поверхности трубы, если
тепловой поток на единицу длины трубы равен 500 Вт/м. Найти-также сум*
марный коэффициент теплопередачи, рассчитанный по площади наружной по-
поверхности трубы.
Решение. Схема теплопередачи через трубу показана на рисунке. Теп*
ловой поток определяется формулой
К примеру 2.4.
he Bnrxl)
In (r2/n)
Тепловой поток на единицу длины трубы составляет
<¦-+¦
j
In (r{jr2) *
2nkx
500 = .
100 — T2
1
300-2я-0,015 +
Т2 = 36,5° С.
In B/1,5) *
2зх • 0,5
64 Глава 2
Суммарный коэффициент теплопередачи, рассчитанный по Ло, выражается
соотношением
г, „ 1
|
In(r2/rt) '
4- + -
hc2nrxl 2nkxl
1
2 0,02-10B/1,5)
1,5-300 0,5
-=62,69 Вт/(м2 • град).
В качестве проверки величины U можно найти тепловой поток на единицу
длины, применяя рассчитанное значение Uo,
q' = U0A0 (Г, - Т2) = 62,69 . 2я • 0,02 A00 — 36,53) = 500 Вт/м.
Жидкость
Критическая толщина изоляции цилиндра
Интересная ситуация возникает, когда цилиндр с низким
термическим сопротивлением покрыт слоем изоляции, наружная
поверхность которой омы-
омывается жидкостью. Геомет-
Геометрия задачи показана на рис.
2.8. Предположим, что тем-
температура внутренней поверх-
поверхности изоляции постоянна и
равна Ti. Нужно определить
влияние дополнительной
теплоизоляции на тепловой
поток от цилиндра. Неясно,
приведет ли дополнительная
изоляция к увеличению или
уменьшению теплового по-
потока. В установившихся ус-
условиях кондуктивный тепло-
тепловой поток через цилиндр
и изоляцию должен равняться конвективному тепловому потоку
на наружной поверхности (обозначения указаны на рис 2.8):
Рис- 2.8. Критический радиус теплоизо-
теплоизоляции трубы.
При использовании дополнительной теплоизоляции величина
Ао возрастает, но То снижается. Чтобы определить, какой эф-
эффект преобладает, запишем тепловой поток в виде
т.~т
I о
In (го/г.)/2як/ + \/hc2nrot
Чтобы найти влияние изменения толщины теплоизоляции на
тепловой поток, можно продифференцировать q по г0 и прирав*
Стационарная теплопроводность 65
нять результат нулю, определяя таким образом оптимум. В итоге
получаем условие для оптимального теплового потока:
1. B.44)
Безразмерный параметр hcro/ki называется числом Био. Он вы-
выражает отношение кондуктивного термического сопротивления
теплоизоляции к конвективному термическому сопротивлению
жидкости. Число Био обозначается Bi, оно часто фигурирует
в задачах смешанного (кондуктивного и конвективного) тепло-
теплообмена.
Итак, условие оптимального теплового потока через цилиндр
выражается соотношением
%l. B.45)
Построив график зависимости теплового потока от наружного
радиуса теплоизоляции гОу можно показать, что тепловой поток
достигает максимума при Bi = 1. Если Bi < 1, дополнительная
теплоизоляция приведет к снижению теплового потока.
При числе Био, равном единице, значение наружного радиуса
теплоизоляции называется критическим радиусом, поскольку
тепловой поток от цилиндра максимален при условии
kj
hc
Анализируя порядок величин ki и Йс, с которыми можно встре-
встретиться в практических задачах, легко видеть, что критический
радиус является величиной порядка нескольких миллиметров.
Следовательно, нужно иметь в виду, что дополнительная тепло-
теплоизоляция цилиндров малого диаметра (например, электрических
выводов небольшого датчика) может на самом деле привести
к интенсификации теплоотдачи от провода. С другой стороны,
следует ожидать, что дополнительная теплоизоляция трубопро-
трубопроводов и каналов большого диаметра всегда будет вызывать сни*
жение теплового потока.
Пример 2.5. Электрический провод диаметром 1 мм покрыт слоем пласт*
массовой теплоизоляции [kt = 0,5 Вт/(м-град)] толщиной 2 мм. Провод рас-
расположен в воздухе с температурой 25°С, Не = 10 Вт/(м2-град). Температура
провода 100°С.
Найти тепловой поток от единицы длины провода с изоляцией и без нее,
предполагая, что наличие изоляции не влияет на температуру провода.
Решение. Прежде всего вычислим число Био:
10 B+ 0,5) Ю-3
Поскольку число Био меньше единицы, теплоизоляция приведет к возраста-
возрастанию теплового потока от провода. Тепловой поток на единицу длины провода
3 Зак 487
66 Глава
с изоляцией находим следующим образом:
7. - Т 100 - 25
Ш(го//г) 1 " Ш B,5/0,5) ,
Zh 2 05
2nk1 Znrohc 2я • 0,5 2я B,5 • 10~3) • 10
Тепловой поток без теплоизоляции равен
q' » Й, = А (Га - fj = 10 • 2я @,5-10~3) A00 - 25) = 2,36 Вт/м.
Итак, применение теплоизоляции привело к возрастанию теплового потока
от проволоки в 4,6 раза.
2.4. ВЛИЯНИЕ ПЕРЕМЕННОСТИ КОЭФФИЦИЕНТА
ТЕПЛОПРОВОДНОСТИ
Коэффициент теплопроводности большинства материалов не
является постоянной величиной, а зависит от температуры. До
сих пор мы предполагали, что величина коэффициента тепло-
теплопроводности постоянна. Однако в этом разделе мы найдем влия-
влияние переменности коэффициента теплопроводности на тепловой
поток и распределение температуры для плоской стенки, по-
полого цилиндра и полого шара.
Если при выводе уравнения теплопроводности в прямоуголь-
прямоугольной системе координат (разд. 2.2) предположить, что величина
коэффициента теплопроводности переменна, то уравнение B.5)
примет вид
Для стационарного одномерного распределения температуры в
прямоугольном твердом теле при отсутствии внутреннего тепло-
тепловыделения уравнение B.47) упрощается и сводится к следую-
следующему:
4D5] B-48)
Прежде чем перейти к решению этого уравнения, следует знать
закон изменения коэффициента теплопроводности от темпера-
температуры k{T) в рассматриваемом диапазоне температур. Для мно-
многих материалов можно получить достаточно точные результаты,
предполагая, что существует линейная зависимость коэффи-
коэффициента теплопроводности от температуры,
*оA+рГ), B-49)
где р — постоянная.
Интегрируя уравнение B.48) по лс, получаем
(Г)-S—С,. B.50)
Стационарная теплопроводность 67
В установившихся условиях через стенку течет постоянный
тепловой поток. Применяя закон Фурье, находим
<l" = -k(T)?. B.51)
Сравнивая соотношения B.50) и B.51), видим, что
Подставляя соотношение B.49) в уравнение B.50) и проводя
интегрирование по х, получаем
Значения двух постоянных интегрирования можно найти, задав
два граничных условия. Предполагая, что температуры гранич-
граничных поверхностей твердого тела известны (рис. 2.3), получаем
граничные условия:
Теперь можно определить значения постоянных С\ и С2:
В таком случае распределение безразмерной температуры в
стенке имеет вид
4 ?[?4ё?] B.52,
Профиль температуры в плоской стенке с переменным коэф-
коэффициентом теплопроводности нелинеен, но если коэффициент
теплопроводности постоянен, т. е. р = 0, распределение B.52)
сводится к линейному распределению B.24).
Плотность теплового потока через стенку определяется со-
соотношением
которое можно переписать в форме
я = ^о (^ 1 + Э —2—)—Г~-
Величина в скобках —это значение коэффициента теплопровод-
теплопроводности при средней температуре стенки:
68 Глава 2
Коэффициент теплопроводности при Тт равен
Применяя km, получаем простое выражение для плотности те-
теплового потока:
Соотношение B.53) имеет особенно удобную для расчетов
форму. Оно показывает, что плотность теплового потока через
стенку, коэффициент теплопроводности которой линейно зависит
от температуры, можно вычислить по формуле, полученной для
случая постоянного коэффициента теплопроводности, если коэф-
коэффициент теплопроводности принять равным значению при сред-
средней температуре двух поверхностей стенки.
Если коэффициент теплопроводности материала стенки ци-
цилиндра или шара линейно зависит от температуры, можно ана-
аналогичным образом найти профиль температуры и тепловой по-
поток для этих тел. Подробный вывод мы оставляем для само-
самостоятельных упражнений (задачи в конце главы).
Тепловой поток через цилиндрическую стенку с линейно из-
изменяющимся коэффициентом теплопроводности и заданными
температурами граничных поверхностей определяется формулой
4 In (ro/ri)/2nkml '
а для стенки шара
4 (г0 ~
[ Р(+ )/]
Теперь мы видим, что полученные ранее выражения для
теплового потока через плоскую, цилиндрическую и шаровую
стенки с постоянным коэффициентом теплопроводности приме-
применимы и в случае переменного коэффициента теплопроводности,
если в этих выражениях использовать значение коэффициента
теплопроводности при средней температуре стенки.
Если зависимость коэффициента теплопроводности от темпе-
температуры нелинейна, можно показать, что тепловой поток можно
представить с помощью закона Фурье, записанного в форме за-
закона Ома: q = №/Rm, где Rm — среднее термическое сопротив-
сопротивление твердого тела. Независимо от геометрии твердого тела
среднее термическое сопротивление рассчитывается по сред-
среднему коэффициенту теплопроводности тела, определенному со-
соотношением
Стационарная теплопроводность 69
где Т\ и Т2 — температуры на граничных поверхностях твердого
тела, т. е. AT = Т\ — Г2. В таком случае среднее термическое
сопротивление для плоской стенки определяется по формуле
для цилиндрической стенки — по формуле
Rm = In (r
и для стенки шара — по формуле
Пример 2.6. Большая плоская стенка имеет толщину 0,35 м. Темпера-
Температура одной поверхности 35°С, второй 115°С. Известны лишь два значения
коэффициента теплопроводности материала стенки: k = 26 Вт/(м-град) при
0°С и k = 32 Вт/(м-град) при 100°С. Найти плотность теплового потока че-
через стенку, предполагая, что коэффициент теплопроводности линейно зави-
зависит от температуры.
Решение. Средняя температура стенки равна
Т{ + Т2 35+115 0
Тт= 2 в 2 = 75С
Средний коэффициент теплопроводности можно найти с помощью линейной
интерполяции между двумя заданными значениями:
32 — km _ 100 — 75
32 — 26 — 100 — 0 *
Отсюда km = 30,5 Вт/(м-град). Плотность теплового потока через стенку на-
находится следующим образом:
2.5. ОДНОМЕРНАЯ СТАЦИОНАРНАЯ ЗАДАЧА
ТЕПЛОПРОВОДНОСТИ ПРИ НАЛИЧИИ ВНУТРЕННЕГО
ТЕПЛОВЫДЕЛЕНИЯ
До сих пор мы не рассматривали задач теплопроводности
с тепловыделением внутри материала. Подход к решению задач
с внутренним тепловыделением аналогичен тому, который при-
применялся в предыдущих разделах. Во-первых, из решения соот-
соответствующей формы уравнения энергии определяем распреде-
распределение температуры в материале. Решение зависит от двух по-
постоянных интегрирования, которые нужно найти, задавая два
граничных условия. Затем с помощью закона Фурье вычисляем
плотность теплового потока через материал.
Внутреннее тепловыделение может происходить при различ-
различных явлениях. В твердом материале могут протекать химические
реакции, как эндотермические, так и экзотермические. Экзотер-
Экзотермические реакции протекают с выделением тепла, а эндотер-
эндотермические— с поглощением тепла из материала, создавая отри-
отрицательный источник тепла или тепловой сток. Электрический ток
70 Глава 2
вызывает омический нагрев проводника. Кроме того, тепловы-
тепловыделение может происходить в радиоактивных материалах при
ядерных реакциях внутри материала.
Прямоугольные координаты
В качестве примера задачи с внутренним тепловыделением
рассмотрим плоскую стенку с равномерно распределенными по
ее объему источниками тепла. Интенсивность тепловыделения
в единице объема q'^ в нашем примере является постоянной
величиной. Предположим,
что одна поверхность пло-
плоской стенки имеет темпера-
температуру 7\, а вторая теплоизо-
теплоизолирована. Геометрия и гра-
граничные условия задачи по-
показаны на рис. 2.9.
Уравнение теплопровод-
теплопроводности для рассматриваемой
задачи имеет вид
q"G = constant
/с= constant
/// nnRPnXHOCTb
I
поверхность
d2T
///
Рис» 2.9. Теплопроводность через пло-
плоскую стенку при равномерном тепловы-
тепловыделении.
—0, B.54)
поскольку предполагается,
что распределение темпера-
температуры является установив-
установившимся и одномерным. Двукратно интегрируя уравнение B.54),
находим распределение температуры в виде
B.55)
где постоянные интегрирования С\ и С2 определяются из гра-
граничных условий.
Первое граничное условие имеет простой вид:
П0) = 7\. B.56)
Второе граничное условие требует, чтобы поверхность х = L
была теплоизолированной, или адиабатической. Поскольку к
этой поверхности происходит только кондуктивный перенос теп-
тепла, уравнение теплоизолированной поверхности записывается
следующим образом:
= 0,
пли
Я U-L й -JJ
¦?г =0.
Таким образом, на теплоизолированной границе твердого мате-
рияла градиент температуры равен нулю. Используя граничные
Стационарная теплопроводность 7\
условия B.56) и B.57) и соотношение B.55), находим распре-
распределение температуры в твердом теле:
Т(х)-Т{ q'?'x
Распределение температуры по х подчиняется параболическому
закону, причем максимум температуры достигается на теплоизо-
теплоизолированной поверхности х = L. Условие максимума темпера-
температуры dT/dx = 0 удовлетворяется на теплоизолированной по-
поверхности при х = L. Следовательно, максимальная темпера-
температура стенки определяется соотношением
Это соотношение можно переписать в безразмерной форме, как
показано в примере 1.10:
Следует также отметить, что вся энергия, генерируемая внутри
стенки, должна войти в кондуктивный тепловой поток, снимае-
снимаемый с поверхности х = 0. Через противоположную поверхность
тепло не может переноситься, поскольку она теплоизолирована;
аккумулироваться в материале энергия тоже не может, по-
поскольку предполагалось, что достигнуты установившиеся усло-
условия. Следовательно, баланс энергии на поверхности х = 0 тре-
требует, чтобы q |^0 = — q%'V, или
ах #«¦()
Дифференцируя соотношение B.58), можно показать, что это
условие автоматически удовлетворяется.
Задачи с неравномерным тепловыделением или с иными гра-
граничными условиями можно решить методом, аналогичным опи-
описанному выше.
Цилиндрические координаты
Типичной задачей теплопроводности в цилиндрических коор-
координатах с внутренним тепловыделением является задача о про-
проводе, по которому течет электрический ток (рис. 2.10). Сила
тока /, электрическое сопротивление провода R. Задана темпе-
температура поверхности проволоки 7V Интенсивность тепловыделе-
тепловыделения в единице объема провода q'^' = I2R/V. Если сила тока и
электрическое сопротивление постоянны, интенсивность внутрен*
него тепловыделения также постоянна.
72 Глава 2
Одномерное стационарное уравнение теплопроводности с по-
постоянной интенсивностью тепловыделения записывается в ци-
цилиндрических координатах в виде B.21)
B.59)
Двукратно интегрируя уравнение B.59), находим распределение
температуры в проволоке, выраженное через две произвольные
постоянные Сх и С2:
Т(г)=Сх\пг-
С2. B.60)
4k
Чтобы найти Ci и С2, нуж-
нужно задать два граничных усло-
условия. На первый взгляд мы
имеем лишь одно граничное
условие
Известно также, что темпера-
температура должна оставаться конеч-
конечной во всех точках проволоки.
Если попытаться рассчитать
температуру на оси проволоки
при г = 0 по формуле B.60),
то получим бесконечное значе-
значение, если сохранить в формуле
член с In r. Чтобы избежать физически нереального значения
температуры на оси проволоки, следует принять С\ = 0.
Можно определить второе граничное условие и по-другому,
если учесть, что на оси проволоки должно выполняться условие
теплоизолированности
dr |r=o
Ось должна быть теплоизолированной, поскольку она является
линией симметрии. Это условие приводит к тому же результату,
что и раньше, С\ = 0.
После того как из двух граничных условий найдены значения
С\ и С2, распределение температуры в проволоке выражается
соотношением
Рис. 2.10. Теплопроводность в цилин-
цилиндре при равномерном тепловыделе-
тепловыделении.
На оси проволоки достигается максимальная температура
„Г"Л
— ль i l о*
Стационарная теплопроводность 73
Пример 2.7. Найти максимальную силу тока, который можно пропускать
по алюминиевой проволоке [k = 204 Вт/(м-град)] диаметром 1 мм, чтобы
ее температура не превышала 200°С. Проволока подвешена в воздухе с тем-
температурой 25°С, коэффициент конвективной теплоотдачи от проволоки к воз-
воздуху равен 10 Вт/(м2-град). Электрическое сопротивление на единицу длины
проволоки 0,037 Ом/м.
Решение. Условия этого примера несколько видоизменены по сравнению
с ситуацией, для которой выведено уравнение B.61). Здесь известна темпе-
температура окружающего воздуха, а не температура поверхности проволоки. Сле-
Следовательно, граничным условием является условие равенства кондуктивного
теплового потока, подводимого к поверхности изнутри проволоки, конвектив-
конвективному тепловому потоку, отводимому воздухом. Математически это граничное
условие выражается следующим образом:
B.62)
Второе граничное условие, как и раньше, имеет вид
dT
dr
— 0. B.63)
Это граничное условие означает, что максимальная температура достигается
на оси проволоки.
Уравнение теплопроводности для этой задачи записывается в форме
B.59), а решение при постоянной интенсивности внутреннего тепловыделе-
тепловыделения выражается соотношением B.60). Применяя граничные условия B.62) и
B.63), находим распределение температуры в проволоке:
B.64)
_ . п.
2k "~ 2rokJ
Следовательно, максимальная температура проволоки равна
2hc \ 2k
Член, определяющий внутреннее тепловыделение, выражается через силу тока
и сопротивление на единицу длины соотношением
q° V A
и тогда
г т . /2
200 = 25 + . ^,м 0,037
2A0~3/2I0
. ,м 0,037 Г1 +
2яA0~3/2I0 L 2-204
Отсюда находим силу тока / = 12,2 А.
В ходе изложения принципов теплопроводности еще раз об-
обратим внимание читателя на безразмерные комплексы, появив-
появившиеся в этой главе. Уравнение B.64) записано в безразмерной
форме. Следовательно, комплексы q'a'rjhjr^ и hcrojk тоже яв-
являются безразмерными. Первый комплекс действительно являет-
является безразмерным параметром тепловыделения, а произведение
74 Глава 2
обоих комплексов является также безразмерным параметром
тепловыделения, впервые определенным соотношением B.16).
Второй безразмерный комплекс представляет собой число Био,
которое появляется в задачах смешанного (кондуктиэного и
конвективного) теплообмена.
Следует не только знать о существовании числа Био, но и
понимать его влияние на теплообмен. Число Био является отно-
отношением кондуктивного термического сопротивления твердого
тела к конвективному термическому сопротивлению жидкости.
Следовательно, физическими предельными значениями числа
J3ho являются
Bi-*0 при
и
или
или
оо.
Bi —> ОО ПрИ Лконв' или ii,c-
Когда число Био стремится к нулю, твердое тело практиче-
практически изотермично и изменение температуры происходит в основ-
основном в жидкости. При очень больших числах Био, наоборот, тер-
термическое сопротивление твердого тела существенно больше тер-
термического сопротивления жидкости, жидкость приблизительно
изотермична, а изменение температуры происходит в основном
в твердом теле.
2.6. ПЕРЕНОС ТЕПЛА В РЕБРАХ
Кондуктивный тепловой поток через твердое вещество часто
отводится от твердого тела посредством конвекции. Поскольку
конвективный тепловой по*
-Окружа-
-Окружающая
Периметр
ток пропорционален площа*
ди поверхности, интенсив*
ность рассеяния тепла с по*
верхности можно повысить,
просто увеличивая эту по-
поверхность. Это достигается
при помощи ребер.
На рис. 2.11 показано
простое прямое ребро по-
постоянного поперечного сече-
сечения А. Тепло распространя-
распространяется вдоль твердого мате-
материала ребра посредством
теплопроводности и отводит-
отводится от его поверхности окружающей жидкостью посредством кон-
конвекции. Температура окружающей среды Гоо, средний коэффи-
коэффициент теплопередачи равен Яс, причем обе эти величины счи-
считаются постоянными.
Чтобы найти распределение температуры в ребре, а затем
тепловой поток от его поверхности, необходимо сначала 9
Рис. 2.11. Ребро постоянного поперечно-
поперечного сечения.
Стационарная теплопроводность 75
вить тепловой баланс для элементарного объема ребра. Мы не
можем использовать уравнение теплопроводности, выведенное
в разд. 2.2, так как оно учитывает только теплопроводность и не
учитывает конвективный перенос тепла от поверхности тела.
В установившихся условиях кондуктивный тепловой по-
поток, подведенный к элементарному объему ребра в сечении х
(рис. 2.11), равен сумме кондуктивного теплового потока, отво-
отводимого из объема в сечении х + Дя, и конвективного теплового
потока, отводимого с поверхности элементарного объема:
Qx = qx+Ax + Яс Выражая два кондуктивных члена с помощью
заксша Фурье, а конвективный член с помощью закона охлаж-
охлаждения Ньютона, получаем
где Р —периметр ребра. Разделив все члены на Ах и перейдя
к пределу при Ajc->0, получаем дифференциальное уравнение
второго порядка относительно температуры:
S%-roo] = 0. B.65)
Уравнение B.65) можно привести к безразмерному виду, вводя
безразмерную температуру Q(x) = [T(x)— Too]/(Tb — Too) и без-
безразмерную линейную координату ? = x/L, где Ть — температура
основания ребра (х = 0). В новых переменных уравнение B.65)
записывается следующим образом:
-а B.66,
Безразмерный комплекс (HcPL2/kA) можно упростить, приведя
его к форме, напоминающей число Био. Произведение пери*
метра на длину равно общей площади поверхности ребра,
As = PL. В таком случае
где Л —площадь поперечного сечения ребра. Комплекс, выра-
выраженный формулой B.67), имеет размерность длины, и, следова*
тельно, его можно рассматривать как характерный линейный
размер ребра / = PL2/А. Теперь можно выразить безразмерный
комплекс, входящий в уравнение B.66), в виде
hcPL2 _ hcl f0 ft5n
аналогичном числу Био, применявшемуся при решении преды*
дущих задач сложного (кондуктивного и конвективного) тепло*
обмена. Следовательно, число Био для ребра имеет вид
B-69)
76 Глава 2
Можно было ожидать появления в какой-либо форме числа Био
в задаче о переносе тепла в ребре, поскольку в этой задаче со-
совместно действуют теплопроводность и конвекция.
Безразмерное уравнение переноса тепла в ребре B.66) мож-
можно теперь записать, используя число Био:
|g--(Bi)8 = 0. B.70)
Решение уравнения B.70) выражается соотношением
+ C2e<Bi>1/2 *. B.71)
Значения двух постоянных интегрирования можно опреде-
определить, как только будут заданы два граничных условия. Чаще
всего известна температура основания ребра Ть\ запишем это
в виде граничного условия:
Т@) = Ть. B.72)
Это соотношение будет служить первым граничным условием.
Возможны несколько вариантов второго граничного условия.
Рассмотрим три наиболее часто встречающихся граничных
условия.
Случай I. Очень длинное ребро, такое, что температура на
его торце равна температуре окружающей среды:
Т (/,-00) = ^, B.73)
или 9A) = 0.
Случай II. Ребро с теплоизолированным торцом при x=L:
или ir
Случай III. Ребро с конвективным отводом тепла от поверх-
поверхности торца. В этом случае граничное условие имеет вид
k\ TJ, B.75)
или
Используя граничное условие B.72) и одно из трех граничных
условий B.73) —B.75), мы получим три различных распределе-
распределения температуры в ребре постоянного поперечного сечения.
Если распределение температуры в ребре известно, можно
найти суммарный тепловой поток, отводящийся от ребра. Про-
Стационарная теплопроводность 77
ще всего найти этот тепловой поток, рассчитав кондуктивный
тепловой поток через основание ребра:
IL* BJ6)
Теперь определим распределение температуры в ребре и тепло-
тепловой поток, отводящийся от ребра, при задании каждого из трех
граничных условий.
Случай I. Для ребра бесконечной длины распределение тем-
температуры определяется выражением
9 (I) = Т® -/" = e-VSTt».
* Ь — 1 оо
Но длина ребра является неопределенной, поэтому удобнее найти
распределение температуры по х:
Q (*) = 'т. _ т— = e v * • (*•'')
J D -1 oo
Тепловой поток выражается формулой
^реб— \ исгк/± \1 ь 1 qq) — /VD1 ^ К1 b l <x>)% \4-1O)
Случай II. Для ребра с теплоизолированным торцом распре-
распределение температуры имеет вид
Ть - г» ch i
а тепловой поток от ребра определяется соотношением
<7реб= (BiI'2 ^ (Ть - Г..) th (BiI/2. B.80)
Случай ПК Для ребра с конвективной теплоотдачей на по-
поверхности торца распределение температуры выражается фор-
формулой
Q/gv_ Г F) — Poo _ ch [(BiI/2 (I — ?)] + (BiI/2 (Л/PL) sh [(BiI/2 A — ?)]
Ть — Т^ ~~~ ch(Bi)l/2 + (BiI/2(,4/PL)sh(BiI/2
B.81)
а тепловой поток определяется следующим образом:
_ /Ши/2 М /г _ т ^MBQ^+CBQ^WPDchCBi)/2 , . ,
_ (Bi) — (Гь - roo)ch(Bi)l/2+(BiI/2^//>L)sh(B.I/2. B.82)
Пример 2.8. Ребро из нержавеющей стали fife = 20 Вт/(м-град)] с круг-
круглым поперечным сечением имеет диаметр 2 см и длину 10 см. Ребро установ-
установлено на стенке, температура которой 300°С. Температура окружающей среды
50°С, коэффициент конвективной теплоотдачи 10 Вт/(м2-град). Торец ребра
теплоизолирован. Найти: а) тепловой поток от поверхности ребра; б) темпе-
температуру торца ребра; в) тепловой поток от поверхности, занятой основанием
78 Глава 2
ребра, если бы это ребро отсутствовало; г) тепловой поток, отдаваемый этим
же ребром, если нержавеющую сталь заменить гипотетическим материалом
с бесконечно большим коэффициентом теплопроводности.
Решение. Распределение температуры в ребре и тепловой поток от его
поверхности выражаются соответственно формулами B.79) и B.80). Прежде
всего рассчитаем характеристики ребра:
А = я/?2 = я @,01J = я • 10~4 м2,
10-я-0,02'@,1J
20-я-10
20-я-10
0,06283 Вт/град.
0,1
а) Тепловой поток равен
<7реб = (BiI/2-^- (Tb - Т„) th (BiI/2= 1,0 • 0,06283 C00—50) th (l,0)=l 1,96 Вт.
б) Температура торца ребра равна температуре при | = 1
е A) = ch° 1 L_ - o,648,
ch(BiI/2 ch A,0) 1,543
Г (L) = Гоо + 0,648 (Tb — Too) = 50 + 0,648 C00 — 50) = 212°C.
в) Если предположить, что коэффициент конвективной теплоотдачи от
поверхности стенки такой же, как от поверхности ребра, то тепловой поток
от стенки без ребра определяется следующим образом:
q s. hcA (Tb - Гоо) = 10 • я • 10~4 C00 - 50) = 0,785 Вт.
Применение ребра позволяет усилить теплоотдачу от поверхности, занятой
основанием ребра, в 11,96/0,785 = 15,2 раза.
г) Если коэффициент теплопроводности очень велик, число Био стре-
стремится к нулю. Кондуктивное термическое сопротивление ребра будет равно
нулю, и вся поверхность ребра будет иметь постоянную температуру, равную
температуре его основания. Тепловой поток от такого идеального ребра qaA
равен
дял = hcAs (Tb - Г,») — Юя • 0,02 • 0,1 C00 - 50) = 15,71 Вт.
Этот идеальный тепловой поток является максимально возможным потоком,
который отводится от ребра заданной формы. Ребро из нержавеющей стали
отдает тепло на A5,71—11,96)/15,71 =24% слабее, чем идеальное ребро.
Коэффициент эффективности ребра
Описанный выше метод расчета распределения температуры
в ребре и теплового потока от ребра применим только для
ребра постоянного поперечного сечения. Если ребро суживается
к концу, площадь поперечного сечения переменна и распределе-
распределение температуры определяется более сложным соотношением.
Распределение температуры и тепловой поток в случае трапе-
трапециевидного ребра выражаются через функции Бесселя. Полный
анализ этой задачи можно найти в работах [1,2].
Удобным параметром для расчета теплового потока от ребра
является коэффициент эффективности ребра. Коэффициент эф-
Стационарная теплопроводность 79
фективности ребра определяется как отношение теплового по-
потока от ребра к тепловому потоку от идеального ребра:
B.83)
^реальн
^идеальн
Идеальное ребро рассеивает максимальное количество тепла
при заданных форме ребра и температуре его основания. Иде-
Идеальное ребро имеет бесконечно большой коэффициент тепло-
теплопроводности, и, следовательно, температура его поверхности по
Окружающая
среда
Периметр Р
лПлощадь сечения А
20
Рис. 2.12. Коэффициент эффективности ребра постоянного поперечного сече-
сечения с теплоизолированным торцом.
всей длине постоянна и равна температуре основания. Реаль-
Реальное и идеальное ребра имеют одинаковую форму и одинаковую
температуру основания. Тепловой поток от идеального ребра
<7иДеальн = hcAs{Tb — Гоо), где As — площадь поверхности ребра,
омываемой жидкостью с температурой 7'«>.
Тепловой поток от реального ребра выражается соотноше-
соотношением
Яреальп = ^Л(Ть-Тж). B.84)
Теперь можно найти конкретные выражения для коэффициента
эффективности ребра. Например, коэффициент эффективности
ребра с постоянным поперечным сечением и теплоизолирован-
теплоизолированным торцом определяется следующим образом:
Уреальн
<7идеальн
ИЛИ
Т]=-
(В!I'2
hcPL (Tb -
th (Bi).
B.85)
График зависимости B.85) представлен на рис. 2.12. Видно, что
коэффициент эффективности быстро снижается с ростом числа
80 Глава 2
Окружающая
среда
К.
Био. Ребро с большим числом Био рассеивает тепло хуже, чем
ребро с меньшим числом Био. Если коэффициент эффективности
ребра мал, то может возникнуть ситуация, когда поверхность
без ребра отдает тепло интенсивнее, чем поверхность с ребром.
Этого следовало ожидать. Число Био выражает отношение кон-
дуктивного термического сопротивления к конвективному тер-
термическому сопротивлению. При большом числе Био кондуктив-
ное термическое сопротивление велико по сравнению с конвек-
конвективным, и поэтому температура
существенно падает вдоль рёб-
рёбра. Если число Био велико,
площадь, которая могла бы
эффективно отдавать тепло по-
посредством конвекции, занята
ребром с низкой теплопровод-
теплопроводностью, и в итоге наличие реб-
ребра вызывает снижение тепло-
теплоотдачи от стенки.
Для ребер нужно выбирать
высокотеплопроводные мате-
материалы: следовательно, метал-
металлические ребра предпочтитель-
предпочтительнее ребер из теплоизоляцион-
теплоизоляционных материалов. Если коэффи-
1,0
0;8
0,6
0,4
0,2
10
Рис. 2.13. Коэффициент эффективно-
эффективности ребра треугольного профиля.
циент конвективной теплоот-
теплоотдачи велик, число Био возрас*
тает и ребра не столь эффек-
эффективно усиливают теплоотдачу. Если в среде происходит фазо-
фазовый переход в результате кипения или конденсации, коэффи-
коэффициент теплоотдачи становится очень большим, как показывают
данные, приведенные в табл. 1.2. Следовательно, при фазовом
переходе в окружающей среде действительно возможна ситуа-
ситуация, когда ребро будет снижать теплоотдачу от плоской
стенки.
На рис. 2.12 представлены значения коэффициента эффек-
эффективности ребра постоянного поперечного сечения, когда его то-
торец теплоизолирован. Представленную зависимость в несколько
модифицированном виде можно применять для ребра с тепло-
теплоотдачей на торцевой поверхности. Тепловой поток от торцевой
поверхности можно компенсировать, фиктивно удлиняя ребро.
Величина приращения длины ребра должна выбираться таким
образом, чтобы тепловой поток от торца был равен тепловому
потоку с дополнительной поверхности ребра при теплоизолиро-
теплоизолированном торце.
В монографии Якоба [3] рекомендуется выбирать дополни-
дополнительную длину, равную отношению площади поперечного сече-
сечения ребра к его периметру. В таком случае скорректированная
Стационарная теплопроводность 81
длина ребра Lc, необходимая для удовлетворения граничного
условия теплоизолированного торца, равна Lc = L + А/Р. По-
Погрешность такого приближенного подхода, связанного с удли-
удлинением ребра для компенсации теплоотдачи с его торца, меньше
1%, если (hct/kI^2 < 1/4, где / — толщина ребра.
На рис. 2.13 и 2.14 представлены значения коэффициента
эффективности для некоторых других типов ребер. Дополни-
Дополнительные сведения о коэффициенте эффективности ребра приво-
приводятся в работе [4].
Рис. 2.14. Коэффициент эффективности кольцевого ребра прямоугольного про-
профиля.
Пример 2.9. Найти тепловой поток от прямоугольного ребра, показанного
на рисунке. Торец ребра не теплоизолирован, коэффициент теплопроводности
материала ребра 150 Вт/(м-град). Температура основания ребра 100°С, тем-
температура окружающей среды 20°С, коэффициент конвективной теплоотдачи
от ребра к окружающей среде 30 Вт/(м2трад),
К примеру 2.9.
82 Глава 2
Решение. Определим скорректированную длину ребра, учитывающую теп-
теплоотдачу с его торца:
Lc = L + -i = 20 + -^- = 20,95 см.
Число Био, рассчитанное по этой скорректированной длине ребра, равно
hcPl\ 30 • 0,84. @,2095J
М-ТГ- 150-0,008
а площадь поверхности ребра длиной Lc составляет
As » LCP =» 0,2095 .0,84 = 0,176 м2.
Коэффициент эффективности ребра (рис. 2.12) х\ = 0,775. Теперь находим
тепловой поток:
q = x\RcAs (Tb - rj == 0,775 • 30 • 0,176 A00 - 20) = 327 Вт.
Пример 2.10. На медном трубопроводе, по которому течет жидкость, ус-
установлено алюминиевое [/г = 200 Вт/(м-град)] кольцевое ребро. Наружный
диаметр трубопровода 8 см, температура жидкости 250°С, толщина ребра
0,5 см, его внешний диаметр 16 см. Температура окружающей среды 70°С,
коэффициент конвективной теплоотдачи 60 Вт/(м2-град). Найти тепловой по-
поток от ребра.
Окружающая
среда
т
I
x4f
К примеру 2.10.
Решение. Скорректированная длина ребра, учитывающая теплоотдачу с
его торца (рис. 2.14), равна
Lc = L + i = (.8-4) + -^- = 4,25 см.
Площадь поперечного сечения равна
Ар = Lct = 4,25 • 0,5 = 2,125 см2,
L3/2 (±\Ч> _ @>0425K/2 / 60 уП _
с \kAp) \ 200- 2,125 .10-V
Стационарная теплопроводность 83
Коэффициент эффективности ребра определяем с помощью рис. 2.14: ц =
= 0,89, а тепловой поток от ребра рассчитываем следующим образом:
Я = r\hcAs (Tb - Гто) = 4hc2n (г|с - г?) (Tb - Т^) =
= 0,89 • 60 • 2 • я @.08252 — 0,042) B50 — 70) = 314 Вт.
Предполагается, что температура основания ребра равна температуре жид-
жидкости внутри трубопровода, так как перепад температур на медной стенке
будет мал.
2.7. НЕОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ ЗАДАЧИ
ТЕПЛОПРОВОДНОСТИ
До сих пор мы предполагали, что температура в твердом
теле зависит только от одной пространственной координаты;
т. е. мы рассматривали одномерный процесс теплопроводности.
Однако теперь необходимо познакомиться с методами расчета
теплового потока и распределения температуры, которые могут
использоваться, когда температура зависит от двух или трех
пространственных координат. Решать двумерную или трехмер-
трехмерную задачу теплопроводности значительно сложнее, чем одно-
одномерную, и поэтому мы будем применять приближенные методы
и непрямой метод расчета — метод электротепловой аналогии.
Ввиду сложности и трудоемкости решения двумерной или
трехмерной задачи теплопроводности желательно решать по-
подобные задачи численным методом с использованием ЭВМ. По-
Поэтому в данный раздел мы включили две программы численного
расчета, написанные на алгоритмическом языке Фортран IV.
Мы выбрали в качестве примера программы довольно простого
типа, поэтому читатель может без особых затруднений просле-
проследить за ходом составления этих программ. Для задач, приве-
приведенных в конце главы, предлагаются более сложные программы.
Аналитические методы
Если требуется найти распределение температуры в твердом
теле в случае, когда температура зависит от двух или трех
пространственных координат, самый очевидный подход — попы-
попытаться получить точное решение основного уравнения. Уравне-
Уравнение стационарной теплопроводности в твердом теле с постоян-
постоянным коэффициентом теплопроводности при отсутствии внутрен-
внутреннего тепловыделения выведено в разд. 2.2 и имеет вид
Это уравнение Лапласа. Формы уравнения Лапласа в различ-
различных системах координат представлены в приложении I.
Уравнение Лапласа является линейным дифференциальным
уравнением в частных производных. Известно несколько стан-
стандартных методов его решения. Один из них, метод разделения
84 Глава
переменных, особенно полезен для решения задач теплообмена.
Мы не будем его здесь рассматривать; подробное описание этого
и других методов решения уравнения Лапласа можно найти в
работах [5—7].
После того как тем или иным методом распределение темпе-
температуры найдено, тепловой поток определяется с помощью закона
Фурье. В двух- и трехмерных си-
системах этот закон удобнее всего
выразить в векторной форме:
B.86)
•¦ constant
Рис. 2.15. Векторы плотности теп-
теплового потока (обозначены чер-
чертой сверху) и их геометрическая
связь с изотермами.
где VT — градиент температуры
(скалярной величины). В прило-
приложении I приведены формы запи-
записи градиента в прямоугольной,
цилиндрической и сферической
системах координат.
Градиент скалярной величи-
величины, такой, как температура, яв-
является вектором, т. е., согласно
векторной записи закона Фурье
B.86), плотность теплового пото-
потока q" — это вектор. Обычно мы
не рассматриваем плотность теп-
теплового потока как вектор, по-
поскольку она имеет размерность
мощности на единицу площади,
а ни одна из этих величин не яв-
является вектором. Однако удобно
вообразить, что тепло «течет»
в некотором направлении; по-
этому величину q" часто называют вектором плотности тепло-
вого потока.
Вектор плотности теплового потока обладает важным гео-
геометрическим свойством, присущим градиентам: он направлен по
нормали к изотерме, линии постоянной температуры, во всех
точках твердого тела. Для иллюстрации этого свойства на
рис. 2.15 показаны несколько изотерм и типичных векторов
плотности теплового потока в точках А, В я С твердого тела.
Длина каждого из трех векторов плотности теплового потока
пропорциональна местному градиенту температуры. Это зна-
значит, что в области тесного расположения изотерм градиент ве-
велик и плотность теплового потока также велика. В области, где
расстояние между изотермами больше, плотность теплового по-
потока соответственно меньше. На рис. 2.15 плотность теплового
потока в точке А больше, чем в точке В, где градиент темпера-
температуры меньше.
Стационарная теплопроводность 85
Поскольку мы считаем плотность теплового потока вектор-
векторной величиной, она должна обладать всеми свойствами векто-
векторов. Следовательно, можно разложить вектор плотности тепло-
теплового потока на составляющие в направлении осей координат.
Выражения для этих составляющих вектора можно найти, ис-
исходя из формы градиента. В прямоугольной системе координат
вектор плотности теплового потока выражается следующим об-
образом:
I+J +
Следовательно, плотность теплового потока в направлении х
равна
«;--*?•
Аналогичными соотношениями описываются составляющие век-
вектора плотности теплового потока в направлениях у и г.
Тепловой поток в направлении х через плоскую поверхность
Р, лежащую в плоскости (yf z), равен
$
Ар
Индекс Р означает, что в каждой точке поверхности нужно
найти производную температуры, а затем уже проводить инте-
интегрирование по поверхности.
Графический метод
Часто невозможно получить точные аналитические решения
уравнения теплопроводности для двумерных или трехмерных за-
задач. В случаях когда решение задачи аналитическими методами
найти трудно, можно использовать приближенные методы. Из
них сравнительно простым является графический метод, кото-
который позволяет определить тепловой поток с поразительной точ-
точностью.
Графический метод основан на геометрическом представле-
представлении векторной формы закона Фурье, согласно которому изо-
изотермы и линии постоянной плотности теплового потока (^'-ли-
(^'-линии) должны пересекаться только под прямым углом. Следова-
Следовательно, можно нанести изотермы и линии постоянной плотности
теплового потока и корректировать их, пока не будет удовлетво-
удовлетворяться условие их взаимной перпендикулярности.
Точность изображенного распределения температуры будет
непосредственно определяться точностью нанесения линий. При
небольшом опыте можно довольно быстро получать достаточно
точные результаты.
86 Глава 2
При использовании графического метода нужно проделать
следующие операции:
Операция 1. Начертить точную масштабную модель тела, для
которого нужно найти распределение температуры и тепловой
поток.
Операция 2, Нанести на модели линии постоянной плотности
теплового потока (^-линии) и изотермы. Во всех точках пере-
пересечения /'-линий и изотерм касательные к этим кривым долж-
должны быть взаимно перпендикулярны. Диагонали криволинейных
четырехугольников должны быть взаимно перпендикулярными
и делить друг друга пополам. Следует помнить, что соседние
изотермы и /'-линии не могут пересекаться. Изотермы перпен-
перпендикулярны адиабатическим границам, поскольку каждая адиа-
адиабатическая граница является линией постоянного теплового по-
потока (/' = 0). Кроме того, адиабатическими границами явля-
являются линии симметрии.
Операция 3. Корректировать изотермы и /'-линии до тех
пор, пока не будут удовлетворяться условия операции 2.
Когда вы сами будете удовлетворены точностью вашего ри-
рисунка, можно считать, что распределение температуры полу-
получено, после чего плотность теплового потока вычисляется, как
обычно, с помощью закона Фурье. Чтобы проиллюстрировать
графический метод решения, рассмотрим задачу определения
теплового потока через несущую двутавровую балку в стенке
печи. С двух сторон балка окружена изоляцией, расположенной
в стенке печи (рис. 2.16, а). Температура поверхности балки,
обращенной внутрь печи, равна Ти а температура наружной по-
поверхности балки 7Y Коэффициент теплопроводности материала
балки равен k.
Средняя линия балки является линией симметрии и, следо-
следовательно, адиабатической границей. На рис. 2.16,6 показаны
линии постоянной плотности теплового потока и изотермы на
масштабном чертеже балки.
Тепло течет по четырем каналам, ограниченным с каждой
стороны /'-линиями. Следовательно, суммарный тепловой по-
поток через половину балки равен
<7сум — II 4i*
На вставке показана типичная криволинейная четырехугольная
ячейка, тепловой поток через которую равен q?>. Применяя закон
Фурье для одиночной криволинейной ячейки на единицу длины
балки по нормали к чертежу, получаем
Tt. B.88)
Стационарная теплопроводность 87
Если каждую криволинейную ячейку нарисовать таким обра-
образом, чтобы выполнялось условие Дл: = Ауу то перепад темпера-
температур между каждыми соседними изотермами будет одинаков.
В таком случае перепад температур между двумя соседними
Линии
постоянных
значений
Я"
^Теплоизо-
^Теплоизолированная
поверхность
Изотермы
Рис. 2.16. Применение графического метода для двутавровой балки,
а-—физическая модель; б—масштабный чертеж балки и схема линий постоянных значе-
значений плотности теплового потока q" и изотерм.
изотермами можно выразить через полный температурный на-
напор поперек всей поверхности и число равных температурных
промежутков между изотермами М:
Т т (А-Ополн ¦* 1 — Т2 /о ОГк\
Тм-Т,=—ш— = ___. B.89)
Если <7"-линии делят тепловой поток на Af равных частей,
тепловые потоки по всем каналам, образованным (/"-линиями,
одинаковы, и суммарный тепловой поток через балку равен
B.90)
88 Глава 2
Подставляя соотношения B.88) и B.89) в равенство B.90),
находим суммарный тепловой поток для «квадратной» сетки,
т. е. для случая Ал: = Ау
7 сум
B.91)
Итак, можно найти тепловой поток, начертив сетку криволи-
криволинейных ячеек, а затем подсчитав число равных промежутков
температуры М и равных промежутков плотности теплового
потока N.
Пример 2.11. Найти тепловой поток через балку (рис. 2.16) при 7\ =
= 500°С, Т2 = 200°С и k = 70 Вт/(м-град).
Решение. В этом примере М = 13, N ш* 4, (ДГ)П0Лн = 300°С. Тепловой
поток на единицу длины балки определяется соотношением B.91)
q' = 2 [jL k (АПполн] - 12,923 Вт/м.
Коэффициент 2 вводится потому, что число N соответствует только половине
балки.
Формфактор теплопроводности S для тел различной формы.
q'^kS^-To) ?11 — 14]
Таблица 2.1
Форма тела
Обозначения
Формфактор
теплопроводности S
Труба, эксцентрично
расположенная в круглой
изоляции длиной L
Труба в квадратной
изоляции длиной L
arch
Ьг,2-е2\
2гоГ\ )
Щ0,54а/Г1)
Прямоугольный канал в изоляции т
равномерной толщины; уо
площадь поверхности канала Ах,
площадь наружной
поверхности изоляции Аг
t
i
7
А
\*~
а
/
/ 1
t
t
/
если а,Ь,с> -
если а,Ьгс<-
Стационарная теплопроводность 89
Форма тела
Обозначения
Формф актор
теплопроводности 5
Тонкая прямоугольная пластина
длиной!, в полуограниченной
среде
(z«0)
lira
Горизонтальная труба длиной L
в полуограниченной среде
2irL
arch (г/г,)
B>2ri)
Сфера в полуограниченной среде
Две параллельные трубы длиной L
в неограниченной среде
Тонкий горизонтальный диск
в полуограниченной среде
1 —L,
(z->oo)
arch
I 2/y0 )
r, (z-0)
8r,
Вертикальный цилиндр длиной L
в полуограниченной среде
L
L
к
1
-*|2r.U-
lnBL/r,)
Полусфера, заглубленная
в полуограниченную среду
96 Глава 2
Отношение N/M, входящее в выражение B.91), называется
формфактором теплопроводности S = N/M1), так что тепловой
поток можно выразить через S
q' = kS (ЛГ)ПОЛН. B.92)
В табл. 2.1 указаны значения формфактора теплопроводности
для некоторых тел различной формы.
Известны значения формфактора теплопроводности для неко-
некоторых тел простой формы. Например, если преобразовать вы-
выражение B.26) к виду соотношения B.92), то формфактор
теплопроводности для плоской стенки равен A/L. Для полого
цилиндра длиной / формфактор теплопроводности равен
2зг//1п (го/ri). Отметим, что формфактор имеет размерность
длины.
Метод электротепловой аналогии
Установившийся электрический потенциал Е в материале с
постоянным удельным сопротивлением без внутренних источни-
источников потенциала определяется уравнением Лапласа, тем же урав-
уравнением, которому подчиняется распределение температуры в
твердом теле с постоянными теплофизическими свойствами без
внутренних источников тепла. Аналогичны и соотношения для
скорости переноса тепла (закон Фурье) и для скорости пере-
переноса заряда (закон Ома), как показано в приведенной ниже
таблице. Поскольку процессы переноса тепла и заряда описы-
описываются аналогичными уравнениями, говорят, что имеет место
аналогия между этими процессами.
Аналогия уравнений переноса электричества и тепла
Тепло
Закон сохранения у2?г=0 у2Г = 0
Скорость переноса / * ^- ц * -=—
Безразмерный потенциал в электрической системе аналоги*
Чен безразмерной температуре в тепловой системе. В наших
интересах использовать эту аналогию, так как напряжение легче
измерять, чем температуру. Определяя положение линий по-
постоянного потенциала, можно найти положение изотерм.
Аналогия используется следующим образом. Из электропро*
водной бумаги, имеющейся в продаже, вырезают масштабную
1) Данное выражение для формфактора характеризует тепловой поток
на единицу длины балки. В общем случае полного потока тепла через тело
формфактор имеет размерность длины. — Прим. ред.
Стационарная теплопроводность 91
модель исследуемого тела и к бумаге подключают электриче-
электрическую батарею для создания электродвижущего потенциала на
модели. Электрические граничные условия на бумаге должны
быть аналогичны соответствующим тепловым граничным усло-
условиям. Изотермическая граница соответствует на модели гранич-
граничному условию в виде постоянного потенциала. Это легко осу-
осуществить, если покрыть границу краской, имеющей высокую
электропроводность, и подключить ее к батарее. Условие тепло-
изолированности границы можно смоделировать в электриче-
электрической системе путем электрической изоляции границы, для чего
служит просто край бумаги.
Определив с помощью пробника, соединенного с вольтмет-
вольтметром, положение линий постоянного потенциала, можно отклю-
отключить граничные условия и найти положение ортогональных ли-
линий— линий постоянной силы тока. Эти линии соответствуют
линиям постоянной плотности теплового потока. Применяя опи-
описанный метод, можно точно построить всю совокупность криво-
криволинейных четырехугольных ячеек на поверхности модели и опре-
определить величину формфактора теплопроводности точнее, чем
с помощью графического метода.
Преимущество метода электротепловой аналогии заклю-
заключается в том, что он позволяет найти положение изотерм и линий
постоянной плотности теплового потока без помощи метода проб
и ошибок, как в графическом методе, но его недостатком яв-
является применение специального оборудования. Для графиче-
графического же метода требуются лишь карандаш, бумага и терпение.
Однако практически применимость обоих методов ограничена
двумерными задачами с простыми граничными условиями, та-
такими, как изотермические и теплоизолированные границы. Бо-
Более подробное описание метода электротепловой аналогии мож-
можно найти в работах [8, 9].
Численные методы
Численные методы являются мощным и гибким средством
решения задач стационарной теплопроводности. Их можно
успешно применять для решения задач, которые трудно решить
другими методами. Например, с помощью численных методов
можно решать задачи с излучением на границах или с внутрен-
внутренним тепловыделением. Графический метод и метод электро-
электротепловой аналогии неэффективны для решения задач этих двух
типов.
При использовании численного метода конечных разностей
твердое тело представляют в виде совокупности узлов. Для
каждого узла записывают баланс энергии, получая в итоге алге-
алгебраическое уравнение для температуры в каждом узле. Отдель-
Отдельные уравнения записывают для каждого узла, расположенного
92 Глава 2
на границе твердого тела. В результате применения метода
конечных разностей получают п алгебраических уравнений для
п узлов в твердом теле. Эти п алгебраических уравнений заме-
заменяют одно уравнение в частных производных с соответствую-
соответствующими граничными условиями.
Если узлов в твердом теле сравнительно мало, можно решить
полученную систему алгебраических уравнений стандартными
математическими методами. При возрастании числа узлов для
Рис. 2.17. Расположение узлов внутри двумерного твердого тела; толщина
тела d, коэффициент теплопроводности k.
получения точного решения требуется слишком много времени.
В этом случае полезно применить приближенные методы реше-
решения. Одним из них является метод релаксации, который мы рас-
рассмотрим прежде всего.
Когда уравнений становится много, необходимо использовать
программируемые калькуляторы и ЭВМ. В этот раздел вклю-
включены две программы численного расчета, чтобы показать, какие
типы двумерных задач теплопроводности лучше всего решать
численными методами на цифровых вычислительных машинах.
Чтобы проиллюстрировать метод конечных разностей, рас-
рассмотрим двумерную задачу теплопроводности. Во-первых, раз-
разделим твердое тело на равные элементарные прямоугольники.
Представим, что масса каждого элементарного прямоугольника
сосредоточена в его центре, называемом узлом. На рис. 2.17
показана внутренняя область типичного двумерного твердого
Стационарная теплопроводность 93
тела. Каждый элементарный прямоугольник имеет длину Ах в
направлении х и длину Д# в направлении у. Узел, обозначен-
обозначенный символом 0, окружен четырьмя соседними узлами. Пред-
Представим, что каждый узел связан с соседними узлами тонкими
теплопроводными стержнями. Тепло может передаваться только
по этим воображаемым стержням. Другими словами, кондук-
тивный перенос тепла между узлами 0 и 1, который в действи-
действительности происходит в непрерывном материале через поверх-
поверхность раздела высотой Ду, мысленно заменяется переносом теп-
тепла через воображаемый стержень, соединяющий узлы 0 и 1.
В установившихся условиях баланс энергии для узла 0 при
отсутствии внутреннего тепловыделения записывается в форме
Е^о = О. B-93)
Затем, применяя закон Фурье для каждого члена, выражаем
это уравнение через температуры в узлах. Например, первый
член принимает вид
Та-То
где градиент температуры определяется посередине между
двумя узлами, a d — толщина двумерного тела по нормали к
плоскости чертежа. Аналогичные выражения можно записать
для остальных трех членов:
* kAxd
qA+t~kbxd—^—.
Если ячейки сетки имеют квадратную форму, то Ах = Ау>
и каждое из уравнений для теплового потока становится неза-
независимым от формы тела. Однако погрешность замены градиента
температуры конечной разностью двух температур зависит от
размера каждой ячейки. Чем меньше ячейка, тем точнее аппрок-
аппроксимируется градиент температуры.
Подставляя четыре конечно-разностных соотношения в урав-
уравнение B.93), можно видеть, что для сетки с квадратными ячей-
ячейками при постоянном коэффициенте теплопроводности баланс
энергии для узла 0 сводится просто к соотношению между тем-
температурой в этом узле и температурами в четырех соседних
узлах:
Тх + Т2 + Т3 + Т4 - 4Г0 = 0. B.94)
Соотношение вида B.94) применимо ко всем внутренним
узлам, т. е. ко всем узлам, не лежащим на границе твердого
94 Глава 2
Окружающая
среда
тела и окруженным со всем сторон равноотстоящими квадрат-
квадратными ячейками сетки.
Иначе выражается баланс энергии для узлов, расположен-
расположенных на границе твердого тела. Рассмотрим, например, узел О,
расположенный на границе твердого тела, которая находится в
контакте с окружающей средой. Температура среды равна Гоо,
коэффициент конвектив-
конвективной теплоотдачи от окру-
окружающей среды к твердо-
твердому телу равен Яс. Соот-
Соответствующая схема пред-
представлена на рис. 2.18.
Каждый граничный узел
расположен в центре со-
соответствующего элемен-
элементарного прямоугольника.
Отметим, что масса, со-
соответствующая каждому
граничному узлу, равна
половине массы, соответ-
соответствующей каждому вну-
внутреннему узлу.
Узел 0, расположен-
расположенный на границе, может
обмениваться кондуктив-
ным потоком тепла с тре-
тремя соседними узлами в
твердом теле и, кроме
того, конвективным теп-
тепловым потоком с окру-
окружающей средой. Следовательно, баланс энергии для узла 0 за-
записывается следующим образом:
Рис. 2.18. Расположение узлов в двумерном
твердом теле, омываемом жидкостью; тол-
толщина тела d> коэффициент теплопроводно-
теплопроводности ?.
Первые три члена выражают кондуктивный тепловой поток в
твердом теле, а последний — конвективный тепловой поток к
узлу 0 от окружающей среды, параметры которой обозначены
индексом оо. Подставляя конечно-разностные аппроксимации
закона Фурье для первых трех членов и закона Ньютона для
последнего члена, получаем
~2~ Дй ' ~2~ Ди *""
Дл:
B.95)
Соотношение B.95) можно упростить, если выбрать сетку с
квадратными ячейками, Ах = Ау. В этом случае оно сводится
Стационарная теплопроводность 95
к виду
\(Т2 + Т3)
То = 0. B.96)
Температуры в граничных узлах зависят от температур в со-
соседних узлах и от параметра hckx/k. Этот безразмерный комп-
комплекс имеет форму числа Био.
Применение конечно-разностного метода иллюстрируется на
следующем примере.
Пример 2.12. Определить стационарное распределение температуры и теп-
тепловые потоки от всех четырех поверхностей двумерного твердого тела, пока-
показанного на рисунке. Две поверхности изотермичны, третья теплоизолирована,
а на четвертой происходит конвективный теплообмен.
Поверхность В
Поверхность А |
Лс=5ОВт/(м2.град)
7!=50°С
20 см
А:=1 Вт/(м-град)
«7с=0
Толщина d
L
^лтеплоизолиро
I
^лтеплоизолиро-
I
20 см
.Поверхность/)
7J °C
Ay
2
Ay
L
О
5
К примеру 2.12.
Решение. Сначала нанесем на тело сетку с квадратными ячейками, как
показано на рисунке. Пронумеруем узлы цифрами от 1 до 9. Основная ячей-
ячейка сетки представляет собой квадрат со стороной Ах = Ау = 10 см. Неиз-
Неизвестны температуры только в трех узлах: 4, 5 и 6. Узел 5 является внутрен-
внутренним, так что применимо соотношение B.94):
Узел 4 лежит на границе, на которой осуществляется конвективный перенос
тепла, поэтому применимо соотношение B.96)
Y Gi + Т7) + Т5 + (В1) Т„ - B + BI) Г4 -0,
96 Глава 2
где
hcAx 50-0,10
.
Узел 6 расположен на теплоизолированной границе, и для него баланс энер-
энергии записывается следующим образом:
или j (Г. + Г9) + Г5 - 2Гб = 0.
Температуры в остальных шести узлах известны, так что для них записывать
баланс энергии не нужно. В этих шести узлах достигаются следующие тем-
температуры: Т{ = Т2 = Ть = 200°С, Т7 = Т8 = Т9 = 100°С. Подставляя эти
значения в уравнения энергии для узлов 4—6, получаем
400 + Г5 - 7Г4 = 0 (узел 4),
300 + ТА + Гб — 4Г5 = 0 (узел 5),
150 + Гб —2Гв = 0 (узел 6).
Температуры Г4 Т5 и Г6 можно найти, решая эту систему трех уравнений.
В результате получаем Г4 = 75,5°С, Тъ = 128,7°С, Т6 = 139,4°С.
Чтобы определить тепловые потоки на единицу толщины для каждой по-
поверхности, используем конечно-разностную форму закона Фурье для кондук-
тивного теплового потока и закона Ньютона — для конвективного.
На поверхности Л теп |овой поток на единицу толщины, направленный в
твердое тело, равен
я а - К ьу [Тоо7Тх + (г~ - т<) + Тоо7Т?]в 27>5 Вт/М-
Следовательно, с поверхности А твердого тела отводится конвективный теп-
тепловой поток 627,5 Вт/м. Знак минус показывает, что тепловой поток отдается
твердым телом.
На поверхности В тепловой поток на единицу толщины, направленный
в твердое тело, равен
7 + ? + <7з->б + <7'->оо =
^ 7 2 ^д^~)+ с~2 ^i-^)8* 538>8
Поверхность С теплоизолирована, поэтому <7С = 0. На поверхности D
f (T7 - Г^) = 88,8 Вт/м.
Чтобы проверить полученные значения теплового потока, используем извест-
известное требование, чтобы в установившихся условиях суммарный тепловой по-
поток в твердое тело был равен нулю:
<4м = Яа + Яв + Яс + Яо^- 627,5 + 538,8 + 0 + 88,8 «* 0,1 Вт/м.
Величина результирующего теплового потока в твердое тело показывает уро*
вень точности решения данной задачи методом конечных разностей.
Стационарная теплопроводность 97
Метод релаксации
В примере 2.12 твердое тело делилось на элементарные
ячейки с помощью сетки, в трех узлах которой температура
была неизвестна. Получалась система трех алгебраических урав-
уравнений с тремя неизвестными. Если бы требовалось повысить точ-
точность решения, применяя более частую сетку, появилось бы
больше узлов с неизвестными температурами и надо было бы
решать дополнительные уравнения для их определения. В об-
общем случае каждый узел с неизвестной температурой приводит
к появлению одного алгебраического уравнения, которое нужно
решать совместно с уравнениями для остальных узлов.
Когда число узлов сравнительно мало, как это было в при-
примере 2.12, решение системы уравнений находится без особого
труда. Однако, когда уравнений становится много, приходится
решать систему уравнений приближенным методом. При реше-
решении задач теплопередачи иногда применяют метод релаксации.
Хотя этот метод редко используют для решения практических
задач, он является хорошим педагогическим приемом, позво-
позволяющим показать, как можно решить простые задачи числен-
численными методами. Кроме того, принципиальная схема применения
метода релаксации поможет нам понять чаще используемые на
практике численные методы, которые будут описаны ниже в
этой главе.
Цель метода релаксации —определить температуры в каж-
каждом узле твердого тела таким образом, чтобы приближенно
удовлетворялись уравнения энергии в узлах. Вместо того чтобы
полагать правые части уравнений энергии, например B.94) и
B.96), равными нулю, их можно принять равными некоторой
величине, называемой остаточным членом. Затем следует систе-
систематически изменять температуры до тех пор, пока остаточный
член не станет достаточно малым. Величина остаточного члена
характеризует степень точности определения температур во всех
узлах. Если остаточные члены в уравнениях энергии для всех
узлов становятся равными нулю, температуры в узлах являются
точными решениями системы уравнений энергии.
Чтобы показать, как пользоваться методом релаксации, при-
применим его к системе трех уравнений, полученных в примере
2.12. Три уравнения энергии в этом примере имеют вид
150 + Г5 —2Г6 = /?6.
Правые части этих уравнений заменены остаточными членами
Ri, где индекс — это номер соответствующего узла. Наша задача
состоит в нахождении таких значений Г4, Г5 и Гб, чтобы вели-
величины остаточных членов были достаточно малыми. Величины
4 Зак. 487
§8 Глава 2
остаточных членов будут определять точность приближения
температуры. Отметим, например, что при ошибке Г4 в один
градус остаточный член будет равен семи градусам. Остаточные
члены имеют размерность температуры. После того как полу-
получены уравнения энергии для всех узлов, применяем метод ре-
релаксации, выполняя последовательно действия в соответствии
со следующими четырьмя операциями.
Операция 1. Сначала нужно задать приближенные значения
всех неизвестных температур в узлах. Мы должны использовать
наши знания теории теплопередачи, чтобы задать температуры
как можно точнее. Предельные значения температур в рассма-
рассматриваемой задаче — это 50°С (температура окружающей среды)
и 200°С (температура верхней поверхности твердого тела). Сле-
Следовательно, ожидаемые температуры в установившихся усло-
условиях должны быть заключены между этими значениями. Можно
ожидать, что самой низкой из трех температур будет Г4, а са-
самой высокой — Г6, поскольку узел 6 находится на теплоизолиро-
теплоизолированной границе. В качестве начального приближения зададим
следующие значения температур: Г4 = 80°С, Г5=100°С, Гб =
= 150°С.
Операция 2. Следующая операция состоит в подстановке на-
начальных температур в приближенные уравнения энергии для уз-
узлов и вычислении остаточных членов. В нашем примере R* =
= — 60°С, /?5=130°С, /?6 = —50°С. Поскольку остаточные чле-
члены не равны нулю, следует продолжать изменять температуры,
стремясь свести остаточные члены к нулю.
Операция 3. Чтобы уменьшить остаточные члены, изменим
температуру, соответствующую наибольшему по абсолютной
величине остаточному члену, стремясь свести величину этого
остаточного члена к нулю. Часто можно ускорить сходимость
к истинным значениям температур, если изменить температуру
в рассматриваемом узле таким образом, чтобы остаточный член
был равен не нулю, а некоторой малой величине, противополож-
противоположной по знаку остаточному члену до изменения температуры. Та-
Такой процесс называется избыточной релаксацией.
В нашем примере наибольший остаточный член соответ-
соответствует узлу 5. Из разностного уравнения баланса энергии для
узла 5 следует, что, если увеличить Г5 на 35°С, значение R5
уменьшится на 140°С и станет равным сравнительно небольшой
величине противоположного знака. Заметим, что при изменении
Тъ изменятся также 7?4 и R&. Итак, получаем новые значения
(второе приближение) трех температур и соответствующих оста-
остаточных членов:
Г4 = 80°С, /?4 = -25°С,
Г5=135°С, /?5 = -Ю°С,
Г6=150°С, Яб=-15°С.
Стационарная теплопроводность 99
Операция 4. Следующая операция процесса релаксации со-
состоит в повторении действий предыдущей операции, пока не бу-
будет достигнута требуемая точность. Теперь наибольшим явля-
является остаточный член #4, поэтому изменяем Г4 таким образом,
чтобы член /?4 стал равным малой положительной величине.
Например, уменьшаем Г4 на 4°С. Получаем новые значения
(третье приближение) температур и остаточных членов:
Г4 = 76°С, /?4==3°С,
Г5=135°С, Я5-=-14°С,
, #6=- 15°С.
Повторяем эту операцию дважды, изменяя сначала Гб, а затем
7V Уменьшая Гб на 10°С, получим
Г4 = 76°С, /?4 = 3°С,
Г5==135°С, /?5 = -24°С,
76=140°С, /?6 = 5°С.
Уменьшая Т$ на 7°С, получим
Г5=128°С, /?5 = 4°С,
Г6=140°С, RQ=-2°C.
После четырех операций релаксации все температуры отклоня-
отклоняются от точных значений, найденных в примере 2.12, не более
чем на ГС. Результаты действий при предыдущих операциях
лучше всего свести в таблицу типа табл. 2.2. Систематизируя
операции релаксации и регистрируя получаемые результаты в
таблице, можно свести к минимуму выполняемую работу.
Таблица 2.2
Сводка значений температур и остаточных членов для примера 2.12
Операция
Начальная оценка
Начальные остаточные члены
Увеличение Ть на 35
Новые остаточные члены
Уменьшение П на 4
Новые остаточные члены
Уменьшение Те на 10
Новые остаточные члены
Уменьшение Т$ на 7
Новые остаточные члены
т<
80
80
76
76
76
-60
-25
3
3
—4
100
135
135
135
128
130
-10
-14
-24
4
150
150
150
140
140
#6
-50
-15
-15
5
—2
100 Глава 2
Метод конечных разностей с использованием релаксации
можно распространить на случай цилиндрических координат;
соответствующие разностные уравнения приведены в работе
"[5].
Таблица 2.3
Разностные уравнения баланса энергии для граничных узлов
двумерных тел; сетка с квадратными ячейками (^x = Ку)
Рассматриваемый случай
Схема
Разностное уравнение
Плоская поверхность,
изотермическая граница
Плоская поверхность,
теплоизолированная граница
Плоская поверхность,
омываемая жидкостью
Внешний угол,
обе поверхности
теплоизолировании
Внешний угол,
обе поверхности
омываются жидкостью
--¦ Окружающая
~2~ Окружающая
. среда"
\ 1
*
q"— плотность теплового
потока на поверхности)
-B+В1OЪ=Л0
-A+Bi)ro-J?o
Стационарная теплопроводность 101
Внутренний угол,
обе поверхности
теплоизолированы
Внутренний угол,
обе поверхности
омываются жидкостью
Окружающая/
среда/
Если в твердом теле происходит внутреннее тепловыделение,
метод релаксации применим без каких-либо усложнений. Пред-
Предположим, что в некотором внутреннем узле 0 интенсивность
тепловыделения на единицу объема составляет q^. Баланс
энергии для этого узла в двумерном теле, окруженного четырьмя
соседними узлами (рис. 2Л7), записывается в виде
Заменяя каждый член, выражающий составляющую теплового
потока, конечно-разностной аппроксимацией закона Фурье, по-
получаем
kAyd
Ал: Ayd ^ 0. B.97)
Если сетка с квадратными ячейками, уравнение B.97) сводится
к следующему:
т -4-Г JL.T 4-Г —47 4- агп = Q A ОЯТ
Если узел находится на границе твердого тела, форма раз-
разностного, уравнения баланса энергии зависит от типа гранич-
граничного условия на поверхности. Например, такое уравнение ба-
баланса энергии для узла, расположенного на плоской поверхно-
поверхности, омываемой жидкостью, имеет вид B.96). В табл. 2.3 ука^
заны разностные уравнения баланса энергии при других гранич-
граничных условиях. В каждом случае разностное уравнение баланса
энергий записано для узла 0, ' -. .¦ _ .
102 Глава 2
До сих пор мы рассматривали задачи, в которых температура
зависела только от двух линейных координат. Однако методы,
разработанные для двумерных задач, можно легко распростра-
распространить и на трехмерные задачи. Например, если рассмотреть ти-
типичный узел 0 в твердом теле с постоянными теплофизическими
Рис. 2.19. Расположение узлов внутри трехмерного твердого тела.
свойствами при отсутствии внутреннего тепловыделения, кото-
который окружен шестью узлами (рис. 2.19), то баланс энергии для
узла 0 записывается в виде
<7i»o + Я2+0 + ?з-»о + ?4-*о + <75->о + «Wo — 0. B.99)
Уравнение B.99) можно записать через температуры в каждом
узле, применяя для каждой составляющей теплового потока за-
закон Фурье:
= 0. B.100)
Если сетка состоит из кубических ячеек, т. е. Ал; = Ау = Дг,
уравнение B.100) можно упростить, получая в итоге
Tx + T2 + Tz + TA + Ts + Tt-bT0 = 0. B.101)
Следовательно, разностное уравнение баланса энергии для узла
в трехмерной задаче при отсутствии тепловыделения, если узел
находится внутри твердого тела и каждый из узлов расположен
в центре кубической ячейки, означает просто, что сумма темпе-
температур всех окружающих узлов равна ушестеренной температуре
Стационарная теплопроводность 103
центрального узла. Уравнение B.101) подобно по форме ба-
балансу энергии для узла в двумерной задаче B.94).
Если в трехмерном теле имеются внутренние источники энер-
энергии с интенсивностью тепловыделения в единице объема q^',
разностное уравнение баланса энергии для внутреннего узла
имеет вид
T{ + T2 + TZ + TA + T5 + TQ-6Г0 + Чо \ = 0. B.102)
Приведенные в табл. 2.3 разностные уравнения баланса энер-
энергии для узла, расположенного на границе двумерного тела,
можно обобщить на случай трехмерных задач. Предлагается
вывести эти уравнения в качестве упражнения.
Матричный метод
Методом релаксации удобно решать задачи теплообмен^
когда число разностных уравнений баланса энергии сравни-
сравнительно невелико. Однако он неудобен для численных расчетов
на ЭВМ, поскольку необходимо выбирать уравнение с наиболь-
наибольшим остаточным членом. ЭВМ работает последовательно, й
трудно добиться, чтобы процесс выбора максимального значен
ния из некоторого ряда проходил достаточно эффективно. При
решении задачи на ЭВМ вместо метода релаксации применя-
применяются другие методы.
Если для повышения точности или при больших размерах
тела требуется решить систему большого числа разностных
уравнений, желательно применять ЭВМ. При расчете на ЭВМ
распределения температуры в двумерном или трехмерном твер-
твердом теле удобно использовать метод обращения матрицы. Это?
метод основан на представлении системы уравнений баланса
энергии для узлов в форме матрицы. Например, если мы пред^
ставили твердое тело в виде совокупности п узлов, система раз*
ностных уравнений баланса энергии может быть записана в виде
B.103)
+ ... + аппТп = Ьп,
где ац и bi — известные постоянные, а Г/ — неизвестные темпе-
температуры.
Используя матричные обозначения, систему уравнений
B.103) можно записать в сжатом виде:
АТ = В, B.104)
104 Глава 2
где А — квадратная матрица коэффициентов (#
форму
ап п
' °22 '"
> имеющая
B.105а)
а Т и В — столбцовые матрицы, состоящие из п элементов каж-
каждая:
¦ в-
B.1056)
Чтобы вычислить неизвестные температуры, нужно найти обра-
обращенную матрицу А, после чего температура определяется из
уравнения
Т = А~1В. B.106)
Если элементы обращенной матрицы записать в виде
С2п
B.107)
то неизвестные температуры в узлах определяются уравнениями
B.108)
+cnnbn =
Поскольку все величины bi известны, задача вычисления темпе-
температур сводится к определению обращенной матрицы А. Обра-
Обращенную матрицу можно найти с помощью стандартных матема-
математических методов [6], если число узлов не слишком велико. При
большом числе узлов элементы обращенной матрицы можно
быстро рассчитать на ЭВМ с помощью подпрограмм из библио-
библиотеки стандартных программ. Методика численного расчета ил-
иллюстрируется на следующем примере.
Пример 2.13. Найти стационарное распределение температуры в двумер-
двумерном твердом теле, показанном на рисунке а. Использовать сетку с квадрат-
квадратными ячейками Д* = Ау = 5 см. Две границы изотермичны, третья теплоизо*
Стационарная теплопроводность 105
лирована, а на четвертой происходит конвективный теплообмен. Сравнить ре-
результаты расчета с решением примера 2.12.
Г=200°С
Окружающая
среда
Лс=50Вт/(м2-К)
Т=50°С
V/
у. Поверхность
^теплоизоли-
у рована
К примеру 2.13(а).
Решение. На теле строится сетка с квадратными ячейками, как показано
на рисунке б. Все узлы с неизвестными температурами пронумерованы. Тем-
Температуры в узлах верхней и нижней поверхностей известны, нужно найти
температуры в 15 узлах. Для решения системы 15 уравнений методом релак-
релаксации требуется много времени, поэтому разумной альтернативой является
проведение численного расчета на ЭВМ с использованием подпрограммы об-
обращения матрицы.
-t—-1—
kjl-U-
1—L
o i <
о I с
О 1 <
-±4_jl5
К примеру 2.13F).
Прежде всего нужно найти значения элементов матриц А и В, входящих
в уравнение B.103). Все разностные уравнения баланса энергии для вну-
внутренних узлов имеют вид B.94). Разностные уравнения для граничных уз-
узлов можно выписать из табл. 2.3. В эти уравнения входят следующие по-
постоянные параметры: Bi = ПЛх/k = 50-0,05/1 = 2,5; (В1)Гоо = 2,5-50 =
= 125°С; 2 + Bi = 4,5. Система 15 разностных уравнений баланса энергии в
матричной форме B.103) записывается следующим образом:
узел 1: — 4.571, + Т2 + 0,5Гб = —225,
узел 2: Тх — 4Т2 + Тг + Т7 = —200,
узел 3: Т2 — 4Г3 + Г4 + Г8 = —200,
узел 4: Г3 — 4Г4 + Т5 + Т9 = —200,
узел 5: ТА — 2Т5 + 0,5Гш = —100,
узел 6: 0,57, — 4,5Г6 + Т7 + 0,5Гп = —125,
узел 7: Т2 + Т6 - 4Т7 + ТЬ + Т12 = 0,
106 Глава 2
узел 8: Г3 + Т7 - 4Т8 + Г9 + Г13 = О,
узел 9: Т4 + Т% — 4Г9 + Г10 + Г14 = О,
узел 10: 0,5Г5 + Т9 — 2Т]0 + 0,5Г15 = О,
узел 11: 0,5Гб — 4,5ГП + Г12 = —175,
узел 12: Т7 + Ти — 4712 + Ji8 = —100,
узел 13: Гв + Тп — 4Г18 + Гн = —100,
узел 14: Т9 + Г18 - 4Г14 + Г1Б = —100,
у?ёл 15: 0,5710 + Ти — 2715 = —50.
Теперь можно найти элементы матриц А и В, анализируя коэффициенты этих
15 уравнений. Постоянные в правых частях уравнений являются элементами
столбцевой матрицы В. Многие элементы матрицы А равны нулю, а ненуле-
ненулевые элементы группируются около главной диагонали.
Следующей операцией является обращение матрицы А. Элементами об-
обращенной матрицы являются величины сц [см. уравнение B.107)]. Обраще-
Обращение матрицы такого размера вручную потребует много времени. К счастью,
имеются стандартные библиотечные подпрограммы, которые можно приме-
применить в короткой программе численного расчета 15 неизвестных температур.
Ниже мы приводим пример программы численного расчета температур
в узлах, написанной на алгоритмическом языке Фортран. Она написана в об-
общей форме, чтобы заинтересованный пользователь мог скопировать ее и при-
применить для решения своей конкретной задачи, которая может отличаться от
задачи, рассмотренной здесь в качестве примера. Входной информацией яв-
являются N — число узлов с неизвестными температурами, N2 элементов мат-
матрицы А и N элементов матрицы В.
В примере программы используется подпрограмма обращения матрицы
MATINV. Эта подпрограмма представлена в приложении XI. Имеются и дру-
другие подпрограммы обращения матрицы. Пользователю нужно проверить, нет
ли в его вычислительном центре соответствующей подпрограммы, чтобы не
снимать копию с подпрограммы MATINV.
Основная программа имеет следующий текст;
Текст программы численного решения примера 2.13
PIMENSIONAE0.50),BE0),CE0,5Q),T(SO)
READ , N
READ . ((A(I,J),J«1,N),H1.N),(B(I),I = 1,N)
CALL MATINV (A.N.O)
DO 20 1 = 1,N
DO10J*1,N
10 SUM»SUM+C(I,J)*B(J)
20 T(I)»SUM
WRJTEF,40)
WRITE F,50) (I,T(I), 1-1.N)
STOP
40 FORMAT AH /••• STEADY TEMPERATURE DISTRIBUTION IN DEGREES',/,
1'CELSIUS DETERMINED BY-A MATRIX INVERSION TECHNIQUE ***',//)
60 FORMAT D('T(',I2/) • ',F8.2,2X))
END
Ниже представлена входная информация программы. Первая строка со*
держит единственное значение N — число узлов в данной конкретной за-
задаче. В следующих N строках указаны значения элементов ац матрицы А.
Каждая из 15 строк содержит 15 значений, каждой строке соответствует фик-
фиксированная величина индекса и Последние две строки содержат 15 значений
элементов bi столбцевой матрицы В.
Стационарная теплопроводность 107
Входная информация программы для примера 2.1$
-4.5, 1., 0., 0., 0., 0.5, 0., 0., 0., 0., 0., 0., 0., 0., 0.,
1., -4., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 1., -4., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 1., -4., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 1., -2., 0., 0., 0., 0., 0.5, 0., 0., 0., 0., 0.,
0.5, 0., 0., 0., 0., -4.5, 1., 0., 0., 0., 0.5, 0., 0., 0., 0.,
0,1,0., 0., 0., 1 , -4,1., 0., 0., 0., 1., 0., 0., 0.,
0., 0., 1., 0., 0., 0., 1., -4., 1., О , 0., 0., 1., 0., 0.,
0., 0., 0„ 1., 0., 0., 0., 1., -4., 1., 0 , 0., 0., 1., 0.,
0., 0., 0., 0., 0.5, 0., 0., 0., 1., -2., 0., 0., 0., О , 0.5,
О., 0., 0., 0., 0., 0.5, 0., 0., О , 0., -4.5, 1., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 1., -4., 1., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 1., 0., О , 0., 1., -4., 1., O.f
0., 0., 0., 0., 0., 0., О., 0., 1., 0., 0., 0., 1., -4., 1.,
0., 0., 0., 0., 0., 0., О., 0., 0., 0.5, 0., 0., 0., 1., -2.,
-225., -200., -200., -200., -100., -125., 0., О, 0., 0., -175.,
-100., -100., -100., -50.
Приведем выходную информацию программы:
Выходная информация программы для примера 2.13
*** Стационарное распределение температуры в градусах
Цельсия, рассчитанное методом обращения матрицы •••
ТA)« 88.57 ТB) = 138.91 ТC)=158.56 ТD)-166.30
ТE)« 168.38 ТF)= 69,30 ТG)-108.51 Т(8)« 129.01
Т(9)-138.23 ТA0)-> 140.91 ТA1)= 68.11 ТA2)» 96.83
ТA3)-110.69 ТA4)»116,91 ТA5)»118.68
Рассмотренный пример аналогичен примеру 2.12, за исключением лишь того,
что использована более частая сетка. В табл. 2.4 сравниваются результаты
расчета для эквивалентных узлов, что позволяет выявить влияние размера
ячейки сетки на значения местной температуры.
Таблица 2.4
Сравнение результатов численного расчета
температуры, полученных при использовании
редкой и частой сеток
Температура,
сетка 10X10 см
(пример 2.12)
Г4 = 75,5°С
Г5=128,7°С
Гб = 139,4°С
Температура,
сетка 5X5 см
(пример 2.13)
Т6 = 69,3°С
Г8 =» 129,0°С
Г10 = 140,9°С
Программа для примера 2.13 носит общий характер. Ее
можно в точности скопировать и применять для решения целого
ряда различных задач стационарной теплопроводности. Она
108 Глава 2
позволяет найти распределения температуры в одномерных, дву-
двумерных и трехмерных телах при наличии внутреннего тепловы-
тепловыделения и при самых различных граничных условиях. Пользова-
Пользователю нужно сначала вывести все разностные уравнения баланса
энергии и найти элементы матриц А и В. Эти элементы и число
узлов N следует упорядочить в виде входной информации точно
так, как в примере программы.
При числе узлов больше 50 программу обращения матрицы
не следует применять. В этом случае для решения системы
уравнений используются более сложные математические методы,
например метод Чолески [10]. Метод Чолески требует меньше
машинного времени, чем программа MATINV, поскольку он ис-
исключает из рассмотрения нулевые элементы матрицы и поэтому
сводит к минимуму необходимый объем памяти.
Чтобы облегчить пользование программой, в приведенной
ниже таблице перечисляются принятые в программе обозначе-
обозначения, их определения и типичные единицы измерения.
Обозначения, принятые в программе численного решения примера 2.13
Обозначение
A (I, J)
ВA)
С (I, J)
N
ТA)
Определение
Элемент квадратной матрицы А, см. B.105а)
Элемент столбцевой матрицы В, см. B 1056)
Элемент квадратной матрицы С = А-1, см.
B.107)
Число, равное числу узлов
Элемент столбцевой матрицы Т, 'см. B.1056)
Единицы
измерения
о 1 III
Итерационный метод
Для численного решения задач на ЭВМ очень удобен итера-
итерационный метод, основанный на непосредственном определении
температуры в каждом узле из разностного уравнения баланса
энергии для этого узла. Например, если мы рассматриваем урав-
уравнение баланса энергии для внутреннего узла двумерного твер-
твердого тела, то получаем уравнение B.94):
Разрешая это уравнение относительно температуры в узле 0, по-
получаем
П =4 (Г,+ 7-2 + 7-3 + 7-4).
Это соотношение типично для внутреннего узла в твердом теле
с постоянными теплофизическими свойствами при отсутствии
внутреннего тепловыделения, если применяется сетка с квадрат-
Стационарная теплопроводность 109
ными ячейками. Аналогичное соотношение получается для тем-
температуры в узле, расположенном на границе тела. Например,
если узел 0 находится на границе, где происходит конвективный
теплообмен с окружающей средой, температуру То можно найти
из уравнения B.96):
т _ 0,5 (Т2 + Г3) + Л + Bi т„
l°~~ 2 + Bi
Соответствующие выражения для других граничных условий
можно легко получить из уравнений, приведенных в табл. 2.3.
Итак, температуру в каждом узле можно выразить через
температуры в соседних узлах. Число полученных соотношений
равно числу узлов с неизвестными температурами.
При использовании итерационного метода последовательно
выполняются следующие четыре операции.
Операция 1. Выводят разностные уравнения, записав баланс
энергии для каждого узла с неизвестной температурой. Из каж-
каждого уравнения выражают в явном виде температуру узла, для
которого составлялся баланс энергии. Уравнения для всех вну-
внутренних узлов одинаковы по форме. Уравнения для граничных
узлов будут различными в зависимости от типа граничных усло-
условий в конкретной задаче. Данные табл. 2.3 помогут определить
уравнения для граничных узлов.
Операция 2. Задают ряд значений температур во всех узлах.
Если задача будет решаться вручную, разумная начальная
оценка всех температур позволит снизить затраты времени на
вычисление истинных значений температуры в каждом узле.
Если проводится численный расчет на ЭВМ, удобно принять все
начальные температуры равными нулю.
Операция 3. Вычисляют новые значения температур, исполь-
используя уравнения, полученные при операции 1. Как только полу-
получено новое значение какой-либо температуры, немедленно за-
заменяют ее старое значение новым, так что новые значения тем-
температур в узлах все время вычисляют с использованием самого
последнего приближения для остальных температур. Это позво-
позволяет уменьшить время сходимости решения к конечным стацио-
стационарным значениям температур. Этот частный вид итерационного
метода часто называют методом Гаусса — Зайделя.
Операция 4. Повторяют операцию 3 до тех пор, пока раз-
разность между новым и предыдущим приближениями для всех
температур не станет меньше заданной величины.
Применение итерационного метода иллюстрируется на сле-
следующих двух примерах. Первая задача (система всего лишь из
трех уравнений) решается вручную. Во второй фигурирует
15 уравнений, и такую задачу нужно решать на ЭВМ. Выше обе
задачи были решены другими методами, поэтому можно прове-
проверить точность итерационного метода.
ПО Глава 2
Пример 2.14. Найти температуры в узлах 4, 5 и б для примера 2.12, при-
применяя итерационный метод. Сравнить результаты расчета с точными зна-
значениями для примера 2.12 и с данными, полученными методом обращения
матрицы (табл. 2.4).
Решение. В примере 2.12 нужно было определить температуры в узлах
4, 5 и 6. Уравнения баланса энергии для этих трех узлов имеют вид
Чу о И и. «у уаьнепии идлдпса
узел 4: 400 + Тъ — 7Г4 = 0,
узел 5: 300 + Т, + Т6 — 4Г5 =
узел 6: 150 + Г5 — 2Г6 = 0.
0,
Теперь выполним четыре операции, описанные выше при рассмотрении итера-
итерационного метода.
Операция 1. Выразим в явном виде температуру в каждом узле:
узел 4: Г4 = 400/7 + Г5/7,
узел 5: Тъ = 300/4 + Г4/4 + Г6/4,
узел 6: Т6*= 150/2 + Т5/2.
Операция 2. Зададим начальные значения температур в узлах. Разумной
оценкой для начальных значений этих трех температур будут значения Г4 =
= 80°С, Ть = 100°С, Т6 = 150°С. Это те же начальные значения, которые
были использованы при решении системы трех уравнений методом релакса-
релаксации.
Операция 3. Вычислим новые значения температур, используя уравнения,
полученные в ходе выполнения операции 1. Как только будет получено новое
значение температуры, сразу используем его при последующих операциях:
Т4 = 400/7 + 100/7 = 71,43°С,
Т5 = 300/4 + 71,43/4 + 150/4 = 130,36°С,
Г6 == 150/2 + 130,36/2 = 140,18°С.
Операция 4. Повторяем операцию 3 до тех пор, пока значения темпера-
температур, полученные при двух последовательных приближениях, не будут схо-
сходиться с заданной степенью точности. Предполагая, что температуры, полу-
полученные при двух последовательных приближениях, не должны отличаться бо-
более чем на 0, ГС, повторяем операцию 3. Ниже приведена таблица, в которой
собраны результаты расчетов.
100
130,36
128,99
128,77
128,73
150
140,18
139,50
139,39
139,37
Номер итерации Т4, °С Г5, °С Т6, °С
Начальное приближение 80
1 71,43
2 75,77
3 75,57
4 75,54
После четвертой итерации все температуры отличаются не более чем на 0,ГС
от соответствующих значений после третьей итерации, поэтому итерационный
процесс на этом останавливается. С точностью 0,ГС полученные значения
согласуются с результатами точного решения той же самой системы уравне-
уравнений (пример 2.12). Следует также отметить, что при тех же начальных зна-
значениях температур результаты расчета методом релаксации для этого кон-
конкретного примера после четырех приближений отличаются от точного реше-
решения на величину порядка ГС. Результаты расчета методом релаксации пред-
представлены в табл. 2.2. Значения температур в трех узлах, полученные путем
Стационарная теплопроводность 111
точного решения разностной системы уравнений, решения методом релаксации
D приближения) и решения итерационным методом D приближения) отли-
отличаются друг от друга менее чем на 1°С.
Пример 2.15. Определить итерационным методом значения температур
в 15 узлах для примера 2.13. Сравнить полученные результаты с результа-
результатами решения методом обращения матрицы.
Решение. Решение системы 15 уравнений вручную итерационным мето-
методом требует много времени, поэтому следует решать задачу на ЭВМ. При ис-
использовании итерационного метода выполняются 4 операции.
Операция 1. Простым преобразованием разностных уравнений для всех
узлов в примере 2.13 получаем требуемую систему 15 уравнений:
Тх = 50-г-0,222Г2+ 0,111^6, '
Т2 = 50 + 0,25 (Т, + Гз + Т7),
Г4 = 50 + 0,25 (Г3 + Тъ + Г9),
Тъ = 50 + 0,5 Г4 + 0,25Г10,
Т6 = 27,778 + 0,1117\ + 0,222Г7 + 0,111 Гц,
Т7 = 0,25 (Г2 + Т6 + Т8 + Т12),
Т8 = 0,25 (Г3 + Т7 + Т9 + Г13),
Г10 = 0,25Г5 + 0,5Г9 + 0,25Г15,
Тп = 38,889 + 0,1117б + 0,2227112,
Г13 = 25 + 0,25 (Г8 + Г12 + 7\4),
Т15 = 25 + 0,25710 + 0,5Г14.
Эти уравнения составляют часть приведенной ниже программы численного
расчета между пунктами 21 и 22.
Операция 2. Все начальные температуры принимаем равными нулю. Это
начальное приближение далеко от ожидаемых значений температуры при за-
заданных граничных условиях. Несомненно, что использование такого прибли-
приближения приведет к излишним затратам времени при получении решения. Од-
Однако нулевую величину удобно вставлять в программу, а излишние затраты
времени не имеют особого значения, когда расчет проводится на ЭВМ. Все
начальные температуры полагаются равными нулю (см. пункт 15 про-
программы).
Операция 3. Проведя вычисления, указанные между пунктами 21 и 22
программы, находим новые значения температур в 15 узлах.
Операция 4. Новое значение температуры в каждом узле сравнивается со
старым, и, если их разность меньше допустимого отклонения, заданного во
входной информации, итерационный процесс заканчивается и значения темпе-
температур выводятся на печать. Текущие значения температур запоминаются в
строке ТA), а значения температур на предыдущей итерации запоминаются
в строке ТТA). Проверка величины отклонения осуществляется в логическом
пункте IF.
112 Глава 2
Ниже приведен текст программы.
Тенет программы численного решения примера 2.15
DIMENSION ТA00),ТТA00)
READ , N.TOLER
WRITE F,10)
10 FORMAT AH ,ЗХ;*** STEADY TEMPERATURE DISTRIBUTION IN',/,
1'DEGREES CELSIUS DETERMINED BY AN ITERATION TECHNIQUE **¦',//)
DO20l = 1,N
15 T(l) = 0.0
20 TT(I) = T(I)
DO 70 1 = 1,50
21 TA) = 50.0+ 0.222*TB) +0.111*TF)
T{2) - 50.0 + 0 250»(TA)+TC) + TG))
TC) - 50.0 + 0.250»(TB) + TD) + T(8))
TD) - 50.0 + 0.250«(TC) + TE) + T(9))
TE) - 50.0 + 0.500*TD) + 0 250*TA0)
TF) - 27.778 + 0.111 »TA) + 0.222»TG) + 0.111 «TCI1)
TG) - 0.250»(TB) + TF) + T(8) + TA2))
T(8) - 0.250*(TC) + TG) + T(9) + TA3))
T(9) - 0.250*(TD) + T(8)+TA0)+TA4))
TA0) - 0 250*TE) + 0.500*T(9) + 0.250*TA5)
TA1) - 38.889 + 0.111 *TF) + 0.222*TA2)
TA2) = 25.0 + 0.250*(TG) + TA1) + TA3))
TA3) - 25.0 + 0.250*(T(8) + TA2) + TA4))
TA4) - 25.0 + 0 250»(T(9) + T( 13) + TA5))
22 TA5) = 25.0 + 0.250*TA0) + 0.500*TA4)
DO30J = 1,N
IF (ABS(TT(J)-T(J)).GT. TOLER) GO TO 50
30 CONTINUE
WRITE F,40) (K.T(K).K-1,N)
40 FORMAT AH ,T(M2,') = ',F,8.2)
STOP
50 DO60J-1.N
60 TT(J)=»T(J)
70 CONTINUE
WRITE F,80) TOLER
80 FORMAT AH1 /TEMPERATURES DO NOT CONVERGE TO WITHIN' «F6.3,/,
1'DEGREES IN 50 ITERATION STEPS')
STOP
END
Входная информация программы состоит из двух чисел, расположенных
в одной строке в следующем порядке: N — число узлов, TOLER — допусти-
допустимое отклонение (°С) между значениями на двух последовательных итера-
итерациях. Если разность температур, полученных на двух последовательных ите-
итерациях, в каждом узле меньше TOLER, итерационный процесс заканчивается
и значения температур выводятся на печать. Таким образом, входная инфор-
информация для данной программы имеет следующий вид:
Входная информация программы
для примера 2.15
15,0.1
Стационарная теплопроводность 113
Ниже представлена выходная информация программы численного решения
примера 2.15.
Выходная информация программы для примера 2.15
*** Стационарное распределение температуры в градусах Цельсия,
расчитанное итерационным методом***
ТA) =
ТB) =
ТC) =
Т<4) =
ТE)«
ТF)=
ТG)-
Т(8)-
88.48
138.78
158.41
166.16
168.25
69.19
108.36
128.84
Т(9) =
Т(Ю)=
ТA1)-
ТA2)=
ТA3)~
ТA4)=
ТA5)=
138.12
140.76
68.04
96.73
110.59
116.82
118.60
Программа численного решения примера 2.15 написана в
общей форме, так что ее можно скопировать и применить для
решения самых разнообразных задач стационарной теплопро-
теплопроводности. В качестве входной информации пользователю тре-
требуется задать лишь два числа. Одно из них — число узлов N,
в которых неизвестна температура, а второе — допустимое от-
отклонение TOLER результатов расчета.
Ввиду ограничения по емкости оперативной памяти про-
программа позволяет вести расчет для 100 узлов, хотя пункт
DIMENSION можно изменить и занять программой больший
объем оперативной памяти. Если после выполнения 50 итераций
не достигается сходимости решения, на печать выводится сооб-
сообщение об отсутствии сходимости.
В случае если программа применяется для другой задачи,
нужно вывести новые разностные уравнения и из них выразить
в явном виде температуры в отдельных узлах. Эти N уравнений
должны быть введены в программу между пунктами 21 и 22.
Литература
1. Schneider P. J., Conduction Heat Transfer, Addison-Wesley, Mass., 1955.
[Имеется перевод: Шнейдер П., Инженерные проблемы теплопроводности.—
М.: ИЛ., 1970.]
2. Kern D. Q., Kraus A. D., Extended Surface Heat Transfer, McGraw,
N. Y., 1972. [Имеется перевод: Керн Д., Краус А., Развитые поверхности
теплообмена — М : Энергия, 1977].
3. Jakob М., Heat Transfer, I, Wiley, N. Y., 1949. [Имеется перевод изда-
издания 1957 г.: Якоб М., Вопросы теплопередачи. — М.: ИЛ., I960.]
4. Gardner К. A., Efficiency of Extended Surfaces, Trans. ASME, 67,
p. 621 A945).
5. Arpaci V., Conduction Heat Transfer, Addison-Wesley, Mass., 1966.
6. Ozisik M. N., Boundary Value Problems of Heat Conduction, Intext
Publishers Group, N. Y., 1968.
7. Myers G. E., Analytical Methods in Conduction Heat Transfer, McGraw,
N. Y., 1971.
8. Kazan C. F., An Electrical Geometrical Analogue for Complex Heat
Flow, Trans. ASME, 67, p. 113 A945).
114 Глава 2
9. Kazan С. F., Heat Transfer Temperature Patterns of a Multicomponent
Structure by Comparative Methods, Trans. ASME, 71, p. 9 A949).
10. James M. L., Smith G. M., Wolford J. C, Applied Numerical Methods
for Digital Computation with FORTRAN and CSMP, 2nd ed., Crowell, N. Y.,
1977.
11. Holman J. P., Heat Transfer, 4th ed., McGraw, N. Y., 1976, p. 66.
12. Kreith F., Principles of Heat Transfer, 3rd ed., Intext Publishers
Group, N. Y., 1973, p. 93.
13. Rohsenow W. M, Hartnett J. P., eds., Handbook of Heat Transfer,
McGraw, N. Y., 1973, ch. 5, p. 3.
14. Welty J. R., Engineering Heat Transfer, Wiley, N. Y., 1974, p. 98.
ЗАДАЧИ
Задачи в этой главе сгруппированы по тематике разделов, как указано
в таблице. В четырех задачах B.70—2.73) требуется получить численное ре-
решение на ЭВМ, причем нет необходимости составлять новые программы, так
как все нужные программы представлены при рассмотрении примеров в этой
главе.
Номера задач
2.1-2.23
2.24—2.27
2.28-2.34
2.35—2.46
2.47—2.48
2.49-2.58
2.59 -2.73
Раздел
2.1—2.3
2.4
2.5
2.6
2.7
2.7
2.7
Тема
Одномерная стационарная теплопроводность при
отсутствии внутреннего тепловыделения
Влияние переменного коэффициента теплопро-
теплопроводности
Одномерная стационарная теплопроводность при
наличии внутреннего тепловыделения
Перенос тепла в ребрах
Двух- и трехмерная стационарная теплопровод-
теплопроводность, аналитические методы
Двух- и трехмерная стационарная теплопровод-
теплопроводность, графические методы
Двух- и трехмерная стационарная теплопровод-
теплопроводность, численные методы
2.1. Рассчитать плотность теплового потока через плоскую кирпичную
стенку [k = 0,65 Вт/(м-град)] толщиной 15 см, если температура ее наруж-
наружной поверхности 35°С, а температура внутренней поверхности 25°С. Вычис-
Вычислить термическое сопротивление на единицу площади поверхности стенки.
Найти температуру в среднем сечении стенки.
2.2. Плотность теплового потока через алюминиевую пластину толщиной
10 см равна 5-Ю4 Вт/м2. Температура одной поверхности пластины 150°С.
Найти температуру второй поверхности пластины.
2.3. Алюминиевая пластина, рассматриваемая в задаче 2.2, заменена пла-
пластиной из нержавеющей стали 304 той же толщины. Плотность теплового по-
потока и температура одной поверхности такие же, как и в задаче 2.2. Найти
температуру второй поверхности. Сравнить это значение с температурой, по-
полученной в задаче 2.2. Объяснить причину различия между двумя значениями
температуры.
2.4. Площадь поверхности стены здания 500 м2, коэффициент теплопро-
теплопроводности 0,7 Вт/(м-град), толщина стены 20 см. Зимой температура наруж-
наружной поверхности стены 0°С, температура внутренней поверхности 20°С. Найти
мощность отопительной системы (в ваттах), способной возместить потери
тепла через стену. Рассчитать тепловой поток через стену.
2.5. Лист оконного стекла имеет толщину 4 мм и площадь поверхности
2 м2. Найти тепловой поток через стекло, если температура одной поверхно-
поверхности 0°Q а другой 20°С. Рассчитать плотность теплового потока через стекло.
116 Глава 2
2.6. Сравнить значения плотности теплового потока, полученные в зада-
задачах 2.4 и 2.5. Куда больше уходит тепла при одинаковом перепаде темпера-
температур? Через стену или стекло? Предложить способы снижения потери тепла
через стекло.
2.7. Цилиндр диаметром 20 см и длиной 50 см теплоизолирован по пери-
периметру. Температура одного торца цилиндра 300°С, а температура в попереч-
поперечном сечении на расстоянии 25 см от этого торца 100°С. Коэффициент тепло-
теплопроводности 2 Вт/(м-град). Найти тепловой поток вдоль оси цилиндра й
рассчитать температуру второго торца цилиндра.
2.8. По длинной алюминиевой проволоке диаметром 1 см течет электриче-
электрический ток силой 1000 А. Проволока покрыта слоем резиновой изоляции тол-
толщиной 3 мм [? = 0,15 Вт/(м-град)]. Температура наружной поверхности
изоляции 30°С. Найти температуру внутренней поверхности изоляции. Оми-
Омическое сопротивление проволоки на единицу длины 3,7-10~4 Ом/м.
2.9. Паропровод с наружной температурой 120°С и наружным диаметром
10 см покрыт слоем асбеста толщиной 5 см [& = 0,15 Вт/(м-град)]. Рассчи-
Рассчитать тепловой поток от паропровода на единицу его длины, если температура
наружной поверхности изоляции 35°С. Найти термическое сопротивление изо-
изоляции на единицу длины паропровода.
2.10. По круглому каналу выводятся из печи газообразные продукты сго-
сгорания. Диаметр канала 0,5 м, температура стенки 500°С. Найти толщину изо-
изоляции [& = 0,2 Вт/(м-град)], обеспечивающую снижение температуры на-
наружной поверхности до такой величины, чтобы человек, коснувшийся ее, не
обжегся. Удельная теплоемкость газа 1000 Дж/(кг-град), расход 1 кг/с, па-
падение температуры на длине канала 40 м составляет 10°С. Предположить,
что термическое сопротивление стенки канала мало по сравнению с термиче-
термическим сопротивлением изоляции и что максимальная температура, не вызываю-
вызывающая ожога, равна 65°С.
2.11. Найти термическое сопротивление и тепловой поток через стенку по-
полого шара внутренним диаметром 5 см, наружным диаметром 10 см и коэф-
коэффициентом теплопроводности 20 Вт/(м-град). Температуры внутренней и на-
наружной поверхностей равны соответственно 100 и 50°С.
2.12. Стенка большой печи толщиной 1,5 см изготовлена из чугуна. Тем-
Температура горячего газа 1100°С, коэффициент конвективной теплоотдачи на
внутренней поверхности стенки 250 Вт/(м2-град). Наружная поверхность печи
окружена воздухом [Яс = 20 Вт/(м2-град)] с температурой 30°С. Нарисовать
тепловую цепь и указать все сопротивления. Рассчитать значения всех тер-
термических сопротивлений на единицу площади. Найти плотность теплового
потока через стенку печи. Рассчитать температуры внутренней и наружной
поверхностей стенки.
2.13. Найти толщину изоляции [& = 0,5 Вт/(м-град)], которую нужно
нанести на стенку печи (задача 2.12), чтобы снизить тепловой поток вдвое.
Предположить, что изоляция не повлияет на коэффициент теплоотдачи на
наружной поверхности. Рассчитать температуры обеих поверхностей изоля-
изоляции.
2.14. Пенопластовая камера для льда имеет форму полого цилиндра с
внутренним диаметром 0,5 м, наружным диаметром 0,6 м и длиной 1 м. Ка-
Камера полностью заполнена льдом с температурой 0°С. Температура наруж-
наружного воздуха 30°С, коэффициент конвективной теплоотдачи между воздухом
и пенопластом йс = 10 Вт/(м2-град). Найти время, за которое лед полностью
растает, и температуру наружной поверхности пенопласта. Рассчитать терми-
термическое сопротивление пенопласта и воздуха. Пренебречь подводом тепла с
концов камеры. Скрытая теплота плавления льда 3,35-105 Дж/кг.
2.15. Изготовлено две модели подогревателя воды. Обе модели имеют
форму цилиндра с двойными металлическими стенками. В более дешевой мо-
модели нет изоляции между стенками, а коэффициент конвективной теплоотдачи
между стенками на обеих поверхностях равен 20 Вт/(м2-град). В более до-
дорогой модели зазор между стенками заполнен стекловолокном [k =
= 0,05 Вт/(м-град)]. У обеих моделей внутренний диаметр стенки 0,G м, на-
Стационарная теплопроводность 117
ружный диаметр 0,7 м, высота 3 м. Температура внутренней стенки 60°С, а
температура воздуха, омывающего наружную поверхность подогревателя,
равна 25°С при hc = 15 Вт/(м2-град). Предполагая, что происходит одно-
одномерный перенос тепла в радиальном направлении, и пренебрегая термическим
сопротивлением металлических стенок, найти требуемый стационарный под-
подвод мощности для обеих моделей, если из подогревателя вода не отводится.
Найти в процентах экономию энергии, которую дает более дорогая модель.
2.16. Температура поверхности длинного цилиндрического стержня диа-
диаметром 4 см равна 200°С. Стержень покрыт изоляцией двоякого типа, как по-
показано на рисунке. Поверхность раздела двух материалов идеально теплоизо-
теплоизолирована. Толщина обоих материалов 5 см, kA = 5 Вт/(м-град), kB =
= 10 Вт/(м-град). Наружная поверхность изоляторов омывается воздухом
с температурой 20°С и hc = 15 Вт/(м2-град). Рассматривая только стацио-
стационарный перенос тепла в радиальном направлении, а) нарисовать тепловую
цепь и указать все сопротивления, б) найти суммарный тепловой поток на
единицу длины стержня, в) найти температуру наружной поверхности обоих
изоляторов.
К задаче 2.16.
2.17. Для составной стенки, показанной на рисунке, найти коэффициент
теплопроводности kx. Определить, кроме того, температуры поверхностей раз-
раздела Тх и Ту,
_ 6=5 Вт/(м-град)
Окружающая среда /
hc= 20 Вт/(м2-град) / *=15 Вт/(м-град)
Г700°С
:г=5оо°с-
-10 см-
6 см-
К задаче 2.17.
2.18. Воздух, имеющий температуру, 120°С, омывает большую горизон-
горизонтальную пластину из нержавеющей стали толщиной 5 см, температура верх-
верхней поверхности которой поддерживается равной 250°С. Коэффициент кон-
конвективной теплоотдачи равен 30 Вт/(м2-град). Верхняя поверхность теряет
излучением в воздух 700 Вт/м2. Найти установившуюся температуру нижней
поверхности пластины.
118 Глава 2
2.19. Хоккейная площадка спортивного сооружения имеет площадь
1600 м2. Чтобы лед сохранялся, сквозь него по змеевику циркулирует хладо-
агент, как показано на рисунке. На лед с зазором 1,5 см кладется пол баскет*
больной площадки. Эффективный коэффициент конвективной теплоотдачи
Зсм
1,5 см
т-
to
I
9
Излучение ламп
Г-Л; Дерево
WWW
о
WWi
Воздух
О лел|
Змеевик Теплоизолированная
поверхность
К задаче 2.19.
в воздушном зазоре равен 5 Вт/(м2-град). Поверхность пола находится в
контакте с воздухом, имеющим температуру 25°С; коэффициент конвектив-
конвективной теплоотдачи 3 Вт/(м2-град). Результирующий радиационный теплозой по-
поток от освещения равен 250 Вт/м2. Коэффициент теплопроводности дерева
0,2 Вт/(м-град), льда —2,6 Вт/(м-град). Предполагается, что нижняя по-
поверхность льда теплоизолирована. Если пол баскетбольной площадки остает-
остается на льду 24 ч, рассчитать минимальное количество энергии, которое нужно
отвести ото льда, чтобы предотвратить его таяние. Вычислить стоимость
работы холодильной установки, предполагая, что к. п. д. ее равен 0,5, а стои-
стоимость электроэнергии 4 коп/(кВт-ч).
2.20. Большая плоская стенка омывается жидкостью с температурой
200°С. Стенка покрыта слоем изоляции [k = 0,5 Вт/(м-град)] толщиной
5 см. Температура поверхности раздела между изоляцией и стенкой 100°С.
Найти величину коэффициента конвективной теплоотдачи, которую необхо-
необходимо поддерживать на наружной поверхности изоляции, чтобы ее темпера-
температура не превышала 150°С.
2.21. Резервуар состоит из центральной цилиндрической секции и двух
торцевых полусферических секций. В резервуаре находится горячая жид-
жидкость, поддерживающая температуру внутренней поверхности стенки на уро-
уровне 350°С. Резервуар изготовлен из нержавеющей стали и имеет постоянную
толщину стенки 2,5 см. Наружный диаметр цилиндрической секции 2 м, дли-
длина ее 2 м. Температура атмосферного воздуха, окружающего резервуар, 25°С.
Коэффициент конвективной теплоотдачи от резервуара к воздуху 7 Вт/(м2Х
Хград). Найти количество тепла, которое нужно подводить к жидкости в ре-
резервуаре, чтобы поддерживать ее температуру постоянной. Считать, что
происходит только радиальный перенос тепла через стенку резервуара.
2.22. Медный провод диаметром 2 мм, покрытый слоем изоляции толщи-
толщиной 1 мм [^ = 0,18 Вт/(м-град)], при использовании в лабораторном при-
приборе перегревается. Коэффициент теплоотдачи от изоляции к воздуху равен
34 Вт/(м2-град). Приведет ли утолщение изоляции к повышению теплоот-
теплоотдачи от проволоки? Если приведет, то какого максимального повышения теп-
лоотвода (в %) можно добиться путем утолщения изоляции? Найти крити*
ческую толщину изоляции, при которой достигается максимальный теплоот-
вод от провода.
2.23. Используя методику расчета критической толщины изоляции для
цилиндра, описанную в разд. 2.3, показать, что критическая толщина изоля-
изоляции для шара определяется соотношением Bi == #сго/6из = 2,0 или гкрИт =*
= 2&из/Йс
2.24. Найти выражения для распределения температуры и плотности теп-
теплового потока через плоскую стенку, имеющую переменный коэффициент теп-
Стационарная теплопроводность 119
лопроводности k(T) = ko(\ + ЬТ + сТ2). Толщина стенки L, граничные усло-
условия Т@) = Т\ и T(L) = Т2. Коэффициенты b и с постоянны.
2.25. Найти выражение для стационарного распределения температуры
в длинном полом цилиндре при заданных температурах поверхностей, если ко-,
эффициент теплопроводности цилиндра линейно зависит от температуры,
ЦТ) =*оA + РП.
2.26. На рисунке показано стационарное распределение температуры в
составной стенке из четырех пластин. Перечислить коэффициенты теплопро-
теплопроводности пластин в порядке возрастания. Обосновать свой ответ.
К задаче 2.26.
2.27. На рисунке показано стационарное распределение температуры в
плоской стенке. Возрастает или снижается коэффициент теплопроводности
материала при увеличении температуры? Обосновать свой ответ.
К задаче 2.27.
2.28. Ток силой 200 А пропускается через проволоку из нержавеющей
стали диаметром 2 мм и длиной 1 м. Электрическое сопротивление прово-
проволоки 0,125 Ом, коэффициент теплопроводности 17 Вт/(м-град). Температура
поверхности проволоки 150°С.
а) Найти определяющее уравнение для стационарного распределения тем-
температуры Т(г) в проволоке.
б) Найти граничные условия.
в) Решить дифференциальное уравнение.
г) Рассчитать температуру на оси проволоки.
д) Предположить, что проволока покрыта слоем изоляции [k =
= 0,15 Вт/(м-град)] и что коэффициент конвективной теплоотдачи
на поверхности изоляций равен 60 Вт/(м2-град). Как надо изменить
силу тока (увеличить или уменьшить), чтобы температура поверхно-
поверхности проволоки осталась постоянной и равной 150°С?
2.29. Показать, что стационарное распределение температуры в полом ци-
цилиндре с постоянными теплофизическими свойствами при равномерном вну-
внутреннем тепловыделении в единице объема интенсивностью qG описывается
выражением
* V / ~~" *¦ О 4J и j | 1 I ь
Граничные условия суть: Г{/-()= Ti и Г(го)== То
120 Глава 2
2.30. Стенка, показанная на рисунке, имеет постоянный коэффициент теп-
теплопроводности. Поверхность х = 0 теплоизолирована, а поверхность х = L
омывается жидкостью, которая обеспечивает постоянную температуру Т\.
В стенке равномерно распределены источники тепла с интенсивностью вну-
внутреннего тепловыделения в единице объема qfQ . Найти максимальную ин-
интенсивность тепловыделения в единице объема стенки, при которой темпера-
температура Т\ не превышает 120°С, если L = 0,1 м, ?=15 Вт/(м-град). Рассчи-
Рассчитать температуру теплоизолированной поверхности стенки.
A:*=constant
q'^~ constant
Лс=15Вт/(м2-град)
7\=80°С
i
К задаче 2.30.
2.31. Плоская стенка толщиной L имеет постоянный коэффициент тепло-
теплопроводности k. Температуры поверхностей Г@) = Th T(L) = T2. Интенсив-
Интенсивность внутреннего тепловыделения в единице объема стенки изменяется по
закону qfQ = Вх2. Выразить через &, В, Гь Т2 и L следующие величины:
а) стационарное распределение температуры Т(х)у б) координату плоскости
максимальной температуры, в) плотность теплового потока на поверхности
х = L
2.32. Одна поверхность (х = 0) плоской стенки толщиной 1 м теплоизо-
теплоизолирована, а температура другой поверхности (х = L) постоянна и равна
350°С. Коэффициент теплопроводности стенки 25 Вт/(м-град), интенсивность
равномерного внутреннего тепловыделения в единице объема стенки 500 Вт/м3.
Найти безразмерное выражение для распределения температуры стенки. Оп-
Определить максимальную температуру и координату плоскости, где достигает-
достигается максимальная температура.
2.33. Длинный сплошной цилиндр радиусом го имеет постоянный коэф-
коэффициент теплопроводности k. Интенсивность внутреннего тепловыделения в
единице объема цилиндра qQ = Ar\ поверхность цилиндра имеет постоян-
постоянную температуру 7Y Найти стационарное распределение температуры в ци-
цилиндре, выраженное через k, r0, Т\ и Л.
2.34. По длинному полому цилиндру длиной L пропускается в осевом
направлении ток постоянной силы /. Внутренняя поверхность цилиндра (г =
= п) теплоизолирована, температура наружной поверхности (г = го) под-
поддерживается равной То. Электрическое сопротивление цилиндра R. Найти
выражение для стационарного распределения температуры в цилиндре. Ответ
можно выразить через /, i?, k, Lt Гц го и То.
2.35. На печь поставили кастрюлю из нержавеющей стали диаметром
30 см с толщиной стенки 2 мм. В кастрюле кипятят воду, расстояние между
водой и краем кастрюли 15 см. Коэффициент конвективной теплоотдачи от
кастрюли к воздуху 300 Вт/(м2-град). Средняя температура воздуха внутри
и снаружи кастрюли 50°С. Рассчитать температуру края кастрюли.
• 2.36. Ребро круглого сечения .диаметром d и длиной L омывается жид-
жидкостью с температурой Too. Коэффициент конвективной теплоотдачи от по-
поверхности ребра к жидкости Яс, а коэффициент теплопроводности ребра k.
Построить графически зависимость безразмерной температуры 0 = (Т —
— Тоо)/(Ть — Too) от безразмерной координаты вдоль оси ребра g = x/L при
трех значениях числа Био: Bi = hcPL2/kA = 0,1, 1, 10, предполагая, что по-
поверхность торца теплоизолирована.
Стационарная теплопроводность 121
2.37. Алюминиевое ребро треугольного профиля установлено на поверх-
поверхности с температурой 200°С. Длина ребра 10 см, толщина основания 4 см,
температура окружающей среды 100°С, коэффициент конвективной теплоот-
теплоотдачи 35 Вт/(м2-град). Найти тепловой поток, отводимый от единицы ширины
ребра.
2.38. Ребро из нержавеющей стали толщиной 5 мм, наружным диамет-
диаметром 3 см охватывает трубу внешним диаметром 1 см. Температура окружаю-
окружающей среды 50°С, коэффициент конвективной теплоотдачи 40 Вт/(м2-град).
Температура стенки трубы 150°С. Рассчитать тепловой поток от ребра.
2.39. Медное ребро круглого сечения площадью 0,25 см2, длиной 2,5 см
установлено на стенке с температурой 175°С. Температура окружающей сре-
среды 20°С, hc = 35 Вт/(м2-град). Рассчитать тепловой поток и температуру
торца ребра для двух случаев: а) торец теплоизолирован и б) на поверхно-
поверхности торца происходит конвективная теплоотдача.
2.40. Две очень длинные алюминиевые проволоки нужно спаять друг
с другом. Проволоки находятся в воздухе [Яс = 20 Вт/(м2-град)] с темпе-
температурой 25°С. Температура плавления припоя 250°С. Определить количество
тепла, которое необходимо подвести к торцу проволок при стационарном рас-
распределении температуры в проволоке.
2.41. Сплошной стержень круглого сечения диаметром D, длиной 2L с ко-
коэффициентом теплопроводности k соединяет две стенки, имеющие одинако-
одинаковую температуру Ть. Температура окружающего воздуха Гоо, коэффициент
конвективной теплоотдачи hc. Найти выражения для стационарного распре-
распределения безразмерной температуры в стержне и суммарного теплового по-
потока от стержня. Ответ можно выразить через L, D, Яс, Т<х> и 7V
2.42. Требуется провести точные измерения плотности теплового потока
от исследуемого образца. Образец нагревается до 300°С, а его температура
измеряется термопарой с двумя термоэлектродами диаметром 1 мм и коэф-
коэффициентом теплопроводности 75 Вт/(м-град). Температура окружающего воз-
воздуха 20°С, коэффициент конвективной теплоотдачи от термоэлектродов к возду-
воздуху 25 Вт/(м2-град). Найти возможную ошибку измерения плотности теплового
потока от образца, обусловленную теплопроводностью термоэлектродов.
2.43. Одноцилиндровый двигатель косилки с воздушным охлаждением
работает в стационарных условиях. Температура цилиндра не должна пре-
превышать 300°С. Для охлаждения цилиндра предусмотрены чугунные кольце-
кольцевые ребра. Внешний диаметр цилиндра двигателя у основания ребра 0,3 м.
Предполагая, что двигатель работает в воздухе с температурой 30°С, а ко-
коэффициент теплоотдачи на боковых поверхностях и торце ребра 12 Вт/(м2Х
X град), рассчитать тепловой поток от одного ребра. Определить число ребер,
необходимое для охлаждения двигателя мощностью 3 кВт до заданной тем-
температуры, если к. п. д. двигателя 30%, а ребрами отводится 50% всего тепла,
выделяемого двигателем.
2.44. Один конец стальной [? = 55 Вт/(м-град)] кочерги круглого сече-
сечения находится в пламени. Диаметр кочерги 1 см, длина от конца кочерги до
рукоятки 0,6 м. Температура конца кочерги, находящегося в пламени, 350°С;
температура воздуха, окружающего кочергу, 80°С [hc = 25 Вт/(м2-град)].
Рассчитать температуру рукоятки кочерги.
2.45. В ребре постоянного сечения площадью Л, периметром Р и длиной L
интенсивность равномерного тепловыделения на единицу объема составляет
qQ . Ребро окружает среда с постоянной температурой Тж и. постоянным
коэффициентом теплоотдачи Яс. Показать, что распределение безразмерной
температуры в ребре определяется выражением
rrr
где 9 A) = (Г (|) - Т^Ть - Т^), Qa = qQ A/hcP (Tb - Г^-безразмерная
интенсивность внутреннего тепловыделения, Bi <= ftcPL2/kA. Граничные
122 Глава 2
условия: 9@)= 1; (d9/dg) | ^=1 =0 (теплоизолированный торец). Показать,
что при отсутствии внутреннего тепловыделения (QG = 0) распределение тем-
температуры сводится к полученному в разд. 2.6 распределению для ребра с
теплоизолированным торцом.
2.46. Паяльник имеет мощность 50 Бт. Нагревательный элемент паяль-
паяльника показан на схеме. Его длина примерно 10 см, он имеет квадратное се-
сечение 3X3 мм и его коэффициент теплопроводности 55 Вт/(м-град). Темпе-
Температура окружающего воздуха 25°С, Яс = 15 Вт/(м2-град). Температура осно-
основания нагревательного элемента 400°С. Рассчитать температуру конца паяль-
паяльника в стационарных условиях. Учтено ли в ваших расчетах, что паяльник
не используется непрерывно? Применить распределение температуры, найден-
найденное в задаче 2.45.
К задаче 2.46.
2.47. Распределение температуры в твердом теле [/> = 2,5 Вт/(м-град)]
описывается законом Т(х, у) = ах2 + by2 -f ex + dy где температура выра-
выражена в Кельвинах, а х и у — сантиметрах; значения коэффициентов: а =
= 2,0 К/см2, 6=1,5 К/см2, с =1,0 К/см, d = 300 К. Найти направление
и величину вектора плотности теплового потока в точках @,0), A 1)
и C, 0).
2.48. Для распределения температуры, указанного в задаче 2.47, найти
тепловой поток на единицу толщины вдоль поверхностей х = 0 от у = 0 до
у = 3 см и у = 0 от х = 0 до х = 5 см.
2.49. Два паропровода находятся в контакте, как показано на рисунке,
и окружены асбестовой изоляцией для снижения потерь тепла. Внутренний
диаметр паропроводов 10 см, наружный диаметр изоляции 30 см. По паро-
паропроводам течет пар с температурой 150°С и расходом 0,08 кг/с; средняя тем-
температура наружной поверхности изоляции 35°С. Рассчитать тепловой поток
через изоляцию на единицу длины паропровода. Найти формфактор тепло-
теплопроводности изоляции. Определить длину паропровода, на которой темпера-
температура пара снизится на 5°С.
Г=35°С
Г=150°С
К задаче 2.49.
2.50. Трубопроводы горячей воды расположены в бетонной плите [k =
1,5 Вт/(м-град)] с шагом 0,5 м, как показано на рисунке; температура
Стационарная теплопроводность 123
наружной поверхности бетона 30°С, средняя температура воды 90°С. Рассчи-
Рассчитать тепловой поток на единицу длины каждого трубопровода.
30°С
0,5 м
-0,5 м
К задаче 2.50,
30° С
2.51. Температура внутренней поверхности высокой дымовой трубы, пока-
показанной на рисунке, 170°С, температура наружной поверхности 50°С. Рассчи-
Рассчитать тепловой поток на единицу высоты трубы, если k = 2,0 Вт/(м-град).
50°С
1,5 м
К задаче 2.51.
2.52. Температура одной поверхности длинного стального [?=43 Вт/(м X
Хград)] уголка, показанного на рисунке, равна 100°С, температура другой по-
поверхности поддерживается равной 200°С. Рассчитать тепловой поток между
двумя поверхностями на единицу длины.
i
20 см
100°С
см
-20см-
200°С
К задаче 2.52.
2.53. Температура стенки канала квадратного сечения, по которому те-
течет горячий газ, равна 300°С. Канал проходит внутри длинной асбестовой
трубы [k = 0,25 Вт/(м-град)], как показано на рисунке. Температура наруж-
наружной поверхности асбеста 45°С. Рассчитать тепловой поток от газа на единицу
длины канала.
124 Глава 2
К задаче- 2 53.
2.54. Радиоактивные отходы помещены в сферический контейнер диамет-
диаметром 1 м и захоронены в землю на глубину 25 м, где коэффициент теплопро-
теплопроводности почвы 2,0 Вт/(м-град). Поверхность земли имеет постоянную тем-
температуру 15°С. Отходы генерируют тепло с мощностью 1000 Вт. Какую тем-
температуру должен выдерживать контейнер?
2.55. По подземному трубопроводу перекачивается нефть со средней тем-
температурой 15°С. Трубопровод с наружным диаметром 0,5 м и внутренним
диаметром 0,45 м находится на глубине 5 м, температура поверхности земли
5°С. Рассчитать стационарный тепловой поток от нефти на единицу длины
трубопровода. На какое расстояние можно перекачать нефть, пока ее сред-
средняя температура не упадет до 12°С, если удельная теплоемкость нефти
2000 Дж/(кг-град), а расход 50 кг/с? Коэффициент теплопроводности почвы
1,0 Вт/(м-град).
2.56. Подземный силовой электрический кабель диаметром 10 см прохо-
проходит на глубине 1,5 м. Коэффициент теплопроводности почвы 1,5 Вт/(м-град),
а температура поверхности земли 20°С. Электрическое сопротивление кабеля
на единицу длины 10~4 Ом/м. Рассчитать максимально допустимую силу тока
в кабеле, если температура изоляции провода не должна превышать 120сС.
2.57. Небольшая электрическая печь имеет форму параллелепипеда. Стен-
Стенка печи изготовлена из асбеста толщиной 10 см. Внутренний объем печи вы-
выполнен в форме куба со стороной 0,5 м. Найти мощность печи в стационар-
стационарном режиме работы, если температура внутренней поверхности асбеста 220°С,
а температура наружной поверхности 45°С.
2.58. Ось подземного нефтепровода находится на глубине 6 м. Наруж-
Наружный диаметр металлической трубы 1 м, внутренний диаметр 0,95 м. Коэффи-
Коэффициент теплопроводности почвы 1,5 Вт/(м-град), температура поверхности
земли —20°С. Найти требуемый подвод тепла на единицу длины нефтепро-
нефтепровода для поддержания средней температуры нефти на уровне 20°С, если рас-
расход нефти 900 кг/с.
2.59. Температура основания ребра, показанного на рисунке, 200°С. На
торце ребра расположен источник энергии, создающий плотность теплового
Площадь торца 0,1 м2
а"= 5 кВт/м2
2
О
3 4
О О
rr I-, // \ [*¦ 5 см-»-|
: = 5Вт/(м-град)
Теплоизолировано
задаче 2.59.
Стационарная теплопроводность 125
потока 5000 Вт/м2. Наружная поверхность ребра теплоизолирована. С по-
помощью метода релаксации рассчитать температуры в узлах 1—5.
2.60. Предполагая, что температуры в узлах 1—8, указанных на ри-
рисунке, равны 50, 51, 52, 53, 54, 55, 56 и 57°С, рассчитать остаточные члены в
узлах 1, 2, 4 и 5 Численные значения параметров, указанных на рисунке:
hex = 5 Вт/(м2-град), Яс2 = 10 Вт/(м2-град), Т* = 40рС, L = 5 см, ? =
= 20 Вт/(м-град). Изменяя температуру в узле с наибольшим остаточным
членом, определить температуру в этом узле, при которой остаточный член
равен нулю.
К задаче 2.60.
2.61. На рисунке показана твердая стенка, имеющая коэффициент тепло-
теплопроводности k, которая помещена в среду с температурой Too. Вывести раз-
разностные уравнения баланса энергии для узлов 1, 2 и 3, выраженные через
температуры в узлах 4—9 и Bi = hcLjk.
Окружающая
среда
К задаче 2.61.
2.62. Проверить все разностные уравнения баланса энергии, приведенные
в табл. 2.3.
2.63. Решить систему пяти уравнений методом релаксации. Значения всех
неизвестных находятся в диапазоне от 0 до 10.
х + Ьу — Зг = 22,
6у — 2z + и = 35,
2z — bw — 14м = — 9,
3* —4z + 3o> = —11,
2х + bw — 20« = %
126 Глава 2
2.64. Рассчитать стационарные температуры в узлах 1—4 двумерного
тела, показанного на рисунке. Температуры поверхностей приведены на ри-
рисунке, коэффициент теплопроводности материала 2 Вт/(м-град). Вычислить
температуры для двух случаев: а) внутреннее тепловыделение отсутствует;
б) интенсивность внутреннего тепловыделения на единицу объема тела равна
1000 Вт/м3.
100°О> —+"--+——+— -200eC
N300eC
К задаче 2.64.
2.65. Решить задачу 2.64 итерационным методом.
2.66. Рассчитать температуры в девяти узлах тела, показанного на ри-
рисунке, методом релаксации; коэффициент теплопроводности материала
30 Вт/(м-град).
Лс= 20Вт/(м2-град)
т = 50°С
„Теплоизо-
лировано
К задаче 2.66.
2.67. Решить задачу 2.66 итерационным методом.
2.68. Сосуд Дьюара прямоугольного сечения для жидкого азота поддер-
поддерживается двумя подставками из нержавеющей стали, как показано на ри-
рисунке (а). Подставки фиксируют промежуток между внутренней и наружной
стенками сосуда. Из этого промежутка выкачан воздух, и он заполнен тепло-
теплоизоляционным материалом. Найти скорость выкипания жидкого азота вслед-
Стационарная теплопроводность 127
ствие подвода тепла по подставкам с помощью двух методов: а) метода ре-
релаксации для решения разностных уравнений энергии; б) графического ме-
метода. Эскиз элемента подставки приведен на рисунке (б).
Жидкий азот
-196°С
Объем 0,3 м3
р = 807,5 кг/м3
Л -2-105Дж/кг
/8
Изоляция
Длина
70 см/Нержавеющая
сталь
20°С
К задаче 2.68(а).
U 15см >l
К задаче 2.68F).
15 см
2.69. Две смежные поверхности длинного прямоугольного стержня, сече-
сечение которого показано на рисунке, имеют постоянную температуру, а на
остальных двух поверхностях происходит конвективный теплообмен. Числен-
Численные значения параметров: к = 30 Вт/(м-град), hc\ = 50 Вт/(м2-град), Йс2 =
= 70 Вт/(м2-град), Too = 100°С. Применяя разбивку по узлам, показанную
на рисунке, рассчитать методом релаксации стационарные температуры в
15 узлах.
10 см-
150°С
К задаче 2.69.
2.70. Применить в задаче 2.69 метод обращения матрицы. Вывести урав-
уравнения баланса энергии для каждого узла и определить элементы матриц А и
В. Использовать программу численного решения примера 2.13. Сравнить от*
вет с результатами предыдущего решения задачи 2.69.
128 Глава 2
2.71. Решить задачу 2.69 итерационным методом. Модифицировать про-
грамму численного решения примера 2.15 и применить ее для вычисления тем-
температур в 15 узлах Сравнить ответы с результатами решения задач 2.69 и
2.70.
2.72. На рисунке показано сечение длинного стального канала [k =
= 45 Вт/(м-град)]. Температура верхней теплоизолированной поверхности
100°С, нижней 300°С. Одна боковая поверхность омывается воздухом с тем-
температурой 40°С [Не = 100 Вт/(м2-град)], а вторая теплоизолирована. Вну-
Внутренняя часть канала омывается жидкостью с температурой 200°С [hc =
= 25 Вт/(м2-град)]. Найти стационарные температуры в 20 узлах методом
обращения матрицы, используя программу численного решения примера 2.13.
100Вт/(м2трад)
0,6 м-
1 1 1 г
till
—I. + 4. 4. 4. (___
О i (
/IOO°C
о I о ! о
16 I 17 I 18
I '10 I
о i с
12 I 13
j j
о <\
5 I 6
—г +—
^Теплойзо-
^Теплойзонировано
300°C hc= 25Вт/(м2-град) 300°С
?l200oC
К задаче 2.72.
2.73. Решить задачу 2.72 итерационным методом; применяя программу
численного решения примера 2.15.
Глава 3
НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
3.1. ВВЕДЕНИЕ
В гл. 2 мы рассматривали лишь стационарный теплообмен.
Поскольку в большинстве инженерных задач происходит изме-
изменение характеристик по времени, необходимо рассмотреть ме-
методы расчета температур и тепловых потоков для физических
систем, которые находятся в нестационарных, или переходных,
условиях.
Мы назовем задачу о теплообмене нестационарной, если тем-
температурное поле в рассматриваемой системе изменяется по вре-
времени. Нестационарный теплообмен встречается во многих прак-
практических ситуациях. Например, при различных процессах обра-
обработки требуется, чтобы продукт нагревался или охлаждался во
время его производства. Топки и печи работают циклично, и при
этом происходят нестационарные изменения температуры их со-
содержимого и стенок печи. Здания претерпевают суточные и се-
сезонные изменения температуры. Металлы часто нагревают и
охлаждают, чтобы получить требуемые физические свойства,
В двигателях происходят переходные процессы при запуске, а
также более быстрые периодические нестационарные процессы
на каждой части термодинамического цикла.
В общем случае нестационарную задачу решать труднее,
чем стационарную. В следующем разделе будут выведены со-
соотношения для систем с пренебрежимо малым изменением тем-
температуры по пространству, когда основное уравнение теплопро-
теплопроводности сводится к обыкновенному дифференциальному урав-
уравнению. В последующих разделах мы будем решать более
сложные задачи. Мы рассмотрим аналитические решения и чис-
численные методы, которые могут быть использованы для расчета
тепловых потоков в твердых телах при изменении температуры
как по времени, так и по пространству.
3.2. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
ПРИ ПРЕНЕБРЕЖИМО МАЛОМ
ВНУТРЕННЕМ ТЕРМИЧЕСКОМ СОПРОТИВЛЕНИИ
Чтобы найти нестационарное распределение температуры и
в итоге тепловой поток, необходимо решить общее уравнение
теплопроводности, в которое на первых порах входит член,
б Зак. 487
130 Глава 3
учитывающий аккумулирование тепла. Уравнение теплопровод-
теплопроводности, которое требуется решить, имеет следующий вид:
Л + ^-ТТ' <3-»
Это дифференциальное уравнение в частных производных, и для
нахождения его общего решения требуются сложные математи-
математические методы. Опубликовано несколько содержательных моно-
монографий [1—4], в которых можно найти решения уравнения
C.1) для ряда конкретных случаев.
Один из способов упрощения подхода к решению нестацио-
нестационарных задач теплопроводности состоит в том, чтобы рассмо-
рассмотреть класс задач,_в которых поле температур в твердом теле
изменяется по времени, но в любой момент времени не изме-
изменяется по пространству. Это означает, что температура во всех
точках твердого тела равномерно изменяется по времени.
Если предположить, что энергия передается от твердого тела
к жидкости путем конвекции, то условие равномерного измене-
изменения температуры в твердом теле будет удовлетворяться в том
случае, если сопротивление теплопроводности будет намного
меньше сопротивления конвекции на поверхности. Системы,
удовлетворяющие этому условию, называются системами с пре-
пренебрежимо малым внутренним термическим сопротивлением,
хотя некоторые авторы называют их системами с сосредоточен-
сосредоточенной теплоемкостью.
Если тело имеет пренебрежимо малое внутреннее термиче-
термическое сопротивление, то градиенты температуры внутри тела
существенно меньше, чем в окружающей среде. Чтобы опреде-
определить, имеет ли тело, окруженное жидкостью, пренебрежимо
малое внутреннее термическое сопротивление, следует прежде
всего сравнить величины этих двух соответствующих термиче-
термических сопротивлений. Это можно сделать, определив число Био,
которое является безразмерным параметром — отношением кон-
дуктивного термического сопротивления к конвективному тер-
термическому сопротивлению. Следовательно, если
Bi==M-<l,0, C.2)
то внутреннее термическое сопротивление действительно мало
по сравнению с внешним, или конвективным, термическим со-
сопротивлением. Величина L в соотношении C.2) — это характер-
характерный линейный размер твердого тела. В дальнейшем мы убе-
убедимся, что при решении задач теплопередачи характерный
линейный размер будет различным для тел различной геоме*
трии. Для тел неправильной формы характерный линейный раз*
мер часто определяется как отношение объема к площади по*
верхности. Если число Био существенно меньше единицы, можно
Нестационарная теплопроводность 131
труда получить соотношения для нестационарной темпера-
температуры тела и теплового потока от поверхности твердого тела к
жидкости. Рассмотрим тело произвольной формы (рис. 3.1). Из
баланса энергии для твердого тела следует, что уменьшение
энергии, аккумулированной в твердом теле, должно быть равно
тепловому потоку, отводимому от поверхности конвекцией:
- pVc ^ж1=К*А* fr w -т^ <3-3>
Здесь р —плотность твердого тела, V — его объем, с — удельная
теплоемкость материала, As — площадь поверхности тела. Урав-
Уравнение C.3) представляет _ dT__
СОбоЙ Обыкновенное ДИффе- Окружающая *= ~Р 57 ~Лс * в
ренциальное уравнение, среда
причем единственной неза-
независимой переменной явля-
является время. Решение для
мгновенной температуры
T(t) будет определять тем-
температуру во всех точках те-
тела, включая его поверх-
поверхность, поскольку мы предпо-
предположили, что внутреннее Рис- зл-- Баланс энергии для твердого
трпмичргкор гпппотияпение тела с пРенебРежимо малым внутренним
термическое сопротивление термическим сопротивлением.
пренебрежимо мало.
Уравнение C.3) можно несколько упростить, введя новую
искомую функцию
9(/) = Г (/)-7^. C.4)
Чтобы решить уравнение C.3), нужно задать температуру тела
в некоторый момент времени. Если предположить, что в на-
начальный момент времени t = 0 температура тела известна и
равна Го, то начальное условие для уравнения C.3) имеет вид
0О = ГО — Т„ при / = 0. C.5)
Решение уравнения C.3) при начальном условии C.5) выра-
выражается формулой
Q @ o~~(hcAsl&Vc) t (rx a\
Формула C.6) записана в безразмерном виде и, следовательно,
параметр HcAst/pVc должен быть безразмерным.
Этот параметр является в действительности произведением
двух безразмерных критериев, уже использованных нами. Один
из них — это число Био C.2), а второй — число Фурье BЛ5).
Произведение чисел Био и Фурье равно
5*
132 Глава 3
Характерный линейный размер L для рассматриваемого нами
тела произвольной геометрии определяется как отношение объ-
объема твердого тела к площади его поверхности
Число Фурье не участвовало в рассмотренных ранее задачах
стационарной теплопроводности. Оно является важным безраз-
безразмерным параметром для задач нестационарной теплопроводно-
теплопроводности. Если ввести числа Био и Фурье, то формула C.6) прини-
принимает вид
В (О f
е,
'о
C.8)
Следует помнить, что она позволяет точно определить изменение
температуры твердого тела по времени лишь при условии пре-
пренебрежимо малого внутреннего термического сопротивления.
Первым шагом при решении любой нестационарной задачи яв-
является определение числа Био. Известно, что если Bi<0,l, то
ошибка в значениях температуры, рассчитанных по формуле
C.8), не превышает 5%. При меньших значениях Bi точность
повышается. Если число Био больше 0,1, то следует примириться
с большими ошибками или решать задачу другим методом. Ме-
Методы, учитывающие пространственное изменение температуры
в твердом теле, будут описаны в следующих разделах.
После того как изменение температуры твердого тела по
времени определено, можно рассчитать суммарную теплоот-
теплоотдачу и мгновенный тепловой поток от поверхности твердого тела,
определив количество тепла, отводимое от поверхности. Вели-
Величина мгновенного теплового потока в момент времени t равна
Подставляя сюда значение мгновенной температуры из C.8),
можно выразить в безразмерной форме величину мгновенного
теплового потока от твердого тела с пренебрежимо малым вну-
внутренним термическим сопротивлением:
hcAs (To —
C.9)
Суммарное количество тепла, отданное твердым телом в пе-
период от 1 = 0 до произвольного момента времени /, можно
найти, интегрируя соотношение C.9) в этом интервале времени.
В результате получаем
Q@ =
или в безразмерном виде
Q@ ^м rmpni I C10)
hcAs (Го — Гоо) / Bi Fo *
Нестационарная теплопроводность 133
Здесь q(t) — мгновенный тепловой поток от твердого тела,
который обычно выражается в ваттах; Q(t)— полное количество
тепла, отданное телом, которое выражается в ватт-секундах, или
джоулях. Соотношения для q(t) и Q(t) являются точными лишь
для систем с пренебрежимо малым внутренним термическим
сопротивлением, т. е. при Bi <С 1,0.
а. Тепловая система 6. Электрическая система
Физическая схема: T{t\
Окружающая среда r-r4
*с ?>т- \Х Ч
/ТвердоеХ \
( тело \ I
УА) Е±
Уравнение сохранения:
Начальное условие:
0@)= 7*0-7^ = 00
Решение для потенциала:
Рис. 3.2. Аналогия между нестационарными процес-
процессами переноса тепла и электричества.
Соотношения для изменения температуры по времени и теп-
теплового потока в случае пренебрежимо малого внутреннего тер-
термического сопротивления применимы и для другого важного
класса задач. Если твердый материал заменить жидкостью, ко-
которая непрерывно перемешивается, так что в любой момент вре-
времени в жидкости отсутствуют перепады температуры, жидкость
будет иметь очень малое внутреннее термическое сопротивление
по сравнению с внешним конвективным термическим сопротив-
сопротивлением. Для такой хорошо перемешанной жидкости, как ее на-
называют, применимо соотношение C.8), определяющее мгновен-
мгновенную температуру жидкости; мгновенный тепловой поток опре-
определяется формулой C.9), а суммарные потери тепла — соотно-
соотношением C.10).
В разд. 2.7 отмечалась аналогия между потоком тепла и
электрическим током для установившейся системы. Такая
же аналогия существует и для нестационарного потока теп-
тепла от тела с пренебрежимо малым внутренним термическим
134 Глава 3
сопротивлением. Две такие аналогичные системы проиллюстри-
проиллюстрированы на рис. 3.2, где выписаны аналогичные друг другу урав-
уравнения сохранения и решения для температуры в тепловой си-
системе и для электрического потенциала в электрической системе.
Если сравнить уравнения сохранения для обеих систем
(рис. 3.2), то можно видеть, что термическое сопротивление
конвективного слоя равно i/HcAs. Кроме того, теплоемкость
твердого тела Ct = pVc. Теплоемкость пропорциональна про-
произведению массы на удельную теплоемкость твердого мате-
материала. Следовательно, тело из материала с большей удельной
теплоемкостью будет медленнее реагировать на внешнее изме-
изменение температуры, чем тело той же массы из материала с более
низкой удельной теплоемкостью. Об объекте с более медленной
реакцией на изменение температуры говорят, что он имеет боль-
большую теплоемкость.
Пример 3.1. Шарикоподшипники из хромистой стали [k = 50 Вт/(м X
Хград), а= 1,3-10 м2/с] подвергаются термической обработке. Они нагре-
нагреваются до температуры 650°С, а затем резко охлаждаются в ванне с маслом,
имеющим температуру 55°С. Диаметр шарикоподшипника 4,0 см. Коэффи-
Коэффициент теплоотдачи от шарикоподшипника к маслу 300 Вт/(м2-град). Опреде-
Определить: а) сколько времени подшипники должны оставаться в масле, пока их
температура не снизится до 200°С; б) общее количество тепла, отданное
каждым подшипником за это время; в) значения мгновенного теплового по-
потока от подшипников в моменты времени, когда они погружаются в масло
и когда их температура достигает 200°С.
Решение. Чтобы определить, выполняется ли для подшипников условие
пренебрежимо малого внутреннего термического сопротивления, проверим
сначала величину числа Био:
ш_ hcL __ hc(V/As) _ hc(r/3) __ 300@,02/3)
Поскольку число Био меньше 0,1, применимы соотношения, полученные в
этом разделе, и погрешность результатов расчета будет невелика. Можно
выразить число Фурье через искомое время:
F - at — at — 1»3-1(Г5
L2 ~" (г/3J "" @,02/3J '
а) Время, необходимое для снижения температуры шарикоподшипников
до 200°С, определяется с помощью формулы C.8):
200 - 55 _
650 — 55
@,04) @,2930
Отсюда t = 120,5 с, что соответствует числу Фурье 35,31.
б) Общее количество тепла, отданное каждым подшипником в течение
первых 120,5 с, равно
Q = hcAs (Го - Г,) [1 - е~т Fo] -gj^- =
= 300 • Ы @.02J F50 - 55) [l - е~<°.°№0] ]2^ = 5,79 ¦ 104 Дж.
Нестационарная теплопроводность 135
в) Мгновенный тепловой поток при t = О (или Fo = 0) составляет
q = hcAs (Го - Гоо) = 300 • 4л; @,02J F50 - 55) = 897 Вт,
а при / = 120,5 с (Fo = 35,31) мгновенный тепловой поток равен
q = hcAs (Го - Т^) e~Bi Fo = 300. An @,02J F50 - 55)
218 Вт.
3.3. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
В ПОЛУБЕСКОНЕЧНОМ ТВЕРДОМ ТЕЛЕ
Полубесконечным твердым телом можно считать большое
тело с одной плоской поверхностью. Хорошим примером полу-
полубесконечного тела является земля. Если температура поверхно-
поверхности земли изменяется, тепло отводится в землю, и поскольку
ее размеры можно считать бес-
бесконечными, температура зави-
зависит от расстояния от поверхно-
поверхности земли х и от времени t,
т. е. в математической форме
T=T(xf t). Основное уравне-
уравнение B.6) для случая нестацио-
нестационарной теплопроводности в
полубесконечном твердом теле
упрощается и принимает вид
где координата х измеряется
от поверхности (рис. 3.3).
Прежде чем перейти к ре-
решению уравнения C.11), сле-
следует задать одно начальное и
два граничных условия. На-
Начальное условие записывается
следующим образом:
Пу П\ Т (Ч 1 9^
Рис. 3.3. Полубесконечное твердое
тело.
Это означает, что в начальный момент времени t = 0 все полу*
бесконечное твердое тело имеет постоянную температуру Го,.
Одно из граничных условий требует, чтобы температура ма-
материала на бесконечно большом расстоянии от поверхности
оставалась постоянной по времени:
T(oo,t) = TQ. C.13)
Теперь, задавая различные варианты второго граничного усло-
условия, можно найти соответствующие решения. Рассмотрим два
возможных случая.
Случай К Изотермическое граничное условие
136 Глава 3
Одно из возможных грацичных условий, которое физически
сравнительно легко осуществить, состоит в том, чтобы внезапно
изменить температуру поверхности (х = 0) до величины fs и
поддерживать ее постоянной. Изотермическое граничное усло-
условие можно выразить математически следующим соотношением:
Г @,0 = Г.. C.14)
Решение уравнения C.11) при двух граничных условиях C.13)
и C.14) и начальном условии C.12) выражается соотношением
Т(х t)-Ts _ f
C.15)
Способ получения этого решения приведен в работе [5]1).
Функция ошибок Гаусса erf часто встречается в инженерной
практике:
v 0
Значения функции ошибок Гаусса затабулиррваны в приложе-
приложении III и представлены графически на рис. 3.4.
1 г
^'0,6-
Рис. 3,4. Распределение температуры в полубесконечном твердом теле при
внезапном изменении температуры пове^хноей.
Плотность ^кондуктивного теплового потока, поступающего в
полубесконечное твердое тело, можно найти, применяя закон
1) Многочисленные аналитические решения дифференциального уравнения
теплопроводности для тел различной формы при разнообразных граничных
условиях приведены в монографиях А. В. Лыкова: Теплопроводность и диф-
диффузия.— М.: Гостехиздат, 1941; Теплопроводность нестационарных процес-
процессов.— М. — Л.: Госэнергоиздат, 1948; Теория теплопроводности. — М.: Выс-
Высшая школа, 1967. Там же широко представлены вспомогательные графики
и диаграммы, — Прим. ред.
Нестационарная теплопроводность 137
Фурье на поверхности:
= _k(TQ-Ts)-?-\eri(-±=)]\ ,
с-о дх L \2<s/at /Л*=о
или ?//@=-^^^1. C.16)
Общее количество тепла, поступающее в тело вследствие тепло-
теплопроводности за период времени от t = 0 до t = /, составляет
•Л,
Л/ ТГГГ J
или
(ЗЛ7)
Случай II. Конвективное граничное условие
Вместо изменения температуры поверхности полубесконеч-
полубесконечного тела можно принять условие воздействия на поверхность
жидкости с температурой Too при среднем значении коэффици-
коэффициента конвективной теплоотдачи Ис. Тепло, поступающее к по-
поверхности тела от жидкости вследствие конвекции, распростра-
распространяется в нем посредством теплопроводности. Граничное условие
для задачи такого типа имеет вид
Ac[71oo-r@,0I = -^(|j)L0. C.18)
Решение уравнения C.11) при начальном условии C.12) и двух
граничных условиях C.13) и C.18) определяется соотношением
[5]
Т ? - ГрГ° = 1 - erf g - {exp [Bi + л] [ 1 - erf (s + Vq)l). C.19)
где | = V*74a/ = Fo-J/2/2; Fo = at/x2;
Bi = hcx/k; ц = hlat/k2 = Bi2 Fo.
Итак, распределение безразмерной температуры в полубес-
полубесконечном твердом теле с постоянной начальной температурой,
на поверхность которого начиная с момента t = 0 воздействует
жидкость с температурой Гоо, является функцией только чисел
Био и Фурье. Для наглядности на рис. 3.5 представлены резуль-
результаты расчета по формуле C.19).
Соотношения для распределения температуры и теплового
потока, полученные в этом разделе, справедливы только для
полубесконечного тела. В этой связи возникает логичный вопрос:
насколько велики должны быть размеры твердого тела, чтобы
его можно было считать полубесконечным? Разумеется, если
значения времени, при которых требуется найти решение, так
138 Глава 3
малы или коэффициент теплопроводности так низок, что тем-
температура на рассматриваемой глубине твердого тела конечных
размеров не изменяется по сравнению с начальным значением,
такое тело тоже можно считать полубесконечным. Согласно
Рис. 3.5. Распределение температуры в полубесконечном твердом теле, на
поверхности которого происходит конвективная теплоотдача к внешней среде,
имеющей температуру Too.
Крейту [6], большую пластину толщиной L можно считать па*
лубесконечной, если выполняется условие
Fo = -~-<l,0. C,20)
Следовательно, распределение температуры в пластине конечной
толщины, удовлетворяющей условию C.20), будет описываться
соотношением C.15) или C.19) в зависимости от граничного
условия (случай I или случай II соответственно).
Пример 3.2. Большой плоский нагреватель с температурой поверхности
100°С положен на землю (& — 2,0 Вт/(м-град), а = 5-10-7 м2/с). Почва
вначале имела постоянную температуру 15°С. Найти температуру на глубине
5 см под нагревателем через 2 ч его работы. Определить общее количество
тепла на единицу площади, отведенное в почву за первые 2 ч.
Решение. Земля является полубесконечным телом, а нагреватель нахо-
находится в непосредственном контакте с землей. Следовательно, граничное усло-
условие соответствует случаю I, и распределение температуры определяется соот-
соотношением C.15)
~
erf 0.417,
7200
Т (*, t) — 100
15— 100
= erf 0,417 = 0,445,
или T(xt t) =62,2°C.
Нестационарная теплопроводность 139
Общее количество тепла на единицу площади, отведенное в течение 2 ч, рас-
рассчитывается по формуле C.17):
Q" @ « 2k (Г, - Го) д/— = 2 B,0) A00 - 15) a/ J^-a -
V яа V лE-10 ')
=з 2,3 • 107 Вт • с/м2 =* 6,39 кВт • ч/м2-
Пример 3.3. Большая стальная пластина имеет вначале постоянную тем-
температуру 300°С. Пластину нужно охладить воздухом с температурой 50°С,
омывающим одну ее сторону. Толщина пластины 10 см, коэффициент темпе-
температуропроводности 10~5 м2/с, коэффициент теплопроводности 40 Вт/(м-град),
коэффициент конвективной теплоотдачи от пластины к воздуху 400 Вт/(м2Х
Хград). Сколько времени нужно пропускать воздух над поверхностью пла-
пластины, чтобы температура ее поверхности понизилась до 200°С? Каковы тем-
температуры на расстоянии 1 и 10 см от поверхности в момент времени, когда
температура поверхности достигнет 200°С?
Решение. Сначала проверим величину числа Био, чтобы установить, вы-
выполняется ли условие пренебрежимо малого внутреннего термического сопро-
сопротивления системы:
Ei=M, = 400@,1) =1Д
Ei= =
Система имеет существенное внутреннее термическое сопротивление, так что
нельзя применять соотношения, полученные в разд. 3.2.
Затем проверим величину числа Фурье, чтобы установить, можно ли счи-
считать пластину полубесконечным телом
*°~ L2 ОД2 -10 U
Следовательно, согласно условию C.20), пластину можно Считать полубеско*
нечной в течение промежутка времени, не превышающего 1000 с A6,67мин).
Чтобы найти время, за которое температура поверхности снизится до
200°С, можно либо провести расчет по формуле C.19), либо использовать
данные рис. 3.5. Применяя данные рис. 3.5, замечаем, что поверхность пла-
пластины, х = 0, соответствует абсциссе
х/2 л/аГ = 0,
а безразмерная температура поверхности в неизвестный момент времени
равна
Г @,/)-Го __ 200-300 0
T^-Tq "" 50-300 '
Снимая данные с рис. 3.5, находим
ИЛИ t
Поскольку температура поверхности снижается до 200°С за время, меньшее
1000 с, пластину действительно можно считать полубесконечным твердым те-
телом.
140 Глава 3
Чтобы определить местные температуры в сечениях х = 1 см и х =
= 10 см в момент времени 250 с, проведем расчеты в соответствии со сле-
следующей таблицей:
Координата
xIIocm
х/2\Я
0,1
1,0
0,50
0,5Q
0,325
0,039
T(x,t)
219°C
290°C
В течение первых 250 с температура в сечении х = 10 см снизилась всего
на 10°С, т. е. сравнительно на небольшую величину, что подтверждает пра-
правильность использования соотношений для полубесконечного тела в случае
пластины конечной толщины.
3.4. ДИАГРАММЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ
НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Решение одномерных задач
Для тел простой геометрии, часто встречающихся в инженер-
инженерной практике, были получены аналитические решения нестацио-
нестационарного уравнения теплопроводности. Наибольшее практическое
значение имеют тела трех видов:
1. Бесконечная пластина шириной 2L, для которой Т =
= Т(х, t)f где координата х отсчитывается от средней плоско-
плоскости пластины.
2. Бесконечно длинный сплошной цилиндр радиусом го, для
которого Т =T{r,t).
3. Сплошной шар радиусом го, для которого Т = T(r, t). Гра-
Граничные условия для всех трех тел аналогичны. Первое — это
условие теплоизолированности в средней плоскости пластины,
на оси цилиндра и в центре шара.
Второе граничное условие требует, чтобы тепловой поток с
внешней поверхности твердого тела отводился жидкостью с тем-
температурой Гоо при коэффициенте теплоотдачи Яс. Это граничное
условие выражается математически следующим образом:
hc(Ts-TJ k%[,
где индекс s относится к параметрам на поверхности твердого
тела, а п — координата по нормали к поверхности тела.
Можно принять и другое граничное условие, если рассмо-
рассмотреть предельный случай бесконечно большого коэффициента
конвективной теплоотдачи. При Нс-^<х> термическое сопротив-
сопротивление конвективного слоя пренебрежимо мало и температура
поверхности тела равна температуре жидкости. Следовательно,
Сводка безразмерных параметров, необходимых при использовании расчетных данных (рис. 3.6 — 3.8)
Таблица 3.1
Форма тела
Обозначения
Безразмерная линейная координата
Число Био
Число Фурье
Безразмерная температура в сред-
среднем сечении (на оси, в центре)
9@, О/во
Безразмерная местная температура
9(х, 0/9@, 0 или 9(г, 0/9@,0
Безразмерный теплоотвод
Q @ Q' @ Q" @
Qo Qo Qo
Бесконечная пластина толщиной 2L
Окружающая
среда
1
Окружающая
среда
X
т
hcL
к
at
L2
Рис. 3.6а
Рис. 3.66
Рис. З.бв
ао~рсцто-т„)
Бесконечно длинный
цилиндр радиусом г«
Окружающая среда
г
Го
hcr0
к
at
Л
Рис. 3.7а
Рис. 3.76
Рис. 3.7в
QQ «a pcnrl (Tq — Гто)
Шар радиусом п
Окружающая среда
г
hcro
к
at
Т
Рис. 3.8а
Рис. 3.86
Рис. 3.8в
Q — С4 ЯГ3 (Г
о
л оо/
142 Глава 3
ГО
= 8
^2
rf
Hi
II
II
II
/
J
/
1
I
ШЪИ'М
VMM
ti't.vr*
i V.V.f/.
1 НИИ
tllMMf
ИН.'ГЛ!
fflflfi
i firm
IJtrffl
пиши/
rffluT
Hnwl
и
№
Rffffl
нШ
Htnf
1
i
ш
Ш:
НтН-
-
1
-
/
It
ft
*t
1
1
j
3"
с
^e
У
z
Z2
T
9
T
С
%
or
II
7
' <
//
//
-f
1
II
ft
r
//
/у
' /
/
/ /
/у
' /
?-f
ft
y>
/ 1
/ /
//
/ /
у
-Л
щ
у-,
if '
^^ t
f /to ^
f // '
У i ¦
f 1
j 7*
//
у *
iff'1'
%?? *
' J
r> -
^<.
. p.2
1-е
?; =
.
z
g
z
.^
¦^"_
/
—p
г—
*^\
{*+
\^*
—-p
_^
У у
^^.¦И*" | i a
/
у
У
у ¦'
"^^У.. -
¦ = ¦:
!is
life
—
¦и:
Г
^»
ее:
/
—-;
\-^
р-
У
у1
у
\ ¦ '
у
У
У^~
^-¦"**
§
я
I
03
о
о
S
я
а
I
со
ев
о" оЧГо- о" сГ
Нестационарная теплопроводность 143
хотя представленные ниже результаты получены в предположе-
предположении о наличии конвективного переноса тепла с поверхности
тела, можно получить решение для изотермического граничного
условия, рассмотрев предельный случай hc—> оо или Bi->oo.
1
0,9
1"
^ -0,6
аз
0,2
0,1
о
0,01
Г"
°4-
0,5..
0,6..
0/7
0,8 „
°49''
1
/
/
/
/
— - ¦
.- - ¦
-*'
/ t
/ /
/ '
у
ж
Him
к
I
ОД 1,0 10 100
Рис. 3.66. Безразмерная местная температура бесконечной пластины шириной
2L в зависимости от температуры в среднем ее сечении.
1
0,9
0,8
0,7
0,3
0,2
к —
а.
7
11
/ / /
¦<^:
Y/
\\/,
\\i 1
n
' /
/ у
'У
i
i
i
/
I 1
111
If
1 /
1
1
) V
/
* /
/
<^
* I
I
1 /
' i
j
/ f.
?<
i j
j
) t
T~ j
'' \
f f
1
j
( f
/
I
1
7
10
10 '
10
(BiJ(Fo)
Ю l
hUt
кг
10
Рис. З.бв. Безразмерный теплоотвод от одной поверхности бесконечной пла-
пластины шириной 2L.
Начальное условие одинаково для всех трех тел. В момент
времени t = 0 твердое тело имеет постоянную температуру Го.
3 этот момент времени внешняя поверхность твердого тела по-
погружается в жидкость с температурой Too и начинается процесс
нестационарного теплообмена.
Решения для распределения температуры и теплового потока
для трех рассматриваемых конфигураций обычно представляю?
144 Глава 3
rt
I
f
4
№
in
ii
in
in
in
in
in
№
№
Ш
IT
-
-1
\—
s -
2
Mlflfl
I U lit I
ill 111
шШ HI1
¦II flff ffi
¦ Iff ШГМ
llflfJ/J
IliffirWi
ШШ1
тш
щи.
Witt
Штп
Ш
Wv-
WWIM
¦wniik
unit/
il'Mi7i
ниш
1ШШ
ПШЙ
пиши
ЧШАГ/,
mil/мм
tHJtW
Ш
1
h-H'
//
у
' /
/1
Mi
ЙШ
r
H
* t
ft
—f-
/j
//
/ /
fj
If
I
1 ,
f (
1 i
f i
JJ
11
I I
1
J
' j
/ i
II
j/
'/j
? /
'Ф
/
/
t '
/ / '
{/'/
//
у У
Уу* '
УУУ
^Уу''
II 1
1 / ч
' 1 *\
/ 1
J 1
/
/ /
/ /
/ J
J /
J / /
/ if '
f //
//
i/ У .
У У
у^' '
*?у
г/
/ / ^
/ <f
у у
У У
У У '
У**У**
¦ -1
;
/
' г
2
У
t-
\
7
у
/
с
/
о?
у*
J
d.
с?
~7
/*
(
> N
y.
у
/
/
/
•/*-
у
У
5^
у
J
/
у
у
У
у
у
У
Лъ*
у
??
/
у
у "^с
у
уг *
У у
У ' '
У^ .'
у
у
у
/
'V '
\ ГУ
Fa.
>\ *'
У
У* -
^^
у
у
У t <•
» н ' ,
А?"
^ 3
^^. «:
i- * -
?и *
Г -
7 j
I . ~.л
7
^ г
^- '
г
>*
=i
У-
л
"^*
у
W
у
у
У\
'—
у
*•*
\у
\-^
—¦' lllJi
у
у
у
у*
у
у
у
—¦
у
у
у
у
у
^у
у
—-_,
у
^у
у^
^у
8
1
о" о'о" о" о*
о оо о о
8888 8 8
о<э<э<э а о
8
СЗ
ч
о
я
1
о
I
о
8
2
cd
I
СО
i
Си
Нестационарная теплопроводность 145
в графической форме с использованием безразмерных перемен-
переменных. Мы убедились, что определяющими параметрами в зада-
задачах нестационарной теплопроводности с конвективным гранич-
граничным условием являются числа Био и Фурье. Три рассматривае-
Рис. 3.76. Безразмерная местная температура бесконечно длинного цилиндра
радиусом г0 в зависимости от температуры на его оси.
1
0,9
0,8
0,7
0,6
0,4
0,3
0,2
0,1
7/,
/У L
// /// /
1 10 102 103
104
Рис. 3.7в. Безразмерный теплоотвод от бесконечно длинного цилиндра радиу-
радиусом Го.
мых нами случая не служат исключением. Значения местной
температуры зависят от безразмерной линейной координаты
внутри тела, числа Био и числа Фурье. Сводка выражений для
всех безразмерных параметров представлена в табл. 3.1.
Значения безразмерной температуры представлены графи-
графически на рис. 3.6а, 3.66; 3.7а, 3.76 и 3.8а, 3.86. На рис. 3.6 при-
приведены значения для бесконечной пластины шириной 2L, на
рис. 3.7 — для бесконечно длинного цилиндра, на рис. 3.8 —для
146 Глава 3
Illl 1 1
jO
1,5-;
7
Ш
MfUftt
ШмшШ
iiSintt i
ШШ
Пя/тгм
If н ft Vnfl
ft i If Witt}
ttthffluJi
WfNjtf
Wjjht
Иг7
/
Ууу,' J
^ У/ '
ES
7_
а!
1
т.
~7
ц
?
Z
г
?
i
/ /
¦А
t?
<
/у
л/
^
У у
1
1
f I
I
j
I
I
,111 Jfi/JV
W>9'/.'A
/И
2
7~7 i^> ^
у?т :?'
If/ '
/ / j t
/ / ' t
/yy ; '"
У У "
у j, * +
f f
/ v
/ / '/
/// ''
/// ' '
/"ууУ .'
' У* • '
p »- ^5
^ ^-
^ 2_
7~~7
*~ У.
z-z
у
r.
V
/
^1
Us
у
у
У
у *
гу~^ ':
У
^f 1 '
/ / ,.
у у t
*, у s'
= = = =
/>
^у^:Х
¦¦; -
•>
~*
У
—
-и ^
К
***
2!
>
у
.^¦=
*?-
у
—L
-^
у
у
У*
yS
у*
С—?
у
+*-~~ j-
—¦ ¦—
у
<-г——
^—
<<
i j
у
«о
CS
о
сч
90110 130 170
о
с-»
о
«о
?
20 25 30
иусом г
1015
а
vo о.
3 4
фа в це
со ?»
°^ Л
О.
<N С
- г
з 1
СО
«л cd
) (
Без]
Г- «/I^f ГЛ CM г— Г» fnrt П M —* Г- »^Tt f> CN —«W' ,
, о ооо о- о о goo о о. gogo о § g
о" оо о о о ^
(; 'о)е^
Нестационарная теплопроводность 147
шара. На рисунках 3.6а, 3.7а и 3.8а представлены серии кривых,
выражающих безразмерную температуру на оси тела:
6 @, t) = т (О, t) - т^
е0 т0 - т^ *
C.21)
Чтобы найти местную температуру вне осевой линии, нужно
использовать результаты, приведенные на рис. 3.66, 3.76 и 3.86.
1
0,9
ггя
0,8
*f 0,7
С 0,6
S 0,5
II 0,4
В 0,3
* п?
0,2
0,1
0
0
0
/
I5-
0,6.
0,7.
-0
-0
-
Г'
= 0,2
ТШ1—Т
/
у
J
/
/
/
/
'
'
/ ,
У
У/
1
у
ш
1
111
¦J [¦ 111
к
0,01
0,1
10
100
вг
Рис. 3.86. Безразмернал местная температура шара радиусом гов зависимости
от температуры в центре шара.
1
0,9
0,8 -
0,7
0,6
i|<S 0,5
0,4
0,3
0,2
0,1
0
/
? у
||
%
т
г
1
j
7 )
/f'
А'*
it !
ш
i 7 /
7 / /
! (
m
1
II
> f
t J
f
11
п
1 1
I
T
/\,
?'¦'
7
/ ^
/
/
/ /
i
1
i
1
I
/
< V
//
/
1
I
/ /
: <*
1
i
f
/
I 1
1
/
1
f-
у
У
' i
1
\t
,.'
hcr0
к
Illllll
О
ю-5 ю-4
(BiJ(Fo) =
1
Ic2oct
10
102
Ю3
104
Рис. 3.8в. Безразмерный теплоотвод от шара радиусом r0.
Представленные на указанных рисунках серии кривых выра-
выражают зависимость местной температуры от температуры на оси
тела; отношение этих величин для бесконечной пластины выра-
выражается формулой
Т (х, t) - То
e @, t) т (o, /) -:
C.22)
148 Глава 3
Аналогичные выражения получаются для бесконечного цилиндра
и шара. Чтобы найти значение местной температуры, следует
использовать произведение соотношений C.21) и C.22):
Т (*, 0 - т„ __ 9 @, t) е (л:, О
т0 -т^ dQ e (о, t)'
Как только найдено распределение температуры, можно рас-
рассчитать тепловой поток от поверхности твердого тела, применяя
закон Фурье на поверхности раздела тела и среды. Значения
безразмерного теплоотвода от поверхности представлены гра-
графически на рис. З.бв для бесконечной пластины, на рис. 3.7в —
для бесконечно длинного цилиндра и на рис. 3.8в — для шара.
Каждое значение Q(t) представляет собой общее количество
тепла, отводимое от поверхности к греде за период времени от
t = 0 до t = t. Нормирующая величина Qo — это начальная
энергия твердого тела в момент времени t = 0, если нулевая
энергия соответствует температуре Too. В табл. 3.1 для удобства
приведены значения Qo для трех рассматриваемых форм тела.
Поскольку объем пластины бесконечен, безразмерный теплоот-
вод для этой конфигурации выражен на единицу площади по-
поверхности и обозначен Q"(O/Qo- Объем бесконечно длинного
цилиндра также бесконечен, поэтому относительный теплоотвод
Q' @/Q6 выражен на единицу длины цилиндра. Объем шара
конечен, и для этого тела относительный теплоотвод равен про-
просто Q(t)/Qo. Если величина Q(t) положительна, тело отдает
тепло в окружающую среду, т. е. тело охлаждается. Если вели-
величина Q(t) отрицательна, тело нагревается окружающей средой.
Представленные диаграммы позволяют решить два общих
класса нестационарных задач. К первому классу относятся за-
задачи определения местной температуры, если задано время. Ко
второму классу относятся задачи определения времени, по исте-
истечении которого местная температура принимает заданное зна-
значение. Задачи первого класса можно решить непосредственно с
помощью диаграмм. Задачи второго класса иногда решают ме-
методом проб и ошибок. Приведем примеры решения задач обоих
классов.
Пример 3.4. Длинный чугунный [k = 70 Вт/(м-град), а=*210-р ь2/с)
цилиндр диаметром 20 см имеет вначале постоянную температуру 400°С. На-
Наружная поверхность цилиндра охлаждается воздухом с температурой 50°С
при коэффициенте конвективной теплоотдачи 420 Вт/(м2-град). Найти тем-
температуру поверхности и температуру на оси цилиндра после его охлаждения
воздухом в течение 20 мин. Рассчитать общее количество тепла, отданное
единицей длины цилиндра за 20 мин.
Решение. Найдем число Био, чтобы проверить, имеет ли система прене-
пренебрежимо малое внутреннее термическое сопротивление:
Отсюда следует, что в рассматриваемом теле должны существовать большие
Нестационарная теплопроводность 149
температурные градиенты, поэтому необходимо применить решение в виде
диаграмм.
Рассчитаем необходимые параметры, указанные в табл. 3.1:
hlat D20J B • 1<Г5) B0 • 60)
(Bi)* (Fo) ¦—|s— щг 0,86,
90 = Го - Т„ = 400 - 50 = 350°С,
Qf0 = рскг* (Го - Гте) = -t-nrl (Г0-Гоо)=-^г-5 л @,1J C50)=3,85 • 107 Дж/м.
(X a* 1U
С помощью диаграммы 3.7а находим значение безразмерной температуры на
оси цилиндра при Fo = 2,4, Bi-1 = 1,66:
6@,0 по, Q-Гоо nnQ
или Т @, *) = 0,09 (Го - Гто) + Гоо = 81,5°С.
По диаграмме 3.76 найдем отношение температуры поверхности (г/г0 = 1,0)
к температуре на оси цилиндра:
иг., о L 075
6@,0
так что температура поверхности равна
. = 0.75 • 0,09 = 0,0675,
U (и, t)
или Т (го, 0 « 0,0675.350 + 50 = 73,6°С.
Количество тепла, отданного поверхностью, можно найти с помощью диа-
диаграммы 3.7в:
'j0,88,
или Q'(t) = 0,88-3,85-107 = 3,39-107 Вт-с/м = 9,41 кВт • ч/м.
Пример 3.5. Большая плита из нержавеющей стали (к = 30 Вт/(м-град),
а = 1,5-10 м2/с) толщиной 30 см выходит из прокатного стана, имея по-
постоянную температуру 800°С. Плита охлаждается с обеих сторон высокоско-
высокоскоростными воздушными струями. Температура воздуха 30°С, коэффициент кон-
конвективной теплоотдачи от поверхности плиты к воздуху 500 Вт/(м2-град). На
поверхность плиты нужно положить слой пластиковой теплоизоляции, но тем-
температура поверхности стальной плиты при этом не должна превышать 200°С.
Определить минимальное время, в течение которого нужно обдувать плиту,
чтобьд можно было положить слой теплоизоляции.
Решение. Находим число Био (табл. 3.1)
V, 500-0,15
ш
ш-~-—зо—
Следовательно, необходимо применить решение в виде диаграмм. Нельзя не-
непосредственно использовать диаграмму на рис. 3.6а, поскольку на ней приво-
приводятся температура в среднем сечении и время, а обе эти величины неиз-
неизвестны. Сначала нужно с помощью рис. 3.66 найти температуру в среднем
сечении плиты:
6(L, t) _ 200-30 _ 170 _
е (о, t) ~ т (о, /) - зо ~~ т (о, *) - зо ~~ • ¦
или Т @, 0 « 444,6°С.
150 Глава 3
Безразмерная температура в среднем сечении плиты равна
9 @, 0 444,6 - 30
800 - 30
s 0,538.
Теперь по диаграмме на рис. 3.6а находим, что при Bi~1 = 0,4 и безразмер-
безразмерной температуре в среднем сечении 0,538 число Фурье Fo = at/L2 == 0,60,
или t = 900c = 15 мин.
Решение двумерных и трехмерных задач
Диаграммы для одномерных нестационарных задач можно
применить к решению двумерных и трехмерных задач, используя
произведения значений, снятых с диаграмм для одномерной за-
задачи (рис. 3.6—3.8). Решения двумерных и трехмерных задач
с помощью диаграмм для одно-
одномерной задачи можно найти на
том основании, что решение диф-
дифференциального уравнения в част-
частных производных можно предста-
представить в виде произведения реше-
решений двух или трех обыкновенных
дифференциальных уравнений.
Доказательство этого положения
можно найти в работе [3]
(разд. 5.2).
Метод представления решения
в виде произведения лучше все-
всего проиллюстрировать на при-
примере. Предположим, что нужно
Рис. 3.9. Цилиндр конечной длины.
найти нестационарную температуру в точке Р цилиндра конеч-
конечной длины (рис. 3.9). Положение точки Р определяется двумя
координатами (х, г), где х — координата вдоль оси, измеряемая
от среднего сечения цилиндра, а г — радиальная координата.
Начальное и граничные условия такие же, как при решении
одномерной нестационарной задачи. Вначале цилиндр имеет по-
постоянную температуру Го. В момент времени t=0 вся поверх-
поверхность цилиндра вступает в контакт со средой, имеющей постоян-
постоянную температуру Г<х>, при постоянном коэффициенте конвектив-
конвективной теплоотдачи поверхности тела к среде Яс.
На рис. 3.76 представлено распределение температуры по
радиусу бесконечно длинного цилиндра. Для цилиндра конечной
длины распределение температуры по г и х выражается произ-
произведением решений для бесконечно длинного цилиндра и беско-
бесконечной пластины:
где С (г) и Р(х) — распределения безразмерной температуры для
бесконечно длинного цилиндра и бесконечной пластины соот-
Нестационарная теплопроводность 151
Таблица 3.2
Решения двумерных задач нестационарной теплопроводности
в виде произведения решений одномерных задач
Форма тела
Обозначения
Безразмерная
температура
в точке Р
Полубесконечная
пластина
Бесконечно
длинный
прямоугольный
брус
Окружающая
к:
Окружающая
^ среда
Окружающая
среда
Четверть
бесконечного
. тела Окружающая
к, а
Окружающая
Полубесконечный среда
цилиндр hc, Х
Окружающая/
среда /
Цилиндр конечной
длины
-оГ
*Р(х)С(г)
ветственно: C(r)=B(r, t)/Qo\ P(x) = Q(x, t)/Qo. Распределение
С (г) находится по данным рис. 3.7а и 3.76, а распределение
Р(х) — по данным рис. 3.6а и 3.66.
Решения для других двумерных и трехмерных тел можно
получить методом, аналогичным примененному для цилиндра
152 Глава 3
Таблица 3.3
Решения трехмерных задач нестационарной теплопроводности
в виде произведения решений одномерных задач
Форма тела
Обозначения
Безразмерная
температура
в точкеР
Полубесконечный
прямоугольный
бруо -
Окружающая
среда ^
*?Ч
Параллелеп^ед
Окружающая
среда
Четверть
бесконечной
пластины
Окружающая .4 'х
Ьдна восьмая сР?да
бесконечного h
тела
конечной длины. Решение трехмерной задачи является произве-
произведением трех решений одномерной задачи, а двумерную задачу
можно решить, используя произведение двух решений одномер-
одномерной задачи.
В табл. 3.2 представлена сводка всех двумерных конфигура-
конфигураций, для которых получены решения в виде диаграмм.
В табл. 3.3 представлены трехмерные конфигурации. В обеих
таблицах использованы следующие обозначения:
Нестационарная теплопроводность 153
S(x)= Q{x, t)/% — решение для полубесконечного твердого
тела (рис. 3.4 или 3.5);
Р(х) = Q(x, t)/Qo — решение для бесконечной пластины,
(рис. 3.6а и 3.66);
Р(г) = в(г, t)/Qo — решение для цилиндра бесконечной дли-
длины (рис. 3.7а и 3.76).
Применяя решения одномерных задач для двумерных и трех-
трехмерных тел, можно решить много задач нестационарной тепло-
теплопроводности.
Пример 3.6. Цилиндр диаметром 10 см и длиной 16 см (k = 0,5 Вт/(м X
X град) и а = 5-Ю*-7 м2/с) имеет вначале постоянную температуру 20°С. Его
помещают в печь с температурой воздуха 500°С и Нс — 30 Вт/(м2-град).
Найти минимальную и максимальную температуры в цилиндре после 30-ми-
30-минутной выдержки его в печи.
Решение. Число Био, рассчитанное по радиусу цилиндра, равно
Следовательно, задачу нельзя решить упрощенным методом в предположе-
предположении о пренебрежимо малом внутреннем термическом сопротивлении, и тре-
требуется применить решение в виде диаграмм.
Данные, приведенные в табл. 3.2, показывают, что распределение темпе-
температуры в цилиндре конечной длины можно найти как произведение решений
для бесконечной пластины и цилиндра бесконечной длины. В любой момент
времени минимальная температура достигается в точке х = 0, г = 0, а мак-
максимальная — на окружностях х = ±L, г = г0. Сводка результатов расчета
представлена в следующих таблицах.
Бесконечная пластина
Fo-g
E-1(Г7I8ОО
M),14
FoV
Ei0~7I800
@,05J
=0,36
Kb
(Рис. 3.6а)
0,90
(Рис. 3.6а, 3,66)
Бесконечно длинный цилиндр
Vo
с@)=М
(Рис. 3.7а)
0.47
(Рис. 3.7а, 3.76) .
0,47 -0,33 «0,155
Минимальная температура цилиндра равна
QjSSL = р @) С @) « 0,90 • 0,47 = 0,423,
"о
^мин = 0,423 B0 - 500) + 500 — 297°С.
154 Глава 3
Максимальная температура цилиндра равна
Омакс
P(L)C (rо) = 0,243 -0,155 = 0,0377,
Гмакс = 0,0377 B0 - 500) + 500 = 482°С.
3.5. ЧИСЛЕННЫЕ РЕШЕНИЯ ЗАДАЧ
НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ
Явный метод
Методика численного решения задач нестационарной тепло-
теплопроводности аналогична описанной в разд. 2.7 методике решения
задач стационарной теплопроводности. Вначале твердое тело
делят на ряд ячеек. В центре каждой ячейки помещают вообра-
воображаемый узел. Записывая ба-
баланс энергии для каждого
узла, получают алгебраиче-
алгебраическое уравнение, выражаю-
выражающее температуру в рассма-
рассматриваемом узле через темпе-
температуры в соседних узлах,
геометрические характери-
характеристики и теплофизические
свойства материала. При ре-
решении нестационарных за-
задач для каждого узла нужно
дополнительно учесть акку-
аккумулирование энергии в мате-
материале. Эта аккумулированная энергия представляет собой воз-
возрастание внутренней энергии в узле, которое определяется тер-
термодинамической характеристикой материала, называемой удель-
удельной теплоемкостью с.
Рассмотрим сначала одномерную задачу для внутреннего
узла (рис. ЗЛО). В дальнейшем можно обобщить этот анализ
для двумерных и трехмерных задач. Закон сохранения энергии
для узла 0, расположенного между узлами 1 и 2, при отсутствии
внутреннего тепловыделения можно выразить в виде
Твердое тело
Свойства к,р? с
Рис. ЗЛО. Расположение узлов внутри
твердого тела (одномерная задача).
Скорость изменения внутренней \
энергии в узле 0 по времени /
C.23)
Соотношение C.23) аналогично соотношению B.93) с той лишь
разницей, что в нестационарной задаче учитывается скорость
изменения внутренней энергии. В стационарной задаче изме-
изменение внутренней энергии равно нулю.
Нестационарная теплопроводность 155
Используя принятые обозначения, перепишем соотношение
(ЗЩ в виде
flWo + ?2->oeir. C*24)
где Uq — внутренняя энергия в узле 0.
Кондуктивные члены в соотношении C.24) можно выразить
с помощью конечно-разностной формы закона Фурье:
rpt *pt
кЛ * °
C-25>
Верхний индекс / в этих членах означает, что температуры
должны рассчитываться в момент времени /. Нижние индексы
отражают положение узлов. Следовательно, они определяют
изменение температуры по пространству, или по х, а верхние
индексы — изменение температуры по времени.
Изменение внутренней энергии в узле 0 в предположении,
что плотность и удельная теплоемкость материала постоянны,
выражается соотношением
i^L „ mc ?l = рЛ Axe I±lflk. (з.26)
Подставляя соотношения C.25) и C.26) в уравнение C.24), по-
получаем уравнение энергии для узла 0:
Разрешая это уравнение относительно Го+Л', получаем
= Fo (fi + Tl) + [1 - 2Fo] To, C.27)
где число Фурье определяется в виде Fo = a(At)/(hxJ. Выра-
Выражение C.27) показывает, что температуру в момент времени
t-\-At в произвольном внутреннем узле 0 можно рассчитать,
зная текущие температуры в момент времени t в узле 0 и сосед-
соседних узлах. Для всех внутренних узлов можно записать уравне-
уравнения, аналогичные C.27), получая в итоге систему алгебраиче-
алгебраических уравнений для температур в п соседних узлах. Каждое из
этих уравнений энергии в явном виде определяет температуру
рассматриваемого узла в будущий момент времени; поэтому
такой способ численного решения называется явным методом.
Кроме того, этот метод называется методом с использованием
156 Глава 3
правых производных, поскольку производная по времени аппрок-
аппроксимируется разностью, направленной вперед по времени:
dt
Если узел расположен на границе твердого тела, то для
него необходимо вывести специальное уравнение энергии. Форма
уравнения энергии зависит от граничного условия на поверхно-
поверхности. Одним из наиболее часто встречающихся условий является
наличие конвективной тепло-
теплоотдачи поверхности. Снова
рассмотрим одномерную зада-
чу, причем узел 0 расположен
на поверхности (рис. 3.11).
Уравнение энергии для узла О
имеет вид
Окружающая
среда
или
kA-
1""" °
A*
dUQ
dt
+ hcA (Tl - Tl) =
Рис. 3.11. Расположение узлов для
поверхности твердого тела, находя-
находящейся в контакте с внешней средой
(одномерная задача).
рльхс г?+Л'-;г$
C.28)
Отметим, что узлу, лежащему
на поверхности, соответствует
объем (Дл:)Л/2, поскольку ширина ячейки в этом случае со-
составляет половину ширины ячейки внутреннего узла. Всем вну-
внутренним узлам соответствует ячейка шириной Да:, в то время
как граничным узлам — ячейка шириной Д#/2.
Разрешая уравнение C.28) относительно температуры в гра-
граничном узле в момент времени t + Д*, получаем
2Fo [T{ + Bi TL] + [l- 2Fo - 2Fo Bi] Tl C.29)
где Fo = а (ДО/(Да:J, Bi = Ec(&x)/k. Если узлы расположены
близко друг к другу, масса, соответствующая граничному узлу,
мала и можно пренебречь энергией, аккумулирующейся в гра-
граничном узле; другими словами, можно пренебречь теплоемко-
теплоемкостью граничного узла. В случае пренебрежимо малой теплоем-
теплоемкости Го+Л* = То и соотношение C.29) сводится к следующему:
t т\ + Bi TJ,
Т«= 1 + Bi '
Если теплоемкостью граничного узла нельзя пренебречь и для
расчета изменения температуры поверхности применяется соот-
Нестационарная теплопроводность 157
ношение C.29), то для нахождения температуры поверхности
в момент времени / + А/ необходимо знать текущие значения
температуры на поверхности твердого тела и в первом узле от
поверхности. Если можно пренебречь теплоемкостью поверх-
поверхности и применить соотношение C.30), то достаточно знать
текущие значения температуры Т\ и Too, чтобы найти текущее
значение температуры поверхности Го.
Чтобы решить задачу нестационарной теплопроводности чис-
численным методом, необходимо знать начальное распределение
температуры в твердом теле. Обычно в качестве начального
условия задают начальные температуры в твердом теле. Часто
тело вначале изотермично, а это условие легко учесть, приняв
начальные температуры во всех узлах равными известной на-
начальной температуре тела. Затем начинают численное решение,
вычисляя температуры в момент времени At с помощью соотно-
соотношения C.27) для всех внутренних узлов и соотношения C.29)
для граничных узлов, если на поверхности происходит конвек-
конвективная теплоотдача к окружающей среде, имеющей темпера-
температуру Г». После расчета всех температур в момент времени At
процесс повторяют и рассчитывают распределение температуры
в момент времени 2А/. Эту процедуру повторяют до тех пор,
пока не будет достигнут момент времени, для которого тре-
требуется знать распределение температуры.
До сих пор мы считали, что выбор расстояния между узлами
Д* и временного интервала At является произвольным. Однако
при некоторых значениях Ах и At можно получить результаты,
противоречащие основным законам термодинамики. Предполо-
Предположим, например, что в некоторый момент времени температуры
в трех соседних узлах (рис. 3.10) равны Т\ = 100°С, Т2= 100°С,
Го = 50°С. Мы хотим рассчитать температуру в узле 0 в сле-
следующий момент времени с помощью соотношения C.27). Кроме
того, предположим, что при заданном коэффициенте температу-
температуропроводности материала мы выбрали Да: и At таким образом,
чтобы число Фурье было равно единице Fo = aAt/(AxJ = 1,0.
Подставляя это значение числа Фурье в соотношение C.27), на-
находим температуру в узле 0 в следующий момент времени:
Г?+ Г2 —Го,
или Г$+А' = 100 + 100 - 50 = 150°С.
Однако мы знаем, что температура в узле 0 не может стать
выше 100°С, поскольку тепло подводится к нему из областей с
температурой 100°С. Тот факт, что, согласно численным расче-
расчетам, температура в узле 0 превышает 100°С, противоречит вто-
второму началу термодинамики. Если бы мы подставили другие
значения числа Фурье, чтобы определить его влияние на буду-
будущую температуру в узле 0, то мы бы нашли, что результаты
Таблица 3.4
Явные разностные уравнения баланса энергии и критерии устойчивости для некоторых задач
Рассматриваемый случай
Схема
Одномерная задача,
внутренний узел
Двумерная задача,
внутренний узел,
квадратная ячейка
Трехмерная задача,
внутренний узел,
кубическая ячейка
Одномерная задача,
граничный узел,
конвекция на границе
Разностное уравнение
Критерий
устойчивости
О)
Г/+ Г5*+ Tj)
Fo < i
+[l-<KFo)]r0*
Окружающая
среда
Двумерная задача,
граничный узел,
конвенция на границе
Двумерная задача,
внешний угол,
граничный узел,
конвекция на границе
Двумерная задача,
внутренний угол,
граничный узел,
конвекция на границе
r1'+ Ц- + Ц-
Ц- + Ц
+[l-4(Fo)-2(Fo)Oi)]r0'
Fo<2+BQ< I
дх Окружающая
— среда
+[l-4(Fo)-4(FoXBi)]ro'
Ц- +
+[l-4(Fo)-!(Fo)(Bi)]7o*
FoC+B0 < I
Окружающая
160 Глава 3
расчета по формуле C.27) не будут противоречить второму на-
началу термодинамики в том случае, если
Fo < 0,5,
l-2Fo>0.
Это ограничение на величину числа Фурье часто рассматри-
рассматривается в качестве критерия устойчивости. Если число Фурье
больше 0,5, то говорят, что решение для температуры не-
неустойчиво. Отметим, что критерий устойчивости удовлетворя-
удовлетворяется, если коэффициент при То в соотношении C.27) положите-
положителен. Это условие является общим, и его можно доказать мате-
математически [7].
Критерий устойчивости для граничных узлов отличается от
критерия устойчивости для внутренних узлов. Если мы хотим
найти критерий устойчивости для граничного узла, в котором
происходит конвективная теплоотдача к окружающей среде, мы
можем потребовать, чтобы коэффициент при То в соотношении
C.29) был положительным:
l-2Fo —2FoBi>0,
или Fo(l + Bi)<0,5. C.32)
В конкретной задаче теплопроводности разностные уравне-
уравнения баланса энергии как для внутренних, так и для граничных
узлов должны быть устойчивыми. Например, если мы выберем
значение Fo = 0,25, чтобы, согласно критерию C.31), темпера-
температуры во внутренних узлах были устойчивыми, для устойчивости
решения в граничном узле необходимо выполнить условие
Bi <: 1,0 согласно критерию C.32). Если число Фурье принять
равным 0,5, то критерий устойчивости для граничного узла
удовлетворить невозможно, поскольку, согласно соотношению
C.32), требуется, чтобы число Био было отрицательным.
Уравнения баланса энергии для внутренних узлов в двумер-
двумерных и трехмерных задачах можно вывести без труда с помощью
метода, аналогичного методу, используемому при выводе соот-
соотношения C.27). Можно также вывести уравнения баланса энер-
энергии для граничных узлов в двумерных и трехмерных задачах
при различных граничных условиях.
В табл. 3.4 представлена сводка уравнений баланса энергии
для внутренних и граничных узлов. Для каждого уравнения
приведен критерий устойчивости. Этот критерий должен удов-
удовлетворяться для каждого уравнения, чтобы результаты расчета
температуры были устойчивыми. Каждое уравнение записано
для рассматриваемого узла 0, а нумерация остальных узлов по*
казана на специальных рисунках в таблице.
Нестационарная теплопроводность 161
Пример 3.7. Большая толстая плита [k = 40 Вт/(м-град), а = 3 X
X Ю" м2/с] имеет постоянную температуру 200°С. Поверхность плиты вне-
внезапно погружается в жидкость с температурой 100сС, коэффициент конвек-
конвективной теплоотдачи к жидкости от поверхности плиты 500 Вт/(м2-град). Най-
Найти изменение температуры плиты в течение первой минуты после погружения
в жидкость.
Окружающая
среда
К примеру 3.7.
Решение. Плита разделяется на слои с узлами, как показано на рисунке,
и нумерация узлов начинается от поверхности. Если учесть теплоемкость гра-
граничного узла, то температура T(t + At) в граничном узле определяется со-
соотношением C.29):
— 2Fo [Tf2 + Bi
- 2Fo - 2Fo Bi ] T\.
Все остальные узлы являются внутренними, и поэтому для произвольного
узла, обозначенного индексом i, применимо соотношение C.27):
¦ Fo [r^t + T*i+l] + [1 - 2Fo] T\.
Критерий устойчивости для граничного узла
-Bi)<0,5,
Fo<0,5.
Выберем удовлетворяющие этим критериям значения Fo *= <Ш/(Д#J а*
*= 0,25 и Bi = fickx/k = 0,5. Поскольку число Бйо выбрано, известна вели*
чина шага по пространству
а для внутренних узлов
k
2hc
40
2-500
^0,04 ms4 см.
Шаг по времени ограничивается выбранной величиной числа Фурье:
А/:
(А*J
4а
@,04J
4 C • 10Г
13,33 е.
Выбор чисел Био и Фурье осуществлен произвольно, но с учетом критериев
устойчивости. Можно применить другой подход к решению задачи. Можно
сначала выбрать величины А* и А?, а затем вычислить значения Fo и Bi. Если
найденные значения Fo и Bi не удовлетворяют критериям устойчивости, ве*
личины Ал; и Д? изменяют таким образом, чтобы эти критерии удовлетворя*
лись.
Теперь проведем расчет температур в узлах, отстоящих друг от друга на
4 см в последовательные моменты времени с интервалом 13,33 с. Темпера-
Температуры в промежуточных точках или в промежуточные моменты времени можно
6 Зак* 487
162 Глава 3
найти путем интерполяции. Температуры во всех внутренних узлах рассчиты-
рассчитываем' по формуле
Г<+д* = 0,25 (Г{_, + Г{
а температуру в граничном узле — по формуле
0,5 {т{ + 0,
Результаты расчета температур представлены в таблице.
Время,
с
0
13,33
26,67
40,00
53,33
56,67
Узел1,
*~0
200
175
168,8
164,1
160,6
157,8
Узел 2,
х*4см
200
200
193,9
189,1
185,2
181,9
Температура,
УзелЗ,
х«8см
200
200
200
198,5
196,5
194,5
?С
Узел 4
*«12см ^
200
•200
200
200
199,6
198,9
Узел 5,
х«16см
200
200
200
200
200
199,9
Пример 3.7 можно решить аналитически, решение выражается соотно-
соотношением C.19). Для проверки точности численного решения в приведенной
ниже таблице результаты расчета температур по формуле C.19) сравнивают-
сравниваются с численным решением в момент времени t = 66,67 с.
Значения температуры (°С) в момент времени f=66,67 с для примера 3.7
Узел
1
2
3
4
§
X СМ
•о
4
8
12
16
Численное
решение
157,8
181,9
194,5
198,9
199,9
Точное
решение
158,7
182,2
. 194,2
198,6
199,8
Графическая интерпретация численного метода
Можйо получить довольно простое графическое решение за*
Дач нестационарной теплопроводности, если выбрать величину
числа Фурье 0,5. При Fo *= 0,5 разностное уравнение для вну-
внутреннего узла( 3.27) упрощается и принимает вид
^= 0,5G1 + 71) C,33)
Это соотношение показывает, что будущая температура во внут-
внутреннем узле равна среднеарифметическому значению текущих
температур в двух соседних узлах. На рис. 3.12 иллюстрируется
Нестационарная теплопроводность 163
процесс графического определения будущей температуры во
внутреннем узле с помощью соотношения C.33). Температуру
в узле 0 в момент времени i-\- At находим, соединяя точки
Т\ и Т\ прямой линией.
Описанное графическое построение поля температур назы-
называется методом Биндера — Шмидта. Недостатком этого метода
является то, что могут получаться одни и те же значения
температур в узлах для двух последовательных моментов вре-
времени. Такая физически неправильная картина обусловлена не-
необходимостью выбора числа Фурье, точно равного критерию
Рис. 3.12. Определение будущей температуры во внутреннем узле методом
Биндера — Шмидта.
устойчивости Fo =5 0,5. Были предложены модификации графи-
графического метода Биндера — Шмидта, в которых использовались
значения числа Фурье, отличные от 0,5 [8]. В этих усовершен-
усовершенствованных методах применяется более сложное геометрическое
построение, но они приводят к более точным результатам ра-
расчета изменения температуры по времени. J
Метод Биндера — Шмидта применяется только для одномер-
одномерных задач. Он позволяет получить решение для составных сте-
стенок и при наличии конвективного теплообмена на поверхности
твердого тела. Более подробно этот способ решения описан в
работе [9]. Хотя применимость и точность графического метода
ограничены, он прост и позволяет визуально следить за измене-
изменением распределения температуры по времени. Рассмотрим при-
пример использования этого метода.
Пример 3.8. Большая плита толщиной 30 см имеет коэффициент темпера-
температуропроводности 5-Ю м2/с Вначале плита имеет постоянную температуру
0°С. Обе поверхности плиты внезапно вступают в тепловой контакт с твер-
твердым телом, имеющим температуру 500°С. Найти изменение распределения
температуры плиты по времени в течение первых 100 с контакта с нагретым
твердым телом.
6*
164 Глава 3
Решение. Нарисуем сечение плиты в масштабе и разделим его на шесть
равных частей. В результате получим семь узлов, отстоящих друг от друга
на 5 см. По оси ординат отложим температуру от начального значения 0°С
до максимальной величины 500°С, как показано на рисунке.
Узел 7
V
О 5 10. 15 20 25 30
К примеру 3.8.
Величина шага по времени определяется выбором числа Фурье:
или
(Ал:J = @,05J
2а 2E-Ю-5)
:25 С.
Теперь последовательно применяем метод Биндера — Шмидта, как показано
на рисунке, определяя графически температуру в каждом узле. Символом
Т\ обозначена температура в узле 3 в момент времени 2At = 50 с. По ис-
истечении 100 с температуры в узлах 1—4 принимают следующие значения:
Г, = 500°С, Г2 = 312°С, Г3 = 218°С, Г4 = 125°С.
Неявный метод
Основной недостаток явного численного метода состоит в том,
что разностное уравнение баланса энергии для каждого узла
должно удовлетворять критерию устойчивости. Чтобы удовле-
удовлетворить этому критерию, часто приходится выбирать очень ма-
дый шаг по времени, а это приводят к возрастанию объема рад*
Нестационарная теплопроводность 165
четов. В настоящем разделе описан несколько иной численный
метод, который устойчив при любых значениях чисел Био и
Фурье.
Рассмотрим внутренний узел в двумерном теле (рис. ЗЛО).
Явнойч формой разностного уравнения баланса энергии для
этого случая является соотношение C.27). Если уравнение ба-
баланса энергии, на основании которого получено соотношение
C.27), модифицировать и выразить через температуры в мо-
момент времени t + А/, то получим это уравнение для узла О
в виде
Tt+At Tt+At
Преобразуя полученное уравнение и применяя число Фурье,
находим
[1 + 2Fo] Tl+At - Fo (T{+At + Tl+At) - ТЪ = 0, C.34)
где, как обычно, Fo = а (А/)/(Ал;J. Если разностное уравнение
баланса энергии записать в этой форме, то можно видеть, что
температура T(t-j-At) во внутреннем узле зависит от темпера-
температур в момент времени t + At в соседних узлах, каждая из ко-
которых неизвестна. Следовательно, нужно записать разностные
уравнения баланса энергии для всех узлов и решить их одновре-
одновременно, получая в результате распределение температуры в твер-
твердом теле. Этот метод решения называют неявным методом в от-
отличие от явного метода, при использовании которого можно, ре-
решая по отдельности разностные уравнения баланса энергии для
каждого узла, найти в явном виде местную температуру. Этот
метод называют также методом с использованием левых произ-
производных, поскольку производная по времени аппроксимируется
разностью, направленной назад по времени.
Неявный численный метод устойчив при всех величинах ша-
шагов по пространству и времени. Однако чем мельче шаги, тем
точнее значения температур, поскольку уменьшаются ошибки
аппроксимации производных конечными разностями.
Существенное преимущество неявного метода — отсутствие
критерия устойчивости; его недостаток — необходимость реше-
решения системы алгебраических уравнений. При большом числе
уравнений полезно применить в расчетах на ЭВМ методы ре-
релаксации или методы обращения матрицы.
Мы рассмотрели здесь явный и неявный разностные методы.
В работах [10, 11] применяется конечная разность, представ-
представляющая собой среднеарифметическое значение левой и правой
разностей. Еще более общий метод получается при аппрокси-
аппроксимации производной температуры по времени средневзвешен-
средневзвешенным значащем левой ш правой разностей [11]. В работад
166 Глава 3
5
г
+
ь- i
+
СI
I
Ь7
I
I
Нестационарная теплопроводность 16?
г т
I i
|
О
i?
I
о
II
^ I >
1-Г 1
Sh +
11 =
H
168 Глава 3
[12—14] применяются «шахматные» методы («Hopscotch me-
methods»), являющиеся комбинацией явного и неявного методов.
«Неявные» уравнения баланса энергии для граничных узлов
выводятся аналогично «явным» с той лишь разницей, что теку-
текущее значение температуры в узле заменяется значением в
момент времени t-\-At. Рассмотрим, например, граничный узел
О, расположенный на поверхности одномерного твердого тела,
на которой происходит конвективный теплообмен с жидкостью,
имеющей температуру Гоо. Коэффициент конвективной теплоот-
теплоотдачи равен Яс, геометрия задачи показана на рис. 3.11. Баланс
энергии для граничного узла записывается следующим обра-
образом:
Tt+At Tt+At
М
C.35)
Сравнивая соотношения C.28) и C.35), можно видеть различие
между уравнениями баланса энергии, используемыми в явной
и неявной схемах. Преобразуя соотношение C.35), получаем
[1 + 2Fo A + Bi)] Го+А* - 2Fo [т{+А* + Bi f+At] - Т\ = 0. C.36)
Можно вывести разностные уравнения баланса энергии для
граничных узлов с другими граничными условиями для тел
другой формы. Сводка этих уравнений представлена в табл. 3.5.
После того как записаны и преобразованы уравнения ба-
баланса энергии для всех узлов, нужно решить систему п уравне-
уравнений для п узлов и найти температуры во всех узлах. Методика
решения показана на следующих двух примерах. Оба примера
решены с помощью программы численного расчета, использую-
использующей метод обращения матрицы. В примере 3.9 рассматривается
одномерная задача, в примере 3.10 —двумерная. Как и прежде,
программа численного расчета написана в общей форме, чтобы
ее можно было применить для решения неявным методом широ-
широкого класса задач.
Мы приводим в этой главе несколько программ. Мы наме-
намеренно приводим довольно простые программы, но при этом чи-
читателю, прежде чем пользоваться программой, необходимо са-
самому вывести систему уравнений баланса энергии. Это позво-
позволит ему познакомиться с современными численными методами
и счетными машинами, не теряя навыков расчета теплообмена.
С более современными программами решения задач теплооб-
теплообмена читатель может познакомиться в работах [15, 16].
Заслуживает упоминания не использованный нами метод ко-
конечных элементов. Этот метод является очень гибким и мощным
численным методом и имеет ряд преимуществ перед конечно-
Нестационарная теплопроводность 169
разностными методами, употребленными при решении приведен-
приведенных выше примеров.
Методом конечных элементов можно составить весьма об-
общую программу численного решения, применимую для очень
широкого класса задач теплообмена. Практически невозможно
создать общую программу решения конечно-разностным мето-
методом, позволяющую решить тот же самый класс задач. Границы
неправильной формы и смешанные граничные условия не пред-
представляют особых трудностей при решении задачи методом ко-
конечных элементов. Этому методу посвящено несколько содержа-
содержательных монографий [17—20].
Пример 3.9. Решить пример 3.7 неявным численным методом. Плита
имеет следующие теплофизические характеристики: k = 40 Вт/(м-град), а =
= 3-10-5 м2/с, Яс = 500 Вт/(м2трад), Гто = 100°С, То = 200°С. Геометри-
Геометрические характеристики задачи показаны на рисунке,
Окружающая
среда
К, rm
К примеру 3.9
Решение. Делим плиту на слои равной толщины и в середине каждого
слоя располагаем узел, как и при использовании явного метода. Для гра-
граничного узла 1 неявная форма разностного уравнения баланса энергии имеет
вид C.36)
+ 2Fo A + Bi)]
- 2Fo
Bi
- т\
0.
Неявная форма уравнения баланса энергии для произвольного внутреннего
узла / выражается в виде соотношения C.34)
J(^^ ^)-^ = 0 (/ = 2, 3, ...).
Будем решать систему алгебраических уравнений методом обращения мат-
матрицы, поэтому запишем все разностные уравнения баланса энергии в мат-
матричной форме:
Уравнение баланса энергии для граничного узла в матричной форме
имеет вид
+ 2Fo A + Bi)] T\+At - 2Fo
[утренних уз
ом:
- Fo T\tff + [1 + 2Fo]
2Fo Bi
а для всех внутренних узлов уравнения баланса энергии записываются сле-
следующим образом:
- Fo
т\.
170 Глава 3
Если выбрать значения шагов по пространству и времени Д* = 0,04 м, Д/ =»
*= 13,333 с, то Fo = а(Д/)/(Д*J *= 0,25, Bi = hc(&x)/k = 0,5. Ограничим
Текст программы численного решения примера 3.9
DIMENSION ТE0),АE0,50),ВE0),СE0,50)
READ , N,NTIME,DELX,DELT JO
READ , ((A(I,J).J»1,N),I-1,N)
WRITE F,10) DELX.DELT.TO
10 FORMATAH ,'•¦• TRANSIENT TEMPERATURE DISTRIBUTION IN DEGREES' ,/ty
1 'CELSIUS DETERMINED BY AN IMPLICIT NUMERICAL TECHNIQUE ••¦',/,
2 'NODE SPACING -' ,F8.4,# METERS' ,/,'TIME INTERVAL-' ,F8.3,
3 ' SECONDS'./.'ORIGINAL TEMPERATURE*',F8.2,< DEG.REES C)
CALL MATINV (A.N.C)
DO15I = 1,N
15 T(I)=TO
DO80JJ~1,NTIME
30 BA)*=25.0 + TA)
BA0) = 50.0+TA0)
KK-N-1
DO30l = 2,KK
30 B(!)»T(I)
DO50l«1,N
SUM-0.0
DO40J«1,N
40 SUM = SUM + C(I,J)*B(J)
50 T(I)=SUM
TIME«AJ*DELT
WRITE F,70) TIME, (I,T(I),I-1 ,N)
70 FORMAT (/.25X.TIME IS-f,F10.3/ $ECS',/,4CT(M2,
80 CONTINUE
STOP
END
область решения 10 узлами. В таком случае используем 10 разностныл урав-
уравнений баланса энергии:
узел 1: {? i
узел 2: -0,25Г{+д' + 1,5Г?+Д* - 0,25Г?+д' %
узел 3: -0,25Г?+А* + 1,5Г^+А/ - 0,25Г*4+Л/ = Т%
узел 4: -0,257^+Л< + 1,5Г$+Д' - 0,25Г?+д' — Т%
узел 5: -0,25Г<+А? + 1,5Г^+АГ - 0,25Г?+А' - Т%
узел 6: -0,25Г?+ *' + 1,5Г|+ дг - 0,25Г?+Д' - Г|,
узел 7: -0,25Г?+^ + I,5jj+Af - 0,25Г?+ *' = Т\%
узел 8; -0,25Г?+А< + 1,5Г|+Л^ - 0,25Г?+ д/ = Т%,
узел 9: -0,257^+А' +
узел 10: -0,257^+А' +
Нестациднарная теплопроводность 1?1
В эти 10 уравнений входят значения температуры в 11 узлах. Температуру
в 11-м узле можно найти из граничного условия, требующего, чтобы она
оставалась равной начальной температуре 200вС, пока время, в течение ко-
которого отыскивается решение, не слишком велико. Отметим, что на осно-
основании полученного ранее решения примера 3.7 температура в узле 5 практи-
практически не изменяется в течение первой минуты. Поэтому, приняв температуру
в узле 11 равной Го, мы не получим сколько-нибудь существенных ошибок.
Итак, уравнение энергии для узла 10 принимает вид
- 0,25Г?+д' + 1,5Г(+Л* *- 50 + Т\о.
Обращение матрицы проводится с помощью подпрограммы MATINV. Эта
подпрограмма использовалась при решении примера 2.13, и ее текст представ-
представлен в приложении П.Х1. Входной информацией для подпрограммы MATINV
являются элементы матрицы А и число уравнений энергии N. В качестве вы-
выходной информации эта подпрограмма выдает элементы обращенной матрицы
С. Текст программы численного расчета приведен на стр. 170.
В следующей таблице представлены входная информация программы и
соответствующие обозначения на алгоритмическом языке Фортран.
Обозначения входной информации для примера 3.9
Обозначение
N
NTIME
DELX
DELT
ТО
A(I, J)
Определение
Число узлов
Число шагов по времени
Шаг по пространству
Шаг по времени
Начальная температура в
Элементы аи матрицы
2, ..., N; /-1, 2, ...
узле
А (/ = 1,
, п)
Единицы
измерения
_
—
М
С
°С
—
Первые пять величин нужно расположить в одну строку. Следующие N
Строк содержат элементы матрицы А. Каждая строка содержит N величин.
Эти величины ац являются коэффициентами разностных уравнений баланса
энергии, приведенных выше. Матрица называется тридиагональной, поскольку
все ее элементы равны нулю, за исключением элементов, стоящих на главной
диагонали и с двух сторон по соседству с ней.
Входная информация программы и результаты расчета записываются еле*
дующим образом:
Входная информация программы
для примера 3.9
10,5,0.04,13.3333,200.
1.75, -0.5, О., О., 0., 0., 0., О., О., О.,
-0.25,1.5, -0.25, О., 0., 0., 0., 0., 0„ О*
О., -0.25,1.5, -0.25, 0., О., 0., 0., 0., 0.*
О., 0., -0.25,1.5, -0.25, 0., 0., 0., 0., 0.»
О., О., 0., -0.25,1.5, -0.25, 0., 0., О., 0.»
О., 0., 0., 0., -0.25,1.5, -0.25, 0., 0., 0.*
О.. О., 0., О., О., -0.25, 1.5, -0.25, 0., 0.*.
О., 0., 0., 0., О., 0., -0.25,1.5, -0.25. 0.,
О., 0., О., О.. О., 0., 0., -0.25,1.J5, -0.25»
О., О., О., 0., 0.. а, О., 0., -0.25,1.5
172 Глава 3
Выходная информация программы для примера 3.9
*¦*Нестационарное распределение температуры в градусах
.Цельсия, рассчитанное неявным численным методом ***
Шаг по пространству=0,0400 м
Шаг по времени =13,333 с
Начальная температура 200,00° О
*
ТA) = 184.98
ТE)« 199.99
Т(9) = 200.00
ТA)« 175.40
ТE)« 199.94,
Т(9)=200.00
ТA)« 168.90
Т(б)-199.85
Т(9)« 200.00
ТA)~ 164.21
ТE)« 199.69
Т(9)-200.00
ТA) = 160.62
ТE)~ 199.46
Т(9)- 200.00
t=13,3330
ТB) = 197.42
Т(ё)=200.00
ТA0)« 200.00
ТC)«199.56
ТG)« 200.00
*=26,667о
ТB)~ 193.96
ТF)« 199.99
Т(Ю)« 200.00
ТC)« 198.65
ТG)« 200.00
t=40,000c
ТB)« 190.35
ТF)» 199.97
ТA0)« 200.00
ТC) = 197.38
ТG) = 199.99
t= 53,333с
ТB)=» 186.92
ТF) = 199.92
ТA0) = 200.00
ТC) = 195.88
ТG)« 199.98
^«66,6^70
ТB)« 183.75
ТF)« 199.85
ТA0)«200.00
ТC)« 194.24
ТG)« 199.96
ТD)« 199.92
Т(8)«200.00
ТD)« 199.71
Т(8)»200.00
ТD)« 199.35
Т(8)-200.00
ТD) = 198.83
Т(8)-200.00
ТD)» 198.17
Т(8)* 199.99
Для проверки точности результатов численного расчета неявным мето-
методом в следующей таблице проводится сравнение полученных при численном
расчете значений температур с данными точного решения C.19) в момент
времени t =»= 66,67 с.
Сравнение результатов численного расчета
неявным методом с точным решением примера 3.9
Узел
1
2
3
4
5
Температура, °С, при *=66,67 с
Точное решение
158,7
182,2
194,2
198,6
199,6
Численное решение
неявным методом
160,6
183,8
194,2
198,2
199,5
Пример 3.10. Нужно нагреть длинный брус прямоугольного сечения. Из-за
недостатка места тепло можно подвести только с одной поверхности бруса.
Нагреватель прижимается к одной стороне бруса и работает до тех пор, пока
температура противоположной стороны не достигнет требуемого минималь-
минимального значения.
Нестационарная теплопроводность 178
Окружающая среда
—I +—
Нагреватель,
Температура Ts-
о
4
H j
О
з
--+ 1
О
2
I— L j_j
1 I .6
20 см
Окружающая
среда
Окружающая среда
К примеру ЗЛО.
Первоначально брус имеет постоянную температуру 50°С. Коэффициент
температуропроводности материала бруса равен 2,5-10 м2/с, коэффициент
теплопроводности 25 Вт/(м-град). Остальные три поверхности окружены воз-
воздухом с температурой 30°С, а коэффициент конвективной теплоотдачи на
всех трех поверхностях постоянен и равен 75 Вт/(м2-град). Температура по-
поверхности нагревателя Ts = 300°С, и он находится в хорошем тепловом кон-
контакте с длинной стороной бруса, как показано на рисунке. Какое время дол-
должен работать нагреватель, чтобы минимальная температура на противопо-
противоположной стороне бруса составила 120сС?
Решение. Разделим прямоугольное сечение бруса на квадратные ячейки
со стороной Ах = 0,05 м и обозначим узлы с неизвестными температурами
индексами от 1 до 10.
В табл. 3.5 приведена неявная форма разностного уравнения энергии для
любого узла. Для всех внутренних узлов
+ 4Fo] Т\+д' - Fo
Ts) - Г{ - 0 (/ - 2, 3, 4)
Уравнения энергии для граничных узлов, не расположенных в углах тела, за-
записываются следующим образом:
узел 1: [1 + 2Fo B + Bi)]
[Tt+Ai T
узел 5: [1 + 2Fo B + Bi)]
узлы 7-9: [1 + 2Fo B + Bi)]
[
¦pt+M yt
+ T'fti* + Bi
- T\
0 (/ -7, 8, 9).
174
Уравнения энергии для граничных узлов, находящихся в углах тела, записы-
записываются следующим образом:
узел 6: [1 + 4Fo (I + Bi)]
t+M Tt+At
узел 10: [ 1 + 4Fo A + Bi)] 7^A*-
Tt+At
1
[
Выберем шаг по времени Д* = 30 с; в таком случае
о(AQ B,5-Ю-5K0
Fo = lEF (о^р : °'30'
Е[_ hc(Ax) = 75» 0,05 _015<
Подставляя значения Bi, Fo, Ts и Г» в уравнения баланса энергии, получаем
10 уравнений в матричной форме
АТ = В
узел 1: 2,29Г{+А* - О,6Г?+А* - 0,ЗГ?+А'= 92,7 + Г{,
узел 2: -0,ЗГ{+А' + 2,2Г2+Л* - 0,ЗГ|+А* - 0,ЗГ?+А' = 90 + Т%
узел 3: ~0,ЗГ?+Л' + 2,2f^+At -0,ЗГ^+А^ — 0,ЗГ|+л^ = 90 + Т%
узел 4: -0,ЗГ?+А' + 2,ZT\+At - 0,ЗГ^+А^ -0,ЗГ?+А' = 90 + Т%
узел 5: -0,6Г^+А' + 2,29Г^+А/ - 0,ЗГ[+А^ = 92,7 + Г|,
узел 6: -0,6Г[+Af + 2,38r|+Af - О,6Г?+А* = 5,4 + T\t
узел 7: -0,6Г?+А* - 0^+А* + 2,29Г?+А* - 0эЗГ|+АГ = 2,7 + Т*ь
узел 8: -0,6Г?+А' - 0,3^+At + 2,29Г?+А' - 0,ЗГ^+А' = 2,7 + г|,
узел 9: —0,6Г^+А* — 0,з|+Л* +2,29f^+Af - Q,3T\?At = 2,7 + г?
узел 10: -0,6Г|+А* - 0,6$+А* +2,387^ = 5,4 + Г^
Коэффициенты этих 10 уравнений являются элементами квадратной мат-
матрицы А, служащими входной информацией программы численного расчета.
Элементы столбцевой матрицы В вычисляются самой программой.
Программа численного расчета аналогична программе, использованной
при решении примера 3.9, и отличается лишь элементами матрицы В. Зна-
Значения этих N элементов вычисляются в программе, написанной на языке
Фортран, между операторами 20 и 30. Это единственное отличие между дан-
данной программой и программой, использованной при решении примера 3.9.
Ниже приводится текст программы численного расчета.
Нестационарная теплопроводность 175
Тенет программы численного решения примера 3.10
DIMENSION ТE0),АE0,50).ВE0),СE0,50)
READ , N.NTIME.DELX.DELT.TO
READ , ((A(l,J),J -1 ,N),I -1 ,N)
WRITE F,10) DELX.DELT.TO
10 FORMATAH ,'*•• TRANSIENT TEMPERATURE DISTRIBUTION IN DEGREES',/.
1 'CELSIUS DETERMINED BY AN IMPLICIT NUMERICAL TECHNIQUE *•*',/ /,
2 'NODE SPACING -'.F8.4,1 METERS'./.TIME INTERVAL«\F8.3,
3 ' SECONDS'./.'ORIGINAL TEMPERATURE - ^8.2/ DEGREES C)
CALL MATINV (A,N,C)
DO15I-1.N
15 T(I)-TO
DO80JJ-1.NTIME
20 BA)-92.7 + TA)
BE)-92.7 + TE)
BF)«5.4+TF)
BA0)-5.4 + TA0)
DO 22 1*2,4
22 B(l)«90.0+T(l>
DO 30 1-7,9
30 B(l)-2.7+T(l)
DO50I-1.N
SUM-0.0
DO40J-1.N
40 SUM«SUM + C(I,J)*B(J)
50 T(I)-SUM
AJ-JJ
TIME-AJ*DELT
WRITE F,70) TIME, (I,T(I),I = 1 ,N)
70 FORMAT (/,25X,TIME IS-\F10.3,
1 ')-'.F8.2.2X))
80 CONTINUE
STOP
END
Число узлов N = 10, число шагов по времени NTIME = 5, шаг по про-
пространству DELX = 0,05 м, шаг по времени DELT = 30,0 с, начальная тем-
температура ТО = 50,0°С. Входная информация программы и ее формат остают-
остаются такими же, как в примере 3.9. Входная информация программы имеет
вид
Входная информация программы
для примера 3.10
10,5,0.05,30.0.50.0
2.29, -0.6, О., 0., 0., -0.3, 0., 0., 0., 0.,
-0.3, 2.2, -0.3,0., 0., 0., -0.3, 6., 0., 0.,
0., -0.3, 2.2,,-0.3, 0., 0., 0., -0.3, 0., О..
О., 0., -0.3, 2.2, -0.3. 0., 0., 0., -0.3, 0.,
0.. 0.. 0.. -0.6, 2.29, 0., 0., 0., О.. -0.3,
-0.6, 0., 0., 0., О., 2.38, -0.6, 0., 0., О., ,
О., -0.6, 0., 0., 0..-0.3, 2.29. -0.3, 0.,0., \
О., О., -0,6, 0., О., 0., -0.3, 2.29, -0.3, О.,
О., 0., 0., -0.6, О., 0., 0., -0.3, 2.29, -0.3,
О., 0., 0., О.( -0.6, 0., О., 0., -0.6. 2.36
176 Глава 3
Выходная информация программы представлена ниже.
Выходная информация программы для примера 3.10
**• Нестационарное распределение температуры в градусах
Цельсия, расчитанное неявным численным методом *•*
Шаг по пространству-0,0500 м
Шаг по времени - 30,000 с
Начальная температура-50,00°С
ТE)-96.81
T(9)-66.23
TA)-128.89
ТE)=128.89
Т(9)-87.84
ТA)-152.09
ТE)-162.09
Т(9)-109.36
ТA)-169.55
ТE)« 169.55
Т(9)-128.69
ТA)-183.04
ТE)-183.04
Т(9)-145.22
ТF):
ТОО)'
и
7X2)'
ТF)»
ТОО)'
/'
ТB).
ТF)«
ТA0)«
/-
ТB)-
ТF)«
ТA0) =
/«
ТB)«
ТF).
ТA0)-
-30,000с
= 99.48
-64.38
»64.38
-60,000с
= 134.08
¦83.96
• 83.96
•90,000с
¦ 159.44
•103.46
И 03.46
• 120,000с
«178.67
-120.92
И 20.92
'150,000 с
• 193.60
'135.83
'135.83
ТC) - 99.84 ТD) - 99.48
ТG)-66.23 Т(8)«66.52
ТC)«134.94 ТD)«134.08
ТG)- 87.84 Т(8) = 88.60
ТC)-160.82 ТD)« 159.44
ТG)-109.36 Т(8)-110.66
ТC)-180.53 ТD)-178.67
ТG)«128.69 Т(8)-130.52
ТC)- 195.89 ТD)« 193.60
ТG)-145.22 Т(8)-147.55
Самые низкие температуры в сечении достигаются в углах (узлы 6 и 10),
которые дальше всех отстоят от источника тепла и имеют наибольшую
(относительно объема ячейки) поверхность, омываемую холодным возду-
воздухом. На рисунке показаны температурные зависимости в зонах наиболее бы-
быстрого (узел 3) и Наиболее медленного (узлы 6 и 10) нагрева. Согласно пред-
представленным на рисунке данным, минимальная по сечению температура достиг-
достигнет 120°С примерно через 2 мин.
2001-
150
100
50
УзелЗ
Узлы 6 и 10
О 30 60 90 120 15Q
Время, о
Нестационарная теплопроводность 177
Литература
1. Carslaw H. S., Jaeger J. С, Conduction of Heat in Solids, 2nd ed.,
Oxford University Press, N. Y., 1959. [Имеется перевод: Карслоу Г., Егер Д.
Теплопроводность твердых тел. — М.: Наука, 1964.]
2. Eckert E. R. G., Drake R. M., Jr., Analysis of Heat and Mass Transfer,
McGraw, N. Y., 1972. [Имеется перевод первого издания: Эккерт Э. Р.,
Дрейк Р. М., Теория тепло- и массообмена. — М.: Госэнергоиздат, 1961.]
3. Arpaci V., Conduction Heat Transfer, Addison-Wesley, Mass., 1966.
4. Ozisik M. N., Boundary Value Problems of Heat Conduction, Intext
Publishers Group, N. Y., 1968.
5. Schneider P. J., Conduction Heat Transfer, Addison-Wesley, Mass., 1955.
[Имеется перевод: Шнейдер П., Инженерные проблемы теплопроводности.—
М.: ИЛ., 1960.1
6. Kreith P., Principles of Heat Transfer, 3rd ed., Crowell, N. Y., 1973.
7. Richtmyer R. D., Difference Methods for Initial-Value Problems, Wiley,
N. Y., 1957.
8. Paul В., Generalization of the Schmidt Graphical Method for Transient
Heat Conduction, ARS. /., 32, p. 1098 A962). [Имеется перевод: Паул, Об-
Обобщение графического метода Шмидта для расчета нестационарной тепло-
теплопроводности.— Ракетная техника, 1962, № 7, с. 124.]
9. Jakob M., Heat Transfer, vol. 2, Wiley, N. Y., 1949. [Имеется перевод
издания 1957 г.: Якоб М., Вопросы теплопередачи.— М.: ИЛ., I960.]
10. Crank J., The Mathematics of Diffusion, 2nd ed., Oxford University
Press, N. Y., 1975.
11. Richtmyer R. D., Morton K. W., Difference Methods for Initial Value
Problems, Wiley, N. Y., 1967. [Имеется перевод: Рихтмайер Р. Д., Mop-
тон К. У., Разностные методы решения краевых задач. — М.: Мир, 1972.]
12. Gourlay A. R., McGuire G. R., General Hopscotch Algorithm for the
Numerical Solution of Partial Differential Equations, /. Inst. Math, and its
Applications, 7, 216 A971).
13. Gourlay A. R., Hopscotch: A Fast Second-Order Partial Differential
Equation Solver, /. Inst. Math, and its Applications, 6, p. 375 A970).
14. Gourlay A. R., Some Recent Methods for the Numerical Solution of
Time-dependent Partial Differential Equations, Proc. Roy. Soc. London, 323,
p. 219 A971).
15. Adams J. A., Rogers D. F., Computer-aided Heat Transfer Analysis,
McGraw, N. Y, 1973.
16. Schenck H., Jr., Fortran Methods in Heat Flow, The Ronald Press Co.,
N. Y., 1963.
17. Segerlind L. J., Applied Finite Element Analysis, Wiley, N. Y., 1976.
[Имеется перевод: Сегерлинд Л. Д., Применение метода конечных элемен-
элементов.—М.: Мир, 1979.]
18. Huebner К. N., A Finite Element Method for Engineers, Wiley, N. Y.,
1975.
19. Myers G. E., Analytical Methods in Conduction Heat Transfer,
McGraw, N. Y., 1971.
20. Zeinkiewicz О. С, The Finite Element Method in Engineering Science,
McGraw, N. Y., 1971. [Имеется перевод: Зенкевич О., Метод конечных эле-
элементов в технике. — М.: Мир, 1975.]
ЗАДАЧИ
Задачи к этой главе сгруппированы по тематике разделов, как указано
в таблице. Для четырех задач, 3.27, 3.29, 3.30 и 3.38, требуется найти чис*
ленные решения с помощью ЭВМ. Составления специальных программ не
требуется. Все программы, необходимые для решения задач, приведены в этой
главе при рассмотрении примеров.
Номера
задач
3.1-3.7
3.8-3.11
3.12—3.25
3.26—3.38
Раздел
3.2
3.3
3.4
3.5
Тема
Нестационарная теплопроводность тела с
пренебрежимо малым внутренним тер-
термическим сопротивлением
Нестационарная теплопроводность в полу-
полубесконечном твердом теле
Нестационарная теплопроводность, реше-
решения в виде диаграмм
Нестационарная теплопроводность, числен-
численные решения
3.1. Колба медицинского термометра имеет диаметр 7 мм и длину 10 мм.
Термометр вынимают из спиртового раствора и помещают в рот пациента.
Вследствие испарения спиртового раствора начальная температура термо-
термометра 18°С. Найти минимальное время, по истечении которого медсестра дол-
должна вынуть термометр, причем показание термометра не должно отличаться
от истинной температуры более чем на 0,5°С. Теплофизические свойства кол-
колбы термометра можно приближенно принять равными средним значениям ме-
между свойствами ртути и стекла. Найти требуемое время при трех значениях
среднего коэффициента конвективной теплоотдачи к колбе термометра: hc =
в 10, 50 и 100 Вт/(м2-град).
3.2. Небольшой медный наконечник после отливки вынимают из формы
при температуре 650°С и охлаждают в баке с жидкостью [Яс = 790 Вт/(м2 X
Хград), Too = 75°C]. Объем наконечника 1,75 см3, площадь его поверхности
3,5 см2. Сколько времени должен оставаться в жидкости наконечник, чтобы
его температура снизилась до 100°С?
3.3. При движении по сборочному конвейеру нужно нагревать цилиндри-
цилиндрические алюминиевые детали диаметром 1,5 мм и длиной 10 мм. Перед вхо-
входом в нагревательную секцию конвейера [Яс = 100 Вт/(м2-град), Гто =
= 300°С] алюминиевые детали имеют постоянную температуру 30°С. Сколь-
Сколько времени должна оставаться в нагревательной секции каждая деталь, что-
чтобы выйти из нее с температурой 200°С? Найти мсщность нагревательного эле-
элемента этой секции, предполагая, что только 30% тепла идет на нагрев дета-
деталей, а производительность конвейера составляет 10 тыс. деталей в час.
3.4. Кубик алюминия со стороной 1 см нужно нагреть в открытом пла-
мени от 50 до 300°С. Сколько времени нужно держать кубик в пламени, если
Нестационарная теплопроводность 179
температура пламени 800°С, а коэффициент конвективной теплоотдачи от
пламени к алюминию 190 Вт/(м2*град)?
3.5. Показать, что нестационарная температура твердого тела с прене-
пренебрежимо малым внутренним термическим сопротивлением в условиях конвек-
конвективного теплообмена на поверхности (hCi Too) при постоянной интенсивности
тепловыделения на единицу объема qfQ определяется формулой
Г @ - Г» = в (t) = 42- [1 - e~Bi Fol
hcAs
Начальное условие: 0 @) = 0, т. е. вначале температура твердого тела равна
температуре окружающей среды.
3.6. Предположим, что нужно нагреть кусок алюминиевой проволоки,
пропуская по ней электрический ток. Диаметр проволоки 1 мм, длина 10 см,
электрическое сопротивление 0,2 Ом. Какова будет температура проволоки,
если по ней пропускать в течение 1 мин постоянный ток силой 1 А и если
ее начальная температура была 25°С? Предположить, что проволока нахо-
находится в воздухе с температурой 25°С и пс = 20 Вт/(м2-град). Использовать
решение задачи 3.5.
3.7. Электродетонатор имеет форму цилиндра диаметром 0,1 мм и дли-
длиной 5 мм. Он находится в воздухе [Гоо = 30°С, Яс = 10 Вт/(м2-град)]. Теп-
лофизические свойства детонатора: k = 20 Вт/(м-град), а = 5-10~5 м2/с,
электрическое сопротивление 0,2 Ом, температура плавления материала дето-
детонатора 900°С. Пренебрегая излучением и утечками тепла в крепления на кон-
концах детонатора, определить время, по истечении которого детонатор взорвет-
взорвется, если по нему пропускать постоянный ток силой 3 А. Использовать реше-
решение задачи 3.5.
3.8. Поверхность толстой плиты [а = 2-10~6 м2/с, & = 10 Вт/(м-град)],
имеющей начальную температуру 50°С, внезапно нагревается до 80°С. Найти:
а) время, за которое температура на расстоянии 3 см от поверхности достиг-
достигнет 65°С; б) количество тепла, которое нужно подвести на 1 м2 поверхности
плиты, чтобы достичь этой температуры.
3.9. Решить задачу 3.8а, предполагая, что нагреватель заменен газом с
температурой 80°С, а коэффициент конвективной теплоотдачи от газа к плите
120 Вт/(м2-град).
3.10. Предложен метод измерения коэффициента температуропроводности
почвы с помощью термопары, погруженной в землю на известную глубину.
На поверхности земли в хорошем тепловом контакте с ней размещен нагре-
нагреватель с температурой 90°С, и после 15 мин нагрева термопара зарегистри-
зарегистрировала температуру 27°С. Начальная температура почвы 22°С, термопара по-
погружена на глубину 6 см. Найти коэффициент температуропроводности почвы.
3.11. Большая плита из мягкой стали толщиной 0,25 м имеет начальную
температуру 45°С Одна ее поверхность начинает омываться воздухом с тем-
температурой 200°С и he = 210 Вт/(м2-град). Найти температуру поверхности и
температуру на расстоянии 2 см от нее после 3 мин воздействия горячего
воздуха.
3.12. Найти температуру на глубине 3 см от поверхности эбонитового ша-
шарика диаметром 10 см через 10 ч после того, как он был погружен в ванну
с маслом, имеющим температуру 100°С. Перед погружением в масло шарик
имел постоянную температуру 200°С, а коэффициент теплоотдачи от масла к
шарику 1,5 Вт/(м2-град). Найти количество тепла, отданное шариком в те-
течение 10 ч.
3.13. Начальная температура хлорвинилового шарика \k = 0,15 Вт/(м X
Хград), а = 8-Ю-8 м2/с] диаметром 5 см равна 90сС. Он погружается в бак
с водой, имеющей температуру 20°С. Коэффициент теплоотдачи от шарика к
воде 20 Вт/(м2-град). Найти время пребывания шарика в воде, по истечении
180 Глава 3
которого температура в его центре достигает 40°С. Найти температуру по-
поверхности шарика по истечении этого периода времени.
3.14. Длинные металлические стержни [k = 45 Вт/(м град), <х = 2 X
X 10 м2/с] диаметром 0,5 м помещены в печь для термической обработки.
Температура в печи 600°С, начальная температура стержней 60°С. Сколько
времени стержни должны оставаться в печи, чтобы их минимальная темпера-
температура достигла 400°С? Какова температура их поверхности в этот момент вре-
времени? Принять, что коэффициент конвективной теплоотдачи 120 Вт/(м2«град).
3.15. Стенка толщиной 0,2 м изготовлена из огнеупорного материала
[? = 6 Вт/(м-град), а — 8-10 м2/с]. Этот материал не воспламеняется,
пока его температура ниже 650°С. При испытаниях стенку помещают в пла-
пламени, охватывающем обе ее поверхности. Средняя температура пламени
875°С, начальная температура стенки 30°С. Определить минимальный и мак-
максимальный промежутки времени, в течение которых стенка может пробыть
в огне до воспламенения, предполагая, что коэффициент конвективной тепло-
теплоотдачи от пламени к стенке составляет от 100 до 250 Вт/(м2 град). Найти
значения температуры в среднем сечении стенки в эти моменты времени.
3.16. Телефонные столбы пропитывают смолистым составом, чтобы пре-
предотвратить их гниение и порчу насекомыми. Пропитка дерева происходит при
повышенных температурах и давлениях. Столб диаметром 0,3 м, имеющий на-
начальную температуру 20°С, помещают в печь под давлением и вынимают из
печи, когда он просмолится на глубину ~10 см. Установлено, что при этом
температура на глубине 10 см составляет М0°С. Найти время выдерживания
столба в печи, если температура в ней 350°С, hc = 145 Вт/(м2-град). Тепло-
физические свойства дерева: k = 0,2 Вт/(м-град), а= 1,1-10—7 м2/с.
3.17. Апельсины могут в течение короткого времени без ущерба выдер-
выдержать отрицательные температуры. Предположим, что апельсин диаметром
0,1 м [р = 940 кг/м3, с = 3,8-103 Дж/(кг-град), k = 0,47 ВтДмтрад)] имеет
начальную температуру 5°С. Температура воздуха внезапно падает до —5°С.
За какое время температура поверхности апельсина достигнет 0°С, если
he = 10 Вт/(м2-град)?
3.18. Найти температуру в центре яйца, вынутого из холодильника
(Т = 5°С) и опущенного на 3 мин в кипящую воду [hc = 3000 Вт/(м2„ град)!
Считать, что яйцо имеет сферическую форму, его диаметр 3,6 см, а теплофизи-
ческие свойства следующие: р= 1080 кг/м3, с = 4,0-103 Дж/(кг-град), k ==
= 0,75 Вт/(м-град). Найти количество энергии, необходимое для нагрева
яйца.
3.19. Нагреватели с температурой 250°С смонтированы в прямом тепло-
тепловом контакте с двумя сторонами стенки из обычного строительного кирпича
толщиной 0,25 м. Стенку, имеющую начальную температуру 10°С. нужно на-
нагревать до достижения температуры в среднем сечении 140°С. Сколько вре-
времени должны работать нагреватели?
3.20. Сырой материал перед применением на сборочном конвейере нужно
предварительно нагреть до минимальной температуры 200°С. Материал имеет
следующие теплофизические свойства: р = 4000 кг/м3, ?==2,0 Вт/(м-град),
ос = 8-10" м2/с. Материал нагревают на ленте конвейера, которая движется
через открытую печь с температурой 700°С и коэффициентом конвективной
теплоотдачи от горячего воздуха к материалу 450 Вт/(м2-град). Сырой ма-
материал продается в виде гранул двух размеров: диаметром 8 и 4 см. На-
Начальная температура материала на входе в печь 30°С. Сколько времени зай-
займет предварительный нагрев гранул обоих размеров? С точки зрения наи-
наименьших затрат тепловой энергии какие нужно покупать гранулы: меньшего
или большего размера? Длина ленты транспортера 8 м, ширина 1 м, на 1 м2
ленты помещается 100 больших гранул или 400 маленьких. Найти массовую
производительность конвейера для гранул обоих размеров, если скорость дви-
движения ленты регулируется таким образом, чтобы обеспечить требуемую ми-
минимальную температуру тех и других шариков.
3.21. Бетонный цилиндр диаметром 10 см и длиной 25 см имеет началь-
начальную температуру 90сС. Он охлаждается в воздухе при температуре 10°С. За
Нестационарная теплопроводность 181
какое время температура в его центре достигнет 30°С, если коэффициент кон-
конвективной теплоотдачи от бетона к воздуху 18 Вт/(м2-град)?
3.22. Вы хотите зажарить кусок мяса, скатанный в виде короткого ци-
цилиндра диаметром 15 см и длиной 20 см. Теплофизические свойства говя-
говядины: р = 960 кг/м3, k = 0,9 Вт/(м-град), с = 5-Ю3 Дж/(кг-град). Сколько
времени нужно жарить мясо, чтобы прожарить его середину, предполагая, что
говядина прожаривается при 75°С? Мясо, взятое из холодильника, имеет тем-
температуру 10°С. Духовка предварительно прогрета до 160°С, а коэффициент
конвективной теплоотдачи от горячего воздуха к мясу 30 Вт/(м2-град). На
сколько уменьшится время жарки, если мясо предварительно прогрето до
25°С?
3.23. Брикет размерами 20 X 30 X 50 см, имеющий после нагрева по-
постоянную температуру 120°С, вынимают из печи и оставляют на воздухе с
температурой 30°С. Теплофизические свойства материала брикета: k =
= 2,5 Вт/(м-град), р = 2,8-103 кг/м3, с = 800 Дж/(кгтрад). Коэффициент
конвективной теплоотдачи от брикета к воздуху равен 75 Вт/(м2-град). Най-
Найти температуру в центре брикета через 1 ч после выемки из печи.
3.24. Короткий алюминиевый цилиндр диаметром 0,6 м и длиной 0,6 м
имеет начальную температуру 200°С. Его внезапно помещают в среду с тем-
температурой 70°С и hc = 85 Вт/(м2-град). Рассчитать температуру в точках
цилиндра, расположенных по окружности радиусом 10 см на расстоянии
10 см от его торца, через 1 ч после начала охлаждения.
3.25. В магазине продается мороженое. Его начальная температура
—10°С. Температура окружающего воздуха 25°С, Яс = 25 Вт/(м2-град). Раз-
Размеры упаковки 10 X 15X20 см; теплофизические свойства мороженого: k =
= 0,76 Вт/(м-град), с = 5-Ю3 Дж/(кг-град), р = 845 кг/м3. За какое время
мороженое, вынутое из морозильника магазина, растает (температура плав-
плавления мороженого ~0°С). Если мороженое сразу завернуть в пакет, чтобы
уменьшить приток тепла, коэффициент конвективной теплоотдачи снижается
до 5 Вт/(м2-град). Рассчитать время таяния в этом случае.
3.26. Для условий задачи 2.66 найти нестационарные температуры в
9 узлах, если вначале тело имеет постоянную температуру 20°С, а начиная
с момента времени / =* 0 действуют граничные условия, указанные на ри-
рисунке к задаче 2.66. Коэффициент температуропроводности твердого тела
1,2 -10—6 м2/с. Применить явный численный метод.
3.27. Решить задачу 3.26 неявным численным методом. Модифицировать
программу численного решения примера 3.9 и применить ее для расчета не-
нестационарных температур в 9 узлах.
3.28. Для условий задачи 2.69 найти нестационарные температуры в ^уз-
^узлах, если вначале твердое тело имеет постоянную температуру 250°С, а на-
. чиная с момента времени t = 0 действуют граничные условия, указанные на
рисунке к задаче 2.69. Коэффициент температуропроводности твердого тела
8-10—6 м2/с. Применить явный численный метод.
3.29. Решить задачу 3.28 неявным численным методом. Модифицировать
программу численного решения примера 3.9 и применить ее для расчета не-
нестационарных температур в 15 узлах.
3.30. Для условий задачи 2.72 найти нестационарные температуры в 20 уз-
узлах, если вначале твердое тело имеет постоянную температуру 25°С, а начи-
начиная с момента времени t = 0 действуют граничные условия, указанные на
рисунке к задаче 2.72. Коэффициент температуропроводности твердого тела
2-10~в м2/с. Использовать неявный численный метод. Модифицировать про-
программу численного решения примера 3.9 и применить ее для расчета неста-
нестационарных температур в 20 узлах.
3.31. Проверить все уравнения энергии для узлов и критерии устойчиво-
устойчивости, представленные в табл. 3.4.
3.32. На рисунке показано поперечное сечение длинного прямоугольного
стержня [k = 20 Вт/(м-град), а = 3-10~5 м2/с], имеющего вначале постоян-
постоянную температуру 160°С. Внезапно температура двух поверхностей снижается
До 100°С, а остальные две поверхности становятся теплоизолированными.
182 Глава 3
Найти нестационарные температуры в 6 узлах, показанных на рисунке, с по-
помощью явного численного метода.
К задаче 3.32,
3.33. Проверить «неявные» разностные уравнения баланса энергии, приве-
приведенные в табл. 3.5.
3.34. Решить задачу 3.8, а графическим методом Биндера — Шмидта.
Сравнить ответ с полученным ранее решением задачи 3.8.
3.35. Два больших листа фанеры (а=1,Ы0-7 м2/с) толщиной 2 см
нужно склеить термоклеем. Начальная температура обоих листов фанеры
20°С, и их нужно сжимать друг с другом, пока температура клея не достиг-
достигнет 50рС. Два нагревателя с температурой 120°С расположены в прямом теп-
тепловом контакте с обеими сторонами фанеры. Пренебрегая термическим сопро-
сопротивлением клея, рассчитать время нагрева, чтобы температура клея достигла
50°С. Применить метод Биндера — Шмидта.
3.36. Длинный цилиндр из нержавеющей стали диаметром 20 см, имею-
имеющий вначале температуру 20°С, теплоизолирован по периферии. Торец ци-
цилиндра находится в прямом тепловом контакте с нагревателем, имеющим
температуру 180°С. Найти температуры в плоскостях, расположенных на рас-
расстояниях 1, 2 и 3 см от торца цилиндра, через 1, 2 и 3 мин после начала
нагрева. Применить метод Биндера — Шмидта.
3.37. Решить задачу 3.36 явным численным методом.
3.38. Решить задачу 3.36 неявным численным методом. Модифицировать
программу численного решения примера 3.9 и применить ее для расчета не*
стационарных температур в цилиндре.
Глава 4
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
4.1. ВВЕДЕНИЕ
Прежде чем приступить к расчету коэффициента теплеют*
дачи, несколько подробнее рассмотрим процесс конвективного
переноса и установим связь между конвективным теплообменом
и движением жидкости. На рис. 4.1 показана обогреваемая пло-
плоская пластина, охлаждаемая обтекающим ее потоком воздуха.
Поток жидкости
Т(у)
Тепловой
поток
Рис. 4.1. Распределение скоростей и температур при вынужденной конвекции
около нагретой пластины.
Прежде всего отметим, что в направлении к поверхности пла-
пластины скорость воздуха уменьшается под действием сил вяз-
вязкости. Так как скорость слоя жидкости, примыкающего к стен-
стенке, равна нулю, то теплоотдача от поверхности к этому слою
должна осуществляться только теплопроводностью:
дТ hATTJ D.1)
„ft
'f ду
0-0
Хотя с этой точки зрения основным процессом переноса тепла
и является теплопроводность, но сам градиент температуры на
поверхности (дТ/ду)\у=о определяется интенсивностью пере-
передачи энергии от стенки в основной поток более удаленными
от стенки слоями жидкости. Следовательно, градиент темпера-
температуры на стенке зависит от поля течения, и при более высоких
скоростях достигаются более высокие градиенты температуры
и более высокие тепловые потоки. В то же время важную роль
играет коэффициент теплопроводности жидкости. Например,
184 Глава 4
значение kf для воды на порядок превышает его значение для
воздуха; именно поэтому приведенное в табл. 1.2 значение коэф-
коэффициента конвективной теплоотдачи для воды больше, чем для
воздуха.
Как следует из рис. 4.2, весьма близкая картина наблюдает-
наблюдается и при свободной конвекции. Принципиальное отличие состоит
в том, что если при вынужденной конвекции скорость обуслов-
обусловлена действием внешних сил и приближается к своему значению
в набегающем потоке, то
при свободной конвекции
с увеличением расстоя-
расстояния от пластины она вна-
вначале возрастает вследст-
вследствие довольно быстрого
уменьшения действия вяз-
вязкости и более медленного
снижения разности плот-
плотностей. Однако в конце
концов по мере прибли-
приближения плотности к значе-
значению в окружающей жид-
жидкости подъемная сила по-
понижается. Это приводит к
тому, что скорость снача-
сначала достигает максимума,
а затем по мере удаления
от обогреваемой поверх-
поверхности приближается к ну-
нулю. Профили температур при свободной и вынужденной конвек-
конвекции имеют аналогичную форму, и в обоих случаях механизмом
теплоотдачи на поверхности раздела жидкости и твердого тела
является теплопроводность.
Согласно приведенным рассуждениям, коэффициент конвек-
конвективной теплоотдачи должен зависеть от плотности, вязкости и
скорости жидкости, а также от ее теплофизических свойств
(коэффициента теплопроводности и удельной теплоемкости).
Если при вынужденной конвекции скорость в системе обычно
создается насосом или вентилятором и может быть определена
непосредственно, то при свободной конвекции она зависит от
разности температур поверхности и жидкости, коэффициента
теплового расширения жидкости (который определяет измене-
изменение плотности на единицу разности температур) и силового
поля, которое для находящихся на земле систем определяется
просто силой тяжести.
Для понимания роли различных параметров при вынужден-
вынужденной конвекции рассмотрим подробнее поле скоростей. На рис. 4.3
доказаны распределения скоростей на различных расстояниях
8
Рис. 4.2. Распределение скоростей и темпе-
температур при свободной конвекции около на-
нагретой пластины, наклоненной под углом р
к горизонтали.
Конвективный теплообмен 185
от передней кромки пластины. Сразу за этой кромкой разви-
развивается область течения, в которой силы вязкости вызывают тор-
торможение потока. Эти силы зависят от касательного напряже-
напряжения т. В случае обтекания плоской пластины это напряжение
можно определить через скорость жидкости, параллельную пла-
пластине, в виде
где du/dy — градиент скорости, а коэффициент пропорциональ-
пропорциональности \i называют коэффициентом динамической вязкости. Если
\* Ламинарный режим
Переходный
Jрежим^
Турбулентный режим
ггп:
Ламинарный подслой
Рис. 4.3. Ламинарный, переходный и турбулентный режимы течения в погра-
пограничном слое при обтекании плоской пластины.
касательное напряжение выражено в Н/м2, а градиент скорости
в с-1, то размерностью \х является Н-с/м2.
Область течения около пластины, в которой скорость жид-
жидкости замедляется под действием сил вязкости, называют погра-
пограничным слоем. Расстояние от пластины, на котором скорость до-
достигает значения, равного 99% скорости невозмущенного по-
потока, условно принято считать толщиной пограничного слоя, а
область, более удаленную от пластины, называют невозмущен-
невозмущенным, или потенциальным, потоком.
Вначале течение в пограничном слое является полностью ла-
минарным. Толщина пограничного слоя возрастает с увеличе-
увеличением расстояния от передней кромки, и на некотором крити-
критическом расстоянии хс влияние инерционных сил становится су-
существенно большим по сравнению с влиянием вязкого демпфи-
демпфирования, и в результате в потоке начинают возрастать слабые
возмущения. Так как они становятся все более интенсивными, то
нарушается упорядоченность вязкого течения и происходит пе-
переход от ламинарного течения к турбулентному. В области
186 Глава 4
турбулентного течения линии тока пересекаются макроскопиче-
скими порциями жидкости. В результате происходит интенсив-
интенсивный перенос как тепловой энергии, так и количества движения.
В курсах по гидродинамике (например, [1]) указывается пара-
параметр, который количественно связывает силы вязкости и инер-
инерции и значение которого определяет переход от ламинарного
течения к турбулентному. Это — безразмерное число Рейнольд-
са Re*, определяемое по формуле
Re, = bf. D.3)
где Voo — скорость набегающего потока, х — расстояние от
передней кромки, Vf = [if/pf — коэффициент кинематической вяз-
вязкости жидкости. Критическое значение Re* , при котором проис-
происходит переход от ламинарного течения к турбулентному, зави-
зависит от шероховатости поверхности и интенсивности турбулент-
турбулентных пульсаций, или степени турбулентности, в основном потоке.
Если в потоке имеются значительные возмущения, то переход
начинается при Re* = 105, но в их отсутствие переход может
затянуться до Re* = 2-105. Переходный режим существует до
значения числа Рейнольдса, примерно вдвое превышающего его
значение в начале перехода; но при большем значении числа
Рейнольдса течение в пограничном слое турбулентное.
Приблизительные формы профилей скоростей при ламинар-
ламинарном и турбулентном режимах течения показаны на рис. 4.3.
При ламинарном режиме течения профиль скорости в погра-
пограничном слое близок к параболическому. При турбулентном ре-
режиме течения существует очень тонкий слой около поверхности,
называемый ламинарным подслоем, в котором профиль ско-
скорости почти линейный. Вне этого подслоя профиль скорости яв-
является более наполненным по сравнению с профилем в лами-
ламинарном пограничном слое.
Из других типов течений наибольший интерес представляет
течение в трубе или канале. Это течение может быть ламинар-
ламинарным или турбулентным в зависимости от числа Рейнольдса,
формула для расчета которого в данном случае имеет вид
где Vm — средняя скорость, D — внутренний диаметр. По дости-
достижении ReD = 2300 начинается переход от ламинарного течения
к турбулентному, обычно заканчивающийся при ReD«6000.
Действительные значения ReD зависят от шероховатости стенок
трубы и степени турбулентности.
На рис. 4.4 показаны профили скорости при ламинарном и
турбулентном режимах течения. За входным сечением на вну-
внутренней поверхности трубы развивается пограничный слой, ко*
Конвективный теплообмен 187
торый по мере удаления от входа все более заполняет площадь
поперечного сечения. В случае ламинарного течения профиль
скорости становится параболическим, причем средняя скорость
составляет 1/2 своего значения на оси трубы. При турбулент-
турбулентном течении профиль становится более наполненным и средняя
скорость составляет ~83% от значения на оси трубы.
шшшжшяш
б
Рис. 4.4. Профили скоростей при ламинарйом (а) и турбулентном (б) тече-
течениях в трубе.
Иногда оказывается более удобным относить число Рей-
нольдса Re к плотности потока массы G, определяемому по еле*
дующей формуле:
G V Ж/Л D.4)
где th — массовый расход жидкости, Ас — площадь поперечного
сечения, Vm — средняя скорость жидкости. Уравнение D.4)
можно также использовать для определения средней скорости.
Легко показать, что число Рейнольдса для канала диаметром D
может быть записано в виде
ReD = GDJ\i. D.5)
Если поперечное сечение канала не круглое, то вместо диа-
диаметра трубы D используется эквивалентный (гидравлический)
диаметр, определяемый по формуле
?ч л ( Площадь поперечного сечения \
н \ Смоченный периметр /
Например, при течении в кольцевом канале, образованном тру-
трубой с наружным диаметром Do и большей трубой с внутренним
диаметром D/, эквивалентный диаметр равен
Если поперечное сечение канала является прямоугольным и
имеет ширину w и высоту h, то
wh I» ( wh
При h<w,DH ~ 2Л,
188 Глава 4
Коэффициент конвективной теплоотдачи изменяется с рас-
расстоянием от передней кромки плоской пластины или от входа
в трубу или в канал; параметром, отражающим это изменение,
является местный коэффициент теплоотдачи hex, где х— рас-
расстояние от передней кромки пластины или от входа в трубу.
Если необходимо рассчитать общую теплоотдачу от ^ластины,
то следует знать средний коэффициент теплоотдачи Не Между
hex и Нс существует следующая зависимость:
**™Т ] h°*dx* <4'7)
Другие параметры также зависят от расстояния от передней
кромки пластины или от входа в трубу. Местный коэффициент
сопротивления трения определяется как
D-8)
Средний коэффициент сопротивления трения для пластины дли-
длиной L равен
L
{ J Cfxdx. D.9)
0
Коэффициент трения является безразмерной величиной, харак-
характеризующей касательное напряжение или силу сопротивления
на границе с твердым телом.
4.2. УРАВНЕНИЯ СОХРАНЕНИЯ МАССЫ,
КОЛИЧЕСТВА ДВИЖЕНИЯ И ЭНЕРГИИ
ПРИ ЛАМИНАРНОМ ОБТЕКАНИИ ПЛОСКОЙ ПЛАСТИНЫ
При классическом подходе к конвективному переносу сле-
следует вывести дифференциальные уравнения сохранения коли-
количества движения и баланса энергии в пограничном слое и ре-
решить их относительно градиента температуры в жидкости на
границе раздела со стенкой, с тем чтобы затем получить коэф-
коэффициент конвективной теплоотдачи. Несколько более простым,
но практически более полезным является подход, при котором
вместо дифференциальных уравнений получают интегральные
уравнения и для определения коэффициента теплоотдачи ис-
используют приближенный анализ. В данном разделе будут вы-
выведены дифференциальные уравнения, описывающие течение
жидкости вдоль плоской пластины, что позволит продемонстри-
продемонстрировать аналогию между переносом тепла и переносом количе-
количества движения^ а также ввести число Прандтля (Рг), которое
Конвективный теплообмен 189
связывает два этих процесса. Затем будут выведены интеграль-
интегральные уравнения для случая обтекания плоской пластины и полу-
получено их решение, что позволит продемонстрировать аналитиче-
аналитический подход, который можно также использовать для определе-
определения коэффициентов теплоотдачи в турбулентном потоке.
Рассмотрим элементарный объем внутри пограничного слоя
(рис. 4.5) и предположим, что течение является стационарным,
dx
v^2^%2%^^
pdy
км*
-НЙ
Рис. 4.5. Элементарный объем в пограничном слое, рассматриваемый при вы-
выводе уравнений сохранения массы и количества движения.
а жидкость — несжимаемой. Тогда массовые расходы на входе
и выходе из элементарного объема в направлении х будут соот-
соответственно равны
pudy и
Результирующий массовый расход в элемент в направлении х
составит
ди
p
Аналогично результирующий массовый расход в элемент в на-
направлении у составит
-p—dydx.
Так как результирующий массовый расход из элементарного
объема должен быть равен нулю, то получаем
ди , d
190 Глава 4
откуда следует, что при двумерном установившемся течении из
условия сохранения массы
f + f-0. D.10,
Уравнение сохранения количества движения для элемен-
элементарного объема получаем с помощью второго закона Ньютона.
Предполагая, что жидкость ньютоновская и что в направлении
оси у градиенты давления отсутствуют, а силы вязкости пре-
пренебрежимо малы, получаем, что в направлении оси х левую и
правую вертикальные поверхности элементарного объема
(рис. 4.5) пересекают потоки количества движения pu2dy и
p[u-\-(du/dx)dx]2dy. Следует отметить, что поток жидкости че-
через горизонтальные поверхности также сказывается на балансе
количества движения в направлении оси х. При этом в направ-
направлении оси х нижнюю поверхность пересекает поток количества
движения puvdxy а верхнюю поверхность, также имеющую еди*
яичную ширину,
Касательное напряжение на нижней поверхности составит
—\k{du/dy)dXy а на верхней поверхности —
~W
Таким образом, результирующее касательное напряжение в на-
направлении х оказывается равным \xdx(d2u/dy2)dy.
Сила давления на левую поверхность составляет pdyy а на
правую — [р + (др/дх) dx] dy. Следовательно, результирующая
сила давления в направлении течения равна —(др/дх)dxdy.
Приравнивая сумму рассмотренных сил изменению количества
движения на выходе из элементарного объема в направлении х,
получаем
dv _ j_ jmm , _. ди j_ , _ dv ди - -
dp
Если пренебречь производными второго порядка и использовать
уравнение неразрывности, то уравнение сохранения количества
движения можно упростить:
ди . ди \ д2и др ,л 11Ч
Выведем уравнение сохранения энергии при допущении о не-
независимости всех физических свойств от температуры и о доста-
достаточно малой скорости потока, что позволяет пренебречь работой
Конвективный теплообмен 191
сил трения. На рис. 4.6 показаны потоки энергии, поступающие
и выходящие из элементарного объема благодаря теплопровод-
теплопроводности и конвективному переносу. В дополнение к членам, свя-
связанным с теплопроводностью и использованным ранее в гл. 2
[уравнение B.5)], имеются четыре конвективных члена. Для
pcpuTdy
Эх2
Рис. 4.6. Элементарный объем в пограничном слое, рассматриваемый при вы-
выводе уравнения сохранения энергии.
баланса энергии необходимо, чтобы сумма всех членов, связан-
связанных с теплопроводностью и конвекцией, была равна нулю. При
этом получаем
Используя уравнение неразрывности и пренебрегая членами вто-
второго порядка, как и при выводе уравнения сохранения количе-
количества движения, получаем следующее уравнение сохранения
энергии:
и
дТ
дх
При нормальных условиях член, учитывающий теплопроводность
в направлении г, мал по сравнению с другими членами. Следо-
Следовательно, первым членом в скобках в правой части уравнения
можно пренебречь. Кроме того, в уравнении количества движе-
движения обычно малым по сравнению с другими членами оказывает-
оказывается член, учитывающий градиент давления, и им также можно
1§2 Глава 4
пренебречь. Теперь становится очевидной аналогия между урав-
уравнениями сохранения количества движения и энергии:
ди , ди (д2и \ /л 1О\
и -з—h v -т— = v (-г-т ), D.13)
дх 1 ду \ду2 J9 х }
дТ . дТ
В приведенных уравнениях v = |л/р — коэффициент кинемати-
кинематической вязкости, который часто называют коэффициентом пере-
переноса количества движения, a v/a — (\x/p)/(k/pcp)=Pr— число
Прандтля. Если v = а, то Рг = 1, и тогда уравнения количества
движения и энергии идентичны. При этом идентичными ока-
оказываются и безразмерные решения для и (у) и Т(у). Отсюда
видно, что число Прандтля Рг, которое представляет собой от-
отношение физических свойств жидкости, определяет соотношение
между распределением скоростей и температур. Число Прандт-
Прандтля изменяется от низких значений порядка 0,004 для жидкого
металла до высоких значений порядка 4000 для очень вязкого
масла.
4.3. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
И ЭНЕРГИИ ДЛЯ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ
Приводимый ниже интегральный подход позволяет изба-
избавиться от проблем, возникающих при решении дифференциаль-
дифференциальных уравнений пограничного слоя в частных производных. Рас-
Рассмотрим элементарный объем, который начинается на стенке и
простирается в направлений оси у, выходя за пределы погра-
пограничного слоя (рис. 4.7). Причем он имеет толщину dx в направ-
направлении оси х и единичную ширину в направлении оси г. Для
получения зависимостей для результирующего количества дви-
движения и результирующего количества энергии, вносимых в объем,
поступим таким же образом, как и при выводе уравнений по-
пограничного слоя в предыдущем разделе.
Через поверхность АВ (рис. 4.7) передается поток количе-
количества движения
б
^ ри2 dy.
Аналогично через поверхность CD передается поток количества
движения
б б
Конвективный теплообмен 193
Однако жидкость поступает в элементарный объем также через
б
поверхность BD с расходом (d/dx) [pudydx. Эта величина яв-
о
ляется разностью между расходом, вытекающим через поверх-
поверхность CD, и расходом, втекающим через поверхность АВ. Так
как жидкость, поступающая в объем через поверхность BD,
имеет составляющую скорости в направлении оси х, равную
скорости внешнего потока У<х>, то через эту верхнюю поверхность
в элементарный объем в направлении х поступит поток коли-
количества движения
а
Суммируя все составляющие
потока количества движе-
движения вдоль оси ху получаем
dx J
Рис. 4.7. Элементарный объем в лами-
нарном пограничном слое, рассматривае-
и) dtl мый ПРИ выв°Де интегральных уравне-
' v% ний сохранения.
На поверхности BD касательное напряжение отсутствует, так
как эта поверхность находится вне пограничного слоя, и
du/dy = 0. Однако существует касательная сила трения тю,
действующая на поверхности раздела жидкости и твердой стен-
стенки, а также имеются силы давления, действующие на поверх-
поверхности АВ и CD. Записывая все силы, действующие на элемен-
элементарный объем, и суммируя их, получаем соотношение
-Twdx = -6-%Ldx--%wdx. D.15)
При обтекании плоской пластины градиентом давления в на*
правлении оси х можно пренебречь, и тогда уравнение коли-
количества движения можно переписать в следующем виде:
Tw. D.16)
Интегральное уравнение энергии можно получить аналогич-
аналогичным способом. Однако в этом случае при выводе должен
7 Зак. 487
194 Глава 4
использоваться элементарный объем, выходящий за пределы как
теплового, так и динамического пограничного слоев (рис. 4.8).
В соответствии с первым законом fepMOAHHaMiiKH энергию еле-,
дует рассматривать 8 виде внутренней энергии (энтальпии),
кинетической энергии й теплоты, а также работы сил трения.
При низких скоростях члены, учитывающие кинетическую энер-
энергию и работу сил трения, малы по сравнению с другими чле-
членами, и ими можно пренебречь. Тогда увеличение энтальпии
Динамический
пограничный слой 6
Тепловой
пограничный слой St
Рис. 4.8. Элементарный объем в динамическом и температурном пограничных
слоях,
элементарного объема за счет втекания жидкости через поверх-
поверхность А В будет составлять
Уз
^ cppuTdy,
о
а ее снижение за счет вытекания жидкости через поверхность
CD
J -jz\ cppuTdydx.
о о
Увеличение энтальпии элементарного объема за счет втекания
жидкости через верхнюю поверхность равно
И наконец, теплота, подводимая вследствие теплопроводности
через поверхность раздела жидкости и твердой стенки, составит
ду
Конвективный теплообмен 195
Суммируя все эти величины, получаем интегральное уравнение
сохранения энергии в виде
=0,DЛ7)
0 0
Следует отметить, что за пределами теплового пограничного
слоя температура равна температуре невозмущенного потока Г*,,
и поэтому интегрирование следует проводить только до у = 6*.
Уравнение D.17) при этом упрощается и принимает вид
D.18)
Это уравнение обычно известно как интегральное уравнение
энергии для ламинарного пограничного слоя при низких скоро-
скоростях течения.
4.4. РАСЧЕТ КОЭФФИЦИЕНТОВ ТЕПЛООТДАЧИ И ТРЕНИЯ
В ЛАМИНАРНОМ ПОТОКЕ
Первым шагом в приближенном интегральном методе ра-
расчета является представление распределений скоростей и темпе-
температур в виде степенных рядов — полиномов. При выборе коэф-
коэффициентов этих рядов должны удовлетворяться граничные усло-
условия. Предположим, что распределение скоростей описывается
степенным рядом из четырех членов:
и (у) = а + by + су2 + dy\ D.19)
Выбор коэффициентов проводим с использованием следующих
граничных условий:
при у = 0: и = 0 и поэтому а = 0,
w = y = 0, и поэтому из уравнения D.11) получаем
д2и/ду2 = 0,
при у и б: и в= 1/оо и ди/ду = 0.
Эти граничные условия позволяют получить четыре уравнения
для расчета четырех неизвестных коэффициентов в зависимости
от скорости невозмущенного потока и толщины пограничного
слоя. Легко показать (см. задачу 4.14), что этим граничным
условиям удовлетворяют коэффициенты
Подставляя их в уравнение D.19) и приводя его к безразмер-
безразмерному виду путем деления на скорость невозмущенного потока
196 Глава 4
получаем
При подстановке выражения D.20) для распределения скоро-
скоростей в интегральное уравнение количества движения [уравнение
D.16)] получаем
Касательное напряжение на стенке тт можно найти, определяя
градиент скорости из уравнения D.20) при у = 0 (см. задачу
4.14). После подстановки xw в уравнение D.21) и интегрирова-
интегрирования последнего получаем
Преобразуя уравнение D.22) и интегрируя полученное уравне-
уравнение, находим зависимость толщины пограничного слоя от вяз-
вязкости, расстояния от передней кромки и скорости невозмущен-
невозмущенного потока в виде
б2 _ 140ул; . с D 2Ч\
Так как на передней кромке (т. е. при х = 0) 6 = 0, то коэф-
коэффициент С в этой зависимости должен быть равен 0, и тогда
e9 280vx
б 4,64
Чтобы определить коэффициент трения, подставим выраже-
выражение D.20) в уравнение D.21):
du
з vo
_ ,0"^ 2 б •
Подставляя сюда б из выражения D.24), получаем
*» 9,28 х
и тогда коэффициент трения CfX будет равен
п %wx 0,647
D.5
Конвективный теплообмен 197
Пример 4.1. Определить ламинарное касательное напряжение на расстоя-
расстоянии 0,2 м от передней кромки плоской пластины в потоке воды, имеющем
температуру 293 К и скорость 1 м/с.
Решение. Для воды при 293 К
ц 993. 10"°
и так как течение ламинарное, то
rw = ~~ 993 • Ю-6 М B ¦ 10*I'2 = 0,718 Н/м2.
Обратимся теперь к уравнению энергии и допустим, что
распределение температур в пограничном слое имеет такой же
вид, как и распределение скоростей:
Т (//)== е + fy + gy2 + hy3. D.26)
Граничные условия для поля температур таковы, что при у = 0
7 = Ts, а при у = St (толщина теплового пограничного слоя)
Т = Too и dT/dy = 0. Кроме того, как следует из уравне-
уравнения D.13), d2T/dy2 = 0 при # = 0, так как на поверхности раз-
раздела и = у = 0. При этих условиях константы равны (см. за-
задачу 4.15)
Зт т
i оо л S. * оо
"""" S> 2 ~б7' ~~ ' 262 "
Если для удобства переменную в уравнении энергии выбрать в
виде разности между температурами жидкости и стенки, то
тогда выражение для безразмерной температуры можно запи-
записать в виде
t-ts _ з у \ ( у
Определив Т—Ts и и соответственно из выражений D.27) и
D.20), можно переписать интеграл в уравнении D.18) в виде
G\. - Т) и dg = \ [(Тп - Т.) - (Т - Ts)] udy =
о
Произведя перемножение иод знаком интеграла, получаем вы-
выражение
198 Глава 4
которое после интегрирования принимает вид
V оо 2 s) V оо ^ 4 6 4 6 -f 20 б 8 б3 "^ 20 б3 28 б3 )'
Если ввести обозначение ? = б*/б, то последнее выражение за-
запишется в виде
Для жидкостей, у которых Pr ^ 1, оказывается, что ?^1, и
тогда вторым членом в скобках по сравнению с первым членом
можно пренебречь 1). Подставляя это приближенное выраже-
выражение для интеграла в уравнение D.18), получаем
VJ?b
Из уравнения D.24) получаем
дд
что дает
fe ~ 10,75 v •
или
б^ = 0,9766 Рг/3. D.28)
За исключением числового значения константы @,976 по сравне-
сравнению с 1,0), этот результат полностью совпадает с точным реше-
решением Польгаузена [2].
Из уравнений D.1) и D.27) величина конвективного тепло-
теплового потока от пластины, приходящегося на единицу ее пло-
площади, равна
А Т ду
3 k
3 kf (т т\
Подставляя сюда значения б и б* из выражений D.24) и D.28),
получаем
а 3 k Pr1/3Re1/2 k
и локальное число Нуссельта
= л (Г.-г.) Т
'> Это допущение несправедливо для жидких металлов, у которых
Рг < 1.
Конвективный теплообмен 19§
Эта формула очень хорошо согласуется с точным решением, по-
полученным в работе [2].
Приведенный пример иллюстрирует эффективность прибли-
приближенного метода расчета пограничного слоя. Если исходить из
физического смысла протекающих процессов и следовать ин-
интуиции, то с помощью этого метода можно получить вполне
удовлетворительные результаты, минуя математические трудно-
трудности, возникающие при решении точных уравнений пограничного
слоя. Приближенный метод применялся для решения многих
задач, и результаты этих решений описаны в литературе.
4.5. АНАЛОГИЯ МЕЖДУ ТЕПЛООБМЕНОМ
И ПЕРЕНОСОМ КОЛИЧЕСТВА ДВИЖЕНИЯ
ПРИ ТУРБУЛЕНТНОМ ОБТЕКАНИИ ПЛОСКОЙ ПЛАСТИНЫ
В большинстве практических задач течение в пограничном
слое бывает турбулентным, а не ламинарным. Качественно ме-
механизм переноса в турбулентном потоке можно представить себе
как усиление молекулярного переноса в ламинарном потоке,
В установившемся ламинарном потоке частицы жидкости сле-
следуют по вполне определенным линиям тока. Перенос тепла и
количества движения поперек линий тока происходит только
посредством молекулярной диффузии, поперечные же потоки
столь малы, что при введении в некоторой точке окрашенной
жидкости она следует строго по линиям тока без заметной диф-
диффузии. Но в турбулентном потоке такая окрашенная жидкость
уже на небольшом расстоянии ниже по потоку от места впры-
впрыскивания распространяется на значительную площадь. Меха-
Механизм перемешивания связан с быстро пульсирующими молями,
которые неупорядоченно переносят частицы жидкости. Группы
частиц (моли) сталкиваются друг с другом в этих беспорядоч-
беспорядочных поперечных перемещениях, обеспечивая эффективное пере-
перемешивание жидкости. Так как это перемешивание при турбу-
турбулентном течении происходит на макроскопическом уровне груп-
группами частиц, движущимися в жидкости зигзагообразно, то
механизм поперечного переноса оказывается во много раз эффек-
эффективнее, чем при ламинарном течении. В результате потоки тепла
и количества движения при турбулентном течении, а также
значения соответствующих коэффициентов трения и теплоотдачи
оказываются во много раз большими, чем при ламинарном те-
течении.
Если производится осреднение параметров турбулентного по-
потока в некоторой точке за некоторый промежуток времени, до-
достаточно продолжительный по сравнению с периодом одиночной
пульсации, то значительный интерес представляет случай, когда
осредненные йо времени физические свойства и скорость жид*
кости постоянны, если само осредненное течение является
200 Глава 4
установившимся. При этом каждое из физических свойств и ско-
скорость жидкости в турбулентном потоке можно выразить в виде
суммы не изменяющегося во времени среднего значения и пуль-
сационной составляющей, являющейся функцией времени. Для
упрощения задачи рассмотрим двумерный поток (рис. 4.9), в ко-
котором средняя скорость параллельна направлению оси я. Мгно-
венные значения составляю-
\dyy\ щих скорости и и v можно'
^ -/у- выразить в следующем виде:
1
L_
Рис. 4.9. Длина смешения при переносе
количества движения.
v = v', D.31)
где черта сверху означает
величину, осредненную во
времени, а штрих означает
мгновенное отклонение от
этой средней величины. Со-
Согласно модели, используе-
используемой для описания потока,
е*
Рис. 4.10. Изменение во времени мгно-
мгновенной скорости.
где 8* — интервал времени,
достаточно продолжитель-
продолжительный по сравнению с перио-
периодом пульсаций. На рис. 4.10
показано качественно изме-
изменение и к и' во времени. Из
уравнения D.32) или из
рассмотрения рис. 4.10 сле-
следует, что осреднение состав-
составляющей по времени и' дает нуль (т. е. и! = 0). Аналогично мож-
можно показать, что осредненные по времени v1 и (pv)' также рав-
равны нулю.
Пульсационные составляющие скорости непрерывно перено-
переносят массу, а следовательно, и количество движения через по-
поверхность, перпендикулярную оси у. Мгновенная скорость пере-
переноса продольной составляющей количества движения в направ-
направлении оси у на единицу площади составляет
где знак минус, как будет показано ниже, учитывает статисти-
статистическую корреляцию (взаимосвязь) между и! и г/.
Осреднение во времени переноса количества движения по
оси х приводит к кажущемуся напряжению турбулентного тре-
Конвективный теплообмен 201
ния %и которое определяется выражением
rt = - -Jr \ (pv)' (п + и') dQ: D.33)
о
Разделяя эту величину на два члена и осредняя первый из них,
получаем
¦grj (pv)'udQ = 0,
о
поскольку и — величина постоянная, а осреднение (pv)' дает
нуль. Интегрирование второго члена уравнения D.33) приво-
приводит к
е*
= - "г S
о
или при постоянном значении р
??)9 D.35)
где v'u! — осреднение по времени произведения и' и v'.
Нетрудно показать, что такие осреднения смешанных произ-
произведений пульсаций скоростей, как v'u\ отличны от нуля. Из
рис. 4.9 видно, что частицы, перемещающиеся вверх (?/>0),
переходят в слой жидкости, средняя скорость которой п выше,
чем в слое, из которого они поступили. В предположении, что
частицы жидкости в среднем сохраняют свою первоначальную
скорость п во время этого перемещения, получаем, что они
должны замедлять другие частицы жидкости после перехода
в новое положение. Это приводит к появлению отрицательной
составляющей и'. И наоборот, если v' является отрицательной,
то на новом месте и' будет положительной. В среднем положи-
положительная v' связана с отрицательной и', и наоборот. Следова-
Следовательно, осредненная величина u'v' оказывается в целом нерав-
неравной нулю и притом отрицательной. В результате турбулентное
касательное напряжение, определяемое по уравнению D.35),
положительно и имеет тот же знак, что и соответствующее ла-
ламинарное напряжение:
du du
x^9V
Следует при этом иметь в виду, что ламинарное касательное
напряжение является действительным напряжением, в то время
как кажущееся турбулентное касательное напряжение является
202 Глава 4
просто понятием, вводимым для объяснения переноса количе-
количества движения турбулентными пульсациями. Эта величина по-
позволяет выражать общее касательное напряжение в турбулент-
турбулентном потоке в следующем виде:
Сила вязкого сопротивления , /гт А /л ос\
Т = ^ - (- (Поток турбулентного D.36)
Площадь количества движения).
Чтобы связать поток количества движения, переносимого
турбулентностью, с осредненным градиентом скорости du/dy,
примем, что пульсации макрочастиц жидкости в турбулентном
потоке в среднем аналогичны движению молекул в газе [т. е.
они переносятся в среднем на расстояние /, перпендикулярное
п (рис. 4.9), прежде чем потерять скорость в другой плоскости
у]. Расстояние / известно как длина пути перемешивания
Прандтля и качественно соответствует средней длине свобод-
свободного пробега молекул газа. Предполагая, что при поперечных
перемещениях сохраняются как сами частицы жидкости, так и
их физические свойства и что возникновение турбулентных пуль-
пульсаций обусловлено в основном различием значений осредненных
физических свойств в плоскостях у, отстоящих друг от друга на
расстояние I, получаем, что при движении частицы от слоя у
к слою у + 1
«'-*-§• D.37)
При такой модели турбулентное касательное напряжение п
имеет вид, аналогичный виду ламинарного касательного напря-
напряжения:
T/ = «pPy-pBM^-t D.38)
где гм — коэффициент турбулентной вязкости, или коэффициент
турбулентного переноса количества движения. Формально коэф-
коэффициент турбулентной вязкости ем аналогичен коэффициенту
кинематической вязкости v; но если v является физическим
свойством, то ЕМ зависит от гидродинамических условий. Объ-
единяя уравнения D.37) и D.38), получаем, что eM = — v'U и
тогда уравнение D.36) дает общее напряжение трения в виде
T = p(v + eA1)^. D.39)
В турбулентном потоке ем оказывается намного больше v, и,
следовательно, членом с кинематической вязкостью можно пре-
пренебречь.
Перенос тепловой энергии в турбулентном потоке можно
представить аналогичным образом. Будем рассматривать дву-
Конвективный теплообмен 203
мерное осредненное распределение температур (рис. 4.11). Пуль-
сационные составляющие скорости непрерывно переносят ча-
частицы жидкости и запасенную в них энергию через плоскость,
перпендикулярную оси у. Плотность потока энергии в данный
момент времени и в произвольном положении вдоль оси у со-
составляет
(pv')(cpT), D.40)
где Т = Т + Г'. Путем рассуждений, аналогичных тем, что при-
привели к уравнению D.35), получаем осредненное количество
Рис. 4.11. Длина смешения при переносе энергии.
энергии, переносимое пульсациями и называемое турбулентным
тепловым потоком qt\
qt^A9cpVf\ D.41)
Используя введенное Прандтлем понятие пути перемешивания,
можно получить следующую зависимость между пульсациями
температуры и осредненным температурным градиентом:
«•""¦?¦
D.42)
Физический смысл этой зависимости состоит в том, что при
перемещении частицы жидкости из одного слоя у в другой, рас-
расположенный выше или ниже первого на расстояние /, резуль*
тирующие пульсации температуры вызываются в основном раз-
различием между осредненными температурами в этих слоях. Пред-
Предполагая, что механизмы переноса температуры (или энергии)
и скорости аналогичны, получаем, что длины пути перемешива-
перемешивания в уравнениях D.37) и D.42) одинаковы. Но произведение
vfTr в среднем оказывается положительной величиной, так как
положительному значению v' соответствует положительное зна-
значение Т\ и наоборот.
204 Глава 4
При подстановке уравнения D.42) в уравнение D.41) полу-
получаем плотность теплового потока, переносимого турбулентностью
-5- = cpPVT' = - cp9Vl -g-, D.43)
где знак минус является следствием второго закона термодина-
термодинамики (гл. 1). Чтобы выразить плотность турбулентного тепло-
теплового потока в форме, аналогичной уравнению теплопроводности
Фурье, будем определять величину е#, называемую коэффициен-
коэффициентом турбулентного переноса температуры, или коэффициентам
турбулентной температуропроводности по_у равнению sH = v'l.
Подставляя гн в уравнение D.43) вместо v'l, получаем
А^-^р^ — . D.44)
Общий поток тепла, который переносится через единицу пло-
площади поверхности, перпендикулярной направлению средней ско-
скорости потока, можно записать в виде
jj_ Молекулярная теплопроводность , Турбулентный теплоперенос
"X Площадь ' Площадь
или с помощью обозначений
¦J—-^(о + вя)-^-. D.45)
где а = k/Cpp — коэффициент молекулярной температуропро-
температуропроводности. Вклад в теплоперенос молекулярной теплопроводности
пропорционален ос, а турбулентная составляющая пропорцио-
пропорциональна гн. Для всех жидкостей, за исключением жидких метал-
металлов, гн в турбулентном потоке намного больше а. Отношение
молекулярной кинематической вязкости к молекулярной темпе-
температуропроводности v/a, как отмечалось ранее, называется чис-
числом Прандтля. Аналогично отношение турбулентной вязкости
к турбулентной температуропроводности гм/гн можно рассма-
рассматривать как турбулентное число Прандтля Рг*. Согласно тео-
теории длины__пути перемешивания Прандтля, Рг/=1, так как
ел* = ея = <//.
Хотя такое описание турбулентного движения является весь-
весьма упрощенным, из экспериментальных результатов следует,
что, по крайней мере качественно, этот подход верен. Нагревая
ртуть при ее турбулентном течении в трубе, можно получить
значения Рг* от 1,0 до 1,6 [3]. Для газов Рг* составляет ~0,7
и существенно не зависит от значения ламинарного числа
Прандтля, а также от типа эксперимента. В предположении, что
Рг/=1, объединяя уравнения D.38) и D.44), можно устано-
Конвективный теплообмен 205
вить следующую зависимость между плотностью турбулентного
теплового потока и турбулентным напряжением трения
х —war- <4-46>
Эта зависимость впервые была предложена в 1874 г. англий-
английским ученым О. Рейнольдсом и называется аналогией Рейнольд-
са. Для турбулентного течения она вполне удовлетворительно
описывает экспериментальные результаты и может применяться
как к турбулентным пограничным слоям, так и к турбулентному
течению в трубах или каналах. Однако аналогия Рейнольдса
не подходит для ламинарного подслоя. Так как этот слой ока-
оказывает значительное термическое сопротивление тепловому по-
потоку, то уравнение D.46) в целом не пригодно для получения
количественных результатов. Лишь для жидкостей, у которых
число Прандтля равно единице, его можно использовать непо-
непосредственно для расчета плотности теплового потока. Именно
этот случай будет рассмотрен в следующем разделе.
4.6. АНАЛОГИЯ РЕЙНОЛЬДСА
ПРИ ТУРБУЛЕНТНОМ ОБТЕКАНИИ ПЛОСКОЙ ПЛАСТИНЫ
Прежде чем установить связь между теплопереносом и по-
поверхностным трением при обтекании плоской пластины, напом-
напомним, что ламинарное касательное напряжение т определяется
формулой
da
а плотность теплового потока через любую поверхность, пер-
перпендикулярную оси у, — формулой
А ~ dy '
Объединяя две эти формулы, получаем
Из сопоставления уравнений D.46) и D.47) следует, что при
cp = k/\x (т. е. при Рг = 1) как в ламинарном, так и в турбу-
турбулентном пограничном слое применимо одно и то же уравнение
для расчета плотности теплового потока.
Для определения теплового потока от плоской пластины к
обтекающему ее турбулентному потоку при Рг = 1 заменим
k/\i на ср и разделим переменные в уравнении D.47). Предпо-
Предполагая, что q и т являются постоянными, получаем
dT, D.48)
206 Глава 4
где индекс s указывает на то, что как q> так и т берутся на по-
поверхности пластины. Интегрируя уравнение D.48) от и = 0
при Т = Ts до и = Foo при Т = Гоо, получаем
Й--<7.-Г->. D-49)
Но так как по определению локальные коэффициенты тепло-
теплоотдачи и трения соответственно равны
то уравнение D.49) можно переписать в виде
нс* д Nu* ^ cfx
Уравнение D.50) справедливо для газов, в которых число
Прандтля близко к единице. Это уравнение можно также при-
применять для жидкостей, у которых число Рг имеет значения от
0,6 до ~50, если только это уравнение модифицировать в соот-
соответствии с экспериментальными результатами и рассматривать
в виде
J^ -^. D.51)
Здесь индекс х означает расстояние от передней кромки пла-
пластины.
Чтобы на практике применять аналогию между переносом
тепла и переносом количества движения, необходимо знать
коэффициент трения С^. При турбулентном обтекании плоской
пластины эмпирическая зависимость для локального коэффи-
коэффициента трения
Cfx = 0,0576 (—У'15 D.52)
хорошо согласуется с экспериментальными данными при Re «
= 5-105ч- 107, если только нет отрыва пограничного слоя. Если
предположить, что турбулентный пограничный слой начинается
на передней кромке пластины, то путем интегрирования уравне-
уравнения D.52) можно получить следующее выражение для среднего
коэффициента трения при обтекании плоской пластины дли*
ной L:
Cf - -г $ с>*dx e °'072 (^Ф) 1/5 ¦ D-бз)
о
Однако з действительности на расстояниях от х — 0 до
х = хс турбулентному пограничному слою предшествует лами-
ламинарный пограничный слой. Так как локальное сопротивление
Конвективный теплообмен 207
трения в ламинарном пограничном слое меньше, чем в турбу-
турбулентном при том же Re, то среднее сопротивление трения, рас-
рассчитываемое по формуле D.53) без поправки, учитывающей ла-
ламинарный пограничный слой, оказывается завышенным. Дей-
Действительное сопротивление можно рассчитать достаточно точно,
если предположить, что за точкой перехода турбулентный погра-
пограничный слой ведет себя так же, как если бы он начинался на
передней кромке.
Прибавляя сопротивление ламинарного пограничного слоя
между х==*0их==хск сопротивлению турбулентного погранич-
пограничного слоя между х = хс и х = L, получаем
[0,072Re?-I/5L - 0,072Re ~115хс + 1,33 ReJ1/2*c]
Cf=— jf c- .
Для критического значения Re*c = 5-Ю5
Cf = 0,072 (ReZ * - ^f^. D.54)
Подставляя выражение для CfX [уравнение D.52)] в урав-
уравнение D.51), получаем, что локальное число Нуссельта при
произвольном значении х> превышающем хс, равно
Шх = ^f- = 0,0288Рг1/3 (^f^H'8. D.55)
Можно видеть, что при конвективном теплообмене в турбулент-
турбулентном пограничном слое локальный коэффициент теплоотдачи
уменьшается с увеличением расстояния х следующим образом:
ftc*e© 1/х0'2. Из уравнения D.55) следует, что по сравнению с
ламинарным течением, при котором hcx ®о 1/л:1/2, коэффициент
теплоотдачи при турбулентном течении уменьшается с увеличе-
увеличением х менее интенсивно и что при данном числе Рейнольдса
этот коэффициент оказывается намного больше своего значения
для ламинарного течения.
Средний коэффициент теплоотдачи при турбулентном обте-
обтекании плоской поверхности длиной L в первом приближении
может быть рассчитан путем интегрирования уравнения D.55)
от х в 0 до х = L:
В безразмерном виде получаем
Шь = -^ = 0,036Pr ^Ref. D.56)
В уравнении D.56) не учитывается ламинарный пограничный
слой, и поэтому оно справедливо только при L » хс. Ламинар-
Ламинарный пограничный слой можно учесть, если при определении кем
208 Глава 4
выполнять интегрирование уравнения D.30) от х = 0 до х = хс
и уравнения D.55) от х = хс до x = L. Тогда при Rec = 5-105
получаем
"NUL = СОЗбРг1'3 (Re0/ - 23200). D.57)
Пример 4.2. Картер автомобильного двигателя имеет следующие разме-
размеры: длина 0,6 м, ширина 0,2 м и высота 0,1 м. Считая температуру поверх-
поверхности картера равной 350 К, оценить тепловой поток от картера к атмосфер-
атмосферному воздуху, имеющему температуру 276 К, при скорости движения автомо-
автомобиля 30 м/с. Предположить, что вибрация двигателя и шасси автомобиля
вызывает переход ламинарного течения к турбулентному очень близко к пе-
передней кромке, в результате чего можно считать для практических целей,
что на всей поверхности картера пограничный слой турбулентный. Радиацион-
Радиационным теплопереносом пренебречь, а для передних и задних поверхностей кар-
картера принять такой же средний коэффициент конвективной теплоотдачи, как
для дна и его боковых поверхностей.
Решение. С использованием физических свойств воздуха при 313 К
(табл. П. VI. 1) получаем число Рейнольдса
L \i 19,123-10
Среднее число Nul получаем из уравнения D.56):
NuL = 0,036Pr1/3Re?8 = 0,036 • 0,711/3 (l,03 • 106H'8 = 2075.
При этом средний коэффициент теплоотдачи будет равен
Шгк 2075-0,0265
hc = —^- = ^ =91,6 Вт/(м2 • град).
Площадь поверхности, на которой происходит теплоотдача, составляет 0,28 м2,
и, следовательно, потери тепла картером составят
q = hcA (Ts - Tj) = 91,6 • 0,28 C50 - 276) = 1898 Вт.
4.7. ВЫНУЖДЕННАЯ КОНВЕКЦИЯ
ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ В ТРУБЕ
Коэффициент теплоотдачи при ламинарном течении в трубе
будем определять для полностью развитого течения и постоян-
постоянного теплового потока на стенке. Для вывода уравнения сохра-
сохранения энергии в данном случае рассмотрим небольшой цилин-
цилиндрический элементарный объем, имеющий длину dx, внутренний
радиус г и наружный радиус г + dr (рис. 4.12). Тепло входит
в объем и выходит из него в радиальном направлении в резуль-
результате теплопроводности, в то время как конвективный перенос
энергии происходит в осевом направлении. Тепловой поток, вхо-
входящий в элементарный объем вследствие теплопроводности,
равен
qr = — k2nr dx -j^r.
Конвективный теплообмен 209
%+dr
Результирующий тепловой поток, выходящий из элементарного
объема вследствие теплопроводности, равен
E3JL Иг —
дг аг~~
Скорость движения через элементарный объем в осевом на-
направлении постоянна, но при этом в нем происходит изменение
температуры. В результате конвективного переноса в элемен-
элементарный объем входит тепло-
тепловой поток
qx = 2nrdrpucpT,
а выходит из него тепловой по-
поток
2лг dr риСр \ Т + -gj dx\.
Приравнивая результирующие
тепловые потоки, обусловлен-
обусловленные теплопроводностью и кон-
конвекцией при установившихся
условиях, получаем уравнение
энергии для ламинарного тече*
идя в трубе:
1 д / дТ \ _ рср дТ
uf дг \ дг ) k дх ' ^ '
При постоянной плотности теплового потока на стенке q"s и
постоянных физических свойствах жидкости ее температура при
любом значении г должна линейно возрастать в направлении
течения, так что величина dT/dx будет постоянной. Другие усло-
условия для такой системы следующие: при г = 0 (ось трубы)
дТ /дг = 0, а при r — rs Т = Ts. Кроме того, при г = rs тепловой
поток связан с градиентом температуры следующей зависи-
зависимостью:
«:--*(?)„•
При допущении о постоянстве (dT/dx) дифференциальное
уравнение в частных производных D.58) превращается в обык-
обыкновенное дифференциальное уравнение, в котором скорость на
любом радиальном расстоянии г является функцией скорости на
оси трубы Имакс- При полностью развитом ламинарном течении
распределение скоростей в трубе является параболическим и
может быть записано в безразмерном виде в зависимости от ра-
радиального расстояния следующим образом:
Рис. 4.12. Элементарный объем при
ламинарном течении в трубе.
210 Глава 4
где rs — радиус трубы. После подстановки распределения ско-
скоростей D.59) в уравнение D.58) и некоторых преобразований
получаем выражение
д ( дТ\ 1 дТ г, /г VI ,л СЛ\
) "[1 () ]г D.60)
интегрирование которого дает
/г2 г4 \ „ /л ^
С)Cl> (
После второго интегрирования получаем распределение темпе-
температур по радиусу в виде
Константы С\ и С2 определяем с помощью следующих гранич-
граничных условий. Так как дТ/дг = 0 при г = 0, то С\ = 0. А по*
скольку при г = rs T = TSt то
** ~ о" 1Г"макс vТ ~ ITJ + Сз D-63)
«макс
D.64)
Подстановка Ci и С2 в уравнение D.62) дает следующее распре-
распределение температур:
Обозначая Г (г)—Ts через 6, получаем профиль температур в
безразмерном виде:
где ••—•(^)
Теперь можно получить коэффициент теплоотдачи, определив
градиент температуры при г = rs. Используя определение коэф-
коэффициента теплоотдачи и подставляя градиент температуры на
стенке, получаем
)(??)—? <4-68>
ИЛИ Л=^". D-70)
Конвективный теплообмен
Таблица 4.1
Теплоотдача и потери на трение при полностью развитом
ламинарном течении ньютоновских жидкостей в каналах
различной формыа) [8; см. также 6 и 7]
Форма поперечного
сечения канала
<L/Dh>100)
Г -а
i 60е
la Л W.VJ
?_Л 2а 2
1 п
7Ь
i
2а
О
•ПН
2а
О
»c=zig-t
_,«,,. ь п 0
Теплоизолировано
3,014
3,111
3,608
4,002
4,123
4,364
5,099
5,331
6,490
8,235
5,385
N11*2
1,474
1,892
3,091
3,862
3,017
4,364
4,35е)
2,930
2,904
8,235
Nur
2,39е
2,47
2,976
3,34В>
3,391
3,657
3,66
4,439
5,597
7,541
4,861
/Re
12,630
13,333
14,227
15,054
15,548
16,000
18,700
18,233
20,585
24,000
24,000
iJHx/ff
0,269
0,263
0,286
0,299
0,299
0,307
0,307
0,329
0,353
0,386
0,253
МиЯ1
Nur
1,26
Г,26
1,21
1,20
1,22
1,19
1,39
1,20
1,16
1,09
1,11
a)Индекс Н\ означает постоянную плотность теплового потока
вдоль канала при постоянной температуре стенок в каждом попе*
речном сечении; индекс Я2 означает постоянную плотность тепло*
вого потока на стенке как по ее периметру, так и вдоль канала;
индекс 7 означает постоянную температуру стенок канала.
б) Эта величина представляет собой то же, что и Nu#iPr~
при Рг«0,7.
в) Значения, полученные путем интерполяции
212 Глава 4
Последнюю зависимость можно переписать с помощью обычного
числа Нуссельта:
N*d-¦?—f D.71)
Здесь число Нуссельта определяется по разности температур
на оси трубы и на ее поверхности, т. е. при rs = D/2. С прак-
практической точки зрения обычно удобнее. относить число Нус-
Нуссельта к разности между среднемассовой температурой жид-
жидкости и температурой на поверхности стенки. Среднемассовую
температуру жидкости обычно называют температурой смеше-
смешения (см. задачу 4.32) и получают путем сбора жидкости, исте-
истекающей из канала в специальный сосуд, и ее полного переме-
перемешивания. Естественно, что на входе в трубу температура по-
постоянная, и поэтому среднемассовая температура и температура
на оси трубы идентичны. Если число Нуссельта и коэффициент
теплоотдачи определяются по разности температур между
среднемассовой температурой жидкости и температурой поверх-
поверхности стенки, то можно получить следующее значение этого
числа [6]:
NuD = 4,36. D.72)
Следует отметить, что значение числа Нуссельта при полностью
развитом ламинарном течении не зависит от числа Рейнольдса,
так как в этом случае толщина пограничного слоя просто равна
радиусу трубы. Однако на начальном участке трубы значение
числа Нуссельта будет больше, чем при полностью развитом
течении. В гл. 5 будут представлены эмпирические уравнения
для расчета числа Нуссельта на начальном участке трубы.
В табл. 4.1 приведены значения числа Нуссельта для полностью
развитого течения в каналах с различной формой поперечного
сечения.
Пример 4.3. Рассчитать коэффициент теплоотдачи при полностью разви-
развитом ламинарном течении глицерина, имеющем среднемассовую температуру
293 К, в канале сечением 0,5 X 0,5 м при температуре его стенок 400 К и
скорости потока 0,1 м/с.
Решение» Из уравнения D.6) определяем эквивалентный диаметр
Из табл. 4Л для квадратного сечения при постоянной температуре стенок
имеем
Nun =2,976-%^-
DH Ь
Этот результат хорошо согласуется со значением числа Нуссельта, определен-
определенным по формуле D.71).
Из табл. П. V. 3 при 293 К имеем
к — 0,285 Вт/(м. град).
Конвективный теплообмен 213
Подставляя это значение в выражение для Nu^ и разрешая последнее от-
относительно коэффициента теплоотдачи, получаем
2,976 • 0,285
0,5
« 1,70 Вт/(м2-град).
4.8. АНАЛОГИЯ РЕЙНОЛЬДСА
ДЛЯ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ В ТРУБЕ
Допущения, которые необходимо принять для получения про-
простой аналогии, справедливы лишь для жидкостей, у которых
число Прандтля равно единице. Но общую взаимосвязь между
теплообменом и трением в жидкости при ее турбулентном тече-
течении в каналах можно продемонстрировать без дополнительных
математических выкладок. Результаты такого простого анализа
можно распространить и на другие жидкости с помощью эмпи-
эмпирических поправочных коэффициентов, как это будет показано
в гл. 5.
Связь между плотностью теплового потока и градиентом
температуры следует из ранее полученного уравнения:
T- D>45)
Аналогично для определения касательного напряжения, обуслов-
обусловленного совместным действием сил вязкости и турбулентного
переноса количества движения, можно использовать уравнение
Согласно аналогии Рейнольдса, перенос тепла и количества дви-
движения в турбулентном потоке происходит подобным образом.
Следовательно, аналогично должны изменяться величины q и т
с изменением расстояния от поверхности у. Для полностью раз-
развитого турбулентного течения в трубе локальное касательное
напряжение линейно уменьшается с увеличением радиального
расстояния г. Следовательно, можно записать
i-i-1-JL D,73)
Зй* <4-74>
где индекс 5 обозначает условия на внутренней поверхности
трубы. Подстановка выражений D.73) и D.74) соответственно
в D.39) и D.45) дает
*('-*)-({¦+««)¦?¦
214 Глава 4
Если гн = ем, то выражения в скобках в правых частях урав-
уравнений D.75) и D.76) равны при условии, что молекулярная ки-
кинематическая вязкость |х/р равна молекулярной температуро-
температуропроводности k/pCp, т. е. при условии, что число Прандтля равно
единице. Делением уравнения D.76) на D.75) получаем
. D.77)
Проинтегрируем уравнение D.77) от стенки, где и = О и Т = 7V
до оси потока, где и = Vm и Т = Ть. Путем интегрирования по-
получаем зависимость
? D.78)
которую можно переписать в виде
1 h .
D.79)
так как коэффициент Яс по определению равен qs/As{Ts — Tb).
Умножая числитель и знаменатель в правой части уравнения
D.79) на DHiik и производя перестановку, получаем
где St — «*«ело Стантона.
Чтобы привести левую часть уравнения D.79) к более удоб-
цому виду, рассмотрим баланс сил, действующих на цилиндри-
цилиндрический объем жидкости (рис. 4.13). Разность давлений р\ — р2
О {)-•
Рис. 4.13. Обозначения, используемые при рассмотрении баланса сил, дей-
действующих на элемент жидкости в трубе.
создает силу (p\ — p2)nD2/4, которая в стационарном случае
компенсируется трением на стенках:
D.81)
Находим из этой зависимости выражение для касательного на-
напряжения на стенке:
т J?jj-g2i?. D.82)
Конвективный теплообмен 215
Выражая падение давлением через коэффициент трения /, по-
получаем
L pFi
fV1 <483)
Подставляя это выражение для р\ — р% в уравнение D.82),
имеем
r.-f^S. D.84)
И наконец, подставляя это xs в уравнение D.79), получаем
уравнение
St^-p7^7=?' D.85)
известное как аналогия Рейнольдса для течения в трубе1). Ра-
Расчеты по этому уравнению хорошо согласуются с эксперимен-
экспериментальными данными по теплоотдаче к газам в случае, когда
число Прандтля близко к единице.
Согласно экспериментальным результатам, при течении жид-
жидкостей в гладких трубах в интервале чисел Рейнольдса от
10 000 до 120 000 коэффициент трения определяется эмпириче*
ской зависимостью
С помощью этой зависимости можно переписать уравнение
D.85) в следующем виде:
St = -—^ = 0,023 Re*0'2. D.86)
Поскольку число Прандтля считается равным единице,
Ш = 0,023 Re0/, D.87)
или Ас = 0,023 vSfD"'^ (—) . D.88)
Можно видеть, что при полностью развитом турбулентном
течении в трубе коэффициент конвективной теплоотдачи прямо
пропорционален скорости в степени 0,8 и обратно пропорциона-
пропорционален диаметру трубы в степени 0,2. При заданном расходе
увеличение диаметра трубы приводит к снижению скорости,
вследствие чего Нс снижается пропорционально 1/D1»8. Поэтому
использование труб малого диаметра и высоких скоростей при-
приводит к более высоким коэффициентам теплоотдачи, но при
!> Аналогия Рейнольдса может быть распространена и на массообмен.
Аналогия между переносом массы, тепла и количества движения рассматри-
рассматривается в гл. §,
216 Глава 4
этом возрастают затраты энергии на преодоление сапротивле-
ния трения. Поэтому при разработке теплообменного оборудо-
оборудования необходимо соблюдать баланс между выигрышем в коэф-
коэффициенте теплоотдачи, достигаемым за счет использования ка-
каналов с меньшей площадью поперечного сечения, и соответ-
соответствующим увеличением требований к насосному оборудованию.
Литература
1. Schlichting H., Boundary Layer Theory, 6th ed., N. Y., McGraw, 1968.
[Имеется перевод с немецкого издания: Шлихтинг Г., Теория пограничного
слоя. — М.: Наука, 1974.]
2. Pohlhausen Е., Der Warmeaustausch zwischen festen Korpern und Flus-
sigkeiten mit kleiner Reibung und kleiner Warmeleitung, ZAMMt 1, p. 115
A921).
3. Isakoff S. E., Drew Т. В., Heat and Momentum Transfer in Turbulent
Flow of Mercury, Inst. Mech. Eng. and ASME, Proc. General on Heat Transfer,
p. 405, 1951.
4. Forstall W., Jr., Shapiro A. H., Momentum and Mass Transfer in Co-
Coaxial Jets, /. Appl Mech.t 17, p. 399 A950).
5. Colburn A. P., A Method of Correlating Forced Convection Heat Trans-
Transfer Data and a Comparison with Fluid Friction, Trans. AlChE, 29, p. 174
A933).
6. Shah R. K., Laminar Flow Friction and Forced Convection Heat Trans-
Transfer in Ducts of Arbitrary Geometry., Int. J. Heat Mass Transfer, 18, p. 849
A975).
7. Shah R. K-, London A. L., Thermal Boundary Conditions and Some
Solutions for Laminar Duct Flow Forced Convection, /. Heat Transfer, 96,
p. 159 A974). [Имеется перевод: Шах, Лондон, Тепловые граничные условия
и некоторые решения для ламинарной вынужденной конвекции в каналах. —
Труды Амер. об-ва инж.-мех., сер. С. Теплопередача, 1974, № 2, с. 45.]
8. Shah R. К., London A. L., Laminar Flow Forced Convection in Ducts,
Academic Press, N. Y., 1978.
ЗАДАЧИ
Задачи в данной главе сгруппированы по тематике разделов, как указа-
указано в таблице.
Номера
задач
4.1—4.13
4.14-4.17
4.18-4.25
4.25—4.31
4.32—4.44
Разделы
4.1 и 4.2
4.3
4.4 и 4.5
4.6
4.7 и 4.8
Тема
Ламинарное обтекание плоской пла-
пластины
Интегральные уравнения для лами-
ламинарного течения
Ламинарное и турбулентное обтека-
обтекание плоской пластины
Аналогия Рейнольдса
Ламинарное и турбулентное течение
в трубе
4.1. Жидкость с температурой 40°С течет в круглой трубе диаметром
15 см. Средняя скорость жидкости 2 м/с. Рассчитать число Рейнольдса, если
жидкость представляет собой: а) воздух, б) СО2, в) воду, г) моторное масло.
Использовать физические свойства, приведенные в приложениях.
4.2. При тех же условиях, что и в задаче 4.1, определить, каким является
течение в каждом случае: ламинарным, переходным или турбулентным?
4.3. Принять, что изменение скорости в поперечном сечении круглой тру-
трубы является параболическим и описывается зависимостью
¦[-(тЛ-
где Умакс = 30 м/с (максимальная скорость, или скорость на оси трубы),
R = 20 см (внутренний радиус трубы). Путем интегрирования профиля ско-
скоростей по площади поперечного сечения трубы определить среднюю скорость
жидкости.
4.4. Воздух при 20°С обтекает плоскую пластину при скорости невозму-
невозмущенного потока 10 м/с. Определить расстояние от передней кромки пластины,
на котором: а) начинается переходный режим течения; б) начинается турбу-
турбулентное течение.
Принять, что критическое число Рейнольдса Rec, при котором начинается
переходное течение, составляет 2-IQ5, а для полностью развитого турбулент-
турбулентного течения оно равно 5-Ю5.
4.5. Решить задачу 4.4 в случае, когда жидкость представляет собой:
а) воду, б) ртуть.
4.6. Жидкость при температуре 40°С течет по трубе диаметром 7 .см. Рас-
Рассчитать среднюю скорость жидкости, необходимую для возникновения пере*
ходного и турбулентного режимов течения. Принять в качестве жидкости:
а) воздух, б) воду, в) моторное масло-
218 Глава 4
4.7. Воздух при температуре 20°С движется по трубе внутренним диа-
диаметром 15 см. Массовый расход воздуха 1,05-10~3 кг/с. Определить значение
числа Рейнольдса воздуха.
4.8. Принять, что профиль температур воздуха около поверхности изо-
изотермической плоской пластины описывается уравнением
см).
где Ts — температура пластины, Too — температура воздуха в невозмущенном
потоке, у — расстояние по нормали от поверхности пластины, см.
Рассчитать коэффициент конвективной теплоотдачи от пластины и общее
количество отдаваемого пластиной тепла при площади ее поверхности 2 м2 и
Ts = 100°C, Too = 0°С.
4.9. Вода при 60°С течет по каналу прямоугольного сечения 10 X 15 см со
средней скоростью 8 м/с. Рассчитать значение числа Рейнольдса воды.
4.10. Профиль скорости при обтекании воздухом, имеющим температуру
60°, поверхности квадратной пластины площадью 1,8 м2 описывается форму-
формулой
где у — расстояние от поверхности пластины, измеренное в сантиметрах. Оце-
Оценить толщину пограничного слоя в потоке воздуха.
4.11. Для условий задачи 4.10 рассчитать касательное напряжение на
пластине при ее обтекании воздухом при V<x> = 3 м/с. Определить также
общую силу сопротивления пластины.
4.12. Изменение локального коэффициента теплоотдачи с расстоянием х>
отсчитываемым от передней кромки плоской пластины, описывается следую*
щей безразмерной зависимостью:
Найти выражение для среднего коэффициента теплоотдачи Я при длине пла-
пластины в направлении течения, равной L. Принять физические свойства жид-
жидкости постоянными.
4.13. Локальный коэффициент теплоотдачи при турбулентном обтекании
плоской пластины определяется выражением
Кхх
~- = 0,0288
где х отсчитывается от передней кромки пластины. Предполагая, что турбу-
турбулентное течение начинается на передней кромке и физические свойства по*
тока постоянны, найти выражение для среднего коэффициента теплоотдачи
от пластины длиной L в направлении течения.
4Л4. Профиль скорости в пограничном слое при обтекании плоской пла-
пластины принят в виде
и =*= а + by + су2 + dyzt
где у — координата, отсчитываемая перпендикулярно пластине. Использовать
соответствующие граничные условия, найти коэффициенты а, Ь, с и d и по*
казать, что профиль безразмерной скорости описывается зависимостью
и г у
Конвективный теплообмен 219
С использованием этого профиля скорости определить расчетную зависимость
касательного напряжения на стенке от б.
4.15. Профиль температуры внутри пограничного слоя около плоской пла-
пластины можно представить в виде
Т = е + fy + gy> + hy\
где у — координата, отсчитываемая перпендикулярно пластине. Использовать
соответствующие граничные условия и показать, что уравнение для профиля
температур при этом будет следующим:
T~TS
3 у I fy \з
2~ 6*~2Лб77 '
4.16. Предполагая, что профиль скорости при обтекании жидкостью пло-
плоской пластины является линейным
а) использовать соответствующие граничные условия и выразить и в за-
зависимости от б и V<x>\
б) подставить выражение для профиля скорости в интегральное уравне-
уравнение количества движения D.16) и найти выражение для локальной толщины
пограничного слоя б(*);
в) сравнить найденное для б (я) выражение с выражением D.25), кото-
которое получено аналогичным образом, но для более сложного профиля скорости,
описываемого уравнением третьей степени;
г) с использованием найденного для б (я) выражения найти зависимость
для Cfx и сравнить ее с полученной ранее в примере 4.1.
4.17. Принимая линейный профиль температуры
в жидкости, обтекающей плоскую пластину,
а) использовать соответствующие граничные условия и найти зависи-
зависимость Т от би Ts и 7V,
б) принять, что профиль скорости также линейный (см. задачу 4.16),
подставить его выражение в интегральное уравнение энергии D.18) и найти
зависимость б/б/ от числа Прандтля;
в) сравнить найденный для б/б/ результат с уравнением D.28), получен-
полученным с использованием более сложных профилей скорости и температуры,
описываемых уравнениями третьей степени;
г) с использованием полученной для б/б* зависимости найти выражение
для Nil* и сравнить результат с уравнением D.30).
4.18. Температура квадратной плоской пластины длиной 35 см поддержи-
поддерживается равной 120°С. Воздух при температуре 20°С обтекает пластину со
скоростью 22 м/с. Рассчитать тепловой поток от пластины.
4.19. Прямоугольная пластина имеет длину в направлении потока 120 см
и ширину 200 см. Температура пластины поддерживается равной 80°С при
обтекании ее азотом, имеющим скорость 2,5 м/с и температуру 0°С. Опреде-
Определить: а) средний коэффициент трения; б) силу вязкого сопротивления пла-
пластины; в) средний коэффициент конвективной теплоотдачи; г) общий тепло-
тепловой поток от пластины.
4.20. Воздух при атмосферном давлении обтекает плоскую пластину дли-
длиной 3 м и шириной 5 м. Температуры воздуха и пластины 15 и 65°С, а ско-
скорость воздуха 35 м/с. Рассчитать на задней кромке пластины (т.е. при
х = 3 м): а) локальный коэффициент трения, б) локальный коэффициент
теплоотдачи.
4.21. Для условий задачи 4.20 рассчитать те же величины для того сече-
сечения пластины, где течение становится турбулентным. Принять Rec==5-105.
220 Глава 4
4.22. Вода обтекает квадратную пластину со стороной 2 м. Температура
воды составляет 90йС, а ее скорость 10 м/с. Пластина имеет постоянную тем-
температуру 30°С. Определить силу сопротивления пластины и теплоотдачу от ее
поверхности.
4.23. Мощность плоского электрического нагревателя 400 Вт. Нагреватель'
охлаждается воздухом, имеющим температуру 30°С и движущимся парал-
параллельно поверхности со скоростью 28 м/с. Размер нагревателя в направлении
течения 75 см, а поперек течения 125 см. Определить температуру нагрева-
нагревателя. С целью упрощения расчетов физические свойства воздуха брать при
температуре окружающей среды.
4.24. Принять, что турбулентное течение начинается у передней кромки
плоской пластины. С использованием выражения для локального коэффициен-
коэффициента трения D.52) показать, что средний коэффициент трения на пластине дли-
длиной L определяется уравнением D.53).
ч 4.25. Проверить, справедливо ли выражение D.57) для расчета среднего
числа Нуссельта при обтекании плоской пластины длиной L? Для локального
числа Нуссельта использовать формулу D.30) при ламинарном режиме те-
течения и формулу D.55) при турбулентном режиме. Критическое значение
числа Рейнольдса принять равным 5-Ю5.
4.26. Коэффициент трения при обтекании обогреваемой поверхности воз-
воздухом, имеющим среднюю температуру 40°С и скорость 20 м/с, составляет
0,075. Определить средний коэффициент конвективной теплоотдачи от поверх-
поверхности.
4.27. Число Стантона St определяется по формуле St = Nu/Re Рг. Вы-
Выразить St через свойства Жидкости, коэффициент теплоотдачи и скорость
жидкости. ¦
4.28. Тело с площадью поверхности 0,55 м2 нагрето до 110°С. Его обте-
обтекает вода с температурой 10°С и скоростью 5 м/с. Сила сопротивления тела
составляет 4,0 Н. Рассчшать тепловой поток от тела.
4.29. Плоский электрический нагреватель с площадью поверхности 0,1 м2
имеет поддерживаемую постоянной температуру поверхности 80°С. Нагрева-
Нагреватель обогревает газ СОг, имеющий исходную* температуру 10°С и обтекающий
поверхность нагревателя со скоростью 20 м/с. При силе сопротивления нагре-
нагревателя 0,2 Н рассчитать мощность нагревателя в ваттах.
4.30. Измерения на теле,' помещенном' в аэродинамической трубе, пока-
показали, что сила сопротивления трения, приложенная к телу, составляет 100 Н.
Площадь поверхности тела 0,8 м2, а его температура 200°С. Температура на-
набегающего воздуха 30°С, а его скорость 35" м/с. Вычислить средний коэффи-
коэффициент теплоотдачи и общее количество тепла, отдаваемого телом.
4.3Г. Блок с электронным "оборудованием "для измерения физических
свойств-воды погружен позади судна. При скорости судна 24 м/с натяжение
кабеля, удерживающего блок, составляет 370 Н. Блок с измерительной аппа-
аппаратурой имеет площадь поверхности 3 м2 и потребляет мощность 8500 Вт.
Вычислить температуру поверхности блока, если. температура окружающей
его воды равна 15^/' -
"' 4.32. Температуру смешения, или среднюю температуру, жидкости-движу-
жидкости-движущейся по трубе, определяют гипотетически путем' сбора жидкости из трубы
и адиабатического ее 'перемещивднйя до достижения постоянной температуры.
' .а) Показать, что средняя температура'жидкости при ее течении со ско-
скоростью^ (О -в трубе с внутренним ра'диусом rw равна ; ; - -
9(r)Cp(r)u(r)T(r)rdr
г-0 - - • -
r - • '
\ 9(r)cp(r)u(r)rdr
Конвективный теплообмен 221
б) Показать, что при постоянных физических свойствах жидкости это
выражение можно упростить и свести к виду
rw
jj u(r)T(r)rdr
r=0
r dr
[ u(r)
io
в) Показать, что для течения с постоянным профилем скоростей
(и = const) зависимость для Тт может быть упрощена до выражения
rw
r Tm = ^- [ T(r)rdr,
в котором А — площадь поперечного сечения трубы.
4.33. Рассчитать среднюю температуру жидкости, имеющей постоянные
"физические свойства и движущейся по трубе диаметром 6 см; при изменении
ее температуры по радиусу по закону
Т — 50 _ (г_у .
100 V 3 ) ' '
где Г — в градусах Цельсия, а г — в сантиметрах. Принять равномерный
профиль скоростей и использовать результаты, приведенные в задаче 4.32.
4.34. В трубе диаметром 1 см имеет место полностью развитое ламинар-
ламинарное течение насыщенной жидкости — фреона-12. Изотермическая стенка трубы
имеет температуру 0°С. Средняя температура фреона 20°С. Определить теп-
теплоотдачу от фреона в случае, когда длина трубы 1,7 м.
4.35. Моторное масло со средней температурой 100°С удаляется из дви-
двигателя через трубку диаметром 5 мм, температура стенок которой 40°С. Для
полностью развитого ламинарного течения рассчитать коэффициент конвек-
конвективной теплоотдачи масла и тепловой поток от масла на 1 м длины
трубы.
4.36. Двуокись углерода движется по каналу с треугольным поперечным
сечением. Изотермическая стенка канала имеет температуру 20°С, а средняя
температура СО2 равна 120°С. Длина каждой стороны канала 1,2 см. Рас-
Рассчитать тепловой поток на единицу длины канала в осевом направлении для
случая полностью развитого ламинарного течения.
4.37. Вода течет по прямоугольному каналу сечением 10X4 мм. Сред-
Средняя температура воды 10°С, течение является ламинарным и полностью раз-
развитым. Рассчитать коэффициент конвективной теплоотдачи воды в случаях:
а) постоянной температуры стенок канала; б) постоянной плотности тепло-
теплового потока в направлении течения и постоянной температуры стенок канала
в заданном поперечном сечении; в) постоянной плотности теплового потока
по всей поверхности канала.
4.38. Азот со средней температурой 40°С при атмосферном давлении дви-
движется в гладкой трубе внутренним диаметром 15 см и длиной 20 м. Массо-
Массовый расход N2 составляет 120 г/с. Температура поверхности трубы поддержи-
поддерживается постоянной и равной 100°С. Определить: а) коэффициент поверхност-
поверхностного трения; б) перепад давлений на всей длине трубы; в) коэффициент кон-
конвективной теплоотдачи к азоту; г) тепловой поток к N2 от поверхности стенок
трубы.
4.39. Коэффициент трения при течении в круглой трубе водяного пара,
поступающего в нее при атмосферном давлении, составляет 0,02. Диаметр
222 Глава 4
трубы 18 см, а ее длина 40 см. Средняя температура пара 200°С, а темпера-
температура изотермической стенки трубы 154°С. Определить тепловой поток к трубе.
Рассчитать давление на выходе из трубы.
4.40. Труба в химико-технологической установке используется для транс-
транспортировки скипидара с массовым расходом 23 кг/с. Труба имеет длину 10 м
и внутренний диаметр 13 см. Средняя температура скипидара в трубе 80°С,
а его температура на входе в трубу 100°С. Если температура поверхности
трубы поддерживается постоянной и равной 30°С, то какой тепловой поток
передается от скипидара и какова его температура на выходе из трубы?
4.41. Водород при атмосферном давлении и числе Рейнольдса 1,7-10* дви-
движется по гладкой трубе диаметром 1,5 см и длиной 1 м. Температура водо-
водорода на входе 20°С, а температура стенок трубы поддерживается равной
40°С. Рассчитать тепловой поток от стенок и определить температуру водо-
водорода на выходе из трубы.
4.42. Заводской паропровод имеет внутренний диаметр 6 см и длину
100 м. Падение давления на длине трубы 100 м составляет 6 кН/м2. Скорость
водяного пара 24 м/с. Средняя температура пара 140°С, температура трубы
70°С. Определить тепловой поток от пара.
4.43. Жидкий фреон-12 движется по гладкой трубе диаметром 1,3 см.
Скорость фреона 2,9 м/с, его среднемассовая температура — 10°С. Рассчитать
тепловой поток к фреону на единице длины трубы при условии, что темпе-
температура последней составляет +10°С.
4.44. Этиленгликоль на выходе из химико-технологической установки имеет
температуру 45°С и поступает в гладкую трубу диаметром 4 см со скоростью
15 м/с. Труба имеет постоянную температуру 20°С. Рассчитать, на какой дли-
длине трубы температура жидкости понизится до 35°С.
Глава &
ИНЖЕНЕРНЫЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА
КОНВЕКТИВНОГО ТЕПЛООБМЕНА
5.1. ВВЕДЕНИЕ
Как показано в гл. 4, величину коэффициента теплоотдачи
можно определить из теоретического рассмотрения процесса
конвективного теплообмена. Однако теоретические решения воз-
возможны лишь для систем достаточно простой геометрии. В инже-
инженерной практике коэффициенты теплоотдачи в реальных систе-
системах вычисляют по эмпирическим формулам, полученным путем
совместного использования теории размерностей и эксперимен-
экспериментальных данных.
5.2. БЕЗРАЗМЕРНЫЕ КОМПЛЕКСЫ, ИСПОЛЬЗУЕМЫЕ
ДЛЯ ОБОБЩЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
ПО КОНВЕКТИВНОМУ ТЕПЛООБМЕНУ
В общем случае выбор физических параметров, необходимых
для решения данной задачи по конвективному теплообмену, тре-
требует определенного предварительного рассмотрения физического
смысла процесса. Но после того, как такие параметры установ-
установлены, теория размерностей позволяет связать их в несколько
безразмерных комплексов, точная функциональная зависимость
между которыми может быть определена из эксперимента. Что-
Чтобы проиллюстрировать такой подход, найдем безразмерные
комплексы, определяющие число Нуссельта при вынужденном
течении в длинной гладкой трубе.
Зависимой переменной в рассматриваемом случае является
коэффициент конвективной теплоотдачи hc. Для несжимаемого
низкоскоростного течения независимыми переменными, опреде-
определяющими коэффициент теплоотдачи, являются скорость жидко-
жидкости У, линейный размер (т. е. диаметр трубы D) и такие физи-
физические свойства жидкости, как коэффициент теплопроводности
ky коэффициент динамической вязкости ji, удельная теплоем-
теплоемкость ср и плотность р.
Независимые размерные величины, используемые в теории
размерностей — масса М, длина L, время 8 и температура Т.
Переменные, их обозначения и формулы размерности приве-
приведены в табл. 5.1.
Итак, имеется семь физических величин и четыре основные
размерности. Можно ожидать, что для обобщения эксперимен-
экспериментальных данных потребуются три безразмерных комплекса. Для
224 Глава 5
Таблица 5.1
Переменные для конвективного теплообмена в трубе
Переменная
Диаметр трубы
Коэффициент теплопроводности жидкости
Скорость жидкости
Плотность жидкости
Коэффициент динамической вязкости жидкости
Удельная теплоемкость при постоянном давле-
давлении
Коэффициент теплоотдачи
Обозначение
D
k
V
Р
ср
Формула
размерности
[Ц
[ML/&T]
[L/8]
[M/L3]
[М/Щ
[L4WT]
[м/езг]
( ' /
нахождения этих комплексов запишем их в виде произведения
всех переменных с неизвестными показателями степени и обо-
обозначим через я:
. n = DakbVcpd»ecffi. E.1)
Подставим сюда формулы размерности из табл. 5.1:
я=[?] [-p^rj [T] IttJ LttJ LwJ Ыг\ • E-2)
Чтобы величина я была безразмерной, сумма показателей сте-
степени каждой основной размерности должна равняться нулю.
Проведя соответствующее суммирование, получаем следующую
систему уравнений:
b + d + e + g = 0 для М,
a + b + c-3d — e_+2f = 0 для L,
— 3b-c-e — 2f-3g = 0 для 9, /
— ft —/ —ff = 0 для Т.
Так как имеется семь неизвестных и всего четыре уравнения,
то три показателя степени можно выбрать произвольно для
каждого безразмерного комплекса. Единственное ограничение
при этом состоит в том, что каждый из произвольно выбранных
показателей степени не будет зависеть от других показателей.
Это требование выполняется, если определитель, образованный
коэффициентами оставшихся членов, не равен нулю.
Так как коэффициент конвективной теплоотдачи является
зависимой переменной, которую мы хотим в конечном итоге
определить, примем показатель степени g в первом безразмер-
безразмерном комплексе щ равным единице. Для упрощения математи-
математических выкладок произвольно примем с = d = 0. Это означает,
что. в первом безразмерном комплексе скорость и плотность' бу-
будут отсутствовать.
Формулы для расчета конвективного теплообмена 225
Решая систему уравнений E.3), получаем а = 1, 6 = —1 и
e = f — Q. При этом первый безразмерный комплекс будет иметь
вид
и это не что иное, как описанное в гл. 4 число Нуссельта Nii?>.
Чтобы избежать появления зависимой переменной hc во вто-
втором безразмерном комплексе, примем g = 0. Пусть также
а = 1 и / = 0. Решая систему уравнений, получаем второй
комплекс
^ E.5)
представляющий собой число Рейнольдса Re/), в котором в ка-
качестве линейного размера взят диаметр трубы.
Пусть в третьем безразмерном комплексе будет присутство-
присутствовать удельная теплоемкость, отсутствовавшая в двух предыду-
предыдущих комплексах, причем примем /= 1. Пусть в Яз не входят
коэффициент теплоотдачи и диаметр трубы, т. е. а = g = 0.
Тогда третий безразмерный комплекс будет иметь вид
Щ=^-> E.6)
а это не что иное, как описанное в гл. 4 число Прандтля Рг.
Итак, коэффициент теплоотдачи в щ может быть функциональ-
функционально связан с безразмерными комплексами яг и яз зависимостью
вида
f Pr). E.7)
Хотя теория размерностей не позволяет установить функцио-
функциональную зависимость, она дает возможность уменьшить число
переменных с семи до трех и обеспечивает основу для проведе-
проведения экспериментов с целью нахождения связи между тремя
комплексами в уравнении E.7).
Корреляция экспериментальных данных
Из уравнения E.7) следует, что безразмерный коэффициент
теплоотдачи, или число Нуссельта, зависит от чисел Рейнольд-
Рейнольдса и Прандтля. Удобной и сравнительно простой зависимостью
для обобщения экспериментальных данных является следую-
следующее уравнение:
Nu^=CRewPrrt, E.8)
где С, m и п — константы, которые необходимо определить эк-
экспериментально.
Для получения значений этих констант удобно отложить эк-
экспериментальные результаты для данной жидкости на графиках.
8 Зак. 487
226 Глава б
Сначала устанавливается зависимость между числами Нус-
сельта и Рейнольдса, т. е. значение показателя степени т. Это
легко сделать при помощи логарифмических координат, когда
данные получены для одной жидкости и температура относи-
относительно неизменна, т. е. когда отсутствует влияние числа Прандт-
ля. Определив показатель т, можно отложить данные для не-
нескольких жидкостей на графике зависимости lg(Nu?>/Rew) от
ю4
103
ж
<
V
Ца
г"
а?1 о о
?, од
10»
Рис. 6.1. Экспериментальные данные по конвективному теплообмену при те-
течении в трубе.
lgPr и найти значение показателя степени п. Затем при из-
известном п можно отложить данные для многих жидкостей на
графике зависимости lg(Nuzj/Prn) от lg Re и уточнить значение
показателя т, а также определить значение константы С. При-
Пример такого обобщения результатов приведен на рис. 5.1 для
турбулентного вынужденного течения в гладких трубах. Полу-
Получаемые таким образом соотношения обычно описывают экспе-
экспериментальные данные с точностью ±25%.
5.3. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
ПРИ ТЕЧЕНИИ В ТРУБАХ И КАНАЛАХ
В практических задачах обычно требуется определять изме-
изменение температуры при течении жидкости в канале с заданной
скоростью при заданных температурах жидкости на входе и
стенке канала. Для течения в трубе длиной L и при температуре
Формулы для расчета конвективного теплообмена 227
стенки Ts тепловой поток к жидкости можно записать в виде
Чс==срРУср-
E.9)
4 ' Фь* — ¦
где Ть2 и Тьх являются средними по сечению температурами,
или температурами смешения, соответственно на выходе и вхо-
входе. Если использовать коэффициент теплоотдачи, то тепловой
поток на элементарной длине dx (рис. 5.2) будет связан с из-
изменением среднемассовой температуры, а также с разностью
я
Направлениеи^
течения
Рис. 5.2. Схема теплового баланса при течении в трубе.
температур стенки Ts(x) и среднемассовой температуры жидко-
жидкости Ть(х) на этой длине, следующей зависимостью:
dqc = thcp dT = hc (nD) dx {Ts - Tb). E.10)
Тогда средний коэффициент теплоотдачи при течении жидкости
в канале можно представить в виде
где А — общая площадь поверхности контакта жидкости с теп-
лопередающей поверхностью. Вполне очевидно, что как TSf так
и Ть может изменяться по длине трубы, и поэтому для практи-
практического использования уравнения E.11) необходимо разрабо-
разработать удобный процесс осреднения температуры. В данной главе
основное внимание уделяется вопросу определения значения
коэффициента теплоотдачи, а вопрос об осреднении температуры
в различных практических приложениях будет рассмотрен в
гл. 7.
Турбулентное течение в трубах и каналах
Экспериментальные данные при турбулентном течении в
длинной трубе жидкостей, имеющих число Прандтля от 0,5 до
100, обобщаются зависимостью [1]
NuD = 0,023 Rei)8Pr0'33. - - E.12)
В этой формуле все физические свойства жидкости следует
брать при так называемой определяющей температуре ff, яв-
являющейся среднеарифметической величиной для температуры
228 Глава 5
стенки и среднемассовой температуры жидкости,
lf = - -, (оЛо)
где Ть, ср является в свою очередь среднеарифметической вели-
величиной для температуры жидкости на входе и выходе:
гр * &> вх "Г *»> вых
* Ы ср — о
Причиной использования средней температуры является изме-
изменение физических свойств жидкости в результате теплообмена.
Другой метод учета такого изменения физических свойств пред-
предложен в работе [2], где рекомендована следующая формула для
оценки числа Нуссельта при вынужденном течении жидкости
в длинном канале:
Шо = 0,027 ReW-33(^Y-14, E.14)
где |i& — коэффициент динамической вязкости при среднемассо-
среднемассовой температуре Га, ср:
Ть, ср = (Ть, вх + ТЪу вых)/2,
[is — коэффициент динамической вязкости при температуре Ts.
Все другие физические свойства жидкости следует определить
ПрИ ТЪ, ср.
Уравнения E.12) и E.14) применимы к полностью разви-
развитому турбулентному течению в трубах. Их можно также при-
применять к полностью развитым течениям в каналах с другой
формой поперечного сечения, но тогда необходимо использовать
эквивалентный диаметр (гл. 4).
Пример 6.1. Поток воздуха с давлением 2 атм и температурой 490 К дви-
движется в трубе с внутренним диаметром 2 см со скоростью 10 м/с. Рассчи-
тать коэффициент теплоотдачи, когда температура трубы равна 510 К, и оп-
определить тепловой поток, передаваемый воздуху на единице длины трубы,
если плотность теплового потока поддерживается постоянной.
Решение. Из табл. П.VI. 1 теплофизические свойства воздуха при среднем
значении температуры между температурой стенки и среднемассовой темпе-
температурой жидкости E00 К) следующие: \i = 29,37- 10~б Н-с/м2, k =,
= 0,0386 Вт/м-град, ср = 1038 Дж/кгтрад, р = 0,689-2 = 1,378 кг/м3, Рг =¦
= 0,71. Число Рейнольдса Rep составляет
о» 1,378-10.0,02
ReD ~ 29,37-Ю-6
Следовательно, течение турбулентное и коэффициент теплоотдачи определяет-
определяется по формуле E.12):
4
= @,0386/0,02) 0,023 (9384H'8 @,71 H-33 = 59,7 Вт/(м2 - град).
Если плотность теплового потока поддерживается постоянной, разность тем-
температур Ts — Ть будет неизменной, но среди ем ассовая температура будет воз-
Формулы для расчета конвективного теплообмена 229
растать. Если пренебречь изменением коэффициента теплоотдачи, связанным
с изменениями физических свойств жидкости, то тепловой поток, передавае-
передаваемый жидкости на одном метре длины трубы, составит
q' = hc7iD (Ts — Tb) = 59,7 . n • 0,02 • 20 = 75,0 Вт/м.
Однако во многих практических задачах трубы и каналы
недостаточно длинные, чтобы достигалось полностью развитое
течение. В работе [3] рекомендована формула, которая содер-
содержит поправочный коэффициент, учитывающий наличие вход-
входного, или начального, участка
Мщ>я - 0,036 Re^Pr0'33 (%¦)"" <5' 15>
(справедливая при 10 < L/DH < 400),
где l — длина трубы, Dh — эквивалентный диаметр канала. Фи-
Физические свойства в приведенных выше уравнениях следует
брать при определяющей температуре, рассчитываемой в фор-
формуле E.13).
Ламинарное течение в трубах и каналах
Коэффициент теплоотдачи при ламинарном течении в трубах
и каналах при (ReDPrD/L) > 10 может быть определен по
эмпирической формуле, предложенной в работе [2]:
, E.16)
в которой все физические свойства берутся при среднемассо-
вой температуре Г&, а для учета влияния изменения температуры
на вязкость вводится эмпи- ::
рический поправочный коэф-
коэффициент (lXb/[lsH>U. В ЖИД-
ЖИДКОСТЯХ с увеличением темпе-
температуры вязкость понижает-
понижается, а в газах повышается.
При нагреве жидкость, на-
находящаяся ОКОЛО стенки, рис g3 профили скорости при лами*
Имеет меньшую ВЯЗКОСТЬ, Нарном течении жидкости с нагревом,»
чем жидкость в центре. Сле- охлаждением.
ДОВатеЛЬНО СКОРОСТЬ НаГре- / — нагревание жидкости или охлаждение газа;
диосиыюпи, слири^ю n«xFv 2—изотермическое течение (параболический
ТОЙ ЖИДКОСТИ будет ООЛЬШе, профиль); 3—нагревание газа или охлаждение
чем ненагретой, при тех же жидкости.
средних скорости и темпе-
температуре. При охлаждении жидкости искажение параболического
профиля скорости происходит в противоположном направлении
(рис. 5.3). В газах наблюдается картина, обратная той, которая
наблюдается в жидкости, что связано с увеличением их вязко-
вязкости при повышении' температуры; возможно дополнительное
230 Глава 5
искажение профиля скорости, связанное с изменением плот-
плотности.
Пример 5.2. Вода движется в капиллярной трубке с внутренним диамет-
диаметром 2,54-10~3 м и длиной 0,3 м со скоростью 0,2 м/с; температура воды на
входе 333 К. Считая, что температура трубки поддерживается постоянной и
равной 353 К, рассчитать температуру воды на выходе.
Решение. Теплофизические свойства воды при ЗЗЗК, согласно табл. FLV. 1,
следующие р = 983 кг/м3, ср = 4181 Дж/(кг-град), ц = 4,72-10 Н-с/м2,
k = 0,658 Вт/(м-град), Рг = 3,0.
Чтобы удостовериться, что течение ламинарное, определим число Рей-
нольдса Re/? при температуре жидкости на входе:
Re -?VD ,983-0,2-0,00254
KeD~ ц - 4,72 • Ю-4 ~1U0Bl
Следовательно, течение ламинарное, и поскольку
то для расчета коэффициента теплоотдачи можно воспользоваться формулой
E.16). Так как средняя среднемассовая температура жидкости неизвестна,
то вначале возьмем все физические свойства при среднемассовой температуре
жидкости на входе Ть, и затем определим среднемассовую температуру на
выходе и вновь повторим все операции для получения более точного значе-
значения. Обозначая условия на входе и выходе соответственно индексами 1 и 2,
запишем уравнение баланса энергии
q = hcnDL (js- Tbl + Tb2 ) = mcp (Tb2 - Tbl). (a)
Из табл. П.V.I имеем при температуре стенки 353 К м« — 3,52-10~4 Н-с/м2.
Среднее число Нуссельта рассчитываем по формуле E.16) f
и, следовательно,
кШп 0,658.5,74
Массовый расход равен
р igl V^ m ¦«(°-°40254J (°'2) = 0.996 • Ю-' кг/с.
Подставляя рассчитанные значения hc и m в уравнение (а) с учетом того,
что Tbl = 333 К и Т8 = 353 К, имеем
1487 • я. 0,00254 • 0,3. ГзбЗ - 333 + Ть* \ « 0,996. Ю-3.4181 (ТЬ2 - 333)#
(б)
Решая это уравнение, получаем
Повторный расчет проводим, беря физические свойства жидкости при но*
вой средней среднемассовой температуре:
fb_ 345^333^339 К.
Формулы для расчета конвективного теплообмена 231
Из табл. П.У. 1 при этой температуре имеем: р = 980 кг/м3, ср =
= 4185 Дж/(кгтрад), р, = 4,36-10~4 Н-с/м2, 6 = 0,662 Вт/(мтрад), Рг =
= 2,78.
Рассчитывая вновь Re^ при новых значениях физических свойств, полу-
получаем
Re __ рКД_ 980-0,2-2,54-10-'
KeD~~~ir 4,36-10-4
Теперь при этом значении ReD рассчитываем коэффициент теплоотдачи.
При второй итерации получаем ReDPr (D/L = 25,9, NuD = 5,61 и hc =
= 1490 Вт/(м2 • град). Подставляя новое значение Нс в уравнение (б), полу-
получаем Тьг = 345 К. Последующие итерации в данном примере не приведут к
существенному изменению результатов, что связано с малой разностью сред-
немассовой температуры жидкости и температуры стенки. Когда эта раз-
разность температур велика, может понадобиться вторая итерация.
Формулу E.16) нельзя использовать для длинных труб, так
как она может привести к нулевому значению коэффициента
теплоотдачи. Для обычных жидкостей и газов при L/D <
< 0,0048 ReD в трубах и при L/DH < 0,0021 ReDff в каналах с
прямоугольным поперечным сечением в условиях постоянной
температуры стенки или постоянного теплового потока более
подходит следующая формула, рекомендованная в работе [5]:
\п\ р тггхгр Хъч>- E.17)
| 1 [2654/Pr0'167 (RePr ZtyL0'5)] J V '
4L | 1 - [2,654/Pr0'167 (ReD//Pr Zty
Для очень длинных каналов значение числа Нуссельта следует
брать из табл. 4.1.
Осреднение вычисляемого по формулам E.16) или E.17)
числа Нуссельта по длине трубы производится следующим
образом:
l
где индекс х характеризует расстояние от входа. Такое число
Нуссельта часто называют среднелогарифмическим, так как его
можно непосредственно использовать в формулах, применяемых
при проектировании теплообменников, которые рассматриваются
* в гл. 7.
Жидкие металлы
Приведенные выше формулы для расчета коэффициентов
теплоотдачи при ламинарном и турбулентном течении приме-
применимы к жидкостям, у которых число Прандтля больше 0,5.
Только жидкие металлы имеют числа Прандтля, существенно
меньшие 0,5. Это обусловлено их высокими коэффициентами
теплопроводности. Жидкие металлы отводят значительно боль-
большие тепловые потоки, чем другие жидкости или газы, и поэтому
232 Глава 5
их широко применяют в ядерных реакторах, в активной зоне
которых развиваются чрезвычайно высокие тепловые потоки.
Работать с жидкими металлами трудно, поскольку многие из
них являются коррозионно-активными, а при их непосредствен-
непосредственном контакте с водой или воздухом происходят интенсивные хи-
химические реакции. Несмотря на эти недостатки, жидкие металлы
применяются в теплонапряженных системах. Эмпирические фор-
формулы для определения числа Нуссельта для жидких металлов
собраны в работах [6, 7]. Установлено, что при теплоотдаче к
жидким металлам число Нуссельта зависит от произведения
чисел Рейнольдса и Прандтля, называемого числом Пекле Ре.
При полностью развитом турбулентном течении в трубах и по-
постоянной плотности теплового потока экспериментальные дан-
данные обобщаются соотношением [6]
Шв = 0,625 Ре0'4, E.19)
если все физические свойства определяются при средней средне-
массовой температуре жидкости. Соотношение E.19) справед-
справедливо при 100 < Ре < 10 000 и отношениях длины к диаметру,
больших 60. Для случая постоянной температуры стенок в ра-
работе [8] рекомендуется соотношение
NUD = 5,0 + 0,025 Ре0'8, E.20)
справедливое при Ре > 100, отношениях длины к диаметру,
больших 60, если все физические свойства определяются при
средней среднемассовой температуре жидкости. В проблеме
теплопередачи к жидким металлам существует еще много нере-
нерешенных вопросов. Более подробная информация об этом содер-
содержится в работах [6, 7].
Пример 5.3. В ядерном реакторе по трубе внутренним диаметром 5 см
движется жидкий металл с расходом 3 кг/с. Температура жидкого металла
473 К, а температура стенок обогревающей его трубы на 30 К выше. Опре-
Определить длину трубы, требуемую для повышения среднемассовой температуры
жидкого металла на 1 К, используя следующие физические свойства: р =
= 7,7-103 кг/м2, v = 8,0-10"8 м2/с, ср = 130 Дж/(кг-град), k = 12 Вт/
/(м-град), Рг = 0,011.
Решение. Для увеличения температуры на 1 К требуется тепловой поток
q = тсрЬТ = 3,0 • 130 • 1 = 390 Вт.
Число Рейнольдса равно
ре ™° - 3'0'05 -121 10»
Коэффициент конвективной теплоотдачи рассчитываем по формуле E.19):
hc = 40'625 (Re^Prf4-
0,625 A,24 • 105 • 0,011H'4 * 2692 Вт/(м2 • град).
Формулы бля расчета конвективного теплообмена 233
Площадь поверхности составляет
А = nDL :
390
= 0,00483 м2.
hc{Ts-Tb) 2692-30
Длина трубы, требуемая для увеличения температуры на 1 К, равна
Л 0,00483
л; • 0,05
: 0,0307 м.
Вынужденная конвекция при переходном режиме течения
Механизм теплообмена при переходном режиме течения
жидкости B000 < Re^ < 6000) существенно изменяется от си-
системы к системе. В этой области течение может быть неустойчи-
неустойчивым, возможны пульсации перепада давления и характеристик
од
0,07
0,05
* 0,04
сГ—^ 0,03
^ 0,02
^Г^ 0,01
, ^ 0,007
*? 0,005
"Т^ 0,004
И? * 0,003
^—' 0,002
0,001
ч,
Ч
s,
—
—
Ч
ч
>
40(
hi
у
)
л
>H =
50-
00
-/-
^:
II!
ч. "Ч„
4 4,
\
s
ч
/
/
J
¦ * -
102
103
104
ю5
106
Рис. 5.4. Число Нуссельта в зависимости от числа Рейнольдса в переходном
режиме течения.
теплообмена. Существует большая неопределенность в основных
данных по теплоотдаче и потерям на трение, и конструкторам
рекомендуется так проектировать оборудование, чтобы его ра-
работа никоим образом не проходила в переходном режиме. Для
оценки числа Нуссельта в переходном режиме можно использо-
использовать кривые рис. 5.4, однако действительные характеристики мо-
могут существенно отличаться от полученных с помощью этих
>кривых [5].
5.4. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН В УСЛОВИЯХ
ВЫНУЖДЕННОЙ КОНВЕКЦИИ ПРИ ВНЕШНЕМ ОБТЕКАНИИ
Уметь рассчитывать конвективный тепловой поток нужно не
только при течениях в каналах, но и при обтекании плоских
пластин, цилиндров, сфер и пучков труб, что важно для многие
инженерных приложений.
234 Глава 5
Плоская пластина
Теплообмен при обтекании плоской пластины рассматри-
рассматривался в гл. 4, где было показано, что для данной жидкости
среднее число Нуссельта прежде всего зависит от числа Рей-
нольдса, вычисленного по скорости невозмущенного течения и
длине пластины в направлении потока. В некоторых случаях
бывает необходимо знать местный коэффициент теплоотдачи, и
тогда характерным размером, используемым в числах Нуссельта
и Рейнольдса, будет расстояние от передней кромки. В инже-
инженерных расчетах локальное число Нуссельта при ламинарном
обтекании плоской пластины (Re*<5«105) определяют по фор-
формуле
Nu* = -^f? = 0,332 RefPr1/3, E.21)
тогда как среднее число Нуссельта определяют по формуле
Шь = -*?¦ = 0,664 Re[/2Pr1/3. E.22)
Средний коэффициент теплоотдачи в формуле E.22) получают
интегрированием
Lt
hc=]:\hcxdx. E.23)
о
При турбулентном обтекании (Rei>5*105) на части пла-
пластины, непосредственно следующей за передней кромкой, тече-
течение ламинарное, и лишь далее оно становится турбулентным.
Локальное значение числа Нуссельта при любом х за местом
смены режима течения, т. е. при х > хс, определяется по фор-
формуле
Nu*=^f =0,0288
в то время как среднее его значение, если переход происходит
при Re* = 5-105, равно
Ь^ о,О36 Рг1/3 (Re?8 - 23 200). E.25)
Одиночный цилиндр и сфера
Принципиальное отличие отбекания цилиндра или сферы от
обтекания плоской пластины состоит в том, что при этом может
происходить не только переход от ламинарного течения к тур-
турбулентному в пограничном слое, но и отрыв самого погранич-
пограничного слоя от поверхности раздела жидкости и тела в кормовой
его части. Причиной отрыва является возрастание давления §
Формулы для расчета конвективного теплообмена 235
направлении течения, что и приводит к образованию области
отрывного течения за телом в случае, когда скорость невозму-
невозмущенного потока достаточно велика. Образование такой области
при обтекании цилиндра схематически показано на рис. 5.5, а
¦~+ Граница
*j пограничного
слоя
течение
Рис. 5.5. Схема развития отрывного течения.
ее снимок приведен на рис. 5.6. Вполне очевидно, что в области,
где пограничный слой оторван от поверхности, будут совер-
совершенно другие значения числа Нуссельта, чем в области, где он
примыкает к поверхности. Это подтверждают данные, получен-
полученные при числах Рейнольдса в невозмущенном потоке 70 000 <
< Re < 220 000 (рис. 5.7). На рис. 5.7 приведены значения
Рис. 5.6. Область отрыва за одиночным цилиндром.
локального числа Nue = hc, eD/k в зависимости от углового рас-
расстояния 8 от критической точки. Можно видеть, что сначала,
как и при ламинарном обтекании пластины, локальное число
Нуссельта понижается по мере удаления от передней образую-
образующей цилиндра, но затем оно резко возрастает при переходе те-
течения от ламинарного к турбулентному и снова понижается в
области турбулентного пограничного слоя. Однако в задней
части цилиндра в области отрывного течения число Нуссельта
236 Глава б
800
вновь возрастает. При двух самых низких значениях числа Рей-
Рейнольдса G0 000 и 100 000) отрыв происходит до начала перехода
от ламинарного режима течения в пограничном слое к турбу-
турбулентному. При этом, как
следует из работы [9],
минимальное значение
коэффициента теплоотда-
теплоотдачи достигается примерно
в точке отрыва.
В обычной инженер-
инженерной практике не обяза-
обязательно рассчитывать ло-
локальные значения числа
Нуссельта, а достаточно
знать среднее значение
коэффициента теплоотда-
теплоотдачи. Среднее число Нус-
Нуссельта, hcD/k можно пред-
представить в зависимости от
числа Рейнольдса pFocZVix
невозмущенного потока и
числа Прандтля- cp\x/k;
причем эта эмпирическая
зависимость аналогична
ранее полученной для те-
течения в каналах, с той
лишь разницей, что ха-
характерным размером в
числах Рейнольдса и Нус-
100
Рис. 5.7. Число Нуссельта в зависимости
от угловой координаты при поперечном об-
обтекании цилиндра.
0 40 80 120 160
Угловое расстояние от критической точки в
сельта для цилиндра и
сферы является наруж-
наружный диаметр тела D. Для
газов и обычных жидко-
жидкостей средний коэффи-
коэффициент теплоотдачи при обтекании одиночного цилиндра можно
рассчитать по формуле
E.26)
где Foo — скорость набегающего потока, а значения коэффи-
коэффициента С и показателя степени п для различных интервалов
значений ReD приведены в табл. 5.2.
. Все физические свойства в формуле E.26) следует опреде-
определять при среднеарифметическом значении температур поверхно-
поверхности и жидкости. Значения Сип при обтекании цилиндрических
тел с некруглыми поперечными сечениями приводятся в табл. 5.3.
Формулы для расчета конвективного теплообмена 237
Таблица 5.2
Значения констант в формуле E.26)
0,4-4
4-40
40-4 000
4 000-40 000
40 000-400 000
С
0,989
0,911
0,683
0,193.
0,0266
п
0,330 -
0,385 .
0,466 -
0,618
0,805
В работе [13] получена следующая простая аппроксима-
ционная формула:
Шо = 2 + @,4 Reb/2 + 0,06 Re2/3) Pr0'4 (\ioo/\xsf2\ E.27)
которая справедлива при 3,5 < ReD < 8-Ю4 и 0,7 < Рг < 380.
Все физические свойства, за исключением \xs, в этой формуле
следует определять при температуре набегающего потока.
Таблица 5.3
Значения констант в формуле E.26) для расчета теплообмена
при поперечном обтекании цилиндрических тел
с некруглым поперечным сечением [12]
Форма поперечного сечения Re/>/ С л
1
5 • 10М05
5 • ltf-lO5
0,246
0,102
Or588
0,675
5 • l
1,95
104
0,160
0,0385
0,638
0,782
5 • 10M05
0,153
0,638,
4 • 10M,5 • 104
0,228'
0,731
При обтекании сфер жидким металлом коэффициент тепло-
теплоотдачи можно рассчитывать по формуле из работы [14]:
Шо = 2,0 + 0,386 (ReD PrH'5, E.28)
справедливой в интервале значений числа Рейнольдса 3-104<
^ 1>5-105.
238 Глава б
Пример 5.4. Определить тепловой поток к атмосферному воздуху, имею-
имеющему температуру 358 К и скорость 5 м/с. Воздух движется по трубе диа-
диаметром 0,5 м и длиной 10 м; температура поверхности трубы 373 К-
Решение. Прежде всего путем интерполяции найдем физические свойства
воздуха из табл. П.VI. 1 при определяющей температуре Tf — (Ts + Гоо)/2 =
= 365,5 К: р = 0,936 кг/м3, fx = 21,3-10 Н-с/м2, 6 = 0,0302 Вт/(мтрад),
Рг = 0,71.
Рассчитаем теперь число Рейнольдса:
-т/ п 0,936 • 5 • 0,5
Rer
21,3-Ю-6
05.
Из табл. 5.2 получаем
С = 0,0266 и п = 0,805.
Средний коэффициент теплоотдачи рассчитываем по формуле E.26):
h0 = M^2_00266 A>1 . 1(NH,805 0>710,33 = 164 Вт/(м2 . град)>
и тогда тепловой поток составит
q = hc = (nDL) (Ts — 7\J = 16,4яО,5 • 10 • 15 = 3864 Вт.
Пучки труб
Знание характеристик теплообмена при обтекании пучков
(или пакетов) труб важно при конструировании теплообменни-
теплообменников, которое более подробно рассматривается в гл. 7. Формула
иг.— Л". —ьи— Л' —у
Рис. 5.8. Обозначения к таблице 5.4.
а—коридорное расположение труб; б—шахматное расположение труб.
для расчета теплообмена при обтекании пучков труб предло-
предложена в работе [15]; она имеет такой же вид, как и формула
E.26), которая приводилась при рассмотрении обтекания оди-
одиночной трубы. Однако значения коэффициента С и показателя
степени п зависят от расстояния между соседними трубами и
расстояния между рядами труб в направлении течения, а также
от способа расположения труб, коридорного или шахматного
(рис. 5.8). В табл. 5.4 приведены значения Сип, которые сле-
следует использовать в формуле E.26) при различном расположе-
Формулы для расчета конвективного теплообмена 239
Таблица 5.4
Значения констант в формуле для расчета теплообмена
при обтекании пучков труб с десятью и более рядами [15]1)
1,25
1,5
2,0
3,0
0,6
0,9
1,0
1,125
1,25
1,5
2,0
3,0
1
С
0,386
0,407
0,464
0,322
—
—
—
0,575
0,501
0,448
0,344
,25
n
0,592
0,586
0,570
0,601
—
—
—
—
0,556
0,568
0,572
0,592
I
С
sn
,5
п
2,0
С
п
Коридорное расположение
0,305
0,278
0,332
0,396
0,608
0,620
0,602
0,584
0,111
0,112
0,254
0,415
0,704
0,702
0,632
0,581
Шахматное расположение
—
—
0,552
—
0,561
0,511
0,462
0,395
—
—
0,558
—
0,554
0,562
0,568
0,580
—
0,495
0,531
0,576
0,502
0,535
0,488
—
0,571
0,565
0,556
0,568
0,556
0,562
3,0
С
0,0703
0,0753
0,220
0,317
0,236
0,445
0,575
0,579
0,542
0,498
0,467
п
0,752
0,744
0,648
0,608
0,636
0,581
0,560
0,562
0,568
0,570
0,574
1) В первой вертикальной колонке приведены значения S (D
нии труб в пучках и наличии 10 или более рядов в направлении
течения.
Для меньшего числа рядов в табл. 5.5 приводится доля, ко-
которую составляет hc при N рядах труб от соответствующего
значения при 10 рядах. Число Рейнольдса ReMaKC для потока
через пучок труб определяется по диаметру трубы и максималь-
максимальной скорости течения (т. е. скорости потока через минимальную
площадь проходного сечения).
Таблица 5.5
Отношение hc при N ряд$х труб в пучке
к соответствующему значению при 10 рядах [16]
N
Отношение при шахмат-
шахматном расположении труб
Отношение при коридор-
коридорном расположении труб
•
0,68
0,64
2
0,75
0,80
3
0,83
0,87
4
0,89
0,90
5
0,92
0,92
6
0,95
0,94
7
0,97
0,96
8
0,98
0,98
9
0,99
0,99
ю
1,0
1,0
Для определения коэффициентов теплоотдачи при обтекании
пучков труб жидкими металлами в работе [17] рекомендована
формула
NuD = 4,03 + 0,228 (ReMaKCPrH'67, E.29)
справедливая в интервале значений 20 000 < ReMaKc < 80 000,
240 Глава 5
Падение давления (Н/м2) в потоке газа через пучок труб
можно рассчитать по соотношению
\0'14
) , ¦ E.30)
где бмакс — массовая скорость при минимальной площади про-
проходного сечения, кг/(с-м2); р — плотность при условиях в не-
невозмущенном потоке, кг/м3; N — число поперечных рядов.
Эмпирический коэффициент трения f определяется по ре-
рекомендованным в работе [18] формулам
при шахматном расположении труб и
.044 + [Eд°У+,,,з^} Re?? F-32)
Г - 2-J0.
при коридорном расположении труб.
Для расчета коэффициента теплоотдачи при турбулентном
обтекании пучка труб при наличии 10 и более рядов труб как
при коридорном, так и шахматном их расположении и ReMaKc >
>'6ООО рекомендуется формула
^)°>6?3 E.33)
которая, согласно полученным в работе [5] результатам, с до-
достаточной точностью описывает экспериментальные данные.
•JM. СВОБОДНАЯ КОНВЕКЦИЯ
В условиях свободной, или естественной, конвекции теплопе-
ренос к телу или от него приводит к образованию градиентов
температуры и плотности в покоящейся жидкости, если ее тем-
температура не равна температуре тела. В отличие от вынужден-
вынужденной конвекции, при которой скорость жидкости определяется
внешними силами, при свободной конвекции движение жидко-
жидкости возникает под действием подъемных (архимедовых) сил,
которые связаны с изменениями температуры и плотности
в самой жидкости и которые невозможно точно определить.
Как и при вынужденной конвекции, движение жидкости под
действием подъемных сил может быть либо ламинарным,
либо турбулентным. Однако в условиях свободной конвекции
пограничный слой имеет нулевую скорость не только на границе
раздела твердое тело — жидкость, но и на внешней своей гра-
границе, удаленной от тела. Движение жидкости может быть на-
Формулы для расчета конвективного теплообмена 241
правлено вверх, как в случае нагрева воздуха от плоской пла-
пластины, или вниз, как в случае, когда холодный цилиндр поме-
помещен в емкость с неподвижной теплой водой.
Прежде чем использовать теорию размерностей для установ-
установления определяющих критериев при свободной конвекции, рас-
рассмотрим природу возникновения движущей силы. Если роо —
плотность холодной невозмущенной жидкости, а р— плотность
более нагретой жидкости, то подъемная сила, действующая на
единицу объема в поле земного тяготения, равна (р«> — p)g, где
g— ускорение свободного падения.
Разность плотностей можно выразить в зависимости от тер-
термического коэффициента объемного расширения жидкости р, ко-
который по определению равен
ft_ 1 / dV X _ 1 V — Vqq _ Pop — р /ХОЛ\
При подстановке полученного из E.34) выражения для р«> — р
в формулу для подъемной силы она принимает вид pg$(Ts—Гоо),
где Т? — температура тела. Отсюда следует, что подъемная сила
зависит от переменных р, g и (Ts — Too). Помимо этих трех пе-
переменных и характерного размера системы L при использова-
использовании теории размерностей необходимо также учесть соответствую-
соответствующие физические свойства жидкости р, [г, ср и k. При нормаль-
нормальных условиях поле тяготения является неизменным, и поэтому
в теории размерностей вместо р и g можно использовать одну
переменную р#.
Записывая все переменные, каждую с неизвестным показа-
показателем степени, и применяя теорию размерностей аналогично
тому, как это делалось в гл. 1 (см. также задачу 5.2), можно
показать, что для корреляции экспериментальных данных по
-теплообмену в условиях естественной конвекции достаточно
иметь следующие три безразмерных критерия:
¦?-*.
Первый из них — это число Нуссельта, второй — число Прандтля
и третий известен как число Грасгофа. Gr/, — это отношение
подъемной силы к силе внутреннего трения. Подъемная сила
при свободной конвекции заменяет действие импульса при вы-
вынужденном течении. Следует также отметить, что так как
$gp(Ts — Too)—подъемная сила, действующая на единицу объ-
ема, то \$gp{Ts — Too)L] представляет собой подъемную силу,
242 Глава 5
приложенную к единице площади. Следовательно, отношение
подъемной силы к силе внутреннего трения на единицу пло-
площади равно $gp(Ts — Too)L/(\iV/L). Но скорость V является
103
102
80
60
40
20
< Ламинарный >
режим течения
10 Ъ
10s
Переходный
*— режим ^
—течения—
Z_
ж
У_
Nu==0,0210(GrLPrffs
Турбулентный режим течения-»
107
109
1011
10 и
Рис. 5.9. Экспериментальные данные по теплообмену для вертикальных пла-
пластин и цилиндров в условиях свободной конвекции [40].
О-—вертикальный цилиндр; D —вертикальная пластина; Л —пластина высотой 23 см;
V — пластина высотой 7,6 см.
зависимой переменной, пропорциональной \i/pL, и поэтому отно-
отношение подъемной силы к силе внутреннего трения принимает
вид
GrA = jjg • (э.дЬ)
На основе многочисленных экспериментальных данных было
установлено, что среднее число Нуссельта можно связать с чис-
числами Грасгофа и Прандтля соотношением
щ = С (Grf Prfy\ E.36)
Индекс f здесь указывает на то, что все физические свойства
должны браться при Tf = (Ts + Too)/2. Произведение Gr Pr из-
известно как число Релея Ra, через него обычно выражают ре-
результаты в инженерной практике. При этом число Грасгофа
часто приходится находить с помощью итерации при данном
числе Прандтля, что связано с невозможностью точного опре-
определения разности температур Ts — Too в числе Грасгофа.
При свободной конвекции наблюдаются как ламинарный, так
и турбулентный режимы течения. Смена режима течения проис-
Формулы для расчета конвективного теплообмена 243
ходит в интервале значений 107 < Gr Рг < 109 и зависит от гео-
геометрии системы. На рис. 5.9 обобщены экспериментальные дан-
данные по теплоотдаче к вертикальной плоской пластине и от нее
в условиях свободной конвекции при высоте пластины L. Дан-
Данные представлены в координатах Nui. f и (GrLPr)ft
Вертикальная пластина и цилиндр
В табл. 5.6 приведены значения констант для расчета сред-
среднего числа Нуссельта по уравнению E.36) для изотермических
вертикальных поверхностей высотой L и изотермических верти-
вертикальных цилиндров с D/L > 35/Gr?25. Так как для горизонталь-
горизонтальных пластин можно использовать уравнение того же типа, то в
таблице приведены соответствующие константы и для этого слу-
случая. Уравнения для расчета теплоотдачи от изотермической
Таблица 5.6
Значения констант в формуле E.36)
Форма тела
Вертикальные плас-
пластины и вертикаль-
вертикальные цилиндры
Горизонтальные ци-
цилиндры
Верхняя поверхность
нагретых пластин
или нижняя поверх-
поверхность охлажденных
пластин
Верхняя поверхность
нагретых пластин
* или нижняя поверх-
поверхность охлажденных
пластин
Нижняя поверхность
нагретых пластин
или верхняя поверх-
поверхность охлажденных
пластин
GrfPrf
104-109
109-1013
109-1013
0—10~5
10~5—104
104-109
109-1012
2- 104—8-Ю6
8 • 106—10й
105—1011
[19]
С
Использовать
рис. 5.9
0,59
0,021
0,10
0,4
Использовать
рис. 5.10
0,53
0,13
0,54
0,15
0,58
п
Использовать
рис. 5.9
1/4
2/5
1/3
0
Использовать
рис. 5.10
1/4
1/3
1/4
1/3
1/5
Работа
[33]
[33]
[34]
[35, 36]
[33]
[33]
[33]
[33]
[37, 38]
[37, 38]
[37, 39]
244 Глава 5
вертикальной пластины при ламинарной свободной конвекции
можно применить также к поверхностям с постоянной плот-
плотностью теплового потока, если брать температуру поверхности
в середине пластины [5].
Если нагретая пластина отклонена от вертикали на неболь-
небольшой угол 9, то массовая сила, действующая вдоль оси ху стано-
становится равной g$(Tw Too)cos 0 и среднее число Нуссельта для
верхней поверхности можно рассчитать по формуле E.36), если
использовать эффективное число Грасгофа йгЭфф в виде
Or — fo?P2 cos 6 G^-7^I* „ п
иГэфф — jjs - @.6 ()
Горизонтальный цилиндр, сфера и прямоугольные блоки
Среднее число Нуссельта при теплоотдаче к горизонтальным
цилиндрам и от них в условиях свободной конвекции также
можно рассчитать по формуле E.36), но при соответствующих
значениях констант, приведенных в табл. 5.6, или по уравнению
из работы [19]:
0,60 + 0,387 {[l + @|56;prf)U]16/9} J E.38)
в интервале значений 10~5<Ra< 1012. На рис. 5.10 обобщены ч
экспериментальные данные для различных жидкостей при
Рг > 0,5.
Теплоотдачу от горизонтальных цилиндров к жидким метал-
металлам можно рассчитать по соотношению [20]
Шо. f = 0,53(GrD, fPr2H'25. E.39)
Для расчета теплоотдачи к сферам диаметром D и от них в
условиях свободной конвекции при Gtd, f > 1 в работе [21] по-
получено соотношение
ШВ9 f = 2,0 + 0,45 (Gr* f Prf)°.25. E.40)
Если GrD,f->0, то Nud,f-^2, что соответствует случаю чистой
теплопроводности через слой неподвижной жидкости, окружаю-
окружающей сферу.
Коэффициент теплоотдачи от вертикального прямоугольного
блока с горизонтальным размером Lh и вертикальным размером
Lv можно рассчитать, как это предложено в работе [22], по
формуле E.36), в которой при 104 < GrL Рг < 109 С == 0,6, п =
= 0,25 и l/L=*l/Lh+l/Lv.
Пример 5.5. Определить величину тепловых потерь от горизонтальной па-
паровой трубы наружным диаметром 0,3 м и длиной 10 м. Температура наруж-
наружной поверхности трубы 510 К, а температура воздуха в помещении, в кото*
ром находится труба, 300 К.
Формулы для расчета конвективного теплообмена 245
I
2,0
1,8
1,6
li4
1,2
1,0
0,8
0,6
0,4
0,2
0
-0,2
-0,4
_5 _4 _з _2 -1 0 1 2 3 4 5 6 7 8 9
i
Рис. 5.10. Экспериментальные данные по теплообмену для горизонтальных
цилиндров в условиях свободной конвекции [33].
+
i
— о
•
•
•о-
а
t
- в
¦
о
#
Аппр
-А
4
5
6
7
8
,§
11
12
13
14
15
16
17
18
юксимаци
|__A924 r.)j
ч Раиса ^
А
6
X Нуссельт
A929 г.)
J\
<
II
/
•\
•/
\
Аппроксимация
A
324 г.
)
Источник
Кеннеди
Лэнгмюр
Эйртон, Килгур
Райе
Петавал
Дзвис
Эберли
Аккерман
Кох
УЪмслер
СГаундерс
Поряд-
Порядковый
номер
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Текучая
среда
Воздух
>
Водород
СО2
Анилин
ССЦ
Глицерин
Толуол
Воздух
Вода
Воздух
Азот 0,11
Диаметр, см
0,01-0,07
0,004-0,05
0,003-0,035
4,3-11,3
0,11
0,11
0,11
0,015
0,015
0,015
0,015
7,6-16
5
1,4-10
2,05-8,9
250 1000
Кривая, рекомендованная
Кривая, рекомендованная
Давление,
МН/м2
0,1-2,2
0,1
0,1
0,011-0,1
0,097-16,8
0,097-11,4
0,1-3,5
0,1
ОД
0,1
0,1
0,1
0,1
0,1
0,1
[ Девисом
Кингом
Темпера-
Температура жид-
жидкости, °С
20
27
10-14
12-103
16
16
16
14
13
19
15,5
20
30-50
20
15-30
Темпера-
Температура ци-
цилиндра, °С
185
1027
300
82-150
916
916
916
19-64
18-63
24-69
20-65
140-180
34-92
30-190
55-240
Nuf
GrfPrf
Координаты рекомендуемой кривой:
0,49 -0,55 -0,661 -0,841 1,08 1,51 2,11 3,16 5,37 9,33 16,2 28,8 51,3 93,3
ю-
о-1 о
10 102 103 104 105 10б 107 108 Ю9
246 Глава 3
Решение. Произведение GroPr/ вычислим, используя теплофизические
свойства из табл. П. VI. 1 при
Число Релея получаем путем интерполяции также по данным табл. 6.1:
= @,373 • 108) E10 — 300) 0,33 • 0,71 = 1,5 • 108.
Из табл. 5.6 находим С = 0,53 ип = 0,25. Затем вычисляем
Шо = 0,53 (GrDPrfH*25 = 0,53 A,6 • 108H'25 = 58,7,
kNun 0,0327-58,7
hc - —^- ^ 6,4 Вт/(м* • град).
Следовательно, тепловые потери составляют
qc = hcA {Ts - Г,») = 6,4 • jt • 0,3 .10 • 210 = 12,7 кВт.
Свободная конвекция в замкнутом пространстве
Свободная конвекция в замкнутом пространстве представ-
представляет интерес при разработке таких теплоизоляционных систем,
как окна с двойным остеклением. Свободная конвекция внутри
замкнутых объемов осложняется большим разнообразием тече-
течений, которые могут при этом образовываться. Самое простое из
них соответствует случаю жидкости, заключенной между двумя
большими горизонтальными пластинами, удаленными одна от
другой на расстояние Ъ. Когда температура нижней пластины
меньше, чем верхней пластины, процесс передачи тепла осу-
осуществляется только теплопроводностью через слой жидкости,
если пренебречь концевыми эффектами. При этом, когда темпе-
температурный напор принимается равным разности температур меж-
между пластинами, число Нуссельта равно единице:
Ш6 = М=1Д E.41)
Для воздуха, заключенного между горизонтальными пласти-
пластинами, у которых температура нижней пластины выше, чем верх-
верхней, в работе [23] рекомендуются приведенные ниже формулы
для расчета среднего числа Нуссельта. В качестве характерного
размера в этом числе используется расстояние между пласти-
пластинами 6, физические свойства берутся при среднеарифметическом
значении температур двух пластин, а в качестве температурного
напора берется разность температур пластин. Эти формулы
имеют вид
Nu* = 0,195GriDf. E.42)
Формулы для расчета конвективного теплообмена 247
При 104<GrM<3,7-105 и
Nub = 0,068 Griff E.43)
при 3,7-105<Grft,f < 107.
Для жидкости, заключенной между двумя параллельными
горизонтальными пластинами, когда температура нижней пла-
пластины выше, в работе [24] путем обобщения экспериментальных
данных для воды, силиконовых масел и ртути получено соотно-
соотношение
Wub = 0,069 (Gr* PrI/3 Pr?'074, E.44)
справедливое при 1,5-105 < Ra < 109.
В работе [23] обобщены результаты нескольких исследова-
исследователей для воздушных промежутков между двумя вертикальными
пластинами, удаленными друг от друга на расстояние b и имею-
имеющими по вертикали высоту L. Рекомендованы следующие фор-
формулы для числа Нуссельта в зависимости от числа Gr*,, f:
Nu6==M = i,o E.45)
при Gr&, f < 2000,
(L/6I/a
при 2*- 104<GrM <2- 105 и
^b=0'°(Llb){®f E'47)
при 2- 105<GrM <107.
В числах Нуссельта и Грасгофа в формулах E.45) — E.47) в
качестве характерного размера используется расстояние между
пластинами &, физические свойства берутся при среднеарифме-
среднеарифметическом значении температур поверхностей двух пластин, а в
качестве температурного напора используется разность этих
температур. Требуется также выполнение условия
Lib > 3. E.48)
Можно ожидать, что при L/b < 3 коэффициенты теплоотдачи
для вертикальных поверхностей в условиях свободной конвек-
конвекции в большом объеме жидкости будут, по крайней мере при-
приближенно, одинаковыми для обеих этих поверхностей.
В работе [25] изучался теплообмен в замкнутых вертикаль-
вертикальных слоях жидкости при 3 < Рг < 30 000 и были рекомендо*
ваны следующие формулы:
248 Глава 5
при Ra& < 103 и
при 103 < Ra& < 107.
5.6. СМЕШАННАЯ СВОБОДНАЯ И ВЫНУЖДЕННАЯ КОНВЕКЦИЯ
При малых значениях числа Рейнольдса, особенно в случае
больших разностей температур или большого эквивалентного
диаметра канала, роль свободной конвекции может быть су-
существенной. Дополнительный вклад свободной конвекции ока-
оказывается особенно важным при ламинарном течении в каналах.
Совместное влияние свободной и вынужденной конвекции ока-
оказывается весьма сложным, и мы ограничим его рассмотрение
только случаем наложения свободной конвекции на вынужден-
вынужденную в горизонтальных и вертикальных круглых трубах.
Смешанная свободная и вынужденная конвекция
в горизонтальных круглых трубах
В горизонтальных трубах свободная конвекция приводит к
возникновению вторичных течений в любом поперечном сечении,
интенсифицирующих конвективный процесс. Поэтому коэффи-
коэффициент теплоотдачи и число Нуссельта при смешанной конвекции
выше, чем при чисто вынужденной конвекции. Наиболее интен-
интенсивный теплообмен происходит в нижней части трубы. Когда
влияние свободной конвекции в ламинарном потоке становится
существенным, около стенок возникают большие градиенты тем-
температуры и становится существенным изменение температуры
в вертикальном направлении. Измерения распределений скоро-
скоростей в горизонтальном и вертикальном направлениях также ука-
указывают на существенное отличие от пуазейлевского течения.
В работе [26] проведена классификация режимов свободной,
смешанной и вынужденной конвекции для горизонтальных труб
при условии постоянства температуры стенки по длине трубы
(рис. 5.11). Граница между режимами вынужденной и смешан-
смешанной конвекции при этом определяется из условия, что вклад
в тепловой поток свободной конвекции составляет ~10%. По-
Поэтому с помощью рис. 5.11 можно определить, является ли су-
существенным вклад свободной конвекции.
В работе [27] приведены результаты экспериментального ис-
исследования теплоотдачи к воде при ламинарном ее течении в го-
горизонтальной трубе с постоянной температурой стенки в уело
виях совместного влияния свободной и вынужденной конвекции.
Экспериментальные результаты описываются соотношением
= 1J5 [Gz + 0,012 (Gz Gr}? L/3]1/3 (^-)~°М, E.60)
Формулы для расчета конвективного теплообмена 249
где
Gz = nD Re Pr/4L.
E.51)
Все физические свойства в Nuz>, Gz, GvD и \xm берутся при
среднемассовой температуре жидкости. Соотношение согла-
согласуется с экспериментальными данными для воды с точностью
±8% и с большинством опубликованных экспериментальных
юб
ю5
ю4
Re
102
ю
Вынужденная конвекция
Турбулентное течение I
_Nu=0,116 [l +(? )Vi] (Re2"-.25)Pr(gH'H_
Хаузен
""Переход ламинарного"
течения в турбулентное
о Турбулентное течение
Вынужденная конвекция*>г
~Ламинарное течение *^г
Сидер и Тэйт
Смешанная
конвекция-
Д36
Nu=4569Rea27Pr°'21Gr°'07(f)
I Мотойл VL/
TР
Смешанная конвекция
Ламинарное течение
/JUf\ 014
Nu=l,75 \j~) [Gz+0,0083(GrPr)°'75J1/3
Оливер
Свободная
конвекция
а Холден
v Керн"
о Метэйс.
а Петухов
х Шервуд
10
102
104 105 106
GtVi(D/L)
ю8
Рис. 5.11. Режимы свободной, вынужденной и смешанной конвекции при тече-
течении в горизонтальных трубах [10~2 < Pr (d/L) < 1] [26].
данных для воды, этилового спирта и вязких масел с точностью
±50%.
В работе [28] предложено следующее соотношение для ра-
расчета теплообмена в условиях смешанной конвекции при тече-
течении в горизонтальной круглой трубе с постоянной плотностью
теплового потока вдоль оси трубы q"\
Wuh = {D,36J + [0,145
где
E.52)
E*53)
a KP = kwa'/kDH — параметр теплопроводности в радиальном
направлении. Индекс h указывает на условие постоянства плот-
плотности теплового потока вдоль оси трубы и наличие конечной
теплопроводности в радиальном направлении. Все физические
250 Глава $
свойства, используемые в NU&, Gr*, Pr и KPt берутся при опре-
определяющей температуре.
Длина теплового начального участка под влиянием свобод-
свободной конвекции существенно уменьшается. Поэтому в большин-
большинстве случаев наложения свободной конвекции течение можно
10б
ю5
ю4
ю3
ю2
10
ынужденная конвекция
Турбулентное течение
Переход ламинарного
_ течения в турбулентное
Вынужденная конвекция
-—- Ламинарное '
течение
jgf
&
А Свободная конвекция
Турбулентное течение
Свободная конвекция Ламинарное течение\
.' ! Ппптияппплпмшпа V
Сопутствующее течение
Противоположное
1 течение 1
105 10б
GrPrB>/Z,)
Рис. 5.12. Режимы свободной, вынужденной и смешанной конвекции при тече-
течении в вертикальных трубах [10~2 < Рг (d/L) < 1] [26].
/ — Браун, постоянный тепловой поток; 2—Эккерт, постоянная температура стенки;
3—Кемени, постоянный тепловой поток; 4—Холмен, переход ламинарного течения в тур*
булентное, постоянный тепловой поток; 5—Мартинелли, смешанная конвекция, постоян*
ная температура стенки; б—Метэйс, постоянная температура стенки; 7—Петухов, постоян-
постоянная температура стенки; 8 — Шеде, постоянный тепловой поток; 9— Вотцингер, постоян-
постоянная температура стенки; 10—Браун, постоянный тепловой поток; 11 — Метэйс, постоянная
температура стенки; 12— Вотцингер, постоянная температура стенки; Хенрэти, постоян-
постоянный тепловой поток, постоянная температура стенки.
считать полностью развитым, и формулы E.50) или E.52)
позволяют определить число Нуссельта для любой длины трубы.
При смешанной конвекции получаются также более высокие
значения коэффициента трения. С использованием опытных
данных для этиленгликоля в работе [28] получена следующая
расчетная формула:
/из
E.54)
Формулы для расчета конвективного теплообмена 251
где /из = 16/Re —изотермический коэффициент трения. Как /,
так и Ra в этой формуле рассчитываются при физических свой-
свойствах жидкости, которые берутся при определяющей темпера-
температуре.
Влияние наложения свободной конвекции
при течении в вертикальной круглой трубе
В отличие от горизонтальных труб влияние наложения сво-
свободной конвекции в вертикальных трубах зависит от направле-
направления течения и от того, нагревается жидкость или охлаждается.
При нагревании жидкости и ее течении вверх или при ее охлаж-
охлаждении и течении вниз свободная конвекция усиливает действие
вынужденной конвекции, и результирующий коэффициент тепло-
теплоотдачи оказывается выше, чем в случае чисто вынужденной кон-
конвекции. Однако при охлаждении жидкости и течении вверх или
при нагревании жидкости и течении вниз свободная конвекция
противодействует вынужденной конвекции, что приводит к более
низким значениям коэффициента теплоотдачи. Классификация
режимов свободной, вынужденной и смешанной конвекции для
вертикальных труб из работы [26] представлена на рис. 5.12.
Она позволяет судить о вкладе свободной конвекции. Приведен-
Приведенные на рис. 5.12 результаты справедливы как при условии по-
постоянства плотности теплового потока, так и при условии по-
постоянства температуры стенок.
5.7. ТЕПЛООБМЕН В ВЫСОКОСКОРОСТНОМ ПОТОКЕ
Конвективный теплообмен в высокоскоростном потоке важен
для таких систем, как самолеты и ракеты, скорости которых
приближаются к скорости звука или превышают ее. В совершен-
совершенном газе скорость звука можно рассчитать по формуле
E.55)
где у = Cp/Cv — отношение удельных теплоемкостей (с~ 1,4 для
воздуха), Ru — универсальная газовая постоянная, Т — абсолют-
абсолютная температура, Ш1 — молекулярный вес газа. Когда скорость
газа, обтекающего нагретую или охлажденную поверхность,
близка к скорости звука или превышает ее, поле течения не-
невозможно характеризовать только числом Рейнольдса и нужно
учитывать также отношение скорости газа к скорости звука
(т. е. число Маха, М = Voo/поо). При достижении газом скоро-
скорости, составляющей около половины скорости звука, повышается
роль вязкости диссипации в пограничном слое. При этом темпе-
температура поверхности, которую обтекает газ, может фактически
превышать температуру набегающего потока. На рис. 5.13
252 Глава 5
схематически показаны профили скорости и температуры при об-
обтекании адиабатической поверхности (т. е. идеально теплоизоли-
теплоизолированной стенки). Высокая температура на поверхности яв-
является совместным результатом нагрева в результате вязкости
диссипации и подъема температуры жидкости из-за преобра-
преобразования ее кинетической энергии
во внутреннюю энергию при тор-
торможении в пограничном слое.
Действительная форма профиля
температур определяется соотно-
соотношением между скоростью, с ко-
которой работа сил трения увели-
увеличивает внутреннюю энергию жид-
^%^^^^ кости, и скоростью, с которой теп-
тепло передается новозмущенному
потоку.
Хотя процессы, протекающие
в высокоскоростном погранич-
пограничном слое, не являются адиабати-
адиабатическими, их обычно таковыми
считают. Преобразование кинети-
кинетической энергии газа при его адиабатическом торможении до
нулевой скорости описывается зависимостью
V2
i^i^ + l^L, E.56)
где to — энтальпия торможения, a /«>— энтальпия газа в невоз-
невозмущенном потоке. В совершенном газе уравнение E.56) при-
принимает вид
Рис. 5ЛЗ. Профили скорости и
температуры при обтекании тепло-
теплоизолированной пластины высоко-
высокоскоростным потоком.
7—профиль температуры; 2— профиль
скорости; 3—поверхность пластины.
или в зависимости от числа Маха
) j" * 1 2
E.57)
где 70 — температура торможения и Г*, — температура невоз-
невозмущенного потока.
Процесс торможения в реальном пограничном слое не может
быть обратимым, так как процесс, связанный с работой сил тре-
трения, термодинамически необратим. Для учета необратимости в
пограничном слое введем коэффициент восстановления г, опре-
определяемый как
r = ^zT~, E.58)
где Tas — адиабатическая температура поверхности.
Формулы для расчета конвективного теплообмена 253
Согласно экспериментальным данным, при ламинарном тече-
течении в пограничном слое
г = Рг{'2, E.59)
а при турбулентном течении
г = Рг1/3. E.60)
Когда поверхность не теплоизолирована, конвективный теп-
тепловой поток от высокоскоростного газа к этой поверхности
определяется соотношением
-?l = — ъ дТ
А ~. ду
На рис. 5 14 показано, как влияет теплоотдача к поверхности
и от нее на профиль температуры. Видно, что в высокоскорост-
высокоскоростном потоке тепло может передаваться поверхности даже в том
случае, когда ее температу-
температура выше температуры невоз-
невозмущенного потока. Такое яв-
явление оказывается следстви-
следствием действия сил трения, и
его часто называют аэроди-
аэродинамическим нагревом. Теп-
Тепловой поток при этом мож-
можно рассчитывать m форму-
формулам для низкоскоростного
потока, если определять
средний коэффициент кон-
конвективной теплоотдачи с по-
помощью соотношения
E.61)
Рис. 5.14. Профили температуры в высо-
высокоскоростном пограничном слое при на-
нагревании и охлаждении.
7 — профиль температуры при тепловом потоке,
направленном от поверхности; 2—профиль тем-
температуры при тепловом потоке, направленном
к поверхности.
в соответствии с которым при равенстве температуры поверх-
поверхности Ts адиабатической температуре поверхности тепловой по-
поток равен нулю.
Так как в высокоскоростном потоке градиенты температуры
в пограничном слое велики, то изменения физических свойств
жидкости также будут значительными. Тем не менее можно ис-
использовать соотношения для теплообмена, полученные при по-
постоянных физических свойствах, если только всё физические
свойства взять при характерной температуре Г*, определяемой
по рекомендованной в работе [29] формуле
= ТС0 + 0,5 (Ts - TJ + 0,22 (Tas - TJ.
E.62)
Локальные значения коэффициента теплоотдачи, определяе-
определяемого выражением
QlA
h -
Т Т
254 Глава 5
могут быть рассчитаны по следующим формулам:
St*, = (-^- )• = 0,332 (Re*,)-1'2 (РгГ
)-1'2 (РгГт E.63)
для ламинарного пограничного слоя (Re* < 105),
0,0288 (Re;)-1/5 (Рг*)~2/3 E.64)
для турбулентного пограничного слоя при 105 < Re* < 107.
для турбулентного пограничного слоя при 107 < Re* < 109. Вид
последней формулы обусловлен тем, что экспериментальные дан-
данные по локальным коэффициентам трения в высокоскоростном
газовом потоке при 107 < Re* < 109 обобщаются зависимостью
4,92
(m
\2,584 '
E.66)
Если нужно определить средние значения коэффициента тепло-
теплоотдачи, следует проинтегрировать приведенные выше выраже-
выражения, полученные для низкоскоростного потока, от х = 0 до x=L.
0,001 0,01 0,1
ю
ю2
ю3
ю4
ю5 ю6 ю7
Число Рейнольдса
Рис. 5.15. Диаграмма режимов течения.
В большинстве практических случаев приходится проводить чис-
численное интегрирование, поскольку, как следует из формул
E.59) и E.60), характерная температура Г* не одинакова в
ламинарной и турбулентной частях пограничного слоя.
В определенных ситуациях (например, на очень больших
высотах) плотность газа может оказаться столь малой, что рас-
расстояние между его молекулами станет соизмеримым с толщиной
Формулы для расчета конвективного теплообмена 255
пограничного слоя. В таких случаях газ нельзя рассматри-
рассматривать как сплошную среду и необходимо выделять характерные
режимы течения. Эти режимы характеризуются отношением
средней длины свободного пробега молекул к характерному раз-
размеру системы, называемым числом Кнудсена Кп. Режим тече-
течения сплошной среды соответствует малым значениям числа
Кнудсена, в то время как при более высоких значениях этого
числа столкновения молекул происходят главным образом на
поверхности и в основном потоке. Поскольку в последнем слу-
случае перенос энергии осуществляется путем свободного переме-
перемещения молекул между поверхностью и основным потоком, такой
режим течения называется свободномолекулярным. Между сво-
бодномолекулярным режимом и течением сплошной среды
имеется переходный режим, который называют режимом те-
течения со скольжением, поскольку при этом принимается, что
на поверхности раздела жидкости и твердого тела имеет место
проскальзывание, или скачок, температуры и скорости. На
рис. 5.15 приведена диаграмма режимов течения. Сведения о
методах расчета теплообмена и трения для этих особых режи-
режимов течения можно найти в работах [30—32].
Литература
1. Colburn A. P., A Method of Correlating Forced Convection Heat Trans-
Transfer Data and a Comparison with Fluid Friction, Trans. AlChEy 29, p. 174
A933).
2. Sieder E. N., Tate С. Е., Heat Transfer and Pressure Drop of Liquids
in Tubes, Ind. Eng. Chem., 28, p. 1,429 A936).
3. Nusselt W., Der Warmeaustausch zwischen Wand und Wasser im Rohr,
Forsch. Geb. Ingenieurwes., 2, p. 309 A931).
4. Hausen H., Darstellung des Warmeuberganges in Rohren durch verall-
gemeinerte Potenzbeziehungen, VDI Z., No 4, p. 9 A943).
5. Kreith F., Principles of Heat Transfer, 3rd ed., Harper and Row, N. YM
1973.
6. Lubarsky В., Kaufman S. J., Review of Experimental Investigations
of Liquid-Metal Heat Transfer, NACA Tech. Note 3336, 1955.
7. Lyon R. D., ed., Liquid Metals Handbook, 3rd ed. Atomic Energy Com-
Commission and U. S. Navy Department, Washington, D. C, 1952.
8. Seban R. A., Shimazaki Т. Т., Heat Transfer to a Fluid Flowing Turbu-
lently in a Smooth Pipe with Walls at Constant Temperature, Trans. ASME,
73, p. 803 A951).
9. Giedt W. H., Investigation of Variation of Point Unit-Heat-Transfer
Coefficient Around a Cylinder Normal to an Air Stream, Trans. ASME, 71,
p. 375'A949).
10. Hilpert R., Warmeabgabe von geheizen Drahten und Rohren, Forsch.
Geb. Ingenieurwes., 4, p. 220 A933).
11. Knudsen J. D., Katz D. L., Fluid Dynamics and Heat Transfer,
McGraw, N. Y., 1958.
12. Jakob M., Heat Transfer, vol. 1, Wiley, N. Y., 1949. [Имеется перевод
издания 1957 г.: Якоб М., Вопросы теплопередачи. — М.: ИЛ, I960.]
13. Whitaker S.. Forced Convection Heat-Transfer Correlations for Flow
in Pipes, Past Flat Plates, Single Cylinders, Single Spheres, and Flow in
Packed Beds and Tube Bundles, AIChE, 18, p. 361 A972).
256 Глава б
14. Witte L. С, An Experimental Study of Forced-Convection Heat Trans-
Transfer from a Sphere to Liquid Sodium, /. Heat Transfer, 90, p. 9 A968). [Име-
[Имеется перевод: Витте, Бейкер мл., Хейворт, Теплоотдача от сферы к жидкому
недогретому натрию при вынужденной конвекции. — Труды Амер об-ва инж-
мех., сер. С, Теплопередача, 1968, № 4, с. 26.]
15. Grimison E. D., Correlation and Utilizatioh of New Data on Flow
Resistance and Heat Transfer for Cross Flow of Gases over Tube Banks,
Trans. ASME, 59, p. 583 A937).
16. Kays W. M., Lo R. K., Basic Heat Transfer and Flow Friction Data
for Gas Flow Normal to Banks of Staggered Tubes: Use of a Transient Tech-
Technique, Stanford Univ. Tech. Rpt. 15, Navy Contract NC-ONR25i Т. О., 6, 1952.
17. Kalish S., Dwyer О. Е., Heat Transfer to NaK Flowing Through Un-
baffled Rod Bundles, Int. J. Heat Mass Transfer, 10, p. 1533 A967).
18. Jacob M., Heat Transfer and Flow Resistance in Cross Flow of Gases
over Tube Banks; Trans. ASME, 60, p 384 A938).
19. Churchill S. W., Chu H. H. S. Correlating Equations for Laminar and
Turbulent Free Convection from a Horizontal Cylinder, Int. J. Heat Mass
Transfer, 18, p. 1049 A975).
20. Hyman S. C, Bonilla C. F., Ehrhch S VV. Heat Transfer to Liquid
Metals from Horizontal Cylinders, AIChE Symp. Heat Transfer,, Atlantic
City, N. J., 1953, p. 21.
21. Yuge Т., Experiments on Heat Transfer from Spheres Including Com-
Combined Natural and Forced Convection, /. Heat Transfer, ser C, 82, p. 214
A960).
22. King W. J., The Basic Laws and Data of Heat Transmission, Mech.
Eng.y 54, p. 347 A932).
23. Jakob M., Free Heal Convection Through Eaclo^ed Plane Gas Layers,
Trans. ASME, 68, p. 189 A946).
24. Globe S., Dropkin D., Natural Convection Heat Transfer in Liquids
Confined by Two Horizontal Plates and Heated from Below, /. Heat Trans-
Transfer, 81, p. 24 A959).
25. Emery A., Chu N. C, Heat Transfer Across Vertical Layers, J. Heat
Transfer, 87, Ser. C, № 1, p. 110 A965) [Имеете* перевод: Эмери, Чу, Теп-
Теплопередача через вертикальный слой жидкости.- - • Труды Амер. об ва инж.-
мех., сер. С, Теплопередача, 1965, № 1, «. ?32.]
26. Metais В., Eckert E. R. G., Forced, Mixed and Free Convection Re-
Regions, /. Heat Transfer, 86, Ser. C, p. 295 A964). [Имеется перевод: Метэйс,
Эккерт, Режимы вынужденной, смешанной и свободной конвекции. — Труды
амер. об-ва инж.-мех., сер С. Теплопередача, 1964, № 2, с. 196.]
27. Brown A. R., Thomas M. A., Combined Free and Forced Convection
Heat Transfer for Laminar Flow in Horizontal Tubes, /. Mech. Eng. ScL, 7,
p. 440 A965).
28. Morcos S. M., Bergles A. E, Experimental Investigation of Combined
Forced and Free Laminar Convection in Horizontal Tubes, /. Heat Transfer,
97, ser. C> p. 212 A975). [Имеется перевод: Моркос, Берглес, Эксперименталь-
Экспериментальное исследование смешанной, вынужденной и свободной конвекции в гори-
горизонтальных трубах —Труды Амер. об-ва инж.-мех., сер. С, Теплопередача,
1975, № 2, с. 54.]
' 29. Eckert E. R., Engineering Relations for Heat Transfer and Friction in
High-Velocity Laminar and Turbulent Boundary Layer Flow over Surface with
Constant Pressure and Temperature, Trans. ASME, 78, p. 1273 A956).
30. Van Driest E. R., Turbulent Boundary Layer in Compressible Fluids,
/. Aeronautical ScL 18, No 3, p. 145 A951).
31. Oppenheim A. K-, Generalized Theory of Convective Heat Transfer
in a Free-Molecule Flow, / Aero, ScL, 20, p. 49 A953).
32. Hayes W. D., Probstein R. F., Hypersonic Flow Theory, Academic
Press, N. Y. 1959. [Имеется перевод: Хейз, Пробстин, Теория гиперзвуковых
течений. — М.: ИЛ, 1962.]
Формулы для расчета конвективного теплообмена 257
33. McAdams, Heat Transmission, 3rd ed., McGraw, 1954. [Имеется пере-
перевод: Мак-Адаме, Теплопередача. Металлургиздат, 1961.]
34. Eckert E. R. G. Jackson T. W., Analysis of Turbulent Free Convection
Boundary Layer on a Flat Plate, NACA Rpt. 1015, 1951.
35. Warner C. Y., Arpaci V. S., An Experimental Investigation of Turbu-
Turbulent Natural Convection in Air at Low Pressure Along a Vertical Heated Flat
Plate, Int. J. Heat Mass Transfer, 11, p. 397 A968).
36. Bayley F. J., An Analysis of Turbulent Free Convection Heat Transfer,
Proc. Inst. Mech. Eng., 69, No. 20, p. 361 A955).
37. Fujii Т., Imura H., Natural Convection Heat Transfer from a Plate
with Arbitrary Inclination, Int. J. Heat Mass Transfer, 15, p. 755 A972).
38. Lloyd J. R., Moran W. R., Natural Convection Adjacent to a Horizon-
Horizontal Surface of Various Planforms, ASME Paper 74 — WA/HT — 66.
39. Singh N., Birkebak R. C, Drake R. M. Laminar Free Convection Heat
Transfer from Downward-Facing Horizontal Surfaces of Finite Dimensions.
Prog. Heat Mass Transfer, 2, p. 87 A969).
40. Gebhart B,, Heat Transfer, 2nd ed., McGraw, N. Y., 1970.
§ Зак. 48?
ЗАДАЧИ
Задачи в данной главе сгруппированы по тематике разделов, как ука-
указано в таблице
Номера задач
5.1-5,4
5.5-5.15
5.16—5,38
6.39-5,58
6,59—5,61
5,62-5,69
Раздел
5,2
5,3
5.4
5,5
5,6
5.7
Тема
Безразмерные комплексы
Конвективный теплообмен при тече*
нйи в трубах и каналах
Конвективный теплообмен при внеш-
внешнем обтеканий
Теплообмен в условийх естествен-
естественной конвекции
Теплообмен в условиях смешанной
естественной и вынужденной кон-
т} О ТУ Т Т t^IJf
ЬсКЦИИ.
Теплообмен в высокоскоростных по-
потоках
5.1. Известно, что конвективный тепловой поток для коротких каналов
Определяют следующие параметры: V — скорость жидкости, D — диаметр ка-
канала, L — длина канала, р — плотность жидкости, ср — удельная теплоемкость
жддкостй, k — коэффициент ее теплопроводности. Показать с помощью тео-
теории размерностей, что безразмерным комплексом, включающим все эти пара»
Метры, является число Гретца Gz, которое определяется выражением
5.2. Известно, что тепловой поток в условиях свободной конвекции Опре-
Определяют следующие параметры: р — плотность жидкости, \i — коэффицент ди-
динамической вязкости жидкости, р — термический коэффициент объемного рас-
расширения жидкости, g — ускорение свободного падения, D — характерный
размер тела, (Ts — Tw) — разность температур тела и окружающей его жидко-
жидкости. С помощью теории размерностей показать, что безразмерным комплек-
комплексом, включающим все эти параметры, является число Грасгофа, которое оп*
ределяется выражением
5.3. Известно, что сопротивление тела, обтекаемого жидкостью, опреде*
Ляют следующие Параметры: р — Плотность жидкости, р, — коэффициент дй*
намической вязкости жидкости, У* — скорость набегающего потока, D — ха-
характерный размер тела, т* — касательное напряжение на поверхности тела.
Формулы для расчета конвективного теплообмену 269
С использованием я-теоремы показать, что безразмерное сопротивление
х^рУ^ можно выразить в зависимостей от числа Рейнольдса Re = pVooD/ц.
5.4. Предположим, что экспериментальным путем получен коэффициент
теплоотдачи Яс при вынужденной конвекции воздуха около сферы диаметром
D. Если эти результаты нанести на график зависимости Niu> от Re^ Pr, то
они ложатся на этот график, как показано на рисунке
10'
101
101 102 103
К задаче 5.4.
Написать безразмерное критериальное уравнение для среднего числа Нус-
сельта, обобщающего эти экспериментальные данные, и определить границы
применимости полученного уравнения.
15.5. При течении с расходом 4 кг/с в трубе с внутренним диаметром 5 см
вода нагревается от 30 до 50°С. Определить требуемую длину трубы, если
температура ее стенки поддерживается равной 80°С.
5.6. Сухой воздух при давлении 1400 кН/м2 движется в трубе с внутрен-
внутренним диаметром 7,5 см и длиной 5 м; расход воздуха 0,5 кг/с. Средняя тем-
температура стенки канала поддерживается равной 200°С, а средняя темпера-
температура воздуха на входе в канал 260°С. Рассчитать коэффициент теплоотдачи
и определить, насколько понизится температура воздуха в канале.
5.7. Средняя температура воды на входе в трубу с внутренним диамет-
диаметром 2,5 см соствляет 10°С, а ее расход 0,5 кг/с. Электрический нагреватель-
нагревательный элемент обеспечивает постоянную плотность теплового потока от стенки
трубы и ее среднюю температуру 50°С. Определить коэффициент теплоотдачи
и рассчитать, как изменится температура воды при длине трубы 5,6 м.
5.8. Вода со среднемассовой температурой 20° поступает в трубу вну-
внутренним диаметром 2,5 м и длиной 1,5 м. При расходе воды 1,0 кг/с опреде-
определить, какова температура воды на выходе из трубы, если температура ее сте-
стенок поддерживается постоянной и равной 50°С.
5.9. Атмосферный воздух с температурой 10°С поступает в прямоуголь-
прямоугольный канал сечением 7,5 X 15 см и длиной 6 м. Все четыре поверхности этого
канала благодаря солнечному облучению поддерживаются при температуре
70°С. Рассчитать, при каком расходе воздуха его температура на выходе из
канала будет на 20°С превышать его температуру на входе.
5.10. Вода со средней температурой 20°С и средней скоростью 0,1 м/с по-
поступает в трубу внутренним диаметром 3 мм. Труба имеет электрический обо-
обогрев, обеспечивающий постоянную плотность теплового потока стенки, состав-
составляющую 1,0 кВт/м2. Определить изменение температуры воды по радиусу
трубы.
5.11. Атмосферный воздух, имеющий температуру 120°С с расходом
0,22 м3/с, поступает в трубу внутренним диаметром 7 см. В предположении,
что температура стенки трубы поддерживается постоянной и равной 20°С,
определить длину трубы, необходимую для охлаждения воздуха до 80°С.
5.12. Измерения, проведенные в экспериментах с трубой эллипсоидаль-
эллипсоидального поперечного сечения, показали, что коэффициент конвективной тепло-
9*
260 Глава 5
отдачи к движущемуся в ней воздуху составил 35 Вт/(м2-град) при скорости
воздуха 15 м/с и эквивалентном диаметре трубы 0,4 м. Каким стал бы коэф-
коэффициент теплоотдачи, если бы эквивалентный диаметр трубы с аналогичным
поперечным сечением уменьшился до 0,2 м, а скорость воздуха возросла до
30 м/с?
5.13. Ртуть движется в трубе диаметром 3,4 см со скоростью 3 м/с и
температурой 80°С. Определить коэффициент теплоотдачи, если длина трубы
6 м.
5.14. Жидкий натрий движется в трубе диаметром 2 см; его массовый
расход на входе в трубу равен 0,2 кг/с. Обеспечивается постоянная плот-
плотность теплового потока от стенок трубы к натрию, причем разность между
температурами стенок и натрия составляет 10°. Температура натрия на входе
378 К, и по мере прохождения трубы он нагревается на 2,8°С. Определить
тепловой поток к натрию.
5.15. Канал длиной 4 м имеет треугольное поперечное сечение с длиной
стороны 3 см. Температура жидкого натрия на входе в канал 478 К, а его
массовый расход 3,6 кг/с. Стенки канала поддерживаются изотермическими
при температуре 525 К. Взять все физические свойства натрия при его вход-
входной температуре и определить: а) температуру натрия на выходе и б) теп-
тепловой поток к натрию.
5.16. Пусть распределение скоростей при обтекании водой плоской пла-
пластины определяется безразмерным выражением ti/V^ = (у/4л:) Re]/2, где х —•
расстояние, измеряемое вдоль пластины, а у — расстояние по нормали к ней.
Средняя температура воды 60°С (Ts = 80°С, Г«> = 40°С), а ее скорость при
обтекании одной стороны пластины, имеющей площадь 3X3 м, составляет
VTO = 5 м/с. Определить следующие данные: а) общее сопротивление пла-
пластины; б) формулу для расчета локальной толщины пограничного слоя 6(х);
в) толщину пограничного слоя на конце пластины (х = 3 м).
5.17. Пусть локальное число Нуссельта при обтекании пластины опреде-
определяется выражением Nu^ = 0,5Re^3Pr1/3. Определить вид зависимости сред-
среднего числа Нуссельта Ntu от Rei.
5.18. Ветер дует вдоль улицы, имеющей асфальтовое покрытие. Скорость
ветра 4 м/с, температура воздуха 22°С, температура асфальта 58°С, ширина
улицы 12 м. Определить тепловой поток от поверхности асфальта.
5.19. Плоская горизонтальная крыша имеет зимой температуру 10°С.
Крыша квадратная и имеет площадь 40 X 40 м. Определить конвективный
тепловой поток от крыши к воздуху с температурой — 10°С при скорости
ветра: а) 2 м/с; б) 6 м/с и в) 12 м/с.
5.20. Стальная пластина площадью 2 X 20 м выходит из прокатного стана
и движется по транспортеру со скоростью 4 м/с. Температура стали 835 К, а
температура окружающего воздуха 305 К. Определить конвективный тепло-
тепловой поток от верхней поверхности пластины.
5.21. Плоская пластина имеет длину 3 м и ширину б м. Температура пла-
пластины 160°С, а температура окружающего воздуха 40°С. Воздух движется
параллельно пластине вдоль ее длины. Рассчитать коэффициент конвективной
теплоотдачи от пластины при скоростях воздуха: а) 0,1 м/с; б) 10 м/с;
в) 20 м/с.
5.22. Среднее число Нуссельта при вынужденном обтекании газом сферы
рассчитывается по формуле Nud = 0,37Re^'6, справедливой при 17 < Red <
< 70 000. Определить тепловой поток, который следует подвести к сфере диа-
диаметром 4 см, чтобы температура ее поверхности оставалась постоянной и рав-
равной 90°С при условии, что сфера находится в потоке а) воздуха и б) воды,
температура которых равна ЗОХ. Скорость потоке в обоих случаях состав-
составляет 1 м/с.
5.23. Сферическая капля воды диаметром 4 мм свободно падает в не-
неподвижном воздухе. Рассчитать средний коэффициент конвективной теплоот-
теплоотдачи в момент достижения каплей скорости 10 м/с. Принять температуру
Формулы для расчета конвективного теплообмена 261
капли равной 10°С, а температуру воздуха 30°С. Испарением от капли пре-
пренебречь. Если бы не пренебрегали массообменом, то увеличилась бы или
уменьшилась теплопередача к капле? Приведите ваши доводы.
5.24. Форма воздушного шара, заполненного горячим воздухом, близка
к сферической, и его диаметр составляет 18 м. Общий вес гондолы, газовой
горелки, полезного груза и материала воздушного шара 1050 Н. Определить
мощность газовой горелки (кВт), необходимую для снабжения шара горячим
воздухом. Предположить, что воздушный шар летает на высоте, где темпе-
температура равна 18°С, а скорость ветра 0,1 м/с. Термическим сопротивлением
материала шара можно пренебречь.
5.25. Вязкая жидкость закачивается в трубу, уложенную в поверхно-
поверхности земли между двумя цехами химического предприятия. Чтобы уменьшить
вязкость жидкости и, следовательно, энергию, требуемую для ее прокачки,
жидкость нагревается до 40°С. Наружный диаметр трубы 22 см, а ее длина
110 м. Расход жидкости в трубе 20 кг/с. Направление ветра перпендикулярно
оси трубы, а его скорость 14 м/с. Пренебрегая термическим сопротивлением
трубы, определить тепловой поток, отводимый от жидкости в тот день, когда
температура воздуха равна 0°С. Определить падение температуры жидкости
в трубе при условии, что удельная теплоемкость жидкости равна 1,3 кДж/
/(кг-град).
5.26. Емкость для хранения сжиженного природного газа имеет сфериче-
сферическую форму с диаметром 5 м. Согласно измерениям температура наружной
поверхности сферы составляет 10°С, а температура окружающего воздуха
30°С. Пренебрегая влиянием радиационного теплопереноса, рассчитать тепло-
тепловой поток к сжиженному газу при средней скорости ветра 7 м/с.
J5.27. Воздух обтекает внешнюю поверхность одиночного цилиндра диа-
диаметром 5 см. Направление воздушного потока перпендикулярно оси цилиндра.
Скорость воздуха 35 м/с, а его температура 100°С. При температуре цилинд-
цилиндра 200°С определить отношение среднего коэффициента теплоотдачи к его
локальному значению на критической линии цилиндра в предположении, что
число Нуссельта здесь определяется выражением Nu^ = <y/ReD.
5.28. Толуол с температурой 20°С обтекает одиночную трубу диаметром
4 см со скоростью 2 м/с. Направление потока перпендикулярно оси трубы.
Вычислить коэффициент теплоотдачи.
5.29. Вода с температурой 20°С обтекает ряд параллельных труб со ско-
скоростью 8 м/с. Расстояние между осями труб 8 см, а их наружный диаметр
4 см. Определить значение максимального числа Рейнольдса ReMaKC.
5.30. Фреон-12 с температурой 5°С обтекает пучок труб, расположенных
в шахматном порядке, с наружным диаметром 1,8 см. Скорость фреона до
входа в пучок труб 10 м/с. Расстояние между осями соседних труб в одном
ряду 3,5 см, а расстояние между осями труб в смежных рядах 3,0 см. Рас-
Рассчитать максимальное число Рейнольдса ReMaKc.
5.31. Кислород с температурой 100°С поступает при давлении 1 атм и
средней скоростью 4 м/с перпендикулярно оси труб в теплообменник с кори-
коридорным расположением труб. Всего имеется 12 рядов труб, имеющих наруж-
наружный диаметр 3 см. Расстояние между осями труб в одном ряду 6 см, а в
смежных рядах в направлении потока 9 см. Длина труб 6 м, а температура
их поверхности 50°С. Определить следующие параметры: а) коэффициент
конвективной теплоотдачи от потока кислорода, обтекающего трубы; б) теп-
тепловой поток от кислорода к одной трубе; в) давление, при котором кислород
покидает пучок труб.
5.32. Ответить на вопросы задачи 5.31 при условии, что трубы в пучке
распочожены не в коридорном, а в шахматном порядке.
5.33. Ртуть поступает в пучок труб с коридорным расположением пер-
перпендикулярно осям труб. Наружный диаметр труб 3 см, расстояние между
их осями в одном ряду 6 см. Расстояние между осями труб в смежных ря-
рядах 4,5 см. Температура ртути на входе 423 К, а ее скорость 7 ем/с. Опре-
Определить коэффициент конвективной теплоотдачи,
262 Глава 5
5.34. Натрий на входе в пучок труб имеет температуру 644 К и скорость
60 см/с. Диаметр труб 0,8 см, а расстояние между осями труб поперек пб-
тока составляет 3,1 см. Трубы в пучке расположены в шахматном порядке,
и расстояние между осями в смежных рядах 3,8 см. Определить величину Я.
5.35. Газы, выходящие из печи, используются для нагревания воды, дви-
движущейся внутри пучка труб с шахматным расположением. Общий массовый
расход воды 25 кг/с. Отработанные газы на входе в пучок имеют скорость
35 м/с и температуру 320°С. Расстояние между осями труб перпендикулярно
направлению потока газа 2,4 см, а параллельно потоку газа 1,6 см. Пучок
состоит из 36 труб (по шесть труб в каждом из шести рядов); длина трубы
5 м и наружный диаметр 1,6 см. Температура поверхности труб 80°С. Фи-
Физические свойства отработанных газов можно считать такими же, как у воз-
воздуха при 1 атм. Определить следующие параметры: а) коэффициент конвек-
конвективной теплоотдачи от газов; б) тепловой поток к воде; в) прирост темпера-
температуры воды; г) падение давления при течении отработанных газов в пучке
труб.
5.36. Было предложено транспортировать айсберг из Антарктики в юж-
южные страны с засушливым климатом для снабжения их пресной водой. Пред-
Предположим, что айсберг является цилиндром, погруженным в воду на глубину
320 м и имеющим диаметр 730 м. Пусть средняя скорость буксировки айс-
айсберга составляет 1,0 м/с, а средняя температура воды 10°С. Определить ко-
количество льда, которое будет потеряно при 3-месячной его буксировке за счет
конвективной теплоотдачи к боковой поверхности и донной части айсберга.
Скрытая теплота плавления льда составляет 3,35-105 Дж/кг.
5.37. Пучок труб с коридорным расположением в 50 рядах по 50 труб
в каждом имеет длину 4 м. Наружный диаметр труб 1,1 см. Расстояние ме-
между осями труб в ряду и смежных рядах составляет 1,65 см. Воздух посту-
поступает в пучок труб со скоростью 6 м/с и температурой 180°С. Определить теп-
тепловой поток к трубам и падение давления при движении воздуха через пу-
пучок труб, если температура всех труб одинакова и составляет 20°С.
5.38. Воздух с температурой 40°С при максимальном числе Рейнольдса
4-10§ поступает в пучок труб с шахматным расположением, состоящий из
5 рядов. Наружный диаметр труб 1 см. Определить коэффициент конвек-
. тивной теплоотдачи.
5.39. Вертикальная плоская пластина высотой 25 см нагрета до темпера-
температуры 90°С. Жидкость с температурой 30°С находится в контакте с этой пла-
пластиной. Рассчитать число Грасгофа для случаев, когда жидкость представ-
представляет собой: а) воздух при атмосферном давлении, б) воду, в) моторное мас-
масло и г) ртуть.
5.40. Для тех же условий и тех же жидкостей, что и в задаче 5.39, рас-
рассчитать тепловой поток от пластины в условиях свободной конвекции при
площади поверхности пластины 0,5 м2.
5.41. Паровая труба проходит вертикально через помещение. Температура
наружной поверхности трубы 60°С, а температура неподвижного воздуха в
помещении 20°С. Наружный диаметр трубы 6,8 см, а длина ее учасша в по-
помещении 3,4 м. Определить тепловой поток от трубы в условиях свободной
конвекции. Предполагая, что стены помещения полностью теплоизолированы,
а его объем составляет 900 м3, рассчитать, за какое время температура воз-
воздуха в помещении повысится на 1°С.
5.42. Мощность обогрева электроподушки размером 0,3 X 0,3 м состав-
составляет 12,5 Вт. Определить, какой будет температура подушки, если она подве-
подвешена вертикально в покоящемся воздухе с температурой 25°С. Предполо-
Предположить, что теплоотдача с обеих сторон подушки одинакова.
5.43. При условиях, приведенных в задаче 5.42, рассчитать температуру
подушки, если она лежит горизонтально на хорошо теплоизолированной по-
поверхности.
5.44. Нагревательный канал из металлических листов предназначен для
переноса теплового воздуха с одного этажа на другой в вертикальном на-
направлении. Температура канала 55°, а температура окружающего канал воз-
Формулы для расчета конвективного теплообмена 263
духа 25°С. Поперечное сечение канала 0,8 X 0,8 м, а его длина 4 м. Рассчи-
Рассчитать потери тепла теплого воздуха в канале.
5.45. Площадь помещения 12X14 м, а высота от пола до потолка 2,6 м.
Температура воздуха в помещении 25°С, а температура внутренней поверх-
поверхности стен 15°С. Определить тепловой поток через поверхности стен.
5.46. Рассчитать коэффицинт теплоотдачи от горизонтального цилиндра
, наружным диаметром 2,8 см, имеющего температуру 300°С, к окружающему
его натрию с температурой 110°С.
5.47. Наружный диаметр горизонтальной паровой трубы 4,6 см. Труба
расположена в комнате, температура в которой 20°С. Температура наружной
поверхности трубы 40°С. Определить тепловой поток от единицы длины трубы.
5.48. Электрический элемент осветителя из древесного угля имеет диа-
диаметр 1 см, длину 70 см и номинальную мощность 425 Вт. Элемент располо-
расположен в горизонтальном положении на улице, где температура воздуха 28°С.
Излучательная способность элемента ~0,3. Скоростью ветра можно прене-
пренебречь. Определить температуру поверхности элемента после его включения и
достижения установившихся условий. Подтверждает ли ваш ответ рекоменда-
рекомендацию изготовителей: не оставлять осветитель включенным более 8 мин?
5.49. Крытый каток имеет размеры 100 X 120 м и температуру поверхно-
поверхности льда —4°С. Температура воздуха в помещении 20°С. В предположении,
что тепло от поверхности льда передается воздуху в основном благодаря сво-
свободной конвекции, определить холодопроизводительность холодильной уста-
установки, необходимую для поддержания льда при —4°С. Принудительная вен-
вентиляция воздуха в помещении отсутствует.
5.50. Лампа дневного света мощностью 40 Вт имеет наружный диаметр
3,2«рм и длину 136 см. При температуре окружающего воздуха 24°С темпера-
температура поверхности лампы 36°С. Какой процент общего рассеяния тепловой
энергии лампы составляет теплоотдача вследствие свободной конвекции? Лам*
па расположена горизонтально в покоящемся воздухе.
5.51. Горизонтальная паровая труба наружным диаметром 14 см нахо-
находится в покоящемся воздухе в помещении промышленного предприятия. Тем-
Температура наружной поверхности трубы 55йС, а температура воздуха 25°С.
Рассчитать тепловой поток от пара при длине трубы 20 м.
5.52. Тонкостенный бак из нержавеющей стали, предназначенный для
сушки картофельных ломтиков, помещен в покоящемся воздухе с темпера-
турой 25°С. Бак имеет квадратное поперечное сечение и заполнен раститель*
ным маслом, которое нагревается до 205°С от газовых горелок, находящихся
под дном бака. Площадь сечения бака равна 3X3 м2, а высота слоя масла
в нем 1 м. Определить расход газа (м3/с), потребляемый при нормальных
условиях, когда достигнут установившийся режим работы. При стандартных
давлении и температуре теплотворная способность природного газа состав-
составляет 3,7-107 Дж/м3. При стоимости газа в США 0,07 долл./м3 определить за*
траты на него в течение 1 ч работы бака для компенсации потерь тепла через
стенки, связанных со свободной конвекцией.
5.53. Кирпичи вынимают из печи для обжига при температуре 420°С и
охлаждают в покоящемся воздухе при температуре 30°С. Высота кирпича
10 см, а размеры его основания 14X7 см. Рассчитать тепловой поток от кир-
кирпичей в результате естественной конвекции сразу после извлечения из печи.
Кирпичи лежат на теплоизолированной поверхности.
5.54. Электронный блок потребляет 75 Вт электроэнергии. Для защиты
его помещают в кубический оловянный корпус с размером стороны 28 см.
Определить температуру поверхности корпуса, если температура окружаю-
окружающего его воздуха равна 20°С. Основание корпуса покоится на хорошо тепло-
теплоизолированной поверхности. Потерями излучением можно пренебречь.
5.55. Оконная рама с двойным остеклением состоит из двух стекол тол-
толщиной 1 см каждое, разделенных слоем воздуха толщиной 1,8 см. Опреде-
Определить тепловой поток через раму, когда температура наружной поверхности
внешнего стекла рамы —10°С, а температура внутренней поверхности другого
стекла 20°С.
264 Глава 5
5.56. Верхняя часть печи выполнена из двух горизонтальных металличе-
металлических пластин, разделенных слоем покоящегося воздуха. Температура нижней
пластины 380°С, а верхней 120°С. Пластины отстоят друг от друга на 2 см.
Определить коэффициент конвективной теплоотдачи от нижней пластины к
верхней.
5.57. Большой бак с нагретой жидкостью имеет двойные металлические
стенки, разделенные слоем воздуха. Каждая стенка имеет высоту 12 м и го-
горизонтальное основание 15 м. Слой разделяющего воздуха имеет толщину
3,5 см. Рассчитать тепловой поток между стенками, если температура вну-
внутренней стенки 90°С, а наружной 30°С.
5.58. Две большие вертикальные пластины разделены слоем воздуха тол-
толщиной 3 см. Температура одной пластины 10°С, а другой 70°С. Определить
тепловой поток от одной пластины к другой при площади поверхности каж-
каждой из них 20 м2 и высоте пластин по вертикали 5,6 м.
5.59. Вода с температурой 30°С и скоростью 0,15 м/с поступает в гори-
горизонтальную трубу. Температура изотермической стенки трубы 90°С. Внутрен-
Внутренний диаметр трубы 3 мм, а ее длина 250 см Рассчитать коэффициент тепло-
теплоотдачи для случая смешанной свободной и вынужденной конвекции. Сравнить
свой результат со случаем чисто вынужденной конвекции.
5.60. Горизонтальная труба длиной 1 м имеет температуру поверхности
100°С и внутренний диаметр 5 см. В нее поступает кислород при атмосфер-
атмосферном давлении с температурой 60°С и скоростью 0,4 м/с. Определить коэффи-
коэффициент теплоотдачи для случая смешанной свободной и вынужденной кон-
конвекции.
5.61. Насыщенный жидкий аммиак поступает в горизонтальную трубу с
температурой 40°С. Температура изотермической поверхности трубы 0°С. Дли-
Длина трубы 85 см, а ее внутренний диаметр 0,25 см. Скорость аммиака 13,5 см/с.
Рассчитать коэффициент теплоотдачи в условиях: а) чисто вынужденного те-
течения, б) смешанной свободной и вынужденной конвекции.
5.62. Плоская пластина помещена в поток воздуха, имеющего число Маха
М = 2,0 и давление 25 000 Н/м2. Температура невозмущенного потока —15°С.
Температура пластины не может превышать 120°С. При длине пластины в на-
направлении течения 30 см рассчитать плотность теплового потока, который не-
необходимо отвести в систему охлаждения, чтобы поддержать температуру пла-
пластины ниже указанного предельного значения.
5.63. Спутник входит в атмосферу Земли со скоростью 2700 м/с. Опреде-
Определить максимальную температуру защитной тепловой оболочки при отсутствии
уноса материала оболочки и теплообмена излучением. Температура верхних
слоев атмосферы —50°С.
5.64. Масштабная модель секции крыла самолета помещена в аэродина-
аэродинамическую трубу, где проводятся ее испытания при числе Маха М = 1,5. Дав-
Давление воздуха и температура в рабочей части трубы составляют соответ-
соответственно 20 000 Н/м2 и —30°С. Требуется охладить секцию крыла до темпе-
температуры 60°С. Рассчитать плотность теплового потока, отводимого от этой
секции, с тем чтобы поддерживать указанную температуру. Предположите,
что крыло представляет собой плоскую пластину, а его длина в направлений
потока составляет 30 см.
5.65. Воздух с температурой 0°С при давлении 23 000 Н/м2 обтекает со
скоростью 500 м/с плоскую пластину, нагретую до температуры 80°С. Длина
пластины в направлении потока 20 см, а ее ширина в поперечном направле-
направлении 40 см. Определить следующие параметры: а) температуру адиабатической
поверхности; б) расстояние от передней кромки пластины хкр, на котором
поток становится турбулентным; в) локальный коэффициент теплоотдачи в
сечении хкр; г) локальный коэффициент трения в конце пластины; д) локаль-
локальный тепловой поток в конце i ластины.
Глава 6
ИЗЛУЧЕНИЕ
6.1. ВВЕДЕНИЕ
Радиационный способ теплопередачи характеризуется энер-
энергией, передаваемой в форме электромагнитных волн. Волны
распространяются со скоростью света. Передача энергии излу-
излучением может происходить между поверхностями, разделенными
вакуумом. Солнце, например, передает энергию Земле через
миллионы километров космического вакуума исключительно
излучением. Кроме того, это единственный способ передачи
энергии к космическому кораблю или от него.
Для объяснения поведения теплового излучения использу-
используются как волновая, так и корпускулярная теории. Согласно вол-
волновой теории, излучение можно представить волновыми колеба-
ниями, имеющими частоту v и длину волны X. Произведение ча-
частоты и длины волны есть скорость распространения, равная
скорости света с:
c = Xv. F Л)
Согласно корпускулярной теории, энергия излучения передается
в виде порций энергии, называемых фотонами. Каждый фотон
движется со скоростью света и имеет определенную энергию,
заданную соотношением
e — hv,
в котором h — постоянная Планка. Фотоны с более высокими
частотами обладают большей энергией, чем фотоны с более йиз-
кими частотами. Когда тело нагрето, свободные электроны мо-
могут переходить на более высокие, или возбужденные, уровни.
Когда электрон возвращается на свой более низкий энергетиче-
энергетический уровень, он испускает фотон, энергия которого равна
разности энергий возбужденного и равновесного состояний. Для
любой поверхности в любой данный момент многочисленные
электроны совершают переходы на разные энергетические уров-
уровни, и поэтому энергия фотонов, покидающих поверхность, рас-
распределена по спектру частот. Испускание фотонов зависит
исключительно от температуры тела. Энергия фотонов, поки-
покидающих поверхность таким образом, называется тепловым излу-
излучением.
Есть другие способы кроме нагревания поверхности, которые
могут быть причиной испускания телом фотонов. На коротко-
коротковолновом конце спектра, например, находится рентгеновское
266 Глава 6
излучение, которое может быть вызвано бомбардировкой куска
металла потоком электронов. На другом конце спектра находятся
радиоволны с большими длинами волн, которые могут генери-
генерироваться электронным оборудованием и кристаллами. Между
1км
-14 -13-12-11-10-9 -8-7-6-5-4-3-2-10 12 3 4 5 6 7 8
Частотау; \0П 21 20 19
с 1 | Рен!
)*—ci
Космические лучи
Рентгенов-
кие—
17 16 15 14 13 12 И 10 9 8 7 6 5 4 3 2 1
Видимое
излучение
Гамма-
лучи
лучи
Тепловое
излучение
Радио-
Радиоволны .
-Волны Герца-
Электро-
^энергия^
Рис. 6.1а. Электромагнитный спектр.
этими двумя предельными случаями находится тепловое излу-
излучение, которое испускается телом и зависит только от его тем-
температуры. Полный диапазон излучения всех длин волн назы-
называется электромагнитным спектром.
Длина волныЛ,м 10
Частота у, с"*1
,-7
Ультрафиолетовый | В ид и-|Б л иж ни и! Средний
Дальний
нфракрасный
Рис. 6.16. Часть электромагнитного спектра, приходящаяся на тепловое излу-
излучение.
Электромагнитный спектр подразделяется на ряд диапазо-
диапазонов, (рис. 6.1а). Тепловое излучение, испускаемое с поверхности
и определяемое только его температурой, сосредоточено между
длинами волн 10~4 и 10~7 м. Часть спектра, относящаяся к теп-
тепловому излучению, показана более подробно (рис. 6.16).
Глаз человека способен воспринимать электромагнитное из-
излучение в диапазоне между длинами волн приблизительно
Излучение 267
3,8-10—7 и 7,6* 10~7 м, и поэтому излучение между этими дли-
длинами волн называется видимым излучением. Видимая часть
спектра составляет очень малую часть всего спектра и лежит
полностью внутри области теплового излучения. Для измерения
длин волн используются различные единицы:
1А = 1 ангстрем = 10~10 м=1(Г8 см=10"~4 мкм.
1 мкм = 1 микрометр = 1 микрон = 10 м=1СГ4 см = 104А.
Следующий раздел посвящен физике теплового излучения.
В нем введено понятие теплового черного тела и представлено
распределение энергии как функция длины волны и темпера-
температуры для излучающего абсолютно черного тела.
6.2. ФИЗИКА ИЗЛУЧЕНИЯ
Понятие черного тела
Не все поверхности, нагретые до одной и той же темпера-
температуры, излучают или поглощают одно и то же количество лучи-
лучистой энергии. Поверхность тела, которая излучает и поглощает
максимальное количество энергии при данной температуре, на-
называется черной поверхностью или просто черным телом. Чер-
Черное тело — это эталон, к которому можно приблизиться на прак-
практике покрытием поверхности тела или видоизменением формы
его поверхности. Черное тело — это эталон, с которым можно
сравнивать все другие излучатели. В этом отношении оно по-
похоже на изоэнтропийный насос или турбину, используемые как
эталон для сравнения в термодинамике.
Закон Планка
При нагревании черного тела до температуры Т поверхностью
тела испускаются фотоны. Фотоны имеют определенное распре-
распределение энергии, зависящее от температуры поверхности Г.
Макс Планк в 1900 г. показал, что энергия излучения длиной
волны X, испускаемой черным телом с температурой Г, равна
где Еъ% — плотность потока монохроматического, или спек-
спектрального, излучения черного тела при температуре Г, Вт/м3;
С\ чя 3,7418- Ю-16 Вт-м2 — первая постоянная излучения; С2==
==sa 1,4388-10~2 м-К —вторая постоянная излучения. Изменение
монохроматической плотности потока излучения черного тела в
зависимости от температуры и длины волны, выраженное фор-
формулой F.2), известно как закон Планка.
268 Глава в
График монохроматической плотности потока излучения чер-
черного тела представлен на рис. 6.2. Видно, что энергия излучения,
испускаемого черной поверхностью, возрастает с температурой.
Кроме того, плотность потока достигает максимального значе-
значения при длине волны, которая уменьшается с ростом темпера-
температуры поверхности.
Закон смещения Вина
Длина волны, при которой плотность потока излучения чер-
черного тела достигает максимального значения для данной тем-
ю14
1012
!s io8
g 10'
102
Положение максимумов Дмак Т'вв21898<10~3м-град
i t i i I i
4 6 8 10 12
Длина волны Л, мкм
14
Рис. 6.2. Плотность потока монохроматического излучения черного тела.
пературы, может быть определена из закона Планка посредст-
посредством выполнения условий максимума:
*** _ й Г
d% dh L
d% dh L Я5 (eCilKT - 1) Jr=const
Результат этой операции дает
А>максГ = 2,898 • 10~3 м • К, F.3)
где Ямакс — длина волны, при которой достигается максимум
монохроматической плотности потока излучения черного тела с
температурой Т. Формула F.3) называется законом смещения
Вина. Положение точек, описываемых законом Вина, показано
на рис. 6.2.
Максимальное значение плотности потока монохроматиче-
монохроматического излучения черного тела можно получить подстановкой
Излучение 269
формулы F.3) в F.2), что в результате дает
. F.4)
Мы знакомы с проявлением закона смещения Вина. Допу-
Допустим, что электрический ток протекает через тонкую нить,
нагревая ее. При сравнительно низкой температуре нити (не
выше 900 К) длина волны, на которой энергия излучения дости-
достигает максимума, составляет примерно 3,2-10~6 м, что соответ-
соответствует инфракрасной области. Мы можем ощутить энергию из-
излучения, испускаемого нитью, почувствовав повышение темпе-
температуры кожей рук, когда мы держим их около нити. Однако
наши глаза не способны обнаружить видимое излучение, испу-
испускаемое нитью, потому что на видимую часть спектра прихо-
приходится незначительная доля энергии.
По мере возрастания температуры нити количество энергии
излучения возрастает и все большая ее доля относится к более
коротким длинам волн. При превышении 1000 К некоторая доля
энергии приходится на длинноволновый, или красный, конец
видимого спектра. Наши глаза способны обнаружить это излу-
излучение, и нить кажется тусклого красного цвета. При дальнейшем
возрастании температуры все больше энергии относится к ви-
видимой области, и выше 1600 К излучением охвачена вся види-
видимая область, так что нить кажется раскаленной добела при этой
температуре.
Солнце является примером источника энергии с высокой
температурой. Внешняя поверхность Солнца имеет температуру
~5800 К. Согласно закону Вина, Ямакс при этой температуре
равняется 5,2-10—7 м, что соответствует приблизительно сере-
середине видимой области. Глаз человека идеально приспособлен
к восприятию максимума энергии монохроматического излуче-
излучения Солнца.
Наши глаза являются надежным приемником энергии излу-
излучения, которое приходится на видимую область длин волн.
Предмет, который окажется белым, если его поместить на солн-
солнце, отражает почти все излучение и практически ничего не по-
поглощает в видимой области. С другой стороны, черное тело
поглощает все видимое излучение, ничего не отражая, поэтому
кажется черным для наших глаз.
Поскольку глаз человека не реагирует на энергию излучения,
не входящую в видимую область спектра, он может только пред-
предсказывать поведение поверхности в пределах этого очень уз-
узкого диапазона длин волн. Позже, в разделе, посвященном
монохроматическим свойствам, будет показано, что некоторые
поверхности ведут себя как хорошие поглотители в видимой об-
области и кажутся темными для наших глаз. В инфракрасной об-
области их поведение изменяется и они могут стать слабыми
поглотителями. С другой стороны, некоторые поверхности могут
270 Глава 6
быть слабыми поглотителями в видимой области и казаться
белыми на вид. Те же самые поверхности могут стать отлич-
отличными поглотителями за пределами видимой области.
Закон Стефана — Больцмана
Общее количество энергии излучения, покидающего поверх-
поверхность с абсолютной температурой Г, на единицу площади для
всех длин волн называется плотностью потока интегрального
излучения. Если поверхность — черное тело, плотность потока
интегрального излучения описывается интегралом от распреде-
распределения Планка по всем длинам волн:
Eb (T) - j Ebk (T) dX = j %Чес%_х) dk. F.5)
После интегрирования получается выражение
Еь{Т) = оТ\ F.6)
которое известно как закон Стефана — Больцмана. Символ о
обозначает постоянную Стефана — Больцмана, величина кото-
которой равна
(^Ly^ = 5,67. 10-8 Вт/(м2.К4). F.7)
Постоянные С\ и Сг те же, что и в формуле Планка; Еь имеет
размерность плотности теплового потока, Вт/м2.
Из закона Стефана — Больцмана следует, что влияние излу-
излучения в большинстве случаев незначительно при низких темпе-
температурах вследствие малого значения а. При комнатной темпе-
температуре, или около 300 К, интегральная плотность потока излу-
излучения черной поверхности достигает только ~460 Вт/м2. Эта
величина составляет около 1/10 плотности теплового потока,
передаваемого конвекцией от поверхности к жидкости, когда
коэффициенты конвективной теплоотдачи и перепад температур
имеют достаточно низкие значения — 100 Вт/(м2-град) и 50 К
соответственно. Поэтому при низких температурах теплообме-
теплообменом излучения часто можно пренебречь. Однако его следует учи-
учитывать при высоких температурах, поскольку плотность потока
излучения возрастает как четвертая степень абсолютной темпе-
температуры.
Радиационные функции
Если проинтегрировать плотность потока монохроматиче-
монохроматического излучения, выраженную законом Планка, по всем длинам
волн от % = 0 до % = %и то в результате получим полное коли-
количество энергии излучения в интервале длин волн от 0 до %и
Излучение 271
испущенного черной поверхностью с температурой Т. Проведя
интегрирование, можно показать, что результат является функ-
функцией только произведения Х\Т. Интеграл обозначается
F.8)
Общее количество энергии излучения, испущенного в интер-
интервале длин волн Х\ ч- Х2 для черной поверхности с температурой
Г, определяется разностью
двух таких интегралов:
F.9)
Физический смысл раз-
разности интегралов в уравне-
нииЦб.9) показан на рис. 6.3 . Длина волны Я
как площадь под кривой рИс. 6.3. Смысл радиационных функций.
ЕЪк{Т) между Х\ и Х2.
Чтобы найти долю полной энергии излучения черного тела,
испущенного во всем спектре, которая приходится на интервал
длин волн Х\ < X < Я2, необходимо разделить уравнение F.9) на
F.10)
в результате чего получим
"Доля полной энергии"
излучения черного те-
тела, приходящаяся на
интервал длин волн
В работе Данкла [1] табулированы величины
?>уг) F.П)
— функции произведения XT. Эти величины в системе единиц
СИ приведены в табл. 6.1. Их обычно называют радиационными
Функциями. Использование этих величин иллюстрируется сде-
Дующим примером,
272 Глава 6
Радиационные функции черного тела
Таблица 6.1
XT,
(wi-KxlO3)*'
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
5,0
5,2
5,4
5,6
5,8
6,0
Eb(O->\T)
oT4
0,341796 X1O~26
0,186468X10-"
0,929299 ХКГ7
0,164351 X10
0,320780 X1O~3
0,213431 ХНГ2
0,779084 X10
0,197204XKT1
0,393449 X10"!
0,667347 X10-!
0,100897
0,140268
0,183135
0,227908
0,273252
0,318124
0,361760
0,403633
0,443411
0,480907
0,516046
0,548830
0,579316
0,607597
0,633786
0,658011
0,680402
0,701090
0,720203
0,737864
XT,
(M-KXIO3K1
6,2
6,4
6,6
6,8
7,0
7,2
7,4
7,6
7,8
8,0
8,5
9,0
9,5
10,0
10,5
11,0
11,5
12
13
14
15
16
18
20
25
30
40
50
75
100
Eb(Q-±\T)
oT4
0,754187
0,769282
0,783248
0,796180
0,808160
0,819270
0,829580
0,839157
•0,848060
0,856344
0,874666
0,890090
0,903147
0,914263
0,923775
0,931956
0,939027
0,945167
0,955210
0,962970
0,969056
¦0,973890
0,980939
0,985683
0,992299
0,995427
0,998057
0,999045
0,999807
1,000000
а) Относительно использования числовых множителей, кратных 10, см. приложение
IV. с, 479.
Пример 6.1. Предположим, что Солнце (Т = 5800 К) и лампа накали-
накаливания (Т = 2800 К) являются черными телами. Рассчитать для обоих этих
источников излучения следующие параметры: а) плотность потока интеграль-
интегрального излучения; б) максимум плотности потока монохроматического излуче-
излучения; в) длину волны, на которой имеет место максимум плотности потока
излучения; г) долю полной энергии излучения, которая приходится на види-
видимую область спектра.
Решение.
а) Плотность потока интегрального излучения выражается законом Сте-
Стефана — Больцмана (формула F.6)):
Для Солнца ЕЬ{Т) = E,67-Ю-8) E800L =- 6,42-107 Вт/м2.
Для лампы ЕЬ(Т) = E,67-Ю-8) B800L = 3,49-106 Вт/м2.
б) Максимум плотности потока монохроматического излучения черного
тела определяется по формуле F.4).
Для Солнца
О»28? ' 10~5) E800M = 8>45 • W* ^Т/М3.
Излучение 273
Для лампы накаливания
(^я)макс *= О»287'10") B80°M = 2>21'1012 Вт/м3-
в) Величина А,Макс определяется по закону Вина [формула F.3)].
2 898 • 10
Для Солнца Ямакс= * =~5,00-1(Г7м (в видимой области длин
ооии
™Лмакс=2'898-10 --—7
волн). _з
Для лампы ЛМакс — ' няни "¦ 1>04'10 м ^в инФРа1КРасной ча^ти спек-
тра).
г) Долю полной энергии излучения, приходящуюся на видимую C,8 X
X 10~7 м < К < 7,6-10~7 м) область, можно определить с помощью радиа*
ционных функций табл. 6.1.
Для Солнца
%J *= C,8. 10~7) 580Q *= 2,204 • Ю-3 м • К,
%2Т ** G,6 • Ю-7) 5800 === 4,408 • I0-8 м • К.
[¦
Доля полной энергии излучения"] ?у{0 -> %2Т) — ?& @ -> Х\Т)
в видимой области J gt4
= 0,5500 - 0,1017 = 0,4483 = 44,83%.
Для лампы
%{Т = C,8 • 10~7) 2800 = 1,064 • Ю-3 м • К,
%2Т == G,6 • Ю-7) 2800 =* 2,128 • 10~3 м • К.
[Доля полной энергии излучения! Еь @ -» ЯгГ) + Еь @ -> к\Т)
в видимой области J а74 """*
= 0,0886 - 0,0009 = 0,0877 = 8,77%.
Заметим, что максимум солнечной энергии находится в видимой части
спектра и более 40% полной солнечной энергии может воспринимать глаз че-
человека. С другой стороны, энергия излучения ламп накаливания на участке
видимого спектра составляет менее 10% полной энергии. Остальные 90% энер*
гии рассеиваются в виде инфракрасного излучения, и эту часть энергии наши
глаза не воспринимают, но мы можем ощущать ее своей кожей как тепло.
6.3. РАДИАЦИОННЫЕ СВОЙСТВА
Радиационные свойства количественно описывают взаимо-
взаимодействие энергии излучения с поверхностью материала, в част-
частности как поверхность излучает, отражает, поглощает и пропу-
пропускает энергию излучения.
В общем случае радиационные свойства зависят от длины
волны. Например, поверхность может хорошо отражать в види-
видимой части спектра и быть плохим отражателем в инфракрасной
области. Свойства, которые описывают поведение поверхности
в зависимости от длины волны, называют монохроматическими,
или спектральными, свойствами. Радиационные свойства зави-
зависят также от направления, по которому излучение падает на по-
поверхность. Свойства, которые описывают изменения распреде-
распределения энергии в зависимости от угла, называют направленными
Шйств
274 Глава 6
При составлении баланса энергии на поверхности, например,
с целью определения ее температуры, необходимо знать радиа-
радиационные свойства этой поверхности и всех других поверхностей,
которые обмениваются энергией с данной поверхностью. Даже
когда известны спектральные и направленные свойства всех этих
поверхностей, анализ процесса весьма сложен. Сложность за-
задачи, а чаще полное отсутствие детальных свойств заставляют
искать упрощенный подход. Такой подход допускает использо-
использование одной величины радиационного свойства, осредненной по
всем длинам волн и всем направлениям. Свойства, которые
осреднены по всем длинам волн и углам, называют интеграль-
интегральными свойствами. При использовании интегральных свойств в
анализе радиационного теплообмена полученные результаты до-
достаточно точны для большинства инженерных целей и, конечно,
очень сложная задача расчета сводится к более простой.
Даже если мы хотим использовать исключительно интеграль-
интегральные радиационные свойства, важно иметь представление о спек-
спектральных и направленных характеристиках поверхностей, что-
чтобы учесть их изменение в задачах, в которых эти эффекты имеют
существенное значение.
Рассмотрим радиационные свойства в порядке возрастания
их сложности: сначала интегральные, затем спектральные и,
наконец, направленные свойства.
Падающее излучение
(облученность) G
Интегральные радиационные свойства Л
Рассмотрим пучок излучения, падающий на поверхность
(рис. 6.4). Полную энергию падающего излучения будем назы-
называть интегральной облученно-
отраженное с*ь1?г и обозначим ее символом
излучение pG G. Когда падающее излучение
достигает поверхности, часть
его поглощается в материале,
часть отражается от поверхно-
поверхности, а остальная пропускается
сквозь тело. Три радиацион-
радиационных свойства — поглощатель-
ная, отражательная и пропу-
Пропущенное излучение тО
Рис. 6.4. Определение интегральных
радиационных свойств.
скательная способности — опи-
описывают распределение энергии
падающего излучения по этим
трем категориям.
Поглощательная способность а поверхности определяется
как часть потока падающего излучения, поглощенная телом,
отражательная способность р поверхности — как часть потока
падающего излучения, отраженная от поверхности, пропуска-
у§льная способность % — как часть падающего излучения, пропу-
Излучение 275
щенная телом. Из рассмотрения энергетического баланса тела
(рис. 6.4) известно, что падающее излучение должно либо по-
поглотиться, либо отразиться, либо пройти сквозь тело. Матема-
Математически баланс энергии можно выразить следующим образом:
или а+р + т = 1. F.12)
Часто поверхность бывает непрозрачна. Это означает, что она
не пропускает падающее излучение. Для непрозрачной поверх-
поверхности
т = 0
и уравнение F.12) сведется к следующему:
а + Р = 1. F.13)
Если поверхность представляет собой идеальный отражатель, то
все падающее излучение отразится, или
Р = 1, F.14)
и баланс энергии для идеально отражающей поверхности будет
выражен в виде
т==а=:0. F.15)
Черное тело поглощает максимальное количество падающего
излучения, или
о=1, F.16)
и, следовательно, для черного тела
т = р = 0. F.17)
Другим очень важным интегральным радиационным свойст-
свойством является излучательная способность тела (степень черно-
черноты), которая определяется как отношение потока собственного
излучения, испущенного телом, к потоку излучения, испущен-
испущенного черным телом при той же температуре. Математическое
определение интегральной изЛучательной способности 8 будет
следующим:
Е(Т) __ Е(Т) , ,
ь~1ш=-^-- FЛ8>
Поскольку черное тело испускает максимальное количество
излучения при данной температуре, излучательная способность
поверхности всегда заключена между нулем и единицей. Когда
поверхность является черным телом, Е(Т) = Еь и е==ос=1,0.
Закон Кирхгофа
Между поглощательной и излучательной способностью мате-
материала существует важная зависимость. Эту зависимость можно
без труда вывести, поместив испытуемое тело с поглощательной
276 Глава в
Изотермическая замкнутая полость
с температурой Т
способностью а и излучательной способностью г в изотерми-
изотермическую полость (рис. 6.5). Предположим, что тело и полость
находятся в тепловом равновесии, т. е. температуры испытуе-
испытуемого тела и полости одинаковы. При равновесии энергия погло-
поглощенного излучения должна быть равна энергии испущенного
излучения, или если G — падающее на испытуемое тело излуче-
излучение, то
axG = Ex. F.19)
Представим теперь, что испытуемое тело удалено и заменено
вторым испытуемым телом такого же размера при сохранении
неизменными условий в полости.
Когда снова будут достигнуты
условия равновесия, второе тело
примет ту же температуру, что и
первое испытуемое тело. Пред-
Предположим, что второе испытуемое
тело —черное тело. Условия рав-
равновесия требуют, чтобы выполня-
выполнялось равенство
?2 = ?b. F.20)
Рис. 6.5. К выводу закона Кирх-
Кирхгофа.
Испытуемое тело
с температурой?
и свойствами
и е
Взяв отношение уравнений F.19)
и F.20), получаем
а2
Поскольку второй материал является черным, о&2 = 1. Тогда
а, =-
F.21)
Уравнение F.21) идентично определению излучательной способ-
способности первой поверхности. Таким образом,
а{=гх. F.22)
Этот результат выражает закон Кирхгофа, согласно которому
при тепловом равновесии поглощательная способность тела рав-
равна его излучательной способности. Этот результат не справед-
справедлив, если тело не находится в равновесии с его окружением.
Из закона Кирхгофа следует, что хорошие поглотители, т. е.
тела, имеющие высокие значения поглощательной способности,
будут также хорошими излучателями теплового излучения. Этот
результат подсказывает простой способ имитации черного излу-
излучателя с помощью изотермической полости, имеющей маленькое
отверстие в поверхности (рис. 6.6).
Излучение, которое проходит через отверстие, будет много-
многократно отражаться от внутренней поверхности полости, и неза-
Излучение 277
Третье отражение
Падающее
излучение (г
Второе
висимо от состояния поверхности полости падающее излучение
в основном поглотится. Следовательно, практически все падаю-
падающее на отверстие излучение будет поглощено и отверстие в изо-
изотермической полости будет вести себя подобно черному телу.
Способность изотермической полости поглощать практически все
излучение, падающее на
маленькое отверстие в его
поверхности, называется
эффектом полости. Эф-
Эффективная поглощатель-
ная способность ряда из-
известных форм, таких, как
Сферические, ПрЯМОуГОЛЬ- поглощение/
ные или цилиндрические
полости, рассмотрена в
работах [3—5].
Изотермические обо-
оболочки или полости могут
быть использованы в ла-
лабораторной работе для
создания источника чер-
черного излучения. Полость
должна быть нагрета до
постоянной температуры
Г. Тогда внутреннее пространство полости заполнится равномер-
равномерным черным излучением с плотностью потока, равной <тГ4. Из-
Излучение, выходящее через малое отверстие в полости, будет
также иметь плотность потока
Первое
отражение
и частичное
поглощение
Изотермическая
замкнутая полость
Рис. 6.6. Изотермическая замкнутая по-
полость, моделирующая поведение черного
тела.
Монохроматические радиационные свойства
До сих пор были рассмотрены интегральные свойства, яв-
являющиеся величинами, осредненными по всему электромагнит-
электромагнитному спектру. Определим монохроматические свойства, относя*
щиеся к отдельным длинам волн. Монохроматическая погло-
щательная способность а^ представляет собой поглощенное
излучение с длиной волны i, деленное на падающее на поверх-
поверхность излучение с длиной волны К. Соотношение между
монохроматической поглощательной способностью тела и его
интегральной поглощательной способностью а определяется
в виде
F.23)
278 Глава в
где индекс к обозначает монохроматическую величину. Подоб-
Подобные соотношения можно записать для зависимостей между
монохроматическими и интегральными отражательной и пропу-
скательной способностями.
При составлении баланса энергии на поверхности для моно-
монохроматического излучения уравнение F.12) будет иметь вид
Ч + 9х + Ч=1. F.24)
Монохроматическая, или спектральная, излучательная спо-
способность определяется в виде
а соотношение между монохроматической и интегральной излу-
чательной способностью определяется в виде
$*»х(г)л
Если сравнить уравнения F.23) и F.26), то можно заметить
существенное различие между интегральной поглощательной и
интегральной излучательной способностями. Как поглощател^-
ная, так и излучательная способности являются свойствами по-
поверхности и зависят от типа материала, состояния поверхности
и ее температуры. Кроме того, поглощательная способность —
функция свойств всех окружающих поверхностей, дающих вклад
в падающее излучение G\, как это видно из уравнения F.23).
Излучательная способность поверхности, согласно определению
[уравнение F.26)], не зависит от свойств других поверхностей.
Она является функцией только свойств собственного материала
поверхности, состояния поверхности и температуры. Это иллю-
иллюстрируется следующим примером.
Пример 6.2. Поверхность имеет постоянную монохроматическую погло-
щательную пособность, равную 0,6 в диапазоне длин волн 4-10~7^А,^
^ 4-Ю*6 м. Поглощательная способность равна нулю для всех других длин
волн. Предположим, что монохроматические излучательная и поглощательная
способности равны. Рассчитаем интегральные поглощательную и излучатель-
ную способности, если температура поверхности 3000 К для следующих двух
случаев: а) падающее излучение от черной поверхности при 3000 К; б) па-
падающее излучение от черной поверхности при 1000 К.
Излучение 279
Решение. Интегральная излучательная способность поверхности равна
оо 4 • Ю-6
# S
S
4. Ю-7
= 0,6 @,9452 - 0,0021) « 0,566,
где два определенных интеграла вычислены при XT =1,2-10 м-К и
1,2-10» м-К с помощью радиационных функций, представленных в
табл. 6.1. Излучательная способность поверхности не зависит от падающего
излучения, поэтому излучательная способность для случаев а) и б) одна и
та же. Поглощательная способность поверхности при черном падающем излу-
излучении от поверхности с температурой 3000 К равна
«« 4 • ю—6
0,6
4 • И)"?
U О
или о, = 0,61 =п 7fA I ¦
L а/ о Г J
Интегралы те же, что и при расчете излучательной способности, поэтому
а — 0,6 @,9452 — 0,0021) = 0,566.
Поглощательная способность поверхности при черном падающем излуче-
излучении от поверхности при 1000 К равна
: 0,6 @,4809 - 0) = 0,289.
Здесь произведения XT равны: Х2Т = D-10~6) 1000 = 4-Ю" м-К и XJ =
= D-10-7I000=4.10-4м-К.
Заметим, что излучательная способность не зависит от спек-
спектра падающего излучения, в то время как поглощательная спо-
способность зависит от Gx. Можно заметить также, что, даже когда
монохроматические излучательная и поглощательная способно-
способности идентичны, интегральные величины а и е могут различаться.
Однако в случае, когда падающее излучение исходит от черной
поверхности с температурой, равной температуре приемной по-
поверхности, излучательная способность приемной поверхности
равна ее поглощательной способности. Этот результат следует
из закона Кирхгофа [уравнение F.22)].
Пример 6.3. Автомобиль остановился на стоянке, расположенной на солн-
солнцепеке. Переднее стекло машины имеет пропускательную способность 0,92 для
Длин волн в интервале значений 3-10~7 < л < 3-10~6 м и непрозрачно для
9се? других 4ЛИН волн. Салон автомобиля можно рассматривать как черн.ое
280 Глава б
тело с температурой 300 К. Солнце представляет собой черный источник с
температурой 6800 К, плотность потока падающего излучения которого равна
1100 Вт/м2.
Рассчитать а) интегральную пропускательную способность переднего стек-
стекла для солнечного излучения; б) интегральную пропускательную способность
переднего стекла для излучения салона автомобиля; в) плотность потока
энергии солнечного излучения, проходящего сквозь стекло; г) плотность по-
потока энергии излучения салона автомобиля, проходящего сквозь стекло.
Решение.
а) Интегральная пропускательная способность определяется по формуле
о
Когда излучение падает от черного тела, G% =*= Е^, или
со 3 • К)-6
X 0,92 J Eb%d%
0 3 ¦ 10~7
х = ¦
оТ4 оТ4
Используя радиационные функции для источника с температурой 5800 К,
получаем
%гТ = C • Ю-6) 5800 = 1,74 . Ю-2 м • К,
XJ = C. Ю-7) 5800 = 1,74 • Ю-3 м • К
и т = 0,92 @,977 - 0,033) = 0,868.
б) Когда источником излучения служит черное тело с температурой
300 К, имеем
%2Т » C • Ю-6) 300 = 9 • Ю-4 м • К,
%ХТ = C • Ю-7) 300 = 9 • Ю-5 м • К
и т = 0,92 A,686 • Ю-4 — 0) = 1,55 • Ю-4
в) Плотность потока проходящего через стекло солнечного излучения
будет равна
(^) °>868 ' 1100 = 955 Вт/м2.
г) Плотность потока проходящего через стекло излучения салона автомо-
автомобиля будет равна
(Т(?)салон = №)салон — (тоТ4)салон
= 1,55 . Ю-4 - 5,67 . Ю-8 . 3004 = 0,0712 Вт/м2.
Каждый, кто входил в автомобиль после его стоянки на солнцепеке, мо-
может оценить этот результат. Переднее стекло пропускает 87% солнечного из-
излучения в салон и практически не пропускает излучение в противоположном
направлении. Характеристики стекла, обеспечивающие пропускание большого
процента коротковолнового солнечного излучения и блокирование пропуска-
пропускания низкотемпературного и инфракрасного излучения, приводят к так назы-
называемому парниковому эффекту. Он объясняет, как может получать тепло ин-
интерьер автомобиля или парник от солнца даже в холодный зимний день,
Излучение 281
Закон Кирхюфа, который был ранее выведен для интеграль-
интегральных свойств, можно также вывести для монохроматических
свойств:
аЛ = ех. F.27)
Монохроматическая форма закона Кирхгофа не ограничена
условием теплового равновесия. Таким образом, монохромати-
монохроматическая излучательная и поглощательная способности тела рав-
равны, даже если поверхности, которые вносят вклад в падающее
на тело излучение, находятся не при одной температуре.
Понятие серого тела
Понятие серого тела сильно упрощает расчеты излучения.
Серое тело — это поверхность, монохроматические свойства ко-
которой постоянны для всех длин волн. Если поверхность серая, то
е^ s*= const,
(fy ss* Const.
Другие монохроматические свойства, такие, как пропуска-
тельная и отражательная способности, для серого тела также
постоянны.
Интегральная поглощательная способность для серого тела
определяется следующим образом:
F-28)
Это означает, что интегральная и монохроматическая погло-
{Цательные способности серой поверхности равны. Можно вы*
вести подобные выражения и для других свойств серого тела,
а именно
в = вь, р = ря, т = тх. F.29)
Если применить к серому телу закон Кирхгофа в форме урав*
нения F.27), то получим
«A, = ev
Подставляя сюда выражения F.28) и F.29), приходим к заклЮ*
чению, что для серой поверхности
а = е. F.30)
Интегральные излучательные и поглощательные способности
Для серого тела равны, даже если тело не находится в тепловом
Равновесии с окружающей средой. Это важная характеристика
282 Глава в
серого тела. Если известна излучательная способность серого
тела на одной длине волны, известны также интегральные излу-
излучательная и поглощательная способности поверхности.
Понятие серого тела является идеализированным, поскольку
серые тела на практике не существуют. Типичные монохрома-
0,2
0,5 1 2 3 4 5 6
Длина волны Я, мкм
а
1,0
o,s
0,6
0,4
0,2
0,5 1 2 34 5 б
Длина волны Я, мкм
б
Рис. 6.7. Монохроматические излучательная и поглощательная способности
некоторых реальных поверхностей:
а—диэлектрики; б—электропроводники; /-—огнеупорная глина (белая); 2—кирпич (белый);
3—штукатурка; 4 — полированный алюминий; 5—анодированный алюминий; ff—полиро-
ff—полированная медь.
<ч
4
. /
1
ч-
\
—
—
/
/
/.
тические излучательйые и поглощательные способности некото-
некоторых реальных поверхностей показаны на рис. 6.7. Даже если
поведение реальных поверхностей только приближенно соответ-
соответствует поведению серых поверхностей, расчеты излучения, осно-
основанные на приближении серого тела, дают удовлетворительные
результаты. Если монохроматические свойства сильно изменя-
изменяются, интегральные свойства могут быть приближенно представ-
представлены делением электромагнитного спектра на части, в пределах
которых свойства можно считать постоянными. Этот процесс
Излучение 283
показан ка рис. 6.8, где представлены монохроматическая излу-
чательная способность реальной поверхности и аппроксимирую-
аппроксимирующее ее распределение, используемое для оценки интегральной
излучательной способности. В обозначениях величин, представ-
представленных на рис. 6.8, можно следующим образом выразить инте-
интегральную излучательную способность поверхности:
dk
¦ ГЕЬ(О->ХЖТ)
+ 2L of*
, rEb@->XsT) ' Eb(Q->K2T)-\
"Г «3 [ oT4 aT4 J •
где для оценки членов в скобках можно использовать радиа-
радиационные функции, приведенные в табл. 6.1.
Рис. 6.8. Метод определения интегральных свойств для несерой поверхности.
i-^свойство реальной поверхности; 2—аппроксимирующее распределение.
Рис. 6.7, б иллюстрирует другой момент, связанный с радиа-
радиационными свойствами материалов. Монохроматические излуча-
гельная и поглощательная способности полированного и аноди-
анодированного алюминия сильно отличаются друг от друга, даже
если материал один и тот же в обоих случаях. Так как излуче-
излучение поглощается и испускается в пределах очень тонкого слоя
на поверхности, радиационные свойства в основном определя-
определяется состоянием поверхности материала. В результате окисные
с«лои, покрытия, загрязнения поверхности, такие, как масло или
смазка, и общее состояние поверхности, например чистота обра-
обработки, могут сильно влиять на радиационные свойства.
Интегральная излучательная способность ряда конструк-
конструкционных материалов представлена в табл. I1.VIII. 1—П.УШ.З.
284 Глава б
Материалы классифицированы в соответствии с обработкой их
поверхности. Можно заметить большие изменения в свойствах
в зависимости от состояния поверхности материалов.
Направленные радиационные свойства
До сих пор мы предполагали, что радиационные свойства
являются функциями только длины волны и условий, характе-
характеризующих поверхности приемника и излучателя. Дальнейшее
0,Н 0,12 0,10 0,08 0,06 0,04 0,02 0 0,02 0,04 0,06 0,08 0,10 0,12 0,14
е €
40°,
60°,
40*
60'
1,0 0,8 0,6 0,4 0,2 0 0,2 0,4 0,6 0,8 1,0
6
Рис. 6.9. Направленная излучательная способность некоторых реальных по-
поверхностей [6J.
а—электропроводники, б—диэлектрики; /—полированный никель; 2—тусклый никель;
3—мокрый лед; 4—дерево; 5—стекло; 6—бумага; 7—глина; 8—окись меди; 9 — окись
алюминия.
усложнение связано с учетом зависимости свойств от направле-
направления, в котором излучение падает на поверхность или покидает
ее. Свойства, которые описывают угловые изменения, называ-
называются направленными свойствами. Направленные излучательные
способности нескольких реальных поверхностей приведены на
рис. 6.9 в полярных координатах. Угол 9 — это угол между нор-
нормалью к поверхности и направлением излучения с поверхности.
Направленная излучательная способность для электропро-
электропроводных материалов характерна тем, что для больших углов б
Излучение 285
она выше, чем для малых. Следовательно, проводник будет
испускать больше излучения по касательной, чем по нормали
к поверхности. Иначе ведут себя диэлектрики. Они испускают
больше излучения в направлениях, близких к нормали, тогда
как при увеличении Э до 90° их излучательная способность па-
падает до нуля.
Перед тем как установить соотношение между направлен-
направленными и интегральными свойствами, следует рассмотреть две ве-
величины. Первая величина — телесный угол, который является
= dA cos в
Нормаль к
Нормаль к dAxr
Рис. 6.10. Телесный угол.
мерой угла в стереометрии. Рассмотрим элементарную пло-
площадку dA (рис. 6.10), которая стягивает элементарный телес-
телесный угол da) в точке О. Телесный угол — это безразмерная вели-
величина, определяемая как нормальная проекция dA, деленная на
квадрат расстояния между точкой О и проектируемой площад-
площадкой. Телесный угол do по определению равен
dA.. dA cos 8
Телесный угол измеряется в стерадианах, сокращенно ср.
Можно заметить подобие между плоским и телесным угла-
углами. Плоский угол стягивается нормальной проекцией линии, де-
деленной на расстояние до этой линии. Плоский угол безразмерен
и измеряется в радианах. Угол в 2я рад стягивается замкнутой
линией, например окружностью. Число стерадиан в угле, огра-
ограниченном замкнутой поверхностью, например сферой, может
определено интегрированием уравнения F,31) по сфере.
286 Глава 6
Согласно рис. 6.11, в сферическом угле будет содержаться сте-
стерадиан
«*=$*»= J^= \ \ ^уе^Ф,4п. F.32)
сф сф ф=0 6=0
Вторая величина, которая должна быть введена при обсуж-
обсуждении направленных свойств, — это интенсивность излучения,
г sin в d<p
Рис. 6.11. К определению телесного угла, стягиваемого сферой.
которая определяется как энергия излучения, испускаемого в
единицу времени, в единицу телесного угла, на единицу площади
Интенсивность излучения
п 1F, <р)
Излучающая площадка dA
Телесный угол d(O
Рис. 6.12. Интенсивность излучения.
поверхности, перпендикулярной направлению переноса излуче-
излучения. Интенсивность излучения обозначается символом /. Со-
Согласно рис. 6.12, интенсивность излучения определяется следую-
следующим образом:
Излучение 287
где через q" обозначена, как и в других главах, энергия в еди-
единицу времени на единицу площади. Единица интенсивности
Вт/(м2-ср).
Если известно распределение интенсивности, то интегрирова-
интегрированием уравнения F.33) по полусфере можно определить плот-
плотность потока излучения, покидающего плоскую поверхность:
? = ?" = J /(8,<p)cos8rf®. F.34)
полусф
Подстановка результатов для dco при использовании уравнения
F.32) дает
2л я/2
Е= ^ ^ /(8, q>)sin9cos8rf8d<p. F.35)
Уравнение F.35) нельзя проинтегрировать, если неизвестно
распределение интенсивности по углам 8 и ср. Простейший вид
распределения интенсивности по углам — постоянная интенсив-
интенсивность^ Поверхность, которая излучает с постоянной интенсив-
интенсивностью по всем углам, называется диффузной поверхностью или
иногда поверхностью, подчиняющейся закону косинусов Лам-
Ламберта, поскольку энергия излучения, покидающая его диффуз-
диффузную поверхность в данном направлении, изменяется пропорцио-
пропорционально косинусу угла между этим направлением и нормалью
к поверхности. Поэтому для диффузной поверхности
/(8, ф) = const,
и плотность потока излучения диффузной поверхности будет
равна
2я я/2
J j sin9cos8rf8rf<p===:rt/. F.36)
Черная поверхность является также диффузной, потому что,
если бы она не излучала с одинаковой интенсивностью по всем
направлениям, она не характеризовалась бы максимальной энер-
энергией излучения при данной температуре. Поэтому плотность
потока излучения черного тела и интенсивность его излучения
связаны уравнением F.36):
Еь = я1ь. F.37)
Направленные радиационные свойства не могут быть опре-
определены через плотность потока излучения, поскольку плотность
потока излучения не зависит от направления. Направленные ра-
радиационные свойства должны определяться через интенсивность
излучения. Например, направленная излучательная способность
288 Глава в
е (9, ф) определяется как интенсивность излучения, испущенного
поверхность^ в направлении, определенном углами 8, ср, делен-
деленная на интенсивность излучения черного тела в том же самом
направлении:
8F, ф) = /(9, Ф)//ь. F.38)
Интегральная излучательная способность поверхности была
определена уравнением F.18) в виде
8 = Е/ЕЬ. F.39)
Если поверхность недиффузная, интенсивность ее излучения яв-
является функцией направления. Подставляя уравнение F.35) в
числитель и уравнение F.37) в знаменатель, приходим к выра-
выражению
2л я/2
\ [ I @, ф) sin 8 cos 9 dB dq>
±i2
H = je±i=2 _ . F.40)
Далее, подставляя из уравнения F.38) интенсивность излу-
излучения, получаем связь между интегральной и направленной из-
лучательными способностями:
2л я/2
e = -i- ^ С 8(9, <p)sin9cos9d9tfq>. F.41)
ч
Если направленная излучательная способность не зависит от
угла ф, то направленные свойства становятся подобными пока-
показанным на рис. 6.9. Когда е зависит только от 9, интегрирование
уравнения F.41) дает
Я/2
е=^=2 \ e(9)sin9cos9rf9. F.42)
eio
Пример 6.4. Направленная излучательная способность окисленной меди
Может быть приблизительно описана выражением
t F) =* 0,70 cos G.
Определить количество энергии излучения, испускаемого й единицу времени
поверхностью окисленной меди площадью 0,5 м2 при температуре 800 К.
Решение. Интегральный поток энергии излучения, испущенного поверх-
поверхностью, равен
q -= ЕА т вЕьЛ
где е — интегральная излучательная способность поверхности. Направленная
излучательная способность связана с интегральной по формуле F.42):
Т -14 I*2
\ 0,70 cos' в sin G dQ =*= —-^- cos3 8 .
о
Излучение 289
Подставляя пределы интегрирования, получим
8=1,4/3 = 0,467.
Поток энергии излучения будет тогда равен
q = еЛоТ4 = 0,467. 0,5 .5,67 • Ю-8.8004 = 5422 Вт.
Направленные поглощательная1), отражательная и пропу-
скательная способности зависят от распределения интенсивности
как падающего, так и исходящего (эффективного) излучения.
Эти направленные свойства относятся к двунаправленным свой-
свойствам, т. е. для определения этих направленных свойств должны
быть указаны оба угла. Двунаправленные свойства рассматри-
рассматриваются в работах [7, 8].
Интенсивность
падающего
излучения
Равномерно
распределенная
интенсивность
отраженного
излучения
Интенсивность
падающего
излучения
Интенсивность
отраженного
излучения
Рис. 6.13. Предельные случаи отражающих поверхностей,
а—диффузный отражатель; б—зеркальный отражатель.
Для упрощения расчетов радиационного обмена введены два
типа отражающих поверхностей, соответствующих двум предель-
предельным случаям. Первый — диффузно отражающая поверхность.
Эта поверхность отражает отдельный падающий луч так, что его
энергия имеет одну и ту же интенсивность для всех углов отра-
отражения. Когда поверхности отражают диффузно, нет необходи-
необходимости следить за каждым отраженным лучом по мере его отра-
отражения от каждой поверхности, поскольку, отражаясь, луч теряет
свою индивидуальность. Поэтому предположение о диффузном
отражении поверхностей заметно упрощает расчеты радиацион-
радиационного обмена.
Другой тип отражающей поверхности — зеркальный отража-
отражатель. Подобно зеркалу, зеркальный отражатель изменяет на-
направление падающего луча так, что угол падения равен углу
отражения. Поверхность становится зеркальной, когда ее шеро-
шероховатость очень мала по сравнению с длиной волны падающего
излучения. Более детальное обсуждение зеркальных свойств к
Расчет теплообмена излучением между диффузно и зеркально
1) Направленная поглощательная способность зависит только от рас-
пРеделения интенсивности падающего излучения. — Прим. ред.
10 Зак. 487
290 Глава 6
отражающими телами можно найти в работах [9, 10]. Поведе-
Поведение диффузно и зеркально отражающих тел иллюстрируется на
рис. 6.13.
6.4. УГЛОВОЙ КОЭФФИЦИЕНТ ИЗЛУЧЕНИЯ
Чтобы рассчитать теплообмен излучением между двумя по-
поверхностями, необходимо определить долю полной энергии из-
излучения, исходящую от одной поверхности и достигающую не-
непосредственно вторую поверхность. Определим угловой коэффи-
коэффициент излучения F\.+2 как часть полной энергии излучения, исхо-
Интенсивность
излучения /j
Площадка йЛ
Площадка */Л
Рис. 6.14. Угловой коэффициент излучения.
дящую от поверхности 1 и достигающую непосредственно поверх-
поверхности 2. Угловой коэффициент является безразмерной величи-
величиной. В некоторых книгах его также называют коэффициентом
видимости, или конфигурационным коэффицентом, или коэф-
коэффициентом формы1).
Выражение для углового коэффициента можно получить из
рассмотрения рис. 6.14, где через dA\ обозначена излучающая
площадка, a dA2— приемная площадка. Поток энергии излуче-
излучения на единицу площади dA\, который исходит с dA\ и дости-
достигает dA2i определяется уравнением F.33):
COS
F.43)
Индекс 1 -> 2 означает, что излучение исходит от поверхности 1
и достигает поверхности 2. Символом d(Di->2 обозначен телесный
1) Автор использует термин коэффициент формы; в отечественной литера-
литературе используется термин угловой коэффициент, принятый в настоящем пе-
переводе. — Прим. перев.
Излучение 291
угол, стягиваемый площадкой dA2 над dA\. Подставляя выраже-
выражение F.31) для телесного угла, получаем
« // l\ COS Вх COS Э2 rfi42 /л . мч
aq = -2 F.44)
Допустим, что излучающая площадка диффузная, тогда интен-
интенсивность излучения, исходящего от dAu не зависит от направ-
направления. Полный поток излучения, исходящего от dAu должен
достичь полусферы, расположенной над dA\. Плотность этого
потока определяется выражением F.36):
F.45)
Угловой коэффицент излучения между двумя элементарными
площадками dA\ и dA2 будет равен отношению выражений
F.44) и F.45):
„ cos 9) cos 92 dA2 /д „дч
FdA^dA, = —2 . F.46)
Очень редко требуется определять теплообмен излучением
между двумя бесконечно малыми площадками, так как в боль-
большинстве случаев обмен излучением происходит между поверх-
поверхностями конечных размеров. Выражения для угловых коэффи-
коэффициентов для площадок конечных размеров можно получить ин-
интегрированием уравнения F.46) как по излучающей, так и по
приемной площадкам.
Угловой коэффициент между диффузной элементарной излу-
излучающей площадкой и приемной площадкой конечных размеров
определяется в виде
cos 8j cos Q2 dA2 (Cs A7X
—• F.47)
J J2
Аг А2
Угловой коэффициент между диффузно излучающей площад-
площадкой конечных размеров А\ и приемной площадкой конечных раз-
размеров А2 определяется в виде
j(( (dA^dA2) dAu F.48)
1 л! А
или
- «.— л, „ „
А. А,
W-ЯГ S S "***"*?*****. F.49)
Приведенные выражения для угловых коэффициентов F.46),
F.47) и F.49) справедливы лишь для диффузно излучающих
яоверхностей. Допущение диффузной поверхности — сильное
Упрощение, поскольку при этом условии угловой коэффициент
зависит только от геометрии и не зависит от распределения ин-
Тенсивности излучения,
292 Глава в
Если поменять индексы 1 и 2 в выражении F.49) местами,
предположив, что поверхность 2 излучающая, а поверхность 1
приемная, то получим
F.60)
Индекс А\-*А2 в уравнении F.49) заменен более простым ин-
индексом 1->2. Упрощенный индекс будет использован в даль-
дальнейшем в выражениях для угловых коэффициентов, он обозна-
обозначает угловой коэффицеинт между двумя диффузными площад-
площадками 1 и 2 конечных размеров. Со-
Соотношение F.50) называют соотно-
соотношением взаимности. Это соотноше-
соотношение может быть применено к любым
двум поверхностям i и /. Общая
форма соотношения взаимности
AiFt+, = AjFi+t. F.51)
Дополнительную связь между угло-
угловыми коэффициентами можно полу-
получить в случае, когда отдельные по-
поверхности образуют замкнутую си-
/-1,2,а стему. Рассмотрим три поверхности,
которые образуют замкнутую си-
Рис 6.15. Замкнутая система. стему (рис. 6.15). Все излучение,
исходящее, например, от поверх-
поверхности 1, должно непосредственно попасть на какую-либо из трех
поверхностей, образующих замкнутую систему: . .
["Энергия излуче- ["Энергия излуче-1
I ния, испущенного = I ния, падающего I +
^поверхностью 1 J Ьна поверхность Ы
ГЭнергия излуче-Т ГЭнергия излуче-"]
+ I ния, падающего + I ния, падающего . F.52)
l-на поверхность 2 J Ьна поверхность 3 J
Если все члены соотношения F.52) поделить на величину,
состоящую в левой его части, то каждый член станет угловым
коэффициентом:
+ Л->з = 1,0. F.53)
Это соотношение известно как соотношение замкнутости; в фор-
форме F.53) оно относится к трем поверхностям. В общем случае,
когда замкнутую систему образуют п поверхностей, соотноше-
соотношение имеет вид
п
= 1,0 /=1,2, ...,«. F.54)
Излучение 293
0,01
0,2
0,4 0,6 0,8 1
У/D
6 8 10
Рис. 6.16. Угловой коэффициент излучения для расположенных друг против
друга диффузных прямоугольников.
0,2
0,4 0,6 0,8 1
Z/X
6 8 10
рис. 6.17. Угловой коэффициент излучения для перпендикулярно расположен-
расположении относительно друг друга диффузных прямоугольников с общим ребром,
294 Глава 6
Член Fi+i необходимо включать в соотношение замкнутости,
когда поверхность / вогнутая. Такая поверхность может «ви-
«видеть» себя, и некоторая доля излучения, испущенного поверхно-
поверхностью, упадет на другую часть этой же поверхности. Если i-я по-
поверхность выпуклая или
плоская, то она не может
1,0
0,8
cs 0,6
0,4
0,2
/
ни
видеть себя; тогда
1
dlx
Рис. 6.18. Угловой коэффициент для распо-
расположенных друг против друга диффузных
дисков.
Соотношения взаимности
и замкнутости очень важ-
важны. При их применении к
задаче вычисления угло-
угловых коэффициентов часто
удается сэкономить вре-
время, избавившись от про-
проведения детального инте-
интегрирования.
Угловые коэффициен-
коэффициенты излучения для многих
поверхностей, встречающихся в инженерной практике, вычисле-
вычислены и представлены в графической форме. Некоторые угловые
коэффициенты представлены на рис. 6.16—6.18. Более подроб-
подробный перечень угловых коэффициентов приведен в монографиях
Гамильтона и Моргана [11], а также Зигеля и Хауэлла [12].
Алгебра угловых коэффициентов *)
Таблицы угловых коэффициентов можно использовать для
определения значений этих коэффициентов для гораздо боль-
большего класса геометрических форм, применяя метод, известный
как алгебра угловых коэффициентов. Допустим, нужно вычис-
вычислить угловой коэффициент F\+2 для поверхностей 1 и 2
(рис. 6.19). Угловой коэффициент F\ + представлен на графике
рис. 6.17, где поверхность 3 есть сумма поверхностей 2 и а.
Алгебра угловых коэффициентов означает просто сохранение
энергии, т. е. энергия излучения, исходящего от поверхности 1
(рис. 6.19) и достигающего поверхности 3, должна быть равна
сумме энергий излучений, исходящих от поверхности 1 и дости-
достигающих поверхностей, из которых составлена поверхность 3.
Поскольку Лз = А2 + Аа, условие сохранения энергии требует,
чтобы
Fi+z = Fx+a + Fi+2. F.55)
Как Fi-^, так и F\-+a представлены на рис. 6.17, следовательно,
F\-+2 можно определить из уравнения F.55).
1) В отечественной литературе более распространен термин поточная ал*
гебра. — Прим. перев,
Излучение 295
Если применить соотношение взаимности к каждому члену
соотношения F.55), то получим равенство
AzFz^i = AaFa^x + A2F2+U F.56)
которое означает, что полная энергия излучения, падающего на
поверхность 1 от поверхности 3, равна сумме энергий излучения
от поверхности а и 2, падающего на поверхность 1. Заметим,
Рис. 6.19.эАлгебра угловых коэффициен-
коэффициентов.
Рис. 6.20. Метод натянутых ни-
нитей.
что соотношение F.56) содержит площади, в то время как со-
соотношение F.55) их не содержит. В соотношении F.56) пло-
площади сохраняются, поскольку излучающие площадки не равны.
В соотношении F.55) площади сокращены, поскольку все излу-
излучающие площадки равны. Методика использования алгебры
угловых коэффициентов проиллюстрирована примерами в конце
этого раздела.
Метод натянутых нитей
Существует очень полезный и простой метод расчета угловых
коэффициентов для двумерных поверхностей, бесконечно про-
протяженных в одном направлении и характеризуемых идентично-
идентичностью всех поперечных сечений, нормальных к направлению бес-
бесконечной протяженности. Метод назван методом натянутых
нитей, его обоснование дано Хоттелем и Сэрофимом [13]!). На
Рис. 6.20 показаны две поверхности, удовлетворяющие указан-
указанным выше геометрическим ограничениям. Согласно этому
1) Метод натянутых нитей для расчета угловых коэффициентов был пред-
предложен в 1935 г. Г. Л. Поляком. — Прим. перев.
296 Глава 6
методу, угловой коэффициент F\-+2 равен сумме длин пересекаю-
пересекающихся нитей, натянутых между краями двух поверхностей, ми-
минус сумма длин непересекающихся нитей, деленной на удвоен-
удвоенную длину А\. Таким образом, угловой коэффициент Li->2 равен
Л->2 = 22-- [Ы + ~cb) — (ab + ей)]. F.57)
Пример 6.5. Определить угловой коэффициент Р\^2 Для указанной гео-
геометрии. Поверхности диффузны.
'¦Аа + Аи
К примеру 6.5.
Решение. Применяя принципы, отраженные в соотношениях F.65) и
F.56), получаем
V = AaFa-*b + A
получим
Комбинируя эти три уравнения и решая их относительно
= -д^ (i43F3-»4 ~ AaFa->4 " А
Уо крэфф^циенты в правой части этого уравнения представлены на гра-
графике рис. 6.17. Они имеют значения
: 0,19,
'¦ 0,32,
. 0,08,
= 0,19.
Затем можно определить
F 1
-1~
[50 • 0,19 - 20 . 0,32 - 50 • 0,08 + 20 • 0,19] = 0,097.
Это означает, что 9,7% излучения, .диффузно исходящего от поверхности 1»
дадает непосредственно на поверхность 2.
Излучение 297
Пример 6.6. Замкнутая система состоит из трех диффузных бесконечно
длинных плоскостей, поперечное сечение которых представляет собой прямо-
прямоугольный треугольник, как показано на рисунке. Определить угловые коэф-
коэффициенты ^ ^ ^ ^
г
Поверхность 1
Li s3m *
К примеру 6.6(а).
Решение. Двумерные поверхности бесконечно протяженны в направлении
нормали к плоскости рисунка, а площади всех поперечных сечений идентич-
идентичны, поэтому для определения Fi^,2 можно использовать метод натянутых
нитей.
К примеру 6.6F).
Слегка раздвинем две поверхности А\ и А2, чтобы яснее показать распо-
расположение нитей. Согласно соотношению F.57), угловой коэффициент /ri->2
определяется следующим образом:
Если две поверхности будут касаться друг друга, то точки а и Ь совпадут,
и тогда
аЬ = 0, ad = L2,
Угловой коэффициент будет равен
298 Глава 6
Подставляя длины, получим
Остальные угловые коэффициенты можно подсчитать, используя соотноше-
соотношения взаимности и замкнутости. Применяя соотношение замкнутости, полу-
получаем
Поверхность 1 плоская, поэтому Flmt>l=0. Тогда
F =1-F =1-1 = 1
Поскольку угловой коэффицент F{m^2 известен, можно использовать соотно-
соотношение взаимности для определения F2^x:
Г*->1~"А2 1 + 2~ 4 U;'
Применение соотношения взаимности к угловому коэффициенту Р\+з дает
F z=^Lp = — (lS\—jL9
6.5. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
МЕЖДУ ЧЕРНЫМИ ПОВЕРХНОСТЯМИ
В этом разделе будет изложен способ определения радиа-
радиационных тепловых потоков между черными поверхностями.
Практически удобно начать анализ теплообмена с черных по-
поверхностей, так как черная поверхность лишена усложняющей
особенности — отражения части падающей энергии. В следую-
следующем разделе будут рассмотрены серые поверхности и анализ
станет более сложным.
Приведенный ниже анализ основан на нескольких упрощаю-
упрощающих предположениях. Примем условия стационарными, а все
поверхности черными и изотермическими. Любая неизотермиче-
неизотермическая поверхность делится на части до тех пор, пока более мел-
мелкие поверхности не будут иметь приближенно постоянную тем-
температуру. Поверхности разделены средой, которая не испускает
излучения, а также не поглощает и не рассеивает излучения,
проходящего между черными поверхностями1). Наконец, при-
примем, что интенсивность излучения постоянна на каждой поверх-
поверхности и все поверхности — диффузные излучатели и отража-
отражатели. При этих допущениях справедливы выражения для угло-
угловых коэффициентов, выведенные в предыдущей части. Допуще-
Допущение диффузности поверхностей не ставит ограничений при рас-
рассмотрении только черных поверхностей, так как черное тело
всегда является диффузной поверхностью.
Такая среда называется диатермичеокой. — Прим. ред.
Излучение 299
При анализе переноса излучения важны определения раз-
различных видов тепловых потоков. Три наиболее важных тепловых
потока определяют следующим образом:
q . = поток энергии излучения, испущенного поверх-
">/ ностью / и поглощенного поверхностью /, F.58)
= результирующий поток энергии, которую нужно
подвести к поверхности / для поддержания ее
температуры постоянной2), F.59)
q _>= результирующий поток теплообмена излучением
*" между поверхностями i и /. F.60)
Далее будут приведены некоторые общие приемы расчета
этих потоков на примере простой геометрической системы, по-
показанной на рис. 6.21. Геометрическая система состоит из двух
Поверхность 1_%Я \ Поверхность 3
Темперагура Г^ЯЯ \_^-~---(окружающее
v пространство)
» Температура 7^=0 Н
» Поверхность 2
Температура
Рис. 6.21. Теплообмен излучением в системе из трех черных поверхностей.
черных плоскостей и третьей поверхности, представляющей со*
бой окружающее пространство. Эти три поверхности образуют
замкнутую систему. Две плоские поверхности имеют известные
температуры Т\ и Г2, а температура окружающего пространства
принята равной 0 К.
Таким образом, окружающее пространство не испускает из-
излучения на две плоскости, а излучение, которое, покидая любую
плоскость, попадает в окружающее пространство, никогда не
может вернуться ни на одну из этих плоскостей, поскольку оно
полностью поглотится черным окружающим пространством.
Рассматриваемая система поверхностей, будучи замкнутой,
обладает рядом полезных свойств. Анализ излучения в замкну-
замкнутой системе гарантирует учет излучения, поступающего со всех
направлений. Даже когда в задаче поверхности не образуют
пот ^ отечественной литературе используется понятие результирующего
вепх °Т повеРхности> определяющего энергию излучения, уносимого от по-
НОстЛ' что количественно то же самое, но имеет противоположный
— Прим. ред.
300 Глава 6
замкнутой системы, полезно построить воображаемые поверхно-
поверхности, дополняющие замкнутую систему.
Замкнутую систему можно образовать, проведя воображае-
воображаемые поверхности, которые стягивают отдельные твердые поверх-
поверхности. Каждой воображаемой поверхности придаются эквива-
эквивалентная температура и такие свойства, чтобы радиационные ха-
характеристики воображаемых поверхностей имитировали условия
действительной задачи. Например, допустим, что две относи-
относительно маленькие твердые поверхности расположены в большом
помещении, имеющем температуру Ts. Чтобы имитировать усло-
условия этой задачи, можно построить замкнутую систему из двух
твердых поверхностей плюс воображаемой поверхности между
этими двумя поверхностями, которая дополняет замкнутую си-
систему. Воображаемая поверхность заменит помещение, если ее
участие в радиационном теплообмене будет таким же, как и
помещения.
Геометрия задачи такова, что излучение, исходящее от двух
твердых поверхностей, которое уходит в окружающее простран-
пространство, имеет очень малую вероятность обратного отражения и
попадания на первоначально испустившую его поверхность. Сле-
Следовательно, большое помещение можно заменить воображаемой
черной поверхностью с эквивалентной температурой Ts. Черная
поверхность не отражает излучение обратно на излучатель и,
следовательно, ведет себя подобно большому помещению. Сооб-
Сообщение температуры Ts воображаемой черной поверхности также
обеспечивает точное воспроизведение энергии излучения, испу-
испускаемой помещением и падающей на две плоскости.
Поток энергии излучения, испущенного поверхностью 1
(рис. 6.21), которое падает на поверхность 2 и ею поглощается,
определяется по формуле
ЛЛ-А» F.61)
а поток энергии излучения, испущенного поверхностью 2 и по-
поглощенного поверхностью 1, — по формуле
« F-62)
Результирующий поток теплообмена излучением между поверх-
поверхностями 1 и 2 определяется разностью F.61) и F.62);
А- F-63)
Если применить свойство взаимности к уравнению F.63), по-
получим
4Л (?*) F-64)
Уравнение F.64) можно записать в общей форме закона Ома
как разность потенциалов, деленную на тепловое сопротивле-
Излучение 301
ние. Общее выражение для результирующего потока теплооб-
теплообмена излучением между поверхностями i и / будет следующим:
^=ж?г- F-65)
Тепловое сопротивление обусловлено тем, что не все излучение,
испущенное поверхностью i, достигает поверхности /. Сопротив-
Сопротивление 1/AiFi^i называют поэтому геометрическим сопротивле-
сопротивлением. Потенциалами в тепловой цепи служат плотности потоков
черного излучения обеих поверхностей, и определяются они
через температуру поверхности по закону Стефана — Больцмана.
Если применить уравнение F.65) ко всем трем поверхностям,
образующим замкнутую систему, то можно построить частичную
тепловую цепь (рис. 6.22). Результирующий поток энергии, ко-
который необходимо сообщить поверхности 1, чтобы поддержи-
поддерживать ее температуру установившейся, равен разности между
потоком энергии испущенного поверхностью 1 излучения и по-
потоком энергии, поглощенной поверхностью 1 излучения. Поток
результирующего теплообмена, сообщаемый поверхности 1, обо-
обозначен в выражении F.59) (<7i)pe3.
Поток энергии излучения, испущенного поверхностью 1,
равен
а поток энергии излучения, поглощенного поверхностью 1,—
это поток энергии излучения, падающего на нее от поверхно-
поверхности 2,
^2->Л2. F.67)
От поверхности 3 излучение не поступает, так как она имеет
температуру абсолютного нуля; никакого излучения не может
попасть и с поверхности 1, поскольку она плоская и не может
«видеть» себя. Результирующий поток энергии излучения для
поверхности 1, (<7i)pes, таким образом, будет определяться раз-
разностью между выражениями F.66) и F.67):
Используя подобную процедуру, можно показать, что выраже-
выражение для (92)рез будет следующим:
(Чез-^-^^Л,- F-69)
величины (<7i)pe3 и (#2)рез могут быть включены в тепловую
Цепь на рис. 6.22. Поток теплообмена (<7i)pe3 — это количество
энергии, которую необходимо сообщить в единицу времени по-
поверхности 1 для поддержания ее температуры на постоянном
302 Глава б
уровне. Сообщаемая результирующая энергия может быть смо-
смоделирована электрическим источником напряжения, который
Рис. 6.22. Частичная тепловая цепь
для трех черных поверхностей, обра-
образующих замкнутую систему.
Рис. 6.23. Полная тепловая цепь для
трех черных поверхностей, образую-
образующих замкнутую систему.
подсоединен к потенциальному узлу, обозначенному Еьк. До-
Добавление величин (#i)pe3, (#2)рез и (<7з)рез завершает построение
электрической цепи (рис. 6.23)
для геометрической системы
(рис. 6.21).
Тепловая цепь является
удобным и компактным сред-
средством выражения потоков теп-
теплообмена. В узле цепи, обозна-
обозначенном Еьг (рис. 6.23), из усло-
условия сохранения энергии в ста-
стационарных условиях следует
равенство нулю суммы всех
тепловых потоков:
Это уравнение эквивалентно
закону Кирхгофа для тока,
применяемому к стационарно-
стационарному состоянию в электрических
^пях. Подставляя уравнение
(о.Ь5) в оба слагаемых в пра-
вой части уравнения F.70),
применяя соотношения взаим-
взаимности и замкнутости и, наконец, полагая Еь3 = 0, получим ре-
результат, представленный уравнением F.68). Аналогичное усло-
условие сохранения энергии в точке тепловой цепи Еъ, можно при-
привести к уравнению F.69). Кроме того, анализируя цепь, изобра-
Рис. 6.24. Тепловая цепь для четы-
рех черных поверхностей, образую-
щих замкнутую систему,
Излучение 303
женную на рис. 6.23, можно определить следующее:
Мреэ + Ырез + Ырез = 0, F.71)
?2*3 = Л/2+А,. FJ2)
qlts = A{F{^Ebx. F.73)
Методику анализа радиационных задач путем построения тепло-
тепловых цепей можно распространить на произвольное число черных
поверхностей, образующих замкнутую систему. Например, теп-
тепловая цепь для четырех таких черных поверхностей показана
на рис. 6.24. Применение закона Кирхгофа для тока дает
-li (?i*/) (^=1.2,3,4),
F.74)
где член с / = i не включают в сумму. Применение закона Ома
к цепи (рис. 6.24) требует, чтобы
UA.F
F.75)
Огнеупорные поверхности
Иногда встречаются такие условия, когда результирующий
тепловой поток к отдельной поверхности излучающей системы
равен нулю:
В этих условиях поверх-
поверхность называют огнеупор-
огнеупорной, или переизлучающей,
поверхностью1). Если огне-
огнеупорная поверхность пере-
передает тепло только излуче-
излучением, а теплообмен другими
видами переноса пренебре-
пренебрежимо Мал, ЭНерГИЯ Падаю-
б
реэ
(Огнеупорная поверхность)
Щего излучения, ИЛИ облу- Рис. 6.25. Тепловая цепь для двух чер-
ченность, должна быть рав- ных поверхностей и огнеупорной поверх-
На энергии Эффективного ИЗ- ности, образующих замкнутую систему,
лучения поверхности2).
Можно легко преобразовать тепловую цепь, чтобы учесть
любое число огнеупорных поверхностей, просто приняв (^)рез =
= 0 для каждого узла цепи, представляющего собой огнеупор-
огнеупорную поверхность. Такой узел тогда становится точкой с плаваю-
1) Более строго такую поверхность следовало бы назвать адиабатиче-
адиабатической. — Прим. перев.
2) В отечественной литературе по теплообмену такие поверхности назы-
называют теплоизолированными. — Прим. ред.
304 Глава б
щим потенциалом, для которой плотность потока излучения чер-
черного тела, а следовательно, и ее температура определяются
температурами всех других поверхностей. Тепловая цепь для
двух черных поверхностей (поверхности 1 и 2) и огнеупорной
поверхности (поверхность 3), образующих замкнутую систему,
показана на рис. 6.25.
Температура огнеупорной поверхности может быть опреде-
определена из тепловой цепи с учетом того, что
или
\/A2
F.77)
Уравнение F.77) можно использовать для определения Г3, если
известны температуры Т\ и Т2 и задана геометрическая система.
Пример 6.7. Черная пластина с площадью поверхности 2 м2 зарыта в
землю так, что верхняя ее поверхность находится на одном уровне с поверх-
поверхностью земли. Нижняя поверхность пластины теплоизолирована. Верхняя по-
поверхность омывается воздухом при температуре 300 К, при этом коэффи-
коэффициент конвективной теплоотдачи от воздуха к пластине равен 10 Вт/(м2Х
Хград). Рассчитать равновесную температуру пластины для двух условий:
а) пластина излучает при ясном ночном небе с эффективной радиационной
температурой неба 100 К; б) пластина излучает при облачном ночном небе
с эффективной температурой неба 250 К.
/ \
/ Черная Г.-300Н \
/ пластина, hc = 10 Вт/(м2 • град)
I Ч \ \
К примеру 6.7 (а)
-AAV
К примеру 6.7 (б).
Решение. Система показана на рисунке. Пластина обозначена как по-
поверхность 1, небо — как поверхность 2. Небо можно принять черным телом,
так как оно будет отражать ничтожную долю излучения обратно на пла-
пластину и будет поглощать практически все излучение, испускаемое пластиной.
Излучение 305
образом, излучающая система представляет собой замкнутый объем,
образованный двумя черными поверхностями, между которыми происходит
теплообмен. Тепловая цепь для этих двух черных поверхностей, показанных на
стр. 304, является простейшей (рис. 6.23).
Все излучение, исходящее от пластины, должно попасть на небо, так что
При этом предполагается, что пластина расположена на открытой площадке
и на нее не падает излучение от окружающих зданий, деревьев и т. п.
Результирующий тепловой поток в пластину обусловлен конвективной
теплоотдачей от воздуха, поэтому
(<7i)pes = hcAi (Г*, — ГО, F.78)
и в соответствии с тепловой цепью тепловой поток, передаваемый пластине
конвекцией, должен быть равен результирующему тепловому потоку излуче-
излучением от пластины к небу, или
VI/рез 1^2 1 1 ->2 V Ь\ Ьг)
Подставляя уравнение F.78) и используя для плотности потока излучения
закон Стефана — Больцмана, получим
Tt). F.79)
а) При 7*2 = ЮО К из уравнения F.79) получим
10 C00 - Т{) = 5,67 • 10"e (Г4 - ЮО4),
решение относительно Т\ дает
Тх = 270,2 К = - 3 °С.
б) При Гг = 250 К, решая уравнение F.79), получим для равновесной
температуры пластины
71! = 284,8 К —11,6 °С.
Этот результат показывает, что поверхность, обращенная к небу в холодную
ясную ночь, может принять температуру ниже точки замерзания воды. Во-
Водяной пар из воздуха может затем сконденсироваться на поверхности и за-
замерзнуть, образуя слой инея, даже если температура воздуха выше точки
замерзания.
Слой облаков увеличивает эффективную температуру неба и будет пре-
препятствовать образованию инея. Окружающие здания или деревья, которые
закрывают видимость неба в ясную ночь, дают такой же эффект, как и воз-
возрастание эффективной температуры неба. Это объясняет, почему на перед-
переднем стекле автомобиля на открытой стоянке утром может быть слой инея, а
на стекле автомобиля, стоящего около здания или под деревьями, инея мо-
может и не быть, хотя температура воздуха одинакова в обоих случаях.
Пример 6.8. Две части космического корабля можно приближенно пред-
представить расположенными друг против друга прямоугольниками, как пока-
показано на рисунке. Прямоугольники черные и поддерживаются при температу-
температурах 500 и 400 К внешними средствами. Энергия падающего излучения от дру-
других источников пренебрежимо мала, а обратные стороны обеих поверхностей
теплоизолированы. Рассчитать: а) результирующий поток энергии, который
нужно сообщить более теплой поверхности для поддержания ее температуры;
б) результирующий поток энергии, который нужно сообщить более холодной
поверхности для поддержания ее температуры; в) результирующий поток
306 Глава 6
энергии, который нужно сообщить окружающему пространству для поддер-
поддержания его температуры; г) результирующий поток теплообмена между двумя
поверхностями и окружающим пространством.
Изоляция
Поверхность!
rj = 500K
Окружающее
пространство
Поверхность 3
К примеру 6.8 (а).
Решение. Тепловая цепь задачи идентична показанной на рис. 6.23. По-
Поскольку излучение, падающее от окружающего пространства, пренебре-
пренебрежимо мало, окружающее пространство можно заменить черной поверхностью
при О К, которая образует вместе с двумя прямоугольниками замкнутую си-
систему.
1
К примеру 6.8 (б).
Значения трех потенциалов цепи будут следующими:
Ьх = оТ\ - 3,543 • 103 Вт/м2; Ebi - оТ\ « 1,451.103 Вт/м2;
0.
Три угловых коэффициента этой тепловой цепи можно определить, используя
данные рис. 6.16, соотношение замкнутости и симметрию геометрической си-
системы:
• 0,52;
а) Результирующий поток энергии к поверхности 1 определяется урав-
уравнением F.68):
8 I3»543 •
0.52 A,451. 103)]=*2,231. 104 Вт.
Это означает, что поверхность 1 следует подогревать внешним источником
энергии мощностью 22,31 кВт, чтобы поддерживать ее температуру при
500 К.
Излучение 307
б) Выражение для результирующего потока энергии к поверхности 2
дается уравнением F.69):
Поверхность 2 следует охлаждать, отводя от нее поток энергии 3,13 кВт,
чтобы сохранить ее температуру равной 400 К. Отрицательный знак у
(<7г)рез означает, что результирующий поток энергии на поверхности 2 на-
направлен от поверхности или что ее следует охлаждать внешними средствами.
в) Рассмотрение тепловой цепи дает следующее выражение для резуль-
результирующего потока энергии к окружающему пространству:
в _ AXFX+Z (Ebi + ЕЬя) = - 8 • 0,48 C,543 • 103 + 1,451.103) — - 1,918 • 104 Вт.
Окружающее пространство следует охлаждать, отводя от него поток
энергии 19,18 кВт, иначе его температура будет увеличиваться.
В качестве проверки этих расчетов заметим, что результирующий тепло-
теплообмен всех трех поверхностей должен быть равен нулю, как это следует из
уравнения F.71):
* Мрез + Ырез + Ырез - 2,231 • 10* - 3,13 . 103 - 1,918 • 10* - 0.
г) Результирующие потоки теплообмена между поверхностями, согласно
уравнению F.64), будут равны
В качестве заключительной проверки решения следует убедиться, что
6.6. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
МЕЖДУ СЕРЫМИ ПОВЕРХНОСТЯМИ
Расчеты теплообмена в системе, включающей серые поверх-
поверхности, более сложны, чем в системе, состоящей только из черных
поверхностей. При падении излучения на серую поверхность
часть излучения отражается и оно должно учитываться в ба-
балансе энергии. В предыдущем разделе отраженное излучение
не учитывалось, поскольку там рассматривались только черные
поверхности.
Сначала выведем общие уравнения для стационарного тепло-
теплообмена между серыми поверхностями на примере трех серых
изотермических поверхностей, образующих замкнутую систему,
которая заполнена радиационно нейтральной (диатермической)
средой. Все поверхности изотермические, и падающее на каж-
каждую поверхность излучение распределено равномерно. Серые
308 Глава 6
поверхности считаются диффузными, и поскольку они серые, то
на основании закона Кирхгофа излучательная способность по-
поверхности равна ее поглощательной способности. Кроме того,
предполагается, что поверхности непрозрачны, так что уравне-
уравнение F.13) дает
а = е=1— р. F.80)
Если над серой поверхностью поместить воображаемую пло-
плоскость (рис. 6.26), то для обеспечения баланса энергии этой
плоскости в стационарных условиях результирующая энергия,
Падающее излучение G Отраженное излучение pG
Собственное излучение еЕ^
Воображаемая плоскость
Рис. 6.26. Баланс энергии на воображаемой плоскости около серой поверх-
поверхности.
которую необходимо сообщить серой поверхности для поддер-
поддержания ее температуры, должна быть равна разности между
энергией исходящего с поверхности и энергией падающего на
нее излучения.
Излучение, исходящее от серой поверхности, называется эф-
эффективным излучением1). Плотность потока эффективного из-
излучения обозначается символом /, она равна сумме плотностей
потоков собственного излучения, испущенного единицей поверх-
поверхности, и отраженного излучения:
F.81)
Результирующий тепловой поток от серой поверхности, обо-
обозначенной индексом /, будет равен разности тепловых потоков
эффективного и падающего излучений на поверхность:
(?*)« = Л* (/!-<?*)¦ F.82)
Подстановка уравнений F.80) и F.81) в уравнение F.82) дает
= :да7- F.83)
Если записать уравнение F.83) в форме закона Ома, то его
знаменатель представит собой тепловое сопротивление, которое
находится между двумя потенциалами Еъ. и /. (рис. 6.27). Со-
Сопротивление pi/^iAi обусловлено тем, что серая поверхность
!) Автор использует термин светимость.—Прим перев.
Излучение 309
л-
отражает часть падающего излучения, и его можно назвать
поверхностным сопротивлением. Заметим, что поверхностное
сопротивление равно нулю для черной поверхности, для которой
Если поверхностное сопротивление Еи ^W Л
добавить в тепловую цепь, образован-
образованную для черных поверхностей (рис.
6.23), то цепь можно изменить так,
чтобы она учитывала теплообмен меж-
между серыми поверхностями. Основная
структура цепи для черных поверхно-
поверхностей может оставаться неизменной,
если мы рассматриваем серые поверх-
поверхности, так как сопротивления являют-
являются геометрическими сопротивлениями,
зависящими только от геометрии и не
зависящими от свойств поверхностей.
Полная тепловая цепь для теплообмена излучением между
тремя серыми поверхностями, образующими замкнутую систему,
показана на рис. 6.28.
Рис. 6.27. Поверхностное со-
сопротивление для серой по-
поверхности.
Рис. 6.28. Тепловая цепь для трех серых поверхностей, образующих замкну-
замкнутую систему.
Тепловая цепь является чрезвычайно удобным средством
анализа радиационных задач. Применяя закон Ома к каждому
сопротивлению и закон Кирхгофа для тока в каждой точке вет-
ветвления цепи, можно в небольшой диаграмме сконцентрировать
большое число уравнений, связывающих тепловые потоки и
свойства. Примененние тепловых цепей проиллюстрировано на
примерах в конце этого раздела.
310 Глава 6
В предыдущем разделе было введено понятие огнеупорной
поверхности, для которой (^)рез = 0. Если принять равным
нулю результирующий тепловой поток в тепловой цепи на
рис. 6.27, то можно видеть, что для огнеупорной поверхности
Jt = Ehr F.84)
Кроме того, если (<?,)рез = 0 в уравнении F.82), то для огнеупор-
огнеупорной поверхности
/, = Gf. F.85)
Из уравнений F.84) и F.85) следует, что для огнеупорной
поверхности плотности потоков падающего излучения, эффек-
эффективного излучения и черного излучения равны между собой.
Поверхность, для которой плотности потоков падающего на нее
и исходящего от нее излучения равны, можно рассматривать
как идеально отражающую поверхность. Таким образом, огне-
огнеупорная поверхность — просто поверхность, которая изменяет
направление падающего излучения, ничего не поглощая из него.
Огнеупорная поверхность примет равновесную температуру,
определяемую температурой других поверхностей, так что плот-
плотность потока черного излучения для огнеупорной поверхности
равна плотности потока эффективного излучения и падающего
излучения на поверхности.
Две серые поверхности, образующие замкнутую систему
Часто приходится иметь дело с задачами, которые включают
только две серые непрозрачные диффузные поверхности, обра-
образующие замкнутую систему. Тепловая цепь для этого случая
показана на рис. 6.29. Приведем несколько примеров геометри-
геометрических систем, удовлетво-
удовлетворяющих допущениям двух
поверхностей, образующих
замкнутую систему.
1) Две бесконечно боль-
большие параллельные пластины.
Рис. 6.29. Тепловая цепь для двух серых ^Г
поверхностей, образующих замкнутую альн-ых цилиндра,
систему. 3) Две сферы, одна за-
замыкающая другую.
4) Небольшое тело, окруженное второй замкнутой поверх-
поверхностью.
Для тепловой цепи (рис. 6.29) этих геометрических систем
должны выполняться следующие условия:
(Ч- F-86)
й (<7l)»e3== P./M. + l/Vjl + PV'Ha • F>87)
Излучение 311
Если рассматриваются две бесконечные параллельные пластины
одинаковой площади, то А\ = А2 и F\-*2 = 1,0. Подстановка этих
результатов в уравнение F.87) дает
Еъ —Еь
Если две поверхности, образующие замкнутую систему, — бес-
бесконечно длинные цилиндры, причем цилиндр 1 охватывает ци-
цилиндр 2, то F\+2 =1,0 и выражение для (<7i)pe3 будет сле-
следующим:
Уравнение F.89) также применимо для случая двух сфер, когда
сфера 1 полностью охватывается сферой 2.
Если поверхность 1 представляет собой небольшое серое
тело, которое полностью охватывается большой замкнутой по-
поверхностью 2, то А\/А2~*0 и уравнение F.89) можно еще более
упростить:
«¦>* =
Три серые поверхности, образующие замкнутую систему
Когда замкнутая система состоит из трех серых поверхно-
поверхностей, выражения для потоков радиационного теплообмена зна-
чительнЬ сложнее, чем для двух поверхностей, но они полу-
получаются аналогичным способом. Пусть две серые непрозрачные
э
(Огчеупорная поверхность)
0
Рис. 6.30. Тепловая цепь для двух серых поверхностей и огнеупорной поверх-
поверхности, образующих замкнутую систему.
поверхности и одна огнеупорная поверхность образуют замкну-
замкнутую систему. Тепловая цепь для этого случая показана на
рис. 6.30, где поверхность 3 выбрана в качестве огнеупорной по-
поверхности. Из условия сохранения энергии следует, что
8=-Ыреа. F-91)
312 Глава 6
Кроме того, результирующий тепловой поток к поверхности 1
равен разности потенциалов Еъх — Еь2, деленной на полное со-
сопротивление между этими потенциалами:
где Яжв — сопротивление, эквивалентное геометрическому со-
сопротивлению между точками J\ и /2, соединенному параллельно
с двумя геометрическими сопротивлениями между ]\ и /з и
между /2 и /3. Эквивалентное сопротивление будет
[ 1 \
Подстановка F.93) в F.92) и упрощение дают следующее вы-
выражение:
;
е2
Пример 6.9. Длинная серая металлическая труба отводит нагретую жид-
жидкость от одного технологического агрегата к другому. Труба имеет внешний
диаметр 0,8 м и излучательную способность поверхности 0,5. Труба окружена
второй серой трубой с внутренним диаметром 1,0 м и излучательной способ-
способностью 0,3. Пространство между трубами вакуумировано для уменьшения
тепловых потерь от жидкости. Внутренняя труба имеет температуру 550 Kt
внешняя 300 К.
Оценить теплопотери от жидкости на 1 м длины трубы. Определить сни-
снижение потерь тепла от жидкости, если внутреннюю трубу покрыть серой
краской, имеющей излучательную способность 0,15.
Решение. Пространство между двумя трубами вакуумировано, поэтому
единственным видом потерь энергии жидкостью является теплоперенос излу-
излучением между внутренней и внешней поверхностями труб. Две серые непро-
непрозрачные концентрические трубы образуют замкнутую систему, поэтому для
определения тепловых потерь от жидкости можно использовать уравнение
F.89).
Обозначим поверхность внутренней трубы 1, а поверхность внешней тру-
трубы 2, тогда результирующий тепловой поток от жидкости определяется по
формуле
„ (?l)pe3Ebj — Eb2
8j A2 82
где Ebx = oT\ = 5,67 • 10~8 • 5504 = 5187 Вт/м2
10"8 • 3004 = 459 Вт/м2,
Излучение 313
и площадь поверхности внутренней трубы на единицу длины
ndi = 0,8л;.
Подстановка этих значений в выражение для (<7i)Pe3 дает результирую-
результирующий тепловой поток на единицу длины
/ 0,8я E187-459)
(?1)рез
:3073 Вт/м.
¦ 0,5/0,5 + 0,8 @,7/0,3)
Если 8i заменить на 0,15, то потери тепла от жидкости составят
Вт/м,
или снизятся на 54,7%.
Пример 6.10. Серый круглый нагреватель диаметром 10 см расположен
параллельно второму серому круглому приемнику на расстоянии 5 см от него,
как показано на рисунке. Мощность нагревателя 300 Вт. Тыльные стороны
нагревателя и приемника теплоизолированы. Конвекция от обеих поверхно-
поверхностей пренебрежимо мала. Нагреватель и приемник расположены в большом
помещении, поддерживаемом при 350 К. Нагреватель имеет излучательную
способность 0,8. Рассчитать: а) температуру нагревателя; б) температуру
приемника; в) результирующий тепловой поток излучением к окружающему
пространству; г) результирующий поток теплообмена излучением между на-
нагревателем и приемником.
Теплоизолировано
Теплоизолировано
10см
Поверхность 1,
нагреватель
К примеру 6.10 (а).
Поверхность 2,
приемник
Решение. Заданная в задаче информация включает результирующий теп-
тепловой поток от нагревателя и температуру окружающего пространства.
Если обозначить нагреватель как поверхность 1, приемник как поверх-
поверхность 2 и окружающее пространство как поверхность 3, то
(?l)pe3 = 30° Вт»
Г3= 350 К.
Температура приемника, а также результирующий тепловой поток в при-
приемник являются неизвестными величинами. Однако в задаче задано, что при-
приемник теплоизолирован и конвекция к нему пренебрежимо мала. Внешняя
энергия к приемнику не подводится, поэтому результирующий тепловой поток
излучением для него должен быть равен нулю. Приемник — это просто огне-
Упорная поверхность, для которой
(^)рез = °>
и из уравнения F.84) следует
314 Глава 6
Поскольку окружающее пространство велико по сравнению с размерами
нагревателя и приемника, оно ведет себя как черное тело, поэтому
8з = 1,0
Wpeaf JQ
К примеру 6.10 (б).
Тепловая цепь для этой задачи подобна показанной на рис. 6.28, за исключе-
исключением того, что поверхностное сопротивление для окружающего простракства
равно нулю, так как оно черное, и результирующий тепловой поток к поверх-
поверхности 2 равен нулю. Угловые коэффициенты могут быть получены с по-
помощью рис. 6.18:
Площадь нагревателя и приемника равна
Ах = Л2 = яг2 = я • 0,052 = 7,85 • 10~3 м2.
Плотность потока излучения из окружающего пространства составляет
ЕЬз « оТ\ = 5,67 • 10~8-3504 = 851 Вт/м2.
Обращаясь к схеме тепловой цепи, можно видеть, что из условия сохранения
энергии на поверхности 2 следует, что
Л-'2 >2~ЕЬ,
а для поверхности 1
Единственными неизвестными в приведенных выше уравнениях являются J\
и /а. Решая совместно эти уравнения, получим
Jx = 45 134 Вт/м2,
/2 = 17 234 Вт/м2.
Излучение 315
а) Температуру нагревателя можно определить из выражения
ИЛИ I 1 :
N v • L. v J
|!/4
Г f ! 2iE—-^300 + 45 134 1
V 0,8. 7,85 .Щ-У
L 5.67-10""8 J
:991K=718eC.
5,67-10 M
б) Температуру приемника можно определить по плотности потока чер«
ного излучения приемника:
Г, = (±)Ш = ( 172348У/4 = 743 К = 470'G
\oj V5.67-10 V
> в) Результирующий тепловой поток излучения к окружающему простран-
пространству, определяемый из тепловой цепи, будет равен
4^ ^ А^ (% ')
= 7,85.10" • 0,63 B • 851 - 45 134 - 17 234) = - 300 Вт#
Для проверки этой величины сумма результирующих потоков для трех
поверхностей должна быть равна нулю, если полная энергия системы сохра-
няетая:
(?.)рез - (?2)рез + Ырез = 300 + 0 - 300 = 0 Вт.
г) Результирующий поток теплообмена излучением между нагревателем
и приемником будет равен
q{ + 2 = А{Рх+2 (]х - /2) =» 7,85 ¦ 10" • 0,37 D5134 - 17234)«- 81,0 Вт.
6.7. МАТРИЧНЫЕ МЕТОДЫ
Если радиационная задача содержит более четырех или пяти
отдельных поверхностей, усилия и время, необходимые для опре-
определения плотностей тепловых потоков и температур поверхно-
поверхностей методами, описанными в предыдущих разделах, становятся
слишком большими, так что оправдано получение решения с
помощью вычислительной машины. С увеличением числа по-
поверхностей необходимо привести определяющие уравнения в си-
систематический вид и применять стандартные математические
методы для их решения. Одним из простейших, но и наиболее
мощных методов, который можно использовать для анализа
задач по излучению такого типа, является матричный метод.
Мы видели, что уравнения, связывающие тепловой поток
с температурой поверхности, например уравнения F 65), F.74)
316 Глава 6
и F.83), являются алгебраическими уравнениями. Если урав-
уравнения для плотности теплового потока можно привести к ма-
матричному виду, то для определения неизвестных параметров
можно применить стандартные матричные методы, такие, как
обращение матрицы. Когда число поверхностей, входящих в за-
задачу, становится большим, обращение матрицы может быть
запрограммировано для ЭВМ и решения, которые обычно тре-
требуют большого количества времени при ручном счете, можно
получить очень быстро.
Матричные уравнения, используемые в случае, когда на по-
поверхностях заданы температуры, несколько отличаются от ма-
матричных уравнений, используемых, когда на поверхностях за-
заданы плотности тепловых потоков. Обсудим отдельно эти оба
случая, рассмотрев сначала задачу с поверхностями, темпера-
температуры которых известны.
Поверхности с заданными температурами
Первой задачей в матричном методе является приведение
определяющих уравнений к матричной форме. Допустим, что
температуры всех поверхностей известны и нужно найти резуль-
результирующие плотности тепловых потоков на всех поверхностях.
Все поверхности — непрозрачные, серые, и распределения энер-
энергии излучения по поверхностям равномерные. Поверхности обра-
образуют замкнутую систему, и каждая поверхность изотермична.
Поверхности, которые не изотермичны, необходимо разбивать
на меньшие площадки до тех пор, пока разделенные площадки
не будут близки к изотермичным. Одно из отличительных преи-
преимуществ матричного метода при использовании его для решения
на ЭВМ состоит в том, что увеличение числа поверхностей в
задаче незначительно увеличивает объем работы, необходимой
для решения задачи.
Для простоты выведем уравнения в матричной форме, рас-
рассматривая только три поверхности, образующие замкнутую си-
систему. Соответствующая тепловая цепь для этого случая пред-
представлена на рис. 6.28. Результирующую плотность потока для
каждой из трех поверхностей можно получить, комбинируя урав-
уравнения F.82) и F.83). В результате для поверхности 1 получим
Падающее на поверхность 1 излучение G\ обусловлено энер-
энергией эффективного излучения, исходящего от поверхности 1
(если она вогнута и может «видеть» себя) и от двух других по-
поверхностей, которые образуют замкнутую систему:
h + A*F 3W3. F.96)
Излучение 317
Применяя соотношения взаимности к уравнению F.96), по-
получим
Gi =Fx + iJi + Л->2/2 + Л->з/з. F.97)
Подстановка уравнения F.97) в уравнение F.95) дает зависи-
зависимость
которая может быть представлена в виде
= ±-Ebl. F.99)
Аналогичные выражения можно написать для поверхностей 2
и 3. Они будут следующими:
-^) /
з =77^- FЛ00)
~^) h=-^Ebi. F.101)
Уравнения F.99) — F.101) можно записать в матричной форме:
AJ = B. F.102)
Для общего случая п поверхностей, образующих замкнутую
систему, А есть яХ я-мерная матрица, имеющая вид
F.103)
в то время как J и В —столбцевые матрицы, состоящие из п
элементов:
F.104)
F.105)
Анализируя уравнения F.99) — F.101), можно видеть, что вне-
Диагональные элементы матрицы А имеют вид
«*/ = —Fi+i ' С Ф \)> F.106а)
318 Глава 6
а диагональные члены — вид
а„-1-/>„ + -?. F.1066)
Элементы матрицы В будут следующими:
FЛ07)
Если в замкнутой системе имеется черная поверхность, то
для нее уравнение F.99) упрощается. Для черной поверхности
Jt = Ebv F.108)
Следовательно, элементы матриц А и В для черного тела запи-
записываются в виде
Я// = 0 AФ1), F.109а)
а« = 1Д F.1096)
Ьл = Еъй. F.110)
Если температуры всех поверхностей известны, задача опреде-
определения результирующих плотностей тепловых потоков на всех
поверхностях решается следующим образом. Сначала вычис-
вычисляют элементы матриц А и В. Для всех нечерных поверхностей
элементы матрицы А определяют по уравнению F.106). Если
i-я поверхность черная, тогда i-й ряд элементов матрицы А
определяется уравнением F.109). Заметим, что все элементы
этой матрицы известны, поскольку определены геометрия и
свойства поверхностей.
Элементы столбцевой матрицы В определяются уравнением
F.107) для всех нечерных поверхностей и уравнением F.110),
если поверхность черная. Элементы матрицы В зависят от
свойств поверхностей и известных температур.
После того как определены матрицы А и В, обращают ма-
матрицу А. Обратной матрице А будет матрица С
A-J = C =
cncn"'<
F.111)
в которой все элементы — известные величины. Элементы J мож-
можно теперь определить, решая уравнение F.102);
J = CB, F.112)
Излучение 319
которое можно записать в развернутом виде следующим
образом:
h ^ + ^ + • • • + Clrfin
F.113)
СппЬп.
После того как из уравнения F.113) определены значения плот-
плотности потока эффективного излучения на всех поверхностях,
можно воспользоваться уравнением F.95) для определения
значений плотностей результирующих тепловых потоков для
всех поверхностей. Плотность результирующего теплового по-
потока для нечерной поверхности i будет равна
Если поверхность i черная, выражение для плотности резуль-
результирующего потока получится из совместного рассмотрения
уравнений F.95) и F.97) »):
<*&. =/| - О, = /, - t Ft+iJi. F.115)
Поверхности с заданной плотностью результирующего
теплового потока
Допустим, что температуры всех поверхностей, которые об-
образуют замкнутую систему, неизвестны, но плотность результи-
результирующего теплового потока на всех поверхностях задана. Урав-
Уравнение F.98) можно преобразовать в матричную форму с извест-
известными величинами, исключив неизвестные Еь и включив извест-
известные (<7)ре3- В результате для поверхности 1 замкнутой системы,
состоящей из трех поверхностей, получим
A-Л+.)Л + (-^2Н2+(-Л.»з)'з==№з- F.П6)
Аналогичные выражения можно записать для других двух по-
поверхностей.
Для задачи, в которой температуры не известны, а задана
плотность результирующего теплового потока на каждой по-
поверхности, уравнение F.116) означает, что внедиагональные
элементы матрицы А в матричном уравнении F.102) будут
следующими:
ati^-Fi+t {1ф})у F.117а)
а элементы диагонали будут равны
т ati = l-Ft+i. F.1176)
1) Сл|?ует заметить, что уравнение F.115) справедливо и для случая,
когда поверхность i нечерная. — Прим. перев.
320 Глава 6
Элементы матрицы В имеют вид
.. F.118)
При такой форме записи элементы обеих матриц А и В из-
известны.
Как только определены элементы А и В, получаем следую-
следующее решение. Выполняя обращение матрицы А, в результате
получаем матрицу С. Элементы матрицы плотности потока эф-
эффективного излучения определяются уравнением
J = CB.
Температуры поверхностей можно определить из уравнения
F.95):
или
Г Р*
i L
Если i-я поверхность черная (р/ = 0), то выражение для ее
температуры упростится:
Описанная выше методика и уравнения также могут быть ис-
использованы в задачах со смешанными граничными условиями.
Когда температуры некоторых серых поверхностей известны, но
неизвестны плотности потоков, соответствующие строки в ма-
матрицах А и В записывают в форме уравнений F.106) и F.107)
соответственно. Плотность результирующего теплового потока
для каждой из этих поверхностей определяется уравнением
F.114). Если на поверхности известна плотность результирую-
результирующего потока, но неизвестна температура, то соответствующая
строка матриц А или В определяется уравнениями F.117) и
F.118) соответственно. Температура поверхности определяется
уравнением F.119).
Матричный метод является удобным и мощным средством
для решения задач радиационного теплообмена. Если в про-
программе численного расчета используют стандартную библио-
библиотеку подпрограмм для обращения матрицы, то задачи с боль-
большим числом отдельных поверхностей могут быть решены по
относительно простой программе.
Поскольку матричный метод крайне полезен для решения
радиационных задач, остановимся в дальнейшем на программе
расчета, основанной на матричном методе. Эта программа на-
написана на языке Фортран IV. Она является довольно общей, с
ее помощью можно рассчитывать либо температуру поверхно-
поверхности, либо результирующую плотность теплового потока для
Излучение 321
каждой отдельной поверхности в замкнутой системе. Программа
составлена так, что позволяет анализировать большое число
изотермических серых непрозрачных поверхностей, образую-
образующих замкнутую систему. Если задана температура поверхности,
то программа позволяет определить плотность результирую-
результирующего потока на поверхности. Если известна плотность результи-
результирующего потока, программа позволяет рассчитывать темпера-
температуру поверхности.
Для обращения матриц в программе используется подпро-
подпрограмма MATINV. Текст подпрограммы MATINV приведен в
приложении IV. В подпрограмму MATINV вводят матрицу А
и число поверхностей N, образующих замкнутую систему, и
получают матрицу С, обратную матрице А.
Ниже приведен текст программы решения радиационных за-
задач матричным методом (стр. 322).
Программа достаточно общая и может быть применена к
целдму ряду радиационных задач. Пользователь может в точ-
точности переписать программу и добавить подпрограмму MATINV
из приложения IV. Вместо подпрограммы MATINV для обра-
обращения матрицы А можно использовать подпрограммы из мест-
местных библиотек.
Входные данные программы и порядок, в котором они долж-
должны располагаться в массиве исходных данных, следующие:
N—целочисленная величина равна общему числу поверх-
поверхностей, образующих замкнутую систему.
L*—целочисленная величина равна числу поверхностей,
имеющих известные температуры и неизвестные плот-
плотности результирующих тепловых потоков.
Для всех N. поверхностей должны быть известны либо темпе*
ратуры, либо плотности результирующих тепловых потоков, т. е.
0^.L^.N. Когда L меньше N, программа учитывает, что для
N— L поверхностей заданы плотности результирующих тепло-
тепловых потоков и не известны температуры.
F(I, J) —двумерный массив из N2 угловых коэффициен*
тов, расположенных в следующем порядке:
, n+\i » nn
EMIS (I) — одномерный массив из N излучательных спо*
собностей для N поверхностей.
ТA) —одномерный массив из L значений температуры
для L поверхностей, имеющих заданные тем-
температуры.
QNET (I) — одномерный массив из N—L значений плотно-
плотностей результирующих тепловых потоков для
N—L поверхностей, имеющих заданные плот-
плотности результирующих тепловых потоков»
11 Зак. 487
322 Глада в
Текст
программы численного решения радиационных задач
матричным методом
1
1
20
40
50
60
80
DIMENSION AE0,50),BE0),CE0l50),EMISE0),FE0,50),GE0),JE0)v .
QNETE0)JE0)
REALJ
SIGMA -5.67E- 08
READ , N.L
M-N-L
LL-L+1
READ , ((F(I,K),K -1 ,N),I -1 ,N),(EMIS(I),I -1 ,N)
(T@,l -1 ,L).(QNET(I),I - LL.N)
DO20I-1.N
DO20K-1.N
A(I,K)--F(I,K)
DO60I-1.L
IF (EMIS(I).EQ. 1.0) GO TO 40
A0.I).-1.0 - Ffl.l) + EM IS(I)/A.0 - EMIS(I))
GO TO 60
DO50K-1.N
A(l,K)-0.0
CONTINUE
DO80I-1.L
B(I)-SI.GMA*T(I)**4
IF (EMIS(I) .EQ. 1.0) GO TO 80
B(l) - EMIS(I)*B(I)/A.0 - EMIS(I))
GO TO 80
CONTINUE
DO85I-LLN
B(I)-QNET(I)
85 CONTINUE
CALL MATINV (A.N.C)
DO100I-1.N
SUM» 0.0
DO90K-1.N
00 SUM-SUM-*-C(l,K)*B(K)
100 J(I)*SUM
DO120l*1,N
SUM «0.0
DO110K-1,N
110 SUM«SUM + F(I,K)M(K)
120 G(I)=SUM
DO125I-1.L
125 QNET(I)-J(I)-G(I)
DO140l = LL,N
If (EMIS(I) .EQ. 0.0) GO TO 130
T(I) - ((A.0 - EMIS(I))*QNET(I)/EMIS(I) + J(I))/SIGMA)* *0 25
GO TO 140
130 T(l)-(J(l)/SIGMA)**0.25
140 CONTINUE
WRITE F,150)
150 .FORMAT AH ,20X,'RADIATION ANALYSIS BY MATRIX METHOD',//
1 IX/SURFACEMX.'EMISSIVITY'^X/TEMPERATURE.SX.QNET'.eX,
Z.'RADIOSITY'^X.'IRRADIATION'./^X.'CKELVINX.SX/CW/SQ.M)'
3 i6X,((W/SQ.M)i,4X,i(W/SQ.M)tI/)
WRITE F,160) (I,EMIS(I),T(I),QNET(I)>J(I),G(I)>I«1,N)
160 FORMAT DX,I2,6X,F5.315XIF7.2J4X,E11.5,2Х,Е11.5,2X,E11.5)
STOP
END
Излучение 323
Программа предполагает, что поверхности пронумерованы та-
таким образом, что первые L поверхностей имеют известные тем-
температуры, а остальные N—L поверхностей — известные плотно-
плотности результирующих тепловых потоков. Например, предполо-
предположим, что замкнутая система состоит из 20 поверхностей и
только 5 из них имеют известные температуры. Остальные
15. поверхностей имеют известные результирующие плотности
тепловых потоков. Для этого случая N = 20 и L = 5. Первые
5 поверхностей имеют известные температуры. Поверхности с
6 по 20 имеют известные результирующие плотности тепловых
потоков.
В приведенной ниже таблице символы, использованные в
программе, сопоставляются с обозначениями, использованными
в тексте. Кроме того, в таблице приведены единицы, которые
использованы в программе.
Символы,
1
Символ
A(I, J)
ВЦ)
С (I, J)
EMIS (I)
F (I, J)
G(I)
J(I)
L
N
QNET (I)
SIGMA
T(I)
использованные в радиационной программе
ач
bi
cij
e*
G(
J l
(<7/)рез
a
Tt
Определение
— элементы матрицы А, определенные уравне-
уравнением F.103)
— элементы матрицы В, определенные уравне-
уравнением F.105)
— элементы матрицы С, определенные уравне-
уравнением F.111)
— излучательные способности всех N поверхно-
поверхностей
— угловые коэффициенты (всего N2 значений)
— плотность потока падающего излучения для
всех поверхностей
— плотность потока эффективного излучения
для всех поверхностей
Число поверхностей с известными темпера-
температурами @ ^ L ^ N)
Общее число поверхностей, образующих зам-
замкнутую систему
— плотность результирующего теплового потока
для N — L поверхностей
= 5,67-Ю-8
— температуры L поверхностей
Единицы
Вт/м2
—
—
—
Вт/м2
Вт/м2
—
—
Вт/м2
Вт/(м2Х
ХК4)
к
_ Программа используется в двух следующих примерах. За-
Задачи иллюстрируют матричный метод и, кроме того, показы-
вают, как можно использовать программу для анализа более
сложных задач.
Пример 6.11. Длинный конструкционный элемент космического корабля
имеет прямоугольное поперечное сечение, как показано на рисунке. Телеме-
рические измерения показывают, что температуры на четырех поверхностях;
324 Глава 6
Тх = 200 К, Т2 = 300 К, Тг = 400 К, Т4 = 500 К. Излучательные способно-
способности четырех поверхностей: ei = 0,2, е2 == 0,3, е3 = 0,4 и е4 = 0,5. Рассчитать
плотность результирующего радиационного теплового потока для каждой из
четырех поверхностей,
IT
# 0,2 м
I i
К примеру 6.11.
Решение. В открытом космосе конвекция незначительна, кроме того, мы
будем предполагать, что теплопроводность между элементами пренебрежимо
мала. Поэтому единственным способом теплопередачи между четырьмя по-
поверхностями является перенос тепла излучением.
Определение тепловых потоков для четырех поверхностей требует сов-
совместного решения четырех алгебраических уравнений. Для нахождения плот-
плотностей тепловых потоков будем использовать только что описанную програм-
программу на языке Фортран IV.
Входными величинами программы должны быть все 16 угловых коэффи-
коэффициентов. Угловые коэффициенты для прямоугольной геометрической системы
даны на рис. 6.16:
F Fz->\ = 0,82.
Из симметрии конструкции имеем
а из условия замкнутости
Поэтому
^4 = ^+2= уA-^з) = 0,09.
Кроме того,
^ ^ ^ ^ °
Из условий взаимности и симметрии
^^^^^Л^@.09) =0,45,
1,0 — 0,45 — 0,45 = 0,Ь
Из угловых коэффициентов формируется массив Ft+f.
/«1
/«З
i-4
У-1
0
0,45
0,82
0,45
0,09
0
0,09
0,10
У-3
0,82
0,45
0
0,45
j -4
0,09
0,10
0,09
0
Заметим, что из соотношения замкнутости следует, что сумма элементов каж-
каждой строки массива должна быть равна единице,
Излучение 325
Входная информация программы имеет вид
Входная информация программы для
примера 6.11
4,
0 0.
0.45,
0.82,
0.45,
0.20,
200.,
4
0.09,
0.0.
0.09,
0.10,
0 30,
300.,
0.82,
0.45,
0.0,
0.45,
0.40,
400.,
0.09
0.10
0,09
0.0
0.50
500.
Первая строка содержит две целочисленные величины. Первая величина
N— общее число поверхностей, образующих замкнутую систему. Вторая ве-
величина L — число поверхностей с заданными температурами. В этой задаче
обе величины равны 4.
Следующие 4 строки входных данных содержат 16 значений угловых ко-
коэффициентов, представленных выше. В приведенном тексте программы
операторы ввода не снабжены метками операторов FORMAT, так как соответ-
соответствующие операторы FORMAT должны быть предусмотрены при использо-
использовании программы в зависимости от числа размещаемых в одной строке угло-
угловых коэффициентов. При этом пользователь должен обратить внимание на
то, чтобы величины вводились в следующем порядке:
Следующая строка входных данных содержит излучательные способности
четырех поверхностей: ei, e2, вз, е4.
Последняя строка входных данных содержит температуры в Кельвинах
для L поверхностей. Значение L вводится в первой строке. В данной задаче
L = ?, и поэтому температуры четырех поверхностей вводятся в последова-
последовательности Ти Т% Г3, Т4. Число значений температур всегда должно быть
равно L.
Когда N = L, как в настоящей задаче, просто опускают величины (<7)р'ез
поскольку поверхностей с заданными значениями плотностей результирующих
тепловых потоков нет. Когда L = О, опускают значения температур и по-
последнюю строку заполняют N значениями (<7)рез«
Выходная информация программы представлена ниже.
Выходная информация программы для примера 6.11
По-
верх-
верхность
1
2
•з.
4
Изл.
способ н.
.200
.300
.400
.500
Расчет излучения
Температура,
К
200.00
300.00
400.00
500.00
матричным методом
QNET,
Вт/м2
-.26190Е + 03
-.26654Е + 03
.82610Е + 02
.11630Е + 04
Эфф.изл.,
Вт/м2
.11383Е + 04
.10812Е + 04
.13276Е + 04
.23808Е + 04
Падающее изл.,
Вт/м*
.14002Е + 04
/I3477E + 04
.12450Е + 04
.12177Е + 04
В выходной информации программы приводятся номер каждой поверх-
поверхности, ее излучательная способность, температура, плотность результирую-
результирующего теплового потока, эффективного и падающего потоков излучения. В вы-
выходных данных указаны также единицы измерения каждой величины.
Можно легко проверить результаты счета, сравнивая величины (^/)рез
с расчетом по уравнению F 82),
326 Глава 6
Пример 6.12. Две длинные серые параллельные пластины расположены
друг против друга, как показано на рисунке. Поверхности пластин диффуз-
диффузные, пластины непрозрачные. Они изготовлены из материала с плохой тепло-
теплопроводностью, и поэтому поперек обеих пластин существует значительный
градиент температуры. Между краями обеих пластин расположены идеально
отражающие (огнеупорные) поверхности. Излучательная способность верхней
поверхности 0,6, нижней поверхности 0,2.
В нашем анализе задач теплообмена всегда предполагается, что каждая
поверхность является изотермической. Чтобы удовлетворить этим условиям,
разделим обе пластины на три полосы равной ширины. Полосы пронумеро-
пронумерованы от 1 до 6, как показано на рисунке, а отражающие поверхности имеют
номера 7 и 8. Измерения локальной температуры на шести участках поверх-
поверхностей дали следующие результаты: Т\ = Г3 = 400 К; Т2 = 500 К; Г4 =
= Т6 = 700 К; П = 800 К.
Определить полные плотности результирующих тепловых потоков для
верхней и нижней пластин и температуры двух крайних огнеупорных пластин.
Серая поверхность
?=0,6
Огнеупорная
поверхность
Серая поверхность
?=0,2
К примеру 6.12.
Решение. *В этой задаче замкнутая система состоит из восьми поверхно-
поверхностей и объем работы, требуемый для решения задачи «вручную», оправды-
оправдывает использование программы для ЭВМ. Сначала следует представить исход-
исходные данные в форме входной информации для программы, как это описано
в примере 6.11. Поверхности пронумерованы, начиная с поверхностей, имею-
имеющих известные температуры. Последние номера присвоены поверхностям с из-
известными плотностями результирующего теплового потока. Огнеупорные по-
поверхности 7 и 8 имеют нулевые плотности результирующих потоков:
Используя алгебру угловых коэффициентов, соотношения взаимности и замк-
замкнутости, а также данные, приведенные на рис. 6.16, получим следующий мас-
массив угловых коэффициентов /*W/.
1-1
' = 2 ,
i-3
i = 4
i-5
i«7
1-8
7=1
0
0
0
0,42
0,20
0,05
0,29
0,04
7-2
0
0
0
0,20
0,42
0,20
0,09
0,09
7 = 3
0
0
0
0,05
0,20
0,42
0,04
0,29
7-4
0,42
0,20
0,05
0
0
0
0,29
0,04
7=5
0,20
0,42
0,20
0
0
0
0,09
0,09
7 = 6
0,05
0,20
0,42
0
0
0
0,04
0,?9
7-7
0,29
0,09
0,04
0,29
0,09
0,04
0
0,16
7-8
0,04
0,09
0,29
0,04
0,09
0,29
0,16
0
Излучение 327
Входная информация программы представлена ниже.
Входная информация программы для примера 6.12
8,
0.0,
0.0,
0.0.
0.42,
0.20,
0.05,
0.29,
0.04,
0.6.
400.,
0.0.
6
0.0,
0.0.
0.0,
0.20,
0.42.
0.20,
0.09,
0.09.
0.6.
500.,
0.0
0.0,
0.0,
0.0.
0.05,
0.20.
0.42,
0.04,
0.29,
0.6,
400.,
0.42,
0.20,
0.05.
0.0,
0.0.
0.0.
0.29,
0.04,
0.2,
700..
0.20,
0.42,
0.20,
0.0,
0.0.
0.0.
0.09.
0.09,
0.2,
800.,
0.05.
0.20,
0.42,
0.0.
0.0.
0.0.
0.04,
0.29.
0.2.
700.
0.29,
0.09,
0.04,
0.29,
0.09.
0.04.
0.0.
0.16,
0.0,
0.04
0.09
0.29
0.04
0.09
0.29
0.16 ,
0.0
0.0 *
Первая строка содержит два целых числа. Первое — общее число по-
поверхностей, второе — число поверхностей с известными температурами. Сле-
Следующие восемь строк содержат величины F^f Десятая строка данных содер-
содержит перечисленные по порядку излучательные способности восьми поверхно-
поверхностей. В предпоследней строке перечислены по порядку заданные температуры.
В последней строке приведены известные плотности результирующих тепловых
потоков для двух отражающих поверхностей.
Выходная информация программы имеет вид
Выходная информация программы для примера 6.12
Расчет излучения матричным методом
Поверх-
Поверхность
1
2
3
4
б
6
7
в
Изл.
способн.
.600
.600
.600
.200
.200
.200
0.000
0.000
Температура
К
400.00
500.00
400.00
700.00
800.00
700.00
547.11
547.11
QNET, Эфф.изл.,
Вт/м* Вт/м2
-.28190Е+04 .33307Е + 04
-.19153Е + 04 .48205Е + 04
-.28190Е + 04 .33307Е + 04
.18814Е + 04 .60872Е + 04
.37905Е + 04 .80619Е + 04
.18814Е + 04 .60872Е + 04
0. .50802Е+04
0. .50802Е + 04
Падающее изл.,
Вт/м*
.61498Е + 04
.67353Е+04
.61498Е + 04
.42060Е + 04
.42713Е + 04
.42060Е+04
.50802Е+04
.50802Е + 04"
Полная результирующая плотность теплового потока к верхней поверх*
ности равна
@)?ез == (- 0,28190 - 0,19153 - 0,28190) 104 = - 7553 Вт/м2.
Полная результирующая плотность теплового потока к нижней поверх*
ности равна
@)?з =± @,18814 + 0,37905 + 0,18814) 104 = 7553 Вт/м2.
Заметим, что сумма полных' результирующих плотностей теплового потока по
всем поверхностям равна нулю, что удовлетворяет условию сохранения энер-
энергии для всей замкнутой системы. Результат счета на ЭВМ показывает ожи-
ожидаемую симметрию для поверхностей 1 и 3 и для поверхностей 4 и 6. Тем-
Температуры обеих огнеупорных поверхностей равны
Г7 = Г8= 547,11 К,
что еще раз подтверждает условие симметрии для двух торцевых поверхно^
стей.
328 Глава 6
6.8. ПЕРЕНОС ИЗЛУЧЕНИЯ
В ПОГЛОЩАЮЩИХ ПРОПУСКАЮЩИХ СРЕДАХ
В предыдущих разделах считалось, что все излучающие по-
поверхности непрозрачны, так что падающее на поверхность из-
излучение не проходит через эту поверхность. Такое допущение
сильно упрощает расчеты теплообмена излучением. Многие ве-
вещества, имеющие важное значение в технике, такие, как стекла,
некоторые пластмассы и газы, являются прозрачными, и по-
поэтому следует расширить анализ радиационных задач, чтобы
Пове хность 1 учесть перенос энергии излуче-
сероенепрозрачноЛвердоетело,^, тх нием через такие материалы.
Z^^^^^^ Для развития общего мето-
метода рассмотрим простой случай
теплообмена излучением меж-
Поглощающий ду ДвуМЯ бОЛЬШИМИ СерЫМИ
пропускающий серый газ, непрозрачными ПОВерхНОСТЯ-
9 ми, разделенными пропускаю-
щей средой. Допустим да-
лее> ч/0 частично поглощаю-
серое непрозрачное твердое тело, 62,Т2 ЩаЯ Среда ЯВЛЯетСЯ ИЗОТер-
о< _ . мической и серой и не отра-
Рис. 6.31. Две бесконечные пластины, пяляюшего ичлучения
разделенные поглощающим пропу- ^ает падающего излучения,
екающим газом. Это допущение, в частности,
верно применительно к га-
газам, хотя стекла и другие частично прозрачные твердые тела
могут отражать часть падающего излучения. Геометрия задачи
показана на рис. 6.31. Две твердые поверхности названы по-
поверхностями 1 и 2, в то время как свойства пропускающего газа
отмечены индексами g. Допустим, что свойства и температуры
двух поверхностей известны и что нужно определить потоки
теплообмена излучением между этими тремя материалами и
температуру газа.
Закон Кирхгофа, примененный к пропускающему газу, тре-
требует, чтобы
<** —V
и, так как отражательная способность среды равна нулю,
г8 = 1 — ag = 1 — eg.
Выведем уравнения для теплообмена излучением между по-
поверхностями, применяя электроаналогию для данной задачи.
Выражения для потока эффективного излучения от поверхно-
поверхности 1 [уравнение F.81)] и результирующего теплового потока
[уравнение F.82)] не зависят от присутствия газа, поэтому вы*
ражение для результирующего потока от поверхности 1 опре-
Излучение 329
деляется уравнением F.83):
Поток падающего на поверхности 1 излучения равен сумме по-
потока эффективного излучения, идущего от поверхности 2 через
газ, и потока собственного излучения газа:
Gx=xgJ2 + zgEbg. F.121)
Выражение для (<7i)pe3 имеет вид
foiU-iM'i-Gi)- FЛ22)
Подстановка F.121) в F.122) дает
- Мрез = Аг (JX - Tg/2 — ZgEbg),
что можно преобразовать к виду
<* W - 4 К d - '«> + •. (Л - \)\ - -fesT"+JW •
F.123)
Аналогичный вывод для поверхности 2 дает следующее выра-
выражение для (<7г)рез:
Уравнения F.120), F.123) и F.124) составляют основу для
элеетроаналогии рассматриваемой задачи. Соответствующая
схема показана на рис. 6.32.
Рис. 6.32. Электрический аналог схемы, показанной на рис. 6.31.
Тепловая цепь на рис. 6.32 показывает, что плотность по-
потока черного излучения Еь газа является плавающим потен-
потенциалом, и поэтому температура газа представляет собой функ-
функцию его свойств, а также температур и свойств двух непроз-
непрозрачных поверхностей. Фактически газ является огнеупорным
(адиабатическим) веществом, поскольку к нему не подводится
внешняя энергия, или (^pe3)g = 0.
330 Глава 6
Пример 6.13. Две большие серые пластины (ei = 0,2, Т\ = 600 К; ег ==
= 0,6, Т2 = 800 К) разделены серым газом (ег = 0,1). Рассчитать: а) плот-
плотность результирующего теплового потока к поверхности 1 и плотность ре*
зультирующего потока теплообмена излучением между двумя непрозрачными
поверхностями при наличии газа; б) температуру газа; в) плотность потоков
п. (а) для случая, когда газ между пластинами заменен вакуумом.
Решение.
а) Из схемы тепловой цепи на рис. 6.32 следует выражение для (^i)pe^
через известные величины:
pi . Р2
8 6
E,67.10-8)F004-8004)
0Д A/0,9) B/0,1)
^+^6+ A/0,9) + B/0,1)
Поверхность 1 должна охлаждаться с отводом 2,776 кВт/м2, чтобы ее
температура поддерживалась на уровне 600 К. Значение q _> адожцо опре*
делить, если известны величины J\ и /г:
Подставляя значения свойств, а также (<7i)pe3> ^, и ?$,» получаем
/j « 18450 Вт/м2, /2 == 21370 Вт/м2.
Результирующий поток теплообмена излучением между поверхностями 1 и 2
будет
б) Температура газа может быть определена из уравнения
^- 2776 + 2628
в) Когда газа между поверхностями нет, значения (аЛ" и q" рав-
4 /рез 1 ^> 2
ны и определяются уравнением F.88):
// nbi nb2
з = ^2!=1 + р1/е1 + р2/82 1+0,8/0,2 + 0,4/0,6
Заметим, что плотность результирующего теплового потока, подводимого
к поверхности 1, уменьшается при наличии газа благодаря излучению газа.
Плотность результирующего потока теплообмена излучением между пласти*
нами также уменьшается при наличии газа, потому что газ поглощает часть
энергии излучения, проходящего между пластингвд.
Излучение 331
В примере 6.13 были рассмотрены две бесконечные пласти-
пластины, для которых Fi-+2 = 1, и поэтому угловые коэффициенты не
учитывались. Если поверхности имеют конечные размеры, то
схему тепловой цепи нужно изменить для того, чтобы учесть
неравенство единице угловых коэффициентов. Например, нужно
рассчитать теплообмен для двух непрозрачных, параллельных
плоскостей конечных размеров, разделенных серым изотерми-
изотермическим неотражающим газом. Выражение для плотности потока
излучения, падающего на поверхность 1, имеет вид
F.125)
Подставляя F.125) в F.122), получаем
Ырез = A\h — A2F2+\%gJ2 — A{BgEbg. F.126)
После преобразований
(<7l)pes =
Уравнения F.120) и F.127) записаны в форме закона Ома
и могут быть представлены в виде тепловой цепи (рис. 6.33).
Рис. 6.33. Электрический аналог для излучения между конечными пласти-
пластинами, разделенными газом.
Отметим сходство с тепловой цепью для бесконечных плоско-
плоскостей (рис. 6.32).
6.9. РАДИАЦИОННЫЕ СВОЙСТВА ГАЗОВ
Излучение, испущенное газами, существенно отличается от
излучения, испущенного твердыми телами. В то время как
монохроматическая плотность потока излучения для твердого
вещества сравнительно изменяется во всем спектре, испускание
й поглощение излучения в газах происходят в узких полосах
Длин волн. Для примера на рис. 6.34 приведена монохромати-
монохроматическая поглощательная способность водяного пара.
332 Глава 6
Вид спектра поглощения водяного пара типичен и для дру-
других газов. Испускание и поглощение в очень узких полосах
длин волн значительны, но в соседних смежных полосах они
могут падать до нуля. Газы с симметричным строением моле-
молекул, такие, как О2, N2 и Н2, не относятся к сильно поглощающим
или излучающим веществам. В большинстве случаев при темпе-
температуре, меньшей температуры ионизации этих газов, излучением
1,0
0,8
0,6
А 0,4
0,2
О
0,8 0,9 i 1,5 2
Длина волны Л,мкм
1
1
1
л
л
1
л
м
1 1
1
1 \
/ \
/ у
А \
1 1
\А
1
/
/
i
1
\
~г
1
L j
ill
1 \
0,8
0,6
0,2
0
"Г
л
а
J
К
т
г
г
i
"А
\
iflf1\ III
г 11 Л!i
у I ||L
1 1 г
1
Ц
1
|
II.
fV
1
b
./
А
Г
я
л
А
у
и
Л
/
/
/
./
/
J
III
'\
V
|
Г
С
1
'1
,/
1
1
, /
V
II
ни
(\
(
)
б 7 8 9 10 12 14 16 18 20
Длина волны Д,мкм
30
Рис. 6.34. Монохроматическая поглощательная способность водяного пара
[28].
газов с симметричным строением молекул можно пренебречь.
С другой стороны, излучение и поглощение газов с несимметрич-
несимметричной структурой молекул могут быть значительными. Наиболее
важными для техники газами с несимметричной структурой яв-
являются Н2О, СО2, СО, SO2, NH3 и углеводороды. Ограничимся
рассмотрением свойств двух из них: Н2О и СО2. Свойства дру-
других газов рассмотрены в работах [14—19].
Еще одно важное различие между радиационными свойст-
свойствами непрозрачных твердых тел и газов состоит в том, что
форма газового объема влияет на его свойства, тогда как свой-
свойства непрозрачного твердого тела не зависят от его формы.
Толстые слои газа поглощают больше излучения, чем тонкие, и
пропускают меньше излучения, чем тонкие. Поэтому кроме
общепринятых свойств, определяющих состояние газа, таких,
как температура и давление, необходимо еще указать харак*
Излучение 333
терный размер массы газа, прежде чем определять его радиа-
радиационные свойства. Характерный размер в газе называется
средней длиной пути луча. Средние длины пути луча в объемах
газа различных простых геометрических форм даны в табл. 6.2.
Средняя длина пути луча в объемах газа
различных геометрических форм [24]
Таблица 6.2
Форма объема газа
Сфера
Бесконечный цилиндр
Бесконечные параллельные пластины
Полубесконечный цилиндр, излучающий на центр
основания
Прямой круговой цилиндр с высотой, равной
Хиаметру
излучающий на центр основания
излучающий на всю поверхность
Бесконечный цилиндр полукруглого поперечного
сечения, излучающий на точку в середине пло-
плоской стороны
Прямоугольные параллелепипеды
куб
1:1:4, излучающий на грань 1 X 4
излучающий на грань 1 X 1
излучающий на все грани
Пространство вне пучка бесконечных труб с цен-
центрами в вершинах равностороннего треуголь-
треугольника
диаметр трубы равен промежутку между тру-
трубами
диаметр трубы равен 1/2 промежутка между
трубами
2/3 диаметра
Диаметр
Два расстояния между
пластинами
Диаметр
Диаметр
2/3 диаметра
Радиус
2/3 стороны
0,9 меньшего ребра
0,86 меньшего ребра
0,891 меньшего ребра
3,4 промежутка
4,44 промежутка
Для других геометрических форм, не перечисленных в таблице,
средняя длина пути луча в газе может быть приближенно опре-
определена по формуле
()
где V — объем газа, А — площадь поверхности газа.
В работах Хоттеля [20—22] измерены зависимости излуча-
тельной способности ряда газов от температуры, полного давления
и средней длины пути луча. Кривые для излучательных способно-
способностей паров 'Н2О и СО2 показаны на рис. 6.35 и 6.36. На этих двух
графиках Рн2о и Рсо2 — парциальные давления газов. Полное
Давление для обоих случаев 0,10133 МН/м2 Aатм). В случае
334 Глава 6
когда полное давление газа не равно 0,10133 МН/м2, значения
8н о и 8со2 с Рис> ^-35 и ^-36 Д°лжны быть умножены на попра-
поправочные коэффициенты. Поправочные коэффициенты Сн2о и Ссо2
представлены на рис. 6.37 и 6.38. Излучательные способности
250 500 750 1000
1250 1500 1750 2000 2250 2500 2750
Температура, К
Рис. 6.35. Излучательная способность водяного пара при полном давлении
0,10133 МН/м2 A атм) [20].
Н2О и СО2 при полном давлении Рт, отличном от 0,10133 МН/м2
A атм), определяются выражениями
В случае когда оба газа, Н2О и СО2, образуют смесь, излу-
чательную способность смеси можно рассчитать как сумму из-
лучательных способностей газов, определенных при допущении,
что каждый газ существует отдельно, за вычетом коэффициен-
коэффициента Де, который учитывает излучение в перекрывающихся
0,006
0,005
0,004
о.ооз
^ 2
оз L
250
i i ¦
500 750 1000 1250 1500 1750 2000 2250 2500 2750
Температура, К
Рис. 6.36. Излучательная способность углекислого газа при полном давлении
0,10133 МН/м2 A атм) [20].
1,8
1,6
1,4
1,2
1,0
СН2О 0,8
0,6
0,4
0,2
0
У/
у
4
—152—
0,02
0,04
0,06
0,08
ОД
0,12
Рис. 6.37. Поправочный коэффициент для излучательной способности водя-
Woro пара при давлениях, отличных от 0,10133 МН/м2 A атм) [21, 23].
336 Глава б
спектральных полосах. Коэффициент Ае для Н2О и СОг пред-
представлен на рис. 6.39. Излучательная способность смеси НгО и
СО2 поэтому определяется_выражением
есм = Сн2о (ен2о)ргг=1 ~Ь Ссо2 (eco2)pr=»i — Ае. F.129)
2,0
1,5
1ьо
с 0|8
2 0,6
0,5
0,4
0,3
0,005 0,008 0,01 0,02 0,03
р ь
-76
—-^\
^^
^>
¦ - ¦• ]
3.7
з\ ^
1
15,2
0,05 0,08 0,1
т, МН/м2
0,2 0,3
0,5
Рис. 6.38. Поправочный коэффициент для излучательной способности СО2 при
давлениях, отличных от 0,10133 МН/м2 A атм) [21].
0 0,2 0,4 0,6 0,8 1,0 0 0,2 0,4 0,6 0,8 1;0 0 0,2 0,4 0,6 0,8 1,0
^Н2О ^НзО ^Н2О
Рис. 6.39. Поправочный коэффициент Аб для излучательной способности смеси
водяного пара и СОг [21].
Пример 6.14. Определить излучательную способность газовой смеси, со-
состоящей из N2, H2O и СО2 при температуре 800 К и имеющей форму сферы
диаметром 0,4 м. Парциальные давления газов PN =0,1 МН/м2, РцъО**
= 0,04 МН/м2, ЯСО2 = 0,06 МН/м2.
Решение. Из табл. 6.2 определяем значение средней длины пути луча для
сферы
L = B/3) D = 0,27 м
(по формуле F.128) L = 0,24 м). Значения параметров, используемых на
рис. F.35) и F.36), равны
Т = 800 К, PHz0L = 0,0104 (МН/м2)м, pQQ2L = 0,0156 (МН/м2)м, .
Излучение 337
Излучательные способности для полного давления 0,1 МН/м2 равны
(вн,о)рг-ол в °'15' (есо2)яг«ол - °>125-
Считаем, что N2 при 800 К существенно не излучает. Поскольку полное
давление газа 0,2 МН/м2, необходимо ввести поправку в значения 8, рассчи-
рассчитанные для 0,1 МН/м2. Величины СНа0 и ССОа берем с графиков (рис. 6.37
и 6.38)
Сн2О = 1>62> ССО2 = 1,12.
Наконец, с помощью рис. 6.39 определяем величину Де, используемую
для учета излучения в перекрывающихся полосах спектра:
Де а 0,005.
Излучательная способность смеси определяется по формуле F.129):
8см — 1,62 • 0,15 + 1,12 • 0,125 - 0,005 » 0,378.
Определение поглощательной способности газа несколько сложнее по
сравнению с определением 8. Используются графики для излучательной спо-
способности, описанные выше, однако параметры графиков должны быть моди-
модифицированы. Например, рассмотрим водяной пар при температуре Уц2о» на
который падает излучение с поверхности, имеющей температуру Ts. Погло-
щательную способность Н2О можно приближенно рассчитать по уравнению
«н2о = СН2овн2о (л?гH'45' FЛ30)
в котором величина Сн2о берется с рис. 6.37, a e?j2o — значение излуча-
излучательной способности водяного пара с рис. 6.35, определенное при температуре
Ts и при произведении давления на среднюю длину пути луча, равном
Значение поглощательной способности СО2 определяется аналогично по
уравнению
(^)°l65 (M31)
где величина Сс02 берется с рис. 6.38, а величина е?о2 определяется по
рис. 6.36 при Pqo2L (^s/^co2)« Для смеси Н2О и СО2 поглощательная спо-
способность равна
«см в аН2О + аСО2 - Аа'
где ан2о и асо20пРеДеляются по уравнениям F.130) и F.131) соответст-
венно, а Да = Де оценивается по рис. 6.39 при температуре 7Y
Пример 6.15. Определить поглощательную способность смеси О2 и водя-
водяного пара с полным давлением 0,2 МН/м2 и температурой 400 К. Средняя
Длина пути луча для газов 1,5 м, а падающее излучение испускается по-
поверхностью с температурой 800 К. Парциальное давление Н2О составляет
°02 МНМ
М
Решение. Считаем, что кислород не поглощает заметного количества па-
Дающего излучения и поглощательная способность смеси равна поглощатель-
*;ои способности водяного пара. Поглощательная способность Н2О определяет*
^я Уравнением F.130):
5
/ Гн2о\
н2оен2о \ т§ J
338 Глава 6
Параметры, используемые для определения СНзО и е^2О, следующие:
Н2О
= 0,11 (МН/м2)м,
= 0,06 (МН/м2)м.
.-1,45,
По графику с рис. 6.37 находим
а по графику с рис 6.35 находим
Поглощательная способность водяного пара, следовательно, равна
«НоО - Ь45 * 0,33 ( S)°'45 - °>350-
6.10. СОЛНЕЧНОЕ ИЗЛУЧЕНИЕ
Солнце —это маленькая звезда в нашей Галактике, которая
выделяет энергию в результате термоядерных реакций. Подсчи-
Подсчитано, что поток энергии излучения Солнца составляет 3,8» 1026 Вт,
¦1300
\
\
\
\
\
\
\
ч
~>
/
/
/
'/
г
/
/
/
/
г-
"¦
—
ЙФМАМИИАСОНД
Месяц
Рис. 6.40. Изменение отношения плотности потока внеатмосферного солнеч*
ного излучения к солнечной постоянной и плотности потока внеатмосферного
излучения в зависимости от времени года.
из которого около 1,7-1017 Вт достигают Земли. Средняя плот-
плотность потока энергии солнечного излучения, падающего на
внешнюю границу земной атмосферы, при среднем расстоянии
между Землей и Солнцем 1,495-1011 м A а. с.) называется сол-
солнечной постоянной. Солнечная постоянная приблизительно
равна 1353 Вт/м2. Благодаря движению Земли вокруг Солнца
по эллиптической орбите солнечное излучение, падающее на
атмосферу, изменяется по временам года (рис. 6.40). В начале
января, когда Солнце ближе всего к Земле, внеатмосферное
солнечное излучение возрастает до 1,43 кВт/м2? а в июле, когда
Внеатмосферное солнечное излучение3 [29]
Таблица 6.3
Л,
%
%
0,115
0,14
0,16
0,18
0,20
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0Д4
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,007
0,03
0,23
К25
10,7
57,5
66;/
63,0
70,9
130
232
222
482
514
689
830
1059
1074
1093
1068
1181
1120
1098
1429
1751
1747
IX КГ4
5ХИГ4
6Х10
1,6ХИГ3
8ДХКГ*
0*M
0,10
0,14
0,19
0,27
0,41
0,56
0,81
121
1,66
2,22
2,93
3,72
4,52
5,32
6,15
7,00
7,82
8,73
9,92
11,22
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50.
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,75
0,80
1639
1810
2006
2066
2033
2074
1950
1942
1822
1833
1842
1783
1725
1695
1712
1715
1700
1666
1602
1544
1486
1427
1369
1314
1235
1109
12,47
13,73
15,14
16,65
18,17
19,68
21,15
22,60
24,01
25,38
26,74
28,08
29,38
30,65
31,91
33,18
34,44
35,68
38,10
40,42
42,66
44,81
46,88
48,86
51,69
56,02
0,90
1,00
1,2
1,6
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,5
5,0
6,0
7,0
8,0
10,0
15,0
20,0
50,0
891
748
485
337
245
154
103
79
62
48
39
31
22,6
16,6
13,5
11,1
3,5
5,9
3,8
1,8
1,0
0,59
0,24
0,0048
0,0015
0,0004
63,37
69,49
78,40
84,33
88,61
91,59
93,49
94,83
95,86
96,67
97,31
97,83
98,22
98,50
98,72
98,91
99,06
99,34
99,51
99,72
99,82
99,88
99,94
99,98
99,99
100,00
р
а Солнечная постоянная равна 1353 Вт/м2.
б ЕХ—среднее значение плотности спектрального потока солнечного излучения в узком интервале длин воли
с центром, соответствующим Я.
в D4 — Доля (в %) солнечной постоянной, соответствующая длинам волн, меньшим К
340 Глава 6
100%
Отражение от
атмосферы
в космоо
Поглощение,
Солнце дальше всего от Земли, оно уменьшается до
1,33 кВт/м2.
Солнце излучает приблизительно как черное тело при тем-
температуре 5762 К. Для точных вычислений в табл. 6.3 приведены
стандартные значения плотности спектрального потока солнеч-
солнечного излучения, падающего на внешнюю границу атмосферы,
для среднего расстояния от
Солнца до Земли (по данным
NASA). Приблизительно 99%
прямого солнечного излучения
приходится на интервал длин
волн 0,1—4 мкм. Однако при
прохождении солнечного излу-
излучения через атмосферу часть
энергии рассеивается и погло-
поглощается атмосферой. Солнеч-
Солнечное излучение, достигающее
земной поверхности, таким
образом, состоит из прямого
пучка лучей и диффузного
(рассеянного) излучения. Сум-
Сумма прямого и диффузного из-
- лучения называется полным
(или глобальным) солнечным
излучением, а поток солнечно-
солнечного излучения, получаемый го-
горизонтальной поверхностью,
Рис. 6.41. Поглощение и рассеяние называют инсоляцией.
солнечного излучения при ясном небе. При прохождении СОЛНеч-
Рассеяние,
%
2-10
Суммарное^ у Диффузное
поглощение \ / солнечное
11-23% \/ Излучение (кЗемле)
Прямое 6-15%
солнечное
излучен и е
83-56%
снижается за счет
1) поглощения и рассеяния молекулами сухого воздуха, на-
называемого релеевским рассеянием;
2) поглощения и рассеяния пылью;
3) селективного поглощения водяным паром, окисью угле-
углерода и углекислым газом;
4) отражением и поглощением излучения слоями облаков. •
На рис. 6.41 иллюстрируются эти процессы в условиях яс-
ясного неба; на рис. 6.42 показаны спектр излучения черного тела;
при температуре 5762 К и спектральное распределение инсоля-
инсоляции в верхней атмосфере и на поверхности земли для массы
атмосферы, равной 1. Массой атмосферы называется длина пути
излучения в атмосфере, она равна единице на уровне моря,
когда Солнце расположено прямо в зените. Точное значение ко-
количества излучения, получаемого на Земле, зависит от высоты
над уровнем моря и положения Солнца на небе относительно
Излучение 341
точки наблюдения, определяющего длину пути сквозь атмо-
атмосферу, которую преодолевает излучение, достигающее поверх-
поверхности земли. На средних широтах при ясном небе плотность
потока излучения, получаемого площадкой, расположенной пер-
перпендикулярно к солнечным лучам в пределах ±4 ч от полудня,
2400
1.4
Длина волнь! X, мкм
Н2О, СО/
Ptic. 6.42. Спектральное распределение внеатмосферного солнечного излучения;
также показаны спектры эквивалентного черного излучения и солнечного из-
излучения, ослабленного атмосферой.
1—солнечный спектр при массе атмосферы, равной нулю; плотность потока интегрального
излучения 1353 Вт/м2; 2—распределение (нормализованное) излучения черного тела при
температуре 5762 К; плотность потока интегрального излучения 1353 Вт/мг; Я—солнечный
спектр при массе атмосферы, равной двум; а=0,66, р* =0,085; НгО—2 см, Оз—0,34 см;
плотность потока интегрального излучения 691,2 Вт/м2; 4—солнечный спектр при массе
атмосферы, равной двум, без учета молекулярного поглощения.
составляет в среднем ~70% солнечной постоянной (т. е,
~1 кВт/м2).
Пример 6.16. Рассчитать долю энергии солнечного излучения, приходя-
приходящуюся на видимую часть спектра в интервале длин волн (т. е. 0,40—
.0,75 мкм).
Решение. В первой колонке в табл. 6.3 приведены длины волн. Во вто-
второй колонке даны средние солнечные спектральные плотности потока падаю-
падающего излучения в полосе спектра с центром, совпадающим с длиной волны,
Указанной в первой колонке. Третья колонка, Dx, содержит выраженную в
процентах часть полного солнечного излучения, приходящуюся на более ко-
короткие длины волн, чем величина А,, указанная в первой колонке. При длине
волны 0,40 мкм 8,7% полного солнечного излучения приходится на более ко-
Р°ткие длины волн. При длине волны 0,75 мкм 51,7% излучения приходится
^а более короткие длины волн. Следовательно, 43% полного солнечного из-
Учения лежит в пределах полосы 0,40 — и 0,75 мкм, а суммарная энергия,
обучаемая внешней атмосферой Земли, в пределах той же спектральной об-
облети будет 582 Bt/iA
342 Глава 6
Чтобы рассчитать поток солнечного излучения, падающий
на поверхность заданного наклона и ориентации, необходимо
дать определение некоторым основным терминам. Смысл этих
терминов станет ясным при решении конкретной задачи.
Высота Солнца а — угол между направлением на Солнце и
горизонтальной поверхностью в заданном месте на Земле
(рис. 6.43). Высота для данного дня года и времени дня изме-
изменяется в зависимости от положения точки на Земле.
Вертикаль
Рис. 6.43. Высота Солнца а и его азимут а5.
Азимут Солнца as — угол между горизонтальной проекцией
солнечного луча и линией, направленной на юг в северном по-
полушарии. Азимут Солнца измеряется угловым смещением к во-
востоку или к западу от направления на юг в горизонтальной
плоскости (см. рис. 6.43).
Склонение Солнца б5 — угловое положение Солнца относи-'
тельно плоскости земного экватора. Как показано на рис. 6.44
и 6.45, из-за того, что ось вращения Земли наклонена на угол
23,5° относительно оси плоскости орбиты вращения вокруг Солн-
Солнца, величина склонения будет меняться в течение года между
+23,5° и —23,5°. Склонение обычно выражается в радианах
(или градусах) к северу или к югу от экватора. Склонение R
северу от экватора (т. е. летом в северном полушарии) принято
положительным.
Плоскость эклиптики — плоскость, в которой движется в те-
течение дня Солнце относительно стационарного наблюдателя,
расположенного в точке Р (рис. 6.44).
Солнечное время — время в часах до или после полудня при
определении полудня как времени, когда Солнце занимает с&#
мое высокое положение в небе.
Излучение 343
Угловое солнечное время hs — угловое смещение Солнца от
полудня A ч соответствует я/12 рад, или 15° углового смеще-
смещения). Смещения на восток от юга (т. е. утренние значения)
считаются положительными.
Зенит
/ Плоскость
/ эклиптики
/ ^^
X 1
\ Экватор
V
А
/л
о
L
с \d ¦
Направление
на Солнце
Рис. 6.44. Определение углового солнечного времени hs (CND), солнечного
склонения 6s (VOD) и широты L (РОС); Р — положение наблюдателя на
земле; 5 — Солнце.
Широта места на Земле L — его угловое значение выше или
ниже плоскости экватора, измеренное от центра Земли, как по-
показано на рис. 6,44. Широта положительна к северу от экватора,
21 марта.
-154,3 млн км
22 июня
144,5 млн км
----" 22 декабря
Экватор
Тропик Козерога
23 сентября
Рис. 6.45. Движение Земли вокруг Солнца.
Долгота — это угол, образованный полуплоскостью, прохо-
проходящей через ось Земли и рассматриваемое место на ее поверх-
поверхности, и плоскостью, проходящей через Гринвич. Полуплоскость,
яроходящая через Гринвич, произвольно принята за нулевую,
^ линия ее пересечения с земной поверхностью называется
Гринвичским меридианом. Долгота измеряется к востоку и за-
ПаДУ от Гринвича. Широта и долгота являются координатами,
^пределяющими положение точки на поверхности З
344 Глава 6
Зенитный угол z — угол между направлением в зенит и на-
направлением на Солнце. Этот угол является дополнительным по
отношению к высоте солнцестояния.
Возможность использования солнечной энергии на Земле
зависит от широты, времени года и погоды. Причина влияния
первых двух переменных становится ясной из рассмотрения
10-15°
/Солнечный Г~~Т"широта
коллектор
:vv Летнее
% солнцестояние
jg B2 июня)
Весеннее
равноденствие
.-.{'».:•?.. B1 марта)
ffi Осеннее
^ равноденствие
{23 сентября)
#:{ солнцестояние
B2 декабря)
Рис. 6.46. Связь между положением Солнца и Земли и солнечного коллектор
ра, наклоненного под углом Р, в зависимости от времени года.
траектории Земли вокруг Солнца, показанной схематически яш
рис. 6.45. Путь Земли вокруг Солнца является эллипсом о
Солнцем в одном из фокусов. Расстояние между Солнцем й
Землей изменяется в течение года. Земля ближе всего к Солнцу
в декабре A,445-1011 м) и дальше всего в июне A,543-10й м)*
Как показано на рис. 6.40, это относительно небольшое измене?
ние расстояния приводит к ощутимому различию в инсоляции!
которая обратно пропорциональна квадрату расстояния.
. Рис. 6.46 показывает взаимное расположение Земли и Соли*
ца с точки зрения неподвижного наблюдателя на Земле, кото*
рому Солнце представляется движущимся телом. С этой точки
зрения, часто называемой Птолемеевой точкой зрения, Солнце
перемещается дальше всего к северу 22 июня, когда оно распо*
ложено прямо над тропиком Рака. Осеннее и весеннее равно?
действия наступают, когда Солнце пересекает экватор, 23 се#
тября и 21 марта соответственно. Солнце никогда не бывзе?
Излучение 345
1000
6 7 8 9 10 11 12 1 2 3 4 5 6
80
70
60
. Sr 50
I 40
| 30
1 20
10
6 7 8 9 10 11 12 1 2 ^3 4 5 6
* Время, ч
Рис. 6.47. Высота Солнца (июнь, сентябрь, январь) и инсоляция горизонталь-
горизонтальной поверхности, расположенной на 40° с. ш., при безоблачном небе в зави-
зависимости от времени дня.
1200
/
/
/
/ '*
:";:::" *::.;- 21 июня
*'-;;';¦•'• Ч
.:.*-.::.:.21 \
:-•':' "^сентябрях
¦•'I*. •*»'•* ^ч *
:4:< "v.'-*.21 января^. ч
%^\ \\
1 лэнгли=4,186 Дж/см2
I
Широта
ЯФМАМИ ИАСОНД
•Месяц
^ис. 6.48. Годовые изменения дневной инсоляции на отдельных широтах се-
веРного полушария [30].
346 Глава 6
прямо над головой на территории США, но его максимальная
высота достигается во время летнего солнцестояния.
Высота Солнца, определяемая углом подъема Солнца над
горизонтом, важна по двум причинам. Во-первых, при большей
ЯФМАМИИАСОНД
Зима
4:00 5.00
6:00
1 • ¦ i ¦ • •' ¦" • ¦: ¦ i ¦ •
8:00 „ /7:00
Лето
I....T....1.
10
20
30 40
Широта, град
б
50
Рис. 6.49. а — график для определения солнечного склонения; 6 — номограм-
номограмма захода Солнца. Пример определения времени захода Солнца летом
G ч 08 мин после полудня) и зимой D ч 52 мин после полудня) на 39° с. 1Ш
при угле солнечного склонения 20° [31]. *
высоте Солнца солнечное излучение проходит более короткое
расстояние, пересекая атмосферу, в то время как при меньшей
солнечной высоте излучение Солнца пересекает гораздо боль§
Шую массу воздуха. Затеняющий эффект промежуточной массН
воздуха снижает солнечную инсоляцию. При большей высоте
Солнца увеличивается число дневных световых часов, во вреМв
которых можно аккумулировать солнечную энергию. Связэ
между временами года и высотой Солнца иллюстрируется схе*
Излучение 347
матически на рис. 6.47, где показаны высота Солнца и инсоля-
инсоляция в зависимости от времени дня на широте 40° с. ш. для
января, сентября и июня месяцев. На рис. 6.48 представлены
годовые изменения дневной инсоляции поверхности, располо-
расположенной на заданной широте северного полушария за пределами
атмосферы.
Влияние относительного движения Солнца и Земли можно
выразить математически через а и z, используя сферическую
геометрию для определения инсоляции на горизонтальной по-
поверхности, расположенной на внешней границе атмосферы. Од-
Однако высота Солнца и азимут не являются фундаментальными
величинами и сами рассчитываются по зависимостям, содержа-
щим угловое солнечное время, широту и солнечное склонение.
Из рис. 6.44 следует (вывод этих уравнений приведен в [25])
sin а = sin L sin 6S + cos L cos 6S cos hs F.132)
» . cos 6o sin h» /
й Sma= (
cosa
Склонение Солнца дано на номограмме рис. 6.49 в зависимости
от времени года, но для получения более точных величин 8S
необходим солнечный календарь. В табл. 6.4 представлен сокра-
сокращенный вариант солнечного календаря. Номограмма также дает
число солнечных часов в сутки. Для инженерных расчетов скло-
склонение может быть принято постоянным в течение дня.
»
Пример 6.17. Рассчитать высоту Солнца и азимутальный угол в 10 ч
утра по солнечному времени 25 декабря в г. Денвер (шт. Колорадо).
Решение. Денвер расположен на 40° с. ш. Из рис. 6.49, а для 25 декабря
б$ = —23,5°. Угловое солнечное время hs в 10 ч утра будет равно +30°. Под-
Подстановка этих значений в уравнения F.132) и F.133) дает
a ==20,6° и as = + 29,3°.
Наклонные поверхности
Количество прямого солнечного излучения, улавливаемого
поверхностью, /&, с, зависит от угла падения /, определяемого
как угол между нормалью к поверхности и направлением лу-
лучей от Солнца. Рассмотрим сначала обращенную на юг поверх-
поверхность в северном полушарии, наклоненную под углом р к гори-
горизонтали. Инсоляция может быть разложена на две составляю-
составляющие перпендикулярную и параллельную наклонной поверхности.
Только перпендикулярная составляющая падает на поверхность,
и если угол падения между нормалью к поверхности коллектора
и направлением на Солнце будет / (рис. 6.50), то действующая
на поверхность компонента инсоляции /&, с определится следую-
следующим образом;
hhi FЛ34)
348 Глава t
Солнечный календарь
Дата
Январь 1
5
9
13
17
21
25
29
Март 1
5
9
13
17
21
25
29
Май 1
5
9
13
17
21
25
29
Июль 1
5
9
13
17
21
25
29
Сентябрь 1
5
9
13
17
21
25
29
Ноябрь 1
5
9
13
17
21
25
29
Скло-
Склонение
Град
-23
22
22
21
20
20
19
18
-7
б
4
3
1
-0
+ 1
3
+ 14
16
17
18
19
20
20
21
+ 23
22
22
21-
21
20
19
18
+ 8
7
5
4
2
+ 1
-0
2
-14
15
16
17
18
19
20
21
¦ !>
Угловые
минуты
4
42
13
37
54
5
9
8
53
21
48
14
39
5
30
4
50
2
9
11
9
2
49
30
10
52
28
57
21
38
50
57
35
7
37
6
34
1
32
6
11
27
38
45
48
45
36
21
Уравнение
времени
мин
-3
5
б
8
9
И
12
13
«12
11
10
9
8
7
6
5
f2
3
3
3
3
3
.3
2
-3
4
4
5
5
6
6
6
-0
+ 1
2
3
5
6
8
9
+ 16
16
16
15
15
14
13
11
с
14
6
50
27
54
10
14
5
38
48
51
49
42
32
20
7
50
17
35
44
44
34
16
51
31
16
56
30
57
15
24
23
15
2
22
45
10
35
0
22
21
23
- 12
47
10
18
15
59
Дата
Февраль
Апрель
Июнь
Август
Октябрь
Декабрь
1
5
9
13
17
21
'25
1
5
9
13
17
21
25
29
1
5
9
13
17
21
25
29
1
5
9
13
17
21
25
29
1
5
9
13
17
21
25
29
1
5
9
13
17
21
25
29
Снло-
нение
Град
-17
16
14
13
12
10
9
+4
5
7
.8
10
11
12
14
+21
22
22
23
23
23
23
23
+ 18
17
16
14
13
12
И
9
•—2
4
5
7
8
10
11
13
-21
22
22
23
23
23
23
23
Таблица 6.4
Уравнение"
Угловые времени
минуть
19
10
55
37
15
50
23
14
46
17
46
12
35
56
13
57
28
52
10
22
27
25
17
14
12
б
55
41
23
2
39
53
26
58
29
58
25
50
12
41
16
45
6
20
26
25
17
1 МИН
-13
14
14
14
14
13
13
-4
3
1
-0
+0
1
1
2
+2
1
1
+0
-0
1
2
3
-6
5
5
4
4
3
2
1
+ 10
11
12
13
14
15
15
16
+ 11
9
8
6
4
2
+0
-1
с
34
2
17
20
10
50
19
12
1
52
47
13
б
53
33
27
49
б
18
33
25
17
7
17
59
33
57
12
19
18
10
1
17
27
30
2*
10
46
Ш
\6
АУ
X
12
17
№
20?
]) Так как каждый год имеет 365,25 суток, величины склонения меняются из года в го?
Точные величины для каждого дня каждого года содержатся в ежегодном Государстве^
ном издании США [32].
Уравнение времени—это разность между средним и истинным солнечным времен**
Эта величина учитывает неравномерность движения Земли по орбите и наклон плоское*»
«клиптики ж плоскости экватора.—Ярил*, перев,
Излучение 349
где h — прямое солнечное излучение и
cos / = sin 6S sin (L — p) + cos 6S cos (L — p) cos hSi F.135)
где L — широта.
Если наклонная поверхность в северном полушарии обра-
обращена, в направлении, отличающемся от направления на юг, то
Вертикаль
к горизонтальной
плоскости
z
Нормаль к
наклонной плоскости
Восток
Рис. 6.50. Определение солнечных и поверхностных углов для наклонной пло-
площадки, обращенной в направлении на юг.
для расчета угла падения i используют уравнения F.136) и
F.137):
cos / = cos (as — awa) cos a sin P + cos a cos p, F.136)
где as — азимут Солнца; aWa — азимутальный угол нормали к
облучаемой поверхности, измеряемый таким же способом, как и
солнечный азимут:
/ cos 6с sin hs\ ,~ 1 о_ч
^ *) F.137)
Для получения результатов, описываемых предыдущими урав-
уравнениями, удобно использовать диаграммы движения Солнца,
такие, как представленные в Смитсоновскюг метеорологических
таблицах. Одна из этих диаграмм воспроизведена на рис. 6.5L
Использование этих диаграмм проиллюстрировано на следую*
^ем примере.
Пример 6.18. Найти высоту и азимут Солнца в 10 ч утра солнечного вре-
Мени 23 февраля на 30° с. ш
Решение. Широта для каждой диаграммы движения Солнца указана в
П0Дписи к рисунку. Рис. 6.51 относится как раз к 30° с. ш. Время года можно
ЮЗ
16Р
190 Юг 170
Рис. 6.51. Диаграммы движения Солнца: для 30° с. ш. (а) и для 40° с. ш. (б)*
позволяющие определить высоту и азимут [33].
Склонение
Приблизи-
Приблизительные
Даты
+23°27'
22
июня
+20°
21 мая
24
июля
+ 15° | +10°
1 мая
12 авг.
16 апр.
28 авг.
+5°
3
апр.
10
сент.
0°
21
марта
23
сент.
-5°
8
марта
6
окт.
-10°
23
февр.
ОКТ.
-15°
9
февр.
3
нояб-
ноября
-20°
21
янв.
22
нояб-
ноября
декаб-
декабря
д. д.—до долу дня; д. п.—досле долу дня.
Излучение 351
учесть, выбрав соответствующую линию движения Солнца по таблице, поме-
помещенной на диаграмме. Для 23 февраля движение Солнца изображает линия,
обозначенная —10°. Следуя по ходу этой линии от положения полудня (т. е.
Qh I I I I I I 1 I I М 1 1 t N I I I М I I I I 1 I 1 I I
20 40 60
Южная широта, град
80 90
Рис. 6.52. Внеатмосферная суточная инсоляция поверхности для средних чи-
чисел каждого месяца года.
Управления на юг) направо до линии солнечного времени 10 ч утра, опреде-
определяем положение азимута а5, равного 40° на юго-восток. Для определения вы-
высоты Солнца (т. е. его восхождения над горизонтом) заметим, что пересече*
**Ие линий —10° ч до полудня лежит при 41°.
Полную энергию незатененного излучения, падающего за
Убранный период времени At на поверхность, /Полн можно
352 Глава 6
получить интегрированием уравнения F.134):
/полн=5 Ib(t) COS i(t)dt. F.138)
о
Для внеатмосферного, или незатененного, излучения h(t)
равно солнечной постоянной, умноженной на коэффициент экс-
эксцентричности орбиты es (рис. 6.40),
Ib(t)=es(t)I0, F.139)
где es @ = 1 + 0,034 cos -g~, F.140)
п — порядковый номер дня начиная от первого дня года.
Воспользовавшись уравнениями F.132) и F.140), можно про-
проинтегрировать уравнение F.138) за время одних суток для го-
горизонтальной поверхности, тогда получим
/Сут „ - Ц- /о [l + 0,034 cos (-§§-)] (cos L cos 6S sin hss + !
+ hss sin L sin 6S), F.141)
i
где /0 — солнечная постоянная (часовая) и hss — угловое сол-;
нечное время для часа захода Солнца при нулевой высоте в]
радианах для п-х суток. 1
Воспользовавшись уравнением F.132), hss можно опреде-1
лить из соотношения \
sin а = 0 = sin L sin 6S + соз L cos 65 cos hss (а = 0), FЛ 42)j
или hss (а = 0) = hsr (а = 0) = arccos (— tg L tg 68). FЛ43|
(Заметим, что для наклонных поверхностей восход Солнца ино<
гда бывает при i = 90°.) На рис. 6.52 представлены график»
изменения внеатмосферной суточной инсоляции на горизон*4
тальной поверхности для средних чисел каждого месяца то{
Да, Но. i
Солнечное излучение на Земле |
Проникновение солнечного излучения к поверхности Земл|
важно для проектирования систем преобразования солнечно!
энергии. Как отмечено выше, поток солнечного излучения, д$
стигающий поверхности Земли, зависит не только от времен!
года, месторасположения и времени суток, но также и от nor
годы. Практически невозможно предсказать заранее величий?
инсоляции для данного момента времени, но, исходя из опыт*,
и имеющихся данных, можно предсказать величину инсоляции
ожидаемую в среднем в течение даЙного периода времени (я*
пример, месяца или суток).
Излучение 353
X
03
о
и
¦5
?
« Ч
с со
К
S
?^
12 Зак 48?
354 Глава 6
Излучение 355
Многие годы под эгидой национальной службы погоды
США (NWS) работают многочисленные метеостанции, которые
регистрируют полное солнечное излучение Нн на горизонталь-
горизонтальной поверхности с помощью прибора, называемого пираноме-
пиранометром. Результаты этих измерений осреднены и опубликованы
в виде солнечных карт, на которых нанесены линии постоянной
среднесуточного солнечного излучения, получаемого в течение
заданного месяца на территории США. На рис. 6.53 и 6.54 при-
приведены примеры солнечных карт для февраля и июня соответ-
соответственно. Единица плотности энергии излучения, используемая
t в NWS-лэнгли (Ла):
1 Ла = 4,186Дж/см2.
Для инженерного проектирования систем преобразования
солнечной энергии необходимо знать не только полную инсоля-
инсоляцию, но и какую долю от нее составляет прямое и какую диф-
диффузное излучение. Это очень сложная задача, но Луи и Джор-
Джордан [26] разработали простой метод, с помощью которого изме-
измеренная полная инсоляция может быть разложена на прямое и
диффузное излучение. Ключевым параметром этого разложения
является месячный показатель чистоты неба Кт9 определяемый
в виде __
Кт=-=г> FЛ44)
/70
где Ен — среднемесячная наземная инсоляция горизонтальной
поверхности; Яо — среднемесячная внеатмосферная инсоляция
горизонтальной поверхности, определенная для середины ме-
месяца по уравнению F.141).
Имеющиеся данные по излучению Солнца, приведенные на
рис. 6.55, показывают, что отношение среднемесячного рассеян-
рассеянного излучения Dh к среднемесячному полному излучению Ин
зависит от месячного показателя чистоты неба. Клейн [27] по-
показал, что эта зависимость может быть представлена следую-
следующей^ эмпирической формулой:
М = 1,39 -4,03^г + 5,53Ат -3,1 М& F.145)
Ни
если солнечная постоянная принимается равной 1,394 кВт/м2.
После того как определена диффузная составляющая излу-
излучения, среднемесячная прямая составляющая излучения на го-
горизонтальной поверхности Вн может быть рассчитана по соотно-
соотношению
Bh = Hh-Dh. F.146)
12*
366 Глава 6
Для наклонной поверхности составляющая прямого солнечного
излучения, согласно уравнению F.134), равна
= RbIb'h'
F.147)
где jbt h _ проекция текущего значения составляющей прямого
солнечного излучения на горизонтальную поверхность, а отно-
fete
0,8
0,6
0,4
0,2
п
\
Экстраполяция-
>
а
ч
u
ч
: j
д
Г1
i
)г\
¦>.
ОД 0^2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
v- ^ н _ Среднемесячное суточное полное излучение
гв//0~* Внеатмосферная суточная инсоляция
Рис. 6.55. Зависимость между среднемесячным суточным диффузным излуче-
излучением В и среднемесячным суточным полным излучением Я для горизонталь-
горизонтальных поверхностей [26].
О—расчет; •—обсерватория «Блю Хилл» A947-1956); Д —Нис, Франция A931-1933);
X—Мелсингфорс, Финляндия A928-1931); ? — обсерватория Кью, Лондон A947-1951).
щение (cosf/cosa), которое называют коэффициентом наклона
Rb> определяется зависимостью
cos/ __ sjn 6g sin (L — ft) + cosds cos (L — ft) coshs /g J4gv
Ab cos ^ sjn i s-in 5^ _|. cos i cos 5S cos hs
Rb — это геометрический параметр, связывающий прямое излу-
излучение для горизонтальной поверхности с прямым излучением
для наклонной поверхности. Хотя он является непрерывно из-
изменяющейся величиной, для инженерных расчетов можно ис-
использовать средние значения, определяемые по формуле [26]
cos (L — Р) cos 6S sin hss + hss sin (L — ft) sin 6S
cos L cos 65 sin/*55 (a = 0) + hss (a = 0) sin L sin 6S '
F.149)
где угловые солнечные времена /i5s(a = 0) и /г55 должны быть
выражены в радианах и рассчитаны для середины месяца. Ис-
Используя F.149), находим среднемесячное прямое излучение для
наклонной поверхности Бс:
B<.=zRbBh. F.150)
Излучение 357
В табл. 6.5 приведены коэффициенты наклона Яь для широт
20, 30, 40 и 50° и углов наклона, представляющих интерес для
гелиотехники.
Таблица 6.5
Коэффициенты наклона солнечного коллектора для различных широт
Широта
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
?-=20°
/3-20°
1,36
1,22
1,08
1,00
0,92
0,87
0,89
0,95
1,04
1,17
1,30
i.li
/3=40°
1,52
1,28
1,02
0,83
0,70
0,63
0,66
0,78
0,95
1,20
1,44
1,60
0-30°
1,68
1,44
1,20
1,00
0,87
0,81
0,83
0,93
1,11
1,36
1,60
1,76
30°
0-50*
1,88
1,52
1,15
0,84
0,66
0,58
0,62
0,76
1,00
1,36
1,76
1,99
?«40°
0=40°
2,28
1,80
1,36
1,05
0,88
0,79
0,82
0,96
1,24
1,62
2,08
1,48
/3=60°
2,56
1,90
1,32
0,90
0,66
0,60
0,64
0,78
1,12
1,64
2,24
2,80
/3=50°
3,56
2,49
1,65
1,16
0,90
0,80
0,84
1,02
1,44
2,10
3,16
4,Q4
50°
0=70°
3,94
2,62
1,62
1,00
0,64
«ft
6,61
0,83
№
ZM
3,32
Помимо прямого излучения наклонная поверхность будет
также получать диффузное излучение от части неба в пределах
видимости. Если предположить, что небо — изотропный истбч-
ник излучения, то по уравнению F.57) угловой коэффициент
Rd определяется в следующем виде:
/?(l+cosp). F.161)
Если поверхность расположена вблизи поверхности земли, на-
например плоский коллектор на крыше дома, она может также
получать прямое и диффузное излучение, отраженное от земли
с угловым коэффициентом Rr, приблизительно равным
F.162)
где (is — отражательная способность поверхности грунта, обра-
обращенной к югу. Точных измерений величины ps не проводили, но
климатологические измерения альбедо Земли позволяют пред-
предположить, что можно предложить значения: ps = 0,7 для снега
и льда, ps = 0,2 для бетона, р5 = 0,1 для асфальта, воды или
темной земли и ps = 0,4 для песка.
Комбинируя уравнения F.149) — F.152), получаем полное
среднемесячное излучение Солнца, 7С, падающее на поверхность^
расположенную на земле,
(в.163)
358 Глава 6
Среднесуточная или среднечасовая энергия солнечного излу-
излучения, падающего на поверхность, вычисляется аналогично; по-
подробности этого расчета можно найти в работе [25].
Пример 6.19. Рассчитать полную среднесуточную энергию солнечного из-
излучения, падающего на обращенный к югу солнечный коллектор, наклонен-
наклоненный под углом 40°, для февраля и июня месяцев в г. Боулдер (шт. Коло-
Колорадо). В феврале земля на южной стороне покрыта снегом, а в июне — тра-
травой (р* = 0,3).
Решение. Боулдер расположен на 40° с. ш. Из солнечных карт определяем
среднемесячную инсоляцию горизонтальной поверхности Яа, равную
268 Ла/сутки(= 11,218 кДж/(м2-сутки)) в феврале и 525 Л а/сутки
(= 21,977 кДж/(м2-сутки)) в июне. По номограмме (рис. 6.49) определяем
долготу дня 15 февраля FS = 14°) 10,5 ч, а 15 июня FS = 22°) 14,5 ч.
Среднее значение показателя чистоты неба Кт, получаем из рис. 6.55.
Сначала рассчитаем или определим по графику внеатмосферное излучение в
середине месяца.
Из рис. 6.52 или уравнения F.141) Но равно 500 Л а/сутки ==
= 20 930 кДж/(м2-сутки) в феврале и 1000 Ла/сутки = 41 860 кДж/(м2-сут-
ки) в июне. Из рис. 6.55 получаем
для февраля Кт = -— = 0,536 и -т=~ = 0,36,
Но Hfi
для июня Кт = -=Д- = 0,524 и -—- = 0,35.
Но Н\
Таким образом, диффузное излучение будет 0,36-11 218 = 4038 кДж/(м2Х
X сутки) в феврале и 0,35-21 977 = 7692 кДж/м2-сутки) в июне.
Из уравнения F.148) или табл. 6.5 имеем Яь = 1,8 в феврале и 0,79 в
июне. _
В результате из уравнения F.153) получаем 1С= 1,8 A1 218 — 4038) +
+ 4038 1+^766 +11218 °'7AТ°'766) = 17 400. кДж/(м2 • сутки) для фев-
раля и Тс - 0,79 B1 977 - 7692) + 7692 1 + %Ш + 21 977 °'3 A ~ °'766) -
= 18 850 кДж/(м2 • сутки) для июня.
Литература
1. Dunkle R. V., Thermal-Radiation Tables and Applications, Trans. ASME,
65, p. 549 A954).
2. Touloukian Y. S., DeWitt D. P., Thermal Radiative Properties-Metallic
Elements and Alloys, vol. 7, IFI/Plenum, Publishing Corp., N. Y., p. 10a, 1970.
3. Sparrow E. M., Radiant Emission, Absorption and Transmission Cha-
Characteristics of Cavities and Passages, NASA—SP—55, p. 103, 1965.
4. Truenfels W., Emissivity of Isothermal Cavities. /. Opt. Soc. AmertJ 53,
No. 10, p. 1162 A963).
5. Sparrow E. M., Jonsson V. K., Radiant Emission Characteristics of
Diffuse Conical Cavities, /. Opt. Soc. Amer., 53, p. 816 A963).
6. Schmidt E., Eckert E., Uber die Richtungs-verteilung der Warmestrab
lung, Forsch. Gebeite Ingenieurwesen, 6 A935).
7. Sparrow E. M., Cess R. p., Radiation Heat Transfer, Brooks/Cole Pub-
Publishing Company, Monterey, Calif., 1966, pp. 56—63. [Имеется перевод: Спэр-
роу, Сесс, Теплообмен излучением. — Л.: Энергия, 1971.]
* 8. Torrance К. Е., Sparrow E. М., Biangular Reflectance of an Electrical
Nonconductor as a Function of Wavelength and Surface Roughness, /. Heat
Излучение 359
Transfer, 87, p. 283 A965). [Имеется перевод: Торренс, Спэрроу, Двупарамет-
рическая отражательная способность непроводника электричества как функ-
функция длины волны и шероховатости поверхности. — Труды Амер. об-ва инж.-
мех., сер. С, Теплопередача, 1965, № 2, с. 145.]
9. Eckert F. R. G., Sparrow E. M., Radiative Heat Exchange Between
Surfaces with Specular Reflection, Int. J Heat Mass Transfer, 3, p. 42 A961).
. 10. Sparrow E. M., Eckert E. R. G., Jonsson V. K«, An Enclosure Theory
for Radiative Exchange Between Specular and Diffusely Reflecting Surfaces,
/. Heat Transfer, 84, p. 294 A962). [Имеется перевод: Спэрроу, Эккерт, Джон-
Джонсон, Теория радиационного теплообмена в полости при зеркальном и диффуз-
диффузном отражении от поверхностей.— Труды Амер. об-ва инж.-мех., сер. С, Теп-
Теплопередача, 1962, № 4, с. 27.]
11. Hamilton D. С, Morgan W. R., Radiant-Interchange Configuration Fac-
Factors, NACA Tech. Note 2836, 1952.
12. Siegel R., Howell J. R., Thermal Radiation Heat Transfer, McGraw,
N. Y., 1972. [Имеется перевод: Зигель, Хауэлл, Теплообмен излучением. — М.:
Мир, 1975.]
13. Hottel Н. С, Sarofim A. F., Radiative Transfer, McGraw, N. Y., p. 31—
39, 1967.
14. Schmidt E., Forsch. Gebiete. Ingenieurs, 3, No. 57 A932).
15. Guerrieri S. A., S. M. Thesis in Chemical Engineering, MIT, Cambridge,
Mass., 1932.
\ 16. Malkmurs W., Thompson H., J. Quant. Spectro. Radiative Transfer, 2,
No. 16 A962).
17. Lee R. H. C, Happel J., Thermal Radiation of Methane Gas, Ind. Eng.
Chem. Fundamentals, 3, No. 167 A964).
18. Ullrich W., Sc. D. Thesis in Chemical Engineering, MIT, Cambridge,
Mass., 1953.
19. Eckert E. R. G., Forschungsheft, 387, p. 1 A937).
20. Hottel H. C, in McAdams W. H., Heat Transmission, 3rd ed., ch. 4,
McGraw, N. Y., 1954. [Имеется перевод: Мак-Адаме, Теплопередача, Метал-
лур«издат, 1961, с. 87—175.]
21. Hottel Н. С, Egbert R. В., Trans. AlChE, 38, p. 531 A942).
22. Hottel H. С, Sarofin A. F., Radiative Transfer, McGraw, N. Y., 1967.
23. Egbert R. В., Sc. D. Thesis in Chemical Engineering, MIT, Cambridge,
Mass., 1941.
24. Rohsenow M., Hartnett J. P., eds., Handbook of Heat Transfer, McGraw,
N. Y, 1973.
25. Kreith F., Kreider J. F., Principles of Solar Engineering, McGraw, N. Y.,
1978.
26 Liu B. Y. H., Jordan R. C, Availability of Sojajr Energy for Flat Plate
Solar Heat Collectors, in Low Temperature Engineering Application 6f Solar
Energy, ch. 1, ASHRAE, N. Y., 1967.
27. Klein S. A., A Design Procedure for Solar Heating Systems, Ph. D. The-
Thesis, University of Wisconsin, Madison, 1976.
28. Kreith F., Principles of Heat Transfer, 3rd ed., Crowell T. Y., Harper
and Row, 1973.
29. Thekaokaw, Solar Energy Outside the Earth's Atmosphere, Solar Ener-
Energy, vol. 14, 1973, pp. 109—127.
30. Strahler A. N., The Earth Sciences Harper and F&w, N. Y., 1^63.
31. Whillier A., Solar Radiation Graphs, Solar Eneffy, Pergamori, vol. 9,
p. 164 A965).
32. The American Ephemeris and Nautical Almanac, U. S. Government
Printing Office.
33. Kreider J. F., Kreith F., Solar Heating and Cooling, McGraw-Hill, N. Y.,
№. 1st ed., 1977.
ЗАДАЧИ
Задачи в данной главе сгруппированы по тематике разделов, как ука-
указано в таблице. Три задачи предполагают численное решение на ЭВМ. Это
задачи 6.61—6.63. Для их решения не требуется составления никаких спе-
специальных программ. Все необходимые для решения программы представлены
в примерах этой главы.
Номера
задач
6.1-6.9
6.10-6.18
6.19-6.28
6.29—6.35
6.36-6.56
6.57—6.63
6.64—6.73
6.74-6.80
Раздел
6.2
6.3
Ч
6.5
6.6
6.7
6.8 и 6.9
6.10
Тема
Физика излучения
Радиационные свойства
Угловые коэффициенты излучения
Теплообмен излучением между чер-
черными поверхностями
Теплообмен излучением между се-
серыми поверхностями
Матричные методы
Перенос излучения через поглощаю*
щую среду
Солнечное излучение
6.1. Рассчитать максимальное значение плотности монохроматического по*
тока излучения черного тела для поверхностей, имеющих температуру:
а) 100 К, б) 500 К, в) 1000 К и г) 5000 К.
6.2. Определить длину волны, при которой достигается максимум плот-
плотности потока черного излучения для поверхностей, имеющих температуру:
а) 100 К, б) 500 К, в) 1000 К и г) 5000 К.
6.3. Построить график плотности монохроматического потока черного
излучения для температур поверхности: 200, 1000, 50Q0 и 10 000 К.
6.4. Нить лампы накаливания имеет температуру 3?00 К, и излучдет как
черное тело. Какова доля (в %) энергии испущенного излучения, приходящая-
приходящаяся на а) инфракрасную область длин волн й о) на видимую область длин
волн?
6.5. Определить температуру, до которой необходимо нагреть черную по*
верхность, чтобы 40% ее энергии излучения приходилЪсь на инфракрасную
область спектра.
6.6. Определить температуру, до которой нужно нагреть черную поверх-
поверхность, чтобы 20% ее энергии излучения приходилось на видимую область
спектра.
6.7. Вольфрамовая нить лампы фотософита имеет температуру 3500 К
Предполагая, что нить излучает как черное тело, йайти, в каком соотноше-
Излучение 361
нии распределяется полная энергия излучения, испускаемого нитью в ультра-
ультрафиолетовой, видимой и инфракрасной областях. Повторить расчеты для обыч-
обычной вольфрамовой нити, имеющей "температуру 2500 К.
6.8. Вывести закон Вина [уравнение F.3)] путем дифференцирования за-
закона Планка.
6.9. Показать, что постоянная Стефана — Больцмана равна
4 С
6.10. Предположим, что требуется выбрать один из двух материалов, ко-
который предполагают использовать для облицовки большого административ-
административного здания. Первый материал пропускает 60% энергии падающего излуче-
излучения в интервале длин волн 0,3-10~6 — 0,6-10~6 м и 20%—в интервале
0,6-Ю — 40«10~6 м. Второй материал пропускает 40% энергии падающего
излучения в интервале длин волн 0,3 «Ю" — 2-10~6 м и 30% в интервале
2-10" — 30-10~6 м. При других длинах волн материалы непрозрачны. Здание
расположено в местности, где приблизительно 80% потребляемой энергии ис-
используется для кондиционирования воздуха и только 20% для нагревания.
Какой материал Вы выберете и по каким причинам?
N,6.11. Теплица сооружена из кварцевого стекла, которое пропускает 92%
энергии падающего излучения в интервале длин волн 0,35-10~6 — 2,7-10"*6 м.
Полагая, что стекло совершенно непрозрачно для малых и больших длин
волн, рассчитать долю солнечного излучения (в %%), которая достигает
грунта, если Солнце излучает как черное тело при температуре 5550 К. Если
средняя температура грунта 300 К и он излучает как черное тело, рассчи-
рассчитать долю энергии излучения (в %%), испускаемого грунтом, которую про-
пропускает стекло в окружающее пространство.
6.12. Поверхность имеет температуру 500 К и монохроматическую излу-
чатеяьную способность
ел = 0 при 0<Я<5-10~6 м,
е^ = 0,002Л • 106 — 0,01 при 5 • 10~б м < А, < 100 -10 м,
6^ = 0,19 при 100-10" м<Я<200-10-6 м,
при 200 • 10~6 м < Я< оо,
где А измеряется в метрах. Определить интегральную излучательную способ-
способность/ поверхности.
6.13. Определить поглощательную способность поверхности из задачи 6.12,
если падающее на поверхность излучение исходит от черного тела при тем-
температуре а) 500 К и б) 1000 К.
6.14. Поверхность имеет температуру 1000 К и монохроматическую по-
поглощательную способность
ах = 0 при 0<Я<0,5-10~6 м,
ак = 0,5 (Я • 106 - 0,5) при 0,5.1(Г6 м < X < 1,5 -10 м,
ал = 0,5 при 1,5-10" м<Л<2,0-10 м,
ал = 0 при 2-Ю м <Л< оо,
362 Глава 6
где Я измеряется в метрах. Определить интегральную поглощательную спо-
способность поверхности, если источником падающего излучения является чер-
черное тело при а) 5000 К и б) 500 К.
6.15. Монохроматическая излучательная способность реальной поверхно*
сти аппроксимируется выражениями
е*=°
при 0 < X < 2 • 10 6 м,
при 2 • Ю м < Л < 8 • 10 м,
для 8 • 10~6 м < Я< 25 • 10~6 и,
для 25 • 10~6 м < Л < оо.
а) Рассчитать интегральную излучательную способность поверхности,
когда ее температура 800 К. б) Рассчитать интегральную поглощательную
способность поверхности, если падающее на поверхность излучение исходит
от черного тела при температуре 1000 К.
6.16. Спутник Земли нужно покрыть специальным терморегулирующим
покрытием Имеются две краски. Монохроматические излучательные способ-
способности красок показаны на рисунке. Принимая, что Солнце излучает как чер-
черное тело при 5550 К, рассчитать интегральную поглощательную способность
обеих красок по отношению к солнечному излучению. Какая из красок будет
поглощать больше солнечной энергии?
0,8
0,6
0,4
0,2
Краска 2
Краска 1
1 2 3-
Длина волны Я, мкм
К задаче 6.16.
6.17. Спутники, покрытые красками, описанными в задаче 6.16, перед вы-
выводом их на орбиту испытывают в имитаторе космоса. Спутник, покрытый
краской 1, принимает равновесную температуру 550 К, а покрытый краской
2, — температуру 450 К. Определить интегральную излучательную способ-
способность обеих красок.
6.18. Поверхность имеет направленную излучательную способность, опре*
деляемую зависимостью 8(8) =0,60 cos 0, где 6 — угол, измеренный относи*
тельно нормали к поверхности. Определить величину полусферической излу*
чательной способности поверхности.
6.19. Используя метод натянутых нитей, получить выражение для угло-
углового коэффициента излучения F\^2 для показанной на рисунке геометрий,
бесконечно протяженной в направлении, перпендикулярном к плоскости стра*
ницы. Построить график F{_^2 B функции Ь/а и сравнить с результатами, ДО*
Излучение 363
казанными на рис. 6.16.
1 ¦
<—¦ Ь А
К задаче 6.19.
6.20. Определить величину углового коэффициента между небом и бес*
конечно длинной трубой радиусом г, лежащей на земле.
6.21. Определить величину углового коэффициента между небом и беско*
нечно длинной трубой радиусом г, наполовину закопанной в землю.
^ 6.22. Показать, что угловой коэффициент fdAi^,A2 для элемента плоской
поверхности и прямоугольника будет равен
К задаче 6.22.
arctg
( Y \
arctg
где
6.23. Рассчитать выражение для углового коэффициента F^Ax-^A* для
круглого диска и элемента плоской поверхности в ситуации, показанной на
рисунке.
К задаче 6.23.
364 [лава 6
6.24. Рассчитать величину/г1_>2 Для каждой пары поверхностей, показан*
ных на рисунке.
К задаче 6.24.
6.26. Определить величину углового коэффициента /7i->2 Аля геометрии,
показанной на рисунке.
Г
1м
,6 М
0,4м
-1м з
К задаче 6.25.
6.26. Определить величину углового коэффициента /7i-^2 Для геометрии!
показанной на рисунке.
О
¦«-1м-»-
Зм
5м
К задаче 6.26.
6.27, Определить угловые коэффициенты ^1^3» ^1-м» ^1^5 и ^"i->6 Для
геометрии, поперечное сечение которой показано на рисунке. Поверхности, бес-
бесконечно протяженные в направлении, перпендикулярном к плоскости стра-
страницы.
Излучение 365
< 1 м >j*-
.1 !
i
- 1M—+
%
\
5 1М
I
3 4
К задаче 6.27.
6.28. Определить угловые коэффициенты
и Л
-»4
Для ци-
цилиндрической геометрии, показанной на рисунке. Поверхности 1 и 4 — торце-
цые плоскости цилиндра, а поверхности 2 и 3 — криволинейные внешние по-
поверхности цилиндра.
1м
к 1м
К задаче 6.28.
з /
Г
I
I
6.29. Два параллельных черных прямоугольника размером 5 X Ю м Рас"
положены прямо друг против друга на расстоянии 5 м. Примем, что окру-
окружающее пространство черное и имеет температуру О К. Прямоугольники обо-
обозначены как поверхности 1 и 2. Температуры поверхностей Т\ = 100 К и
Т2 = 2000 К. Построить тепловую цепь для системы, обозначив все потен-
потенциалы, сопротивления и токи:
а) Определить результирующий теплообмен излучением между поверхно-
поверхностями 1 и 2.
б) Определить результирующий поток энергии к поверхности 1.
в) Определить результирующий поток энергии к поверхности 2.
г) Определить результирующий теплообмен излучением между поверх-
поверхностью 1 и окружающим пространством.
д) Определить результирующий теплообмен излучением между поверх-
поверхностью 2 и окружающим пространством.
6.30. Решить задачу 6.29, когда окружающее пространство заменено ог-
огнеупорной (адиабатической) поверхностью. Рассчитать температуру огнеупор-
огнеупорной поверхности.
6.31. Черный солнечный коллектор расположен на крыше дома. Площадь
поверхности коллектора 50 м2. Падающее от Солнца излучение создает на
коллекторе плотность потока излучения 800 Вт/м2. Окружающее простран-
пространство можно считать черным при эффективной температуре 30°С. Кондуктив-
ным и конвективным потоками от коллектора можно пренебречь. Рассчитать:
а) равновесную температуру коллектора; б) результирующий теплообмен из-
излучением между коллектором и окружающим пространством.
6.32. Решить задачу 6.31, учитывая теплообмен конвекцией от поверхно-
поверхности коллектора к окружающему воздуху при 30°С, если hc = 60 Вт/(м2-град).
6.33. Два параллельных черных диска диаметром 30 см расположены
на расстоянии 20 см. Один диск имеет температуру 800 К, другой 400 К. Ди-
Диски помещены в вакуум, и тыльные стороны обоих дисков теплоизолированы.
Окружающее пространство — черное, при температуре 300 К.
Ш Рлава 6
а) Построить тепловую цепь для этой задачи, обозначив все потенциалы,
сопротивления и токи.
б) Рассчитать результирующий теплообмен излучением между двумя ди-
дисками.
в) Рассчитать результирующие тепловые потоки для двух дисков и окру-
окружающего пространства. Убедиться, что сумма трех результирующих потоков
равна нулю.
г) Рассчитать результирующий теплообмен излучением между двумя ди-
дисками и окружающим пространством.
6.34. Решить задачу 6.33, принимая, что окружающее пространство заме-
заменено огнеупорной (адиабатической) поверхностью. Рассчитать температуру
огнеупорной поверхности.
6.35. Изолированная черная прямоугольная поверхность на космическом
корабле ориентирована перпендикулярно солнечным лучам. Космический ко-
корабль находится на расстоянии 1,5-108 км от Солнца; диаметр Солнца 1,39 X
X 10б км. Принимаем, что Солнце —- черное тело при температуре 5550 К.
Энергия излучения, падающего от других частей космического корабля и от
планет, пренебрежимо мала. Окружающее пространство имеет эквивалентную
радиационную температуру 0 К. Рассчитать равновесную температуру черной
поверхности.
6.36. Асфальтированная улица имеет излучательную способность 0,6 для
испускаемого длинноволнового излучения и поглощательную способность 0,95
для коротковолнового излучения, падающего от Солнца. В ясный день плот-
плотность потока падающего солнечного излучения от Солнца составляет
1000 Вт/м2. Определить равновесную температуру асфальта, если темпера-
температура воздуха 290 К, а коэффициент конвективного теплообмена между ас-
асфальтом и воздухом 10 Вт/(м2-град). Теплопроводностью в землю прене-
пренебречь.
6.37. Решить задачу 6.36, заменив асфальт бетонным покрытием, которое
имеет излучательную способность 0,5 для длинноволнового излучения и по-
поглощательную способность 0,65 для коротковолнового излучения, падающего
от Солнца.
6.38. Сосуд Дьюара для жидкого азота изготовлен в виде двух концен-
концентрических сфер, разделенных вакуумом. Внутренняя сфера имеет внешний
диаметр 1 м, а внешняя сфера имеет внутренний диаметр 2 м. Обе сферы
являются серыми поверхностями се = 0,20. Температура кипения азота при
давлении 0,1 МН/м2 A атм) 78 К, а скрытая теплота испарения 2-Ю5 Дж/кг.
Определить скорость выкипания N2, когда внутренняя сфера заполнена жид-
жидким азотом, а внешняя сфера имеет температуру 300 К.
6.39. Две большие серые пластины расположены параллельно друг другу
и разделены узким зазором. Одна пластина имеет излучательную способ-
способность 0,8 и температуру 500 К, а другая — излучательную способность 0,2 и
температуру 400 К. Пространство между пластинами вакуумировано, а тыль-
тыльные поверхности обеих пластин теплоизолированы. Рассчитать:
а) плотность результирующих тепловых потоков для обеих поверхностей;
б) плотность результирующего потока теплообмена излучением между по-
поверхностями.
6.40. На фабрике одежды введена новая линия легких курток, на кото-
которой используется «технология космического века». Куртки покрывают сереб-
серебристым материалом, который снижает радиационные потери от тела. Посереб-
ренная внутреннняя поверхность куртки имеет излучательную способность
0,10. Рассчитать радиационные потери человека, одетого в куртку, принимая
температуру куртки 270 К и предполагая, что платье имеет температуру 295 К
и излучательную способность 0,70. Так как куртка плотно облегает фигуру,
примем, что теплообмен излучением между платьем и курткой соответствует
случаю теплообмена между двумя бесконечными параллельными пластинами.
Сравнить потери тепла излучением с конвективными потерями тепла, если Не
на внешней поверхности куртки 200 Вт/(м2-град), а температура окружаю*
Излучение 367
щего воздуха 260 К. Какова доля потерь тепла излучением от полных теп-
тепловых потерь?
6.41. Замкнутая система состоит из трех бесконечно длинных серых по-
поверхностей, которые образуют равностороннее поперечное сечение. Поверх-
Поверхность 1 имеет известную температуру Т\\ на поверхности 2 известна плотность
его результирующего теплового потока (<72)рез> но неизвестна температура;
поверхность 3 имеет известную температуру Г3. Построить тепловую цепь для
данной задачи. Обозначить все сопротивления и определить их величины.
Рассчитать плотность потока эффективного излучения для каждой поверх-
поверхности. Также рассчитать величины (<7i)pe3> ^2 и (^з)рез-
с2'= 0,7 2
Ц)"е~500Вт/м2
К задаче 6.41.
6.42. Длинная труба уложена на уровне земли. Труба серая, с излуча-
тельной способностью 0,50. Диаметр трубы 1 м. Температура трубы, воздуха
и грунта 285 К. Рассчитать результирующий поток обмена энергией излучения
на единицу длины трубы между трубой и небом в ясную ночь, когда эффек-
эффективная температура неба 150 К.
6.43. Решить задачу 6.42, когда труба наполовину закопана в землю.
6.44. В печи нагревают плоские квадратные AX1 м) листы пластика,
которые можно рассматривать как серые тела с излучательной способностью
0,40. Нагреватели расположены выше и ниже пластика, как показано на ри-
рисунке. Нагреватели имеют температуру 700 К и излучательную способность
0,90. Тыльная сторона обоих нагревателей хорошо теплоизолирована. Темпе-
Температура стенок 450 К и е = 0,2. Пренебречь конвекцией и рассчитать равно-
равновесную температуру пластика.
Нагреватель,
J=700 К
е=0,9
К задаче 6.44,
368 Глава 6
6.45. В печи нагревают стальные слитки. Верх печи занят радиационными
электронагревателями общей мощностью 100 кВт. Излучательная способность
нагревателей 0,75. Боковые стенки печи хорошо теплоизолированы и имеют
огнеупорные (адиабатические) поверхности. Слитки серые (г = 0,40) и рас-
расположены на полу печи, как показано на рисунке. Начальная температура
слитков 300 К. Для этой начальной температуры рассчитать: а) температуру
нагревателя; б) температуру боковых поверхностей печи; в) результирующие
тепловые потоки для нагревателя и слитков; г) результирующий поток тепло-
теплообмена излучением между нагревателем и слитками.
Нагреватель, с = 0,75
Тепловыделение 100 кВТ
Огнеупорная
поверхность
Стальные слитни, с =¦ 0,40
К задаче 6.45.
6.46. Решить задачу 6.45, когда стальные слитки достигнут температуры
600 К.
6.47. Нить лампы в 100 Вт окружена сферической колбой. Колба серая,
с т = 0,88 и а = 0,12. Допустим, что нить выключена и быстро достигла рав-
равновесной температуры 300 К. Определить выражение для нестационарной
температуры колбы, если она имеет внутренний диаметр 10 см, наружный диа-
диаметр 10,2 см, плотность 2,7-103 кг/м3 и теплоемкость 840 Дж/кг-град. Энер-
Энергией излучения, падающего на колбу из окружающего пространства, прене-
пренебречь.
6.48. Солнечный коллектор размером 10X2 м состоит из труб, в кото-
которых циркулирует теплоноситель и которые размещены в основании коллек-
коллектора. Коллектор имеет однослойное стеклянное покрытие, а пространство ме-
между покрытием и поглощающей пластиной коллектора вакуумировано. По-
Поглощающая пластина зачернена, а боковые стенки коллектора представляют
собой огнеупорные (адиабатические) поверхности. Нижняя поверхность кол-
коллектора хорошо теплоизолирована. Свойства стекла для коротковолнового из-
излучения а = 0,05, т = 0,88, для длинноволнового излучения а = 0,90, т =
= 0,04. Расход теплоносителя достаточен для поддержания поверхности по-
поглощающей пластины коллектора при температуре 55°С. При плотности по-
потока солнечного излучения 950 Вт/м2 рассчитать: а) температуру стекла, пре-
пренебрегая теплопроводностью и конвекцией; б) результирующий поток излу-
излучения, переносимый в поглощающую пластину коллектора.
Стенло
Огнеупорная стенка
Поглощающая пластина
коллектора
Трубы с теплоносителем
Теплоизоляция
W////////M
К задаче 6.48.
Излучение 369
6.49. Решить задачу 6.48, принимая, что воздух над стеклом имеет тем-
температуру 25°С, а коэффициент конвективного теплообмена между воздухом
и стеклом 25 Вт/(м2-град).
6.50. Лампа накаливания в диапроекторе имеет мощность 400 Вт. Отра-
Отражатель, размещенный за нитью накала, направляет 30% энергии в сторону
слайда. Слайд серый с т = 0,50, е = 0,20. Площадь слайда 8,9 см2. Прини-
Принимаем, что энергия излучения, исходящего от слайда, не возвращается обрат-
обратно. Определить равновесную температуру слайда, если: а) конвективные по-
потери от слайда пренебрежимо малы; б) вентилятор обдувает воздухом при
35°С обе стороны слайда с h = 500 Вт/(м2-град).
6.51. Небольшой электронный блок размещен на полу большой комнаты.
Площадь поверхности блока 0,5 м2, излучательная способность поверхности
0,70. Мощность источников электронного блока 850 Вт, а коэффициент конвек-
конвективного теплообмена между блоком и воздухом 15 Вт/(м2-град). Температура
комнаты и воздуха 25°С. Определить температуру блока, принимая его изо-
изотермичным и хорошо теплоизолированным от пола.
6.52. Для сушки краски на прямоугольной плите используют тепловые
лампы. Окрашенная поверхность размером 4 X 4 м имеет излучательную спо-
способность 0,25. Тепловые лампы размещены на прямоугольнике, соответствую-
соответствующего по размерам крашеной поверхности, и могут рассматриваться как диф-
диффузные излучатели. Мощность ламп 50 КВт. Краска покрывается пузырями,
если ее температура превышает 450 К. Примем, что тыльные поверхности
тепловых ламп и окрашенной плиты теплоизолированы, и пренебрежем кон-
конвекцией от обеих поверхностей. Процесс сушки происходит в большой ком-
комнате с температурой 20°С. Определить минимальное расстояние между теп-
тепловыми лампами и окрашенной поверхностью.
6.53. Решить задачу 6.52, используя данные, приведенные в задаче, но
принимая во внимание конвекцию от лампы и окрашенной поверхности. До-
Допустим, что 15% энергии, выделенной лампами, рассеивается конвекцией в
окружающий воздух. Окрашенная поверхность ориентирована вертикально, а
температура окружающего воздуха 20°С. Использовать соответствующую за-
зависимость для числа Нуссельта для учета конвекции от окрашенной поверх-
поверхности. Определить минимальное расстояние между тепловыми лампами и
окрашенной поверхностью для этого случая. ^
6.54. Куски мяса помещены над угольной жаровней на расстоянии 20 см
выше углей. Слой древесного угля имеет площадь 60 X 80 см, излучатель-
излучательную способность 0,8 и температуру 1000 К. Куски мяса расположены парал-
параллельно углям и имеют площадь, равную площади слоя древесного угля. Из-
Излучательная способность кусков мяса 0,40. Мясо жарится на открытом воз-
воздухе, температура которого 300 К. Во время поджаривания конвективный по-
поток между углем и мясом составляет в среднем приблизительно 600 Вт. Теп-
Теплообменом от верхней поверхности кусков мяса и нижней поверхности слоя
углей можно пренебречь.
а) Определить равновесную температуру кусков мяса.
б) Определить расход угля для поддержания стационарных условий, при-
принимая теплотворную способность древесного угля 2,8-107 Дж/кг.
6.55. Решить задачу 6.54, приняв, что пространство между жаровней и
углем полностью закрыто идеально отражающей фольгой.
6.56. Печь цилиндрической формы используется для нагрева круглого объ-
объекта, расположенного наверху печи, как показано на рисунке. Нагревателем
является круглое дно печи, имеющее мощность тепловыделения 1,3 кВт. Ци-
Цилиндрические стенки печи являются огнеупорными поверхностями. Излуча-
Излучательная способность нагревателя 0,75, а нагреваемого объекта 0,50. Тепло-
Теплопроводностью и конвекцией между поверхностями пренебречь. Температура
нагреваемого объекта измерена и равна 500 К. Определить: а) температуру
Нагревателя; б) температуру огнеупорной поверхности; в) плотность потоков
Падающего и эффективного излучения на всех трех поверхностях; г) плот-
плотность результирующего теплового потока к нагреваемому объекту.
370 Глава 6
60 см
Нагреваемый объект,
Огнеупорная
поверхность
Нагреватель, е= 0,75
К задаче 6.56.
6.57. Рассмотрим замкнутую систему, состоящую из трех серых поверх-
поверхностей известной геометрической формы с известной излучательной способ-
способностью. Поверхности 1 и 2 имеют заданные результирующие плотности теп-
тепловых потоков, но неизвестные температуры. Для поверхности 3' известна
температура, но не задана плотность результирующего теплового потока. Вы-
Вывести три алгебраических выражения, которые можно использовать для рас-
расчета Ти Т% и (<7з)рез-
6.58. Четыре серые диффузные изотермические непрозрачные поверхности
образуют замкнутую систему. Поверхности 1 и 2 имеют заданные плотности
результирующих тепловых потоков, в то время как на поверхностях 3 и 4
заданы температуры. Допустим, что свойства всех поверхностей и их геоме-
геометрическая форма известны. Вывести уравнения, которые можно использо-
использовать для определения 7\, Г2, (<7з)рез и (?4)рез» и представить уравнения в
стандартной матричной форме.
6.59. Решить пример 6.8 матричным методом.
б!бО. Решить пример 6.10 матричным методом.
6.61. Длинный конструкционный элемент имеет поперечное сечение в фор-
форме шестиугольника. Все поверхности шестиугольника серые, непрозрачные и
диффузные. Рассчитать плотность результирующего теплового потока для
каждой из шести поверхностей. Пренебречь конвекцией и теплопроводностью
между поверхностями. Для определения величин (flt)"^ использова1Ь вычис-
вычислительную программу, описанную в разд. 6.7. Геометрия сечения показана на
рисунке. Температуры и излучательные способности поверхностей равны
Тх = Тг - 400К, Т2 = Г4 = 500К, Ть — Т6 = 300К,
ej а 8г = 0,2, бз = е4 = 0,3, е5 = е6 = 0,4.
3 0,5 м
Излучение 371
6.62. Для элемента с шестиугольным поперечным сечением, показанного
в задаче 6.61, заданы следующие условия: 8i = 0,1, е2 = 0,2, 83 = 0,3, 64 =
= 0,4, е5 = 0,5, е6 = 0,6, Тх = 300 К, Т2 = 350 К и Гз = 400 К. Поверхно-
Поверхности 4—6 огнеупорные. Используя вычислительную программу, описанную в
разд. 6.7, определить температуры трех огнеупорных поверхностей и плотно*
сти результирующих тепловых потоков для поверхностей 1, 2 и 3.
6.63. Печь новой улучшенной конструкции, подобная описанной в за-
задаче 6.56, предназначена для нагрева объектов до повышенных температур.
Ее новые конструктивные особенности — донный нагревательный элемент
плюс нагреватель, занимающий половину боковой поверхности цилиндра, как
показано на рисунке. Остальная часть цилиндрической поверхности представ-
представляет собой огнеупорную поверхность. Оба нагревателя имеют излучательную
способность 0,9. Нагреваемый объект с излучательной способностью 0,5, по-
помещенный в верхней части топки, принимает равновесную температуру 650 К.
А&ощность донного нагревателя 1,3 кВт, а мощность бокового нагревателя
1,0 кВт. Используя вычислительную программу, описанную в разд. 6.7, опре-
определить: а) температуры обоих нагревателей; б) температуру огнеупорной по-
поверхности; в) плотность потоков падающего и эффективного излучения для
всех поверхностей; г) плотность результирующего теплового потока для на-
нагреваемого объекта.
г
25 см
25 см
L
-50
Нагреваемый
' объект, с«0,50
Огнеупорная
поверхность
Боковой
нагреватель,
е=0,9
Донный
' нагреватель,
С-0,9
К задаче 6.63.
6.64. Смесь СО2 и N2 нагрета до 1000 К. Парциальное давление СО2
0,1 МН/м2, а полное давление смеси 0,1 МН/м2. Форма объема газовой сме-
смеси — полусфера с радиусом 0,8 м. Определить излучательную способность га*
зовой смеси.
6.65. Смесь сухого воздуха и водяного пара имеет полное давление
0,2 МН/м2. Парциальное давление водяных паров 0,01 МН/м2. Смесь газов
занимает пространство между двумя большими параллельными пластинами,
размещенными на расстоянии 1,5 м друг от друга. Рассчитать излучательную
способность смеси газов при температуре 800 К.
6.66. Смесь СО2 и Н2О имеет полное давление 0,05 МН/м2 и температуру
700 К. Смесь газов заключена в кубический контейнер, сторона которого 1 м.
Определить излучательную способность смеси, если парциальное давление СОг
0,02 МН/м2.
6.67. Смесь Н2О и СО2 при полном давлении 0,15 МН/м2 находится ме-
между двумя большими параллельными пластинами, расположенными на рас-
расстоянии 0,5 м друг от друга. Парциальное давление водяного пара
0,07 МН/м2. Температура газов 800 К. Определить излучательную способ-
способность газовой смеси.
372 Глава б
6.68. Определить поглощательную способность газовой смеси из за-
задачи 6.67 по отношению к падающему излучению от поверхности при 400 К.
6.69. Рассмотреть данные задачи 6.67 и предположить, что газ серый.
Верхняя пластина (поверхность 1) серая (б = 0,4), с температурой 500 К.
Нижняя пластина (поверхность 2) серая (е = 0,8), и ее температура 1000 К.
Рассчитать плотность результирующего теплового потока для поверхности
1 (<7i)pe3 при наличии и отсутствии газа. Определить температуру газа.
6.70. Используя данные задачи 6.65, определить поглощательную способ-
способность газовой смеси для падающего потока излучения от поверхности при
900 К.
6.71. Большой лист стали (е = 0,5) выходит из прокатного стана с тем-
температурой 1000 К. На расстоянии 1 см от листа расположен небольшой при-
прибор для контроля поверхностных свойств стали. Пространство между при-
прибором и сталью заполнено серым газом с излучательной способностью 0,15.
Рассчитать плотность теплового потока на поверхности, необходимую для
поддержания температуры корпуса прибора при 500 К, если прибор черный.
Рассчитать плотность теплового потока, если поглощающий газ отсутствует.
6.72. Рассчитать результирующий теплообмен излучением между двумя
Серыми (е = 0,6) бесконечными пластинами, отстоящими друг от друга на
4 см. Пространство между пластинами наполнено СОг при давлении 0,1 Мн/м2
а температуры пластин 800 и 600 К. Принять, что СОг — серый газ. Рассчи-
Рассчитать также результирующие потоки энергии, подводимые к каждой пластине.
Рассчитать результирующий теплообмен излучением между двумя пласти-
пластинами, когда газ отсутствует.
6.73. Выхлопные газы после процесса горения истекают из трубы диа-
диаметром 20 см при температуре 2200 К. Газы состоят из СО2 и Н2О при пол-
полном давлении 0,1 МН/м2 и парциальных давлениях 0,05 и 0,01 МН/м2. Вбли-
Вблизи выхлопных газов расположена черная поверхность, чтобы охлаждать их
до температуры менее 500 К. Какая требуется минимальная охлаждающая
способность на единицу площади поверхности? Принять газ серым.
6.74. Рассчитать долю внеатмосферного солнечного излучения, прихо-
приходящуюся на длины волн менее 1 мкм.
6.75. Определить солнечное склонение на 30 января и 1 сентября.
6.76. Рассчитать угол падения солнечных лучей в 2 ч после полудня по
солнечному времени 15 февраля на 40° с. ш. на поверхностях со следующей
ориентацией: а) горизонтальной; б) обращенной на юг с наклоном 40°; в) на-
наклоненной на 40°, но отклоненной на угол 30° к западу от юга; г) вертикаль-
вертикальной, обращенной на юг; д) вертикальной, обращенной на запад.
6.77. Рассчитать для г. Денвер (шт. Колорадо) на 1 марта часовую сум-
суммарную солнечную радиацию от восхода до захода Солнца, поступающую на
поверхность, которая наклонена под углом, равным широте, и обращена на
юг. Принять, что земля покрыта снегом, имеющим отражательную способ-
способность 0,7.
6.78. Рассчитать равновесную температуру черной горизонтальной пла-
пластины, изолированной снизу, в г. Мэдисон (шт. Висконсин) в полдель 11 мая
при скорости ветра 5 м/с и температуре воздуха 10°С. Повторить расчет для
плоской поверхности, имеющей отражательную способность 0,8 при длинах
волн менее 1 мкм и излучательную способность 0,2 при длинах волн более
1 мкм. Затем определить плотность потока тепла, который мог бы отво-
отводиться от пластины, если бы ее температура понизилась на 30°С.
6.79. Решить задачу 6.78, приняв, что пластина закрыта тонкой пленкой
пластика, которая пропускает 95% солнечного излучения и только 10% ин-
инфракрасного излучения и расположена на расстоянии 1 см над пластиной.
6.80. На приведенной ниже схеме показана солнечная установка, пред-
предназначенная для выработки электроэнергии. Определить максимальную моШ-
ность, которую может произвести эта установка, когда плотность падаю*
щего излучения равна 3200 кДж/(ч-м2). Характеристики коллектора следу*0*
щие: полный коэффициент тепловых потерь Ui = 7,0 кДж/(ч*м2-град); эф*
Излучение 373
фективность коллектора F' =» 0,92. Расходы воды через коллектор т =
s= 30 кг/(ч-м2). Произведение пропускательной способности на поглощатель-
ную способность та равно 0,80. Окружающая температура Токр = 20°С. Пло-
Площадь коллектора Ас = 50 000 м2. Принять, что тепловая машина имеет к. п. д.,
"полезн.
^_
Теговая
машина
т
н, вх
К задаче 6.80.
^отработ*
приблизительно равный 1/3 к. п. д. цикла Карно для работы между тем-
температурой окружающей среды как стока и температурой коллектора ТКг вых
как источника тепла.
Глава 7
ТЕПЛООБМЕННИКИ
7.1. ВВЕДЕНИЕ
В этой главе представлен тепловой анализ различных типов
теплообменников. В частности, описаны два метода расчета
тепловых характеристик промышленных теплообменников и
представлены методики оценки необходимого размера и наибо-
наиболее подходящего типа теплообменника для решения определен-
определенной задачи. Будут также рассмотрены в рамках тепловых ха-
характеристик теплообменника его гидравлическое сопротивление
и оборудование, необходимое для прокачки жидкости через
теплообменник.
При выполнении полного проектного расчета теплового обо-
оборудования важно знать не только тепловые характеристики, но
и экономические показатели системы. В последние годы роль
теплообменников непрерывно возрастает, поскольку инженерам
приходится заниматься проблемами общего потребления энер-
энергии и они стремятся оптимизировать конструкцию не только с
точки зрения теплового анализа и экономических соображений
возмещения капиталовложений, но и с точки зрения возврата
энергетических затрат, потребляемых тепловой системой. По-
Поэтому должны быть рассмотрены экономические аспекты, а так-
также вопросы потребления энергии и сырья для решения задан-
заданной задачи.
При использовании теплообменника в системе теплоснаб-
теплоснабжения для передачи тепла необходим температурный напор.
Величину температурного напора можно уменьшить путем ис-
использования более крупного теплообменника, однако это в
свою очередь приведет к возрастанию экономических, а также
энергетических затрат. Проблемы подобного рода будут играть
все возрастающую роль в последующие годы, однако такой ана-
анализ выходит за рамки данной главы. Тем не менее рассмотрим
среди теплообменных аппаратов различного назначения не
только кожухотрубные теплообменники, но также теплообмен-
теплообменники с неподвижной насадкой, солнечные коллекторы и тепло-
тепловые трубы.
7.2. ОСНОВНЫЕ ТИПЫ ТЕПЛООБМЕННИКОВ
Теплообменник простейшего типа состоит из трубы, внутри
которой расположена другая труба (рис. 7.1). Такое устройство
может работать либо в режиме противотока, либо в режиме
Теплообменники 3715
прямотока, когда горячая или холодная жидкость течет внутри
кольцевого пространства, а другая жидкость течет во внутрен-
внутренней трубе.
Наиболее распространенным типом теплообменника, который
широко используется в химической и других отраслях промыш-
промышленности, является кожухотрубный теплообменник (рис. 7.2),
С, В*
Рис. 7.1. Простой противоточный теплообменник типа «труба в трубе».
В теплообменнике такого типа одна жидкость течет внутри
труб, тогда как другая жидкость прокачивается в межгрубном
пространстве внутри кожуха в поперечном направлении. При-
Причина выбора схемы движения потока жидкости поперек, а не
i i
Рис. 7.2. Кожухотрубный теплообменник с сегментными перегородками; в
трубном пучке два хода, в межтрубном пространстве один ход.
вдоль труб заключается в том, что более высокие коэффициенты
теплоотдачи достигаются при поперечном, а не при продольном
обтекании труб. Для создания перекрестного обтекания труб в
межтрубном пространстве внутри кожуха устанавливают пере-
перегородки (рис. 7.2). Эти перегородки установлены таким обра-
образом, что в каждой образованной ими секции поток обтекает тру-
трубы в поперечном направлении сначала в первой секции вниз, за-
затем во второй секции вверх и т. д. В зависимости от устройства
Коллекторов, расположенных на двух концах теплообменника,
376 Глава 7
можно обеспечить один или более ходов труб. В двухходо-
двухходовом аппарате входной коллектор разделен таким образом,
что жидкость течет через половину труб в одном направлении,
Перегородка^
Tpy6as
Проходное сечение
1 воерегородке
Проходное сечение
между перегородками
Кожух
Кольцевая
перегородка
Проходное сечение
диска
Проходное сечение
кольцевой перегородки
Проходное сечение
перегородни
Кожух
Рис. 7.3. Три типа перегородок, используемых в кожухотрубных теплообмен-
теплообменниках [18].
а—перегородка с отверстиями; б—перегородка типа диск—кольцо; в—сегментная
перегородка.
затем поворачивает и возвращается обратно через другую по-
половину труб к началу своего движения (рис. 7.2). Три или
четыре хода труб можно получить путем установки дополнитель-
дополнительных перегородок внутри коллектора. В промышленных уста-
установках применяются разнообразные типы перегородок, устанав-
устанавливаемых в межтрубном пространстве, однако наиболее распро-
распространенным типом являются перегородки в виде дисков и колей
(рис. 7.3,6).
Теплообменники 377
При нагревании или охлаждении газа часто удобно исполь-
использовать теплообменник с перекрестным током (рис. 7.4). В теп-
теплообменнике такого типа жидкость прокачивается внутри труб,
тогда как газообразный теплоноситель продувается поперек
трубного пучка. Течение внешнего теплоносителя может осу-
осуществляться путем вынужденной или свободной конвекции.
В теплообменнике такого типа газ, проходящий поперек труб-
трубного пучка, рассматривается как смешивающийся, тогда как
Поток
газа,
вход
Поток
газа,
выход
* Нагревающая или охлаждающая
жидкость
Рис. 7.4. Перекрестноточный воздушный подогреватель при перекрестном те-
течении неперемешивающейся жидкости и перемешивающегося газа.
жидкость, протекающая внутри трубы, рассматривается как не*
смешивающаяся. Внешний поток газа считается смешиваю-
смешивающимся, поскольку он может почти свободно перемещаться в
межтрубном пространстве в процессе переноса тепла, тогда как
жидкость, протекающая внутри труб, не может смешиваться
ни с каким другим потоком в процессе переноса тепла.
Другой тип теплообменника с перекрестным током, который
широко используется в космической технике и для отопления
Жилых помещений, показан на рис. 7.5. В этом аппарате газовый
поток, обтекающий оребренный трубный пучок, не смешивается,
поскольку он протекает через отдельные каналы в процессе
переноса тепла. Как показано на профиле температуры
(рис. 7.5,а), когда теплоноситель не перемешивается, в нем
существует градиент температуры как вдоль, так и поперек на-
направления потока. С другой стороны, если теплоноситель хо-
хорошо перемешивается, его температура стремится выровняться
в направлении, нормальном к движению потока, и поэтому в
378 Глава 7
нем устанавливается градиент температуры только в направ-
направлении потока. При проектировании теплообменников важно
определить, будут ли теплоносители перемешиваться и какие
из них будут перемешиваться. Также важно выровнять темпера-
температурный напор путем достижения приблизительно одинаковых
коэффициентов теплоотдачи снаружи и внутри труб. Если этого
Рис. 7.5. Перекрестноточный теплообменник, широко используемый в косми-
космической технике и для отопления жилых помещений. :
не сделать, одно из термических сопротивлений окажется слиш-
слишком высоким, что приведет к неоправданно высокому значению
полного температурного напора для заданного теплового по*
тока и соответственно к увеличению размеров теплообменногв
аппарата и, следовательно, к низким экономическим пока-
показателям.
Кожухотрубный теплообменник (рис. 7.2) имеет на каждом
конце фиксированные трубные доски, к которым приварива*
ются или развальцовываются трубы. Теплообменник такой кон-
конструкции имеет самую низкую стоимость, но может использо-
использоваться лишь при малых разностях температур между горячим
и холодным теплоносителями, поскольку в его конструкции йе
предусмотрены мероприятия по предотвращению термически*
напряжений, обусловленных неодинакррым р^сщи^щием трУ|
и кожуха. Другой недостаток заключается в том", ЭД6 трубЯМ"
Теплообменники 379
пучок нельзя извлечь из теплообменника для очистки поверх-
поверхностей. Модифицированная конструкция теплообменника, не
имеющая указанных недостатков, показана на рис. 7.6. В этом
аппарате одна трубная доска жестко зафиксирована, а другая
прикреплена болтами к плавающему коллектору, что позволяет
трубному пучку перемещаться относительно кожуха. Плаваю-
Плавающая трубная доска зажата между плавающим коллектором и
1 22 20
18 17
Рис. 7.6. Кожухотрубный теплообменник с плавающим коллектором. (С раз-
разрешения Ассоциации фирм-изготовителей трубчатых теплообменников.)
/—днище кожуха; 2—плавающий коллектор; 3—разъем для продувки; 4—-ответный фла-
фланец для крепления трубной доски плавающего коллектора; 5—фланец для крепления
днища кожуха; 6—поперечные перегородки или поддерживающие пластины; 7—кожух;
8—стяжки и распорки; 9—патрубок кожуха; 10— отражающая перегородка; // —стацио-
—стационарная трубная доска; 72—патрубок коллектора; 13—коллектор; 14—подъемное кольцо;
15—разделительная перегородка; /5 —крышка коллектора; 17—фланец для крепления
коллектора; 18—опоры; 19—теплоотдающие трубки; 20— щтуцер для проведения испыта-
испытаний; 21 ~-фланец плавающего коллектора: 22—штуцер для дренажа; 23 — плавающая
трубная доска.
фланцем таким образом, что позволяет извлекать трубный пу-
пучок для очистки поверхностей, Теплообменник, показанный на
рис. 7.5, имеет один ход в межтрубном пространстве и два
хода труб.
Для некоторых специальных типов теплообменников, таких,
как регенеративные теплообменники для авиационных и авто-
автомобильных газовых турбин, определяющими являются пока-
показатели плотности теплового потока на единицу веса или еди-
единицу объема. Компактные легкие теплообменники для этих це-
целей были использованы Кейсом и Лондоном [1]. Полное опи-
описание и расчет компактных теплообменников, в особенности
°ребренных с целью увеличения эффективности таких устройств,
Можно найти в работах [2—4].
7.3. СУММАРНЫЙ КОЭФФИЦИЕНТ ТЕПЛОПЕРЕДАЧИ
Одной из основных задач при тепловом анализе кожухо-
тРубного теплообменника является расчет суммарного коэффи-
коэффициента теплопередачи между двумя потоками жидкости. Как
Сказано в гл. 1, суммарный коэффициент теплопередачи между
380 Глава 7
горячей жидкостью с температурой Th и холодной жидкостью
с температурой Тс, разделенными твердой плоской стенкой, опре-
определяется из уравнения
q = UA(Tk-TJ9 G.1)
ПА _ 1 1
где ил— з — (\ihxA) + (L/kA) + A/М) '
Площадь внутренней поверхности теплообменника типа «труба
в трубе» (рис. 7.1) 2w*L, а площадь наружной поверхности
2nr0L. Таким образом, если суммарный коэффициент теплопере-
теплопередачи приведен к наружной поверхности Ао, то
U G2)
Ао
2nkL ^ hQ
а если он приведен к внутренней поверхности Аи то
{
ht + 2nkL + ЛоАо
Хотя для тщательного и строгого конструкторского расчета не-
необходимы значения коэффициентов теплопередачи, вычислен-
вычисленные для конкретных условий, для предварительных оценок ча-
часто полезно иметь приближенное значение U, типичное для
условий, встречающихся на практике. В табл. 7.1 приведены
некоторые типичные значения U для различных теплообменни-
теплообменников и рабочих условий [б]. Следует отметить, что во многих
случаях значение U почти полностью определяется термиче*
ским сопротивлением на одной из поверхностей раздела жид-
жидкость— твердое тело, например когда одним теплоносителем
является таз, а другим — жидкость или когда один из теплоно-
теплоносителей представляет собой кипящую жидкость с очень высо-
высоким значением коэффициента теплоотдачи. „1
Коэффициенты загрязнения Я
Суммарный коэффициент теплопередачи теплообменника в
рабочих условиях часто нельзя рассчитать на основании одного
только теплового анализа. При работе с большинством жидко*
стей и некоторыми газами на поверхности теплообмена посте-
постепенно происходит отложение пленки загрязненией. Этими от-
отложениями могут быть ржавчина, котельная накипь, осадки*
кокс и многие другие вещества. Этот эффект, который назы-
называется загрязнением, приводит к увеличению термического со*
Суммарные коэффициенты теплопередачи, Вт/(м 2 • град) [19]
Таблица 7.1
Тепловой поток -> к
от
Газа (свободная кон-
конвекция), Ас = 5—15
Газа (вынужденная
конвекция),
ЛС=Ю—100
Жидкости (свобод-
(свободная конвекция),
?с = 50—10 000
Жидкости (вынуж-
(вынужденная конвекция)
воды,
йс = 3 000—10 000,
других жидкостей,
hc = 500-3 000
Конденсирующегося
пара
воды,
fic = 5 000—30 000,
других жидкостей,
hc == 1 000—4 000
Газу (свободная
конвекция),
Йс = 5—15
Теплопередача
из комнаты
к наружному
воздуху через
стекло, U — 1—2
Радиатор цент-
центрального отоп-
отопления, U = 5—15
Радиаторы паро-
парового отопления,
?/ = 5-20
Газу (вынуж-
(вынужденная конвек-
конвекция), йс= 10—100
Пароперегрева-
Пароперегреватели, ?/ = 3—10
Газовые тепло-
теплообменники,
?/=10-30
Охладители газа,
?/=10-50
Воздухоподогре-
Воздухоподогреватели,
?/=10-50
Жидкости (сво-
(свободная конвек-
конвекция),
Йс = 50—1000
Жаротрубный
котел, ?/= 10—15
Масляная ванна
для обогрева,
U == 25—500
Нагревательный
змеевик в сосуде
вода — вода
без перемешива-
перемешивания, U = 50—250,
с перемешива-
перемешиванием,
U = 500—2 000
Паровые рубаш-
рубашки вокруг сосудов
с мешалками
вода,
?/ = 300—1000,
другие жидкости,
U = 150—500
Жидкости (вынуж-
(вынужденная конвекция)
воде,
йс = 3 000—10 000
другим жидкостям,
hc = 500—2 000
Камера сгорания,
?/ = Ю—40 + излу-
излучение
Охлаждающий змее-
змеевик с перемешива-
перемешиванием, ?/ = 500—1 500
Теплообменник
вода — вода,
U = 900—2 500,
вода — другие жид-
жидкости, ?/ = 200— 1 000
Конденсаторы
водяной пар — вода,
?/=100—4 000,
пары других жид-
жидкостей — вода,
U = 300—1000
Кипящей жидкости
воде,
йс = 3 500—60 000,
другим жидко-
жидкостям,
hc = 1 000—20 000
Пароводяной
котел,
?/=10—40 + из-
излучение
Испарители хо-
холодильников или
охладители соля-
соляных растворов,
^7 = 300—1 000
Испарители
водяной пар —
вода,
U = 1 500—6 000,
водяной пар —
другие жидкости,
U = 300—2000
382 Глава 7
противления. Изготовитель оборудования обычно не может
учесть природу отложения загрязнений или скорость загрязне-
загрязнений. Поэтому он может гарантировать только характеристики
теплообменников с чистыми поверхностями. Термическое сопро-
сопротивление отложения в общем случае можно определить только
на основе натурных испытаний или эксплуатации. Если прове-
проведены испытания по определению характеристик теплообменника
с чистыми поверхностями, а затем испытания проведены по-
повторно после того, как устройство проработало в течение неко-
некоторого времени, то удельное термическое сопротивление отло-
отложения (или коэффициент загрязнения) можно определить из
соотношения
_1_
и
G.4)
где U — коэффициент теплопередачи теплообменника с чисты-
чистыми поверхностями нагрева; Ud— коэффициент теплопередачи
теплообменника с загрязненными поверхностями; Rd — удель-
удельное термическое сопротивление отложения. Удобной рабочей
формой записи уравнения G.4) является следующая:
'd=-
Коэффициенты загрязнения для различных приложений собра-
собраны и опубликованы Ассоциацией фирм-изготовителей трубча-
трубчатых теплообменников [6]. Некоторые из этих значений приве*
дены в табл. 7.2. Коэффициенты загрязнения необходимо учи-
учитывать, как это показано на примере следующего уравнения
Таблица 7.2
Обычные коэффициенты загрязнения [6]
Жидкость
Морская вода
ниже 325 К
выше 325 К
Обработанная питательная вода в котле
свыше 325 К
Нефтепродукты
Закалочное масло
Пары спирта
Водяной пар, не загрязненный маслом
Промышленный воздух
Хладагент
Коэффициент
загрязнения
Rd, м2-град/Вт
0,00009
0,0002
0,0002
0,0009
0,0007
0,00009
0,00009
0,0004
0,0002
Теплообменники 383
для суммарного коэффициента теплопередачи
труб:
неоребренных
где Ud — суммарный коэффициент теплопередачи, Вт/(м2-град),
приведенный к наружной поверхности трубы; Яо — средний ко-
коэффициент теплоотдачи от наружной поверхности трубы,
Вт/(м2-град); hi — средний коэффициент теплоотдачи внутрен-
внутренней поверхности трубы, Вт/(м2-град); Ro— удельное термиче-
термическое сопротивление загрязнения наружной поверхности трубы,
м2- град/Вт; Ri— удельное термическое сопротивление загряз-
загрязнения внутренней поверхности трубы, м2-град/Вт; Rk — удель-
удельное термическое сопротивление материала трубы, приведенное
к площади наружной поверхности трубы, м2- град/Вт; Ao/Ai —
отношение площади наружной поверхности трубы к площади
ее внутренней поверхности.
\
7.4. СРЕДНЕЛОГАРИФМКЧЕСКАЯ РАЗНОСТЬ ТЕМПЕРАТУР
В теплообменнике в общем случае температуры теплоноси-
теплоносителей не постоянны, а изменяются по длине, по мере того как
тепло передается от горячего теплоносителя к холодному. По-
Площадь поверхности
с, вых
полн
, вых
Площадь поверхности
Рис. 7.7. Распределение температуры Рис. 7.8. Распределение температуры
в одноходовом конденсаторе. в одноходовом испарителе.
этому даже при постоянном термическом сопротивлении плот-
плотность теплового потока будет изменяться по ходу потока жид-
жидкости в теплообменнике, поскольку ее значение зависит от раз-
разности температур между горячим и холодным теплоносителями
в Данном сечении теплообменника. Рисунки 7.7—7.10 иллюстри-
Руют изменение температур либо в одном, либо в обоих тепло-
теплоносителях для простого кожухотрубного теплообменника
(Рис. 7.1). Расстояние между двумя сплошными линиями про-
п°рционально разности температур АГ между двумя теплоно-
теплоносителями.
384 Глава 7
На рис. 7.7 представлен случай, когда пар конденсируется
при постоянной температуре, а другой теплоноситель нагре-
нагревается. На рис. 7.8 показан случай, когда жидкость испаряется
при постоянной температуре, а тепло передается от другого
вых
Площадь поверхности
Рис. 7.9. Распределение температуры в одноходовом прямоточном теплооб-
теплообменнике.
теплоносителя, температура которого понижается по мере про-
прохождения через теплообменник. Для указанных выше случаев
направление движения каждого теплоносителя несущественно
и жидкость с постоянной температурой может также находиться
вхГ
, вых
ict вых
Площадь поверхности
Рис. 7.10. Распределение температуры в одноходовом противоточном тепло-
теплообменнике.
в неподвижном состоянии. На рис. 7.9 представлены распреде-
распределения температуры для прямоточного теплообменника, а на
рис. 7.10 — для противоточного. В двух последних случаях не
происходит изменения агрегатного состояния вещества. Из
рис. 7.9 видно, что при прямотоке независимо от длины тепло-
теплообменника конечная температура холодного теплоносителя ни-
никогда не может достигнуть выходной температуры горячего теп-
Теплообменники
лоносителя. С другой Стороны, при противотоке конечная тем-
температура холодного теплоносителя может превышать темпера-
температуру на выходе горячего теплоносителя вследствие наличия бла-
благоприятного перепада температур по всей длине теплообмен-
теплообменника. Дополнительное преимущество схемы противотока состоит
в том, что для заданного теплового потока здесь необходима
меньшая площадь теплоотдающей поверхности, чем для схемы
прямотока.
Для определения теплового потока в любом рассмотренном
выше случае необходимо проинтегрировать уравнение
dq = VdA АГ G.6)
пЬ всей площади теплоотдающей поверхности А по длине теп-
теплообменника. Если суммарный коэффициент теплопередачи V
постоянный, изменение кинетической энергии не учитывается,
а кожух теплообменника теплоизолирован, то уравнение G.6)
легко проинтегрировать для случаев прямотока и противотока.
Уравнение теплового баланса для элементарной площади dA
имеет^вид
dq = - mhcph dTh = ± тссрс dTc = U dA (Th - Tc)9 G.7)
где m — массовый расход, кг/с; ср — удельная теплоемкость при
постоянном давлении, Дж/(кг-град), и Т — среднемассовая тем-
температура теплоносителя, К. Индексы h и с относятся к горячему
и холодному теплоносителям соответственно, знак плюс в
третьем члене уравнения соответствует прямотоку, а знак ми-
минус—противотоку. Если удельная теплоемкость теплоносите-
теплоносителей не зависит от температуры, можно записать уравнение теп-
теплового баланса от входного сечения до произвольного попереч-
поперечного сечения теплообменника
- С„ (Т„ - ГА, ах) = Се (Тс - Г, вх), G.8)
где Ch = rhnCph — расходная теплоемкость горячего теплоноси-
теплоносителя, Вт/град; Сс = fhccpc — расходная теплоемкость холодного
теплоносителя, Вт/град.
Решая уравнение G.8) относительно Thy получаем
^ = ^BX--^(rc-7c>BX), G.9)
откуда
(^)c+?j-TCiEK + ThtBX. G.10)
Подставляя выражение G.10) в уравнение G.7), после неко-
некоторых преобразований получаем
13 Зак. 487
366 Глава 7
Интегрирование уравнения G.11) по всей длине теплообмен-
теплообменника (т. е. от А = О до А = АПОлн) дает выражение
. | - [1 + (Cc/ch)] тСш вых + (Сс/сн) тСш
(CC/CAO'c..x+7'ft.Bx
lnW+cc/ch)ir -т
которое можно упростить:
G-12)
Из уравнения G.8) для полной длины теплообменника полу-
получаем выражение
п т т
с h, вых fi, вх in I q\
— , \i.LQ)
с. вых с, вх
которое можно использовать, чтобы исключить расходные теп-
теплоемкости из уравнения G.12). После некоторых преобразова-
преобразований имеем
Т4 Т1 v ТТЛ
h> вых с, вых 1 г/т* Т \ (Т Т м
~т -zrj J — l^y h*вых "" с*вых'"~' h>вх"" с«вх^"~^~ •
А. вх с. вх / ^
G.14)
поскольку ^ = СС(ГС, вых — ГС| вх) = Ch(Th, вх — Thi вых). Пусть
7/i—Г<: = Д7\ тогда уравнение G.14) можно записать в виде
GЛ5)
где индексы а и b относятся соответственно к разностям тем-
температур на входе и выходе теплообменника (рис. 7.9, 7.10). На
практике удобно использовать среднюю эффективную разность
температур AT для всего теплообменника, определяемую сле-
следующим образом:
q = UAkT. G.16)
Сравнивая уравнения G.15) и G.16), находим, что для пря-
прямотока или противотока
Величина ЛГ называется среднелогарифмической разностью
температур1). Она также используется в случае, когда темпе-
температура одного из теплоносителей постоянна (рис. 7.7, 7.8). Когда
!> В отечественной литературе распространен термин «среднелогарифмй-
ческий температурный напор».— Прим. ред.
Теплообменники 387
= thcCpc, разность температур при противотоке принимает
постоянное значение и AT = АТа = АТь. Если разность темпе-
температур АТа не более чем на 50% превышает АТЬ, то среднеариф-
среднеарифметическая разность температур отличается от AT не более чем
на 1% и ее можно использовать для упрощения расчетов.
0,2 0,3 0,4 0,5 0,6 0>7 0,8 0,9
J
lS, ВЫХ
Рис. 7.11. Поправочный коэффициент к значению Д7\ рассчитанному при про-
противотоке, для теплообменника с одним ходом в межтрубном пространстве и
с двумя или кратными двум ходами в трубном пучке. (С разрешения Ассо-
Ассоциации фирм-изготовителей трубчатых теплообменников.)
Использование среднелогарифмической разности температур
представляет по существу аппроксимацию, удобную для прак-
практических расчетов, поскольку в общем случае величина U не
постоянна. При проектировании, однако, суммарный коэффи-
коэффициент теплопередачи обычно рассчитывается для средней сек-
секции теплообменника, посредине между его концами, и прини-
принимается постоянным. Если U существенно изменяется, то для ре-
решения уравнения G.6) необходимо численное интегрирование
по шагам.
Для теплообменников более сложных типов, таких, как ко-
жухотрубные аппараты с несколькими ходами в трубном пучке
и в межтрубном пространстве, для противоточных теплообмен-
теплообменников со смешивающимися и несмешивающимися потоками
определение средней разности температур представляет сложную
13*
388 Глава 7
задачу. Обычная методика расчета заключается в модифи-
модификации простого выражения для АГ с помощью поправочных
коэффициентов, которые представлены в виде диаграмм [6, 7].
На рис. 7.11—7.14 приведены четыре из упомянутых диа-
диаграмм1). По оси ординат каждого графика отложен поправоч-
поправочный коэффициент F. Для получения истинной средней разности
1 I
11, вых
г
Ts, вых
Рис. 7.12. Поправочный коэффициент к значению Af, рассчитанному при про-
противотоке, для теплообменника с двумя ходами в межтрубном пространстве
при числе ходов в трубном пучке, кратном двум. (С разрешения Ассоциации
фирм-изготовителей трубчатых теплообменников.)
температур для_любого из этих аппаратов необходимо расчет-
расчетное значение АГ для противотока умножить на соответствую-
соответствующий поправочный коэффициент, т. е.
G.18)
На оси абсцисс отложены отношения разностей температур
т Т
1 /, вых ' U вх
1 5, ВХ J t> BX
G19)
1) Поправочные коэффициенты для некоторых других теплообменных.
аппаратов представлены в работе [6].
Теплообменники 389
где индексы t и s относятся к теплоносителям в трубах и в
межтрубном пространстве соответственно, а индексы «вх» и
«вых» означают условия на входе и выходе из теплообменника
1,0
0,9
0,8
0,7
0,6
'О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
к \
n1_
S
\
д
\
О
\
V
\
=z
-*+
к,
\
Л
1
\
\
¦*>
fa»
\
\
—
ч
\
\
кг
ч
\
^>
\°
\
\
—,
N
\
1
\
\
\
\
\-
1
1
';,вых
Рис. 7.13. Поправочный коэффициент к значению AT, рассчитанному при про-
тлвотоке, для перекрестноточного теплообменника; один теплоноситель в
межтрубном пространстве перемешивающийся, другой — неперемешивающий-
ся; один ход в трубном пучке [20].
соответственно. Отношение Р характеризует эффективность на-
нагревания или охлаждения и может изменяться от нуля при по-
постоянной температуре одного из теплоносителей до единицы в
случае, когда температура на входе горячего теплоносителя
JS, BX '
Jf,Bb»X
s
\
\\
и
!5
ч
>
>
в
\
V
=;
\
>
\
\
\\
\
\
У
-—.
s
\
s
\
-—.
¦-*>,
ч
\
\
\
\
\
\
1
С
s
\
\
\
\
\
7
\
\
\
\
\
\
\
л
llf
°'5.0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
S, ВЫХ
Рис. 7.14. Поправочный коэффициент к значению ДГ, рассчитанному при про-
противотоке, для перекрестноточного теплообменника; обе жидкости не переме-
перемешивающиеся; один ход в трубном пучке [20].
равна температуре на выходе холодного теплоносителя. Пара-
Параметр Z, характеризующий отдельные кривые, равен отношению
произведений массовых расходов на теплоемкости двух тепло-
теплоносителей rhtCpt/rhsCps. Это отношение также равно изменению
температуры теплоносителя в межтрубном пространстве, делен-
деленному на изменение температуры теплоносителя в трубах:
G.20)
J Т
S, ВХ S,
т — т
5, BblX t
Щ
390 Глава 7
При использовании поправочных коэффициентов не имеет зна-
значения, где течет поток горячего теплоносителя в межтрубном
пространстве или трубах. Если температура одного из тепло-
теплоносителей остается постоянной, направление течения не имеет
значения, поскольку F равно l^ji в расчетах можно использо-
использовать непосредственно значение Д7\
Пример 7.1. Определить площадь теплопередающей поверхности тепло-
теплообменника, требуемую для охлаждения 95%-ного раствора этилового спирта
(ср = 3810 Дж/кг-град) от 65,6, до 39,4°С потоком воды при температуре
на входе 10°С. Теплообменник изготовлен из труб с наружным диаметром
0,0254 м, расход спирта 6,93 кг/с, расход воды 6,3 кг/с. Предполагается, что
суммарный коэффициент теплопередачи, отнесенный к наружной поверхности
трубы, равен 568 Вт/(м2-град). Рассмотреть каждое теплообменное устрой-
устройство с различными схемами течения теплоносителей:
а) Прямоточный теплообменник.
б) Противоточный теплообменник.
б) Прямоточно-противоточный теплообменник с двумя ходами в меж-
межтрубном пространстве и 72 трубами в пучке; спирт течет в межтрубном про-
пространстве, вода — по трубам.
г) Перекрестный ток с одним ходом в трубном пространстве и одним хо-
ходом в межтрубном пространстве, жидкость в межтрубном пространстве пере-
перемешивается.
Решение.
а) Температуру воды на выходе для любой из четырех схем теплообмен-
ных устройств можно определить из общего уравнения теплового баланса
в предположении, что тепловыми потерями в атмосферу можно пренебречь.
Записывая уравнение теплового баланса
™ЦСрк (ГА, вх ~ Гй, вых) = Ксрс (Тс, вых ~ Тс, вх)
и подставляя в это уравнение исходные данные, получаем
6,93 • 3810 F5,6 — 39,4) = 6,30 • 4187 (TCi выХ — 10),
откуда температура воды на выходе равна 36,2°С. Тепловой поток от спирта
к воде равен
1 - **сд* (Гй, вх ~ Tk. вых) - 6'93 • 3810 <65>6 - 39-4) - 691 800 Вт.
Из уравнения G.17) для прямотока находим
т*_ ДГд-АГ, _ 55,6-3,2 _1д1оГ
"" In (ДГа/ДГ6) " In E5,6/3,2) ~ ' '
Из уравнения G.12) определяем площадь теплопередающей поверхности
Л --JU- 6918°° =66,2 и*.
U-Ы 568-18,4
Теплообменник длиной 830 м с диаметром наружной трубы 0,0254 м имеет
слишком большие размеры, чтобы его можно было использовать на прак-
практике.
б) Для аппарата с противотоком средняя разность температур равна
65,3 — 36,2 = 29,4°С, поскольку thcCpc = rhhCph. Требуемая площадь поверх-
поверхности равна
Л q 619 800 < .
А == _ = = 41,4 м2,
UAT 568 • 29,4
что на 40% меньше площади, необходимой для прямоточного теплообмен-
йика.
Теплообменники 391
в) Для прямоточно-противоточного аппарата соответствующая средняя
разность температур вычисляется с помощью поправочного коэффициента, ко-
который определяется из рис. 7.12 при средней температуре для противотока:
°' '
а отношение расходных теплоемкостей теплоносителей равно
Из диаграммы (рис. 7.12) находим F = 0,97, и площадь теплоотдающей по-
поверхности равна
41 4
Л = = 42 7 м2
0,97 ' "
Длина теплообменника из семидесяти двух труб с наружным диаметром
0,0254 м, установленных параллельно, равна
Л/72^ 42,7/72
jtD я-0,0254
Эта длина вполне приемлема для практических целей, однако если необхо-
необходимо укоротить теплообменник, то можно использовать большое число труб,
г) Для аппарата с перекрестным током (рис. 7.3) поправочный коэффи-
коэффициент, определенный из диаграмм (рис. 7.13), равен 0,88. Требуемая площадь
теплоотдающей поверхности, таким образом, равна 48,5 м2, что на 10% боль-
больше площади поверхности прямоточно-противоточного теплообменника.
7.5. ЭФФЕКТИВНОСТЬ ТЕПЛООБМЕННИКА
При тепловом анализе теплообменников различных типов,
рассмотренном в предыдущем разделе, использовалось уравне-
уравнение G.16), записанное в виде
Эта форма записи уравнения удобна, когда известны все гра-
граничные температуры, необходимые для расчета соответствую-
соответствующей средней разности температур, и поэтому уравнение G.16)
широко используется в конструкторских расчетах теплообмен-
теплообменников различного назначения. Однако встречаются многочис-
многочисленные случаи, когда характеристика теплообменника (т. е. U)
известна, или, по крайней мере, ее можно оценить, в то время
как температуры теплоносителей на выходе из теплообменника
неизвестны. Проблема такого рода возникает при выборе тепло-
теплообменника или когда проведено его испытание для одного рас-
расхода, а условия эксплуатации требуют других значений расхо-
расходов одного или обоих теплоносителей. Значения выходных тем-
температур и тепловой поток можно найти только с помощью
утомительного метода последовательных приближений, используя
диаграммы, представленные в предшествующем разделе. В та-
таких случаях желательно привлекать любые справочные мате-
материалы для расчета логарифмической или другой средней раз-
разности температур. Подобный метод предложен Нуссельтом [8]
и Тен Броеком [9].
392 Глава 7
Для вывода уравнения, описывающего тепловой поток, ко-
которое не содержит значений температур на выходе, введем
понятие эффективности теплообменника Е. Эффективность теп-
теплообменника определяется как отношение фактического тепло-
теплового потока в данном теплообменнике к максимально возмож-
возможному тепловому потоку в теплообменнике. Последнее значение
может быть получено в противоточном теплообменнике с бес-
бесконечно большой поверхностью теплообмена. В устройстве та-
такого типа при отсутствии потерь тепла наружу температура
холодного теплоносителя на выходе равна температуре горя-
горячего теплоносителя на входе, если mccpc <C fhhcpc'f если же
thhCph < rhcCpc, то температура горячего теплоносителя на вы-
выходе равна температуре холодного теплоносителя на входе.
Другими словами, эффективность означает сравнение фактиче-
фактического теплового потока с максимальным возможным тепловым
потоком, величина которого ограничена только требованиями
второго закона термодинамики. В зависимости от того, какая
расходная теплоемкость меньше, выражения для эффективно-
эффективности имеют вид
Q /Т Т \
F h\ й.вх /г, вых/,
Ь — -Q 7f 7т Г.
мин V h, вх с, вх/
или
Е = г(т-т\ ' <
мин \ /г. вх с, вх/
где Смин наименьшая из величин rhhCPh и тссрс. Если эффектив-
эффективность теплообменника известна, тепловой поток можно непо-
непосредственно определить из уравнения
? = ЕСМИН(ГЙ,ВХ-~ГС,ВХ), G.22)
ПОСКОЛЬКУ ЕСминG\ вх — Тс, вх) = Ch{ThiBX — 7\ вых) =
= СС(ТС,вых — Тс,вх). Уравнение G.22) является основным соот-
соотношением для данного анализа, поскольку оно позволяет выра-
выразить тепловой поток в зависимости от эффективности, наимень-
наименьшего значения расходной теплоемкости и разности между тем-
температурами теплоносителей на входе. Оно заменяет уравнение
G.16) при анализе АГ, но не включает значения температур на
выходе. Естественно, уравнение G.22) можно также использо-
использовать для конструкторского расчета вместо уравнения G.16).
Проиллюстрируем методику нахождения выражения для эф-
эффективности теплообменника применительно к устройству пря-
прямоточной схемы. Эффективность можно получить, подставляя
в уравнение G.12) вместо (Tc,BX—TC)Bblx)/(ThfBX~Tc,BX) вы-
выражение для эффективности из уравнения G.21). Тогда имеем
или
Теплообменники 393
Решая относительно Е, получаем
ЖсГ' G'23)
Если Ch < Сс, выражение для эффективности принимает вид
1 — е'
а если Сс < Chi то
г+еш— G'24б)
Поэтому выражение для эффективности, соответствующее обоим
случаям, можно записать в виде
. G.25)
Проведенный выше анализ показывает, каким образом эффек-
эффективность для заданной схемы движения потоков в теплообмен-
теплообменнике можно выразить в виде зависимости от двух безразмерных
100
Го
Те
1
/
/
Ха
ряч
/
плс
пов
ин/(
//
у
рактеристики прямоточнс
теплообменника
ая жидкость/тс)А= Ch
/Холодная жидкость, (тс)
>отдающая
ерхность
чма
<^1
-0 ^
^*
-о,
*-**
50-
0f7
—•-¦
1Т
JU
)ГО
с =
Характеристики противоточного
теплообменника
Горячая жидкость, (mc)h=Ch
100
80
О
X
I 40
О 20
Рис. 7.15. Эффективность прямоточ- Рис. 7.16. Эффективность противоточ-
ного теплообменника [1]. ного теплообменника [1].
параметров: отношения расходных теплоемкостей Смнн/Сыакс и
отношения суммарного коэффициента теплопередачи к наи-
наименьшей по величине расходной теплоемкости жидкости
М/Смин. Последний из двух параметров называется числом
единиц переноса тепла (Number of heat-Transfer Units (NTU)].
Теплоотдающая
поверхность
NTU,
394 Глава 7
Безразмерный коэффициент теплопередачи представляет собой
меру теплообменной способности теплообменника. Чем больше
значение NTU, тем ближе теплообменник к своему термодина-
термодинамическому пределу. На основе анализа, который в принципе
100
20
Ха
ВО'
Ш
Bi
BTf
см
эан
04*
Л
\
ид
эуб
J{
//
ш
F
/
л
теристини, прямоточно-проти-
¦юго теплообменника по схеме
1-2
Жидкость в межтрубном
ii пространстве (mc)$ = cs
r< -+ \-
\\ -д— I—
чость в трубах (mc)t = Ct Ш
ктрубном пространстве 1 ход,
ном пучке 2,4,6 и т. д. ходов
"ма
/
g
й
s
1
-
-
1—
1.00
—
2
NTU
Характеристики перекрестноточного
теплообменника (обе жидкости непе-
ремешивающиеся) Холодная
Jt жидкость (тс)с
Горячая
жидкость
100
80
60
40
20
Рис. 7.17. Эффективность кожухо- Рис. 7.18. Эффективность перекрест-
трубного теплообменника с одним хо- ноточного теплообменника с непере-
непередом в межтрубном пространстве с мешивающимися теплоносителями [l].
перегородками и двумя или кратны-
кратными двум ходами в трубном пучке [I].
аналогичен рассмотренному здесь анализу для прямотока, мож-
можно оценить эффективность большинства схем движения потока,
представляющих практический интерес. Такие результаты были
приведены Кэйсом и Лондоном [1] в удобном графическом
виде, позволяющем определить эффективность для заданных
значений NTU и СМин/СМакс. На рис. 7.15—7.19 приведены кри-
кривые эффективности некоторых наиболее общих схем движения
потоков. На этих рисунках по оси абсцисс отложены значения
NTU теплообменников. В качестве постоянного параметра для
каждой кривой выбрано отношение расходных теплоемкостей
СМин/Смакс, а по оси ординат отложена эффективность теплооб-
теплообменника. Отметим, что для испарителя или конденсатора
СМин/СМакс = 0, поскольку если в теплообменнике температура
одного теплоносителя остается постоянной, то ее эффективная
Теплообменники 395
удельная теплоемкость, а следовательно, и ее расходная тепло-
теплоемкость по определению равны бесконечности.
Пример 7.2. При испытании теплообменника с разделительными перего-
перегородками, одним ходом в межтрубном пространстве и двумя ходами в труб-
трубном пучке получены следующие данные: масло (ср = 2100 Дж/(кг-град))
при турбулентном режиме течения входит в трубный пучок при температуре
340 К с расходом 1,00 кг/с и выходит из трубного пучка при температуре
310 К; вода входит в межтрубное пространство при температуре 290 К и
выходит из него при температуре
300 К. В условиях эксплуатации тре-
требуется охлаждение масла, поступаю-
поступающего в теплообменник при темпера-
температуре 370 К с расходом, составляю-
составляющим три четверти расхода в условиях
проведения испытания. Рассчитать
температуру масла на выходе, если
расход воды и ее температура на
входе остались без изменения.
Решение. На основе данных ис-
испытаний можно определить расход-
расходную теплоемкость воды и суммарный
коэффициент теплопередачи в тепло-
теплообменнике. Из уравнения G.13) нахо-
находим расходную теплоемкость воды
100
••С,
h, вх
р
/ь вых
Т —7
с% вых с, вх
340 - 310
_Ь21М__- 6300 Вт/град,
а из уравнения G.19) находим отно-
отношение разностей температур Р:
D *» ВЫХ U ВХ _
Характеристики перекрестно-точного
теплообменника (одна жидкость пере-
перемешивающаяся)
-4
Л.^.
Неперемешйвающ. жидкость
ремеши-
ающ.
жидкость
'Г Т
1 s, вх t, вх
340 — 310
340 — 290
= C00 - 290) C40 - 310) - 0,33.
0,6,
Рис. 7.19. Эффективность перекрест-
ноточного теплообменника, один теп-
теплоноситель перемешивающийся, дру-
другой неперемешивающийся. Когда
Ссмеш/Снесмеш > 1, NTUMaKc раССЧИТЫ-
ВаетСЯ ДЛЯ Снесмеш-
0,94, тогда средняя разность температур равна
C40 — 300) — C10 — 290)
= 28,9 К
Из рис. 7Л1 определяем F =
А;Гср =vF АГ = 0,94 1п[(з40-300)/C10-290)]
'Из уравнения G.16) суммарный коэффициент теплопередачи
= 2180 Вт/град.
АГ
1-2100C40 — 310)
28,9
» Поскольку термическое сопротивление в трубном пучке со стороны масла
зависит от скорости потока, уменьшение скорости до 75% первоначального
значения приводит к увеличению термического сопротивления на величину,
приблизительно равную отношению скоростей в степени 0,8. В этом можно убе-
убедиться из рассмотрения уравнения D.88). Следовательно, для новых усло-
условий коэффициент теплопередачи, NTU и отношение расходных теплоемкостей
396 Глава 7
будут приблизительно равны
UА « B180) 0,750'8 = 1730 Вт/град;
U А 1730
мтп _
Смасло 0,75- Ь 2100 "
масло _ Смин _ 0,75.1-2100
1,1
6300
= 0,25.
Из рис. 7.17 эффективность равна 0,61. Следовательно, из уравнения
G.21а) температура масла на выходе будет равна
Гмасло, вых = ^масл0) вх - Е ЛГмакс = 370 - [0,61 C70 - 290)] = 321,2 К.
Пример 7.3. Плоский пластинчатый нагреватель (рис. 7.20) должен ис-
использоваться для нагревания воздуха горячими выхлопными газами из тур-
турбины. Требуемый расход воздуха 0,75 кг/с, температура воздуха на входе
Вход
воздуха
7,62 -10 М
Воздух1™
j
8,2296-10-3Mv
i
6,7056*10М'
Сечение Л — А
(не в масштабе)
^0,3048 М-
аза во.
Рис. 7.20. Подогреватель пластинчатого типа.
Выход
воздуха
290 К; горячие газы входят при температуре 1150 К, расход газа 0,60 кг/с.
Определить температуру воздуха на выходе из теплообменника.
Ра = 0,703 м — смоченный периметр со стороны воздуха;
Pg = 0,416 м — смоченный периметр со стороны газа;
Аа = 2,275-Ю-3 м2 — площадь поперечного сечения воздушного потока,
отнесенная к одному каналу;
/4g=l,6-10~3 м2 — площадь поперечного сечения газового потока, от-
отнесенная к одному каналу;
число каналов на воздушной стороне 19;
число каналов на газовой стороне 18.
Решение. Из рис. 7.20 видно, что данное устройство относится к пере-
крестноточному типу, когда оба теплоносителя не смешиваются. В качестве
первого приближения пренебрегаем концевыми эффектами. Схема движения
воздушного и газового потоков аналогична схеме движения в прямых тру-
трубах, имеющих следующие размеры: длину воздушного канала L = 0,2 м;
эквивалентный диаметр воздушного канала DHa = -^- = 0,0128 м; длину
газового канала Lg = 0,35 м; эквивалентный диаметр газового канала
4Л
Z)t
: 0,0154 м; площадь теплоотдающей поверхности А = 2,52 м2'
Теплообменники 397
Коэффициенты теплоотдачи можно рассчитать из уравнения E.15), описы-
описывающего теплообмен при течении газа в каналах (La/&Ha = 15,6; LJD^ =
= 22,7). Однако при расчете возникают определенные трудности, связанные
с тем, что температуры обоих теплоносителей изменяются вдоль трубы. По-
Поэтому сначала необходимо оценить определяющую среднюю температуру теп-
теплоносителя, а затем уточнить расчеты после вычисления температуры на вы-
выходе и температуры стенки. Выбираем определяющую среднюю температуру
воздуха, равную 573 К, определяющую среднюю температуру газа 973 К, а
теплофизические свойства при этих температурах находим из табл. ILVI. 1
(в предположении, что свойства газа близки к свойствам воздуха):
^возд = 3,932 • Ю-5 Н • с/м2, РгВозд = 0,71, 6ВОЗД = 0,0429 Вт/(м - град),
Цгаз = 4,085 • 10~5 Н • с/м2, Рггаз = 0,73, ?газ = 0,0623 Вт/(м • град),
1047 Дж/(кг • град), сп =1101 Дж/(кг • град).
^газ
Массовые расходы на единицу площади равны
О 75
19 ¦ 2,275-10*3"
(т/Л)газ = — гз = 20,83 кг/(м2. с).
^ 18- 1600- 10 d
Числа Рейнольдса равны
_ (*M)rMDffg 20,83-0,0154
Квга3 ^ " 4,085-Ю-5 =
Используя уравнение E.15), находим средние коэффициенты теплоотдачи:
(к \ / D \ 0,055
0,036-^
= [0,036 Jg|f 5650^0,710-33] (^_H-055_ 93>0 Вт/(м*. град),
[0,036 ^|| 7850°-80,730-33] (-^У™ - 144 Вт/(м» • град).
Эти значения коэффициентов теплоотдачи показывают, что примерно 60%
общего падения температуры происходит на стороне воздуха. Если прене-
пренебречь термическим сопротивлением металлической стенки, суммарный коэффи-
коэффициент теплопередачи равен
UА = — —¦ j Х- j = 142 Вт/град.
haA hgA 93-2,52 144-2,52
Безразмерный коэффициент теплопередачи, рассчитанный по параметрам бо-
более горячего теплоносителя, который имеет меньшую расходную теплоемкость,
равен
NTU = -^- - ftfi14.2.m = 0,215.
t-мин 0,0-1101
398 Глава 7
Отношение расходных теплоемкостей равно
= 0,841.
Сгаз 0,6-1101
0,75-1047
Из рис. 7.18 находим, что эффективность равна 0,13. В итоге средние темпе-
температуры газа и воздуха на выходе равны
Ггаз, вых = 7*аэ, вх - Е ДГмакс = 1150 - 0,13 A150 - 290) = 1038 К,
^возд, вых = ^возд, вх + г Е дгмакс = 290 + 0,841 • 0,13 A150 — 290)==384 К.
^возл
Проверка определяющих средних температур воздуха и газа дает значения
567 и 946 К, которые достаточно близки к принятым значениям 573 и 973 К,
поэтому нет необходимости проводить повторный расчет. Для оценки преиму-
преимущества подхода, основанного на понятии эффективности теплообменника,
представьте, что такая же задача решается методом последовательных при-
приближений с использованием уравнения G.16) и диаграммы рис. 7.14,
Эффективность теплообменника, рассмотренного в приме-
примере 7.3, очень низка A3%), поскольку площадь поверхности
теплообмена слишком мала, чтобы эффективно использовать
располагаемую тепловую энергию. Улучшение характеристик
теплообменника, которого можно достигнуть увеличением пло-
площади поверхности теплообмена, хорошо иллюстрируется кри-
кривыми эффективности. Пятикратное увеличение площади при-
приводит к возрастанию эффективности до 60 %. Если, однако,
для определенной конструкции теплообменника расчетная точка
окажется вблизи изгиба этих кривых или над ним, увеличение
площади поверхности не приведет к существенному улучшению
характеристик, а может вызвать лишь чрезмерное увеличение
потерь давления на трение.
7.6. СОЛНЕЧНЫЕ КОЛЛЕКТОРЫ
Солнечный коллектор представляет собой теплообменное
устройство, использующее энергию излучения Солнца для уве-
увеличения внутренней энергии и температуры теплоносителя. Кол-
Коллектор простейшего типа представляет собой трубу, восприни-
воспринимающую солнечное излучение. Солнечное излучение частично
поглощается трубой, температура стенки трубы возрастает, и
если теплоноситель при температуре окружающей среды про-
протекает по трубе, тепло передается от трубы к жидкости и тем-
температура последней возрастает до тех пор, пока тепловые по-
потери трубы в окружающую среду не сравниваются по величине
с энергией поглощенного солнечного излучения. Тепловые ха-
характеристики этой простейшей системы можно улучшить оребре-
нием труб, что позволяет увеличить площадь поверхности, вос-
воспринимающей солнечное излучение, а тепловые потери можно
уменьшить размещением одного или двух слоев стекла между
падающим солнечным излучением и поверхностью, поглощаю-
Теплообменники 399
щей это излучение. На рис. 7.21 показано поперечное сечение
типичного плоского солнечного коллектора. Если теплоноси-
теплоноситель, например вода, протекает по трубам, то сообщаемая ему
полезная тепловая энергия равна
9и = тср(ГЬвых--7>,вх), G.26)
где т — массовый расход жидкости через коллектор; ср —
удельная теплоемкость теплоносителя при постоянном давле-
1 /
//у Стеклянное покрытие
jSyS /Воздух / Воздух
/
бы с теплоносителем-^
* Соединительная пластина'
Рис. 7.21. Поперечное сечение плоского коллектора.
Изоляция
нии; Г/, вых — Tf} вх — прирост температуры теплоносителя при
прохождении через коллектор.
Баланс энергии для плоского коллектора
Тепловые характеристики солнечного коллектора можно рас-
рассчитать из уравнения баланса энергии, которое позволяет опре-
определить долю энергии падающего излучения как полезную энер-
энергию, передаваемую теплоносителю. Для плоского коллектора
площадью Ас уравнение баланса энергии имеет вид
— а 4-/7 -±-***-
dt
G.27)
где 1с — плотность потока солнечного излучения, падающего на
поверхность коллектора; %с — эффективная пропускательная
способность покрытия (покрытий) солнечного коллектора;
as> с— поглощательная способность поверхности поглощающей
пластины солнечного коллектора; qu — тепловой поток от по-
поглощающей пластины коллектора к теплоносителю; gw — теп-
тепловой поток (или тепловые потери) от поглощающей пластины
коллектора в окружающую среду; dec/dt — поток тепла, акку-
аккумулированный коллектором за счет его внутренней энергии.
400 Глава 7
Мгновенное значение коэффициента полезного действия
коллектора цс представляет собой просто отношение полезно
используемой энергии к полной энергии падающего солнечного
излучения:
Практически коэффициент полезного действия должен быть из-
измерен за некоторый конечный период времени. При проведении
стандартных испытаний тепловых характеристик NBS1) необ-
необходимый период времени для расчета эффективности состав-
составляет 15 или 20 мин, в то время как для конструкторского ра-
расчета представляет интерес более длительный период времени
(сутки или месяц). Тогда средний коэффициент полезного дейст-
действия равен
t
«k^-i . . G.29)
\ Aclc dt
S
где t — продолжительность периода времени, в течение кото-
которого осредняется указанная характеристика.
Детальный и строгий анализ коэффициента полезного дейст-
действия солнечного коллектора представляет собой сложную задачу
вследствие нелинейного характера уравнений, описывающих
радиационный теплообмен. Однако упрощенный анализ на
основе решения линеаризованных уравнений радиационного
теплообмена обычно достаточно точен для практических целей.
Он позволяет проиллюстрировать влияние тепловых параметров
на к. п. д. солнечного коллектора и указать, каким образом эти
параметры взаимодействуют между собой. Хотя для конструк-
конструкторских и экономических расчетов солнечных систем в общем
случае используются результаты стандартных испытаний теп-
тепловых характеристик NBS, для надлежащего анализа и интер-
интерпретации результатов этих испытаний крайне необходимо по-
понимание существа происходящих тепловых процессов.
Коэффициент тепловых потерь коллектора
Для лучшего понимания значения параметров, которые опре-
определяют тепловой коэффициент полезного действия солнечного
коллектора, важно ввести понятие суммарного коэффициента
l) NBS— Национальное бюро стандартов США,
Теплообменники 401
тепловых потерь коллектора1). Если коэффициент тепловых
потерь коллектора Uc задан, а пластина коллектора находится
при средней температуре Тс, то второй член в правой части
Солнце
Верхнее
отражающее[
А покрытие
ТеМПера1ура 0HPWaK>^ среды Та
Полезная
энергия
Солнце
Температура верхнего
покрытия Tgj
Температура нижнего понрытия Tg7
R,
Отражение излучения
поглощающей пластиной
Температура пластины
коллектора' Тс
Температура основания корпуса коллектора
Температура окружающей среды Та
Рис. 7.22. Тепловые цепи для плоского коллектора, показанного на рис. 7.21.
а—подробная схема, б —приближенная схема, эквивалентная схеме а. Для обеих схем
поглощающая пластина воспринимает энергию падающего излучения, равную &sls> где
уравнения G.27) можно записать при заданной температуре
окружающего воздуха Та в простом виде:
п II А (Т — Т \ G Qfl\
Ч ион "~~ ^ с^с V с шщ \* *&**/
Простота этого соотношения может ввести в заблуждение, ко-
коэффициент тепловых потерь коллектора нельзя определить без
детального анализа всех тепловых потерь. На рис. 7.21 приве-
приведена схема коллектора с двумя стеклянными покрытиями, а на
рис. 7.22, а показана тепловая цепь, элементы которой должны
быть рассчитаны прежде, чем они могут быть объединены
1> По существу этот коэффициент есть не что иное, как коэффициент
теплопередачи, с помощью которого рассчитываются тепловые потери с по-
поверхности коллектора в окружающую среду. — Прим. перев.
402 Глава 7
в эквивалентный коэффициент тепловых потерь, как это показа-
показано на рис. 7.22,6.
На рис. 7.23 качественно показано распределение темпера-
температуры в плоском коллекторе. Излучение падает на верхнюю по-
поверхность пластины, соединяющую две расположенные рядом
трубы, в которых течет теплоноситель. Это излучение равно-
равномерно поглощается пластиной и передается теплопроводностью
Пластина коллектора
Теплоноситель Труба
а
В заданном
сечении у
Рис. 7.23. Распределение температуры в поглощающей пластине плоского кол-
коллектора.
а—схема поглощающей пластины; б —профиль температуры в направлении течения тепло-
теплоносителя; в— профиль температуры в заданном сечении у: «—распределение температуры
в поглощающей пластине.
в поперечном направлении трубам, внутри которых тепло пере-
передается конвекцией движущемуся теплоносителю. Очевидно, что
в любом поперечном сечении, перпендикулярном направлению
течения, температура имеет максимум в средней точке между
двумя соседними каналами и уменьшается вдоль пластины по
направлению к трубе (рис. 7.23,6). Поскольку тепло перено-
переносится к теплоносителю, его температура, а также температура
всей коллекторной системы будут возрастать в направлений
течения. Увеличение температуры в среднем сечении между
двумя трубами качественно показано на рис. 7.23, в. Распреде-
Распределения температур в направлениях осей х и у показаны в трех-
трехмерном изображении на рис. 7.23, г.
Для построения модели, подходящей для теплового расчета
Теплообменники 403
плоского коллектора, будут сделаны следующие упрощающие
допущения:
1. Коллектор находится в стационарном тепловом состоянии.
2. Температурный напор между верхней и нижней поверх-
поверхностями поглощающей пластины пренебрежимо мал.
3. Тепловой поток через покрытия и изоляцию является
одномерным.
4. Гидравлические коллекторы, соединяющие трубы, зани-
занимают небольшую площадь солнечного коллектора и обеспечи-
обеспечивают равномерное течение жидкости в трубах.
5. В области инфракрасного излучения небосвод можно рас-
рассматривать как абсолютно черное тело при некоторой эквива-
эквивалентной температуре.
6. Поток солнечного излучения распределен равномерно по
пластине коллектора.
Для численного анализа рассмотрим точку с координатами
х, у на поверхности типичного плоского коллектора (рис. 7.23, а).
Пусть температура в этой точке Тс(х,у), и предположим, что
солнечное излучение поглощается с заданным потоком^ погло-
поглощенного излучения /sa5. Если нижняя поверхность коллектора
хорошо изолирована, то в основном тепловые потери происходят
через*верхнюю поверхность. Коэффициент тепловых потерь для
верхней поверхности коллектора можно рассчитать, определив
термические сопротивления /?3, /?4 и ^5 (рис. 7.22). Тепло пере-
передается между поглощающей пластиной и вторым стеклянным
покрытием, а также между двумя стеклянными покрытиями
конвекцией и излучением одновременно. За исключением потока
солнечного излучения, поглощаемого вторым стеклянным по-
покрытием, соотношения для теплового потока между телами с
температурой Тс и Tg2 и между телами с температурой Tg2 и Tg\
одинаковы. Таким образом, плотность теплового потока между
поглощающей пластиной и вторым стеклянным покрытием равна
<7верх, пот = ЛсНс2 (Тс Tg2) + -щ +1/8 ^Т ' G.31)
где Нс2 — коэффициент теплообмена между поглощающей пла-
пластиной и вторым стеклянным покрытием; ер,,— излучательная
способность пластины в инфракрасной области спектра; гё2, i —
излучательная способность второго стеклянного покрытия.
Как было показано в гл. 1, если линеаризовать радиацион-
радиационный член в уравнении G.31), то его можно записать в виде
<7веРх, пот = (hc2 + hr2) Ас (Тс - Tg2) = Тс~*82 , G.32)
где h а(т' + т#)(т2с + т*) ,7 33)
404 Глава 7
Аналогичное преобразование для теплового потока между
двумя стеклянными покрытиями дает
пот
= (ha + Ari) Ae (Tg2 - Tgl) = Tg2*el , G.34)
rAe
и hc\ — коэффициент теплообмена между двумя прозрачными
покрытиями.
Разумеется, излучательные способности двух покрытий бу-
будут одинаковыми, если они изготовлены из одинакового мате-
материала. Однако экономические показатели можно иногда улуч-
улучшить, если использовать между верхним стеклянным покрытием
и поглощающей пластиной пластиковое покрытие, и, следова-
следовательно, в такой конструкции типа сэндвича радиационные свой-
свойства двух покрытий могут оказаться различными.
Уравнение для термического сопротивления между верхней
поверхностью наружного покрытия коллектора и окружающим
воздухом по форме аналогично двум рассмотренным выше соот-
соотношениям, однако коэффициент теплоотдачи на верхней поверх-
поверхности необходимо рассчитывать иначе. Когда окружающий воз-
воздух неподвижен, необходимо использовать соотношения для
теплообмена в условиях свободной конвекции, а когда над по-
поверхностью коллектора дует ветер, необходимо использовать
соотношения для теплообмена при вынужденной конвекции, как
показано в гл. 5. Между верхним покрытием и небосводом при
Гнеб происходит теплообмен излучением, тогда как между верх-
верхним покрытием при температуре Тё\ и окружающим воздухом
при Гвозд происходит конвективный теплообмен. Для удобства
обе величины удельной тепловой проводимости отнесем к тем-
температуре воздуха. Это дает
Ср, по, - {К, со + К. .) (Tgl - ТВ03Л) - 'gl ~'возд . G.36)
где Аг.. - 8gl> to (Tgl + Гнеб) (Tgl + Т1б) ^'Г^ • G-37)
Для плоского коллектора с двумя стеклянными покрытиями
суммарный коэффициент тепловых потерь коллектора Uc, сумм
можно представить в виде
Ve. СУММ = -?7 + #з
где R]—термическое сопротивление нижней поверхности.
Для расчета коэффициента тепловых потерь коллектора с
использованием уравнения G.38) требуется решение уравнений
G.35) и G.36) итерационным методом, поскольку удельные
радиационные проводимости являются функциями температур
Теплообменники 405
покрытия и пластины, которые заранее неизвестны. Клейн [11]
предложил эмпирический метод расчета Uc для коллекторов
с покрытиями, изготовленными из одинакового материала, ко-
который оказывается достаточно точным и более удобным для ис-
использования. Для такого подхода тепловые потери с верхней
поверхности коллектора в ваттах записываются в виде
п - - (Тс-Та) Ас _j_
чверх,пот
N
1
G.39)
где f = A - 0,04ACf во + 0,0005А^ов)A+0,09 Ш); С = 365,9 A -
— 0,00883р + 0,00013Р2); Л; — число покрытий, hCt „ = 5,7 +
+ 3,8F (V в м/с), egl — сте-
пень черноты покрытий. 1
Значения qBepxf пот, рас-
рассчитанные по формуле
G.39), « хорошо согласу-
согласуются со значениями, вы-
вычисленными по формуле
G.38).
Для определения ко-
коэффициента полезного
действия солнечного кол-
коллектора необходимо рас-
рассчитать тепловой поток к
теплоносителю. Если пре-
пренебречь нестационарными
тепловыми эффектами, то
тепловой поток к тепло-
теплоносителю, протекающему
Через коллектор, зависит Рис. 7.24. Коэффициент эффективности реб-
только ОТ температуры Ра Ц? Для плоских солнечных коллекторов
поверхности коллектора, типа лист~~ тРУба-
от которой тепло переда-
передается конвекцией к теплоносителю, температуры теплоносителя и
коэффициента теплообмена между коллектором и жидкостью.
Для расчета теплового потока сначала рассмотрим условия в
поперечном сечении коллектора, показанном на рис. 7.21. Сол-
Солнечное излучение, поглощенное на верхней поверхности солнеч-
солнечного коллектора, передается в поперечном направлении к потоку
теплоносителя в каналах. Температура максимальна в некото-
1,0
0,9
0,8
0,7
0,6
-
i i i i
\
\
i i i i
о ;
iiit
iiii
-
/llll
; о
0,5 1,0
(Uc/kt) w
1,5
406 Глава 7
рой средней точке между соседними каналами, и пластина кол-
коллектора действует как ребро, прикрепленное к стенкам канала
с потоком жидкости. Тепловую характеристику плоского ребра
можно выразить через коэффициент эффективности ребра %, ко-
которая определяется как отношение теплового потока, проходя-
проходящего через реальное ребро, к тепловому потоку через ребро с
бесконечной теплопроводностью.
Если Uс — суммарный коэффициент тепловых потерь с по-
поверхности плоского коллектора к окружающему воздуху, то
тепловой поток для данного сегмента пластины коллектора при
х, у на рис. 7.24 равен
Я (х, У) = Uс [Тс (х, У) - Та] dx dy, G.40)
где Тс — местная температура пластины коллектора, а Та — тем-
температура окружающего воздуха.
Если пренебречь теплопроводностью в направлении оси х,
то уравнение теплового баланса на данном расстоянии xq для
поперечного сечения плоского коллектора на единицу длины
в направлении * можно записать в виде
- ш
J - (- ш%-\^ J]=
=o.
l IJ ( ^
G.41)
Если толщина пластины t постоянна, а коэффициент теплопро-
теплопроводности материала пластины не зависит от температуры, урав-
уравнение G.41) можно представить в виде дифференциального
уравнения второго порядка
d2Tc
dy2
G>42)
Это уравнение имеет следующие граничные условия:
1. В центре между любыми двумя каналами тепловой поток
равен нулю, dTc/dy = О при у = 0.
2. У трубы температура пластины равна Ть(хо), или Тс =
= Ть(хо), при у = w = [(/' — ?)/2], где ^(лго) — температура
основания ребра.
Если принять, что пг2 = Uc/kt и Ф = Тс —(Та + asIs/Uc)i
уравнение G.42) принимает вид
G.43)
dy2 '
удовлетворяющий граничным условиям:
-as—° при у==
И ф = Ть(Х0)— \Ta-f--ff-) ПРИ У
Теплообменники 407
Общее решение уравнения G.43)
Ф = Сх sh ту + С2 ch my. G.44)
Постоянные С\ и С2 можно определить подстановкой двух гра-
граничных условий и решением двух результирующих уравнений
для С\ и С2. Это дает
Тс — (Та + o,s/s/Uc) ch my
Ть (*o) — (Ta~\~ cts/s/?/c) ch mw
На основе приведенного выше уравнения тепловой поток к
трубопроводу от части пластины между трубами можно опре-
определить путем расчета градиента температуры у основания
ребра для единицы ширины ребра, или
<7Реб = -kt^[f \y_w = ~k ^s - ^с (Ть (х0) - Та) th mw]. G.46)
Поскольку трубопровод соединен с ребрами с обоих сторон, пол-
полный тепловой поток равен
<7полн (*о) = 2w [аЛ - Uc (Ть (х0) - Та)] ^~. G.47)
Если все ребро находится при температуре Ть(х), что физически
соответствует пластине с бесконечно большим коэффициентом
теплопроводности, тепловой поток будет иметь максимальное
значение ?Полн, макс Как отмечалось ранее, отношение теплового
потока в реальном ребре к максимально возможному тепловому
потоку есть коэффициент эффективности ребра %. С использо-
использованием этого определения уравнение G.47) можно записать в
виде
?полн (х) = 2wr\f [аЛ - Uс (Ть (х0) - Та)], G.48)
th mw
'f mw *
Ha рис. 7.24 представлена зависимость коэффициента эф-
эффективности ребра % от безразмерного параметра {Uc/kt)xl2w.
Когда коэффициент эффективности ребра стремится к единице,
на нагрев жидкости расходуется максимальная доля энергии
излучения, поглощаемой ребром.
Кроме тепла, передаваемого через ребро, создается и по-
полезный поток энергии излучением, поглощаемым частью пла-
пластины непосредственно над трубой. Полезный поток энергии из
этой области пластины, который расходуется на нагрев тепло-
теплоносителя, равен
<7тРУба (х) = D [аЛ - Uс (Ть {х,) - Та)]. G.49)
м образом, полезная энергия на единицу длины в направ-
направлении потока теплоносителя равна
Я и (х) = (D + 2wi\f) [asls - Uc (Tb (x0) - Ta)]. G.50)
408 Глава 7
Энергия qu(x) должна передаваться в виде тепла теплоноси-
теплоносителю. Если термическое сопротивление металлической стенки
трубы пренебрежимо мало и отсутствует контактное сопротив-
сопротивление между трубой и пластиной, то тепловой поток к жидко-
жидкости равен
qu (х) = (я/),) hc, t [Tb (xQ) - Tf (xQ)]. G.51)
Коэффициент эффективности коллектора
Чтобы найти соотношение, связывающее полезную энергию,
получаемую коллектором, с известными физическими параме-
параметрами, температурой жидкости и температурой окружающей
среды, из уравнений G.50) и G.51) необходимо исключить
температуру коллектора. Решая уравнение G.51) относительно
Ть(х0) и подставляя полученное соотношение в уравнение G.50),
получаем
qu (х) = (D + 2w) F' [asls - Uc (Tf (x0) - Ta)]9 G.52)
где F'— коэффициент эффективности коллектора, определяе-
определяемый по формуле
F'
(D
Физически знаменатель в уравнении G.53) означает термиче-
термическое сопротивление между теплоносителем и окружающей сре-
средой, тогда как числитель представляет собой термическое со-
сопротивление между коллектором и окружающим воздухом.
Коэффициент эффективности пластины коллектора Р зависит
Таблица 7.3
Типичные значения параметров, которые определяют
коэффициент эффективности плоского коллектора F'
в уравнениях G.46) и G.53)
Г
1_
два стеклянных покрытия, 4 Вт/(м2-град)
одно стеклянное покрытие, 8 Вт/(м2-град)
Г медная пластина толщиной I мм, 0,4 Вт/град
[.стальная пластина толщиной 1 мм, 0,005 Вт/град
ламинарное течение воды при вынужденной конвекции,
300 Вт/(м2 • град)
турбулентное течение воды при вынужденной конвек-
конвекции, 1500 Вт/(м2-град)
турбулентное течение воздуха при вынужденной кон-
конвекции, 100 Вт/(м2-град)
Теплообменники 409
от Uсу hc,i и r[f. Он лишь слабо зависит от температуры, и для
всех практических случаев его можно рассматривать в качестве
расчетного параметра. Типичные значения параметров, которые
определяют значение F\ даны в табл. 7.3.
Коэффициент эффективности коллектора увеличивается с
увеличением толщины пластины и ее теплопроводности и умень-
уменьшается с увеличением расстояния между каналами для прохода
жидкости. Кроме того, увеличение коэффициента теплоотдачи
между стенками канала и рабочей жидкостью приводит к воз-
возрастанию F', а увеличение суммарного коэффициента тепловых
потерь ис вызывает уменьшение F'.
Коэффициент отвода тепла из коллектора
Уравнение G.52) позволяет определить тепловой поток к
теплоносителю в данном сечении х вдоль пластины для рас-
рассматриваемого коллектора и заданных температур теплоноси-
теплоносителя. Однако в реальном коллекторе температура теплоносителя
возрастает в направлении течения вследствие подвода тепла к
жидкости. Уравнение баланса энергии для элементарного объ-
объема тегуюносителя длиной dx можно записать в виде
- пгср (Tf \x+dx - Tf \х) = qu (x) dx. G.54)
Подставляя уравнение G.52) для qu{x) и принимая
в уравнении G.54), получаем следующее дифференциальное
уравнение:
- тср ^^ = (D + 2w)F' [asls - Uc (Tf (x) - Ta)]. G.55)
Разделяя переменные, после некоторых преобразований по-
получаем
dTf(x) _ (D + 2w)F'Uc
Tf (x) - Та- (asIs/Uc) ~ mcp dX' {7'ЬЬ)
Уравнение G.56) можно проинтегрировать и решить относи-
относительно температуры теплоносителя на выходе 7^;вых для трубы
Длиной L и температуры теплоносителя на входе 27, Вх, если
предположить, что F' и Uc постоянные, или
Tf,BX-Ta-asls/Uc -exP{ тср
410 Глава 7
Для сравнения характеристик реального коллектора и коллек-
коллектора с оптимальной термодинамической характеристикой удобно
определить коэффициент отвода тепла FR как отношение факти-
фактического теплового потока к теплоносителю к тепловому потоку
при максимальной разности температур между поглощающей
пластиной и окружающей средой. Предельное термодинамиче-
термодинамическое значение соответствует условию, когда температура тепло-
теплоносителя при прохождении через коллектор сохраняется равной
температуре на входе. Это условие можно достичь при очень вы-
высоких значениях скорости жидкости.
По определению FR можно выразить в виде
где Gc = т/Ас — расход жидкости на единицу площади поверх-
поверхности коллектора. Преобразуя правую часть уравнения G.58) и
комбинируя с уравнением G.57), можно легко показать, что
F -°*С0 Fi К/*/PC)~(rf, вы»-ГаП
Г*~ Uc V (as!s/Uc)-(TfiBX-Ta) J'
Анализ приведенного выше соотношения показывает, что Fr
возрастает с увеличением расхода жидкости и стремится к
верхнему пределу, равному коэффициенту эффективности кол-
коллектора F'. Поскольку числитель в правой части уравнения
G.58) равен qu, полезный тепловой поток можно теперь выра-
выразить в зависимости от температуры жидкости на входе:
Qu = ACFR [<xA - Ue G>, вх - Та)}. G.60)
Это уравнение имеет удобную форму для расчета, поскольку
температура теплоносителя на входе обычно известна или мо-
может быть задана.
Пример 7.4. Рассчитать среднечасовой и среднесуточный к. п. д. солнеч-
солнечного коллектора, в котором в качестве теплоносителя используется воде»
15 января в г. Боулдер (шт. Колорадо). Коллектор установлен под углом 6°
к горизонту, и на верхней его поверхности суммарный коэффициент тепло-
тепловых потерь равен 8 Вт/(м2-град). Коллектор изготовлен из медных труб внУ*
тренним диаметром 1 см и толщиной стенки 0,05 см, соединенных пластиной
толщиной 0,05 см; расстояние между осями труб 15 см. Коэффициент тепл0^
отдачи к воде, текущей в трубах, 1500 Вт/(м2-град), пропускательная cflO'
собность покрытия 0,9, поглощательная способность поверхности медной пл»*
стины по отношению к солнечному излучению 0,9. Коллектор имеет шйРй?
1 м и длину 2 м, температура воды на входе 330 К, расход воды 0,02
Значения солнечной инсоляции (полной) и температуры окружающего
Теплообменники 411
духа приведены в таблице. Предположить, что диффузное излучение состав-
составляет 25% полного солнечного излучения.
Время, ч
7-8
8-9
9-10
10-11
11-12
12-13
13-14
14-15
15-16
16-17
Hs, Вт/м2
12
80
192
320
460
474
395
287
141
32
Та, К
270
280
283
286
290
290
288
288
284
280
Решение. Полный поток излучения, воспринимаемый коллектором, рассчи-
рассчитывается из уравнения F.153):
1с - /с, диф + 1-е, пр - Hs X 0,25 A+C2OS6° ) + Hs A - 0,25) Rb
Коэффициент наклона Rb находится по определению из уравнения F.148):
cos / sin 65 sin (L — ft) + cos 6S cos (L — ft) cos hs
b cos a sin L sin 6S + cos L cos 6S cos /*s
где L = 40°, 6s = —21,1° на 15 января (из уравнения F.10)) и ft = 60°.
Угловое солнечное время hs составляет 15° для каждого часа после полудня.
Коэффициент эффективности ребра находится из уравнения G.48):
th mw
(Uс \V2 / 8 V/2 Л А
при т == (—- 1 = [ г | = 6,4,
У \kt) V390-6.10-V
th [6,4 @,15-0,01)/2]
4f" 6,4@,15 — 0,01)/2
Коэффициент эффективности коллектора F' определяется из уравнения G.53):
р,^ VVc
(D + 2w)\ rt _ 1 ^ г+т-^—
1/ад . = о,92о:
0>15[ 8,0 @,01+0,14-0,938) + 1500я-0,01 J
Среднесуточное значение к. п. д. находится суммированием полезной энергии
в Дневные часы, в течение которых коллектор воспринимает тепло, и деле-
и на полную солнечную инсоляцию между восходом и заходом солнца,
дает
412 Глава 7
Затем из уравнения G.59) находится коэффициент отвода тепла
Р -2#L\X- е W'Vp)] = Ml_l^i [! _ ,-(8,0.0.920/0.0.-4.84)] =
к ис о
Полезный тепловой поток определяется из уравнения G.60):
В приведенном выше соотношении h представляет собой поток падающего
излучения на коллектор. Если пропускательная способность стекла 0,9, то
Is = Т/С) полн = 0,9/Cj полн»
qu = 2 . 0,844 [Ie% t. 0,81 - 8,0 G>, вх - Га)].
Коэффициент полезного действия коллектора равен Ць = qu/AIc, t. Резуль-
Результаты расчета среднечасовых значений приведены в таблице ниже.
Время,
ч
7-8
8-9
9-10
10-11
11-12
12-13
13-14
14-15
15-16
16-17
Вт/м2
12
80
192
320
460
474
395
287
141
32
10,89
3,22
2,44
2,18
2,08
2,08
2,18
2,44
3,22
10,89
/диф'
Вт/м2
2.3
15
36
60
86
89
74
54
26
6
7прям>
Вт/м2
92
193
351
523
718
739
646
525
341
261
«4837
Аюлн»
Вт/м2
94
208
387
583
804
828
720
579
367
267
1ОЛН
Вт/м2
fl-гВт
0
0
0
221
584
619
438
237
0
0
=2099 Вт
га,к
270
280
283
286
290
290
288
288
284
280
Ъ
0
0
0
0,190
0,363
0,374
0,304
0,2Q5
0
0
7.7. ТЕПЛООБМЕН И ТЕЧЕНИЕ В НАСАДКАХ
Кроме обычных теплообменников, в которых горячий и хо-
холодный теплоносители разделены твердой стенкой и которые
действуют стационарным образом, существуют теплообменники
нестационарного типа. Устройства такого рода состоят из слоя
твердых частиц (насадки), которые могут нагреваться горячим
теплоносителем1). При этом частицы могут передавать акку-
аккумулированную ими энергию этому же или другому теплоноси-
теплоносителю через некоторый промежуток времени, когда теплоноси-
теплоноситель становится холоднее частиц и его необходимо нагреть. При-
Примером такой теплообменной аккумулирующей системы является
галечная насадка систем солнечных коллекторов, в которых в
качестве теплоносителя используется воздух.
1) В отечественной литературе такие теплообменники называются реге-
регенеративными. — Прим. ре$,
Теплообменники 413
В технике обычно используются два типа слоев частиц для
тепло- и массообменных систем: неподвижный и псевдоржижен-
ный (кипящий) слой. В первом частицы лежат друг на друге
в состоянии покоя, и их положение не изменяется при течении
теплоносителя через пары. Однако, если теплоноситель в слое
движется вверх и его скорость возрастает настолько, что сила
лобового сопротивления преобладает над силой тяжести, тепло-
теплоноситель будет поднимать частицы в слое и они будут нахо-
находиться во взвешенном состоянии. Слой, находящийся в таком
состоянии, называется псевдоожиженным (кипящим) слоем, он
характеризуется хорошим перемешиванием частиц, что приво-
приводит к существенному уменьшению градиента температуры в
слое. Такой характер протекания процесса часто наблюдается
в химической промышленности, особенно в процессах, сопро-
сопровождающихся одновременным переносом тепла и массы.
При анализе течения и конвективного теплообмена в не-
подвия#ном слое галечной насадки предполагается, что частицы
имеют сферическую форму («шаровая» насадка). Леф и Хаули
[12] исследовали теплообмен в таком слое насадки и для ра-
расчета коэффициента теплоотдачи предложили следующее эмпи-
эмпирическое соотношение:
где hv — объемный коэффициент теплоотдачи, Вт/(м3-град);
ть — массовый расход, кг/с; Аъ — площадь поперечного сечения
слоя насадки, м2; Ds — эквивалентный диаметр сферических
частиц, м, определяемый с помощью выражения
р. /_6_ Суммарный объем частицу/3
5 \ п Число частиц ) ^ '
Справедливость этого соотношения проверена эксперимен-
экспериментально в следующем диапазоне значений переменных: темпе-
температура входящего воздуха 300—380 К, размер частиц 0,5—
3,8 см, объемный расход воздуха 0,66—3,6 м3/с, отнесенный к
площади пустот в поперечном сечении слоя, причем объемы пор
измерялись обычным методом заполнения жидкостью.
Для слоя частиц, имеющих приблизительно сферическую
форму, полная площадь поверхности частиц Ар опреде-
определяется
где ev — объемная доля пустот (или пористость) в слое, L —
Длина в направлении движения потока. Хэндли и Хэггс [13]
исследовали теплообмен и потери давления на трение при те-
течении газа в слое насадки и обобщили свои результаты, а такж§
414 Глава 7
данные других авторов. Они показали, что коэффициенты тепло-
теплоотдачи для слоя, состоящего из приблизительно сферических
частиц, можно обобщить с помощью безразмерного уравнения
. 0,255
Ь= о,зз' G-64)
где jb = NnDJReDs Рг1/3 — число Стантона; Re^ = GDs/\x — число
Рейнольдса; Ds — эквивалентный диаметр сферы; NuD5 =
= hcDsДтеплоносит — число Нуссельта; G — массовая скорость
фильтрации газа, отнесенная к площади поперечного сечения
слоя, кг/(м2-с); hc — коэффициент теплоотдачи, отнесенный к
площади поверхности частиц в слое, определяемой из уравнения
G.63).
Для воздуха (Рг = 0,71) это соотношение сводится к виду
Nil*,-—^ G.65)
Перепад давления в слое длиной L можно определить из выра-
выражения
^^^(^У G-66)
G-67)
a Vs = rh/Аьр — средняя скорость фильтрации. Для слоя ша-
шаровой насадки sv принимает значения от 0,35 до 0,45.
Более детальный анализ, касающийся рассмотрения неста-
нестационарного теплообмена и данных о влиянии формы частиц на
коэффициенты теплоотдачи, представлен в работе [4]. Сведе-
Сведения о применении неподвижных насадок для аккумулирования
тепла в солнечных коллекторах, работающих на воздухе, при-
приведены в работе [15].
7.8. ТЕПЛОВЫЕ ТРУБЫ
Одной из основных проблем систем преобразования энергии
является передача энергии от одного приемника тепла к дру-
другому, расположенному на некотором расстоянии от первого,
где эта энергия может быть использована для нагрева тепло-
теплоносителя. Относительно новым устройством, которое может пе-
передавать большие количества тепла через малые площади пои
верхности, является тепловая труба. Принцип работы тепловой
трубы схематически показан на рис. 7.25. Это устройство со-
состоит из круглой трубы с расположенным внутри нее кольце-
кольцевым слоем материала фитиля. По полой центральной части
Теплообменники 415
системы свободно перетекает теплоноситель от левого ее конца,
где тепло подводится, к правому концу, где тепло отводится.
Конец трубы с подводом тепла эквивалентен испарителю, а ко-
конец трубы, на котором происходит отвод тепла, соответствует
конденсатору. Конденсатор и испаритель соединены изолирован-
изолированной секцией длиной L. Жидкость проникает в материал фитиля
под действием капиллярных сил, и когда тепло подводится к
зоне испарения тепловой трубы, жидкость испаряется в фитиле
Подвод тепла
в испарителе
t ) \
—i— ——
() ) \
Корпус
Изоляция
_ ^
Фитиль
L
1
^ i ,
/ |
Ч- |-
Пар j
J
Отвод теп лав
конденсаторе
) \ \
т
) \ )
Рис. 7.25. Схема тепловой трубы.
и образующийся пар движется по центральной части трубы к
зоне конденсации, где происходит отвод тепла. Затем пар кон-
конденсируется в фитиле и цикл повторяется.
Для тепловых труб используется широкое многообразие
комбинаций теплоносителей и материалов труб. Некоторые ти-
типичные комбинации теплоносителей и материалов, а также
интервалы рабочих температур представлены в табл. 7.4. В чет-
четвертой и пятой колонках таблицы приведены измеренные зна-
значения плотностей тепловых потоков на поверхности труб и в осе-
осевом направлении. Видно, что в тепловых трубах могут быть до-
достигнуты очень высокие плотности тепловых потоков.
Для расчетов широко используется соотношение, устанавли-
устанавливающее связь между максимальной достижимой мощностью,
передаваемой тепловой трубой, и ее определяющими размерами,
а также рабочими параметрами [16]:
q = 2AwgHe9f (-^Ly/2ML, G.68)
где Aw — площадь фитиля, g — ускорение свободного падения,
Не — теплота испарения, р/ — плотность жидкости, р^, — плот-
плотность пара, [xi — вязкость жидкости, ^ — вязкость пара, 1т —
высота капиллярного поднятия жидкости в фитиле, Ki — пара-
параметр фитиля, L — длина тепловой трубы.
Таблица 7.4
Некоторые типичные рабочие характеристики тепловых труб [21]
Интервал
температур.
230—400
280—500
360-850
673—1073
773—1173
Теплоноситель
Метиловый спирт
Вода
Ртуть + 0,02%,
магний+0,001 %
Калий
Натрий
Материал корпуса
Медь, никель, нержа-
нержавеющая сталь
Медь, никель
Нержавеющая сталь
Никель, нержавеющая
сталь
Никель, нержавеющая
сталь
Измеренная
плотность теплового
потока а)
в осевом
направлении,
Вт/см2
0,45 при 373 К
0,67 при 473 К
25,1 при 533 К
5,6 при 1023 К
9,3 при 1123 К
Измеренная
плотность теплового
потока
на поверхности а),
Вт/см2
75,5 при 373 К
146 при 443 К
181 при 533 К
181 при 1023 К
224 при 1033 К
Примечания
Использовался артери
альный фитиль в тру-
трубе с резьбой
На основе данных по
звуковому пределу в
тепловой трубе
Зависит от температуры.
Теплообменники 411
Высота капиллярного поднятия жидкости в фитиле опреде-
определяется по формуле
jL G.69)
где у — коэффициент поверхностного натяжения, гс — эффектив-
эффективный радиус поры.
Максимальная высота капиллярного поднятия в фитиле с
натрием, используемым в качестве теплоносителя, составляет
~38,5 см в предположении, что эффективный диаметр поры
8,6 «1 О* см. Это значение характерно для сетки с восемью
проволочками диаметром 4,Ы0~3 см на один миллиметр. При-
Присущие данной тепловой трубе гравитационные напоры связаны
с диаметром тепловой трубы и процессами перетекания жидко-
жидкости в фитиле. В рабочих условиях гравитационные напоры воз-
возникают при наклоне тепловой трубы или эффективных изгибах
в вертикальной плоскости испытания тепловых труб. Если теп-
тепловая труба работает при некотором гравитационном напоре
Те, движущая сила уменьшается на величину этого напора и
высота капиллярного поднятия жидкости в фитиле 1т в урав-
уравнении G.68) должна быть заменена величиной
Из приведенного выше выражения следует, что тепловая
труба утратит свою способность к передаче тепловой мощности,
когда полный гравитационный напор в тепловой трубе превысит
располагаемый движущий напор, обусловленный действием по-
поверхностного натяжения.
Основными определяющими параметрами, влияющими на
суммарную передаваемую мощность, являются площадь сече-
сечения фитиля Aw, эффективная высота капиллярного поднятия
жидкости в фитиле lw и длина тепловой трубы. Для любой эф-
эффективной высоты капиллярного поднятия жидкости в фитиле
lw можно подобрать площадь сечения фитиля Aw и достичь тре-
требуемой полной передаваемой мощности, если известны рабочая
температура, а также разность температур на испарительной и
конденсаторной секциях. Однако, когда существуют ограниче-
ограничения по верхнему пределу рабочей температуры, а также по тем-
температуре в конденсаторной секции тепловой трубы, толщину
фитиля можно определить из рассмотрения этих температур-
температурных условий. В общем случае разности температур и рабочая
температура возрастают с увеличением толщины фитиля. Если
толщина фитиля выбрана с учетом рабочей температуры и раз-
разностей температур, то для заданной передаваемой мощности
можно определить максимальную длину тепловой трубы.
Уравнение G.68) представляет собой соотношение между
полной передаваемой мощностью и геометрическими размерами
14 Зак. 487
418 Глава 7
тепловой трубы в предположении постоянной площади сече-
сечения фитиля Aw. Для уменьшения разности температур в испа-
испарителе и конденсаторе можно отдельно уменьшить толщину
фитиля в каждом из этих двух участков тепловой трубы. В этом
случае уравнение G.68) необходимо преобразовать с учетом
неоднородности площади сечения
фитиля к следующему уравнению:
q = 2gHe9l
- lc) K\ X
Температура
где индексы е, а и с относятся к
испарительной, адиабатической и
конденсаторной секциям тепловой
трубы.
Хотя тепловая труба аналогична
материалу с очень высокой тепло-
теплопроводностью, она имеет ограниче-
ограничения по переносу тепла, которые опи-
описываются определенными законами
механики жидкости. Возможные
Рис. 7.26. Ограничения перено-
переносу тепла в тепловой трубе.
A-2) — звуковой предел; B-3) — унос ,.
ФеГ;ТЬ^3кип7ниаеПИЛЛЯрный эф" эффекты проявления этих ограни-
чений на характеристики тепловой
трубы с жидким металлом в качестве теплоносителя показаны
на рис. 7.26.
Ограничения, указанные на рисунке, обсуждаются ниже.
Для более полного рассмотрения теории и практического ис-
использования тепловых труб читателю рекомендуется обратиться
к работе [17].
Звуковой предел
Когда тепло передается от испарительной секции к конден-
конденсаторной секции тепловой трубы, тепловой поток между этими
двумя секциями определяется из выражения
q = rhvhfg9
G.71)
где thv — массовый расход пара на выходе из испарителя и
hfg — скрытая теплота испарения жидкости. Поскольку в теп-
тепловой трубе используется скрытая энергия теплоносителя вме-
вместо его теплоемкости, можно достичь больших тепловых пото-
потоков при относительно малых массовых расходах. Кроме того,
если тепло передается при высокой плотности и низкой скоро-
скорости пара, его перенос происходит практически в изотермиче-
Теплообменники 419
ских условиях, поскольку для перетекания пара необходимы
очень малые градиенты давления.
Чтобы продемонстрировать влияние плотности и скорости
пара на перенос тепла, можно преобразовать уравнение G.71),
используя уравнение неразрывности
thv=pvVAf G.72)
где pv — средняя по радиусу плотность пара на выходе из испа-
испарителя, а Л — площадь поперечного сечения парового канала.
Комбинируя уравнения G.71) и G.72) и производя соответ-
соответствующие перестановки, получаем
JL — л Vh* G 7*Х\
где q/A — аксиальная плотность теплового потока, отнесенная
к»площади поперечного сечения парового канала.
Из уравнения G.73) следует, что плотность теплового по-
потока в осевом направлении тепловой трубы может поддержи-
поддерживаться постоянной, а регулирование охлаждения конденсатора
приводит к понижению давления, температуры и плотности пара
до тех пор, пока поток пара на выходе из испарителя не достиг-
достигнет скорости звука. В этом случае изменения давления потока
в зоне конденсации не будут передаваться в зону испарения.
Это условие звукового предела на рис. 7.26 описывается сплош-
сплошной кривой, проходящей между точками 1 и 2. Некоторые зна-
значения плотностей тепловых потоков, соответствующих звуко-
звуковому пределу, в зависимости от температуры на выходе из зоны
испарения приведены в табл. 7.5 для Cs, К, Na и Li.
Таблица 7.5
Звуковой предел для теплоносителей тепловых труб
Температура
на выходе
испарителя,
°С
400
500
600
700
800
900
1000
1100
1200
1300
Предельные значения плотности
теплового потока, kBt/cn
Cs
1,0
4,6
14,9
37,3
—
—
—
—
К
0,5
2,9
12,1
36,6
—
—
—
Na
_
0,6
3,5
13,2
38,9
94,2
—
—
L!
—
—
—
1,0
3,9
12,0
31,1
71,0
143,8
Хотя тепловые трубы обычно не работают при звуковом
течении потока, такие условия могут возникать при запуске
420 Глава 7
тепловых труб с теплоносителями, указанными в табл. 7.5. При
запуске тепловой трубы температура в начале зоны испарения
всегда выше, чем в конце этой зоны. Разность температур мож-
можно рассчитать, используя уравнение количества движения для
системы с добавкой массы:
Pi=P2 + PvV\ G.74)
где Pi — статическое давление в начале зоны испарения, Р2 —
статическое давление в конце зоны испарения и pvV2 — динами-
динамическое давление в конце этой зоны. Если выразить скорость
через число Маха, соотношение для идеального газа дает
-?l = 1+M2Y, G.75)
* 2
где М — число Маха в конце зоны испарения и у — отноше-
отношение удельных теплоемкостей пара. Использование уравнения
G.75) и соответствующих кривых зависимостей давления от
температуры пара позволяет определить градиенты темпера-
температуры в испарителе при звуковых и дозвуковых условиях тече-
течения потока.
Ограничения, вызываемые уносом жидкости
Обычно звуковые ограничения не вызывают высыхания фи-
фитиля, сопровождающегося перегревом испарителя. В действи-
действительности они часто предотвращают достижение других огра-
ограничений при запуске тепловой трубы. Однако если увеличение
плотности пара не сопровождается уменьшением его скорости,
то возможен унос некоторого количества жидкости при ее воз-
возвращении в фитиль. Условие возникновения уноса можно вы-
выразить в виде зависимости от числа Вебера:
где Lc — характеристическая длина и as — поверхностное натя-
натяжение жидкости. Выражение G.76) является просто отноше-
отношением инерционных сил пара к силам поверхностного натяжения.
Если это отношение превышает единицу, возникают условия,
аналогичные тем, которые наблюдаются на поверхности воды
под действием сильного ветра, когда образуются волны, распро-
распространяющиеся до тех пор, пока жидкость не срывается с их
гребней. При возникновении срыва жидкости в тепловой трубе
усиливается циркуляция жидкости до тех пор, пока система
возврата жидкости не перестает справляться с возрастающим
потоком. Это вызывает высыхание фитиля и перегрев испа-
испарителя.
Теплообменники 421
Поскольку длина волны возмущений на границе раздела
пар — жидкость в тепловой трубе определяется структурой фи-
фитиля, ограничение по уносу жидкости можно оценить, комби-
комбинируя выражения G.73) и G.76), что дает
д _ 2n9vohfg
С помощью выражения G.77) можно построить кривые типа
представленной на рис. 7.26 сплошной линией между точками
2 и 3.
Ограничение, связанное с капиллярной структурой фитиля
Циркуляция жидкости в тепловой трубе поддерживается ка-
капиллярными силами, которые действуют в структуре фитиля
на границе раздела жидкость — пар. Эти силы уравновеши-
уравновешиваются потерями давления в потоке жидкой и паровой фаз; они
показывают, насколько велики мениски, которые позволяют
давлению в паре быть больше давления в прилегающей жид-
жидкости во всех участках системы. Если типичный мениск харак-
характеризуется двумя основными радиусами кривизны (г\ и гг), па-
падение давления АРС поперек поверхности жидкости определя-
определяется формулой
Эти радиусы, которые являются наименьшими на испари-
испарительном конце трубы, становятся еще меньше с увеличением
теплового потока. Если жидкость хорошо смачивает фитиль,
величины радиусов кривизны будут точно определяться раз-
размером поры фитиля, когда достигается предел по переносу
тепла. Любое дальнейшее увеличение теплового потока будет
вызывать удаление жидкости из фитиля, сопровождающееся
высыханием и перегревом фитиля на испарительном конце си-
системы. \
Как видно из уравнения G.78), капиллярную силу в тепло-
тепловой трубе можно увеличить путем уменьшения размера пор
фитиля, обращенных к потоку пара. Однако, если размер пор
уменьшается также и в остальной части фитиля, ограничение,
связанное с капиллярной его структурой, в действительности
может быть ослаблено за счет увеличения перепада давления
в жидкой фазе. Это видно из уравнения Пуазейля, описываю-
описывающего перепад давления в капиллярной трубке
-> ¦ G.79)
где ^ — вязкость жидкости, те — массовый расход жидкости,
г~~ радиус трубы, р — плотность жидкости и L — длина трубы.
422 Глава 7
Уравнение G.79) можно преобразовать для определения
давления в жидкости при заданном тепловом потоке q и раз-
различных структурах фитиля. Ниже приводятся уравнения для
структур фитиля, показанных на рис. 7.27:
а) артерия
APL = ^1' , G.80)
б) канавки
в) сетка
L nr4eNphfg '
b\iqZe
г) концентрический кольцевой фитиль
G.81)
G.82)
G.83)
G.84)
Входящие в уравнения величины обозначают следующее:
Ze — эффективная длина тепловой трубы; ге —- эффективный ра-
радиус канавки; N — число канавок; Ъ — фактор кривизны сетки;
д) серповидный кольцевой фитиль
Рис. 7.27. Поперечные сечения фитилей различных структур.
а—артерия; б—канавки; в—сетка; г—концентрический кольцевой фитиль; д—серповид-
д—серповидный кольцевой фитиль.
Rи? — внешний радиус сетчатой структуры; R — радиус канала
для прохода пара; 8 — проницаемость сетки; гс — эффективный
радиус отверстий в сетке; D — средний диаметр кольцевого фи-
фитиля, w — ширина кольцевого фитиля.
Уравнения G.81) — G.84), за исключением уравнения G.82),
представляют собой простые модификации уравнения G.79).
Во всех случаях q/L подставляется вместо m*., a Ze — вместо Z.
Первая подстановка следует из уравнения G.71), поскольку
mL = mv для тепловой трубы. Вторая подстановка следует из
соотношения
Ze = IiL±I^ + Zh G.85)
Теплообменники 423
где Zh — длина обогреваемого участка, Zc — длина охлаждае-
охлаждаемого участка и Z/ — длина изолированного участка между обо-
обогреваемым и охлаждаемым участками. Когда средняя часть
тепловой трубы обогревается, а остальная часть охлаждается,
эффективная длина равна
Ze = -Z/* + Zg. G.86)
Хотя артериальная система фитиля представляется идеаль-
идеальной, необходима дополнительная капиллярная сетка для распре-
распределения жидкости по всем поверхностям, на которых осущест-
осуществляются подвод и отвод тепла. Вследствие этого осложнения
артерии обычно используются для систем, в которых возможно
возникновение кипения в фитиле, если сетка, служащая для
поддержания возвращающейся жидкости, размещена на пуги
подвода тепла. (Последствия такого кипения будут рассмотрены
ниже.)
Уравнение G.81) по существу аналогично уравнению G.82),
за исключением того, что оно учитывает число канавок N и
эффективный радиус канавки ге, определяемый из соотношения
для эквивалентного радиуса:
~ / Площадь поперечного сечения потока \ ,- ~-ч
е V Смоченный периметр / * v • /
Хотя открытые канавки подвержены взаимодействию пара
и жидкости, которое вызывает возникновение волн, но не унос
жидкости, это взаимодействие можно подавить, закрыв ка-
канавки сеткой с мелкими ячейками. Поскольку сетка разме-
размещается на границе раздела жидкости и пара, мелкие поры
сетки способствуют развитию значительных капиллярных сил
для циркуляции жидкости, тогда как канавки обеспечивают
меньшее ограничение движению потока возвращающейся жид-
жидкости. Этот основной тип фитиля называется составным фи-
фитилем.
Сетчатые составные фитили изготавливают, наматывая слой
мелкоячеистой сетки на оправку, а затем второй слой более
крупной сетки. Эту сборку помещают в обойму, диаметр ко-
которой уменьшают до тех пор, пока внутренняя стенка не кос-
коснется сетки с крупной ячейкой. Величину b\zr\ в уравнении
G.82) можно затем определить путем измерений потока жид-
жидкости через сетку, прежде чем оправка будет удалена.
Идеальный фитиль для жидких металлов, используемых в
качестве теплоносителя, состоит из внутренней пористой трубы,
отделенной от внешней обоймы зазором, образующим свобод-
свободный кольцевой канал для возврата жидкости. Падение давле-
давления в концентрическом кольцевом фитиле (уравнение 7.83) по-
получено из уравнения Пуазейля для потока между двумя
424 Глава 7
параллельными пластинами. Хотя это уравнение не обладает
точностью уравнения, описывающего течение потока между кон-
концентрическими цилиндрами, им легче пользоваться, и можно по-
получить достаточно точные результаты при условии, что ширина
кольцевого канала мала по сравнению с его средним диаметром.
Уравнение G.84) получено для серповидного кольцевого фитиля
в предположении, что смещение фитиля описывается косину-
соидальной функцией; ширина канала принимает удвоенное
значение на вершине трубы, становится равной нулю у ее осно-
основания и остается без изменения на боковых сторонах трубы.
На рис. 7.26 ограничение, связанное с капиллярной структу-
структурой фитиля, представлено сплошной линией, соединяющей
точки 3 и 4. Хотя это ограничение соответствует температурам,
при которых существенную роль играет падение давления в
жидкой фазе, влияние значительного перепада давления в па-
паровом потоке при низких температурах указано пунктирной
линией.
Ограничения, связанные с кипением
В большинстве двухфазных потоков образование паровых
пузырей в жидкой фазе (кипение) усиливает конвекцию, по-
посредством которой происходит перенос тепла. Такое кипение
обычно трудно воспроизвести в жидкометаллических системах,
поскольку жидкость стремится заполнить центры парообразо-
парообразования, необходимые для зарождения пузырей. В тепловой трубе
конвекция в жидкости не обязательна, поскольку тепло подво-
подводится к тепловой трубе теплопроводностью через тонкий насы-
насыщенный жидкостью фитиль. Более того, образование паровых
пузырей нежелательно, поскольку они могут вызвать образова-
образование перегретых участков и нарушить работу фитиля. Поэтому
тепловые трубы перед использованием обычно подвергают изо-
изотермическому нагреву, что позволяет жидкости смочить внутрен-
внутреннюю стенку тепловой трубы и заполнить все, даже самые наи-
наименьшие центры парообразования.
Кипение может начаться при высоких плотностях теплового
потока и высоких температурах. Кривая, соединяющая точки
4 и 5 на рис. 7.26, рассчитана с помощью уравнений
Pi-Pl=~> G.88)
где Pi — давление пара внутри пузыря; Pl — давление в окру-
окружающей жидкости; г — радиус наибольшего центра парообра-
парообразования; S — площадь поверхности, к которой подводится теп-
тепловой поток; k — эффективный коэффициент теплопроводности*
Теплообменники 425
насыщенного жидкостью фитиля; Tw — температура внутрен-
внутренней поверхности тепловой трубы; 70 — температура на границе
раздела жидкость — пар и / — толщина фитиля.
Поскольку обычно размеры центров парообразования в лю-
любой системе неизвестны, невозможно рассчитать момент воз-
возникновения кипения. Однако уравнения G.88) и G.89) пока-
показывают, какие факторы влияют на процесс кипения. Например,
если центры парообразования малы, то для роста пузырей не-
необходимы большие разности давлений. При заданной плотности
подводимого теплового потока разность давлений будет зависеть
от толщины и коэффициента теплопроводности материала фи-
фитиля, температуры насыщения пара и падения давления в паро-
паровой и жидких фазах. Падение давления часто не учитывается,
поскольку оно не является определяющим фактором при обыч-
нс/й обработке данных по кипению.
Кипение не является ограничивающим фактором при исполь-
использовании жидких металлов, но, когда в качестве теплоносителя
используется вода, кипение может стать основным ограничением
переносу тепла вследствие низкой теплопроводности жидкости
и затрудненного заполнения ею центров парообразования. К со-
сожалению, экспериментальных данных, относящихся к этому
ограничению, недостаточно.
Литература
1. Kays W. M., London A. L., Compact Heat Exchangers, 2nd ed.,
McGraw, N. Y., 1964. [Имеется перевод: Кэйс В, М., Лондон А. Л., Компакт-
Компактные теплообменники.— М.: Энергия, 1967.]
2. Kays W. M., London A. L., Remarks on the Behavior and Application
of Compact High-Performance Heat Transfer Surfaces, Inst. Mech. Eng. and
ASME, Proc. General Discussion on Heat Transfer, 1951, p. 127.
3. Boelter L. M. K., Martinelli R. C, Romie F. E, Morrin E. H, An In-
Investigation of Aircraft Heaters XVIII — A Design Manual for Exhaust Gas and
Air Heat Exchangers, NACA Wartime Rep., ARR5AO6, Aug., 1945.
4. London A. L., Kays W. M., The Gas Turbine Regenerator — the Use
of Compact Heat Transfer Surfaces, Trans. ASME, 72, p. 611 A950).
5. Kreith F., Principles of Heat Transfer, 3rd. ed., Intext Publishers Group,
N. Y., 1973.
6. Standards of Tubular Exchanger Manufacturers Association, 4th ed.,
1959.
7. Bowman R. A., Mueller A. C, Nagle W. M., Mean Temperature Diffe-
Difference in Design, Trans. ASME, 62, 283 A940).
8. Nusselt W., A New Heat Transfer Formula for Cross-Flow, Technische
Mechanik und Thermodynamik, 12 A930).
9. Ten Broeck H., Multipass Exchanger Calculations, Ind. Eng. Chetn., 30,
p. 1041 A938).
10. Hill J. E., Kusuda Т., Methods of Testing for Rating Solar Collectors
Based on Thermal Performance, NBS, U. S. Department of Commerce, Washing-
Washington, D. C, Interim Rept NBSIR 74-635, Dec, 1974.
11. Klein S. A., The Effects of Thermal Capacitance upon the Performance
of Flat Plate Collectors, University of Wisconsin, Madison, 1973 (диссертация
магистра наук).
426 Глава 7
12. Lof G. О. G., Hawley R. W., Unsteady Heat Transfer Between Air and
Loose Solids, Ind. Eng. Chem., 40, p. 1061 A948).
13. Handley D., Heggs P. J., Momentum and Heat Transfer Mechanisms
in Regularly Shaped Packings, Trans. Inst. Chem. Eng., 46, p. 251 A968).
14. Handley D., Heggs P. J., The Effect of Thermal Conductivity of the
Packing Material on the Transient Heat Transfer in a Fixed Bed, Int. J. Heat
Mass Transfer, 12, p. 549 A969).
15. Kreith F., Kreider J., Principles of Solar Engineering, McGraw, N. Y.,
1978.
16. Richter R., Solar Collector Thermal Power System, vol. I, Rept.
AFAPL-TR-74-89-1, Xerox Corp., Pasadena, Calif.; NTIS AD/A-000-940, 1974.
17. Chi S. W., Heat Pipe Theory and Practice, Hemisphere, Washington,
D. C, 1976. [Имеется перевод: Чи, Тепловые трубы. Теория и практика. — М.:
Машиностроение, 1981.1
18. Cramer С. В., Heat Transfer, 2nd ed., Intext Publishers Group, N. Y.
19. Beek W. J., Muttzall K. M. K., Transport Phenomena Wiley, N. Y.,
1975.
20. Bowman R. A., Mueller A. C, Nagel W. M., Mean Temperature Diffe-
Difference in Design, Trans. ASME, 62 A940).
21. Dutcher C. H., Burke M. R., Heat Pipes: A Cool Way to Cool Circuits,
Electronics, Febr. 16, p. 93 A970). [Имеется перевод: Датчер, Бурке, Тепловые
трубки — средство для охлаждения электронных схем и приборов. Электро-
Электроника № 4, 1970, с. 3.]
ЗАДАЧИ
Задачи в данной главе сгруппированы по тематике разделов, как указано
в таблице.
Номера
задач
7.1-7.6
7.7-7.14
7.15—7.24
Раздел
7.3
7.4
7.5
Тема
Суммарный коэффициент теплопереда-
теплопередачи
Среднелогарифмическая разность тем-
температур-
Эффективность теплообменника
' 7.1. В теплообменнике поток воздуха обтекает латунные трубы, внутри
которых течет водяной пар. Коэффициенты конвективной теплоотдачи от во-
водяного пара к поверхности нагрева и от поверхности нагрева к воздуху равны
соответственно 210 и 70 Вт/(м2-град). Все трубы имеют внутренний диаметр
1,8 и наружный диаметр 2,1 см. Рассчитать суммарный коэффициент тепло-
теплопередачи теплообменника: а) отнесенный к площади внутренней поверхндсти
трубы; б) отнесенный к площади внешней поверхности трубы.
7.2. Хладагент течет внутри медной трубы с внутренним диаметром
2,6 см и наружным диаметром 3,2 см. Воздух омывает трубы снаружи. Ко-
Коэффициент конвективной теплоотдачи для хладагента равен 120 Вт/(м2* град),
а для воздуха 35 Вт/(м2-град). Рассчитать суммарный коэффициент тепло-
теплопередачи, отнесенный к наружной поверхности трубы: а) с учетом термиче-
термического сопротивления стенки трубы; б) пренебрегая термическим сопротивле-
сопротивлением стенки трубы.
7.3. Решить задачу 7.1 в предположении, что коэффициент загрязнения
на внутренней поверхности трубы равен 0,00018 м2-град/Вт.
7.4. Решить задачу 7.2 в предположении, что коэффициент загрязнения
на внутренней поверхности трубы 0,00023 м2-град/Вт, а на внешней поверх-
поверхности 0,00011 м2-град/Вт.
7.5. Коэффициент конвективной теплоотдачи на внутренней поверхности
латунной трубы A,9 см — внутренний диаметр и 2,4 см—наружный диа-
диаметр) равен 560 Вт/(м2-град), а на наружной поверхности 105 Вт/(м2-град).
Коэффициент загрязнения на внутренней поверхности равен 0,00065 м2 X
X град/Вт. Вычислить увеличение теплоотдачи (в %), которого можно до-
достигнуть путем удаления отложения, при условии, что о^тложение вызывает
пренебрежимо малое изменение температур теплоносителей внутри и снаружи
труб.
7.6. В длинной алюминиевой трубе течет вода, которая обогревается по-
поперечным потоком воздуха, обтекающим трубу. Внутренний диаметр трубы
1,85 см, наружный 2,3 см. Массовый расход воды в трубе 0,65 кг/с,
а средняя температура воды в трубе 30°С. Скорость свободного потока и
428 Глава 7
температура воздуха 10 м/с и 120°С соответственно. Используя соотношения
для расчета теплообмена (гл. 4 и 5), рассчитать суммарный коэффициент
теплопередачи теплообменника.
7.7. Масло используется для нагрева воды в противоточном теплообмен-
теплообменнике от 20 до 40°С. Температура масла изменяется от 95 до 60°С. Рассчи-
Рассчитать среднелогарифмическую разность температур для этих условий.
7.8. Для условий, рассмотренных в задаче 7.7, рассчитать тепловой по-
поток между водой и маслом, если суммарный коэффициент теплопередачи
325 Вт/(м2-град), а площадь поверхности теплообмена 1,6 м2.
7.9. Суммарный коэффициент теплопередачи, отнесенный к площади
14 м2, нового кожухотрубного противоточного теплообменника составляет
230 Вт/(м2-град). Горячий теплоноситель входит в теплообменник при темпе-
температуре 150°С и выходит из него при температуре 90°С, а холодный тепло-
теплоноситель входит при температуре 20°С и выходит при 75°С. Определить
тепловой поток между теплоносителями. После нескольких лет работы ин-
интенсивность теплообмена уменьшилась вследствие отложения ржавчины вну-
внутри трубы. Коэффициент загрязнения отложения 0,0003 м2-град/Вт. Опреде-
Определить тепловой поток для этого условия и рассчитать в процентах уменьшение
теплового потока вследствие образования ржавчины.
7.10. Кожухотрубный теплообменник имеет один ход в межтрубном про-
пространстве и четыре хода в трубном пучке. Теплоноситель входит в трубный
пучок при температуре 250°С и выходит из него при 110°С. Температура теп-
теплоносителя на входе в межтрубное пространство 10°С, а на выходе 90°С.
Суммарный коэффициент теплопередачи на поверхности ¦ теплообмена пло-
площадью 12 м2 равен 320 Вт/(м2-град). Рассчитать тепловой поток между теп-
теплоносителями.
7.11. Отработавшие газы теплоэлектростанции используются для подо-
подогрева воздуха в перекрестноточном теплообменнике. Отработавшие газы по-
поступают в теплообменник при 450°С и выходят из него при 200°С. Воздух с
'массовым расходом 10 кг/с входит в теплообменник при 70°С и выходит из
него при 250°С. Предполагается, что свойства отработавших газов близки к
свойствам воздуха. Суммарный коэффициент теплопередачи теплообменника
равен 154 Вт/(м2-град). Рассчитать площадь поверхности теплообмена, если:
а) воздух не смешивающийся, а отработавшие газы смешивающиеся; б) оба
теплоносителя не перемешивающиеся.
7.12. Кожухотрубный теплообменник используется для нагрева воды за
счет конденсации водяного пара в межтрубном пространстве. Вода с расхо-
расходом 15 кг/с нагревается от 60 до 80°С. Водяной пар конденсируется при
140°С; суммарный коэффициент теплопередачи теплообменника 820 Вт/(м3Х
Хград). Теплообменник имеет два хода в трубном пучке и один ход в меж-
межтрубном пространстве. Пучок состоит из 45 труб наружным диаметром
2,75 см. Рассчитать требуемую длину труб.
7.13. Для нагрева комнаты требуется мощность 5 кВт. Тепло подводится
с горячей водой, которая с расходом 0,8 кг/с течет в медной трубе внешним
"диаметром 2,9 см при температуре на входе 110°С. Определить: а) необходи-
необходимую длину трубы при условии, что коэффициент конвективной теплоотдачи
от поверхности трубы к воздуху равен 150 Вт/(м2-град), а температура в
комнате 25°С; б) температуру воды на выходе из трубы и в) среднюю тем-
температуру поверхности трубы.
7.14. Рассчитать тепловой поток в кожухотрубном теплообменнике яля
следующих условий: шесть ходов в трубном пучке, один ход в межтрубном
пространстве; температура горячего теплоносителя на входе 500°С, на выходе
250°С; температура холодного теплоносителя на входе 100°С, на выходе
300°С; суммарный коэффициент теплопередачи на поверхности теплообмена
площадью 14,5 м2 равен 175 Вт/(м2-град).
7.15. В теплообменнике вода обогревается горячим воздухом; расход
воды112 кг/с, расход воздуха 2 кг/с. Вода входит при температуре 40°С, воз-
воздух — при температуре 460°С. Суммарный коэффициент теплопередачи на по-
поверхности теплообмена площадью 14 м2 равен 275 Вт/(м2-град). Определить
Теплообменники 429
эффективность теплообменника: а) прямоточного типа, б) перекрестноточного
типа.
7.16. Рассчитать тепловые потоки для двух типов теплообменников, рас-
рассмотренных в задаче 7.15.
7.17. Рассчитать температуры на выходе горячего и холодного теплоно-
теплоносителей для условий задачи 7.15.
7.18. Масло (Ср = 2,1 кДж/кг-град) используется для нагревания воды
в кожухотрубном теплообменнике с одним ходом в межтрубном пространстве
и двумя ходами в трубном пучке. Суммарный коэффициент теплопередачи
525 Вт/(м2-град). Массовый расход масла 7 кг/с, а воды — 10 кг/с. Масло и
вода входят в теплообменник при 240 и 20°С соответственно. Теплообменник
сконструирован таким образом, что вода выходит из него при минимальной
температуре 80сС. Рассчитать площадь поверхности теплообмена, необходи-
необходимую для поддержания этой температуры.
7.19. Водяной пар при температуре 125°С конденсируется на наружной
поверхности труб в кожухотрубном теплообменнике. Вода с массовым расхо-
расходом 1,3 кг/с входит в трубный пучок при температуре 35°С. Массовый рас-
расход /водяного пара 2,5 кг/с, а суммарный коэффициент теплопередачи по-
поверхности теплообмена площадью 3,7 м2 равен 1650 Вт/(м2-град). Рассчи-
Рассчитать: а) эффективность теплообменника; б) фактический тепловой поток к
воде и в) температуру воды на выходе.
7.20. Перекрестноточный теплообменник (суммарный коэффициент тепло-
теплопередачи U = 45 Вт/(м2-град), поверхность теплообмена 53 м2) используется
на электростанции для предварительного подогрева входящего газа теплом
отработавших газов. Расход отработавших газов 2,7 кг/с, а расход входящего
воздуха 2 кг/с. Температуры на входе отработавших газов и воздуха равны
350 и 35°С соответственно. Предполагая, что свойства отработавших газов
близки к свойствам воздуха, рассчитать эффективность теплообменника, если:
а) оба теплоносителя неперемешивающиеся и б) отработавшие газы непереме-
шивающиеся, а воздух перемешивающийся.
7.21. Рассчитать тепловой поток к воздуху для обоих типов теплообмен-
теплообменников, рассмотренных в задаче 7.20.
7.22. Рассчитать выходные температуры обоих теплоносителей для обоих
типов теплообменников, описанных в задаче 7.20.
7.23. Вода, движущаяся с расходом 10 кг/с в пучке из 50 труб в двух-
двухходовом кожухотрубном теплообменнике, нагревает воздух, который дви-
движется в межтрубном пространстве. Латунные трубы имеют длину 6,7 м и
наружный диаметр 2,6 см. Коэффициенты конвективной теплоотдачи от воды
к поверхности нагрева и от поверхности нагрева к воздуху равны 470 и
210 Вт/(м2-град) соответственно. Воздух входит в межтрубное пространство
при температуре 15°С с расходом 1,6 кг/с. Температура воды на входе в
трубы 75°С. Рассчитать: а) эффективность теплообменника, б) тепловой по-
поток к воздуху и в) выходные температуры воздуха и воды.
7.24. После нескольких лет работы на трубах теплообменника, рассмо-
рассмотренного в задаче 7.23, произошло отложение накипи. Коэффициент загряз-
загрязнения для накипи равен 0,0006 м2- град/Вт. Решить задачу 7.23 с учетом этого
нового условия.
Глава 8
КОНДЕНСАЦИЯ, КИПЕНИЕ И МАССООБМЕН
8.1. ВВЕДЕНИЕ
В этой главе рассматриваются три особых вида процессов
переноса: теплообмен при конденсации, теплообмен при кипе-
кипении и массообмен. Все эти три процесса имеют сложный харак-
характер, и о каждом из них написаны отдельные книги. Подробное
обсуждение вопросов кипения и конденсации можно найти в
книге Кольера [16], а для детального изучения массообмена
можно рекомендовать монографию Трейбала [47]. Здесь будут
рассмотрены только наиболее характерные особенности каж-
каждого из этих процессов и будут представлены некоторые корре-
корреляционные формулы для расчета коэффициентов тепло- и массо-
массообмена.
8.2. ТЕПЛООБМЕН ПРИ КОНДЕНСАЦИИ
Когда насыщенный пар соприкасается с поверхностью, имею-
имеющей более низкую температуру, происходит конденсация. При
х.« о
Рис. 8.1. Пленочная конденсация на вертикальной поверхности.
а—рост пленки; б—профиль скорости; в—распределение температуры.
нормальных условиях на всей поверхности образуется непре-
непрерывный поток жидкости и конденсат стекает вниз под действием
силы тяжести. Пока скорость пара не слишком высокая или
Конденсация, кипение и массообмен 431
жидкая пленка не слишком толстая, течение пленки конденсата
ламинарное и тепло передается от границы раздела пар — жид-
жидкость к твердой поверхности просто посредством теплопровод-
теплопроводности. Поэтому тепловой поток зависит главным образом от
толщины пленки конденсата, которая в свою очередь зависит
от массовых расходов при конденсации пара и при удалении
конденсата. Как показано на рис. 8.1, толщина пленки на вер-
вертикальной поверхности непрерывно возрастает от ее верхнего
края к основанию. При отклонении пластины от вертикального
положения массовая скорость стекания пленки уменьшается, а
толщина жидкой пленки увеличивается. Это, естественно, вызы-
вызывает уменьшение интенсивности теплообмена.
Пленочная конденсация
* Теоретические соотношения для расчета коэффициентов теп-
теплоотдачи при пленочной конденсации чистых паров на поверх-
поверхностях труб и пластин впервые были получены Нуссельтом [1]
в 1916 г. Чтобы проиллюстрировать классический подход Нус-
сельта, рассмотрим плоскую вертикальную поверхность при по-
постоянной температуре TSy на которой конденсируется чистый
пар при температуре насыщения Tsv. Как показано на рис. 8.1,
непрерывная пленка жидкости стекает вниз под действием силы
тяжести и ее толщина увеличивается по мере конденсации пара
на границе раздела жидкость — пар. На расстоянии х от верх-
верхнего края пластины толщина пленки равна б. Если течение жид-
жидкости ламинарное и происходит под действием только силы тя-
тяжести, то можно оценить скорость жидкости путем рассмотрения
баланса сил, действующих на элемент dxhl. Направленная
вниз сила, действующая на жидкость на расстоянии от поверх-
поверхности, большем у, равна
(б — у) dxptg.
В предположении, что пар вне слоя конденсата находится в
условиях гидростатического равновесия,
dp/dx = pvg,
частично уравновешенная сила, равная
(б — у) dxpvg,
будет представлять собой результат действия разности давле-
давлений между верхней и нижней поверхностями элемента. Другие
силы, замедляющие движение жидкости вниз, представляют со-
собой силы сопротивления на внутренней границе элемента. Если
пар не течет с очень высокой скоростью, касательное напряже-
напряжение на свободной поверхности весьма мало и им можнд
432 Глава 8
пренебречь. Тогда оставшаяся сила — просто касательное напря-
напряжение \xi(du/dy)dx в вертикальной плоскости у. При стационар-
стационарных условиях силы, направленные вверх и вниз, равны
где б — толщина слоя конденсата; р/ — плотность жидкости; pv —
плотность пара; g — ускорение свободного падения; и — скорость
при координате у\ \ц — вязкость жидкости.
Скорость и при координате у может быть получена методом
разделения переменных и интегрированием. Это дает следую-
следующее выражение:
и {у) = (P/~^)g (бу - { /) + const. (8.2)
Постоянная интегрирования равна нулю, поскольку и равна
нулю на поверхности (т. е. и = 0 при у = 0).
Массовый расход конденсата Гс на единицу ширины получен
путем интегрирования местного удельного массового расхода
ри(у) на высоте х в пределах от у = 0,до у = б:
y=^l^638 . (8.3)
Изменение массового расхода конденсата Тс по толщине слоя
конденсата б равно
db
¦б2. (8.4)
Тепло передается через слой конденсата только посредством
теплопроводности. В предположении, что распределение темпе-
температуры в пленке линейное, изменение средней энтальпии пара
при его превращении в жидкость в процессе конденсации и пере-
переохлаждении до средней температуры пленки конденсата равно
б
hf* + ТГ S и™"{т™ -T)dy = кы + 4 cpi Wsv - ts), (8.5)
о
а плотность теплового потока на стенке равна (k/8)(Tsv—Ts),
где k — коэффициент теплопроводности конденсата. При ста-
стационарном состоянии скорость изменения энтальпии конденси-
конденсирующегося пара должна быть равна плотности теплового потока
на стенке:
JL = k isv^JH e [A/g + | Ср1 (г5р _ ту] «к.. (8.6)
JL = k i^JH e [A/g + | Ср1 (г5р _ ту] к
Конденсация, кипение и массообмен 433
Приравнивание выражения для dTc из уравнений (8.4) и (8.6)
дает
891 {9l - 9V) hfg
где h'fg = hfg + -| cpl (Tsv — T8). Интегрируя в пределах от б = О
при х = 0 до 8 = 6 при х==х и разрешая относительно 6(jc),
получаем
[^(ГУГ, (8.7)
Местный коэффициент теплоотдачи Л(х) равен k/8(x). Подста-
Подстановка сюда выражения для б из уравнения (8.7) дает коэффи-
коэффициент теплоотдачи (удельную тепловую проводимость поверх-
поверхности)
и безразмерное местное число Нуссельта в сечении х:
Анализ уравнения (8.8) показывает, что коэффициент тепло-
теплоотдачи при конденсации уменьшается с увеличением расстояния
от верхнего края пластины, поскольку толщина пленки возра-
возрастает. Утолщение пленки конденсата аналогично росту толщины
пограничного слоя на плоской пластине в условиях конвекции.
В то же время наблюдается интересный факт, заключающийся
в том, что увеличение разности температур Tsv — Ts вызывает
уменьшение коэффициента теплоотдачи. Это вызвано ростом
толщины пленки в результате увеличения массового расхода
при конденсации пара. Аналогичного явления для случая про-
простого конвективного течения не существует.
Среднее значение коэффициента теплоотдачи Я для пара, кон-
конденсирующегося на пластине высотой L, получается путем ин-
интегрирования местного значения hx по высоте пластины и деле-
делением на площадь поверхности. В результате для вертикальной
пластины единичной ширины и высотой L получаем
L
\hxdx = jhx-L% (8.10)
434 Глава 8
Можно легко показать, что для поверхности наклоненной под
углом г|) к горизонтали, средний коэффициент теплоотдачи равен
— 0 913 Г
»iL(Tsv-Ts) J • (8Л2)
Розенау [2] использовал для решения этой задачи модифи-
модифицированный интегральный метод, который лучше описывает
экспериментальные данные при Рг > 0,5 и cpl (Tsv — Т&}Щ < 1,0^
и получил выражения, идентичные формулам (8.8) —(8.12), за
исключением того, что h'fg заменено на [hfg + 0,68ср/(Г5&—- Ts)].
Влияние касательного напряжения пара на ламинарную пленку
при конденсации обычно мало, однако его можно учесть в пред-
предшествующем анализе [3].
Хотя рассмотренный выше анализ проведен для вертикаль-
вертикальной плоской пластины, он применим также для внутренних и
наружных поверхностей вертикальных труб при условии, что
диаметр труб больше толщины пленки. Эти результаты, однако,
не могут быть распространены на наклонные грубы. В таких
случаях течение пленки не будет параллельным оси трубы и
эффективный угол наклона будет изменяться в зависимости
от х.
Средний коэффициент теплоотдачи чистого насыщенного
пара, конденсирующегося на наружной поверхности горизон-
горизонтальной трубы, можно рассчитать с помощью метода, аналогич-
аналогичного использованному для получения выражения (8.12). Для
трубы диаметром D это приводит к выражению [4]
и 0725
Нс — 0,725
Dlll(Tsv-Ts)
При конденсации пара на N горизонтальных трубах, уста-
установленных таким образом, что конденсат с одной трубы стекает
на трубу, расположенную снизу, средний коэффициент теплоот-
теплоотдачи для всей системы труб можно рассчитать, заменив диа-
диаметр трубы D в уравнении (8.13) на DN. В общем случае этот
метод дает заниженные результаты, поскольку трудно избежать
турбулентности в пленке для систем такого типа [8].
Лучше согласуются с экспериментальными данными резуль-
результаты анализа, который был проведен Ченом [5], предполо-
предположившим, что поскольку пленка жидкости недогрета, то на слое
жидкости между трубами будет происходить дополнительная
конденсация пара. Предполагая, что весь недогрев жидкости
идет на дополнительную конденсацию пара, на основе анализа
Чена для N горизонтальных труб можно получить следующее
Конденсация, кипение и массообмен 435
выражение:
hG = 0,728[l + 0,2 Ср{Т™~ Ts) (N- 1)] X
- Ts
которое достаточно хорошо согласуется с экспериментальными
данными, при условии, что [(N—\)cp{Tsv — Ts)/hfg] < 2.
В предыдущих выражениях размерность коэффициента теп-
теплоотдачи— Вт/(м2'град) при условии, что размерности других
величин следующие: cpi — удельная теплоемкость жидкости,
Дж/(кг-град); ki — коэффициент теплопроводности жидкости,
Вт/(м • град); р/ — плотность жидкости, кг/м3; pv — плотность
пара, кг/м3; g — ускорение свободного падения, м/с2; hfg — скры-
/ о
та^теплота конденсации или испарения, Дж/кг; hffg=hfg -f §ер/ X
y((Tsv — Tsy,\xi —вязкость жидкости, Н-с/м2; D — диаметр тру-
трубы, м; L — вертикальный размер плоской поверхности, м; Tsv —
температура насыщенного пара, К; Ts — температура поверхно-
поверхности стенки, К.
Теплофизические свойства жидкой пленки в выражениях
(8.7) — (8.14) необходимо рассчитывать при среднеарифметиче-
среднеарифметическом, значении температур пара и стенки. При этих условиях
формулы Нуссельта позволяют удовлетворительно рассчитать
коэффициенты теплоотдачи при конденсации паров. Экспери-
Экспериментальные данные в целом согласуются с расчетами по теории
Нуссельта, если физические условия соответствуют допущениям,
принятым при анализе. Когда течение конденсата становится
турбулентным, когда скорость пара очень высокая [6] или когда
приняты особые меры, чтобы сделать поверхность несмачивае-
мой, наблюдаются отклонения от результатов, рассчитанных на
основе пленочной теории Нуссельта. Все эти факторы способ-
способствуют увеличению коэффициента теплоотдачи, и поэтому пле-
пленочная теория Нуссельта всегда будет давать заниженные ре-
результаты.
Пример 8.1. Водяной пар конденсируется в трубе длиной 1,5 м наруж-
наружным диаметром 0,013 м при давлении 40 кН/м2 и Tsv = 349 К. Рассчитать
коэффициенты теплоотдачи для этой трубы, находящейся а) в горизонталь-
горизонтальном и б) в вертикальном положениях. Принять, что средняя температура
стенки трубы 325 К.
Решение.
а) При средней температуре пленки конденсата [Tf = C49 + 325) /2 =*
= 337 К] условиям данной задачи соответствуют следующие значения тепло-
физических свойств: &/ = 0,661 Вт/(м-град), р/ = 980,9 кг/м3, hfg = 2,349 X
X 10б Дж/кг, ц/ = 4,48-Ю-4 Н-с/м\ cpt = 4184 Дж/(кг • град).
Для горизонтальной трубы можно использовать выражение (8.13), тогда
коэффициент теплоотдачи равен
г п _о, Г 930,9 -980,6. 9,81 -2,387. КГ- 0,6613 W 1ЛСЛЛО „ 7 .
hc = 0,725[ 0>013,4,48. ю-4 C49-325) J =">600 Вт/(ы'. град).
436 Глава 8
б) Труба, расположенная вертикально, может рассматриваться как вер-
вертикальная пластина площадью ndL, и, согласно выражению (8.11), средний
коэффициент теплоотдачи равен
, Л ПАО Г 980,9 . 980,6 • 9,81 • 2,387. 106 • 0,6613 11/4
he = 0,943 [ 4,48-10-'-1,6(849-326) J ~ 423° Вт/(М ' ГрНД)'
Влияние турбулентности в пленке
Результаты предыдущих расчетов показывают, что при за-
заданной разности температур средний коэффициент теплоотдачи
значительно больше, когда труба находится в горизонтальном
положении, при котором путь стекания конденсата короче и
пленка тоньше, чем в вертикальном положении, при котором
путь стекания длиннее и пленка толще. В общем случае этот
вывод справедлив, когда длина вертикальной трубы более чем
в 2,87 раза превышает наружный диаметр, как это видно из
сравнения выражений (8.11) и (8.13). Однако оба этих выраже-
выражения получены на основе допущения, что течение пленки конден-
конденсата ламинарное, и, следовательно, они неприменимы, когда
течение конденсата турбулентное. Турбулентное течение трудно
получить на горизонтальной трубе, но оно может возникнуть в
нижней части вертикальной поверхности. Когда это происходит,
средний коэффициент теплоотдачи возрастает с увеличением
длины поверхности конденсации, поскольку конденсат уже не
обладает большим термическим сопротивлением, как в случае
ламинарного течения. Такое поведение в известной степени ана-
аналогично поведению пограничного слоя.
Подобно тому как в жидкости, текущей по поверхности, про-
происходит переход от ламинарного режима течения к турбулент-
турбулентному, так и движение конденсата становится турбулентным,
когда число Рейнольдса превышает критическое значение
~2000. Число Рейнольдса для пленки конденсата Re6, вычис-
вычисленное с использованием эффективного (гидравлического) диа-
диаметра в качестве определяющего размера, можно записать как
Re6 = DA/P)Tc/8\ii> где Р — смоченный периметр, равный nD
для вертикальной трубы, и А — площадь поперечного сечения
потока, равная Рб. Местный коэффициент теплоотдачи для тур-
турбулентного течения конденсата можно рассчитать по фор-
формуле [7]
( AV 10,2 Г аЗ.2 U/3
Л,-0,056 РЧ Р^| Рг!/2. (8.15)
Чтобы получить средние значения коэффициента теплоотдачи,
необходимо проинтегрировать hx по поверхности с помощью
уравнения (8.8) для значений 4Тс/\хи меньших 2000, и с по*
мощью уравнения (8.15) для значений этого параметра, боль*
ших 2000. Результаты таких расчетов для двух значений числа
Конденсация, кипение и массообмен 437
Прандтля нанесены линиями на рис. 8.2, где также приведены
некоторые экспериментальные данные, полученные для дифе-
нила при турбулентном течении пленки [8]. Пунктирная линия
на том же графике представляет собой эмпирическую кривую.
1,0
0,8
0,6
* 0,4
' 0,3
г 0,2
0,1
—^
Лами
>
2
нарн
эет
еч
<
•
•
pr = е.
Турбупе
— I
f l
знтнс
ет
Н
<ie
|
3 4 6 8 103
3 4 6 8 104 2 3 4 6 8 10s
Г
Ри? 8.2. Влияние турбулентности в пленке на теплообмен при конденсации.
1 —кривые, рекомендованные для расчета пленочной конденсации на вертикальной поверх-
поверхности; 2—-расчет.
рекомендованную Мак-Адамсом [9] для расчета среднего коэф-
коэффициента теплоотдачи для однокомпонентных паров, конденси-
конденсирующихся на вертикальных поверхностях.
Пример 8.2. Определить, будет ли течение конденсата в примере 8.1 ла-
ламинарным или турбулентным на нижнем конце трубы.
Решение. Число Рейнольдса для конденсата на нижнем конце трубы мож-
можно записать с помощью уравнения (8.3) следующим образом:
4ТС
Re6 = —- =
Подстановка выражения (8.7) для б дает
„1/3
Подстановка в это выражение приведенных выше численных значений задачи
дает
_ ± Г 4 - 0,661 * 1,5 C49 - 325) 980,92/3. 9,81 ^3 13/4 = 5?б
66 ~" 3 L D,48 • 1(Г4M/3 • 2,349 • 106 J
Поскольку число Рейнольдса на нижнем конце трубы меньше 2000, течение
конденсата ламинарное и, следовательно, справедлив результат, полученный
из уравнения (8.11).
Влияние высокой скорости пара
Согласно одному из допущений в пленочной теории Нуссель-
та, сопротивление трения между конденсатом и паром пренебре-
пренебрежимо мало. Это допущение несправедливо, когда скорость не-
сконденсированного пара значительна по сравнению со скоро-
скоростью жидкости на поверхности раздела пар — конденсат. Когда
438 Глава 8
пар движется вверх, к вязкому касательному напряжению до-
добавляется тормозящая сила, которая вызывает утолщение плен-
пленки. При движении пара вниз толщина пленки уменьшается и
коэффициенты теплоотдачи значительно выше расчетных значе-
значений, которые могут быть получены из уравнения (8.11). Кроме
того, при высоких скоростях пара переход от ламинарного тече-
течения к турбулентному происходит при числах Рейнольдса для
пленки конденсата порядка 300. Карпентер и Колберн [10] опре-
определили коэффициенты теплоотдачи при конденсации чистых па-
паров некоторых углеводородов и водяного пара в вертикальной
трубе длиной 2,44 м и внутренним диаметром 1,27 см при скоро-
скоростях пара у верхней части трубы до 152 м/с. Их данные хорошо
обобщаются корреляционной формулой
—^_Prj/2 = 0,046 Л/—/ • (8.16)
где Рп — число Прандтля для жидкости; р/ — плотность жидко-
жидкости, кг/м3; р0 — плотность пара, кг/м3; ср/— теплоемкость жид-
жидкости, Дж/(кг-град); Дс — средний коэффициент теплоотдачи,
Вт/(м2-град); / — коэффициент трения для круглой трубы, рас-
считанный по средней скорости napa;Gm =д/(°? + GiG2 + Gl)/^ ""
среднее значение массовой скорости пара, кг/(м2-с); G\ — мас-
массовая скорость у вершины трубы; G2 — массовая скорость у ос-
основания трубы.
Все теплофизические свойства жидкости в формуле (8.16)
должны рассчитываться при определяющей температуре, рав-
равной 0,25 TSv + 0,75 Ts. Эти результаты расчета не были под-
подтверждены для других систем, но в общем случае могут быть
использованы для доказательства влияния скорости пара на
коэффициент теплоотдачи конденсирующих паров, когда на-
направления течения пара и конденсата совпадают.
Конденсация перегретого пара
Хотя все рассмотренные выше уравнения строго применимы
только для случая конденсации насыщенных паров, их можно
также использовать с достаточной точностью для случая кон-
конденсации перегретых паров. Следовательно, тепловой поток от
перегретого пара к стенке при температуре Т$ будет равен
q = Ah(Tsv-Ts)f (8.17)
где Я — среднее значение коэффициента теплоотдачи, опреде-
определяемое из уравнения, справедливого для геометрической кон-
конфигурации с таким же паром, находящимся на линии насыще-
насыщения; TSv — температура насыщения, соответствующая преобла-
преобладающему давлению в системе.
Конденсация, кипение и массообмен 439
Капельная конденсация
Когда поверхность конденсации покрыта веществом, которое
препятствует конденсату смачивать поверхность, пар будет кон-
конденсироваться в виде капель, а не в виде сплошной пленки [11].
Это явление известно как капельная конденсация. В таких усло-
условиях большая часть поверхности не покрыта изолирующей плен-
пленкой и коэффициенты теплоотдачи в 4—8 раз выше, чем при
пленочной конденсации. До сих пор капельная конденсация до-
достаточно надежно получена только для водяного пара. Для прак-
практического расчета коэффициента теплоотдачи предполагается
существование пленочной конденсации, поскольку даже для во-
водяного пара возникновение капельной конденсации можно ожи-
ожидать только при тщательно регулируемых условиях, которые
не всегда можно поддерживать на практике [12, 13]. Однако
капельная конденсация водяного пара может оказаться полез-
полезным способом улучшения теплообмена в некоторых отраслях
промышленности.
Таблица 8.1
Приближенные значения коэффициентов теплоотдачи
при конденсации чистых паров
Пар
Водяной
Водяной
Этилового
спирта
Бензоловый
Этилового
спирта
Аммиачный
Система
Горизонтальные трубы, наруж-
наружный диаметр 25—75 мм
Вертикальная поверхность вы-
высотой 3 м
Вертикальная поверхность высо-
высотой 0,15 м
Горизонтальная труба, наруж-
наружный диаметр 25 мм
Горизонтальная труба, наруж-
наружный диаметр 50 мм
Горизонтальный кольцевой ка-
канал с размерами 50 и 75 мм
Приблизи-
Приблизительный
диапазон
значений
T8V-T8'
К
3—20
3-20
10-55
15-45
5—20
1-4
Приблизитель-
Приблизительный
диапазон
значений
среднего
коэффициента
теплоотдачи,
Вт/(м2-град)
11 000—23 000
5 700—11 000
1 100-1900
1 400—2 000
1 700—2 600
1 400—2 600 а)
а) Суммарный коэффициент теплопередачи V при скоростях охлаждающей воды
1,2—2,4 м/с внутри трубы [14].
В табл. 8.1 приведены некоторые приближенные значения
коэффициентов теплоотдачи при конденсации паров на горизон-
горизонтальных трубах и вертикальных поверхностях.
440 Глава 8
Смеси паров и неконденсирующихся газов
Анализ конденсирующейся системы, содержащей смесь па-
паров или чистый пар в смеси с неконденсирующимся газом, зна-
значительно сложнее по сравнению с анализом системы, содержа-
содержащей только чистый пар. Присутствие заметных количеств некон-
неконденсирующегося газа в общем случае уменьшает интенсивность
теплоотдачи. Если желательно получить высокую интенсивность
теплоотдачи, необходимо в практических целях продуть некон-
денсирующий газ, который в противном случае будет покрывать
газовой подушкой охлаждающую поверхность и значительно
увеличивать термическое сопротивление. Неконденсирующиеся
газы препятствуют массообмену, создавая диффузионное сопро-
сопротивление. Полное рассмотрение вопросов, касающихся конден-
конденсации смесей, выходит за рамки этого раздела, и поэтому чита-
читателю можно рекомендовать работы [8, 15] в качестве исчерпы-
исчерпывающего обзора существующих данных по этим вопросам.
8.3. ТЕПЛООБМЕН ПРИ КИПЕНИИ
Кипение может возникнуть, когда поверхность, находящаяся
в контакте с жидкостью, поддерживается при температуре выше
температуры насыщения жидкости. В отличие от конвективного
теплообмена однофазной жидкости, при котором плотность теп-
теплового потока зависит от разности температур между поверхно-
поверхностью и объемом жидкости, в случае теплообмена при кипении
движущим потенциалом для теплового потока является разность
между температурой поверхности и температурой насыщения
при заданном давлении в жидкости. Когда подогреваемая по-
поверхность погружена в неподвижную жидкость, процесс кипения
называется кипением в большом объеме. Когда температура
жидкости ниже температуры насыщения и происходит кипение,
то этот процесс называется кипением с недогревом. Если, с дру-
другой стороны, жидкость находится при температуре насыщения,
такой процесс известен как кипение насыщенной жидкости, или
объемное кипение.
Различные режимы кипения в большом объеме схематично
показаны на рис. 8.3. На рис. 8.3 плотность теплового, потока
представлена в зависимости от разности температуры поверхно-
поверхности и температуры насыщения, для краткости называемой тем-
температурным напором АТХу для случая нагретой платиновой про-
проволоки, погруженной в воду при атмосферном давлении [17].
В области 1 теплообмен осуществляется свободной конвекцией.
В этой области жидкость вблизи проволоки перегрета, однако
степень перегрева недостаточна для образования паровых пу-
пузырей. По мере увеличения температуры нагретой поверхности
энергетический уровень жидкости вблизи поверхности стано^
Конденсаций,, кипение и массообмен 441
вится достаточно высоким, чтобы отдельные молекулы жидкости
отрывались от остальных молекул с образованием паровых за-
зародышей, которые в конце концов вырастают в пузыри пара.
Этот процесс происходит одновременно на благоприятных для
образования пузырей участках поверхности нагрева [18]. Перво-
Первоначально паровые пузыри малы и конденсируются прежде, чем
достичь свободной поверхности, но с ростом температуры число
1 500 000
5
30 000
1,0
10
100
1000
10 000
AT'
Рис. 8.3. Типичные кривые кипения воды на проволоке, трубе или горизон-
горизонтальной поверхности в большом объеме при атмосферном давлении.
1 —чистая конвекция; тепло переносится перегретой жидкостью, поднимающейся к границе
раздела фаз, на поверхности которой происходит процесс испарения; 2—режим образова-
образования одиночных пузырей; 3—режим образования непрерывных трубок пара; 4—переходный
режим кипения; 5—режим устойчивого пленочного кипения; 6—режим пузырькового ки-
кипения.
пузырей увеличивается и они становятся более крупными. На-
Наконец, пузыри достигают свободной поверхности. При дальней-
дальнейшем росте температурного напора пузыри образуются более
быстро, и в области 3 они сливаются в более или менее непре-
непрерывные паровые трубки, поднимающиеся к поверхности жидко-
жидкости. Оба режима, 2 и 3, называются режимом пузырькового ки-
кипения.
Если продолжать увеличивать температурный напор, пузыри
образуются настолько быстро, что сливаются на проволоке в
сплошную пленку пара, которая покрывает поверхность. В этих
условиях тепло передается через образовавшуюся пленку тепло-
теплопроводностью. Поскольку коэффициент теплопроводности пара
мал, термическое сопротивление этой пленки велико, что факти-
фактически вызывает уменьшение плотности теплового потока при
возрастании температурного напора, как показано пунктирной
кривой в области 4. Эта область соответствует переходу от пу-
пузырькового кипения к пленочному и является неустойчивой.
Устойчивое пленочное кипение устанавливается в области 5,
442 Глава 8
когда плотность теплового потока снова начинает возрастать
с увеличением температурного напора. Поскольку температура
Рис. 8.4. Пузырьковое кипение воды на проволоке. (С разрешения Дж. Кастл-
са.)
Рис. 8.5. Пленочное кипение воды на проволоке (С разрешения Дж. Кастл-
са.)
стенки в этом режиме устойчивого пленочного кипения довольно
высока, значительная часть суммарного количества тепла пере-
передается излучением.
Конденсация, кипение и массообмен 443
Максимальная плотность теплового потока при пузырьковом
режиме кипения, отмеченная точкой а на рис. 8.3, требует осо-
особого внимания. Температурный напор, соответствующий точке
а, известен как критический температурный напор. Если прово-
проволока или поверхность, от которых отводится тепло, обогреваются
электрическим током, увеличение плотности теплового потока
выше точки а требует перехода к точке 6, чтобы отвести выде-
выделяющееся тепло. Поскольку во многих случаях температурный
напор в точке b настолько велик, что температура поверхности
превышает точку плавления, проволока плавится и происходит
«пережог» [19]. Только если очень быстро уменьшить подвод
тепла ниже критической плотности теплового потока в момент,
когда система достигает точки а, можно реализовать переход-
переходный режим кипения и, наконец, достигнуть устойчивого пленоч-
котб режима кипения (область 5 на рис. 8.3). Фотографии на
рис. 8.4 и 8.5 иллюстрируют механизмы пузырькового и пленоч-
пленочного режимов кипения соответственно.
Корреляция данных по теплообмену при кипении
При пузырьковом кипений интенсивность теплообмена в силь-
сильной степени зависит от турбулентности жидкости, генерируемой
пузырями вблизи поверхности. Пузыри образуются вследствие
расширения захваченного газа или пара в небольших впадинах
или трещинах на поверхности. Их поведение зависит от темпе-
температуры и давления жидкости [20J, а также от поверхностного
натяжения на границе раздела жидкость — пар.
Для корреляции экспериментальных данных по теплообмену
при пузырьковом кипении используется безразмерный параметр,
учитывающий турбулизацию и смешение в процессе кипения.
Этот параметр представляет собой число Рейнольдса Re6, кото-
которое построено по среднему диаметру пузыря D&, массовой ско-
скорости пузыря Оь и вязкости жидкости |х/ в виде
Reft=-^- (8.18)
Этот параметр можно рассматривать в качестве числа Рейнольд-
Рейнольдса для пузыря и использовать его для расчета числа Нуссельта
N\ib с использованием уравнения вида
где Prr—число Прандтля насыщенной жидкости и Я&— коэф-
коэффициент теплоотдачи при пузырьковом кипении, определяемый
как
К = -jir7' (8-20)
При пузырьковом кипении температурный напор заменяет раз-
разность температур между поверхностью и объемом жидкости,
444 Глава 8
которая используется при определении обычного конвективного
коэффициента теплоотдачи в однофазной жидкости.
Кипение в большом объеме
На основе анализа экспериментальных данных Розенау [21]
модифицировал уравнение (8.19) с помощью упрощающего
предположения и получил следующее корреляционное безраз-
безразмерное уравнение для пузырькового кипения в большом объеме:
^- /=Z
(8.21)
но^
I
где Ci — теплоемкость насыщенной жидкости, Дж/ (кг• град);
АТХ = Ts — Гнас — температурный напор, К; q/A — плотность
теплового потока, Вт/м2;
5.юб| 1 r-h Лту\ I—Н hfg — скрытая теплота ис-
испарения, Дж/кг; g —
ускорение свободного па-
падения, м/с2; р/ — плот-
плотность насыщенной жид-
жидкости, кг/м3; pv — плот-
плотность насыщенного пара,
кг/м3; а — поверхностное
натяжение на границе
раздела жидкость — пар,
Н/м; \ц — вязкость жид-
жидкости, Н-с/м2; CSf — без-
безразмерная эмпирическая
постоянная, зависящая от
природы поверхности на-
нагрева и жидкости, числен-
численное значение которой из-
изменяется от системы к
системе; Рп — число
Прандтля для жидкости
(безразмерное).
Эмпирическая посто-
постоянная CSf зависит от ше-
шероховатости поверхности
кипения и ее смачиваемо-
смачиваемости данной жидкостью.
Ее значение необходимо
определять опытным путем для каждой комбинации поверх-
поверхность— жидкость. На рис. 8.6 показаны экспериментальные
данные, полученные Аддомсом для случая кипения воды в боль-
большом объеме на платиновой проволоке малого диаметра при
различных давлениях насыщения [22]. На рис. 8.7 представлена
ыо5
5-Ю4
?!
/
1
if/
/// /
///
'in
i
fx
/
/
10
20 30
Рис. 8.6. Плотность теплового потока в за-
зависимости от температурного напора при
пузырьковом кипении воды на электрически
нагреваемой платиновой проволоке диамет-
диаметром 0,6 мм [49].
Конденсация, кипение и массообмен 445
корреляция этих данных с помощью уравнения Розенау с ис-
использованием комплекса параметров, входящего в квадратных
скобках в правую часть уравнения (8.21)
mhfg
— Pv)
в качестве ординаты и комбинации параметров в левой части
уравнения (8.21)
в качестве абсциссы. Тангенс угла наклона линии, проходящей
через экспериментальные точки, равен 0,33, а эмпирическая по-
постоянная CSf равна 0,013. С помощью этих двух эмпирических
100
10
1,0
0,1
1—ГТ77ТП
1 Mil!
о 1 МНм
а 2,6МН/м2
• 5,2МН/м2-
а 8,2 МН/м2
жЮ,9МН/м2
°16,8МН/м2
I I II I ММ
\ \ 1 I I I I
0,01
0,1
1,0
Рис. 8.7. Корреляция данных по теплообмену при кипении в большом объеме
по методу Розенау [49].
постоянных экспериментальные данные, охватывающие диапа-
диапазон давлений 1—15 МПа, обобщаются достаточно удовлетвори-
удовлетворительно. Значения постоянной CSf для различных комбинаций
жидкость — поверхность приведены в табл. 8.2. Некоторые зна-
значения поверхностного натяжения для воды на границе раздела
пар — жидкость при различных температурах насыщения даны
в табл. 8.3.
446
Глава 8
Значения коэффициентов Csj в уравнении (8.21)
для различных комбинаций жидкость — поверхность нагрева
Таблица 8.2
Комбинация жидкость—поверхность нагрева
Вода — медь
Четыреххлористый углерод — медь
35%-ный раствор КгСОз — медь
н-бутиловый спирт — медь
50%-ный раствор КгСОз — медь
Изопропиловый спирт — медь
н-пентан — хром
Вода — платина
Бензол — хром
Вода — латунь
Этиловый спирт — хром
н-пентан на меди, обработанной наждаком
н-пентан на никеле, обработанном наждаком
Вода на меди, обработанной наждаком
Четыреххлористый углерод на меди, обработанной
наждаком
Вода на меди, обработанной наждаком и покрытой
парафином
н-пентан на отшлифованной меди
н-пентан на меди, обработанной наждаком
Вода на шероховатой поверхности меди
Вода на притертой и полированной нержавеющей
стали
Вода на нержавеющей стали, покрытой тефлоном
Вода на химически протравленной нержавеющей
стали
Вода на механически полированной нержавеющей
стали
Csf
0,0130
0,0130
0,0054
0,0030
0,0027
0,0025
0,0150
0,0130
0,0100
0,0060
0,0027
0,0154
0,0127
0,0128
0,0070
0,0147
0,0049
0,0074
0,0068
0,0080
0,0058
0,0133
0,0132
Источник
23
23
23
19
23
19
24
22
24
25
24
26
26:
26
26
[26]
26
26
26
26
[26
[26
[26]
Основное преимущество соотношения Розенау состоит в том,
что характеристики теплообмена для любой комбинации жид-
жидкость — поверхность при пузырьковом кипении при любом дав-
давлении и плотности теплового потока можно рассчитать на осно-
основании данных одного опыта. Одно значение плотности теплового
потока и соответствующее ему значение температурного напора
позволяют определить значение CSf в уравнении (8.21). Необхо-
Необходимо отметить, однако, что уравнение (8.21) строго применимо
только для чистых поверхностей. Для загрязненных поверхно-
поверхностей показатель степени при Рп изменяется от 0,8 до 2, хотя, по-
видимому, загрязнение не влияет на другой показатель степени
в уравнении (8.21). Геометрическая форма поверхности нагрева
не оказывает существенного влияния на механизм пузырькового
кипения, поскольку влияние движения пузырей на характер те-
течения жидкости ограничено областью вблизи поверхности
[27, 28],
Конденсация, кипение и массообмен
Таблица 8.3
Коэффициент поверхностного натяжения
на границе раздела нар — жидкость
для воды
Поверхностное натяжение,
ffXlO3 Н/м
75,6
72,6
69,4
66,0
62,5
.58,8
48,2
37,6
26,4
14,7
3,7
0,0
Температура
насыщения, °С
0
20
40
60
80
100
150
200
250
300
350
374,1
Пример 8.3. Рассчитать коэффициент теплоотдачи для воды, кипящей при
атмосферном давлении на медной поверхности при 120°С.
Решение. Плотность теплового потока можно определить с помощью со-
соотношения Розенау, используя теплофизические свойства воды из табл. ILV. 1
и CSf из табл. 8.2.
421V20 ,у - 0,013 Г fid г ЛИШ
' 2,257 • 106 • 1.741'7 L 278 • 10~6 • 2,257 • 10~6 V 9,81 (957 - 0,6)
Отсюда плотность теплового потока равна
q/A = 358 кВт/м2
и коэффициент теплоотдачи
НЬ = -g^-= ^-== 17,9 кВт/(м*. град).
Пузырьковое кипение в условиях вынужденной конвекции
Когда жидкость течет вдоль поверхности, температура кото-
которой выше температуры насыщения жидкости, или когда жид-
жидкость движется по каналу, температура стенок которого выше
температуры насыщения, то в этих случаях может возникнуть
кипение при вынужденной конвекции. На рис. 8.8 показаны ти-
типичные экспериментальные результаты по теплообмену при ки-
кипении недогретой жидкости в условиях вынужденного течения
в трубах или каналах. По ординате отложена плотность тепло-
теплового потока, а по абсциссе — разность температуры поверхности
нагрева и среднемассовой температуры жидкости. Пунктирные
линии соответствуют условиям вынужденной конвекции при
различных скоростях и степенях недогрева, тогда как сплош-
сплошные линии указывают на изменение теплообмена по сравне-
сравнению с вынужденной конвекцией, обусловленное поверхностным
448 Глава 8
кипением. После начала кипения температура стенки практиче-
практически не зависит от скорости жидкости, и это свидетельствует о том,
что перемешивание жидкости, вызванное пузырями, гораздо эф-
эффективнее турбулентного перемешивания при вынужденной кон-
конвекции без кипения. Данные по теплообмену при поверхностном
5-106
МО
5-Ю5
1-105
5-104
200
AT, °C
Рис. 8.8. Типичные данные по теплообмену при кипении недогретой жидкости
в условиях вынужденной конвекции: зависимость плотности теплового по-
потока от разности температур между поверхностью и массой жидкости [30].
кипении с рис. 8.8 перенесены на рис. 8.9, где представлены в
виде зависимости плотности теплового потока от температур-
температурного напора. Видно, что результирующая кривая аналогична
кривой на рис. 8.6 для пузырькового кипения насыщенной жид-
жидкости в большом объеме. Это подчеркивает подобие процессов
кипения при наличии и в отсутствие вынужденной конвекции;
в обоих случаях плотность теплового потока зависит от темпе-
температурного напора между поверхностью и температурой насыще-
насыщения, а не от разности температуры поверхности и среднемассо-
вой температуры жидкости. Суммарную плотность теплового
потока при кипении в условиях вынужденной конвекции можно
получить, прибавляя плотность теплового потока при кипении,
Конденсация, кипение и массообмен 449
рассчитанную по формуле (8.21), к плотности теплового потока
при вынужденной конвекции без кипения:
V Л )сумм ~[а )кип + ( Л )
вынужд. конв
(8.22)
Однако, чтобы рассчитать плотность теплового потока при вы-
вынужденной конвекции без кипения, необходимо использовать
5-Ю6
1.1 Лб
$•1П5
б 7
8
9
Обозн.
D
Л
О
Скоросп
м/с
3,66
1,22
0,305
о
"о*
0
д ?
г О/
А /
о /о
о /о
°/
10
2С
\J°a
а
4
н8
г> /Л
7°
Q
о
> j
f
40 50
дг,-г,- гнас,°с
Рис. 8.9. Приближенная корреляция данных для пузырькового кипения в
условиях вынужденной конвекции, представленная в виде зависимости плот-
плотности теплового потока от температурного напора [30].
разность температуры стенок и среднемассовой температуры, а
не температурный напор между стенкой и температурой насы-
насыщения, поэтому Розенау и Гриффите [32] рекомендуют для
течения в трубах заменить коэффициент 0,023 в уравнении E.12)
на 0,019 для случая кипения в условиях вынужденной конвек*
ции. Метод суперпозиции дает удовлетворительные результаты,
когда в процессе кипения испаряется лишь незначительная часть
жидкости.
15 Зак. 487
450 Глава $
Максимальная плотность
теплового потока при пузырьковом кипении
Корреляционное уравнение Розенау (8.21) связывает плот-
плотность теплового потока с температурным напором при кипении,
но не позволяет определить температурный напор, при котором
плотность теплового потока достигает максимума, после чего
возможен пережог (кризис теплопередачи при кипении). Мак-
Максимально достижимая плотность теплового потока при пузырь-
пузырьковом кипении представляет большой интерес для конструкто-
конструкторов, поскольку для эффективности теплоотдачи и в целях без-
безопасности, особенно для теплонапряженных систем, необходимо
избегать работы в условиях пленочного режима кипения.
На основе рассмотрения устойчивости границы раздела фаз
между пленкой пара и жидкостью при пузырьковом кипении
Зубер и др. [31] получили аналитическое выражение для расче-
расчета максимальной плотности теплового потока
— J = — pvhfg I g I ( " 1 » (8.23)
А /макс. 24 |_ Ро J \ Р/ /
которое хорошо согласуется с экспериментальными данными.
Упрощенный вариант выражения (8.23) был предложен Розе-
Розенау и Гриффитсом [32, 33]. В общем случае тип материала по-
поверхности нагрева не влияет на максимальную плотность теп-
теплового потока, хотя известно, что для загрязненных поверхностей
значения максимальной плотности теплового потока могут воз-
возрастать на 15%. Когда объем жидкости недогрет до темпера-
температуры насыщения, максимальная плотность теплового потока мо-
может быть рассчитана из соотношения [31]
где
(8 24)
1/2Г р2 -11/4
U]
a (q/A)макс.нас определяется из уравнения (8.21). Неконденси-
Неконденсирующиеся газы и несмачиваемые поверхности могут уменьшать
максимальную плотность теплового потока при данной средне-
массовой температуре.
Кипение и парообразование при вынужденной конвекции
Характеристики процесса парообразования при вынужденной
конвекции исследованы достаточно широко, однако вследствие
большого числа переменных, которые могут влиять на этот про-
Конденсация, кипение и массообмен 451
цесс, в литературе дано только качественное его описание [34,
35]. Предположим, что жидкость при температуре ниже темпе-
температуры кипения входит в канал, в котором она нагревается и
постепенно переходит в пар. На рис. 8.10 схематично показано,
о
Недогрев
Паросодержание,%
д
Перегрев
Рис. 8.10. Характер зависимости коэффициентов теплоотдачи при кипении в
условиях вынужденной конвекции от паросодержания и режимов течения
двухфазного потока:
а—пузырьковый режим, б—снарядный режим, в—кольцевой режим, г —дисперсный ре-
режим, д—режимы течения; 1 — вынужденная конвекция (жидкость); 2— пузырьковый и сна-
снарядный режимы течения (режимы а, б); 3—кольцевой режим течения (режим в); 4— пере»
ходный дисперсно-кольцевой режим течения; 5—дисперсный режим течения (режим г);
6—вынужденная конвекция (пар).
что происходит в трубе, в которой испаряется жидкость. На
рис. 8.10,<? качественно представлена зависимость коэффициента
теплоотдачи от местного паросодержания в характерных точках.
По мере продвижения жидкости по каналу ее среднемассовая
температура возрастает до температуры насыщения. Это обычно
происходит только на коротком расстоянии от входа в систему,
предназначенную для испарения жидкости. Затем на центрах
парообразования начинают формироваться пузыри, которые пе-
переносятся в основной поток, как и при пузырьковом кипении
в большом объеме. Этот режим, известный как пузырьковый ре-
15*
452 Глава 8
жим кипения, схематически показан на рис. 8.10, а. Пузырько-
Пузырьковый режим возникает только при очень малых паросодержа-
ниях, и в этом случае течение состоит из отдельных пузырей
пара, уносимых в основной поток. В очень узком интервале па-
росодержаний, при котором существует пузырьковый режим
течения, коэффициент теплоотдачи можно рассчитать методом
суперпозиции, используя уравнения для конвективного теплооб-
теплообмена при вынужденном течении однофазной жидкости и для
пузырькового кипения в большом объеме. Так можно поступать
до тех пор, пока температура стенки не станет столь велика, что
произойдет переход к пленочному кипению.
По мере возрастания объемной доли пара отдельные пузыри
начинают сливаться с образованием пробок или «снарядов»
пара (рис. 8.10,6). Хотя в этом режиме, известном как снаряд-
снарядный режим течения, массовая доля пара обычно много меньше
1%, объемная доля пара может составлять 50% и скорость жид-
жидкости может значительно возрасти. Пробки пара представляют
собой сжимаемые объемы, которые вызывают пульсации потока
внутри трубы, даже если на входе в канал поток стационарный.
Пузыри могут продолжать образовываться на стенке, и меха-
механизм теплообмена при снарядном режиме течения, вероятно,
аналогичен механизму пузырькового режима: суперпозиция вы-
вынужденной конвекции в жидкости и пузырькового кипения в
большом объеме. Вследствие увеличения скорости потока коэф-
коэффициент теплоотдачи возрастает, как это можно видеть из
рис. 8.10,6.
По мере дальнейшего движения жидкости вдоль трубы и
роста паросодержания развивается третий режим течения,
обычно называемый кольцевым режимом течения. В этом ре-
режиме стенка трубы покрыта тонкой пленкой жидкости и тепло
передается через эту жидкую пленку. В центре трубы пар течет
с более высокой скоростью, и хотя может существовать доста-
достаточное количество активных центров парообразования на стен-
стенке, пар в основном генерируется за счет испарения на границе
раздела жидкость — пар внутри трубы, а не за счет образования
пузырей внутри кольцевого слоя жидкости. Кроме жидкости в
кольцевой пленке на стенке существует значительное количество
жидкости, диспергированной в виде капель в паровом ядре. Ин-
Интервал паросодержаний для этого режима течения в сильной
степени зависит от свойств жидкости и геометрии канала, но
обычно полагают, что переход к следующему, дисперсному, ре-
режиму течения происходит при паросодержаниях ~25% или
выше.
Переход от кольцевого режима течения к дисперсному пред-
представляет большой интерес, поскольку, по-видимому, этот пере-
переход соответствует точке, в которой коэффициент теплоотдачи
резко уменьшается (рис. 8.10,б). Следовательно, в этой точке
Конденсация, кипение и массообмен 453
возможен пережог при парообразовании в условиях вынужден-
вынужденной конвекции, если своевременно не уменьшить плотность теп-
теплового потока до возникновения этого явления. При переходе
от кольцевого к дисперсному режиму течения происходит важ-
важное изменение: в первом случае стенка покрыта жидкостью с
относительно высокой теплопроводностью, тогда как во втором
случае стенка покрыта паром с низкой теплопроводностью.
Основной перенос тепла в дисперсном режиме течения про-
происходит от нагретой стенки к пару, а затем тепло, поступившее
в паровое ядро, идет на нагрев находящихся там капель жид-
жидкости. Фактически в дисперсном потоке испарение происходит
внутри трубы, а не на ее стенке. По этой причине температура
пара в дисперсном режиме течения может превышать темпера-
температуру насыщения и в трубе возможно нарушение теплового рав-
^новесия. Хотя объемная доля капель жидкости мала, они со-
составляют значительную массовую долю вследствие большого
отношения плотности жидкости к плотности пара.
Для расчета теплообмена при течении парожидкостных сме-
смесей в трубах для жидкостей, смачивающих стенку, предложено
эмпирическое соотношение [42]
U)=°'06(-^) (иг) Pr?* (8-25>
где % — массовая доля пара, или паросодержание. Это уравне-
уравнение описывает результаты ряда исследований с точностью
-20%.
Дисперсный режим течения существует до тех пор, пока
паросодержание не достигнет 100%. По достижении этого
уровня паросодержания коэффициент теплоотдачи можно снова
рассчитывать по уравнениям, справедливым для вынужденной
конвекции пара в трубе или канале.
Гриффите [36] предложил эмпирическое соотношение для
расчета кризиса теплоотдачи при кипении в условиях вынуж-
вынужденной конвекции, охватывающее широкий диапазон условий
проведения опытов. Он обобщил данные по кризису кипения
для воды, бензола, н-гептана, н-пентана и этилового спирта при
давлениях, составляющих 0,5—96% критического давления, ско-
скоростях 0—30 м/с, недогревах 255—535 К и паросодержаниях
0—70%. Данные, использованные для этой корреляции, были
получены в круглых трубах и каналах прямоугольного сечения.
На рис. 8.11 приведена корреляция опытных данных, из которой
следует, что кризис кипения можно рассчитать с погрешностью
±33% для исследованного диапазона параметров. На рис. 8.11
hg — энтальпия насыщенного пара, a hb — среднемассовая эн-
энтальпия жидкости, которая может представлять собой недогре-
тую жидкость, насыщенную жидкость или двухфазную смесь
при паросодержании, меньшем 70%.
454 Глава 8
Необходимо отметить, однако, что точность расчетов крити-
критической плотности теплового потока при кипении в условиях вы-
вынужденной конвекции значительно хуже, чем при кипении в
большом объеме, и поэтому корреляция, представленная на
рис. 8.11, слишком упрощает сложность рассматриваемого яв-
явления. На рис. 8.12 показано качественное изменение темпера-
температуры вблизи кризиса теплоотдачи при кипении в условиях вы-
102
10
~F = 1 +0,0144
~ +O.51O-3
0
-33%
-4
44-1 1—M
(PiC^Tg-Tt)
{ Pvh
17™*
л
)(
Pi
i
И-4-
tfH
1J
33%
II ^*
. /VD
1Л-6 f
\ p
's-Tb)\
hfgPv 1
AN
•
Pl\
J
0,5
Гл
Этилое
p
Г
Г
E
E
= :::: E
--¦ b
-¦¦ E
S\
V
\
Зода
5ЫЙ СПИ
эензод
1ептан
"еп тан
Зода
Зода
Зода
Зода
Зода
Зода
Шй\
1
in
III
1 L_l_L .
• ¦ ..
эт* .
0
о
t Щ
\ ¦
—
i i i
...
М
...
0,001
0,01
0,1
1,0
10
Рис. 8.11. Корреляция данных по критическим плотностям теплового потока
при кипении и испарении в условиях вынужденной конвекции. (С разреше-
разрешения П, Гриффитса и Американского общества инженеров-механиков.)
нужденной конвекции [19]. На оси абсцисс приведены вели-
величины, кратные критической плотности теплового потока. При
превышении критической точки температура поверхности резко
возрастает и начинает колебаться в переходном режиме III,
пока стенка не станет полностью сухой и не установится пленоч-
пленочное кипение, если, конечно, материал стенки способен выдер-
выдержать воздействие температур, характерных для работы системы
в пленочном режиме кипения IV. Характеристики течения и
теплообмена при кипении в условиях вынужденного течения
имеют большое значение для техники безопасности и эксплуата-
эксплуатации ядерных реакторов, и, хотя удовлетворительный теоретиче-
теоретический анализ всех режимов кипения и отсутствует, были пред-
предприняты значительные усилия для получения соотношений, обоб-
обобщающих экспериментальные данные. Наиболее всеобъемлющее
соотношение было предложено Макбетом [48], который в серии
отчетов обобщил существовавшие в мире до 1963 г. данные по
кризису теплоотдачи при кипении воды. На критическую плот-
Конденсаций, кипение и массообмен 455
ность теплового потока влияет множество различных факторов,
например энтальпия на входе, длина канала, диаметр и форма
трубопровода, давление, ориентация в пространстве, паросодер-
жание, расход, распределение плотности теплового потока вдоль
Колебания
Критическая
плотность
теплового потока
(я/4)нр
0,90 0,95 1,00 1,05 1,10 1,15 1,20
Значения, кратные (ч/Л)^
Рис. 8.12. Характерное изменение температуры вблизи критический плотности
теплового потока при кипении в условиях вынужденной конвекции.
Режимы течения: I —вынужденная конвекция; II— пузырьковое кипение; III —переходный
режим; IV—пленочное кипение.
канала. Тонг [34] и Розенау [19] рассмотрели и систематизиро-
систематизировали многие из предложенных соотношений, и читателю реко-
рекомендуется ознакомиться с указанными источниками для более
детального изучения этой трудной и сложной темы.
Переходное и пленочное кипение
Переходную область между пузырьковым и пленочным ре-
режимами кипения трудно охарактеризовать количественно [37].
В переходной области кипения количество генерируемого пара
недостаточно для поддержания устойчивой паровой пленки и в
то же время слишком велико, чтобы позволить жидкости в до-
достаточном количестве достигать поверхности для поддержания
пузырькового кипения. Поэтому Беренсон [38] предположил,
что пузырьковое и пленочное кипение происходит поочередно на
одних и тех же участках поверхности. Этот процесс имеет не-
неустойчивый характер, и фотографии показывают, что волны
жидкости иногда движутся по направлению к поверхности на-
нагрева, а иногда в противоположном направлении. Временами
эти турбулентные жидкие образования столь сильно перегрева-
перегреваются, что взрывообразно переходят в пар [39]. С технической
456 Глава 8
точки зрения переходный режим кипения представляет ограни-
ограниченный интерес; оборудование, предназначенное для работы в
пузырьковом режиме кипения, может быть рассчитано доста-
достаточно надежно и давать воспроизводимые результаты.
Для пленочного кипения характерно существование паровой
пленки, покрывающей поверхность нагрева. Поскольку пар
имеет низкую теплопроводность по сравнению с жидкостью, то
для передачи тепловых потоков, соответствующих пузырьковому
режиму кипения, требуются очень большие разности темпера-
температур. Поэтому пленочное кипение используется в технике только
в тех обстоятельствах, когда этот режим является неизбежным.
Примером такой ситуации является кипение при обычных тем-
температурах сжиженных газов, как кислород или водород. Кроме
того, пленочное кипение может наблюдаться в потоках криоген-
криогенных жидкостей.
Пленочное кипение происходит при большой разности тем-
температур между твердой поверхностью и жидкостью, однако не-
невозможно точно рассчитать минимальное значение температур-
температурного напора, необходимое для поддержания устойчивой пленки.
Для большинства органических жидкостей при атмосферном
давлении это значение составляет по крайней мере 100 К, в то
же время известно, что нижний предел температурного напора
в значительной степени зависит о г давления. По-видимому, не
существует верхнего предела температурного напора для под-
поддержания устойчивой пленки, но при высоких температурах зна-
значительное количество тепла передается путем излучения, кото-
которое влияет на процесс кипения.
Процесс пленочного кипения классифицируется в зависимо-
зависимости от типа течения плейки пара — вязкого или турбулентного.
Течение является вязким, если длина пути пара в пленке корот-
короткая (например, на горизонтальных проволоках, небольших го-
горизонтальных трубах или вертикальных поверхностях неболь-
небольших размеров). На рис. 8.5 иллюстрируется вязкое пленочное
кипение на проволоке.
При вязком течении пленки можно достаточно точно рассчи-
рассчитать толщину паровой пленки и плотность теплового потока.
Бромли [40, 41] экспериментально и теоретически исследовал
устойчивое пленочное кипение на наружной поверхности гори-
горизонтальных труб, и его экспериментальные результаты с удовле-
удовлетворительной точностью могут быть описаны выражением
где kv — коэффициент теплопроводности насыщенного пара,
Вт/(м«град); Do — наружный диаметр трубы, м; \iv— вязкость
насыщенного пара, Н-с/м2; другие обозначения такие же, как
Конденсация, кипение и ма^сообмен 457
и в уравнении (8.21), за исключением АЛ Величина Я' опреде-
определяется по формуле
где cPv — удельная теплоемкость насыщенного пара,
Дж/ (кг -град).
Средний коэффициент теплоотдачи Нь в выражении (8.26)
учитывает только количество тепла, переданное путем тепло-
теплопроводности через пленку пара и путем конвекции от поверхно-
поверхности пленки к окружающей жидкости при кипении. При расчете
суммарного переноса тепла дополнительно к этому потоку тепла
необходимо учитывать вклад излучения. Поскольку радиацион-
радиационный теплообмен вызывает увеличение толщины пленки, коэф-
коэффициент hb> учитывающий теплопроводность и конвекцию, при
•наличии заметного вклада излучения меньше, чем в его отсут-
отсутствие. Суммарный коэффициент удельной тепловой проводи-
проводимости поверхности при существенном влиянии излучения можно
определить из эмпирического отношения
Л = АЛ^| +hr (8.28)
в предположении, что излучательная способность жидкости рав-
равна единице. Для определения коэффициента теплоотдачи в слу-
случае, когда жидкость обтекает поверхность трубы, Бромли и др.
[41] предложили формулу
Ч = <
(8-29)
при условии, что скорость Voo больше 2 л]gDo. Тогда в этом
случае суммарный коэффициент удельной тепловой проводимо-
проводимости поверхности с учетом излучения равен
h=hb + ^hr. (8.30)
При скоростях, меньших 2 уgDo, течение не является полно-
полностью развитым турбулентным и коэффициент Я можно рассчи-
рассчитать на основе данных работы [41].
8.4. МАССООБМЕН
Массообмен — процесс переноса некоторой компоненты сме-
смеси из области с высокой концентрацией этой компоненты в
область с меньшей концентрацией. Наше обсуждение проблемы
массообмена будет проведено на относительно элементарном
уровне. Для более глубокого изучения массообмена рекомен-
рекомендуется обратиться к работам [43, 47].
458 Глава 8
В двух последующих разделах будут рассмотрены две ши-
широкие категории массообмена. Этими категориями являются
диффузионный массообмен и конвективный массообмен. Диф-
Диффузионный массообмен в среде (также часто называемый моле-
молекулярным массообменом) происходит главным образом в
результате молекулярного движения. Диффузия одного компо-
компонента в смеси, находящейся по существу в стационарном со-
состоянии, в направлении уменьшения концентрации этого ком-
компонента аналогична переносу тепла теплопроводностью в
направлении уменьшения температуры. Хорошо известным при-
примером диффузионного массообмена является перенос распыляе-
распыляемого из баллончика аэрозоля в неподвижном воздухе комнаты.
Аэрозоль из места распыления распространяется по всей ком-
комнате. Аналогично мокрая одежда, находящаяся в комнате, в ко-
конечном счете высыхает, поскольку водяной пар с высокой кон-
концентрацией, окружающий одежду, диффундирует в более сухой
воздух. Существуют другие многочисленные примеры процесса
диффузионного массообмена.
Конвективный массообмен включает перенос компонента
вследствие движения всей массы жидкости. Процесс конвектив-
конвективного массообмена аналогичен процессу конвективного теплооб-
теплообмена. Конвективный массообмен может быть вынужденным и
свободным. Если движение жидкости обусловлено разностью
плотностей, процесс является свободным конвективным массо-
массообменом, а если движение жидкости вызывают внешние устрой-
устройства, такие, как вентилятор или насос, процесс принято класси-
классифицировать как массообмен при вынужденной конвекции. Су-
Существуют многочисленные примеры процессов конвективного
массообмена, такие, как увлажнение, дистилляция, экстракция
жидкости, абсорбция газа, выщелачивание.
Наши представления о массообмене в большой степени осно-
основаны на аналогии с соответствующим процессом теплообмена.
Мы обсудим уравнение для диффузионного потока массы, ко-
которое аналогично закону Фурье для переноса тепла теплопро-
теплопроводностью. Кроме того, поскольку уравнения сохранения для
конвективного переноса тепла и массы подобны, найдем, что
многие из безразмерных корреляционных соотношений для кон-
конвективного теплообмена дают приемлемые результаты и приме-
применительно к задачам конвективного массообмена.
Диффузионный массообмен
Скорость диффузии частиц типа А в смеси частиц А и В
(такой процесс переноса часто называют бинарной диффузией,
поскольку в смеси присутствуют только два типа частиц) опре-
определяется первым законом диффузии Фика. Этот закон можно
записать на основе массовых представлений, когда поток массы
Конденсация, кипение и массообмен 459
измеряется в кг/с, или на основе молярных представлений, когда
поток массы измеряется в моль/с.
При использовании массовых представлений первый закон
Фика в одномерном виде имеет вид
тА = <йА (тА + т'в) — рОлв Wy , (8.31)
%
где т% т'в— плотность потока массы в направлении х частиц
типа Л и частиц типа В соответственно, кг/м2-с; сои — массовая
долевая концентрация частиц типа Л, которая представляет со-
собой безразмерную величину, определяемую как масса частиц
типа Л, деленная на массу смеси частиц Л и В; р — плотность
смеси частиц Л и В, кг/м3; DAB — коэффициент диффузии частиц
типа Л в частицах типа 5, м2/с; л: —направление, в котором из-
^меряется поток массы, м.
Первый член в правой части уравнения (8.31) представляет
перенос частиц типа Л и В вследствие движения массы частиц
обоих типов.
Второй член в правой части уравнения (8.31) представляет
собой диффузию частиц Л вследствие градиента концентрации
частиц Л внутри смеси. Этот член аналогичен по форме записи
закону Фурье для теплопроводности [уравнение A.2)]. Отрица-
Отрицательный знак перед этим членом указывает, что масса перено-
переносится в направлении +#, если концентрация частиц гипа Л
уменьшается в направлении х.
Уравнение (8.31) можно значительно упростить, если плот-
плотность потока массы частиц Л точно равна плотности потока
массы частиц В в противоположном направлении. Это условие
называется эквимассовой противодиффузией. Если условия та-
таковы, что существует эквимассовая противодиффузия, то
тА = — т'в
и первый член в правой части уравнения (8.31) исключается.
Тогда первый закон Фика принимает упрощенный вид:
ЛХ = -рАиг^-. (8.32)
Уравнение (8.32) справедливо также еще для одного усло-
условия. Если массовая долевая концентрация частиц типа Л мала
(т. е. юл «С 1,0), член сол (т^ + /п?) мал по сравнению с членом,
учитывающим перенос массы вследствие градиента концентра-
концентрации, и уравнение (8.32) можно использовать даже в том слу-
случае, если условие существования эквимассовой противодиффу-
зии не выполняется.
460 Глава S
Закон Фика можно также записать на основе молярных пред-
представлений, когда плотность потока компоненты измеряется в
моль/(м2-с). Первый закон Фика при использовании молярных
представлений аналогичен по виду уравнению (8.31):
N"A = XA (Na + Nb) - CDAB ЦЬ-% (8.33)
где Na, Nb — плотности мольного потока массы частиц А и В
соответственно в направлении х, моль /(м2-с); Хд — мольная до-
долевая концентрация частиц Л, которая представляет собой без-
безразмерную величину, равную числу молей частиц Л, деленную
на число молей смеси частиц Л и В; С — суммарная мольная
концентрация смеси Л и В, моль/м3.
Если существуют условия, когда на каждый моль типа Л,
переносимый в одном направлении, существует равное число
молей типа В, переносимых в противоположном направлении,
то такой процесс называется эквимолярной противодиффузией.
Для эквимолярной противодиффузии Afл = — N"b и условие
(8.33) сводится к виду
N'^-CDab^. (8.34)
Уравнение (8.34) также применимо, когда мольная долевая кон-
концентрация частиц Л мала (ХА <С 1,0), даже если условие экви-
эквимолярной противодиффузии не выполняется.
Аналогично коэффициенту теплопроводности в законе Фурье
коэффициент диффузии Dab представляет собой величину, кото-
которую можно измерить. Для коэффициента диффузии используется
двойной индекс, поскольку его значение является функцией
обоих типов частиц, образующих бинарную смесь. Значения
Dab зависят не только от температуры, давления и концентрации
обоих типов частиц, но также от фазового состояния каж-
каждого типа частиц. Измеренные значения коэффициентов диффу-
диффузии для бинарных систем, в которых оба типа частиц представ-
представляют собой газы, приведены в табл. П. IX. 1. Некоторые значе-
значения коэффициентов диффузии для жидкой фазы приведены в
табл. П. IX. 2. Значения коэффициентов диффузии в жидкой
фазе на несколько порядков величины меньше, чем в газовой
фазе, поскольку подвижность молекул жидкости намного мень-
меньше, чем молекул газа. Некоторые известные значения коэффици-
коэффициентов бинарной диффузии твердых тел указаны в табл. П. IX. 3.
Чтобы определить плотность диффузионного потока массы,
нужно проинтегрировать выражение для первого закона Фика.
В предположении существования эквимассовой противодиффу-
противодиффузии, постоянной плотности потока массы, постоянной плотности
и постоянного коэффициента диффузии интегрирование уравне-
Конденсация, кипение и массообмен 461
ния (8.32) для стационарного одномерного процесса диффузии
дает
со. (L) — со. @)
*1а = 9DABA А' L аК> , (8.35)
где L — ширина диффузионного слоя, на поверхностях которого
массовая долевая концентрация частиц А равна о)д(?) и @^@).
Можно получить аналогичное уравнение на основе молярных
представлений путем интегрирования уравнения (8.34). В пред-
предположении постоянных Dab, С и плотности мольного потока
массы в одном направлении при эквимолярной противодиффу-
зии интегрирование дает следующий результат:
AS^L'm. ,8.36)
> Используя понятие диффузионного сопротивления, плотность
.диффузионного мольного потока массы можно выразить следую-
следующим образом:
. XA(L)-XA@)
NA — р ,
где Rd — сопротивление диффузии массы. Можно видеть, что
величина этого сопротивления при эквимолярной противодиффу-
зии в прямоугольных координатах равна
где А — площадь поперечного сечения, через которое происхо-
происходит диффузия вещества. Отметим, что сопротивление диффузии
массы обратно пропорционально коэффициенту диффузии.
Нетрудно распространить понятие о сопротивлении диффу-
диффузии массы для других систем координат. Например, можно по-
показать, что сопротивление при эквимолярной противодиффузии
через цилиндрическую трубу с радиусами rt и го и длиной L
равно
l(/)
2nCDABL
а сопротивление при эквимолярной противодиффузии через сфе-
сферическую оболочку равно
Уравнение (8.40) подобно уравнению B.40), а уравнение (8.39)
подобно уравнению B.35).
Если предполагается, что оба диффундирующих вещества
представляют собой идеальные газы, то часто удобнее выражать
462 Глава 8
первый закон Фика или его интегральную форму через темпе-
температуры и парциальные давления вместо массовых или мольных
концентраций.
Уравнение состояния идеального газа для смеси можно за-
записать в виде
^f (8.41)
где Р — полное давление смеси, Ru — универсальная газовая по-
постоянная (Ru = 8,314» 103 Дж/(кмоль-град) и М — молекуляр-
молекулярный вес смеси. Уравнение состояния идеального газа можно
также записать для одиночных компонент, которые образуют
идеальную газовую смесь. Например, для вещества А уравне-
уравнение состояния имеет вид
ЬЦf (8-42)
В этом уравнении Ра — парциальное давление вещества Л. Сле-
Следовательно, массовая долевая концентрация вещества А в иде-
идеальном газе может быть выражена в виде
р- РЛМЯ
»i-T—Ав*- (8-43)
В предположении, что идеальная смесь газов находится в изо-
изотермических условиях и при постоянном полном давлении, урав-
уравнение (8.35) для эквимассовой противодиффузии можно выра-
выразить через парциальные давления путем подстановки уравнений
(8.41) — (8.43). Это приводит к результату
МА pA(L) — PA@)
™*=TJ l/dJ¦
Если стационарная эквимассовая противодиффузия происходит
при постоянной температуре и постоянном полном давлении в
радиальном направлении сквозь полый цилиндр, то диффузион-
диффузионный поток массы будет равен
m*-
МА
RJ in (ro/rl)/2nDABL ¦
Уравнения, соответствующие уравнениям (8.44) и (8.45), при
эквимолярном массообмене имеют вид
Конденсация, кипение и массообмен 463
для диффузии идеальных газов при постоянной температуре и
полном давлении в прямоугольных координатах и
для аналогичных условий в цилиндрических координатах.
Пример 8.4. Два больших резервуара разделены трубой длиной 0,75 м
и внутренним диаметром 2 см. Один резервуар содержит чистый СО2 при тем-
температуре 0°С и давлении 1 атм A,0133-105 Н/м2), а другой — чистый Н2 при
0°С и при давлении 1 атм. Рассчитать начальный диффузионный поток массы
СО2 в сосуд с Н2.
Решение. Из табл. П.1Х.1 Dab = 5,5-10~5 м2/с, а уравнение (8.46) даег
мольный поток массы в предположении, что поведение газа отвечает идеаль-
идеальному газу и условия соответствуют эквимолярной противодиффузии:
д-0,012-5,5.10-5
/ РЛ @I - 8,314 ^103-27
= 1,029 • Ю-9 кмоль/с = 3,7 • Ю-3 моль/ч.
Можно проверить допущение о существовании эквимолярной противодиффу-
противодиффузии путем расчета мольного диффузионного потока Н2 с помощью уравнения
(8.46):
** Чёт 1Рв №> - рв @)] - 4^Г [рл <°> - рл
= —1,029- 10~9 кмоль/с.
Следовательно, допущение о существовании эквимолярной противодиффузии
справедливо.
Пример 8.5. Чистый гелий при давлении 10 атм и температуре 20°С на-
находится в трубке из стекла пирекс наружным диаметром 5 см с толщиной
стенки 4 мм. Рассчитать утечку гелия через стенку трубки в кг/с на 1 м длины.
Решение. Гелий имеет следующие свойства: МА = 4 кг/моль, РА(п) =
= 10 атм = 1,0133-106 Н/м2, а значение DAb для диффузии гелия через пи-
пирекс определяется из табл. П.1Х.З: Dab — 4,49 • 10~15 м2/с. Предполагая, что
концентрация гелия с наружной стороны трубки практически равна нулю, по-
получаем Ра (го) = 0. Если предположить, что массовая долевая концентрация
гелия в пирексе очень мала (ХА < 1,0), то из уравнения (8.45) можно
точно рассчитать диффузионный поток массы через стенку трубки на 1 м ее
длины:
МА PA(ri)~PA(ro)
4-1,0133-1» -2 69.10-» кг/с
8,314 '103- 293 -1п B,6/2,1 )/2я- 4,49-10-15 • 1
Оценка показывает, что 1 г гелия будет диффундировать через стенку труб-
трубки в течение приблизительно 120 лет.
Конвективный массообмен
Предположим, что надо определить скорость испарения воды
с поверхности озера, когда над его поверхностью дует сухой
воздух. Поскольку массообмен определяется конвективным про-
процессом, то удобно определять поток массы пропорционально
464 Глава 8
разности между массовыми концентрациями на поверхности и
в окружающей среде:
тА = hmA (СА$ - СДоо). (8.48)
Уравнение (8.48) является основным уравнением для расчета
конвективного массообмена при малых значениях потока массы,
и оно определяет смысл коэффициента конвективного массооб-
массообмена ftm. Уравнение (8.48) аналогично по форме записи закону
Ньютона при охлаждении A.16).
На рис. 8.13 показана схема физической задачи испарения
воды из озера. Эта задача подобна задаче о переносе тепла от
Концентрационный пограничный слой
Вода
Поверхность воды, CAs
Рис. 8.13. Концентрационный пограничный слой на плоской пластине.
горизонтальной плоской пластины, на поверхности которой раз-
развивается тепловой пограничный слой. Аналогичным образом
образуется концентрационный пограничный слой, внутри кото-
которого концентрация изменяется в направлении, перпендикуляр-
перпендикулярном горизонтальной поверхности озера. Снаружи пограничного
слоя концентрация водяного пара остается постоянной и равной
своему значению в окружающей среде.
Пример задачи об испарении воды из озера далее иллюстри-
иллюстрирует подобие между процессами конвективного теплообмена и
массообмена. Действительно, если вывести уравнения сохране-
сохранения для процессов конвективного переноса тепла и массы, то
эти уравнения окажутся подобными, причем массовая концен-
концентрация СА аналогична температуре Г, а коэффициент диффузии
Dab аналогичен коэффициенту температуропроводности а.
Эта аналогия предполагает, что простым методом расчета
коэффициента массообмена является использование соответ-
соответствующего безразмерного соотношения для конвективного тепло-
теплообмена с подстановкой соответствующих безразмерных комплек-
комплексов, описывающих процесс массообмена. Безразмерным комплек-
комплексом, описывающим теплообмен, в который входит коэффициент
теплоотдачи, является число Нуссельта
Конденсация, кипение и массообмен 465
Аналогичный безразмерный комплекс, описывающий массооб-
мен, называется числом Шервуда и определяется следующим
образом:
Sh = ^-. (8.49)
В теории теплообмена безразмерным комплексом, который ха-
характеризует отношение переноса количества движения к тепло-
теплопроводности, является число Прандтля
Pr = j. (8.50)
В теории массообмена коэффициент диффузии заменяет коэф-
коэффициент температуропроводности и новый безразмерный ком-
комплекс называется числом Шмидта:
Sc=-J-. (8.51)
Число Шмидта характеризует отношение переноса количества
движения к массовой диффузии.
Число Нуссельта является функцией чисел Рейнольдса и
Прандтля:
Nu = f(Re, Рг).
С учетом подобия между процессами конвективного тепло- и
массообмена можно ожидать, что число Шервуда будет анало-
аналогичной функцией чисел Рейнольдса и Шмидта:
Sh = /(Re, Sc). (8.52)
Например, при турбулентном течении в трубе безразмерное со-
соотношение для теплоотдачи E.12) имеет вид
Nuz> = 0,023 Re?8 Pr0'33. (8.53)
Используя это соотношение, можно приближенно описать поток
массы от жидкости, которая полностью смачивает внутреннюю
поверхность трубы, к турбулентному потоку газа, протекающему
вдоль трубы, с помощью уравнения
= 0,023 Re%8 Sc0'33. (8.54)
В этом случае жидкость переходит в газовую фазу в результате
испарения и уравнение (8.54) можно использовать для расчета
скорости испарения жидкости.
В качестве второго примера рассмотрим снова задачу об
испарении воды с поверхности озера. Для этого случая конвек-
конвективный теплообмен описывается соотношением
Ргь% (8.55)
466 Глава 8
которое представляет собой соотношение E.22) для расчета
теплоотдачи от плоской пластины в предположении ламинар-
ламинарного режима обтекания. Соответствующее соотношение для ра-
расчета ламинарного массообмена будет иметь вид
Shc = 0,664 Re[/2 Scl/3. (8.56)
Если в задаче о массообмене перенос осуществляется сво-
свободной конвекцией, выражение для коэффициента массообмена
можно вывести на основе аналогичной задачи о теплообмене в
условиях свободной конвекции. Известно, что теплообмен при
свободной конвекции описывается соотношением
Nu = /(Gr, Рг). . (8.57)
Число Грасгофа для массообмена определяется следующим
образом:
8lLZJCA (8.58)
где g определяется в виде
S P dC,
сА
Можно ожидать, что для массообмена при свободной конвекции
будет справедливо соотношение в виде
Sc).
Для определения вида конкретных функциональных зависимо-
зависимостей при рассмотрении каждой задачи массообмена следует
обращаться к гл. 5.
Аналогию Рейнольдса, которая связывает плотность тепло-
теплового потока и касательное напряжение на поверхности, можно
распространить на случай массообмена. Выражение для анало-
аналогии Рейнольдса D.50) имеет вид
N" =4- (S.59)
RePr ~ 2 #
Аналогия Рейнольдса для турбулентного массообмена записы-
записывается так:
Sh cf
-тппг—т
Используя уравнение (8.60), можно рассчитать коэффициенты
массообмена по известному коэффициенту трения.
Пример 8.6. Рассчитать скорость испарения воды с поверхности озера,
имеющего размеры приблизительно 500 X 500 м. Скорость ветра 5 м/с. Тем-
Температура воздуха и воды в озере равна 25°С. Рассчитать скорость испарения
воды для случаев, когда окружающий воздух имеет относительную влаж-
влажность а) 10% и б) ™п/
Конденсация, кипение и массообмен 467
Решение. Эта задача определяется процессом массообмена при вынуж-
вынужденной конвекции от плоской пластины. Прежде чем подобрать соответствую-
соответствующее безразмерное соотношение для числа Шервуда, следует определить, бу-
будет ли течение ламинарным или турбулентным. Число Рейнольдса в конце
озера равно
p^Z. 1,146.5.500 =0з
1 ц 18,46-Ю"
Следовательно, течение воздуха полностью турбулентное и, таким образом,
соответствующее безразмерное соотношение аналогично соотношению D.56)
NuL = 0,036 Prl/3Re?8,
которое используется для расчета турбулентного теплообмена на плоской
пластине. Следовательно, соответствующее соотношение для расчета массо-
массообмена имеет вид
ShL==: 0,036 Sc1/3Re?8,
Используя физические свойства из табл. ILVL 1 и ПЛХ. 1, имеем
/>лв = 2F.10- „«/с, Sc= ^--Ш^-- 0,6223.
Число Шервуда равно
ShL = 0,036 • 0,62231/3 A,55 • 108H'8 = 1,096 • 105.
Коэффициент конвективного массообмена равен
.10- м/с.
Ь096 • 105 • 2,6 • 10
Л*~Г= 500 = 5
Далее необходимо определить концентрацию паров воды у поверхности озера
и в окружающем воздухе., У поверхности воды воздух насыщенный и его от-
относительная влажность равна 100%. Соотношение между парциальным дав-
давлением водяного пара, относительной влажностью и температурой насыще-
насыщения имеет вид
Из таблиц для водяного пара давление насыщения при 25°С равно Рнас =
= 3098 Н/м2. Парциальное " давление пара у поверхности озера равно
p^s = рнас = 3098 Н/м2. Концентрация водяного пара у поверхности озера
в предложении, что водяной пар представляет собой идеальный газ, равна
MWPW, 18-3098 ЛЛООС| , о
s 0,02251 кг/м3.
=
RJ 8,314 • 103 • 298
а) При относительной влажности окружающего воздуха 10% концентрация
водяного пара в воздухе равна
18.0,10.3098
UUU^^° КГ/М '
с в
Л» RuT 8,314 . 103 • 298
Скорость испарения воды равна
^А = КА (CAS - Сд^) = 5»7 * 10~3 # 25 * 1СL @,02251 - 0,00225) =* 28,9 кг/с.
468 Глава 8
б) Если относительная влажность окружающего воздуха 80%, концентрации
водяного пара у поверхности озера и в окружающем воздухе равны
Сд =0,02251 кг/м3, 6^^ = 0,0180 кг/м3, а скорость испарения воды равна
тА = 5,7 . Ю-3 • 25. 104 @,02251 - 0,0180) = 6,43 кг/с,
что на 78% меньше скорости испарения воды при относительной влажности
окружающего воздуха 10%.
Литература
I. Nusselt W., Die Oberflachenkondensation des Wasserdampfes, Z. Ver.
Deutsch. Ing., 60, p. 541 A916).
2. Rohsenow W. M., Heat Transfer and Temperature Distribution in La-
Laminar-Film Condensation, Trans. ASME, 78, p. 1645 A956).
3. Rohsenow W. M., Choi H., Heat, Mass, and Momentum Transfer, Pren-
Prentice-Hall, Englewood Cliffs, N. Y., 1961
4. Kreith F., Principles of Heat Transfer, Harper and Row, N. Y., 1973.
5. Chen M. M., An Analytical Study of Laminar Film Condensation: Pt. 1,
Flat Plates, Pt. 2, Single and Multiple Horizontal Tubes, Trans ASME, ser. C,
83, p. 48 A961). [Имеется перевод: Минг Чен Аналитическое исследование
процесса конденсации при ламинарном течении пленки. Части I и II.— Труды
Амер. об-ва инж.-мех., сер. С. Теплопередача, 1961, № 1, с. 60.]
6. Rohsenow W. M., Weber J. MM Ling А. Т., Effect of Vapor Velocity
on Laminar and Turbulent Film Condensation. Trans. ASME, 78, p. 1637
A956).
7. Colburn A. P., The Calculation of Condensation where a Portion of the
Condensate Layer is in Turbulent Flow, Trans. AIChE, 30, p. 187 A933).
8. Kirkbridge C. G., Heat Transfer by Condensing Vapors on Vertical
Tubes, Trans. AIChE, 30, p. 170 A933).
9. McAdams W. H., Heat Transmission, 3rd ed., McGraw, N. Y., 1954.
[Имеется перевод: Мак-Адаме, Теплопередача. — M.: Металлургиздат, 1961.]
10. Carpenter E. F., Colburn A. P., The Effect of Vapor Velocity on Con-
Condensation-Inside Tubes, Inst. Mech. Eng. ASME, Proc. General Discussion on
Heat Transfer, 1951, p. 20.
II. Drew Т. В., Nagle W. M., Smith W. Q., The Conditions for Dropwise
Condensation of Steam, Trans. AIChE, 31, p. 605 A935).
12. Rose J. W., On the Mechanism of Dropwise Condensation, Int. /. Heat
Mass Transfer, 10, p. 755 A967).
13. Criffith P., Lee M. S., The Effect of Surface Thermal Properties and
Finish on Dropwise Condensation, Int. /. Heat Mass Transfer, 10, 697
A967).
14. Katz A. P., Macintire H J., Gould R. E., Heat Transfer in Ammonia
Condensers, Univ. Illinois Eng. Expt. Sta. Bull., 209, 1930.
15. McAdams W. H., Heat Transmission, 3rd ed., McGraw, N. Y., 1954.
[Имеется перевод: Мак-Адаме, Теплопередача. — M.: Металлургиздат, 1961.]
16. Collier J. С, Convective Boling and Condensation, McGraw, N. Y., 1972.
17. Farber E. A., Scorah R. L., Heat Transfer to Water Boiling under
Pressure, Trans. ASME, 70, p. 36У A948).
18. Gunther F. C, Kreith F., Photographic Study of Bubble Formation in
Heat Transfer to Subcooled Water, Jet Propulsion Laboratory, California In-
Institute of Technology, Prog. Rept. 4-120, March 1950.
19. Rohsenow W. M., Boiling, Section 13, in Handbook of Heat Transfer,
W. M. Rohsenow, J P. Hartnett, eds., McGraw, 1973, p. 13.
20. Falh H. S., Judd R. L., Influence of System Pressure on Microlayer
Evaporation Heat Transfer, J. Heat Trans., 100, p. 49 A978). [Имеется пере-
перевод: Фатх, Джад. Влияние давления на теплоотдачу при испарении микро-
микрослоя. — Труды Амер. об-ва инж.-мех., сер. С. Теплопередача, 1978, № 1, с. 52.]
Конденсация, кипение и массообмен 469
21. Rohsenow W М., A Method of Correlating Heat Transfer Data for
Surface Boilfng Liquids, Trans. ASME, 74, p. 969 A952).
22. Addoms J. N.. Heat Transfer at High Rates to Water Boiling Outside
Cylinders, MIT, Cambridge, Mass., 1948 (диссертация доктора химических
наук).
23. Piret E. L., Isbin H. S., Natural Circulation Evaporation Two-Phase
Heat Transfer, Chem. Eng. Prog., 50, p. 305 A954).
24. Cichelli M. Т., Bonilla C. F., Heat Transfer to Liquids Boiling under
Pressure, Trans. AIHE, 41, p. 755 A945).
25. Cryder D. S., Finalbargo A. C, Heat Transmission from Metal Surfaces
to Boiling Liquids: Effect of Temperature of the Liquid on Film Coefficient,
Trans. AlChE, 33, 346 A937).
26. Vachon R. L., Nix G. R, Tanger G. E., Evaluation of Constants for
the Rohsenow Pool-Boiling Correlation, /. Heat Transfer, 90, p. 239 A968).
[Имеется перевод: Вачон, Нике, Тэнджер, Оценка постоянных для зависи-
зависимости Росеноу при объемном кипении. — Труды Амер. об-ва инж.-мех., сер. С.
Теплопередача, 1968, № 2, с. 62.]
27. McAdams W. Н.> et al., Heat Transfer from Single Horizontal Wires to
Boiling Water, Chem. Eng. Prog., 44, p. 639 A948).
» 28. McAdams W. H., Heat Transmission, 3id ed., McGraw, N. Y., 1954.
[Имеется перевод: Мак-Адаме, Теплопередача. — М.: Металлургиздат, 1961.]
29. Kxeith F., Foust A. S., Remarks on the Stability and Mechanism of
Surface Boiling Heat Transfer, ASME Paper 54-A-16, Aug. 1954.
30. McAdams W. H., Kennel W. E., Minden C. S., Carl R., Picornell P. M.,
Dew J. E., Heat Transfer at High Rates to Water with Surface Boiling, Ind.
Eng. Chem.,4\, 1945 A944).
31. Zuber N., Tribus M., Westwater J. W., The Hydrodynamic Crisis in
Pool Boiling of Saturated and Subcooled Liquids, Proceedings of the Interna-
International Conference on Developments in Heat Transfer, ASME, N. Y., 1962,
p. 230.
32. Rohsenow W. M., Griffith P., Correlation of Maximum Heat Flux Data
for Boiling of Saturated Liquids, Reprint, Heat Transfer Symposium, AIChE,
Louisville, Ky., March 1955.
33. Rohsenow W. M., Choi H., Heat, Mass, and Momentum Transfer, Pren-
Prentice-Hall, Englewood, Cliffs, N. J., 1961.
34. Tong L. S., Boiling and Two-Phase Flow, Wiley, N. Y., 1965. [Имеется
перевод: Тонг, Теплоотдача при кипении и двухфазное течение. — М.: Мир,
1969.]
35. Konmutsos К., Moissis R., Spyridonos A., A Study of Bubble Depar-
Departure in Forced Convection Boiling, /. Heat Transfer, 90, p. 223 A968). [Имеется
перевод: Кумутсос, Мойсис, Спиридонос, Исследование отрыва пузырьков в
кипящей жидкости при вынужденной конвекции. — Труды Амер. об-ва инж.-
мех., сер. С, Теплопередача, 1968, № 2, с, 44.]
36. Griffith P., Correlation of Nucleate-Boiling Burnout Data, ASME Paper
57-HT-21.
37. Jordan D. P., Film and Transition Boiling, in Advanced in Heat Trans-
Transfer, 5, Irvine T. F., Jr., Hartnett J. P., eds., Academic Press, N. Y., 1968, p. 55.
[Имеется перевод: Джордан Д. П. Пленочное кипение и кипение в переход-
-ном режиме. Ё сб. Успехи теплопередачи. — М.: Мир, 1971, с. 68.]
38. Berenson P. J., Experiments on Pool-Boiling Heat Transfer, Int. J. Heat
Mass Transfer, 5, p. 985 A962).
39. Westwater J. W., Boiling Heat Transfer, Amer. Scientist, 47, p. 427
40. Bromley L. A., Heat Transfer in Stable Film Boiling, Chem. Eng. Prog.,
46, p. 221 A950).
41. Bromley L. A., et al.,, Heat Transfer in Forced Convection Film Boiling,
Ind. Eng. Chem., 45, p. 2639 A953).
42. Davis E. J., David M. M., Two-Phase Gas-Liquid Convection Heat
Transfer, I and E С Fundamentals, 3, 1964, p. ill.
470 Глава 8
43. Bird R., Stewart W. E., Lightfoot E N., Transport Phenomena, Wiley,
N. Y., 1960. [Имеется перевод: Берд, Стыоард, Лаитфут, Явления переноса. —
М.: Химия, 1974.]
44. Crank J., The Mathematics of Diffusion, 2nd ed., Oxford University
Press, N. Y., 1975.
45. Jost W., Diffusion in Solids, Liquids and Gases, rev. ed., Academic
Press, N. Y, 1960.
46. Sherwood T. K., Pigford R. C, Wilke C. R., Mass Transfer, McGraw,
N. Y., 1975.
47. Treybal R. D., Mass Transfer Operations, 2nd ed., McGraw, N. Y.,
1968.
48. Macbeth R. V., Forced Convection Burnout in Simple Uniformly Heated
Channels: A. Detailed Analysis of World Data, European Atomic Energy Soc.
Symp. on Two-Phase Flow, Steady State Burnout and Hydrodynamic Instabi-
Instability, Sweden, 1963
49. Rohsenow W. M , A Method of Correlating Heat Transfer Data from
Surface Boiling Liguids, Trans. ASME, 75 A955).
ЗАДАЧИ
Задачи в данной главе сгруппированы по тематике разделов, как указано
в таблице
Номера задач
8.1-8.6
8.7-8.14
8.14-8.26
Раздел
8.2
8.3
8.4
Тема
Конденсация
Кипение
Массообмен
8.1. Вывести соотношение для пленочной конденсации Нуссельта при кон-
конденсации пара внутри коротких вертикальных труб, когда пленка жидкости
течет в виде кольцевого слоя.
8.2. Рассмотреть вертикальную трубу с внутренним диаметром 1 см при
температуре поверхности 90°С, внутри которой течет насыщенный пар при
атмосферном давлении. Определить длину трубы, при которой конденсат
заполнит все сечение трубы и течение пара прекратится.
8.3. Рассчитать средний коэффициент теплоотдачи при пленочной конден-
конденсации водяною пара при давлениях 0,005 и 0,1 МН/м2 для а) вертикальной
поверхности высотой 2 м; б) наружной поверхности вертикальной трубы диа-
диаметром 1 см и длиной 2 м; в) наружной поверхности горизонтальной трубы
диаметром 1 см и длиной 2 м и г) вертикального конденсатора, состоящего из
10 горизонтальных труб диаметром 1 см и длиной 2 м. Во всех случаях пред-
предполагается, что скоростью пара можно пренебречь и что все поверхности нахо-
находятся при постоянной температуре на 10°С ниже температуры насыщения.
8.4. Тонкостенная горизонтальная медная трубка с наружным диамет-
диаметром 9 мм помещена в объем воды при атмосферном давлении и температуре
100°С. Внутри трубки происходит конденсация пара органической жидкости,
а температура наружной поверхности трубки постоянна и равна 220°С. Рас-
Рассчитать средний коэффициент теплоотдачи наружной поверхности трубки.
8.5. Рассчитать а) необходимую площадь поверхности теплообмена и
б), предложить соответствующую конструкцию для конденсатора холодиль-
холодильной машины холодопроизводительностью 70 кВт. Теплоносителем является
аммиак, конденсирующийся на наружной поверхности горизонтальных труб
при давлении 1,2 МН/м2. Конденсатор необходимо сконструировать из сталь-
стальных труб C см—наружный диаметр, 2,5 см — внутренний диаметр), темпе-
температура охлаждающей воды 25°С, а средняя скорость воды в трубах не дол-
должна превышать 2 м/с.
8.6. Внутренняя поверхность вертикальной трубы с внутренним диамет-
диаметром 1 см и длиной 1 м поддерживается при температуре 120°С. Для насы-
насыщенного водяного пара, конденсирующегося внутри трубы при давлении
0,34 МН/м2, рассчитать средний коэффициент теплоотдачи и расход конден-
конденсата при условии, что скорость пара мала.
8.7. Рассчитать коэффициент теплоотдачи при пузырьковом кипении воды
при атмосферном давлении на наружной поверхности вертикальной трубы на-
наружным диаметром 1 см и длиной 2 м. Предположить, что температура по-
поверхности трубы постоянна и превышает температуру насыщения на 10°С.
8.8; Рассчитать максимальную плотность теплового потока при пузырь-
пузырьковом кипении в большом объеме на чистой поверхности а) воды на латуни
при давлении 0,1 МН/м2, б) воды на латуни при давлении 1 МН/м2 и в) н-бу-
тилового спирта на меди при давлении 0,3 МН/м2.
8.9. Определить температурный напор, соответствующий половине значе-
значения максимальной плотности теплового потока для комбинаций жидкость —
поверхность нагрева в задаче 8.8.
8.10. Рассчитать время, необходимое для замораживания слоя воды тол-
толщиной 2 см вследствие радиационного теплообмена с окружающим воздухом
в ночное время при начальной температуре воды 5°С. Эффектом испарения
пренебречь..
472 Глава 8
8.11. Рассчитать максимальную плотность теплового потока при кипении
насыщенной воды в большом объеме при давлениях, составляющих 10, 20, 40,
60 и 80% критического давления рКр, и представить полученные результаты
в виде зависимости cwc от р/ркр. Коэффициент поверхностного натяжения
воды можно рассчитать из выражения о = 0,242 — 6,3-10~4 Т, где величина
а выражена в Н/м и Т — в °С.
8.12. Плоская пластина из нержавеющей стали толщиной 5 мм, шириной
1,5 см и длиной 35 см погружена в вертикальном положении при начальной
температуре 1000°С в большую водяную ванну, находящуюся при 100°С и
атмосферном давлении. Определить длительность охлаждения пластины до
температуры 600°С.
8.13. Рассчитать безопасное максимальное значение плотности теплового
потока при пузырьковом режиме кипения воды, текущей со скоростью 15 м/с
в трубе с внутренним диаметром 1 см и длиной 0,5 м, если вода входит в
трубу при давлении 0,1 МН/м2 и температуре 100°С, а на стенке трубы за-
задана постоянная плотность теплового потока 16 МВт/м2.
8.14. Вода при атмосферном давлении кипит в баке с плоским медным
дном на электрической плите, которая поддерживает температуру поверхно-
поверхности 110°С. Рассчитать коэффициент теплоотдачи при кипении.
8.15. Сферический резиновый баллон диаметром 1м содержит гелий при
избыточном давлении 0,3 МН/м2 и температуре 30сС. Толщина материала
баллона 0,1 мм. Рассчитать диффузионный поток массы гелия через материал
баллона, если коэффициент диффузии гелия в резине равен 3-10~п м2/с.
8.16. Труба длиной 3 м и внутренним диаметром 1 см соединяет два ре-
резервуара, содержащие газы при давлении 0,1 МН/м2 и температуре 0°С. Рас-
Рассчитать плотность диффузионного потока между двумя газами в случае эк-
вимолярной противодиффузии. В качестве газов рассмотреть воздух и водо-
водород.
8.17. Решить задачу 8.16 для двуокиси углерода и водорода.
8.18. Конец металлической трубы внутренним диаметром 2 см соединен
с диафрагмой толщиной 3-10~2мм. В трубе находится водород при темпера-
температуре 20°С и давлении 0,5 МН/м2. Коэффициент диффузии водорода в мате-
материале диафрагмы считается равным 6-10~~12 м2/с. Рассчитать скорость диф-
диффузии водорода через диафрагму.
8.19. Рассчитать плотность диффузионного потока массы газообразного
аммиака при давлении 0,1 МН/м2 и температуре 0°С через слой неподвижного
воздуха толщиной 25 см при тех же условиях.
8.20. Рассчитать скорость диффузии слоя азота с площадью поверхности
0,5 м2 через слой двуокиси углерода толщиной 2 м при полном давлении
0,1 МН/м2 и температуре 25°С.
8.21. Проверить, что числа Шервуда, Шмидта и Грасгофа для массооб-
мена являются безразмерными.
8.22. Рассчитать скорость испарения воды из озера размером 100 X
X ЮО м. Скорость окружающего сухого воздуха 20 м/с, температура воды
в озере 25°С.
8.23. Решить задачу 8.22 при условии, что окружающий воздух имеет
относительную влажность 50% и температуру 25°С.
8.24. Ванна с толуолом размерами 30 X 30 см помещена в комнату при
температуре 25°С. Воздух циркулирует над поверхностью толуола со ско-
скоростью 10 м/с: Определить скорость испарения в воздух толуола.
8.25. Горизонтальный цилиндр наружным диаметром 3 см изготовлен из
пористого материала, который насыщен водой. Цилиндр обдувается по нор-
нормали к оси сухим воздухом при температуре 25°С со скоростью 100 м/с. Рас-
Рассчитать скорость испарения воды с поверхности на единицу длины цилиндра.
8.26. Рассчитать скорость испарения в воздух воды с поверхности оди-
одиночной капли диаметром 2 мм, если капля падает в неподвижном воздухе со
скоростью 170 м/с. Относительная влажность воздуха 50%.
Приложение I
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
ЛАПЛАСИАН
Часто удобно описывать поле теплового потока с помощью
векторного анализа. Такие понятия векторного анализа, как
лапласиан и градиент, позволяют очень удобно и компактно вы-
выразить некоторые основные уравнения теплопередачи.
Применяя оператор Лапласа, можно записать общее урав-
уравнение теплопроводности B.6) следующим образом:
Функциональная форма оператора Лапласа, обозначаемого
V2, зависит от используемой системы координат. В табл. П. 1.1
приведены выражения для лапласиана в прямоугольной, цилин-
цилиндрической и сферической системах координат.
Таблица П. 1.1
Форма Лапласиана
Система координат Лапласиан V2T
Прямоугольная, T=(x,y,z) ?j^ +•?-?. + ?-|.
Цилиндрическая*,*) I|(?)
1
Сферическая,^,*,*) 7
1 Ь2Т
r2sin20 Эф2
Уравнение теплопроводности, записанное в форме равенства
(П. 1.1), применимо во всех трех системах координат. При
переходе от одной системы к другой нужно только подставить
соответствующее выражение лапласиана из табл. П. 1.1.
Лапласиан производит операцию над скалярной величиной,
в данном случае температурой, и дает в результате скалярную
величину. Произведение лапласиана температуры на коэффи-
коэффициент теплопроводности физически выражает результирующий
поток энергии на единицу объема, подводимый к элементарному
объему твердого тела вследствие теплопроводности.
474 Приложение I
ГРАДИЕНТ
В теории теплопередачи часто применяется еще одно поня-
понятие векторного анализа — градиент. Используя понятие гради-
градиента, закон Фурье для теплопроводности можно записать в век-
векторной форме:
где градиент температуры VT является векторной величиной.
Градиент обладает тем важным свойством, что он является век-
вектором, направленным в сторону максимального изменения тем-
температуры. Другими словами, тепло течет в направлении макси-
максимального изменения температуры.
Тепловой поток не является векторной величиной, но если
закон Фурье для теплопроводности записывается в форме соот-
соотношения (П.1.2), тепловой поток можно считать вектором,
имеющим три составляющие (в направлении трех осей коор-
координат). Например, в прямоугольной системе координат вектор
теплового потока выражается в виде q" = q"i -\-q"y\ + <?"k, где
i, j, k — единичные векторы в направлениях х, у и z соответ-
соответственно. Аналогичными соотношениями можно выразить вектор
теплового потока в цилиндрической и сферической системах ко-
координат.
В табл. П.1.2 приведены выражения для градиента в раз-
различных системах координат.
Таблица П.1.2
Форма градиента
Система координат Градиент уГ
дТ . дТ , дТ
Прямоугольная 'дхХ + "ду^ + 'Шк
дТ . 1 дТ , дТ
Цилиндрическая ~дГ{г + Т~дФ Ч + ~дГ1г
ОТ . 1 дТ , 1 дТ
Сферическая *аГ^ + ТЖ !6 + ТТ^д'дФ *Ф
Приравнивая коэффициенты уравнения (П.1.2) соответ-
соответствующим членам градиента, находим составляющие вектора
теплового потока в прямоугольной системе координат:
ft L- di ff i дТ ff i дТ
Ях = — «-§7. (iy = ^k'j^* qzZS=~~klte
и в цилиндрической системе координат:
Яг дг » Чф у "g?-, Яг к дг '
Приложение II
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Некоторые комбинации экспоненциальных функций имеют
специальные названия. Поскольку они связаны с гиперболой,
подобно тому как тригонометрические функции связаны с
окружностью, их называют гиперболическими, функциями. Три
из этих гиперболических функций, встречающиеся в теории теп-
теплопередачи, определяются формулами
eh*
V
sh
th*—2?i-
ex - e-x
ch x ел + e~
Производные функций sh# и chx равны соответственно
d
— (ch x = sh x.
В табл. П. П. 1 представлены значения функций shx, chx и th#.
Таблица П. И. *
Значения гиперболических функций
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
U
1,8
1,9
2,0
2,5
3,0
3,5
4,0
4,5
5,0
shx
0,00000
0,10017
0,20134
0,30452
0,41075
0,52110
0,63665
0,75858
0,88811
1,02652
' 1,17520
1,33565
1,50946
< 1,69838
1,90430
2,12928
2,37557
2,64563
2,94217
3,26816
3,62686
6,05020
10,01787
16,5426
27,2899
45,0030
74,2032
chx
1,0000
1,00500
1,02007
1,04534
1,08107
1,12763
1,18547
1,25517
1,33743
1,43309
1,54308
1,66852
1,81066
1,97091
2,15090
2,35241
2,57746
2,82832
3,10747
3,41773
3,76220
6,13229
10,06766
16,5728
27,3082
45,0141
74,2099
thx
0,00000
0,09967
0,19738
0,29131
0,37995
0,46212
0,53705
0,60437
0,66404
0,71630
0,76159
0,80050
0,83365
0,86172
0,88535
0,90515
0,92167
0,93541
0,94681
0,95624
0,96403
0,98661
0,99505
0,99818
0,99933
0,99975
0,99991
Приложение HI
ФУНКЦИЯ ОШИБОК ГАУССА
Функция ошибок Гаусса определяется формулой
Cl 1
Функция ошибок
X
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0.18
0,20
0,22
0,24
0,26
0,28
Р,зо
0,32
Q,?4
0,36
0,38
0,40
0,42
0,44
0,46
0,48
0,50
0,52
0,54
0,56
Q,58
9,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
erf л:
0,00000
0,02256
0,04511
0,06762
0,09008
,11246
0,13476
0,15695
0,17901
0,20094
0,22270
0,24430
0,26570
0,28690
0,30788
0,32863
0,34913
0,36936
0,38933
0,40901
0,42839
0,44749
0,46622
0,48466
0,50275
0,52050
0,53790
0,55494
0,57162
0,58792
0,60386
0,61941
0,63459
0,64938
0,66278
0,67780
0,69143
0.70468
л —
V
X
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
0,94
0,96
0,98
1,00
1,02
1,04
1,06
1,08
1,10
1,12
1,14
1,16
1,18
1,20
1,22
1,24
1,26
1,28
1,30
1,32
1,34
1,36
1,38
1,40
1,42
1,44
1,46
1,48
1,50
'— J
0
erfx
0,71754
0,73001
0,74210
0,75381
0,76514
0,77610
0,78669.
0,79691
0,80677
0,81627
0,82542
0,83423
0,84270
0,85084
0,85865
0,86614
0,87333
0,88020
0,88079
0,89308
0,89910
0,90484
0,91031
0,91553
0,92050
0,92524
0,92973
0,93401
0,93806
0,94191
0,94556
0,94902
0,95228
0,95538
0,95830
0,96105
0,96365
0,96610
Таблица
X
1,52
1,54
1,56
1,58
1,60
1,62
1,64
1,66
1,68
1,70
1,72
1,74
1,76
1,78
1,80
1,82
1,84
1,86
1,88
1,90
1,92
1,94
1,96
1,98
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,20
3,40
3,60
я. ///. /
erf*
0,96841
0,97059
0,97263
0,97455
0,97635
0,97804
0,97962
0,98110
0,98249
0,98379
0,98500
0,98613
0,98719
0,98817
0,98909
0,98994
0,99074
0,99147
0,99216
0,99279
0,99338
0,99392
0,99443
0,99489
0,995322
0,997020
0,998137
0,998857
0,999311
0,999593
0,999764
0,999866
0,999925
0,999959
0,999978
0,999994
0,999998
1,000000
Производная функции ошибок
(eif x
dx
e
-X*
Степенное разложение функции ошибок
V* V 3 ^5-2! 7-3!,
В табл. П. III. 1 представлены значения функции ошибок.
)
Приложение IV
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
ПОЯСНЕНИЯ К ТАБЛИЦАМ
В приведенных ниже таблицах указаны теплофизические
свойства материалов, используемые при решении задач тепло-
теплопередачи. Все свойства выражены в единицах самосогласован-
самосогласованной системы СИ.
Если некоторая величина намного меньше или больше еди-
единицы, ее удобно выразить в виде численного значения, умно-
умноженного на определенную степень десяти. Это позволяет до-
добиться существенной экономии места без потери точности. Од-
Однако при этом возможны недоразумения при использовании зна-
значений, указанных в таблицах. В приведенных ниже таблицах
головка столбца типа
а • 106 м2/с
означает, что численное значение коэффициента температуро-
температуропроводности, указанное в таблице, умножено на 106. Следова-
Следовательно, если в таблице приведена величина 5,06, то действи-
действительное значение коэффициента температуропроводности
а. Ш6 = 5,06,
или а = 5,06- 1(Г6 м2/с.
Если в головке стоит
р-1(Г3кг/м3,
то численное значение плотности, указанное в таблице, умно-
умножено на 10~3. Например, если в таблице приведена величина
, 1,84, то действительное значение р равно
р. 1(Г3 =1,84,
или р = 1,84 • 103 кг/м3.
Читателю всегда следует проверять головки столбцов при ис-
использовании табличных значений, чтобы правильно определить
порядок интересующей его величины.
Таблица П. IV. 1
Теплофизическж
Элемент
Алюминий
Бериллий
Борв)
Ванадий
Висмут в)
Вольфрам в)
Гафний
Германий
Железо
Золото
Индий
Иридий
Кадмий в)
Калий
Кобальт в)
Кремний
Литий
Магний
Марганец.
! свойства металлов а)
[1-31
Коэффициент теплопроводности К ВтДмтрад) б)
200 К
-73 °С
237
301
52,5
31,5
9J
197
24,4
96,8
94
327
89,7
153
99,3
104
122
264
88,1
159
7Д7
273 К
0вС
236
218
31,7
31,3
8,2
182
23,3
66,7
83,5
318
83,7
148
97,5
104
104
168
79,2
157
7,68
400 К
127 °С
240
161
18,7
32,1
162
22,3
43,2
69,4
312
74,5
144
94,7
52
84,8
98,9
72,1
153
600 К
327 °С
232
126
11,3
34,2
139
21,3
27,3
54,7
304
138
64,9
149
800 К
527 °С
220
107
8,1
36,3
128
20,8
19,8
43,3
292
132
42,2
146
1000 К
727 °С
89
6,3
38,6
121
20,7
17,4
32,6
278
126
31,2
1200 К
927 °С
73
5,2
41,2
115
20,9
17,4
28,2
262
120
25,7
Р.
кг/м3
2 702
1850
2 500
6100
9 780
19 300
13 280
5360
7 870
19 300
7 300
22 500
8 650
860
8 862
2 330
534
1740
7290
Свойства при 293
V
Дж/(кгтрад)
896
1750
1047
502
124
134
452
129
134
231
741
389
703
3 391
1017
486
К или 20 °С
k.
Вт/(м«град)
236
205
28,6
31,4
7,9
179
23,1
61,6
81,1
316
82,2
147
97
103
100
153
77,4
156
7J8
а-10е,
М2/С
97,5
63,3
10,9
10,3
6,51
69,2
22,8
126,9
48,8
48,5
161,6
29,0
93,4
42,7
88,2
Темпера-
Температура
плавле-
плавления,
К
933
1550
2 573
2 192
545
3 653
2 495
1211
1810
1336
430
2 716
594
337
1765
1685
454
923
1517
Медь
Молибден
Натрий
Никель
Ниобий
Олово в)
Палладий
Платина
Рений
Родий
Ртуть в)
Рубидий
Свинец
Серебро
Сурьма
Тантал
Титан в)
Уран в)
Хром
Цезий
Цинк
Циркбний
413
143
138
106
52,6
73,3
75,5
72,4
51
154
28,9
58,9
36,6
403
30,2
57,5
24,5
25,1
111
36,8
123
25,2
401
139
135
94
53,3
68,2
75,5
71,5
48,6
151
58,3
35,5
428
25,5
57,4
22,4
27
94,8
36,1
122
23,2
392
134
80,1
55,2
62,2
75,5
71,6
46,1
146
33,8
420
21,2
57,8
20,4
29,6
87,3
116
21,6
383
126
65,5
58,2
75,5
73,0
44,2
136
31,2
405
18,2
58,6
19,4
34
80,5
105
20,7
371
118
67,4
61,3
75,5
75,5
44,1
127
389
16,8
59,4
19,7
38,8
71,3
21,6
357
112
71,8
64,4
75,5
78,6
44,6
121
374
60,2
20,7
43,9
65,3
23,7
342
105
76,1
67,5
82,6
45,7
115
358
61
22
49
62,4
25,7
8933
10 240
971
8 900
8 570
5750
12 020
21450
21 100
12 450
13 546
1530
11340
10 500
6 684
16 600
4 500
19 070
7 160
1873
7 140
6 570
383
#251 {
1206
446
270
227
247
133
137
248
348
129
234
208
138
611
113
440
230
385
272
399
138
133
91
53,6
67,0
75,5
71,4
48,1
150
58,2
35,3
427
24,6
57,5
22,0
27,4
91,4
36
121
22,8
116,6
53,7
113,6
22,9
23,2
51,3
25,4
25,0
16,6
48,6
109,3
24,1
173,8
17,7
25,1
8,0
12,7
29,0
83,6
44,0
12,8
1356
2 883
371
1726
2 741
505
1825
2 042
3 453
2 233
234
312
601
1234
904
3 269
1953
1407
2 118
302
693
2125
а) Чистота всех элементов выше 99%. ч
б) Возможная погрешность коэффициента теплопроводности составляет примерно ±5% при комнатной температуре и около ±10% при
остальных температурах.
в) Свойства кристаллических веществ даны для поликристаллов.
480 Приложение IV
Таблица П. IV. 2
Теплофизические свойства сплавов [1,4]
Металл
Алюминий
дюралюминий
силумин
Железо
пудлинговое
железо
чугун
Медь
алюминиевая
бронза
бронза
константан
латунь
нейзильбер
томпак
Сталь
вольфрамовая
кремнистая
марганцевая
нержавеющая
никелевая
никельхроми-
стая
углеродистая
хромистая
хромоникелевая
Состав, %
94-96 А1, 3—5 Си,
следы Mg
87 Al, 13 Si
0,5 С
-4 С
95 Си, 5 А1
75 Си, 25 Sn
60 Си, 40 Ni
70 Си, 30 Zn
62 Си, 15 Ni,22 Zn
85 Си, 9 Sn, 6 Zn
1 W
5 W
1 Si
5 Si
1 Mn
5 Mn
марка 304
марка 347
10 Ni
20 Ni
40 Ni
60 Ni
80 Ni, 15 Cr
40 Ni, 15 Cr
1 С
1 5 С
1 Cr
5 Cr
10 Cr
15 Cr, 10 Ni
20 Cr, 15 Ni
Свойства при
P.
кг/м3
2787
2659
7849
7272
8666
8666
8922
8522
8618
8714
7913
8073
7769
7417
7865
7849
7817
7817
7945
7993
8169
8378
8522
8073
7801
7753
7865
7833
7785
7865
7833
V
Дж/(кгтрад)
833
871
460
420
410
343
410
385
394
385
448
435
460
460
460
460
461
461
460
460
460
460
460
460
473
486
460
460
460
460
460
293 К, или 20 <
К
Вт/(м»град)
164
164
59
52
83
26
22,7
111
24,9
61
66
54
42
19
50
22
14,4
14,3
26
19
10
19
17,0
11,6
43
36
61
40
31
19
15,1
>С
а* 10*,
м*/с
6,676
7,099
1,626
1,702
2,330
0,859
0,612
3,412
0,733
1,804
1,858
1,525
1,164
0,555
1,388
0,637
0,387
0,387
0,720
0,526
0,279
0,493
0,444
0,305
' 1,172
0,970
1,665
1,110
0,867
0,526
0,415
Теплофизические свойства твердых тел 481
Таблица П. IV. 3
Теплофизические свойства изоляционных и строительных материалов [1, 2, 4]
.Материал
Асбест
Асфальт
Бакелит
Бетон (сухой)
Глина D8,7% влажно-
влажности)
Гранит
Дерево
¦ дуб
сосна, пихта, ель
Дерево листовое
целлотекс
Земля глинистая B8%
влажн.)
диатомовая
песчаная (8% влажн.)
Капок
Картон
Кирпич карборундовый
E0% SiC)
магнезитовый E0%
MgU)
обычный
силикатный (95%
0IU2)
строительный
цирконный
F2% ZrO2)
Кора сосновая
Лед @°С)
Линолеум
Опилки древесные
Песок
влажный
<:ухой
Плексиглас
Полистирол
Пробка (пластина)
Пробка пористая
Резина, буна
губчатая
твердая (эбонит)
Слюда
Стекло оконное
Стекловата
Стекловолокно
Свойства при 293 К, или 20 °С
Р.
кг/м3
383
2120
1270
500
1545
2750
609—801
416—421
200
400
1500
466
1500
25
2200
2000
1800
1900
1700
3600
342
913
535
215
1640
1180
1050
150
L20
1250
224
1150
2900
2800
50
100
200
220
V
Дж/(кгтрад)
816
837
880
2390
2720
879
840
837
1830
1880
2009
800
670
К
ВтДм'Град)
о,пз
0,698
0,233
0,128
1,26
3,0
0,17—0,21
0,15
0,047
0,055
1,51
0,126
1,05
0,035
0,14-0,35
5,82
2,68
0,38-0*52
1,07
0,658
2,44
0,080
2,22
0,081
0,071
1,13
0,582
0,195
0,157
0,042
0,036
0,465
0,055
0,163
0,523
0,81
0,037
0,036
0,040
0,035
а» 10»,
М2/С
0,036
0,049
0,101
0,0111-0,0121
0,0124
0,031
0,028-0,034
0,046
0,124
0,015-0,044
0,0062
0,034
0,028
16 Зак. 487
482 Приложение IV
Продолжение табл. П.1У.З
Материал
Уголь, антрацит
Фанера (клееная)
Цемент (твердый)
Шерсть
Штукатурка
Свойства при 293 К, или 20 °С
Р.
кг/м3
1370
590
200
1800
V
Дж/(кг-град)
1260
Вт/(м-град)
0,238 *
0,109
1,047
0,038
0,814
а-10»,
м*/с
0,013-0,015
Приложение V
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
Обозначения: Т — температура; р — плотность; ($— термический коэффициент объемного
расширения; ср — удельная теплоемкость при постоянном давлении; k — коэффициент
теплопроводности; а — коэффициент температуропроводности; \х — коэффициент динами-
динамической вязкости; v — коэффициент кинематической вязкости; Рг — число Прандтля.
!
Таблица П. V. 1
Вода при давлении насыщения [2]
Т, р, 0x10*, ср, *, охШ6, /iXlO6, pxlO6, Рг ^хЮ"9, §
К °С кг/мЗ 1/град Дж/(кгград) Вт/(м-град) м2/с Н-с/м2 м2/с ^(град-м3}
273 0 999,3 -0,7 4226 0,558 0,131 1794 1J89 13,7
§
293
313
333
353
,373
.473
573
20
40
60
80
100
200
300
998,2
992,2
983,2
971,8
958,4
862,8-
712,5
2,1
3,9
5,3
6,3
7,5
13,5
29,5
4182
4175
4181
4194
4211
4501
5694
0,597
0,633
0,658
0,673
0,682
0,665
0,564
0,143
0,151
0,159
0,165
0,169
0,170
0,132
993
658
472
352
278
139
92,2
1,006
0,658
0,478
0,364
0,294
0.160
0,128
7,0
4,3
3,00
2,25
1,75
0,95
0,98
2,035
8,833
22,75
46,6» .
85,09
517Д
1766
Хладагент фреон-12 (CC12F2) (насыщенная жидкость) [1]
Таблица П. V. 2
aXlO8, /iXlO4,
°С кг/мз 1/град Дж/(кг.град) Вт /(м- град) м2/с
М2/с
Рг
^х10-ю
v2
1/(град-м3)
s
223
233
243
253
263
273
283
293
303
313
323
-50
-40
-30
-20
-10
0
10
20
30
40
50
1547
1519
1490
1461
1429
1397
1364
1330
1295
1257
1216
2,63
875,0
884J
895,6
907,3
920,3
934,5
949,6
965,9
983,5
1001,9
1021,6
Д067
0,069
0,069
0,071
0,073
0,073
0,073
0,073
0,071
0,069
0,067'
5,01
5,14
5,26
5,39
5,50
5,57
5,60
5,60
5,60
5,55
5,45
4,796
4,238.
3,770
3,433
3tl'58
2,990
2,769*
2,633
2,512
2,401
2,310
0,310
0,279
0,253
0,235
0,221
0,214
0,203
0,198
0,194
0,191
0,190
6,2
5,4
4,8
4,4
4,0
3,8
3,6
3,5
3,5
3,5
3,5
26,84
Хладагент аммиак (NH3) (насыщенная жидкость) [1]
Продолжение табл. Я. V, 2
К
223
233
243
253
263
273
283
293
303
313
323
т,
°с
-50
-40
-30
-20
-10
0
10
20
30
40
50
Р,
кг/мз
703,7
691,7
679,3
666,7
653,6
640,1
626,2
611,8
596,4
581,0
564,3
J3X103,
1/град
2,45
ср,
Дж/(кг-град)
4463
. 4467
4476
4509
4564
4635
4714
. 4798
4890
4999
5116
К
Вт /(мк град)
0,547
0,547
0,549
0,547
0,543
0,540
0,531
0,521
0,507
0,493
0,476
«Х10>,
М2/С
17,42
17,75
18,01
18,19
18,25
18,19
18,01
17,75
17,42
17,01
16,54
jiXlO4,
• Н-с/м2
3,061
2,808
2,629
2,540
2,471
2,388
2,304
2,196
2,081
1,975
1,862
УХ106,
М2/С
0,435
0,406
0,387
0,381
0,378
0,373
0,368
0,359
0,349
0,340
0,330
Рг Щ X Ю-0,
1/(град-м3)
2,60
2,28
2,15
2,09
2,07
2,05
2,04
2,02 18,64
2,01
.2,00
1,99
Таблица П. V. 3
Органические соединения при 20
Жидкость
Анилин
Аиетон
Бензол
н-Бутиловый спирт
н-Гептан
Глицерин
Изобутиловый спирт
Метиловый спирт
н-Октан
н-Пентан
Терпентин
Толуол
Уксусная кислота
Хлороформ
Этилацетат
Этиленгликоль
Этиловый спирт
Химиче-
Химическая
формула
C6H7N
С3Н6О
СбНб
с4н10о
c7HlE
СзН8О3
С4Н,0О
СН4О
CeHig
СзН12
CioHi6
с7н8
С2Н4О2
СНС13
С4Н8О2
С2Нб02
С2НбО
°С [2t i
p.
км/м3
1 022
791
879
810
684
1260
804
792
702
626
855
866
1 049
1489
901
1 113
789
Ч
рхю4,
1/К
8,5
14,3
10,6
8,1
12,4
5,0
9,4
11,9
11,4
16,0
9,7
10,8
10,7
12,8
13,8
.11,0
V
Дж/(кг-град)
2 064
2 160
1738
2 366
1 884
2 428
2 303
2 470
2 177
2 177
1800
1675
2 031
967
2010
2 382
2 470
Вт/<м*град)
0,172
0,180
0,154
0,167
0,140
0,285
0,134
0,212
0,147
0,136
0,128
0,151
0,193
0,129
0,137
0,258
0,182
ах Ю-9,
м*/с
81,5
105,4
100,8
87,1
108,6
93,2
72,4
108,4
96,2
99,8
83,2
104,1
90,6
89,6
75,6
97,3
93,4
М- X ю<,
Н-с/м*
44,3
3,31
6,5
29,5
4,09
14 800
39,5
5,84
5,4
2,29
14,87
5,86
5,8
4,49
199
12,0
vxio«,
М2/С
4,34
0,418
0,739
3,64
0,598
1 175
4,91
0,737
0,769
0,366
1,74
0,677
0,390
0,498
17,9
1,52
Рг
53,16
3,97
7,34
41,79
5,50
12 609
67,89
6,80
8,00"
3,67
20,91
6,50
4,35
6,59
183,7
16,29
1/(град-м8)
4,43
802,6
190,3
5,99
340,1
0,0000355
3,82
214,9
189,1
1 171
31,4
231,1
825,3
545,7
46,7
Таблица П. V, 4
Не бывшее в употреблении моторное масло (насыщенная жидкость) [1]
к
273
293
313
333
353
373
393
413
433
т,
°с
0
20
40
60
80
100
12Q
140
160
Р,
кг/м3
899,1
888,2
876,1
864,0
852,0
840,0
829,0
816,9
805,9
р X103,
1/град
0,70
,Дж/(кг-град)
1796
1880
1964
2047
2131
2219
2307
2395
2483
*.
Вт/(м* град)
0,147
0,145
0,144
0,140
0,138
0,137
0,135
0,133
0,132
аХ\0ю,
м2/с
911
872
834
800
769
738
710
686
663
fix 103,
Н-с/м2
3848
799
210
72,5 ,
32,0
17,1
10,3
6,54
4,51
М2/С
4280
900
240
83,9
37,5
20,3
12,4
8,0
5,6
РгХЮ Щ>
1/(град.м3)
471
104 8475
28,7
10,5
4,90
2,76
1,75
1,16
0,84
I
R
Продолжение табл. П. VA
Трансформаторное масло (стандарт 982-68) [5]
К
223
233х
243
253
263
273
283
293
303
313
°С
-50
-40
-30
-20
-10
0
10
20
30
40
.Р,
кг/м3
922
916
910
904
898
891
885
879
873
867
0Х1О3,
1/град
ср>
Дж/(кг-град)
1700
1680
1650
1620
1600
1620
1650
1710
1780
1830
К
Вт/(м-град)
0,116
0,116
.0,115
0,114
0,113
0,112
0,111
0,111
0,110
0,109
аХ\0ю,
М2/С
742
750
764
778
788
778
763
736
70Г
688
/iX Ю3;
Н-с/м2
29320
3 866
1 183
365,6
108,1
55,24
33,45
21,10
13,44
9,364
.Х106,
м2/с
31800
4220
1300
404
120
67,5
37,8
24,0
15,4
10,8
PrXlO-2 if,
1/(град-м3)
4286
563
170
52
15,3
8,67
4,95
3,26
2,18
1,57
Приложение VI
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Сухой воздух при атмосферном давлении [2J
Таблица П. VI. 1
•к
273
293
313
' 333
353
373
473
573
673
773
1273
т,
°С
0
20
40
60
80
100
2(КУ
300
4<Ю
500
1000
Р>
йг/м3
1.252
1,164
1,092
1,025
0,968
0,916
0,723
0,596
0,508
0,442
0,268
Двуокись углерода
К
220
250
t 300
, 350
400
450
500
550
600
т,
°С
-53
-23
27
77
127
!77
227
277
327
Pt
кг/м3
2,4733
2,1657
1,7973
1,5362
1,3424
1,1918
1,0732
0,9739
0»8938
0Х1О3,
1/град
3,66
3,41
3,19
3,00
2,83
2,68
2,11
1,75
1,49
1,29
0,79
ср>
Дж/(кг град)
1011
1012
1014
1017
1019
1022
1035
1047
1059
1076
1139
*,
Вт/(м-град)
0,0237
0,0251
0,0265
0,0279
0,0293
0,0307
0,0370
0,0429
0,0485
0,0540
0,0762
при атмосферном давлении [1, 4]
?ХШ3,
1/град
3,33
2,86
2,50
2,22
2,00
1,82
1,67
Дж/&гград)
783
804
871
900
942
980
1013
1047
1076
к,
Вт/(м-град)
0,010805
0,012884
0,016572
0,02047
0,02461
0,02897
0,03352
0,03821
0,04311
аХЮ6,
М2/С
19,2
22,0
24,8
27,6
30,6
33,6
49,7
68,9
89,4
113,2
240
«Х104,
К/.2/С
0,05920
0,07401
0,10588
0,14808
0,19463
0,24813
0,3084
0,3750
0,4483
МХ106,
Н-с/м2
17,456
18,240
19,123
19,907
20,790
21,673
25,693
39,322
32,754
35,794
48,445
цх 10*
Н-с/м2
11,105
12,590
14,958
17,205
19,32
21,34
23,26
25,08
26,83
?Х106,
М2/С
13,9
15,7
17,6
19,4
21,5
23,6
35,5
49,2
64,6
81,0
181
ГХ106,
М2/С
4,490
5,813
8,321
11,19
14,39
17,90
21,67
25,74
30,02
Рг
0,71
0,71
0,71
0,71
0,71
0,71
0,71
0,71
0,72
0,72
0,74
1/'(град-м3)*
1,85
1,36
1,01
0,782
0,600
0,472
0,164
0,0709
0,0350
0,0193
0,00236
Таблица П. VI. 2
Рг
0,818
0,793
0,770
0,755
0,738
0,721
0,702
0,685
0,668
Щ Х10-6,
V
1/(град.м3)-
472
224
118
67,9
41,8
26,9
18,2
Таблица /7. VL 3
Окись углерода при атмосферном давлении [1, 4]
К
220
250
300
350
400
450
500
550
600
Гелий
К
3
33
144
200
255
366
477
589
700
800
900
т,
°С
-53
-23
27
77
127
177
227
277
327
Р,
кг/мз
1,554
0,841
1,139
0,974
0,854
0,758
0,682
0,620
0,569
0Х1О3,
1/град
3,33
2,86
2,50
2,22
2,00
1,82
1,67
ср>
Дж/(кг-град)
1043
1043
1042
1043
1048
1055
1064
1076
1088
при атмосферном давлении [1, 4]
т,
°С
-270
-240
-129
-73
-18
93
204
316
427
527
627
Р.
кг/м3
1,466
3,380
0,2435
0,1906
0,1328
0,1020
0,08282
0,07032
0,06023
0,05286
0X10*,
1/град
6,94
5,00
3,92
2,73
2,10
1,70
1,43
1,25
1.Н
ср>
Дж/(кг-град)
5200
5200
5200
5200
5200
5200
5200
5200
5200
5200
5200
к
ВтДм-град)
0,01906
0,02144
0,02525
0,02883
0,03226
0,04360
0,03863
0,04162
0,04446
к,
Вт/(м« град)
0,0106
0,0353
0,0928
0,1177
0,1357
0,1691
0,197
0,225
0,251
0,275
0,298
аХ10*
М2/С
0,1176
0,1506
0,2128
0,2836
0,3605
0,4439
0,5324
0,6240
0,7190
«Х104,
М2/С
0,04625
0,5275
0,9288
1,3675
2,449
3,716
5,215
6,661
8,774
10,834
11X10»,
Н-с/м2
13,88
15,40
17,84
20,09
22,19
24,18
26,06
27,89
29,60
/1X10*,
Н-с/м2
0,842
5,02
12,55
15,66
18,17
23,05
27,50
31,13
34,75
38,17
41,36
»Х10б,
м2/с
8,90
11,28
15,67
20,62
25,99
31,88
38,19
44,97
52,06
,XlO«
М2/С
3,42
37,11
64,38
95,50
173,6
269,3
375,8
494,2
634,1
781,3
Рг
0,758
0,750
0,737
0,728
0,722
0,718
0,718
0,721
0,724
1/(град.м3)
133
65,9
36,3
21,4
13,4
8,83
6,04
Таблица П. VI. 4
Рг
0,74
0,70
0,694
0,70
0,71
0,72
0,72
0,72
0,72
0,72
1/(град-м3)
49,4
11,8
4,22.
0,88а
0,284
0,118
0,0574
0,0305
0,0178
¦51
Водород при атмосферном давлении [1, 4]
Таблица /7. VI. 5
р.
кг/м3
aXlO4,
1/град Дж/(кгград) Вт/(м-град)
Н-с/м2
FX106,
М2/С
Рг
ifxHT6,
1/(град-м3)
50
100
150
200
250
300
350,
400
450
500
600
700
800
1000
1200
-223
-173
-123
-73
-23
27
77
127
177
227
327
427
527
727
927
0,50955
0,24572
0,16371
0,12270
0,09819
0,08185
0,07016
0,06135
0,05462
0,04918
0,04085
0,03492
0,03060
0,02451
0,02050
10,0
6,67
5,00
4,00
3,33
2,86
2,50
2,22
2,0t)
1,67
1,43
1,25
1,00
0,833
10501
11 229
12602
13 540
14059
14314
14436
14491
14499
14507
14537
14574
14675
14 968
15 366
0,0362
0,0665
0,0981
0,1282
0,1561
0,182
0,206
0,228
0,251
0,272
0,315
0,351
0,384
0,440
0,488
0,0676
0,2408
0,475
0,772
1,130
1,554
2,031
2,568
3,164
3,817
5,306 '
6,903
8,563
11,997
15,484
2,516
4,212
5,595
6,813
7,919
8,963
9,954
10,864
11,779
12,636
14,285
15,89
17,40
20,16
22,75
4,880
17,14
34,18
55,53
80,64
109,5
141,9
177Д
215,6
257,0
349,7
455,1
569
822
1107
0,721
0,712
0,718
0,719
0,713
0,706
0,697
0,690
0,682
0,675
0,664
0,659
0,664
0,686
0,715
333,8
55,99
15,90
6,03
2,72
1,39
0,782
0,468
0,297
0,134
0,0677
0,0379
0,0145
0,00667
Азот
К
при атмосферном
Т, р.
°С кг/мз
давлении
/JX1O3,
1/фад
[1, 4]
Дж/(кг-град)
Вт/(м-
град)
М2/С
Н-
с/м2
М2/С
Таблица Я. VI. 6
Рг МхнГ6,
1/(град-м3)
100
200
300
400
500
600
700
800
900
1000
1100
1200
-173
-73
27
127
227
327
427
527
627
727
827
927
3,4808
1,7108
1,1421
0,8538
0,6824
0,5687
0,4934
0,4277
0,3796
0,3412
0,3108
0,2851
5,00
3,33
2,50
2,00
1,67
1,43
1,25
1,11
1,00
0,909
0,833
1072
1043
1041
1046
1056
1076
1097
1123
1146
1168
1186
1204
0,00945
0,01824
0,02620
0,03335
0,03984
0,04580
0,05123
0,05609
0,06070
0,06475
0,06850
0,07184
0,0253
0,1022
0,2204
0,3734
0,5530
0,7486
0,9466
1,1685
1,3946
1,6250
1,8591
2,0932
6,86
12,95
17,84
21,98
25,70
29,11
32,13
34,84
37,49
40,00
42,28
44,50
1,97
7,57
15,63
25,74
37,66
51,19
65,13
81,46
91,06
117,2
136,0
156,1
0,786
0,747
0,713
0,691
0,684
0,686
0,691
0,700
0,711
0,724
0,736
0,748
855,6
133,7
37,00
13,83
6,25
3,31
1,85
1,31
0,714
0,482
0,335
Кислород при атмосферном давлении [1, 4]
Таблица Я. VI. 7
к
100
150
200
250
300
350
400
450
500
.550
600
т,
°С
-173
.-123
-73
-23
27
77
127
177
227
277
3?7
Р,
кг/м3
3,992?
2,619
1,956
1,562
1,301
1,113
0,9755
0,8682
0,7801
0,7096
0,6504
fixtf,
1/град
6,67.
5,00
4,00
3,33
2,86
2,50
2,22
2,00
1,82
1,67
ср,
Д ж/(кг-град)
948
918
913
916
920
929
942
957
972
988
1004
к,
Вт/(м-град)
0,00903
0,01367
0,01824
0,02259
0,02676
О;03О7О
0,03461
0,03828
0,04173
0,04517
0,04832
а X104,
М2/С
0,0239
0,0569
0,1021
0,1579
0,2235 k
0^68
0,3768
0,4609
$5502
0,6441
0,7399
jiXlO6,
Н-с/м2
7,768
11,49
14,85
17,87
20,63
23,16
25,54
27,77
2921
31,97
33,92
ГХ10»
М2/С
1,946
4,387
7,593
11,45
15,86
20,80
26,18
31J99
3834
45-05
52,15
Рг
0,815
0,773
0,745
0,725
0,709
0,702
0i695
0,694
0,697
0,700
0,704
1/(град-м3)
3398
850,5
299,2
129,8
64,8
35,8
21,3
13,3
8,79
6,02
Водяной пар при атмосферном давлении [1, 4]
Таблица П. VI. 8
К
380
400
450
'500
550
600
650
700
750
800
850
т,
°0
107
, 127
177
227
277
327
377
427
477
527
577
Р,
кг/м3"
0,5863
0,5542
0,4902
0,4405
0,4005
0,3652
0.3380
0,3140
0,2931
0,2739
0,2579
/?ХШ>
1/град
2,50
2,22
2,00
1,82
1,67
1,54
1,43
1,33
1,25
1,18
с,,
Дж/(кг-град)
2060
2014
1980
1985
1997
2026
2056
2085
2119
2152
2186
к,
Вт Дм-град)
0,0246
0,0261
0,0299
0,0339
0,0379
0,0422
0,0464
0,0505
0,0549
0,0592
0,0637
«Х104,
М2/С
0,204
0,234
0,307
0,387
0,475
0,573
0,666
0,772
0,883
1,001
1,130
JAX106,
Н-С/М2
12,71
13,44
15,25
17,04
18,84
20,67
22,47
24,26
26,04
27,86
29,69
FXW,
М2/С
21,6
24,2
31,1
38,6
47,0
56,6
66,4
77,2
88,8
102,0
115,2
Рг
1,060
1,040
1,010
0,996
0,991
0,986
0,995
1,000
1,005
1,010
1,019
1/(град-м3)
41,86
22,51
13,16
8,08
5,11
3,43
2,35
1,65
0^872
Приложение VII
ТЕПЛОФИЗИЧЕСКИЕ
Висмут [4]
СВОЙСТВА ЖИДКИХ МЕТАЛЛОВ
Таблица П. VII. I
Т, р, jSxlO3, cp7 kt
К °С кг/мЗ 1/град ДжДкгград) Вт/(мград)
М2/С
1/(градмЗ)
589
700
811
922
1033
316
427
538
649
760
10011
9 867
9 739
9611
9 467
0,117
0,122
0,126
144,5
149,5
154,5
159,5
164,5
16,44
15,58
15,58
15,58
15,58
1,14
1,06
1,03
1,01
1,01
16,22
13,39
11,01
9,23
7,89
1,57
1,35
1,08
0,903
0,813
.0,014
0,013
0,011
0,009
0,008
46,5
65,6
106
Ртуть
7
К
(насыщенная
Р»
°С кг/м3
жидкость)
fix\(f,
1/град
[1]
Дж/(кгград)
К
Вт/(м-фад)
аХЮ7,
МХ104,
УХ106,
М2/С
Таблица Я. У//. 2
Рг ^Х1О~10,
1/(град-м3)
273
293
323
373
423
473
523
588,7
0
20
50
100
150
200
250
315,5
13 628
13 579
13 506
13 385
13 264:
13 145
13 026
12 847
1,82
140,3
139,4
138,6
137,3
136,5
157,0
135,7
134,0
8,20
8,69
9,40
10,51
11,49
12,34
13,07
14,02
42,99
46,06
50,22
57,16
63.54
69,08
74,06
81,50
16,90
15,48
14,05
12,42
11,31
10,54
9,96
8,65
0,124
0,114
0,104
0,0928
0,0853
0,0802
0,0765
0,0673
0,0288
0,0249
0,0207
0,0162
0,0134
0,0116
0,0103
0,0083
13,73
Натрий
т,
К
[4]
°С
Р>
кг/м3
ДХ103,
1/град
ср>
Дж/(кг-град)
^,
Вт/(м-град)
«Х105,
М2/С
/1X10*,
Н-С/М2
уХЮ7,
М2/С-
Таблица П. VII. 3
Рг Щ X КГ9,
1/(град-м3)
367
478
644
811
978
94
205
371
538
705
929
902
860
820
778
0,27
0,36
1382
1340
1298
1256
1256
86,2
80,3
72,4
65,4
59,7
6,71
6,71
6,45
6,19
6,19
6,99
4,32
2,83
2,08
1,79
7,31
4,60
3,16
2,44
,26
0,0110
0,0072
0,0051
0,0040
0,0038
4,96
16,7
Приложение VIII
ИЗЛУЧАТЕЛЬНАЯ СПОСОБНОСТЬ РАЗЛИЧНЫХ
ВЕЩЕСТВ В НАПРАВЛЕНИИ НОРМАЛИ
Таблица Я. VIII. I
Излучательная способность металлов [2]
Металл
Алюминий
Вольфрам
Железо
Золото
Латунь
Медь
Молибден
Никель
Олово
Платина
Свинец
Серебро
Сталь
Хром
Цинк
Состояние поверхности
Полированная пласти-
пластина
Полированный лист
Шероховатая пластина
Нить
Блестящее
Окисленное гладкое
Полированное
Неполированное
Полированное
Окисленная
Полированная
Тусклая
Окисленная
Слегка тусклая
Полированная
Нить
Окисленный
Полированный
Блестящее
Полированная
Серый окисленный .
Полированный
Полированное
Окисленная шерохова-
шероховатая
Листовая
Полированный
Тусклый
Полированный
Температура,
К
296
498
443
298
3300
293
398
698
293
293
611
292
573
329
293
293
293
998
373
373
293
498
898
293
403
293
313
1213
423
293
503
Степень
черноты ejjj*
0,040
0,039
0,039
0,070
0,39
0,24
0,78
0,144
0,47
0,025
0,22
0,05
0,032
0,202
0,780
0,037
0,030
0,096
0,41
0,045
0,070
0,054
0,104
0,28
0,056
0,025
0,94
0,520
0,058
0,25
0,045
а) Полусферическую излучательную способность 8 можно приближенно выразить
формулами: 8=1,28^—для блестящих металлических поверхностей; е л""
гих гладких поверхностей; е=0,98ел—для шероховатых поверхностей.
И злу нательная способность различных веществ 493
Таблица П. VIII. 2
Степень черноты неметаллов [2]
Материал
Асбестовый картон
Бумага
Дерево
бук
дуб
Кварц
Кирпич
Кирпичная кладка
Лед
Резина
мягкая
твердая
Стекло
Угольная нить
Фарфор
Штукатурка, известь
Состояние поверхности
Строганый
Строганый
Плавленый шерохова-
шероховатый
Красный шероховатый
Оштукатуренная
Гладкий
Шероховатый
Серая
Черная шероховатая
Гладкое
Глазурованный
Белая шероховатая
Температура,
К
297
293
343
294
293
293
273
273
273
297
297
293
1313
293
293
Степень
черноты,
0,96
0,80
0,935
0,885
0,93
0,93
0,93
0,966
0,985
0,86
0,95
0,93
0,53
0,93
0,93
Таблица П. VIIL 3
Степень черноты красок
Материал
Алюминиевая бронза
Алюминиевая краска
Алюминиевая эмаль
Бакелитовая эмаль
Масляная краска
Свинцовая грунтовка
Шеллак черный
Эмаль
белая
черная
и покрытий [2]
Состояние поверхности
Нагретая до 325 °С
Шероховатая ;
Блестящий
Матовый
Шероховатая
Блестящая
Температура,
К
373
423-588
293
353
273—473
293-373
294
348-418
293
298
Степень
черноты
*п
0,20—0,40
0,35
0,39
0,935
0,885
0,93
0,82
0,91
0,90
0,876
Приложение IX
КОЭФФИЦИЕНТЫ ДИФФУЗИИ
Таблица П.1Х.1
Коэффициенты бинарной диффузии смеси газов при атмосферном
давлении [6, 7]
Бинарная смесь газов
Водород — азот
Воздух — аммиак
Воздух — анилин
Воздух — бензол
Воздух — вода
Воздух — водород
Воздух — йод
Воздух — кислород
Воздух — нафталин
Воздух —ргуть
Воздух — углекислый газ
Воздух — сероуглерод
Воздух — толуол
Воздух — углекислый газ
Воздух — хлор
Воздух — этиловый спирт
Кислород — азот \
Кислород — аммиак
Кислород — бензол
Кислород — водород
Углекислый газ — азот
Углекислый газ — бензол
Углекислый газ — вода
Углекислый газ — водород
Углекислый газ — сернистый ангид-
ангидрид
Углекислый газ — этиловый спирт
Температура
К
236
273
298
298
298
273
298
273
298
614
273
273
298
273
273
-298
285
293
296
285
298
318
298
273
318
273
°с
13
0
25
25
25
0
25
0
25
341
0
0
25
0
0
25
12
20
23
12
25
45
25
0
45
0
mVc
7,376
1,98
0,726
0,962
2,60
5,472
0,834
1,75
0,611
4,73
1,22
0,883
0,844
1,36
1,24
1,32
2,025
2,53
0,39
7,748
1,58
0,715
1,64
5,50
0,715
0,693
Коэффициенты, диффузии 495
Таблица П. IX. 2
Коэффициенты бинарной диффузии растворов
А — растворенное вещество, В — растворитель [6]
Бинарный раствор
Водные растворы
азота
брома
водорода
глюкозы
йода
кислорода
метанола
углекислого газа
хлора
Растворы в бензоле
брома
йода
уксусной кислоты
хлороформа
четыреххлористого углерода
Растворы в метаноле
анилина
йодоформа
молочной кислоты
хлороформа
четыреххлористого углерода
Температура,
К
295
285
298
288
298
298
288
291
285
285
293
288
288
298
288
288
288
288
288
°С
22
12
25
15
25
25
15
18
12
12
20
15
15
25
15
15
15
15
15
DAB.l0>.
м2/с
2,02
0,90
3,36
0,52
1,25
2,60
1,28
1,71
1,40
2,00
1,95
1,92
2,11
2,00
1,49
1,33
1,36
2,07
1,70
Таблица П. IX. 3
Коэффициенты бинарной диффузии твердых тел [8]
Диффундирующее
вещество
Алюминий
Висмут
Водород
»
Гелий
>
Кадмий
Ртуть
Сурьма
Среда
Медь
Свинец
Двуокись кремния
Никель
Двуокись кремния
Пирекс
Медь
Свинец
Серебро
Температура,
К
293
293
773
358
438
293
293
773
293
293
293
°С
20
20
500
85
165
20
20
500
20
20
20
DAB.\Q".
м2/с
1,зо.ю-^
uo.io-'0
0,573-2,1 • 1<Г*
1,16-10
0,105
2,40-5,50 • 10"*
4,49- Ю-5
2,00- 10~f
2,71 • 10~*
3,51 • 105
Приложение X
БЕЗРАЗМЕРНЫЕ КРИТЕРИИ
Таблица /7. Я.
Безразмерные критерии, используемые в теплопередаче
Критерий
Био
Грасгофа
Гретца
Льюиса — Се-
Семенова
Нуссельта
Пекле
Прандтля
Рейнольдса
Релея
Обозна-
Обозначение
Bi
Gr
Gz
Le
Nu
Pe
Pr
Re
Ra
Формула а)
Bi = hfL
RS
ft A7V 3
s>r §P ^-* "
V2
Gz = RePrf—)-=
\ L» J
pV d*cp
AB
Nu - hr
k
Pe = Re Pr =
pVLcn
p
R
pr _ №P _ V
k a
^e= qVL = —
u v
Ra = Gr Pr =
gp AiTcpp2L3
*№
Физический смысл
Отношение термического со-
сопротивления твердого тела
к термическому сопротивле-
сопротивлению жидкости
Отнпшрнир полъбмной силы к
силе вязкости
Используется в задачах вы-
вынужденной конвекции
Отношение коэффициента
диффузии к коэффициенту
температуропроводности; ис-
используется в задачах мае-
сообмена
Основной безразмерный коэф-
коэффициент конвективной теп-
теплоотдачи
Отношение конвективного теп-
теплового потока к кондуктив-
ному тепловому потоку;
применяется в задачах вы-
вынужденной конвекции
Отношение потока количества
движения к потоку тепла
Отношение силы инерции к
силе вязкости
Применяется в задачах сво-
свободной конвекции
Безразмерные критерии 497
Продолжение табл. П.ХЛ
Критерий
Стантона
Фурье
Шервуда
Шмидта
Обозна-
Обозначение
St
Fo
Sh
Sc
St
Sc
Формула а)
= Nu = hc
Re Pr qVcp
Fo = —
h J
Sh = nJ"L
DAB
Ц V
~ <>DAB DAB
Физический смысл
Отношение количества тепла
на стенке к количеству теп-
тепла, переносимому жидко-
жидкостью
Отношение скорости кондук-
тивного переноса тепла к
скорости аккумулирования
тепла в материале; приме-
применяется в задачах нестацио-
нестационарной теплопроводности
Отношение коэффициента кон-
конвективного массообмена к
коэффициенту диффузии
Отношение потока количества
движения к диффузионному
потоку
а) Обозначения:
с —удельная теплоемкость при постоянном давлении;
&АВ—коэффициент диффузии,
d—диаметр;
g—ускорение свободного падения;
Л-—коэффициент конвективной теплоотдачи;
/z —коэффициент конвективного массообмена;
Л—коэффициент теплопроводности жидкости;
&з—коэффициент теплопроводности твердого тела;
L—характерная длина;
*—время;
V—скорость;
а—коэффициент температуропроводности;
Р—термический коэффициент объемного расширения;
ДГ—разность температур;
р,—коэффициент динамической, или абсолютной, вязкости;
V—коэффициент кинематической вязкости;
р—плотность.
Литература
1. Eckert E. R. G., Drake R. M., Analysis of Heat and Mass Transfer,
McGraw, N. Y., 1972. [Имеется^ перевод первого издания: Эккерт Э. Р.,
Дрейк Р. М., Теория тепло- и массообмена, — М.: Госэнергоиздат, 1961.]
2. Raznjevi5 К., Handbook of Thermodynamic Tables and Charts, 3rd ed.,
McGraw, N. Y., 1976.
3. Touloukian Y. S., ed., Thermophysical Properties of Matter, IFI/Plenum,
N. Y., 1970.
4. Kreith R, Principles of Heat Transfer, 3rd ed., Crowell, N. Y., 1973.
5. Vargaftik N. В., Tables oi the Thermophysical Properties of Liquids and
Gases, 2nd ed., Hemisphere, Washington, D. C, 1975.
6 Reid R. D., Sherwood Т. К., The Properties of Gases and Liquids,
McGraw, N. Y., 1966.
7. Handbook of Chemistry and Physics, 39th ed., CRC Press, Cleveland,
Ohio, 1957—1958.
8. Barrer R. M., Diffusion in and Through Solidsf Macmillan, N, Y.? 1941,
Приложение XI
ПОДПРОГРАММА ОБРАЩЕНИЯ МАТРИЦЫ
Ниже приведен текст подпрограммы MATINV обращения
матрицы АА формата Ny^N. Входной информацией MATINV
являются NX.N элементов матрицы АА и число N строк (или
столбцов) квадратной матрицы. Выходной информацией
MATINV являются N2 значений элементов обращенной матрицы
AINV.
Представленная здесь подпрограмма ограничена форматом
матрицы 50X50, хотя пользователь может увеличить предель-
предельный размер программы, чтобы она могла обращать матрицу
большего формата, просто увеличив объем информации в опе-
операции DIMENSION. MATINV предусмотрен вызов специальной
подпрограммы ЕХСН, которая производит обмен строк и столб-
столбцов матрицы АА и обеспечивает перевод наибольшего элемента
в положение АА(К, К). Подпрограммы MATLNV и ЕХСН имеют
следующие тексты [ 1 ]:
SUBROUTINE MATINV (AA.N.AINV)
DIMENSION AAE0M0),AINVE0,50)lAE0I OO),IDEO)
NN«N+1
N2-2*N
D0100I=*1,N
ID(I)-I
DO100J-1,N
100 A(I,J)-AA(I,J)
DO200I-1.N
DO 200 J-NN,N2
200 Atf,J) = 0.
DO300I-1.N
300 A(I,N + I)-1
K-1
1 CALL EXCH (A.N.N.N^KJD)
2 IF (A(K,K)) 3,999,3
3 KK-K+1
Подпрограмма обращения матрицы 499
41
42
4
5
8
101
10
999
1000
21
2
31
32
3
41
42
4
Литература
DO 4 J-KK.N2
DO4I-1,n'
IF (К-I) 41,4,41
W-A(L,K)*A(K,J)
IF (ABS(A(i,J))-0.0001 *AB$(W)) 42,4,4
A(l,J)-0.0
CONTINUE
K-KK
IF (K-N) 1,2,5
DO10I-1.N
DO.10J-1,N
IF (ID(J)-1) 10,8,10
DO 101 K-1.N
AINVO.KJ-A^N + K)
CONTINUE
RETURN
PRINT 1000
RETURN11
FORMAT A9H MATRIX IS SINGULAR)
END
SUBROUTINE EXCH (A.N.NA.NB.K.ID)
DIMENSION AE0t100),IDE0)
NROW-K
NCOL-K
B-ABS(A(K,K))
DO 2 1=K,N
DO 2 J-K.NA
IF (ABS(A(I,J))-B) 2,2,21
NROW.-I ,
NCOL-J
B-ABS(A(I,J))
CONTINUE
IF (NROW-K) 3,3,31
DO32J-K.NB
C=A(NROW.J)
A(NROW,J)-A(K,J)
A(K,J)-C
CONTINUE
IF (NCOL-K) 4.4,41
DO 42 1-1,N
C-A(I.NCOL)
A(I,NCOL)-A(I,K)
A(I,K)-C
I-ID(NCOL)
ID(NCOL)-ID(K)
CONTINUE
RETURN
END . v
1. Pennington R. R, Introductory Computer Methods and Numerical Analy-
Analysis, 2nd ed., Macmillan, London, 1970.
ОТВЕТЫ НА НЕЧЕТНЫЕ НОМЕРА ЗАДАЧ
Глава 1
1.1. 105 Вт/м2.
1.3. 91,07°С.
1.5. 22.3ГС, 26,15аС.
1.7. Стекловолокно 2,86; штукатурка 0,123; фанера 0,917; обыч-
обычный кирпич 0,358. Все значения в м2-град/Вт.
1.9. а) 31,3 Вт; б) 18,7 Вт; в) 1,13 Вт; г) 8,88-10-» Вт;
д) 1,96-Ю-2 Вт; е) 2,75-КН Вт.
1.11. 1066 Вт.
1.13. 31089 Вт/м2.
1.15. 29740 Вт; 397,4°С.
1.17. 7,109 Вт/(мтрад).
1.19. 48000 Вт; 680000 Вт.
1.21. 51000 Вт.
1.23. 500 см2.
1.25. 187,5 Вт/(м2-град); 5625 Вт/м2.
1.27. б) 23662 Вт/м2; в) 236,6°С; г) 57931 Вт/м2.
1 29 60 83°С* 15°С
1.31* а)'45,92 Вт; б) 2322 Вт; в) 16191 Вт.
1.33. 17,01 Вт.
1.35. 37,18 Вт/(м2-град).
1.37. 0,3397 Вт/(м2-град).
1.41. ni == hL/k, я2 = pVL/pL, я3 = цСр/k.
Глава 2
2.1. —43,33 Вт/м2; 0,231 м2трад/Вт; 30°С
2.3. — 197,2°С.
2.5. 8,1 кВт; 4050 Вт/м2.
2.7. 50,27 Вт; —100°С.
2.9. 115,6 Вт/м; 0,735 м • град/Вт.
2.11. 7,96-Ю-3 град/Вт; 6283 Вт.
2.13. 2,71 см; 522,8°С; 1058°С.
2.15. 1319 Вт; 201,5 Вт; 84,7%.
2.17. 0,804 Вт/(м-град); 420°С; 121,3°С.
2.19. 1520 кВт-ч; 122 р.
2.21. 56,48 кВт.
Ответы на нечетные номера задач 501
2.25. (Т-
2.27. При возрастании температуры k увеличивается.
2.31. а) Т = Г, + .*.(ra_r1)
Л\ г \Ък IT 7MJ- L$T/3.
в) 9"' = -^--?¦ (Г,-Г,).
2.35. 50°С.
2.37. 693 Вт/м.
2.39. 0,9526 Вт; 173,8°С; 1,006 Вт; 173,6°С.
241 0- ch[BiA~EI - 1—Z-. Ы—
РпВА
kA ' P~nD' A~
q = 2 Bi1/2 ^- (Tb - TJ th Bi1/2.
2.43. 130,9 Вт; 27 ребер.
2.47. —2,5 • 10-2 i Bt/m2; —(lOi + 7,5j) 10 Вт/м2; —3/103 i Вт/м2.
2.49. 118,1 Вт/м; 2,27; 6,77 м.
2.51. 574 Вт/м.
2.53. 403 Вт/м.
2.55. 17 Вт/м; 17,6 км.
2.57. 364 Вт.
2.59. Тл = 250°С; Т2 = 300°С; Т3 = 350°С; Г4 = 400°С.
2.61. 4(Г4 +
i (Г, + Т9) + Bi Гте - A + Bi) Т2 = /?2;
T7 + T6 + T5 + T4-4T3 = R3.
2.63. д: = 3; у = 8; z = 7; ы = 0,6; w = 3.
2.65. а) Г,=287,5°С, 712 = 312,5°С, Г3 = 237,5°С, Г4 = 262,5°С;
б)Г,=290°С, Г2 = 315ОС, Г3 = 240°С, Г4 = 265°С.
2.67. 7*! = 160°С, Г2 = 140,7оС, Г3=140,5оС, Г4 = 162,4ОС,
Г5=142°С, 7'6=137ОС, 717 = 147,6°С, Г8=128,2°С,
7'9=123,4°С.
2.69. 7", = 170°С, Т2 = 178°С, Т3 = 180°С, Г4 = 178°С,
Т5 = 172°С, Т6 = 158°С, Т7 = 162°С, Г8 = 164°С,
Гв = 160°С, Г,о = 150°С, Г,, = 140°С, Т12 =- 150°С,
Г13=152ОС, Г14=152°С, Г15 = 150°С.
2.71. Г, =171,53°С, Г2 =178,28°С, Т3 = 180,24°С,
Г4 = 178,75°С, Г5=171)80°С, Т6 = 158,43°С,
502 Ответы на нечетные номера задач
Т7 = 162,99°С, Ts = 163,94°С, Т9 = 161,39°С,
7110 = 154,53°С, 7111 = 143,05°С, Г1а = 148,80°С,
7-13 = 151,16°С, Г14=150,84°С, Г^ = 148,96°С.
2.73. 7", =207,64°С, Т2 =225,56°С, Т3 =227,09°С,
Г4 = 237,12°С, Г5 =241,54°С, Г6 =243,13°С,
Т7 = 153,07°С, 7*8 = 167,51°С, Г9 = 162,28°С,
Г10 = 148,84°С, Гц = 171,67°С, Т12 = 185,92°С,
Г1з=189,46°С, Г14 = 119,18°С, 7115 = 129,17°С,
Г16 = 129,99°С, Ти = 128,53°С, Г18 = 135,31°С,
Г19 = 141,03°С, Г2о = 142,88°С.
Глава 3
3.1. 20,43 мин; 4,08 мин; 2,04 мин.
3.3. 9,12 с; 73,1 Вт.
3.7. 7,62-Ю-3 с.
3.9. 1 ч 35 мин.
3.11. 79°С, 65°С.
3.13. 40,8 мин; 26°С.
3.15. 41,7 мин; 166,6 мин.
3.17. 1,06 ч.
3.19. 5,88 ч.
3.21. 33,3 мин.
3.23. 84°С.
3.25. 5 мин; 13,3 мин.
3.35. 15,15 мин.
3.37. При / = 64 с Г1 = 130,0°С, 7'2 = 80,0оС, 7\, = 55,0°С;
при /=116 с Г, = 140,6°С, Г2=101,3°С, 7\, = 75,0°С;
при / = 181 с 7'1 = 146,5ОС, 7=117,2°С, Г3 = 87,8°С.
Глава 4
4.1. а) 1,705-104; б) 3,31-Ю4; в) 4,56-105; г) 1,25-103.
4.3. 15 м/с.
4.5. а) 0,02 м, 0,05 м; б) 0,0023 м, 0,0057 м.
4.7. 488,6.
4.9. 2,01-106.
4.11. 1,19-Ю-2 Н/м2; 2,15-Ю-2 Н.
/ цс„ у/з (V L V/5 k
4.13. h = 0,036 (^J (-^-J T.
4 15 т~т» =3 У ' («Л
4.17. a) *~Jf =-f; б) ¦|- = Pr1'3;
г) N"u = 0,29Re1/2Pr1/3.
Ответы на нечетные номера задач 503
4.19. а) 3,706-Ю-3; б) 2,55-Ю-2 Н; в) 5,63 Вт/(м2трад);
г) 1082 Вт.
4.21. а) 9,16-Ю-4; б) 22,11 Вт/(м2трад).
4.23. 37,3°С.
4.27. -J-J-.
4.29. 722°°Вт.
4.31. 15,5°С.
4.33. 100°С.
4.35. 101,7 Вт/(м2трад); —95,8 Вт/м.
4.37. а) 448,6 Вт/(м2-град); б) 538,8 Вт/(м2трад);
в) 296,1 Вт/(м2-град).
4.39. а) —28,763 кВт; б) 101,183 кН/м2.
4.41. 34,23°С; 366 Вт.
4.43. 2567 Вт/м.
Глава 5
5... »_(»¦
О.и« 21\ = 5^J . Ji2 = •
рУ [л
5.5. 6,62 м.
5.7. 3912 Вт/(м2трад); 32,9°С.
5.9. 2,27 м3/с.
5.И. 2,67 м.
5.13. 20,98 кВт/(м2-град).
5.15. 550,3 К; 349 кВт.
5.17. NUt=l,5RefPr1/3.
5.19. а) 141,7 кВт; б) 361,1 кВт; в) 639 кВт.
5.21. а) 0,0683 Вт/(м2трад); б) 17,5 Вт/(м2трад);
в) 36,1 Вт/(м2-град).
5.23. 186 Вт/(м2трад).
5.25. 142 кВт; 5,5°С.
5.27. 0,64.
5.29. 6,36-105.
5.31. а) 79,7 Вт/(м2-град); б) 2,25 кВт на трубу;
в) 101,239 кН/м2.
5.33. 8306 Вт/(м2-град).
5.35. а) 406,8 Вт/(м2-град); б) 883 кВт; в) 8,4°С; г)" 8284 Н/м2.
. 5.37. 9,79 МВт; 787 Н/м2.
5.39. а) 7,33-107; б) 2,13-1010; в) 9,14-105; г) 1,61-10".
5.41. 125,4 Вт; 140,9 мин.
5.43. 52,7°С.
5.45. 3,35 кВт.
5.47. 17,28 Вт/м,
504 Ответы на нечетные номера задач
5.49. 45,7 кВт.
5.51. 1305 Вт.
5.53. 233 Вт.
5.55. 620 Вт.
5.57. 17,1 кВт.
5.59. 792 Вт/(м2-град); 648 Вт/(м2-град).
5.61. а) 762 Вт/(м2трад); б) 974 Вт/(м2трад).
5.63. 3173°С.
5.65. а) 111°С; б) 1,7 см; в) 155,4 Вт/(м2трад); г) 3,52- Ю-3;
д) 8,09 кВт/м2.
Глава 6
6.1. а) 128,7 кВт/м3; б) 4,022-Ю8 Вт/м3; в) 12,87 ГВт/м3;
г) 40,22 ТВт/м3.
6.5. 6245 К.
6.7. а) ультрафиолетовая область 0,58%, видимая 19,0%, ин-
инфракрасная 80,4%; б) ультрафиолетовая область 0,024%,
видимая 5,28%, инфракрасная 94,7%.
"• —Штк-
6.11. Солнечное излучение 83,7%, грунт 0,0015%.
6.13. а) 0,0118; б) 0,00292.
6.15. а) 0,2365; б) 0,2123.
6.17. i — 0,2; 2 — 0,6.
6.21. 0,8183.
6.23.
6.25. 0,060.
6.27. -F,+4 = 0,204, F^3 =0,414, FlH.e = 0,089. Л-в = 0,293.
6.29. a) —12,7 МВт; б) —12,69 МВт; в) 45,35 МВт; г) 204,1 Вт;
д) 32,65 МВт.
6.31. а) 114°С; б) 40 кВт.
6.33. б) 440,1 Вт; в) 1589 Вт; —390 Вт; —1199 Вт; г) 1149 Вт»
50 Вт.
6.35. 104°С.
6.37. 50°С.
6.39. 398,4 Вт/м2.
6.41. /, = 404,8 кВт/м2; /2 = 637,3 кВт/м2; /3 = 868,5 кВт/м2;
K)pes= - 348,0 кВт/м2; «)рез = 346,9 кВт/м2; Г2= 1831 К.
6.43. 244,1 Вт/м.
6.45. а) 1095 К, б) 995 К; в) 0,1 МВт; г) 59,136 кВт.
6.47. -^- = 0,1651-5,647- 10~12Гз (Т -в Кельвинах, /-в се-
секундах),
Ответы на нечетные номера задач 505
6.49. а) 20°С; б) 11,64 ,
6.51. 105°С.
6.53. 1,0 м.
6.55. а) 962 К; б) 2,88 кг/ч.
6.59. а) 22,31 кВт; б) —3,13 кВт; в) —19,18 кВт; 9,^2=8,703 кВт,
' 91^з=13>61 кВт> ^з^5'572 кВт< *"
6.61. —30,1 Вт/м2, 409 Вт/м2, —14,5 Вт/м2, 613 Вт/м2,
—482 Вт/м2, —496 Вт/м2.
6.63. а) 906 К, 922 К; б) 855 К; г) -11,714 кВт/м2.
6.65. 0,38.
6,67. 0,66.
6.69. а) —16,612 кВт/м2, 919 К; б) —19,326 кВт/м2.
6.71. а) —25,538 кВт/м2; б) —26,573 кВт/м2.
• 6.73. —39,734 кВт/м2.
Глава 7
7.1. а) 58,8 Вт/(м2-град); б) 50,3 Вт/(м2-град).
7.3. а) 58,2 Вт/(м2-град); б) 49,8 Вт/(м2-град).
7.5. 4,95%.
7.7. 47, ГС.
7.9. а) 233 кВт; б) 218 кВт, 6,52%.
7,11. а) 53,7 м2; б) 51,4 м2.
7.13. а) 4,31 м; б) 108,5°С; в) 109,3°С.
7,15. а) 81%; б) 82%.
7.17. а) ГВОда = 54,5°е; 7"8Озд = 120°С; б) ТВОАЛ = 54,7°С; Г„озд=
= 115,8°С.
7.19. а) 67%; б) 48,8 кВт; в) 44,0°С.
7.21. а) 357 кВт; б) 313 кВт.
7.23. а) 90,5%; б) 87,9 кВт; в) Твоаа = 72,9°С; ГВОэД = 69,3°С.
УКАЗАТЕЛЬ КЛЮЧЕВЫХ ТЕРМИНОВ,
ИСПОЛЬЗОВАННЫХ В КНИГЕ
Азимут Солнца — Altitude of the sun
342
Активный центр парообразования —
Active bubble nucleation 452
Алгебра угловых коэффициентов —
Shape-factor algebra 294
Аналогия Рейнольдса — Reynolds ana-
analogy 205
Безразмерный комплекс параметров—
Dimensionless group 36
Бинарная диффузия — Binary diffu-
diffusion 458
Вектор плотности теплового потока—
Heat-flux vector 84
Вынужденная конвекция — Forced
convection 23
Динамический пограничный слой —
Velocity boundary layer 194
Дисперсный режим течения — Mist
flow regime 451
Диффузионный (молекулярный) мас-
сообмен — Diffusion (molecular)
mass transfer 458
Диффузная поверхность—Diffuse sur-
surface 287
Диффузно отражающая поверх-
поверхность— Diffusely reflecting surface
289
Длина пути перемешивания Прандт-
ля — Prandtl's mixing length 202
Долевая массовая концентрация —
Mass fraction 459
Естественная (свободная)
ция — Free convection 23
конвек-
Загрязнение — Fouling 380
Зенитный угол — Zenith angle 344
Зеркальный отражатель — Specular
reflector 289
Излучательная способность (степень
черноты) — Emissivity, emittance
275
Излучение в видимой области спектра
(видимое излучение) —Visible ra-
radiation 267
Инсоляция — Insolation 340
Интегральная облученность — Total
irradiation 274 -
Интегральные радиационные свой-
свойства— Total radiation properties
274
Интенсивность излучения — Intensity
of radiation 286
Интенсивность тепловыделения в еди*
нице объема — Rate of heat genera-
generation per unit volume 70
Кажущееся напряжение турбулент-
турбулентного трения — Apparent turbulent
shear 200
Капельная конденсация — Dropwise
condensation 439
Кипение в большом объеме — Pool
boiling 440
Кипение насыщенной жидкости (объ-
(объемное кипение) — Saturated (bulk)
boiling 440
Кипение с недогревом — Subcooled
boiling 440
Кожухотрубный теплообменник —
Shell and tube heat exchanger 375
Кольцевой режим течения — Annular
flow regime 451
Конвективный массообмен — Convecti-
ve mass transfer 458
Концентрационный пограничный
слой — Concentration boundary lay-
layer 464
Коридорное расположение труб --
In-line tube arrangement 238
Указатель ключевых терминов 507
Кризис кипения (пережог) — Burnout
443
Критический температурный напор —
Critical excess temperature 443
Коэффициент восстановления — Reco-
Recovery factor 252
Коэффициент динамической вязко-
вязкости — Dynamic (absolute! viscosity
185 *
Коэффициент диффузии — Mass dif-
fusivity 459
Коэффициент загрязнения — Fouling
- factor 380
у Коэффициент кинематической вязко-
вязкости (коэффициент переноса количе-
- ства движения) — Kinematic vis-
viscosity (Momentum diffusivity) 192
Коэффициент конвективного массо-
обмена — Convective mass transfer
coefficient 464
¦Коэффициент молекулярной темпера-
температуропроводности — Molecular dif-
diffusivity of heat 204
Коэффициент наклона — Tilt factor
356
Коэффициент отвода тепла из коллек-
коллектора — Collector-heat-removal factor
409
Коэффициент полезного действия кол-
коллектора — Collector efficiency 400
Коэффициент тепловых потерь кол-
коллектора — Collector-heat-loss condu-
conductance 400
Коэффициент трения — Friction factor
39
Коэффициент турбулентного переноса
температуры (коэффициент турбу-
турбулентной температуропроводности) —
Turbulent exchange coefficient for
temperature (eddy diffusivity of
heat) 204
Коэффициент турбулентной вязкости
, (коэффициент турбулентного пере-
переноса количества движения) — Eddy
viscosity (turbulent exchange coef-
coefficient for momentum) 202
Коэффициент турбулентной темпера-
температуропроводности — Eddy diffusivity
of heat 204
Коэффициент эффективности коллек-
коллектора—Collector efficiency factor 408
Коэффициент эффективности ребра —
' Fin efficiency 79
Критерий устойчивости — Stability li-
limit 160
Ламинарный подслой — Laminar sub-
sublayer 186
Массообмен—Mass transfer 457
Местный коэффициент сопротивления
трения — Local friction coefficient
188 -
Местный коэффициент теплоотдачи —
Local heat-transfer coefficient
188
Метод конечных элементов — Finite-
element method 168
Метод натянутых нитей — Crossed-
string method 295
Метод обращения матрицы — Matrix-
inversion method 103
Мольная долевая концентрация —
Mole fraction 460
Мольная концентрация—Molar con-
concentration 460
Монохроматические (спектральные)
радиационные свойства—Monochro-
свойства—Monochromatic (spectral) radiation proper-
properties 273
Направленные радиационные свой-
свойства— Directional radiation proper-
properties) 273
Насадка (слой твердых частиц) —
Packed bed 412
Невозмущенный (потенциальный) по-
поток — Undisturbed (potential) flow
185
Недогрев — Subcooling 453
Несмешивающаяся жидкость — Unmi-
Unmixed fluid 398
Нестационарная задача теплообме-
теплообмена— Transient heat transfer prob-
problem 129
Нестационарная (переходнаяI зада-
задача — Unsteady (transient) problem
48
Неявный численный метод (метод с
использованием левых производ-
производных) —¦ Implicit numerical method
(backward difference technique) 165
Объемная доля пара — Vapor volume
fraction 452
Объемная доля пустот (пористость) —
Void fraction (porosity) 413
Огнеупорная (переизлучающая) по-
поверхность — Refractory (reradiating)
surface 303
Одноходовой теплообменник—Single-
pass heat exchanger 384
Определяющая температура — Film
temperature 227
608 Указатель ключевых терминов
Отражательная способность — Refle-
Reflectivity, reflectance 274
Отрицательный источник тепла (теп-
(тепловой сток) — Negative source (heat
sink) 69
Парниковый эффект — Greenhouse ef-
effect 280
Паросодержание (массовая доля
пара) — Quality (vapor mass frac-
fraction) 451, 452, 453
Перегрев — Superheat 451
Перекрестноточный теплообменник —
Cross-flow heat exchanger 377
Переходный дисперсно-кольцевой ре-
режим течения — Annular mist transi-
transition 451
Переходный режим кипения — Tran-.
sition boiling regime 441
Пленочная конденсация — Filmwise
condensation 431
Пленочное кипение — Film boiling 456
Плоскость эклиптики — Ecliptic plane
342
Плотность потока массы —Mass flux
density 459
Плотность потока падающего излу-
излучения — Irradiation (incident radiant
flux) 323
Поверхностное натяжение — Surface
tension 444
Поверхностное сопротивление — Sur-
Surface resistance 309
Поглощательная способность — Ab-
Absorptivity, absorptance 274
Подогреватель пластинчатого типа —
Flat-plate-type heater 396
Подъемная (архимедова) сила —
Buoyancy force 240
Полное (глобальное) солнечное излу-
излучение— Total (global) solar radia-
radiation 340
Поток массы — Mass transfer rate 458
Поток турбулентного количества дви-
движения— Turbulent momentum flux
202
Пропускательная способность—Trans-
missivity, transmittance 274
Противоточный теплообменник —
Counterflow heat exchanger 375
Псевдоожиженный (кипящий) слой—
Fluidized bed 413
Пузырьковое кипение — Nucleate boi-
boiling 441 ., .ь!
Пузырьковый режим : течения — Bub-
Bubbly flow regime 451 : ¦
Пудьсационная составляющая — Flue,
tuating component 200
Радиационно нейтральная (диатерми-
(диатермическая) среда — Radiatively nonpar-
ticipating medium 307
Радиационные свойства — Radiative
properties 273
Радиационные функции — Radiation
functions 270
Расходная теплоемкость — Heat-capa-
Heat-capacity rate 385
Режим образования непрерывных тру-
трубок пара — Continuous column re-
regime 441
Режим образования одиночных пу-
пузырей — Individual bubble regime
441
Режим течения со скольжением—
Slip flow regime 255
Режим течения сплошной среды —
Continuum flow regime 254
Режим устойчивого пленочного кипе-
кипения-Stable film boiling regime 441
Релеевское рассеяние — Rayleigh scat-
scattering 340.
Свободно-молекулярный режим тече-
течения — Free molecule flow regime
255
Сила вязкого сопротивления — Vis-
Viscous force 202
Скорость фильтрации — Superficial ve-
velocity 414
Смешивающаяся жидкость — Mixed
fluid 377
Снарядный режим течения — Slug
flow regime 451
Солнечное время — Sun time 342
Солнечное излучение — Solar radia-
radiation 338
Солнечный коллектор — Solar energy
collector 398
Соотношение замкнутости — Enclosure
relationship 292
Сопротивление диффузии массы —
Resistance to diffusion mass transfer
461
Среднее значение — Mean value 200
Среднелогарифмическая разность тем^
ператур (среднелогарифмический
температурный напор) — Logarith-
Logarithmic mean" temperature difference 386
Среднелогарифмическое число Нус-
сельта — Logarithmic mean Nusselt
number 383
Среднемассовая. температура — Bui К
temperature 407
Указатель ключевых терминов 509
Средний коэффициент сопротивления
трения — Average friction coefficient
188
Средний коэффициент теплоотдачи —
Average heat-transfer coefficient 188
Стационарная (установившаяся) за-
v дача — Steady (steady-state) prob-
problem 48
Степень турбулентности —Turbulence
level 186
Суммарный коэффициент теплопере-
теплопередачи-Overall heat transfer coeffi-
coefficient 62
Телесный угол — Solid angle 286
Температура насыщения — Saturation
temperature 438
Температура смешения — Mixing cup
temperature 212
Температурный напор — Excess tem-
temperature 440
Тепловая проводимость — Thermal
conductance 16
Тепловая труба —Heat pipe 414
Тепловое излучение — Thermal radia-
radiation 265
Тепловое равновесие — Thermal equi-
equilibrium 276
Тепловой пограничный слой — Tempe-
Temperature boundary layer 194
Теплообмен при «кипении — Boiling
heat transfer 440
Теплообменник — Heat exchanger 275
Теплообменник типа «труба в тру-
трубе»— Tube-within-a-tube heat ex-
exchanger 375
Термический коэффициент объемного
расширения — Volumetric thermal
expansion 485
Термическое сопротивление —Thermal
resistance 18
Трубный пучок (пучок труб) — Tube
bank 378
Турбулентный тепловой поток — Tur-
Turbulent rate of heat transfer 203
Угловое положение Солнца относи*
тельно плоскости земного эквато*
pa — Declination of the sun 342
Угловое солнечное время — Solar hour
time 343
Угловой коэффициент (коэффициент
видимости, конфигурационный коэф-
коэффициент, коэффициент формы) —
Shape factor (view factor, configu-
configuration factor) 290
Удельная тепловая проводимость —
Unit thermal conductance 16
Формфактор теплопроводности — Con-
Conduction shape factor 90
Хорошо перемешанная жидкость —
Well-stirred fluid 133
Число единиц переноса тепла — Num-
Number of heat-transfer units (NTU)
393
Шахматное расположение труб —
Staggered tube arrangement 238
«Шахматные» методы — «Hopscotch»
methods 168
Эквивалентный (гидравлический) диа-
диаметр— Hydraulic diameter 187
Эквимассовая противодиффузия —
Equimass counterdiffusion 459
Эквимолярная противодиффузия —
Equimolar counterdiffusion 460
Эффект полости — Cavity effect 277
Эффективное излучение (свети-
(светимость) — Radiosity 308
Эффективность теплообменника —
Heat-exchanger effectiveness 391
Явный численный метод (метод с ис-
использованием правых производных)
— Explicit numerical method (For-
(Forward-difference technique) 165
ОГЛАВЛЕНИЕ
Предисловие редактора русского издания 8
Предисловие 7
Обозначения 9
Глава 1. Принципы теплопередачи .11
1.1. Введение . 11
1.2. Теплопроводность (кондуктивный перенос тепла) 12
1.3. Конвективный теплообмен 23
1.4. Радиационный теплообмен < 27
1.5. Сложный теплообмен 29
1.6. Размерные величины и единицы измерения 33
1.7. Теория размерностей 34
Литература ч 40
Задачи 41
Глава 2. Стационарная теплопроводность 47
2.1. Введение 47
2.2. Уравнение теплопроводности 48
2.3. Одномерная стационарная задача теплопроводности при отсут-
отсутствии внутреннего тепловыделения 55
2.4. Влияние переменности коэффициента теплопроводности .... 66
2.5. Одномерная стационарная задача теплопроводности при наличии
внутреннего тепловыделения 69
2.6. Перенос тепла в ребрах 74
2.7. Неодномерные стационарные задачи теплопроводности .... 83
Литература ИЗ
Задачи 115
Глава 3. Нестационарная теплопроводность 129
3.1. Введение 129
3.2. Нестационарная теплопроводность при пренебрежимо малом внут-
внутреннем термическом сопротивлении 129
3.3. Нестационарная теплопроводность в полубесконечном твердом
теле 135
3.4. Диаграммы для решения задач нестационарной теплопроводности 140
3.5. Численные решения задач нестационарной теплопроводности . . 154
Литература 177
Задачи • .... 178
Глава 4. Конвективный теплообмен . . . 183-
4.1. Введение • 183
4.2. Уравнения сохранения массы, количества движения и энергии при
ламинарном обтекании плоской пластины 18S
4.3. Интегральные уравнения количества движения и энергии для ла-
щщарного пограничного слоя ,*,,,.,,, . „ , . ч , . *9*
Оглавление 511
4.4. Расчет коэффициентов теплоотдачи и трения в ламинарном по-
потоке 195
4.5. Аналогия между теплообменом и переносом количества движе-
движения при турбулентном обтекании плоской пластины 199
4.6. Аналогия Рейнольдса при турбулентном обтекании плоской пла-
пластины 205
4.7. Вынужденная конвекция при ламинарном течении в трубе . . . 208
4.8. Аналогия Рейнольдса для турбулентного течения в трубе . . .213
Литература 216
Задачи 217
Глава 5. Инженерные формулы для расчета конвективного теплообмена 223
5.1. Введение * 223
5.2. Безразмерные комплексы, используемые для обобщения экспери-
экспериментальных данных по конвективному теплообмену 223
5.3. Конвективный теплообмен при течении в трубах и каналах . . 226
5.4. Конвективный теплообмен в условиях вынужденной конвекции
при внешнем обтекании . 233
5.5. Свободная конвекция 240
5.6. Смешанная свободная и вынужденная конвекция 248
5.7. Теплообмен в высокоскоростном потоке 251
Литература 255
Задачи 258
Глава 6. Излучение 265
6.1. Введение 265
6.2. Физика излучения 267
6.3. Радиационные свойства 273
6.4. Угловой коэффициент излучения 290
6.5. Теплообмен излучением между черными поверхностями .... 298
6.6. Теплообмен излучением между серыми поверхностями .... 307
6.7. Матричные методы 315
6.8. Перенос излучения в поглощающих пропускающих средах.. . . 328
6.9. Радиационные свойства газов 331
6.10. Солнечное излучение 338
Литература 358
Задачи 360
Глава 7. Теплообменники 374
7.1. Введение 374
7.2. Основные типы теплообменников 374
7.3. Суммарный коэффициент теплопередачи 379
7.4. Среднелогарифмическая разность температур 383
7.5. Эффективность теплообменника 391
7.6. Солнечные коллекторы . 398
7.7. Теплообмен и течение в насадках 412
7.8. Тепловые трубы 414
Литература 425
Задачи 427
Глава 8. Конденсация, кипение и массообмен 430
- 8.1. Введение 430
8.2. Теплообмен при конденсации 430
8.3. Теплообмен при кипении 440
8.4. Массообмен 457
612 Оглавление
Литература 468
Задачи 471
Приложение I \ 473
Приложение И \ 475
Приложение III [ 476
Приложение IV 477
Приложение V 483
Приложение VI 487
Приложение VII 491
Приложение VIII .' 492
Приложение IX 494
Приложение X 496
Приложение XI 498
Ответы на нечетные номера задач 500
Указатель ключевых терминов, использованных в книге 506
Фрэнк Крейт, Уильям Блэк
ОСНОВЫ ТЕПЛОПЕРЕДАЧИ
Старший научный редактор О. Н. Вишнякова
Младшие научные редакторы Н. И. Сивилева, Л. С. Сысоева
Художник В. И. Харламов
Художественный редактор Л. Е. Безрученков
Технический редактор Н. И. Борисова
Корректор В. И. Киселева
ИБ № 3141
Сдано в набор 11.11.82. Подписано к печати 23.05.83. Формат 60Х90!/1в. Бумага типограф-
типографская № 2. Гарнитура литературная. Печать высокая. Объем 16 бум. л. Усл. печ. л. 32.
Усл. кр.-отт. 32. Уч.-изд. л. 31,26. Изд. № 20/1960., Тираж 7000 экз. Зак. 487. Цена 3 р. 70 к.
ИЗДАТЕЛЬСТВО «МИР» 129820, Москва, И-110, ГСП 1-Й Рижский пер., 2.
Ленинградская типография Нч 2 головное предприятие ордена Трудового Красного Зна-
Знамени Ленинградского объединения. «Техническая книга* им. Евгении Соколовой Союз-
полиграфпрома при Государственном комитете СССР по делам издательств, полиграфии
и книжной торговли. 198052, г. Ленинград, Л-52, Измайловский проспект, 29.