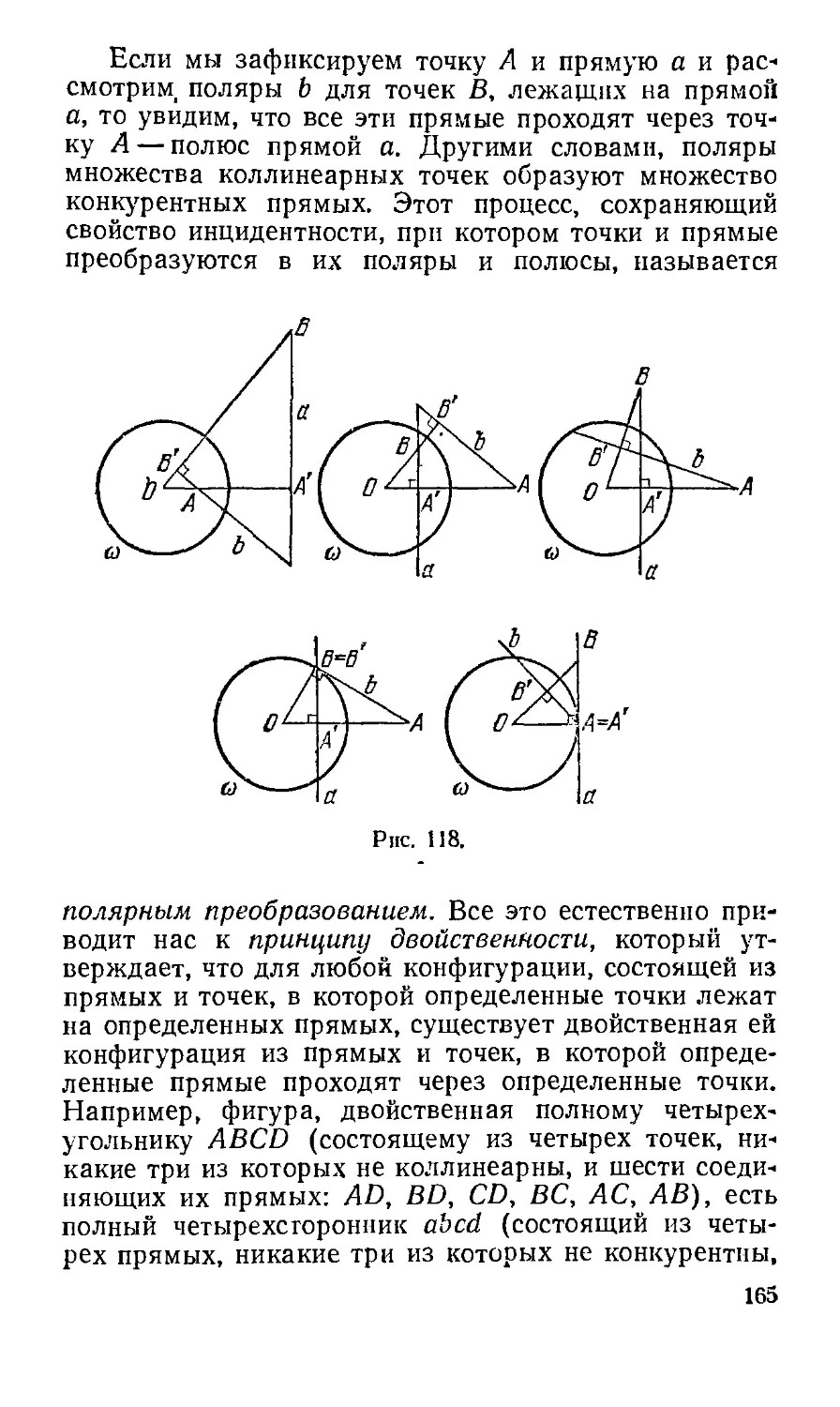
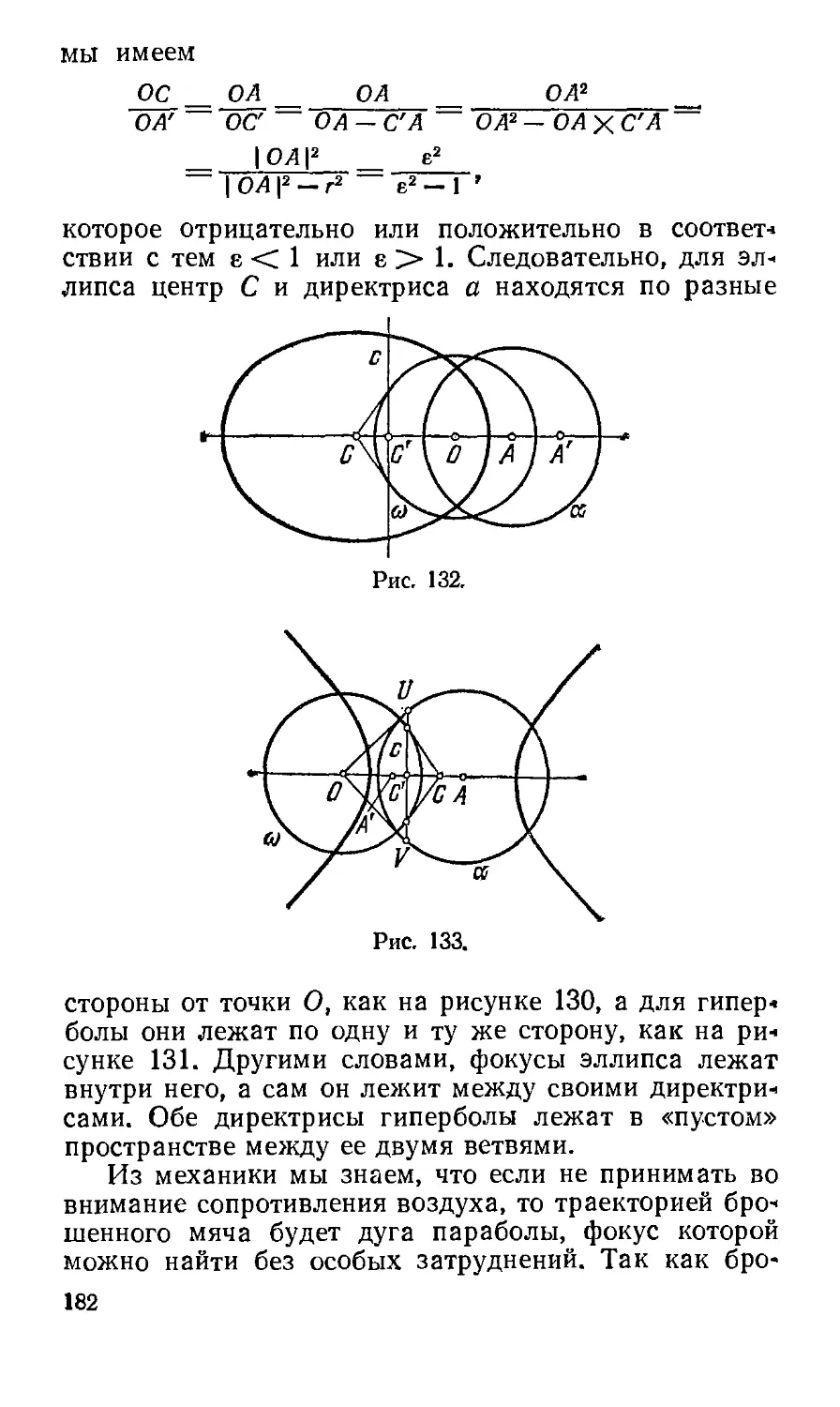
Text
Г.СМ. Коксетер, СП. Грейтцер
С ГЕОМЕТРИЕЙ
БИБЛИОТЕКА МАТЕМАТИЧЕСКОГО КРУЖКА
ВЫПУСК Н
Г. С. М. КОКСЕТЕР, С. Л. ГРЕЙТЦЕР
НОВЫЕ ВСТРЕЧИ
С ГЕОМЕТРИЕЙ
Перевод с английского -
' А. П. САВИНА и Л. А. САВИНОП
Под редакцией
А. П. САВИНА
МОСКВА «НАУКА»1
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1978
513
K59
УДК 513
GEOMETRY
REVISITED
by
H. S. M. Coxeter
and
S. L. Greitzer
TORONTO — NEW YORK
1967
20202—163 , © Перевод на русский язык.
"~Псо/по\ тя 81-78 Главная редакция
и*}0\Ш)-1в физико-математической литературы
издательства «Наука», 1978
СОДЕРЖАНИЕ
От редактора русского перевода 5
Предисловие ... . . .10
Глава 1. Точки и линии, связанные с треугольником ... 13
§ 1. Обобщенная теорема синусов 13
§ 2. Теорема Чевы 15
§ 3. Замечательные точки 17
§ 4. Вписанная и вневписанные окружности . -21
§ 5. Теорема Штейнера — Лемуса 23
§ 6. Ортотреугольник 27
§ 7. Серединный треугольник и прямая Эйлера ... 28
§ 8. Окружность девяти точек 31
§ 9. Педальный треугольник 34
Глава 2. Некоторые свойства окружностей 39
§ 1. Степень точки относительно окружности ... 39
§ 2. Радикальная ось двух окружностей ... 43
§ 3. Соосные окружности 47
§ 4. Еще раз о высотах и ортоцентре треугольника . . 49
§ 5. Прямые Симеона 53
§ 6. Теорема Птолемея . ...... . . 55
§ 7. Еще раз о прямых Симсопа 57
§ 8. Теорема о бабочке 59
§ 9. Теорема Морлея . . 61
Глава 3. Коллинеарность и конкурентность 65
§ 1. Четырехугольники; теорема Вариньона . ... 65
§ 2. Вписанные четырехугольники; теорема Брахма-
гупты 71
§ 3. Треугольники Наполеона .... . . . . 76
§ 4. Теорема Менелая . .82
§ 5. Теорема Паппа 85
§ 6. Перспективные треугольники; теорема Дезарга . . 86
1* 3
§ 7. Шестиугольники ,90
§ 8. Теорема Паскаля Р2
§ 9. Теорема Брианшона 95
Глава 4. Преобразования . . 99
§ 1. Параллельный перенос 100
§ 2. Поворот 102
§ 3. Разворот 105
§ 4. Симметрия 106
§ 5. Задача Фаньяно 108
§ 6. Задача о трех кувшинах ПО
§ 7. Дилатация 116
§ 8. Спиральное подобие 118
§ 9. Генеалогия преобразований 124
Глава 5. Введение в инверсивную геометрию 127
§ 1. Разбиение 127
§ 2. Сложное отношение 131
§ 3. Инверсия 132
§ 4. Круговая плоскость 138
§ 5. Ортогональность 141
§ 6. Теорема Фейербаха 145
§ 7. Сооскые окружности 148
§ 8. Инверсное расстояние 152
§ 9. Гиперболические функции 157
Глава 6. Введение в проективную геометрию ...... 163
§ 1. Полярное преобразование 163
§ 2. Полярная окружность треугольника 168
§ 3. Конические сечения 170
§ 4. Фокус и директриса 173
§ 5. Проективная плоскость 176
§ 6. Центральные конические сечения 179
§ 7. Стереографическая и гмономическая проекции . . 183
Ответы и указания к упражнением . 188
Библиография ... , 212
Словарь основных терминов, используемых в книге . . . 215
Указатель 220
ОТ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
«Вновь я посетил...»
А. С. Пушкин
Дословным переводом названия этой книги явля-
является «Вновь посещенная геометрия». Авторы как бы
проводят читателя по наиболее красивым местам
древней, но нестареющей страны — Геометрии. i
Когда-то геометрия олицетворяла всю математику.
Но математика росла и развивалась, особенно бурно в
последние 200 лет. Возникли новые направления: ма-
математический анализ, теория множеств, топология,
совсем иначе стала выглядеть алгебра. Конечно, раз-
развивалась и геометрия, однако некоторые математики
начали в последнее время относить ее к числу второ-
степеннык математических направлений. Это мнение
нашло свое отражение и в содержании школьны к
программ по математике, как в США, так и в ряде
других стран.
Книга Г. С. М-. Коксетера и С. Л. Грейтцера явля-
является ярким документом в защиту геометрии, за
утверждение геометрии на подобающем ей месте в
системе школьного образования.
В то же самое время она является прекрасным
материалом для работы школьных математических
кружков. Изучение этой книги дает возможность
взглянуть на геометрию в целом и в то же время
познакомиться с отдельными ее жемчужинами.
Именно поэтому книга включена в серию «Библиотека
математического кружка».
5
Большинство книг этой серии (исключение состав-
составляет лишь «Числа и фигуры» Г. Радемахера и О. Теп-
Теплица) написано в «эвристической» манере изложения,
а именно, читатель входит в круг рассматриваемых
вопросов, решая последовательно серию задач. Если
задача оказывается для него слишком сложной, он
может прочесть ее решение. Таким образом, читатель
сам становится как бы исследователем, самостоятель-
самостоятельно открывающим эту область математики. Однако,
при этом полностью исчезает исторический аспект
рассматриваемого вопроса.
Книга Г. С. М. Кокстера и С. Л. Грейтцера, хотя и
содержит много задач, но написана в обычной манере
последовательного изложения материала. При этом
авторы насытили изложение большим количеством
интересных сведений по истории появления идей и
результатов, что делает книгу еще более привлека-
привлекательной.
Несколько слов об авторах книги. Гарольд Скотт
Макдональд Коксетер — профессор университета в
Торонто (Канада)—один из крупнейших современ-
современных геометров, автор ряда книг, две из которых
«Введение в геометрию» и «Действительная проектив-
проективная плоскость» ([17] и [18]) переведены на русский
язык. Заметим, что транскрипция его имени в этих
книгах (Г. С. М. Кокстер и X. С. М. Кокстер) отлича-
отличается от примененной здесь; однако было решено пе-
перейти на эту более правильную транскрипцию, тем
более, что она уже стала встречаться в русской лите-
литературе по математике.
Самуэль Грейтцер, профессор математики Рутгер-
ского университета (США), более 25 лет проработал
школьным учителем математики. Он является основ-
основным организатором Всеамериканских математических
олимпиад, которые по стилю сходны со Всесоюзными
математическими олимпиадами. В течение ряда по-
6
следних лет он руководит командой США на Между-
Международной математической олимпиаде школьников.
Перевод книги был осложнен двумя обстоятель-
обстоятельствами: во-первых, в настоящее время средняя школа
СССР только-только перешла на новые программы по
математике и одновременно на новую терминологию и
новые обозначения, непривычные для лиц, закончив-
закончивших среднюю школу до 1977 года, а, во-вторых, Кок-
сетером разработана своя стройная и логичная систе-
система обозначений, например, площадь треугольника
ABC обозначается через (ABC), и т. д. В результате
перед переводчиками встал трудный вопрос о выборе
терминологии и обозначений.
Поскольку эта книга адресована в первую очередь
школьникам, то за основу была взята система обо-
обозначений, применяющаяся сейчас в средней школе.
При этом были сделаны небольшие отклонения, по-
позволяющие без труда читать эту книгу и человеку,
незнакомому с новой терминологией и новыми
обозначениями.
В частности, здесь употребляется термин «конгру-
«конгруэнтность фигур» вместо ранее существовавшего тер-
термина «равенство фигур», однако, во многих случаях по
отношению к отрезкам и углам сохранен термин «ра-
«равенство», причем имеется в виду равенство длин от-
отрезков и величин углов. Этого же принципа придер-
придерживаются и авторы учебников, принятых в настоящее
время в школе. Заметим, .что пунктуальное примене-
применение терминов «конгруэнтность» и «равенство длин от-
отрезков» привело бы к существенному утяжелению
текста, не говоря уже о появлении таких «монстров»,
как «равновеличинобедренный треугольник» или
«конгруэнтносторонний треугольник».
Длина отрезка АВ здесь обозначается через
\АВ\, как и принято сейчас в школе, но не применя-
применяются обозначения [АВ], ]АВ[, {АВ) для отрезка,
интервала и прямой, а просто указывается, что именно
имеется в виду: прямая АВ, отрезок АВ или интервал
АВ. Такое указание невозможно в формуле, однако
там фигурирует лишь длина отрезка, для которой есть
четкое обозначение. Однако в этой книге рассматрива-
рассматриваются также и направленные отрезки. В формулах они
обозначаются просто через АВ, CD и т. д., а произве-
произведение направленных отрезков (лежащих на одной
прямой), например, АВ и CD обозначается через
АВ X CD, в то время как произведение длин этих
отрезков обозначается через \АВ\ • \CD\.
Употребление знака X в качестве знака умноже-
умножения направленных отрезков существенно еще и пото-
потому, что через AB-CD авторы книги обозначают точку
пересечения прямых АВ и CD.
Теперь несколько слов о терминологии. Суще-
Существенную роль в тексте книги имеет поворот плоскости
на 180°, названный авторами «half-turn» и переведен-
переведенный как разворот. Хотя такое преобразование пло-
плоскости и совпадает с хорошо известной центральной
симметрией, однако употребление термина централь-
центральная симметрия оказалось невозможным, поскольку
свойства этого преобразования выводились из свойств
поворота.
Далее, сохранен термин «изометрия» вместо более
привычного термина «движение», так как в тексте
акцентируется именно сохранение расстояний при та-
таких преобразованиях.
Систематическое использование в книге термина
«коллинеарность» привело к сохранению авторского
термина «коллинеация» (collineation) для преобразо-
преобразований, переводящих прямые в прямые, вместо обычно
употребляемого термина «аффинные преобразования».
Последним терминологическим новшеством книги
является употребление термина «дилатация» (от
dilatation — расширение) для обозначения преобра-
8
зований плоскости, при которых каждая прямая пе-
переходит в параллельную ей прямую. Этот класс пре-
преобразований состоит из гомотетий и параллельных
переносов, однако в русской математической литера-
литературе еще не было термина для обозначения этого
весьма естественного класса преобразований.
При • переводе была существенно расширена биб-
библиография (добавленные книги отмечены звездочка-
звездочками). В их числе широкодоступные книги из серии
«Популярные лекции по математике» [1], [2], [6],
[12], [25], [32], [35], изучение которых даст возмож-
возможность взглянуть на изложенные в этой книге вопросы
с другой точки зрения (в частности, на конические
сечения, изложение которых в этой книге весьма
нетрадиционно). Желающим глубже познакомиться с
рассматриваемой тематикой окажут помощь книги
[14], [15], [18], [33], [44], [45], [46], достаточно
доступные для широкого круга читателей.
Я приношу искреннюю благодарность И. М. Ягло-
му, чьи замечания и предложения существенно со-
содействовали улучшению перевода этой книги.
Также благодарю В. Г, Шнитке за помощь при
переводе эпиграфов.
А. П. Савин
ПРЕДИСЛОВИЕ
Тот, кто ни во что не ставит евклидову
геометрию, подобен человеку, который,
вернувшись из чужих краев, поносит свой
дом.
Г. Фордер
В программу по математике средней школы
(США) входит годичный курс геометрии плоскости
или курс геометрии и элементарной аналитической
геометрии, называемый «математика-10». Обычно для
ученика средней школы на этом и заканчивается зна-
знакомство с геометрией. В противоположность этому,
математически одаренным школьникам программы
средней школы дают возможность дальнейшего изуче-
изучения элементарной алгебры, дополнительных ее глав и
даже высшей алгебры. Поэтому естественно наблю-
наблюдаемое пристрастие к алгебре и предубеждение про-
против геометрии. Более того, введенные в заблуждение
энтузиасты пытаются убедить учащихся, что геомет-
геометрия находится «где-то в стороне от основного направ-
направления математики» и что анализ или теория множеств
должны вытеснить ее.
Возможно, тот факт, что в школьной программе
геометрия занимает одно из последних мест, объясня-
объясняется тем, что педагоги мало знают о природе геомет-
геометрии и об успехах, которые были достигнуты ее иссле-
исследователями. Мы имеем в виду многие блестящие
результаты, такие, как теорема Брианшона (§9 гл. 3),
теорема Фейербаха (§6 гл. 5), теорема Петерсона—
ю
Шута (§8 гл. 4) и теорема Морлея (§9 гл. 2). Как
известно из истории, Евклид писал для зрелых людей,
которые готовились изучать философию. И вплоть до
нашего столетия одной из основных причин обучения
геометрии было то, что ее аксиоматический метод счи-
тался лучшим введением в дедукцию. Естественно,
что на этот формальный метод делался акцент в про-
процессе обучения. Однако ни древние, ни современные
геометры не боялись использовать менее ортодок-
ортодоксальные методы, когда это их устраивало. Если мето-
методы тригонометрии, аналитической геометрии или век-
векторные методы подойдут, геометры их используют.
Кроме того, они создали свои собственные современ-
современные методы, элегантные и мощные. Один из них—■
применение преобразований таких, как поворот,
симметрия и подобие, что дало возможность доказать
ряд теорем более рациональным способом, а также
связать геометрию с кристаллографией и искусством.
Этому «динамическому» аспекту геометрии посвяще-
посвящена глава 4. Другим является метод инверсивной гео*
метрии, рассматривающий точки и окружности, при
этом и прямая считается окружностью, проходящей
через бесконечно удаленную точку. О некоторых осо-
особенностях этой геометрии рассказывается в главе 5,
И, наконец, третий — метод проективной геометрии,
который совсем не рассматривает расстояния и углы,
а выделяет аналогию между точками и прямыми.
В проективной геометрии не только через любые две
точки проходит прямая, но и любые две прямые имеют
точку пересечения; при этом параллельные прямые
пересекаются на «бесконечно удаленной прямой». Из-
Изложению небольшого фрагмента этой темы посвящена
глава 6.
Геометрия и сейчас обладает всеми теми достоин-
достоинствами, за которые ее ценили педагоги прошлых по-
поколений. На свете еще есть геометрия, которая ждет,
П
чтобы ее познали и оценили. Геометрия (особенно
проективная геометрия) остается отличным средством
введения учащихся в аксиоматику. Геометрия сохра-
сохранила всегда присущую ей эстетическую привлекатель-
привлекательность, и не поблекла красота ее результатов. Более
того, для специалистов в чистой и прикладной мате-
математике геометрия стала еще более полезной и необхо-
необходимой, чем она была когда-либо раньше. Возьмите,
например, формы орбит искусственных спутников и
четырехмерную геометрию пространства-времени.
Геометрия росла. На протяжении веков были раз-
разработаны новые понятия и методы, которые будут для
учащихся интересными и удивительными, если мы,
приложим все усилия, чтобы донести до них эти по-
понятия. Так давайте же вновь перелистаем Евклида,
познакомимся с некоторыми новыми результатами.
Возможно, мы снова сможем испытать тот же восторг
и трепет, как и при первых встречах с геометрией.
Авторы приносят искреннюю благодарность док-
доктору Аннелии Лаке за ее терпеливое сотрудничество и
многие полезные предложения.
Г. С. М. Коксетер
С. Л. Гргйтцер
Торонто н Нью-Йорк, 1967
Глава 1
ТОЧКИ И ЛИНИИ, СВЯЗАННЫЕ
С ТРЕУГОЛЬНИКОМ
Обладая литературой более обширной, чем
алгебра и арифметика вместе взятые, и
по крайней мере столь же обширной как
м анализ, геометрия в большей степени,
чем любой другой раздел математики,
является богатейшей сокровищницей инте-
интереснейших, но полузабытых вещей, кото-
которыми спешащее поколение ие имеет вре-
времени насладиться.
Е. Т. Белл
Цель этой главы состоит в том, чтобы вспомнить
некоторые из тех полузабытых вещей, к которым от-
отсылал доктор Белл, вывести новые теоремы, появив-
появившиеся после Евклида, и применить все это к инте-
интересным ситуациям. Мы рассматриваем произвольный
треугольник и самые знаменитые связанные с ним
точки и линии: центр описанной окружности, медиа-
медианы, центроид, биссектрисы углов, центр вписанной ок-
окружности, центры вневписанных. окружностей, высо-
высоты, ортоцентр, прямую Эйлера и окружность девяти
точек.
Изучение биссектрис углов естественно подводит
нас к теореме Штейнера — Лемуса, которая сотни лет
считалась трудной для доказательства, хотя, как мы
видим сейчас, ее довольно легко доказать.
Наконец, по треугольнику и точке Р^ находящейся
в общем положении, мы получаем новый треугольник,
вершины которого являются основаниями перпенди-
перпендикуляров из точки Р к сторонам данного треугольни-
треугольника. Эта идея приводит к занимательным результатам,
с некоторыми из них мы встретимся в следующей
главе.
§ 1. Обобщенная теорема синусов
Теорема синусов — это тригонометрическая теоре-
теорема, которой мы будем часто пользоваться. К сожале-
сожалению, она обычно появляется в учебниках в урезанной
форме, и в этом виде она не приносит всей той пользы,
которую могла бы дать обобщенная теорема, Поэтому
13
мы позволим себе доказать теорему синусов в жела-
желательной для нас форме.
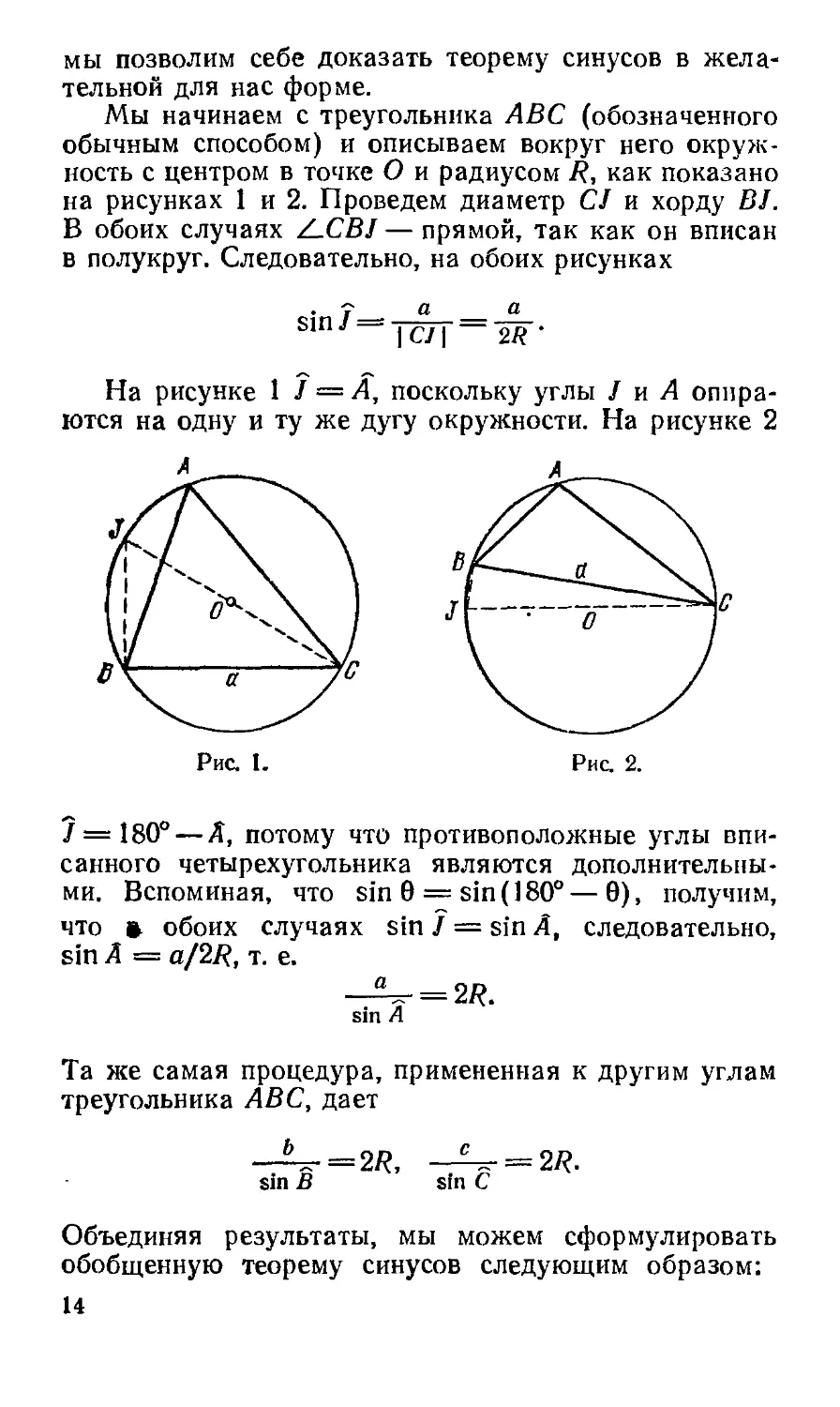
Мы начинаем с треугольника ABC (обозначенного
обычным способом) и описываем вокруг него окруж-
окружность с центром в точке О и радиусом R, как показано
на рисунках 1 и 2. Проведем диаметр CJ и хорду BJ.
В обоих случаях /LCBJ— прямой, так как он вписан
в полукруг. Следовательно, на обоих рисунках
sin/ =
\Cl\
а
W
На рисунке 1 ? = А, поскольку углы / и Л опира-
опираются на одну и ту же дугу окружности. На рисунке 2
Рис 1.
Рис. 2.
7 = 180° — А, потому что противоположные углы впи-
вписанного четырехугольника являются дополнительны-
дополнительными. Вспоминая, что sin 9 = sin A80° — 9), получим,
что » обоих случаях sin 7= sin Л, следовательно,
sin A = a/2R, т. е.
sin A
= 2R.
Та же самая процедура, примененная к другим углам
треугольника ABC, дает
sin В
sin С
Объединяя результаты, мы можем сформулировать
обобщенную теорему синусов следующим образом:
14
Теорема 1.11. Для треугольника ABC с ради-
радиусом описанного круга R выполнены соотношения:
sin A sin В sin С
Упражнения
1. Покажите, что *) для любого треугольника ABC, даже
если угол В или С тупой, а = Ъ cos С + с cos Б. Используйте тео-
теорему синусов для вывода «формулы сложения»
sin(B + С) = sin В-cosС + sin С-cos В.
2. В любом треугольнике ABC
a (sin В — sin С) + Ъ (sin С — sin А) + с (sin А — sin С) = 0.
3. В любом треугольнике ABC Sabc = abc/iR.
4. Пусть р и q — радиусы двух окружностей, проходящих
через точку А и касающихся стороны ВС в точках В и С соот-
соответственно. Тогда pq = R2.
§ 2. Теорема Чевы
Отрезок, соединяющий вершину треугольника с
некоторой точкой па противоположной стороне, назы-
называется чевианой. Таким образом, если в треугольнике
ABC X, Y и Z — точки, лежащие на сторонах ВС, С А,
АВ соответственно, то отрезки АХ, BY, CZ являются
чевианамн. Этот термин происходит от имени италь-
итальянского математика Джованни Чевы, который в
1678 году опубликовал следующую очень полезную
теорему:
Теорема 1.21. Если три чевианы АХ, BY, CZ (no
одной из каждой вершины) треугольника ABC конку-
конкурентны, то
\ВХ\ \CY\ \А2\
\ХС\ ' \YA\ ' \ZB\
Когда мы говорим, что три прямые (или отрезка)
конкурентны, то мы имеем в виду, что все они прохо-
проходят через одну точку, которую обозначим через Р.
Для доказательства теоремы Чевы вспомним, что
*) В следующих упражнениях для экономии места мы опу-
опускаем слова «Покажите, что» или «Докажите, что». Таким обра-
som, каждое упражнение, появляющееся в форме теоремы, нужно
доказать.
15
площади треугольников с равными высотами пропор-
пропорциональны основаниям треугольников. Ссылаясь на
рисунок 3, мы имеем:
I AC I SAXC
Аналогично,
\CY\
s
РХС
SAXC SPXC
'CAP
JBCP
ABP
\AZ\
"CAP
Теперь, если мы перемножим их, то получим
\ВХ\ \CY\ \AZ\
\кс\
\zb\
'АВР
^САР
ВСР
АВР
S
'САР
ВСР
= 1.
Теорема, обратная к этой теореме, также верна:
Теорема 1.22. Если
три чееианы АХ, BY, CZ
удовлетворяют соотноше-
соотношению
\ВХ\ \CY\ \AZ\
\ХС\ \УА\ \ZB\
= 1,
то они конкурентны.
Чтобы это показать,
предположим, что две
первые чевианы пересе-
рис. з. каются в точке Р, как и
прежде, а третья чевиана,
проходящая через точку Р, будет CZ'. Тогда, по тео-
теореме 1.21,
\ВХ\ \CY\ \AZ'\
\ХС\ \YA\
Но по предположению
\ВХ\ \CY\
\Z'B\
= 1.
\КС\ \YA\
= 1.
Следовательно,
\AZ'\ _ \AZ\
\Z'B\~ \ZB\'
точка Z' совпадает с точкой Z, и мы доказали, что от*
резки АХ, BY и CZ конкурентны ([13], стр. 54 и [42],
стр. 48, 317;.
Упражнения
1. Если X, Y, Z — середины сторон, то соответствующие им
три чевианы конкурентны.
2. Чевианы, перпендикулярные противоположным сторонам,
конкурентны.
3. Пусть ABC и А'В'С — два неконгруэнтных треугольника,
соответствующие стороны которых параллельны, как на рисун-
рисунке 4. Тогда три прямые /4.4', ВВ\ СС конкурентны.^(Такие тре-
треугольники называются гомотетичными. Мы рассмотрим их далее
в § 7 гл. 4.)
Рис. 4.
4. Пусть АХ — чевиака длины р, причем \ВХ\ —m и
\ХС\ = п, как на рисунке 5. Тогда
а (р2 + тпп) = Ьгш + с2п.
-Указание. Сложите выражения для косинусов двух до-
дополнительных углов в точке х через стороны треугольников АВХ
и С АХ соответственно. Этот результат называется теоремой
Стюарта в честь М. Стюарта, который сформулировал ее в
1746 году. Возможно, что она была открыта Архимедом около
300 г. нашей эры, но первое известное доказательство было дано
Р. Симеоном в 1751 году.
§ 3. Замечательные точки
Существует много специальных точек и линий, свя-
связанных с треугольником, но нам придется ограничить-
ограничиться только небольшим их числом. Мы уже упоминали
одну такую точку — центр окружности, описанной во-
вокруг треугольника. Мы условимся обозначать ее бук-
буквой О. Она является точкой пересечения трех перпен-
перпендикуляров, делящих пополам стороны треугольника
(рис. 6). Радиус описанной окружности был уже обо-
обозначен буквой R.
17
Чевианы, которые связывают вершины треугольник
ка с серединами противоположных сторон, называются
медианами. На рисунке 7 отрезки АА', ВВ' и СС —
медианы, так что |ВЛ'| = |Л'С|, \СВ'\ = \В'А\ и
|ЛС"| = |С"В|. Применяя теорему 1.21, мы делаем
вывод, что медианы конкурентны. Их общая точка G
называется центроидом треугольника. Если бы тре*
угольник был вырезан из однородного материала, то
он оставался бы в равновесии, будучи подвешенным
А
"— .
А
Рис. 6.
в этой точке. Другими словами, центроид есть «центр
тяжести» треугольника.
Рассмотрев вновь рисунок 7, мы обнаруживаем,
что Scba' = Sca'c, так как эти треугольники имеют
одинаковые основания и одну и ту же высоту. Вот
почему на рисунке мы обозначили эти площади одной
и той же буквой х. Из тех же соображений мы имеем
Sgcb1 — Sgb'a и Sgac =
Поэтому обозначим эти площади через у и г, как и
показано. Однако мы также имеем Scac' = Sccb, т.е.
2у -\- z = z -\- 2х, следовательно, х = у. Аналогично,
Saba' = Saa'c, следовательно, y — z. Таким образом,
мы показали, что х — y — z, а это есть
Теорема 1.31. Треугольник делится своими ме-
медианами на шесть меньших" треугольников равной
площади.
Продолжая наше рассмотрение рисунка 7, мы от-
отмечаем, что Sgab = 2Sgba'- Так как эти треугольники
18
имеют общую высоту, то отсюда следует, что |ЛС| =
= 2\GA'\. Аналогично, \BG\=2\GB'\ и \CG\ =
= 2] GC'\, т. е. имеет место:
Теорема 1.32. Медианы треугольника делят
одна другую в отношении 2:1. Другими словами,
каждая медиана треугольника отсекает треть другой.
Чевианы AD, BE, CF (рис. 8), перпендикулярные
прямым ВС, СА, АВ, соответственно, называются вы-
высотами треугольника ABC. Как мы видели'в упраж-
Рис. 8.
нении 2 § 2, теорема, обратная теореме Чевы,
устанавливает их конкурентность. Их общая точка Н
называется ортоцентром *).
Сами точки D, E, F называются основаниями вы-
высот. Соединяя их попарно, мы получим треугольник
DEF — ортотреугольник треугольника ABC.
Другое важное семейство чевиан образуют бис-
биссектрисы внутренних углов. На рисунке 9 показана
одна такая биссектриса AL. Применяя теорему 1.11
к двум треугольникам ABL и ALC (углы которых в
точке L, являясь дополнительными, имеют равные си-
синусы), мы получаем
\BL\ с_ | LC | _ b
sin - A sin 2 Л
Следовательно,
sinL
*) Историю этого термина см. J. Satterly, Mathematical Ga-
Gazette 45 A965), стр. 51.
19
Так как мы можем получить аналогичные результаты
для биссектрис внутренних углов В и С, то мы таким
образом доказали
Теорему 1.33. Каждая биссектриса внутреннего
угла в треугольнике делит противоположную сторону
на отрезки, длины которых пропорциональны длинам
прилегающих сторон.
Любая точка на прямой AL (рис. 9) равноудалена
от прямых СА и АВ. Аналогично, любая точка на бис-
биссектрисе внутреннего уг-
угла В равноудалена от
прямых АВ и ВА. Следо-
Следовательно, точка /, в кото-
которой эти две биссектрисы
пересекаются, находится
на равных расстояниях г
от всех трех сторон:
Теорема 1.34. Бис-
Биссектрисы трех внутренних
углов треугольника кон-
конкурентны.
Рис 10. Окружность с центром
в точке / и радиуса г
(рис. 10) касается всех трех сторон и поэтому яв-
является вписанной окружностью.
Упражнения
1. Центр описанной окружности и ортоцентр тупоугольного
треугольника лежат вле этого треугольника.
2. Нгпдые отношение площадей данного треугольника и тре-
треугольника, стороны которого имеют те же длины, что и медианы
данного.
3. Любой треугольник, имеющий две равные медианы, явля-
является равнобедренным.
4. Любой треугольник, имеющий две равные высоты, яв-
является равнобедренным.
5. Используя теоремы 1.22 и 1.33, получите другое доказа-
доказательство теоремы 1.34.
6. Выразите длину медианы АА' (р'ис. 7) через а, Ь, с.
Указание. Используйте теорему Стюарта (упражнение 4
7. Квадрат длины биссектрисы AL (рис. 9) равен
20
8. Найдите длину биссектрисы прямого угла треугольника со
сторонами 3, 4, 5.
9. Произведение длин двух сторон треугольника равно про-
произведению длины диаметра описанной окружности на длину вы-
высоты, опущенной на третью сторону.
§ 4. Вписанная и вневписанные окружности
На рисунке 11 изображена вписанная окружность,
касающаяся сторон ВС, СА и АВ в точках X, Y, Z.
Так как две касательные к окружности, проведенные
из внешней точки, равны,
то мы получаем, что
|ЛУ| = |Лг|, |BZ| =
= |сЛ|, |СЛ| = |СУ|.
На рисунке 11 длины
этих отрезков обозначе-
обозначены буквами х, у, z, так
что
Складывая эти равенства Рис п.
и используя введенное
Эйлером обозначение s для полупериметра (от «semi-
perimeter»), получим
поэтому
x-\-y-\-z —
т. е. справедлива
Теорема 1.41. x — s — а, у = s — b,z — s — c.
Так как треугольник IBC имеет основание а и вы-
высоту г, то его площадь равна S/Bc = -2"ar* Прибавив
к нему аналогичные выражения для Sica и Siab, мы
получим -g- (а + Ь + с) г = sr; следовательно, доказана
Теорема 1.42. Sabc = sr,
JHa рисунке 12 изображен треугольник Iahh, сто-
стороны которого являются биссектрисами внешних
углов треугольника ABC. Любая точка на биссектрисе
IJa угла В равноудалена от прямых АВ и ВС. Анало-
Аналогично, любая точка на прямой IaIb равноудалена от
21
прямых ВС и СА. Следовательно, точка 1а, в которой
эти биссектрисы пересекаются, находится на одинако-
одинаковом расстоянии га от всех трех сторон. Так как /„
равноудалена от сторон^ЯВ и АС, то она должна при-
принадлежать множеству точек, равноудаленных от этих
прямых, т. е. она должна лежать на прямой AI, внут-
внутренней биссектрисе угла А:
Теорема 1.43. Внешние биссектрисы любых двух
углов треугольника конкурентны с внутренней биссек-
биссектрисой третьего угла.
Окружность с центром в точке /о радиуса га, ка*
сающаяся всех трех сторон треугольника, является
одной из трех вневписанных окружностей. Каждая из
вневписанных окружностей касается одной из сторон
треугольника внутри, а двух других сторон (продол-
женных) извне.
Обозначив точки касания как на рисунке 12, мы
замечаем, что так как две касательные из одной точ-
точки к окружности имеют одинаковые длины, то
\BXb\=\BZb\
22
Следовательно, касательная из точки В (или любой
другой вершины) к вневписанной окружности, распо-
расположенной за противолежащей стороной, имеет дли-
длину s. Действительно,
Кроме того, так как | СХЬ \ — \ ВХЬ \ — \ ВС \ = s — аи
т.д., то также и
\ ВХС\ = \ BZc\ = \CXb\ = \CYb\ = s - а,
Упражнения
1. Если три окружности с центрами в точках А, В, С по-
попарно касаются, то их радиусы равны s — a, s — b, s — с.
2. abc = bsrR (s, г, R имеют их обычные значения).
3. Чевианы АХ, BY, CZ треугольника ABC, где X, Y, Z —
точки касания вписанной окружности со сторонами треугольника,
конкурентны. (Их общая точка называется точкой Жергона тре-
треугольника ABC.)
4. Треугольник ABC является ортотреугольником треуголь-
треугольника lahlc (рИС. 12).
5- SA ABC = (s—°) ra = (s~&) rb =* (s—c) rc (CP- теорему 1.42).
§ 5. Теорема Штейнера — Лемуса
Существует ряд геометрических задач, которые
околдовывают каждого, кто по воле случая сталки-
сталкивается с ними. По-видимому, это было характерно для
геометрии даже в древнее время. Стоит только вспом-
вспомнить три знаменитые задачи древности — удвоение
куба, трисекцию угла и квадратуру круга. Попытки
решить эти задачи привели к развитию новых ветвей
математики. Даже сейчас существуют псевдоматема-
псевдоматематики, которые присылают в редакции «решения» этих
23
вадач и требуют публикации или доказательства лож-
ложности своих «решений».
Одна всегда возбуждавшая интерес теорема мо-
может быть сформулирована следующим образом:
Теорема 1.51. Любой треугольник, у которого
равны длины биссектрис двух углов- (измеряемые от
вершины до противоположной стороны), является
равнобедренным.
Эта теорема была- послана великому шведскому
геометру Якобу Штейнеру в 1840 году С. Л. Лемусом
(имя которого, если бы не этот случай, было бы давно
забыто) с просьбой дать чисто геометрическое доказав
тельство. Штейнер дал довольно сложное доказатель-
доказательство, которое вдохновило многих других на поиски
более простых методов. Работы по теореме Штей-
нера — Лемуса появлялись в различных журналах
в 1842, 1844, 1848 годах и почти каждый год с 1854 го-
года по 1864 год, а также в большом количестве и в те-
течение следующего столетия.
Одно из простейших доказательств опирается на
следующие две леммы:
Л'емма 1.511. Если две хорды окружности стя-
стягивают различные острые углы с вершинами на этой
окружности, то меньшему углу соответствует меньшая
хорда.
Доказательство. Две равные хорды стяги-
стягивают равные углы с вершиной в центре окружности и
равные углы (как их половины) с вершинами в соот-
соответствующих точках на окружности. Из двух неравных
хорд более короткая,~находясь дальше от центра, стя-
стягивает меньший угол с вершиной в центре и, следова-
следовательно, меньший острый угол с вершиной на окруж-
окружности.
Лемма 1.512. В треугольнике с двумя различны'
ми углами меньший угол обладает большей биссеК'
триссй ([22], стр. 72).
Доказательство. Пусть ABC— треугольник,
в котором В < С, как на рисунке 13; пусть отрезки
ВМ и CN делят пополам углы В и С. Мы хотим до-
доказать, что \ВМ\ > \CN\. Возьмем точку ЛГ на от*
резке ВМ так, чтобы M'CN — -^B. Так как этот угол
24
равен углу M'BN, то четыре точки N, В, С, М' лежат
на одной окружности. Поскольку
то
CBN < М'СВ < 90°.
По лемме 1.511 \CN\ <\М'В\.Следовательно,
>\BM'\>\CN\.
Доказательство теоремы. Часто случает-
случается, что теорема может быть выражена в форме «про-
«противоположной к обрат-
обратной» — эквивалентной
первоначальной. На-
Например, вместо того,
чтобы сказать: «.Все
люди смертны», мы мо-
можем также сказать
«.Бессмертные не есть
люди». Вместо доказа-
тельстЕа самой теоре-
теоремы 1.51 для нас будет
достаточно доказать,
что если в треугольни-
треугольнике ABC ВфС, то
\ВМ\Ф\СЩ. Но это
есть прямое следствие
леммы 1.512.
Вышеприведенное Рис 13.
доказательство этой
леммы имеет занятную историю. Оно было придумано
двумя английскими инженерами Г. Джильбертом и
Д. Мак-Доннеллом и опубликовано в American Ma-
Mathematical Monthly 7 A963), стр. 79—80, со следую-
следующим редакционным примечанием:
«Мартин Гарднер в своем обзоре книги Коксетера
«Введение в геометрию» (Scientific American 2C4
A961), стр. 166—168) описал эту знаменитую теорему
столь интересно, что сотни читателей прислали ему
свои доказательства. Он взял на себя труд по обра-
обработке этого громадного материала и совершенствовал
его до тех пор, пока не 'заблистала, очищенная от на-
наслоений, жемчужина, которую мы приводим здесь.»
25
Некоторые читатели могут испытать чувство не-
неудовлетворенности потому, что доказательство Д жил ь-
берта и Мак-Доннелла, подобно большинству других
(например, [22], стр. 73 [17], стр. 32), является кос-
косвенным: вместо самой теоремы Штейнера — Лемуса
они доказывают теорему, противоположную к обрат-
обратной (лемма 1.512). Было предложено несколько яко-
якобы прямых доказательств (например, [17], стр. 589 и
[42], стр. 31, 249); но каждое из них в действительно-
действительности является в скрытой форме косвенным. Это не-
несложно понять, если вспомнить, что практически толь-
только самые элементарные теоремы доказываются пол-
полностью. Все остальные доказываются с помощью
других, уже известных теорем, которые выстраиваются
в ряд, ведущий к аксиомам. Нельзя, строго говоря,
утверждать, что некое доказательство —прямое, если
хоть одна из этих вспомогательных теорем имеет кос-
косвенное доказательство. Более того, некоторые из са-
самых простых и самых основных теорем имеют кос-
косвенные доказательства; следовательно, если бы мы
настаивали на абсолютно прямом доказательстве, то
существующее великое множество теорем свелось бы
к небольшому числу тривиальных. Стоит ли об этом
сожалеть? Великий английский математик Г. Харди
говорил по этому поводу ([40], стр. 34):
«Reductio ad absurdum*), столь любимое Евкли-
Евклидом, является тончайшим инструментом математика.
Оно является намного более тонким гамбитом, чем
любой шахматный гамбит: шахматист может предло-
предложить в жертву пешку или другую фигуру, а матема-
математик предлагает в жертву всю игру.»
Упражнения
1. В треугольнике ABC даны величины углов В = 12°,
С = 132°. Проведены -внешние биссектрисы ВМ и CN этих углов
до пересечения с продолжениями противоположных сторон. Срав-
Сравните длины этих биссектрис, не используя тригонометрические
функции (О. Боттема) **).
*) Приведение к абсурду (лат.). — Прим. перев.
**) См. Archibald Henderson, Scripta Mathematica 21 A956),
стр. 309—310.
26
2. Где доказательство теоремы 1.51 нарушается, если мы по-
попытаемся применить его к внешним биссектрисам треугольника
Боттемы (в котором, как каждый согласится, В < С)?
3. Используйте упражнение 7 § 3 для получения «прямого»
доказательства теоремы Штейнера — Лемуса.
§ 6. Ортотреугольник
Можно многое узнать, исследуя рисунок 14, на ко-
котором изображены остроугольный треугольник ABC,
центр О описанной вокруг него окружности, ортоцентр
И и ортотреугольник DEF. Объясним, почему мы обо-
обозначили несколько углов на рисунке одним и тем же
символом а, имеющим
значение 90° — А. Во-пер-
Во-первых, так как треугольник
О А'С подобен треуголь-
треугольнику JBC, изображенно-
изображенному на рисунке 1, то
А'ОС=А. Таким образом,
величина каждого из уг-
углов при основании равно-
равнобедренного треугольника
ОВС равна 90° —Л. Из
прямоугольных треуголь-
треугольников A BE и ACF мы по-
поВ
Рис. 14.
лучаем те же значения
для углов ЕВА и ACF. Равенство последних дЕух
углов можно было бы увидеть из того факта, что че-
четырехугольник BCEF является вписанным, так как
углы ВЕС и BFC — прямые. Аналогично, используя
четырехугольники BDHF и CEHD, мы находим, что
Таким образом, отрезок HD является биссектрисой
угла EDF.
Из тех же соображений получаем, что отрезок НЕ
делит пополам угол FED, а отрезок HF — угол DFE.
Поэтому мы можем сформулировать следующий весь-
весьма интересный результат: высоты в треугольнике яв-
являются биссектрисами его ортотреугольника. Этот ре-
результат можно иначе записать в следующем виде:
27
Теорема 1.61. Ортоцентр остроугольного тре-
треугольника является центром окружности, вписанной
в его ортотреугольник.
Мы уже отметили на рисунке 14, что HDF = DBO
А так как отрезок HD перпендикулярен отрезку DB,
то и отрезок FD должен быть перпендикулярен отрез-
отрезку ОВ. Аналогично показывается перпендикулярность
отрезков DE и ОС, а также EF и ОА.
Упражнения
1. ДЛЕРсл ADBF ел ДОЕСсл ААВС (рис. 14).
2. Нарисуйте другой вариант рисунка 14, в котором угол при
вершине А — тупой. Какое из вышеприведенных заключений
должно быть изменено?
3. Ортоцентр тупоугольного треугольника является центром
вневписанной окружности к ортотреугольнику.
4. ЯЛО=|В-С|.
§ 7. Серединный треугольник и прямая Эйлера
Треугольник, полученный соединением середин сто-
сторон данного треугольника, назовем серединным тре~
угольником. На рисунке 15 треугольник А'В'С есть
серединный треугольник треугольника АВ~С. Рассмот-
Рассмотрим также две медианы АА' и ВВ', пересекающиеся
в точке С, две высоты треугольника ABC, пересекаю-
пересекающиеся в точке И, и две высоты треугольника А'В'С,
пересекающиеся в точке О. Поразительно, как много
можно обнаружить, лишь изучая этот рисунок.
Во-первых, стороны треугольника А'В'С парал-
параллельны сторонам треугольника ABC, поэтому эти тре-
треугольники подобны. Далее, | С В' \ = -^\ВС\, поэтому
отношение длин любых двух соответствующих отрез-
отрезков (а не только соответствующих сторон) будет рав-
равно 1:2. В действительности, отрезки В'С, С А', А'В'
разбивают треугольник ABC на четыре конгруэнтных
треугольника. Кстати, точка Р — середина отрезка
В'С — также является и серединой отрезка АА'.
Далее мы видим, что АС'А'В' — параллелограмм,
следовательно, прямая АА' делит пополам отрезок
В'С, Поэтому медианы треугольника А'В'С лежат на
28
медианах треугольника ABC, а это означает, что оба
треугольника имеют один и тот же центроид G.
Высоты треугольника А'В'С, изображенные нами
на рисунке, являются серединными перпендикулярами
сторон АВ и ВС треугольника ABC. Отсюда мы де-
делаем вывод, что точка О — ортоцентр треугольника
А'В'С — является в то же время и центром окружно-
окружности, описанной вокруг треугольника ABC.
Так как точка Н — ортоцентр треугольника ABC,
а точка О — ортоцентр подобного ему треугольника
А
А'В'С, то \АН\ =2|ОЛ'|. Вспомним, что по теоре-
теореме 1.32 \AG\ =2|СЛ'|. И, наконец, так как оба от-
отрезка, AD и ОА', перпендикулярны стороне ВС, то
они параллельны. Следовательно,
и
HAG = OA'G, A HAG go Д OA'G,
AGH = .
Этим показано, что точки О, G, И коллинеарны *) и
\HG\ = 2|GO|, т.е. справедлива
Теорема 1.71. Ортоцентр, центроид и центр опи-
описанной окружности произвольного треугольника ле-
лежат на одной прямой. Центроид делит расстояние от
*) Точки называются коллинеарными, если они лежат на од-
одной прямой. — Прим. перев. _
29
ортоцентра до центра описанной окружности в отно-
отношении 2:1.
Прямая, на которой лежат эти три точки, назы-
называется прямой Эйлера этого треугольника.
Давайте изучим рисунок 15 более тщательно. Мы
отметили точку N, где прямая Эйлера НО пересекает
прямую, проходящую через точку Р перпендикулярно
отрезку В'С. Все три прямые АН, PN и А'О, перпен-
перпендикулярные к отрезку В'С, параллельны. Так как
\АР\ = \РА'\, то прямая PN равноудалена от пря-
прямых АН и А'О. Следовательно, точка N — середина
отрезка НО.
До сих пор в наших рассуждениях фигурировала
сторона В'С треугольника А'В'С. Если мы проведем
те же рассуждения, но применительно к какой-либо
другой стороне этого треугольника, то отрезок НО
останется тем же, и он будет делиться пополам сере-
серединным перпендикуляром к новой стороне. Так как
у отрезка НО только одна середина, то мы можем
утверждать, что серединные перпендикуляры всех
трех сторон треугольника А'В'С будут проходить че-
через точку N. Другими словами, точка N должна быть
центром окружности, описанной вокруг треугольника
А'В'С.
Итак, центр окружности, описанной вокруг сере-
серединного треугольника, лежит в середине отрезка НО
прямой Эйлера исходного треугольника. Кроме того,
так как треугольник А'В'С подобен треугольнику
ABC, то радиус окружности, описанной вокруг сере-
серединного треугольника, равен половине радиуса окруж-
окружности, описанной вокруг исходного треугольника.
Имя Эйлера появляется столь часто и в столь
многих областях математики, что невозможно не ска-
сказать о нем несколько слов. Леонард Эйлер родился
в 1707 году в г. Базеле (Швейцария). В 1727 году он
был приглашен в Россию в Санкт-Петербургскую ака-
академию. В 1741 году он уехал в Берлин, чтобы полу-
получить кафедру математики Прусской академии. Он
вернулся в Санкт-Петербург в 1766 году и оставался
там вплоть до своей смерти в 1783 году.
Эйлер был неутомимым работником, его деятель-
деятельность обогатила каждую область математики. Куда
ни глянешь, всюду либо теорема Эйлера, либо фор-
30
мула Эйлера, либо метод Эйлера. Эйлер написал
473 мемуара, которые были опубликованы при его
жизни, и еще 200, которые были опубликованы вскоре
после его смерти, и еще 61 мемуар, которые были из-
изданы позже. И все это несмотря на то, что в 1735 году
он перестал видеть одним глазом, а в 1766 году обои-
обоими. Он обладал исключительным комбинаторным да-
даром, н его интуитивное понимание математики было
огромным. Мы еще не раз встретимся с его именем
в этой книге.
Упражнения
1. Начертив новый вариант рисунка 15, основанный на ри-
рисунке 2 (вместо ранее использованного рисунка 1), проверьте,
что наше доказательство теоремы 1.71 остается справедливым и
для случая тупоугольное™ треугольника ABC.
2. IOW|2 = 9tf2 — а2 — Ь2 — с2.
3. |D/l'| = |b2 — с2|/2а.
4. Если треугольник ABC обладает тем свойством, что его
прямая Эйлера параллельна стороне ВС, то tgfl-tgC = 3.
§ 8. Окружность девяти точек
Чтобы облегчить восприятие дальнейшего, мы убе-
уберем некоторые линии на рисунке 15 и добавим не-
несколько других; в результате получим рисунок 16.
Рассмотрим внимательно новый чертеж, на котором
К, L, М — середины отрезков АИ, ВИ, СИ, лежащих
на высотах. Так как ВС — общая сторона двух тре-
треугольников ABC и ИВС, а точки С, В' и L,M являют-
являются серединами других их сторон соответственно, то
отрезки С'В' и LM параллельны прямой ВС (а их
длины равны половине длины отрезка ВС). Аналогич-
Аналогично, так как АИ — общая сторона двух треугольников
ВАН и САИ, то оба отрезка CL и В'М параллельны
прямой АИ (а их длины равны половине длины отрез-
отрезка АИ). Следовательно, B'C'LM — параллелограмм.
Так как отрезки ВС и АИ — перпендикулярны,
то этот параллелограмм —прямоугольник. Аналогич-
Аналогично, A'B'KL — прямоугольник (как и С'А'МК). Следо-
Следовательно, А'К, B'L, CM являются тремя диаметрами
окружности, как показано на рисунке 17.
Так как ZA'DK — прямой, эта окружность (по-
(построенная на отрезке А'К, как на диаметре) проходит
31
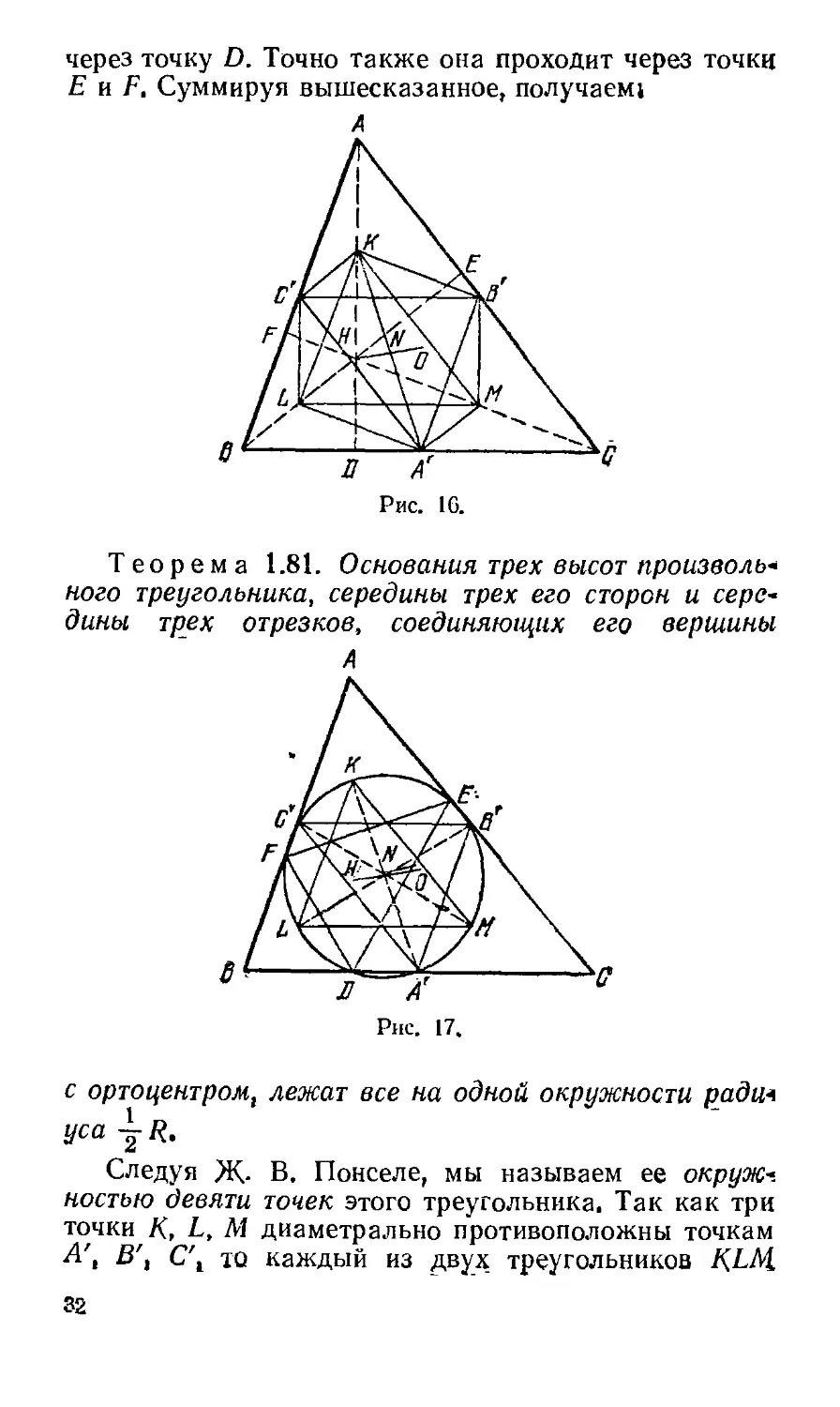
через точку D. Точно также она проходит через точки
Е и F. Суммируя вышесказанное, получаем!
C'l
Fr
1
IL,
1
J
л
7
r
\
\
M \
Л Аг
Рис. 16.
Теорема 1.81. Основания трех высот произвола
ного треугольника, середины трех его сторон и сере-
середины трек отрезков, соединяющих его вершины
А
с ортоцентром, лежат все на одной окружности рада*
уса -j R.
Следуя Ж- В. Понселе, мы называем ее окруж-.
ностью девяти точек этого треугольника. Так как три
точки К, L, М диаметрально противоположны точкам
Л', В\ С\ то. каждый из двух_ треугольников K.LM.
32
или А'В'С может быть получен из другого поворотом
На 180° вокруг центра этой окружности. Очевидно,
что этот поворот, который меняет местами эти два
конгруэнтных треугольника, должен также поменять
местами и их ортоцентры И и О. Следовательно, цент-
центром окружности девяти точек является середина от-
отрезка НО, которую уже ранее мы обозначили через N,
имея в виду ее будущую роль центра окружности де-
девяти точек. Другими словами:
Теорема 1.82. Центр окружности девяти точек
лежит на прямой Эйлера, точно в середине отрезка
между ортоцентром и центром описанной окружности.
История этих двух теорем несколько запутана. За-
дача Б. Бивана, опубликованная в английском жур-
журнале в 1804 году, по-видимому, указывает на то, что
эти теоремы уже тогда были известны. Иногда они
ошибочно приписываются Эйлеру, который уже в
1765 году доказав, что ортотреугольник и серединный
треугольник имеют общую описанную окружность.
И в самом деле, европейские авторы часто называют
эту окружность «окружностью Эйлера». По-видимому,
первое полное доказательство было опубликовано в
1821 году Понселе. К. Фейербах переоткрыл частич-
частичный результат Эйлера еще позже и добавил новое
свойство, которое является настолько замечательным,
что побуждает многих авторов называть окружность
девяти точек «окружностью Фейербаха». Теорема
Фейербаха (которую мы докажем в § 6 гл. 5) утвер-
утверждает, что окружность девяти точек касается вписан-
вписанной и всех вневписанных бкружностей.
Упражнения
1. Четырехугольник АКА'О (см. рис. 16) — параллелограмм.
2. В окружности девяти точек (см. рис. 17) точки К, L, М
делят пополам соответственно дуги EF, FD и DE.
3. Окружность, описанная вокруг треугольника ABC, явля-
является окружностью девяти точек треугольника hhh-
4. Пусть три конгруэнтные окружности имеют общую точку
и пересекаются еще в трех точках Л, В и С. Тогда радиус каж-
каждой из этих окружностей равен радиусу окружности, описанной
вокруг треугольника ABC, и их общая точка является ортоцен-
ортоцентром этого треугольника.
5. Окружность девяти точек пересекает стороны треуголь-
треугольника под углами \8 — С\, \С—Д|, |Д — Й|.
2 _Г. С. М. Коксетер. С. Л. ГреПтцер 33
§ 9. Педальный треугольник
Ортотреугольник и серединный треугольник явля-
являются двумя примерами сопутствующих треугольников
более общего типа. Пусть Р — любая точка внутри
данного треугольника ABC, и пусть перпендикуляры,
опущенные из точки Р на стороны ВС, СА, АВ тре-
треугольника будут РА\, РВ\ и РС\, как на рисунке 18.
Треугольник AiB\Cx, вершинами которого являются
основания этих перпендикуляров, называется педаль-
педальным треугольником треугольника ABC для «педаль-
«педальной точки» Р. Требование, чтобы точка Р находилась
А
внутри треугольника, можно ослабить, запретив лишь
точке Р находиться на окружности, описанной вокруг
треугольника ABC (по причинам, которые будут объ-
объяснены в § 5 гл. 2). Ясно, что*если точка Р — орто-
ортоцентр, то образуется ортотреугольник, а если она —
центр описанной окружности, то образуется середин*
ный треугольник.
Разберем рисунок 18 более детально. Прямые углы
в точках С\ и В\ указывают на то, что эти точки ле-
лежат на окружности с диаметром АР; другими слова-
словами, точка Р лежит на окружности, описанной вокруг
треугольника АВхС\. Применив теорему синусов к это-
этому треугольнику, а также к самому треугольнику-
ЛВС, мы получаем
sin A sin A
34
откуда
\ в г \— а\АР\
\b1c1\ — —w-
Аналогично,
|_ Ь\ВР\ , л о ,_. с\СР\
\ — —щ— и 1Л1#|| =—2R—
Таким образом, нами доказана
Теорема 1.91. Если расстояния от педальной
точки до вершин треугольника ABC равны х, у, z, то
длины сторон педального треугольника равны
ах by сг
~2R' ~2R' ~2R'
Разумеется, в частном случае х— у — z — R это
утверждение общеизвестно.
Перейдем к одной очень интересной задаче, в ко-
которой рассматриваются педальные треугольники пе-
педальных треугольников. Она в то же самое время
прекрасно демонстрирует роль воображения в геомет-
геометрии. Эта задача, по-видимому, впервые появилась в
1892 году, когда она была добавлена редактором
Ж- Нейбергом в шестое издание классического труда
Джона Кейси «Продолжение первых шести книг На-
Начал Евклида»*). На рисунке 19 внутренняя точка Р
использована для определения треугольника А\В\С\
(первого) педального треугольника треугольника
ABC. Та же самая педальная точка Р снова использо-
использовалась для определения педального треугольника тре-
треугольника Л1В1С1, который мы обозначим через А2В2С2
и, естественно, назовем «вторым педальным треуголь-
треугольником» треугольника ABC. Третья операция дает тре-
треугольник А3В3Сз — педальный треугольник треуголь-
треугольника А2В2С2. Мы подразумеваем, что и для «третьего
педального треугольника» использовалась та же са-
самая точка Р. В этих терминах открытие Нейберга
можно выразить следующим образом:
Теорема 1.92. Третий педальный треугольник
подобен исходному.
Доказательство является удивительно простым.
Оно легко следует из чертежа, стоит лишь соединить
♦) J. Casey, A Sequel to the First Six Books of the Elements
of Euclid Fth ed.), Hodges Figgis, Dublin, 1892,
2* 35
точки Р и А. Если рассмотреть окружности, описан-
описанные вокруг треугольников АВ\Си A2BtC2, А3ВЪС2,
А2В2С\ и А3В2С3, то точка Р принадлежит каждой из
них, поэтому
CiAP =
= А2ВХР = А2С2Р — В3С2Р = ВзА3Р
и
РАВ{ = PQBi = ЯС,Л2 = РВ2А2 = ЯВ2С3 = ЯЛ3С3.
Другими словами, две части, на которые прямая АР
делит угол А (обозначенные на чертеже одинарной и
А
двойной дугами), имеют двойников: одна — при вер-
вершине В\, а Другая — при вершине С\, далее — при
вершинах С2 и В2 и, наконец, обе — при вершине А3.
Следовательно, треугольник ABC и треугольник
А3В3С3 имеют равные углы при вершинах А и Л3.
Аналогично, они имеют равные углы при вершинах В
и В3. Таким образом, теорема доказана.
Интересно проследить на чертеже «шествие углов»
из положения А в положение А3 — столь же четкое,
как и маневры вымуштрованной команды.
Это свойство продолжающихся педальных тре«
угольников было обобщено доктором А. Оппенгеймом,
проректором Малайского университета в Сингапуре,
36
Он установил, что п-й педальный п-угольник любого
п-угольника подобен первоначальному п-угольнику.
Довольно поучительно провести подобное построение
для четвертого педального четырехугольника некото-
некоторого четырехугольника, про-
проследив еще более длинное «ше-
«шествие углов»,
На этом месте мы преры-
прерываем наши исследования. Мы
выполнили часть того, что на-
намеревались сделать; начав с
хорошо известных элементар-
элементарных утверждений, мы выявили
ряд простых, но важных фак-
фактов. Методы, описанные здесь,
позволяют решить многие за-
задачи. Некоторые из них — это широко известные труд-1
ные задачи, которые читатель, возможно, видел рань-
раньше. Мы хотим закончить эту главу пятью из этих не*
увядающих трудных задач,
А
Рис. 20.
Рис. 21.
Рис. 22.
Упражнения
1 Если продолжение чевианы AQ равностороннего треуголь-
треугольника ABC пересекает описанную окружность в точке Р, то
\РВ\ "г \РС\ ~ \PQ\m
37
2 Если внутри квадрата A BCD построен равнобедренный
треугольник РАВ с углами по 15° при основании АВ, как на ри-
рисунке 20. то точки Р, С, D являются вершинами равностороннего
треугольника.
3. Если прямые РВ и PD, проведенные вне параллелограмма
ABCD, составляют равные углы со сторонами ВС и DC соответ-
соответственно, как на рисунке 21, то СРВ — DP А. (Конечно, это пло-
плоский, а не пространственный чертеж.)
4. Пусть ABC — равнобедренный треугольник с углами по 80°
при вершинах В и С. Чевиана BD делит угол В на углы в 60°
и 20°, а чевиана СЕ делит угол С на углы в 30° и 50°, как на
рисунке 22. Найдите EDB.
5. Если две прямые, проходящие через одну из вершин рав-
равностороннего треугольника, делят полуокружность, построенную
извне на противоположной стороне, на три равных дуги, то этн
прямые делят саму сторону на три равных отрезка.
Глава 2
НЕКОТОРЫЕ СВОЙСТВА ОКРУЖНОСТЕЙ
Наряду с геометрией греки плодотворно
разрабатывали также многие другие обла-
области математики, но в настоящее время мы
всюду, несомненно и в геометрии, суще-
существенно перегнали их.
Ф. Клейн
Во все века окружность пользовалась наивысшим
уважением. Ее совершенная форма одинаково волно-
волновала как философов, так и астрономов. До открытия
Кеплером его законов мысль о том, что планеты мог-
могли бы двигаться иначе, чем по круговым орбитам, бы-
была невероятной. В наши дни слова «квадрат», «пря-
«прямая» и им подобные иногда имеют пренебрежительный
оттенок, но слово «окружность» — никогда. Очищен-
Очищенное от суеверного вздора и псевдонауки, это слово
и сейчас достойно уважения, как и всегда.
Из-за недостатка места мы* смогли изложить лишь
несколько самых интересных свойств окружности, об-
обнаруженных после Евклида, которые связывают ее
с треугольником и другими многоугольниками.
§ I. Степень точки относительно окружности
Мы начинаем наши исследования с напоминания
о двух теоремах Евклида: теореме о произведении
длин частей, на которые две хорды круга делят друг
друга (т.е. в обозначениях рисунка 23 |ЯЛ|-|РЛ'| =
= \РВ\ • \РВ'\), и теореме, сравнивающей секущую и
касательную, проведенные из одной и той же точки Р
вне круга (на рисунке 24 \РА\ ■ \РА'\ = \РТ\2). Если
мы договоримся рассматривать касательную как пре-
предельное положение секущей, то сможем соединить эти
результаты следующим образом:
Теорема 2.11. Если две прямые, проходящие че-
через точку Р, пересекают окружность: одна — в точках
А и А' {возможно совпадающих) ,ja другая — в точках
39
В и В' (возможно совпадающих), то
\РА\-\РА'\ = \РВ\-\РВ'\.
Для доказательства достаточно заметить, что из
подобия треугольников РА В' и РВА' (с общим углом
в точке Р, рис. 23) следует, что
\РА\ _ \РВ\
\РВ'\~ \РА'\'
В случае, изображенном на рисунке 24, мы можем с
Рис. 23.
Рис. 24.
тем же успехом использовать подобные треугольники
РАТ и РТА', получая
\РА\
\РТ\
\РТ\
\РА'\'
а затем записать \РА\ • \РА'\ = \РТ\2=\РВ\- \РВ'\.
Обозначим через R радиус окружности и через d
расстояние от точки Р до центра окружности. Пост-
роив диаметр ВВ', проходящий через точку Р (нахо-
(находящуюся дальше от точки В, чем от точки В'), мы ви-
видим, что если точка Р находится внутри окружности
(как на рис. 23), то
а если точка Р — вне ее (как на рис. 24), то
Равенство
40
\AP]-\PA'\ = R2-d2
дает короткое доказательство формулы, принадлежа*
щей Эйлеру:
Теорема 2.12. Пусть точки О и I являются
центрами (соответственно) описанной и вписанной
окружностей треугольника, радиусы которых равны R
и г; пусть d есть расстояние \О1\, Тогда
B.121)
= R2-2rR.
На рисунке 25 изображена внутренняя биссектри-
биссектриса угла А, продолженная до пересечения с описанной
окружностью в точке L, яв-
являющейся серединой той ду-
дуги ВС, которая не содержит
точку A. LM — диаметр, пер*
пендикулярный стороне ВС.
Обозначая для удобства
1 с-
а=*-А и
мечаем, что
\ = —В, мы за-
Так как внешний угол треугольника ABI в вершине /
удовлетворяет соотношению:
то треугольник LBI — равнобедренный. Таким обра-
образом,
sina
\LB\I\LM\
т. е. d2 = R2 — 2rR, что мы и хотели доказать.
Для любой окружности радиуса R и любой точки
Р, отстоящей на расстояние d от i^eHTpaj мы называем
ЧИСЛО
2
41
степенью точки Р относительно окружности. Эта сте-
степень является положительным числом, когда точка Р
лежит вне окружности, нулем, когда точка Р лежит
на окружности, и отрицательным числом, когда точка
Р лежит внутри нее. Для первого из этих случаев мы
уже получили выражение
\РА\-\РА'\,
где А и А' — любые две точки на окружности, колли-
неарные с точкой Р (как в теореме 2.11). Это выра-
выражение для степени точки Р останется справедливым
для любого положения точки Р, если мы согласимся
принять ньютоновскую идею о направленных прямо-
прямолинейных отрезках, как в одномерной векторной
алгебре, в которой
АР=-РА.
Произведение (или отношение) двух направленных
отрезков на одной прямой рассматривается как поло-
положительное или отрицательное число в зависимости от
того, совпадают или не совпадают их направления.
При таком соглашении равенство
d2 - R2 = РА X РА' *)
выполняется во всех случаях. Если точка Р — внутри
окружности, то d2 — R2 = — (R2 — d2) = —АР X РА'—
= РА X РА', а если точка Р — на окружности, то ли-
либо точка А, либо точка А' совпадает с точкой Р; по-
.этому один из этих отрезков имеет длину, равную
нулю. С другой стороны, заметив, что произведение
РА X РА' имеет одно и то же значение для любой се-
секущей (или хорды), проходящей через точку Р, мы
могли бы использовать эту величину для определения
степени точки Р относительно окружности.
*) Следуя установившейся традиции, мы будем обозначать
направленные отрезки и в тексте, и в формулах просто парой
букв (без стрелок или других знаков): первой ставится буква,
которой отмечена начальная точка, а затем буква, которой отме-
отмечена конечная точка (при этом АВ = —БА). Для обозначения
произведения направленных отрезков будет использован косой
крест. Путаница с обычными отрезками исключается тем, что в
тексте всегда будет оговорен случай использования направленных
отрезков, в формулах же участвуют для обычных отрезков лишь
их длины, имеющие специальное обозначение. — Прим. перее.
42
Слово степень было впервые использовано в этом
значении Якобом Штейнером, чье имя уже упомина-
упоминалось в первой главе.
Упражнения
1. Какую наименьшую (алгебраически) величину может иметь
степень точки относительно окружности данного радиуса Rf Ка-
Какая точка имеет эту экстремальную степень?
2. Каково множество точек, имеющих постоянную степень
(большую, чем —R2) относительно данной окружности?
3. Пусть степень точки имеет положительное значение t2.
Дайте геометрическую интерпретацию длины t.
4. Если РТ и PU — касательные из точки Р к двум концен-
концентрическим окружностям, причем точка Т находится на меньшей
из них, и если отрезок РТ пересекает большую окружность в
точке Q, то
|РГ|2— \PU\2 = \QT\2.
5. Радиус окружности, описанной вокруг треугольника, по
крайней мере вдвое больше радиуса вписанной окружности.
6. Выразите (в терминах г и, R) степень центра вписанной
окружности относительно описанной.
7. Применение направленных отрезков дает нам возможность
выразить теорему Стюарта (упражнение 4 § 2 гл. 1) в следую-
следующей симметричной форме ([22], стр. 152): Если Р, А, В, С—че-
С—четыре точки, из которых последние три коллинеарны, то
РА2. ВС + РВ2 ■ С А + PC2 -AB+BCXCAXAB = O.
» 8. Прямая, проходящая через центроид G треугольника ABC
пересекает стороны треугольника в точках X, У, Z. Используя
понятие направленных отрезков, докажите, что
"gT + 'gF + 'gz а
9. Сколь далек горизонт, если смотреть с вершины горы вы-
высотой в 1 милю A миля = 1,609 км)? (Считайте, что Земля —
сфера диаметра 7920 миль.)
§ 2. Радикальная ось двух окружностей
Е. Т. Белл рассказывает интересную историю ([4],
стр. 48). Молодая принцесса Елизавета, высланная из
Богемии, применяя метод координат, выполнила ре-
решение одной геометрической задачи, которая, по
утверждению Белла; «являлась прекрасным образцом
задач, неприспособленных для прямого применения
к ним грубой силы элементарной декартовой геомет-
геометрии». Ее учителем был Рене Декарт (в честь которого
43
декартовы*) координаты и получили свое назва«
ние**)). Узнав об этом, он заметил, что «не взялся
бы выполнить ее решение даже за ... месяц».
Урок ясен: если у нас имеется метод, с помощью
которого можно получить решение задачи, то это ре-
решение может еще и не быть наилучшим или самым
экономным. Во всяком случае, аналитическое доказа-
доказательство следующей теоремы, будучи нисколько не
сложнее, чем обычное синтетическое доказательство
([7], стр. 32), влечет за собой ряд интересных резуль-
результатов.
Теорема 2.21. Множество точек, для которых
степени относительно двух неконцентричных окруж-
окружностей равны, является прямой, перпендикулярной ли~
нии центров этих окружностей.
В терминах декартовых координат квадрат рас-
расстояния d между любыми двумя точками (х, у) и
[а, Ь) выражается как
(х-аJ + (у-ЬJ.
Поэтому степень точки (х, у) относительно окружно-
окружности радиуса г с центром в точке (а, Ь) равна
d2 г г2 = (х - аJ + (у - Ь2) - г2.
В частности, сама окружность, являясь множеством
точек (х, у) степени нуль, имеет уравнение
B.211) (х-аJ + (у-ЬJ-г2 = 0.
То же самое уравнение в форме (х — аJ-\-(у—ЬJ=
t=r2 выражает окружность как множество точек, уда*
ленных от точки (а, Ь) на постоянную величину г.
Когда эта окружность выражена в форме
B.212) х2 + у2 — 2ах —
{c = a2'-sfb2— г2), степень произвольной точки [х,у)
снова выражается левой частью уравнения, а именно:
х2 + У2 — 2ах — 2Ьу + с.
*) Их еще называют картезианскими также в честь Декар*
та, латинизированное имя которого — Renatus Cartesius. — Прим.
перев.
**) Некоторые считают, что создание аналитической геомет»
рии в действительности принадлежит Пьеру Ферма A601—1665).
Оии утверждают, что ее основная идея была им изложена в од-
одном из писем к Декарту,
44
Другая окружность с тем же центром (а, Ь), но иным
радиусом, описывается уравнением такой же формы,
но с другим с, а любая окружность с отличающимся
центром описывается уравнением вида
B.213) x* + y2-2a'x-2b'ij + c'=:0,
где либо а ф а', либо Ь Ф Ь', либо одновременно и то,
н другое. Таким образом, мы можем использовать
уравнения B.212) и B.213) для описания двух некон-
центрическнх окружностей, упомянутых в теореме 2.21.
Множество всех точек (х, у), степени которых относи-
относительно этих двух окружностей равны, описывается
уравнением
.v2 + У2 - 2ах - 2Ьу + с = х2 + у2 - 2а'х - 2Ъ'у + с',
а так как х2 + У2 сокращается, то это множество есть
прямая
Выбрав нашу систему отсчета так, чтобы ось х
проходила через оба центра, мы сможем описать эти
две окружности в более простой форме,
B.214)
х2 + У2 ~ 2ах + с<= 0, .v2 + У2— 2а'х + с' = О,
где а! Ф а. Тогда наше множество описывается урав-
уравнением
_ с'-с
Х— 2(а'-а) •
Эта прямая, параллельная оси Оу, перпендикулярна
оси Ох, которая является линией центров. Так как
прямая может быть определена геометрически через
эти окружности (как множество, содержащее все точ-<
ки с одинаковыми степенями), то мы могли бы при-
принять ее га саму ось Оу, как изображено на рисунке 26.
Таким образом, любые две неконцентрические окруж-
окружности могут быть описаны в еще более простой форме
B.215)
Теперь наше множество описывается уравнением х=0.
И, наоборот, каждая точка @, у) прямой х = 0 имеет
45
одну и ту же степень у2 + с относительно обеих
окружностей.
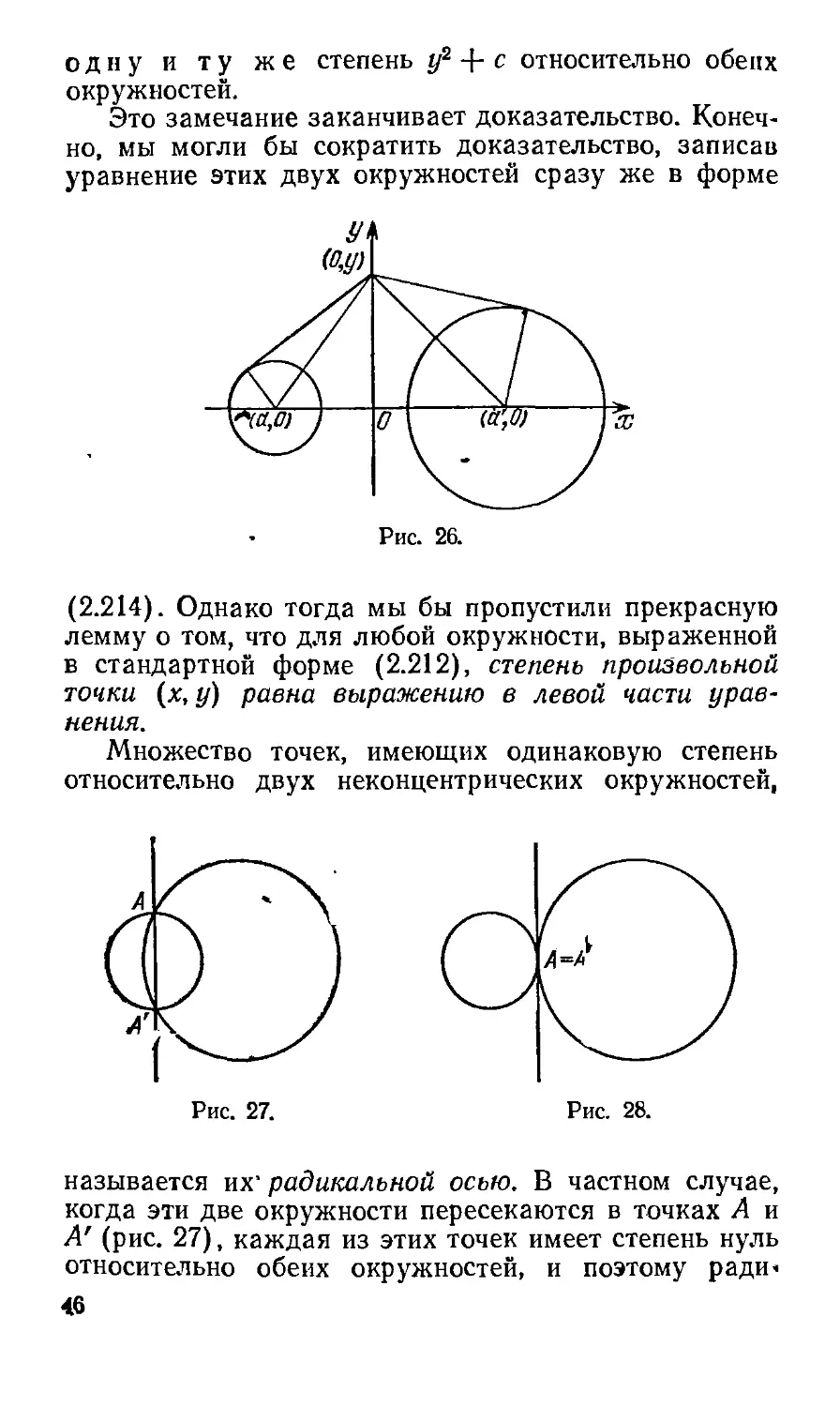
Это замечание заканчивает доказательство. Конеч-
Конечно, мы могли бы сократить доказательство, записав
уравнение этих двух окружностей сразу же в форме
Рис. 26.
B.214). Однако тогда мы бы пропустили прекрасную
лемму о том, что для любой окружности, выраженной
в стандартной форме B.212), степень произвольной
точки (х, у) равна выражению в левой части урав-
уравнения.
Множество точек, имеющих одинаковую степень
относительно двух неконцентрических окружностей,
Рис. 27.
Рис. 28.
называется их1 радикальной осью. В частном случае,
когда эти две окружности пересекаются в точках А и
А' (рис. 27), каждая из этих точек имеет степень нуль
относительно обеих окружностей, и поэтому ради*
46
кальная ось—просто прямая АА'. Аналогично, когда
две окружности касаются друг друга (рис. 28), их ра-
радикальная ось является их общей касательной в точке
их касания.
Упражнения
1. Каково множество точек, для которых касательные к двум
данным окружностям имеют равные длины?
2. Если расстояние между центрами двух окружностей боль-
больше, чем сумма их радиусов, то окружности имеют четыре об-
общие касательные. Середины этих четырех отрезков коллииеарны.
3. Пусть РАВ, AQB, ABR, Р'ВА,
BQ'A, BAR' — шесть подобных
треугольников*, лежащих по одну сто-
сторону от их общей стороны АВ (три
из них показаны на рисунке 29, а
остальные могут быть получены сим-
симметрией *) относительно серединного
перпендикуляра к отрезку АВ). Те
вершины этих треугольников, кото-
которые не лежат на отрезке АВ (а
именно, Р, Q, R, P', Q', R') все ле-
лежат на одной окружности.
Указание. Сравните степени
точек А и В относительно окружно-
окружности PQR.
4. Пусть даиы числа а и Ь. Для
каких значений с уравнение B.212) Рис. 29.
описывает окружность?
5. Опишите построение радикальной оси двух данных некон-
неконцентрических окружностей: [построение должно быть применимо
и в том случае, когда одна окружность содержит другую.
§ 3. Соосные окружности
Как мы видели, любые две неконцентрические
окружности могут быть описаны уравнениями B.215)
и, следовательно, являются элементами бесконечного
семейства, описываемого уравнением
где с — фиксировано, в то время как а меняется
во всем интервале действительных значений (за
*) Операция симметрии бывает полезна при решении многих
геометрических задач. Смотри, например, Яглом [43], т. 1.—
Прим. ред.
47
исключением интервала от — /\[с до -(- *\Jc в случае
положительного с). Это семейство называется пучком
соосных окружностей, так как каждые две окружности
из этого семейства имеют одну и ту же линию цент-
центров и одну и ту же радикальную ось. Если с отрица-
отрицательно, то каждый элемент семейства пересекает ось
у в одних и тех же двух точках @, ± У— c)> и пучок
состоит просто из всех окружностей, проходящих че-
через эти две точки. Аналогично, если с = 0, то пучок
состоит из всех окружностей, которые касаются оси
Оу в начале координат. Случай, когда с положитель-
положительно, проиллюстрирован на рисунке 30.
Рис. 30.
Пусть три окружности не являются соосными, и
кроме того, никакие две не концентричны, тогда, рас-
рассмотрев их попарно, мы сможем найти три радикаль-
радикальные оси. Любая точка, которая имеет одну и ту же
степень относительно всех трех окружностей, должна
лежать на всех этих трех прямых. Наоборот, любая
точка пересечения двух из трех радикальных осей,
имеющая одну и ту же степень относительно всех трех
окружностей, должна также лежать и на третьей пря-
~мой. Если две из этих осей параллельны, то и все три
должны быть параллельны. В частности,
Теорема 2.31. Если центры трех окружностей
образуют треугольник, то существует только одна
точка, степени которой относительно этих трех окруж-
окружностей равны.
Эта общая точка трех радикальных осей называ-
называется радикальным центром трех окружностей,
48
Упражнения
1. Две окружности касаются внутренним образом в точке Т,
Пусть хорда АВ большей окружности касается меньшей окруж«
ностп в точке Р. Тогда прямая ТР делит угол АТВ пополам.
2. Если О — радикальный центр трех окружностей, .каждая
из которых лежит вне других, то точки касания шести касатель-
касательных, проведенных из точки О, лежат все на одной окружности.
§ 4. Еще раз о высотах и ортоцентре треугольника
Окружность, описанная вокруг треугольника, ко-
торая уже встречалась нам в предыдущей главе, за-
заслуживает дальнейшего изучения. На рисунке 31 по-
показана окружность, описанная вокруг треугольника
ABC с центром в точке О, диаметром АА0, прохо-
проходящим через точку А, и радиу-
радиусом OL (\OL\ = R), перпенди-
перпендикулярным стороне ВС. Мы так-
также видим высоту \AD\ = ha.
Равенство углов в точках В
и Ао указывает нам на подобие
треугольников ABD и АА0С,
откуда
ha Ь
с | ААй |
и
в
B.401)
и _
_
2R '
Рис. 31.
Вычитая из величины угла ВАС величины двух равных
углов:
А^АС = BAD = 90° -В,
мы получаем:
X = A- 2(90°~В) =
Это выражение для угла DAA0, равного углу DAO,
было получено нами для того случая (изображенного
на рисунке), когда В > С. Если бы мы взяли В < С,
то угол DAO стал бы пересечением двух равных углов
АоАС и BAD, а, следовательно, его величина стала бы
49
равной С—В. Теперь мы можем объединить оба слу-
случая, записав
B.402) DAO = | В — С \.
На рисунке 32 показаны три высоты AD.BE, CF,
продолженные до пересечения с описанной окруж-
окружностью в точках D', Е', F'. Точка Н, как ввегда, г—
ортоцентр. Теперь DAB—FCB, причем оба угла
являются дополнительными углами к углу В до пря-
прямого угла. Это объясняет использование нами одного
и того же символа 6 для
обозначения обоих углов.
Также BCD' = BAD', поэто-
поэтому мы обозначили угол
BCD' тем же символом. Из
конгруэнтности прямоуголь-
прямоугольных треугольников CDH и
CDD' следует, что
B.403) \HD\ = \DD'\.
Аналогично, I HE I = I ЕЕ' I и
\HF\ = \FF'\.
Так как окружность с
диаметром АВ проходит че-
через точки D и Е, то из теоре-
теоремы 2.11 мы получаем, что
Рис.32. \HA\-\HD\ = \HB\.\HE\.
Подобным же образом,
\HB\-\HE\ = \HC\-\HF\. Следовательно,
B.404) \HA\-\HD\ = \HB\-\HE\ = \HC\-\HF\.
Если X, Y, Z — любые точки, взятые на сторонах
ВС, СА, АВ соответственно, то окружности, построен-
построенные на чевианах АХ, BY и CZ как на диаметрах, бу-
будут проходить через основания высот: точки D, E, F
соответственно. (Вторая и третья окружности изобра-
изображены на рисунке .33.) Три равных выражения в соот-
соотношении B.404) являются степенями точки Н относи-
относительно этих трех окружностей. Следовательно, Н есть
радикальный центр этих окружностей. Таким обра-
образом, мы доказали две интересные теоремы, которые
появились в разное время, как трудные задачи.
БО
Теорема 2.41. Если окружности построены на
двух чевианах как на диаметрах, то их радикальная
ось проходит через ортоцентр этого треугольника.
Теорема 2.42. Для любых трех несоосны к
окружностей, имеющих чевианы в качестве диамет-
диаметров, точка Н — их радикальный центр.
С другой стороны, т$ же результаты могут быть
получены с помощью следующих простых соображе-
соображений. Если AD—rвысота, опущенная из точки А, то пу-
пучок соосных окружностей, проходящих через точки А
и D, может быть описан как совокупность окружно-
окружностей, имеющих чевианы, проходящие через точку А,
в качестве диаметров. Две из
этих чевиан есть стороны АВ и
'АС. Таким образом, окружно-
окружности, построенные на сторонах
ВС, С А, АВ как на диаметрах
и взятые попарно, имеют вы-
высоты в качестве своих ради-
радикальных осей и точку А в
качестве своего радикального
центра. (Таким образом, вид-
видно, что конкурентность вы-
сот является частным случаем
теоремы 2.31.) Из этого сле-
следует, что точка Н имеет одну Рис. за
и ту же степень относительно
всех окружностей, имеющих чевианы в качестве диа-
диаметров.
Обратите внимание на слово «несоосный» в фор-
формулировке теоремы 2.42. Оно означает, что три рас-
рассматриваемые чевианы не все исходят из одной вер-
вершины треугольника ABC. В следующей теореме мы
увидим, что это понятие означает даже немного
больше1
Из теоремы 2.42 можно вывести ряд любопытных
задач (применив ее к чевианам АХ, BY, CZ), если до-
дополнительно ввести некоторые несущественные дета-
детали. Пусть вас не смущает тот факт, что хотя три
чевианы треугольника, как правило, не имеют общей
точки, мы будем рассматривать и случаи их конку-
конкурентности. Например, докажите, что для окружностей,
построенных на медианах (или высотах, или биссек-
51
трисах) как на диаметрах, их радикальный центр яв-
является ортоцентром этого треугольника.
Самый интересный случай для неконкурентных че->
виан возникает тогда, когда точки X, Y, Z, лежащие
на отрезках ВС, С А, АВ (или их продолжениях), ока-
оказываются коллинеарными, как на рисунке 34.
Тогда мы можем с равным успехом утверждать, что
точки X, В, С—коллинеарные точки на сторонах тре-
треугольника AYZ и что точки Y, С, А —»коллинеарные
точки на сторонах треугольника BZX, и что точки Z,
Рис. 34.
А, В — коллинеарные точки на сторонах треугольник
ка CXY.
Следовательно, окружности, построенные на отрез-
отрезках АХ, BY и CZ как на диаметрах, расположены
так, что их радикальные оси проходят через точку Н,
а также, по тем же соображениям, и через ортоцент-
ортоцентры других трех треугольников. Так как эти четыре
ортоцентра очевидно различны, то эти радикальные
оси должны совпасть. Таким образом, нами доказана
Теорема 2.43. Если четыре прямые пересекают-
пересекаются в шести точках А, В, С, X, Y, Z так, что образуются
множества коллинеарных точек: {X, В, С}, {Y,C,A},
{Z,A,B}, {X, Y,Z), то окружности, построенные на от-
отрезках АХ, BY, CZ как на диаметрах, соосны, а орто-
ортоцентры четырех треугольников AYZ, BZX, CXY и ABC
коллинеарны.
52
Другое свойство треугольника и его высот проил-
проиллюстрировано на рисунке 8. Если мы внимательно
рассмотрим этот рисунок, то мы придем к выводу, что
по тем же причинам, по которым точка Н является
ортоцентром треугольника ABC, точка А является
ортоцентром треугольника НВС, точка В — орто-
ортоцентром треугольника НАС, а точка С — ортоцентром
треугольника НАВ. Рассмотренная здесь конфигура-
конфигурация АВСН называется ортоцентрическим четырех'
угольником и обладает рядом интересных свойств.
Здесь мы рассмотрим только одно из них, а именно:
если АВСН — ортоцентрический четырехугольник, то
для четырех треугольников, вершины которых являют-
являются вершинами этого четырехугольника, описанные во~
круг них окружности имеют равные радиусы.
Простейшее доказательство этого свойства осно-
основано на уравнении B.403) и рисунке 32. На ето,м ри-
рисунке треугольники НВС и D'BC конгруэнтны, а по-
потому окружности, описанные вокруг них, конгруэнтны.
Следовательно, окружность, описанная вокруг тре-
треугольника D'BC (или ABC), конгруэнтна окружности,
описанной вокруг треугольника НВС. Аналогично про-
проводятся рассуждения и для остальных треугольников.
Упражнения
1. Точки, в которых высоты или их продолжения пересекают
описанную окружность, образуют треугольник, подобный ортоцен«
трическому.
2. Биссектрисы внутренних углов треугольника ABC продол-
продолжаются до пересечения с описанной окружностью в точках L,
М, N соответственно. Выразите углы треугольника LMN через
углы треугольника ABC.
§ 5. Прямые Симеона
Если из точки Р опущены перпендикуляры на сто-
стороны треугольника ABC, то основания этих перпенди-
перпендикуляров, как правило, образуют вершины треугольни-
треугольника AiBiCi (это педальный треугольник, рассмотрен-
рассмотренный в § 9 гл. 1). *
Теперь давайте рассмотрим тот особый случай,
когда точка Р лежит на описанной окружности, как
на рисунке 35. Для определенности будем считать, что
53
точка Р находится на дуге СА, не содержащей
точку В.
Все остальные случаи могут быть получены пере-
переобозначением вершин буквами А, В, С. Так как углы
Аи Вх и С\ — прямые, то точка Р также лежит на
окружностях, описанных вокруг треугольников А\ВС\,
ABC и ABid. Поэтому
и, вычитая АРА\, мы выводим, что
Но так как точки А\, С, Р, Вх лежат на окружности, то
и, так как точки А, Ви Р, С\ лежат на окружности, то
Таким образом,
-■--, Р
отсюда следует, что точки А\, В\, С\ — коллинеарны,
т. е. педальный треугольник «вырождается».
Наоборот, если точка Р рас-
расположена так, что педальный
треугольник треугольника ABC
вырождается, то, . очевидно, что
точка Р должна лежать внутри
одного из углов треугольника
ABC и вне противолежащей ему
стороны. Переобозначая верши-
вершины, если это необходимо, мы мо-
можем предположить, что этот
«один угол» является углом- В и
что точка С\ лежит на продолже-
продолжении стороны ВА за точку А, как
на рисунке 35. Повторяя приве-
приведенные выше рассуждения об углах в обратном по-
порядке, мы сможем получить, что точка Р лежит на
описанной окружности. Следовательно, справедлива
Теорема 2.51. Основания перпендикуляров, опу-
опущенных из точки на стороны треугольника, коллине-
Ы
Рис. 35.
арны тогда и только тогда, когда эта точка лежит на
описанной окружности. ,
Прямая, содержащая эти основания, известна как
прямая Симеона данной точки относительно данного
треугольника. Роберт Симеон A687—1768) внес зна-
значительный вклад как в геометрию, так и в арифме-
арифметику. Например, именно он открыл, что если fn есть
п-й член ряда Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, .... то ffl_.-ffl+1-ft = (-l)'1 ([17], стр. 243-
247). Прямая Симеона приписывалась ему, поскольку
она казалась типичной для его геометрических идей.
Однако историки тщетно пытались найти ее в его ра-
работах. В действительности,
она была открыта в 1797 го- А
ду Вильямом Уоллесом.
Упражнения
1. Нуждается ли наше доказа-
доказательство теоремы 2.51 в каких-либо
изменениях для того случая, когда
треугольник ABC — тупоугольный?
2. Какая точка окружности
имеет прямую СА своей прямой
Симсоиа?
3. Существуют ли какие-либо
точки, лежащие на своей прямой
Симеона? Какими прямыми они
могут быть в этом случае?
4. Две касательные к окружности, касающиеся ее в точках
В к С, пересекаются в точке А. Пусть Ai, Bi, Ci — педальный
треугольник равнобедренного треугольника ABC для произволь-
произвольной точки Р"на этой окружности, как на рисунке 36. Тогда
Рис. 36.
§ 6. Теорема Птолемея
Понятие прямой Симеона может быть использова-
использовано для вывода очень полезной теоремы. Рассмотрим
вновь рисунок 35. Хотя «педальный треугольник»
*А\В\С\ вырожден, длины его «сторон» все еще могут
быть вычислены с помощью теоремы 1.91:
55
Так как | АХВХ \-\-\BxC\ | = | ЛА |, мы выводим, что
с\СР\ + а\ АР\ = Ь\ВР\,
\АВ\-\СР\ + \ВС\-\АР\ = \АС\-\ВР\.
т. е.
Так как АВСР — вписанный четырехугольник, то та*
ким образом мы доказали теорему Птолемея:
Теорема'2.61. Если четырехугольник вписан в
окружность, то сумма произведений длин двух пар
его противоположных
сторон равна произве-
произведению длин его диаго-
диагоналей.
Теорема Птолемея
имеет обратную, кото-
которая может быть усиле^
на, если принять во
внимание, что в случае,
когда точка В\ не ле-
лежит на отрезке А\С\,
C| должно быть заме-
замеРис. 37.
равенство |/4i
нено «неравенством треугольника»
\AlBl\ + \BlCl\>\AlCl\,
что дает
\АВ\-\СР\ + \ВС\-\АР\>\АС\-\ВР\.
Следовательно, справедлива ~~
Теорема 2.62. Если точка Р не лежит на дуге
СА окружности, описанной вокруг треугольника ABC,
то
\АВ\.\СР\ + \ВС\.\АР\>\АС\-\ВР\.
Упражнения
1. Пусть Р — любая точка в плоскости равностороннего тре-
треугольника ABC. Тогда \РС\ + \РА\ = \РБ\ или \РС\ + \РА\>
>\РВ\ в зависимости от того, лежит или иет точка Р на
дуге СА описанной окружности. (Интересные применения этого
результата см. [31], стр. 11—12.)
2. Если точка Р лежит на дуге CD окружности, описанной
вокруг чвадрата ABCD, то
Б6
3. Если окружность пересекает две стороны и диагональ па-
параллелограмма ABCD в точках Р, R, Q, как показано на рисун-
рисунке 37, то
\AP\-\AB\+\AR\-\AD\ = \AQ\.\AC\.
Указание. Примените теорему 2.61 к четырехугольнику
PQRA, а потом замените стороны треугольника PQR соответ-
соответствующими сторонами подобного ему треугольника СВА.
§ 7. Еще раз о прямых Симеона
Прямая Симеона обладает многими интересными
свойствами и стоит рассмотреть некоторые из них.
Начнем с рассмотрения рисунка 38, который повто-
повторяет рисунок 35, за исключением перпендикуляра РАи
Рис. 38.
В
продолженного до пересечения с описанной окруж*
ностью в точке U, и добавленной прямой All.
Поскольку четырехугольники РАИС и РВ\А\С впи-
вписанные, то
PUA = РСА = РСВх = P/UBl
Поэтому прямая AU параллельна прямой Сим,'
сона А\В\.
Сравним теперь прямую Симеона точки Р с пря-
прямой Симеона другой точки Р' (лежащей, конечно, на
той же описанной окружности). Угол между этими
двумя прямыми Симеона, очевидно, равен углу UAU'
между параллельными им прямыми А V и А V
(рис. -39). Две хорды PLJ и P'V, перпендикулярные
Б7
отрезку-ВС, параллельны друг другу и отсекают рав-
равные дуги РР' и ULJ'. Таким образом,
uau' = | иди' =±
или, если мы различаем положительные и отрица-
отрицательные углы, то
UAU' = у UOUf = - -[ POP'.
Таким образом, нами доказана
Теорема 2.71. Величина угла между прямыми
Симеона двух точек Р и Р', лежащих на описанной
окружности, равна угловой ме-
мере величины дуги РР'.
Если мы вообразим точку Р
равномерно двигающейся по
описанной окружности, то пря-
прямая AU будет равномерно вра-
вращаться вокруг точки А со вдвое
меньшей угловой скоростью и
направленной в обратную сто-
сторону; при этом она переменит
первоначальное направление
на противоположное к тому
моменту, когда точка опишет
полную окружность. Тем вре-
временем, прямая Симеона будет
поворачиваться соответствую-
соответствующим образом вокруг непрерыв-
непрерывно меняющегося центра вра-
вращения. На самом деле, прямая
Симеона при движении посто-
постоянно касается красивой симметричной кривой, кото-
которая называется дельтоидой или «гипоциклоидой
Штейнера» [24]. Это движение можно было бы легко
проследить, если нарисовать последовательные поло-
положения прямой и составить из них мультфильм.
Для продолжения наших исследований давайте
рассмотрим сейчас рисунок 40, который является ком-
комбинацией рисунков 34 и 38 с добавлением прямой HP,
прямой D'P (пересекающей отрезок ВС в точке Q) и
прямой HQ (продолженной до пересечения с прямой
Б8
Рис. 40.
PU в точке V). Так как и отрезок HD', и отрезок PV
перпендикулярны стороне ВС, то из уравнения B.403)
следует, что треугольники QHD' и QPV являются рав-
равнобедренными. Другими словами, отрезок HV являет-
является образом отрезка D'P при симметрии относительно
прямой ВС. Так как
ЕП1V = Р\/Ъ = Г/PLJ = /f/Ш,
то прямая HV параллельна прямой AU, которая,
как мы уже показали, параллельна прямой Симеона
точки Р.
И, наконец, отметим, что в треугольнике PHV пря-
прямая Симеона А\В\ параллельна стороне HV и делит
пополам отрезок PV (в точке А\). Следовательно, она
также обязана делить пополам оставшуюся сторо-
сторону РН:
Теорема 2.72. Прямая Симеона точки (лежащей
на описанной окружности) делит пополам отрезок,
соединяющий эту точку с ортоцентром.
Все это было только введением в круг идей, свя*
занных с прямой Симеона. Существует много других
свойств, рассмотрение которых мы, к сожалению, вы-
вынуждены предоставить другим авторам.
Упражнения
1. Прямые Симеона диаметрально противоположных точек
описанной окружности перпендикулярны между собой и пересе-
пересекаются на окружности девяти точек. *
2. Пусть ABC — равносторонний треугольник, вписанный в
окружность с центром О. и пусть Р — произвольная точка на этой
окружности. Тогда прямая Симеона точки Р делит пополам ра-
радиус О Р.
§ 8. Теорема о бабочке
Теорема о бабочке была популярна довольно дол-
долго. Мы ее формулируем следующим образом (рис.41):
Теорема 2.81. Пусть через точку М, являющую-
являющуюся серединой хорды PQ некоторой окружности, прове-
проведены две произвольные хорды АВ и CD. Хорды AD
и ВС пересекают отрезок PQ в точках X и Y. Тогда
точка М является серединой отрезка XY.
Было найдено много доказательств этой теоремы
различной длины и трудности. Три доказательства
59
были получены от доктора Золля из Ньюаркского
колледжа. Он сообщил при этом, что одно из них бы-
было предложено в 1815 году В. Г. Горнером, открыв-
открывшим метод приближенного вычисления корней много-
многочленов. (Согласно Е. Т. Беллу, метод Горнера был
предвосхищен китайскими математиками.) Другое до-
доказательство см. Р. Джонсон [11], стр. 78 и [42],
стр. 33, 259. Самое короткое доказательство исполь-
использует проективную геометрию ([19], стр. 78, 144). До-
Доказательство, представленное здесь, хотя и не очень
коротко, но довольно про-
простое и легкое для запоми-
запоминания. »
Сначала опустим перпен-
перпендикуляры Х\ и у\ из точек X
и У на прямую АВ, затем
перпендикуляры х2 и у2 из
точек X и У на прямую CD.
Обозначая для удобства
г/ = |7ИУ|, мы замечаем, что
рис 41. из рассмотрения пар подоб-
подобных треугольников Мх\ *) и
Му\, Мх2 и Му2, Ах\ и Су2, Dx2 и Ву\ вытекает, что
X
У '
откуда
X* X
Ух
• Х2
Уг
\CY\
У\-Уг
и х— уГ
_ Х.-Х2 _ \AX\.\XD\ _
У2-У1 ~ \CY\-\YB\ ~
(а — х)-(а + х)
(« + У) ■ (« - У) '
мы и хотели доказать.
У\
\РХ\.
\PY\-
а2-
я2-
\YB\'
\XQ\
№\
х2 а2
и1 а2
а- «
"Г5" *
Упражнения
1. На рисунке 41 прямые АС и BD пересекают прямую PQ
в двух точках, которые, как и точки X и У, равноудалены от
точки М.
*) Обозначение Mxi означает треугольник с вершиной М й
противолежащей ей стороной xi\ аналогично и дальше. — Прим.
черев.
2. Пусть РТ и РВ — две касательные к окружности, АВ —
диаметр, проходящий через точку В, и ТН — перпендикуляр, опу-
опущенный из точки Т на АВ. Тогда прямая АР делит пополам от-
отрезок ТН.
3. Пусть окружность (с центром в точке /), вписанная в тре-
треугольник ABC, касается стороны ВС в точке X и пусть А' — се-
середина этой стороны. Тогда прямая А'1 делит пополам отре-
отрезок АХ.
§ 9. Теорема Морлея
Одна из самых удивительных теорем элементарной
геометрии была открыта в 1904 году Франком Мор-
леем (отцом Кристофора Морлея, в романе которого
«Гроза слева» было приме-
применено «закручивание» тече-
течения времени, особенно по-
понравившееся геометрам). Он
упоминал об этой теореме
своим друзьям в Кембридже
(Англия) и опубликовал ее
двадцать лет спустя в Япо-
Японии. Тем временем она была
переоткрыта и представле-
представлена, как задача в журнале
«Educational Times». Было
прислано два решения, одно Рис. 42.
из которых, принадлежащее
М. Т. Нараньенгару*), столь же лаконично, как и
масса других, найденных с тех пор. Теорема утверж-
дает:
Теорема 2.91. Точки пересечения смежных три-
трисектрис углов произвольного треугольника являются
вершинами равностороннего треугольника.
Доказательство Нараньенгара нуждается в сле-
следующей лемме (проиллюстрированной на рисунке 42) :•
Лемма. Если четыре точки Y', Z, Y, Z' удовлет~
воряют условиям
YZY' = rYZ = 180° — 2а > 60°,
*) Mathematical Questions and Their Solutions from Educa-
lional Times -(New Series) 15 A909), стр, 47.
61
то они лежат на одной окружности. Кроме того, если
точка А, расположенная по другую сторону от прямой
Y'Z', нежели точка У, образует угол Y'AY = За, то эта
пятая точка А также лежит на той же окружности.
Докажем эту лемму. Пусть биссектрисы равных
углов YZY' и Z'YZ пересекаются в точке О. Тогда
OY'Z, OZY и OYZ' — три конгруэнтных равнобедрен-
равнобедренных треугольника с углами при основании, равными
90° — а. Их равные стороны OY', OZ, OY и OZ' яв-
являются радиусами окружности с центром в точке О,
а углы при их общей вершине равны по 2а. Другими
Рис. 43.
словами, каждая из равных хорд Y'Z, ZY и YZ' проти-
противолежит углу 2а с центром в точке О и, следователь-
следовательно, противолежит углу а с вершиной на дуге Y'Z', не
содержащей точку У. Эта дуга может быть описана
как множество точек (по ту сторону от прямой Y'Z',
на которой не лежит точка У), из которых отрезок
Y'Z' виден под углом За. Одной из таких точек яв-
является точка А, поэтому она лежит на этой окруж-
окружности.
Теперь мы готовы приступить к доказательству са-
самой теоремы 2.91. Как показано на рисунке 43, три-
трисектрисы углов В = Зр и С = Зу пересекаются в точ-
62
ках LJ и X. В треугольнике BCU углы В и С делятся
пополам прямыми ВХ и СХ, следовательно, X — центр
окружности, вписанной в треугольник BCU, и прямая
UX является биссектрисой угла U. Если мы построим
точки У и Z на прямых CU и BU так, чтобы прямые
XY и XZ образовали равные углы, по 30° каждый,
с прямой XV по разные стороны от нее, то Л UXY я?
шЬ,\]Х1, \XY\ = \XZ\. Так как угол при вершине
равен 60°, то отсюда следует, что треугольник XYZ —
равносторонний.
Кроме того, треугольник UZY — равнобедренный.
Его угол при вершине U тот же, что и в треугольнике
LJBC, у которого остальные углы равны 2р и 2у; по-
поэтому равные углы треугольника LJYZ при вершинах
У и Z равны по р + у каждый.
Обозначая сс = Д/3, мы выводим из равенства А-\-
+Е+С=180°, что a+p+v=60°, откуда р+у=60°—«•
•Таким образом,
YZV = 60° — а и iz£/=120P — a.
Следующий наш шаг состоит в том, что мы нане-
нанесем на рисунок отрезки BY'ш ВХ на прямой В А и
CZ' ¥lCX на прямой С А. Теперь мы имеем
и
так что
| Y'Z | = | ZX | = | ZY |=| YX | = | YZ' \.
Прежде чем мы сможем применить лемму, мы еще
должны оценить величины углов YZY' и Z'YZ. Однако
это довольно просто.
Так как конгруэнтные углы BZY' и BZX имеют и
конгруэнтные дополнения, то
UZY' = XZU= 120° — a
YZY' = YZU + UZY = F0° —a) + A20° —a)= 180°- 2a_
Аналогично, Z/YZ = 180° — 2a, и конечно, a =
= -|"Л<6СР.
63
Применяя лемму, мы получаем, что пять точек Y't
Z, У, Z', А все лежат на одной окружности. Так как
равные хорды Y'Z, ZY, YZ' стягивают равные углы а
в точке А, то прямые AZ и AY делят угол А в тре«
угольнике ABC на три равные части. Другими слова-
словами, точки X, Y, Z, которые были искусственно построе-
построены так, чтобы образовался равносторонний треуголь-
треугольник, на самом деле оказались точками, описанными
в теореме Морлея. Доказательство теперь закончено.
Упражнения
1. Пусть трисектрисы AZ и СХ при продолжении пересе-
пересекаются в точке V, а ВХ н AY— в точке W. Тогда три прямые
UX, VY и WZ конкурентны. (На языке проективной геометрии это
означает, что UVW и XYZ — перспективные треугольники, при
этом треугольник UVW не обязан быть равносторонним.)
2. Для каких треугольников ABC пятиугольник AY'ZYZ' бу-
будет правильным?
3. Если треугольник ABC — равносторонний, .то четыре точки
У, Z, У-, Z' находятся среди вершин правильного девятиуголь»
ника, у которого вершина А противоположна стороне ZY,
4. Для треугольника с углами За, 3E, Зу и радиусом опи*
санной окружности R треугольник Морлея имеет стороны, длины
которых равны 8R sin a-sin p-sin у.
5. Если точки Y и Z, лежащие на стороне Z'Y' прямоуголь-
прямоугольника BCZ'Y', обладают тем свойством, что \Z'Y\ = \YZ\ = \ZY'\,
и центр этого прямоугольника — точка X — вместе с точками Y
и Z образует равносторонний треугольник, то прямые ВХ и BZ
делят прямой угол В на три равные, части.
Глава 3
КОЛЛИНЕАРНОСТЬ И КОНКУРЕНТНОСТЬ
Он же. не смутясь нимало.
Развернул пазы и петли.
Стал вертеть их так и эдак.
Пока все вдруг не предстало
В виде плоскостей, квадратов.
Точно сложная фигура
Из Эвклидова трактата.
Ч, Л. Доджсон
(перевод В. Г. Шнитке)
В этой главе мы рассмотрим ряд новых свойств
треугольников и четырехугольников. Обсуждение этих
свойств подведет нас вплотную к владениям проектив-
проективной геометрии, и мы даже частично нарушим ее гра-
границы. К сожалению, систематическое изложение этой
очаровательной теории мы вынуждены перепоручить
другим книгам, но четыре из ее самых основных тео-
теорем мы сочли возможным поместить здесь, так как
они могут быть доказаны методами, изложенными
еще у Евклида. На самом деле три из них являются
столь давними, что в ту пору еще не было других ме-
методов, пригодных для их доказательства. Все эти тео-
теоремы касаются либо -коллинеарности (принадлежно-
(принадлежности некоторого множества точек одной прямой), либо
конкурентности (наличия у некоторого множества
прямых общей точки). И вот тогда, когда мы обнару-
обнаружим, что многие свойства параллельных прямых ока-
оказываются подобными свойствам конкурентных пря-
прямых, в наших рассуждениях начнет проявляться дух
проективной геометрии.
§ 1. Четырехугольники; теорема Вариньона
Многоугольник может быть определен заданием
некоторого числа точек (называемых вершинами) и
равного ему количества отрезков (называемых сторо-
сторонами), а именно, циклически упорядоченного множе-
множества точек на плоскости, причем такого, что никакие
три последовательные точки не должны быть колли-
неарными, и отрезков, соединяющих последователь-
последовательные точки. Другими словами, многоугольник — это
3 Г. С. М. Коксетер, С. Л, Грейтцер 65
замкнутая ломаная, лежащая на плоскости. Много-
Многоугольник, имеющий п вершин и п сторон, называется
п-угольником. Иногда употребляются греческие на-
названия n-угольников: Пентагон (п = 5), гексагон (п=
=6) и т.д. (а от греческого названия треугольника —
«тригон» произошло название «тригонометрия»). Оче-
Очевидно, что мы должны воздержаться от тенденции
называть четырехугольник «четырехсторонником», по-
поскольку в проективной геометрии под стороной пони-
понимают всю прямую, а не отрезок, и мы будем нуждать-
нуждаться в обоих терминах с различным значением.
Две стороны четырехугольника называются смеж-
смежными, если они имеют общую вершину, в противном
Л
С А
Рис. 44.
случае они называются противоположными. Анало-
Аналогично, две вершины называются смежными, если они
принадлежат одной стороне и противоположными в
противном случае. Прямые, соединяющие пары проти-
противоположных вершин, называются диагоналями. Таким
образом, четырехугольник ABCD имеет стороны АВ,
ВС, CD, DA и диагонали АС и BD.
На рисунке 44 мы видим четырехугольники трех
явно различных типов: выпуклый четырехугольник,
обе диагонали которого находятся внутри него, четы-
четырехугольник с входящим углом, имеющий одну диа-
диагональ внутри себя, а другую вне, и скрещенный че-
четырехугольник, обе диагонали которого находятся
снаружи. -
Мы, естественно, определяем площадь выпуклого
четырехугольника как сумму площадей двух треуголь-
треугольников, на которые он разбивается диагональю:
— $bcd "I"
66
Для того чтобы эта формула могла быть применена
для четырехугольника с входящим углом, мы считаем
площадь треугольника положительной или отрица-
отрицательной в соответствии с тем, указаны ли вершины
в порядке, обратном направлению движения часовой
стрелки или по ее движению. Таким образом,
Sabc — $вса = Scab = — $сва-
Например, четырехугольник с входящим углом, изо-
изображенный в центре рисунка 44, имеет площадь
Sabcd = Sbcd "T" Sdab = $cda — $сва = Scda "Ь
Наконец, эта формула заставляет нас рассматривать
площадь скрещенного четырехугольника как разность
между площадями маленьких треугольников, из ко-
которых он составлен.
Если соединить идею направленных отрезков (§ 1
гл. 2) с соглашением Sabc = —Scba, to это дает нам
возможность расширить наше доказательство теоре-
теоремы Чевы и ей обратной A.21 и 1.22) и на те случаи,
когда некоторые из точек X, Y и Z делят соответст-
соответствующую сторону треугольника ABC в отрицательном
отношении, т. е. внешним образом.
Следующая теорема, принадлежащая Пьеру Ва-
риньону A654—1722), столь проста, что вызывает
удивление ее публикация лишь только в 1731 году.
Теорема 3.11. Фигура, образованная путем по-
последовательного соединения середин сторон четырех'
угольника, является параллелограммом, и его пло-
площадь равна половине площади четырехугольника.
Напомним, .что отрезок, соединяющий середины
двух сторон треугольника, параллелен третьей сторо-
стороне и имеет длину, равную половине длины этой сто-
стороны. Возьмем четырехугольник ABCD; пусть середи-
серединами его сторон АВ, ВС, CD и DA будут точки Р, Q,
R и S.-как на рисунке 45. Рассматривая треугольники
ABD и CBD, мы заключаем, что отрезки PS и QR оба
параллельны диагонали BD, а их длины равны —| BD |.
Следовательно, четырехугольник PQRS — параллело-
3* 67
грамм*); его часто называют параллелограммом Ва-
риньона четырехугольника ABCD.
Что касается площади, то мы имеем
" $abc f $cda " $bcd — "
= Sabcd 4" Sabcd " Sabcd =
Читатель может при желании нарисовать четырех-
четырехугольник ABCD с входящим углом и убедиться, что
такое разложение справедливо и в этом случае.
Так как диагонали любого параллелограмма при
пересечении делятся пополам, то середины отрезков
о
с
Рис. 45.
PR и QS совпадают с центром параллелограмма Ва-
риньона (т. е. с точкой О на рисунке 46). Теперь, по-
подобно тому, как отрезки АС и BD являются диагона-
диагоналями четырехугольника ABCD, отрезки AD и ВС яв-
являются диагоналями четырехугольника ABDC. Так
как отрезок PR имеет только одну середину, то па-
параллелограмм Вариньона нового четырехугольника
ABDC имеет тот же центр О. Следовательно, спра-
справедлива
Теорема 3.12. Отрезки, соединяющие середины
пар противоположных сторон произвольного четырех-
четырехугольника, и отрезок, соединяющий середины диаго-
*) Он останется параллелограммом даже в том случае, когда
A BCD будет не плоским, а пространственным четырех-
четырехугольником.
налей, конкурентны и делят друг друге, пополам.
(Это — первая наша теорема о конкурентности.)
Большую пользу нам принесет следующий ре-
результат:
Теорема 3.13. Если одна диагональ делит четы-
четырехугольник на два треугольника равной площади, то
она делит пополам другую диагональ. И, наоборот,
если одна диагональ делит пополам другую диаго-
диагональ, то она делит пополам площадь этого четырех-
четырехугольника.
Для того чтобы увидеть, почему это так, предпо-
предположим, что отрезок BD делит четырехугольник ABCD
на два треугольника DAB и
BCD равной площади, как на
рисунке 47. Так как эти тре-
треугольники имеют одно и то же
основание BD, то они имеют и
равные высоты АН и CJ. Из
конгруэнтности треугольников
AHF и CJF мы выводим, что
\AF
\AF
ники
CF
CF
. И, наоборот, если
то эти треуголь-
конгруэнтны, |ЛЯ| =
и Sdab = Sbcd-
Теперь мы в состоянии доказать заключительную
теорему этого параграфа:
Теорема 3.14. Если противоположные стороны
AD и ВС четырехугольника ABCD пересекаются (при
69
продолжении) в точке W, а точки X и Y являются се*
рединами диагоналей АС и BD, то S S
Сначала отметим середины Р и R отрезков АВ и
CD, как на рисунке 48, и нарисуем отрезки РХ, PY,
RX,RY,RW. Прямая RY, соединяющая середины двух
сторон треугольника BCD, параллельна отрезку ВС и
делит пополам «другую» диагональ DW четырех-
А
угольника DYWR, Следовательно, по «обратной» ча*
сти теоремы 3.13
Подобным образом мы находим, что
Также, по теореме Вариньона, примененной к четы-
четырехугольнику ABDC,
S S = " SaBDC = ~4"$САВ "Г" ~£ ^BDC =\
4 "^АВС
Складывая последние три выражения, мы получаем
S^^ I ^^ I ^^ ^^ ^^ I
(С |*о *о i ' о *
70
Упражнения
1, Периметр параллелограмма Вариньона равен сумме длин
диагоналей первоначального четырехугольника.
2, Сумма квадратов сторон произвольного четырехугольника
равна сумме квадратов диагоналей плюс учетверенный квадрат
длины отрезка, соединяющего середины диагоналей (рис, 49),
3, Для параллелограмма сумма квадратов длин его сторон
равна сумме квадратов длин его диагоналей,
4, Если равнобочная трапеция имеет боковые стороны дли-
длины о, параллельные стороны длины Ь и с и диагонали длины d,
то d2 — а2 + be.
§ 2. Вписанные четырехугольники;
теорема Брахмагупты
Множество, состоящее из Е прямолинейных отрез-
отрезков, соединяющих попарно V точек, рассмотрим как
«систему», в которой отрезки играют роль твердых
стержней, шарнирно соединенных
между собой так, чтобы они все
время оставались в одной пло-
плоскости. Ясно, что треугольник
{Е = V = 3) является жестким, в
то время как четырехугольник
([£ = V = 4) имеет одну степень
свободы: один из его углов мо-
может быть увеличен или уменьшен,
что влечет за собой изменение В'
других углов. Говорят, что систе-
система строго жесткая, если она ис- 49*
жесткая, но перестает быть тако-
таковой после удаления любого из стержней. Сэр Гораций
Лэмб ([23], стр. 93—94) дал простое доказательство
того, что необходимым (хотя и не достаточным)
условием строгой жесткости системы является соот-
соотношение
Например, Е = 5, а V = 4. В этом случае мы имеем
четырехугольник с одной диагональю; устранение
Этой диагонали дает упомянутую ранее степень
Свободы.
Любые четыре длины а, Ь, с, d, каждая из которых
меньше суммы остальных трех, могут быть использо-
использованы в качестве длин сторон выпуклого четырехуголь-
71
ника. Степень свободы дает нам возможность умень-
уменьшать или увеличивать два противоположных угла до
тех пор, пока они ни станут дополнительными, и тог-
тогда, как мы помним, все его четыре вершины будут
лежать на окружности. Предположим, что длины диа-
диагоналей такого вписанного четырехугольника равны I
и п (как обозначено на первом чертеже рис, 50). Раз-
Разрезая четырехугольник abed вдоль его диагонали / и
вновь соединяя его, при этом перевернув треугольник
dal, мы получим новый четырехугольник bead, вписан-
вписанный в ту же окружность (как на втором чертеже
рис. 50). Одной из его диагоналей является снова от-
отрезок I. Рассекая вписанный четырехугольник вдоль
Рис. 50.
другой еп> диагонали m и соединяя его вновь после
переворачивания треугольника dbm, мы получаем
третий четырехугольник cabd, вписанный в ту же са-
самую окружность (как на последнем чертеже рис. 50).
Так как этот третий четырехугольник мог бы быть
получен из первого рассечением вдоль диагонали п,
то его диагонали имеют длины т и п, и никакие но-
новые преобразования такого вида невозможны (исклю-
(исключая перевороты всего четырехугольника такие, как
abed в deba).
По теореме Птолемея (теорема 2.61)
тп = bc-\- ad,
ca-\- bd, lm = ab-\- cd.
Так как эти четырехугольники выпуклы, то мы мо-
можем считать площадь каждого суммой положитель-
положительных площадей двух треугольников. Переворачивание
треугольника описанным способом не меняет его по-
положительной площади. Следовательно, все три четы-
четырехугольника имеют одну и ту же площадь (хотя ни-
72
какие два из них не конгруэнтны, если никакие две
длины из а, Ь, с, d не окажутся равными). Эти наблю-
наблюдения мы суммируем в следующем утверждении:
Теорема 3.21. Любые четыре неравные длины,
каждая из которых меньше суммы остальных трех,
могут быть длинами сторон трех различных впи-
вписанных четырехугольников, имеющих одинаковую
площадь.
Следствие. Площадь вписанного четырехуголь-
четырехугольника является симметрической функцией длин четы-
четырех его сторон.
Точное выражение для этой функции было найде-
найдено в седьмом столетии нашей эры индийским матема-
математиком Брахмагуптой:
Теорема 3.22. Если вписан-
вписанный четырехугольник имеет дли-
длины сторон а, Ъ, с, d и полупери-
полупериметр s, то его площадь К равна
K= V(s —a) (s — Ь) (s — с) (s — d).
Изложим один из простей-
простейших методов получения формулы
Брахмагупты, использующий три-
тригонометрию. На рисунке 51 изо- Рис- 51-
бражен вписанный четырех-
четырехугольник abed, где Е — вершина, принадлежащая сто-
сторонам о и b, F — вершина, принадлежащая сторонам
с и d, и п — диагональ, соединяющая две другие вер-
вершины. (Мы будем обозначать внутренние углы в вер-
вершинах Е и F теми же буквами Е и F) Так как £ + Р =
=180°, мы имеем
cos/7 — — cosE "и sinf = sin£'.
По теореме косинусов
а2 + Ь2 — 2ab cos Ё=п2 = с2 + d2 — led cos F,
следовательно,
C.221) 2 {ab + cd) cos Ё = a2 + b2 - c2 - d2.
Так как
' = 4" ab sin Ё + 4" cd sin F = -^ (afc + cd) sin £,
73
мы также имеем
C.222) 2 {ab + cd) sin Ё =
Возводя в квадрат и складывая выражения C.221) и
C.222), мы получаем
4 {ab + cdJ = {a2 + Ь2 - с2 - d2J + 16/С2.
Следовательно,
16/С2 = {2аЬ + 2cdJ — {а2 + Ь2-с2- d2J.
Повторно применяя тождество А2—В2—{А—В) {А + В),
мы находим
= [2аЬ + 2cd - (а2 + Ь2 — с2 — d2)] ■
• [2ab + 2cd + (а2 + b2 - с2 - d2)] =
«= [с2 + 2cd + d2-a* + 2ab — b2] •
■ [a2 + 2afc + b2 — c2 + 2cd - d2] =
= [{c + df - (a - fcJ] • [(a + bf -{c- df] >
J] =
• [(a + b - с + d) (a + b + с - d)] =*
*= Bs - 2a) Bs - 26) Bs — 2c) Bs - 2d),
где 2s = a + 6 + c + d. Это заканчивает доказа-
доказательство.
Положив d = 0 в теореме 3.22, мы получаем фор-
формулу Герона для величины площади треугольника че-
через длины сторон а, Ь, с и полупериметр s
Sabc = Vs (s — a)(s — b) (s — c).
Хотя она называется в честь Герона Александрийско-
Александрийского (около 60 года нашей эры), однако ван дер Варден
([8], стр. 314, 373) разделяет мнение Белла ([3],
стр. 58), приписывающего ее Архимеду (третье столе-
столетне до нашей эры).
Другое открытие Брахмагупты касается вписанных
четырехугольников некоторого специального вида.
Теорема 3.23. Если вписанный четырехугольник
имеет перпендикулярные диагонали, пересекающиеся
в точке Р, то прямая, проходящая через точку Р и
74
перпендикулярная одной из его сторон, делит противо-
противоположную ей сторону пополам.
Ссылаясь на рисунок 52, где вписанный четырех-
четырехугольник ABCD имеет перпендикулярные диагонали
АС и BD, а прямая РН перпендикулярна стороне ВС
и пересекает сторону DA в точке X, мы имеем
Следовательно, треугольник XPD — равнобедренный.
Аналогично, равнобедренным будет и треугольник
ХАР. Поэтому •
\ = \XP\=\XD\.
Упражнения
1. Если четырехугольник со сторо-
сторонами, имеющими длины а, Ь, с, d, впи-
вписан в одну окружность и описан вокруг
другой окружности, то его площадь вы-
выражается как
2. Найдите по формуле Герона площади треугольников со
сторонами а) 13, 14, 15; б) 3, 14, 15.
3. Для треугольника ABC выразите радиус вписанной
окружности г через s, s — a, s — b, s — с,
4. В обозначениях § 4, гл. 1
S. ., =
'а'Ь'с
, — г = /т и
5. В обозначениях рисунка 50 К = /
6. Как изменится результат упражнения 5, если мы поло-
положим d = 0?
7. Если выпуклый четырехугольник со сторонами а, Ь, с, d
вписан в окружность радиуса R, то его площадь К выражается
как
(be + ad) (ca + bd) (ab + cd)
8. Пусть две противоположные стороны вписанного четырех-
четырехугольника при продолжении. пересекаются в точке V, а две дру-
другие стороны — в точке W. Тогда внутренние биссектрисы углов
V и W перпендикулярны. •
9. Если произвольная точка Р, лежащая в плоскости пря-
прямоугольника ABCD, соединена с его четырьмя вершинами, то
| РА |2 - | РВ |2 + | PC j2 - IPD |2 = 0.
75
10. Если четырехугольник вписан в окружность, то произве-
произведение расстояний точки, лежащей на этой окружности, до двух
противоположных сторон равно произведению расстояний этой
точки до других двух сторон, а также произведению расстояний
той же точки до диагоналей.
§ 3. Треугольники Наполеона
Теперь мы будем изучать некоторые фигуры, по-
построенные с помощью треугольников и четырехуголь-
четырехугольников. Следующая легкая теорема была удивитель-
удивительным образом упущена из виду.
Теорема 3.31. Пусть на сторонах произвольного
треугольника построены во внешнюю сторону некото-
некоторые треугольники, обладающие тем свойством,
сумма их «.отдаленных» углов равна 180°. Тогда окру-
окружности, описанные вокруг этих трех треугольников,
имеют общую точку.
(Вот еще одна теорема о конкурентности!) Ее до-
доказательство совсем просто. Пусть имеются, как на
рисунке 53, треугольники СВР, ACQ, BAR, построен-
построенные на сторойах данного треугольника ABC и подо-
подобранные так, что углы Р, Q, R удовлетворяют соотно-
соотношению Р + Q + Й = 180°. Окружности, описанные во-
вокруг треугольников СВР и ACQ, пересекаются в точке
С, а другую точку их пересечения обозначим, скажем,
F. Соединяя точку F с точками А, В, С, мы видим, что
= 180°—Р,
— Q,
76
поэтому
AFB = 360° - (BFC + CFA) =
= 360° - A80° - P + 180° - Q) = P + Q = 180° - R.
Следовательно, точка F лежит не только на окружно-
окружностях, описанных вокруг треугольников СВР и ACQ,
но и на окружности, описанной вокруг треуголь-
треугольника BAR.
Особый интерес представляют два частных случая:
Теорема 3.32. Если вершины А, В, С треуголь-
треугольника ABC лежат соответственно на сторонах QR, RP,
PQ треугольника PQR, то три окружности СВР, ACQ,
BAR имеют общую точку.
Теорема 3.33. Если подобные треугольники РСВ,
CQA, BAR построены извне на сторонах треугольника
ABC, то окружности, описанные вокруг этих трех тре-
треугольников, имеют общую точку. (Заметьте, что из по-
порядка, в котором мы назвали вершины подобных тре-
треугольников, следует, что углы при вершинах Р, Q,-R
не являются соответственными углами этих треуголь-
треугольников.)
Теорема 3.32 была названа Фордером ([38],
стр. 17) теоремой о центре вращения. Она была от-
открыта А. Микелем в 1838 году. Меняя обозначения
PQRABC на ABCAiB\C\ для приведения в соответ-
соответствие с обозначениями на рисунке 18, мы можем столь
же легко доказать ее и в несколько расширенной фор-
форме: если ABC — треугольник и А\, В\, С\ — любые три
точки на прямых ВС, СА, АВ, то три окружности
AB\CU A\BCy, A\BiC имеют общую точку Р. В част-
частном случае, когда отрезки АР, ВР, СР являются их
диаметрами, треугольник А\В\С\ является педальным
треугольником треугольника ABC относительно точки
Р. Закрепив треугольник ABC и точку Р, мы можем
вращать три прямые РАи РВ^ и PC] как единое целое
вокруг «центра вращения» Р на любой угол; при этом
получается «косой педальный треугольник» Л1В1С1.
Ясно, что окружности АВ\С\, А\ВС\, А\В\С продол-
продолжают проходить через точку Р.
Точки А\, В\, С] не обязательно должны являться
вершинами треугольника, они могут быть и коллине-
арными, как на рисунке 35. В этом случае точки Аи
It
В, С лежат на прямых В\С\, С\А, АВХ и* тогда та же
теорема утверждает, что три окружности ABC, А\В\С,
AjBCi имеют общую точку. Так как единственными
общими точками последних двух окружностей являют-
являются точки А\ и Р, то нами доказана
Теорема 3.34. Если четыре прямые пересекают'
ся в шести точках А, В, С, А\, В\, С\ так, что множе-
ствами коллинеарных точек являются .{Аи В', С},
{А, Ви С}, {А, В, Ci}, {Аи Вх, С), то четыре окружно-
окружности АВ\Си AiBCi, AB\C, ABC имеют общую точку.
В частном случае, когда у первых трех окружно-
окружностей отрезки АР, ВР, СР являются диаметрами, пря-
прямая А\В\ есть прямая Симеона точки Р для треуголь-
треугольника ABC. Закрепив треугольник ABC и точку Р, мы
можем вращать три прямые РА\, РВи РС\ как единое
целое вокруг точки Р на произвольный угол и, таким
образом, получить «косую прямую Симеона». Эта пря-
прямая содержит новые «основания> Аи Ви С\, обладаю-
обладающие тем свойством, что три прямые РАи РВи РС\ об-
образуют равные углы (отсчитываемые в одну и ту же
сторону) с тремя прямыми ВС, СА, АВ.
Теорема 3.33 имеет интересное следствие, связан-
связанное с треугольником из центров OiO2O3 (рис. 53).чТак
как стороны О2О3, ОгО\, ОУО2 этого треугольника пер-
перпендикулярны общим хордам (или радикальным
осям) пар окружностей, его угол б\ должен быть до-
дополнительным к углу BFC, а это означает, что
б\=Р. Аналогично, <52 = <3 и 63 = Й. Они являются
тремя различными углами наших трех подобных тре-
треугольников.
Следовательно, справедлива
Теорема 3.35. Если на сторонах произвольного
треугольника ABC во внешнюю сторону построены по-
подобные треугольники PC В, CQA, BAR, то центры опи-
описанных вокруг них окружностей образуют треуголь-
ник, подобный этим трем треугольникам.
Ее частным случаем, изображенным на рисунке 54,
является
Теорема 3.36. Если на сторонах произвольного
треугольника во внешнюю сторону построены равно-
равносторонние треугольники, то их центры образуют рав-
равносторонний треугольник.
Гв
Известно, что Наполеон Бонапарт был немного ма-
математиком, причем он интересовался в основном гео-
геометрией. Рассказывают, что однажды Наполеон, тогда
еще не ставший правителем Франции, вел дискуссию
с великими математиками Лагранжем и Лапласом, во
время которой Лаплас его резко прервал: «Менее все-
всего мы хотим от вас, генерал, урока геометрии».
В дальнейшем Лаплас стал его главным военным ин-
инженером.
Теорему 3.36 приписали Наполеону, хотя являются
сомнительными его знания геометрии для такого под-
Ог /
Рис. 54.
вига, равно -как и его знания английского языка для
составления знаменитого палиндрома *)
ABLE WAS I ERE I SAW ELBA.
Во всяком случае, удобно называть треугольник из
центров О\О%Ог (в случае, когда треугольники РСВ,
CQA и BAR — равносторонние) внешним треугольни-
треугольником Наполеона для треугольника ABC. По аналогии,
если равносторонние треугольники построены внутрь
на сторонах треугольника ABC, как на рисунке 55, то
их центры являются вершинами внутреннего треуголь~
ника Наполеона NiN2Na, Таким образом, теорема 3.36
*) Палиндром — «перевертыш» —слово или фраза, имеющие
одинаковый смысл при чтении слева направо и обратно, напри-
например, «искать такси». Смысл данного палиндрома можно переве-
перевести как «я был силен, пока не увидел Эльбу». — Прим. перев.
7?
может быть кратко сформулирована следующим об-
образом:
Внешний треугольник Наполеона является равно-
равносторонним.
И. М. Яглом ([43], т. I, стр. 40, 159) доказал это
другим методом, совсем не похожим на наш, но имею-
имеющим то преимущество, что при помощи него также
получается и аналогичная
Теорема 3.37. Внутренний треугольник Наполе-
Наполеона является равносторонним.
Иг
Рис. 55. •
Другой подход, который тоже дает интересный
промежуточный результат, состоит в применении тео-
теоремы косинусов к треугольнику АО3О2 (см. рис. 54).
Так как АО2 — радиус окружности, описанной вокруг
равностороннего треугольника со стороной |СЛ| = &,
то его длина равна Ь/^/3. Аналогично, ЛОз = с/УЗ.
Кроме того,
ОИО2==/4+ 60°.
Следовательно,
I О2О3 Р = j Ь2 +1 с2 -1 be cos (A + 60°).
Так как вершины ./V2 и #з внутреннего треугольника
Наполеона могут быть получены из точек О3 и Оз сим-
80
метрией относительно прямых СА и АВ соответствен-
соответственно, a N^AN2 = A — 60°, то мы также имеем
Путем вычитания получаем
I П П Р I Л/ Л/ Р .
= -| fee [cos (Л - 60°) - cos {A + 60°)] =
4 ^ 2 4
= — Ьс sin Л cos 60° = —j= be sin Л = —j= SABC.
3 ^y 3 д/З
Аналогичным образом,
I O,O2 P-I W,W2 P = |O3O,P-| W3M P =
и так как | О2О3 | = | О3О{ \ = \ OtO2 \, то мы выводим,
что
Вспоминая, что площадь равностороннего тре-
V3
угольника равна -!^-, умноженному на квадрат дли-
длины его стороны, мы можем сформулировать «интерес-
«интересный промежуточный результат»:
Теорема 3.38. Разность площадей внешнего и
внутреннего треугольников Наполеона произвольного
треугольника ABC равна площади треугольника ABC.
В действительности (как мы видим на рисунке 55),
внутренний треугольник Наполеона и треугольник
ABC имеют противоположные направления обхода,
так что площадь треугольника NiN2N3 является отри-
отрицательным числом (или нулем) и точной формулой
будет не
или
N3 = Sabc-
81
J пражнсния
1. Если на двух сторонах треугольника построены квадраты,
то окружности, описанные вокруг них, пересекаются на окруж-
окружности, построенной на третьей стороне, как на диаметре, и цен-
центры этих трех окружностей являются вершинами равнобедрен-
равнобедренного прямоугольного треугольника.
2. В обозначениях рисунка 54:
а) прямые POi, QOz, ROa все проходят через точку О —
центр окружности, описанной вокруг треугольника;
б) прямые AOi, BO2, СОз конкурентны;
в) отрезки АР, BQ, CR имеют равные длины, проходят через
общую точку F трех описанных окружностей и пересекают друг
друга под углом 60°. (Эта точка получила обозначение F в честь
Ферма, установившего, что для этой точки сумма расстояний до
вершин А, В и С является наименьшей, если углы треугольника
не превышают 120°.)
3. В обозначениях рисунка 55 прямые ANU BNz, CN3 кон-
конкурентны.
4. Внешний и внутренний треугольники Наполеона имеют
один и тот же центр.
§ 4. Теорема Менелая
Менелай Александрийский (приблизительно 100 год
нашей эры, не путайте с Менелаем из Спарты) напи-»
сал трактат, называемый «Sphaerica» (Сферика), в
котором он использовал некоторое свойство сфериче-
сферического треугольника; он писал так, как будто аналогич*
ное свойство плоского треугольника было уже хорошо
известно. Может быть, это так и было, но поскольку
никаких более ранних письменных упоминаний об
этом не сохранилось, нам ничего не остается, как на«
звать соответствующее высказывание теоремой Мене-
лая. Используя обозначения направленных отрезков
(§ 1 гл. 2), ее можно сформулировать следующим об*
разом (см. рис. 56 и 57):
Теорема 3.41. Если точки X, У, Z, лежащие на
сторонах ВС, СА, АВ {соответственно продолженных)
треугольника ABC коллинеарны, то
ВХ CY AZ _.
СХ ' AY ' BZ ~1'
Обратно, если это уравнение выполняется для точен
X, Y, Z, лежащих на трех сторонах треугольника, то
эти три точки коллинеарны,
82
. Пусть заданы коллинеарные точки X, Y, Z как на
рисунке 56 или 57. Обозначим через hi, hi, hz длины
перпендикуляров, опущенных из точек А, В, С на пря-
прямую XY, считая те из них положительными, которые
находятся по одну сторону от этой прямой, и отрица-
А
Рнс. 56.
тельными те, которые лежат по другую сторону. Пере*
множив следующие три уравнения:
J^L^h. SL — h. AZ — й'
СХ ~ hi' AY hi ' BZ h2'
мы получим желаемый результат. (Заметим, что для
того, чтобы разместить на сторонах треугольника ABC
три различные коллинеарные точки X, Y, Z, всегда не-
необходимо продолжить либо все три, либо только одну
из сторон треугольника.)
Обратно, если точки X, Y, Z расположены на трех
сторонах таким образом, что
ВХ CY AZ _.
СХ ' AY ' BZ
то, обозначив через Z' точку пересечения прямых АВ
и XY, получим
ВХ CY AZ' _,
СХ ' AY ' BZ' 1*
83
Следовательно,
AZ' _ AZ
ВГ ~~BZ'
т. е. точка Z' совпадает с точкой Z, и мы доказали,
что точки X, Y, Z — коллинеарны.
Мы замечаем, что теорема Менелая дает критерий
коллинеарности, так же как теорема Чевы A.21 и
1.22) дает критерий конкурентности. Чтобы подчерк-
подчеркнуть их противоположность, мы можем выразить урав-
уравнение Менелая в другой форме:
• _ВХ_ CY_ AZ _
Упражнения
1. Биссектрисы внешних углов разностороннего треугольника
пересекают соответствующие противоположные стороны в трех
коллинеарных точках.
2. Биссектрисы двух внутренних углов разностороннего тре-
треугольника и биссектриса внешнего угла при третьей вершине пе-
пересекают соответствующие противоположные стороны в трех
коллннеарных точках.
§ 5. Теорема Паппа
Теперь мы подходим к одной из важнейших тео-
теорем планиметрии. Она впервые была доказана Пап-
пом Александрийским около 300 года нашей эры. Но
лишь шестнадцать столетий спустя была признана ее
роль в создании проективной геометрии. И тогда Папп
был назван последним великим геометром древности.
Эта выдающаяся теорема, носящая его имя, может
быть сформулирована различными способами, один из
которых дается ниже.
Теорема 3.51. Если А, С, Е — три точки на од-
одной прямой, а В, D, F — на другой, и если три прямые
АВ, CD, EF пересекают прямые DE, FA, ВС, соответ-
соответственно, то три их точки пересечения L, М, N колли-
коллинеарны.
«Проективная» природа этой теоремы видна из
того, что она использует только принадлежность точек
прямым или прохождение прямых через точки, без из-
измерения длин или углов и даже без какой-либо ссыл-<
ки на порядок: в каждом множестве из трех коллине*
84
арных точек безразлично, какая из них лежит между
двумя другими. Рисунок 58 реализует одну из воз-
возможностей нарисовать чертеж, а рисунок 59 — другую
такую возможность. Мы можем циклически переста-
переставить буквы А, В, С, D, Е,
F при условии, что соот-
соответственно переименуем
точки L, М, N. Чтобы из-
избежать рассмотрения бес-
бесконечно удаленных точек,
которое завело бы нас
'слишком далеко в напра-
направлении $ проективной гео-
геометрии, давайте предпо-
предположим, что три прямые
АВ, CD, EF образуют тре-
треугольник UVW, как на рисунке 60. Применяя теорему
Менелая к пяти тройкам точек
{L, D, Е), {А, М, F}, {В, С, N}, {А, С, Е}, {В, D, F},
А
Рис. 59.
лежащих на сторонах этого треугольника, мы полу-
-1,
-1,
чаем:
VL
LW
VB
BW
WD
DU "
WC
си
UE
EV
UN
NV
VB
BW
1
- ■ 1,
1
1,
WD
DU
VA
AW
VA
AW
UF
FV
WM
MU
WC
cu
1
UF
FA
UE
EV
85
Разделив произведение первых трех соотношений на
произведение последних двух и с наслаждением
F
Рис. 60.
Л
произведя массу сокращений, мы получаем
VL_ WM UN _ ,
LW ' MU ' NV ~~
т. е. точки L, M, N коллинеарны, что и требовалось
([11], стр. 237 и [1],стр. 12).
Упражнения
1. Если А, С, Е— три точки на одной прямой, В, D, F— на
другой, и если две прямые АВ и CD параллельны прямым DE и
FA соответственно, то прямая EF параллельна прямой ВС.
2. Пусть А, В, D, E, N, М — шесть точек, обладающих тем
свойством, что прямые АЕ, DM, NB конкурентны и прямые AM,
DB, NE конкурентны. Что можно сказать о прямых АВ, DE, NM?
3. Пусть С и F — произвольные точки соответственно, на сто-
сторонах АЕ и BD параллелограмма AEBD. Обозначим через М и
N точки пересечения прямой CD с прямой FA и прямой EF,
с прямой ВС. Пусть прямая MN пересекает прямую DA в точ-
точке Р, а прямую ЕВ в точке Q. Тогда 1ЛР| = |<ЗВ|.
4. Сколько точек и прямых, обозначенных буквами, находит-
находится на рисунке 58 (или рисунке 59)? Сколько таких прямых про-
проходит через каждую из этих точек? Сколько таких точек лежит
на каждой из этих прямых?
§ 6. Перспективные треугольники; теорема Дезарга
Первые шаги в разработке геометрической теории
перспективы были сделаны архитектором Филиппом
Брунеллески A377—1446), которому принадлежи^
£6 »
проект восьмиугольного купола собора во Флоренции,
а также проект палаццо Питти. Более глубокое изуче-
изучение этой теории было проведено другим архитектором
Жераром Дезаргом A591—1661), чья теорема «о двух
треугольниках», как было обнаружено позже, столь
же важна, как и теорема Паппа. Хотя она может быть
выведена из теоремы Паппа, однако этот вывод насы-
насыщен сложными деталями, и намного легче вывести ее
из теоремы Менелая.
Если две одинаковые конфигурации, составленные
из точек и прямых, могут быть приведены в соответ-
соответствие так, что пары соответствующих точек соеди-
соединяются прямыми, пересекающимися в одной точке, то
мы говорим, что эти две конфигурации перспективны
относительно этой точки. Если соответствие таково,
что пары соответствующих прямых пересекаются в
точках, лежащих на одной прямой, то мы говорим, что
эти две конфигурации перспективны относительно этой
прямой *).
Утверждение теоремы Дезарга о двух треугольни-
треугольниках, записанное в духе проективной геометрии, вы-
выглядит следующим образом: если два треугольника
перспективны относительно точки, то они перспектив-
перспективны и относительно прямой. Однако, чтобы избежать
сложностей, связанных с рассмотрением случаев па-
параллельности прямых, мы удовлетворимся следующей
ее перефразировкой:
Теорема 3.61. Если два треугольника перспек-
перспективны относительно точки и если их пары Соответ-
Соответствующих сторон пересекаются, то эти три точки пере-
пересечения коллинеарны.
Вновь мы имеем теорему лишь о принадлежности
точек прямым и пересечении прямых. Рисунки 61 и 62
являются двумя из многих способов нарисовать такой
чертеж. Здесь треугольники PQR и P'QR' перспектив-
перспективны относительно точки О, а пары их соответствующих
сторон пересекаются в точках D, E, F. (Некоторые
примеры перспективных треугольников уже были рас-
рассмотрены в упражнении 2 § 3, где каждые два из трех
*) В русской математической литературе указанную точку
принято называть центром перспективы, а прямую — осью пер-
перспективы. — Прим. перев.
87
треугольников ABC, PQR, OiO2O3 перспективны отно-
относительно точки.)
Рис. 61.
Для доказательства мы применим теорему 3.41 к
тройкам точек
{D. Rf, Q% {Е, Р', /?'}, {F, Qf, P'},
лежащих на сторонах трех треугольников
OQR, ORP, OPQ,
£8
получив при этом
QD RR' OQ' __ . RE PP' OR' __ .
RD ' OR' ' QQ' ~~ l' PE OP' ' /?/?''
PF QQ' OF__.
QF ' OQ' ' PP' -
Перемножив эти три выражения и проделав умерен-
умеренное число сокращений, получим
QD RE PF _
RD ' РЕ ' QF ~~ '
откуда следует, что точки D, Е, F коллинеарны, что и
требовалось ([11], стр. 231 и [1] стр. 17).
Теорема Дезарга, как легко видеть, подразумевает
существование обратной к ней: если два треугольника
перспективны относительно прямой, то они перспек-
перспективны относительно точки. Удовлетворимся следую-
следующей ее записью:
Теорема 3.62. Если два треугольника перспек-
перспективны относительно прямой и если две пары соответ-
соответствующих вершин соединяются пересекающимися пря-
прямыми, то эти треугольники перспективны относительно
точки пересечения этих прямых.
Объявляя, что треугольники PQR и P'Q'R' пер-
перспективны относительно прямой, мы подразумеваем,
что имеются три коллинеарные точки *)
D = QR-Q'R', E = RP-R'P', F = PQ-P'Q',
как на рисунке 61. Если определить точку 0 =
= PP'-RR', то утверждение теоремы можно перепи-
переписать в следующем виде: точка О коллинеарна с точ-
точками Q и Q'. Так как треугольники FPP' и DRR' пер-
перспективны относительно точки Е, то мы можем к ним
*) Из контекста будет ясно, в каком случае символом типа
АВ обозначается вся прямая, проходящая через точки А н В, а
не просто отрезок, ограниченный ими. Общую точку двух непа-
непараллельных прямых АВ и DE удобно обозначать через ABDE.
Это обозначение не так страшно, как символ (Л iBB) Л {D (БЕ),
предпочитаемый некоторыми авторами.
89
применить теорему 3.61 и сделать вывод, что точки
пересечения пар соответствующих сторон, а именно
O = PP'-RR', Q'^P'F-R'D, Q = FP-DR,
'коллинеарны, что и требовалось.
Это пример чисто «проективного» доказательства.
Упражнения
1. Если два треугольника перспективны относительно точки и
две пары соответствующих сторон параллельны, то и две остав-
оставшиеся стороны параллельны. (В этом случае говорят, что два
треугольника гомотетичны, как в упражнении 3 § 2 гл. 1.)
2. Сколько точек н прямых, обозначенных буквами, имеется
иа рисунке 61 (или 62)? Сколько таких прямых проходит через
каждую из этих точек? Сколько таких точек лежит на каждой
из прямых?
3. Назовите два треугольника, которые перспективны относи-
относительно а) точки Р, б) точки Р", в) точки D.
4. Что можно сказать о вершинах и сторонах двух пяти-
пятиугольников DFP'OR и EPQQ'R' (см. рис. 61). Имеются ли на
рисунке другие пятиугольники, обладающие теми же свойствами?
5. Две непараллельные прямые нарисованы на листе бумаги
так, что их точка пересечения находится вне этого листа. Через
■Точку Р, находящуюся между этими прямыми на листе бумаги,
постройте прямую, которая проходила бы (при достаточном про-
продолжении) через точку пересечения данных прямых. Что дало бы
то же самое построение, если бы мы его применили к двум па-
параллельным прямым?
§ 7. Шестиугольники
Говорят, что две вершины шестиугольника являют-
являются смежными, чередующимися или противоположны'
ми в зависимости от того, разделяются они одной сто-
стороной, двумя или тремя сторонами. Таким образом, в
шестиугольнике ABCDEF вершины F и В смежны с
вершиной А, вершины Е и С— чередующиеся с верши-
вершиной А и вершина D противоположна вершине А. Отре-
Отрезок, соединяющий две противоположные вершины, на-
называется диагональю. Таким образом, шестиугольник
ABCDEF имеет три диагонали: AD, BE, CF. Анало-
Аналогично, этот шестиугольник имеет три пары противопо'
ложных сторон: АВ и DE, ВС и EF, CD и FA.
Данный шестиугольник может быть обозначен как
ABCDEF двенадцатью способами: любая из шести его
вершин может быть обозначена буквой А, любая из
00
двух смежных с ней вершин может быть обозначена
буквой В, и тогда обозначения остальных определяют-
определяются алфавитным порядком.
Шесть данных точек, никакие три из которых не
коллинеарны, могут быть обозначены буквами А, В, С,
D, E, F 6! = 720 способами. Каждый способ опреде-
определяет шестиугольник ABCDEF, имеющий в качестве
вершин шесть данных точек. Следовательно, число
различных шестиугольников, определяемых шестью
точками, равно
тг-»
На рисунке 63 показаны три из шестидесяти шести-
шестиугольников, определяемых шестью точками, лежащи-
лежащими на окружности. Хотя мы привыкли к первому («вы-
(«выпуклому») типу, мы не должны пренебрегать и дру-
Рис. 63.
гими пятьюдесятью девятью возможными шестиуголь-
шестиугольниками, которые могут быть получены с помощью тех
же шести точек.
В § 1 мы потребовали, чтобы никакие три последо-
последовательные вершины многоугольника не были колли-
коллинеарны. Однако коллинеарность других вершин допу-
допустима. В частности, теорема 3.51 (теорема Паппа) мо-
может быть перефразирована следующим образом:
Если каждое множество из трех чередующихся
вершин шестиугольника является множеством трех
коллинеарных точек, и три пары противоположных
сторон пересекаются, то эти три точки пересечения яв-
являются коллинеарными.
Упражнения
1. Если две противоположные стороны ВС и EF шестиуголь-
шестиугольника ABCDEF параллельны диагонали AD, а две противополож-
противоположные стороны CD и FA параллельны диагонали BE, и при этом
91
оставшиеся стороны DA и АВ также параллельны, то третья
диагональ CF .параллельна стороне АВ, и центроиды треугольни-
треугольников АСЕ и BDF совпадают.
2. Даны две тройки коллинеарных точек. Сколько существует
способов построить шестиугольник так, чтобы точки каждой трой-
тройки были его чередующимися вершинами?
§ 8. Теорема Паскаля
Мы подошли к замечательной теореме, -открытой
философом и математиком Блезом Паскалем A623—-
1662) в шестнадцатилетнем возрасте.
Теорема 3.81. Если все шесть вершин шести-
шестиугольника лежат на окружности и три пары противо-
противоположных сторон пересекаются,
то эти три точки пересечения кол-
линеарны.
Никто не знает, как Паскаль
доказывал ее, потому что подлин-
подлинный текст доказательства был
утерян. Однако до того, как он
был потерян, его видел и хвалил
Г. В. Лейбниц (открывший одно-»
временно с Ньютоном дифферен-
дифференциальное и интегральное исчисле-
исчисления). Такое положение вещей сти-
стимулирует попытки восстановить
потерянное доказательство, т. е.
дать доказательство, используя
только результаты и методы, су-
существовавшие во времена Паска-
Паскаля. Одно такое доказательство, использующее только
первые три книги Евклида, было дано Фордером
([39], стр. 13); но это tour de force*), а вероятнее
всего, Паскаль использовал теорему Менелая так же,
как и в приведенном здесь доказательстве.
На рисунке 64 показан один из многих способов
расположения шестиугольника ABCDEF, вписанного
в окружность. (Читатель может легко увидеть, какие
изменения понадобятся в рассуждениях при ином его
расположении, например, если те же самые шесть вер-
вершин соединить одним из пятидесяти девяти других
Рис. 64.
*) Ловкий трюк (франц.) — Прим. перев.
92
возможных способов.) Мы хотим доказать, что ель-
дующие три точки пересечения
L = AB-DE, M = CD-FA, N = ВС • EF
коллинеарны.
Предположим, что три прямые А В, CD, EF обра-
образуют треугольник UVW, как на рисунке 64. Применяя
теорему 3.41 к трем тройкам точек LDE, AMF, BCN,
лежащих на сторонах этого треугольника UVW, мы
получим
VL WD UE__. V_A_ WM UF _.
WL ' UD ' VE ~~ .' WA ' UM ' VF ~~ '
VB WC UN .
-= 1.
WB UC VN
Перемножая все эти три выражения и замечая, что
по теореме 2.11 —
WD UE VA UF VB WC _
UD ' VE ' WA ' VF ' WB UC ~~
_ UE• UF VA-VB WC-WD _ .
~ UC-UD ' VE-VF ' WA-WB ~ '
мы получаем
VL WM UN _.
WL ' UM ' VN ~~ V'
поэтому точки L, М, N коллинеарны, что и требова-
требовалось*).
Прямая, содержащая эти три точки L, M, N, назы-
называется прямой Паскаля шестиугольника ABCDEF.
Как мы видели в § 7, эти же шесть точек определяют
шестьдесят шестиугольников; следовательно, они опре-
определяют (вообще говоря) шестьдесят прямых Паскаля.
Эти шестьдесят прямых образуют очень интересную
конфигурацию: некоторые их подмножества конкурен-
конкурентны, а некоторые подмножества "точек их пересечения
коллинеарны, и т. д.
*) Эта попытка реконструкции доказательства Паскаля по-
появилась в 18-м издании книги Теодора Спикера (Theodor Spieker,
«Lehrbuch der ebenen Geometrie, Potsdam, 1888). См. также [11],
стр. 235, [29], стр. 26 или [43] т. II, стр. 80, 115, 193. Другая
попытка была предложена авторами этой книги — см. Н. S. М. Со-
xeter and S. L. Greitzer «L'hexagramme de Pascal. Un essai pour
reeonstituer cette decouverte» Le Jeune Scientifique (Joliette, Que-
Quebec) 2 A963), стр. 70—72.
9Я
Как следует из сохранившейся короткой работы
Паскаля «Опыт о конических сечениях» («Essay pour
les coniques»), он хорошо знал, что его теорема при-
применима не только к шестиугольнику, вписанному
в окружность, но и к шестиугольнику, вписанному в
коническое сечение. Обратная к ней теорема, доказан-
доказанная независимо Вильямом Брекенриджем и Колином
Маклореном, содержится в любом учебнике по проек-
проективной геометрии, например ([18], стр. 125).
Если три пары противоположных сторон шести-
шестиугольника пересекаются в трех коллинеарных точках,
то шесть его вершин лежат на коническом сечении,
которое может вырождаться в пару прямых (как в
теореме 3.51).
В
Рис. 65.
Если позволить вершинам вписанного шестиуголь-
шестиугольника сливаться, при этом внимательно следя за тем,
чтобы сохранились их обозначения, то мы сможем
вывести несколько интересных теорем о вписанных
пятиугольниках и четырехугольниках. В таких случаях
сторона, конечные точки которой сливаются, превра-
превращается в точку, а прямая, содержащая ее, переходит
в касательную к этой окружности (или коническому
сечению) в этой точке. Рассмотрим, например, вписан-
вписанный четырехугольник ADBE, изображенный на рисун-
рисунке 65. Считая, что скрещенный четырехугольник ADBE
является вырождением шестиугольника, при котором
вершина В совпала с вершиной С, а вершина Е — с
вершиной F, мы можем применить теорему Паскаля,
утверждение которой будет состоять в том, что каса-
касательные в точках В и Е пересекаются в точке N, лежа-
лежащей на прямой, соединяющей точки
L = AB-DE и M = BD-EA.
94
Упражнения *
1. Если пять из шести вершин шестиугольника лежат на
окружности и три пары противоположных сторон пересекаются
в трех коллинеарных точках, то и шестая вершина лежит на той
же окружности.
2. У вписанного четырехугольника АВСЕ с непараллельными
сторонами касательные в точках А и С пересекаются на прямой,
соединяющей точки АВ-СЕ и ВС-ЕА.
§ 9. Теорема Брианшона
Ш. Ж- Брианшон A760—1854) открыл интересную
теорему (в некотором смысле связанную с теоремой
Паскаля) о свойстве шестиугольника, описанного
вокруг конического сече-
сечения. Доказательство Бри-
Брианшона использует «двои-
ственность» точек и пря-
прямых, характерную для
проективной геометрии.
Однако случай, когда ко-
коническое сечение является
окружностью, был вызо-
вызовом математикам на по-
поиски для него евклидов-
ского доказательства. На
этот вызов успешно ответил А. С. Смогоржевский
([34], стр. 28). Для понимания его доказательства
необходима следующая лемма:
Пусть к окружности в точках Р и Q проведены ка-
касательные и пусть точки Р' и Q' лежат на этих каса-
касательных (соответственно) по одну сторону от прямой
PQ, так что |PP'| = |QQ'|. Тогда существует окруж-
окружность, касающаяся прямых РР' и QQ' в точках Р' и Q'
соответственно. Л
Действительно, фигура, изображенная на рисун-
рисунке 66, симметрична относительно серединного перпен-
перпендикуляра к отрезку PQ, являющегося также середин-
серединным перпендикуляром к отрезку P'Q', а кроме того, и
диаметром данной окружности. Перпендикуляры к от-
отрезкам РР' и QQ' в точках Р' и Q' пересекают эту
«среднюю линию» — ось симметрии — в одной и той
же точке, которая является центром искомой окруж-
окружности.
95
Теперь мы можем перейти к доказательству Смо-
горжевского:
Теорема 3.91. Если все шесть сторон шести-
шестиугольника касаются окружности, то три его диагонали
конкурентны (или параллельны).
Пусть R, Q, Т, S, Р, U — точки касания шести ка-
касательных АВ, ВС, CD, DE, EF, FA, как на рисунке 67.
Для простоты предположим, что шестиугольник
ABCDEF — выпуклый, тогда все его три диагонали
Рис. 67.
являются секущими вписанной окружности (и исклю-
исключается возможность их параллельности). На прямых
EF, CB, АВ, ED, CD, AF (продолженных) возьмем
точки Р', Q', R', S', Г, W так, что
| PP'\ = \QQ' | = | RR' | = | SS' | = | ТГ | = | UU'\,
(длина этих отрезков может иметь любое удобное
значение) и построим окружность I (касающуюся
прямых РР' и QQ' в точках Р' и Q'), окружность II
(касающуюся прямых RR' и SS' в точках R' и S') и
окружность III (касающуюся прямых ТТ' и UW в точ-
точках Т и V) в соответствии с леммой.
96
Теперь мы используем тот известный факт, что две
касательные к окружности, проведенные из одной точ-
точки, имеют равные длины. Так как |Л/?| =
AU\
AR'\ =
\RR'\ = \UU'\, то, сложив их, мы получаем
= |Л^'|.Таккак \DS\ = \DT\ n\SS'\ = \TT'\ то, вы-
вычитая, мы получаем \DS'\ = \DT'\. Таким образом,
точки А и D имеют равные степени (§ 2 гл. 2) относи-
относительно окружностей II и III, а соединяющая их пря-
прямая AD совпадает с радикальной осью этих двух окру-
окружностей. Аналогично, отрезок BE лежит на радикаль-
радикальной "оси окружностей I и II, а отрезок CF лежит на
радикальной оси окружностей III и I. Как мы видели
в § 3 гл. 2, радикальные оси трех несоосных окружно-
окружностей, взятых попарно, конкурентны (или параллель-
параллельны). Мы представили диагонали нашего шестиуголь-
шестиугольника в качестве радикальных осей трех окружностей.
Так как эти диагонали, очевидно, не могут совпасть,
то эти окружности не являются соосными, и доказа-
доказательство закончено.
Обратная теорема, относящаяся к проективной гео-
геометрии, формулируется следующим образом ([19],
стр. 83).
Если три диагонали шестиугольника конкурентны,
то шесть его сторон касаются конического сечения,
которое может вырождаться в пару точек (подобную
паре точек FL для шестиугольника ABDENM в упра-
упражнении 2 § 5).
Если позволить сторонам сливаться, при этом вни-
внимательно следя за тем, чтобы сохранились их обозна-
обозначения, то мы сможем вывести несколько интересных
теорем о пятиугольниках и четырехугольниках, опи-
описанных вокруг окружности. В таких случаях общая
вершина двух совпадающих сторон становится их точ-
точкой касания с окружностью (или коническим сече-
сечением).
Рассмотрим, например, пятиугольник ABCDE, опи-
описанный вокруг окружности (как показано на рисун-
рисунке 68). Считая, что он является вырождением шести-
шестиугольника ABCDEF с «развернутым углом» в точке F,
мы можем применить теорему Брианшона, утвержде-
утверждение которой будет состоять в том, что точка касания
стороны ЕА пятиугольника ABCDE, описанного
4 Г. С. М. Кокеетер. С. Л. Грейтцер 97
вокруг окружности, лежит на отрезке, соединяющем
точку С с точкой пересечения AD • BE.
Подобным же образом, четырехугольник BCEF,
описанный вокруг окружности, стороны которого FB
и СЕ касаются окружности в точках А и D, мож-
можно рассматривать как вырожденный шестиугольник
(рис.* 69). В результате этого мы приходим к выводу,
Е
Рис. 68.
что диагонали BE и CF четырехугольника пересекают*
ся на прямой AD, которая соединяет точки касания
сторон FB и СЕ с окружностью.
Упражнения
1. На рисунке 69 прямая PQ, соединяющая две другие точки
касания, также проходит через точку пересечения диагоналей.
2. На рисунке 69 считайте, что фигура ABQCEF является
шестиугольником. Какие прямые являются конкурентными в этом
случае?
3. Дает ли теорема Брианшоиа новый подход к упражне-
упражнению 3 § 4 гл. 1?
Глава 4
ПРЕОБРАЗОВАНИЯ
Господь с тобоП, MotokI Господь с тобоШ
Тебя преобразили.
В. Шекспир. «Сон в летнюю ночь»
(перевод М. Лозинского).
В замечании, приведенном в конце § 6 гл. 1, мы
(установили перпендикулярность прямых FD и 0D
(см. рис. 14) как следствие того, что они могут быть
получены из перпендикулярных прямых HD и СВ по-
поворотом на равные углы а вокруг точек D и В соот-
соответственно. В преамбуле к теореме 1.71 мы видели,
что у подобных треугольников ABC и А'В'С центро-
центроиды совпадают и что, так как их ортоцентрами яв-
являются точки Я и О, то \АН\ =2|ОЛ'|. Наконец, в
обсуждении, последовавшем за теоремой 1.81, мы
использовали разворот, чтобы поменять местами орто-
ортоцентры двух конгруэнтных треугольников А'В'С' и
K.LM. Поворот, дилатация и разворот являются тремя
примерами преобразования, которое мы будем пони<
мать, имея в виду рассматриваемый здесь круг вопро-<
сов, как отображение всей плоскости на себя такое,
что каждая точка Р отображается в единственную
точку Р', а каждой точке Q' соответствует единствен-
единственный прообраз Q. Идея «отображения» имеет первосте-
первостепенное значение во многих областях математики, на*
пример, когда мы описываем функцию у = f(x), то мы
отображаем множество значений переменной х на
множество соответствующих значений переменной у.
Евклидова геометрия является только одной из
многих геометрий, каждая из которых имеет свои соб*
ственные исходные понятия, аксиомы и теоремы. Фе<
лике Клейн в речи, прочитанной им в 1872 году при
вступлении на кафедру в немецком городе Эрлангене,
предложил классификацию геометрий в соответствии
с теми группами преобразований, использование кото-
которых не меняет понятий, аксиом и теорем, Обычная
4* 99
евклидова геометрия характеризуется группой подо-
подобий, которые могут быть описаны как преобразования,
сохраняющие углы. Важным частным случаем подобия
является изометрия, которая может рассматриваться
как преобразование, сохраняющее длины, например,
поворот и, в частности, разворот. Изометрия лежит в
основе известного нам понятия конгруэнтности: две
фигуры конгруэнтны в том и только в том случае, если
можно преобразовать одну в другую с помощью изо-
метрии.
§ 1. Параллельный перенос
Помимо тождественного преобразования, при кото-
котором каждая точка переходит в ту же самую точку,
наиболее известным является параллельный перенос,
сохраняющий расстояния между любыми двумя точ-
точками и направление прямой, проходящей через них.
А' В'
с * о о • о
А В
Рис. 70. Рис. 71.
Если отрезок А'В' является образом отрезка А В
при параллельном переносе, то либо точки А, В, А', В'
лежат на прямой, как на рисунке 70, либо АА'В'В—
параллелограмм, как на рисунке 71. (В первом слу-
случае мы, естественно, говорим о вырожденном паралле-
лограмме АА'В'В.) Таким образом, параллельный пе-
перенос определяется заданием направленного отрезка
АА', и с тем же успехом он может быть определен при
помощи любого отрезка из бесконечного множества
других, имеющих ту же длину и направление, напри-
например, ВВ'. Другим названием параллельного переноса
служит слово вектор, и мы будем пользоваться обо-
значением АА' = ВВ'. В частности, тождественное
преобразование может рассматриваться как парал-
параллельный перенос на нулевое расстояние или как нуль-
вектор.
100
Тот факт, что параллельный перенос сохраняет
форму и размеры любой фигуры, используется в до-
доказательствах различных теорем о площадях. Напри-
Например (рис. 72), при выводе обычной формулы площади
параллелограмма ABCD с острым углом при верши-
вершине А мы отрезаем прямоугольный треугольник AHD и
н
Рис. 72.
приклеиваем его вновь, перенеся параллельно в поло-
положение ВН'С, в результате чего получается прямо-
прямоугольник HH'CD.
Рисунок 73 иллюстрирует задачу о вписывании в
данную окружность прямоугольника, обладающего
тем свойством, что две его противоположные стороны
Су'
ч
Рнс. 73.
параллельны данному отрезку а и имеют с ним одина*
ковую длину. Эта задача может быть решена при по-
помощи параллельного переноса данной окружности на
любой из двух векторов, соответствующих отрезку а.
Если старое и новое положения окружности имеют
общие точки В и С, то они будут двумя вершинами
искомого прямоугольника A BCD, стороны которого
АВ и CD параллельны отрезку а и имеют с ним оди-
одинаковую длину,
101
Упражнения
1. «Впишите» в треугольник ABC (рис. 74)" отрезок, равный
П параллельный данному отрезку а.
А
Рнс. 74.
2. Нарисуйте несколько нз бесконечного множества положе-
положении, которые может занимать образ равностороннего треуголь-
треугольника при параллельных переносах на векторы, равные сумме век-
вектора АВ, умноженного на целое число, н вектора АС, умножен-
умноженного на целое число.
у
§ 2. Поворот
Другим видом преобразований, сохраняющих рас-
расстояния, является поворот. При этом вся плоскость
поворачивается вокруг некоторой точки на заданный
угол. Таким образом, размеры и форма любой фигуры
остаются неизменными, а все ее точки движутся по
дугам концентрических окружностей. Центр вращения
(который может как принадлежать, так и не принад-
принадлежать вращаемой фигуре) является единственной
неподвижной точкой.
В качестве примера использования поворота рас->
смотрим следующую ситуацию. Пусть дан треуголь-
треугольник ABC (рис. 75) и пусть на его сторонах построены
внешним образом равносторонние треугольники ВРС,
CQA и ARB. Нарисовав прямые BQ и CR, пересекаю-
пересекающиеся в точке F, мы замечаем, что поворот на 60° во-
вокруг точки А переводит треугольник ARC в треуголь-
треугольник ABQ. Следовательно, RFB = 60° и \RC\ = \BQ\.
Подобными рассуждениями показывается, что |РЛ|=*
«=|С/?|. Таким образом,
\AP\~\BQ\ = \CR\.
Более того, так как
и
102
То четырехугольники ARBF и CQAF являются вписан-
вписанными; и так как BFC = 120°, а СР£ = 60°, то и четы-
четырехугольник BPCF также является вписанным. Поэто-
Поэтому окружности, описанные вокруг трех треугольников
ВРС, CQA, ARB, проходят через точку F. Она назы-
называется точкой Ферма треугольника ABC. Определив
ее как точку пересечения прямых BQ и CR, мы теперь
видим, что она должна также лежать и на прямой АР.
В евклидовом доказательстве теоремы Пифагора
квадраты CBIG, ACKJ, BADE построены внешним об-
образом на сторонах данного прямоугольного треуголь-
треугольника ABC, при этом последний квадрат разбивается
продолжением высоты СИ на две части, как на ри-
рисунке 76. Точками О\, О2, О3 обозначены центры этих
frpex квадратов, а связь точек U, V, W, X, Y с другими
точками и линиями видна из рисунка. Хотя существуют
более легкие способы доказать теорему Пифагора, до-
доказательство Евклида интересно уже тем, что из рас-
рассматриваемого рисунка можно получить много неожи-
неожиданных результатов.
Нарисовав прямые AI, BJ, CD и СЕ, мы видим, что
поворот на 90° вокруг точки А переводит треугольник
'ADC в треугольник ABJ, Поэтому \BJ\ = \DC\ и
103
отрезок BJ перпендикулярен отрезку CD. Аналогично,
отрезки AI и СЕ равны и перпендикулярны.
И
_ Рис. 76.
Из подобия треугольников ВСХ и BKJ, а также
CAY и GAI, вытекают следующие соотношения:
\СХ\ _ \СХ\ _ \ВС\ _ а
Ь — \K1\~ \BK\~ а + Ь'
откуда
I CY | _ | CY | _ | С A | b_
a ~ | G/ | ~ | CM | ~ я + i
I-CXI -^r 1СУ1.
Упражнения
1. Центры квадратов, построенных внешним образом иа сто-
сторонах параллелограмма, являются вершинами квадрата ([43],
т. 1, стр. 21, 161).
2. В обозначениях рисунка 76 докажите, что
а) три прямые Л/, BJ, CH — конкурентны;
б) отрезки OiO2 и СО3 перпендикулярны, а их длины равны;
в) точки U, V, W являются серединами отрезков GK, JD, E1.
3. На плоскости дана точка Р. Постройте равносторонний
треугольник, одна из вершин которого отстоит от точки Р на
расстояние 2; вторая — 3, а третья — 4 (выбранных единиц
длины).
104
§ 3. Разворот
Один из случаев поворота, подобно параллельному
переносу, обладает свойством переводить каждую пря-
прямую в параллельную ей прямую. Это разворот или по-
поворот на 180°, который переводит каждый луч в проти-
противоположно ему направленный луч. Очевидно, что раз-
разворот полностью определяется заданием его центра.
Так как параллельный перенос переводит каждый луч
в параллельный ему луч, то результат двух последо-
последовательно выполненных разворотов является таким же,
как и в случае параллельного переноса. Короче говоря,
«сумма» двух разворотов есть параллельный перенос,
который превращается
в тождественное преоб-
преобразование, если оба
разворота имеют один
и тот же центр. Чтобы
А
Рис. 77. Рис. 78,
лучше понять действие этого преобразования, рассмот-
рассмотрим следующий пример: пусть точки А, В к С лежат
на прямой так, что точка В является серединой отрез-
отрезка АС. Рассмотрим разворот, оставляющий точку А
неподвижной, и разворот относительно точки В, пере-
переводящий точку А в точку С. Сумма этих двух разворо-
разворотов является параллельным переносом АС, а также
суммой разворотов вокруг точек В и С.
На рисунке 77 проиллюстрирована сумма разворо-
разворотов вокруг точек О\ и О2. Отрезок АВ сначала пере-
переводится в отрезок А'В' (противоположно направлен-
направленный), а затем в отрезок А"В"; таким образом, их сум-
суммой является параллельный перенос АА" = ВВ".
Многие старые и хорошо знакомые теоремы можно
доказать гораздо проще, используя развороты. На ри-
рисунке 78 точка О одновременно является серединой
105
двух отрезков АС и BD. Разворот вокруг точки О, пе-
переводящий отрезок АВ ъ отрезок CD, показывает, что
четырехугольник ABCD является параллелограммом.
Рассмотрим рисунок 79, на котором точки М и N — се-
середины отрезков АВ и АС. Мы видим, что сумма раз-
Ёоротов вокруг этих двух точек вновь является парал-
параллельным переносом ММ" = ВС, откуда следует, что
А,В'
Рис. 79.
отрезок MN параллелен отрезку ВС, а его длина
вдвое меньше длины отрезка ВС.
Упражнения "»
1. Пусть А—общая точка двух пересекающихся окружно-
окружностей. Постройте прямую, проходящую через точку А так, чтобы
Высекаемые ею хорды имели одинаковую длину.
2. Через точку А, лежащую вне данной окружности, прове-
проведите прямую, пересекающую окружность в точках Р и Q таких,
что \AP\ = \PQ\.
3. Если противоположные стороны шестиугольника равны и
параллельны, то диагонали (соединяющие противоположные вер-
вершины) конкурентны.
§ 4. Симметрия
Третьим типом преобразований,-сохраняющих рас-
расстояния, является симметрия относительно прямой
НК, называемой осью симметрии. Каждая точка, при-
принадлежащая оси (например, И или К), остается на
месте, т. е. является симметричной самой себе. Образ
точки Л, не принадлежащий оси, есть точка А', кото-
которая лежит на перпендикуляре, проходящем через точ-
точку А, причем ось делит пополам отрезок АА'. На рп-
сунке 80 отрезок А'В' является образом отрезка АВ.
Довольно просто показать, что если точка С лежит на
прямой АВ, то ее образ С принадлежит прямой А'В'.
106
В трапеции АА'В'В диагонали АВ' и А'В являются об-
образами друг друга; их общая точка X, являясь симме-
симметричной самой себе, лежит на оси НК. Из свойств вер-
вертикальных углов следует, что АХН = В'ХК, а из кон-
конгруэнтности треугольников ВХК и В'ХК вытекает, что
В'ХК = КХВ. Следовательно,
= КХВ.
Отсюда можно сделать вывод, что кратчайшим пу-
путем от произвольно заданной точки А до оси и далее
к данной точке В, лежащей по ту же сторону от оси,
является ломаная АХВ. Действительно, как видно из
Рис. 80.
Рис 81.
рисунка 81, если взять любую другую точку У на оси,
то длина ломаной AYB будет равна |ЛУ|-)-| У£?| =
= И'У| + |У5| и будет больше, чем длина отрезка
\А'В\ = \АХ\ + \ХВ\.
Это, в частности, дает нам способ геометрического
решения известной экстремальной задачи, не прибе-
прибегая к помощи вычислений. Физики утверждают, что
луч света, движущийся из точки А к зеркалу, и далее
к другой точке В, выбирает такой путь, при котором
время движения было бы наименьшим. В' однородной
среде это время пропорционально пройденному пути.
Поэтому луч света, который идет из точки А в точку
В, отражаясь в зеркале и падая на зеркало под уг-
углом а, отражается от него под тем же углом. Итак,
107
это является следствием требования, что путь должен
иметь наименьшую длину. Физики обычно измеряют
углы, отсчитывая их от нормали — перпендикуляра к
Рис 82.
зеркалу, вместо того чтобы отсчитывать их от самого
зеркала. Угол i, изображенный на рисунке 82, назы-
называется углом падения, а угол г — углом отражения.
Упражнения
1. Дан разносторонний треугольник ABC со сторонами, спо-
способными отражать свет. Определите, где на стороне АВ нужно
установить источник света, чтобы выпущенный из него луч, по-
последовательно отразившись в двух других' сторонах, вернулся
в ту же точку?
Указание. См. § 6 гл. 1.
2. Среди всех треугольников с заданными основанием и пло-
площадью равнобедренный имеет наименьший периметр.
3. Проделайте упражнение 1 § 3, используя симмефию.
§ 5. Задача Фаньяно
Свойства зеркального отражения могут быть ис-
использованы для вывода (притом весьма изящного)
многих интересных теорем. Мы применим эти свой-
свойства для решения задачи нахождения треугольника
наименьшего периметра, вписанного в данный остро-
остроугольный треугольник, известной как задача Фань-
Фаньяно*).
Решение начнем с того, что в произвольный остро-
остроугольный треугольник ABC (рис. 83) впишем его орто-
треугольник (изображенный штриховой линией) и лю-
*) Она была предложена в 1775 г. Фаиьяно, который решил
ее при помощи вычислений. Доказательство, приведенное здесь,
принадлежит Г. А. Шварцу. Другие доказательства, также ис-
использующие симметрию, см. Кокстер [17], стр. 39 или Казаринов
[26], стр. 76—77, или Курант и Роббннс [21], стр. 380. Метод
Шварца был перенесен с треугольников иа Bл + 1) -угольники
Франком Морлеем и Ф. В. Морлеем в книге: Frank Morley and
F. V. Morley, Inversive Geometry, Boston, GInn, 1933, стр. 37.
108
бой другой треугольник (изображенный пунктирной
линией). Затем последовательно будем отражать
Л ABC вместе с проведенными внутри него линиями
относительно сторон АС, СВ, В А, АС, СВ. Теперь ис-
исследуем полученный рисунок, чтобы увидеть все, что
произошло с нашими треугольниками.
Если не принимать во внимание две точки, поме-
помеченные буквой С, то остальные вершины образуют ло-
ломаную линию ВАВАВА, углы которой (измеряемые
против движения часовой стрелки) равны: 2Д в пер-
первой точке А (верхняя слева), 2В во второй точке В (в
середине), —2Д во второй точке А (снизу) и —2В в
третьей точке В (справа). Из того, что сумма этих че
тырех углов равна нулю, следует, что сторона В А, по-
полученная в результате последнего отражения, являет-
является образом стороны ВА исходного треугольника при
параллельном переносе; при этом пары со-
соответствующих точек на этих двух сторонах образуют
параллелограмм такой, как, например, PP'Q'Q.
Теперь мы вспомним, что высоты треугольника
ABC делят пополам углы его ортотреугольника. От-
Отсюда следует, что после указанных отражений сто-
стороны этого ортотреугольника будут последовательно
отложены на прямой РР', как показано на рисунке 83.
Аналогично, стороны любого другого треугольника та-
такого, как треугольник, изображенный на рисунке пун-
пунктирной линией, образуют ломаную, которая связы-
связывает точку Q (на исходной стороне АВ) с точкой Q'
109
'(на последней из полученных сторон АВ). Так как от-
отрезок PQ равен и параллелен отрезку P'Q', то длина
отрезка QQ' равна длине отрезка РР', которая в свою
очередь равна удвоенному периметру ортотреуголь-
ника. Ясно, что отрезок QQ' короче, чем ломаная, свя-
связывающая точки Q и Q', длина которой равна удвоен-
удвоенному периметру другого треугольника. Следовательно,
треугольником с минимальным периметром является
ортотреугольник.
§ 6. Задача о трех кувшинах
Любопытно применение симметрии *) к решению
задач, в которых требуется разделить жидкость на
определенные порции с помощью инструментов, каза-
казалось бы, совсем не приспособленных для этого. Для
того чтобы показать, как это делается, необходимо
предварительно описать трилинейные координаты, что
мы сейчас и сделаем.
Как правило, для нанесения точек с заданными де-
декартовыми координатами используется обычная мил-
миллиметровая бумага. Для наших же целей лучше ис-
использовать «триангулированную» бумагу, т. е. бумагу,
на которой проведены три системы параллельных
линий, разбивающих ее плоскость на маленькие рав-
равносторонние треугольники. На такой бумаге удобно
наносить точки, задаваемые трилинейными координа-
координатами относительно (большого) равностороннего тре-
треугольника. В плоскости такого треугольника ABC со
стороной а и высотой h трилинейные координаты точ-
точки Р определяются, как расстояния х, у, г точки Р от
трех его сторон ВС, СА, АВ. Эти расстояния считают-
считаются положительными, когда точка Р внутри треуголь-
треугольника. Введем для точки Р обозначение (х, у, г). Так
как
1 ,1 .1
~к ЦХ ■+■ -к О-У ~т тг az ==
I
— ^РВС I ^РСА Ч^ ^РАВ — "^АВС — о '
*) M. С. К. Tweedie, Mathematical Gazette 23 A939),
стр. 278—282; Я. И. Перелыиан, Занимательная геометрия, М.,
Физматгиз, 1958; Т. Н. Cfieirne, [27], стр. 49—75.
ПО
то мы имеем
Такими координатами можно идеально предста*
вить любую ситуацию, в которой три переменные ве-
величины имеют постоянную сумму. В том случае, когда
одна из величин остается постоянной, а две другие
изменяются (с постоянной суммой), точка (х, у, z)
движется по прямой, параллельной одной из сторон
треугольника. В частности, сами стороны описываются
уравнениями
х = 0, «/ = 0, z = 0,
а вершины А, В, С имеют координаты (ft, 0, 0),
@, ft, 0), @, 0, ft).
Именно такая ситуация возникает в том случае,
когда ft литров жидкости разливается по трем сосудам
так, чтобы в первом сосуде было х литров, во вто-
втором — у литров и в третьем — z литров. Постепенному
переливанию жидкости из второго сосуда в третий
соответствует движение точки (х, у, z) по прямой х =
= const в направлении, соответствующем уменьшению
у и соответственному увеличению z. Если каждый со-
сосуд может вмещать ft литров (такую ситуацию мы
будем обозначать символом [ft; ft, ft, ft]), то каждая из
координат может принимать любое значение от 0 до ft,
и множество точек, в которые можно попасть, как-то
переливая жидкость из одного сосуда в другой — это
множество мы назовем областью операций, — совпа-
совпадает с треугольником ABC и задается неравенствами
0<x<ft, 0<«/<ft, 0<z<ft.
Гораздо больший интерес представляет случай [ft; a,
Ъ, с], где ft ^ а > b > с. Теперь три данных сосуда
имеют емкости а, Ь, с, и задача состоит в том, чтобы
отмерить определенную величину а жидкости, много-
многократно переливая ее из одного сосуда в другой; при
этом мы или полностью опорожняем один сосуд, или
до краев наполняем другой (или, возможно, делаем и
то, и другое сразу)^ Область операций теперь примет
вид
Ш
Она, как правило, будет (правильным или неправиль*
ным) шестиугольником, ограниченным шестью пря-
прямыми
Но в частных случаях она может превратиться в пяти-
пятиугольник, трапецию, параллелограмм или (как мы
уже видели) охватывать весь равносторонний тре-
треугольник.
Например, на рисунках 84 и 85 проиллюстриро-
проиллюстрирована ситуация [8; 7, 6, 3], в которой 8 литров жидкости
503
л АЛЛАЛЛЛ/У л/\лллллл/\л
('80 06Z 053 008 080 061053 008
Рис. 84. Рис. 85.
некоторым заданным образом разлиты в сосуды ем-
емкостью 7, 6, 3 литров. Мы хотим отмерить, скажем,
4 литра. Теперь областью операций станет шести-
шестиугольная область
которая ограничена шестью прямыми
х = 7, z = 0, у = 6, л: = 0, 2 = 3, у = 0,
и имеет вершины
G, 1, 0), B, 6, 0), @, 6, 2), @, 5, 3), E, 0, 3), G, 0, 1)
или в сокращенной форме: 710, 260, 062, 053, 503, 701.
На рисунке 84 выделена точка 332, которая пред-
представляет общий случай: 3 литра в первом сосуде,
И2
820
столько же во втором и 2 литра в третьем. Ломаная,
исходящая из этой точки, указывает шесть возмож-
возможных операций по переливанию. Путь от точки 332 до
■точки 530 соответствует процессу опорожнения послед-
последнего сосуда в первый, а движению в противополож-
противоположную сторону от точки 332 до точки 233 соответствует
процесс наполнения третьего сосуда из первого. Пути
от точки 332 до точки 062 соответствует процесс опу-
опустошения первого сосуда во второй, который тем са-
самым наполняется.
Заштрихованные прямые на рисунке 85 показы-
показывают один из нескольких способов прохождения из
точки 332 в точку 440 и, таким образом, деления
8 литров на две равные
порции. Весь путь есть
ломаная, которая идет
всегда параллельно од-
одной из сторон исходно-
исходного треугольника и пово-
поворачивает только тогда,
когда она достигает
какой-нибудь стороны
или вершины шести-
угольника, ограничи-
вающего область опе-
операций. Если бы мы,
придерживаясь тех же
правил, продолжали
этот путь (минуя точ-
точку 440), то, в конце концов, достигли бы всех точек на
границе области операций, имеющих целые координа-
координаты. Из этого следует, что в ситуации [8; 7,6, 3] ука-
указанным образом может быть отмерено любое целое
число литров (меньше, чем 8).
На рисунке 86 проиллюстрирована ситуации [10;
8, 7, 6], в которой требуется разлить 10 литров жидко-
жидкости в сосуды, вмещающие 8, 7 и 6 литров, соответ-
соответственно. Здесь мы легко можем отмерить 1, 2, 3 или
4 литра. Но мы никогда не сможем отмерить 5 литров
(если не известно, что с самого начала в одном из со-
сосудов содержится 5 литров), потому что путь, прохо-
проходящий через точки 055, 505, 550, крутится подобно по-
порочному кругу, и в него нельзя войти ни с какого
ИЗ
073
055 OfyB
Рис. 86.
другого пути. Такие явления встречаются в любой си*
туации [h; a, b, с] при
Несколько другой случай аномалий встречается в
ситуации [10; 8, 6, 4] (рис. 87), где пути, проходящие
через точку 550, образуют узор из маленьких* равно-
равносторонних треугольников и правильных шестиугольник
ков. Это подтверждает тот очевидный факт, что нечет*
ное число литров нельзя измерить сосудами, все емко-
емкости которых четны. Та»
кие затруднения моьут
встретиться в любой
ситуации [h; a, ft, с], в
которой числа а, Ь, с
имеют общий делитель,
больший единицы.
Наиболее известны
ситуации [hya, ft, с], в
которых
h = а = Ы = Ъ + с,
и поэтому сфера опера-
операций ограничена парал-
параллелограммом, верши-
вершинами которого являются аОО, cbO, Obc, ЬОс. На рисун-
рисунках 88 и 89 в ситуации [8; 8, 5, 3] показаны шести-
этапное и восьмиэтапное решения задачи, которая мо-
может быть выражена следующим образом: два челове-
человека имеют сосуд, наполненный 8 литрами какой-то
жидкости, и два пустых сосуда; емкостью 5 литров и
3 литра. Они хотят разделить эти 8 литров жидкости
поровну.
Первое, что нужно сделать, — это либо наполнить
сосуд емкостью 5 литров, как на рисунке 88, либо со-
сосуд емкостью 3 литра, как на рисунке 89. После этого,
всякий раз, когда путь достигает одной из четырех
прямых у = 0, у = 5, z = 0, z = 3, которые являются
сторонами нашего параллелограмма (область опера-
операций), мы рассматриваем одну прямую как зеркало.
Другими словами, мы следуем по траектории билли-
ардного шара, который ударили так, чтобы он дви-
двигался вдоль одного края стола, имеющего эту несколь-
114
ко необычную форму. (Правило последовательных
отражений объясняется тем фактом, что каждый отре-
отрезок ломаной, параллельный стороне исходного тре-
треугольника, соответствует операции переливания
800
620
АЛЛЛЛЛлЛ
Рис. 88.
Рис. 89.
жидкости из одного сосуда в другой, а третий сосуд
в это время не трогают). Таким образом, мы получаем
семиэтапное решение
800, 350, 323, 620, 602, 152, 143, 440
и восьмиэтапное решение
800, 503, 530, 233, 251, 701, 710, 413, 440.
Ясно, что такую задачу (с а = Ь + с) можно ре-
решить только тогда, когда целые числа b и с — взаим-
взаимно просты, т. е. не имеют общего делителя, большего
единицы.
Упражнения
1. Нам даны сосуд емкостью 12 пиит, наполненный жидко-
жидкостью, и два пустых сосуда емкостью 9 пинт и 5 пинт. Каким об-
образом мы можем разделить жидкость на две равные порции?
2. Три грабителя украли у лавочника флакои с 24 унциями
бальзама. Убегая, они встретили по дороге продавца стеклянной
посуды, у которого купили три сосуда. Добравшись до надежного
места, они захотели разделить добычу, но оказалось, что куп-
купленные сосуды вмещают 13, 11 и 5 унций соответственно.
Как они мог,ли бы разделить добычу на равные доли? ([5],
стр. 28, 40).
3. Пусть две точки Р и Р' имеют трилинейные координаты
j[x, у, г) и (*', у1, г') относительно треугольника ABC. Если эти
115
координаты удовлетворяют уравнениям
хх' = уу' = zz',
то эти две точки являются изогонально сопряженными, т. е.
Р^АС = ВАР, Р^ВА = СВР, РТВ = АСР.
§ 7. Дилатация
Преобразования, которые мы до сих пор рассма-
рассматривали, объединяет то, что они переводят каждую
фигуру в конгруэнтную ей фигуру. Всякое преобразо-
преобразование, которое обладает свойством сохранять расстоя-
расстояния, мы назовем изометрией.
Однако во многих случаях бывает полезным ис-
использование преобразования фигуры в подобную
ей фигуру. Такое подобие сохраняет углы, но может
изменять расстояния. При этом все расстояния увели-
увеличиваются (или уменьшаются) в одном и том же отно-
отношении, называемом коэффициентом подобия. Таким
образом, любой отрезок АВ переводится в отрезок
А'В', длина которого равна
\A'B'\=k\AB\.
Коэффициент k может быть как большим, так и рав-
равным или меньшим единицы. Подобие содержит, как
частный случай, и изометрию, для которой k=l.
Эти рассуждения можно сделать более строгими,
если определить подобие как преобразование, сохраня-
сохраняющее отношение расстояний, откуда следует, что при
этом сохраняются углы, а прямые переходят в прямые.
Простейшим случаем подобия является дилатация,
которая переводит каждую прямую в параллельную
ей прямую. Любая дилатация, не являющаяся парал-
параллельным переносом, называется центральной дилата-
цией или гомотетией, потому что все прямые, соеди-
соединяющие соответствующие точки фигуры и ее образа,
пересекаются в одной точке. Чтобы убедиться в спра-
справедливости этого, рассмотрите рисунки 90 и 91, на
которых соответствующие отрезки АВ и А'В' (лежа-
(лежащие на параллельных прямых) удовлетворяют вектор-
векторному соотношению
АГВ' = ±А~В.
116
Для любой точки С, образующей вместе с точками А
и В треугольник, ее образ С является точкой пересе-
пересечения прямой, проходящей через точку А' параллель-
параллельно отрезку АС, с прямой, проходящей через точку В'
Рис. 90.
параллельно отрезку ВС. Если эта дилатация не яв-
является параллельным переносом, то прямые АА' и
ВВ' не параллельны, а пересекаются в точке О, обла-
обладающей тем свойством, что либо
и OB' = kOB,
как на рисунке 90, либо
~ и OB'=—kOB,
как на рисунке 91. Вспоминая, что параллельные пря-
прямые делят пересекающие их прямые на пропорцио-
пропорциональные отрезки, мы можем легко сделать вывод, чго
точка С лежит на отрезке ОС. Действительно,
117
Передвигая точку О все дальше и дальше влево на
рисунке 90, мы видим, что параллельный перенос яв-
является предельным случаем гомотетии А'В' = kAB,
когда коэффициент k стремится к единице. Еще проще
изменить рисунок 91 таким образом, чтобы точка О
стала серединой отрезка АА'. Отсюда следует, что
частным случаем гомотетии А'В' = — kAB является
центральная симметрия или разворот
А7В' = — АВ;
при этом четырехугольник АВА'В' является паралле-
параллелограммом с центром в точке О.
Упражнения
1. Определите множество середин отрезков, у которых один
конец находится в заданной точке, а другой — на заданной
окружности.
2. Постройте квадрат, две смежные вершины которого лежат
на стороне ВС остроугольного треугольника ABC, а две другие
вершины — на сторонах СА и АВ соответственно.
§ 8. Спиральное подобие
Если сначала произвести дилатацию, а затем па-
параллельный перенос, то любая прямая переходит в па-
параллельную ей прямую; следовательно, результатом
этого преобразования вновь является просто дилата-
ция. И вообще, по тем же соображениям, сумма лю-
любых двух дилатаций (т. е. к результату первой приме-
применяется следующая дилатация) есть дилатация. С дру-
другой стороны, если вначале произвести дилатацию, а
затем поворот, то тогда уже соответствующие прямые
не параллельны. Таким образом, сумма дилатаций и
поворота (отличного от тождественного преобразова-
преобразования или разворота) не является дилатацией, хотя и
остается прямым подобием, т. е. преобразованием, со-
сохраняющим как величину углов, так и их знак.
Сумма гомотетии и поворота вокруг того же
центра называется спиральным подобием. Это ма-
малоизвестное преобразование может быть прекрасно ис-
поЛьзовано для решения многих задач,
118
Если рассмотреть спиральное подобие с центром
в точке О, как на рисунке 92, которое переводит отре-
отрезок АВ в отрезок А'В', то треугольники ОАВ и ОА'В
связаны прямым подобием и
АОА' = ВОВ'.
Кроме того, как и в случае обычной дилатации, коэф-
коэффициент подобия
\ОА'\ _\А'В'\
\ОА\ \АВ\ '
Так как любое спиральное подобие полностью опреде-
определяется его центром О, коэффициентом k и углом пово-
поворота G, то мы будем его
обозначать символом
О (k, 8).
(Как обычно, поворот
в направлении против
движения часовой
Стрелки будем считать
положительным, а в
направлении по движе-
движению часовой стрелки — отрицательным.) В частности,
O(k, 0°) и O(k, 180°) являются дилатациями, проил-
проиллюстрированными на рисунках 90 и 91 соответственно,
i 0A, 6) является поворотом.
В качестве примера использования спирального
подобия докажем следующую теорему:
Теорема 4.81. Если на сторонах ВС, СА, АВ
треугольника ABC построены внешним образом квад-
квадраты с центрами в точках О\, Ог, Оз, то отрезки О1О2
и СО3 равны и перпендикулярны.
В обозначениях рисунка 93 спиральное подобие
/l(V2~*. 45°) преобразует треугольник САОз в тре-
треугольник КАВ, а спиральное подобие C(V2~. —45°)
преобразует треугольник О\СО^ в треугольник ВСК.
Так как первое преобразование переводит отрезок
О3С в отрезок ВК, а второе — отрезок О\О2 в тот же
отрезок ВК и так как коэффициент подобия один и
тот же у обоих преобразований, то и стороны исход-
исходных треугольников должны были быть равными,
119
Кроме тего, так" как угол между образами отрезков
ОзС и O\Oi (при подобиях, сопровождающихся пово-
поворотами на 45° и —45°) равен нулю, то эти отрезки и
первоначально должны были быть перпендикулярны-
перпендикулярными. Теперь доказательство закончено. (Заметим, что
три отрезка АО\, ВО^, СО3, являясь высотами тре-
треугольника О]О2Оз, конкурентны.)
Определив спиральное подобие как сумму гомоте-
гомотетии и поворота с одним и тем же центром, естествен-
естественно задаться вопросом: что же будет суммой гомоте-
гомотетии и поворота, если их центры различны. Простой и
К
Рис. 93.
неожиданный ответ — спиральное подобие —
является следствием того факта, что не существует бо-
более сложных случаев прямого подобия, а именно:
Теорема 4.82. Любые две прямо подобные фи-
фигуры могут быть переведены одна в другую парал-
параллельным переносом или спиральным подобием.
Для доказательства рассмотрим два соответствую-
соответствующих отрезка АВ и А'В' прямо подобных фигур. Если
отрезок АВ параллелен отрезку А'В' и имеет ту же
длину, то тогда это преобразование является парал-
параллельным переносом. Чтобы увидеть это, возьмем про-
произвольную точку С, не Лежащую на отрезке АВ, и ее
образ точку С. Тогда из.прямого подобия этих фигур
мы можем вывести, что треугольники ABC и А'В'С
конгруэнтны, а их соответствующие стороны парал-
120
лельны. Из этого следует, что все отрезки, соединяю-
соединяющие точки с их образами, параллельны и равны, т.е.
преобразование является параллельным переносом.
Далее предположим, что отрезки АВ и А'В' имеют
разные длины (если четыре точки А, В, А', В' не об-,
разуют четырехугольник, то выберите новую пару со-
соответствующих отрезков таких, чтобы они образовали
четырехугольник, и назовите их АВ и А'В'. Например,
если точка В лежит на отрезке АА', как на рисунке 94,
то возьмите вместо точки А середину отрезка АВ, а
вместо точки А' — середину отрезка А'В'). Тогда пря-
прямые АА' и ВВ' пересекаются в точке D, как на рисун-
рисунке 95. Пусть окружности ABD и A'B'D, имеющие об-
щук> точку D, пересекаются еще раз в точке О (если
же D — точка их касания, то буква О будет другим
обозначением точки D). Сравнивая углы ОАВ, ODB,
ODB' и О А'В', мы видим, что ОАВ=ОА'В'. Ана-
Аналогично ОВА = ОВ'А'. Таким образом, треугольни-
треугольники ОАВ и ОА'В', являясь прямо подобными, связа-
связаны спиральным подобием О (к, 9), где
*= и е
Другими словами, каждое прямое подобие, кото-
которое не является лараллельным переносом, имеет не-
неподвижную точку. Кроме того, неподвижная точка
только одна. Действительно, в противном случае, от-
отрезок, соединяющий две такие точки, скажем, А и В,
перешел бы сам в себя. А так как
R~ \AB\ ~1'
то подобие было бы изометрией, оставляющей эти две
точки неподвижными. И если при этом треугольник
ABC является образом некоторого треугольника
ABC, то мы можем считать, что точка С' лежит на
каждой из окружностей с центрами в точках Л и В и
радиусами АС и ВС. Однако такой изометрией мо-
может быть лишь тождественное преобразование, являю-
являющееся параллельным переносом (на нулевое расстоя-
расстояние), и симметрия, которая не является прямым подо-
подобием (потому что она меняет знаки углов).
121
•<=-_!
Рис. 94.
9
Рис. 95.
Рассмотрим следующий интересный факт: если на-
нарисовать на кальке две карты некоторого государства
в различных масштабах и совместить их*), то только
в одном месте обе карты будут изображать один и
тот же участок местности.
Идея спирального подобия легла в основу очень
красивой теоремы, сформулированной Юлиусом Пе-
терсеном (в 1880 году) и Р. Г. Шутом (в 1890 го-
ДУ) **). частным случаям которой является следую-
следующая
Теорема 4.83. Если ABC и А'В'С — два прямо
подобных треугольника и, кроме того, АА'А", ВВ'В",
СС'С" — три прямо подобных треугольника, то тре-
треугольник А"В"С" прямо подобен треугольнику ABC.
Если треугольники ABC и А'В'С совмещаются при
параллельном переносе, то утверждение очевидно,
если нет, то пусть О (k, 9) — то единственное спираль-
спиральное подобие, которое преобразует треугольник ABC
в треугольник А'В'С, так что
'\\ОВ'\\ ОС |
R ~
| О А | ~~ | ОБ | ~ | ОС
как на рисунке 94. Отсюда следует, что G = АО А' =•
= ВОВ' = СОС. Но мы допускаем, что
Л АА'А" оо Л ВВ'В" оо Л СС'С".
Следовательно,
| О А" | |Off4 | ОС" | .,
|ОЛ I ~~ \ОВ\ ~ \ОС\ ~R »
ЛОА" = ВОВ" = СОС" = 6',
и существует спиральное подобие O(k', 9'), переводя-
переводящее треугольник ABC в треугольник А"В"С".
Другим частным случаем теоремы Петерсена —■
Шута, который доказывается таким же образом, яв-
является
*) Здесь слово «совместить» используется в том смысле,
что меньшая карта целиком лежит В пределах большей. В этом
Случае легко показать, что центр спирального подобия действи-
действительно является точкой, лежащей внутри страны.
**) См. Ю. Петерсен [30], стр. 71 или Г. Г. Фордер [37],
стр. 53.
123
Теорема 4.84. Пусть задано подобие, переводя-
переводящее каждую точку Р отрезка АВ в точку Р' отрезка
А'В'; тогда точки, лежащие на отрезках РР' и деля-
делящие их в заданном отношении, либо различны и кол-
линеарны, либо все совпадают.
Упражнения
1. Если треугольник ABC преобразуется при помощи спи-
спирального подобия вокруг вершины А, при котором вершина В
движется по отрезку ВС, то вершина С будет двигаться прямо-
прямолинейно.
- 2. Если треугольник ABC является разносторонним, то его
внутренний треугольник Наполеона NiN2Ns является.обратно на-
направленным по отношению к нему в том смысле, что его ориен-
ориентация противоположна ориентации треугольников ABC и О^О
(это утверждалось без доказательства в § 3 гл. 3).
§ 9. Генеалогия преобразований
Существенной особенностью всех рассмотренных
нами преобразований является тот факт, что они ото-
отображают взаимно однозначно всю плоскость на себя.
Среди них мы рассмотрели только непрерывные пре-
преобразования (или «гомеоморфизмы»), т.е. преобразо-
преобразования, переводящие близкие точки в близкие точки *).
Среди непрерывных преобразований (которые, в неко-
некотором смысле, являются предметом рассмотрения кни-
книги О. Оре [28]) мы обсудили линейные преобразова-
преобразования, которые сохраняют коллинеарность точек и, сле-
следовательно, переводят параллельные прямые в парал-
параллельные прямые. Среди линейных преобразований мы
рассмотрели подобия, которые сохраняют отношения
расстояний, но мы не касались их более причудливых
видов, таких, как прокрустово растяжение (которое
переводит окружность в эллипс той же площади).
Частными случаями подобий, которые мы рассмотре-
рассмотрели, являются изометрия, сохраняющая расстояния,
•) Точнее: если А — некоторая точка, а А' — ее образ при
непрерывном преобразовании, то образ В' точки В будет лежать
внутри произвольно малого круга с центром в точке А', как
только точка В будет достаточно близка к точке А.
124
дилатация, переводящая каждую прямую в парал-
параллельную ей прямую, и спиральное подобие, которое
(так же как и во многих случаях изометрии и дилата-
ции) оставляет одну точку неподвижной и сохраняет
знак поворота (по движению часовой стрелки или
против ее движения). Эти категории частично пере-
перекрываются: среди изометрнй мы рассмотрели симмет-
симметрии, параллельные переносы (которые являются ди-
латациями согласно вышеприведенному определению)
и повороты (которые являются спиральными подобия-
подобиями с коэффициентом растяжения 1). Оставшимся ви-
видом дилатации является центральная дилатация или
гомотетия (которая является спиральным подобием
с нулевым вращением). И, наконец, разворот являет-
является как поворотом (на 180°), так и гомотетией. Все эти
связи могут быть сведены воедино в генеалогическом
дереве, где каждый «ребенок» является частным слу-
случаем своего «родителя»
^Преобразование |
у/влрерывнае преобразования^
\ \дилата^пА \ Спиральное поооби^
Симметрия Параллельный перенос Поворот Гомотетия
Упражнения
В терминах декартовых координат прокрустово растяже-
растяжение*) переводит каждую точку (х, у) в точку (х', у'), где
х' = kx, #' = k~ly. Запишите аналогичные выражения для:
*) В русской математической литературе это преобразование
носит название «гиперболический поворот». — Прим. перев.
125
1) параллельного переноса, переводящего точку (О, 0J в
точку (а; Ь),
2) симметрнв относительно оси Оу,
3) симметрии относительно прямой х — у = О,
4) разворота вокруг начала координат — точки О,
5) гомотетии O(k, 0°),
6) спирального подобия O(fe,90°),
7) изометрии, которая еще не была упомянута,
8) подобия, которое еще не было упомянуто,
9) непрерывного преобразования, не являющегося линейны^
10) преобразования, не являющегося непрерывным.
Глава 5
ВВЕДЕНИЕ В ИНВЕРСИВНУЮ ГЕОМЕТРИЮ
Помещаем круглую клетку в заданную
точку пустыни, входим в нее н запираем
изнутри. Производим инверсию простран-
пространства по отношению к клетке. Теперь лев
внутри клетки, а мы — снаружи.
Г. Петард *)
До сих пор мы рассматривали лишь взаимно одно*
значные преобразования всей евклидовой плоскости.
В настоящей главе это ограничение будет в значи-
значительной степени ослаблено — мы позволим одной из
точек, — точке О, — не иметь образа. Точнее, рассмат-
рассматриваемые преобразования будут состоять в том, что
мы фиксируем окружность с центром в точке О и
«выворачиваем» через нее плоскость. При этом проис-
происходит следующее: все окружности, проходящие через
точку О, преобразуются в прямые, а остальные окруж-
окружности— вновь в окружности (а более сложные фигу-
фигуры претерпевают радикальные изменения формы).
Использование такого преобразования часто ynpti-
щает решения многих задач, в которых фигурируют
прямые и окружности.
§ 1. Разбиение
Рассмотрим теорему, которая настолько интересна,
что была включена в 1965 году в число вопросов на
известном американском конкурсе по решению задач
«William Lowell Putnam Competition». Предлагаемое
нами доказательство этой теоремы является квинтэс-1
сенцией представленных решений.
Теорема 5.11. Если четыре точки А, В, С, D не
все лежат на одной окружности или прямой, то
*) «Другие математические способы охоты», см. American Ma-
Mathematical Monthly, авг. — сент., 1938, стр. 446—447. [См. также
«Физики продолжают шутить», М., «Мир», 1968, стр. 261; Мате-
Математическое просвещение, вып. 4, М., Физматгиз, 1959, стр, 188,
196. — Прим. перев.]
127
существуют две непересекающиеся окружности, одна
из которых проходит через точки А и С, а другая —
через точки В и D.
Прежде всего отметим, что если р — серединный
перпендикуляр отрезка AC, a q— серединный перпен-
перпендикуляр отрезка BD, то они не могут совпасть. В том
случае, когда прямые р и q пересекаются (как на ри-
рисунке 96), их общая точка О является центром двух
концентрических окружностей, одна из которых
проходит через точки Л и С, а другая — через точки
В и D. Если же прямые р и q параллельны (как на
рисунке 97), то также параллельны и прямые АС и
Рис. 96.
Рис. 97.
BD. Рассмотрим точки Р и Q на прямых р и ц (соот-
(соответственно), лежащие строго посередине между па-
параллельными прямыми АС и BD. Очевидно, что
окружности АРС и BQD не имеют общих точек.
Говорят, что две различные пары точек А, С и В,
D разбивают друг друга, если все точки А, В, С, D
лежат на одной окружности (или прямой), притом
так, что на каждой из дуг АС (или отрезке АС) ле-
лежит ровно одна из двух оставшихся точек В и £).Это
соотношение мы будем обозначать
AC//BD.
Заметим, что с тем же успехом мы сможем записать
это соотношение еще семью другими способами, на-
например, AC//DB или ВВЦ АС.
Если две пары точек Л, С и В, D, лежащие на од-
одной прямой или окружности, не разбивают друг дру-
друга, то легко построить две непересекающиеся окруж-
окружности, одна из которых проходит через точки Л и С,
128
Рис. 98.
а другая — через точки В и D. В том случае, когда
точки коллинеарны (рис. 98), мы воспользуемся
окружностями, построенными на отрезках АС и BD
как на диаметрах. В случае же, когда точки лежат на
одной окружности (рис. 99), мы можем принять в ка-
качестве их центров точки пересечения касательных в
точках Л и С, а также В и D.
Если, с другой стороны, AC//BD, то любая окруж-
окружность, проходящая через точки Л и С, но не проходя-
проходящая через точку В, «разбивает» точки В и D в том
смысле, что одна из
этих точек лежит вну-
внутри этой окружности,
а другая — вне ее. По-
Поэтому данная окруж-
окружность, проходящая че-
через точки Л и С, пере-
пересекает каждую окруж-
окружность, проходящую че-
через точки В и D.
Теорема 5.11, запи-
записанная в форме проти-
противоположной обратной,
утверждает, что если
каждая окружность,
преходящая через две
заданные точки, имеет
по крайней мере две
общие точки с каждой
окружностью, проходя-
проходящей через две другие данные точки, то эти четыре точ-
точки должны лежать либо на одной прямой (рис. 100),
либо на одной окружности (рис. 101). Очевидно, при
этом указанные пары точек разбивают'друг друга. Это
замечание позволяет нам определить разбиение дру-
другим способом — симметричным и не использующим
принадлежность этих четырех точек прямой или окру-
окружности.
Говорят, что две различные пары точек А, С и В,
D разбивают друг друга, если любая окружность, про-
проходящая через точки А и С, пересекает любую окруж-
окружность, проходящую через точки В и D {или совпадают
с ней).
5 Г. С. М. Коксетер, С. Л. Грейтцер 129
Рис. 99.
В действительности, существует и третий способ
определения понятия разбиения вообще без упомина-
упоминания окружностей:
Теорема 5.12. Попарные расстояния между че-
четырьмя различными точками А, В, С, D удовлетво-
удовлетворяют соотношению '
\BC\-\AD\^\AC\-\BD\,
причем равенство возможно только тогда, когда
AC//BD.
Хотя для того, чтобы понять это доказательство,
требуется внимательно следить за его ходом, оно до-
довольно интересно. Рассмотрим случай, когда все четы-
четыре точки лежат на одной
прямой и, следовательно,
\27
Рис 100. Рис. 101.
мы можем временно вновь использовать обозначения
для направленных отрезков (положительных или от*
рицатёльных, как в § 1 гл. 2), Обозначим
тогда
АВ = х — у, BC = y — z, AC--
и мы имеем
E.124)
Если AC//BD (как на рисунке 101), то на отрезке АС
лежит ровно одна из двух точек В или D, поэтому от*
ношения АВ/ВС и AD/DC имеют противоположные
знаки, так же и произведения ABXDC и BCXAD
имеют противоположные знаки, а произведения ЛВХ
X CD и BCXAD имеют одинаковые знаки, Следова*
130
тельно, соотношение E.121) будет выполнено и в том
случае, если выражения АВ, CD и т. д. мы будем по-
понимать как обычные положительные длины отрезков.
Если же, с другой стороны, точки Л и С не разбивают
точек В и D (см. рис. 98), то эквивалентные утвержде-
утверждения меняются на обратные, например: АВУ^СР и
BCXAD имеют противоположные знаки. Теперь, если
использовать лишь положительные длины, то соотно-
соотношение E.121) означает, что положительное число
\АС\ • \BD\ равно разности между двумя положитель-
положительными числами |ЛВ|-|"С£)| и |ВС|-|Л£)|. А так как
их сумма больше их разности, из этого следует, что
| Л В | • | CD | +1 ВС | • \AD | > J АС | • | BD |.
На этом заканчивается доказательство теоремы 5.12
для случая коллинеарных точек.
И, наконец, если эти четыре точки не лежат на
одной прямой, то некоторые три из них должны обра--
зовывать треугольник, и мы можем переобозначить их
(если необходимо) так, чтобы этот треугольник имел
обозначение ABC, а оставшаяся точка (возможно, ле-
лежащая на одной из сторон этого треугольника) — D,
Теперь мы видим, что теорема 5.12 есть следствие тео-
теоремы Птолемея B.61) и ее обратной B.62), которая
утверждает, что попарные расстояния между четырь-
четырьмя точками Л, В, С, D (первые три из которых обра-
образуют треугольник) удовлетворяют соотношению
\AB\-\CD\ + \BC[-\AD[>[AC['\BD\
(знак равенства появляется только тогда, когда
ABCD — вписанный четырехугольник с диагоналями
AC nBD).
Упражнение
1. Запишите все восемь соотношений, эквивалентных соотно-
соотношению АС ИBD.
§ 2. Сложное отношение
Для любых четырех различных точек А, В, С, D
определено число {АВ, CD}, называемое сложным от-
отношением этих точек в указанном порядке; оно
Б* 131
определяется через их попарные расстояния с по-
помощью следующей формулы:
Разделив обе стороны неравенства в теореме 5.12 на
|ЛС|-|В/)| и использовав введенное обозначение,мы
получаем следующее утверждение:
Теорема 5.21. Сложные отношения четырех то-
точек А, В, С, D удовлетворяют соотношению
{AD, ВС} + {АВ, DC} = 1
тогда и только тогда, когда AC//BD.
Этот критерий разбиения, записанный в терминах
сложных отношений, позволяет нам поменять ролями
рассматриваемые понятия: вместо определения раз-
разбиений через окружности, мы теперь сможем опреде-
определить окружности через разбиения! Любые три различ-
различные точки А, В, С определяют единственную
окружность (или прямую) ABC, состоящую из самих
точек А, В, С и точек X, для "которых выполняется
одно из следующих соотношений:
ВС//АХ, или СА//ВХ, или АВ//СХ.
Упражнения
1. {АВ, CD] = {В A, DC) = {CD, AB] = {DC, В А].
2. Вычислите {AD, ВС) + {АВ, DC} при условии, что:
а) точки В и D делят отрезок АС внутренним и внешним
образом в одном и том же отношении, т.е. \АВ\1\ВС\ =
= \AD\I\CD\;
б) точка D —^цеитр равностороннего треугольника ABC;
в) ABDC—квадрат;
г) ABCD — квадрат.
§ 3. Инверсия
В 1831 году Л. Магнус предложил следующее «ква-
зипреобразование». Пусть даны окружность со с цент-
центром в точке О и радиусом k, как на рисунке 102, и
точка Р, отличная от точки О. Образом точки Р при
инверсии относительно окружности со назовем точку
132
Р', лежащую на луче OP, расстояние которой до точ-
ки О удовлетворяет соотношению
Из этого определения следует, что образом точки Рг
является точка Р, а следовательно, инверсия (так же
как и известные нам разворот и симметрия) обладает
тем свойством, что двукратное ее применение приво-
приводит к тождественному преобразованию. Кроме того,
каждая точка, лежащая вне окружности инверсии со,
имеет своим образом точку, лежащую внутри ее: ин-
инверсия «выворачивает внутренность окружности со на-
наружу». Единственными точками, которые переходят
в себя при этом преобразо-
преобразовании, являются точки, ле-
лежащие на окружности со.
Рассмотрим, во что пере-
переходят при инверсии некото-
некоторые кривые. Окружность с
центром в точке О и радиу-
радиусом г, очевидно, переходит
в концентричную ей окруж-
окружность радиуса k2/r. Любая
прямая, проходящая через точку О, переходит в себя
при условии, что мы не рассматриваем саму точку О
(попытку избежать этой оговорки, принимая в каче-
качестве образа точки О саму точку О, следует признать
неудачной, поскольку при этом нарушается непрерыв-
непрерывность преобразования: при приближении точки Р к
точке О точка Р' удаляется от нее).
. Пусть точка Р лежит внутри окружности со (не
совпадая с точкой О). Рассмотрим хорду TV, прохо-
проходящую через точку Р перпендикулярно к отрезку ОР,
и точку Р', в которой пересекаются касательные, про-
проведенные к окружности в точках Т и U. Так как тре-
треугольники ОРТ и ОРТ подобны, то точка Р', пост-
построенная таким образом, удовлетворяет соотношениям:
и, следовательно, является образом точки Р.
И, наоборот, чтобы построить образ произволь-
произвольной точки Р', лежащей вне окружности со, нужно
133
построить окружность на отрезке ОР' как на диаметре,
а точки ее пересечения Т и U с окружностью со соеди-
нить отрезком TU. Тогда его середина и будет иско-
искомой точкой Р (являющейся точкой пересечения отрез-
отрезков TU и ОР).
Рисунок 103 показывает, что образом любой пря-
прямой а, не проходящей через точку О, является окруж-
окружность, проходящая через точку О (за исключением
самой точки О), а ее диаметр, проходящий через точ-
точку О, перпендикулярен прямой а. Докажем это стро-
строго. Пусть точка А — основание перпендикуляра, опу-
опущенного из точки О на прямую а, и пусть А' — образ
.точки Л, Возьмем произвольную точку Р на прямой
а и обозначим через Р' точку пересечения луча ОР
с окружностью, построенной на отрезке ОА' как на
диаметре. Тогда из подобия треугольников ОАР и
ОР'А следует, что
\ОР\ _ \ОА'\
\ОА\
\ОР'\
\\\\ \\\
И, наоборот, все точки Р', лежащие на окружно-
окружности с диаметром ОА' (за исключением точки О), пе-
переходят в точки прямой а. Следовательно, образом
любой окружности, проходящей через точку О (с вы-
выколотой точкой О), является прямая, перпендикуляр-
перпендикулярная ее диаметру, проходящему через точку О, т. е.
прямая, параллельная касательной к этой окружно-
окружности в точке О.
Из этого следует, что пара пересекающихся окруж-
окружностей, точками пересечения которых являются точки
О и Pt переходит в пару пересекающихся прямых,
134
проходящих через точку Р' — образ точки Р, а пара
касающихся окружностей, имеющих точку О в каче-
качестве точки касания, переходит в пару параллельных
прямых.
Существует инструмент не намного сложнее цир-
циркуля, с помощью которого мы рисуем окружности,
позволяющий нарисовать образ при инверсии любой
данной кривой. Это приспособление, открытое Л. Лип-
киным в 1781 году, было переоткрыто А. Поселье поч-
почти девяносто лет спустя и получило известность как
инверсор Поселье*). Оно состоит из шести шарнирно
соединенных стержней, четыре из которых образуют
ромб PQP'R (длина стороны
которого равна Ь), а два
других (длины а, большей
Ь) соединяют два противо-
противоположных угла Q и R этого О'
ромба с фиксированной точ-
точкой О (см. рис. 104). Если
вставить кончик карандаша
в точку Р', а в точку Р —
острие следящей иглы (или Рис- 104-
наоборот) и передвигать
иглу вдоль заданной кривой, то карандаш будет вы-
вычерчивать образ этой кривой при инверсии. Действи-
Действительно, если точка X — центр ромба, то
\ = (\OX\-\PX\)(\OX\
= \ ОХ Р -1РХ р = | ОХ Р +1 RX Р -1 RX Р -1РХ Р =
т.е. произведение |ОР|-|ОР'| является постоянным.
Естественно, что конструкция прибора позволяет пре-
преобразовывать лишь кривые, лежащие внутри кольца,
ограниченного окружностями с центром в точке О и
радиусами а± Ь.
*) Другие конструкции и теорию рычажных механизмов см.,
например, А. В. Kemple, How to Draw a Straight Line, стр. 1—51
(в книге Hobson и др., Squaring a Circle, Chelsea, New York,
1953); для более глубокого изучения см. И. И. Артоболевский,
Теория механизмов для воспроизведения плоских кривых, Мо-
Москва, Изд-во АН СССР, 1959 г. или Е. Н. Lockwood [24].
135
В частности, если седьмой стержень SP соединяет
точку Р с фиксированной точкой S, расстояние кото-
которой от точки О равно длине этого стержня, то точка Р
будет вынуждена двигаться по окружности, проходя-
проходящей через точку О и, следовательно, точка Р' будет
описывать прямую или, точнее, отрезок. Таким обра-
образом, инверсор Поселье решает старую задачу — по-
построение прямой без использования линейки (прямиз-
(прямизна которой теоретически зависит от прямизны ранее
построенной прямой).
Образом треугольника при инверсии обычно явля-
является довольно странная фигура, образованная дугами
трех окружностей, про-
ходящих через точку О.
Однако, если ограни-
ограничиться рассмотрением
только вершин тре-
треугольника ABC, то мо-
можно получить интерес-
интересный результат. Если
Рис. 105. вершины А, В, С пере-
переходят при инверсии в
точки А', В', С, как на рисунке 105, и точка О лежит
внутри треугольника ABC, то из равенств
| ОА 1.1 OA'\ = k2 = \ OB |-1 OB' |
следует, что треугольник ОА'В подобен треугольнику
OB А и углы, помеченные цифрой 1, равны. То же са-
самое справедливо для углов, помеченных цифрой 2.
Следовательно, угол ВОС равен сумме углов при вер-
вершинах Л и Л' в треугольниках ABC и А'В'С. А так
как
ВОС = 1 + Л'В'О + 2 + Л'С'О
и
А&О = ВАд, А^О = САО,
то мы имеем
ВОС = Т + 2 + ВАО + САд = ВГАУС + ВАС.
Аналогично
СОА = В + В'.
136
Отсюда следует, что для данного треугольника ABC
можно легко подобрать такое положение точки О,
чтобы получился треугольник А'В'С с любыми напе-
наперед заданными углами при вершинах А' и В'. Найдя
такое положение точки О, мы можем изменить k и,
таким образом, изменить размер треугольника А'В'С'
(см. упражнение 6). Можно легко подобрать указан-
указанное положение точки О и в том случае, если она на-
находится вне треугольника ABC, более того, даже если
точки А, В, С коллине.арны. Следовательно, справед-
справедлива
Теорема 5.31. Для любого данного треугольни-
треугольника и любых точек А, В, С можно подобрать окруж-
окружность инверсии так, чтобы образы А', В', С этих то-
точек стали вершинами треугольника, конгруэнтного
данному.
Упражнения
1. Постройте образ квадрата, описанного вокруг окружности
инверсии.
2. Найдите положения точки О, для которых стороны дан-
данного треугольника переходят в три конгруэнтные окружности.
3. Дана окружность <в с центром в точке О и некоторая
точка Р, отличная от точки О. Постройте образ точки Р, исполь-
используя только циркуль (без линейки) *):
а) при OP > k/2;
б) при -А-<0Р< 2{nk_x) ([4], стр. 144).
4. Как связаны треугольники ABC и А'В'С, если точка О
является для треугольника:
а) центром описанной окружности;
б) ортоцентром;
в) центром вписанной окружности?
5. Найдите координаты образа точки (х, у) при инверсии
относительно окружности
х2 + у2 = k2.
6. Даны треугольники ABC и DEF. Опишите в общих чер-
чертах процесс нахождения центра О и радиуса k окружности ин-
инверсии, обладающей тем свойством, что образы точек А, В, С
являются вершинами треугольника А'В'С, конгруэнтного тре-
треугольнику DEF.
*) Используя инверсию, можно показать, что все построения,
выполнимые с помощью циркуля и линейки, могут быть выпол-
выполнены с помощью только одного циркуля; см. [21], стр. 176—188
или Н. P. Hudson, Ruler and Compasses, стр. 131—143 (статья,
содержащаяся в упомянутой выше книге «Squaring a Circle»).
137
§ 4. Круговая плоскость
В предыдущем параграфе мы видели, что любая
окружность, проходящая через точку О (с выколотой
точкой О) переходит при инверсии в прямую и что
любая окружность с центром О переходит при инвер-
инверсии в окружность. Естественно задать вопрос: что
случится с иначе расположенной окружностью. Сна-
Сначала рассмотрим, как изменяется расстояние между
двумя точками при инверсии.
Теорема 5.41. Если при инверсии относительно
окружности с центром в точке О и радиусом k пара
точек А, В переходит в пару
точек А', В', то расстояния
между ними удовлетворяют
равенству:
|Л '~ \OA\-\OB\'
Действительно, так как
треугольники ОАВ и ОВ'А
подобны (рис. 106), то
| А'В' | _ | О А' | _
\АВ\ — \ОВ\
_ | О А | • | О А' | fe2
~~ | ОА | • | ОВ | ~~ I О А | • | ОВ Г
Рис. 106.
Отсюда легко следует сохранение величины слож-
сложного отношения*).
Теорема 5.42. Если точки А, В, С, D переходят
при инверсии в точки А', В', С, D', то
{А'В', CD'} = {AB, CD}.
Действительно,
fe21АС|
fe21BD|
\'R' Г'П'\— \A'C'\-\B'D'\ \OA\-\OC\ \OB\-\OD\ _
i d , и и ) — | A,D, | _ | B,c, | — k2 | AD | fe2 | ВС | ~
|0Л | -| 0£>| "|OB|-|OC|
_ \AC\-\BD\ _
~~ \AD\-\BC\
*) J. Casey, A Sequel to the First Six Books of the Elements
of Euclid Fth ed.), Hodges Figgis, Dublin, 1892, стр. 100.
138
В свою очередь, отсюда следует сохранение раз-
разбиения:
Теорема 5.43. Если при инверсии точки А, В, С,
D переходят в точки А', В', С, D' и AC//BD, то
A'C'1/B'D'.
На самом деле, используя теоремы 5.21 и 5.42, мы
получаем, что отношение AC//BD означает, что
{A'D1, В'С'} + {А'В', D'C'} = {AD, ВС} + {АВ, DC} = 1,
откуда A'C'1/B'D'.
В конце § 2 мы установили, что любая окружность
полностью определяется тремя своими точками как
множество, состоящее из этих точек А, В, С и всех то-
точек X, удовлетворяющих либо ВС//АХ, либо СА//ВХ,
либо АВ//СХ. Следовательно, образ данной окружно-
окружности при инверсии состоит из точек А', В', С и всех
точек X', удовлетворяющих либо С А'//В'Х', либо
А'В'ЦС'Х', либо В'С'ЦА'Х', т. е. ее образом является
окружность (или прямая) А'В'С. Как мы установили
в § 3, окружность переходит при инверсии в прямую
тогда и только тогда, когда она проходит через точку
О. Тем самым доказана
Теорема 5.44. Образом при инверсии любой
окружности, не проходящей через точку О, является
окружность, не проходящая через точку О.
Описание окружности (или прямой) через разбие-
разбиения наводит на мысль, что может оказатьей полезным
следующее изменение нашей терминологии: пусть по-
понятие окружность включает как частный случай и
прямые, т. е. мы будем рассматривать прямую как
окружность бесконечного радиуса. Одновременно до-
договоримся присоединить к евклидовой плоскости един-
единственную бесконечно удаленную точку Рх и считать
ее образом центра для любой окружности инверсии.
Так пополненная плоскость называется круговой плос-
плоскостью. Так как при инверсии с центром в точке О
любая окружность, проходящая через точку О, пере-
переходит в прямую, то мы будем рассматривать прямую
как окружность, проходящую через точку Рх. Далее,
поскольку две окружности, касающиеся друг друга
в точке О, переходят при инверсии в параллельные
прямые, то мы будем рассматривать параллельные
прямые как окружности, касающиеся в точке />„,. При
139
этом соглашении из теоремы 5.44 в сочетании с ре-
результатами § 3 получается для круговой плоскости
Теорема 5.45. При инверсии образом любой
окружности является окружность.
Присоединение точки Р^, к евклидовой плоскости
позволяет нам объявить инверсию взаимно однознач-
однозначным преобразованием всей круговой плоскости: каж-
каждая точка (без исключения) имеет образ, и каждая
точка является образом некоторой точки.
Любые две окружности могут быть отнесены к од-
одному из трех типов: пересекающиеся, касающиеся и
непересекающиеся, которые характеризуются количе-
количеством общих точек B, 1 и 0). Поэтому пара окружно-
окружностей при инверсии переходит в пару окружностей,
принадлежащих к тому же типу (при этом к «касаю-
«касающимся окружностям» причисляются как окружность
с касательной к ней прямой, так и две параллельные
прямые).
Упражнения
1. Пусть Л—любая точка вне окружности ш, Л'— ее образ
при инверсии и Р—точка, движущаяся по окружности ш. Тогда
для любого положения точки Р отношение |РЛ[/|РЛ'| постоянно.
Обратно, если точки В и С делят данный отрезок АА' внешним
и внутренним образом в одном и том же заданном отношении
(отличном от единицы, как в упражнении За § 3), то окружность,
построенная на отрезке ВС, как иа диаметре, является множе-
множеством точек, отношение расстояний которых от точек Л и Л'
постоянно. (Это множество называется окружностью Аполлония.)
2. Пусть через произвольную точку на окружности <в про-
проведены прямые, проходящие через концы некоторого диаметра
этой окружности. Обозначим через Р и Р' точки пересечения
этих прямых с другим диаметром, перпендикулярным первому
Тогда точка Р' является образом точки Р.
3. Через любые две точки, лежащие внутри данной окружно-
окружности, можно провести только две окружности, касательные к
данной.
4. Для любых трех различных точек можно построить три
попарно касающиеся окружности, для которых данные точки
являются центрами. Если а, Ь, с — попарные расстояния между
этими точками, то радиусы этих окружностей, как легко видеть,
равны s — a, s — b, s — с, где s=(a + 6 + c)/2. (Эти точки ие
обязательно должны образовывать треугольник. Они могут быть
и коллинеарными.) При этом существуют ровно две окружности,
касающиеся всех этих трех окружностей. Эти две окружности
не пересекаются. (Они называются окружностями Содди ([17],
стр. 29—32)).
5. Дайте короткое доказательство теоремы 5.12, используя
инверсию ([31], стр. 10—11),
140
6. При' инверсии относительно окружности ш с центром в
точке О окружность а, проходящая через точку О, переходит
в прямую являющуюся радикальной осью (см. § 2 гл. 2) окруж-
окружностей ш и а.
7. Если рассматривать прямую как частный случай окруж-
окружности, то чему соответствует пара пересекающихся прямых?
Паре касающихся или паре пересекающихся окружностей? Объ-
Объясните ваш ответ в терминах количества общих точек у двух
прямых.
§ 5. Ортогональность
Итак, мы обнаружили, что при инверсии окружно-
окружности сохраняются (вновь переходят в окружности). Те-
Теперь нам остается сделать лишь один шаг, чтобы уви-
увидеть, что при этом сохраняются также и углы. Угол
между двумя пересекающи-
пересекающимися окружностями есте-
естественно определить как угол
между касательными к ним
в точке пересечения. Из
симметрии относительно ли-
линии центров ясно, что углы
имеют одну и ту же величи-
величину в обеих точках пересече-
пересечения. Посмотрим, как на ве-
величину углов влияет инвер-
инверсия относительно окружно-
окружности с центром в точке О. Рис- 107-
Пусть 0 — один из углов
между двумя прямыми а и Ь, проходящими через
точку Р, как на рисунке 107. При обсуждении ри-
рисунка 103 мы заметили, что прямая а при инверсии
переходит в окружность а, проходящую через точку О,
касательная к которой в точке О параллельна пря-
прямой а. Аналогично, прямая b переходит при инверсии
в окружность р, проходящую через точку О, касатель-
касательная к которой в точке О параллельна прямой Ъ. Так
как угол 6 является углом между их касательными в
точке О, то он является углом пересечения и самих
окружностей аир. Однако эти окружности пересе-
пересекаются не только в точке О, но и в точке Р' — образе
точки Р. Следовательно, окружности образуют тот же
самый угол бив точке Р'.
Читатель может легко сообразить, какие необхо;
димы изменения в том случае, если прямая а (или Ь)
141
проходит через точку О. (Если обе прямые проходят
через точку О, то они переходят при инверсии в са-
самих себя, и неизменность угла становится очевидной.)
Пусть некоторые две окружности проходят через
точку Р. Мы можем считать, что прямые а и b явля-
являются их касательными в точке Р. Образы этих окруж-
окружностей при инверсии касаются окружностей аир
(соответственно) в точке Р'. Следовательно, спра-
справедлива
Теорема 5.51. Если две окружности пересекают-
пересекаются под углом 0, то образы этих окружностей при ин-
инверсии пересекаются под тем же углом 0.
Две окружности называются ортогональными, если
они пересекаются (дважды) под прямым углом, при
этом в каждой из точек пересечения касательная к
одной из них является диаметром другой. Частным
случаем теоремы 5.51 является
Теорема 5.52. Ортогональные окружности пере-
переходят при инверсии в ортогональные окружности.
Рассмотрим вновь рисунок 24 и заменим на нем
обозначение точки Р на О. Изображенную там окруж-
окружность мы можем рассматривать в качестве произвола
ной окружности, проходящей через точки А и А' (каж*
дая из которых, как и следует из обозначения, являет-
является образом другой при инверсии с центром в точке
О). Тогда, так как
£2 = | ОА \-\OA' | = | ОВ\-\ОВ' | = | ОТ?,
то любая другая секущая ВВ', проходящая через точ-
точку О, порождает новую пару точек В и В', переходя-
переходящих друг в друга при этой инверсии. А если рассмот-
рассмотреть касательную, проведенную из точки О к этой
окружности, то точка касания Т будет точкой, перехо-
переходящей в себя при этой инверсии, т. е. точкой, лежа*
щей на окружности инверсии со. Следовательно, имеет
место.
Теорема 5.53. Любая окружность, проходящая
через две различные точки, каждая из которых явля-
является образом другой при инверсии относительно
окружности со, переходит в себя при этой инверсии и
ортогональна к окружности со.
Обратно, каждая окружность, ортогональная к
окружности со, переходит в себя при инверсии относи-
142
тельно этой окружности. -Действительно, если она пе-
пересекает окружность со в точке Т и А — любая ее дру-
другая точка, то прямая ОА пересекает ее также в точке
А', обладающей тем свойством, что
Кроме того, если две окружности, ортогональные к
окружности со, пересекаются, то их общие точки пере-
переходят друг в друга при этой инверсии. На самом де-
деле, если точка А — одна из этих точек, то прямая ОА
пересекает каждую из окружностей в точке, являю-
являющейся образом точки А.
Эти замечания позволяют нам дать определение
инверсии, используя понятие ортогональности, так что
в результате получим «инверсивное» определение ин-
инверсии:
Любая точка на окружности со является своим об-
образом при инверсии относительно этой окружности;
образом любой другой точки Р при этой инверсии
является вторая точка пересечения любых двух окруж-
окружностей, проходящих через точку Р и ортогональных к
окружности со.
Если вместо окружности со мы возьмем прямую, то
согласно приведенному определению инверсия превра-
превращается в симметрию относительно этой прямой и, сле-
следовательно, симметрию можно считать частным слу-
случаем инверсии.
Из того же определения инверсии следует, что для
любой окружности а и двух точек, переходящих друг
в друга при инверсии относительно этой окружности,
их образами при инверсии относительно окружности ю
будут окружность а' и две точки, переходящие друг
в друга при инверсии относительно окружности а'. Те-
Теперь, соединив идеи инверсивной геометрии и евкли-
евклидовой, мы можем установить влияние инверсии на по-
положение центра А окружности а. Мы могли бы пред-
предположить, что при инверсии точка А переходит в центр
окружности а', но это было бы слишком просто! (Это-
(Этого не происходит даже в том случае, когда окруж-
окружность а совпадает с окружностью со.) В действитель-
действительности, при инверсии относительно окружности со
окружность а переходит в окружность а', а две точки
А и Рос, переходящие друг в друга при инверсии
ИЗ
относительно окружности а, преобразуются в две точ-
точки А' и О, переходящие друг в друга при инверсии от-
относительно окружности а'. Таким образом, точка А'
(являясь образом точки А при инверсии относительно
О)
Рис. 108. _
окружности со) не будет центром окружности а', а
будет образом точки О (при инверсии относительно
окружности а', рис. 108).
Упражнения
1. Дана окружность <в и точка А вне нее. Постройте окруж-
окружность с центром в точке А, ортогональную окружности <в.
2. Дана окружность ш и две точки Р и Q, не переходящие
друг в друга при инверсии относительно этой окружности. По-
Постройте окружность, проходящую через точки Р и Q, ортогональ-
ортогонально к окружности ш.
Рис. 109.
3. Дана точка Р и две окружности a>i и а>2, не проходящие
через точку Р. Постройте окружность, проходящую через точку Р
и ортогональную к обеим окружностям u>i и <в2.
4. Пусть при инверсии относительио окружности а (радиуса k
и с центром в точке О) окружность а переходит в окружность а'.
Найдите, как связаны между собой степени точки О относитель-
относительно окружностей а и а'.
144
5. Для любой окружности а, точки Р, лежащей иа ней, и
точки О, не лежащей на ней, существует единственная окруж-
окружность, проходящая через точку О и касающаяся окружности ее
в точке Р (рис. 109).
§ 6. Теорема Фейербаха
В § 8 гл. 1 мы кратко упомянули теорему Фейер-
Фейербаха, доказательство которой может быть проведено
с помощью инверсии по крайней мере тремя спосо-
способами. Один из них изложен в книге Д. Пидо ([31],
стр. 9—10). Прежде чем изложить другой способ*),
вновь сформулируем теорему Фейербаха, а именно":
3-,
Теорема 5.61. Окружность девяти точек произ-
произвольного треугольника касается вписанной и всех трех
вневписанных окружностей этого треугольника.
На рисунке ПО изображены треугольник ABC, его
серединный треугольник А'В'С, окружность, вписан-
вписанная в треугольник ABC (с центром в точке /), касаю-
касающаяся стороны ВС в точке X, одна из вневписанных
окружностей (с центром в точке /„), касающаяся сто-
стороны ВС в точке Ха, и общая касательная В\С\ к этим
двум окружностям (которые одновременно касаются
всех трех сторон треугольника ABC). На этом рисун-
рисунке также изображены окружность со, построенная на
отрезке ХХа как на диаметре, и точки S, В", С", в ко-
которых отрезок В\С\ пересекает отрезки ВС, А'В',
*) См. [29], стр. 76-77.
145
А'С. Так как окружность со ортогональна к вписан-
вписанной и к вневписанной окружностям, то при инверсии
относительно окружности со обе эти окружности пе-
переходят в себя: Теперь мы переходим к доказатель-
доказательству того, что инверсия относительно окружности со
переводит окружность девяти точек А'В'С' в прямую
Bid.
Из теоремы 1.41 'и последующих замечаний мы
имеем
(где £ = (а + Ь + с) /2), откуда следует, что центром
окружности со является точка А'— середина отрезка
ВС, а длина диаметра окружности со равна
(эту величину мы предполагаем положительной; в
противном случае проведем те же построения по от-
отношению к другой стороне, соответственно переимено-
переименовав вершины А, В, С). Окружность девяти точек про-
проходит через точку А — центр окружности со; следова-
следовательно, при инверсии относительно окружности со она
переходит в прямую. Показав, что точки В" и С" яв-
являются образами при инверсии относительно окруж-
окружности со точек В' и С, лежащих на окружности девя-
девяти точек, мы получим, что эта прямая проходит через
точки В" и С" (а поэтому и через точки В\ и С\).
Так как точка S (так же как и точки / и /„) ле-
лежит на биссектрисе угла Л, а по теореме 1.33 точка S
делит отрезок СВ (длины а) в отношении Ъ : с, то мы
имеем
Я Со = -
аС
Ь + с ' ' Ь + с
и полуразность этих двух длин равна
1 ол ' ~ 2 (Ь + с)'
Также |ВС,| = |ЛС,| — \АВ\ = \АС\ — \АВ\ =;
= b — си, аналогично, |СВу\ =Ь — с.
146
Так как треугольник SA'B" подобен треугольнику
SBC\ и треугольник SA'C" подобен треугольнику
SCB\, то мы имеем
\А'В"\ \А'В"\ _ \SA'\ _ Ь-с
Ъ — с |ВС,| ~ \SB\ ~ 2с
И
\А'С"\ \А'С"\ _ \SA'\ _ Ъ — с
Ъ~с ~ |СВ,! ~ \SC\ ~ 26 '
И
\А'С | • \А'С" |=-*.
Таким образом, при инверсии относительно окружно-
окружности со, радиус которой равен (Ь — с) /2, точка В' пере-
переходит в точку В", а точка С — в точку С", что и тре-
требовалось.
Более того, инверсия относительно окружности со
переводит вписанную окружность и рассмотренную
вневписанную окружность в самих себя, а их общую
касательную В\С\ в окружность девяти точек. Следо-
Следовательно, окружность девяти точек, как и прямая
В\С\, касается этих двух окружностей и, аналогично,
касается двух оставшихся вневписанных окружностей.
В связи с этим, окружность девяти точек может
быть определена с помощью точек D, E, F, которые
являются точками пересечения пар противоположных
сторон ортоцентрического четырехугольника АВСН
(см. конец § 4 гл. 2). Другими словами, все четыре
треугольника ABC, BCH, САН, АВН имеют одну и ту
же окружность девяти точек. Однако каждый из этих
треугольников имеет свое собственное множество че-
четырех окружностей (вписанную и три вневписанные).
Таким образом, ортоцентрический четырехугольник
определяет множество из шестнадцати окружно-
окружностей, касающихся окружности DEF.
Упражнения
1. Угол пересечения прямых BiCi и ВС (см. рис. ПО) равен
В —С.
2. При инверсии относительно окружности ш точка о пере-
переходит в точку D (основание высоты, опущенной из вершины А
На прямую ВС),
147
§ 7. Соосные окружности
В § 3 гл. 2 мы установили, что любые две некон-
неконцентрические окружности аир определяют «пучок»
ар соосных окружностей, обладающих тем свойством,
что радикальная ось окружностей аир является ра-
радикальной осью и для любой пары окружностей, при-
принадлежащих этому семейству. При этом любая точка
Р на радикальной оси имеет одну и ту же степень
относительно всех окружностей этого пучка. В тех
случаях, когда она положительна, квадратный корень
из нее равен длине касательной от точки Р до любой
из этих окружностей. Этот отрезок может рассматри-
рассматриваться как радиус окружности с центром в точке Р,
ортогональной ко всем этим окружностям. Любые две
из таких окружностей, назовем их у и б (ортогональ-
(ортогональные ко всем окружностям пучка ар) принадлежат
пучку уб, двойственному к первоначальному, такому,
что каждая окружность одного пучка ортогональна к
любой окружности из другого пучка. Каждый пучок
содержит в качестве одного из своих элементов пря-
прямую, являющуюся, с одной стороны, радикальной
осью окружностей этого пучка, а с другой стороны, —
линией центров окружностей второго пучка. Разумеет-
Разумеется, эти две прямые перпендикулярны. Если использо-
использовать эти прямые в качестве координатных осей, как в
§ 3 гл. 2, то эти окружности могут быть заданы урав-
уравнениями
х2 + у2-2ах + с = 0 и х2 + у2-2Ьу-с = 0,
где число с фиксировано, а числа а и Ъ могут изме-
изменяться. Если с > 0, то первый пучок состоит из непе-
непересекающихся окружностей, как на рисунке 30, а вто-
второй— из пересекающихся окружностей, проходящих
через граничные точки (± Vе • 0)> которые могут рас*
сматриваться как вырожденные элементы
+ y2 = 0 и (х
первого пучка. Если же с < 0, то мы получим то же
самое расположение окружностей, лишь повернутое
на прямой угол вокруг начала координат; при этом
первый пучок будет состоять из пересекающихся, а
второй из непересекающихся окружностей. Наконец,
148
если с = О, то мы получим два ортогональных пучка
касающихся окружностей, причем все они будут ка-
касаться своих осей в начале координат.
Элементы пучка непересекающихся соосных окруж-
окружностей располагаются в естественном порядке, опре-
определяемым порядком точек, в которых они пересекают
отрезок, соединяющий граничные точки. Этот порядок
позволяет нам точно указать, какой из трех элементов
лежит «между» двумя другими.
Мы можем описать пучок сф как состоящий из
всех окружностей, ортогональных к окружностям у и
б, и пучок уб, как состоящий из всех окружностей,
Рис. 111.
ортогональных к окружностям аир. Другими слова-
словами, пучок оф состоит из всех окружностей, ортого-
ортогональных любым двум различным окружностям, кото-
которые ортогональны к окружностям аир.
Если точки О и Р — общие точки двух пересекаю-
пересекающихся окружностей у и 6. то инверсия относительно
любой окружности с центром в точке О переводит эти
окружности в прямые, проходящие через точку Р' —
образ точки Р. При этом окружности, ортогональные
к этим прямым, образуют «пучок» концентрических
окружностей с центром в точке Р', а пучок уб перехо-
переходит в совокупность диаметров этих концентрических
окружностей. Такая же картина может быть получена
из любых двух непересекающихся окружностей аир.
Действительно, мы можем легко найти (рис. 111) две
149
пересекающиеся окружности у и б, ортогональные
одновременно к окружностям а и В, а именно, две
окружности соответствующих радиусов, центры кото-
которых лежат на радикальной оси окружностей а и В.
Следовательно, справедлива
Теорема 5.71. Любые две непересекающиеся
окружности могут быть переведены при помощи ин-
инверсии в две концентрические окружности.
Окружностью, относительно которой производится
такая инверсия, может быть любая окружность с цент-<
ром в любой из граничных точек (О или Р) непересе-
непересекающегося пучка аВ. Если окружность а предшест-
предшествует окружности В в естественном порядке от точки О
к точке Р, то любая окружность с центром в точке О
(или Р) будет переходить при инверсии относительно
окружности а в большую (или меньшую) из концент-
концентрических окружностей. Если мы изменим радиус
окружности инверсии, оставив на месте ее центр, то
получим новую пару концентрических окружностей,
отношение радиусов которых будет тем же, что и у
предыдущей пары. Действительно, новая инверсия
эквивалентна ранее рассмотренной инверсии с после-"
дующим применением подходящей дилатации. Прово-"
дя инверсию относительно окружности с центром в
точке Р, мы получим пару концентрических окружно-
окружностей, отношение радиусов которых обратно отношению
радиусов окружностей, полученных при инверсии от-
относительно окружности с центром в точке О.
Если а и со — любые две различные окружности, то
образ окружности а при инверсии относительно
окружности со принадлежит пучку асо. Действительно,
любые две окружности, одновременно ортогональные
к окружностям а и со, переходят при этом в себя. Если
окружность а переходит в окружность В при инверсии
относительно окружности со, то мы будем называть
окружность со серединной окружностью окружностей
а и В. Так как окружность р принадлежит пучку асо,
то окружность со принадлежит пучку ар. Теперь мы
готовы доказать теорему, обратную теореме 5.45.
Теорема 5.72. Любые две окружности имеют по
крайней мере одну серединную окружность. Две непе-
непересекающиеся или касающиеся окружности имеют,
только одну серединную окружность. Две пересекаю-i
150
щиеся окружности имеют две серединные окружно-
окружности, ортогональные друг к другу.
Если окружности аир пересекаются, то при помо-
помощи инверсии мы можем перевести их в пересекающие*
ся прямые, которые переводятся одна в другую' сим-
симметрией относительно любой из биссектрис углов
между ними. Окружности, которые переходят при ин-
инверсии в эти биссектрисы, и будут двумя искомыми
серединными окружностями.
Если окружности аир касаются, то при инверсии
они переходят в параллельные прямые. Поэтому та-
такие окружности имеют одну-единственную серединную
окружность.
Если окружности а и р не пересекаются, то при
инверсии они переходят в концентрические окружное
сти, радиусы которых обозначим через а и Ь. Они пе*
реводятся одна в другую при инверсии относительно
концентричной им окружности, радиус которой равен
•V'а.Ъ — среднему геометрическому радиусов этих
окружностей. Окружность, которая переходит при_ин-
версии в рассмотренную окружность радиуса ^ab, и
будет той единственной серединной окружностью дан-^
ных окружностей аир.
Заметим также, что если окружности аир конгру-
конгруэнтны, то их серединная окружность совпадает с их
радикальной осью.
Упражнения
1. Найдите соотношение между числами с и с', при котором
окружности
х2 + у2 — 2ах + с = 0 и х2+у2 — 2Ьх + с' = 0
ортогональны.
2. Радиус серединной окружности для двух касающихся
окружностей (лежащих по одну сторону от их общей касатель-
касательной) является средним гармоническим радиусов этих двух дан-
данных окружностей.
3. Во что перейдут два ортогональных пучка касающихся
окружностей, если провести инверсию относительно окружности
с центром в их общей точке?
4. Любые две окружности могут быть переведены при по-
помощи инверсии в конгруэнтные окружности.
5. Радикальная ось любых двух конгруэнтных окружностей
является их серединной окружностью.
6. Любые четыре различные точки А, В, С, D могут быть
переведены при помощи инверсии в вершины параллелограмма
151
А'В'С'ТУ (который может быть и вырожденным в том случае,
когда эти четыре вершины лежат на одной прямой, и при этом
\А'В'\ = \D'C'\k \A'D'\ = Ifi'C'l).
Указание. Рассмотрите отдельно три случая: а) АС//BD;
б) АВ II CD или AD II ВС; в) точки А, В, С, D не лежат на одной
окружности.
7. Постройте серединную окружность для двух данных непе-
непересекающихся окружностей (разных радиусов).
Указание. Считайте известным (исходя из упражнения 3,
§ 5) положение граничных точек пучка соосных окружностей оф,
где а и р — две данные непересекающиеся окружности (с раз-
разными центрами).
§ 8. Инверсное расстояние
Так как при инверсии биссектрисы углов перехо-
переходят в биссектрисы углов, то каждая из серединных
окружностей двух пересекающихся окружно-
окружностей делит пополам углы между ними. Соответствен-
Соответственно, разумно задать вопрос: нельзя ли определить по-
подобную числовую характеристику для двух непере-
непересекающихся окружностей, которая бы «делилась
пополам» их единственной серединной окружностью.
Так поставленный вопрос приводит нас к созданию
для любых двух непересекающихся окружностей а и
Р их инверсного расстояния (а, р), обладающего тем
свойством, что если окружность у принадлежит пучку
непересекающихся окружностей аР и окружность р
лежит между окружностями а и у, то
E.801) (а, Р) + (Р, V) = (а, V).
Произведя инверсию относительно окружности с цент-
центром в одной из граничных точек, мы получаем три
концентрические окружности, радиусы которых а, Ъ, с
удовлетворяют либо условию а~>Ъ>с, либо условию
а<Ь<.с и, конечно, тождеству
а_ Ъ_ а_
b с с
Заметив, что при логарифмировании произведение пе-
переходит в сумму, мы определяем
E.802) (a, p) = |log||,
т.е. равное log (a/b), если а> b, или log (b/a), если
b > а. Для рассмотренных концентрических окружно-
152
стей таким образом введенное расстояние, очевидно,
удовлетворяет уравнению E.801).
Под знаком log можно было бы понимать «лога-
«логарифм при основании десять», так что соотношение л:—
= log у обозначало бы, что г/= 10-*. Однако привычка
использовать основание десять сложилась в силу того,
что у большинства людей на руках десять пальцев.
Математически же гораздо удобнее заменить чисчо
десять на трансцендентное число
е= Y, -^- = 2,7182818284590....
при этом соотношение х = log у (часто записываемое
1пг/, где п отражает название—«натуральный лога-
логарифм») означает, что
у = ех =
„1
0
а сам натуральный логарифм*) может быть выражен
столь же замечательным рядом
/2 /3 /4
Договоримся определять инверсное расстояние
между любыми двумя непересекающимися окружно-
окружностями как натуральный логарифм отношения радиу-
радиусов (большего к меньшему) двух концентрических
окружностей, в которые данные окружности могут
быть переведены при помощи инверсии.
Так как концентрические окружности при инвер-
инверсии переходят в соосные окружности, то так введен-
введенное расстояние аддитивно, в смысле соотношения
E.801), для элементов соосного пучка. В частности,
серединная окружность любых двух непересекающих-
непересекающихся окружностей делит пополам инверсное расстояние
между ними. Рассматривая две параллельные прямые
как предельное положение двух концентрических
окружностей, мы видим, что две касающиеся окруж-
окружности могут соответственно рассматриваться как на-
находящиеся на инверсном расстоянии нуль.
*) См. ([41], стр. 37 и следующие).
153
Если мы имеем две (неконцентрические) окружно-
окружности, одна из которых находится внутри другой, и еще
несколько окружностей, последовательно касающих-
касающихся друг друга, а также касающихся двух первона-
первоначально заданных окружностей, как на рисунке 112, то
может случиться так, что последовательность касаю-
касающихся окружностей замкнется в кольцо из п окруж-
окружностей, в котором последняя окружность касается пер-
первой. В этом случае, очевидно, в качестве первой
окружности кольца мы можем принять произволь-
произвольную окружность, касающуюся, двух первоначально
данных. Подобным образом построенное кольцо вновь
замкнется и будет содержать также п окружностей.
Рис. 112. Рис. 113.
Из теоремы 5.71 следует удивительно простое доказа-
доказательство этого результата, известного как поризм*)
Штепнера ([38], стр. 53 и [43], т. II, стр. 199, 507).
А именно: произведем инверсию, переводящую перво-
первоначальные окружности в концентрические; тогда
остальные образуют кольцо конгруэнтных окружное
стей с центрами в вершинах правильного п-угольника,
как на рисунке 113. Здесь точка А — центр одной из
окружностей, Т — точка ее касания с одной из сосед-
соседних окружностей кольца, и точка О — общий центр
двух концентрических окружностей. Обозначим pa-
диус внешней окружности через а, а радиус внутрен-
*) Поризмом называют математическое предложение, зани-
занимающее промежуточное положение между теоремой и задачей на
построение. — Прим. иерее.
154
ней — через b; тогда в прямоугольном треугольнике
([20], стр. 3). Так как радиусы этих концентрических
окружностей равны а и Ь, то инверсное расстояние
между ними 6=log (a/b) удовлетворяет соотношению
_ а-Ъ _ (а/Ь)-1 гь-\
cin __
и \ОА\ a + b (a/b) + l еб+\ '
Отсюда следует, что поризм Штейнера выполняется
всякий раз, когда инверсное расстояние между рас-
рассматриваемыми первоначальными окружностями удов-
удовлетворяет этому же уравнению
п ее-1
sin — — ■
n e° + 1
Решая это уравнение относительно е6, мы получим
1 + sin — / 1 + sin —
1 — sin — \ cos —
П V П
откуда находим
E.803) 6 = 2 log (sec -J-) .
В частности, задавая п = 4, мы получаем, что лю*
бые две окружности, инверсное расстояние между ко->
торыми равно
21og(V2+l),
принадлежат к конфигурации из шести окружностей,
каждая из которых касается четырех других. Эти
шесть окружностей распадаются на три пары «проти-
«противоположных», так что каждая окружность касается
всех других, кроме своей противоположной. Инверс-
Инверсное расстояние между любыми двумя противопо-
противоположными окружностями равно 2Iog(V2~+0> a
оставшиеся двенадцать расстояний, конечно, равны
нулю.
Поризм Штейнера остается справедливым и в том
случае, если цепочка окружностей замыкается не
155
после одного, а после d полных оборотов. В этом слу-
случае мы должны заменить во всех формулах число п
на дробь n/d.
Так как окружность может иметь произвольный
радиус и так как ее центр задается двумя координа-
координатами, то множество всех окружностей в евклидовой
плоскости (а также и в круговой плоскости) пред-
представляет собой трехпараметрическое семейство или
совокупность троек чисел, каждое из которых может
принимать бесконечное число значений. Если мы рас-
рассмотрим интерпретацию этого семейства окружностей
на круговой плоскости в виде совокупности плоско-
плоскостей трехмерного пространства, то мы сможем полу-
получить знаменитую «неевклидову» геометрию, которая
была открыта независимо (между 1820 и 1830 годами)
Гауссом, Больаи и Лобачевским. Углы между двумя
пересекающимися окружностями соответствуют углам
между двумя плоскостями, пересекающимися по пря-
прямой; две касающиеся окружности соответствуют двум
«параллельным» плоскостям; инверсное расстояние
между двумя непересекающимися окружностями со-
соответствует расстоянию между двумя «ультрапарал-
«ультрапараллельными» плоскостями, которые имеют общую пер-
перпендикулярную прямую, причем расстояние между
ними измеряется вдоль этой прямой *).
Упражнения
1. В случае торизма Шгейиера точки касания смежных
окружностей кольца лежат на серединной окружности двух пер-
первоначальных окружностей. (Более того, серединная окружность
двух произвольных окружностей а и Р мо'жет быть описана как
множество точек Р, таких, что две окружности, касающиеся одно-
одновременно окружностей а и Р, касаются друг друга в точке Р.)
2. Равенство E.803) эквивалентно равенству
3. Нарисуйте три конгруэнтные окружности, касающиеся
друг друга, н второе множество из трех таких же окружностей,
каждая из которых касается двух окружностей из первого мно-
множества. Каковы инверсные расстояния между этими шестью
окружностями?
*) См. Н. S. M. Coxeter, Non-Euclidean Geometry, Eth ed.),
Toronto, 1965, стр. 265—266, или [35], или [44].
156
§ 9. Гиперболические функции
В этом параграфе мы рассмотрим красивую ана-
аналогию между тригонометрическими функциями углов,
образованных пересекающимися окружностями, и тдк
называемыми гиперболическими *) функциями ин-
инверсных расстояний между парами непересекающихся
окружностей. Гиперболический синус, гиперболический
косинус и гиперболический тангенс определяются че-
через показательную функцию формулами
— е
thx--=
2 2
из которых, как легко видеть, следует, что
ch х + sh к = ех, chx — shx = e~x.
Некоторые важные тождества указаны в левой ко-
колонке приведенной ниже таблицы, а в правой колонке
даются аналогичные тригонометрические тождества.
shO = O, chO=l
th 0 = 0, th оо = 1
ch2x — sh2x=l
sh x
ch*
ch
ch
ch
x —
2
x +
2
x —
1
1
1
sh x
sin 0 = 0, cosO=l
tgO=0, tgi= 1
cos2x+ sin2x^ 1
sin x
cos*:
1 — cos x
2
1 + cos x
2
1 — COS X
sin x
В этих обозначениях равенство E.803) может быть
переписано как
thT =
n
I —, ИЛИ
2
я
n
*) Почему «гиперболические»? См. [17], стр. 189—190 и
[41], стр. 24. Неевклидову геометрию Гаусса, Больаи н Лоба-
Лобачевского 'называют гиперболической геометрией. Обоснование
этого названия можно иайти в [44],
157
или
, б п
2 п
Возможно, покажется не слишком странным срав-
сравнение роли гиперболических функций в математике
С ролью радикала аммония NH4 в химии*). Этот ра-
радикал ведет себя как атом натрия или калия, хотя
его можно разложить на атомы азота и водорода. Что-
то похожее происходит и с гиперболическими функ-
функциями: они ведут себя подобно тригонометрическим
функциям, хотя их можно выразить через показатель-
показательные функции. (Нужно признать, что такой экскурс в
область химии меньше понравится читателю, который,
изучив функции комплексной переменной, понимает
значение формул cos х = ch ix, i sin x = sh ix.)
Возвращаясь к нашему обсуждению углов и' рас-
расстояний между парами окружностей, давайте рассмот-
рассмотрим две окружности с радиусами а и Ъ такие, что
(обычное) расстояние между их центрами равно с.
Если каждая из величин а, Ь, с меньше, чем сумма
двух других, то окружности пересекаются в двух точ-
точках. Любая из этих точек вместе с центрами окруж-
окружностей образует треугольник, длины сторон которого
равны а, Ъ, с. Один из двух дополнительных углов,
образующихся при пересечении окружностей, равен
углу между сторонами ал\ Ь треугольника, и поэтому
его косинус (из теоремы косинусов) равен
а2 + Ь* - С2
2аЪ
Посмотрим, не сможем ли мы указать геометриче-
геометрический смысл этого выражения
г»2 Л- Л2 — /*2
У=^
2аЬ
В том случае, Когда одно из чисел а, Ъ, с больше, чем
сумма двух других, т. е. когда окружности не пересе-
пересекаются. Например, они могут быть двумя концентри-
концентрическими окружностями (если с = 0), диаметры кото-
которых АА' и ВВ' лежат на одной прямой и удовлетво-»
•) А. Е. Н. Tutton, Crystals, Kegan Paul, London, 1911,
стр. 82.
158
ряют соотношению АВ'//А'В, как на рисунке 114. Те-
Теперь используем инверсное расстояние б = log (a/b)
в выражении для сложного отношения
(АА' ЯЯ'1 — \ЛВ\-\А'В'\ _
{АА , вд )___т____
\АВ'\
е6 + е~6 - 2
ch б - 1
Пусть эти окружности являются образами при инвер*
сии двух непересекающихся окружностей, тогда дл;
Рис. 114.
Рис. 115.
удобства мы вновь обозначим через с- расстояние
(обычное) между центрами этих окружностей, а через
а и Ь их радиусы; соответственно, точки А, А', В, В'
будут точками их пересечения с линией центров (при
этом АВ'//А'В,как и раньше).Согласно теоремам5.42
и 5.43, сложное отношение и свойство быть разбие-i
нием сохраняются при инверсии, поэтому останется
справедливым
{АА', ВВ'}
однако это сложное отношение нам нужно выразить
теперь через новые значения а, Ъ и с. Если а — Ь> с,
как на рисунке 115, то мы имеем
| А'В' | = (а + с - Ь) (а - с - Ь)
(а + с + Ь) (а - с + Ь) ^
{АА', ВВ'}-
\АВ\
| АВ' | • | А'В I
(а— ЬJ — с" _ а2 + 6" — с2 —
(а + ЬJ + с2 ~ а2 + Ь*
_ V-1
с2 + 2аЬ ~~ у + 1 '
159
с2.
откуда ch6=v. Аналогично, если a-\-b<c, как на
рисунке 116, то
'\ _(c-a-b)(c + a + b) _
в ( — (с _ а + ft) (с + а - ft) ~
__ — а2 — ft2 + с2 — 2aft _ — у — 1
~ с2 - (а - ftJ ~ - а2 - ft2 + с2 + 2aft ~ - у + 1 '
откуда ch б = —у. Объединяя эти результаты, мы ви-
видим, что доказана
Теорема 5.91. Если с—(обычное) расстояние
между центрами двух непересекающихся окружностей
ftJ
Рис. 116.
с радиусами а и Ь, то инверсное расстояние б между
этими окружностями задается формулой *)
г-ft8 —с2
2aft
Интересное приложение этой теоремы можно по-
получить при рассмотрении четырехугольника, все вер-
вершины которого лежат на одной окружности (радиуса
а), а все стороны касаются другой окружности (ра-
(радиуса Ь). Известно**), что (обычное) расстояние
между центрами таких окружностей удовлетворяет
равенству
1 ■ + ■
(а-с? т (а + сJ
1
*) График функции у = ch x обычно называют цепной ли-
линией: такую форму принимает цепочка, подвешенная за оба кон-
конца ([17], стр. 455).
**) ([11], стр. 91—95 или [42], стр. 34, 267). В книге
J. L. Coolidge, A Treatise on the Circle and the Sphere, Oxford,
1916, стр. 45—46, утверждается, что открытие этой формулы при-
принадлежит Л. Эйлеру, как и открытие аналогичной формулы
п __ j + р , ■■ = — для треугольника (см. теорему 2.12).
160
которое может быть выражено в виде
\а2 + Ь2- с2| =
или
Так как
ch26 = l + sh26,
то отсюда следует, что инверсное расстояние между
окружностями, которые имеются у вписанно--описан-
ного четырехугольника, выражается через их радиусы
с помощью простой формулы
ъ
Упражнения
1. Пусть (обычное)' расстояние между центрами двух окруж-
окружностей радиуса 1 равно 2 (л/3 + \). Рассмотрим окружность,
которая делит пополам инверсное расстояние между этими
окружностями. Является ли она их серединной окружностью?
2. Инверсное расстояние б между окружностями Содди
(упражнение 4 § 4) удовлетворяет уравнению
3. Пусть две окружности лежат одна вне другой и, следова-
следовательно, имеют четыре общие касательные; тогда отношение дли-
длины большей касательной к длине меньшей равно th—, где б —
инверсное расстояние между этими двумя окружностями.
4 Рассмотрим прямую на расстоянии р от центра окружно-
окружности радиуса Ь. Если р <Ь, то прямая пересекает окружность
под углом б, для которого cos 6 = dzp/b. Если же р ^ 6, то ин-
инверсное расстояние б между ними задается.равенством ch б=р/Ь.
5. Если R и г — радиусы описанной и вписанной окружно-
окружностей треугольника, то инверсное расстояние б между этими
окружностями выражается с помощью равенства
, б 1
h
Указание. Используйте теорему 2.12.
6. Рассмотрим описанную окружность и окружность девяти
точек треугольника ABC. Если этот треугольник тупоугольный,
то рассматриваемые окружности пересекаются под углом б,
6 Г. С. М, Коксетер, С. Л. Грейтцер 161
удовлетворяющим равенству
sins — = — cos A • cos В • cos С.
i
Если же треугольник прямоугольный или остроугольный, то ин-
инверсное расстояние б между этими окружностями удовлетворяет
равенству
sh2 — = cos A • cos S- cos С.
7. Инверсное расстояние между окружностями
х2 + у2 — Чах + й2 = 0 (а > d > 0)
x2 + y* — 2bx + d2 = 0 {b>d>Q}
равно | а — р |, где
= -^-, a ihp = j.
Главе. 6
ВВЕДЕНИЕ В ПРОЕКТИВНУЮ ГЕОМЕТРИЮ
Так как вы сейчас изучаете геометрию и
тригонометрию, то я хочу предложить вам
одну задачу. Корабль плывет в океане.
Ои отплыл из Бостона с грузом шерсти.
Он веснт 200 тонн. Он направляется в
Гавр. На 6opiy 12 пассажиров. Ветер дует
на восток-северо-восток. На часах чет-
четверть четвертого. Месяц —май. Сколько
лет капитану?
Гюстав Флобер
Во всех преобразованиях, которые мы рассматри-
рассматривали до сих пор, точки переходили в точки. Наиболее
характерной чертой «проективной» плоскости являет*
ся принцип двойственности, который дает нам воз*
можность преобразовывать точки в прямые, а прямые
в точки. Одним из таких преобразований, несколько
похожим на инверсию, является «полярное преобразо-
вание» относительно данной окружности. Каждая точ-
точка, за исключением центра О этой окружности, преоб*
разуется в некоторую прямую; каждая прямая, на
проходящая через точку О, преобразуется в некото-
некоторую точку, а каждая окружность преобразуется в
«коническое сечение», у которого точка О является
«фокусом». В этой главе мы обсудим различные виды
конических сечений, а в конце проведем тщательное
сравнение инверсивной и проективной геометрий.
§ 1. Полярное преобразование
Здесь, как и при инверсии (§ 3 гл. 5), мы исполь-
используем окружность со с центром в точке О и радиусом k.
Каждой точке Р (отличной от точки О) ставится в со-
соответствие прямая р, называемая полярой точки Р,
перпендикулярная к прямой ОР и проходящая через
точку Р' — образ точки Р при инверсии относительно
окружности со (рис. 117). И, наоборот, каждой пря-
прямой р (не проходящей через точку О) ставится в со-
соответствие точка Р, называемая полюсом прямой р, —»
образ при инверсии относительно окружности со осно-
основания перпендикуляра, опущенного из точки О на пря-
прямую р. Меняя местами точки Р и Р' на рисунке 102,
б* 163
мы видим, что в том случае, когда точка Р лежит вне
окружности со, ее поляра проходит через точки каса-
касания двух касательных, проведенных из точки Р. В том
случае, когда точка Р лежит на окружности со, оче-
очевидно, что ее полярой является касательная к этой
окружности в точке Р. Это единственный случай, ког-
когда точка Р и прямая р—инцидентны (т.е. точка Р
лежит на прямой р, и прямая р проходит через точ-
точку Р). Нам будет удобно использовать согласованные
обозначения для точек и прямых так, чтобы поляры
точек А, В, ... были прямыми а, Ъ, .... а полюс любой
Рис. 117.
прямой обозначался соответствующей большой бук*
вой.
Для любой точки А (за исключением точки О) обо-
обозначим через А' ее образ при инверсии, а через а — ее
поляру (как на рисунке 118). Для произвольной точ-
точки В, лежащей на прямой а, построим прямую АВ'',
перпендикулярную прямой ОВ. Тогда треугольники
ОАВ' и ОБА' подобны и
\OB\-\OB'\=\OA\-\OA'\=k2.
Следовательно, точка В' является образом точки В
при инверсии относительно окружности со, и прямую
АВ' мы сможем обозначить через Ъ, так как она яв-
является полярой точки В. Обратно, любая прямая Ь,
проходящая через точку А (за исключением прямой
ОА) порождает перпендикулярную ей прямую ОВ,
что дает нам возможность восстановить тот же рису-
рисунок. Итак, доказана
Теорема 6.11. Если точка В лежит па прямой а,
то прямая Ъ проходит через точку А.
164
Если мы зафиксируем точку А и прямую а и рас-
рассмотрим, поляры b для точек В, лежащих на прямой
а, то увидим, что все эти прямые проходят через точ-
точку А — полюс прямой а. Другими словами, поляры
множества коллинеарных точек образуют множество
конкурентных прямых. Этот процесс, сохраняющий
свойство инцидентности, при котором точки и прямые
преобразуются в их поляры и полюсы, называется
в
полярным преобразованием. Все это естественно при-
приводит нас к принципу двойственности, который ут-
утверждает, что для любой конфигурации, состоящей из
прямых и точек, в которой определенные точки лежат
на определенных прямых, существует двойственная ей
конфигурация из прямых и точек, в которой опреде-
определенные прямые проходят через определенные точки.
Например, фигура, двойственная полному четырех-
четырехугольнику ABCD (состоящему из четырех точек, ни-
никакие три из которых не коллинеарны, и шести соеди-
соединяющих их прямых: AD, BD, CD, ВС, АС, АВ), есть
полный четырехсторонник abed (состоящий из четы-
четырех прямых, никакие три из которых не конкурентны,
165
и шести их точек пересечения: а-й, b-d, c-d, b-c, а-с,
а-Ь).
Мы будем рассматривать окружность в двух аспек-
аспектах: первый — обычный — как множество точек и вто-
второй — как совокупность всех касающихся ее прямых,
которую мы будем называть оболочкой (рис. 119).
Каждая касательная является предельным положе-
положением секущей, при сближении точек ее пересечения с
окружностью. Соответственно каждая точка касания
является предельным положением точки пересечения
двух касательных, при сближении этих касательных*).
Таким образом, полярное преобразование меняет ме-
местами точечные множества и их оболочки. Окружность
^множествоточен 'оболочка
Рис. 119.
со, рассматриваемая как множество точек или как
оболочка, переходит при полярном преобразовании в
ту же самую окружность, рассматриваемую в проти-
противоположном аспекте. Аналогично, окружность с цент-
центром в точке О радиуса г переходит при полярном пре-
преобразовании (с таким же изменением- аспекта) в кон-
концентричную ей окружность радиуса k2/r.
Теорему, двойственную к данной теореме, как и
построение, двойственное к данному построению, мож-
можно очень просто получить при помощи замены слов
в соответствии со следующим «словарем». (Если нам
встречается слово, принадлежащее одной из колонок,
то мы должны его заменить на соответствующее слово
из другой колонки.)
*) Подробнее см. [6]. Прим. перев.
166
точка
лежит на
прямая, проходящая через
две точки
конкурентны
четырехугольник
полюс
множество точек
касательная
прямая
проходит через
точка пересечения двух прямых
коллинеарны
четырехсторонник
поляра
оболочка
точка касания
В
(о
Рис. 120.
В том случае, когда две точки и две прямые рас-
расположены так, как указано в-теореме 6.11 (т. е. каж-
каждая из точек лежит на поляре другой точки), мы на*
зываем точки Л и В сопря-
сопряженными точками, а пря-
прямые а и Ь — сопряженными _ & Ы-Ь
прямыми. Таким образом,
поляра точки Л есть множе-
множество точек, сопряженных с
точкой Л, а полюс прямой а
есть оболочка из прямых,
сопряженных с прямой а.
(Устремляя радиус окруж-
окружности к нулю, мы можем
обосновать представление
точки в виде «оболочки» из
прямых, проходящих через
нее. В частности, любая
точка на касательной а сопряжена с точкой касания
Л, которая является самосопряженной точкой, а лю-
любая прямая, проходящая через точку Л (лежащую на
окружности со), сопряжена с прямой а, которая яв-
является самосопряженной прямой.
Полюс любой прямой АВ (не проходящей через
точку О) лежит на полярах обеих точек Л и В и, та-
таким образом, может быть описан как точка пересече-
пересечения а-b. Например, если точки Л и В лежат на окруж-
окружности со, как на рисунке 120, полюс секущей АВ есть
точка пересечения касательных а и Ъ. Соответственно,
любая точка, лежащая вне окружности со, принадле-
принадлежит двум касательным, скажем, а и Ь, а ее поляра
может быть построена как секущая, соединяющая
точки касания Л и В.
У любой прямой р существуют точки, лежащие вне
окружности со. Если прямая р не является диаметром,
167
то ее полюс Р принадлежит полярам всех этих внеш*
них точек и может быть построен как точка пересече-
пересечения поляр двух из них. Соответственно любая точка
Р лежит на некоторых секущих. Если она не совпа-
совпадает с точкой О, то ее поляра р содержит полюсы всех
этих секущих и может быть построена как прямая,
соединяющая полюсы двух из них. Мы можем подыто-
подытожить эти результаты в следующем утверждении:
Теорема 6.12. Полюс любой секущей АВ (за
исключением диаметра) является общей точкой каса-
касательных в точках А и В. Поляра любой внешней точки
является прямой, соединяющей точки касания двух
касательных, проходящих через эту точку. Полюс лю-
любой прямой р (за исключением диаметра) является
общей точкой поляр двух внешних точек, лежащих на
прямой р. Поляра любой точки Р (за исключением
центра) является прямой, соединяющей полюсы двух
секущих, проходящих через точку Р.
Стоит заметить, что если заданы окружность w,
относительно которой производится полярное преоб-
преобразование, и все ее касательные, то рассмотренные
построения используют лишь инцидентность точек и
прямых; при этом нет необходимости в каких-либо из-
измерениях. Эта черта характерна для проективной гео-
геометрии.
Упражнения
1. Поляра произвольной точки А относительно окружности <в
с центром О (не совпадающим с точкой А) может быть построена
как радикальная ось двух окружностей: окружности <в и окруж-
окружности, построенной на отрезке ОА как на диаметре.
2. Один из углов между полярами точек А я В равен углу
АОВ.
3. Вершины и стороны (рассматриваемые как прямые) пра-
правильного и-угольника с центром в точке О переходят при поляр-
полярном преобразовании в стороны и вершины другого правильного
п-угольника.
4. Прямоугольник с центром в точке О переходит при поляр-
полярном преобразовании в ромб.
§ 2. Полярная окружность треугольника
Если все четыре точки А, В, А', В', изображенные
на рисунке 118, различны, то треугольник ABC (точка
С является точкой пересечения прямых а и Ь) обладает
тем свойством, что каждая вершина является полюсом
168
противоположной стороны, а любые две вершины яв-
являются сопряженными точками, и любые две стороны
являются сопряженными прямыми. Более того, любые
две сопряженные (но не самосопряженные) точки
можно рассматривать как две вершины такого авто-
автополярного треугольника ABC.
Так как три части рисунка 121 (воспроизводящие
первые три части рисунка 118) представляют все раз-
различные возможности выбора точек Л и Б, то каждый
автополярный треугольник является тупоугольным,
причем вершина тупого угла лежит внутри окружно-
окружности со, а остальные две вершины — вне нее. Обратно,
Рис. 121.
любой тупоугольный треугольник ABC имеет единст-
единственную полярную окружность, относительно которой
этот треугольник является автополярным. Центр и ра-
радиус этой окружности могут быть найдены следую-
следующим образом. Так как прямые ОА и ОВ являются вы-
высотами треугольника ABC, то точка О служит его
ортоцентром. Если вернуться к обозначениям, исполь-
использованным нами в равенстве B.44), то центром поляр-
полярной окружности будет точка Н, а ее радиус будет
равен
л/\НА\-\НБ\= т/\НВ\-\НЕ\= \\HC\-\HF\.
Поэтому инверсия относительно этой окружности пе-
переводит вершины треугольника ABC в основания его
высот. Рассмотрев окружности, проходящие через эти
тройки точек, и вспоминая, что при инверсии окруж-
169
ности переходят в окружности, мы видим, что спра-
справедлива
Теорема 6.21. Для любого тупоугольного тре-
угольника описанная вокруг него окружность и окруж-
окружность девяти точек переходят друг в друга при инвер-
инверсии относительно полярной окружности этого тре-
треугольника.
Другими словами, полярная окружность является
одной из двух серединных окружностей для описанной
окружности и окружности девяти точек (они пересе-
пересекаются, поскольку треугольник является тупоуголь"
ным). Отсюда следует, что описанная окружность,
окружность девяти точек и полярная окружность
(центры которых лежат на прямой Эйлера) соосны
и что (для любого тупоугольного треугольника)
окружность девяти точек проходит не через девять, а
через одиннадцать замечательных точек, причем
последние две являются точками пересечения описан-
описанной и полярной окружностей.
Упражнение
1. В любом тупоугольном треугольнике полярная окружность
пересекает описанную окружность под углом G, для которого
coss G = — cos Л• cos В • cos С
§ 3. Конические сечения
Здесь мы рассмотрим интересные кривые, назы*
ваемые коническими сечениями, которые кратко упо-
упоминались в §§ 8 и 9 гл. 3. Эти кривые могут быть
определены многими различными способами. Одним
из них является определение конического сечения как
образа окружности при полярном преобразовании. Бо«
лее точно, пусть а — окружность с центром А и ра-
радиусом г. Рассмотрим полярное преобразование этой
окружности относительно окружности со с центром в
точке О. Величина радиуса k окружности со не суще-
существенна, так как она влияет только на размер, а
не на форму конического сечения. Форма опреде-
определяется отношением
е = |ОЛ|/л,
170
которое называется эксцентриситетом конического ее*
чения. Точка О называется его фокусом.
Описывая коническое сечение как образ при по-
полярном преобразовании окружности а, мы рассматри-
рассматриваем его в обоих аспектах: как множество полюсов
прямых, касательных к окружности а, так и как обо-
оболочку из поляр точек, лежащих на окружности а. Если
е <! 1, т.е. точка О лежит внутри окружности а, то
существует точка конического сечения на каждом
луче, выходящем из точки О, и коническое сечение
является овальной кривой, называемой эллипсом
(рис. 122). В частности, эллипс с е = 0 есть просто
окружность. С увеличением эксцентриситета е кони-
коническое сечение все больше и больше отличается от
Рис. 122.
окружности. Если е = 1, т. е. \ОА\ = г и точка О ле-
лежит на окружности а, то множество точек окружно-
окружности а содержит единственную точку, а именно, точку
О, которая не имеет поляры (относительно окружно-
окружности со), а множество касательных к окружности а со-
содержит одну касательную, а именно, касающуюся
окружности в точке О, которая не имеет полюса. Сле-
Следовательно, коническое сечение, которое мы назовем
параболой (рис. 123), простирается до бесконечности
в направлении луча АО. Коническое сечение называ-
называется гиперболой (рис. 124), если е > 1, т. е. точка О
лежит вне окружности а. Две касательные к окруж-
окружности а, проходящие через точку О, не имеют полю-
полюсов, а поляры точек их касания U и V с окружностью
со называются асимптотами этой гиперболы. Эти
две прямые и и v принадлежат оболочке и, таким
171
образом, являются касательными, которые не имеют
точек касания! Если мы будем двигаться вдоль одной
из них в любом направлении, то мы увидим, что кри-
кривая все больше и больше приближается к асимптоте,
никогда ее не достигая.
Рис. 123.
Рис 124.
Сэр Исаак Ньютон A642—1727) объяснил заме-
замеченную Кеплером закономерность движения планет
по эллиптическим орбитам с фокусом, находящимся
на солнце. С тех пор были измерены эксцентриситеты
е для орбит различных планет и комет. Некоторые из
них даются в следующей таблице:
172
Планбты
Меркурий
Венера
Земля
Марс
Юпитер
Сатурн
Уран
Нептун
Плутон
0,2056
0,0068
0,0167
0,0934
0,0484
0,0557
0,0472
0,0086
0,2481
Кометы
Энке
Биэлы
Холмса
Брукса
Галлея
Доиати
Коджиа
Даниэля
Морхауза
0,85
0,76
0,41
0,47
0,967
0,9963
0,9988
1,000
1,000
Упражнения
1. Нарисуйте две окружности а и Р с почти равными ра-
радиусами и почти совпадающими центрами так, чтобы окруж-
окружность а лежала внутри окружности р. Выберите точки А\, Аз,
Аь, ... на окружности а и Во, Вг, Вк, ... на окружности Р так,
чтобы прямые ВоВг, В2В4, ... касались окружности а в точ-
точках А\, Аз, ... Обозначим через Ьг, bt ... прямые А\Аз, АзА5, ...,
а через Си Сз, ... точки пересечения касательных к окружно-
окружности Р, проведенных в точках Во и Вг, Вг и Bt, ... Тогда прямые
Ьг, bi, ... являются касательными к образу окружности Р при
полярном преобразовании относительно окружности а, а точки
Си Сз, ... лежат на образе окружности а при полярном преоб-
преобразовании относительно окружности р.
2. Образ окружности а при полярном преобразовании отно-
относительно неконцентричной с ней окружности со симметричен отно-
относительно линии их центров. Может ли коническое сечение иметь
вторую ось симметрии? г
3. Основания перпендикуляров, опущенных из фокуса пара-
параболы на касательные к ней, лежат на одной прямой.
4. Угол G между любой асимптотой гиперболы и прямой ОА
(рис. 124) определяется из равенства sec 6 = е. Получите отсюда
эксцентриситет прямоугольной гиперболы, угол между асимпто-
асимптотами которой является прямым.
5. Что случится с кометой, орбита которой имеет эксцентри-
эксцентриситет е ^ 1?
§ 4. Фокус и директриса
Если коническое сечение рассматривается как об-
образ при полярном преобразовании окружности с цент-
центром в точке А (относительно окружности и), то по-
поляра точки А называется директрисой (соответствую.?
щей фокусу О) этого конического сечения. Расстояние
от фокуса до произвольной точки называется фокаль'
175
цым расстоянием этой точки. Теперь мы приступаем
к выводу одного из самых замечательных свойств ко-
конического сечения (доказательство которого в IV веке
н.э. было найдено Паппом Александрийским; однако,
возможно, оно было известно уже Евклиду, жившему
шестью столетиями раньше).
Теорема 6.41. Для любой точки Р на коншеч
ском сечении с эксцентриситетом е, фокусом О и ди-
директрисой а ев фокальное расстояние \ОР\ равно про-
изведению числа е на расстояние от точки Р до ди-
директрисы а.
На рисунках 125—127 точка Р является полюсом
(относительно окружности и) прямой р, которая ка-
касается окружности а в точке Т, пересекает прямую
ОА в точке М и пересекает прямую ОР в точке Р'
(образе точки Р при инверсии относительно окружное
сти и). Директриса и поляра точки М пересекают
прямую ОА в точках А' (образе точки А при инвер-
инверсии) и М' (образе точки М при инверсии); кроме
того, точка К является основанием перпендикуляра,
опущенного из точки Р на прямую а. Мы хотим дока*
зать, что \ОР\ =е|Р/С|, Для того чтобы учесть все
возможности, мы будем считать все расстояния, рас-
рассматриваемые на прямой О А, направленными
расстояниями *) (т. е. ОМ — ОА = AM, даже если
точка О лежит между точками М и А). Введя А: и г —
радиусы окружностей и и а, мы получим
'\РК\ _\ОА'-ОМ'\ k \ОА' ОМ' I
\OP\~ \ОР\ ~~ \ОР\ I k k \~
_\ОР'\\ Н k I _ | ОР'\ I ОМ |
—" k \ ОА ОМ | ~ | ОМ | " | О А 1\~
| AT | | AM | _ г _ 1
^ | AM | | ОА | ~ | О A | ~ e '
что и требовалось.
Обратно,
Теорема 6.42. Для любой точки О, любой пря-
прямой а, не проходящей через точку О, и любого поло-
положительного числа е множество точек, расстояние
каждой из которых от точки О равно расстоянию
*)' То есть обращаться с ними как с направленными отрез-
отрезками (см. § 1, гл, 2\,*~Прим. перев,
174
Рис. 125.
а
Рис. 126.
Рис. 127.
до прямой а, умноженному на е, является коническим
сечением.
Это легче всего увидеть, приняв в качестве окруж-
окружности и с центром в точке О такую окружность, ко-
которая касается прямой а; при этом точка А становит-
становится точкой касания. Тогда окружностью а является
окружность с центром в точке А радиуса |ОЛ|/е.
Упражнения
1. Получите уравнение, связывающее декартовы координаты
множества точек Р, расстояния которых от начала координат
равны произведению числа е на расстояния их до прямой
х = Це.
2. Если е Ф 1, то множество, описанное в упражнении 1, пе-
пересекает ось Ох дважды. Передвиньте ось Оу так, чтобы новое
начало координат находилось ровно посередине между двумя
этими точками пересечения. Упростите уравнение, используя кон-
константы а = j- и Ь2 = 1а вместо ей/. Какие выводы
можно сделать из этого уравнения о симметричности рассматри-
рассматриваемой кривой?
§ 5. Проективная плоскость
Изучая полярное преобразование, мы установили,
что оно переводит почти каждую точку в прямую и
почти каждую прямую в точку. Исключение состав-
составляют точка О, не имеющая поляры, и прямые, прохо-
проходящие через точку О, не имеющие полюсов. В случае
инверсии мы избавились от исключений, расширив ев-
евклидову плоскость до круговой плоскости. В рассмат-
рассматриваемом случае мы избавляемся от исключений с
помощью другого ее расширения — расширения до
проективной плоскости. Мы вводим бесконечно уда-
удаленную прямую /оо, которая будет полярой точки О,
и ее точки (бесконечно удаленные точки), являюшие-
ся полюсами прямых, проходящих через точку О.
Свойства новой прямой и новых точек определяются
тем, что при проективном преобразовании все точки,
лежащие на прямой а, переходят во все прямые, про-
проходящие через ее полюс А. Если прямая а проходит
через точку О, то поляры точек, лежащих на ней, об-
образуют «пучок» параллельных прямых, состоящий из
всех прямых, перпендикулярных к прямой а. Следова-
176
тельно, бесконечно удаленная точка, подобно полюсу
прямой а, должна рассматриваться как общая точка
пучка параллельных прямых. Отсюда следует, что на
проективной плоскости отсутствуют исключения для
утверждения:
Любые две различные прямые а и Ъ определяют
единственную точку а-Ъ.
Фактически любая теорема об инцидентности точек
и прямых порождает двойственную ей теорему о пря-
прямых и точках, а именно, о полярах и полюсах точек
и прямых первоначальной теоремы. Например, мы
можем считать, что стороны шестиугольника, описан-
описанного вокруг окружности и, являются касательными в
вершинах шестиугольника, вписанного в ту же самую
окружность. Таким образом, теорема Паскаля (§ 8
гл. 3) и теорема Брианшона (§ 9 гл. 3) двойственны,
и любая из них может быть выведена из другой при
помощи полярного преобразования относительно
окружности и. Более того, теорема Паскаля (или Бри-
Брианшона), примененная к произвольной окружности,
порождает теорему Брианшона (или Паскаля) для
конического сечения, в которое переходит при поляр-
полярном преобразовании эта окружность.
Теперь мы можем упростить формулировку теоре-
теоремы 6.12, опустив исключения, помещенные в круглых
скобках. Более того, если мы рассмотрим эту теорему
по отношению к произвольной окружности а вместо
окружности и, то мы сможем использовать окруж-
окружность и для перевода окружности а в коническое се-
сечение а'. Тогда наши построения для полюсов и поляр
по отношению к окружности а перейдут в построения
из «поляр» и «полюсов» по отношению к коническому
сечению а'. Таким же способом мы сможем обобщить
полярное преобразование, рассматривая его уже не
относительно окружности, а относительно любого ко-
конического сечения (см. [6], стр. 363). Теорема 6.12
(в которой опустим заключенные в скобки исключе-
исключения) состоит из четырех частей, двойственных одна
другой; поэтому она остается верной при замене
окружности, относительно 'которой производится по-
полярное преобразование, на коническое сечение.
Если вновь рассмотреть рисунок 65, то нетрудно
заметить, что прямая LM проходит через точку N =
177
= b-e и, аналогично, через точку a-d. Это замечание
позволяет нам преобразовать последнюю часть теоре*
мы 6.12 так, что она укажет способ прямого построен
ния поляры произвольной точки Р (рис. 128):
Теорема 6.51. Если точка Р не лежит на кони'
ческом сечении, то ее поляра проходит через точки
пересечения прямых AB'DE и AE'BD, где AD и BE —
любые две секущие, проходящие через точку Р.
Мы видели, что любой полюс и любая поляра по
отношению к окружности а переходят при полярном
Рис 128,
преобразовании (относительно другой окружности и)
в поляру и полюс относительно конического сечения
а'. В частности (см. рис. 122—124), центр А окружно-
окружности а и прямая /«> являются полюсом и полярой по
отношению к окружности а; поэтому прямая а и точ-
точка О являются полярой и полюсом по отношению к
коническому сечению а' и, следовательно, справед-
справедлива
Теорема 6.52. По отношению к любому коничв'
скому сечению, за исключением окружности, директ-
директриса является полярой соответствующего фокуса,
178
Упражнения
1. Запишите теорему 8.61 (Дезарга)" в проективной форме,
а также запишите ей двойственную.
2. Запишите теорему З.Б1 (Паппа) в проективной форме, а
также запишите' ей двойственную.
3. Если автополярный треугольник для некоторой окружно-
окружности имеет прямую /«> одной из своих сторон, то что можно ска«
зать о двух других его сторонах?
4. Коническое сечение является эллипсом, если оно не пере-
пересекается с прямой /оо, параболой, если касается ее, и гиперболой,
если пересекает ее.
5. Асимптоты гиперболы касаются этой гиперболы в точках
ее пересечения с прямой /■».
6. Касательные, проведенные из любой точки, лежащей на
директрисе параболы, к этой параболе перпендикулярны.
7. Для любого конического сечения, проходящего через че-
четыре вершины полного четырехугольника, точки пересечения трех
Пар «противоположных» сторон являются вершинами автополяр-
автополярного треугольника.
§ 6. Центральные конические сечения
Естественно возникает вопрос, являются ли эллипс
И гипербола в действительности более симметричны-
симметричными, чем это непосредственно следует из наших по-
построений этих фигур, т. е. одинаковы ли оба «конца»
эллипса и одинаковы ли две отдельные «ветви» гипер-
гиперболы. Из последующего обсуждения мы увидим, что
предполагаемая нами дополнительная симметрия дей-
действительно имеет место.
Возвращаясь к обозначениям, использованным в
теореме 6.51, мы можем утверждать, что если точка С
не лежит на коническом сечении, то ее поляра прохо-
проходит через точки пересечения прямых PQ-PiQi и
PQi'PiQ, где РР\ и QQi — любые две секущие, про-
проходящие через точку С. Если поляра точки С есть
бесконечно удаленная прямая (как на рисунке 129),
то это означает, что вписанный четырехугольник
PQPiQi есть параллелограмм. Так как точка С не
лежит на коническом сечении, то ее поляра /«> не яв-
является касательной к нему. Следовательно, кониче-
коническое сечение не может быть параболой. Так как диа-
диагонали параллелограмма при пересечении делятся по-
пополам, то эта точка С (являющаяся полюсом прямой
2оо) есть середина каждого из отрезков РР\ и QQi,
а эти отрезки могут быть любыми двумя хордами,
179
проходящими через точку С. В соответствии с этим,
точка С называется центром конического сечения, а
эллипс и гипербола называются центральными кони-
коническими сечениями. Таким образом, доказана
Теорема 6.61. Центральное коническое сечение
центрально-симметрично относительно его центра.
При этой центральной симметрии относительно
точки С фокус О и директриса а (см. § 4) переходят
во второй фокус О\ и вто-
вторую директрису ai, как на
рисунках 130 и 131. Если мы
применим это же преобразо-
преобразование к окружностям а и ю,
рассмотренным в § 3 гл. 6,
то мы 'получим новые окру-
окружности а»1 и ai, такие, что
то же самое коническое се-
сечение а' будет образом
окружности ai при поляр-
полярном преобразовании относи-
относительно окружности fi>i.
Отбрасывая тривиальный
случай, когда точки О и Л
совпадают, мы видим, что
каждое коническое сечение
симметрично относительно
прямой ОА. В случае цен-
центрального конического сече-
сечения отсюда следует, что
точка С лежит на этой пря-
прямой. Мы можем получить
центральную симметрию относительно точки С в виде
суммы симметрии относительно двух перпендикуляр-
перпендикулярных прямых, проходящих через точку С; в качестве
одной из них можно взять прямую ОА. Следователь-
Следовательно, центральное коническое сечение также симметрич*
но относительно прямой, проходящей через точку С
перпендикулярно прямой ОА. Другими словами,
центральное коническое сечение обладает симмет-1
рией, аналогичной симметрии ромба или прямоуголь-
прямоугольника.
Рассмотрим теперь центр конического сечения —
точку С и ее поляру с относительно окружности и, как
180
Рис. 129.
на рисунках 132 и 133. Так как точка С и прямая
/оо — полюс и поляра относительно конического сече-
сечения а', то прямая с и точка О должны быть полярой
и полюсом относительно окружности а. Таким обра-
образом, точка С есть и-полюс прямой с, которая в свою
Рис. 130.
Рис. 131.
очередь есть а-поляра точки О. Другими словами,
если С' — точка, в которой прямая с пересекает пря-
прямую ОА, то точка С есть образ при инверсии относи^
тельно окружности а точки С, которая является обра-
образом точки О при инверсии относительно окружности а.
Так как
\OC\-\OC'\ = k2 = \OA\-\OA'\
и
г2 = \АО\-\АС'\ = \ОА\-\С'А\,
то (используя обозначения направленных расстояний)
181
МЫ имеем
ОС
ОА'
ОА
ОС
. \0А\
\0А\2-
ОА
2
-Г2
ОА
- С А ОА2
в2
е2-1 '
ОА2
-ОА
ХС'А
которое отрицательно или положительно в соответ*
ствии с тем е < 1 или е > 1. Следовательно, для эл-
эллипса центр С и директриса а находятся по разные
Рис. 132.
Рис. 133.
стороны от точки О, как на рисунке 130, а для гипер*
болы они лежат по одну и ту же сторону, как на ри-
рисунке 131. Другими словами, фокусы эллипса лежат
внутри него, а сам он лежит между своими директри-
директрисами. Обе директрисы гиперболы лежат в «пустом»
пространстве между ее двумя ветвями.
Из механики мы знаем, что если не принимать во
внимание сопротивления воздуха, то траекторией бро«
шенного мяча будет дуга параболы, фокус которой
можно найти без особых затруднений. Так как бро-
182
шенный мяч на несколько секунд становится малень*
ким искусственным спутником, то эта наблюдаемая
парабола на самом деле является сильно вытянутым
эллипсом, эксцентриситет которого лишь немного
меньше единицы. Где же второй ее фокус? В центре
Земли!
Упражнения
1. Для любой точки Р, лежащей на эллипсе, сумма ее фо-
фокальных расстояний |OP| + |OiP| постоянна (см. рис. 130).
2. Для любой точки Р, лежащей на гиперболе, разность
||ОР|—I Oii311 ее фокальных расстояний постоянна (см. рис. 131).
3. Основания перпендикуляров, опущенных из фокуса цен-
центрального конического сечения на касательные к нему лежат на
одной окружности (она называется вспомогательной окруж-
ностью конического сечения; [24], стр. 13, 25, 155 и [33],стр.577).
§ 7. Стереографическая и гномоническая проекции
Как мы видели в § 3 гл. 5, единственной точкой
евклидовой плоскости, не имеющей образа при инвер-
инверсии, является центр О. окружности инверсии со. Для
того чтобы устранить это исключение и превратить
инверсию во взаимно однозначное преобразование
всей плоскости, мы расширили евклидову плоскость,
добавив единственную идеальную точку, называемую
бесконечно удаленной точкой, которая становится об-
образом точки О. Эта расширенная плоскость называет*
ся круговой плоскостью.
Как мы видели в § 1 настоящей главы, единствен-!
ной точкой евклидовой плоскости, не имеющей поля-
поляры, является центр О окружности со, относительно ко-
которой производится полярное преобразование. Для
того чтобы устранить это исключение и превратить
полярное преобразование в преобразование всей
плоскости, переводящее каждую точку в прямую, а
каждую прямую в точку, мы расширили евклидову
плоскость, добавив единственную идеальную прямую,
называемую бесконечно удаленной прямой, которая
становится полярой точки О. Эта расширенная пло-
плоскость называется проективной плоскостью.
Таким образом, существуют два различных, но в
равной степени эффективных способа расширения ев-
евклидовой плоскости. К сожалению, они известны го«
раздо меньше, чем того заслуживают. Эти два расши-
183
рения получат новое истолкование, если мы перейдем
от плоскости к пространству и проведем сравнение
двух самых простых из возможных способов отобра-
отображения сферы на плоскость.
Наше первое определение инверсии относительно
окружности (§ 3 гл. 5) легко обобщается на случай
пространства. Зададим сферу со радиуса k с центром
в точке О и точку Р, отличную от точки О. Образом
точки Р при этой инверсии назовем точку Р', лежа-
лежащую на луче ОР, расстояние которой до точки О удо-
удовлетворяет соотношению
\OP\-\OP'\ = k2.
Поместив плоскость рисунка 103 в трехмерное про-
пространство и произведя вращение вокруг линии цент-
центров ОА, мы сразу же увидим, что сферы (включая и
плоскости, рассматриваемые как сферы бесконечного
радиуса) переходят при инверсии в сферы. В частно-
частности (рассмотрите среднюю часть рисунка 103), если
а — касательная плоскость в точке А к сфере инвер-
инверсии со, то образом плоскости а будет сфера а', постро-
построенная на отрезке О А как
на диаметре. Точки на
плоскости а и сфере а',
переходящие друг в дру-
друга при этой инверсии, мо-
могут быть получены и без
помощи сферы со. Взяв
точку Р на плоскости а
(см. рис. 134), мы смо-
сможем построить соответ-
соответствующую ей точку Р',
как вторую точку пересе-
Рис. 134. чения сферы о! с прямой
ОР. Обратно, задав на
сфере о! произвольную точку Р', отличную от точ-
точки О, мы сможем построить соответствующую ей точ-
точку Р как точку пересечения прямой ОР' с плоскостью
а. Наше естественное желание избегать исключений
вынуждает нас заменить плоскость а на круговую
плоскость, добавляя единственную бесконечно удален-
удаленную точку. Эта точка будет положением точки Р в
184
том случае, когда точка Р' совпадает с точкой О
([17], стр. 145).
Такое отображение сферы а' на плоскость а назы-
называется стереографической проекцией. Тот факт, чго
этот вид проекции возникает в результате инверсии
пространства, позволяет нам легко увидеть, что окру-
окружности проектируются в окружности. Действительно,
так как при инверсии сферы переходят в сферы (или
плоскости), а любая окружность может рассматри-
рассматриваться как линия пересечения двух сфер, то отсюда
следует, что окружности (расположенные где-либо в
пространстве, в частности, на сфере ос') переходят при
инверсии в окружности.
Другим способом отображения сферы а' на касаю-
касающуюся ее плоскость а является гномоническая проек*
ция (или «центральная проекция»). Теперь вместо
проектирования из точки О (диаметрально противопо-
противоположной точке Л), мы проектируем из центра сферы а'
(который является серединой отрезка О А). Так кик
любая плоскость, проходящая через эту точку, пересе-
пересекает сферу по большому кругу, а плоскость а-—
по прямой, то каждая пря-
прямая на плоскости а порож-
порождается большим кругом на
сфере а', а каждая точка
на плоскости а — парой диа-
диаметрально противополож-
противоположных точек сферы (таких,как
Р[ и Р'2 на рисунке 135).
Обратно, любой большой
круг, за исключением боль-
большого круга, плоскость кото-
которого параллельна плоско- Рис- ' -1
сти а, позволяет нам по-
построить соответствующую ему прямую на плоскости а
как линию пересечения плоскости а с плоскостью
этого большого круга. Наше естественное желание
избегать исключений вынуждает нас заменить пло-
плоскость а на проективную плоскость, добавляя един-
единственную бесконечно удаленную прямую, соответ-
соответствующую исключенному большому кругу. Точки этой
идеальной прямой («бесконечно удаленные точки»)
185
соответствуют парам диаметрально противоположных
точек этого большого круга. Проективное утвержде-
утверждение о том, что любые две прямые имеют общую точку,
соответствует тому очевидному факту, что любые два'
больших круга имеют общую пару диаметрально про-
противоположных точек (т. е. что любые две плоскосги,
проходящие через центр сферы, пересекаются по пря-
прямой линии; [38], стр. 56).
Так как все точки проективной плоскости (вклю-
(включая и бесконечно удаленные точки) возникают при
гномонической проекции из пар диаметрально проти-
противоположных точек на сфере, то полезно рассматривать
проективную плоскость как полученную из сферы при
помощи абстрактного отождествления каждой пары
диаметрально противоположных точек, т. е. изменения
значения слова «точка» так, чтобы называть такую
пару одной точкой ([17], стр. 419).
Для практического картографирования ни стерео-
стереографическая, ни гномоническая проекции не являются
идеальными, хотя каждая из них имеет свои достоин-
достоинства. Преимущество первой состоит в том, что углы
между двумя направлениями в точке сохраняются и,
следовательно, формы маленьких островов изобра-
изображаются без изменений. Одно из преимуществ другой —
то, что кратчайшие пути между двумя точками на
сфере изображаются прямолинейными отрезками.
В теореме 5.41 мы установили, что сложное отно-
отношение сохраняется при инверсии. Будет ли оно сохра-
сохраняться при полярном преобразовании? Нет, оно будет
сохраняться только лишь для коллинеарных точек
(см. [19], стр. 118—119). Точное утверждение состоит
в том, что сложное отношение четырех точек, лежа-
лежащих на прямой р, равно сложному отношению четырех
точек, в которых поляры этих точек пересекают про-
произвольную прямую, не проходящую через точку Р —
полюс прямой р. Это целый рассказ, слишком длин-
длинный, чтобы быть изложенным здесь.
Любой, кто понял изложенные здесь идеи, будет
готов воспринять аксиоматическую трактовку проек-
проективной геометрии, как в [19]. Там он вновь встретится
с теоремами Дезарга, Паппа и Паскаля, взглянув на
них с совершенно другой точки зрения, но будет иметь
то преимущество, чго узнает в них старых друзей.
186
Упражнения
1. Стереографическая проекция сохраняет углы.
2. На плоскости а- существует окружность, обладающая тем
свойством, что стереографическая проекция каждого большого
Круга на сфере с/ является окружностью (или прямой), пересе-
пересекающей эту Окружность в диаметрально противоположных точках.
3. Пусть Pj и Р^ — паРа диаметрально противоположных
Точек на сфере а', а точки Pi и Pi получены из них при стерео-
стереографической проекции. Какое преобразование плоскости перево-
переводит каждую такую точку Pi в соответствующую ей точку Р2?
4. Получите с помощью стереографической проекции шесть
окружностей, описанных в упражнении 3 § 8 гл. 5 из окруж-
окружностей, вписанных в шесть граней куба.
ОТВЕТЫ И УКАЗАНИЯ К УПРАЖНЕНИЯМ
Его ответ проскочил через мою голопу,
как вода через решето,
Ч. Л. Доджсон
ГЛАВА 1
§ 1
1. Высота, опущенная на сторону ВС, делит ее длину а на две
части: Ъ cos Сие cos В. Далее, произведите сложение (или вычи-
вычитание).
2. Подставьте sm A = a/2R, sin В ■— b/2R, sin C = c/2R и упро-
упростите.
1 ^ ^
3. SABC = -каЬ sin С, sin С = c/2R.
4. с = 2р sin В = pb/R, b=2qs\nC= qc/R. Перемножьте эти
выражения и упростите. ,
§2
1. Используйте теорему Чевы для случая \ВХ\ = \ХС\,
\СГ\щ=\¥А\. \AZ\ = \ZB\.
2. Используйте теорему Чевы для случая | ВХ | = с cos В,
\XC\ = b cos С и т. д.
3. Пусть отрезок ВВ' пересекается с отрезком СС в точке О,
а отрезок ОА пересекает отрезок А'В' в точке А\. Так как
А А'В'С со Д ABC, то
\А'В'\ ^_ \В'С'\ _ \ОВ'\
\Ali\ \BC\ \OB\ \АВ\ '
Поэтому точка А\ совпадает с точкой А'.
4. Так как углы СХА и АХВ являются дополнительными, то
члены, содержащие их косинусы, сокращаются.
§3
1. Тупоугольный треугольник вписан в дугу, меньшую полу-
полуокружности. Две из высот пересекают противоположные стороны
в точках, лежащих на нх продолжениях.
2. Используя рисунок 7, нарисуйте отрезок A'D, равный и
параллельный отрезку ВВ'; при этом A'CDB' будет параллело*
183
граммом с центром в точке Е, являющейся серединой отрезка СВ'.
Тогда стороны треугольника DAA' равны и параллельны трем
медианам треугольника ABC и
SABC = SCAA' _ \СА\ _4
SDAA' SEAA,~ \EA\- 3-
3. Пусть равные медианы ВВ' и СС пересекаются в точке G,
как на рисунке 8. Так как | BG | = |-1 ВВ' | = -fr | СС | = | CG |,
то треугольник GBC является равнобедренным и С'СВ = В'ВС.
И по известному признаку А С'СВ с£ Д В'ВС, откуда В = С.
4. Пусть .Ш? н CF — равные высоты. Так как b \ BE I =
= 2SABC = c\CF\, то 6= с.
5. В обозначениях рисунка 9, | BL |/| LC \ = c/b и т. д.
6. По теореме Стюарта (упражнение 4 § 2)
откуда
р = j V2b2 + 2с2 - а2.
7. Используйте теорему Стюарта для случая tn — kc, n = fefe,
fe = а/F + с).
8. 12л/2~/7
9. Добавляя высоту CF на рисунках 1 и 2, мы замечаем, что
!С/ со Д FCA откуда | ВС |/| С/1 = | FC |/| СА |.
Д ВС/
§4
1. В обозначения рисунка 11 их радиусы равны х, у, г и,
таким образом, у + z = a, z + x = 6, x + j/ = с. Сложив их,
получим x + j/ + z = s и т. д.
2. Используйте теорему 1.42 и упражнение 3 § 1.
3. Используйте теорему Чевы для случая | AY | = | AZ \ = х,
Z\ = \BX\ = y. \CX\ = \CY\ = z.
4. Внутренняя и внешняя биссектрисы угла А образуют пря-
прямой угол.
5- SABC = SIaCA + SIaAB ~ SIaCB=-2 (*+'-«) ^«=(
Обратно, так как Д AIaYa <*> AA1Y, то rjr = s/(s — a).
6. JL + JL + _L e IZLlL + ^Z± + iZl£ = i.
^ ^ ^ s s s
§5
1. Так как ВСМ = 48° = CMB, а СШ = \2° = BNC, то
| ВМ | = | ВС | = | CN |. Заметьте, что центр вневписанной окруж-
окружности, точка /, лежит на отрезке ВМ, а не на отрезке CN.
2. Если применить лемму 1.512 к треугольнику Боттемы,
то она, конечно, выполняется и в этой ситуации. Но если мы
189
попытаемся заменить слово «внутренний» на «внешний», мы увя-
дим, что окружность BCN пересекает прямую ВМ в точке М'г
причем точки М и М' лежат по разные стороны от точки С. Такям
образом, мы не сможем больше утверждать, что | ВМ\ > | ВМ' |.
3. Равенство | ВМ | = | CN | означает, что
откуда
a(a + b + c){(a + b + c) (а2 + be) + 2аЬс} (Ь - с) = 0.
§ 6
1. Так как четырехугольник BCEF может быть вписан
В окружность, то AEF — В н A AEF со Д ABC. Аналогично и для
других треугольников.
2. Хотя точка Я все еще лежит на внутренней биссектрисе
угла EDF, она станет лежать на внешних биссектрисах углов FEu
и DFE.
3. См. ответ к упражнению 2.
4. #ЛС=90° — С, ОЛС = 90°-В.
§7
2. Из рисунка 14 мы видим, что | О А' |2 = R2 — Г -^ . Обо-
зкачая"| СА' \ = и, мы имеем | .ЛО | = 2п и | АА' | = Зп. Из упраж-
упражнения 6 § 1
Применяя теорему Стюарта (упражнение 4 § 2) к треуголь-
треугольнику ОАА', мы получаем
Зп (| OG |2 + 2и2) = 2и | О А' |2 + и I О А |2 = и (г^2 -1 а2
откуда
| ОЯ |2 = C \OG | J = 9/?2 - -| а2 - 18к2 = ЗД2 - (а2 + Ь2 + с2).
3. Предположим, для определенности, что b > с. (В противном
случае переобозначим вершины В и С.) По теореме Пифагора
I ВА |2 — | BD |2 = | А4' |2 - | ЯЛ' |2, т. е.
и поэтому а | ДЛ' | = — (Ь2 — с2).
4. Если прямая Эйлера параллельна отрезку ВС, то она делит
отрезок AD в отношении 2: 1, так что
| ОА' | = | AD |/3.
190
Теперь подставим вместо \AD] к \ О А' | следующие выражения!
\AD | = Ъ sin C = 2R sin В- sin С,
| О А' | = R cos Л = R (sin В • sin С — cos В • cos С).
§8
1. \OA'\ = -j\AH\ = \AK\, а отрезок О А' паралделен от-
отрезку АК.
2. По замечанию в конце § 6 отрезок EF перпендикулярен
отрезку ОА, параллельному отрезку А'К.. Таким образом, диа-
диаметр А'К делит пополам хорду EF и дугу EF.
3. Треугольник ABC является ортотреугольником треуголь-
треугольника 1а1ь1с-
4. Пусть Р — общая точка, а Оа, Оь, Ос — центры трех кон-
конгруэнтных окружностей РВС, РСА, РАВ. Тогда четырехуголь-
четырехугольники РОьАОг. и РОцСОъ — ромбы. Следовательно, Д POi,Oa c£
Щ, А ОьАС и | АС | = | ОсОа |. Аналогично, | В А \ = \ ОаОь | и
| СВ | = | О6ОС |. Следовательно, A ABC ^2 А ОаОьОс и, конечно,
конгруэнтные треугольники имеют одинаковые радиусы описанных
вокруг них окружностей. Так как отрезок АР перпендикулярен
отрезку Офс, который параллелен отрезку ВС, то высотами
треугольника ABC являются прямые АР, ВР и СР. Поэтому
точка Р совпадает с точкой Н ([11], стр. 75).
5. Так как отрезок DK. перпендикулярен отрезку ВС,
а КА' — диаметр, то окружность пересекает сторону ВС под
углом ^
DKA'' = 1ШГ = ЙАО = \В - С\.
{ал. упражнение 4 § 6).
§9
1. Продолжите отрезок СР до точки D так, чтобы образо-
образовался равносторонний треугольник BDP. Так как A DC Boo A PCQ,
то | DB |/| PQ | = | DC |/| PC | = 1 + (I DP |/| PC \). Разделив на
\DB\ = \PB\=\DP\, мы выводим, что 1/| PQ | = A/f PB \) +
1«М)
/1М)
2. Доказательство проведем методом «от противного». Пред-
Предположим, что | PDI < | CD |. Тогда CPD > 60°, DPB < 75°,
| /Ш |< | PD | < | CD \. Если, с другой стороны, | PD \ > | CD |, то
все неравенства меняются на противоположные. В любом случае
четырехугольник не был бы квадратом. Следовательно, если
четырехугольник ABCD — квадрат, мы должны иметь | PD \ = | CD |.
Или: постройте A BQC tg А АРВ (см. рис. 20). Тогда тре-
треугольник BPQ равносторонний, отрезок CQ (продолженный) пер»
пендикулярен отрезку РВ и делит его пополам; отсюда | СР \ =«
= | СВ 1 = | CD J. Аналогично, | DP \ = | DC |.
191
3. Обозначая различные углы через а, Р, \, 6, е, как указано,
и используя теорему синусов, мы находим
sin F +
sin Y
8)
|C£»|
\PC\
sin F +
sin a
\PC\
\BC\ '
e) • sin a
• sin Y
\CD\
\BC\
sin
\AB\
\AD\
(Y + e) • sin
sin (a + P) •
\AB\
\PA\
(a + P)
sin 6
\PA\
\AD\
sin
(Y
sin
+ e)
6
откуда
sin у • sin (y + e) = sin 6» sin F + e),
cos e — cos By + e) = cos e — cos B6 + e),
4. Пусть отрезок DF, параллельный отрезку ВС, пересекает
отрезок АВ в точке F. Пусть отрезок CF пересекает отрезок BD
в точке G. Так как треугольник BCG равносторонний, то | BG | =
= | ВС |. Так как треугольник СВЕ равнобедренный, то | BE | =
= I ВС |. Следовательно, треугольник BGE равнобедренный,
BGE = 80°, FGE = 40°. Так как EFG = 40°, то треугольник FEG
равнобедренный и | FE \ = \ FG \ Но также | DF \ = | DG \ Следо-
Следовательно, AGDE^QAFDE, прямая DE делит пополам угол FDG,
а EDB— 30°.
5. Концы равных дуг являются четырьмя вершинами пра-
правильного шестиугольника, двумя другими вершинами которого
являются середины двух сторон равностороннего треугольника.
Продолжая эти стороны на половину их длины, мы получаем
больший равносторонний треугольник, три стороны которого со-
содержат чередующиеся стороны шестиугольника. Теперь дальаей-
шая схема решения становится ясной.
ГЛАВА 2
§ 1
1. - R2. Центр.
2. Концентричная ей окружность.
3. Длина любой касательной.
4. |РГ|2-|Р£/|2=|О£/|2-|ОГ|2 |Э1|| |Э|
5. R {R — 2r) = R2 — 2rR = d2 > 0. Но R > 0. Следовательно,
2>
6. Степень есть d2 — R2=— 2rR.
7. Написав Р вместо А и А вместо X на рисунке 5, мы имеем
ВС (РА2 + ВА X АС) = PC2 • В А + РВ2 • АС,
т. е.
ВС(РА2 + С А X АВ) + РВ2 -CA
192
f. Разделите отрезок ВС иа три части точками U и V так,
чтобы BU=UV — VC. Так как отрезок GU параллелей отрезку АВ,
и отрезок GV параллелен отрезку АС, то
GX \~GX + ~GY + ~GZ ) = ' + ~Ш + VF ™
_. . УХ-UX VU
~1 + —vc—-1 + W=0-
9. 89 миль.
§2
1. Радикальная ось или, если окружности пересекаются, ра-
дчкчльиая ось без общей хорды.
2. Все четыре середины лежат на радикальной оси.
3 Так как А РАВ со Д AQB, то РВА = ABQ, точка Q лежит
на отрезке ЪР иДРВ \1\А.В \ = | АВ |/| QB |. Так как A AQB со
со Д ABR, то B^4Q = ^у4В. точка R лежит на отрезке АО и
| AQ |/| АВ\=\АВ |/| ЛЯ |. Так как
то точки А и В находятся на равном" расстоянии от центра
окружности PQR и эта окружность симметрична относительно
серединного перпендикуляра к отрезку АВ. Поэтому все точки Р',
Q', R' лежат иа этой окружности (и являются ее остальными
точками пересечения с прямыми BR, АР', АР).
4. Записывая уравнение в форме (х — аI + (у — Ь)г =*
t=a2-\-b2 — с, мы видим, что оно представляет окружность, если
с < а2 +Ь\
5. Нарисуйте окружность, центр которой не лежит на линий
центров данных окружностей, так, чтобы оиа пересекала одну
окружность в точках А и В, а другую —в точках С и D. Из
точки пересечения прямых АВ и CD проведите прямую, перпен-
перпендикулярную прямой, проходящей через центры окружностей Это
и есть радикальная ось.
§3
1. Пусть касательная в точке Т пересекает хорду АВ
в точке О. Так как А О AT со Д ОТВ и | ОТ \ = | ОР \, то
|771| \ОР±_ \ОА\ \OP\-\OA\ _ \АР\
\ТВ\=" \OB\~ \ОР\ = \OB\-\OP\ ~~ \РВ\ •
Теперь используйте теорему, обратную теореме 1.33.
2. Все касательные к окружности, проведенные из точки О,
равны.
7 Г. С. М, Коксетер, С. Л. Грейтцер 193
§4
I. На рисунке 32 точки D, E. F — середины отрезков HD',
НЕ', HF'. Следовательно стороны треугольника D'E'F' парал-
параллельны сторонам ортотреугольника DEF.
2. MLN = MLA + ALN = JfWA + ACN
Аналогично NML = у (С + А) и ZJVM = -i- W + В)
§5
1. Нет.
2. Точка, диаметрально противоположная точке В
3. Вершины треугольника лежат на своих собственных пря-
прямых Симеона.
4. Проведите отрезки РВ PC, C\AU A\BU Вписанные четы-
четырехугольники AiPBiC и AtBC\P дают
ВСР
= РСВ1 = РВС
и A Py4iBi со А РС,Л,
§6
1. Используйте теоремы 2.61 и 2.62 для случая | АВ \ = I ВС I =
= \АС\.
2. Проведите диагонали ЛС, BD и примените теорему Пто-
Птолемея к четырехугольникам РАВС и PDAB^ Тогда | /М | +
3. Так как QPR = QAR = CAb = АСВ и ^Q =
то A PQ# со Д СВА.
По теореме Птолемея \AP\-\RQ\ + \AR\-\QP\ = \AQ\ \RP\.
Поэтому \АР\ ■ \AB\ + \AR\ ■ \ВС\ = \AQ\- \AC\.
§7
1. Пусть ОН — прямая Эйлера треугольника ABC и. РР' —
диаметр описанной вокруг него окружности. По геореме 2.72
прямые Симеона точек Р и Р' делят пополам отрезки HP и HP',
скажем, в точках М и М' соответственно. Так как точки О, М,
М', N — середины отрезков РР', HP, HP', ОН (теорема 1.82),
то точка N также является и серединой отрезка ММ'. Так как
| NM | = -j | ОР | = —- R есть радиус окружности девяти точек
(теорема 1.81), то отрезок ММ' — диаметр. Если прямые Сим-
Симеона пересекаются в точке X, то МХМ' = 90° (теорема 2.71), и
точка X лежит на окружности девяти точек.
2. В равностороннем треугольнике ортоцентр и центр описан-
описанной окружности совпадают.
194
§8
1. Доказательство в основном то же самое, что и для теоре-
теоремы «о бабочке», за исключением нескольких изменений знака.
2. Пусть точка О — центр окружности, а X — точка в кото-
которой отрезок АР пересекает отрезок НТ. Так как А ЛЯХ со Д АВР
и А НТВ со ATOP то
\НХ\ \ВР\ \НТ\
\АН\'=*\АВ\ И \HB\
Следовательно.
\НХ\ \HX\-\HT\_\HX\-\HT\ \ВР\ \ТО\ _ 1
\ТН\ \НТ\2 \AH\-\HB\ = |77>| \AB\~2-
3. Предположите, что Ь>с (в противном случае переобо-
переобозначьте вершины В и С). На отрезке ВС возьмите точку X' так,
чтобы | ВХ' | = | ХС | = s — с и поэтому
Постройте высоту AD. Из упражнения 3 § 7 | DA'\
(Ь2 — с2)/2а. Таким образом.
Так как | AD | = 2SABC/a = 2rs/a
| ХЛ71 \ХА'\
2л г = \1Х\ '
то А ЛДХ'со Д /ХЛ', и прямая ЛХ' параллельна прямой /Л'.
Так как прямая 1А' делит пополам отрезок XX', то оиа также
делит пополам отрезок ЛХ.
§9
1. Прямые VX, VY, WZ делят пополам углы равностороннего
треугольника XYZ.
2. А =108°, g = C = 36°.
3. Описанная окружность делится на три равные дуги точ-
точками Л, Y', Z', а дуга Y'Z' делится на три равные части точ-
точками X и У.
4. В обозначениях рисунка 43
60° + a и ВХС=120°
Отсюда
I ZX1 _ | ВХ 1 \ВХ\ а _^_ 2R sin За
sin P ~~ sin F0° + а) ' sin y ~~ sin A20° + а) = sin F0° — а)
7* 195
I /у. 2^? sin За• sin P • sin у
1 ' ~~ sin F0° + a) • sin F0° - u) =
4R sin a • C — 4 sin2 a) sin 8 • sin V o -. .
Cos2a-cosl20° = 8R sin a • s.n В • sin Y.
5. Если взять сторону треугольника XYZ за единицу изме-
измерения, мы получаем
| ВС Г= | Y'Z' | = 3,
отсюда tg CBX = tg CBZ = V3"/3, tg ZBY' = l/Уз",
C£W = ZBT= 30°.
ГЛАВА 3
§ 1
1. На рисунке 45 | PS | = | QR\ = y BD \, поэтому | PS | +•
R
q | | BD |. Аналогично, | PQ | + | RS | = | AC |.
2. Используйте результат упражнения 6 § 3 гл. 1 для тре-
треугольников ABC, CDA, BDX рисунка 49. (Интересно отметить,
что в этой теореме можно считать «любой четырехугольнш»
даже пространственным четырехугольником, у которого пары при-
прилежащих сторон лежат в четырех различных плоскостях.)
3. Используйте упражнение 2, приняв |ЛТ| =0.
4. Используйте теорему Птолемея 2.61.
§2
" 1. Заметьте, что касательные к окружности из внешней точки
равны, и используйте_теорему 3.22 для случая s = a + c—b + d.
2. а) 84, б) 4 V26 .
3. г =. SABC/s = V(s - a) (s - b) (s - c)/s.
4. Из упражнения 5 § 4 гл. 1 и упражнения 3 § 1 гл. 1
/1,1,1 1
rc~r — Ъ +
cr — ЪАВС\ s _ а +71Г
SABC'abc ahc
s(s — a)(s — b) (s — c)
196
5W =
We
= T (ara + 4 + crc) +sr =
113
— j (s - 6) rb — — (s — c) rc -f — sr =
_ „ _ абя , cdn (ab + erf) n tmn
Л ~ 4# "^ 4^ 4^ "" ~4ДГ*
6. / = a, m = 6, n = c, K = abc/4R.
7. Примените упражнение 3 § 1 гл. 1 к двум треугольникам
рисунка 51 и сложите результаты. Получите второе выражение
для площади К, используя другую диагональ / вместо п. Пере»
множьте два выражения и используйте теорему Птолемея 2.61.
8. Сравните дуги, на которые окружность делится биссек»
трисами углов V и W.
9. Проведите через точку Г перпендикуляры к парам па-
параллельных сторон прямоугольника и используйте теорему Пифа*
гора четыре раза. (Отсюда следует, что точка Р могла бы также
лежать вне плоскости прямоугольника.)'
10. Пусть ABCD—четырехугольник, вписанный в окруж-
окружность с диаметром d, и пусть Р — заданная точка иа этой окруж-
окружности. Из упражнения 9 § 3 гл. 1 произведение расстояний от
точки Р до прямых АВ и CD равно
\PA\-\PB\ |РС|-1^Д| _ \PB\-\PC\ | PD | • | РА |
d ' d ~ d ' d =
1 РА | • | PC | \PB\-\PD\
= 2 2 .
§3
1. Проведите диагонали СР н CQ в квадратах, построенных
иа первых двух сторонах ВС и СА и постройте равнобедренный
прямоугольный треугольник BAR, гипотенуза которого будет
третьей стороной АВ. Так как APCB<y>ACQA соДД4#, то
можно применить теоремы 3.33 и 3.35.
2. a) POi, QO2, ROi — серединные перпендикуляры к сторо-
сторонам треугольника ABC.
б) Пусть отрезки AOi, BO2, COs пересекают стороны тре*
угольника ABC в точках X, Y, Z. Тогда
\ВХ\ SABOi с sin (В + 30°)
SCAOi Ь sin (С +30°)'
SCAOi
197
также имеют место подобные выражения для |СУ|/|УЛ| и
\AZ\/\ZB\, ылорые дают нам возможность применить теорему,
обратную к теореме Чевы.
в) Так как APCA^ABCQ, то мы получаем \PA\ = \BQ\,
и аналогично \BQ\ = \CR\, а также PFC = РВС = 60°, анало-
аналогично
CFQ — GO", 0?Л = 60°
и, складывая, получаем, что PFA = 180°. Отсюда следует, что
точка F лежит на прямой АР. Подобным же образом можно по-
показать, что точка F лежит на прямой BQ, иа прямой CR и эти
три прямые образуют шесть углов по 60° в точке F ([17],
стр. 42).
3. Используйте теорему, обратную к теореме Чевы, как в
упражнении 26).
4. Представьте себе, что рисунки 54 и 55 соединились вместе.
Так как шесть треугольников BOiNit CNiOu CO2N2, AN2O2,
AO1N1 и BNiOs являются равносторонними, а другие шесть тре-
треугольников AN3O2, AO3N2, O3BN1, NaBOu N2O1C, O2N1C прямо
подобны треугольнику ABC и конгруэнтны друг к другу, то мы
получаем
| = | O2N2 | = | BNl I = I BOi I = J OiC I = I NiC I ■■
= I CO2 I = I O2A I = I N2A I =
Так как
BChN2 = ВО^А - NiChA = 120° - В,
то четырехугольник BO1N2O3 (противоположные стороны кото-
которого равны) является параллелограммом. Если через X обозна-
обозначим середину отрезка ОгОз, а через В' — середину отрезка СА
(которая также является и серединой отрезка OiN2), то мы смо-
сможем вывести, что прямая ХВ' параллельна прямой OiN2 и пря-
прямой ВОъ Так как |ВО,|= 2\ХВ'\, то прямые OiX и ВВ' пере-
пересекаются в точке G такой^что |O,G| =2\GX\ и \BG\ =2|GB|,
Но прямые OiX и ВВ' являются медианами треугольника OiOiO3
и треугольника ABC. Следовательно, для этих двух треугольни-
треугольников точка G является их общим центроидом. Заменяя параллело-
параллелограмм BO1N2O3 на параллелограмм .ЙЛ^ОгЛ'а, мы, аналогично, на-
находим, что точка G является также центроидом треугольника
NNN
§4
1. Пусть АХ, BY, CZ — биссектрисы внешних углов тре-
треугольника. Тогда
BX CY _AZ__c_ а_ _6
CX ' AY ' BZ ~ b ' с ' а
198
2. Пусть АХ' и BY' — биссектрисы внутренних углов, a CZ —
биссектриса внешнего угла. Тогда
BXf CY'
СХ' ' AY'
§5
1. Если две прямые АС и BD параллельны, то из рассмотре-
рассмотрения параллелограммов ABCD и CDFA следует, что \BD\i
рр еду, что |ДО| |Л£|
и |£)Л = 1СЛ|, откуда, произведя сложение, мы получаем
\BF\ = \CE\. Таким образом, EFBC—параллелограмм, а отре-
отреEF ВС. Если, с другой стороны, отрез
сть они пересекаются в точке
и \OC\I\OD\=\OA\I\OF\,
\\ \C\. Тким обро, Cпарлллограмм, а отре
зок EF параллелен отрезку ВС. Если, с другой стороны, отрезки
АС и BD не параллельны, пусть они пересекаются в точке О.
Так как
то мы получаем
\OB\-\OE\*=\OA\.\OD\=\OC\.\OF\,
откуда \OE\I\OF\=\OC\I\OB\.
2. Пусть С и F — точки пересечения, как на рисунках 58 и 59,
и пусть L — точка, в которой прямая АВ пересекает прямую DE.
По теореме Паппа точка L лежит иа прямой MN, т.е. прямые
АВ, DE и NM конкурентны.
3. Согласно теореме Паппа прямая MN проходит через
центр L параллелограмма и, таким образом, делит противопо-
противоположные стороны на попарно равные отрезки.
4. 9 точек; 9 прямых; 3 прямые через каждую точку; по
3 точки на каждой прямой.
§ 6
1. Если два треугольника PQR и P'Q'R' перспективны от-
относительно точки О и при этом прямая QR параллельна пря-
прямой Q7/?', а прямая RP параллельна прямой R'P', то мы имеем
I OQ |/| OQ' | = | OZ? |/| OR' | = | OP |/| OP' |.
Поэтому прямая PQ параллельна прямой P'Q'.
2. 10 точек; 10 прямых; 3 прямые через каждую точку; по
3 точки на каждой прямой.
3. а) треугольники OQR и P'FE,
b) треугольники OQ'R' и PFE,
c) треугольники ERR' и FQQ?.
4. Вершины каждого пятиугольника лежат на сторонах
другого. Да, иа рисунке есть всего шесть таких пар взаимно
вписанных пятиугольников. Одной парой из оставшихся является
RPP'Q'D, EFQOR'.
5. Пусть Р — вершина треугольника PQR, две другие вер-
вершины которого Q и R лежат на двух данных прямых е и f.
Возьмите точку D на продолжении отрезка QR и точку Е на
продолжении отрезка RP. Пусть прямая DE пересекает от«
резок QP (продолженный) в точке F. Для любой точки Q',
лежащей иа прямой е, обозначим точку пересечения отрезка DQ'
199
с прямой / через /?', а точку пересечения прямых ER' и EQ' че-
через Р'. Тогда РР' есть искомая прямая, проходящая через точ-
точку Р. Если бы мы применили то же самое построение к парал-
параллельным прямым е и /, то мы получили бы прямую, прохо-
проходящую через точку Р и параллельную обеим прямым ей/ (так
как в противном случае это противоречило бы теореме 3.62).
§7
1. Продлите отрезки АВ, CD, EF так, чтобы образовался
треугольник UVW с точками А и В на стороне UV, точками С
и D на стороне VW и точками Е и F на стороне WU. Так как
\UE\=>\AD\=\FW\, мы имеем \UF\ = \EW\ = \BC\. Таким
образом, BCFU — параалелограмм и диагональ CF параллельна
стороне АВ. Чтобы рассмотреть центроиды, обозначим через X
и Y точки, в которых диагональ BE пересекает диагонали CF и
AD соответственно. Тогда CDEX и BCDY — параллелограммы, а
их центры А' и F', которые являются серединами диагоналей DB
и DX, лежат на прямой, параллельной прямым ВХ и AF. Так как
"" ' \AF\ = \BX\=2\F'A'\,
то прямые АА' и FF' пересекаются в точке G, так что \FG\ =
=2\GF'\ и |v4G| =2|СЛ'|. Но отрезки АА' и FF' —медианы
треугольников АСЕ и BDF. Следовательно, у этих двух тре-
треугольников точка G — общий центроид.
2. Шестью способами.
§8
1. Пусть вершины А, В, С, D, Е шестиугольника ABCDEF
лежат на окружности, которая вновь пересекает отрезок AF в
точке F'. Три точки L = AB-DE, М = CD-FA и N = BC-EF по
условию коллинеарны, как на рисунке 64. Применяя теорему
Паскаля к шестиугольнику ABCDEF', мы видим, что прямая EF',
так же как и прямая EF, проходит через точку N = BC-LM.
Следовательно, точка F' совпадает с точкой F.
2. На рисунке 65 показано, как теорема Паскаля применяет-
применяется к вырожденному шестиугольнику ABBDEE. Требуемый ре-
результат можно получить подобным же образом, рассматривая
шестиугольники ААВССЕ или АВССЕА.
§9
1. Используйте вырожденный шестиугольник BQCEPF.
2. Прямые AC, BE, QF.
3. Используйте вырожденный шестиугольник AZBXCY.
ГЛАВА 4
§ 1
1. Рассматривая отрезок а двумя способами как вектор, пе-
переведите треугольник ABC в треугольник А'В'С направо и в
треугольник А"В"С" налево. Соедините точки АС-А'В' и
АВ-А"С".
200
2. Мы получим мозаику из равносторонних треугольников,
причем каждую вершину окружают шесть треугольников.
§2
1. Примените поворот на 45° вокруг центров этих квадратов.
2. а) Так как | СХ \/Ь •= а/(а + Ь), то
\СХ\ \СХ\ а д
I лл | о — I ел | о + о — a i
Аналогично, | BY \I\YC\ —alb. Также
Так как теперь
\BY\ \CX\ \АН\ а а_ &__.
\YC\' \ХА\' \HB\~ b' b' a* ~ •
то результат следует из теоремы Чевы.
б) Треугольник ABC является одной половиной параллело-
параллелограмма ABFC, центр которого — точка М — середина стороны ВС,
Применяя результаты упражнения 1 к этому параллелограмму,
мы получаем, что 1Л10а| = |Л103|, и эти прямые перпендикуляр»
ны, а также, что (AJOi| = |AlC|, и эти прямые тоже перпенди-
перпендикулярны. Следовательно, поворот на 45° вокруг точки М пере-
переводит треугольник MO\Oi в треугольник МСОз.
в) Дорисуйте чертеж, чтобы образовались прямоугольник
KCGC' и параллелограммы DAJA' и IBEB'. Произведя положи-
положительные и отрицательные повороты на 45° вокруг точек 04, 02,
03, мы получим, что шесть треугольников B'lB, CCG, CCR,
JA'A, DAA', ВЕБ' прямо конгруэнтны треугольнику ABC. Следо-
Следовательно, точки U, V, W являются центрами рассмотренных пря-
прямоугольника и параллелограммов.
3. Рассмотрите результат поворота на 60° вокруг одной из
вершин искомого равностороннего треугольника.
§3
1. Пусть В — точка пересечения одной из окружностей с об*
разом другой при развороте вокруг точки А. Прямая АВ и буде*
искомой прямой.
2. Пусть точка О —центр данной окружности, а г — ее ра-
радиус. Постройте две окружности с центрами в точках А и О
радиусов г и 2г, которые пересекаются в точках Oi и О2. Иско-
Искомая прямая соединяет точку А с точкой Р — серединой отрез-
отрезка OOi или отрезка ОО2-
3. Рассмотрите разворот вокруг середины одной из диаго-
диагоналей.
201
§ 4
1. В основании высоты, проведенной к стороне АВ.
2. Пусть АВ — основание. треугольника. Третья вершина С
должна лежать на прямой, параллельной отрезку АВ, и мы
должны минимизировать сумму |ЛСЦ-|Св|.
3. Ось симметрии соединяет точку А с серединой линии цен-
центров.
§ 6
1. Одним из способов является: A2,0,0)', G,5,0), G,0.5),
B,5,5), B,1,9). A1,1,0), A1,0,1), F,5,1), F,0,6).
2. Сначала нужно налить бальзам в сосуды емкостью И ун-
унций и 5 унцнй, затем отдать одному грабителю флакон с остав-
оставшимися в нем 8 унциями бальзама, что и является его долей
добычи. Осталось разделить на равные части 16 унций бальзама
с помошью сосудов емкостью 5, И и 13 унций, т.е. в ситуации
[16; 13, 11, 5] решить задачу деления на равные части, которая
может быть решена в четыре этапа.
3. Используя обозначения рисунка 19, мы находим, что че-
четырехугольники ACiPBi и АВ1Р'С1 подобны.
§7
1. Окружность, радиус которой равен половине радиуса дан-
данной окружности.
" 2. Постройте квадрат CBED внешним образом на стороне ВС.
Прямые AD и АЕ пересекают сторону ВС в двух вершинах иско-
искомого квадрата.
§8
1. Пусть треугольник АВ'С—некоторое ночое положение
нашего подвижного треугольника ABC. Так как ДЛСС со ДЛбб,
то АСС''•= ABB'' = ABC.
1. Рассмотрев множество конгруэнтных отрезков, которые
выписаны в ответе к упражнению 4 § 3 гл. 3, мы видим, что
вращение на 120° вокруг точки G, которое переводит точку О\
в точку Ог, точку Ог — в точку Оз и точку Оз — в точку О\,
также переводит точку Л^ в точку Nz, точку Nz в точку Nt и
точку Ni в точку Ns. Конечно, существует подобие, которое пере-
переводит точки Oi, Ог, Оз в точки Nt, N2, Na, соответственно. Одна-
Однако это подобие является обратным, а не прямым и может
быть представлено как сумма дилатации и симметрии ([17],
стр. 116—117).
1.
2.
3.
4.
5.
10.
202
х' =
х' =
х' =
х' =
х' =
*'=
х +
— х.
</.
— х.
kx,
X.
а.
У'
у' = у +
{/' = {/.
у' = х.
у'--у.
у' = *».
1-у.
§9
Ъ. 6.
7.
8.
9
если
если
х' = — ky.
х' = х + а
х' = kx.
х' = х\
х>0,
х < 0.
•y' = kx
»' = -
*' = -
У' = У-
ГЛАВА 5
§ 1
1. AC//BD, ACI/DC, CAI/BD, CA//DB, BD/IAC, ВВЦАС.
BDUCA, DBI/CA.
§2
, Ш DC,\BD\-\AC\_\AC\.\BD\
Лт {ВАг DCi \BC\-\AD\ \AD\.\BC\-lAB- CD]- и
аналогично в остальных случаях.
2. а) 1; б) 2; в) 3; г) 1.
§ 3
1. Это будет фигура в форме цветка, состоящая из четырех
конгруэнтных полуокружностей (построенных внешним образом
на сторонах меньшего квадрата).
2. В тех случаях, когда точка О — центр вписанной окруж-
окружности или центр вневписанной окружности.
3. а) Пусть окружность с центром в точке Р и радиусом РО
пересекается с окружностью инверсии ю в точках А и В. Цен-
Центрами окружностей, проходящих через точку О, являются точки
А п В. Эти окружности вновь пересекаются в точке, являющейся
образом точки Р.
б) Используя окружности, мы можем для любой точки Pi
построить точку Р2 такую, что |OPa|=2|OPi| ч, аналогично,
точку Р„ такую, что |ОР„|= ra|0Pi|. Если \OPt\ > k/2n, то
\ОРЛ> kj2, т.е. мы можем построить образ точки Р„ — точ-
точку Р„,как и в предыдущем случае а).Тогда образ точки Рх, точка
/"j, описывается равенством | ОР\ | = га | ОР'п\.
4. а)" треугольник А'В'С подобен треугольнику ABC;
б) треугольник А'ВС подобен ортотреугольнику DEF (со-
(согласно соотношению 2.44);
в) треугольник А'В'С' подобен треугольнику 1ahh с верши*
нами в центрах вневписанных окружностей (согласно упражне»
нию 4 § 4 гл. 1 и теореме 1.61).
г (
у" х*+у2.
6. Постройте равнобедренный треугольник BOtC с равными
углами Л + D — 90" при вершинах В и С и равнобедренный тре-
треугольник СОгА с равными углами В + Ё— 90° при вершинах С
и А Окружности, проходящие через точку С с центрами в точ«
ках О4 и О2, пересекаются снова в искомом центре О. Радиус
k определяется из соотношения
I О А | • I ОВ | ■ | РЕ |
к - \АВ\
203
§4
1. Пусть точка О — центр окружности инверсии fi). Тогда
ДОЛРооДОРЛ' и \РА\/\РА'\ = \ОА\/\ОР\.
2. Пусть ВС — диаметр. Тогда АРОВ оо АСОР' и
|РО|/|ОВ|=|СО|/|ОР'|, \ОР\-\ОР'\ = **.
3. Пусть Р и Q — точки внутри данной окружности а. Ин-
Инверсия относительно любой окружности с центром в точке Р
дает точки Р«>, Q' и окружность а'. Так как точка Ра, лежит
вне окружности а', то точка Q' тоже лежит вне ее. Две каса-
касательные, проведенные из точки Q' к окружности а', являясь
двумя «окружностями», проходящими через точки Р«> и Q', яв«
ляются и образами двух окружностей, проходящих через точки Р
и Q и касающихся окружности а.
4. Используйте окружность инверсии, с центром в одной из
трех точек касания. Фигура переходит в две параллельные пря*
мые и окружность, касающуюся обеих прямых.
5. Инверсия относительно любой окружности с центром в
точке А дает три точки В', С, D" так, что точка С лежит на
отрезке B'D' тогда и только тогда, когда АС // BD. По теоре-
теореме 5.41 «неравенство треугольника» \В'С'\ + \С'1У\ ^\В'1У\ эк-
эквивалентно
|6С| |С£>| |б£>|
\AB\-\AC\ "•" \AC\-\AD\ ** \AB\-\AD\'
т.е. |Л£>|-|бС| + ИВ|-|С£>| £г \AC\-\BD\.
6. Если окружности ю и а пересекаются или касаются, то
утверждение очевидно. В противном случае, пусть окружности ю
и а описываются уравнениями х2 + уг = к1 и хг + уг = ах. Со-
Согласно упражнению 5 § 3 образ окружности а относительно
окружности ю описывается уравнением
k2x \2 / k2y \2 / k2x
* + уЧ +\х2+у2) '==a{x2 + y
т. е. k2 = ах.
7. Парой пересекающихся окружностей. Вторая точка пере-
пересечения — точка Роо.
§5
1. Построенная вами окружность должна проходить через
точки пересечения окружности инэерснн ю с окружностью, по-
построенной на отрезке ОА как на диаметре.
2. Это окружность PP'Q, где точка Р' является образом
точки Р.
3. Это окружность PPiPzy где точки Р± и Рг являются обра-
образами точки Р.
4. Их произведение равно kK
5. Инверсия относительно любой окружности с центром в
точке О дает окружность а' и точку Р' на окружности а'.
Только одна прямая касается окружности а' в точке Р1. И, иа-
204
оборот, инверсия относительно любой окружности с центром в
точке Р дает прямую а и точку О', не лежащую на прямой а.
Только одна прямая, проходящая через точку О', параллельна
прямой а.
§ 6
1. Так как треугольник ABiCi является конгруэнтным тре-
треугольнику ABC при симметрии относительно прямой AS, то
SBA —
В— С.
2. Согласно упражнению 3 § 7 гл. 1, |Д'£>| = (Ь2 —сг)/2а.
Мы только что видели, что \A'S\ = a(b — с)/2F + с). Следова-
Следовательно,
|4'S|.M'D|-(£=^.J.
§7
1. Уравнению с + с' = 0.
2. Пусть г — радиус серединной окружности двух касаю-
касающихся окружностей с радиусами а и Ь. Инверсия относительно
окружности, центром которой является точка касания, цает пря-
прямую на расстоянии ft2 /2т- от нее, т. е. посередине между двумя
параллельными прямыми, находящимися на расстояниях fe2/2a и
№]2Ь. Следовательно,
2 1,1
3. Мы получаем два ортогональных пучка параллельных пря-
прямых подобно двум пучкам прямых, описываемых уравнениями
к = const и у = const.
4. Возьмите точку О на серединной окружности. Тогда се-
серединная окружность переходит при инверсии в прямую, а ин-
инверсия относительно нее переходит в симметрию.
5. Симметрия относительно прямой является частным слу-
случаем инверсии относительно окружности.
6. а) Если АС IIBD, то пусть у — окружность, на которой
лежат четыре заданные точки. Пусть аир — две окружности,
ортогональные к окружности Vi одна из которых проходит через
точки Л и С, а другая — через точки В и D. Окружности аир
пересекаются, скажем, в точках t и О. Инверсия относительно
любой окружности с центром в точке L будет переводить окруж-
окружности а и р в два диаметра окружности y'". при этом параллело-
параллелограмм A'B'C'D' становится прямоугольником с центром в точ-
точке О'.
б) Если AB//CD или AD // ВС, определите окружности Y.
а, р, как прежде. Но теперь окружности а и р не пересекаются.
Пусть L и О — граничные точки соосного пучка ар, другими
словами, пусть L и О — точки, в которых окружность у пересе-
пересекает прямую, соединяющую центры окружностей а и р. При ин-
инверсии относительно любой окружности с центром L окружности
аир будут переходить в две окружности, имеющие один и тот
205
же центр О. Так как отрезки А'С в B'D' (лежащие на одной
прямой) являются диаметрами этих концентрических окружно-
окружностей, то A'B'C'D' — вырожденный параллелограмм.
в) Если точки А, В, С, D не все лежат на одной окружности,
то они определяют четыре различные окружности ABC, ACD,
ABD, BCD. Пусть (х — одна из серединных окружностей для
окружностей ABC и ACD, а именно та, которая разбивает точ-
точки В и D (так что одна из этих точек лежит внутри окружно-
окружности (х, а другая — вне нее или, если окружность (х окажется
прямой, то точки В и D лежат по разные стороны от нее). Ана-
Аналогично, пусть v — серединная окружность окружностей ABD и
BCD, разбивающая точки Л и С. Окружности ц и v пересе-
пересекаются, скажем, в точках L и О. При инверсии относительно
любой окружности ю с центром в точке L окружности ABC и
ACD преобразуются в две конгруэнтные окружности А'В'С и
A'C'D", причем радикальная ось ц' разбивает точки В' и D' так,
что
'ft'C' С Г)' А'
Аналогично, при инверсии относительно окружности ю окружно-
окружности ABD и BCD преобразуются в две конгруэнтные окружности
A'B'D' и B'C'D', причем их радикальная ось v' разбивает точки
А' и С так, что D'A'B' = B'C'D'. Следовательно, A'B'C'D' —
параллелограмм ([11], стр. 99).
В каждом случае пара точек L, О называется якобианом
двух пар точек А, С и В, D (см. Coxeter, Abh. Math. Sem. Univ.
Hamburg 29 A966), стр. 233).
7. Пусть диаметры данных окружностей, лежащие на нх ли-
линии центров, обозначены через АВ и CD так, чтобы АС Ц BD.
Пусть а и Э обозначают окружности, диаметрами которых яв-
являются отрезки AD и ВС. Пусть L и М — граничные точки со-
осного пучка ар. Искомая серединная окружность имеет диа-
диаметр LM. (Так как при инверсии относительно этой окружности,
ортогональной к окружностям аир, точка А переходит в точ-
точку D, а точка В — в точку С.)
§8
1. Используйте упражнение 4 § 7.
2. Подставьте 6 = — -\ в тригонометрическое тождество
cosec е — ctg е = tg — е.
3. С точки зрения инверсивной геометрии такое расположе-
расположение окружностей — это просто чертеж поризма Штейнера при
п = 4. Поэтому три инверсных расстояния равны по
2 log (V2"+ l) i а остальные двенадцать — нулю.
206
§9
1. Меньшее инверсное расстояние С определяется из урав-
уравнения
ch6 =
Гиперболический косинус большего инверсного расстояния
равен
+ 1-4 (V3+ IJ
■ 4 Уз~+ 7 = 2 ch2 б — 1 «= ch 26.
Нет; окружность между двумя данными окружностями ра-
радиуса 1 не может быть их серединной окружностью, потому что
она несоосна с ними.
2. Окружности Содди являются частным случаем поризма
Штейнера при п = 3; следовательно,
ch- = secT=2.
3. Квадрат отношения длин равен
с2 - (а + ЬJ с2 - а2 - Ь2 - 2аЪ ch б - 1 _ б
2 *
с2-(а- ЬJ c2-a2-b2 + 2ab ch б + 1 2
4. Первая часть утверждения ясна из чертежа. Для решения
второй части используйте теорему 5.91 при а = b и с = 2р:
+ l
6. Из рисунка 8 мы видим, что
| АН | = Ь cos i"cosec В = 2R cos A.
Используя также упражнение 4 § 6 гл. 1, мы выводим, что
I ОН |2 = R2 + B#cos АJ — AR2 cos /cos (B — C) =
= /?2 A — 8 cos A • cos В • cos б).
Так как | ОЛ/1 =—-| ОЯ |, то из этого следует, что
cos б или ch б =
= 1 + 2 cos A • cos В • cos б
7. Если использовать упражнение 4 и принять, что указан-
указанная там прямая есть радикальная ось х = 0, то мы имеем, что
ch а = а/л/а2 — d2 и ch p = bl^¥ — d2.
207
ГЛАВА в
1. Так как при инверсии относительно окружности ю окруж-
окружность, построенная на отрезке О А как на диаметре, преобразуется
в поляру а, то эти две окружности и прямая принадлежат одно-
одному пучку соосных окружностей, поэтому а — радикальная ось
этих окружностей.
2. Поляры А и В перпендикулярны отрезкам ОА и ОВ соот-
соответственно.
3. Так как образ любой фигуры при полярном преобразова-
преобразовании относительно окружности с центром в точке О подобен
образу этой фигуры при полярном, преобразовании относительно
любой другой окружности с тем же центром О, то мы можем
считать, что окружность ю есть окружность, вписанная в
данный правильный многоугольник ABC... Тогда полюсами сто»
рон АВ, ВС, .. являются середины отрезков АВ, ВС, .... а по-
полярами вершин А, В, С, ... являются прямые, соединяющие
смежные пары этих середин. Аналогично, если мы будем считать,
что окружность ю является описанной окружностью, то об-
образом многоугольника при полярном преобразовании будет мно-
многоугольник, полученный из прямых, касательных к этой окруж-
окружности в каждой из его вершин.
4. Полюсы двух противоположных сторон прямоугольника
равноудалены от точки О н лежат с ней на одной прямой. Это
Также справедливо н для других сторон, т. е. полюсы этих сто-
сторон равноудалены от точки О и лежат с ней на одной прямой.
При этом рассмотренные прямые перпендикулярны. Таким обра-
образом, мы получаем четырехугольник, диагонали которого делят
пополам друг друга под прямыми углами, т. е. ромб. И наоборот,
две оси симметрии прямоугольника высекают конгруэнтные от-
отрезки касательных, проведенных в его вершинах.
§2
1. Согласно теореме 6.21 полярная окружность делит попо-
пополам углы между описанной окружностью и окружностью девяти
точек, причем те углы, которые стремятся к нулю, когда тупой
угол треугольника стремится к 180°. Следовательно, используя
обозначения из упражнения 6 § 9 гл. 5, мы получаем, что
§ з
1. Относительно окружности а полярой точки Вг является
прямая i>2 и т. д. Относительно окружности р полюсом пря-
прямой ВоВ2 является точка Ci и т. д.
2. Каждая из фигур, рассматриваемых в этом параграфе,
симметрична относительно прямой ОА: все, что производится
над этой прямой, може* быть продублировано под ней. Из рас-
рассмотрения рисунков 122 и 124 можно предположить существо-
ванне другой оси симметрии, перпендикулярной к прямой ОА,
для эллипса и гиперболы (это будет установлено в § 6).
208
3. Из рисунка 123 мы видим, что каждая касательная t па-
параболы является полярой точки Т на окружности а. Основание
перпендикуляра, опущенного из точки О на прямую t, является
образом точки Т при инверсии относительно окружности ю. Все
полученные таким образом точки, являясь образами точек, ле-
лежащих на окружности а (проходящей через точку О) лежат на
одной прямой.
4. Из рисунка 124 мы видим, что асимптота ы, являясь поля-
полярой точки U, перпендикулярна стороне OU прямоугольного тре-
треугольника OAU. Следовательно, этот треугольник имеет угол 8
при вершине А и
\ОА\ \ОА\
Для прямоугольной гиперболы 6 = 45°, а е = л]2.
5. Комета с параболической или гиперболической орбитой
никогда ие вернется в окрестность Солнца. Однако нет убеди-
убедительных доказательств, что такую комету видели когда-либо. Хотя
участок орбиты, который мы можем наблюдать, иногда похож
на гиперболу из-за возмущений, создаваемых планетами (осо-
(особенно такими массивными, как Юпитер), а некоторые эллипти-
эллиптические орбиты так вытянуты, что их нельзя отличить от парабол,
все известные кометы (включая и «непериодические», которые
ненадолго посещают нас и никогда снова не видны) обычно счи-
считаются членами Солнечной системы. Их скорость относительно
Солнпа никогда не бывает достаточно велика, чтобы дать им
возможность уйти во «внешнее пространство», где притяжение
другой звезды могло бы оказаться более существенным, чем при-
притяжение Солнца.
§4
1. х2 + у2 = (/ - ехJ.
2. Серединой отрезка между точками *i = //(e+ 1) и х2 =
= //(е — 1) является точка * = — га. Таким образом, новым
уравнением будет
(* - гаJ + у2 = [/ - е (* - еа)]2 = (а - ел;J,
или
A - е2) *2 + у2 = A - е2) а2 = la = ± Ъ2,
а2 ^ Ь2 ~ '
причем знак плюс или минус берется в соответствии с тем е < 1
или е > 1. Так как в уравнение входят только четные степени
переменных х и у, то эллипс и гипербола симметричны относи-
относительно обеих координатных осей.
§8
1. Если два треугольника перспективны относительно точки,
то они перспективны относительно прямой. Если два треуголь-
треугольника перспективны относительно прямой, то они перспективны
относительно точки.
209
2. Если шесть вершин шестиугольника лежат, чередуясь, на
двух прямых, то три пары противоположных сторон пересекаются
в коллннеарных точках. Если шесть сторон шестиугольника про-
проходят, чередуясь, через две точки, то три его диагонали конку-
конкурентны (f 19], стр. 38, 90).
3. Они являются перпендикулярными прямыми, проходящи-
проходящими через ее центр.
4. Так как прямая /«, является полярой точки О, то любая
точка на бесконечности конического сечения является полюсом
(относительно окружности to) касательной к окружности а, кото-
которая проходит через точку О. Следовательно, числситочек на бес*
конечности конического сечения будет 0, 1 или 2 в зависимости
от того, находится точка О внутри окружности а, на ней или
вне нее.
5. Используя обозначения рисунка 124, можно сказать, что
прямая ОН касается окружности а в точке U. Поэтому одной
из точек на бесконечности для гиперболы является точка касания
касательной и и, конечно, другой точкой касания является точка
касания прямой V.
6. Так как директриса является полярой точки Л, то любая
точка, лежащая на ней, является полюсом некоторого диаметра
окружности а, и касательные к параболе из такой точки явля-
являются полярами двух концов этого диаметра. Так как эти диа-
диаметрально противоположные точки окружности а стягивают пря-
прямой угол в точке О, то их поляры перпендикулярны.
7. Каждая из трех «диагональных точек» в свою очередь
может быть рассмотрена как точка Р в теореме 6.51, и тогда две
другие лежат на ее поляре.
§6
1. | ОР | + | OtP | = е | РК | + е | К,Р | = е | KVK |.
Отсюда она равна произведению е на расстояние между дирек-
директрисами.
2. Если точка Р лежит на левой ветви этой гиперболы, как
на рисунке 131, то
IОР| - | О,Р| = в | РК| - в | Р/Г,| = - в | /Г/Г,|.
Для первой ветви знак будет обратным
3. Эта окружность является образом окружности а при
инверсии относительно окружности ю (сравните с упражне-
упражнением 3 § 3).
§7
1. Стереографическая проекция является частным случаем
инверсии.
2. Плоскость, проходящая перпендикулярно к диаметру ОА
через его середину (см. рис. 134), пересекает сферу а' вдоль
особого большого круга, который мы, естественно, назовем эква-
экватором. Каждый другой большой круг пересекает его в паре диа-
диаметрально противоположных точек. Характерной особенностью
экватора является то, что его диаметры проектируются в диа-
210
метры (окружности на плоскости а с центром в точке А и ра-
радиусом 2k).
3. Мы можем рассмотреть точки />, и Р2 как точки пересе-
пересечения двух больших кругов на сфере а', один из которых про-
проходит через точки О и Л. Таким образом, точки Pi и Рг на пло-
плоскости а являются точками пересечения прямой, проходящей
через точку А, с окружностью, проходящей через две диаметраль-
диаметрально противоположные точки, скажем, Qt и Q2, «проективного эква-
тора> (с центром в точке А и радиусом 2fe). Так как
АР1 X АР2 = AQl
то точки Pi и Pi переводятся друг в друга при помощи антиин-
антиинверсии: суммы инверсии относительно проективного экватора и
разворота вокруг его центра А.
4. Пусть а' — сфера, касающаяся двенадцати ребер куба (з
их серединах), а точка О — одна из точек пересечения сферы а
с прямой, соединяющей две противоположные вершины. (Пере-
(Передвигая точку О к одной из точек пересечения сферы а' с прямой,
соединяющей центры двух противоположных граней, мы полу-
получим симметричный чертеж для поризма Штейнера при п = 4.)
БИБЛИОГРАФИЯ
1*. Аргунов Б И. и Скорняков Л. А., Конфигура*
пионные теоремы, М, Гостехиздзт, 1957.
2*. Бакельмаи И. Я., Инверсия, М., «Наука>, 1966.
3. Белл Е. Т. (Bell E. Т.), Development of Mathematics,
New York, McGraw Hill, 1945.
4. Белл E. T. (Bell E. Т.), Men of Mathematics, New
York, Simon and Schuster, 1937.
5. Бол л У. У. Р. (Ball W. W. R.), Mathematical Recrea-
tions and Essays A1th ed.), London, Macmillan, 1939.
6*. Болтянский В. Г., Огибающая, М., Физматгиз, 1961.
7*. Васильев Н. Б. и Гутенмахер В. Л., Прямые и
кривые, М., «Наукв>, 1978.
8. в а н дер ВарденВ. Л., Пробуждающаяся наука, Мч
Физматгиз, 1959.
9*. В о л ь б е р г О. А., Основные идеи проективной геомет-
геометрии, М. — Л., Учпедгиз, 1949.
10. Гильберт Д. и Кон-Фоссен С, Наглядная геомет-
геометрия, М. — Л., Гостехиздат, 1951.
П. Д ж о н с о н P. A. (J о h n s о n R. A.), Advanced Euclidean
Geometry, New York, Dover, 1960.
12*. Дорфман А. Г. Оптика конических сечений, М., Физ-
Физматгиз, 1959.
13. Д юр ель С. В. (Durell С. V.), A Course of Plane
Geometry for Advanced Students, Part I, II, London, Macmillan,
1909—10.
14*. 3 e т е л ь С. И, Новая геометрия треугольника, М, Уч-
Учпедгиз, 1962. _
15*. Зетель С. И., Геометрия циркуля и геомегрия линей-
линейки, М., Учпедгиз, 1957.
16. К as ар и нов Н. Д. (Kazarinoff N. D.), Geometric
Inequalities, New Mathematical Library, vol. 4, Random House,
New York and the L. W, Singer Co., Syracuse, 1961,
212
17. Ко кет ер Г. С М., Введение в геометрию. М., «Наука»,
1966.
18*. Кокстер X. С. М., Действительная проективная пло«
скость, М., Физматгиз, 1959.
19. Коксетер Г. С. М. *) (Coxeter H. S. M.), Projective
Geometry, New York, Blaisdell, 1964.
20. Коксетер Г. С. М. (Coxeter H. S. M.), Regular Po-
lytopes Bnd ed.), New York, Macmillan, 1963.
21. К у р а н т Р. н Р о б б и н с Г., Что такое математика? М.,
«Просвещение», 1967.
22. Курт Н. A. (Court N. A.), College Geometry Bnd ed.),
New York, Barnes and Noble, 1952.
23. Лэмб Г. (Lamb H.), Statics, Cambridge University
Press, 1916.
24. Л оквуд Е. X. (Lock wood E. H.), A Book of Curves,
Cambridge University Press, 1961.
25*. Маркушевич А. И., Замечательные кривые, М,
«Наука», 1978.
26*. Моиз Э. Э. и Дауне Ф. Л., Геометрия, М., «Просве-
«Просвещение», 1972.
27. О'Бейрн Т. X. (O'Beirne Т. Н.), Puzzles and Parado-
Paradoxes, London, Oxford University Press, 1965.
28. О р е О., Графы и их применение, М., «Мир», 1965.
29. Перфект Г. (Perfect H.), Topics in Geometry, Lon-
London, Pergamon, 1963.
30. Петерсен Ю., Методы и теория решения геометриче«
ских задач на построение с приложением более 400 задач, Харь-
Харьков, книжный магазин Кервнли и К", 1883.
31. Пи до Д. (Pedoe D.), Circles, London, Pergamon, 1963."
32*. Розенфельд Б. А. и Сергеева Н. Д., Стереогра-
Стереографическая проекция, М., «Наука», 1973.
33*. Скопец 3. А., Конические сечения. Энциклопедии эле-
элементарной математики, кн. V, М., «Наука», 1966.
34. С м о г о р ж е в с к н и А. С, Линейка в геометрических
построениях, М., Гостехиздат, 1957.
35*. Смогоржевский А. С, О геометрии Лобачевского,
М., Гостехиздат, 1956. ■
36. Фейеш Тот Л. (Fejes T6th L.), Regular Figures,
Oxford (England), Pergamon, 1964.
*) По поводу различий написании имени Г. С. М. Коксетера
в [17], [18], [19], [20] см. «От редактора русского перевода»,
помещенное в начале книги, — Прим. перев.
213
37. Фор дер Г Г (Forder H. G.), The Calculus of Exten-
Extension. New York, Chelsea, I960. ■
38. Фор дер Г. Г. (Forder H. G.), Geometry, London,
Hntchinson, 1960.
39. Фор дер Г. Г. (Forder H. G.), Higher Course Geo-
Geometry, Cambridge University Press, 1949.
40. Харди Г. X. (Hardy G. H.), A Mathematician's Apo-
Apology. Cambridge University Press, 1940.
41. Шерватов В. Г., Гиперболические функции, М. Гос-
Гостехиздат, 1958.
42*. Шклярский Д. О., Ченцов Н. Н„ Яглом И. М.,
Избранные задачи и теоремы элементарной математики, ч. 2,
геометрия (планиметрия), М., Гостехиздат, 1952.
43. Я г л о м И. М., Геометрические преобразования, т. I, 2,
М.. Гостехиздат, 1955—1956.
44*. Яглом И. М., Принцип относительности Галилея и не«
евклидова геометрия, М., «Наука», 1969.
45*. Яглом И. М., Окружности. Энциклопедия элементар-
элементарной математики, кн. IV, М., Физматгиз, 1963.
46*. Яглом И. М. и Атанасян Л. С, Геометрические
преобразования. Энциклопедия элементарной математики, кн. IV,
М., Физматгиз, 1963.
СЛОВАРЬ ОСНОВНЫХ ТЕРМИНОВ,
ИСПОЛЬЗУЕМЫХ В КНИГЕ
«Когда я употребляю какое-нибудь сло-
слово, — сказал Шалтай-Болтай довольно пре-
врительно, — оно означает только то, что
я хочу, чтобы оно означало, — ни больше,
ни меньше.»
Ч. Л. Доджсон
Автополярный треугольник. Треугольник, вершины которого
являются полюсами соответственно противоположных сторон.
Антиподные точки на сфере. Концы диаметра.
Асимптота к кривой. Касательная, точка касания которой на-
находится в бесконечности.
Бесконечно удаленная прямая. Идеальная прямая; каждому
пучку параллельных прямых соответствует точка этой прямой,
которая принимается за точку пересечения прямых этого пучка.
Бесконечно удаленная точка. Идеальная точка, которая при-
принимается за общую точку всех прямых в круговой плоскости,
рассматриваемых как окружности бесконечного радиуса.
Большой круг на сфере. Сечение сферы плоскостью, прохо-
проходящей через центр сферы.
Вектор. См. параллельный перенос.
Вневписанная окружность треугольника. Окружность, касаю-
касающаяся одной из сторон треугольника и продолжений двух других
его сторон.
Вписанный четырехугольник. Выпуклый четырехугольник, все
вершины которого лежат на одной окружности (при этом проти'
воположные углы являются дополнительными).
Высота треугольника. Отрезок перпендикуляра, опущенного
из вершины треугольника на противоположную сторону (или ее
продолжение), заключенный между ними.
Гипербола. Коническое сечение с эксцентриситетом е > 1;
при этом точка О находится вне окружности а (см. определение
конического сечения).
Асимптоты гиперболы. Поляры точек касания с окруж-
окружностью а касательных, проведенных через точку О.
Гномоническая проекция. Проекция сферы из ее центра на
касательную к ней плоскость.
Граничные точки пучка окружностей, задаваемого двумя
окружностями а и р. Две точки, принадлежащие одновременно
всем окружностям, ортогональным как окружности а, так и ок-
окружности р.
Дилатация. Преобразование, переводящее каждую прямую в
параллельную ей прямую. Подобие, сохраняющее'направления
прямых.
Директриса конического сечения. Поляра точки А относитель-
относительно окружности со (см. определение конического сечения).
215
Изометрия. Преобразование, сохраняющее длины. Движение.
Инверсное расстояние между двумя непересекающимися ок-
окружностями. Натуральный логарифм отношения радиусов кон-
концентрических окружностей, в которые данные окружности могут
быть переведены при помощи инверсии.
Инверсор Поселье. Шарнирный инструмент, с помощью кото-
которого можно произвести инверсию заданного множества точек.
Коллинеарность множества точек. Существование прямой, на
которой находятся все точки этого множества.
Коллинеация. Преобразование, переводящее прямые в пря-
прямые.
Коническое сечение. Полярное преобразование окружности а
(радиуса г с центром в точке А) относительно окружности со ра-
радиуса k с центром в точке О).
Конгруэнтность. См. изометрия.
Конкурентность прямых. Существование точки, через кото-
которую все эти прямые проходят.
Круговая плоскость. Евклидова плоскость, дополненная одной
идеальной точкой (см. бесконечно удаленная точка).
Медиана треугольника. Чевиана, проходящая через середину
стороны.
Многоугольник. Замкнутая ломаная на плоскости.
п-угольник. Многоугольник с п вер'линам и га сторонами.
Оболочка. Множество всех касательных к кривой.
Образ точки Р при инверсии относительно окружности -со.
Вторая точка пересечения двух окружностей, проходящих через
точку Р ортогонально окружности со.
Образ точки Р при симметрии относительно- прямой I. Вто-
Вторая точка пересечения двух окружностей с центрами на пря-
прямой /, проходящих через точку Р.
Ортогональные окружности. Две пересекающиеся окружно-
окружности, касательные к которым в точках пересечения ортогональны.
Ортотреугольник треугольника ABC. Треугольник, вершины
которого являются основаниями высот треугольника ABC.
Ортоцентр треугольника. Точка пересечения его высот.
Парабола. Коническое сечение с эксцентриситетом е = 1; при
этом точка О лежит на окружности а (см. определение кониче-
конического сечения).
Параллелограмм Вариньона данного четырехугольника. Па-
Параллелограмм, образованный отрезками, соединяющими середины
смежных сторон четырехугольника.
Параллельный перенос. Преобразование, при котором направ-
направленные отрезки, 'соединяющие точки с их образами, имеют оди-
одинаковые длины и направления. Иначе, дилатация, не имеющая
неподвижных точек.
Педальный треугольник точки Р относительно треугольника
ABC. Треугольник, вершинами которого являются основания пер-
перпендикуляров, опущенных из точки Р на стороны треугольника
ABC (или их продолжения).
Поворот. Преобразование, являющееся результатом враще-
вращения всей плоскости вокруг точки на этой плоскости на заданный
угол.
Подобие. Преобразование, сохраняющее отношение расстоя-
расстояний.
216
Полюс прямой р относительно окружности и с центром в
точке О. Образ основания перпендикуляра, опущенного из точ-
точки О на прямую р при инверсии относительно окружное™ со,
нли, иначе, точка пересечения поляр любых дзух точек, лежащих
на прямой р.
Поляра точки Р относительно окружности со. Прямая, соеди-
соединяющая точку пересечения прямых АВ и DE с точкой пересече-
пересечения прямых АЕ и BD, где AD и БЕ — две хорды окружности со,
высекаемые двумя прямыми,- проходящими через точку Р.
Полярная окружность. Окружность, при инверсии относи-
относительно которой вершины тупоугольного треугольника переходят
в основания высот, или, иначе, окружность, относительно которой
данный тупоугольный треугольник является автополярным.
Полярное преобразование. Преобразование точек в их по-
поляры, а прямых в их полюсы.
Правильный многоугольник. Многоугольник, центр которого
расположен на равном расстоянии R от всех его вершин и рав-
равном расстоянии г от всех его сторон.
Преобразование плоскости. Отображение плоскости на себя
такое, что каждая точка Р имеет единственный образ — точку Р',
а каждой точке Q' соответствует единственный прообраз — точ«
ка Q.
Проективная плоскость. Евклидова плоскость, дополненная
идеальной прямой (см. бесконечно удаленная пряная).
Произведение двух преобразований. Результат применения
сначала первого преобразования, а потом второго.
Пучок окружностей ар. Совокупность окружностей, ортого-
ортогональных двум различным окружностям, которые б свою очередь
ортогональны окружностям аир.
Пучок прямых. Совокупность всех прямых' (на одной пло-
плоскости), проходящих через одну точку.
Прямая Паскаля шестиугольника, вершины которого лежат
на окружности или любом другом коническом сечении. Прямая,
содержащая три точки пересечения пар противоположных сторон
этого шестиугольника.
Прямая Симеона точки Р, лежащей на окружности, описан-
описанной вокруг треугольника ABC. Прямая, в которую вырождается
педальный треугольник точки Р относительно треугольника ABC.
Прямая Эйлера треугольника ABC. Прямая, на которой ле-
лежат ортоцентр, центроид и центр описанной окружности тре-
треугольника ABC.
Прямое подобие. Коллинеация, при которой сохраняются
углы и их знаки.
Радикальная ось двух неконцентрических окружностей. Мно-
Множество всех точек, имеющих одинаковую степень относительно
этих окружностей.
Радикальный центр трех окружностей с неколлинеарными
центрами. Общая точка пересечения всех трех радикальных осей,
каждая из которых является радикальной осью двух из этих трех
окружностей.
Разбиение АС // BD (для любых четырех различных точек,
лежащих в одной плоскости). Любая окружность, проходящая
через точки А к С пересекает любую окружность, проходящую
через точки В и D.
217
Разворот. Поворот на 180е, или, иначе, центральная сим-
симметрия.
Серединная окружность или окружность антиподобия. Ок-
Окружность, при инверсии относительно которой две дачные окруж-
окружности переходят одна в другую.
Серединный треугольник треугольника ABC. Треугольник,
образованный отрезками, соединяющими середины сторон тре-
треугольника.
Симметрия относительно прямой I. Преобразование, которое
переводит каждую точку плоскости в ее образ при симметрии
отражения относительно этой прямой.
Сложное отношение четырех точек \АВ, CD) =*
«= (ACIBC)l(ADIBD).
Соосные окружности. Семейство окружностей, любая пара
из которых определяет одну и ту же радикальную ось, или,
иначе, окружности, ортогональные к двум данным.
Сопряженные прямые. Прямая а и любая прямая, проходя-
проходящая через полюс прямой а.
Сопряженные точки. Точка А и любая точка, лежащая на
поляре точки А.
Спиральное подобие (или дилатационный поворот). Произве-
Произведение поворота и дилатации или наоборот.
Степень точки Р относительно окружности. Число d2— R2,
где d—расстояние от точки Р до центра окружности, a R — ра-
радиус окружности.
Стереографическая проекция. Проекция из точки О сферы,
проходящей через эту точку на плоскость, касающуюся сферы
в точке, антиподной к точке О.
Топология. Геометрия, рассматривающая взаимно однознач-
однозначные и взаимно непрерывные преобразования.
Точка Жергона треугольника ABC. Точка пересечения че-
виан, проходящих через точки касания вписанной окружности со
сторонами этого треугольника.
Треугольник Наполеона для треугольника ABC.
Внутренний. Треугольник, вершины которого являются цен-
центрами равносторонних треугольников, построенных внутрь
на сторонах треугольника.
Внешний. Треугольник, вершины которого являются цен-
центрами равносторонних треугольников, построенных снару-
снаружи на сторонах треугольника.
Фокус конического сечения. Центр О окружности, относи-
относительно которой производится преобразование (см. определение
конического сечения).
Центральная дилатация. Дилатация, составляющая одну из
точек неподвижной. Гомотетия.
Центральное коническое сечение. Эллипс или гипербола.
Центроид треугольника. Точка пересечения медиан.
Чевиана. Отрезок, соединяющий вершину треугольника с
точкой на противоположной ей стороне (или ее продолжении).
Четырехсторонник См. четырехугольник.
Четырехугольник. Многоугольник с четырьмя вершинами и
четырьмя сторонами.
218
Выпуклый четырехугольник. Обе диагонали лежат внутри
него.
Четырехугольник с входящим углом. Одна из диагоналей
лежит внутри, а другая вне него.
Скрещенный четырехугольник. Обе диагонали лежат вне
него.
Эксцентриситет конического сечения, е =• \ОА\/г (см. опреде-
определение конического сечеиия).
Эллипс. Коническое сечение с эксцентриситетом е < 1, при
этом точка О находится внутри окружности а (см. определение
конического сечения).
УКАЗАТЕЛЬ
Автополярный треугольник 169,
179
Антиинверсия 211
Аргунов В. И. 212
Артоболевский И. И. 135
Архимед из Сиракуз 17, 74
Асимптоты гиперболы 171 —
173, 179
Атанасян Л. С. 213
Бакельман И. Я. 212
Белл Е. Т. 13, 43, 60, 74, 212
Бесконечно удаленная прямая
176
точка 139, 176, 214
Биван Б. 33
Биссектриса угла внешняя 26
■ внутренняя 19
Болл У. У. Р. 212
Болтянский В. Г. 212
Больаи Я. 156
Боттема О. 26
Брахмагупта 73, 74
Брекенридж В. 94
Брианшон Ш. Ж- 95
Брунеллески Ф. 87
Ван дер Варден Б. Л. 74, 212
Вариньон П. 67
Васильев Н. Б. 212
Вектор 100, 214
Взаимная простота 115
Вольберг О. А. 212
Высота 19
Гарднер М. 25
Гаусс К. Ф. 156
220
Геометрия гиперболическая 156
— инверсивная 108, 163
— неевклидова 156
— проективная 65, 168
Герон из Александрии 74
Гильберт Д. 212
Гипербола 171
— прямоугольная 173
Гиперболическая геометрия 156
Гиперболические функции 157
Гипоциклоида 58
Гномоническая проекция 183,
185, 214
Гомеоморфизм 124
Гомотетия 17, 90
Горнер В. Г. 60
Граничные точки 148
Грейтцер С. Л. 93
Гутенмахер В. Л. 212
Дауне Ф. Л. 213
Декартовы координаты 43
Дельтоида 58
Джильберт Г. 25
Джонсон Р. А. 60, 212
Диаметрально противополож-
противоположные точки 185
Дюрель С. В. 212
Евклид из Александрии 13, 39,
174
е 153
Задача о трех кувшинах НО
— Фаньяно 108
Зетель С. И. 212
Идеальная прямая 183
— точка 183
Инверсия 132 и далее
—, инверсивное определение
143
— относительно сферы 183
Инверсное расстояние 152, 215
Инверсор Поселье 135
Инцидентность 164
Искусственный спутник 183
Казаринов Н. Д. 108, 212
Квадрат 82, 119
Кейси Д. 35, 138
Кеплер И. 39, 172
Коксетер Г. С. М. 93, 212,
213
Коллинеарность 65
Комета 172, 209
Конгруэнтность 99
Коническое сечение 163, 170,
210, 215
центральное 179
Конкурентность 65
Конфигурация 155, 165
— двойственная 165
Кон-Фоссен С. 212
Коэффициент подобия 116
Круговая плоскость 138, 139,
183, 184
Курант Р. 108, 213
Курт Н. А. 213
Лагранж Ж- 79
Лаплас П. 79
Лейбниц Г. В. 92
Лемус С. Л. 24
Линейные преобразования 124.
158
Липкин Л. 135
Лобачевский Н. И. 156
Логарифм (натуральный) 153
Локвуд Е. X. 135, 213
Лэмб Г. 71, 213
Магнус Л. И. 132
Мак-Доннел Д. 25
Маклорен К. 94
Маркушевич А. И. 213
Медиана 18
Микель А. 77
Многоугольник 65
Мозаика 201
Моиз Э. Э. 213
Наложение карт 123
Наполеон Бонапарт 79
Нараньенгар М. Т. 61
Нейберг Ж. 35
Неподвижная точка 121
Ньютон И. 42, 92, 172
Оболочка 166
Образ (при инверсии} окружи
ности 139
— прямой 134
— точки 133, 184, 215
— треугольника 137
Окружности Содди 140, 161,
Окружность 39, 132
— Аполлония 140
— вневписанная 22
— вписанная 20
— девяти точек 31—33, 145,
161
— инверсии 133
— описанная 17, 41, 137
— Эйлера 33
Оппенгейм А. 36
Орбита 172
Оре О. 213
Ортогональность 141
Ортотреугольник 19, 27, 108
Ортоцентрический четырех»
угольник 53, 147
Отображение 99
Отражение 108
Палиндром 79
Папп из Александрии 84, 174,
179
Парабола 171, 179, 215
Параллелограмм 67
— Вариньона 67
— вырожденный 100, 151, 206
Параллельный перенос 100, 213
Паскаль Б. 92, 176
Педальная точка 34
Педальный треугольник 34, 53,
215
Перельман А. И. ПО
221
Перспективность относительно
прямой 86
точки 86
Перспективные треугольники
64, 86
Перфект Г. 213
Петард Г. 127
Петерсен Ю. 123, 213
Пи до Д. 213
Планеты 39, 172
Площадь 16
— отрицательная 67
— положительная 67
Поворот 100, 102, 119
Подобие 99, 116, 215
— прямое 118
Подобные треугольники 47, 77
Полюс 163
Поляра 163, 183
Полярная окружность тре-
треугольника 169, 216
Полярное преобразование 163,
216
Понселе Ж. В, 32
Поризм Штейнера 154, 206,
211
Поселье А. 135
Правильный многоугольник 216
Преобразование 99 и далее
— линейное 124
— непрерывное 124
Приведение к абсурду 26
Принцип двойственности 165
Проективная геометрия 65, 168
— плоскость 163, 176, 183, 185
Проекция гномоническая 183,
185, 214
— стереографическая 183, 185,
217
Прокрустово растяжение 125
Прямая Паскаля 93, 216
— Симеона 53—55, 57, 78
— Эйлера 30, 170, 190, 194,
216
Пучок окружностей 48, 216
Пятиугольник 64, 66, 97
Равносторонний треугольник
38, 78, 194
Радикальная ось 46, 97, 151,
193, 216
Радикальный центр 48, 51
Разбиение 127, 216
222
Разворот 33, 99, 105, 118
Роббинс Г. 108, 213
Розенфельд Б. А. 213
Рычажный механизм 135
Самосопряженная прямая 167
— точка 167
Сергеева Н. Д. 213
Серединная окружность 150
Серединный треугольник 28
Симметрия 180
Симеон Р. 17, 55
Скопец 3. А. 213
Скорняков Л. А. 212
Сложное отношение 131, 133,
186, 217
Смогоржевский А. С. 95, 213
Соосные окружности 47, 148,
170, 217
Сопряженные прямые 167
— точки 167
Сохранение углов 141
Степень точки 39, 42
Стереографическая проекция
183, 185, 217
Стюарт М. 17
Теорема Брианшона 95, 97, 177
— Вариньона 65 и далее
— косинусов 73
— о бабочке 59, 195
— о центре вращения 77
— Паппа 84
— Паскаля 92, 200
— Петерсена — Шута 123
— Птолемея 55, 131, 197
— Стюарта 17, 43, 190
— Фейербаха 33, 145
— Чевы 15, 67
— Штейнера — Лемуса 24
Тождественное преобразование
100
Точка Жергона 23
— Ферма 103
Траектория 182
Треугольник Боттемы 189
— Наполеона внешний 79, 124
внутренний 79
— равносторонний 38, 78, 194
— центров 78
Треугольника неравенство 204
Треугольники Наполеона 76,
217
Трехпараметрическое семейство
156
Трилинейные координаты ПО
Трисекция угла 61
Угол отражения 108
— падения 108
Ультрапараллельные плоскости
156
Фаньяно Д. Ф. Т. 108
Фейербах К. 33
Фейеш Тот Л. 213
Ферма П. 44, 82
Флобер Г. 163
Фокус 163, 173
Фордер Г. Г. 92, 123, 213
Формула Брахмагупты 73
— Герона 74
Функции гиперболические 157
Функция показательная 157
Харди Г. X. 213
Центроид 18
Цепная линия 160
Чева Д. 15
Чевиана 15
Чепцов Н. Н. 213
Четырехсторонник полный 165
Четырехугольник вписанный 72
— выпуклый 66
— ортоцентрический 53, 147
— полный 165
— с входящим углом 66
— скрещенный 66
Шварц Г. А. 108
Шерватов В. Г. 213
Шествие углов 36
Шестиугольник 90, 210
Шклярский Д. О. 213
Штейнер Я. 24, 43
Шут Р. Г. 123
Эйлер Л. 30, 41, 160
Эксцентриситет 171
Эллипс 171
Юпитер 209
Центр конического сечения 180
— тяжести 18
Яглом И. М. 47, 80, 213
Якобиан 206
Гарольд Коксетер, Самуэль Грейтцер
НОВЫЕ ВСТРЕЧИ С ГЕОМЕТРИЕЙ
(Серия: «Библиотека математического кружка»)
М., 1978 г., 224 стр. с илл.
Редактор Ф. И. Кмзнер
Технический редактор В. Н. Кондакова
Корректоры Е. А. Белицкая, Л. С. Сомова
ИБ № 11192
Сдано н набор 01.02.78. Подписано к печати 25.10.78. Бумага 84XIU87;,.
тип. Лг 2. Литературная гарнитура. Высокая печать Уеловн. печ. л. 11.76.
Уч.-изд. л. 10.14. Заказ № 953. Тираж 148 000 экз. Цена книги 50 коп.
Издательство «Наука»
Главная редакция физико-математической литературы
117071. Москва, В-71. Леииискнй проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении Соколовой
«Союзполиграфпрома» при Государственном комитете Совета
Министров СССР по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект. 29.